*■ -; - -J.
*fcfc
^■2^-'-*-*:с*^?:^ :^,^пшй£<
^■'v=c
3*
Л«-;>;^1
■*■ *
^УЗ&л.рд 'Т
: ♦
ч тошя
■--#*
;^ та 'ст i

Северо-Западное отделение Российской академии медицинских наук
Новгородский научный Центр
Новгородский государственный университет имени Ярослава Мудрого
В. А. Медик, М. С. Токмачев, Б. Б. Фишман
СТАТИСТИКА
В МЕДИЦИНЕ И БИОЛОГИИ
Руководство в 2-х томах под редакцией профессора Ю. М. Комарова
том
1
Теоретическая статистика
э
Москва
«МЕДИЦИНА»
2000

УДК61+57]:31
ББК 51.1(2)
М42
РЕЦЕНЗЕНТЫ: член-корреспондент РАМН, доктор
медицинских наук, профессор В. 3. Кучеренко, доктор
медицинских наук, профессор В. Г. Кудрина.
Медик В. А., Токмачев М. С, Фишман Б. Б.
М42 Статистика в медицине и биологии: Руководство. В 2-х
томах / Под ред. Ю. М. Комарова. Т. 1. Теоретическая
статистика. — М.: Медицина, 2000. — 412 с. ISBN 5-225-
04630-4
В первом томе представлены основные понятия и методы
математической статистики, изложен курс основ теории вероятностей, где
рассмотрены случайные события, случайные величины и системы случайных
величин. Приведены материалы по анализу данных, статистические
критерии, исследование зависимости групп наблюдений, причем
использованы как параметрические, так и непараметрические современные методы.
Представлены многочисленные примеры, иллюстрирующие прикладную
направленность статистики.
Руководство предназначено для студентов медицинских и
биологических специальностей, медицинских работников и организаторов
здравоохранения, а также ученых и исследователей — специалистов НИИ
медицинского и биологического профилей.
Рассмотрено, одобрено и рекомендовано секцией по социальной
гигиене и организации здравоохранения Ученого Совета МЗ РФ
ББК 51.1(2)
ISBN 5-225-04630-4 © В. А. Медик, М. С. Токмачев,
Б. Б. Фишман, 2000
Все права автора защищены. Ни одна часть этого издания не может быть
занесена в память компьютера либо воспроизведена любым способом без
предварительного письменного разрешения издателя.

Авторский коллектив
МЕДИК Валерий Алексеевич, член-корреспондент РАМН, доктор
медицинских наук, профессор, директор Новгородского научного Центра СЗО
РАМН, заведующий кафедрой социальной медицины, экономики и
управления здравоохранением института медицинского образования
Новгородского государственного университета имени Ярослава Мудрого.
ТОКМАЧЕВ Михаил Степанович, кандидат физико-математических наук,
доцент кафедры прикладной математики Новгородского государственного
университета имени Ярослава Мудрого.
ФИШМАН Борис Борисович, доктор медицинских наук, профессор
кафедры социальной медицины, экономики и управления здравоохранением
института медицинского образования Новгородского государственного
университета имени Ярослава Мудрого.

Оглавление
Предисловие 8
Глава I. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ 12
1.0. О теории вероятностей и вероятностных методах 12
1.1. Основные понятия и определения 15
1.2. Понятие о вероятности случайного события 19
1.3. Классическое определение вероятности 20
1.4. Элементы комбинаторики 21
1.5. Примеры 26
1.6. Вероятность суммы событий. Противоположные события 30
1.7. Условная вероятность. Зависимые и независимые события 32
1.8. Формула полной вероятности. Формула Байеса 37
1.9. Геометрическая вероятность 42
1.10. Статистическое определение вероятности 45
1.11. Понятие об аксиоматическом построении теории вероятностей 48
1.12. Последовательность независимых испытаний. Формула Бернулли.
Наивероятнейшее число успехов 50
1.13. Приближенные формулы, используемые в схеме Бернулли 56
1.14. Функция Лапласа. Интегральная теорема Муавра—Лапласа 60
1.15. Теорема Бернулли (закон больших чисел) 66
Задачи и упражнения 68
Глава II СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 73
2.1. Начальные понятия и определения 73
2.2. Закон распределения случайной величины.
Функция распределения вероятностей 75
2.3. Дискретные случайные величины и их числовые характеристики 80
2.4. Числовые характеристики дискретных случайных величин
(продолжение) 87
2.5. Биномиальное распределение 90
2.6. Распределение Пуассона 92
2.7. Примеры 95
2.8. Некоторые дискретные распределения 104
2.9. Непрерывные случайные величины 111
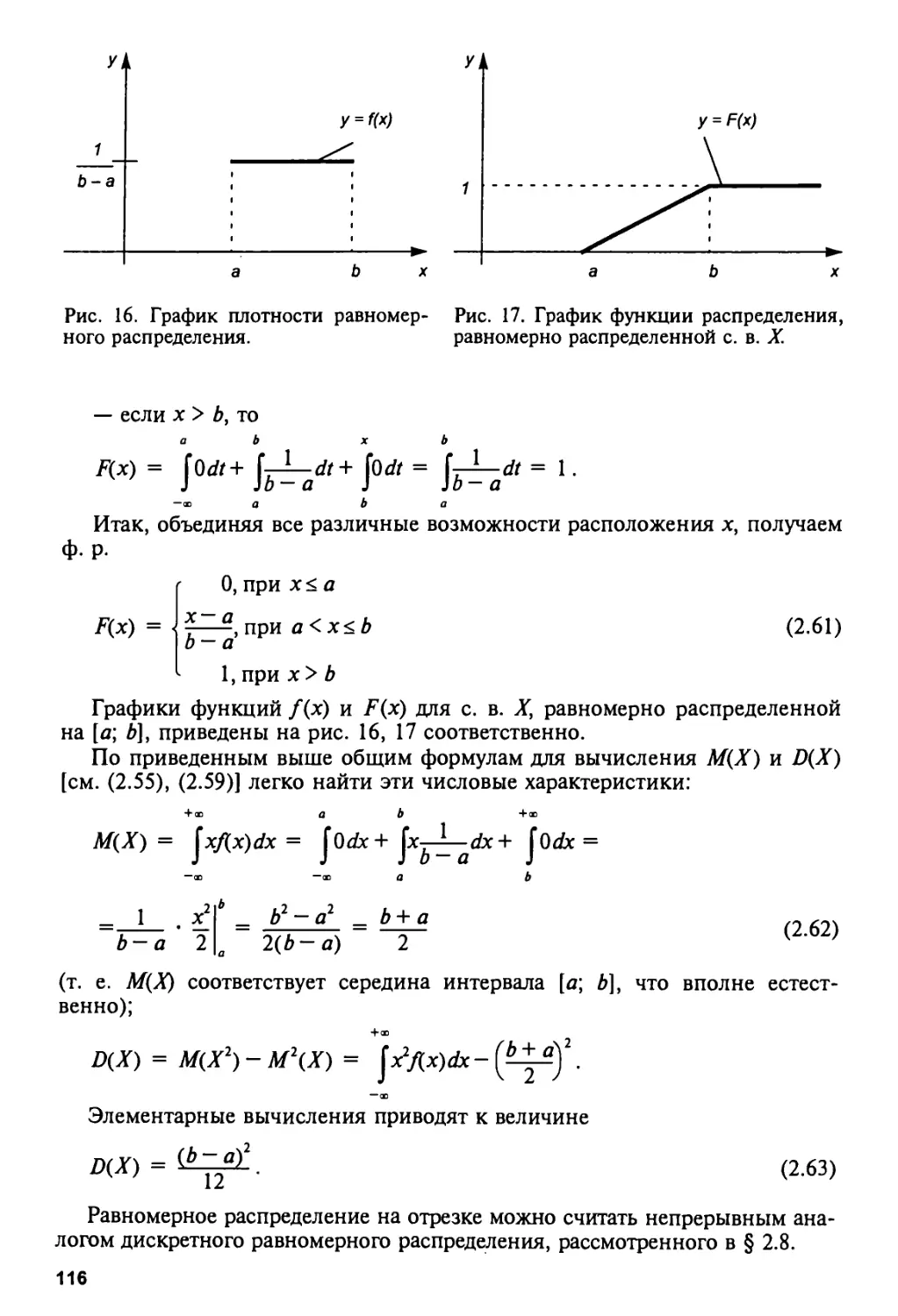
2.10. Равномерное распределение на отрезке 114
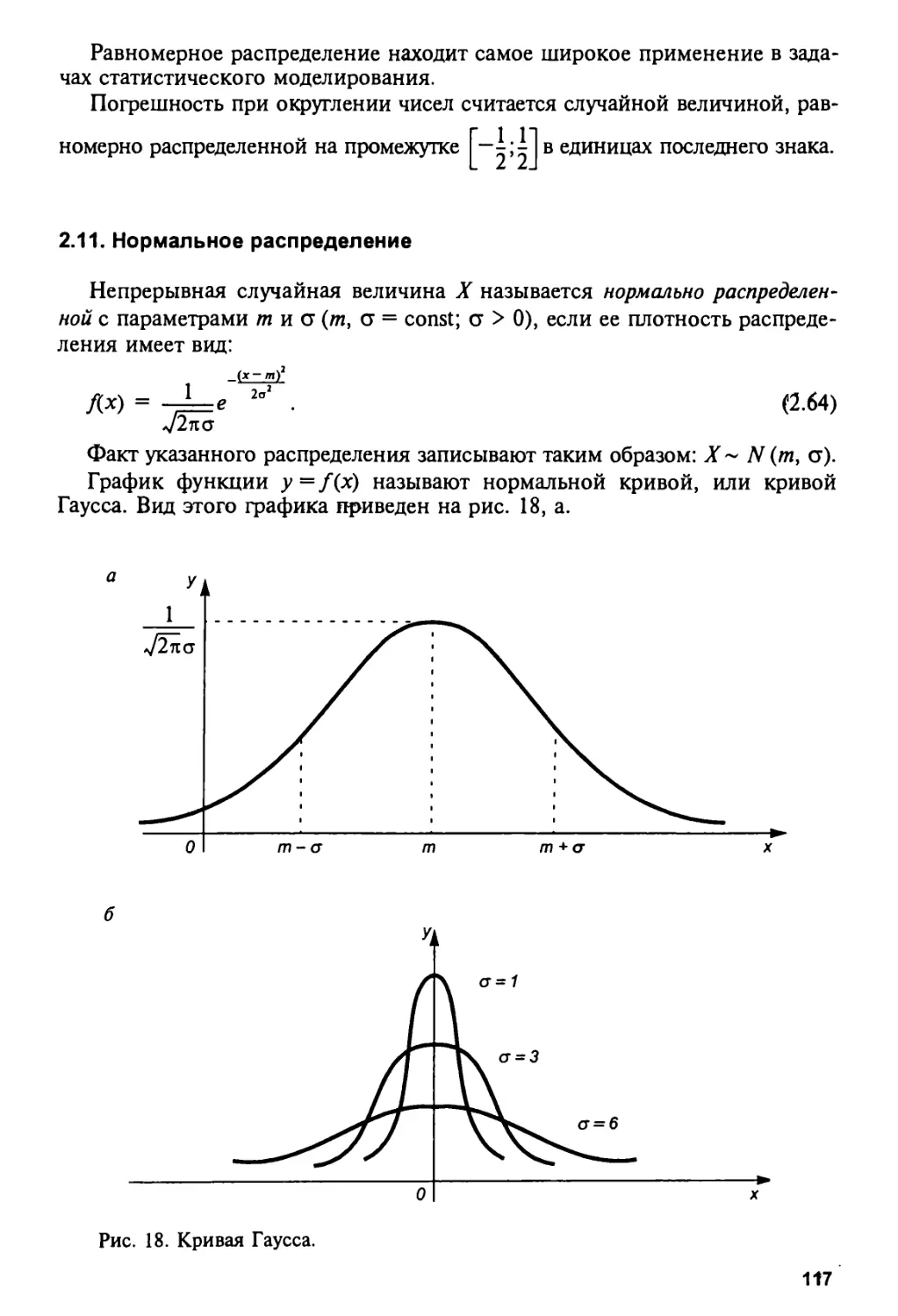
2.11. Нормальное распределение 117
2.12. Числовые характеристики распределений 120
Задачи и упражнения 122
4

Глава III. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН 127
3.1. Функция распределения и плотность распределения
системы случайных величин 127
3.2. Зависимые и независимые случайные величины 130
3.3. Моменты системы случайных величин. Ковариация 131
3.4. Свойства моментов 133
3.5. Независимость и некоррелированность случайных величин.
Коэффициент корреляции 135
3.6. Система двух дискретных случайных величин 137
3.7. Функции случайных величин 140
3.8. Специальные распределения (Пирсона, Стьюдента, Фишера) 144
3.9. Условное распределение. Регрессия. Среди еквадратическая регрессия . . 148
3.10. Предельные теоремы 153
Задачи и упражнения 158
Глава IV ВЫБОРОЧНЫЙ МЕТОД 162
4.1. Предмет и задачи 162
4.2. Основные понятия выборочного метода 163
4.3. Выборочное распределение и его характеристики 164
4.4. Преобразования выборок 170
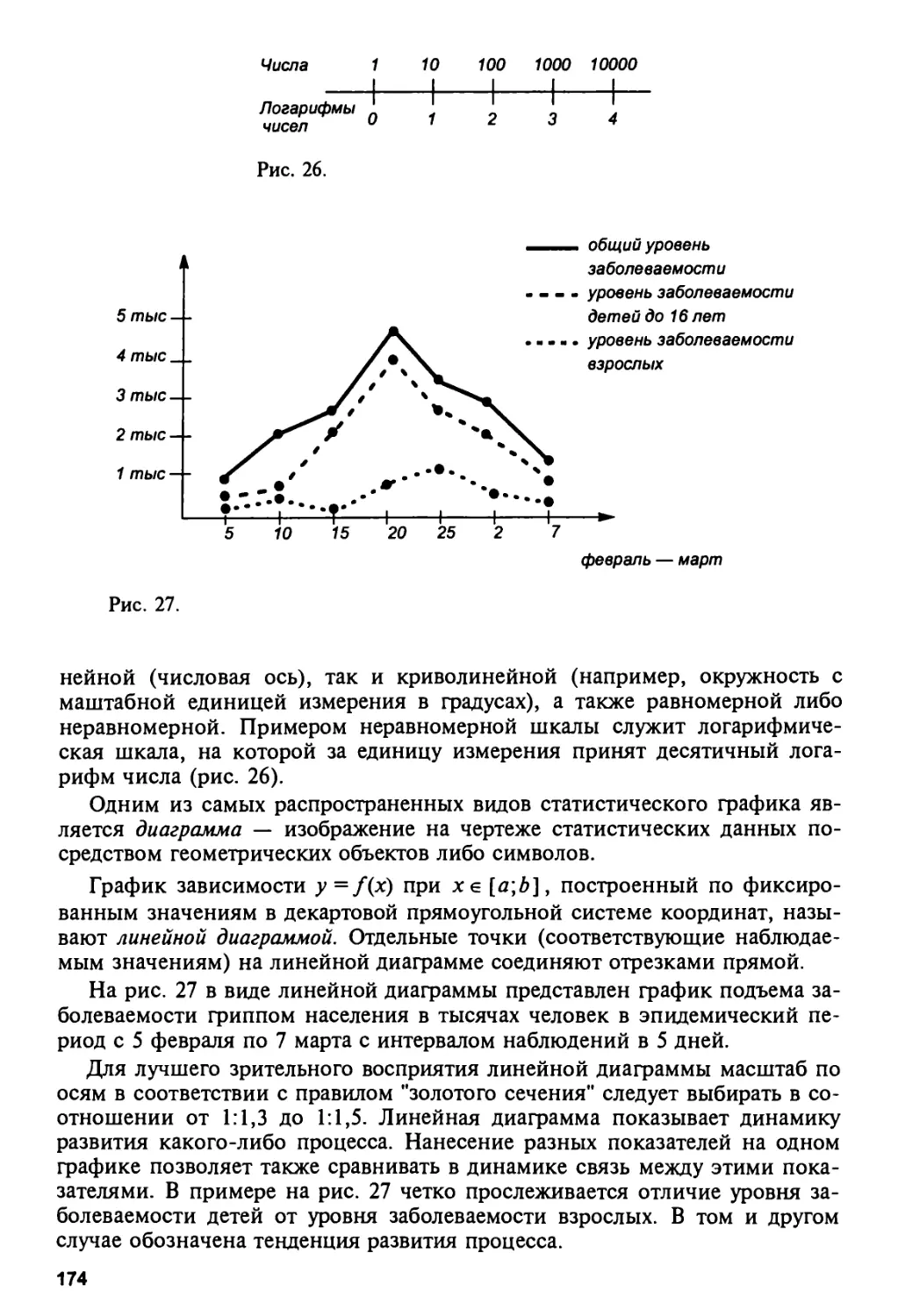
4.5. Графический метод представления статистических данных 173
4.6. Методика выравнивания статистических рядов 180
4.7. Критерии согласия 183
4.8. Практический пример применения критерия согласия (закон Менделя) . 187
4.9. Приближенная проверка гипотезы о нормальном распределении 189
Задачи и упражнения 191
Глава V ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ 196
5.1. Особенности малых выборок. Точечные оценки 196
5.2. Точечные оценки для математического ожидания и дисперсии 199
5.3. Распределения некоторых статистик 203
5.4. Интервальные оценки. Доверительные интервалы 208
5.5. Построение доверительных интервалов для математического ожидания . 209
5.6. Доверительные интервалы для дисперсии 215
5.7. Доверительный интервал для разности средних 220
5.8. Оценка вероятности по частоте 222
5.9. Ошибка выборки. Оптимальная численность выборки 227
Задачи и упражнения 230
Глава VI ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ 235
6.1. Статистическая гипотеза 235
6.2. Статистические критерии 238
6.3. Сравнение дисперсий двух нормальных генеральных совокупностей . . . 242
6.4. Проверка гипотезы о равенстве неизвестной дисперсии
конкретному значению 246
6.5. Сравнение средних двух нормальных генеральных совокупностей
при известных дисперсиях 251
5

6.6. Критерий Стьюдента. Сравнение средних двух нормальных
генеральных совокупностей при неизвестных одинаковых
дисперсиях 256
6.7. Сравнение выборочной средней с известной величиной.
Наблюдения до и после эксперимента 262
6.8. Мощность критерия 267
6.9. Проверка гипотез о вероятности в схеме Бернулли
(одна генеральная совокупность) 275
6.10. Проверка гипотез о вероятности в схеме Бернулли
(две сравниваемые генеральные совокупности) 279
6.11. Таблицы сопряженности и критерий у} 283
6.12. Критерий для процента смертности с учетом возрастных параметров. . . 289
6.13. Критерий Кочрена сравнения дисперсий нескольких
нормальных генеральных совокупностей 292
6.14. Критерий Бартлетта сравнения дисперсий нескольких
генеральных совокупностей 294
Задачи и упражнения 296
Глава VII. ДИСПЕРСИОННЫЙ АНАЛИЗ.
МНОЖЕСТВЕННЫЕ СРАВНЕНИЯ 304
7.1. Основные понятия дисперсионного анализа 304
7.2. Суммы квадратов отклонений.
Общая, факторная и остаточная дисперсии 307
7.3. Однофакторный дисперсионный анализ 311
7.4. Однофакторный дисперсионный анализ
в случае разного числа испытаний на различных уровнях 315
7.5. Схема двухфакторного дисперсионного анализа 319
7.6. Множественные сравнения.
Критерий Стьюдента с поправкой Бонферрони 324
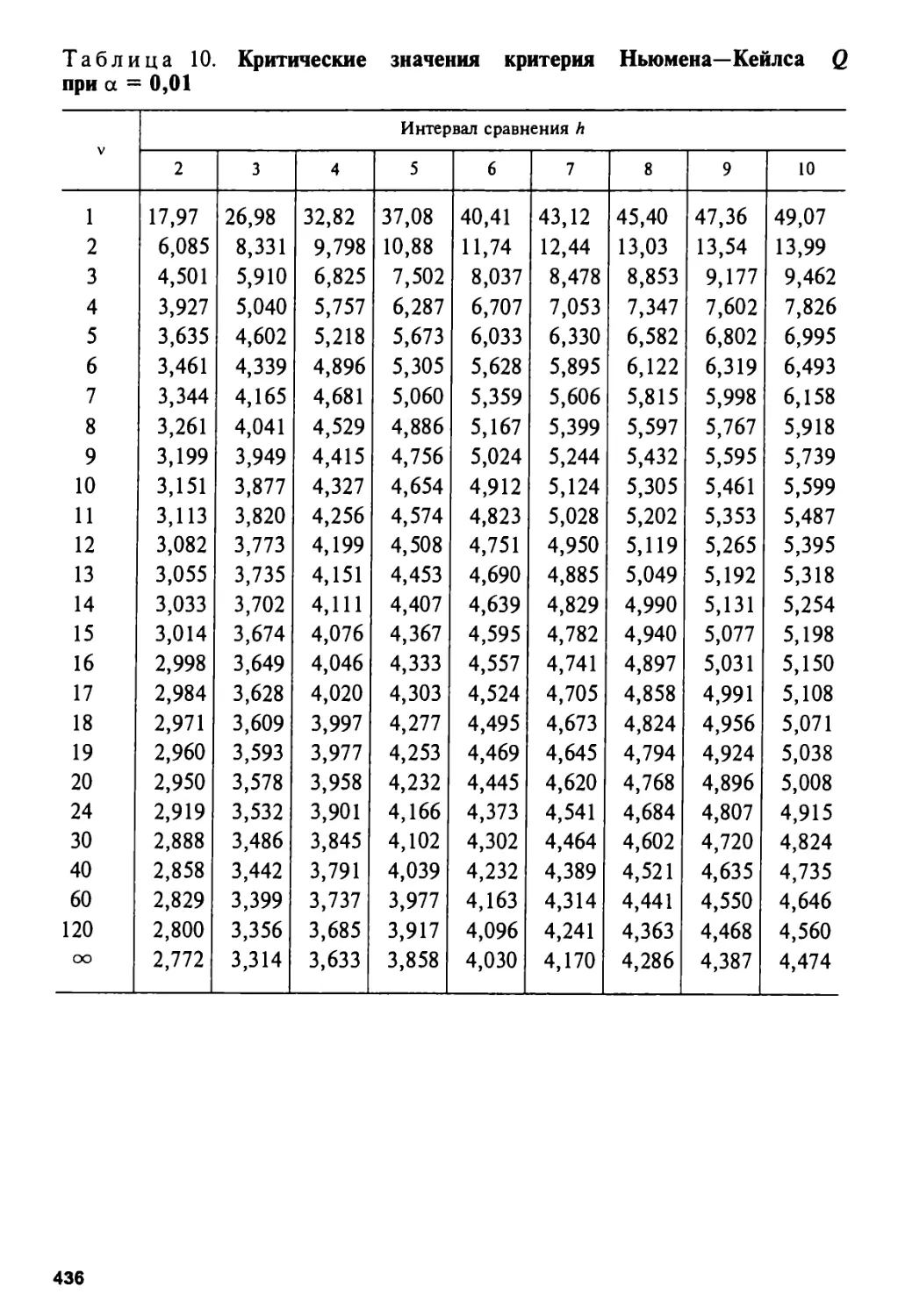
7.7. Критерий Ньюмена—Кейлса 328
Задачи и упражнения 330
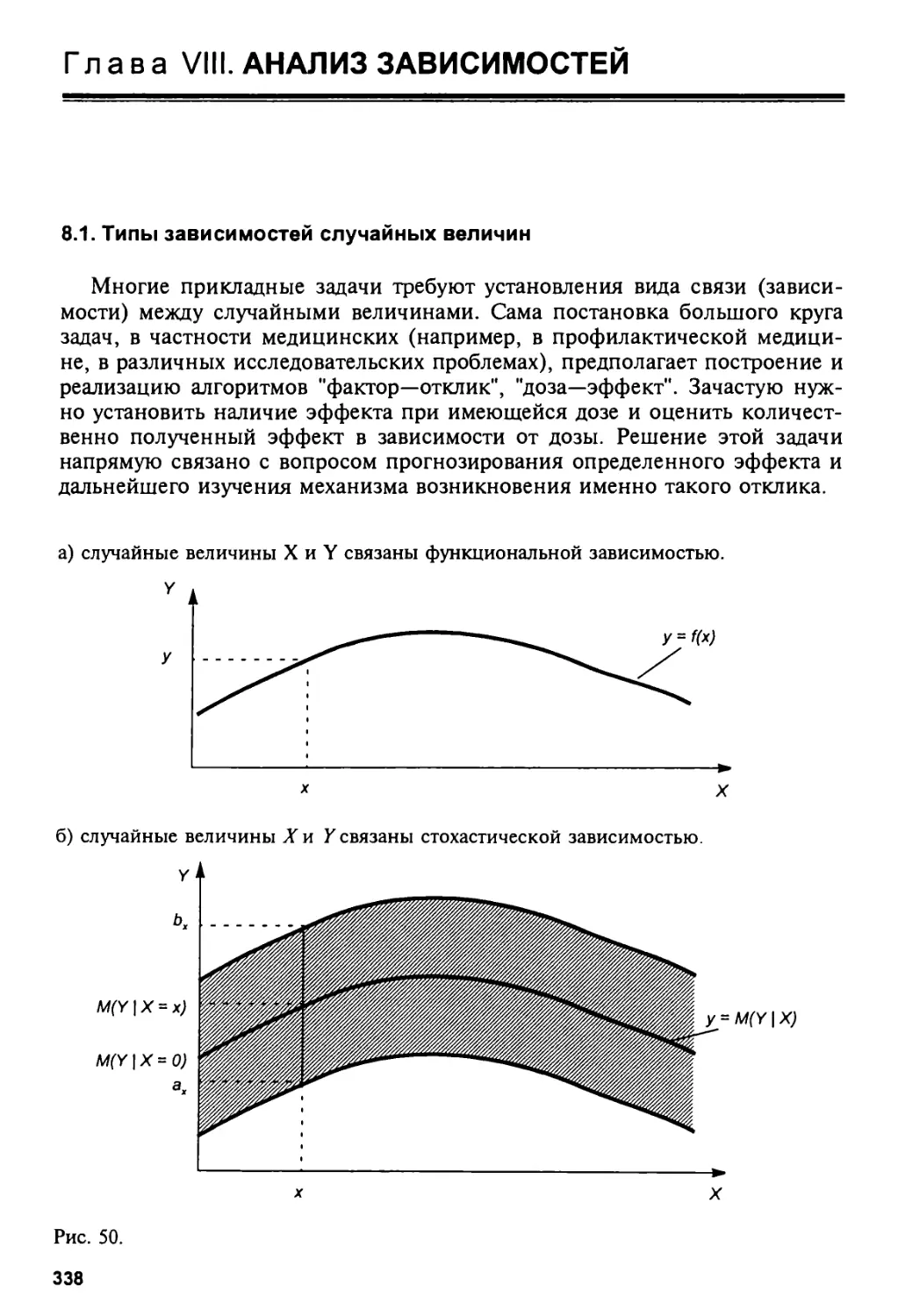
Глава VIII. АНАЛИЗ ЗАВИСИМОСТЕЙ 338
8.1. Типы зависимостей случайных величин 338
8.2. Выборочный коэффициент корреляции 341
8.3. Проверка независимости признаков 345
8.4. Проверка гипотезы о силе линейной связи двух признаков 347
8.5. Выборочная регрессия 348
8.6. Параметры выборочного уравнения регрессии при линейной зависимости 352
8.7. Проверка гипотез о параметрах уравнения регрессии 357
8.8. Использование линейной регрессии в случае нелинейной зависимости. . 358
8.9. Мера любой корреляционной связи.
Выборочное корреляционное отношение 360
8.10. Простейшие случаи нелинейной регрессии 363
8.11. Выборочный коэффициент ранговой корреляции Спирмена 368
8.12. Непараметрические методы оценки корреляционной зависимости . . . . 373
Задачи и упражнения 377
6

Глава IX. НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ 383
9.1. Условия использования критериев 383
9.2. Критерий Манна—Уитни (критерий однородности) 383
9.3. Критерий Уилкоксона (наблюдения до и после эксперимента) 391
9.4. Критерий Краскела—Уоллиса
(проверка однородности нескольких групп) 397
Задачи и упражнения 400
Приложение 1 404
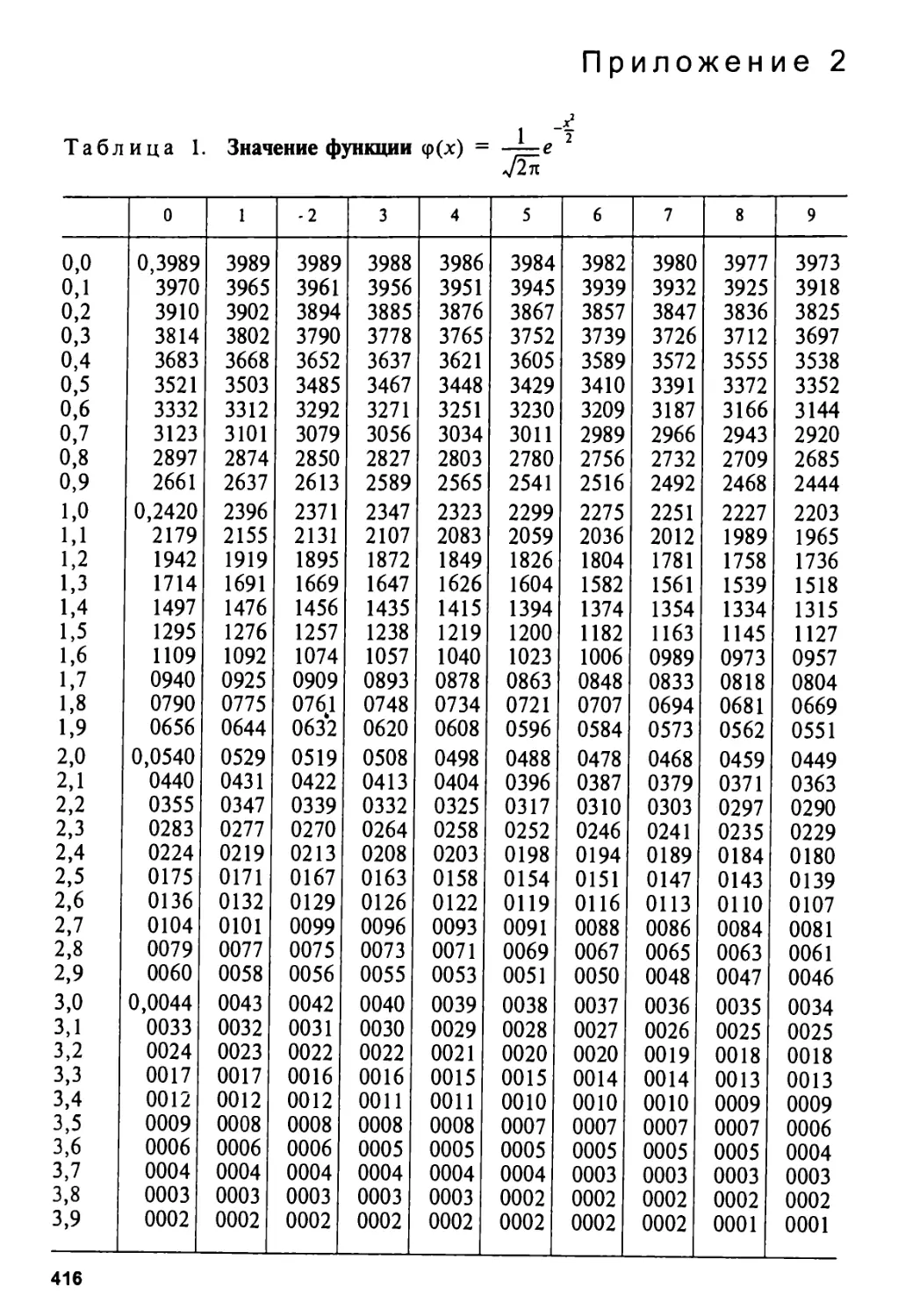
Приложение 2 416
Приложение 3 450
Литература 451

... не проникнуться
воинственностью и мужеством на поле боя от
одной хорошей речи, так же как нельзя
стать музыкантом, прослушав одну
хорошую песню. Этим можно
овладеть только после длительного и
основательного обучения."
Мишель Монтень
Предисловие
Уважаемый читатель!
Вы берете в руки эту новую книгу и, конечно же, начинаете ее
просматривать с оглавления, и сразу же бросается в глаза, что в одном руководстве
фактически объединены три книги, которые могут носить вполне
самостоятельный характер, первые две из которых посвящены математическим
аспектам статистики (теоретической и практической), а третья
(прикладная) — статистике здоровья и здравоохранения.
Ранее на эти темы для медицинских работников существовали
фундаментальные руководства, выпущенные как в России (Козлов, Медков,
Поляков, Шиган и др.), так и за рубежом с переводом на русский язык
(Сепетлиев, Фишер, Бейли и др.). К сожалению, эти руководства в
настоящее время стали раритетами и, естественно, не очень доступными
современному читателю. С другой стороны, за последние годы в
статистике произошел целый ряд коренных изменений, связанных прежде
всего с использованием современных компьютеров и адекватного
программного обеспечения. Если раньше достаточно было, исходя из
обработки данных пробного исследования, рассчитать основные параметры
вариационного ряда и с учетом необходимой достоверности и
устойчивости результатов можно было определить численность выборки, то в
последние годы наряду с этим традиционным подходом, зародившимся в
недрах Эдинбургской школы, все чаще используются вероятностные
методы и подходы. Если раньше для оценки взаимосвязей и других
отношений между изучаемыми явлениями достаточно было использовать ме-
8

тоды оценки достоверности различий, Г-критерий Стьюдента, хи-квад-
рат, коэффициенты сопряженности Пирсона и Чупрова, метод Спирмена
и т. д., а затем стали применяться более сложные методы и модели
(линейные и многофакторные корреляционный, регрессионный,
дисперсионный анализы и т. д.), то в настоящее время можно использовать
готовый пакет программных средств, значительно облегчающий всю
вычислительную работу. К этому следует добавить необходимость понимания
возможностей каждого метода и разной интерпретации полученных
результатов, ибо очень часто применение методов математической
статистики отражает дань моде, а не целесообразности для данного
конкретного исследования.
Вместе с тем остаются незыблемыми основные постулаты и атрибуты
любого исследования: методы планирования исследования и
эксперимента, случайного, непреднамеренного и многоступенчатого отбора,
правильного выбора объекта и предмета исследования, формирования выборки и
расчета ее численности, определения этапности и уровней проведения
исследования, определения необходимости контрольной группы и ее
численности, оценки достоверности, устойчивости и представительности
полученных результатов и т. д. и т. п.
Как представляется, уровень требовательности к применению
статистических методов в медицине и здравоохранении, несмотря на
возросшие возможности, в последние десятилетия несколько снизился, что
заметно на примере и плановых и даже диссертационных исследований. С
чем это связано? На наш взгляд, с тем, что традиционно существовавшие
в нашей стране медико-статистические школы, локализованные главным
образом в Москве и Санкт-Петербурге, со сменой поколений постепенно
утрачивали свои позиции, и в наши дни осталось считанное число
носителей этих идей. Конечно же, все это не могло не сказаться на качестве
преподавания статистики в медицинских вузах и средних учебных
заведениях, на формировании мировоззрения у молодых ученых и
специалистов. И если в клинике, гигиене, социальной гигиене эти методы еще
применяются, то в работах по организации здравоохранения они
становятся редкостью.
Таким образом, вопрос о преемственности поколений, сохранении и
развитии научных школ носит далеко не риторический характер.
Вследствие того, что нередко руководители органов и учреждений
здравоохранения не всегда владеют статистическими методами, становятся нередкими
случаи неверной интерпретации исходных данных и рассчитанных
показателей, а выводы, сделанные на этой основе, не просто неверны, но и
зачастую вредны. До сих пор у нас продолжаются сравнения несравнимых
данных, без понимания различий в определениях, методах измерения, без
стандартизации и т. д.
До сих пор, анализируя демографические показатели, показатели
ресурсов и деятельности здравоохранения, делаются неправильные выводы, что
свидетельствует о чрезвычайно поверхностной подготовке целого ряда
политических, общественных и медицинских деятелей. Когда их спрашива-
9

ешь, например, какое население Вы использовали (наличное, постоянное,
на начало года, на конец года, среднегодовую численность, в том числе
рассчитанную как среднеарифметическое, среднегеометрическое, средне-
гармоническое или взвешенное и т. д.) или что входит в ВВП и как он
исчисляется, то в глазах видишь полное изумление.
Именно по указанным выше причинам мы допустили отставание от
многих западных стран в проведении широкомасштабных
эпидемиологических исследований (еще недавно термин "эпидемиология" у нас
относился к инфекционным болезням и применялся не только для изучения их
распространенности, но и для оценки триады Л. В. Громашевского:
источник — механизм — реципиент) и особенно в области клинической
эпидемиологии, оформленной в виде науки 30 лет назад. А это в свою очередь
повлияло на доказанность и верность выводов, на политику в области
здоровья и здравоохранения, на проведение рандомизированных
исследований, на развитие доказательной медицины, т. е. на установление связей
между результатами и технологиями, а значит, на обеспечение качества
медицинской помощи. Еще раз напомню, что в основе этого отставания
находится отсутствие достаточных и широких взглядов в области
статистики.
Вот почему так актуально и необходимо настоящее руководство,
представленное на рассмотрение читателю. Оно получилось большим,
сложным, достаточно математизированным и имеет известные достоинства и
недостатки. В то же время оно просто необходимо для использования в
первую очередь в преподавании дисциплины, а затем — для
исследовательской и аналитической работы.
В настоящем руководстве будет сделана системная попытка показать,
каким образом методы математической статистики, распознавания образов
и прогнозирования можно применить к описанию и моделированию такой
"диффузной", плохо организованной системы, как здоровье населения.
Действительно, принципиально невозможно установить жесткие
функциональные зависимости между величинами заболеваемости,
нетрудоспособности, смертности населения и др. и полом, возрастом, профессией,
социально-бытовыми условиями и т. д., хотя, несомненно, зависимости каких-
то типов здесь все же существуют.
Во введении в настоящее руководство мною сформулированы основные
принципы применения методов математической статистики в медицине и
биологии, изложенные в виде обзора.
В дальнейшем авторами в первом томе представлены случайные
события, случайные величины и системы случайных величин, методы
анализа полученных данных, статистические критерии, исследование
зависимости групп наблюдений, причем рассматриваются как
параметрические, так и непараметрические методы. Существенное внимание
уделено интерпретации полученных результатов. Рассмотрены
многочисленные примеры. Во втором томе проанализированы современные
представления о статистике здоровья и здравоохранения.
10

Таким образом, заинтересованный читатель может получить достаточно
подробную информацию о статистических подходах, методах и приемах и
использовать их в своей повседневной работе.
Комаров Ю. Л/., доктор медицинских наук,
профессор, заслуженный деятель науки РФ

Посвящается светлой памяти
первого президента Новгородского
государственного университета академика
Сороки Владимира Васильевича
Глава I. СЛУЧАЙНЫЕ СОБЫТИЯ. ВЕРОЯТНОСТЬ
1.0. О теории вероятностей и вероятностных методах
Окружающий нас мир представляет огромное многообразие различных
явлений, процессов, событий, взаимосвязанных между собой
бесчисленными нитями причинно-следственных зависимостей. В большинстве
явлений хитросплетение множества различных связей настолько сложно, что
предсказать заранее осуществление того или иного события не
представляется возможным. Например, невозможно предсказать точно, сколько лет
проживет конкретный ребенок, родившийся сегодня абсолютно здоровым.
Невозможно точно предсказать, когда и какими болезнями он
переболеет, с какими последствиями, каковы параметры его здоровья будут через
20 лет и вообще доживет ли он до этого возраста. Даже внешние данные
(рост, масса тела) заранее вычислить невозможно. Точно так же мы до
определенного времени не можем знать, в каком возрасте этот человек
вступит в брак (и женится ли вообще?), сколько будет иметь детей, сколько
мальчиков и сколько девочек, какую профессию он изберет и в какой
местности будет жить и т. д. За словами "т. д." кроется бесконечное
количество вопросов, на которые невозможно до определенного момента (до
осуществления испытания) дать однозначные ответы. Причина этого
"незнания" объясняется обилием случайностей, которые сопровождают нашего
новорожденного на протяжении всей жизни. И если каких-то
случайностей можно сознательно избежать, то на их место придут другие
случайности. Следует отметить, что случай играет как негативную, так и
позитивную роль, примеров тому любой читатель может привести предостаточно.
Наличие неопределенности исхода проявляется не только на большом
временном отрезке, но и в каждое следующее мгновение. Например,
подбрасывая стандартную монету, мы не можем гарантировать исход данного
испытания: однозначно выпадение "орла" или выпадение "решки". Даже если
испытания будут проводиться при сравнительно одинаковых условиях (в
частности, пусть монетка подбрасывается специальной сверхточной
"бросательной машиной"), нет никакой гарантии, что малейшее неуловимое
отклонение от начальных условий не приведет наши испытания к
различным исходам.
Случайность всеобъемлюща, она проявляет себя во всех явлениях
окружающего нас мира, будь то физические, химические, биологические,
социальные и другие процессы.
12

Однако доля неопределенности, доля случая в разных ситуациях
совершенно различна. И если исход одних явлений становится полной
неожиданностью, то в других компонента случайности столь мала, что результат
прогнозируется практически однозначно. Например, набирая номер
телефона, мы не сомневаемся, что на другом конце провода раздастся звонок,
или, смешивая растворы Ва(ОН)2 и H2S04, обязательно получим осадок
молочно-белого цвета. В то же время мы с гораздо меньшей уверенностью
можем утверждать, что набираемый нами абонент окажется у телефона,
или, смешивая произвольные растворы, получим предполагаемый эффект.
Резюмируя сказанное, можно утверждать, что практически все явления
окружающего нас мира происходят с той или иной степенью
неопределенности, спектр которой простирается от полной непредсказуемости до
несомненной однозначности исходов.
При такой точке зрения естественно ввести некоторую характеристику
явлений, выражающую меру неопределенности или меру нашей
уверенности в исходе испытания. Рассматривая численное выражение этой меры,
можно случайность не только описывать, но и исследовать, учитывать и
использовать для прогноза.
Меру нашей уверенности восходе испытания.и . ^шыдавдизюэдято-
стью. Вероятность — объективная характеристика. Во избежание возмож-
ньТхНнедоразумений, разночтения, субъективности исследователя
необходимо ввести более точное определение термина "вероятность" и подчинить
ее (вероятность) некоторым правилам, соответствующим здравому смыслу
и не противоречащим жизненному опыту. Наука, в основу которой
положено понятие вероятности и которая занимается_выявлением_и изучением
закономерностей в случайных явлетШ^з^ы^ё^^Т^Ш^ЗЁРШТМО&Х^-
Теория вероятностей — наука математическая, так как широко
использует математический аппарат, но область приложений этой науки
безгранична. Численная интерпретация случайности позволяет находить
специфические закономерности, специфические вероятностные законы, что в
конечном итоге опровергает тезис о хаотичности, бессистемности
случайных явлений. В настоящее время появились новые науки,
разрабатывающие тактику и методы действия в среде со случайными факторами: теория
массового обслуживания, теория случайного поиска, теория игр, теория
катастроф и некоторые другие.
Чем далее развивается наука, тем более аргументированными
становятся положения о вероятностной основе окружающего мира: мир построен
на вероятности.
Классическая наука исследует, как правило, детерминистические
закономерности: например, площадь любого треугольника равна '/2 ah, длина
пути при равномерном движении всегда равна vt. Эти соотношения
справедливы при любом исходе испытания (в данных конкретных случаях при
измерениях используемых параметров). В случае с подбрасыванием
стандартной монеты исход испытания неоднозначен и детерминистической
закономерности выпадения "орла" или "решки" нет. Используя
вероятностный подход, можно утверждать, что «вероятность выпадения "орла" равна
У2» (т. е. 50 %). Смысл этого утверждения в следующем: если данное
испытание производить достаточно большое количество раз, то "орел"
появится в среднем в 50% исходов. Детерминистические закономерности, та-
13

ким образом, являются частным случаем вероятностных, т. е. события
npoHcxoAHT^js^ofliimcii^J^^j'pp^^cnbiTaHHft). Для многих задач
вероятностная оценка результата является вполне удовлетворительной.
Следует отметить, ЧТО TPnjwg_ggpnirmnr.Tfttt ичучяр/г только массовые яв-
ления, а именно: явления, которые могут быть повторены достаточно
большое количество раз, а теоретически и бесконечное число раз. Теория
вероятностей изучает события, обладающее статистической, устойчиво^
стью, т. е. события, относительная частота появления которых с ростом
количества испытаний стабилизируется, колеблется около некоторого
значения (именно это значение и будем считать вероятностью
рассматриваемого события). Этот факткакраз jl выражает, закономерность в среде
случайности. Как известно из курса философии, поихт^а^ШЧййнодх^лз^н&о^-
ходимостй,_ случайности и закономерности (порядка) диалектически
йаТтао^ЖаньГ.Хвязующеё звено между этими"антагонисте
тйямй — комплекс условий, при которых происходит случайное явление
(испытание). Дри многократном повторении испытаний комплекс условий
должен оставаться неизменным. При этом из^ножества случайностей
вырисовываются закономерность и"гТорядо"к, которые и находят свое выражё-
ние в понятии вероятности. ф&ШТЯ&£^У№зШ&&Т'Ш 'Нал*йчйеГ*а также
[степе^^вязи^комплекса условий и осуществления случайного события. _
^ори^_МР^ятностёи не изучает уникальные^события: события, которые
заведомо нельзя считать многократно повторяющимися или массовыми.
Например, события (высказывания) —
к 2005 г. будет найдено эффективное лекарство против СПИДа;
в 1980 г. нынешнее поколение будет жить при коммунизме;
следующим президентом страны будет избран гражданин N;
в 1994—1996 гг. в Ядранском (Адриатическом) море будет выловлена
"дивная рыба с человеческой головой" (предсказание Нострадамуса) —
относятся к уникальным. И хотя указанные события, безусловно, содержат
в себе элементы случайности — могут произойти или не произойти, они
(так же как, впрочем, и их авторы) к теории вероятностей отношения не
имеют. Произойдут ли данные события — может показать только время.
Рассматривая вероятность как меру неопределенности, следует
опираться на знания, на информацию, извлеченную из наблюдения и из
предшествующего опыта. Ни в коем случае нельзя при отсутствии
информации объявлять возможные исходы испытания равновероятными,
ибо в этой ситуации наши рассуждения базируются на незнании, что
обычно не приводит к позитивным результатам. По той же причине в
теории вероятностей не рассматриваются и уникальное события: нельзя
основываться на незнании, а знание закономерностей, следовательно, и
вероятностей извлечь неоткуда, так как отсутствует "пЪТГгбр^ёмость собы"~
тий и их массовость.
Отметим также не только субъективность, но и объективную природу
случайности, которой присущи в массовых явлениях свои специфические
черты, не проявляющиеся в отдельных испытаниях.
Следует подчеркнуть особую роль в вероятностных исследованиях
статистики, которая является практической копией теории вероятностей.
Именно статистика поставляет данные, необходимые для применения
вероятностных методов.
14

Учитывая эту специфику, можно утверждать, что во многих
практических задачах в самых различных областях естествознания и деятельности
человека вероятностный подход является наиболее целесообразным и
соответствующим объективной истине.
В частности, современная медицина, имеющая объектом
исследования множество индивидуумов, отличающихся друг от друга по
всевозможным различным показателям, имеет вероятностную основу и широко
использует вероятностные и статистические методы. Без знания этих
методов невозможно осмысление целого ряда медико-биологических
научных дисциплин, и эффективная деятельность медицинского работника
существенно зависит от его компетентности в области применения
указанных методов.
1.1. Основные понятия и определения
В предыдущем параграфе мы вольно, исходя из обыденного смысла,
употребляли многие термины, значение которых необходимо определить
более четко. В противном случае неминуемо придем к разночтению,
двусмысленности и в конечном итоге к непониманию. Поэтому
представляется крайне важным для многих используемых понятий определить их в
нужном нам смысле. Строгость таких определений различна и зависит в
основном от уровня математичности изложения.
Условимся испытанием называть ася^ш_0ДЬ1тг при проведение
которого задана совокупность условий, неоднозначно пр!гдЪпределяющая исход
этого опыта. — — - —
Несколько примеров испытаний:
— подбрасывание игральной кости с выпадением какой-то грани, на
каждой из которых указано количество очков от одного до шести;
— перепад атмосферного давления и температуры воздуха;
— способ лечения данного заболевания;
— некоторый период жизни человека и т. д.
Результатом данного испытания будет какое-то произошедшее явление,;
а точнее одно из возможных явлений, которые могли бы осуществиться/
Эти явления принято называть случайными событиями. Таким образом,
случайным co6Tirae~M~~no отношению к данному испытанию называют
явление, которое может произойти или не произойти в зависимости от
исхода этого испытания.
Условимся обозначать случайные события большими буквами
латинского алфавита: А, В, С, .... Например, при испытании, заключающемся в
подбрасывании игральной кости, возможные случайные события — это:
Ах — выпадение одного очка;
А2 — выпадение двух очков;
А€ — выпадение шести очков.
Эти события простые (элементарные), однако по отношению к данному
испытанию можно найти и другие случайные события, получающиеся из
элементарных: А — выпадение четного числа очков; В — выпадение числа
очков, больших чем 4; С — выпадение числа очков, кратного 3 и т. д.
15

Таким образом, с испытанием связывают некоторое множество
случайных событий, осуществление которых возможно в результате данного
испытания. Например, степени обострения ишемической болезни
сердца, включая случаи смерти, являются случайными событиями при
испытании — резком повышении температуры воздуха зимой.
Чтобы со случайными событиями производить какие-то операции типа
арифметических — сложения, умножения1, необходимо к множеству
случайных событий добавить еще два: невозможное событие (играет роль
нуля или, точнее, пустого множества — (0) и достоверное событие
(охватывает все множество возможных событий).
Случайное.j£o§^1^.M^M^1^t достоверным по- оти©1некикг-к~ данному
испытанию, если оно осуществляется при любом исходе этого испытания.
УслбвТшся достоверное событие обозначать буквой U.
Случайное событие называют невозможным по отношению к данному
испытаниГО7"е"слтгоно неосуществимо при любом исходе этого испыта«ия.
Также условимся обозначать невозможное £o6biiHeJ5jKj3oJM^
Следует отметить, что все события определяются по отношению к
данному испытанию, т. е. события являются следствием определенного
комплекса условий, предполагаемых при испытании. Изменение этих условий
влечет изменение результата испытаний: меняется взаимосвязь множества
случайных событий, вплоть до того, что событие) невозможное при одном
комплексе условий, может оказаться вполне реальным (или даже
достоверным) при других условиях. Поэтому теория вероятностей, изучая
случайные события, всегда связывает их с определенным испытанием. Если же
испытания повторяются, то предполагается, что комплекс условий,
сопровождающий испытания, неизменен.
Два события А и В называют эквивалентными (или равносильными) по
отношению к данному испытанию, если из факта осуществления одного
из них следует обязательное осуществление другого: например, из
осуществления А следует осуществление В, а из осуществления В следует
осуществление А. Эквивалентные события обозначают обычным равенством:
А = В. Пример эквивалентных событий при бросании игральной кости: А —
выпадение "шестерки", В — выпадение четного числа очков, большего
четырех.
Введем операции сложения и умножения случайных событий.
Суммой случайных событий А и В называют случайное событие С,
состоящее в осуществлении хотя бы одного из событий-слагаемых.
Обозначение: А + В = С. Если события представить как множества А и В (рис.1),
то суммой событий называют объединение этих множеств (AvB). На рис.1
объединением множеств является заштрихованная область, которая
состоит из трех частей: 1-я — осуществляется только событие А и не
осуществляется В; 2-я — осуществляется только событие В, и не осуществляется А;
3-я — осуществляется и событие А, и событие В (общая часть, т. е. их
пересечение).
'Более точное соответствие случайных событий не с числами, а с множествами. Тогда
операции сложения соответствует объединение множеств (AKJB), а операции умножения —
пересечение множеств (АГ\ В).
16

А* В АВ
Рис. 1. Рис. 2.
Произведением случайных событий А и В называют случайное событие С,
состоящее в осуществлении и события А, и события В. Обозначение
А • В = С. Если события представить как множества А и В, то
произведением событий является пересечение множеств (Агл В) (см. заштрихованную
часть на рис. 2).
Пример. Испытание заключается в извлечении случайным образом из
тщательно перетасованной стандартной колоды, состоящей из 36 карт,
одной карты. Случайное событие А — извлечение карты бубновой масти;
случайное событие В — извлечение туза любой масти.
При данном испытании предполагаемым комплексом условий является
следующая система:
— имеется стандартная колода из 36 карт определенного состава (4
различные масти по 9 карт от "шестерки" до "туза");
— карты в колоде располагаются случайным образом, что достигается
тасованием, и извлекаемая карта берется наудачу.
При этих условиях суммой событий А + В является событие, состоящее
в появлении либо любой бубновой масти (от "шестерки" до "туза"), либо
появление "туза" любой масти, включая бубновую.
Произведением событий А • В является событие, состоящее в появлении
туза бубновой масти.
Заметим, что в данном примере при изменении комплекса условий,
например при замене колоды на стандартную из 52 карт, приходим к
изменению структуры события А и события А + В, а также изменению всего
множества случайных событий, связанных с испытанием.
Для действий над событиями справедливы следующие свойства:
I. А + В = В + А;
2.{А + В)+С = А + (В+С);
З.А + А = А;
4.А-В = В-А;
5. (А-В)- С = А-(В-С);
6.А-А = А;
7.{А + В)-С = А- С+ В-С.
Свойства достаточно простые и естественные, однако следует обратить
отдельное внимание на 3 и 6, справедливость которых непосредственно
следует из определений суммы и произведения случайных событий.
Далее сформулируем некоторые определения, еще раз подчеркивая, что
все они вводятся по отношению к данному испытанию.
2 — 3529
17

Случайные события А и В называют несовместными, если их
произведение является событием невозможным: А • В = V (т. е. А и В не могут вместе
одновременно осуществиться в одном испытании).
Систему п случайных событий Ех, Е2, ..., Еп называют полной, если
сумма событий является событием достоверным: Ех+Е2+ ...+ Еп= U. Таким
образом, хотя бы одно из событий системы Ех, Е2, ..., Еп происходит при
любом исходе испытания.
Систему п случайных событий Ех, Е2, ..., Еп называют несовместной,
если любые два события системы являются событиями несовместными:
Е/' Ej= Уддя всех i = 1, 2, ..., n;j = 1, 2, ..., п; i*j.
Систему п случайных событий Ех, Е2, ..., Еп называют равновозможной,
если никакое из событий системы в своем осуществлении не имеет
приоритетов по отношению к другим событиям системы.
Систему случайных событий называют полной системой элементарных
событий, если эта система полная, несовместная и равновозможная. При
этом слово "элементарное" применительно к случайному событию,
предполагает, что данное событие является простым, а не составным и не
разбивается на систему более простых. Заметим, что понятие элементарного
события столь же неопределяемо, как и понятие точки в геометрии.
Например, при испытании, заключающемся в случайном выборе одной
карты из стандартной колоды в 36 карт, полная система элементарных
событий содержит 36 событий: Ех, Е2, ..., Е^. Каждое их этих событий
состоит в появлении одной из 36 различных карт. Эта система действительно
полная (одна из 36 карт обязательно появится), несовместная (извлеченная
карта одновременно не может быть, например, "шестеркой пик" и "валетом
треф"). Равновозможность обеспечивается случайным выбором. При этом
наряду с элементарными мы можем рассматривать и другие случайные
события, в частности:
А — появление "туза" (состоит из объединения четырех элементарных
событий);
В — появление карты бубновой масти (состоит из объединения девяти
элементарных событий) и т. д.
Событие А называют благоприятствующим событию В, если из
осуществления А следует осуществимость события В.
Событие А называют неблагоприятствующим событию В, если из
осуществления события А следует неосуществимость события В.
Например, испытание — подбрасывание игральной кости. Полная
система элементарных событий состоит их шести случайных событий Ех, Е2,
..., Е6 — выпадение соответствующего количества очков. Событие В —
выпадение четного числа очков. Для события В благоприятствующими
являются следующие события: Е2 — выпадение "двойки", ЕА — выпадение
"четверки", Е6 — выпадение "шестерки". Неблагоприятствующими для события
В будут следующие события: Ех — выпадение "единицы", Е3 — выпадение
"тройки" и Е5 — выпадение "пятерки".
18

1.2. Понятие о вероятности случайного события
Введенные выше случайные события должны иметь некоторую
характеристику, опираясь на которую можно судить о степени ожидаемости того
или иного события. Данная характеристика должна быть объективной, т. е.
зависеть не от мнения автора прогноза, а от комплекса условий, при
которых происходит испытание, и соответствующей многократно
повторяющимся наблюдениям. Данная характеристика должна быть универсальной,
так как призвана характеризовать случайные события самой различной
природы. Вводимая характеристика должна позволять сравнивать и
сопоставлять различные события по степени их достоверности.
Вывод — всем перечисленным условиям удовлетворяет числовая
характеристика, т. е. каждому случайному событию в испытании ставят в
соответствие некоторое число, которое и называют вероятностью
рассматриваемого события. Обозначают вероятности так же, как и функции: Р(А) —
вероятность события А в заданном испытании. Часто для удобства записи
аргумент не пишут, а для значения вероятности используют строчные
латинские буквы, например Р(А) = р, Р(В) = q , Р(АХ) = рх и т. д.
На виде рассматриваемого соответствия и правилах вычисления
остановимся позднее в последующих параграфах. Однако следует подчеркнуть, что
понятие вероятности вводится точно так же, как многие понятия в известном
школьном курсе геометрии. Например, никого не удивляет и не вызывает
особых трудностей понятие площади плоской фигуры, в основе которого тоже
лежит соответствие между свойствами фигуры и числами. По определению
вводится число а2, соответствующее одной из самых простых фигур, квадрату со
стороной а, затем указываются способы вычисления площадей
прямоугольника, прямоугольного треугольника, произвольного треугольника,
многоугольников. Используя понятия предела, а затем определенного интеграла,
вычисляются площади круга, криволинейной трапеции и далее площади фигур
произвольной формы, а также и площади поверхностей различных объемных тел.
Аналогично вводится в геометрии и понятие объема тел. По мере усложнения
структуры исследуемых объектов возникают новые связи между понятиями,
новые определения, выявляются новые закономерности.
Аналогично построена и теория вероятностей. В роли простейшей
геометрической фигуры — квадрата — выступает полная система
элементарных событий, введенная в § 1.1. Простота этой системы определяется
конечным числом элементарных событий и особенно условием равновоз-
можности (сравните с равенством сторон квадрата). Для полной аналогии
можно сопоставить условие несовместности событий в полной системе
элементарных событий с наличием прямых углов в квадрате.
Таким образом, если Вы хотите в теории вероятностей достичь уровня,
соответствующего умению в геометрии вычислять площади квадрата и
некоторых близких к нему фигур, достаточно изучить классическое определение
вероятности и некоторые приемы комбинаторики. Однако если Вы занимаетесь
более сложными проблемами, нежели задачи, связанные с простым
пересчетом вариантов, следует иметь представление и о более общем определении
вероятности, а также оперировать понятиями: случайная величина, функция
распределения, закон распределения, числовые характеристики случайных
величин, корреляция, регрессия и др. Обо всем этом далее и пойдет речь.

1.3. Классическое определение вероятности
Пусть по отношению к данному испытанию имеем полную систему
элементарных событий Ех, Е2, ..., Еп. Событие А таково, что любое из
событий системы либо благоприятствует осуществлению А, либо не
благоприятствует. Обсуждаемую ранее возможность осуществления события А
определим с помощью числовой характеристики (меры), которую и
назовем вероятностью случайного события.
Определение. Вероятностью случайного события А называют число,
обозначаемое Р(А) и равное отношению т/п, где п — число всех
элементарных событий системы; т — число элементарных событий в системе,
благоприятствующих осуществлению А.
Таким образом, введена простая формула
Р(А) = 2.
п
В соответствии с этой формулой справедливы свойства вероятности:
Свойство 1. Вероятность любого случайного события является числом
неотрицательным.
Справедливость данного соотношения следует из неотрицательности
чисел тип.
Свойство 2. Вероятность любого случайного события всегда
удовлетворяет двойному неравенству
0<Р(А)<\.
Справедливость данного соотношения следует из простого факта, что
О < т < п, который означает, что число событий, благоприятствующих А,
не больше, чем число всех элементарных событий системы и, конечно же,
не меньше нуля.
Свойство 3. Вероятность достоверного события равна 1. (P(U) = 1).
Это верно, так как для достоверного события благоприятствующими
являются все п событий системы:
P(U) = n/n= 1.
Свойство 4. Вероятность невозможного события равна нулю.
(P(V) = 0).
Утверждение верно, так как для невозможного события среди полной
системы элементарных событий благоприятствующих нет:
P(V) = О/л = 0.
Пример. Из стандартной колоды в 36 карт наудачу выбирается одна
карта. Найти вероятность, что выбранная карта является тузом (масть роли
не играет).
Решение. Обозначим искомое случайное событие символом А. Полная
система элементарных событий состоит из 36 событий (п = 36), среди
которых благоприятствующими для осуществления А являются 4 события,
так как в колоде 4 туза (т = 4). Таким образом, по введенной выше
формуле получаем
Р(А) = т/п = 4/36= 1/9.
Смысл найденного числа (вероятности) состоит в следующем: если
данное испытание — извлечение карты — проводить многократно, то в
среднем доля случаев появления туза (безразлично какой масти) составит при-
20

близительно % среди всех исходов испытаний. И чем больше испытаний
проводится, тем точнее эта доля соответствует %.
Отметим, что однократное появление туза в 9 испытаниях является
наиболее вероятным событием, наиболее ожидаемым и не более того: в
конкретных 9 испытаниях туз может появиться любое число раз от нуля до
девяти. А для проявления вероятности необходима массовость испытаний.
1.4. Элементы комбинаторики
Вычисление вероятностей случайных событий в условиях классического
определения в конечном итоге сводится к пересчету различных вариантов,
к пересчету количества комбинаций. А эти вопросы о количестве
комбинаций, которые можно составить, имея элементы произвольной природы,
относятся к компетенции раздела дискретной математики, называемого
комбинаторикой. Отметим, что многие формулы, методы и приемы
комбинаторики используются не только в собственно математических
дисциплинах, но и в областях визуально исторически достаточно далеких от
математики: биологии, медицине, логике, лингвистике и др.
Вначале рассмотрим примеры.
Пример 1. В магазине в продаже имеется 5 видов хлеба и 15 видов
колбас. Сколькими способами можно составить бутерброд (имея в виду
определенный вид хлеба и определенный вид колбасы)?
Решение. Хлеб можно выбрать пятью различными способами, и с
каждым из этих способов комбинируется один из 15 видов колбасы, т. е. с
хлебом первого вида можно составить 15 различных бутербродов, с хлебом
второго вида — 15 бутербродов и т. д. Суммируя все способы, получаем:
общее количество видов бутербродов равно 5 • 15.
Ответ: существует 75 способов составить бутерброд.
Пример 2. Из пункта А в пункт В ведут 4 дороги. Из пункта В в пункт С
ведут 3 дороги. Сколькими способами можно проехать из А в С через В?
Решение. Для наглядности сделаем рисунок.
Пронумеруем дороги от А до В (рис. 3). Если из А в В ехать по 1-й
дороге, то из А в С можно добраться тремя способами (от В до С — три
дороги); если из А в В ехать по второй дороге, то до С можно добраться опять
тремя способами и т. д. еще дважды по три способа для дорог 3-й и 4-й.
Всего, суммируя, получаем 4 • 3.
Ответ: существует 12 способов проехать из А в С через В.
1
Рис. 3.
21

В каждом из приведенных примеров мы применяем правило
умножения: перемножаем количество способов выполнения одного действия с
количеством способов выполнения второго действия.
Количество рассматриваемых действий может быть и более двух.
Рассмотрим соответствующий пример.
Пример 3. В первенстве университета по волейболу участвует 20
команд. Сколькими способами могут быть распределены золотая, серебряная
и бронзовая медали?
Решение. Золотую медаль может получить одна из 20 команд,
следовательно, имеется 20 способов. После того как золотая медаль нашла своего
владельца, серебряную медаль может получить одна из оставшихся 19
команд. Таким образом, золотую медаль можно распределить 20 способами,
с каждым из которых сочетается 19 способов распределения серебряной
медали. Всего 20* 19 = 380 способов распределения золотой и серебряной
медалей. После определения владельцев золотой и серебряной медалей
остается 18 претендентов на бронзовую медаль, т. е. для каждого из 380
способов имеется по 18 вариантов распределения бронзовой медали. А всего
380-18 = 6840 способов.
Ответ: существует 6840 различных вариантов распределения золотой,
серебряной и бронзовой медалей среди 20 команд.
Замечание. Во всех трех рассмотренных примерах мы пересчитываем
все возможные варианты, не отдавая предпочтения наиболее вкусному
бутерброду в примере 1, кратчайшему пути в примере 2 или наиболее
сильным командам в примере 3, т. е. пересчитывается количество возможных
комбинаций без учета вероятностей выбора отдельных вариантов. Точнее,
все возможные варианты предполагаются равновероятными.
Исходя из рассмотренных примеров, сформулируем правило
умножения, называемое основным правилом комбинаторики -
Пусть необходимо выполнить одно за другим А:-действий (например,
выбрать объект из какого-то множества). При этом первое действие
возможно выполнить /и, способами, второе действие — т2 способами и т. д.
до к-го действия, которое выполнимо тк количеством способов. Тогда все
^-действия можно выполнить т способами, где
Задание. Вернитесь к рассмотрению предыдущих примеров 1, 2, 3 и в
каждом из них найдите, чему равно к и какие значения принимают
величины тх, т2,..., тк.
Рассмотрим следующие примеры.
Пример 4. Изменим условия примера 2, а именно (см. рис. 4): из
пункта А в пункт В ведут 4 дороги; из пункта В в пункт С ведут 3 дороги; из
пункта А в пункт D ведут 2 дороги, а из D в С ведут 5 дорог. Сколькими
способами можно добраться от пункта А до пункта С?
Решение. По условию задачи (см. рис. 4) из пункта А в пункт С можно
добраться либо через В, либо через D. Согласно правилу произведения (см.
пример 2), существует 12 способов выбора пути через В. Аналогично через
22

Рис. 4.
D в С можно добраться 10 способами (2 • 5). Общее количество возможных
путей можно найти, объединив число путей, проходящих через В с числом
путей, проходящих через D: 12+10.
Ответ: существует 22 различных способа выбора пути из пункта А в
пункт С.
Пример 5. Имеются три серии книг: "фантастика" — 20 различных книг,
"приключения" — 25 различных книг, "детектив" — 30 различных книг.
Сколькими способами можно выбрать две книги обязательно различных
серий?
Решение. С учетом различных серий можно выбрать либо "фантастика"
и "приключения" (20 • 25 способов), либо "фантастика" и "детектив" (20 • 30
способов), либо "приключения" и "детектив" (25 • 30 способов). Общее
количество вариантов выбора двух книг получаем, объединяя все возможные
способы: 20 • 25 + 20 • 30 + 25 • 30 = 1850.
Ответ: существует 1850 различных способов выбора.
Резюмируя примеры 4, 5, сформируем правило суммы.
Пусть некоторое действие Ах (например, выбор объекта из какого-то
множества) можно выполнить /и, способами, а другое действие А2 можно
выполнить т2 способами. Тогда выполнить только одно из действий, либо
Ах, либо А2, можно т способами, где)т = тх + т?\
Замечание. Данное правило легко распространяется с двух действий на
^-действий, где к = 3, 4, 5, ... . Тогда соответственно количество способов
выполнить лишь одно действие равно т = /и, + т2 + ... + тк.
Задание. Вернитесь к примерам 4, 5 и в каждом из них найдите, чему
равно к и какие значения принимают т = тх + т2 + ... + тк.
Далее введем некоторые определения и формулы.
Определение. Произведение первых п натуральных чисел.,1 ■ 2- 3 •... • п
обозначаютд^и называют п-факториал, т. е. «J,= 1 • 2. • 3 •... • п.
~~ В"частностиГ1Г= Т,"2\~=X # ="6, 4Г= 24 и'т. д!
Для существования некоторых формул удобно ввести величину 0!, по
определению полагая 0! = 1.
Определение. Комбинации п различных элементов, отличающиеся
лишь порядком расположения этих элементов, называют перестановками.
Найдем, сколько перестановок можно получить, меняя местами п
различных элементов при конкретных п. Пусть имеется один элемент а. В
23

этом случае комбинировать не с чем, следовательно, имеется лишь одна
перестановка. Обозначим ее Рх, тогда Рх = 1 = 1!
Пусть имеется два элемента: а, Ь. Тогда количество перестановок равно
2, а именно: аЬ и Ьа, т. е. Р2 = 2 = 2!
Рассмотрим три элемента: а, Ь, с. В этом случае возможных
перестановок 6, а именно: abc, acb, bac, bca, cab, cba. Рг = 6 = 3!
В общем случае справедлива формула Рп = п! Действительно, если
имеется п элементов, то упорядочить их можно следующим образом: на первое
место поставить любой из п элементов, на второе место — любой из
(л — 1) оставшихся, на третье — любой из (л — 2) оставшихся и т. д., на
последнее л-е место претендует лишь один оставшийся элемент.
Применяя правило произведения, находим
Рп = п{п- 1)(л-2) ... 21 =п\ (1.1)
Пример 6. Сколько различных чисел можно составить, используя в
записи числа лишь пять неповторяющихся цифр: 1, 2, 3, 4, 5?
Решение. Каждое из чисел, например 12 3 4 5 или 5 4 3 2 1, является
перестановкой из пяти различных элементов. Тогда общее количество
возможных чисел равно Р5 = 5! = 120.
Пусть снова имеется л-различных элементов. Усложним задачу:
требуется выбрать из п элементов ровно т, где т — некоторое целое число,
0 < т <п. Например, из 10 элементов нужно выбрать 3 элемента. При этом
необходимо различать два случая: важен порядок выбора элементов или
неважен. К примеру, выбраны из 10 три элемента: а,Ь,с. В первом случае,
когда учитывается порядок следования элементов при выборе,
комбинации (перестановки) abc, acb, bac, bca, cab, cba считаются различными и их
ровно Р3 = 3! (в общем случае т!). Во втором случае, когда порядок
следования элементов при выборе безразличен, все 3! приведенных комбинаций
(в общем случае т!) считаются за одну. Следовательно, таких комбинаций
в общем случае выбора т элементов из п ровно в т\ раз меньше, чем в
случае упорядоченного выбора.
Найдем, сколько же их в обоих случаях.
При упорядоченном выборе т элементов из п первый элемент может
быть любым и выбран соответственно п способами. Для выбора второго
элемента остается (л — 1) способов и т. д., для выбора m-го элемента
остается (п — т + 1) способов. По правилу произведения в итоге получаем
п(п — 1)...(« — т + 1) способов.
Заметим, что при т = п получается произведение всех натуральных
чисел от 1 до п, т. е. множество перестановок Рп. В нашем случае, когда т,
вообще говоря, меньше п, это множество неполное.
Определение. Комбинации по т элементов, выбранные из множества п
различных элементов, отличающиеся либо составом элементов, либо их
порядком, называют размещениями.
Количество всех возможных размещений принято обозначать Апт, и, как
только что установлено, справедлива формула:
Апт=п(п- 1) ... (п- т+ 1), (1.2)
где т = 1, 2, 3, ..., п.
24

Отметим, что если данное произведение домножить на
1 • 2 • 3 •... • (п — т) = (п — т)\ , то получим п!
Таким образом Апт • (л - т)\ = п!, следовательно,
Апт=—^—. (1.3)
Найденная формула имеет смысл и при т = 0, а именно: Ап°= 1.
Рассмотрим второй случай: случай, когда т выбранных элементов не
различают по порядку выбора.
Определение. Комбинации по т элементов, выбранные из множества п
различных элементов, отличающиеся по составу хотя бы на один элемент,
называют сочетаниями по т элементов из п.
Количество сочетаний по т элементов из п принято обозначать Спт.
Как уже установлено ранее, количество сочетаний Спт меньше
соответствующего количества размещений в т\ раз. Таким образом, справедлива
формула (1.3).
Ст = я- (\ л)
m!(/i-m)!' v ' ;
где т = 0, 1,2 ... п.
Пример 7. В спортивной секции занимается 10 человек. Сколькими
способами можно отобрать команду, состоящую из 6 человек?
Решение. Поскольку порядок отбора игроков в команду несуществен,
то всего имеется С,60 способов; см. (1.4). Вычислим это значение, сокращая
одинаковые сомножители в числителе и знаменателе дроби:
пв _ 10! _ 10! _ 10 ■ 9 ■ 8 ■ 7 _ 10 ■ 9 • 8 ■ 7 _ 1П о 7-ип
Cl0~6!(10-6)! " 614! 4! 1 .2-3-4 " Ю ' 3 ' 7 - 210.
Ответ: существует 210 способов отбора.
Пример 8. В аудитории 25 мест. Сколькими способами можно
рассадить на них 4 студентов?
Решение. Судя по условию задачи, порядок размещения студентов
должен быть учтен, т. е. речь идет не о сочетаниях, а о количестве
размещений A*s\ см. (1.2):
А" = Щ=Т) = Ш. = 25' 24 ' 23 ' 22 = 303 600'
Ответ: 303 600 способов.
Отметим, что количество сочетаний по m элементов из п используется в
формуле бинома Ньютона:
(а + л:) =С°аПх°=СП1ап-1х1 + ... +Cnma"-mxm + ... +С"а°хп. (1.5)
\ / л л л л л х'
Данная формула является обобщением известных равенств для п = 2 и
л = 3:
{а + х)2= а2+ 2ах+ х2=С°а2х°+С}а1х1 + С2а°х2
(а + хУ = а3 + За2х+ Зах2 + х3 =C3Vjc° +C3W + C2alx2+ C]a'x\
25

Используя знак суммирования, формулу бинома Ньютона можно
записать короче:
л
(а + х)п = £ Смпап~мхм. (1.6)
/п = 0
Величины Спт, являющиеся коэффициентами при степенях а и х,
называют биномиальными коэффициентами.
Биномиальные коэффициенты обладают многими интересными
свойствами.
Из формулы (1.4) следует, что Спт= Спп~т. (1.7)
Полагая в (1.5) а = 1, х = 1, получаем равенство, справедливое для
любого натурального п\
Сл°+ С,,1 + ... + СЛЛ = 2Л. (1.8)
Полагая в (1.5) а = 1, х= 1, получаем другое равенство, также
справедливое для любого натурального числа п:
С" С + Сп2 - ... + (-l)-C; = 0. (1.9)
Используя комбинаторные формулы и методы, можно вычислять
вероятности многих достаточно сложных событий.
1.5. Примеры
Рассмотрим некоторые примеры на применение формул
комбинаторики и нахождение вероятностей, используя классическое определение.
Пример 1. Назовем "словом" любую (даже бессмысленную)
комбинацию букв. Сколько "слов" можно получить, переставляя буквы в словах
a) ВРАЧ,
b) МЕДИЦИНА,
c) ПОЛИКЛИНИКА?
Решение, а) В слове ВРАЧ 4 различные буквы, В, Р, А, Ч, можно
переставить 4! = 24 способами.
b) В слове МЕДИЦИНА имеются две одинаковые буквы И. Очевидно,
что если в "слове" эти буквы И поменять местами, то само "слово" не
изменится. Также понятно, что если эти буквы считать разными, например,
пометив их И, и И2, to различных "слов" получится 8!. Снимаем пометки с
букв И, и тогда оказывается, что в количество из 8! слов все слова входят
попарно (например, МЕДИ, ЦИ2 НА и МЕДИ2 ЦИ, НА без пометок
становятся одинаковыми). Таким образом, различных "слов" вдвое меньше:
8!/2 = 20 160.
c) В слове ПОЛИКЛИНИКА 11 букв. Если бы они все были различны,
то количество их возможных комбинаций равно 11!. Однако наличие пары
букв Л уменьшает это количество в два раза, наличие пары букв К еще в
два раза, а три одинаковые буквы И уменьшают количество различных
слов еще в 3! раз (три буквы можно расставить по трем позициям 3! = 6
26

способами). Следовательно, различных "слов", получаемых из данного на-
0|
бора в 11 букв, всего = -—-^—— 1680.
2-2-3!
Пример 2. Ребенок играет четырьмя карточками из азбуки, на которых
написаны буквы М, М, А, А. Найти вероятность, что, расположив
случайным образом карточки в ряд, он получит слово "МАМА".
Решение. Используем классическое определение вероятности
Р{А) = т/п, где А — искомое случайное событие. Тогда п, аналогично
рассуждениям в примере 1, вычисляется как -—'—. Благоприятствующих
исходов т, причем т = 1. Таким образом, Р(А) = 1/61.
Пример 3. Генератор случайных чисел выдает на экран компьютера
шестизначное число. Считая все комбинации цифр равновозможными,
найти вероятность, что в записи числа присутствуют лишь нечетные
цифры.
Решение. Поскольку все комбинации цифр равновозможны,
используем классическое определение вероятности Р(А) = т/п, где А — искомое
случайное событие, п — количество всех шестизначных чисел:
п = 999 999 - 99 999 = 900 000. Число т найдем, используя правило
умножения. Шестизначное число — это шесть цифр, каждая из которых
записана на своей позиции. Таким образом, если все цифры нечетные (а
нечетных цифр всего пять), то на каждой из шести позиций шестизначного
числа может оказаться одна из пяти цифр. По правилу умножения общее
количество комбинаций из нечетных цифр т = 5-5-5-5-5-5 = 56.
Следовательно, искомая вероятность равна
Р(А) = т/п = ——-«0,0174.
9 • 105
Замечание. В примере 3 число п также можно было найти по правилу
умножения, учитывая, что всего различных цифр десять, и нуль не может
находиться на первой позиции:
я = 9 • 10 • 10 • 10 * 10 • 10 = 9 • 105.
Пример 4. Игральный кубик бросают 12 раз. Найти вероятность, что
каждое число очков выпадет дважды.
Решение. Считаем кубик правильным (симметричным, сделанным из
однородного материала), тогда все возможные исходы одного испытания
равновероятны, и вероятность выпадения любого количества очков от 1 до
6 равна 1/6. Проведя испытание 12 раз и опираясь на равновозможность
исходов в каждом испытании, также используем классическое определение
вероятности Р(А) = т/п, где А — искомое случайное событие. Найдем п и
т. Согласно правилу умножения и учитывая, что в каждом из 12
испытаний может осуществляться любой из шести исходов, п = б12 (см.
аналогичные вычисления в примере 3). Число благоприятствующих
событий-исходов равно числу различных последовательностей по 12 элементов таких,
1 В данной задаче можно количество всех исходов считать равным 4!, имея в виду
количество комбинаций из 4 различных карточек. Но тогда благоприятствующими для искомого со-
4 1
бытия окажутся ровно 4 способа размещения карточек, и вновь Р(А) = — = -? .
4 о
27

что все элементы обязательно входят парами: две единицы, две двойки и
т. д., две шестерки. Итак,
т - —-.
26
Тогда искомая вероятность:
ПА) = ^. = 0,0034-
Пример 5. В картотеке из 100 карточек имеется одна разыскиваемая.
Наудачу извлекается 10 карточек. Найти вероятность, что среди них
окажется требуемая.
Решение. Используем классическое определение вероятности. При этом
л-количество способов, которыми можно извлечь 10 элементов из
множества в 100 элементов, а именно: п = С,1^. Число благоприятствующих
способов т находится сложнее. Все множество карточек разбиваем на два
подмножества: одна карточка разыскиваемая и остальные 99 карточек.
Искомое событие А осуществляется, если одна карточка извлекается из
одноэлементного множества (количество способов —С\), а остальные девять —
из множества в 99 элементов (количество способов — С|9). Тогда т
находим по правилу умножения:
т= CiC999.
Зная тип, получаем:
рт_ С\С\\ = 99!Ю!90!
С,! 9!90!100!"
Сокращая близкие факториалы-сомножители в числителе и
знаменателе, находим
РШ=99!Ш! _ 1 ■ 10 _ 0 j
FW 10019! 100-1 U,i'
Пример 6. Из колоды в 36 карт выбирают наудачу три карты. Найти
вероятность, что
а) выбраны три туза; б) выбраны два туза.
Решение. Аналогично предыдущему примеру, все множество из 36 карт
разбиваем на два подмножества: 4 туза и оставшиеся 32 карты. Тогда в
случае а) все три карты извлекаются из первого подмножества, а в случае б)
две карты извлекаются из первого подмножества и одна — из второго
подмножества. Запишем ответы:
гл р(А) = С< = 4!3!33! = 4! _ 0 000.
*)Р(А) ~Щ6 ЗШ36! 34 • 35 • 36 ~ 0'°006'
&\ P(R\ = С4 • Сп _ 4!32!3!33! _ 3-2-32-3! _ п тм
)П) ~С]Г ~ 2!2!1!31!36! " 34-35-36 ~ °'0269'
Пример 7. Некто, имея 10 друзей, решил ежедневно приглашать
некоторых из них в гости так, чтобы компания ни разу не повторялась. В
течение какого времени это возможно?
28

ooo ooo oooo oooo
Рис. 5.
Решение. Искомое количество дней равно числу возможных компаний.
Компания может состоять из любого количества человек от одного до
десяти. Компанию из одного человека можно составить С,'0 способами, из
двух человек — С?0 способами и т. д. Тогда общее количество возможных
компаний равно сумме
Согласно формуле (1.8), доказанной в предыдущем параграфе,
С+С+...+ СЛ"=2Л,
при п = 10 получаем
Гх 4- Г2 4- 4- Г1'0 = 910— Г"
Так как С10°= 1, то общее число компаний и соответственно количество
дней, в которые эти компании могут быть приглашены, равно
210- 1 = 1023.
Пример 8. Сколькими способами 15 одинаковых шаров можно
разложить по 5 различным ящикам при условии, что ни один из ящиков не
окажется пустым?
Решение. Расположим шары в ряд (рис. 5).
Так как шары одинаковы, то их порядок в данном ряду не имеет
значения, а так как ящики различны, то пронумеруем их от одного до пяти.
Данное множество шаров разобьем на пять подмножеств. На рис. 5
разбиение осуществляется с помощью перегородок (вертикальных черточек):
шары, расположенные до первой перегородки, попадают в первый ящик,
от первой до второй перегородки — во второй ящик и т. д. Таким образом,
количество способов разложить шары равно количеству способов
расставить перегородки. Как легко заметить, для разбиения множества шаров на
пять подмножеств перегородок требуется всего четыре (на одну меньше
количества ящиков). И эти четыре перегородки должны быть расставлены
по 14 позициям (на рис. 5 место перегородок — пространство между
шарами). Итак, 4 перегородки можно расставить по 14 позициям C,J
способами.
°14 4!Ш! 4! ШЩ'
Таким образом, существует 1001 способ разложить 15 одинаковых
шаров по 5 различным ящикам, причем ни один из ящиков не окажется
пустым.
Замечание. Рассматривая в примере 8 п одинаковых шаров и т {т <п)
различных ящиков, в ответе аналогично получим С'"1Х способов.
29

1.6. Вероятность суммы событий. Противоположные события
Поскольку над случайными событиями возможны арифметические
операции сложения и умножения, то представляется разумным исследовать
вероятности, связанные с этими действиями. В частности, справедливо
следующее утверждение.
Теорема сложения. По отношению к любому испытанию и для любых
случайных событий А и В имеет место равенство:
Р(А + В) = Р{А) + Р(В) - Р(АВ). (1.10)
Доказательство. Пусть 2?„ Е2, ..., Е„ — полная система элементарных
событий. В зависимости от благоприятствования или неблагоприятствования
событиям А и В, разобьем систему на непересекающиеся группы. Не теряя
общности из-за нумерации, можно считать, что:
a) первые к событий Ех, ..., Ек благоприятствуют и событию А, и
событию В;
b) следующие г событий Ек+Х, ..., Ек+Г благоприятствуют событию А и не
благоприятствуют событию В;
c) следующие s событий £*+,+,, ..., Ek+r+s не благоприятствуют событию А
и благоприятствуют событию В;
d) остальные события Ek+I+S+1, ..., Еп не благоприятствуют ни событию А,
ни событию В.
Найдем все вероятности, представленные в (1.10):
Р(А) = £iT, P(B) = £±^,
п п
Р(АВ) = -, Р(А+В) = k+r + s
п п
(напомним, что благоприятствующими для произведения АВ являются
события, благоприятствующие и событию А, и событию В, а
благоприятствующими для суммы А + В являются события, благоприятствующие либо
А, либо В, либо и тому и другому).
Проверим справедливость равенства (1.10), используя найденные
вероятности:
Р(А) + Р(В)- Р(АВ)= k±I+!i±l-k = k + r+s = Р(А + Ву
п п п п
Утверждение доказано.
Следствие 1. Если А и В — несовместные случайные события, то из
теоремы сложения следует
Р(А + В) = Р{А) + Р(В). (1.11)
Формула (1.11) получается из формулы (1.10), так как для несовместных
событий А и В имеем Р(АВ) = P(V) = 0.
Замечание. Аналогичная формула справедлива и для суммы п попарно
несовместных событий (л > 2).
30

Следствие 2. Для трех случайных событий А, В, С теорема сложения
имеет вид:
Р(А+В+С) = Р(А) + Р(В) + Р(С) -
- Р{АВ) - Р(АС) - Р(ВС) + Р(АВС). (1.12)
Формула (1.12) получается неоднократным применением теоремы
сложения для двух слагаемых:
Р(А + В + С) = Р((А + В) + С) = Р(А + В) + Р(С) - Р((А + В)С) =
= Р(А) + Р(В)~ Р(АВ) + Р(С) - Р(АС+ ВС) = Р(А) + Р(В) +
+ Р(С) - Р{АВ) - [Р(АС) + Р(ВС) - Р(АСВС)\.
Учитывая в последнем слагаемом свойство С' С= Си, следовательно,
АСВС = АВСС = ABC, раскрывая квадратные скобки, приходим к формуле
(1.12).
Для иллюстрации применения формулы рассмотрим пример.
Пример. На стеллаже библиотеки в случайном порядке расставлены 15
учебников. Из них 5 учебников по медицине и 10 по биологии.
Библиотекарь наудачу берет 3 книги. Найти вероятность, что хотя бы один из
взятых учебников по медицине.
Решение. Обозначим искомое случайное событие символом А. Событие
А — сложное событие, которое происходит, если произойдет одно из
следующих событий: Ах — из трех выбранных учебников один по медицине и,
соответственно, два по биологии; А2 — из трех выбранных учебников два
по медицине и соответственно один по биологии; Аг — из трех выбранных
учебников все три по медицине. Таким образом, случайное событие А
(хотя бы один учебник из трех выбранных — по медицине) происходит, если
осуществляется либо Аи либо А2, либо Ау Заметим, что других событий,
благоприятствующих А, кроме Ах, А2, Аг, нет, т. е. А = Ах + А2 + Аг, и задача
сводится к нахождению вероятности суммы трех случайных событий:
Р(А) = Р(А{ + А2 + Аг).
Привлекаем формулу (1.12). Однако в нашем примере, как легко
заметить, все события-слагаемые Ах, А2, Аг попарно несовместны.
Действительно, не могут осуществляться одновременно, например, Ах (ровно одна
книга из трех по медицине) и А2 (ровно две книги из трех по медицине).
Поэтому все произведения АХА2, АхАг, А2Аг и АхА2Аг являются событиями
невозможными, и их вероятности, естественно, равны нулю. Тогда
формула (1.12) приобретает простой вид:
Р{А) = Р(АХ +А2 + А,) = Р(АХ) + Р(А2) + Р(А3).
Найдем вероятности, записанные в правой части равенства, используя
классическое определение вероятности и посчитав количество возможных
комбинаций. Извлечь три книги из 15 возможно С]5 способами. Заметим,
что 15 учебников состоят из двух множеств в 5 и 10 элементов.
Осуществление события Ах означает, что один из учебников извлечен из множества
в 5 элементов (что возможно С\ способами), а два учебника извлечены из
множества в 10 элементов (что возможно С2Х0 способами). Применив
правило умножения, получаем по классическому определению:
31

P(A \ = С^С?о = 5!10!3!12! = 45
y x) c\5 1!4!2!8!15! 9Г
Аналогично находим:
C]C\0 _ 5!10!3!12! _ 20
P(A2) =
PW =
C]5 2!3!1!9!15! 9V
_ С]С°10 = 5!3!12! = _2_
C\ 3!2!15! 91"
67
Тогда искомая вероятность Р{А) = —.
Приведенный пример показывает, как непосредственно можно
использовать теорему о вероятности суммы случайных событий.
Введем новое понятие: случайное событие, противоположное данному.
Пусть имеется некоторое случайное событие А. Рассмотрим событие,
которое дополняет А_до достоверного события. Обозначим это новое
событие А. Тогда А + А = U, а также А • А = V, где U — достоверное
событие, V — невозможное событие. Последние два равенства определяют
событие А, противоположное событию А. Однако, как легко заметить, в
равенствах оба события А и А совершенно равноправны, поэтому аналогично
событие А является противоположным событию А, т. е. случайные события
А и А — противоположные события. Для вероятностей противоположных
событий справедливо следующее утверждение:
Р(А) = 1 - Р(А). (1.13)
Действительно, так как А + А= U, то Р(А + А) = P(U).
Поскольку события А и А несовместны, то, согласно _следствию 1 из
теоремы сложения и факту P(U) = 1, получаем Р(А) + Р(А) = 1, откуда и
следует формула (1.13).
Вернемся к приведенному выше примеру. Используя противоположное
событие — все три выбранных учебника по биологии — по формуле (1.13)
легко находим
Г3
10
.3
Р(А) = \-Р(А)=\-
/.(/0 = , - ]0!3!U! = ! - 24 = 67
v ; 3!7!15! 91 91
Как видим, обращение к вероятности противоположного события в
данном примере существенно облегчает вычисления.
1.7. Условная вероятность. Зависимые и независимые события
Пусть при некотором комплексе условий проводится испытание, в
результате которого могут произойти случайные события А и В с
вероятностями Р(А) и Р(В) соответственно. Например, испытание — бросание
правильной игральной кости; А — выпадение четного числа очков; В —
выпадение "шестерки". Очевидно, что Р(В) = \ безотносительно
6
32

события А. Усложним задачу: полагаем известным, что событие А
произошло, и требуется найти вероятность события В с учетом данной
информации. Условие обязательного осуществления события А означает
изменение комплекса условий, при котором проводится испытание, а это может
повлечь изменение вероятности события В. В рассмотренном примере
выпадение четного числа очков (событие А) уменьшает полную систему
элементарных событий до п, равном 3: выпадение "двойки", "четверки" и
"шестерки". Тогда вероятность события В при условии, что событие А
произошло, равна 1/3, т. е. в нашем примере вероятность события В различна
в зависимости от того, учитывается событие А или нет.
Определение. Условной вероятностью события В при гипотезе А
называется вероятность события В при условии, что событие А обязательно
происходит. Обозначим соответствующую условную вероятность Р(В\А).
Как отмечено выше, обязательное осуществление случайного события А
связано с изменением комплекса условий, при котором производится
испытание. И тогда при измененном комплексе условий относительно
события В возможны два варианта: вероятность события В сохраняет прежнее
значение или изменяется.
Определение. Событие В называется независимым от события А, если
условная вероятность события В при гипотезе А равна безусловной
вероятности события В:
Р(В\А) = Р(В).
Определение. Событие В называется зависимым от события А, если
Р{В\А)*Р(В).
Далее, используя понятие условной вероятности, сформулируем
теорему умножения.
Теорема. По отношению к любому испытанию и для любых двух
случайных событий А и В справедливы соотношения
Р(АВ) = Р(А)-Р(В\А), (1.14)
Р(АВ) = Р(В)-Р(А\В).
Доказательство. Как легко заметить, вторая формула (1.14) получается
из первой, если А и В поменять местами. Поэтому достаточно доказать
лишь одно равенство, например первое.
Пусть Ех, Е^, ..., Е„ — полная система элементарных событий. Среди
этих п событий выделим следующие группы:
первые к событий 2?,,..., Ек благоприятствуют осуществлению и события
А и события В (т. е. АВ);
следующие г событий, Ек+Х, ..., Ек+п благоприятствуют осуществлению
события А и не благоприятствуют осуществлению события В (т. е. АВ);
следующие s событий, Ек+Г+Х, ..., Ek+I+S, не благоприятствуют
осуществлению события А и благоприятствуют осуществлению события В (т. е. АВ);
оставшиеся события, Ек+1^.^х, ..., Еп-не благоприятствуют осуществлению
ни события А, ни события В (т. е. АВ).
Используя классическое определение, найдем вероятности,
используемые в первой из формул (1.14):
Р(А) = £±-г, Р{АВ) = *, Р{В\А) = JL
П И К -г Г
3 — 3529
33

Проверяем справедливость формулы:
Р(А)-Р(В\А) = £±± • т^- = - = Р(АВ).
п к + г п
Теорема доказана.
Приведем важные следствия из теоремы умножения.
Следствие 1. По отношения к любому испытанию и для любых
случайных событий А и В с ненулевыми вероятностями Р(А) и Р(В) условные
вероятности можно вычислить по формулам:
Р{В\А) = ЕпВ' (115)
v ' ' Р(В)
Формулы (1.15) элементарно следуют из (1.14).
Следствие 2. В любом испытании, если событие В не зависит от
события А, то и событие А не зависит от события В при условии, что
Р(АВ)*0.
Действительно, используя оба равенства (1.14), получаем
Р(АВ) = Р(А)-Р(В\А) = Р(В)-Р(А\В).
Предполагая независимость В от А, т. е. Р(В\А) = Р(В), последнее из
равенств получаем в виде
Р{А)-Р{В) = Р(В)-Р(А\В).
Отсюда при Р(В) Ф О следует равенство Р(А) = Р(А\В), а это и
означает, что событие А не зависит от события В. Следствие 2 доказано.
Исходя из следствия 2, в дальнейшем, говоря о независимости двух
событий, всегда будем иметь в виду взаимную независимость как события А
от события В, так и события В от события А.
Следствие 3. Для независимых случайных событий А и В справедливо
равенство
Р(АВ) = Р{А)-Р{В). (1.16)
Равенство (1.16) следует из первой формулы (1.14) при использовании
равенства Р{В\А) = Р{В), справедливого для независимых событий, либо
из второй формулы (1.14) при использовании равенства Р(А\В) = Р(А).
Следствие 4. Для трех случайных событий А, В, С из теоремы
умножения следует формула
Р{АВС) = Р{А)- Р(В\А)- Р(С\АВ). (1.17)
Действительно, рассматривая ABC как произведение двух
сомножителей, АВС—{АВ)-С, согласно теореме умножения, получаем
Р(АВС) = Р(АВ)- Р(С\АВ) и далее Р{АВ) представляем по первой из
формул (1.14).
Следствие 4 доказано.
Выше было определено понятие независимости для двух случайных
событий. Если рассматриваются более двух событий, то аналогично можно
ввести понятие попарной независимости, т. е. каждое событие системы не
зависит от любого другого события. Однако для совокупности п случайных
событий при п > 2 часто необходимо более сильное требование, нежели
попарная независимость. Например, в формуле (1.17) из попарной незави-
34

симости А, В, С еще не следует равенство вероятности произведения и
произведения вероятностей событий-сомножителей (имеются
соответствующие примеры). Причина в наличии сомножителя Р(С\АВ),
требующего независимости С не только от А и В, но и от произведения АВ. Введем
соответствующее обобщение понятия независимости.
Определение. Случайные события Ах, А2, ..., Ап, где п >2, называют
независимыми в совокупности, если они попарно независимы, и каждое
событие независимо от любого из произведений оставшихся событий.
В частности, для двух событий понятия независимости и независимости
в совокупности совпадают. Для трех событий А, В, С требование
независимости в совокупности предполагает независимость А и В, А и С, В и С, А и
ВС, В и АС, С и АВ.
Утверждение. Если случайные события Ах, А2, ..., Ап, где п >2,
независимы в совокупности, то справедливо равенство
Р(АХА2 ... Ап) = Р(АХ) • Р(А2) •... • Р{Ап). (1.18)
В общем виде приведенную формулу доказывать не будем, однако
отметим, что при л = 3 данное равенство следует из (1.17) и определения
независимости в совокупности.
Также следует заметить, что если случайные события Ах, А2,_...,_Лп
независимы в совокупности, то и противоположные им события Ах, А2, ..., Ап
независимы в совокупности.
При решении практических задач о независимости случайных событий
часто судят по смыслу задачи: например, при двукратном бросании
игральной кости выпадение "шестерки" при первом бросании (событие Ах) и
втором (событие А2) — события независимые. О независимости событий А
и В более строго можно говорить, проверяя справедливость равенства
(1.16).
Приведем примеры использования условных вероятностей и теоремы
умножения.
Пример 1. Студент знает 20 из 25 вопросов программы. Найти
вероятность, что он знает 3 вопроса, предложенных экзаменатором.
Решение. Обозначим искомое случайное событие — А. А — сложное
событие, которое состоит из простых событий:
Ах — знает первый вопрос;
А2 — знает второй вопрос;
Аг — знает третий вопрос.
Тогда по определению произведения случайных событий А = АхА2Аг.
Вероятность А находим по формуле вида (1.17):
Р(А) = Р(АХА2А,) = Р{АХ) Р(А2\АХ) Р(А,\АХА2).
Вычислим вероятности в правой части равенства:
Р(А2\АХ) = ^, так как при обязательном осуществлении Ах остается 24
возможных вопроса (24 = 25 - 1), из них благоприятствующих 19 вопросов
(19 = 20- 1).
з*
35

18
Р(Аг\АхА2) = —, так как при обязательном осуществлении и Ах и А2
остается 23 возможных вопроса (23 = 25 — 2), из них благоприятствующих 18
вопросов (18 = 20 — 2).
Таким образом,
Р(А\ = 20 • 12 . I? = Л
к ' 25 24 23 115*
Искомая вероятность найдена. В качестве информации к размышлению
отметим невысокое значение этой вероятности: — < - .
Замечание. Искомую вероятность можно было найти и
непосредственно по классическому определению:
Р(А\ - т - ^20 ^ 57
ПА) п ch US'
Пример 2. Студент разыскивает нужную ему химическую формулу в
трех различных справочниках. Вероятность того, что формула имеется в
первом справочнике, равна рх = 0,6, во втором — р2 = 0,7, в третьем —
/?3 = 0,8. Найти вероятность, что а) формула имеется хотя бы в одном
справочнике; б) формула имеется только в одном справочнике.
Решение. Введем обозначения случайных событий:
А — формула имеется хотя бы в одном справочнике;
В — формула имеется только в одном справочнике;
Ах — формула имеется в первом справочнике;
А2 — формула имеется во втором справочнике;
у43 — формула имеется в третьем справочнике.
Тогда сложное случайное событие А можно представить в виде
комбинации событий Ах, А2, Аг и противоположных им событий, а затем перейти
к вероятностям. Однако более простой путь — использование события,
противоположного событию А:
где случайное событие А означает, что формула отсутствует во всех трех
справочниках. Как видим, сложное событие А значительно проще по своей
структуре, нежели сложное событие А. Находим искомую вероятность:
Р{А) = 1- Р(А) = 1 - Р(Л,Л2Л3).
Задача сводится к отысканию вероятности произведения трех событий.
Поскольку справочники различны, т. е. основание предполагать
независимость событий Ах, А2, Аг (в данном случае независимость в совокупности),
а следовательно, и событий АХА2АУ А тогда вероятность произведения
равна произведению вероятностей^независимых событий-сомножителей:
Р(АХА2А,) = Р(АХ) Р(А2) Р(Аг) = (1 - Рх){\ - р2)(\ - Л) = чхЫу
Так как qx = 1 - рх = 0,4; q2 = 1 - р2 = 0,3 и яг= \ - рг = 0,2, то
Р(А)= 1 -0,4-0,3-0,2 = 0,976.
Для вычисления Р(В) к противоположному событию переходить
нецелесообразно, поскольку по своему составу сложное случайное событие В,
вообще говоря, не проще события В (проверьте!). Выразим случайное со-
36

бытие В через более простые: событие В имеет место, когда нужная
формула имеется в первом справочнике и не имеется во втором и третьем,
либо имеется во втором справочнике и не имеется в первом и третьем и
либо, наконец, имеется в третьем и отсутствует в обоих первых, т. е. В равно
сумме трех сложных событий:
В = АХА2А) + ~АхА2~Аг + AlA2Ay
События-слагаемые попарно несовместны (почему?), поэтому
вероятность суммы этих событий равна сумме вероятностей слагаемых. События-
сомножители в каждом из слагаемых предполагаем независимыми в
совокупности, поэтому вероятность каждого произведения оказывается равной
произведению вероятностей. Тогда
Р{В) = Р(А;А2А,) + Р{АхА2Аг) + P(AlA2Ai)=plq2q, + qxp2q, + qxq2p, =
= 0,6 • 0,3 • 0,2 + 0,4 • 0,7 • 0,2 + 0,4 • 0,3 • 0,8 = 0,188.
Итак, Р(А) = 0,976; Р(В) = 0,188.
1.8. Формула полной вероятности. Формула Байеса
Предположим, что некоторое случайное событие А может
осуществиться лишь при условии осуществления одного из случайных событий Я,,
#2, ..., #„. В дальнейшем такие события Я,, Я2, ..., Я„ будем называть
гипотезами.
Определение. Систему случайных событий Я,, Н2, ..., Я„ называют
полной системой гипотез, если эта система полная и несовместная, т. е.
Я, + Я2 + ... + Hn=U; (1.19)
Я, • Hj= V, при i */
Сформулируем и докажем теорему, которая представляет формулу,
называемую формулой полной вероятности.
Теорема. Если система событий Я,, Я2, ..., Я„ является полной системой
гипотез, то для любого события А выполнено равенство
л
/>(Л) = £/>№) ' Р(А\Н,). (1.20)
/= 1
Доказательство. Любое случайное событие А можно представить в виде
произведения А • U, тогда
A = A-U=A(HX + Я2+...+ Нп)=АНх +АН2+...+ АНп.
События, составляющие сумму, попарно несовместны, так как по
определению несовместны любые Я,, Н} при / Ф j (события АН{ и АН} не могут
осуществиться вместе). Вычисляя вероятность суммы п попарно
несовместных событий, получаем
Р{А) = Р{АНХ + АН2 +...+ АНп) = Р(АНХ) + Р(АН2) +...+ Р{АНп).
Применяя к каждому слагаемому в правой части равенства теорему
умножения, получаем
Р(А) = Р{НХ) • Р{А\НХ) + Р(Н2) • Р(А\Н2) +...+ Р{Нп) • Р{А\Нп) =
37

= £Р(Я,)- Р(А\Н,).
Формула (1.20) доказана, а тем самым доказана и теорема.
Пример 1. Студент выучил не все из п (п > 3) экзаменационных
билетов. Какая тактика для него предпочтительнее: среди трех экзаменующихся
выбирать билет первым, вторым или третьим?
Решение. Для определенности предположим, что студент выучил т
билетов, где, по условию задачи, 1 < т < п. И тогда множество из п билетов
разбивается на два: т билетов "хороших" и п — т билетов "плохих".
Причем понятие "хороший" или "плохой" билет рассматривается только по
отношению к нашему студенту. Обозначим искомое событие, выбор
"хорошего" билета, буквой А и найдем Р(А) во всех трех предложенных случаях.
a) Если студент выбирает билет первым, то по классическому
определению
Р(Л)=-.
п
b) Пусть наш студент берет билет вторым. Тогда возникает ситуация
неопределенности: какой же билет уже взят первым экзаменующимся
студентом, "хороший" или "плохой". Введем две возможные гипотезы: Я, —
первый студент выбрал "хороший" билет, Я2 — первый студент выбрал
"плохой" билет. Нетрудно видеть, что Я,, Я2 образуют полную систему
гипотез (Я, + Я2 = U, Я, • Я2 = V). Воспользуемся формулой полной
вероятности, предварительно вычислив все необходимые вероятности.
Р(Н1)=^;Р(Н2)=^=^;
п п
Р(А\НХ)=™-4;Р(А\Н2)- т
/1-1 ' ч '" п-\
Следовательно,
Р{А) = Р{НХ) • Р{А\НХ) + Р(Н2) • Р{А\Н2) =
_ т . т — 1 + п — т . т _ т2 — т + пт — т2 _ т
п /1—1 п /1—1 п(п— 1) п '
с) Пусть наш студент берет билет третьим. Таким образом до него уже
взято два билета, и студент выбирает из п — 2 оставшихся. Сколько среди
этих /1 — 2 билетов "хороших" (благоприятствующих) можно предполагать
и выстроить полную систему гипотез Я,, Я2, Я3> Я4:
Я, — и первый, и второй выбранные билеты — "хорошие";
Я2 — первый билет — "хороший", второй — "плохой";
Я3 — первый билет — "плохой", второй — "хороший";
Я4 — и первый, и второй билеты — "плохие".
Тогда
п /1—1 п /1—1
р/ггч_ п- т . т . р/17ч _ п — тп — т—1.
38

P{A\Hx) = *-*\P{A\HJ = !!L-±\
П ~ L П~ 2.
Р(А\Н,) = ™^±;Р(А\Н4) = т
/i-2' v ' v /i-2
Следовательно, по формуле полной вероятности имеем
Р(А)= УР(Н.) ■ Р(Л\Ид = Щ^ • "Г2 + МЛ^ • ffizl +
£-j n{n-\) /i — 2 /i(/i— 1) /i — 2
/= i
+ (я — m)m . m— 1 + /i — m . /i —m— 1 . _/w__
n(n— 1) /i — 2 /i /i—1 /i — 2
m [(m - l)(m - 2) + 2(/i - m)(m - 1)+(л - m)(/i - m - 1)] =
/i(/i- l)(/i~2)
_ m(n2 — 3/i + 2) _ m
/i(/i — l)(/i —2) /i'
Ответ: вероятности вытащить "хороший" билет одинаковы во всех трех
случаях.
Замечание 1. При т = 1 или п - т = 1 система гипотез будет Я2, Я3, Я4
или соответственно Я,, Я2, Я3, так как при т = 1 следует
Р(НХ) = P(V) = О, а при л - т = 1 следует Р(Я4) = Р(Ю = 0. Однако
искомая вероятность и в этих случаях Р(А) = —(проверьте!).
л
Замечание 2. В случае, когда студент выбирает билет третьим, полную
систему гипотез можно построить иначе: Я, — осталось т "хороших"
билетов, Я2 — осталось т — 1 "хороших" билетов, Я, — осталось т — 2
"хороших" билетов. Тогда необходимые вероятности могут быть вычислены
следующим образом:
Р{А\НХ) = -2Ц, Р(А\Н2) = ^-i, Р(Л|Я3) = .
/1 — 2 /1 — 2 /1 — 2
Применив формулу полной вероятности по-прежнему получим
/>(Л) = -.
л
В рассмотренном примере мы дважды строили полную систему гипотез
и применяли формулу полной вероятности. Эта формула в условиях
неопределенности позволяет вычислять некоторую среднюю вероятность,
взвешенную по вероятностям возможных гипотез. В случае, когда все гипотезы
считаются равновероятными, полная вероятность Р(А) является равной
просто среднему арифметическому условных вероятностей P(A\Ht), где
/= 1, 2, ..., п.
При формулировке условий для справедливости формулы полной
вероятности мы предполагали, что искомое событие А может осуществиться
только с одной из гипотез Я,, Я2, ..., Я„. При этом вероятности самих
гипотез считались известными. Однако на практике данные вероятности
гипотез, введенные до опыта (так называемые априорные вероятности), после
39

опыта могут оказаться иными. Причина — появление в результате опыта
дополнительной информации, а чем больше информации, тем,
естественно, точнее значения неизвестной нам рассматриваемой вероятности.
Вероятность, найденную после опыта, называют апостериорной.
Выведем формулу для апостериорной вероятности гипотез.
Предположим, что в результате опыта искомое событие А осуществилось (это и есть
дополнительная информация). Апостериорной вероятностью гипотезы Нк
назовем условную вероятность Р(Нк\А), где к = 1, 2, ..., п.
Из теоремы умножения для двух событий А и Нк справедливо
соотношение [см. (1.14)]
Р(АНк) = Р(А)- Р(Нк\А) = Р(Нк)- Р(А\Нк).
Поделив в последнем равенстве обе части на сомножитель Р{А),
отличный от нуля (иначе Р{АНк) = 0, и Нк не входит в число гипотез по
условию), получаем апостериорную вероятность:
Р(Нк\А) = Р(Нк)рР^Нк\ (1.21)
Формулу (1.21) называют формулой Байеса. При этом Р{А)
вычисляется по формуле полной вероятности:
л
Р(А) = ^ПЪ)' Р(А\Н<).
/= 1
Полученная формула Байеса может быть применена к любой гипотезе
Нк, к = 1, 2, ..., п, полной системы гипотез. Таким образом, найдя
апостериорные вероятности гипотез Р(Нк\А), к = 1, 2, ..., п, можно снова
проделать опыт и вновь уточнить вероятности гипотез. С каждым новым опытом
увеличивается объем информации и соответственно уточняются
рассматриваемые вероятности. Данный процесс, особенно с использованием
возможностей компьютера, находит самое широкое применение в различных
областях, поскольку позволяет весьма эффективно корректировать
различные выводы, решения, планы и прогнозы.
Пример 2. В некотором коллективе среди мужчин курящих 30%, среди
женщин курящих 10%. Наугад выбранное лицо курит. По данной
информации найти процентное соотношение мужчин и женщин в этом
коллективе.
Решение. Построим гипотезы относительно "наугад выбранного лица":
Ям — выбранное лицо — мужчина, Яж — выбранное лицо — женщина.
События Ям и Яж образуют полную систему гипотез. Поскольку
информация о вероятности выбранных гипотез отсутствует, естественно
предположить априорные вероятности гипотез равными Р(НМ) = Р(НЖ) = 0,5.
Пусть случайное событие А — наугад выбранное лицо курит, тогда
условные вероятности легко находятся из известного процента курильщиков:
40

Используем информацию, что событие А произошло. По формуле Байе-
са получаем
Р(Н хАЛ Р(НМ)Р(А\НМ) = 0,5-0,3 = 0 7-
V м| } Р(НМ)Р(А\НМ) + Р(НЖ)Р(А\НЖ) 0, 5 • 0, 3 + 0, 5 • 0, 1
Р(И \А\ Р(НЖ)Р(А\НЖ) = Q,5 • 0, 1 = 0 ~
К ж1 ; Р(НМ)Р(А\НМ) + Р(НЖ)Р(А\НЖ) 0,5 • 0,3 + 0, 5 • 0, 1 U,ZJ"
Учитывая, что вероятность 0,75 по классическому определению
означает отношение числа мужчин к суммарному числу работающих, заключаем:
в данном коллективе мужчин — 75%. Аналогично, женщин, работающих в
данном коллективе, оказывается 25%.
Если мы хотим уточнить далее эти данные, то необходимо иметь
больше информации, т. е. продолжить наблюдения. Также следует еще раз
подчеркнуть, что полученный ответ основывается только на имеющейся
информации, носит вероятностный характер и в данном конкретном
коллективе может отличаться от реального соотношения. Суть же найденного
нами соотношения, 75%—25%, в том, что при имеющихся данных оно
является наиболее правдоподобным (вероятным).
Пример 3. При постановке диагноза болезни конкретного больного
возникло подозрение на одно из трех заболеваний: Я,, Я2, Я3. Статистическая
практика показывает, что при наблюдаемых симптомах вероятности этих
заболеваний соответственно равны 0,6; 0,3; 0,1. Существует
специфический анализ, выдающий некоторый положительный отклик на заболевание
Я, с вероятностью 0,1, на заболевание Я2 с вероятностью 0,8 и на
заболевание Я, с вероятностью 0,2.
Анализ произведен 4 раза, из них трижды получен положительный
отклик. Задача — поставить диагноз, т. е. найти наиболее вероятное
заболевание.
Решение. Заболевания Я,, Я2, Я3 являются вероятностными гипотезами,
и по условию Р(НХ) = 0,6, Р(Н2) = 0,3, Р(Нг) = 0,1. Поскольку других
гипотез нет, то эта система полная. Допустив, что крайне маловероятно
одновременное наличие двух или трех заболеваний, получаем в виде Я,, Я2,
Я, полную систему гипотез. Согласно имеющимся вероятностям,
естественно предположить наличие заболевания Я, как наиболее вероятного
среди рассматриваемых, однако вероятности Р(Н2) и Р(Нг) не так уж малы,
чтобы ими пренебречь. Требуется дополнительная информация, которую и
содержат результаты проводимого анализа.
Обозначим через А свершившееся случайное событие: трижды
положительный отклик в четырех анализах. Далее воспользуемся формулой Байеса,
которая и предоставит нам апостериорные вероятности гипотез —
заболеваемости с учетом свершившегося события А. Для применения формулы
вычислим условные вероятности Р(А\НХ), Р(А\Н2), Р(А\Нг). Поскольку А —
сложное событие, то введем простые события Ах, А2, Аг, А4 — появление
положительного отклика соответственно при_1-м, 2-м, 3-м и 4-м анализе.
Тогда А = AlA2AiA4 + АхА2АгАА + АХА2А3А4 + АхА2АгАл.
При заболеваемости Я, вероятность появления положительного отклика
равна 0,1, а непоявления — 0,9 (0,9 = 1 - 0,1 — вероятность противопо-
41

ложного события). Тогда, считая анализы независимыми, а
события-слагаемые несовместными_(почему?2, получаем _
Р(А\НХ) = Р(АХА2А3АА + АхА2АгАА + АхА2АгАА + АхА2АгАА) =
= 0,1-0,1-0,1-0,9 + 0,1-0,1-0,9-0,1 +0,1-0,9-0,1-0,1 +
+ 0,9-0,1-0,1-0,1 =4-(0,1)3-0,9.
Заметим, что в последнем произведении 4 = С\ ив вычислениях
фактически получена формула Бернулли (см. далее § 1.12).
Аналогично находим
Р(А\Н2) = 4 • (0,8)3 • 0,2, Р{А\Нг) = 4 • (0,2)3 • 0,8.
По формуле Байеса имеем выроятности гипотез, уточненные после
анализов:
Р(НЫ) = Р(НХ)Р(А\НХ) =
* '' ' Р(НХ)Р(А\НХ) + Р(Н2)Р(А\Н2) + Р{Нг)Р{А\Нг)
= 0,6 • 4 - (0, I)3 • 0,9 =
0, 6 • 4 • (0, I)3 • 0,9 + 0, 3 • 4 • (0, 8)3 • 0,2 + 0, 1 • 4 • (0, 2)3 • 0, 8
= 0^002^ ж001?
0, 1276 ' '
Р1Й1\Л)- OJ^JMlllM, 0,963;
РЫЛ)-0-1 -\«$''Ь* .0,02.
Таким образом, полученные вероятности позволяют весьма уверенно
принять гипотезу (поставить диагноз) наличия заболеваемости Н2.
Вероятность гипотезы Н2 утверждает, что по имеющейся информации, данных
четырех анализов и данных статистической практики, при достаточно
большом количестве случаев наш диагноз окажется верным в среднем в
963 случаях из 1000. Отметим математический факт, что сумма
вероятностей гипотез по-прежнему остается равной 1:
0,017 + 0,963 + 0,02 = 1.
1.9. Геометрическая вероятность
Вводя классическое определение вероятности случайного события
Р(А) = —, мы предполагали, что тип — конечные числа, т. е. полная
п
система элементарных событий Ех, Е2, ..., Еп представляет собой конечное
число исходов испытания. Но на практике нередки испытания, когда
полная система элементарных событий является несовместной, равновозмож-
ной, но имеет бесконечное количество исходов. Например, случайные
события, связанные с измерениями: рост и масса тела новорожденных,
время между двумя ударами пульса больного, время инкубационного периода
инфекционного заболевания и т. д. Поскольку измеряемая величина
может принять любое значение из некоторого интервала, а множество таких
значений бесконечно (и даже несчетно), то и возможных исходов испыта-
42

ния имеем бесконечное множество. Таким образом, классическое
определение в явном виде неприменимо: нельзя делить бесконечность на
бесконечность.
На помощь приходит принцип геометрии. В геометрии простейшим
элементом является точка, а рассматриваемыми объектами — множества
точек (отрезки, различные кривые, треугольники, трапеции, пирамиды,
шары, эллипсоиды и т. д.). Для численного сравнения геометрических
объектов не пересчитывают количество точек, а используют понятие меры
соответствующего множества: длину, площадь, объем.
В нашем случае все бесконечное множество элементарных событий также
рассматривают как множество точек, совокупность которых образует
некоторую область, которую можно численно измерить: для кривой найти длину,
для плоской области — площадь, для пространственной — объем. Выделяя
множество благоприятствующих событий как часть множества элементарных
событий, получаем область, для которой находится численная мера.
Таким образом, приходим к обобщению классического определения
вероятности на случай бесконечного множества элементарных событий. При
этом непременно должна иметь место равновозможность всех исходов
(т. е. все точки в множестве равноправны).
Определение. Если множество элементарных событий понимается как
область, то геометрической вероятностью события А называется
отношение меры области, благоприятствующей осуществлению события А, к мере
всей области.
Геометрическая интерпретация задачи такова.
Пусть задана некоторая область G, включающая в себя другую область
g. В область G бросается наугад точка. Требуется найти вероятность, что
точка, обязательно попав в область G, попадет также и в область g.
Условие равновероятности выглядит следующим образом: бросаемая точка
может попасть в любую точку области G, а вероятность попасть в какую-то
часть области G (в область g) пропорциональна мере этой части (длине,
площади, объему) и не зависит от ее формы и расположения.
Обозначив через А искомое событие, получаем
Р(А) = !™*-1, (1.22)
mes G
где mes g — мера соответствующего множества.
Пример 1. Цена деления шкалы термометра равна О, ГС. Показания
округляются до ближайшего целого деления. Найти вероятность, что
появляющаяся при измерении ошибка не превосходит 0,0ГС.
Решение. Рассмотрим шкалу термометра в виде прямой линии.
Выберем любое деление на шкале, до которого производится округление,
например Зб,00вС (рис. 6).
43

Тогда округление до 36°С произойдет лишь в том случае, когда
показание термометра будет в интервале от 35,95е до 36,05вС. Множество точек
этого интервала и есть множество элементарных событий. Мера этого
интервала (mes G) — это его длина, равная 0,1. Искомое событие обозначим
через А, т. е. осуществление А означает, что ошибка измерения не
превосходит 0,0Г. Следовательно, случайное событие А происходит лишь в
случае попадания точного значения в интервал от 35,99е до 36,0ГС.
Множество точек этого интервала — множество событий, благоприятствующих
осуществлению А. Мера данного множества (mes g) — длина интервала,
равная 0,02.
Согласно геометрическому определению, искомая вероятность равна
v ' mes G 0, 1
Пример 2. (Задача о встрече.) Двое студентов договорились встретиться
в определенном месте в течение часа. Пришедший первым ожидает
второго 20 мин, затем уходит. Время прихода каждого студента не зависит от
времени прихода другого и выбирается наудачу. Найти вероятность, что
встреча состоится.
Решение. Обозначим время прихода первого и второго студентов через
х и у соответственно. Так как каждый из студентов приходит в течение
часа, то, перейдя в качестве единицы измерения к минутам, принимаем
хе[0;60], уе[0;60]. Исходя из независимости х и у, считаем, что время
прихода каждого соответствует точке на плоскости декартовой
прямоугольной системы координат Оху (рис. 7).
Таким образом, множество элементарных событий — множество точек
квадрата со стороной 60. Это область G.
Найдем множество событий, благоприятствующих встрече. Встреча
состоится только в том случае, когда х и у отличаются друг от друга не более
чем на 20, причем учитываются два случая: х > у и у > х. Этим условиям
удовлетворяет соотношение \у - х\ < 20, которое равносильно двойному
неравенству
-20<у- х<20,
т. е., получаем систему
44

у-х<20 или (y<x + 20
y-x>-20 [у>х~20
Данной системе уравнений удовлетворяет заштрихованная область на
рис. 7. Это область g.
Далее находим геометрическую вероятность встречи (вероятность
события А):
Р(А) = mes s = плои<а^ь£ = 602 - 2 • 0, 5 • 402 _ 5
mes G площадь G 602 9"
Пример 3. В квадрат со стороной а случайным образом брошена точка.
Найти вероятность, что эта точка попадет точно в центр квадрата.
Решение. Используем геометрическое определение вероятности.
Множество элементарных событий (область G) — все точки квадрата.
Множество событий, благоприятствующих искомому событию А — всего одна
точка (множество g). Тогда
Р(А) = mes 8 = ги1ои^адь^ = .2. = о
mes G площадь G а2
Замечание. Пример 3 демонстрирует любопытный факт, связанный с
геометрическим определением вероятности: вероятность события А равна
нулю, но само событие А не является невозможным. Дело в том, что в
данном случае использовано понятие бесконечности, которая по сравнению с
конечным числом элементов имеет свою специфику, которую нужно
учитывать.
1.10. Статистическое определение вероятности
Классическое определение вероятности предполагает допустимость
построения полной системы элементарных событий и обязательное условие
равновозможности, которое в простейших задачах базируется на
соображениях симметрии (равноправность обеих поверхностей монеты, правильный
ифальный кубик из однородного материала и т. д.). Та же схема работает
и в случае геометрического определения с той лишь специфической
разницей, что речь идет о бесконечных множествах элементарных событий.
Но переход к более сложным задачам сразу же приводит к проблемам
принципиального порядка. Например, проведение хирургической
операции является испытанием, для которого составить полную систему
элементарных событий представляется весьма сомнительным. Во многих
задачах также нет оснований сводить рассматриваемые события к равновоз-
можным случаям. Равновозможность, основанная на симметрии, как
правило, встречается либо в очень простых, либо в искусственно
организованных опытах (например, в азартных ифах). Природа устроена более
мудро и обычно не преподносит примитивных задач. Например, вероятность,
что родившийся ребенок окажется мальчиком, вовсе не равна 0,5, и эта
вероятность 0,5 пригодна лишь для очень приближенных расчетов. Вывод —
классическое определение вероятности имеет практическое применение
для достаточно узкого круга проблем.
45

И тем не менее вероятность, как было отмечено ранее, — это
объективная характеристика любых случайных событий. Следовательно,
необходимо найти другие, более общие способы определения вероятности, не
затрагивающие вопрос ограниченности полной системы элементарных событий
и не привязанные к постулату равновозможности.
Преодолеть создавшееся затруднение можно, лишь расширив кругозор:
перенести внимание с индивидуальных экспериментов, в которых все
зерно истины заслонено различными случайными отклонениями,
колебаниями, ошибками наблюдения, на всю последовательность экспериментов. В
достаточно длинной последовательности опытов случайные отклонения в
ту и иную сторону взаимно компенсируются, уравновешиваются,
суммарно уменьшаются и почти исчезают, и вот она — истина, выплывающая
перед взором благодарного терпеливого исследователя. Достаточно давно
было замечено, что с ростом количества испытаний средние величины
начинают стабилизироваться, колебание значений происходит около
некоторого постоянного числа, и чем больше испытаний, тем больше
затухание этих колебаний.
Для проявления указанной закономерности необходимо, чтобы
испытания могли быть проведены (по крайней мере теоретически) достаточно
большое (бесконечное) число раз при неизменных условиях.
В качестве среднего значения можно взять относительную частоту
осуществления \х раз контролируемого события в п независимых испытаниях,
проводимых при неизменных условиях: ^.
п
Относительная частота ^, являясь средним значением, также обладает
п
стабилизационным свойством стремления к некоторой постоянной с
ростом п. Экспериментальная проверка показывает, что в случае
применимости классического определения вероятности, константа, к которой
стремится относительная частота, есть не что иное, как значение
теоретической вероятности. Самый простой опыт — подбрасывание монетки — был
проделан в студенческой аудитории 10, 20, 50, 100, 500, 1000, 2000 раз.
Если сюда же добавить более объемные по числу испытаний известные
опыты Бюффона, Керриха, Пирсона и др., то данные можно представить в
виде таблицы.
Как видим, относительная частота с ростом числа испытаний п
стремится к значению 0,5, что наглядно иллюстрирует последний столбец
таблицы. Следует отметить неравномерность убывания чисел в последнем
столбце, что вполне естественно, так как теоретически допустимо
появление "герба" в п независимых испытаниях даже п раз. Разумеется, повторяя
наши испытания вновь, мы почти наверняка получим при тех же п другие
значения относительных частот. Но общая тенденция стремления ^ к 0,5
п
сохранится. Вместе с тем, применяя специальные вероятностные методы,
возможно установить, что выпадение "герба" и "монеты" не равновероятно.
Расхождение с вероятностью 0,5 объясняется неидеальной
симметричностью монет. Однако модель с двумя равновозможными исходами чрезвы-
46

Опыт Бюффона
Опыт Феллера
Опыт Керриха
Первый опыт Пирсона
Опыт Джевонса
Второй опыт Пирсона
Опыт Романовского
Число
испытаний
10
20
50
100
500
1000
2000
4040
10000
10000
12000
20480
24000
80640
Частота
появления
"герба"
6
10
22
46
263
507
988
2048
4979
5087
6019
10379
12012
39699
Относительная
частота
(статистическая
вероятность)
0,6
0,5
0,44
0,46
0,526
0,507
0,494
0,5069
0,4979
0,5087
0,5016
0,5068
0,5005
0,4923
Отклонение
относительной
частоты от 0,5
0,1000
0
0,0600
0,0400
0,0260
0,0070
0,0060
0,0069
0,0021
0,0087
0,0016
0,0068
0,0005
0,0077
чайно полезна для многих практических задач, поэтому допущение о
полной симметричности монеты является вполне оправданным.
Можно проделать и другие эксперименты: например, при подбрасывании
трех игральных костей фиксировать относительную частоту события — по-
5 4 5
явление различного числа очков (вероятность р = 1 • ^ • ■? ~ 5) или ПРИ
извлечении наудачу двух карт из тщательно перетасованной колоды в 36
карт фиксировать относительную частоту события — появление одинако-
о
вой масти (вероятность р = 1 • —) и т. д. Во всех случаях относительная
частота контролируемого события с ростом п устойчиво стремится к своей
вероятности.
Отметим также, что стремление относительной частоты события к его
вероятности экспериментально лишь проиллюстрировано, а на самом деле
имеется глубокое теоретическое обоснование этого факта в виде теоремы
Бернулли, называемой также законом больших чисел (см. § 1.15).
Таким образом, естественно считать, что относительная частота
события стремится к своей объективно существующей вероятности не только в
случае применимости классического определения, но и в любом другом. И
тогда вероятность любого случайного события определяется статистически
на основании многочисленных испытаний как значение, близкое к
относительной частоте. Отметим, что для относительной частоты ^ справедливы
свойства, характерные для вероятности:
а) вероятность достоверного события равна единице;
47

b) вероятность невозможного события равна нулю;
c) если случайное событие А представлено в виде суммы несовместных
случайных событий Ах и А2, то Р(А) = Р(АХ) + Р(А2).
Отметим также и недостатки статистического определения вероятности.
Во-первых, если мы приравниваем относительную частоту ^ к объективно
существующему числу вероятности, то в зависимости от наших опытов мы
неизбежно допускаем ошибку. Например, в случае с выпадением "герба"
при подбрасывании монеты на роль вероятности претендует любая из
относительных частот, приведенных в нашей таблице, и даже выбор при
наибольшем п может оказаться не наилучшим (сравните относительные
частоты в таблице при п = 24 000 и п = 20). Следовательно,
неоднозначность выбора вероятности приводит к проблемам в теории, решением
которых и занимается математическая статистика. Во-вторых, вопрос
неоднозначности выбора вероятности можно разрешить, взяв в качестве
определения вероятности предел
р = lim^.
п-*<х>П
Это определение несет принципиальные проблемы практического
применения, ведь чтобы найти вероятность, согласно последнему равенству,
нужно произвести бесконечное количество испытаний и перейти к
пределу. Требование беспрецедентное. Например, поступая аналогично, для
измерения температуры больного следует произвести бесконечное
количество измерений и найти предел.
И все же статистическое определение вероятности, являющееся
обобщением классического определения, находит свои многочисленные
применения в самых разнообразных областях исследований и в том числе в
медицине, но с учетом поправок на погрешности измерений, с учетом
оценок различных параметров, доверительных вероятностей, приближений.
Математические методы статистического исследования, включающие в
себя общепринятый математический аппарат, имеют свою специфику,
сформировались сравнительно недавно и с началом компьютерной эры
переживают бурный расцвет своего развития.
1.11. Понятие об аксиоматическом построении теории вероятностей
Впервые классическое и статистическое определения вероятности были
сформулированы Якобом Бернулли около трехсот лет назад и
опубликованы в посмертном трактате "Искусство предположений" (Ars conjectandi,
1713 г.). С того времени более двух веков практически не затухал интерес к
вероятности, происходило уточнение формулировок, решение частных
задач, появление новых понятий. Эти исследования подстегивались
потребностями статистических исследований, в частности демографии. Однако
не было опоры, фундамента у нарождающейся науки, без которого
предыдущие знания представляют собой всего лишь в той или иной степени
совокупность разрозненных фактов и задач.
Новым своим рождением с последующим бурным расцветом теория
вероятностей обязана аксиоматике А. Н. Колмогорова, введенной в 30-е го-
48

ды двадцатого столетия. Аксиомы Колмогорова позволили объединить
известные факты на единой основе, применить наработанный к тому
времени аппарат других математических дисциплин. Образно говоря, теория
вероятностей как наука встала на ноги и научилась ходить. Заметим, что
также, основываясь на системе аксиом, построены и многие другие
естественные науки, например евклидова геометрия, геометрия Лобачевского,
теоретическая механика.
В основе аксиоматики Колмогорова лежит понятие множества
(пространства) элементарных событий Q. Кроме элементарных событий, как
мы видели ранее, необходимо использовать невозможное событие;
событие, противоположное исходному; суммы и произведения событий.
Поэтому на множестве элементарных событий рассматривается множество F
подмножеств элементарных событий.
Пример. Пусть пространство элементарных событий Q состоит всего из
четырех элементарных событий: Q = {Ех, Е2, Ег, Е4}.
Найдем все элементы множества F. Во-первых, это сами элементарные
события (множества из одного элемента):
■^1) -^2» Аз> -^4-
Во-вторых, это суммы двух элементарных событий (множества из двух
элементов):
{£„ Е2), {£„ Ег), {£„ Е4}, {Е2, Е3}, {Е2, Е4), {Ег, Е4).
В-третьих, это суммы трех элементарных событий (множества из трех
элементов):
{-£[, Ь2, /2-зЬ \^1> ^2» ^4'» l^l» Аз> ^41» 1-^2» Аз> ^4»-
В-четвертых, это сумма четырех элементарных событий (множество из
четырех элементов), само множество Q:
{£-!, Ь2, £-3> ^4i"
Далее, рассматривая все возможные произведения найденных событий,
мы придем либо к невозможному событию V (которое также часто
обозначают символом 0), либо к событию, уже выписанному ранее, например по
определению произведения событий
Ег Е2 = V,
{Ех, Е2, Ег) - {£,, Е2, Е4) = {£,, Е2).
Событие {£,, Е2, Ег, Е4} является достоверным событием.
Находя события, противоположные любому из записанных, мы
непременно получим события из того же множества, например
Й = 0.
Таким образом, множество F состоит из одного невозможного события
(0), из четырех "одноэлементных" событий (элементарных), из шести
"двухэлементных" событий, из четырех "трехэлементных" событий, одного
"четырехэлементного" (Q).
Итого: 1+4 + 6 + 4+1 = 16 всевозможных событий.
Заметим, что в нашем случае четырех элементарных событий
16 = С°4 + С\ + С] + С\ + С4 [см. формулу (1.8)].
4 — 3529
49

Аналогично в случае п элементарных событий множество F состоит из
2" различных подмножеств, так как согласно формуле (1.8)
с°п+с1п+с2п+...+спп = г.
В более общем случае множество подмножеств F вводится как
множество, составленное по правилам:
l)QefH0eFL
2) если А е F, то А е F;
3) если А е Fn Be F, то А + В е FuAB e F
Такое множество F называют алгеброй множеств.
Введя множество элементарных событий Q. и множество
подмножеств F, получаем, что все возможные случайные события являются
элементами F.
Для таких событий и имеют место аксиомы Колмогорова.
Аксиома 1. Каждому случайному событию А можно поставить в
соответствие неотрицательное число, которое обозначим Р(А) и назовем
вероятностью события А.
Аксиома 2. P(Q) = 1.
Аксиома 3. Если случайные события Ах, А2, ..., А„ попарно несовместны,
то Р(А{+А2+...+Ап) = Р(АХ) + Р(А2) +...+ Р(Ап).
Несмотря на кажущуюся простоту, приведенные аксиомы имеют
глубокий смысл. Они непротиворечивы, поскольку многие реальные задачи
укладываются в схему, созданную аксиомами. Классическое и
статистическое определения вероятности — частные случаи аксиоматического
определения, в которых вероятность Р(А) задана конкретным соотношением.
Вместе с тем свобода выбора неотрицательного числа Р(А) в аксиоме 1
позволяет использовать вероятность не только в случае конечного числа
элементарных событий и условия равновозможности, но и, что весьма
существенно, в случае достаточно сложных и хитроумно запутанных задач,
непрерывно преподносимых нам природой и обществом.
, Отметим также справедливость основных свойств и теорем,
рассмотренных нами ранее в классическом варианте; в частности, справедливы
теоремы сложения и умножения, формула полной вероятности и
формула Байеса.
Вместе с тем, рассматривая вероятность как функцию множества Р(А),
аксиоматика Колмогорова приглашает применить к вероятности мощный,
серьезно разработанный математический аппарат метрической теории
функций, что и предопределило успех развития.
Тройку символов (Q, F, Р) для рассматриваемой вероятностной задачи
называют вероятностным пространством.
1.12. Последовательность независимых испытаний. Формула Бернулли.
Наивероятнейшее число успехов
а) В различных областях исследовательской деятельности возникает
необходимость проверки каких-либо фактов опытным путем. Например, на
заводе, прежде чем запустить в серийное производство новый прибор или
устройство (транзистор, электролампочка, часы, термометр, дверной за-
50

мок, парашют, телевизор, станок, автомобиль и т. д.), производится
достаточно продолжительная последовательность испытаний. По этим
испытаниям судят о качественных и количественных характеристиках изделия,
таких как надежность, долговечность, устойчивость к внешним
воздействиям, ошибка показания прибора, степень удобства в эксплуатации и т. д.
Исследование контролируемых свойств или степени воздействия с
помощью серии испытаний необходимо не только в массовом промышленном
производстве, но и в медицине (эффективность нового лекарства или
новых методов лечения и профилактики), биологии (преимущества одного
сорта или вида растительных и животных организмов по сравнению с
другими), химии (исследование некоторых свойств тех или иных веществ),
экономике (эффективность в организации тех или иных производственных
процессов), обучении (разработка новых методик) и т. д. В приведенных
выше примерах, как правило, речь идет об активном эксперименте:
исследователь сам проводит испытания. Возможна и другая ситуация, когда
исследуется объективный процесс, ниспосланный нам свыше. Например, в
метеорологии эксперимент пассивный, исследователь не организует
испытания, а лишь снимает необходимые наблюдения (температура, осадки,
направление ветра, облачность) в нужный момент в нужном месте. Здесь
своя специфика в выборе этих момента и места, но суть также в
последовательности испытаний.
Термин "последовательность испытаний" имеет самый широкий смысл,
поскольку испытания можно организовать и наблюдать всевозможными
способами. Разберем следующую схему. Испытание рассматриваем только
по отношению к исследуемому случайному событию А: отвлекаясь от всех
нюансов, фиксируем лишь два исхода испытания: произошло А или нет.
Предполагаем, что испытание проводится в неизменных условиях и
вероятность осуществления А постоянна и равна р. Тогда вероятность
неосуществления события А естественно обозначить q, где q = 1 — р. Данная схема
организации последовательности испытаний играет фундаментальную роль
во многих прикладных исследованиях. Однако предполагаемая
неизменность условий в различных испытаниях является своего рода идеализацией
реальности, поэтому обычно вместо неизменности условий при
проведении испытаний используют более осязаемое понятие, а именно:
независимость испытаний, имея в виду, что любая комбинация любого количества
исходов среди п испытаний является последовательностью независимых
событий. Проще говоря, осуществление или неосуществление события А в
любом испытании не зависит, появилось или не появилось это событие в
любых других испытаниях, предыдущих или последующих.
Последовательность п испытаний, организованных подобным образом,
называют схемой Бернулли.
Испытания, в которых событие А осуществляется с постоянной
вероятностью, будем называть однотипными. Таким образом, схема Бернулли —
последовательность однотипных, независимых испытаний.
Если проводится одно испытание^ то пространство элементарных
событий состоит из двух элементов А и А. Если проводится два испытания, то
пространство элементарных событий содержит четыре (22) элемента: АА,
АА, АА, АА. Легко вычислить, что если проводится п испытаний, то
пространство элементарных событий содержит 2" элементов: от АА...А до

AA...A (сравните задачу "Сколько различных _л-буквенных слов можно
составить, используя алфавит из двух букв А и AT').
b) Поставим вопрос: Какова вероятность, что в п испытаниях,
проводимых по схеме Бернулли, событие А осуществится ровно т раз, где
О < т < п ? Следовательно, требуется найти вероятность события В,
состоящего из произведения т сомножителей А и (п — т) сомножителей А_ При
этом такие произведения различаются порядком сомножителей А и А,
поскольку место каждого сомножителя соответствует номеру испытания,
т. е., например, произведения AAA и AAA означают разные
последовательности: в первой последовательности событие А не осуществилось при
первом испытании и осуществилось при втором и третьем, а во второй
последовательности событие А не осуществилось уже при втором испытании и
осуществилось при первом и третьем.
Итак, поскольку каждое из указанных произведений влечет
осуществление события В,тоВ— сумма всех таких возможных произведений, причем
любые два слагаемых в этой сумме — события несовместные. Таким
образом, вероятность события В представляет собой сумму вероятностей каж-
дого_отдельного произведения из m сомножителей А и (п — ш)
сомножителей А. Все произведения отличаются лишь порядком сомножителей.
В = А...АА...А +...+ А...АА...А
tn n~tn n~tn tn
P(B) = P(A...AA..J) + ... + P(A...AA...A).
Используя независимость событий-сомножителей в каждом из
произведений (независимость испытаний), получаем
Р(В) =2^(1^+ ... +j^^p.
tn n—tn n—tn tn
Поскольку вероятности р и q — это конкретные числа, а в
произведении порядок чисел безразличен, то оказывается, что в правой части
последнего равенства все слагаемые одинаковы pmq"~m. Таких слагаемых
всего С™ (именно столько способов в последовательности из п элементов
выбрать /и элементов, их мы обозначим А, остальные — А). Таким образом,
приходим к формуле
Р(В) = Cmnpmqn-m.
С целью выделить числа пит обозначим Р(В) = Рп(т), и тогда
полученная формула приобретает окончательный вид:
Рп(т) = C'Zpnq"-", (1.23)
где р — вероятность осуществления события в одном испытании,
q= 1 - р.
Данное соотношение называют формулой Бернулли.
Замечание 1. Заметим, что в случае равновозможного исхода АиАв
одном испытании, р = q = - , данная формула соответствует классическому
определению вероятности, ибо тогда
Р(т) = ±л
52

где как раз число элементарных событий и есть 2", а число событий,
благоприятствующих осуществлению А ровно т раз в п независимых
испытаниях, конечно же, Стп. В случае р Ф q классическое определение для
вычисления Рп(т), естественно, неприменимо.
Замечание 2. Используя бином Ньютона для выражения (q + /?)",
получаем
(Я + Р)" = CV+ Clnpq"-lClp2qn-2+ ...+ СГУ-'<7+ CV
или, согласно введенным обозначениям,
(я + ру = ад + ад + р„о) +-+ Л(« - о + ад. (1-24)
Ввиду указанной зависимости вероятности Р„(т) называют
биномиальными вероятностями.
Заметим также, что при р + q = 1 из (1.24) получаем
РпФ) + ВД + /»,<2) +...+ Рп(п - 1) + />я(л) = 1. (1.25)
Условия (1.25) удобно использовать для контроля вычислений.
Замечание 3. Формула Бернулли (1.23) используется лишь в случае
организации испытаний по схеме Бернулли, к которой принято относить п
бросаний монеты, п последовательных (с возвращением) извлечений карт
из колоды, выбор п объектов (например, обследуемых больных) из
достаточно большой однородной совокупности и т. д.
Пример 1. В многодетной семье 6 детей. Используя статистическую
вероятность рождения мальчика р = 0,516, найти вероятности всех
возможных случаев распределения детей по признаку пола (все дети — девочки,
один мальчик и пять девочек, два мальчика и четыре девочки и т. д.).
Решение. Рассматривая рождение мальчика как случайное событие с
постоянной вероятностью, мы находимся в условиях схемы Бернулли.
Применяя формулу Бернулли, получаем:
Л(0) = C°6p°q6 = q6 = (1 -pf = 0,4846« 0,013-
вероятность, что среди шести детей нет мальчиков;
Л(1) = C\pqs = 6 • 0,516 • 0,4845«0,082-
вероятность, что среди шести детей один мальчик;
Л(2) = C26p2q4 = 15 • 0,5162 • 0,4844« 0,219-
вероятность, что среди шести детей два мальчика;
Л(3) = CjpV = 20 • 0.5163 • 0,4843«0,312-
вероятность, что среди шести детей три мальчика;
Л(4) = ClpW = 15 • 0.5164 • 0,4842«0,249-
вероятность, что среди шести детей четыре мальчика;
Л(5) = C\pq = 6 • 0,5165 • 0,484« 0,
Невероятность, что среди шести детей пять мальчиков;
Л(6) = C66p6q° = р6 = 0,5166«0,019-
вероятность, что все шестеро детей — мальчики.
Таким образом, все искомые вероятности найдены. Заметим, что их
сумма равна 1 [см. (1.25)].
53

с) Пусть п испытаний проводятся по схеме Бернулли (т. е. однотипны и
независимы), вероятность осуществления события в одном испытании
(назовем это осуществление "успехом") равна р.
Так как количество испытаний п, то число "успехов" может быть 0, 1,
2, ..., п. Все эти значения обладают, вообще говоря, различными
вероятностями. Поставим вопрос: какое из этих значений имеет наибольшую
вероятность?
Обозначим наиболее вероятное значение т0 и будем называть его наи-
вероятнейшим числом успехов в п испытаниях.
Установлено, что вероятности Р„(т) при изменении т от 0 до п вначале
возрастают и, достигнув наибольшего значения при т = т0, далее
убывают. Таким образом, чтобы найти т0 достаточно решить при
фиксированных пир неравенства относительно т:
Рп(т0)>Рп(т0-\); 6
Рп(т0)>Рп(т0+1).
Используя формулу Бернулли (1.23) и записывая биноминальные
коэффициенты через факториалы, вместо первого из неравенств (1.26) имеем
П! т0 п-гпо . П\ та-\ п-та+\
;Р Я >, 1Ч„ _,_ 1ч,/> Я
mQl(n-mQ)l ~(/я0- 1)!(й-/я0+ 1)!
Сокращая в неравенстве одинаковые положительные сомножители,
получаем
т0 п — т0 + 1
Следовательно,
р(п- т0+ 1)- qm0
>0
т0(п- т0+ 1)
А так как т0(п — т0+1) > 0, то справедливо неравенство
р(п — т0 + 1) — qm0 > 0 , т. е.
pn-pm0+p-qm0>0,
(л+ l)p>mQ(p + q).
Учитывая, что/? + q = 1, приходим к
т0 < (п + 1 )р.
Аналогично, расписав второе из неравенств (1.26), получаем
т0 > пр - q.
Объединяя последние два выражения, имеем границы для т0:
np-q<m0<(n+\)p. (1.27)
Заметим, что числа пр -qn (п+ 1)р отличаются на величину q + р, т. е.
на 1. Следовательно, значение т0 можно определить как целую часть числа
(п+\)Р.
Также отметим, что в случае, когда число (п+\)р целое, будет целым и
пр - q, поскольку они отличаются на 1, и наивероятнейших чисел
оказывается два. В этом случае, разумеется, Р„((п+\)р) = Рп(пр - q) = т0.
54

В рассмотренном ранее примере 1 наивероятнейшим числом т0, как
видно из вычислений, является число 3, именно вероятность Р6(3) я 0,312 —
наибольшая по сравнению со всеми другими. По нашей формуле
(и + 1)/? = 7-0,516 = 3,612.
Целая часть этого числа равная 3 и есть т0, что соответствует
непосредственно проведенным вычислениям.
Пример 2. При проведении сложного химического опыта
вероятность положительного исхода постоянна и равна 0,2. Произведено
14 независимых опытов. Найти наивероятнейшее число опытов, в
которых получен положительный исход. Вычислить соответствующие
вероятности.
Решение. В данном случае п = 14, р = 0,2 и испытания однотипны и
независимы (т. е. проводятся по схеме Бернулли). Тогда найдем
величину (п+\)р, а именно: (п+\)р = 15 -0,2 = 3. А так как это число
является целым, то и оно само является наивероятнейшим, и число 2, на
единицу меньшее, чем 3, также наивероятнейшее. Вычислим искомые
вероятности:
Л4(2) = С]4 • (0,2)2 • (0,8)12 = -Ili-0,220,812 = Я2'8'2 -
2!12! ' ' ю14
38 in-14
= 91 • 2JB • 10
Л4(3) = С]4 • (0,2)3 • (0,8)" = -liLo,230,8" = 91 • 4^ =
J. 11. 10
= 91 • 238 • 10~14.
Итак, />14(2) = Л4(3) = 91 • 238 • 10"14«0,25.
Пример 3. Всхожесть семян некоторого растения оценивается в 85%.
Сколько нужно посеять семян, чтобы получить наивероятнейшее число
всходов в количестве 20 растений?
Решение. Посадку семян рассматриваем как проведение испытаний с
двумя исходами (есть всход или нет). Испытания однотипны с
вероятностью р = 0,85, и предполагаем, что они также и независимы.
Следовательно, мы находимся в условиях схемы Бернулли и имеем основания
применять соответствующую теорию. Итак, р = 0,85; т0 = 20, требуется найти п.
Воспользуемся двойным неравенством (1.27), согласно которому
п • 0,85-0, 15 < 20,
20<(л+ 1) • 0,85.
Тогда
f <20 + 0,15
0, 85
^ 20 ,
т. е. 22,53 < п < 23,71, и поскольку п — число натуральное, то п = 23.
Ответ: чтобы наивероятнейшим числом всходов было 20 нужно посеять
23 штуки семян.
55

1.13. Приближенные формулы, используемые в схеме Бернулли
Схема Бернулли, как указано в предыдущем параграфе, имеет
фундаментальное значение и является универсальным инструментом многих
теоретических и прикладных исследований. Однако использование формулы
Бернулли (1.23), лежащей в основе соответствующей схемы и, безусловно,
справедливой при любых натуральных пит, часто сопряжено с большими
трудностями вычислений. Действительно, сомножители в формуле
Бернулли являются факториалами и степенными выражениями, которые с ростом
п становятся практически недоступными для вычислений (факториалы
быстро стремятся к бесконечности, а степени соответственно стремятся к
нулю). Владея абсолютно точной формулой для вычисления вероятностей
Р„(т), мы оказываемся остановленными стеной вычислений.
Разумеется, можно искусственным образом, группируя и сокращая
отдельные сомножители в формуле, преодолеть этот вычислительный барьер
и вычислить точное значение вероятности. Но обычно поступают проще:
пожертвовав некоторой точностью вычислений, применяют
приближенные формулы, беспроблемно используемые для расчета вероятностей Рп(т)
даже в докомпьютерные времена.
1. Приближенная формула Пуассона.
Теорема Пуассона. Пусть для вычисления вероятности Рп (т)
справедлива формула Бернулли (1.23):
PnW = C>V"m-
Полагаем п -> а>, р -> 0, причем пр = а, где а — некоторая
положительная константа. Тогда при любом фиксированном целом неотрицательном
т справедливо равенство
т
НтЛОя) = -е~°. (1-28)
п-*т Ш1
Доказательство. Так как по условию пр = а, то р = -, следовательно,
q = 1 — р = 1 — - . Тогда вероятность Р„(т) можно записать в виде
/..(„) = OV- = ^L . (2)"(,--«)- =
= п(п- 1)(я-2)...(я-т+ 1) . аГ_ . Л _ qX(x_qXm =
ml пт ^ п' ^ п'
mil п'п ]{ nJ \ nJ '
Выражение в квадратных скобках имеет в числителе ровно т
сомножителей. Вынося в каждом из них за скобку число п, получаем
«■• 1 -fi - IVi -2-)..U -s^l)
— "V " Ч-внН'-^)-
56

Таким образом,
Переходя далее к пределу в обеих частях полученного равенства при
w->oo, имеем (см. Приложение 1):
все сомножители выражения в квадратных скобках стремятся к 1, а в
пределе равны 1;
сомножитель (1 — -J при фиксированных а и т в пределе равен 1;
сомножитель (1 — -J в пределе равен числу е", где число е — известная
общеупотребительная математическая константа — определяется именно
как предел
limfl +-У = е, е = 2,71828...
Следовательно, получаем
т
НтЛСя) = -е~а.
п -»» /72!
Теорема доказана.
Соотношение (1.28) позволяет при достаточно больших п и
соответственно малых вероятностях р полагать
т
Рп{т)*^е-°. (1.29)
При этом погрешность нашего приближения, т. е. разность между
истинным значением вероятности и приближенным, оценивается
неравенством (приводимым без доказательства)
РЛт)--е-°
ml
<пр2. (1.30)
Приближение Пуассона обычно применяют для вычисления
вероятностей редких событий (малая вероятность р) и при соответствующих п
таких, что число пр = а невелико. Как мы увидим далее (см. § 2.6), число а
является средним числом успехов в испытаниях, проводимых по схеме
Бернулли. Зная это значение, можно вычислять вероятность Р„(т) и при
неизвестных пир. Поэтому в записи данной вероятности индекс п можно
опустить и записывать Р{т).
Если известно среднее число успехов X за единицу времени
(называемое интенсивностью), то среднее число успехов за время t определяется по
формуле a = Xt. Тогда формула, соответствующая (1.28), имеет вид
адяМ!е"". (1.31)
ml
Отметим, что значения е~а затабулированы при различных а либо легко
находятся на микрокалькуляторе.
57

Пример 1. В санатории 600 отдыхающих. Полагая вероятность
рождения в любой день года равной г^т > найти вероятность, что: а) один из от-
365
дыхающих родился 1 января; б) двое из отдыхающих родились 1 апреля.
Решение. Поскольку полагаем, что общество отдыхающих (п = 600)
подобрано независимо от дней рождения, вероятность рождения в
какой-либо день (например, 1 января или 1 апреля) постоянна (р = г^т), то мы на-
365
ходимся в условиях схемы Бернулли. Тогда по формуле Бернулли
ЛооО) " СЧзб5Лзб5)
Лоо(2) = С2т[ш) [ш)
599
598
Однако довести до числа подобные выражения нелегко. И так как р —
число малое, п — число достаточно большое, воспользуемся
приближенной формулой Пуассона (1.29). При этом пр = -^-^ 1,6438 и, полагаем,
365
а = 1,6438. Следовательно,
Лоо(1)«^«~в = l,6438c-,6438«0, 3177,
Aoo(2)*fV* = OiipiV'-^-cutti.
Отметим, что, согласно оценке (1.30), наша погрешность метода не
более чем пр2 = ар < 0,005, так что две последние цифры в полученных
ответах роли не играют.
Пример 2. Известна средняя плотность болезнетворных микробов: 200
на 1 м3 воздуха. На пробу взято 3 дм3 воздуха. Найти вероятность
обнаружения хотя бы одного микроба.
Решение. Данную постановку задачи также можно свести к схеме
Бернулли. Хотя в данной ситуации неизвестны ни п, ни р, но зато
фактически задано среднее значение а = пр, а именно: поскольку среднее
число микробов в 1 м3 равно 200, то в 3 дм3 среднее количество
микробов 200* 0,003 = 0,6. Итак, а — 0,6, что соответствует в схеме Бернулли
большим значениям п и малым вероятностям р. Знания числа а
достаточно для вычисления искомой вероятности:
Р(т>\) = 1-/>(0) = 1-^е~а = 1-е"0,б«0,451.
Замечание. В рассмотренном примере в записи вероятностей Р(0) и
Р(т> 1) индекс п опущен, так как он в данном случае принципиального
значения не имеет.
Пример 3. На станцию скорой помощи поступает в среднем 2 вызова в
минуту. Найти вероятность, что в ближайшие 3 мин поступит: а) ровно 5
вызовов; б) менее 5 вызовов.
58

Решение. Для решения задачи воспользуемся приближением Пуассона
вида (1.31). Интенсивность вызовов X равна 2, тогда Xt = 2*3 =6.
Следовательно,
а) />(5) = 1M1-V" = ^е~6*0, 1606.
б) Р(/л < 5) = Р(0) + Р(1) + Р(2) + Р(3) + Р(4) =
= ^°е~6 + £е_6 + |V6 + |V6 + ^е"6 = е"6(1 + 6 + 18 + 36 + 54) » 0, 2851.
2. Локальная теорема Муавра—Лапласа.
Пусть вновь п испытаний проводятся по схеме Бернулли. Тогда,
естественно, имеет место точная формула (1.23):
лею = cmnPmqn-m.
Предположим, что ввиду больших п точной формулой пользоваться
затруднительно. Приведем без доказательства еще одно приближение.
Теорема (локальная теорема Муавра—Лапласа). Если п испытаний
проводятся по схеме Бернулли относительно события А, то вероятность
осуществления А ровно т раз (т <п), можно найти по формуле
РМ = -L=<?(x) + a(n,p,m), (1.32)
<jnpq
где р — вероятность осуществления события А в одном испытании,
q=\- P,
х _ т-пр
Jnpq '
а(п,р, т) некоторая убывающая с ростом п функция, т. е.
lima(w,/>, m) = 0.
В формулировке локальной теоремы приведено точное выражение для
вероятности Р„(т). Обычно при достаточно больших п слагаемым
а(п,р, т) пренебрегают, и тогда
Л0я)«-р=Ф(*). (1-33)
Jnpq
Таким образом, функция а(п,р, т)является пренебрегаемым значением
разности между точным значением Рп{т) и приближенным <р (х).
Функция а(п,р,т) стремится к нулю с ростом п быстрее в случае, когда р
и q близки к 0,5 (естественно, р + q = 1). Если же какая-то из величин р
или q значительно отклоняется от 0,5, то точность приближения (1.33)
ухудшается, и тогда более эффективным является приближение Пуассона,
рассмотренное выше.
59

Заметим, что используемые в (1.32) значения х и ф(х) легко
вычисляются с помощью микрокалькулятора. Ранее, в докомпьютерные времена,
численные значения функции ф(х) для различных х табулировались.
Сейчас использование таблицы продиктовано исключительно условием
удобства (см. Приложение 2, табл.1).
Пример 4. Вероятность рождения мальчика /7 = 0,516. Найти
вероятность, что среди 100 новорожденных 50 мальчиков.
Решение. В задаче выполнены условия схемы Бернулли, п — 100,
т = 50, р = 0,516, q = 0,484. Требуется найти вероятность Р100(50). В
данном случае совершенно точная формула Бернулли приводит к
вычислительным проблемам, поэтому воспользуемся приближенной формулой
локальной теоремы Муавра—Лапласа (1.33):
Лоо(50)« 1 , Ф (*),
7100 • 0,516 • 0,484
где х = 50-100-0,516 ( = _^/1
V100 • 0,516 • 0,484 72я
Тогда х« —0, 32. Значение ф(х) можно вычислить с помощью
микрокалькулятора, а можно воспользоваться таблицей (см. Приложение 2, табл. 1). При
этом так как функция ф(х) четная, то ф(-0,32) = ф(0,32) я 0,379. И
окончательно получаем ответ:
Лоо(50)«^ . 0,379*0,076.
1.14. Функция Лапласа. Интегральная теорема Муавра—Лапласа.
Определение. Функцией Лапласа называют неэлементарную функцию
Ф(х) вида:
х -'1
Ф(*) = -р= U 2dt, (1.34)
определенную при хе (—оо;+оо).
В интеграле выражения (1.34) t — переменная интегрирования, которая
в процессе вычисления заменяется пределами интегрирования. Таким
образом, выражение в правой части (1.34) остается зависящим только от
верхнего предела х, что и отмечено в (1.34) как Ф(х).
Интеграл в элементарных функциях не вычисляется, поэтому значения
функции Ф(х) для различных х затабулированы (см. Приложение 2, табл. 2).
Приведем основные свойства функции Лапласа Ф(х).
1. Ф(х) — функция, возрастающая во всей области определения. Для
доказательства вычислим производную по х:
1 (х -- V 1
ф'(х) = _±J [e 2dt = -L.
j2n\J J Jbk
■e . (1.35)
60

При нахождении производной от интеграла с переменным верхним
пределом по этому переменному пределу использовано соотношение теоремы
Барроу (см. Приложение 1):
jf(t)dt\ =/(*)
Так как Ф'(*) > 0 при любых х [см. (1.35)], то, как известно, функция
Ф(х) является возрастающей. Свойство доказано.
2. При х-> — оо функция Лапласа Ф(х) -> 0, т. е. lim Ф(х) = О.
Выпишем предел.
- 1 i;~ ГЛл - 1
lim Ф(х) = -L lim [e 2dt = — [е 2 dt = О,
х->_аз J2nx^~m J Ля J
так как последний интефал вычисляется по нулевому промежутку, что и
требовалось доказать.
3. При х-> +оо функция Лапласа Ф(х) -> 1, т. е. lim Ф(х) = 1.
Х-» + аэ
Выпишем предел
lim Ф(х) = -L lim f e * dt = -L f e 2 dt.
—т —т
Несобственный интефал вида
+ » ,2
ji'2dt
—т
известен как интефал Пуассона и равен Ля (см. Приложение 1). Таким
образом,
lim Ф(лг) = -L • Ля = 1 .
*^+- Ля
Что и требовалось доказать.
4. Ф(-х) + Ф(х) = 1 (1.36)
Доказательство.
1 ~х, -г- ^ +1 -'-
^ 1 Г. 2 . , 1 Г 2
Ф(-*) + Ф(х) = -L fe 2<£ + -L f
Ля J Ля J
е 'Л.
Выносим общий множитель за скобку и в первом интефале проводим
замену переменной z = ~t. Тогда
( х -i х -'1 \
= 1 - [а 2W,4- [а 2Ht =
е 'Л =
Ф(-х) + Ф(х) = -L - f e 2dt+ f
(+т i1 X i1 \ +» ;2
61

У А
у . .
0,5
X
Рис. 8. График функции у = Ф(х).
В последнем равенстве мы воспользовались свойством аддитивности
определенного интеграла. Далее, используя интеграл Пуассона (см.
доказательство свойства 3), имеем
Ф(-х) + Ф(х) = -L • J2n = 1.
Свойство доказано.
5. Ф(0) = 0,5 (1.37)
Доказательство.
По свойству 4 можно записать Ф(-0) + Ф(0) = 1, т. е. 2Ф(0) = 1, а
следовательно, Ф(0) = 0,5.
Используя доказанные свойства, можно построить график у = Ф(х), вид
которого приведен на рис. 8
Следует отметить, что функцией Лапласа также часто называют
неэлементарную функцию
Ф„(*) = -j=U2dt,
хе (—оо;+оо)
(1.38)
Как видно, функции Ф(х) и Ф0(х) отличаются лишь нижним пределом
интегрирования и по свойству аддитивности определенного интеграла
следует:
0 _£ X ,2
1К 2dt = -L. [в 2dt+-1
Согласно свойству 5 функции Лапласа, первое слагаемое равно 0,5, а
второе слагаемое по (1.38) есть Ф0(х). Таким образом, справедливо простое
соотношение
Ф(х) = -L f
J_ [е 2dt+-±-[e 2dt.
Ф(х) = 1 + Ф0(х)
(1-39)
Значения функции Ф0(х) также затабулированы, а равенство (1.39)
легко позволяет находить одну из функций Лапласа Ф(х) или Ф0(х),
зная другую.
График функции у = Ф0(х) приведен на рис. 9. Отметим, что, исходя из
формулы (1.39), график одной из функций получается параллельным пере-
62

У А
0,5
^Sv
-0,5
X
Рис. 9. График функции у = Ф0(х).
носом фафика другой функции на 0,5 по оси ординат. Однако свойство
функций Ф(х) и Ф0(х) различны. В частности, Ф0(х) = 0 и
Ф0(-х) = -Ф0(х), т. е. функция Ф0(х) — нечетная в отличие от Ф(х).
Функция Лапласа используется в одном из важнейших соотношений
схемы Бернулли — интефальной теореме Муавра—Лапласа.
Теорема. Пусть п испытаний относительно события А проводятся по
схеме Бернулли. Тогда для вероятности осуществления события А ровно т
раз при тх < т < т2справедлива формула
Р(тх<т<т2) = ф(?±^)-ф(г!±^)+а(п,р,тхт2),
4 Jnpq J ч Jnpq J
(1.40)
где Ф(...) — функция Лапласа,
р — вероятность осуществления события А в одном испытании,
Я = 1 ~ Р,
а(п,р, тхт2) — некоторая функция, стремящаяся к нулю с ростом п,
т. е. lima (л, р, т^т2) = 0.
Теорему Муавра—Лапласа примем без доказательства. Разъясним смысл
этой теоремы и ее особенности.
Замечание 1. Теорема Муавра—Лапласа позволяет без излишних
затруднений рассчитывать вероятности не отдельных значений т, как в
локальной теореме, а значений т из некоторого интервала [/и„ т2]. Фактически
правая часть выражения (1.40) является суммой вероятностей Рп(т),
вычисленных по формуле (1.32) локальной теоремы, при т = /и„ т = тх +
+ 1, ..., т = т2. При этом суммирование сведено к интефалу, который в
свою очередь низведен до функции Ф{х), значения которой находятся по
таблице, и для этого не требуется ни навыков интефирования, ни каких-
либо других специальных математических знаний.
Замечание 2. В левой части равенства (1.40) вместо нестрогих
неравенств тх<т<т2 можно использовать строгие неравенства /л, < т, т < т2
(одно или оба). Равенство (1.40) не нарушится, так как слагаемое
а(п,р, тхт2) в теореме не конкретизировано и, изменив величину в левой
части [например, вместо Р(тх<т<т2) взяли Р(тх <т < т2)], в правой
63

части на то же самое число [в нашем примере уменьшение на Рп(т2)]
изменим слагаемое а(п,р,тхт2).
Замечание 3. В формуле (1.40) равенство не нарушится, если вместо
функции Лапласа Ф (х) использовать функцию Ф0(х). Данный факт
следует из формулы связи функций (1.39), согласно которой в (1.40):
гт2 — пр^
Jnpq
Ф-Ф
гтх — л/Л
Jnpq
= Ф,
т2 — пру
. J*4>q j
+ 0, 5 - Фс
гтх — пру
Jnpl j
-0,5 =
= Ф,
т2 — пр
Jnpq
-Фс
тх — пр
Jnpq
Замечание 4. Ввиду того что с ростом п слагаемое а(п,р,
тхт2)стремится к нулю, на практике обычно используют приближенное равенство
Р(тх <т<т2)~Ф
т2 — пр
Jnpq
-Ф
тх — пр
Jnpq
(1-41)
и тогда величина а(п,р, mim2)ecTb не что иное, как разность между
истинным значением, которое находится исходя из формулы Бернулли, и
приближенным значением
( W, —
Ф
т2 — пр
Jnpq
-Ф
/и,
пр
Jnpq
Пример 1. Вероятность рождения мальчика равна р = 0,516. Найти
вероятность, что на 1000 новорожденных количество мальчиков находится в
пределах: а) от 496 до 536; б) не менее 500.
Решение. Согласно постановке задачи, мы находимся в условиях схемы
Бернулли. Ввиду вычислительных трудностей применения формулы
Бернулли воспользуемся приближенной формулой Муавра—Лапласа (1.41).
а) По условию п = 1000, р = 0,516, q = 0,484, m, = 496, т2 = 536.
Тогда
Р(496 <т< 536)« Ф
536-1000 - 0,516
7Ю00 • 0,516 • 0,484
-Ф
496-1000 ■ 0,516 >
V1000 • 0,516 • 0,484,
«Ф(1,27)-Ф(-1,27).
Значение Ф(1,27) равно 0,8980 согласно таблице (см. Приложение 2,
табл. 2). Однако в таблице отсутствуют значения функции Лапласа от
отрицательного аргумента, и, чтобы найти Ф(—1,27), используем свойство
функции Лапласа [см.(1.36)]:
Ф(-1,27) = 1 - Ф(1,27) = 1 - 0,8980 = 0,1020.
Тогда
Р(496 <т< 536) *0, 8980 -0,1020 = 0, 796.
б) По условию п = 1000, р = 0,516, q = 0,484, m, = 500, т2 = 1000.
Таким образом,
64

Р(500</л<1000)«Ф
1000-1000 • 0,516
71000 • 0,516 • 0,484
-Ф
500-1000 ■ 0,516
ЛООО- 0,516 -0,485 я Ф<30'63) " ф<~1' 01)-
Воспользуемся таблицей значений функции Ф(х) (см. Приложение 2,
табл.2);
Ф (—1,01) = 1—0(1,01) * 1 - 0,8438 = 0,1562. Значения функции
Ф(30,63) в таблице нет, но наибольшее из имеющихся значений
Ф(5) = 0,999997, и так как функция Ф(х) возрастающая и шпФ(х) = 1 (см.
свойства функции Лапласа), то смело можно полагать Ф(30,63) я 1.
Следовательно,
Р(500<т< 1000)«1—0,1562 = 0, 8438.
Пример 2. Смертность среди населения некоторой возрастной
категории составляет в среднем 0,5% в год. Найти вероятность, что за текущий
год число умерших превысит уровень 5 человек на каждую 1000 человек
населения. Решить задачу различными методами и сравнить результаты.
Решение. Условию задачи соответствует схема Бернулли с п = 1000,
р = 0,005 (что соответствует статистическим 0,5%). Требуется найти
Р(5 < т< 1000). Решим задачу двумя приближенными методами
(интегральная формула Муавра—Лапласа и формула Пуассона), найдем точное
значение по формуле Бернулли, затем сравним результаты.
а) Воспользуемся приближением Муавра—Лапласа.
Р(5<т<1000)«Ф
Г 1000-1000 • 0,005
-Ф
( 5-1000-0,005
VI000 • 0,005 • 0,995 J ^VlOOO • 0,005 • 0,995
« Ф(446, 09) - Ф(0)« 1 - 0, 5 = 0, 5 .
б) Рассмотрим приближение Пуассона.
i>(5<m<1000) = \-Р{т<5) =
= 1 - [Р(т=0) + Р(т=\) + Р{т=2) + Р(т=3) + Р{т=А) + Р(т=5)] *
« 1 - r*Va + If + £е~а + ^е~а + ^-еа + £еа\
L0! 1! 2! 3! 4! 5! J
Поскольку в формуле Пуассона а = пр, то а = 1000 • 0,005 = 5,
следовательно,
P(5<m<1000) = l-e"5(l + 5 + ^ + ^ + ^ + ^)*0, 3840394.
Как видим, полученный результат существенно отличается от
приближения по формуле Муавра—Лапласа. Для сравнения обоих ответов
вычислим точное значение искомой вероятности, используя формулу Бернулли.
Р(5<т< 1000) = 1 - Р(т< 5) =
= 1 - [СУУ + су<г' + cW"2 + сУ<Г3 + судп-4+с5пр5дп-5].
5 - 3529 65

Подставив п = 1000, р = 0,005, q = 0,995 и произведя на
микрокалькуляторе утомительные вычисления, получим с точностью до шестого знака
после запятой
Р(5<т< 1000) = 0, 384079.
Сравним это значение с ранее полученными величинами.
Вывод. В данной задаче приближение Пуассона дает верный результат с
точностью до четвертого знака после запятой. Интефальное приближение
Муавра—Лапласа приводит к ошибке уже на первом знаке. Это
превосходство метода Пуассона объясняется малым значением вероятности р = 0,005
(и небольшим числом пр = 5). Если бы вероятность р была близка к 0,5,
как, например, в примере 1, то более эффективным оказалось бы
приближение Муавра—Лапласа.
1.15. Теорема Бернулли (закон больших чисел)
Пусть п испытаний проводятся по схеме Бернулли. Итогом каждого
испытания является осуществление или неосуществление события А.
Вероятность осуществления А в одном испытании равна числу р. Отметим, что
вероятность р — это объективная характеристика изучаемого явления.
Предположим, что в п испытаниях событие А осуществилось ровно т
раз, тогда число — — относительная частота осуществления события А.
п
Ставится задача — сравнить две величины: объективно существующую
(теоретическую) вероятность р и наблюдаемую (эмпирическую),
изменяющуюся в различных сериях по п испытаний относительную частоту — .
п
Как уже было отмечено при статистическом определении вероятности
(§ 1.10), с ростом п относительная частота стремится к своей соответст-
п
с ростом п должен быть
вующеи вероятности, т. е. модуль разности
меньше любого сколь угодно малого положительного числа е:
<е. (1.42)
-Г'
Однако если рассматривать стремление относительной частоты к
вероятности подобным образом, то придется исключить возможность в
реальном опыте (серии из п испытаний) для относительной частоты оказаться
вне интервала (р — е; р + е). Практика подобные запреты не приемлет и
показывает, что в единичной серии из п испытаний относительная частота
— может оказаться любым возможным числом: 0,-,-,...,п ~ , 1, а не
п п п п
обязательно находиться в (р — е; р + е).
Чтобы избежать противоречий с реальностью, поступают следующим
образом: неравенство (1.42) интерпретируют как случайное событие,
поскольку в результате испытания данное соотношение может быть выпол-
66

ненным, а может быть и нет. И далее рассматривается вероятность этого
события:
(£-'<•)
(1.43)
Если это событие (1.42) действительно происходит в громадном
большинстве испытаний, то вероятность (1.43) должна быть близка к 1. Тем
самым учитывается и возможность для события (1.42) в некоторой доле
испытаний не осуществляться. Такая сходимость называется сходимостью по
вероятности. При изучении статистического стремления — к р использует-
п
ся именно этот вид сходимости.
Теорема Бернулли. Если испытания проводятся по схеме Бернулли, р —
вероятность осуществления события в одном испытании, — — относитель-
п
ная частота осуществления события в п испытаниях, то для любого сколь
угодно малого положительного числа Е справедливо соотношение
Х\тР(--р <z\ = 1
(1.44)
Доказательство. Преобразуем неравенство (1.42). Оно равносильно
двойному неравенству
—е < — — р< е.
п
Далее
р-Е<-<р + г,
п
пр — пг<т< пр + ле. (1-45)
Таким образом, случайное событие (1.42) эквивалентно случайному
событию (1.45), суть которого заключается в том, что частота т
осуществления события А в п испытаниях по схеме Бернулли находится в пределах от
числа пр - we до числа пр + п£. Налицо все условия применимости
интегральной теоремы Муавра—Лапласа, причем роль /и, и т2 выполняют
числа пр — лЕ и пр + /iE соответственно.
Применяем эту теорему:
р(--р <е\ = Р(пр-ПЕ<т<пр + пг) =
= Ф
ПР + /IE — ПР
Jnpq
-Ф
пр—пе — пр
Jnpq
+ «(/!,/?, е) =
5*
67

= ф
1Е_\
Jnpq) ^{Jnpqj
-Ф
+ сс(л,/?,е) =
= Ф
-Ф
—zjn
pq \+a(n,p,E).
(1.46)
sjn
Устремляем п к бесконечности. Тогда -^= -> +°о, а, следовательно, по
свойству 3 функции Лапласа (см. § 1.14) ФР^1->1. Аналогично
Jpq'
-zjn v_.
и по свойству 2 функции Лапласа (см. § 1.14) Ф[ zdll 1 -» 0.
Функция а(п,р, е), согласно интегральной теореме, также стремится к
нулю с ростом п.
А значит, переходя к пределу в (1.46), получим
limPl
л-»»
(^-/? <е) = 1-0 + 0=1
Теорема доказана.
Теорема Бернулли играет фундаментальную роль в теории вероятностей
и математической статистике, ибо она по существу узаконивает
статистическое определение вероятности.
Теорема утверждает, что с ростом п относительная частота
осуществления события по вероятности стремится к вероятности появления события
в одном испытании. Тем самым в практических расчетах вместо
теоретического абстрактного понятия вероятности мы на законных основаниях
получаем право использовать в качестве аналога вероятности реальную
величину — относительную частоту.
Теорема Бернулли относится к группе предельных теорем, называемых
законом больших чисел.
Задачи и упражнения
1. Сколько различных последовательностей "гербов" и "монет" можно
получить при четырехкратном подбрасывании монеты?
Указание. Используйте правило произведения событий.
2. В потоке студентов отобрана контрольная группа, состоящая из 20
человек. Контролируется посещение лекций: отсутствующему на лекции
ставится 0, присутствующему — 1. Сколько существует возможных двадца-
тиэлементных последовательностей из нулей и единиц?
3. В языке некоторого племени всего три буквы: А, В, С. Словом
является любая последовательность, состоящая не более чем из 5 букв.
Сколько слов содержится в этом языке?
Указание. Требуется по отдельности сосчитать количество одно-, двух-,
трех-, четырех- и пятибуквенных слов и найти сумму.
68

4. Сколько существует четырехзначных чисел, в записи которых
присутствуют лишь нечетные цифры?
Указание. На каждой из четырех позиций может находиться любая из
пяти возможных цифр.
5. Сколько существует четырехзначных чисел, в записи которых
присутствуют лишь четные цифры?
Указание. Нуль не может находиться на первой позиции.
6. Сколько существует четырехзначных чисел, в записи которых
обязательно имеются как четные, так и нечетные цифры?
Указание. Найдите, сколько всего четырехзначных чисел, и отбросьте
неудовлетворяющие условию задачи (см. 4, 5).
7. Сколько способов поставить на шахматную доску белую и черную
ладьи, чтобы они не "били" друг друга? Какова вероятность, что
поставленные случайным образом на шахматную доску белая и черная ладьи не
"бьют" друг друга?
8. Сколькими способами белую, красную, синюю и зеленую бусины
можно выложить в ряд? Сколькими способами белую, красную, синюю и
две зеленых бусины можно выложить в ряд?
Указание. Используйте перестановки.
9. Из колоды в 36 карт выбирают наудачу одну карту. Какова
вероятность, что: эта карта достоинством от "восьмерки" до "десятки"?
10. Из колоды в 36 карт выбирают наудачу две карты. Какова
вероятность, что а) обе карты одной и той же масти; б) обе карты бубновой
масти; в) обе карты разных мастей? Сравните найденные вероятности и
объясните соотношения между ними.
Ответ: а) —; б) — ; в) — .
35 ' } 35 ' } 35
11. Сколькими способами можно выбрать три тома из
двенадцатитомного собрания сочинений?
Указание. Используйте сочетания.
12. Сколькими способами можно выложить в стопку три тома, наудачу
извлеченных из двенадцатитомного собрания сочинений?
Указание. Сравните условие с условием задачи 11 и используйте
размещения.
13. На прямой зафиксировано 5 точек, а на параллельной ей прямой —
10 точек. Сколько существует треугольников с вершинами в указанных
точках?
Указание. Рассмотрите две группы способов возможного расположения
вершин. Используйте сочетания.
Ответ: 325.
14. В лотерее необходимо отметить 6 номеров из 36, имеющихся в
карточке. В розыгрыше "счастливыми" объявляются также 6 номеров. Какова
вероятность угадать: а) все 6 номеров; б) ровно 5 номеров; в) менее 5
номеров; г) ни одного номера?
15. По данным переписи населения Англии и Уэльса (1891 г.)
установлено: среди обследованных лиц темноглазые отцы и темноглазые сыновья
(АВ) составили 5%, темноглазые отцы и светлоглазые сыновья (АВ) —
7,9%, светлоглазые отцы и темноглазые сыновья (АВ) — 8,9%, светлогла-
69

зые отцы и светлоглазые сыновья (А В) — 78,2%. Найти зависимость
между цветом глаз сына и отца.
Указание. По условию _
Р(АВ) = 0,05; Р{АВ) = 0,079; Р(АВ) = 0,089; Р(АВ) = 0,782.
Требуется найти условнью вероятности
Р(В\А),Р(В\А),Р(В\А),Р(В\А).
Используйте теор_ему умножения_вероятностей и формулы
Р{А_) = Р[А(В +В)} = Р(АВ + АВ) = Р{АВ) + Р(АВ).
Р(А) = Р(АВ) + Р(АВ).
После вычисления значений условных вероятностей найдите пары
противоположных событий и проконтролируйте у_словие нормировки^
Ответ: Р(В\А) = 0,39; Р(В\А) = 0,10; Р(В\А) = 0,61; Р(В\А) = 0,90.
16. Вероятность преодоления планки при прыжке в высоту для первого
прыгуна равна рх = 0,3; для второго — р2 = 0,7; для третьего — рг = 0,5.
Каждый из прыгунов совершает по одной попытке. Найти вероятность,
что:
а) только один из спортсменов возьмет данную высоту;
б) хотя бы один из спортсменов возьмет высоту.
Ответ: а) 0,395; б) 0,895.
17. Если в условиях предыдущей задачи спортсменам дается по три
попытки, то найти вероятность, что: а) первый прыгун преодолеет высоту
лишь с третьей попытки; б) каждый из прыгунов преодолеет высоту лишь
с третьей попытки.
Ответ: а) 0,147; б) «0,001.
18. Схема дорог некоторой
местности изображена на рисунке.
Туристы вышли из пункта О,
выбирая на разветвлении дорог
дальнейший путь наугад (исключая
дорогу, по которой только что шли).
Найти вероятность, что туристы
попадут в пункт К.
Указание. Использовать формулу
полной вероятности.
7
Ответ: —.
12
19. В условиях предыдущей задачи дано, что туристы добрались до
пункта К. Найти вероятность, что они шли через М.
Указание. Использовать формулу Байеса.
3
Ответ: —.
14
20. В некотором коллективе соотношение мужчин и женщин 1 : 2.
Предположим, что 4% всех мужчин и 2,5% всех женщин носят очки.
Наугад выбранное лицо носит очки. Найти вероятность, что это мужчина.
Указание. Использовать формулу Байеса.
4
Ответ: -.
70

21. У рыбака имеется три излюбленных места для ловли рыбы, которые
он посещает с равной вероятностью каждое. Если он закидывает удочку,
то на первом месте рыба клюет с вероятностью /?, = 0,8; на втором месте —
с вероятностью р2 = 0,7; на третьем — с вероятностью рг = 0,9. Известно,
что, выйдя на ловлю рыбы, рыбак трижды закинул удочку, и рыба
клюнула только один раз. Найти вероятность, что он удил рыбу на втором месте.
Ответ: Р(Н2\А)= Q.
22. В группе из 10 студентов, пришедших на экзамен, 3 подготовленных
отлично, 4 — хорошо, 2 — посредственно и 1 — плохо. В
экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может
ответить на все 20 вопросов, хорошо подготовленный — на 16,
посредственно — на 10, плохо — на 5. Вызванный наугад студент ответил на три
произвольно заданных вопроса. Найти вероятность, что этот студент
подготовлен: а) отлично; б) плохо.
Ответ: Р(Н, |Л)«0,58, Р(Н4 \ А) я 0,002.
23. Шахматист играет с равносильным противником шахматный матч.
Учитываются только победы одного из соперников. Какое событие
вероятнее: выиграть две партии из четырех или три из шести?
Указание. Используя формулу Бернулли, вычислить Р4(2) и Р6(3).
24. Всхожесть семян оценивается в 80%. Какова вероятность, что среди
посеянных 12 семян взойдут: а) не менее 10; б) менее 10? Найти
наивероятнейшее число всходов среди этих 12 посеянных семян.
Указание. Р12(т > 10) = Р12(\0) + Рп(П) + Рп(\2). Каждую из
вероятностей в правой части равенства вычислить по формуле Бернулли (р = 0,8).
Рп(т < 10) = 1 - Рп(т > 10).
25. Человек, выбранный случайным образом из определенной группы
населения, с вероятностью 0,2 оказывается брюнетом, с вероятностью
0,3 — шатеном, с вероятностью 0,4 — блондином и с вероятностью 0,1 —
рыжим. Наугад выбирается группа из 6 человек. Найти вероятности
следующих событий:
А — в группе два брюнета;
В — в группе не менее четырех блондинов;
С — в группе хотя бы один рыжий;
D — в группе нет ни блондинов, ни шатенов.
Ответ: Р{А) я 0,246; Р(В) я 0,455; Р(С) я 0,468; P(D) я 0,0007.
26. Статистические наблюдения показывают, что в некоторой местности
в сентябре в среднем 10 дождливых дней. Найти вероятность, что из 10
наугад выбранных сентябрьских дней дождливыми окажутся: а) менее 4
дней; б) не более 4 дней. Найти наивероятнейшее число дождливых дней
среди 10 выбранных.
27. Учебник имеет тираж 10 000 экземпляров. Вероятность
неправильной брошюровки книги для типографии, в которой учебник напечатан,
составляет 0,0002 (0,0002 — средняя доля книг, сброшюрованных
неправильно). Найти вероятность, что в тираже неправильно сброшюрованных
учебников: а) ровно 4; б) не более 4; в) более 4; г) таковые отсутствуют.
Указание. Использовать приближение Пуассона.
Ответ: а) 0,09; б) 0,947; в) 0,053; г) 0,135.
71

28. Найти вероятность, что случайное событие А в 243 независимых
испытаниях наступит ровно 70 раз, если вероятность осуществления А в
одном испытании постоянна и равна 0,25.
Указание. Использовать локальную теорему Муавра—Лапласа.
Ответ: я 0,023.
29. Вероятность рождения мальчика 0,516. В первый класс школы
принимается 200 детей. Найти вероятность, что окажется девочек и мальчиков
поровну.
Ответ: я 0,05.
30. Всхожесть семян некоторого растения равна 0,9. Определить
вероятность, что при посадке 500 семян проросших окажется от 440 до 460.
Указание. Использовать интегральную теорему Муавра—Лапласа.
Ответ: я 0,8638.
31. Вероятность появления некоторого события А в каждом из
независимых испытаний постоянна и равна 0,8. Сколько необходимо произвести
испытаний, чтобы с вероятностью 0,9 можно было ожидать осуществления
А не менее 75 раз?
Указание. Использовать интегральную теорему Муавра—Лапласа для
нахождения неизвестного числа испытаний п. Очевидно, что п > 75.
Возникшую в процессе решения величину ф(^ ) принять приближенно
равной 1, так как для возрастающей функции Лапласа справедливо
ф(з£1) > ф(^) * Ф(4, 33) * 0,99999,
и функция Лапласа не может быть больше 1.
Ответ: п > 100.
32. Сколько нужно произвести опытов с бросанием монеты, чтобы с
вероятностью 0,95 можно было ожидать отклонение относительной частоты
выпадения "герба" — от теоретической вероятности 0,5 на величину, по
п
модулю меньшую чем 0,01.
Указание. Требуемое значение п можно найти из соотношения
интегральной теоремы Муавра—Лапласа
[см. §1.15, (1.46)]. В нашей задаче р = ^ = 0,5; е = 0,01;
< е) = 0, 95.
Ответ: п > 9604.
-»-"
т

Глава II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.1. Начальные понятия и определения
Понятие случайного события, являющееся одним из основных в теории
вероятностей, все-таки носит несколько описательный характер. А во
многих задачах практики используются величины, принимающие то или иное
значение в зависимости от обстоятельств (от случая). Понятие случайной
величины тесно связано с понятием случайного события, но наличие
численной характеристики позволяет применить к случайным величинам
мощный математический аппарат.
Определение. Переменная X называется случайной величиной, если в
результате испытания она однозначно принимает некоторое численное
значение, но какое именно, до испытания неизвестно.
Условимся далее случайные величины обозначать большими буквами
латинского алфавита: X, Y, Z, Г и т. д. и использовать для случайных
величин сокращение "св.".
Каждая случайная величина в результате испытания может принять
одно из значений некоторого множества. Значения св. будем обозначать
соответствующими малыми буквами: х, у, z, t и т. д. Также для значений
будем пользоваться индексами, например значения св. X — это х„ х^, ..., хк.
Пример 1. В группе 15 студентов. Пусть св. X — число студентов,
явившихся на лекцию. До начала лекции мы не можем сказать, какое значение
примет X, хотя множество возможных значений известно: это числа 0, 1,2,
..., 15.
Как только испытание завершено (в нашем примере наступило время
начала лекции), св. X принимает некоторое значение (например, Х= 12).
В этом случае мы говорим, что произошло случайное событие: св. X
приняла значение, равное 12. Тогда случайные события ^=0, Х=\, ...,
Х= 15 образуют множество элементарных событий. Таким образом, св. X
выступает в роли функции, заданной на множестве элементарных
событий. В данном случае функция очень простая: элементарному событию "на
лекцию явились к студентов" соответствует значение функции X = к
(к = 0, 1,2,..., 15)
В других случаях принцип определения случайной величины тот же
самый: св. — однозначная числовая функция, определенная на множестве
элементарных событий, т. е. каждому элементарному событию полной
системы элементарных событий поставлено в соответствие число, находимое
по некоторому правилу. Понятно, что это правило мы можем определить
(т. е. задать функцию) произвольно. Например, в рассмотренном выше
случае пусть св. Y — это квадрат числа студентов, явившихся на лекцию.
Тогда множество возможных значений Y — числа 0, 1, 4, 9, 16, 25, ..., 225.
Очевидно, что рассмотренные св. связаны зависимостью Y= X2,
следовательно, Y — функция X, а А'является функцией множества элементарных
73

событий. Таким образом, зафиксируем важный факт: св., являясь
числовой функцией множества элементарных событий, сама может выступать в
роли аргумента для других функций (других случайных величин).
Даже если пространство элементарных событий внешне не располагает
к численной интерпретации (например, имеются качественные
характеристики), все равно можно поставить в соответствие каждому событию
численное значение. Например, двум возможным исходам испытания
(происходит событие или нет) ставятся в соответствие 1 и 0; каждому из семи
цветов радуги можно соответственно сопоставить числа 1, 2, ..., 7 и т. п.
Далее, поскольку св. являются числовыми функциями, то даже для
совершенно различных св. имеют место математические операции:
сложение, умножение, деление, дифференцирование, интегрирование и т. д.
Пример 2. Пусть св. X может принимать лишь три значения: 0, ^, п.
С. в. У может принимать значения: 2, 3, 4. Задана функция Z— Y+sinX.
Найти все возможные значения св. Z
Решение. Так как X — св., то sin Л'также является случайной
величиной. Ее возможные значения sin 0 = 0, sin?; = 1, sinrt = 0. Поскольку
первое и последнее значения совпадают, то всего св. sin X принимает два
различных значения: 0 и 1. Возможные значения св. Z — это сумма
любого из возможных значений св. sin Л' (т. е. 0 и 1) и любого из возможных
значений св. У (т. е. 2, 3, 4). Итак, получаем: 0+2, 0+3, 0+4, 1+2, 1+3,
1+4. Учитывая, что среди этих сумм имеются одинаковые, различных
значений св. Z будет всего четыре: 2, 3, 4, 5.
Используя различные функции и действия, мы можем математически
неограниченно оперировать со случайными величинами. Но так как св.
связаны со случайными событиями, а те в свою очередь имеют
определенную вероятность, то, математически манипулируя случайными
величинами, необходимо ясно представлять, что происходит с соответствующими
вероятностями. Оказывается, что вероятности также подчинены
определенным правилам и изучаются методами математики вне зависимости от
природы случайности, будь то задачи медицины, экономики, сельского
хозяйства, социологии или космические проблемы. Исследованию этих
закономерностей в поведении вероятностей в связи со случайными
величинами и посвящен данный раздел.
Случайные величины классифицируют в зависимости от множества
принимаемых ими возможных значений. Наиболее важными для
статистических исследований и приложений являются св. двух типов: дискретного
и непрерывного.
Определение. Св. X называют дискретной св., если множество ее
значений конечно или счетно.
Напомним, что множество называется счетным, если всем его
элементам можно поставить в соответствие натуральный ряд чисел (проще
говоря, все элементы можно пересчитать). Счетное множество содержит
бесконечное количество элементов.
В приведенном выше примере 1 X — дискретная св., так как
количество возможных значений конечно (16 значений). Св. X, Y, Z в примере 2
также оказываются дискретными случайными величинами.
74

Примерами дискретных св., в частности, являются:
1) количество новорожденных в городе за текущие сутки;
2) число ударов пульса больного в минуту;
3) количество звонков на станцию скорой медицинской помощи в
течение определенного периода времени (например, часа);
4) количество заболевших гриппом во время подъема заболеваемости;
5) количество осложнений после операции в данной больнице:
6) число атомов радиоактивного вещества, распадающихся за
определенный период времени;
7) число метеоритов, достигающих поверхности Земли в течение года.
Определение. Св. Л'называется непрерывной св., если все ее значения
заполняют сплошь некоторый промежуток.
Примерами непрерывных св., в частности, являются:
1) температура тела больного (обычно точное значение округляют до
ближайшего деления);
2) величина ошибки, допускаемой при округлении точных значений;
3) время инкубационного периода заболевания;
4) характеристики запыленности и освещенности рабочего места,
измеренные в соответствующих единицах;
5) время безотказной работы прибора (например, электрической
лампочки, компьютера и т. д.);
6) дальность полета артиллерийского снаряда;
7) количество расходуемого автомобилем бензина на 100 км пробега.
Круг примеров св. как дискретных, так и непрерывных читатель легко
может расширить.
2.2. Закон распределения случайной величины.
Функция распределения вероятностей
Каждая случайная величина в результате испытания принимает одно из
значений некоторого множества. Однако знание множества значений
характеризует с. в. далеко не достаточно, ибо необходимо еще знать, как
часто (с какой вероятностью) принимаются те или иные значения.
Рассмотрим простой пример. Пусть два лучника стреляют по мишени. Попадание
в мишень позволяет набрать от 1 до 10 очков, промах 0 очков. Введем с. в.
Хх и Х2 — число выбитых очков первым и вторым лучниками
соответственно. Испытание — выстрел. Обе с. в. Хх и Х2 обладают одинаковым
множеством возможных значений: 0, 1,2, ..., 10. Но можно ли считать Хх и Х2
"одинаковыми"? Разумеется, нет, поскольку первый стрелок может
оказаться Робин Гудом, и тогда Хх принимает, как правило, значение 10 и
гораздо реже все остальные; а если второй стрелок является начинающим
лучником, то с. в. Х2 с тупым упорством будет принимать значение 0 в
большинстве случаев и только иногда другие значения. Как видим, с. в. Хх
и Х2 , обладающие одним и тем же множеством возможных значений,
реализуют эти возможности по-разному. Знание этих возможностей
(вероятностей) делают с. в. предсказуемой настолько, что позволительно
употребить слово "закон".
75

Законом распределения вероятностей с. в. называют множество ее
значений и соответствующих этим значениям вероятностей.
Для дискретной с. в. X имеется возможность перечислить все значения
х,, Xj, ..., х„, ... и их вероятности />,, р2, ..., рп, ..., и тогда законом
распределения называют таблицу:
X;
Pi
*1
Р\
*г
Pi
х„
Рп
Причем обязательно должно быть выполнено условие
2>=1, (2-D
называемое условием нормировки.
Равенство (2.1) легко доказывается.
Так как х,, д^, .... х„, ... — все возможные значения, то сумма случайных
событий
(Х=х,) + (Х=х2) + ... + (Х=хп) + ...
является событием достоверным (£/). Переходя к вероятностям и учитывая,
что все слагаемые в сумме попарно несовместны (все х,, х^, ..., х„, ... —
различны), получаем
Р((Х = х.) + (Х=х2) + ... + (Х=хп) + ...) = P(U),
Р(Х=хх) + Р(Х=х2) + ... + Р(Х=хП) + ... = 1,
Р\ +р2+...+ рн+... = 1.
Записав последнее равенство в виде V/7, = 1 , и приходим к (2.1).
Теперь становится ясным и термин "распределение вероятностей":
суммарная вероятность равна 1, и она распределена (разложена) некоторым
образом по всем возможным значениям х,, х2, ... . В зависимости от этих
разложений единичной вероятности и говорят о различных
распределениях.
Существует бесконечное число способов задания значений с. в. и
соответствующих им вероятностей, поэтому и распределений с. в. существует
сколь угодно много. Однако среди всего их многообразия можно вьщелить
определенные типы распределений, отличающихся только параметрами.
Пример 1. Бросается игральная кость. С. в. X — число выпавших очков.
Тогда закон распределения с. в. X имеет вид
х;
Pi
1
1
6
2
1
6
3
1
6
4
1
6
5
1
6
6
1
6
Такое распределение называют дискретным равномерным
распределением. В общем случае вместо шести значений можно взять п равноотстоя-
76

щих чисел с соответствующими вероятностями -. Тогда п является пара-
п
метром типичного распределения, называемого дискретным равномерным.
Некоторые другие типичные распределения, характеризуемые одним
или более параметрами (биномиальное, геометрическое, пуассоновское)
будут рассмотрены в последующих параграфах.
Для непрерывных с. в. понятие закона распределения конкретизируем
далее в § 2.9.
Итак, с. в. полностью характеризируется своим законом распределения.
Но закон распределения не обязательно задавать в виде таблицы (в
частности, для непрерывных св. это и невозможно), а достаточно ввести
функцию, связывающую значения с. в. и соответствующие вероятности.
Определение. Функцией распределения (ф. р.) случайной величины X
называют функцию одной переменной F(x) такую, что
F(x) = Р(Х<х). (2.2)
Ф. p. F(x) оказывается обычной функцией одной переменной,
определенной при всех х е (—оо, +оо), включая и те значения х, которые с. в. л'не
может принимать (проходя через такие точки, функция не изменяет свое
значение). К такой функции применимы все возможные математические
операции; в частности, можно найти характерные точки и построить
график. По данной функции для дискретных с. в. легко восстановить закон
распределения в виде таблицы. Ф. p. F(x) представляет собой
накопленную вероятность, т. е. суммарную вероятность всех значений с. в. X,
меньших чем х.
Если х интерпретировать как точку на числовой оси, то ф. p. F{x) равна
вероятности попадания с. в. Хв интервал (—оо; х). При разных х этот
интервал изменяется, и тем самым, вообще говоря, изменяется вероятность.
Суть данной ф. р. в том, что она представляет нам вероятность,
являющуюся функцией множества (которая сложна, громоздка, хитро устроена,
непонятна), в виде функции одной переменной, хорошо знакомой и
любимой нами еще в средней школе.
Приведем основные свойства ф. p. F(x).
1. Для любых х значение ф. р. заключены в промежутке [0; 1].
Данное свойство следует из того факта, что F(x) является вероятностью,
а вероятность по определению всегда находится в пределах от 0 до 1.
2. lim F(x) = 0. (2.3)
х-*— «
Доказательство.
lim F{x) = lim Р(Х<х) = Р(Х<-<х>) = P(V) = О,
Х->— 3D Х-*- «
где V обозначает невозможное событие (Х< —оо).
3. lim F(x) = 1 (2.4)
Х-> +«1
Доказательство.
lim F(x) = lim P(X<x) = Р(Х< +оо) = P(U) = 1,
где U обозначает достоверное событие (X < +оо).
4. F(x) является функцией неубывающей.
77

Рис. 10.
Доказательство. Чтобы F(x) была функцией неубывающей, необходимо
доказать, что для любых значений х, и х,, таких как х, < х,, справедливо
соотношение F(xx) < Fipc,).
Нанесем на числовой оси точки х, и х,, причем х, < х,.
По определению F(xx) = Р(Х< х,), F(xJ = Р(Х< xj. Так как
интервалы (-оо; х,) и (х,; х,) не пересекаются, можно записать
Fix,) = Р(Х< xj = Р(Хе(-со; х)) = Р(Хе(-со; x,))U [х,; х,)) =
= Р((*е(-оо; х,)) + (^е[х1; х^)) = Р(Хе(-со; х,)) + /»(^Гб[дг1; х^) =
= Р(Х<Х]) + PiXefaxJ).
Таким образом, учитывая, что Р(Х< х,) = /\х,), получаем
F(x2) = F(xl) + P(Xe[xl;xJ. (2.5)
Так как в равенстве (2.5) последнее слагаемое неотрицательно, то Fix,)
превосходит F(xx) на величину этого слагаемого. Следовательно,
F{Xj) > F(xx), при этом равенство достигается лишь в случае, когда
Р(Хе[хх\ x2)) = 0. Свойство доказано.
5. Вероятность попадания св. Хв интервал [х,,д^) находится по формуле
P(Xe[x];x2)) = F(x2)-F(xl). (2.6)
Равенство (2.6) получается из (2.5).
Замечание. Из равенства (2.6) следует важное свойство вероятности св.,
а именно: если ф.р. F{x) непрерывна в некоторой точке Х= а, то
Р(Х=а) = 0.
Действительно, положив в (2.6) обозначение х, = а, х, = b и, устремляя
Ь—>а, получим
Р(Х= а) = UmP(Xe [а,Ь)) = Um(F(b) - F(a)) = F(a)~ F(a) = 0.
b-* a b-*a
Пример 2. Производится два независимых выстрела по мишени.
Вероятность попадания в мишень при каждом выстреле р = 0,8. Св. X —
число попаданий. Найти закон распределения с. в. Л" и построить график
ф. p. F{x).
Решение. В результате двух выстрелов св. X может принять лишь три
возможных значения: 0, 1,2. Так как выполнены условия схемы Бернулли,
то вероятности, соответствующие значениям 0, 1, 2 и обозначенные pQ, /?,,
р2, найдем по формуле Бернулли:
Ро = С\р\г = (0,2)2 = 0,04;
Р\ = C\pq = 2 • 0,8 • 0,2 = 0,32;
Рг = Clp2q° = (0,8)2 = 0,64.
Заметим для контроля, что условие нормировки pQ + pi + р2 = 1
выполнено.
78

У
1
0,36
0,04
0
i
I I
1 2
X
Рис. 11.
Закон распределения представим в виде таблицы.
х\
Р\
0
0,04
1
0,32
2
0,64
Найдем значения ф.р. F(x). Они изменяются лишь в точках
сосредоточения вероятности 0, 1, 2 . Поэтому рассмотрим значения функции F(x)
отдельно для интервалов (—оо; 0), (0; 1), (1; 2), (2; +оо) и для конкретных
точек х = 0, х = 1, х = 2.
Пусть х е (—оо;0), тогда по определению
F(x) = P(X<x) = P(V) = 0,
так как (X < х) — невозможное событие, поскольку св. X таких значений
не принимает.
Пусть х е (0; 1), тогда
F(x) = Р(Х< х) = Р(Х= 0) = 0,04,
так как при х е (0;1) события (Х< х) и (Х= 0) равносильны.
Пусть х е (1; 2), тогда
F(x) = Р(Х< х) = Р((Х= 0) + (Х= 1)) = Р(Х= 0) + Р(Х= 1) = 0,04 +
+ 0,32 = 0,36,
так как событие (X < х) равносильно сумме несовместных событий
(*=0)+(*=1).
Пусть х е (2;+оо), тогда
F(x) = Р(Х<х) = Р((Х=0) + (Х=1) + (Х=2)) = Р(Х=0) +
+ Р(Х= 1) + Р(Х= 2) = 0,04 + 0,32 + 0,64 = 1.
Аналогично найдем
/"(О) = Р(Х< 0) = 0, F(l) = Р(Х< 1) = Р(Х= 0) = 0,04,
F(2) = Р(Х< 2) = Р((Х= 0) + (Х= 1)) = 0,36.
Исходя из полученных значений, строим график у = F(x) (рис. 11).
79

Отметим, что график функции распределения нашей дискретной с. в. X
имеет ступенчатый вид, "ступенька" начинается в точках сосредоточения
вероятности, и "высота ступеньки" в точности равна соответствующей
вероятности: при х = О — это /70, при х = 1 — это /?, и при х = 2 — это р2.
Сама функция F(x) может быть записана в виде
ад =
О, при хе (—оо; 0]
О, 04, прихе(0; 1]
0, 36, при хе (1; 2]
1, при х е (2; +оо).
2.3. Дискретные случайные величины и их числовые характеристики
В предыдущем параграфе были введены понятия закона распределения
и функции распределения для произвольных с. в., рассмотрен пример
закона распределения и функции распределения дискретной св., получено
условие нормировки. Отметим, что для любой дискретной с. в.
a) закон распределения можно задать в виде таблицы, может быть,
бесконечной (если число значений счетно);
b) условие нормировки выполняется обязательно;
c) зная закон распределения, можно найти функцию распределения, и
наоборот, зная функцию распределения, можно восстановить закон
распределения в виде таблицы;
d) график ф. р. всегда имеет вид ступенчатой линии, с началом
"ступенек" в точках значений, принимаемых случайной величиной, и "высотой
ступеньки", равной вероятности данного значения.
Указав общие характерные особенности дискретных с. в., подчеркнем
различие: все дискретные с. в. отличаются одна от другой числовыми
характеристиками. Различие числовых характеристик обусловлено разным
количеством значений и местоположением этих значений (точек на
числовой оси) и разным распределением единичной вероятности между
значениями.
И хотя закон распределения является исчерпывающей характеристикой
с в., числовые характеристики играют наиважнейшую роль в теории
вероятностей. Достаточно указать, что существует много вероятностных задач,
для решения которых не обязательно полностью знать закон
распределения, а можно обойтись лишь знанием некоторых чисел, характерных для
данной с. в., которые и называют числовыми характеристиками
(например, среднее значение с. в., степень разброса значений относительно
среднего, наиболее вероятное значение и т. д.).
Введем упомянутые выше характеристики, по которым можно судить о
поведении дискретной с. в.
Определение. Начальным моментом к-го порядка, где к = О, 1, 2, ...,
дискретной с. в. X называют число
ак(Х) = £*?/>,., (2.7)
80

^—i—i—i—h
Рис. 12.
Pp
*л
Pr,
где x, представляют все возможные значения с. в. X; /?,. — вероятности,
соответствующие значениям х,.
Часто наряду с обозначением ак(Х) употребляют а*.
Пример 1. Дискретная с. в. X имеет закон распределения
х\
Pi
1
о,з
2
0,4
4
0,2
10
0,1
Найти начальные моменты нулевого, первого и второго порядков.
Решение. Так как с. в. X может принимать лишь четыре возможных
значения, то сумма в формуле (2.7) будет содержать всего четыре
слагаемых. Вычислим соответствующие моменты:
а0(Х) = £х°/>, = J>/ = 0,3 + 0,4 + 0,2 + 0,1 = 1;
а,(А) = ^/м = 1 • 0, 3 + 2 • 0,4 + 4 • 0,2 + 10 • 0,1 = 2, 9;
i
а2(Х) = Y^Pt = I2 ' 0, 3 + 22 • 0, 4 + 42 • 0, 2 + 102 • 0,1 = 15,1.
Таким образом, искомые начальные моменты найдены.
Замечание. Начальный момент нулевого порядка а0(Аг)мы посчитали
исключительно в учебных целях, а фактически при любом распределении
вероятностей случайной величины X всегда а0(Х) = 1, так как
а0(АО = Yx°iPi = 2/"
и последняя сумма по условию нормировки обязана быть равной 1.
Среди начальных моментов различных порядков особую роль играет
первый начальный момент.
Определение. Математическим ожиданием дискретной с. в. X называют
ее первый начальный момент.
Обозначим математическое ожидание с. в. X посредством М(Х)Х. Тогда
по определению
М(Х) = а,(Х) = Y*iPi
(2.8)
Дадим механическую иллюстрацию понятия математического
ожидания. Пусть на числовой оси имеется система материальных точек х,, Xj, ...,
х„, в которых сосредоточены массы />„ р2, ..., рп соответственно.
'В литературе также математическое ожидание обозначают Е(Х).
6 — 3529
81

Как известно, координаты центра тяжести системы находятся по
формуле
Y = xipl+x2p2 + ...+хпрп
А если массы таковы, что рх + р2 + ... + рп = 1, то получаем
х„.т. = Х\Р\ +х2р2+ ... +ад, = ]£ед-,
что соответствует математическому ожиданию из формулы (2.8). Таким
образом, в вероятностном смысле математическое ожидание является
"центром вероятности" или, иначе, "центром тяжести вероятности".
Если все значения х,, х,, ..., хп равновероятны, т. е. все р. = -(/ = 1, 2,
п
..., п), то М(Х) есть просто среднее арифметическое чисел х,, Xj, ..., х„. При
произвольных значениях вероятностей р„ число М(Х) — это то же среднее,
но с учетом "веса" каждого значения х„ выражающегося вероятностью ph
т. е. с учетом вероятностного вклада каждого значения х, во всю систему
значений х,, Xj, ..., х„. Поэтому часто вместо математического ожидания
употребляют термин "среднее".
В рассмотренном выше примере 1 число М(Х) оказалось равным 2,9.
Исходя из этого примера, заметим, что математическое ожидание не
обязательно должно совпадать с каким-либо из значений с. в. Заметим также,
что в любом случае, как бы ни были разбросаны значения с. в. и
рассредоточены их вероятности, математическое ожидание всегда находится между
наименьшим и наибольшим значениями.
Определение. Центральным моментом к-го порядка, где к = 1, 2, ...,
дискретной св. ^называют число
Ц*№ = Yjfri-M{X))kpit (2.9)
где х, представляют все возможные значения с. в. X, pt — вероятности,
соответствующие значениям х„ М(Х) — математическое ожидание с. в. X.
Для любой с. в. X справедливы следующие утверждения:
1) ц0(Л = О,
так как ц0№ = УЧ*«- M(X))°Pi = J]Pi = 1 согласно условию норми-
ровки;
2)ц,№ = 0, (2.10)
так как
Ц.№ = %{х,-М(Х))р, = ^(ед-Щ)А) =
= £зд-ОДГ)]£а = М(Х)-М(Х) -1=0.
Определение. Дисперсией дискретной с. в. X называют ее второй
центральный момент.
82

Обозначив1 дисперсию D(X), по определению имеем
D(X) = ц2(ЛГ) = £(*,•- M(X))2Pi. (2.11)
i
Рассмотрим данное выражение подробнее.
В формуле дисперсии (2.11) присутствуют величины х,- — М(Х), которые
являются отклонениями значений х,- от среднего М(Х). Эти отклонения
возведены в квадрат, и тем самым положительные и отрицательные
отклонения уравнены в своем влиянии на всю сумму. Далее полученные
квадраты просуммированы с учетом "веса" каждого отклонения (т. е.
вероятностей р.) по всем /, где / = 1, 2, ....
Таким образом, сумма в формуле (2.11) характеризует степень
отклонения (вариацию) значений с. в. X от среднего М(Х). Чем больше значения
с. в. отдаляются от М(Х), тем большую величину принимает D(X), и
наоборот, чем больше D(X), тем больше значения с. в. отклоняются от числа
М(Х). Если рассмотреть предельный случай, когда св. ^принимает только
одно значение а с вероятностью 1, тогда М(а) = а и D(a) = (а — а)2' 1 = 0.
Заметим также, что из (2.11) следует неотрицательность дисперсии.
Дисперсия является мерой рассеяния значений с. в. относительно
среднего.
Во многих задачах знание среднего значения далеко не достаточно.
Например, два исследователя измеряют одну и ту же величину с разной
точностью, и хотя средние значения их измерений могут совпасть, суммарные
ошибки измерений одного исследователя гораздо больше суммарных
ошибок измерения другого. Большее значение дисперсии для больших ошибок
и констатирует указанный факт.
Другой пример. Испытываются на эффективность два лекарства.
Процесс выздоровления больного, кроме применяемого лекарства, зависит
еще и от различных субъективных (случайных) факторов: возраст
больного, степень запущенности болезни, наличие каких-либо сопутствующих
заболеваний, различие погодных условий, влияющих на больного во время
испытания, и т. д. Эффективность применяемого лекарства
характеризуется средним количеством процентов выздоровевших. При равенстве этих
средних процентов при применении того и другого лекарства, которому же
следует отдать предпочтение? И вот здесь на первый план также
выдвигается характеристика рассеяния (дисперсия). Наиболее эффективным
следует признать то лекарство, применение которого наименее подвержено
влиянию случайных факторов, которое наиболее стабильно в своем
действии вне зависимости от группы испытуемых. Например, препараты А и В,
излечивающие некоторое инфекционное заболевание, испытываются на
двух численно равных группах пациентов, имеющих сопутствующее
сердечно-сосудистое заболевание и не имеющих такового. Процент
выздоровевших при применении препарата А по группам 72 и 78, для препарата
В — соответственно 65 и 85. Как видим, средний процент для каждого
лекарства равен 75. Однако разброс значений по группам совершенно
различен, и наиболее эффективным по результатам данного исследования сле-
'В литературе для дисперсии также используют обозначения Var(X) и У(Х), полагая в
качестве синонима "дисперсии" слово "вариация".
6*
83

дует признать лекарство А как наиболее стабильное. (Отметим, что
численный пример представлен в упрощенном виде чисто в учебных целях. На
самом деле для констатации эффективности необходимо более
разностороннее исследование.)
Замечание. Обозначение М(Х), введенное для математического
ожидания, удобно использовать и в других случаях, например для обозначения
моментов:
ак(Х) = £дс*Л = М(Хк),
i
Ц*№ = ^(x-M(X))kPi = M(X- М(Х))к. (2.12)
Тогда а2(Х) = М(Х2), а3(Х) = М(Х>), ц2(ЛГ) = М(Х~ М(Х))2и т. д.
Следовательно, если с. в. Л" имеет распределение
*,■
Pi
х\
Р\
*г
Рг
\
Рп
то распределение с. в. Хк — это
х?
Р,-
xf
Р\
*/
Рг
хк
Рп
Утверждение. Для любой с. в. X справедливо равенство
D(X) = М(Х2) - М\Х), (2.13)
где М(Х2) = а2(Х), М2(Х)— математическое ожидание в квадрате.
Доказательство. По определению дисперсии:
D(X) = J^[x,-M(X)]2Pi = J^(x2pi-2M(X)xiPi + M\X)Pi) =
i i
/ i i
= M(X2)-2M(X) • M(X) + M\X) • 1 = M(X2)-M\X).
Утверждение доказано.
Замечание. Аналогично приведенному утверждению можно найти и
другие формулы, связывающие центральные моменты ц„и начальные
моменты порядка не выше п:
Из = а3-3а,а2 + 2а{, (2.14)
ц4 = сц- 4а|Сс3 + 6а?а2 — За),
Определение. Средним квадратическим отклонением с. в. X называют
число a = JD(X).
84

Таким образом, используя новое обозначение а, можно записать
D(X)=g2.
Заметим, что среднее квадратическое отклонение — величина
неотрицательная.
Среднее квадратическое отклонение, так же как и дисперсия,
характеризует степень рассеяния значений с. в. относительно среднего Л/да, но
имеет по сравнению с дисперсией другую размерность [размерность
дисперсии равна 2, так как в формуле (2.11) представлены значения в
квадрате, а размерность среднего квадратического отклонения равна 1, так же
как, впрочем, и размерность М(Х)].
В литературе среднее квадратическое отклонение также называют
стандартным отклонением.
Наряду со средним квадратическим отклонением ст (или дисперсией ст2)
для определения степени рассеяния значений с. в. относительно
математического ожидания используется и другая характеристика, называемая
средним отклонением.
Определение. Средним отклонением с. в. X называют математическое
ожидание с. в. \Х— М(Х)|.
Для дискретной с. в. Переднее отклонение имеет вид
Мх = ^\х,-М{Х)\р„ (2.15)
i
т. е. для каждого значения х, с. в. X рассматривается его отклонение от
среднего М(Х),полученные разности берутся по модулю \х,- М(Х)\ и
находится их среднее с учетом "весов" /?,., что и отражено в названии "среднее
отклонение".
Среднее отклонение также является числовой характеристикой с. в.,
однако наличие в соотношении модуля привносит некоторые трудности в
дальнейшие теоретические исследования, поэтому в практических задачах
в качестве характеристики рассеяния, как правило, используется среднее
квадратическое отклонение.
Пример 2. Заданы две св. Хи /законами распределения
х,
Pi
-0,1
0,8
0,4
0,2
yj
Pj
-90
0,25
30
0,75
Найти для каждой св. и сравнить: а) средние квадратические
отклонения; б) средние отклонения.
Решение. Легко найти математические ожидания св.
Л/ДО = -0,1-0,8 + 0,4-0,2 = 0; Л/(У) =-90-0,25 + 30-0,75 = 0.
Вычислим дисперсии для св. Хи У:
с2х = М(Х2) - Л/2(ЛГ) = М(Х2) = (-0,1)2 • 0,8 + (0,4)2 • 0,2 = 0,04;
с2у= Л/(У2) " Л/2(У) = Л/(У2) = (-90)2-0,25 + 302-0,75 = 2700.
Тогда ах= 0,2; ау = 72700«51, 96.
85

Как видим, ох и ау отличаются весьма существенно: большему
рассеянию значений относительно среднего [М(Х) = М(У) = 0] у св.
Yсоответствует и большее значение среднего квадратического отклонения.
Вычислим средние отклонения для св. Хи Y.
2
Мх= £|х,.- М(Х)\р, = |-0,1| -0,8 + |0,4| -0,2 = 0,16,
I-1
2
Му= £|Уу" ЩУ)\Р;= |-90|-0,25 + 1301-0,75 = 45.
Хотя значения Мх и Му отличаются от ох и оу, тенденция
характеризовать степень рассеяния значений св. относительно среднего проглядывает
достаточно определенно.
В соотношении (2.15) представлено математическое ожидание от
модуля случайной величины [Х- М(Х)]. Аналогично, можно ввести и другие
моменты от модуля св., называемые абсолютными моментами
(начальными или центральными):
М\Х\к= Y)x\kPi, (2.16)
М\Х- М(Х)\к= ^\х-М{Х)\кр-„ (2.17)
где к = 0, 1, 2, .... В данной ситуации |ЛЧ и \Х — М(Х)\ также выступают в
качестве случайных величин.
Отметим, что в случае бесконечного количества значений св. X ее
моменты, начиная с некоторого порядка к, могут не существовать.
Существование моментов зависит от сходимости соответствующего числового ряда
типа Vxf/7/.
/= 1
В качестве меры рассеяния также часто используется отношение
среднего квадратического отклонения и математического ожидания,
называемое коэффициентом вариации (С. V.):
С V = CTW
• М{ХУ
Коэффициент вариации не зависит от размерности, поскольку
размерности ст(Л) и М(Х) одинаковы. Поэтому величина С. V. характеризует
относительную вариабельность распределений. Следовательно, С. V.
удобно использовать для сравнения вариабельности распределений св.,
измеряемых в разных единицах (например, в различных распределениях
масса представлена в килограммах и фунтах или стоимость в рублях и
долларах и т. д.).
86

2.4. Числовые характеристики дискретных случайных величин
(продолжение)
Во многих прикладных задачах является весьма важным описание
исследуемого распределения посредством некоторых параметров (чисел).
Наряду с математическим ожиданием и дисперсией рассмотрим и другие
характеристики.
Определение. Медианой распределения св. Л" называют значение х0, при
котором для функции распределения Fix) выполняется равенство
F(x0) = 0,5.
Таким образом, медиана представляет собой середину распределения,
т. е. точку, в которой вся вероятностная масса (единица) делится пополам.
Обозначим Xq = Ме(Х).
Замечание. В конкретных задачах может оказаться так, что функция
распределения F(x) принимает значение 0,5 на целом интервале (рис. 13).
В этом случае любое значение из интервала, на котором справедливо
равенство F(x) = 0,5, является медианой распределения.
Возможна и другая ситуация: функция распределения F(x)
"перескакивает" через ординату 0,5 (рис. 14), и тогда равенство Fix) = 0,5 не
выполнено. В этом случае медианой распределения называют точку, в которой
происходит соответствующий "скачок" функции.
Следовательно, учитывая замечания, получаем, что каждое
распределение имеет по крайней мере одну медиану.
Определение. Модой распределения дискретной с. в. X называют то
значение с. в., для которого вероятность является наибольшей по сравнению с
соседними значениями.
Обозначим моду распределения с. в. ^посредством MQ(X).
Пример. Пусть с. в. X имеет закон распределения
*,■
Pi
-1
0,05
0
0,15
2
0,1
5
0,25
6
0,4
9
0,05
<
У
1
0,5~
к
а Ь
y = F(x)
X
Рис. 13. Любая точка интервала (а, Ь) на оси абсцисс является медианой
распределения.
87

A
У
y = F(x)
1 ~4
;•* ■
0,5
a x
Рис. 14. Точка х = а является медианой распределения, несмотря на то что
равенство F(x)=Q,5 не выполнено ни для каких значений х.
Найти моду распределения.
Решение. Как видно из таблиц, наибольшие вероятности по сравнению
со своими соседними значениями имеют два значения х = 0
(соответствующая вероятность, равная 0,15, превосходит и 0,05 и 0,1) и х= 6
(соответствующая вероятность 0,4 превосходит и 0,25 и 0,05). Таким образом,
распределение с. в. А" имеет две моды М0(Х) = 0 и М0(Х) = 6.
Если мода распределения единственна, то распределение называют
унимодальным. Если имеется две моды или более, то распределение называют
соответственно бимодальным или мультимодальным.
Аналогично определению медианы равенством F(x) = 0,5, можно
определить и другие точки разбиения вероятностной массы, если вместо числа
0,5 рассмотреть некоторые значения р, где 0 < р < 1.
Определение. Квантилью распределения порядка р называют значение
хр с. в. X, для которого справедливо равенство F(x) = р, где р может быть
любым числом из интервала (0; 1).
Согласно данному определению, медиана распределения — это
квантиль порядка 0,5. Это значение удобно обозначить не х0 , а х05 в
соответствии с обозначением, введенным в определении квантили.
Квантили порядка 0,25 и 0,75 называют соответственно нижней и
верхней квартилями (х025 и Xq 75).
Квантили Xq ,, х02, ..., Xq9 называют дицилями.
Квантили Xqo,, д^02, ..., л^09 называют процентилями (персентилями).
Знание некоторого заранее выбранного количества квантилей
(например, процентилей) позволяет получить определенное представление о
характере распределения: его рассредоточении и степени рассеяния.
Для характеристики рассеяния используют также значение
5(хо,75 — *о,25). называемое вероятным отклонением (или семи-интерквар-
тильной широтой).
88

Степень рассеяния характеризуется также широтой распределения —
длиной интервала между граничными значениями х, при которых F(x) = О
и F(x) = 1.
Можно ввести характеристику симметричности распределения
относительно среднего. Для симметричных распределений отклонения от
среднего в ту или иную сторону взаимно компенсируются, поэтому все
центральные моменты нечетного порядка, ц„ ц3> Щ. •••» обязаны быть равными
нулю. Поскольку Ц, = 0 для любых распределений (см. § 2.3), то каждый из
моментов нечетного порядка, начиная с ц3> может служить мерилом
симметричности распределения. Обычно используют момент наименьшего
порядка, ц3- Чтобы придать характеристике абсолютный характер, делением
на значение ст3 получают величину нулевой размерности (напомним, что
а = JD(X) — среднее квадратическое отклонение).
Определение. Коэффициентом асимметрии распределения с. в. X
называют число
Ъ=Ц. (2.19)
а
Для симметричного распределения у, = 0. Если у, > 0, то ц3 > 0.
Следовательно, кубы положительных отклонений превышают кубы
отрицательных отклонений, и более "длинная часть" распределения находится справа
от среднего. Асимметрия положительна.
Аналогично, в случае у, <0 асимметрия отрицательна, т. е. более
длинная часть распределения расположена слева от среднего.
Используя центральный момент четвертого порядка в абсолютных
единицах, можно получить характеристику, называемую коэффициентом
эксцесса распределения:
y2 = Hi-3. (2.20)
а
Коэффициент эксцесса характеризует сглаженность (плавность
поведения) распределения относительно центра. Эталоном для сравнения служит
нормальная кривая (см. § 2.11), для которой у2 = 0. Если у2 > 0, то пик
распределения находится выше, чем у нормальной кривой (более резкий),
и наоборот, если у2 < 0, то пик распределения ниже пика нормальной
кривой, и само распределение рассредоточено более плавно.
Последние характеристики, коэффициенты асимметрии и эксцесса,
наиболее показательны для непрерывных распределений.
Отметим, что наряду с рассмотренными характеристиками
расположения, рассеяния и формы распределения используются и другие численные
характеристики поведения случайных величин.
89

2.5. Биномиальное распределение
Одними из типичных распределений случайных величин дискретного
типа являются распределения, связанные со схемой Бернулли. Среди таких
распределений выделим распределение, называемое биномиальным.
Итак, пусть п испытаний относительно некоторого случайного события А
проводятся по схеме Бернулли. Вероятность осуществления события А в
одном испытании постоянна и равна р. В качестве с. в. X рассмотрим число
испытаний, в которых событие А осуществляется (назовем эти испытания
удачными). Тогда с. в. ^принимает возможные значения 0, 1, 2, 3, ..., п, а
вероятности значений хт = т находятся по формуле Бернулли
рт= OV", (2.21)
где q = 1 - р.
Определение. Биномиальным распределением с. в. X называют
распределение вида
(2.22)
где вероятности рт представлены, исходя из формулы (2.21).
Таким образом, биномиальное распределение в каждом конкретном
случае зависит от двух чисел пир, называемых параметрами
распределения. Задавая пир, мы полностью определяем биномиальное
распределение, так как по существу оказываются однозначно предопределены все
значения случайной величины и их вероятности.
Проверим условие нормировки и установим значения математического
ожидания и дисперсии.
Для этого воспользуемся известной формулой бинома Ньютона, уже
встречавшейся ранее [см. (1.6)], а также двумя формулами,
получающимися из данной путем дифференцирования по х обеих частей равенства:
*,„
Рт
0
Ро
1
Р\
2
Рг
п
Рп
Л1 „Л1 _ Л — /Л
(х+а)п = £ Стпхта
т = 0
п(х+а)П-1 = ^ С
im т- I п- т
тпх а
(2.23)
(2.24)
m - О
n(n-l)(x+a)n 2= Y^C^m(m-l)xm~2a"~m.
(2.25)
m = 0
Причем в двух последних формулах суммирование ведется, начиная с
m = 0, чисто формально, поскольку в (2.24) первое слагаемое равно нулю,
а в (2.25) два первых слагаемых — нули.
Итак, запишем условие нормировки:
90

m"0 m = 0
Последнее равенство следует из (2.23) при х = р, а = q. А так как по
условию формулы Бернулли р + q = 1, то и
!> = '•
т = 0
Утверждение 1. Для с. в. Л", имеющей биномиальное распределение с
параметрами пир, математическое ожидание равно произведению пр.
По определению математического ожидания и биномиального
распределения (2.22) получаем
л л
М(Х) = ^тРт = J>0'Y~'n. (2.26)
т = 0 /л = 0
Сравним полученное выражение с правой частью (2.24) при х = р,
а = q:
л
n(p+q)n~l = £C>/,"Y"'\ (2.27)
т = 0
Как видим, данные суммы отличаются одним сомножителем р.
Умножив обе части равенства (2.27) на р и с учетом р + q = 1, получаем
л
n(p + q)n-lp=np = £ Cmnmpmqn-m = М(Х),
/п = 0
т. е. Л/(Л) = л/7, и утверждение 1 доказано.
Утверждение 2. Для с. в. X, имеющей биномиальное распределение с
параметрами пир, дисперсия равна произведению npq, где q = 1 — р.
Для доказательства воспользуемся формулой (2.13):
D(X) = М(Х2) - М\Х).
При этом, как только что установлено, М(Х) = пр, т. е. М2(Х) = (пр)2, и
остается найти лишь М(Х2). По определению М(Х2) и биномиального
распределения (2.22) имеем
М(Х2) = j^x2mPm = ^т2СтпртЯп-т. (2.28)
т = 0 т = 0
Для дальнейших преобразований запишем (2.25) при х = р, а = q
(причем р + q = 1):
n(n-\)(p+q)n-2 = п(п-\) = ^C>(w-1/-V
m - 0
Умножим обе части последнего равенства на р2:
л
л(л-1)/>2 = £ С>(т-1)/У"т.
т = 0
91

И далее
л
п(п-\)р2 = £ Cmn{m2-m)pmqn-m =
/71 = 0
- 2^K^nfn p q - Lnmp q ) -
m = 0
л л
= ^ Cmnm2pmqn-m- £ Cmnmpmqn~m = M(I2)-M(I).
m = 0 m = 0
Последнее соотношение следует из (2.28), (2.26).
Итак,
п(п-\)р2 = М(Х2)-М(Х),
следовательно,
М(Х2) = п(п -\)р2 + М(Х) = (п2р2 - пр2) + пр.
Далее находим дисперсию:
D(X) = М(Х2)-М2(Х) = п2р2-пр2 + пр-(пр)2 =
= — пр2 + пр = пр( 1 — р) = npq.
Утверждение 2 доказано.
В завершение данного параграфа отметим важный частный случай
биномиального распределения.
Определение. Биномиальное распределение при п = 1 называют
распределением Бернулли.
Таким образом, с. в., имеющая распределение Бернулли, принимает
лишь два значения, 0 и 1, с вероятностями соответственно q и р:
*т
Рт
0
Ч
1
Р
Для такой с. в. А" легко найти непосредственно М(Х) = р, D(X) = pq, что
соответствует и соотношениям, установленным в утверждениях 1, 2, при
п= 1.
Замечание. Биномиальное распределение с. в. А" с параметрами пир
принято обозначать
Х~В(пур), (2.29)
при этом знак ~ читается "распределена как" или "распределена по закону".
2.6. Распределение Пуассона
Со схемой Бернулли также связано и дискретное распределение,
обобщающее биноминальное распределение на случай бесконечного
количества значений с. в. А" и называемое распределением Пуассона. При этом
сошлемся на соотношение (1.26):
ton Л(»0 = -е~\
92

характеризующее поведение вероятностей Рп(т), найденное по формуле
Бернулли, с ростом п и при а = пр. Учитывая, что число пр при
биноминальном распределении есть не что иное, как среднее (математическое
ожидание), фиксирование этой величины с ростом п означает фактически
неизменность среднего значения в различных сериях испытаний.
Определение. Распределением Пуассона с. в. X называют распределение
вида
, (2.30)
хт
рт
0
А)
1
Р\
2
Рг
т
Рт
...
где все вероятности рт вычисляются по формуле
п - а а~а
Рт ~ ~^\е
(2.31)
(а — положительная постоянная).
Согласно определению, распределение Пуассона зависит лишь от
одного параметра а, смысл которого прояснится далее. Отметим также, что
ограничение а > 0 совершенно необходимо, ибо в противном случае либо
все рт = 0 (при а = 0), либо формула (2.31) содержит отрицательные
значения вероятности (при а < 0, т — нечетное), что для вероятности
недопустимо.
Проверим условие нормировки, а также найдем математическое
ожидание и дисперсию пуассоновской с. в. X. Для этого нам потребуется
известная формула представления функции е? в виде бесконечного количества
слагаемых (числового ряда):
= ! + *. + £. + ... + :*!!+... = "V —,
1! 2! т\ £~чп\
(2.32)
/71 = 0
справедливо при любом х (см. Приложение 1).
Утверждение 1. Для вероятностей рт, рассчитываемых по формуле
(2.31), справедливо условие нормировки
т = 0
Действительно,
еа = 1.
/71 = 0 /71=0 /71 = 0
Отметим, что мы воспользовались равенством (2.32) для функции & при
х= а.
Утверждение 2. Для с. в. X, имеющей распределение Пуассона с
параметром а, математическое ожидание равно указанному параметру:
М(Х) = а.
93

По определению математического ожидания и распределения Пуассона
(2.30), (2.31), получаем
OD 00 00 00
М(Х) = УхтРт = У т^е-° = У т^е-° = e"aV/ a , .
\ j ^ тит ^ m! ^ m\ Z^(m-l)!
/п = 0 /л = О /п=1 /л = I
Чтобы к последней сумме применить равенство (2.32), необходимо
привести в соответствие суммирование (с 0, а не с 1). Для этого введем другую
переменную суммирования: s = т — 1. Тогда т = s + 1, и суммирование
слагаемых будет начинаться с нуля, а именно:
<х> ао . . <х>
М(Х) = е-" У °т = е~аУ^— = е-"аУ°-.
т=I s=0 j=0
Далее используем (2.32) при х = а и, учитывая, что обозначение
индекса суммирования буквами т или j или какой-то другой совершенно
никакой роли не играет, получаем
т. е. М(Х) = е~а а е? = а.
Утверждение 2 доказано.
Утверждение 3. Для с. в. X, имеющей распределение Пуассона с
параметром а, дисперсия равна указанному параметру: D(X) = a.
Поскольку математическое ожидание нам известно, для нахождения
дисперсии достаточно вычислить М(Х2).
00 00 00 00
.2а „-в _ „-ov1 J" — „-" v ^. о
т-
щ*) = Zx»p» - ЪтЪ'° - «-1»Ъ - -Т
m! L-i m\ £~i (т— 1)!
/л = О /п = 0 /л = I /п=1
Далее, как и при доказательстве утверждения 2, вводим новую
переменную суммирования: s = т— 1. Следовательно, т = s + 1, и
j=0 J-0 j=0
j - I J - О J = I
Чтобы преобразовать сумму в последнем выражении к виду формулы
(2.32), вновь переобозначим переменную суммирования к = s — 1, тогда
s = к + 1. Таким образом,
i+\ " к+2 " *
L^{s- 1)! L^ k\ L^k\
s=\ к =О *= О
= ё~аа2еа+а = a2 + a.
Следовательно,
ДАТ) = М(Х2)-М\Х) = (а2 + а)-а2 = а.
Утверждение 3 доказано.
94

2.7. Примеры
Биномиальное распределение и распределение Пуассона по своей
значимости, особенно в вопросах приложений, имеют ключевое значение
среди обширного множества дискретных распределений. Приведем примеры
использования указанных распределений (часть примеров заимствована из
известной монографии В. Феллера "Введение в теорию вероятностей и ее
приложения". — М.: Мир, 1984)
Пример 1. Комбинации полов в многодетных семьях.
Среди многодетных семей с пятью детьми вычислить процентные доли
семей с различным соотношением детей по половому признаку.
Вероятность рождения мальчика и девочки считать равной 0,5.
Среди пятерых детей в семье возможны следующие соотношения:
— все 5 детей — девочки;
— 4 девочки и 1 мальчик;
— 3 девочки и 2 мальчика;
— 2 девочки и 3 мальчика;
— 1 девочка и 4 мальчика;
— все 5 детей — мальчики.
Взяв в качестве события А рождение в рассматриваемой семье,
например мальчика, мы оказываемся в условиях схемы Бернулли. Полагаем с. в.
X — количество мальчиков в семье из 5 детей. Тогда с. в. А" имеет
биномиальное распределение с параметрами п = 5, р = 0,5:
*i
Pi
0
А)
1
Pi
2
Pi
3
Л
4
Ра
5
Ръ
где вероятности р{ находятся по формуле Бернулли.
Вычислив соответствующие вероятности с точностью до 10~5 и переведя
их в соответствующие проценты, получим искомые процентные доли
семей.
*i
Pi
Доли в %
0
1
32
3,125
1
5
32
15,625
2
10
32
31,25
3
10
32
31,25
4
5
32
15,625
5
1
32
3,125
I-1
£ = 100%.
Найденные процентные соотношения являются теоретическими.
Отклонение реальных данных, найденных статистически, от теоретических
при достаточно большом наблюдаемом количестве семей и при
вероятности р = 0,5 не должно быть существенным. В противном случае есть повод
усомниться в предположении р = 0,5 и необходимо уточнить значение
этой вероятности статистическими методами.
Пример 2. Контроль качества продукции.
Проверяется на соответствие качеству большая партия изготовленных
препаратов. Для контроля случайным образом отбирается 100 изделий, у
95

которых контролируются некоторые параметры. Препарат бракуется, если
эти параметры не соответствуют допустимому уровню. Известно, что брак
в данном производстве составляет в среднем 2%. Какова вероятность, что
среди 100 исследуемых будет: а) ровно 2 бракованных изделия; б) более
четырех бракованных изделий?
В данной задаче с. в. X — число бракованных изделий среди 100
отобранных. Можно ли считать распределение с. в. X биномиальным? Если
партия изделий невелика, то с каждым испытанием (извлечением по
одному 100 изделий из партии) вероятность р появления бракованного изделия
изменяется весьма существенно, так как заметно меняется от испытания к
испытанию отношение — , количество благоприятствующих событий к об-
п
щему числу возможных элементарных событий, т. е. испытания не будут
однотипными. Если же партия изделий достаточно велика по сравнению с
числом испытаний, то с каждым испытанием вероятность р = — хотя и
п
изменяется, но столь незначительно, что возможно считать значение р
неизменным. И тогда можно использовать биномиальное распределение.
Параметры п = 100, р = 0,02. Находим соответствующие вероятности:
Лоо(2) = С?оо(0,02)2(0, 98)98« 0, 273411,
Лоо(т>4)= 1-Лоо(/л<4)= 1-[/>,оо(0) + Лоо(1) + Лоо(2) + Лоо(3) +
+ Лоо(4)] = 1-[0,98|00+ С||00(0,02)(0,98)"+ С;оо(0,02)2(0,98)98 +
+ С;оо(0,02)3(0, 98)97 + CUO, 02)4(0, 98)96] «
* 1 - [0, 132618 + 0, 270650 + 0,273411 + 0, 182274 + 0,090207] =0, 05084.
Данные вероятности без учета ошибок округления являются точными
значениями. Заметим, что в данном случае можно было воспользоваться
приближением Пуассона при а = пр = 2, тогда приближенные вероятности
будут равны:
Лоо(2)«|^е"2« 0, 270671
[расхождение с точным значением на третьем знаке после запятой; см.
соотношение (1.28), согласно которому модуль разности точного и
приближенного значений не более пр1 = 0,04];
Рт(т > 4) * 1 - \£е~2 + 1е~2 + %е~2 + ^е~2 + §-V2l =
L0! 1! 2! 3! 4! J
= 1 - е~2[\ +2 + 2 + | +|) «0,05265
(расхождение с точным значением снова на третьем знаке после запятой).
Полученная вероятность Рт(т > 4)« 0,05084 является теоретической
вероятностью и свидетельствует о редкости появления в выборке из 100
изделий более четырех бракованных. Поэтому предполагается, что в
единичном испытании (одной выборке) это событие (т > 4) не должно
происходить. Если же в одной выборке в 100 элементов получили значение т,
96

большее 4, т. е. основания усомниться, что процент бракованных изделий
во всей партии равен в среднем 2%.
Пример 3. Проверка эффективности сывороток или вакцин.
Пусть известен средний процент заболеваемости некоторой болезнью
среди крупного рогатого скота. Для проверки новой вакцины отбирается
случайным образом группа из п животных, которым делаются прививки.
Можно ли судить об эффективности вакцины по результатам
заболеваемости животных, получивших прививку? Оказывается, вполне определенные
выводы можно сделать, сравнивая данные, полученные
экспериментальным путем, с теоретическими. И решающую роль здесь играет
биномиальное распределение.
Предположим, что вакцина абсолютно не влияет на численность
заболевших животных. Тогда с. в. X — число заболевших животных среди п
отобранных — подчинена биномиальному закону распределения с
известными п и р (в данном случае вероятность р получается из среднего
процента заболеваемости, а каким быть числу п мы решаем сами, отбирая п
животных для прививки). Вычисляем биномиальные вероятности
Рт = C"pmqn~mH сравниваем с ними полученные эмпирические значения
соответствующих частот. Например, р = 0,25; п = 10, тогда закон
распределения с. в. А'имеет вид
хт
Рт
0
0,0563
1
0,1877
2
0,2816
3
0,2503
4
0,1460
5
0,0584
6
0,0162
7
0,0031
8
0,0004
9
0,0000
10
0,0000
При р = 0,25; п = 12 имеем
хп
Рт
0
0,0317
1
0,1267
2
0,2323
3
0,2581
4
0,1936
5
0,1032
6
0,0401
7
0,0115
8
0,0024
9
0,0004
10
0,0000
11
0,0000
12
0,0000
При/7 = 0,25; п = 17:
Хт
Рт
0
0,0075
1
0,0426
2
0,1136
3
0,1893
4
0,2209
5
0,1914
17
0,0000
И наконец, при р = 0,25 и п = 23:
хт
Рт
0
0,0013
1
0,0103
2
0,0376
3
0,0878
4
0,1463
5
0,1853
6
0,1853
7
0,1500
8
0,1000
23
0,0000
Заметим, что все значения вероятностей округлены до четвертого знака
после запятой.
Согласно рассчитанным вероятностям, значения pQ = Рп(0) —
достаточно малые числа: />|0(0) = 0,0563; />2(0) = 0,0317; />7(0) = 0,0075;
Р23(0) = 0,0013. При столь малых вероятностях обычно полагают, что в
единичном испытании это маловероятное событие (Х= 0) не происходит.
7-3529 97

Если же с. в. Л" все-таки в нашей выборке п животных приняла значение О,
то возникает повод усомниться в наших предположениях, а именно:
отнести данный факт на счет действия вакцины. И если вопреки меньшей
вероятности данное событие происходит, тем сильнее свидетельство в
пользу вакцины. Отметим, что вероятность оказаться не более одного
заболевшего животного из 17, не получивших прививки, приближенно
равна 0,0075 + 0,0426 = 0,0501, т. е. факт наличия такого события (X < 1 при
п = 17) — более сильный аргумент эффективности вакцины, нежели
отсутствие заболевания среди 10 животных, вероятность которого, 0,0563,
большая чем 0,0501. Аналогично, при п — 23, вероятность не более двух
заболеваний равна 0,0013 + 0,0103 + 0,0376 = 0,0492 (т. е. меньше чем 0,0501) и
поэтому может еще лучше свидетельствовать в пользу вакцины, чем одно
заболевание из 17.
Пример 4. Эффективность лекарства.
Проверяется на эффективность некоторое лекарство, понижающее
кровяное давление. Имеется группа из п человек, которым измеряется
давление до приема лекарства и после. Получены две последовательности чисел:
х,, х2, ..., хп и ух, у2, ..., уп. Полагаем, что /-е испытание закончилось
успехом, если х < х„ и закончилось неудачей, если у{ > xt. Таким образом, в
каждом испытании имеется всего два возможных исхода. Если бы лекарство
не являлось эффективным, то п испытаний можно считать
производящимися по схеме Бернулли с постоянной вероятностью успеха в одном
испытании р = 0,5.
Число успехов в п испытаниях — это с. в. Z, имеющая биномиальное
распределение:
Zm
Рт
0
Ро
1
Рх
2
Pi
3
ft
п
Рп
гяеРт = Cmnpmqn-m = С:(0,5)я.
Если в эксперименте произойдет существенно большее число успехов,
чем предусмотрено соответствующей вероятностью, то данный факт
следует рассматривать как свидетельство эффективности лекарства.
Пример 5. Самки в популяции грызунов.
Исследуется распределение количества самок среди новорожденных
детенышей в популяции грызунов. Имеется фактическое распределение
самок в 240 пометах с 4 детенышами в каждом помете:
0
23
1
72
2
91
3
47
4
7
2=240
В данной таблице хт — число самок в помете среди 4 детенышей, пт —
количество пометов с числом самок хт. Найдем относительные частоты
98

встречаемости значений 0, 1, 2, 3, 4 самок в помете, поделив пт на 240
(суммарное количество пометов), тогда
240
0
0,096
1
0,3
2
0,379
3
0,196
4
0,029
I=1
Относительные частоты, являясь аналогом соответствующих
вероятностей (вспомним статистическое определение вероятности (§ 1.10) и
теорему Бернулли (§ 1.15)), вначале возрастают, затем убывают, т. е. ведут себя
так же, как вероятности в биномиальном распределении. Полагая, что
количество самок в помете из 4 детенышей — с. в., принимающая значения
0, 1,2, 3, 4, можно предположить наличие биномиального распределения
этой с. в. Такое предположение, разумеется, в первую очередь оправдано
приложимостью схемы Бернулли к ситуации появления 4 детенышей в
помете. Итак, с. в. X — количество детенышей в помете. Полагая наличие
биномиального распределения и зная п (п = 4), по фактическим данным
находим другой параметр р. Как известно, при биномиальном
распределении среднее равно пр. Фактическое среднее обозначим х, и тогда
- _ 0 • 23+ 1 • 72 + 2 • 91 + 3 • 47 + 4 • 7 _ 425 , п,
Х 240 240 е1'76-
Тогда х= пр, следовательно, 1,76 = 4р и р = 0,44. Вычислив значение р,
по формуле Бернулли легко находим соответствующие вероятности рт, а
следовательно, и закон распределения:
х,„
Рт
0
0,098
1
0,309
2
0,364
3
0,191
4
0,038
Z=1
Полученные вероятности несколько отличаются от соответствующих
относительных частот, приведенных выше. Однако чисто визуально
соответствие достаточно заметно. Оценить эту зависимость более точно можно
математическими методами, называемыми критериями согласия, которые
будут рассмотрены в дальнейшем (см. § 4.7).
Заметим, что, умножив вероятность рт на 240 и округлив результат до
целых, мы получим теоретическую частоту (вместо пт). В этих
обозначениях теоретическое распределение самок среди детенышей в 240 пометах
будет выглядеть так:
х,„
rim meopem.
0
24
1
74
2
87
3
46
4
9
Е=24°
Пример 6. Столетние старцы в стабильном обществе.
Статистика свидетельствует, что для каждого конкретного родившегося
человека вероятность прожить более 100 лет крайне мала, т. е. смерть после
7* 99

100 прожитых лет — это редкое событие. Естественно предположить, что
частоты тех лет, в которые умирает ровно т стариков, проживших более 100
лет, соответствуют пуассоновским вероятностям с некоторым параметром а.
Для данного предположения существенным фактором является стабильность
общества: отсутствие войн и революций, крупных эпидемий, природных
катаклизмов. В этом случае есть основания продолжительности жизни
отдельных индивидуумов считать приближенно независимыми, что необходимо.
Значение пуассоновского параметра а для каждого общества определяется
отдельно в зависимости от размера этого общества, как физического, так и
морального здоровья его членов, экологии и т. д. Согласно ссылке В. Фелле-
ра, данные по Швейцарии подтверждают указанное предположение.
Пример 7. Падение самолетов-снарядов в Лондоне.
Хотя данный пример пуассоновского распределения внешне далек от
вопросов медицины, он столь иллюстративен и нагляден, что не привести
его невозможно. В. Феллер использовал статистику падения самолетов-
снарядов в южной части Лондона во время второй мировой войны. Всего
было Т= 537 таких падений. Вся область поделена на N участков, каждый
площадью примерно 0,25 км2, оказалось N = 576. Рассматривается
распределение случайных точек (падений снарядов) по поверхности (по N
участкам). Все участки рассортированы по числу падений m на шесть групп:
m = 0, m = 1, m = 2, m = 3, m = 4, m> 5. Посчитаны значения Nm — число
участков с m падениями снарядов. Получилась таблица:
m
0
229
1
211
2
93
3
35
4
7
>5
1
Z=576
Предположив, что с. в. X — число падений самолетов-снарядов на
одном участке — распределена по закону Пуассона, найдем, каковы должны
быть теоретические значения частоты Nm(meop). Среднее число падений
Т пт
а = —«0,9323 , тогда пуассоновские вероятности равны рт = —е~а:
/V /и!
т
Рт
NPm
0
0,3936
226,741
1
0,3670
211,390
2
0,1711
98,540
3
0,0532
30,623
4
0,0124
7,137
>5
0,0027
1,569
*г(теор.)
Значения рт « т , поэтому в последней строке таблицы
представлены именно теоретические частоты. Для сравнения приведем совместную
таблицу:
т
N
хт(теор.)
1У т
0
229
226,74
1
211
211,39
2
93
98,54
3
35
30,62
4
7
7,14
>5
1
1,57
100

Соответствие частот удивительное, что свидетельствует о действительно
случайности точек падения и равновозможности попадания на любой из
отмеченных участков.
Пример 7 является характерным примером распределения случайных
точек по некоторой области, что весьма существенно и для многих
медико-биологических задач. Приведем еще аналогичные примеры, по сути
близкие к примеру 7.
Пример 8. Гнездование белых аистов.
По данным биологов, на территории Новгородской области (точнее в ее
западной и юго-западной части) летом гнездятся 324 семейства белых
аистов, птицы, достаточно редкой для данной местности. Каково же
распределение этих гнезд по рассмотренному району? По аналогии с
предыдущим примером есть основания рассматривать распределение случайных
точек по поверхности и предполагать наличие именно пуассоновского
распределения. Разобьем весь очерченный район («30 тыс. км2) на N
участков, приближенно равных по площади, например на N= 1000 участков.
Предполагая природные условия на каждом из участков приближенно
одинаковыми для расселения птиц, можно считать и вероятность прилета
аистов для каждого участка также одинаковой. Тогда среднее число гнезд на
участке равно а = 324/1000 = 0,324. Полагая количество гнезд на участке в
качестве с. в. ЛГ и используя распределение Пуассона с параметром а,
приходим к таблице:
т
Рт
jy(meop.)
0
0,7233
723,3
1
0,2343
234,3
2
0,0380
38
3
0,0041
4,1
4
0,0003
о,з
>5
0,0000
0
Числа N„p) = pm' 1000 — теоретические частоты встречающихся
значений с. в. X. Таким образом (округляя до целых), на 723 участках гнезд нет,
на 234 участках по одному гнезду, на 38 участках по два гнезда и т. д.
Можно рассмотреть и другое разбиение района: например, положить
N = 500, тогда а = 324/500 = 0,648, и вновь воспользовавшись
распределением Пуассона, приходим к новой таблице
т
Рт
*j(meop.)
1У т
0
0,5231
261,55
1
0,3390
169,5
2
0,1098
54,9
3
0,0237
11,85
4
0,0038
1,9
>5
0,0006
0,3
Отклонение наблюдаемых данных от теоретических возможно
вследствие некоторого различия участков разбиения (близость или, наоборот,
отдаленность от городов, наличие или отсутствие болот и др.), вследствие
индивидуальных запросов птиц (прежде чем строить гнездо, аисты
выбирают место), а также вмешательства человека.
101

Пример 9. Островки Лангерганса}.
Исследуется распределение островков Лангерганса в поджелудочной
железе обезьяны макаки резус. Проецировались на экран гистологические
срезы. При этом вся рассматриваемая область оказалась разбитой на
N = 900 квадратов, в каждом из которых фиксировалось количество
островков Лангерганса. Как оказалось, их количество т колеблется в каждом
из квадратов от 0 до 6 и с учетом частоты Л^ суммарно равно 904.
Данные представлены в таблице:
т
0
327
1
340
2
160
3
53
4
16
5
3
6
1
£= 900
Nm — частота встречаемости квадратов с т островками.
0 • 327 + 1 • 340 + 2 • 160 + 3 • 53 + 4 • 16 + 5 • 3 + 6 • 1 = 904 - всего
выявленных островков.
Предполагая, что с. в. X — количество островков Лангерганса в одном
квадрате — имеет распределение Пуассона, найдем относительные частоты
Nm am -а
-—£ и соответствующие пуассоновские вероятности рт = —е , где
900 тп\
904
а = ^лл» 1,0044. Исходя из вероятностей рт, вычислим и теоретические
частоты = Nmneop') = pm' N. Данные занесем в таблицу:
т
0
1
2
3
4
5
6
К
327
340
160
53
16
3
1
£= 900
Nm
900
0,3633
0,3778
0,1778
0,0589
0,0178
0,0033
0,0011
I=1
Рт
0,3663
0,3679
0,1848
0,0619
0,0155
0,0031
0,0005
E=1
xj(meop.)
1У т
329,62
331,09
166,28
55,67
13,98
2,81
0,55
£= 900
Как видим из сравнения частот Nm и Nm р)или из сравнения относи-
N
тельных частот ^ и рт (что по существу то же самое), соответствие
данных распределению Пуассона достаточно хорошее.
'Данные заимствованы из книги: П. Ф. Рокицкий. Биологическая статистика. — Минск:
"Вышэйшая школа", 1967.
102

Рис. 15.
Пример 10. Распределение бактерий и клеток крови.
Рассмотрим рис. 15, на котором воспроизведена фотография чашки
Петри с колониями бактерий, которые под микроскопом смотрятся как
темные пятнышки. Вся поверхность разбита на маленькие квадраты, в
каждом из которых указано количество колоний бактерий. Число колоний —
с. в., распределение которой предполагается пуассоновским. Приведем
таблицу1 наблюдений и теоретических частот, составленную по восьми
экспериментам с различными видами бактерий.
т
т
хтОпеор.)
*т(теор.)
1У т
\т(теор.)
1У т
хг(теор.)
1У т
хт(теор.)
1У т
хг{теор.)
1У т
т
*т(теор.)
■•* т
*г(теор.)
1У т
0
5
6,1
26
27,5
59
55,6
83
75,0
8
6,8
7
3,9
3
2,1
60
62,6
1
19
18,0
40
42,2
86
82,2
134
144,5
16
16,2
11
10,4
7
8,2
80
75,8
2
26
26,7
38
32,5
49
60,8
135
139,4
18
19,2
11
13,7
14
15,8
45
45,8
3
26
26,4
17
16,7
30
30,0
101
89,7
15
15,1
11
12,0
21
20,2
16
18,5
4
21
19,6
7
9,1
20
15,4
40
43,3
9
9,0
7
7,9
20
19,5
9
7,3
5
13
11,7
16
16,7
7
6,7
8
7,1
19
15
6
8
9,5
7
7,4
7
9,6
7
9
9,6
х1-
уровень
97
66
26
63
97
53
85
78
1 Таблица приведена в книге В. Феллера "Введение в теорию вероятностей и ее приложе>
ния" и заимствована у Ю. Неймана.
103

В приведенной таблице х2_УРОвень указывает процент случаев, в
котором данные наблюдений привели бы к худшему результату согласования с
распределением Пуассона. Вопросы нахождения вероятности (процентов)
по критерию х2 будут рассмотрены в дальнейшем (§ 4.7). Пока же
отметим, что согласие наблюдаемых значений с теоретическими весьма
существенное.
Пример 11. Травматизм на производстве.
Рассматривается количество случаев травматизма с ВУТ (временной
утратой трудоспособности) на крупном промышленном предприятии за
определенный промежуток времени (например, за месяц или неделю). Все
работники предприятия разбиты на N подразделений примерно с равным
количеством рабочих. С. в. X — количество случаев травматизма в
подразделении — распределена по закону Пуассона с параметром а, где а —
статистическое среднее количество случаев травматизма с ВУТ на данном
предприятии или среднее по отрасли. Сравнивая наблюдаемые частоты с
теоретическими, можно судить об уровне техники безопасности.
Пример 12. Неэпидемическая заболеваемость.
Пусть исследуется число неэпидемических случаев заболеваемости в
день в течение длительного промежутка времени. Например, можно
рассмотреть заболеваемость ОРЗ в холодное время года с 1 ноября по 31
марта среди п студентов и сотрудников университета. С. в. X — количество
зарегистрированных случаев в день. N — количество испытаний (в данном
случае N = 151 — число учетных дней), в каждом из которых с. в. Л" может
принять одно из значений 0, 1,2, ..., п, где п — достаточно большое число.
Предполагая в среднем одинаковую и достаточно малую вероятность
заболеваемости каждого потенциального больного в конкретный день (р), а
также независимость случав заболеваемости (так как отсутствует
эпидемическая ситуация), неизбежно приходим к распределению Пуассона с
параметром а = пр. Фактически, а — среднее число зарегистрированных
случаев в день. (Разумеется, наши допущения о постоянной вероятности р,
абсолютной независимости случаев несут определенную степень условности,
вполне допустимую для рассматриваемой математической модели. Право
же, мы ничуть не страдаем, измеряя рост или массу тела человека и при
этом жертвуя точностью до миллиметра или грамма.)
Пуассоновским вероятностям р0, /?,, р2, ... должны соответствовать отно-
»,»»»,„„« „о„~~™, ^ ^ ^ ™» — число дней с к случаями
сительные частоты шп, ш,, ш„ ..., где со* = — z .
N
В данной ситуации распределение Пуассона служит приемлемой
моделью фактического распределения.
2.8. Некоторые дискретные распределения
Как уже было отмечено выше, биномиальное и пуассоновское
распределения являются наиболее распространенными и уважаемыми
дискретными распределениями. Однако существует бесконечное количество
всевозможных законов распределения, так как имеет место достаточный
произвол в выборе значений с. в. и соответствующих вероятностей. Читатель
без особого труда может сфантазировать свое собственное распределение:
104

для этого достаточно придумать ряд чисел (значений с. в.) и разделить
(распределить) каким-либо образом между этими значениями суммарную
единичную вероятность. И весь вопрос сведется лишь к тому, к каким
задачам применимо полученное распределение, что в конечном итоге наряду
с удобством и простотой применения и определяет ценность данного
распределения.
Далее приведем примеры некоторых распределений, которые "нашли"
свой круг задач (или же появились на свет, исходя из запросов
поставленной задачи) и которые в настоящее время считаются классическими.
а) Вырожденное распределение.
Говорят, что с. в. X имеет вырожденное распределение,
сосредоточенное в точке а, если с. в. X принимает лишь одно значение а с
вероятностью 1:
Р(Х=а)=\. (2.33)
Таким образом, вырожденное распределение описывает неслучайные
величины, которые, как было указано ранее, можно считать простейшим
представителем множества случайных величин.
Для с. в. X, имеющей вырожденное распределение, легко найти
[l,x> a
(2.34)
М(Х) = а, М(Хк) = 0м, D(X) = 0. (2.35)
Наличие нулевой дисперсии подчеркивает отсутствие какого-либо
разброса значений относительно среднего. Таким образом, мы приходим к
обратному утверждению: если с. в. X имеет конечное математическое
ожидание и нулевую дисперсию, то Р[Х= М(Х)] = 1, т. е. Л" можно полагать
величиной неслучайной.
б) Дискретное равномерное распределение.
С. в. X имеет дискретное равномерное распределение, если все ее
возможные различные значения х,, х^, ..., хп равновероятны. Следовательно,
закон распределения имеет вид:
(2.36)
Простейшим примером указанного распределения является с. ъ. X —
число выпавших очков при бросании игральной кости. Здесь п = 6, и все
возможные значения (1, 2, 3, 4, 5, 6) имеют вероятности, равные 2 ■
о
Другой пример. Элементы некоторой конечной совокупности
перенумерованы, т. е. каждое значение имеет шанс встретиться в совокупности
лишь один раз. Такой совокупностью может быть спортивная команда,
список больных, множество автомобилей, зарегистрированных в
конкретном городе, и т. д. И если провести испытание — извлечение наудачу
какого-то элемента, то появление в результате испытания любого элемента
**
Р/с
х\
1//I
*2
1//I
х„
\/п
105

совокупности имеет одну и ту же вероятность (см. классическое
определение): \/п, где п — количество всех элементов совокупности.
Функция распределения с. в. X, имеющей дискретное равномерное
распределение, возрастает скачкообразно в точках х,, Xj, ..., хп с величиной
"скачка" \/п. Таким образом, график у = F(x) представляет собой
ступенчатую линию, у которой число (вероятность) \/п — высота "ступеньки".
По определению следует, что
М(Х) = Vx*I = Iy
к" 1
к" 1
l*i
(2.37)
т. е. М(Х) — среднее арифметическое всех возможных значений. Заметим,
что в статистике среднее арифметическое чисел х,, Xj, ..., х„ принято
обозначать х. Таким образом, М(Х) = х. Также по определению найдем
дисперсию с. в. X
п п
D(X) =У[хк- М(Х)]2 • i = 1У (х, - х)2. (2.38)
к"1 к- 1
в) Геометрическое распределение.
Пусть испытания проводятся по схеме Бернулли. В каждом испытании
вероятность успеха полагаем р (О < р < 1), а вероятность неудачи — q
(естественно, q = 1 — р). Пусть с. в. X — число неудач до первого успеха,
тогда ^принимает значения х0 = 0, х, = 1, Xj = 2, ... с соответствующими
вероятностями р0 = р, /?, = qp, p2 = фр, ....
Следовательно, закон распределения имеет вид:
(2.39)
Заметим, что вероятности р, pq, фр, ..., qkp, ... образуют бесконечно
убывающую геометрическую прогрессию со знаменателем q.
Легко проверить условие нормировки:
_ р _ р _
**
Рк
0
р
1
ЯР
2
Ч2Р
к
qkp
YPk = p + qp + q2p + ...+qkp+... = ^- = F- = 1
^ 1 - 0 0
*=0
Введенное распределение называют геометрическим распределением с
параметром р.
Можно доказать, что
М(Х) = I D(X) = 4,
Р р-
а также найти коэффициенты асимметрии (у,) и эксцесса (у2):
yi-i±f, b.6+i.
Jq 9
(2.40)
(2.41)
106

г) Отрицательное биноминальное распределение (распределение Паскаля).
Отрицательное биноминальное распределение является обобщением
геометрического распределения.
Вновь вернемся к схеме Бернулли, при которой вероятность успеха в
каждом испытании обозначим р, а вероятность неудачи — q. Возьмем
некоторое натуральное число г и рассмотрим с. в. X — число неудач до
появления r-го успеха.
Найдем все возможные значения с. в. X. Понятно, что r-й успех может
появиться не раньше чем в r-ом испытании. Итак, если r-й успех появился
в r-м испытании, то все г первых испытаний успешные, т. е. неудач в
испытаниях не было, и Х= 0. Соответствующая вероятность р0 = рг. Если же
r-й успех пришел в (г + 1)-м испытании, то, значит, среди первых г
испытаний только (г— 1) успешное, и в каком-то из этих г испытаний была
одна неудача, т. е. Х= 1. Соответствующая вероятность /?, = C\prq. Далее,
если r-й успех пришел в (г+2)-м испытании, то Х= 2 и р2 = C2r+ xprq2.
Рассуждая аналогично, приходим к распределению введенной с. в. X
(2.42)
Как видим, отрицательное биномиальное распределение зависит от двух
параметров г и р.
Для с. в. X, имеющей отрицательное биномиальное распределение,
можно найти числовые характеристики:
xt
Pk
0
/
1
C\prq
2
г2 nrJ-
k
r2 *r„k
M(X) = rq-, D{X) = Д;
(2.43)
= rl+g
Jrq '
У 2 + — ■
r rq
(2.44)
Легко видеть, что при г = 1 распределение (2.42) превращается в
геометрическое распределение (2.39). Те же превращения претерпевают и
параметры (2.43), (2.44) при г= 1. Следовательно, геометрическое
распределение — частный случай отрицательного биномиального при г = 1.
Замечание. Отрицательное биномиальное распределение (2.42)
рассматривают также и для нецелых г, понимая в этом случае коэффициенты
С r+k- 1 КаК
г* - (r+k- l)(r+k-2)...r
Таким образом имеет место некоторое обобщение нашего
распределения, представленного в схеме.
Отметим, что отрицательное биномиальное распределение имеет
значительные приложения в медицине и биологии, в частности к статистике
заболеваний и несчастных случаев.
107

д) Гипергеометрическое распределение.
С вероятностями гипергеометрического распределения мы встречались
ранее (см. § 1.5, Примеры 5,6). Поскольку гипергеометрическое
распределение наиболее распространено в задачах контроля качества выпускаемой
продукции, приведем типичную постановку подобной задачи. Пусть в
множестве из N изделий ровно М годных, остальные (N — М) —
бракованные. Из всего множества наудачу отбирают ровно п изделий. При этом
отбор производится без возвращения, т. е. для каждого последующего
извлекаемого изделия вероятность оказаться годным изменяется.
Следовательно, испытания не являются однотипными, и схема Бернулли в данной
ситуации неприменима. Рассмотрим с. в. X — число годных изделий среди
п отобранных. Очевидно, что это число годных изделий ограничено не
только числом л, но и не может быть больше, чем М, т. е. возможные
значения с. в. А"— это 0, 1,2, ..., min (M, п).
Соответствующие вероятности находим, исходя из следующих
соображений. Все множество изделий состоит из двух частей (подмножеств):
годных (М элементов) и бракованных (N — М элементов). Если же среди
извлеченных п элементов годных лишь т (т. е. Х= т), то эти т годных
элементов взяты из первого подмножества, и извлечь их можно
Стмспособами. В то же время оставшиеся п — т бракованных элементов
должны быть извлечены из второго подмножества, для этого имеется
С"N~-mMспособов. Учитывая, что всего п элементов возможно получить из TV-
элементного множества C"Nспособами применяем классическое
определение вероятности и получаем
Р(Х=т) = Рт=С"^-».
(2.45)
Таким образом, для рассматриваемой с. в. X записываем закон
распределения, обозначив для определенности число min (М, п) = пм:
(2.46)
где все вероятности рт(т = О, 1, ..., пм) находятся по формуле (2.45).
Распределение с. в. X, заданное выражениями (2.46), (2.45), и называют
гипергеометрическим распределением. Можно вычислить М(Х) и D(X):
хт
Рт
0
Ро
1
Рх
2
Рг
пм
Рп„
М(Х) = Щ; D(X) = nM(N-n)(N-Af) .
N N2(N-l)
(2.47)
Это распределение характеризуется тремя параметрами — N, М, п и
используется обычно в случаях, когда число п не слишком мало по
сравнению с N. На практике выражение "не слишком мало" означает
соотношение п > 0,\N. В противном случае (при п < 0,1N) вероятности извлечения
годной детали в каждом из п извлечений (испытаний) меняются незначи-
108

м
тельно, поэтому, считая их равными (обычно р = —), мы пренебрегаем
некоторой малой погрешностью, но зато взамен приобретаем более
простое и удобное распределение: биномиальное с параметрами пир, где
М М
р = — . Заметим, что р = — — вероятность успеха (извлечение годной
детали) при первом испытании. Таким образом, при п < 0,1 TV оказывается
С/л (~ч п ~ т
_M~N-M „ Гтпт(\ — п\п~т
— ^пР K^ Р)
Понятно, что вместо схемы "годные — бракованные" можно
рассматривать любую пару противоположных состояний: например, "здоровые —
больные", "неинфицированные — инфицированные", "незаразные —
заразные" и т. д. Следовательно, данное распределение находит свои
приложения и для ряда чисто медицинских задач.
Биологи используют гипергеометрическое распределение для оценки
размера популяций животных. Например, необходимо оценить количество
рыб в замкнутом водоеме. Обозначим число рыб в водоеме через N.
Именно это значение и нужно оценить. Далее вылавливают в водоеме М рыб
(например, М= 1000), каким-то способом помечают их и выпускают
обратно. Таким образом, все множество из N элементов разбивается на два:
из М элементов и N—M элементов соответственно. Далее, производится
повторный отлов п рыб (например, пусть для простоты также п = 1000) и
среди этих п рыб рассматривается число помеченных т. Вероятность, что
с. в. X — число помеченных рыб в повторном отлове — окажется равной
т, вычисляется по формуле (2.45), причем М, п, т — конкретные
наблюдаемые числа, а величина N — неизвестна; следовательно, эта вероятность
зависит от N. Для оценки N используют статистический принцип
максимума правдоподобия: если случайное событие (Х = т) осуществилось в
единичном испытании, то оно обладает наибольшей вероятностью рт по
сравнению с другими возможными событиями. Исходя из этого принципа,
и можно найти число N. Естественно, что N является не точным
значением, а лишь оценкой этого значения. Отметим также, что здесь приведена
лишь постановка задачи, не затрагивающая детали организации
эксперимента.
е) Распределение Пойа (Полиа).
При моделировании различных эпидемий заразных заболеваний
широко используется следующая схема эксперимента. В урне находится Ь белых
шаров и с — черных. Всего b + с = N шаров. Наудачу вынимают один шар,
фиксируют его цвет и отправляют обратно в урну, еще добавив s шаров
того же цвета (сопоставьте с этой моделью схему процесса заражения). Таких
извлечений шара производится п. Введем с. в. X — число появлений белого
шара в п экспериментах. Очевидно, что значения с. в. X — 0, 1, 2, ..., п.
Найдем соответствующие вероятности, аналогично выводу формулы Бер-
нулли, только в нашем случае вместо постоянных вероятностей р и q
фигурируют вероятности, изменяющиеся от испытания к испытанию. Итак,
109

P(X=Q) =p0 = т,
c + s . с + 2s
. С + (П- 1)5.
N+(n-l)s'
N N+s N+2s
P(X=\\ = D = rlb ' (c + s)(c + 2s)...[c + (n-2)s]
y } yi nN(N+s)(N+2s)...[N+(n-\)s]
Аналогично, для произвольного к (к = 0, 1, 2, .... п) можно получить
формулу
Р(Х=к) =Рк =
_скЬ - (b + s)(b + 2s)...[b + (k- 1)5 • c(c + s)]...[c + (n- к- 1)5]
N(N+s)...[N+(n-l)s]
Таким образом, найдено распределение с. в. X:
(2.48)
**
Рк
0
Ро
X
Р\
2
Рг
к
Рк
п
Рп
(2.49)
где вероятности рк вычисляются по формуле (2.48). Это распределение
известно как распределение Пойа.
Для указанного распределения можно вычислить
ЩХ) = ^; D{X) = n<£-
1+™
_ N
1 + ^
N
(2.50)
Распределение Пойа является четырехпараметрическим с
параметрами (Ь, с, п, 5). В литературе данные параметры иногда вводят иначе:
b с
b + c= N, — = р; следовательно, — = q — тогда вместо b и с выступают
параметры N и р.
Легко видеть, что при 5 = 0 формула (2.48) превращается в формулу
Бернулли:
* - ^Г-
где обозначения — = р и 4v = Я весьма уместны.
N N
Также следует отметить, что в случае п < 0,1 W справедливо
приближенное равенство
Р(Х=к)»Скпркдп-к.
Пример. Данные результатов исследования заболевания оспой в
Швейцарии в 1877—1900 гг., проведенного Ф. Эггенбергером и Д. Пойа (Polya),
занесены в таблицу
Число
случаев смерти за
месяц

Наблюдаемое
количество месяцев
0
100
1
39
2
28
3
26
4
13
5
6
6
11
7
5
8
5
9
6
10
1
11
6
12
2
13
2
14
3
15
3
110

За единицу времени (одно наблюдение) принят месяц. Всего 256
наблюдений. Поделив каждое наблюдаемое количество месяцев на 256,
получим относительную частоту для каждого из значений числа случаев смерти
за месяц. Напомним, что относительная частота является статистическим
аналогом вероятности. Рассматривая распределение Пойа случайной
величины X с соответствующими параметрами (которые мы не приводим)
можно найти вероятности значений X О, 1, 2, ..., 15. Для сравнения
полученных относительных частот с соответствующими вероятностями найденные
значения занесем в таблицу.
Число
случаев
смерти
за месяц

Относительная
частота
случаев

Вероятность из

распределения
Пойа
0
0,39
0,39
1
0,15
0,14
2
0,11
0,09
3
0,10
0,07
4
0,05
0,05
5
0,025
0,04
6
0,04
0,04
7
0,02
0,03
8
0,02
0,03
9
0,025
0,02
10
0,005
0,02
11
0,025
0,02
12
0,01
0,02
13
0,01
0,02
14
0,01
0,01
15
0,01
0,01
Соответствие данных второй и третьей строк таблицы весьма наглядно
и дает основания полагать случайную величину — число случаев смерти —
распределенной по закону Пойа с соответствующими параметрами.
2.9. Непрерывные случайные величины
Напомним, что случайную величину называют непрерывной, если
множество ее возможных значений заполняет сплошь некоторый интервал. Из
этого определения следует, что множество значений непрерывной с. в. не
только бесконечно, но и несчетно. Суммарная единичная вероятность
поделена (распределена) между этом бесконечным множеством значений, и
для каждого значения вероятность оказывается практически равной нулю.
Поэтому методы, используемые для дискретных с. в., в данной ситуации
бессильны: мы не можем даже перечислить все возможные значения, не
можем оперировать одними лишь нулевыми вероятностями, даже просто
просуммировать все эти вероятности с помощью элементарного сложения
невозможно. Выходом из возникшего тупика является смена подхода к
проблеме: значения с. в. следует рассматривать не персонально, а
объединив их в интервалы (сравните с геометрической вероятностью). В этом
случае операция суммирования обобщается в операцию интегрирования, а
каждое индивидуальное значение с. в. вносит свой вклад в формирование
интеграла и тем самым и проявляет себя. Логически это вполне
естественно: чем большее число значений имеет случайная величина, тем меньше
внимания уделяется каждому конкретному значению и все операции
осуществляются на уровне объединений, групп этих значений. Отметим, что
все значения в интервале, вообще говоря, не являются равновероятными.
Таким образом, аппарат изучения поведения случайности также
выходит на новый уровень: используются методы и понятия теории функций,
пределов, дифференциального и интегрального исчисления. Мы не будем
111

использовать сложные математические выкладки и приводить строгие
определения и доказательства. Однако для знакомства со многими важными
понятиями и особенно для эффективного применения этих понятий
необходимы определенные математические действия. Все используемые в
изложении математические определения, формулы и теоремы, как правило, не
выходящие за рамки школьного курса математики, представлены в
Приложении 1, куда и следует обращаться по мере надобности.
Взамен определения вероятности в точке введем для непрерывных
случайных величин понятие плотности распределения вероятностей.
Определение. Плотностью распределения вероятностей случайной
величины Л" называют функцию/(х), удовлетворяющую следующим условиям:
1) /(*) определена при всех х: —оо < х < +<х>;
2)/(х) > О во всей области определения;
ь
3) Р(Хе[а,Ь)) = j/(x)dx.
а
Таким образом, функция плотности распределения вероятностей
должна быть всюду определенной, неотрицательной и связана с вероятностью
попадания случайной величины в заданный промежуток [а, Ь) посредством
определенного интеграла с пределами интегрирования а и Ь.
Приведем основные свойства функции плотности.
1. Функция распределения Fix) выражается через функцию плотности
распределения fix) по формуле
X
т = \Mdt. (2.51)
Доказательство. По определению функции распределения
F{x) = Р(Х<х) = Р(Хе(-оо ;*)).
Далее используем условие 3 в определении плотности и получаем
№) = JAOdt.
Свойство доказано.
2. Плотность распределения f(x) равна производной от функции
распределения:
f{x) = Р{х) (2.52)
Доказательство. Воспользуемся соотношением в свойстве 1. Тогда
F'(x) = jf(t)dt\ = f(x)
Последнее равенство следует из теоремы Барроу.
3. Для плотности распределения f(x) справедливо условие нормировки
\Ax)dx =
= 1. (2.53)
112

Доказательство. Из свойств ф. р. известно, что lim F(x) = 1. Тогда, ис-
Х-+ + OD
пользуя свойство 1, получаем
X +0О
1 = lim F(x) = lim \f{t)dt = [f(t)dt.
—<x> —<x>
Поскольку величина интеграла не зависит от того, какой буквой
обозначена переменная интегрирования, то (2.53) доказано.
4. Вероятность, что непрерывная св. X примет конкретное значение, а
равняется нулю, т. е. Р(Х = а) = О для любого числа а (также см.
замечание в § 2.2).
Свойство верно, так как по определению плотности
Р(Х=а) = [f(x)dx = О
Замечание 1. Равенство (2.52) объясняет использование термина
"плотность":
Ях) = F(x) = lim F{x + Ax)-F(x) = и Р(Хе[х,х+Ах)) {2М)
JK ' v ' дж-о Ах дж-о Ах
Последнее равенство следует из свойства ф. р.
P(Xe[a,b)) = F(b)-F(a).
Таким образом, согласно (2.54), функция/(х) и является не чем иным,
как плотностью вероятности в точке х. Вместо "плотность вероятности"
часто используют термин "плотность распределения". Также f{x) называют
дифференциальной функцией распределения.
Отметим, что распределение непрерывной с. в. Л" в дальнейшем также
будем называть непрерывным распределением или распределением
непрерывного типа.
Замечание 2. Условие нормировки (2.53) графически означает, что
площадь бесконечной криволинейной трапеции, ограниченной кривой
у = f{x) и осью абсцисс, всегда равна единице.
Замечание 3. Исходя из свойства 4, в дальнейшем вероятность
попадания непрерывной св. в интервалы [а\ Ь), [а; Ь), (а\ Ь) и (а; Ь) считаем
одинаковой.
Определение. Начальным моментом к-го порядка (к = 0, 1,2, ...)
непрерывной с. в. X называют число
+ <Е
о-к = jxk/[x)dx.
Справедливо утверждение а0 = 1, поскольку приходим к условию
нормировки
+ OD +00
«о = jx°f(x)dx = j/(x)dx = 1
8 — 3529
113

Определение. Математическим ожиданием непрерывной с. в. X
называют ее первый начальный момент
+«
М(Х) = ос, = jxf(x)dx. (2.55)
— <и
Смысл понятия "математическое ожидание" тот же, что и для
дискретных с. в. — среднее значение с. в. с учетом вероятностного "веса" каждого
значения.
Используя обозначение М(Х), получаем
+«
а* = \x"f(x)dx = M(Xk). (2.56)
—ас
Определение. Центральным моментом k-го порядка (к = О, 1,2, ...)
непрерывной с. в. X называют число
+ QO
ц, = j(x-M(X))kf(x)dx. (2.57)
— <и
Справедливы утверждения: |а0=1. Hi=0- Первое из равенств следует из
определения |Д,0 и условия нормировки. Проверим (д,,:
ц, = j(x-M(X))f(x)dx= jxf(x)dx-M(X) jf(x)dx=
=М(Х)-М(Х) -1=0.
Определение. Дисперсией непрерывной с. в. X называют ее второй
центральный момент:
+«
D(X) = ц2 = Ux-M(X))2/[x)dx. (2.58)
Как и в случае дискретных с. в. легко доказать формулу, упрощающую
вычисление дисперсии:
D(X) = М(Х2) - М\Х). (2.59)
Определение. Средним квадратическим отклонением (стандартным
отклонением) непрерывной с. в. X называют число а = JD(X).
Смысл понятий дисперсии и среднего квадратического отклонения тот
же, что для дискретных с. в. — мера рассеяния значений случайной
величины относительно математического ожидания.
2.10. Равномерное распределение на отрезке
Так же как и для дискретных случайных величин, существует
бесконечное количество распределений непрерывного типа, ибо речь идет о
количестве возможных способов рассредоточить единичную суммарную
вероятность между значениями, составляющими некоторый интервал.
114

Простейшим из подобного типа распределений является распределение,
в котором единичная вероятность распределена поровну между всеми
значениями из конечного интервала [а; Ь], где a, b — любые действительные
числа, а < Ь. С этим распределением мы встречались в случае
геометрического определения вероятности (см. § 1.9).
Рассмотрим данный способ распределения с точки зрения общей
теории. Пусть имеется с. в. X, все значения которой заполняют сплошь
промежуток [а; Ь] и имеют равные вероятности. Следовательно, это
распределение непрерывного типа и плотность этого распределения всюду на [а; Ь]
постоянна и равна какому-то числу с, а вне указанного промежутка
f{x) = 0, так как этих значений с. в. ^не принимает. Итак,
дх) = к при хе[а\Ь]
[О, при х«ё [а;Ь]
Конкретное значение постоянной с находим из условия нормировки
(2.53):
+<х> a b +<*>
\f{x)dx = fOrfx+ [cdx+ fOdx = 1.
—<x> —<x> a b
Так как определенный интеграл от нуля равен нулю, то получаем
ь
[cdx = 1, т. е. сх\ьа = с(Ь- а) = 1 , следовательно, с = .
а
Таким образом,
1
Л*) =
b_a,np» Xe[a;b] ^щ
О, при хё [а;Ь].
Распределение с. в. Л" с плотностью вида (2.60) называют равномерным
распределением на отрезке [а, Ь].
Найдем функцию распределения F{x) с. в. X, равномерно
распределенной на [а; Ь]. По формуле (2.51) записываем
F{x) = jf(t)dt.
Далее, поскольку функция/(0 в разных интервалах задана разными
выражениями, F{x) вычисляется в зависимости от значений х.
— если —оо < х < а, то
F(x) = ГОЛ = 0;
—ас
— если а<х<Ь, то
8*
115

У,
1
b-a
y = f(x)
a b x
y = F(x)
Рис. 16. График плотности равномер- Рис. 17. График функции распределения,
ного распределения. равномерно распределенной с. в. X.
— если х > Ь, то
а о ко
Итак, объединяя все различные возможности расположения х, получаем
ф. р.
О, при х < а
F(x) =
х— а
, при а<х<Ь
(2.61)
Ь-а
1, при х> b
Графики функций f(x) и F{x) для с. в. X, равномерно распределенной
на [а; В], приведены на рис. 16, 17 соответственно.
По приведенным выше общим формулам для вычисления М(Х) и D(X)
[см. (2.55), (2.59)] легко найти эти числовые характеристики:
М(Х) = \xf{x)dx = J0dx+ jx—L- dx+ fo^c =
_ 1
x_
b-a 2
= b2-a2 = b + a
2(b-a) 2
(2.62)
(т. е. М(Х) соответствует середина интервала [a; b], что вполне
естественно);
+«
D(X) = M{X2)-M\X)= |х2Лх)^с-(^)2.
Элементарные вычисления приводят к величине
D(X)
= (b-a)7
12
(2.63)
Равномерное распределение на отрезке можно считать непрерывным
аналогом дискретного равномерного распределения, рассмотренного в § 2.8.
116

Равномерное распределение находит самое широкое применение в
задачах статистического моделирования.
Погрешность при округлении чисел считается случайной величиной,
равномерно распределенной на промежутке
L Т2\
в единицах последнего знака.
2.11. Нормальное распределение
Непрерывная случайная величина X называется нормально
распределенной с параметрами т и а (т, а = const; а > 0), если ее плотность
распределения имеет вид:
/(*) = 1
-(х-т)1
2с2
2ла
(2.64)
Факт указанного распределения записывают таким образом: Х~ N(m, a).
График функции y=f(x) называют нормальной кривой, или кривой
Гаусса. Вид этого графика приведен на рис. 18, а.
Рис. 18. Кривая Гаусса.
117

Заметим, что в точке х = т график функции имеет максимум, а точки
х = т±о — точки перегиба графика.
Непосредственным вычислением, используя формулы (2.53), (2.55),
(2.58), можно проверить условие нормировки и найти М(Х) и D(X).
Оказывается, что параметры распределения тис имеют определенный
смысл:
М(Х) = т, D(X) = a2. (2.65)
Тогда а — среднее квадратическое отклонение.
Замечание. Вид кривой Гаусса зависит от численных значений
параметров т и а. Как известно из школьного курса элементарной математики,
графики функций f(x) и fix — т) имеют одинаковую форму и отличаются
один от другого сдвигом на т единиц вдоль оси абсцисс. Следовательно,
параметр т входит в выражение (2.64) так, что изменение т влечет лишь
сдвиг кривой Гаусса. В частности, при т = О вершина кривой Гаусса
лежит на оси ординат. Совсем иное влияние на график оказывает параметр
а: изменение значений а меняет форму кривой Гаусса. Так как ордината
вершины равна -——, то с ростом значений а кривая становится более
/2 я а
пологой (наибольшее значение на кривой уменьшается). И наоборот, с
уменьшением а число -—= увеличивается и соответственно кривая стано-
л/2яа
вится "пикообразной" (вид графика при т = 0 и различных значениях а
см. на рис. 18. б).
Поведение кривой Гаусса в зависимости от а объясняется смыслом
параметра а: среднее квадратичное отклонение а характеризует степень
рассеяния (сосредоточения) значений св. относительно среднего. Чем больше
а, тем чаще встречаются значения, отдаленные от среднего (больший
разброс значений св.), и обратно, чем меньше а, тем сильнее значения св.
концентрируются около среднего т (меньший разброс значений св.).
Найдем функцию распределения:
-С-"»2
X X г'
_ 1 - 2°
ад = \At)dt =-L= \e dt.
В последнем интеграле введем новую переменную интегрирования по
формуле z = , тогда получаем
а
х—т х—т
F(x)=-L= \e"2odz=-±= \e~~2dz = <b(X^»l),
118

где ф( —J — функция Лапласа, введенная ранее (см. § 1.14), от
аргумента -—— . Таким образом, установлено
а
F(x) = Ф(^) • (2.66)
График функции Лапласа представлен на рис. 8 (см. § 1.14). Изменение
аргумента на приводит к сдвигу этого графика вдоль оси абсцисс и
а
растяжению (сжатию) его в горизонтальной полосе при у е [0;1]. Заметим,
что при т = 0, а = 1 получаем
F{x) = Ф(х).
Зная функцию распределения, легко получаем формулу для вероятности
попадания с. в. А" в заданный промежуток:
P(Xe[a;b)) = F(b)~F(a) = ф(^) - ф(£^»?) , (2.67)
где Ф(...) — функция Лапласа.
Выведем еще одно важное соотношение. Найдем вероятность
отклонения значения нормальной с. в. от ее математического ожидания т в
единичном испытании, т. е. вероятность попадания в некоторый интервал
(т — е; т + е), где е — любое положительное выбранное нами число.
Р(\Х-т\<е) = Р( т - е < Х< т + е) = ф(т + е " т) - ф(т " е " т) =
= Ф(£)-Ф^) = ф(£)-(1-Ф(?))=2Ф(£)-1.
Выражая число е через а, т. е. 8 = tG, где / — частное от деления 8 на
а, для искомой вероятности можно получить конкретное значение:
Р(\Х- т\ < to) = 2Ф(0 - 1. (2.68)
Напомним, что функция Лапласа затабулирована (см. Приложение 2),
и, полагая / конкретным числом, можно найти, например,
Р(\Х-т\<а) = 2Ф(1)-1 «0,68268,
Р(\Х- т\ < 2а) = 2Ф(2) - 1 * 0, 9545,
Р(Х\Х- т\ < За) = 2Ф(3) - 1 « 0, 9973.
Таким образом, вероятность, что в единичном испытании нормально
распределенная с. в. X отклонится от своего математического ожидания
меньше чем на а, равна 0,68268, меньше чем на 2а равна 0,9545 и,
наконец, меньше чем на За равна 0,9973. В последнем случае вероятность
принято считать столь близкой к 1, что данное событие \Х— т\ < За для
единичного испытания полагается практически достоверным (оно происходит
в среднем в 9973 случаях из 10 000 испытаний). Исходя из этого, сформу-
119

лируем правило проверки распределения на нормальность, широко
известное как "правило трех сигм":
Если с. в. X имеет нормальное распределение с параметрами т и а, то
попадание ее в интервал (т — За; т + За) в единичном испытании
является практически достоверным событием. В противном случае имеются
веские основания усомниться в нормальности распределения этой с. в.
Разумеется, данное правило является достаточно грубым и более
призвано работать на отвержение гипотезы о нормальном распределении,
нежели на принятие этой гипотезы, и тем не менее при исследовании св. на
предмет нахождения ее закона распределения в первом приближении
данным правилом пользуются.
Нормальное распределение имеет все моменты, причем все
центральные моменты нечетного порядка — нули: ц2*+1 = 0. что следует из
симметричности распределения (см. рис. 18). Все центральные моменты
четного порядка выражаются через дисперсию а2:
li2k = 1 • 3 • ... • (2*-1)а2*,*=1,2, 3, ... (2.69)
Нормальное распределение впервые было найдено Муавром в первой
половине XVIII в. как предельное распределение для биномиального
распределения. Затем при изучении теории ошибок наблюдений
использовано в работах Гаусса и Лапласа в начале XIX в. и по существу было открыто
заново. В настоящее время в литературе нормальное распределение
называют также законом Гаусса, законом Лапласа—Гаусса, вторым законом
Лапласа.
Роль нормального распределения в вероятности и статистике
совершенно особая — это самое распространенное в практических приложениях
распределение. Оно является предельным для многих других
распределений, что связано со справедливостью центральной предельной теоремы
(которая будет представлена в дальнейшем). Под влиянием классических
работ Гаусса и Лапласа долгие годы считалось непререкаемой истиной, что
все возможные распределения при достаточно большом количестве
наблюдений приближаются к нормальному распределению как некоему идеалу.
Подобное утверждение, безусловно, слишком смелое, но тем не менее
многие из распределений, используемых в приложениях, в частности в
физике, биологии, медицине, демографии и других дисциплинах, являются
приближенно нормальными.
В дальнейшем с этим важнейшим из вероятностных распределений мы
будем встречаться постоянно во всех статистических исследованиях.
2.12. Числовые характеристики распределений
Для непрерывных случайных величин числовые характеристики
определяются по тому же принципу, что и для дискретных с в. (см. § 2.3, 2.4).
Основными среди них являются моменты (начальные и центральные),
среди которых особую роль играют математическое ожидание и дисперсия.
Эти понятия введены в § 2.9. Определим и другие характеристики
непрерывных случайных величин.
120

У i
1_1
р
0.75
0.5-
0.25-
ол,,
А х °
[
S
Х0.25
X0.S XO.TS Х
в
y = F(x)
X
Рис. 19. Квантили распределения.
Определение. Абсолютным начальным моментом к-го порядка
непрерывной с. в. X называют число
М\Х\к = j\x\kf(x)ax,k = Q, 1,2,....
(2.70)
Определение. Абсолютным центральным моментом к-го порядка
непрерывной с. в. X называют число
М\Х-М(Х)\к = \\х-М(Х)\к/[х)ах, к = 0, 1,2, ... .
(2.71)
Определение. Модой распределения непрерывной с. в. X называют
значение с. в., при котором функция плотности f{x) достигает своего
максимума.
Распределения, имеющие моду, могут быть унимодальными,
бимодальными и мультимодальными. Например, нормальное распределение с
параметрами тис является унимодальным распределением, и мода его
совпадает со значением математического ожидания: MQ(X) = т.
Определение. Квантилью порядка р распределения непрерывной с. в. X
называют значение хр такое, что для ф. p. F(x) справедливо равенство
F(XP) = />, где 0 </>< 1.
Квантиль порядка 0,5 называют медианой распределения. Квантили
порядка 0,25 и 0,75 называют соответственно нижней и верхней квартилями.
Аналогично *„,, х02, ..., Xq9 — децили, а числа х^01> х^02> ..., XQfi9 —
процентами (персентили).
Если рассмотреть график функции распределения F(x), отложить на оси
ординат значения вероятности р, то на оси абсцисс проявятся
соответствующие квантили порядка р. На рис. 19 отмечены некоторые из
квантилей: дециль х0,, квартили Xq2S и XqJS, медиана XqS, произвольная квантиль
порядка р.
Расстояние между точками А и В — широта распределения.
121

Так же как и для дискретных с. в., определяются коэффициенты
асимметрии и эксцесса:
Yi - —у Уг-^-З.
а а
Отметим, что для нормального распределения yj=0, у2=0.
Также следует подчеркнуть, что все указанные характеристики
достаточно легко вычисляются на компьютере с помощью стандартных
статистических программ.
Задачи и упражнения
1. Случайная величина X — количество "шестерок" при двух
подбрасываниях игральной кости. Найти закон распределения случайной величины X.
Указание. Очевидно, что случайная величина X может принимать лишь
три возможных значения: 0, 1,2. Требуется найти вероятности этих
значений и оформить данные в виде таблицы.
2. Случайная величина X имеет закон распределения
*,■
Pi
-2
0,1
-1
0,3
0
0,4
1
0,1
2
0,1
Найти функцию распределения F(x) и построить ее график. Найти
вероятности следующих событий:
\Х\< I; \Х\> 1; 0,5 <Х<2.
3. а) Может ли функция распределения быть отрицательной?
б) Может ли функция распределения быть больше 1?
в) Какое ограничение имеется на вероятности /7, значений
дискретной случайной величины?
г) Какой смысл разности F(b) — F{a), где F(x) — функция
распределения случайной величины XI
4. Рассматривая неслучайную величину а как частный случай случайной
величины: а) построить ее закон распределения; б) найти функцию
распределения F{x)\ в) вычислить математическое ожидание.
5. По данным задачи 2 для случайной величины X вычислить М(Х) и
ДА).
6. Случайная величина X имеет биномиальное распределение с
параметрами п = 5; р = 0,2. Найти все возможные значения X и
соответствующие им вероятности. Найти наивероятнейшее значение т0.
7. Случайная величина X имеет распределение Пуассона с параметром
а = 3. Найти: а) Р(Х= 1); б) Р(Х< 2); в) М(Х2).
8. Случайная величина Л" имеет закон распределения
*,■
Pi
1
0,1
3
0,2
5
0,3
7
0,4
Вычислить: а) М(Х); б) D(X); в) |а3; г) коэффициент асимметрии у,;
д) |а4; е) коэффициент эксцесса у2.
122

9. Записать первые четыре значения и соответствующие им вероятности
для случайной величины X
а) имеющей геометрическое распределение с параметром р = 0,4;
б) имеющей отрицательное биномиальное распределение с параметрами
/> = 0,2;г=3.
10. Найти все возможные значения и их вероятности для случайной
величины X
а) имеющей гипергеометрическое распределение с параметрами N= 10,
М=6, л = 8;
б) имеющей распределение Пойа с параметрами b = \\ с = 2; п = 3;
5 = 4.
11. Непрерывная случайная величина Л" задана функцией распределения
0, при х< 2
Rx) = \х-2, при 2<х<3
1, при х> 3.
Найти вероятность, что в результате испытания случайная величина X
примет значение из интервала (2,5; 4).
Указание. Воспользоваться формулой
Р(Хе[а,Ь)) = F(b)-F(a).
Ответ: 0,5.
12. По данным задачи 11 найти плотность распределения/(х).
0, при х < 2
Ответ: f(x) = < 1,при2<х<3
0, при х> 3.
13. Непрерывная случайная величина Л" имеет плотность распределения
0, при х<0
а) Ах) =
б) Ах) =
sinx, при 0<х<^ .
0,прих> =
0, при х < 0
Хе Хх, при х> 0, где X — положительный параметр.
Найти функцию распределения F(x).
0, при х < 0
Ответ: a) F(x) =
l-cosx,npn 0<x<J [ 0,прих<0
н 2; б) F(x) = _
[1-е ,при х>0
1,придг>^
123

14. Случайная величина Л" имеет плотность распределения
дх) = |0,5х,при хе(0;2)
1 0, прих*(0;2)
Найти: а) М(Х); б) F(x)\ в) медиану Ме(Х); г) нижнюю и верхнюю
квартили х025, х075.
О, при х < О
Ответ: а) |; б) f(x) =
-,при 0<х<2; в) Ме(Х) = 72;
4
1,при х> 2
*/ *0,25 1> *0,75 **^ *
15. Случайная величина Л" имеет плотность распределения
/(*) =
--х2 + 6х-^, при хе(3;5)
4 4
0,
при х« (3;5)
Найти математическое ожидание, моду и медиану X.
Указание. Постройте график у = /(х) и воспользуйтесь его свойствами.
Ответ: М(Х) = М0(Х) = Ме(Х) = 4.
16. Нормально распределенная случайная величина X имеет плотность
распределения
/(*) = 1
18
Найти: М(Х), D(X).
Ответ: М(Х) = 1, Я(ЛГ) = 9, т. е. ЛГ~ Л^(1; 3).
17. Заданы параметры распределения нормально распределенной
случайной величины X М(Х) = 25; D(X) = 4. Найти: а) функцию плотности
распределения; б) Р(Хе (20;25)).
Указание, б) В качестве функции распределения для нормальной с. в. X
выступает функция Лапласа (см. § 2.11). Значения функции Лапласа найти
в таблице.
Ответ: б) 0,4938.
18. Случайная величина А" имеет нормальное распределение с
параметрами т = 1 и а = 2. Найти вероятность, что в результате испытания X
примет значение из интервала: а) (—1; 3); б) (—3; 5); в) (—5; 7).
Найти квантили распределения: х03; х09; х099.
Ответ: х03 «—0,05; х09 « 3,564; х099 « 5,652.
19. Обследуется группа животных, каждое из которых с вероятностью р
является больным. Обследование проводится путем анализа крови. Если
смешать кровь п животных, то анализ этой смеси будет положительным в
случае, когда среди п животных хотя бы одно больное. Требуется
обследовать N животных, где N — число достаточно большое. Предлагается два
способа обследования:
124

1) обследовать всех TV животных; при этом придется провести N
анализов;
2) вести обследование по группам, смешав сначала кровь группы из п
животных; если анализ отрицательный, считать, что все животные группы
здоровы, и переходить к следующей группе из п животных; если анализ
положительный, обследовать каждое из п животных и после этого
переходить к следующей группе (при отрицательном результате на группу
приходится 1 анализ, а при положительном — п + 1 анализ).
Определить, какой способ обследования выгоднее — первый или
второй — в смысле минимального среднего числа анализов. Рассмотреть
решение в двух случаях: а) при п = 3, р = 0,2; б) при п = 3, р = 0,6.
Указание. Число анализов на группу из п животных при первом способе
равно п, при втором способе — это случайная величина Хп, имеющая
распределение
*,■
Pi
1
<г
п+ 1
\-cf
Требуется найти среднее число анализов для группы (п для первого
способа и ЩХп) для второго способа) и сравнить найденные значения.
Ответ: а) выгоднее второй способ; б) выгоднее первый способ.
20. Известно, что 20% населения Болгарии — долгоголовые
(долихоцефалы)1. Необходимо при исследовании 10 человек, отобранных случайным
образом, найти вероятности, что среди них окажется ровно т
долихоцефалов (т = 0, 1, 2, ..., 10).
Указание. Рассмотреть биномиальное распределение случайной
величины X — числа долихоцефалов среди 10 отобранных. При этом число
испытаний п = 10, вероятность осуществления события в одном испытании
Р = 0,2.
21. По данным польского статистика В. Борткевича по 200
кавалерийским корпусам старой прусской армии число смертей солдат от удара
копытом коня за год составило 122 случая, которые распределились
следующим образом:
Число случаев в корпусе
за год
Количество корпусов с
данным числом случаев
Относительная частота
числа случаев
0
109
0,545
1
65
0,325
2
22
0,110
3
3
0,15
4
1
0,005
У=200
I-1
Полагая в качестве случайной величины X — число смертных случаев
солдат-кавалеристов от удара копытом коня, сравнить вероятности
теоретического распределения Пуассона — Р(0), Р(\), Р(2), Р(3), Р(>4) (заме-
'Пример заимствован из книги болгарского автора: Д. А. Сепетлиев. Статистические
методы в научных и медицинских исследованиях. — М.: Медицина, 1968.
125

тим, что Р{4) & Р(>4)) — с соответствующими наблюдаемыми
относительными частотами. Имеются ли основания считать распределение X пуассо-
новским? Являются ли указанные случаи редкими и независимыми
событиями?
Указание. В распределении Пуассона параметр а принять равным сред-
122
нему числу случаев а = -?— = 0,61.
Ответ: Р(0) = 0,544; Р(\) = 0,331; Р(2) = 0,101; Р(3) = 0,021;
Р(>4) = 0,003.

Глава III. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
3.1. Функция распределения и плотность распределения
системы случайных величин
Системой случайных величин будем называть п случайных величин, Хх,
Х2, ..., Хп, рассматриваемых в совокупности. Значения случайных величин
обозначим соответствующими малыми буквами: х,, х2, х3, .... хп, т. е. хк —
переменная величина, включающая в себя все возможные значения св. Хк.
Если каждому значению одной случайной величины соответствует
точка на прямой, то каждой паре значений (х,, х2,) системы двух св. Хх, Х2
соответствует точка на плоскости (рис 20). Аналогично для системы трех
св. Хх, Х2, Х3 тройке значений (х,, х2, х3) соответствует точка в трехмерном
пространстве. При п > 3 формально говорят о точке л-мерного
пространства.
Совместные вероятности будем обозначать, используя индексы:
Р(ХХ = Xi,X2 = Xj) = pJk,
Р(ХХ = xh,X2 = xh, ...,Xn = хл) = pJtJi h.
Определение. Функцией распределения системы случайных величин Хи
Х2, ..., ^„называют функцию п переменных F{xu x2, ..., х„), равную
вероятности произведения событий Хх < хх, Х2 < х2, ..., Хп < хп:
F(xux2,...,xn) = Р(Хх<хьХ2<х2,...,Хп<хп). (3.2)
Замечание. Хотя в формуле (3.2) случайные события записаны в виде
последовательности, речь идет именно о произведении событий, т. е. об их
совместном осуществлении.
Геометрически при п = 2 функция распределения F{xx, x^ означает
вероятность попадания в область, удовлетворяющую условиям Хх < х, и
Х2 < х2 (см. заштрихованную область на рис. 21). Данная область является
прямоугольником с бесконечными сторонами. Аналогично при п = 3 ф.р.
. (*Т- Х2>
►
Рис. 20.
127
Х2
*2

Рис. 21.
F(xu x2, x3) равна вероятности попадания значений случайных величин
Xv X2, Х3 в бесконечный параллелепипед и т. д.
Сформулируем свойства ф.р. системы:
1. 0< F(xbx2, ...,*„)< 1 , так как по определению функция
распределения является вероятностью.
2. lim F(xu ...,xk,...,xn) = 0. (3.3)
Xt~* —41
По определению функции распределения получаем:
lim F(xu ...,хк, ...,хп) = Р(Хх<хь ...,Хк<-со, ...,Хп<хп).
xt-*— «1
Учитывая, что в последнем соотношении записана вероятность
произведения событий, один из сомножителей которого — событие
невозможное, а следовательно, и все произведение является невозможным
событием, получаем в итоге нуль.
3. Если имеется система св. Хи ..., Хк, ..., Хп и ф.р. системы
F(xuxk, ••,хп), то ф.р. одной св. Хк, записываемая в виде Fk(xk), равна:
Fk(xk) = limF(xu...,xk,...,xn),
(3.4)
где в пределе все аргументы х^,х2, ...,хп за, исключением хк, стремятся к +оо.
Заметим, что случайные события X, < +оо — достоверные события (U),
и тогда UmF(xu...,xk,...,xn) = P(U • ... • (Хк<хк) • ... • U) =
= Р(Хк<хк) = Fk(xk).
4. lim F(xh...,xn) = 1. (3.5)
все xt-* +<r
Соотношение справедливо, так как по определению ф.р. получаем
lim F(xh...,xn) = P(U) = 1.
все xt-* +<n
Далее, опираясь на свойства ф.р., введем понятие совместной
плотности распределения.
Определение. Совместной плотностью распределения системы п
непрерывных св. Хи Х2, ..., Хп называют функцию п переменных/(х,, х2, ..., х„),
такую, что:
1 )/(*,, х2, ..., хп) определена при всех хк е (—оо; + оо);
2) во всей области определения/(х,, Xj, ..., хп) > 0;
128

3) для любой области т„ л-мерного пространства вероятность попадания
значений системы случайных величин в эту область вычисляется по
формуле:
Р((хьх2, ...,х„)ет„) = J ...^f(xux2,...,xn)dxxdx2...dxn (3.6)
Как видим, в формуле (3.6) фигурирует л-кратный интеграл от функции
плотности, непосредственное вычисление которого несет определенные
проблемы. В ряде частных случаев, опираясь на свойства и известные
соотношения, эти проблемы удается разрешить.
Заметим, что определение плотности распределения одной св. (см.
§ 2.9) является частным случаем приведенного определения при п = 1.
Рассмотрим свойства совместной плотности:
X, X, X.
1. F(xx, %, .... хп) = J J... j/(th ...,tn)dtxdt2...dtn. (3.7)
Для простоты докажем (3.7) при л = 2, т. е.
х, х2
F{xux2) = \ JAtu h)dtxdt2.
— <х> — <х>
По определению ф.р. F(xx, xj следует
F(xx, х,) = Р(ХХ < х2, Х2 < х2) = Р(ХХ е (-со;*,), Х2 е (-оо;х2)).
В данном соотношении указана область изменения переменных хх и Xj,
т. е. область т2 (заметим, что доказательство проводится при л = 2), и тогда
по условию 3 определения плотности [см.(3.6)] получаем
X, Х2
*X*i. Ь) = JJ/C'i. t2)dtxdt2 = J j/to, t2)dtxdt2.
*2 — <Ц — <H
Свойство доказано.
2.дхи ь,.... *„) = ^^;;^я). о-8)
т. е. совместную плотность можно получить, продифференцировав ф.р.
F(xx, х2, ..., хп) последовательно по всем переменным. Доказать данное
свойство можно, продифференцировав обе части равенства (3.7) по каждой
из переменных и используя теорему Барроу.
3. Плотность распределения одной с. в. Хк можно получить, зная
совместную плотность системы с. в. Хх, ..., Хк, ..., Хп, по формуле
/i(*i) = ^ jf(th...,tk.x,xk,tk+h...tn)dtx...dtk-xdtk+x...dtn. (3.9)
Отметим, что интеграл в (3.9) имеет кратность л — 1.
9-3529 12д

Частным случаем равенства (3.9) при п = 2 является следующее:
+»
/i(*i) = JAxbx2)dx2,
7 (зл°)
fi(x2) = jf(xux2)dxl.
—<XJ
Ввиду громоздкости оставим данные формулы без доказательства.
4. Для совместной плотности/(х,, х2, .... xj справедливо условие
нормировки:
j...JAxu...1xH)dxl...dx„ = 1. (3.11)
—<х> —in
Данное равенство следует из равенства (3.7), в котором необходимо
перейти к пределу всех х,, .... хп, стремящихся к +оо, и справедливости
соотношения (3.5).
В данном параграфе ф. р. и плотность вероятности введены в общем
случае для произвольных с. в. Хх, ..., Хп.
3.2. Зависимые и независимые случайные величины
Для того чтобы избежать зачастую излишне сложных соотношений и
используя аналогию со случайными событиями, введем еще одну
совместную характеристику случайных величин: независимость.
Определение. Случайные величины Xv X2, ..., Хп называют
независимыми, если вероятность произведения событий Хх < х,, Х2 < Xj, ..., Хп < хп
равна произведению вероятностей событий-сомножителей для любых
значений х,, х2, ...,x„:
P(Xx<xhX2<x2t...,Xn<xn) = Р(Хх<хх) • Р(Х2<х2)- ...
- • Р(Хп<хп). (3.12)
В противном случае случайные величины Хх, Х2, ..., Хп называют
зависимыми.
Легко видеть, что в соотношении (3.12) фигурируют вероятности,
являющиеся функциями распределения. Исходя из этого факта и введенного
определения, сформулируем утверждение:
Для того чтобы св. Хх, Х2, ..., Хп были независимыми, необходимо и
достаточно, чтобы выполнялось равенство:
F(xbx2,...,xn) = Fx(xx)F2(x2)...Fn(xn), (3.13)
где F(xx, х2, ..., хп) — совместная ф.р. системы св., a Fx(xx), F^xJ, ..., Fn(xn) —
функции распределения соответственно одной из св. Хх, X2, ..., Хп.
Используя соотношение (3.13), математически легко можно доказать
еще одно важное утверждение:
130

Для того чтобы непрерывные св. Хи Х2, ..., Хп были независимыми,
необходимо и достаточно, чтобы выполнялось равенство:
/(*„ х2, ..., хп) = /,(х,)/2(х2) • ... • /„(*„), (3.14)
где /(*,, Xj, ..., хп) — совместная плотность системы св., а
/i(*i)> /2(^2). •■■,fn(xn)— плотности распределения каждой случайной
величины персонально.
Заметим, что (3.14) получается из (3.13) последовательным
дифференцированием по всем переменным.
Из того, что (3.13) (3.14) являются необходимыми и достаточными
условиями независимости случайных величин следует что при
невыполнении этих условий имеем дело с зависимыми случайными величинами.
3.3. Моменты системы случайных величин. Ковариация
Пусть имеем систему Хх, Х2, ..., Хп. Рассматривая случайные величины
как аргументы, введем функцию Y = <p(Xlt X2, ..., Х„), где Y, разумеется,
тоже будет являться случайной величиной, для которой можно вычислять
различные характеристики.
Определение. Математическим ожиданием функции (р (Xlt X2, ..., Хп)
называют л-кратный интеграл
М(ч>(ХьХ2,...,Хп)) = J... |ф(х1,...,хп)Лх1,...,хп)^1...^„, (3.15)
-<х> —<х>
где/(х,, х2, ..., хп) — совместная плотность распределения системы св. Хи
Х2, ..., Хп .
Исходя из приведенного определения, рассмотрим некоторые моменты
случайных величин.
Определение. Начальным моментом порядка кх + /q + ... + кп системы
св. Xlt X2, ..., Хп называют математическое ожидание функции
Х\х • Х22 • ... • Хкп", а именно:
J... l№...xkMxlx2...xH)dxldx2...dxHy (3.16)
— <и —<xj
В соответствии с этим определением запишем первые начальные
моменты:
«Чо,...^ = ЩХ\Х\ ' ••• * Х°п) = М(Х\)>
а0>1 о = М{Х\Х2Х\ • ... • Х°п) = М(Х2),
(3.17)
ссо.0 = М{Х\- ... • Х°п-М = М(Хп).
9* 131

Проверим, например, первое из равенств, используя определение (3.16):
«i.o о = М(ХХХ\ • ... • Х\) = J... jxxf(xx,x2, ..., xn)dxxdx2...dxn =
— <XJ —txj
I-+CC +CC
Jx, J... J/(x,,x2, ..., xn)dx2...dxn
-cc — <n
dfri.
Интеграл кратности п — 1, представляемый в квадратных скобках,
согласно формуле (3.9), равен плотности распределения одной св. fx(xx),
тогда
+«
a i,o о = pi/i(^i)^i = ЩХХ).
—<х>
Соотношение верно.
Определение. Центральным моментом порядка кх, к^, ..., кп системы св.
Хх, Х2, ..., Хп называют число \ikttkl кя, равное
ц*,.*а *. = М[(ХХ- М(ХХ))\Х2- М(Х2))к\..(Хп- М(Хп))к'] =
(3.18)
+ Х) +СС
= J... j(xx- М(Хх))к\х2- М(Х2))к\..(хп- М(Хп))к'/(хх, .... x„)dxxdx2...dxn.
-<и —<xj
Исходя из этого определения, находим
Ц2.о о = М[(ХХ- М(ХХ))2(Х2- М(Х2))°...(ХП- М(ХП))°] =
=М(ХХ - М(ХХ))2 = D(XX),
Цо.2.0 о = М(Х2 - М(Х2))2 = D(X2), (3.19)
Цо.о 2 = ЩХ„-ЩХЯ))2 = ОД,).
Данные формулы можно проверить с помощью интеграла аналогично
соотношению для М(ХХ).
Рассмотрим далее центральные моменты для двух случайных величин
Хх, Х2 порядка 1 + 1.
Определение. Корреляционным моментом двух случайных величин Хх, Х2
называют их смешанный центральный момент |ап. Обозначая
корреляционный момент К(ХХ, Х2), получаем:
ед, х2) = Цп = м[(хх - м{хх)) • (х2 - м(х2т. (3.20)
Для непрерывных св. Хх, Х2 с совместной плотностью f(xx,x2) следует
+ сс + сс
ВД, Х2) = J J(*. - М(Хх))(х2 - M(X2))f(xx,x2)dxxdx2. (3.21)
— 41— X)
132

Для дискретных св. X, У получаем
К(Х, Y) = ££(*,. - M(X))(yj - М{ Y))Pij, (3.22)
* j
где х0 у} — все возможные значения св. Хи У, а вероятность
р„= P(X = xitY=yj).
Отметим, что другое название корреляционного момента — ковариация
и соответствующее обозначение: соу(Хх,Х2).
Корреляционный момент (ковариация) имеет два очевидных из
определения (3.20) свойства:
1) ед, х2) = к{х21 хх)\
2) К(Х, X) = D(X). (3.23)
Пусть имеется система Хи Х2, ..., Хп. Тогда корреляционный момент
можно определить для каждой пары св. X,, Хт. Всего из п случайных
величин можно составить п2 пар, включая пары, состоящие из одинаковых
элементов. Для простоты обозначим К(Х,,Хт) = klm. Упорядочивая
корреляционные моменты, можно их записать в виде квадратной таблицы,
содержащей п строк и п столбцов. Такую таблицу принято называть матрицей (см.
Приложение 1).
Определение. Матрица, элементами которой являются корреляционные
моменты, называется корреляционной матрицей:
К =
fk\\k\2...k\n
k2\ k22... k2n
^kn\kn2...knJ
(3.24)
В корреляционной матрице на главной диагонали (из верхнего левого
угла в нижний правый угол) стоят элементы с одинаковыми индексами:
Согласно второму из равенств (3.23), эти величины есть не что иное,
как дисперсии соответствующих св. Xv Х2, ..., Хп.
Также отметим, что, согласно первому свойству (3.23), корреляционные
моменты klm и kml равны для любой пары индексов, следовательно,
корреляционная матрица (3.24) оказывается симметричной относительно
главной диагонали.
3.4. Свойства моментов
а) Свойства математического ожидания
1. Если а — неслучайная величина, то М(а) = а.
Это естественное свойство можно доказать используя, например,
формулу (3.15) при Ф(х,, ..., хп) = а и возможность выносить постоянный
сомножитель за знак интеграла.
М(а) = j ...jaf(xh...,xH)dxl...dxn =
133

=aj ...jf(xx,...,xn)dxx...dxn = a • 1 = a
Последний интеграл равен 1 по условию нормировки (3.11).
2. Математическое ожидание обладает свойством линейности:
М{аХх + ЬХ2) = аМ{Хх) + ЬМ(Х2), (3.25)
где а, Ь — постоянные, Xlt X2 — случайные величины.
Для доказательства предположим, что/(х,, xj — совместная плотность
св. Хх, Х2, тогда согласно формуле (3.15),
М(аХх + ЬХ2) = С... \{ахх + bx2)f{xbx2)dxxdx2 =
по свойству линейности интеграла
= а^ jxj(xux2)dx,dx2 + b^ jx2/[xhx2)dx,dx2 = аМ(Х,) + ЪМ(Х2).
3. ЩХХ • Х2) = ЩХХ) • М(Х2) + К(ХЬХ2). (3.26)
Доказательство. По определению корреляционного момента
К(ХЬХ2) = М[{ХХ- М{ХХ)){Х2- М{Х2))}=
=М[ХХХ2-ХХМ(Х2)~Х2М(ХХ)+ М{ХХ) - М(Х2)]=
согласно свойствам 1 и 2 и с учетом, что М(ХХ), М(Х2) — постоянные
= М(ХХХ2) - М(Х2) ♦ М(ХХ)- М(ХХ)М(Х2)+ М(ХХ) • М(Х2).
Приводя подобные члены, получаем
ВД, Х2) = М(ХХ • Х2) - М(ХХ) • М(Х2), (3.27)
откуда и следует доказываемое соотношение.
б) Свойства дисперсии
1. Дисперсия — величина неотрицательная (установлено ранее).
2. Если а — неслучайная величина, то
D{a) = 0. (3.28)
Доказательство.
D(a) = М(а-М(а))2 = М(а~а)2 = М(0) = 0.
3. D(aXx + ЬХ2) = a2D(Xx) + b2D(X2) + 2abK(Xx, X2). (3.29)
Доказательство.
D(aXx + ЬХ2) = М[аХх + ЬХ2 - М(аХх + ЬХ2)}2 = М[аХх + ЬХ2 - аМ(Хх) -
-ЬМ(Х2)]2 = М[а(Хх- М(ХХ)) + b(X2- М(Х2))]2 = а2М(ХХ - М(ХХ))2 +
+ Ь\Х2 - М(Х2)) = +2аЬМ[(Хх - М(ХХ))(Х2 - М(Х2))] =
= a2D(Xx) + b2D(X2) + 2abK(XuX2).
Равенство верно при любых а и Ь.
4. D(aX) = a2D(X). (3.30)
Данное равенство следует из свойства 3 при b = 0 (ХХ=Х).
134

в) Свойства корреляционных моментов
1. ВД, Х2) = М(Хи Х2) - М(ХХ) • ЩХ2). (3.27)
Данная формула, полученная ранее как формула (3.27), позволяет
вычислять корреляционный момент проще, чем непосредственно по
определению.
2.К(Х,а) = 0. (3.31)
Доказательство.
К(Х,а) = М[(Х-М(Х))(а-М(а))] = М[(Х- М{Х))(а- а)] = М(0) = 0.
3. |ВД Y)\ <ахау, где ах = ЩХ), ау = Щ7). (3.32)
Доказательство. В равенстве (3.29), справедливом для любых чисел а и
Ь, полагаем Хх = X, Х2 = У, а = су, b = Gx и, учитывая неотрицательность
дисперсии, получаем
D(aX+bY) = a2D(X) + b2D(Y) + 2abK(X, У)>0;
ауах + охоу + 2ayaxK(Xh X2) > 0;
2ахау(ахау + К(Х, У))>0.
А так как сомножители схсу положительны, то
ахау+ К(ХьХ2)*0,
т. е.
K(XuX2)>-Gxay. (3.33)
Аналогично, полагая в равенстве (3.29) Хх = X, Х2 = Y, а = —о , b = ах,
приходим к неравенству
К(ХьХ2)<схсу. (3.34)
Объединяя (3.33), (3.34), получаем неравенство с модулем (3.32).
Улучшить неравенство (3.32) нельзя, так как корреляционный момент
К(Х, Y) может быть равен произведению GxGyили (~GxGy).
3.5. Независимость и некоррелированность случайных величин.
Коэффициент корреляции
Рассмотрим необходимое условие независимости св. Хи Y.
Утверждение 1. Если X, У независимые св., то К(Х, Y) = 0.
Доказательство. Пусть св. Хи У имеют совместную плотность
распределения/^, у). А так как X,Yнезависимы, то, согласно равенству (3.14),
Аъу) =Л(хШу)-
Тогда
ВД Y) = M[(X-M(X))(Y-M(Y))] =
= [° j(x~ М(Х))(у- М{ Y))A(x)f2(y)dxdy =
135

= j(x- M(X))A(x)dx • j(y-M(Y))f2(y)dy =
=M(X-M(X)) • M(Y-M(Y)) = 0.
Последнее равенство — законное равенство нулю первых центральных
моментов. Утверждение доказано.
Заметим, что обратное утверждение, вообще говоря, неверно. Из
равенства нулю корреляционного момента еще не следует независимость
случайных величин1.
Определение. Св. Хи /называют некоррелированными, если К(Х, Y) = 0.
Из приведенного выше замечания следует, что свойство
некоррелированности св. более слабое, нежели независимость, ибо независимые
величины обязательно некоррелированы, а некоррелированные могут и не
быть независимыми. Однако нормально распределенные
некоррелированные с. в. всегда независимы (см. сноску).
Сформулируем достаточный признак зависимости св. Хи Y.
Утверждение 2. Для того чтобы св. Xи Убыли зависимыми,
достаточно, чтобы
ад Y) * 0.
Доказательство. Предположим противное: К(Х, Y) Ф 0, а св. Хи У все-
таки независимы. Тогда по утверждению 1 из независимости X, У следует,
что К(Х, У) = 0. Пришли к противоречию, следовательно, что
предположение о независимости ложно, т. е. X, У зависимы. Утверждение доказано.
Заметим, что условие К(Х ,У) Ф 0 только достаточное условие
зависимости св., ибо для некоторых зависимых величин (некоррелированных)
может оказаться К(Х, У) = 0.
Определение. Коэффициентом корреляции св. X, У называют число г^,
равное
rxy = -SML=. (3.35)
JD{X)MT)
Рассмотрим свойства г^.
1. Для того чтобы гху = 0 необходимо и достаточно, чтобы К(Х, У) = 0.
Данное свойство следует из равенства (3.35) в определении
коэффициента корреляции.
Таким образом, говоря о некоррелированности св. вместо равенства
нулю корреляционного момента, можно использовать условие г = 0.
2. |гх,|<1. (3.36)
Данное неравенство следует из условия (3.32) и определения
коэффициента корреляции /"^[см. (3.35)].
3. Если св. X и У связаны линейной функциональной зависимостью
Y=aX+ Ь, то
1/^1 = 1 , причем г^ = 1 при а> 0, и гху= -I при а < 0.
1 Для нормально распределенных с. в. А" и У из условия К{Х, Y) = 0 следует независимость
Хи Y.
136

Доказательство. Пусть Y = аХ + Ь. Тогда полагаем
D(X) = al
D(Y) = D(aX+b) = a2D(X) + b2D(l) + 2abK(X, 1) = a2D(X) = a2a2x,
согласно свойству 2 дисперсии и свойству 2 корреляционных моментов,
ВД Y) = M[(X-M(X))(Y-M(Y))) =
= М[(Х- М(Х))(аХ+ Ь- М(аХ+ Ь))] = аМ(Х- М(Х))2 = aD(X) = аа2х.
Таким образом,
г = ЭД У) = а°* = ± = +1
JD(X)MT) сх • J7?x lfll
Из последнего равенства и следует справедливость свойства.
Исходя из свойств коэффициента корреляции, можно заметить, что
значение коэффициента корреляции, изменяясь по модулю от нуля до 1,
характеризует степень зависимости св.: от независимости при гху= 0 через
некоррелированность (также при гху= 0) с возрастанием |гжу|до
сильнейшей из функциональных зависимостей, линейной зависимости,
при \гху\= 1.
Коэффициент корреляции — показатель степени зависимости св. При
этом если гху= 1, то Хи /связаны прямой линейной зависимостью: с
ростом значений врастут и значения У; если гху= —1, то Хи /связаны
обратной линейной зависимостью: чем больше значения X, тем меньше
значения Y
При \гху\ * 1 обычно строгого соответствия возрастания (убывания)
значений одной св. с ростом другой нет, однако имеется тенденция к
возрастанию (убыванию) соответствующих значений, проявляющаяся в
наибольшей вероятности больших (меньших) значений.
Также отметим, что для некоррелированных св. Хи У некоторые
свойства упрощаются, например:
а) М(Х • Y) = М(Х) • M(Y) [см. (3.26)];
б) D(X± Y) = D(X) + D(Y) [см. (3.29)].
Замечание. В частности, последние две формулы, разумеется,
справедливы и для независимых с. в. X и Y
3.6. Система двух дискретных случайных величин
Закон распределения системы двух св. X,Yможно задать аналитически,
например, в виде функции распределения F(x, у). Однако для дискретных
св. возможно задание закона распределения в виде таблицы, в которой
указаны все возможные значения переменных и соответствующие этим
значениям совместные вероятности:
Ри= Р(Х = xhY= yj).
137

Продемонстрируем на примере, как, зная совместное распределение Хи
Y, найти распределение каждой св. и вычислить корреляционные
характеристики.
Пример 1. Задано совместное распределение системы св. Хи Yb виде
таблицы
0
2
1
0,05
0,05
3
0,14
0,06
5
0,25
0,15
10
0,26
0,04
Найти:
а) законы распределения составляющих;
б) cov {X, 7), v
Зависимы ли св.?
Решение, а) Чтобы найти закон распределения св., необходимо указать
все значения этой св. и соответствующие этим значениям вероятности.
Значения св. Л"указаны в таблице: 1, 3, 5, 10. Вычислим вероятности.
Р(Х = 1) = Р[(Х = 1,7 = 0) + (Х = 1, Y = 2)] = 0,05 + 0,05 = 0,1;
Р(Х = 3) = Р[(Х = 3,7 = 0) + (Х = 3, Y= 2)] = 0,14 + 0,06 = 0,2;
Р(Х = 5) = Р[(Х = 5,7 = 0) + (Х = 5, Y= 2)] = 0,25 + 0,15 = 0,4;
Р(Х = 10) = Р[(Х = 10,7= 0) + (Х = 10,7= 2)] = 0,26 + 0,04 = 0,3.
Тогда закон распределения св. X
(3.37)
Аналогично найдем закон распределения св. 7, принимающей всего
два значения: 0 и 2.
P(Y= 0) = Р[(Х = 1,7= 0) + (Х = 3,7= 0) + (Х = 5,7= 0) +
+(Х= 10, 7=0)] = 0,05 + 0,14 + 0,25 + 0,26 = 0,7;
P(Y= 2) = Р[(Х = 1,7= 2) + (Х = 3,7= 2) + (Х = 5,7= 2) +
+(Х= 10, 7=2)] = 0,05 + 0,06 + 0, 15 + 0,04 = 0,3;
*,■
Pi
1
0.1
3
0.2
5
0.4
10
о.з
yj
Pi
0
0.7
2
о.з
(3.38)
б) Для нахождения cov (X, 7) или, что то же самое, K{X,Y) необходимо
знать М(Х), M(Y), которые легко находятся из (3.37), (3.38)
соответственно. М(Х) = 5,7, M(Y) = 0,6. Можно найти К(Х, 7) по определению (3.22),
рассматривая сумму всевозможных произведений:
138

ВДУ) = ££(х,-5,7)О;,-0,6)/>, = (1-5,7)(0-0,6)- 0,05 +
+(1-5, 7)(2 - 0, 6)0, 05 + (3 - 5, 7)(0 - 0, 6)0, 14 +
+(3 - 5, 7)(2 - 0, 6)0,06 + (5 - 5, 7)(0 - 0, 6)0, 25 +
+(5-5,7)(2-0,6)0, 15 + (10-5,7X0-0,6)0, 26 +
+(10-5, 7)(2-0,6)0,04 = -0,66.
Можно найти К(Х, У) проще, если воспользоваться свойством (3.27):
4 2
ВД Y) = М(Х • Y) - М(Х) • M(Y) = YYaXiyjPiJ~ 5' 7 " °' 6 =
=(1 • 0 • 0, 05 + 1 • 2 • 0, 05 + 3 • 0 • 0, 14 + 3 • 2 • 0, 06 + 5 • 0 • 0, 25 +
+ 5 • 2 • 0, 15 + 10 • 0 • 0, 26 + 10 • 2 • 0,04)-5, 7 • 0, 6 = -0, 66.
Чтобы вычислить коэффициент корреляции г^, воспользуемся
формулой (3.35), предварительно найдя D(X) и D(Y) из (3.37) и (3.38).
D(X) = М(Х2) - М\Х) =
=(1 • 0,1 + 9 • 0,2 + 25 • 0,4+ 100 • 0,3)-5,72 = 9,41;
D(Y) = M(Y2)- M\Y) = (0 • 0,7 + 4 • 0, 3) - 0, б2 = 0,84;
r = -ВД у) _ = ~0,66 _ю-о 2348.
JD(X)JD(T) 79,41-/0Г84
Так как корреляционный момент отличен от нуля (то же самое
относится и к г^), то с. в. Хи /зависимы, причем (поскольку /^ < 0)
преобладает тенденция обратной зависимости: большим значениям с. в. X
наиболее вероятно соответствие меньших значений с. в. Y. Данное соответствие
отчетливо видно из таблицы совместного распределения.
Пример 2. По данным примера 1 найти закон распределения с. в.
Z= X + Y
Решение. Требуется найти все возможные значения с. в. Z и указать
соответствующие этим значениям вероятности.
Складывая значения с. в. Л" и с. в. У, каждое с каждым, получим восемь
чисел: (1+0), (3+0), (5+0), (10+0), (1+2), (3+2), (5+2), (10+2). Среди этих
чисел различных только шесть: 1, 3, 5, 7, 10, 12, так как числа 3 и 5 могут
быть получены двумя способами 3 = 3+0 = 1+2, 5 = 5+0 = 3+2. Итак,
всего с. в. Z может принять любое из шести возможных значений.
Найдем соответствующие вероятности.
P(Z= 1) = Р{Х= 1, Y= 0) = 0,05 — вероятность найдена из таблицы
закона распределения с. в. Л" и У;
P{Z= 3) = Р((Х= 3, У= 0)+(Х= 1, У= 2)) = 0,14 + 0,05 = 0,19 -
использована формула вероятности суммы несовместных событий;
P(Z= 5) = Р((Х= 5, У= 0)+(Х= 3, У= 2)) = 0,25 + 0,06 = 0,31;
P(Z= 7) = Р{Х= 5, У= 2) = 0,15;
P(Z= 10) = Р(Х= 10, У= 0) = 0,26;
P(Z= 12) = Р(Х= 10, У= 2) = 0,04.
139

Заносим данные в таблицу, которая и представляет искомое
распределение:
Zi
Pi
1
0,05
3
0,19
5
0,31
7
0,15
10
0,26
12
0,04
5>-1
Условие /Pt= 1 является контрольным для рассеяния сомнений в
правильности вычислений.
3.7. Функции случайных величин
До сих пор мы рассматривали распределение одной св. Резонно
поставить вопрос: что произойдет с законом распределения, если вместо одной
св. Л" взять некоторую функцию У=ц>(Х). Также интересно рассмотреть
законы распределения св. Y, являющейся некоторой функцией от системы
св. ХЬХ2, ...,Хпс известными законами распределения.
Пример 2 предыдущего параграфа показывает в простейшем случае
дискретных случайных величин метод нахождения закона распределения
функции двух случайных аргументов Z = ф(Л", У) = Х+ Y.
Рассмотрим более сложный случай.
Пусть Хь Х2, ...,Хп — система непрерывных св.
F(xhx2, ...,*„) — функция распределения системы св.
f(xhx2, ...,*„) — плотность распределения системы св.
Задана функция Y = у(ХиХ2, ...,Хп).
Очевидно, что Y — случайная величина. Полагаем, что
G{y) — функция распределения св. У,
g(y) — плотность распределения св. Y.
Тогда по определению ф.р. и согласно определению плотности
распределения (см. § 3.1) получаем
G(y) = P(Y<y) = P(4>(X]tX2,...,Xn) <у) =
= j ...jf(xux2,...,xn)dxldx2...dxn, (3.39)
где область л-мерного пространства т„ определяется появившимся
условием
у(ХиХъ...,Хн)<у. (3.40)
Зная функцию распределения G{y), легко найти плотность
распределения g (у) = G'{y).
Записав общие соотношения, перейдем к частным случаям.
140

Линейная функция одной с. в.
Пусть X — св. с плотностью распределения f(x). Задана линейная
функция Y= аХ + Ь, где a, b — постоянные, а * 0. Требуется определить
ф.р. G{y) и плотность распределения g(y).
Согласно (3.39),
G(y) = J f(x)dx, (3.41)
ах н Ь < у
где условие ах + b < у это и есть условие (3.40), задающее область
интегрирования. Конкретизируем это условие: явно выпишем пределы изменения
переменной х. Именно х является переменной интегрирования, а наша
переменная у с точки зрения интеграла ничем не отличается от обычной
постоянной (для интеграла у = const).
Итак: ах + b < у, следовательно, ах < у — b и
х<¥ при а >0,
а
х>¥- , при а < 0,
а
т. е. получим два случая:
l)XG(-oo,£zi), приа>0;
2)хе
(V44
при а < 0.
Значит, равенство (3.41) следует рассмотреть отдельно при
положительных и отрицательных значениях а.
G(y)
>-ь
ff(x)dx, при а > 0
+ т
l/[x)dx, при а < 0.
(3.42)
к-6
Функция распределения найдена и в зависимости от знака числа а
необходимо выбрать в (3.42) тот или иной интеграл и вычислить его для
конкретной функции fix).
Найдем плотность распределения: g{y) = G'iy).
Для этого необходимо продифференцировать по у каждый из
интегралов в (3.42). Заметим, что в данном случае у представляет функцию G{y) и
является переменной. Дифференцирование осуществляем, используя
теорему Барроу и учитывая, что предел интегрирования (^ J является не
переменной у.ав свою очередь является функцией от у. Следовательно,
141

при дифференцировании вычисляем производную сложной функции.
Тогда
g(y) = -
>-ь
jf(x)dx
\ -о
1-Ь
jf(x)dx
\ + „
, при а > О
, при а<О
v a J a
f(lLLb)±t приа<0.
v а ' — а
Используя равенство для \а\:
. - = f а, при а>0
\ — а, при а < О,
оба отношения можно объединить, вводя |а|. Окончательно получаем
зависимость между плотностями распределения св. У и X.
'«-^lii
(3-43)
Также отметим, что при использовании формул необходимо учитывать
области определения для св. У и X.
Пример. Пусть св. Х~ N(mx;ax), Y= aX + />. Найти плотность
распределения св. Y.
Решение. Для нормально распределенной св. X с параметрами тх,ох
функция плотности / (х) известна:
_(х-/п,Я
Ах) = —Ue 2o'
л/2яах
Для нахождения функции плотности g(y) воспользуемся соотношением
(3.43). Тогда
v a yN Л™*
1
_(у— am, — by
2^?
J2ncsx \a\ j2nox\a
и функция g(y) найдена. Однако в данном примере заметим еще один лю
бопытный факт. Из свойства линейности математического ожидания полу
чаем
М(У) = М(аХ+Ь) = аМ(Х) + Ь = атх+ Ь = ту\
Из свойств дисперсии (см. § 3.4) следует:
142

D(Y) = D(aX+b) = a2D(X)+bD(\) + 2abK(X, 1) = a2a2x = a};
следовательно, ay = \a\ax. Исходя из полученных соотношений, можно
записать
g(y) = ^±-e 2о' ,
J2llGy
где -оо < у < +оо.
Последнее равенство доказывает, что линейная функция нормальной
распределенной св. также имеет нормальное распределение с
соответствующими параметрами.
Мы не будем рассматривать доказательства соотношений для более
сложных функций, приведем лишь конечные результаты. Источник
приводимых соотношений — это формула (3.39) и равенство g(y) = G'{y).
Линейная функция двух случайных величин
Пусть Y = aXi + ЬХ2 + с,
где а, Ь, с — числа, причем а, Ь*0, хь х2 — св. с совместной плотностью
распределения/(л,, х2).
Тогда плотность распределения св. /вычисляется по формуле
Л*" И**^)ЙЛ- (344)
—сю
В частности, для суммы У= Х^+Х2 из (3.44) имеем
+«
g(y) = \Ax,y-x)dx. (3.45)
—сю
Замечание. Используя (3.45)j можно доказать, что в случае нормально
распределенных с. в. Хх и Х2 их сумма также имеет нормальное
распределение с соответствующими параметрами. То же верно и для суммы п
случайных величин.
Произведение двух случайных величин
Пусть У = Хх • Х2, где Xv Х2 — с в. с совместной плотностью
распределения/(*,, Xj).
Тогда плотность распределения с. в. У равна
м- |/(*.£)гаЛ- <3-46>
143

Частное от деления двух случайных величин
Пусть Y = -г?, где Хи Х2 — с. в. с совместной плотностью распределе-
Х-1
ния/(х„ xj.
Тогда плотность распределения с. в. У равна
g(y) = JAyx,x)\x\dx. (3.47)
Заметим, что в последних формулах (3.44) — (3.47) в случае
независимых с. в. Хх, Х2 совместную плотность/(х,, д^) можно представить в виде
произведения плотностей f\(xx) • /2х2в соответствии со свойством (3.14).
3.8. Специальные распределения (Пирсона, Стьюдента, Фишера)
Распределения Пирсона, Стьюдента, Фишера находят широкое
применение в статистических исследованиях. С использованием этих
распределений встретимся позднее, при обработке статистических данных, а в
текущем параграфе введем распределения.
Нам потребуются специальные функции: гамма-функция и
бета-функция. Определим их.
Определение. Гамма-функцией (у-функция) называют неэлементарную
функцию Г(х) вида
Г(х) = [e~uux~xdu, при х > 0. (3.48)
о
Гамма-функция обладает интересными свойствами:
1)Г(х+ 1) = хГ(х); (3.49)
2) Г(л + 1) = п\, где п = 0, 1, 2, ...; (3.50)
3)г(л + 1) = (л-1)(л-|)...1^,гдел = 0, 1,2,...; (3.51)
4) г(|) = Л. (3.52)
Первое и четвертое свойства можно доказать непосредственным
вычислением, а свойства второе и третье доказываются методом математической
индукции.
Определение. Бета-функцией называют неэлементарную функцию двух
переменных р и q:
1
B(p,q)= jxp-\l-x)q-ldx,(p>Q,q>0). (3.53)
о
144

Известно, что бета-функция связана с гамма-функцией равенством
Г(Р + q)
Распределение Пирсона (распределение у})
Пусть Xv Х2, ..., Хп — система случайных величин, которые
а) независимы;
б) распределены по нормальному закону с параметрами т = О, а = 1.
Составим функцию Х\ + Х\ + ... + Х\, которую обозначим у} (хи-квад-
рат). Таким образом, получаем с. в.
X2 = X] + Xl+... + Xl
(3.55)
Значения с. в. %2 обозначим через у. Заметим, что у может принимать
лишь неотрицательные значения.
Можно найти ф. р. Кп{у), а затем и плотность распределения кп{у). Для
этого нужно рассмотреть совместную плотность системы /(*,, Xj, ..., х„),
которая ввиду независимости и одинаковой распределенности нормальных
случайных величин равна
/„(*„) = 1
-1<*?+*2 + ...+*2>
Дх,,х2, ...,*„) =/i(x,) -/2(x2)
(Тад"
Функция распределения Кп{у) находится, исходя из формулы (3.39):
Км = 1-Ш
1 -\(*\+х\+ ...+£)
dxxdx2... dxn,
где область т„ определяется соотношением хх + х2 + ... + хп < у.
Рассматривая ф. р. Кп{у) при п = 1, 2, ... и применяя метод
математической индукции, можно доказать, что
■Ту 1_2
кп(у) =
Г1
Г г(5)о
W x" xdx, приу>0
(3.56)
. О, при ,у<0
Тогда плотность вероятности кп(у) = Хп(у) имеет вид
к„(у)
1
I О,
-У 2-1
е 2у2 , при у > О
(3.57)
при у < О
Заметим, что распределение с. в. %2 зависит лишь от одного параметра
п, называемого числом степеней свободы.
10 — 3529
145

A yl
II
l-0<n<2
II -n = 2
lll-n>2
III
►
Рис. 22. График функции z = kn{y) при различных п {у > 0).
Заметим также, что распределение х2 рассматривают и при нецелых
значениях п. Приведем вид соответствующих графиков функции z = кп(у) при
разных значениях п на рис. 22.
Распределение Стъюдента (t-распределение)
Рассмотрим с. в. Х~ N (0; 1) и с. в. х2 с п степенями свободы.
Предполагаем, что св. X и х2 независимы, т. е. их совместная плотность равна
произведению плотностей/(х) и кп{у), где
*.г
кп{у) имеет вид (3.57).
Составим новую случайную величину
Jk
J?
(3.58)
Распределение случайной величины Т и называют распределением
Стьюдента.
Значения с. в. Т обозначим t.
Используя формулу (3.39), можно по совместной плотности
Дх) • кп(у) определить ф. р., а затем и плотность распределения частного
у у
——, потом, рассматривая линейную функцию этого частного (Jn-^-), по
Vx2 Jx2
соответствующей формуле (3.43) находим и плотность распределения с в. Т.
В конечном итоге, обозначив искомую плотность распределения стьюден-
товой случайной величины Г посредством sn(t), приходим к формуле
*„(0
ЩГ)
7Гпг(-«)
4(1 + ")
л+1
-00 < t< +00
(3.59)
146

z = sjt)
Рис. 23. График функции z = s„(t).
В распределении Стьюдента с плотностью sn(t) единственный параметр
распределения п называют числом степеней свободы.
На рис. 23 приведен график плотности распределения Стьюдента.
Заметим, что график функции плотности распределения Стьюдента
симметричен относительно оси абсцисс, так как sn(t) — функция четная.
Также отметим наиважнейший факт: кривые z = sn(t) с ростом п
стремятся к кривой Гаусса (см. рис. 18) с параметром т = 0, и практически
при п = 30 эти кривые уже совпадают.
Замечание. При п = 1 распределение Стьюдента называют
распределением Коши. Соответствующая плотность распределения равна
,2ч-1
ДО = Ji(0
г(1)
7Г.<1)
пЮ
1
я(1 + Г)
(3.60)
поскольку по свойствам гамма-функции [см. (3.50), (3.52)] Г(1) = 1,
г(1) - Л.
Распределение Фишера '(F-распределение)
Рассмотрим частное двух независимых с. в.: Хи имеющей распределение
X2 с т, степенями свободы, и Хъ имеющей распределение у} с т2
степенями свободы.
Введем новую с. в.
XiJlTli Ш\ X-l
(3.61)
Обозначим значения с. в. /'посредством и.
Используя формулу совместной плотности с. в. Хх и Хъ и
кт (У\) ' кт 0>2) соотношение (3.47) плотности распределения частного
Данное распределение также называют распределением Фишера—Снедекора.
10*
147

z = q»)
Рис. 24. График плотности /-распределения.
двух случайных величин -^, а также формулу (3.43) для плотности линей-
ной функции с. в., получим выражение для плотности с. в. F:
/П( /Л;
Ш\ Ytli
Л") =
/Л| /Л 2
(m2 + /Wju) , при о > О
(3.62)
В(тьт2)
I. О, при и <0
где Дт,, т2) — бета-функция вида (3.54).
Как видим, /'-распределение зависит от двух параметров: т, и т2,
называемых также числом степеней свободы распределения. График функции
плотности представлен на рис. 24.
3.9. Условное распределение. Регрессия. Среднеквадратическая
регрессия
Ранее в § 1.7 были определены условные вероятности событий [см.
(1.15)] в виде
Р(В\А) = %Ш.
Введем аналогичные формулы применительно к случайным величинам.
Пусть с. в. А" имеет значения: хь хъ ..., хп\ случайная величина У имеет
значения: уи у2, ..., ут.
Тогда Х= х, или Y= y} есть не что иное, как случайные события, для
которых можно определить условную вероятность аналогично
приведенной выше:
ПГ Ъ\* xt) P{X=xi)
или, сократив запись, то же самое запишем в виде
P(v\x) = ^*"у^
КУА ,} P(Xi) ■
(3.63)
(3.64)
148

Таким образом, для дискретных с. в. X и Y введено понятие условной
вероятности значений. Р Q>;. \x,) означает вероятность, что У = у} при
обязательном условии X = xt.
Рассмотрим пример, для которого используем данные примера из § 3.6.
Пример 1. Совместное распределение системы с. в. Хи /задано в виде
таблицы
^^^^^1
0
2
1
0,05
0,05
3
0,14
0,06
5
0,25
0,15
10
0,26
0,04
Найти: а) условный закон распределения с. в. ^при условии, что У = 0;
б) условный закон распределения с. в. Упри условии, что Х= 5.
Решение. Выпишем найденные ранее в § 3.6 безусловные законы
распределения Хи У:
*|
Pi
1
0,1
3
0,2
5
0,4
10
0,3
>
yj
Pj
0
0,7
2
0,03
а) Тогда условные вероятности значений с. в. X при У = 0 находим по
формуле
РШУ= 0) = Р(х"0)
Р(У= 0)'
Следовательно,
P(X=l\Y=0) = № = ^; р(Х=3\¥=0) = ^ = Щ-
д*=5|У=0) = ^у = Ц;Р(Х=ЩУ=0) = ^ = Щ-
Условный закон распределения с. в. X при условии У = 0:
x,\Y=Q
PMY=0)
1
5
70
3
14
70
5
25
70
10
26
70
E=1
б) Условные вероятности значений с. в. У при X = 5 находим по
формуле
Г(уЛХ = 5) = -$Щ-у
Следовательно,
149

и условный закон распределения с. в. Упри ^=5 имеет вид
У]\Х=3
P(yj\X=3)
0
25
40
2
15
40
Далее рассмотрим непрерывные с. в. Л" и Ус совместной плотностью
fix, у)\А(х) — плотностью распределения с. в. Хи/2(у) — плотностью
распределения с. в. У
По аналогии с условной вероятностью события определим условную
плотность распределения.
Определение. Условной плотностью распределения с. в. У при заданном
значении с. в. Х= х называют функцию fyai{y \ х), равную отношению
плотностей:
Аналогично можно ввести условную плотность
JycA ]У) /200
(3.65)
(3.66)
(3.67)
Из (3.65), (3.66) следуют равенства
f(x,y) = fyjy I x) •/(*),
f(x,y)=fyc/l(x\y)-f2(y).
Заметим, что для независимых с. в. Хи У в этом случае получаем
/уаку\х)=Ш),/усл{х\у)=/х{х).
Используя понятие условной плотности, введем условные математиче
ское ожидание и дисперсию.
Для непрерывных с. в. Л" и У:
+ СС +41
М(У\Х= х) = jyfycAy\x)dy = \yj^dy,
D(Y\X = x) = j[y-M(Y\X= x)}%Xy\x)dy.
Аналогично,
M(X\Y=y) = jxfycjl(x\y)dx = \xJj^dx,
(3.68)
(3.69)
D(X\Y = y) = j[x-M(X\Y= y))2fyM\y)dx,
(3.70)
(3.71)
При фиксированных значениях х условные характеристики M(Y\ X= x)
и D(Y\ X= х) являются постоянными. Однако если рассматривать х в ка-
150

честве переменного значения, то с изменением х будут, вообще говоря,
меняться и условные характеристики.
Определение. Регрессией с. в. Уна св. Л"называют условное
математическое ожидание М(У\ Х=х) в предположении, что с. в. Л" пробегает свое
множество значений.
Таким образом, М(У\ Х = х) оказывается функцией от переменной х.
M{Y\X=x) = y{x). (3.72)
Аналогично введенная регрессия св. ^на с. в. /является функцией
переменной у:
ЩХ\Г=у) = у(у). (3.73)
В зависимости от вида функций ср (х) и vj/ (у) регрессия бывает
постоянной, линейной, полиномиальной и т. д.
Функция регрессии ср(х) = M(Y\ X= х) характеризует изменение
среднего значения с в. Упри изменении значений св. Хи широко
используется в статистических исследованиях.
Подобная зависимость средних значений одной св. от значений другой
с. в. называется регрессионной зависимостью.
Определение. Если регрессия У на Л" и регрессия Л" на У суть линейные
функции, то зависимость между У и X называют линейной
корреляционной зависимостью.
Можно доказать, что любые нормально распределенные с. в. X и У
связаны линейной корреляционной зависимостью, причем
М(У\Х=х) = ту+г^(х-тх), (3.74)
М(Х\У=у) = тх+г^(у-ту), (3.75)
Gy
где х, у — переменные, а тх, ах, ту, оу, г — числовые характеристики
распределений. В правых частях формул (3.74), (3.75) фигурируют именно
линейные функции от переменных х и у соответственно. Если с. в. X и Уне-
коррелированы, т. е. их коэффициент корреляции г = 0, то регрессия
оказывается постоянной:
M(Y\X=x) = my,
М(Х\ Y=y) = mx,
а, значит, условные математические ожидания равны безусловным.
В случае произвольного распределения св. Хи У зависимые св. не
обязаны иметь именно линейную корреляционную зависимость.
Пример 2. По данным примера 1 найти регрессию М (У| Х= х).
Решение. Поскольку с. в. ^принимает лишь четыре значения, то
требуется найти условное математическое ожидание У при четырех условиях:
Х= \,Х= 3, Х=5, Х= 10.
2 2
M(Y\ х= 1) = |>,7>ед*=1) = ^Л-Ш^1=
151

M(Y | X) A
1—
0,6_l_M(Y)
0,5
I I I L
13 5 10 x
Рис. 25. Линия регрессии, построенная по четырем значениям.
M(Y
M(Y
х=3)=у ЛЗ.Уу)
°> LyjP(X=3)
У-1
2
Jr-5)-5>^
У-1
2
5)
= О
°Л4 + 2
0,2
0.25 ?
0.4 +2
. 0,26 +
0.06 _ ..
0.1 1*
0.15 _ 0
0.4 U>
2.°'04«0.
ЛГ(Г|ЛГ-10)-5:Л^^-О.йМ + 2.йМ.0,2667.
Полученные значения можно соединить отрезками, и тогда получим
линию регрессии, которая дает представление о тенденции изменения
условного среднего значения св. У в зависимости от X.
Заметим, что в данном примере линия регрессии проведена
исключительно ради наглядности, а фактически регрессия наших дискретных
случайных величин характеризуется лишь четырьмя точками.
В случае непрерывных с. в. Хи У линии регрессии Уна Л" и Л" на У
определяются формулами (3.68), (3.70).
Как уже было указано, регрессия представляет зависимость среднего
значения одной с. в. от другой с. в. Зададимся вопросом: если Хи У —
зависимые св., то нельзя ли построить функцию этой зависимости 1и У?
Вообще говоря, точную зависимость между X и У можно воспроизвести
лишь в исключительных случаях, когда Хи У связаны функционально
(например, У= 2Х3 + 1 и т. д.). Корреляционная же зависимость
предполагает более слабую связь между случайными величинами, к тому же
подвергнутым неодинаковым случайным воздействиям: например, одному и тому
же значению с. в. Смогут соответствовать разные значения с. в. У.
Исходя из этого, вместо точной функциональной связи между X и У
ищут некоторую приближенную зависимость переменных, "наилучшую" в
некотором классе функций: Y»g(X), где g(X), например, линейная
функция вида аХ + Ь. Чтобы функция действительно была "наилучшей" по
сравнению с другими функциями из того же класса, необходимо
определить соответствующим образом ее параметры (в нашем случае g(X) = aX+b
нужно подобрать числа а и Ь).
Итак, пусть ищем зависимость У»g (X) среди линейных функций
g(X) = aX+b.
152

Функцию g(X) = аХ + be конкретными значениями а и Ъ называют
наилучшей в смысле метода наименьших квадратов, если величина
ЩУ~8(Х))2 принимает наименьшее значение по сравнению с другими
функциями вида g (X) = аХ+ Ь.
Сама функция g(X), являющаяся наилучшим приближением,
называется среднеквадратическойрегрессией Уна X.
Найдем значения параметров а и Ь, при которых величина
M{Y — g(X))2 = M(Y— аХ— b)2 имеет наименьшее из возможных значений.
Исследуя на экстремум эту функцию F(a, b) = M(Y' — аХ - b)2 двух
переменных а и Ь, неминуемо придем к равенству
g(X) = my + r^(X-mx). (3.76)
Таким образом, как нетрудно заметить, линейная среднеквадратическая
регрессия (3.76) совпадает с регрессией вида (3.74) при нормальном
распределении.
Коэффициент а = г—* называют коэффициентом регрессии Y на. X, а
соответствующую прямую
у = ту+гЪ:(х-тх) (3.77)
ох
называют прямой среднеквадратической регрессии Y на X.
Прямая (3.77) указывает приближенную линейную зависимость между
с. в. X и Y, причем наилучшую в смысле метода наименьших квадратов.
Ошибку, допускаемую при замене у на величину ту + г—*(дс — тх), на-
зывают остаточной дисперсией, и она равна значению функции F(a,
b) = M(Y — aX - b)2 при наилучших найденных а и b. Эта остаточная
дисперсия равна о2у( 1 - г2). Как видим, при г = ± 1 остаточная дисперсия
(ошибка) оказывается равной нулю, что совершенно справедливо, ибо в
этом случае Хи У связаны точной линейной зависимостью Y = aX+ b.
Можно искать аналогично зависимость Yx g(X) и в классе других
функций, например полиномов заданной степени или в классе показательных
функций g(x) = Ь- а* пт. R. Лучшим среди различных приближений
считается то, для которого стандартная ошибка меньше.
3.10. Предельные теоремы
Как уже упоминалось многократно, теория вероятностей изучает
закономерности, возникающие в массовых явлениях, т. е. в испытаниях,
которые можно повторить сколь угодно много раз. Так же изучаются
случайные величины (законы их поведения), значения которых складываются
под влиянием множества случайных факторов. Массовость случайных
явлений приводит к устойчивости некоторых показателей (средних
значений), для которых случайные отклонения в единичном явлении при по-
153

вторяемости испытаний суммарно взаимно компенсируются. Свойство
устойчивости средних показателей и составляет суть предельных теорем,
называемых "законом больших чисел". Эта суть такова, что при
многократных повторениях испытаний среднее значение каких-то характеристик
стабилизируется настолько, что на некотором этапе его можно считать уже
практически не случайным значением, т. е. с ростом числа испытаний
средние показатели стремятся к каким-то константам. Закономерности,
выражаемые законом больших чисел, определяют простор для
практических приложений теории вероятностей.
Другие задачи решает группа теорем, называемых центральной
предельной теоремой. В этих теоремах речь идет не о стремлении отдельных
показателей в массовых явлениях, а о предельных законах распределения.
Следовательно, если случайная величина может быть представлена в виде
суммы большого количества других случайных величин, вклад каждой из
которых не превуалирует над другими, то при некоторых условиях закон
распределения суммарной случайной величины "стабилизируется", а
именно: стремится к нормальному закону распределения. В этом и заключается
особая роль нормального закона, как своего рода идеала для случайных
величин, к которому при определенных условиях "стремятся" другие законы
распределения.
К предельным теоремам теории вероятностей относят две группы
теорем: закон больших чисел и центральную предельную теорему.
Закон больших чисел
Одной из теорем, относящихся к закону больших чисел, является
теорема Бернулли (см. § 1.15), обосновывающая статистическое определение
вероятности.
Приведем еще две теоремы из той же группы: теорему Маркова и
теорему Чебышева. Вначале запишем две леммы.
Лемма 1 (неравенство Маркова).
Для любой неотрицательной с. в. X, имеющей математическое
ожидание, при любом положительном числе е справедливо неравенство
Р(Х<е)>\-^^. (3.78)
е
Данное неравенство можно доказать, произведя оценку вероятности
Р(Х< е) = 1 - Р(Х> е).
Лемма 2 (неравенство Чебышева).
Для одной с. в. X, имеющей дисперсию, при любом положительном е
справедливо неравенство
Р(\Х- МХ\ < е) > 1 - Щ±. (3.79)
е
Для системы с. в. Xlt Х2, ..., Хп, имеющих дисперсии, при любом
положительном е справедливо неравенство
^Хк ]ГЛ/(^)
к = 1 _ к=1
<е
41
X
>1- *-\ . (3.80)
п г
154

Доказательство. 1. Докажем неравенство (3.79), опираясь на
неравенство Маркова (3.78), записанное в других обозначениях,
Р(Г<а)>1-^Д а>0
(3.81)
Полагаем Y= (X — М (X))2, а = е2 и подставим эти величины в (3.81).
Тогда
Р«Х- М(Х))2 < е2) > 1 - М(Х~ f <X»2.
е
Заменив событие в левой части неравенства эквивалентным и учитывая,
что М(Х— М (X))2 = D(X), получаем доказываемое соотношение
Р(\Х-М(Х)\<е)>\-Щр.
е
2. Для доказательства неравенства Чебышева (3.80) воспользуемся
только что доказанным неравенством (3.79). Введем новую переменную
Х =
_ 1
к = 1
Тогда
М(Х) = М Ц^д - \^М(Хк),
к = 1
к= 1
4 к = 1 ' \ = 1 у
Подставив X, М(Х) и D(X) в (3.79), получим доказываемое соотношение
(3.80).
Лемма 2 доказана.
Теорема Маркова. Пусть Xlt Х2, ..., Хп — произвольные с. в., для
которых справедливо условие
lim
4Z
к= 1
= 0.
(3.82)
Тогда для любого е > 0 выполняется соотношение
limP
1-ухк-1-УМ(Хк)
к= 1
<е = 1.
(3.83)
Доказательство. Для вероятности, фигурирующей в (3.83), справедливо
двойное неравенство
1>Р
±ухк-±ущхк)
Аг = 1 *= 1
<е >1-
°\Ъ
к= 1
2 2
п е
(3.84)
155

поскольку вероятность всегда не превосходит 1, и для указанной
вероятности выполнено соотношение (3.80).
Далее переходим к пределу в каждом из неравенств:
1>НтР
л л
х-ухк-х-ум{хк)
к= 1
к= 1
<е >1.
Из полученных ограничений следует, что нашему пределу не остается
ничего иного, кроме как быть равным 1.
Тем самым выполнено (3.83), и теорема доказана.
Теорема Чебышева. Пусть Xv Х2, ..., Хп — независимые с. в., имеющие
ограниченную дисперсию D(Xk)<A (при к = 1, 2, ..., п). Тогда для любого
е > 0 выполняется соотношение
limP
л л
Jt= 1
k= 1
<e
= 1
(3.85)
Доказательство. Для вероятности соотношения (3.85), так же как и в
доказательстве предьщущеи теоремы, можно записать соотношение вида
(3.84)
\>Р
л л
-Yxk--YM(Xk)
<е|>1- '-'
2 2
п е
(3.84)
к=1 к= 1
Так как с. в. Хи Хъ ..., Хп независимы и имеют ограниченные
дисперсии, то
*= 1
2 2
п е
U* 1ДЛ) ZA
= t=_L
2 2
п е
<к-\ = пА _ А
п\2
п2е2
пе
2 '
Очевидно, что неравенство (3.84) не нарушится, если в нем вместо
Хк
хк= 1
2 2
п е
записать величину не меньшую: -^-.
пе
Тогда из (3.84) получаем
\>Р
л л
n*-j п*—*
к= 1
* = 1
<е >1-А.
ле
Переходя к пределу в каждом из неравенств, приходим к
1>НтР
\ix*-\iM^
*=i
к= 1
<е >1
Из полученных ограничений вытекает, что указанный предел,
ограниченный сверху и снизу единицей, сам равен 1.
Теорема доказана.
156

Значение доказанных теорем трудно переоценить. Эти теоремы (при
разных условиях) утверждают, что среднее арифметическое суммы
достаточно большого количества случайных величин утрачивает характер
случайности и стремится к конкретному числу — среднему арифметическому
математических ожиданий. Если все случайные величины одинаково
распределены, то они имеют одно и то же математическое ожидание т, и
среднее арифметическое равных математических ожиданий оказывается
также равным т.
Теорема Чебышева позволяет находить истинное значение некоторого
измерения как среднее арифметическое значений, полученных в
некоторой последовательности измерений.
По существу на теореме Чебышева основывается выборочный метод,
применяемый в статистике.
Центральная предельная теорема
Если в законе больших чисел рассматривалась сходимость по
вероятности случайных величин и их характеристик к некоторым постоянным, то
центральная предельная теорема оперирует распределениями случайных
величин. Все теоремы, входящие в центральную предельную теорему,
представляют собой набор условий, при которых случайная величина,
представленная как сумма достаточно большого числа слагаемых, имеет
нормальное распределение или распределение, близкое к нормальному.
Набор условий на случайные величины-слагаемые обычно включает
различные комбинации предположений: независимости, одинаковой
распределенности, соотношений на первые моменты и т. д.
Приведем одну из самых простых теорем центральной предельной
теоремы.
Теорема. Пусть Хи Х2, ..., Хп — независимые, одинаково распределенные
случайные величины с математическим ожиданием т и дисперсией а2.
Тогда с ростом п закон распределения суммы Yn = Хх + Х2 + ...+ Хп стремится
к нормальному закону.
Заметим, что доказательство подобных утверждений обычно проводится
методом характеристических функций, который можно найти в более
математически строгих пособиях по теории вероятностей.
В практических задачах центральная предельная теорема часто, решая
вопрос о распределении, по существу предлагает и метод решения задачи.
В частности, если для св. Yn = Хх + Х2 + ...+ Хп выполнены условия
центральной предельной теоремы, то независимо от того, как распределены
случайные слагаемые, зная лишь их математические ожидания и
дисперсии, можно найти вероятность попадания с. в. Yn в заданный интервал {а,
Ь) по формуле
Р(а< Yn<b) = ф(^^Ь)-ф(а^Ь) ,
V Оу J ^ Оу J
справедливой для нормально распределенных св. (см. 2.11).
В данной ситуации математическое ожидание ту и среднее квадратиче-
ское отклонение с. в. Yn, как суммы независимых случайных величин,
легко вычисляются.
157

На практике закон распределения с. в. Yn обычно полагают
приближенно нормальным уже при п = 10.
Также отметим как частный случай центральной предельной теоремы
для дискретных случайных величин теорему Муавра—Лапласа (см. § 1.14).
Задачи и упражнения
1. Бросают две помеченных (например, различно раскрашенных)
игральных кости. Задание: для данного испытания рассмотреть систему двух
случайных величин, найти закон распределения этой системы.
2. Случайные величины Х{, Х2, ..., Хп независимы и одинаково
распределены: каждая из них имеет нормальное распределение с параметрами
М(Х,) = 0, D(X) = 4. Найти совместную плотность распределения системы:
f(Xlt *2> •••> Хп)-
Ответ:/(х,, х^, ..., хп) = -е
2\2nf
3. Дискретная случайная величина X имеет закон распределения
*/
Pi
-1
од
0
0,4
1
0,3
2
0,2
Найти закон распределения случайной величины, являющейся
функцией от X a.)Y=X+ 1; б) Z=X2.
4. Независимые дискретные случайные величины X и Y имеют законы
распределения
xi
Pi
0 1 2
0,2 0,5 0,3
У)
Pj
-1 3
0,3 0,7
Найти закон распределения случайной величины Z= 2X + Y. Какую
роль играет условие независимости случайных величин?
Ответ:
Zi
Pi
-1
0,06
1
0,15
3
0,23
5
0,35
7
0,21
5. Случайные величины X и Y имеют распределения: X ~ N(\; 2),
Y~ N(3; 5). Найти плотность распределения суммы Z= X + Упри условии,
что Хи У: а) независимы; б) некоррелированы. Как связаны независимость
и некоррелированность при нормальном распределении?
Указание. Воспользоваться свойством, что сумма нормально
распределенных случайных величин распределена также нормально, и найти
параметры распределения Z: mv oz.
158

6. Задан закон распределения системы дискретных случайных величин
Хи Y:
yj ~—^^_
1
2
-10 12
0,1 0,3 0 0,15
0,2 0,05 0,15 0,05
Найти: а) закон распределения составляющих Хи У; б) М(Х), M(Y).
Ответ: б) М(Х) = 0,25; М( Y) = 1,45.
7. Задан закон распределения системы двух случайных величин Хи Y.
-1
1
0 1 2
0,35 0,1 0,15
0,05 0,3 0,05
Найти числовые характеристики системы: а) М(Х), Л/(У); б) ДА'),
ДУ); в) cov(A; У), V
Ответ: а) М(Х) = 0,8; M(Y) = -0,2; б) D(X) = 0,56; ДУ) = 0,96;
в) cov(A;r) = -0,5376; Гху * -0,733.
8. Функция распределения системы случайных величин X, У имеет вид
Fix, у) =
sin* sin;', при 0<х<^, 0 < >> < ^
0, при х< 0 или у< 0.
Найти значение функции плотности распределения: а) во второй
координатной четверти; б) в точке 1х = j, у = 5); в) в области
0<x<j,0<y<j.
Указание. Использовать формулу, связывающую совместную плотность
распределения с соответствующей функцией распределения [см. § 3.1, (3.8)].
Ответ: а) 0; б) ^-; в) cos x cos у.
9. По данным задачи 7 найти условный закон распределения: а)
случайной величины А^при условии, что Y= 1; б) случайной величины Упри
условии, что X = 2.
Указание. Значения случайных величин известны, требуется найти
условные вероятности Р(х,\ Y— 1) в случае а и P{yj \ Х= 2) в случае б.
Ответ: а)
*,|У=1
Р(х,\ Y= 1)
0
0,125
1
0,75
0,125
159

б)
yj\X=2
P(yj\X=2)
-1
0,75
1
0,25
10. Совместная плотность распределения системы случайных величин
X, Yравна /(*,у) = 1е-'.5(^ + ^+Л при _оо< х < +оо, -оо< у < +оо.
71
По формулам типа (3.10) (см. § 3.1) вычислены плотности
распределения каждой из случайных величин:
JTk
Определить условные плотности распределения /^(у \ х) и/уо1(х \ у).
Ответ:
fyjy I x) =
_ 1 -0,5(x + ^)J .
Jb.
fyjx I У) = ^—e
11. Совмест
распределения
_ /5 -0, \{Ьх + у)2
11. Совместное распределение случайных величин X и Y задано законом
^>V>>V>-v^ Х>
-1
0
1
-2
0,05
0,15
0
0
0,2
од
0,05
l
0
0,05
0,1
2
0,15
0,1
0,05
Найти: а) условные законы распределения Упри Х= —2, 0, 1, 2; б)
регрессию Уна X. Построить график функции регрессии.
Ответ: M(Y\X=-2) = -0,25; M(Y\X= 0) =-1; M(Y\X=\)=1;
M{Y\X=2) = -\.
12. Случайные величины Хи У подчинены нормальному закону
распределения X~N(l; 3), Y~N(2; 4). Найти уравнения регрессии Уна X и X на У в
случаях: а) X и У некоррелированы; б) X и У коррелированы, и cov(Ar,
Y) = —J3. Построить графики регрессионной зависимости.
Указание. Для нахождения уравнения регрессии воспользоваться
равенствами (3.74), (3.75).
160

13. Дискретная случайная величина X имеет закон распределения
*/
Pi
од
0,05
0,4
0,2
0,8
0,3
1
0,25
1,2
0,2
Используя неравенство Чебышева (3.79) (см. § 3.10), оценить
вероятность события \Х- М(Х)\ < 0,5.
Ответ: Р(\Х- М(Х)\ < 0,5) > 0,6069.
14. Пусть Хх, Х2, ..., Хп — независимые одинаково распределенные
случайные величины с известным математическим ожиданием т и конечной
дисперсией. Какова тенденция изменения значений среднего
арифметического
к= 1
с ростом количества слагаемых л?
Указание. См. теорему Чебышева, § 3.10.
15. Как приближенно вычислить математическое ожидание (среднее) п
независимых одинаково распределенных случайных величин Xv X2, ..., X?.
Указание. См. теорему Чебышева, § 3.10.
Ответ: М(ХХ) = М(Х2) = ... = М(Хп) = т (почему?).
к= 1
16. Пусть случайные величины Х{, Х2, ..., Хп — независимые и одинаково
распределенные, обладающие математическим ожиданием т и дисперсией
а2, л^Ю. Определить вид приближенного распределения случайной
величины Yn = Хх + Х2 + ... + Хп, указать параметры этого распределения.
Каким распределением обладает среднее арифметическое
х= 1-Ухк,
к= 1
каковы его параметры?
Указание. См. центральную предельную теорему (§ 3.10).
11 — 3529

Глава IV. ВЫБОРОЧНЫЙ МЕТОД
4.1. Предмет и задачи
Теория вероятностей, являясь по своей сути дисциплиной
математической, строго определяет свои понятия, методы и законы действий с
различными объектами и тем самым носит некоторый отпечаток
абстрактности. Однако фундаментальная, объективно существующая вероятность в
любой практической задаче определяется конкретно, исходя из реального
комплекса условий или наблюдений. Нередко вероятность определяется
статистически, т. е. в основе изучения случайности всегда лежит
эксперимент, в массовых явлениях многократно повторяемый. Если задача носит
вероятностный характер, то на первом этапе необходимо собрать
экспериментальные данные. Далее эти данные подвергаются обработке и анализу
на основе теоретических вероятностных законов, и только потом делаются
выводы и строятся прогнозы.
Наука, занимающаяся методами сбора, обработки, анализа и
интерпретации экспериментальных данных, называется математической
статистикой. В данной последовательности действий между сбором и
интерпретацией данных безраздельно господствует теория вероятностей,
предоставившая статистике свой аппарат и методы исследования, которые для данных
задач также имеют и свою особую специфику.
Среди многообразия задач математической статистики можно выделить
следующие:
1) задача нахождения закона распределения случайной величины по
наблюдаемым данным;
2) задача нахождения параметров распределения;
3) проверка согласованности теории с данными опыта (проверка
гипотез);
4) задача установления и исследования различного рода зависимостей
на основании экспериментальных данных.
Как правило, в результате наблюдений массовых явлений мы получаем
некоторым образом ряд экспериментальных численных данных. По этим
данным с определенной долей уверенности (с вероятностью) можно судить
об определенных объективных закономерностях. Например, по
наблюдаемой последовательности значений с. в. требуется сделать какие-либо
возможные выводы о самой случайной величине.
Таким образом, математические статистические методы являются
универсальным аппаратом исследования числовых данных. Сами данные,
предоставляющие область медицины, биологии, экономики или социологии,
вносят свою специфику в постановку задачи и интерпретацию результатов.
162

4.2. Основные понятия выборочного метода
Одним из важнейших в статистике является понятие генеральной
совокупности (г. с). Генеральной совокупностью называют множество
качественно однородных объектов. Генеральная совокупность может быть
конечной или бесконечной, например множество граждан России или
множество всех действительных чисел на отрезке [а, Ь]. Генеральная совокупность
может быть гипотетической (т. е. реально несуществующей), например
множество исходов при бесконечном повторении некоторого опыта.
Любое подмножество объектов генеральной совокупности называют
выборочной совокупностью или просто выборкой. Количество элементов
генеральной совокупности называют объемом г. с. Аналогично говорят об
объеме выборки. Суть выборки в том, что она, являясь частью генеральной
совокупности, в определенной мере может характеризовать саму
генеральную совокупность, т. е., обследуя часть объектов, возможно сделать
выводы обо всем их множестве. Как правило, генеральная совокупность имеет
достаточно большое, а в идеале и бесконечное, количество элементов.
Понятно, что чем больше объем выборки, тем лучше она представляет
генеральную совокупность. Однако обследование больших выборок или
проведение сплошных обследований зачастую просто невозможно или
экономически нецелесообразно. Например, если в результате эксперимента
исследуемый объект портится либо вообще уничтожается, либо сам
эксперимент является чересчур дорогостоящим, то естественно желание не
увеличивать объем выборки, но при этом малом объеме получить максимум
информации о генеральной совокупности. При этом возникают вопросы:
каков объем выборки достаточен? Каким образом должен осуществляться
выбор, чтобы обеспечить представительность? А также необходимо уметь
обработать эти выборочные данные и оценить величины неизбежно
допускаемых ошибок.
В реальных задачах обычно исследуется некоторый признак, а не сам
объект, носитель этого признака. Причем данный признак связывается с
численным значением, которое у каждого носителя признака свое
собственное, возможно, совпадающее со значениями у других объектов. Таким
образом, вместо генеральной совокупности можно рассматривать
множество всех возможных значений этого признака, среди которых, вообще
говоря, имеются повторяющиеся. Одни значения встречаются чаще, другие
крайне редко и т. д. Все сказанное подводит нас к факту, что,
во-первых, в дальнейшем генеральной совокупностью мы будем
называть не только множество объектов, но и сам исследуемый признак,
обладающий совокупностью значений;
во-вторых, определенная таким образом генеральная совокупность
является случайной величиной X;
в-третьих, выборку объема п можно считать набором значений,
принимаемых св. X в результате п испытаний (обозначим эти значения х,,
в-четвертых, выборку объема п можно интерпретировать как набор
случайных величин Xlf Хъ ..., Хп, каждая из которых распределена так же, как
и генеральная совокупность X.
11*
163

В такой постановке с. в. Хк является копией с. в. X, связанной с к-ы
экспериментом, и тогда хк — это значение, принимаемое случайной
величиной Хк (т. е. той же самой случайной величиной X, но в к-ы.
эксперименте), где к= 1, 2, ..., п.
В дальнейшем выборкой г. с. X будем называть и набор значений х,,
Xj, ..., х„ и набор случайных величин Xlt Х2, ..., Хп. Обычно с. в. Хх, X2, ..., Хп
используются для различных теоретических выкладок, а реализации этих
с. в. х,, %, ..., х„ для конкретного применения этой теории. (Отметим, что
введенная условность не является оригинальной: например, в геометрии в
формуле площади треугольника мы полагаем в зависимости от задачи
SA = -а • h и в то же время численно^ = - • 3 • 5).
Выборка объема п получается в результате экспериментов. Чтобы
выборка была представительной, необходимо организовать эти эксперименты с
одинаковыми возможностями для каждой выборочной случайной величины,
иначе говоря, с. в. Хх, Х2, ..., Хп должны реализовываться при одном и том же
комплексе условий, как и с. в. X, и должны быть независимы друг от друга.
Определение. Выборка Xlt Х2, ..., Хп из г. с. X называется
репрезентативной (представительной), если
— с. в. Xv Х2, ..., Хп имеют то же самое распределение, что и с. в. X;
— с. в. Xlt Х2, ..., Хп независимы.
Реально на практике репрезентативность выборки обеспечивается
способом отбора значений. Отбор должен гарантировать каждому возможному
значению равные шансы быть выбранным, и тогда появление или
непоявление конкретного значения определяется его частотой встречаемости в
генеральной совокупности, т. е. мы подошли к вероятности появления тех
или иных значений. А потому отбор должен быть случаен. Наиболее
распространенным способом обеспечить простой случайный отбор является
выбор "наудачу", однако этот выбор не лишен некоторой доли
субъективизма. И наиболее корректным следует признать выбор с использованием
таблицы случайных чисел или генератора случайных чисел, имеющегося
во многих компьютерных программах. В этом случае каждый объект г. с.
получает свой порядковый номер, а таблица случайных чисел поставляет
нам совершенно произвольные номера, которые следует использовать при
выборе.
Отметим также, что выбор бывает с возвращением и без возвращения в
г. с. В случае бесконечной г. с. и выборки конечного объема это различие
оказывается несущественным.
4.3. Выборочное распределение и его характеристики
Пусть рассматривается г. с. X. В результате п независимых наблюдений
получена выборка, состоящая из п значений (чисел), среди которых,
вообще говоря, имеются и равные.
Если все значения в выборке упорядочены по возрастанию, то такую
выборку называют вариационным рядом, а элементы выборки —
вариантами.
164

Предположим, что выборка состоит из к различных значений хх, Xj, ...,
хк, при этом значение хх встречается тх раз; значение Xj — т2 раз;...;
значение хк — тк раз. Числа тх, т2, ..., тк называют частотами
соответствующих выборочных значений. Разумеется, тх + т2 + ... + тк = п. Отношения
тх mi mk
п п п
называют относительными частотами выборочных значений. Обозначим
их соответственно со,, со2, ..., (ьк. Отметим, что относительные частоты
являются аналогами вероятностей в дискретных распределениях.
Справедливо равенство
со, + со2 +...+ ®к = 1.
Статистическим распределением (распределением выборки) называют
последовательность всех различных значений выборки вместе с их
относительными частотами:
*/
со,-
хх х^ ... хк
со, со2 ... соЛ
ZC0/=/I
Таким образом, статистическое распределение является некоторым
приближением теоретического (истинного) распределения г. с. X. Таблицу
вида (4.1) называют также статистическим рядом.
Поскольку статистическое распределение имеет такой же вид, что и
распределение дискретной с. в. с конечным множеством значений, то для
описания статистического распределения можем использовать
аналогичные характеристики. К характеристикам, связанным со статистическим
распределением, обычно добавляют прилагательное "выборочная",
"эмпирическая" либо "статистическая" и в отличие от соответствующих
теоретических характеристик каким-либо образом помечают: чертой сверху,
волной, звездочкой, индексом (например, X, S, 0*). Условимся в дальнейшем
выборочные характеристики отмечать, как правило, сверху чертой, хотя
придется использовать и другие обозначения. При этом, если речь идет о
случайных величинах, будем использовать прописные буквы, а если о
численных значениях, то соответствующие строчные буквы; например, св. X,
имеет значение xt, с. в. X имеет значение х и т. д.
Введем эмпирическую функцию распределения. Пусть х — некоторое
действительное число. Обозначим посредством тх количество выборочных
значений, меньших чем х. При этом учитывается кратность каждого
значения. Тогда отношение mjn — относительная частота наблюдаемых
значений с. в. X, меньших чем х\ при разных х эта величина принимает
различные значения, следовательно, она является функцией от х.
Определение. Эмпирической функцией распределения выборки объема п
называют функцию
К(х) = ^. (4-2)
п
165

Легко заметить, что для статистического распределения вида (4.1)
эмпирическая ф. р. равна
Fn(x) =
0, при х<хх
^со,, при хк<х<хк+1 (4.3)
iuk
1, прих>х„.
Здесь индекс к изменяется от 1 до п - 1, а суммирование при каждом х
из промежутка (хк; хк+1] ведется по всем индексам /таким, что / < к.
Графиком функции ~Fn(x) служит ступенчатая линия (как и для
дискретной с. в. см. § 2.3), которая в точках х{, х^, ..., хп изменяется скачкообразно
с соответствующими величинами скачков со,, со2, ..., со„. Т„(х) — функция
неубывающая, и все ее значения находятся в интервале [0; 1].
Найдем выборочное математическое ожидание (выборочное среднее) и
выборочную дисперсию. Обозначим их соответственно М(Х) = х и
-2
D(X) = Г. Согласно (4.1),
к к к
х = ухр, = Yxp = iy^ni,. (4.4)
1=1 i = 1 i = 1
В данном равенстве выборочное среднее х записано с учетом, что все х,.,
/ = 1, 2, ..., к, под знаком суммы различны, а т{ — соответствующие
кратности (частоты) значений. Если не использовать кратность, а
рассматривать все значения выборки объема п (х,, х^, ..., хк,..., хп), то та же формула
получится без учета повторяемости значений:
-х = 1 £*.. (4.5)
1 = 1
Понятно, что сумма в (4.4) отличается от суммы в (4.5) объединением
одинаковых слагаемых.
Аналогично выборочную дисперсию вычисляем как второй
центральный момент статистического распределения при найденном среднем х:
к к к
? = £(*-х)2со,. = 5>-*)2^ = ^(x-x)V (4.6)
i= 1 i=l i= 1
При записи без совместного учета повторяющихся значений среди п
элементов выборки можно записать
л
? = 1-^(х-х)2. (4.7)
1= 1
166

При этом так как статистическое распределение (4.1) есть дискретное
распределение, то справедливы и все соответствующие формулы для
числовых характеристик, в частности
к ( к \ /к
J = 5>-X)2CD,. = JVCD,- -(X)2 = I^x'l -(К)
1= 1
i= 1
-.ч 2
(4.8)
Подобным образом можно получить формулы и для других выборочных
моментов. Например, для выборочных начальных и центральных моментов
имеют место соотношения
Д, = !у (х-х)к,к = 0,1,2,3,
1= 1
а* = ±У*А*= 0,1,2,3,...
i= 1
(4.9)
Зная выборочные моменты, можно найти выборочные коэффициенты
асимметрии и эксцесса, также аналогично находятся и другие выборочные
числовые характеристики.
Совершенно очевидно, что эти найденные характеристики
статистического распределения отличаются от соответствующих характеристик
теоретического распределения г. с. X. Об их соответствии и поведем речь далее,
в последующих параграфах.
Пример. В течение 25 дней фиксировалось количество обратившихся за
экстренной врачебной помощью. В результате получена выборка объема
п = 25 элементов:
1, 0, 4, 2, 3, 5, 2, 4, 0, 1, 8, 5, 2, 4, 3, 3, 2, 5, 1, 3, 2, 5, 1, 3, 2.
Требуется:
а) представить выборку в виде вариационного ряда;
б) представить выборку в виде статистического ряда;
в) найти эмпирическую функцию распределения;
г) найти следующие числовые характеристики: выборочное среднее,
выборочную дисперсию, выборочные коэффициенты асимметрии и эксцесса;
д) найти моду и медиану выборки.
Решение, а) Запишем элементы выборки в порядке возрастания
(упорядочим). Получим в результате вариационный ряд:
0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 8.
б) Из вариационного ряда видно, что среди 25 элементов различных
только семь. Запишем эти значения х, с соответствующими частотами т„
где i = 1, 2, ..., 7.
V ffl; = П = 25.
*,
щ
0
2
1
4
2
6
3
5
4
3
5
4
8
1
167

Зная частоты значений, легко найдем относительные частоты со. = —,
п
и тогда получим статистический ряд:
*,■
СО;
0
0,08
1
0,16
2
0,24
3
0,20
4
0,12
5
0,16
8
0,04
1>
= 1
вд =
в) Для нахождения эмпирической ф. р. воспользуемся формулой (4.3).
Так как статистический ряд имеет семь различных значений, то запись
Fn(x) будет несколько громоздкой.
0, при х<0
0,08, при 0<х<1
0,24, при 1<х<2
0,48, при 2<х<3
0,68, при 3<х<4
0,80, при 4<х<5
0,96, при 5<х<8
1, при х>8.
Графиком данной функции является ступенчатая линия с высотами
ступенек, равными наращенной вероятности (0,08; 0,16; 0,24; 0,20; 0,12; 0,16;
0,04).
г) Выборочное среднее удобно вычислять, воспользовавшись формулой
(4.4), поскольку у нас уже сформирован статистический ряд (т. е. над
выборкой уже проделана некоторая работа, а иначе по формуле (4.5)
пришлось бы суммировать вместо 7 значений все 25).
7
х = ^х/со, = 0 • 0, 08 + 1 • 0, 16 + 2 • 0, 24 + 3 • 0, 20 + 4 • 0, 12 +
+ 5 • 0, 16 + 8 • 0,04 = 2,84.
Выборочную дисперсию ? вычисляем по формуле (4.6):
7
? = ^(х.-х)2©, = (0 - 2, 84)2 • 0,08 + (1 - 2, 84)2 • 0,16 +
+ (2 - 2, 84)2 • 0,24 + (3 - 2, 84)2 • 0,20 + (4 - 2, 84)2 • 0,12 +
+ (5 - 2, 84)2 • 0,16 + (8 - 2, 84)2 • 0,04 = 3, 3344.
Выборочный коэффициент асимметрии найдем по формуле [см.
формулу (2.19), § 2.4], аналогичной формуле для теоретического коэффициента
асимметрии:
_ Дз _ Дз
Yi
(j2)2 (3,3344)2
Необходимо вычислить Д3
168

Дз = ^(х,--*)3©/ = (0 - 2, 84)3 • 0,08 + (1 - 2, 84)3 • 0,08 +
1= 1
+ (2 - 2, 84)3 • 0,24 + (3 - 2, 84)3 • 0,20 + (4 - 2, 84)3 • 0,12 +
+ (5 - 2, 84)3 • 0,16 + (8 - 2, 84)3 • 0,04 * 4, 3246.
Таким образом,
у, = 4'3246 3 «0,7103 .
(3, 3344)2"
Аналогично выборочный коэффициент эксцесса равен [см. формулу
(2.20), § 2.4].
7
(j2)2 (3,3344)2£
Отметим, что наши вычисления можно было выполнить проще,
используя для вычисления ? формулу (4.8), а для ц3 и ц4 соответствующие
формулы, выражающие центральные моменты через начальные [см.
формулы (2.14), § 2.3], поскольку рассматриваемые эмпирические
распределения по своей структуре не отличаются от дискретных распределений, для
которых эти формулы справедливы.
Заметим также, что подробные вычисления в примере проведены
исключительно в учебных целях. На практике указанные характеристики,
как и многие другие, вычисляются с помощью компьютерных программ,
имеющихся в любом стандартном статистическом пакете.
д) Моду выборки Мо(Х) найдем, исходя из статистического ряда. Как
видим, наибольшими вероятностями (относительными частотами со,) по
сравнению со своими соседними значениями обладают два элемента
выборки: х3 = 2 и х6 = 5. Соответствующие им значения
а) со3 > со2, со3 > со4 (численно 0,24 > 0,16 и 0,24 > 0,20), т. е. М0(Х) = 2;
б) со6 > со5, со6 > со7 (численно 0,16 > 0,12 и 0,16 > 0,04), т. е. М0(Х) = 5.
Таким образом, статистический ряд имеет две моды, и выборочное
распределение бимодальное.
Медиану выборки можно найти двумя способами. Во-первых, из
эмпирической функции распределения, как корень уравнения 1гп(х) = 0,5;
тогда Ме(Х) = 3 (в этой точке функция Уп{х) "перескакивает" со значения
0,48 на значение 0,68, минуя нужное нам число 0,5). Во-вторых,
медиана — это середина распределения, т. е. среди всех 25 возможных
значений вариационного ряда — это тринадцатое значение; как легко видеть,
на тринадцатой позиции вариационного ряда находится число 3.
Итак, Ме(Х) = 3.
Рассмотренный пример показывает, как, применяя приведенные выше
формулы, можно найти значения числовых характеристик конкретной
выборки *,, Xj, ..., хп, полученной по результатам наблюдений генеральной
совокупности X. Для записи числовых характеристик, не привязанных к
169

конкретной выборке, а являющихся функциями случайных величин Xv Х2,
..., Хп, используем соответствующие обозначения в виде прописных букв.
Тогда формулы типа (4.5), (4.7) имеют вид
*=±УХ ? =l-j\(Xi-X)2.
i=l i=l
Разумеется, аналогичные формулы справедливы и для других числовых
характеристик, которые в этом случае интерпретируются не как числа, а
как случайные величины.
4.4. Преобразования выборок
Для выборок большого объема, при количестве наблюдений порядка
сотен, хотя все приведенные выше определения и формулы остаются
справедливыми, применение их оказывается весьма громоздким. Разумеется,
использование компьютерных программ значительно упрощает
вычисления, но все-таки не уменьшает проделанную работу. Особенно очевидное
неудобство работы с большими выборками возникает, когда наблюдения
производятся над непрерывной с. в. X, и все наблюдаемые значения
фактически оказываются различными, даже если незначительно отличаются
одно от другого.
В подобных случаях рекомендуется уменьшить объем выборки,
используя метод группировки. Для этого весь диапазон из п значений с. в. X
разбиваем на непересекающиеся интервалы. Пронумеруем их и обозначим
количество выборочных значений, попадающих в /'-й интервал,
посредством /я,. Затем в каждом из интервалов наблюдаемые значения усредняем:
вместо т{ различных значений в /'-м интервале рассматриваем лишь одно
значение, середину интервала, но повторяющееся ровно т, раз. Проделав
такую группировку значений и усреднив их, мы получаем выборку
меньшего объема и, конечно же, отличающуюся от исходной. При такой
замене, добиваясь упрощения в вычислительном аспекте, мы неминуемо
теряем часть информации, содержащейся в выборке. Поэтому при выборе
количества интервалов разбиения необходим разумный компромисс между
упрощением выборки и сохранности первоначальной информации в
выборке. Оптимальным принято считать число интервалов к, где
**2 1пл. (4.10)
Например, при п = 100 должно быть, согласно формуле, к = 9, а при
п = 1000 можно взять к = 14.
Обычно весь промежуток длины хп — х, разбивают на равные интервалы
длиной h = -2-j-—1 лишь в случае распределения выборочных значений по
интервалу более или менее равномерно. Если же на каких-то участках
повышенная концентрация значений, то удобнее выбирать здесь интервалы
меньшей длины, чем на участках с редко встречающимися значениями.
Часто размеры интервалов при группировке определяются однородностью
рассматриваемых объектов. Например, при наблюдении температуры
пациентов является неверным включать в одну группу больных и с
повышенно

ной, и с пониженной температурой; является более целесообразным
развести их по разным группам.
В случае нахождения значения точно на границе двух интервалов его
можно считать в равной мере принадлежащим обоим промежуткам, т. е. к
количествам значений mt того и другого интервала следует добавить по 0,5.
Пример 1. Пусть в качестве выборочных значений выступает рост в
сантиметрах группы из п детей (п = 40). Обычно рост не измеряется точно,
а берется с точностью до ближайшего целого числа сантиметров.
Например, все значения из интервала (124,5 см; 125,5 см) считаются равными
значению середины интервала: 125 см. Следовательно, все п полученных,
вообще говоря, различных нецелых чисел заменяются ближайшими
целыми. При этом выборка объема п оказывается разбитой на к групп, каждую
из которых представляет одно значение, но встречающееся столько раз,
сколько значений попало в данную группу (интервал). Исходя из
конкретной выборки с размахом хп— хи возьмем к = 12. Таким образом, получаем
статистический ряд
(4.11)
£ = п = 40
В рассмотренном примере в качестве типичного представителя группы
берется значение середины интервала, что позволяет использовать в
качестве элементов выборки лишь целые числа. Это технически удобно,
особенно в случае разбиения на интервалы равной длины. Однако в других
случаях типичным значением группы может выступать, например, среднее
арифметическое в группе. Следовательно, получается преобразованная
выборка, состоящая из групповых средних.
Иногда вычислительные удобства диктуют переход к выборкам с
равноотстоящими вариантами. В этом случае, как уже отмечалось, весь интервал
делят на равные частичные интервалы длины А.
Представителем каждого из таких интервалов выступает значение
середины этого интервала, повторяющееся столько раз, сколько вариант
оказалось в интервале. Подобный переход от выборок с неравноотстоящими
вариантами к выборкам с равноотстоящими вариантами изменяет и
числовые характеристики выборки. Особенно это касается выборочной
дисперсии. С целью уменьшения ошибки, вызванной группировкой
значений, для вычисления выборочной дисперсии используют некоторое
исправление допускаемой погрешности, называемое поправкой Шеппарда.
Эта поправка заключается в уменьшении выборочной дисперсии на вели-
Рост в см
Частота
Щ

Относительная
частота
ю,
119
1
1
40
121
3
3
40
122
2
2
40
123
4
4
40
125
6
6
40
126
5
5
40
128
7
7
40
129
2
2
40
130
3
3
40
132
4
4
40
134
2
2
40
135
1
1
40
-
чину —, т. е. Dw
- С2 _ П
~S 12'
где h — длина интервала. Особенно важно использовать поправку
Шеппарда при разбиении на малое число интервалов.
171

Пример 2. По данным примера 1 преобразовать выборку с
неравноотстоящими вариантами в выборку с четырьмя1 равноотстоящими
вариантами. Вычислить выборочную дисперсию с учетом поправки Шеппарда.
Решение. Весь интервал от 119 см до 135 см разбиваем, согласно усло-
135 — 119
вию, на четыре интервала, каждый длины А, где И = —- = 4.
Получаем новый статистический ряд, варианты которого — середины
интервалов (119-123), (123-127), (127-131), (131-135).
Рост в см
Частота
Относительная
частота
121
8
8
40
125
13
13
40
129
12
12
40
133
7
7
40
Е =п =40
Z = 1
Заметим, что 4 значения варианты 123 в исходных данных, оказавшиеся
на границе интервалов, поделены поровну между интервалами (119—123) и
(123—127). Вычислим х и найдем выборочную дисперсию i2no (4.6):
х = 121
8_
40
+ 125
li + U9
12
40
+ 133
j2 = (121-126, 8)2
А+ (125-126, 8)2
*>=126'8'
±jj + (129- 126, 8)2
12
40
+
+ (133-126, 8)2 • ± = 15,96.
Тогда выборочная дисперсия с учетом поправки Шеппарда равна
А-^-П = 15'96-7Г14>6267.
Отметим, что использование средних значений является не только
техническим приемом упрощения вычислений. Средние величины сохраняют
в себе общие закономерности, присущие данной совокупности и не столь
заметные в единичных наблюдениях. При этом случайные факторы,
влияющие на каждое единичное наблюдение, в вычислении среднего
взаимно компенсируются (т. е. отклонения от истинного значения в
положительную и отрицательную сторону при сложении уравновешиваются и
сокращаются). А то общее, что присуще любому наблюдаемому значению в
однородной совокупности, освобождаясь от случайного, и проявляет себя
через среднее значение. При помощи средних значений различия,
возникшие у отдельных элементов совокупности в силу случайных обстоятельств,
сглаживаются. Например, инкубационный период развития вирусной
инфекции для каждого отдельного больного есть величина индивидуальная,
зависящая от защитных свойств организма, от внешних условий, но
значение средней продолжительности инкубационного периода отметает, ниве-
1 Вообще говоря, число интервалов с равноотстоящими вариантами и число вариант
исходной выборки могут быть равными или различными. Для более достоверного результата
каждый интервал должен содержать не менее 7—10 значений.
172

лирует случайные факторы, являющиеся внешними для развития
заболевания, и в значительной степени характеризует саму инфекцию, т. е.
потенциал конкретного типа вируса и общие закономерности, присущие этому
типу.
4.5. Графический метод представления статистических данных
Для наглядного представления и исследования статистической
совокупности наряду со статистическими таблицами, которые играют крайне
важную роль в сортировке, классификации, а также восприятии
статистической информации широко применяются графические методы
представления наблюдаемых данных.
Статистическим графиком называют чертеж, на котором статистические
данные изображены с помощью точек, линий, геометрических фигур
(плоских или пространственных), а также иных символов. Подобные
разнообразные символы называют графическим образом.
Целью построения статистических графиков является в первую очередь
представление информации зрительно ощутимой, наглядной,
выразительной и легко воспринимаемой. Наглядно воспроизведенные статистические
данные позволяют не только представлять, но и исследовать имеющиеся
данные, находить возможные закономерности, вьщвигать определенные
гипотезы, которые затем можно подтвердить или опровергнуть более
точными аналитическими методами. В частности, с помощью графиков
можно проследить участки возрастания, убывания или стабильности
каких-либо показателей, выделить промежутки сосредоточения значений, указать
имеющиеся экстремумы, составить некоторое представление о возможной
группировке значений, сделать определенные предположения о
неизвестном законе распределения г. с. X, проконтролировать резко выделяющиеся
наблюдения, установить тенденцию развития и найти другие
закономерности изучаемого явления.
Основными атрибутами статистического графика являются следующие
понятия: поле графика, заголовок и экспликация графика, графический
образ, пространственные ориентиры, масштаб.
Полем графика называют объект, на котором воспроизводится график,
будь то лист бумаги, географическая карта, экран компьютера или
берестяная грамота. Каждый график должен иметь свое название — заголовок, а
также пояснение к его содержанию и основным составляющим,
называемое вместе с заголовком экспликацией графика.
Пространственными ориентирами являются декартова прямоугольная
система координат либо полярная система координат для круговых
графиков, определяемая расстоянием от начала координат и углом поворота
соответствующего радиус-вектора точки. К пространственным ориентирам
также относят координатные сетки (например, параллели и меридианы на
географической карте) и контурные линии, нанесенные на поле графика.
Масштаб графика — единица перевода численного значения в
графическую величину (например, площади 1 см2 соответствует 10 000 населения
некоторого района). Масштабной шкалой называют линию, на которой
указан принятый масштаб. Масштабная шкала может быть как прямоли-
173

Числа
Логарифмы
чисел
Рис. 26.
1 10 100 1000 10000
общий уровень
заболеваемости
уровень заболеваемости
детей до 16 лет
уровень заболеваемости
взрослых
февраль — март
Рис. 27.
нейной (числовая ось), так и криволинейной (например, окружность с
маштабной единицей измерения в градусах), а также равномерной либо
неравномерной. Примером неравномерной шкалы служит
логарифмическая шкала, на которой за единицу измерения принят десятичный
логарифм числа (рис. 26).
Одним из самых распространенных видов статистического графика
является диаграмма — изображение на чертеже статистических данных
посредством геометрических объектов либо символов.
График зависимости у=/(х) при хе [а\Ь], построенный по
фиксированным значениям в декартовой прямоугольной системе координат,
называют линейной диаграммой. Отдельные точки (соответствующие
наблюдаемым значениям) на линейной диаграмме соединяют отрезками прямой.
На рис. 27 в виде линейной диаграммы представлен график подъема
заболеваемости гриппом населения в тысячах человек в эпидемический
период с 5 февраля по 7 марта с интервалом наблюдений в 5 дней.
Для лучшего зрительного восприятия линейной диаграммы масштаб по
осям в соответствии с правилом "золотого сечения" следует выбирать в
соотношении от 1:1,3 до 1:1,5. Линейная диафамма показывает динамику
развития какого-либо процесса. Нанесение разных показателей на одном
фафике позволяет также сравнивать в динамике связь между этими
показателями. В примере на рис. 27 четко прослеживается отличие уровня
заболеваемости детей от уровня заболеваемости взрослых. В том и другом
случае обозначена тенденция развития процесса.
174

25-,
20-
15-
10-
5-
0-.
16,67
23,33
11,67
№1
№2
болезнь
№3
№4
Рис. 28.
Другим методом представления статистических данных являются
столбиковые диаграммы. Столбиковые диаграммы также используют декартову
прямоугольную систему координат. При этом рассматривается некоторое
дискретное множество значений аргумента, каждое из которых
фиксируется по оси абсцисс (например, моменты или промежутки времени: 1991 г.,
1992 г., ... 1999 г.; либо номера, присвоенные некоторому множеству
объектов: поликлиника №1, поликлиника №2, центр профилактической
медицины, городская больница и т. д.). Рассматриваемый показатель,
соответствующий каждому из введенных аргументов, представляют в виде
прямоугольника, высота которого и является численным значением этого
показателя, указываемым на оси ординат. Длины оснований всех
прямоугольников одинаковы.
Приведем пример использования столбиковой диаграммы. На
некотором производстве предельно допустимая концентрация вредных веществ в
течение месяца оказалась превышенной в среднем на 50%, что вызвало
рост заболеваемости работников. Контролировалось 4 вида болезней: №1,
№2, №3, №4. В абсолютных цифрах количество заболевших
соответственно составило 3; 10; 14; 7 из 600 работающих. В пересчете на тысячу
работающих эти данные соответствуют 5; 16,67; 23,33; 11,67 заболевших.
Столбиковая диаграмма для данного процесса представлена на рис. 28.
Аналогично столбиковой диаграмме строится ленточная диаграмма.
В этом случае аргумент (название показателя) откладывается на
вертикальной оси, а значение показателя — на горизонтальной оси. Таким образом,
ленточная диаграмма представляет собой ряд прямоугольных полос,
вытянутых вдоль оси абсцисс. Так же как и в столбиковой диаграмме, ширина
полос (по оси ординат) должна быть одинаковой.
Приведем пример ленточной диаграммы. Исследуется мнение
населения по некоторому вопросу. Предлагается четыре варианта ответа.
Количество утвердительных ответов по каждому варианту ответа фиксируется на
ленточной диаграмме (рис. 29).
Ленточные диаграммы особенно удобны в случае нарастающего во
времени потока итоговых значений.
175

вариант 4
вариант 3
вариант 2
вариант
Рис. 29.
О 10 20 30 40 50 60 70 80 90
I&I пенсионеры, > бОлет
Щ дети до 17 лет
П трудоспособное население
от 17 до 60 лет
Рис. 30. Распределение жителей района по возрастам.
При изучении статистической совокупности, разбитой на отдельные
подмножества, часто используют круговые диаграммы. В круговой
диаграмме мерой признака является площадь: вся статистическая совокупность —
площадь круга. Весь круг представлен в виде отдельных секторов, площадь
каждого из которых представляет соответствующую долю всей
совокупности. Обычно эти составляющие доли выражены в процентах, площадь
круга — 100%. Так как площади секторов пропорциональны их центральным
углам, при этом 1% соответствует углу в 3,6е, то секторы на диаграмме
строятся достаточно легко и в то же время визуально весьма доходчиво
указывают на вклад каждой из частей во всю наблюдаемую совокупность.
Пример круговой диаграммы см. на рис. 30.
С целью наглядного сопоставления различных значений статистической
совокупности, изменяющихся, например, во времени, часто используют
радиальные диаграммы. В радиальных диаграммах начальной точкой отсчета
служит точка начала координат, из которой через определенный угол
выходят лучи. На этих лучах последовательно откладываются отрезки, прямо
пропорциональные имеющимся статистическим значениям. Например, в
случае годичных наблюдений, проводимых помесячно, вся координатная
плоскость пронизана 12 лучами, исходящими из начала координат, а углы
между соседними лучами оказываются равными 360е: 12 = 30е. Отложив на
176

Количество случаев
январь
декабрь 25"'
февраль
сентябрь
ноябрь
октябрь i 1 1 ^
март
\ апрель
май
август
июнь
июль
Рис. 31. Уровень заболеваемости ОРЗ на предприятии в пересчете на 100
работающих.
каждом из лучей отрезки соответствующей длины, соединяем
последовательно их концы и получаем ломаную, располагающуюся внутри угла в
360°. Полученную таким образом ломаную и называют радиальной
диаграммой. Можно продолжить наблюдение и нанести данные, например, за
следующий год на тот же график, и тогда наша ломаная будет совершать
следующий оборот вокруг начала координат. Получится подобие спирали.
Приведем пример радиальной диаграммы (рис. 31).
Для графического отображения сразу трех показателей, один из которых
равен произведению двух других, используют прямоугольники, в которых
длина основания, высота и площадь прямоугольника и являются
рассматриваемыми показателями. Такие прямоугольники называют знаками Варза-
ра, по имени известного российского статистика. Сопоставляя знаки Вар-
зара, примененные к разным объектам, можно сравнивать сразу три
показателя. Приведем пример (рис. 32).
Для изображения статистического показателя, изменяющегося в
пределах определенной местности, используют картограмму. Картограммой
называют контурную карту, на которой указано значение показателя в
каждой местности. При этом большему или меньшему значению показателя
соответствует разная интенсивность нанесенных на карту точек (точечная
картограмма) либо карта разбита на участки с нанесением разного вида
штриховки (фоновая картограмма).
Картодиаграммой называют карту, на которой статистические
показатели в разных местностях проставлены в виде диаграмм (столбиковой,
круговой и т. д.).
12 — 3529
177

500 ед
1200ед
1050 ед
Объект 1 Объект 2 Объект 3
Условные обозначения: ^^_ - интенсивность облучения
\ - время облучения
■
Рис. 32. Сравнение показателей интенсивности облучения, времени облучения и
полученной дозы (в условных единицах измерения) при радиотерапии.
Для статистического ряда вида (4.1) также можно составить различные
диаграммы.
Полигон частот. Полем графика служит декартова прямоугольная
система координат. На оси абсцисс отмечаем интервалы наблюдаемых
значений. Типичным представителем каждого интервала выбираем середину
интервала и в этих точках (серединах) откладываем по оси ординат значения
соответствующих частот тх или относительных частот, где / = 1, 2, ..., к.
Построенные таким образом к точек соединяем отрезками. Полученная в
результате ломаная называется полигоном частот (в случае частот /и,) или
полигоном относительных частот (в случае относительных частот).
Гистограмма. Как и в случае построения полигона частот, интервалы
наблюдаемых значений откладываем по оси абсцисс декартовой
прямоугольной системы координат. Каждому /-му интервалу соответствует своя
частота т, или относительная частота со,, в зависимости от того, какие
частоты мы хотим изобразить на графике. Это соответствие частоты
интервалу представляем в виде прямоугольника, основанием которого служит
данный интервал, а высоту (по оси ординат) выбираем так, чтобы площадь
прямоугольника равнялась этой частоте: если длину /-го интервала
обозначить ait то высота соответствующего прямоугольника равняется — для
я,
со,
гистограммы частот и соответственно равняется —' для гистограммы отно-
сительных частот.
Можно построить полигон и гистограмму частот применительно к
рассмотренному выше примеру статистического ряда (4.11). При этом
возникает вопрос выбора количества интервалов. В случае, когда число
интервалов велико сравнительно с объемом выборки, частоты оказываются
разбросанными по большому количеству интервалов и обнаруживают резкие
незакономерные колебания — график оказывается невыразительным.
178

т, к
10-
В-
6--
4-
2-
-£Н 1 1 1 1 1 1 1 1—
119 121 123 125 127 129'131 133 135
Рис. 33. Полигон частот.
J
0 1 ■
0,05 -
l
-»-
X;CM
CD,
Рис. 34. Гистограмма относительных частот (высоты прямоугольников равны —'
площади прямоугольников равны со,). 2
В противном случае, слишком малом числе интервалов, происходит
неоправданная концентрация частот, и закономерности растворяются в
случайной среде, результат получается чересчур грубым. Чтобы избежать
подобных крайностей, желательно пользоваться формулой (4.10): к « 21п п. В
примере 1, § 4.4, число интервалов 21п 40 « 7,4; округлим это значение
ради удобства до 8.
Длины интервалов не обязательно брать равными, однако ради
простоты и удобства полагаем длину каждого интервала^авной (135 — 119):8 = 2.
При таком разбиении некоторые значения оказываются на границе
интервалов, поделим их частоты поровну между обоими соседними
интервалами. Типичными значениями считаем середины интервалов.
Тогда (4.11) преобразуется в новый статистический ряд
(4.12)
*,
щ
со,-
120
2,5
1
16
122
5,5
11
80
124
5
1
8
126
8
1
5
128
8
1
5
130
4
1
10
132
4
1
10
134
3
3
40
1=40
I = 1
12*
179

Построим, например, полигон частот и гистограмму относительных
частот (рис. 33, рис. 34).
Заметим, что полигон частот можно было построить и непосредственно
по статистическому ряду (4.11) в виде линейной диаграммы.
Также следует отметить весьма существенный факт, что фигура на
рис. 34, составленная из прямоугольников, имеет суммарную площадь,
равную 1, а ломаная линия, очерчивающая эту фигуру, есть выборочный
аналог графика функции плотности теоретического распределения.
Точнее, рассматривая наблюдаемые данные как репрезентативную выборку из
генеральной совокупности X, получаем, что наша гистограмма
представляет собой некоторое грубое приближение функции плотности fix)
случайной величины X.
4.6. Методика выравнивания статистических рядов
Как известно, выборка дает некоторое представление о генеральной
совокупности X. Однако для генеральной совокупности достаточно большого
объема (теоретически, бесконечного объема) при малом объеме выборки
все выборочные характеристики являются всего лишь приближениями к
соответствующим точным значениям. В частности, статистические
графики, построенные по выборке, следует рассматривать лишь как грубые
копии, приближенные отражения истинных графиков, построенных исходя
из г. с. X.
Отклонения от истинных значений при статистическом распределении
вызваны различного рода случайностями: проведением этих, а не других
наблюдений, в результате которых произошли именно эти, а не другие
исходы. Также важным обстоятельством является ограниченность объема
выборки по сравнению с объемом всей генеральной совокупности. При
малом числе наблюдений случайные факторы могут оказаться весьма
значительными и существенно исказить истинную картину. При больших
объемах выборок ошибки, вызванные случайными факторами, в разных
наблюдениях бывают как положительными, так и отрицательными и, как
правило, суммарно уравновешиваются, взаимно погашаются,
сглаживаются, а, следовательно, полученные результаты более точно соответствуют
истинным, присущим генеральной совокупности. Однако на практике
обычно имеются малые выборки, что связано с естественными причинами
организации и сбора наблюдений. Поэтому возникает задача подбора
теоретического распределения, наилучшим образом соответствующего
выборочным данным. Подбор такого теоретического распределения по данным
статистического распределения называют выравниванием статистического
ряда.
Подбор кривой распределения часто осуществляют методом
наименьших квадратов, при котором по выборочным данным в некотором классе
функций (например, среди линейных функций ах+b или квадратичных
ах2+Ьх+с) теоретическая кривая подбирается таким образом, чтобы сумма
квадратов отклонений всех наблюдаемых значений от этой кривой
оказалась наименьшей. Вместе с тем, если имеются основания судить о виде
распределения, исходя из условий задачи, то задача нахождения искомой
180

кривой [например, графика плотности у = fix) или графика функции
распределения у = F{x)] фактически сводится к нахождению параметров
распределения. В частности, для ошибок измерения Х> представляющих собой
сумму некоторого числа других случайных ошибок, есть повод считать
распределение с. в. X нормальным согласно центральной предельной теореме.
В некоторых случаях строить гипотезу о виде распределения можно,
исходя из вида гистограммы или полигона частот.
При этом параметры выбранного распределения обычно выражаются
через первые выборочные моменты. Например, для равномерного
распределения, заданного на отрезке [а;Ь], числа а и b являются параметрами
распределения. Чтобы найти эти параметры, вычисляем выборочное
математическое ожидание и выборочную дисперсию: х и s2. Зная из теории,
что для равномерного распределения М(Х) = £—?, D(X) = ( ~'а' , и
приравнивая соответствующие теоретические и выборочные моменты,
получаем систему двух уравнений
г - а+ b
-2 = jb-af
^ 12 •
В этой системе х и s2 — конкретные числа, найденные из выборки, а
неизвестными являются а и Ь. Решая систему, и находим искомые
параметры а и Ь. Такой метод приравнивания выборочных и теоретических
моментов с целью нахождения параметров распределения называют обычно
методом моментов. Выборочных первых моментов требуется столько,
сколько параметров имеет соответствующее предполагаемое
распределение. В частности, для нормального распределения одной с. в. — два
момента, для показательного распределения — один момент, для
распределения х2 — один момент и т. д. Предпочтение обычно отдается
распределениям с числом параметров не более 3—4, так как в противном случае резко
ухудшается точность вычисления моментов, что в конечном итоге
обесценивает и результат.
Рассмотрим пример выравнивания статистического ряда.
Пример. Статистическое распределение по репрезентативной выборке
генеральной совокупности X задано в виде статистического ряда.
*,•
т,
со,-
1
2
0,01
2
6
0,03
3
14
0,07
4
28
0,14
5
46
0,23
6
44
0,22
7
32
0,16
8
17
0,085
9
8
0,04
10
3
0,015
^] =200
Z=1
Требуется выровнять данный статистический ряд с помощью
подходящего распределения.
Решение. Построим гистограмму относительных частот для
статистического ряда (4.13). Указанные значения будем считать серединами
интервалов.
181

0,2 -■
0.1
Рис. 35. Гистограмма относительных частот и выравнивающая кривая.
Исходя из вида гистограммы, сравнивая ее число визуально по форме с
кривой Гаусса, можно предположить, что г. с. X имеет нормальное
распределение.
Проведем выравнивание статистического ряда (4.13) с помощью
нормального закона с плотностью распределения вероятности
/(*) = 1
л/2яа
В этом распределении параметры т и а неизвестны, но т = М(Х),
а2 = D(X). Поэтому, согласно методу моментов, приравняем их к
соответствующим выборочным характеристикам.
Итак, вычисляем х и s2:
10 10 / 10 \
х = ^Х/О,-, s2 = ^(х,-х)2со, = ^х2со; -х2.
1=1 i= I i = 1
Тогда
m = x = 1 • 0, 01 + 2 • 0,03 + 3 • 0, 07 + 4 • 0,14 + 5 • 0, 23 +
+ 6 • 0, 22 + 7 • 0, 16 + 8 • 0,085 + 9 • 0,04 + 10 • 0,015 = 5, 62 ;
о2 = s2 = (1 • 0, 01 + 4 • 0, 03 + 9 • 0,07 + 16 • 0,14 + 25 • 0, 23 +
+ 36 • 0,22 + 49 • 0,16 + 64 • 0,085 + 81 -0,04+ 100 • 0,015)-
-(5, 62)2 = 3,1056;
о = J?* 1,7623.
Следовательно, формула для плотности распределения вероятности с. в.
X имеет вид
Ах) =
1
.2-3, 1056
Дп 1,7623
182

Вычислим значения этой функции в соответствующих точках заданного
статистического ряда:
*/
Л*,)
1
0,0073
2
0,0275
3
0,075
4
0,1484
5
0,2128
6
0,2212
7
0,1666
8
0,0909
9
0,036
10
0,0103
(4.14)
/О) = /(5, 62) =
1
0, 2264.
Jb. 1,7623
Далее, соединяя найденные точки плавной линией, получим
выравнивающую кривую для гистограммы распределения (см. кривую на рис. 35).
Замечание 1. В случае больших значений в выборке вычисление
математического ожидания можно упростить, используя свойства
математического ожидания. Случайную величину X можно представить как
X = Х1 + а, где в качестве постоянной а можно выбрать, например, одно из
выборочных значений (обычно из середины выборки). Тогда значения с. в.
XI будут меньше соответствующих значений X. Число М(ХХ) в результате
вычислить проще, а значение М(Х) оказывается равным М(ХХ) + а.
Замечание 2. Вычисления в данном примере проделаны чисто в
учебных целях. Разумеется, использование специальных компьютерных
программ позволяет значительно упростить все вычисления и, что самое
важное, использовать возможность выбора "наиболее подходящего"
распределения среди различных распределений, предлагаемых в программе.
4.7. Критерии согласия
Как мы видели в предыдущем параграфе, эмпирическое распределение
можно выровнять подбором некоторой теоретической кривой и чисто
визуально определить соответствие эмпирического распределения
теоретическому. Далее следует проверить нашу гипотезу о предполагаемом
теоретическом распределении более точными методами.
Методы проверки согласованности эмпирических данных с гипотезой о
предполагаемом законе распределения называют критериями согласия.
Критерии согласия призваны дать ответ на вопрос: отклонение
эмпирических данных от соответствующих теоретических вызвано случайными
обстоятельствами, например малым объемом выборки, или это
расхождение существенно, т. е. подобранная нами выравнивающая кривая
принципиально не соответствует истинной?
Следовательно, задача состоит в том, чтобы найти некоторые
характеристики выборочного распределения, соответствующие характеристикам
предполагаемого теоретического распределения, выявить различие
(которое желательно оценить численно) и, исходя из полученного результата,
сделать выводы о согласии этого теоретического распределения с
выборочными данными. От того, в каком виде рассматривается величина,
характеризующая различие эмпирического и теоретического распределений,
зависит и метод дальнейшего исследования. В соответствии с выбором этой
величины, называемой обычно критерием, имеется несколько критериев
согласия: Пирсона, Колмогорова, Смирнова и др.
183

Ограничимся подробным разбором критерия согласия Пирсона,
называемого также критерием хи-квадрат (х2).
В данном критерии в качестве характеристики распределений
используется функция распределения F{x), являющаяся общей характеристикой
для всех распределений — и дискретных, и непрерывных, в отличие,
например, от плотности распределения. Гипотезу о соответствии
эмпирического распределения предполагаемому теоретическому назовем нулевой
гипотезой Я0. Таким образом, Н0 — гипотеза, что генеральная
совокупность Х> из которой произведена выборка, имеет функцию распределения
F{x).
Далее для проверки соответствия необходимо выбрать критерий К,
величину, характеризующую различие (расхождение) между
рассматриваемыми распределениями, выборочным и теоретическим. В качестве К в
критерии согласия хи-квадрат выбирают сумму
y(jniZnp1l = x2 (415)
^ "Pi
i — 1
Данную сумму принято обозначать х2, поскольку эта величина является
случайной и, как можно доказать, имеет распределение х2 с {к — 1 - s)
степенями свободы, где s — число параметров теоретического распределения
(например, для нормального распределения s = 2, тогда число степеней
свободы х2 равно к — 3; для пуассоновского распределения s = 1 и,
следовательно, число степеней свободы (2 равно к — 2). В данной ситуации
число параметров s — число ограничений на распределение, которое
необходимо учитывать.
Поясним смысл значений, фигурирующих в (4.15):
п — число элементов выборки (объем выборки);
к — число групп (интервалов) разбиения выборки;
т{ — число значений выборки, попавших в i-й интервал (обычно это
число не должно быть меньше 5);
pt — теоретическая вероятность попадания значения с. в. 1в i-й
интервал, следовательно, npt— теоретическая частота попадания значений с. в. X
в /-й интервал в п испытаниях (вспомните, что пр — среднее число
осуществления событий в п испытаниях при биномиальном распределении).
Следовательно, разность m, - npiy записанная в (4.15), представляет
собой отклонение наблюдаемой частоты т, от теоретической npt. Во
избежание компенсации отклонений в положительную и отрицательную сторону
данная разность возведена в квадрат. Затем, чтобы учесть отклонения во
всех интервалах, полученные квадраты разностей необходимо
просуммировать по всем к интервалам. Сумма может оказаться очень большой, во
избежание чего каждое слагаемого можно предварительно уменьшить
пропорционально его вкладу в распределение, т. е., поделив каждый из
квадратов на npt.
В результате характеристика (4.15) представляет суммарное отклонение
частот и имеет известное нам распределение х2 (см. § 3.8), но при условии,
что наше предположение о теоретическом распределении, существенно
используемом при построении величины (4.15), истинно.
184

Как же проверить эту истинность? По таблице распределения х2 (см.
Приложение 2, табл. 4) всегда можно определить, какие значения и с
какими вероятностями может принимать случайная величина х2, имеющая
известное число степеней свободы.
У нас уже есть это значение х2, получаемое из формулы (4.15) по
результатам наблюдений. По данному значению в табл. 4 определяем
вероятность появления этого значения. Если найденная вероятность мала, а это
маловероятное событие все-таки произошло, т. е. повод усомнится в
справедливости наших предположений нулевой гипотезы. В противном случае
нет оснований отвергнуть нулевую гипотезу, и она принимается при
найденной вероятности. Вопрос, какую вероятность полагать малой, зависит
от сути рассматриваемой задачи, от эффекта принятия неверной гипотезы.
Обычно стандартный уровень отвержения нулевой гипотезы —
вероятность, меньшая чем 0,05. При вероятностях, больших 0,1, гипотеза обычно
принимается, а при вероятностях от 0,05 до 0,1 (сомнительный случай)
желательно повторение эксперимента, в результате которого гипотеза
отвергается более решительно.
Рассмотрим конкретный пример применения критерия согласия.
Пример. По данным примера § 4.6 проверить согласование
статистического распределения с нормальным.
Решение. Статистическое распределение задано таблицей (4.13)
*,■
щ
со,-
1
2
0,01
2
6
0,03
3
14
0,07
4
28
0,14
5
46
0,23
6
44
0,22
7
32
0,16
8
17
0,085
9
8
0,04,
10
3
0,015
£=200
I=1
Все выборочные значения необходимо разместить по интервалам,
например, как это сделано на рис. 35. Однако заметим, что в крайних
интервалах наблюдаемые частоты малы (т, = 2, т|0 = 3); обычно
предполагается, что все частоты т, должны быть, как правило, не менее 5, иначе это
может негативно повлиять на точность результата. Исходя из этого,
объединим крайние интервалы с соседними. Также заметим, что поскольку
нормальное распределение имеет значения в интервале (-°°, +°°), то
крайние интервалы можно раздвинуть влево и вправо до —со и +°о
соответственно, что может несколько улучшить результат. Итак, преобразуем
заданную таблицу к виду
№
Интервал
Щ
1
-°°; 2,5
8
2
2,5; 3,5
14
3
3,5; 4,5
28
4
4,5; 5,5
46
5
5,5; 6,5
44
6
6,5; 7,5
32
7
7,5; 8,5
17
8
8,5;+°°
11
Поскольку интервалы изменились, пронумеруем их.
185

Далее найдем теоретические вероятности попадания генеральной
совокупности X при X ~N(m;o) в соответствующие интервалы [ah bt] по
формуле
Л = Ф(^) -ф(^) ' "РИ ' = !• 2 8> (417)
где Ф(...) — функция Лапласа, а параметры т и а найдены ранее (см. §
4.6): т = 5,62, а = 1,7623.
Тогда
Рх = ф(2,15762362) " °* Ф(_1'77) = 1_ф(1'77) = 1-0,9616 = 0,0384;
А = «А 5 ~ 5> 621 - фГ2> 5 ~ 5> 621 * 0 0767-
А V 1,7623 J ^ 1,7623 ) ' '
Л = 0,146; р4 = 0,211; />5 = 0,2194;
/?б = 0,1662; р7 = 0,0907; рг = 0,0516.
Умножая каждую из полученных вероятностей /?, на п, где л = 200,
получим теоретические частоты.
Занесем эти частоты пр{ в таблицу частот
щ
"Pi
8
7,68
14
15,34
28
29,2
46
42,2
44
43,88
32
33,24
17
18,14
11
10,32
Далее, вычисляем наблюдаемое значение критерия х2 по формуле (4.15)
2= у(т,-пР1) ю0682>
i = 1
Так как всего 8 интервалов, нормальное распределение связано двумя
параметрами, то число степеней свободы св. х2 равно 8-1-2 = 5.
В табл. 4 приложения 2 при числе степеней свободы 5 и наблюдаемом
значении х2 = 0,682 ищем вероятность, с которой могло произойти это
событие. Это значение вероятности находится между 0,98 и 0,99.
Следовательно, соответствие эмпирических данных нормальному распределению
очень хорошее. Этот результат означает, что при повторении эксперимента
в среднем более чем в 98% случаев соответствие было бы худшим.
Замечание. Столь хорошее соответствие может навести на мысль, что
данные выборки были предварительно обработаны: например, удалены
резко выделяющиеся наблюдения.
Критерии согласия широко используются в статистических
исследованиях. Особенно удобно использование критериев с привлечением
компьютера, который берет на себя все вычислительные процедуры.
186

4.8. Практический пример применения критерия согласия
(закон Менделя)
Критерии согласия не обязательно играют вспомогательную роль для
дальнейших исследований. В некоторых вопросах они способны
выдвигаться на передний план проблемы. Блестящий пример применения
критерия согласия Колмогорова был продемонстрирован самим А. Н.
Колмогоровым в статье "Об одном новом подтверждении законов Менделя",
вышедшей в 1940 г.1 в разгар борьбы с генетикой, объявленной в Советском
Союзе последователями Т. Д. Лысенко лженаукой. Воспроизведем
изложение этой работы, следуя брошюре В. Н. Тутубалина2.
Законы, открытые монахом Грегором Иоганном Менделем в 1865 г. в
результате 8-летних опытов, являются одним из краеугольных камней
современной теории наследственности. Мендель проводил опыты по
гибридизации различных сортов гороха — с желтыми и зелеными семенами — и
обнаружил, что при таком скрещивании первое поколение гибридов все
имеет желтые семена, а в следующем, втором, поколении снова
появляются растения с зелеными семенами.
Признак, который проявляется в первом поколении (желтые семена)
Мендель назвал доминантным, а другой признак, который временно
исчезал до второго поколения (зеленые семена), он назвал рецессивным.
Тщательно посчитав число особей с желтыми и зелеными семенами (т. е. с
доминантным и рецессивным признаками), Мендель получил соотношение
6022 : 2001 «3,01 : 1.
Проведя еще параллельно шесть опытов относительно других свойств
гороха, в которых семена различаются по определенному свойству
(например, гладкие и морщинистые), Мендель вновь наблюдал в первом
поколении появление только одного из признаков (доминантного). Во втором
поколении соотношения доминантного и рецессивного признаков по шести
опытам получились следующие:
5474: 1850 «2,96: 1;
705 : 224 «3,15 : 1;
882 : 299 «2,95 : 1;
428 : 152 «2,82 : 1;
651 : 207 «3,14: 1;
787 : 277 «2,84: 1.
Как легко заметить, во всех случаях отношение доминантного и
рецессивного признаков близко к отношению 3:1, причем чем больше особей
участвует в опыте, тем точнее это отношение. Различные колебания около
указанного соотношения вызваны случайными причинами. Мендель
проследил проявление доминантного и рецессивного признаков и в
дальнейших поколениях гибридов, которые также подтвердили его теорию переда-
1 ДАН СССР, 1940, т. 27, №1, с. 38—42.
2 Тутубалин В. Н. Границы применимости (вероятностно-статистические методы и их
возможности). — М.: Знание, 1977. — 61 с. Также см. Тюрин Ю. Н., Макаров А. А. Анализ
данных на компьютере / Под ред. В. Э. Фигурнова. — М.: ИНФРА-М, Финансы и статистика,
1995. — 384 с.
187

чи различных свойств растений по наследству независимо друг от друга,
причем с вполне определенной закономерностью.
Работы Менделя намного опередили свое время. Лишь в 1900 г. его законы
были заново переоткрыты, а затем были найдены публикации Менделя с
описаниями этих законов. В начале XX века законы Менделя были объяснены и
обобщены, исходя из генетической теории наследственности. Однако в
Советском Союзе в 30—50-х годах генетика была объявлена буржуазной лженаукой,
занимающиеся ею ученые преследовались советским режимом, а официальная
биологическая школа, возглавляемая Т. Д. Лысенко, старалась показать, что
генетические законы, в частности законы Менделя, вообще не действуют. Так,
некто Н. И. Ермолаева, пытаясь опровергнуть законы Менделя (см. журнал
"Яровизация", 1939, 2(23), с.79—86), рассматривала гибриды второго
поколения не в совокупности, а по семействам — группам растений, выросших в
одном ящике из плодов одного растения первого поколения. При обработке
данных по отдельным "семействам" было обнаружено, что отношение числа
растений с сильным (доминантным) признаком к числу растений со слабым
(рецессивным) признаком от группы к группе достаточно заметно колеблется
и в точности никогда не совпадает с предсказанным Менделем отношением
3:1. На основании полученных наблюдений, чисто визуально, опираясь лишь
на свою интуицию, Н. И. Ермолаева и другие сторонники Т. Д. Лысенко
сделали вывод об опровержении законов Менделя1.
В своей работе А. Н. Колмогоров показал, что результаты опытов Н. И.
Ермолаевой можно объяснить как раз на основе простейшей модели
Менделя. Если для к семейств численностью nv n2, ..., пк числа проявления
рецессивного признака т{, т2, ..., тк, то из классической теоремы Муавра—
Лапласа следует, что случайные величины
т. — п.р
/я,. = ' 'S ,
Jn-,P4
1 Подобная методика "доказательства" или "опровержения" законов природы, когда самые
общие умозаключения основаны лишь на конкретном наблюдении, а переход от частного
наблюдения к глобальным выводам вместо доказательства (теоретической аргументации) обосновывается
лишь интуитивно, позволяет "доказать" практически любое, даже очевидно нелепое, утверждение.
Рассмотрим тривиальный пример: в двух испытаниях, заключающихся в подбрасывании монетки,
"герб" появился оба раза. Можно ли на основании этого опыта утверждать, что "герб" появляется
в любом испытании, и тем самым опровергнуть утверждение, что появление "герба" в одном
испытании имеет вероятность р — 0,5? Разумеется, можно, если руководствоваться лишь одним
созерцанием полученного факта и голой интуицией. Однако если к такой интуиции добавить еще
хотя бы частичку знаний по теории вероятностей и статистике, то никакого опровержения не
получится, а окажется, что данный факт появления двух "гербов" в двух испытаниях совершенно не
противоречит теории (т. е. вероятности появления "герба" в одном испытании р — 0,5), и в
среднем такой результат будет получаться в четвертой части всех опытов, и появление подобной
комбинации в единичном наблюдении из двух испытаний вовсе не удивительно.
То же опровержение объективно существующей вероятности р = 0,5 можно облечь в
более "наукообразную" форму, рассмотрев, например, выборку появлений "герба" и "монеты" в
20 испытаниях
ГМММ ГТМГ МГММ ГМГТ ММГМ
и, разбив ее на пять групп, в каждой из которых "герб" появляется либо один раз, либо три раза
во всех четверках испытаний и ни разу не появляется два раза из четырех. Так что же р * 0,5?
По существу подобную методологию использует и Н. И. Ермолаева, рассматривая всю
выборку по семействам. В данной ситуации выпячивается лишь голый факт и полностью
игнорируются законы статистики, которые этот факт могут объяснить. Малое количество
особей в рассматриваемых семействах и приводит к ощутимым (но вполне объяснимым)
отклонениям наблюдаемых значений от теоретических.
188

где р —вероятность осуществления искомого события в одном испытании
в серии испытаний, проводящихся по схеме Бернулли, q = 1 — р, имеют
приближенно нормальное распределение с параметрами (0;1). В данном
случае из-за соотношения Менделя 3:1 вероятность р равна -, а точность
результатов нормального приближения вполне достаточна при л, порядка
нескольких десятков. Следовательно, если модель Менделя верна, то т,*,
т2\ ..., тк*— выборка из генеральной совокупности, нормально
распределенной с параметрами (0;1).
А. Н. Колмогоров рассмотрел две наиболее многочисленные серии
опытов Н. И. Ермолаевой, которым соответствуют две выборки объемов: 98 и
123 элемента. Для проверки согласия между эмпирической и
теоретической функциями распределения в качестве критерия использовалась
статистика Колмогорова. При выполнении нулевой гипотезы о справедливости
законов Менделя вероятности получить такое же или большее
расхождение между выборочным и теоретическим распределением оказались равны
0,51 для первой выборки и 0,63 для второй выборки. Если сравнить эти
значения вероятностей со стандартными уровнями значимости а = 0,05
или а = 0,01, то совершенно очевидно, что эти вероятности существенно
больше и отвергать статистическую гипотезу, а вместе с нею и закон
Менделя, нет совершенно никаких оснований.
Тем самым применение статистического критерия позволило доказать,
что данные, визуально опровергающие закон Менделя, на самом деле этот
закон, наоборот, подтверждают.
Приведенный фактический пример показывает, сколь важно зачастую
бывает не только собрать данные, но и грамотно ими распорядиться.
Любые статистические наблюдения, даже на первый взгляд весьма
противоречивые, в руках специалиста открывают порой путь к истине.
4.9. Приближенная проверка гипотезы о нормальном распределении
Все используемые далее параметрические критерии проверки
статистических гипотез, как правило, предполагают, что рассматриваемые выборки
извлечены из нормальных генеральных совокупностей. Поэтому проверке
выборочных распределений на принадлежность к нормальному в
статистических исследованиях отводится особое место.
Вывод о нормальном распределении генеральной совокупности может
быть сделан из теоретических соображений (например, применимости
центральной предельной теоремы) или использовании для эмпирического
распределения критерия согласия. Однако наряду с этими методами существует
ряд "быстрых" приближенных методик проверки по выборке гипотезы о
нормальном распределении соответствующей генеральной совокупности.
Одним из таких приближенных методов является "правило трех сигм"
(см. § 2.11), согласно которому является практически несомненным, что
нормально распределенная случайная величина X в единичном испытании
попадает в интервал (т — За; т + За), где т = М(Х), а = JD(X). Точнее,
вероятность этого события приближенно равна 0,9973:
189

P(m - За < X< m + За) * 0,9973.
Используя данное соотношение не для одного испытания, а для п,
получим, что вероятность попадания св. Хв интервал (т — За; т + За) все п
раз при п независимых испытаниях равна
Л(я) = (0,9973)".
Эта вероятность достаточно велика при п < 20, например
Ло( Ю) * 0,973 ; Р19(19) * 0, 95 ; Ло(20)* 0,947 . Таким образом, если
генеральная совокупность X ~ N(m;o), то среди всевозможных выборок объема
л=19 будет 95%, содержащих лишь значения из интервала (т — За;
т + За). При одной выборке (единичном испытании) предполагается, что
это событие — практически достоверное. Вероятность события, равная
0,95^ считается стандартной (граничной) для таких случаев и является
своеобразным уровнем достоверности. Наличие в выборке объема п < 20
значений вне интервала (т — За; т + За) — веский повод усомниться в
нормальности распределения генеральной совокупности X.
Обратимся к данным примера в § 4.3, в котором задана выборка объема
п = 25 и вычислены числовые характеристики х = 2,84, s2 = 3,3344.
Полагая М(Х) и D(X) равными найденным эмпирическим характеристикам,
получаем соответствующий интервал для значений X (—2,638; 8,318). Как
видим, все выборочные значения принадлежат указанному интервалу,
следовательно, есть основание предполагать, что генеральная совокупность X
распределена нормально1.
Другой приближенный метод проверки гипотезы о нормальном
распределении основан на свойстве равенства нулю коэффициентов асимметрии
и эксцесса нормально распределенных случайных величин.
Приближенными значениями (оценками) коэффициентов асимметрии и эксцесса
генеральной совокупности X являются соответствующие эмпирические
характеристики у! и у2, найденные по выборке объема п. Понятно, что в силу
различных случайных причин значения у, и у2 окажутся, как правило,
отличными от нуля, даже если X имеет в точности нормальное
распределение. Наша задача — оценить найденные конкретные числа, т. е. указать, в
каком случае отклонение от нуля можно отнести на счет случайных
обстоятельств, и признать незначимым (тем самым подтвердить гипотезу о
нормальности распределения) или же констатировать, что получено
достаточно существенное отклонение, чтобы считать его случайным. В
последнем случае отклонение признается значимым и гипотеза о нормальном
распределении отвергается.
В качестве допустимых границ отклонения эмпирических
характеристик от нуля обычно используют средние квадратические отклонения, вы-
1 Заметим, что наша проверка приближенным методом вовсе не утверждает, что
случайная величина X действительно имеет нормальное распределение. Речь идет о том, что при
данной проверке гипотезы о нормальной распределенности X не найдено веских доводов
против этой гипотезы.
190

числяемые для у, и у2, интерпретируемых как случайные величины. Эти
значения вычисляются по формулам
-■■/orngbj- (418>
а,- I 24"<Г2)(""3) . (4.19)
где л — объем выборки. Таким образом, если найденное значение у,
принадлежит интервалу (—оас; аос), то можно считать, что теоретическая
величина у, = 0; если значение у2 принадлежит интервалу (~o3K; оэк), то можно
считать, что у2 = 0. Равенство нулю коэффициентов асимметрии и
эксцесса у, и у2 подтверждает справедливость гипотезы о нормальном
распределении X, а отличие от нуля у,, у2 высказанную гипотезу опровергает.
Обратимся вновь к примеру § 4.3, в котором по выборке объема
п = 25 были вычислены коэффициенты асимметрии у, = 0,7103 и
эксцесса у2= 0,6238. Найдем
= 6(25-1)
ас V(25+l)(25 + 3) ' Э'
а.- /24- 25(25-2)(25-ЗТю0>792
V(25-l)2(25 + 3)(25 + 5)
Поскольку коэффициент асимметрии у, не укладывается в рамки
интервала (—аос; а^), то гипотеза о нормальном распределении X считается
опровергнутой: распределение слишком асимметрично, чтобы быть нормальным.
Задачи и упражнения
1. Абитуриент на вступительном экзамене может получить любое число
баллов — от 0 до 20. В результате наблюдений над группой из 40
абитуриентов получены следующие значения баллов:
16, 10, 12, 8, 15, 11, 17, 13, 12, 19, 16, 2, 19, 11, 14, 13, 17, 20, 19, 5, 14,
18, 9, 15, И, 17, 19, 10, 16, 14, 17, 19, 15, 13, 20, 12, 18, 14, 16, И.
Записать эти данные в виде: а) вариационного ряда; б) статистического
ряда. Что в данном примере подразумевается под генеральной
совокупностью?
2. Выборка записана в виде статистического ряда
X:
1 5 10
т:
8 10
Найти эмпирическую функцию распределения этой выборки.
Построить график.
191

3. Все значения выборки объема п = 100 записаны как представители
соответствующего интервала
Границы интервала
Частота попадания
в интервал
0-4
10
4-8
15
8-12
20
12-16
25
16-20
20
20-24
10
Yj= n = 100
Построить: а) гистограмму частот; б) гистограмму относительных
частот.
4. При исследовании отрицательного времени при пробе на остроту
зрения на 12 учениках в возрасте 10 лет были получены следующие
результаты отрицательного времени в секундах.
78, 63, 82, 92, 73, 66, 67, 60, 94, 78, 53, 70.
Найти среднее значение отрицательного времени, исходя из данной
выборки значений.
Ответ: х = 73 с.
5. Из генеральной совокупности X извлечена выборка объема п = 80:
*,■
mi
5
12
10
24
20
30
25
14
Найти выборочное значение х и выборочную дисперсию ?.
Ответ: х~= 15,625; 72 « 48,98.
6. Из генеральной совокупности X извлечена выборка объема п = 60:
*,■
щ
1 2 3
10 30 20
Найти начальные и центральные выборочные моменты до четвертого
порядка включительно. Вычислить выборочные коэффициенты
асимметрии и эксцесса.
7. По данным задачи 1 найти моду и медиану выбор_ки. _ _
8. По данным задачи 1 найти квантили х025; х04; х05; х075; х095
выборочного распределения. Можно ли точно и однозначно определить эти
характеристики?
9. По данным задачи 4 преобразовать выборку в выборку с четырьмя
равноотстоящими вариантами. Вычислить выборочную дисперсию с
поправкой Шеппарда. Объясните, чем вызвано в данной ситуации
расхождение значений выборочной дисперсии со случаем исходных данных.
10. Выборка объема п = 200 из генеральной совокупности X
представлена в виде статистического ряда
*,
щ
0,3
6
0,5
9
0,7
26
0,9
25
1,1
30
1,3
26
1,5
21
1,7
24
1,9
20
2,1
8
2,3
5
Проверить гипотезу о нормальном распределении генеральной
совокупности Хс помощью коэффициентов асимметрии и эксцесса.
Указание. Вычислить коэффициенты у, и у2 и проверить значимость их
отклонения от нуля.
192

11. По данным задачи 10, используя критерий х2> при уровне
значимости а = 0,05 проверить, согласуются ли выборочные данные с гипотезой о
нормальном распределении генеральной совокупности X.
Ответ: xlP = х\0,05; 8) = 15,51; хна6л* 7, 71. Так как xL* < xlP, то нет
оснований отвергнуть гипотезу о нормальном распределении генеральной
совокупности X.
12. Из генеральной совокупности X извлечена выборка объема п = 130,
все значения которой объединены в накрывающие их интервалы:
Границы интервала
Частота т,
3,0-3,6
2
3,6-4,2
8
4,2-4,8
35
4,8-5,4
43
5,4-6,0
22
6,0-6,6
15
6,6-7,2
5
Е=13°
При уровне значимости а = 0,05, используя критерий согласия х2.
проверить гипотезу о нормальном распределении генеральной совокупности
X.
Ответ: Х1Р = хФ, 05; 4) = 9,49; xL* = 6, 22. Так как XL, < xlP, то нет
оснований отвергнуть гипотезу о нормальном распределении генеральной
совокупности X.
13. С помощью критерия согласия х2 проверить гипотезу о том, что
генеральная совокупность X — число долихоцефалов среди 10 наудачу
отобранных жителей Болгарии1 — имеет биномиальное распределение с
параметром р = 0,2. Выборка наблюдаемых значений имеет вид:
*,
щ
0 12 3 4 5
9 27 32 22 7 3
Yj= n = 100
Здесь п = 100 — это число опытов по отбору десяти жителей, каждая
такая группа из 10 человек выдает одно значение случайной величины X.
Таким образом, обследовано 1000 человек и получена выборка объема
п = 100.
Указание. Критерием, служащим для проверки гипотезы о
биномиальном распределении, так же как и в случае гипотезы о нормальном
распределении, является случайная величина
2 = у (т, - при1
L npt
(суммирование ведется по всем группам наблюдений, т. е. от 0 до 5), но в
отличие от нормального закона в данном случае, гипотезы о
биномиальном распределении, вероятности вычисляются по формуле Бернулли:
р0 = С010(0,2)\0,Ъ)1\Р1 = С!00,2(0,8)9,..., р5 = С\0(0, 2)5(0, 8)5.
Поскольку значение вероятности р = 0,2 задано (а не найдено по
выборке), то число степеней свободы критерия х2 равно 6—1, где 6 — число
групп наблюдений [если бы вероятность р была найдена по выборке, то
число степеней свободы равно (6 — 2)].
1 См. гл. 2, Задачи и упражнения, задача 20.
13 — 3529 193

Ответ: нет оснований отвергнуть гипотезу о биномиальном
распределении генеральной совокупности X.
14. Бросая монету п = 4040 раз, Бюффон получил тх = 2048 появлений
"герба" и т2 = 1992 появлений "монеты". Проверить по критерию х2
совместимость этих данных с гипотезой о вероятности появления "герба"
р = k(T. е., что монета была правильной). Уровень значимости а принять
равным 0,05.
Указание. Введем случайную величину X, которой при появлении
"герба" ставим в соответствие 1, а при появлении "монеты" — 0. Поскольку
вероятность появления "герба" в одном испытании постоянна и равна /?, то
распределение X является распределением Бернулли с параметром р.
Именно эту гипотезу о распределении Бернулли с параметром р = - для
случайной величины X необходимо проверить. В нашем случае X — это
генеральная совокупность, из которой Бюффон извлек свои наблюдаемые
значения. Следовательно, имеется выборка
*,•
щ
0 1
2048 1992
£= п = 2040
В качестве критерия используется величина
2 = у (т, - npif = (тх - прУ + (т2 - пд)2
2-t np np nq
Ответ: хнабД = 0,776, xlP = Х2(0>51;1) = 3,8. Данные Бюффона
совместимы с гипотезой о правильности монеты, т. е. р = -.
15. Аналогично задаче 14 проверить гипотезу о вероятности появления
"герба" р = - по данным опыта Романовского (см. § 1.10): количество
испытаний п = 80 640, частота появления "герба" тх = 39 699, частота
появления "монеты" т2 = 40 941.
16. 'Данные статистика В. Борткевича о случаях смерти солдат в
прусской армии от удара копытом коня приведены в таблице.
Число случаев в корпусе за год, xt
Количество корпусов с данным числом
случаев, т{
0
109
1
65
2
22
3
3
4
1
1=200
Полагая в качестве генеральной совокупности X число погибших
солдат, по указанной выборке объема п = 200 с помощью критерия х2
проверить гипотезу о распределении X по закону Пуассона.
1 См. гл. 2, Задачи и упражнения, задача 21.
194

Указание. По выборке вычислить х и принять в распределении
Пуассона а = х.
В качестве критерия проверки гипотезы использовать случайную
величину
2 _ sp(mi-npi)2
*=Г
пр
где pi вычисляются как пуассоновские вероятности:
о
_ а -а _ а -а
Ро ~ О!6 ' Рх ~ Vе ' •-
Число степеней свободы х2 равно s — 2, где s — число групп
наблюдений (в нашем случае s = 5 ', т. е. число степеней свободы равно 3).
Ответ: а = 0,61; хиа6д = 0,32; хкрф, 05;3) = 7,82; гипотезу о пуассонов-
ском распределении X можно принять (нет оснований отвергнуть).
17. Проведена анкета о числе абортов у 1000 замужних женщин
20-летнего возраста, и получены следующие результаты2:
0 1 2 3 4 >4
т,
610 300 75 10 5 0
1=» =
=п = 1000
где х,- — число абортов, mi — количество женщин с соответствующим
числом абортов. По критерию х2 при а = 0,05 проверить соответствие
распределения генеральной совокупности X — число абортов — распределению
Пуассона со средним а = 0,5.
Замечание. Значение а = 0,5 получено из соотношения а = М(Х),
М(Х) « х, х = -±- (0 • 610 + 1 • 300 + 2 • 75 + 3 • 10 + 4 • 5) = 0,5.
Ответ: гипотезу о пуассоновском распределении X можно принять.
18. Как и в опыте Менделя, наблюдали за доминантным и рецессивным
признаками у семян гороха. Наблюдаемые 10 растений, у которых
фиксировалось количество гладких (х,) и количество морщинистых (у,) горошин,
привели к двум выборкам относительно этих признаков
*,■
У,
28
7
20
11
25
6
21
10
24
6
43
11
24
7
30
8
72
20
45
12
С помощью критерия х2 проверьте соответствие полученных данных
ожидаемому соотношению 3:1.
1 Малочисленные группы наблюдений можно объединить; например, в нашем случае
вместо двух последних групп может быть группа со значением х, > 3, тогда соответствующая
частота равна 3+1.
2 Данные из книги: Сепетлиев Д. А. Статистические методы в научных и медицинских
исследованиях. — М.: Медицина, 1968.
13*

Глава V. ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
5.1. Особенности малых выборок. Точечные оценки
Как показано в предыдущей главе, обладая большим количеством
выборочных данных (порядка сотен), можно определить выборочные
характеристики, достаточно точно соответствующие теоретическим, и с
определенной долей уверенности возможно подобрать наиболее подходящее
распределение. Таким образом, с большой вероятностью мы располагаем
информацией о всей генеральной совокупности, и эту почти точную
информацию можем использовать для изучения конкретных процессов и
явлений, а также для различного рода вероятностных прогнозов.
Совсем иная ситуация возникает в случае малых выборок, когда
количество наблюдений представлено не сотнями, а ограничено буквально
одним—тремя десятками. Это может быть связано с технической сложностью
постановки эксперимента или большими финансовыми затратами. Но так
или иначе по столь малому количеству информации невозможно с
достаточной степенью уверенности определить исчерпывающую характеристику
случайной величины — закон распределения. Однако во многих задачах о
виде закона распределения можно судить, исходя из каких-либо
теоретических соображений. Например, применимость к случайной величине
центральной предельной теоремы выводит исследователя на нормальный
закон распределения; условие равновозможности всех значений случайной
величины на некотором интервале влечет использование гипотезы о
равномерном распределении; схема Бернулли может указывать на
биномиальное или пуассоновское распределения; сумма квадратов независимых
нормально распределенных случайных величин с параметрами т = 0, о = 1
согласуется в распределением х2 и т. д. Также имеются многочисленные
задачи, в которых вид закона распределения вероятностей вообще
несуществен. И в тех и других задачах оказывается необходимым определить
лишь параметры распределения или числовые характеристики.
Определяемые параметры и их количество индивидуальны для каждого закона
распределения; например, при нормальном законе — это математическое
ожидание и дисперсия; для распределения Пуассона — это математическое
ожидание; при равномерном распределении — значения на концах
интервала и т. д. Как правило, все используемые параметры либо сами являются
моментами рассматриваемой случайной величины, либо могут быть
выражены через моменты с помощью математических операций. В подобных
задачах определения и исследования параметров распределения возможно
обойтись информацией, извлекаемой и из выборки небольшого объема.
В предлагаемой главе рассмотрим такого рода задачи определения
параметров.
Пусть Х{, Х2, ..., Хп — репрезентативная выборка из генеральной
совокупности X. Напомним, что, согласно определению, последовательность
196

X{, X2, ..., Xn понимается как система независимых случайных величин,
распределенных так же, как и с. в. X. Отметим, что любую функцию от
выборочных значений Х{, Х2, ..., Хп обычно называют статистикой. Находя
выборочные характеристики распределения на основе наблюдаемых
значений случайных величин Xv Х2, ..., Хп (см. § 4.3), мы неизбежно получаем не
точные, а лишь приближенные значения параметров, различные для
различных конкретных выборок. Хотя выборки извлекаются из одной и той
же генеральной совокупности X, значения, принимаемые случайными
величинами Xv Х2, ..., Хп в каждом наблюдении, вообще говоря, отличны
одно от другого, поэтому и находимые по выборке параметры оказываются
численно различными. Следовательно, генеральная совокупность X как
случайная величина, объективно имеющая некоторое распределение (пусть
и неизвестное нам), характеризуется конкретными параметрами
[например, М(Х) = О, D(X) = 3,6 и т. д.]. Находимые по выборке значения
параметров отличаются от истинных, поскольку в каждом случае зависят от
случайных значений, принимаемых Xv Х2, ..., Хп.
Обозначим точное значение исследуемого параметра генеральной
совокупности X посредством 0. Любое приближенное значение этого
параметра, находимое по выборке Х{, Х2, ..., Хп, назовем оценкой 0 и обозначим 0.
Отметим, что величина зависит от Х{, Х2, ..., Хп, точнее, является функцией
этих случайных величин (т. е. статистикой)
0 = ©(*„ Х2, ..., Хп),
а следовательно, и сама оценка 0— случайная величина, закон
распределения которой продиктован законом распределения Хх, Х2, ..., Хп и видом
зависимости оценки от указанных случайных величин. Также особо
подчеркнем, что распределение оценки 0 существенно зависит от объема
выборки п.
Для параметра 0 генеральной совокупности X по выборке Xlt Х2, ..., Хп
приближенное значение можно определять самыми разными путями.
Например, в качестве оценки среднего значения [0 = М(Х)] допустимо
использовать не только среднее арифметическое выборки
X=l-fxk, (5.1)
k= 1
но и другие зависимости от с. в. Хь Хъ ..., Хп, приводящие к
приближенным значениям 0:
1) среднее геометрическое (для положительных с. в.)
2) медиана статистического ряда;
3) середина интервала наблюдаемых значений =(xmtH + хтах) и т. д.
Отметим, что для симметричных распределений при достаточно
больших л среднее арифметическое, среднее геометрическое, медиана и мода
197

почти совпадают или совпадают, для асимметричных распределений
расхождение может оказаться существенным.
Таким образом, оценку 0 параметра 0, характеризующего генеральную
совокупность, можно определять самыми разными соотношениями.
Однако из всего множества оценок хотелось бы пользоваться наилучшей.
Прежде всего отметим, что оценки подразделяются на точечные и
интервальные. Точечные оценки представляют собой одно значение,
приближенно равное оцениваемому параметру 0. Интервальные оценки
характеризуются двумя значениями, концами интервала, в котором с
определенной долей уверенности (т. е. с вероятностью, близкой к 1) содержится
параметр 0. К интервальным оценкам мы обратимся в последующих
параграфах, а сейчас отметим, что все рассматриваемые нами ранее оценки
являются точечными.
Итак, среди точечных оценок наилучшими считаются оценки
несмещенные, состоятельные и эффективные.
Определение. Статистика 0, найденная по репрезентативной выборке
Xv Х2, ..., Хп, называется несмещенной оценкой параметра 0 генеральной
совокупности X, если
Л/(0) = 0. (5.2)
Несмещенность оценки означает, что при использовании вместо
параметра 0 его оценки 0 мы не допускаем систематических ошибок, т. е.
ошибок одного знака в сторону завышения или занижения истинного
значения, а неизбежно возникающие ошибки при разных конкретных
выборках в сумме взаимно компенсируются. Требование несмещенности оценок
особенно существенно при малых выборках.
Определение. Оценка 0, найденная по репрезентативной выборке Х{,
Х2, ..., Хп, называется состоятельной оценкой параметра 0 генеральной
совокупности X, если эта оценка с ростом п сходится по вероятности к
оцениваемому параметру:
ИтР(|0„-0|<е) = 1 (5.3)
Л -> XI
для любого сколь угодно малого положительного числа е.
Поясним смысл введенного понятия. Прежде всего отметим, что оценка
обозначена 0„ вместо 0 с целью подчеркнуть ее зависимость от числа п,
используемую в данном определении. Соотношение (5.3) означает, что с
ростом п подавляющее большинство значений оценки 0„ отличается от 0
(напомним, что параметр 0 — число) менее чем на число е.
Следовательно, при возрастании п значения состоятельной оценки 0„,
взятые в различных конкретных выборках, имеют тенденцию
концентрироваться около числа 0 и тем теснее, чем больше п. А это означает, что
198

при п -> оо разброс значений оценки 0„ относительно 0 должен
неограниченно уменьшаться, т. е.
£(©„)-> 0. (5.4)
Определение. Оценка 0, найденная по репрезентативной выборке Хи
Хъ ..., Хп называется эффективной оценкой параметра 0 генеральной
совокупности X, если она обладает наименьшей дисперсией по сравнению с
дисперсиями других оценок, составленных по той же репрезентативной
выборке Xlt Хъ ..., Хп.
Эффективность оценки 0 означает, что при одном и том же объеме
выборки п оценка 0 обладает наименьшим разбросом своих возможных
значений, получающихся в каждом конкретном случае, сравнительно со
всеми другими оценками рассматриваемого параметра 0, т. е. при каждом
фиксированном п значения эффективной оценки 0 оказываются наиболее
сконцентрированными вокруг 0.
Эффективность или неэффективность оценки — свойство более
сложное, нежели несмещенность или состоятельность, потому как это свойство
зависит не только от вида статистики 0, являющейся оценкой параметра
0 генеральной совокупности X, но и от закона распределения X
(напомним, что при репрезентативности выборки все с. в. Xv X2, ..., Хп имеют то
же распределение, что и Л). Оценка, эффективная при одном
распределении X, может вовсе не оказаться таковой для другого распределения
генеральной совокупности X.
Заметим, что в практических задачах не всегда возможно подобрать
оценку, наилучшую во всех отношениях, поэтому допустимо
использование незначительно смещенных оценок или оценок, не являющихся
эффективными в строгом смысле. Понятно, что применение таких не очень
"доброкачественных" оценок может повлиять на статистические выводы.
Следовательно, прежде чем использовать конкретные оценки для
рассматриваемой задачи, необходимо взвесить как позитивные (например,
простота вычислений), так и негативные последствия (возможность появления
ошибочных результатов). Особенно внимательно нужно относиться к
выбору оценок в случае малых выборок.
5.2. Точечные оценки для математического ожидания и дисперсии
Пусть генеральная совокупность X является случайной величиной,
имеющей математическое ожидание М(Х) = т и дисперсию D(X) = о2. Из
г. с. ^извлекается репрезентативная выборка Xv X2, ..., Хп. Исходя из
выборки, исследуем оценки параметров т и о2.
Рассмотрим статистику X как оценку математического ожидания
т = М(Х). Таким образом, в данной ситуации оцениваемым параметром
0 является число М(Х), т. е. 0 = М(Х) = т, а в качестве оценки 0 этого
параметра берется статистика X, т. е.
199

0 = х= ±ухк.
k = 1 _
Проверим оценку X на несмещенность. В соответствии с определением
несмещенности оценки должно быть выполнено равенство (5.2)
Л/(0) = 0, т. е.
М(Х) = М(Х). (5.5)
Воспользуемся свойством линейности математического ожидания (см.
§ 3.4), и тогда
М(Х) = mU^XA = \^М(Хк). (5.6)
Далее используем определение репрезентативности выборки, согласно
которому все с. в. выборки Хх, Х2, ..., Хп распределены одинаково с
генеральной совокупностью X, а значит, имеют все свои параметры точно
такие же, как и соответствующие параметры X, в частности
М(Хк) = М(Х), при к = 1, 2, ..., п. (5.7)
Продолжая далее равенство (5.6), приходим к (5.5):
М(Х) = !]ГЛ/№) = ~(М(Х) + М(Х) + ... + М(Х))=
^-'т —-1
к= 1
= -пМ(Х) = М(Х) = 0.
п
Тем самым доказано утверждение:
Оценка X, составленная по репрезентативной выборке Хх, Х2, ..., Хп
генеральной совокупности X, является несмещенной оценкой М(Х).
Из доказанного утверждения следует еще один важный факт: найдено
математическое ожидание статистики X:
М(Х) = М(Х). _
Далее вычислим D(X), аналогично используя свойства дисперсии (см. §
3.4) и репрезентативность выборки.
*^ ■ 4й*) ■ Hj4
Так как Хх, Х2, ..., Хп — независимые с. в. (согласно определению
репрезентативности выборки), то
V4 - 1
D(X) = -2^D(Xk)
п *-i
А так как распределены с. в. Х{, Х2, ..., Хп одинаково с г. с. X, то
D(Xk) = D(X), при к = 1, 2, ..., п, (5.8)
и, следовательно,
200

л
D(X) = -2YD(Xk) = \(D(X) + D(X) + ... + D(X))=
"*=, n
= l7nD(X) = Ш1.
n2 "
Таким образом, получено соотношение
D(X) = 2& , (5.9)
в котором указана простая зависимость дисперсии выборочного среднего X
и дисперсии генеральной совокупности X.
Из равенства (5.9) вытекает, что с ростом числа наблюдений_л,
произведенных над генеральной совокупностью X, дисперсия оценки X убывает, и
при п -> оо следует D(X) -> 0. Сопоставляя этот факт с (5.4), делаем вывод
о том, что оценка X математического ожидания генеральной совокупности
X— состоятельная оценка.
Итак, оценка доказывается несмещенной и состоятельной оценкой
параметра 0 = М(Х) независимо от распределения г. с. X. Но эффективной
данная оценка при произвольном распределении X не является. Как было
отмечено в предыдущем параграфе, эффективность оценок зависит от
закона распределения г. с. X. Без доказательства примем утверждение, что
оценка X, составленная по репрезентативной выборке Хх> X2, ..., Хп из
генеральной совокупности X, распределенной по_нормальному закону,
является оценкой, эффективной для М(Х). Также Сбудет эффективной оценкой
М(Х) в случае пуассоновского распределения г. с. X.
Далее займемся оценками дисперсии г. с. X, т. е. полагаем оцениваемый
параметр 0 = D(X).
Поскольку по определению дисперсии D(X) = М(Х - М(Х))2, и для
оценки М(Х) удобно выбрать статистику X, то вполне естественно в
качестве оценки дисперсии по выборке объема п использовать дисперсию
л
S2 = 1у(*,-лУ, (5.10)
i= l
соответствующей выборочной дисперсии (4.7). В формуле (5.10) в отличие
от (4.7) речь идет не о численном значении выборочной дисперсии S2, а о
случайной величине S2(S2— функция случайных величин выборки Xv X2,
..., Х„), что и отражено в соответствующих обозначениях: случайные
величины обозначаются прописными буквами, например X, Хь S, а
соответствующие значения — строчными буквами, например х, х,., s.
Отметим двойственность величины S2, которая, с одной стороны в
качестве оценки дисперсии г. с. Охарактеризует эту дисперсию и для каждой
конкретной выборки имеет численное значение s2, а с другой — сама
является случайной величиной, для которой можно найти и математическое
ожидание, и дисперсию, и другие численные характеристики.
201

Также укажем на справедливость формулы
?-sI*4;M =)ZX]-X*- (5ll)
i = 1 » = 1 »= 1
являющейся аналогом формулы для вычисления дисперсии [см. § 2.3,
соотношение (2.13)]
D(X) = М(Х2) - М\Х). (5.12)
Проверим оценку S2 на несмещенность, т. е. ответим на вопрос:
выполнено ли соотношение (5.2), которое при 0 = D(X), 0 = S принимает вид
M(S2) = DiX)?
Согласно (5.11) и свойству линейности математического ожидания,
запишем
Mis1) = ^тхЬ-Ы^х) = !£*(*?)-±a^£a?+;£i;a;) ,
»= 1 i=l «= 1 «' = 1 l*J
где в последней сумме фигурируют все возможные произведения XtX} при
/, у, изменяющихся от 1 до л и не равных между собой (эти произведения
вида Х,Х, вошли в предыдущую сумму).
Далее, еще раз воспользуемся линейностью математического ожидания
и репрезентативностью выборки (см. определение репрезентативности в
§ 4.2, согласно которому из одинаковой распределенности с. в. Xv X2, ..., Хп
и г. с. X следует, что все параметры их распределений совпадают, в
частности М(Х2) = М(Х2), M(Xj) = M(X), а из независимости случайных
величин следует, что M(X;Xj) = Л/(Л0 • M(Xj), см. § 3.5, замечание). Тогда
л л
M(S2) = ly MX2 - \У M(X2)-\YM(X)M(X),
nLu «2Zj n2bi
<•= i <•= i i*j
и поскольку под знаком каждой из сумм находятся постоянные слагаемые,
то, учитывая количество слагаемых, получаем
M(S2) = ^пМ(Х2)--пМ(Х2)--п(п-\)М2(Х) =
п п п
= й^±М(Х2)-^^-М2(Х) = ^^-(М(Х2)-М2(Х)).
п п п
Используя (5.12), окончательно находим
M(S2) = !L^±D(X). (5.13)
п
Таким образом, равенство для несмещенности оценки S2 не выполнено,
фактически величина M(S2) оказывается несколько меньше оцениваемого
параметра D(X), и оценка S2— смещенная относительно D(X).
202

Данный недостаток поправим: чтобы получить несмещенную оценку
дисперсии, нашу оценку S2 необходимо исправить, умножив ее на
компенсирующий сомножитель п , :
п — 1
л
S2 = -?—S2 = —{— У(Х{- Х)\ (5.14)
Эту оценку S2 будем называть в отличие от S2 исправленной
выборочной дисперсией (см. разницу в обозначениях), и она является
несмещенной оценкой D(X):
M(S2) = D(X). (5.15)
Следует отметить, что сомножитель п t , связывающий оценки S2 и
п — 1
£2, с ростом п стремится к 1, так что при больших п разница между S2 и
S2 практически несущественна, чего нельзя сказать в случае малых
выборок (обычно при п < 30).
Можно доказать, что дисперсия оценки S2 выражается через четвертый
и второй центральные моменты г. с. Zno формуле
D(S2) = 1ц4--р1-ц2, (5.16)
п п(п— 1)
где, конечно же, ц2 = D(X).
Сравнивая (5.16) с условием состоятельности оценок (5.4), получаем,
что так как D(S2)-+Q с ростом п, то оценка S2 является состоятельной
оценкой D(X). Также очевидно, что и выборочная оценка S2,
отличающаяся от S2 сомножителем - , стремящимся к 1 с ростом л, оказывается
состоятельной оценкой D(X).
В случае нормального распределения г. с. X эффективной оценкой
дисперсии является оценка S2.
Оценками среднеквадратического отклонения JD(X) служат
статистики s = J¥ и s = Js*.
Замечание. Все оценки, получаемые с помощью метода моментов, о
котором шла речь в § 4.6, являются состоятельными оценками
соответствующих параметров генеральной совокупности. В частности, свойством
состоятельности обладают все выборочные моменты: начальные ак и
центральные Цк [см. (4.9)].
5.3. Распределения некоторых статистик
Как было определено ранее, статистиками мы называем функции от
выборочных значений Хи Х2, ..., Хп. Таким образом, статистики сами
являются случайными величинами и, вполне естественно, имеют свои
распределения. Для исследования генеральной совокупности X по выборке ис-
203

пользуются статистики определенного вида, например^ выборочные
моменты или некоторые функции от этих моментов, знание законов
распределения которых часто оказывается решающим звеном в решении
поставленной задачи.
Особую роль играет нормальное распределение, ибо в соответствии с
центральной предельной теоремой многие случайные величины
оказываются нормальными или приближенно нормальными. Например, считается,
что статистика X, являющаяся суммой п случайных величин распределена
приближенно нормально, и соответствие тем лучше, чем больше п. Также
если случайные величины представляют собой средние в группах
наблюдений, т. е. основания считать, что они нормально распределенные.
Рассмотрим распределения некоторых функций от выборочных с. в. Хх,
Х2, ..., Хп в "идеальном случае", случае, когда Xv X2, ..., Хп —
репрезентативная выборка нормально распределенной генеральной совокупности Хс
параметрами т и а, т. е. все с. в. Хх, Х2, ..., Хп независимы, и все Хк~ N(m;o).
Утверждение 1. Статистика
х= 1-ухк
к= 1
распределена нормально с параметрами т и -^ .
Нормальное распределение статистики X следует из ее структуры
(сумма нормальных случайных величин, умноженная на постоянную -), заме-
п
чания в § 3.7 относительно распределения суммы и примера в § 3.7,
доказывающего, что линейная функция от нормально распределенной с. в.
сама является нормальной с. в. (в нашем случае линейная функция — это
сумма, умноженная на постоянную -).
п
Параметры с. в. X вычислены в предыдущем параграфе: М(Х) = т,
дХ)=°_ [см. (5.5) и (5.9)]. Напомним, что т = М(Х), o = jD(X),
тогда -^ = JD(X) — среднее квадратическое отклонение для X.
Утверждение 2. Статистика
Г=^р (5.17)
является нормально распределенной с. в. с параметрами 0 и 1, т. е. Y~N
(0;1).
Действительно, как только что было доказано, X имеет нормальное
распределение с параметрами т и -^. Случайная величина Y, являющаяся
л/Л
линейной функцией нормальной с. в. X, согласно примеру в § 3.7, тоже
нормальна. Значения параметров 0 и 1 вычисляются непосредственно:
204

м(Х—™) = JuM(X-m) = ^М(Х-М(Х)) = О,
4 o/JnJ <* ст
поскольку первый центральный момент всегда равен 0 [см. § 2.3,
равенство (2.10)];
I&1M) = Л/f^-oV = (Щ'мСХ-т)1 = Ип(Х) = ^ = 1.
Va/7^; W-Л ; V°J о2 о2п
Утверждение 3. Если S2 — исправленная выборочная дисперсия вида
(5.15), а2 = D(X) — дисперсия генеральной совокупности, то статистика
X2 = ^-F"2 (5-18)
a
имеет распределение х2 с (п — 1) степенями свободы. Напомним, что п —
объем выборки.
Подробное доказательство здесь не воспроизводим, а лишь отметим,
что структура величины х2 вида (5.18) — это сумма квадратов нормально
распределенных случайных величин:
х2 = ^Ч^-2 = -^-У(Хк-1)2 = У(^)\
°2c-ive, & ° '
что соответствует распределению х2, рассмотренному в § 3.8.
Утверждение 4. Если S2— исправленная выборочная дисперсия вида
(5.15), т = М(Х), то статистика
TH-X = j£^ (5.19)
имеет распределение Стьюдента с (п - 1) степенями свободы.
Структура случайной величины, распределенной по закону Стьюдента с
(п — 1) степенями свободы, указана в § 3.8, см. (3.58). Преобразуем нашу
с. в. вида (5.19) следующим образом:
fEEl Х-т
г — гХ—т _ г-Х—т N о2 _ г о / г
Тп-Х = 4п—— - 4п—=- ■ \ = Jn =Jn- l.
Js2 JS2 rrz± IS2(n-\)
2 i i
О A/ a2
у fn
Поскольку с. в. — (обозначим ее У) имеет нормальное распределе-
o/Jn
ние с параметрами 0 и 1, а с. в. ^—^- имеет распределение х2с (п - 1)
a
степенями свободы (см. утверждение 3), то оказывается, что в случае
независимости св. У и х2 случайная величина
Тп.х = -j=Jn=\
J?
как раз соответствует распределению Стьюдента с (п — 1) степенями
свободы, введенному в § 3.8. Условие независимости статистик Y и х2 имеет
205

место для нормальной г. с. X (принимаем без доказательства), и тогда
утверждение 4 доказано.
Утверждение 5. Пусть имеются две выборки объемов пх и п2
соответственно из нормальной генеральное совокупности X. Обозначим
соответствующие выборочные средние Хх, Х2, а исправленные выборочные
дисперсии — S] и 1У2. Тогда статистика
ТП1+П1.2 = Хх~Х\ (5-20)
п\ п2
имеет распределение Стьюдента с пх + п2 — 2 степенями свободы.
Отметим, что индекс у с. в. T„l + nj-2 соответствует числу степеней
свободы, и в этом его смысл. Вместо выборочных дисперсий S] и S\ в (5.20)
можно использовать выборочную дисперсию S2, объединенную по двум
выборкам:
^2 = (Я|-1)^+(Я2-1)^2 (521)
П\ + п2 ~ 2
которая является более точной оценкой дисперсии а2, чем S] и S\, так
как получена по выборке большего объема. Тогда
т- _ Х\ — Хг _ Х\ — Х2
п, + п7 — 2
(5.22)
Пх П2 Ч"\ П2
Далее, умножив и поделив дробь на одну и ту же величину
oJnx + п2 — 2 и попутно сгруппировав сомножители, получаем
Tni + ni-2 = f ~Xx~~Xl Jnx + n2-2.
цпх п2^о /
Можно проверить, что случайная величина
Хх-Хг
*lnx п2
имеет нормальное распределение с параметрами 0 и 1 (линейная функция
нормально распределенных Хх, Х2 также нормально распределена, а
параметры вычисляются непосредственно). Случайная величина, в последнем
равенстве заключенная в скобки, может быть записана как
^(я, + я2-2)
и тогда, учитывая, что пх + п2 — 2 — число степеней свободы, выражение
под знаком корня имеет тот же вид, что и (5.18) в утверждении 3, а значит,
распределено как х2.
206

Таким образом, структура с. в. T„l + nj-2 и значения соответствующих
параметров приводят нас к распределению Стьюдента (см. § 3.8).
Утверждение 6. Пусть имеются две выборки объемов л, ил2
соответственно, полученные, вообще говоря, из разных нормальных генеральных
совокупностей. Обозначим тх и т2 математические ожидания генеральных
совокупностей, Хх, Х2 — выборочные средние, S] и S\ — исправленные
выборочные дисперсии. Тогда статистика
т _ Х\ ~%2 — (гп\ — т2) ,с 0,ч
^л, + л,-2 , 2 2 p.zj;
~А + ~2
имеет распределение Стьюдента с пх + п2 — 2 степенями свободы.
Данное утверждение можно проверить, рассматривая структуру с. в.
Тщ+пг-2 вида (5.23) аналогично предыдущему утверждению.
Утверждение 7. Пусть имеются две выборки Хх, Х2, ..., ХП{ и У„ У2, ..., Yni
объемов пх и п2 из нормальных генеральных совокупностей X и У
соответственно с параметрами (тх, ох) и (ту, оу), причем ох = оу = о. Тогда
статистика
F=^, (5.24)
sl
где
S
2 = ^Z«-v2> ^ = ^т1(^-7)2-
имеет распределение Фишера с (л, - 1), (п2 — 1) степенями свободы.
Преобразуем статистику F вида (5.24) следующим образом:
г 2 (/ii — l)^f
f = Sx = п2- 1 . (пх- \)SX _ п2~ 1 . о2
S] nx-\ (n2-\)S2y nx-\ (П2_{)£'
о
Сопоставив выражения в числителе и знаменателе последней дроби со
статистикой (5.18) из утверждения 3, получаем, что эти выражения имеют
распределения х2 с (л, - 1), (л2 — 1) степенями свободы. Следовательно, их
отношение с соответствующим коэффициентом из степеней свободы
подчинено распределению Фишера (см. выражение (3.61), § 3.8).
Утверждение 7 доказано.
В дальнейшем статистики, фигурирующие в приведенных
утверждениях, будут использованы для статистических выводов.
207

5.4. Интервальные оценки. Доверительные интервалы
Пусть оценка 0 неизвестного параметра 0 строится по выборке
Хи Х2, ..., Хп небольшого объема. Тогда точечная оценка при малых п
существенно подвержена случайным воздействиям, что может привести к
ощутимому расхождению между 0 и 0. В этом случае вместо точечных
оценок обычно пользуются интервальными оценками.
Интервальные оценки задают двумя выборочными значениями:
концами интервала, в котором оказывается наш параметр 0 с некоторой
заранее оговоренной вероятностью у. Таким образом, конечные значения
интервала являются как функции выборочных значений случайными
величинами, обозначим их 0i и 02. Следовательно, правильнее говорить не о
попадании параметра (числа) 0 в случайный интервал, а речь идет о том,
что случайный интервал (0i ,02) накрывает исследуемый параметр 0:
осуществляется случайное событие
0i(*„ Хъ ..., Хп) < 0 < ®2(Хи Хъ ..., Х„). (5.25)
Выбрав вероятность у, называемую доверительной вероятностью (или
надежностью), как вероятность осуществления случайного события (5.25),
т. е.
i>(0,<0<02) = у, (5.26)
можно вычислить граничные значения этого интервала. В реальных
задачах доверительную вероятность у обычно назначают близкой к 1, например
0,95; 0,99, тогда событие (5.25) можно считать практически достоверным.
Интервал (0i,02), отвечающий выбранной доверительной вероятности
у, называют доверительным интервалом.
Граничные значения 0i и 02— доверительные границы.
Как явствует из смысла введенных понятий, чем больше число у
(напомним, что у — вероятность, т. е. 0 <у < 1), тем выше надежность и,
следовательно, полученная оценка является более достоверной. В то же время
для получения более точной оценки мы заинтересованы в малой величине
доверительного интервала. Заметим, что надежность и размеры
доверительного интервала взаимосвязаны (подробнее об этом в § 5.5). Одной из
проблем исследователя является оптимальный выбор соотношения между
этими характеристиками, исходя из смысла рассматриваемой задачи.
Доверительный интервал для параметра 0, найденный по выборке,
называют интервалом значений 0, не противоречащих опытным данным.
Если 0 — выбранная оценка параметра 0, то построение интервала,
симметричного относительно 0, проще, чем построение произвольного
доверительного интервала, поскольку оба граничных значения можно
охарактеризовать лишь одним положительным числом е — расстоянием от
центра интервала 0. Тогда соотношение (5.26) имеет вид
Р(\® - 0| < е) = у, (5.27)
208

где случайное событие |© — ©| < е равносильно случайному событию
0 — е<0<0 + е,т. е. доверительные границы
0, = 0-е, 02 = 0 + е. (5.28)
А так как оценка 0 находится по выборке, то при заранее назначенном
нами числе у единственным неизвестным в (5.27) оказывается величина е,
которую и вычисляем. Значение е — точность оценки.
5.5. Построение доверительных интервалов для математического
ожидания
Как отмечалось в предыдущем параграфе, границы доверительного
интервала (0i ,0г), симметричного относительно оценки 0, можно найти из
(5.27). Однако вероятность, представленная в левой части этого равенства,
при различных распределениях 0 вычисляется по-разному. А поскольку
закон распределения 0 напрямую зависит от распределения генеральной
совокупности X, особенно для малых выборок, то и доверительные
границы (5.28) определяются с учетом закона распределения X.
Ограничимся рассмотрением наиболее распространенного случая
распределения г.с. X, а именно Х~ N(m;o). При этом объективно
существующие характеристики т и о нам, как правило, неизвестны и требуют
оценки.
В данном параграфе разберем методику построения доверительного
интервала для параметра т = М(Х) при фиксированной доверительной
вероятности у.
Оценить М(Х) с надежностью у — задача, имеющая многочисленные
приложения. Например, по результатам измерений некоторой физической
величины, имеющей точное значение т, требуется определить это точное
значение. При этом наше наблюдаемое значение оказывается случайной
величиной, которая равна сумме точного значения т и ошибки измерения,
зависящей от многих факторов и, следовательно, являющейся случайной
величиной:
Х= т + (ошибка измерения). (5.29)
Распределение случайной величины, выражаемой ошибкой измерения,
в силу центральной предельной теоремы принято считать нормальным.
Тогда из линейной зависимости св. X и св., выражаемой ошибкой
измерения [см. (5.29)], следует, что X также имеет нормальное распределение
(см. § 3.7, пример). Если ошибка измерения не является систематической
(т. е. однозначно в сторону завышения или занижения истинного
значения), то ее математическое ожидание равно нулю, и тогда, согласно (5.29),
получаем М(Х) = т.
А это и означает, что для нахождения истинного значения измеряемой
величины т нужно оценить М(Х), где св. X — результат измерения.
Можно воспользоваться точечной оценкой для М(Х), например статистикой X,
однако в случае, когда число измерений п невелико, представляется более
14 — 3529
209

надежным использовать интервальные оценки с заданной доверительной
вероятностью у. Таким образом, пришли к нашей постановке задачи.
При построении доверительного интервала для М(Х) существенную
роль играет значение а2 — дисперсия генеральной совокупности X.
Поэтому рассмотрим решение задачи в двух вариантах: при известном значении
а (например, из каких-либо физических соображений) и при неизвестном
значении а (в этом случае придется пользоваться соответствующей
оценкой).
а) Пусть а известно. Случайная величина Х~ N(m; a).
Исследуемый параметр —
0 = т = М(Х).
Воспользуемся утверждением 2 из § 5.3, согласно которому статистика
X— т
о
л/л
имеет нормальное распределение с параметрами 0 и 1. Для удобства
восприятия заменим обозначение т на 0 и рассмотрим вероятность
( \
Х-®
о
л/л
<е
= Y,
(5.30)
где у — назначаемая исследователем доверительная вероятность, а
значение необходимо вычислить, исходя из известного у. Заметим, что
равенство (5.30) имеет вид (5.27), но с целью упрощения еще введена постоянная
л/л
Так как *^®~N(0;\),
о
л/л
то вероятность попадания этой св. в интервал (-е, е) можно найти с
помощью функции Лапласа Ф(...), свойства которой и связь с нормально
распределенными с. в. известны [см. § 2.11, (2.67)]:
f \ ( \
Х-®
о
4п
<е
= Р
—е < < е
о
Jn
= ф(^)-ф(=^)=2Ф(с)-1.
Таким образом, оказывается у = 2Ф(е) - 1, т. е.
Ф(е)
- Y+1
(5.31)
Точность е при известной надежности у легко найти по таблице
функции Лапласа (см. Приложение 2, табл. 2); например, при у = 0,95 следует,
что Ф(е) = 0,975, и тогда е = 1,96. Ради удобства можно на основании
таблицы функции Лапласа составить новую таблицу зависимости е от у для
210

значений у, близких к 1. Полагаем значения у, начиная от 0,8 с интервалом
в 0,01, и по (5.31), обращаясь к табл. 2 Приложения 2, получаем
соответствующие значения е, которые, чтобы отразить зависимость, обозначим еу.
Дополнительно внесем в таблицу значения при е=1,е = 2, е=3, а также
при у = 0,999. Итак, разрабатываем таблицу.
Таблица 5.11
Y
0,6826
0,8
0,81
0,82
0,83
0,84
0,85
0,86
ег
1
1,282
1,310
1,340
1,371
1,404
1,439
1,475
Y
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
ег
1,513
1,554
1,597
1,643
1,694
1,750
1,810
1,880
Y
0,95
0,9544
0,96
0,97
0,98
0,99
0,9973
0,999
еу
1,960
2
2,053
2,169
2,325
2,576
3
3,290
Теперь, после того как по надежности у установлено значение е = еу, не
составляет труда найти доверительный интервал для исследуемого
параметра. Для этого преобразуем запись случайного события в равенстве
(5.30). Из неравенства *-0
а
л/л
<е
следует
|©-Л]<
Л
(5.32)
и далее двойное неравенство для параметра©
Таким образом, задача решена. Подставив в (5.32) вместо е найденное
значение еу, запишем доверительный интервал, указав его граничные
значения
(*-
л/Й
х+
Jn
4
(5.33)
Замечание 1. Из приведенной выше таблицы легко заметить, что с
повышением надежности у растут и значения е, а следовательно, согласно
(5.33), расширяется доверительный интервал. При больших значениях у
(слишком близких к 1) доверительный интервал может оказаться столь
обширным, что полученная оценка теряет свой смысл. При фиксированном
п, чтобы уменьшить доверительный интервал, необходимо пожертвовать
Таблица 5.1 воспроизведена в Приложении 2 (см. табл. 16).
14*
211

некоторой долей надежности и назначать у в разумных пределах.
Единственный путь и сохранения высокого значения надежности, и приемлемый
доверительный интервал — это увеличение объема выборки п [см. (5.33)],
что вполне естественно.
Замечание 2. Формулой (5.33) можно пользоваться для построения
доверительного интервала и при неизвестной дисперсии а2. В этом случае
вместо стандартного отклонения а используют оценку s Вследствие
использования оценки (т. е. приближенного значения) границы
доверительного интервала получаются приближенными. При достаточно больших
п (обычно при /2 > 30) приближение считается удовлетворительным ввиду
близости значения s1 к а2. При п < 30 более удачным является
использование другого соотношения [см. далее (5.37)].
б) Построим доверительный интервал для 0 = М(Х) в случае, когда
дисперсия а2 = D(X) неизвестна.
Рассмотрим статистику вида (5.19), введенную в § 5.3,
тп., = ^Цт,
имеющую распределение.Стьюдента с (п — 1) степенями свободы.
Обозначим оцениваемый параметр посредством 0, тогда
Тл-Х = ^,где0 = m = М(Х).
Тп
Далее, рассматривая вероятность случайного события 17^,_ || < е,
приходим к доверительному интервалу для 0. Итак,
Б
Л|3:-||<е) = |vi(0*sT. (5.34)
—е
где Vi(0 — плотность распределения Стьюдента с (л — 1) степенями
свободы для св. Тп_1 (см. § 3.8), а интефал от плотности распределения по
промежутку (—е, е) — это и есть вероятность попадания соответствующей
св. Тп^ в данный промежуток (см. определение плотности распределения,
§ 2.9).
Рассмотрим последнее равенство в (5.34)
е
Jj.-i(0<*e Y, (5.35)
в котором надежность у — число, назначаемое исследователем; V-i(0 —
функция плотности распределения, где п — число наблюдений, также
известна. Единственным неизвестным в этом уравнении оказывается
значение е, которое можно найти как решение уравнения (5.35). Это решение
зависит от надежности у и количества степеней свободы п — 1. Для
удобства значения е при различных у и п — 1 принято оформлять в виде таблицы,
при этом величину е обычно обозначают ty, так как другое название рас-
212

пределения Стьюдента — ^-распределение, индекс у подчеркивает
зависимость от надежности (на самом деле более точным было бы обозначение
tyn-1). Таблица значений ty в зависимости от у и от п — 1 приведена в
Приложении 2 (табл. 3), причем ввиду четности подинтегральной функции
Vi(0 вместо интеграла в соотношении (5.35) записан равный ему
удвоенный интеграл по половинному промежутку (см. Приложение 1), а е
заменено на ty, т. е. другой вид (5.35) — это
2Ji„-,(0A = Y, (5.36)
о
что и отражено в табл. 3.
Определив из таблицы величину tJt соответствующую числам у и п — 1,
построим доверительный интервал для 0. Исходим из случайного
события! 7; _ ,| < е в (5.34), т. е.
Х-®
<е
или
1*-0|<е4.
следовательно,
Jn Jn
Тогда
x-eJL<&<x+eJL
Jn Jn
и, заменив е на найденное конкретное значение tv окончательно получаем
доверительный интервал для 0 = М(Х):
X-tyA <@<X+tyAL. (5.37)
Jn Jn
При этом фаницы доверительного интервала — случайные величины.
Если мы хотим получить конкретный интервал, то соответствующие
статистики X и S нужно заменить их численными значениями х и s,
находимыми по выборке х,, Х2, ...,хп.
Замечание 3. В соотношении (5.37) приведены точные значения границ
доверительного интервала. Соотношение (5.37) обычно используется в
случае малых выборок (п < 30). С ростом п, как известно (см. § 3.8),
распределение Стьюдента стремится к нормальному распределению, и при п = 30
эти распределения фактически совпадают, в то же время статистика S2 с
ростом п стабилизируется относительно дисперсии генеральной
совокупности и при п = 30 уже мало отличается от а2. Следовательно, для больших
п получаем S -> о, ty -> е, где еу— значение из доверительного интервала
213

вида (5.33), и оказывается, что интервал (5.37) практически не отличается
от интервала (5.33).
Пример. Исследуется состояние дыхательных путей курильщиков. В
качестве характеристики используется показатель функции внешнего
дыхания — максимальная объемная скорость середины выдоха, которая имеет
численное значение в л/с. Требуется найти среднее значение этого
показателя с надежностью у = 0,95 и у = 0,99. В обследуемой группе из 20
случайным образом отобранных курильщиков среднее значение этого показателя
оказалось равным 2,2 л/с, а среднее квадратическое отклонение составило
0,73 л/с.
Переведем нашу задачу в вероятностную плоскость. Все множество
курильщиков — это генеральная совокупность, а отобранные 20 — выборка
из генеральной совокупности. При этом наша выборка должна быть
репрезентативной, т. е. представлять весь спектр объектов генеральной
совокупности. А значит, осуществляя отбор объектов в выборку, мы должны были
подумать о равных шансах попасть в эту выборку любому из курильщиков
генеральной совокупности. Поэтому наш вывод может быть справедлив
лишь для ограниченного множества объектов, объединенных в
генеральную совокупность. Например, если случайный отбор произведен
исключительно в среде курильщиков Новгородского университета, то и
генеральная совокупность ограничивается лишь университетскими курильщиками;
если же репрезентативность выборки обеспечена для всех курильщиков
города, то и генеральная совокупность соответственно — это множество
горожан, которые курят. Использование полученных данных применительно
к другой генеральной совокупности является необоснованным.
Итак, в очерченной возможностью обеспечения случайности отбора
генеральной совокупности исследуется характеристика максимальной
объемной скорости середины выдоха. Эта характеристика является случайной
величиной, принимающей для каждого выбранного объекта (для каждого
испытания) определенное значение из некоторого множества. В
поставленной задаче и требуется определить среднее значение всего этого
множества, исходя из двадцати наблюдаемых значений. Обозначим эту св. Хи
будем называть генеральной совокупностью, так же как и все множество
объектов (курильщиков). Тогда искомое среднее значение показателя —
это М(Х), отобранные 20 курильщиков представляют выборку Хь Х2, ..., Х20,
п = 20, статистика X имеет значение_2,2, а выборочное среднее
квадратическое отклонение S равно 0,73, т. е. х = 2,2; s = 0,73. Задача сводится к
нахождению доверительного интервала для параметра 0 = М(Х).
Предполагая распределение св. Анормальным (что обосновывается либо
возможностью применения центральной предельной теоремы, либо проверкой
нормальности по выборке, например, с помощью критериев согласия),
используем соотношение (5.37), согласно которому при конкретных
значениях х и s имеем
2,2 - L^J^- < 0 < 2, 2 + L^Il.
\/20 Y720
Находя по табл. 3 Приложения 2 значение ty при п - 1 = 19, т. е.
tQ95 = 2,09, t099 = 2,86, получаем:
1) при надежности у = 0,95
214

2, 2 - 2,09^ < 0 < 2,2 + 2,09^,
720 720
т. е.
1,858 <0<2,542;
2) при надежности у = 0,99
2, 2 - 2, 86^ < 0 < 2, 2 + 2, 86^ ,
720 720
т. е.
1,733 <0<2,667.
Таким образом, установлено, что для всех курильщиков данной
генеральной совокупности среднее значение рассматриваемого показателя с
надежностью 0,95 находится в интервале (1,858; 2,542) и с надежностью
0,99 находится в интервале (1,733; 2,667).
Заметим, что при наших предположениях мы получили точные
значения (с точностью округления) доверительных границ. Приближенные
значения можно было получить, используя формулу (5.32) с заменой точного
значения а на оценку ^и находя еу из табл. 5.1 данного параграфа. Тогда
при у = 0,95 приближенный доверительный интервал (1,880; 2,520), а при
у= 0,99 приближенный доверительный интервал (1,770; 2,620). Сравнивая
доверительные интервалы, полученные точным и приближенным
методами при одинаковой надежности, видим, что они мало отличаются.
Фактически при нашем значении п = 20 доверительные границы имеют различие
на втором знаке после запятой. И еще раз отметим тот факт, что отличие
доверительных интервалов при п < 20 было бы, вообще говоря, более
существенным, а при п > 20, наоборот, приближенный интервал более
соответствовал бы точному.
5.6. Доверительные интервалы для дисперсии
Доверительный интервал для дисперсии генеральной совокупности X,
так же как и для математического ожидания, можно построить точно (что
важно при малом числе наблюдений п) либо приближенно (при п > 30
приближенный интервал, как правило, незначительно отличается от
точного). Понятно, что точный доверительный интервал лучше
приближенного, однако для построения точного интервала важно знать закон
распределения X, в то время как для построения приближенного интервала
возможно и проигнорировать закон распределения. Именно этот факт
произвола на вид распределения влечет значительную долю погрешности
при построении приближенного доверительного интервала.
Рассмотрим метод построения доверительного интервала приближенно
с некоторой погрешностью.
В качестве оценки параметра 0 = D(X) воспользуемся статистикой 5е,
составленной по репрезентативной выборке объема п:
п
2 _ 1 ХР / V V42
s2 =-i-Y(xk-X)
п — 1 ^-»
215

Величина S2 представляет собой сумму п случайных величин
п,
{Хк f)2, где к =1,2,
п— 1
и, хотя эти случайные величины не являются независимыми (в каждой из
них имеется св. X, зависящая от всех других св.), используя центральную
предельную теорему, можно доказать, что с ростом п закон распределения
их суммы стремится к нормальному. Следовательно, начиная уже с п = 20,
закон распределения св. S2 считается приближенно нормальным. А тогда
можно оценить математическое ожидание этой случайной величины,
которое ввиду несмещенности оценки S2 [см. (5.15)] как раз и равно
оцениваемому параметру M(S2) = D(X) = 0.
Таким образом, задача нахождения доверительного интервала для D(X)
сводится к уже рассмотренной в предьщущем парафафе задаче построения
доверительного интервала для математического ожидания, где в роли
исследуемой св. X [см. (5.33)] выступает на этот раз св. S2. В доверительном
интервале (5.33) фигурирует величина -^ = JD(X), а в нашем случае вме-
сто D(X) нужно использовать D(S2), которая известна [см. (5.16)].
п п(п— 1)
Далее, для реальных расчетов вместо теоретических моментов ц2 и ц4 мы
вынуждены использовать их оценки, т. е. эмпирические моменты ц2» S2 и
ц4«|14. Обозначив Jd(S2) = osiy можем записать доверительный интервал
для параметра 0 = D(X) аналогично доверительному интервалу (5.33):
^2 - asj • еу; S2 + CTj, • ет) y (5.38)
где значение еу вычисляется по надежности у и может быть найдено в
табл. 5.1, см. § 5.5 (или Приложение 2, табл. 16). Соответствующий
доверительный интервал для среднего квадратического отклонения о = D(X)
легко получается из доверительного интервала для дисперсии (5.38):
(JS2 - о? - еу; Js2 + о^ • еу).
Замечание. Как можно заметить, вычисление osi = JD(S2) требует
использования момента четвертого порядка |i4, замена которого
эмпирическим моментом ц4 существенно повлияет на точность наших вычислений,
поскольку известно, что чем выше порядок момента цк, тем хуже
приближение ц* * \ik. Особенно пофешность велика при малом числе
наблюдений я. Однако этой пофешности можно избежать, зная закон
распределения генеральной совокупности X. Например, при нормальном
распределении X известно, что ц4 = Зц2;, тогда
216

D(S2) = -2-.I?(X)*-2-(S2)2 (5.39)
n — 1 n—1
[соотношение выводится из (5.16)]. В этом случае доверительный интервал
(5.38) имеет вид
Аналогично для равномерного распределения щ = 1, %\l\ ,
D(S2) = °>*n+]>2D2(X) * 0.8"+l>2(tS.2 2 4
л(л- 1) /i(/i- 1)
и доверительный интервал
(>_ №8«+l,2fl ^ + /0,8„+12лд (5 42)
V а/ л(л-1) Y' V л(л-1) v
Пример 1. Найти приближенно с надежностью 0,9 доверительный
интервал для D(X) в условиях примера § 5.5, предполагая X нормально
распределенной случайной величиной.
Решение. В рассматриваемом примере генеральная совокупность X —
максимальная объемная скорость середины выдоха в л/с, х = 2,2 л/с,
s = 0,73 л/с, п = 20.
Для построения доверительного интервала воспользуемся
соотношением (5.40), полученном для нормальной генеральной совокупности X, в
котором S2 = (0,73)2, а еу находим из табл. 5.1 в § 5.5 (по
условию у = 0,9): еу = е0>9 = 1,643. Тогда доверительный интервал для
дисперсии:
((0,73)2-^Х1(0,73)2 • 1,643; (0, 73)2 + J^^(0, 73)2 • 1,64з)
или (0,5329 - 0,2841; 0,5329 + 0,2841),
и окончательно (0,2488; 0,8170).
Таким образом, с надежностью 0,9, исходя из имеющихся выборочных
данных, можно утверждать, что D(X) находится в пределах от 0,2488 до
0,8170. Это означает, что, взяв сколь угодно много выборок объема п = 20
из генеральной совокупности X и вычислив для каждой из выборок
исправленную выборочную дисперсию s2, мы получим множество
конкретных интервалов. Среди этих интервалов 90% таких, что в них
действительно содержится истинное значение D(X). Точнее, мы гарантируем с
вероятностью 0,9, что любой интервал, вычисленный по соответствующей
формуле и исходя из конкретных выборочных значений, накрывает число
D(X).
В рассмотренном примере доверительный интервал для стандартного
отклонения а = 4ЩХ) — это
(70,2488; V0,8170),t. е. (0,4984; 0,9039).
Зная закон распределения генеральной совокупности X, доверительный
интервал для дисперсии можно построить точными методами.
217

*».!l
т, т2 у
Рис. 36.
Для построения точного доверительного интервала предполагаем, что X
имеет нормальное распределение (что на практике встречается достаточно
часто), и используем статистику вида (5.18), рассмотренную в § 5.3,
2-{n-\)S2
а
которая имеет распределение %2 с (л — 1) степенями свободы.
Следовательно, плотность распределения кп-\(у) данной св. х2> зависящая лишь
от числа степеней свободы, известна и задана соотношением вида (3.57), в
котором вместо значения п всюду следует записать п — 1.
По известной плотности кп-\(у) можно определить интервал (т,,т2), в
который св. х2 попадает с некоторой известной вероятностью у (т. е. с
надежностью у).
На рис. 36 изображен график плотности распределения кп-х(у)\ где в
данном случае у независимая переменная, как она и обозначена в § 3.8
при описании распределения х2 • Площадь фигуры, ограниченной этой
кривой плотности и осью абсцисс, конечно же, равна 1. Указать значения
Т|,т2 по надежности у — означает выделить часть рассматриваемой
криволинейной трапеции с площадью у (на рис. 36 эта часть криволинейной
трапеции не заштрихована). Оставшиеся две части всей фигуры, слева от т, и
справа от т2 (на рис. 36 эти кусочки криволинейной трапеции
заштрихованы), имеют суммарную площадь 1 — у. Таким образом, вероятность
попадания св. х2 в интервал (т,;т2) равна у, а вероятность попадания в
интервалы (0;т|) или (т2;+°о) равна 1 —у. Понятно, что интервал (т,;т2) по
надежности у определяется неоднозначно так как сумма площадей
заштрихованных кусочков должна быть равна 1 — у, но соотношение меж-
1 Заметим, что при числе степеней свободы п — 1, равном 2 или меньшем чем 2, графики
функции плотности fc^Cv) имеют другой вид (см. рис. 22), нежели представленный на рис. 36
график, соответствующий числу степеней свободы, больших чем 2. Однако для построения
доверительных интервалов в данном случае конкретный вид этой кривой при различных
значениях п - 1 принципиального значения не имеет. Полученные в дальнейшем формулы
справедливы и при п - 1 - 2 и при п - 1 < 2.
218

ду этими двумя площадями может быть самым разным. Для
определенности выберем т, и т2так, чтобы площади заштрихованных фигур, слева от т,
и справа от т2, оказались одинаковыми, тогда каждая из площадей равна
—т-^, а это означает, что вероятности попадания значений св. х2 в
интервалы (0;т|) и (т2;+°°) одинаковы и равны —^ каждая.
Определенные таким образом величины т,, т2, зависящие от надежности
у и от числа степеней свободы п — 1 распределения х (напомним, что
рассматривается плотность именно кп-х(у)), можно вычислить. Однако
вместо самостоятельного проведения этих вычислений проще воспользоваться
готовыми таблицами. В Приложении 2 представлена табл. 4, где указаны
значения величины т, для которой выполнено соотношение
Р(Х2 > т) = р (5.43)
в зависимости от г и р.
В этом равенстве *£— св., имеющая распределение "хи-квадрат" с г
степенями свободы, р — вероятность. Для нашего случая, чтобы
определить значение т2, нужно взять г=п— 1, р = р2= ——% и найти требуемое
значение в таблице на пересечении соответствующих строки и столбца.
Чтобы определить по таблице значение т,, нужно учесть, что в нашем
случае табличная вероятность р — это вероятность попадания св. в интервал
1 —у V + 1
(т,;+оо),т. е./? = />, = y + -j-L = ly~'
Итак, пользуясь таблицей, нашли т, и т2 такие, что для рассматриваемой
статистики справедливо
,(tl<("^i^<t1)-r, (5-44)
и а2 = D(X) — оцениваемый параметр. Но рассматриваемое случайное
событие
т,0 f— <т2
а
легко преобразуется в равносильное
С"1)^ < ст2 < ("~1)S2, (5.45)
т2 т,
и тогда вместо (5.44) получаем
p(in-\)S2 < G2< {n-\)S\ = (5 46)
^ т2 т, J
219

Следовательно, оцениваемый по выборке объема п параметр
0 = D(X) = о2 генеральной совокупности X с надежностью у находится в
доверительном интервале
ГС-1)Д';(я-1)Д'У (5.47)
Пример 2. По данным примера 1 найти с надежностью у = 0,9 точные
границы доверительного интервала для дисперсии D(X).
Решение. Точные границы искомого интервала указаны в (5.47). Таким
образом, задача сводится к подстановке в (5.47) конкретных значений
п — 1 = 19, i?2 = (0,73)2 и т,, т2, которые необходимо найти из таблицы.
Значение т2 находим, полагая табличным параметрам г и р числа
г= п - 1 = 19, р = р2 = ^y1 = 1 ~ °' 9 = 0,05. Тогда т2 = 30,1. Анало-
V + 1
гично, для нахождения т, полагаем г=п— 1 = 19, р = Р\ = L-^— = 0, 95,
тогда т, = 10,11. Следовательно, согласно (5.47), точный доверительный
интервал для дисперсии
»2 ,п /Л tin2
С9 з<0173) i 1Jj£tl) »»" (0,3364; 1,0015).
Как видим, точный интервал с точностью до десятых отличается от
доверительного интервала, найденного приближенными методами в
примере 1. Различие объясняется малым объемом выборки п (с ростом п
погрешность уменьшается).
Доверительный интервал для стандартного отклонения а: (0,58; 1,0007).
5.7. Доверительный интервал для разности средних
Пусть имеются две выборки из различных нормальных генеральных
совокупностей Хх и Х2. Обозначим т1 и т2 математические ожидания этих
генеральных совокупностей, т. е. т1 и щ — истинные средние значения.
Требуется сравнить эти значения: оценить разность тх — т2. В качестве
такой оценки используем доверительный интервал, который будем строить,
исходя из выборочных характеристик.
Пусть л, и п2 — объемы рассматриваемых выборок; Х1 и Х2 —
выборочные средние; S] и S\ — исправленные выборочные дисперсии. Все эти
характеристики легко вычисляются по выборочным данным, поэтому, не
останавливаясь на процедуре вычисления, считаем их известными. Для
построения доверительного интервала воспользуемся утверждением 6 в § 5.3,
согласно которому статистика (5.23)
Т _ Х\ - X2-(ml - m2)
1 л, + л2-2
£] + £!
л, п2
220

имеет распределение Стьюдента с пх + п2 — 2 степенями свободы.
Оцениваемый параметр 0 = т] — т2. Обозначив точность оценки t,
подчеркивая зависимость ее от надежности у, рассмотрим вероятность
^|т;1+Я1-2|<д = у.
По введенному нами значению у и известному числу степеней свободы
Л| + п2 — 2 из табл. 3 (см. Приложение 2) находим численное значение ty.
Далее, при конкретном ty случайное событие 17,Л( + Л1-г| < Ц заменяем
равносильным
_t < Х\-Х2-{тх -т2) < f
S\ + S2
я, п2
или, что то же самое,
_, < {тх-т2)-(Х\-Х2)
2 2 Y '
§А + §Л
П\ «2
откуда после несложных преобразований следует
S\_ j. $2 г т //v._v>x* \S\,S2
(Я- Х2)~ t, Z± + Ш < mi- т2< (К - Х2) + L ^ + Ш . (5.48)
\ п\ п2 V Л1 Л2
Полученное соотношение (5.48) представляет доверительный интервал
для разности средних тх — т2 при заданной надежности у. Заменив
выборочные характеристики числами, приходим к конкретному интервалу,
соответствующему рассмотренным выборкам.
Пример. Для проверки эффективности нового препарата, понижающего
артериальное давление, выбрана группа добровольцев из 20 человек.
Контролируемый параметр — среднее артериальное давление (САД) в мм
рт. ст. После двухдневного приема лекарства значение САД оказалось
равным 135 мм рт. ст. при значении исправленной выборочной дисперсии
iS*^ = 10 мм рт. ст. Для сравнения результатов была отобрана еще одна
контрольная группа из 25 добровольцев, примерно однородная по составу
с первой группой (возраст, пол, род занятий, отсутствие сопутствующих
заболеваний) и с САД на начальном этапе, соответствующим САД первой
группы. Во избежание психотерапевтического эффекта, который
параллельно с приемом лекарства мог повлиять на результат и посему должен
быть учтен, вторая группа вместо лекарства получала плацебо1.
Контролируемые параметры через те же два дня для второй группы оказались
следующими: значение САД равно 145 мм рт. ст., S] = \5 мм рт. ст. И хотя
1 Сам факт лечения уже может привести к положительному эффекту. Для выявления
психотерапевтического воздействия лечения в клинических исследованиях и применяют
неактивные препараты (например, сладкие пилюли), называемые плацебо, которые не оказывают
физиологического действия на процесс лечения. Статистические данные свидетельствуют,
что в ряде случаев, не требующих серьезного медицинского вмешательства, плацебо
"улучшает" состояние каждого третьего больного.
221

значение САД в первой группе (135 мм рт. ст.) оказалось ниже, чем во
второй (145 мм рт. ст.), выводы об эффективности лекарства делать рано.
Необходимо более взвешенно сравнить результаты. Для этого оценим с
помощью доверительного интервала разность между истинными значениями
САД в обеих генеральных совокупностях, которые представлены нашими
выборками: больных, принимающих лекарство, и больных, не
использующих этот препарат.
Пусть обе генеральные совокупности имеют нормальное распределение
с математическими ожиданиями т1 и щ соответственно. Разность mi — щ
и требуется оценить. Для нахождения интервальной оценки параметра
т, — т2 воспользуемся доверительным интервалом (5.48). Чтобы
вычислить интервал, кроме известных нам значений, необходимо знать
коэффициент tr Найдем его в табл. 3 Приложения 2, полагая у = 0,95 и у = 0,99.
Тогда при у = 0,95 и числе степеней свободы л,+ п2 — 2 = 43 имеем
у095 = 2,02 и
(135 - 145) - 2,02^ + i| </и, - т2 < (135 - 145) + 2,02^ + i| ,
т. е.
-12,12 < т, - т2< -7,88.
Доверительный интервал найден, однако удобнее рассмотреть разность
не т1 — т2, а т2 — /и,, чтобы доверительный интервал имел положительные
значения. Умножив обе части каждого из неравенств в последнем двойном
неравенстве на (—1), получаем доверительный интервал с надежностью
0,95 для разности т2 — /и,:
7,88 < т2- /и, < 12,12.
Таким образом, применение нового препарата понижает САД
(понижает, так как т, < т2) при двухдневном приеме в 95% случаев на величину от
7,88 до 12,12 мм рт. ст.
Аналогично, при у = 0,99 и числе степеней свободы, равным 43,
находим в таблице t099 = 2,70. Тогда доверительный интервал с надежностью
0,99 для разности средних т2 — т1 — это интервал (7,17; 12,83).
Следовательно, у 99% больных двухдневный прием препарата понижает
САД на 7,17—12,83 мм рт. ст.
Обратим внимание на уже отмеченный факт: повышение надежности
расширяет доверительный интервал (ухудшает точность).
5.8. Оценка вероятности по частоте
В первой главе представлено одно из утверждений закона больших
чисел: теорема Бернулли (см. § 1.15), в которой при условиях схемы Бернул-
ли исследуется стремление относительной частоты события ( —J к
вероятности осуществления события в одном испытании (р). Для удобства далее
относительную частоту — будем обозначать со.
п
222

Рассмотрим относительную частоту со = — подробнее с точки зрения
статистики. Пусть испытания проводятся по схеме Бернулли относительно
некоторого события А, которое в каждом из независимых испытаний либо
происходит (с вероятностью р), либо не происходит (с вероятностью
q= 1 — р). Введем св. X — число наступлений события А в одном
испытании. Как легко видеть, св. X может принимать лишь два возможных
значения 0 и 1 с вероятностями q и р соответственно, т. е. имеет место
распределение Бернулли. Естественно, М(Х) = р, D(X) = pq = p{\ — р).
Полагая св. Хв качестве генеральной совокупности и производя п независимых
испытаний, получим репрезентативную выборку Xlt X2, ..., Хп, в которой
каждая из случайных величин является копией генеральной совокупности
X. Далее рассмотрим выборочное среднее
Х=1-УХк,
к= I
которое оказывается как раз равным относительной частоте — осуществ-
п
ления события А в п испытаниях. Таким образом, со = — — случайная ве-
п
личина1, являющаяся статистикой Х,_в то же время постоянная
вероятность р = М(Х). Поскольку среднее X является оценкой М(Х), то можно
говорить, что относительная частота со является оценкой вероятности р.
При достаточно больших значениях п для многих задач точечная оценка со
вероятности р является удовлетворительной. Однако для ряда других задач
предпочтительнее использовать интервальные оценки.
Построим для параметра р доверительный интервал, опираясь на
теорию построения доверительного интервала для среднего (сгл. § 5.5).
Вначале отметим, что при больших значениях п статистику X (j. е. со) можно
считать распределенной приближенно нормально, так как X — сумма
независимых одинаково распределенных св. Xlf X2, ..., Хп, деленная на л, и
можно применить центральную предельную теорему. Следовательно,
используя доверительный интервал (5.33) для М(Х) = 0
X ~ ——Еу', X + ——EY
^ Jn 4n )'
заменяя X на со и М(Х) на р, получаем с надежностью у
со--^еу</Ксо + -^еу. (5.49)
Найденный интервал, однако, не может служить для точной оценки
параметра р, поскольку входящее в соотношение стандартное отклонение а
1 В данной ситуации имеет место отступление от правила обозначать случайные величины
прописными буквами латинского алфавита. Надеемся, что это не вызовет недоразумений.
223

определяется через р, а именно: а = JD(X) = Jp(\ — р). Таким образом,
оказывается
Ъ-М1-Р\<р<п + М1-Р\. (5.50)
Но можно разрешить это двойное неравенство относительно р и тем
самым найти доверительный интервал. От двойного неравенства переходим
к неравенству с модулем:
Возводя обе части последнего неравенства в квадрат, получаем
квадратное неравенство относительно р, которое имеет решение рх< р < ръ где
Р* =
1 +Ь.
(5.51)
2/i ya/ n 4W
P2 =
Таким образом, доверительный интервал для вероятности р найден: /?, и
р2 вида (5.51) — доверительные границы.
Но из-за громоздкости соотношений (5.51) при больших п (порядка со-
2
тен) обычно слагаемыми вида -* можно пренебречь без особого ущерба
точности, так как с ростом п эта величина уменьшается и незначительно
влияет на величину доверительного интервала. Тогда приближенные
границы доверительного интервала {рх\ р2) оказываются такими:
со + ^ - е _л
2/1 т^ п
4W
2
1 +£г
п
« j. еу - j. h (1_
со + ^- + еу —±
2/1 т^ п
2
1 +Ь.
a»+lfeV
4W
Я. -c.-e./.J-j—I;
. (5-52)
Структура этих фаничных значений, учитывая, что оценкой
стандартного отклонения а является выражение Vco(l —со), как раз соответствует
виду фаниц доверительного интервала (5.33). Также заметим, что (5.52)
соответствует фаницам (5.50) при замене истинного значения дисперсии
р{\ — р) на эмпирическую дисперсию со О — со).
Замечание. Обычно формулами (5.51) пользуются при условии больших
значений п, обязательно контролируя значения пр и nq, каждое из которых
должно быть не менее 4, ибо в противном случае приближение
распределения со к нормальному оказывается слишком фубым, что влечет и сомне-
224

ния в точности приближения (5.51). Для использования формул (5.52) \
ограничения оказываются еще более жесткими: значения пр и nq должны
быть не менее 10. В противном случае полученные результаты не
представляют ценности.
Пример 1. Некоторый анализ, исход которого определяется двумя
значениями (положительный и отрицательный), повторяется 100 раз. В
результате этих 100 испытаний положительный исход наблюдался 72 раза.
Требуется оценить с надежностью у = 0,8 неизвестную вероятность
положительного исхода при одном анализе.
Решение. Так как каждое испытание (проведение анализа) имеет ровно
два возможных исхода, вероятности которых считаем постоянными в
любом испытании, и испытания являются независимыми (ибо из
формулировки задачи нет оснований полагать противное), то мы находимся в
условиях схемы Бернулли. Оцениваемую вероятность появления
положительного исхода в одном испытании обозначим р, тогда по данным
наблюдений точечная оценка параметра р — это относительная частота со,
72
и численно со = j~-z = 0,72. Чтобы использовать соотношения (5.51),
(5.52) для построения доверительного интервала, необходимо оценить пр и
nq. Так как со — точечная оценка р, то полагаем р «со, и тогда
пр&па — 72, nqxn(l —со) = 28.
Следовательно, применение как формул (5.51), так и формул (5.52)
является обоснованным, поскольку значения пр и nq достаточно велики (см.
приведенное выше замечание).
По надежности у = 0,8 из табл. 16 Приложения 2 (см. ту же таблицу в
§ 5.5) находим е08 = 1,282. Тогда доверительный интервал (р,; р2), исходя
из (5.52), имеет границы
рх = 0, 72 - 1, 2*2^°>72' ^-Ш2) « 0, 662,
Рг = 0, 72 + 1, 282 /°'72 ' |]. ~ °» 72) * 0, 778.
Следовательно, истинное значение вероятности с надежностью 0,8
находится в интервале (0,662; 0,778); этот интервал для значений р совместим
с опытными данными.
Воспользовавшись более точным представлением (5.51), приходим к
доверительному интервалу (0,659; 0,774). Как видим, при наших данных
разница в значениях границ обоих интервалов составляет несколько
тысячных, т. е. незначительна.
Как уже отмечалось, построение доверительных интервалов для
вероятности р с использованием формул (5.51), (5.52) предполагает нормальное
распределение относительной частоты со. Приближенную нормальность
распределения со обеспечивают условия на п и р . При малых значениях л,
а также при р, близких к нулю или единице, полученные формулы,
основанные на нормальном распределении, неприменимы. При малом числе
наблюдений п используют точное распределение со, которое, как мы знаем
(см. § 2.5, 1.12), является биномиальным. В этом случае доверительный
интервал для вероятности р имеет другую структуру, нежели при нормаль-
15 — 3529
225

ном распределении. При выбранной надежности у и известной частоте
осуществления события в п испытаниях к, где к — /ко, граничные
доверительные вероятности рх и р2 находятся как решения соответствующих
уравнений, содержащих суммы биномиальных вероятностей:
-„.V— = iZJ
£070-/>.)""" = "—
СтпР?(1-р2У
т'к (5.53)
т = 0
Как видим, в каждом конкретном случае решение уравнений (5.53) —
задача достаточно не тривиальная, поэтому ради удобства пары решений /?,
и р2 , являющихся доверительными границами, при различных п, к и у для
пользователей представляют в виде таблиц. В частности, при у = 0,95 и
у = 0,99 и для п от 1 до 20 см. Приложение 2, табл. 5.
Пример 2. В 20 независимых испытаниях некоторое событие А
наблюдалось трижды. Требуется установить с надежностью у = 0,95
доверительный интервал для вероятности р осуществления события А в данном
испытании.
Решение. По условию п = 20, к = 3, у = 0,95. Обращаемся к табл. 5 и
находим /?, = 0,042, р2 - 0,372. Таким образом, доверительный интервал
получен: (0,042; 0,372). Большая величина найденного интервала
обусловлена малым числом наблюдений п и высокой надежностью у = 0,95. При
у = 0,99 доверительный интервал оказывается еще шире (0,023; 0,446).
Рассмотрим отдельно случай, когда наблюдаемое значение
относительной частоты со равно нулю. При малом числе наблюдений п
доверительный интервал можно найти из табл. 5, при больших значениях п из
формул (5.51), которые выдают интервал
4 п + е у у
Однако в этой ситуации доверительный интервал для вероятности р
можно найти проще: нижняя граница /?, известна, она должна иметь
значение 0, так как 0 является наблюдаемым и обязан входить в интервал, а
меньше нуля вероятность не бывает. Значение р2 вычисляется по
приводимой ниже формуле. Если обозначить посредством Д, событие, что в п
испытаниях контролируемое событие не появилось ни разу, то р2 —
максимальная величина вероятности р, совместимой с наблюдаемым событием
Д, при надежности у. Тогда событие Д,, согласно биномиальному
распределению, имеет вероятность (f, т. е. Р(А0) = q - (1 - /?)".
Полагая вероятность неосуществления события Д, малой величиной и
связывая ее с надежностью у, граничное значение таких вероятностей р2
можно определить из условия Р(Д) = 1 — у, следовательно,
Р(Ло) = а-ргУ = 1-У-
226

Отсюда находим вторую границу доверительного интервала.
р2 = Х-ч/Т^у. (5.55)
Заметим, что при малых значениях р и большом числе наблюдений п
биномиальное распределение стремится к распределению Пуассона (см.
§ 1.13, 2.6) со средним а = пр. И тогда
Р(Л)*^-° = *"",
следовательно,
Р(А0)*е-пр*1-у
и соответственно из последнего равенства находим р2:
Р2*=ЩЦ). (5.56)
Пример 3. Некоторый анализ, имеющий два возможных исхода,
проводится 25 раз. Во всех 25 испытаниях положительный исход не появился ни
разу. С надежностью 0,95 оценить вероятность положительного исхода
анализа в одном испытании.
Решение. Рассмотрим разные методы нахождения доверительного
интервала для вероятности р, положительного исхода анализа в одном
испытании.
По табл. 5 Приложения 2 при у = 0,95 получаем доверительные
границы:
Pl =0;p2 = 0,134.
_L
По формуле (5.55) находим р2 = 1 - 4J1 - 0,95 = 1-(0,05)25*0,113;
естественная нижняя граница рх = 0.
По формуле (5.56) пуассоновского приближения
Л s -ln(l-0,95) = Qj 120. разумеется, Pl = 0.
Доверительные интервалы (0, р2), полученные тремя способами,
различаются незначительно, фактически на величину сотых. Различие
объясняется малым количеством наблюдений п, весьма существенным для
приближенных методов.
Также заметим, что формулы (5.52) в данной ситуации неприменимы, а
приближенный интервал, согласно (5.54), такой: (0; 0,133).
5.9. Ошибка выборки. Оптимальная численность выборки
В предыдущих параграфах мы строили доверительные интервалы для
параметров распределения генеральной совокупности X. Легко заметить,
что в случае нормального (или приближенно нормального) распределения
доверительные интервалы оказывались симметричными относительно
соответствующей точечной оценки параметра. Таким образом, сама точечная
оценка оказывается в середине интервала. Истинное значение параметра (с
надежностью у) находится где-то внутри доверительного интервала,
следовательно, разность между точечной оценкой и значением параметра не
15*
227

превышает длины половины интервала. Эту разность между точечной
оценкой и оцениваемым параметром называют ошибкой выборки. Ошибка
выборки может иметь наибольшую величину, равную длине половины
интервала. Такую наибольшую из возможных ошибок (при заданной
надежности) называют предельной ошибкой выборки. Предельная ошибка выборки
характеризует точность оценки.
Обозначим предельную ошибку выборки величиной А и из структуры
доверительных интервалов вида (5.33), (5.37), (5.40), (5.52) и др. замечаем,
что Д состоит из произведения двух величин
А = t • ц,
где
Ц= R (5.57)
V п
а2 — дисперсия генеральной совокупности, t — коэффициент, зависящий
от надежности у. Величину ц вида (5.57) называют средней ошибкой
выборки. Напомним, что
D(X) = ЯНЬ = <L
п п
[см. (5.9)]. Исходя из этого соотношения для среднего X, величину
ц U гп
л/л
называют также стандартной ошибкой среднего, и ее можно обозначить о^.
В практических вычислениях стандартное отклонение о не всегда
известно, и тогда используют его оценку . Стандартная ошибка
оказывается равной
c-x*S-x=±. (5.58)
л/Л
В случае оценки вероятности р по частоте со дисперсия а2, используемая
в (5.57), равна р(\ — р), а эмпирическая дисперсия соответственно —
со(1 - со), и тогда стандартная ошибка
= РО-Р)^ со(1-со)
^-^-/^-Гт^- (559)
В случае, когда генеральная совокупность имеет объем N, где N —
конечное значение, и объем выборки п сравним с объемом генеральной
совокупности, для вычисления стандартной ошибки вводят поправочные
коэффициенты: вместо (5.57) рассматривают величину
228

Соответственно для стандартной ошибки в (5.59)
При этом используется только повторный отбор элементов из
генеральной совокупности, т. е., выбрав какой-то элемент, его помечают и
отправляют вновь в генеральную совокупность с равными шансами для всех
элементов быть отобранными. Разумеется, при достаточно больших значениях
N, а в идеале для N, стремящемся к бесконечности, введенные поправки и
условие повторного отбора оказываются несущественными. В генеральной
совокупности объема N предельную ошибку выборки А можно записать
также с поправочным сомножителем
д - 'Щг¥) <5-б2>
для среднего и
Д» " 'J^(l-f) (5.63)
для вероятности р.
Стандартная ошибка ц — это средняя ошибка выборки. Истинное же
значение ошибки выборки находится в границах, регулируемых
коэффициентом t в соответствии Д = t • ц. Коэффициент t зависит от выбранной
надежности у и является ранее используемым значением еу для больших
выборок или значением ty для малых выборок. Величина t определяет
кратность стандартной ошибки. Например, для больших выборок, при t = 1 из
табл. 16 Приложения 2 получаем надежность у = 0,6826, при t = 2
получаем у = 0,9544, а при t— 3 имеем у = 0,9973. Следовательно, при.*= 3 в
10 000 испытаний оцениваемый параметр попадает в найденный
доверительный интервал (X— Зц, Х+ Зц)в среднем 9973 раза [для оценки р
соответственно в интервал (со — 3|iffl, со + Зцш) ]. Для малых выборок связь между
/ = / и надежностью у указана в табл. 3 Приложения 2.
Таким образом, пользуясь таблицами для еу или ty, по известному_значе-
нию у можно построить доверительные интервалы для параметров X или р
и, наоборот, выбрав доверительные интервалы в долях от стандартной
ошибки (т. е. вычислив кратность t для стандартной ошибки), можно
установить надежность у этих интервалов.
Коэффициент t называют коэффициентом доверия.
На формулах предельной ошибки выборки основывается способ
определения оптимальной численности выборки. Для среднего предельная
ошибка выборки вычисляется исходя из общей формулы А = t • ц,
следующим образом:
V п
229

Тогда, выбрав надежность у (а следовательно, однозначно определив t из
соответствующих таблиц) и указав предельную ошибку выборки Д, получаем
п = Щ. (5.64)
Д2
В случае генеральной совокупности объема ./V из (5.62) аналогично
можно найти
_ МУ2
NA2 + fa2
п = — —. (5.65)
Равенства (5.64), (5.65) определяют необходимую численность выборки,
обеспечивающую величину предельной ошибки Д по заданной надежности
У-
При исследуемом параметре р из формулы
--'ГЧ
д* =
ш}
при фиксированных предельной ошибке Дш выборки и надежности у
находим п:
^ = Лв(1-ш) (566)
Аналогично, в случае генеральной совокупности объема ./V из формулы
(5.63) определяем
М»а>(1-а») (567)
ЛГД2 + Ло(1-ш)
Равенства (5.66), (5.67) определяют необходимую численность выборки
с гарантией заданных величин Дш и у.
Задачи и упражнения
1. Из генеральной совокупности Л" извлечена выборка объема п = 100:
*,•
т.,
0
63
2
17
4
9
7
6
10
5
Найти несмещенные оценки М(Х) и ДЛГ).
Указание. См. статистики Хи S2> § 5.2.
2. По данным выборки объема п = 50 генеральной совокупности А"
найдена смещенная оценка генеральной дисперсии D(X), равная s2 = 4.
Найти несмещенную оценку генеральной дисперсии.
Указание. См. зависимость между смещенной оценкой S2 и
несмещенной оценкой S2, § 5.2, (5.14).
Ответ: s2 * 4,082.
230

3. Пусть случайные величины Хх и Х2 независимы и имеют нормальное
распределение с параметрами т = 0, о= 1. Определить распределение
случайных величин: a) Y = Х\; б) Z = X2 + Х\.
Указание. См. § 3.8.
4. Каково распределение статистики X, составленной по
репрезентативной выборке Хь Х2У ..., Хп генеральной совокупности X в случае: а) X
нормально распределена с параметрами т и а; б) X имеет произвольное
распределение и п — достаточно большое число?
Указание, а) см. § 3.8; б) см. центральную предельную теорему, § 3.10 и
вывод о распределении линейной функции нормально распределенной св.
5. Пусть Хи Х2, ...,ХПх и Yu Y2t.... Y„2 — репрезентативные выборки
объемов л, и п2 из нормальных генеральных совокупностей X и Y
соответственно. Исправленные выборочные дисперсии, составленные по этим
выборкам, — S2X и S2y.
Какое распределение имеет статистика
2
а)|; б)|?
Какое распределение имеет статистика
в) Jn\ р , где m = M(X) известно;
г)
Х\ — Хг 9
'S + J.2
Щ п2
6. Для оценки неизвестного математического ожидания М(Х) = 0
нормально распределенной генеральной совокупности X найти доверительный
интервал с надежностью: а) у = 0,95; б) у = 0,99. Выборка объема п = 25
дает оценку х =10, а среднее квадратическое отклонение X известно
априори а = 5.
Указание. См. § 5.5, выражение (5.33); значение еу находится из табл.
5.1.
Ответ: а) е095 = 1,96; 8,04 < М(Х) < 11,96;
б) е099 = 2,576; 7,424 < М(Х) < 12,576.
7. Из нормальной генеральной совокупности Л" извлечена выборка
объема п = 12:
-10 12 3 4
т.
1
2> = 12
При надежности у = 0,95 оценить с помощью доверительного интервала
математическое ожидание генеральной совокупности.
Ответ: х = 1,25; s= 1,603; /у = Г(0,95; 11) = 2,2; 0,232 < М(Х) < 2,268.
8. Одним и тем же прибором произведено 33 измерения некоторой
величины (без систематических ошибок). Для случайных ошибок измерений
231

исправленное среднее квадратическое отклонение получилось равным
s = 0,5. Найти точность прибора с надежностью: а) у = 0,95; б) у = 0,99.
Указание. Точность прибора определяется величиной среднего квадра-
тического отклонения случайных ошибок измерения. Требуется оценить
параметр а с доверительной вероятностью у. Используя общепринятое
предположение о нормальном распределении ошибок измерения,
доверительный интервал для дисперсии а2 можно найти по формуле (5.40),
откуда легко находится и доверительный интервал для а.
Ответ: а) (0,357; 0,610); б) (0,298; 0,641).
9. Пусть имеются две выборки объемов л, = 30 и п2 = 20 из двух
нормальных генеральных совокупностей Хх и Х2 соответственно. По выборкам
найдены выборочные характеристики х, = 8,5; х^ = 7,7; s] = 4; s\ = 3, 61.
Требуется оценить различие средних М(Х{) = тх и М(Х2) = т2, т. е. найти
доверительный интервал для разности средних т, — т2.
Указание. Воспользоваться формулой (5.48), § 5.7. Надежность у
принять стандартной 0,95.
10. Проводятся однотипные независимые испытания, причем
вероятность р осуществления контролируемого события А в одном испытании
неизвестна. В проведенных п = 200 испытаниях событие А осуществилось
140 раз. Требуется оценить неизвестную вероятность р с
надежностью у = 0,97.
Указание. Воспользоваться точными формулами (5.51), § 5.8, значение
е097 найти в табл. 5.1.
Замечание. Так как п = 200 — достаточно большое число, то вместо
(5.51) можно воспользоваться приближенными формулами (5.52) без
особого ущерба. Рассмотрите оба способа, результаты сравните.
11. При п = 4040 бросаниях монеты Бюффон получил 2048 появлений
"герба". Полагая, что монета не обязательно должна быть правильной,
оценить с надежностью у = 0,99 вероятность р — появления "герба" при одном
бросании монеты.
Ответ: ш = 0,50693; е099 = 2,576; 0,48668 < р < 0,52718.
12. Найти наименьший объем выборки из нормальной генеральной
совокупности X, при котором с надежностью у = 0,95 точность оценки (т. е.
предельная ошибка выборки) математического ожидания М(Х) равна 0,2,
если среднее квадратическое отклонение генеральной совокупности
известно и равно а = 1,5.
Указание. Воспользоваться формулой (5.64) при t = е095 = 1,96.
Ответ: наименьший объем выборки п = 217.
13. Оценивается средний месячный расход на медицинские нужды в
семьях работников данного предприятия, причем средняя ошибка
полученной оценки должна быть равна 15 руб. Сколько семей должно быть
отобрано для проведения обследования?
Указание. Средняя ошибка оценки, находимой по выборке (средняя
ошибка выборки), равна -^ = 15. Оценивая а, исходя из выборки, o»s,
можно найти п.
14. Новый сорт пшеницы высеян на 10 опытных участках. После
урожая в пересчете на центнеры с 1 га получены следующие данные:
232

25,4; 28,0; 20,1; 27,4; 25,6; 23,9; 24,8; 26,4; 27,0; 25,4.
С надежностью у = 0,9 требуется: а) определить доверительный
интервал для среднего значения урожайности т этого сорта пшеницы; б)
построить доверительный интервал для дисперсии урожайности.
Ответ: 24,1 < т < 26,7; 2,65 < а2 < 13,5.
15. При наблюдении над п = 100 случайным образом выбранными
детьми дошкольного возраста с речевыми расстройствами установлено, что
т = 15 из них левши. Учитывая, что процент левшей — величина
случайная (для другой выборки она примет скорее всего иное значение), с
надежностью 0,95 найти доверительный интервал для величины процента
левшей среди детей дошкольного возраста с речевыми расстройствами.
Указание, ш = 0.15, Pi = ш -eY /ш(1 ~ °^ , р2 = ш + еу/ш(1 ""0 .
Ответ: (0,08; 0,22), т. е. истинный процент левшей с надежностью 0,95 —
от 8 до 22%.
16. Предыдущую задачу решить при п = 400 и т = 60. Хотя значение
ш = —— = 0, 15 и не изменилось, с ростом выборки в 4 раза
доверительный интервал уменьшился в к раз. Найдите к, объясните это соотношение.
17. Из предварительного исследования известно, что среди детей
дошкольного возраста с речевыми расстройствами левши составляют 15%.
Найти необходимый объем выборки л, чтобы предельная ошибка выборки
при надежности у = 0,95 составила 4%.
Указание. См. формулу (5.66), § 5.9.
Ответ: л = 307.
18. При изучении количества левшей среди детей дошкольного возраста
установлено, что среди наблюдавшихся л, = 400 здоровых детей процент
левшей равен 7%, а среди наблюдавшихся л2 = 100 детей, страдающих
теми или иными расстройствами речи, этот процент равен 15%. С
надежностью у =0,95 требуется установить наблюдаемая разность
15% — 7% = 8% является существенной или вызвана случайными
причинами, например недостаточными объемами выборок.
Указание. Требуется построить доверительный интервал для разности
средних, точнее, найти при у = 0,95 предельную ошибку выборки, которую
нужно сравнить с 0,08 (т. е. 8%). Для нахождения предельной ошибки
выборки воспользуйтесь формулой доверительного интервала разности
средних (5.48). В нашем случае оценки S] и SJ соответственно равны
Ш!(1 — ш,) и ш2(1 — ©2), где ш, = 0,07; ш2 = 0,15. Значение коэффициента ty
при л, и л2 порядка сотен практически равно соответствующему значению
еу для нормального распределения и находится из табл. 5.1, § 5.5.
Ответ: Предельная ошибка выборки Д« 0,0743 (т. е. 7,43%). Отклонение
в 8% превышает 7,43% и должно быть с надежностью 0,95 признано
существенным.
19. При исследовании вопроса о семейной наследственности у больных
шизофренией и эпилепсией обследовано л, = 900 больных шизофренией и
п2= 1100 больных эпилепсией. Среди обследованных больных
шизофренией имели наследственность заболевания 63 (т. е. 7%), среди обследован-
233

ных больных эпилепсией — ПО (т. е. 10%). Разность, полученная по этим
данным, составляет 10% — 7% = 3%. Можно ли утверждать, что семейная
наследственность более выражена при заболевании эпилепсией, чем
шизофренией? Привести ответ с надежностью
а) у = 0,95; б) у = 0,99.
Указание. Задача аналогична задаче 18. t095 = 1,96; t099 = 2,576
Ответ: а) Д = 0,0243(2,43%); отклонение с надежностью у = 0,95
существенно; б) Д = 0,0320(3,2%); с надежностью у = 0,99 отклонение не может
быть признано существенным.
20. Из специальной литературы известно, что семейная
наследственность заболевания у больных шизофренией составляет ш, = 0,07 (т. е. 7%),
а у больных эпилепсией — ш2 = 0,10 (т. е. 10%). Если наблюдалось 1100
больных эпилепсией (и у 10% — наследственность заболевания), то
сколько больных шизофренией должно наблюдаться (с наследственностью
заболевания 7%), чтобы считать разность в 3% существенной при надежности
выводов у = 0,99.
Указание. Искомое значение л, находится из соотношения (см.
значение Д из формулы (5.48), причем эмпирические дисперсии S] и S\
выражены через частоты ш, и ш2 соответственно).
д = /ш1(1-ш1) + ш2(1-ш2) де д = = fi = поо
TV л, л2
Следовательно, в указанном выражении л, оказывается единственным
неизвестным.
Ответ: л, = 1210.

Г л а в а VI. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
6.1. Статистическая гипотеза
При решении прикладных задач, имеющих вероятностную постановку,
зачастую необходимую установить неизвестный закон распределения
генеральной совокупности. В других случаях при известном законе
распределения требуется уточнить параметры распределения, равенство их
определенному числу, либо сравнение параметров по различным выборкам, либо
сравнение самих выборок.
Во всех подобных случаях выдвигаются определенные гипотезы:
например, закон распределения генеральной совокупности является
биномиальным или среднее генеральной совокупности, распределенной по
нормальному закону, равно нулю и т. д. Возможны и другие гипотезы
относительно параметров и выборок.
Статистической гипотезой называют предположение о неизвестном
законе распределения генеральной совокупности либо о параметрах
известных распределений. Статистическая гипотеза проверяется, исходя из
выборочных данных, статистическими методами. К статистической проверке
гипотез сводятся задачи сравнительной проверки и оценки различных
процессов: эффективности лечения, продолжительности болезни и
восстановительного периода, тяжести заболевания, сравнение лечебных методик,
сравнение различных характеристик процесса, характеристик препаратов и
медицинской техники, экономичности, мер профилактики и т. д.
Утверждения типа "в 2023 г. Земля может сойти со своей орбиты"
(Нострадамус), "тысячу лет назад нашу планету посещали инопланетяне"
являются гипотезами, но не статистическими, так как в них не присутствуют
ни закон распределения, ни параметры.
Статистические гипотезы, не использующие допущений о конкретном
законе распределения, называют непараметрическими гипотезами, в
противном случае гипотезы называют параметрическими. Непараметрические
гипотезы являются более общим понятием, нежели параметрические, ибо
методика их проверки не требует знания закона распределения, что,
несомненно, является их достоинством. Однако методы проверки
параметрических гипотез более эффективны, так как используют большее количество
информации о случайных величинах (закон распределения известен).
Статистические гипотезы бывают простыми и сложными. Простой
называют гипотезу, которая полностью однозначно определяет функцию
распределения (т. е. закон распределения) случайной величины. Гипотезу
называют сложной, если она состоит из объединения конечного или
бесконечного числа простых гипотез. Например, гипотеза "математическое
ожидание генеральной совокупности, имеющей пуассоновское
распределение, равно 2" — гипотеза простая, поскольку пуассоновское распределение
полностью определено одним проверяемым параметром. Гипотеза
"математическое ожидание нормальной генеральной совокупности равно 2" —
235

Таблица 6.1
^\^^ В действитель-
^^\^^ ности
Принята ^^^->^^^
гипотеза на ^^-^^^
основании исследования -^^
принята Я0
принята Я,
верна Я0,
ложна Я,
1
гипотеза Я0
верна и принята
3
верна гипотеза Я0,
но принята
ложная гипотеза Я,
верна Я,,
ложна Я0
2
верна гипотеза Я,,
но принята ложная
гипотеза Я0
4
гипотеза Я, верна
и принята,
ложная гипотеза Я0
отвергнута
гипотеза сложная, так как нормальное распределение определяется
однозначно двумя параметрами, т и а, и при фиксированном m = 2 и
произвольном а получаем объединение бесконечного множества простых
гипотез (при каждом фиксированном а своя простая гипотеза).
Основную гипотезу, которую намереваются проверять, называют
нулевой гипотезой} и обычно обозначают Я0.
Для каждой нулевой гипотезы обязательно существует альтернативная
гипотеза, противоречащая нулевой. Такую альтернативную гипотезу
называют конкурирующей гипотезой. Обозначим ее Я,.
Нулевая и конкурирующая гипотезы всегда не совместны, но не
обязательно образуют полную систему событий.
Выдвинутые гипотезы Я0 и Я, проверяются на истинность на основе
выборочных наблюдаемых данных статистическими методами.
Следовательно, обладая лишь информацией по выборке (неполной
информацией), о генеральной совокупности можно судить не однозначно, а с
определенной вероятностью. При этом, полагая нулевую гипотезу
справедливой (потому она и считается основной, что из каких-то соображений мы
верим в ее истинность), мы заинтересованы в наибольшей вероятности
признать нулевую гипотезу верной, а конкурирующую гипотезу отвергнуть.
Но вполне возможно, что справедлива не нулевая, а конкурирующая
гипотеза. В этом случае мы заинтересованы, наоборот, в наибольшей
вероятности принятия гипотезы Я, и, следовательно, в отвержении нулевой
гипотезы Я0. Рассмотрим ситуацию подробнее. Из двух взаимоисключающих
гипотез Я0 и Я, справедлива лишь одна. Для каждой из гипотез возможны
два решения: принять либо отвергнуть. Для наглядности представим
возникающие возможности в виде табл. 6.1.
1 Нулевую гипотезу мы уже использовали ранее в § 4.7.
236

Как видим, имеются четыре различных случая (в таблице
пронумерованы). Из них в двух (во 2-м и 3-м) мы допускаем ошибки, приняв вместо
истинной ложную гипотезу. Таким образом, возможны два вида ошибок.
Ошибка первого рода заключается в том, что верная нулевая гипотеза
Я0 отвергается, а принимается конкурирующая ложная гипотеза Я, (в
таблице — случай 3).
Ошибка второго рода заключается в том, что ложная гипотеза Я0
принимается, хотя на самом деле верна конкурирующая гипотеза Я, (в
таблице — случай 2).
Отметим, что гипотезы Я0 и Я, в исследовании не равноправны.
Статистическая проверка осуществляется для нулевой гипотезы Я0, поэтому
гипотезу Я0 и называют основной. Проверить нулевую гипотезу необходимо
так, чтобы возможности ошибок обоих типов свести к минимуму.
Вероятность — допустить ошибку первого рода обозначим а. Число а —
вероятность ошибки первого рода — называют уровнем значимости.
Аналогично, вероятность — допустить ошибку второго рода обозначим р.
Вероятность — не допустить ошибку второго рода, т. е. при
справедливости конкурирующей гипотезы Я, вероятность — принять эту гипотезу,
называют мощностью критерия (иногда говорят "чувствительность
критерия'). Мощность критерия равна 1 — р. Понятно, что чем больше это
значение, тем лучше, качественнее работает наш критерий. Подробнее о
зависимости мощности критерия от некоторых условий поговорим позднее в
§6.8.
Задача исследователя — минимизировать обе вероятности: и а, и р. Но
обе вероятности оказываются взаимосвязанными, и, уменьшая одну из них
при фиксированных условиях, мы неизбежно это уменьшение
компенсируем ростом вероятности другой ошибки. Единственный способ
одновременного уменьшения вероятностей обеих ошибок — это увеличение
объема выборки (вполне естественно, что, увеличивая объем выборки,
получаем больше информации о генеральной совокупности, и вероятность
ошибок уменьшается).
Обычно поступают следующим образом: фиксируют уровень
значимости а, т. е. задают границу вероятности отклонить нулевую гипотезу Я0,
когда она верна, и пытаются провести исследование так, чтобы р
оказалось наименьшим. Стандартными уровнями значимости а, для которых
построены соответствующие таблицы, считаются числа 0,2; 0,1; 0,05; 0,02;
0,01; 0,005; 0,002; 0,001.
Естественным является желание выбрать а как можно меньше, но тогда
вероятность ошибки второго рода р может оказаться слишком большой
(мощность критерия невелика). Разумное соотношение между аир
находят, исходя из тяжести последствий каждой из ошибок. Например, пусть
проверяется гипотеза отсутствия у пациента некоторого заболевания.
Признаком заболевания служит значение определенного показателя (к
примеру, артериальное давление), тогда нулевая гипотеза Я0 — значение
показателя в норме, т. е. пациент здоров. Конкурирующая гипотеза Я, —
значение показателя отличается от нормы, т. е. пациент болен. В этом случае
ошибка первого рода — отклонение нулевой гипотезы, когда она верна,
т. е. признаем человека больным, когда он на самом деле здоров. Эта
237

ошибка приводит к некоторым неудобствам для пациента, который должен
пройти дополнительное обследование или курс лечения, и обычно не
несет тяжелых последствий. Совсем иная картина в случае допуска ошибки
второго рода — принять нулевую гипотезу, когда она неверна, т. е.
признать человека здоровым, когда он на самом деле болен. Фактически
происходит отказ от лечения больного, и в этом случае последствия ошибки
второго рода могут оказаться самыми плачевными. Следовательно, в
рассмотренном примере возможно пожертвовать высоким уровнем
значимости а с целью уменьшить вероятность ошибки второго рода р. Можно
привести примеры других случаев, когда, наоборот, более существенным по
тяжести последствий оказывается выбор наименьшего разумного значения
а, а не р.
Выбор уровня значимости а также продиктован нашей априорной
уверенностью в справедливости гипотезы Н0. Чтобы переубедить нас в
обратном, должны быть веские доказательства против нулевой гипотезы, и для
этого уровень значимости а выбирают достаточно малым.
Особо отметим тот факт, что принятие или отбрасывание нулевой
гипотезы происходит с определенной вероятностью и не является
доказательством ее справедливости или ложности. Например, принятие нулевой
гипотезы #0 при уровне значимости а = 0,01 означает, что наша гипотеза не
противоречит наблюдаемым опытным выборочным данным и для других
выборок того же объема из той же генеральной совокупности принятая
гипотеза в среднем будет справедлива в 99 случаях из 100 (точнее, не менее
чем в 99 случаях на 100 рассматриваемых). Таким образом, принимая эту
нулевую гипотезу, мы рискуем ошибиться в среднем не чаще чем в 1%
случаев.
6.2. Статистические критерии
Обсудив в предыдущем параграфе статистические гипотезы, мы
подошли к вопросу о методах проверки их справедливости или опровержения.
Следовательно вопрос в том, подтверждается наша гипотеза
наблюдаемыми данными или же противоречит этим данным.
Как известно (см. § 1.10, 1.15), теоретическая вероятность обладает
статистической копией в виде относительной частоты. В результате имеет
место частотная интерпретация вероятности:
"Если случайное событие А при некотором комплексе условий имеет
вероятность р, то практически несомненно, что при многократном
повторении испытания с тем же комплексом условий относительная частота
осуществления события А окажется приближенно равной теоретической
вероятности р".
Следовательно, для проверки согласованности теории с опытными
данными мы можем потребовать, чтобы полученная нами теоретическая
вероятность р подтверждалась соответствующей частотной интерпретацией.
Согласно частотной интерпретации случайное событие, имеющее
малую вероятность, в длинной последовательности испытаний будет
осуществляться достаточно редко. А значит, мы можем считать практически
несомненным, что в одном-единственном испытании это редкое событие не
238

произойдет (сравните по своему опыту, сколь часто, приобретя один
лотерейный билет, его обладатель получает приз; разумеется, при условии, что
в этой лотерее число призов гораздо меньше числа проданных билетов).
Аналогично, столь же практически несомненным представляется факт
осуществления случайного события в одном испытании, если теоретическая
вероятность этого события близка к 1. На этих принципах и строится
теория проверки статистических гипотез. Теория допускает возможность
появления ошибок при проверке статистических гипотез (см. § 6.1) и
предлагает методы, минимизирующие вероятности (возможности) ошибок. В то
же время при принятии ответственных решений необходимо принимаемую
гипотезу проверить неоднократно, используя как различные выборки, так
и различные методы.
Рассмотрим схему методов проверки гипотез. Пусть, например, нулевая
гипотеза провозглашает некоторое гипотетическое распределение
генеральной совокупности с определенными параметрами и функцией
распределения F(x). Проверка гипотезы — проверка принадлежности выборки к
этой гипотетической генеральной совокупности, т. е. соответствия
эмпирической функции распределения Fn(x) (см. § 4.3), являющейся
приближенным значением функции распределения генеральной совокупности, к
предполагаемой в нулевой_ гипотезе функции распределения F(x). Для
оценки степени различия Fn(x) и F{x) вводится некоторая мера
отклонения, которая зависит от выборки и, следовательно, будет случайной
величиной.
Эту случайную величину, служащую для проверки нулевой гипотезы,
называют статистическим критерием. Статистический критерий, являясь
случайной величиной, имеет какое-то вероятностное распределение.
Обычно критерий выбирают таким, чтобы он имел одно из следующих
распределений: нормальное, х2, распределение Стьюдента, распределение
Фишера. Это объясняется тем, что нормальное распределение — особое
распределение, наиболее распространенное, тесно связанное со многими
распределениями и являющееся предельным для некоторых распределений
или возникающим согласно центральной предельной теореме; другие
упомянутые распределения оказываются удобными в применении ввиду их
зависимости лишь от числа степеней свободы. Обозначают критерии так же,
как и случайные величины: Z, T> Fn т. д. В качестве статистических
критериев мы будем использовать статистики, представленные в § 5.3.
Выбрав критерий (обозначим его в общем случае А), все множество
значений, принимаемых К, разобьем на два подмножества: значения в
одном из них соответствуют принятию, а значения в другом подмножестве
соответствуют отвержению нулевой гипотезы.
Совокупность значений, при которых нулевую гипотезу следует
отвергнуть, называют критической областью.
Совокупность значений, при которых нулевую гипотезу следует
принять, называют областью принятия гипотезы.
Поскольку все возможные значения критерия К образуют интервал, то
критическая область и область принятия гипотезы также являются
интервалами. Эти интервалы не могут пересекаться, и, следовательно, имеются
граничные точки, разделяющие данные области.
239

"кр
д ШШШ|
1
0
1
1
0
1—
Ш///////////А^
^шшш.^
Рис. 37.
Точки, отделяющие критическую область от области принятия
гипотезы, называют критическими точками. Обозначим их ккр.
Критические области могут быть односторонние (рис. 37, а, б) и
двусторонние (рис. 37, в).
На рис. 37 критические области отмечены штриховкой. В случае а
критическая область определяется неравенством К > ккрУ где ккр > 0, и
называется правосторонней.
В случае б критическая область определяется неравенством К < kKpi где
ккр < 0, и называется левосторонней.
В случае в двусторонняя критическая область определяется двумя
неравенствами: K<kKPi, K> ккрг где kKPi<kKPi. Часто двустороннюю
критическую область выбирают симметричной относительно нуля, тогда
~КРх = kKPi = kKp и тогда \К\ > ккр.
Как видим, критическая область полностью определяется одним или
двумя (в случае двусторонней и несимметричной области) критическими
значениями. И здесь возникают два вопроса: по какому принципу
выбирать критическую область и каким образом определить критические
значения кКП?
Принцип построения критической области таков: эта область
возможных значений критерия К, принимаемых крайне редко, т. е. достаточно
мала вероятность, что в результате наблюдения за одной выборкой
случайная величина К, созданная по этой выборке, примет значение из
критической области. Обозначим эту вероятность попадания критерия К в
критическую область символом а (это значение а является уровнем значимости,
введенном в предыдущем параграфе).
Тогда критическая область при выбранном малом значении а
определяется условием
Р (А" принимает значение из критической области) = а. (6.1)
Согласно частотной интерпретации вероятности при справедливости
нулевой гипотезы, критерий К в одном-единственном испытании
практически не может принять значение из критической области. (Заметим, что
для критерия К нахождение его численного значения по одной имеющейся
выборке — это и есть единственное испытание.)
Далее, по таблицам, которые имеются для каждого критерия в
зависимости от его распределения и приведены в Приложении 2, при принятом
240

уровне значимости а находим граничные значения ккр. Зная kKpi
определяем критическую область (заметим, что вид критической области, см.
рис. 37, диктуется распределением используемого критерия, проверяемой
гипотезой Я0 и особенно видом конкурирующей гипотезы). Условия
определения критической области (6.1) в случае правосторонней критической
области имеет вид
Р(К>ккр) = <х, (6.2)
в случае левосторонней критической области —
Р(К<ккр) = а, (6.3)
и в случае двусторонней критической области —
P(K<kKPi) + P(K>kKP2) = a. (6.4)
Заметим, что в последнем равенстве критические точки kKPi и ккрг
определяются неоднозначно. Если же распределение критерия К симметрично
относительно нуля (например, распределение Стьюдента или нормальное
распределение ./V (0; а)), и критические точки —kKPi = ккрг = ккр, то
P(K<kKPt) = P(K>kKpi)t
и, следовательно, вместо (6.4) имеем
Р(К> ккр) = |, Р(К< -ккр) = 2. (6.5)
Определив критическую область, а следовательно, и область принятия
гипотезы, по выборке вычисляем наблюдаемое значение критерия К.
Частотная интерпретация влечет вывод:
— если найденное по выборке значение К принадлежит области
принятия гипотезы, то нулевая гипотеза Я0 не противоречит наблюдениям и
принимается;
— если найденное по выборке значение К принадлежит критической
области, то тем самым нулевая гипотеза Я0 опровергнута, и принимается
конкурирующая гипотеза Я,.
В случае принятия нулевой гипотезы считается, что различия между
наблюдаемыми значениями и истинными обусловлены случайными
причинами и являются не значимыми (не принципиальными).
В случае отторжения нулевой гипотезы говорят, что различия между
наблюдаемыми значениями и теоретическими (согласно нулевой гипотезе)
значимы, т. е. обусловлены принципиальными причинами: ошибочностью
нулевой гипотезы.
Еще раз отметим, что опровержение опытом гипотезы Я0 вовсе не
равноценно логическому опровержению. Вполне возможно, что нам в нашей
единичной выборке просто не повезло: среди множества всех возможных
выборок заданного объема п попалась именно такая редкая, которая
приводит значение критерия К в критическую область. Утешением в
предчувствии таких случаев может служить знание, что при справедливой нулевой
гипотезе это возможно в среднем лишь в а • 100% случаев. Осознание этого
факта и степень тяжести последствий принятия решения Я0 или Я,
позволяют в каждом конкретном случае либо решительно отвергнуть нулевую
16 — 3529
241

гипотезу, либо принять, либо продолжить исследование иными методами;
можно, например, увеличить объем выборки, а также использовать другие
критерии.
Критерии общего характера проверки статистических гипотез называют
критериями значимости. В случае проверки гипотез о согласии
выборочного и теоретического распределений критерии значимости называют
критериями согласия (см. § 4.7).
6.3. Сравнение дисперсий двух нормальных
генеральных совокупностей
Пусть имеются две нормальные генеральные совокупности X и Y,
дисперсии которых D(X) и D(Y) неизвестны. По выборкам Хи Х2, ..., Хп и У,,
Y2, ..., Ym объемов пит соответственно требуется сравнить дисперсии.
Подобные задачи сравнения дисперсий возникают в случаях сравнения
точности измерений, точности приборов, сравнения методик. Поскольку
дисперсия характеризует степень сосредоточения (рассеяния) значений
относительно среднего, то наилучшей характеристикой является та, у которой
дисперсия меньше.
Из различных гипотез относительно дисперсий (соотношений между
дисперсиями) в качестве нулевой гипотезы обычно выдвигают гипотезу
равенства дисперсий:
Я0: D(X) = D(Y). (6.6)
Тогда для конкурирующей гипотезы остаются следующие возможности:
1) D(X)*D(Y)\ 2) D(X) >D(Y)\ 3) D(X) <D(Y).
Понятно, что последние два случая принципиального различия в
методике не имеют, так как любое из этих неравенств получается из другого,
если X и Y поменять местами. Таким образом, достаточно рассмотреть два
случая конкурирующей гипотезы.
В нулевой гипотезе (6.6) числа D(X) и Д Y) заменим характеристиками,
связанными с выборками:
D(X) = M(S2X), D{Y) = M{S])y (6.7)
где S\ и S2y — исправленные выборочные дисперсии рассматриваемых
генеральных совокупностей. Равенства (6.7) следуют из несмещенности этих
оценок (см. § 5.2). Следовательно, нулевая гипотеза (6.6) оказывается
такой:
Я0: M(S2X) = M(S2y). (6.8)
Для проверки нулевой гипотезы используем в качестве критерия
статистику F отношения двух исправленных выборочных дисперсий S\ и S2y с
п — 1 и т — 1 степенями свободы соответственно (см. § 5.3).
242

Для определенности условимся в отношении оценок S2X и S2y
числителем ставить большую из этих оценок, а знаменателем меньшую. Обозначив
их S] и S2M, получим критерий
F= Ц. (6.9)
Si
Число степеней свободы для числителя обозначим ки для
знаменателя — к2\ разумеется, одно из этих чисел п — 1, а другое — т — 1.
Заметим, что всегда оказывается F> 1.
Из § 5.3 известно, что статистика .Твида (6.9) имеет распределение
Фишера с ки к2 степенями свободы, и распределение целиком определяется
этими двумя параметрами. Так что при справедливости нулевой гипотезы
случайная величина F для. нас полностью открыта: известен ее закон
распределения и точные значения параметров к{ и к2. Следовательно, мы
беспрепятственно можем разбить все множество значений F — а это интервал
от 0 до +оо _ на область принятия гипотезы Я0 и критическую область.
Для этого достаточно выбрать уровень значимости а (например, наиболее
распространенные в медицинских приложениях уровни
значимости а = 0,05 или 0,01) и по таблицам (см. табл. 7 Приложения 2)
определить критические точки распределения F. Критические точки — это
не что иное, как соответствующие квантили нашего рассматриваемого
распределения. И вот здесь мы подходим к вопросу выбора критической
области: односторонней либо двусторонней. Наш выбор зависит от вида
конкурирующей гипотезы Я,. Если есть основания предполагать одну из
дисперсий обязательно не меньше другой, например D(X)> D(Y), тогда
Я0 : D(X) = D(Y);
Я,: D(X)>D(Y).
В этом случае критическая область односторонняя, а именно:
правосторонняя.
Если же нет оснований полагать одну из дисперсий обязательно больше
другой, тогда конкурирующая гипотеза
Я,: D(X)*D(Y)t
и критическая область оказывается двусторонней, а значит, уровень
значимости а должен быть поделен между двумя интервалами критической
области.
Далее находим реальное значение F, наблюдаемое, а точнее,
вычисляемое по выборочным данным. Обозначим его FHa6r Если окажется, что FHa6jl
приняло значение из критической области, то нулевую гипотезу Я0
отбрасываем и принимаем конкурирующую Я,; в противном случае, когда FHa6a
оказывается в области принятия гипотезы, нулевую гипотезу принимаем и
полагаем, что она не противоречит опытным данным.
Рассмотрим оба возможных случая конкурирующей гипотезы по
отдельности.
16*
243

I. Пусть
Я0 : D(X) = D(Y);
Я,: D(X)>D(Y).
Тогда
по выборкам Xlt X2i ..., Х„ и У,, Y2, ..., Ym вычисляем конкретные
значения исправленных выборочных дисперсий S2X, S2y;
находим число
^.=4> (6-ю)
где 4 и s], — большее и соответственно меньшее из чисел sx, ^;
выбираем уровень значимости а и для правосторонней критической
области находим по табл. 7 Приложения 2 граничное значение: критическую
точку ккр (при этом &,, &2 — количество степеней свободы числителя и
знаменателя соответственно);
обозначим ккр = FKp(a\kM\ сравниваем FHa6jl. и ккр\
делаем выводы: если FHa&l > kKp, то при выбранном уровне значимости
различие дисперсий значимо, нулевая гипотеза отбрасывается и
принимается конкурирующая Я,; если же FHa6jt < kKpt то принимается гипотеза Я0
как непротиворечащая опытным данным.
И. Пусть
Щ: D(X) = D(Y);
Я,: D(X)*D(Y).
Далее поступаем так же, как и в предыдущем случае: находим s\, s] и
по отношению (6.10) — FHa6jt.
Для нахождения критической области нужно определить две
критические точки: kKPi и ккРг.
На рис. 38 эти точки указаны и отмечена критическая область, причем
обычно критические точки выбирают так, чтобы вероятности попадания
св. F в каждый из двух интервалов критической области были равны (это
обеспечивает наибольшую мощность критерия). Поскольку суммарная
вероятность — это уровень значимости а, то оказывается
P(F<kKPi) = P(F>kKPi) = |. (6.11)
Если посмотреть на график плотности распределения Фишера (см.
рис 38), то можно заметить, что, начиная от нуля, график круто взмывает
вверх, и вследствие этого интервал от нуля до kKPi достаточно мал.
Поэтому обычно в рассматриваемом случае ищут только одну критическую точку
ккРг, исходя из соотношения (6.11)
P{F>kKPi) = |, (6.12)
244

Рис. 38. Плотность распределения Фишера с. в. Fc обозначением критической
области.
а левую часть критической области игнорируют. Так как FHa&l > 1 [в (6.10)
числитель всегда больше знаменателя], то FHa&l в левую часть критической
области не попадает, но использование в (6.12) вероятности ^ эту область
учитывает.
Итак, по (6.12), используя табл. 7 Приложения 2, находим критическую
точку: kKPi = /ц|;*,;*2).
Далее сравниваем FHa&l и kKPi: если FHa6jt > kKPi, то различие дисперсий
значимо, и Я0 отвергается; если же Fm6ji < kKPi, то гипотеза Я0 принимается
как непротиворечащая опытным данным.
Пример. Пусть при лечении некоторого заболевания применяются две
методики: А и В. Эффективность методик характеризуется изменением
численных значений определенного показателя. Отобраны две однородные
группы больных, первая численностью п = 20, а вторая — т = 15 человек.
В первой группе (с методикой А) значения рассмотренного показателя
Xlt Х2, ..., Х20, во второй (с методикой В) — Ylt Уъ .... Yl5. Известно, что
соответствующие генеральные совокупности X и Y имеют нормальное рас^
пределение. Оказалось, что для обеих групп средние значения показателя х
и у практически равны, а исправленные выборочные дисперсии s\ = 21,5,
s2y = 32, 8 . Требуется сопоставить две методики лечения при уровне
значимости а = 0,1.
Поскольку средние значения наблюдаемого показателя в обеих группах
равны, то эффективность методик в среднем одинакова. Оценим
стабильность результата, т. е. различный разброс значений показателя в группах
значим (вызван сутью применяемых методик) или незначим (вызван
случайными причинами: например, объясняется конкретным подбором
больных в группы, малым объемом выборок и т. д.).
Выдвигаем нулевую гипотезу
Я0: D(X) = D(Y)t
конкурирующую гипотезу
Я,: D(X)*D(Y).
245

При такой конкурирующей гипотезе критическая область должна быть
двусторонней и критическую точку ищем, исходя из соотношения (6.12),
т. е. при половинном значении уровня значимости а. Так как выбранное
значение а равно 0,1, то ^ = 0,05. Чтобы воспользоваться таблицей,
необходимо определить также к{ и к^. Поскольку большее значение
исправленной выборочной дисперсии s2y = 32, 8 соответствует второй группе, то
кх = т — 1 = 14, к2 = п — 1 = 19. По табл. 7 находим критическую точку
FKp(f,kuk2) = /уо,05;14;19) = 2,26.
Замечание. В табл. 7 Приложения 2 не оказалось критического
значения при кх = 14, но ближайшие к нему значения /^(0,05; 15; 19) = 2,23 и
/^(0,05; 12; 19) = 2,31 позволяют методом линейной интерполяции
приближенно определить нужное значение как FKp(0>05; 14; 19) = 2,26.
Вычислим Гмбд по формуле (6.10). По нашим данным, s] = s2y = 32,8,
s2M = s2x = 21,5, тогда
Рнабл. = ~-р7 ~ 1» 526 .
Сравнивая FHa6jl = 1,526 с FKp = 2,26, получаем, что значение FHa6jt
попадает не в критическую область, а в область принятия гипотезы.
Вывод. Принимается нулевая гипотеза как непротиворечащая опытным
данным. Следовательно, разброс значений показателя при обеих методиках
не позволяет судить о значимых различиях: D(X) = D(Y). Различие
выборочных дисперсий s2x и s2y объясняется случайными причинами. Таким
образом, статистически значимых различий методик не установлено.
6.4. Проверка гипотезы о равенстве неизвестной дисперсии конкретному
значению
Пусть генеральная совокупность X имеет нормальное распределение.
Дисперсия генеральной совокупности известна, но на основании
дополнительной информации есть повод предполагать, что дисперсия равна
определенному числу: D(X) = а2,. Требуется проверить указанное
предположение.
Итак, нулевая гипотеза налицо. Проверять гипотезу будем по выборке
Хи Хъ ..., Хп объема и, извлеченной из рассматриваемой генеральной
совокупности X. Исходя из выборки, считаем найденной исправленную
выборочную дисперсию S2. Учитывая несмещенность S2 как оценки D(X) (см.
§ 5.2), нулевую гипотезу запишем в виде
Я0: M(S2) = a2,.
Проверка гипотезы о значимости различий выборочной и генеральной
дисперсий находит практическое применение в задачах оценки точности
измерительных приборов, устойчивости методов исследования, стабильно-
246

к
Рис. 39. Плотность распределения х2 с обозначением правосторонней критической
области.
сти протекания различных процессов, характеризующихся численными
показателями.
Критерием проверки представленной нулевой гипотезы назначим уже
использованную ранее, при построении доверительных интервалов,
статистику
Х2 = -2(п-\), (6.13)
которая имеет распределение "хи-квадрат" с (и — 1) степенями свободы
(см. § 5.3).
Построение критической области зависит от конкурирующей гипотезы,
для которой возможны три случая: D(X) > al, D(X) < а\, D(X) * al.
Попадание значения xL&i, найденного подстановкой в (6.13) вместо S2
конкретного значения исправленной выборочной дисперсии, в область
принятия гипотезы или в критическую область и решает вопрос: принять
нулевую гипотезу или отвергнуть.
Рассмотрим все три возможных случая построения критической
области.
I. Пусть
Я0 : D(X) = а2,;
Я, : D(X) > al
Тогда, исходя из вида конкурирующей гипотезы Я,, заключаем, что
критическая область правосторонняя и сосредоточена в одном интервале
справа от критической точки (рис. 39).
Вероятность попадания критерия у} вида (6.13) в критическую
область — это величина уровня значимости а:
^(Х2 > ккР) = а.
Значение критической точки кКр находим из таблицы распределения у}
(см. табл. 4 Приложения 2) по выбранному уровню значимости а и числу
степеней свободы п — 1 (в табл. 4 эти величины обозначены
соответственно р и г). Тем самым очерчена критическая область, и остается вычислить
247

Ъшбл по формуле (6.13) и конкретным числам j2, а\, n и сравнить
найденные значения XL. и ^.
Если xL&i < £к/)> то нулевая гипотеза принимается, т. е. наблюдаемые
различия между л2 и aj вызваны случайными причинами и незначимы,
можно полагать М(^2) = aj. Если же хна6л > ккр, то различия между j2 и
а] значимы, продиктованы действительно объективными причинами, и
нулевая гипотеза отвергается, а принимается конкурирующая Я,.
Пример 1. При производстве лекарственных препаратов
руководствуются стандартом. Контролируется определенный показатель, допустимая
характеристика рассеяния которого определена числом а0 = 10. Из
произведенной партии продукции извлекается контрольная выборка объема
п = 15 единиц продукции. Исправленная выборочная дисперсия
контролируемого показателя j2 = 15,8. Требуется по выборке проверить значимость
различий дисперсий, наблюдаемой M(S2) и контрольной ol, полагая
уровень значимости a = 0,1. Также известно, что генеральная совокупность
распределена по нормальному закону.
В данной постановке задачи необходимо проверить нулевую гипотезу
Я0 : D(X) = 10.
Так как по стандарту дисперсия не может превышать допустимое
значение а2) = 10, то в качестве конкурирующей гипотезы примем гипотезу
Я,: D(X)>\0.
Тем самым критическая область определяется как правосторонняя. По
уровню значимости a = 0,1 и числу степеней свободы х2> равному
п — 1 = 14, из табл. 4 находим критическую точку ккр = ккр(0,\;\4) = 21,1.
Вычислим
xL*. = ^(15-1) = 22,12.
Поскольку значение %на6л > kKpi т. е. xLm попадает в критическую
область, то нулевая гипотеза отвергается на уровне значимости a = 0,1, а
принимается конкурирующая гипотеза Я,.
Вывод. Данный процесс производства требует корректировки, так как
статистическая проверка показывает значимое отклонение от стандартных
параметров.
II. Пусть
Я0 : D(X) = a2,;
Я, : D(X) < a2,.
Вид конкурирующей гипотезы предопределяет левостороннюю
критическую область (рис. 40).
Уровень значимости a — вероятность попадания критерия х2 в интервал
от 0 до ккр.
Р(Х2 < ккр) = а .
248

Рис. 40. Плотность распределения х2 с обозначением левосторонней критической
области.
Чтобы воспользоваться знакомой нам табл. 4 для нахождения ккрУ
необходимо знать вероятность Р(х2 < ккр), ибо именно вероятности таких
событий представлены в таблице. А так как случайные события х^Ькр и
X > ккр противоположны, то получаем
Р(Х2 > ккр) = 1 - Р(х2 * К) = 1 - Р(х2 < ккр) - Р(х2=ккр) =
= 1 -<х-0 = 1 -<х.
Следовательно, ккр в данном случае можно найти по табл. 4 из условия
Р{Х>К) = 1-а. (6.14)
Далее поступаем стандартно: вычисляем xLm и сравниваем с xlP- Если
х1абл<х1Ру т0 нулевая гипотеза отвергается и принимается конкурирующая.
Если х2шбл>х1Р> т0 принимается именно нулевая гипотеза.
III. Пусть
Н0 : D(X) = al;
Нх: D(X)*al
При рассматриваемой конкурирующей гипотезе следует выбрать
критическую область двусторонней (рис. 41).
Вероятность попадания критерия в критическую область равна а. Но
поскольку критическая область состоит из двух непересекающихся
интервалов, то и вероятность разбивается на сумму двух вероятностей:
Pix2<kKPl) + P{x2>kKpi) = a.
Теория подсказывает, что для обеспечения минимальной ошибки
второго рода (т. е. наибольшей мощности критерия) следует эти
вероятности — слагаемые взять равными:
P(x2<kKPl)=P(x2>kKPl) = \-
249

Рис. 41. Плотность распределения х2 с обозначением двусторонней критической
области.
Тогда критические точки кк?х и ккрг легко найти в табл. 4, исходя из
условий
Дх2 > кКРг) = |, Дх2 > ккр) = 1 - Р(Х2 < kKPi) = 1 " f • (6.15)
Далее, найдя значение kKPx, kKPl, поступаем аналогично предыдущему:
вычисляем х1абл и в зависимости от того, попадает это значение в область
принятия гипотезы (kKPi < х\абА < kKPi) или в критическую область (либо
xLw<£*/>, либо х1абл> ккРг)> нулевую гипотезу принимаем или отвергаем,
принимая конкурирующую.
Пример 2. Из нормальной генеральной совокупности X извлечена
выборка Xxt Хъ ..., Х22 объема п = 22. Вычисленная исправленная выборочная
дисперсия S2 оказалась равной 25. При уровне значимости а = 0,02
необходимо проверить нулевую гипотезу Я0: D(X) = 15 при конкурирующей
гипотезе Я,: D(X)*-\5.
Исходя из вида конкурирующей гипотезы Я,, полагаем критическую
область двусторонней. Ищем критическую область для нулевой гипотезы,
для чего достаточно определить значения критических точек ^и^ (см.
рис. 41), полагаясь на условия (6.15)
P{X>kKPl) = % = 0,01,
Р{г>ккр) = 1-f = 0.99.
Из табл. 4 при числе степеней свободы п — 1 = 21 и найденных
вероятностях 0,01 и 0,99 соответственно следует
КРх = 8,9; kKPi =38,9.
Таким образом, интервал (8,9; 38,9) — область принятия гипотезы Я0;
все остальные значения принадлежат критической области.
Вычисляем наблюдаемое значение критерия
_ s
— \\ = 25хоо _ 1 \ _
ТС** = -2(Я"1) = f?(22-\) = 35
250

Как видим, значение хна6л находится в области принятия гипотезы,
следовательно, нулевая гипотеза принимается.
Замечание. Хотя значение хна6л = 35 при рассматриваемом уровне
значимости а = 0,02 действительно принадлежит области принятия гипотезы
(8,9; 38,9), близость этого значения к критической области, граничное
значение которой 38,9, должна привлечь внимание исследователя. Чтобы
рассеять сомнения в правильности выводов, необходимо дополнительное
исследование. Например, более точного результата можно достичь,
увеличивая объем выборки.
6.5. Сравнение средних двух нормальных генеральных совокупностей
при известных дисперсиях
Пусть имеются две генеральные совокупности X и Y. Исходя из
выборочных данных, требуется сравнить математические ожидания М(Х) и
МП-
Подобная задача возникает при сравнении двух групп элементов
(например, двух групп больных), подвергшихся определенному воздействию
(например, проходящая курс лечения по различным методикам одна
группа больных принимает определенный лекарственный препарат, а другая
группа — контрольная — принимает плацебо). При этом сравнение
средних позволяет судить о степени воздействия, о значимости возможных
эффектов воздействия или, наоборот, об их отсутствии.
В данном параграфе рассмотрим случай, когда генеральные
совокупности Хи Yимеют нормальное распределение, что в различных прикладных
задачах бывает достаточно часто. Проверить условие нормальности по
выборочным данным можно с помощью критериев согласия либо других
методик. Также предположим, что дисперсии D(X), D(Y) известны.
Данными для исследования будут служить две независимые выборки:
Хи Х2, ..., Хп объема п и У,, Y2i ..., Ym объема т. Схема исследования:
выдвижение гипотез, нулевой и конкурирующей, и использование статистики
определенного вида в качестве критерия.
Нулевая гипотеза о равенстве математических ожиданий М(Х) = M(Y)
равносильна гипотезе
Я0: M(X) = M(Y),
так как ввиду несмещенности оценок математического ожидания [см. (5.5)
§5.2] М{Х) = М(Х) и M(Y) = M(Y). Поскольку значения выборочных
средних Хи Y, вообще говоря, различны, то необходимо проверить,
значимо это различие (вызвано принципиальными соображениями) либо
незначимо (вызвано случайными обстоятельствами, методами отбора именно
этих, а не других элементов в выборку, малым количествам наблюдений).
Критерием для проверки гипотезы Я0 может служить статистика
7= ~Х~_^ _- (6Л6)
Jd(X- Y)
251

Так как обе генеральные совокупности Хи Yнормальны, то также
нормальны и случайные величины выборок Хх, Хъ ..., Хп и К„ Y2i ..., Ym
(согласно определению репрезентативности выборок, см. § 4.2). Поскольку
линейные функции нормальных случайных величин нормальны (см. заме^
чание в § 3.7), то также нормально распределенными оказываются и Хи Y
и их линейная функция (6.16) (заметим, что в знаменателе дроби (6.16) не
случайная величина, а число: стандартное отклонение случайной
величины Jf- Y). Таким образом статистика Z вида (6.16) имеет нормальное
распределение. _ _
В случае спр_аведливости_нулевой гипотезы М(Х) = M(Y) получается,
что М(Х) - M(Y) = M(X- Y) = 0, следовательно, и
M(Z) = М\ *~^_ = _* _ М(Х- Y) = 0.
^JD(X- Y)J JD(X- Y)
Непосредственно вычисляется и D{Z)\
D(Z) = D\ i*~^_ 1 = f , _? _ У™*- Y) = 1.
\JD(X- Y)' JD{X- Y)
Итак, вывод: случайная величина Z~ N(0; 1).
Уточним выражение (6.16), упростив знаменатель:
D(X- Y) = D(X) + D(Y),
согласно свойству дисперсии (3.29) (см. § 3.4), примененному к
независимым случайным величинам Хи К (см. также замечание в § 3.5). И так как
D(X) = ШУ
п
[см. (5.9)] и аналогично
т
Ю-Ъ-Ш + ОШ.
п т
Следовательно, критерий Zbhrsl (6.16) можно записать в более удобной
для расчета форме:
Z = *~Y • (6.17)
п т
Вернемся к проверке выдвинутой нулевой гипотезы. Схема действий та
же самая, что и в предьщущих параграфах. В противовес Я0 назначается
конкурирующая гипотеза Я,, и в зависимости от вида Я, и уровня
значимости а строится критическая область. Далее по выборочным значениям
вычисляется значение ZHa6ay которое и определяет справедливость Я0 (в
случае попадания в область принятия гипотезы) либо Я, (в случае попадания
в критическую область).
Учитывая сказанное, приведем методику нахождения критических
областей.
252

Рис. 42.
Рис. 43.
I. Пусть
Я,: М(Х) > M(Y).
Тогда критическая область правосторонняя, и чтобы ее определить,
достаточно для критерия Z найти одно граничное значение zKp. (рис. 42),
соответствующее уровню значимости а.
Учитывая, что Z~ N(0;\), вероятность попадания Zb критическую
область легко найти, вспомнив свойства нормально распределенных
случайных величин [см. (2.67), § 2.11]:
P(Z> zKp) = P(Ze (zKp', + со)) = 1 - ф(^г?) ,
где Ф(...) — функция Лапласа [которая, напомним, стремится к 1 при
стремлении аргумента к +°° (см. § 1.14, свойство 3)].
Данная величина равна назначенному числу а, уровню значимости
следовательно,
Ф(4„)=1-а- <6Л8>
Обращаясь к табл. 2 (Приложения 2) значений функции Лапласа,
находим конкретное значение zKp, для которого справедливо (6.18), а тем самым
и критическую область (zKp, +°°).
II. Пусть
Н{.М(Х) < M(Y).
В этом случае критическая область левосторонняя (~°°; zKp), (рис. 43).
253

Рис. 44.
Тогда вероятность попадания критерия Z в критическую область равна
[см. (2.67), §2.11]
P(Z< zKp) = P(Ze (-co;Zkp)) = Ф^т-5) - О
1
(напомним, что функция Лапласа Ф(...) стремится к нулю при стремлении
аргумента к —°°, см. § 1.14, свойство 2).
Поскольку найденная вероятность попадания Z в критическую
область — уровень значимости а, то получаем
®(zKp) = а.
Далее по табл. 2 (Приложения 2) легко находим конкретное число zKp, a
значит, и критическую область.
III. Пусть
Я,: M(X)*M(Y).
Следовательно, критическая область двусторонняя, состоящая из
объединения двух интервалов: (—<n',ZKPl) v (ZKP2',+<n), (рис. 44).
Вероятность попадания критерия Z в критическую область равна,
разумеется, уровню значимости а и равна сумме вероятностей попадания Z в
каждый из двух указанных интервалов.
Поскольку представить наше выбранное число а в виде суммы двух
положительных слагаемых (тем самым разбив критическую область на два
интервала) можно бесконечным количествам способов, то критическая
область определяется вовсе не однозначно (вид одной из возможных
критических областей и представлен на рис. 44). Как же поступить? Вспомним о
такой важной характеристике критерия, как мощность. Доказано, что
наиболее мощным критерий будет, когда вероятности попадания Z в каждый
из интервалов двусторонней области равны, т. е.
P(Z<zKPl) = P(Z>zKP2). (6.20)
А так как
P(Ze(-ao;^u(^2;+ao)) = P(Z< zKPl) + P(Z> zKP2) = a,
то каждая из вероятностей в (6.20) равна ^.
Более того, из равенства вероятностей в (6.20) и симметричности
распределения Z (вспомните график кривой Гаусса, см. рис. 18, § 2.11) следу-
254

Рис. 45.
ет, что критические точки zKPi и zKPl симметричны относительно нуля, что
позволяет упростить обозначения критических точек:
Zap} ~ Z,ept ZKpl ~ ZKp-
Таким образом, чтобы найти критическую область в случае наиболее
мощного критерия (а именно в этом мы заинтересованы), вычислять
придется лишь одно значение т^р- (рис. 45).
Вычислим zKO-
P(Z>Zkp) = P(Ze(zKp;+<»)) = l-of^^ = \.
следовательно,
Ф(^) = 1 " ?
(6.21)
Конкретное значение zKp находим по табл. 2 значений функции Лапласа;
автоматически проявляется и вторая критическая точка (~zKp)- Тем самым
критическая область установлена.
Пример. Пусть две независимые выборки Xlt Хъ ..., Хт и У,, Y2i ..., Y30
извлечены из нормальных генеральных совокупностей с известными
дисперсиям^ D(X) = 37,5; ДК) = 42,9. Вычислены выборочные средние
х = 17,8; у = 15,3. Требуется проверить нулевую гипотезу Я0: М(Х) = M(Y)
при уровне значимости а = 0,05. Конкурирующую гипотезу выбрать Н{.
M(X)*M(Y).
Для решения поставленной задачи используем критерий Z вида (6.17).
При конкурирующей гипотезе Я,: М(Х) * M(Y) критическая область будет
двусторонней. Значение критической точки zKp находим из выражения
(6.21):
кр) = 1-^ = 0,975
Фа
Из табл. 2 следует z^ = 1,96, тогда другая критическая точка
(~ZKP) = — 1,96. Таким образом, при заданном а = 0,05 область принятия
гипотезы — интервал (-1,96; 1,96). Находим ZHa&lt исходя из выборок и
формулы (6.17):
255

7 _ 17,8 15,3 _ i o7r
37,5 ,42,9
V 20 30
Как видим, ZHa6ji находится в области принятия гипотезы,
следовательно, нулевая гипотеза М(Х) = M(Y) не противоречит опытным данным на
уровне значимости а = 0,05 и принимается. Различия выборочных средних
Хи К вызваны случайными причинами и не принципиальны.
Замечание 1. При нахождении критических точек используется
функция Лапласа Ф(...) вида (1.32) (см. § 1.14). Если же в имеющейся таблице
представлена функция Лапласа Ф0(...) вида (1.36), то необходимо либо
использовать равенство, связывающее эти функции, Ф(х) = - + Ф0(х), либо
соответствующим образом изменить вычислительные формулы (6.18),
(6.19), (6.21).
Замечание 2. В рассмотренном критерии существенными условиями
являются нормальная распределенность^ и_К (на самом деле, нам требуется
нормальное распределение статистик Хи Y) и известные дисперсии D(X) и
D(Y). Критерий применим в этом случае для выборок произвольного
объема. Однако при больших выборках (начиная с п = 30, т = 30 и далее)
распределения статистик X и Y оказываются приближенно нормальными
согласно центральной предельной теореме, а исправленные выборочные
дисперсии S\ и S2y в силу состоятельности этих оценок уже мало отличаются
от своих оцениваемых параметров D(X) и Д Y) вне зависимости от
распределений Хи Y.
Поэтому статистика
Z = *~ Y (6.22)
V п т
оказывается приближенно нормальной с параметрами 0 и 1 и может быть
использована в качестве критерия проверки нулевой гипотезы
М(Х) = M(Y) описанным выше методом. Естественно, что в данном
случае критерий оказывается приближенным, и к его результатам следует
относиться с известной долей сомнения, которое уменьшается с ростом
объемов выборок.
6.6. Критерий Стьюдента. Сравнение средних двух нормальных
генеральных совокупностей при неизвестных одинаковых дисперсиях
Пусть имеются генеральные совокупности X и Y, нормально
распределенные. Требуется сравнить математические ожидания М(Х) и M(Y), как и
в случае, рассмотренном в § 6.5. Но в отличие от предыдущего дисперсии
генеральных совокупностей неизвестны. Причем удовлетворительных
точечных оценок для этих дисперсий также невозможно получить, например
в случае малых выборок. Поэтому метод, рассмотренный ранее, не
работает (для него дисперсии должны быть известны).
256

Рассмотрим другую методику, используя взамен утраченного условия
известности дисперсий условие равенства неизвестных нам дисперсий:
ЩХ) = D{Y). Это условие может быть принято из физических
соображений (например, две партии препаратов, изготовленных одним и тем же
коллективом работников) либо проверено (что весьма желательно) с
помощью критерия Фишера (см. § 6.3).
Для сравнения М(Х) и M(Y) в качестве нулевой гипотезы естественно
выбрать
Н0 : М(Х) = M(Y)y
которая равносильна
H^.M(X)=M(Y).
где Хи Y — выборочные средние, найденные из независимых выборок Xv
Х2, ..., Хп объема п и К,, Y2i ..., Ym объема т. Предполагаем числа тип
достаточно малыми (обычно не более 30), чтобы усомниться в справедливости
применения метода предыдущего параграфа (см. замечание 2 § 6.5).
Для нулевой гипотезы используем в качестве критерия статистику вида
(6.22):
X-Y
п т
При справедливости нулевой гипотезы оказывается, что нормальные
случайные величины Хи У имеют одинаковые математические ожидания и
одинаковые дисперсии (по условию). А поскольку нормально
распределенная случайная величина полностью определяется этими двумя своими
параметрами (математическим ожиданием и дисперсией), то генеральные
совокупности Хи Yодинаковы (совпадают) и их можно считать одной и той
же генеральной совокупностью. И тогда, если верна нулевая гипотеза, обе
наши выборки представляют одну генеральную совокупность.
Обратимся к утверждению 5, § 5.3, в котором представлена статистика
(5.20), составленная по двум выборкам из одной и той же нормальной
генеральной совокупности, т. е., как раз наш случай. Приведя в соответствие
обозначения, получаем статистику (обозначим ее Т, без индексов).
Т = ~X~~Y , (6.23)
r.2 r.2
°Х _|_ °у
п m
которая имеет распределение Стьюдента с п + m — 2 степенями свободы.
Поскольку обе выборки из одной и той же генеральной совокупности, то
вместо S2X и S2y можно использовать в качестве оценки дисперсии
исправленную выборочную дисперсию ^2 типа (5.21), посчитанную по двум
выборкам. Тогда статистика Т, которую будем использовать в качестве
критерия для проверки гипотезы Я0, принимает вид
т= X-Y = X-Y_
Isl + sl s2^±^
п m V nm
17 — 3529
257

и далее, подставляя вместо S2 выражение вида (5.21), получаем
окончательно
т= X-Y
J{n-\)S\ + {m-\)S
lnm(n + m-2) (6 24)
V п + m
Статистический критерий, использующий для проверки нулевой
гипотезы стьюдентову статистику Т вида (6.24), называют критерием
Стьюдента. Критерий применяется в случае малых выборок, что свойственно
медицинским и биологическим задачам, а это обусловливает
многочисленные приложения критерия Стьюдента.
Для проверки гипотезы Я0 необходимо ввести конкурирующую гипотезу
Я,, вид которой и определяет критическую область: двустороннюю,
правостороннюю или левостороннюю. Дальнейшие действия стандартны:
требуется вычислить значение Тна6д, исходя из формулы (6.24) и конкретных
характеристик выборки,
7- = ~Х~~У lnm(n + m-2) (6 25)
Если полученное значение Тна6л принадлежит критической области, то
гипотезу Я0 отвергаем, а принимаем конкурирующую гипотезу Я,,
различие М(Х) и M(Y) значимо, т. е. вызвано принципиальными причинами.
Если Тнава оказывается в области принятия гипотезы, то расхождение
средних незначимо, вызвано случайными причинами, и принимается
нулевая гипотеза Я0 как не противоречащая опытным данным.
Далее укажем методику нахождения критической области в зависимости
от конкурирующей гипротезы Я, и уровня значимости а.
I. Пусть
Я, :M(X)*M(Y).
В этом случае критическая область двусторонняя, состоящая из двух
интервалов. Для определения такой критической области достаточно найти
две граничные точки, что при заданном а возможно бесконечным
количеством способов. Однако, используя симметрию распределения Стьюдента,
которому подчинен наш критерий Т, можно доказать, что критерий
обладает наибольшей мощностью тогда, когда вероятности попадания в
каждый из интервалов одинаковы, т. е. критические точки симметричны
относительно нуля (рис. 46).
В этом случае достаточно найти значение одной критической точки, а
значение другой будет отличаться лишь знаком. При этом критические
точки ищутся из условий
Р(Т< -V^,.) = Р(Т> ^.к/,) = | (6.26)
(следовательно, суммарная вероятность попадания в критическую область
равна | + | = а).
Критическую точку tdeycm.Kp. = ^.^(а; n + m-2), т. е. зависящую от
выбранного уровня значимости а и числа степеней свободы критерия
258

двуст. кр
дшуст.кр.
Рис. 46.
(п + т - 2), находим в табл. 6 Приложения 2. Причем в рассматриваемой
таблице критическую точку необходимо выбирать при уровне значимости
а по шкале двусторонней критической области (верхняя часть таблицы):
например, при уровне значимости а = 0,05 и числе степеней свободы
п + т - 2 = 16 находим tdeycmKp (0,05; 16) = 2,120.
И. Пусть
Я, : M(X)>M(Y).
Исходя из конкурирующей гипотезы Я, критическая область является
правосторонней. При уровне значимости а критическая точка tnpaeocmKp
Определяется из условия
Р(Т>гправост.кр) = а. (6.27)
Значение tnpaeocmKp_ = tnpaeocmKp(a; n + т - 2) находим в табл. 6
Приложения 2. При этом следует использовать шкалу односторонней
критической области (нижняя часть таблицы): например, при уровне
значимости а = 0,05 и числе степеней свободы п + т — 2 = 16
имеем tnpaeocmKp(0y05; 16)= 1,746.
III. Пусть
Я, : M(X)<M(Y).
В данном случае критическая область левосторонняя. Критическая
точка Liocm. кР. удовлетворяет условию
Р(Т<глев0С) = а.
(6.28)
Значение tAeeocmKp. = -tnpaeocm.Kp.> а число ^авосткр_ находим в табл. 6
Приложения 2 описанным выше способом.
Пример1. Препарат из группы антагонистов кальция, нифедипин,
обладает способностью расширять сосуды, и его применяют при лечении ише-
1 Данные примера заимствованы из S. L. Hale, К. I. Alker, S. H. RezJcalla et al. Nifedipine
protects the heart from the acute deleterious effects of cocaine if administered before but not after
cocaine. Circulation, 83: 1437-1443, 1991.
17*
259

мической болезни сердца. Ш. Хейл и соавт. измеряли диаметр коронарных
артерий после приема нифедипина и плацебо и получили следующие две
выборки данных диаметра коронарной артерии (в мм).
Плацебо: 2,5; 2,2; 2,6; 2,0; 2,1; 1,8; 2,4; 2,3; 2,7; 2,7; 1,9.
Нифедипин: 2,5; 1,7; 1,5; 2,5; 1,4; 1,9; 2,3; 2,0; 2,6; 2,3; 2,2.
Позволяют ли приведенные данные полагать, что нифедипин влияет на
диаметр коронарных артерий?
Переведем задачу в вероятностную плоскость. Необходимо исследовать,
значимо или нет различаются средние, представленные двумя выборками.
Обозначим генеральную совокупность, из которой извлечена первая
выборка (плацебо), через Х\ соответственно обозначим генеральную
совокупность, из которой извлечена вторая выборка (нифедипин), через Y. Авторы
полагали, что обе генеральные совокупности Хи Y имеют нормальное
распределение (эту гипотезу желательно проверить).
По выборкам из обеих генеральных совокупностей вычислим
соответствующие выборочные характеристики:
и
х = ЛУ^ = Л(2, 5+ 2, 2+ 2, 6+ 2, 0 + 2, 1 + 1,8 + 2,4 + 2,3 +
11^-| 11
» = 1
+ 2,7 + 2,7+1,9) = ^«2,29;
и
У = ^£^(2,5 + 1,7 + 1,5 + 2,5 + 1,4+1,9 + 2,3 + 2,0 +
У'=1
+ 2,6 + 2,3 + 2,2) = Ц£ «2,08;
и
si = yjrryS^'"^2 = ^[(°.21)2 + (-0,09)2 + (0,31)2 + (-0,29)2 +
»•= 1
+ (-0, 19)2 + (-0,49)2 + (0,11 )2 + (0,01)2 + (0,41)2 + (0,41)2 +
+ (-0,39)2] = 0,1009;
^ = тт^2>-^2 = 0>1716-
У'= 1
Поскольку выборки малого объема, п = т = 11, для проверки
значимости различий средних применим критерий Стьюдента. При использовании
критерия, согласно излагаемой выше теории, необходимо иметь равные
дисперсии: D(X) = D(Y). В нашем случае эти дисперсии неизвестны, но
это равенство можно проверить, воспользовавшись, например, критерием
Фишера (см. § 6.3) проверки гипотезы о равенстве дисперсий. Итак,
нулевая гипотеза в критерии Фишера
Я0: D(X) = D(Y).
В качестве конкурирующей гипотезы рассмотрим
Hl:D(X)^D(Y)i
откуда следует, что критическая область двусторонняя. Уровень
значимости полагаем стандартным а = 0,05. По табл. 7 Приложения 2 находим
критическую точку, исходя из равенства (6.12):
260

P(F>kKP2) = |
Следовательно,
К, = Fj& k{\ *2) = /^(0,025; 10; 10) = 3,74.
.2 „ _2
Вычислим F^a,. Поскольку большей дисперсией среди sx и sy является
syi то согласно (6.10)
р . =sjl = °»1716~i 701
на6л- si 0,1009 '
Таким образом, получим, что FHa6jl< kKp/, следовательно, значение FHa6ji
принадлежит области принятия гипотезы, и нулевая гипотеза о равенстве
дисперсий принимается как не противоречащая опытным данным.
Установленный факт равенства дисперсий D(X) и D(Y) нормальных
генеральных совокупностей позволяет сравнить средние М(Х) и M(Y) с
помощью критерия Стьюдента.
Для средних вновь выдвигаем нулевую гипотезу
Я0: М{Х) = M{Y)
и конкурирующую гипотезу
Я,: M(X)*M(Y).
В качестве критерия проверки гипотезы Я0 выступает стьюдентова
статистика Т вида (6.24). Уровень значимости снова берем
стандартным а = 0,05. При рассматриваемой альтернативной гипотезе Я,
критическая область оказывается двусторонней, и критические точки
находим по табл. 6 Приложения 2 для двусторонней критической области:
*двуап.кр. = <*eycm.KP. (0,05; 11 + 11 - 2) = 2,086,
-<двуап.кр. = -2,086.
Таким образом, критическая область: (-оо; -2,086) и (2,086; +оо), а
область принятия гипотезы — это интервал (-2,086; +2,086). Вычисляем ТнабД
согласно (6.25):
Т =
2, 29 - 2,08
/11 • 11(11 + 11^2),,) зз4
Ы 11 + 11 '
V(H - 1)1,1009 + (11 -1)0,1716'
Как видим, значение Тнабд находится в области принятия гипотезы; и,
следовательно, должна быть принята нулевая гипотеза М(Х) = M(Y) как
не противоречащая опытным данным.
Вывод. В рассматриваемом примере критерий Стьюдента не выявил
существенных различий в диаметрах коронарных артерий при сравнении двух
групп обследуемых. Проведенный статистический анализ не позволяет
считать значимым влияние нифедипина на диаметр коронарных артерий.
261

6.7. Сравнение выборочной средней с известной величиной.
Наблюдения до и после эксперимента
Пусть имеется выборка Xv Хъ ..., Хп из нормальной генеральной
совокупности X. Математическое ожидание генеральной совокупности
неизвестно, но имеются основания предполагать, что М(Х) равно некоторому
конкретному числу /я, какому-то стандартному значению: например,
среднее артериальное давление призывников, признанных годными к службе в
армии, равно т. Требуется проверить гипотезу
Я0: М(Х) = т,
исходя из полученной выборки. Число т — гипотетическое среднее.
Для проверки гипотезы Я0 необходимо учитывать дисперсию, т. е.
степень разброса значений относительно среднего. В связи с этим
рассмотрим два случая: дисперсия генеральной совокупности известна
(D(X) = а2), и дисперсия генеральной совокупности неизвестна.
а) Дисперсия известна.
В качестве критерия используем статистику
Х-т
о I Jn
имеющую нормальное распределение (см. утверждение 2, § 5.3).
Обозначим эту случайную величину посредством Z, тогда при справедливости
нулевой гипотезы имеем Z~N(0\ 1).
Вычислим наблюдаемое значение критерия
Z_ х ~ т
набл г- •
a/ Jn
Далее, задав уровень значимости а, строим критическую область в
зависимости от конкурирующей гипотезы.
I. Конкурирующая гипотеза
Я,: М(Х) * т.
Следовательно, критическая область двусторонняя, и, полагая ее
симметричной относительно нуля, находим правостороннюю критическую
точку ZkP, тогда левосторонняя критическая точка равна (—z^)- Значение zKp
ищем из соотношения
P(Z>z*P) = P(Ze(zKp; +00)) = l -o(5a-J!) = |,
следовательно,
Ф(^р) = 1 - \ ■ (6.29)
Для определения z*p используем таблицу значений функции Лапласа
(см. табл. 2 Приложения 2).
Таким образом, зная критическую область, полагаем: гипотеза Я0
принимается, если
Кнабл! 2кр>
гипотеза Я0 отвергается и принимается гипотеза Я,, если
1А<абл1 ^ 2кр-
262

II. Конкурирующая гипотеза
Я,: М(Х) > т.
Критическая область правосторонняя. Критическая точка одна ^р и
определяется по табл. 2 Приложения 2 из соотношения
Ф(гкр)=\~а. (6.30)
Гипотеза Я0 принимается, если
^набл ^кр>
и гипотеза Я0 отвергается, а принимается Я,, если
■^набл ^кр*
III. Конкурирующая гипотеза
Я,: М(Х) < т.
Критическая область левосторонняя. Критическая точка одна z^ и
определяется из соотношения
Ф(гкР)=сх. (6.31)
Однако при малых значениях а число ^р будет отрицательным, и
непосредственно найти гкр из табл. 2 не удастся. Воспользуемся свойством
функции Лапласа:
Ф(х) + Ф(-х) = 1,
тогда
Ф(-^р) = 1 - Ф&р) = 1 - а. (6.32)
Значение 1 — а уже имеется в табл. 2, и, следовательно, легко
определить значение (_^р). Поменяв знак найденного числа, находим искомое
значение т^р-
Далее гипотеза Я0 принимается, если
^набл ^кр>
и отвергается (принимается Я,), если
■^набл ^-кр*
Пример 1. Пусть выборка Хх, Хъ ..., Х25 извлечена из нормальной
генеральной совокупности X с известной дисперсией D(X) = а2 = 0,75.
Выборочное среднее оказалось равно х = 27,9. При уровне значимости а = 0,01
требуется проверить соответствие выборочных данных стандартному
значению среднего М(Х) = 30.
Полагаем в качестве нулевой гипотезы проверяемое равенство:
Я0: М(Х) = 30.
Поскольку наше выборочное среднее А"приняло значение (х = 27,9),
существенно меньшее гипотетического среднего (т = 30), то естественно
предположить конкурирующую гипотезу
Я,: М(Х) < 30.
Тогда критическая область будет левосторонней, и единственная
критическая точка определяется из соотношения (6.31):
Ф(^Р)=сх = 0,01.
В табл. 2 значений функции Лапласа величина 0,01 отсутствует. Но по
свойству функции Лапласа вместо гкр из той же таблицы легко найти
Ф(-^р) = 1 ~ 0,01 = 0,99,
263

следовательно,
("О = 2>33 и *кР = ~2>33-
Вычислим ZHa6„:
2набл = i^ = gZiZ"3^ = -12,125.
Поскольку ^абл < ZkP (-12,125 < -2,33), то нулевая гипотеза должна быть
отвергнута на уровне значимости а = 0,01, а принимается конкурирующая
гипотеза
М(Х) < 30.
Ь) Дисперсия неизвестна.
В случае неизвестной дисперсии нормальной генеральной совокупности
А'для больших выборок можно воспользоваться оценкой дисперсии S2,
которая фактически мало отличается от своего истинного значения
D(X) = а2, и тогда изложенный выше метод можно использовать в
качестве приближенного. Совсем иная картина в случае малых выборок:
выборочная дисперсия S2 может существенно отличаться от D(X), и,
следовательно, для оценки М(Х) требуется другой критерий.
В качестве критерия проверки гипотезы о равенстве М(Х) некоторому
гипотетическому значению т используем статистику
Т = KzJHt (6.33)
S/Jh_
где величины X и S найдены по выборке объема п. Нулевая гипотеза
Я0: М(Х) = т.
При справедливости нулевой гипотезы критерий Т имеет распределение
Стьюдента с (л - 1) степенями свободы (см. утверждение 4, § 5.3).
Критическая область строится в зависимости от вида конкурирующей гипотезы.
Критические точки находятся в табл. 6 по уровню значимости а и числу
степеней свободы п — 1 аналогично методике, рассмотренной в § 6.6.
Пример 2. Пусть выборка Xv X2, ..., Х16 извлечена из нормальной
генеральной совокупности X. Выборочное среднее х = 117,2, а исправленная
выборочная дисперсия s2 = 2,88. Требуется проверить гипотезу о равенстве
М(Х) гипотетическому значению m = 115 при уровне значимости а = 0,05.
Гипотезу, которую требуется проверить, введем в виде нулевой
гипотезы
Я0: М(Х) =115.
Конкурирующую гипотезу рассмотрим
Я,: М(Х) > 115,
исходя из наблюдаемого расхождения между выборочным средним
х= 117,2 и гипотетическим средним m = 115. Критическая область
оказывается правосторонней. Находим критическую точку '„pa^c^p из табл. 6,
используя заголовок для уровня значимости внизу таблицы
'правост.кр 'правост.кр J,">"^> 13) 1,/JJ.
Далее вычислим
т _ х- m _ 117,2-115 _ г 10/-
унабл . г — ~г==~Т~7т7 ~ 3,160.
s/Jh 72Г88/У16
264

Поскольку Гнабл > fnpaB0CT-1Cp, т. е. Тна6л оказывается в критической области,
то нулевая гипотеза отвергается, а принимается конкурирующая:
М(Х) > 115.
Пример 3. Исследуется эффективность специальной диеты,
позволяющей сбросить избыточную массу больным, страдающим ожирением.
Фиксируется масса тела больного до начала эксперимента и через месяц после
соблюдения диеты. Исходя из полученных результатов, необходимо
сделать выводы о влиянии данной диеты на уменьшение массы тела.
В проводимом исследовании можно сравнивать изменение массы тела
больных в двух группах: экспериментальной, представители которой
соблюдали диету, и контрольной, в которой диета не соблюдалась. Однако
более продуктивным оказывается сравнение не групп разных
индивидуумов, а каждого больного с самим собой до и после эксперимента. В этом
случае используется большее количество информации, а следовательно, и
результат получается точнее и надежнее.
Рассмотрим конкретные данные по группе из пяти испытуемых.
Численные значения потерянной массы в кг обозначим через х, (разумеется, х,
представляют генеральную совокупность X):
х, 4,3 3,7 -0,5 2,5 3,0
Заметим, что отрицательное значение —0,5 означает, что в этом
наблюдении масса тела больного не уменьшилась, а выросла на 0,5 кг.
Предположим, что наши *,. извлечены из нормальной генеральной
совокупности X (вообще говоря, данное предположение о нормальности
необходимо проверить, особенно это касается выборок большого объема).
Применим критерий Стьюдента. Нулевая гипотеза заключается в том, что
диета неэффективна, т. е. среднее равно нулю, а фактическое отклонение от
нуля выборочного среднего незначимо.
Итак,
Я0: ЩХ) = 0,
конкурирующая гипотеза
Я,: М(Х) * 0.
Критерий Т имеет вид
Т= *~°
S_/J~n'
Тогда х = 2,6; J2 = 2,17, п = 5, следовательно,
Т = ^»в ~ 3 947
2, 17
5
По табл. 6 Приложения 2 находим при уровне значимости а = 0,05 и
числе степеней свободы 5-1=4 критическую точку
t = t (0,05; 4) = 2,776.
'двуст.кр. 'двуст.кр. Vuiw"'i V ■"> ' v'
Сравнивая это значение с Тиа6п, приходим к выводу, что отклонение от
нуля значимо, нулевая гипотеза опровергнута, и, значит, диета
действительно влияет на показатель массы.
265

Замечание. Исходя из табл. 6 критических точек распределения Стью-
дента, видим, что отклонение среднего от нуля будет значимо (нулевая
гипотеза отвергается) также и при уровне значимости а = 0,02, так как
W.kp. (0.02; 4) = 3,747, |Гнабл| > 3,747.
При уровне значимости а = 0,01 находим
W.kp. (0,01; 4) = 4,604, |Гнабл| < 4,604,
и должна быть принята нулевая гипотеза.
Таким образом, принятие решения сводится к выбору уровня
значимости (т. е. зависит от тяжести последствий принятия ложной гипотезы).
Напомним, что уровень значимости а — вероятность ошибки первого рода, т.
е. вероятность отвергнуть верную нулевую гипотезу.
Используемый в примере 3 критерий Стьюдента, применяемый к
показателю разности значений до и после эксперимента, называют парным
критерием Стъюдента. В таком виде он широко используется в медицинских
исследованиях.
Пример 4. Измерена температура тела у 10 новорожденных детей под
мышкой (генеральная совокупность А) и в прямой кишке (генеральная
совокупность У). Получены следующие результаты:
х,
У,-
X; ~ У,
36,8
36,9
"0,1
37,1
37,2
"0,1
37,3
37,2
0,1
37,0
37,2
-0,2
37,1
37,3
-0,2
36,9
37,0
"0,1
36,7
36,8
"0,1
37,2
37,1
"0,1
37,0
37,2
-0,2
36,9
37,1
-0,2
I = 370,0
1 = 371,0
1 = -1
Можно ли считать, что температура в прямой кишке выше, чем под
мышкой?
Решение. Используем парный критерий Стьюдента. Предполагаем, что
разности d, = xt — yt (где / = 1, 2, ..., 10) представляют случайную величину
X—Y, имеющую нормальное распределение; это условие выполнено,
например, когда и Хи Y— нормально распределенные случайные величины,
следовательно, их линейная функция также распределена нормально с
соответствующими параметрами. Среднее значение
5 = 1у <ц
П^>
/= 1
также в этом случае имеет нормальное распределение, а статистика
/= 1
имеет распределение у}с п — 1 степенями свободы.
Предполагая, что верна нулевая гипотеза об отсутствии различий между
Хи К, т. е. M(d) = 0, можно записать случайную величину
имеющую распределение Стьюдента с п — 1 степенями свободы.
Далее решение задачи находится достаточно тривиально.
266

Гнабл = -л/Л = . * У ' -ДО = 2, 02
V » = 1
'кР = Wtkp. (°»°5; 9) = 2,26.
Следовательно, так как \THaSa\ < t^, гипотеза о равенстве средних X и Y
на уровне значимости а = 0,05 принимается.
Замечание. Ввиду близости значений Гнабл и t^, исходя из табл. 6
критических точек распределения Стьюдента, можно установить, что
наблюдаемому значению Гнабл соответствует уровень значимости а = 0,07, лишь
незначительно превышающий стандартный 0,05. В данной ситуации соотношение в
пользу принятия нулевой гипотезы всего лишь 7:93, поэтому нулевая
гипотеза может быть отвергнута на уровне значимости а = 0,07, и различие
температур X и Y признано существенным. Для более определенного ответа на
вопрос задачи требуется дополнительное исследование: использование
выборки большего объема обеспечит большую достоверность результатов.
6.8. Мощность критерия
В предыдущих параграфах, подробно разбирая процесс принятия или
отвержения нулевой гипотезы, мы рассматривали лишь вероятность
ошибки первого рода (уровень значимости а). Далее обсудим возможность
допуска ошибки второго рода. Как уже введено ранее (см. § 6.1), вероятность
такой ошибки р — вероятность принятия ложной нулевой гипотезы при
справедливости конкурирующей. Вероятность противоположного события
(отвержение ложной нулевой гипотезы в случае справедливости
конкурирующей) — это мощность (чувствительность) критерия, выражаемая
числом 1 — р. Разумеется, чем больше мощность критерия, тем лучше.
При построении гипотезы мы можем оказаться в ситуации, когда
нулевая гипотеза Я0 ложна, конкурирующая гипотеза Я, верна. Методика
принятия или отвержения гипотезы основывается по существу на одной
выборке (или паре сравниваемых выборок). И вполне возможно, что нам
просто не повезет с выборкой, и тогда верная гипотеза Я, на законных
основаниях не будет принята. Исключить такой вариант мы не можем, но
можем свести до минимума вероятность ошибки. Для этого рассмотрим
вопрос, отчего же зависит мощность критерия и как ее повысить.
Обратимся к критерию Стьюдента. Проиллюстрируем зависимость
мощности критерия от уровня значимости, величины действительных
различий средних в двух группах, дисперсии и объемов выборок.
Уровень значимости
Пусть имеются две группы наблюдений, т. е. две выборки,
различающиеся своими средними. Полагаем, что выборки из нормальных
совокупностей с одинаковыми дисперсиями. Изобразим кривые плотности
распределения критерия Т при справедливости нулевой гипотезы
267

a) a = 0,1
df=15
-2-1 0 1 1.753 2
Мощность критерия 1-0 = 0,6 (60%).
б)а = 0.02
df=15
Справедлива Н(
-3 -2-1 0 1
Мощность критерия 1-0 = 0,4 (40%).
2 2.602 3
Рис. 47. Изменение мощности критерия в зависимости от уровня значимости. С
уменьшением уровня значимости при фиксированных других параметрах мощность
критерия уменьшается.

M(X) - M(Y) и справедливости конкурирующей гипотезы. Для
определенности возьмем в качестве конкурирующей гипотезу Я,: М(Х) *М(У). Тогда
обе кривые по форме будут одинаковы, но вторая кривая окажется
смещена относительно первой на величину d, называемую расстоянием между
гипотезами. Связь между мощностью критерия 1 — р и уровнем
значимости продемонстрируем графически.
На рис. 47, а верхняя кривая изображает график плотности критерия Т
при справедливости нулевой гипотезы Я0, а нижняя кривая — при
справедливости конкурирующей гипотезы Я,. Число степеней свободы df взято
равным 15, а уровень значимости а =0,1. При этих данных
(иауст.кр. = 1>753. Таким образом, область принятия нулевой гипотезы —
интервал (-1,753; 1,753), критическая область — это объединение интервалов
(—°°; —1,753) ^ (1,753; +°°). Вероятность попадания критерия Тъ
критическую область при справедливости Я0 (т. е. ошибка первого рода) равна а и
равна сумме площадей заштрихованных фигур на верхнем рисунке.
Если же справедлива конкурирующая гипотеза Я,, то область принятия
нулевой гипотезы (-1,753; 1,753) является областью допуска ошибки
второго рода. Вероятность этой ошибки обозначена р и равна площади
заштрихованной фигуры на нижнем рисунке. Соответственно вероятность
недопущения ошибки второго рода при справедливости Я, — это
мощность критерия, равная 1 - р, и на нижнем рисунке равна площади неза-
штрихованной области, ограниченной кривой плотности и осью абсцисс.
Заметим, что эта область состоит из двух частей: при t> 1,753 и при
t< -1,753 (ввиду малости на рисунке не отмечена). Судя по нашему
графику, вероятность ошибки второго рода составляет 0,4 (т. е. 40%), тогда
мощность критерия равняется 0,6 (или 60%).
Далее при том же числе степеней свободы df= 15, и при том же
расстоянии d между гипотезами уменьшим уровень значимости а до 0,02.
Полученные графики изображены на рис. 47, б. Верхний график представляет
плотность распределения Т при справедливости нулевой гипотезы. При
таком уровне значимости (nBycT.Kp.(0,02; 15) оказывается равным 2,602, т. е.
область принятия нулевой гипотезы — интервал (-2,602; 2,602), а
критическая область — (-°°; -2,602) ^ (2,602; +°°). Как видим, по сравнению с
предыдущим случаем (при а =0,1) область принятия нулевой гипотезы
расширилась. При справедливости конкурирующей гипотезы — это
область допуска ошибки второго рода. Вероятность такой ошибки равна
площади заштрихованной области на нижнем рисунке, и величина ее возросла
с уменьшением а. Соответственно понизилась мощность критерия 1 - р,
судя по нашему рисунку, до 0,4 (40%).
Итак, приходим к выводу: с уменьшением уровня значимости а
вероятность ошибки второго рода возрастает, а мощность критерия падает
(уменьшается).
Величина различий (параметр нецентральности)
Вновь рассмотрим две выборки из нормальных генеральных
совокупностей X и Y. Проиллюстрируем, как величина разности средних влияет на
мощность критерия. Разность средних по двум выборкам численно харак-
269

теризует величину различий двух генеральных совокупностей X и Y.
Например, если две группы больных получали: одна группа — плацебо, а
другая — эффективный препарат, то разность средних — это величина
эффекта, вызванного применением препарата.
Критерий Стьюдента использует статистику вида (6.23)
п m
Ради наглядности возьмем выборки одинакового объема п, тогда
Т= X-Y . (6.34)
п п
Пусть М(Х) = mxt M(Y) = myi D(X) = D(Y) = a2.
Следовательно, статистика Г является оценкой истинного значения
j _ ™х i^i = ЧЬ. ЧЬ. И (6.35)
При а = 0,1 и фиксированных значениях аил графики плотности
распределения св. Т приведены на рис. 48. Причем на рис. 48, а изображен
график при справедливости нулевой гипотезы, тогда тх — ту = 0
(отсутствие эффекта), т. е. Т0 = 0. Область принятия нулевой гипотезы — интервал
(-1,753; 1,753), критическая область — объединение интервалов (—°°;
-1,753) ^ (1,753; +оо). Вероятность попадания наблюдаемого значения Г в
критическую область оценивается уровнем значимости а и равна сумме
площадей заштрихованных криволинейных трапеций.
В случае справедливости конкурирующей гипотезы Я, разность тх — ту
оказывается не равной нулю (наличие эффекта), Т0 также отлично от нуля,
и графики плотности распределения св. Т представлены на рис. 48, б, в.
При этом чем больше различие средних тх и туу тем больше Т0 [см. (6.35)]
и тем больше смещение графика плотности распределения вдоль оси
абсцисс. На рис. 48 б), в) продемонстрирована эта зависимость смещения
графика от разности mx — my. При справедливости конкурирующей гипотезы
Я, область принятия нулевой гипотезы (-1,753; 1,753) оказывается
областью принятия ложной гипотезы, т. е. областью допуска ошибки второго
рода. Вероятность этой ошибки р равна площади заштрихованной области
(см. рис. 48, б, в). Тогда мощность критерия 1 — р определяется площадью
оставшейся (незаштрихованной) части криволинейной трапеции на рис. 48,
бив. Заметим, что эта область состоит из двух частей: при t < -1,753 и при
t > —1,753. Чем больше смещение графика, тем более мощным является
критерий.
Вывод: мощность критерия увеличивается с ростом разности тх — ту (с
ростом величины эффекта). Данная зависимость является совершенно
естественной, так как чем больше различия тх и ту, тем больше шансов
(больше вероятность) эти различия установить.
270

а) Справедлива Н0
тж-ту = 0
Рис. 48. Изменение мощности критерия в зависимости от разности средних тх — ту
При фиксированных значениях а, а и я с увеличением разности средних тх — ту
мощность критерия возрастает.
Из формулы (6.35) также следует, что с ростом стандартного
отклонения о значение Т0 уменьшается, т. е. меньше смещение графика плотности
распределения св. Т, и мощность критерия падает. Таким образом,
величина о (степень разброса значений относительно среднего) также влияет
на мощность критерия: чем больше значение а, тем меньше мощность
критерия.
271

На практике обычно эти зависимости мощности критерия, прямую от
разности средних тх — ту и обратную от величины стандартного
отклонения а, объединяют, вводя общий коэффициент
= тх-т^ (6 36)
а
называемый параметром нецентральности.
Итак, при фиксированных п А а мощность критерия возрастает с
ростом параметра нецентральности <р.
Для определения мощности критерия при фиксированных а составляют
таблицы мощности критерия 1 - р в зависимости от (р А п.
Объем выборки
Наряду с рассмотренным уровнем значимости, величиной различий и
стандартным отклонением, влияющими на величину мощности критерия,
несомненно, должна быть зависимость мощности критерия от объемов
выборок, ибо с ростом объемов выборок растет количество информации о
генеральных совокупностях, а следовательно, должна возрастать и точность
различных числовых характеристик и применяемых методов.
При этом оказывается, что объемы выборок — это практически
единственный показатель, с помощью которого мы имеем возможность
положительно повлиять на мощность критерия. Отметим, что величина эффекта
т—ту и стандартное отклонение о — объективно существующие
показатели, мы не можем их изменить в конкретной задаче. Выбирая уровень
значимости а (увеличивая число а), мы можем увеличить мощность критерия
до приемлемого значения, но это увеличение мощности критерия
достигается за счет уменьшения области принятия нулевой гипотезы (см. рис. 47:
при а = 0,02 область принятия нулевой гипотезы — интервал (—2,602;
2,602), а при а = 0,1 — (—1,753; 1,753), т. е. длина интервала при таком
росте а уменьшилась примерно в полтора раза), что увеличивает
вероятность ошибки первого рода, а именно: чревато отвержением нулевой
гипотезы, когда она верна. Таким образом, увеличение мощности критерия с
помощью увеличения значения а просто перераспределяет вероятности
ошибок первого и второго рода. Это может быть важно с точки зрения
тяжести последствий ошибок первого и второго рода (см. § 6.1), но
принципиально уменьшить вероятности обеих ошибок одновременно выбор а не в
состоянии.
Вернемся к объемам выборок. Вновь для простоты предположим, что
обе рассматриваемые выборки одинакового объема п. Тогда обратимся к
значению 7^ [см. (6.35)]:
j, _ тх — ту ш
о ^2
Как видим, с ростом п увеличивается и значение Т0, следовательно,
кривая плотности стьюдентова распределения при положительной
разности тх — ту сдвигается вправо, и тем дальше, чем больше п. Тенденция
сдвига данной кривой показана на рис. 49 (при этом отметим, что на
рисунке продемонстрирована именно тенденция: данный рисунок преследует
272

а) Справедлива Hg,
п=16.
в) Справедлива Hv
n=25.
д) Справедлива Hv
n = 40.
мощность
критерия - 0,6 (60%)
1 1,711
Р = 0,05
мощность
критерия - 0,95 (95%)
Рис. 49. Зависимость мощности критерия от объема выборки п при а = 0,1 и
фиксированном параметре нецентральности ср. С ростом п мощность критерия
увеличивается, а вероятность ошибки второго рода р уменьшается.
18 — 3529

целью наглядность, а не вычисление конкретных значений мощности).
При справедливости конкурирующей гипотезы, когда тх— ту*0
(действительно имеется различие между средними двух выборок и существует
эффект), мощность критерия — площадь заштрихованной области на рис. 49,
б, в и г. Заметим, что с ростом п мощность критерия увеличивается по
двум причинам: одна составляющая величины мощности продиктована
сдвигом кривой плотности, а другая составляющая вызвана уменьшением
'двуст.кр.(а; Л ~ О ПРИ растущем п и фиксированном а. Обе эти области
наглядно фигурируют на рис. 49, в, г, где при фиксированном а = 0,1 из
табл. 6 Приложения 2 находим 'двусткр(0,1; 16 - 1) = 1,753; ^„.^.(0,1; 25 -
1)= 1,711; гдвусТ1ср.(0,1; 40-1) = 1,685.
Таким образом, следует вывод, что с ростом п мощность критерия
увеличивается, причем без практического ущерба для области принятия
нулевой гипотезы.
Справедливости ради, отметим, что при растущих п и фиксированном
уровне значимости а эта область несколько сужается, но крайне
незначительно, в чем можно убедиться, анализируя значения критических точек в
табл. 6 при фиксированных а.
Подводя итоги данного параграфа, сделаем выводы:
— мощность критерия определяется при справедливости
конкурирующей гипотезы Я,;
— мощность критерия зависит от уровня значимости а: чем больше
уровень значимости, тем больше мощность критерия;
— мощность критерия пропорциональна параметру нецентральности <р,
т. е. прямо пропорциональна величине эффекта тх— туи обратно
пропорциональна стандартному отклонению а;
— мощность критерия растет с увеличением объема выборки;
— увеличение объема выборки — наиболее эффективный и
безболезненный путь повышения мощности критерия.
Также отметим, что для различных критериев мощность вычисляется по-
разному в зависимости от вида распределения, критических точек и т. д.
Обсудив вопрос зависимости мощности критерия от различных
факторов, неизбежно приходим к новым вопросам. Как определить мощность
критерия в реальной задаче? Каков объем выборки достаточен для
обеспечения желаемой мощности критерия при фиксированных других
показателях? Теоретически мощность критерия — это площадь криволинейной
трапеции (см., например, заштрихованные области на рис. 49, б, в, г, которую
можно вычислить с помощью определенного интеграла от функции
плотности, предварительно определив из конкретных данных пределы
интегрирования. В случае нормального распределения рассматриваемая кривая —
это кривая Гаусса и, естественно, можно воспользоваться таблицей
функции Лапласа.
Практически же проделывать громоздкие вычисления в каждом
конкретном случае, рискуя также ошибиться в дебрях вычислений, является
довольно-таки неблагодарной задачей. Гораздо проще воспользоваться готовым
результатом, который представляет зависимость мощности критерия от
различных параметров в виде соответствующих таблиц или графиков,
рассчитанных с заданной точностью на компьютере. Один из таких
графиков зависимости мощности критерия от параметра нецентральности ф при
274

фиксированном уровне значимости а приведен в табл. 8 Приложения 2.
Например, при ф = 1 и п = 5 мощность критерия Стьюдента 1 - р составляет
примерно 0,36 (36 %), а при ср = 1, п = 10 получаем 1 — р ~ 0,55 (55%).
Из той же табл. 8, задавая мощность критерия при известном значении
Ф и а = 0,05, можно определить примерный объем выборок,
обеспечивающих заданную мощность. Например, при мощности критерия 1 — р = 0,8 и
параметре нецентральности ф = -1,25 находим на графике объем выборок
п = 10, обеспечивающий данную мощность.
Если рассматриваются выборки разных объемов пит, то, взяв
наименьшее из этих чисел и используя таблицу, мы не ухудшим результат, так
как найденная мощность окажется даже несколько меньшей, чем реальное
значение 1 - р.
В заключение отметим, что структура, принципы, методика,
рассмотренные для критерия Стьюдента, различаясь в деталях, в общем остаются
справедливыми и для других критериев значимости.
6.9. Проверка гипотез о вероятности в схеме Бернулли
(одна генеральная совокупность)
Пусть испытания проводятся по схеме Бернулли относительно
некоторого события А. Это событие А в каждом из независимых испытаний
может произойти с вероятностью р либо не произойти с вероятностью q, где
q = 1 — р. Так же как и в § 5.8, введем с. в. X — число осуществлений
события А в одном испытании. С. в. X имеет всего два возможных значения:
0 и 1, вероятности которых соответственно q и р. Распределение с. в. А"
является распределением Бернулли с параметром р. Следовательно,
M(X)=pt D(X) = pq = р(\ - р).
Полагаем с. в. ^генеральной совокупностью, и тогда п испытаний,
проводящихся по схеме Бернулли, представляют нам репрезентативную
выборку Хи Х2У ..., Хп из указанной генеральной совокупности. Выборочное
среднее X, составленное по выборке, оказывается не чем иным, как
относительной частотой осуществления события А в п испытаниях:
Х= У,
п
где т — количество испытаний, в которых А произошло, т. е.
относительная частота — это случайная величина, принимающая в результате п
испытаний некоторое численное значение. Более правильным будет
переобозначить относительную частоту как случайную величину символом ш,
оставив обозначение т/п для численного значения относительной частоты,
тогда ш = X.
Используя относительную частоту как оценку вероятности р в
испытаниях, проводимых по схеме Бернулли, в § 5.8 для параметра р указан метод
построения доверительного интервала. Наша задача в текущем параграфе —
проверка гипотезы о равенстве этой теоретической вероятности р
конкретному числу (гипотетической вероятности р0). Таким образом нулевая
гипотеза имеет вид
Щ- Р = Ро-
18*
275

Поскольку р = М(Х), то Я0 фактически является гипотезой о равенстве
среднего (математического ожидания) известной величине р0, а эта задача
рассмотрена подробно в § 6.7.
Критерием проверки нулевой гипотезы будет статистика
Z = Х-ро _ Х-р0
№
V п
Применительно к нашему случаю X = ш, D(X) = р{\ - р), получаем
критерий
}
Z = ш Р° . (6.37)
п
При больших п (начиная с нескольких десятков), с. в. ш можно считать
приближенно нормально распределенной, так как ш = X, а X представляет
собой сумму достаточно большого числа случайных величин, и
нормальную распределенность гарантирует центральная предельная_теорема.
При этом М(а)_= М(Х). Ввиду несмещенности оценки X для М(Х) (см.
§ 5.2) имеем М(Х) = М(Х), т. е. М(ш) = М(Х) = р. Следовательно, при
справедливости нулевой гипотезы (р = р0) оказывается M(Z) = 0. Также
несложно показать, что при верной нулевой гипотезе будет D(Z) = 1:
Х=г-2 • D(X-Po) = -^гДА) = 1
D(Z) = D ^^ ^_ _х._ г„,
>Щху (да 1КХ)
Таким образом, при справедливости нулевой гипотезы получаем
Z = ®~Ро
!рь(1 ~Ро)
п
nZ~ N(0; 1).
Вид конкурирующей гипотезы Я, определяет и вид критической
области: двусторонняя, правосторонняя или левосторонняя. При заданном уровне
значимости а соответствующие критические точки находятся из табл. 2
функции Лапласа, аналогично действиям в § 6.7.
Для двусторонней критической области критические точки
определяются из равенств
Ф(7 ) = 1 - <*
■Члевост.кр 'М]равост.кр"
Для правосторонней критической области единственная критическая
точка ZkP определяется из соотношения Ф^) = 1 - а.
Для левосторонней критической области единственную критическую
точку можно найти из соотношения Ф(гкр) = а, но так как а — малое
число, то соответствующее значение в табл. 2 отсутствует. Однако,
воспользовавшись свойством функции Лапласа [см. § 1.14, равенство (1.34)] Ф(^р) +
+ 0(~ZkP) = 1, получаем Ф(-^кр) = 1 - 0(ZkP) = 1 — а, и значение (-^р) в
табл. 2 имеется. Тем самым, поменяв знак, найдем и нужное значение z^.
276

Наблюдаемое значение критерия Z находится подстановкой конкретных
чисел ш = — и /?0:
п
т - „
гиабл = —^—=Л. (6.38)
V/>oO ~Ро)
Далее, зная критическую область и ZHa6n, проверяем нулевую гипотезу
(принимаем или отвергаем) на уровне значимости а.
Пример 1. В § 1.10 представлена таблица с данными опытов
подбрасывания монетки. По опытам Бюффона, Керриха и Романовского проверить
совместимость полученных данных с гипотезой о том, что вероятность
выпадения "герба" р0 = -. Уровень значимости принять 0,05.
Проверим высказанную гипотезу по каждой из трех групп опытов. В
качестве конкурирующей гипотезы Я, рассмотрим гипотезу р * ^, тогда
критическая область — двусторонняя.
Опыт Бюффона
Количество испытаний п = 4040. Количество удачных испытаний (т. е.
выпадений "герба") т = 2048. Воспользуемся критерием вида (6.37). Из
соотношения для двусторонней критической области
ФОправос.кр) = 1 " f = 0,975
из табл. 2 находим ърлвост.кр = 1,96. Тогда zneBOCT.Kp = —1,96.
Согласно (6.38), имеем
(Ш - 1)^4040
Z.,„ = U04° ^ *0.8771
К1-9
Сравнивая найденное число с критическими значениями, получаем
|ZHaJ < Ър, значит, гипотеза Я0: р = - не противоречит данным опыта
Бюффона.
Опыт Керриха
Количество испытаний п = 10 000, количество удачных испытаний
т = 5087, тогда относительная частота — « 0, 5087. Критическая область та
п
же самая, что и в опыте Бюффона.
7 = (0, 5087 - 0, 5)Л(Шб = , 74
\г ' 2
277

Поскольку ^равост.кр = 1,96, то |^абл| < ZkP и нулевая гипотеза Я0: р = | не
противоречит данным опыта Керриха.
Опыт Романовского
Количество испытаний п = 80 640, количество удачных испытаний
т = 39 699, относительная частота — » 0,4923. Критическая область та же
самая, что и в предыдущих рассмотренных опытах: ^p^^p = 1,96. Найдем
7
■'набл
z - (0,4923 - 0, 5)У80 640 ^ 373
/ПЛ
а/2 2
Сравнивая полученное значение с критическими точками, получаем
1Д«абл1 > ^правост.кр» следовательно, нулевая гипотеза р = - несовместима с
данными опыта Романовского. Вероятность появления "герба" в одном
испытании в опыте Романовского отлична от -. В данном случае число
испытаний достаточно большое, чтобы отклонение наблюдаемой частоты
0,4923 от значения ^, равное всего 0,0077, признать значимым. Видимо,
монетка, используемая в опыте Романовского, имеет нарушения
симметрии, которые и проявили себя. Истинная вероятность для этой монетки
иная, более близкая к статистическому значению 0,4923, чем к -.
Например, можно проверить значение р0 = 0,49. Тогда оказывается ZHabn = 1,3065,
и поскольку |ZHa&I| < 1,96, то гипотеза р = 0,49 подтверждается опытными
данными Романовского.
Замечание. Если сравнить отклонения относительной частоты от
р0 = 0,5 в опытах Романовского и Керриха, то окажется, что в опыте
Романовского это отклонение (0,0077) даже меньше, чем в опыте Керриха
(0,0087), однако при меньшем различии (отклонении) гипотеза р = 0,5
отвергается, а при большем принимается. Данное противоречие легко
разрешимо, если обратиться к соответствующим значениям количества опытов п.
При достаточно большом количестве опытов даже мельчайшее отклонение
может оказаться значимым. Чем больше количество наблюдений, тем
более значимым становится любое отклонение от теоретического значения.
Это также указывает на свойство средних величин стабилизироваться
относительно истинного (теоретического) значения и свидетельствует в
пользу статистического определения вероятности, представленного в § 1.10.
Пример 2. По статистическим данным смертность среди больных,
страдающих легочным туберкулезом в открытой форме, в течение первого года
после заболевания в среднем составляет 32,61%. В результате наблюдений
над группой таких больных, состоящей из 415 заболевших, за первый год
умер 151 больной, что составляет 36,39%. При уровне значимости а = 0,05
проверить совместимость полученных данных с гипотезой о постоянной
вероятности доли умерших р0 = 0,3261.
278

Итак, относительная частота — наших выборочных данных при объеме
выборки п = 415 составила 0,3639, гипотетическая вероятность/^ = 0,3261.
Объем выборки достаточно велик и позволяет использовать
рассмотренный выше критерий. Нулевая гипотеза — Я0: р = р0. В качестве
конкурирующей рассмотрим гипотезу Я,: р> р0, поскольку наблюдаемая частота
заметно превосходит значение р0. Следовательно, критическая область
правосторонняя, и единственная критическая точка находится из
соотношения Ф(гкр) = 1 — а = 0,95.
По табл. 2 получаем гкр = 1,69.
Исходя из (6.38), имеем ZHa6n = (0,3639-0, 3261W5JS
70,3261(1-0,3261)
Так как \ZHa6n\ < z^, то нулевая гипотеза р = 0,3261 на уровне
значимости а = 0,05 принимается, наблюдаемые отклонения от
гипотетического значения р0 = 0,3261 вызваны случайными причинами. Вместе с
тем близость ZHa6jI к ^р несколько настораживает, случайные причины,
влияющие на величину ZHa6n, на поверку могут оказаться тенденциозными.
Поэтому, подойдя к вопросу менее формально, желательно
проанализировать исходные данные: является ли наша выборка репрезентативной? Не
повлияли ли на столь высокий процент смертности другие причины,
кроме легочного заболевания? После проведенного анализа данные могут
быть уточнены (например, выяснится, что из 151 умершего смерть 15
вызвана острой сердечной недостаточностью, а еще 7 больных закончили
жизнь в результате автомобильной катастрофы или каких-либо природных
катаклизмов, тогда оказывается, что на самом деле число умерших
т = 129, а число наблюдаемых больных п = 393 вместо 415, и
относительная частота — = 0,3282). Пересмотренные результаты наблюдений вновь
проверяются с помощью статистического критерия. Если возможно, то
желательно увеличить объем выборки.
Приведенный пример подчеркивает важность качества данных, ибо в
противном случае математический результат, полученный
беспристрастными формальными методами, будет соответствовать не истине, а ложным
данным со всеми вытекающими отсюда последствиями.
6.10. Проверка гипотез о вероятности в схеме Бернулли
(две сравниваемые генеральные совокупности)
Пусть вновь, как и в предыдущем параграфе, испытания проводятся по
схеме Бернулли относительно некоторого события А. Имеются две
генеральные совокупности. Вероятность осуществления события А для первой
генеральной совокупности обозначим /?,, для второй — соответственно р2.
Требуется на заданном уровне значимости а проверить нулевую гипотезу о
равенстве этих вероятностей:
Hq. Pi= Р2= Р-
279

Для проверки гипотезы Я0 используем две выборки данных: выборка из
первой генеральной совокупности Хх имеет объем л,, и контролируемое
событие А осуществилось /я, раз; выборка из второй генеральной
совокупности Х2 имеет объем п2, и событие А произошло т2 раз. Тогда
относительные частоты осуществления события А для выборок — это случайные
величины ш, и ш2 соответственно, причем
М©,) = Pi, М((и2) = р2.
Аналогично рассуждениям предыдущего параграфа о D(X) = pq для
одной выборки, в нашем случае получаем
Л, Л,
дш) = Pii\~Pi)m
п2
Далее находим Дш, — ш2). Для независимых св. ш, и ш2, согласно
свойству дисперсии суммы [см. (3.29) и замечание в § 3.5], получаем
Дш, - ш2) = Дш,) + Дш2) = /?l(1~/?l) + /?2(1"/?2). (6.39)
л, п2
Теперь рассмотрим случайную величину
(Ш1-Ш2)-(/?1-/?2)
7Дш,-ш2)
(6.40)
которая, как легко проверить, обладает нулевым математическим
ожиданием и единичной дисперсией и распределена по нормальному закону при
достаточно больших объемах выборок.
В случае справедливости нулевой гипотезы рх= р2= р наша случайная
величина имеет вид [см. также (6.39)]:
Z = Ш'~Ш2 — (6.41)
и является критерием проверки рассматриваемой нулевой гипотезы.
Замечание 1. Число осуществлений события А в л испытаниях,
проводящихся по схеме Бернулли, разумеется, является случайной величиной с
биномиальным распределением. Но, как уже отмечалось ранее, при
больших л и вероятностях р и q, близких к 0,5, биномиальное распределение
приближается к нормальному распределению, о чем свидетельствуют, в
частности, предельные теоремы Муавра—Лапласа (см. § 1.13; 1.14).
Условиями, гарантирующими приближенную нормальность случайных величин ш,
и ш2, обычно полагают следующие:
ВДО _ Pi) > 9, ВДО _ Рг) > 9-
Таким образом, при вероятностях, близких к 0,5, объемы выборок
должны быть порядка 40 элементов и более. В противном случае
вычисления (соответственно и выводы) окажутся чересчур приближенными.
Нормальная распределенность ш, и ш2 приводит к нормальной
распределенности Z, так как Z — линейная функция ш, и ш2.
280

Итак, Z~ N(0;l). Ввиду нормального распределения Z критические
точки по уровню значимости а находятся из табл. 2 значений функции
Лапласа, а сама критическая область строится в зависимости от конкурирующей
гипотезы так же, как и в предыдущем параграфе.
Далее вычислим значение ZHafin. Вместо со, и ш2 в (6.41) подставим их
статистические аналоги, относительные частоты —1 и —. Точное значе-
л, п2
ние вероятности р в (6.41) нам неизвестно, и можно воспользоваться
приближенным значением этой вероятности: при справедливости нулевой
гипотезы либо р = р. ~ —, либо р = р7 ~ —. Но более-логичным и точным
л, п2
представляется использование данных не из одной из выборок, а сразу
обеих: при справедливости Я0 обе генеральные совокупности становятся
одинаковыми и, объединяя обе выборки в одну объема (п{+п2), получаем
приближенное значение р более близким к истинному:
р *^!±^. (6.42)
л, + п2
Тогда
Ш\ _ Ш2
гил6л= , *' "2 . (6.43)
т{ + т2Г{ _ тх + т2\П + П
Пх + П2 V Пх +П2'\П\ Л/
Вычислив ZHa&I, выясняем, попадает это число в область принятия
гипотезы либо оказывается в критической области; в зависимости от этого
нулевая гипотеза р{ = р2= р либо принимается, либо отвергается, и
принимается гипотеза конкурирующая. В случае принятия Я0 параметр р
оказывается определенным соотношением (6.42).
Замечание 2. Статистика Zbwisl (6.41), служащая критерием для
проверки нулевой гипотезы, является нормально распределенной случайной
величиной лишь приближенно. Строго говоря, Z имеет дискретное
распределение (напомним, что ш, и ш2, входящие в структуру Z, — случайные
величины с биномиальным распределением). Вследствие того, что исходное
распределение дискретно, а приближенное, которым мы пользуемся,
непрерывно, оказывается, возникает дополнительная погрешность между
истинными значениями и теми, которые мы используем. В частности, Д,а6л,
вычисляемое по формуле (6.43), принимает значения, несколько большие,
чем должны быть при нормальном распределении. Для компенсации этого
расхождения используется поправка на непрерывность, называемая также
поправкой Йейтса, которая представляет критерий Z в виде:
Z = 2 П{ -^-. (6.44)
fi^ti)
281

Тогда с поправкой Йейтса имеем
7 =
ТП\ _ ТП2
Л, П2
2^ nJ . (6.45)
/Л! + /я2Л _ /я1 + /я2У1 + П
«! + Л2 ^ /Ii + /I2A/I, Л/
Таким образом, поправка Йейтса уменьшает значение ZHa6n> и нулевая
гипотеза будет отвергаться не так часто.
Пример 1. При подбрасывании монеты вероятность выпадения "герба"
точно равна 0,5 только в случае идеально симметричной монеты. По
данным таблицы в § 1.10 результатов опытов с подбрасыванием монеты
проверить гипотезу о равенстве вероятностей выпадения "герба" для монет,
используемых в опыте Феллера и опыте Джевонса. Уровень значимости
принять равным 0,05.
Из таблицы § 1.10 имеем: а) в опыте Феллера л, = 10 000, т, = 4979,
^ = 0,4979; б) в опыте Джевонса л, = 20 480, пи = 10 379, —2 = 0, 5068 .
л, пг
Тогда в качестве вероятности р принимаем число
= тх + т2 = 15 358 _ n Sfm
Р пх + п2 30 480 * **
Проверим гипотезу о равенстве вероятностей выпадения "герба" в обоих
опытах:
Щ- Pi = Рг = 0,5039.
Конкурирующая гипотеза:
#,: рх *р2.
Двусторонняя критическая область при уровне значимости а = 0,05
имеет две критические точки: z^ = —1,96, ^ = 1,96.
Вычисляем наблюдаемое значение критерия по формуле (6.43):
7 _ 0,4979 - 0,5068 , ^
Аы>л _ «-1,461.
1 ^
Jo, 5039- 0,496.у.
+
000 20 480^
Поскольку |ZHaJ < 1,96, т. е.
^набл находится в области принятия
гипотезы, то полагаем рх = р2 = 0,5039 не противоречащим опытным данным.
Следовательно, монетки, используемые в опыте Феллера и опыте
Джевонса, в смысле симметричности можно считать одинаковыми.
Пример 2. Исследуется проблема смертности среди больных,
страдающих легочным туберкулезом в открытой форме, в течение первого года
после заболевания. Рассматриваются две группы больных: мужчины и
женщины. В первой группе (мужчины) количество заболевших п{ = 221, из
них количество умерших тх = 68; во второй группе (женщины) количество
заболевших п2 = 194, из них количество умерших т2 = 83. Соответственно
смертность в группе мужчин составляет — = 0, 308 (30,8%) а, в группе
п\
женщин = 0,428 (42,8%). Как видим, смертность в группе женщин
п2
282

на 12% выше. Требуется определить, значимо или незначимо различаются
относительные частоты по группам, т. е. их различие вызвано
принципиальными причинами или же обусловлено случайным стечением
обстоятельств.
Итак, две имеющиеся выборки достаточно большого объема
представляют две соответствующие генеральные совокупности Хх и Х2. Для каждого
больного к концу года имеются два возможных исхода: жив или умер.
Предполагая вероятность смерти каждого больного вследствие
рассматриваемой болезни постоянной (р{ для первой генеральной совокупности и р2
для второй генеральной совокупности) и исход к концу года для каждого
больного независящим от исходов течения болезни других заболевших, мы
имеем справедливость условий, фигурирующих в схеме Бернулли. Задача
заключается в проверке гипотезы
Щ- Р\= Р2= Р>
исходя из данных имеющихся выборок.
Рассмотрим конкурирующую гипотезу
Н{. Рх * Р2>
тогда, как мы неоднократно находили в табл. 2, для двусторонней
критической области две критические точки при уровне значимости а = 0,05
имеют координаты ±1,96. Находим Д,а6л по формуле (6.43):
2набл = 0,308-0,428 - -2,53. (6.46)
68 + 83
221 + 194
fi- 68 + 83 V_L+n
v 221 + 194Л221 194/
Как видим |ZHa6J > 1,96, т. е. находится в критической области,
следовательно, принимается конкурирующая гипотеза /?, * р2. Разность между
наблюдаемыми долями смертности в обеих выборках признается значимой.
Заметим, что использование при вычислении ZHa6n поправки Йейтса
приводит к значению [см. (6.45)] ZHa6jI = 2,43, которое также принадлежит
критической области.
Следовательно, смертность среди женщин, страдающих легочным
туберкулезом в открытой форме, в течение первого года после заболевания,
согласно имеющимся данным, признается принципиально отличной от
соответствующих значений смертности мужчин.
а ~2
6.11. Таблицы сопряженности и критерий х
Метод проверки гипотез о вероятностях, рассмотренный в § 6.9; 6.10,
применим к схеме Бернулли, когда имеются всего два возможных исхода
испытания (произошло событие А либо не произошло). На практике число
возможных исходов испытания часто бывает более чем два, что не
укладывается в схему Бернулли. Также во многих задачах мы располагаем более
чем двумя выборками, что не предполагает предыдущая постановка задачи.
Приведем другие методы проверки статистических гипотез,
использующие в качестве критерия статистику %2- Эта статистика имеет более
сложную структуру, чем нормально распределенный критерий Z, что и
обусловливает более обширную область применения (в случае нескольких возмож-
283

Таблица 6.2. Смертность от легочного туберкулеза среди мужчин и
женщин (наблюдаемые значения)
Наблюдаемые значения
Мужчины
Женщины
Итого
Живы
153
111
264
Умерли
68
83
151
Всего
221
194
415
ных исходов испытания и нескольких выборок). Методика проверки
гипотез с помощью критерия х2 точно такая же, как и в других ранее
рассмотренных критериях: вводятся гипотезы Н0 и Нх\ по уровню значимости
а строятся область принятия гипотезы и критическая область (критические
точки получаем из таблицы); находится наблюдаемое значение критерия;
проверяется принадлежность полученного значения области принятия
гипотезы, и в зависимости от этого нулевая гипотеза принимается либо
отвергается в пользу конкурирующей Нх. Все это нам уже хорошо известно,
и весь вопрос заключается в том, как построить соответствующий
критерий х2 и найти хнабл •
Во избежание громоздких формул и сложных обозначений начнем
изложение принципов метода с простого наглядного примера 1.
Воспользуемся данными примера 2 § 6.10 смертности среди больных, страдающих
легочным туберкулезом в открытой форме, в течение первого года после
заболевания. Рассматриваются две группы (выборки) больных: группа
мужчин в количестве пх = 221, среди них умерших тх = 68, и группа
женщин в количестве п2 = 194, среди них умерших т2 = 83. Требуется
установить, значимо ли различие в смертности по обеим группам больных.
Имеющиеся данные занесем в таблицу, называемую таблицей
сопряженности признаков (табл. 6.2)
В таблице данные по каждой из двух групп (мужчин и женщин)
располагаем по строкам, а признаки (живы, умерли) — по столбцам. Таким
образом, таблица сопряженности состоит из четырех клеток и имеет
размерность 2 х 2. В таблице имеются две графы "Всего", где выписаны суммы
значений по строкам (численность групп) и по столбцам (численность
элементов в обеих группах, обладающих конкретным признаком). Эти клетки
считаются вспомогательными, в них значения предполагаются не
случайными, а фиксированными.
Далее выдвигаем нулевую гипотезу Я0, что смертность в генеральных
совокупностях, соответствующих нашим выборкам, одинакова. Если
показатель смертности в обеих генеральных совокупностях один и тот же, то в
нашем случае имеем
Hq- P\= Рг= Р>
где рх и р2 — теоретические показатели смертности (доли умерших от
общего числа заболевших) соответственно в первой и второй генеральных
284

Таблица 6.3. Смертность от легочного туберкулеза среди мужчин и
женщин (ожидаемые значения)
Ожидаемые значения
Мужчины
Женщины
Итого
Живы
140,6
123,4
264
Умерли
80,4
70,6
151
Всего
221
194
415
совокупностях; р — общее значение /?, и р2. Конкурирующая гипотеза Я,,
как и ранее, это либо рх * р2, либо рх > ръ либо рх < р2.
При справедливости нулевой гипотезы, предполагая, что показатель
смертности не зависит от пола больного (от генеральной совокупности, к
которой причислен конкретный больной), можно вычислить ожидаемые
значения смертности в каждой из групп, исходя лишь из численности
элементов группы. Итак, в табл. 6.2 находим: всего наблюдаемых больных
415, из них умер 151 больной. Следовательно, при справедливости Я0
смертность составляет 151/415 « 0,3639 (36,39%), а в живых остается
соответственно 264/415 ~ 0,6361 (63,61%). Пересчитаем эти доли для каждой
группы. В группе мужчин из 221 больного смертность 36,39% составляет
число 80,4 умерших, а 63,61% составляет число 140,6 оставшихся в живых.
По второй группе из 194 больных получаем 194-0,3639 ~ 70,6 умерших и
194*0,6361 ~ 123,4 оставшихся в живых. Заметим, что полученные числа
являются теоретическими, выражающими средние значения, поэтому
вполне допустимо, что эти числа нецелые. Округление же полученных
значений до целых, разумеется, придаст большую осмысленность нашим
данным, но зато негативно повлияет на точность вычислений. Обычно просто
так точностью вычислений не жертвуют, лучше смириться с дробными
числами. Далее, заносим полученные данные в таблицу ожидаемых
значений, аналогичную табл. 6.2 (см. табл. 6.3).
Сравнивая две таблицы, наблюдаемых значений и ожидаемых значений
при справедливости Я0, заметим, что данные в графах "Всего" в обеих
таблицах одинаковы, различаются лишь наблюдаемые и ожидаемые значения
по группам и признакам.
Далее, рассматривая значения в соответствующих графах обеих таблиц,
можно заметить, что числа несколько различаются. Но сколь
существенным является это отличие, значимо либо незначимо различие выборочных
показателей, чисто визуально мы ответить не можем. Нужны более строгие
характеристики сравнения.
Введем критерий проверки нулевой гипотезы, т. е. статистику (св.,
зависящую от выборочных случайных величин), которая бы учитывала
различие наблюдаемых и ожидаемых значений. Причем речь идет об
относительном различии, ибо даже незначительное отклонение наблюдаемых
значений от ожидаемых, вполне объяснимое случайными причинами для
285

Таблица 6.4
-»-~>^II признак
I признак^^""--*-^^^
Да
Нет
Итого
Да
а
с
а + с
Нет
Ъ
d
b+ d
Всего
а+ b
с + d
n=a+b+c+d
малых выборок, может оказаться весьма существенным для выборок
большего объема.
Таким критерием является статистика
= У^ Г-К набл ~ -Кож4] 2 = \"*(^набл ~ ^ож)
2 _
Дж
2J
Ло
(6.47)
где Л^а, — наблюдаемое значение в графе таблицы сопряженности, Кож —
ожидаемое значение в той же графе, суммирование распространяется по
всем графам таблицы за исключением граф "Всего". Следовательно, в
нашем примере сумма вида (6.47) состоит из четырех слагаемых. Статистика,
представленная в (6.47), имеет распределение х2 с числом степеней
свободы df= 1 для нашей таблицы сопряженности размерности 2x2.
Замечание 1. Для таблицы размерности 2x2, включающую два
признака с альтернативными исходами, типа табл. 6.2 (см. табл. 6.4),
где а, Ьу су d — конкретные значения, величину х2 вида (6.47) можно найти
по другой формуле:
2 _
(ad-bcfn
(a + b)(c+d)(a + c)(b+d)' ( A *
Замечание 2. В общем случае статистика вида (6.47), составленная по
таблице сопряженности с размерностью г х к, где г — число
рассматриваемых групп, а к — число признаков, имеет распределение х2 с числом
степеней свободы df= (г - \)\к — 1). Как легко заметить, в таблице
размерности 2x2 число степеней свободы для х2 равно (2 - 1)(2 - 1) = 1.
Замечание 3. Для того чтобы наш критерий вида (6.47) можно было
считать действительно распределенным по закону х2 с df= (г - 1)(к — 1),
необходимо выполнение условия: в любой из граф таблицы
сопряженности ожидаемое число должно быть не менее 5. В противном случае
используют не приближенный критерий х2, а точный критерий Фишера,
основанный на переборе всевозможных способов заполнения таблицы
сопряженности1.
Вернемся к нашему конкретному примеру и табл. 6.2, 6.3. Рассматривая
наблюдаемые и ожидаемые значения признаков в каждой из клеток,
получаем конкретное значение критерия х2:
В данном пособии указанный критерий не рассматривается.
286

2 = (153- 140,6)' + (68-80,4)' . (111-123,4)' ,
Хнабл 140,6 80,4 123,4
+ (83-70,6)2 , ,2?
70,6 ~°>^/'
Отметим, что, используя формулу (6.47.), мы приходим к тому же
значению:
2 = (153 ■ 83-68 ■ 111)2 • 415 , юп
Хнабл 221 • 194 • 264 • 151 *°>42/'
Для проверки нулевой гипотезы необходимо найти критическую
область. Критическая область критерия х2 строится правосторонняя. Тогда из
табл. 4 Приложения 2 находим критическую точку (напомним, что х2 в
рассматриваемом примере имеет число степеней свободы 1): при уровне
значимости а = 0,02 значение xlP = 5,41, а при а = 0,01 значение %lP = 6,64.
Следовательно, можно утверждать, что при уровне значимости а = 0,02
значение Хнабл попадает в критическую область (хна&л > xlP),
следовательно, гипотеза о незначимости различий смертности от легочного
туберкулеза в группах мужчин и женщин отвергается.
Замечание 4. Критерий х2, построенный по таблице сопряженности
размерности 2x2, связан с критерием Z вида (6.41) простым соотношением
X2 = Z2, что можно проиллюстрировать, сопоставив ZHa6n = -2,53 из (6.46)
и Хнабл = 6,427 [небольшое различие значений (—2,53)2 и 6,427 связано с
погрешностью вычислений].
Замечание 5. В случае построения критерия х2 по таблице
сопряженности признаков размерности 2x2 для достижения более точных значений
критерия применяется поправка на непрерывность, называемая поправкой
Иейтса. С учетом этой поправки
М^набл _ -Кож! _ ^J
В рассмотренном примере поправка Йейтса уменьшает х
набл
2 = (153-140,6-0,5)' , (160-80,41-0,5)' + (ЦП- 123,4|-0,5) +
Хнабл 140,6 80,4 123,4
+ L°£— ' „—»_£i_-5,919, но тем не менее при том же самом уровне
70,6
значимости а = 0,02 по-прежнему Хнабл > xlP > и нулевая гипотеза о
незначимости различий в группах отвергается.
Рассмотрим пример использования таблицы сопряженности
размерности, большей чем 2x2. Отметим, что в этом случае поправка Йейтса
обычно не применяется.
Пример 2. Изучается влияние процесса обучения на результаты
некоторого психологического теста. Проведенные для 100 школьников
испытания выявили следующие результаты, представленные в табл. 6.5.
287

Таблица 6.5
Возраст школьников
Младшие
Средние
Старшие
Итого
Результаты теста
Низкие
10
6
7
23
Средние
15
16
13
44
Высокие
5
8
20
33
Всего
30
30
40
100
Таблица 6.6
Возраст школьников
Младшие
Средние
Старшие
Итого
Результаты теста
Низкие
6.9
6.9
9.2
23
Средние
13,2
13,2
17,6
44
Высокие
9.9
9.9
13,2
33
Всего
30
30
40
100
Используя критерий у} , требуется исследовать наличие влияния
обучения на результаты теста.
Решение. Приведенная таблица представляет собой таблицу
сопряженности размерности 3 х 3. В ней указано количество школьников каждой
группы, показавших те или иные результаты тестирования. Таким образом
в девяти графах таблицы выписаны значения Лнабл. Найдем
соответствующие им девять значений Лож. Исходим из долей результатов тестирования
среди всех 100 школьников (см. последнюю строку таблицы): 23% —
низкий результат; 44% — средний результат; 33% — высокий результат. Для
каждой группы школьников (30, 30 и 40 человек) найдем соответствующие
доли, которые и являются теоретическими значениями Кож. В частности,
для младших школьников численностью в 30 человек имеем:
30 • 0,23 = 6,9; 30 • 0,44 = 13,2; 30 • 0,33 = 9,9.
Аналогично найдем оставшиеся шесть значений Д,ж, и полученные
числа занесем в таблицу ожидаемых значений (табл. 6.6).
Записанные в таблице значения /^ж имели бы место в случае, когда
возраст школьников (время их обучения) не оказывает никакого влияния на
результаты тестирования (нулевая гипотеза). Находя конкретное
(наблюдаемое) значение критерия х2, устанавливаем, сколь сильно реальные
значения Л„абл отличаются от теоретических /^ж.
288

v2 = уС^набл ^ож) =
Хнайл L к^ж
= (Ю-6,9)2 + (15-13,2)2 (5 - 9, 9)2 + (6~6,9)2 + (16- 13, 2)2 +
6,9 13,2 9,9 6,9 13,2
+ (8 ~ 9,9)2 + (7 - 9,2)2 (13 - 17, б)2 + (20 - 13, 2)2 01
9,9 9,2 17,6 13,2 '
Для проверки справедливости нулевой гипотезы о незначимости
различий наблюдаемых и теоретических значений находим ХкР> учитывая, что
число степеней свободы равно (г — \){к — 1), где г х к — размерность
таблицы сопряженности; т. е. в нашем случае df=(3 — 1)(3 - 1) = 4.
Итак, ХкР = ХкР(0,05; 4) = 9,49 (см. табл. 4 Приложения 2). Следовательно,
при стандартном уровне значимости а = 0,05 получим Хнабл > Х*р > и
нулевая гипотеза должна быть отклонена: расхождение между наблюдаемыми
результатами теста и теоретическими (при справедливости нулевой
гипотезы) достаточно велико и признается существенным. Различие в результатах
тестирования может быть отнесено на счет различия в сроках обучения
школьников в разных группах. Однако из полученных результатов вовсе не
следует, что различие во времени обучения школьников целиком
определяет результаты тестирования. Речь идет лишь о том, что фактор времени
обучения оказывает влияние на результаты тестирования, что и удалось
обнаружить критерию х2- О степени этого влияния критерий говорит лишь
косвенно: если бы значение Хнабл оказалось больше, то и влияние первого
признака на второй, наверное, было бы сильнее. Более точные оценки
этого влияния будут получены в гл. 8 (см. § 8.12).
6.12. Критерий для процента смертности с учетом возрастных
параметров
Пусть имеются две группы, А и В, лиц различающихся по некоторому
признаку: методика лечения болезни, пол, профессия, место проживания и
т. д. Лица обеих групп подвержены риску смерти от некоторой общей
причины, например наличия общего заболевания и вредных условий труда.
Изучается различие показателей смертности этих групп. Все обследуемые в
группах разбиты на отдельные возрастные подгруппы, в каждой из
которых наблюдается свое значение показателя смертности. Данные оформим
в виде табл. 6.7.
Таким образом, по каждой группе получается своя последовательность
показателя смертности, состоящая из г элементов:
— для группы А последовательность
Ш\ nil mr.
— для группы В последовательность
т± т£ /и/
пх% п2 пг
19 — 3529
289

Таблица 6.7. Данные по группам при сравнении процентов смертности
Возрастные
подгруппы
1
2
г
Группа А
количество
обследуемых
«1
п2
"г
количество
умерших
/Я,
т2
тг
смертность
П\
т2
п2
т_г
Группа В
количество
обследуемых
количество
умерших
/Я,'
т2
т;
смертность
т±
т2'
п2'
ml
Таблица 6.8
Наблюдаемые значения
Группа А
Группа В
Итого
Живы
Щ - т,
n't -ml
П/ + itf — m, - т,-
Умерли
Щ
ml
т( + ml
Всего
nl
n, + nl
Задача заключается в сравнении данных последовательностей совместно
по всем возрастным подгруппам. Требуется сделать вывод о значимости
или незначимости различий указанных числовых последовательностей.
Рассматривая по отдельности каждую возрастную подгруппу, можно для
нее составить таблицу сопряженности размерности 2*2. Для каждой /-й
возрастной подгруппы получаем данные, приведенные в табл. 6.8.
Методом предыдущего параграфа, составив таблицу сопряженности
ожидаемых значений, можно вычислить значения критерия х/ 0 — номер
возрастной группы). Затем значения по каждой возрастной группе
просуммируем, и тогда
г
является критерием проверки гипотезы о равенстве показателей
смертности в обеих группах с учетом всех возрастов. Однако чем больше число г
(большая градация по возрастам), тем более громоздкими становятся вы-
290

Таблица 6.9. Смертность среди больных, страдающих легочным
туберкулезом в открытой форме, в течение первого года после заболевания
Возрастная
подгруппа
15-19
20-24
25-29
30-34
35-39
40-44
45-49
50-54
55-59
> 60
Всего...
Мужчины

количество
заболевших п,
406
695
585
454
274
221
153
ПО
69
89
3056
количество
умерших /я,
156
204
169
128
82
68
41
34
36
43
961

смертность в %
38,4
29,4
28,9
28,2
29,9
30,8
26,8
30,9
52,2
48,3
—
Женщины

количество
заболевших п\
500
816
619
433
257
194
94
58
29
47
3047
количество
умерших
174
246
184
150
92
83
39
20
13
28
1029

смертность в %
34,8
30,1
29,7
34,6
35,8
42,8
41,5
34,5
44,8
59,6
—
2
XI
1,25
0,11
0,09
4,22
2,10
6,43
5,75
0,23
0,45
1,57
22,20
числения х2- На практике удобнее пользоваться формулой для вычисления
X?, а не вычислять все заново по таблицам сопряженности. Применяя
формулу (6.47'), можно доказать, что в нашей задаче для /-й возрастной
подгруппы справедливо
(6.49)
2 = n,nj(n, + nj) (™i-™£\
' (т, + т-,)(п; + п\ — rrii — m/)v л,- п\)
где величина х« имеет распределение "хи-квадрат' с одной степенью
свободы1. Следовательно, записав равенство (6.49) для всех / от 1 до г и
просуммировав, получим критерий
2 _
= !><
(6.50)
с г степенями свободы. Дальнейшее использование критерия для проверки
нулевой гипотезы о равенстве показателей смертности в обеих группах
является вполне стандартным: находится критическая область, находится
Хнабл и делаются выводы.
1 В качестве упражнения рекомендуется доказать справедливость формулы (6.49), исходя
из (6.47).
19*
291

Пример.1 По данным, приведенным в табл. 6.9, требуется установить,
имеется ли разница среди смертности мужчин и женщин в течение
первого года после постановки диагноза заболевания.
В последнем столбце табл. 6.9 вычислены по формуле (6.49)
наблюдаемые значения х? для каждой из 10 возрастных подгрупп (в обозначении х/
индекс / изменяется от 1 до 10).
Каждая из статистик х/ — это критерий проверки нулевой гипотезы о
незначимости различий смертности мужчин и женщин в /-й возрастной
подгруппе. Заметим, что данные для возрастной подгруппы 40—44 года
были использованы в примере 2 § 6.9, 6.10 и в рассмотренном примере
§ 6.11. Значение х2 — сумма всех х* — это критерий проверки нулевой
гипотезы совместно по всем возрастным подгруппам. Наблюдаемое значение
X2 равно 22,20, что, исходя из табл. 4 Приложения 2, соответствует уровню
значимости а ~ 0,014 (напомним, что число степеней свободы ^критерия
X2 равно числу возрастных подгрупп, т. е. df= 10). Таким образом, барьер
уровня значимости а = 0,05 превзойден (при а = 0,05 критическая
точка ХкР = 18,31, но при а = 0,01 находим %lP = 23,2), и различие между
процентами смертности в группах мужчин и женщин следует признать
значимым.
Проанализировав последний столбец табл. 6.9 значений х2 > можно
констатировать, что наибольшее различие показателей смертности в группах
приходится на возраст от 30 до 50 лет, при этом показатель смертности в
группе женщин существенно выше, чем в группе мужчин.
6.13. Критерий Кочрена сравнения дисперсий нескольких нормальных
генеральных совокупностей
Пусть X/ обозначает /-ю генеральную совокупность. Известно, что т
генеральных совокупностей Хи Хъ ..., Хт имеют нормальное распределение
(т > 2). На уровне значимости а требуется проверить гипотезу о равенстве
дисперсий рассматриваемых генеральных совокупностей (также говорят об
однородности дисперсий):
Я0: ОД) = D(X2) = ... = D(Xm). (6.51)
Для проверки этой нулевой гипотезы взяты выборки одного и того же
объема п каждая и вычислены исправленные выборочные дисперсии S\,
S%, ..., iS^,, которые, как известно, имеют число степеней свободы к = п — 1.
Численные значения исправленных выборочных дисперсий, естественно,
обозначим s], s\, ..., s2m.
1 Представленные данные по наблюдению за туберкулезом принадлежат Г. Бергу и
заимствованы из кн. Г. Крамера "Математические методы статистики". — М., 1975.
292

В качестве критерия проверки выдвинутой гипотезы (6.51) используем
статистику
К = ?тах , (6.52)
$ + $ + ... + &
называемую критерием Кочрена, где S*max — та из исправленных
выборочных дисперсий, значение которой наибольшее.
Критическую область выбираем правосторонней, и тогда имеется
единственная критическая точка к^, которую при фиксированном уровне
значимости а можно найти из соответствующих таблиц (для а = 0,05 и
а = 0,01, см. табл. 9 Приложения 2).
Далее, по имеющимся данным вычисляем А"набл и, если Кна6л < kKpi то
нулевая гипотеза (6.51) принимается, в противном случае, Киа6л > &кр, делаем
вывод, что дисперсии в рассматриваемых генеральных совокупностях
различны. Уточнить, в каких именно генеральных совокупностях различаются
дисперсии, можно с помощью того же или другого критерия, сравнивая
меньшее количество выборок, например выборки попарно.
В случае справедливости гипотезы Я0 в качестве оценки генеральной
дисперсии полагают среднее арифметическое значение имеющихся т
исправленных выборочных дисперсий.
Пример. Три лаборатории произвели анализ 9 проб исследуемого
препарата для определения процентного содержания в нем эфирного масла.
Исправленные выборочные дисперсии оказались: в первой лаборатории
s\ = 0,037, во второй лаборатории s\ = 0,063, в третьей лаборатории s] =
= 0,052. Предполагая, что процентное содержание эфирного масла в
препарате имеет нормальное распределение, требуется при уровне
значимости а = 0,01 проверить гипотезу об однородности дисперсий.
Процентное содержание эфирного масла в препарате — это случайная
величина (генеральная совокупность). Для каждой из лабораторий
рассматриваемая генеральная совокупность своя. Таким образом, имеются
три генеральные совокупности Xv Хъ Х3, из которых извлечены по одной
выборке одинакового объема п = 9. По вычисленным значениям s], s\,
s\ проверим нулевую гипотезу однородности дисперсий:
Я0: D{XX) = D(X2) = ад)-
Так как все три генеральные совокупности по условию нормальны, а
выборки одинакового объема п = 9, то можно применить критерий Кочрена
(6.52). Критическую точку находим из табл. 9 Приложения 2 при а = 0,01:
К, = Ма; Ь т) = ^(0,01; 8; 3) = 0,7107
(напомним, что к = п — 1, где п — объем каждой из выборок; т —
количество выборок).
Вычислим наблюдаемое значение критерия:
К = Smax = 0» 063 ,л 4257
s] + s22 + s] 0,037 + 0,063 + 0,052 ~ '
Так как Кна6п < ккр (0,4257 < 0,7107), то на уровне значимости а = 0,01
различие выборочных дисперсий незначимо, и гипотеза об однородности
293

дисперсий принимается. Оценка дисперсии одна и та же для любой из
трех рассматриваемых генеральных совокупностей — это среднее
арифметическое
s2 = s] + s\ + s] = О,037 + 0,063 + 0, 052 я Q Q493
6.14. Критерий Бартлетта сравнения дисперсий нескольких
генеральных совокупностей
Пусть имеется т нормальных генеральных совокупностей. Обозначим
их Хи Х2, ..., Хт. При уровне значимости требуется проверить нулевую
гипотезу о равенстве соответствующих генеральных дисперсий:
Я0: D(XX) = D(X2) = ... = D(Xm)t
называемую также гипотезой об однородности дисперсий.
Из каждой генеральной совокупности X, извлечена выборка объема л,.
Если все п, равны, то для проверки Я0 можно использовать критерий Коч-
рена (см. § 6.13). В противном случае, когда выборки, вообще говоря,
разного объема, нам необходим другой критерий проверки нулевой гипотезы.
Рассмотрим критерий Бартлетта.
Пусть по выборкам найдены исправленные выборочные дисперсии S\,
iS^, ..., SJ,, при этом каждая статистика S* имеет число степеней свободы
к, = п, — 1. Обозначим суммарное число степеней свободы по всем
выборкам
к=кх + к2 + ... + кт,
и среднее арифметическое исправленных выборочных дисперсий,
взвешенное по числу степеней свободы,
? = \(kxS\ + Ь^ + ... +к,Л)- (6-53)
(Внимание: не путать величину S1 с введенной ранее в гл. 5
выборочной дисперсией.)
Введем еще две величины:
т
V= fcln^-^r^lntf; (6.54)
c=i+ 1 fyl-l
3(m-l)l^A:1 к
(6.55)
Заметим, что V — статистика, т. е. случайная величина, а С—
постоянная, причем О 1.
у
Отношение В = ^,, где Уи С имеют вид (6.54), (6.55) соответственно, и
является критерием Бартлетта проверки гипотезы Я0. При справедливости
нулевой гипотезы критерий В имеет приближенное распределение х2 с
294

Таблица 6.10
Номер
генеральной
совокупи./
1
2
3
Объем
выборки п,
10
12
17
Число
степеней
свободы kj
9
11
16
к= 36
J?
0,045
0,033
0,040
KjSj
0,405
0,363
0,640
5s = 0,039
Ins?
-3,101
-3,411
-3,219
In? = -3,2414
kilns2
-27,910
-37,523
-51,502
1
k(
m—\ степенями свободы. Причем приближение оказывается
удовлетворительным лишь в случае, когда каждая из выборок имеет объем, не
меньший четырех: все п, > 4.
Критическая область строится правосторонняя, а единственная
критическая точка Хкрит при выбранном уровне значимости а находится из
табл. 4 Приложения 2. Вычислив наблюдаемое значение критерия, Вна6пУ
исходя из (6.56) и конкретных значений s], s\, ..., s2n и соответствующих
чисел степеней свободы, сравниваем его с Хкрит- Если Вна6л < xlPm> то
нулевая гипотеза о равенстве дисперсий принимается; если же Вна6л > xlPm, то
различие выборочных дисперсий признается значимым и гипотеза Н0
отвергается.
В случае принятия нулевой гипотезы оценка генеральной дисперсии —
это значение s2, вычисленное по конкретным значениям выборочных
дисперсий.
Замечание. Критерий Бартлетта достаточно резко реагирует на
отклонения от нормального закона распределения, поэтому, если имеются
сомнения в плане распределения, лучше использовать выборки одинакового
объема и обратиться к критерию Кочрена.
Пример. Три лаборатории производили анализ исследуемого препарата на
процентное содержание в нем эфирного масла. Первая лаборатория исследовала
10 проб, вторая — 12 и третья — 17 проб. Исправленные выборочные дисперсии
оказались соответственно s] = 0,045; s\ = 0,033; s] = 0,040. Предполагая, что
процентное содержание эфирного масла в данном препарате имеет нормальное
распределение, требуется при уровне значимости а = 0,01 проверить гипотезу об
однородности дисперсий.
Поступаем так же, как и в примере предыдущего параграфа: переходим
к вероятностной постановке задачи. Процентное содержание эфирного
масла в препарате — случайная величина, т. е. генеральная совокупность —
своя персональная для каждой лаборатории. Поскольку объемы выборок
295

для каждой генеральной совокупности различны, для проверки гипотезы
Я0, равенстве генеральных дисперсий, воспользуемся критерием Бартлетта.
Так как используется много данных, удобнее их оформить в виде
таблицы.
Исходя из найденных значений, вычисляем наблюдаемое значение V:
V= 0,245, тогда Янабл=^.
Из табл. 4 Приложения 2находим ХкРит(0,01; 2) = 9,2.
Заметим, что постоянная С всегда больше 1, следовательно,
^набл q x U,ZtJ
и, разумеется Вна6п < 9,2. Следовательно, вычислять значение постоянной
С нет необходимости, поэтому последний столбец табл. 6.10 остался
незаполненным. Значение Вна6л попадает в область принятия гипотезы, тем
самым статистически доказано равенство дисперсий всех трех генеральных
совокупностей. Оценка их общей дисперсии равна s2 = 0,039.
Задачи и упражнения
1. По двум независимым выборкам, объемы которых л, = 14 и п2 = 10,
извлеченным из нормальных генеральных совокупностей X и Y,
вычислены исправленные выборочные дисперсии s\ = 0,84; s2y = 2,52. При уровне
значимости а = 0,1 проверить нулевую гипотезу о равенстве дисперсий
H0:D(X) = D(Y)
при конкурирующей гипотезе
Н{. D{X)*D(Y).
Указание. Использовать критерий Фишера F. По виду конкурирующей
гипотезы установить вид критической области (двусторонняя,
левосторонняя или правосторонняя). Найти FmSn и FKpy сравнить их и сделать выводы.
2. Измерения одной и той же величины проведены двумя методами по
нескольку раз. Получены две выборки результатов:
X 9,6; 10,0; 9,8; 10,2; 10,6;
Y: 10,4; 9,7; 10,0; 10,3.
Предполагая, что выборки независимы и извлечены из нормальных
генеральных совокупностей, сравнить точность измерений при уровне
значимости а = 0,1.
Указание. Я0: D(X) = D(Y)\
Н{. D{X) * D{Y).
Применить критерий Фишера.
Ответ: = FHa6n = 1,48; /^(0,05; 4; 3) = 9,12. Так как FHa6n < FKpi то
исправленные выборочные дисперсии различаются незначимо, нулевая
гипотеза принимается, т. е. оба метода обеспечивают одинаковую точность
измерений.
296

3. Из нормальной генеральной совокупности извлечена выборка объема
л = 31:
х,
Щ
од
1
0,3
3
0,6
7
1.2
10
1.5
6
1.8
3
2,0
1
При уровне значимости а = 0,05 проверить нулевую гипотезу
Я0: а2 = 0,18
при конкурирующей
Я,: а2 > 0,18.
Указание. В качестве критерия проверки гипотезы Я0 использовать
статистику
X = ^(л-1),где а2, =0,18.
Ответ: Хнабл = 45,0; xlP = 43,8. Принимается конкурирующая гипотеза.
4. Из нормальных генеральных совокупностей Хи Yизвлечены выборки
объемов л, = 50 и л2 = 70 соответственно. Найдены выборочные средние х
= 25; у = 27. Известны генеральные дисперсии D(X) = 10; D(Y) = 14.
Требуется проверить нулевую гипотезу
Я0: М(Х) = M(Y)
при конкурирующей гипотезе
а) Я,: М(Х)* M(Y);
б) Я,: М(Х) < МП-
Уровень значимости в обоих случаях взять а = 0,05.
Указание. Использовать критерий Z[cm. (6.17), § 6.5].
Ответ: ZHa6jI = 3,162; а) ^р = 1,96; б) zKp = 1.645.
Нулевая гипотеза отвергается в обоих случаях.
5. Пусть имеются две независимые выборки объемов л, = 12 и щ = 18,
извлеченные из нормальных генеральных совокупностей X и Y соответственно.
Вычислены выборочные характеристики: х = 28,7; у = 26,7; sx = 0,75; sy = 0,45.
При уровне значимости а = 0,05 проверить нулевую гипотезу о равенстве
генеральных средних
HQ: M(X) = M(Y)
при конкурирующей гипотезе
Я,: М(Х) *M(Y).
Указание. Для проверки гипотезы Я0 использовать критерий Стьюдента
[см. (6.24), § 6.6]. Предварительно необходимо проверить условие
равенства дисперсий: D(X) = D(Y). Для проверки этого условия используется
критерий Фишера F[cm. (6.9), § 6.3].
Ответ: Для критерия Фишера: Fm6n = 1,667; FKp = 2,41. Так как FHa6n < F^,
то полагаем D(X) = D(Y).
Для критерия Стьюдента: Тнл6п = 7,122; >двусткр = 2,05. Выборочные
средние различаются значимо.
297

6. Имеются две выборки из нормальных генеральных совокупностей X
и Y
х,
Щ
12,3
1
12,5
2
12,8
4
13,0
2
13,5
1
I = пх = 10
Я
/я,
12,2
6
12,3
8
13,0
2
I = л2 = 16
На уровне значимости а = 0,05 проверить нулевую гипотезу о равенстве
генеральных средних
Я0: М(Х) = M(Y)
при конкурирующей гипотезе
Н{. М(Х) > M(Y).
Указание. Использовать критерий Стьюдента. Предварительно
проверить гипотезу о равенстве генеральных дисперсий.
Ответ: Выборочные средние различаются значимо, нулевая гипотеза
должна быть отвергнута.
7. Нормальная генеральная совокупность X имеет дисперсию
D(X) = 1600. Извлеченная из генеральной совокупности Л" выборка объема
п = 64 имеет выборочную среднюю х = 136,5. При уровне значимости а = 0,01
требуется проверить нулевую гипотезу
Я0: М(Х) = 130
при конкурирующей гипотезе
Н{. М(Х) * 130.
Ответ: ZHa6jI = 1,3; z^ — 2,57. Нулевая гипотеза принимается.
8. Установлено, что средняя масса таблетки сильнодействующего лекарства
должна быть равна 0,50 мг. Выборочная проверка 121 таблетки полученной
партии лекарства показала, что средняя масса таблетки этой партии х = 0,53 мг.
Требуется при уровне значимости а = 0,01 проверить нулевую гипотезу
Я0: М(Х) = 0,50
при конкурирующей гипотезе
Н{. М(Х) > 0,50,
где масса таблетки — генеральная совокупность X. Многократными
предварительными опытами по взвешиванию таблеток, поставляемых
фармацевтической фирмой, было установлено, что масса таблеток распределен
нормально со средним квадратическим отклонением а = 0,11 мг.
Ответ: ZHa6jI = 3; ^р = 2,33. Средняя масса таблетки значимо отличается
от допустимого; больным давать такое лекарство нельзя.
9. Решить предыдущую задачу при условии, что значение а заранее
неизвестно, а его оценка s найдена по имеющейся выборке: s = 0,10.
Указание. Использовать критерий Стьюдента [см. (6.33), § 6.7].
VBocT.kp.(0,01;120) = 2,36.
10. Для двух выборок объемов л, = п2 = 20, извлеченных из нормальных
генеральных совокупностей Хи Y, вычислены выборочные средние х = 17,2;
у = 19,0. Многократными предварительными опытами установлено, что Хи
Y имеют стандартное отклонение а = 1,5. Найти мощность критерия
Стьюдента, применяемого для проверки гипотезы о равенстве средних.
298

Указание. Воспользоваться табл. 8 Приложения 2.
Ответ: мощность критерия ~ 0,93 (~ 93%).
11. Предполагается, что некоторое событие в результате испытания
осуществляется с постоянной вероятностью р0 = 0,20. По 100 независимым
испытаниям найдена относительная частота осуществления этого
события ш = 0,16. Требуется при уровне значимости а = 0,05 проверить
нулевую гипотезу
Щ- Р = Ро = 0,20
при конкурирующей гипотезе
Я,: р * 0,20.
Указание. В качестве критерия проверки нулевой гипотезы используйте
статистику Zbhhsl (6.38), § 6.9.
Ответ: ZHa6n = — 1; zKp= 1,96. Так как |ZHa6J < z^, to наблюдаемая
относительная частота ш = 0,16 незначимо отличается от гипотетической
вероятности р0 = 0,2. Нет оснований отвергнуть нулевую гипотезу.
12. В двух цехах завода работают соответственно 200 и 300 человек.
Заболеваемость простудными заболеваниями в течение наблюдаемого
периода составила 13% для первого цеха и 20 % для второго. При уровне
значимости а = 0,05 проверить нулевую гипотезу о равенстве вероятностей
заболеваемости одного работающего в 1-м и во 2-м цехах: рх= р2 = 0,13 при
конкурирующей гипотезе /?, * р2.
Указание. В качестве критерия проверки нулевой гипотезы
использовать статистику Zbviasl (6.41), § 6.10.
Ответ: ZHa6j] = —2,28; ^р = 1,96. Нулевая гипотеза отвергается, так как
13. В предыдущей задаче вместо гипотетической вероятности р = 0,13
использовать среднюю вероятность р, вычисляемую по наблюдаемым
данным (6.42).
Ответ: р = 0,172. Нулевая гипотеза р1 = р2 = 0,172 принимается.
14. Решить предыдущую задачу, используя поправку Йейтса.
Указание. См. (6.44), § 6.10.
Зная выводы задачи 13, можно ли заранее предвидеть, что поправка
Йейтса не изменит вывод относительно принятия нулевой гипотезы?
15. Сравниваются методы лечения некоторого заболевания,
применяемые в государствах А и В. Показателем эффективности лечения является
разница в смертности больных, находящихся на излечении. Данные
смертности этих больных в течение определенного срока после установления
диагноза приведены в табл. 6.11.
По имеющимся данным требуется установить наличие (или отсутствие)
существенной разницы в смертности больных в государствах А и В.
Уровень значимости стандартный а = 0,05.
Указание. Заполните пустые графы таблицы. Для вычисления х.
используйте формулу (6.49), § 6.12. Критерием проверки нулевой гипотезы
об отсутствии различий является критерий х вида (6.50).
16. По шести независимым выборкам одинакового объема п = 37,
извлеченным из нормальных генеральных совокупностей, найдены
исправленные выборочные дисперсии: 2,34; 2,66; 2,95; 3,65; 3,86; 4,54. Используя
299

Таблица 6.11
Возрастная
подгруппа
20-30
30-40
40-50
50-60
>60
Всего...
Государство А
количество

заболевших л,
732
1005
990
665
324
количество
умерших п%
65
ПО
123
87
49

смертность, %
—
Государство В
количество

заболевших п!
790
1211
1370
805
305
количество
умерших
т\
92
262
193
121
45

смертность, %
—
2
критерий Кочрена, требуется проверить нулевую гипотезу об однородности
дисперсий. Уровень значимости а = 0,05.
Ответ: Кнл6п = 0,227; ккр = 0,2612. Дисперсии при выбранном уровне
значимости можно считать однородными.
17. По четырем независимым выборкам, объемы которых л, = 17,
п2 = 20, щ = 15, п4= 16, извлеченным из нормальных генеральных
совокупностей, найдены исправленные выборочные дисперсии: 2,5; 3,6; 4,1;
5,8. Используя критерий Бартлетта на уровне значимости 0,05 проверить
гипотезу об однородности дисперсий. Оценить генеральную дисперсию.
Ответ: к= 64; V= 2,8; Вна6л < 2,8; xlP = 7,8. Гипотеза об однородности
дисперсий принимается. Генеральная дисперсия имеет оценку 3,95.
18. Двум лаборантам поручено определить число эритроцитов в крови,
взятой у одних и тех же лиц (для точности эксперимента лаборантам этот
факт не известен). Каждый из них проводит по 21 исследованию. Исходя
из полученных результатов, вычислено стандартное отклонение: а, = 100 000
у первого лаборанта и а2 = 60 000 у второго лаборанта. Имеются ли
основания предполагать, что второй лаборант работает точнее первого? Уровень
значимости примите равным 0,05.
Указание. Используйте для сравнения /'-критерий Фишера, число
степеней свободы в обоих случаях равно 20.
Ответ: Нулевую гипотезу об одинаковой точности работы лаборантов
следует отвергнуть, а принять гипотезу альтернативную.
19. При исследовании новых режимов питания детей в возрасте от 6 до
9 мес требуется установить, ускоряет ли увеличение их массы тела добавка
к ежедневному питанию витамина D. Для этой цели были отобраны 100
6-месячных младенцев и разделены случайным образом на две равные
группы по 50 детей. Первая группа в суточной норме питания получала
витамин D (это экспериментальная группа), а вторая — не получала
витамин D (это контрольная группа). Через 3 мес после начала эксперимента
300

средняя масса тела детей экспериментальной группы оказалась х = 9,114
кг, а детей контрольной группы — у = 8,614 кг. Среднее квадратическое
отклонение в первой группе sx = 0,800 _кг, а. во второй — sy = 0,833 кг.
Можно ли считать полученную разность х — у = 0,500 кг результатом
изменения режима питания?
Указание. Используйте критерий Стьюдента. Уровень значимости
стандартный а = 0,05. Принимаем, что обе выборки извлечены из нормальных
генеральных совокупностей.
Ответ: Гнабл = 3,061; tKp = 2,01. Действие витамина D следует признать
значимым.
20. Известно, что метод Вестергрина обеспечивает среднюю РОЭ,
равную 15 мм при показателе рассеивания о = 2 мм. Модификация метода
Вестергрина обеспечивает среднюю х = 11 мм при 10 наблюдениях и
неизменном значении а. Определить, существенно ли полученное различие
средних. Принимаем, что выборка принадлежит нормальной генеральной
совокупности.
Указание. Использовать критерий Z сравнения выборочной средней с
известной величиной при известной дисперсии (см. § 6.7). Уровень
значимости принять стандартный а = 0,05.
Ответ: ZHa6jI = 6,32, ^р = 1,96. Модификация метода Вестергрина
обеспечивает более низкий уровень РОЭ.
21. При исследовании продолжительности отрицательного времени при
пробе на остроту зрения в двух группах учеников — мальчиков и девочек в возрасте
12 лет — были получены следующие результаты: у мальчиков х = 70 с, sx = 5
с при л, = 20 наблюдениях; у девочек у = 75 с, sy = 6 с при щ = 30
наблюдениях. Требуется определить, существенна ли разность средних в двух выборках.
Уровень значимости принять равным а = 0,05.
Ответ: Гнабл = 2,177, tKp = 2,01. Различие средних продолжительности
отрицательного времени в группах мальчиков и девочек существенно.
22. Во время ежегодного обследования для улучшения организации
здравоохранения и социального обеспечения исследуется показатель
распространенности заболеваний на 1000 человек населения. В результате
опроса на начало и конец периода обследования получены следующие
значения показателя за 10 лет.
Начало периода
обследования, х,
Конец периода
обследования, у,
46,1
50,5
43,8
40,3
37,9
42,2
41,6
40,1
40,7
36,9
46,3
43,4
45,9
52,5
46,9
54,7
50,3
42,1
53,7
52,2
Используя парный критерий Стьюдента, проверить эффективность
принятых мер за время обследования.
Указание. Предполагая разности d, = х, — у; в качестве выборочных
значений из нормальной совокупности, проверить нулевую гипотезу
H0:M(X) = M(Y)
при конкурирующей гипотезе
Нх: М(Х) < M(Y).
301

Таблица 6.12
С прививкой
Без прививки
Итого...
Количество заболевших
72
303
375
Количество незаболевших
7988
9322
17 310
Всего
8060
9625
17 685
Таблица 6.13
Г
с
Итого...
о
13
6
19
но
4
14
18
Всего
17
20
37
В качестве критерия проверки нулевой гипотезы использовать
статистику
имеющую распределение Стьюдента с п — 1 степенями свободы (см. § 6.7).
23. Исследуется эффективность прививки против сыпного тифа. Под
наблюдением находится 17 685 человек. Наблюдаемые результаты
занесены в таблицу 6.12.
Используя критерий х , сделайте выводы об эффективности прививок.
Указание. Указанная таблица размерности 2x2 включает два признака
с альтернативными исходами. Используйте формулу (6.47) или (6.470.
24. Во время эпидемии под наблюдением оказалось 47 больных. Из них
к 30 был применен новый лекарственный препарат, а 17 лечились
прежними средствами. Итог: из 30 лечившихся с помощью нового препарата
умерли 4, выздоровели 26; из 17 лечившихся прежними средствами умерли
9, выздоровели 8 человек. Используя критерий х2, сделайте выводы об
эффективности нового препарата.
Указание. Воспользуйтесь формулой (6.47) или (6.47). Найдите
значение х2 также с учетом поправки Йейтса (см. (6.48)).
25. Согласуются ли следующие данные относительно числа
общительных (О) и необщительных (НО) солдат, призванных из городов (Г) и
сельской местности (С), с предположением о том, что горожане более
общительны, нежели сельские жители (табл. 6.13)?
Ответ: Хнабл = 7,9435 (без поправки Йейтса). Солдаты-горожане более
общительны.
302

Таблица 6.14
Я,
в2
в,
Итого...
А
45
32
4
81
Аг
26
50
10
86
Аг
12
21
17
50
Всего
83
103
31
217
26. По ряду школ собраны данные относительно дефектов речи (Л,, А2,
А3) и физических недостатков школьников (Вь В2, В3) (табл. 6.14).
Проверить гипотезу о независимости признаков, используя статистику х2-
Ответ: Ожидаемые значения:
30,982 32,894 19,124
38,447 40,820 23,733
11,571 12,286 7,143
Хнабл = 34,8828 при 4 степенях свободы. Гипотеза не подтверждается
при а = 0,01.
27. Из нормальной генеральной совокупности X с известным
стандартным отклонением а = 4 извлечена выборка объема п = 36. Выборочное
среднее х = 23,5. Полагая уровень значимости а = 0,05: а) проверить
нулевую гипотезу Я0: М(Х) = 20 при конкурирующей гипотезе Я,: М{Х) > 20;
б) определить мощность критерия при фактическом М(Х) = 22; какова
величина р, ошибки второго рода? в) найти объем выборки, при котором
мощность критерия равнялась бы 0,8.
Указание, б) При нахождении мощности критерия используйте
функцию Лапласа как функцию нормального распределения и соответствующие
рисунки плотности нормального распределения с М(Х) = 20 и М(Х) = 22
типа рис. 49; в) при неизвестном п и М(Х) = 20 выразите критическую
точку хкр, где zKp = Х|ф Jn, положив а = 0,05. Исходя из этой
критической точки хкр, при М(Х) = 22 представьте мощность критерия 0,8 как 1 -
Of^L——^J. и вновь, выразив хкр через Jn, составьте уравнение и
решите его относительно Jn.
Ответ: a) ZHa6jI = 5,25, zKp = 1,645;
б) мощность критерия равна 0,9115, р= 0,0885;
в) п = 25.
28. Известно, что некоторый антибиотик помогает при инфицировании
определенным вирусом в 70% случаев. Усовершенствовав данный
препарат, его решили опробовать на 200 пациентах, инфицированных данным
вирусом. Найти критическое значение относительной частоты ш при
нулевой гипотезе Я0: р = 0,7, конкурирующей гипотезе Я,: р > 0,7 и уровне
значимости а = 0,05. Полагая фактической вероятностью р = 0,8, найти
мощность используемого критерия.
Указание. Воспользуйтесь материалом § 6.9 и функцией Лапласа.
Ответ: шкрит = 0,753, мощность критерия равна 0,952.

Глава VII. ДИСПЕРСИОННЫЙ АНАЛИЗ.
МНОЖЕСТВЕННЫЕ СРАВНЕНИЯ
7.1. Основные понятия дисперсионного анализа
Дисперсионным анализом называют группу статистических методов,
разработанных Р. Фишером для ряда экспериментальных задач биологии и
сельского хозяйства. Однако математическая постановка задачи указывает на
универсальность этих методов, которые в настоящее время с успехом
применяются и в медицинских исследованиях, и в экономике, и в других самых
разных областях, где исследуются экспериментальные наборы данных.
Вероятностная постановка задачи такова. Пусть имеются генеральные
совокупности Xlt Хъ ..., Хк, такие что
— все к генеральных совокупностей распределены нормально;
— дисперсии всех генеральных совокупностей одинаковы.
Условие нормальности устанавливается либо из каких-то физических
соображений, либо согласно центральной предельной теореме, либо
проверяется с помощью критериев согласия. Равенство всех генеральных
дисперсий также желательно проверить, например, используя критерии Барт-
летта или Кочрена (см. § 6.13, 6.14). При этих условиях и заданном уровне
значимости а требуется проверить нулевую гипотезу равенства средних
Я0: лед = М(Х2) = ... = М(Хк). (7.1)
Таким образом, извлекая из каждой генеральной совокупности по
выборке, требуется установить значимость или незначимость различия
полученных к выборочных средних. Очевидный метод попарного сравнения
средних (каждого с каждым) может оказаться неэффективным при
достаточно больших к или по крайней мере громоздким. Методика,
предложенная Р. Фишером, основана на сравнении дисперсий, о виде которых речь
пойдет ниже (отсюда и название "дисперсионный анализ").
Можно предполагать, что все к генеральных совокупностей в чистом
виде идентичны, т. е. имеют не только равные дисперсии, но и
одинаковые математические ожидания. Однако каждая из генеральных
совокупностей подвержена влиянию одного или нескольких качественных факторов,
входящих в эксперимент, которые могут изменять средние значения
mi = M(X) наших генеральных совокупностей. Например, некоторое
количество больных гипертонией разбиты случайным образом на к групп,
каждой из которых предписан прием определенного лекарства. В итоге
контролируется среднее значение показателя изменения артериального
давления. В данном примере значения показателя в i-й группе, состоящей из л,
больных — это i-я выборка объема л, (количество выборок равно
количеству групп к); лекарство — это фактор, влияющий на величину
контролируемого показателя; сам показатель изменения артериального давления — это
отклик на воздействие фактора. Предполагается, что по группам прини-
304

Таблица 7.1
Номер испытания
1
2
nj
Групповая средняя
Уровень фактора А
А
*п
х12
*-,!
*ф>
Лг
хп
х22
Х»>2
*ф2
\
Х\к
*2*
Хпкк
Хгрк
маемые лекарство различаются либо видом, либо дозой, либо еще каким-
то образом, и тогда воздействующий фактор подразделяется на некоторые
составляющие, называемые уровнями фактора.
Если фактор оказывает воздействие на величину отклика, то нулевая
гипотеза о равенстве средних (7.1) неверна, и задача заключается в
установлении того уровня фактора, при котором воздействие на отклик
наиболее эффективно (т. е. происходит наибольшее изменение среднего
значения показателя). Эту процедуру можно провести методом попарных
сравнений средних после выводов дисперсионного анализа.
Исследуемый фактор может быть не единственным, в соответствии с
этим различают однофакторный и многофакторный дисперсионный
анализ (в частности, двухфакторный, трехфакторный и т. д.). В нашем
примере с изменением артериального давления можно исследовать фактор
времени года (уровни: зима, весна, лето, осень), фактор места эксперимента
(уровни: лечение в стационаре или дома), фактор режима (уровни:
постельный, обычный или регулярные пешие прогулки на свежем воздухе) и т. п.
Уровни фактора часто называют способами обработки. Эта
терминология связана с классической задачей применения дисперсионного анализа в
агрономии, где откликом является урожайность некоторой
сельскохозяйственной культуры, а факторами — агротехнические приемы: внесение
удобрений, полив, освещенность, температура, глубина вспашки и др. Каждый
из факторов подразделяется на ряд уровней, являющихся способами
обработки почвы.
Выборочные данные обычно оформляют в виде таблицы. Приведем
такую таблицу для одного фактора Л, имеющего к уровней: Alt A2> ..., Ак.
В приведенной табл. 7.1 выборки (группы наблюдений) соответствуют
уровням фактора и расположены в виде столбцов. Каждый элемент
выборки снабжен двумя индексами: второй индекс — номер выборки (группы), а
первый индекс — номер элемента в выборке (номер испытания). Число п} —
объем у-й выборки, тогда общее число наблюдений
п = л, + п2 + ••• + пк.
20 — 3529
305

Групповые средние — средние арифметические элементов по каждому
уровню фактора (по каждой группе): при уровне фактора А} получаем
*фу = hxu + x2j+...+x^). (7.2)
Вообще говоря, числа п} различны, однако дальнейшие вычисления
существенно упрощаются, если все выборки имеют одинаковый объем.
При справедливости нулевой гипотезы (7.1) все к генеральных
совокупностей оказываются имеющими одинаковые параметры, математическое
ожидание и дисперсию. Каждая нормально распределенная случайная
величина, как известно, полностью определяется этими двумя параметрами;
следовательно, все наши к генеральных совокупностей являются
идентичными и фактически можно считать все выборки извлеченными из одной и
той же генеральной совокупности. А это позволяет выборки объединить в
одну объема п и для нее вычислить оценку дисперсии а2. Мы знаем (см.
§ 5.2), что несмещенной оценкой дисперсии будет статистика
ТЛ2
п— 1^-<
В нашем случае в роли Х- выступают все п случайных величин, разбитых
на к выборок: Хи, Х2], ..., X и Хп, ..., Х„кк. Среднее Л"также вычисляется по
всем п значениям.
Основная идея дисперсионного анализа состоит в разбиении этой
выборочной дисперсии на две компоненты, одна из которых соответствует
влиянию фактора на изменчивость средних значений (факторная
дисперсия), а вторая обусловлена случайными причинами и не влияет на
изменчивость средних (остаточная дисперсия).
Дальнейшее сравнение с помощью критерия Фишера этих компонент
(факторной и остаточной дисперсий) позволяет численно оценить влияние
исследуемого фактора.
Отметим, что в случае нескольких факторов идея остается той же
(сравнение факторных и остаточной дисперсий), но усложняется само
представление данных в виде таблицы и величина & представляется в виде
соответствующего числа компонент. Например, в случае двух факторов Аи В
необходимо учитывать влияние фактора А, влияние фактора В и
совместное влияние обоих факторов АВ. В трехфакторном дисперсионном анализе
с факторами А, В, С учитывается влияние каждого фактора по отдельности
(А, В, С), совместное влияние каждой пары факторов (АВ, АС, ВС) и
совместное влияние всех трех факторов (ABC). Как видим, с ростом числа
исследуемых факторов сложность и громоздкость вычислений резко
возрастают, поэтому все вычисления, особенно в случае многофакторного
анализа, проводятся с использованием соответствующих компьютерных
программ.
306

7.2. Суммы квадратов отклонений. Общая, факторная и остаточная
дисперсии
Предполагаем, что на нормально распределенный признак X (общая
генеральная совокупность) действует некоторый фактор А, имеющий к
уровней. Над генеральной совокупностью X проведено одинаковое число
наблюдений (испытаний) на каждом уровне, а именно: г испытаний. Таким
образом, получено к выборок, каждая объема г, следовательно, всего
проведено п испытаний, где п = кг. Значения X, наблюдаемые в результате
испытаний, обозначим xip где индекс /' означает номер испытания (/' = 1,2, ...,
г), индексу — номер уровня фактора, т. е. номер выборки (/ = 1,2, ..., к).
Все Ху можно занести в табл. 7.2 вида 7.1, в которой все выборки имеют
равный объем:
пх = п2 = ... = пк = г.
Для осознания теоретической сущности метода дисперсионного анализа
предварительно вместо дисперсий рассмотрим суммы квадратов, которые
будем обозначать SS (Sum of Squares). При этом будем различать суммы
квадратов общие, факторные и остаточные.
Общей суммой квадратов отклонений называют сумму
ss06iu = Y,Y,{Xij~~x)2> (7-3)
где х общая средняя для всей выборки объема п.
Факторной суммой квадратов отклонений называют сумму
^фагг, = ^(ДСрУ _ *)2 • (7.4)
У-1
Сумма SSq^ характеризует отклонения групповых средних от общей
средней, т. е. степень рассеяния групповых средних (межгрупповое
рассеяние).
Таблица 7.2
Номер испытания
1
2
г
Групповая средняя
Уровень фактора А
Л,
хи
*2.
ХЛ
*гр.
А2
хп
*22
Хг2
*П>2
Л
X\k
*2к
Хгк
Хгрк
20*
307

Таблица 7.3
Номер испытания
1
2
Уровень фактора А
Л,
*21
*П>1
^2
Х12
Xj2
*гр2
Остаточной суммой квадратов отклонений называют сумму
г г г
SS0„ = ^ (Хп - Хгр,)2 + ^ (*,2 - *гр2)2 + ... + ^ (*,* - ДСгр*)2 •
(7.5)
/ = 1 i = 1 ; = 1
Сумма SS0CT характеризует степень рассеяния значений внутри групп
(внутригрупповое рассеяние).
Рассмотрим внимательнее смысл введенных SS.
Если фактор А на каком-то уровне оказывает влияние на признак X, то
в выборке, соответствующей этому уровню, он изменяет групповую
среднюю, и эта групповая средняя будет отличаться от общей средней х тем
сильнее, чем больше воздействие фактора. А чем больше различие
групповой средней и общей средней, тем [см. формулу (7.4)] больше и величина
^Факт- Оказывается, имеет место прямая зависимость степени воздействия
фактора и величины »S^aKT-
Совсем иначе дело обстоит в выражении (7.5). Как бы ни изменял
фактор значения групповых средних на разных уровнях, это не меняет степени
рассеяния_ значений ху в конкретной у'-й группе относительно группового
среднего х^р ибо отклонения ху от x^j вызваны не воздействием
рассматриваемого фактора, а некоторыми другими случайными причинами,
возможно, другими факторами с иной разбивкой по уровням. Численная
величина суммы квадратов таких отклонений, безучастных к воздействию
фактора, и представляет значение SS^. Можно доказать, что для
введенных сумм квадратов справедливо равенство
•ЯУобш = ^факТ + SSocr (7-6)
В качестве упражнения рекомендуем доказать равенство (7.6) в
простейшем случае, когда фактор имеет всего два уровня и число наблюдений на
каждом уровне также равно 2. Тогда таблица данных имеет простой вид.
В этом случае
Z = *11 + *21 + *12 + *22 " _ *11 + *21 " _ *12 + *22
Л л > ЛП>1 j > ХП>2 Ту .
Дальнейшие выкладки по доказательству (7.6) предлагается проделать
самостоятельно.
Для исследования влияния фактора на групповые средние можно
использовать найденные суммы квадратов отклонений, однако более удоб-
308

ным представляется переход от SS к средним квадратам отклонений.
Средний квадрат принято обозначать MS (Mean Sqare), и он получается в
результате деления соответствующей суммы квадратов SS на присущее ей
число степеней свободы:
SS*
п-\
Л^обш = *"? — общая дисперсия; (7.7)
SS±
к-\
^Уфмп- = I.JT — Факторная дисперсия; (7.8)
SS
^ост= ^ — остаточная дисперсия. (7.9)
Число степеней свободы для SSo6ui равно п — 1, где п — суммарное
количество значений во всех к группах.
Число степеней свободы для SS^^ равно к — 1, где к — количество
групп (количество уровней фактора).
Число степеней свободы для SS0CT равно к{г— 1), где к — количество групп,
г— количество значений в каждой группе [заметим, что к(г— 1) = п — к].
Деление SS на отвечающее ей число степеней свободы не изменяет
смысла этой характеристики, но приводит данные характеристики во
взаимное соответствие. К тому же все приведенные средние квадраты
оказываются несмещенными оценками генеральной дисперсии.
Заметим также, что для вычисления SS формулы можно преобразовать
к более простому виду. Для этого введем обозначения:
Tj = J^Xjj — сумма значений признака на уровне А} (следовательно,
;= 1
Т
y-i y-ii-i
г
Rj = y^xjj — сумма квадратов значений признака на уровне Af
i= l
R - 2>
j= i
Тогда в (7.3), (7.4), выполняя операцию возведения в квадрат и
используя новые введенные обозначения, получаем
^ = 2>-fe)2 = *-?- (7Л0)
у-1 ;=i
SS„ = £ Tf -1W 7} = £ TJ - L. (7.11)
У-1 7-1 У-1
309

Учитывая равенство (7.6), находим
SS^-SS^-SS^ (7.12)
Формулы (7.10 — 7.12) являются расчетными для вычисления сумм
квадратов отклонений. Общую, факторную и остаточную дисперсии
можно найти, используя соотношения (7.7) — (7.9).
Замечание 1. Формулу вычисления остаточной дисперсии можно
представить в виде, более удобном для восприятия [используем (7.9) и (7.5)]:
М*ост к(г-\) к
г
+ _ « / ' (xik ~ хгрк)
<•=1
= i(5? + ^+...+4),
где s] — исправленная выборочная дисперсия /-й выборки (/ = 1, 2, ... , к).
Итак, MS^ в случае равного количества наблюдений на каждом уровне
фактора Л — это среднее арифметическое исправленных выборочных
дисперсий выборок, соответствующих уровням фактора:
MS0CT= ±(s2 + s22+...+s2k). <7-13)
Замечание 2. Формулу вычисления факторной дисперсии также можно
представить в более запоминающемся виде [используем (7.8) и (7.4)]:
где s\ — исправленная выборочная дисперсия выборки, состоящей из к
средних х^, Хгр2, ..., х^к.
Итак,
MS^ = rs\. (7.14)
Замечание 3. Факторную дисперсию МЯфаКТ, характеризующую разброс
средних значений групп относительно общей средней [см. (7.14)] часто
называют межгрупповой дисперсией. А остаточную дисперсию MS^,
являющуюся средним арифметическим для исправленных выборочных
дисперсий групп, [см. (7.13)], называют внутригрупповой дисперсией.
Замечание 4. Полагая MS не значениями средних квадратов,
вычисляемых по конкретным выборкам, а статистиками (т. е. случайными
величинами) вместо (7.13), (7.14) можно записать соответственно
ms„= i(tf +.S3+ ... + .£),
Подведем выводы данного параграфа. Для проведения дисперсионного
анализа нам потребуются общая, факторная и остаточная дисперсии (MS),
которые можно найти по формулам (7.7)—(7.9). В этих формулах
задействованы суммы квадратов (SS) — общая, факторная и остаточная, которые
310

можно вычислить по формулам (7.3)—(7.5) или по преобразованным
формулам (7.10)—(7.12), и тогда вычисления оказываются менее громоздкими.
Однако более простым способом вычисления MS является использование
формул (7.13), (7.14).
7.3. Однофакторный дисперсионный анализ
Рассмотрим постановку задачи.
Пусть имеется некоторая нормально распределенная генеральная
совокупность X, над которой производятся наблюдения. Результатом этих
наблюдений является выборка объема п. Есть основания предполагать, что
на формирование значений св. X влияет некоторый качественный фактор А.
По предполагаемой степени воздействия разбиваем фактор А на к групп,
называемых уровнями фактора: Лх, А2, ..., Лк. При построении выборки
учитываем соответствие значений уровням фактора, и тогда вся выборка
объема п разбивается на к групп (назовем их также выборками), каждая из
которых оказывается привязанной к данному уровню фактора. Поскольку
все к выборок представляют одну и ту же генеральную совокупность X, то
теоретические средние, находимые по этим выборкам, не должны
отличаться одна от другой и от генеральной средней, а различия выборочных
средних носят случайный характер и незначимы. Но это имеет место лишь
в случае репрезентативности всех к выборок, которая обеспечивается
случайным отбором значений из генеральной совокупности. А что же
происходит на самом деле? Фактически, разбивая все п выборочных значений в
соответствии с уровнями фактора, мы полностью отвергаем условие
репрезентативности, наоборот, наш выбор значений тенденциозен, он изменяет
истинные (теоретические) средние в каждой группе. В то же время,
формируя группы значений, мы, нарушив условие репрезентативности
(повлияли на значения групповых средних), нисколько не затронули
случайную составляющую, под влиянием которой формируются наблюдаемые
значения во всех к выборках. Таким образом, показателем влияния
фактора является неравенство групповых средних в выборках, составленных
тенденциозно по уровням фактора. Чем сильнее влияние фактора на X, тем
существеннее различие средних в группах. И наоборот, если исследуемый
фактор не оказывает воздействия на формирование значений X, то как бы
мы ни разбивали выборку объема п на к выборок, наш выбор именно этих
значений оказывается случайным, и различие выборочных средних
получится незначимым. Разумеется, сказанное верно, если в дело не вмешается
другой фактор, действительно влияющий на X, и осуществленное
разбиение не будет соответствовать уровням значимости этого фактора. Такая
возможность в принципе не исключена, поэтому вопрос
репрезентативности выборок требует особого внимания.
Итак, задача проверки влияния некоторого фактора А на значения
генеральной совокупности X сводится к вопросу проверки значимости
различия выборочных средних, найденных по выборкам, которые соответствуют
уровням фактора А.
Пусть верна нулевая гипотеза о незначимости различий выборочных
средних, тогда рассматриваемый фактор не влияет на значения выбороч-
311

Таблица 7.4
Источник
вариации
Общий
Фактор А
Случайные
отклонения
Сумма
квадратов SS
^обш
^Лракт
^ост
ост
Число
степеней свободы df
кг- 1
к- 1
к{г-\)
Средний
квадрат MS
Щракт
MS0CT
F
1 наблюдаемое
р — М. Офа1СТ
F
л критическое
F
л кр
ных средних х^,, хф2, ..., х^, и факторная и остаточная дисперсии
являются несмещенными оценками одной и той же генеральной дисперсии и
оказываются приближенно равными. Если же нулевая гипотеза неверна,
различие выборочных средних значимо, тогда М^5факг заметно превосходит
MS0CT. Остается установить ту грань, начиная с которой различие МУфает и
МУ0СТ следует признать существенным. Рассмотрим статистику
(7.15)
которая имеет распределение Фишера, как частное двух оценок дисперсий
(см. утв.7, § 5.3), с к — 1 и к(г— 1) степенями свободы. Напомним, что (см.
замечание 4, § 7.2) статистики в соотношении (7.15) имеют вид
МУфмгг = л$,
MS0CT=^(S\ + Sl2 + ... + S1k).
По условленному уровню значимости а (например, а = 0,05 или а = 0,01)
критическую точку распределения Фишера можно найти в
соответствующей таблице (см. табл. 7 Приложения 2). Таким образом, поведение
статистики F, являющейся критерием, напрямую связано с принятием или
отвержением нулевой гипотезы о равенстве средних, рассчитанных по
выборкам. Если FHa6n < F^, то при заданном уровне значимости нулевая
гипотеза принимается; если же FHi6n > FKp, то нулевая гипотеза отвергается
и влияние фактора признается существенным. На каком уровне влияние
фактора наибольшее, можно установить, используя попарные сравнения
средних.
В этом и состоит суть дисперсионного анализа: с помощью /'-критерия
проверить нулевую гипотезу о незначимости различий выборочных
средних и в соответствии с полученным ответом сделать выводы о влиянии
рассматриваемого фактора.
Рассчетные и итоговые данные удобно оформить в виде таблицы
дисперсионного анализа (табл. 7.4).
Также отметим, что критерий F называют дисперсионным отношением,
что вполне соответствует его структуре отношения дисперсий.
Пример. Влияние курения на заболеваемость дыхательных путей.
312

Среди взрослого населения определенной возрастной категории
фиксировалось число заболеваний дыхательных путей за два года. Цель
исследования — статистическое доказательство влияния курения на
заболеваемость органов дыхания. Случайным образом были отобраны 3 группы по 4
человека каждая, из них: I группа — некурящие; II группа — стаж
курильщика до 5 лет; III группа — стаж курильщика более 5 лет.
Таким образом, исследуемый фактор А — курение, уровни фактора, Alt
А2, А3 — стаж курильщика1. Отклик на фактор курения — число
заболеваний дыхательных путей. Были получены 12 значений количества
заболеваний — это значения х^, где у — номер уровня фактора (/' = 1, 2, 3), / —
номер элемента в соответствующей выборке (группе), / = 1, 2, 3, 4:
х\1 х\2 х13
Х2\ *22 Х23
*Э1 *Э2 *ЭЭ
Х4\ Х42 *4Э_
=
1 3 3
0 24
1 2 5
2 1 3_
Предполагаем, что Ц,} — выборка из нормальной генеральной
совокупности.
Замечание. Выписанная таблица значений называется матрицей.
Каждый элемент матрицы имеет свое определенное место, определяемое двумя
индексами /, у (сам элемент ху), где / — номер строки, у — номер столбца.
(Вспомните запись корреляционной матрицы, § 3.5, также см.
Приложение 1.) Представление данных в матричном виде типично для
компьютерных программ.
До проведения дисперсионного анализа убеждаемся по критерию Коч-
рена (см. § 6.13), что выборочные дисперсии в группах отличаются
незначимо.
В учебных целях проведем дисперсионный анализ наших данных двумя
способами, которые различаются видом применяемых формул, о чем шла
речь в конце предыдущего параграфа.
I способ. Для вычисления ^используем формулы (7.10)—(7.12).
Предварительно занесем данные (7.16) в таблицу. Далее непосредственно
вычислим и дополнительно занесем в таблицу значения, фигурирующие в
формулах (7.10)—(7.12): Тр Т/, Т, Т\ Rp R (табл. 7.5).
Таким образом, все данные для вычисления сумм квадратов SS у нас
найдены. И тогда, согласно (7.10)—(7.12),
if
9<Г = 1V772-— = I • W5 - — = IS V
1 Разумеется, можно было взять и другую, большую численность групп и другое разбиение
фактора курения на уровни (стаж 10 лет, 20 лет и т. д.), что, несомненно, сделало бы наше
исследование более ценным. Однако пример рассматривается исключительно в учебных
целях, и приоритет отдается наглядности использования метода, поэтому и малая численность
групп, и малое число уровней фактора.
313

Таблица 7.5
Номер испытания /
1
2
3
4
Уровень фактора
Л
1
0
1
2
Г, =4
Т* = 16
Л, = 6
*гр. = 1
*г
3
2
2
1
Г2 = 8
Т22 = 64
Л2 = 18
*гр2 = 2
^3
3
4
5
3
Т3= 15
7^ = 225
Д3 = 59
*п>з = 3,75
Т= 27
Г2 = 729
Г,2 + Г22 + Г32 = 305
R= 83
Таблица 7.6
Источник
вариации
Общий
Фактор А

Случайные
отклонения
Сумма
квадратов SS
22,25
15,5
6,75
Число
степеней
свободы df
11
2
9
Средний
квадрат MS
7,75
0,75
F
* набл
7,75 я 10 33
0,75 '
Ъ
FKP(0,05; 2; 9) = 4,26
FKp(0,01; 2; 9) = 8,02
SSQCl = SSo6ui - SS^ = 22,25 - 15,5 = 6,75.
Найдем число степеней свободы для каждой суммы квадратов SS и
вычислим средние суммы квадратов MS (т. е. остаточную и факторную
дисперсии) по формулам (7.7)—(7.9).
Полученные значения удобно занести в таблицу дисперсионного
анализа (см. табл. 7.4), в которой также кстати привести наблюдаемое и
критическое значения критерия F.
Число степеней свободы для SSo6lu \ п — 1 = 12— 1 = 11,
для SS^ :k-l=2,
для SS0CT : k(r - 1) = 3(4 - 1) = 9.
Составим таблицу.
Как видим из табл. 7.6, значение критерия FHa6n оказалось большим, чем
FKp, как при уровне значимости а = 0,05, так и при а = 0,01, т. е.
наблюдаемое значение критерия попало в критическую область, и, следователь-
314

Таблица
7.7
Номер
испытания i
1
2
3
4
*п>у
*гр; " *
К.,"*)2
'/
Уровень фактора
Л
1
0
1
2
*гр. = 1
-1,25
1,5625
j,2 = 0,666
*г
3
2
2
1
*гр2 = 2
-0,25
0,0625
j22 = 0,666
4
3
4
5
3
*п>. = 3>75
1,5
2,25
s32 = 0,917
но, нулевую гипотезу о равенстве групповых средних нужно отвергнуть.
Фактор курения значимо влияет на заболеваемость дыхательных путей.
II способ. Для вычисления MS используем формулы (7.13) и (7.14), не
вычисляя предварительно суммы квадратов SS. В применяемых формулах
фигурируют величины x^j, х, (x^j — х)2, s2. Вычислим и занесем эти
значения в табл. 7.7.
В табл. 7.7 имеются все необходимые данные для вычисления
/"-критерия. Вначале найдем факторную и остаточную дисперсии. Согласно
формулам (7.13) и (7.14), при к = 3, г = 4 получаем
Щ»акТ = rs-2 = r- FLT^(iipy-i)2 = 4^ (1,5625 + 0,0625 + 2,25) = 7,75;
У= 1
MS0CT = 1 (s2 + s2 + s2) = I (0,666 + 0,666 + 0,917) = 0,75.
Как видим, значения факторной и остаточной дисперсий получились те
же самые, что и при вычислении первым способом, что вполне
естественно. Далее, используя F-критерий, получаем FHaSn = 10,33, находим по
таблице критических точек распределения Фишера FKp при выбранном уровне
значимости и делаем выводы о существенном влиянии фактора курения на
заболеваемость органов дыхания. Итог исследования — табл. 7.6 и выводы.
7.4. Однофакторный дисперсионный анализ в случае разного числа
испытаний на различных уровнях
В предыдущих параграфах мы рассматривали случай проведения
дисперсионного анализа при одинаковом числе наблюдений в группах. В
разобранном примере о влиянии курения на заболеваемость мы сознательно
выбирали равное количество наблюдений в группах. В этом случае наше
исследование носит экспериментальный характер, исследователь может
315

влиять на эксперимент. К числу достоинств экспериментального
исследования относится возможность выбрать одну из групп, являющуюся
контрольной (группа некурящих, группа, принимающая вместо лекарства
плацебо, и т. д.). Такое исследование называется рандомизированным
контролируемым испытанием. Однако обработку данных можно проводить и при
обсервационном исследовании, когда исследователь не может вмешиваться
в ход процесса, и при ретроспективном исследовании, когда данные уже
получены ранее для каких-то целей. Ретроспективное исследование —
исследование обсервационное. При таком исследовании может быть
поставлена под сомнение случайность разбиения значений по уровням фактора,
ибо в этом случае, как правило, данные были собраны для других целей и
здесь возможно проявление неучтенного влияния на репрезентативность
выборок.
При изучении некоторого признака, в частности, при обсервационном
и ретроспективном исследовании, может оказаться, что количество
наблюдений в группах различно. Сводить к случаю равного числа наблюдений
путем отбрасывания части данных — неоправданная потеря информации.
Поэтому важен вопрос применения метода дисперсионного анализа и в
случае неодинакового числа наблюдений в группах, соответствующих
разным уровням фактора.
Оказывается, что дисперсионный анализ успешно справляется со своей
задачей и в этом случае. Точно так же необходимо вычислить суммы
квадратов, затем остаточную и факторную дисперсии и применить критерий
Фишера. Формулы для вычисления SSw MS легко обобщаются и на случай
неравного числа наблюдений в группах.
Итак, пусть фактор Л, как и ранее, имеет к уровней. Количество
наблюдений ву'-й группе равно пр где у =1,2, ..., к. Тогда общее число
наблюдений п равно сумме
п = л,+ п2+...+ пк.
Указанным данным соответствует табл. 7.1.
Обозначим суммы элементов ву'-й группе посредством Т/.
"|
У, = /*/1 = х\\ "•" -*21 "•" ••• "•" -К/,,1 ,
/' = 1
Т2 = ]Гхя = х12 + х22 + ... + хП{2, (7.17)
;= 1
*к = 2^Xik = Х1к + *2* + "• + Хпкк-
;= 1
Введем сумму
Т= Тх+ Т2 + ... + Тк. (7.18)
Суммы квадратов элементов ву'-ой группе обозначим R.:
Л, = 2^*м = *Ц + *21 + ••• + *л,1 ,
/= 1
316

Таблица 7.8
Номер испытания /'
1
2
3
4
5
Уровень фактора А
4
59
53
А
60
54
57
59
4
63
61
68
62
64
Л
67
68
74
72
69
4
73
79
71
75
я2 = jya =
/= 1
*2п
+ Х?3 + ... + X,
п{1 >
(7.19)
-Я* — /*«* — *1* ~*~ *2* +
/• = 1
Введем сумму
R = Rx + R2 +
+ Л
+ X
лД
Запишем формулы, аналогичные формулам (7.10)—(7.12).
•Юобш = (Л, + *2 +
+Л*) - 1 (Г, + Г2 + ... + Тк)2 = R - L.
SS,
факт
= fIl + Il + _ + I±]-Ilf
NA2, П2 Пк' П
^ост — ^обш
1 «2
"ОД
факт"
(7.20)
(7.21)
(7.22)
Далее факторная и остаточная дисперсии находятся по формулам (7.8), (7.9),
(7.24)
\7\7
ост л-Г
и можно применять /"-критерий и делать выводы.
Пример. Известно, что масса тела человека зависит от его роста. На
конкретных числовых данных проследим влияние роста человека на его массу.
Рассмотрим группу студентов из 20 человек, в качестве отклика полагаем
массу в кг; рост индивидуума — фактор, влияющий на переменную отклика,
разобьем его на пять уровней: Ах - (155—160 см); А2 - (160—165 см); А3 -
(165-170 см); Д, - (170-175 см); Аь - (175-180 см). Тогда все 20 значений
массы тела размещаются в таблице следующим образом (табл. 7.8).
Как видим, группы наблюдений, составленные по уровням фактора А,
имеют различную численность.
317

Таблица 7.9
Номер
испытания i
1
2
3
4
5
Уровень фактора А
4
-6
-12
Яр. = "9
Г, = -18
Т2 = 324
Rx = 180
4
-5
-11
-8
-6
Лр2 = _7'5
Г2 = -30
Г22 = 900
R2 = 246
4
-2
-4
3
-з
-1
Г3 = -7
Г32 = 49
Д3 = 39
4
2
3
9
7
4
Лр4=5
Г4 = 25
Г42 = 625
R, = 159
4
8
14
6
10
Яр5 = 9,5
Т5 = 38
Г52 = 1444
R5 = 396
Также заметим, что имеющиеся для исследования числа достаточно
большие, чтобы осложнить наши вычисления и сделать их громоздкими.
Упростим наши данные: поскольку в вычислениях речь идет о дисперсиях,
а для дисперсии любой случайной величины ^справедливо равенство
D(X+a) = D(X), где а - const,
то, вычитая из каждого значения случайной величины одну и ту же
постоянную, мы дисперсию не изменим (т. е. произойдет лишь сдвиг всех
значений на число а, при неизменной характеристике рассеяния). В качестве
а удобно выбрать число в середине интервала наблюдаемых значений; для
упрощения наших данных полагаем а = -65. Обозначим величину X = 65
через К и составим новую таблицу данных для ys, где уц = х^ - 65.
Предполагаем, что данные извлечены из нормальной генеральной
совокупности, что, кстати, можно проверить, используя критерий согласия (см.
§ 4.7). По критерию Бартлетта также устанавливаем, что выборочные
дисперсии s2, s22, s2, j42, ss2 различаются незначимо.
По новым данным вычислим величины, необходимые для нахождения
SS и MS: Тр Т, Т2, Rp R. Эти значения также занесем в табл. 7.9.
Далее находим суммы квадратов SS:
•ЯУобш = R - ^ = 1020 - Ц = 1016,8;
ф ^л, п2 п5у п
_ (324 , 900 , 49 , 625 , 1444^ 64 _ С70 ,.
"l-2- + T + T + -T + ^rJ"20"879'6'
SSm = SS^ - SS^ = 1016,8 - 879,6 = 137,2.
318

Таблица 7.10
Источник
вариации
Общий
Фактор А
Случайные
отклонения
Сумма
квадратов SS
1016,8
879,6
137,2
Число
степеней свободы df
19
4
15
Средний
квадрат MS
219,9
9,147
р

наблюдаемое
24,04
F
л критическое
/у0,05; 4; 15) = 3,06
FKp(0,01; 4; 15) = 4,89
Зная SS, по формулам (7.23), (7.24) находим факторную и остаточную
дисперсии:
MS,
факт
= SS^ = 879,6 _
к- 1
5-1
= 219,9;
MS = SS°" = 137,2 = 9 147
ост п-к 20-5 *'
Применяем /"-критерий:
= MS^ = 219,9 = 24 04
набл MS0CT 9,147 ' '
FKp (0,05; 4; 15) = 3,06, FKp (0,01 ;4; 15) = 4,89.
Таким образом, Fmbn попадает в критическую область и при уровне
значимости а = 0,01, причем FHa6n значительно превосходит FKp, что
свидетельствует о несомненно сильном влиянии роста человека на его массу тела.
Для большей наглядности данные можно занести в таблицу
дисперсионного анализа вида табл. 7.4 (табл. 7.10).
7.5. Схема двухфакторного дисперсионного анализа
Приведем схему исследования в случае воздействия на отклик X
одновременно двух факторов Aw В. Как уже отмечалось выше, кроме
воздействия на отклик собственно факторов Aw В возможно также наличие
влияния, вызванного взаимодействием А и В, которое также необходимо
учесть. Тогда общая сумма квадратов SSo6lli раскладывается на четыре
составляющие:
^Факт л — сумма квадратов, характеризующая рассеяние между
группами фактора А;
^Факт в — сумма квадратов, характеризующая рассеяние между
группами фактора В;
^Факт лв ~ сумма квадратов, характеризующая рассеяние между всеми
группами — фактора А и фактора В;
SS0CT — сумма квадратов, характеризующая рассеяние внутри групп.
319

Рассмотрим схему подробнее. Каждый из двух воздействующих на
отклик факторов разбивается на определенное количество уровней. В общем
виде уровни фактора А условимся обозначать индексом /' и количество
уровней полагаем равным а (а — натуральное число), тогда At - /'-й
уровень фактора А, где / = 1,2, ..., а. Аналогично уровни фактора В условимся
обозначать индексом у и количество уровней полагаем равным b (b -
натуральное число), тогда В} — у'-ый уровень фактора В, где у =1,2, ..., Ь. Пусть
в качестве отклика исследуется генеральная совокупность X, из которой
извлечены п значений. Эти значения мы должны рассортировать по
уровням факторов А и В. Следовательно, каждое наблюдаемое значение,
записанное в общем виде, получает три индекса: xijk, где первый индекс /
свидетельствует о принадлежности значения уровню А;, второй индекс у
говорит о принадлежности значения уровню В/, а третий индекс к позволяет
различать между собой значения, относящиеся к группе (блоку)
совместных значений уровней А-, и В}. Например, элемент х537 — это седьмое из
значений, имеющихся на уровне As и Ву
Все наблюдаемые значения мы можем упорядочить по уровням
факторов А и В, занеся эти значения в прямоугольную таблицу (см. табл. 7.11).
Для упрощения дальнейших выкладок рассмотрим равное число
наблюдений, соответствующих каждой паре уровней А{ и Вр т. е. полагаем, что
третий индекс в наблюдениях х^к может принимать значения от 1 до
некоторого числа г. к = 1,2, ..., г.
Таким образом, начальные данные оформлены в виде таблицы.
Переходим к вычислениям SS и затем MS. Для получения формул, удобных для
использования, введем обозначения:
г
Tij = У\хик — сумма наблюдаемых значений в графе, соответствующей
уровням А-„ В/,
ь
Т,. = V Ту■ — сумма значений Ту по /-й строке;
7=1
а
Т., = V Ту — сумма значений Ту поу'-му столбцу;
;= 1
а Ь
Т = У\У\Ту — общая сумма всех значений во всех ячейках.
; = \j = 1
Заметим, что всего ячеек (клеток в таблице) у нас оказывается ab, а
всего значений п = abr.
Для полученных новых величин на основании табл. 7.11 составим еще
табл. 7.12.
Используя новые обозначения, выпишем формулы для вычисления SS
и MS
2 Г
320

Таблица 7.11
\ Уро-
\ вень
\ факто-
\ ра В
Уро- \
вень \
факто- \
pa A \
Л
А2
А;
Аа
в,
*111
ххх2
ХХХг
-*211
-*212
-*21л
XiXX
ХП2
ХПг
Xall
Ха\2
Ха\г
в2
ХХ2Х
хт
Х\2г
-*221
Xj22
-*22л
ха\
хаг
Хйг
Ха2\
Ха22
Ха2г
Bj
x\j\
х\д
X\jr
Хух
Xljl
Xljr
xifl
*ijl
XUr
Xaj\
Xaj2
X ■
Bb
X\b\
X\b2
X\br
-*2Л1
*2W
Xlbr
XibX
Xm
Xibr
XabX
Xab2
Xabr
(тройная сумма — это сумма квадратов всех возможных наблюдений х^к);
,2
abr
SS^
' = -Lx"1 т2 — ^
фжа Ъг2^ «•• abr
(7.26)
/ = 1
[сумма в формуле — сумма квадратов величин, находящихся в последнем
(вертикальном) столбце табл. 7.12];
SS;
_ 1
факт В
ar*^ %i abr
(7.27)
;-'
[сумма в формуле — сумма квадратов величин, находящихся в нижней
(горизонтальной) строке табл. 7.12];
21—3529
321

Таблица 7.12
^^^ Уровень
>. фактора В
Уровень ^ч.
фактора A >v
4
А2
А;
Аа
Сумма по
уровням фактора В Т.}
Д,
Тп
Т2Х
Тп
тах
т.,
4
Тп
Т22
Та
то2
Т.г
Bj
Tij
Ту
т
т.
т.
вь
тхь
Т1ь
Т
1 \ъ
таь
Т.ь
Сумма
по уровням
фактора A Tt.
тх.
т2.
т,
т..
т
SS*
+
(7.28)
(7.29)
i = 1У = 1 / - 1 У = 1
i= lj= lk= l i = 1У - 1
Все суммы квадратов SS имеют соответствующее число степеней
свободы (df):
Для SS^: df=abr-l,
Для SS„aKTA: df=a-l,
Для SS^ktB: df=b-\,
Для SS^AB: df=(a-l)(b-l),
Для SS^: df=ab(r-l).
Исходя из найденных сумм квадратов SS и указанного числа степеней
свободы, легко найти средние суммы квадратов MS.
SS,
общ
Шо6ш abr-V
JlfC = ^^факт В .
УКУОфакт В t 1 >
а- 1
ss^
b- 1
MS,
SS,
факт АВ
факт АВ
(a-l)(b-\y
MS0CT = LSSocTt
0CT ab(r- 1)
(7.30)
(7.31)
(7.32)
(7.33)
(7.34)
322

Таблица 7.13
Источник
вариации
Общий
Фактор А
Фактор В

Взаимодействие А и В
Случайные
отклонения
Сумма

квадратов SS
(7.25)
^фактЛ
(7.26)
^факт В
(7.27)
ЗЗфяктАВ
(7.28)
(7.29)
Число
степеней
свободы df
abr- l
а- 1
Ь- 1
(a-D(fr-l)
ab{r- l)
Средний
квадрат
MS
Щ>6ш
(7.30)
(7.31)
Щ^акт*
(7-32)
MS^„AB
(7.33)
(7.34)
F
* нобл
Л» *5факт А
MS0CT
Л/£факт Л
Л/£ост
MS* акт Л5
M5-0CT
*,
**,(<*;
^кР(а;
a- l;^(r- 1))
b- l;ab(r- 1))
FKp(a;(a-l)(6-l);^(/-l))
Ввиду большого количества полученных данных желательно их
упорядочить: занести в итоговую таблицу дисперсионного анализа. В той же
таблице обычно указывают и дисперсионное отношение F для каждого из
факторов и их взаимодействия.
Итак, заполняем табл. 7.13.
Пояснение. В табл. 7.13 в столбцах SS и MS в скобках указан номер
формулы для нахождения соответствующего значения. В последнем
столбце значения FKp находятся по табл. 7 Приложение 2 критических точек
распределения Фишера при выбранном уровне значимости а и двух значениях
числа степеней свободы.
Чтобы установить наличие влияния фактора А, фактора В и их
взаимодействия, необходимо сравнить соответствующую пару значений Fm6at FKp.
Если FHu6n > FKp для какого-то фактора (или их взаимодействия), то тем
самым считается установленным факт влияния этого фактора (или
взаимодействия факторов) на отклик. В противном случае, когда Fm6n < FKP,
влияние не доказано.
Замечание. Для вычисления сумм квадратов SS и средних сумм
квадратов MS вместо сумм Tijy 7)., T.j, T можно было использовать
соответствующие средние значения хр *,-., х.р х и получить соответствующие формулы.
Однако наши формулы (7.25)—(7.29), по мнению авторов, более удобны
именно в вычислительном плане, им и отдано предпочтение. Для полноты
изложения приведем формулы, выражающие суммы квадратов SS через
средние:
^обш= УУ Y(*,v*-i)2,
i = \j = 1 k = 1
21*
(7.35)
323

Жфжл= br^Cxi--*)2, (7-36)
/= i
b
Жфжв= аг^ГСх-j-x)2, (7-37)
a b
Жф^АВ = /•££(*,-*/. -~x.j-x)\ (7.38)
i = \j = i
^ocT= 222(^*-^)2- (7-39)
i- \j= Ik- \
Разумеется, все вычисленные по этим формулам значения равны
соответствующим значениям, найденным по (7.25)—(7.29).
Можно привести много примеров влияния двух исследуемых факторов
на некоторый отклик. Например, можно осуществить двухфакторный
анализ, исследующий влияние фактора А — времени, потраченного
студентами на изучение статистики, и фактора В — школьной оценки по
математике на отклик — число баллов, полученных на экзамене по статистике.
Другие примеры: влияние уровня доходов в семье (фактор А) и уровня
образования родителей (фактор В) на число детей в семье; влияние
возраста и профессии работников промышленного предприятия на
заболеваемость органов дыхания; влияние времени суток и температуры воздуха на
число автомобильных аварий; влияние длины волос и цвета глаз на возраст
вступления в брак и т. д. Вы и сами можете придумать достаточное
количество примеров возможного применения методов дисперсионного
анализа, однако наибольшая польза будет, если Вы, собрав данные, доведете их
до аргументированных выводов.
Методика проведения дисперсионного анализа с тремя и более
факторами аналогична приведенной выше с меньшим числом факторов.
Обратим внимание на возможное взаимодействие различных факторов, которое
должно быть учтено. С ростом числа исследуемых факторов резко
возрастает сложность и громоздкость вычислений, поэтому весьма желательно
использование соответствующих компьютерных программ, применение
которых сводит задачу исследователя к начальной подготовке данных и
интерпретации итогов анализа, отраженных в таблице дисперсионного
анализа типа табл. 7.13.
7.6. Множественные сравнения. Критерий Стьюдента с поправкой
Бонферрони
Дисперсионный анализ позволяет проверить гипотезу о равенстве
средних в к нормальных генеральных совокупностях с одинаковой дисперсией,
исходя из данных выборок. Ту же задачу решает и критерий Стьюдента, но
в частном случае к = 2. Хорошо известен факт, что критерий Стьюдента
связан тесными родственными связями с дисперсионным анализом,
проводимым относительно двух групп (двух уровней фактора). В частности,
дисперсионное отношение Фишера
324

для однофакторного анализа и статистика Т вида (6.23) в критерии Стью-
дента связаны простым соотношением F= Г2, которое в случае выборок
одинакового объема проверяется элементарно (рекомендуем доказать это
утверждение в качестве самостоятельного упражнения).
Зададимся вопросом: поскольку дисперсионный анализ и критерий
Стьюдента столь близки, что критерий Стьюдента является просто
вариантом дисперсионного анализа в частном случае к = 2 (и в свою очередь
дисперсионный анализ при к = 2 может рассматриваться как вариант
критерия Стьюдента), то нельзя ли избежать дисперсионного анализа? В случае
к выборок (групп) при к > 2 можно просто применить критерий
Стьюдента к каждой паре выборок и найти попарное равенство или различие
средних, т. е. использовать так называемые множественные сравнения.
Рассмотрим применение множественных сравнений на примере
сравнения эффективности различных препаратов, результатом применения
которых является численное значение определенного показателя (среднее
артериальное давление, уровень глюкозы плазмы, время лечения и т. д.). Для
эксперимента отобраны случайным образом несколько групп больных. И
каждая группа получила не разные препараты, а всего-навсего плацебо.
Результат применения такого "лекарства" нам априори известен: все
групповые средние различаются незначимо просто по определению плацебо;
все выборки оказываются извлеченными из одной и той же генеральной
совокупности, и для каждой выборки оцениваемое генеральное среднее
едино.
А что же преподнесет наше исследование множественных сравнений с
помощью критерия Стьюдента? На практике проведенный подобным
образом эксперимент чисто математически может указать на значимое
различие выборочных средних для какой-то пары наблюдаемых групп, на
основании чего вполне реально получить абсурдный результат о различном
влиянии плацебо в разных группах. Для пущей важности мы вообще
можем брать пилюли - плацебо из одной упаковки и обвинять в полученной
несуразности математику, либо построить "супертеорию" о влиянии,
например, цвета пилюль на исследуемый показатель. И чем больше будет
исследуемых групп, т. е. больше пар выборок, тем чаще будет встречаться
подобная ситуация, противоречащая здравому смыслу. Появление такого
факта называют эффектом множественных сравнений.
Рассмотрим подробнее, в чем же причина возникновения эффекта
множественных сравнений. Вспомним определение уровня значимости а. Если
у нас справедлива нулевая гипотеза о равенстве средних, то малое число а —
вероятность отвергнуть эту верную гипотезу. При этом число а столь мало,
что в единичном испытании нулевая гипотеза практически не отвергается.
Сравнивая выборки попарно, мы проводим не одно, а большее количество
испытаний и фактически увеличиваем вероятность отвержения верной
гипотезы.
Уровень значимости а — вероятность отвергнуть верную нулевую
гипотезу, тогда вероятность противоположного события — принять верную
нулевую гипотезу — равна 1 - а. Если проводится к попарных сравнений, то
вероятность все к раз принять верную нулевую гипотезу оказывается рав-
325

ной (1 — а)*. Следовательно, вероятность противоположного события -
хотя бы раз ошибиться — это а, = 1 - (1 - а)*.
Пусть а — стандартное значение уровня значимости, равное 0,05. Тогда
для трех групп требуется три попарных сравнения (к = С32 = 3), и
вероятность хотя бы одной ошибки равна 1 — (1 — 0,05)3 ~ 0,143. Следовательно,
по сравнению с а = 0,05 вероятность ошибки выросла почти втрое. При
сравнении четырех групп к= С42 = 6, и тогда вероятность ошибки хотя бы
при одном сравнении равна 1 - (1 - 0,05)6 ~ 0,265, а это уже совсем не
малые вероятности, фактически при четырех группах абсурдная ошибка
допускается в среднем более чем в четверти всех экспериментов. Это и
есть объяснение появления эффекта множественных сравнений.
Оценим вероятность появления ошибки хотя бы в одном сравнении.
Если в выражении 1 - (1 - а)* для вероятности ошибки произвести
упрощение, то окажется при разных к:
к = 2, а, = 1 - (1 - а)2 = 2а - а2 < 2а;
к = 3, а, = 1 - (1 - а)3 = За - За2 + а3 = За - а2(3 - а) < За;
а, < ка.
Последнее неравенство а, < ка называют неравенством Бонферрони.
Согласно этому соотношению, при числе парных сравнений к уровень
значимости а следует выбирать таким, чтобы а, также оказывалось достаточно
малым числом. Например, если мы хотим при трех сравнениях а,, т. е.
вероятность ошибиться хотя бы раз, иметь не более чем 0,05, то необходимо в
каждом сравнении проверять нулевую гипотезу при а = -Ц-— » 0, 0165.
Величину уровня значимости
где а, выбирается заранее, называют поправкой Бонферрони. Обычно
поправку Бонферрони используют при малых значениях к, т. е. при
небольшом количестве групп, ибо тогда значение а не является чересчур малым,
что могло бы повлиять в реальной задаче на рост вероятности ошибки
второго рода - возникновение новых неприятностей. Однако во всех случаях,
особенно при больших значениях к, рекомендуется начинать исследование
сравнения средних с дисперсионного анализа. В этом случае, если
гипотеза о равенстве генеральных средних подтверждается, прибегать к
попарным сравнениям критерием Стьюдента с поправкой Бонферрони нет
смысла. Если же нулевая гипотеза будет опровергнута, то искать
значимость различий генеральных средних методом множественного сравнения
(множество попарных сравнений) мы будем с достаточным оптимизмом.
Пример. Для иллюстрации методики множественных сравнений при
помощи критерия Стьюдента с поправкой Бонферрони вернемся к данным
примера о влиянии курения на заболеваемость дыхательных путей (см. § 7.3)
Все испытуемые разбиты на три группы по числу уровней фактора.
Обозначения Alt А2, А3 фактически являются обозначениями групп.
Численность всех групп_одинакова и равна 4. Вычислены групповые средние
*гр1 — 1> *гр2 — 2, -КгрЭ = 3,75.
326

Найдена остаточная дисперсия MS^ = 0,75. Напомним, что термины
"остаточная дисперсия" и "внутригрупповая дисперсия" обозначают одну и
ту же величину, обозначим ее ^нутр (slHyiv = 0,75).
Дисперсионный анализ показал различие генеральных средних групп
Alt А2, Ау Проведем попарные сравнения, используя критерий Стьюдента Т.
Уровень значимости для каждой пары сравнений выбираем, исходя из
поправки Бонферрони а,. Если полагаем а, = 0,05, то, следовательно, для
каждой сравниваемой пары групп уровень значимости
„=£ = 0,05 „0,0165.
Итак, для групп Ах, А2 имеем
Т =
_ Х\ Л2
9 Т2
^•"внутр
П
Данное выражение следует из соотношения (6.23), в котором средние
обозначены Хх и Х2, п = m - численность групп, равная 4, и
_ 1
*5внутр — ^(^, "*" 'Sjcj)
В наших вычислениях воспользуемся значением sBHylp = 0,75,
найденном для всех групп.
Тогда для групп Alt А2:
Т — *гр 1 -Угр2 _ 1— 2 1 1 £ 11
1 набЛ _ | _ , = ~ л /СП/1 ~ А' DJJ *
pZ jlZAH °-6124
Аналогично для групп Alt Ay'
f — -Угр! ~ -Угрз ,, (1 ~ 3, 75) л до]
БТ~ ~ 0,6124 ~ ' *
4
Для групп А2, Ау
Гнабл = ^п^фз и (20"631>2745), -2, 858
'внутр
4
Вычислим fKp, исходя из двусторонней критической области, по таблице
критических точек распределения Стьюдента. Во всех трех сравнениях
'кР = 'кР = («; 3(п - 1)) = Гкр(0,0165; 9) - 2,97.
Поскольку ^нутр оценивалась по трем группам, то число степеней
свободы 3(п - 1) = 3(4 - 1) = 9. (Заметим, что численное значение Гкр
найдено из табл. 6 Приложения 2 с использованием линейной интерполяции.)
Сравнивая наблюдаемые значения критерия Гкр с критической точкой,
получаем для пары Ах, А2 |Гнабл| < Гкр, следовательно, в таких группах средние
различаются незначимо. Аналогично в группах А2, А3 различие средних не-
327

значимо, однако данный результат желательно перепроверить, так как
слишком близко значение Гнабл к критической точке (-2,97).
Средние в группах Ах, А3 различаются значимо. Таким образом, курение
оказывает наибольшее (значимое) влияние на заболеваемость дыхательных
путей при стаже курильщика более 5 лет (третья группа).
7.7. Критерий Ньюмена—Кейлса
С ростом числа сравниваемых групп к поправка Бонферрони для
критерия Стьюдента ос = -— значительно уменьшается при выбранном истин-
ном уровне значимости а, (например, а, = 0,05). Такое существенное
уменьшение уровня значимости а в каждом попарном сравнении приводит
к падению мощности критерия и жесткому отвержению гипотезы (при
достаточно больших к, возможно, неоправданному).
Рассмотрим более мягкий критерий для множественных сравнений,
называемый критерием Ньюмена—Кейлса. Мощность этого критерия выше,
нежели у критерия Стьюдента с поправкой Бонферрони, и он представляет
уровень значимости а, более точно.
Прежде чем приступать к попарным сравнениям групп, методом
дисперсионного анализа проверяется нулевая гипотеза о равенстве
генеральных средних в группах. В случае отвержения нулевой гипотезы мы знаем,
что различие групповых средних значимо, и исследуем это различие по
группам. Схема исследования следующая.
Все групповые средние упорядочиваем по возрастанию. Затем проводим
проверку критерия для пары групп, имеющих наибольшее различие
средних, потом для следующей пары и т. д. Таким образом, если имеется т
групп и они упорядочены по возрастанию в зависимости от значений
групповых средний, то вначале сравнивается пара (1; т), затем (2; т), ...,
(т — 1; т). При этом если на каком-то шаге средние различаются
незначимо, то в паре групп, имеющих меньшую разность средних, средние также
будут различаться незначимо. Например, пусть мы установили различие
средних для пары (1; т), далее для средних пары (2; т) различие
отсутствует, тогда не будет значимого различия средних и для оставшихся пар (3;
т), ..., (т - 1; т) можно не проверять. Далее исследуем пары (1; т - 1),
(2; т - 1), ..., (т — 2; т — 1). При этом если установлено отсутствие
различий между какими-то парами, то для всех пар внутри различий также не
будет, поскольку их средние различаются еще меньше. Например,
отсутствие значимого различия групповых средних в паре (2; т - 1) позволяет не
проверять все оставшиеся пары с номерами, заключенными в промежутке
от 2 до т - 1. Таким образом, "принцип стягивания" может значительно
уменьшить количество сравнений.
Попарные сравнения средних X-t и Xj (у > /) проводятся с помощью
статистики
328

Q = % %
ly» (
J 2 U
n
где л,, л,. — численность групп, Лвнутр — внутри групповая дисперсия,
вычисленная для всех т групп. Статистика Q — критерий Ньюмена—Кейлса.
Найденное наблюдаемое значение критерия Q сопоставляется с
критическим значением qKp, которое находится по таблице (см. табл. 10
Приложения 2). В этой таблице для определения qKp необходимо знать три
параметра: а, — уровень значимости (а, = 0,05 или а, = 0,01); v — число
степеней свободы, определяемое из соотношения ("суммарная численность всех
групп" — "число групп"), v = N - m\h — интервал сравнения, который для
/-й иу-й сравниваемых групп в упорядоченной последовательности равен
h = J - i + 1 при j > /.
Ввиду упорядоченности групп по величине средних критическая
область является правосторонней, т. е. сравниваемые групповые средние
различаются значимо, если (?набл > qKp, и различаются незначимо, если
>^набл " кр •
Пример. Для применения критерия Ньюмена—Кейлса используем
данные примера о влиянии курения на заболеваемость дыхательных путей (см.
§ 7.3, 7.7).
Согласно дисперсионному анализу, групповые средние х^, = 1, х^ = 2,
х^з = 3,75 различаются значимо. Осуществим их попарное сравнение.
Заметим, что групповые средние уже упорядочены по возрастанию,
следовательно, менять местами их не приходится.
Начинаем сравнение с групп 1 и 3. Для них
*J ниитп f 1 I 1 1 ~ '
'2!ш( 1 + 1
2 Ч 4>
Находим при уровнях значимости а, = 0,05 и а, = 0,01, v = 12 - 3 = 9,
h = 3 - 1 + 1 = 3:
qKp = <7кр(0,05; 9; 3) = 3,949,
<7КР(0,01; 9; 3) = 5,428.
Как видим, (?набл превосходит qKp как при а = 0,05, так и при а = 0,01, т.
е. различие средних в группах 1 и 3 значимо. (Заметим, что если бы это
различие оказалось незначимым, то для следующей пары групп 2 и 3
проверка бы не потребовалась).
Для групп 2 и 3 имеем
<2набл = (3'75~Д>" 2* 4,0415.
Значения qKP те же, что и найдены ранее. Таким образом, (2набл попадает
в критическую область при а, = 0,05 (на уровне значимости а, = 0,05
различие групповых средних значимо) и попадает в область принятия
гипотезы на уровне значимости а, = 0,01 (различие групповых средних
незначимо). Какое принять решение, зависит от исследователя. Кстати, вспомните
329

результат сравнения тех же групп с помощью критерия Стьюдента (пример
§ 7.6), где решение о незначимости различий также находилось на грани
принятия и отвержения нулевой гипотезы.
Для групп 1 и 2 имеем
<2„абл = (2~iJJ 2«2,309.
70/75
Сравнивая с найденным ранее qKp гипотезу о равенстве средних в
группах 1 и 2, принимаем как при а, = 0,05, так и при а, = 0,01.
Таким образом, критерий Ньюмена—Кейлса подтвердил наши
результаты попарного сравнения групп при помощи критерия Стьюдента с
поправкой Бонферрони. При этом сравнение групп 2 и 3 оказалось более тонким,
чем в критерии Стьюдента.
Замечание. Если в критерии Ньюмена—Кейлса при определении
критической точки дкр интервал сравнения h положить равным числу групп т
для любой сравниваемой пары средних, то получим критерий, известный
как критерий Тьюки. Критерий Тьюки более прямолинейный и отвергает
нулевую гипотезу несколько решительнее, чем критерий
Ньюмена—Кейлса. Вопрос в пользу выбора того или иного критерия при решении
конкретной задачи решается субъективным мнением исследователя, точнее,
его отношением к выдвигаемой нулевой гипотезе: сколь решительно ее
следует отвергать в проблемных случаях.
Задачи и упражнения
1. Произведено по пять испытаний на каждом из четырех уровней
фактора F. Результаты испытаний занесены в таблицу, в которой также
указаны и групповые средние (табл. 7.14).
При уровне значимости а = 0,05 методом дисперсионного анализа
требуется проверить гипотезу о равенстве генеральных (теоретических)
групповых средних (или, что то же самое, требу_ется установить, значимо ли
различие наблюдаемых групповых средних х^.). Предполагается, что все
Таблица 7.14
Номер испытания /
1
2
3
4
5
**
Уровень фактора F
Рх
36
47
50
58
67
51,6
Рг
56
61
64
66
66
62,6
Рг
52
57
59
58
79
61,0
Р*
39
57
63
61
65
57,0
330

Таблица 7.15
Номер
испытания i
1
2
3
4
**
Уровень фактора F
Ъ
1,38
1,38
1,42
1,42
1,40
F,
1,41
1,42
1,44
1,45
1,43
F,
1,32
1,33
1,34
—
1,33
F<
1,31
1,33
—
—
1,32
четыре выборки извлечены из нормальных генеральных совокупностей с
одинаковыми дисперсиями.
Указание. Использовать методы и формулы однофакторного
дисперсионного анализа при одинаковом числе наблюдений на каждом уровне
фактора, изложенные в § 7.3. Для упрощения вычислений данные желательно
преобразовать, как это сделано в примере § 7.4: вместо наблюдаемых
значений ху можно использовать уу = xs + а. В качестве такого удобного
значения а, упрощающего вычисления, возьмите а = -58.
Ответ: SSo6ui = 1851; SS^ = 360,55; SS0CT = 1490,45; MS^ = 120;
MS0CT = 93;
^набл = 1,29; FKp(0,05; 3; 16) = 3,24. Групповые средние различаются
незначимо. Отвергнуть нулевую гипотезу о равенстве генеральных средних
оснований нет, следовательно, влияние исследуемого фактора
несущественно.
2. Проверяется воздействие некоторого фактора F на генеральную
совокупность X. Фактор F разбит на четыре уровня. Произведено 13
наблюдений, из них 4 на первом уровне фактора, 4 — на втором, 3 — на третьем и
2 — на четверном. Данные представлены в виде таблицы (табл. 7.15).
При уровне значимости а = 0,05 методом дисперсионного анализа
требуется проверить гипотезу о равенстве генеральных групповых средних.
Предполагается, что выборки извлечены из нормальных совокупностей с
одинаковыми дисперсиями.
Указание. Использовать методику, изложенную в § 7.4.
Ответ: SS^ = 2,629; SS0CT = 0,3; МУфакт = 0,876; MS^ = 0,033;
Fmtn = 26,32; 7^(0,05; 3; 9) = 3,86. Нулевую гипотезу о равенстве
групповых средних отвергаем. Влияние фактора F следует признать существенным.
3. На 5 самках дрозофилы поставлен опыт по изучению развития мушек
из оплодотворенных яиц при разных температурах (20°; 25°; 30°С). От
каждой самки при каждой температуре брали по 40 яиц. Их разделяли на 2
группы по 20 яиц в каждой. Таким образом, получено 30 групп по 20 яиц в
каждой. Наблюдаемое значение — число неразвившихся яиц среди каждых
20. Так как наблюдаемых групп 30, то всего имеется 30 наблюдений,
каждое из которых получено от определенной самки (фактор А с 5 уровнями,
331

Таблица 7.16
^^^-^^^Уровень фактора В (темпе-
^"""-"■^^^ ратура, вС)
Уровень фактора Л^^-—«^^
(самки) --^^^
1
2
3
4
5
20*
1
11
4
10
2
1
9
3
7
0
25*
0
5
3
8
2
4
5
2
6
0
30*
0
10
1
5
2
1
14
1
7
4
Таблица 7.17
Источник вариации
Общий
Фактор А
Фактор В
Взаимодействие А и В
Случайные отклонения
SS
412
306
9
63
34
df
29
4
2
8
15
MS
14,2
76,5
4,5
7,9
2,3
/г
набл
/О, J _ -J-} -J
2,3
4-5 = 19
2,3 '
L9 = 34
2,3 '
*,
3,06
3,68
2,64
по количеству самок) и при определенной температуре (фактор В с 3
уровнями, по количеству рассматриваемых температур). Все 30 наблюдений
занесены в таблицу (табл. 7.16).
В каждой из 15 ячеек таблицы оказалось по два наблюдения. При
уровне значимости а = 0,05 методом двухфакторного дисперсионного анализа
требуется исследовать влияние факторов А (индивидуальность самки), В
(температура) и АВ (взаимодействие факторов индивидуальности самки и
температуры) на развитие мушек дрозофилы из оплодотворенных яиц.
Указание. По данным задачи составьте таблицу вида табл. 7.12 (см.
§ 7.5), в каждой ячейке которой - сумма наблюдаемых элементов, в
частности (см. данные) Ти = 1 + 1 = 2; Т21 = 11 + 9 = 20 и т. д. Далее,
используя формулы (7.25) - (7.34), заполните таблицу дисперсионного анализа
вида табл. 7.13. Сравнивая Fm6n с соответствующим FKp, сделайте вывод о
влиянии каждого из факторов и их взаимодействия на рассматриваемую
случайную величину - количество неразвившихся яиц.
Ответ: Приведем итоговую таблицу дисперсионного анализа (табл. 7.17).
332

Таблица 7.18
Час кормления
6
9
12
15
18
21
Кормящие матери
1-я
100
92
101
127
111
69
2-я
141
119
87
83
84
86
3-я
147
122
88
80
83
80
4-я
126
104
105
87
96
82
5-я
133
115
93
96
83
80
6-я
101
102
102
106
90
99
7-я
148
128
74
68
101
81
8-я
128
146
94
97
64
71
Таблица 7.19
Номер испытания /
1
2
3
4
5
6
7
8
V-
Уровень фактора (час кормления)
6
100
141
147
126
133
101
148
128
128
9
92
119
122
104
115
102
128
146
116
12
101
87
88
105
93
102
74
94
93
15
127
83
80
87
96
106
68
97
93
18
111
84
83
96
83
90
101
64
89
21
69
86
80
82
80
99
81
71
81
Таким образом, существенное влияние на развитие потомства оказывает
фактор А (индивидуальность самки), влияние фактора В (температуры) не
доказано, имеется заметное влияние взаимодействия факторов.
4. Данные о количестве сцеженного и высосанного молока (в процентах
к среднесуточному) у 8 кормящих матерей, страдающих гипогалактией, в
течение 6 суточных кормлений представлены в таблице (табл. 7.18).
Необходимо проверить, действительно ли в течение суток за шесть
кормлений количество сцеженного и высосанного молока у кормилиц с
гипогалактией уменьшается или это различие случайно. Исследование
провести при уровне значимости а = 0,01.
Указание. Имеющиеся данные записать в таблицу по уровням фактора —
часа кормления (табл. 7.19).
333

Таблица 7.20
6
9
12
15
18
21
Кормящие матери
1-я
100
—
101
—
—
69
2-я
—
119
87
83
84
86
3-я
—
122
88
—
83
80
4-я
126
104
105
87
96
82
5-я
133
115
93
96
83
80
6-я
101
102
102
—
90
99
7-я
—
128
74
—
101
81
8-я
128
—
94
97
64
71
X ■
ЛПУ
117,60
115,00
93,00
90,75
85,86
81,00
Ответ: SS^ = 22 390; SS^ = 12 960; SS0CT = 9430; МУфакт = 2592; MS0CT =
= 224,52; Fwtn = 11,54; ^кр(0,01; 5; 42) = 3,49. Различие в количестве
сцеженного и высосанного молока у матерей с гипогалактией за шесть
кормлений в течение суток существенно.
5. При экспериментальном изучении предыдущего примера было
решено устранить "выделяющиеся" результаты наблюдений, используя
определенную методику. Оставшиеся данные занесены в таблицу (табл. 7.20).
Применяя однофакторный дисперсионный анализ, требуется
установить, имеется ли существенное различие между количеством сцеженного и
высосанного молока во время шести кормлений в течение суток.
Ответ: ^=11 087; ^факт = 7196; SS0CT = 3891; MS^„ = 1439,20;
MS0CT = 121,59; Fm6n = 11,84; FKp(0,0l; 5; 32) = 3,66. Различие в зависимости
от времени кормления существенно.
6. При изучении методов лечения гипогалактии требовалось
предварительно уточнить влияние, оказываемое некоторыми факторами на состав
материнского молока. В частности, в отношении содержания жиров в
материнской молоке были получены следующие результаты (табл. 7.21).
Требуется изучить влияние двух факторов: фактор А (на двух уровнях:
первородящие и повторнородящие кормящие матери) и фактор В - час
кормления (на шести уровнях: 6, 9, 12, 15, 18 и 21 час). Комбинации
уровней обоих факторов исследовались по 6 раз (6 наблюдаемых первородящих
и 6 наблюдаемых повторнородящих женщин).
С помощью двухфакторного дисперсионного анализа необходимо
установить наличие влияния на количество жира в молоке фактора А, фактора
В и взаимодействия обоих факторов АВ.
Ответ: SSo6lu = 88,34; SS^A = 0,83; SS^ в = 47,44;
SS^AB = 1,01; SS0CT = 39,06; MS^A = 0,83;
№ф^в = 9,488; MS^AB = 0,202; MS0CT = 0,651;
F***A = 1,275; FKpA = 7,08; FHli6nB = 14,576;
F^ab = 0,31; FKpB = 3,34; FKpAB = 9,20.
Выводы: фактор А (число родов) не оказывает влияния на количество
жиров в материнском молоке; фактор В (час кормления) оказывает
влияние; взаимодействие факторов несущественно.
334

Таблица 7.21
N. ЧИСЛО
N. родов FA
Час ^ч
кормле- N.
ния FB n.
6
9
12
15
18
21
Первородящие (А,)
1,6 3,5 2,2 3,0 3,9 2,8
2,9 2,4 5,0 3,2 3,3 2,6
3,5 3,3 3,5 4,0 3,8 3,9
4,0 6,0 4,5 3,9 5,0 3,5
3,8 5,9 4,4 5,0 5,5 5,0
4,0 6,1 6,9 4,9 4,1 5,8
Итого
17,0
19,4
22,0
26,9
29,6
31,9
Повторнородящие (А2)
2,9 4,0 4,5 3,0 4,0 3,0
4.1 3,4 2,8 2,9 3,2 2,8
2,8 4,2 3,2 3,5 4,1 3,6
5,0 6,0 5,0 4,0 5,1 3,5
4.2 5,6 4,2 6,0 4,9 3,8
4,0 6,2 6,0 5,0 5,3 4,2
Итого
21,4
19,2
21,4
28,6
28,5
30,7
Таблица 7.22
Fm (старшие дети)
Fn (младшие дети)
FM (до занятий)
2 0 3 4
2 4 4 6
FA2 (во время занятий)
2 3 5 6
0 5 6 7
FM (после занятий)
4 5 6
7 8 9
7. Шесть групп детей исследуются при помощи психологического теста
работоспособности. Одним из показателей, при помощи которого
определяют работоспособность, является количество ошибок, допускаемых
каждым из детей за единицу времени. Экспериментальным путем исследовали
влияние двух факторов: FA — изменения в работоспособности во время
учебных занятий и FB — изменения в работоспособности в зависимости от
возраста. Фактор FA имеет три уровня: FM — до учебных занятий, FA2 — во
время учебных занятий и FA3 — после учебных занятий. Фактор FB имеет
два уровня: FBl — дети старшего возраста и FB2 — дети младшего возраста.
Результаты эксперимента (количество ошибок за единицу времени)
занесены в таблицу (табл. 7.22).
Требуется определить: 1) снижается ли работоспособность во время
учебного процесса вследствие наступившего утомления; 2) находится ли
работоспособность в зависимости от возраста; 3) оказывает ли влияние на
работоспособность комбинированное воздействие факторов утомляемости
и возраста.
Ответ: FM6nA = 7,49; ^ = 6,51;
^бл* = 9,99; ^р*=8,8б;
^абл^ = 0,83< 1; FKpAB = 6,5l.
Выводы: 1) Работоспособность учеников снижается в течение учебного
процесса. Видимо, причиной этого является утомление.
335

Таблица 7.23
Группа
Контрольная
Доза 100 р.
Доза 200 р.
Число мышат от отдельных самок
10
8
7
12
10
9
11
7
6
10
9
4
Таблица 7.24
Туберкулез
Прочие заболевания
Сельские
районы
4,9
21,9
Пригородные
районы
8,9
20,7
Небольшие
города
6,8
21,7
Средние
города
8,4
20,4
Крупные
города
11,2
20,0
Таблица 7.25
Причина смерти
(фактор В)
Новообразован ия

Сердечно-сосудистые болезни
Несчастные случаи
Цирроз печени
Самоубийства
Вид занятий (фактор А)
руководители
высшего звена
150
130
45
15
20

преподаватели
140
150
30
16
25
руководители
среднего звена
205
180
75
33
36
с/х рабочие
290
190
175
75
30

промышленные рабочие
350
185
95
95
45
2) Работоспособность учеников находится в зависимости от их возраста:
у старших учеников работоспособность выше.
3) Влияния взаимодействия факторов "возраст" — "время" не установлено,
т. е. утомляемость у тех и других детей проявляется в одинаковой степени.
8. Имеются данные о плодовитости мышей при облучении
рентгеновскими лучами (табл. 7.23).
Установить методами дисперсионного анализа, влияет ли облучение на
плодовитость мышей. Если различие между группами по уровням фактора —
дозы облучения — существенно, то провести попарное сравнение групп,
используя критерий Стьюдента для множественных сравнений.
9. Имеются данные о заболеваемости в различных районах страны1 (на
1000 человек населения) (табл. 7.24).
lTakemune Soda. Общенациональное выборочное обследование и заболеваемость в
Японии. См. Тенденции в изучении заболеваемости и смертности. ВОЗ, Женева, 1966.
336

Методами дисперсионного анализа требуется установить влияние
фактора местности на заболеваемость населения. Проследите отдельно данные
по туберкулезу. Какие напрашиваются выводы?
10. Имеются данные о причинах смертности в разных социальных
группах населения Франции за 1986 г. (на 100 тыс. занятых) (табл. 7.25).
I. Методами однофакторного дисперсионного анализа требуется
установить влияние профессионального фактора А на смертность.
Если различие по группам (уровням фактора) существенное, то
провести сравнения групп: а) используя критерий Стьюдента для множественных
сравнений; б) используя критерий Ньюмена - Кейлса.
11. Методами однофакторного дисперсионного анализа установить
влияние заболеваемости и бытового фактора (причина смерти) на
смертность населения.
Если различие по группам причин смертности (фактор В) существенно,
то провести сравнение групп: а) используя критерий Стьюдента для
множественных сравнений; б) используя критерий Ньюмена - Кейлса.
II. В задаче 10 провести двухфакторный дисперсионный анализ.
22 — 3529

Глава VIII. АНАЛИЗ ЗАВИСИМОСТЕЙ
8.1. Типы зависимостей случайных величин
Многие прикладные задачи требуют установления вида связи
(зависимости) между случайными величинами. Сама постановка большого круга
задач, в частности медицинских (например, в профилактической
медицине, в различных исследовательских проблемах), предполагает построение и
реализацию алгоритмов "фактор—отклик", "доза—эффект". Зачастую
нужно установить наличие эффекта при имеющейся дозе и оценить
количественно полученный эффект в зависимости от дозы. Решение этой задачи
напрямую связано с вопросом прогнозирования определенного эффекта и
дальнейшего изучения механизма возникновения именно такого отклика.
а) случайные величины X и Y связаны функциональной зависимостью.
У
y = f(x)
б) случайные величины X и У связаны стохастической зависимостью.
M(Y | X = х)
М(У\Х= 0)
y = M(Y\X)
Рис. 50.
338

Как известно (см. § 3.1), случайные величины X и У могут быть либо
независимыми, либо зависимыми. Зависимость случайных величин также
подразделяется на функциональную и статистическую. В математике
функциональной зависимость переменной У от переменной X называют
зависимость вида Y = f{X), где каждому допустимому значению вставится
в соответствие по определенному правилу единственно возможное
значение У (рис. 50, а).
Однако если Хи У— случайные величины, то между ними может
существовать зависимость иного рода, называемая стохастической
(статистической). Дело в том, что на формирование значений случайных величин X и
У оказывают влияние различные факторы. Под воздействием этих
факторов и формируются конкретные значения X и Y. Допустим, что на А" и У
влияют одни и те же факторы, например Z,, ^, Z3, тогда Хи У находятся в
полном соответствии друг с другом и связаны функционально.
Предположим теперь, что на св. Аг воздействуют факторы Z„ ^, Z3, а на случайную
величину У — только Z, и 7^. Обе величины и А", и У являются
случайными, но так как имеются общие факторы Z, и ^, оказывающие влияние и
на X, и на У, то значения А"и У обязательно будут взаимосвязаны. И связь
в) случайные величины X и Y некоррелированы и независимы
(M(Y\X) = M(Y) = const, область изменения У постоянная при любых X).
M(Y)
y = M(Y\X)
г) случайные величины X и Y некоррелированы, но зависимы
(M(Y\X) = M(Y) = const, область изменения У зависит от значений Х= х).
M(Y)
y = M(Y\X)
Рис. 50.
22*
339

эта уже не будет функциональной: фактор Z3, влияющий лишь на одну из
случайных величин, разрушает прямую (функциональную) зависимость
между значениями X и Y, принимаемыми в одном и том же испытании.
Связь носит вероятностный, случайный характер, в численном выражении
меняясь от испытания к испытанию, но эта связь определенно
присутствует и называется стохастической.
При этом каждому значению X может соответствовать не одно значение
Y, как при функциональной зависимости, а целое множество значений. На
рис. 50, б для наглядности эти границы изменения У очерчены, например,
при указанном значении X = х, значения Y находятся в пределах от ах до
Ьх. Среди этого множества значений Yможно найти среднее M(Y\ X= x),
которое для каждого значения х свое. Множество этих значений на
графике образуют линию
y=M(Y\X=x), (8.1)
вид которой может быть самым разнообразным (прямая, парабола,
экспонента и т. д.) и определяется случайными величинами X и Y. Напомним
(см. § 3.9), что график (8.1) называют линией регрессии Уна X. Также
заметим, что часто условное математическое ожидание М (Y\ X= х)
записывают в сокращенном виде М (Y\ X).
Зависимость случайных величин называют стохастической
(статистической), если изменения одной из них приводит к изменению закона
распределения другой. Изменения закона распределения могут проявляться
по-разному. В частности, если изменение одной из случайных величин
влечет изменение среднего другой случайной величины, то стохастическую
зависимость называют корреляционной. Зависимость между случайными
величинами X и Y, представленная на рис. 50, б, является корреляционной,
так как при разных значениях х соответствующие значения средних для Y,
заданные величиной M(Y\ X= х), вообще говоря, различны. Сами
случайные величины, связанные корреляционной зависимостью, оказываются
коррелированными.
Классическим примером корреляционной зависимости является
зависимость урожайности сельскохозяйственной культуры (Y) от количества
внесенных удобрений (X). Зависимость Y от X в данном случае ни у кого
не вызывает сомнений. Однако, если на разных участках поля внести
равное количество удобрений, урожайность на этих участках одинаковой,
вообще говоря, не будет, так как, кроме удобрения, на урожайность /влияет
и множество других факторов (влажность, освещенность, структура почвы,
способ внесения удобрений, различие в методике обработки культуры на
разных участках и т. д.). Таким образом, в рассматриваемом примере Y
связан с А" не функциональной, а именно корреляционной зависимостью
(различие урожайности — это и есть различие средних значений).
Корреляционной является зависимость массы от роста: каждому
значению роста (X) соответствует множество значений массы (Y), причем,
несмотря на общую тенденцию, справедливую для средних, большему
значению роста соответствует и большее значение массы — в отдельных
наблюдениях субъект с большим ростом может иметь и меньшую массу.
Корреляционной будет зависимость заболеваемости от воздействия
внешних факторов, например запыленности, уровня радиации, солнечной
активности и т. д. Имеется корреляция между дозой ионизирующего излуче-
340

ния и числом мутаций, между пигментом волос человека и цветом глаз,
между показателями уровня жизни населения и процентом смертности,
между количеством пропущенных студентами лекций и оценкой на
экзамене. Именно корреляционные зависимости наиболее часто встречаются в
природе в силу взаимовлияния и тесного переплетения огромного
множества самых различных факторов, определяющих значения изучаемых
показателей.
Некоррелированные случайные величины, как бы они ни изменялись, не
влияют на средние значения друг друга. Пример такого рода см. на рис. 50,
в, из которого видно, что при любых возможных значениях случайной
величины Л'среднее значение У остается неизменным: M(Y \ Х = х) = M{Y). На
этом рисунке исключительно для наглядности очерчена область возможных
значений случайной величины Y. a<Y<b.
Напомним, что независимые случайные величины — это частный
случай некоррелированных. Случайные величины могут быть
некоррелированными и в то же время зависимыми. Пример такой зависимости
представлен на рис. 50, г, где хотя среднее M(Y\ X = х) = M{Y) и остается
постоянным при разных х (некоррелированность), сама область значений Y
меняется при изменении х, т. е. зависимость У от Л'имеется, несмотря на
некоррелированность.
При корреляционной зависимости Y и X возможно наблюдать
тенденцию роста: с увеличением значений X растет и среднее значение Y или с
увеличением значений А" среднее значение Y уменьшается. В этих случаях
говорят соответственно о положительной и отрицательной корреляции.
Заметим, что наряду с рассматриваемой зависимостью Y от X с тем же
успехом во многих примерах можно рассмотреть и зависимость А'от Y.
8.2. Выборочный коэффициент корреляции
Как известно (см. § 3.5), степень зависимости случайных величин X и Y
характеризуется значением коэффициента корреляции [см. (3.35)].
r=r - K(X, Y)
ху Щх)Щ7)
При этом коэффициент корреляции, как и всякая другая теоретическая
характеристика, вычисляется, исходя из всех возможных значений X и Y
[этим значениям на рис.50, б, в, г соответствует множество точек (х, у)
заштрихованных областей]. На практике же мы не имеем возможности
охватить наблюдениями все означенное множество, а используем лишь
ограниченное число наблюдений: двухмерную выборку значений (х, у).
Полученные числа можно занести в таблицу:
X
У
хх
Ух
*2
Уг
*i
У;
Хп
Уп
По данным наблюдений мы можем вычислить значение коэффициента
корреляции так же, как вычисляли его в случае системы дискретных
случайных величин (см. пример 1, § 3.6), с той лишь разницей, что вместо из-
341

вестных вероятностей для каждой пары возможных значений будем
использовать соответствующий аналог: относительную частоту - .
п
Формула для вычисления выборочного коэффициента корреляции
случайных величин Хи У выглядит так:
R* =
п
(8.2)
l&^-ffEI^-tf
У-i
где X, Y — выборочные средние, a RB означает, что коэффициент
корреляции выборочный (а не теоретический). Сокращая в числителе и
знаменателе дроби (8.2) одинаковые сомножители, получаем
%(Х,-Х)(Г,-Г)
R* =
'•-1
(8.3)
ТЛ2
ТЛ2
1 j = 1 У = 1
Для вычисления численного значения RB нужно в соотношение (8.3)
вместо случайных величин поставить их значения, тогда наблюдаемое
значение гв имеет вид:
£(*;-*) СИ/-У)
г в =
'= 1
;=i y=i
(8.4)
(Отметим, что в последних формулах выборочный коэффициент
корреляции в качестве случайной величины обозначен RB, а в качестве
конкретного числа обозначен соответственно гв.)
Пример. Имеется выборка из 10 наблюдений роста в см. отцов (X) и их
взрослых сыновей (Y).
*,■
У,
180
186
172
180
173
176
169
171
175
182
170
166
179
182
170
172
167
169
174
177
Требуется найти выборочный коэффициент корреляции, составленный
исходя из представленных данных.
Для удобства вычислений по формуле (8.4) разместим наши
выборочные значения в табл. 8.1, в которой удобно и наглядно можно представить
и результаты вычислений.
В нижней части таблицы выписаны суммы, используемые в формуле
(8.4). Итак,
342

Таблица 8.1
/
1
2
3
4
5
6
7
8
9
10
xi
180
172
173
169
175
170
179
170
167
174
Z = 1729
x= 172,9
yt
186
180
176
171
182
166
182
172
169
177
1= 1761
у =176,1
x,— x
7,1
-0,9
0.1
-3,9
2,1
"2,9
6,1
"2,9
"5,9
1,1
(*, - x)2
50,41
0,81
0,01
15,21
4,41
8,41
37,21
8,41
34,81
1,21
Z = 160,90
у,- у
9,9
3,9
-o,i
"5,1
5,9
-10,1
5,9
"4,1
"7,1
0,9
(у. ~ у)2
98,01
15,21
0,01
26,01
34,81
102,01
34,81
16,81
50,41
0,81
Z=378,90
(*, ~ x){yt - у)
70,29
-3,51
-0,01
19,89
12,39
29,29
35,99
11,89
41,89
0,99
1=219,10
г в = 219>1 - * 0, 887 .
7160, 9 • 378, 9
Поставленная задача решена.
Если число наблюдений достаточно велико и особенно если
наблюдения объединяются поинтервально, т. е. все значения, попавшие в
интервал, округляются до значения середины интервала (как, например, рост
измеряется с точностью до целых см., а масса — с точностью до целых
килограмма), то каждая из наблюдаемых пар значений может встретиться
неоднократно. В этом случае обычно данные заносят в таблицу с учетом
частот встречаемости. Такую таблицу со сгруппированными данными
называют корреляционной. Приведем пример корреляционной таблицы с
конкретными данными (X — рост в см, У — масса в кг).
В первом столбце и первой строке табл. 8.2 указаны наблюдаемые
значения соответственно случайных величин Хи К На пересечении
рассматриваемых строки и столбца записано число — частота встречаемости этой
пары в данной выборке. Например, пара значений А'= 174, У = 75
[запишем в виде (174;75)] встречается 16 раз, а пара (17б;85) не встречается ни
разу. В общем случае частоту пары (х, у) в выборке обозначим пху, или
более конкретно пара (х„ уу) имеет частоту пг В последнем столбце
представлены суммарные значения частот встречаемости в выборке пар с каждым
из наблюдаемых значений X: например, Х= 170 встречается с различными
значениями У суммарно 32 раза (8+15+7+2 = 32), 172 — 44 раза и т.д.
Аналогично, в последней строке корреляционной таблицы выписаны
суммарные частоты встречаемости в наблюдениях каждого из значений Y.
Сумма всех частот, записанных в таблице для каждой пары значений X, У,
равна п и, естественно,
343

Таблица 8.2
^\ Y
X \.
170
172
174
176
178
180
182
"у;
65
8
4
—
2
—
—
—
14
70
15
19
11
5
—
1
—
51
75
7
10
16
11
3
—
—
47
80
2
8
12
3
1
1
2
29
85
—
3
2
—
5
4
5
19
пх,
32
44
41
21
9
6
7
п = 160
В нашей таблице п = 160.
Формула для выборочного коэффициента корреляции гв вида (8.4),
вычисляемого по корреляционной таблице, т. е. с учетом частот
встречаемости в наблюдениях каждой пары (х, у), принимает вид
гв
^пху(х-х)(у-у)
(8.5)
где х и у — соответствующие выборочные средние
i = ]£>*, у = £>■
а суммирование распространяется в знаменателе на все возможные х или у
соответственно и в числителе — на все возможные пары (х, у).
Если в числителе выражения (8.5) под знаком суммы выполнить
умножение, то данная формула преобразуется к виду
гв
^пхуху-пху
JY, пх(х~х)2^ "у(У - У)2
(8.6)
Заметим, что в знаменателе выражение под знаком корня равно
ns2 • nsy2, где sx2, sy2 — выборочные дисперсии [см. § 4.3, выражения (4.6),
(4.7)].
Проведя вычисления непосредственно по числовым данным табл. 8.2,
получаем
х= 173,7125; у = 74,625;
г в =
^Пхху-пху
^пх(х-х)2 • ^пу(У~У)2
344

= 2 075 700-160 • 173,7125 • 74,625 = Q 54?
71566,9 • 5277,51
Итак, выражения (8.2)—(8.6) являются различной формой
представления одной и той же величины: выборочного коэффициента корреляции.
Как известно, коэффициент корреляции случайных величин
(генеральных совокупностей) Хи Y, изменяясь по модулю в пределах от 0 до 1,
характеризует тесноту линейной связи: от полной независимости (или по
крайней мере некоррелированности) при г = 0 до линейного соотношения,
У= аХ + Ь, при | г | = 1. Причем при г > 0 возрастание одной переменной
влечет и рост другой (положительная корреляция), а при г < 0 возрастание
одной переменной влечет убывание другой (отрицательная корреляция). В
данном случае речь идет не об однозначном возрастании или убывании
переменной по всем значениям, а об общей тенденции.
Выборочный коэффициент корреляции RB — оценка коэффициента
корреляции г, рассчитанного по всей генеральной совокупности, т. е. rB ~ г.
Следовательно, рассчитав гв, мы также можем судить о силе линейной
связи. В случае если выборка имеет достаточно большой объем л, порядка
сотен, то можно воспользоваться RB как точечной оценкой коэффициента
корреляции г.
8.3. Проверка независимости признаков
Рассмотрим два признака. Первый из них характеризуется рядом
значений *,, ^2, ..., хп, а второй — соответствующими значениями ух, у2, ..., уп.
Исходя из имеющихся данных, требуется установить, зависимы ли эти
признаки. Полагаем, что наблюдаемые значения х, представляют
генеральную совокупность X, а значения yt — генеральную совокупность Y, и тогда
задача сводится к проверке независимости случайных величин X и Y. В
этом нам поможет коэффициент корреляции. Предположим, что с. в Хи Y
имеют нормальное распределение. Следовательно, согласно § 3.5 (см.
сноску), условие некоррелированности нормально распределенных Хи
/равносильно их независимости. Следовательно, гху= 0 гарантирует
независимость случайных величин (а значит, и независимость признаков), а г^ * 0
означает зависимость Хи Y, причем величина коэффициента г^ говорит о
силе имеющейся зависимости.
Итак, в качестве нулевой гипотезы полагаем Я0: г^ = 0, тогда
конкурирующая гипотеза Я0: гху * 0.
Для проверки гипотезы Я0 требуется подобрать, исходя из выборочных
данных, статистику-критерий, которая бы через выборочный коэффициент
корреляции RB характеризовала и гху и распределение которой было бы
хорошо известно. Таким критерием является статистика
Т = Яв^п ~ 2 , (8.7)
л/1 - R'b '
которая при справедливости нулевой гипотезы имеет распределение Стью-
дента с п — 2 степенями свободы.
345

Следовательно, для проверки Я0 используется критерий Стьюдента, т. е.
по выбранному уровню значимости а и числу степеней свободы п — 2
необходимо по табл. 6 Приложения 2 найти гкр, затем определить Гнабл по
формуле
Гнабл = ^^О (8.8)
и сравнить полученные значения гкр и Гнабл. Если |Гнабл| < /кр, то
наблюдаемое отклонение гв от нуля незначимо, и нулевая гипотеза принимается,
случайные величины независимы; если же |Гнабл| > г^, то принимается
гипотеза Я,, св. Хм У зависимы.
Замечание. Вместо использования табл. 6 критических значений
(квантилей) распределения Стьюдента можно воспользоваться специальной
таблицей "наибольших случайных значений коэффициента корреляции" (см.
табл. 11 Приложения 2). В этой таблице при заданном уровне значимости
а (а = 0,05; 0,01; 0,027; 0,001) и известном числе степеней свободы т = п
— 2 представлены максимальные значения, которые может иметь величина
| гв | при справедливости нулевой гипотезы.
Пример. По данным примера § 8.2 требуется определить, зависит ли
рост взрослых сыновей (У) от роста их отцов (X). Распределение св. Хи У
предполагается нормальным.
Используем критерий Стьюдента для проверки гипотезы Я0: г^ = 0.
В нашем примере число наблюдений п = 10, выборочный коэффициент
корреляции гв = 0,887. Найдем Гнабл [см.(8.8)]:
Гнабл = 0^2^ = 5,4327.
Vl-0,8872
Выберем уровень значимости а = 0,05 и по табл. 6 находим t^ = /^(0,05; 8) =
= 3,833.
Так как |Гнабл| > гкр, то нулевую гипотезу отвергаем, следовательно, св. X
и У зависимы, т. е. рост взрослых сыновей зависит от роста их отцов.
К данному выводу можно было прийти, используя табл. 11 наибольших
случайных значений коэффициента корреляции. В этой таблице при
уровне значимости а = 0,05 и числе степеней свободы т = 10 — 2 = 8
наибольшее возможное значение |rj, вызванное случайными причинами (а на
самом деле Гц = 0), может быть 0,65'. Наше наблюдаемое значение
|rj = 0,887, следовательно, наблюдаемое отклонение коэффициента
корреляции от нуля вызвано не только случайными причинами, а и
зависимостью Хи У. Таким образом, У зависит от X, рост взрослых сыновей зависит
от роста их отцов.
'Значения 0,65 в таблице нет, оно получено линейной интерполяцией соседних значений:
при т = 5 находим |rmJ = 0,75 и при т = 10 соответственно |rmJ = 0,58.
346

8.4. Проверка гипотезы о силе линейной связи двух признаков
Допустим, что гипотеза о независимости двух исследуемых признаков
отвергнута, как в примере предыдущего параграфа. Значит, статистически
установлена зависимость признаков. Идем дальше: требуется установить,
сколь сильна эта зависимость. Для решения вопроса о линейной
зависимости нужно знать величину коэффициента корреляции. Мы же
располагаем лишь его полномочным представителем, выборочным
коэффициентом корреляции, который в силу разных случайных обстоятельств
несколько отличается от своего теоретического оригинала г . Строим гипотезы: в
нулевой гипотезе предполагаем равенство г конкретному числу,
отличному от нуля
Я0: Гху = а,
тогда конкурирующая гипотеза Я0: гху * а.
Далее для проверки нулевой гипотезы необходимо подобрать
подходящий критерий.
Фишером установлено, что статистика
lV=l2lnT^fBf (8,9)
построенная по выборкам из Хи Y достаточно большого объема п (п > 50)
имеет приближенно нормальное распределение. В случае справедливости
нулевой гипотезы, г^ = а, параметры этого распределения
mw= M{W)= llni±5 + —5—, (8.10)
2 \ — а 2{п — 1)
с]у = D{W) = -1_. (8.11)
Для использования в качестве критерия более удобна нормированная
величина, т. е. с нулевым средним и единичной дисперсией. Полагаем
Z= W-m*. (8.12)
<3уу
Это и есть наш критерий, Z ~ N(0; 1).
Далее схема простая: находим ZHa6jl, при выбранном уровне значимости
а находим по табл. 2 функции Лапласа ^р и сравниваем эти величины. В
зависимости от полученных значений ZM6n и ^р нулевая гипотеза
принимается либо нет.
Пример. Вернемся к примеру предыдущего параграфа1. Нами
установлено, что рост взрослых сыновей зависит от роста их отцов. Найдем
степень этой корреляционной зависимости.
Вычислено значение гв = 0,887. Проверим нулевую гипотезу Я0: гху = 0,9
при уровне значимости а = 0,05 (число а = 0,9 выбрано, исходя из
численного значения гв = 0,887). Конкурирующая гипотеза Я0: г^ *0,9.
'В данном примере объем выборки л = 10 явно недостаточен. Проведем выкладки
исключительно в учебных целях.
347

Для использования критерия Z вначале вычислим mw [см. формулу
(8.10)], аЛсм. (8.11)]:
m-"2lnr^t9 + 2(10^T)w1'522'
Тогда
7= Ff-1,522
0,378 '
Используя (8.9), находим наблюдаемое значение критерия:
li^l +0,887 _ ! „9
21п1 -Q ЯЯ7 1)522
7 - l l и>°й/ я-0 302
При уровне значимости а = 0,05 критическое значение критерия zKp нам
хорошо известно из табл. 2 значений функции Лапласа: ^р = 1,96.
Сравнивая ZHa6jl с найденным критическим значением. Видим, что наблюдаемое
значение критерия находится в области принятия гипотезы: |2^a6J < z*v.
Нулевая гипотеза принимается: при уровне значимости а = 0,05 (т. е. с
вероятностью ошибиться не более чем в 5% реальных случаев)
коэффициент корреляции равен 0,9. Эта зависимость очень сильная (при г = 1
зависимость уже функциональная Y = аХ + Ь, где a, b — некоторые числа).
8.5. Выборочная регрессия
Пусть для системы случайных величин Хи Y наблюдаемые пары
значений (х, у) оформлены в виде корреляционной табл. 8.3. В этой таблице в
отличие от табл. 8.2 данные представлены в общем виде.
Случайная величина X принимает к различных значений, а случайная
величина Y — I различных значений. На пересечениях строк и столбцов
Таблица 8.3
X \.
*1
*2
*/
Хк
П>,
У\
ти
Щ\
/И;,
Щ\
"у,
Уг
т\2
т22
та
mk2
ПУ2
У}
mxj
m2j
ГПу
тк,
%
У,
ти
т21
ти
mki
"у,
Пх,
пх
х2
пх
х\
пх
п
348

Таблица 8.4
X
Ух
Пх
хх
У*,
"*,
*2
Уч
П*2
Xk
yxt
"Хк
имеющихся значений указана соответствующая частота: например, пара
(*,, У]) встречается в нашей выборке т^ раз (какие-то ту могут равняться
нулю). В последнем столбце и строке выписаны суммы соответствующих
частот для значений X и Y. Например,
пхх = /и„ + тп + ... + /и,,,
пп = Щг + Щг + ••• + «iQ-
Сумма всех возможных частот ту равна п и, конечно же, равна сумме
этих частот, рассматриваемых отдельно по строкам и столбцам таблицы:
п = ZZm*= 2л= 1л- (813)
i = \j = 1 / = 1 У = 1
Каждому числу х-, соответствует целый набор значений ylt у2, ..., у, с
конкретными частотами тл, та, ..., ти (вновь отметим, что какие-то из
частот могут быть равны нулю). Вычислим среднее этих значений, которое
обозначим ух:
yXi = — (yxmix + у2та + ... + у/п„).
(8.14)
Среднее значение (условное среднее значение у при условии, что Х= х,)
можно вычислить для каждого х,. Занесем полученные данные в табл. 8.4.
Из табл. 8.4 легко прослеживается зависимость (соответствие) средних
значений ух от значений X, т. е.
Я = Ф'(*). (8-15)
Напомним, что в корреляционной табл. 8.3 представлены выборки
случайных величин X и Y, значения которых рассматриваются попарно. Если
бы мы имели возможность рассмотреть все возможные значения X и У, то
наше среднее ух оказалось бы не чем иным, как условным математическим
ожиданием М (Y\ X= x), которое при разных х представляет собой
функцию ф (х), называемую регрессией (см. § 3.9). Равенство вида (3.72)
M(Y\X=x) = y(x) - (8.16)
это уравнение регрессии Уна ^(теоретическое выражение).
В нашем случае, когда генеральные совокупности X и Y представлены
конкретными наборами выборочных значений, ух является оценкой
теоретической величины M(Y\ X= х), а уравнение (8.15) — выборочный аналог
уравнения регрессии. Уравнение (8.15) называют выборочным уравнением
регрессии Yна X. Функция ф*(*) — это выборочная регрессия Y на X, а график
функции — выборочная линия регрессии Y на X.
349

Таблица 8.5
У
Ху
"у
Ух
**
пп
Уг
Хуг
пп
У/
Ху,
ПУ,
Совершенно аналогично выборочным уравнением регрессии X нъ Y
является уравнение
*, = v/0>), _ (8.17)
где выборочные средние ху при различных значениях Y находятся из
корреляционной табл. 8.3; и уравнение (8.17) — выборочный аналог
теоретического уравнения регрессии типа (3.73):
М(Х\У=у) = ц,(у). _ (8.18)
Для выборочных значений ху можно, пользуясь корреляционной
табл. 8.3, построить таблицу^ аналогично табл. 8.4:
Как видно из (8.15), Хи ух связаны некоторой функциональной
зависимостью, аналогично из (8.17) — К и ху также связаны функциональной
зависимостью. В то же время непосредственно X и Y имеют зависимость
лишь корреляционную [если ф(х) и ц/(у) отличны от const].
Исходя из табл. 8.4, 8.5, ^южно определить, какой вид функциональной
зависимости связывает X и ух или Y и ху.
Далее необходимо подобрать коэффициенты функций ф*(*), ц/'(у) так,
чтобы зависимость была "наилучшей" в смысле соответствия наблюдаемым
значениям.
Также необходимо оценить степень корреляционной связи между Хи Y,
т. е. величину рассеяния значений относительно среднего: у относительно
ух или х относительно ху.
Так как средние обладают свойством стабилизироваться, нивелировать
случайные отклонения, то регрессия представляет собой истинные
значения без различного рода случайных факторов.
Таким образом, задача регрессионного анализа — определить
приближенное уравнение регрессии и оценить допускаемую ошибку.
Важнейшим является вопрос выбора вида функции регрессии ср*(*) [или
v/(y)]t например линейная
у = а + Ьх
или нелинейная (показательная, логарифмическая и т. д.).
Если обратиться к рис. 50, б, в, г, на котором обозначены
теоретические линии регрессии М (Y \ X = х), то видим, что в случае б зависимость
нелинейная, похожа на зависимость вида у = ах2 + Ьх + с, где а, Ь, с —
некоторые постоянные; в случаях в) и г) регрессия постоянная М(Y \
Х= х) = М (X) = const, т. е. корреляционная зависимость отсутствует.
На практике вид функции регрессии можно определить, построив на
координатной плоскости множество точек, соответствующих всем
имеющимся парам наблюдений (х, у). Например, на рис. 51 отчетливо видна
тенденция роста значений у с ростом х, при этом средние значения у рас-
350

Рис. 51. Линейная регрессия значима. Модель У= а + ЬХ.
У п
Рис. 52. Линейная регрессия незначима. Модель Y = Y.
У и
Рис. 53. Линейная регрессия значима. Желательно проверить нелинейную модель
Y=aX2 + ЬХ + с.
полагаются визуально на прямой. Имеет смысл использовать линейную
модель1 зависимости у от х. На рис. 52 средние значения у не зависят от х,
следовательно_линейная регрессия незначима (функция регрессии
постоянна и равна у). На рис. 53 прослеживается тенденция нелинейности
модели. Поэтому наряду с линейной моделью возникает необходимость
рассмотреть и нелинейную, в частности квадратическую Y= aX2+ ЬХ+ с.
'Отметим, что вид зависимости Кот Л'(или Хот У) принято называть моделью. Далее
будем придерживаться этой терминологии.
351

8.6. Параметры выборочного уравнения регрессии при линейной
зависимости
Выбрав вид функции регрессии, т. е. вид рассматриваемой модели
зависимости У от Л'(или Л'от Y), например, линейную модель Y= ЬХ + а,
необходимо определить конкретные значения коэффициентов модели.
Обратимся к линейной модели. При различных значениях аи b можно
построить бесконечное число зависимостей вида Y= ЬХ + а (т. е. на
координатной плоскости имеется бесконечное количество прямых), нам
же необходима такая зависимость, которая соответствует наблюдаемым
значениям наилучшим образом. Как установлено в § 3.9, в случае модели
линейной зависимости Хи Yфункция регрессии имеет вид (3.76)
ту + &(Х- тх)
или, что то же самое,
[т г^тЛ+г^Х. (8.19)
Мы же линейную функцию а + ЬХ ищем, исходя лишь из некоторого
количества имеющихся наблюдений. Для нахождения функции с
наилучшим соответствием наблюдаемым значениям используем метод
наименьших квадратов. Следовательно, находим коэффициенты а и b так, чтобы
сумма квадратов отклонений наблюдаемых значений от значений на
прямой линии регрессии оказалась наименьшей:
Vq>- (а + Ьхд)2 - min.
i
Исследуя на экстремум эту функцию аргументов а и b с помощью
производных, можно доказать, что функция принимает минимальное
значение, если коэффициенты а и b являются решениями системы
!Lx)a+{lLxbb = lLXiyi
' ' (8-20)
Решая эту систему уравнений относительно а и Ь, получаем
"(5>)-(2»(2>)
* = —'-( л-7 ^— (8-2|>
i i
(Х*И2>)-(2>И5>)
а = — / Л / V—'■ • (8-22)
»(5>0-(5»
352

Чтобы отличать найденные наилучшие значения коэффициентов b и а
вида (8.21)—(8.22) от всех других, обозначим их соответственно р и ос.
Тогда линейная модель, наилучшая в смысле метода наименьших квадратов,
имеет вид у = ос + $х.
Заметим, что р, коэффициент при х, равный Ь в выражении (8.21),
можно представить как
^(Xi-xXyi-y)
Р = -^=- Z-T-. (8.23)
2j.Xi-x)
i
Домножив числитель и знаменатель этой дроби на
Щ^)'
и сравнив полученное выражение с выражением выборочного
коэффициента корреляции (8.4), легко удостовериться, что
Р = г/*, (8.24)
где sx, s — выборочные стандартные отклонения
Число из соотношения (8.24) называют выборочным коэффициентом
регрессии Y на X. В дальнейшем для него также будем использовать
обозначение рух, т. е. [см. (8.24)]
Рух = 'А (8.25)
Коэффициент а в линейной модели у = а + $х [напомним, что
посредством а обозначено число а, являющееся решением системы (8.20)] можно
находить не по формуле (8.22), а непосредственно из второго уравнения
системы (8.20):
а = а = у - Рухх. (8.26)
Итак, по числовым данным парных наблюдений (х, у) найдено
выборочное уравнение линейной регрессии Уна X.
у = а + рх,
где р и а определяются как решения системы (8.20) в виде (8.21), (8.22)
либо, в другой записи, по формулам (8.24), (8.26).
Чтобы отличать значения у, относящиеся к уравнению регрессии,
пометим их: будем обозначать у. Тогда выборочное уравнение линейной
регрессии
у = а + р*
или в другой записи
у = у + РуЛх - х). (8.27)
23 - 3529 353

Таблица 8.6
Xj
167
169
170
170
172
173
174
175
179
180
Yfi = 1729
У,
169
171
166
172
180
176
177
182
182
186
5> = 1761
*,2
27 889
28 561
28 900
28 900
29 584
29 929
30 276
30 625
32 041
32 400
£x? = 299 105
i
Х.У;
28 223
28 899
28 220
29 240
30 960
30 448
30 798
31 850
32 578
33 480
V х,у; = 304 696
Согласно последнему уравнению, каждому наблюдаемому значению х,
соответствует не только наблюдаемое yif но и значение у-,,
удовлетворяющее уравнению регрессии, т. е.
У1=У+ Р„(*/ " *)■ (8.28)
Коэффициенты аир, полученные по выборочным данным,
естественно, отличаются от соответствующих коэффициентов в уравнении
регрессии генеральных совокупностей Y на X, т. е. являются их оценками. По
этим оценкам мы можем проверить гипотезы о равенстве коэффициентов
а и b в уравнении регрессии конкретным числам.
Однако предварительно рассмотрим конкретный числовой пример
нахождения выборочного уравнения регрессии Уна X.
Пример. По данным примера § 8.2 о зависимости роста взрослых
сыновей (Y) от роста их отцов (X) требуется найти выборочное уравнение
регрессии Уна X. Напомним данные десяти парных наблюдений:
*/
У;
180
186
172
180
173
176
169
171
175
182
170
166
179
182
170
172
167
169
174
177
Поскольку мы после нахождения уравнения регрессии будем строить
график, то гораздо удобнее пользоваться упорядоченными данными.
Проведем упорядочивание данных по значениям *,. Получаем новую таблицу:
*/
У;
167
169
169
171
170
166
170
172
172
180
173
176
174
177
175
182
179
182
180
186
Для упрощения вычислений составим расчетную табл. 8.6, в которую
занесем необходимые численные значения.
354

186 --
184 --
182 —
180 ~-
178 --
176 -~
174 —
172 —
170 —
168 —
166 --
л.
у = -59,349 + 1,3617х
166 168 170 172 174 176 178 180 182
Рис. 54.
Согласно формуле (8.21), вычисления коэффициента регрессии,
_ 10 • 304 696- 1729 • 1761
Рух
10 • 299 105 - 17292
а по формуле (8.22) (где а = а)
_'299 105 • 1761 - 1729 • 304 696
1,3617,
а =
-59,349.
10 • 299105- 17292
Таким образом, выборочное уравнение регрессии имеет вид
у = -59,349 + 1,3617*.
Нанесем на координатной плоскости точки (*,-, у,) и отметим прямую
регрессии (см. рис. 54).
Замечание. Чтобы начертить график прямой, достаточно задать две ее
точки. Например, полагая х = 167 из уравнения прямой, получаем
у~ 168,055, при х= 180 находим у ~ 185,757. Далее наносим полученные
две точки на координатную плоскость и соединяем их прямой.
На рис. 54 видно, как располагаются наблюдаемые значения
относительно линии регрессии. Для численной оценки отклонений у( от yt, где у., —
23*
355

Таблица 8.7
х,
167
169
170
170
172
173
174
175
179
180
У,-
169
171
166
172
180
176
177
182
182
186
h
168,055
170,778
172,140
172,140
174,863
176,225
177,587
178,949
184,395
185,757
h - у»
-0,945
-0,222
6,140
0,140
-5,137
0,225
0,587
-3,051
2,395
-0,243
наблюдаемые, а у, — определяемые регрессией значения, составим табл. 8.7.
Значения yt вычислены согласно уравнению регрессии [также см. (8.28)].
Заметное отклонение некоторых наблюдаемых значений от линии
регрессии объясняется малым числом наблюдений. При исследовании
степени линейной зависимости Y от X число наблюдений учитывается. Сила
зависимости определяется величиной коэффициента корреляции,
вычисленного ранее. В нашем примере гв = 0,887, что свидетельствует о достаточно
высокой зависимости Y от X.
Замечание. Совершенно аналогично можно найти и уравнение
регрессии Jif на Yвида (8.27), но, поменяв местами х и у, т. е. положив у в
качестве независимой переменной, ах — функция от у. Тогда уравнение
регрессии
х = х+ рху(у - у), где рху = /v?. (8.29)
sy
В математической постановке задачи безразлично, какую из
переменных выбрать независимой, а какую зависимой от нее, поскольку речь идет
лишь о двух наборах чисел. Заметим, что уравнения (8.29) и (8.27), как
правило, не совпадают. В практических задачах обычно имеет смысл лишь
односторонняя зависимость. Например, в рассмотренном выше примере
нелогично рассматривать зависимость X от Y (рост отца в зависимости от
роста сына), хотя такая постановка задачи также не исключается.
Итак, вернемся к нашей теории. Линия регрессии представляет
множество средних значений. Мы можем вычислить характеристику разброса
значений у относительно линии регрессии. Определим эту характеристику
выражением
л
/- 1
356

Величина } называется остаточной дисперсией или дисперсией
относительно линии регрессии. Эта величина — одна из оценок дисперсии
случайной величины Y. Деление в (8.30) на (п - 2) обеспечивает несмещенность
этой оценки.
Выбор коэффициентов а и р в уравнении регрессии с помощью метода
наименьших квадратов гарантирует минимальное значение }2. Остаточная
дисперсия } связана с коэффициентом корреляции гв равенством
регулирующим взаимоотношения между линейной регрессией и линейной
корреляцией.
8.7. Проверка гипотез о параметрах уравнения регрессии
Коэффициенты линейной регрессии аир, находимые по выборочным
данным, являются лишь оценками соответствующих коэффициентов
теоретической регрессии. Проверим гипотезы о равенстве аир конкретным
значениям, которые, как мы предполагаем, являются истинными
значениями коэффициентов.
Начнем с коэффициента регрессии Ь. Введем нулевую гипотезу:
Я0: Ъ = Ь0,
где Ь0 — число. Альтернативная гипотеза
Я,: Ь ф Ь0.
В качестве критерия используем статистику Ть, реализацией которой
является величина
tB = ^^, (8.32)
где
s, = . s , (8.33)
J(n-l)s2x
т. е.
th = (P ~.bo)SxJh~zr\. (8.34)
s
Статистика Ть имеет распределение Стьюдента с п — 2 степенями
свободы. Следовательно, для проверки нулевой гипотезы можно применить
критерий Стьюдента. Значение ТЬнабл определяется выражением (8.34), а
критическое значение гкр при выбранном уровне значимости и имеющемся
числе степеней свободы находим из табл. 6 Приложения 2. Если \ tb\ < tKp,
то гипотеза Я0 принимается, следовательно, b = b0, иначе, если | tb \ > tKp, то
принимается альтернативная гипотеза b ф Ь0.
Далее проверим гипотезу о равенстве конкретному числу свободного
члена в уравнении регрессии, т. е.
Я0: a = aQ
357

при альтернативной гипотезе
Я,: а ф а0.
Критерием проверки нулевой гипотезы возьмем статистику Та,
реализацией которой служит величина
t„ =
во
(8.35)
где
*.-*! +
^ . (8.36)
(л-1)4
Статистика Та имеет распределение Стьюдента с (п — 2) степенями
свободы. Следовательно, tKp можно найти по табл. 6 Приложения 2, задав уровень
значимости и число степеней свободы. Значение Гонабл находится по (8.35).
Для проверки нулевой гипотезы нужно сравнить, как обычно, Гонабл и гкр.
Задание. Используя данные примера о зависимости роста взрослых
сыновей от роста их отцов в уравнении регрессии (см. § 8.6)
у = -59,349 + 1,3617*,
проверьте нулевые гипотезы относительно коэффициента регрессии, Ь = О
и Ь = 1, и нулевые гипотезы относительно свободного члена, а = -60,
а = -50.
Коэффициенты аир находятся по конкретной выборке, для различных
выборок они будут разными, т. е. а и р являются случайными величинами,
оценками истинных коэффициентов регрессии. Естественно, что эти
случайные величины имеют свои средние (истинные значения
коэффициентов) и свои стандартные отклонения. Стандартные отклонения
коэффициентов, ар и оа, называются стандартными ошибками коэффициентов
регрессии. Значения jp и sa, вычисляемые по формулам (8.33), (8.35), — это
соответствующие оценки для ар и аа. Стандартные ошибки также
используют при построении доверительных интервалов для оценки
коэффициентов регрессии.
8.8. Использование линейной регрессии в случае нелинейной
зависимости
Пусть имеются числовые данные парных наблюдений (х, у), всего п пар.
Исследуется корреляционная зависимость Y от X. Построение линейной
модели у = а + Ьх оказывается неэффективным; например, малое значение
коэффициента корреляции обесценивает построенную модель. В этом
случае можно попытаться построить нелинейную модель, которая "внутренне
линейна", а именно: можно попытаться преобразовать исходные данные
так, чтобы построенная по новым данным линейная модель оказалась
лучше предыдущей. Поясним сказанное конкретными преобразованиями.
Предположим, что исходные данные записаны в виде таблицы
X
У
*.
Ух
*2
Уг
х,
У;
*п
Уп
358

Вначале преобразуем данные независимой переменной X.
Обратное преобразование. В строке значений х запишем величины -
X;
(естественно, в случае, когда все х,. отличны от нуля), тогда
преобразованные данные имеют вид
\
X
У
Xi
У\
х2
Уг
1
X;
У!
Хп
Уп
Соответствующая линейная модель, построенная по этим данным,
У = а+Ь-,
оказывается относительно х нелинейной, но относительно величины - эта
X
модель, конечно же, линейна, что и позволяет для нахождения
коэффициентов а и b использовать приведенную выше теорию линейной рефессии.
Этим и объясняется термин "внутренне линейна", характеризующий ре-
фессионную модель.
Возможно, эта модель будет более удачной, чем предыдущая.
Логарифмическое преобразование. Если все наблюдаемые значения х-,
положительны, то вместо исходных данных х,- можно взять величины In х,- ,
тогда преобразованные данные запишутся в виде
In х
У
In х,
Ух
In Xj
Уг
In х,-
У;
lnx„
Уп
и по ним можно построить линейную модель
у = а + b In x,
которая линейна относительно In x, но, конечно же, нелинейна
относительно х.
Преобразование типа степени. Если все х,- положительны, то вместо
исходных данных х-, можно взять значения (х,)с, где с — некоторая
постоянная (например, при с = 3 все х, возводятся в куб, а при с = - из х,-
извлекается квадратный корень и т. д.). Тогда преобразованные данные
запишутся в виде
Xе
У
*.с
Ух
*/
Уг
х?
У;
хс
лп
Уп
а соответствующая линейная модель окажется такой:
у = а + bxf (с — заранее заданная постоянная).
Преобразование отрицательных данных. Если среди наблюдаемых
значений X/ имеются нули или отрицательные значения, то операция
логарифмирования или извлечения квадратного корня для этих величин
невозможна. В этом случае все х( можно сместить на одно и то же число, а затем вы-
359

полнить выбранную операцию логарифмирования, извлечения корня и
т. д. Например, вместо (х, : -1, 0, 1, 2) можно исследовать, добавив 2,
последовательность (2 + дс,: 1, 2, 3, 4), значения которой уже допускают,
например, логарифмирование. Таким образом, построенная модель,
линейная относительно новых данных, имеет вид
у = а + Ь 1п(2 + х).
Можно строить модели и преобразовывая зависимую переменную у.
Например, модель у = ах* легко сводится к линейной модели в
результате операции логарифмирования обеих частей равенства:
In у = In a + b In х.
Таким образом, вместо значений xt можно взять преобразованные
величины In X/, а вместо yt - In yr
Замена ys на - приводит к модели
у а + Ьх'
Таким образом, метод построения линейной модели может быть
использован и для построения нелинейных моделей.
Разумеется, множество нелинейных моделей, которые являются
"внутренне линейны", не ограничивается рассмотренными выше случаями.
8.9. Мера любой корреляционной связи.
Выборочное корреляционное отношение
Коэффициент корреляции г^ позволяет определить силу линейной
корреляционной связи. Если же зависимость между Хи Удалека от линейной,
то для определения тесноты корреляционной связи необходим другой
показатель.
Рассмотрим регрессию Уна X, т. е. полагаем Хв качестве независимой
величины, а У зависит от X, причем зависимость корреляционная: X влияет
на значения, принимаемые У, но не предопределяет их однозначно в силу
наличия еще каких-то случайных воздействий на У В наших рассуждениях
функциональная зависимость Кот Хне исключается, а просто является
частным случаем корреляционной.
Пусть парные наблюдения оформлены в виде корреляционной таблицы
вида 8.3 (см. § 8.5). Из таблицы видно, что все выборочные значения
оказываются разбитыми на группы: при X = х, и различных значениях У —
первая группа, при X = х^ и различных значениях У — вторая группа и т. д.
Всего к групп. В каждой /-й группе мы вычисляли среднее значение у [см.
(8.14)], которое называли условным средним при Х=х,. Фактически
условные средние в соответствии с нашим разбиением являются групповыми
средними.
Далее в каждой группе мы можем вычислить выборочную дисперсию, т.
е. величину, характеризующую разброс значений в группе. Среднее
арифметическое значение выборочных дисперсий, взвешенное по объемам
групп — это выборочная внутригрупповая дисперсия.
360

Зная групповые средние ух. и общую среднюю у, можно найти
выборочную межгрупповую дисперсию, т. е. дисперсию групповых средних
относительно общей средней. Если использовать терминологию "X —
воздействующий фактор, a Y — отклик на это воздействие", то межгрупповая
дисперсия — это факторная дисперсия по фактору X.
И наконец, рассматривая все имеющиеся значения у, можно вычислить
общую дисперсию, т. е. дисперсию у относительно общей средней у.
Заметим, что в дисперсионном анализе мы уже рассматривали общую,
межгрупповую и внутригрупповую дисперсии. Только разбиение на
группы осуществлялось по уровням фактора, и в соответствии с этим
межгрупповую дисперсию мы называли факторной, а внутригрупповую —
остаточной дисперсией.
Для любой совокупности (генеральной или выборочной) справедливо
соотношение дисперсий
А*ц = А™, + А.СЖП,- (8-37)
Обратим внимание на DBHrp. Внутригрупповая дисперсия зависит от
групповых дисперсий (она — их среднее арифметическое значение): чем
меньше групповые дисперсии, тем меньше и DMn>. В частном случае
функциональной зависимости (не обязательно линейной), когда каждому х
соответствует только одно значение у, все групповые дисперсии равны нулю,
и, следовательно, DBHrp = 0. Если же корреляционная зависимость далека
от функциональной, то каждому значению х соответствует много
различных далеко разбросанных значений у\ следовательно, растут групповые
дисперсии, и чем сильнее они отличаются от нуля, тем больше значение
/)внгр. Ввиду соотношения (8.37) внутригрупповая дисперсия не может быть
больше общей дисперсии. Таким образом, DBHrp является характеристикой
силы корреляционной зависимости Y от X: чем меньше Д,нгр, тем сильнее
корреляционная зависимость, и при Z)BHrp = 0 зависимость функциональная.
Однако для практического применения гораздо удобнее использовать не
Д,нгр, а /)межгр, которая, согласно соотношению (8.37), оказывается при
функциональной зависимости равной Do6ul (поскольку Dmrp = 0), тогда
■^межгр _ 1
А>бщ
С уменьшением корреляционной связи Y от X также уменьшается и
отношение
А>бш
которое при отсутствии корреляционной зависимости (т. е. при
Ашгр = А>бш) Равно нулю. Точно так же, но для линейной зависимости,
ведет себя и коэффициент корреляции.
Определение. Коэффициентом детерминации (причинности) называют
число R2:
R2 = Дмежгр (838)
D,
общ
361

Коэффициент детерминации R2 указывает долю факторной дисперсии
фактора X в общей дисперсии, т. е. численно выражает, какая часть
вариации Y связана с воздействием фактора X.
Определение. Значение R = J1? называют выборочным корреляционным
отношением.
Легко заметить, что R равно отношению соответствующих средних
квадратических отклонений.
Если перейти к нашим выборочным данным, то
А,ежп> = l£nXiCyXl-'y)2 (8-39)
I
А*ш = -УЧСи-й2- (8-4°)
I
Следовательно, рабочая формула для вычисления R2 имеет вид
-2
R2 = ± —■ (8-41)
Сформулируем свойства корреляционного отношения R.
1. 0< R< 1.
2. При R = О признаки X и Y не связаны корреляционной
зависимостью.
3. При R = 1 зависимость между Хи Y функциональная.
4. Для любой выборки признаков Хи Yсправедливо соотношение:
Л > \гв |,
где гв — выборочный коэффициент корреляции.
5. Если R = | гв |, то корреляционная зависимость между Xw Y —
линейная, и все точки парных наблюдений (х„ yt) лежат на прямой линии
регрессии.
Коэффициент детерминации, полученный в виде (8.41), исходя из
выборочных данных, является оценкой истинного значения (теоретического)
для коэффициента детерминации. Проверить значимость R2 можно,
используя критерий Фишера. Нулевая гипотеза
Щ: R = О,
соответственно
Н{. R>0.
В качестве критерия используется статистика
Fr = —^— ' п~т (8 42)
1-Я2 л»" Г К '
где т — число параметров уравнения регрессии. Статистика FR имеет
распределение Фишера с (т - 1; п - т) степенями свободы. Критическая
точка находится по табл. 7 Приложения 2, а наблюдаемое значение
критерия вычисляется непосредственно. Если наблюдаемое значение FR превос-
362

Таблица 8.8
R

Характеристика зависимости
0,1 - 0,3
Слабая
0,3 - 0,5
Умеренная
0,5 - 0,7
Заметная
0,7 - 0,9
Высокая
0,9 - 0,99
Весьма
высокая
ходит критическое значение, то нулевая гипотеза отвергается, и величина
R2 признается значимой.
При использовании R как показателя силы связи между X и Y можно
применить качественную оценку зависимости. Для этих целей имеется так
называемая шкала Чеддока (табл. 8.8).
При значениях R, меньших чем 0,7, коэффициент детерминации R2
оказывается меньше 0,5, т. е. на долю вариации факторным признаком
приходится менее 50% от влияния всех признаков, воздействующих на
отклик. В этом случае полученная модель большой ценности не
представляет, лучше попытаться найти другую модель (другой вид зависимости) с R2,
большим чем 0,5.
8.10. Простейшие случаи нелинейной регрессии
Выборочная функция регрессии подбирается в соответствии с
имеющимися наблюдениями. Если график регрессии
ух = ф(х) или ху = \\i(y)
не является прямой линией, т. е. ср(х), ц/(у) — нелинейные функции, то и
соответствующую корреляцию называют нелинейной.
Наиболее распространенной нелинейной регрессией является
параболическая модель
ух= ах2 + Ьх + с (или у = ах2 + Ьх+ с). (8.43)
Конкретные значения коэффициентов вычисляются, исходя из метода
наименьших квадратов. Следовательно, коэффициенты а, Ь, с
определяются таким образом, чтобы сумма квадратов отклонений наблюдаемых
значений от значений на линии регрессии
2^[у,-((и4 + Ьх, + с)]2
I
была бы наименьшей. Вновь, как и в случае линейной регрессии,
используя производные для нахождения экстремума функции, можно доказать,
что коэффициенты а, Ь, с должны удовлетворять системе уравнений:
(х\а + (х3)пЬ + (х\с = (х2у)п
(?)па + (?)пЬ + хпс = (х~у)п
(х2)па + хпЬ + с = у„,
(8.44)
363

где
_ 1
хп = -Y*,, уп = -Y>,-, (x2),, = -Ух],
ni—i п*-< п*-*
1 = 1
~3ч _ lv- 3 ,~л _ 1
1
(*3)«= пТ,х''(ху)п = JLXiyi>(ху)»= ^Lx]yi- (845)
1=1 1=1 1=1
В системе трех линейных алгебраических уравнений (8.44) неизвестными,
искомыми значениями являются а, Ь, с; используемые в системе суммы
вычисляются по формулам (8.45), исходя из данных парных наблюдений.
Вычислив, согласно (8.45), значения коэффициентов системы и решив
ее, найдем а, Ь, с.
Подставив найденные из системы параметры в (8.43), получим искомое
уравнение регрессии.
Рассмотрим пример подбора регрессионной модели, наиболее
соответствующей имеющимся числовым данным.
Пример. В результате эксперимента над случайными величинами X и Y
получены парные наблюдения.
х,
У!
1
3,2
2
4,2
3
2,7
4
0,7
5
1,2
6
2,4
7
3,7
8
3,1
9
4,3
10
4,9
Требуется подобрать наиболее подходящую модель, отражающую
зависимость Y от X.
Заметим, что наши десять парных наблюдений можно оформить в виде
корреляционной таблицы размером 10 х 10, в 10 клетках которой частота
встречающихся пар значений равна 1, а в остальных 90 клетках частота
равна 0 (в таблице типа 8.3 частоты miy = 0 при / *Д Поэтому все формулы
и соотношения, основанные на данных корреляционной таблицы, без
труда переносятся и в наш случай.
Поиск подходящей регрессионной модели начнем с линейной
регрессии. Рассмотрим зависимость вида
у = а + Ьх.
Согласно формулам (8.21), (8.22) вычисления коэффициентов линейной
регрессии, можно найти а и Ь. Для этого вычисляем
£х, = 55, ]>>,- =30,4, J^xj = 38,5, £зд = 181,3.
i i i i
Подставляя в формулы (8.21), (8.22), находим
а = 2,11, Ъ = 0,17.
Таким образом, уравнение линейной регрессии имеет вид
у = 0, 17jc + 2, 11.
Определим, сколь точно полученное уравнение отражает истинную
зависимость Y от X. Для этого вычислим значение коэффициента
детерминации R2. Воспользуемся рабочей формулой (8.41)
364

Таблица 8.9
Таблица 8.10
_
Ух,
2,28
2,45
2,62
2,79
2,96
3,13
3,30
3,47
3,64
3,81
_
У*-У
-0,76
-0,59
-0,42
-0,25
-0,08
0,09
0,26
0,43
0,6
0,77
_
(Ух,~ У)2
0,5776
0,3481
0,1764
0,0625
0,0064
0,0081
0,0576
0,1849
0,36
0,5929
Z = 2,3745
У,
3,2
4,2
2,7
0,7
1,2
2,4
3,7
3,1
4,3
4,9
У:~ У
0,16
1,16
-0,34
-2,34
-1,84
-0,64
0,66
0,06
1,26
1,86
(У:-у)7
0,0256
1,3456
0,1156
5,4756
3,3856
0,4096
0,4356
0,0036
1,5876
3,4596
Z = 16,244
-2
YnXi(yXl-y)
52 _
Rl = -l
ПУ,{У;-У)2
В нашей корреляционной таблице все пх. = 1 и все п = 1. Значение у
легко вычисляется: у = 3,04. Найдем средние значения ух., исходя из
найденного уравнения регрессии:
Л, = 0,17 • 1 +2,11=2,28
^ = 0,17 • 2 + 2,11=2,45
Л, = 0,17 • 3 + 2,11 = 2,62
£,„ = 0,17 • 10+2,11 = 3,81.
Занесем полученные данные в табл. 8.9.
Далее вычислим знаменатель в выражении (8.41), заполнив для этого
табл. 8.10.
И наконец, получаем
R2 = 1>™1 * 0, 1462 , R ~ 0,3824.
16,244 '
Таким образом, ввиду малости величины R зависимость между X и У,
выражаемая линейной регрессионной моделью, умеренная. Для
практического использования модель непригодна.
Проверим гипотезу Я0: R = 0. Для этого воспользуемся критерием
Фишера [см. (8.42)]
_ R2
п — т
Fr l-R2 rn-V
При п = 10, т = 2 получаем
365

F = 0,1462 10-2 , .7ft
набл 1-1462 2-1 ~1':>/u-
По таблице критических значений распределения Фишера (см. табл. 7
Приложения 2) находим
FKp(0,05; 1; 8) = 5,32.
Следовательно, FHa&n находится в области принятия гипотезы и вполне
возможно, что теоретическое значение R равно нулю.
Продолжим исследование с помощью другой модели: например, в
линейной модели вместо величины х введем слагаемое е*. Тогда получаем
модель
у = а + be*,
которая относительно х, конечно же, нелинейна, но является линейной
относительно переменной е*. Преобразуем исходные данные для х„ составим
соответствующую таблицу.
*••
е*
У:
1
2,718
3,2
2
7,389
4,2
3
20,086
2,7
4
54,598
0,7
5
148,413
1,2
6
403,429
2,4
7
1096,633
3,7
8
2980,958
3,1
9
8103,084
4,3
10
22026,47
4,9
Введя вместо х новую переменную е*, мы тем самым расширили
диапазон значений х, что хорошо видно из таблицы, и колебания значений У,
возможно, окажутся не столь резкими, как на малом промежутке
изменения х, что в конечном итоге позволит более явно проявиться зависимости
у от х.
Проделав вычисления, так же как и в предыдущем случае модели
линейной по х, для новой модели с преобразованными данными получаем
— уравнение регрессии: у = 0,000117е* + 2,63248;
— R2 = 0,370258, R = 0,608488;
— Fm6a = 4,703607, что соответствует уровню значимости 0,061936.
(Заметим, что данные вычисления были проведены на компьютере,
который избавляет нас от вычислительных трудностей.)
Итак, в исследуемой модели, согласно шкале Чеддока, зависимость
вариации У от вариации X следует признать заметной, изменение У на
37,0258% объясняется изменением Хл хотя все-таки эта величина,
характеризующая влияние X, остается менее 50%. Уровень значимости F- критерия
близок к стандартному 0,05, что позволяет с некоторой уверенностью
отвергнуть нулевую гипотезу R = 0.
Однако, несмотря на то что эта модель лучше предыдущей объясняет
зависимость вариации Y от X, все же она не очень пригодна для
практического применения: и недостаточно большое значение коэффициента
детерминации R2, и балансирование на грани стандартного уровня
значимости подчеркивают это.
Продолжим исследование, вводя новую модель в надежде, что она
окажется лучше предыдущих. Рассмотрим квадратическую зависимость, т. е.
модель параболического типа (8.43)
у = ах2 + Ьх + с.
366

Таблица 8.11
xi
1
2
3
4
5
6
7
8
9
10
_
Л
3,73451
2,92966
2,36875
2,05178
1,97875
2,14966
2,56451
3,22330
4,12603
5,27270
_ _
yXi - у
0,69451
-0,11034
-0,67125
-0,98822
-1,06125
-0,89034
-0,47549
0,18330
1,08603
2,23270
(Л," У?
0,482344
0,012175
0,450577
0,976579
1,126252
0,792705
0,226091
0,033599
1,179461
4,984949
I = 10,26473
Построение модели, привлекая статистические компьютерные
программы, не представляет труда. Однако в учебных целях представим и процесс
вычислений с использованием изложенной выше теории.
Коэффициенты а, Ь, с модели параболического типа находим из
системы линейных алгебраических уравнений (8.44). Предварительно
вычисляем по формулам (8.45)
х|0 = 5,5, ую = 3,04, (?)10 = 38,5, (?)10 = 302,5,
(?)10 = 2533,3, (^),о = 18,13, (7у)10 = 138,99.
Тогда система уравнений (8.44) такова:
2533, За + 302, 5Ь + 38, 5с = 138, 99
« 302, 5а + 38, 5Ь + 5, 5с = 18,13
38, 5а + 5, 5Ь + с = 3,04.
Единственное решение этой системы (которое можно также найти с
помощью компьютера или в результате громоздких вычислений) — это
а = 0,12197; b = -1,17076, с = 4,7833.
Таким образом, модель параболического типа имеет вид
у = 0.12197Х2 - 1,17076л: + 4,7833.
Найдем значения ух., т. е. значения у, удовлетворяющие найденному
уравнению регрессии при всех десяти наблюдаемых значениях х:
уХ1 = 0,12197 • I2 - 1,17076 • 1 + 4,7833 = 3,73451,
3^ = 0,12197 • 22 - 1,17076 ■ 2 + 4,7833 = 2,92966,
Все полученные значения занесем в таблицу. Также вычислим все
значения ~ух. - у и (ух. - у)2. Получаем табл. 8.11.
367

Итоговая сумма в табл. 8.11 позволяет вычислить коэффициент
детерминации R2:
-2
У\Пх,(Ух,~ У)
R2 = =£ = Щ^Т- = 0,631909
yOi-y)2 16'244
Напомним, что знаменатель в последней дроби был вычислен ранее
(см. табл. 8.10). Следовательно,
R = 0,794925.
Это значение R позволяет считать связь Y и Ху описываемую моделью
параболического типа, высокой (по шкале Чеддока). Эта модель объясняет
зависимость вариации Yот вариации Хна 63,1909%, что значительно
больше 50%; остальные почти 37% влияния на изменение случайной величины
Yопределяются другими причинами.
Соответственно столь большое отличие R2 от нуля позволяет полагать
это отличие значимым. Численно данное утверждение вновь можно
проверить по критерию Фишера:
J7 - r2 n-m _ 0,631905 .10-3 , пШ1г
*- " ГГЙ5 в ЙГМ " 0^68095 J3T-M08415,
FKp (0,05; 2; 7) = 4,74.
Так как FHa&n > FKp, то гипотеза R = 0 отклоняется, о чем мы
догадывались с самого начала.
Итак, модель параболического типа из трех рассмотренных является
наилучшей, наиболее адекватно отражающей зависимость Уот X.
Разумеется, можно попытаться построить и другие, более пригодные
для практического использования модели.
Для исследования корреляционной зависимости трех и более признаков
разработаны методы множественной корреляции, которые в данном
пособии не рассматриваются.
8.11. Выборочный коэффициент ранговой корреляции Спирмена
При исследовании зависимости признаков с помощью коэффициента
корреляции и исследовании зависимости регрессионными методами,
подбирая подходящие модели, мы за основу брали числовые значения
признаков, т. е. количественные показатели. При этом рассматриваемые
статистические критерии связаны с проверкой параметрических гипотез в
предположении известного закона распределения генеральной совокупности
вплоть до отдельных параметров. Однако в целом ряде задач признаки
имеют не количественные, а качественные характеристика. Таким образом
значение признака невозможно измерить, но разные значения можно
сравнивать между собой и располагать их в порядке возрастания или
убывания качества. Следовательно, все множество значений признака мы
можем упорядочить по качественной характеристике. Для каждого объекта
такого упорядоченного множества можно поставить в соответствие
некоторое число: его порядковый номер. Обычно значения признака (или
объекты, как носители этого признака) принято располагать в порядке ухудше-
368

ния качества (например, I сорт, II сорт и т. д. Или 1-е место, 2-е место,
3-е место и т. д.), т. е. любой последующий объект по своему качеству
уступает предыдущему. Порядковый номер каждого объекта назовем рангом,
тогда упорядочивание объектов — ранжирование. Таким образом, каждому
наблюдаемому значению качественного признака поставлено в
соответствие натуральное число, и мы вновь имеем набор чисел — выборку. Но эти
числа (ранги) не представляют закон распределения признака и
характеризуют не внутренние особенности объекта, а лишь указывают его место по
отношению к другим объектам. Часто данной информации бывает
достаточно для сравнения различных признаков и определения их степени
зависимости.
Такие порядковые признаки нередко встречаются в клинических
испытаниях, а также при оценке различных психологических тестов.
Для исследования качественных показателей мы можем строить
некоторые гипотезы, которые проверяются с помощью соответствующих
критериев, использующих ранги. Эти критерии непараметрические и не
используют какие-либо данные о законах распределения. Если применить
ранговый критерий к количественным показателям, то он окажется менее
эффективным, чем соответствующий параметрический критерий. Дело в
том, что при переходе от конкретных чисел к рангам часть информации,
имеющейся в выборке, теряется, потому что выборка конкретных
значений более содержательна в информационном плане, нежели простое
упорядочивание. При применении к количественным признакам ранговые
критерии реже, чем параметрические, отвергают нулевую гипотезу. И если
нулевая гипотеза отвергнута ранговым критерием, то и параметрические
критерии не приведут к иному результату.
К достоинствам непараметрических критериев, в частности ранговых,
кроме области применимости, следует отнести простоту вычислений и
быстрые способы опровержения нулевой гипотезы.
Пусть имеются п независимых объектов, для которых рассматриваются
два качественных признака Aw В. Требуется оценить силу связи этих
признаков.
Для подобной оценки мы можем использовать коэффициент
корреляции, вычисляемый по значениям рангов, которые проставляются объектам
в соответствии с рассматриваемыми признаками. Такой показатель
называется коэффициентом ранговой корреляции. Этот коэффициент можно
определить по-разному, мы рассмотрим коэффициент ранговой корреляции
Спирмена1.
Итак, имеющиеся п объектов рассортируем по признаку А в
соответствии с ухудшением качества. Объекту, оказавшемуся на /-м месте,
припишем ранг xif где х, = i — порядковый номер, / = 1, 2, ..., п. Для признака А
получим последовательность рангов дс„ Xj, ..., хп (Указанная
последовательность рангов фактически является последовательностью 1, 2, ..., п, если все
объекты различны по качественному признаку. Если же какие-то объекты
одинаковы по качеству, то им присваивается один и то же ранг, равный
'Можно упомянуть также коэффициент ранговой корреляции Кендалла, не
рассматриваемый в этой книге, который обобщается на случай нескольких независимых переменных.
Отметим, что используемый нами ранее коэффициент корреляции г называют коэффициентом
корреляции Пирсона.
24 — 3529
369

среднему арифметическому занимаемых ими мест. Например, 3-й и 4-й
объекты в последовательности одинаковы по качеству, тогда
*3 = *4 = ^ = 3,5.)
Теперь наши л объектов упорядочим по признаку В в порядке убывания
качества и каждому из них припишем ранг уь где у, уже не равно
порядковому номеру /. Методика проставления рангов у,- такая: индекс / при у,- по-
прежнему равен порядковому номеру объекта по признаку Л, а само
значение у, равно порядковому номеру объекта по признаку В. Например, если
объект по признаку А находится на 5-м месте, а по признаку В — на 9-м
месте, то х5 = 5, у5 = 9.
Таким образом, получаем две последовательности рангов:
по признаку А: *,, ^, ..., хп\
по признаку В: уь у2, ..., у„.
Данные последовательности из л элементов будем рассматривать как
выборки из генеральных совокупностей X и Y соответственно.
Следовательно, можно вычислить выборочный коэффициент корреляции гв.
±У(х,-х)(у,-у)
г = Ц±±
'в »
SxSy
где sx, sy — выборочные стандартные отклонения Хи Y соответственно.
Поскольку наши значения xit у, — не произвольные числа, а вполне
определенные от 1 до л, то формула для вычисления гв конкретизируется.
Можно доказать, что получится величина (обозначим полученное значение
вместо гв посредством рв, чтобы отличать коэффициент ранговой
корреляции от коэффициента корреляции Пирсона):
Рв= 1-г-У^, (8.46)
I = 1
где d, = х, - у,.
Значение рв, вычисляемое по формуле (8.46), называют коэффициентом
ранговой корреляции Спирмена. Рассмотрим его свойства.
1. Если между признаками А и В имеется полная прямая зависимость, т.
е. и по тому и по другому признаку все соответствующие ранги х, и у,
одинаковы, то рв = 1.
Действительно, при всех х, = у, следует, что все d, = 0, и тогда из (8.46)
получаем рв = 1.
2. Если между признаками Аи В имеется противоположная зависимость
[т. е. для признака А ранги: 1, 2, ..., л, а для признака В ранги: п, (п - 1),
..., 1], то рв = -1.
В этом случае
dx = 1 - п, d2 = 3 - л, ..., dn = (2л - 1) - л.
Можно доказать, что
JT^d] = (1-„)2 + (3-л)2 + ... + [(2л-1)-л]2 = ... = ^,
i= 1
370

Таблица 8.12
Объект
Ранг по 1-му признаку
Ранг по 2-му признаку
Разность рангов (d)
А
4
5
-1
В
1
4
-3
С
2
1
1
D
5
3
2
Е
3
2
1
а тогда, согласно (8.46),
_ 1 6 п — п _ ,
Pj- I"- ' —з -1-
п — п J
3. Если между признаками А и В отсутствует полная как прямая, так и
противоположная зависимость, то коэффициент рв находится в пределах
от -1 до +1, и чем меньше он отличается от нуля, тем меньше и
зависимость между признаками.
Свойство 3 примем без доказательства.
Так же как и в случае количественных признаков, значение рв подвержено
случайным воздействиям и, вообще говоря, отличается от истинного
(теоретического) значения коэффициента ранговой корреляции р, имеющего
место для генеральных совокупностей Хи Y. Проверить гипотезу Я0: р = О
можно с помощью соответствующего критерия. При п < 50 значение рнабл
вычисляется непосредственно по формуле (8.46), а значение ркрит можно
найти по табл. 12 Приложения 2 критических значений коэффициента
ранговой корреляции Спирмена.
В случае п > 50 применяется критерий Стьюдента. При этом
используется в качестве критерия статистика
Т= , р Л^!. (8.47)
имеющая распределение Стьюдента с п — 2 степенями свободы. Тогда
Т = рв In-7
1 набл . V" ^ ,
л/1 ~Рв
а значение t находят по табл. 6 Приложения 2 критических точек
распределения Стьюдента.
Если |Гнабл| < /кр, то нулевая гипотеза р = 0 принимается, если |Гнабл| > /кр,
то принимается гипотеза р * 0.
Пример 1. Исследуется группа из 5 студентов, Л, В, С, D, Е, по двум
качественным признакам: 1) свойства характера (жизнерадостность); 2)
успехи в учебе. Проранжируем наших студентов по обоим признакам.
Полученный результат занесем в табл. 8.12.
По найденным значениям разностей di и п = 5 находим выборочный
коэффициент ранговой корреляции Спирмена. Предварительно вычислим
24* 371

Таблица 8.13
Рост
значение, см
167
169
170
170
172
173
174
175
179
180
отца
Ранг
1
2
3,5
3,5
5
6
7
8
9
10
Рост сына
Значение, см
169
171
166
172
180
176
177
182
182
186
Ранг
2
3
1
4
7
5
6
8,5
8,5
10
d,
-1
-1
2,5
"0,5
-2
1
1
"0,5
0,5
0
df
1
1
6,25
0,25
4
1
1
0,25
0,25
0
I d} = 15
5
Y^d] = 1 + 9+1+4+1 = 16.
i= 1
Тогда
_ 1 6 • 16 _ Л л
Далее проверим нулевую гипотезу Я0: р = 0.
Найдем ркрит по табл. 12 Приложения 2: при уровне значимости а = 0,02
значение ркрит равно 1.
Значение рнабл = рв = 0,2. Следовательно, |рнабл| < Р|Срит , и на уровне
значимости а = 0,02 гипотеза р = 0 принимается. Вывод по имеющимся
данным: зависимость между жизнерадостностью и успехами в учебе студентов
не доказана. Если данная зависимость имеется, то она носит нелинейный
характер и для ее нахождения нужны другие методы.
Применим наш критерий к данным примера о зависимости признаков
роста взрослого сына от роста отца (см. § 8.2).
Пример 2. По имеющимся данным
*,•
У,
180
186
172
180
173
176
169
171
175
182
170
166
179
182
170
172
167
169
174
177
требуется исследовать зависимость роста сына (Y) от роста отца (X) с
помощью коэффициента ранговой корреляции Спирмена.
Проранжируем имеющиеся данные и полученные результаты занесем в
табл. 8.13.
372

Находим значение коэффициента ранговой корреляции Спирмена:
Рв = 1-
6 • 15
103 — 10
«0,9091
Сравниваем полученное значение рв = рнабл с табличным значение ркрит,
найденным по табл. 12 Приложения 2. Из таблицы видим, что даже при
самом высоком уровне значимости а = 0,001 значение р, = 0,903, и
(I лт к КрИТ ' '
Рнабл I > Ркрит- Тем самым гипотеза р = 0 уверенно должна быть отвергнута
и принята гипотеза р * 0. Таким образом, вновь статистически
подтверждена гипотеза о зависимости роста взрослого сына от роста его отца.
Заметим, что данный метод применен к количественным признакам,
для которых ранжирование — простое упорядочивание (по возрастанию
или убыванию значений безразлично).
Также заметим, что найденное значение рв = 0,9091 несколько
превосходит вычисленное ранее значение коэффициента корреляции гв = 0,887
(см. § 8.2).
8.12. Непараметрические методы оценки корреляционной зависимости
В предыдущем параграфе рассмотрен один из непараметрических
методов исследования корреляционной зависимости, коэффициент ранговой
корреляции Спирмена, который основывается лишь на рангах и не
использует информацию о конкретных законах распределения случайных
величин. Он, как и коэффициент корреляции Пирсона, характеризует
тесноту корреляционной связи признаков.
Приведем еще ряд характеристик, оценивающих тесноту связи
различных факторов (признаков), причем не только количественных, но и
качественных. В первую очередь это касается признаков, представленных
двумя альтернативными исходами типа "да - нет", "жив — умер", "заболел —
не заболел" и т. д. В этом случае показатели тесноты связи вычисляются с
использованием расчетных таблиц вида таблиц сопряженности
размерности 2 х 2 (см. табл. 6.3, § 6.11).
В табл. 8.14. а, Ь, с, d — конкретные наблюдаемые значения,
соответствующие различным исходам в каждом из двух признаков.
Таблица 8.14
^^•^^2-ой признак
1-ый ^\^^
признак ^^\^
Да
Нет
Итого
Да
а
с
а + с
Нет
Ь
d
b + d
Всего
a + b
с + d
n=a+b+c+d
373

Определение. Коэффициент ассоциации Д. Юла 1С, в соответствии с
приведенной таблицей находится по формуле
К = ad-be (8<48)
а ad+bc'
Коэффициент ассоциации К„ может принимать значения от -1 до +1.
Эти граничные значения могут достигаться в случае, когда одно из четырех
чисел а, Ь, с, d оказывается равным 0. Допустимо так же равенство нулю
сразу двух чисел, не находящихся в одной строке или одном столбце:
а = д = 0 или с = b = 0. В этих случаях Ка = ±1, и теснота связи между
признаками считается наиболее сильной. Причем также как и для
коэффициента корреляции, положительный или отрицательный знак К„
свидетельствует о прямой или соответственно обратной зависимости значений
признаков.
Замечание 1. В случае равенства нулю двух чисел в таблице,
находящихся в одной строке или одном столбце, один из признаков лишается
альтернативы. В этой ситуации коэффициент ассоциации неопределен и не
рассматривается.
Равенство нулю коэффициента ассоциации возможно в случае ad = be,
т. е. при пропорциональной зависимости значений. Такая зависимость, т.
е. 1^ = 0, свидетельствует об отсутствии связи между признаками.
Другой характеристикой тесноты связи между признаками служит
коэффициент контингенции К. Пирсона Кк :
К|:= t ad~bc (8.49)
J(a + d)(c + b)(a + c)(b + d)
Формулы для коэффициента контингенции (8.49) и коэффициента
ассоциации (8.48) различаются лишь знаменателями соответствующих дробей.
Коэффициент контингенции также изменяется от —1 до +1, но его значения
всегда (за исключением граничных случаев К^ = ±1) несколько меньше
значений коэффициента ассоциации. Значит, эта характеристика имеет тот же
смысл, что и 1^, но оценивает тесноту связи менее категорично.
Для качественной оценки силы связи при использовании
коэффициентов ассоциации Д. Юла и коэффициентов контингенции К. Пирсона
можно воспользоваться шкалой Чеддока (см. табл. 8.8, § 8.9).
Рассмотрим конкретный пример вычисления Ка и Кк. Воспользуемся
данными примера 1, § 6.11, смертности от легочного туберкулеза среди
мужчин и женщин (см. табл. 6.1) (табл. 8.15).
В § 6.11 с помощью критерия х2 мы установили, что различие в
смертности от легочного туберкулеза (признак 2) среди мужчин и женщин
(признак 1) существенно. Значит признак 2 тесно связан с признаком 1. Теперь
оценим эту тесноту связи численно с помощью коэффициента ассоциации
Ка и коэффициента контингенции Кк.
к = ad-be = 153 • 83-68 • 111 = ft 9<-4.
а ad + bc 153 • 83 + 68 • 111 ' '
к = ad-be = 153 • 83-68 • 111 = Q n5
J(a + d)(c + d)(a + c)(b + d) V221 • 194 • 264 • 151
374

Таблица 8.15
^^\2-ой признак
1-ый ^-^^
признак ^^-^^
Мужчины
Женщины
Итого
Живы
153
111
264
Умерли
68
83
151
Всего
221
194
415
Хотя значения обоих коэффициентов К„ и Кк отличаются один от
другого, согласно шкале Чеддока, качественная характеристика тесноты связи
одна и та же: сила связи слабая. Логически эта характеристика вполне
закономерна, так как в нашем примере градация "мужчина - женщина" не
является определяющей для второго признака "живы — умерли", а лишь
оказывает некоторое влияние, наличие которого зафиксировал критерий х2
в § 6.11, а величину этого влияния и описывают коэффициент ассоциации
и коэффициент контингенции.
Замечание 2. Шкала Чеддока, предусматривающая использование лишь
положительных значений коэффициента в данной ситуации, может быть
применена к модулям соответствующих коэффициентов: | KJ и IKJ.
Заметим также, что шкала Чеддока представляет условную качественную
характеристику силы связи и не является математически строгой.
В случае, когда каждый из двух качественных признаков содержит более
чем два уровня значений (т. е. более двух групп значений), тесноту связи
признаков измеряют с помощью числовой характеристики: коэффициента
взаимной сопряженности. Для этой характеристики также нет единообразия:
следует различать коэффициент взаимной сопряженности К. Пирсона
Сп =
JL
1 + Ф2
и коэффициент взаимной сопряженности А. А. Чупрова
Сч =
JL
(8.50)
(8.51)
'V(*-1)(j-1)
где к х s — размерность соответствующей таблицы сопряженности
признаков, а значение ф2, называемое Показателем взаимной сопряженности,
находится по определенным формулам. Далее укажем способ вычисления
значения ф2 по имеющейся таблице сопряженности.
Пусть таблица сопряженности двух признаков Aw В имеет размерность
к х s, где к — количество уровней (групп) признака A, a s — количество
уровней признака В. Количество наблюдаемых значений, одновременно
относящихся к уровню А-, и к уровню Вр обозначим аг Тогда таблица
сопряженности имеет вид, представленный в табл. 8.16.
375

Таблица 8.16
n. Уровень при-
^n. знака В
Уровень ^*^^
признака А ^"^^^
А
А
А
Итого
*.
*11
°21
ак\
Щ
Вг
*12
а22
йю.
т2
в<
<*и
<hs
aks
*,
Всего
п\
П2
пк
В данной таблице в графе "Итого" проставлены суммарные значения по
строкам и по столбцам.
Вычисляем ф2 по следующей схеме:
из первой строки находим
г, = ('£L + 5i3 + ... + £L):„,;
из второй строки находим
<,-(£ + £ + ...+£):„,;
из последней строки находим
*-(# + £ + ••• + **):'*
далее
Ф2 = (г, + г2 + - + zk) - 1. (8.52)
Определив значение ф2, легко вычислить и коэффициенты взаимной
сопряженности Сп и Сч по формулам (8.50), (8.51).
Заметим, что хотя оба коэффициента Сп и Сч характеризуют одну и ту же
величину — силу связи признаков, наиболее употребительным является
коэффициент взаимной сопряженности Чупрова, поскольку он наряду с
показателем взаимной сопряженности учитывает и число групп в признаках.
Для практической иллюстрации вычисления коэффициентов Сп и Сч
обратимся к примеру 2, § 6.12, в котором установлено влияние процесса
обучения на результаты некоторого психологического теста.
Воспроизведем соответствующую таблицу сопряженности (табл. 6.4) (табл. 8.17).
По приведенной выше схеме вычислим значение показателя взаимной
сопряженности признаков ф2:
376

Таблица 8.17
Возраст школьников
Младшие
Средние
Старшие
Всего
Результаты теста
Низкие
10
6
7
23
Средние
15
16
13
44
Высокие
5
8
20
33
Всего
30
30
40
100
* = (IM+S:30=o-3ii;
*-ffi + £ + f> 40 = 0,452;
Ф2 = (Zi + Z2 + Zi) - 1 = (0,341 + 0,311 + 0,452) - 1 = 0,104.
Далее вычисляем коэффициенты взаимной сопряженности Сп и Сч
согласно формулам (8.50), (8.51):
Сп =
сч =
1 + ср
Ф2 = Ю7Т04 =
1,104
0,307;
_Ф_
0,104
= 0, 228
'V(*-i)(j-i) W(3-i)(3-i)
Найденные значения указывают на наличие связи между исследуемыми
признаками: результаты данного теста зависят от времени обучения.
Однако зависимость не слишком велика (шкала Чеддока классифицирует такую
зависимость как слабую или умеренно слабую), что вполне объяснимо
наличием других причин, влияющих на результаты тестирования. Фактор
времени обучения, хотя и влияет на изменение зависимого признака, все
же не является определяющим.
Задачи и упражнения
1. Какая зависимость называется корреляционной? В чем отличие
корреляционной зависимости от функциональной?
2. Какой смысл несет понятие "некоррелированности" случайных
величин? Как связаны понятия независимости и некоррелированности? При
каких условиях на случайные величины понятия некоррелированности и
независимости совпадают?
3. При каких значениях коэффициента корреляции зависимость
случайных величин является: а) прямой; б) обратной?
377

Таблица 8.18
№
1
2
3
4
5
6
7
8
9
10
Сумма
ЛГ
15
18
21
24
27
30
33
36
39
42
285
Y
ПО
100
105
ПО
105
90
95
90
85
80
970
X1
Y1
XY
4. Имеются выборки наблюдений двух случайных величин X и У
*;
У,
1
10
3
6
5
6
7
4
9
1
Найти выборочный коэффициент корреляции. До вычисления
попробуйте, исходя из конкретных выборочных данных, определить знак
коэффициента корреляции.
Ответ: гв = -0,962.
5. Под наблюдением находятся 10 физиологически здоровых
первородящих матерей. Наблюдается количество сцеженного и высосанного молока
во время шестого кормления в 21 час. Полученные результаты занесены в
таблицу. Необходимо определить степень связи между X — возрастом
матерей и У— количеством сцеженного и высосанного молока (табл. 8.19).
Указание. Вычислите коэффициент корреляции. Для этого заполните
оставшихся три последних столбца таблицы и воспользуйтесь
соответствующей формулой.
Ответ: г = -0,88. Связь между Хи У обратная и достаточно сильная (см.
шкалу Чеддока).
6. Вычислить коэффициент корреляции гв генеральных совокупностей X
и У по выборочным данным, представленным в корреляционной таблице
(табл. 8.19).
Указание. Воспользуйтесь формулой (8.6) (см. § 8.2).
Ответ: х = 31,7; у = 35,6; гв = 0,76.
7. По данным задачи 6 проверить гипотезу о независимости признаков
Хи У
Указание. См. § 8.3.
378

Таблица 8.19
\ Y
X \.
20
25
30
35
40
ПУ,
16
4
6
—
—
—
10
26
—
8
10
—
—
18
36
—
—
32
3
9
44
46
—
—
4
12
6
22
56
—
—
—
1
5
6
"*,
4
14
46
16
20
л = 100
Ответ: Гнабл « 11,58. Гипотеза о независимости X и У отвергается даже
при уровне значимости а = 0,001. Признаки зависимы.
8. По данным задачи 6 проверить гипотезу гху= 0,8.
Указание. См. § 8.4.
Ответ: ZHa6n ~ -1,048. Гипотеза принимается.
9. По данным задачи 5 найти выборочное уравнение линейной
регрессии Уна X.
Ответ: у = а + $х = 126, 36 - 1, ОЗх.
10. По данным задачи 6 найти выборочное уравнение линейной
регрессии Уна X.
Ответ: у = -10, 36 + 1,45л:.
11. По данным задачи 5 найти выборочное уравнение регрессии
х
Указание. Преобразуйте переменную х заменой Zi = - ■ Тогда для слу-
чайной величины Z получится выборка значений
J_J_J_J_J_J_J_J_J_J_
15' 18' 2Г 24' 27' 30' 33' 36' 39' 42'
Далее найдите выборочное уравнение линейной регрессии Y на Z вида
у = а + р.г. Следовательно, искомое уравнение — у = а + Е .
Ответ: у = 73, 84 + 594,81.
х
12. По данным задачи 5 найти выборочное уравнение квадратической
регрессии. Вычислить коэффициент детерминации R2. Оцените
зависимости Y от X в данной модели по шкале Чеддока.
Указание. Требуется найти коэффициенты параболической модели
ух = ах + bx + с, как решения системы уравнений (8.44), полученной по
конкретным данным (см. § 8.10). Значение i?2 вычисляется по формуле (8.41).
379

Таблица 8.20
Вакцинировано
Не вакцинировано
Итого
Заболели
10
990
1000
Не заболели
490
510
1000
Всего
500
1500
2000
Ответ: ух = 101, 5 + 0, 89*- 0,034х2, Л2 = 0,828, R= 0,91.
13. Знания 12 студентов по двум различным предметам оценены по
стобалльной шкале. В результате получены две выборки значений:
48 52 64 74 91 78 62 53 74 66 93 99
56 60 63 80 94 76 51 58 80 61 88 98
Найти выборочный коэффициент ранговой корреляции Спирмена
между оценками.
Ответ: рв = 0,92.
14. Два члена жюри, оценив мастерство 13 участников конкурса,
расставили их по местам следующим образом (проранжировали):
1-й: 12345 678910111213
2-й: 6342110789 5 111312
С помощью коэффициента ранговой корреляции Спирмена требуется
оценить согласованность членов жюри. Проверить гипотезу об отсутствии
согласованности: р = 0.
Ответ: рв = 0,75; Гнабл = 3,76; гипотеза об отсутствии согласованности
отвергается.
15. Имеются данные о вакцинации против гриппа и заболеваемости
гриппом во время эпидемии: вакцинированных всего 500 человек, из них
заболели 10; невакцинированных 1500, из них заболели 990. Требуется определить
величину зависимости между проведенной вакцинацией и заболеваемостью.
Указание. Вычислить коэффициент контингенции Пирсона, используя
табл. 8.20.
Ответ: Кк ~ —0,6. Найденное значение коэффициента контингенции
свидетельствует об обратной связи: вакцинированные заболевают реже,
чем невакцинированные.
16. Требуется проверить, одинаково ли содержание дифтерийного
антитоксина в крови детей двух детских садов А и В. Распределение детей по
содержанию антитоксина приведено в табл. 8.21.
а) Найдите коэффициент ранговой корреляции Спирмена и проверьте
гипотезу р = 0.
б) Вычислите коэффициенты взаимной сопряженности Сп и Сч.
в) Проверьте гипотезу по критерию х2 (см. гл. 6, § 6.11).
17. Опрошены жители 130 населенных пунктов в отношении жилищных,
бытовых и трудовых условий (фактор Л) и о размерах заболеваемости
туберкулезом (отклик Y). Фактор X отмечался посредством четырех разновидностей:
Хх — плохие условия; Х2 — средние; Хъ — хорошие; ХА — отличные. Для
отклика У также приняты четыре разновидности: Yx - отсутствие заболеваемости ту-
380

Таблица 8.21
Детский сад
А
В
Итого
Содержание антитоксина
До 0,1
46
52
98
0,1 -0,3
22
30
52
0,3 - 0,5
12
20
32
Более 0,5
12
16
28
Всего
92
118
210
Таблица 8.22
X, (плохие)
Х2 (средние)
Х3 (хорошие)
Х4 (отличные)
Итого...
Заболеваемость туберкулезом Y
У, (отсутствует)
—
5
5
20
30
У2 (низкая)
10
5
20
5
40
Yj (средняя)
10
20
5
5
40
У4 (высокая)
20
—
—
—
20
Итого
40
30
30
30
130
Таблица 8.23
X
3,36
2,88
3,63
3,41
3,78
4,02
Y
65
156
100
134
16
108
X
4,00
4,23
3,73
3,85
3,97
4,51
Y
121
4
39
143
56
26
X
4,54
5,00
5,00
4,72
5,00
Y
22
1
1
5
65
беркулезом; У2 — низкая заболеваемость; У3 ~ средняя; УА — высокая.
Необходимо определить степень связи жилищных, бытовых и трудовых условий с
заболеваемостью туберкулезом. Числовые данные приведены в табл. 8.22.
Требуется найти коэффициент взаимной сопряженности Пирсона.
Дайте качественную оценку зависимости.
Ответ: Сп = 0,668.
18. Имеются данные наблюдений продолжительности жизни (отклик У)
в неделях от момента постановки диагноза и соответствующих значений
381

Таблица 8.24
Город
Алма-Ата
Ашхабад
Баку
Вильнюс
Горький
Душанбе
Ереван
Киев
Кишинев
Куйбышев
Ленинград
Минск
Москва
Новосибирск
Рига
Свердловск
Таллин
Ташкент
Тбилиси
Фрунзе
Харьков
Число родившихся
на 1000 населения
16,1
23,0
18,2
16,7
14,0
23,5
21,0
16,9
18,7
14,5
13,6
18,3
12,6
16,2
13,4
15,8
15,6
20,5
16,7
20,2
14,9
Число умерших до 1 года
на 1000 родившихся
30,9
36,4
23,4
13,6
18,4
47,7
28,4
16,8
17,4
28,9
18,0
16,6
21,2
23,9
15,5
21,9
14,9
40,8
26,3
21,6
23,8
(фактор X) величины lg (исходное количество лейкоцитов в крови) для 17
пациентов, страдавших лейкемией. Данные представлены в табл. 8.23.
Постройте различные регрессионные модели зависимости Y от X.
Оцените степень соответствия моделей выборочным данным.
Для вычисления используйте компьютерные программы.
19. Имеются данные1 о рождаемости и детской смертности в крупных
городах бывшего СССР в 1972 г. (табл. 8.24).
Требуется определить, имеется ли зависимость между числом
родившихся и долей умерших до 1 года.
Указание. Для нахождения зависимости определите коэффициент
корреляции, проверьте гипотезу о независимости признаков. Если коэффициент
корреляции значимо отличается от нуля, найдите уравнение линейной
регрессии признаков. Для вычислений используйте компьютерные программы.
'Вестник статистики, 1974, №2, с. 88.
382

Глава IX. НЕПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ
9.1. Условия использования критериев
Для установления эффективности влияния некоторых факторов
(лекарственного препарата, метода лечения, курения, занятия спортом и т. д.) на
определенный контролируемый показатель ранее мы использовали критерий
Стьюдента1 и дисперсионный анализ. При этом указанные методы
применимы лишь для показателей, определяемых числовыми значениями, имеющими
нормальное распределение и одинаковые (отличающиеся незначимо)
дисперсии по сравниваемым группам. Эти ограничительные условия, подлежащие
предварительной проверке, на практике выполняются достаточно часто.
Однако если имеются сомнения в применимости указанных критериев,
или исследуемый признак является качественным, то следует использовать
непараметрические критерии, в основе которых лежит упорядочивание
(ранжирование) имеющихся значений по отношению друг к другу, типа
"больше - меньше" или "лучше - хуже". Это разграничение значений не
предполагает точных количественных соотношений, а следовательно, и
ограничений на параметры и вид распределения. Следовательно, для использования
непараметрических критериев нужно меньше информации, нежели для
использования критериев параметрических. Поэтому в случае применимости
параметрических критериев (нормальное распределение признака и
незначимо отличающиеся групповые дисперсии) они, как учитывающие большее
количество информации, оказываются более мощными, чем
непараметрические критерии, и именно им следует отдать предпочтение.
Справедливости ради отметим, что мощность непараметрических
критериев, как правило, лишь незначительно меньше мощности
соответствующих параметрических критериев, а значит, используя непараметрические
критерии даже в случае применимости параметрических, мы не слишком
рискуем ошибиться.
Непараметрические критерии также, как правило, существенно проще в
вычислительной части, что позволяет их использовать для "быстрой
проверки" результата.
9.2. Критерий Манна—Уитни (критерий однородности)
Непараметрическим аналогом критерия Стьюдента является критерий
Манна —Уитни2.
■Напомним, что критерий Стьюдента используется только для сравнения двух групп, а для
множественных сравнений — критерий Стьюдента с поправкой Бонферрони или критерий
Ньюмена—Кейлса.
2Мы рассмотрим критерий, известный как Г-критерий Манна-Уитни. Существует еще
вариант, называемый £/-критерием Манна -Уитни, который в данном руководстве не
рассматривается.
383

В критерии Стьюдента мы рассматривали две выборки из нормальных
генеральных совокупностей и при условии равенства дисперсий (которое
проверялось заранее) устанавливали, значимо или нет различие средних в
этих генеральных совокупностях. Если это различие оказывалось
незначимым, то исходя из того, что нормальное распределение полностью
определяется двумя параметрами (средним и дисперсией), а они в обеих
совокупностях получились одинаковыми, мы делали вывод о совпадении этих
генеральных совокупностей'. Следовательно, можно считать, что обе
выборки извлечены из одной и той же генеральной совокупности, т. е.
однородны. Если же выборочные средние различаются значимо, то выборки
извлечены из разных генеральных совокупностей, тот есть неоднородны.
При нарушении условий на нормальность распределений и равенство
дисперсий наша схема рассуждений рушится, хотя и может быть
преобразована применительно к другому конкретному распределению, с другим
количеством параметров, характеризующих распределение. Но этот путь
исследования нестандартный. Гораздо проще и удобнее использовать
критерии, не связанные с конкретными законами распределения. Одним из
таких непараметрических методов установления однородности двух
выборок и является критерий Манна—Уитни.
Сущность этого критерия в следующем. Рассматриваются две группы
наблюдений. Требуется установить однородность этих групп, т. е. можно
ли считать эти выборки полученными из одной и той же генеральной
совокупности или они получены из различных генеральных совокупностей.
а) Обе группы наблюдений объединяем в одну, упорядочиваем ее по
возрастанию и каждому элементу группы предписываем его ранг. При
этом элемент, обладающий наименьшим значением, получает ранг 1,
следующий — ранг 2 и т. д. Последний ранг N, где N — суммарная
численность групп, получает элемент, принимающий наибольшее значение. Если
несколько элементов имеют одинаковые значения, то всем им
предписывается один и тот же ранг, равный среднему арифметическому номеров,
под которыми стоят элементы в упорядоченной группе. Например, после
упорядочения на 5-м и 6-м месте оказались элементы с равными
значениями, тогда ранг каждого из них равен 5,5 (так как —-— = 5, 5).
б) Присвоив элементам ранги, опять разводим их по своим группам.
Вычисляем значение критерия Т, где Т — сумма рангов элементов
меньшей из групп.
Замечание. С тем же успехом, если условиться, можно вычислять Т как
сумму рангов элементов большей из групп. Эта условность не
принципиальна. В случае равного количества элементов в группах берем любую.
в) Вводим нулевую гипотезу об однородности двух выборок.
г) Полученное наблюдаемое значение критерия Т сравниваем с двумя
критическими значениями, взятыми из соответствующей таблицы (см.
табл. 13 Приложения 2). Если наблюдаемое значение Г находится между
'Разумеется, речь идет о совпадении случайных величин, предполагающем равенство
законов распределения, т. е. обе случайные величины имеют одинаковые множества значений
и одинаковые вероятности появления этих значений (подмножеств) в результате испытания,
что в конечном итоге определяется набором параметров распределений.
384

Таблица 9.1
Экспериментальная группа
потерянная масса, кг
6,2
3,0
3,9
ранг
8
3,5
6
Т= 17,5
Контрольная группа
потерянная масса, кг
4,0
"0,5
3,3
1,5
3,0
ранг
7
1
5
2
3,5
этими критическими значениями, то принимаем нулевую гипотезу:
выборки извлечены из одной генеральной совокупности.
Чтобы понять сущность применения критерия Манна—Уитни и
методику построения табл. 13 Приложения 2, рассмотрим конкретный пример
с малыми объемами обеих выборок.
Пример. Исследуется эффективность препарата, позволяющего
сбросить лишнюю массу больным, страдающим ожирением. При этом группе
добровольцев предписана определенная диета. Через месяц подобного
режима, соблюдения диеты и регулярного приема препарата фиксируется
величина потерянной массы в килограммах. Для проведения эксперимента
отобрана группа из 8 добровольцев, причем 3 их них действительно
получали исследуемый препарат (экспериментальная группа), а 5
довольствовались плацебо (контрольная группа). Отбор 3 добровольцев из 8 в
экспериментальную группу осуществлялся случайным образом (репрезентативно).
Ради чистоты эксперимента, естественно, испытуемые не знали, кто из
них какой препарат принимает, точнее, все добровольцы считали, что
принимают лекарство. В этом состоит сущность так называемого слепого
метода проведения эксперимента', позволяющего в определенной мере
исключить субъективную составляющую воздействия на отклик.
Полученные данные проранжированы и занесены в табл. 9.1.
В таблице указана сумма рангов элементов меньшей из групп: Т= 17,5.
Нулевая гипотеза для двух рассматриваемых групп — однородность
групп, т. е. утверждение, что обе полученные выборки рангов извлечены
из одной генеральной совокупности, а следовательно, препарат
неэффективен. Для проверки (или опровержения) этой гипотезы воспользуемся
критическими точками табл. 13 Приложения 2. Находим, что эти критиче-
'Заметим, что если и экспериментаторы, принимающие участие в эксперименте, не
обладают информацией о принадлежности пациентов к той или другой группе, то метод называют
двойным слепым методом.
Особенно важно использовать слепой метод или двойной слепой метод, когда
субъективное влияние на ход эксперимента со стороны пациента или врача способно, зачастую даже
помимо их воли, существенно исказить результаты.
25 — 3529
385

ские точки равны 6 и 21 при уровне значимости а = 0,036 и равны 7 и 20
при уровне значимости а = 0,071. В таблице приведены критические точки
при двух значениях а, так как оба этих значения, 0,036 и 0,071, близки к
стандартному уровню значимости а = 0,05.
Наше наблюдаемое значение критерия Т, равное 17,5, находится между
критическими точками даже при а = 0,071 > 0,05, т. е. в области принятия
нулевой гипотезы (7 < Т < 20 — область принятия нулевой гипотезы при
уровне значимости а = 0,071). А это означает, что отвергнуть нулевую
гипотезу о неэффективности препарата нет оснований: исследуемый
препарат неэффективен, а снижение массы объясняется другими причинами,
возможно, диетой. Если обратиться к таблице данных, то все-таки
заметно, что в экспериментальной группе наблюдается превышение значений
потерянной массы над соответствующими значениями в контрольной
группе. Однако то, что мы предполагаем интуитивно, статистический
критерий не почувствовал по очень простой причине: слишком мал объем
выборки. Ведь, наблюдая при подбрасывании монетки три раза троекратное
выпадение "герба", мы не станем утверждать, что "герб" появляется чаще,
чем "монета", ибо вероятность этого события достаточно велика,
р = (Л = -, и оно вполне может произойти в единичном испытании.
Возвращаясь к нашему примеру, отметим, что нулевая гипотеза принята не
потому, что она верна в этом конкретном случае, а потому, что при
скудности имеющейся информации у нее значительно больше шансов (больше
вероятность) оказаться верной. А оснований отвергнуть нулевую гипотезу
явно недостаточно. С большей степенью уверенности мы можем судить о
справедливости наших выводов, лишь увеличивая объемы выборок.
Больше данных, больше информации — точнее выводы.
Далее, основываясь на нашем примере, рассмотрим подробнее, как
получена используемая нами табл. 13 Приложения 2.
При справедливости нулевой гипотезы — отсутствия какого-либо
влияния препарата на снижение массы — обе группы, и экспериментальная, и
контрольная, оказываются в одинаковых условиях. Следовательно, любой
из возможных рангов с равной вероятностью может быть в той или другой
группе. Напомним, что разбиение 8 испытуемых на две группы
производилось случайным образом. Исходя из этого, мы можем установить закон
распределения случайной величины Т — суммы рангов в группе с
меньшим числом наблюдений. При равной вероятности каждого из возможных
рангов (равновероятности элементарных событий), мы находимся в
условиях применимости классического определения вероятности'. Также
используем приемы комбинаторики. В рассмотренном примере суммарное
'Таким образом, предполагается условие, что ранги, предписываемые всем наблюдениям,
различны и являются натуральными числами. Использование одинаковых рангов в случае
наличия равных выборочных значений влияет лишь на точность наблюдаемого Т, которое в
конкретном случае может оказаться и нецелым числом. Таблицей пользуются и в этом
случае. Наш пример показывает, что, используя для вычисления Г лишь целые ранги, мы были
бы поставлены перед выбором, какой ранг, 3 или 4, имеет значение 3,0 в экспериментальной
группе, и следовательно, чему равно наблюдаемое значение Г, 17 или 18. Среднее
арифметическое значение ранга 3,5 разрешило наши сомнения и сделало выводы более точными:
Г= 17,5.
386

число наблюдений — 8, в меньшей группе - 3 наблюдения (три ранга),
следовательно, значение Т — сумма трех натуральных чисел от 1 до 8. Эта
сумма будет наименьшей для чисел 1, 2, 3 и наибольшей для чисел 6, 7, 8,
т. е. случайная величина Г принимает значения от 6 до 21. Три числа из
восьми возможных можно выбрать Cj = 56 способами. Оставшиеся пять
чисел для другой группы с точностью до перестановки целиком
определяются составом чисел первой группы (например, если в первой группе —
1, 3, 5, то во второй обязательно — 2, 4, 6, 7, 8). Поэтому, чтобы посчитать
вероятности возможных значений случайной величины Т, нам не нужно
рассматривать обе группы, а достаточно найти для каждого значения
количество благоприятствующих ему комбинаций слагаемых в сумме значений
Т. Для наглядности занесем все возможные значения слагаемых в табл. 9.2.
Символом * в таблице обозначены ранги элементов меньшей группы.
Таблица 9.2. Возможные способы разбиения 8 рангов на две группы по 3
и 5 рангов
№ п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Ранг
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
2
*
*
*
*
*
*
3
*
*
*
*
*
*
4
*
*
*
*
*
*
5
*
*
*
*
*
*
6
*
*
*
*
*
*
7
*
*
*
*
*
*
8
*
*
*
*
*
*
т
i
6
7
8
9
10
11
8
9
10
11
12
10
11
12
13
12
13
14
14
15
16
25* 387

Продолжение табл. 9.2.
№ п/п
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
1
2
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
3
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Ранг
4
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
5
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
6
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
7
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
8
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Т
9
10
11
12
13
11
12
13
14
13
14
15
15
16
17
12
13
14
15
14
15
16
16
17
18
15
16
17
17
18
19
18
19
20
21
388

7/56+
5/56
3/56"|-
1/56
Рис. 55.
• ••
I I I I I I I I I I I I I—►
°1 3 5 7 91113151719212325 T
В последнем столбце таблицы указаны все 56 возможных случаев
значений случайной величины Т. Частота встречаемости каждого из значений —
это количество комбинаций, благоприятствующих появлению именно
этого значения. Поскольку всего возможных комбинаций 56, то по
классическому определению легко посчитать вероятности возможных значений:
Р(Т= 6)= ^ «0,018
56
Р(Т=8) = -^«0,036
56
Р(Т=7)
_1_.
56'
ДГ=9) = ^*0,054;
Запишем закон распределения дискретной случайной величины Т,
принимающей (в нашем примере) 16 возможных значений tlt t2, , ..., tl6:
h
Pi
6
1/56
7
1/56
8
2/56
9
3/56
10
4/56
11
5/56
12
6/56
13
6/56
14
6/56
15
6/56
16
5/56
17
4/56
18
3/56
19
2/56
20
1/56
21
1/56
Для наглядности представим полученный закон распределения
графически (рис.55).
В данном случае, так как случайная величина Т является дискретной (а
не непрерывной) графиком будет не кривая линия, а последовательность
точек. Поэтому при проверке нулевой гипотезы для построения
критической области мы не можем по заранее выбранному стандартному уровню
значимости а (а = 0,05 или а =0,01) указать соответствующие
критические точки, как поступали ранее, когда в качестве критерия
использовалась непрерывная случайная величина. В нашем распоряжении имеются
лишь 16 конкретных точек. Рассмотрим крайние из них: Т= 6 и Т= 21.
Если эти точки отнести к критической области, то получим уровень
значимости а = Р(Т= 6 или Т= 21) = ДГ= 6) + ДГ= 21) = 1/56 + 1/56 « 0,036.
Этот уровень значимости а = 0,036 близок к стандартному 0,05 — им и
удовлетворимся. Таким образом, критическая область при численности
групп 3 и 5 — это два граничных значения случайной величины Т. 6 и 21.
Заметим, что, расширив критическую область, взяв в качестве критических
точек значения 7 и 20, получим другой уровень значимости
а = Р((Т= 6) + (Т= 7) + (Т= 20) + (Т= 21)) = 1/56 + 1/56 + 1/56 +
+ 1/56 = 4/56 « 0,071.
389

Это значение уровня значимости также достаточно близко к
стандартному 0,05, поэтому приведено в табл. 13 Приложения 2. Вместе с тем
заметим, что если строго следовать стандартному уровню значимости а = 0,05,
то следует однозначно остановиться на фактическом значении уровня
значимости 0,036, которое не ухудшит наши выводы относительно нулевой
гипотезы, чего нельзя сказать об а = 0,071. Область принятия нулевой
гипотезы при а = 0,036 — это 6 < Т < 21 (т. е. критические значения 6 и 21
исключены), а при а = 0,071 — это (7 < Т < 20). Уменьшить уровень
значимости при данных объемах выборок невозможно, однако, как видно из
табл. 13 Приложения 2, это вполне реально с ростом объемов выборок.
Критические значения для групп другой численности вычисляются
аналогично. Заметим, что в табл. 13 Приложения 2 представлены наибольшие
значения численности групп — это 8 и 8. Приведенным выше методом
границы таблицы можно раздвинуть, но, например, для следующего
значения численности групп, 8 и 9, количество различных вариантов
представления величины Т равно Cj7 = 24 310, что уже приводит к громоздким
вычислениям. Обычно при численности групп, большей 8, используют не
точные значения уровня значимости (с точностью до округления), а
приближенные. В Приложении 2 табл. 14 содержит критические значения
критерия Манна—Уитни для двух стандартных уровней значимости а
= 0,05 и а = 0,01, которые в данном случае являются приблизительными,
но большими, чем фактические. Точные значения уровней значимости,
как уже отмечалось выше, близки к указанным приближенным. Объемы
выборок (численность групп) в данной таблице от 6 до 25 значений, что
существенно выше, чем в табл. 13.
При большой численности групп (фактически, начиная с п = 20)
обычно используют нормальный закон распределения. Оказывается, что с
ростом численности групп распределение случайной величины Т стремится к
нормальному N(m; а) при
ст = пмпБ(пм + пъ+ 1)
где пм и пБ — численности меньшей и большей групп соответственно.
Иллюстрацией данного утверждения служит графическое изображение
распределения Т, представленное выше и являющееся дискретным аналогом
кривой Гаусса.
В качестве критерия используют нормированную случайную величину
Z-1^*, (9.3)
т. е. Z~ N(0; i).
Ввиду того что случайная величина Г дискретная, а нормальное
распределение является непрерывным, в качестве компенсации обычно исполь-
390

зуется поправка Йейтса, применение которой приводит к более точным
значениям. Случайная величина с поправкой Йейтса имеет вид:
\T-m\-\
Для нашего примера ввиду малого объема выборок лучше применять
точный метод. Чисто в учебных целях воспользуемся приближенно
нормальным распределением Z:
„, = 3(3 + 5+1) = 13|5. g = J3- 50 + 5 + 1)^,35;
^ = '17-5-3133f-°-5,l,04.
При уровне значимости а = 0,05 область принятия нулевой гипотезы —
это интервал (-1,96; 1,96). Так как ZHa6n принадлежит этой области, то
нулевая гипотеза о неэффективности препарата принимается.
9.3. Критерий Уилкоксона (наблюдения до и после эксперимента)
Критерий Уилкоксона является непараметрическим аналогом парного
критерия Стьюдента, рассмотренного в § 6.7. Поскольку критерий
непараметрический, то для его применимости не требуется какой-либо
определенный закон распределения генеральной совокупности (напомним, что
для критерия Стьюдента необходимы выборки из нормальной
совокупности). Распределение может быть любым — в этом и заключается
преимущество рассматриваемого критерия. Критерий Уилкоксона — ранговый
критерий, причем присваиваемые значениям признака ранги могут быть
как положительными, так и отрицательными.
Так же как и при применении парного критерия Стьюдента, для одних
и тех же объектов наблюдения снимаются дважды: до эксперимента и
после эксперимента. Под экспериментом понимается некоторое воздействие
на объект, в результате которого наблюдаемые показатели могут
измениться в ту или иную сторону: например, прием лекарственного препарата или
определенная методика лечения приводят, вообще говоря, к некоторым
изменениям контролируемых показателей. При этом у различных
индивидуумов эти изменения также будут различными. Задача критерия — по
статистическим данным установить эффективность воздействия.
Поскольку изменения показателя у каждого объекта могут быть
вызваны самыми различными случайными причинами, а нас интересует
влияние именно нашего эксперимента, то, чтобы исключить случайные
воздействия, требуется рассматривать группу объектов. И чем больше объем этой
группы, тем более взаимно сокращаются положительные и отрицательные
случайные отклонения и, наоборот, ярче проявляются отклонения
систематические, вызванные эффектом эксперимента.
Группа наблюдений до эксперимента выступает в роли контрольной
группы, а группа наблюдений после эксперимента — в роли
экспериментальной группы. Однако в данной ситуации мы располагаем гораздо
большей информацией, чем информация из двух произвольных групп наблю-
391

дений: парные данные выдают непосредственно для каждого объекта
зависимость наблюдаемого показателя от произведенного воздействия
(возросло значение показателя или уменьшилось и на сколько единиц
измерения).
Исходя из сказанного, в качестве наблюдаемого значения удобно
использовать разность наблюдаемых показателей до и после эксперимента
для каждого индивидуума. Таким образом, из двух групп наблюдений
получается одна выборка значений, среди которых могут быть как
положительные (уменьшение показателя), так и отрицательные (увеличение
показателя). При нулевой разности наблюдение не учитывается.
Далее производится ранжирование этой выборки, причем несколько
иначе, чем, например, в критерии Манна—Уитни, где используется
простое упорядочивание. В нашем случае, прежде чем приступить к
упорядочиванию выборочных значений, их вначале заменяют соответствующими
абсолютными величинами, а затем полученные положительные числа
ранжируют по возрастанию. Расставленные таким образом ранги изменения
показателя являются промежуточными, далее каждому такому рангу
предписывается знак "+" или "—" в зависимости от знака соответствующей ему
разности. Значит, часть рангов окажется положительными числами, а
другая часть — отрицательными. Такие ранги называют знаковыми. Сумма
знаковых рангов — случайная величина W, называемая критерием Уилкок-
сона.
В случае, когда исследуемое воздействие неэффективно, количество
положительных и отрицательных разностей (а также и знаковых рангов) в
среднем должно уравновешиваться, так как нет превуалирующего
изменения показателя в ту или иную сторону. Следовательно, среднее значение
критерия Уилкоксона W должно быть равно нулю [М( W) = 0 — нулевая
гипотеза]. Далее действия стандартны: для конкретной выборки разностей
вычисляем WHa6n, по табл. 15 Приложения 2 находим соответствующие
критические точки (с учетом желаемого уровня значимости а) и
определяем принадлежность WHabn критической области или области принятия
нулевой гипотезы.
Проиллюстрируем подробно приводимую теорию на конкретном
примере по данным примера 3 § 6.7, а также поясним суть и использование
соответствующей таблицы.
Пример. Выявляется эффективность специальной диеты, позволяющей
избавиться от избыточного массы.
Фиксируется масса каждого участника до начала эксперимента и через
месяц соблюдения диеты. Данные для группы из пяти добровольцев
представлены в табл. 9.3.
В первом столбце таблицы проставлен номер участника эксперимента,
второй и третий столбцы представляют данные наблюдений массы в
килограммах до и после эксперимента. Оставшиеся четыре столбца
таблицы заполнены на основании этих данных. Уменьшение (изменение)
показателя массы — это случайная величина, которую, как и ранее, мы
обозначаем X. Значения, представленные в соответствующем столбце (4,3; 3,7;
—0,5; 2,5; 3,0) — не что иное, как выборка из генеральной совокупности X.
Для парного критерия Стьюдента важно, чтобы случайная величина X
имела нормальное распределение. В нашем случае распределение X неиз-
392

Таблица 9.3
№
1
2
3
4
5
Масса (кг)
до
эксперимента
93,2
98,2
105,6
86,8
95,5
Масса (кг)
после
эксперимента
88,9
94,5
106,1
84,3
92,5
Уменьшение
показателя
массы (кг), X
4,3
3,7
-0,5
2,5
3,0
Модуль
уменьшения
показателя массы (кг)
4,3
3,7
0,5
2,5
3,0
Ранг
5
4
1
2
3
Знаковый
ранг
5
4
-1
2
3
W= 13
вестно, и для получения выводов мы привлекаем другую случайную
величину W — сумму знаковых рангов, которые получаются на основании
сравнения различных значений случайной величины X с учетом
положительности и отрицательности (т. е. знаков) этих значений. В последнем
столбце выписаны значения знаковых рангов, сумма которых и есть
наблюдаемое значение случайной величины W, выступающей в роли
критерия. В нашем примере наблюдаемое значение критерия W оказалось
равным 13: \¥т&я = 13.
Далее мы должны определить, что означает значение 13 для нулевой
гипотезы, хорошо это или плохо. Напомним, что нулевая гипотеза — это
теоретическое предположение HQ : M{W) = 0, и, следовательно,
отклонение наблюдаемого значения W от теоретического среднего составляет 13
единиц. Необходимо решить вопрос о значимости этого отклонения: можно
ли считать, что это несоответствие вызвано случайными причинами или же
существенное влияние оказывает диета питания. Обратимся к табл. 15
Приложения 2, согласно которой при п = 5и уровне значимости а = 0,062
критическое значение равно 15: WKpm = 15. Поскольку | WHa6„ | < ^крит, то на
уровне значимости а = 0,062 принимается нулевая гипотеза: исходя из
наших данных (напомним, что в данном случае критерий "не знает" тип
распределения случайной величины X — изменения показателя массы, в
отличие от парного критерия Стьюдента, § 6.7), возможная допускаемая
ошибка имеет вероятность не более чем 0,062.
Проследим подробно за работой критерия W в нашем случае малого
числа наблюдений, п = 5, и рассмотрим подробно, каким образом
получается значение а = 0,062 и соответствующее критическое значение ^=15,
фигурирующее в табл. 15 Приложения 2. Следовательно, внесем ясность в
вопрос составления этой таблицы.
Итак, п = 5, и справедлива нулевая гипотеза, согласно которой
воздействие диеты не оказывает на массу никакого влияния, а это означает, что
знаковые ранги, один относительно другого, не имеют никаких
приоритетов, т. е. все допустимые комбинации знаковых рангов равновероятны.
Поскольку в нашем примере всего рангов 5 и каждый из них имеет два воз-
393

р к
3/32
2/32
1/32
111 I I M I I d I I I I I I J I J I J J J J I ...
-15 -13 -11 -9-7-5-3-11 3 5 7 9 11 13 15 W
Рис. 56.
можных знака, "+" или "-", то всего возможно различных комбинаций
25 = 32 (см. § 1.4, правило умножения). Перечислим все эти 32 возможные
комбинации знаковых рангов и в каждом случае вычислим их сумму, т. е.
значение критерия W. Результаты занесем в табл. 9.4.
Так как возможные комбинации равновероятны, и всего различных
комбинаций знаковых рангов 32, то вероятность каждой из комбинаций по
классическому определению вероятности равна 1/32. Зная эту вероятность
и все допустимые значения случайной величины W, которые выписаны в
последнем столбце таблицы, с учетом их кратности мы можем найти закон
распределения W.
Как видим, W имеет своими значениями w,. все целые нечетные числа
от —15 до +15. Найдем вероятности этих 16 значений согласно
классическому определению:
P(W = -15) = 1/32 = 0,03125; P(W = -13) = 1/32;
P(W = -11) = 1/32; P(W = -9) = 2/32 = 0,0625;
P(W = +13) = 1/32; P{W= +15) = 1/32.
Таким образом, получаем закон распределения случайной величины W:
щ
Pi
-15
1/32
-13
1/32
-11
1/32
-9
2/32
-7
2/32
-5
3/32
-3
3/32
-1
3/32
+1
3/32
+3
3/32
+5
3/32
+7
2/32
+9
2/32
+ 11
1/32
+ 13
1/32
+ 15
1/32
Построим график распределения дискретной случайной величины W.
Построенный на рис. 56 график симметричен относительно нуля.
Поскольку случайная величина дискретная, то наименьшей двусторонней
критической областью является область, состоящая из двух крайних
значений W= —\5 и W= +\5. Вероятность попадания в эту область (уровень
значимости) равна вероятности суммы несовместных событий (IV = -15) и
(W= +15):
P((W= -15)+ (W= +15)) = P{W= -15)+ P{W= +15) = 1/32+1/32 = 0,0625.
394

Таблица 9.4. Возможные комбинации 5 знаковых рангов
Знак ранга
Ранг
1
—
+
-
-
-
-
+
+
+
+
-
-
-
-
-
-
+
+
+
+
+
+
-
-
-
-
+
+
+
+
-
+
г
—
-
+
-
-
-
+
-
-
-
+
+
+
-
-
-
+
+
+
-
-
-
+
+
+
-
+
+
+
-
+
+
3
—
-
-
+
-
-
-
+
-
-
+
-
-
+
+
-
+
-
-
+
+
-
+
+
-
+
+
+
-
+
+
+
4
—
-
-
-
+
-
-
-
+
-
-
+
-
+
-
+
-
+
-
+
-
+
+
-
+
+
+
-
+
+
+
+
5
—
-
-
-
-
+
-
-
-
+
-
-
+
-
+
+
—
-
+
-
+
+
-
+
+
+
-
+
+
+
+
+
Сумма знаковых рангов (W)
-15
-13
-11
-9
-7
-5
-9
-7
-5
-3
-5
-3
-1
-1
+1
+3
-3
-1
+ 1
+ 1
+3
+5
+3
+5
+7
+9
+5
+7
+9
+ 11
+ 13
+ 15
Именно это значение, как наименьшее и наиболее близкое к
стандартному а = 0,05, и является уровнем значимости критерия Уилкок-
сона при п = 5. В табл. 15 это число округлено до 0,062. Если же в качест-
395

ве критических точек выбрать значение W= -13 и W= +13, то
соответствующий уровень значимости окажется равен
а = P{(W= -15) + (W= -13) + (W= +13) + Д W= +15)) = 4/32 = 0,125.
Заметим, что в нашем примере lVHa6n =13, и, следовательно, нулевую
гипотезу мы можем отвергнуть на уровне значимости а = 0,125, а на уровне
значимости а = 0,0625 нулевая гипотеза должна быть принята.
Замечание. Анализируя одни и те же данные с помощью парного
критерия Стьюдента (см. § 6.7) и критерия Уилкоксона, мы получили различные
результаты: наблюдаемые значения критериев приводят к
соответствующим разным уровням значимости, вероятностям отвержения нулевой
гипотезы. Отличие этих вероятностей объясняется двумя причинами.
Во-первых, оба критерия используют разный объем информации; в
основе работы парного критерия Стьюдента лежит нормальное распределение
генеральной совокупности X, а критерий Уилкоксона вид распределения
игнорирует, его выводы справедливы независимо от распределения, т. е.
являются более грубыми; напомним также, что вероятность — это мера
неопределенности знаний о явлении и, вполне естественно, что разный
объем используемой информации приводит к разным значениям вероятностей.
Во-вторых, случайные величины Т и W, используемые в качестве
критериев, различны по своей структуре: одна непрерывна, другая дискретна,
изменяется скачками в отдельных точках; в частности, в рассмотренном
примере изменение наблюдения х3 = -0,5 в пределах от 0 до -2,5 не
нарушит ситуацию, по-прежнему \Уна&л = 13, в то время как значение Тна6п при
малейшем изменении данных окажется иным, что повлечет и изменение
соответствующего уровня значимости.
Вывод: тот факт, что при применении разных критериев к одним и тем
же данным мы получили разные значения вероятностей, является вполне
объяснимым и закономерным.
Исходя из приведенного замечания, напрашивается естественный
вопрос: которым же критерием необходимо воспользоваться, чтобы получить
наиболее достоверный результат? Ответ фактически уже был: если данные
изменения показателя до и после эксперимента извлечены из нормальной
генеральной совокупности X (что необходимо проверить), то парный
критерий Стьюдента выдает точный результат, им и следует воспользоваться;
если же имеются сомнения в нормальности распределения X, то лучше не
рисковать ошибиться и воспользоваться более грубым, но гарантирующим
правильность критерием Уилкоксона1.
В табл. 15 Приложения 2 указаны критические точки критерия
Уилкоксона лишь до п = 20. Чем больше объем выборки, тем вычисления
становятся более громоздкими, однако есть и другая закономерность: с ростом п
распределение случайной величины W стремится к нормальному с
нулевым средним и легко вычисляемым стандартным отклонением
*„=рЕ±ШпШ. (9.5)
'Можно привести следующую численную аналогию: какая оценка вероятности лучше
0 < р < 0,01 — более точная, но, возможно, неверная, или 0 < р < 0,1 — более грубая, но
гарантированно верная?
396

Уже при п = 5, соединяя точки на графике (см. рис. 56), мы можем
наблюдать грубое сходство полученной ломаной с кривой Гаусса. Обычно
при п > 20 уже полагают приближенное соответствие W~ N(0; aw). Таким
образом, при п > 20 наши табличные вычисления можно значительно
упростить, используя вместо критерия W критерий
Z--g^°- W . (9.6)
aw n(n+ 1)(2лТТ)
V 6
Погрешность при переходе от дискретного распределения W к
непрерывному распределению Z можно несколько сгладить, введя поправку
Йейтса:
щ-\ _ \щ-\
°w jn(n+l)(2n+ l)
(9.7)
Далее вместо WHa6n вычисляем ZHa6n, а критические точки при уровне
значимости а находим из соответствующей табл. 2 Приложения 2.
Отметим, что для непрерывного критерия Z уровень значимости а мы можем
выбирать любым, например, 0,05, или 0,01, или 0,0123, в отличие от
дискретного критерия W, когда уровень значимости предлагается выбрать из
набора фиксированных дискретных значений.
9.4. Критерий Краскела—Уоллиса
(проверка однородности нескольких групп)
Задачу проверки однородности нескольких групп наблюдений мы
решали методами дисперсионного анализа в гл. 7. (Напомним, что группы мы
формировали в зависимости от исследуемого фактора.) Однородность
групп (выборок) означает возможность считать их выбранными из одной и
той же генеральной совокупности. При этом мы полагали генеральную
совокупность X подчиненной нормальному закону и, следовательно,
полностью определяемую двумя параметрами: математическим ожиданием
т = М (X) и дисперсией a2 = D (X). Таким образом, для проверки
однородности нескольких групп методами дисперсионного анализа (однофак-
торного) необходимо установить принадлежность всех групп именно к
нормальной генеральной совокупности; проверить гипотезу о равенстве
групповых дисперсий; проверить гипотезу о равенстве групповых средних.
Если же окажется, например, что генеральная совокупность А'имеет
закон распределения, отличный от нормального, то, увы, рассмотренная
нами теория становится неприменимой. В этом случае требуются критерии
проверки однородности групп, которые не зависят от вида закона
распределения (т. е. от всевозможных параметров) и называются
непараметрическими. Непараметрическим аналогом дисперсионного анализа, в
частности, является критерий Краскела — Уоллиса, основанный на рангах.
Изложим методику применения критерия Краскела — Уоллиса для к
групп наблюдений. Задача — проверить однородность этих групп (выбо-
397

рок), т. е. принадлежность к одной и той же генеральной совокупности.
Такая задача возникает при исследовании эффективности различных
лекарственных препаратов, методов лечения и т. д.
Итак, однородность групп наблюдений — нулевая гипотеза. Для
построения критерия проверки нулевой гипотезы используем ранги, как и в
критерии Манна — Уитни. Пусть числа элементов по группам
соответственно равны nlt пъ ..., пк. Общее количество наблюдений по всем группам
обозначим N:
N = щ + п2 + ... + пк. (9.8)
Упорядочим все N элементов независимо от группы по возрастанию.
Тогда каждый из элементов получает свой ранг: номер места в
упорядоченном ряду. Если среди элементов ряда имеются совпадающие, то всем
из них присваивается один и тот же ранг, равный среднему
арифметическому их номеров, мест упорядоченного ряда. Заметим, что сумма всех N
рангов, согласно формуле суммы арифметической прогрессии, равна
1+2 + ... + ЛГ- N{N+\) (99)
Далее вычислим средние ранги по группам , как средние
арифметические соответствующих величин. Аналогично общий средний ранг равен
Tt - l£Lfr±M - Ц±. (9.Ю)
Если верна нулевая гипотеза, выборки однородны, то сами наблюдения,
а следовательно, и ранги должны быть по величине рассредоточены по
группам более-менее равномерно, т. е. средние ранги /?„ R2, ..., Rk не
должны существенно различаться между собой. При их сравнении можно
использовать отклонения от общего среднего:
(я-ад.-С*-*?1)
2 J ' ' v"* 2
Для суммарной характеристики таких отклонений с учетом численности
групп введем случайную величину
называемую статистикой Краскела—Уоллиса.
Эта статистика Н — критерий проверки нулевой гипотезы. Его структура
такова, что распределение Н с ростом численности групп стремится к
распределению х2_2 (к — 1) степенями свободы (действительно,
распределения средних Rp по центральной предельной теореме, стремятся к
нормальному распределению; разности Лу - R также распределены нормально;
сумма квадратов таких величин имеет распределение х2, а
соответствующие значения параметров, необходимых для этого распределения, обеспе-
п 10
чивают сомножители N L )• Фактически при численности каждой из
групп 5 элементов уже обеспечивается удовлетворительное приближение.
398

Таблица 9.5
№
1
2
3
4
5
6
Рост 155 - 165 см
масса
(кг)
59
53
60
54
57
59
Ранг
4,5
1
6
2
3
4,5
*,=3,5
Рост 165 — 170 см
масса
(кг)
63
61
68
62
64
Ранг
9
7
12,5
8
10
Л2=9,3
Рост 170 — 175 см
масса
(кг)
67
68
74
72
69
Ранг
11
12,5
18
16
14
7?з=14,3
Рост 175 — 180 см
масса
(кг)
73
79
71
75
Ранг
17
20
15
19
^=17,75
При количестве групп, большем 3, возможно использование и меньшей
численности чем 5.
Итак, подставляя наши данные в приведенную выше формулу критерия
Я, получаем Яна6л. Критическую точку распределения х2 с г= (к — 1)
степенями свободы находим при выбранном уровне значимости а (по табл. 4
Приложения 2. Если оказывается, что Яна6л < xiUr. то на выбранном
уровне значимости нулевая гипотеза об однородности выборок принимается
(опытные данные этой гипотезе не противоречат). Если же Яна6л > Хкрит, то
нулевая гипотеза об однородности групп наблюдений отвергается и группы
следует сравнить попарно.
Замечание. Для вычисления наблюдаемого значения критерия Краске-
ла—Уоллиса Я вместо приведенной выше формулы (9.11) можно
использовать равносильную ей
Я =
2
12 у^ п2
^(#+1)2.^
3(N+l).
(9.12)
Пример. Данные примера в § 7.4 (см. табл. 7.8) применения
дисперсионного анализа вполне пригодны для иллюстрации работы критерия Крас-
кела—Уоллиса. Ввиду малочисленности первой из групп объединим ее со
второй. Итак, для определения влияния роста человека на его массу
отобрано 20 студентов, которые разбиты на 4 группы в зависимости от их
роста. Требуется установить (или опровергнуть) однородность полученных
групп по массе. Данные занесем в таблицу, в которой также укажем ранги
всех 20 наблюдений (табл. 9.5).
Далее оперируем только с рангами. Находим средние ранги по группам
(они занесены в нижнюю строку таблицы) и вычисляем
Я = 20 + 1 = Ю, 5. По формуле (9.12) критерия Я вычисляем его
наблюдаемое значение:
399

H^=whl[6 ' (3'5)2 + 5 ' <9'3>2 + 5 • (14'3)2 + 4 * (17, 75)2] -
- 3(20 + 1) = 16,676.
Согласно табл. 4 Приложения 2, при уровне значимости а = 0,01 и
числе степеней свободы г= 4 - 1 = 3 находим хКРит = 11,34.
Поскольку Яна6л > х^рит, то нулевая гипотеза об однородности выборок
должна быть отвергнута. Следовательно, масса человека зависит от роста.
Результат тот же, что и в методе дисперсионного анализа.
Задачи и упражнения
1. Предложены два метода лечения: А и В. Эффективность каждого
метода выражена в процентах изменения некоторого показателя. Проведено
6 опытов по методике А и 7 опытов по методике В. Результаты
представлены в виде двух выборок:
А: 0,3 0,4 0,6 0,10 0,12 0,16
В: 0,1 0,2 0,5 0,7 0,15 0,19 0,20
При уровне значимости а = 0,05 проверить гипотезу об однородности
двух методов лечения. Используя табл. 13 Приложения 2, найдите
фактический уровень значимости, приближенно соответствующий 0,05.
Таблица 9.6
Порядковый номер семьи
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Доля расходов на культурные
нужды, %
12,1
6,2
6,0
8,4
4,2
6,8
6,9
20,0
13,5
7,2
8,5
10,7
7,9
1,3
6,9
Доля расходов на транспорт, %
5,3
5,7
4,2
4,6
10,8
5,0
5,2
12,7
6,3
3,2
5,0
4,8
5,7
8,4
6,7
400

Таблица 9.7
Страна
Финляндия
Франция
Япония
Канада
Норвегия
Новая Зеландия
(белое население)
Португалия
США
Швеция
Великобритания
Италия
Коста-Рика
Сальвадор
Польша
Югославия
50-е годы
Число
рождений на 1000
населения
23,1
19,3
23,5
27,9
18,8
24,1
24,7
23,5
16,4
15,7
17,2
47,6
48,8
29,1
28,3
Средняя
продолжительность жизни
для новорожденных
62,2
66,4
63,7
68,6
71,0
70,4
58,0
68,2
70,3
69,7
64,7
55,7
51,2
61,4
58,7
70-
Число
рождений на 1000
населения
12,2
16,5
19,4
15,5
15,5
20,5
20,1
15,0
13,5
13,7
16,0
28,3
40,3
17,9
18,1
е годы
Средняя
продолжительность
жизни для
новорожденных
71,4
73,4
73,6
73,3
74,7
72,0
68,5
71,5
75,2
72,4
72,1
70,8
64,4
70,9
69,0
Ответ: Тна6„ = 41. Гипотеза об однородности выборок должна быть
принята.
2. Проверить нулевую гипотезу об однородности двух выборок объемов
пх = 25 и п2 — 30:
14 15 18 21 25 26 27 30 31 32 35
41 43 46 48 52 56 57 60 65 68 73
12
38
75
11
33
53
13
34
55
16
36
58
17
37
61
19
39
63
20
40
66
22
42
23 24
44 45
26
47
28
49
29
51
Указание. Для проверки гипотезы используйте в качестве критерия
статистику Zc поправкой Иейтса вида (9.4).
Ответ: Тна6л = 736,5; ZHa6n = 0,609. Гипотеза об однородности двух
выборок должна быть принята.
3. Проведен случайный отбор 15 семей, состоящих каждая из 5 человек
и имеющих одинаковый месячный доход. Обследовано, какую долю
доходов каждая семья тратит на культурные нужды и на транспорт. При уровне
значимости а = 0,05 необходимо проверить гипотезу Н0, что средние доли
расходов на эти цели в генеральной совокупности семей, из которой взята
26 — 3529
401

Таблица 9.8
Номер испытания /
1
2
3
4
5
*П>У
1-я группа
36
47
50
58
67
51,6
2-я группа
56
61
64
66
66
62,6
3-я группа
52
57
59
58
79
61,0
4-я группа
39
57
63
61
65
57,0
Таблица 9.9
Причина смерти
Новообразования

Сердечно-сосудистые болезни
Несчастные
случаи
Цирроз печени
Самоубийства
Вид занятий
руководители
высшего звена
150
130
45
15
20

преподаватели
140
150
30
16
25

руководители среднего
звена
205
180
75
33
36
с/х рабочие
290
190
175
75
30

промышленные рабочие
350
185
95
95
45
выборка, в среднем одинаковы. Результаты обследования представлены в
табл. 9.6.
Указание. Используйте критерий однородности Манна — Уитни.
Ответ: На уровне значимости а = 0,05 нулевая гипотеза должна быть
отвергнута.
4. Имеются данные о рождаемости и рассчитанной средней
продолжительности жизни для новорожденных в 50-е и 70-е годы1 (табл. 9.7).
Используя критерий Уилкоксона, проверить справедливость гипотезы о
падении рождаемости и гипотезы о рассчитываемом для новорожденных
росте средней продолжительности жизни.
Найдите коэффициент корреляции числа рождений и средней
продолжительности жизни, установите его значимость. Имеется ли зависимость
между этими величинами?
'См. Э. Фильрозв. Очерк потенциальной демографии. Ежегодник мировой санитарной
статистики. ВОЗ., Женева, 1978. С. 12 - 15, 1114 - 1115.
402

Таблица 9.10
Возрастная
группа
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
70-74
75-79
80-84
85 и старше
Городское население
оба пола
31,2
56,6
103,8
168,6
294,6
492,1
890,9
1518,2
2964,4
5213,2
8932,8
15 101,4
мужчины
44,1
83,9
156,5
263,4
450,8
750,4
1296,6
2116,5
3741,5
6182,9
10080,7
16 562,3
женщины
18,5
30,1
55,1
104,9
194,3
338,0
666,2
1238,2
2664,1
4837,4
8547,1
14 682,5
Сельское население
оба пола
44,5
72,7
106,9
163,5
262,0
400,9
734,3
1267,2
2590,9
4348,8
7915,9
13 896,9
мужчины
59,2
98,1
153,8
246,8
394,8
617,3
1048,4
1697,0
3169,2
5044,6
8680,5
14 489,4
женщины
30,7
48,2
65,8
109,3
185,9
293,8
569,6
1055,0
2319,2
4012,1
7587,0
13 671,9
5. По данным задачи 3 с помощью критерия Уилкоксона проверить
нулевую гипотезу о равенстве доли расходов на культурные нужды и на
транспорт в генеральной совокупности семей, из которой извлечена
выборка.
6. По данным задачи 1 гл. 7 с помощью критерия Краскела—Уоллиса
требуется проверить гипотезу об однородности четырех рассматриваемых
групп (табл. 9.8).
7. По данным задачи 10 гл. 4 о причинах смертности в разных
социальных группах населения Франции (на 100 тыс. населения) с помощью
критерия Краскела — Уоллиса требуется проверить гипотезу об однородности
пяти рассматриваемых групп населения (табл. 9.9).
8. Имеются данные1 о смертности населения бывшего СССР от
болезней системы кровообращения в 1971 г. (на 100 тыс. населения) (табл. 9.Ю).
Требуется: а) с помощью критерия Краскела—Уоллиса проверить
гипотезу об однородности четырех групп: мужчин и женщин городского и
сельского населения; б) если группы неоднородны, то провести попарное
сравнение групп, используя критерий Манна—Уитни; в) используя критерий
Уилкоксона, сравнить две группы — "оба пола" для городского и сельского
населения.
'Я. А. Быстрова, Р. К. Игнатьева. Смертность от сердечно-сосудистых заболеваний в
СССР. - Терапевтический архив, 1974, № 6, с. 59.
26*
403

П риложен ие 1
Сформулируем некоторые математические понятия и обозначения,
используемые в данном руководстве. Причем наша цель — это не
математически строгое обоснование фактов, а доступность изложения. Более
точные, с точки зрения математики, определения и формулировки можно
найти в соответствующих курсах высшей математики.
1. Запись вида
1= 1
означает сумму п слагаемых, каждое из которых обозначено единым
общим выражением хг Значение /' называют индексом суммирования, Z —
символ, означающий суммирование. В выражении (1) указано, что индекс
/ изменяется, принимая натуральные значения, от 1 до п, т. е. запись (1)
означает не что иное, как
х1+х2 + ... +хп.
В качестве п можно взять любое натуральное число, х{ — также любое
условленное выражение, каким-то образом связанное с индексом /. В
качестве индекса суммирования обычно используют буквы /, у, к. Индекс
суммирования не обязательно начинается с 1. Рассмотрим примеры записи
выражений:
5
а = а + а2 + а3 + а4 + а5;
к= 1
Е('+!И1+И1+И1+!);
к= 2
L г jJ ? зг
п = 1
Последнее выражение содержит бесконечное количество слагаемых и
называется числовым рядом. Сумма бесконечного количества слагаемых
(сумма ряда) может быть для одних выражений равна конечному числу, а
для других может не существовать (например, быть равной
бесконечности). В зависимости от этого говорят о сходимости ряда к некоторому
числу или о расходимости ряда, если такого числа не существует.
Аналогично вместо чисел можно суммировать функции. Например,
п
£V = x° + xl+x2 + ...+xn.
к=0
404

£Y= l+q + q2 + ....
л = 0
В случае | q \ < 1 последняя сумма представляет собой геометрическую
прогрессию (ряд) со знаменателем q, которая сходится к числу —-— [см.
\- q
далее (11)].
Можно использовать двойное суммирование, тогда выражение под
знаком сумм должно иметь два индекса, например j и к, каждый из которых
относится к своей сумме. Например,
2 3 2
X 2 Xjk = 2(*У1 + Xjl + Xj^ = (*И + ХП + Xl^ + ^21 + X22 + *23) '
/=1*=1 j=\
Иногда вместо подробного описания изменения индекса суммирования
п
V**, используют сокращенную запись V'jc,, имея в виду, что индекс / из-
i=i '
меняется в пределах, определенных в условии задачи.
Также используют обозначение суммирования без указания области
изменения индексов или вообще без индексов; например, запись вида
Vx, или Vjc
или означает, что суммирование в первом выражении ведется по всем
возможным имеющимся в задаче значениям х{, а во втором выражении — по
всем возможным значениям х, фигурирующим в условиях задачи. При
этом в случае бесконечного числа слагаемых необходимо заботиться,
чтобы рассматриваемые суммы действительно существовали.
Запись V* *,.>>, означает, что суммирование производится по всем
возможным произведениям пар чисел xt и yjt т. е. данная запись равносильна
записи выражения при двойном суммировании.
2. Приведем обозначения, используемые в комбинаторике.
п\ = 1 • 2 • 3 •... • л, т. е. 1! = 1, 2! = 2, 3! = 6,... .
По определению полагают 0! = 1.
Читается п\ (п — факториал) и определяется только для целых
неотрицательных значений п.
С = „ Я! ч,, где т = 0, 1, 2, ..., п. (2)
т\(п- т)\
С1 — число сочетаний по т элементов из множества, содержащего п
элементов. Например,
5 3!2!
означает, что из множества в 5 элементов можно выбрать 3 элемента
десятью различными способами. Количество сочетаний не учитывает, в каком
порядке выбирались элементы.
Атп = —2Ц- гдет = 0, 1,2,..., л. (3)
(п-.т)\
405

A™ — число размещений по т элементов из множества, содержащего п
элементов. Число размещений в отличие от числа сочетаний учитывает и
порядок выбора элементов. Например, выбор трех элементов 1-го, 4-го и
7-го — это одно размещение, а выбор последовательно в другом порядке 1-
го, 7-го и 4-го — это другое размещение.
Для любых чисел хи а справедлива формула бинома Ньютона.
(х + а)п = Y,Cmxman = С°пх°ап + С1пха"-1 + ... + Сп-1хп~1а + Спхпа°. (4)
3. Сформулируем определение предела последовательности ах, а2, ...,
ап, ..., где перечисленные значения — некоторые числа, зависящие от
индекса, например 1, -, -, ..., -,... — бесконечная последовательность.
2 3 п
Число а называют пределом числовой последовательности ах, а2, ..., ап,
... при п->оо и обозначают
lima,, = a, (5)
Л-Ю>
если с ростом п разность между ап и числом а неограниченно уменьшается,
т. е. какое бы малое положительное число е мы ни взяли, найдется в
последовательности такой номер п, начиная с которого все разности \ап — а\
будут меньше этого е.
Например,
lim ± = 0.
В этом примере ап = -, а = 0 — предел последовательности а,, а2, ...,
ап, ..., т. е. последовательности -, -, -, ..., -,....
12 3 п
Аналогично,
limfl +^) = liml +51im- = 1 +5 • 0 = 1.
Заметим, что в данном примере использованы правила (теоремы)
действий с пределами:
— предел суммы величин равен сумме пределов слагаемых при условии,
что каждый из этих пределов существует;
— постоянный множитель можно выносить за знак предела;
— предел постоянной равен самой постоянной.
Найдем limfl +-) , где т — какое-либо фиксированное число, не за-
висящее от п. Вид зависимости (1 + 0)т. Вычисляется этот предел
следующим образом:
limfl + Ц = flimfl + ±ТГ" = flimfl + Щ\ = Г = 1.
406

Однако как только мы в показатель выражения вместо т поставим п:
картина изменится, появится зависимость вида (1 + 0)°°, т. е.
неопределенность. Можно доказать, что данный предел (6) существует и равен
некоторому числу. Более точный расчет показывает, что это число
иррациональное, как, например, знакомое всем число л, и приближенно равно 2,71828.
Определяемое таким образом число обозначают символом е.
Следовательно,
lim(l + Л" = е* 2, 71828. (7)
Числу е отводится особая роль во многих математических формулах.
Логарифмы по основанию е называют натуральными логарифмами и
обозначают символом In. Значит,
log^x = lnx. (8)
Одна из наиболее распространенных функций, е*, называется
экспоненциальной, также эту функцию называют экспонентой.
4. Многие функции можно представить в виде суммы сходящегося ряда,
только в этом случае суммируемыми значениями будут не числа, а
функции.
Примеры:
ж^г" X Г2 ХП
е* = у*- = !+£ + £ + ...+^L + ... (9)
*-~т\ 1! 2! п\
л = 0
1 = \+х + х2 + ... +У + ..., при -1 < х< 1. (11)
1
5. Понятие производной, первообразной и определенного интеграла
известно из курса средней школы.
Напомним некоторые свойства определенного интеграла.
а) Численное значение интеграла
ь
jf(x)dx
а
равно площади криволинейной трапеции, ограниченной осью абсцисс,
линией y-f(x) и прямыми х= а, х= b (рис. 57 — криволинейная трапеция
заштрихована);
Отметим, что конкретный определенный интеграл может и не
существовать. Например, в случае, когда на промежутке интегрирования [а, Ь]
подынтегральная функция/[х) стремится к оо, и тогда может оказаться, что
407

y = /W
соответствующая криволинейная трапеция имеет бесконечную площадь
(рис. 58). В этом случае говорят, что интеграл не существует (расходится).
ь ь
(12)
(13)
б) JAx)dx = -jf(x)dx.
а а
Ь Ь
в) [СЛ*)<& = с [Д^)^с, где с — постоянная.
а а
Ь Ь Ь
г) j(Ax)+g(x))dx = j/{x)dx+ jg(x)dx.
(147
Замечание. Свойства виг называют свойством линейности
определенного интеграла.
д) Свойство аддитивности определенного интеграла:
Ь с Ь
jf(x)dx = jf(x)dx+ JAx)dx, (15)
а а с
где с — любое число, причем не обязательно из промежутка [а, Ь] (т. е.
свойство верно и при с £ [а, Ь], важно лишь, чтобы все рассматриваемые
интегралы существовали).
408

/ = /W
Рис. 60.
e) Если определенный интеграл вычисляется по симметричному
промежутку [—а, а], и подынтегральная функция f(x) — четная, то
\f(x)dx = 2 j/{x)dx = 2 jf(x)dx,
(16)
Соотношения (16) проиллюстрированы на рис. 59. Ввиду четности
функции J[x) площади криволинейных трапеций на интервалах [—а; 0] и
[0; а] оказываются равными, что и означает справедливость равенств (16).
ж) Определенный интеграл по симметричному промежутку [-а, а] от
нечетной функции/(х) равен нулю:
jf(x)dx =
= 0.
(17)
Соотношение (17) проиллюстрировано на рис. 60.
Так как в соответствии с (15)
409

a 0 a
j/[x)dx= jf(x)dx+ f/Lx)dx,
-a -a 0
а значения интегралов — слагаемых отличаются лишь знаком, то и
оказывается, что их сумма равна нулю.
Для вычисления определенного интеграла обычно используют формулу
Ньютона—Лейбница
ь
jf(x)dx = F(b) - F(a), (18)
а
где F(x) — любая из первообразных подынтегральной функции / (х) (т. е.
F=/[x)), а величины F(b) , F{a) — значения выбранной первообразной
соответственно в точках b и а.
Из формулы (18) непосредственно следует, что значение определенного
интеграла не зависит от того, какой буквой обозначена переменная
интегрирования, а зависит от вида подынтегральной функции/(...) и пределов
интегрирования а, Ь.
6. Определенный интеграл, у которого имеются бесконечные пределы
интегрирования, называют несобственным интегралом, т. е.
jf(x)dx, jf(x)dx, jf(x)dx -
а ~~<ю — <х>
несобственные интегралы. Основные свойства указанных интегралов такие
же, как и у определенных интегралов. Однако если для вычисления
определенного интеграла справедлива теорема Ньютона—Лейбница [см. (18)]:
ь
jf(x)dx = F(b) - F(a),
а
то при вычислении несобственного интеграла соотношение этой теоремы
неприменимо, поскольку нельзя подставлять в функцию F(x) вместо х
"бесконечность". При вычислении несобственного интеграла поступают
следующим образом, используя предел функции:
+» в
[f(x)dx = lim [f{x)dx = lim [F(B) - F(a)]. (19)
J B-*+a>J B-*+a>
a a
Если последний предел существует, то говорят, что интеграл сходится,
и вычисляют его конкретное значение. Если этот предел не существует, то
говорят, что интеграл расходится, и какие-либо действия вычислительного
плана с таким интегралом не производятся. Аналогично
+ <х> В
\Ax)dx = lim \f{x)dx = lim [F(B) - F(A)]. (20)
—» B-*+*>A Д->+ао
Рассмотрим пример вычисления несобственного интеграла.
410

+ 30 В
-2 + 1
f-2dx= lim [x-2dx= Um-^гЦ- = lim (-Г)| =
}X В-у+odJ B-*+od— 2+1 Д->+оЛ JC/
-/sH-H))-»*1-1-
7. У определенных интегралов (как обычного вида, так и
несобственных) один или оба предела интегрирования могут быть не постоянными, а
переменными величинами:
\Mdt.
Тогда и сам интеграл в итоге оказывается функцией от этой
переменной, стоящей в пределе интегрирования. Действительно, по теореме
Ньютона—Лейбница [см. (18)]
X
\f{t)dt = F(x) - F{a).
а
Если обе части последнего равенства продифференцировать по х (т. е.
по переменному верхнему пределу интеграла), то окажется
\\f{t)dt\ = F\x) - (F(a)Y = f(x) - 0 = f(x) (21)
a x
(напомним, что по определению первообразной F'{x) = f[x), а
производная постоянной F(a) равна нулю).
Соотношение (21), позволяющее находить производную от интеграла с
переменным верхним пределом, называют теоремой Барроу.
Замечание. Если переменным окажется нижний предел
интегрирования, то можно поменять местами верхний и нижний пределы
интегрирования, при этом знак самого интеграла изменится на противоположный:
jf(t)dt= -JMdt.
8. Интеграл Пуассона.
Интегралом Пуассона называют несобственный интеграл
+ 30
\e~Ut. (22)
— <ю
В курсе математического анализа доказывается, что интеграл (22) равен
числу л/я.
9. Кратные интегралы.
Кратный интеграл (двойной, тройной и т. д.) является обобщением
обычного (однократного) определенного интеграла, вычисляемого от
функции одной переменной, на случай, когда подынтегральная функция
является функцией многих переменных.
411

z A
Рис. 61.
В случае определенного интеграла интегрирование осуществляется по
некоторому интервалу (конечному или бесконечному). В случае двойного
интеграла область интегрирования определяется значениями двух
переменных, т. е. это некоторое множество точек на плоскости (плоская область);
для тройного интеграла область интегрирования — область трехмерного
пространства и т. д.
Если пределы изменения каждой переменной интегрирования
известны, то они указываются для каждого интеграла по отдельности. Например,
пусть V — область интегрирования функции fix, у, z), определяемая
неравенствами
а<х<Ь
c<y<d,
\<Z<2
(23)
тогда соответствующий тройной интеграл по области V можно записать в
виде
Ь (12
| | \/(х, У, Z)dxdydz = jjJAx, У, Z)dxdydz.
(24)
(v)
В выражении (24) первый из интегралов относится к переменной х,
второй — к переменной у, а третий — к переменной z- Область
интегрирования, т. е. область изменения переменных х, у, z, можно нарисовать
(рис. 61).
Интегрирование в (24) проводится последовательно по каждой из
переменных. Таким образом, вычисление тройного интеграла сводится к
вычислению трех обычных (однократных) определенных интегралов: вначале
вычисляется внутренний интеграл (в данном случае по переменной z), за-
412

тем следующий интеграл (в данном случае по переменной у) от функции,
получившейся при первом интегрировании, и последним вычисляется
внешний интеграл (по переменной х) от функции, получившейся при
двукратном интегрировании. Изобразим порядок вычисления (24):
Ь (12 Ь d 2
\\\ЯХ> У> Z)dxdydz = jjjfix, У, Z)dzdydx. (25)
а с А
Для иллюстрации вычисления возьмем конкретную функцию/(х) = х +
+ у + z~ 1, конкретную область (прямоугольный параллелепипед)
О <jc< 1
V:\~\<y<\
0<z<2
и вычислим тройной интеграл (ради удобства обозначим его J)
/= J f kx + y + z- \)dxdydz.
(у)
Расставим пределы интегрирования для каждой переменной
1 1 2
/= f f {(x + y + z~\)dxdydz = f f ((x + y + z~\)dzdydx.
(V> o-io .
I I
I I
Вначале вычислим внутренний интеграл по переменной z, с другими
переменными (х и у) в этом интеграле обращаемся как с постоянными:
2 2 2 2 , z=2
\(x + y+z-\)dz= j(x + y-\)dz+ jzdz = (x + y-\)jdz+i
z=0
= (* + y-l)Co + (y-°) = (x + y-\)(2-0) + 2 = 2(x + y).
Далее получаем уже двойной интеграл (переменные — х и у, а все, что
касается переменной z, уже посчитано):
1 1
/= f h(x + y)dydx.
°Ь I
Вновь вычисляем внутренний интеграл (в данном случае по переменной у):
1 11 1 2 у=1
\2(x + y)dy = 2 \xdy+ 2 \ydy = 2х Uy+2y-
-i -i -i -i
y=-l
= 2xy\£ll + 2(£-L-p) = 2x(l-(-l)) + 0 = Ax.
2 2
После вычисления значения внутреннего интеграла наш двойной
интеграл оказался сведенным к однократному, который и находим
413

= Uxdx = 4 f;
xdx = 4-
2(1-0) = 2
Итак, значение тройного интеграла найдено. Аналогичным образом
вычисляются и другие кратные интегралы.
Заметим, что пределы интегрирования во внешнем интеграле должны
быть постоянными, а во внутренних интегралах могут быть и
переменными (зависеть от переменных интегрирования). Пределы интегрирования
могут быть как конечными, так и бесконечными (в последнем случае
важно, чтобы несобственные интегралы существовали), как, например,
кратные интегралы, представленные в гл. 3. При представлении кратного
интеграла в виде повторного переменные интегрирования можно
рассматривать в любом порядке, контролируя лишь условие, чтобы каждая
переменная получила интеграл со своими пределами интегрирования
(следовательно, в рассмотренном примере в качестве внешнего интеграла
можно было использовать интеграл по переменным у и z)-
10. Матрица.
Пусть имеется некоторое множество элементов. Упорядочим его,
расположив элементы в виде прямоугольной таблицы. Последовательности
элементов, расположенных в таблице слева направо, называют строками, а
расположенных сверху вниз называют столбцами. Таким образом, каждый
элемент оказывается в некоторой строке и некотором столбце.
Следовательно, пронумеровав строки и столбцы, мы каждому элементу однозначно
предпишем его место.
Такую таблицу, в которой место каждого элемента определено
соответствующими номерами строки и столбца, называют матрицей. Запишем ее
в общем виде, обозначив элементы atj, где / — номер строки, j — номер
столбца, на пересечении которых и расположился элемент матрицы
А =
ап а12 а13 ... аХп
а2х а22 а23 ... а2п
ап ап о3з ••• Язл
ат\ ат2 атЗ ••• атп
(26)
Например, элемент а23 расположен во второй строке и третьем столбце.
Количество строк и столбцов определяют размерность матрицы. В нашем
случае размерность матрицы А — это т х п. Если количество строк равно
количеству столбцов, т. е. т = п, то матрицу называют квадратной.
Для квадратной матрицы элементы с одинаковыми индексами, ап, а22, ...,
ат образуют диагональ, называемую главной диагональю. Элементы ai} и ajt
располагаются симметрично относительно главной диагонали. Если все
элементы а у и aj( попарно равны, то матрицу называют симметричной.
Рассматриваемая в нашем курсе корреляционная матрица всегда квадратная и
симметричная.
Элементами матрицы могут быть числа, переменные, некоторые
выражения или даже другие матрицы.
414

Квадратная матрица, у которой элементы на главной диагонали —
единицы, а все остальные элементы — нули, называется единичной матрицей.
Единичные матрицы — это
1- -1
1 0
0 1
>
_ J
1 0 0
0 1 0
0 0 1_
, . . .,
1 00
0 1 0
00 1
000 ... 1
(27)
Матрица, все элементы которой — нули, называется нулевой матрицей.
В частном случае матрица может состоять из одной строки (вектор-строка)
или одного столбца (вектор-столбец).
В курсе алгебры рассматриваются действия с матрицами (сложение,
вычитание, умножение, нахождение матрицы, обратной к данной),
аналогичные действиям с числами. При этом роль единицы выполняет единичная
матрица, а роль нуля — нулевая. Число можно рассматривать как матрицу
размерности 1 х 1, т. е. понятие матрицы есть обобщение понятия числа.
Понятие матрицы находит широкое применение не только в
математике (например, при решении систем уравнений), но и в других
дисциплинах. В частности, при использовании компьютерных программ часто
данные требуется представить в виде матрицы определенной размерности.
Особенно это касается статистических программ, где любая выборка по
существу является вектор-строкой или вектор-столбцом соответствующей
размерности.
В заключение отметим, что в Приложении 1 дано лишь первичное
знакомство с некоторыми важными математическими понятиями, призванное
несколько облегчить восприятие математической 'части курса. Однако
систематическое, серьезное изучение курса статистики требует более
детального знакомства и с основами высшей математики, которые
рассматриваются в соответствующих учебных пособиях.

o\
oo
r~
VO
<o
rf
m
rs
-
о
со oo m r-~ oo
as as oo чо in
M fl fl fl fl
r-~ in чо cm in
r-~ см со —i in
as as oo r-~ in
CO CO CO CO CO
о см r-~ чо см
oo со -«3- см r-
as as oo r-~ in
CO CO CO CO CO
3352
3144
3372
3166
3391
см as r-~ as as о
OO CO 1П CO OO ~^
as as oo r-~ in
Tiro го го го со со
Tf in t-~ CM 1П
OO ■«*■ ЧО 1П О
as as oo r-~ чо
со го со со со
чо —* чо in ~-
oo in r-~ чо см
CO CO CO CO CO
см оо ■«*■
о\ чо ■«*■
см см см
2943
3187
2966
3209
3429
3230
2709
2468
2732
2492
ON ЧО ЧО
00 1П ^
as r-~ in
см см см
зон
OO ~ -гГ
Tt 1П СО
■«з- см о
со со со
oo so in oo r— r-~
oo in oo г- со чо
as as oo r-~ so ■«*■
со го со со со со
oo so as as in
as as oo r- so
CO CO CO CO CO
On in см см oo
OOVDOOVO
as as as oo so
CO CO CO CO CO
OO Г"» ^^ •—i OO
as as as oo \o
CO CO CO CO CO
o~
3485
3503
3521
3271
3056
3292
3312
3332
О *-* CM CO Tj" in SO
о о о о о
о
о
2780
2541
2803
2565
2827
2589
ON О СО
г- in ^
О ОО ЧО
со см см
3101
3123
г-
2874
2637
2897
2661
oo as
о о о
со in чо оо
о чо со ~^
см as r-~ in
2227
1989
2251
2012
2275
2036
1758
1539
1781
1561
1804
1582
ON 1П СМ О
см о oo чо
CM CM ^^ ^
2323
2083
2347
2107
2371
2131
2396
2155
1849
1626
1872
1647
in r- r- ■«*■ as ~*
~ CM 1П О SO 1П
со ^ as oo чо in
~* ~ о о о о
т1- in со оо -^ см
n ^t r^ ^oovo
со ^ as oo чо in
~ ~ о о о о
Tf ГО OS СО Tf ГО
in чо оо со as r-~
со —i as oo чо in
-и ^ О О О О
Tt СМ ЧО ОО Г- т1-
r-~ oo о ■«*■ о оо
со *-* о оо г- in
^ ^ ^н О О О
■«3- О со со -н чо
On О см чо см On
со см о оо г» in
^ ^н ^ о О О
in ст\ о оо -«з- оо
~^ ~н -«3- г- со о
■«*■ СМ О ОО Г-~ ЧО
^ ^ ^ о о о
in оо г-~ со оо о
СО СО 1П OS -rt CM
Tl- CM О OO t- ЧО
_ ^н ^ о О О
in as so r- ■«*■ as ^..см
O\4oininr-~040co
оочо-«з-смоо\г-чо
^^^^^ooo
1919
1691
(N1 Г- Tj- ^M
■«*■ -и as r-~
CM^CM ^ ~^
o"
О -H
CM CO
чо чо см in in ■«*■
r-~ r- as см г- ■«*■
■«*■ см о as г- чо
^н ^ ~* о О О
r- in on о О чо
On СТ\ О ■«*■ On in
■«*■ см ~^ On г- чо
^н ^ -и о О О
■«*■ in чо r-~ oo as
'«3-ЧОО\СМООСООООЧО'«3-
oooooooooo
ON^r^inTl-rOO'^-COr-
тг-^гооо-^-^^оочо-^-
■«3-сосмсм~-^^ооо
oooooooooo
00CTNrO^^ONr-~CO4Oin00
чог-о-^-оо-^-^^оочо-^-
TtnntN^i-'-hOOO
oooooooooo
OOt^OVOTfrtVOOOt^O
^оо^^омл^оочош
■^■COCOCM^^^^OOO
oooooooooo
00CTN^^inONin^^ON4Oin
■«3-cOrocM^^^OOO
oooooooooo
оо-^тоосооосмсо^со
ONOcMinoincMONr-in
■^■«Э-сосмсм^^ооо
oooooooooo
оососм^оосочочосот
Шт^СОСМСМ^^ООО
oooooooooo
т-^-сосмсм^^ооо
oooooooooo
о\^г-~г-~о\^см^г-~оо
СМГОт1-Г-~^-Г-~СООГ^1П
oooooooooo
оотсотз-1пчо-«з-о\о
т1-т1-1ПООСМГ-~ГООГ-~ЧО
1Пт1-СОСМСМ^^^^ОО
o^ooooooooo
o"
О^СМСОт1-1ПЧОГ-~ООСТ\
CMCMCMCMCMCMCMCMCMCM
Tj-in00COaN4O'^-COCM^^
COCM^^OOOOOO
oooooooooo
oooooooooo
minoocoo\r-~incocM^
COCM^^OOOOOO
oooooooooo
oooooooooo
чочоо\-«з-ог-1псосмсм
СОСМ^~н^ООООО
oooooooooo
oooooooooo
r-r^o-^-or-incocMCM
тсмсм^н^ооооо
oooooooooo
oooooooooo
oooooinor-in-^-смсм
COCMCM^^OOOOO
oooooooooo
oooooooooo
aNON^^in^^ooin-^-rocM
COCMCM^^OOOOO
oooooooooo
oooooooooo
ООсмчо^оот-^тсм
tJ-cOCM^^OOOOO
oooooooooo
oooooooooo
СМ^СМЧОСМООЧО^СПСМ
tJ-cOCM^^OOOOO
oooooooooo
oooooooooo
госмсог^смоочо-^-тсм
■^•COCM^^OOOOO
oooooooooo
oooooooooo
■^-COTl-r-~CMCTN40'^-COCM
■«3-COCM^^OOOOO
oooooooooo
o^ooooooooo
o"
о ^(Nn ^-"луом»^
СОСОГОСОСОГОГОСОГОСО
«о

ооооpoopppppppppppppopо р
ророрррро
1-iNJ —0430C~-JOly>-*M-iNJ —ОЧЗСЮ~-1С\1л.(и^1Ю
28
^^РРР' °'РРР'РРРРРР °'s's о о о о о о
llflfilliilffiflflifK
ттттттжтж
pppppppppppppppppppppppp
nmmmmmmmmm
S^f|fS-SSSSg-S-S-S-;-S-S§-S-5-S-S
lyt.£.UJNJ-
)<10Ovl(MJlJkUIM —0>000~J(Mn*UIM
pppppppppppppppppppppppp
NJNJNJNJ —— — —OOO43~04343000000~J~J~J^JO(7\
осты —аилыр--1июч)Ли1-юим>р17\ы0^1Ь
^1j1j7>j1j^1jVjVjV<VjVjVjVjVjToVj^^^^""-^^^""-^"poo"poTpooo"pvo^ovo^o
op p о op op о оррр oppppppppppppppppppppppppopо
ю*о *o о *o *o *o *o *o*o *o *o *o *o *o *© *o*o *o *o *o *o *o *o *o *o *o *o *o *o *o *o *tf *o *o *o *o *o vo *o *o
JkUNJ —04300~JO\iy>jM4j--p4300~Jl-'>-ibbJ —
l-INJNJNJNJNJNJNJ ————
i'Uj'Kj'ivjToTsjTsj^-^-^-^-'h-'o'o'q o^'vc vO^O^p'vO^p^O^O ^O vp oo oo oo oo oo oo ос ею oo с
" юооДДмО'ооо-JCT\iy>-bi*iNj —ОЧЗс -—------■
■tbNJOOCO.tb.NJOOOO-tb.NJC
)ОС«-JOMy>*.UINJ—ОЧЗОО
ssi-s&s-s-SyS&s-s-si^^^
)0000000000000000000000000000**J-^**J**J**J-^-^**J-^-^-^-^*>^-^04<
\ ^^ *?^ V* 9^ ^^
8Й8
J> L^LU^j^J UJ MtJSI Ю NJJ-J^NJJONJ NJNJ IsJJOJvJ^^JO JOJsJJO JOJOJOJOJsJJsJJO JOJsJ NJNJJ-J
*ооЪ\"л1о7э^^^о^^о^Тх*ооооЪо^1^1^^1^Ъ\"«>Ъ\"о\Ъ\\л\л\л\лЯл"л%"л"^"*"1^1и
>ао\^юоооол njOooo
-.1
Я>рс>с>р
' >voJ ... - -
_ _ _ _ _ Л \o О "*0 Ш "*0 Ш "»0 ^ >£>^0 Ш "*0 Ш Ю ^O "*0 vO vO Ш "»0 Ю "»0 "»0 VO "»0 ^ ^ "*0 Ш Ш >£>^0 ч
>o >o so "*o oo *^> "»o oo no^ *5 "*o ^o "*o "*o ^o "*o Ф "»o ч5 v *o ^> "5 "5 Ф "*o v "»o "*o ^5 Ф v v "*o ^o ^o чо "»o \
^^^IO^^LUO\000000000000^^^^^^^^0^^^U»VAU»U»^^^L»JL»JL»J|sJ|sJ*-*-<
nJnJ0000^O\^V/i^V^^K)^O>0^OAAU^\0nJU(U^n0(M^^00^1^00^^nJ|O00UV

о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о
hOhOhOhOhOhOhOhOhOhOhOhOhOhOtOhOhOhOhOhOhOhOhOhOhOtOU>U>U>U>U)U>Jblsi
0\0\0\C\v|v|vJv4vJv|v|v|vJvJ-g-gvJOOOOOOOOOOOOVOVO>000 — MJk-JKJOO
о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о
"ю "ю "ю "ю Vj "ю Vj Vj "ю "ю "ю Vj Vj To "ю Vj To To "ю lo lo "ю "ю "ю Vj Vj Vj Vj "ю To To То To "u>
WA*WO\0\0\0\0\»0\0\0\vJ4vlN|-goOOCOOVOVOOOi-MWWv4Mv4VOW
0 ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °
U> U> U) *U> U) *U> *U> \ti *U> *U> \ti *U> *U> "u> 1*> \ti 1»J *U> *U> *U> 1*) 1*) *U> *U> *U> "u> "l*> ^U ^U 4> Jb -U -U \n
m^slOOVCvOVOtCOOOOOMi-oKJMMWWALnOVvJOOVOtOJkMAAUiO
о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о
i^i^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^(^Crt(^(^\y>(^(-ni-»<ON-«J
N)N)N)S)WU>U>UWU1U1UIUIU>WU>U>UIUIUIUIU1U1AAAAAUiUiO\!»'-N)
о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о _>—
0\0\0\0\0\0\0\0\0\0\O\0\0\0\0\0\O\0\0\0v0\0\O\0\v|-~lv|vtv|vJvJvJ00O
•g-g.goooooooowoooooooooooooooowoovovovovcvovoooOH'^MAOSH'O
о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о о oj— —
oooooooooobooobobooooobobobobobobobooobooooobobobo'oooo'oovovovovoou)
MLn00i-*AWWl0\0\-g0000V0Of-WWLftON00O0J0\V0UI>O0\0\OH'00H-0\
ооооооооооооооооооооооооо-—•—•—•—•—•—>ou>vo
UA4kWLnWLftLftLftLnLft0\0\0\0\0\0\0\v|vJ-g-g0000>eOO'-ULn>fiUlUI0\
o\"0\ouiua\viMoovoo"W^a\s)\CH<Aa\vcuoouooovoAo\ooa\w
oooovoo>—~->—►—--►—►—~-totototou>u>u>jkj^i^<iy<ON-~ioovo~-.U-«ju>u>oor-:
O\O\O\O\O\O\-gvJvl-gvJvJvJvJv|v|-g-4|v|vl-4|-4|v|v|00000000VC
-u<-*-~ioovovooooo — — ►—ююю
Ui CO — А Ч^О —
Адта\'ч1сп<£н<ыо\\оА
0\МмД>дмт«АОО\ЫммМО\Ми01пи
OnWVOW
ю u> <-* ю ►—
JO JO JO JO K) Ю Ю Ю Ю Ю Ю Ю IO Ю Ю Ю Ю Ю Ю Ю Ю Ю Ю IO Ю JO JO y\ bJ _U> J> J3
oooooooooooooo
OSIAAlnlna\0\0\'>Js|M«vCOMMWAO\000
K)K)Wwu*oivj —
o\'-o\Lft-gvj»o^;
K)K)bJhOKJK)bJKJbjK)K)K)K)K)hJK)K)K)K)bJK)KiK)K)K)KiK)uiuuiwAa\u
<-* o\o\-j -~i Vi -~i Vi Vj Vi bo Ъо Ъо "оо Ъо "оо Ъо vo vo vo vo о о >— — "ю u> lx -~i To Tjn oo vo »
WWUWlXUlUIUIUIWWUUIWUIWWUlAAAAAAAAWLflUlOVCeKl^y
Mu^w on "on on"onVi Vj Vj Vj Vibo'oo'oo vo vo о oV-ToT*) ji. u->jo avooo owe '—. on
<evia\WiWiO\-JO'-K)A-J40K)LftCeK)0\K)-4l44s)K)4040Ce4kOO\0\H'*^"ov
Q tOON-tbUttOtOtOtOtOtOtOtOtOtO*— *— •— *-*"-" •—•—•—•— •—

Таблица 4. Критические значения случайной величины х1 с г степенями
свободы, для которой выполнено равенство Р(хг > т) = р
ч
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0,99
0,000
0,020
0,115
0,297
0,554
0,872
1,239
1,646
2,09
2,56
3,05
3,57
4,11
4,66
5,23
5,81
6,41
7,02
7,63
8,26
8,90
9,54
10,20
10,86
11,52
12,20
12,88
13,56
14,26
14,95
0,98
0,001
0,040
0,183
0,429
0,752
1,134
1,564
2,03
2,53
3,06
3,61
4,18
4,76
5,37
5,98
6,61
7,26
7,91
8,57
9,24
9,92
10,60
11,29
11,98
12,70
13,41
14,12
14,85
15,57
16,31
0,95
0,004
0,103
0,352
0,711
1,145
1,635
2,17
2,73
3,32
3,94
4,58
5,23
5,89
6,57
7,26
7,96
8,67
9,39
10,11
10,85
11,59
12,34
13,09
13,85
14,61
1538
16,15
16,93
17,71
18,49
0,90
0,016
0,211
0,584
1,064
1,610
2,20
2,83
3,49
4,17
4,86
5,58
6,30
7,04
7,79
8,55
9,31
10,08
10,86
11,65
12,44
13,24
14,04
14,85
15,66
16,47
17,29
18,11
18,94
19,77
20,6
0,80
0,064
0,446
1,005
1,649
2,34
3,07
3,82
4,59
5,38
6,18
6,99
7,81
8,63
9,47
10,31
11,15
12,00
12,86
13,72
14,58
15,44
16,31
17,19
18,06
18,94
19,82
20,7
21,6
22,5
23,4
0,70
0,148
0,713
1,424
2,20
3,00
3,83
4,67
5,53
6,39
7,27
8,15
9,03
9,93
10,82
11,72
12,62
13,53
14,44
15,35
16,27
17,18
18,10
10,02
19,94
20,9
21,8
22,7
23,6
24,6
25,5
0,50
0,455
1,386
2,37
3,36
4,35
5,35
6,35
7,34
8,34
9,34
10,34
11,34
12,34
13,34
14,34
15,34
16,34
17,34
18,34
19,34
21,3
21,3
22,3
23,3
24,3
25,3
26,3
27,3
28,3
29,3
0,30
1,074
2,41
3,66
4,88
6,06
7,23
8,38
9,52
10,66
11,78
12,90
14,01
15,12
16,22
17,32
18,42
19,51
20,6
21,7
22,8
23,9
24,9
26,0
27,1
28,2
29,2
30,3
31,4
32,5
33,5
0,20
1,642
3,22
4,64
5,99
7,29
8,56
8,80
11,03
12,24
13,44
14,63
15,81
16,98
1815
19,31
20,5
21,6
22,8
23,9
25,0
26,2
27,3
28,4
29,6
30,7
31,8
32,9
34,0
35,1
36,2
0,10
2,71
4,60
6,25
7,78
9,24
10,64
12,02
13,36
14,68
15,99
17,28
18,55
19,81
21,1
22,3
23,5
24,8
26,0
27,2
28,4
29,6
30,8
32,0
33,2
34,4
35,6
36,7
37,9
39,1
40,3
0,05
3,84
5,99
7,82
9,49
11,07
12,59
14,07
15,51
16,92
18,31
19,68
21,0
22,4
23,7
25,0
26,3
27,6
28,9
30,1
31,4
32,7
33,9
35,2
36,4
37,7
38,9
40,1
41,3
42,6
43,8
0,02
5,41
7,82
9,84
11,67
13,39
15,03
16,62
18,17
19,68
21,2
22,6
24,1
25,5
26,9
28,3
29,6
31,0
32,3
33,7
35,0
36,3
37,7
39,0
40,3
41,7
42,9
44,1
45,4
46,7
48,0
0,01
6,64
9,21
11,34
13,28
15,09
16,81
18,48
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44,3
45,6
47,0
48,3
49,6
50,9
0,001
10,83
13,82
16,27
18,46
20,5
22,5
24,3
26,1
27,9
29,6
31,3
32,9
34,6
36,1
37,7
39,3
40,8
42,3
43,8
45,3
46,8
48,3
49,7
51,2
52,6
54,1
55,5
56,9
58,3
59,7
27*
419

ы
о
«-ft -t±
о о
IaJ Ю
-d. to
>— «-ft
о о
SO OO
-Ц. -J
~-J p—
О О
Ю —
OJ -t*.
ON Ю
О О
S£) ЧО
-J Ю
~-J SO
IaJ
О
>-^
Ю
SO
О
~-J
~-J
l-ft
О
О
~-J
О
OO
«-ft
OO
to
о
о
t-ft
OJ
о
ON
l-ft
SO
о
о
to
U->
о
~-l
ON
-tb
-
о
о
-J
о
о
«-ft
«-ft
-Рь
о
о
1-^
о
ON
-fcb
IaJ
s
II
~-J
о
о
о
о
о
о
UJ
-J
-J
о
о
о
о
о
«-ft
о
о
ON
о
l-ft
оо
ЧО
о
о
о
о
-и.
ON
-и.
^
о
о
о
«-ft
о
-и.
1—1
о
SO
SO
о
to
SO
-и.
о
SO
SO
OO
-n.
о
to
~-J
о
SO
UJ
~-J
о
1—I
~-J
IaJ
о
SO
~-J
IaJ
IaJ
о
>-^
«-ft
IaJ
о
OO
-n.
~-J
о
о
OO
«-ft
о
SO
1—I
«-ft
to
о
о
ON
IaJ
о
~-J
to
SO
о
о
to
~-J
о
OO
to
~-J
-
о
о
SO
о
о
«-ft
OO
SO
о
о
to
о
о
~-l
о
ON
3
II
ON
о
о
о
о
о
о
-ц.
1—1
о
о
о
о
о
«-ft
IaJ
ON
«-ft
о
«-ft
о
о
о
о
о
о
IaJ
SO
OO
^
о
о
о
-и.
о
1лЛ
-и.
IaJ
о
so
SO
о
о
to
to
to
о
SO
SO
OO
IaJ
о
1-^
OO
SO
о
SO
to
-n.
о
1—>
о
ON
о
SO
ON
~-J
to
о
о
~-J
ON
о
OO
1-^
о
о
1>J
о
о
OO
SO
-n.
-
о
о
о
о
ON
«-ft
~-J
о
о
to
о
о
~-J
~-J
OO
3
II
«-ft
О -U
о о
О -U
О -J
О IaJ
о •—
«-ft О
о о
о о
о о
о «-<->
о —
О ON
о —
ON О
о о
Ю О
IaJ
о
to
-fcb
so
о
so
OO
--J
о
1—>
J».
о
so
so
-J
to
о
о
SO
OO
о
SO
о
to
о
о
-n.
to
о
SO
«-ft
OO
-
о
о
IaJ
о
~-J
«-ft
о
о
IaJ
о
о
OO
«-ft
SO
3
II
-n.
О IaJ
о о
О «j->
О ON
о оо
о •—
«-ft О
to О
-J О
о о
О to
о —
О «-ft
о •—
ON О
оо о
-и. о
to >—
о о
— о
1лЛ >—
«-ft -J
оо
so оо
ОО ON
IaJ «-ft
о о
о о
«-ft «Jj
о о
SO
о о
SO so
SO Л-
~-J >—
з
II
IaJ
о
о
о
о
о
о
ON
IaJ
to
о
о
о
о
о
-J
оо
«-ft
to
о
to
to
-ц.
о
о
о
о
1—>
о
о
^-
о
о
о
-
о
о
to
«-ft
о
so
-J
«-ft
о
о
«-ft
о
о
SO
SO
«-ft
3 3
II II
to •—
о — о
о о о
о о о
О «-ft О
о о о
о •— о
~-J О so
-■J О «-ft
ON О О
о о о
о о о
о •— о
о о о
о •— о
SO О SO
О О so
о о о
а
*-
5>
•о
м
ч>
•о
*■"
о
ЧО
о
ЧО
ЧО
2 »
s< к
S Д
a ^
| у
в
5я
^» S
Ё i
|i
я s
ъ 3
M «a
S
ro
a
s
s
о
н
о
•а
о
a
a
s
s<
la
о
в
n
•а
s

О чО
О О
~-J чЛ
О чЛ
ЧО ^
*- О
О so
О so
О чЛ
о о
on -и
*- оо
~-J ОО
~ сэ
"о "чо
О чо
О so
оо
о
-и.
-и.
ON
о
чО
ON
UJ
о
UJ
оо
UJ
о
SO
оо
-и.
~-J
о
UJ
оо
о
чО
1—1
UJ
о
Ю
чо
~-J
о
SO
чЛ
Ю
ON
о
Ю
SO
о
оо
чЛ
о
о
Ю
1-^
оо
о
ЧО
О
~-J
чЛ
о
Ю
Ю
Ю
О
~-J
~-J
ОО
о
>—1
чЛ
О
о
оо
чЛ
о
-и.
о
1—1
чЛ
о
о
~-J
о
чо
о
о
ЧО
UJ
о
~-J
оо
Ю
UJ
о
о
оо
~-J
о
on
1—1
чо
о
о
-и.
оо
о
~-J
о
UJ
Ю
о
о
UJ
о
о
чЛ
чЛ
-и.
о
о
>-^
ON
о
ON
1—'
~-J
3
II
^-
о
*- о
о о
о о
чЛ О
о о
о о
•Сь (О
-&. чо
ON *-
о о
о о
— о
о о
о о
чЛ UJ
^- оо
Ю UJ
so
о
on
■~~i
■~~i
^
о
о
о
о
чЛ
ON
оо
о
о
о
оо
о
чЛ
чЛ
~-J
о
SO
чо
-р».
о
-и.
UJ
Ю
о
чо
чО
SO
-J
о
л.
л.
to
о
SO
чЛ
SO
о
UJ
-и.
-n.
о
SO
оо
UJ
ON
о
UJ
to
UJ
о
SO
о
to
о
to
чЛ
о
о
SO
-Ц.
~-J
чЛ
о
to
чЛ
о
оо
UJ
о
1-^
~-J
о
оо
SO
чЛ
-и.
о
1-^
on
SO
о
~-J
-и.
SO
о
>—'
о
чЛ
о
оо
to
SO
UJ
о
о
SO
оо
о
on
■~~i
■~~i
о
о
чЛ
UJ
о
~-J
чЛ
о
to
о
о
-и.
о
чЛ
чЛ
оо
о
о
1-^
~-J
о
on
чЛ
ON
о
о
ON
о
о
-и.
-и.
UJ
о
о
^^
о
о
чЛ
ON
оо
3
II
SO
о
о
о
о
о
о
UJ
to
UJ
о
о
о
о
о
-и.
UJ
to
оо
о
on
UJ
чЛ
^
о
о
о
о
чЛ
-и.
SO
о
о
о
~-J
о
чЛ
о
о
о
SO
SO
-и.
о
-и.
^^
о
о
SO
SO
SO
ON
о
UJ
ON
чЛ
о
SO
чЛ
-n.
о
to
SO
UJ
о
SO
oo
ON
чЛ
о
to
oo
SO
о
oo
oo
SO
о
1—I
so
oo
о
SO
UJ
SO
-n.
о
1—1
SO
UJ
о
oo
о
~-J
о
1—1
to
о
oo
~-J
SO
UJ
о
>—1
1—ь
о
~-J
1—1
о
о
ON
о
oo
о
to
to
о
о
-n.
ON
о
ON
UJ
чЛ
о
о
to
о
о
~-J
о
~-J
о
о
ON
о
о
чЛ
о
о
о
о
м^
о
о
чЛ
SO
о
3
II
оо
о
о
о
о
о
о
UJ
ON
чЛ
о
о
о
о
о
-и.
чЛ
~-J
о
ON
to
UJ
^
о
о
о
о
чЛ
о
о
о
о
ON
о
-и.
-и.
ON
о
SO
SO
UJ
о
UJ
чЛ
~-J
о
SO
SO
SO
a
?r
•o
""
^3
t>
""
33
б'О
(-*
j=>
ЧО

го
ы
SO
о
-р».
1-^
UJ
о
оо
оо
~-J
о
UJ
NJ
чЛ
О
SO
UJ
оо
о
UJ
-р».
NJ
О
оо
UJ
-р».
о
NJ
~-J
UJ
О
ОО
оо
SO
~-J
О
NJ
ON
ON
О
~-J
~-J
ON
О
NJ
i-^
UJ
О
оо
-Рь
ON
О
NJ
NJ
-P».
О
~-J
-Рь
О
о
*~
Ul
SO
о
~-J
oo
~-J
Lti
о
>—'
ON
ON
О
ON
«-fi
OO
о
^^
1-^
о
~-J
NJ
~-J
-Рь
О
>-—
i-^
UJ
о
«-fl
oo
~-J
о
о
ON
SO
О
ON
~-J
«-fi
UJ
о
ON
ON
ON
О
«-fi
NJ
О
О
о
UJ
О
ON
О
чЛ
SO
-Рь
NJ
О
О
NJ
OO
о
-Рь
UJ
-Pb
о
о
1—I
NJ
О
чл
NJ
UJ
О
О
-Рь
О
о
UJ
-p».
ю
о
о
>-—
о
о
-Рь
ю
SO
S
II
^
UJ
о
о
о
о
о
о
NJ
NJ
чЛ
О
о
о
о
о
UJ
NJ
чЛ
NJ
О
~-J
чл
~-J
о
о
о
о
ON
-Рь
чЛ
^
О
о
о
о
ON
UJ
О
о
SO
ЧО
ON
о
Ul
-Рь
~-J
о
SO
SO
SO
о
о
«-fl
-p».
UJ
о
SO
~-J
о
о
-Рь
чл
UJ
о
SO
oo
~-J
SO
о
-p».
t^i
~-J
о
SO
NJ
oo
о
UJ
t^i
«-fl
о
SO
ON
oo
о
UJ
~-J
о
о
oo
~-J
~-J
о
UJ
о
NJ
о
SO
NJ
-Pb
~-J
о
NJ
SO
-Pb
о
oo
1—1
SO
о
NJ
UJ
«-f|
О
oo
~-J
SO
ON
О
NJ
-Рь
UJ
О
~-J
Ul
~-J
о
^^
~-J
«-fl
о
oo
NJ
«-ft
СП
О
1—*
oo
о
-J
о
ON
о
_
(О
JO
Vj
ON
Ul
-Pb
о
1—1
NJ
UJ
О
ON
UJ
О
О
о
~-J
ON
О
ON
SO
OO
UJ
О
о
~-J
NJ
О
Ul
-Pb
UJ
О
о
UJ
SO
о
ON
-P».
«-f|
3
II
,—
Ю
NJ ^- О
О О О
о о о
ы д о
о о о
о о о
-Р». U-> Ю
1Л v) Ji
~-J О OJ
о о о
о о о
*- к- О
UJ О О
о о о
ISl .Рь UJ
-Рь чЛ чЛ
~-J L«J чЛ
о
~-J
UJ
Ul
о
о
о
о
ON
•Рь
^—
о
о
о
о
о
чл
so
ON
о
SO
SO
«-fl
о
Ul
о
о
о
SO
SO
SO
SO
о
«-fl
о
о
о
SO
ON
~-J
о
•Рь
o
~-J
о
SO
oo
ON
oo
о
-p».
о
•Рь
o
SO
NJ
о
UJ
-Pb
о
о
SO
«-fl
~-J
~-J
о
UJ
UJ
IaJ
о
oo
ON
«-fl
о
NJ
ON
NJ
О
SO
>-^
ON
ON
О
NJ
ON
«-f|
О
oo
о
о
о
*~
SO
•Рь
о
оо
ON
ON
Ul
о
NJ
О
о
о
~-J
UJ
^л
о
^^
UJ
•U
о
оо
о
ON
•Рь
О
I—»
UJ
^л
о
ON
ON
~-J
О
О
оо
•Рь
о
~-J
UJ
оо
UJ
о
о
--J
so
о
и\
so
ON
о
о
-Рь
L«J
о
ON
ON
О
NJ
О
О
UJ
IaJ
О
^Л
О
о
о
о
»—'
•Рь
о
^л
SO
UJ
о
о
^л
о
о
•U
о
•Рь
о
о
1-^
о
о
^л
о
о
3
II
^^
о
о
о
о
о
о
NJ
ON
«-fl
о
о
о
о
о
UJ
^л
so
а
?т
\з
•о
ы
у
•о
м
о
\0
с>
\0
ЧО
■^

ы
ы
чЛ -Р*
О О
-■J ON
~-J ЧО
оо оо
— о
О чО
О "-О
О -J
о о
--J ON
NJ *-
о *-
*- о
О ЧО
О so
О "-О
UJ
о
ON
о
UJ
о
чО
~-J
ON
о
чЛ
UJ
~-J
о
•^о
чо
о
NJ
о
чЛ
UJ
-Рь
о
•^о
-Рь
UJ
о
-Рь
ON
UJ
о
чО
ON
"-О
о
-Рь
ON
ON
о
•^о
о
UJ
о
UJ
оо
чО
о
чО
-р*
о
о
UJ
чО
~-J
о
оо
чЛ
оо
о
UJ
NJ
ОО
о
•^о
о
ON
ЧО
О
UJ
UJ
NJ
О
оо
о
чо
о
ю
оо
о
о
оо
ON
чЛ
оо
о
NJ
"-О
-р*
о
~-J
~-J
оо
о
ю
ю
"-О
о
оо
ю
~-J
о
NJ
ю
NJ
о
~-J
о
ON
О
(—1
--J
"-О
о
~-J
~-J
ON
о
1-^
"-О
о
ON
ON
ОО
О
i-^
UJ
чЛ
О
~-J
NJ
О
чЛ
О
^^
-Рь
NJ
О
ON
О
UJ
О
О
ЧО
-Рь
О
ON
~-J
NJ
-Р*
О
О
"-О
■~~л
о
чЛ
UJ
-Рь
о
о
чЛ
"-О
о
ON
i-^
UJ
о
о
чЛ
--J
О
-р*
ON
ON
О
О
UJ
о
чЛ
UJ
--J
NJ
О
о
NJ
-Р*
О
UJ
чО
--J
О
О
^^
о
о
•Рь
ON
UJ
о
о
UJ
о
о
UJ
о
NJ
О
о
^^
о
о
UJ
оо
чО
3
II
1—1
чЛ
о
о
о
о
о
о
NJ
NJ
NJ
О
о
о
о
о
NJ
ОО
о
•Рь
о
--J
ON
NJ
О
О
О
о
ON
"-О
"-О
О
О
О
UJ
О
ON
оо
UJ
о
•^о
"-О
ON
о
чЛ
оо
о
•^о
"-О
"-О
NJ
о
чЛ
--J
-рь
о
•^о
■~~л
•Рь
о
чЛ
о
о
о
^о
оо
"-О
о
чЛ
о
о
о
•^о
UJ
чо
о
-Рь
1-^
"-О
о
•^о
ON
~-J
о
о
•Рь
NJ
ON
о
оо
"-О
ON
о
UJ
ON
-Рь
о
•^о
UJ
ON
^D
о
UJ
~-J
о
оо
-Рь
~-J
о
UJ
о
о
оо
"-О
оо
оо
о
UJ
1-^
--J
о
~-J
"-О
•Рь
о
NJ
-Рь
ЧО
о
оо
чЛ
-Рь
~-J
о
NJ
UJ
ОО
о
~-J
ON
NJ
О
i-^
"-О
чЛ
О
оо
о
чЛ
ON
О
NJ
О
ON
О
ON
ОО
UJ
О
1-^
-Рь
ON
О
~-J
чЛ
чЛ
О
1-^
чЛ
UJ
О
ON
NJ
ЧО
О
(—1
О
NJ
О
ON
"-О
"-О
-Рь
О
^^
О
-р».
о
чЛ
~-J
-р».
о
о
ON
•Рь
о
ON
UJ
ON
UJ
О
О
ON
О
чЛ
О
о
о
о
UJ
UJ
о
чЛ
оо
NJ
О
о
NJ
ON
О
•Рь
NJ
ON
О
О
^^
о
чЛ
о
о
о
о
-Рь
о
о
UJ
1—1
~-J
о
о
^^
о
о
•U
1—1
\о
75
II
^
•U
о
о
о
о
о
о
NJ
UJ
ОО
о
о
о
о
о
UJ
о
UJ
о
~-J
~-J
чЛ
о
о
о
о
ON
~-J
чЛ
о
о
о
NJ
О
ON
чЛ
ОО
о
•^о
"-О
ON
О
чЛ
~-J
О
ЧО
ЧО
"-О
О
1Л
ON
ON
О
чО
~-J
NJ
О
•U
~-J
~-J
О
•^о
оо
оо
о
о
•Рь
оо
ON
о
ЧО
UJ
•U
о
•Рь
о
ON
о
•^о
ON
•Рь
а
?г
•о
•о
•о
•«э
о
чо
О
ЧО
ЧО
о

-J ON
о о
ОО -~J
о *-
-fck OJ
*- о
О ЧО
о so
О -J
о о
-4 ON
(О чЛ
SO -U
*- о
О so
О so
О so
U1
о
on
чл
о
о
SO
~-J
SO
о
«-fl
ON
чл
о
SO
SO
-fcb
о
«-fl
oo
UJ
о
SO
«-fl
о
о
чл
о
о
SO
~-J
UJ
UJ
о
Ul
1-^
о
ЧО
1-^
1Л
о
-fcb
UJ
«-fl
о
SO
-fcb
oo
NJ
о
-fcb
t^i
ON
о
oo
~-J
on
о
UJ
oo
о
о
SO
I-—
oo
-
о
-fcb
о
ON
о
oo
UJ
-fcb
о
UJ
UJ
oo
о
oo
oo
OJ
о
о
UJ
Ul
о
о
oo
о
-&>
о
ю
-J
о
oo
-fcb
U\
SO
о
ю
oo
-J
о
-J
-fcb
-J
о
ю
-&ь
ю
о
oo
о
IaJ
oo
о
ю
U\
IaJ
о
-J
^^
IaJ
о
1—'
so
~-J
о
--J
t/l
oo
~-J
о
»-^
SO
ON
о
a\
U\
о
о
1—'
t/l
t/l
о
-J
NJ
so
a\
о
^^
ON
ON
о
«-ft
so
-fc*
о
1—»
1—»
-о
о
OS
OS
NJ
«-ft
о
1-^
NJ
-fcb
о
Ul
-fcb
-fcb
о
о
oo
NJ
о
ON
NJ
о
-fcb
о
о
oo
«-ft
о
-fcb
oo
so
о
о
«-ft
NJ
о
«-ft
ON
«-ft
IaJ
о
о
«-ft
о
о
-fcb
1-^
~-J
о
о
NJ
~-J
о
«-ft
о
NJ
о
о
NJ
о
UJ
«-ft
о
о
о
SO
о
о
-U
UJ
«-ft
-
о
о
UJ
о
о
NJ
ОО
~-J
о
о
1—1
о
о
UJ
-U
On
3
II
^
~-J
о
о
о
о
о
о
1—1
SO
ON
о
о
о
о
о
NJ
~-J
ON
о
~-J
SO
NJ
о
о
о
о
о
~-J
UJ
ON
о
о
о
«-ft
о
ON
SO
«-ft
о
SO
SO
~-J
о
ON
1>J
-J
о
SO
SO
SO
-fcb
о
ON
Ю
oo
о
SO
-J
-J
о
«-ft
-fcb
SO
о
SO
so
о
IaJ
о
«-ft
ON
-fcb
о
SO
-Pb
-J
о
-Рь
~-J
«-ft
о
so
~-J
(O
о
«-ft
о
о
so
^-t
о
о
J».
(О
о
so
-fcb
«-ft
-
о
-fc>
1>J
ON
о
oo
ON
oo
о
1>J
ON
1>J
о
SO
1—»
NJ
о
о
IaJ
-о
(О
о
oo
(О
ю
о
(О
SO
«-ft
о
ОО
~-J
«-ft
SO
о
IaJ
о
«-ft
о
~-J
SO
NJ
о
NJ
ON
о
oo
UJ
-fcb
oo
о
NJ
~-J
NJ
о
~-J
(O
oo
о
NJ
1—1
NJ
о
~-J
oo
oo
~-J
о
NJ
о
oo
о
ON
SO
«-ft
о
I-—
ON
ON
о
~-J
IaJ
SO
ON
о
>-^
~-J
oo
о
ON
NJ
oo
о
I-—
NJ
«-ft
о
~-J
о
^л
Lti
о
1-^
UJ
NJ
о
^л
ON
•Сь
о
о
ОО
ОО
о
ON
UJ
~-J
•Сь
о
о
SO
о
о
^л
о
о
о
^л
^л
о
^л
~-J
SO
UJ
о
о
^л
UJ
о
•U
UJ
ON
о
о
NJ
SO
о
^л
NJ
^л
ю
о
о
ю
OJ
о
UJ
-J
ю
о
о
1—1
о
о
^
и\
S
II
1—1
ON
и- О
о о
о о
oj О
о о
о о
u-> to
о о
^Л ОО
о о
о о
*- о
о о
о о
UJ Ю
ON ON
u-> ^
а
?г
ч>
ъ
^3
•ъ
о
р
ЧО
■&

ы
ел
чЛ -t±
о о
Чл Чл
чЛ О
-U О
о о
Чо Ъо
NJ ЧО
чЛ О
О О
-fcb -U
ОО OJ
чЛ ON
о о
ЧО ЧО
чЛ NJ
-Ц. -~J
UJ
о
-U
-U
о\
о
Ъо
чЛ
UJ
о
UJ
ОО
~-J
о
ОО
"-О
■~~i
to *- о
о о о
W W Ы
SO -U *-
Ю У| Ю
о о о
ОО --1 --1
Ю vl ^
^ ОО W
о о о
Ы 1ч) М
to чО -U
ОО Ы 1ч)
о о о
ОО ОО s)
ON NJ ОО
W ч) ОО
чО
о
NJ
чЛ
~-J
о
о\
ОО
ОО
о
NJ
1-^
NJ
о
~-J
чЛ
ОО
ОО
о
NJ
NJ
NJ
О
о\
чЛ
чЛ
О
1—1
~-J
UJ
о
~-J
о
~-J
~-1
о
1-^
~-1
о\
о
ON
о
00
о
1-^
UJ
-J
о
о\
-J
ю
ON чЛ
о о
^^ м^
Ji. *-
-J О
о о
чЛ чЛ
чЛ О
-U
о о
*- о
О ~-J
UJ UJ
о о
ON чЛ
*- ON
OJ -fck
-U
о
о
~-J
чЛ
о
-U
-U
о\
о
о
-U
о\
о
чЛ
1—1
чЛ
UJ
о
о
-U
-U
о
UJ
ЧО
NJ
о
о
NJ
-р».
о
-U
чЛ
чЛ
NJ
о
о
1-^
"-О
о
UJ
1-^
о\
о
о
ОО
о
о
UJ
ОО
~-J
-
о
о
UJ
о
о
NJ
чЛ
~-J
о
о
^^
о
о
UJ
NJ
ОО
S
II
^
^о
о
о
о
о
о
о
1-^
~-J
о\
о
о
о
о
о
NJ
-U
ю
ОО -О
о о
ОО ~-J
*- .ю
чЛ SO
*- о
О "-О
О SO
О -J
о о
-■J ON
-Сь сп
-fck OJ
*- о
О чО
О чО
о so
С\
о
ON
~-J
о
о
"-О
ОО
о
о
чЛ
чО
о
о
"-О
"-О
NJ
чЛ
о
чЛ
ОО
ON
о
"-О
чЛ
UJ
о
чЛ
UJ
о
о
чО
~-J
чЛ
-U
о
чЛ
NJ
ЧО
о
"-О
NJ
о
о
-U
~-J
о
о
"-О
чЛ
UJ
о
-U
~-J
о
ОО
ОО
-U
о
-U
^^
о
о
"-О
NJ
UJ
ю
о
-&>
^^
-t^
о
ОО
£
о
OJ
-U
~-J
о
ОО
ЧО
о
-
о
UJ
~-J
чЛ
о
ОО
1-^
чЛ
о
UJ
1-^
-U
о
ОО
чЛ
чЛ
о
о
UJ
UJ
о
о
~-J
ON
•u
о
NJ
чЛ
ON
о
ОО
1-^
о\
ЧО
о
NJ
~-J
о
~-J
NJ
ЧО
о
NJ
NJ
о\
о
~-J
~-J
•u
ОО
о
NJ
UJ
о\
О
о\
~-J
о
о
1—1
ОО
•U
о
~-J
•U
•U
~-J
о
1-^
ОО
чЛ
о
о\
NJ
чЛ
о
1-^
•U
чЛ
о
о\
ОО
о\
ON
о
»—»
чЛ
о\
о
чЛ
ОО
о\
о
»—»
1-^
о
о
о\
чЛ
UJ
чЛ
о
1-^
»-^
ON
о
чЛ
NJ
чО
о
о
~-J
~-J
о
чЛ
"-О
о
•U
о
о
ОО
о
о
•U
~-J
о
о
•U
"-О
о
чЛ
и>
о
L»J
о
о
-ц.
~-J
о
Ji.
н^
Ji.
о
о
(О
чЛ
о
Ji.
--J
о
NJ
о
о
NJ
о
о
^U)
u>
о
о
о
ОО
о
•U
1—1
о
-
о
о
UJ
о
о
"(О
~-J
о
о
^^
о
о
UJ
•U
~-J
S:
II
^^
ОО
о
о
о
о
о
о
1—1
ОО
чЛ
о
о
о
о
о
"(О
чЛ
о\
а
?г
•о
*"
•о
w
•о
*"
^з
о
о
ЧО
ЧО
о

ы
О»
о so
о о
ОО ~-J
IaJ «-ft
IaJ ON
*- о
о so
о so
О -J
О О
--J ON
-~J ОО
*- ЧО
*- о
о so
О so
О so
ОО
О
ON
ОО
о
о
SO
ОО
ю
о
on
ю
l-ft
о
SO
SO
ю
~-J
о
ON
(О
ОО
о
so
«-ft
ОО
о
«-ft
«-ft
-fcb
о
so
-J
-J
ON
о
l-ft
~-J
ON
о
SO
NJ
SO
о
l-ft
о
о
о
SO
«-ft
ON
«-ft
о
«-ft
NJ
«-ft
о
ОО
so
ON
о
-n.
-n.
ON
о
SO
UJ
-n.
о
-n.
~-J
l-ft
о
ОО
ON
о
о
UJ
SO
SO
о
SO
о
NJ
UJ
о
-n.
NJ
-n.
о
ОО
OJ
OJ
о
OJ
ON
OJ
о
ОО
-J
(О
о
1>J
~-J
(О
о
~-J
so
о
OJ
N-^
о
ОО
IaJ
--J
о
IaJ
NJ
о
о
-J
«-ft
ON
о
NJ
-o
-n.
о
ОО
о
о
о
о
NJ
SO
UJ
о
~-J
о
~-J
о
NJ
NJ
SO
о
~-J
~-J
SO
о
NJ
-Ц.
-Ц.
О
ON
00
О
О
NJ
О
О
~-J
NJ
ON
00
О
NJ
О
SO
о
ON
NJ
00
О
1—I
ON
UJ
О
ON
00
SO
~-l
О
N-^
ON
~-l
О
«-ft
-J
ON
О
H—l
Ю
so
О
ON
1>J
-J
ON
О
^-*
-fc».
О
о
«-ft
NJ
«-ft
О
о
SO
00
о
ON
о
«-ft
о
^^
о
-n.
о
-n.
~-J
«-ft
о
о
ON
SO
о
«-ft
«-ft
-n.
-n.
о
о
~-J
о
-n.
NJ
-Ц.
О
о
-n.
-n.
о
«-ft
о
о
UJ
о
о
-n.
NJ
О
1>J
~-J
NJ
О
О
NJ
IaJ
О
-Ц.
-Ц.
ON
Ю
О
о
t—*
ОО
о
UJ
ю
о
о
о
ОО
о
о
IaJ
~-1
«-ft
о
о
IaJ
о
о
(О
-fcb
-fcb
о
о
N^
о
о
1>J
1—1
II
(О
о
о
о
о
о
о
о
1—1
ON
~-J
о
о
о
о
о
NJ
NJ
so
SO
о
ОО
NJ
-и.
о
о
о
о
~-J
«-ft
ОО
о
о
о
ОО
о
~-J
-и.
IaJ
о
SO
SO
~-J
о
ON
~-J
NJ
о
SO
SO
SO
~-J
о
ON
oo
-n.
о
SO
oo
о
ON
1-^
1>J
о
SO
SO
NJ
ON
О
ON
О
OO
О
SO
«-ft
ON
О
«-ft
-Рь
«-ft
О
SO
-J
ON
a
?T
Ъ
•o
ъ
•o
_o
_o
ЧО
s

ы
-J
Уро!
n
X
«г
u
£u
ЧИМОСТИ
а (одно
а
роння
а
.рит
ичес
^
1я обла
Ц
«г
о
(-*
0,10
_о
о
_о
к»
j=>
о
_о
о
Ln
о'о
о
к»
_о
о
о
W
~-J
о
681
й
1Л
ON
OO
Ю
"о
Ю
ON
Ю
W
^-
Ю
~-J
1Л
Ю
SO
oo
1Л
W
W
Ю
ON
W
1Л
~-J
-p».
W W
ON Ul
О О
ON ON
OO OO
и- Ю
.-.-
ON ON
OO О
Ю Ю
О О
&s
Ю (О
-P». -P»
w w
-Б OO
Ю Ю
-J -J
H- Ю
чо 4».
Ю Ю
чо чо
чо чо
О ON
W W
W W
W -P».
W О
W Lb)
1Л Ul
OO ЧС
Ю *-
U Ы W
д ы to
о о о
ON ON ON
OO OO OO
M M NJ
ЙЙ8
s) OO^D
W
о
682
--
so
ON
*- Ю ^ ON
to м to
о о о
www
(О (О (О
£££
к- U1 чо
(О (О (О
~о ~о ~о
Ю W W
ОО Ы 00
W Ы U
о о о
о о ^-
Ю OO U
ы ы ы
ы ы ы
-Р». 1Л ON
00 ОМЛ
ы ы ы
ON ON ON
О н- (О
н- н- (О
(О
ср
5
(О
W
(О
~о
£
W
о
(О
(О
W
W
~о
1Л
W
ON
W
W
W Ю Ю
о чо оо
о о о
ON ON ON
oo oo oo
www
www
О ^- W
ON ON -O
so so О
~o so H-
Ю Ю Ю
Ю1ЛЮ
Ю Ю Ю
1Л ON ON
~-J Ю -J
Ю Ю Ю
~o ~o ~-j
1Л1Л C\
oo\w
www
о о о
W W -P»
О OO ~-J
www
W W -P»
oovoo
1Л ON O0
www
ON ON ON
-P». 1Л -J
ON ЧО -P»
Ю
~o
о
684
w
-Рь
vj
О
w
Ю
о
M
Ю
а
W
Ю
vj
vj
K-
W
о
1Л
V)
W
-p».
Ю
^
w
ON
so
О
to
ON
О
684
w
1Л
V)
Sn
Ю
о
&
Ю
so
Ю
•o.
•o
so
W
о
ON
•o
W
-p».
W
1Л
W
V)
о
vt
Ю
1Л
о
684
W
ON
~o
s
Ю
о
о
(О
&
1Л
(О
~о
ОО
~о
W
о
~о
ОО
W
-р».
1Л
о
W
~о
(О
1Л
ю
*.
о
to
w
о
to
to
о
to
о
СЛ 1Л ON ON
W
oo
-J
J~*
to
о
л£
to
so"
to
to
-J
so
-J
w
о
so
^
w
-p».
ON
~-J
w
~-J
-p».
Ul
w
so
~-J
£
to
690
to
«£
<->
to
oo
о
~-J
w
K-
о
-p».
UJ
-p».
oo
Ul
UJ
~-J
ON
oo
w
to
^-
~-J
^J
to
о
s
to
Й
oo
to
oo
>-^
so
w
K~
^^
so
UJ
1Л
о
Ul
UJ
~-J
so
to
w
to
w
-o
to
to
о
8
to
1Л
oo
to
oo
w
^
UJ
K^
UJ
Ul
UJ
Ul
to
-J
w
oo
>—1
so
to
о
о
687
w
to
1Л
~-J
to
to
о
oo
ON
to
и
oo
to
2
1Л
w
K~
Ul
UJ
w
1Л
Ul
to
UJ
oo
1Л
о
SO
о
oo
о
oo oo
to
oo
~-J
to
so
to
093
to
1Л
UJ
so
to
oo
ON
^-
UJ
^^
~-J
•u
UJ
^Л
~-J
SO
UJ
oo
oo
w
w
w
о
~-J
-J
о
689
w
w
w
-J
ON
о
069
w
w
~-J
~-J
££&
to
о
to
to
to
oo
~-J
oo
UJ
K^
SO
~-J
UJ
ON
1—I
о
w
so
to
to
to
о
to
&
-J
to
oo
SO
oo
w
to
to
to
w
ON
^
ON
w
so
ON
Cfl
to
а
to
1Л
oo
w
to
^p
U\ 4±
о о
UJ
о
ON ON ON
^^
^- LTI
-J -J
^Л ON
w *-
to to
OJ -Pi.
to to
8S
to -p».
to to
SO SO
lO^v]
^-
w
to
«-fl
to
w
ON
oo
ON
•Pb
o
>—*
Lti
~-J ~-J
UJ W
to w
oo to
ON ON
w w
~-J ~-J
w oo
W ~-J
-p». Ji.
о ^-
-J -Рь
UJ О
1,350
~-J
~-J
to
8
to
650
w
о
to
w
w
~-J
to
w
oo
«-fl
to
•P*
to
to
^-
to
о
695
w
ON
~-J
oo
to
to
so
to
©
^-
UJ
о
Ul
1Л
UJ
•u
to
oo
w
SO
w
о
•Рь
w
1-^
oo
о
о
о
ON -J
^S8
o<
UJ
~-J
&
to
to
о
to
~-J
oo
UJ
l_>
8
w
•Pb
SO
~-J
•u
о
to
«-fl
•u
•u
w
~-J
-J
to
oo
to
to
to
&
to
764
w
1—1
ON
SO
w
LH
oo
,—
^
_
^
^
^
CTi
oo
-J
SO
о
703
oo
w
oo
w
w
to
to
ON
to
to
oo
to
^-
w
K)
>-/l
о
w
ON
SO
о
•Рь
to
SO
~-J
•u
~-J
oo
^-
oo
о
706
w
SO
~-J
oo
8
to
UJ
8
to
896
w
w
«-fl
^Л
w
oo
w
w
•Pb
Lti
о
^-
^Л
о
•Рь
^-
~-J
о
711
•Рь
Ltt
oo
SO
to
w
ON
to
$
oo
w
•Pb
«
•Pb
o
to
SO
•u
~-J
oo
^Л
Ltt
•u
о
oo
ON
о
718
-r
о
943
to
s
w
£
w
w
~-J
о
~-J
•u
UJ
^^
~-J
Lti
to
о
oo
Lti
SO
^Л
SO
^Л
о
727
•Рь
ON
to
о
1Л
to
^Л
~-J
UJ
a<
^Л
•u
о
w
to
•Pb
~-J
~-J
UJ
^Л
oo
so
w
ON
oo
ON
SO
•Pb
o
741
w
to
l_^
to
to
~-J
ON
UJ
2
~-J
•u
Ф»
r^
^
Lti
Lti
SO
oo
~-J
^-
~-J
UJ
oo
ON
о
w to
о о
->J OO
ON *-
1Л ON
ON OO
IX> OO
OO ON
to to
w so
СЛ tO
t>J О
w -fc».
i— UJ
oo о
to uj
-t». ON
£Ж
i— ^Л
«-Г| SO
S2i8
и- ^Л
-~J Ji.
-t>. о
СЛ OO
w so
i— tO
О to
to w
^- to
Cfl ~-J
>— UJ
to *-
SO Ltt
to so
^ SO
000
3,07
oo
ON
w
£
to
~-J
Ы
w
oo
to
ON
w
ON
1Л
~-J
^^
to
OJ
to
318
w
о
SO
ON
w
ON
ON
SO
<
о
о
0,20
_o
о
j=>
о
j=>
о
к»
_o
о
j=>
О
Ln
_o
О
к»
о
<
•о
вень з
X
ачимост
S
а (двус
н
о
о
X
S
н
п
X
ая облас
н
ч_^
£
н
S
д
Р5
S S
ГР О
о н
» л
* s
о С °^
^^
» о W
н^
го го
St О
о s
я го
о
a\ w
fs
v>
< X
х о
о 2
» g
w 2
s s
i M
«9
s
Р )а
го
ю &»
ТЭ ft}
о S
ЕЕ s
S °
м s

Продолжение табл. 6.
V
38
39
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
90
100
120
140
160
180
200
со
Уровень значимости а (односторонняя критическая область)
0,50
0,681
0,681
0,681
0,680
0,680
0,680
0,680
0,679
0,679
0,679
0,679
0,679
0,679
0,678
0,678
0,678
0,678
0,678
0,678
0,678
0,678
0,678
0,678
0,677
0,677
0,677
0,676
0,676
0,676
0,676
0,6745
0,25
0,20
1,304
1,304
1,303
1,302
1,301
1,300
1,299
1,299
1,298
1,297
1,297
1,296
1,296
1,295
1,295
1,295
1,294
1,294
1,293
1,293
1,293
1,292
1,292
1,291
1,290
1,289
1,288
1,287
1,286
1,286
1,2816
0,10
0,10
1,686
1,685
1,684
1,682
1,680
1,679
1,677
1,676
1,675
1,674
1,673
1,672
1,671
1,670
1,669
1,668
1,668
1,667
1,666
1,666
1,665
1,665
1,664
1,662
1,660
1,658
1,656
1,654
1,653
1,653
1,6449
0,05
0,05
2,024
2,023
2,021
2,018
2,015
2,013
2,011
2,009
2,007
2,005
2,003
2,002
2,000
1,999
1,998
1,997
1,995
1,994
1,993
1,993
1,992
1,991
1,990
1,987
1,984
1,980
1,977
1,975
1,973
1,972
1,9600
0,025
0,02
2,429
2,426
2,423
2,418
2,414
2,410
2,407
2,403
2,400
2,397
2,395
2,392
2,390
2,388
2,386
2,384
2,382
2,381
2,379
2,378
2,376
2,375
2,374
2,368
2,364
2,358
2,353
2,350
2,347
2,345
2,3263
0,01
0,01
2,712
2,708
2,704
2,698
2,692
2,687
2,682
2,678
2,674
2,670
2,667
2,663
2,660
2,657
2,655
2,652
2,650
2,648
2,646
2,644
2,642
2,640
2,639
2,632
2,626
2,617
2,611
2,607
2,603
2,601
2,5758
0,005
0,005
2,980
2,976
2,971
2,963
2,956
2,949
2,943
2,937
2,932
2,927
2,923
2,918
2,915
2,911
2,908
2,904
2,902
2,899
2,896
2,894
2,891
2,889
2,887
2,878
2,871
2,860
2,852
2,846
2,842
2,839
2,8070
0,0025
0,002
3,319
3,313
3,307
3,296
3,286
3,277
3,269
3,261
3,255
3,248
3,242
3,237
3,232
3,227
3,223
3,218
3,214
3,211
3,207
3,204
3,201
3,198
3,195
3,183
3,174
3,160
3,149
3,142
3,136
3,131
3,0902
0,001
0,001
3,566
3,558
3,551
3,538
3,526
3,515
3,505
3,496
3,488
3,480
3,473
3,466
3,460
3,454
3,449
3,444
3,439
3,435
3,431
3,427
3,423
3,420
3,416
3,402
3,390
3,373
3,361
3,352
3,345
3,340
3,2905
0,0005
Уровень значимости а (односторонняя критическая область)
428

Таблица 7. Критические точки Fраспределения Фишера в зависимости
от числа степеней свободы большей дисперсии кх и числа степеней свободы
меньшей дисперсии /^
Значения /'при а = 0,05
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
со
1
161,4
18,51
10,13
7,71
6,61
5,99
5,59
5,32
5,12
4,96
4,84
4,75
4,67
4,60
4,54
4,49
4,45
4,41
4,38
4,35
4,32
4,30
4,28
4,26
4,24
4,22
4,21
4,20
4,18
4,17
4,08
4,00
3,92
3,84
2
199,5
19,00
9,55
6,94
5,79
5,14
4,74
4,46
4,26
4,10
3,98
3,88
3,80
3,74
3,68
3,63
3,59
3,55
3,52
3,49
3,47
3,44
3,42
3,40
3,38
3,37
3,35
3,34
3,33
3,32
3,23
3,15
3,07
2,99
3
215,7
19,16
9,28
6,59
5,41
4,76
4,35
4,07
3,86
3,71
3,59
3,49
3,41
3,34
3,29
3,24
3,20
3,16
3,13
3,10
3,07
3,05
3,03
3,01
2,99
2,98
2,96
2,95
2,93
2,92
2,84
2,76
2,68
2,60
4
224,6
19,25
9,12
6,39
5,19
4,53
4,12
3,84
3,63
3,48
3,36
3,26
3,18
3,11
3,06
3,01
2,96
2,93
2,90
2,87
2,84
2,82
2,80
2,78
2,76
2,74
2,73
2,71
2,70
2,69
2,61
2,52
2,45
2,37
5
230,2
19,30
9,01
6,26
5,05
4,39
3,97
3,69
3,48
3,33
3,20
3,11
3,02
2,96
2,90
2,85
2,81
2,77
2,74
2,71
2,68
2,66
2,64
2,62
2,60
2,59
2,57
2,56
2,54
2,53
2,45
2,37
2,29
2,21
6
234,0
19,33
8,94
6,16
4,95
4,28
3,87
3,58
3,37
3,22
3,09
3,00
2,92
2,85
2,79
2,74
2,70
2,66
2,63
2,60
2,57
2,55
2,53
2,51
2,49
2,47
2,46
2,44
2,43
2,42
2,34
2,25
2,17
2,09
8
238,9
19,37
8,84
6,04
4,82
4,15
3,73
3,44
3,23
3,07
2,95
2,85
2,77
2,70
2,64
2,59
2,55
2,51
2,48
2,45
2,42
2,40
2,38
2,36
2,34
2,32
2,30
2,29
2,28
2,27
2,18
2,10
2,02
1,94
12
243,9
19,41
8,74
5,91
4,68
4,00
3,57
3,28
3,07
2,91
2,79
2,69
2,60
2,53
2,48
2,42
2,38
2,34
2,31
2,28
2,25
2,23
2,20
2,18
2,16
2,15
2,13
2,12
2,10
2,09
2,00
1,92
1,83
1,75
24
249,0
19,45
8,64
5,77
4,53
3,84
3,41
3,12
2,90
2,74
2,61
2,50
2,42
2,35
2,29
2,24
2,19
2,15
2,11
2,08
2,05
2,03
2,00
1,98
1,96
1,95
1,93
1,91
1,90
1,89
1,79
1,70
1,61
1,52
оо
254,3
19,50
8,53
5,63
4,36
3,67
3,23
2,93
2,71
2,54
2,40
2,30
2,21
2,13
2,07
2,01
1,96
1,92
1,88
1,84
1,81
1,78
1,76
1,73
1,71
1,69
1,67
1,65
1,64
1,62
1,52
1,39
1,25
1,00
429

Продолжение табл. 7.
Значения /'при а = 0,025
*2\
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
со
1
647,79
38,51
17,43
12,22
10,01
8,81
8,07
7,57
7,21
6,94
6,72
6,55
6,41
6,30
6,20
6,12
6,04
5,98
5,92
5,87
5,83
5,79
5,75
5,72
5,69
5,66
5,63
5,61
5,59
5,57
5,42
5,29
5,15
5,02
2
799,50
39,00
16,04
10,65
8,43
7,26
6,54
6,06
5,72
5,46
5,26
5,10
4,96
4,86
4,76
4,69
4,62
4,56
4,51
4,46
4,42
4,38
4,35
4,32
4,29
4,27
4,24
4,22
4,20
4,18
4,05
3,92
3,80
3,69
3
864,16
39,16
15,44
9,98
7,76
6,60
5,89
5,42
5,08
4,83
4,64
4,47
4,35
4,24
4,15
4,08
4,01
3,95
3,90
3,86
3,82
3,78
3,75
3,72
3,69
3,67
3,65
3,63
3,61
3,59
3,46
3,34
3,23
3,12
4
899,58
39,25
15,10
9,60
7,39
6,23
5,52
5,05
4,72
4,47
4,28
4,12
4,00
3,89
3,80
3,73
3,66
3,61
3,56
3,52
3,48
3,44
3,41
3,38
3,35
3,33
3,31
3,29
3,27
3,25
3,13
3,01
2,89
2,79
5
921,85
39,30
14,88
9,36
7,15
5,99
5,28
4,82
4,48
4,24
4,04
3,89
3,77
3,68
3,58
3,50
3,44
3,38
3,33
3,29
3,25
3,22
3,18
ЗД6
3,13
3,10
3,08
3,06
3,04
3,03
2,90
2,79
2,67
2,57
6
937,11
39,33
14,74
9,20
6,98
5,82
5,12
4,65
4,32
4,07
3,88
3,73
3,60
3,50
3,42
3,34
3,28
3,22
3,17
3,13
3,09
3,06
3,02
3,00
2,97
2,94
2,92
2,90
2,88
2,87
2,74
2,63
2,52
2,41
8
956,66
39,37
14,54
8,98
6,76
5,60
4,90
4,43
4,10
3,86
3,66
3,51
3,39
3,28
3,20
3,12
3,06
3,00
2,96
2,91
2,87
2,84
2,81
2,78
2,75
2,73
2,71
2,69
2,67
2,65
2,53
2,41
2,30
2,19
12
976,71
39,42
14,34
8,75
6,52
5,37
4,67
4,20
3,87
3,62
3,43
3,28
3,15
3,05
2,96
2,89
2,82
2,77
2,72
2,68
2,64
2,60
2,57
2,54
2,52
2,49
2,47
2,45
2,43
2,41
2,29
2,17
2,06
1,94
24
997,25
39,46
14,12
8,51
6,28
5,12
4,42
3,95
3,61
3,36
3,17
3,02
2,89
2,79
2,70
2,62
2,56
2,50
2,45
2,41
2,37
2,33
2,30
2,27
2,24
2,22
2,20
2,17
2,15
2,14
2,01
1,88
1,76
1,64
оо
1018,3
39,50
13,90
8,26
6,02
4,85
4,14
3,67
3,33
3,08
2,88
2,72
2,60
2,49
2,40
2,32
2,25
2,19
2,13
2,08
2,04
2,00
1,97
1,94
1,91
1,88
1,85
1,83
1,81
1,79
1,64
1,48
1,31
1,00
430

Продолжение табл. 7.
Значения fnpn a = 0,01
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
со
1
4052
98,49
34,12
21,20
16,26
13,74
12,25
11,26
10,56
10,04
9,65
9,33
9,07
8,86
8,68
8,53
8,40
8,28
8,18
8,10
8,02
7,94
7,88
7,82
7,77
7,72
7,68
7,64
7,60
7,56
7,31
7,08
6,85
6,64
2
4999
99,00
30,81
18,00
1327
10,92
9,55
8,65
8,02
7,56
7,20
6,93
6,70
6,51
6,36
6,23
6,11
6,01
5,93
5,85
5,78
5,72
5,66
5,61
5,57
5,53
5,49
5,45
5,42
5,39
5,18
4,98
4,79
4,60
3
5403
99,17
29,46
16,69
1203
9,78
8,45
7,59
6,99
6,55
6,22
5,95
5,74
5,56
5,42
5,29
5,18
5,09
5,01
4,94
4,87
4,82
4,76
4,72
4,68
4,64
4,60
4,57
4,54
4,51
4,31
4,13
3,95
3,78
4
5625
99,25
28,71
15,98
11,39
9,15
7,85
7,01
6,42
5,99
5,67
5,41
5,20
5,03
4,89
4,77
4,67
4,58
4,50
4,43
4,37
4,31
4,26
4,22
4,18
4,14
4,11
4,07
4,04
4,02
3,83
3,65
3,48
3,32
5
5764
99,30
28,24
15,52
10,97
8,75
7,46
6,63
6,06
5,64
5,32
5,06
4,86
4,69
4,56
4,44
4,34
4,25
4,17
4,10
4,04
3,99
3,94
3,90
3,86
3,82
3,78
3,75
3,73
3,70
3,51
3,34
3,17
3,02
6
5859
99,33
27,91
15,21
10,67
8,47
7,19
6,37
5,80
5,39
5,07
4,82
4,62
4,46
4,32
4,20
4,10
4,01
3,94
3,87
3,81
3,76
3,71
3,67
3,63
3,59
3,56
3,53
3,50
3,47
3,29
3,12
2,96
2,80
8
5981
99,36
27,49
14,80
10,29
8,10
6,84
6,03
5,47
5,03
4,74
4,50
4,30
4,14
4,00
3,89
3,79
3,71
3,63
3,56
3,51
3,45
3,41
3,36
3,32
3,29
3,26
3,23
3,20
3,17
2,99
2,82
2,66
2,51
12
6106
99,42
27,05
14,37
9,89
7,72
6,47
5,67
5,11
4,71
4,40
4,16
3,96
3,80
3,67
3,55
3,45
3,37
3,30
3,23
3,17
3,12
3,07
3,03
2,99
2,96
2,93
2,90
2,87
2,84
2,66
2,50
2,34
2,18
24
6234
99,46
26,60
13,93
9,47
7,31
6,07
5,28
4,73
4,33
4,02
3,78
3,59
3,43
3,29
3,18
3,08
3,00
2,92
2,86
2,80
2,75
2,70
2,66
2,62
2,58
2,55
2,52
2,49
2,47
2,29
2,12
1,95
1,79
оо
6366
99,50
26,12
13,46
9,02
6,88
5,65
4,86
4,31
3,91
3,60
3,36
3,16
3,00
2,87
2,75
2,65
2,57
2,49
2,42
2,36
2,31
2,26
2,21
2,17
2,13
2,10
2,06
2,03
2,01
1,80
1,60
1,38
1,00
431

Продолжение табл. 7.
Значения /"при а = 0,005
*2 \
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
со
1
16211
198,50
55,55
31,33
22,78
18,64
16,24
14,69
13,61
12,83
12,23
11,75
11,37
11,06
10,80
10,58
10,38
10,22
10,07
9,94
9,83
9,73
9,64
9,55
9,48
9,41
9,34
9,28
9,23
9,18
8,83
8,50
8,18
7,88
2
20000
199,00
49,80
26,28
18,31
14,54
12,40
11,04
10,11
9,43
8,91
8,51
8,19
7,92
7,70
7,51
7,35
7,22
7,09
6,99
6,89
6,81
6,73
6,66
6,60
6,54
6,49
6,44
6,40
6,36
6,07
5,80
5,54
5,30
3
21615
199,17
47,47
24,26
16,53
12,92
10,88
9,60
8,72
8,08
7,60
7,23
6,93
6,68
6,48
6,30
6,16
6,03
5,92
5,82
5,73
5,65
5,58
5,52
5,46
5,41
5,36
5,32
5,28
5,24
4,98
4,73
4,50
4,28
4
22500
199,25
46,20
23,16
15,56
12,03
10,05
8,80
7,96
7,34
6,88
6,52
6,23
6,00
5,80
5,64
5,50
5,38
5,27
5,17
5,09
5,02
4,95
4,89
4,84
4,78
4,74
4,70
4,66
4,62
.4,37
4,14
3,92
3,72
5
23056
199,30
45,39
22,46
14,94
11,46
9,52
8,30
7,47
6,87
6,42
6,07
5,79
5,56
5,37
5,21
5,08
4,96
4,85
4,76
4,68
4,61
4,54
4,49
4,43
4,38
4,34
4,30
4,26
4,23
3,99
3,76
3,55
3,35
6
23437
199,33
44,84
21,98
14,51
11,07
9,16
7,95
7,13
6,54
6,10
5,76
5,48
5,26
5,07
4,91
4,78
4,66
4,56
4,47
4,39
4,32
4,26
4,20
4,15
4,10
4,06
4,02
3,98
3,95
3,71
3,49
3,28
3,09
8
23925
199,37
44,13
21,35
13,96
10,57
8,68
7,50
6,69
6,12
5,68
5,34
5,08
4,86
4,67
4,52
4,39
4,28
4,18
4,09
4,01
3,94
3,88
3,83
3,78
3,73
3,69
3,65
3,61
3,58
3,35
3,13
2,93
2,74
12
24426
199,42
43,39
20,70
13,38
10,03
8,18
7,02
6,23
5,66
5,24
4,91
4,64
4,43
4,25
4,10
3,97
3,86
3,76
3,68
3,60
3,54
3,48
3,42
3,37
3,32
3,28
3,25
3,21
3,18
2,95
2,74
2,54
2,36
24
24940
199,46
42,62
20,03
12,78
9,47
7,64
6,50
5,73
5,17
4,76
4,43
4,17
3,96
3,79
3,64
3,51
3,40
3,31
3,22
3,15
3,08
3,02
2,97
2,92
2,87
2,83
2,79
2,76
2,73
2,50
2,29
2,09
1,90
оо
25465
199,51
41,83
19,32
12,14
8,88
7,08
5,95
5,19
4,64
4,23
3,90
3,65
3,44
3,26
3,11
2,98
2,87
2,78
2,69
2,61
2,55
2,48
2,43
2,38
2,33
2,29
2,24
2,21
2,18
1,93
1,69
1,43
1,00
432

Таблица 8. Мощность критерия Стьюдента при уровне значимости
а = 0,05 в зависимости от параметра нецентральности ср и объема выборки п
433

fret
8
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
к-
ю
о
к-
ю
ю
чЛ
о
-J
чЛ
чо
о
U\
оо
U\
о
4^
оо
чо
о
4^
ю
чо
о
и>
оо
-J
о
U)
ил
-J
о
U)
4^
4^
о
U)
^—
о\
о
и>
о
ю
о
ю
4^
ю
о
к—
-J
оо
о
^—
ю
U\
о
о
оо
U)
0\
о
с>
То
^^
U\
—
_©
'м
и>
-J
^-
j=>
~^-
о
Оч
чо
j=>
Ъ>
чо
о
ю
j=>
ъ>
-J
чо
Оч
j=>
"о
-J
ю
ю
j=>
ъ>
Оч
Оч
оо
j=>
"о
Оч
ю
ел
о
о
U\
чо
4^
j=>
ъ>
ел
Оч
-J
j=>
"о
4^
Оч
^-
j=>
о
U)
4^
4^
j=>
Ъ>
ю
4^
ел
j=>
ъ>
1—1
Оч
-J
4^
о
ю
чо
4^
о
м
чо
к—
ел
К'
U\
о
оо
к~
ю
оо
^-
н—
^—
U)
U\
^—
о
U)
U)
о
чо
U\
-J
о
оо
чо
оо
о
оо
U\
U)
о
оо
к^
о\
о
Оч
Оч
оо
о
U\
о
4^
о
и>
Оч
и>
о
ю
U\
о
U)
о
U)
о\
U)
ю
ю
4^
к—
ю
К'
чо
^^
и>
^-
Оч
U)
ел
к~
4^
ел
4^
к~
и>
ю
-J
к~
ю
U)
ю
к~
^^
ел
-J
1—^
^^
о
о
к~
о
ел
4^
о
оо
о\
-J
о
Оч
U\
оо
о
4^
оо
о
о
и>
U)
U)
ю
4^
о
V
ю
4^
-J
о
То
оо
-J
^-
j=>
То
ю
чо
ил
j=>
*^-
чо
-J
о
j=>
*^-
-J
U\
чо
j=>
*^-
Оч
о
оо
j=>
*^—
4^
чо
U\
с>
*^-
4^
о
о\
о
^^
U)
U)
оо
j=)
~^-
ю
оо
и>
j=)
>^-
о
о\
о
j=>
ъ>
оо
^^
о
j=)
"о
(^
чо
^л
j=)
"о
4^
к^
-J
ю
о
4^
-J
чо
чо
U)
ю
чо
-J
ю
о\
(У\
4^
ю
ю
оо
оо
ю
о
4^
оо
1—»
оо
-J
-J
к~
-J
4^
оо
к^
as
4^
OS
^^
ил
о\
-J
к~
(^
о
^-
н-
ю
4^
оо
о
чо
о\
о
о
-J
о
чо
о
(У\
о
о
к^
U\
U\
-J
4^
-J
4^
о
о\
чо
U)
U)
^^
-J
ю
оо
оо
ю
ю
U\
чо
U)
ю
U)
оо
о\
ю
ю
ю
оо
ю
^^
о
4^
ю
о
о
ю
к^
чо
1—1
оо
к^
Оч
1—»
ю
к^
ю
^л
^-
о
чо
U)
4^
о
о\
о\
-J
к^
ю
j=>
Ъч
(^
ю
оо
о
V
-J
U\
^-
j=>
"oj
чо
^^
чо
j=>
"и»
4^
ю
оо
j=>
1*>
о
чо
чо
j=>
То
оо
Оч
^-
j=>
То
Оч
оо
о
с>
То
(^
и>
(^
о
ю
4^
^^
чо
j=>
То
U)
ю
о
j=>
^
чо
Оч
^-
с>
>^-
(^
U)
(^
j=>
^^
(^
-J
j=)
"о
оо
U)
U)
ни
о
--J
I—+
-J
и»
U\
U)
и»
оо
4^
<У\
чо
U)
чо
U)
4^
и>
t-r»
-J
ю
OJ
OJ
о
оо
OJ
^^
о
Оч
ю
чо
4^
ил
ю
оо
^^
и>
ю
-J
о
4^
ю
ю
чо
-J
к^
оо
^^
^-
U)
-J
о\
о
о
о
чо
-J
U\
4^
4^
(^
-J
ю
-J
4^
оо
^^
о
4^
ю
U\
^-
U)
оо
-J
о
U)
^л
чо
ю
и>
OJ
-J
оо
U)
ю
о
-J
U)
о
Оч
-J
ю
чо
U\
о
ю
U\
к^
4^
к^
чо
чо
ю
U\
ю
^-
к^
к^
к-
оо
с>
"-J
чо
4^
(^
j=>
Ъч
^^
(^
ю
j=)
1л
ю
о
чо
j=>
V
Оч
ю
-J
о
V
ю
ю
о\
с>
"и)
чо
U)
ю
j=>
Lj
-J
о
4^
с>
Lj
(^
ю
ю
о
U)
U)
-J
U)
j=>
"и>
ю
4^
оо
с>
То
-J
-J
чо
с>
То
ю
^^
4^
с>
-J
о
о
j=)
ю
U\
о
-J
оо
U)
-J
Оч
Оч
Оч
4^
4^
U\
о\
оо
U\
U\
о
оо
о
4^
о\
U\
чо
4^
и>
4^
-J
4^
о
U\
и>
чо
^-
U)
-J
U\
^-
U)
Оч
к^
Оч
U)
к^
о
U\
ю
4^
чо
4^
чо
ю
чо
4^
ю
чо
0\
оо
оо
ю
оо
-J
ю
оо
0\
ю
U\
оо
U\
о\
и>
U\
U\
^^
чо
U\
4^
оо
Оч
Оч
4^
о\
о
оо
4^
о
^-
4^
ю
ю
чо
4^
о
оо
4^
U)
U\
ю
чо
ю
оо
U\
оо
ю
ю
ю
чо
0\
о\
-J
U\
j=>
VO
ю
-J
чо
о
"-J
оо
оо
U\
j=>
Ъч
чо
(^
-J
j=>
Ъч
U)
ю
чо
j=>
1л
оо
-J
U\
с>
~U\
U\
и>
^-
j=)
1л
ю
1Л
чо
j=>
1л
о
U)
-J
о
4^
оо
U\
4^
с>
V
Оч
чо
-J
j=>
V
о
чо
4^
j=)
1*>
U)
(^
^-
JO
То
Оч
4^
4^
j=)
То
о
о
о
4^
чо
о\
-J
о\
оо
Оч
4^
U)
-J
оо
^^
4^
-J
ю
1—к
ю
Оч
-J
о\
^-
Оч
4^
к^
о
0\
^^
ю
чо
U\
оо
чо
-J
^л
-J
о
ю
U\
U\
U)
о\
4^
оо
оо
4^
4^
о
U\
-J
U)
ю
(^
^-
ю
U\
о
о
U)
чо
чо
U)
U)
чо
4^
ю
U)
оо
оо
U)
^-
оо
и>
U)
(^
-J
чо
U)
U)
-J
о\
о
Оч
-J
и>
U)
(^
-J
^^
о
--о
0\
чо
^^
ю
0\
-J
4^
U)
Оч
о
U\
чо
^л
к^
U\
и>
4^
ю
U)
о
U)
U)
и>
и>
ю
JO
чо
чо
чо
чо
j=>
чо
чо
(^
о
JO
чо
-J
чо
4^
j=)
"чо
(^
оо
о\
j=>
1о
U)
-J
и>
j=)
чо
^^
-J
ю
j=)
Ъо
чо
оо
оо
с>
Ъо
оо
ю
U)
о
оо
Оч
-J
4^
с>
Ъо
(^
4^
чо
j=>
"-J
чо
4^
чо
j=>
Vl
о
Оч
-J
с>
"as
о
Оч
ю
j=)
1л
о
о
°
а
N>
LU
^
t/<
СТч
^J
00
VO
—
о
—
СТч
UJ
а\
^
■и
8
?р
•<
ровень
и
X
ачимос
н
S
р
II
"о
бор
о
я
3
н
о
ta
5
с
р
■В1
5
го
•о
S
«
о
л
•о
го
S
о
н
S
ta
вэ
н
го
я
го
S
го
о
а\
о
1
S
о

■§■
o^
о"
II
a
s
H
о
ЧИМО
пз
X
n
л
овен
а.
J*
8
^
■ч-
ЧО
ЧО
о
СТ\
00
f~
ЧО
ч->
■ч-
СП
СМ
—
Б
о
о
О
in
о"
го
^^
оо
о"
rs
о
чо
чо^
о"
_н
Tf
ГО
0,7
о
оо
оо
0,7
о
^^
о
оо
о"
о>
in
^^
°я.
о"
CS
ГО
ГО
оо
о
Tf
ГО
in
°я.
о"
CS
f-
f-
°ч,
о"
f»
1П
о
о>
о"
CS
as
ГО
о>
о"
о
in
f-
°\
о"
in
оо
as
о\
о"
CS
ГО
ГО
ГО
ГО
_н
ГО
о
Tf
оо
Tf
f-
Tf
чо
чо
Tf
in
in
rs
о
чо
f-
чо
^^
чо
ГО
ГО
ГО
чо
о
ГО
in
чо
^
f»
f-
чо
^
f-
о
f»
f-
in
Tf
f-
f-
f-
o>
f-
o>
о
f-
oo
as
ЧО
ЧО
ON
ГО
о
о
in
rs
ro
as
о
ГО
о
rs
f-
ГО
ЧО
ЧО
ГО
Tf
Tf
oo
oo
Tf
f-
^^
о
in
in
f-
^^
wo
in
ЧО
ГО
in
oo
as
in
m^
©"
in
as
oo
in
f-
oo
rs
ЧО
^
Tf
oo
ЧО
as
f-
ЧО
f-
in
ЧО
о
as
■sf
o
о
о
°i
о"
ГО
^^
о
0,2
чо
чо
о
е'о
in
Tf
чо
0,3
оо
^н
^н
о"
^
Tf
rs
■^
о"
f-
оо
ГО
■^
о"
3
in
Tf
о
ГО
оо
f»
Tf
ГО
чо
о
т^
о"
о
■sf
■sf
in
о"
^
оо
as
in
о"
оо
ГО
ГО
чо^
о"
CS
^^
Tf
°я.
о"
in
f-
чо
чо
as
^^
^^
rs
CS
^^
чо
rs
in
ГО
f-^
ГО
оо
чо
in
ГО
CS
оо
чо
ГО
f»
^н
оо
ГО
о
оо
as
ГО
Tf
оо
^^
Tf
f-
Tf
Tf
Tf
ГО
о
оо
Tf
^
rs
ГО
in
^
чо
^н
чо
оо
о
оо
f»
чо
as
CS
Tf
ГО
ГО
оо
оо
f»
rs
rs
чо
in
f-
rs
Tf
in
^H
ГО
as
in
rs
CO
Tf
oo
ГО
ГО
in
ГО
in
rO
ЧО
CN
r-
ГО
Tf
f-
as
ГО
f-
o
ГО
Tf
o
о
oo
Tf
CN
^^
ЧО
in
^
f-
rs
f-
f-
o
in
rs
©"
ЧО
^^
ЧО
©"
rs
rs
о
0,2
rs
ЧО
Tf
0,2
as
rs
oo
©"
ЧО
rs
as
°i
©"
ГО
Tf
о
ГО^
©"
in
oo
^^
ГО
о
rs
ЧО
ГО
ГО^
©"
in
as
in
r*\
©"
о
^H
as
ГО
©"
f»
t--
ГО
■^
o"
f»
in
^H
**\
о"
oo
as
f»
чо^
o"
oo
^
^^
^^
ЧО
Tf
,^-
о
rs
oo
ЧО
rs
rs
rs
oo
ЧО
in
rs
as
in
ЧО
rs
oo
ЧО
f-
rs
^^
о
as
rs
f»
ЧО
о
ГО
ЧО
oo
rs
ГО
Tf
oo
in
ГО
f-
CN
о
Tf
in
f-
f-
,^-
in
oo
CO
ЧО
as
о
о
о
oo
о
ГО
in
in
чо
rs
ГО
о
rs
ГО
in
ГО
rs
as
ГО
Tf
rs
^^
Tf
in
rs
ЧО
ЧО
ЧО
rs
CO
rs
oo
rs
as
rs
о
ГО
^
^H
ГО
ГО
CO
CO
f-
ГО
о
in
3
о
rs
о
чо
о
ГО
ГО
оо
©^
о"
о
о
^^
о"
ГО
о
Tf
0,1
f»
ГО
f-
0,1
о
rs
о
о"
oo
as
о
°i
о"
f»
oo
^^
°i
o"
as
as
rs
rs
о
as
ГО
Tf
°i
o"
Tf
rs
ЧО
°i
o"
о
oo
oo
°i
o"
Tf
rs
ЧО
ГО^
o"
Tf
rs
as
rr\
o"
о
^^
Tf
in^
o"
rs
^^
f-
ЧО
ЧО
о
as
OO
oo
о
■sf
■sf
o>
rs
Tf
^
f-
ЧО
ЧО
ГО
f»
^^
in
^H
oo
—->
^
^H
as
^н
Tf
ГО
о
rs
in
as
^^
rs
as
^н
Tf
rs
oo
in
f»
rs
ЧО
Tf
CO
CO
as
о
f»
,^-
in
^^
о
о
in
о
in
f»
ЧО
о
as
f»
oo
о
oo
о
^^
CO
о
ГО
f»
in
ГО
-^
rs
rs
Tf
*•^
^^
о
in
^H
rs
о
чо
-^
•n
ГО
f-
-^
^^
rs
as
-^
in
о
rs
rs
in
о
f»
rs
Tf
as
oo
oo
о
rs
t--
i-^
Tf
o^
o"
f-
ЧО
in
o'o
CO
Tf
f»
o'o
rs
Tf
as
0,0
CO
^H
^H
I'O
о
чо
^^
-^
o"
ЧО
^H
rs
—->
©"
ЧО
oo
rs
^H
о
Tf
f-
ГО
-^
©"
CO
as
Tf
o"
ЧО
in
ЧО
^^
o"
f»
o
as
-^
o"
Tf
in
ГО
°i
o"
Tf
ГО
Tf
r*\
o"
Tf
rs
ГО
CO
ГО
о
f»
in
Tf
о
Tf
o
ЧО
о
^H
f»
f-
o
^^
rs
as
о
oo
in
as
о
rs
о
о
—■*
^^
чо
о
^н
f»
ГО
^^
-^
f-
ГО
rs
-^
f-
f-
ГО
-^
CO
as
in
-^
о
oo
as
-^
as
rs
as
rs
о
ГО
о
in
rs
о
f»
,^-
CO
о
rs
ЧО
Tf
о
•n
as
in
о
ГО
^H
f-
o
in
Tf
f-
o
о
oo
f»
o
f-
rs
oo
о
f-
oo
oo
о
oo
ЧО
as
о
$
о
as
in
rs
-^
ЧО
f-
in
-^
о
f-
ГО
rs
о
Tf
f-
ЧО
^^
©^
o"
Tf
CO
rs
o'o
ЧО
^^
CO
0,0
_H
^H
Tf
o'o
f-
o>
Tf
o'o
о
rs
in
©^
o"
rs
in
in
©^
©"
CO
oo
in
©
о
ГО
rs
чо
©^
©"
rs
oo
ЧО
©^
©"
in
ЧО
f»
©^
©"
in
as
oo
©^
©"
^H
ГО
^H
-^
©"
r~
ГО
f»
—•*
©"
©
ЧО
CO
oo
©
©
©
rs
^^
©
in
ЧО
^H
©
oo
^H
rs
©
ЧО
ЧО
rs
©
as
f»
rs
©
rs
as
rs
©
rs
^H
ГО
©
f-
ГО
ГО
©
^^
f-
ГО
©
as
^н
Tf
©
in
as
■sf
©
rs
ГО
ЧО
©
oo
as
as
©
©
<N
^^
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
©
О
©
©
©
©
©
©
©
©
©
©
О
о
о
о
о
о
8
435

ы
О»
8 §
Ю Ю
~-J OO
~-J О
Ю О
OJ U>
U> U>
^- СЛ
-P». ON
u> u>
ON ON
U> OO
U) СЛ
U> U>
OO SO
1Л и-
OO -J
-p». *.
о о
UJ ЧО
о on
-p». *.
H- Ю
~-l *.
О H-
-p». *.
to oj
OO ON
ON LO
-p». -p*
U> -P».
oo on
-J OO
-p». -p».
■P» <~л
--J ON
-P». О
ON -P».
о о
Ю Ю
OO OO
Ю 1Л
SO OO
u> u>
OJ -P»
S£) .£».
SO Ю
U) UJ
-J -J
UJ SO
~-J H-
OJ -P»
SO О
~-J U)
~-J SO
-p». -p».
H- Ю
ON UJ
U) Ю
-P». -P».
U> U>
и- OO
■P» SO
-p». -p».
-P». 1Л
-Pi. NJ
и- Н-
-p». -p».
1Л ON
1Л U)
О 1Л
-p». -p».
ON -J
-P». U>
ON 1Л
U)
о
to
OO
OO
OO
U)
-P-
OO
ON
UJ
OO
-P-
«-П
-Pb
^
о
to
-P*
U)
о
to
-P*
-Pb
ON
-Pb
-Pb
ON
о
to
-P*
~-J
to
о
-p».
OO
to
-p».
to
-p».
to
SO
>—L
SO
u>
1Л
u>
to
u>
SO
о
K-
-p».
K~
ON
on
-p».
UJ
~-J
u>
-p».
1Л
-p».
K-
-p».
ON
OO
-p».
-p».
OO
о
~-J
-p».
SO
(—1
1Л
О so
to to
so so
СЛ OS
о о
U) U)
Ul 1Л
~-J SO
OO U>
U) U)
SO SO
Ul ~-J
OO -J
-p». -p».
to to
IaJ 1Л
to u>
-p* -p».
-p». -p».
-p». on
ui so
-p». -p».
ON ON
to -p».
О 1Л
-p* -p».
-J -J
ON SO
OO -P».
-p* -p».
oo so
so to
ON -P».
1Л 1Л
о о
О U)
OO OO
OO
to
SO
~-J
^
u>
ON
о
SO
u>
SO
SO
~-J
-p».
to
~-J
~-J
-p».
-p».
SO
1Л
-p».
ON
~-J
u>
-p».
OO
to
-p».
-p».
SO
1Л
ON
1Л
о
~-J
K-
~-J
to
SO
OO
-p».
u>
on
to
OO
-p».
о
to
о
-p».
u>
о
u>
-p».
Ul
to
-p».
-p».
~-J
о
Ul
-p».
OO
Ul
OO
-p».
SO
SO
K-
Ul
t—k
о
OO
ON
to
SO
SO
OO
u>
o\
-p».
SO
-p».
о
-p».
o\
-p».
u>
u>
u>
-p».
Ul
Ul
~-J
-p».
~-J
-p».
K-
-p».
OO
SO
~-J
Ul
о
u>
K-
Ul
»-^
Ul
о
U1 -P».
u> u>
о о
к- U)
-pi. U>
U) UJ
On ^1
-J О
-P». to
-p». -p».
О H-
-J H-
o\ ^-
-p». -p».
u> -P».
o\ о
-J -J
-p». -p».
ui o\
SO U>
ui so
-p». -p».
-J OO
oo to
to so
-p». -p».
so so
-P». SO
о о
V\ U\
о ^~
~J L«J
-J H-
U1 Ul
^- to
SO Ul
OO -Pi.
u>
u>
о
V\
V\
OJ
~-J
UJ
Ul
-p».
>—1
Ul
H-
-p».
-p».
Ul
u>
.*».
o\
SO
о
-p».
OO
OO
V\
Ul
о
-p».
SO
Ul
»—I
SO
to
Ul
u>
1—1
OO
to H-
UJ U)
О H-
OO H-
tO U)
U) UJ
~-J OO
~~j to
U) О
-p». -p».
и- tO
so ui
SO ON
-p». -p».
Ul Ul
О ^
OO -P».
-p». -p».
-J OO
ui to
^- UJ
*■ Ul
SO О
СП NJ
О OO
Ul Ul
и- tO
и- О
so to
Ul Ul
to u>
On ui
Ul U)
Ul Ul
U> -Рь
so oo
Ul -J
о
U)
>—'
Ul
U)
OO
-o
-J
-Pk
U)
to
-o
-Pk
ON
Ul
-P*
-Pk
SO
>—ь
to
Ul
K^
to
-Pk
Ul
U)
о
Ul
Ul
-Pk
ON
^
Ul
Ul
SO
SO
SO OO
u> u>
^- to
SO ON
SO ►—
OJ -Pi.
SO О
-p». -p»l
SO и-
-p». -p».
-P». U1
H- tO
Ul SO
-p». -p»l
~-J OO
un oo
ON ON
Ul СЛ
О и-
tO ON
-p». -J
Ul СЛ
to u>
-Pi. SO
-Pi. SO
Ul СЛ
-P». U1
UJ SO
to ~-j
Ul V\
U\ ~~J
SO ON
Ul ~~J
Ul СЛ
~-J SO
UJ ►—
SO OO
si 0\ (Л Д W M
Ы W W U) A ON
1>J *■ ON SO U1 О
4*. ON U) tO О OO
^ и- Ul v) и- У)
^ A A U U OO
^- U) ON О SO UJ
On U) О -P». ►— U)
Ul SO to О О н-
^ Д 1Л У) 0\ SO
о\ oo w si и si
OO SO H- Ul tO SO
м ON OO n) W OO
Ul Ul Ul ON ~-J О
О 1>J ON tO U1 OO
ON О ^J OO О OO
О Ul 1>J sj tO
H-
Ul Ul ON 0\ 00 м
U) ON О ^J О ~-J
Ul tO U) О U) *■
SO OO U) ~-J --J
^
W 1Л ON n) OO Ю
ON OO UJ О 4^ -P».
О SO U) Ul -J 4*.
ON Ul О UJ OO
H-
Ul ON ON ~-J OO UJ
OO м yi w 00 О
м W OO * W W
ui to to ^j u>
^^
Ul ON ON ~-J SO U)
SO U) OO ON ►— Ul
SO H- О О -J ^
oo so to to ~-j
^^
ON ON ON ~-J SO U)
м Д \Д CO ^ VO
Ul SO SO tO ON SO
00 W in ON Ю
~-J
SO
~-J
to
ON
SO
OO
to
OO
to
о
OO
-p».
о
-p».
^^
-p».
UJ
K^
to
-p».
Ul
-p».
о
-p».
~-J
UJ
ON
-p».
SO
о
~-J
<
Ю
l*>
■U
i-n
o\
-~l
00
SO
о
s
[тервал
о
•о
№
внен
s
а
а-

Продолжение табл. 10.
Критические значения критерия Ньюмена—Кейлса Q при а = 0,05
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
24
30
40
60
120
со
Интервал сравнения А
2
90,03
14,04
8,261
6,512
5,702
5,243
4,949
4,746
4,596
4,482
4,392
4,320
4,260
4,210
4,168
4,131
4,099
4,071
4,046
4,024
3,956
3,889
3,825
3,762
3,702
3,643
3
135,0
19,02
10,62
8,120
6,976
6,331
5,919
5,635
5,428
5,270
5,146
5,046
4,964
4,895
4,836
4,786
4,742
4,703
4,670
4,639
4,546
4,455
4,367
4,282
4,200
4,120
4
164,3
22,29
12,17
9,173
7,804
7,033
6,543
6,204
5,957
5,769
5,621
5,502
5,404
5,322
5,252
5,192
5,140
5,094
5,054
5,018
4,907
4,799
4,696
4,595
4,497
4,403
5
185,6
24,72
13,33
9,958
8,421
7,556
7,005
6,625
6,348
6,136
5,970
5,836
5,727
5,634
5,556
5,489
5,430
5,379
5,334
5,294
5,168
5,048
4,931
4,818
4,709
4,603
6
202,2
26,63
14,24
10,58
8,913
7,973
7,373
6,960
6,658
6,428
6,247
6,101
5,981
5,881
5,796
5,722
5,659
5,603
5,554
5,510
5,374
5,242
5,114
4,991
4,872
4,757
7
1 215,8
28,20
/5,00
11,10
9,321
8,318
7,679
7,237
6,915
6,669
6,476
6,321
6,192
6,085
5,994
5,915
5,847
5,788
5,735
5,688
5,542
5,401
5,265
5,133
5,005
4,882
8
227,2
29,53
15,64
11,55
9,669
8,613
7,939
7,474
7,134
6,875
6,672
6,507
6,372
6,258
6,162
6,079
6,007
5,944
5,889
5,839
5,685!
5,536
5,392
5,253
5,118
4,987
9
237,0
30,68
16,20
11,93
9,972
8,869
8,166
7,681
7,325
7,055
6,842
6,670
6,528
6,409
6,309
6,222
6,147
6,081
6,022
5,970
5,809
5,653
5,502
5,356
5,214
5,078
10
245,6
31,69
16,69
12,27
10,24
9,097
8,368
7,863
7,495
7,213
6,992
6,814
6,667
6,543
6,439
6,349
6,270
6,201
6,141
6,087
5,919
5,756
5,559
5,447
5,299
5,157
437

ы
00
ooooooouitoosooo--jaNt^-p»-uj
оооооооооооооооо^л
5
о
О)
О)
Л
° Р Р Р Р Р3 Р Р Р Р3 Р Р Р Р Р Р Р
л
0 Р Р Р -0 Р Р »0 Р Р Р Р Р J0 -0 -0 vP
О "о "н— "%- "к- ^- "%- "ю "ы "ы "ю "ю 1>J 1>J 1>J 1*> "*■
л
0 Р vP Р Р Р Р -0 Р Р Р Р J0 Р ,Р J0 vP
*— к- V- к- h- "h- "(О "(О "(О К) Ы W Ы W V "^ "■£»■
ООн-ЫУ|ч1мДч1\СмЫ1Лч1м1ЛОО
л
р р р) р3 р р р р р р3 р р р р р р р3
UJ Ы Ы ^- н-
О ^л О «-ft О d
р р р р р р3
Ы Ы ^ Д Ui Ч
Ui ОО М М ОО Ui
о о о о о о
"*. ^ 1л Ъ\ ~--J "oo
U \С W и- h- ч]
р3 р р р р р
1л 1л Ъ\ Ъ\ Vj 1o
ь- Ui ь- 00 ОО Ы
р р3 р р р р
1л Ъ\ Ъ\ Vj Ъо 1о
^л о ^л ю ы и\
свободы т
0,05
0,01
0,0027
0,001
Число степеней
Уровень значимости a
н
х
я
р
Я
S
о
О"
Е
s
го
I
i
S
н
о
•о
•о

ы
(О
UJ L«J
C\ U\
О О
>-^ >-^
o\ oo
° -°
"to To
^- Ю
SO Ю
о о
1o "to
--J OO
SO OJ
о о
1aj 1*J
L«J UJ
О U\
о о
1>J IaJ
oo so
OO -P».
о о
V V
tO IaJ
-vj OJ
-° °
V "*■
C\ ON
to OO
о о
^л ^л
О и-
-Р* О
о о
^Л Cf|
OJ UJ
UJ SO
UJ
-р».
о
to
о
о
to
to
^л
о
to
оо
--J
о
UJ
-р».
о
о
UJ
SO
SO
о
-р».
UJ
SO
о
-р».
--J
^л
о
Lti
>-^
--J
о
Lti
-р».
--J
UJ
UJ
о
to
^
о
to
to
ЧО
о
to
SO
^
о
UJ
-р».
^л
о
-р».
о
^л
о
-р».
-р».
о\
о
-р».
оо
to
о
Lti
to
^л
о
^л
^л
-р».
UJ
to
о
to
-р».
о
to
UJ
to
о
to
SO
о\
о
UJ
^л
о
о
-р».
>-^
to
о
-р».
^л
to
о
-р».
оо
SO
о
Lti
UJ
UJ
о
Lti
о\
UJ
OJ
о
ю
о\
о
to
OJ
о\
о
UJ
о
^
о
UJ
^л
ON
о
-р».
>-^
оо
о
-р».
^л
so
о
-р».
SO
ON
о
«-fl
-р».
^
о
Lti
--J
^^
UJ
о
о
to
оо
о
to
-р».
о
о
UJ
о
ON
о
UJ
ON
to
о
-р».
to
^л
о
-р».
о\
--J
о
^л
о
-р».
о
^л
-р».
SO
о
Lti
оо
о
to
so
о
UJ
о
о
to
-р».
^л
о
UJ
>-^
to
о
UJ
ON
оо
о
-р».
UJ
UJ
о
-р».
--J
«-fl
о
^л
>-^
UJ
о
Lti
^л
оо
о
Lti
оо
so
to
оо
о
UJ
UJ
о
to
^л
о
о
UJ
>-^
--J
о
UJ
--J
^л
о
-р».
-р».
о
о
-р».
оо
UJ
о
^л
to
to
о
Lti
о\
--J
о
Lti
SO
оо
to
--J
о
UJ
ON
о
ы
^л
^л
о
UJ
ы
-р».
о
UJ
оо
ы
о
-р».
•Pv
оо
о
-р».
SO
к-
о
^л
UJ
к-
о
Lti
■-J
■-J
о
ON
о
оо
ы
о\
о
UJ
оо
о
ы
^л
SO
о
UJ
UJ
к-
о
UJ
so
о
о
-р».
^л
■-J
о
^л
о
к-
о
^л
-р».
к-
о
^л
оо
■-J
о
ON
>-^
SO
ы
^л
о
-р».
ы
о
ы
о\
^л
о
UJ
UJ
■-J
о
UJ
SO
оо
о
-р».
о\
о\
о
^л
>-^
к-
о
^л
^л
к-
о
^л
SO
оо
о
ON
UJ
о
ы
-р».
о
-р».
-р».
о
ы
■-J
к-
о
UJ
-р».
-р».
о
-р».
о
о\
о
-р».
--J
о\
о
^л
ы
к-
о
^л
ON
ы
о
ON
>-^
о
о
ON
-р».
ы
ы
UJ
о
-Рь
оо
о
ы
--J
оо
о
UJ
^л
UJ
о
-р».
»—'
^л
о
-р».
оо
ON
о
^л
UJ
ы
о
^л
■-J
UJ
о
ON
ы
ы
о
ON
^л
-р».
ы
ы
о
Lti
ы
о
ы
оо
-р».
о
UJ
о\
к-
о
-р».
ы
^л
о
-р».
SO
о\
о
^л
-р».
-р».
о
^л
оо
ON
о
ON
UJ
-р».
о
ON
ON
--J
ы
о
Lti
о\
о
ы
SO
ы
о
UJ
■-J
о
о
-р».
UJ
^л
о
^л
о
оо
о
^л
^л
ON
о
^л
SO
SO
о
ON
-р».
оо
о
ON
оо
^^
ы
о
о
ON
к-
о
ю
so
so
о
UJ
оо
о
о
-р».
-р».
--J
о
^л
ю
о
о
Lh
■-J
о
о
о\
»-^
ю
о
ON
ON
ю
о
ON
SO
ON
SO
о
ON
«-fl
о
UJ
о
so
о
UJ
SO
K-
о
-p».
o\
о
о
«-fl
UJ
«-fl
о
^л
оо
-p».
о
o\
to
OO
о
ON
--J
--J
о
■-J
>—L
to
OO
о
■-J
о
о
UJ
(—1
■-J
о
-p».
о
к-
о
-р».
■-J
ы
о
^л
^л
о
о
ON
о
о
о
ON
-р».
UJ
о
ON
so
«-fl
о
--J
to
оо
■-J
о
--J
о\
о
UJ
to
оо
о
•Рь
^^
•Pv
о
-р».
оо
^л
о
^л
ON
ON
о
ON
>-^
1Л
о
ON
ON
to
о
--J
»-^
UJ
о
--J
•Pv
оо
OS
о
оо
to
о
UJ
-р».
к-
о
-р».
to
SO
о
t/l
о
IaJ
о
t/l
оо
to
о
о\
UJ
t/l
о
ON
--J
SO
о
■-J
to
SO
о
--J
ON
to
Lti
о
OO
so
о
UJ
^л
-p».
о
-p».
-p».
o\
о
^л
to
K-
о
ON
о
-p».
о
o\
«-fl
-p».
о
--J
о
о
о
■-J
«-fl
о
о
■-J
■-J
SO
-р».
о
to
о
о
о
UJ
о\
■-J
о
-р».
о\
-р».
о
^л
UJ
оо
о
ON
to
о\
о
ON
--J
so
о
--J
to
UJ
о
--J
■-J
к-
о
оо
о
to
UJ
о
to
о
SO
о
UJ
оо
«-fl
о
-р».
оо
-р».
о
^л
ON
о
о
ON
-р».
оо
о
Vj
о
UJ
о
■-J
-р».
■-J
о
■-J
so
к-
о
оо
to
-р».
to
о
to
>-^
■-J
о
■р».
о
ON
о
^л
о
UJ
о
СГ|
оо
-J
о
ON
■-J
оо
о
-J
to
■-J
о
-J
ON
so
о
оо
»-^
оо
о
оо
■р».
ON
о
to
UJ
о\
о
-р».
to
■-J
о
^л
UJ
о\
о
ON
(—1
оо
о
■-J
о
SO
о
--J
^л
U1
о
оо
о
о
о
оо
-р».
^л
о
оо
--J
UJ
о
о
to
-р».
оо
о
-р».
^л
^л
о
^л
ON
•Рь
о
о\
•Pv
оо
о
--J
•Pv
^л
о
--J
SO
•Pv
о
оо
UJ
о
о
оо
■-J
so
о
so
о
UJ
so
о
to
о\
--J
о
-р».
оо
UJ
о
ON
о
о
о
■-J
о
о
о
--J
оо
UJ
о
Ъо
UJ
UJ
о
оо
ON
■-J
о
so
>-^
■-J
о
so
UJ
UJ
оо
о
UJ
>-^
о
о
Lti
to
-р».
о
о\
-р».
UJ
о
--J
UJ
оо
о
оо
UJ
UJ
JD
Ъо
оо
к-
о
so
о
U1
о
so
^л
to
о
so
--J
о\
■-J
о
UJ
to
к-
о
1л
■-J
к-
о
■-J
1—ь
-р».
о
Vj
оо
ON
о
оо
so
UJ
о
1о
to
so
о
so
ON
-р».
к-
о
о
о
к-
о
о
о
ON
о
UJ
■-J
к-
о
Ъ\
^л
■-J
о
"оо
to
so
о
"оо
оо
ON
о
"so
-р».
UJ
, .
о
о
о
, .
о
о
о
^л
о
^л
о
о
о
"оо
о
о
о
1о
о
о
, .
о
о
о
, .
о
о
о
-р».
о
ON
о
о
, .
о
о
о
, .
о
о
о
а
0,50
о
о
о
о
о
"о
о
"о
to
о
1,01
о
о
о
Ln
о
"о
о
к»
_о
"о
о
<
•о
шень :
X
0*
[ИМ0СТ1
г*
р
■а °^

Продолжение табл. 12.
ft
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Уровень значимости а
0,50
0,114
0,113
0,111
0,110
0,108
0,107
0,105
0,104
0,103
0,102
0,101
0,100
0,098
0,097
0,20
0,216
0,212
0,210
0,207
0,204
0,202
0,199
0,197
0,194
0,192
0,190
0,188
0,186
0,184
0,10
0,275
0,271
0,267
0,264
0,261
0,257
0,254
0,251
0,248
0,246
0,243
0,240
0,238
0,235
0,05
0,325
0,321
0,317
0,313
0,309
0,305
0,301
0,298
0,294
0,291
0,288
0,285
0,282
0,279
0,02
0,383
0,378
0,373
0,368
0,364
0,359
0,355
0,351
0,347
0,343
0,340
0,336
0,333
0,329
0,01
0,421
0,415
0,410
0,405
0,400
0,395
0,391
0,386
0,382
0,378
0,374
0,370
0,366
0,363
0,005
0,456
0,450
0,444
0,439
0,433
0,428
0,423
0,419
0,414
0,410
0,405
0,401
0,397
0,393
0,002
0,497
0,491
0,485
0,479
0,473
0,468
0,463
0,458
0,453
0,448
0,443
0,439
0,434
0,430
0,001
0,526
0,519
0,513
0,507
0,501
0,495
0,490
0,484
0,479
0,474
0,469
0,465
0,460
0,456
440

Таблица 13. Критические значения критерия Манна—Уитни Тдля
двусторонней критической области
ЧИГПРННПГТЧ. гп\/ттп1Л
^JlvJl^nriv
меньшей
3
4
5
6
7
8
Wl U к £SJ IIIIUI
большей
4
5
5
6
7
7
8
4
5
5
6
7
8
8
5
5
6
7
8
6
6
7
7
8
8
7
8
8
Приблизительный уровень значимости а
0,05
критические значения
6
6
7
7
7
8
8
11
11
12
12
13
14
17
18
19
20
21
26
28
29
30
37
39
49
18
21
20
23
26
25
28
25
29
28
32
35
38
38
37
41
45
49
52
56
61
60
68
73
87
точное
значение а
0,057
0,036
0,071
0,048
0,033
0,067
0,042
0,057
0,032
0,063
0,038
0,042
0,048
0,032
0,056
0,052
0,048
0,045
0,041
0,051
0,043
0,059
0,053
0,054
0,050
0,01
критические значения
6
6
6
10
10
10
10
11
12
15
16
16
17
18
23
24
24
25
25
26
33
34
44
24
27
30
26
30
34
38
41
40
40
39
44
48
52
55
54
60
59
65
64
72
78
92
точное
значение а
0,024
0,017
0,012
0,026
0,016
0,010
0,012
0,008
0,016
0,008
0,016
0,010
0,010
0,011
0,009
0,015
0,008
0,014
0,008
0,013
0,011
0,009
0,010
29 — 3529
441

Таблица 14. Критические значения критерия Манна—Уитни Г для
двусторонней критической области (расширенная таблица)
Численность группы
меньшей
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
6
7
7
7
7
7
7
7
7
7
7
7
7
большей
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
7
8
9
10
11
12
13
14
15
16
17
18
Критические значения
при а = 0,05
нижнее
26
27
29
31
32
34
35
37
38
40
42
43
45
46
48
50
51
53
54
56
36
38
40
42
44
46
48
50
52
54
56
58
верхнее
52
57
61
65
70
74
79
83
88
92
96
101
105
ПО
114
118
123
127
132
136
69
74
79
84
89
94
99
104
109
114
119
124
Критические значения
при а = 0,01
нижнее
23
24
25
26
27
28
30
31
32
33
34
36
37
38
39
40
42
43
44
45
32
34
35
37
38
40
41
43
44
46
47
49
верхнее
55
60
65
70
75
80
84
89
94
99
104
108
113
118
123
128
132
137
142
147
73
78
84
89
95
100
106
111
117
122
128
133
442

*
\0\O^VO^^\O^OOOOOOOOOOMOOOOOOOOOOOOIX10000000000s]s)v)41v)n4s]
0\W*WM^OVOWAWWmO^000v)0\WAUM^OV000U.UI>JIO^O^
00v)v)vlN)O\O\O\00000000v)vls)'s)s)O\^a*ONUllAUlUl^vlNl0\O\O\O\O\
MVO0\W^00UiWV00\*^\OslASJO4WlWO00UiWi-\0IOO000\AWO
WAAWIOSJMOOOslvlONONUiUAWlfJNJM^MOVO^OOOWU^AWWW
v)o\o\a>o\o\uiUiv)vj^s]0\a»o\o\o\wiuuiAUA^A^o\uuiuuiuiui
WVOs)UlWi-ai^UiWHOOOO\AWOOO^AWMyOslUiWOOOs)WWWO
Ю^У0М1Л00Ю1Лч)м1Л00Ю0\О*00Ю0\О1»)Чм1Л\ОЫи0\Ои|О5\0
меньшей
большей
нижнее
верхнее
нижнее
верхнее
Численность группы
Критические значения
при a = 0,05
Критические значения
при a = 0,01
о

^000n10\UiAW(OmUiAU)IOmO\000vJ0\Ui^WWmOUi^I>JSJmO^00v)
4^K-^UJ©0NUJS00\0NtOVO0NWO^VAJO--J4bb-00*.b-00-'-J-£k^-
W Ю W i- k-k-i— ммЮЮЮЮЮЮми-м >— ^-к-к-к-к-к-ЮЮ>— >— к- >— >— ►— к-
K-oovoooc»-^aNtyiUJ(ONJ^-oo^ooooo--jaNtyityi-P».ujujoo404ooo-^j--jaNtyi
^soto«^^oto«^^4bOOK-4b^ow^oujaNVO(ooNso»oootooNO.t»---~4»—• t/i чо
^OOOVOSOVOSO(»b-00040SOSOVO(»(»(»(»^--J--J--J404000???2 2^rT?^
^-CX«^tOVOONUJO^O^«^tOSO^^NJVOaN^b-SOa\UJ^-NJOOOuov>Jt'-,WA"^'
WIOmOVO\OOOvJO\Ui^WWS)m OVOS000-JO\ON«-fl-fklAJlOK-OOS00000--JON
oto^a\(xoto4^aNOL^«^ooH-uja\(x^-^aN4o^-^».--j4oojaN4ouja\vouja\s£)
s
n
X
E
en
о
шей
X
^
X
n
Ш
X
X
X
i
X
rt
ш
•a
iXHee
X.
ислен
X
о
a
«r
•3
v:
э
a
!*
s
9 3
[ческие
1ри а =
о а
-/-> X
О с>
х
S
a
!*
•о
S
a s
•о л
х «
о
R g
II а.
О w
О ia
— Л
п
х
§
о
§

Продолжение табл. 14.
Численность группы
меньшей
11
11
11
11
11
11
12
12
12
12
12
12
12
12
12
12
12
12
12
12
13
13
13
13
13
13
13
13
13
13
13
13
13
14
большей
20
21
22
23
24
25
12
13
14
15
16
17
18
19
20
21
22
23
24
25
13
14
15
16
17
18
19
20
21
22
23
24
25
14
Критические значения
при а = 0,05
нижнее
128
131
135
139
142
146
115
119
123
127
131
135
139
143
147
151
155
159
163
167
136
141
145
150
154
158
163
167
171
176
180
185
189
160
верхнее
224
232
239
246
254
261
185
193
201
209
217
225
233
241
249
257
265
273
281
289
215
223
232
240
249
258
266
275
284
292
301
309
318
246
Критические значения
при а = 0,01
нижнее
114
117
120
123
126
129
105
109
112
115
119
122
125
129
132
136
139
142
146
149
125
129
133
136
140
144
148
151
155
159
163
166
170
147
верхнее
238
246
254
262
270
278
195
203
212
221
229
238
247
255
264
272
281
290
298
307
226
235
244
254
263
272
281
291
300
309
318
328
337
259
445

Продолжение табл. 14.
Численность группы
меньшей
14
14
14
14
14
14
14
14
14
14
14
15
15
15
15
15
15
15
15
15
15
15
16
16
16
16
16
16
16
16
16
16
17
17
большей
15
16
17
18
19
20
21
22
23
24
25
15
16
17
18
19
20
21
22
23
24
25
16
17
18
19
20
21
22
23
24
25
17
18
Критические значения
при а = 0,05
нижнее
164
169
174
179
183
188
193
198
203
207
212
184
190
195
200
205
210
216
221
226
231
237
211
217
222
228
234
239
245
251
256
262
240
246
верхнее
256
265
274
283
293
302
311
320
329
339
348
281
290
300
310
320
330
339
349
359
369
378
317
327
338
348
358
369
379
389
400
410
355
366
Критические значения
при а = 0,01
нижнее
151
155
159
163
168
172
176
180
184
188
192
171
175
180
184
189
193
198
202
207
211
216
196
201
206
210
215
220
225
230
235
240
223
228
верхнее
269
279
289
299
308
318
328
338
348
358
368
294
305
315
326
336
347
357
368
378
389
399
332
343
354
366
377
388
399
410
421
432
372
384
446

-J
Юк-^-к-^-к-ООООООЧОЧОЧОЧОЧОЧОЧООООООООООООООООО-^-^
IOWAWIOmUi^WKJmOUi^WWmO'iOUiAWIOmO^OOUA
mO^OOOOvJsI^WW^W^WWWm О О »— OO4D4000--J--J0000
Ui U Ul Ul Ui Ul (^(^(^(^^ь^ь^^ь^ь^ь^ь^ь^ь-Рь-Рь-Рь-Рь-Рь-Рь-Рьил-Рь-Рь
■-J OO --J «-ft -P». IaJ AUJ(OO^0(»^V000sl0\UWsia\Lft^W^OV0Al»J
^WO^WO^^^VOONWmVOvIWWmOOONWWWO^OvIONUJIO
UJUJUJUJUJUJUJUJUJUJUJUJUJUJUJUJtOtOtOtOtOtOtOtOtOtOtOtOtO
00s1s1O\W***WWIOmmmOOVOI»I»\O00I»s)0N0\UiUi0\0\
0\s)OW0\^M^Ui00WUi\0Ws1mUiV0WIO^OW^W00WUO
О^\0000\1А^1ЛДЫмОЫ1Ом\О1Х1ч)иО00ч10\1ЛЫЮм0\и
--J --J
Ю Ю
UJ Ю
Ю Ю
-J -J
ON О
Ю H-
H- О
Ю Ю
Ltt ЧО
Ю ь-
--J
Ю
264
399
244
419
-j -j
Ю H-
O ЧО
Ю Ю
oo to
OO --J
OO -vj
to to
О ЧО
меньшей
большей
нижнее
верхнее
нижнее
верхнее
Численность группы
Критические значения
при a = 0,05
Критические значения
при a = 0,01
S

Продолжение табл. 14.
Численность группы
меньшей
22
22
22
23
23
23
24
24
25
большей
23
24
25
23
24
25
24
25
25
Критические значения
при а = 0,05
нижнее
419
427
435
451
459
468
492
501
536
верхнее
593
607
621
630
645
659
684
699
739
Критические значения
при а = 0,01
нижнее
393
400
408
424
431
439
464
472
505
верхнее
619
634
648
657
673
688
712
728
770
Таблица 15. Критические значения критерия Уилкоксона И7для
двусторонней критической области в зависимости от количества наблюдений п при
уровне значимости а
п
5
6
7
8
9
10
11
12
w
15
21
19
28
24
32
28
39
33
45
39
52
44
58
50
а
0,062
0,032
0,062
0,016
0,046
0,024
0,054
0,020
0,054
0,020
0,048
0,018
0,054
0,020
0,052
п
13
14
15
16
17
18
19
20
w
65
57
73
63
80
70
88
76
97
83
105
91
114
98
124
106
а
0,022
0,048
0,020
0,050
0,022
0,048
0,022
0,050
0,020
0,050
0,020
0,048
0,020
0,050
0,020
0,048
448

Таблица 16. Значения точности ег в зависимости от надежности у при
нормальном распределении
У
0,6826
0,8
0,81
0,82
0,83
0,84
0,85
0,86
ет
1
1,282
1,310
1,340
1,371
1,404
1,439
1,475
У
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
ет
1,513
1,554
1,597
1,643
1,694
1,750
1,810
1,880
У
0,95
0,9544
0,96
0,97
0,98
0,99
0,9973
0,999
ет
1,960
2
2,053
2,169
2,325
2,576
3
3,290

П риложение 3
Греческий алфавит
Буквы
А а
в Р
г у
Д 5
Е е
z С
Н л
Т 0
I I
К к
Л X
М ц
Названия
альфа
бета
гамма
дельта
эпсилон
дзета
эта
тета
йота
каппа
ламбда
ми
Буквы
N
Н
О
п
р
£
Т
Y
Ф
X
ч*
Q
V
%
о
п
р
а
т
о
ф
X
Ч>
со
Названия
ни
кси
омикрон
пи
ро
сигма
тау
ипсилон
фи
хи
пси
омега

Литература
1. Агапов Г. И. Задачник по теории вероятностей. — М.: Высшая школа,
1994.
2. Айвазян С. Статистическое исследование зависимостей. — М.:
Металлургия, 1968.
3. Айвазян С. А., Енюков И. С, Мешалкин Л. Д. Прикладная статистика.
Исследование зависимостей. — М.: Финансы и статистика, 1985.
4. Андерсон Т. Введение в многомерный статистический анализ. — М.:
Физматгиз, 1963.
5.Аптон Г. Анализ таблиц сопряженности. — М.: Финансы и
статистика, 1982.
6. Афифи А., Эйзен С. Статистический анализ. Подход с использованием
ЭВМ. - М.: Мир, 1988.
7. Бейли Н. Математика в биологии и медицине. — М.: Мир, 1970.
8. Бендат Дж., Пирсон А. Прикладной анализ случайных данных. — М.:
Мир, 1989.
9. Бикел П., Доксум К. Математическая статистика. — М.: Финансы и
статистика, 1983.
10. Большее Л. И., Смирнов И. В. Таблицы математической статистики. —
М.: Наука, 1983.
11. Борель Э. Вероятность и достоверность. — М.: Наука, 1969.
12. Боровков А. А. Теория вероятностей. — М.: Наука, 1986.
13. Булдык Г. М. Теория вероятностей и математическая статистика. —
Минск: Вышэйшая школа, 1989.
14. Вентцель Е. С, Овчаров Л. А. Теория вероятностей, задачи и
упражнения. — М.: Наука, 1973.
15. Вентцель Е. С. Теория вероятностей. — М.: Высшая школа, 1998.
16. Виленкин Н. Я. Комбинаторика. — М.: Наука, 1969.
17. Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975.
18. Гаскаров Д. В., Шаповалов В. И. Малая выборка. — М.: Статистика,
1978.
19. Генкин С. А., Итенберг И. В. Комбинаторика и вероятность, учебное
задание для ЗМШ при ЛГУ. - Л., 1989.
20. Гланц С. Медико-биологическая статистика. — М.: Практика, 1999.
21. Гмурман В. Е. Руководство к решению задач по теории вероятностей и
математической статистике. — М.: Высшая школа, 1979.
22. Гмурман В. Е. Теория вероятностей и математическая статистика. —
М.: Высшая школа, 1977.
23. Гнеденко Б. В. Курс теории вероятностей. — М.: Наука, 1988.
24. Гнеденко Б. В., Хинчин А. Я. Элементарное введение в теорию
вероятностей. — М.: Наука, 1982.
25. Гурский Е. И. Сборник задач по теории вероятностей и
математической статистике. — Минск: Вышэйшая школа, 1984.
451

26. Гурский Е. И. Теория вероятностей с элементами математической
статистики. — М.: Высшая школа, 1971.
27. Дайменд С Мир вероятностей. — М.: Статистика, 1970.
28. Демиденко Е. 3. Линейная и нелинейная регрессия. — М.: Финансы и
статистика, 1981.
29. Дрейпер Н. Смит Г. Прикладной регрессионный анализ: В 2-х книгах. —
Кн. 1. — М.: Финансы и статистика, 1986. — Кн. 2. — М.: Финансы и
статистика, 1987.
30. Дружинин Н. К. Выборочное наблюдение и эксперимент. — М.:
Статистика, 1977.
31. Ежов И. И., Скороход А. В., Ядренко М. И. Элементы комбинаторики. —
М.: Наука, 1977.
32. Езекиел М., Фокс К. Методы анализа корреляций и регрессий. М.:
Статистика, 1966.
33. Журавлева К. И. Статистика в здравоохранении. — М.: Медицина,
1981.
34. Занимательная статистика / Под ред. Г. И. Бакланова, Г. С. Кильди-
шева — М.: Статистика, 1980.
35. Зубков А. М., Севастьянов Б. А., Чистяков В. П. Сборник задач по
теории вероятностей. — М.: Наука, 1989.
36. Калинина В. И., Панкин В. Ф. Математическая статистика. — М.:
Высшая школа, 1994.
37. Каминский Л. С. Медицинская и демографическая статистика. — М.:
Статистика, 1974.
38. Каминский Л. С. Обработка клинических и лабораторных данных.
Применение статистики в научной и практической работе врача. —
Л.: Медгиз, 1959.
39. Карасев А. И. Теория вероятностей и математическая статистика. —
М.: Статистика, 1979.
40. Кендэлл М. Ранговые корреляции. — М.: Статистика, 1975.
41. Кендэлл М., Стьюарт А. Статистические выводы и связи. — М.:
Наука, 1973.
42. Кендэлл М., Стьюарт А. Теория распределений. — М.: Наука, 1966.
43. Кокрен У. Методы выборочного исследования. — М.: Статистика,
1976.
44. Кокс Д. Р., Оукс Д. Анализ данных типа времени жизни. — М.:
Финансы и статистика, 1988.
45. Кокс Д., Снелл Э. Прикладная статистика. Принципы и примеры. —
М.: Мир, 1984.
46. Колмогоров А. Н. Об одном новом подтверждении законов Менделя //
ДАН СССР. - 1940. - Т. 27, № 1. - С. 38 - 42.
47. Колмогоров А. Н. Основные понятия теории вероятностей. — М.:
Наука, 1974.
48. Колмогоров А. И., Журбенко И. Г., Прохоров А. В. Введение в теорию
вероятностей. — М.: Наука, 1982.
49. Кордемский Б. А. Математика изучает случайности. — М.:
Просвещение, 1975.
50. Корн Г., Корн Т. Справочник по математике (для научных работников
и инженеров). — М.: Наука, 1974.
452

51. Крамер Г. Математические методы статистики. — М.: Мир, 1975.
52. Кудрин А. И, Пономарева Г. Т. Применение математики в
экспериментальной и клинической медицине. — М.: Медицина, 1967.
ЪЪ.Лакин Г. Ф. Биометрия. — М.: Высшая школа, 1980.
54. Леман Э. Проверка статистических гипотез. — М.: Наука, 1964.
55. Леман Э. Теория точечного оценивания. — М.: Наука, 1991.
56. Ликеш И., Ляга И. Основные таблицы математической статистики. —
М.: Финансы и статистика, 1985.
57. Лисенков А. Н. Математические методы планирования
многофакторных медико-биологических экспериментов. — М.: Медицина, 1979.
58. Лихолетов И. И. Высшая математика, теория вероятностей и
математическая статистика. — Минск: Вышэйшая школа, 1976.
59. Лихолетов И. И., Мацкевич И. П. Руководство к решению задач по
высшей математике и математической статистике. — Минск:
Вышэйшая школа, 1976.
60. Лоэв М. Теория вероятностей. — М.: ИЛ, 1962.
61. Лютикас В. С. Школьнику о теории вероятностей. — М.:
Просвещение, 1983.
62. Майстров Л. Е. Теория вероятностей. Исторические очерки. — М.:
Наука, 1967.
63. Мацкевич И. П., Свирид Г. П. Высшая математика, теория
вероятностей и математическая статистика. — Минск: Вышэйшая школа, 1993.
64. Медик В. А., Токмачев М. С. Математическая статистика в медицине и
биологии. — Новгород: НовГУ, 1998.
65. Мерков А. М. Общая теория и методика санитарно-статистического
исследования. — М.: 1969.
66. Мерков А. М., Поляков Л. Е. Санитарная статистика. — Л.: Медицина,
1974.
67. Митропольский А. К Техника статистических вычислений. — М.:
Наука, 1971.
68. Мостеллер Ф. Пятьдесят занимательных вероятностных задач с
решениями. — М.: Наука, 1975.
69. Мостеллер Ф., Рурке Р., Томас Дж. Вероятность. — М.: Мир, 1969.
70. Мюллер П., Найман П., Шторм Р. Таблицы по математической
статистике. — М.: Финансы и статистика, 1982.
71. Общая теория статистики / Под ред. А. А. Спирина, О. Э. Башиной.
— М.: Финансы и статистика, 1995.
72. Общая теория статистики / Под ред. А. Я. Боярского, Г. Л. Громыко.
Издательство Московского университета, 1985.
73. Павловский 3. Введение в математическую статистику. — М.:
Статистика, 1967.
74. Пасхавер И. С. Закон больших чисел и статистические
закономерности. — М.: Статистика, 1974.
75. Поллард Дж. Справочник по вычислительным методам статистики. —
М.: Финансы и статистика, 1982.
76. Пугачев В. С. Теория вероятностей и математическая статистика. —
М.: Наука, 1979.
77. Райзер Г. Комбинаторная математика. — М.: Мир, 1966.
453

78. Рао С. P. Линейные статистические методы и их применения. — М.:
Наука, 1968.
79. Реньи А. Письма о вероятности. — М.: Мир, 1970.
80. Розанов Ю. А. Лекции по теории вероятностей. — М.: Наука, 1986.
81. Рокицкий П. Ф. Биологическая статистика. — Минск: Вышэйшая
школа, 1967.
82. Руннон Р. Справочник по непараметрической статистике. — М.:
Финансы и статистика, 1982.
83. Рыбников К. А. История математики: Учебник. — М.: Изд-во МГУ,
1994.
84. Савельев Л. Я. Комбинаторика и вероятность. — М.: Наука, 1975.
85. Сепетлиев Д. Статистические методы в научных медицинских
исследованиях. — София: Медицина и физкультура, 1965.
86. Смирнов И. В., Дунин - Борковский И. В. Курс теории вероятностей и
математической статистики для технических приложений. — М.:
Наука, 1969.
87. Солодовников А. С. Теория вероятностей. — М.: Просвещение, 1983.
88. Справочник по прикладной статистике. В 2-х т. / Под ред. Э. Ллойда,
У. Ледермана, Ю. Н. Тюрина. — М.: Финансы и статистика, 1989,
1990.
89. Справочник по теории вероятностей и математической статистике /
Под ред. В. С. Королюка. — М.: Наука, 1985.
90. Статистические методы исследования в медицине и
здравоохранении. / Под ред. Л. Е. Полякова — Л.: Медицина, 1971.
91. Тарасов Л. В. Мир, построенный на вероятности. — М.: Просвещение,
1984.
92. Тутубалин В. Н. Границы применимости
(вероятностно-статистические методы и их возможности). — М.: Знание, 1977.
93. Тьюки Дж. Анализ результатов наблюдений. Разведочный анализ. —
М.: Мир, 1983.
94. Тюрин Ю. И., Макаров А. А. Анализ данных на компьютере / Под ред.
В. Э. Фигурнова. — М.: ИНФРА — М.: Финансы и статистика, 1995.
95. Уилкс С. Математическая статистика. — М.: Наука, 1967.
96. Урбах В. Ю. Биометрические методы. — М.: Наука, 1964.
97. Урбах В. Ю. Математическая статистика для биологов и медиков. —
М.: Изд-во АН СССР, 1963.
98. Федоров А. И. Методы математической статистики в биологии и
опытном деле. — Алма-Ата: Крайнар, 1967.
99. Феллер В. Введение в теорию вероятностей и ее приложения. — М.:
Мир, 1984.
100. Фишман Б. Б., Токмачев М. С, Медик В. А. Применение методов
математического моделирования в практике санитарно-гигиенического
мониторинга. — В сб.: Совершенствование статистики здоровья и
здравоохранения в РФ. Материалы 6-й ежегодной Российской НПК
НПО "МедСоцЭкономИнформ", 27-28 мая 1999 г. — С.127-132.
101. Халамайзер А. Я. Комбинаторика и бином Ньютона. — М.:
Просвещение, 1980.
102. Халамайзер А. Я. Математика гарантирует выигрыш. — М.:
Московский рабочий, 1981.
454

103. Хальд А. Математическая статистика с техническими приложениями. —
М.: ИЛ, 1956.
104. Хастингс И., Пикок Дж. Справочник по статистическим
распределениям. — М.: Статистика, 1980.
105. Хеттсманпергер Т. Статистические выводы, основанные на рангах. —
М.: Финансы и статистика, 1987.
106. Хилл А. Б. Основы медицинской статистики. — М.: Медгиз, 1958.
107. Холл М. Комбинаторика. — М.: Мир, 1970.
108. Холлендер М., Вулф Д. Непараметрические методы статистики. — М.:
Финансы и статистика, 1983.
109. Четыркин Е. М., Калахман И. Л. Вероятность и статистика. — М.:
Финансы и статистика, 1982.
ПО. Шварц Г. Выборочный метод. — М.: Статистика, 1978.
111. Ширяев А. И. Вероятность. — М.: Наука, 1980.
112. Шторм Р. Теория вероятностей. Математическая статистика.
Статистический контроль качества. — М.: Мир, 1970.

В. А. Медик, М. С. Токмачев, Б. Б. Фишман
СТАТИСТИКА В МЕДИЦИНЕ И БИОЛОГИИ
ЛР № 010215 от 29.04.97.
Сдано в набор 30.07.2000. Подписано к печати 29.10.2000. Формат
бумаги 70х 100'/|6. Бумага офсетная. Гарнитура Тайме. Печать офсетная.
Усл. печ. л. 36,9. Усл. кр.-отт. 30,3. Уч.-изд. л. 35.0. Тираж 1000 экз.
Заказ № 3529.
Ордена Трудового Красного Знамени издательство «Медицина».
101000, Москва, Петроверигский пер., 6/8.
ЗАО «Шико». Москва, 2-й Сетуньский пер., 11-27.
Отпечатано с оригинал-макета в ГУП ордена «Знак Почета»
Смоленской областной типографии им. В. И. Смирнова.
214000, г. Смоленск, проспект им. Ю. Гагарина, 2.
J
ISBN 5-225-04630-4
lllllllipil 11111111
785225||04630911