Вертолеты. Расчет и проектирование. Книга II. Колебания и динамическая прочность. - Миль М.Л.

Автор: Миль М.Л.

Теги: техника средств транспорта самолетостроение проектирование вертолеты теория колебаний

Год: 1967

Похожие

Вертолеты. Расчет и проектирование. Книга I. Аэродинамика

Расчет самолета на прочность

Вертолет Ми-6. Устройство эксплуатации и техническое обслуживание. Книга 1

Расчет самолета на прочность

Текст

Посвящается 50-й годовщине
Великой Октябрьской
социалистической революции
М. Л. МИЛЬ, А. В. НЕКРАСОВ, А. С. БРАВЕРМАН,
Л. Н. ГРОДНО, М. А. ЛЕЙКАНД
Вертолеты
расчет
и проектирование
2
Колебания и
динамическая
прочность
Под редакцией
д-ра техн, наук М. Л. МИЛЯ
ИЗДАТЕЛЬСТВО
•МАШИНОСТРОЕНИЕ*
Москва . 12 Ь7
УДК 629.135.4 ; (534-9.014.4+539.43)
Труд «Вертолеты (расчет и проектирование)» издается в трех книгах.
Книга первая — Аэродинамика;
Книга вторая — Колебания и динамическая прочность;
Книга третья — Проектирование.
В настоящей второй книге изложены некоторые вопросы теории коле-
баний и методы расчета напряжений, возникающих при этих колебаниях
в конструкции вертолета в полете и, в частности, в лопасти несущего винта.
Приводятся методы расчета ресурса конструкции, а также методы
расчета вибраций вертолета, позволяющие определить амплитуды этих
вибраций и сопоставить их с нормами комфорта. При этом впервые в оте-
чественной литературе рассмотрена задача о совместных колебаниях несу-
щего винта и фюзеляжа.
Подробно изложена теория самовозбуждаюшихся колебаний особого
типа, носящих название «земной резонанс». Рассмотрены особенности
возникновения таких колебаний у вертолета на земле, во время взлета и
посадки с пробегом и в условиях полета.
В отдельной главе рассмотрены особые, мало освещенные в общей
литературе, случаи расчета подшипников, работающих в специфических
условиях качательного движения. Здесь же изложена теория и метод
расчета нового типа упорных подшипников повышенной грузоподъемности,
а также подшипников, воспринимающих комбинированные нагрузки.
Книга предназначена для инженеров конструкторских бюро, научных
работников, аспирантов и преподавателей высших учебных заведений.
Она может быть полезна инженерам вертолетостроительных заводов и сту-
дентам при углубленном изучении колебаний и динамической прочности
вертолетов. Некоторые разделы книги будут полезны также летному и тех-
ническому составу вертолетных авиационных подразделений.
Таблиц 35. Иллюстраций 246. Библиографий 47.
Рецензент канд. техн, наук Р. А. Михеев
3-18—6
233—66
ПРЕДИСЛОВИЕ
Первая книга труда «Вертолеты (расчет и проектирование)», вы-
шедшая в 1966 г., была посвящена аэродинамике: теории и методам
расчета аэродинамических характеристик несущего винта и аэродинами-
ческому расчету вертолетов различных схем в целом.
В эту же книгу' включено изложение теории флаттера несущего
винта, относимой обычно к аэроупругости — области, пограничной меж-
ду аэродинамикой и прочностью.
Настоящая, вторая книга является логическим продолжением пер-
вой и посвящена колебаниям и динамической прочности вертолетов.
Вопросы статической прочности вертолетов в принципе не содержат
чего-либо нового по сравнению с известным в самолетостроении. Что
касается колебаний и динамической прочности, то вертолеты имеют ряд
особенностей, которые обозначились с первых же шагов вертолетов как
нового типа летательных аппаратов. Эти особенности приобрели боль-
шую остроту в процессе, если можно так выразиться, «борьбы за суще-
ствование» этих новых аппаратов в общей системе безаэродромных ави-
ационных транспортных средств.
Изложение вопросов колебаний и динамической прочности верто-
лета начинается с описания методов расчета упругих колебаний лопасти
его несущего винта, которые близки по основным уравнениям и методам
решения к используемым в теории флаттера, но имеют иную направлен-
ность, так как в конечном счете расчет сводится главным образом к ре-
шению чисто прочностной задачи, — определению переменных напряже-
ний, действующих в лопасти, а затем с использованием данных о пре-
делах усталости конкретной конструкции и к определению срока служ-
бы, т. е. ресурса лопасти.
Проблемы колебаний в динамической прочности важны не только
с точки зрения надежности аппаратов. От решения этих проблем зави-
сит срок службы машин, а значит и их экономичность.
В книге, в частности, рассмотрены современные методы расчета
упругих колебаний лопасти, выполняемого на быстродействующих элек-
тронно-вычислительных машинах, позволяющие определять действую-
щие в лопасти переменные напряжения.
Исследования колебаний типа «земной резонанс», так же как изуче-
ние вибраций конструкции, составляют собственно главную тему теории
колебаний вертолета.
Исключение колебаний типа «земной резонанс», приводящих
в случае их возникновения и развития к разрушению аппарата на земле,
а в многовинтовых схемах и в воздухе, всегда являлось одной из
главных задач, стоящих перед конструкторами. Весьма важным оказы-
вается и вопрос о колебаниях (вибрациях) частей вертолета, рассматри-
ваемый с точки зрения комфорта для экипажа и пассажиров. Остроту
этой проблемы нетрудно оценить, если представить себе мощность их
1578
3
постоянного источника — огромного несущего винта, работающего
в сильно переменном поле скоростей.
Последняя глава книги посвящена расчету специальных подшипни-
ков, необходимому при проектировании многих агрегатов вертолета, и
таким образом является переходной к третьей книге — «Проектиро-
вание».
В книге «Проектирование» будут кратко рассмотрены основные во-
просы компоновки вертолетов, выбора основных параметров вертолетов,
в том числе имеющих крылья, а также вспомогательные пропульсивные
средства: тянущие винты или дополнительные реактивные двигатели.
Будут также изложены соображения об экономичности авиационной
техники, которые необходимо иметь в виду при проектировании.
В этой книге будут рассмотрены также вопросы балансировки,
управляемости и устойчивости с точки зрения выбора параметров сис-
темы управления, а также вопросы проектирования отдельных агрега-
тов вертолета.
М. Миль
- - — — ★ =====
Книгу вторую «Колебания и динамическая прочность» написали:
введение—М. Л. Миль; главу 1—А. В. Некрасов; главы 2 и 3 —
Л. Н. Гродко; главу 4 — М. А. Лейканд. § 11 главы 1 написан А. В. Не-
красовым совместно с инженером 3. Е. Шнуровым.
В подготовке рукописи авторам оказали большую помощь инже-
неры Ф. Л. Заржевская, В. М. Костромина и И. В. Курова.
В книге использованы результаты расчетов, выполненных инжене-
рами Ю. А. Мягковым, О. П. Баховым, В. Ф. Хвостовым, С. А. Голубцо-
вым, В. М. Пчелкиным, С. Е. Сно, В. Г. Пашкиным, Н. Ф. Шевняковой,
Н. М. Киселевой, Л. В. Артамоновой, В. Ф. Семиной, Н. А. А^ацксвич,
В. И. Кирюшкиной и А. Г. Орловой.
Много ценных указаний было сделано рецензентом Р. А. Михеевым.
Окончательную подготовку рукописи к изданию провел инженер
Л. Г. Рудницкий.
Всем этим товарищам авторы выражают искреннюю призна-
тельность.
ВВЕДЕНИЕ
Как только был создан достаточно мощный и легкий авиационный
двигатель и вертолет впервые оторвался от земли, возникли и первые
проблемы, относившиеся к балансировке, управляемости и устойчивости
этой машины. Это были в основном аэродинамические проблемы. Если
считать началом полетов на винтокрылых аппаратах первые полеты
автожиров Сиерва в 1925—26 гг., то можно сказать, что данные пробле-
мы в основном были разрешены уже в первом десятилетии (1926—36 гг.)
их развития. Новый тип летательных аппаратов таким образом был изле-
чен от «детских болезней»..
Однако, как только появились первые серийные машины и началась
их практическая эксплуатация, выявились и более серьезные недостатки
вертолетов, такие, например, как усталость, связанная с недостаточ-
ной динамической прочностью некоторых элементов конструкции.
С более широким практическим применением автожиров, а особенно
геликоптеров, возродившихся в конце тридцатых — начале сороковых
годов на новой, более совершенной технической основе, появились новые
динамические проблемы. К ним относятся в первую очередь колебания
и вибрации отдельных элементов конструкции п вертолета в целом,
опасные по условиям возникающих при этом напряжений или недопу-
стимые с точки зрения создания необходимого комфорта для экипажа
и пассажиров, а также проблема ресурса — срока службы элементов
конструкции, работающих при высоких переменных напряжениях.
Последняя из проблем — увеличение ресурса — приобретает все боль-
шее значение в настоящее время, так как амортизационный и межре-
монтный сроки службы вертолета, определяемые ресурсом его агрегатов,
оказывают влияние на экономику его применения как средства транс-
порта. Ресурс в свою очередь определяется главным образом уровнем
действующих в конструкции переменных напряжений, поэтому точность,
с которой они рассчитываются, составляет одну из основных задач
исследования динамической прочности вертолетов.
Тянущий винт самолета работает практически в осевом потоке
и так же, как и двигатель, не создает в элементах конструкции сколько-
нибудь заметных переменных напряжений. Лишь взлет, посадка и полет
в условиях атмосферной турбулентности (а на боевом самолете и
маневр) создают в конструкции самолета значительные динамические
нагрузки, но с относительно небольшим (порядка десятков и сотен ты-
сяч циклов) числом нагружений за срок службы самолета. В этом слу-
чае можно говорить о повторно-статических нагрузках.
Совсем другой характер нагрузки у вертолета. Его основные сило-
вые элементы нагружаются динамически, причем число нагружений
часто превышает десятки миллионов циклов за срок службы. Это объ-
ясняется прежде всего несимметричным обтеканием несущего винта,
вращающегося и одновременно движущегося поступательно. При этом
5
лопасть испытывает переменные аэродинамические нагрузки вследствие
изменения относительной скорости потока и углов атаки ее сечений. Все
силы и моменты, действующие на лопасти, передаются на втулку и сис-
тему управления несущим винтом. Причем силы и моменты, приходящие
от разных лопастей, взаимно уравновешиваются, за исключением нагру-
зок, действующих с частотами, отношение которых к числу оборотов
винта кратно числу лопастей. Эти нагрузки передаются на фюзеляж и
невращающиеся части системы управления винтом и создают в них
также весьма заметные переменные напряжения.
Таким образом, проблема колебаний и динамической прочности
в вертолетостроении не только значительно шире, чем в самолетострое-
нии, но в целом ряде случаев она не имеет в самолетостроении прямой
аналогии.
Понимание важности вопросов динамической прочности пришло
не сразу. Так, даже причины первых аварий автожиров в 1936—37 гг.,
во время которых автожиры переворачивались в воздухе, долгое время
пытались объяснить недостаточной динамической устойчивостью.
В связи с этим, в частности, и были предприняты исследования дина-
мики несущего винта с шарнирным креплением лопастей при криво-
линейном движении аппарата (см. § 2 гл. 2 первой книги). Эта теория
нашла в дальнейшем широкое применение при разработке вопросов
динамической устойчивости и управляемости вертолетов. Однако она
не вскрыла действительной причины упомянутых аварий. Как выясни-
лось впоследствии, причиной их была недостаточная динамическая
прочность лопастей несущего винта.
Эти вопросы познавались буквально ощупью. Первые экспери-
ментальные автожиры и геликоптеры имели малые размеры и, как
следствие, достаточно высокую жесткость конструкции. Однако первое
же увеличение размеров сразу встретило большие затруднения. Так,
на автожире А-4, имевшем диаметр немного больший, чем его пред-
шественник автожир 2ЭА, возникли серьезные трудности из-за недоста-
точной жесткости лопасти на кручение. Угол установки лопастей в пер-
вом же полете из-за деформации кручения увеличился настолько, что
авторотация оказалась невозможной и полет едва не закончился
аварией.
Исследование этого явления было завершено опубликованием
работы о динамическом закручивании лопасти несущего винта в полете
(см. [2]), в которой впервые были даны рекомендации о необходимости
совмещения центра тяжести и центра давления и рассмотрены сообра-
жения о влиянии профиля лопасти на статическую устойчивость и уп-
равляемость аппарата. Это исследование привело к тому, что в практике
советского вертолетостроения были приняты несимметричные профили,
обеспечивающие больший запас авторотации. При компоновке лопасти
применялся набор различных профилей. Сделанных в указанной работе
рекомендаций оказалось также достаточно для того, чтобы первые
советские вертолеты, имевшие диаметр несущего винта около 14 м,
не испытывали флаттера.
Развитие советского вертолетостроения характеризуется более
крупными шагами, чем зарубежное (это и позволило нашим конструк-
торам, позднее начавшим строить вертолеты, создать машины, значи-
тельно превосходящие современные зарубежные по грузоподъемности
и размерам). В то время как после первого удачного вертолета «Си-
корский» S-51 с диаметром винта 14 м, построенного в 1947 г., амери-
канцы в 1950—51 гг. перешли к работе над машиной с винтом диамет-
ром 15,5 м (S-55), у нас после создания вертолета Ми-1 с 14-метровым
винтом уже в 1952 г. были построены вертолеты Ми-4 и Як-24 с винтами
диаметром 21 м. И не удивительно, что такой скачок в размерах
выявил новое, ранее не встречавшееся явление — на обеих машинах
6
при первом же запуске начался флаттер несущего винта. С этой пробле-
мой практически мы справились быстро, однако вопросы теории флат-
тера еще долго ожидали своего разрешения.
Впервые с новым явлением мы столкнулись в апреле 1952 г. верто-
лет Ми-4 был готов к первому запуску. После начала раскрутки лопасти
начали произвольно взмахивать, все сильнее и сильнее изгибаясь и грозя
задеть за конструкцию. Испытатели поняли, что они имеют дело с новым
явлением, которого никогда никто прежде не наблюдал. Это был флат-
тер лопастей несущего винта. Тогда никому не приходила в голову мысль,
что это тот самый флаттер винта, исследованием которого занимались
многие ученые в СССР и за рубежом. По всем имевшимся в то время
данным, флаттера ожидать не следовало, так как он мог возникать
не при числе оборотов несущего винта 100—НО в минуту, как это было
на вертолете Ми-4 в действительности, а примерно при 500 оборотах.
Решающим для возникновения флаттера оказалось в данном случае
то обстоятельство, что развившиеся на винте такого диаметра большие
силы вызывали значительную деформацию автомата перекоса, что
эквивалентно понижению крутильной жесткости лопастей, а также и то,
что тогда для этих машин было выбрано большое значение коэффициен-
та регулятора взмаха (близкое к единице); в ранних исследованиях
флаттера этот фактор не принимался во внимание. В результате нечего
было и думать о полетах на вертолете, так как флаттер начинался зна-
чительно раньше, чем достигались рабочие числа оборотов несущего
винта.
При наблюдении картины флаттера (взмахивание, изгиб и кручение
лопастей) стало ясно, что это явление можно устранить, только исполь-
зуя крутящие моменты от инерционных сил, возникающих в процессе
перемещения сечений лопасти при ее взмахах. Не связывая флаттер
несущего винта с флаттером крыльев, где, как давно известно, основное
значение имеет взаимное расположение центра тяжести, оси жесткости
и центра давления, а просто установив контргрузы в нескольких точках
по длине лопасти, которые должны были при колебаниях создать инер-
ционные моменты обратного знака, мы повторили запуск несущего винта
и поняли, что в наших руках есть надежное средство для того, чтобы
прекратить флаттер.
Таким образом в короткое время данная задача была решена прак-
тически, а в мае 1952 г. были совершены и первые полеты вертолета
Ми-4.
, В это же время возник флаттер и на вертолете Як-24, который имел
втулку и автомат перекоса те же самые, что и на вертолете Ми-4, а лопа-
сти — совсем другой конструкции (с большей изгибной и крутильной
жесткостью). Однако вследствие того, что при возникновении флаттера
решающее значение имеют жесткость автомата перекоса и параметры
регулятора взмаха, на лопастях вертолета Як-24 возник флаттер той же
самой формы и на тех же оборотах, что и на вертолете Ми-4.
Таким образом в течение нескольких недель было найдено практи-
ческое решение для устранения флаттера, которым пользуются и до сих
пор. Однако научная теория, которая позволила бы получить ответ,
возникнет флаттер или нет, а если и возникнет, то при каких числах
оборотов и какой формы, создавалась нами в течение последующих че-
тырех лет.
Надо сказать, что самое сложное заключалось в том, что, покончив
с наблюдаемым на земле флаттером (с помощью смещения центровки
лопасти вперед удалось «загнать» его за пределы рабочих чисел оборо-
тов и даже выше максимально допустимого числа оборотов двигателя
на земле), все же не была исключена возможность его появления в по-
лете. Это и привело к неприятным последствиям. В январе 1953 г. на вер-
толете Ми-4 произошло летное происшествие, причины которого в тече-
7
ние почти трех лет не были достаточно убедительно объяснены. При рас-
следовании были обнаружены следы удара лопастей о кабину летчика.
Ни в каких других случаях этого не наблюдалось. Следует заметить, что
при нормальном маховом движении лопасть не может задеть за кабину,
так как для этого необходимо, чтобы в воздухе были сбиты нижние огра-
ничители свеса лопастей.
Можно себе представить, как энергично мы должны были продол-
жать искать причины этого происшествия, если вспомнить, что после него
нс были остановлены ни полеты, ни серийное производство этих машин.
В течение 1954 г. многие летчики наблюдали в полете необычное
явление, которое получило название «эффект Калиберного» (по фами-
лии летчика, впервые заметившего его). Калиберный установил, что на
режиме моторного снижения, примерно на угле установки лопастей
6—7°, лопасти начинают вымахивать из описываемого ими конуса вра-
щения. После перекомплектовки лопастей, имевших несколько различ-
ную поперечную центровку, это явление прекращалось. Но однажды, че-
рез два года, при проверке в полете комплекта лопастей на отсутствие
«эффекта Калиберного», т. е. при выполнении в полете моторного сни-
жения с углом шага 6—7°*, это явление проявилось в такой степени,
причем взмахи лопастей были такими сильными, что на машине с тру-
дом совершили вынужденную посадку. При этом надо отметить, что
вблизи земли при переходе на другой режим взмахивание лопастей
прекратилось и машина вела себя нормально. При осмотре вертолета
после полета были обнаружены порванные замки лопастей (так называ-
ются подвижные соединения на разрезанной задней кромке лопасти),
что свидетельствовало об изгибе лопасти в плоскости вращения. Все ос-
тальное было исправно. Было решено подробно исследовать этот верто-
лет с тем же комплектом лопастей. Были проведены летные испытания,
чтобы повторить это явление и изучить его.
Обмеры лопастей показали, что их центровка оказалась примерно
на 1% хорды более задняя, чем была при выпуске лопастей на заводе.
И это объяснимо. Лопасти были обшиты фанерой. Центр тяжести фане-
ры находится примерно на половине хорды. Поэтому при набухании и
утяжелении ее от влаги, центр тяжести всей лопасти смещается к ее
задней кромке. Случай же с этим вертолетом произошел во время от-
тепели, когда влажность воздуха была высокая.
При этих испытаниях было также окончательно установлено, что
характер махового движения лопастей и движения ручки управления
в полете на режиме «эффекта Калиберного» совершенно аналогичны
маховому движению и движению ручки, которые записывались на земле
при испытаниях, когда лопасти вводились во флаттер путем искусст-
венно созданной задней центровки. Этот сложный путь позволил уста-
новить, что явление, возникшее в полете, идентично с тем, которое было
отмечено на земле. Так было установлено, что «эффект Калиберного»
есть не что иное, как начало флаттера в полете. На основе этого заклю-
чения и возникла догадка, что необъясненное ранее летное происшествие
с ударами лопастей пс кабине летчика также не что иное, как флаттер
лопастей в полете, возникший при оборотах несущего винта, при которых
при работе на земле он не проявлялся.
При флаттере колебания шарнирно заделанной лопасти в отличие
от колебаний крыла самолета подобны маховому движению, амплитуда
которого возрастает до тех пор, пока лопасть не ударится об ограничи-
тели свеса, а затем, сбив их, о кабину.
* На вертолете Ми-4 флаттер появляется всегда в первую очередь на этом ре-
жиме.
8
То, что это явление не было вскрыто в течение долгого времени,
объясняется ошибочным предположением, вытекающим из испытаний
на моделях, что если флаттер на земле устранен, то в воздухе при посту-
пательном движении он возникнуть не может. Но практика, а затем и бо-
лее строго поставленный эксперимент на вертолете, наконец, и теория
показали, что есть режимы полета, при которых флаттер при рабочих
оборотах винта хотя и не возникает на земле, но может произойти в
полете.
Следует сказать, что, как было установлено в ходе исследований,
явление флаттера проявлялось на вертолетах и раньше. Еще в 1949 г.
на вертолете Ми-1 для увеличения запаса по срыву был спроектирован
и построен несущий винт с более широкими лопастями. Этот винт в по-
лете вызывал тряску, которую устранить так и не удалось. Когда же была
разработана теория флаттера и объяснены все особенности этого явле-
ния, стало возможным не только объяснить причину тряски на вертолете
Ми-1 с широкими лопастями, вызванную близостью режима к флаттеру,
но и без единого затруднения спроектировать и построить еще в 1956 г.
35-метровый винт для вертолетов Ми-6 и Ми-10. Совершенство этого
винта подтверждается тем, что через неделю после первого вылета но-
вый тяжелый вертолет Ми-6 смог совершить полет для тренировки к уча-
стию в воздушном параде на авиационном празднике в Тушино. Ника-
ких неприятных явлений, связанных с флаттером, на этих машинах ни
тогда, ни позже уже не было. Такова история вопроса о флаттере.
Не менее важной является и задача определения переменных на-
пряжений в лопастях, которая решается путем рассмотрения их вынуж-
денных колебаний.
В течение первого десятилетия своего развития несущие винты вер-
толетов проектировались фактически без предварительного расчета
переменных напряжений, возникающих в полете. В то время расчет этот
был трудоемким и неточным, нередко его заканчивали лишь после вы-
хода машины на аэродром. Только разработка методов расчета пере-
менных напряжений, позволяющих использовать быстродействующие
электронно-вычислительные цифровые машины, позволила конструиро-
вать лопасти с сознательным выбором распределения их жесткостей и
масс таким образом, чтобы избежать опасных резонансов, понизить уро-
вень напряжений и тем обеспечить высокий ресурс п надежность ло-
пастей.
Следует заметить, что уточнения методики расчета лопасти на проч-
ность вызвали дальнейшие углубления и уточнения аэродинамической
теории. Как уже было показано в первой книге, уточнение расчета лет-
ных данных не вызывало большой необходимости в разработке сложной
и трудоемкой для расчетов вихревой теории несущего винта. Однако
только вихревая теория позволяет определить неравномерность поля
индуктивных скоростей, вызывающую переменные нагрузки на лопасть
с частотами, возбуждающими изгибные колебания лопастей по второму,
третьему и более высоким тонам. Поэтому только вихревая теория мо-
жет дать в расчете напряжений результаты, близкие к тем, которые
наблюдаются в действительности.
Другой не менее важной проблемой были вибрации. Эта проблема
всегда была одной из самых трудных в развитии винтокрылых аппара-
тов. Десятки интересных по замыслу и летно-тактическим данным конст-
рукций в СССР и за рубежом не вышли в свет из-за высокого уровня
вибраций.
На самолетах нет таких мощных источников возбуждения колеба-
ний, как на вертолетах. Кроме того, и двигатели, и воздушные винты,
которые являются на самолетах основными возбудителями вибраций,
9
могут быть достаточно хорошо изолированы от конструкции при помощи
специальной амортизации. Резонансы с высокими частотами от этих воз-
будителей довольно легко могут быть устранены путем сравнительно
небольших изменений конструкции. На вертолете же, помимо того, что
сами возмущающие силы от винтов значительно больше, чем па самоле-
те, их частоты от медленно вращающегося несущего винта довольно
низки и при совпадении с собственными частотами колебаний фюзеляжа,
двигателя, крыла или оперения возникают резонансы, приводящие к зна-
чительным вибрациям с амплитудой перемещений, достигающей на уста-
новившихся режимах полета величин порядка 0,3—0,4 мм, а на кратко-
временных режимах перед посадкой вертолета даже 1—2 мм в кабине
экипажа.
Резонансы с основными тонами собственных колебаний фюзеляжа
отстроить изменением жесткости конструкции на построенной уже ма-
шине часто оказывается практически невозможно, так как это равно-
сильно полной переделке фюзеляжа. Поэтому важно уметь правильно
оценивать частоты собственных колебаний фюзеляжа и вычислять
амплитуды вибраций уже в процессе проектирования машины.
Основное внимание в борьбе с вибрациями уделяется снижению
величин переменных сил, приходящих на фюзеляж от несущего винта.
Эти силы вызываются колебаниями лопастей. В свою очередь колебания
лопастей могут быть большими или меньшими в зависимости от близо-
сти их собственных частот к частотам источников внешнего возбуждения.
Во всех случаях близость к резонансу вызывает увеличение напря-
жений в лопастях. Но, если эти колебания происходят с частотой гармо-
ники £л +1 или 2Л—1 для колебаний в плоскости вращения винта или
частотой гармоники £л для колебаний в плоскости взмаха (где £л число
лопастей), то силы суммируются и передаются через шарниры на втулку
и через нее на фюзеляж, вызывая его колебания.
Наиболее неприятные для человека вертикальные вибрации в зна-
чительной степени вызываются силами, действующими в плоскости вра-
щения винта, так как эти силы, будучи приложенными высоко над цент-
ром тяжести вертолета, создают значительные моменты, возбуждающие
колебания изгиба фюзеляжа. При этом естественно, что наибольшие ам-
плитуды вибраций (пучности) достигаются по концам фюзеляжа, а сле-
довательно, и в кабине летчика.
Оказывается, что при определении частот собственных колебаний
лопастей вертолета необходимо считаться с тем, что втулка винта при
колебаниях не остается неподвижной, так как она закреплена на упру-
гом фюзеляже. Таким образом, при определении вибраций вертолет
должен рассматриваться как единая динамическая система с упругими
лопастями, шарнирно подвешенными ко втулке, укрепленной на упругом
фюзеляже.
Само собой разумеется, что такая расчетная схема могла возник-
нуть и оказаться посильной для рассмотрения лишь в последнее время.
Насколько нам известно, в настоящей книге впервые дается изложение
метода расчета вибраций вертолета при его проектировании.
Далее в книге рассматриваются самовозбуждающиеся колебания
вертолета, носящие обычно название «земной резонанс».
Впервые с явлением земного резонанса конструкторы столкнулись
более 30 лет тому назад, когда на одном из первых отечественных авто-
жиров А-6 (конструкции В. А. Кузнецова) применили появившиеся в то
время колеса с шинами низкого давления. Стойки, имевшие воздушно-
масляную амортизацию, были сняты с вертолета. И при первом же
запуске возникли неожиданные колебания. Вертолет качался с колеса
на колесо со все нарастающими амплитудами, пока не начал подпрыги-
вать, отрывая колеса от земли. Запуск закончился поломкой.
10
Благодаря тому, что эти испытания были засняты кинокамерой, уда-
лось установить, что лопасти совершали нарастающие колебания во-
круг вертикальных шарниров. Эти колебания, происходившие в поле
центробежных сил, вызывали периодическое смещение центра тяжести
всей несущей системы относительно центра втулки и таким образом
возбуждали колебания вертолета, стоявшего на земле. Ясно, что если
частота смещений центра тяжести винта совпадает с частотой собствен-
ных колебаний вертолета на иневматиках, то такие колебания могут
нарастать. Вот, казалось бы, и ясна физическая картина явления.
Энергией, питавшей эти нарастающие колебания, была либо энергия
двигателя, вращающего винт, либо, когда двигатель выключен, кине-
тическая энергия вращающегося винта.
Однако для разработки теории земного резонанса, изучения новых
его проявлений, возможно в новых, принципиально отличных схемах и
конструкциях вертолетов, потребовались многочисленные исследования,
которые продолжаются и сейчас.
Первые теоретические работы, прояснившие природу автоколебаний
типа «земной резонанс», были выполнены еще в 1936 г. И. П. Братухи-
ным и Б. Я. Жеребцовым, Результаты проведенных ими исследований
позволили устранить, в частности, земной резонанс на самом крупном из
когда-либо построенных в мире автожире А-15 с несущим винтом диа-
метром 18 .и, созданном в 1936 г. по проекту В. А. Кузнецова и
М. Л. Миля. В конструкции втулки этого автожира были применены
пружины, вмонтированные в ограничители колебаний лопастей вокруг
вертикального шарнира. Пружины изменили собственную частоту коле-
баний лопастей в плоскости вращения, и таким образом «земной резо-
нанс» был устранен.
Нет сомнений в том, что явление земного резонанса было в то время
известно и как-то изучено и на Западе, поскольку уже первые удачные
автожиры Сиерва, например С-19, имели упругие связи (амортизато-
ры), включенные в лопасти через фрикционные демпферы.
Однако многие конструкторы на протяжении некоторого времени
продолжали создавать автожиры без демпферов в вертикаль-
ных шарнирах. Образцом такой машины был автожир А-7, созданный
в 1937 г. Н. И. Камовым. Он успешно летал, не имея демпферов на
втулке несущего винта. Секрет успешных полетов заключался в том, что
это была первая машина с трехколесным шасси, обеспечивающим прак-
тически вертикальное расположение оси несущего винта при раскрутке
его перед взлетом и при остановке после посадки. Это обстоятельство
обусловило малые величины начальных возмущений вследствие откло-
нения лопастей в плоскости вращения, поскольку начальные отклонения
лопастей вызываются проекцией силы тяжести на плоскость вращения.
С другой стороны, имели также значение силы трения в шарнирах
(в то время в шарнирах ставились бронзовые втулки), которыми при
значительных центробежных силах нельзя пренебрегать — они да-
вали в этом случае достаточно большое демпфирование. Однако стоило
однажды летчику С. А. Корзинщикову после одного из полетов сразу
после посадки не отдать ручку от себя и тем самым не перевалить
машину из трехточечного положения (костыль и основное шассн) в стоя-
ночное (с опорой на переднюю ногу), как при последующем падении
оборотов ротора из-за большого начального возмущения в отклонениях
лопастей в плоскости вращения (ось вращения ротора была наклонена
к земле под углом 14°) возник земной резонанс-—лопасти поломались
и повредили вертолет.
Так от одного опытного образца к другому проявлялись все новые
аспекты этой проблемы.
Поскольку точного расчета необходимого демпфирования колебаний
лопастей (а при колебаниях земного резонанса равное значение имеет
И
и демпфирование колебаний аппарата, осуществляемое амортизацией
шасси) в то время не существовало, конструкторы стремились выбрать
минимальное значение момента трения демпфера на втулке. Это дикто-
валось стремлением уменьшить переменные изгибающие моменты, воз-
никавшие при наличии демпфера при вынужденных колебаниях лопа-
стей в полете.
При демпферах трения, как известно, возникают колебания с поро-
гом возбуждения. Если возбуждение мало — возбуждающий момент
меньше момента трения — колебания вообще не проявляются. И вот на
благополучном в отношении земного резонанса вертолете, уже находив-
шемся в эксплуатации, вдруг возникают колебания. Это объясняется
тем, что в данном частном случае начальные возмущения оказались
больше обычных. Этот случай произошел на вертолете Ми-1, когда он
переруливал наискосок через глубокие колеи от автомобиля. При этом
случайное возмущение крена сильно раскачало машину на пневмати-
ках и она приобрела столь большие амплитуды колебаний, что имею-
щегося демпфирования во втулке оказалось недостаточно и возник зем-
ной резонанс. Летчик Г. А. Тиняков тогда справился с ним очень просто,
ок взлетел и колебания прекратились, так как нарушилась упругая
связь — связь с землей.
Этот случай натолкнул на необходимость применения вязкого тре-
ния, т. е. гидравлических демпферов колебаний лопастей во втулке,
у которых момент трения не остается постоянным, а растет с амплитудой
колебаний.
Однако и в дальнейшем практика постоянно требовала совершен-
ствования и развития теории в этой области. Достаточно вспомнить
хотя бы возникновение земного резонанса, когда вертолет работает на
привязи.
Несколько случаев земного резонанса произошло также в момент,
когда вертолет при рулении во время взлета или посадки лишь слабо
касался земли колесами, когда сила тяги несущего винта становится
близкой к весу аппарата и амортизационные стойки с обычной предва-
рительной затяжкой оказывались полностью выпущенными. Разница
между весом и силой тяги аппарата воспринималась только пневмати-
ками колес.
Ясно, что при этом не только меняются частоты колебаний маши-
ны, но и отсутствует демпфирование стоек. Тут-то и возникал земной
резонанс, который на вертолете, не привязанном или не рулившем с
очень малой нагрузкой на колеса, никогда не проявлялся.
Чтобы избежать таких случаев стали применять так называемые
двухкамерные стойки шасси — амортизационные стойки, имевшие вто-
рую камеру низкого давления, поглощавшую энергию колебаний аппа-
рата, когда он касался земли лишь слегка обжатыми пневматиками
и основные стойки не работали.
Особое значение вопросы теории земного резонанса приобретают
на двухвинтовых схемах, когда упругая система, связывающая оба
винта, будь то фюзеляж при продольной или крыло при поперечной
схеме, имеет низкие частоты собственных колебаний. При таких колеба-
ниях могут возникать значительные перемещения втулки несущего
винта, создающие возможность энергообмена между колебаниями лопа-
стей и колебаниями несущей конструкции. Колебания такого типа воз-
можны не только на земле, но и в полете.
Подобная же проблема возникает при конструировании хвостовых
винтов с вертикальными шарнирами, расположенных на упругой хво-
стовой балке.
Создание гармоничной и совершенной машины возможно только
в том случае, когда конструктор достаточно компетентен не только
12
в общих вопросах проектирования, но и в специальных вопросах, связан-
ных с теорией и расчетом отдельных ее элементов.
На современном вертолете имеется большое число ответственных
высоконагруженных механических агрегатов, надежность и ресурс кото-
рых во многом зависят от работоспособности их подшипниковых узлов.
Поэтому конструкторы вертолетов должны быть знакомы с теорией
и расчетом подшипников качения. Это особенно относится к случаям
работы подшипников качения в сложных комбинациях внешних нагру-
зок и при качательном движении с малыми амплитудами.
Поэтому в книгу включена глава, в которой можно найти ответ на
вопросы теории и расчета подшипниковых узлов втулок, автоматов
перекоса и других агрегатов. Одним из наиболее интересных описанных
в гл. 4 вопросов является теория специальных упорных роликоподшип-
ников, в которых благодаря расположению роликов под углом к ра-
диальному направлению сепаратор при качательном движении не только
колеблется вместе с подвижным кольцом, но и непрерывно вращается
в одном направлении. Это предотвращает местный износ дорожек каче-
ния и повышает долговечность подшипника.
Следует отметить, что применение таких подшипников в осевых шар-
нирах втулок несущих винтов обеспечило значительное увеличение их
ресурса.
Вертолетостроение требует высокого общего уровня теоретической
и научной подготовки инженера-конструктора, так как динамические
проблемы для вертолетов (летательных аппаратов с вращающимися
крыльями) имеют намного большее значение, чем для самолетов (аппа-
ратов, имеющих стационарные, хотя теперь уже и поворачивающиеся
и отклоняющиеся назад крылья). Это подтверждается и тем фактом, что
те немногие конструкторы, которым удалось внести значительный вклад
в развитие вертолетостроения, и, даже больше, те, кто имел практиче-
ский успех, являлись одновременно и крупными учеными теоретиками.
Таковы академик Б. Н. Юрьев, профессор А. М. Черемухин и профес-
сор И. П. Братухин — создатели первых советских вертолетов-геликоп-
теров тридцатых годов от 1ЭА до 11ЭА; профессор Фокке — конструк-
тор вертолетов FW-61 и FA-223 в Германии, один из пионеров авиации
Луи Бреге и профессор Доран, создавшие первые французские верто-
леты, ^другие.
Надо отметить, что и в настоящее время теоретическая подготовка
конструкторов, работающих в ведущих фирмах мира в области верто-
летостроения, насколько можно судить по литературе, очень высока.
Поэтому не только инженеру-расчетчику, но и конструктору, работаю-
щему в вертолетостроении не следует боятся трудностей в освоении
изложенного ниже материала.
Авторы надеются, что и эта вторая книга данного труда найдет себе
читателей и будет полезна.
*
На вкладках представлены фотографии основных советских вер-
толетов, находящихся в серийном производстве. Это первые советские
серийные вертолеты с поршневыми двигателями Ми-1 и Ми-4, создан-
ные в 1949 и 1952 годах. Построенные в больших количества каждый,
они являются сейчас одними из наиболее распространенных типов вер-
толетов.
13
Далее показан вертолет Ми-6 с двумя турбовинтовыми двигателя-
ми, созданный в 1957 году, и вертолет Ми-10 (1962 г.) —летающий кран
с высоким шасси, приспособленный для перевозки крупногабаритных
грузов, жестко закрепленных под фюзеляжем. На нем в 1965 году был
установлен мировой рекорд грузоподъемности для вертолетов, 25 тонн
были подняты на высоту в 2830 м.
Затем показаны вертолеты Ми-2 и Ми-8, являющиеся вторым по-
колением советских легких и средних вертолетов. На них были сохра-
нены несущие системы от Ми-1 и Ми-4, но вместо одного поршневого»
установлено по два турбовинтовых двигателя.
ГЛАВА 1
УПРУГИЕ КОЛЕБАНИЯ И ПРОЧНОСТЬ ЛОПАСТИ
Расчет упругих колебаний является обязательным элементом про-
цесса создания новых конструкций лопастей. Он входит как неотъем-
лемая часть в расчет лопасти на прочность.
Для создания лопастей вертолета приходится решать много порой
весьма сложных технологических и конструктивных вопросов. При их
решении следует учитывать самые различные требования и прежде всего
требование обеспечения высокой усталостной прочности конструкции.
Работа по созданию лопастей включает в себя обычно следующие
основные этапы:
— Выбор материалов для отдельных элементов конструкции, опре-
деление оптимальных параметров и проектирование лопасти.
— Выбор лучших технологических процессов, обеспечивающих наи-
более высокую усталостную прочность ее основных силовых элементов,
и изготовление лопасти.
— Летные испытания с измерением действующих в полете на-
пряжений.
— Динамические испытания и оценка ресурса лопасти.
— Проведение комплекса доводочных работ, включающего работы
по снижению действующих напряжений и увеличению усталостной проч-
ности конструкции.
— Завершающие испытания и запуск конструкции в серийное
производство.
— Анализ работы серийных лопастей в различных условиях массо-
вой и длительной эксплуатации и проведение доработок конструкции
в серии по результатам этого анализа.
Расчеты упругих колебаний лопасти приходится выполнять на мно-
гих этапах этой работы, но больше всего на самом начальном этапе,
заканчивающимся проектированием лопасти.
При выборе параметров лопасти и материалов для ее изготовления
одним из основных критериев является величина действующих в полете
переменных напряжений и соотношение между этими напряжениями и
напряжениями, характеризующими усталостную прочность конструкции.
Узнать величину этих напряжений и дать оценку конструкции по ее
прочности на этом этапе можно только при помощи расчета. При этом
для проектирования лопасти в требуемые, обычно весьма сжатые, сроки
в распоряжении конструктора должны быть совершенные методы и сред-
ства выполнения расчета, позволяющие дать быстрый ответ на любой
из возникших вопросов.
Не меньшее значение имеет расчет и при доводочных работах. Как
правило, во вновь созданных лопастях оказываются слишком большие
переменные напряжения и перед конструктором возникает задача их
снижения. Для этого вначале необходимо подтвердить расчетом законо-
15
мерность возникновения измеренных в полете напряжений, а затем
найти возможность путем изменения тех или иных параметров лопасти
уменьшить их величину. Найти решение этой задачи без расчета, как
правило, значит потерять очень много времени на проверку неверных
предложений и затратить немало средств на изготовление лопастей,
которые в дальнейшем после летной проверки будут забракованы.
Снижение переменных напряжений имеет чрезвычайно важное зна-
чение и позволяет не только увеличить надежность и ресурс лопасти, но
и улучшить летно-технические характеристики вертолета такие, напри-
мер, как скорость полета и грузоподъемность, так как у современных
вертолетов они часто ограничены по условиям прочности.
Решение всех этих вопросов не вызывало бы значительных трудно-
стей, если бы расчет давал результаты, достаточно точно совпадающие
с тем, что наблюдается в действительности при измерении напряжений
в полете. К сожалению, это не совсем так, не во всех случаях расчет дает
удовлетворительные для практики результаты
Наиболее надежными оказываются расчеты по определению частот
собственных колебаний. В них достигается точность обычно порядка
±2%. Поэтому все расчеты, связанные с исключением резонансов,
обеспечивают очень высокую надежность. Заметно меньшую надежность
дают расчеты переменных напряжений на крейсерских и максимальных
скоростях полета. Получаемые при этих расчетах напряжения обычно
оказываются на 15—25% меньше напряжений, измеренных в полете.
Поэтому расчет напряжений на этих режимах не всегда удовлетворяет
конструктора. Но надо сказать, что эта погрешность может быть до не-
которой степени компенсирована, если в расчет вводить поправку, учи-
тывающую постоянно наблюдающееся расхождение с экспериментом.
Еще большая погрешность возможна при расчете переменных на-
пряжений на малых скоростях полета.
Из сказанного очевидно, что методика расчета переменных напря-
жений в лопасти требует еще дальнейшей разработки. Тем не менее
практика показывает, что.выбор параметров и доводка лопастей без
использования даже таких еше не совсем совершенных методов расчета
оказывается весьма неэффективной. Поэтому в этой главе приводится
достаточно подробное изложение различных методов расчета. Это, как
нам кажется, позволит дать читателю представление о всех особенно-
стях нагружения лопасти в полете, показать возможные пути подхода
к ее расчету, выявить и оценить преимущества и недостатки различных
методов и, наконец, дать инженерам, занимающимся этим вопросом,
основу для дальнейшего углубления исследований и совершенствования
методов расчета.
Наряду с описанием различных методов расчета упругих колебаний
лопасти, которым уделяется основное внимание, в этой главе изла-
гаются также основные принципы, на которых основаны расчеты лопасти
на прочность и определение ее ресурса (§ 11).
Что касается конкретных данных по выбору параметров лопасти,
то нам представляется целесообразным отнести этот вопрос к разделу
«Проектирование лопасти», который будет включен в третью книгу.
§ 1. ЗАДАЧИ РАСЧЕТА, ОСНОВНЫЕ ДОПУЩЕНИЯ И ВЫВОД
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ИЗГИБНЫХ ДЕФОРМАЦИЙ
ЛОПАСТИ
1. Конечная цель расчета упругих колебаний лопасти
Расчет упругих колебаний лопасти оказывается необходимым для
решения ряда задач, возникающих при проектировании и доводке вер-
толета. Наиболее важная из них — задача определения переменных
16
Б
I ч|д,- iwoidag

BqHo.K'i Ми 4

изгибных напряжений в лопасти. Определение этих напряжений
является основной частью расчета на прочность. Поэтому главной за-
дачей настоящей главы является определение упругих колебаний лопа-
сти для расчета ее прочности.
Определение колебаний лопасти оказывается необходимым и для
решения многих других задач. Без расчета этих колебаний невозможно
найти нагрузки, приходящие на вертолет, его втулку, систему управле-
ния и на трансмиссию привода несущего винта. Определение перемен-
ных нагрузок, приходящих от лопастей несущего винта на вертолет
в значительной мере решает задачу определения вибраций вертолета.
Интерес представляет также вопрос о влиянии колебаний лопасти
на летные характеристики вертолета. Ограничения, накладываемые на
летные характеристики срывом потока с лопастей несущего винта, опре-
деляются прежде всегда допустимой амплитудой колебаний лопасти.
С ростом этих амплитуд увеличиваются переменные усилия в системе
управления и вибрации вертолета. Поэтому расчет упругих колебаний
лопастей позволяет наиболее точно оценить границы допустимых по
условиям срыва режимов полета вертолета.
В известной степени колебания лопасти, и прежде всего ее крутиль-
ные колебания, сказываются на аэродинамических характеристиках
несущего винта н при удалении от режимов со срывом потока.
Остановимся более подробно на первой из поставленных здесь задач.
2. Расчет лопасти на прочность
Расчет лопасти на прочность включает определение постоянных
и переменных напряжений во всех точках конструкции лопасти в раз-
личных условиях нагружения. Наиболее опасные из них выделяются
как случаи, расчетные для прочности конструкции.
Обычно при создании новых лопастей, когда время, отведенное на
выполнение расчетов и их анализ, очень сильно ограничено, число рас-
четных случаев желательно свести к минимуму. Опыт показывает, чтс
достаточно просмотреть один случай нагружения лопастей в условиях
работы вертолета на земле и ряд полетных случаев на различных режи-
мах полета.
Первый случай предусматривает необходимость расчета лопасти,
опертой на вертикальный ограничитель втулки, когда действие центро-
бежных сил прекратилось или почти прекратилось. Это бывает тогда,
когда несущий винт не вращается или находится в начальной стадии
раскрутки, либо останавливается после полета. При отсутствии центро-
бежных сил силы веса или силы инерции, возникающие при ударе лопа-
сти об ограничитель, вызывают в ней значительные изгибные напряже-
ния. При этом особенно тяжелыми для прочности лопасти оказываются
напряжения сжатия. Опыты показывают, что отдельные перегрузки
лопасти, при которых возникают значительные сжимающие напряжения,
могут сказаться на усталостной прочности конструкции, а следова-
тельно, и на ее ресурсе. Обычно статические напряжения от изгиба
лопасти под действием ее собственного веса ограничиваются величи-
нами ffG = 25-r-28 кгс!мм2 для лопасти со стальным лонжероном и
gg = 7,0-4-7,5 кгс^мм'' для лопасти с лонжероном из дуралюмина.
С точки зрения расчета этот случай не представляет никаких труд-
ностей. Поэтому мы здесь не будем на нем подробно останавливаться.
Другие случаи относятся к различным режимам полета вертолета,
когда к постоянно действующим напряжениям от центробежных сил
добавляются постоянные и переменные напряжения от изгиба лопасти.
Это сочетание нагрузок оказывается очень тяжелым для усталостной
прочности конструкции лопасти.
2 1578
17
3. Режимы полета, опасные для усталостной прочности конструкции
Измерения напряжений в полете показывают, что лопасти вертолета
испытывают значительные переменные нагрузки, опасные для прочности
конструкции, на режимах двух различных типов.
К первому типу режимов относятся режимы полета на малых ско-
ростях, когда скорость полета составляет 3—8% от концевой скорости
лопасти ((л = 0,034-0,08). На этих режимах полета наблюдается резкое
возрастание амплитуд изгибных колебаний лопастей, соответственно
увеличиваются и переменные напряжения.
Указанный диапазон скоростей полета вертолет использует при
разгоне, горизонтальном полете с установившейся малой скоростью и
на режиме торможения. Обычно наибольшие переменные напряжения
возникают на режиме торможения. Значительные по величине напряже-
ния могут возникнуть также и на режиме крутого снижения с малой
горизонтальной скоростью.
По условиям нагружения конструкции полеты на малых скоростях
являются, как правило, кратковременными режимами полета, во всяком
случае для вертолетов, выполняющих транспортные работы. Однако
из-за больших напряжений часто именно эти режимы и определяют
ресурс лопасти по условиям выносливости.
Ко второму типу опасных для усталостной прочности режимов
относятся полеты на больших скоростях. Это прежде всего полеты на
крейсерской и максимальной скоростях. Полет на крейсерской скорости
является обычно наиболее продолжительным режимом полета и поэтому
вносит в конструкцию значительную усталостную повреждаемость.
Резкое увеличение переменных напряжений на малых скоростях
объясняется прежде всего значительной неравномерностью поля индук-
тивных скоростей, возникающего на этих режимах в потоке, протекаю-
щем через несущий винт. К тому же и по своей абсолютной величине
индуктивные скорости на этих режимах достигают наибольших значений
по сравнению со всеми другими режимами полета. Поэтому их влияние
на величину напряжений на малых скоростях полета существенно воз-
растает. Переменное поле индуктивных скоростей приводит к возник-
новению переменных аэродинамических нагрузок на лопасть. Под дей-
ствием этих нагрузок лопасть совершает изгибные колебания, отчего
в ней и появляются значительные переменные напряжения.
На больших скоростях полета переменные аэродинамические на-
грузки возникают главным образом вследствие пульсации относитель-
ной скорости потока и изменения углов атаки сечений лопасти по ази-
муту несущего винта. Переменное поле индуктивных скоростей на этих
режимах слабо сказывается на величинах аэродинамической нагрузки.
При расчете на прочность иногда оказывается также необходимым
рассмотреть случай возможной в полете раскрутки несущего винта,
когда значительно возрастают центробежные силы. При этом увеличи-
вается постоянная часть действующих в лопасти напряжений.
4. Допущение о равномерном поле индуктивных скоростей
Из того, что было сказано выше, ясно, что расчет переменных аэро-
динамических нагрузок на малых скоростях невозможен без учета
переменного поля индуктивных скоростей.
С увеличением скорости полета абсолютная величина индуктивных
скоростей падает. Уменьшается и влияние их неравномерности на вели-
чины аэродинамических нагрузок. Поэтому, начиная со средних скоро-
стей полета, когда ц>0,2, при расчете переменных напряжений в лопа-
сти можно приближенно полагать, что поле индуктивных скоростей рав-
номерное, т. е., что индуктивные скорости постоянны по диску несущего
18
винта. Это допущение приводит к очень серьезным упрощениям всех
выкладок и резкому сокращению продолжительности расчета. Поэтому
оно широко применяется в практических расчетах.
Однако точность получаемых с учетом этого допущения результатов
часто не удовлетворяет конструктора. Поэтому во многих случаях при
расчете режимов полета со средней и большой скоростью от этого допу-
щения приходится отказываться.
5. Допущения, используемые при расчете аэродинамических нагрузок
на профиль лопасти
Во всех методах расчета, изложенных в этой главе, предполагается,
что аэродинамические силы, действующие на профиль лопасти, можно
определить, используя аэродинамические коэффициенты, относящиеся
к стационарному обтеканию бесконечно длинного крыла в плоско-
параллельном потоке. Нестационарность обтекания учитывается только
в значениях углов атаки профиля, в которые вводится индуктивный скос
потока.
Следовательно, для определения сил, действующих на элемент
профиля, достаточно определить его угол атаки а и относительную ско-
рость обтекающего его потока U. Тогда, зная а и число М= — (здесь
азв— скорость звука), по поляре профиля можно определить коэффи-
циенты Су и сх, а следовательно, и силы, действующие на профиль.
В случае необходимости определяется также и коэффициент mz.
Если на рассматриваемом режиме полета угол атаки профиля не
превышает а~9°, а число М не более М~0,5, то его влиянием можно
пренебречь и полагать, что
0-1)
где е“ — тангенс угла наклона зависимости cy—f(a).
Это допущение используется при расчете нагрузок на режимах,
достаточно удаленных от срыва, на которых, кроме того, можно прене-
бречь явлениями, связанными со сжимаемостью потока.
Возможность применения тех или иных допущений в отношении
способа определения аэродинамических сил имеет решающее значение
при выборе метода расчета напряжений, который в рассматриваемом
случае должен быть использован. Вследствие этого на разных режимах
полета наиболее целесообразным оказывается применение различных
методов расчета. Поэтому в дальнейшем мы выделим три типа режимов,
отличающихся тем, что на каждом из них наилучшие результаты могут
быть получены различными методами расчета. Это режимы малых, сред-
них и больших скоростей.
На режимах малых скоростей нельзя не учитывать переменное поле
индуктивных скоростей, но при умеренных нагрузках на лопасть можно
пользоваться линейной аэродинамикой. На средних скоростях полета
учет переменного поля индуктивных скоростей оказывается необходи-
мым только при решении специальных задач, связанных с необходи-
мостью выделения отдельных высоких гармоник аэродинамических
нагрузок. Учет нелинейных зависимостей при определении аэродинами-
ческих коэффициентов на этих скоростях оказывается почти всегда из-
лишним. И, наконец, на режимах больших скоростей, лежащих вблизи
границы срыва, учет этих нелинейностей становится обязательным, в то
время как переменность поля индуктивных скоростей в большей части
случаев может не учитываться.
2* 19
Перечисленные соображения приводят к тому, что отдельные мето-
ды расчета могут привязываться к определенным режимам полета.
6. О связи деформаций при изгибе в двух взаимно перпендикулярных
направлениях и принимаемых в связи с этим допущениях в расчетах
Обычно лопасть вертолета проектируется таким образом, что глав-
ные упругие моменты инерции ее сечений оказываются существенно раз-
личными по величине. Поэтому лопасть представляет собой растянутый
центробежными силами стержень, каждый участок которого обладает
различными жесткостями в двух взаимно перпендикулярных направле-
ниях. Чтобы характеризовать эти направления через ось стержня по
направлению главных осей сечения проводятся плоскости, именуемые
плоскостями наибольшей и наименьшей жесткости (рис. 1.1).
Часто для создания аэродинамической крутки лопасти закручи-
внешнюю поверхность, но и
лонжерон лопасти. В этом
случае направления глав-
ных упругих осей сечения
изменяются по длине лопа-
сти, и она становится гео-
метрически закрученным
стержнем. В других случаях
аэродинамическая крутка
выполняется только за счет
поворота каркаса лопасти
относительно лонжерона.
В полете на профиль
лопасти действуют внешние
силы в самых различных
направлениях. Это делает
задачу об изгибе лопасти
очень сложной пространст-
венной задачей.
Вместе с тем величина геометрической крутки у лопастей вертоле-
тов не очень велика (порядка 6—12°) и значительно меньше, чем может
быть у самолетных пропеллеров и лопаток компрессоров и турбин. Как
показывают различные оценки, влияние этой крутки на результаты ра-
счетов невелико. Поэтому во всех приведенных здесь методах расчета
мы пренебрегаем закрученностью упругих осей лонжерона лопасти
и считаем, что направление плоскости наибольшей и наименьшей жест-
кости лопасти постоянно по ее длине.
вается не только каркас,
Плоскость
хорд-к
Д<р
Плоскость
Вращения-
Плоскость наиВольшей
жесткости
Плоскость наименьшей
жесткости
/ \'- Плоскость
/ Взмаха
Рис. 1. 1. Схема расположения лонжерона
в случае, когда геометрическая крутка осуще-
ствляется при помощи поворота каркаса отно-
сительно лонжерона (<рл=const)
ее

Это предположение позволяет спроектировать все внешние силы на
эти плоскости и решать две упруго несвязанные плоские задачи об из-
гибе лопасти в двух взаимно перпедикулярных направлениях. По окон-
чании расчета для определения напряжений в различных точках сечения
лопасти результаты этих двух расчетов можно просуммировать.
Профиль сечения лопасти позволяет увеличить габариты лонжерона
в плоскости хорд и ограничивает их в перпендикулярном направлении.
Поэтому плоскость наибольшей жесткости обычно близка к плоскости,
проходящей через хорду лопасти. Это обстоятельство, а также то, что
в плоскости хорд величина аэродинамических сил обычно меньше, чем
в плоскости ей перпендикулярной, приводит к тому, что величина изгиб-
ных напряжений обычно больше при изгибе в плоскости наименьшей
жесткости и меньше в плоскости наибольшей жесткости. Если рассмат-
ривать современные конструкции лопастей, у которых усталостная
прочность примерно одинакова при изгибе во всех направлениях, то
окажется, что значительно более опасным является изгиб в плоскости
20
наименьшей жесткости. На практике обычно все трудности возникают
в связи с необходимостью обеспечения прочности при изгибе в этой
плоскости. Поэтому в данной главе будут рассмотрены методы расчета
колебаний лопасти только в плоскости наименьшей жесткости. При
расчете в этой плоскости можно применить дополнительное допущение
о том, что плоскость наименьшей жесткости совпадает с плоскостью,
проходящей через ось несущего винта. Эту плоскость мы в дальнейшем
будем называть плоскостью взмаха.
7. Об учете крутильных деформаций лопасти
при расчете изгибных колебаний
Крутильные деформации изменяют углы атаки сечений лопасти,
а следовательно, и действующие на них аэродинамические силы. По-
этому они должны учитываться при расчете аэродинамических нагрузок
и колебаний лопасти. Однако учет крутильных колебаний лопасти пред-
ставляет значительные трудности и сильно усложняет расчет.
В то же время в целом ряде случаев он не приводит к существен-
ным уточнениям результатов. Поэтому учет крутильных деформаций
должен производиться только тогда, когда в этом появляется настоя-
тельная необходимость. Например, в тех случаях, когда изгибпые коле-
бания лопасти усиливаются близостью к изгибному флаттеру, хотя та-
кое положение говорит о недостаточном запасе до флаттера и не может
считаться допустимым.
Для учета крутильных деформаций приходится решать систему
дифференциальных уравнений изгибно-крутильных колебаний лопасти.
Решение этой же системы выполняется и при расчете флаттера. Поэтому
такой метод расчета, названный общим методом расчета флаттера
и изгибных напряжений в лопасти, отнесен в первую книгу (см. § 7 гл. 4).
В этой главе будут изложены только методы расчета свободных
крутильных (§ 5) и изгибно-крутильных колебаний (§ 6).
8. Два этапа расчетов при проектировании лопасти:
расчет частот собственных колебаний и расчет напряжений
Если вновь создаваемая лопасть вертолета не очень сильно отли-
чается по своим геометрическим и массовым характеристикам от уже
изготовленной и проверенной лопасти, то можно утверждать, что на оди-
наковых режимах полета, действующие в ней переменные напряжения
будут примерно такими же, как и в лопасти, являющейся ее прототипом.
Однако это положение нарушается в тех случаях, когда вследствие
некоторого изменения ее параметров лопасть оказывается в резонансе
с какой-либо гармоникой внешних сил.
Практика проектирования лопастей показывает, что достаточно
надежные лопасти могут быть созданы только в том случае, если ни
одна из ее собственных частот не совпадает с частотами внешних сил
и находится от них на достаточном удалении. Это относится к колеба-
ниям лопасти как в плоскости наименьшей, так и в плоскости наиболь-
шей жесткости. Следует, конечно, оговориться, что опасными для проч-
ности являются не все гармоники внешних сил, а только те, величина
которых достаточна для создания существенных по величине напряже-
ний. Практически обычно отсутствие резонансов должно быть обеспе-
чено с гармониками не выше восьмой к оборотам несущего винта. Более
высокие гармоники внешних сил оказываются не существенными.
Таким образом, если не допущена грубая ошибка в выборе харак-
теристик лопасти, то для ограничения переменных напряжений в допу-
стимых пределах, оказывается достаточным только обеспечить отсут-
21

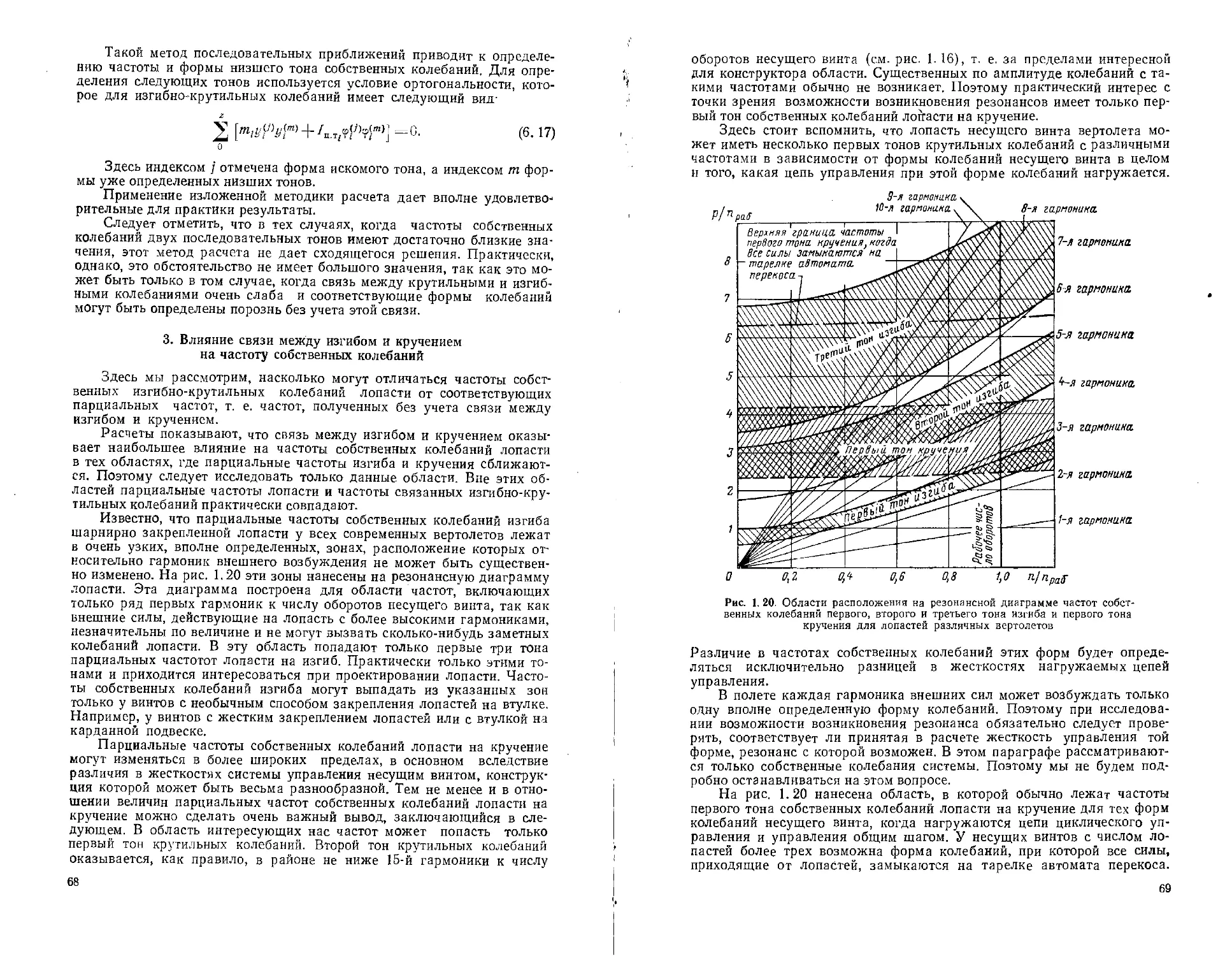
ствие резонансов. Производить расчет величин амплитуд переменных
напряжений в этом случае нет необходимости. Поэтому часто опытный
конструктор может ограничиться только первым этапом расчета лопасти:
определением ее частот собственных колебаний и построением резонанс-
ной диаграммы.
Из сказанного вытекает, что расчет частот и форм собственных
колебаний лопасти не является только вспомогательным этапом для
расчета напряжений, а имеет самостоятельное значение как предвари-
тельный этап расчета лопасти на прочность.
9. Идеализированные модели лопасти, применяемые в расчете
При выполнении расчета необходимо представить лопасть в виде
некоторой идеализированной механической модели, для которой были
бы справедливы все принятые исходные допущения с тем, чтобы в даль-
нейшем, в процессе вычислений, не было необходимости использования
приближенных математических операций.
При расчете на цифровых машинах задача должна быть постав-
лена таким образом, чтобы ее решение было возможно с любой задан-
ной наперед и доступной для машины точностью.
Как показал опыт, применение методов расчета, использующих
приближенные математические операции, очень часто приводит к раз-
личным недоразумениям. В ряде случаев только из-за неточности при
вычислениях может оказаться невозможным довести расчет до конца.
Так, например, при расчете форм собственных колебаний методом после-
довательных приближений приходится вычислять целый ряд интегралов.
Часто это делается методом трапеций. При ограниченном количестве
интервалов интегрирования этот метод дает настолько большую по-
грешность, что при расчете форм колебаний более высоких тонов, орди-
наты которых вычисляются в виде малых разностей больших величин,
метод последовательных приближений перестает сходиться.
Это обстоятельство требует особой осторожности при использовании
приближенных способов вычислений. Поэтому целесообразнее ввести
упрощеную идеализированную модель лопасти, которую было бы удобно
рассчитывать с максимально допустимой для машины точностью.
Известны три различных типа механических моделей, которые
часто используются в расчетах.
Балочная модель с непрерывно распределенными параметрами.
В этой модели лопасть представляется в виде балки с непрерывно рас-
пределенными жесткостями EI, погонной массой т и параметрами,
определяющими величину погонной аэродинамической нагрузки.
Такая модель очень удобна при составлении исходных дифферен-
циальных уравнений и применении к ним известных приближенных ме-
тодов решения, но оказывается малопригодной для завершающего чис-
ленного расчета. Ниже мы будем часто пользоваться такой моделью
для вывода расчетных формул с тем, чтобы на этапе численного расчета
использовать формулы, записанные по аналогии и относящиеся уже
к модели с дискретными параметрами. В этих формулах все интегралы
от функций, зависящих от радиуса лопасти, заменяются суммами дис-
кретных величин, относящихся к ряду фиксированных радиусов лопасти.
Балочная модель с сосредоточенными грузами. В этой модели лопасть
представляется в виде системы связанных между собой сосредоточенных
грузов. Связь между этими грузами осуществляется посредством неве-
сомых балочек, обладающих постоянной по длине жесткостью на изгиб,
равной жесткости соответствующих участков лопасти.
При определении аэродинамических сил предполагается, что к каж-
дому грузу прикреплено отдельное крылышко, площадь которого равна
22
площади соответствующего участка лопасти. Обычно предполагается,
что площадь
+ (1-2)
где и /;t, Н1 — длины смежных участков, на которые разбита ло-
пасть при расчете;
bt — хорда лопасти в сечении между этими участками.
Эта модель наиболее точно отражает свойства реальной лопасти.
Поэтому почти во всех случаях при практических расчетах будет исполь-
зована именно она.
Надо, однако, отметить, что этими положительными свойствами ба-
лочная модель обладает только при числе участков z, равном 25—30 и
больше. С уменьшением числа участков форма деформаций балочной
модели начинает очень сильно отличаться от формы деформаций ло-
пасти. Это обстоятельство более подробно будет проиллюстрировано
в § 10, п. 3. Кроме того, применение балочной модели приводит в ряде
случаев к весьма сложной системе формул и иногда даже затрудняет
выполнение расчета, В этих случаях может быть применена более про-
стая шарнирная модель лопасти.
Шарнирная модель лопасти. В этой модели лопасть представляется
в виде многошарпирной цепочки, состоящей из абсолютно жестких неве-
сомых звеньев с массами, сосредоточенными в шарнирах. Жесткость
лопасти на изгиб имитируется сосредоточенными в шарнирах упругими
элементами. Под действием внешних сил ось такой цепочки примет
форму ломаной линии, а не плавной, как в модели балочного типа. Это
обстоятельство так же, как и операция выбора жесткости упругих эле-
ментов, вносит определенную погрешность при переходе от лопасти
к механической модели.
В то же время применение шарнирной модели создает настолько
существенные упрощения в расчетных формулах, что иногда делает воз-
можным применение и более совершенных методов расчета, которые
были практически неосуществимы при использовании балочной модели.
Это компенсирует недостатки, свойственные этой модели.
Следует еще добавить, что с уменьшением числа участков, на кото-
рые разбивается лопасть в расчете, свойства моделей начинают очень
сильно отличаться от свойств реальной лопасти. Но у шарнирной моде-
ли эти погрешности возрастают не так быстро как у балочной. Вследст-
вие этого шарнирная модель может оказаться выгоднее при применении
грубых методов расчета, когда лопасть разбивается на малое число уча-
стков, скажем порядка 10—12.
10. Вывод дифференциального уравнения изгиба лопасти
в поле центробежных сил при колебаниях в плоскости взмаха
Лопасть представим в виде балки с непрерывно распределенными
параметрами. Выделим для рассмотрения элемент балки длиной dr.
Силы, действующие на этот элемент, показаны на рис. 1.2.
Составим уравнения равновесия этого элемента, ограничившись
величинами только первого порядка малости. Тогда сумма проекций
сил на ось у может быть записана как
Wdr+dQ = Q, (1.3)
и сумма моментов всех сил относительно точки А
Qdr+dM—Ndy = 0, (1-4)
где W—погонная внешняя нагрузка на лопасть;
Q — перерезывающая сила в сечении лопасти;
23
М — изгибающий момент;
N— центробежная сила в сечении лопасти.
Из уравнения (1.3) получим
F=— Q'. (1.5)
Здесь и ниже штрихом обозначается дифференцирование по радиусу
лопасти.
Продифференцировав уравнение (1.4), получим
Q' = —M" + [Ny']'.
(1.6)
Если положить М — Е1у" и подставить выражение (1. 6) в уравнение
(1.5), то получим известное дифференциальное уравнение изгибных
Рис. 1.2. Схема сил, действующих на эле-
мент лопасти
деформаций лопасти в поле
центробежных сил:
[EIy"\"-[Ny']' = W. (1.7)
Представим внешнюю на-
грузку W, состоящей из аэро-
динамической и инерционной
нагрузок:
W—T—my, (1.8)
где Т — погонная аэродинами-
ческая нагрузка;
иг —погонная масса ло-
пасти.
Двумя точками здесь обо-
значено дифференцирование
по времени.
Подставив выражение (1.8) в уравнение (1.7), получим дифферен-
циальное уравнение колебаний лопасти:
[EIy"]’’-[Ny']'+my=T. (1.9)
В пустоте, когда аэродинамическая нагрузка Т равна нулю, урав-
нение (1.9) будет описывать свободные колебания лопасти в поле цент-
робежных сил:
[£//]"-W]'+^=0. (1.Ю)
Решение этого уравнения представляет известные трудности. По-
этому в § 2 будет вначале рассмотрено его решение для случая N=0,
относящееся к невращающейся лопасти.
11. Дифференциальное уравнение изгиба лопасти
в плоскости вращения несущего винта
При изгибе лопасти в плоскости вращения из-за концентричности
поля центробежных сил на элемент лопасти будет действовать дополни-
тельная сила, которая не входила в уравнения в плоскости взмаха.
С учетом этого обстоятельства уравнение (1.8) должно быть перепи-
сано в форме;
W = Q 4- а>2тх—тх, (1. 11)
где Q — аэродинамическая сила в плоскости вращения;
к-—перемещения элементов лопасти в плоскости вращения.
24
Подставив (1.11) в уравнение, аналогичное (1.7), но записанное
для плоскости вращения, получим дифференциальное уравнение изгиба
лопасти в этой плоскости:
— (1.12)
Это уравнение отличается от уравнения (1.9) только дополнитель-
ным членом (f>2tnx.
§ 2. СВОБОДНЫЕ КОЛЕБАНИЯ ЛОПАСТИ
НЕВРАЩАЮЩЕГОСЯ ВИНТА
1. Метод расчета, приводящий к решению
интегрального уравнения колебаний лопасти
Расчет форм и частот собственных колебаний лопасти невращающе-
гося винта достаточно широко освещен в литературе (см. например [1]).
В этом параграфе будут лишь вкратце повторены некоторые основные
положения и несколько уточнены формулы, применяемые при практи-
ческих расчетах.
Рассмотрим дифференциальное уравнение колебаний, полученное
для модели лопасти с непрерывно распределенными параметрами. Если
в уравнении (1. 10) положить N = 0, то оно примет вид:
[E//]"+w=0- (2-D
Положив
Z/=//sin pt (2.2)
и подставив в (2. 1), получим
[ЕГу"]"-р^~у=0. (2.3)
При дальнейших выкладках мы черточку над у опустим. Проинтег-
рируем уравнение (2. 3) с учетом граничных условий закрепления лопа-
сти. Для простоты рассмотрим случай жестко заделанной в комле
лопасти с граничными условиями:
— при г=0; у = 0; у'=0;
— при г = Д; Л1 = 0; Q=0.
В результате четырехкратного интегрирования уравнение (2. 3) пре-
образуется в интегральное уравнение вида
д R
mydE. (2.4)
0 0 г г

Уравнение (2. 4) решается обычно методом последовательных при-
ближений. Задавшись произвольной формой у, нормированной каким-
либо образом, например
№=1, (2.5)
подставим ее в правую часть уравнения (2.4).
Выполнив интегрирование, получим функцию
г г R R
ИШЬ’"*'
0 0 г г
такую, что у — р2и.
(2-6)
25
Откуда, используя условие (2.5), получим
(2 7)
R
где uR — значение и при г=/?.
Повторим ту же операцию, приняв новое значение
у = р2и. (2.8)
Выполнив описанные выше операции несколько раз, можно убедить-
ся, что форма колебаний у и частота р сходится к определенным значе-
ниям, которые и являются решением интегрального уравнения (2.4).
Примененный таким образом метод последовательных приближе-
ний приводит к тому, что определяемая форма у сходится к форме низ-
шего тона собственных колебаний лопасти.
Для определения последующих тонов необходимо еще выполнить
условие отрогональности тонов собственных колебаний. Это условие бу-
дет рассмотрено в п. 3.
При практическом применении изложенного здесь метода расчета
очень важно выбрать достаточно точный способ для вычисления интег-
рального выражения (2.6). Если параметры лопасти заданы в виде
непрерывных функций, то наиболее простым способом вычисления
интегралов (2. 6) является обычно применяемый в таких случаях метод
трапеций. Однако, как уже указывалось выше, при вычислении более
высоких тонов колебаний вносимая этой операцией погрешность приво-
дит к столь существенным ошибкам, что такой способ не может быть
применен для практических целей. Этот недостаток пропадает, если для
вычисления интегралов (2. 6) применить способ, вытекающий из рас-
смотрения механической модели лопасти с дискретно распределенными
параметрами.
2. Расчет форм и частот собственных колебаний
модели лопасти с дискретно распределенными параметрами
Для расчета используем модель балочного типа с сосредоточенными
грузами (см. § 1 п. 9). Для этого разделим лопасть на z участков. Длины
отдельных участков могут быть различными. Вес лопасти сосредоточим
по краям этих участков в виде отдельных дискретных грузов с массой т,-
Изгибную жесткость лопасти представим ступенчатой кривой таким
образом, чтобы на протяжении каждого участка она оставалась постоян-
ной (рис. 1.3).
Так же, как в п. 1, рассмотрим вначале случай заделанной в комле
лопасти. Операция, определяемая уравнением (2.6), в этом случае мо-
жет быть выполнена абсолютно точно.
Действительно, зададимся произвольной формой перемещений гру-
зов модели Уг. Здесь формой перемещений мы называем систему
дискретных значений уг (г = 0, 1, 2, 3, . . . г—порядковый номер сосредо-
точенных грузов модели). Так же, как и выше (см. условие 2.5), поло-
жим г/2=1. Если перемещения у-; известны, то можно определить инер-
ционные силы грузов при их колебаниях с частотой р=\. Они опреде-
ляются по выражению
р1 = т(у{. (2.9)
Зная инерционные силы, можно определить все изгибающие мо-
менты по системе простых рекурентных формул вида:
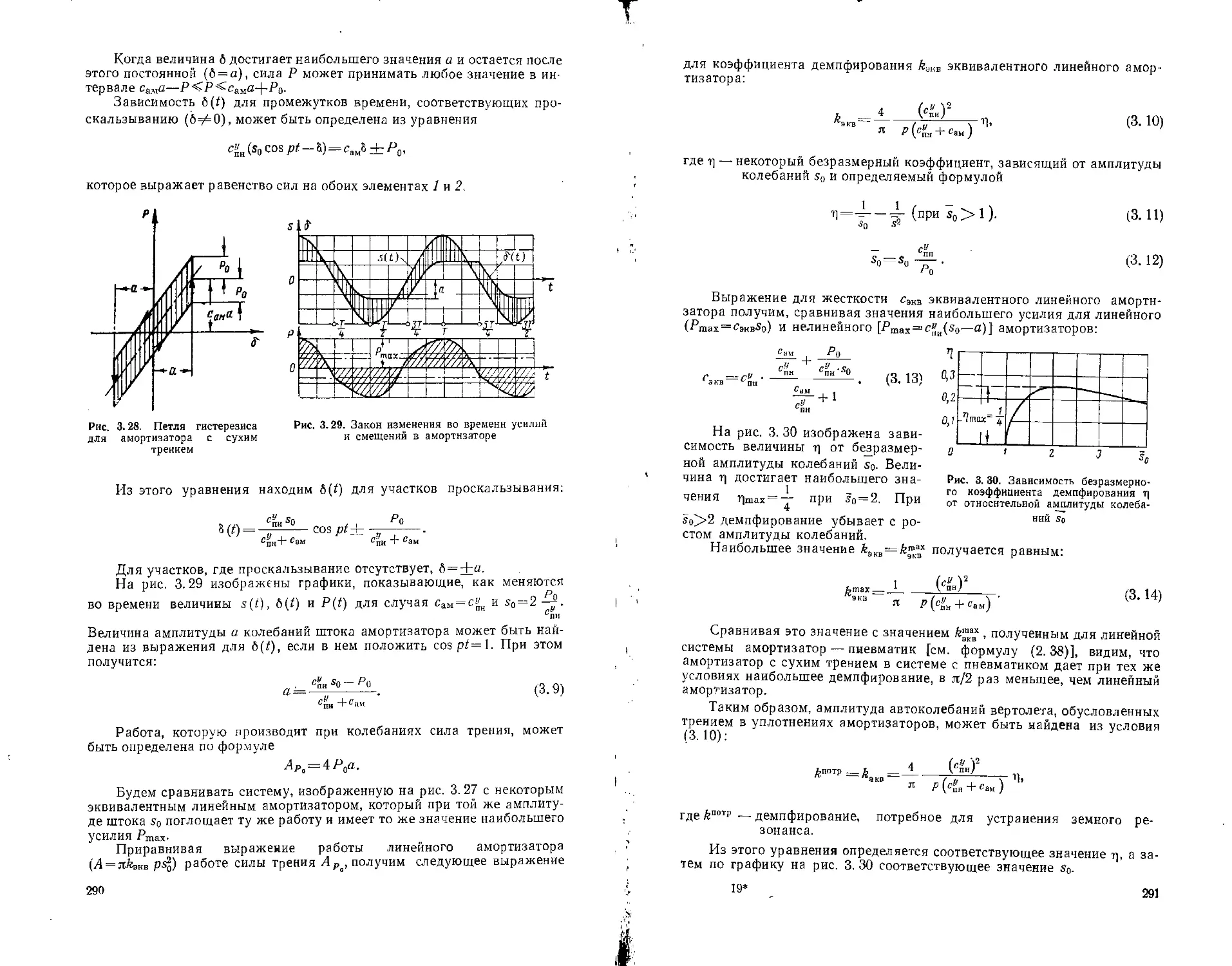
= —fri+iAlj+s], (2. 10)
где Ц, i+i — длина участка лопасти между Z-ой и г+1-ой сосредоточенной
массой.
26
Коэффициенты ai и bz определяются по формулам:
4,1+1
at~~ — bt_x bj.
Вычисление изгибающих моментов по формулам (2. 10) следует
начинать с конца лопасти, положив вначале i = z~*1, а изгибающие мо-
менты М, и Mz+t равными нулю.
После определения изгибающих моментов нетрудно определить
и деформации лопасти. Деформации лопасти при колебаниях с частотой
р=1 будем, как и выше, обозначать буквой и.
Величина этих деформаций определяется по рекурентным форму-
лам вида:
1, i bi_2Ui—2 (2.11)
где
—-d^^ 1+1. (2- 12)
Здесь:

6Е7,.>(. + 1 (2. 13)
Q = 2{dt^
Расчет деформации ил следует начинать с комля лопасти, положив
в соответствии с принятыми здесь граничными условиями и.о—0. Также
равными нулю следует положить все величины с отрицательными индек-
сами.
Таким образом, выполнение операций (2.10) и (2.11) примени-
тельно к балочной модели с дискретным распределением параметров
приводит к вычислению точных значений Ц;.
Определив р2 так же, как и раньше [см. (2.7)]:
/А--’- (2.14)
«г
и новые значения
t/i = p2Ui, (2. 15)
27
повторим все операции столько раз, сколько необходимо для того, чтобы
метод последовательных приближений сошелся. Обычно расчет счи-
тается оконченным, когда разность значений у, в двух последовательных
приближениях оказывается меньше заданной точности еу.
3. Условие ортогональности и вычисление последующих тонов
собственных колебаний
Метод последовательных приближений, изложенный выше, приво-
дит к определению низшего тона собственных колебаний. При опреде-
лении следующих тонов необходимо выполнить еще условия независи-
мости колебаний по различным тонам.
Представим, что свободные колебания лопасти в пустоте происхо-
дят одновременно по двум формам у и Энергию колебаний по
каждой из форм в отдельности можно определить по амплитудным значе-
ниям кинетической энергии*:
[т(П]2;
(2.16)
= [ртУ^У-
I
С другой стороны полную энергию системы, колеблющейся одно-
временно по двум формам, можно определить по амплитудному значе-
нию суммарной кинетической энергии:
I
Этой кинетической энергией система обладает в тот момент времени,
когда лопасть проходит при колебаниях через нейтральное положение
одновременно по двум формам и Из-за различия в значениях
частот собственных колебаний такое положение может возникнуть отно-
сительно редко, но легко может быть создано искусственно путем зада-
ния соответствующих фаз колебаний в начальный момент времени.
Если амплитуда по каждой из составляющих форм колебаний не
меняется с течением времени, то остается постоянной и их энергия,
определяемая по формулам (2. 16).
Полная энергия колебаний всегда должна равняться сумме энергий
составляющих движений, т. е.
К^К^Кт. (2.18)
Как следует из выражения (2. 17), это возможно только при усло-
вии, если
= (2.19)
i
Это условие называется условием ортогональности тонов собствен-
ных колебаний. Более строгий вывод этого условия будет дан в § 2 гл. 2.
При вычислении какого-либо /-го тона все предыдущие тона, кото-
рым соответствует индекс m = 0, 1, 2 /—1, должны быть уже вы-
числены.
* Здесь и дальше в значениях кинетической и потенциальной энергии колебаний
для простоты опущен постоянный коэффициент 1/а.
28
Для выполнения условия ортогональности при определении методом
последовательных приближений формы /-го тона представим искомую
форму как
m—j—l

(2.20)
где у <т> — уже определенные формы собственных колебаний.
Постоянные Ст определяются из условия ортогональности (2. 19)
по формулам:
2

(2.21)
Значение частоты /-го тона вычисляется по формуле:
(2. 22)
771 = 0
Зная р~, можно определить форму колебаний по выражению (2.20).
4. Особенности расчета частот и форм собственных колебаний
шарнирно заделанной лопасти
Все приведенные выше выкладки, относящиеся к жестко заделан-
ной лопасти, легко могут быть распространены и на лопасть с шарнир-
ной заделкой в комле.
Для этого случая интегральное уравнение (2.4) принимает сле-
дующий вид:
У = Р2
(2.23)
где постоянная Со определяется из условия равенства нулю суммы момен-
тов всех инерционных сил относительно шарнира. Для модели с дискрет-
ным распределением параметров это условие может быть записано так:

(2.24)
Нетрудно заметить, что это условие совпадает с условием ортого-
нальности к форме колебаний, которую мы будем условно называть
формой колебаний нулевого тона. Если эту форму нормировать в соот-
ветствии с условием (2. 5), то она может быть записана как
,(0)=C2L£o
' Я-го
(2.25)
Таким образом, при расчете шарнирно заделанной лопасти следует
считать, что форма ее нулевого тона заранее известна и задана форму-
лой (2. 25) и при вычислении всех последующих тонов, начиная с пер-
вого, выполнять условие ортогональности и к нулевому тону (2.24).
При этом определять функции Ui можно по тем же формулам, которые
приведены в п. 2.
Ln
5. Расчет форм и частот собственных колебаний
лопасти как свободной балки
В целом ряде случаев оказывается необходимым вычислять частоты
совместных колебаний лопасти и фюзеляжа вертолета. При этом втулка
несущего винта, являющаяся точкой закрепления лопасти, сама может
перемещаться вместе с фюзеляжем вертолета. Расчеты таких колебаний
очень легко выполнить, если использовать модель лопасти, представ-
ляющую собой свободную балку. Тогда при определении совместных
колебаний несущего винта и фюзеляжа достаточно вычислить приве-
денную к несущему винту массу фюзеляжа т0 (см. рис. 1.3) и произ-
вести расчет частот собственных колебаний лопасти.
Расчет лопасти как свободной балки может быть выполнен по фор-
мулам п. 2, только все формы собственных колебаний должны быть
дополнительно ортогонализированы к форме второго нулевого топа:
,у[°) = 1 = const, (2. 26)
что равносильно выполнению условия равенства нулю суммы всех инер-
ционных сил, действующих при колебаниях.
Эта же методика расчета с небольшими доработками может быть
использована и при расчетах форм и частот собственных колебаний
фюзеляжа, о чем будет сказано в гл. 2,
§ 3. ПРИБЛИЖЕННЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ЧАСТОТ
СОБСТВЕННЫХ КОЛЕБАНИЙ ЛОПАСТИ В ПОЛЕ
ЦЕНТРОБЕЖНЫХ СИЛ
1. Применение метода Б. Г. Галеркина для определения частот
собственных колебаний лопасти
Метод Б. Г. Галеркина очень широко применяется для решения
различных задач об упругих колебаниях лопасти.
Идея метода Б. Г. Галеркина и его применение к решению диффе-
ренциальных уравнений достаточно подробно изложена в литературе
(см. например, справочник «Машиностроение», т. 1, кн. первая, Маш-
гиз, 1947).
Здесь мы не будем повторять выводы, которые могут быть найдены
в других источниках, а проиллюстрируем применение этого метода на
ряде простых примеров.
В п. 10 § 1 этой главы было выведено дифференциальное уравнение
колебаний лопасти в поле центробежных сил. Если подставить в него у
в форме (2. 2), то это уравнение примет следующий вид (черточку над у
мы здесь отбросили):
[EIy"]"—[Ny']'—p2my = 0. (3. 1)
Предположим, что формы собственных колебаний лопасти в поле
центробежных сил не отличаются от соответствующих форм, подсчи-
танных для случая М=0. Тогда, считая, что формы колебаний у^ из-
вестны, подставим какую-либо одну форму в уравнение (3. 1), и,
умножив все члены уравнения на эту же форму г/<Л, проинтегрируем
полученные выражения по длине лопасти.
Полученное уравнение после некоторых преобразований может быть
представлено в форме:
R R R
f El + {m*dr-p^ mly^dr^Q. (3.2)
0 0 о
30
Входящие в это уравнение интегралы
£/[(<?)'W, (3.3)
о
Cv=jAr (3.4)
о
имеют вполне определенный физический смысл, а именно:
Cei — есть упругая потенциальная энергия, накапливаемая лопастью,
когда в процессе изгибных колебаний по форме /'-го тона она до-
стигает крайних отклонений от положения равновесия *;
С*- — есть потенциальная энергия, накопленная лопастью при ее из-
гибе в поле центробежных сил. Здесь так же, как и в выражении
(3.3), могут быть рассмотрены различные тона собственных
колебаний.
Полная потенциальная энергия, накопленная лопастью при ее из-
гибе в поле центробежных сил по формуле t/O) может быть записана как:
Cs = С£/ . (3.5)
При изгибных колебаниях, когда лопасть проходит через положение
равновесия, скорости перемещения ее точек достигают наибольших
величин:
y<i~> = pyth. (3.6)
При этом кинетическая энергия лопасти может быть определена
по формуле
R
К)=р2 ^m[yU^dr. (3.7)
о
В процессе свободных колебаний потенциальная энергия, накоплен-
ная лопастью при ее изгибе по форме у^\ превращается в кинетическую
энергию, когда лопасть проходит положение равновесия. Равенство
амплитудных значений потенциальной и кинетической энергии лопасти
и выражает уравнение (3.2).
Из уравнения (3. 2) можно определить частоту /-го топа собствен-
ных колебаний лопасти в поле центробежных сил. Эта частота опреде-
ляется по формуле
= + (3-8)
где р0^ — частота собственных колебаний лопасти без учета центро-
бежных сил;
Kj — коэффициент, учитывающий влияние центробежных сил.
Здесь:
R
J El[(yj)"Vdr
;----: М
о
У?
-----------• (3.10)
J т [у]\2<1г
о
* Это справедливо с точностью до постоянного множителя, равного 1/а, который
в выражениях (3.3), (3.4) и (3.7) опущен.
31
В выражении (3. 10) — есть центробежная сила в сечении ло-
пасти при (0=1.
Выражение (3.9) для частоты собственных колебаний без учета
центробежных сил может быть получено, если таким же образом при-
менить метод Б. Г. Галеркина к уравнению (2.3).
Полученные здесь выражения Для частот собственных колебаний
лопасти в поле центробежных сил являются приближенными. Однако
расчеты показывают, что в целом ряде случаев эти выражения дают
вполне удовлетворительную для практических целей точность. Более
подробная оценка точности результатов этих расчетов будет дана в § 4.
2. Резонансная диаграмма колебаний лопасти
Выше уже отмечалось, что в процессе проектирования лопасти при-
ходится проводить расчеты с целью исключения возможных резонансов
частот собственных колебаний лопасти с теми гармониками внешних
сил, которые могут вызвать значительные по величине переменные на-
пряжения. Как уже говорилось, гармонические составляющие аэродина-
мических сил, действующие на лопасть в полете, имеют существенную
величину до гармоник не выше восьмой. Более высокие гармоники аэро-
динамических сил настолько малы по величине, что могут не прини-
маться во внимание.
Частоты вынужденных колебаний, которых следует опасаться при
расчете лопасти, могут быть определены по формуле
V = B(», (3.11)
где п= 1, 2, 3, . . . , 8.
Уравнение (3. 8) позволяет построить зависимость частот собствен-
ных колебаний различных тонов от угловой скорости вращения несу-
щего винта. Построенные совместно на одном графике зависимости
(3.8) и (3.11) называются обычно резонансной диаграммой лопасти.
На рис. 1.4 и 1.5 приведены резонансные диаграммы, построенные для
лопастей с различными, встречающимися на практике, параметрами.
Эти диаграммы построены в относительных величинах. И частоты соб-
ственных колебаний р и числа оборотов несущего винта отнесены к опре-
деленному рабочему значению числа оборотов праб.
Резонансная диаграмма позволяет в. наглядной форме проследить,
в каком направлении следует изменять параметры лопасти для того,
чтобы исключить резонансы во всем диапазоне рабочих чисел оборотов
несущего винта.
3. Выбор параметров лопасти для исключения резонансов
при колебаниях в плоскости взмаха
Если просмотреть резонансные диаграммы, построенные для самых
различных пр конструкции лопастей, то оказывается, что они не сильно
различаются между собой. Причем это различие чаще всего объясняется
разницей в жесткостях лопасти на изгиб. Реже, и в меньшей степени,
оно вызывается отклонениями в массовых характеристиках лопасти. Это
обстоятельство объясняется очень просто. Дело в том, что при проекти-
ровании конструктор должен руководствоваться множеством различных
требований, ограничивающих возможности варьирования параметров
лопасти и приводящих в конечном итоге к созданию очень близких по
своим характеристикам лопастей.
Широкому изменению параметров лопасти препятствуют, главным
образом, следующие условия:
1. Высота лонжерона ограничена профилем лопасти и не может
быть существенно увеличена, так как с ростом относительной толщины
32
профиля ухудшается аэродинамическое качество винта. Это обстоятель-
ство ограничивает величину жесткости лопасти на изгиб сверху.
2. Прогиб лопасти под действием собственного веса нс должен быть
очень большим, так как это вызывает затруднения при компоновке вер-
толета. Изгибные напряжения в лонжероне, возникающие от собствен-
ного веса, также не должны превышать известных величин, выбираемых
из условий прочности с учетом возможных динамических перегрузок.
Эти соображения ограничивают возможности снижения жесткости
лопасти.
Рис. 1.4. Резонансные диаграммы различных типов лопастей
в плоскости взмаха
3. Вес лопасти оказывается заключенным в еще более тесных гра-
ницах. Стремление к увеличению весовой отдачи вертолета заставляет
конструктора максимально снижать вес лопасти. Но это приводит
к росту переменных напряжений от изгиба, действующих в лопасти
в полете и, следовательно, к снижению ее ресурса. Поэтому обычно вес
лопасти уменьшается до тех пор, пока лонжерон терпит возрастающие
переменные напряжения. В результате вес лопасти оказывается жестко
связанным с размерами несущего винта и прочностными характеристи-
ками материала, из которого изготовляется со лонжерон.
Как следствие резонансные диаграммы различных лопастей изме-
няются на практике в пределах, которые ограничиваются с одной сто-
роны возможностью создания очень жесткой лопасти, а с другой — воз-
можностью обеспечения удовлетворительного ресурса лопастей, имею-
щих малую жесткость.
3 1578
33
При заданном общем весе конструкции максимально жесткая ло-
пасть получается, если материал ее лонжерона расположить по контуру
профиля, т. е. вписать лонжерон в профиль лопасти. При этом большой
процент веса лопасти можно вложить в ее силовой элемент — лонжерон.
Такие лопасти оказываются обычно наиболее выгодными с точки зре-
ния величины действующих напряжений, но их трудно изготовить. Более
простыми в производстве оказывались лопасти со свободной формой
сечений лонжерона (например, в виде трубы), не вписанной в профиль
лопасти. Такие лопасти обладают малым сопротивлением изгибу и дают
наименее удачную резонансную диаграмму при колебаниях в плоскости
взмаха.
По динамическим характеристикам в плоскости взмаха можно вы-
делить следующие типы лопастей:
Лопасти с малой жесткостью в плоскости взмаха. Такие лопасти
получаются обычно в конструкции, основанной на трубчатом стальном
лонжероне с неработающим при изгибе каркасом. На рис. 1.4 пункти-
ром показана резонансная диаграмма для лопасти, жесткость которой
в плоскости взмаха находится на нижнем пределе жесткостей, встре-
чающихся на практике. При таких параметрах лопасть попадает в резо-
нанс второго тона с 4-й гармоникой и третьего тона с 6-й гармоникой
возбуждающих сил, отчего в ней возникают значительные напряжения
с этими частотами (см. также рис. 1. 66). Особенно резко эти резонансы
проявляются на режимах малых скоростей, где у лопастей этого типа
напряжения оказываются даже выше, чем на максимальной скорости
(рис. 1.64). Поэтому их ресурс, как правило, ограничивается пребыва-
нием на режимах малых скоростей.
Лопасти с малой жесткостью оказываются обычно неудачными по
прочности и ресурсу, но часто применяются, так как их изготовление
в производстве оказывается наиболее простым.
Лопасти со средней жесткостью в плоскости взмаха. С увеличением
жесткости частоты собственных колебаний лопасти уходят от этих резо-
нансов. В этом случае удается создать вполне удачную лопасть. На
рис. 1.4 резонансная диаграмма такой лопасти показана сплошной ли-
нией. Как следует из этой диаграммы, второй тон колебаний такой ло-
пасти еще не приблизился к 5-й гармонике, а третий тон оказался где-то
между 7 и 8-й гармониками. Конструктивно это обычно лопасти с кон-
турным (или близким к этой форме), вписанным в профиль, лонжеро-
ном. Лонжерон может быть как стальным, так и дуралюминовым.
Без увеличения веса лопасти увеличить жесткость больше невоз-
можно. К тому же незначительное увеличение жесткости может привести
к резонансу второго тона с 5-й гармоникой внешних сил. Поэтому сле-
дующими в порядке увеличения жесткости могут быть только утяже-
ленные лопасти с сильно увеличенной жесткостью.
Утяжеленные лопасти с большой жесткостью в плоскости взмаха.
Если пойти на увеличение веса лопасти, вложив этот вес в конструкцию
лонжерона, то можно увеличить ее жесткость настолько, что частота
второго тона окажется выше 5-й гармоники. В этом случае возможна
резонансная диаграмма, показанная на фиг. 1.4 штрих-пунктирной ли-
нией. В лонжероне лопасти с такой резонансной диаграммой будут
действовать еще меньшие переменные напряжения, но лопасти оказы-
ваются несколько более тяжелыми по сравнению с лопастями средней
жесткости. Однако для небольших вертолетов, у которых относительный
вес несущего винта невелик, на такое утяжеление лопастей можно пойти.
Следует отметить, что при оценке динамических характеристик раз-
личных лопастей в плоскости взмаха совершенно не принималось
во внимание расположение первого тона колебаний лопасти. Обычно
первый тон лежит между 2 и 3-й гармониками и существенно изменить
его расположение удается только в конструкциях, отличающихся
34
какими-либо особенностями, например, у реактивных винтов с двигате-
лями на концах лопастей или у винтов с нешарнирным креплением ло-
пастей. Наблюдающееся у обычных винтов незначительное смещение
частоты собственных колебаний первого тона, как правило, сущест-
венно не сказывается на величине действующих переменных напряжений.
4. Выбор параметров лопасти для исключения резонансов
в плоскости вращения
При проектировании лопасти оказывается необходимым обеспечить
отсутствие резонансов и в плоскости наибольшей жесткости лопасти,
которая приближенно может считаться совпадающей с плоскостью вра-
щения несущего винта. Плоскость наибольшей жесткости лопасти
обычно совпадает с плоскостью хорд. Поэтому жесткостные характери-
стики лопасти в этой плоскости могут изменяться в более широких
пределах, чем в плоскости взмаха. Начиная с круглой трубы, сечение
лонжерона может быть увеличено до размеров, занимающих практиче-
ски весь профиль от передней до задней кромки. Однако имеются опре
деленные ограничения и в этой плоскости. Так, увеличение ширины лон-
жерона по хорде обязательно приводит к сдвигу центровки лопасти
к задней кромке, что обычно недопустимо с точки зрения требований,
предъявляемых для исключения флаттера. Кроме того, увеличение ши-
рины лонжерона может сопровождаться увеличением в нем переменных
напряжений. При снижении жесткости лонжерона путем уменьшения
его ширины одновременно падает и крутильная жесткость лопасти. Это
обстоятельство является одним из факторов, препятствующих созданию
лопастей с очень малой жесткостью в плоскости вращения.
При оценке резонансных характеристик в плоскости вращения сле-
дует рассматривать, главным образом, первый тон и в отдельных слу-
чаях также и второй тон колебаний лопасти. Возбуждение колебаний
по более высоким тонам оказывается слабым.
По своим динамическим характеристикам в плоскости наибольшей
жесткости лопасти могут быть разделены на следующие типы:
Лопасти с предельно низкой жесткостью в плоскости вращения.
К этому типу лопастей относятся обычно лопасти с трубчатым лонже-
роном и неработающим при изгибе каркасом. Частоты собственных ко-
лебаний этого типа лопастей в плоскости вращения оказываются при-
мерно такими же, как в плоскости тяги или даже несколько ниже
вследствие того, что значение коэффициента к, [см. формулу (3.8)]
в рассматриваемой плоскости несколько ниже (об этом еще будет ска-
зано в § 4, п. 4). Первый тон колебаний в этом случае оказывается, как
правило, все же несколько выше 2й гармоники внешних сил и серьезных
неприятностей от этого резонанса обычно не бывает. Хуже обстоит дело
со вторым тоном. Он может попасть в резонанс с 4-й гармоникой внеш-
них сил. Это обычно приводит к существенному росту напряжений с этой
частотой в плоскости вращения. На рис. 1.5 пунктиром показана резо-
нансная диаграмма для лопасти, жесткость которой в плоскости враще-
ния лежит на нижней границе жесткостей, встречающихся на практике.
Эта лопасть близка к резонансу второго тона с 4-й гармоникой внешних
сил.
Лопасти с малой жесткостью в плоскости вращения. Если жесткость
лопасти в плоскости вращения несколько увеличить таким образом,
чтобы ее первый тон остался между 2 и 3-й гармониками, а второй тон
вышел из резонанса с 4-й гармоникой, то получится вполне удовлетвори-
тельная по напряжениям в плоскости вращения лопасть. Необходимо
отметить, что при увеличении жесткости следует опасаться резонанса
второго тона с 5-й гармоникой к числу оборотов несущего винта. Прак-
3*
35
тика показывает, что при этом резонансе напряжения в плоскости вра-
щения довольно сильно увеличиваются, что может даже сказаться на их
ресурсе. Резонансная диаграмма лопастей с малой жесткостью в плос-
кости вращения, у которых второй тон расположен между 5 и 6-й гар-
мониками показана на рис. 1.5 сплошными линиями.
Рис. 1.5. Резонансные диаграммы различных типов лопастей
в плоскости вращения
Лопасти с малой жесткостью в плоскости вращения широко приме-
няются на практике и, как правило, не вызывают никаких неприятно-
стей, связанных с колебаниями в этой плоскости. Однако часто по своим
жесткостным характеристикам в плоскости взмаха они приближаются
к лопастям с малой жесткостью в плоскости взмаха, отличающимся
повышенными напряжениями на малых скоростях. При увеличении
жесткости лопасти в плоскости взмаха часто одновременно увеличи-
вается жесткость и в плоскости вращения. Это Обстоятельство застав-
ляет применять лопасти с еще большей жесткостью в плоскости
вращения.
Лопасти со средней и большой жесткостью в плоскости вращения.
К лопастям со средней жесткостью в плоскости вращения относят
обычно лопасти, первый тон которых лежит между 3 и 4-й гармониками
внешних сил, а второй тон выходит в облЯсть частот с настолько слабым
возбуждением, что им можно не интересоваться. На рис. 1. 5 частота
первого тона этих лопастей показана двойной линией.
36
К лопастям с большой жесткостью в плоскости вращения относят
лопасти, частота первого тона которых лежит выше 4-й гармоники
внешних сил (штрих-пунктирная линия на рис. 1. 5).
Лопасти со средней и большой жесткостью в плоскости вращения
могут быть выполнены с вполне умеренными напряжениями. Однако
часто при использовании таких лопастей возникают трудности, связан-
ные с падением частот лопасти вследствие упругости заделки несущего
ьинта на фюзеляже. Это обстоятельство должно обязательно учитывать-
ся при проектировании лопастей этого типа.
§ 4. РАСЧЕТ ФОРМ И ЧАСТОТ СОБСТВЕННЫХ КОЛЕБАНИИ
ЛОПАСТИ В ПОЛЕ ЦЕНТРОБЕЖНЫХ СИЛ
1. О целях и задачах расчета
Выше в § 1, п. 8 уже отмечалось, что необходимость в определении
форм и частот собственных колебаний лопасти возникает при решении
двух типов технических задач, предъявляющих различные требования
к методике расчета.
К первому типу относятся задачи, в которых расчет форм и частот
производится для выбора параметров лопасти, исключающих возмож-
ность появления резонансов. Расчет в этом случае заканчивается по-
строением резонансной диаграммы, а формы собственных колебаний
играют роль только промежуточных результатов и в дальнейшем не
используются. Поэтому в получивших широкое распространение расче_
тах этого типа форма собственных колебаний лопасти в поле центробеж-
ных сил считается совпадающей с формой невращающейся лопасти.
Влияние же центробежных сил учитывается только в значениях частот,
которые подсчитываются из энергетических соотношений, определяемых
уравнением (3.8). Такая довольно простая методика расчета вполне
удовлетворяет целям задач этого типа.
Ко второму типу относятся задачи, в которых формы и частоты
собственных колебаний используются для расчета вынужденных коле-
баний с определением переменных напряжений, действующих в конст-
рукции лопасти. Для получения достаточно точных результатов в этом
случае большое значение имеет учет тех особенностей, которые вносят
в форму колебаний растягивающие центробежные силы.
В этом параграфе будет показано, что центробежные силы сущест-
венно изменяют форму собственных колебаний лопасти. Особенно сильно
влияние центробежных сил проявляется в форме распределения кри-
визны упругой линии по длине лопасти и в меньшей степени в форме
перемещений ее элементов. Изменение формы распределения кривизны
естественно приводит и к перераспределению изгибных напряжений
по лопасти. Влияние центробежных сил на распределение напряжений
по длине лопасти наиболее сильно сказывается в местах резкого пере-
пада изгибной жесткости и крепления сосредоточенных грузов.
Следует заметить, что при определении форм собственных колеба-
ний с учетом центробежных сил встречаются определенные трудности,
которые стоит рассмотреть подробнее.
2. Пределы применимости методов расчета, сводящихся к решению
интегрального уравнения колебаний лопасти
Для расчета свободных колебаний лопасти в поле центробежных
сил было бы очень удобно применить тот же метод, что и для лопасти
невращающегося винта. ОднакО' оказывается, что метод последователь-
ных приближений (см. § 2), заключающийся в решении интегрального
уравнения (2. 1), не может быть во всех случаях применен к решению
37
уравнения (3.1), описывающего собственные колебания лопасти в поле
центробежных сил,
В § 2, п. 1 было показано, что при четырехкратном интегрировании
уравнения (2.1) задача сводится к решению интегрального уравнения
(2.4). Это интегральное уравнение может быть записано в несколько
иной форме:
9 f С Л1инерг/л2
S=p\\—s— <4-1)
о о
R R
где /Иинер=с f mijdr2 — есть изгибающий момент от инерционных сил,
г г возникающих при колебаниях лопасти с часто-
той р = 1.
Аналогично при интегрировании уравнения (3.1) задача сводится
к решению уравнения следующего вида:
y = (^Hep-^a.c)rfr2 , (4.3)
О О
где /Иц с —изгибающий момент центробежных сил при угловой скорости
вращения несущего винта ш=1.
R R
7Иц С= С myrdr— у С mrdr\ (4. 4)
Если метод последовательных приближений, примененный к урав-
нению (4. 1), дает хорошую сходимость во всех случаях, относящихся
к расчету винтов, то в применении к уравнению (4. 3) он сходится лишь
в некоторой области значений параметра у.
На рис. 1. 6 приведена резонансная диаграмма для обычной лопасти
вертолета с шарнирным креплением к втулке. По оси абсцисс на этом
графике отложены числа оборотов несущего винта, а по оси ординат —
частоты собственных колебаний.
Значения частот собственных колебаний, полученные в результате
решения уравнения (4.3) методом последовательных приближений,
отмечены на рис. 1.6 точками. Против каждой точки указано соответ-
ствующее значение параметра у и количество приближений s, необхо-
димое для достижения нужной точности, равной 0,001. Из графика
видно, что при некоторых у значение s начинает быстро увеличиваться
и метод последовательных приближений перестает сходиться.
Из рис. 1.6 следует, что в диапазоне рабочих чисел оборотов для
лопастей вертолетов такой метод позволяет определить частоты соб-
ственных колебаний третьего и более высоких тонов и только в том
случае, если все тона колебаний определяются для постоянного значе-
ния параметра у, что соответствует условиям поставленной физической
задачи лишь приближенно. Если в процессе последовательных прибли-
жений параметр у уточнять под заданное значение угловой скорости ы,
то метод будет сходиться только в диапазоне чисел оборотов, значи-
тельно меньших рабочих.
Это обстоятельство вызывает необходимость применения других
методов, дающих возможность получить надежный результат во всем
диапазоне чисел оборотов несущего винта.
38
3. О возможных методах расчета свободных колебаний лопасти
в поле центробежных сил
Для расчета частот и форм собственных колебаний в поле центро-
бежных сил могут быть применены различные методы расчета. Из опуб-
ликованных по этому вопросу отечественных работ можно указать ра-
боты [4], [8] и [10]. Из иностранных известны работы [33] и [34]. В ра-
Рис. 1.6. Резонансная диаграмма лопасти вертолета в плоскости тяги, построенная
методом последовательных приближений
ботах [33] и [34] изложен весьма громоздкий метод, дающий при том не
очень высокую точность в окончательных результатах, несмотря на то,
что расчет должен вестись с точностью не менее 10—12 знаков.
Здесь будет изложен метод, который с нашей точки зрения является
наиболее удобным для расчета частот собственных колебаний лопасти
в поле центробежных сил. Он основан на использовании метода трех
моментов, который был применен И. Морисом и В. Тай [32] для расчета
изгибных напряжений в растянутой центробежными силами лопасти.
Метод И. Мориса и В. Тай изложен также в работе [12].
Метод трех моментов, примененный к расчету растянутой центро-
бежными силами лопасти, имеет ряд значительных преимуществ. Среди
них главным является то, что он не требует высокой точности в про-
цессе вычисления. Расчеты могут производиться даже на обычной
логарифмической линейке.
39
Метод трех моментов для расчета собственных частот применяется
уже давно. Он запрограммирован на электронно-вычислительных маши-
нах «Стрела» и М-20. Расчет на машине «Стрела» первых восьми тонов
собственных колебаний лопасти занимает всего около трех минут. Про-
делано очень большое количество самых различных расчетов. Их резуль-
таты говорят о значительных удобствах и большой надежности этого
метода.
Следует отметить, что при наличии программы такого расчета нет
необходимости обращаться к каким-либо упрощенным методам расчета,
например, к тем, о которых говорилось в § 3.
4. Метод трех моментов для расчета форм и частот собственных колебаний
лопасти в поле центробежных сил
Для вывода расчетных формул используем балочную модель ло-
пасти с сосредоточенными грузами, которая уже применялась в § 2, п. 2.
Как и раньше, изгибную жесткость лопасти представим в виде ступен-
чатой кривой таким образом, чтобы она оставалась постоянной на про-
тяжении каждого участка (см. рис, 1.3). Центробежную силу будем
считать приложенной только к грузам. Поэтому на протяжении каждого
Чп
Рис. 1.7. Схема сил, действующих Иа два смежных эле-
мента лопасти
участка величина ее не будет изменяться. Будем также считать, что
центробежная сила воспринимается специальным креплением нулевого
груза, который тем не менее может свободно перемещаться по вертикали.
Очевидно, что такая идеализированная расчетная схема может
быть надежно использована, если число участков z взять достаточно
большим. Обычно лопасть разбивается не менее чем на 25—30 участков.
Предлагаемая в дальнейшем методика состоит в определении
частот и форм собственных колебаний такой идеализированной схемы
без каких-либо дополнительных допущений.
Рассмотрим два соседних участка лопасти, отклонившихся под
действием инерционных сил от плоскости вращения винта (рис. 1.7).
Как обычно, будем рассматривать только малые отклонения.
Уравнение равновесия каждого из участков под действием внешних
по отношению к данному участку сил может быть записано в виде ра-
венства нулю суммы моментов всех этих сил относительно какой-либо
точки. При этом в сумму моментов этих сил следует включить и дейст-
вующие в сечении перерезывающую силу Q и изгибающий момент Л4.
40
Тогда сумма моментов сил, действующих на участок лопасти 0—1
относительно точки 0, может быть записана как
Л1]—Л40—№i(#i—Ус) + Qoi^oi ~ 0. (4.6)
Сумма моментов сил, действующих на участках 1—2 относительно
точки 1'.
М2—Mi—N\2(y2—yi) +<212^2 = 0. (4.7)
Здесь:
Qoi= -Ът‘У1'
1
Q12= —
2
Разделив уравнения (4. 6) и (4. 7) соответственно на Zqi^oi и l\2Ni2
и сложив их, получим следующее уравнение равновесия:
Мо + ад + ^'2 = тео^о + ^М14-т1Л42+^ —(4.8)
Л]2 Л'О1
Введенные здесь, а также в уравнениях (4. 12), (4. 13), (4. 14) и
(4. 15), обозначения выписаны ниже (см. выражения 4. 18-М. 25).
Аналогично уравнению (4. 8) могут быть записаны уравнения рав-
новесия и для всех других участков лопасти.
Рассматривая по-прежнему только малые перемещения элементов
лопасти, определим деформации участка 1—2. Уравнение деформаций
элемента 1—2 может быть записано как обычно [см. уравнение (3. 1)].
[E/i2/T-4AW]'=o.
Инерционный член здесь отсутствует, поскольку инерционные силы
приложены только на границах участка. Учитывая, что на длине участка
£7 = const и N=const, а также, что1 Е1у" = М, получим
где
1 £Лз
Решение уравнения (4.9) можно записать через гиперболические
функции следующим образом:
МХ=А sh p,ix + B ch щх. (4. 10)
Коэффициенты А и В находятся из следующих граничных условий:
— при х = 0 =
-- ПрИ Х=112 МХ = М2.
Откуда
д М, _
sh eq th ci,
5 = 34],
где И] —
4Т
Подставив эти значения в уравнение (4.10), получим
Мх=Е1пу"=\-^--Ishpjx+Afj ch^x.
[ sh aj th ct] J
(4.И)
Проинтегрировав дважды уравнение (4.11), полагая, что при
х—О y'=Pi, y=yi, а при х=/]2 у'=Рг, У=У2, получим либо
либо
У1) —
(4- 12)
М*/2-01) = -^2-^1 + ^-
Уравнение деформаций для участка 0—1 может быть записано по
аналогии со вторым уравнением (4.12):
^о(У1—У о) =—еоЛ4]—cZoMj+Pi.
(4.13)
Изменив в уравнении (4.13) все знаки на обратные и сложив с пер-
вым уравнением (4.12), получим:
ЬоУо+Qiyi+bly2=d0M(J+clMi -f-djMz.
(4. 14)
Подставив в уравнение равновесия элементов (4.8) левую часть,
выраженную через изгибающие моменты из уравнения (4. 14), получим
следующее уравнение:
АоЧ+ё1м ]+h,M2=_ goi
(4.15)
Повторив проделанные выкладки для других участков лопасти,
получим выписанную ниже систему дифференциальных уравнений отно-
сительно неизвестных функций времени yi и Л4{.
Эта система, записанная в форме таблиц, состоит из двух семейств
уравнений (4.16) и (4.17), каждое из которых включает в себя г+1
уравнение.
Любое из уравнений, занимающее в табл. 1. 1 одну строку, пред-
ставляет собой многочлен, коэффициенты которого выписаны в клетках
таблицы. Все слагаемые многочлена представляют собой произведения
некоторого коэффициента, определяемого по формулам (4.18), (4.21),
(4. 23) и (4, 24) — (4. 27), на неизвестные функции Mi и yi или на вторую
производную от yi по времени.
В клетках табл. 1. 1 выписаны только коэффициенты при этих функ-
циях, а сами функции, входящие одновременно в несколько уравнений,
вынесены по вертикали в специальную строку, помещенную сверху
таблиц.
В описанную систему уравнений включены также уравнения типа
(4. 12), относящиеся только к комлевому и концевому участку лопасти
и содеожащие краевые значения р0 и (V Эти уравнения необходимы для
учета граничных условий задачи.
Полученная система уравнений имеет следующий вид:
42
Ги£ли.ца 7.7
А Мд М1 мг ••• м*.. мг |А | Л у\ 5 ««• Уг;

1 ho = 0 ^0! .^1. i 13 *о,г-1 *02 (9.rs)
Ь-и ^12 t1z
А Зг s2 ^гз • • • t22
• • • • ••
^г-j ъ-2 ^г-г sz-2 ^z-Z,z
ki-2 Ъ-, hZ-1 S2-1 Ч-1;2
9г 1 SZ
fin Mg Mz • •• • •• мг., Ml fiz
1 A
£1^ ar,
Й,
• •• • •• •••
сг-2 У-г-г
^г-2 ci-i &2-1
^г-1 сг О
(4.77)
При составлении выписанных выше уравнений приняты следующие
обозначения:
£о=п-; ай=~Ь0-,
чн
Z>. = —; a^-bi^bi’,
Ч, 1+1
^=0; a^-bz-t.
(4. 18)
1
т0=-
(4.19)
аг=0.
(4.20)
d^m-t ( 1----— V
' ' \ sh а, /
0^ = 0.
(4-21)
43

(4. 22)
(4.23)
Aq — d0 m0;
hi = dl —mi;
hz = 0.
go—co no’’
gi==Ci-nt-,
gz = Cz — nz.
(4. 24)
(4. 25)
В нижеследующих выражениях (4. 26) и (4. 27) /п}- есть масса г-го
груза.
s0=O;
(4.26)
(4-27)
Здесь индексом k обозначен номер строки в табл. 1.1.
Для решения системы уравнений, записанной в табл. 1. 1, удобно
применить метод последовательных приближений. Применительно к этой
системе уравнений он заключается в следующем. Представим входящие
в систему (4. 16) и (4. 17) функции времени Mj(t) и рДД в сле-
дующем виде:
yt (/)= z/fsin р/;
Л4( — sin pi;
?1 (/) = ₽/ sinp/,
где буквами yit Л1, и рг- обозначены теперь только амплитудные значе-
ния этих функций.
Тогда, имея в виду, что jn(£) =—р2щ sin pf, и сокращая на sin pi,
получим систему алгебраических уравнений, аналогичную системе (4. 16)
и (4.17). Только в правых частях семейства уравнений, аналогичных
(4. 16), появятся значения р2-
44

Метод последовательных приближений начнем с того, что в качестве
нулевого приближения зададимся некоторой функцией yi„ . Вторым ин-
дексом снизу мы здесь обозначили номер приближения. Взятая в каче-
стве нулевого приближения функция t/z0 должна быть каким-нибудь
образом нормирована, например
г/2=1. (4.28)
Если функция yi известна, то с точностью до постоянного множи-
теля р2 могут быть определены и входящие в правую часть уравнений
(4. 16) инерционные силы.
Положим временно р2=1. Тогда из уравнений (4. 16) можно опре-
делить значения изгибающих моментов Л4, и угол поворота лопасти
в комле 0о- После чего по известным уже значениям Л4г и [1о из уравнений
(4. 17) могут быть определены и перемещения оси лопасти при дефор-
мациях, которые мы для случая р2=1 обозначим через таким обра-
зом, что
Уг = р2иг. (4.29)
После определения перемещений и{ может быть определена и ча-
стота собственных колебаний р. Ее величина получается на основании
выражений (4.28) и (4.29) следующим образом:
/?2==J^ = JL. (4.30)
Uz
После чего в соответствии с выражением (4.29) определяется и
уточненная после первого приближения функция
Затем весь процесс повторяется до тех пор, пока не будет достигнута
требуемая точность.
Примененный метод последовательных приближений приводит
к тому, что определяемая форма yt сходится к форме низшего тона соб-
ственных колебаний лопасти.
При определении последующих тонов должно быть соблюдено
условие ортогональности. Операции, вытекающие из соблюдения усло-
вия ортогональности, остаются теми же, что и для лопасти невращаю-
щегос.я винта (см. п. 3 § 2).
Выписанные выше уравнения в равной степени годятся для расчета
частот собственных колебаний как в плоскости взмаха, так и в плоско-
сти вращения винта. Только при расчете в плоскости вращения полу-
ченные выше значения частот следует поправить по формуле
„2 — „2 — о,2 (4.32)
где со —угловая скорость вращения винта.
Методика расчета форм собственных колебаний не меняется от того,
в какой плоскости производится расчет.
Рассмотрим более подробно некоторые операции при выполнении
одного приближения.
5. Определение изгибающих моментов по известным силам
Начнем с определения изгибающих моментов по известным, входя-
щим в правую часть уравнения (4. 16) инерционным силам, которые мы
в каждом приближении определяем, задаваясь вначале значением р2=1.
Задавшись какой-то формой колебаний yt, мы можем определить
коэффициенты правой части уравнений (4. 16), которые мы здесь обо-
значим через Fk-
45
Коэффициенты Fh могут быть определены по формулам?
2 ^У‘ (4-33)
i-A+1
или лучше
f Qk-i, k I Qfe, я-t
Nk—l, k Nk,k+1
z
где Qs-i,*=2/«z^-
ь
Тогда система уравнений (4. 16) может быть переписана в следую-
щем виде (табл. 1.2):
Для решения этой системы необходимо знать еще два дополнитель-
ных уравнения, учитывающих граничные условия. Эти уравнения могут
быть следующими:
— при жесткой заделке комля лопасти
Ро=О;
— при жесткой заделке конца лопасти
₽г = 0.
При шарнирном закреплении концов лопасти или при полностью
свободных концах Л4о = О и Л1г = 0.
В дальнейшем мы будем рассматривать только два наиболее рас-
пространенных случая, когда конец лопасти свободен (Л1г = 0), а в комле
имеется либо шарнирная опора (Mo — Q), либо жесткая заделка (ро = 0).
Рассмотрим вначале первый случай, когда лопасть закреплена шар-
нирно, т. е. Мо = О. В этом случае для определения изгибающих момен-
тов используем только те уравнения, которые в системе (4. 35) обведены
жирной линией, после чего из первого уравнения может быть опреде-
лено и значение угла поворота лопасти в шарнире ро- Из последнего
уравнения системы (4. 35) можно было бы определить и значение pz.
Однако это значение нам для дальнейшего решения не понадобится.
Само же уравнение используется только в редко встречающемся на
практике случае, когда р2 = 0.
При решении системы (4. 35) может быть выбран неудачный путь,
приводящий к появлению в процессе решения малых разностей больших
величин, которые в некоторых случаях могут совершенно испортить ре-
зультат даже при использовании машины, обеспечивающей точность
до девяти знаков.
46
Мы здесь предлагаем неоднократно проверенный путь, который
позволяет производить расчет даже на обычной логарифмической
линейке.
Разделим первое уравнение системы (4.35), выписанной примени-
тельио к шарнирному креплению лопасти, на gi и второе уравнение —
на fti:
+ = (4.36)
ST gl
+ ? + = (4.37)
ft] ft]
Вычтя из уравнения (4.37) уравнение (4.36) и введя следующие
обозначения
„* ДЗ Й1 .
ё2 hi gi ’
hi gi
получим уравнение, аналогичное уравнению (4. 36):
й* F*
+ (4.38)
g2 g2
В сочетании со следующим уравнением системы (4. 35) это уравне-
ние образует систему двух уравнений, аналогичную уравнениям (4.36)
и (4.37), Повторив описанные операции некоторое число раз, мы полу-
чим в конце концов одно уравнение следующего вида:
(4.39)
gz—l
После определения момента Mz-i определяется момент Mz_2 и т. д.
вплоть до момента Mh Другими словами, момент определяется каж-
дый раз, когда момент Mi+i уже определен. Формула для определения
момента Mi может быть записана на основании уравнений (4.36) и
(4.38) следующим образом:
F? й’
------(4.40)
g, gi
После определения изгибающих моментов угол поворота лопасти
в комлевом шарнире 0о определяется по формуле
₽о = /?о—h0Mi. (4. 41)
Второй этап метода последовательных приближений заключается
в определении деформаций лопасти по известным уже значениям изги-
бающих моментов Mi и углу поворота лопасти в шарнире |30-
6. Определение перемещений по известным изгибающим моментам
Перемещения лопасти при ее деформации, которые мы здесь в со-
ответствии со сказанным выше обозначаем могут быть определены
из системы (4. 17). Однако можно показать, что уравнений системы
(4.17) недостаточно для определения всех значений щ.
47
Действительно, для определения положения кривой с известным
распределением кривизны по длине, которая задается значениями Л4,,
п с известным значением угла поворота в одной точке (30 необходимо
еще одно дополнительное условие, наложенное на значения переме-
щений. При этом последнее уравнение системы (4. 17), включающее
в себя значение угла поворота в другой точке [ф, фактически тождест-
венно первому уравнению и выписано нами исключительно по аналогии
с системой (4. 16).
Таким дополнительным условием является либо условие
ио = О, (4.42)
если в комле лопасти имеется опора, либо условие
(4.43)
/-о
если лопасть рассматривается как свободная с двух сторон балка. Усло-
вие (4.43) совпадает с выражением, вытекающим из условия ортого-
нальности с нулевым тоном колебаний
yW — 1 = Const.
Подсчитав коэффициенты, включающие в себя уже определенные
значения АД и (Ь и оставив из двух тождественных уравнений только
первое, получим следующую систему уравнений, которая в сочетании
с уравнениями (4.42) и (4.43) позволяет определить все значения гд
(см. табл. 1.3).
Таблица, гз
U-0 ^2 • • • иг-,
Do Ь0 Do
ьо bl Di
^2 bZ = Dl (4.44)
b2 аз ьз = D3
• • • • • • • • • • • •
bZ-Z а1-1 bZ~l =: Dt-i
bZ~1 az Di
Здесь мы ввели следующие обозначения
Di—di—\M.i—\ CiMiA-(4.45)
причем в этой формуле при 1 =—1 вместо значения Л4_] следует поста-
вить р0, а значение cLi считать равным единице =
При условии (4. 42) решение системы (4. 44) сводится к определе-
нию значений ut из простых рекурентных формул вида:
= (4.46)
*/-1
48
При решении системы (4. 44) с условием (4. 43) значения Ut можно
представить как
нг = ко+йь (4.47)
где йо = О,
и определить йг- по формулам (4. 46), после чего значение «о может быть
определено по формуле
У,
------------ (4.48)
1=0
О дальнейшем ходе последовательных приближений уже было ска-
зано выше.
В рассматриваемом случае шарнирного крепления лопасти в комле
метод последовательных приближений приведет вначале к определению
формы нулевого тона, которая при совпадении шарнира лопасти с осью
вращения винта будет совпадать с прямой линией. Естественно, что
в этом частном случае расчет следует начинать прямо с определения
первого тона, проводя в каждом приближении ортогонализацию к нуле-
вому тону, считая его совпадающим с прямой.
Чаще всего комлевой шарнир лопасти вертолета отнесен от оси
вращения винта на некоторую величину г0, которая может составлять
примерно 3—10% от радиуса лопасти. Наличие этого расстояния при-
водит к тому, что форма нулевого тона шарнирно подвешенной лопасти
может несколько отличаться от прямой линии, а частота собственных
колебаний становится заметно отличной от величины, равной числу обо-
ротов несущего винта. Ниже (см. рис. 1.14) мы для иллюстрации этого
эффекта приводим график формы нулевого тона с очень сильно увели-
ченным расстоянием от оси вращения винта до комлевого шарнира.
7. Случай жестко закрепленной в комле лопасти
Расчет форм собственных колебаний для жестко заделанной в комле
лопасти очень мало отличается от рассмотренного выше случая шарнир-
ного крепления.
Первый этап расчета, заключающийся в определении изгибающих
моментов М{, проводится таким же образом, как это было описано выше,
только при этом решается система, обведенная в (4.35) пунктирной ли-
нией. Эта система включает в себя на одно уравнение больше, в котором
в силу граничных условий принимается 0 = 0.
Это же условие используется и при решении системы (4. 44), в кото-
рой коэффициент Da подсчитывается по формуле
Do = СоМо + doM 1.
8. Возможные упрощения при расчете коэффициентов
Отметим еще, что в тех случаях, когда лопасть разбита на доста-
точно большое количество участков таким образом, что значение коэф-
фициентов а< в формулах (4.20) меньше 0,05—0,08, формулы (4.21) и
(4.22) можно упростить, заменив входящие в них гиперболические
функции первыми членами их разложения в ряды.
Действительно, положим в формулах (4.21) и (4.22)
. । о3 , «5 , , а3
sha=a-l-----------р. . . а-4---;
1 3! 1 5! 1 ' 6
,, а3 2а® а3
tha=a-------- ч---.. . =а------
3 1 15 3
4 1578
49
и пренебрежем значениями а2 по сравнению с единицей. Тогда коэффи-
циенты di и можно подсчитывать по приближенным формулам
d Ji. 1+^.-
SEIi.l+i
Р tj’i+i
1 3EIifl+i
= 4di-
Эти упрощения несколько уменьшают трудоемкость расчета, что
имеет значение при его ручном выполнении.
9. Некоторые результаты расчета форм и частот
собственных колебаний лопасти
Здесь мы выделяем два вопроса, представляющих с нашей точки
зрения наибольший интерес.
Первый вопрос будет касаться тех уточнений, которые вносит расчет
частот и форм собственных колебаний лопасти в поле центробежных
сил в окончательные результаты по сравнению с приближенной методи-
кой расчета, изложенной в § 3. После чего мы остановимся на рассмот-
рении случаев возникновения резких перегибов лопасти под действием
местных особенностей в распределении жесткостных и массовых пара-
метров по длине лопасти. Возникновение этих перегибов характерно для
растянутых центробежными силами балок и без растяжения центро-
бежными силами не наблюдается.
Начнем с первого вопроса. В п. 1 § 3 мы уже отмечали, что прибли-
женный метод расчета частот собственных колебаний лопастей в поле
центробежных сил, в основу которого положено предположение о том,
что формы собственных колебаний при наличии и Отсутствии центробеж-
ных сил не различаются, дает вполне удовлетворительные результаты
в величинах частот.
Для подтверждения этого положения приведем значения частот
собственных колебаний первых трех тонов шарнирно подвешенной и
жестко заделанной в комле Таблица 1.4 допасти одного из вертоле-
Тон колебаний — х - — .гив в виле центробежных Частота собственных сил. Значения чаСтот, под- считанные ППпб.ПиЖАНМТиМ
приближен- ный метод точный энергетическим методом метод (см. § 3), помещены во вто-
Шарнирно подве- шенная в комле ло- пасть Первый Второй Третий Жестко заделан- ная в комле лопасть Первый Второй Третий уже отмечалось вы ние возможности г вполне удовлетвор 405,3 708,5 1069,7 212,1 463,7 821,5 ше, для ра юявления ительные р рои графе табл. 1.4. В третьей графе помещены для сравнения точные зна- чения частот, подсчитанные 404,3 п0 методу, изложенному в 705'9 ЭТОм паРагРаФе- ’ Сравнение приведенных 1069,0 в табл. 1.4 значений частот показывает, что при шар- нирной подвеске лопасти 194,7 различие в их величинах 461,9 весьма незначительное. При 817 5 жесткой заделке оно не- сколько больше, но тоже не- велико. Поэтому, как нами счетов, целью которых является исключе- резонансов, приближенная методика дает езультаты.
50
Влияние центробежных сил сильнее сказывается на формах соб-
ственных колебаний и, особенно, на распределении изгибающих момен-
тов и кривизны упругой линии по длине лопасти.
На рис. 1.8 показаны шарнирные формы первых пяти тонов
(исключая нулевой тон) для той же лопасти, что и в табл. 1.4, а на
рис. 1.9 распределение изгибающих моментов, соответствующее этим
формам. Сплошными линиями на рис. 1.8 и 1.9 (так же, как и на рис.
1.10, 1.11 и Г. 12) показаны
формы собственных колебаний
в поле центробежных сил, а
пунктирными — те же формы
для невращающейся лопасти.
На рис. 1.10 приведены
формы собственных колебаний
и соответствующие им изгиба-
ющие моменты для двух пер-
вых тонов заделанной в комле
лопасти.
Как видно из всех этих
графиков, учет центробежных
сил оказывает в некоторых се
чениях лопасти весьма замет-
ное влияние на форму собст-
венных колебаний, что особен-
но сильно проявляется в эпю-
рах изгибающих моментов, а
следовательно, и в распределе-
нии изгибных напряжений по
длине лопасти. Это влияние
тем сильнее, чем ниже тон соб-
ственных колебаний.
Распределение изгибаю-
щих моментов по длине лопас-
ти при ее колебаниях в поле
центробежных сил характери-
зуется увеличением изгибаю-
щих моментов на некоторых
участках лопасти за счет их
Третий тон _
। । 1 । । | ।
I I I I I II Второй, тон
_ р^ЗбЗмл/мин, рп=7О5нол!мин J
Уг
f,0r
0,6
0,1
О
-0,1
Уг
0,5
0,2
О
-0,2
Уз
0,6
0,2
0
-0,2
Л
0,6
42
О
~0,21
У5
п = 165
р0=664 нпл/мин
р„-1и68 кол/мин
Четвертый тон
. ро=1115кол/мин 1 1
- рп = 1540 кол)мин
n-ISSof/MUH (
n-K5oSlm
д=0
5 I । Пятый, тон
• L р0=17311 юл/мин
' = 2172 нол/мин
0,6
0,2
О
-0,2
-0,6
уменьшения на соседних участ- Рис. i.s Формы первых пяти топов лопасти
ках. Такое местное увеличение в поле центробежных сил и при п=0
изгибающих моментов мы бу-
дем называть концентрацией
изгибающих моментов. Возникновение концентраций изгибающих момен-
тов связано с наличием в конструкции лопасти крупных сосредоточен-
ных грузов и резких перепадов изгибной жесткости.
Концентрации изгибающих моментов приводят к появлению на ряде
участков лопасти повышенных изгибных напряжений, что вызвано рез-
кими перегибами лопасти на этих участках.
Это обстоятельство представляет значительный интерес для прак-
тики и поэтому должно быть рассмотрено более подробно.
Характер колебаний лопасти в поле центробежных сил в большой
мере определяется соотношением между величинами упругих и центро-
бежных сил. Если жесткость лопасти на изгиб достаточно велика (как
это часто бывает, особенно в плоскости вращения винта), а центробеж-
ные силы незначительны (малые обороты винта), то форма колебаний
мало отличается от формы колебаний невращающейся лопасти.
Если же, наоборот, жесткость лопасти на изгиб невелика, а центро-
бежные силы значительны, то форма деформаций лопасти опреде-
4*
51
ляется в основном инерционными и центробежными силами и мало
зависит от упругих свойств лопасти. В этом случае форма деформаций
лопасти при колебаниях очень слабо отличается от формы деформаций
абсолютно гибкой растянутой центробежными силами тяжелой нити.
Такое положение, как правило, наблюдается при колебаниях в плоско-
сти тяги у лопастей современ-
ных вертолетов.
Количественно соотноше-
ние между упругими и центро-
бежными силами может быть
оценено при помощи коэффи-
циента а, представляющего со-
бой отношение упругой потен-
циальной энергии к потенци-
альной энергии, накопленной
лопастью за счет изгиба в поле
центробежных сил:
Рис. 1.9. Распределение изгибающих мо-
ментов по лопасти при колебаниях по фор-
мам первых пяти тонов в поле центробеж-
ных сил и при /1=0
- у
Значения Свт и CN распи-
саны в формулах (3.3) и
(3.4).
При а>1 влияние упру-
гих свойств лопасти сильнее
влияния центробежных сил.
При а<1 наблюдается обрат-
ная картина.
В табл. 1.5 приведены зна-
чения коэффициентов а для
шарнирно подвешенной лопа-
сти, формы колебаний которой
/показаны на рис. 1.8 и 1.9.
'Эта лопасть может рассматри-
ваться как типичная вертолет-
ная лопасть.
Приведенные в табл. 1.5
значения коэффициентов а
подтверждают то положение,
Причем свойства лопасти и гибкой
чем ниже тон собственных колебаний.
что лопасть вертолета по сво-
им характеристикам в плоско-
сти взмаха приближается к
абсолютно гибкой, растянутой
центробежными силами тяже-
лой нити, для которой а=0.
нити сближаются тем сильнее,
Основной особенностью растянутой абсолютно гибкой нити является
то, что ее ось претерпевает изломы в точках приложения сосредоточен-
ных поперечных сил и в местах соединения нити с жесткими элементами.
Такой излом, как правило, возникает в месте заделки нити. Если в гиб-
кую нить вставить жесткий участок, то по краям этого участка возникнут
такие же изломы. Поэтому в тех случаях, когда свойства лопасти и рас-
тянутой гибкой нити сближаются, эти особенности проявляются и при
деформациях лопасти. Конечно, упругая лопасть, как бы низка не была
ее изгибная жесткость, не может претерпевать таких изломов. Тем же
менее изломы, свойственные абсолютно гибкой нити, передаются ло-
52
пасти и проявляются в виде резких перегибов ее оси. Эти перегибы со-
провождаются появлением концентраций изгибающих моментов и повы-
шением изгибных напряжений в местах перегиба.
Рассмотрим несколько примеров, подтверждающих это положение.
На рис. 1.11 приведено распределение изгибающих моментов по
длине лопасти, соответствующее формам собственных колебаний перво-
го и второго топа с грузом,
почти равным весу лопасти
и помещенном на относи-
тельном радиусе г = 0,48.
В точке крепления гру-
за наблюдается резкая кон-
центрация изгибающего мо-
мента, приводящая к увели-
чению напряжений почти в
два раза по сравнению с не-
вращающейся лопастью.
Введение в лопасть участка
с повышенной жесткостью
приводит к появлению кон-
центрации изгибающего мо-
Таблица 1. 5
Тон колебаний Коэффициент а при
деформа- ции в плос- кости взмаха деформа- ции в плос- кости вращения
Первый 0,083 2,2
Второй 0,332 3,7
Третий 0,629 7,7
Четвертый 1,116
мента в районе этого участка (рис. 1. 12). Но поскольку увеличение из-
гибной жесткости приводит к увеличению момента сопротивления на
длине жесткого участка, то наибольшие напряжения возникают по кра-
ям участка, т. е. там, где испытывала бы изломы абсолютно гибкая
нить.
Проявлением тех же свойств абсолютно гибкой растянутой нити объ-
ясняется появление резкой концентрации изгибающего момента в случае
жесткой заделки лопасти, так как гибкая нить имела бы в месте задел-
ки такой же излом, как и шарнирно закрепленная лопасть.
Увеличение изгибающего момента, соответствующего первому тону,
при жесткой заделке лопасти в комле происходит почти в шесть раз
диусе г—0,48, близким по весу к весу лопасти
(см. рис. 1. 10) по сравне-
нию с моментом невращаю-
щейся лопасти. Такая рез-
кая концентрация изгибаю-
щего момента оказывает за-
метное влияние даже на
значения частот собст-
венных колебаний (см.
табл. 1.4). Это существенно
снижает возможности при-
ближенного метода (см.
§ 3) в применении к расчету
лопасти с жесткой заделкой
в комле.
В ряде случаев на прак-
тике возникает необходи-
мость в введении в лопасть
винта дополнительных шар-
ниров или в смещении поло-
жения тех шарниров, кото-
рые уже имеются в конст-
рукции втулки. Потребность
в создании дополнительных
шарниров может быть свя-
зана с необходимостью сни-
жения изгибных напряже-
ний на каком-либо участке
лопасти или с изменением
частот ее собственных коле-
баний.
Посмотрим, как сказы-
вается на изгибных дефор-
мациях лопасти введение
в нее дополнительного шарнира. Раньше уже говорилось, что лопасть
вертолета близка по своим характеристикам к растянутой гибкой нити.
Так же, как и гибкая нить, ведет себя и растянутая цепочка с непрерыв-
но распределенными по длине шарнирами. Поэтому можно считать, что
лопасть вертолета принимает при деформациях примерно такую же
форму, как и растянутая многошарнирная цепь. Естественно поэтому,
что введение в лопасть дополнительного шарнира не может существенно
сказаться на форме ее деформаций. Это обстоятельство проиллюстри-
ровано рис. 1. 13, где показана форма первого тона собственных коле-
баний лопасти с введенным в нее дополнительным шарниром и без него.
Из рис. 1. 13 также видно, что влияние дополнительного шарнира замет-
но сказывается на форме изгибающего момента только на небольшом
участке, близком к шарниру. На удаленных от шарнира участках его
влияние невелико.
Следует особо отметить, что в рассмотренном случае, когда лопасть
имеет два шарнира, формы ее колебаний в поле центробежных сил весь-
54
м
кгс-н
Рис. 1.12. Форма изгибающего момента по
первому тону для лопасти с участком повы-
шенной жесткости
Рис. 1.13. Форма первого тона собственных
колебаний лопасти с дополнительным шар-
ниром и без него:
а и б—формы первого тона в поле центробежных
сил без шарнира (а) и с шарниром (б); в—форма
первого той а неврашаюшихся лопастей с шарни-
ром; г и б—формы изгибающего момента по пер-
вому топу в поло центробежных сил без шарнира
(а) и с шарниром (5)
55
ма сильно отличаются от форм колебаний невращающейся лопасти. При
колебаниях по первому тону невращающаяся лопасть совсем не дефор-
мируется. Поэтому в данном частном случае приближенный энергети-
ческий метод расчета частот в таком виде, как он изложен в § 3, просто
не применим.
Также нельзя пренебрегать полем центробежных сил и при рассмот-
рении деформаций лопасти в винте типа Дершмидта с сильно вынесен-
ным от оси вращения шарниром. Форма колебаний низшего тона лопас-
Рис. 1. 14. Форма низшего тона собственных колебаний ло-
пасти с отнесенным от оси вращения шарниром и соот-
ветствующий этой форме изгибающий момент (при колеба-
ниях в плоскости взмаха Рв/п —1,35, при колебаниях
в плоскости вращения ро/п=0,91)
ти этого винта и соответствующий ей изгибающий момент показаны на
рис. 1. 14. Без учета центробежных сил форма лопасти совпадала бы
с прямой линией и величину показанного на рис. 1. 14 изгибающего мо-
мента, который у этого винта очень велик и фактически определяет воз-
можность его применения, нельзя было бы найти.
Приведенные примеры показывают, что в целом ряде случаев фор-
мы собственных колебаний в поле центробежных сил существенно отли-
чаются от соответствующих форм невращающейся лопасти. Это обстоя-
тельство обязательно должно учитываться при конструировании ло-
пасти. Поэтому при работе в конструкторском бюро, когда все расчеты
ведутся на электронно-вычислительных машинах и степень сложности
методики просто остается незамеченной, нет смысла обращаться к при-
ближенным методам.
§ 5. КРУТИЛЬНЫЕ КОЛЕБАНИЯ ЛОПАСТИ
1. Задачи, решаемые при расчете крутильных колебаний
Выше в параграфах § 1 и 4 отмечалось, что расчет форм и частот
собственных изгибных колебаний лопасти имеет наряду с подсобным
(для расчета напряжений) также и самостоятельное значение как метод
выбора параметров лопасти, исключающих возможность изгибных резо-
нансов. Этой задачи не стоит перед расчетом свободных крутильных ко-
лебаний, так как на практике никогда не наблюдалось значительных по
амплитуде колебаний, которые бы были вызваны крутильным резонан-
сом. Как правило, значительные крутильные колебания возникают
только при флаттере или при вынужденных колебаниях в условиях
близости флаттера. Поэтому величина частоты собственных крутильных
колебаний сама по себе никакого практического интереса не представ-
ляет (если не рассматривать ее как параметр, характеризующий жест-
кость лопасти на кручения), а результаты расчета форм и частот собст-
56
венных колебаний имеют только вспомогательное назначение для
расчета флаттера или расчета изгибных напряжений, подсчитываемых
с учетом крутильных деформаций лопасти. Другой задачи перед расче-
том свободных крутильных колебаний лопасти не ставится.
Перед расчетом вынужденных крутильных колебаний стоят в основ-
ном Две задачи. Первая —это определение упругих деформаций лопасти,
учет которых необходим для расчета изгибных напряжений, и вторая —
это определение величин шарнирных моментов, необходимых для расчета
системы управления несущим винтом.
2. Дифференциальное уравнение крутильных колебаний лопасти
Представим лопасть в виде консольного прямолинейного стержня
с переменной по длине жесткостью на кручение GTKp. Массовый момент
инерции сечений стержня относительно его оси !т будем считать так же,
как и жесткость на кручение, непрерывной функцией, переменной по
длине стержня, центры тяжести всех сечений стержня —лежащими на
его оси, заделку стержня — упругой на кручение.
Естественно, что сведение задачи о колебаниях лопасти к расчету
такой модели предполагает применение целого ряда упрощающих допу-
щений. Будем считать, что ось жесткости лопасти прямолинейна и сов-
падает с осью осевого шарнира втулки несущего винта. Компенсатор
взмаха я положим равным нулю.
Учет сдвига центров тяжести и определение влияния компенсатора
взмаха на частоты собственных колебаний будут рассмотрены в § 6.
Применение перечисленных допущений позволяет решать задачу
о крутильных колебаниях лопасти совершенно независимо, не связывая
их с ее изгибными колебаниями.
Составим дифференциальное уравнение крутильных колебаний ло-
пасти. Крутящий момент в сечении лопасти может быть определен из
дифференциального уравнения:
РИКРГ=-5Ш, (5.1)
где ® —погонный крутящий момент внешних и инерционных сил, дей-
ствующих на элемент лопасти.
Под действием крутящего момента каждый элемент лопасти закру-
чивается на угол:
Лй.:п
(5.2)
кр
где <р — упругий угол поворота сечеиия лопасти.
Значение крутящего момента, полученное из (5.2), подставим в
(5. 1). Тогда дифференциальное уравнение крутильных деформаций ло-
пасти может быть записано в форме
[«Гкр?']' + ЗЛ =0. (5.3)
Рассмотрим крутильные колебания лопасти несущего винта, враща-
ющегося в пустоте. Погонный крутящий момент в этом случае будет
равен:
(5.4)
где 1у и 1Х—массовые моменты инерции сечения лопасти относительно
ее главных осей инерции.
57
Если протяженность профиля вдоль оси х значительно больше, чем
вдоль оси у, а так это обычно и бывает, то можно приближенно поло-
жить
Iy-Ixsilm, (5.5)
где 1т — погонный массовый момент инерции сечения лопасти относи-
тельно оси, проходящей через ось жесткости.
Подставив выражение (5.4) с учетом (5.5) в уравнение (5.3), по-
лучим дифференциальное уравнение крутильных колебаний лопасти
винта, вращающейся в поле центробежных сил:
[GrKP?T-/m(?-W?)=o.
(5-6)
Рассматриваемая здесь модель лопасти имеет следующие гранич-
ные условия:
при г=0:
[G7'K.,y Jo — ^ynp'fth
при r=/?:
[G7\p<p'h=O,
(5.7)
где супр— жесткость системы управления несущим винтом, приведен-
ная к осевому шарниру втулки (жесткость управления
определяет величину жесткости упругой заделки лопасти
в комле);
% —поворот лопасти в осевом шарнире вследствие деформаций
системы управления несущим винтом.
3. Определение форм и частот
собственных колебаний лопасти на кручение
Здесь мы применим тот же способ решения, который был изложен
в п. 1 § 2 для определения форм и частот изгибных колебаний. Положим
<p(/)=cpsin vt. (5-8)
Подставив выражение (5.8) в уравнение (5.6), получим
[G7>']' + (v2-»2) (5.9)
Из этого уравнения сразу следует, что формы собственных колеба-
ний вращающейся и невращающейся лопасти па кручение одинаковы,
а частоты связаны простым соотношением вида
v2 = v2_[_«)2, (5.10)
где V — частота собственных колебаний в поле центробежных сил;
v0 — частота собственных колебаний лопасти невращающегося винта.
Проинтегрировав уравнение (5.9) с учетом граничных условий
(5.7) для случая <о = 0, получим
(5.П)
Здесь и ниже индекс при v, означающий, что частота собственных
колебаний определяется для ы=0, опустим.
Уравнение (5.11) решается методом последовательных приближе-
ний, так же как это было выполнено при решении уравнений (2.4) в § 2.
58
Зададимся произвольной формой колебаний <р. Эта форма должна
•быть каким-либо образом нормирована, например
?я=1, (5.12)
где —упругий угол закрутки конца лопасти.
Тогда, выполнив операции, задаваемые выражением (5. 11), опре-
делим функцию
г Я Я
f /„ffdr. (5. 13)
J J ^vnp J
Частоту собственных колебаний лопасти на кручение можно опре-
делить из условия нормирования (5. 12)
т2 = ~, (5.14)
Я
где Од — значение функции fl при г = /?.
Задавшись новым значением функции
?=т2» (5.15)
и проделав операции (5.13) и (5. 14) еще столько раз, сколько необхо-
димо для обеспечения потребной точности, получим окончательные зна-
чения v и ср. Как и при определении форм и частот собственных изгиб-
ных колебаний такой метод последовательных приближений приводит
к определению низшего тона собственных колебаний кручения. При оп-
ределении последующих тонов необходимо выполнить условие ортого-
нальности
R
j = (5. 16)
о
Здесь индексом / отмечена форма искомого тона колебаний, а ин-
дексом т формы уже определенных низших тонов. Полагая
(5.17)
получим из условия (5.16) выражения для постоянных коэффициентов
^=4--------------• (5-18)
[<р(т>]2Дг
О
Частоты собственных колебаний последующих тонов определяются
при каждом приближении по формуле
т — 1
По окончании определения всех необходимых для дальнейших рас-
четов форм и частот собственных колебаний необходимо подправить
частоты по формуле (5. 10), учитывающей влияние центробежных сил.
Расчеты форм и частот собственных колебаний лопасти на круче-
ние для реальных вертолетов показывают, что решающее значение при
определении величин частот низшего тона колебаний имеет жесткость
59
системы управления несущим винтом. Почти всегда жесткость лопасти
на кручение оказывается намного выше жесткости системы управле-
ния. На рис. 1.15 приведены формы первого тона собственных крутиль-
ных колебаний лопастей различных вертолетов, находящихся в массо-
вой эксплуатации.
По соотношению между деформациями кручения лопасти и системы
управления несущим винтом при колебаниях по первому тону можно
судить о величине крутильной жесткости лопасти по сравнению с жест-
костью системы управления. Соотношение между этими жесткостями
оценивается коэффициентом а (см. рис. 1. 15). Этот коэффициент опре-
деляет собой долю общего угла поворота конца лопасти вследствие де-
формаций только лопасти.
Рис. 1,15. Формы собственных колебаний лопасти на кручение при раз-
личных соотношениях жесткости лопасти и системы управления
Описанная особенность в соотношении жесткостей лопасти и управ-
ления позволяет в некоторых расчетах применить допущение о том, что
крутильные деформации лопасти малы по сравнению с деформациями
управления, и вводить в расчеты только закрутку лопасти вследствие
деформации управления. Это допущение часто применяется при расчете
флаттера (см. гл. 4 книги первой).
Результаты расчета по изложенной методике позволяют судить о ха-
рактере расположения частот собственных колебаний лопасти на кру-
чение относительно гармонических составляющих аэродинамических
сил. На рис. 1. 16 приведена резонансная диаграмма крутильных коле-
баний лопасти, построенная для одного из существующих вертолетов,
а на рис. 1. 17 — формы первых трех тонов.
В п. 1 этого параграфа уже отмечалось, что переменные внешние
силы, скручивающие лопасть, невелики, и поэтому даже при наличии
резонанса амплитуды крутильных колебаний не становятся опасными
для прочности лопасти. Ввиду этого крутильных резонансов обычно не
стараются избегать и приведенная на рис. 1. 16 резонансная диаграмма
дана только для оценки абсолютной величины частот крутильных ко-
лебаний.
Из рис. 1. 16 следует, что даже второй тон крутильных колебаний
оказывается на рабочих оборотах «раб выше пятнадцатой гармоники
к числу оборотов несущего винта. Частоты последующих топов оказы-
ваются еще выше. Поэтому практический интерес может представлять,
вероятно, только частота первого тона собственных колебаний лопасти
на кручение.
60
Рис. 1.16. Резонансная диаграмма крутильных
колебаний лопасти
Рис. 1.17. Формы первых трех тонов крутиль-
ных колебаний лопасти
61
Все приведенные выше соображения относились к крутильным ко-
лебаниям лопасти несущего винта, рассматриваемой изолировано без
учета тех связей, которые накладывает на колебания конструкция за-
крепления лопасти на втулке. Оказывается, что связь между крутильны-
ми колебаниями отдельных лопастей несущего винта через систему уп-
равления может существенно изменить всю картину колебаний.
4. Определение форм и частот
собственных колебаний несущего винта в целом
На рис. 1. 18 приведена схема системы управления углом установки
лопастей, применяемого на большинстве современных вертолетов. Кон-
структивно эта система выполнена таким образом, что нагружение той
или иной цепи управления зависит от того, какая комбинация сил прихо-
дит на тарелку автомата перекоса от лопастей. Вид этой комбинации за-
висит от формы колебаний несущего винта, т. е. от распределения фаз ко-
Рис. 1. 18. Схема автомата перекоса:
/—рычаг поворота лопасти; 2—горизонтальный шар-
нир; 3—вертикальный шарнир; 4—лопасть; 5—тарелка
автомата перекоса; 6—ползун
лебаний по лопастям. Так, на-
пример, в том случае, когда
все лопасти колеблются с оди-
наковой фазой, нагружается
только цепь управления общим
шагом. Когда противоположно
расположенные лопасти ко-
леблются в противофазе, на-
гружаются цепи поперечного
и продольного управлений. На-
конец, если число лопастей в
несущем винте больше трех,
то возможны такие формы ко-
лебаний, когда все силы, при-
ходящие от лопастей, замыка-
ются на тарелке автомата пе-
этими
ления
редки
Так, например, при вертикальных колебаниях тарелки, возникающих
при деформации цепи управления общим шагом, возбуждаются колеба-
ния несущего винта такой формы, при которой фазы всех лопастей
рекоса.
Возникающие при колеба-
ниях лопастей переменные си-
лы вызывают деформации тех
цепей управления, которые
силами нагружаются. При деформациях отдельных цепей управ-
колеблется и тарелка автомата перекоса, причем колебания та-
навязывают вполне определенные фазы колебаниям лопастей.
одинаковы.
Когда тарелка автомата перекоса при колебаниях наклоняется,
противоположно расположенные лопасти возбуждаются в противофазе.
Таким образом, тарелка автомата перекоса связывает колебания от-
дельных лопастей в несущем винте. В результате оказывается, что ко-
лебания лопастей могут происходить только с вполне определенными
формами колебаний всего несущего винта в целом, причем число таких
форм совпадает с числом лопастей в несущем винте. При этом каждой
Форме колебаний соответствует свое приведенное к осевому шарниру
лопасти значение жесткости управления, зависящее от жесткости той
пепи управления, которая при этой форме нагружается. Соответственно
каждой форме колебаний несущего винта присуще свое значение часто-
ты собственных колебаний лопасти на кручение.
62
Следовательно, у несущего винта с числом лопастей 2Л имеется хл
различных частот собственных колебаний, соответствующих каждому
тону колебаний лопасти на кручение. Каждой частоте собственных ко-
лебаний присуща своя определенная форма распределения углов крут-
ки по длине лопасти, но качественно все формы, соответствующие опре-
деленному тону колебаний не различаются, так например, они имеют
одинаковое число узлов колебаний.
В качестве примера можно привести значения частот собственных
колебаний первого тона для четырехлопастного винта вертолета Ми-4.
Низшие значения частот при нагружении продольного и попереч-
ного управления, отнесенные к рабочим числам оборотов несущего винта
составляют —=3,4 -4-- 3,5. При нагружении цепи общего шага эта
1 V, . ..
же величина принимает значение _»ш — 4,6, а когда все силы от несу-
Яраб
щего винта замыкаются на тарелке автомата перекоса— 1ап =6,6.
^раб
Очень важным обстоятельством является то, что в пределах частот
колебаний, соответствующих гармоникам к числу оборотов несущего
винта, по которым внешние силы имеют заметную величину, лежит толь-
ко первый тон собственных колебаний лопасти на кручение. Все после-
дующие тона колебаний лежат выше и поэтому не представляют прак-
тического интереса.
§ 6. СОВМЕСТНЫЕ ИЗГИБНО-КРУТИЛЬНЫЕ КОЛЕБАНИЯ
ЛОПАСТИ
1. О связи между изгибными и крутильными колебаниями
Выше были рассмотрены свободные изгибные и крутильные колеба-
ния лопасти как две не связанные между собой независимые задачи.
В реальной лопасти крутильные и изгибные колебания всегда связаны.
Насколько эта связь оказывается сильной будет показано ниже. Будем
рассматривать колебания лопасти в пустоте, когда связь между кру-
тильными и изгибными колебаниями осуществляется только за счет
сдвига центров тяжести сечений относительно оси жесткости лопасти и
вследствие кинематической связи через компенсатор взмаха. Использу-
ем методику расчета, построенную на базе метода трех моментов,
описанного в § 4, применительно к расчету изгибных колебаний.
Возможность выполнения расчета частот собственных изгибно-
крутильных колебаний может оказаться полезной конструктору при ре-
шении целого ряда конкретных практических задач.
Так, например, необходимость выполнения такого расчета возника-
ет в тех случаях, когда для устранения резонанса предлагается уста-
новка на лопасти вынесенных вперед балансиров. Здесь имеются в виду
те относительно редкие случаи, когда постановка балансиров предлага-
ется не для устранения флаттера, а для изменения частот собственных
колебаний.
Желание учесть связь между изгибными и крутильными колебания-
ми может возникнуть у конструктора также и в том случае, когда рас-
чет частот собственных колебаний лопасти почему-либо не совпадает
с экспериментом. При этом в ряде случаев может показаться, что это
различие объясняется неучетом этой связи. Можно надеяться, что при-
веденные ниже результаты расчетов облегчат разрешение этих сом-
нений.
63
Нужно, однако, отметить, что расчет частот собственных колеба-
ний в пустоте не может дать ответа на многие вопросы, возникающие на
практике в связи с появлением в лопасти повышенных переменных на-
пряжений с какой-либо частотой и оцениваемых как резонансы, так как
аэродинамические силы могут внести во многих случаях очень сущест-
венные поправки в картину явления.
2. Методика расчета совместных колебаний
Выполнение расчета форм и частот собственных изгибно-крутиль-
ных колебаний значительно упрощается, если рассматривать лопасти
только определенного наиболее распространенного типа, при расчете
которых могут быть использованы следующие допущения:
1. Ось жесткости лопасти есть прямая линия, совпадающая с осью
осевого шарнира.
Принципиально методика расчета не изменится и в том случае, ког-
да эти оси не будут совпадать. Только в расчетные формулы придется
внести ряд дополнительных членов, учитывающих расстояние между
этими осями. Для простоты выкладок предполагаем, что ось жесткости
проходит через ось вращения несущего винта.
2. Плоскость наименьшей жесткости лопасти считается совпадаю-
щей с плоскостью взмаха.
3. Лопасть совершает крутильные колебания вследствие крутиль-
ных деформаций самой лопасти, деформаций системы управления углом
установки лопасти и в результате кинематической связи через компенса-
тор взмаха с колебаниями лопасти в плоскости взмаха.
Эти допущения позволяют представить лопасть в виде невесомой
свободной балки, разделенной на z участков, по краям которых с неко-
торым выносом хц,Т/ расположены грузы с массой mi (рис. 1. 19). Каж-
дый груз кроме массы сосредоточенной в центре тяжести соответст-
вующего элемента лопасти, обладает также некоторым моментом инер-
ции /ц.т/ относительно оси, проходящей через центр тяжести груза и
параллельной упругой оси лопасти.
Изгибную и крутильную жесткости представим в виде ступенчатых
кривых таким образом, чтобы они оставались постоянными на протяже-
нии каждого участка.
64
Наличие компенсатора взмаха приводит к кинематической связи
между изгибными и крутильными колебаниями, которая может быть вы-
ражена формулой
Л1..г,
%= — -*&>. (6-1)
£упр
где ?0 — угол поворота лопасти в осевом шарнире;
Л1КР() —крутящий момент относительно осевого шарнира;
супр —жесткость системы управления углом установки лопасти, при-
веденная к осевому шарниру;
•х —компенсатор взмаха;
₽0—угол поворота лопасти относительно горизонтального шарнира.
Кроме того, несколько меняются граничные условия в комле шар-
нирно закрепленной лопасти при ее колебаниях в плоскости тяги. Эти
условия при наличии компенсатора взмаха могут быть записаны как;
Af0 = zAfltPo, (6.2)
где 7И0 —изгибающий, а Л4кро крутящий момент в комле лопасти.
При составлении дифференциальных уравнений колебаний лопасти
в плоскости взмаха мы применим метод трех моментов в том виде, как
это было изложено в § 4. Применение этого метода к рассматриваемому
здесь расчетному случаю приводит к следующим уравнениям:
V1 Mi-l +glMi+^/+1;
'I ' 1 ' У',/+1 ^_llZ (6.3)
Здесь
Qt, t+i = — У
T (6.4)
Qz_j,z= — У m[yl (где г = 0,1,2,..., z);
ft — вертикальные перемещения точек упругой оси лопасти (см.
рис. 1. 19);
yi — вертикальные перемещения центров тяжести масс иг
Выражения для постоянных коэффциентов az, bi, cit hi и gt даны в
§ 4, см. формулы (4.18) -г- (4. 25).
Перемещения упругой оси ft и центров тяжести элементов лопасти
Уг связаны соотношением
(б-5)
где (pi — углы поворота элементов лопасти вокруг ее упругой оси.
Для определения форм и частот изгибно-крутильных колебаний ло-
пасти к уравнениям (6. 3) следует добавить уравнения крутильных ко-
лебаний.
Крутящий момент, если его считать постоянным по величине на
протяжении каждого участка лопасти, может быть определен как:
г .. г г г
z= -щ257п.т,'Р/+(в22"гл.т/п//+ Swzx„.Tzi/z. (6.6)
‘ ’ i I i i
5 1578
65
По величине крутящего момента могут быть определены и крутиль-
ные деформации лопасти
о
где СГкр;_11У—жесткость на кручение участка лопасти длиной, равной
причем <ро определяется по формуле (6.1).
При использовании метода трех моментов граничные условия зада-
чи учитываются в коэффициентах уравнений системы. Так, в рассматри-
ваемом здесь случае граничное условие (6. 2) приводит к изменению ко-
эффициентов первых двух уравнений системы (6. 3). Для лопасти с шар-
нирным креплением в комле эти уравнения могут быть записаны следу-
ющим образом:
— первое уравнение системы (6.3), из которого определяется зна-
чение р0:
(6,8)
/V01
— второе уравнение системы (6. 3):
(6.9)
Л12 "01
Таким образом, система уравнений, включающая в себя уравнения
(6. 3), (6. 5), (6. 6) и (6. 7), представляет собой систему дифференциаль-
ных уравнений изгибно-крутильных колебаний лопасти. Решение этой
системы позволяет определить формы и частоты собственных изгибно-
крутильных колебаний лопасти, что и входит в задачу расчета.
Если положить, что входящие в дифференциальные уравнения
(6.3), (6.5), (6.6) и (6.7) переменные изменяются по синусоидальному
закону вида
sin Р*’
то эти уравнения могут быть преобразованы в систему алгебраических
уравнений относительно неизвестных, представляющих собой амплитуд-
ные значения прежних переменных. Только в некоторые коэффициенты
этих уравнений войдут сомножителями параметры р2 и у= — . Если
положить р2=1, то эти уравнения могут быть переписаны в виде
А2,_1 + ci -!v!i + d-i Mi+l = bt + «,-«, + .
^крг-1,г=(1-У) +
(6.10)
(6.11)
(6. 12)
66
где
'ц/ = й/-хц.Т/&г>
(6. 13)
l-i-1
т‘У‘-
Входящие в эти уравнения величины подчинены следующим соот-
ношениям:
fi = P^
м{ = Р^М г;
=P2M^v
Ъг=Р2%-
(6. 14)
Систему уравнений (6.10), (6.11), (6.12) и (6.13) удобно решать
методом последовательных приближений. При этом в каждом прибли-
жении должно выполняться уточнение параметра у под заданную в рас-
чете угловую скорость вращения несущего винта ы.
Выполнение последовательных приближений производится в следу-
ющем порядке.
Зададимся некоторой величиной параметра у и произвольной фор-
мой нулевого приближения функций у,0 и <р,0.
Взятые в качестве нулевого приближения функции должны быть
каким-нибудь образом пронормированы, например
уг=1.
После этого по формуле (6.5) может быть получена и функция ft,
Затем по уравнению (6.11) может быть определена величина Мкр , не-
обходимая для решения системы уравнений (6. 10). Одновременно опре-
деляется и Мкр
После решения системы уравнений (6Л0) и определения из пер-
вого уравнения этой системы определяется Ро:
% = 1 - xg0MKPo. (6.15)
Л01
Затем по уравнению (6. 12) определяется О,, а по уравнению (6. 13)
и значения vit которые, кроме того, должны удовлетворять условию
Частота собственных колебаний определяется из условия нормиро-
вания на основании первого соотношения (6. 14) так:
Р2=^-. (6.16)
После этого по соотношениям (6. 14) могут быть определены функ-
ции у{ и фц которые используются для следующего приближения, выпол-
няемого в том же порядке. Одновременно уточняется и параметр у.
5* 67
Такой метод последовательных приближений приводит к определе-
нию частоты и формы низшего тона собственных колебаний. Для опре-
деления следующих тонов используется условие ортогональности, кото-
рое для изгибно-крутильных колебаний имеет следующий вид-
Z
у [т^У^ + )<?<"”] = G. (6.17)
о
Здесь индексом / отмечена форма искомого тона, а индексом т фор-
мы уже определенных низших тонов.
Применение изложенной методики расчета дает вполне удовлетво-
рительные для практики результаты.
Следует отметить, что в тех случаях, когда частоты собственных
колебаний двух последовательных тонов имеют достаточно близкие зна-
чения, этот метод расчета не дает сходящегося решения. Практически,
однако, это обстоятельство не имеет большого значения, так как это мо-
жет быть только в том случае, когда связь между крутильными и изгиб-
ными колебаниями очень слаба и соответствующие формы колебаний
могут быть определены порознь без учета этой связи.
3. Влияние связи между изгибом и кручением
на частоту собственных колебаний
Здесь мы рассмотрим, насколько могут отличаться частоты собст-
венных изгибно-крутильных колебаний лопасти от соответствующих
парциальных частот, т. е. частот, полученных без учета связи между
изгибом и кручением.
Расчеты показывают, что связь между изгибом и кручением оказы-
вает наибольшее влияние на частоты собственных колебаний лопасти
в тех областях, где парциальные частоты изгиба и кручения сближают-
ся. Поэтому следует исследовать только данные, области. Вне этих об-
ластей парциальные частоты лопасти и частоты связанных изгибно-кру-
тильных колебаний практически совпадают.
Известно, что парциальные частоты собственных колебаний изгиба
шарнирно закрепленной лопасти у всех современных вертолетов лежат
в очень узких, вполне определенных, зонах, расположение которых от-
носительно гармоник внешнего возбуждения не может быть существен-
но изменено. На рис. 1.20 эти зоны нанесены на резонансную диаграмму
лопасти. Эта диаграмма построена для области частот, включающих
только ряд первых гармоник к числу оборотов несущего винта, так как
внешние силы, действующие на лопасть с более высокими гармониками,
незначительны по величине и не могут вызвать сколько-нибудь заметных
колебаний лопасти. В эту область попадают только первые три тона
парциальных частотот лопасти на изгиб. Практически только этими то-
нами и приходится интересоваться при проектировании лопасти. Часто-
ты собственных колебаний изгиба могут выпадать из указанных зон
только у винтов с необычным способом закрепления лопастей на втулке.
Например, у винтов с жестким закреплением лопастей или с втулкой на
карданной подвеске.
Парциальные частоты собственных колебаний лопасти на кручение
могут изменяться в более широких пределах, в основном вследствие
различия в жесткостях системы управления несущим винтом, конструк-
ция которой может быть весьма разнообразной. Тем не менее и в отно-
шении величин парциальных частот собственных колебаний лопасти на
кручение можно сделать очень важный вывод, заключающийся в сле-
дующем. В область интересующих нас частот может попасть только
первый тон крутильных колебаний. Второй тон крутильных колебаний
оказывается, как правило, в районе не ниже 15-й гармоники к числу
68
оборотов несущего винта (см. рис. 1-16), т. е. за пределами интересной
для конструктора области. Существенных по амплитуде колебаний с та-
кими частотами обычно не возникает. Поэтому практический интерес с
точки зрения возможности возникновения резонансов имеет только пер-
вый тон собственных колебаний логгасти на кручение.
Здесь стоит вспомнить, что лопасть несущего винта вертолета мо-
жет иметь несколько первых тонов крутильных колебаний с различными
частотами в зависимости от формы колебаний несущего винта в целом
и того, какая цепь управления при этой форме колебаний нагружается.
Рис. 1. 20. Области расположения на резонансной диаграмме частот собст-
венных колебаний первого, второго и третьего тона изгиба и первого тона
кручения для лопастей различных вертолетов
Различие в частотах собственных колебаний этих форм будет опреде-
ляться исключительно разницей в жесткостях нагружаемых цепей
управления.
В полете каждая гармоника внешних сил может возбуждать только
одну вполне определенную форму колебаний. Поэтому при исследова-
нии возможности возникновения резонанса обязательно следует прове-
рять, соответствует ли принятая в расчете жесткость управления той
форме, резонанс с которой возможен. В этом параграфе рассматривают-
ся только собственные колебания системы. Поэтому мы не будем под-
робно останавливаться на этом вопросе.
На рис. 1.20 нанесена область, в которой обычно лежат частоты
первого тона собственных колебаний лопасти на кручение для тех форм
колебаний несущего винта, когда нагружаются цепи циклического уп-
равления и управления общим шагом. У несущих винтов с числом ло-
пастей более трех возможна форма колебаний, при которой все силы,
приходящие от лопастей, замыкаются на тарелке автомата перекоса.
69
Жесткость управления, соответствующая этой форме, оказывается обыч-
но очень высокой. На рис. 1.20 верхняя граница области расположения
крутильных колебаний в этом случае отмечена штрих-пунктирной ли-
нией.
Рассмотрим наиболее распространенный на практике случай, когда
парциальные частоты первого тона изгиба и первого тона кручения сов-
падают по величине в зоне рабочих оборотов несущего винта. Исследу-
ем два варианта распределения центров тяжести лопасти по ее длине.
В обоих вариантах в соответствии с принятыми выше допущениями
будем полагать, что ось жесткости лопасти прямолинейна и совпадает
с осью осевого шарнира втулки. Расстояние до центров тяжести сечений
будем отсчитывать от оси жесткости в процентах к хорде лопасти. Все
Рис. 1.21. Ступенчатая центровка лопасти со сменой
знака в узле первого топа собственных изгибных
колебаний
исследования будем проводить применительно к лопасти вертолета с дур-
алюминовым прессованным лонжероном с постоянной по длине хордой.
Такая лопасть имеет примерно постоянный погонный вес по длине. Ее
хорда составляет около одной двадцатой радиуса несущего винта.
Чтобы результаты расчетов были более наглядными, будем считать,
что при изменениях центровки лопасти массовые моменты инерции ее
сечений относительно оси, проходящей через центры тяжести, не изменя-
ются, т. е. выдерживается положение
т = const.
Вначале рассмотрим случай, когда центровки сечений лопасти по-
стоянны по ее длине, т. е.
Хп = const,
Ц.Т ь
где Ь — хорда лопасти.
Этот вариант распределения центровок следует считать весьма рас-
пространенным на практике. Кроме того, он позволяет в очень нагляд-
ной форме проследить влияние центровки и оценить ее значимость как
фактора связи между изгибными и крутильными колебаниями.
На рис. 1.22 приведена резонансная диаграмма лопасти для этого
случая. Сплошными линиями показаны парциальные частоты изгиба и
70
кручения лопастн, а пунктирными — частоты совместных изгибно-кру-
тильных колебаний, подсчитанные для сдвига центровки относительно
оси жесткости, равного 10% хорды лопасти. Расчеты выполнены для
случая, когда х = 0. Поэтому знак сдвига центровки не имеет значения.
Здесь и ниже мы умышленно рассматриваем очень широкий диапа-
зон изменения центровок для того, чтобы в более четкой форме просле-
дить ее влияние. Практически конструктивные возможности и условия,
накладываемые флаттером, позволяют изменять центровку в очень не-
больших пределах. Обычно у лопастей несущих винтов центровка ме-
няется в пределах от 20% до 25% от хорды лопасти (здесь приводятся
Рис. 1. 22. Резонансная диаграмма лопасти с постоянным по длине сдвигом
центровки на 10% хорды
значения, отсчитываемые от передней кромки лопасти), т. е. весь диапа-
зон изменения центровки составляет всего около 5%1 хорды лопасти.
Поэтому из рассмотрения рис. 1.22 можно сделать вывод, что смещение
центровки, постоянной по длине лопасти, очень слабо сказывается на
значениях частот собственных колебаний.
Во втором рассматриваемом здесь случае распределение центровки
выбрано таким образом, при котором ее влияние оказывается наиболее
сильным при колебаниях с частотой, близкой к парциальной частоте из-
гиба первого тона. Центровка принята постоянной по длине лопасти, но
ее знак изменяется в узле первого тона парциальной изгибной формы.
Ступенчатая центровка может быть создана у лопасти в тех случа-
ях, когда противофлаттерный балансир вводится в конструкцию не по
всей длине, а только на небольшом участке на конце лопасти. Резуль
тэты расчета для этого варианта распределения центровки приведены
на рис. 1.23. Влияние центровки в этом случае довольно сильное. Поэ-
тому при таком ее распределении по длине связь между изгибом и кру-
чением следует учитывать при расчете лопасти.
71
Следует рассмотреть еще влияние перемещаемого по хорде сосредо-
точенного груза. Величину груза примем равной 8% веса лопасти. Это,
вероятно, та максимальная величина груза, который может быть ре-
ально закреплен на лопасти. Наиболее эффективным местом закрепле-
ния такого груза с точки зрения создания сильных факторов связи из-
гибных и крутильных колебаний является та точка лопасти, где переме-
щения в плоскости тяги максимальны. Поэтому рассмотрим случай с за-
креплением груза на конце лопасти.
Рис. 1.23. Частоты собственных изгибно-крутильных колебаний лопасти при сту-
пенчатом законе изменения центровки по длине лопасти со сдвигом на 10 и 2Оя/о
по хорде от оси жесткости
На рис. 1.24 показаны результаты расчета для этого случая.'Влияние
сосредоточенного груза на частоту собственных колебаний при больших
его выносах можно считать существенной, однако, применение такого
средства для устранения резонанса вряд ли может быть рекомендовано
конструктору. Тем не менее установка груза может рассматриваться в
качестве временного средства лечения лопастей, испытывающих боль-
шие переменные напряжения вследствие резонанса.
Последний параметр, который должен быть рассмотрен как фактор
связи между изгибом и кручением, это компенсатор взмаха. Для оцен-
ки его влияния на величину частот собственных изгибно-крутильных
колебаний были проделаны расчеты с компенсатором взмаха к= 1,0. Это
наибольшие значения компенсатора взмаха из когда-либо применявших-
ся на практике. Все приведенные выше данные были получены с х=0.
72
Из проделанных расчетов следует, что влияние компенсатора взма-
ха ничтожно. Однако учет компенсатора взмаха может быть в какой-то
f
20% сосредоточенного на конце
собственных изгибно-крутильных
Рис, 1.24. Влияние сдвига по хорде на 10 и
лопасти груза весом 10 кг на величину частот
колебаний лопасти
мере оправдан, поскольку он вносит некоторое уточнение в форму рас-
пределения изгибающего момента в комле лопасти.
§ 7. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ЛОПАСТИ
1. Применение метода Б. Г. Галеркина для расчета деформаций лопасти.
Определение статических деформаций лопасти
Задача об определении деформаций лопасти сводится к решению
уже описанного выше дифференциального уравнения (1-9), вывод кото-
рого дан в § 1.
*
<
где
ная
[Е/у"]"- \Ny']' + my=T, (7.1)
Т — распределенная по радиусу и изменяющаяся во времени погон-
внешняя нагрузка на лопасть.
Выше в § 2, 3 и 4 мы рассматривали решение однородного уравне-
при Т=0, описывающего свободные колебания лопасти. Здесь бу-
рассмотрены вынужденные колебания лопасти, когда Т есть неко-

ния
ДУТ .
торая периодическая функция, изменяющаяся с частотой v.
В частном случае, когда v=0, задача сводится к определению ста-
тических деформаций лопасти от постоянной по времени нагрузки То-
73
♦
Наиболее простым способом решения уравнения (7. 1) является ме-
тод Б. Г. Галеркина.
Для иллюстрации применения метода Б. Г. Галеркина к определе-
нию деформаций лопасти рассмотрим вначале статическую задачу, ког-
да внешняя нагрузка не изменяется во времени. При этом у = 0 и урав-
нение (7. 1) может быть записано как
[Ely"]"—[Nу']'= То. (7.2)
Представим деформации лопасти в виде:
У=2М'Л- (7.3)
i
где yj — формы собственных колебаний лопасти по /-му тону;
— некоторые коэффициенты, которые мы будем в дальнейшем на-
зывать коэффициентами деформаций лопасти. Коэффициенты
деформаций во всех дальнейших выкладках с применением ме-
тода Б. Г. Галеркина будут играть роль обобщенных коорди-
нат системы.
Подставим выражение (7.3) в уравнение (7.2), умножим все члены
уравнения поочередно на £/<°>, у<г\ у& и т. д. и проинтегрируем их по ра-
диусу лопасти.
В силу ортогональности функций г/® проделанная операция преоб-
разует диффернциальное уравнение (7. 2) к ряду независимых уравне-
ний вида:
(7.4)
где
R к
Q = J Е1[у"]^г+^[у']^г-
° (7-5)
A^T^dr.
6
Величину Cj будем называть обобщенной жесткостью лопасти при
деформациях по форме /-го тона в поле центробежных сил. Из рассмот-
рения формул (7.5) следует, что обобщенная жесткость лопасти Cj
равна удвоенной потенциальной энергии, накопленной лопастью при ее
упругих деформациях в поле центробежных сил по нормированной фор-
ме /-го тона. Величину Aj будем называть обобщенной внешней силой,
деформирующей лопасть по форме /-го тона. Величина обобщенной
силы А, равна удвоенной работе внешних погонных сил То на деформа-
циях лопасти по нормированной форме /-го тона ее собственных
колебаний.
Из уравнения (7. 4) могут быть определены коэффициенты дефор-
маций лопасти дд
А,
(7-6)
после чего по формуле (7. 3) определяется и форма статических дефор-
маций лопасти.
Чем больше взять в расчете форм собственных колебаний, тем точ-
нее будет определена форма деформаций. Однако для целей практики
оказывается достаточным ограничиться первыми четырьмя тонами ко-
лебаний лопасти.
74
Если известны коэффициенты деформаций dj, то нетрудно опреде-
лить изгибающие моменты и изгибные напряжения в лопасти. Они опре-
деляются по формулам:
,w=v
8/з<7>-
(7- 7)
Здесь Л1<’> и сг(Л — формы распределения изгибающих моментов и
изгибных напряжений при нормированных деформациях лопасти по /-му
тону ее собственных колебаний.
Входящие в формулы (7. 7) величины подчиняются соотношениям:
t
I
I
Л!
о = — •
W
W '
(7.8)
где IF — момент сопротивления сечений лопасти.
2. Определение деформаций лопасти
при периодическом приложении внешней нагрузки
Рассмотрим случай, когда внешняя нагрузка изменяется по закону;
Т=Т^ sinvL (7.9)
Для решения этой задачи также применим метод Б. Г. Галеркина
Представив деформации лопасти в форме (7.3), подставим выражения
(7.3) и (7.9) в уравнение (7. 1), умножим все члены полученного урав-
нения поочередно на и проинтегрируем по длине лопасти. В силу
ортогональности функций у® получим ряд независимых дифференци-
альных уравнений вида
mySJ.-|-C/8/ = 71/siti v/, (7.10)
где
и
m.j —\ dr•,
\ (7.И)
Aj = J T-.y^dr.
Величину rrij будем называть эквивалентной массой лопасти при ее
колебаниях по форме /-го тона. Если формы колебаний у^ нормированы
таким образом, что уУ} =1, то rrij есть эквивалентная масса лопасти,
приведенная к се концу. Из первой формулы (7. И) также следует, что
эквивалентная масса лопасти равна ее удвоенной кинетической энергии,
когда элементы лопасти перемещаются со скоростью у®.
Для определения установившегося движения положим
= 8U) sin V/.
Подставив это выражение в уравнение (7. 10) и сократив все члены
уравнения на величину sin vt, получим уравнение
~^mj^^Cj^ = Aj, (7.12)
75
Л
откуда значение амплитуды деформаций лопасти оказывается равным
Л‘ V—v <7-13)
Ч1-^)
Нетрудно заметить, что отношение Cjlrrij равно частоте собственных
колебаний /-го тона лопасти. Действительно, если положить в уравнении
(7.12) А/ =0, то значение v в этом случае будет определять частоту сво-
бодных колебаний лопасти и может быть получено из уравнения (7. 12):
v2 = p2j=-Cjlm.j. (7.14)
В соответствии с выражением (7.6) отношение AjlCj определяет
величину деформаций в случае, если бы нагрузка Л была бы приложе-
на статически.
Выражение (7. 13) удобно представить в форме
8(Л=лви>, (7.15)
где коэффициент, определяющий величину деформации при ста-
тически приложенной внешней силе 7\; в дальнейшем этот
коэффициент будем называть коэффициентом квазистатических
деформаций лопасти;
Хд —коэффициент динамического увеличения амплитуды колебаний.
Для рассматриваемого случая
Ч = —(7.16)
Из выражения (7. 16) следует, что при резонансе, когда частота
вынужденных колебаний v равна частоте собственных колебаний pj, ко-
эффициент динамического увеличения амплитуды обращается в беско-
нечность. Этот результат закономерен для задач, в которых рассматри-
ваются вынужденные колебания без демпфирования.
В действительности лопасть вертолета, работающая в воздушной
среде, испытывает при колебаниях значительное аэродинамическое демп-
фирование. Аэродинамическое демпфирование ограничивает амплитуду
колебаний лопасти при резонансе и не может не учитываться, если в за-
дачу расчета входит определение колебаний лопасти и в условиях ре-
зонанса.
При определении колебаний лопасти вертолета, когда колебания
возникают под действием аэродинамических сил, очень трудно строго
отделить силы аэродинамического демпфирования от аэродинамических
сил, вызывающих колебания лопасти. Такое разделение может быть вы-
полнено только условно. Однако в ряде упрощенных методов расчета
такое разделение используется. Поэтому мы здесь такой подход воспро-
изведем более подробно.
3. Упрощенный подход к расчету вынужденных колебаний лопасти
Предположим, что внешние аэродинамические нагрузки, действую-
щие на упругую лопасть в полете, можно разделить на две части: на
внешние нагрузки, действующие на лопасть, и на силы аэродинамическо-
го демпфирования. Будем приближенно полагать, что внешние нагруз-
ки, действующие на упругую лопасть, совпадают с нагрузками, действу-
ющими на абсолютно жесткую на изгиб лопасть. Тогда для выполнения
расчета остается только определить силы аэродинамического демпфи-
рования.
76
Обычно силы аэродинамического демпфирования определяются для
режима с осевым обтеканием несущего винта, после чего используется
предположение, что и на всех других режимах полета с косым обтека-
нием несущего винта коэффициенты аэродинамического демпфирования
не изменяются.
На режиме с осевым обтеканием несущего винта сила аэродинами-
ческого демпфирования может быть определена, исходя из следующего.
При колебаниях элементы лопасти перемещаются со скоростью у.
Вследствие этого углы атаки всех элементов лопасти изменяются на ве-
личину
Да = —.
аг
При изменении угла атаки на элементы лопасти действуют допол-
нительные силы аэродинамического демпфирования
Лемп = у с’б^2г2Да= —~-с^гу. (7.17)
Предположим, что аэродинамическая нагрузка Т может быть пред-
ставлена состоящей из двух составляющих:
(7-18)
где Тж — аэродинамическая нагрузка, действующая на жесткую лопасть;
7'демп —дополнительная нагрузка от аэродинамического демпфирова-
ния, возникающая при упругих колебаниях лопасти.
Тогда уравнение (7. 1) можно переписать в следующей форме:
[f/г/"]"-[W]'+/ny+-y с*аЬи>гу—Тж. (7.19)
Рассмотрим колебаниям лопасти от синусоидальной составляющей
аэродинамической нагрузки, изменяющейся по закону
ТЖ =^Т; sin vf.
Если представить деформации лопасти в форме (7. 3) и применить
к уравнению (7. 19) метод Б. Г. Галеркина, то можно прийти к системе
обыкновенных дифференциальных уравнений относительно коэффици-
ентов деформаций dj. Отдельные уравнения этой системы будут связа-
ны между собой членами, в которые входит интеграл:
я
Dim=^bry<J>yWdr,
О
где y(f> и г/<т> формы собственных колебаний, соответствующие различ-
ным тонам (/#=т).
В упрощенных методах расчета интегралы Djm обычно полагаются
равными нулю, хотя такое допущение во многих случаях не может быть
оправдано.
Если все же принять это допущение, то в результате применения
метода Б. Г. Галеркина получим ряд независимых дифференциальных
уравнений вида
тЛ (7.20)
77
где коэффициент определяет величину аэродинамического демпфиро-
вания:
br [y^]2dr. (7.21)
Разделив все члены уравнения (7. 20) на rrij, получим уравнение
вида
8Z + 2/г/В, + р% = р^ s in vt, (7. 22)
где
2/;, = —--;
♦ Ост — "2 •
Cj
Обычно для характеристики величины демпфирования использует-
ся коэффициент относительного демпфирования
Его величина применительно к аэродинамическому демпфированию
лопасти вычисляется по формуле
R
(7.23)
4- pj ГЛ] J
7 О
Решение уравнения (7.22), выполненное таким же образом, как
это было сделано выше при решении уравнения (7. 10), приводит к
формуле
UJ)
Од —^д°'-т ,
где коэффициент динамического увеличения амплитуды колебаний
Таким образом, решение рассмотренной здесь задачи складывает-
ся из определения квазистатических коэффициентов деформаций и
последующего их умножения на величину коэффициента динамического
увеличения амплитуды Лл.
Такой подход страдает некоторыми неточностями в силу искусст-
венного разделения аэродинамических сил на две составляющие по
формуле (7.18), недостаточно обоснованного допущения о том, что
Djm=Q и приближенного определения коэффициентов аэродинамическо-
го демпфирования для режима с осевым обтеканием несущего винта.
Поэтому в § 8 и 9 будут изложены методы расчета, в которых приведен-
ные здесь упрощения не используются.
Однако такой упрощенный подход очень хорошо описывает качест-
венную картину явлений, наблюдаемых при колебаниях лопасти.
78
4. Амплитудная диаграмма колебаний лопасти
Выше, в § 3, уже указывалось, что для оценки характера колебаний
лопасти широко применяется резонансная диаграмма лопасти. Резо-
нансная диаграмма позволяет оценить, насколько частоты собственных
колебаний лопасти отлича-
ются от частот возбуждения
и не имеется ли опасность
6
возникновения резонансных
колебаний. Однако в тех
случаях, когда частоты соб- 5
ственных колебаний и часто-
ты возбуждения отличаются 4
не сильно, интересно оце-
нить, к каким амплитудам 3
колебаний лопасти это мо-
жет привести. Такую оценку г
можно сделать, используя
амплитудную диаграмму ко- ?
лебаний лопасти. Эта диа-
грамма, построенная для
лопасти с обычными массо- °
выми И жесткостНЫМИ ха- рис> 1,25. Амплитудная диаграмма колебаний
рактеристиками, приведена лопасти
на рис. 1. 25.
По оси абсцисс на этой диаграмме отложена частота возбуждения,
отнесенная к угловой скорости вращения несущего винта,
— V
V—----.
(А
(7.25)
По оси ординат отложены коэффициенты динамического увеличе-
ния амплитуды колебаний. Диаграмма построена только для трех пер-
вых тонов упругих колебаний лопасти с использованием коэффициентов
демпфирования, вычисленных по формуле (7.23).
5, Расчет колебаний в случае, когда фаза приложения внешней нагрузки
переменна по длине лопасти
В п. 3 этого параграфа были приведены формулы для случая, когда
внешняя нагрузка представлена в виде
7^=7, sin vi.
Такая форма записи нагрузки возможна только в том случае, если
фаза ее приложения по длине лопасти постоянна. Как правило, такой
картины при колебаниях лопасти вертолета не возникает. Фаза внеш-
ней нагрузки меняется по длине лопасти, и поэтому нагрузка должна
быть представлена в форме
7Д. - "T cos v/— 7» sin у/, (7.26)
где составляющие внешней нагрузки Г, и 7, изменяются по длине ло-
пасти по разным законам.
79
Подставив выражение (7, 26) в уравнение (7. 19) и применив метод
Б. Г. Галеркина, полагая, что Djm — 6, получим:
ШуВу Cftj — Aj cos v/ A] sin v/,
(7.27)
где
Положим
Тогда
— X —
Aj = J 7\z/(rt dr\
о
_ R _
8/ = 8*s * 7) В cos vt 8д7> sin v/.
(7.28)
Bt7) =
ид ----
v2 '1 - _
1 Вет’ 2n7
v2 I 2
1 — 2
Pi
—.ЙЛ
Pi "
- v2
+ 4л7- —
Pi
(7.29)
о
1 - 4] + 2n>
7^
2 „ v2

°д
где
Pi
i - 4
pj
Ai
UCT —~T~ — 2
Cj Pjmi
s (?) _~Ai _ Л
°CT ---------
Cj Pjmi
(7.30)
есть коэффициенты квазистатических деформаций лопасти.
Формулы (7. 29) позволяют определить динамические коэффициен-
ты деформаций лопасти, если известны квазистатические коэффициенты
деформаций, полученные по аэродинамическим нагрузкам и 7’,.
6. Аэродинамическая нагрузка на жесткую лопасть
В полете на лопасть вертолета действуют переменные нагрузки с
частотами, кратными оборотам несущего винта. При этом, как уже гово-
рилось, наибольшие по величине переменные напряжения в лопасти
вызывают первые шесть — восемь гармоник аэродинамической нагрузки
к оборотам несущего винта. Более высокие гармоники оказываются
обычно настолько малыми, что не вызывают заметных напряжений
в лопасти даже при резонансах.
Вычисление переменных аэродинамических нагрузок на лопасть
представляет известные трудности. Эти трудности связаны прежде все-
го с необходимостью определения переменного поля индуктивных ско-
ростей, учета нелинейности в зависимости аэродинамических коэффици-
ентов от угла атаки профиля, числа М и связи нагрузок с крутильными
колебаниями лопасти. Учет этих особенностей рассматривается в соот-
ветствующих параграфах. Здесь мы составим формулы для определе-
ния переменных аэродинамических нагрузок на жесткую на изгиб и
кручение лопасть при следующих предположениях.
80
а) Будем считать, что угол притекания потока к профилю лопасти
Ф (рис. 1.26) невелик и поэтому можно приближенно полагать:
<D = arctg-^^, (7.31)
и х V х
где ф — угол притекания потока;
Ux и иу — взаимно перпендикулярные составляющие относительной
скорости потока, лежащие в плоскости, нормальной к оси
лопасти (см. рис. 1.26). При этом скорость Ux параллельна
плоскости вращения винта.
Полагая также, что созФ = 1, будем считать, что искомая нагрузка
Т, действующая в плоскости взмаха, не отличается от нагрузки Тсу,
Рис. 1.26. Схема обтекания жесткой на изгиб и кручение лопасти
перпендикулярной к притекающему к профилю лопасти потоку
(рис. 1.26;.
б) Будем полагать, что величина относительной скорости потока
U, обтекающего профиль, мало отличается от величины Ux:
U=UX. (7.32)
в) Будем считать, что при определении нагрузок в плоскости взма-
ха сопротивлением профиля можно пренебречь и полагать, что сх=0.
Коэффициент подъемной силы профиля су будем полагать линейно
зависящим от угла атаки профиля а:
(7.33)
г) Индуктивную скорость потока V, протекающего через несущий
винт, будем считать постоянной по всей площади, ометаемой винтом:
о = const. (7.34)
При этих предположениях существенными по величине оказывают-
ся только постоянная часть и первые две гармоники аэродинамических
сил и то только на средних и больших скоростях полета вертолета. Бо-
лее высокие гармоники оказываются небольшими и их вычисление с пе-
речисленными допущениями не представляет интереса.
Используя эти допущения, погонную аэродинамическую нагрузку
на лопасть можно определить по формуле
(7.35)
Положим далее, что угол атаки профиля
а = ®г+^?, (7.36)
где <рг — угол установки профиля лопасти в сечении на расстоянии г от
оси вращения.
6 1578
81
Тогда формула (7. 35) может быть преобразована к виду:
Т=-^^Ь[ъи^ихиу]. (7.37)
Для абсолютно жесткой на изгиб лопасти, подвешенной ко втулке
при помощи горизонтального шарнира, входящие в формулу (7. 37) ско-
рости могут быть определены по следующим формулам:
77 = <о/? (г -}- р. sin ф);
I 7 \ (7.38)
Uy^4>R Хо —рсозф^о----р0 I.
\ 01 /
Здесь
р0 —угол взмаха лопасти относительно горизонтального шарнира;
^0=^-производная угла 4 по времени;
ot
Хо—относительная скорость потока, протекающего через несущий
винт;
Хо = ц tg ав + г>о,
где ав — угол атаки несущего винта в осях вала;
у о— постоянная по диску несущего винта индуктивная скорость по-
тока, отнесенная к со/?.
Угол установки лопасти можно записать как
фг=9о+Дф—81 sin-ф—О2созф—хро, (7.39)
где 90 — угол установки лопасти на относительном радиусе г = 0,7 или
другом радиусе, принятом для отсчета 90, когда ро=О;
Дф — геометрическая крутка лопасти;
61 и 02 — углы циклического управления лопастью, задаваемые автома-
том перекоса.
Если представить маховое движение лопасти в виде ряда
30=а0-2(«ncosa<H6„stawp) (7.40)
л
и удержать в нем только две первые гармонические составляющие, по-
скольку последующие при принятых допущениях малы, то выражение
(7.37) может быть преобразовано к виду:
А с’е^2/?2 P0+2(pncosa-J>+P„sina<p) ,
п
где
Л = ь рх* -1- -ф А Р;
Л~ рАг0+[г2+ — ) Ь\ — А ?га2 4- рг*Ь2j;
А, = & ^Х*+2 рг®, + (- г2 -Д А- 1*2 - ргад2 - A- ргЬ2
Р2=~ь [ - А. ц2<?г 4- ^ra\+X (г*+А [*2) а2 + 2?2&2 ];
= b Г - А- [12а0 4 - 2?2ст., -ф * (г 2Ц- А ^2 I
(7.41)
(7.42)
82
В процессе выполнения этих преобразований была использована
подстановка, позволяющая осуществить переход к так называемому
эквивалентному несущему винту.
Эквивалентным несущим винтом называется винт, вал которого
мысленно повернут относительно реального винта на такой угол, при
котором те же углы атаки сечений лопасти достигаются без циклическо-
го управления углом установки лопасти. Все формулы, выписанные для
эквивалентного винта, могут быть без изменений использованы для ре-
ального винта, не имеющего автомата перекоса. Эквивалентному несу-
Рис. 1.27. Распределение гармонических составляю
щих аэродинамической нагрузки по радиусу лопасти
при ц=0.28
щему винту обычно также придают свойства винта, не имеющего ком-
пенсатора взмаха. В этом случае эквивалентность формул соблюдается
только с точностью до первых гармоник махового движения.
Преобразование формул для аэродинамических нагрузок примени-
тельно к эквивалентному несущему винту было выполнено с применени-
ем следующих подстановок:
—j— J
Ь\=Ьг V-4®
S — '-о h- (x^i ®i), '
где фист—истинный угол установки лопасти с учетом действия
компенсатора взмаха на том се радиусе, который принят
для отсчета этого угла;
а*. Ь\ и коэффициенты махового движения и относительная ско-
рость протекания у эквивалентного несущего винта.
Более высокие гармоники аэродинамической нагрузки мы здесь
рассматривать не будем.
На рис. 1. 27 показаны постоянная часть и косинусоидальная и си-
нусоидальная составляющие первых двух гармоник аэродинамической
6* 83
нагрузки для типичной лопасти вертолета, получение по формулам
(7.42) для режима горизонтального полета вертолета при р = 0,28.
На рис, 1.28 и 1.29 эти нагрузки сложены и показана суммарная
относительная аэродинамическая нагрузка Р, действующая на лопасти
в продольной плоскости винта при ф = (У и ф=180° (рис. 1.28) и в по-
перечной плоскости при ф = 90° и ф = 270° (рис. 1.29).
вуЮЩая на лопасти в продольной плоскости несущего винта
7. Определение коэффициентов махового движения лопасти
Для определения аэродинамических нагрузок по формулам (7.42)
необходимо знать коэффициенты махового движения жесткой на изгиб
лопасти.
Коэффициенты махового движения могут быть определены из диф-
ференциального уравнения (7. 1), если представить решение уравнения
в виде:
У^лУ['\ (7.44)
где — форма колебаний лопасти по нулевому тону.
Для жесткой лопасти эта форма колебаний совпадает с прямой ли-
нией.
1-/г.ш/Я’
84
Если расстояние от оси вращения до горизонтального шарнира равно
нулю (/г.ш = 0), то

(7. 45)
что справедливо как для жесткой, так и для упругой лопасти (см. § 4).
Положив /г.ш = 0, подставим выражение (7. 45) в дифференциальное
уравнение (7.1) и применим к нему метод Б. Г. Галеркина. Эта опера-
ция приводит к дифференциальному уравнению маховых колебаний
лопасти
7(?o+“0 = J Tdr,
(7.46)
где /—момент инерции лопасти относительно горизонтального шарнира.
Рис. 1.29, Относительная аэродинамическая нагрузка, действую-
щая на лопасти в поперечной плоскости несущего винта
Уравнение (7. 46) может быть также получено из условия равенства
нулю момента всех сил относительно горизонтального шарнира,
Подставив выражения (7.40) и (7.41) в уравнение (7.46) и при-
равняв коэффициенты при одноименных гармонических функциях ази-
мута, получим систему уравнений, из которой могут быть определены
все коэффициенты махового движения. Эту систему уравнений запишем
в виде таблицы (см. табл. 1. 6)
85
Ta,$jiu,ura, 1.6
ч* — ъг. ф
-1-^с Уу+У+т./АУ
fiB ^.8 -JCXB
= 8 f
-Ji в lo С) -2А -2^
У2с -/18 2А 1о
Каждое уравнение полученной системы представляет собой сумму
произведений некоторых коэффициентов, записанных в клетках
табл. 1.6, на неизвестные коэффициенты махового движения лопасти,
входящие одновременно в несколько уравнений и вынесенные по верти-
кали в специальную строку, помещенную сверху таблицы. Известные
коэффициенты каждого уравнения занимают в табл. 1. 6 одну строку.
В правой части таблицы в специальной графе выписаны коэффициенты
Ф, составляющие правую часть уравнений. Незаполненные клетки таб-
лицы соответствуют коэффициентам, равным нулю.
При составлении таблицы использованы следующие обозначения:
1
А = J" br^dr;
о
В = j* bAdr,
6
i _
С = J' brdr.
о )
1 _ _
= J brsvrdr;
О
1 _ _
Bf = f br^fdr,
о
i _
(У — br/rdr.
б
(7.47)
(7.48)
Массовая характеристика жесткой лопасти у определяется следую-
щим выражением;
,__с°РА0,7#4
' 2?
(7-49)
При решении этой системы уравнений оказывается, что коэффициен-
ты а2 и Ь2 значительно меньше коэффициентов а0, а’ и Ь*. Поэтому ими
можно пренебречь при определении коэффициентов а0, Ь*г и а’. Это до-
86
лущение приводит к простым формулам для определения коэффйциёН
тов махового движения лопасти
Л--(Х2С
41 "7^7
° ,8?L ? к (4ЛВ!,; + т-(2ЛСЧ+ ^-’}1;
18Ч-8Д2у£ L \ • * / \ »«/J
Н-4Л^ + у-^ Ы2 (2ЛС?-Зф- а0)1 ,
1О —оЛ2ух [_ \ ’* / \ rz /J
где
(7.50)
8. Упрощенный расчет упругих колебаний лопасти
На основе принятых в этом параграфе упрощающих допущений мо-
жет быть построен расчет упругих колебаний и изгибных напряжений
в лопасти на режимах горизонтального полета вертолета. При этом та-
кой расчет, естественно, не может дать положительных результатов
в приложении к малым скоростям полета, когда основную роль играют
переменные нагрузки, связанные с неравномерным полем индуктивных
скоростей, и при больших скоростях, когда нельзя не учитывать нели-
нейность в зависимости аэродинамических коэффициентов от угла ата-
ки и явления, вызванные сжимаемостью потока.
В соответствии с приведенными выше формулами расчет удобно
производить в осях эквивалентного несущего винта.
Расчет упругих колебаний лопасти выполняется в следующем по-
рядке:
1. Прежде всего определяются параметры режима полета, на ко-
тором должен быть произведен расчет напряжений. Это следующие па-
раметры:
а) угол атаки несущего винта аЭКв;
б) угловая скорость вращения несущего винта ы;
в) высота и скорость полета, представленные в расчете коэффици-
ентами О и |Л.
2. Вычисляется относительная скорость протекания потока через
несущий винт по формуле
X* -= a tg а в J-Сг -, (7.51)
4 1>2+(Хо)2
где Ст — коэффициент тяги несущего винта.
3. Подсчитывается угол установки лопасти в контрольном сечении,
относительно которого задается геометрическая крутка лопасти.
87
Без учета сил, связанных со второй гармоникой махового движения,
этот угол может быть определен по формуле
?ИСт = ‘
В
(7. 52)
Здесь
1
О
1 -
D = J bdr,
о
1_
— j" b\ydr,
6
(7.53)
/ — коэффициент тяги;
з- коэффициент заполнения несущего винта.
4. По формулам (7. 50) вычисляются коэффициенты махового дви-
жения лопасти, а по формулам (7. 41) и (7. 42) внешние нагрузки на
лопасть.
5. Для определения изгибных напряжений необходимо произвести
расчет форм и частот собственных колебаний лопасти.
6. Если такой расчет произведен, то по формулам (7. 30) могут быть
определены квазистатические коэффициенты деформаций по различным
тонам колебаний лопасти от постоянной части первой и второй гармоник
аэродинамической нагрузки.
Подставив выражение (7.41) в формулу (7.30), получим значения
квазистатических коэффициентов деформаций по j-му тону колебаний
лопасти.

= . Y/ [ _^Biao(А} + „1_ ] .
У/ р’оС/ + 2«В?-(ду —all;
(7.54)
— — •?/ Г‘—~—— [12сД а24-2Д/£>21
Pj L \ ~ / J
= 4 . у, Г _ X ^С1аа + (хД; - 2ДА + X (Д; + А Ь,2
Здесь индекс, стоящий внизу при коэффициентах квазистатических
деформаций лопасти, соответствует порядку гармоники аэродинамичес-
ких сил. Индексом j отмечены коэффициенты, относящиеся к /-му тону
колебаний лопасти, yj— массовая характеристика лопасти при дефор-
мациях по j-му тону:
1/2с“еА0.7/?г
Y/ =----------------
т,-
(7. 55)
88
Для входящих в формулы (7.54)
обозначения:
интегралов приняты следующие
J brbfn dr-,
О
1___
В; — j bry^ dr,
о
1__ _
Cj = § by<!> dr\
0
1 _ _
dr-,
0
1 _ __
= J br^ dr,
c}=\b^ty{1}
0 I
J
(7.56)
где yV> — форма колебаний лопасти по /-му тону, нормированная таким
образом, что при r== I у^= I.
7. Запишем деформации лопасти в следующей форме:
у = [с0 — сг cos ф — sin ф — с2 cos 2| — d2 sin 2р] yW -ф
-ф[е0 — ei cos'?—fi зшф —e2cos 2)—- /2sin 2ф] //(2) -ф
-ф[£0 — gi собФ —A] sintp —g2c°s 2ф — A2sin2)] £/(3)-ф... (7. 57)
Здесь для определения деформаций лопасти помимо формы нулево-
го тона, которая в случае Го = О совпадает с прямой линией, использова-
ны три первых тона собственных колебаний лопасти //2) и нор-
мированные таким образом, что при r=R Тогда коэффициенты
деформаций лопасти, входящие в формулу (7.57), могут быть опреде-
лены через квазистатические коэффициенты деформаций в соответствии
с (7.29).
В качестве примера выпишем формулы для определения коэффици-
ентов деформаций по первому тону.
С0---8(Р
(7.58)
d}
Gi2 —1 — .. — (о — /1 х
-7ГГ’ ч’2'" «'!S
w2-
со2
89’
d2=~
1- — SP - 2пг —Ц’
Pl
4ш212
1 — —ЙГ + 4n?
Pl
Pl
-,4<о2
1 р\
(7.58)
Если динамические коэффициенты деформаций известны, то легко
могут быть определены любые компоненты действующих в лопасти на-
пряжений. Об этом более подробно будет сказано в п. 17 § 8 и в п. 8 § 9.
В изложенном здесь упрощенном методе расчета помимо исходных
допущений, касающихся физических свойств модели лопасти, принятых
при выводе уравнения (7. I) и при вычислении правой части этого урав-
нения, сводящегося к формуле (7. 35), используется множество дополни-
тельных допущений вычислительного характера, применяемых почти на
всех этапах расчета. Все эти упрощения, хотя и делают метод расчета
вполне пригодным для выполнения вручную, но вносят множество не-
точностей, которые плохо поддаются количественной оценке. Все же,
несмотря на этот недостаток, описанный упрощенный метод расчета об-
ладает очень важным преимуществом — большой наглядностью. По су-
ти дела все результаты расчетов, получаемые по другим более совершен-
ным методам, оцениваются и анализируются на основе зависимостей,
представленных здесь в упрощенном виде.
Однако даже с применением всех этих упрощений расчет по этому
методу вручную требует работы одного расчетчика в течение не менее
месяца. Современные темпы проектирования лопасти не могут быть
обеспечены при расчете с такой длительностью. Поэтому расчет упругих
колебаний лопасти, используемых для выбора ее параметров в процессе
проектирования, может быть выполнен только на быстродействующих
электронно-счетных машинах. Естественно, что в этом случае нет не-
обходимости в применении допущений, облегчающих процесс вычис-
лений.
Поэтому в § 8 будет изложен метод расчета, основанный на тех же
исходных допущениях, если не считать учета переменных индуктивных
скоростей, но выполняемый без каких-либо допущений вычислительного
характера.
§ 8. РАСЧЕТ ИЗГИБНЫХ НАПРЯЖЕНИЙ В ЛОПАСТИ
НА МАЛЫХ И СРЕДНИХ СКОРОСТЯХ ПОЛЕТА
1. Особенности, отличающие режимы полета
на малых н средних скоростях
Малые и средние скорости вертолета рассматриваются здесь как ре-
жимы, достаточно удаленные от срыва, на которых, кроме того, могут
не приниматься во внимание явления, связанные со сжимаемостью пото-
ка. Исходя из этого, при расчете аэродинамических нагрузок прибли-
женно полагается, что
= (8.1)
Это предположение существенно упрощает выкладки, необходимые
при составлении расчетных формул.
so
С другой стороны режимы полета на малой скорости могут быть вы-
делены как режимы, особенно опасные для усталостной прочности, на
которых часто возникают наибольшие по величине переменные изгибные
напряжения в лопасти.
Эти соображения оправдывают применение метода расчета пригод-
ного только для малых и средних скоростей полета и не пригодного для
больших скоростей и тех режимов, на которых определяющими стано-
вятся явления, связанные с нелинейным характером зависимости су =
= f(a) и с сжимаемостью потока.
Следует отметить, что допущение (8. I) не всегда оказывается спра-
ведливым для режимов полета на малых скоростях. В тех случаях, когда
на лопасти несущего винта приходится чрезмерно большая нагрузка,
расчет следует производить с учетом нелинейной зависимости аэродина-
мических коэффициентов от угла атаки профиля. Метод такого расчета
будет рассмотрен в § 9.
О перегрузке лопастей можно судить по величине коэффициента
тяги несущего винта t. Расчеты показывают, что допущение (8. I) мо-
жет быть использовано на режимах малых скоростей без внесения су-
щественных погрешностей в результаты пока £<Х), 18.
На режимах с вертикальными перегрузками таких, как, например,
режим торможения вертолета перед посадкой, нарушение этого нера-
венства возможно и у тех винтов, у которых на установившемся режиме
полета оно соблюдается. Все эти соображения следует учитывать при
выборе метода для расчета.
2. О методе расчета напряжений
В этом параграфе излагается наиболее распространенный на прак-
тике метод расчета переменных напряжений, основанный на примене-
нии метода Б. Г. Галеркина с разложением коэффициентов деформаций
в ряд Фурье по гармоникам.
В связи с возможностью применения этого метода для расчета ре-
жимов малых скоростей во все расчетные формулы введены гармони-
ческие составляющие индуктивного поля и задача о деформациях
лопасти решается совместно с задачей определения индуктивных ско-
ростей.
Однако такой подход не является обязательной принадлежностью
предлагаемого здесь метода. При расчете напряжений на средних ско-
ростях полета, когда переменные индуктивные скорости вносят нс очень
существенные уточнения в результаты, они могут не учитываться. В этом
случае метод расчета очень сильно упростится.
Если принять допущение (8. 1), то аэродинамическая нагрузка ока-
жется линейной функцией перемещений элементов лопасти и задача
расчета изгибных деформаций сведется к решению линейного дифферен-
циального уравнения (1.9). Для решения этого уравнения и применя-
ется метод Б. Г. Галеркина. Деформации лопасти представляют-
ся в виде ряда по собственным функциям, а временные коэффициенты
этого ряда разлагаются в ряд Фурье. Применение метода Б. Г. Галер-
кина преобразует дифференциальное уравнение колебаний лопасти к
системе алгебраических уравнений относительно неизвестных коэффици-
ентов ряда Фурье, и определение изгибных деформаций лопасти сводит-
ся к вычислению этих неизвестных коэффициентов. Такой метод расчета
и будет здесь изложен.
3. О допущениях при определении индуктивных скоростей
При расчете изгибных напряжений на малых скоростях полета,
когда их величина определяется главным образом степенью неравно-
91
мерности поля индуктивных скоростей, очень важно, на основе каких
допущений это поле определяется.
В первой книге (гл. 2, § 5) уже говорилось, что индуктивные скорос-
ти могут быть представлены в виде суммы внешних и собственных ин-
дуктивных скоростей. Это деление несколько условно, но оказывается
очень полезным, так как позволяет дать оценку влияния отдельных со-
ставляющих индуктивных скоростей по аналогии с тем, что уже извест-
но для крыла самолета, и тем самым оправдать принятие некоторых,
важных для дальнейшего изложения допущений.
Обтекание лопасти вертолета в потоке с неравномерным полем ин-
дуктивных скоростей аналогично обтеканию крыла самолета при полете
в неспокойном воздухе, когда крыло непрерывно встречает воздушные
потоки с различной скоростью и направлением. При вращении несуще-
го винта лопасть тоже встречает на своем пути неравномерное иоле ско-
ростей, только это поле вызвано не атмосферной турбулентностью,
а индуктивным воздействием всей вихревой системы винта. Это поле по
аналогии с крылом называется обычно внешним полем индуктивных
скоростей в отличие от поля скоростей, индуцируемых в районе лопас-
ти ее собственными вихрями, стекающими с нее в связи с изменением
циркуляции по времени и по радиусу лопасти. Эти вихри создают
значительные индуктивные скорости у лопасти только потому, что они
находятся от нее на очень близком расстоянии. При удалении на рас-
стояние 20—30° по азимуту несущего винта их влияние на аэродинами-
ческую нагрузку на лопасть пропадает.
Так же, как и при расчете крыла, для определения аэродинамичес-
ких нагрузок на лопасть можно использовать «гипотезу стационарнос-
ти». По этой гипотезе предполагается, что при нестационарном обтека-
нии профиля на него действуют такие же нагрузки, как если бы возник-
шая в рассматриваемый момент времени картина обтекания оставалась
бы неизменной во времени. В соответствии с этой гипотезой, при расче-
те аэродинамических нагрузок на крыло учитывается изменение угла
атаки только от внешнего поля скоростей, а влиянием собственных ин-
дуктивных скоростей пренебрегается.
Применим аналогичный подход к лопасти. При определении аэро-
динамических нагрузок будем учитывать только внешнее поле индук-
тивных скоростей.
При расчете этого поля могут быть приняты некоторые дополни-
тельные допущения, связанные с особенностями вихревой системы на
режиме малых скоростей.
На рис. 1.30 показан вид в плане на систему свободных вихрей, сте-
кающих с концов лопастей пятилопастного несущего винта на режиме
полета со скоростью, соответствующей ц = 0,05. На этой скорости пере-
менные напряжения в лопастях несущего винта достигают максималь-
ных значений.
Приведенная на этом рисунке картина является неполной, так как
на ней показаны только свободные вихри, сошедшие с концов лопастей
и не показаны вихри, сошедшие со всех других радиусов лопасти. Не
показаны также радиальные (поперечные) вихри. Однако даже из этой
картины можно составить представление о том, насколько тесно распо-
ложены вихри на режимах малых скоростей. Эта особенность вихревой
системы приводит к тому, что индуктивные воздействия отдельных вих-
рей сливаются и проявляются в виде общей неравномерности всего поля
скоростей. Резкие пики индуктивных скоростей, характерные для вих-
ревой системы, с редко расположенными вихрями при этом не возника-
ют. Поэтому на малых скоростях полета, особенно для винтов с большим
числом лопастей, индуктивные скорости можно определить из теории,
рассматривающей схему несущего винта с бесконечным числом лопастей.
92
влияние примыкающих вихрей и, следова-
нп
Рис. 1.30. Вид в плане на систему вихрей, сте-
кающих с концов лопастей на режиме ц=0,05
С увеличением скорости полета система свободных вихрей начина-
ет растягиваться и становится более редкой. В том же направлении из-
меняется вихревая система и с уменьшением количества лопастей в не-
сущем винте. Расчет по схеме с бесконечным числом лопастей стано-
вится при этом менее точным.
При переходе от несущего винта к схеме с бесконечным числом ло-
пастей местный эффект от непосредственно примыкающих к лопасти
вихрей настолько сильно ослабляется, что приближенно можно считать,
что эта схема не учитывает
тельно, определенное, по
ней поле скоростей прак-
тически совпадает с по-
лем внешних индуктив-
ных скоростей.
Изложенные выше
соображения приводят к
выводу, что для расчета
упругих колебаний лопас-
ти на малых скоростях
полета может быть ис-
пользована вихревая тео-
рия, основанная на схеме
с бесконечным числом ло-
пастей.
В полете на малых
скоростях обычно измеря-
ют переменные напряже-
ния, в которых большую
часть составляют высокие
гармоники к числу обо-
ротов несущего винта,
лежащие обычно в диапазоне от 4 до 6-й. Поэтому к методу определения
индуктивных скоростей приходится предъявить еще одно очень важное
требование. Этот метод должен определять поле индуктивных скоростей
с точностью по меньшей мере до 6-й гармоники, что возможно только
в том случае, если и значения циркуляции определяются с точностью до
той же гармоники. Следовательно, все методы, не удовлетворяющие
этому требованию, отпадают и не могут быть использованы при расчете
упругих колебаний.
Выше уже было сказано, что здесь будет изложен метод расчета
напряжений, в котором все переменные величины разлагаются в ряд
Фурье по гармоникам. Поэтому оказывается удобным применить и ме-
тод определения поля индуктивных скоростей, в котором эти скорости
определяются также в виде разложения по гармоникам.
Этим требованиям наилучшим образом удовлевторяет теория
В. Э. Баскина [3] (см. также § 5 гл. 2 первой книги). Поэтому эта теория
и будет использована в этом параграфе при расчете напряжений.
4. Расчетные формулы для определения поля индуктивных скоростей
Рассмотрим систему формул, предложенных В. Э. Баскиным для
расчета поля индуктивных скоростей в плоскости вращения несущего
винта.
Представим поле этих скоростей в виде суммы его гармонических
составляющих. При этом как суммарные скорости потока, так и гармо-
93
НийеСкйе составляющие этой скорости, отнесем к окружной скоростй
вращения концов лопастей несущего винта ыР.
х = У- tg аз + Хо + 2 cos И'О-t- Хл sin «0). (8.2)
п
Здесь X —отнесенная к со/? суммарная скорость потока, протекаю-
щего через несущий винт;
Хо —постоянная часть индуктивной скорости также отнесен-
ная к со/?;
Хл и Хл —гармонические составляющие индуктивной скорости;
у — азимутальный угол лопасти, отсчитываемый от оси, сов-
падающей по направлению с хвостовой балкой одновин-
тового вертолета;
___ V cos ав
!Л— <->А‘
где У —скорость полета вертолета;
ав — угол атаки несущего винта в осях вала.
Погонную аэродинамическую нагрузку, действующую на лопасть,
представим в виде
Т=±с^Ь0^Р, (8.3)
2 J
где с" —угол наклона зависимости су= /(а), которая здесь принимается
линейной в форме (8.1);
Q—плотность воздуха;
^017 —значение хорды лопасти на относительном радиусе г = 0,7.
Входящее в это выражение значение Р будем в дальнейшем назы-
вать относительной аэродинамической нагрузкой.
Представим значение Р в виде:
Р=Р0-|-2 (Pmcosmy4-Pmsinm0). (8.4)
m
Гармонические составляющие скорости /.« представляются в виде
суммы так называемых частичных индуктивных скоростей, каждая из
которых индуцируется только одной гармоникой аэродинамической на-
грузки:
= 3 ^ЛЛ1;
m
В этих выражениях полные суммарные составляющие индуктивных
скоростей имеют один индекс п снизу, а частичные—два индекса п пт.
Значения частичных гармонических составляющих индуктивных
скоростей определяются по следующим выражениям:
— при я —0:
О
— при п ф 0:
+ (- i)'V+m] J(pmy
о
(8.6)
лт= ~ 1х”~т ~ •
О
94
Если степень, в которую возводится т, отрицательна (п—zn<0),
то в формулах (8.6) следует положить тя-т=(—х)т~п-
Входящие в формулы (8. 6) коэффициенты имеют следующие зна-
чения:
1
l^f12 + Хоср
Ef*2 + ^оср — I ^-сср I
3
gab0,7
nR
(8.7)
где
о—коэффициент заполнения несущего винта;
гл — число лопастей в несущем винте.
Значение средней по радиусу лопасти скорости протекания Хоср оп-
ределяется из формулы
Xocp^HtgaB+2 f lordr.
(8-8)
1 = _
fpm(o)J„,(^)dQ dz,
Для определения входящих в уравнения (8.6) функций J (Рт)
> и J(Pm) из теории В. Э. Баскина вытекают следующие формулы:
/(Pm)=Jj„(zr)z
О
JAzbz
о
, где Jn(zr) и Jm(zr) — функции Бесселя первого рода с порядком п и т
J соответственно;
г—параметр интегрирования.
Здесь для того, чтобы уточнить, по какому параметру производится
1 интегрирование, введено новое обозначение для относительного радиуса
лопасти q. Это обозначение будет использоваться только при вычисле-
нии интегралов (8.9).
5. Преобразования расчетных формул в частных случаях
(8.9)
В частных случаях выражения (8. 6) значительно упрощаются. Так
в случае, когда n=m = 0
— (8-10>
8 ” г
Для дальнейших выкладок особенно важным является результат,
полученный для случая, когда п~т. Оказывается, что совпадающие
95
гармоники аэродинамической нагрузки и индуктивной скорости одно-
значно связаны выражениями:
(8.U)
где
W"];
о J
±С^А0[1_(_1)пг2п].
О v
(8.12)
Такая форма выражений делает целесообразным разделение состав-
ляющих индуктивных скоростей на два типа. На основные составляю-
щие индуктивной скорости, индуцируемые той же гармоникой аэродина-
мической нагрузки, что и гармоника индуктивной скорости, и на побоч-
ные составляющие, вызванные всеми остальными гармониками аэроди-
намической нагрузки.
Это разделение позволяет записать выражения (8. 5) в виде
(8.13)
где основные составляющие индуктивной скорости определены по вы-
ражениям (8. 11), а сумма всех побочных составляющих индуктивных
скоростей введена в уравнения при помощи новых обозначений^ и К";
т^п—1
\п= v \т+ 2
rw=0 т=л + 1
тп—л—1
АП Х? ^-пт +
л . пт I пт*
т—0 тЛ“Л4-1
(8-14)
I
Здесь zr — число гармонических составляющих индуктивных ско-
ростей, учитываемых в расчете.
При zz=O первые члены этих выражений следует положить равно-
му нулю, а при n = zT, то же следует сделать со вторыми членами. При
составлении уравнений для расчета напряжений индуктивные скорости
будем представлять в виде (8. 13).
6. Численное определение величин интегралов J(Pm) и J (Рт)
Когда т^=п вычисление интегралов (8.9) представляет известные
трудности. Для определения величин этих интегралов В. Э. Баскиным
предложен метод, в котором составляющие аэродинамической нагрузки
аппроксимируются при помощи тригонометрических многочленов. Для
этого нужно определять значения Рт на заданных заранее радиусах ло-
пасти, не совпадающих с теми, которые используются во всем расчете.
Применительно к излагаемому здесь методу это не очень удобно. Поэ-
тому здесь будет использован другой способ, более подходящий для дан-
ного случая, в котором вычисление интегралов J(Pm) и J(Pm) произво-
ле
дится примерно по той же форме, в какой вычисляются интегралы при
расчете напряжений в лопасти. Для этого лопасть разбивается на от-
дельные участки, в пределах которых аэродинамическая нагрузка пред-
ставляется в виде, пригодном для интегрирования. При этом естествен-
но разбить лопасть на одни и те же участки во всех случаях как при
расчете напряжений, так и при вычислении интегралов (8.9). Предста-
вим нагрузку Рт(о) таким образом, чтобы она на каждом участке ин-
тегрирования изменялась по закону
(8.15)
_ е*
Здесь q—текущее значение относительного радиуса лопасти; пос-
ле выполнения интегрирования и подстановки пределов
значение q без индекса встречаться в формулах не будет.
qa — то же значение относительного радиуса, но с индексом k,
означает, что рассматриваемый радиус совпадает с ра-
диусом, на котором вычислена относительная аэродина-
мическая нагрузка Рм (gft)
Рис. 1.31. Форма относительной аэродинамической нагрузки,
принятая для расчета индуктивных скоростей
В дальнейшем, как уже было сказано, будем отличать относитель-
ные радиусы рь, на которых берется значение аэродинамической нагруз-
ки от относительных радиусов г{, на которых вычисляется индуктивная
скорость. Это позволит избежать возможной путаницы.
Будем считать, что относительная аэродинамическая нагрузка из-
меняется по закону (8. 15) на протяжении каждого участка, ограничен-
ного относительными радиусами
и q = + рл-ы)-
На рис. 1.31 сплошной ступенчатой линией показана форма распре-
деления относительной аэродинамической нагрузки по длине лопасти,
в которой она представляется для расчета индуктивных скоростей выра-
жением (8.15) в случае т = 0. Такой вид представления аэродинамиче-
ской нагрузки может, конечно, внести некоторые погрешности в значения
индуктивных скоростей. Однако расчеты, проделанные для оценки вели-
7 1578 '97
чины этой погрешности, показали, что она невелика и не может внести
существенных изменений в результаты расчета.
Если подставить значение относительной аэродинамической нагруз-
ки, выраженной в форме (8. 15), в выражение подынтегральной функции
уравнения (8.9), то внутренний интеграл в правой части этого уравне-
ния может быть представлен в виде некоторой суммы определенных ин-
тегралов:
1 _ _ <о*+оА+1>
\ Рт (б) Jm (^) \ Qm+1 Jm (ZQ) dQ. (8. 16)
n*' ь 0S -
0 k 112(0^+^)
Входящие в это выражение определенные интегралы могут быть
вычислены аналитически (см. 11]. Подставив в полученные выражения
пределы интегрирования, можно записать:
\ Ря(е)4(ге)^улЛ4+1к^). (8.17)
J z \ 2 )
о к
где
л __ + 8^+1 Рт (8а) Рт (8*+1)
й о ~и+1
z 8ft
nm+l
Sk+1
Подставив выраженное таким образом значение внутреннего интег-
рала в уравнения (8.9), получим:
7(7’m) = J J„{zr)z
О
Или если записать в более простой форме:
к
где
(п) = Jn (zri) Л1+1 (z• - +29iitl) dz.
0
(8. 18)
(8. 19)
(8. 20)
Интеграл (8. 20) является разрывным интегралом, носящим назва-
ние интеграла Вебера и Шафхейтлина 111]. Его аналитическое выраже-
ние в зависимости от соотношения между гг и VzfQfc+pfi+i) имеет следу-
ющий вид:
Если ± (Qftlcft+i)<r„ то
к О
98
Если ^-(е*+ёй+1)>г/, ТО
°-* (Й) =- рл (*Й) Ли-н^ g* ~t2g--1) =
О
-„/ /и+2 + п \
______________' \ 2 }__________х
f г »+2+«. t 27, yi |8 22)
L 2 2 \0А + Qk+i/ J
Здесь Г —гамма-функция с различными аргументами,
F — гипергеометрическая функция от аргументов а, р, у, z.
Эти аргументы, как видно из выражений (8.21) и (8.22), могут
иметь разные значения в зависимости от соотношения между гг- и
(ел + Qfe+i)- Так, например, в выражении (8. 21)
т -J- 2 + п
а —-------!:
2
|3_ т + 2 — п
н— ~ >
y = zn-[-2;
z__+e»+i
При расчете на электронно-цифровых машинах эти функции легко
программируются. Поэтому их вычисление не представляет никаких
трудностей.
7. Допущения, принятые при определении аэродинамических сил
При определении аэродинамических нагрузок помимо допущения
(8.1) применяются те же допущения, которые использовались при оп-
ределении нагрузок на жесткую лопасть (§ 7 п. 6), за исключением до-
пущения (7. 34).
1. Будем считать, что угол притекания потока к профилю лопасти
Ф невелик и что поэтому можно приближенно полагать;
®=arctg^^^, (8.23)
и X
где Ф— угол притекания потока;
Ux и ^ — взаимно перпендикулярные составляющие относительной
скорости потока, лежащие в плоскости, нормальной к упру-
гой оси лопасти (рис. 1.32); при этом скорость Ux параллельна
плоскости вращения винта.
2. Будем считать, что величина относительной скорости потока V,
обтекающего профиль, мало отличается от величины Ux. Поэтому будем
полагать, что U~UX.
3. Будем считать, что при определении нагрузок в плоскости взмаха
(плоскость, проходящая через ось вращения несущего винта) сопротив-
лением профиля можно пренебречь и полагать, что сж = 0.
у*
99
4. Полагая, что собФ=1 будем считать, что нагрузка в плоскости
взмаха не отличается от нагрузки, перпендикулярной к притекающему
к профилю лопасти потоку (см. рис. 1. 32).
Рис. 1.'32. Схема обтекания лопасти, принятая при рас-
чете напряжений на малых скоростях полета
8. Расчетные формулы
При использовании допущений, указанных в п. 7, значение относи-
тельной аэродинамической нагрузки Р, входящее в уравнение (8.3), мо-
жет быть определено по формуле:
P = + (8.24)
где Ъг—величина хорды лопасти на рассматриваемом радиусе,
_ _ отнесенная к хорде на радиусе г = 0,7;
Ux и Uy — те же составляющие относительной скорости потока, что
и в выражении (8.23), но отнесенные к окружной ско-
рости концов лопастей aR:
ту , , о 1 • (8‘25)
Л/₽ = Х — p,cos2) ₽----у.
u>R
Здесь
X —относительная скорость потока, протекающего через несущий
винт; эта скорость определяется по выражению (8.2);
// — перемещения упругой оси лопасти в плоскости, перпендику-
лярной плоскости вращения, от которой эти перемещения
и отсчитываются;
? = у' — угол наклона упругой оси лопасти.
Штрихом здесь, обозначается дифференцирование по радиусу лопас-
ти, а точкой — по времени.
Угол установки лопасти может быть записан в форме
ср = е04-До-0]sinф— 02созф — х0р0. (8. 26)
Здесь 0О —угол установки лопасти на относительном радиусе г = 0,7
или другом радиусе, принятом для отсчета б0, когда угол
поворота лопасти в горизонтальном шарнире Ро равен нулю;
Дер — геометрическая крутка лопасти;
0] и 02 —углы циклического управления, задаваемые автоматом пере-
коса;
х —компенсатор взмаха;
₽0 —угол поворота лопасти в горизонтальном шарнире.
100
Представим деформации лопасти в форме
У=^1У(}),
(8. 27)
где 8;-— коэффициенты деформации лопасти, соответствующие у'-му
тону ее собственных колебаний; эти коэффициенты являются
функциями времени и поэтому называются также временными
множителями.
y{i> формы собственных колебаний лопасти в пустоте, нормирован-
ные таким образом, что у<Р — Ц,
Разложим временные множители 6; в ряд Фурье по гармоникам.
Тогда деформации лопасти можно будет представить в виде;
У = \ «о-2 (a„cos^ + ^sinzzi)]p(°)4-
+ ко — 2 (слcos n^da sin /гф)] у^ -|-
-гко-2 (^coszz^ + /„sin^)lpP)4-
+ Г go — 2(gncoszz'i + A„sin/z^)l-z/<3)4-... (8.28)
Этот вид записи решения является продолжением традиционной
формы записи махового движения лопасти (7. 40).
Продифференцировав (8. 28) по радиусу и по времени и подставив
у вместе с его производными и выражениями (8.2)_и (8.26) в (8.25),
а затем составленные таким образом формулы для Ux и Uy—в (8.24),
получим выражение, из которого можно определить все гармонические
составляющие относительной аэродинамической нагрузки Р.
Эти составляющие можно представить в форме
pn = ~br [fn + кл-1 -k+i)];
К. = к [1 + + -к fx (ХЛ_1 - кп+1) ] .
(8. 29)
Здесь fn и fn — некоторые функции, определяющие величину той
части аэродинамической нагрузки, которая не зависит от величины ин-
дуктивных скоростей.
Если теперь индуктивные скорости и представить в виде сум-
мы основных и побочных составляющих, а основные составляющие вы-
разить через Рп и Рп по выражениям (8. 11), то значения Рп и Рп ока-
жутся как в левой, так и в правой части уравнений (8.29).
101
Определив из этих уравнений значения Рп и Рп, получим следую-
щие выражения:
(8.30)
где
14- ’
О 9
(8.31)
! + [1-(-1А2пНг
О 9
Значения Вп и B,t мы будем в дальнейшем называть эквивалентны-
ми хордами лопасти, так как при расчете они играют ту же роль, что
и действительные хорды и стоят в формулах (8. 30) на тех же местах,
где в формулах (8. 29) стоят значения Ъг.
Таким образом, гармонические составляющие аэродинамических
нагрузок, с учетом переменных индуктивных скоростей, следует опреде-
лять, вводя в формулы только побочные составляющие индуктивных
скоростей, а вместо действительных — эквивалентные хорды лопасти.
Величины эквивалентных хорд лопасти могут быть различными в зави-
симости от режима полета и порядка определяемой гармоники аэроди-
намической нагрузки. Однако они оказываются всегда меньше действи-
тельных хорд. Следовательно, все гармонические составляющие аэроди-
намических нагрузок оказываются меньше тех значений, которые они
имели бы, если бы основные составляющие индуктивных скоростей рав-
нялись бы нулю, и во столько раз, во сколько эквивалентные хорды
меньше действительных. Введение эквивалентных хорд приводит к
уменьшению всех составляющих аэродинамической нагрузки как воз-
буждающих, так и демпфирующих колебания лопасти. Поэтому умень-
шаются и значения относительных коэффициентов аэродинамического
демпфирования, которые определяют амплитуды колебаний при резо-
нансах. Это приводит к тому, что вдали от резонанса переменные дефор-
мации лопасти уменьшаются, а при резонансе остаются примерно та-
кими же, как и при расчете без учета этого эффекта.
Выражения типа (8.30), выписанные для всех гармонических сос-
тавляющих аэродинамической нагрузки, оказываются взаимосвязан-
ными через составляющие индуктивных скоростей. Следовательно, они
представляют собой некоторую сложную систему уравнений относитель-
но неизвестных нагрузок, которая может быть разрешена только в том
случае, если известны значения и fn. А эти значения зависят от вели-
чины коэффициентов деформаций лопасти. Поэтому для решения этой
системы уравнений необходимо составить уравнения для определения
коэффициентов деформаций. Это будет выполнено ниже.
Если расписать подробно входящие в уравнения (8. 30) значения
fn и /п, то выражения для гармонических составляющих аэродинами-
ческой нагрузки можно представить в форме табл. 1. 7.
_ Выражение для каждой гармонической составляющей нагрузки Рч
и Рп занимает в таблице одну строку и представляет собой сумму про-
изведений коэффициентов, записанных в клетках таблицы, на неизвест-
ные множители, входящие одновременно в несколько выражений и вы-
102
несенные по вертикали в специальную строку, помещенную вверху таб-
лицы. Эти множители, как уже говорилось выше, мы называем коэффи-
циентами деформаций лопасти. В правой части таблицы выписан ряд
членов f6n, fan, и /*, не связанных с неизвестными коэффициентами
деформаций. _
Чтобы определить значения Рп и Рп нужно сумму произведений
членов каждой строки на неизвестные коэффициенты деформаций, сло-
женную с членами, не зависящими от коэффициентов деформаций, еще
умножить на значения Вп и Вп. Эти величины для памяти выписаны в
левой части таблицы. _
Количество членов, входящих в выражения для Рп и А, зависит от
числа учитываемых в расчете гармоник и тонов собственных колебаний.
В табл. 1. 7 выписаны выражения для случая, когда в расчете учитыва-
ется только два тона и четыре гармоники переменных сил.
В программах, которые используются при расчетах на электронно-
цифровых машинах, учитывается обычно четыре тона собственных ко-
лебаний и шесть — восемь гармоник переменных сил.
9. О переходе к эквивалентному несущему винту
Чтобы показать возможность перехода к эквивалентному несущему
винту при составлении табл. 1. 7 использовано равенство:
которое справедливо только в случае, когда расстояние от оси вращения
до горизонтального шарнира /г.ш равно нулю.
Если теперь воспользоваться известными формулами для коэффи-
циентов махового движения и угла атаки эквивалентного несущего
винта:
а*—а1 —
6* = 6i4xai-e,;
tg аЭхв=4е«в + ^1 - ei>
то выражения для Рп и Рп можно будет несколько упростить, введя
в первую строку значения а\ и 6* вместо a-i и Ьь При этом коэффициен-
ты окажутся равными нулю, а значения углов в i и 62 вообще не бу-
дут входить в уравнения. Другими словами, известное положение о том,
что нагрузки на лопасть не зависят от отклонения тарелки автомата
перекоса, когда /г.ш = 0, в выражениях табл. 1.7 полностью соблюдается.
Однако возникающие при переходе к эквивалентному несущему
винту упрощения настолько несущественны, что не оправдывают допу-
щения о том, что /г.ш = 0. Поэтому.в дальнейшем будем рассматривать
колебания лопасти только в осях вала и понятием об эквивалентном
несущем винте пользоваться не будем.
10. Основные допущения, используемые при расчете изгибных напряжении
При расчете изгибных напряжений в лопасти используем все те до-
пущения, которые были приняты при выводе дифференциального урав-
нения колебаний лопасти в плоскости тяги (1.9). Представим лопасть
в виде растянутой центробежными силами N упругой балки. Параметры
этой балки — ее погонную массу т и изгибную жесткость Е1 — будем
считать непрерывно распределенными по длине лопасти.
103
Кроме того, примем следующие допущения:
1. Будем считать, что плоскость наименьшей жесткости лопасти сов-
падает с плоскостью взмаха, .поэтому изгибаться в плоскости взмаха
лопасть будет только под действием сил, действующих в этой плоскости.
2. При определении нагрузок в плоскости взмаха не будем учиты-
вать крутильных деформаций лопасти (об учете крутильных деформа-
ций см. "§ 7 гл. 4 первой книги).
3. Будем рассматривать обычный тип несущего винта с шарнирно
подвешенными лопастями, причем расстоянием от оси вращения до го-
ризонтального шарнира пренебрегать не будем, т. е. положим /гш=#0.
Не будем также учитывать силы трения в шарнирах подвески лопасти.
11. Дифференциальное уравнение колебаний лопасти и его решение
При использовании этих допущений расчет изгибных напряжений
сведется к решению дифференциального уравнения, вывод которого дан
в § 1 этой главы:
[£Iy"]"— [Ny']'~j-my = T.
(8.32}
При рассматриваемом закреплении лопасти граничные условия
могут быть записаны так:
уо=О; [W]/?=0;
[W']o = 0; [W]; = 0.
(8.33),
Входящее в правую часть уравнения (8. 32) значение погонной аэ-
родинамической нагрузки определяется по формулам (8.3), (8.4) и по
табл. 1. 7.
Подставив в это уравнение решение в форме (8.28) и применив
к нему метод Б. Г. Галеркина, получим систему алгебраических уравне-
ний относительно неизвестных коэффициентов деформаций. Эту систему
уравнений представим в форме табл. 1. 8.
Каждое уравнение полученной системы представляет собой! сумму
произведений некоторых коэффициентов, записанных в клетках табли-
цы, на неизвестные коэффициенты деформаций, входящие одновремен-
но в несколько уравнений и вынесенные по вертикали в специальную
строку, помещенную сверху таблицы. Известные коэффициенты каждо-
го уравнения занимают в таблице одну строку. Справа от таблицы
в специальном столбце выписаны коэффициенты Фп и Фп, представля-
ющие собой правую часть уравнений.
В табл. 1. 8 так же как и в табл. 1. 7 и 1.9 имеются незаполненные
клетки. Это означает, что коэффициенты уравнений, для которых эти
клетки предназначены, равны нулю.
12. Определение коэффициентов левой части уравнений табл. 1. 8
Для определения коэффициентов левой части уравнений в програм-
ме расчета должен быть создан специальный оператор. Этот оператор
должен выдавать значения всех коэффициентов любого уравнения сис-
темы. Чтобы сделать этот оператор возможно более простым, разделим
всю таблицу коэффициентов на ряд зон по числу тонов собственных
колебаний, используемых в расчете. Этими зонами объединим в отдель-
ные группы те коэффициенты, которые имеют сходный путь образования
при применении метода Б. Г. Галеркина и могут быть подсчитаны по
одним и тем же формулам.
Преобразование дифференциального уравнения (8. 32) с помощью
метода Б. Г. Галеркина к системе алгебраических уравнений табл. 1.8
состоит из следующих операций:
104
1. В дифференциальное уравнение (8.32) подставляется решение
в форме (8. 28), в которое входят различные формы собственных колеба-
ний. Если входящие в решение (8. 28) формы пометить индексом /, то
все члены полученного в результате этой операции уравнения могут
быть разделены на несколько групп, каждая из которых характеризует-
ся определенным индексом I.
2. Затем все члены уравнений умножаются поочередно на те же
формы собственных колебаний у11'1. В результате этой операции образу-
ется уже система уравнений, причем каждое уравнение этой системы
отличается от других формой тона собственных колебаний _г/(/,,на кото-
рую были умножены все члены уравнения. Поэтому полученные таким
образом уравнения нумеруются нами по значениям индекса I.
3. Следующим действием метода Б. Г. Галеркина является интегри-
рование всех функций, полученных в результате предыдущих операций
по длине лопасти. В результате этой операции все члены уравнений, яв-
лявшиеся раньше функциями радиуса лопасти, становятся постоянными
коэффициентами.
4. После этого каждое полученное таким образом уравнение может
быть разделено на целый ряд более простых уравнений, если приравнять
между собой все коэффициенты, стоящие при одноименных значениях
cos mp и sin «ф. В результате этой операции каждое уравнение с номе-
ром I превратится в целое семейство уравнений. Входящие в это семей-
ство отдельные уравнения в табл. 1.8 закоординированы индексом i.
Кроме того, каждая пара уравнений, относящаяся к одноименным гар-
моникам, отмечена индексом п, равным порядку соответствующей гар-
моники.
Анализируя полученную таким образом систему алгебраических
уравнений можно заметить, что все одноименные коэффициенты урав-
нений расположились в табл. 1.8 по диагоналям. Причем такое рас-
положение повторяется во всех зонах, соответствующих различным ин-
дексам / и I. При этом следует оговориться, что из этого правила име-
ются отдельные исключения, которые легко можно заметить при рас-
смотрении табл. 1. 8.
Используя введенные выше индексы I, п, J и I, оказывается возмож-
ным составить общие формулы для всех коэффициентов, входящих в ле-
вую часть уравнений табл. 1. 8. При составлении этих формул будем
пользоваться также специальными функциями fi(a) и /2(a), которые
принимают следующие значения в зависимости от четности и величины
их аргумента:
1 при а четном;
/1(Д)= „
О при а нечетном;
Л(«) =
при а = 0;
при а -/-О.
Эти формулы имеют следующий вид:
R=nfi (г ф-1) 4- (г)
n/j (г)(х'4-1)
105
М = ^7i W (i +1) В,;
и=(/+1) (i) в{-
L==-^^JCB
К=- ^Нл.
(8.34)
Здесь
где
zj = xo%7’«
S(y>—угол поворота в горизонтальном шарнире при колебаниях
по нормированной в соответствии с (8.27) форме /-го тона
собственных колебаний;
У/—массовая характеристика лопасти при
тону:
__g^e^o,7^2 .
v 2^кв ’
колебаниях по /-му
(8.35)
тВКЕ — эквивалентная масса лопасти при ее колебаниях по форме
/-го тона:
R
тэкв = у т |у/)рд(Г;
о

в частном случае, когда / = 0 и можно положить у<М — г, выражение
для у0 совпадает с общепринятым выражением (7.49) для массовой
характеристики жесткой лопасти (7.49);
Pj — частота собственных колебаний лопасти по форме J-го тона;
в процессе выполнения выкладок значение частоты приписано
выражению
R R
f £/[(/)"Frfr+ [(/)']2rfr
/>2=°---------ъ----5-----------; (8. 36)
| т [/]2<Zr
и — угловая скорость (или число оборотов несущего винта в зави-
симости от того, в каких единицах определяется pj); отноше-
ние ру/<» должно быть безразмерной величиной.
Другие входящие в формулы (8.34) величины, имеют следующие
значения:
B^r^ydr-
О
1
в, = f B(i) ry'dr,
О
C^B^ydr,
О
BiiyryJtfdr,
О
(8.37)
106
и
G^B^y'dr;
О
о
(8.37)
Здесь В'('>—эквивалентная хорда лопасти, определяемая по формулам
(8.31) и имеющая, следовательно, различные значения
в зависимости от номера уравнения:
BG) — Bn при I четном;
ВО) = Вп при i нечетном;
у и у — формы собственных колебаний лопасти, тон которых
определяется значением индексов J и 7.
Буквенные обозначения этих форм отмечены сверху чертой. Это
означает, что они нормированы таким образом, что ук=1. В то же вре-
мя значения первой производной от этих форм при дифференцировании
по радиусу лопасти |у не отмечены чертой. Это означает, что эти про-
изводные взяты от форм колебаний у}, нормированных таким образом,
ЧТО £/£=/?.
Формулы (8.34) позволяют определить строчку коэффициентов К,
L, Л1, JV, Л, Q, S, Т, U, L, К для любой зоны табл. 1.8, если заданы ко-
ординаты этой зоны / и I и номер уравнения в зоне I, Таким образом,
задавая последовательно различные значения /, I и i и обращаясь
к оператору, включающему в себя действия, предусмотренные формула-
ми (8. 34), можно определить все коэффициенты левой части уравнений
табл. 1.8.
13. Определение коэффициентов правой части уравнения табл. 1. 8
Для определения коэффициентов правой части Фп и Фп в програм-
ме расчета должен быть составлен специальный оператор, в котором
эти коэффициенты определяются по следующим формулам:
Ф2=(х5/01---1- 112Сг + Фг;
(8.38)
ф2=-1x5/02 Н-Фг;
Ф3 = -^- [х2С/В2 -L Ф3;
ф3 = -^1х2сд + <
107
Для гармоник выше третьей (когда и>3)
ФП=Ф\; Фп=Ф*п.
В формулах (8. 38) использованы новые обозначения для ряда ин-
тегралов:
Aj = ^ Bu)^2yldr-,
О
В°!= J В{‘^ <srry!dr-,
= J В{е> <?ry dr,
О
(8.39)
фЛ = Р(0 fiy'd'r.
о
Здесь
сРг = ?нст + Д?,
где
?ист = ®0 ~ ’*оф) к1(-0 *2^0
<рг — есть постоянная часть угла установки лопасти, отсчитанная от
плоскости вращения несущего винта; по радиусу лопасти эта
величина меняется только за счет ее геометрической крутки Д<р.
Значения f* выписаны в самом правом столбце табл. 1.7.
Таким образом, формулы (8. 38) позволяют определить все коэф-
фициенты правой части уравнений, если задано значение I.
14. Система уравнений после подстановки формул (8.34) и (8.38)
Если значения коэффициентов, определяемые формулами (8. 34) и
(8.38), подставить в уравнения табл. 1.8, то та же система уравнений
может быть представлена в виде табл. 1.9.
Здесь мы для простоты ограничились случаем, когда расчет ведется
с точностью до двух тонов колебаний и четырех гармоник по оборотам
несущего винта. Однако приведенные выше расчетные формулы (8. 34)
и (8. 38) записаны в общем виде и позволяют вести расчет с какой угод-
но точностью.
Оценив реальные потребности практики, можно при составлении
программы ограничиться учетом только четырех тонов собственных ко-
лебаний и шести—восьми гармоник к оборотам несущего винта.
15. Общая схема расчета
Система алгебраических уравнений, выписанная в табл. 1. 8, сов-
местно с системой уравнений, приведенной в табл. 1.7, представляет
собой некоторую сложную систему уравнений, позволяющую определить
все входящие в нее неизвестные величины. Определение этих неизвест-
ных величин и, прежде всего, коэффициентов деформаций лопасти и со-
ставляет цель изложенного здесь метода расчета.
Выше, в § 7, при расчете изгибных напряжений с использованием
метода Б. Г. Галеркина были применены различные упрощения как при
108
выводе приведенных здесь уравнений, так и при их решении. Примене-
ние электронно-цифровых машин позволяет без особого труда решать
эту систему уравнений, не вводя в нее каких-либо упрощений, что поз-
воляет значительно увеличить надежность получаемых результатов. Во
всяком случае погрешности расчета могут быть связаны только с исход-
ными допущениями. Выполнение же всех требуемых математических
операций не вносит каких-либо погрешностей и производится с любой
заданной наперед точностью.
Как же решать эту весьма сложную систему уравнений? Самым
простым методом здесь, без всяких сомнений, оказывается метод после-
довательных приближений в том виде, в котором он здесь ниже будет
изложен. Этот метод был использован при составлении программ и про-
верен большим количеством расчетов. Метод очень быстро сходится
и для получения необходимой для практики точности оказывается до-
статочным всего трех-четырех приближений.
При использовании метода последовательных приближений неиз-
вестные коэффициенты деформаций определяются поочередно в порядке
возрастания индекса, определяющего их принадлежность к соответст-
вующей гармонике. Поэтому, прежде чем перейти к описанию порядка
всех операций при использовании метода последовательных приближе-
ний, нужно остановиться на определении коэффициентов деформаций.
16. Определение коэффициентов деформаций
При определении коэффициентов деформаций во всех случаях ис-
пользуется один и тот же принцип, заключающийся в следующем. Коэф-
фициенты деформаций определяются попарно из двух уравнений
системы табл. 1.8, относящихся к косинусоидальной и синусоидальной
составляющей какой-либо гармоники. Эти уравнения прежде всего пре-
образуются следующим образом. Определяется сумма произведений
АФП и АФИ коэффициентов табл. 1.8 на уже определенные к моменту
выполнения этой операции коэффициенты деформаций, за исключением
тех произведений, в которые входят коэффициенты, обведенные в табл. 8
пунктирной линией. Эти суммы произведений переносятся в правую
часть уравнений. После этого коэффициенты деформаций, относящиеся
к одноименным гармоникам (правда только в случае, когда п> 1)
и формам деформаций, определяются из двух алгебраических уравне-
ний следующего вида:
Qan + Sbn^;
Ran + $b=&n,
(8.40)
где
Фп = Фя —ДФЛ; Ф« = ФЯ-ДФЯ.
Коэффициенты аг и Ьп здесь носят обобщенный характер в том
смысле, что такая же запись уравнений возможна и с коэффициентами
И Фд, вп И fn,.gn и Ия.
Входящие в уравнения (8.40) коэффициенты Q, S, R и Q определя-
ются по формулам (8. 34) для случая, когда J=I. Причем значение i
для первого уравнения является величиной четной, а для второго не-
109
четной. Следовательно, эти коэффициенты в этом частном случае могут
быть записаны в соответствии с (8. 34) в такой форме:
S = —nDf,
R=nDj.
(8.41)
В этом случае, когда J = J,
Dj^B^~r[y^dr.
о
Если в первой формуле (8.41) пренебречь вторым членом и при-
ближенно положить Вп~Вп=Ьг, то уравнения (8.40) можно преобра-
зовать к виду, используемому в упрощенных методах расчета (см. § 7).
Действительно, произведя эти упрощения, умножим все члены
(.8. 40) на Ъ р"-
Введем новые обозначения. Величину nj, определяемую выраже-
нием
<8-42>
2 Р}
будем называть относительным коэффициентом аэродинамического демп-
фирования.
Величину vn=/wo будем называть вынужденной частотой возбуж'
дения колебаний.
Тогда уравнения (8. 40) можно переписать в форме, используемой
в § 7:
[/ V„ \2 <1 V„ w to2 -Т2
-г -Ьп=-^У^п,
\ PJ! J Pj Pj
Из этих уравнений амплитудное значение коэффициентов деформа-
ций, соответствующее Z-му тону собственных колебаний, можно опреде-
лить как
______j »<-')
° ЛИН_ЛД°СТ ,
где Хд —коэффициент динамического увеличения амплитуды;
8^2 — прогиб лопасти по форме J-ro тона при статическом прило-
жении внешних сил.

(8. 44)
Таким образом, принятая форма определения коэффициентов де-
формаций в принципе совпадает с той формой, которая используется в
задачах механики при определении амплитуды колебаний системы
с демпфированием, и описана выше, в § 7.
4
н
г
'V
но
Надо отметить, что при определении коэффициентов деформаций
уравнения системы (см. табл. 1.8) преобразуются к виду (8.40) только
в случае, когда п>1. При определении коэффициентов, относящихся
к первой гармонике, в левую часть уравнений (8. 40) войдут еще неко-
торые дополнительные коэффициенты К, L и U, которые, однако, не ме-
няют существа дела.
Несколько отличным оказывается определение коэффициентов ао,
с0, Со и go, определяющих постоянную часть деформаций. Они могут быть
определены из одного уравнения с номером Z=0. Однако чтобы не на-
рушать общность подхода, оказывается удобным их определить в про-
грамме также из двух уравнений с номерами i = 0 и i=l, коэффициенты
которых определяются по тем же формулам (8.34). При этом следует
положить Фо — 0. Такой подход позволяет несколько упростить програм-
му расчета.
17. Программа расчета
При составлении программы расчета принимается следующая по-
следовательность выполнения необходимых операций:
1. По отдельной программе, которая совершенно необходима при
проектировании лопастей и поэтому обязательно должна быть составле-
на, определяются формы и частоты собственных колебаний лопасти в
плоскости тяги. В процессе этого расчета должны быть получены следу-
ющие величины: у1, д', о7, pj и т“в. Здесь о(7) —распределение изгиб-
ных напряжений по радиусу лопасти при ее колебаниях по нормирован-
ной форме /-го тона.
2. Задаются параметры, характеризующие режим полета вертолета:
ц, р, ы, ав, фист. О I и 9г. Значения ав и <рИст могут быть определены из рас-
чета, если заданы потребная пропульсивная сила и тяга несущего винта.
Углы циклического управления 01 и Оа могут быть определены, если из
условий балансировки вертолета определены потребные моменты Мх и
Mz, действующие на его втулку со стороны лопастей несущего винта.
Эти операции обычно включаются в программу расчета.
3. Для того, чтобы приступить к решению системы уравнений, вы-
писанных в табл. 1. 7 и 1.8, необходимо определить еще коэффициенты
YV и X/. Эта система уравнений решается методом последовательных
приближений, причем в каждом приближении все неизвестные величины
определяются в последовательности, которая выписана в табл. 1. 10.
Сначала определяются коэффициенты, записанные в первой строчке,
затем —во второй и т. д.
4. После определения всех величин, выписанных в табл. 1. 10, мож-
но уточнить параметры режима полета фист, ав, 01 и В2 и выполнить рас-
чет всех коэффициентов в следующем приближении, в том же порядке.
5. Последовательность операций, выписанная в табл. 1.10, повторя-
ется до тех пор, пока разность одноименных коэффициентов деформа-
ций в двух последовательных приближениях не окажется меньше задан-
ной точности расчета ег. Значение es можно принять равным 1/1000
или несколько меньшим.
6. Величины изгибающих напряжений в лопасти на каждом азимуте
могут быть определены по формуле
j
где значения 6/ определяются по коэффициентам деформаций ай ап Ьп
сй сп Ьп и т. д. в соответствии с формулами (8. 27) и (8. 28).
Эта последовательность операций и составляет содержание изло-
женного здесь метода расчета. Выполнение расчета позволяет получить:
ill
о
Определяются по формулам таолицы 1'7 -г fl ft S, “ ]} ]ч и J* 3 7/ U
Суммарные индуктивные скорости Определяются по формулам (8 5) с их а е "X к П-Х 3 е с 11-^ 3 с с 11*^* 3 с? '•ч С |<Х 3 е IX £ iiX 3 e iX e "X 3 e iX
Частичные 'индуктивные скорости 'Определяются [по формулам 1 (S-of е CS 1«Х е п*^ □ с О •Si «-Ч 3 л? IX £ 3 X? . ”> IX е ИХ 3 3 <Х ce и x 3 « ''Ч e <o »x 3 e
Гармонические составляющие нагрузки Определяются по таблице 17 IC? hex а 1еГ II ex' 3 IC? PjU Р3 "Сх 3 lef nej? i<£> nef? 3 ICl?
Коэффициенты деформаций Определяются по уравне- ниям (8 40} сь Ьч JC* J? dt? fti ft
«и" ft* «и" ft1 Qj
ft ft •ft С ч ft ft* ft* <? ft ft ^ft
ft <3 ♦ft ft •ft- ft* <? $ «» О’ ft t? ft*
-* яизвлн еоннаоиюоу ‘Первая ^гармоника Втора я гармоника Третья гармоника u w ftl Пятая гармоника Шестая гармоника
112
— изгибные напряжения и форму деформаций лопасти на каждом
азимуте несущего винта; одновременно определяются и все гармоничес-
кие составляющие этих величин;
— поле осевых индуктивных скоростей в плоскости несущего винта
и все гармонические составляющие этого поля;
— угол атаки и угол установки лопастей несущего винта на режиме
полета с заданными значениями пропульсивной силы и тяги;
— углы отклонения тарелки автомата перекоса, необходимые для
создания потребных для балансировки вертолета моментов Мх и Mz.
18. Сравнение расчета с экспериментом на малой скорости полета
При полетах на малой скорости величина переменных напряжений,
измеряемых в лопасти, обычно носит очень нестабильный характер.
На протяжении одного режима полета, заданного летчику, ампли-
туда напряжений может изменяться по величине в два—три раза. Это
объясняется тем, что угол атаки несущего винта и скорость полета на
этих режимах выдержать постоянными очень трудно. Режим полета
непрерывно меняется. Однако конструктора, в основном, интересуют
значения максимальных амплитуд переменных напряжений, так как они.
как правило, вносят наибольшую усталостную повреждаемость в конст-
рукцию.
Обычно максимальные переменные напряжения в лопасти возника-
ют на режимах полета с наибольшими углами атаки несущего винта.
К этим режимам относятся режимы торможения вертолета и режимы
крутого снижения с большой вертикальной скоростью.
Для сравнения результатов расчета и эксперимента поступим сле-
дующим образом. Рассмотрим все режимы полета с резким торможе-
нием вертолета перед посадкой, в которых производилось измерение
напряжений в лопасти. Из каждого полета выберем значение макси-
мальной по радиусу лопасти амплитуды напряжений, возникающей на
протяжении всего режима посадки. Поле значений этих напряжений на
рис. 1. 33 заштриховано.
Расчет напряжений выполним для режимов с разными скоростями
полета и с одинаковым углом атаки несущего винта, Скорость полета
на режиме будем характеризовать величиной ц: Результаты этих расче-
тов приведены на рис. 1.33. Сплошными линиями показаны зависимос-
ти полученных из расчета максимальных переменных напряжений в ло-
пасти от скорости полета. При этом рассмотрены режимы с углом атаки
а = 0, а = 30°, который может быть достигнут на режиме резкого тормо-
жения, и с углом атаки а = 50°, который возможен при крутом снижении
с большой вертикальной скоростью. Пунктирной линией показана та же
зависимость для а = 0 и а = —6°, но без учета переменного поля индук-
тивных скоростей. При выполнении этих расчетов исследовались режи-
мы полета без перегрузки, когда тяга несущего винта равна весу.
Из проделанных расчетов следует, что наибольшее возрастание пе-
ременных напряжений на малых скоростях наблюдается на тех режимах
полета, на которых пелена свободных вихрей, стекающих с лопастей,
становится плоской. При отходе пелены от плоскости несущего винта пе-
ременные напряжения резко уменьшаются и приближаются по величи-
не к напряжениям, подсчитанным без учета переменного поля индуктив-
ных скоростей.
При сравнении режимов с одинаковыми углами атаки резкое воз-
растание переменных напряжений наблюдается в очень узком диапазо-
не скоростей полета.
Результаты расчета в какой-то степени отражают картину явления,
наблюдающуюся в полете. Так же, как и в полете, расчетные значения
переменных напряжений возрастают на малых скоростях и увеличива-
8 1578
113
ются с ростом угла атаки несущего винта. Однако между расчетом и
экспериментом наблюдается существенное расхождение.
1. На одинаковых режимах полета амплитуды переменных напря-
жений, полученные в расчете, оказываются меньше измеренных при лет-
ных испытаниях.
2. Амплитуды переменных напряжений, полученные в расчете и при
эксперименте, оказываются похожими в количественном отношении,
если сравнивать режимы с различными углами атаки, взяв в расчете
угол атаки несущего винта несколько большим, чем это бывает в полете.
Рис. 1.33. Результаты расчета переменных напряжений
с учетом неравномерного поля индуктивных скоростей
и сравнение их с экспериментом
3. Если сравнивать режимы полета, при которых величины напря-
жений, полученные в расчете и при эксперименте, совпадают, то на-
блюдается существенное различие в их гармоническом составе. В на-
пряжениях, измеренных'Ь полете, содержание высоких гармоник выше,
чем в расчете. Так в напряжениях, измеренных на режиме резкого тор-
можения и приведенных на рис. 1.33 преобладают гармоники в диапа-
зоне от четвертой до шестой. В то же время в составе переменных на-
пряжений, полученных по расчету, преобладают напряжения с первой,
третьей и пятой гармоникой. Здесь они названы в порядке убывания их
амплитуды. В качестве примера на рис. 1.34 показано распределение
напряжений по радиусу лопасти и их гармонический состав на режиме *
полета с а = 50° и ц = 0,048.
114
Следует отметить, что в расчете была исследована лопасть с харак-
теристиками, обеспечивающими отсутствие резонансов на рабочих обо-
ротах. Ее резонансная диаграмма приведена на рис. 1.35. Рабочие
обороты, принятые в расчете,
отмечены на резонансной диа-
грамме вертикальной чертой.
Приведенные данные пока-
зывают, что применение мето-
да расчета с учетом средних
индуктивных скоростей с теми
допущениями, которые были
описаны в п. 3 сближает ре-
зультаты расчета и экспери-
мента па малых скоростях по-
лета. Однако для получения
приемлемых для практических
целей результатов необходимы
дальнейшие уточнения.
19. Сравнение расчета
с экспериментом на средних
скоростях полета
К средним скоростям поле-
та мы здесь относим все ско-
рости, на которых еще не ска-
зывается нелинейность в зави-
симости cy=f(a) и явления,
связанные со сжимаемостью
г м
Рис. 1.34. Распределение напряжений ь >
радиусу лопасти и их гармонический состав
на режимах полета (ц = 0,048 и а = 5СГ)
потока. Во многих случаях по-
этому к средним скоростям
полета можно отнести и крей-
серскую скорость вертолета,
которая особенно интересна с
точки зрения усталостной прочности, так как на этой скорости вертолет
проводит наибольший процент времени при эксплуатации.
На рис. 1.36 дано сравнение амплитуд переменных напряжений
и их первой и второй гармоник к числу оборотов несущего винта, полу-
ченных по расчету, с напряжениями, измеренными в лопасти на крей-
серской скорости при ц = 0,25. Напряжения, полученные в полете пока-
заны точками. Пунктиром показаны напряжения, подсчитанные с учетом
допущения о том, что А, = А,оор = const, а сплошными линиями с учетом
того, что X=var.
Из этого рисунка следует, что результаты расчета и эксперимента
на крейсерской скорости различаются довольно существенно. Суммар-
ная амплитуда расчетных напряжений составляет не более 80% от зна-
чений, измеренных в полете. Это расхождение происходит в основном
вследствие различия в значениях второй гармоники напряжений к числу
оборотов несущего винта. Совпадение в первой гармонике напряжений
достаточно хорошее. Более высокие гармоники напряжений на этом
.режиме полета весьма малы и не оказывают существенного влияния на
амплитуду напряжений.
Приведенные на рис. 1.36 результаты являются типичными для ре-
жимов полета с ц=0,25 и повторяются почти на всех вертолетах.
Из рис. 1.36 также видно, что учет переменных индуктивных ско-
ростей не дает на этом режиме заметных уточнений в значениях пере-
менных напряжений. Однако если говорить только об одной какой-либо
8*
115
гармонике, например, о четвертой, то видно, что ее величина существен-
но возрастает при учете переменного поля индуктивных скоростей. По-
этому если эта гармоника является проходной и определяет величину
сил, приходящих на фюзеляж и вызывающих его вибрации, то это уточ-
нение оказывается очень важным.
Выше ничего не говорилось о постоянной части изгибающих напря-
жений. Обычно их величина, полученная на основании расчета, оказы-
вается настолько точной, что ее измерение в полете, как правило, даже
не производится. Расчет в этом случае дает более надежные результаты.
20. Возможные пути дальнейшего уточнения результатов расчета
Как следует из изложенного выше, расчет переменных напряжений
в лопасти не дает еще результатов, которые бы полностью удовлетворя-
ли конструктора. Если на средних скоростях полета результаты расчета
более или менее удовлетворительно согласуются с экспериментом (хотя
дальнейшие уточнения значений второй гармоники крайне желатель-
ны), то на малых скоростях полета наблюдается весьма отдаленное сов-
падение. -
В связи с этим очень важно, в каком направлении вести поиски по
дальнейшему уточнению результатов. Можно предложить следующие
пути.
При расчете переменных напряжений на малых скоростях полета
наиболее важными уточнениями необходимо считать:
— учет влияния собственных индуктивных скоростей (отказ от
«гипотезы стационарности»);
116
— применение вихревой теории, учитывающей деформации системы
свободных вихрей (отказ от допущения, что вихри отходят от несущего
винта с постоянной скоростью, равной средней скорости протекания по-
тока Хоер).
При расчете переменных напряжений на средних скоростях полета,
где основное расхождение наблюдается в значениях второй гармоники
напряжений, наиболее полезным уточнением было бы применение вих-
ревой теории с конечным числом лопастей и введение в расчет влияния
как внешних, так и собственных индуктивных скоростей.
О 0,1 0,2 0,3 Ofi 0,5 0,6 0,7 0,3 0,9 г 0 0,1 0,1 0,3 0,4- 0,5 0,5 0,7 0,3 0,9 г
Рис. 1.36. Сравнение величин переменных напряжений, подсчитанных с учетом
переменного поля индуктивных скоростей, с напряжениями, измеренными
в полете
В тех случаях, когда лопасть имеет малую жесткость на кручение,
или тогда, когда внешние силы возбуждают форму колебаний винта,
совпадающую с формой флаттера, и их частота близка к частоте флат-
тера, заметные уточнения может дать учет крутильных деформаций ло-
пасти. Метод подобного расчета был приведен в § 7 гл. 4 первой книги.
Во многих случаях при расчете переменных напряжений на крей-
серской скорости полета (так же как и на максимальной скорости) за-
метные уточнения может дать учет нелинейных зависимостей су—/'(а)
и сжимаемости потока, о чем будет говориться в следующем пара-
графе.
117
§ 9. РАСЧЕТ ИЗГИБНЫХ НАПРЯЖЕНИИ В ЛОПАСТИ С УЧЕТОМ
НЕЛИНЕЙНОЙ ЗАВИСИМОСТИ АЭРОДИНАМИЧЕСКИХ
КОЭФФИЦИЕНТОВ ОТ УГЛА АТАКИ ПРОФИЛЯ И ЧИСЛА М
1. Рассматриваемые режимы полета
Учет нелинейной зависимости аэродинамических коэффициентов от
угла атаки профиля необходим на тех режимах полета, когда эти углы
достигают столь значительных величин, что уже нельзя пользоваться ли-
нейной зависимостью (8.1). К таким режимам относятся полеты на ско-
ростях, близких к максимальным, и те режимы полета на малых скоро-
стях, когда вследствие большой нагрузки на лопасть и очень сильной
неравномерности поля индуктивных скоростей на отдельных участках
площади, ометаемой несущим винтом, углы атаки выходят в нелинейную
область зависимости с„=/(а). В ряде случаев учет этих нелинейностей
оказывается необходимым и на других режимах, включая и режим поле-
та на крейсерской скорости.
Учет явлений, связанных со сжимаемостью потока, необходим, как
правило, на больших скоростях полета у вертолетов, имеющих несущие
винты с высокими окружными скоростями.
2. Определение аэродинамических нагрузок
Выше, в § 8, предполагалось, что угол притекания потока к профилю
лопасти Ф есть величина малая, и поэтому использовалась приближен-
ная формула (8.23) для определения этого угла. Здесь предполо-
жим, что угол Ф может изменяться в пределах 360° и его величину будем
подсчитывать по формуле:
® = arctg^-, (9,1)
U X
где значения Ux и Uy определяются по формулам:
Uх=(г ;j. sin б);
п оА 1 А (9-2)
\ “л /
Формулы (9.2) совпадают с формулами, использованными в § 8.
Это означает, что при их составлении предполагалось, что перемещения
лопасти малы и поэтому можно положить:
Значение угла Ф, определяемое по формуле (9.1), при расчетах на
цифровой машине выдается обычно только в диапазоне qz90°. Это следу-
ет учитывать при вычислении угла атаки по формуле
f а=<р-|-Ф. (9-4)
Поэтому формулой (9.1) можно пользоваться только тогда, когда
Гх>0. Если UX<S>, то, как следует из рис. 1.37,
® = n-|-arctg—. (9.5)
Ux
Угол притекания потока, определяемый формулами (9.1) и (9.5),
изменяется в диапазоне —90°<Ф<270°.
118
Если предположить, что угол установки может изменяться, от
Ф = —15° до ф=+45°, то аэродинамические коэффициенты должны быть
заданы в пределах изменения угла атаки от —105° до +315°.
Число М, необходимое для определения аэродинамических коэффи-
циентов, подсчитывается по формуле:
. (9.6)
#зв
Здесь а,в скорость звука:
*зв=]/^, (9.7)
где Л—показатель адиабаты;
р — атмосферное давление.
Рис. 1.37. Схема обтекания профиля для определения угла при-
текания потока Ф
Необходимые для расчета аэродинамические коэффициенты опреде-
ляются в результате круговой продувки профиля в аэродинамической
трубе. При расчетах на машине для определения аэродинамических ко-
эффициентов удобно воспользоваться программой, составленной инжене-
ром М. Н. Тищенко. В этой программе влияние числа М на аэродинами-
ческие коэффициенты учитывается только в диапазоне углов атаки про-
филя от а = —2° до а= + 15°. В остальном диапазоне изменения углов
атаки аэродинамические коэффициенты считаются не зависящими от
числа М.
На рис. 1.38 в качестве примера показана принятая в одном из ва-
риантов этой программы зависимость коэффициента подъемной силы су
от угла атаки а для профиля NACA-230.
119
Если коэффициенты подъемной силы св и силы сопротивления сх
известны, то аэродинамические силы, действующие в плоскости взма-
ха Т и в плоскости вращения Q, могут быть определены по формулам
Рис. 1.38. Принятая в программе зависимость cv=f(a, М)
3. Метод расчета лопасти как системы,
движение которой связано заданными заранее формами колебаний
Как и выше, в § 8, расчет упругих колебаний лопасти сводится к ре-
шению дифференциального уравнения
{Ely’} ’— {Ny'}'-\-my— Т, (9.9)
где при принятых предположениях аэродинамическая сила Т является
нелинейной функцией перемещений элементов лопасти у.
В этом случае для решения уравнения (9. 9) удобно применить ме-
тод, в котором движение лопасти по времени находится численным инте-
грированием обыкновенных дифференциальных уравнений, полученных
из уравнения (9.9) при помощи метода Б. Г. Галеркина. При таком под-
ходе к задаче эти уравнения оказываются связанными только через
аэродинамические силы. Поэтому, если в какой-то произвольный момент
времени аэродинамические силы оказывается возможным вычислить, то
деформации лопасти по каждой заданной форме колебаний определяют-
ся независимо, если эти формы ортогональны.
Представим форму колебаний лопасти в виде суммы некоторого
числа тонов собственных колебаний лопасти:
(9.10)
i
где 7 = 0, 1, 2, ..., /в (j’e — номер высшего тона собственных колебаний
лопасти, учитываемого в решении);
z/W) — форма /-го тона собственных колебаний лопасти, нормирован-
ная таким образом, что при f=R у^1 =R;
bj — некоторые коэффициенты, определяющие величину деформа-
ций лопасти по /-му тону.
120
Коэффициенты б,-, как и выше, будем называть коэффициентами де-
формаций лопасти. Значения 6j являются функциями времени.
Коэффициенты деформации лопасти 6j в настоящем методе расчета
приняты за обобщенные координаты системы. Определение закона их
изменения по времени и составляет содержание расчета.
Дважды продифференцировав выражение (9.10) по времени, по-
лучим:
у=2 W7J;
7
У
j
(9.П)
Если выражения (9. 10) и (9. 11) подставить в уравнение (9.9) и все
члены уравнения (9.9) поочередно умножить на yW (где /=0, 1, 2,...,/в)
и проинтегрировать по радиусу лопасти, то в силу ортогональности форм
собственных колебаний уравнение (9.9) распадается иа /Б+1 независи-
мых уравнений вида:
/ЦуЗу С/Зу — А/.
(9. 12)
Здесь
R R А
C/ = j£/ J\V [(y')Wr;
и о
тп/ = j* m(yJ')2dr;
6
(9. 13)
Ai^Ty^dr.
о
Выше в пп. 1 и 2 § 7 уже отмечалось, что входящие в уравнение
(9. 12) величины имеют вполне определенный физический смысл. Вели-
чина Cj, называемая обобщенной жесткостью лопасти при деформациях
по форме /-го тона, представляет собой также удвоенную потенциальную
энергию, накопленную лопастью при изгибе в поле центробежных сил по
форме того же тона. Величина т.- есть эквивалентная масса лопасти, при-
веденная к ее концу. Она равна также удвоенной кинетической энергии
колебаний лопасти по форме /-го тона с частотой р=1. Интеграл Aj,
стоящий в правой части уравнения (9. 12), представляет собой обобщен-
ную силу и равен удвоенной работе аэродинамических сил на перемеще-
ниях, вызванных деформациями лопасти по j-му тону.
Известно, что частота /-го тона собственных колебаний лопасти мо-
жет быть определена по формуле
Поэтому уравнения (9.12) удобно преобразовать, отнеся все члены
к значениям mj. Тогда их можно записать как
(9-14)
или
s(j)
+ (9-15)
Pj
где Зр7) — коэффициент квазистатических деформаций лопасти по форме
у-го тона от аэродинамических сил Т (см. §7, п. 7).
121
Как следует из формул (9.8) и (9.2), величина аэродинамической
силы меняется по азимуту лопасти и зависит от деформаций лопасти или
точнее от значений у и р, определяющих величины относительной ско-
рости Uy. Поэтому для подсчета аэродинамических сил необходимо пред-
варительно определить значения у и р по формулам:
' (9.16)
kW’-
i
где р0‘)-—угол поворота упругой оси лопасти относительно плоскости
вращения, соответствующий нормированной форме собствен-
ных колебаний /-го тона.
Если коэффициенты деформаций б3- и их первые производные 6j, от-
носящиеся к какому-либо азимутальному положению лопасти или како-
му-либо моменту времени t, известны, то расчет может быть выполнен
в следующем порядке.
Вначале по формулам (9.16) определяются значения у и р. После
этого по формулам (9.2) могут быть определены составляющие относи-
тельной скорости потока Uy и Ux и скорость U;
U = yrU^Ul (9.17)
Правда, для определения скорости Uy еще нужно знать относитель-
ную скорость протекания X, которая в общем случае является перемен-
ной величиной, меняющейся по радиусу и азимуту лопасти. Об опреде-
лении величины X будет сказано в п. 5 этого параграфа.
Если скорости Uy и Ux известны, то по формулам (9.1) и (9.5) мо-
жет быть определен угол притекания потока Ф, а по формуле (9.4) угол
атаки профиля а. Число М определяется по формуле (9.6). Этих данных
достаточно для определения аэродинамических коэффициентов по кру-
говой продувке профиля, а следовательно, и аэродинамических сил Т.
Таким образом, на рассматриваемом азимуте оказываются извест-
ными деформации лопасти, скорости этих деформаций и действующие на
лопасть аэродинамические силы Т. Следовательно, воспользовавшись
формулой (9. 14), можно определить и коэффициенты’ бд определяющие
ускорения элементов лопасти:
После этого путем численного интегрирования уравнений (9.14) по
времени можно определить новые значения коэффициентов деформаций
лопасти б3- и их первые производные б,- на следующем азимуте лопасти
через некоторое время At, определяемое шагом интегрирования. Переход
от момента времени t, на котором коэффициенты деформаций бд их пер-
вые 6j и вторые 6j производные известны, к следующему моменту време-
ни £ + может быть произведен при помощи ряда известных способов
численного интегрирования уравнений.
Здесь, только в качестве примера, выпишем формулы такого пере-
хода, относящиеся к способу, именуемому методом Эйлера:

(9.19)
Ниже особенности различных способов численного интегрирования
будут рассмотрены подробнее. В частности, будет показано, что способ
122
Эйлера, представленный формулами (9.19), не пригоден для расчета
упругих колебаний лопасти.
Применение численного интегрирования уравнений (9.14) по вре-
мени позволяет определить коэффициенты деформаций и их первые про-
изводные на новом азимуте лопасти. Тогда, определив на этом азимуте
новые значения аэродинамических сил, можно определить и новые коэф-
фициенты б;. Этот процесс можно продолжить, пока значения коэффи-
циентов деформаций не будут определены на всех азимутах лопасти на
протяжении одного оборота несущего винта.
Если начальное значение коэффициентов б;- и б,- задать произвольно,
то после интегрирования уравнений на протяжении одного оборота не-
сущего винта значения б; и 6j, полученные на том же азимуте в резуль-
тате интегрирования, окажутся уже другими, отличающимися от значе-
ний, взятых в начальный момент времени произвольно. Однако, если дви-
жение лопастей устойчиво, то численное интегрирование можно продол-
жить. Тогда через несколько оборотов несущего винта движение устано-
вится и будет повторяться в каждом следующем обороте несущего вин-
та. Это установившееся движение и является искомым решением урав-
нения (9. 9).
Таким образом, предлагаемый здесь метод расчета представляет со-
бой решение задачи Коши с интегрированием уравнений движения ло-
пасти по времени при заданных начальных условиях.
4. Расчетные формулы для модели лопасти с дискретными параметрами
Обычно в практических расчетах лопасть несущего винта рассмат-
ривается в виде невесомой балки с закрепленными на ней сосредоточен-
ными грузами, имитирующими ее массу. Аэродинамические силы, дейст-
вующие на лопасть, также удобно представить в виде ряда сосредоточен-
ных сил. Будем считать, что аэродинамические силы приложены в точ-
ках крепления сосредоточенных грузов, как будто к каждому грузу при-
креплено отдельное крылышко с некоторой площадью S, (см. § 1, п. 9).
Тогда аэродинамические силы можно определить по формулам, анало-
гичным формулам (9.8):
+ (9.20)
Q^-^c^-c^qS.U., (9.21)
где индексом i отмечены все величины, относящиеся к сечению лопасти
с номером i (см. рис. 1.51). Величина площади сосредоточенного кры-
лышка S, определяется по формуле (1.2).
Для лопасти несущего винта, представленной не в виде балки с рас-
пределенными параметрами, а в виде модели с конечным числом упруго
связанных между собой сосредоточенных масс, могут быть получены
уравнения, аналогичные уравнениям (9.14). Только входящие в уравне-
ния величины т.- и Aj будут определяться не как интегралы, а как сум-
мы вида;
J
(9. 22)
где — значения сосредоточенных масс системы;
у<р — значения, определяющие форму собственных колебаний /-го
123
тона; форма собственных колебаний должна в этом случае быть
представлена рядом дискретных значений ординат tji, опреде-
ляющих перемещения i-ых масс лопасти;
Ti — дискретные значения аэродинамических сил, определенные по
формуле (9.20).
Во всем остальном расчет модели лопасти с дискретными пара-
метрами не отличается от расчета модели с параметрами, непрерывно
распределенными по длине лопасти. Однако при расчете на цифровых
машинах несравненно удобнее рассматривать модель с дискретными па-
раметрами.
5. Об учете переменного поля индуктивных скоростей
Применение изложенного здесь метода расчета не исключает воз-
можности учета переменного поля индуктивных скоростей, представлен-
ного относительным коэффициентом протекания К в формуле (9.2). Для
этого при определении аэродинамических сил, действующих на лопасть
в рассматриваемый момент времени t, должно быть решено интегро-
дифференциальное уравнение вихревой теории несущего винта (см. фор-
мулу (5. 29) § 5, гл. 2, первой книги).
Сведение задачи об упругих колебаниях лопасти к задаче Коши
с определением движения лопасти, начиная с какого-то начального мо-
мента времени приводит к значительным упрощениям и при решении ин-
тегро-дифференциального уравнения вихревой теории.
При повороте несущего винта на один шаг по азимуту с лопасти сте-
кают вихри, связанные с изменениями циркуляции только на протяже-
нии этого последнего шага. Все вихри, сошедшие с лопасти в предыдущие
моменты времени, только перемещаются в пространстве, а их циркуля-
ция уже не меняется. Поэтому при решении интегро-дифференциального
уравнения, относящегося к какому-то определенному моменту времени,
приходится находить связь только между циркуляцией присоединенных
вихрей и вихрей, сошедших с лопасти за время ее перемещения только
при последнем шаге интегрирования. Величины циркуляций всех осталь-
ных свободных вихрей при этом оказываются уже известными и опреде-
ленными всей историей процесса движения.
Для упрощения задачи в начальный момент времени может быть
принята какая-то схематическая модель вихревой системы, состоящая,
например, только из винтовых вихрей, сошедших с конца лопасти, с по-
стоянной циркуляцией по длине. Предположить, что к моменту начала
расчета никаких свободных вихрей не существует, нельзя, так как при
этом средняя индуктивная скорость через несущий винт окажется равной
нулю.
Рассматриваемый здесь метод позволяет достигнуть максимально
возможной точности, которую только может обеспечить расчет индук-
тивных скоростей по схеме винта с конечным числом лопастей. Приме-
нение этой схемы в других методах расчета упругих колебаний лопасти
приводит к очень серьезным усложнениям.
Использование методов расчета индуктивных скоростей, основан-
ных на схеме несущего винта с бесконечным числом лопастей, примени-
тельно к рассматриваемому в этом параграфе методу расчета связано
со многими трудностями. Так, наиболее простым обычно кажется метод
последовательных приближений. Однако, если применить метод, при
котором индуктивные скорости вычисляются по окончании расчета дви-
жения лопасти на протяжении каждого оборота несущего винта (когда
значения аэродинамических сил Т известны на всех азимутах и радиу-
сах лопасти и, следовательно, могут быть определены и значения цирку-
ляции в тех же точках) и ввести эти скорости в расчет аэродинамических
124
сил на следующем обороте винта, то оказывается, что такой процесс ре-
шения не сходится. Поэтому приходится применять различные приемы,
обходящие эти трудности, что, как правило, приводит к значительным
усложнениям, которые в конечном итоге могут оказаться неоправдан-
ными.
6. Особенности численного интегрирования дифференциальных уравнений
упругих колебаний лопасти
Для успешного выполнения расчета упругих колебаний лопасти
очень важным оказывается выбор наивыгодиейшего способа численного
интегрирования, обладающего хорошей точностью при минимальном чис-
ле операций, связанных с разрешением дифференциального уравнения
движения. На эту операцию идет основная часть машинного времени
при расчете. Причем наибольшая ее часть тратится на определение внеш-
них сил. Поэтому продолжительность расчета определяется, главным об-
разом, числом обращений к уравнению движения. Это число определяет-
ся выбранным способом и шагом интегрирования. Чем мельче шаг, тем
продолжительнее расчет.
Анализ показывает, что при отыскании периодического решения за-
дачи об упругих колебаниях потребный шаг интегрирования меняется
в очень широких пределах в зависимости от того, какой способ числен-
ного интегрирования используется. Очень плохие результаты при этом
дают многие распространенные способы численного интегрирования та-
кие, как уже упоминавшийся способ Эйлера [см. формулы (9.19)]. Таким
же малопригодным для рассматриваемой задачи оказался и широкоиз-
вестный способ решения при помощи ряда Тейлора. Этот способ приво-
дит к следующим формулам перехода от момента времени t к моменту
времени l + At:
а = 8^ -|- AZtif.
(9.23)
! .. Z .
Значение %t+u=f Z(+i() определяется из дифференциального
i уравнения. Здесь Д/— шаг интегрирования.
Более подходящими к данному случаю, но все же недостаточно удоб-
ными оказываются также широко известные способы численного инте-
грирования Рунге-Кутта и Адамса.
* Наилучшим методом проверки применимости способа численного
г интегрирования к решению задачи о колебаниях лопасти является чис-
, й ленное решение уравнения
S —|—2zz6 —й slu (9.24)
описывающего колебания некоторой механической модели, представляю-
щей собой массу на пружинке с демпфером (см. рис. 1.39).
Лопасть несущего винта может рассматриваться как совокупность
некоторого числа таких моделей, обладающих разными частотами соб-
ственных колебаний и разными коэффициентами демпфирования, соот-
ветствующими частотам и коэффициентам демпфирования различных то-
нов колебаний лопасти.
, При относительно малых шагах Д/ применение ряда Тейлора для
интегрирования уравнения (9.24) приводит к решению, представляюще-
му собой колебательный процесс, амплитуда которого стремится к неко-
торому определенному значению, отличному от точного аналитического
значения на величину погрешности расчета. С увеличением шага интегри-
рования при некоторых определенных значениях At решение расходится.
Если решение не расходится, наибольшая погрешность возникает при ре-
125
зонансе, т. е. при v=l. Поэтому в дальнейшем будем оценивать погреш-
ность по этому наиболее тяжелому случаю.
На фиг. 1. 39 показано изменение амплитудных значений колебатель-
ного процесса, полученного в результате численного решения уравнения
(9.24) при помощи ряда Тейлора. Причем в качестве начальных значе-
ний взяты точные аналитические величины б0 и бо. Рассмотрены случаи
с относительными коэффициентами демпфирования, равными 2гё = 0,1
и 2й = 0,2 и различными шагами интегрирования.
Рис. 1.39. Влияние относительного шага интегрирования на точ-
ность решения
Максимальные значения б, полученные на протяжении периода ин-
тегрирования с порядковым номером М, приняты за амплитуду колеба-
ний на этом периоде и отнесены к аналитическому значению ампли-
туды
Л=-1. (9.25)
Из рис. 1.39 следует, что в процессе численного интегрирования ре-
шение уходит от точной аналитической кривой. Установившийся колеба-
тельный процесс имеет амплитуду всегда больше точного значения.
Причем, чем больше относительный шаг интегрирования АТ, тем больше
и погрешность. Относительным шагом интегрирования мы здесь называ-
ем величину
(9.26)
где At — шаг интегрирования по времени;
Т — период колебаний модели.
126
Величина относительного коэффициента демпфирования п также за-
метно влияет на точность решения. Из расчетов следует, что для полу-
чения удовлетворительной точности относительный шаг интегрирования
должен быть порядка 1/200 периода колебаний или даже меньше.
При численном интегрировании уравнений, описывающих упругие
колебания важно не только обеспечить требуемую точность, но приме-
нить такой шаг интегрирования, при котором не было бы расходящегося
решения.
Определение предельного шага интегрирования, при котором реше-
ние будет еще устойчивым может быть выполнено слдующим образом.
Уравнения (9. 23) и (9. 24) можно рассматривать как некоторую сис-
тему разностных уравнений. Для определения устойчивости решения рас-
смотрим однородную систему разностных уравнений [без правой части
в уравнении (9.24)].
Уравнения (9.23) запишем в несколько более общем виде, введя не-
который постоянный коэффициент х:
4“ Д^/ 4~ хД/24;
AZ = 4"
(9. 27)
При х=0 эти формулы совпадают с формулами Эйлера (9.19), а при
х = i- с формулами Тейлора (9. 23).
Из уравнения (9.24) для случая, когда sinv/=0, определим значе-
ние fit и, подставив его в уравнения (9.27), получим следующую систему
разностных уравнений:
8/+д/ = (1 — хд^2) oz4”(A^ — 2/гхД/2)8,;
&t+u= — 2/гД/)йР
Решение эхой системы будем искать в виде:
8/=Дая; 8<+д< = Да(л+1>;
8z = Ban; = .
(9.28)
(9. 29)
Подставив (9.29) в систему однородных разностных уравне-
ний (9.28), получим характеристическое уравнение относительно а. Из
этого уравнения найдем а.
хдг?
а = 1 —
(9.30)
Чтобы значения bt не стремились к бесконечности, при п—>оо необ-
ходимо условие:
При относительно малых Д/ и п значение а, как следует из уравне-
ния (9.30), является величиной комплексной.
Определив модуль а, получим условие нерасходящегося решения:
у/ 1 -ф- Д/2 — 2Д/ п 4~ -у- хД/
Д/ — 2 I п-i-— хД/^ <Г0.
к 2
<1 (9.31)
(9. 32)
или
127
(2х— 1) Д£2-(-4ггД/—-4/>0.
Откуда неустойчивость решения для метода
ступает при Д7)> п~ п—-— и только тогда,
Л
тода Тейлора (х =—) в том случае, когда ДТ>
Откуда
Ы < . (9.33)
1 — %
Если шаг интегрирования отнести к периоду колебаний системы Т,
ранному для рассматриваемой упрощенной модели 2л, то получим усло-
вие нерасходящегося решения
ДГ< --------. (9.34)
^я(1—х) v ’
Тогда для метода Эйлера при х=|0 получим, что решение возможно
при
ДГ<—, (9.35)
Л
а для метода Тейлора при х=-^-
д7<2--. (9.36)
Л
Таким образом, чтобы не получить расходящегося решения, при ис-
пользовании метода Эйлера требуется вдвое меньший шаг, чем в методе
Тейлора. При этом оба метода дают расходящееся решение, как бы мал
ни был взят шаг интегрирования, если относительный коэффициент демп-
фирования п равен нулю.
С увеличением п и L\t значение а становится вещественным числом.
При этом значение а никогда не может быть больше единицы, но может
оказаться отрицательной величиной, большей единицы по абсолютной
величине.
Условие, что а<4 соблюдается, если
(9. 37)
Эйлера при х=0 ни-
когда н)>1, а для ме-
—~. Однако эти ус-
2лп
ловия обычно перекрываются более жестким условием (9.36).
Если эти результаты перенести на систему, которой представлена
лопасть несущего винта, то величину относительного шага нужно выби-
рать исходя из периода наивысшего тона колебаний, возможного в сис-
теме, так как это приведет к наименьшему значению потребного шага,
при котором возможно численное интегрирование.
На рис. 1.40 показан типичный характер изменения периода собст-
венных колебаний лопасти 7\, и относительного коэффициента аэроди-
намического демпфирования п по номеру тона колебаний /. Величина
периода колебаний вычислена в градусах по азимуту лопасти. На этом же
графике приведена зависимость \'р, от номера тона; р3-—частота /-го
тона собственных колебаний лопасти, подсчитанная в колебаниях в ми-
нуту. В области низших тонов величина pj существенно меняется при
изменении числа оборотв несущего винта от п=0 до рабочих чисел обо-
ротов П = «раб-
Если при расчете ограничиться учетом только первых четырех тонов
собственных колебаний, включая нулевой, которых бывает обычно доста-
точно для получения необходимой на практике точности, то шаг интегри-
рования придется выбрать исходя из периода и коэффициента относи-
128
тельного демпфирования наивысшего для этой системы третьего тона
собственных колебаний.
Если принять, что период колебаний по третьему тону не может быть
меньше 45° по азимуту несущего винта, а относительный коэффициент
аэродинамического демпфирования не меньше п = 0,07, то для получения
только нерасходящегося решения шаг интегрирования в соответствии
с выражением (9.36) должен быть меньше 2°, а в соответствии с выра-
жением (9.35) меньше 1° по азимуту. Для получения же удовлетвори-
тельной точности (см. рис. 1.39) шаг пришлось бы уменьшить еще силь-
нее.
Рис. 1. 40. Зависимость периода колебаний отно-
сительного ^коэффициента аэродинамического демп-
фирования п от номера тона собственных колеба-
ний /
Этот пример показывает, что применение указанных способов инте-
грирования к расчету лопасти приводит к весьма неудовлетворительным
результатам. Способы Рунге-Кутта и Адамса позволяют для того же
примера применить шаг интегрирования порядка 3°, но они оказываются
не очень удобными из-за того, что требуют хранения в памяти машины
слишком большого числа переменных, подсчитанных для предшествую-
щих моментов времени.
Хорошие результаты дает уже упоминавшийся в первой книге (гл. 4,
§ 7) способ интегрирования с разложением решения в ряд Тейлора
и с повторным пересчетом каждого шага интегрирования. Этот способ
признан вполне подходящим в применении к рассматриваемой задаче
и в настоящее время используется во многих программах расчета.
Переход от момента времени t к моменту времени t+\t произво-
дится по этому способу численного интегрирования в такой последова-
тельности;
9 1578 129
Первый просчет:
= 8< -j- 4—“ Д/^Вр
^t+^t—в( 4~
bJ+a#=f (о’+д<, в}+д<) определяется из дифференциального уравнения.
Затем определяется 8ср по формуле
®сР =— (4’8{+д«). (9.38)
Повторный пересчет:
С«^4-л^+^-Д/2&еР;
+ Д^ср;
8f+4(=/(8'+Af, 8”+д<) определяется из дифференциального уравнения.
Значения й'+до и 8^д/ считаются окончательными для момен-
та времени /-|-Д/.
Изменение переменной 6 и ее первой и второй производной по време-
ни, определенное в соответствии с формулами (9.38), показано на
рис. 1.41.
На рис. 1.42 приведено установившееся решение уравнения (9.24),
полученное в результате численного интегрирования этим способом. Ре-
шение приведено при разных значениях шага интегрирования. Жирной
линией показано точное аналитическое решение.
При относительном шаге ]/?2 и менее численное интегрирование дает
решение, почти точно совпадающее с аналитическим. При большем отно-
сительном шаге возникает существенное различие между точным и чис-
ленным решением, что видно из рис. 1.42.
При относительном шаге
Д7 > -1- (9.39)
Л
решение расходится.
Для исключения возможности появления в системе расходящихся
решений шаг интегрирования не должен быть больше примерно одной
трети периода наивысшего тона колебаний системы, имеющего самый
малый период. Очень важным преимуществом этого способа является
то, что предельный шаг интегрирования практически не зависит от ве-
личины относительного коэффициента демпфирования.
На рис. 1.43 для лопасти с параметрами, указанными на рис. 1.40,
приведено сравнение предельных шагов Дфпред для рассмотренных спо-
собов интегрирования в зависимости от номера высшего тона /в собст-
венных колебаний системы.
Если ограничиться учетом только четырех первых тонов собствен-
ных колебаний, то в соответствии с выражением (9.39) для получения
нерасходящегося решения достаточно иметь шаг интегрирования око-
ло 15° по азимуту лопасти, т. е. примерно в 7 раз больший, чем в том же
способе без повторного пересчета.
Результаты решения уравнения (9.24) позволяют ориентировочно
определить погрешность в значениях амплитуд, соответствующих раз-
личным тонам колебаний лопасти, в зависимости от применяемого шага
интегрирования. Под погрешностью мы здесь понимаем разность между
точным аналитическим значением амплитуды колебаний и значением,
полученным в результате численного интегрирования. При интегрирова-
ло
Рис. 1.41. Зависимость переменной д и
ее первой и второй производной по вре-
мени
Рис. 1.42. Результаты численного решения уравнения (9.26)
в зависимости от относительного шага интегрирования
V
9*
131
нии с помощью ряда Тейлора с повторным пересчетом эта разность всег-
да положительна. Это означает, что численное решение всегда приводит
к занижению амплитуды колебаний.
Погрешности расчета в процентах от точного значения амплитуды
для разных тонов колебаний лопасти с обычными параметрами в зави-
симости от шага при интегрировании с помощью ряда Тейлора с повтор-
ным пересчетом даны в табл. 1.11.
Рис. 1.43. Сравнение предельных шагов для двух способов
численного интегрирования:
—-------предельный шаг при интегрировании с разложением
решения в ряд Тейлора,
--------предельный шаг при интегрировании с повторным пере-
счетом по формулам (9.38)
Таблица 1.11
Погрешности расчета в % от точного значения
Номер тона амплитуды пр и шаге интегрирования в градусах
о,3 1,0 2,5 5 10 20
Нулевой <0,1% <0,1% <0,1% 0,3% 5% 25%
1-й <0,1% <0,1% 0,4% 6% 12% 50%
2-й <0,1% 0,3 % 5% 25% 45% 80%
3-й <0,1% 0,4% 15% 30% 75%
5-й <0,1% 2% 20% 70%
10-й 1% 30% 90%
20-й 40% Расходящееся решение
30-й 90%
Приведенные данные показывают, что величина потребного шага
интегрирования, а следовательно, и продолжительность расчета опреде-
ляются, главным образом, параметрами той системы, которой представ-
лена лопасть несущего винта. Чем больше система имеет степеней сво-
132
боды, тем больше она имеет тонов собственных колебаний, тем меньше
период колебаний наивысшего тона и тем меньше должен быть шаг ин-
тегрирования. Поэтому продолжительность расчета существенно сокра-
щается, если уменьшить число степеней свободы системы. Все эти сооб-
ражения оказываются особенно важными при применении прямых мето-
дов расчета, не использующих ограничений, накладываемых на формы
колебаний лопасти. Эти методы будут рассмотрены в § 10 этой главы.
7. Способ численного интегрирования, предложенный Л. Н. Гродко
и О. П. Баховым
При численном интегрировании дифференциальных уравнений упру-
гих колебаний лопасти способом, предложенным Л. И. Гродко и О. П. Ба-
ховым, в формулах (9.27) значение коэффициента х принимается рав-
ным единице.
Условие устойчивости (9.31) упрощается и принимает вид
|]/1-2д/«|<1.
(9.40)
Следовательно, при х=1 расходящегося решения с комплексным
значением а быть не может. Из условия, что а есть комплексное число,
условие (9.40) справедливо только для значений Д/<С2 — 2ге.
Из условия (9.37) получим, что решение будет не расходящимся
пока
Д^<2 1/——-г—-
V 2х-1 1 (2%-1)2
Откуда при х= 1 получим, что
уг У 1 + П2 — п
л
2п
27.-1 '
(9.41)
(9.42)
Так же, как и при интегрировании с помощью ряда Тейлора с двой-
ным пересчетом, этот способ не дает расходящегося решения при п = 0
и имеет примерно такое же значение предельного шага.
Применительно к решению задач об упругих колебаниях его точ-
ность не хуже, чем у предыдущего метода. При этом объем счетных опе-
раций снижается почти вдвое. Поэтому данный способ численного инте-
грирования может быть рекомендован для практического применения.
8. Последовательность операций при выполнении расчета
и практическая оценка различных шагов интегрирования
В целом расчет упругих колебаний лопасти ведется в такой последо-
вательности:
1. Задаются произвольные начальные значения б, и б, на азимуте
ф = 0.
2. По формуле (9.20) определяются величины аэродинамических
сил Ti, для определения р.оторых предварительно должны быть подсчита-
ны такие параметры, кай. yt, pj, Uxi, Uyi, ф; a,-, M,, cyi и cxi.
3. Из уравнений (9.18) определяются значения 63-. Входящие в это
уравнение значения и р? подсчитываются заранее, после определения
форм собственных колебаний лопасти и в процессе расчета не изме-
няются.
133
4. Переход к следующему азимуту осуществляется в соответствии
с выбранным способом численного интегрирования, например, по фор-
мулам (9.38).
8}+д< = 8,4- Д/28/;
д/ = 6; -j- д^4;
jl Ai гА1
4+а/ = —— Рг>‘+м,
»• 4 + 5!+а/
% =--------2-----;
Д/З^ф- — Д/58Ср;
8]Дд< = 8Я-Д«ср;
(9.43)
Значения 8/+д/, 8”+д/ и б"+д< для момента времени считаются
окончательными. Для перехода к следующему азимуту весь цикл пов-
торяется заново.
Этот способ интегрирования может быть рекомендован как весьма
точный и достаточно полно проверенный на практике при расчете упру-
гих колебаний лопасти.
Численное интегрирование выполняется на протяжении нескольких
оборотов несущего винта, пока все значения в двух последовательных
оборотах не будут различаться меньше, чем заданная точность расчета.
Выполненные расчеты показывают, что может быть достигнута любая
наперед заданная точность.
Практически, однако, принимается, что расчет закончен, когда точ-
ность в определении коэффициентов деформаций становится равной
/?/1000 (Д — радиус несущего винта). При необходимости может быть
задана и большая точность.
Величины изгибных напряжений на каждом азимуте могут быть оп-
ределены по формуле
(9.44)
j
где о; — нормированные значения изгибных напряжений, т. е. напряже-
ния при изгибе лопасти по нормированной форме собственных
колебаний /-го тона.
Продолжительность периода переходного процесса к установивше-
муся движению очень сильно зависит от заданных начальных значений
коэффициентов деформаций. При правильно заданных начальных зна-
чениях dj и б,- расчет заканчивается после просчета двух оборотов несу-
щего винта. При неудачно определенных начальных значениях б3- расчет
может затянуться на 8—10 оборотов.
В программе расчета должна быть также предусмотрена возмож-
ность уточнения параметров режима полета. о0> aD, р. и Х0Ср после просче-
та каждого оборота. Указанные параметры уточняются таким образом,
чтобы несущий винт обеспечивал заданные в исходных данных значения
тяги и пропульсивной силы. Естественно поэтому, что продолжитель-
ность расчета определяется также правильностью задания параметров
режима полета.
134
Для уточнения параметров режима полета, а также для решения
других вопросов в процессе расчета должны определяться различные ин-
тегральные характеристики несущего винта, такие, как тяга ТцЪ, про-
дольная сила Н, крутящий момент Мк и т. д.
Исходя из потребностей практики, колебания лопасти достаточно
полно могут быть представлены при помощи четырех тонов собственных
колебаний. В этом случае, даже исходя из табл. 1.11, где приведены
наибольшие погрешности, возникающие при резонансе, хорошая точ-
ность может быть получена при шаге интегрирования Дф = 2,5°.
Однако практически в тех случаях, когда явно выраженные резо-
нансы отсутствуют, либо в системе действуют достаточно большие демп-
фирующие силы, обеспечивающие коэффициент демпфирования боль-
ший, чем 2п = 0,1, использованный при составлении табл. 1. 11, точность
расчета фактически не падает н при шаге Дф = 5с, а иногда даже и при
шаге Дф = 10р. Это обстоятельство имеет большое значение для экономии
времени при расчете на машинах со средней скоростью счета. Так при
расчете на машине «Стрела» на определение движения лопасти на про-
тяжении одного оборота несущего винта требуется около 6 мин при
шаге 10;. С уменьшением шага время счета соответственно увеличивает-
ся и при шаге 2,5° продолжительность настолько возрастает, что выпол-
нение расчета на этой машине становится затруднительным. При расче-
те на более быстродействующей машине М-20 эти соображения теряют
свое значение.
На рис. 1.44 в качестве примера приведены значения коэффициентов
деформаций, подсчитанные для одного из вертолетов на режиме полета
со скоростью, соответствующей ц = 0,3. Этот режим для рассматривае-
мого вертолета далек от срыва, и поэтому расчет выполнен в линейной
постановке с допущениями, описанными в п. 3 § 8. При этих допущениях
расчет был сделан с шагом интегрирования 2,5°, 5° и 10°. Результаты
этих расчетов, показанные на рис. 1.44 сплошной линией, практически
полностью совпадают. На основании этих данных можно сделать вывод,
что на режимах полета, достаточно удаленных от срыва, когда исполь-
зуется линейный подход к решению задачи и в решении превалируют
низкие тона колебаний, а на лопасть действуют значительные силы
аэродинамического демпфирования, без существенных потерь в точности
расчет может выполняться с шагом интегрирования Лф=10°,
Картина меняется при рассмотрении режимов, в которых отмечается
начало срыва. Срыв потока приводит к росту колебаний по более высо-
ким тонам и к резкому снижению коэффициентов аэродинамического
демпфирования. Вследствие этого возникает необходимость уменьшения
шага интегрирования.
На рис. 1.45 показаны результаты подсчета коэффициентов дефор-
маций с использованием шага Дф = 5“ и Дф=10р для того же несущего
винта, который был рассмотрен выше, но на режиме с ц = 0,4 с начавшим-
ся срывом. Расчет велся с учетом нелинейной зависимости аэродинами-
ческих коэффициентов от угла атаки профиля а и числа^' М. Возникнове- t
ние срыва приводит к резкому увеличению амплитуд колебаний по фор-
мам высших тонов, которые, как известно, и без срыва имеют меньшие
величины коэффициентов аэродинамического демпфирования. Поэтому
снижение аэродинамического демпфирования при срыве прежде всего
сказывается на амплитудах колебаний по этим формам. Все это приве-
ло к тому, что расчет с шагом Дф=10° внес существенные погрешности
в расчет коэффициентов деформаций ба и 63. На рис. 1.45 это видно из
сравнения с расчетом, где Дф = 5°, Поэтому для снижения погрешности
при расчете деформаций на режимах с начавшимся срывом шаг инте-
грирования необходимо уменьшить до значений порядка Дф = (2,5 : 5)°.
135
9. Сравнение результатов расчета по методу численного интегрирования
с методом расчета по гармоникам
Выше был изложен метод расчета напряжений по гармоникам в ли-
нейной постановке с допущениями, перечисленными в п. 3 § 8. Такой
метод с успехом может быть применен для режимов полета достаточно
удаленных от срыва. Он имеет целый ряд преимуществ и прежде всего
это относительно малая продолжительность вычислений.
Рис. 1.44. Сравнение коэффициентов деформаций, полученных
в результате решения уравнений по методу Б. Г. Галеркина
и численным интегрированием при су = Су а и д=0,3
На рис. 1.44 пунктирной линией для сравнения приведены коэффи-
циенты деформаций, подсчитанные методом расчета по гармоникам, из-
ложенным в § 8, для того же режима полета на ц = 0,3 с линейной зави-
симостью су=с*а. Сравнение методов расчета говорит о хорошем совпа-
дении результатов. Небольшое различие может объясняться некоторой
разницей в исходных параметрах режима полета.
10. Некоторые результаты расчетов
Приведем отдельные результаты, характеризующие те новые воз-
можности для теоретических исследований, которые открывает метод
численного интегрирования с учетом нелинейной зависимости аэроди-
136
намических коэффициентов по углу атаки а и числу М по сравнению
с линейными методами расчета.
Одним из важных преимуществ метода численного интегрирования
является возможность выполнения расчетов напряжений в условиях,
близких к срывным режимам полета.
Расчеты показывают, что с приближением к срыву резко снижается
аэродинамическое демпфирование колебаний лопасти и возрастают амп-
литуды колебаний с теми гармониками, которые находятся в резонансе
или вблизи резонанса с частотами собственных колебаний лопасти. Из
рассмотрения коэффициентов деформации, приведенных на рис. 1.45,
видно, что колебания по первому тону происходят в основном со второй
гармоникой, колебания по второму тону—с четвертой и колебания по
третьему тону — с шестой гармоникой! к оборотам несущего винта, т. е.
только с частотами, близкими к частотам собственных колебаний рас-
сматриваемой лопасти. Особенно резкое возрастание амплитуды колеба-
ний происходит по формам относительно более высоких тонов колебаний,
что на рис. 1.45 можно наблюдать на примере коэффициентов 62 и S3.
Появление срыва характеризуется резким увеличением амплитуд пе-
ременных напряжений в лопасти. На рис. 1.46 приведены значения мак-
137
Рис. 1.46. Зависи-
мость максимальной
амплитуды перемен-
ных напряжений по
лопасти от скорости
полета
6„ кгс/ммг
19
18
17
16
15
1k
13
12
11
10
Рис. 1. 47. Распределение ам-
плитуды переменных напряже-
ний и двух первых гармоничес-
ких составляющих напряжений
по радиусу лопасти на ц=0,4
- 1
Личеаныи.
расчет
О 0,1 0,2 0,3 ОЛ 0,5 0,6 0,7 0,8 0,9 1?
Амплитуда,
переменны*
напряжений
Линейный,
расчет
Нелинейный.
расчет
0,1 0,1 О 0,4 0,5
Линейный
расчет -
0,1 0,2_
Нелинейный,
расчет
0.3 Ос7 0,5 0,6 0,7 0,8 0,3 г
Нелинейный.
138
симальных по радиусу лопасти амплитуд переменных напряжений по
скорости полета, подсчитанные с учетом линейной и нелинейной зависи-
мости cy=f(a, М). Резкое увеличение напряжений является очень удоб-
ным критерием определения начала срыва при расчете аэродинамиче-
ских характеристик несущего винта.
Гармонический состав действующих при срыве переменных напря-
жений и их распределение по радиусу лопасти показаны на рис. 1.47
и 1.48.
Рис. 1.48. Распределение амплитуд третьей, чет-
вертой, пятой и шестой гармонических состав-
ляющих напряжений по радиусу лопасти н2
р = 0,4
* Следует обратить внимание также.и на то, что существенная разни-
; ца в результатах линейного и нелинейного расчета наблюдается и на
режимах, достаточно удаленных от срыва.
На рис. 1.49 показаны коэффициенты деформаций, подсчитанные
для того же вертолета при ц = 0,3 с линейной и нелинейной зависимостью
cy = f(a, А4), а на рис. 1.50 соответствующие им гармонические состав-
ляющие напряжений и их амплитуда <jA, построенниые по радиусу ло-
пасти. Как видно из этого рисунка результаты различаются достаточно
существенно.
Таким образом, даже из тех данных, которые нами здесь приведены,
видно, что расчет переменных напряжений в лопасти с учетом нелиней-
ной зависимости cv=f(a, М) позволяет выявить целый ряд интересных
особенностей, оказывающих существенное влияние на прочность несуще-
го винта.
139
Рис. 1. 49. Сравнение коэффициентов деформаций, подсчитанных
учетом линейной и нелинейной зависимости с„ = )(а, М) для ре-
жима ц = 0,3 вдали от срыва потока
140
G„ кгс/мм2
7
6
3
2
5
О
Линейный расчет _
-Л
р Л
Диплитуда - переменных напряжений * Л Р г S U
/у Нелинейный расчет
'1

1
О
1
О
Нелинейный
расчет
2-я гармоника Нелинейный.
расчет
/S' Линейные. Р\
— расчет
0,2 0,3 0,4 0,5 0,6 0,2 0,8
З-я гармоника Нелинейный расчет --L_ _
—“ZSll I n-i—~ — ] | Линриныи. расчет
4-я гармоника Нелинейный расчет Линейный расчет^
L-J— -—
Рис. 1. 50. Распределение амплитуды переменных напряже-
ний н четырех первых гармонических составляющих по
радиусу лопасти на |Л = О,3
141
§ 10. РАСЧЕТ ИЗГИБНЫХ КОЛЕБАНИЙ
С НЕПОСРЕДСТВЕННЫМ ОПРЕДЕЛЕНИЕМ ТРАЕКТОРИЙ
ДВИЖЕНИЯ ТОЧЕК ЛОПАСТИ
1. Сущность метода расчета
В параграфах § 7, 8 и 9 были изложены методы расчета изгибных
колебаний лопасти, где форма ее деформации определялась при помощи
метода Б. Г. Галеркина. Для этого деформации лопасти разлагались
в ряд по заданным заранее известным функциям. В качестве этих функ-
ций предлагалось использовать формы собственных изгибных колебаний
лопасти в пустоте. При этом утверждалось, что для практических целей
достаточно ограничиться только первыми четырьмя тонами собственных
колебаний.
Здесь будут рассмотрены методы, позволяющие отказаться от этого
допущения и находить деформации лопасти путем непосредственного оп-
ределения траекторий движения некоторого числа точек лопасти без раз-
ложения формы колебаний по заданным заранее функциям. *
Для определения движения отдельных точек лопасти удобно исполь-
зовать модель лопасти с дискретно распределенными параметрами.
В этом случае масса лопасти имитируется при помощи ряда сосредото-
ченных грузов, распределенных по ее длине.
Для такой механической модели может быть написана система диф-
ференциальных уравнений вида:
т^ = Сг\ Т;, (10.1)
где i = 0, 1, 2,..., z;
У; — вторая производная по времени от перемещений /-го сосре-
доточенного груза с массой ту, значения yt отсчитываются от
плоскости вращения несущего винта;
С/ — упругая сила, действующая на /-ю массу mz, со стороны сосед-
них участков механической модели лопасти;
7";- — внешняя аэродинамическая сила, действующая на l-ю точку
лопасти, где расположен один из сосредоточенных грузов.
Система уравнений (10.1) описывает движение всех масс механиче-
ской модели лопасти. Поэтому она состоит из такого числа уравнений
с переменными г/,-, которое равно числу масс рассматриваемой механиче-
ской модели.
Однако не все переменные yt, входящие в систему (10.1), являются
независимыми, так как движение должно удовлетворять условию равно-
весия всей системы:
(т,^-7';) = 0. (10.2)
о
Удобнее всего считать, что независимыми переменными являются
перемещения всех масс, кроме комлевой массы Тогда движение ком-
левой массы, если принять Т0=О, может быть определено в соответствии
с (10.1) как
тоУо = со,
где
с0=2<7’«--т.'И)- (10-3>
1
* Такой метод для расчета лопасти вертолета впервые был применен Р. М. За-
иозиной.
142
Это условие равновесия сил автоматически выполняется при ис-
пользовании приведенных ниже формул.
Таким образом, рассматриваемая система может быть описана не-
зависимыми переменными yt, число которых на единицу меньше числа
сосредоточенных масс механической модели лопасти. Следовательно,
число степеней свободы, которое имеет эта система, равно числу участ-
ков расчетной схемы и на единицу меньше числа сосредоточенных масс.
Решение системы уравнений (10.1) может быть получено при помо-
щи численного интегрирования по времени. Для этого в каждый момент
времени нужно определить силы С, и 7\. Определение сил Т{ может быть
выполнено по формулам (9.20), вывод которых дан в § 9. Определение
же упругих сил С, имеет целый ряд особенностей, на которых следует
здесь остановиться.
2. Определение упругих сил, приложенных к рассматриваемой точке
лопасти со стороны смежных участков
Рассмотрим более подробно принятую для расчета механическую
модель лопасти. Вначале будем рассматривать модель балочного типа.
Представим лопасть в виде невесомой, свободной балки, подчиненной
некоторым граничным условиям на концах и разделенной на z участков,
по краям которых расположены сосредоточенные грузы (рис. 1.51). Дли-
ны участков могут быть различными.
Рис. 1. 51. Модель лопасти, рассматриваемая в расчете
Изгибную жесткость лопасти, как и раньше, представим в виде сту-
пенчатой кривой таким образом, чтобы она оставалась постоянной на
протяжении каждого участка. Центробежную силу будем считать при-
ложенной только к грузам. Поэтому на протяжении каждого участка
величина ее не будет изменяться. Будем также считать, что и аэродина-
мические силы приложены только в точках крепления грузов так, как
будто к каждому грузу прикреплено отдельное крылышко с пло-
щадью
Для создания условий заделки лопасти в комле будем считать, что
центробежная сила воспринимается специальным креплением комлевой
массы т0, которая может свободно двигаться по вертикали. При реше-
нии настоящей задачи создание свободы движения комлевой массы по
вертикали не обязательно. Однако в других задачах, связанных с опре-
143
делением совместных форм колебаний лопасти и фюзеляжа, это условие
оказывается необходимым. Когда колебания фюзеляжа не учитываются
и лопасть считается закрепленной на втулке, как на жестком основании,
условия комлевой заделки в расчете создаются путем задания необходи-
мой, обычно достаточно большой, массы т0.
Естественно, что такая идеализированная схема тем ближе будет
описывать истинную картину колебаний лопасти, чем на большее число
участков будет разбита лопасть. Практически достаточно точно лопасть
может быть представлена схемой в виде балки, состоящей из 25—30
участков и такого же числа сосредоточенных масс.
Рис. 1.52. Схема сил, действующих на смежные элементы
• лопасти
Для определения упругой силы Ci составим уравнения деформаций
лопасти. На рис. 1.52 показаны силы, действующие на два смежных
участка деформированной лопасти. Выпишем уравнения деформаций
этих участков.
Поскольку инерционные и аэродинамические силы для рассматри-
ваемой механической модели лопасти приложены только по краям
участков, деформации каждого участка могут быть определены по урав-
нению
[WT-W]'=o. (10.4)
Величина изгибной жесткости EI и центробежной силы N не ме-
няется на протяжении каждого участка. Поэтому они могут быть выне-
сены за знак дифференцирования. Тогда уравнение (10. 4) может быть
переписано в виде
Л1"~-!х2Л4 = 0, (10.5)
где М — Е1у есть изгибающий момент в сечении лопасти, а ч2 = -— .
EI
Решение уравнения (10. 5) может быть записано как
МЯ=А shjix-j-B ch ух,
(10.6)
144
где коэффициенты А и В могут быть получены из граничных условий.
Так, для участка 1—2 при x = 0 Mx=Mlt а при х = /12 МХ = М2. Подставив
эти условия в (10. 6), получим:
д __ ^2_____Ml _
sh щ th ссj ’
В^Щ.
Здесь а и., = 1/ Аг .
I Е112
С учетом (10.7) и того, что МХ=Е!12у", уравнение (10.6) может
быть записано в виде:
(Ю.7)
W = “-Д’] (10.8)
Проинтегрировав дважды уравнение (10.8) и имея в виду, что при
х=0 у'=^; у—ylt а при х=112 у' = ^2> У—Уъ, получим:
А (//2 У1) — ^1-^г “Ь ei^i I" Pi (10.9)
или
(Уг^~ У1)= — АА-ЬРа- (10.10)
Здесь:
42
d^ —— fl------S-V
Лг-'У12 \ sh ci] /
<?!=-—— ---1V
^12^ 12 \ th Ctj /
Уравнение деформаций для участка 0—1 может быть записано по
аналогии с уравнением (10.10):
^О(У1-УО) = -e0M1-d0M0-\ р,. (10.11)
Изменив в уравнении (10.11) все знаки на обратные и сложив
с уравнением (10.9), получим:
йГ0Л40-1 CjTW!-I djM^Aj, (10.12)
где
С] = е0 б];
А “ ^оУо ~г (*о 4“ &1) У1 I" ^1У2-
Проделав те же операции для других смежных участков, получим
систему z уравнений следующего вида:
Тиолица 712
А Л/, мг • • • ... мг-2 Мг-1

7 А»
А С, = А,
й, ^2 *2
• •• ... ... = « • •
... • • • - • • •
ci, Л г-/ сг-2 = Аг-2
Лг-2 сг-1 -
10 1578
145
•Эта система уравнений записана нами здесь в форме таблицы. Лю-
бое из уравнений системы представляет собой сумму произведений ко-
эффициентов, занимающих в прямоугольной табл. 1. 12 одну строку, на
неизвестные функции Mit входящие одновременно в несколько уравнений
и вынесенные по вертикали в специальную строку, помещенную сверху
табл. 1.12. В эту же строку записана входящая только в первое уравне-
ние неизвестная функция 0о. Правые части уравнений помещены
в специальном столбце.
Система уравнений табл. 1.12 решается методом исключения неиз-
вестных. Этот метод был уже описан в п. 5 § 4.
Таким образом, выписанная выше система уравнений позволяет оп-
ределить значения угла поворота лопасти в комле р0 и все значения из-
гибающих моментов Mi, если известна форма деформаций лопасти как
совокупность значений yi.
Для определения упругой силы С; необходимо выполнить ряд после-
довательных операций, первая из которых заключается в разрешении
системы, представленной таблицей 1.12. В эту последовательность опе-
раций целесообразно включить и определение необходимых в дальней-
шем для подсчета аэродинамических сил углов поворота упругой оси
лопасти р;:
(10. 13)
По известным значениям Mi из условия равновесия элементов мож-
но определить перерезывающую силу Qi, i+b постоянную на протяжении
каждого участка лопасти. Действительно, приравнив нулю суммы мо-
ментов всех сил, действующих на участок 4 »+1, получим уравнение
Qi.i+ili,i+i=N t.i+i Ml+1, (10.14)
из которого может быть определено значение Qi, <+i.
Зная значения перерезывающих сил по длине лопасти, можно опре-
делить и упругую силу Ct, приложенную к массе т{ со стороны соседних
участков:
Ci~Qi.i+i—Qi-i.t- (10.15)
Приведенные выкладки позволяют определить все значения упругих
сил Ci, действующих со стороны соседних участков на данную массу тг-,
если известна форма деформации
3. Особенности численного интегрирования уравнений (10.1)
Выше, в § 9, уже были описаны основные особенности применения
численного интегрирования к решению дифференциальных уравнений
упругих колебаний лопасти. Было показано, что успех численного инте-
грирования в значительной степени определяется величиной предельно
го шага, который прямым образом связан с наименьшим периодом ко-
лебаний механической модели, рассматриваемой в качестве аналога ло-
пасти. Предельный шаг интегрирования не должен быть слишком малым,
так как расчет в этом случае будет чрезмерно растянут по времени.
Особенностью рассматриваемой здесь модели является то, что она
имеет столько тонов собственных колебаний, на сколько участков по
длине разбита в расчете лопасть. Дак уже отмечалось выше, для умень-
шения погрешностей про переходе от лопасти к ее аналогу механиче-
ской модели необходимо представить лопасть при помощи не менее 25—
30 участков с таким же количеством сосредоточенных масс. Поэтому при
определении предельного шага интегрирования в этом случае приходится
исходить из периода наивысшего — тридцатого тона собственных колеба-
ний модели.
146
На рис. 1.40 показана зависимость частоты и периода собственных
колебаний обычной лопасти вертолета по номеру тона. Из этого рисунка
следует, что период тридцатого тона собственных колебаний составляет
около одного градуса по азимуту несущего винта. Выше уже было ска-
зано, что при использовании наиболее выгодного способа численного ин-
тегрирования для получения нерасходящегося решения шаг интегриро-
вания должен быть меньше одной трети периода наивысшего тона. Сле-
довательно, для рассматриваемого здесь метода расчета шаг интегриро-
вания должен быть меньше 0,3° по азимуту несущего винта. В этом слу-
чае решение будет устойчивым, а значительная погрешность, возникаю-
щая при определении амплитуд, соответствующих высоким тонам коле-
баний, может не приниматься во внимание, так как их величины обыч-
но малы и напряжения в лопасти определяются в основном несколькими
первыми тонами собственных колебаний. Амплитуда же колебаний по
этим тонам будет определена с хорошей точностью.
Из приведенных соображений делается понятным, что для исполь-
зования метода расчета с непосредственным определением траекторий
движения точек лопасти выгодно использовать модель с минимальным
числом сосредоточенных грузов. Желательно ограничиться моделями
с числом грузов порядка 12—15 не более. Необходимо отметить, что при
таком малом числе участков рассмотренная выше балочная модель ло-
пасти начинает вносить в расчет погрешности, связанные с особенностя-
ми этой модели. Для иллюстрации этих особенностей на рис. 1. 53 приве-
дена форма изгибающего момента, соответствующая первому тону соб-
ственных колебаний лопасти, подсчитанная для z = 28 (сплошная линия)
и z=12 (пунктирная линия). Из рис. 1.53 следует, что при малом числе
участков изгибающий момент в балочной модели начинает проявлять
особенности, характерные для очень гибких балок, нагруженных попе-
речными силами в поле центробежных сил,— в местах расположения
масс возникают концентрации изгибающего момента. Об этой особенно-
сти уже было сказано в § 4, п. 9. Возникновение этих концентраций
существенно снижает точность расчета. Поэтому применение балочных
моделей с числом участков менее 25 (z=25) не рекомендуется. При ма-
10* 147
лом числе масс такого рода погрешности не возникают при использова-
нии многошарнирной членистой модели, хотя при этом формы колеба-
ний более высоких тонов будут достаточно сильно искажены. Па
рис. 1.53 изгибающий момент, подсчитанный для многошарнирной моде-
ли с числом участков z— 12, показан штрих-пунктирной линией.
Исходя из этих соображений, рассмотрим более подробно изложен-
ный здесь метод применительно к многошарнирной модели. Кроме то-
го, в п. 6 этого параграфа будет показано, что многошарнирная модель
Допускает применение метода расчета упругих колебаний с использова-
нием способа численного интегрирования с обратным порядком опреде-
ления переменных, который практически исключается в балочной мо-
дели.
4. Уравнения движения при рассмотрении
многошарнирной членистой модели лопасти
Представим лопасть в виде цепочки, состоящей из абсолютно жест-
ких невесомых звеньев, соединенных между собой при помощи шарни-
ров. Вес лопасти сосредоточим в шарнирах этой цепочки в виде отдель-
Рис. 1.54. Схема многошарнирной членистой модели лопасти
ных грузов с массой т{. Жесткость лопасти на изгиб также сосредото-
чим в шарнирах, представив, что в каждый шарнир как бы встроена пру-
жина с жесткостью с,, препятствующая излому лопасти в этом шарни-
ре (рис. 1.54).
Систему дифференциальных уравнений колебаний, относящуюся
к этой модели лопасти, выпишем, начиная с уравнения, описывающего
равновесие груза с порядковым номером i=2. Затем по аналогии со-
ставим все остальные уравнения системы.
148
Уравнение равновесия груза с массой т2 может быть записано
в форме:
m2y2=4C, ,-7V (10.16)
Упругая сила С2, действующая на массу т2, со стороны соседних
участков модели, определяется по формуле:
C2-Q23-Q12, (10.17)
где Qi2 и Q23 — перерезывающие силы на смежных с грузом участках
модели лопасти.
Для определения величины перерезывающих сил Qi2 и Q23 запишем
уравнения равенства нулю суммы моментов всех сил относительно точ-
ки расположения груза с массой т2 (точка Л) для обоих участков мо-
дели, смежных с этим грузом. Эти уравнения имеют следующий вид:
Qdi? — Л^127И1 = 0; 1 .jq
Q23'23 ^23 (,Уз М3 ТИ2=0. )
Определив отсюда Q12 и Q23 и подставив их в формулу (10. 17), по-
лучим:
С2 — Q23 Qi2 —
=_2_Ж1+М +Цуи2_2_;Из+
42 V 42 43/ 43
+ У,+^Уз- (10. 19)
42 \ 42 ‘23 1 ‘23
Входящие в это уравнение изгибающие моменты могут быть выра-
жены через перемещения элементов лопасти по формулам:
Mi — ci(₽i2~₽oi)—“4 Уо^е1 hy~'j У1 + у- Уъ
‘01 \ ‘01 42/ 42
Л12 = с2(?23-М=^-у- У2 +-7- Уз,
42 \ 42 43' 43
Ms = с.л (Р34 — Д.) = -у- у2~сз(~,—h —) Уз + у" Уь-
‘23 \ ‘23 ‘34/ ‘34
(10.20)
Подставив выражения (10. 20) для Af1; М2 и М3 в формулу (10. 19),
получим уравнение:
где
С2 — ^1Уо | ^1У1 । /2Г'24 ‘-гГз ! ^зУ^ (10.21)
149
Если аналогично расписать все остальные значения Сг- и поставить
их в (10. 16), то система дифференицальных уравнений колебаний лопас-
ти может быть представлена в форме табл. 1.13.
Таблица 7. 7J
Уо Уз У1 № Уэ У$ ,.а у2-/ Уг
fo ео d, = теУо
fl Ф d-l = KWi-Ti
di ft е1 • = тгУ?~
d-г fl (L if тзУз~Тз
• а а • « « - • a a
•а. а а » а а а = a a .
•аа • # » . а . а а . ••• = a . a
fz-2 е2-2 f 2-7 ez-1 - пг-1Уг-Г\-!
d-z-t ez-1 f z =: mzj'z-Tz
Каждое уравнение полученной системы, занимающее в табл. 1.13
одну строку, представляет собой сумму произведений известных коэффи-
циентов di, е( и ft на переменные у-t, входящие одновременно в несколько
уравнений. Переменные г/{ вынесены по вертикали в специальную строчку,
помещенную в верхней части табл. 1.13. Правая часть уравнений, пред-
ставляющая собой сумму инерционных и аэродинамических сил, поме-
щена в специальном столбце в правой части табл. 1.13.
Эта система уравнений связывает деформации лопасти с действу-
ющими на нее силами непосредственно без промежуточной связи через
изгибающие моменты, как это имело место в аналогичных уравнениях,
относящихся к балочной модели, описанной выше в п. 3 этого парагра-
фа, и в уравнениях, применявшихся ранее для расчета свободных ко-
лебаний лопасти в § 4.
Такой вид дифференциальных уравнений значительно упрощает
расчеты при определении упругих деформаций лопасти, но имеет
и определенные недостатки. Первым из них, как уже отмечалось, сле-
дует считать то, что упругая ось лопасти представляется в виде не плав-
ной, а ломаной линии. Также в виде ломаной линии представлена
и форма распределения изгибающего момента по длине лопасти. Вто-
рым недостатком следует признать известную произвольность в выборе
шарнирных жесткостей Cj.
Приведем один из способов определения этих жесткостей. Для это-
го рассмотрим два смежных участка лопасти. Значение шарнирной
жесткости Ci определим из условия, что углы поворота концов смежных
участков Ро и Рг эквивалентной балочной схемы совпадают с углами
Poi и Р12 для шарнирной схемы (рис. 1.55).
(?2-₽о)бал = (₽12-₽О1)шаРн. (Ю-23)
Если при сравнении этих углов пренебречь влиянием центробеж-
ных сил и считать, что изгибающий момент на протяжении этих двух
150
участков постоянен (Al0=Ali =Л42 = const), то из условия (10.23) для
определения шарнирной жесткости может быть получена формула:
J_ *01 I 112
С1 £/И EI12
(10. 24)
Практически эти допущения могут соблюдаться лишь приближен-
но. Это и создает известные погрешности при применении такой расчет-
ной схемы.
Рис. 1.55. К определению шарнирной жесткости
5. Последовательность операций при расчете упругих колебаний
методом численного интегрирования
В целом расчет лопасти по изложенной методике производится
в следующей последовательности. В начальный момент времени, кото-
рый обычно связывается с азимутом ф = 0, задается произвольная фор-
ма деформаций лопасти у{ и распределение скоростей перемещения
масс г/;. Если все значения уг известны, то по формулам, изложенным
в пп. 2 и 4 этого параграфа, могут быть определены упругие силы Ci.
Одновременно должны быть подсчитаны и углы поворота упругой оси
лопасти Для балочной модели они определяются по формуле (10. 13).
Для членистой модели они могут быть определены в виде полусуммы
углов поворота двух смежных с рассматриваемой точкой звеньев мо-
дели:
--------2 •
Если значения р, и yt известны, то по формулам (9.20) могут
быть получены и аэродинамические силы Т\. Этих данных достаточно
для того, чтобы по формулам (10. 1) определить значения
151
Дальше выполняется переход к следующему азимуту лопасти по
формулам, аналогичным (9.43):
У'+м = + Myt +
t/t+м =yt-\~
У*+м
•• yt+Ht-^u
- - ;
у!+м H- ktyt "1 ^Уср>
J/I+a* — yt + Дг'г/ср!
^+iz=±(Cnw + ^J.
(10. 25)
Значения yt+м, у'+м и yt+м для момента времени t + At счи-
таются окончательными. Индекс I, относящийся к номеру сосредоточен-
ного груза, в формулах (10.25) опущен, чтобы чрезмерно не усложнять
выражения.
Для перехода к новому азимуту все операции повторяются заново.
Этот процесс продолжается в течение нескольких оборотов несущего
винта, пока движение лопасти не станет установившимся. Расчет за-
канчивается на том обороте, когда рейгение сойдется к установившему-
ся с заданной точностью. Точность решения определяется по разнице
в ординатах перемещения масс при расчете движения в двух последо-
вательных оборотах несущего винта.
Обработка результатов расчета может быть выполнена в любом
виде в зависимости от цели расчета. Для решения вопросов, определяю-
щих прочность лопасти, обычно практикуется вывод во внешнюю па-
мять значений изгибающих моментов через 10° по азимуту несуще-
го винта. По окончании расчета по значениям Mi и моментам сопротив-
ления сечений лопасти определяются значения напряжений и их ампли-
туда
дД _— cmax i cmln /
1 2
(10.26)
и производится разложение напряжений по гармоникам.
Расчет упругих колебаний по изложенной методике представляет
собой непрерывное повторение одних и тех же операций, сводящихся
к определению сил С, и и решению уравнения (10. 1). Поэтому про-
должительность расчета прежде всего, будет зависеть от числа этих по-
вторений. Это число определяют только два фактора. Первый из них —
это продолжительность периода перехода к установившемуся процессу,
который зависит только от соответствия начальных условий установив-
шемуся движению и от физических свойств несущего винта и не зависит
от методики расчета. Второй, о котором уже говорилось выше, это по-
требный шаг интегрирования.
6. Метод расчета с обратным порядком определения переменных
при численном интегрировании
Выше, в § 9, и в этом параграфе рассматривались прямые способы
численного интегрирования дифференциальных уравнений, когда при
переходе к новому моменту времени определяются вначале перемен-
152
ная у и ее первая производная у, а затем из дифференциального урав-
нения определяется и вторая производная у. Здесь мы рассмотрим ме-
тод расчета, предложенный В. Э, Баскиным, когда эти величины опре-
деляются в обратном поряд-
ке.
Рассмотрим последо-
вательно три момента вре-
мени: момент времени, в ко-
торый необходимо опреде-
лить деформации лопасти
tn, и два предшествующих
ему момента времени tn-i =
“ И tn— tn Q\t.
Если положить, что вто-
рая производная у сохраня-
ется постоянной на протя-
жении каждого участка ин-
тегрирования, как это пока-
зано на рис. 1.56, в, то зна-
чение уп-л может быть вы-
ражено через у п-2 и yn-i'-
'уп-^п^,п^- (10.27)
at
Если теперь положить,
что и первая производная у
также сохраняется постоян-
ной на протяжении участка
интегрирования, как это по-
казано на рис. 1.56,6 пунк-
тиром, то значения уп-\ и
уп-2 можно определить по
формулам:
Рис. 1.56. Изменение переменной у и ее про-
изводных по времени при численном интегри-
ровании
Уп-1
Уп Уп—\ .
(10. 28)
У п-1 —Уп—2
М
Подставив (10.28) в (10.27), получим выражение для yn-i‘.
Уп—1 д^2^л ^Уп—1Уп—г)-
(10. 29>
Если шаг иитегриования взять достаточно малым, то можно при-
ближенно положить
Уп Уп—1
(10.30)
и выражение (10. 29) записать в виде:
'уп=^АУп-2Уп-1-УУп-2>- ' (10.31)
Подставив значения уп в систему дифференциальных уравнений,
представленную табл. 1.13, получим систему алгебраических уравнений
относительно неизвестных уп. Как и выше, эту систему запишем в фор-
ме табл. 1.14.
155'
У переменных у, входящих в табл. 1. 14, индекс, определяющий
момент времени, записан сверху, а снизу, как и раньше, поставлен ин-
декс, относящийся к номеру сосредоточенного груза модели.
При составлении табл. 1.14 принято также допущение о том, что
аэродинамические силы, вычисленные для момента времени tn-\, мо-
гут быть приближенно положены равными этим силам для момента
Допущение (10.30) позволяет выразить ускорение уп в момент вре-
мени tn через деформации уп~2, уп--\ и уп. Определив инерционные силы
как произведения масс тг на соответствующие ускорения и сложив их
с аэродинамическими силами, можно получить суммарные внешние
силы, действующие на лопасть. Тогда деформации уп определяются,
как в обыкновенной статической задаче. Это и делается в результате ре-
шения системы уравнений, записанной в табл. 1.14. Единственной осо-
бенностью этих уравнений является то, что составляющие инерционных
сил, выраженные через еще не вычисленные значения уп, перенесены
в левую часть и определяются одновременно с решении системы урав-
нений.
Таким образом, определение различных параметров движения ло-
пасти по этому методу производятся в необычном порядке. Вначале как
бы определяются ускорения, а затем уж деформации. Поэтому этот ме-
тод решения нами здесь назван обратным способом численного инте-
грирования. Часто его называют также неявным способом.
Метод расчета с применением обратного способа численного инте-
грирования не приводит к расходящемуся решению даже при доста-
точно большом шаге интегрирования. Поэтому величину потребного
шага интегрирования следует определять исходя только из величины
погрешностей, которые возникают при применении этого метода. Ве-
личина погрешности может быть оценена, если применить обратный
способ численного интегрирования к решению уравнения (9.24). Ре-
зультаты такого расчета приведены на рис. 1.57.
Из этих расчетов следует, что для достижения удовлетворительной
точности в значениях деформаций, соответствующих частотам, равным
числу оборотов несущего винта, шаг интегрирования должен быть
меньше 1° по азимуту несущего винта I ДТ= —I .
154
В процессе расчета с применением метода с обратным порядком
определения переменных решение системы уравнений, записанных
в табл. 1. 14 выполняется последовательно на каждом азимуте с ис-
пользованием уже ранее определенных значений уп~г и уп~' • В на-
чальный момент времени эти
величины могут быть взяты
произвольно.
Изложенный метод расче-
та отличается большей трудо-
емкостью по сравнению с ме-
тодами, использующими раз-
ложение решения по заранее
заданным формам колебаний,
и требует поэтому при расче-
тах на электронно-цифровых
машинах очень большой зат-
раты времени. Однако такой
Рис, 1.57. Результаты численного решения
уравнения (9.26) «обратным способом ин-
тегрирования» в зависимости от относитель-
ного шага интегрирования
метод имеет серьезные преи-
мущества в тех случаях, ког-
да необходимо оценить влия-
ние различных сосредоточен-
ных воздействий на лопасти,
например, при оценке воздей-
ствий со стороны демпферов в шарнирах, и во всех тех случаях, когда
решение не может быть достаточно точно представлено при помощи ог-
раниченного числа заданных заранее форм колебаний.
7. Сравнительная оценка различных методов расчета
изгибных колебаний лопасти
В этой главе было изложено множество различных методов расчета
изгибных колебаний лопасти и, естественно, может возникнуть вопрос,
какой же метод должен быть выбран для практического использования
и на основании каких критериев этот выбор должен осуществляться.
Ответ на этот вопрос очень прост: для практических целей наилучшим
всегда будет тот метод, который наиболее полно и точно учитывает все
особенности работы несущего винта, включая переменное поле индук-
тивных скоростей и нелинейный характер зависимости аэродинамиче-
ских коэффициентов от угла атаки и числа М. Но при этом оказывается
нельзя отбросить и имеющиеся ограничения, состоящие в том, что чем
полнее и точнее метод расчета, тем большего времени вычислений он
требует при расчете на цифровых машинах. Поэтому при выборе наи-
лучшего метода расчета главным критерием оказываются возможности
машины, которые ограничивают применение наиболее совершенных ме-
тодов расчета.
Чтобы выбрать наиболее подходящий метод расчета, приведем
таблицу 1.15 с указанием потребной скорости вычислений при примене-
нии различных методов расчета. В этой же таблице приведены основные
характеристики различных методов расчета.
Здесь мы приводим ориентировочные значения потребной ско-
рости операций в одну секунду УпотР для выполнения расчета в течение
5—10 мин. Потребная скорость приведена для всех методов расчета
в четырех вариантах применяемых допущений. В табл. 1.15 не оцени-
вается потребный объем памяти машины, так как у современных ма-
шин он обычно не стесняет расчетчика.
155

«3
Метод расчета с непосредствен- ным определением траекторий, движения отдельных тачек лопасти II Е 'Ч II : Уравнения не преобразуются Обратный способ численного ин - тегрирования й /'потр - 0,5б 1,0° 1/п 0 j р ~ МО ООО операци идеек тивных скоростей определенных по чпастей /при числе точек по радиу- V'norp - 500000 операций /сек иных зависимостей Cy=f(ot.,M) и dorp - 200000 операций/сек 'Г=М2 /ПО7Р > 1000 000 операцай/сек
Метод расчета с разложением ре- шения по собственным функциям и с определением временных мне - жителей методом численного ин- тегрирования преобразованных уравнений и 4? II Г. Галеркина Прямой спосод численного интег- рирования 'Г потя _ 6,5 . 5 ° /погр = 20000 операцай/сек Методы удобны для учета он вук схеме винта с конечным числом'л, су 1,^121 I'ncTP - 100000 операции /сек Методы удобны для учета нелине. Сх Чпзтр - 50000 операцай/сек | При 1 vpptp ~ 650 000 операций /сек |
Метод расчета с разложением решения по собствен- ным функциям и определением коэффициентов разло- жения временных множителей в ряд Фуоье по гар- моникам ।—। Uj 1 1 у^/ац-а, сояф-ЬчЗьп <р-а2 cos2ip-b2sin 2<р.. .) у10} + + (с0- CtCostji-d/Sini/i- c2cos Zip - йглёп 2ф )-у',1 7- f-!ea-efcosiji-f.iS'i.nili-e2 cos2 ip-f2stn2p...)-y(2^ + 4(gg-g!cosyi-hlsitip-g2 coslip -h2sin Zip...)- y1^ Метод Б. > Коэффициенты разложения временных множителей определяются из системы алгебраических уравнений к'потя = 5000 операций /сек |_ Метод удобен для учета неравномерного поля индуктивных скоростей .разложенного по гармоническим составляющим к1атр =50 000 операции/сек Для учета зависимости су = f/щ м/ и сх= f(y, м) метод практически непригоден —, -- - _ -
о § $ $Г в которой, явлено пр- ение § 3? определения . <ых множи- ли Л = const су = Су а Сх = 0 t- •« S V* '-I Л = cons t СУ Cx=f/U,M} а з -£ " 'L х -х >.?
«л & g'S JK § $ § Метод । времена те. :якпнзБ1биор хпЬючбдвиэ пди нпя /?/ -_с z?r пшэиои swnitcjd поидо пн ппнзже:! - UVH KTlHdlfdpSdUO tfl/p Mlfy DtUJhJ QlL/JL/d - они tfvupddtijou п врЪшлм/ хптшзтнЗзшхвспх
156
Из рассмотрения данных табл. 1. 15 следует, что для машины с ма-
лои скоростью счета I порядка 5000 ——-—J широко может приме-
няться только один метод, носящий название метода расчета по гармо-
никам. В этом методе решение разлагается по собственным функциям.
Временные множители при этих функциях представляются в виде ряда
Фурье по гармоникам. Коэффициенты этого ряда определяются из си-
стемы алгебраических уравнений, полученных из дифференциального
уравнения с помощью метода Б. Г. Галеркина. Этот метод изложен
в § 8.
На машинах с малой скоростью счета этот метод может применять-
ся только с допущением о равномерном распределении индуктивных
скоростей Z = const. Для учета нелинейной зависимости аэродинамиче-
ских коэффициентов от угла атаки профиля и числа М этот метод прак-
тически не пригоден. Учет этих зависимостей при таком методе может
быть выполнен только с очень серьезными допущениями. Но даже
при таком подходе трудоемкость выкладок, необходимых для составле-
ния расчетных формул, настолько велика, что практически просто не-
осуществима.
Для машин со средней скоростью счета (порядка 20 000—
50 000 °-п-рацаа^ наиболее удобным оказывается метод расчета с раз-
ложением решения по собственным функциям и определением времен-
ных множителей при этих функциях с помощью численного интегриро-
вания. Этот метод изложен в § 9. Он очень удобен для учета нелиней-
ных зависимостей аэродинамических коэффициентов от угла атаки
профиля и числа М.
При необходимости учета переменного поля индуктивных скоростей
применение этого метода возможно только на машинах с большой ско-
ростью счета. Если при определении индуктивных скоростей ограничить
число расчетных точек по радиусу и азимуту несущего винта, то расчет
может быть выполнен и на машинах со средней скоростью счета.
Метод расчета с непосредственным определением траекторий дви-
жения отдельных точек лопасти (§ 10) может быть использован только
на машинах со скоростью счета большей 100 000 onePa4au . учет пере-
сек
менного поля индуктивных скоростей и нелинейных зависимостей аэро-
динамических коэффициентов от угла атаки профиля и числа М еще
больше увеличивает потребную скорость счета при этом методе. В по-
следнем столбце табл. 1. 15 рассмотрен только метод с обратным спосо-
бом численного интегрирования уравнений. В случае применения пря-
мого способа численного интегрирования потребная скорость счета для
метода с непосредственным определением траекторий движения отдель-
ных точек лопасти может возрасти еще сильнее.
Потребные скорости счета, приведенные в табл. 1. 15, получены для
случая, когда расчет продолжается в течение 5—10 мин. При такой про-
должительности возможно проведение различных требуемых в процессе
проектирования лопасти исследований с варьированием параметров не-
сущего винта и режима полета.
Если ограничиться расчетом только для одного варианта парамет-
ров, то можно использовать и большую продолжительность счета.
В этом случае приведенные в табл. 1.15 потребные скорости счета могут
быть соответственно уменьшены.
Используя изложенные здесь соображения, можно в каждом отдель-
ном случае выбрать наиболее подходящий метод расчета, исходя из воз-
можности применения тех или иных допущений и располагаемого време-
ни при расчете на машине.
157
§ 11. УСТАЛОСТНАЯ ПРОЧНОСТЬ И РЕСУРС ЛОПАСТИ
1. Испытания конструкции для определения ее ресурса
Ресурс конструкции устанавливается обычно на основании резуль-
татов ее динамических испытаний.
В зависимости от степени ответственности конструкции за безопас-
ность полета проводятся испытания одного или нескольких экземпляров
этой конструкции. Часто испытаниям подвергают только отдельные части
конструкции, прочность которых является определяющей для всего про-
веряемого агрегата в целом.
При определе-
нии ресурса лопасти
проводятся обычно
испытания образцов
отдельных участков
лонжерона с деталя-
ми каркаса, создаю-
щими концентрации
напряжений в лон-
жероне. Испытыва-
ются образцы не ме-
нее трех различных
участков лонжеро-
на. Это, как правило,
участок, включаю-
щий комлевой стык
и два участка по
длине лонжерона.
Иногда приходится
„ , „ „ „ „ подвергать испыта-
Рис. 1.58. Стенд для испытании образцов лопасти ниям дополнитель.
ные образцы для
проверки отдельных конструктивных особенностей лонжерона (напри-
мер, мест перехода сечений лонжерона).
Испытания образцов лопасти почти всегда проводятся на резонанс-
ных стендах с возбуждением от механических вибраторов. Длина образ-
ца выбирается таким образом, чтобы его частота собственных колебаний
на изгиб укладывалась в рабочий диапазон вибратора. Обычно испыта-
ния проводятся с частотой от 1500 до 2500 кол!мин. При этом длины об-
разцов оказываются порядка 3—4 м. Кроме переменных напряжений
изгиба образец обязательно растягивается продольными силами, создаю-
щими постоянную статическую подгрузку, близкую к той, которую ло-
пасть испытывает в полете от действия центробежных сил. На рис. 1.58
показан стенд для испытания образцов лопасти вертолета с центробеж-
ной силой порядка 100 тс.
Испытания лопасти в целом, а не отдельных коротких образцов, как
правило, не проводятся ввиду слишком большой сложности стендов, ко-
торые для этого требуются, и значительной продолжительности испыта-
ний, так как частота колебаний в этом случае не может быть больше
300—400 кол!мин.
2. Рассеяние характеристик выносливости
при усталостных испытаниях
При проведении усталостных испытаний некоторого числа образцов,
изготовленных в одинаковых условиях, обнаруживается значительный
разброс результатов испытаний. Разрушение образцов, испытываемых
при одном и том же уровне напряжений, происходит при различном чис-
158
ле циклов N. Часто отношение наибольшего числа циклов к наименьшему
доходит до 20—40.
Разброс характерестик усталостной прочности объясняется неодно-
родностью структуры материала, различием в условиях изготовления
и обработки образцов. Разрушение образцов конструкции начинается
всегда от мелких дефектов в материале и на поверхности образца. В по-
давляющем большинстве случаев разрушение начинается от дефекта,
расположенного на поверхности. При этом характеристики выносливости
образцов определяются характером и величиной этих дефектов.
Рассеяние долговечности при испытаниях образцов характеризу-
ется обычно функцией распределения чисел циклов N до разрушения об-
разцов. Обработка результатов испытаний показывает, что распределе-
ние логарифмов чисел циклов IgA/ до разрушения достаточно хорошо
подчиняется нормальному закону распределения почти при всех средних
значениях вероятности разрушения, начиная примерно с вероятности,
равной 0,01—0,02.
На рис. 1.59 показаны распределения вероятности разрушения Р
и плотности вероятности ср, соответствующие действительным характе-
ристикам долговечности конструкции (сплошные кривые) и определяе-
мые нормальным законом распределения (пунктирные кривые):
1 21Sh» Ar
<p(lg^)= „ z-x- ; (11.1)'
•big N У
P(lg2V)= р(5Ж (11.2>
Здесь <p(lgAf) —плотность распределения вероятности разрушения кон-
струкции;
P(lgAf)—вероятность разрушения конструкции при числе нагру-
жений, меньшем ЛУ;
£ = lgAf — значение логарифма числа циклов до разрушения кон-
струкции;
SigAr—среднеквадратическое отклонение распределения лога-
рифмов чисел циклов до разрушения конструкции;
—математическое ожидание распределения логарифмов
чисел циклов.
В области малых вероятностей разрушения функция распределения
обычно отклоняется от нормального закона (фиг. 1.59). Это связано
с очень важной особенностью характеристик долговечности. Дело в том,
что усталостное разрушение может произойти только после какого-то
числа циклов нагружения jVq и никогда не происходит раньше. Эта осо-
бенность характеристик долговечности приводит к понятию зоны нечув-
ствительности по N, в которой вероятность разрушения конструкции рав-
на нулю (Р = 0). Отсюда, в частности, следует очень важный вывод о воз-
можности назначения ресурса работы конструкции по условиям вынос-
ливости с Вероятностью разрушения, равной нулю, даже при достаточно
высоких переменных напряжениях.
К сожалению, определение порога чувствительности jV0 со сколько-
нибудь удовлетворительной точностью практически оказывается невоз-
можным. Поэтому при определении ресурса конструкции закон распре-
деления долговечности принимается обычно нормальным, а требование
Р = 0 заменяется требованием очень малой вероятности разрушения.
159'
Отклонение значений логарифмов чисел циклов от нормального за-
кона должно наблюдаться также в области больших вероятностей раз-
Рис. I. 59. Кривые распределения долговечности при испы-
таниях и соответствующие нормальному закону
рушения. При относительно низком уровне переменных напряжений это
связано с тем, что почти всегда имеется какое-то число образцов, не
разрушающихся даже при очень большом числе циклов нагружения.
3. Основные характеристики усталостной прочности конструкции
Усталостная прочность конструкции характеризуется обычно числом
циклов N, которое она выдерживает до разрушения при заданной ампли-
туде переменных напряжений о. Чем больше амплитуда переменных на-
пряжений ст, тем меньшее число циклов нагружения выдерживает конст-
рукция.
Кривая, характеризующая число циклов N до разрушения, в зави-
симости #г амплитуды переменных напряжений о называется кривой Ве-
лера.
Приближенно кривая Велера может быть описана уравнением:
a'njy^const при и
а = %=const при 7V>A\B.
Здесь <yw — наибольшая амплитуда напряжений, при которой конструк-
ция может выдержать какое угодно большое число циклов
нагружения N без разрушения; эта амплитуда называется
обычно пределом выносливости;
Nu — минимальное число циклов нагружения, соответствующее
пределу выносливости;
т — некоторый показатель степени, величина которого опреде-
ляется по результатам испытаний.
Кривая Велера может быть построена для различных значений ве-
роятности разрушения. Для этого необходимо разбить партию образцов
на несколько групп и испытать их при различных амплитудах перемен-
ных напряжений.
Построив функции распределения долговечности при разных уровнях
переменных напряжений (рис. 1.60) и соединив точки с одинаковой ве-
роятностью разрушения, можно получить кривые Велера, соответствую-
щие различной вероятности разрушения. Обычно при этом оказывается,
что рассеяние характеристик долговечности тем меньше, чем выше уро-
вень переменных напряжений, а порог чувствительности Na более четко
выражен при меньших напряжениях. Причем при малых напряжениях
порог чувствительности наблюдается при относительно больших вероят-
(И.З)
160
, ностях Р, а при больших напряжениях он перемещается на столь малые
вероятности, что его обычно не удается заметить.
Результаты испытаний почти всегда подтверждают наличие предела
выносливости Ощ,. При заданном напряжении о какое-то число образцов
обычно не разрушается даже при очень большом числе циклов нагруже-
, ния. Существование предела выносливости подверждается также опытом
J эксплуатации различных машин и механизмов. Известно множество раз-
‘ личных деталей, очень большое число которых постоянно работает при
значительных переменных напряжениях и не разрушается при числе цик-
лов нагружения 108 и более. Из этого общего правила имеются отдель-
Рис. 1.60. Распределение долговечностей при различном уровне
переменных напряжений
ные исключения. Замечено, что для некоторых конструктивных элемен-
тов из алюминиевых сплавов кривая выносливости продолжает снижать-
ся и при долговечностях порядка 108—1010 циклов. Однако это снижение
столь незначительно, что и в этом случае кривая Велера может быть при-
ближенно представлена в форме (11.3). Во всяком случае применитель-
но к основным агрегатам вертолета учет этого снижения не приводит
к сколько-нибудь существенным уточнениям.
В значениях пределов выносливости также наблюдается определен-
ное рассеяние. Для их распределения характерно наличие порога чув-
ствительности по амплитуде напряжений. Этот порог чувствительности
будем в дальнейшем называть минимальным пределом выносливости
%т1п. При напряжениях, меньших ст^п, ни один образец не разрушается
даже при очень большом числе циклов нагружения. В соответствии с
перечисленными особенностями характеристик усталости кривые Веле-
ра должны иметь вид, изображенный на рис. 1.61.
Если кривые, соответствующие разной вероятности разрушения, за-
менить приближенной аналитической зависимостью (11.3), то в логариф-
мическом масштабе кривые Велера будут иметь вид, изображенный на
рис. 1.62. Зона нечувствительности, соответствующая нулевой вероятно-
сти разрушения, на этом графике заштрихована. При таком изображе-
нии кривых Велера число циклов Nw, соответствующее пределу выносли-
вости, и показатели степени т оказываются различными для кривых, со-
ответствующих разным вероятностям разрушения.
11 1578
161
Следует отметить, что построение кривых Велера в том виде, как
они изображены на рис. 1.61 и 1.62 практически возможно только при
испытаниях малых лабораторных образцов, так как для этого оказы-
вается необходимым иметь их очень большое число.
Рис, 1.61. Кривые Велера, соответствующие разной
вероятности разрушения
При оценке прочности конструкции построение таких кривых прак-
тически невозможно, так как приходится ограничиваться испытанием
очень малого числа образцов. Часто это число не превышает «=Зч-5 (где
п — число испытанных образцов). При этом для оценки прочности испы-
тания дают только п значений чисел циклов до разрушения при задан-
ной величине нагрузок. По такому ограниченному числу результатов
Рис. 1.62. Кривые Велера, соответствующие разной
вероятности разрушения, в логарифмическом мас-
штабе
можно составить представление об усталостных характеристиках кон-
струкции только на основе определенных предположений в отношении
кривых Велера.
Величина амплитуды переменных напряжений, при которой конст-
рукция выдерживает заданное число циклов нагружения N до разруше-
ния, зависит также от величины постоянной части напряжений цикла <ут
162
(статической подгрузки). Чем больше статическая подгрузка, тем мень-
ше амплитуда напряжений, при которой конструкция выдерживает за-
данное число циклов. Эта за-
висимость характеризуется
обычно диаграммой Хея. В ка-
честве примера на рис. 1.63
показан примерный вид такой
диаграммы.
Для стальных труб лон-
жеронов при от=20ч-
30 кгфлм2 увеличение ста-
тической подгрузки на величи-
ну Дощ приводит к снижению
предела выносливости на вели-
чину Дото--0,4Аат. Для дур-
алюминовых лонжеронов при
Рис. 1.63. Диаграмма Хея для образцов труб
лонжерона лопасти
qot=6-t-8 кгс/мм? величина
АсГщ.
Следует обратить внима-
ние на то, что в области постоянных напряжений сжатия пределы вы-
носливости существенно возрастают. Это обстоятельство используется
при упрочнении деталей конструкции наклепом (см. пп. 16 и 17).
4. Напряжения, действующие в конструкции лопасти в полете
В § 1 этой главы (п. 3) уже говорилось, что в полете под действием
аэродинамических сил лопасти вертолета испытывают значительные пе-
ременные нагрузки на режимах двух различных типов, именуемых нами
Рис. 1.64. Характер изменения амплитуд
переменных напряжений по скорости
полета в лопастях с малой (стальная
труба) и средней (дуралюмиповый лон-
жерон) жесткостью в плоскости взмаха
режимами малых и больших ско-
ростей.
На рис. 1.64 показан при-
мерный характер изменения ам-
плитуд переменных напряжений
по скорости полета у двух кон-
струкций лопастей: со стальным
и дуралюминовым лонжероном.
Как видно из этого рисунка, мак-
симальные переменные напряже-
ния могут возникнуть и на ма-
лых скоростях (режим торможе-
ния) и на максимальной скорос-
ти полета. При этом, как уже
было показано, лопасти соверша-
ют изгибные колебания так, что
в каждой точке лонжерона на-
пряжения изменяются по перио-
дическому закону, повторяясь за
каждый оборот несущего винта.
На рис. 1.65 в качестве примера
приведена запись напряжений, полученная в сечениях лопасти на отно-
сительных радиусах г=0,73 и г = 0,8 на режиме горизонтального полета
с относительно большой скоростью. На этом же рисунке приведен гар-
монический состав действующих в этих сечениях лопасти напряжений.
Обычно в горизонтальном полете на ц = 0,2н-0,4 наибольших значе-
ний достигает первая гармоническая составляющая напряжений. Вторая
гармоника меньше по амплитуде и составляет обычно 30—70% от первой
гармоники. Первая и вторая гармоники в сумме, как правило, на 70_
90% определяют величину суммарных переменных напряжений на этих
И*
163
режимах в лопасти, так как более высокие гармоники оказываются обыч-
но малыми. Их величина почти всегда уменьшается с увеличением поряд-
ка гармоники. Такой характер изменения величины гармоник связан
с уменьшением величины гармонических составляющих аэродинамичес-
неяряжений.:
Рис. 1. 65. Запись напряжений в двух сече-
ниях лопасти вертолета на режиме гори-
зонтальной скорости (ц=0,3) и их гармо-
нический состав)
У Лопастей со средней жесткостью
ных напряжений на малых скоростях
ких сил при переходе к более
высоким гармоникам.
Из этого общего правила
имеются повторяющиеся для
всех лопастей исключения,
связанные с возникновением
резонансов или близостью к
ним.
На режимах малых ско-
ростей гармонический состав
действующих напряжений ока-
зывается другим. Здесь преоб-
ладающими становятся более
высокие гармоники, причем в
первую очередь выделяются
гармоники, близкие по час-
тотам к частоте собственных
колебаний второго и третьего
тонов. Особенно сильное воз-
растание переменных напря-
жений на этих режимах полета
(см. рис. 1.64) происходит у
лопастей с малой жесткостью
в плоскости взмаха (см. § 3,
п. 3). У таких лопастей силь-
нее всего проявляются напря-
жения с четвертой и шестой
гармониками (рис. 1.66). Ре-
жимы малых скоростей дают у
таких лопастей основную пов-
реждаемость конструкции (см.
табл. 1.21).
в плоскости взмаха рост перемен-
оказывается значительно слабее
(см. фиг. 1. 64) и преобладание более высоких гармоник не наблюдается
столь резко (рис. 1.67). У таких лопастей (так же, как и лопастей с
большой жесткостью) основную повреждаемость дают режимы полета
с большой скоростью.
Наряду с переменными напряжениями от изгибных колебаний, лон-
жерон лопасти растянут и изогнут постоянными по величине центробеж-
ными силами и постоянной частью аэродинамических сил. Поэтому ма-
териал лонжерона работает при переменных напряжениях с большой ста-
тической подгрузкой. Статическая подгрузка сильно снижает усталост-
ную прочность лонжерона.
5. Гипотеза линейного суммирования повреждаемостей
и средняя эквивалентная амплитуда переменных напряжений
На различных режимах полета в конструкции действуют самые раз-
личные по величине переменные напряжения. При этом продолжитель-
ность отдельных режимов полета может быть существенно разной. Так,
наиболее продолжительным режимом полета оказывается обычно полет
на крейсерской скорости. Для вертолетов, используемых на транспорт-
ных перевозках, этот режим занимает 60—70% ресурса. Максимальная
164
пряжений в лопасти со стальным трубчатым лон-
жероном, имеющей малую жесткость в плоскости
взмаха в процессе торможения, и их гармониче-
ский состав
Рис. 1.67. Гармонический состав пе-
ременных напряжений в лопасти
средней жесткости с прессованным
дуралюминовым лонжероном па ре-
жиме торможения
165
скорость полета у транспортных вертолетов, применяемых в народном
хозяйстве, почти не используется. Очень малую продолжительность име.
ют у этих вертолетов также режимы полета на малых скоростях, которые
обычно оказываются только проходными при разгоне и торможении.
Однако вертолеты могут быть использованы на самых различных
видах работ, где продолжительность отдельных режимов полета оказы-
вается иной. В качестве примера в табл. 1.21 приведены значения отно-
сительной продолжительности различных режимов at, принятые для од-
ного из военно-транспортных вертолетов.
Ресурс конструкции должен определяться с учетом временного со-
става пребывания вертолета на режимах с разным уровнем переменных
напряжений, и поэтому вносящих в конструкцию различную долю уста-
лостной повреждаемости. Для учета этого обстоятельства удобно вос-
пользоваться гипотезой линейного суммирования повреждаемостей. Эта
гипотеза предполагает возможность суммирования отдельных долей по-
вреждаемости, вносящихся различными уровнями напряжений и гово-
рит, что разрушение конструкции наступает тогда, когда
4WS= 1,
где

(11.4)
Здесь N{ — число циклов до разрушения при непрерывном поддержа-
нии уровня нагружения с амплитудой щ;
AATi— число циклов нагружения с амплитудой щ. испытываемое
конструкцией на i-м режиме полета.
Отношение АЛ7;=^~ обычно называется повреждаемостью конст-
рукции на режиме с амплитудой напряжений a A2VS — суммарной по-
вреждаемостью.
В некоторых работах доказывается, что при определенном чередова-
нии режимов нагружения разрушение конструкции может наступить и
тогда, когда
Однако рассмотренные в этих работах случаи в основном не соот-
ветствуют условиям нагружения агрегатов вертолета. Поэтому почти
всегда при расчетах можно использовать формулу (11.4).
Вследствие рассеяния характеристик долговечности повреждаемость
отдельных экземпляров конструкции даже при одинаковом по продол-
жительности составе уровней нагружения оказывается различной. Наи-
большую повреждаемость испытывают конструкции с наименьшими зна-
чениями долговечности. Поэтому можно говорить о повреждаемости, со-
ответствующей определенной вероятности разрушения.
Если в формуле (11.4) задавать значения соответствующие за-
данной вероятности разрушения Рзад, то при ДЛ^ = 1 вероятность раз-
рушения также будет равна Рзап. Отсюда может быть получена и фор-
мула для расчета безопасного числа циклов нагружений Л/'без с заданной
вероятностью разрушения Р3ад, определяющая ресурс конструкций по
условиям выносливости:
N без
]__
I IP
J Ni
(И.5)
Здесь а;=---------
'Vpec
относительная продолжительность режима с на-
пряжением аг;
166
— число циклов нагружения за ресурс конструкции
при определении относительной продолжительно-
сти отдельных режимов полета at (вообще говоря,
может быть взят любой произвольный промежуток
времени эксплуатации вертолета с числом циклов
N, вовсе не обязательно равным числу циклов
нагружения за установленный ресурс конструкции
^рес);
N; — число циклов нагружения с амплитудой <зг, при
котором вероятность разрушения равна заданной
Если действующие напряжения ниже минимального предела вы-
носливости, то повреждаемость в конструкцию не вносится. В этом слу-
чае число циклов N{ в формуле (11.5) нужно положить равным беско-
нечности.
Можно ввести понятие об относительной продолжительности режи-
мов е, вносящих повреждаемость в конструкцию:
N повр
^рес
где Мповр — число циклов нагружения за ресурс конструкции, внося-
щее повреждаемость.
Таким образом, за время ресурса Л конструкция повреждается толь-
ко в течение времени, равного еЛ.
Часто для придания расчетам большей наглядности оказывается
удобным ввести понятие о средней эквивалентной амплитуде перемен-
ных напряжений.
Средней эквивалентной амплитудой напряжений называют такую
постоянную по времени и действующую в течение части ресурса, равной
гЛ, амплитуду, которая вносит в конструкцию повреждаемость, равную
повреждаемости, вносимой различными по величине амплитудами пере-
менных напряжений на всех режимах полета, встречающихся при экс-
плуатации вертолета.
При введения этого понятия полагается, что при напряжениях, боль-
ших предела выносливости, долговечность конструкции может быть оп-
ределена как
Nt=Nw^m. (11.6)
Тогда, подставив (11.6) в (11.4), получим:
У, Д.'Лс"'
где суммирование производится только по тем режимам, которые вносят
повреждаемость в конструкцию.
Если ввести один эквивалентный уровень напряжений с амплитудой
(Уэкв и числом циклов, определяемым из условия, что напряжения сгвкв
действуют непрерывно в течение части ресурса еЛ, т. е., что 1УЭкв = е1Урес.
то можно записать
х;дЛУи^£Л'р[С:^. (Ц.8)
i
Следовательно:
167
В качестве примера ниже в пункте 12, см. также табл. 1.21, приведен расчет экви-
валентных напряжений для лопасти _одного из вертолетов в наиболее напряженном
сечении на относительном радиусе г = 0,74. Лонжерон этой лопасти представляет
собой стальную трубу, обжатую па эллипс по всей длине, начиная от радиуса г- 0,3.
Минимальный предел выносливости трубы лопасти в этом ссченни по результатам ди-
намических испытаний может быть принят равным ow mln=13 кге/мм2.
Измерение напряжений в лопасти с лонжероном из стальной трубы производится
обычно в двух плоскостях: в плоскости наименьшей (ав) и в плоскости наибольшей
жесткости (а»), При этом может оказаться, что в какой-то точке периметра сечения
лонжерона амплитуда переменных напряжений достигает величины аа = j/~-I- ,
большей, чем амплитуда оу.
Однако обычно из-за различия в фазах действующих напряжений в этих двух
плоскостях такая величина переменных напряжений почти никогда не достигается.
Поэтому при расчете ресурса лопасти можно пользоваться приближенной формулой:
(/" 2 2 \
У ах + ау ~ ) •
Коэффициент g может быть вычислен, если имеется одновременная запись напря-
жений Ох и Оу. Если нет данных для определения g, то практически достаточно надеж-
ные результаты могут быть получены, если принять 5=0,5.
6. Разброс амплитуд переменных напряжений на заданном режиме полета
При измерении переменных напряжений в полете обнаруживается,
что на заданном режиме полета величины напряжений оказываются
различными на протяжении режима полета и в разных полетах. Поэтому
приходится вводить свою среднеэквивалентную амплитуду переменных
напряжений на всех режимах полета.
Для определения этой амплитуды можно воспользоваться специаль-
ными дешифраторами осциллограмм, позволяющими определить число
амплитуд напряжений п^, лежащих в диапазоне
—°л-1’
где ой и — выбранные для расчета уровни амплитуд переменных
напряжений.
Тогда среднеэквивалентная амплитуда переменных напряжений на
рассматриваемом режиме может быть определена по формуле, анало-
гичной (11.9),
г л
Здесь /гй — относительное число циклов с амплитудой ай.
где пк — число циклов с амплитудой ой, a /zs —общее число циклов, за-
фиксированное дешифратором;
ег- — относительное число циклов с напряжениями, большими мини-
мального предела выносливости на i-м режиме полета.
Суммирование по k производится только для тех промежутков вре-
мени на j-м режиме, где амплитуда напряжений ah больше минимального-
предела выносливости ст.,, .
mln
При определении среднеэквивалентной амплитуды за весь ресурс
вертолета по формуле (11-9) амплитуда на каждом режиме полета долж-
на вычисляться по формуле (11.10), а относительная продолжитель-
ность режимов, вносящих повреждаемость в конструкцию, по формуле:
s=S siai-
I
168
Практически часто для упрощения расшифровки определяют на
каждом режиме не среднеэквивалентную амплитуду, а максимальную,
что идет в запас надежности, но приводит к некоторому уменьшению ре-
сурса конструкции.
7. Метод расчета ресурса с использованием коэффициентов надежности
Задача определения ресурса конструкции сводится к нахождению
такого безопасного числа циклов нагружения при эксплуатации Увеа.
при котором вероятность разрушения конструкции очень мала и равна
заданной. Если бы было можно испытать достаточно большое число об-
разцов, то, определив характеристику распределения их долговечности
(рис. 1. 68), было бы легко найти N5es. На таком подходе основаны мно-
гие методы расчета ресурса (см., например, [43]). Однако обычно ресурс
Рис. 1.68. Определение безопасного числа циклов по кривой распре-
деления долговечности
конструкции приходится определять на основании результатов динами-
ческих испытаний какого-то малого числа образцов конструкции п, ког-
да закон распределения долговечности определить с необходимой точ-
ностью нельзя. Поэтому на практике получил широкое распространение
метод расчета ресурса конструкции, основанный на введении определен-
ных запасов надежности по числу циклов т]лг и амплитуде переменных
напряжений цо.
Для расчета ресурса по этому методу необходимо произвести изме-
рение напряжений в конструкции на ризличных режимах полета, опреде-
лить эквивалентное значение напряжений и провести динамические ис-
пытания одного или нескольких экземпляров конструкции при напряже-
ниях
^ИСп^Л3^ЭКВ‘ (И' И)
Запас ц,, здесь вводится для учета возможного различия в значени-
ях переменных напряжений в одноименных агрегатах различных верто-
летов.
Проведя испытания образцов и получив минимальное значение числа
циклов до разрушения Л'га1п, определяют безопасное число циклов нагру-
жения в эксплуатации по формуле:
(11.12)
16»
Запас надежности тщ вводится для учета рассеяния характеристик
долговечности.
Тогда ресурс конструкции в часах может быть определен по формуле
D__N без
~ 60/ ’
где f—частота нагружения лопасти в эксплуатации (колебаний в ми-
нуту) •
В некоторых случаях долговечность конструкции оказывается зави-
сящей от частоты нагружения. Поэтому, если динамические испытания
ведутся на частоте большей, чем частота нагружения в полете, то прихо-
дится вводить еще дополнительный запас на частоту нагружения ц/.
Этот запас вводится в основном для деталей, изготовленных из дуралю-
мина, и тогда, когда испытания проводятся на частоте в 5—10 раз пре-
вышающей частоту нагружения в полете. В этом случае он принимается
равным ц/= 1,5-^2,0. При учете этих запасов формула для определения
ресурса может быть записана в виде:
Я
бО/Чд^у
(11.13)
Если предположить, что распределение характеристик долговечно-
сти подчиняется нормальному закону и параметры этого закона извест-
ны, то, как уже говорилось, величины потребных запасов надежности по
числу циклов тщ и амплитуде переменных напряжений ц<, можно было
бы определить расчетным путем, задавшись определенной достаточно
малой вероятностью разрушения конструкции в эксплуатации. Однако
такие расчеты не могут претендовать на высокую точность. Поэтому на
тех же правах может быть использован и метод назначения величин этих
коэффициентов на основе опыта эксплуатации вертолетов.
Исходя из этого опыта, коэффициент запаса по амплитуде перемен-
ных напряжений ц, может быть принят равным 1,2, а запас по числу
циклов нагружения тщ различным в зависимости от числа испытанных
образцов и степени ответственности агрегата за безопасность полета.
По степени ответственности за безопасность полета все агрегаты
и детали вертолета можно разделить на четыре группы:
1 группа — агрегаты, разрушение которых приводит к немедлен-
ному и полному нарушению работоспособности и безопасности при
трудно обнаруживаемом начале появления усталостной трещины. К этой
группе можно отнести лопасти, лонжерон которых обшит каркасом и не
позволяет осмотреть его после полета, ряд закрытых для осмотра дета-
лей втулки и системы управления несущим и хвостовым винтом, вал не-
сущего винта и т. д.
II группа — агрегаты, разрушение которых могло бы привести
к немедленному и полному нарушению работоспособности конструкции
и безопасности полета, но имеется возможность раннего обнаружения
появления усталостной трещины. К этой группе можно отнести лопасти
с надежно работающей системой сигнализации появления трещин и все
остальные агрегаты, отнесенные к I группе, если появление в них уста-
лостной трещины может быть обнаружено в предполетном осмотре.
III группа — агрегаты, разрушение которых приводит к частич-
ной потере работоспособности, угрожает безопасности полета, но позво-
ляет совершить вынужденную посадку без поломки вертолета. К этой
группе можно отнести многие элементы фюзеляжа, даже редукторную
раму, если она выполнена по статически неопределимой схеме
170
IV группа — агрегаты, разрушение которых вызывает частичную
потерю работоспособности, позволяет продолжать полет, не влечет за
собой быстрого разрушения других агрегатов и позволяет обнаружить
разрушение при наземном осмотре. К этой группе можно отнести многие
элементы фюзеляжа, стабилизатор вертолета и ряд аналогичных эле-
ментов конструкции.
Чем ответственнее агрегат, тем больше величина запаса по числу
циклов должна быть взята. Могут быть предложены следующие значе-
ния этих запасов (табл. 1.16).
Осуществить запасы по чис-
.лу циклов, требуемые для I и II
групп агрегатов вертолета, на
практике оказывается возмож-
ным только при очень низкой час-
тоте изменения нагрузок в поле-
те. При установлении ресурса с
такими большими запасами для
всех основных агрегатов верто-
лета пришлось бы вести испыта-
ния до очень большого числа
циклов, существенно большего,
чем 107 циклов. На это пришлось
бы затратить очень много време-
ни. Поэтому все большее распро-
странение приобретает ускорен-
ный метод динамических испыта-
ний с запасом по числу циклов
т]№ 1 или даже меньшем едини-
цы. В этом случае обеспечение
требуемой надежности достига-
Таблица /. 16
Запасы надежности
по числу циклов*
Коэффициент запаса 1],у
Число испы- танных образ- цов п I груп- па II груп- па III груп- па IV груп- па
1 12 6,0 6 2,5
2 8 4,0 4 2,0
3 6 3,0 3 1,5
6 4 2,5 2 1,0
* Запасы "Чуу, приведенные для I груп-
пы агрегатов, вдвое больше общеизвест-
ных значений, так как в них включены
также запасы i)s, вводимые часто на не-
точность гипотезы линейного суммирова-
ния повреждаемостей.
ется путем введения только запаса по напряжениям. Для пересчета за-
пасов t]W в запас по гр применяют обычно формулу (11.3) с показате-
лем степени т = 6. При таком подходе потребный запас по амплитуде пе-
ременных напряжений оказывается различным в зависимости от числа
испытанных образцов и большим для дуралюмина, для которого оказы-
вается необходимым ввести дополнительный запас на разницу в часто-
те при испытаниях и в полете. Таблица 1.17 С учетом всего сказанного, для
Число испы- танных образ- цов п VA— ) ппинять запасы по амплитуде пепе-
сталь дуралю- менных напряжений, указанные мин в табл. 1.17.
1 2 3 6 шими запасам 1,8 1,7 1,6 1,5 [И по ам При динамических испытаниях с 2 Q такими запасами безопасное число циклов определяется по минимально- ’ . му числу циклов нагружения образца 1>8 до разрушения V6e3 = .VmSn, I,7 Следует однако иметь в виду, что проведение испытаний с такими боль- плитуде переменных нагрузок возможно только в
тех случаях, когда при увеличении нагрузки характер распределения
напряжений по различным деталям конструкции существенно не изме-
няется. Когда при увеличении нагрузок происходит перераспределение
напряжений вследствие скажем раскрытия стыков, появления взаимных
перемещений соприкасающихся деталей, работающих при рабочих на-
грузках без таких перемещений, или по другим аналогичным причинам,
применение такого метода испытаний нецелесообразно.
171
8. Метод А. Ф. Селихова для подсчета необходимого запаса надежности
ПО ЧИСЛУ ЦИКЛОВ T)jv
Выше, в п. 2, уже говорилось о том, что долговечность конструкции
имеет порог чувствительности по числу циклов No, и поэтому функция
распределения в области малых вероятностей разрушения отклоняется
от нормального закона. В принципе, можно было бы выбрать такой запас
надежности по числу циклов г|Л-, что вероятность разрушения конструк-
ции равнялась бы нулю. Но, как показано в работе [44], для достаточно
точного определения порога чувствительности требуется большое коли-
чество образцов, так что определить его величину для конструкции чаще
всего не представляется возможным. Поэтому обычно предполагают, что
логарифмы чисел циклов до разрушения 1g N распределены по нормаль-
ному закону и назначение ресурса конструкции производят исходя не
из условия, что вероятность разрушения Р = 0, а из условия, что эта ве-
роятность достаточно мала, скажем равна Р = - , Если в действи-
тельности порог чувствительности имеет место, то требование такой
малой вероятности разрушения, подсчитываемое но нормальному закону
распределения, оказывается более жестким, чем требование Р = 0, кото-
рое можно было бы предъявить, если бы значение No оказалось возмож-
ным вычислить. Поэтому можно считать вполне допустимым определение
запасов надежности исходя из несколько большей вероятности разруше-
ния, скажем Р= и даже Р= — .
1000 100
Для определения потребных запасов надежности по числу циклов
может быть использована методика, предложенная А. Ф. Селиховым.
Эта методика заключается в следующем.
Если предположить, что распределение логарифмов чисел циклов
до разрушения конструкции подчиняется нормальному закону
(lgW-migW)2
1 25= N
?(lgA0= g -e , (11.14)
TV r
то распределение минимальных значений долговечности некоторой пар-
тии образцов этой конструкции может быть определено по формуле
п г / т. „ — Ic.'V v-in-l
?П11п(^^) = ^|1 + ф ( v T(lg^V), (11.15)
2 |_ \ У * / J
где /г —число испытанных образцов;
(tn — lg N \
Х =-------------I .
51g N г 2 /
Характер распределения <pmin(lg^) для значений SigAr=O, 15
и п = Ъ, 10 и 100 показан на рис. 1.69. Значения математических ожида-
ний и среднеквадратические отклонения этого распределения в зависи-
мости от Sig.y и п можно найти по кривым, приведенным на рис. 1. 70 и
1.71.
Математическое ожидание минимального значения долговечности
может быть определено по формуле:
Л'тШ - Д/^ig JV-
Значение Amig.v определяется в зависимости от среднеквадратиче-
ского отклонения Sig.v и числа испытанных образцов по кривой на
рис. 1.70.
Среднеквадратическое отклонение минимального значения долго-
вечности Sig.vmin, отнесенное к Sig.v, приведено на рис. 1.71.
172
Таким образом, если известны характеристики распределения долго-
вечности конструкции, то по формуле (11. 15) можно определить распре-
деление минимальных значений долговечности при испытаниях малого
числа образцов п. Зная это распределение, можно определить вероят-
ность разрушения конструкции при числе циклов нагружения
(И.16)
V
где т]д’ — коэффициент запаса надежности по числу циклов;
Мы»—минимальное значение числа циклов до разрушения конст-
рукции при испытаниях.
Рис. 1.69. Распределение минимальных значений долговеч-
ности при разном объеме выборки
Прологарифмировав выражение (11.16), получим
1g ЛГбе3 = Н- 1g ть (11.17)
где
? = ЪЧп1п-
Если динамические испытания натурных образцов проводятся при
нагрузках, эквивалентных нагрузкам, действующим в рассматриваемой
конструкции в полете, то можно полагать, что распределение долговеч-
ности при динамических испытаниях и в условиях эксплуатации одина-
ково. Некоторое различие в этих распределениях может возникнуть толь-
ко вследствие погрешностей при динамических испытаниях и масштабно-
го эффекта в тех случаях, когда объем загруженного материала в конст-
рукции оказывается большим, чем в образце. Например, когда на образ-
це, вырезанном из лопасти, оказывается загруженной при испытаниях
только его средняя часть. Если динамические испытания проводятся при
нагрузках, отличных от действующих в полете, то характеристики рас-
пределения долговечности в эксплуатации оказываются существенно от-
личными от полученных при испытаниях и могут быть определены только
приближенно путем пересчета, основанного на определенных предполо-
жениях в отношении кривой Велера.
Если распределение долговечности в условиях эксплуатации фэкс
определено, то условную вероятность разрушения одного, произвольно
173
взятого экземпляра конструкции, в эксплуатации при данном исходе ди-
намических испытаний £2 можно определить по выражению
E«-ig чЛ-
/’уСЛ = J ?3KcGl)^l-
— 00
(11.18}
Полная вероятность разрушения этого экземпляра конструкции
в эксплуатации будет равна сумме условных вероятностей, умноженных
на абсолютную вероятность каждого исхода (pmta (g2)^fe:
00
J ?т1п(У
5»-Ig Чдг
J Ч’экс (£1)0^1
<й2.
Г(И. 19)
Вычислив величину этого интеграла, можно построить зависимость
вероятности разрушения конструкции Р от принятой величины запаса-
надежности ПО ЧИСЛу ЦИКЛОВ T]2V-
Рис. 1. 71. Зависимость среднеквадратиче-
скнх отклонений минимальных значений
долговечности от числа испытанных об-
разцов
Рис. 1. 70. Изменение величины матема-
тического ожидания минимальных зна-
чений долговечности от числа испытан-
ных образцов
В том случае, когда распределение долговечности в эксплуатации1
и при испытаниях одинаково
от1вЛгИС11==ОТ1гкэкс;
вероятность Р оказывается зависящей только от двух величин: от чис-
ла испытанных образцов п и от отношения логарифма запаса надежно-
сти Igrjjv к среднеквадратическому отклонению логарифмов чисел цик-
лов до разрушения образцов Sig,v (рис. 1- 72),
Таким образом, для определения потребного запаса надежности по
числу циклов нужно провести динамические испытания п образцов кон-
струкции, определить среднеквадратическое отклонение S\%n и и, за-
174
давшись некоторой вероятностью разрушения Рзал, по кривым рис. 1.72
определить tjjv- После этого безопасное число циклов до разрушения
может быть определено по формуле (11. 12).
Такой подход возможен и в том случае, когда испытаниям подвер-
гается малое число образцов. При этом значение Sig.v можно взять по'
результатам других испытаний аналогичных конструкций*.
Рис. 1. 72. Диаграмма для выбора величины запа-
са надежности 4w по числу циклов нагружения
Если положить заранее, что Sigjv = O,2 (это значение близко к мини-
мальным среднеквадратическим отклонениям, наблюдаемым для боль-
шинства агрегатов вертолета)
указанными в табл. 1. 18,
то можно получить величи-
ны запасов, близкие к тем,
которые приведены в
табл. 1. 16. Обычно величи-
ны Sig iv оказываются выше.
Поэтому и запасы, получае-
мые по этому методу выше
тех, которые приведены в
табл. 1. 16.
Основным вопросом,
который встает при пользо-
вании приведенной здесь
методикой, оказывается
вопрос о том, какую вероят-
ность разрушения конструк-
ции следует задать при рас-
чете ресурса. Часто значе-
и задаться вероятностями разрушения,
Таблица I.18
Группа агрегатов с различной ответствен- ностью за безопасность Вероятность разру- шения конструкции
I группа 1
10000
II группа III группа 1
1000 1
100
IV группа 1 10
ния вероятностей, рекомендуемые различными источниками, могут от-
личаться на 3—4 порядка (см. например, [43]). Предлагаемые здесь
* Аналогичный подход применительно к расчету самолетных конструкций был
предложен В. Л. Райхером.
175-
(в табл. 1. 18) значения этой вероятности выбраны из соображения, что
они с большой или меньшей степенью надежности должны соответство-
вать числам циклов, меньшим порога чувствительности No. Поэтому
эти вероятности следует рассматривать как некоторые условные значе-
ния, относящиеся к нормальному закону распределения. Действитель-
ные же значения намного меньше или даже просто равны нулю.
9. Об определении Slg у с заданной доверительной вероятностью
Как следует из предыдущего пункта, логарифм запаса надежности
по числу циклов lg r]N, необходимый для обеспечения заданной вероятно-
сти разрушения, оказывается прямо пропорциональным среднеквадра-
тическому отклонению в распределении логарифмов чисел циклов до
разрушения конструкции SigK. Чем больше SIgJv, тем больше должен
быть взят и запас Поэтому надежность определения ресурса конст-
рукции, зависящая от правомерности многих принятых допущений в зна-
чительной степени связана и с точностью определения SigJv-
Обычно для установления ресурса конструкции проводятся испыта-
ния трех-пяти экземпляров конструкции. Во многих случаях считается
достаточным проведение испытаний даже одного образца. Нет сомнений
в том, что при таком малом числе испытанных конструкций нет возмож-
ности для достаточно точного определения Sig.v- Поэтому в методике,
которая предложена А. Ф. Селиховым (см. п. 8) предполагается, что Sisn
может определяться не во всех случаях. При малом числе испытанных
образцов можно принять Sigw по результатам испытаний аналогичных
образцов другой испытанной ранее конструкции. Такой подход очень
сильно упрощает процесс установления ресурса и оказывается чрезвы-
чайно полезным на практике.
Определение StgJv с достаточной надежностью возможно при испы-
таниях не менее десяти образцов конструкции. Для оценки этой надеж-
ности пользуются часто понятием о доверительной вероятности определе-
ния Sig
Доверительная вероятность р выбирается обычно такой, чтобы мож-
но было считать практически достоверным, что значение Sjgw лежит
в интервале:
где SIg/v—оценка SigN, полученная по ограниченному числу результа-
тов испытаний;
—коэффициент по величине, больший единицы.
Из сказанного следует, что искомое значение 51гЛ? может лежать
в доверительном интервале с вероятностью р. Следовательно, оно может
оказаться и равным qSigN. В этом случае логарифм запаса надежности
по числу циклов 1g в соответствии с изложенной в п. 8 методикой уве-
личится пропорционально величине q, отчего расчетное значение ресур-
са снижается.
Значение коэффициента q оказывается зависящим от числа испытан-
ных образцов и принятого значения доверительной вероятности р.
В табл. 1.19 приведены значения коэффициентов q и соответствую-
щие им значения доверительной вероятности р, взятые нами из книги
Е. С. Венцель «Теория вероятностей».
Как следует из табл. 1. 19, при испытаниях, например, двадцати пяти
образцов и доверительной вероятности не менее 70%, полученное по
эксперименту значение 5ig,v оказывается необходимым при расисте ре-
сурса еще увеличить в 1,15 раза.
176
При задании доверительной вероятности следует однако иметь
в виду, что надежность определения Sig^ не должна превышать надеж-
ности определения всех других параметров, входящих в расчет ресур-
са. Это относится прежде
всего к параметрам, опреде-
ляющим закон распределе-
ния долговечности в облас-
ти малых вероятностей раз-
рушения, таким как порогу
чувствительности No, и к ха-
рактеру самого закона рас-
пределения, который
только приближенно может
быть принят логарифмиче-
ски нормальным.
Поэтому доверительную
Таблица 1.19
Число испытан- ных об- разцов Значения доверительной вероят-
ности р в % при различных 7
1,06 1,1 1,15 1,20 1,25 1,3
п=5 14,6 24,1 35,5 46,1 55,6 63,7
п=10 20,8 34 49 62 72,2 79,7
л=25 32,7 51,8 70,6 83,2 90,5 94,4
/2=50 45,2 68,2 86 94 97,4 98,8
вероятность 0, характеризующую надеж-
ность определения SigN, можно существенно снизить до значений, при
которых коэффициент q будет не намного больше единицы.
Исходя из этих соображений, при определении запасов т]л- часто по-
лагают q — 1 и пользуются значением Sisn, а не тем, которое соответству-
ет верхней границе доверительного интервала при достаточно высоком 0.
10. Разброс в уровнях нагружения различных экземпляров конструкции
и запас надежности по амплитуде переменных напряжений 13 =
Значения амплитуд переменных напряжений, действующих в полете
в отдельных экземплярах одинаковых по конструкции агрегатов верто-
лета, оказываются различными.
Измерения показывают, что на одинаковых режимах полета ампли-
туды переменных напряжений различаются как для лопастей одного вин-
та, так и между лопастями различных несущих винтов. Это объясняется
разбросом параметров лопастей, изготавливаемых серийно, вследствие
различия в их геометрических размерах, а, следовательно, и в их весе.
Обычно всегда имеются отклонения от теоретического контура профиля
и различия в геометрической крутке лопасти. Кроме того, при установке
лопастей на вертолет и регулировании соконусности несущего винта воз-
никают различия и в углах установки лопастей. Все это в конечном итоге
приводит к некоторому различию в условиях работы отдельных лопас-
тей и, как следствие, к разбросу в значениях амплитуд переменных на-
пряжений, действующих на одинаковых режимах полета.
Имеется также различие в параметрах режима полета, связанное
с манерой пилотирования отдельными летчиками.
Не меньшее, или даже существенно большее, различие наблюдается
в значениях амплитуд напряжений и во всех других агрегатах вертолета.
Особенно велик разброс в амплитудах напряжений в тех деталях, где
переменные нагрузки от отдельных лопастей при суммировании должны
быть равны нулю (если лопасти идеально одинаковые) для всех гармо-
ник, за исключением гармоник, кратных числу лопастей. Если же пара-
метры лопастей различны, а так практически всегда и бывает, то в этих
агрегатах, кроме малых переменных, нагрузок с частотами гармоник,
кратными числу лопастей, появляются значительные по величине на-
грузки с другими гармониками, и их величина оказывается пропорцио-
нальной величине различия в параметрах лопастей. Разброс в значе-
ниях переменных напряжений в таких агрегатах может оказаться очень
большим. Обычно это следующие агрегаты-, автомат перекоса, детали
системы управления винтом и фюзеляж, и в первую очередь его редук-
торная рама, которая особенно сильно нагружается переменными на-
грузками.
12 1578 177
Для учета всех перечисленных факторов при расчете ресурса вво-
дится коэффициент надежности по амплитуде переменных напряжений
11,. Этот коэффициент должен обеспечить надежность работы любого
экземпляра конструкции в парке вертолетов с учетом имеющегося раз-
броса в значениях переменных напряжений.
Обычно для измерения переменных напряжений в конструкции
произвольно выбирается некоторый экземпляр вертолета. Полученные
при его испытаниях переменные напряжения аизм используются для про-
ведения динамических испытаний. При этом испытании проводятся с на-
пряжениями <тИсп = 11а аизм. Поэтому изложенная выше (см. п. 8) мето-
дика определения запаса надежности и безопасного срока службы
дает результаты, которые могут быть применены только к тому экзем-
пляру конструкции, в которой действуют напряжения, равные апсп. Для
всех других экземпляров этой конструкции ресурс окажется больше,
если действующие в них напряжения адейст<^ксп> и меньше, если
Писи.
Определим значение коэффициента надежности гр из условия того,
что вероятность разрушения рассматриваемого агрегата вертолета Рц
с учетом имеющегося разброса в значениях амплитуд переменных на-
пряжений равна заданной вероятности Р3ад. Обычно эта величина
принимается такой же, как и вероятность разрушения Pq того агрегата,
в котором действуют переменные напряжения <тиСп, принятые при дина-
мических испытаниях.
Итак, если значение rjjv выбрано из условия, что вероятность раз-
рушения экземпляра конструкции с напряжениями аИсп равна Ро = Рзая,
то вероятность разрушения других экземпляров этой конструкции мо-
жет быть определена по формуле:
Gi)
d^.
(11.20)
Здесь Ра — вероятность разрушения того агрегата вертолета, г, котором
действуют напряжения, равные о. При этом входящее в формулу
(11.20) распределение долговечности факс, определенное на основании
динамических испытаний для некоторого выбранного уровня эквивалент-
ных напряжений, должно быть пересчитано с учетом того, что в раз-
личных экземплярах конструкции действуют различные эквивалентные
напряжения.
Если предположить, что долговечность изменяется в соответствии
с законом
—const, (11.21)
то характеристики распределения фЭНс(?) можно положить равными:
(^^-51еЛ,иСп; (11.22)
(^ig n\ = Nmn + m [1g aKCn - 1g адейСтн], (11.23)
где (Slgjv)a — среднеквадратическое отклонение распределения логариф-
мов чисел циклов при напряжениях адейСтн, отличных от тех,
при которых производятся динамические испытания;
—математическое ожидание этого распределения;
чИСп —напряжения при испытаниях;
апейСтв —напряжения, действующие в каком-то экземпляре вертолета.
Предположим, что распределение амплитуд действующих перемен-
ных напряжений по различным экземплярам конструкции может быть
178
принято логарифмически нормальным. Тогда вероятность разрушения
рассматриваемых агрегатов вертолета будет равна:
^иам= (11-24)
f Ptfiec -
J “1*йсДСИСТВ ° ’
— co
где Ф1ву,|(?П(.тв —закон распределения действующих амплитуд перемен-
ных напряжений (рис. 1.73).
При этом следует иметь в виду, что значение <тИсп, принятое для ди-
намических испытаний, выбрано случайно по результатам измерения
напряжений на одном произвольно взятом вертолете или на нескольких
вертолетах. Поэтому распределение вероятности разрушения Р, по
агрегатам с различными действующими напряжениями будет смещать-
ся вдоль оси 1g ст (см. рис. 1.73) в зависимости от принятого значения
Оисп, таким образом, чтобы при оДейств=<7исл вероятность разрушения Ра
равнялась бы Ряад, ибо из этого условия было выбрано значение t]n- От-
сюда ясно, что и значение Р^м будет зависеть от величины (Тисп.
Следовательно, вероятность Ризм является условной вероятностью
при определенном, случайно выбранном, значении <тИсп- Полная вероят-
ность разрушения, произвольно взятого из парка вертолетов агрегата
Ps может быть получена как сумма условных вероятностей Ризм, умно-
женных на вероятность возникновения в этом агрегате напряжений,
взятых за основу при динамических испытаниях cpig<r rflgfcr:
Оо
Jp..3M<pIg:i3K/lg°==
<₽lgJ flfig а.
т изм °
(11.25)
Если произведено измерение напряжений на одном вертолете, то
можно считать, что
' °изм адейстз‘
12*
179
Если измерение производится на нескольких экземплярах конструк-
ции и при динамических испытаниях задаются напряжения
аиСп
vp
где Зизмср — средняя амплитуда переменных напряжений, измеренная на
нескольких экземплярах конструкции, то параметры распре-
деления м следует определять как параметры распре-
деления средних значений переменных напряжений
^«“изм =='?^’ср •
Из выражения (11. 25) следует, что полная вероятность разрушения
Рв оказывается зависящей от величины гр. Поэтому, задавшись Рв =
= Рзад, можно определить необходимое значение г|3 . Очевидно, что при
этом потребное значение гр оказывается зависящим от закона распре-
деления переменных напряжений по различным экземплярам одноимен-
ных агрегатов вертолета <₽ig =действ Для определения характеристик
этого закона распределения могут быть использованы данные различ-
ных измерений напряжений, выполняемых часто на одних и тех же агре-
гатах вертолета в испытаниях, проводящихся с различными целями.
Естественно, что разброс значений средних эквивалентных пере-
менных напряжений может быть различным для различных агрегатов.
Среднеквадратическое отклонение в распределении переменных
напряжений по различным лопастям несущего винта лежит обычно
в диапазоне:
Sig 0,02 -ч-0,035.
Если принять, как это часто делается, нормальный закон распреде-
ления амплитуд переменных напряжений, то этим значениям Sig» будут
соответствовать значения:
у,=-=0,05-4-0,08, (11.26)
т,
где З3 — среднеквадратическое отклонение в распределении амплитуд
переменных напряжений по различным лопастям;
т, —математическое ожидание этого распределения, т. е. среднее
напряжение в этих лопастях.
При малых у, можно принять Sig „ = у, 1g е.
Для агрегатов, нагрузка которых зависит от качества регулировки
несущего винта, таких как автомат перекоса, редукторная рама и дру-
гие, коэффициент у, оказывается несколько большим.
Из структуры формулы (11.25) следует, что суммарная вероят-
ность разрушения Ръ зависит в основном от двух параметров:
а = ——;
SlgN
, lg1E
b —-----,
Sign
где tn — показатель степени кривой Велера.
Суммарная вероятность разрушения Рв зависит также и от при-
нятой в расчете вероятности разрушения Ро того экземпляра конструк-
ции, в котором действуют напряжения аИсп-
На рис. 1.74 приведены расчеты суммарной вероятности Рв для
различных значений а, b и Ро по формуле (11.25) в случае, когда вы-
180
полнено измерение напряжений только в одном экземпляре конструкции
вертолета. Расчеты были проведены также для различных значений
числа испытанных образцов, но оказалось, что суммарная вероятность
разрушения не сильно зависит от их числа. На рис. 1.74 пунктиром
показаны кривые для /гОбр = 5, а сплошными линиями для /гОбР = 20.
Рис. 1.74. Результаты расчета вероятности разрушения
с учетом разброса в значениях напряжений, действую-
щих в различных экземплярах конструкции
Если потребовать, чтобы Ра =Ро = Рзад, то можно получить оконча-
тельные графики, по которым легко определить необходимый запас т]<„
если известны значения Sigo, Sig дг и Рзад- Эти графики приведены на
рис. 1.75. Причем так же, как и на рис. 1.74, пунктирные линии отно-
сятся к случаю пОбр = 5, а сплошные к случаю попр = 20.
В качестве примера найдем потребный запас’ц, для лопасти вер-
толета, если известно, что у„ =0,08 (Sigo =0,035), a SigN =0,4.
Определим значение коэффициента а:
mSiga 6-0,035
а =----— =--------= 0,525.
Slgiv 0.4
Тогда, задавшись значением = , по кривым рис. 1.75 полу-
чим:
b =1,28 (при /гобр = 5);
1g п,= 1,28-0,035 = 0,0448,
и
Т|,= 1,11.
откуда
181
В тех случаях, когда закон распределения сро неизвестен, обычно
принимается т]а =1,2. Этим значением тр , как уже отмечалось в п. 7,
часто пользуются при практических расчетах.
Рис. 1.75. Диаграмма для выбора запаса надежности по
11. Метод определения запаса надежности т]„
предложенный А. Ф. Селиховым
В нашем изложении некоторые приемы и рассуждения здесь не-
сколько отличаются от тех, которые были предложены А. Ф. Селиховым,
но основной принцип подхода к решению задачи заимствован у автора.
В этом методе для определения запаса т]=. используется та же ме-
тодика, которая была описана в п. 8, но в характеристиках распреде-
ления долговечности учитывается разброс в значениях амплитуд, дей-
ствующих в полете напряжений.
Если, как и раньше, считать, что при изменении амплитуды напря-
жений долговечность в условиях эксплуатации изменяется в соответ-
ствии с законом (11.21), т. е., что
1g = !g -^иеп 4- т (1g °исп - 1g ’действ)’ (11.27)
то можно определить характеристики распределения долговечности
в эксплуатации с учетом разброса в величинах амплитуд действующих
напряжений.
Математическое ожидание этого распределения будет равно:
<v„cn + т (1g аисп - mig ,действ), (11.28)
где mls »дейст11— математическое ожидание распределения амплитуд напря-
жений в различных экземплярах исследуемой конструк-
ции (среднее значение амплитуд переменных напряжений
в различных экземплярах конструкции).
182
Если испытания ведутся при напряжениях
Зисп = г1»т°ср ’
то положив
mlg ° ~ 1gz;7= .
16 девств ° ср
получим
= //г1Вл'ИСп-т« 1g П-
Среднеквадратическое отклонение в значениях логарифмов чисел
циклов до разрушения в условиях эксплуатации может быть определено
по формуле
о1-29)
Если динамические испытания вести при амплитуде напряжений
Опсп=Л“ ffcp (где <Тср — средняя амплитуда, измеренная в полете на раз-
личных экземплярах конструкции), то разброс характеристик долговеч-
ности при испытаниях окажется зависящим от разброса в действующих
напряжениях на различных экземплярах вертолетов. Амплитуда, уста-
навливаемая при испытаниях, оказывается величиной случайной, зави-
сящей от результатов измерения напряжений. Как и раньше (см. п. 8),
нас интересуют характеристики распределения логарифмов минималь-
ных чисел циклов до разрушения.
Положим, что значения минимальных чисел циклов до разрушения
подчиняются закону
1g ТУ2=1g - [- т [1g аИСп- 1g (щаср) J, (11.30)
где N2 — минимальное число циклов до разрушения конструкции с уче-
том того, что амплитуда испытаний может быть установлена
различной в зависимости от результатов измерения средней
амплитуды напряжений оср;
Атт—минимальное число циклов до разрушения конструкции при
определенном фиксированном значении амплитуды напряже-
ний при испытаниях аисп.
Тогда
m2 = m1E ,vmla + т (1g аисп - 1g - т 1g ac„). (11.31)
Если
3ИС11==|'Пз,^зСр I
ТО
Ig3BCn = lg^-rlg^cp-
Положим
Тогда ^2 = /??ig2VralII , а значение среднеквадратического отклонения
логарифмов чисел циклов при испытаниях
(11.32)
где (Sigo)cp - среднеквадратическое отклонение в значениях среднего
логарифма амплитуды напряжений, измеренной в различных
экземплярах конструкции.
Эта величина зависит от числа измерений ПиЗМ:
(Slgo) (11.33)
V «изм
183
При одном измерении (/гИзм=1)
(5igo)Cp = SjgtI. (11.34)
С учетом соотношения (11.33) среднеквадратическое отклонение
в распределении долговечности при испытаниях может быть определено
по формуле
^=1/ -I' • О Ь 35)
И '«"min П„зм
Применяя те же рассуждения, что и выше (см. п. 8), придем к тому,
что вероятность разрушения в этом случае может быть определена по
выражению, аналогичному (11, 19):
Еа-18
J %kcG1)^I
J Тш1п(У
^2-
(11.36)
Если распределение логарифмов минимального числа циклов до
разрушения при испытаниях может быть приближенно представлено
нормальным законом распределения, то выражение (11.36) может быть
переписано в виде:
11
Ps = — — е 2
2л J S2
Если ввести новые переменные
(В 1—) 8
2S“
1 dk}
и Г _ '2 — т2
И Со —-------------— ,
то выражение (11.37) преобразуется к виду:
di2. (11.37)
(11.38)
(11.39)
где верхний предел f(&) определяется по выражению
Подставив сюда значения и т2, получим:
/ (£,) = — m lg + Ig + m ~~ m *g' . (1141)
Si st
Из этого выражения следует, что вероятность разрушения Ря мо-
жет быть определена для каждого ip , если известны значения
Si, 52, tw и A^lgjv = «ig^ICn-«lgyinln-
Можно предложить следующую методику определения потребного
Ignjv +
запаса г].,. Построим зависимости S2/ii от------------------- для за-
данных значений Ps (см. рис. 1.76).
184
Si
gi — mi
«1

4
Тогда, определив Si и S2 по формулам (11.29) и (11.35), можно по
рис. 1.76 для заданного значения Рзая определить
«lgri. + lg^ + ^ , (1142)
откуда, зная r|W, &m!gN (см. рис. 1. 70) и Sb легко определить и п»-
Изложенный здесь метод довольно прост, хотя и требует при опре-
делении ресурса несколько более сложных вычислений, по сравнению
в функции S,/S2 при различных заданных вероятностях разрушения
с методикой, изложенной в п. 10, где запасы г]3 вычисляются по вели-
чинам, взятым прямо с графика.
Из приведенных формул следует, что при принятых здесь допуще-
ниях запасы надежности и т]’ можно объединить в один критерий
il=T]vri7 ИЛи заменять один запас надежности на другой. Это оказы-
вается удобным при выполнении расчетов и проведении динамических
испытаний, о чем уже говорилось в п. 7, но не дает никаких облегчений
при выборе запасов p.v и г]0, так как их величины определяются из
разных условий.
12. Пример расчета ресурса
В качестве примера приведем расчет ресурса для лопасти тяжелого
вертолета с лонжероном в виде стальной трубы.
При определении ресурса лопасти расчет должен быть выполнен
для сечений, расположенных на различных относительных радиусах,
после чего всей лопасти устанавливается ресурс, полученный для самого
слабого сечения.
Пусть самым слабым оказалось сечение на относительном радиусе
г = 0,74.
Предположим, что результаты динамических испытаний пяти об-
разцов лонжерона при амплитуде переменных напряжений ±15 кгс/мм'1
следующие (табл. 1.20).
185
Из результатов испытаний делаем вывод, что пределы выносливо-
сти <тш образцов № 2, 3, 4 и 5 оказались выше ак=15 кгс!мм2. Следо-
вательно, вероятность Р того, что предел выносливости <тш ниже
15 кгс]мм2, может быть принята равной 0,2.
Таблица 1.20
№ образца Число циклов нагружения Результаты испытаний
№ 1 № 2 № 3 № 4 № 5 9,8-105 20-106 20-106 20-106 20-106 Образец разрушился Образцы не разру- шились
Положив Sig равным 0,07 (см. п. 13), получим, что вероятно-
сти 5% соответствует предел выносливости aw =13 кгс/мм'2. Этот пре-
дел выносливости и будем считать минимальным.
Запас по числу циклов может быть принят либо на основе прак-
тического опыта назначения ресурса в соответствии с табл. 1. 16, либо
по методике А. Ф. Селихова (см. п. 8). На основании табл. 1. 16 для
II группы агрегатов (лопасть имеет сигнализатор повреждения лон-
жерона) и /г = 5 запас надежности r].v может быть принят равным при-
мерно 2,7.
Во втором случае необходимо знать -$|гл'- Очевидно, что по ре-
зультатам приведенных испытаний определить значение S\%n невоз-
можно. Однако можно задаться определенным значением S\sn на осно-
вании результатов испытаний аналогичных образцов.
Положим S|g№=0,4. Тогда, задавшись значением Т>зад= —-
(II группа агрегатов), по рис. 1.72 получим lgpN=2,3-SigAS т. е.
tiy = 8,3. Таким образом, требуемый запас надежности по числу циклов
т|л- по методике А. Ф. Селихова оказывается существенно большим, чем
тот, который мог бы быть взят на основании опыта назначения ресурса.
Это различие во многих случаях частично компенсируется введением
в расчет понятия о пределах выносливости и уточнением потребных
запасов надежности г]» .
Как уже говорилось выше при назначении ресурса с использова-
нием коэффициентов надежности, выбранных на основании практиче-
ского опыта, значение Цо принималось всегда равным 1,2. Однако
этот коэффициент может быть уточнен в соответствии с методикой, из-
ложенной в пп. 10 и И. Но для этого необходимо иметь более полные
данные о разбросе амплитуд переменных напряжений по различным
экземплярам конструкции.
Предположим, что произведено измерение напряжений только
в одном экземпляре конструкции. Однако на основании опыта измере-
ний в аналогичных агрегатах других вертолетов можно принять, что
V» =0,08, следовательно, Sigo =0,035. Тогда по методикам, изложенным
в пп. 10 и И, получим, что =1,11. Все же примем гр =1,2.
Минимальное значение Мтт из пяти испытанных образцов (п = 5)
при амплитуде переменных напряжений a=q=15 кес^мя? составляет
Amm = 9,8-106 циклов.
186
Число циклов, соответствующее минимальному пределу выносли-
вости, определим по формуле
I в
^,п11п^тШрМ =23-106,
\ «'mln'
а значения N, по формуле
Д'™ . / . \т
__ mln I in Ы ]
1 Чу \щ®2. /
При расчете ресурса будем считать, что па тех режимах, где дей-
ствующие напряжения ниже минимального значения предела вынос-
ливости, повреждаемость в конструкцию не вносится.
Эквивалентные напряжения на отдельных режимах полета подсчи-
тывать не будем, а примем их равными максимальным измеренным
амплитудам напряжений. В этом случае значение ег- будет равно толь-
ко либо пулю, либо единице.
Расчет эквивалентных напряжений сведем в табл. 1.21.
Таблица-!, 21
Пример расчета ресурса лопасти по сечению
на относительном радиусе г=0,74
”и1 )п=13 кгс/л/ж2; 5=0,5; n=5; SigAi=0,4; д.=1,2;
^=8,3 (рзад=^); ^mln=23.106
Режим полета Е/ 5=0,5; V°5l. Д', а*
Висение Малые скорости: 0 0,1 6,0 8,8 9,7 11,64 со 0
4=20 км/час 1 0,03 7,2 10,5 11,6 13,92 1,84-106 0,016-10-6
4=30 км/час 1 0,02 10,5 13,2 15,02 18,02 0,39-106 0,051-10-6
4=60 км/час 1 0,05 12,4 12,5 15,05 18,06 0,39-106 0,128-10-в
Разгон 1 0,02 9,5 12,4 14,0 16,8 0,59-106 0,034-10-6
Набор 0 0,06 6,0 5,6 6,9 8,28 СЛ 0
Крейсерская ско- рость 0 0,55 8,0 9,0 10,5 12,60 оо 0
Максимальная скорость 1 0,10 8,0 10,5 11,09 13,31 2,4-106 0,042-10-6
Планирование Торможение: 0 0,05 7,5 7,2 8,8 10,56 о<1 0
1-й этап—отах 1 0,002 15,2 18,4 21,11 25,33 0,05-106 0,04-10-6
2-й этап—0,7 <гтах 1 0,007 10,64 12,88 14,79 17,75 0,43-106 0,016-10-6
3-й этап — зависа- ние 0 0,011 6,0 8,8 9,72 11,66 ©О 0
е=0,229 S 0,327-10-6
Если предположить, что долговечность подчиняется закону (11.21)
при всех уровнях переменных напряжений и предела выносливости не
существует (в этом случае е«= 1 на всех режимах), то все режимы по-
лета эквивалентны по повреждаемости режиму с амплитудой напряже-
187
ний аэкв= Н,5 кгс/мм2, действующими в течение всего ресурса лопасти.
В этом случае
7Vrain = ^ -----Y” = 16,2-10e;
Mies -=1,95- 106;
4v
/?=^-=271 час.
60f
Если положить, что минимальный предел выносливости crw =
= 13 кгс/мм2, то всем режимам полета будет эквивалентен один режим
[см. формулу (11.9)] с амплитудой аЭКв=13,6 кгс1мм?. Причем продол-
жительность этого режима, как следует из табл. 1. 21, будет составлять
около 23% ресурса лопасти (е = 0,229).
Тогда ресурс можно определить следующим образом:
M,In = A4 ,п PM” =3,86-10®;
ГП 1-4 \ VI Л /
\ч3аэкв /
Me,= -mhl=0,707-1 о6;
Tv
/^Мез.^429 час
60/е
Тот же результат можно получить по суммарной повреждаемости
без использования понятия об эквивалентных напряжениях [см. формулу
(11.5)]:
---= 3,09-10®;
X 1 а,-
7?=^ =429 час.
GOf
Приведенные результаты показывают, что с введением понятия о
пределе выносливости ресурс лопасти по расчету оказывается больше.
Следует, однако, иметь в виду, что запасы по числу циклов, при-
веденные в табл. 1. 16, вводились в расчеты, не предполагавшие суще-
ствования предела выносливости. Поэтому в расчетах с пределом вы-
носливости они использоваться не должны.
13. Возможные пути определения минимального предела
выносливости конструкции
Из приведенного выше примера видно, что при расчете с исполь-
зованием понятия о минимальном пределе выносливости могут быть
получены существенно большие значения ресурса конструкции. Поэтому
определение его значений во многих случаях оказывается крайне не-
обходимым.
Отыскание значений aWmln по результатам испытаний с достаточ-
но хорошей точностью оказывается практически неосуществимой за-
дачей. Можно только рассчитывать на весьма ориентировочное опре-
деление этой величины. Но даже и для этого требуется существенное
увеличение числа испытываемых образцов. Тем не менее использование
в расчете ресурса даже ориентировочных значений пределов выносливо-
188
F
if,
сти существенно приближает результаты расчетов к действительности
и открывает возможность для принятия более грамотных технических
решений. Поэтому рекомендуется во всех случаях прибегать к опреде-
лению пределов выносливости, используя для этого как ориентировоч-
ные, так и даже просто формальные способы расчета.
Прежде всего следует попытаться определить параметры закона
распределения пределов выносливости. Для этого нужно провести уста-
лостные испытания образцов на нескольких уровнях переменных напря-
жений, лежащих в области распределения пределов выносливости. Ис-
пытания должны проводиться на достаточно большой базе по числу
циклов. При выборе базы испытаний обычно полагают, что для сталь-
ных образцов база может быть установлена несколько большей, чем 107
ill J । *"ЧЧУ!*М
Рис. 1. 77. Распределение
пределов выносливости
циклов (например 2 • 107 циклов), а для дуралюминовых образцов не-
сколько больше, чем 2 • 107 циклов (часто принимается база 5 • 107 цик-
лов) .
Вероятность того, что предел выносливости выше, чем заданный
уровень переменных напряжений, определяется как отношение чисел
образцов, прошедших испытания на заданной базе без разрушения пНер
к общему числу испытанных на этом и на меньшем по напряжению
уровне образцов п:
р”нер
п
Полученное таким образом распределение пределов выносливости
может совпадать с нормальным законом только на небольшом участке,
соответствующем средним значениям вероятности (рис. 1.77). При ма-
лых вероятностях распределение пределов выносливости отклоняется
от нормального закона и имеет некоторый порог чувствительности
%, ( . При больших вероятностях, начиная с каких-то напряжений Ора3р,
все образцы разрушаются, не пройдя заданную базу испытаний.
Распределение пределов выносливости при средних значениях ве-
роятности разрушения лучше всего представлять при помощи логариф-
мически нормального закона распределения. Он же может быть исполь-
зован и для определения минимальных значений пределов выносли-
вости.

189
Имеющиеся результаты испытаний образцов лопасти показывают,
что для этого закона могут быть приняты значения Sig» , равные при-
мерно:
SlKa —0,05-i-0,07,
где — среднеквадратическое отклонение в распределении логариф-
мов пределов выносливости.
Предложить достаточно надежный способ для определения <тШ1|1]|1
не представляется возможным. Поэтому может быть рекомендован толь-
ко сугубо формальный способ, который, однако, на практике дает
достаточно хорошие результаты. Можно считать, что минимальный пре-
дел выносливости совпадает со значением aw, соответствующим 5%
вероятности логарифмически нормального закона распределения пре-
делов выносливости.
Если принять такой подход, то для уточнения значений <Ttt,mlll мо-
жет быть использован метод, основанный на проведении усталостных
испытаний на двух близких по амплитуде уровнях переменных напря-
жений. Испытываемые образцы, которых должно быть не менее 15—
20, разделяются на две группы.
Первая группа испытывается при максимальных по величине пере-
менных напряжениях, которые предположительно не превышают ми-
нимального предела выносливости и поэтому желательно, чтобы ни один
из них не разрушился при числе циклов, соответствующем выбранной
базе испытаний. Результаты испытаний этой группы служат для под-
тверждения того, что минимальный предел выносливости действитель-
но может соответствовать их уровню испытаний.
Вторая группа образцов испытывается при несколько больших пе-
ременных напряжениях таким образом, чтобы какая-то часть нз них
разрушалась, не проработав установленного числа циклов. Определив
вероятность того, что предел выносливости ниже амплитуды второго
уровня испытаний, и задавшись каким-то значением Sig а вычисляют
значение ov:, соответствующее вероятности 5%. Если данные испытаний
первой группы не противоречат этому результату, то полученное таким
образом значение owS% может быть принято за минимальный предел
выносливости.
Иногда для большей надежности полагают, что минимальный пре-
дел выносливости соответствует меньшим значениям вероятности, ска-
жем, вероятности — . Принимать еще более низкие значения этой ве-
роятности, по-видимому, нецелесообразно.
Следует отметить, что во многих случаях для характеристики уста-
лостной прочности используется условное понятие, которое можно было
бы назвать приведенным пределом выносливости.
Приведенный предел выносливости определяется пересчетом ре-
зультатов испытаний по формуле (11.3) на условную базу, принимае-
мую обычно равной Л^баз=Ю7 циклов для стали и Лг5аэ = 2-107 циклов
для дуралюмина:
где Нисп—амплитуда переменных напряжений при испытаниях;
Np— число циклов до разрушения, соответствующее вероятности
разрушения, равной Р;
т. — показатель степени кривой Велера; принимается обычно
т = 6.
190
Если взять Л'р, соответствующее вероятности разрушения, равной
5%, то значение дает ориентировочное представление о величине
минимального предела выносливости. Часто для характеристики уста-
лостной прочности вместо Л7Р принимается минимальное значение чис-
ла циклов до разрушения конструкции Необходимо подчеркнуть,
что приведенный предел выносливости, каким бы образом он не опре-
делялся, не соответствует понятию о пределе выносливости в том смыс-
ле, в котором оно использовалось выше, в этом параграфе.
Важно также и то, что распределение приведенных пределов вынос-
ливости имеет среднеквадратическое отклонение, равное
С
/С х _______ Iff N
?прив — т ’
почти всегда большее, чем значение 51гз .
14. Преимущества и недостатки различных подходов
при определении необходимых запасов надежности
и примерная оценка их точности
Наиболее простым подходом, как уже было показано выше (см.
п. 7), следует считать расчет ресурса с использованием коэффициентов
qir и q«, принятых на основании практического опыта назначения ре-
сурса. Эти коэффициенты проверены на большом числе вертолетов
и многие сотни агрегатов успешно выработали ресурс, установленный
таким образом. Следует однако иметь в виду то, что применение коэф-
фициентов и г]5, взятых таким образом, подтверждено практикой
только в сочетании с определенной методикой подсчета ресурса, которая
отличается, в частности, следующими допущениями:
1. Предела выносливости не существует и кривая Велера описана
формулой (11.21). Соответственно коэффициенты е и принимаются
равными единице.
2. На каждом режиме полета амплитуда напряжений считается
равной максимальному измеренному ее значению на этом режиме.
Однако такой подход к расчету ресурса имеет существенные недо-
статки:
1. При определении ресурса не учитывается различие в рассеянии
характеристик долговечности, которое может оказаться неодинаковым
у агрегатов разной конструкции, отличающихся, кроме того, примене-
нием различных материалов и различной технологии изготовления. Не
учитывается также и величина разброса напряжений, действующих
в различных экземплярах конструкции.
2. Отказ от понятия предела выносливости и использование в рас-
чете только максимальных амплитуд напряжений, действующих на
каждом режиме полета, приводит к неправильным представлениям
о доле повреждаемости, вносимой различными режимами полета.
Поэтому вполне закономерно стремление к использованию более
совершенных методов с привлечением основных положений теории веро-
ятности. Один из возможных вариантов такого подхода приведен в пп. 8,
10 и 11.
Следует отметить, что в том виде, в каком этот метод здесь изло-
жен, он дает вполне удовлетворительные значения ресурсов, довольно
близкие к тем, которые получаются по предыдущему методу. Правда
в значениях коэффициентов запаса происходит некоторое перераспреде-
ление. Запас t]W оказывается существенно большим, но зато уменьшает-
ся запас г|сг . Кроме того, при расчете должно быть использовано поня-
191
тие о минимальном пределе выносливости. В противном случае ресур-
сы оказываются заниженными.
При использовании такого метода часто вызывает сомнение при-
менение столь больших вероятностей разрушения, равных и даже
больших. Действительно, это означает, что один агрегат из тысячи обя-
зательно должен разрушаться в течение ресурса. Поэтому здесь следует
еще раз подчеркнуть, что указанные значения вероятностей являются
чисто условными величинами, соответствующими нормальному закону
распределения долговечности. В действительности в области малых зна-
чений вероятности разрушения этот закон отклоняется от нормального
и в характеристиках долговечности наблюдается порог чувствительно-
сти. Его значения лежат в области вероятностей, равных примерно — ,
или несколько отличающихся от этого значения. Следовательно, зада-
ние условной вероятности в действительности равносильно тре-
бованию очень малой или даже нулевой вероятности. Поэтому нельзя
согласиться с теми авторами, которые считают возможным предъявлять
требование об обеспечении вероятности порядка 10-6 или даже 10-7
с использованием нормального закона распределения долговечности.
Такие требования не имеют достаточных оснований.
У каждого, кто знакомится с изложенной выше методикой, вызы-
вает обычно также возражения возможность отказа от уточнения полу-
ченных по эксперименту значений среднеквадратических отклонений
Sig по принятым в практике применения методов теории вероятностей
обычно достаточно высоким значениям доверительной вероятности.
Если выполнить это уточнение, то в расчете пришлось бы использовать
увеличенное в q раз (см. п. 9) значение Sigjv, что привело бы к увели-
чению требуемого запаса r).v и соответственно к снижению ресурса.
Кроме тех соображений, которые уже были приведены выше (см.
п. 9), здесь следует отметить, что в предложенной методике расчета
существует и другая неточность. Вместо эквивалентных напряжений,
действующих на различных режимах полета, принимаются обычно их
максимальные значения, что приводит к занижению ресурса. Эти две
неточности взаимно компенсируют друг друга и отказ от одной из них
должен обязательно сопровождаться отказом и от другой. В этом
случае значения получаемых по расчету ресурсов существенно не
изменятся.
Нет сомнений, что с течением времени с появлением новых экспе-
риментальных данных в методике расчета ресурса окажется необходи-
мым ввести и более существенные уточнения. Опыт эксплуатации вер-
толетов и все большее число результатов динамических испытаний так-
же, вероятно, выявит такую необходимость.
15. Требования к прочности лопасти при выборе ее конструкции
Лопасть вертолета работает в очень тяжелых для ее прочности
условиях. В течение всего ресурса она испытывает очень большие по
величине постоянные и переменные нагрузки. Эта особенность условий
работы лопасти предъявляет чрезвычайно жесткие требования к ее
конструкции и прежде всего к усталостной прочности ее основного
силового элемента лонжерону. Поэтому лонжерон лопасти должен из-
готовляться только из материалов, обладающих очень высокими харак-
теристиками усталостной прочности.
192
Наибольшее распространение в настоящее время имеют конструк-
ции лопасти с лонжеронами в виде стальной трубы и прессованного
дуралюминового лонжерона.
Очень хороших результатов можно ожидать при изготовлении лон-
жеронов из различных синтетических материалов. Известны конструк-
ции лопастей со стеклопластиковым лонжероном. Однако достаточно
серьезного опыта эксплуатации таких лопастей еще не имеется. Поэто-
му на их прочности мы здесь останавливаться не будем.
Наиболее важным требованием для лопастей со стальным и дуралю-
миновым лонжеронами оказывается требование максимального устране-
ния каких-либо концентраторов напряжений, снижающих их усталост-
ную прочность. В конструкции лопастей недопустимо применение бол-
товых и заклепочных креплений. Каркас лопасти крепится к лонже-
рону только при помощи клеевых соединений.
Применение креплений с большими концентраторами напряжений
допускается только на участках с малыми переменными напряжениями,
например, в комле лопасти вблизи шарниров втулки. При этом, несмотря
на малые переменные напряжения, сечение лонжерона в районе комле-
вого стыка приходится увеличивать в 3—4 раза. Только очень большое
снижение переменных напряжений позволяет применить крепления с кон-
центраторами.
Резко снижают усталостную прочность и мелкие технологические
дефекты, также являющиеся концентраторами напряжений. Поэтому
при изготовлении лонжеронов лопастей применяется только такая тех-
нология, которая приводит к полному устранению всех видимых дефек-
тов лонжерона.
Для исключения возможности пропуска каких-либо дефектов лон-
жероны -должны проходить тщательный контроль с применением всех
современных средств такого контроля.
Рассмотрим более подробно прочностные свойства лопастей со
стальным и дуралюминовым лонжеронами.
16. Прочность лопасти со стальным трубчатым лонжероном
Для лонжерона лопасти применяется обычно холоднокатанная тру-
ба из высоколегированных сталей типа ЗОХГСА или 40ХНМА, закален-
ная и отпущенная на прочность о'ь=П0-?-130 кгс/ллг2.
После горячей и холодной прокатки, формообразования и закал-
ки наружная и внутренняя поверхности трубы полируется. В последнее
время обязательной операцией после полировки стал также наклеп
лонжеронов.
Изготовленный таким образом лонжерон без наклепа может иметь
минимальный предел выносливости порядка стТОш111 = 12ч-13 кгс/мм2 при
средней составляющей цикла о-т = 20ы-25 кгс/мм2. Однако его прочность
может существенно снизиться, если при изготовлении лонжерона будут
допущены различные технологические дефекты и просчеты. В качестве
наиболее опасных из них можно назвать следующие.
Надрывы и закаты. В процессе горячей прокатки пластические де-
формации могут сопровождаться частичным разрывом материала. Это
происходит обычно при понижении температуры прокатываемой заго-
товки, а также в результате загрязнения стали неметаллическими и га-
зовыми включениями, образования плен, высокой пористости, ликвации
и других металлургических дефектов. Образующиеся разрывы направ-
лены в тело заготовки под острым углом, и поэтому выходящий на
поверхность след надрыва часто плохо виден.
При дальнейшей холодной прокатке степень деформации увеличи-
вается и надрыв закатывается в стенку трубы под все меньшим углом
13 1578
193
к ее поверхности. Обычно наблюдается серия таких надрывов. Размеры
их невелики; глубина 0,1—1,0 мм, ширина 3—10 мм.
Закаты появляются при холодной прокатке на наружной поверх-
ности. Происходят они вследствие больших неровностей наружной по-
верхности после горячей прокатки. Последующее пластическое холодное
деформирование приводит к неравномерному движению материала, при
котором и могут образоваться дефекты, называемые закатами. Закаты
также могут образоваться в результате течения металла в зазор между
калибрами валков, возникновения заусенца и заката его при последую-
щем деформировании.
лированной поверхности. На рис. 1.78
Рис. 1.78. Надрывы на внутренней поверхности
стального лонжерона
Оба дефекта могут быть выявлены при магнитном контроле на по-
’ ”3 показаны характерные надрывы
на внутренней поверхности
лонжерона. Фото сделано
при магнитном контроле.
Предел выносливости трубы
с надрывами и закатами
снижается до оЮтп1„=5-г-
7 кгс/мм?.
«Сыпь» на внутренней
поверхности. После горячей
прокатки на поверхности
трубы остается слой окали-
ны, которая имеет большую
твердость, чем металл. Пос-
ле каждого перехода при
холодной прокатке произво-
дится отжиг. Хотя отжиг
производится в инертной
появляются тонкие пленки
атмосфере, тем не менее на поверхности
окалины за счет кислорода металла. Если не полностью удалить окали-
ну, то при прокатке она дробится и вдавливается в металл, образуя так
называемую «сыпь». На открытой наружной поверхности трубы лонже-
рона «сыпь» легко устраняется механической обработкой. На внутрен-
ней поверхности трубы, обработка которой сложнее и возможна только
путем ленточного шлифования или гидрополирования, «сыпь» может
быть полностью не устранена. Поэтому мелкие, но острые углубления,
с размерами, не превышающими 0,1—0,05 мм, и трудно различимые при
контроле, могут остаться даже после шлифования. Усталостная проч-
ность поверхности снижается при этом до о'Ж[п1п = 104-12 кгс/мм2.
«Сыпь» может быть устранена расточкой и шлифованием поверх-
ности заготовки до полного выведения окалины после горячей прокатки
и опескоструиванием после отжига перед каждым переходом холодной
прокатки.
Для полного удаления надрывов, закатов, «сыпи» и других поверх-
ностных дефектов очень эффективным оказывается продольное шлифо-
вание наружной и внутренней поверхности трубы после окончательной
холодной прокатки до ее профилирования (формообразования).
Снижение усталостной прочности от правки труб. После закалки и от-
пуска трубы лонжеронов оказываются несколько искривленными. По-
этому перед сборкой лопасти трубы часто приходится править. При
этом в материале трубы появляются остаточные напряжения. Обычно
при правке вводятся ограничители, не позволяющие увеличить остаточ-
ные напряжения растяжения в трубе более 10—20 кгс[мм2. Эти напря-
жения увеличивают среднюю составляющую цикла и приводят к умень-
шению предела выносливости на 20—25%. Еще большие потери проч-
ности могут произойти при неправильной правке. Чтобы исключить
194
необходимость правки следует производить отпуск закаленных труб
в специальных приспособлениях, устраняющих деформации, возникшие
в процессе закалки.
При оценке усталостной прочности лонжеронов особое внимание
следует обратить на возможность возникновения фрикционной корро-
зии. Фрикционная коррозия оказывается почти обязательным спутни-
ком циклического нагружения лопастей и приводит к существенному
снижению усталостной прочности. Она возникает обычно в местах со-
прикосновения с лонжероном крепящихся к нему деталей, если между
этими деталями и лонжероном имеются
относительные микроперемещепия. Обыч-
ным местом возникновения фрикционной
коррозии на стальном лонжероне являют-
ся места установки хомутов для крепле-
ния каркаса лопасти.
На рис. 1.79 приведена фотография
разрушившегося лонжерона. Начало
усталостной трещины совпадает с пятном
фрикционной коррозии.
Резкое увеличение динамической
прочности стальных лонжеронов проис-
ходит при использовании механического
упрочнения их поверхности, называемого
обычно наклепом.
В настоящее время наклеп лонжеро-
нов стал почти обязательной операцией
при изготовлении лопастей. В вертолето-
стрсении наибольшее распространение
получили три метода механического уп-
рочнения: динамический метод М. И.
Кузьмина, виброударный метод С. В.
Очагова и дробеструйный метод. Выбор
того или иного метода обычно зависит от
Рис. 1.79. Место начала усталост-
ного разрушения от фрикционной
коррозии
особенностей упрочняемой детали конструкции и производственных воз-
можностей. В тех случаях, когда для упрочнения наружной поверхности
лонжерона применяется динамический метод, его внутренняя поверх-
ность упрочняется дробеструйным методом. При создании сложных уста-
новок для виброударного метода обычно следует учитывать, что этим
методом целесообразно обрабатывать одновременно и наружную н внут-
реннюю поверхность лонжерона.
Увеличение усталостной прочности наблюдается при применении
всех методов наклепа. Лучшим методом, дающим наиболее стабильные
результаты при обработке наружной поверхности стального лонжерона,
следует считать динамический метод М. И. Кузьмина.
Рост усталостной прочности от наклепа объясняется в основном
двумя причинами. Наиболее чувствительная к началу усталостного раз-
рушения внешняя поверхность упрочняемой детали становится, во-пер-
вых, более гладкой (рис. 1.80), а, во-вторых, в ней создаются остаточ-
ные напряжения сжатия, что в соответствии с диаграммой Хея (см.
рис. 1.63) приводит к увеличению усталостной прочности поверхност-
ного слоя детали.
На рис. 1.81 показано распределение внутренних напряжений в ма-
териале стального лонжерона, полученных в результате динамического
наклепа и обдува металлическим песком. Обдув металлическим песком
дает почти такие же остаточные напряжения как и дробеструйный ме-
тод наклепа.
13*
195
Особенно велик прирост усталостной прочности от наклепа при
наличии фрикционной коррозии. Видимо, сжимающие напряжения пре-
пятствуют распространению коррозии в глубь материала. На рис. 1.82
а) М
g) М^ОО: 1
Рис. 1.80. Профилограмма поверхно-
сти прессованного из алюминиевого
сплава лонжерона после механиче-
ской обработки (а) и после наклепа
(б)
Рис, 1.81. Распределение внутренних на-
пряжений от наклепа по толщине стенки
стального трубчатого лонжерона:
--------наклеп по методу М. И. Кузьмина;
--------трехкратный обдув металлическим пе-
ском
приведены результаты испытаний стальных лонжеронов с наклепанной
и ненаклепанной поверхностями, работающих в условиях возникновения
фрикционной коррозии.
Усталостная прочность стальных лонжеронов при применении ме-
ханического упрочнения может быть увеличена в 1,5—2 раза, а в при-
сутствии фрикционной коррозии и в 2,5—3 раза.
Рис. 1.82. Распределение приведенных пределов выносливости сталь-
ных трубчатых лонжеронов прн воздействии фрикционной коррозии:
а—поверхность полирована и опескоструена; б—поверхность полирована и ©пе-
скоструена трижды металлическим песком; в—поверхность наклепана по метолу
М. И. Кузьмина
С применением наклепа предел выносливости стального лонжерона
может быть увеличен до значений порядка o®mln=284-30 кге/мм2 при
<тт=20ч-25 кгс!мм2. Поэтому наклеп оказался наиболее действенным
средством увеличения надежности и ресурса лопастей.
196
:. Фрезерованный и опескоструенный
Рис. 1. 83. Микрошлиф сечения стенки лонжерона
через газовый пузырь, образовавшийся в процессе
прессования
17. Прочность лопасти с дуралюминовым лонжероном
Наиболее важной проблемой при создании лопастей такой конст-
рукции является обеспечение достаточно высокой усталостной прочно-
сти лонжерона. Крепление каркаса к лонжерону осуществляется, как
правило, на клее и не создает в лонжероне сколько-нибудь существен-
ных концентраторов напряжений. Концентрации напряжений в лонже-
роне возникают в основном от мелких дефектов, допущенных при его
изготовлении.
Основную роль в уменьшении усталостной прочности лонжерона
играет состояние его поверхности. Фрезерованный и опескоструенный
лонжерон из сплава АВТ-1
без обработки внутренней
поверхности может иметь
предел выносливости поряд-
ка <TWmin = 3,84-4,2 кге/мм2
при средней составляющей
цикла цт = 6 кгс[мм2.
Усталостная прочность
лонжерона может снизиться
в результате дефектов, воз-
никших в процессе прессо-
вания лонжерона и при его
механической обработке.
Часто внутренний канал
лонжерона не обрабатывает-
ся после прессования. Поэто-
му на внутренней поверхно-
сти могут остаться дефекты
процесса прессования: на-
липы, продольные риски,
газовые пузыри (рис. 1.83)
и, наконец, крупнокристал-
лический ободок. Эти дефек-
ты могут снизить усталост-
ную прочность до значений о,
этому внутренняя поверхность лонжеронов лопастей с относительно вы-
сокими напряжениями должна обязательно подвергаться механической
обработке после прессования.
Существенное снижение усталостной прочности происходит также
от неметаллических и газовых включений. Для удаления включений
должна применяться специальная технология плавки (отстой металла,
слив его с определенных уровней, фильтрация через сетчатые фильтры
и т. д.). Наиболее качественным металл получается при плавке в элек-
трических индукционных печах с выдержкой выплавленного металла
в электрических обогреваемых отстойниках (миксерах).
Для исключения возможности пропуска неметаллических и газо-
вых включений каждый лонжерон должен обязательно проходить про-
верку с помощью ультразвука.
Не менее важным является также исключение возможности корро-
зионного повреждения прессованных лонжеронов в процессе производ-
ства (так же как и в условиях эксплуатации). Опыт показывает, что на-
ружная и интеркристаллитная коррозия глубиной до 0,14-0,15 мм может
резко снизить предел выносливости. Поэтому для лонжеронов лопастей
должен выбираться металл с высокой коррозионной стойкостью, а в
производстве приняты специальные меры по защите лонжеронов от
коррозии с применением гальванических покрытий после промежуточ-
ных операций его обработки (например, анодирование).
=2,54-3,0 кгс/лш2 (цт = 6 кге/.и.и2). По-
197
Резкое увеличение усталостной прочности лонжеронов из алюми-
ниевых сплавов может быть достигнуто применением механического
упрочнения лонжеронов. На рис. 1.84 приведены результаты усталост-
ных испытаний упрочненных лонжеронов в сравнении с неупрочненны-
ми. Здесь же показано распределение внутренних напряжений от на-
Рис. 1.84. Распределение приведенных пределов выносливости
(к базе 107 циклов) прессованных лонжеронов из сплава
АВТ-1 с полированной (кружочки) и наклепанной (крестики)
поверхностями (а) и распределение сжимающих напряжений
по толщине стенки лонжерона от наклепа виброударным ме-
тодом С. В. Очагова (б)
клепа. Предел выносливости упрочненных лонжеронов может быть до-
веден до значений (ь,-min—5,54-6,0 кгс/мм1 (<гт = 6,0 кгс/л.и2).
Следует обратить внимание на то, что прочность наклепанных
дуралюминовых лонжеронов может резко снизиться, если при приклеи-
вании каркаса лонжерон будет нагрет до температуры около 200° С
и более. Поэтому температура при склеивании должна тщательно кон-
тролироваться.
18. Влияние условий эксплуатации
на усталостную прочность лонжеронов
Приведенная выше методика определения усталостной прочности
и ресурса может быть применена только в том случае, если в процессе
эксплуатации конструкция не испытывает никаких механических и кор-
розионных повреждений. В противном случае подход к определению
ресурса должен быть полностью изменен и сведен к изучению воздей-
ствия этих повреждений. С этих позиций конструкции всех лопастей
должны быть разделены на два типа: лопасти с защищенным и откры-
тым лонжероном.
В конструкции лопасти, основанной на стальной трубе, лонжерон
обычно полностью защищен каркасом и не может быть механически
поврежден в эксплуатации. Наибольшую опасность для такой конструк-
ции представляет коррозия и поэтому срок службы таких лопастей опре-
деляется качеством антикоррозионных покрытий лонжерона.
В конструкциях лопастей, у которых лонжерон образует контур
носовой части профиля, особое внимание приходится уделять его защи-
те от механических повреждений. Если эта защита слаба, то ресурс
198
резко падает и оказывается зависящим от величины нанесенных лонже-
рону повреждений. Обычно в этих случаях устанавливается допустимая
величина повреждений, контролируемая при предполетном осмотре ло-
пастей.
Для оценки влияния повреждений лонжерона в эксплуатации обыч-
но проводятся динамические испытания образцов, вырезанных из лопа-
стей, отработавших определенное число часов в различных условиях
эксплуатации, и оценивается возможность сохранения ресурса, установ-
ленного им по условиям выносливости неповрежденных в эксплуатации
образцов. При существенном снижении усталостной прочности предпри-
нимаются меры для улучшения защиты лонжерона.
ГЛАВА 2
ВИБРАЦИИ ВЕРТОЛЕТА
§ 1. О СИЛАХ, ВЫЗЫВАЮЩИХ ВИБРАЦИИ ВЕРТОЛЕТА
1. Частоты возбуждения
Так как при поступательном полете вертолета лопасти несущего
винта, находящиеся под действием переменных во времени аэродинами-
ческих сил, совершают колебания и в плоскости тяги винта и в плоско-
сти вращения, то силы реакции, действующие
Рис, 2,1. Силы и моменты, действующие
на вертолет, от несущего винта
ния, которые
на лопасть в шарнирах
втулки, являются также переменны-
ми во времени. Соответственно на
втулку винта действуют переменные
силы, равные по величине этим си-
лам реакции.
Переменные силы, действующие
на втулку винта со стороны колеб-
лющихся лопастей, можно задавать
в виде трех сил X(t), Y(t), Z(t) и
трех моментов относительно коор-
динатных осей Mz(t)
(рис. 2.1). Если у вертолета имеет-
ся рулевой винт, то со стороны ло-
пастей этого винта на вертолет
также действуют переменные во
времени силы того же происхожде-
также удобно задавать в виде трех переменных сил и
трех моментов.
Переменные силы, действующие на вертолет со стороны колеблю-
щихся лопастей винтов, есть главный источник вибраций фюзеляжа.
Вибрации фюзеляжа могут вызываться также непосредственно
аэродинамическими силами, действующими на фюзеляж со стороны
пульсирующего потока воздуха, отбрасываемого винтами. Так, скорость
потока, отбрасываемого винтом в районе фюзеляжа, увеличивается,
когда какая-либо из лопастей винта проходит над фюзеляжем. Однако
многочисленные расчеты и измерения пульсаций давления на фюзеляже
показывают, что эти переменные аэродинамические силы значительно
меньше переменных сил, действующих на втулку винта со стороны ко-
леблющихся лопастей. Например, для вертолета Ми-4 переменная сила,
действующая на фюзеляж от пульсаций потока, отбрасываемого вин-
том, на самом неблагоприятном режиме полета (торможение перед по-
садкой) составляет величину порядка +10Н-15 кгс, в то время как
переменные силы, действующие на втулку винта, на различных режи-
200
мах полета имеют порядок ± (2004-600) кгс. Поэтому при анализе виб-
раций вертолета следует прежде всего интересоваться переменными
силами,. приложенными к втулке винта.
Эти силы могут быть, вообще говоря, определены, как динамиче-
ские реакции при вынужденных колебаниях лопастей в полете, методы
расчета которых изложены в гл. 1. Здесь следует оговориться, указав,
что переменные силы при таком расчете определяются весьма неточно.
Причина этого заключается в том, что при расчете колебаний лопасти
удовлетворительно определяются лишь низшие гармоники нагрузок
и ошибки расчета возрастают с ростом номера гармоник. Между тем,
как это будет показано ниже, для расчета вибраций решающее значе-
ние имеют именно высокие гармоники возбуждения. В этом заключается
причина того, что все методы анализа вибраций, изложенные в данной
главе, носят, главным образом, качествен-
ный характер.
Точный расчет вибраций с помощью ме-
тодов, изложенных в этой главе, возможен
лишь в некоторых особых случаях. Наибо-
лее важным из этих случаев является проек-
тирование нового фюзеляжа вертолета или
даже вертолета другой схемы (например,
поперечной или продольной вместо одно-
винтовой), на котором будут установлены
уже применявшиеся раньше винты, для ко-
торых переменные силы были определены
экспериментальным путем (например, из-
мерением напряжений в вале винта или в
подредукторной раме).
Нужно отметить, что и качественные ме-
тоды оценки вибраций позволяют сделать
Рис. 2.2. Винт, вращающий-
ся в набегающем потоке
воздуха
много весьма полезных выводов при проектировании вертолетов и при
их доводке во время летных испытаний. Так, например, можно судить
о влиянии на вибрации вида резонансной диаграммы лопасти, резонанс-
ной диаграммы фюзеляжа и определять таким образом направление
изменения конструктивных параметров для уменьшения вибраций, а
иногда и оценивать степень уменьшения вибраций.
Чтобы сделать некоторые общие заключения о характере изменения
во времени сил X(t), У(/), Z(t) и моментов обра-
тимся к рис. 2. 2, на котором изображен пятилопастный винт, равномер-
но вращающийся с угловой скоростью со в потоке воздуха, набегающего
на него с постоянной скоростью V. Пусть в некоторый момент времени
t лопасти винта занимают положение, показанное на рисунке, и пусть
в этот момент сила X имеет некоторое значение X(t). Через промежуток
времени, равный 'А от времени полного оборота винта, винт повернется
на Vs полного оборота. При этом лопасть 1 займет положение лопасти 2,
лопасть 2 — положение лопасти 3 и т. д. Ясно, что в этом новом поло-
жении, если только все лопасти винта абсолютно одинаковы, вся карти-
на обтекания, а следовательно, и все силы, действующие на лопасти,
будут точно такими же, как и в первый момент времени t. В частности,
будет таким же и значение силы X. Очевидно, что при последующем
повороте винта на Vs полного оборота ситуация вновь повторится Сле-
довательно, функция X(t) является периодической функцией времени
с периодом, равным Vs времени полного оборота винта. На рис. 2. 3
показан один из возможных видов графика зависимости X = X(t).
Таким образом, сила X будет меняться во времени с угловой ча-
стотой 5со, в то время как переменные силы, действующие на лопасть
винта, меняются с частотой (раз за оборот винта).
201
Функцию X(t), как всякую периодическую функцию, можно раз-
ложить в ряд Фурье. При этом низшей гармоникой в разложении будет
гармоника 5<о, так что разложение будет иметь вид:
X {t)=XQ-\-Xai cos 5W-|-Xbt sin Xai cos A\sin 1(Ы-[-
4~ Xаз cos -(-X&s sin 15«rf-j-...,
то есть основная частота /? = 5ш, а кратные частоты 2р = 10<о, Зр = 15<о,
4/2 = 20ш и т. д.
Очевидно, точно такие же заключения можно сделать в отноше-
нии функций Y(t), Z(t),
Вообще для винта с числом лопастей, равным z, все силы и момен-
ты, действующие на вертолет, периодически меняются во времени с ча-
стотой так называемой основной гармоники несущего винта /?=£to. Раз-
ложение этих сил и моментов в ряд Фурье имеет вид:
X (/) — Xаз cos pt-\- Xbl sin pt-f-Xa, cos 2pt -f-
-|- Xsin 2pt -[-XOli cos 3pt -f- Xь3 sin 3pt -|-..
(/) = Л!Хо-|-ЛН, cos pt-[-M*i sin pt-}-cos 2pt-}-
4-M*sin2p/-|- Turcos3ptsin3pt,
где
p~z^.
(1.1)
(1-2)
Таким образом, на вретолете с числом лопастей z возбуждение виб-
раций возможно только с частотами £to, 2zco, 3za и т. д. Отметим, что
X
х-х(г.)
Один ofopnm Пинта
Рис. 2. 3. Возможный вид зависимости про-
дольной силы по времени
t
этот вывод сохраняется и в том
случае, если рассматривать пуль-
сирующие аэродинамические си-
лы, действующие непосредствен-
но на фюзеляж со стороны пото-
ка, отбрасываемого несущим
винтом.
Если на вертолете имеется
также рулевой винт, имеющий
Zp.B лопастей и вращающийся с
угловой скоростью Ыр.в, то на
возбуждающие силы, содержащие
фюзеляж будут действовать также
ГарМОНИКИ /7р.в= ^р.вЫр.в, 2рр.Е, Зрр.в и т. д.
Все эти выводы справедливы лишь при условии, что лопасти винта
идеально одинаковы. Если это условие не выполнено, то могут появить-
ся низкие частоты возбуждения to, 2о>, Зы и т. д. Однако многочисленные
экспериментальные данные — результаты измерения вибраций и напря-
жений в элементах конструкции фюзеляжей различных вертолетов —
показывают, что содержание низших гармоник всегда настолько незна-
чительно, что ими следует пренебрегать как при анализе вибраций вер-
толета, так и при оценке прочности элементов конструкции фюзеляжа.
Это говорит о том, что существующий уровень производства и требова-
ния, предъявляемые к конструкции лопастей, обеспечивают достаточно
малые отклонения в индивидуальных качествах отдельных лопастей.
Отметим, что все приведенные выше рассуждения можно было бы
точно также повторить, рассматривая переменные силы, действующие
на тарелку автомата перекоса со стороны лопастей несущего винта.
Несмотря на то, что момент сил, действующих на лопасть относительно
осевого шарнира (шарнирный момент), меняется во времени с основной
частотой ы, результирующие силы и моменты, действующие на тарелку
автомата перекоса меняются во времени с основной частотой za>. По-
202
этому переменные силы, действующие в цепях управления общим и цик-
лическим шагом винта, меняются с основной частотой p—za, а также
содержат гармоники 2р, Зр, 4р и т. д. Низшие гармоники возбуждения
могут появиться также лишь в случае отклонений в индивидуальных
свойствах отдельных лопастей.
2. Зависимость спектра частот возбуждающих сил
от гармонического состава колебаний лопасти
Итак, мы выяснили исходя из самых общих соображений, что пере-
менные силы и моменты X, Y, Z, Мх, Mv, Mz, действующие на втулку
винта со стороны колеблющихся лопастей, меняются во времени с ча-
стотой основной гармоники za> винта и содержат также кратные ей гар-
моники 2Эсо, 3z(o и т. д., в то время, как лопасти винта, а следовательно,
и силы, действующие иа втулку со стороны каждой лопасти, совершают
колебания с основной частотой
<о и содержат кратные гармо-
ники 2«, Зсо, 4(о и т. д., среди
которых имеются и гармоники
2(о, 22(0 и т. д. Это наводит на
мысль, что некоторые гармони-
ческие составляющие перемен-
ных сил, приложенных к втул-
ке со стороны каждой лопасти,
уравновешиваются на корпусе
втулки, а некоторые суммиру-
ются. Покажем, что это дейст-
вительно так. Обратимся к
рис. 2.4, на котором схематич-
но изображен корпус втулки
Рис. 2. 4. Схема сил, приложенных к втулке
винта, от лопасти
с шарнирно прикрепленными к
нему лопастями.
Силу, приложенную к кор-
пусу втулки со стороны &-ОЙ
лопасти, можно разложить на три составляющие: Nk, направленную по
радиусу лопасти, Ph, параллельную оси вала винта, и Qk, перпендикуляр-
ную двум первым.
Каждая из этих составляющих является периодической функцией
времени с основной частотой со. Очевидно, что на установившемся ре-
жиме полета функции Л44), Pk(t) и Qk(t) для всех лопастей одинако-
вы, но сдвинуты по фазе для каждой лопасти относительно соседней на
некоторую величину, соответствующую времени поворота винта на угол
2л/а. Это дает основание написать разложения этих функций в ряды
Фурье в виде:
рл = ро + ра, cos («>/ + + Рь, Sin (ш/ 4- <рй) 4-
4-Pa!cos2(o)Z4-%)4-Assin2(<Dz!4-^j!!)4-.. .4- (1.3)
4- Рая cos п (со/ -4 <pft)4- Р„п sin я (ш/ + <pft) 4-..
где
= (£=1, 2, 3...Z),
«ли короче
= cos w(“z + ?ft) + P»„sinra(“z + <Pft)]- О'4)
Л-1
203
Аналогично имеем
Qft=Qo+[Qan cos n И+т») +Q»n sin n (W + %,)]; (1. 5)
rt-I
+ (®/ + ?A)]. (1.6)
л-1
Поставим теперь следующую задачу: зная величины коэффициен-
тов разложения в ряды Фурье функций Р&(0> <?л(0 и или, иначе
говоря, зная гармонические составляющие сил Рь,< Nh, найти пере-
менные силы X, Y, Z и моменты Мх, Му, М, (точнее их гармонические
составляющие) с тем, чтобы проследить зависимость сил, вызывающих
вибрации, от различных гармонических составляющих сил, действую-
щих на втулку со стороны отдельной лопасти.
Суммируя силы, действующие на втулку со стороны каждой лопа-
сти, получаем следующие формулы:
о-7)
Л-1
*;* . о-8)
Z= Ё [Q»cos^+JVftsiny;
fe-i J
(i.9>
Л=1
S sin
7 (1.Ю)
Mz= — j/Vicos^, j
ft-i ‘
где. — азимутальный угол k-й лопасти:
= = А; (1.11)
Л— расстояние от оси вращения до совмещенных горизонталь-
ных и вертикальных шарниров.
Если втулка имеет несовмещенные шарниры, то в формуле (1.9)
надо брать /г=1в.ш, а в формулах (1. 10) /г = /г.ш.
Рассмотрим подробно выражение (1.7) для определения перемен-
ной силы У. Подставляя в него выражение (1.3) для силы Ph, мы при-
ходим к необходимости вычисления сумм вида:
Z Z
S cos п (^+?й) и S sin /г (ю/ + %),
Й-1 Й=1
где п—целые числа (и=1, 2, 3 ...).
Покажем, что тригонометрические суммы такого вида обладают
следующим замечательным свойством: при любом п не кратном числу
204
лопастей z обе эти суммы равны нулю при всяком при п, кратном z,
т. е., если n=sz (s= 1, 2, 3 ...), то
*
2 COSSZ = Z cos (5ZU)/);
7 (i-12:
zsin(szotf).
Так, например, для винта с пятью лопастями (г=5)
5 5
S cos (w -г Сй) v cos 2 (<»/ -L- %) =
Й=1 /г-1
5 5
= £cos3(w/-|-<pA) =2 cos4(a>/-|-<pft)=0
й-1 к-1
при любом значении t, но
S
У, cos 5 (<«/ <рй)=5 cos .
й = 1
Далее
5 5
У COS 6 (ю/ — ой) = у COS 7 («>/ 4- ©й) —
й-1 Л-1
5 5
= 2 cos8(«>/-j-ггй) = У cos9 О,
й-1 й-1
НО
5
£cos 10(«>/-р<рк)—5cos (1СЫ), и т. д.
й-1
Доказать справедливость формул (1. 12) можно различными спосо-
бами. Применим для этого весьма удобный способ, предложенный
Р. А. Михеевым и основанный на применении известной формулы Эйле-
ра, выражающей связь между тригонометрическими функциями и пока-
зательными функциями с мнимым аргументом. Докажем справедли-
вость лишь первой из формул (1. 12). Имеем:
Поэтому
C0S«ift=-L (е‘^+е^ ('?*=»/+-— k).
2 2
cos «ой = y S 1УЛ1|'й+е~''!'|'*1 =
Л-1 Л^1
1
2
S. п
е
/г-1
—inwt
Рассмотрим отдельно сумму
Z
205
Это геометрическая прогрессия со знаменателем е г.
Пользуясь известной формулой для суммы геометрической прогрес-
сии, получаем:
4=1
(2л —
е г (1-е'2*д)
12к —
1-е 2
Так как п — целое число, то числитель этого выражения всегда ра-
вен нулю, потому что е'2,!Л=1 (п=1, 2, 3
Знаменатель этого выражения может обратиться в нуль только
если^—^целое число, т. е. если п кратно числу лопастей г. Таким обра-
зом, рассматриваемая сумма равна нулю при любых п, за исключени-
ем п кратных числу г. В этом последнем случае величина суммы ста-
новится неопределенной Эту неопределенность можно раскрыть
с помощью известного правила Лопиталя. Пусть п меняется непрерыв-
но, приближаясь к некоторому значению sz (s—любое целое число;
$-=1, 2, 3 ...). Дифференцируя числитель и знаменатель по и и перехо-
дя к пределу n-+sz, имеем:
- йле'2"
Z
12« —
= 1!тг гИт-
П-t-SZ П~>$2
Z.
Точно также можно показать, что
4-1
Д- й 0, если
Z ___
z, если
и. не кратно z;
n — sz, где s=l, 2, 3...
В результате приходим к выводу, что, если п не кратно z, то
2
^cos/i'pft=0.
4 — 1
Если же п. кратно z(n=sz; s=l, 2, 3...), то
Z
cos (е'лш(-|= е-!‘лш')=з cos ws>t—-z cos (sz«>t\-
4-1
Аналогично можно показать справедливость второй из формул
(1. 12).
Указанное свойство тригонометрических сумм удобно записать в.
форме:
* г 0, если п не кратно z\ )
У, cos n&k = / I
*_1 I zcos««>/, если n=sz\ s=l, 2, 3..I
* f 0, если n не кратно z\ । 1
>, sin n'->k =
k^i I 2sinn<i< если n—sz\ s=l, 2, 3... J
206
Возвратимся теперь к выражению для силы У из формулы (1.7),
в которое подставлено значение силы Рк из формулы (1.4):
Z
Y = S [Л) + cos 4- Р», Sill + Ра, COS 2'pft
Й=1
н- sin 2.^+... + Pancos п Pbn sin n.^.. ,j
На основании установленного свойства тригонометрических сумм
(1.13) можно утверждать, что при суммировании различных гармоник
в этом выражении исчезнут все гармоники, не кратные числу лопастей z.
Гармоники, кратные г, суммируются в соответствии с формулами (1. 13),
так что окончательно получим:
У — zP0 + гРЯг cos z<s>i -j-zPbz sin z®t--f- zPa
(2^)
cos 2zo)Z 4- zPh sin 2г<о/
1 ^(2г) 1
(1- 14)
Рис. 2.5. Зависимость амплитуды
вибраций в кабине летчика одно-
винтового вертолета от скорости
полета
Таким образом, все гармонические составляющие силы Pk(f), не
кратные числу лопастей, уравновешиваются на втулке винта и не вызы-
вают вибраций фюзеляжа вертолета.
В результате переменная сила У меня-
ется во времени с основной гармони-
кой p — za> винта, а также содержит
кратные гармоники 2р, Зр и т. д. Это
полностью подтверждает основной вы-
вод предыдущего пункта этого пара-
графа, а также дает дополнительные
сведения в этой части, указывающие,
какие именно гармонические состав-
ляющие силы Рк опасны с точки зре-
ния вибраций.
Для иллюстрации рассмотрим
пример. Допустим, что у некоторого
винта имеется резонанс второго тона
колебаний лопасти в плоскости взмаха
с 5-й гармоникой винта (5ц>). При этом в разложении силы Рк для та-
кого винта будет велика гармоническая составляющая, соответствующая
5-й гармонике (Рй5и РЬб).
Если винт имеет пять лопастей, то указанный резонанс приведет
к большим вибрациям вертолета.
Если же винт имеет четыре лопасти, то этот резонанс никак не про-
явит себя в вибрациях вертолета, так как соответствующие этому
резонансу гармонические составляющие силы Рк будут уравновеши-
ваться на втулке. При этом, как будет видно из дальнейшего, могут
оказаться значительными переменные моменты Мх и Afz на втулке, одна-
ко, практически вибрации вертолета определяются, главным образом,
переменными силами X, У, Z. Иногда ошибочно считают, что вибрации
вертолета тем меньше, чем больше лопастей имеет несущий винт. Одна-
ко на этом примере видно, что в действительности дело обстоит не так
просто, а в данном случае, наоборот, уменьшение числа лопастей при-
водит к уменьшению вибраций.
Рассмотрим еще один пример. На рис. 2.5 показаны результаты
экспериментальных измерений вибрации в кабине летчика одновинтово-
го вертолета, который испытывали с двумя винтами: трех- и четырехло-
пастным. Винты имели совершенно одинаковые лопасти и отличались
лишь втулками. На графиках изображены зависимости амплитуды ау
вертикальных вибраций в кабине летчика от скорости полета V для
обоих винтов.
207
Как показали расчеты, проведенные для этих винтов, лопасть вин-
та имела резонанс второго тона колебаний в плоскости взмаха с 4-й
гармоникой винта на рабочих оборотах. В результате вибрации верто-
лета с четырехлопастным винтом на большей части диапазона скоровтей
оказались значительно выше (при У = 40-е-50 км/час более, чем в три
раза), чем вибрации вертолета с трехлопастным винтом. Однако на
большой скорости полета вибрации вертолета с четырехлопастным вин-
том оказались меньше, чем вертолета с трехлопастным винтом. Это
объясняется тем, что на малой скорости полета имеется большая гар-
моническая составляющая аэродинамических сил, соответствующая 4-й
гармонике и обусловленная большой неравномерностью поля индуктив-
ных скоростей винта на малой скорости полета. С ростом скорости
полета происходит выравнивание поля скоростей потока (см. гл. 1, § 8),
протекающего через винт и соответственно быстро уменьшается воз-
буждение колебаний лопасти по 4-й гармонике, в то время, как 3-я гар-
моника уменьшается с ростом скорости не так быстро или даже совсем
не уменьшается. Относительно большая величина 4-й гармоники в поле
индуктивных скоростей на малой скорости полета является, по-види-
мому, обычным явлением для всякого несущего винта.
Возвратимся теперь к определению других сил и моментов, дей-
ствующих на вертолет. Формула (1.9) для момента Му совершенно ана-
логична формуле (1. 7).
Повторяя все рассуждения, как и при выводе формулы (1. 14) для
силы Y, получим следующее выражение:
Му=zh. [Со + cos zwt -]- Qbz sin zu>t -]-
+ C0S 2z“Z + sin 2z<s,t+ •••!•' (h 15)
Переменный момент My опасен не только с точки зрения вибраций
вертолета (в § 3, п. 1 будет показано, что этот момент вызывает лишь
поперечные колебания фюзеляжа). Этот момент является одним из ис-
точников крутильных колебаний в системе трансмиссии вертолета.
Как видно из формулы (1. 15), переменная часть этого момента
определяется исключительно гармоническими составляющими силы
Q(£), кратными числу лопастей.
Обратимся далее к первой из формул (1.8). Подставляя в нее вы-
ражения для Qk(t) и Nk(t) [формулы (1.5) и (1.6)], получим:
X— S(Qosin<pft—^со8фй)+ 1] [Q^cos^+Q^sin^] sin yft —
7г—1 Й=1
— S [7VaJcos^ft-4-M1sm'ift]cosift4-...+J] [Св/г cos «!>*-[-
fe=l Й=1
+ Qbn sin «^] sin - S [A^cos /гФйф- Nba sin яфй] cos +...
s-=i
Первое слагаемое этой суммы равно нулю в соответствии с форму-
лами (1. 13), так как
И [Qo sin ф» — No COS Фй] = Со S s in фй - No £ cos = 0.
7г-I Ы Й=1
Для подсчета остальных слагаемых рассмотрим выражение
XQ = S [Сал cos Лфй+Со„ sin п Фй] Sin
208
которое представляет собой часть силы X, обусловленную п-й гармони-
кой силы Q.
Z 2
Здесь мы встречаемся с суммами вида cos sin 'у* и sin n~k sin Д.
Эти суммы также легко вычисляются с помощью формул (1. 13). В са-
мом деле
Z Z z
cos sin фй=2- J sin (га Ц-1) ----sin (га - 1) < Л.;
A=I fe-1 Й=1
Z Z z
J] sin sin Д = - 2- yj COS (Л + 1) Д + 2- J cos (n - 1/ \-
4-1 4=1 4=1
На основании формул (1. 13) можно утверждать, что эти суммы
будут отличны от нуля только тогда, когда одно из чисел (га-f-l) или
(«—1) кратно числу лопастей. Пусть (п+1)=зг (s=l, 2, 3 ...), следо-
вательно, n—sz—1. Тогда
cos гафЛ sin sin (szw/);
ft-i
Z
sin rai sin cos (sz®/).
k =i
Далее, если (га—l)=sz; « = &гЦ-1, то
Z
cos zz‘pft sin =----------sin (szco/);
Й=1
z
sin nAk sin 6k=~- cos (sz®/).
4-1
В результате получается следующее выражение для части силы X,
которая получается от всех гармонических составляющих силы Q:
Хо = z J^-1) sin ZU)/---Q2^>+Q* <* + > cos zmi _L
Q ( 2 2 П
+ ±^_1)-Qg(2,+1) s!n 2zwt + cos 2zuit+...} _
(1-16)
Для части силы X, обусловленной гармоническими составляющими
силы N(t), аналогично получается выражение вида:
xN - J +221£±1> cos 2toZ + Nb (^1>+-¥иг+1> siI, ZU)i _
1 2 2
^^-n+.^+i) cogsin2ZC0/4-..J. (1. 17)
2 2 J
Сила X может быть определена по формуле
Л- — Xq-^-Xn.
14 1578
209
Если выражение для силы Х(^) записывать в виде (1. 1), то полу-
чаются следующие формулы для ее гармонических составляющих:
Хаг— 2 fQft (г+1) ^6(г-Л) ^(z+I) ^a(z-1)1’
К2о (г-1) ~Qa (г+1) — -^i(2+i)— Nb (г_()Ь
(1. 18)
Составляющие, соответствующие гармоникам, кратным основной,
Хв1> Хь. и т. д. получаются из этих же формул, если вместо индекса z
брать соответственно индекс 2z, Зг и т. д.
Таким образом, переменная часть силы X(t) определяется гармони-
ческими составляющими сил Q(t) и N(t) комбинационными по отно-
шению к основной гармонике винта (z—1; z+1) или к ее кратным гар-
моникам (2z—1; 2z+l) и т. д.
Так, например, для винта с тремя лопастями (21=3) основная гар-
моника силы X (частота Зсо/) будет определяться 2 и 4-й гармониками
сил Q (f) и N (t), 2-я гармоника силы (частота 6«^) будет определяться
5 и 7-й гармониками сил Q(t) и N(t) и т. д.
Совершенно аналогичные формулы получаются для гармонических
составляющих силы Z(t):
— 2 (г+1)"^^а (г-1) (z+D- (z-l)l’
[Q» (г+1)"Ь^6 (г-1)(z-lj — (z+l)!’
(1-19)
Так же, как и в формулах (1. 18), для получения кратных гармоник
Za„ Zb„ Zaw Zbi в этих формулах надо вместо индекса а подставлять
соответственно индексы 2г, 3z и т. д.
Аналогично получаются из формул (1, 10) выражения для гармо-
нических составляющих моментов Л1ж и Л12:
2 ^&(г-1) (2 + 1)1 ’
[^0(2 + 1) “P“(Z-1)H
Ма, 2 [ ^“(г+1) (г-1)1 >
< = ^[-^(г + 1)-^(г_1)1-
(1.20)
(1.21)
Отметим еще следующее обстоятельство, которое иногда может
облегчить качественный анализ вибраций. Если переменная сила в пло-
скости винта (X или Z) или момент (Мх, Mz) определяется какой-либо
одной гармонической составляющей силы, действующей со стороны ло-
пасти, то в результате получается вектор постоянной длины, равномерно
вращающийся в плоскости винта с угловой скоростью za> (или sza>).
Причем, направление вращения получается против вращения винта,
если этот вектор получается от гармонической составляющей 2+1
(или S2+1), и в сторону вращения винта, если этот вектор получается
от гармонической составляющей z—1 (или sz—1).
210
Пусть, например, винт имеет пять лопастей (z = 5) и рассматрива-
ется вектор момента на втулке с составляющими Л4Х и тг, получаю-
щийся от гармонической составляющей (г—1):
Р = Pat cos 4<й/-ф Pbt sin 4W.
Тогда (см. 1.20 и 1.21)
7ИЛ — cos 5со/ — Pai sin 5<в/];
Mz = [ — Pbi s in 5ш/ — cos 5ш].
При этом, как видно из этих формул, вектор
М = Мх-[-Мг
представляет собой вектор постоянной длины
44=^-/^+^
равномерно вращающийся в плоскости винта с угловой скоростью 5а>
в направлении, совпадающем с направлением вращения винта.
Итак, анализ, проведенный выше, показывает, что несущий винт
является своего рода фильтром, который из всех гармонических состав-
ляющих сил на колеблющихся лопастях пропускает на фюзеляж лишь
некоторые, соответствующие основной гармонике винта гы, ее комбина-
ционным гармоникам (z—1)ы и (z+l) и, а также гармоникам, кратным
основной 2z)co, 3zco и т. д., и комбинационным гармоникам (2z—1)со,
(2z+l)(o, (3z—1)со, (3z+l)co и т. д.
Наибольшую опасность, как с точки зрения уровня вибраций, так
с точки зрения динамической прочности элементов фюзеляжа, представ-
ляют, как правило, низшие гармоники zgj, (z+l)w и (z—l)w.
Из гармоник, являющихся следствием колебаний лопасти в пло-
скости взмаха (сила Ръ, см. рис. 2. 4), гармоника гео (и ей кратные) при-
водит к появлению вертикальной переменной силы на винте, а гармо-
ники (г—1) и (z+l) (а также 2г—1, 2г+1 и т. д.) приводят к появле-
нию переменных моментов на втулке относительно осей Ох и Oz.
Из гармоник, являющихся следствием колебаний лопасти в плоско-
сти вращения (силы и JVk, см. рис. 2.4), гармоника zco (и ей крат-
ные) приводит к появлению переменного крутящего момента на валу
винта, а гармоники (z—1)со и (z+l)со (а также 2z—1, 2z+l и т. д.) —
к появлению переменных сил (продольной и поперечной) в плоскости
вращения винта.
Отметим в заключение, что при суммировании сил, действующих со
стороны лопастей на тарелку автомата перекоса получаются точно
такие же формулы для расчета гармонических составляющих верти-
кальной силы У и моментов Л1Ж и Мг, приложенных к тарелке. При этом
можно пользоваться непосредственно формулами (1.14), (1.20)
и (1.21), понимая под силой
во
Pk (0 = Р0 + S (Рап COS + Pbn Sin «<[>*),
п-1
усилие, действующее в поводке управления А-й лопастью (шарнир-
ный момент, деленный на соответствующее плечо), а под величиной
h — радиус тарелки автомата перекоса:
Таким образом, зная гармонический состав шарнирного момента,
не трудно рассчитать переменные силы, действующие в цепях управ-
ления общим и циклическим шагом винта.
14*
211
§ 2. КОЛЕБАНИЯ ИЗГИБА ФЮЗЕЛЯЖА КАК УПРУГОЙ БАЛКИ
Если известны переменные силы, приложенные к фюзеляжу от не-
сущих винтов, то расчет вибраций в различных точках фюзеляжа мо-
жет быть выполнен обычными методами, применяемыми при расчете
вынужденных колебаний упругой балки переменного поперечного сече-
ния. Конечно, фюзеляж реального вертолета только в первом прибли-
жении можно рассматривать как тонкую упругую на изгиб балку.
В действительности поперечные размеры фюзеляжа обычно нельзя
считать малыми по сравнению с продольными. Кроме того, фюзеляж
вертолета одновинтовой схемы может иметь «изломы» в районе хвосто-
вой балки, резкие перепады жесткости по длине и другие особенности.
Эти особенности и их учет при расчете колебаний рассматриваются
в § 3. Здесь же мы рассмотрим методы расчета колебаний упругой бал-
ки, так как они являются основой для дальнейшего. Кроме того, в этом
параграфе будут рассмотрены колебания системы, состоящей из двух
упругих балок, образующих «крест». К такой системе приводится фюзе-
ляж с крылом.
1. Расчет вынужденных колебаний упругой балки методом
разложения по собственным формам
Пусть к упругой на изгиб идеальной балке (рис. 2.6), лишенной
демпфирования, находящейся в свободном состоянии под действием
уравновешенной системы постоянных во времени сил (сила тяги винта
уравновешивает силы тяжести), приложена распределенная по длине
балки переменная во времени нагруз-
ка q, изменяющаяся по гармоническо-
му закону
q (х, t) = q (.v) cos pt. (2. 1)
Уравнение поперечных колебаний
изгиба такой балки имеет вид:
(£/«/")"+ rnij = q (x,f) (2.2)
Это уравнение в частных произ-
Рис. 2.6. Схемы свободной упругой водных выведено в п. 10, § 1, гл. 1 для
балки с приложенной к ней распре упругой балки в поле центробежных
деленной нагрузкой сил. в случае их отсутствия (У = 0)
уравнение принимает вид (2. 2)
Найти движение балки, это значит найти функцию у=у(х, t), удов-
летворяющую уравнению (2.2), а также краевым условиям, которые
в случае балки со свободными концами имеют вид:
при х —0; Л1==£'7(/" = 0; Q=^EIy")' = Q-, )
при x = Z; М = Е1у" = Ъ, Q = (EIy"y=O. )
Функции у(х, t), удовлетворяющие однородному уравнению (без
правой части)
(Е1у"У’ + ту^0
(2-4)
и краевым условиям (2.3), соответствуют собственным колебаниям бал-
ки. Решение уравнения (2.4) отыскивается в виде
у (х, i) = у (х) cos pt.
(2.5)
212
Это выражение после подстановки в уравнение (2.4) приводит
к обыкновенному дифференциальному уравнению с параметром р для
определения функции у(х):
[Е1У)" — р^ту — О. (2.6)
Последнее уравнение имеет решения, отличные от нулевого, только
при определенных значениях параметра р: р = Ро; Р = Р\; р=р2‘, Р~Рз
и т. д. Причем каждому значению p = pk (& = 0, 1, 2, 3, ...) соответствует
определенная функция ук(х), которая удовлетворяет уравнению (2. 6)’
при p = pk, так что;
(jE/уУ — р1тук—0; (£=1,2,3,...). (2.7)
Числа pk (k = 0, 1, 2, 3, ...) называются частотами собственных ко-
лебаний балки, а функции yk(x)—соответствующими формами собст-
венных колебаний.
Движение балки по закону:
у(Х, t) = акук(х) cos pkt, (2.8)
где йй — постоянная величина, на-
зывается собственными колебания-
ми балки по £-му тону.
Общее решение однородного
уравнения (2.4) имеет вид:
у (х, /) = £ акук (х) cos (pkt + Tft),
k
(2.9)
где ал. и ерь — произвольные посто-
янные.
Таким образом, собственные
колебания балки представляют со-
бой движение, получающееся в ре-
зультате наложения колебаний раз-
личных тонов.
Методы нахождения частот соб-
ственных колебаний рн и соответст-
вующих форм yk(x) для балки с за-
данным законом изменения жестко-
сти £/(х) и погонной массы т(х)
изложены в § 2 гл. 1.
На рис. 2. 7 показаны характер-
ные формы собственных колебаний
свободной балки. Две формы соот-
ветствуют колебаниям балки как
твердого тела, и имеют частоты
собственных колебаний, равные
Рис. 2.7. Характерные формы собствен-
ных колебаний фюзеляжа как свобод-
ной балки (р*, pl и т. д. — частоты ко-
лебаний первого, второго и т. д. упру-
гих тонов; вообще следует считать:
Ро=О; Р1=0; р2=р*; Ps^P2 и т. д.)
нулю. Первая из этих форм соответствует поступательным перемещени-
ям балки, а вторая угловому перемещению балки относительно ее цент-
ра тяжести.
Все формулы, которые выводятся в настоящем параграфе, одина-
ково пригодны для расчета колебаний упругой балки с любыми усло-
виями закрепления концов. Однако в случае применения этих формул
к колебаниям свободной балки и, в частности, фюзеляжа, необходимо
помнить, что в число частот р» и форм уь(х) собственных колебаний
должны быть обязательно включены две низшие формы, которым со-
ответствуют нулевые частоты. Так что надо полагать во всех формулах
213
Ро = О и pi = O и учитывать, что соответствующие нормированные формы
имеют вид:
ioW = 1;
I — хс
где — координата центра тяжести балки.
В случае, если указанные формы не будут учтены при расчете виб-
раций фюзеляжа, расчет вибраций будет выполнен без учета колебаний
фюзеляжа, как твердого тела, и это приведет к значительным ошибкам
в величине вибраций.
Рассмотрим задачу о вынужденных колебаниях балки под действи-
ем «чисто» гармонической нагрузки [см. формулу (2, 1)]. В этом случае
уравнение (2.2) принимает вид:
(Е/у"')"ту —у (х) cos pt. (2.10)
Будем искать частное решение этого уравнения, соответствующее
установившимся вынужденным колебаниям балки с частотой р в виде
у — у (х) cos pt. (2.11)
Подставляя это выражение в уравнение (2. 10), придем к обыкно-
венному дифференциальному уравнению для определения функции у(х),
которую естественно называть формой вынужденных колебаний:
{Ely’)" - p2my=q (х). (2. 12)
Будем искать решение этого уравнения в виде разложения по соб-
ственным формам:
У~ X скУк(х)- (2.13)
Если в этой сумме брать ограниченное число членов, то можно,
определяя значения коэффициентов cit, получать лишь приближенные
решения уравнения (2.12). Однако, можно доказать, что при указанном
ниже способе определения коэффициентов Съ приближенное решение
при достаточно большом числе членов в ряде (2.13) будет как угодно
мало отличаться от точного.
Для нахождения коэффициентов Q подставим выражение (2. 13)
в уравнение (2. 12) и, умножив обе части уравнения (2. 12) на уп(х),
проинтегрируем их от 0 до I. При этом получится уравнение:
i _ir i______ i _
S ck j {EIyk) y^dx—p'1 S сь J myky,ldx= J qyjix. (2. 14)
к 0 1 к 0 0
Интегралы, стоящие в первом слагаемом левой части этого урав-
нения, можно упростить, применяя интегрирование по частям:
г _ г_ г г_,
( {EIyk)’y„dx= j ynd{EIyk) =[уп{Е1ук)'] —J у’п {EIyk)'dx,
о о оо
но
[уп(е/УкУ] |>,
так как функции уь(х) удовлетворяют краевым условиям (2. 3).
214
Далее:
Jу’п{Е1упУdx—J y^d(f/уъ)=\уп(Е1 у*)]
о о
1 1 „
— j£7 ynykdx.
о о
В силу условий (2.3)
так что в результате получается:
I 1
J (EIy’b)yndx = (Elyly'kdx. (2.15)
о б
Так как все функции уь(х) (&=1, 2, 3 ...) удовлетворяют уравне-
нию (2.7), то можно записать:
(Ely к) — р1тул=0;
(EfynS— р2„пйу==0.
Умножив первое из этих уравнений на уп, а второе — на уь, затем
вычтем одно из другого и проинтегрируем полученное выражение от О
до I. Получим:
i _ _ i „ i ___
EI^„)’ykdx=(/^— pty ту^Рх.
о
Но левая часть этого уравнения равна нулю в силу условия (2. 15).
Поэтому, если только рь^рп, то
i____
J тУаУ1^х=Ъ', (пф1г). (2.16)
о
Это есть так называемое условие ортогональности форм собствен-
ных колебаний (см. также гл. 1, § 2, п. 3).
Далее, умножая обе части уравнения (2.7) на уп и интегрируя от
О до I, получаем:
i (____
J (Elykyyndx — pl J mykyndx.
0 V
Отсюда можно заключить, что если n^k, то
i _* т i
(Е1 у k)”yndx =§EI y'ny'kdx^Q. (2. 17)
О
Если же n — k, то получается выражение для частоты рп п-го тона
колебаний, через его форму уп(х):
г
С 2
J EIyn dx
—• (2,18)
J nyfyx
о
Это есть известная формула Релея.
На основании условий (2. 16) и (2. 17) можно утверждать, что в вы-
ражении (2. 14) все слагаемые, для которых k=f=n обратятся в нуль.
215
за пе-
отне-
Учитывая это, а также используя формулу (2. 15), перепишем уравне-
ние (2. 14) в виде:
i _ ч _
сп \ Е/уп dx — crlp- my2„dx= J qyndx.
о 0 0
I
Разделив обе части последнего уравнения на J ту\ dx, разрешив
о
его относительно сп и используя формулу Релея (2. 18), найдем:
i
J ЧУпЛх
С‘=~^7'Т~Г (2.19)
J >ny‘ndx
О
Введем обозначения:
i _
An=-^qyndx- (2.20)
о
I
/C„ = J mp2„dx. (2.21)
о
Величина Ап представляет собой работу возбуждающей нагрузки
<?(х) на форме n-го тона колебаний, а величина КГ1— наибольшее
риод значение кинетической энергии данного тона колебаний,
сенное к величине р2а . Итак:
с 1 А“
Р2п~Р2 '
Учитывая выражения (2. 13) и (2. 11), получаем следующее
ние уравнения (2.10):
у (*> =ГУ 21 и Уь W] cos •
/’s—р2 К к
L к J
Из этого выражения можно сделать некоторые весьма важные
выводы.
Прежде всего видно, что если частота изменения возбуждающей
нагрузки р приближается к одной из частот pk собственных колебаний,
то амплитуда колебаний любой точки балки неограниченно возрастает.
Это есть явление резонанса возбуждающей нагрузки с fe-м тоном соб-
ственных колебаний балки. Так как здесь мы не учитывали влияние
демпфирующих сил (это будет сделано далее), то амплитуда колебаний
при резонансах получается неограниченной.
Далее, если величина р близка к частоте рп п-го тона колебаний,
то член с номером п в сумме (2. 23) становится значительно больше
остальных членов. Поэтому приближенно можно полагать вблизи резо-
нанса (р = рп), что
У (х, t) = J у п (х) cos pt с„уп(х) cos pt,
Рл — Р2 Кп
т. е. вблизи резонанса с каким-либо тоном собственных колебаний фор-
ма вынужденных колебаний мало отличается от формы колебаний дан-
ного тона.
(2. 22)
реше-
(2. 23)
216
Наконец, при переходе значения р от величины несколько меньшей,
чем рп, к величине несколько большей, чем рп, величина, стоящая в
квадратных скобках формулы (2.23), меняет знак. Поэтому, если по-
строить график зависимости амплитуды уа какой-либо точки балки от
частоты возбуждения р [при неизменном <y(x)], то этот график будет
иметь вид, изображенный на рис. 2. 8. Кривая графика имеет бесконеч-
ные разрывы в точках p = Pi, р — ръ Р = Рз и т. д.
2. Динамическая жесткость балки. Резонанс и антирезонанс
Рассмотренный в предыдущем пункте случай вынужденных колеба-
ний балки под действием распределенной по ее длине возбуждающей
нагрузки, изменяющейся во времени по гармоническому закону (2. 1),
и выведенные формулы остаются в силе при любом законе изменения
нагрузки по длине балки, т. е. при любом виде функции q(x). Поэтому
Рис. 2.8. Зависимость амплитуды колеба-
ний любой точки фюзеляжа от частоты воз-
буждения
из этих формул нетрудно полу-
чить формулы для определе-
ния вынужденных колебаний
балки, вызываемых сосредото-
ченной возбуждающей силой
F = F0cospt, (2.24)
приложенной в некоторой точ-
ке х = хд (рис. 2. 9).
Рис. 2. 9. К анализу вынужденных
колебаний свободной балки от
сосредоточенной силы
В самом деле, пусть нагрузка q(x) приложена к балке лишь на не-
котором малом участке длиной Ах в окрестности точки х = хо. При этом
формулы (2.22), (2.20) и (2.21) останутся в силе, но в формуле (2.20)
соответствующий интеграл нужно брать не по всей длине балки I,.
а лишь на участке Ах, т. е.
г _
An=\qyndx= \qyndx.
о ix
При малом значении Ах этот интеграл можно приближенно заме-
нить величиной
j qyndx= Рйуп(х^,
Ajr
где
/•"о = J qdx.
Кг
(2.25)
(2.26)
Причем формула (2. 25) становится точной при бесконечно малом Ах,
т. е. в случае сосредоточенной возбуждающей силы.
21У
Таким образом, мы приходим к следующему выводу: в случае, если
колебания балки вызываются сосредоточенной силой (2.24), прило-
женной в точке х=х0, движение балки по-прежнему описывается вы-
ражением (2.23), в котором величина определяется по формуле
Л==ЛМ*о), (2.27)
т. е. величина Ак представляет собой работу возбуждающей нагрузки
«на форме А-го тона колебаний».
Заметим, что такой метод нахождения вынужденных колебаний
остается в силе и в том случае, если колебания вызываются меняющим-
ся по гармоническому закону сосредоточенным изгибающим моментом
Л4 = Л1о cos pt, (2.28)
приложенным в точке х = х0. В этом случае величина Л^ должна опре-
деляться по формуле
А^М^у'к(х0), (2.29)
где (х0) — угол поворота упругой линии в точке x=xQ, соответст-
вующий форме fe-ro тона.
В случае, если колебания балки вызываются продольной силой
Х—Хо cos pt,
(2. 30)
приложенной на некотором плече h (рис. 2. 10), все приведенные фор-
мулы также остаются в силе, так как в этом случае силу можно пере-
нести из точки Л в соответствующую точку В балки, добавив при этом
пару с моментом, равным Mo=Xoh.
Рис. 2.10. Схема действия на упругий
фюзеляж продольной силы от несущего
винта
Продольная переменная сила,
приложенная в точке В, может вы-
звать лишь продольные (осевые)
колебания балки, а поперечные ко-
лебания балки от гармонического
момента Л40 определяются, как было
указано выше.
При рассмотрении поперечных
вынужденных колебаний балки от
сосредоточенной силы F—F0cos pt
удобно ввести понятие динамиче-
ской жесткости балки в точке х=
—х0 приложения силы.
Назовем динамической жесткостью D(p) балки в точке отно-
шение наибольшего значения (амплитуды) возбуждающей силы Fo
к амплитуде уо = у(хо) вынужденных колебаний балки в точке приложе-
ния силы, так что
Уо
(2.31)
Имеется в виду, что при изменении силы по гармоническому зако-
ну F=Fa cos pt, точка ее приложения совершает установившиеся вынуж-
денные колебания по закону y=yvcos pt.
Таким образом, динамическая жесткость балки есть функция часто-
ты р колебаний и считается положительной, если сила и перемещение
меняются во времени «в одной фазе» и отрицательной, если сила и пе-
ремещение меняются в «противофазе».
218
Амплитуда колебаний точки х = хо приложения силы может быть
определена с помощью формулы (2.23):
<2-32>
k
Если построить график изменения величины у» по частоте р при
неизменном значении Fo, то получится кривая, аналогичная изображен-
ной на рис. 2. 8. Поэтому, если построить график зависимости динами-
ческой жесткости D(p) в данной точке балки от частоты колебаний, то
этот график будет иметь вид, изображенный на рис. 2. 11.
Динамическая жесткость D(p) обращается в нуль при резонансах
P = Pi, Р = Р2 и т. д. и в бесконечность при тех значениях частоты р
(р = Р\2, Р = Р23, р = рзл и т. д.),
при которых амплитуда коле-
баний точки приложения силы
обращается в нуль. Эти зна-
чения частоты р называются
частотами антирезонансов и
равны частотам соответствую-
щих тонов собственных колеба*
ний балки с шарнирной опорой
в точке приложения силы F.
В самом деле, представим
себе, что в точке приложения
силы F балка имеет опору с
шарниром (балка в этой точке
не перерезана), так что эта
точка балки остается непо-
движной при колебаниях. Та-
кая балка имеет свои частоты
и формы собственных колеба-
ний. При собственных колеба-
и(р)кгс/см
Рис. 2. 11. График динамической жесткости
ниях некоторого тона такой
балки в опоре (х=х0) будет возникать динамическая реакция, меняю-
щаяся во времени по гармоническому закону с частотой этого тона.
Амплитуда (наибольшее значение) этой силы реакции будет зависеть
от амплитуды (какой-либо точки, например, конца) собственных коле-
баний балки, которая может иметь любую величину (в зависимости от
начальных условий). Поэтому можно всегда так подобрать амплитуду
колебаний балки, чтобы амплитуда силы реакции имела заданную ве-
личину Fo. Если теперь мысленно убрать опору, продолжая приклады-
вать к балке в этой точке силу F, меняющуюся по гармоническому зако-
ну с той же частотой, то свободная балка будет продолжать колебания
по той же форме с той же амплитудой. Однако эти колебания можно
рассматривать как вынужденные колебания свободной балки под дей-
ствием возмущающей силы F. При таких вынужденных колебаниях
точка приложения возмущающей силы неподвижна и поэтому соответ-
ствующая такому режиму динамическая жесткость балки бесконечна.
Это и называется антирезонансом.
На графике динамической жесткости (рис. 2. 11) точки резонанса
jD(p)=O и антирезонанса П(р)=оо чередуются. Можно показать, что
для упругой балки это всегда так.
Итак, при некоторой частоте возбуждения точка приложения воз-
буждающей силы останавливается и в этой точке получается узел фор-
мы вынужденных колебаний. Это явление называется антирезонансом.
Частота каждого антирезонаиса всегда располагается между двумя
соседними частотами собственных колебаний свободной балки.
219
Явление антирезонанса в «чистом виде» может иметь место лишь
в идеальных колебательных системах, лишенных демпфировании. При
наличии демпфирования, амплитуда колебаний точки приложения силы
при антирезонансе не обращается в нуль. Эта амплитуда будет тем
меньше, чем меньше демпфирование (см. например [19] — динамиче-
ский поглотитель колебаний).
3. Применение метода динамической жесткости
к расчету колебаний вертолета поперечной схемы
Понятие динамической жесткости оказывается весьма удобным при
расчете таких колебательных систем, которые можно расчленить на две
или более части такие, что для каждой из них в отдельности колебания
легко находятся.
Рассмотрим колебательную систему, состоящую из двух скрещен-
ных упругих балок 1 и 2, изображенную на рис. 2. 12. К такой системе
сводится фюзеляж с упругим крылом, характерный для вертолетов по-
перечной схемы.
COS pt
Пусть требуется расчитать вы-
нужденные колебания такой систе-
мы, вызываемые переменной силой
F, меняющейся по гармоническому
закону и приложенной в точке А
сопряжения балок 1 и 2 (ниже бу-
дет указан метод расчета для слу-
чая, когда возбуждающие силы при-
Рис. 2. 12. Схема колебательной си- ложены в любых точках). С по-
стемы из двух скрещенных балок мощью метода, изложенного в ПП. 1
и 2, можно рассчитать вынужденные
колебания каждой из балок н отдельности от некоторых сил Fx и F2, при-
ложенных к каждой из них в точке Л. При этом можно найти динамиче-
скую жесткость каждой из балок в точке А. Пусть эти динамические
жесткости будут Щ(р) и D2(p).
Нетрудно показать, что динамическая жесткость Щр) всей системы
будет равна сумме динамических жесткостей обеих балок:
D(P) ^Ditp) +D2(p).
(2. 33)
Действительно, сила F — Fo cos pt, действующая на систему в целом,
будет равна сумме сил cos pi? и F2 = F02 cos pt, действующих на
каждую из балок. Но:
Щ (Р) Уо’
~ В2 (Р) Уо,
где уо—амплитуда колебаний точки А, одинаковая для обеих балок.
Следовательно
Щ=Щ+Щ2=[В1 (р)+Щ(/?)] ц0=D (р)Уо-
Таким образом, динамическая жесткость системы легко находится
по формуле (2. 33), если известны динамические жесткости балок 1 и 2.
График динамической жесткости Щр) можно получить простым сло-
жением ординат графиков O,(p) и О2(р). Значения частоты р, при кото-
рых Щр) =0, дадут значения частот собственных колебаний системы из
двух балок. Отсюда вытекает следующий удобный метод определения
частот собственных колебаний системы. Так как эти частоты есть корни
уравнения
D(p)=Dl(p) +D2(p)=Q,
220
Рис. 2. 13. К определению частот собственных ко-
лебаний системы методом динамических же.стко-
стей
то их можно находить из условия:
Л1(р)=-Г>2(р). (2.34)
Последнее уравнение удобно решать графически, наложением гра-
фиков Di(p) и —D2(p), как это показано на рис. 2. 13. Абсциссы pt, р-
и т. д. точек пересечения графиков Dt(p) и —П2(р) дадут значения ча-
стот собственных колебаний системы.
При таком методе расчета одновременно определяются и формы
собственных колебаний системы. Форма собственных колебаний систе-
мы, соответствующая некоторой частоте рь (й=1, 2, ...), будет состо-
ять из форм вынужденных колебаний каждой из балок при этой часто-
те от сил Foi и F02. Причем,
так как при собственных ко-
лебаниях
Fo = FOi +-^02 = 0,
то
F ot — —Foz,
т. е. сила Fol, приложенная
к балке 1, равна по величи-
не и противоположна по
знаку силе F02, приложенной
к балке 2.
Формы собственных ко-
лебаний такой системы мож-
но нормировать, выбирая
соответствующий масштаб.
Например, можно подбирать
масштаб так, чтобы форма
колебаний балки 1 имела
бы амплитуду, равную еди-
нице на ее конце (х = /). При этом масштаб связанной с ней формы ко-
лебаний балки 2 должен быть выбран из условия одинаковой с балкой 1
амплитуды колебаний в точке сопряжения.
Располагая нормированными формами собственных колебаний си-
стемы можно производить расчет ее вынужденных колебаний от гармо-
нических сил, приложенных в любых точках, методом разложения по
собственным формам аналогично тому, как это делалось в случае одной
изолированной балки. При этом колебания обеих балок ищутся в виде
у(х,/) = 1ХЫ*), (2.35)
где уа(х)—форма колебаний данной балки, соответствующая норми-
рованной форме k-ro тона колебаний системы (совместных
колебаний обеих балок).
Коэффициенты ch по-прежнему определяются формулой (2. 22):
где рк — частота совместных колебаний k-ro тона системы.
Коэффициенты Ah и Kh определяются следующими формулами:
Ak=F07lk(x0). (*=1,2,3,...) (2.37)
Этот коэффициент представляет собой работу возбуждающей на-
грузки на форме k-ro тона собственных колебаний системы. Величина
представляет собой амплитуду нормированной формы колебаний
k-ro тона системы в точке приложения силы, независимо от того, к какой
221
из балок приложено возбуждение [г/л.(хо)—берется со знаком «плюс»,
если направление силы и отклонения совпадают, и со знаком «минус»,
если направление силы и отклонения не совпадают].
АГЙ=У mtjkdx J mtjkdx.
по 1-й балке по 2-й балке
(2.38)
Если колебания системы возбуждаются не одной, а несколькими
гармоническими силами, приложенными в различных точках, то вынуж-
Рис. 2.14. К анализу вибраций вертолета поперечной
схемы
денные колебания нахо-
дятся как результат сло-
жения колебаний, выз-
ванных каждой из сил в
отдельности.
Здесь следует остано-
виться на одной особен-
ности возбуждения от не-
сущих винтов вертолетов
многовинтовых схем. В
зависимости от того, как
связаны между собой ки-
нематически несущие-
винты (системой транс-
миссии) может оказаться,
что переменные возбуж-
дающие силы от различ-
ных винтов меняются во-
времени в одной фазе или
в противоположных фа-
зах. Так, например, если
у вертолета поперечной
схемы несущие винты свя-
заны так, что лопасти
обоих винтов одновремен-
но занимают аналогичные
положения (например, крайнее переднее, как это показано на схеме А
рис. 2. 14), то силы на обоих винтах одновременно достигают наиболь-
шего и наименьшего значения — меняются в одной фазе. Если же вин-
ты связаны так, как это показано
на схеме В, то наоборот возбуж-
дающие нагрузки от обоих вин-
тов меняются в противоположных
фазах. Это приводит к тому, что
в случае А возбуждающие на-
грузки от обоих винтов могут
вызывать лишь симметричные
формы совместных колебаний си-
стемы фюзеляж—крыло, а в слу-
чае В — лишь кососимметричные
(рис. 2. 15). Так как при колеба-
ниях кососимметричных форм от-
сутствуют вертикальные вибра-
ции точек фюзеляжа, то для вер-
толетов поперечной схемы жела-
Кососимметричные
Рис. 2. 15. Формы собственных колебаний
крыла с фюзеляжем вертолета поперечной
схемы
Симметричные
срормы
тельно соединять несущие винты так,
(рис. 2.14). Аналогичные соображения
ношении вертолетов продольной схемы.
как это показано на схеме В
могут быть высказаны в от-
222
Конечно, решая вопрос о наиболее выгодном взаимном расположе-
нии несущих винтов, необходимо также считаться с конкретными значе-
ниями частот собственных колебаний различных тонов фюзеляжа, а так-
же рассматривать наряду с колебаниями фюзеляжа в плоскости сим-
метрии поперечные колебания, о которых будет рассказано в § 3.
4. Метод добавочной массы
Для определения динамической жесткости по методу, изложенному
в п. 2, необходимо иметь результаты расчета собственных колебаний
фюзеляжа. В этом случае амплитуда вынужденных колебаний точки
приложения силы, необходимая для определения динамической жестко-
сти, определяется формулой (2. 32) в виде разложения по собственным
формам. Однако в случае, когда имеется программа расчета собствен-
ляжа (или динамической жесткости) в точке закрепления винта от
частоты возбуждения
ных частот на электронной вычислительной машине и расчет собствен-
ных колебаний занимает мало времени, можно рекомендовать для опре-
деления динамической жесткости фюзеляжа в данной точке так назы-
ваемый метод добавочной массы. При таком методе производится
расчет собственных колебаний фюзеляжа с добавочной массой Ат,
укрепленной в той точке, в которой надо вычислить динамическую жест-
кость. Расчет производится при различных значениях Ат, и по его ре-
зультатам строится график Ат(р) зависимости Ат от частоты собствен-
ных колебаний различных тонов.
На рис. 2.16 показан пример такого графика для одновинтового
вертолета. На этом графике по оси ординат отложены значения веса
дополнительного груза AG = gAm.
Нетрудно показать, что такой график может в известном смысле
полностью заменить график Щр), показанный на рис. 2.11. В самом
деле, при собственных колебаниях балки с дополнительной массой Ат
с частотой р эта балка нагружается соответствующей дополнительной
силой инерции, амплитуда которой
/%= Amp2t0, (2.39)
где уо—амплитуда колебаний в точке закрепления добавочной массы,
223
Сила инерции Fo в момент наибольшего отклонения от положения
равновесия направлена в ту же сторону, что и отклонение у0. Отрица-
тельным значениям Ат физически соответствует прикрепленная к балке
пружина с жесткостью |с| = |Атр2|, дающая силу, пропорциональную
отклонению г/0 и направленную противоположно отклонению.
Естественно, что можно получать точно такие же колебания балки
без добавочной массы, но вынужденные, от действия гармонической
силы с такой же амплитудой Ь'п, меняющейся с такой же частотой! р.
Динамическая жесткость балки определяется по формуле
Уй
Сравнивая это выражение с выражением (2.39), находим:
•°(Р) = /’2Д/И(/’)- (2.40)
Пользуясь этой формулой, нетрудно построить график зависимости
D(p), располагая зависимостью Ат(р). Однако можно этого и не де-
лать, а пользоваться непосредственно графиком Ат(р) или AG(p). Так,
например, для отыскания частот собственных колебаний фюзеляжа по-
перечной схемы можно вместо точек пересечения на графиках D1(p)
и —D2(p) (см. рис. 2.13) отыскивать точку пересечения графиков
AGi(p) и —AG2(p).
5. Влияние демпфирующих сил. Колебания при резонансе
Изложенная выше теория и вытекающие из нее методы расчета
основаны на предположении, что балка идеально упруга и демпфирую-
щие силы отсутствуют. Как и для всякой другой колебательной систе-
мы, при рассмотрении колебаний балки вдали от резонансов, демпфи-
рующие силы можно не учитывать и это не приводит к большим по-
грешностям.
Однако при рассмотрении колебаний балки вблизи резонанса или
непосредственно в резонансе необходимо принимать во внимание силы
демпфирования, так как амплитуда колебаний при резонансе опреде-
ляется исключительно наличием демпфирования и в предположении об
отсутствии демпфирования амплитуда при резонансе получается неогра-
ниченной.
Демпфирующие силы при колебаниях упругой балки появляются
главным образом вследствие трения между элементами конструкции
балки при ее деформациях, а также вследствие так называемого внут-
реннего трения в материале балки, которое для балки составной кон-
струкции, как правило, пренебрежимо мало по сравнению с трением
между элементами конструкции [16].
Уравнение колебаний изгиба балки при наличии демпфирования
можно вывести, полагая, что изгибающий момент Л1
д2у i
пропорционален ее кривизне — (в соответствии с
в сечении балки
законом Гука),
а также скорости изменения кривизны во времени, так что можно
написать:
—V (2-41)
dxi 1 dt \ дх2) v
где т] —некоторый коэффициент, характеризующий демпфирующие
свойства балки в данном поперечном сечении, который предпо-
лагается заданной функцией координаты х.
224
Пользуясь далее известным соотношением:
/ А
где <у*(х, I) —интенсивность поперечной нагрузки, приложенной к бал-
ке, и учитывая, что эта нагрузка складывается при колебаниях из внеш-
ней возмущающей нагрузки q(x, t) и нагрузки от сил инерции, так что
q*(X,t) = q(x,f)~т
пользуясь уравнением (2.41), получаем следующее дифференциальное
уравнение в частных производных, описывающее поперечные колебания
балки с демпфированием:
— + m — = Я{х, t). (2.42)
дх2\ дхУ~ 'di fix'2 1, дху~ dfi к '
Это уравнение отличается от уравнения (2. 2) лишь наличием члена
с множителем г] и при т) =0 совпадает с (2. 2).
В случае, если q{x, t)~0, получается уравнение, описывающее соб-
ственные колебания балки с демпфированием:
— (ei =°- (2.43)
дхЛ дхЧ)' 'dtdx2 \ дх'2,- Й2
Точное решение этого уравнения довольно сложно. Однако при от-
носительно малом демпфировании можно пользоваться простым прибли-
женным решением. Приближенное решение этого уравнения, соответст-
вующее собственным колебаниям балки по k-му тону, можно отыски-
вать, полагая
у =?*(*) , (2.44)
где yk (х)— форма собственных колебаний k-ro тона балки при отсут-
ствии демпфирования.
Подставляя это решение в уравнение (2. 43) и сокращая множи-
тель , умножая на yfe(x) и интегрируя уравнение в пределах от 0
до I, а также учитывая формулы (2. 17) и (2. 18), получим следующее
уравнение для определения
+ = (2.45)
где
i
2zzj=^-Уи dx- (2-46)
Корнями этого уравнения будут:
(2.47)
где
PI = V"PI^- (2-48)
Соответственно выражение (2. 44) можно записать в виде:
cos (/>;/+?), (2.49)
т. е. величина представляет собой коэффициент затухания колебаний
й-го тона, а р\ —частоту собственных колебаний й-го тона при наличии
демпфирования.
15 1578
225
Можно показать, что такое приближенное решение уравнения
(2.43) тем меньше отличается от точного, чем меньше по сравнению
с единицей безразмерный коэффициент затухания k-ro тона, определяе-
мый формулой
(2.50)
Рк
Этот коэффициент является важнейшей характеристикой колебаний
данного тона и может быть определен экспериментально, либо по ана-
лизу осциллограммы затухающих колебаний данного тона, либо по ре-
зультатам измерения амплитуды вынужденных колебаний балки под
действием вибратора (об этом будет сказано ниже).
Для фюзеляжа обычного типа (клепанный фюзеляж с дуралюми-
новой обшивкой) коэффициенты затухания fin различных тонов лежат
в пределах от 0,02 до 0,05. Это весьма малые значения коэффициента
затухания, при которых частоту колебаний k-ro тона можно считать рав-
ной частоте, подсчитанной без учета демпфирования, так как р*ь =
— рк ]/1—п2к. При указанных значениях rlk эта поправка получается
незначительной.
При расчете вынужденных колебаний балки с демпфированием,
описываемых уравнением (2.42), ввиду того, что демпфирование мало,
также целесообразно пользоваться приближенным методом, основан-
ным на том, что вдали от резонансов демпфирование вообще не учи-
тывается, а вблизи резонансов находится приближенное решение, по-
лучаемое в предположении, что форма вынужденных колебаний вблизи
резонанса k-ro тона, так же как и в случае отсутствия демпфирования,
близка к форме собственных колебаний данного тона.
При наличии демпфирования уравнение вынужденных колебаний
балки под действием гармонической нагрузки
q (х, t) — q (л) cos pt (2.51)
удобно писать в комплексной форме:
(EI +ц(EI ^-rn^q(х)е'?<. (2. 52)
дх2 \, дх1} ox2 at \ dx"J at2
Так как вещественная часть правой части этого уравнения совпа-
дает с выражением (2.51), то действительное движение балки будет
описываться в силу линейности уравнения вещественной частью комп-
лексного решения уравнения (2.52). Вблизи резонанса с k-м тоном соб-
ственных колебаний решение этого уравнения в соответствии с изло-
женными соображениями целесообразно искать в форме
,y(x,/)=cft:yft(x)^, (2.53)
где ya (х) — по-прежнему форма k-ro тона колебаний при отсутствии
демпфирования.
Подставим это выражение в уравнение (2.52). Затем умножим обе
части уравнения (2.52) на </й(х) и проинтегрируем от 0 до /. Преобра-
зуя полученные интегралы и учитывая соотношения (2. 17) и (2. 18),
а также (2.46), получим следующее уравнение для определения коэф-
фициента ск:
Ск(Рк + 12пкР~Р2) = ^-,
где Ак и Kk по-прежнему определяются формулами (2.20) и (2.21).
Отсюда
1 Ак
<2'54*
226
Модуль комплексной величины Ck определяет амплитуду колебаний:
_____________]____________ Аь_
]/ (/’г—/’2)2 + 4ns/’2
а аргумент г\:
argCj, = arc tg
(2.55)
(2. 56)
— фазу вынужденных колебаний по отношению к возбуждающей на-
грузке (2.51). При резонансе значение Сь [см. выражение (2.54)] стано-
вится чисто мнимым:
9 Лт; (при Р=Л).
2 пкрКк
Это означает, что при резонансе фазовый угол между возбуждаю-
щей нагрузкой и колебаниями балки равен л/2. При этом, как это легко
проверить непосредственной подстановкой в уравнение, колебания бу-
дут происходить по закону
у (х, /) =: скук (л) sin pt, (2.57)
где
Таким образом, амплитуда колебаний при резонансе полностью
определяется значением пъ. безразмерного коэффициента затухания fe-ro
тона. Этим можно воспользоваться для экспериментального определе-
ния пь. Если возбуждать колебания балки с помощью вибратора, т. е,
заданной, сосредоточенной силой F = Fncos pt, приложенной в определен-
ной точке х~х0, и при резонансе (p — pk) измерить амплитуду у0 коле-
баний в точке приложения силы, то можно легко найти величину пь.
При этом Ak будет определяться формулой (2.27), а величина у0 фор-
мулой
Уо=^кук(Хо).
Поэтому, учитывая выражение (2.58), найдем:
- __ 1 Fo [t/ft(x0)] 3
к 2 уор% Кк
или
1 Fo
пк = — ц—>
2 тьРьУО
(2.59)
где величина /Ид, которую можно называть массой k-ro тона, приведен-
ной к точке x = %o, определяется формулой
тк — J ту% dx. (2.60)
о
Здесь
(2.61)
Значение приведенной массы mh с достаточной точностью определя-
ется по расчету, но может быть определено и экспериментально путем
измерения формы вынужденных колебаний балки при резонансе с k-м
.тоном.
15*
227
В тех случаях, когда необходимо заранее оценить амплитуду при
резонансе фюзеляжа, который находится в проектировании и еще не
изготовлен, можно пользоваться формулой (2.58), принимая значения
пь, известные для другого фюзеляжа аналогичной конструкции, так как
значения пь для аналогичных конструкций мало различаются.
§ 3. РАСЧЕТ ВИБРАЦИЙ С УЧЕТОМ ОСОБЕННОСТЕЙ ФЮЗЕЛЯЖА
1. Особенности фюзеляжа. Поперечные и вертикальные колебания
В предыдущем параграфе излагались методы расчета вибраций фю-
зеляжа как упругой балки (или системы из двух скрещенных балок для
вертолета поперечной схемы), у которой размеры поперечных сечений
малы ио сравнению с длиной. Во многих случаях такой метод расчета да-
ет вполне удовлетворительные результаты. Однако в некоторых случаях,
когда фюзеляж вертолета обладает особенностями, сильно отличающи-
ми его от модели упругой балки, необходимо рассматривать более слож-
ные расчетные схемы. Конструктивные схемы фюзеляжей вертолетов
различных типов (одновинтовых, поперечной схемы, продольной схемы)
весьма разнообразны. Поэтому трудно было бы указать какой-либо
общий метод расчета, который во всех случаях позволял бы достаточно
точно рассчитывать вибрации фюзеляжа от заданных сил.
Рис. 2. 17. к приведению задачи о колебаниях упру-
гого фюзеляжа к задаче о колебаниях упругой балки
Каждая новая конструктивная схема фюзеляжа может потребо-
вать существенных изменений в методе расчета колебаний. И эта зада-
ча подчас может оказаться достаточно сложной. Однако во всех случаях
метод расчета должен быть основан на общих принципах теории коле-
баний упругих систем. Инженер-расчетчик, которому необходимо ана-
лизировать вибрации будущего вертолета новой конструкции, должен
владеть этими общими методами настолько, чтобы суметь видоизменить
расчетную схему применительно к каждой новой задаче. Поэтому из-
ложение материала этой главы построено таким образом, чтобы пока-
зать сущность наиболее важных приемов, применяемых при расчете ко-
лебаний. Так, метод разложения по собственным формам, метод дина-
мической жесткости, понятие о резонансе и антирезонансе могут быть
приложены не только к упругой балке или системе из двух скрещенных
балок, но и к любой другой более сложной колебательной системе. Эти
методы были изложены применительно к балке, так как, с одной сто-
роны, на этом примере их наиболее легко показать, а с другой стороны,
сам по себе метод расчета колебаний балки может быть во многих слу-
чаях применен к расчету вибраций фюзеляжа без всяких изменений.
Для иллюстрации некоторых особенностей реального фюзеляжа об-
ратимся к рис. 2. 17, на котором схематично изображен фюзеляж одно-
винтового вертолета. Особенность такого фюзеляжа состоит в том, что
его ось жесткости представляет собой ломаную линию, центры тяжести
отсеков фюзеляжа не лежат на оси жесткости, а каждый отсек фюзе-4
228
ляжа есть тело, у которого все измерения одного порядка, и при рас-
чете колебаний необходимо принимать во внимание не только массу
отсека, но и моменты инерции его относительно всех трех осей. Расчеты
показывают, что при определении низшего тона колебаний изгиба тако-
го фюзеляжа, как в плоскости хОу (вертикальные колебания), так и в
плоскости xOz (поперечные колебания) можно получить вполне удов-
летворительные результаты, рассчитывая фюзеляж как упругую тонкую
балку с прямолинейной осью.
Если при расчете вибраций можно ограничиться рассмотрением ко-
лебаний фюзеляжа как твердого тела и учесть лишь низший упругий
тон (первые три формы на рис. 2. 7), то расчет вибраций фюзеляжа как
тонкой балки с прямолинейной осью приведет к удовлетворительным
результатам. Однако, ес-
ли второй упругий тон
колебаний имеет частоту,
близкую к частоте основ-
ной гармоники винта гы
(а это часто случается),
то такой расчет может
привести к некоторым по-
грешностям. Причем при
расчете вибраций в каби-
не летчика (в носовой ча-
сти фюзеляжа) ошибка
Рис. 2. 18. Расчетная модель для расчета колеба-
ний упругого фюзеляжа
может получиться незна-
чительной, но амплитуды вибраций в районе хвостовой балки могут
очень сильно отличаться от действительных. Для повышения точности
расчета потребуется определять вибрации с учетом большего числа
упругих тонов (второго и третьего тона). Но уже определение второго
упругого тона с достаточной точностью потребует усложнения расчетной
модели.
Значительное уточнение результатов расчета может быть получено
при использовании расчетной модели, изображенной на рис. 2. 18. Фю-
зеляж здесь заменяется упругой балкой с прямолинейной осью, к ко-
торой прикреплены отдельные грузы 1, 2, 3 и т. д. Центр тяжести каж-
дого груза отстоит от оси балки на некотором расстоянии h*. Для
каждого груза задается его масса mk и моменты инерции 1Х и 1г отно-
сительно осей, параллельных соответственно осям Ох и Oz и проходя-
щих через центр тяжести груза. Для каждого участка упругой балки,
расположенного между грузами k и &+1, задаются жесткости на изгиб
EIzkw Е1&к в обоих плоскостях xOz и хОу и жесткость на кручение
Для такой расчетной модели поперечные колебания (в плоскости
xOz) представляют собой совместные изгибно-крутильные колебания.
Частоты и формы собственных изгибно-крутильных колебаний такой
системы могут быть рассчитаны с помощью метода, изложенного в § 6
гл. 1 (см. рис. 1.19), применительно к лопасти несущего винта. При
этом надо полагать, что центробежная сила ^=0, жесткость проводки
управления 6^=0, Е1у"(0)—0 и (Ely")' |“°0. Это соответствует тому,
что левый конец балки не закреплен. Вместо величины хц.т в расчете
лопасти следует подставлять значения выносов йь.
При расчете вынужденных поперечных колебаний такой системы
можно пользоваться методом разложения по собственным формам
(изгибно-крутильным). При этом можно пользоваться всеми формула-
ми § 2 настоящей главы, в которых под величиной Аь понимать работу
возбуждающей нагрузки на нормированной форме данного тона, а под
величиной Кь — кинетическую энергию данного тона, отнесенную
I !
f*
229
к квадрату его частоты р\ - На рис. 2. 19 показаны характерные формы
собственных поперечных изгибно-крутильных колебаний одновинтового
вертолета.
Совершенно такой же метод расчета и модель, указанная на
рис. 2. 18, могут быть использованы для расчета вертикальных изгиб-
но-крутильных колебаний крыла вертолета поперечной схемы с мото-
z <f И
гондолами на концах (рис. 2.20). Если центры тяжести мотогондол
имеют большие выносы п, то при расчете колебаний такого крыла нель-
зя рассматривать изолированные колебания изгиба в вертикальной пло-
скости, а необходимо рассматривать совместные изгибно-крутильные
колебания. Для расчета совместных колебаний системы фюзеляж—
крыло в этом случае надо применять метод динамической жесткости.
Наибольшей расчетной моделью, иммитирующей реальный фюзе-
ляж вертолета, следует, по-видимому, считать модель, изображенную на
рис. 2.21. Здесь ось жесткости балки задается как некоторая ломаная
Рис. 2.20. Схема мотогопдолы с боль-
шим выносом
Рис. 2.21. Расчетная модель для расчета
колебаний упругого фюзеляжа с ломаной
осью жесткости
линия. Угол наклона k-ro участка ломаной задается углом aft. Такая
расчетная модель хорошо отражает свойства всякого фюзеляжа, кото-
рый имеет плоскость симметрии хОу. Для фюзеляжа, имеющего такую
плоскость симметрии, можно отдельно рассчитывать вертикальные
колебания изгиба (или колебания в плоскости симметрии) и поперечные
изгибно-крутильные колебания.
230
При расчете вертикальных колебаний для каждого груза нужно
учитывать три степени свободы:
— смещение центра тяжести груза вдоль оси Ох:
— смещение центра тяжести груза вдоль оси Оу;
— поворот груза относительно оси Oz.
При расчете поперечных изгибно-крутильных колебаний для каж-
дого груза нужно также учитывать три степени свободы:
— смещение центра тяжести груза вдоль оси Oz;
— поворот вокруг оси Ох;
— поворот вокруг оси Оу.
Расчет вертикальных колебаний такой системы рассматривается
в следующем пункте данного параграфа. При этом иллюстрируется при-
менение так называемого метода остатка для расчета колебаний, кото-
рый часто оказывается весьма удобным.
Расчет поперечных колебаний такой системы здесь вообще не рас-
сматривается, так как для расчета поперечных изгибно-крутильных ко-
лебаний вполне хорошие результаты дает использование расчетной мо-
дели, изображенной на рис. 2. 18. Отметим лишь, что для системы,
изображенной на рис. 2,21, расчет поперечных изгибно-крутильных ко-
лебаний можно было бы также проводить методом остатка.
2. Расчет колебаний фюзеляжа в плоскости симметрии методом остатка
Пусть плоская упругая система, изображенная па рис. 2. 21, совер-
шает установившиеся вынужденные колебания в своей плоскости хоу
под действием гармонической возбуждающей нагрузки, состоящей из
сил и моментов
Ркх=Р°х cos pt;
Ры = cos pt;
Мк—Мь cos pt,
(3-1)
приложенных к каждому грузу (рис. 2.22).
При установившихся колебаниях все точки системы будут совер-
шать гармонические колебания с частотой возбуждения р так, что, если
обозначить через х, у и й соответственно смещения центра тяжести с
груза вдоль осей Ох и Оу и угол поворота груза относительно его цен-
тра тяжести, то для й-го груза можно написать:
x=xk cos pt;
У = Ук cos pt;
(6=1, 2, 3, ...
(3-2)
9 = Cos pt.
Установим зависимости, связывающие силы, приложенные к гру-
зам, с деформациями участков балки. Будем и силы и деформации рас-
сматривать лишь для положения системы, соответствующего наиболь-
шему отклонению от положения равновесия (т. е. будем рассматривать
лишь амплитуды сил и деформаций). Составим уравнения равновесия
для k-ro груза (рис. 2.23). К грузу приложены:
-внешние силы Р0^, Л1°й (приложенные в точке 4);
— силы инерции груза mkp2xl!; mkp2yk; (приложенные в точ-
ке С);
— силы, действующие на груз со стороны левого, примыкающего
ж нему, участка балки: Ук_1г ТИ^-р
231
— силы, действующие на груз со стороны правого, примыкающего
к нему, участка балки: Хк, Yk, Мк.
Уравнения равновесия груза запишем в виде:
=Хк_.+ткРЧк + Plx- (3.3)
(3.4)
Мк (3. 5)
Положительные направления сил и смещений указаны на рис. 2.22;
2.23; 2.24. Величина А представляет собой расстояние от точки при-
Рис. 2.22. Схема сил, действующих на отсек упругой модели
фюзеляжа
ложения внешних возбуждающих сил Рйкх до точки прикрепления груза
к упругой балке.
Из условий равновесия участка балки (рис. 2. 24) имеем:
Х = ^ + УЛС°8 ak — ^Ssinaft- (3.6)
Для рассмотрения деформаций обратимся к рис. 2. 24, на котором
изображен А-й участок упругой балки А^Вк в положении равновесия
и этот же участок в смещенном положении Ак В'к . Пусть величины хц, уь>
и уи+1 есть смещения точек А& и Bk — концов участка, a fy, и 'th+i —
углы поворота касательной к упругой оси на левом и правом концах,.
Пусть далее есть прогиб балки на А-м участке, т. е. смещение правого
конца балки — точки Вц в направлении, перпендикулярном AkBh отно-
сительно касательной к упругой оси на левом конце — в точке Ак. Тогда
можно написать:
^+i=^-(5A-T-WsinaA; j (3. 7>
Уй+1 = Уй+ (sft+VJcos ак, I
Где 1к и ай —соответственно длина и угол наклона Л-го участка балки
(рис. 2. 24).
232
СУ
Рис. 2.23. Схема сил, при-
ложенных к й-му элементу
упругой модели фюзеляжа
Применяя обычные приемы сопротивления материалов, найдем сле-
дующие уравнения, связывающие силы и деформации:
8.=4-[-тл,*+тЧ; <з-8)
L з 6 J
+ (3,9)
(ЗЛО)
Смещения точек балки Хь и связаны
со смещениями центров тяжести грузов оче-
видными формулами:
1 (ЗЛ1)
ХЪ~ХЬ ^k^k-
Рекурентные формулы (3.3), (3.4),
(3.5), (3.7) вместе с выражениями (3.8),
(3.9), (3. 10) и (3. 11) позволяют, зная си-
лы и смещения й-го груза, определять силы
и смещения (&+1)-го груза. Пользуясь эти-
ми формулами, можно решать задачу «ме-
тодом цепочки», а именно: задав амплитуды
х0у0 и <10 на левом конце балки, можно, по-
следовательно переходя от участка к участ-
ку, определить амплитуды и силы на край-
нем правом конце балки, выразив их через
величины хо, уо, бо- Если балка имеет п грузов, то можно таким образом
определить величины Хп, Yn и Мп на правом конце или «остаток». Но
так как правый конец балки свободен, то «остаток» должен быть равен
нулю, т. е. на правом конце балки должны выполняться условия:
Хп — Yn~Xlr/ —0.
Рис. 2.24. Схема сил,
приложенных к отсеку
упругой модели фюзе-
ляжа
Эти условия представляют собой систему трех уравнений для опре-
деления неизвестных хо, уо, бо, через которые уже выражены амплитуды
колебаний и силы на всех грузах балки. 0 .
Такой метод расчета вынужденных колебаний системы (рис. 2. Z1J
совершенно аналогичен известному методу «остатка» метода Толле,
2за
применяемому для расчета крутильных колебаний многодисковых си-
стем [20]. Аналогичный метод применяется и для расчета колебаний
изгиба упругих балок. В американских и английских работах такой
метод называют методом Майклстеда [33], [34]. Он позволяет, найти кри-
вую динамической жесткости (рис. 2. 11) системы в любой точке и в лю-
бом направлении путем вычисления колебаний при различных значе-
ниях р, а также частоты и формы собственных колебаний системы из
рассмотрения вынужденных колебаний системы вблизи резонансов, ког-
да амплитуды вынужденных колебаний неограниченно возрастают.
Этот метод особенно удобен при использовании электронных вычис-
лительных машин, без которых в настоящее время невозможно проведе-
ние в необходимом количестве всех динамических расчетов.
Для практического применения этого метода удобно величины сил
и смещений на k-м участке выражать через значения л'о, Уо, 'в'о в виде:
Wo;
^A^B^C^D^-
^=Л? + Й^о + С^'о+Оро; (ЗЛ2)
Mk=A^BMx0 + CMy0 + D"%,
где А*; В* и т. д. некоторые коэффициенты.
При расчете методом «цепочки» следует по значениям этих коэффи-
циентов для k-ro участка определять их значения для (А+1)-го участка.
Используя рекурентные формулы для сил и перемещений, нетрудно со-
ставить рекурентные формулы для соответствующих коэффициентов.
При этом получаются следующие формулы.
Для коэффициентов А®, В^к, С* и D®'.
9
А» = А»
* A1 1 1 2E/S-,
'Li
sin ah_i
-----А* (3.13
Причем для величин В|; С|; D\ аналогичные
заменой величин А соответственно на В, С и D.
.последующим формулам (3.14) и (3.15).
Для коэффициентов А*, В*, С* и D*-.
формулы получаются
Это же относится и к
4 sin щ
^А+1
дм ЛУ
2£7ft * 6£7А *
+ 4^P^-4sinaftA». (3.14)
Для коэффициентов А», В^, и D;p
ZjCosa,, „ , Z^cos2 ak
АУ =AyA-—----------AMA— ---------A7 —
4+i »"Г 2£/ft ft । &EIk ь
/ь cos a>, sin a*
(3.15)
:234
Для коэффициентов А*, В*, Ск и £)*:
А* = А^ + т^А* - ткрЧкА*к ^Р^-
В^ = ВХ_^ткр^Ах~ткр^кВ\-
Сх= Cx^+mkp4>k - ткрЧкС^
D* = Dx_y Д mkfPD* - m^D*.
(3.16)
(3. 17)
Для коэффициентов А%, В%, Су и
АУ=АУ_^т^АУ^Р^у (3.18)
В^В^т^В»- Cy=Cy_^mkpKPk- ОУ^У_^ткрЮУ. (3. 19)
И, наконец, для коэффициентов А1*, В^, Слк1 и D^:
Ам_у Д cos aft_! - Л^_/яsin -
- P2 Ы Д /ft) Л» --I- (3.20)
+ cos "w -^-14-1 sin
im#W-P2W2s + /S)^- (3-21)
Формулы для C% и DM получаются из последней заменой величин
В соответственно величинами С и D.
Приведенные формулы позволяют определять значения коэффици-
ентов на следующем участке по известным их значениям на предыду-
щем участке. Так, двигаясь от участка к участку слева направо, мы
определим значения коэффициентов на правом конце балки. На правом
свободном конце (k — n) должны выполняться условия:
Хл=^+^ло+С^о + ^»о = О;
Уп = А у + - СУ у. ф-= 0;
М„ = А* + ВМх0 + С*у0+D^a = 0.
(3. 22)
Решая эту систему, найдем интересующие нас значения х0, у0, fl'o'
(3. 23)
где д — определитель системы (3. 22);
Дхи, Да —определители, получаемые из определителя д путем заме
ны соответствующего столбца свободными членами урав-
нений.
Знание величин х<> t/o> 'д'о позволяет по формулам (3.12) найти пере-
мещение и силы, действующие в каждом сечении балки.
235
На рис. 2. 25 показана форма вынужденных колебаний одновинто-
вого вертолета, определенная указанным методом. Форма колебаний
в этом случае должна быть представлена тремя графиками: Xh(x), уь(х)
и ^л(х).
Рис, 2.25. Форма вынужденных колебаний
упругого фюзеляжа одновинтового вертолета,
полученные методом остатка
В табл. 2. 1 приведены исходные данные для проведенного расчета.
Вынужденные колебания были рассчитаны от следующих сил, при-
ложенных к втулке несущего винта (груз № 3)
Р° =0,05G; Р° = 0,036; Л4»=0,
ОЛ 1 йу о
где О —вес вертолета.
Таблица 2.1
Номера участков 0 1 2 3 4 5 6 7 8 9 10
(л) 0 1,7 3.45 5,1 7,2 9,1 12,4 13,7 15,1 16,7 18,2
°й (кгс) 30 1471 1692 3584 3599 259 24 24 22 92 153
th (кг/м сек2} ОЛО 37.65 63,0 260,5 286,7 4,62 0,19 0,10 0,05 0,077 0,185
hfj (м) —0.15 —0,024 —0,025 0,778 0,316 —0,15 0 0 0 0 0
0.00155 0,0066 0,0068 0,207 0,0015 0,00042 0,00028 0,00(117 0,00013 1.0 -
0 0 0 0 0 21 0 0 0 43 -
Одно из достоинств такого метода расчета состоит в том, что для
расчета вынужденных колебаний не требуется проводить предваритель-
ный расчет частот и форм собственных колебаний системы. Кроме того,
проводя такой расчет для различных значений частот р, можно постро-
ить график динамической жесткости системы D(p) в любой точке, a
236
также найти все частоты и формы собственных колебаний. На рис. 2. 26
приведены результаты расчета графика динамической жесткости для
той же системы, заданной табл. 2. 1 для силы . Значения рь, при ко-
торых Z)(p)=O, дают частоты собственных колебаний системы, а форма
Рис. 2.26. Кривая динамической жесткости фюзеля-
жа, полученная методом остатка
вынужденных колебаний при значении р, близком к какой-либо из ча-
стот pk (k=l, 2, 3, ...) собственных колебаний, дает с любой степенью
точности форму собственных колебаний этого тона. Формы трех первых
тонов для рассматриваемой системы, полученные таким способом, по-
казаны на рис. 2. 27.
Рис. 2.27. Формы собственных колебаний трех низших тонов фюзеляжа одновинтового
вертолета, полученные методом остатка
Отметим в заключение, что приведенный здесь метод «остатка»
требует выполнения расчета с очень большой точностью (не менее че-
тырех—пяти значащих цифр). Это делает указанный метод практиче-
ски непригодным для «ручного» расчета. Однако, как уже указывалось,
расчеты колебаний в необходимом объеме, вообще, могут быть прове-
дены лишь с применением быстродействующих вычислительных машин,
для которых указанная точность является обычной.
3. Учет влияния деформаций сдвига
Все рассмотренные методы расчета колебаний фюзеляжа были
основаны на использовании обычных соотношений сопротивления ма-
териалов для изгиба тонкой балки. Эти соотношения учитывают лишь
деформации растяжения и сжатия волокон материала балки и не учи-
тывают деформации сдвига. Между тем учет этих деформаций вносит
некоторые поправки в результаты расчета, причем эти поправки получа-
ются весьма незначительными для первого тона колебаний (снижение
частоты на 5—6%), для второго тона поправки получаются несколько
больше (снижение частоты на 10—15%), для третьего тона еще больше
(20—30%) и т. д. Поэтому, если при расчете вибраций нужно учитывать
высокие тона колебаний, колебания следует рассчитывать с учетом де-
формаций сдвига, обусловленных тангенциальными напряжениями в
обшивке фюзеляжа. Выполнить это можно следующим образом. Если
расчет производится для модели, изображенной на рис. 2.21, то можно
пользоваться всеми формулами метода «остатка», за исключением фор-
мулы (3.8), которую в этом случае следует писать в виде:
,2
(т ’ <3- 24>
\ о о /
где 8^—дополнительный прогиб А-го участка от перерезывающей силы Q„.
СА=Мйзшай —Кйсоз ай. (3.25)
Дополнительный прогиб % может быть определен по формуле (см.,
например [21])
(3.26)
к
где Fk — площадь поперечного сечения фюзеляжа на А-ом участке, а
х некоторый безразмерный коэффициент, определяемый фор-
мулой:
71 J 28(2г)
F
где Д — момент инерции поперечного сечения относительно нейтраль-
ной линии;
Зй(х) —статический момент относительно нейтральной линии части по-
перечного сечения, расположенной выше прямой, параллельной
нейтральной линии и удаленной от нее на расстояние д;
б (г) —толщина общивки фюзеляжа на расстоянии z от нейтральной
линии.
Интеграл в формуле (3. 27) берется по всему поперечному сечению
F фюзеляжа.
238
Соответственно поправке в формуле (3.8) нужно внести поправки
в рекурентные формулы для коэффициентов А*, А%, и т. д.
§ 4. О СОВМЕСТНЫХ КОЛЕБАНИЯХ СИСТЕМЫ
ФЮЗЕЛЯЖ—НЕСУЩИЙ ВИНТ
1. О колебаниях системы фюзеляж—несущий винт
Методы расчета колебаний упругих лопастей, изложенные в гл. 1,
предполагают, что лопасть шарнирно прикреплена ко втулке, которая
закреплена на неподвижной опоре. На самом деле втулка закреплена
па упругом фюзеляже и при колебаниях лопастей возникают силы, вы-
зывающие его движение, так что в действительности при колебаниях
лопасти прогиб в шарнире втулки равен не нулю, а соответствующему
прогибу фюзеляжа.
Результаты летных испытаний во многих случаях показывали, что
расчеты частот собственных колебаний лопастей, выполненные без уче-
та упругости фюзеляжа, могут привести к существенным ошибкам.
В связи с этим М. Л. Милем была сформулирована и поставлена зада-
ча о расчете совместных колебаний системы фюзеляж — несущий винт,
как единой колебательной системы. Ниже приводятся основные резуль-
таты исследований, которые были проведены в этом направлении.
Частоты и формы собственных совместных колебаний системы фю-
зеляж — несущий винт могут быть найдены с помощью метода динами-
ческой жесткости, сущность которого изложена в пп. 2, 3 и 4 § 2.
Однако проведение таких расчетов связано с большим количеством
вычислительной работы. Особенно это относится к определению частот
поперечных собственных колебаний системы фюзеляж—несущий винт,
когда необходимо определять динамическую жесткость винта в плоско-
сти вращения. Кроме того, проведенные расчеты показывают, что связь
колебаний фюзеляжа и лопастей является, как правило, слабой и ча-
стоты собственных колебаний системы фюзеляж—несущий винт можно
всегда разбить на две такие группы, что частоты первой группы весьма
близки к частотам собственных колебаний изолированного фюзеляжа,
при расчете которых масса лопастей считается сосредоточенной в цент-
ре винта, а частоты второй группы достаточно близки к частотам собст-
венных колебаний лопастей, рассчитанным в предположении, что лопас-
ти укреплены на абсолютно жестком и бесконечно тяжелом фюзеляже.
В тех случаях, когда крепление втулки к фюзеляжу недостаточно-
жесткое (упругий вал винта, упругая подредукторная рама, картер ре-
дуктора), может оказаться, что некоторые из частот колебаний второй
группы заметно меняются по сравнению с частотами лопастей, рассчи-
танными обычным методом.
Поэтому, как правило, частоты собственных колебаний первой груп-
пы можно определять с помощью методов, изложенных в этой главе,
как частоты фюзеляжа, не принимая во внимание упругость лопастей.
Исключение могут составить особые случаи, когда, например, несущие-
винты крепятся к легким и упругим крыльям на вертолете поперечной
схемы. В этих случаях надо рассчитывать частоты совместных колеба-
ний системы фюзеляж — несущий винт упомянутым методом динамиче-
ской жесткости.
Что же касается частот собственных колебаний лопастей, то нужно,,
по-видимому, всегда оценивать возможное изменение некоторых из этих
частот, обусловленное местной упругостью крепления несущего винта
к фюзеляжу.
239
Таким образом, для учета связи колебаний фюзеляжа и лопастей
практически достаточно оценивать лишь изменение частот собственных
колебаний лопастей, обусловленное местной упругостью крепления
винта.
В следующем пункте этого параграфа излагается метод такого рас-
чета для определения частот собственных колебаний лопастей в плоско-
сти вращения с учетом упругости вала винта на изгиб. Этот случай яв-
ляется практически наиболее важным.
К упругости вала винта всегда можно присоединить упругость дру-
гих элементов крепления винта (редукторной рамы, картера редуктора
и т. д.). Здесь же мы укажем некоторые важные принципиальные сооб-
ражения, из которых становится ясно, что лишь некоторые из частот
собственных колебаний лопастей могут измениться в результате влия-
ния упругости крепления винта.
В § 1 этой главы было показано, что не все гармонические состав-
ляющие сил от колеблющихся лопастей «проходят» на фюзеляж, так
как многие из этих составляющих уравновешиваются на корпусе втулки
винта.
Так, например, при колебаниях лопастей пяти лопастного винта
в плоскости взмаха первые четыре гармонические составляющие сил,
приложенных к втулке, от лопастей (со, 2со, Зсо, 4со) уравновешиваются
на втулке и лишь пятая гармоническая составляющая передается на
фюзеляж.
Отсюда ясно, что при расчете вынужденных колебаний лопастей
от сил, соответствующих гармоникам со, 2со, Зсо, 4со, нужно рассматри-
вать формы и частоты собственных колебаний лопастей (при методе
разложения по собственным формам), рассчитанные для обычных гра-
ничных условий, когда лопасть предполагается шарнирно опертой на не-
подвижной втулке.
Что же касается вынужденных колебаний по пятой гармонике, то
здесь необходимо считаться с наличием совместных колебаний лопасти
и фюзеляжа.
Физическая сущность этого явления заключается в том, что формы
собственных колебаний несущего винта с упругими лопастями можно
разделить на две группы:
1) формы колебаний винта, при которых силы от отдельных лопа-
стей уравновешиваются на корпусе втулки;
2) формы колебаний винта, при которых силы от отдельных лопа-
стей суммируются на корпусе втулки и передаются на фюзеляж.
На рис. 2. 28 для примера показаны две такие формы колебаний
для винта с четырьмя лопастями, так как для такого винта картина по-
лучается наиболее наглядной. Обе формы колебаний А и В соответст-
вуют частоте р\ колебаний одноузлового тона изолированной лопасти
в плоскости взмаха и отличаются одна от другой лишь распределением
фазы колебаний по отдельным лопастям. Форме колебаний А соответ-
ствует ситуация, когда пары противоположных лопастей колеблются
в противоположных фазах. При этом силы Pt, Р?, Pg и Pt, действующие
на втулку винта, взаимно уравновешены в каждый момент времени
и не передаются на фюзеляж. Форме колебаний В соответствует ситуа-
ция, когда все четыре лопасти колеблются в одной фазе. При этом
силы Pi, Р?, Р3 и Pt суммируются на втулке и дают некоторую силу,
действующую на фюзеляж и меняющуюся во времени с частотой pi.
Если втулка винта укреплена на абсолютно жесткой опоре, то ча-
стоты обеих форм колебаний А и В винта одинаковы и равны частоте pi
собственных колебаний первого тона одной изолированной лопасти
с шарнирно закрепленным комлевым концом. Если же втулку укре-
пить на некотором упругом основании с вертикальной жесткостью с, то
240
частота формы колебаний А не изменится и останется равной plt а ча-
стота формы В снизится и тем сильнее, чем меньше жесткость с.
Можно показать, что формы двух указанных типов существуют для
винта с любым числом лопастей z. Эти формы колебаний можно харак-
теризовать некоторой формулой. Так, например, все формы колебаний
Рис. 2.28, Формы колебаний впита с упругими ло-
пастями
z-лопастного винта, соответствующие k-му тону колебаний изолирован-
ной лопасти, характеризуются следующим законом колебаний лопастей:
Уп (х, t) = yk (х) cos s фп cos pkt, (4.1)
где yn(x, t) —отклонение точки с координатой х, принадлежащей п-й
лопасти;
cossipn— характеризует закон распределения фаз колебаний по от-
дельным лопастям, т. е. характеризует форму колебаний
винта в целом;
s— любое целое число, которое можно называть порядком
данной формы колебаний винта (s— 1, 2, 3, ..., z).
Величины определяются формулой:
Можно легко показать, пользуясь формулами (1.13) § 1, что фор-
мы колебаний порядка s=l, 2, 3, ..., z—1 соответствуют ситуации, при
которой силы от отдельных лопастей уравновешиваются на втулке, и
лишь форма порядка s=z, соответствует ситуации, когда силы от от-
дельных лопастей суммируются и передаются на фюзеляж.
Формы А и В, приведенные на рис. 2. 28, есть формы второго и чет-
вертого порядков для четырехлопастного винта. Из сказанного ясно,
что частоты собственных колебаний несущего винта, соответствующие
формам колебаний всех порядков, за исключением s=z, не зависят от
упругости крепления втулки и лишь частоты, соответствующие форме
колебаний винта порядка s — z, зависят от упругости крепления втулки.
Можно далее показать, что все гармоники сил, возбуждающих ко-
лебания лопастей в плоскости взмаха, за исключением «проходных»
гармоник zm, 2zm, 3zm и т. д. возбуждают лишь те формы колебаний
винта, при которых силы от лопастей уравновешиваются на втулке,
16 1578
241
и только гармонические составляющие возбуждающих сил, соответст-
вующие «проходным» гармоникам, возбуждают формы колебаний вин-
та, при которых силы от лопастей суммируются и передаются на
втулку.
Отсюда можно сделать полезный практический вывод. Если по-
строена обычная резонансная диаграмма лопасти (см. рис. 1.6 гл. 1)
в плоскости взмаха, рассчитанная без учета упругости крепления винта
к фюзеляжу, то резонансы со всеми гармониками, за исключением ре-
зонансов с гармониками za, 2za и т. д. соответствуют действительности.
Резонансы же с гармониками zco, 2za и т. д. надо дополнительно обсле-
довать, принимая во внимание упругость крепления втулки винта и уточ-
няя значения соответствующих собственных частот.
Следует, однако, отметить, что при рассмотрении колебаний лопа-
стей в плоскости взмаха можно обычно и для этих гармоник не учиты-
вать упругость крепления втулки, так как жесткость крепления втулки
в вертикальном направлении, как правило, велика и мало влияет на
частоты собственных колебаний лопастей (исключение составляет слу-
чай крепления винтов вертолета поперечной схемы на легких и гибких
крыльях).
При рассмотрении же резонансной диаграммы лопасти в плоскости
вращения, обязательно надо принимать во внимание влияние упругости
крепления втулки винта к фюзеляжу.
В отношении колебаний лопастей в плоскости вращения также
справедливы все изложенные выше соображения, с той лишь разницей,
что в этом случае «проходными» являются гармоники (г—1) со, (z+l)w,
(2z—1) со, (2z+ 1)<о и т. д. Кроме того, при резонансе с гармониками za,
2z<o и т. д. в плоскости вращения следует учитывать совместные коле-
бания винта с крутильными колебаниями в системе трансмиссии (соот-
ветствующие расчеты могут быть выполнены также на основе метода
динамической жесткости).
2. Расчет частот собственных колебании лопастей винта
в плоскости вращения с учетом упругости вала винта
и его крепления к фюзеляжу
Рассмотрим задачу о собственных колебаниях лопастей винта,
укрепленного на валу, упругом на изгиб (рис. 2.29). Пусть жесткость
вала по отношению к силе Р, приложенной к валу в центре втулки и ле-
жащей в плоскости вращения винта, равна с0- Следовательно, сила Р
и смещение б конца вала, которое она вызывает, связаны соотноше-
нием:
Р = соб. (4.2)
При этом безразлично, происходит ли смещение б от изгиба самого вала
или вследствие упругости его крепления к фюзеляжу.
Рассмотрим лишь случай, когда указанная жесткость одинакова
во всех направлениях в плоскости xOz, т. е., когда упругое основание,
на котором укреплен винт, является изотропным. В действительности
это не так, но обычно жесткости крепления в направлениях осей Ох
и Oz мало различаются и можно считать основание изотропным, пони-
мая под величиной Со среднее арифметическое жесткостей сх и cz:
(4-3)
Расчет собственных колебаний винта на упругом основании можно
проводить на основе метода динамической жесткости.
Прежде всего введем понятие о динамической жесткости лопасти
в плоскости вращения. Пусть упругая на изгиб лопасть, находящаяся
242
. _Ух+<:г
со—'
в центральном поле центробежных сил, закреплена в комлевой части
шарнирно таким образом, что шарнир имеет возможность свободно пе-
ремещаться в направлении, перпендикулярном оси недеформированной
лопасти (см. рис. 2.30).
Рис. 2.29. Схема винта на
упругом валу
Рис. 2. 30. Схема расчета вынужденных коле-
баний лопасти для определения динамической
жесткости винта
Пусть далее лопасть совершает установившиеся вынужденные ко-
лебания под действием поперечной возбуждающей гармонической силы
F~F0 cos pt,
приложенной в шарнире А. При этом точка А приложения силы будет
также совершать колебания по закону
и = «0 cos pt.
Будем называть динамической жесткостью лопасти величину
= (4.4)
«о
Определить динамическую жесткость лопасти можно либо с по-
мощью метода, изложенного в п. 2 § 2, либо методом добавочной массы
(§ 2, п. 4). При этом нужно учитывать, что лопасть находится в поле
центробежных сил, и решать не уравнение типа (2. 2), как это делалось
при расчете фюзеляжа, а уравнение колебаний лопасти в плоскости вра-
щения (см. гл. 1, § 1, п. 11), которое имеет вид:
(£/и")" — (Хи')' mu — ui2tt=q (г, /). (4.5)
Здесь N—центробежная сила в сечении лопасти на радиусе г.
При применении метода добавочной массы следует рассчитывать
частоты и формы собственных колебаний лопасти в плоскости вращения
при закреплении по схеме, изображенной на рис. 2. 30 с различным зна-
чением добавочной массы Лшл в точке А с помощью метода, изложен-
ного в гл. 1, § 2, п. 5.
По результатам такого расчета можно построить график Дтл=/(р).
Пример такого графика приведен на рис. 2. 32. Точки бесконечных раз-
рывов функции f(p) дают значения частот собственных колебаний лопа-
сти с неподвижным шарниром в точке А, т. е. частот собственных коле-
баний лопасти для случая, когда жесткость вала винта бесконечно ве-
лика. Точки, в которых Дтл = 0 дают частоты собственных колебаний
лопасти, свободно закрепленной по схеме, изображенной на рис. 2. 30.
]6* 243
Соответствующее данному значению р значение динамической жест-
кости лопасти может быть определено по формуле
£,л(/') = (/’2 + <!)2) ЬтЛР)- (4-5)
Добавочный член а>2А/пл(р) появляется в этой формуле от состав-
ляющей центробежной силы массы Ашл, направленной по нормали к ло-
пасти.
Покажем далее, что динамическая жесткость винта в целом может
быть найдена, если известна динамическая жесткость лопасти. Обра-
тимся к рис. 2.31, на котором изображен вид в плане втулки винта
с вертикальными шарнирами и k-n упругая лопасть. Пусть хОу — есть
Рис. 2.31. к расчету динамической жесткости винта с упру-
гими лопастями
система координат, вращающаяся вместе с винтом с угловой скоростью
(о. Пусть далее центр втулки винта совершает заданные гармонические
колебания в плоскости вращения по закону
x=x0cospi; 1 (4 6)
z/=^osin^. /
Такие колебания втулки вызывают колебания упругих лопастей
в плоскости вращения и задача состоит в том, чтобы найти силы, кото-
рыми колеблющиеся лопасти нагружают втулку при таком ее дви-
жении.
Выберем дополнительную, вращающуюся вместе с винтом, прямо-
угольную систему координат пОг, у которой ось Or параллельна пря-
мой, проходящей через центр втулки и вертикальный шарнир A k-u ло-
пасти. Ось Or образует с осью Ох некоторый угол Обозначим через
иа и Vo координаты центра втулки в системе пОг. Тогда, очевидно:
«о= -*sMa + */cos%;
®0=%cos<;ft4-^sin(!'ft.
При колебаниях втулки по закону (4.6) координаты и0 и v0 будут
меняться во времени по закону:
«0 = (-X()Sin^)COS^-t-(«/0COS^)sin/7/;|
V0^(X0COS^k)COS -ф (#0 SillSin pt. I
244
Обозначим далее через и отклонение точки упругой оси лопасти на
радиусе г от прямой, проходящей через вертикальный шарнир А лопа-
сти и параллельной оси Or. При колебаниях лопасти величина и явля-
ется функцией радиуса г и времени I, так что « = «(г. f).
Пусть w — есть вектор полного ускорения точки с радиусом г упру-
гой оси лопасти. Тогда
где й?отн— вектор относительно ускорения точки от движения в подвиж-
ной системе координат пОг;
гспер — вектор переносного ускорения от движения точки вместе
с системой координат пОг;
йДор— вектор ускорения Кориолиса.
Введем единичные векторы г и у, направленные соответственно по
осям г и п. Тогда можно написать:
®отн -z (г’о) + 7 («о +«);
®ucp = г (г + г'о)] + Л - “2 («о + «)];
даКор=Л-2“(«о+ «)] + / [(2®Л)].
Если через wn и wr обозначить проекции вектора полного ускорения
на оси On и Or, то для них получаются выражения:
®л = (Ио-ш3«о) + («-(й2«)-г2»Л0Л 8
wr—(v,~ ш-'г’о)— оРг- 2ши0 —2®иЛ
Уравнение равновесия балки в поле центробежных сил имеет вид:
(E/ii")”-(Nu’y = q, (4.9)
где q—интенсивность поперечной нагрузки, приложенной к балке.
При колебаниях лопасти поперечная нагрузка от сил инерции мо-
жет быть записана в виде:
q (г, i)— — mwn - — т f(и0 — m2w0) Д- (« - - w2zz) 2<ira0],
где т—погонная масса лопасти [m = m(r)]_
Подставляя это выражение в уравнение (4.9), получим следующее
дифференциальное уравнение в частных производных для определения
функции и (г, t):
(EIи")'' — (Nu'Y -ф mu — vfiu = q* (r, t), (4. 10)
где
q*(r,t}= — m[u0 w2«()-|2«iwri]. (4.И)
Если движение центра втулки задано выражениями (4.7), то на-
грузка q* (г, I) является известной функцией времени.
Неизвестная функция «(г, I) должна удовлетворять уравнений
(4. 10), а также граничным условиям:
«(0,/) = «"(0,0 = 0; 1
«"(/?, Z)=(E’/«")'|r_J? =0. J
Дифференцируя выражения (4. 7) и подставляя их в (4. И), найдем
q* (г, t)=mAk cos pt—mB* sin pi, (4. 13)
где постоянные Ak и Bk определяются по формулам:
^ft=-[(P2 + (n2)^o + 2w/7Z/0]sill'Lft; 1
fii = [(/?2 + l"s) «/o + 2‘'Wo] cos 4. J
245
Решение уравнения (4. 10), соответствующее установившимся вы-
нужденным колебаниям от нагрузки [см. выражение (4. 13)], ищем
в виде:
«(г, /) = «(г) [ЛЛсоэ р1-\-Вкsinpt\. (4.15)
Подставляя это выражение в (4. 10) с правой частью для q * из
(4. 13), найдем, что функция и (г) должна удовлетворять обыкновенному
дифференциальному уравнению
(Е/йу'-(М1у-(р*+<&)тй=т, (4.16)
а также граничным условиям
Jz (0)=-«" (0)==0; . 1 (4Л7)
«"(Я)=(£7«")'|;_д=0. J
Заметим далее, что при расчете колебаний лопасти, возбуждаемых
колебанием шарнира А по схеме, изображенной на рис. 2.30, нужно
решать уравнение вида:
(Elu,")" — ти — ш2и=0,
где и — полное смещение точки упругой оси лопасти с радиусом г.
При этом функция и (г, t) должна удовлетворять условиям:
«(0, /) = «0 cos РЬ 1
«"(0,^=0. }
и"(7?,/) = 0; 1
(ЕЫУ\г=ц =0.]
Отыскивая решение этого уравнения в виде:
и — [«о -|-«(г)] cos pl,
причем к выводу, что функция й(г) должна удовлетворять уравнению
(Е 1и'У — (Ми')' - (р2-ф-и2) ти = (р2-ф- ш2) тий,
которое отличается от уравнения (4. 16) лишь постоянным множителем
н0(р2 + <в2). Граничные условия для функции й(г) в этом случае полно-
стью совпадают с выражениями (4.17).
Таким образом, при колебаниях лопасти по схеме, показанной на
рис. 2.30, функция и (г) получается той же, что и в интересующей нас
задаче [см. выражения (4. 16) и (4. 17)], если амплитуду «о выбрать так,
чтобы выполнялось условие
Ио(Р2 + ®2) = 1. (4.18)
Физически это означает, что форма вынужденных колебаний ло-
пасти в интересующей нас задаче совпадает с формой колебаний лопа-
сти, возбуждаемой по схеме, показанной на рис. 2. 30. Используя этот
результат, получим одну важную формулу. Для этого заметим, что при
колебаниях лопасти, закрепленной по схеме, показанной на рис. 2. 30,
возбуждаемых силой F = F0cospi, сумма проекций всех поперечных
246
инерционных сил, приложенных к лопасти, должна уравновешиваться
силой F. Отсюда найдем:
/70=Дтл(р)(р2-[-‘»2)«о= — (л’+'о2) J т(«0-]-«)с?г=
/г __
= — (р2+ш2) «оотл — (Р2+“2) J mu dr,
*в.ш
где £ид — масса лопасти до вертикального шарнира
При выполнении условия (4. 18) отсюда получается формула:
R
J mudr —
^В.Ш
Атл 4- тл
р‘2 со2
(4. 19)
т. е. интеграл по лопасти от функции тй [где й— есть решение урав-
нения (4. 16)] выражается через динамическую жесткость лопасти или,
что то же самое, через добавочную массу Дотл(р)-
Теперь уже нетрудно получить выражения для сил, действующих
на втулку со стороны колеблющихся лопастей. Обозначим через Qk
и Nk соответственно проекции на оси On и Or силы, приложенной со
стороны k-n лопасти k вертикальному шарниру втулки. Тогда:
Qk
R Я
j mwn dr — — j m(u — »2«) dr —
(«0 — о)2й0 -|- 2wv0) тл;
R
Nk= ~ J mwrdr=^ — — ш3г’о — 2i0o))-|-
^в.ш
(4. 20)
R R
-'-i'.2 J mrdr^-‘2<s> mu dr.
^в. ш ^B. Ш
Подставляя сюда выражения (4. 15), (4.7), (4. 14) и учитывая фор-
мулу (4.19), найдем:
Qft=Дт, {[(р2+»2) ха 4- 2шр1’0] sin e cos pl —
— [G»2-|-«>2)b'o + 2up->c0] cos sin pl}; (4. 21)
Nh=No + Гm (p2 + u>2) x0 - дтл2ршt,0 - 4 ^‘“^о Icos ‘cos pt +
L (p2 -г J
~ рМУ 4~Uj2) Уо ~ Дтл2р«>ло—+ T 4 P2"^0 ]sin sin pt' (4- 22^
pi + J
R
где jV0 = w2 f mrdr — центробежная сила лопасти на вертикальном шар-
I* ш нире втулки.
247
Обозначая через X и Y силы, приложенные к втулке со стороны ко-
леблющихся лопастей, получаем формулы:
X = 2 (' Q* sln cos
k-i
г== 2 (^cos^ + A^sin^).
к =1
Подставляя сюда выражения (4.21) и (4.22) и учитывая свойства
тригонометрических сумм, описанные в п. 2 § 1 этой главы [формулы
(1. 13)], придем к следующим выражениям:
2С = | — у Дтл ](р2 + («2) х0 + 2шруа] + -^ {Р1 + “2) *0 -
— Дтл2 р<оу0 — Ат'1 тл 4р2o)2jc0] I cos pt-, (4.23)
J J
Г = ~ Хпч [(р2+О)2) у0 + 2<^рх0 ] - ф
+-^-Гмл(р2~| а>2)г/о--дт2р®д'о— ^i^.4p2a)2i/0llsinpt (4.24)
2 L Р2 +0)2 JJ
С другой стороны, можно составить уравнения движения втулки
винта на упругом валу, которые имеют вид:
твт (х — 'jj2x — 2ад/) сох = X;
давт (у — + 2щх) + соУ = И,
где тах — масса корпуса втулки;
с0 — жесткость вала.
Если движение втулки происходит по закону (4.6), то последние
уравнения дадут:
X = Ивт [ - (рг-г “2) — 2шРУо] + Vo) cos Pf',
Y = I — (p24-<«2) i/0 — 2щрх0] 4- coyo} sin pt.
Если приравнять эти выражения к (4.23) и (4.24), то получим си-
стему двух линейных однородных уравнений для определения амплитуд
Хо И Уй-
(4. 25)
где
А = (У + [ v (тй - Д«,) + mJ - 2г pW - с0; (4. 26)
L2 J (Р1 + и2)
В — 2^р [тВТ — гДтл]. (4. 27)
Приравнивая нулю определитель этой системы, получим характе-
ристическое уравнение для определения собственных частот р:
Д Я '
2 | = А2-В2 = 0, (4.28)
откуда
А^=±В.
Ах0 - ф Ву0 — 0; 1
Вх04~Ауо = О, J
248
В случае .4 =—В [как это видно из (4. 25)] х0 = у0. Это соответству-
ет вращению центра втулки в направлении вращения винта [см. форму-
лы (4. 6)].
В случае А=В получается xq =—уо, что соответствует вращению
центра винта против вращения винта.
Характеристическое уравнение (4.28) можно разрешить относитель-
но величины Дтл(р). При этом получается следующее уравнение:
/ Z \ 2s
(?2 + “2) ДД т„ + твт — с0 — ———тд ? 2ш/?твт
4„. („) =---------12----------> ; , (4.29)
— Ар2 + “2)+ -т-—,.'± 2лш/?
2 р2 --I- <о2
Это уравнение можно решать графически, накладывая на кривую
добавочной массы лопасти Дтл=Дтл(р) две кривые, соответствующие
Рис. 2.32, Определение частот колебаний винта на упругом валу
методом динамической жесткости
правой части этого выражения, в которой берутся либо верхние знаки
(знак минус в числителе и знак плюс в знаменателе), либо нижние зна-
ки. Обозначим первую из этих величин ДтИр), а вторую Дтг(р).
Абсциссы точек пересечения кривой Ami (р) с графиком добавочной
массы Дтл(р) лопасти будут давать частоты собственных колебаний
винта на упругом валу, соответствующие таким формам колебаний, при
которых центр втулки вращается в направлении вращения винта
с угловой скоростью р относительно системы координат хОу, связанной
с винтом, и, следовательно, с угловой скоростью р + <в относительно не-
подвижной системы координат (корпус вертолета). Такие формы оче-
видно могут возбуждаться лишь гармониками (г— 1)®, (2г—1)и и т. д.
Абсциссы же точек пересечения кривых Дт2(р) и Дтл(р) будут давать
частоты собственных колебаний винта на упругом валу, при которых
центр втулки вращается в направлении, противоположном направлению
вращения винта. Такие формы колебаний могут возбуждаться лишь
гармониками (z+l)®, (2гф-1)® и т. д.
На рис. 2. 32 приведены графики кривых Дтл(р), Ami(p) и Лт2(р'),
построенные для следующих исходных данных: со = 5ОО кгс[мм;
= 38 кге • сек2!м; тл—\Ъ кге • сек^м; ®0 = 190 об!мин; z=5. Приведенные
графики показывают значительные отличия частот собственных колеба-
ний винта на упругом валу от частот собственных колебаний изолиро-
249
ванной лопасти. Так, например, частоте одноузлового тона собственных
колебаний изолированной лопасти данного винта (при неподвижной
втулке) соответствует точка Н бесконечного разрыва кривой Дтл(р).
При этом р =/4 = 640 кол!мин. На рис. 2.33 изображена форма колеба-
ний этого тона.
У винта на упругом валу, кроме этой частоты собственных коле-
баний, имеются также частоты колебаний, соответствующие точкам А,
В, С и D пересечения кривых ДтДр) и Дт2(р) с кривой Дтл(р). При
этом колебания с формами, соответствующими точкам А и D, могут
а)
'I р=р'

Рис. 2.33. Формы колебаний лопасти:
а—форма колебаний лопасти без учета упругости пала; б—формы колебаний
лопасти с учетом упругости вала
возбуждаться лишь гармониками (г—1)и, (2г—Г) со и т. д. (в данном
случае 4и и 9и и т. д.). Колебания, соответствующие точкам С и В,
могут возбуждаться лишь гармониками (3+1) со, (2г+1)со и т. д. (в
данном случае бсо, 11® и т. д.).
Эти резонансные кривые построены для вертолета, который внача-
ле имел четырехлопастной винт, но затем из-за сильного резонанса ло-
пасти с гармоникой Зсо в плоскости вращения (точка Л), втулку винта
пришлость переделать и сделать винт пятилопастным.
На рис. 2.33 приведены формы собственных колебаний лопасти
в плоскости вращения с учетом упругости вала, соответствующие точ-
кам A (р, =560 кол!мин) и В (Д[ =761 кол)мин).
В заключение укажем, что приведенный здесь метод для нахожде-
ния частот собственных колебаний винта в плоскости вращения с уче-
том упругости вала является одним из наиболее сложных примеров
применения метода динамической жесткости и поэтому было сочтено
целесообразным изложить его здесь. Что же касается нахождения ча-
стот собственных лопастей в плоскости взмаха с учетом упругости
крепления втулки и частот колебаний лопастей в плоскости вращения
с учетом упругости на кручение системы трансмисссии (которые воз-
буждаются гармониками za>, 2гсо, Зг® и т. д.), то эти расчеты намного
проще и вполне могут быть выполнены на основе принципов, изложен-
ных в § 2.
ГЛАВА 3
ЗЕМНОЙ РЕЗОНАНС
Земным резонансом принято называть самопроизвольно возникаю-
щие колебания (раскачивание) вертолета на земле с нарастающей
амплитудой. Явление это стало появляться после того, как в конструк-
цию втулки винтов вертолетов был введен вертикальный шарнир, по-
зволяющий лопасти качаться в плоскости вращения винта.
В истории вертолетостроения было немало случаев, когда вертолет
разрушался от возникновения колебаний такого типа. Попытки устра-
нить земной резонанс на готовом вертолете иногда приводили к необ-
ходимости больших переделок конструкции вертолета. Эти обстоятель-
ства заставляли инженеров работать над созданием теории земного
резонанса и надежных методов его расчета, которые позволяли бы гра-
мотно выбирать характеристики элементов конструкции, определяющих
запас устойчивости вертолета на земле.
В настоящее время имеется теория земного резонанса, которая объ-
ясняет все важнейшие черты этого явления и позволяет рассчитывать
характеристики конструкции, от которых зависит земной резонанс. Эта
теория возникла в результате многочисленных теоретических и экспери-
ментальных исследований земного резонанса, которые проводились как
у нас в Советском Союзе, так и за рубежом. Из отечественных работ
по теории земного резонанса следует отметить в первую очередь рабо-
ты Б. Я. Жеребцова и А. И. Пожалостина.
Исследования земного резонанса показали, что физическая сущ-
ность этого явления заключается в следующем. При собственных коле-
баниях лопастей несущего винта в плоскости вращения (относительно
вертикальных шарниров), которые могут возникнуть от какого-либо
толчка (порыва ветра, грубой посадки и т. п.), появляются инерционные
силы в плоскости вращения винта. Передаваясь на фюзеляж вертолета,
они вызывают его колебания на упругом шасси. Силы, раскачивающие
вертолет, меняются с определенной частотой, зависящей от частоты соб-
ственных колебаний лопасти в плоскости вращения и угловой скорости
вращения винта. Наиболее легко вертолет раскачивается тогда, когда
частота изменения возбуждающих сил близка к частоте собственных
колебаний вертолета на упругом шасси. Одновременно при колебаниях
корпуса вертолета возникают силы, раскачивающие лопасти в плоско-
сти вращения. Наличие такой двусторонней связи между колебаниями
вертолета и лопастей приводит к тому, что при некоторой угловой ско-
рости вращения винта, вертолет может стать неустойчивым, т. е. раз
начавшиеся (вследствие какого-либо толчка) колебания вертолета мо-
гут оказаться не затухающими, а нарастающими.
Основными средствами борьбы с земным резонансом являются:
1. Установка специальных демпферов на вертикальных шарнирах
лопастей несущего винта, демпфирующих колебания лопастей в пло-
скости вращения.
251
2. Введение специальных демпфирующих элементов в конструкцию
амортизаторов шасси или правильный выбор характеристик гидравли-
ческого сопротивления амортизаторов на прямом и обратном ходе,
а также характеристик жесткости амортизаторов и пневматикой.
Основной целью расчета вертолета на земной резонанс является
правильный выбор характеристик демпферов лопастей и характеристик
жесткости и демпфирования шасси.
Теория земного резонанса, которая будет изложена ниже справед-
лива лишь для винтов с числом лопастей
Теория земного резонанса двухлопастного винта обладает рядом
особенностей и значительно более сложна [36].
§ 1. УСТОЙЧИВОСТЬ ВИНТА НА УПРУГОМ ОСНОВАНИИ
1. Постановка задачи и уравнения движения
Все важнейшие черты земного резонанса вертолета могут быть по-
лучены из рассмотрения движения некоторой идеализированной меха-
нической системы, которую мы будем называть «винт на упругом осно-
вании». Такая система схематически изображена на рис. 3. 1/Вал винта
с тяжелыми и абсолютно жестки-
Рис. 3. 1. Схема винта на упругом
основании:
1 корпус; 2- - основание; 3—.лопасть; 4—
шарнир
ми лопастями 3, соединенными с
втулкой винта с помощью верти-
кальных шарниров 4, вращается
в опорах, жестко связанных с не-
которым тяжелым корпусом (те-
лом) 1, который упруго укреплен
на неподвижном основании 2 и
имеет лишь одну степень свобо-
ды — поступательное смешение
вдоль оси Ох, параллельной пло-
скости вращения винта. При сме-
щении тела 1 вдоль оси Ох воз-
никает упругая восстанавливаю-
шая сила от пружины с и демпфи-
рующая сила от демпфера к
Будем считать упругие и демпфирующие характеристики основания ли-
нейными, т. е. предположим, что сила X, действующая на корпус 1 при
его смещении x(t), выражается формулой:
.г tZ. л
X — —сх—к------ ,
dt
(1-1)
где с — коэффициент жесткости пружины;
к — коэффициент демпфирования.
Будем называть величины с и к коэффициентами жесткости и демп-
фирования упругого основания. Если то масса корпуса 1, а Рх — есть
проекция па ось Ох силы, действующей на корпус от винта, то уравнение
движения корпуса может быть записано в виде:
тох t-кх^-сх — Рх. (1-2)
Здесь и в дальнейшем точками обозначено дифференцирование по вре-
мени.
Будем считать далее, что винт вращается равномерно с угловой ско-
ростью w в пустоте, т. е. не будем принимать во внимание аэродинами-
ческие силы. Теория земного резонанса, не учитывающая аэродинами-
ческих сил, достаточно хорошо согласуется с экспериментом. Таким
образом, принимаются во внимание лишь инерционные силы, возникаю-
щие при колебаниях лопастей в плоскости вращения.
252
Для составления уравнений движения лопасти обратимся к рис. 3. 1
и 3. 2.
Выберем неподвижную прямоугольную систему координат Oxyz.
Ось Оу направим по оси вала винта при положении корпуса 1, соответ-
ствующем статическому равновесию. Направление оси Ох выберем та-
ким, чтобы единственно возможное перемещение корпуса было на-
правлено вдоль оси Ох.
Пусть по-.прежнему х смещение оси вала винта вместе с корпусом
~ ” т1’* есть азимутальный угол А-й
вдоль оси их (рис. ,5.2). Пусть далее
лопасти винта, отсчитываемый от по-
ложительного направления оси Ох.
Углы фЛ различных лопастей
винта определяются формулой:
е7г;=ю/-Т — k, (1.3)
п
где п — число лопастей винта;
k= 1, 2,..., п.
Обозначим через )вш расстоя-
ние АВ (рис. 3. 2) от оси вращения А
до оси вертикального шарнира В,
а через угол отклонения /г-й лопа-
сти при повороте ее относительно
вертикального шарнира, считая £&
положительным при отклонении" ло-
пасти в направлении вращения
Рис. 3. 2. К выводу уравнений дви-
жения
(1.4)
винта.
Тогда координаты хк и элемента /г-й лопасти с массой dm, от-
стоящего на расстоянии q от оси вертикального шарнира, выразятся
следующими формулами:
.x^x-H^cos^+ecosCh На);
гк=1в. ш sin 'h + б sin (фй + U•
Дифференцируя дважды эти выражения по времени, получим фор-
мулы для определения составляющих ускорения элемента лопасти:
хк=х — ч>2/вш cos — q (ш 4- у2 cos ($к + У + sin (^ -ф у;
zk= — Sin <|>ft — Q («> 4- Eft)2 sin (4>й 4- у 44Л q cos (6ft 4- У.
При составлении уравнений малых колебаний лопасти относитель-
но вертикального шарнира следует, как обычно, ограничиваться малыми
первого порядка. Поэтому можно считать
Таким образом, с точностью до малых второго порядка, формулы
для ускорений хк и ук можно записать в виде:
хк = х — и2 /в.щ cos — р (w2 4- 2 «у cos (фА 4- у 4q sin 4- У;
4 = - 4.щ sin - Q (о>2 4- 2 ®У sin 4- у 4- Bsc cos (фА 4- у.
При движении системы в пустоте лопасти винта в каждый момент
времени t нагружены лишь инерционными силами. Элементарные инер-
ционные силы, действующие на элемент лопасти, выражаются форму-
лами:
dXk= — dm^k’,
dZ.k~ — dmkzk.
} (1-5)
(1-6)
253
Пусть в вертикальных шарнирах втулки винта имеются линейные
упругие и демпфирующие устройства, которые при вращении лопасти от-
носительно вертикального шарнира нагружают ее моментом
(1-7)
направленным в сторону, противоположную положительному направ-
лению 1*. Будем называть сл и кл соответственно коэффициентами упру-
гости и демпфирования лопасти.
В каждый момент времени момент от сил инерции, приложенных
к лопасти, относительно вертикального шарнира должен уравновеши-
ваться моментом М. Поэтому можно записать:
J [Хе sin fe" Ш - znQ cos Oh -| • ?ft)] dm — -HX,
t
где интегрирование ведется по длине лопасти I.
Из последнего выражения и формул (1.5) после несложных преоб-
разований получается уравнение движения /г-й лопасти. Так как нас
интересуют уравнения малых колебаний лопасти, то можно ограни-
читься лишь членами первого порядка малости относительно величин
х, х, и gh., отбросив члены, содержащие квадраты и произведения этих
величин. Тогда можно положить:
cosh~l;
sin ~
sin (h+h) ~ sin h+4 cos h;
cos (h+ U ~ cos h - h sin h-
После таких упрощений уравнение малых колебаний /г-й лопасти
примет следующий вид:
V2
^+2лА+(/’л.+''о“>2)^='Г2_ xsinh. (1.8)
*в.ш
Здесь применены следующие обозначения:
пл= ——-----относительный коэффициент демпфирования лопасти;
р\ = ---частота собственных колебаний невращающейся лопасти
А.ш (при со = 0) относительно вертикального шарнира;
v0—безразмерный параметр лопасти, определяемый формулой:
v0=l / (1.9)
Г е/в.ш
где 5В ш= f qdm— статический момент лопасти относительно вертикаль-
i ного шарнира;
/в.ш= 4 tfdm — момент инерции лопасти относительно вертикального
i шарнира.
Правая часть уравнения (1.8) представляет собой момент от инер-
ционных сил, действующих на лопасть от смещения вала винта (х).
При неподвижном вале, когда х=0, уравнение (1.8) описывает собст-
венные колебания лопасти равномерно вращающегося винта в плоско-
сти вращения.
254
Общее решение уравнения (1. 8) без правой части имеет вид:
MVcos (/>? + %»)<
где и <fk произвольные постоянные, а величина ря определяется фор-
мулой
р2п — п?
“Л 1/ I о л
и представляет собой угловую частоту собственных колебаний лопасти
в плоскости вращения.
Далее надо определить силу Д, действующую на корпус со сторо-
ны винта. Сила Рх представляет собой равнодействующую сил инерции
колеблющихся лопастей винта и на основании известной теоремы о дви-
жении центра инерции (центра тяжести) механической системы может
быть определена как произведение массы системы лопастей на состав-
ляющую ускорения общего центра тяжести системы лопастей по оси ох.
Составим формулы для определения координат общего центра тя-
жести системы лопастей.
Пусть хкс и гЙ£ координаты центра тяжести й-й лопасти. Тогда
координаты хс и zc центра тяжести системы лопастей могут быть вычис-
лены с помощью выражений:
(МО)
Пусть далее Qc есть расстояние центра тяжести лопасти от оси вер-
тикального шарнира. Тогда в соответствии с формулами (1.4) коорди-
наты хс, zc могут быть определены так:
=х + 4.шСо8фй+рссо8(^ + У;
=4.Msin^ + ecsin(^--H»).
Подставляя эти выражения (1. 10) и учитывая, что при гг^З [см.
гл. 2, § 1, п. 2, формулы (I. 13)]
п | (1.И)
2 sin^fe=0,
получим следующие простые выражения для координат общего центра
тяжести системы лопастей:
Л
хс=—
Й = 1
п
2^cos,v
£-1
(1-12)
Сила Рх, действующая на упругое основание, может быть определе-
на по формуле
Ps= — птлхс.
255
Дифференцируя дважды первое из выражений (1. 12), получим:
Рх = - птлх | SD. ш 2 lUs ~ sin ф* -Ь 2 cos .
ft=i
Подставляя это выражение в уравнение (1.2), получим окончатель-
но следующее уравнение движения корпуса:
(нг0-^лтл)л;.|-кх + сх = 5в.ш [(’?* — “2Usin^ + 2a):\cosOft],
k = l
Это уравнение удобно записать в виде:
п
X 4- 2 пох 4- р2х = V [ (4 - uftk) Sin 4- 2«4 cos Ф4,
к-1
где величина
М = т0 4~ пт, (1. 13)
представляет собой общую массу системы, па— относительный коэффи-
циент демпфирования упругого основания, определяемый формулой
а величина ро представляет собой угловую частоту собственных колеба-
ний жесткого винта (без вертикальных шарниров) на упругом основа-
нии и определяется формулой
Выпишем теперь вместе уравнения движения винта на упругом
основании, которые состоят из уравнений движения лопастей (1.8)
и уравнения движения корпуса основания:
Л -
4- 4- (/>2 + v2o>2) 1к = --х sin фй;
*В.П1
S -Д .. . (1.16)
х 4- 2п^х4- Plx = у [(Eft- ю2^) sin4- 2ш<к cos фЛ],
* = i
где k— 1, 2, . . . , п.
Итак, уравнения малых колебаний винта на упругом основании
представляют собой однородную систему (н+1) линейных дифферен-
циальных уравнений с периодическими коэффициентами для определе-
ния (п-]-1) неизвестных функций x(t), gft(/) (где k=\, 2...п)
2. Анализ устойчивости и основные результаты
Исследования, проведенные Coleman’oM [35] и Б. Я. Жеребцовым
показали, что для винта с числом лопастей л^З эта система уравнений
может быть приведена к системе линейных уравнений с постоянными
коэффициентами, если вместо gfe(0 ввести новые переменные xc(t)
и zc(4, представляющие собой координаты центра тяжести системы ло-
пастей. В случае же двухлопастного винта уравнения (1. 16) не удается
свести к уравнениям с постоянными коэффициентами. Исследование
устойчивости движения двухлопастного винта на упругом основании
весьма сложно. Его изложение можно найти в работе [36]. Б. Я. Жереб-
цов исследовал также случай двухлопастного винта на изотропном
256
упругом основании, когда корпус основания имеет две степени свобо-
ды— в направлении осей Ох и Oz (см. рис. 3.2) —и жесткость основа-
ния в обоих этих направлениях одинакова. В этом исключительном
случае задача также легко приводится к системе уравнений с постоян-
ными коэффициентами.
Здесь будет рассмотрено исследование устойчивости винта с чис-
лом лопастей п^З, имеющее наибольшее практическое значение.
Чтобы получить уравнения движения с постоянными коэффициен-
тами, преобразуем уравнения (1.16) к новым переменным х(/), »](/),
£(/), связанным с прежними формулами:
п
2 ^sinfe
Я=1
п
2 ^cos^'
Z?=l
(1-17)
Новые величины г] и £, как это видно из формул (1. 12),-с точностью
до постоянного множителя рс/л равны координатам центра тяжести
системы лопастей в подвижной системе координат x'Az', оси которой
параллельны осям Ох и Oz неподвижной системы, а начало координат
А совпадает с центром несущего винта (см. рис. 3.2).
Для составления уравнений движения в новых переменных, умно-
жим все уравнения движения лопастей (первое из уравнений (1. 16)
сначала на соэфь и сложим их левые и правые части от k=i до k = n,
а затем на !)1пфь и также сложим. При этом заметим, что для вйнта
с числом лопастей п^З в силу формул (1. 13) гл. 2:
2 SMa COS %
* = 1
(1.18)
Кроме того,

2 ^8й1^=т1—
2 ^сО8^=С + и>п;
k = l
п
У, ^я1пф4=т] — 2»< — «2ц;
2 Ъcos 4-2,|)п—(°2£-
k=i г
(1-19)
Последние формулы получаются путем последовательного диффе-
ренцирования выражений (1. 17).
В результате получим следующую систему уравнений:
х +' 2н0х 4- р%х — ц=0;
П -г 2«лг] р (1 — v2) - ц - 2юС- -
_2L . —0;
2 ш
С+2<t - р (1 - V2) - Р2J С+2^+2«Л0Щ=0.
(1.20)
17 1578 257
Таким образом, получается однородная система из трех линейных
дифференциальных уравнений второго порядка с постоянными коэффи-
циентами, относительно трех неизвестных функций х(/), т](^) и £(£).
Теперь исследование устойчивости системы может быть проведено
обычным путем.
Полагаем:
х=хоеА*;
П = п,т*(;
где х0, т]о и Со — некоторые постоянные.
Подставляя эти выражения в уравнения (1.20), получим систему
трех алгебраических линейных однородных уравнений для определения
величин хо, и £о. Приравнивая нулю определитель этой системы, по-
лучим характеристическое уравнение для определения X. Разворачивая
это уравнение по степеням X, получим:
X6 + aXs + W4 + cX2 + eX+/==0, (1.21)
Здесь и далее введены следующие обозначения:
k= —;
Po
— Cl)
to =— ;
A>
Ь=В0 + В&
c = C0-\-C1oii’,
d—D0-[-D^2 J- D^-
е=-Е0-\-Е^-\-Е^>*-,
f=FQ+F^+E^.
[«о+(2 - 0];
1 — s
Bq —x----[ 1 + 8попл 4гал + /?л0 (2 — г)];
1 — е
И —(2 —e)(l —v§)];
Q [лл+2«о^+(йо+лл)Л];
1 — e
Cl = ----[wo 4~ %] 0 T vo) ’
1 — s
Co = [4/г-л—j— 2 (1 —4/г0 Д1Л) /гл,,];
&i — j _ E [2”*4~0 "b vo) 0 T^o^ J^P-LO ~ vo)] ;
(1.22)
(1-24)
258
fo—~~ (2ил+no pt);
1 — £
£t [4«o«л + 2ra„ (1 -|- vo) — 2 ~рлan0 (1 - vq)] ;
1 — г
2n0(l-v^
1 —г
F _ Pt .
1 0 —, »
1 — £
^1=^- [4^- 2^,(1-v§)J;
F,-^L.
(1.24)
Безразмерные коэффициенты демпфирования no (упругого основа-
ния) и йл (лопасти) определяются формулами:
Безразмерный коэффициент
Ро
е определяется формулой:
S2
°в.ш
Ir mA!
(1.26)
Нетрудно выяснить механический смысл этого важного коэффици-
ента. Величины Зв ,ш и /в.ш можно записать в виде^
откуда =
*^В.Ш
Л.ш=/«ле?-
радиус инерции лопасти относительно вертикаль-
ного шарнира. Поэтому выражение (1.26) можно
переписать в виде:
2
птл / Qc \2
+ птл ' qz }
(1.27)
Величина рс/рс зависит от закона распределения массы по длине
лопасти и лежит для различных лопастей в узких пределах: рс/рг«=*
~0,8-2-0,9.
Поэтому можно приближенно считать, что величина е пропорцио-
нальна отношению общей массы лопастей к массе всей системы (масса
корпуса упругого основания 4-масса лопастей), и может быть названа
относительной массой несущего винта.
Подробный анализ характеристического уравнения показывает, что
в системе возможна лишь колебательная неустойчивость и невозможна
апериодическая неустойчивость [35]. Границы зон колебательной не-
устойчивости (соответствующие значения со) могут быть найдены сле-
дующим способом: на границе зоны неустойчивости имеют место чисто
гармонические (не затухающие и не нарастающие) колебания, что со-
ответствует чисто мнимому значению одного из корней характеристи-
ческого уравнения (1.21). Полагая в этом уравнении 'к = 1р (где р— ве-
17*
259
(1.28)
личина вещественная) и приравнивая нулю вещественную и мнимую
части, получим следующие уравнения:
а// —ср2 ) с = 0;
Так как коэффициенты a, b, с, d, е, f являются известными функция-
ми и [см. формулы (1.23) и (1.24)], то уравнения (1.28) можно рас-
сматривать как_систему двух уравнений с двумя неизвестными р и ы.
Значения ш и р, являющиеся решением системы (1.28), представляют
собой безразмерную угловую скорость <а вращения ротора, при которой
возможны гармонические колебания системы, и соответствующую без-
размерную угловую частоту р колебаний.
Решать систему (1.28) можно пользуясь тем, что первое из урав-
нений (1.28) является_биквадратным по отношению к р. Задаваясь раз-
личными значениями w, можно из этого уравнения определять р, после
чего вычислять значение некоторой величины £)(оз), равной левой части
второго из уравнений (1.28) при этом значении р:
D(u>) = ps — bp*-\-dp2 — f. (1.29)
По результатам такого расчета можно построить кривую зависи-
мости D от о). Значения <о, при которых D обращается в нуль, и будут
границами зоны неустойчивости. Можно показать, что значения ш, при
которых £)>0, соответствуют устойчивому движению системы, а значе-
ния со, при которых D<Q — неустойчивому.
Расчет зон неустойчивости весьма трудоемок и его практически
можно производить лишь на электронных цифровых машинах. На
рис. 3. 3—3. 12 показаны некоторые результаты таких расчетов, выпол-
ненных на электронной цифровой машине «Стрела» инженером
В. Г. Пашкиным. Графики на этих рисунках позволяют определять гра-
ницы устойчивости и запасы демпфирования.
Устойчивость системы определяется вообще следующими пятью па-
раметрами: vo, е, по, пл. Графики построены для двух наиболее час-
то встречающихся значений vo = O,25 и vo=0,3. Значение =0, т. е. рас-
сматривается винт, на вертикальных шарнирах которого имеются лишь
демпферы. Упругие же элементы отсутствуют. Влияние упругих элемен-
тов будет пояснено ниже. Для каждого из значений v0 дается серия
графиков, соответствующих различным значениям е. По оси абсцисс на
каждом графике отложены значения безразмерной угловой скорости со,
соответствующей границам зоны неустойчивости, а по оси ординат без-
размерный коэффициент пп демпфирования лопасти, при котором по-
лучается данная зона неустойчивости. Графики построены для различ-
ных значений по безразмерного коэффициента демпфирования упругого
основания.
Как видно из этих графиков, ширина зоны неустойчивости сущест-
венно зависит от коэффициентов демпфирования пл и По- С увеличени-
ем демпфирования пл (при фиксированном по) зона неустойчивости
сужается и при некотором критическом значении п* зона стягивается
в точку. При значении пл>п*л зона неустойчивости отсутствует при
всех значениях ю. Так, например, при е = 0,02, vo = O,25 (см. рис. 3.3),
если йо = О,О6, зона неустойчивости стягивается в точку при йл = 0,128,
а при йл>0,128 система устойчива при любом и (в этом случае
пл =0,128).
Рис. 3.4. Графики для определения границ неустойчивости (е = 0,04; vo=O,25)
261
Рис. 3.5. Графики дли определения границ неустойчивости (е --0.G6: по = 0,25)'
I
Рис. 3.6. Графики для определения границ неустойчивости (8=0,08;
vo=O,25)
262
«л
0,25
0,15
0,10
Рис. 3.7. Графики для определения границ неустойчивости (г=0,10;
vo=0,25)
Рис. 3.8. Графики Для определения границ неустойчивости
(е=0.02; vo=O,3O)
263
Рис. 3.9. Графики для определения границ неустойчивости (е = 0,04;
vo = 0,30)
f,25
0,20
0,Ю
0,10
0,05
Рис. 3. 10. Графики для определения границ неустойчивости (а = 0,06; vo = 0.30)
264
0,30
Рис. 3. 11. Графики для определения границ неустойчивости (е = 0,08; v0—0,30'
Рис. 3. 12. Графики для определения границ неустойчивости (е = 0,10; vo = 0,30)
Отношение д = в том случае, когда оно больше единицы, удоб-
на
но называть запасом демпфирования.
Значение со, при котором зона неустойчивости стягивается в точку,
называется критическим и может быть вычислено по приближенной
формуле:
“>kp=1-v0'
Ниже мы дадим физически наглядное пояснение этой формулы.
Следует отметить, что увеличение величины йл не всегда приводит
к улучшению устойчивости. При малых значениях пд (это можно про-
следить по графикам) увеличение пл может привести даже к небольшо-
му перемещению нижней границы зоны неустойчивости в сторону мень-
ших значений ы. Это может привести к появлению неустойчивости при
значениях <в, для которых при меньших пл движение было устойчивым.
Увеличение демпфирования п0 упругого основания при средних зна-
чениях пл также приводит к улучшению устойчивости, однако при весь-
ма малых значениях пл увеличение пд может привести к смещению верх-
ней границы зоны неустойчивости вправо и, тем самым, к расширению
зоны неустойчивости.
Анализ графиков позволяет сделать следующий важный вывод:
в тех случаях, когда величины пл и пд одного порядка и различаются
в ту или иную сторону не более, чем в 2—3 раза, всякое увеличение
демпфирования пл или п0 приводит лишь к увеличению устойчивости.
При таких значениях гёл и п0 наибольшее потребное демпфирование по-
лучается приблизительно при
- - 1
------------- •
к₽ 1 - v0
Для этого весьма важного для практики случая может быть полу-
чена простая приближенная формула Б. Я. Жеребцова*, показываю-
щая, что запас демпфирования пропорционален произведению величин
йл и пд. Эта формула дает значение произведения плпд, при котором
зона неустойчивости стягивается в точку:
(L3°)
Эта приближенная формула верна лишь при ра„ =0; ее справед-
ливость можно проследить по графикам. В случае, когда рЛ1> #=0, можно
пользоваться другой приближенной формулой:
-- • (1.31)
8-v0
где безразмерная величина А определяется формулой
А =-------- 1 + v° =-. (1.32)
1 / 1 -а ( 1 “ 'Л
vo + I/ 1 + ^1 9 I
’ \ v0 /
На рис. 3. 13 показана зависимость А от рл„ при vo = O,25. Из гра-
фика видно, что потребное демпфирование может быть существенно
* Эта формула будет выведена в § 3. Там же будет выведена и формула (1.31).
266
упруго-
шарни-
Рис. 3. 13. Влияние
сти в вертикальном
ре на потребное демпфиро-
вание
уменьшено введением упругого элемента в вертикальном шарнире втул-
ки. Улучшение устойчивости системы с увеличением рЛо иллюстрируется
также серией графиков на рис. 3. 14.
Однако при введении упругого элемента в конструкцию вертикаль-
ного шарнира или при введении так называемых упругих межлопаст-
ных связей необходимо помнить, что из-
гибающий момент, действующий на ком-
левую часть лопасти в полете, обуслов-
лен как демпфером, так и упругим эле-
ментом на вертикальном шарнире.
Поэтому при увеличении жесткости упру-
гого элемента (при увеличении рл<> )
одновременно с уменьшением потребного
момента от демпфера будет увеличивать-
ся момент, действующий на лопасть со
стороны упругого элемента (или межло-
пастных связей). Оптимальным значени-
ем Рл0 следует считать такое, при кото-
ром изгибающий момент, действующий
на лопасть в полете, будет наименьшим
при неизменном запасе демпфирования
оптимальное значение рЛа зависит от по и должно специально выби-
раться для каждого вертолета. Подробнее об этом см. в § 6.
по земному резонансу. Это
Рис. 3.14. Графики, иллюстрирующие влияние упругости в вертикальном
шарнире (е = 0,04; vo=O,366)
3. Физическая картина поведения винта при земном резонансе
Для выяснения физической картины поведения винта при земном
резонансе рассмотрим следующую задачу.
267
Пусть корпус упругого основания (рис. 3. 1) совершает гармониче-
ские колебания по заданному закону:
x=xosin pt,
(1.33)
где Хо и р—амплитуда и частота колебаний корпуса.
Рассмотрим вынужденные колебания лопастей при таком движении
корпуса. Уравнение (1.8) движения £-й лопасти винта примет при этом
следующий вид:
vo
— — ----------- р2Х() sin pl sin
7в.ш
(1-34)
2л
Учитывая, что фл=<о/|Н-k (k=l,2, . . . , п) и представляя пра-
вую часть этого уравнения в виде двух гармоник, можно записать урав-
нение в виде:

v0 2
27-7^0
А* В.Ш
cos (<о — p')t -1-— k
п
. 9л
— COS (u) Р) t -]----k
(1.35)
Это обычное уравнение вынужденных колебаний системы с одной
степенью свободы.
Правую часть уравнения (1.35) представляет собой возбуждающую
силу, которая в данном случае состоит из двух частей. Каждая часть
представляет собой нагрузку, меняющуюся по простому гармоническо-
му закону с частотой, соответственно равной (т—р) или (ы + р). В силу
линейности уравнения (1.35) колебания лопасти от каждой из этих
нагрузок можно рассматривать независимо. Вынужденные (установив-
шиеся) колебания лопасти будут происходить по закону:
^(7)=?i cos {(«>-}- р) t-j-'pj cos [(®-}-р)^ -j-'Ps], (1.36)
где £2, fi, f2 —некоторые постоянные, которые можно легко опре-
делить из уравнения (1.35).
Таким образом, при колебаниях корпуса упругого основания по
простому гармоническому закону с частотой р лопасти винта будут со-
вершать вынужденные колебания с двумя комбинационными частотами
(т-|р) и (т—р), зависящими от угловой скорости “ вращения винта.
Наиболее интенсивные колебания лопастей получатся при резо-
нансе, когда одна из частот возбуждения (р + со) или (р—со) будет
близка к частоте собственных колебаний лопасти рл= V /7л0 + уой)2-
Рассмотрим сначала случай резонанса, когда
]/XW4/>-4 (1-37)
В этом случае величина |i в выражении (1.36) будет значительно
больше величины Ь, и поэтому вторым членом в формуле (1.36) можно
пренебречь. При таком упрощении и при условии (1. 37) закон движе-
ния лопасти будет иметь вид:
Eft = Eesin [(р —<»)/—?^-^ , (1.38)
где
268
Вычислим далее силу Рх, действующую на корпус упругого осно-
вания, от инерции колеблющихся таким образом лопастей винта. Для
этого найдем движение центра тяжести системы лопастей по формулам
(1. 12). Подставляя в эти формулы выражение (1.38) для и учиты-
вая, что
п
-Р)/+^ а]=о
sin J(2«> — АИ + —
после несложных преобразований получим следующий закон движения
центра тяжести системы лопастей:

(1-40)

Если учесть, что координаты центра тяжести в системе координат
x'Az', связанной с корпусом, выражаются формулами х'с =хс—х
и z' =zt, то центр тяжести системы лопастей в этой системе координат
движется по закону:
, 1 f J.
= —Qc^C0S Р*\
< = Ye^°Si11 Pt'
(1-41)
Таким образом, при резонансе, когда выполняется равенство
(1.37), центр тяжести системы лопастей описывает в системе коорди-
нат, связанной с корпусом, окружность с радиусом — qc£o- При этом
угловая скорость его вращения по этой окружности равна частоте р за
данных колебаний корпуса.
Определим теперь силу Рх, Действующую на корпус, по формуле
Рх = —птлхс. При этом получится следующее выражение:
Рх= -\-птяр2 [*о+-у Icosp/.
Подставляя сюда выражение для ёо из (1.39), получим:

1
8 ^в-щЯд Р)
х0 cos pt.
(1-42)
Таким образом, при колебаниях корпуса по гармоническому закону
(1.33) и при условии резонанса лопасти (1.37) сила, действующая на
корпус со стороны колеблющихся лопастей, изменяется во времени так-
же по гармоническому закону с той же частотой р, с фазой колебаний
л/2 (по отношению к колебаниям корпуса) и пропорциональна амплиту-
де х0 колебаний корпуса.
Выражение (1.42) можно также представить в виде:
Р г= — птхАппгр1 —.--------------xncoso/.
Х Л Л в («-/’)
269
Если составить уравнение колебаний корпуса (1.2) под действием
силы Рх, заданной таким выражением, то получится:
• • л vo/?2
тпх4-2кх 4- сх = — птх I пт./Р — ---------------- х0 cos pi.
8 (ш Р)
Применяя уже принятые нами ранее обозначения, это уравнение
можно записать в виде:
х-^Пох + рр^—• /—"7------------------------*ocos/rf. (1.43)
то + птл 8 гв,шпл(о1—р)
Если можно найти параметры системы, при которых закон движе-
ния корпуса (1.33) удовлетворяет этому уравнению, то это означает,
что при таких параметрах системы возможно чисто гармоническое дви-
жение (незатухающие колебания) с частотой р. Подставляя выражение
(1.33) в уравнение (1.43) нетрудно видеть, что это получается при вы-
полнении двух следующих условий:
Р = Ро'-
— zPo
° л 8(ш-/,0)
(1-44)
Кроме того, необходимо помнить, что уравнение (1.43) было по-
лучено при условии резонанса лопасти, т. е. при условии (1.37), ко-
торое, учитывая, что Ро = р, можно записать в виде:
(L45)
Из этого уравнения можно определить значение критической угло-
вой скорости (йКр вращения винта, при которой возможны незатухающие
колебания в системе.
Формула же (1.44) дает значение произведения логёп, при котором
возможны незатухающие колебания и, как мы сейчас увидим, из этой
формулы и условия (1.45) получается приближенная формула (1.31).
Таким образом, незатухающие колебания возможны лишь при та-
ком значении ®, когда одновременно имеют место два резонанса: резо-
нанс лопасти [условие (1.45)] и резонанс упругого основания р = ро- При
таком значении m и при выполнении условия (1.44) собственные коле-
бания винта на упругом основании могут поддерживаться переменной
возбуждающей силой, возникающей от колеблющихся лопастей, кото-
рые при этом находятся в состоянии резонанса.
Рассматривая уравнение (1.35) мы видели, что резонанс лопасти
возможен в двух случаях, а именно: когда одна из комбинационных
частот (р + m) или (р—со) совпадает с собственной частотой колебаний
лопасти, т. е.
Рл = |/’- "’I
И
Рл=|р+4
Из двух этих случаев мы рассмотрели лишь первый. Во втором слу-
чае все выведенные формулы получатся такими же, но во всех выраже-
ниях вместо величины m будет величина —со, в том числе и в формулах
(1.44). Из этой формулы видно, что при рл = |р4-(о| незатухающие коле-
бания возможны только при условии попл<О, т. е. в этом случае одна
из величин п0 или пл должна быть отрицательна. Это означает, что зем-
ной резонанс возможен только при рл=|р—т| и невозможен при
Рл= |р-1-<1>].
270
Рассмотрим далее резонансную диаграмму (рис. 3.15). На этом
рисунке изображена кривая зависимости частоты собственных колеба-
ний лопасти рл от угловой скорости m и нанесены прямые р = ро + & и
р=|ро—to|. Диаграмма изображена для случая, когда рЛо <ро-
Как видно из диаграммы, имеются два значения <о, при которых
выполняется условие рл= |ро—®|, соответствующие точкам А и В.
Причем для точки А имеет место
условие ря = ро—w, а для точки В
условие рл = а—ро-
Таким образом, в первом слу-
чае ®<ро, а во втором ш>ро. Обра-
щаясь ко второму из условий (1.44),
мы видим, что оно может удовлет-
воряться (при положительных зна-
чениях п0 и пл) только тогда, когда
й>ро- Следовательно, из двух воз-
можных значений <в, при которых
может быть резонанс лопасти, лишь
ОДНО (й)>ро) может соответствовать Рис. 3. 15. Резонансная диаграмма
незатухающим колебаниям системы.
Определим это значение и и назовем его (шКр) критическим. Решая
уравнение (1.45) относительно и и отбрасывая одно из полученных
значений (ы<р0), найдем
(0кр = Ро
1 + K Vo+/’I(1-Vo)
l-V20
(1.46)
При /?ло = 0 получается формула
СО
кр
Ро t
1 — V0
(1-47)
Подставляя значение о)нр из выражения (1.46) во второе условие
(1.44), найдем:
где
----С ( 1 — V0 ) А
«о«л = -4------- Д,
О Vo
Эти формулы в точности совпадают с приближенными формулами
(1.31) и (1.32).
Рассуждения, приведенные здесь, вместе с анализом устойчивости,
данным в § 2, позволяют сделать следующий вывод: условие
п0Я»> ——— А всегда обеспечивает устойчивость при критической
8vg
угловой скорости вращения винта, определяемой формулой (1.46).
Однако, как указывалось при анализе графиков на рис. 3. 3—3. 12, это
условие верно только, когда величины йл и п0 одного порядка. Это
означает, что обеспечение устойчивости при й = о)Кр еще не обязательно
обеспечивает устойчивость при любом и.
4. Винт иа изотропном упругом основании
Теория устойчивости винта на упругом основании, изложенная в
этом параграфе, справедлива лишь для случая, когда число лопастей
271
винта и когда упругое основание имеет лишь одну степень сво-
боды — перемещение вдоль оси Ох (рис. 3.2).
Однако аналогичная теория устойчивости может быть построена
и для более общего случая, когда упругое основание имеет две степени
свободы: смещение вдоль осей Ох и Oz. Расчеты устойчивости для та-
кой более сложной системы весьма громоздки. С другой стороны, на
практике почти во всех случаях можно пользоваться формулами для
случая упругого основания с одной степенью свободы. Так можно де-
лать всегда, когда частоты собственных продольных и поперечных ко-
лебаний вертолета на упругом шасси (см. § 5) далеки друг от друга.
Предоставляет интерес указать некоторые простые результаты,
которые получаются в теории устойчивости винта на упругом основании
с двумя степенями свободы в особом случае так называемого изотроп-
ного упругого основания, когда жесткость и демпфирование упругого
крепления корпуса основания одинаковы в обоих направлениях (Ох и
Oz). В этом случае упругие и демпфирующие свойства основания оди-
наковы во всех направлениях, параллельных плоскости хОг. Именно
поэтому такое основание называют изотропным.
Пусть жесткость и демпфирование изотропного основания, одина-
ковые в направлениях осей Ох и Oz, характеризуются соответственно
коэффициентами с и к, так что силы Рх и Рг, приложенные к основа-
нию, связаны с соответствующими перемещениями х и z формулами:
Р..= — сх — к---
л dt
Рг= —cz — k —
z dt
(1.48)
Оказывается, что в этом случае также может иметь место неустой-
чивость винта на упругом основании. При этом зона неустойчивости по-
лучается вблизи того же значения <о = <оКр, что и раньше:
1 + )/ *о + /’л0(1~'’о)
----------
(1.49)
В случае рЛо =0 так же, как и раньше, получается более простая
формула:
Рй .
1 —
(»
кр
(1.50)
При этом величины ро, Рп0 и vo по-прежнему определяются фор-
мулами:
(1-51)
Получаются также аналогичные формулы для определения потреб-
ного демпфирования, но потребное демпфирование в этом случае вдвое
больше.
272
Формула для потребного демпфирования, при котором зона не-
устойчивости стягивается в точку, имеет вид:
= (1.52)
4v0
Величины е и А по-прежнему определяются формулами (1.26)
и (1.32).
§ 2. ПОПЕРЕЧНЫЕ КОЛЕБАНИЯ ОДНОВИНТОВОГО ВЕРТОЛЕТА
1. Предварительные замечания
При расчете колебаний вертолета на упругом шасси можно рассмат-
ривать фюзеляж, как абсолютно твердое тело, прикрепленное к непо-
движному основанию (земле) с помощью системы упругих элементов.
Расчет земного резонанса вертолета, как это будет показано ниже,
может быть сведен к расчету винта на упругом основании, рассмотрен-
ному в § 1. Исходные данные для такого расчета (характеристики упру-
гого основания) получаются из некоторого предварительного расчета
собственных колебаний жесткого фюзеляжа на упругом шасси.
Вертолет, рассматриваемый как твердое тело на упругом шасси,
имеет шесть степеней свободы. Однако, так как фюзеляж имеет, как
правило плоскость симметрии, то продольные и поперечные собственные
колебания вертолета можно рассматривать независимо друг от друга.
Для одновинтового вертолета, имеющего удлиненный фюзеляж, рас-
четными с точки зрения земного резонанса являются, как правило, попе-
речные колебания. При продольных колебаниях запас демпфирования
для устранения земного резонанса получается значительно большим.
Поэтому для расчета земного резонанса одновинтового вертолета доста-
точно рассматривать лишь поперечные колебания (см. также § 5).
При рассмотрении поперечных колебаний следует учитывать три сте-
пени свободы:
1) боковое смещение центра тяжести вертолета;
2) поворот вертолета вокруг продольной оси (крен);
3) поворот вертолета вокруг вертикальной оси (рыскание).
Колебания вертолета, соответствующие этим трем степеням свободы,
вообще говоря, нельзя рассматривать как независимые. Так, например,
при боковом смещении центра тяжести вертолета возникают силы, вызы-
вающие крен и т. д.
Однако для одновинтового вертолета, у которого продольный раз-
мер фюзеляжа относительно велик по сравнению с его поперечными раз-
мерами (этого может не быть, например, для вертолетов соосной и попе-
речной схем), колебания рыскания оказываются слабо связанными с бо-
ковыми колебаниями вертолета и его вращением вокруг продольной оси.
Поэтому в первом приближении колебания рыскания для одновинтового
вертолета можно рассматривать как независимые. Кроме того, при коле-
баниях рыскания вертолета перемещения центра несущего винта в пло-
скости вращения относительно малы (по сравнению с поперечными
колебаниями), и поэтому колебания рыскания для одновинтового верто-
лета, как правило, не представляют опасности в части земного резонан-
са. Как мы увидим из дальнейшего (§ 5), такие колебания опасны для
вертолетов продольной и поперечной схем.
Таким образом, при рассмотрении поперечных колебаний одновин-
тового вертолета достаточно в первом приближении рассматривать фю-
зеляж как тело, имеющее две степени свободы:
1) боковое смещение центра тяжести вертолета;
2) поворот вертолета вокруг продольной оси (крен).
18 1578 273
При таких упрощениях задачу о собственных поперечных колебани-
ях вертолета можно свести к задаче о собственных колебаниях плоского
твердого тела, упруго закрепленного в своей плоскости (рис. 3. 16).
2. Боковая и угловая жесткости шасси. Центр жесткости
Пусть жесткое тело А, имитирующее фюзеляж вертолета, укреплено
на неподвижном основании с помощью системы пружин (рис. 3.16).
Выберем неподвижную систему координат усйг, направив ось соу по оси
симметрии тела, а ось CqZ — по оси горизонтальных пружин с’г.
Если к телу А приложить силу Рг, параллельную оси caz, на расстоя-
нии у от точки Со, то вследствие деформации пружин тело А переместится
в своей плоскости так, что его ось симметрии займет некоторое положе-
ние с'оу'. Обозначим через <р угол поворота оси симметрии тела (угол
крена), а через 7 смещение точки со (отрезок СоСоО-
Пусть пружины имеют линейные характеристики. Тогда, как извест-
но, всегда найдется такая точка приложения силы на оси соу (или такое
значение у), для которой
угловое смещение <р тела
будет равно нулю, т. е.
при приложении силы Р,
в этой точке тело получит
чисто поступательное сме-
щение (<р = 0). Назовем
такую точку центром же-
сткости системы аморти-
зации.
Если к телу А прило-
жить пару сил с момен-
том М, то тело получит
лишь угловое смещение—
поворот вокруг центра
жесткости.
Нетрудно видеть, что
для простейшей системы
амортизации, изображен-
ной на рис. 3. 16, центр
жесткости будет нахо-
диться в точке Cq. Положение центра жесткости системы амортизации
удобно характеризовать величиной расстояния е от центра тяжести с
тела до центра жесткости Cq.
Если к телу приложить силу Ру, направленную по оси симметрии
соу, то тело получит лишь поступательное смещение у вдоль оси соу. Так
как характеристики всех упругих элементов системы амортизации ли-
нейны, то силы Р2, Ру и момент пары М линейно связаны с соответствую-
щими смещениями у, г и ср тела А.
Пусть эта зависимость выражается формулами:
Ру=)Суу\ (2.1)
P^c.z-, (2.2)
М — с^. (2.3)
Будем называть величины су, сг и соответственно коэффициента-
ми вертикальной, боковой и угловой жесткости системы амортизации.
Упругие свойства системы амортизации полностью определяются че-
тырьмя параметрами: положением центра жесткости (е) и коэффициен-
тами жесткости су, сг и ст.
274
Для простейшей системы амортизации, изображенной на рис. 3. 16,
коэффициенты жесткости амортизации могут быть определены по фор-
мулам:
Cz^C'z\
с(---2с' а2,
f у ’
(2.4)
где с' и с’г — коэффициенты жесткости вертикальных и горизонтальных
пружин;
2а — расстояние между осями вертикальных пружин (колея
шасси).
Рис. 3.17. Различные схемы шасси:
а—пирамидальное; б—с вертикальными стойками
Конструкции шасси вертолетов бывают, в основном, двух типов:
1) пирамидальное шасси;
2) шасси с вертикальными стойками.
Соответствующие этим двум типам шасси схемы упругой амортиза-
ции изображены на рис. 3. 17, а и б.
Пневматики в такой схеме можно считать абсолютно жесткими, а их
упругость имитировать специальными пружинами с жесткостями с"" и с™',
соответственно равными вертикальной и боковой жесткости пневматика.
Коэффициент вертикальной жесткости пневматика может быть опре-
делен по диаграмме статического обжатия пневматика, которая всегда
имеется в каталоге колес и представляет собой отношение величины
силы, прижимающей пневматик к опорной поверхности, к величине соот-
ветствующего обжатия пневматика. Боковая жесткость пневматика, если
ее значений нет, может быть определена экспериментально. Значение бо-
ковой жесткости пневматика требуется также знать для проведения рас-
чета на шимми. Поэтому, если для данного колеса проводился расчет
шимми, то значение боковой жесткости известно. Для ориентировочного
определения боковой жесткости пневматика можно пользоваться также
табл. 3.1.
18* 275
Амортизационная стойка шасси на рис. 3.17, а и б также заменяется
некоторой пружиной с жесткостью сам. В действительности амортизаци-
онная стойка шасси является нелинейным
упругим элементом и ее характеристика
определяется диаграммой статического об-
жатия стойки, дающей зависимость силы Р,
действующей на стойку от хода s стойки.
При расчете малых колебаний стойку
можно заменять эквивалентным линейным
упругим элементом (пружиной), жесткость
которого определяется по формуле:
dP
с,|М
(2-5)
Таблица 3.1
Тип пневматика «н
Арочные 0,7-0,9
Полубаллон- ные 0,4—0,64
Высокого давления 0,3—0,4
ds |’-?ст
где £ст — стояночное обжатие
тора.
В системе шасси с вертикальными стойками (рис. 3.17,6) центр
жесткости амортизации всегда находится в точке с0, лежащей на поверх-
ности земли. Коэффициенты жесткости такого шасси определяются фор-
мулами (2.4), в которых с'г и с' соответственно равны:
амортиза-
/ч * - /1ПН.
Ст-с™
(2.6)
Для пирамидального шасси (рис. 3.41, а) центр жесткости всегда
находится выше поверхности земли и его положение надо вычислять по
специальным формулам, которые мы дадим ниже.
Пирамидальное шасси является частным случаем некоторой более
сложной системы шасси, разработанной английской фирмой Бристоль
[39] и изображенной (схематично) на рис. 3.18. Эта система шасси отли-
чается от пирамидального шасси наличием качалки АВ и специальной
горизонтальной пружины с жесткостью спр. В такой системе имеется воз-
можность менять высоту положения центра жесткости с0 (т. е. величи-
ну е) путем подбора определенной жесткости пружины спр- В частности,
подбором некоторого значения спр можно добиться положения, при кото-
ром центр жесткости системы амортизации совпадает с центром тяжести
вертолета. При этом, как будет видно из дальнейшего, отсутствует связь
между колебаниями крена и поперечными колебаниями вертолета, что
позволяет получить хорошие характеристики вертолета в отношении зем-
ного резонанса (см. § 4, п. 3).
Для системы шасси, изображенной на рис. 3. 18, можно записать сле-
дующие формулы, которые могут быть легко выведены обычными мето-
дами строительной механики:
(2-7)
(2-8)
(2.9)
276
i* = p j_/ =Л_/ Zl_ ।___
2 ‘ 2 2 caMZ2 c”H fl2/ ’
(2. 10)
где Ao — расстояние от поверхности земли до точки F пересечения осей
амортизационных стоек (см. рис. 3.18);
I— расстояние от оси амортизатора до точки А;
/1 — расстояние между точками F и Д;
/2 — расстояние от точки F до центра тяжести вертолета.
Рис. 3. 18. Схема шасси вертолета «Бристоль 192»
Приведенные формулы содержат в себе как частный случай форму-
лы для расчета пирамидального шасси (см. рис. 3.17,а). Для получения
формул пирамидального шасси следует в формулах (2.7) и (2.8) при-
нять СПр=100-
3. Собственные поперечные колебания вертолета
Обратимся опять к рис. 3.16. При изучении поперечных колебаний
будем рассматривать для тела А две степени свободы, соответствующие
координатам <р и z. Наложим дополнительное ограничение на движение
тела А, а именно: потребуем, чтобы точка ОЛ, принадлежащая телу Д
и отстоящая на расстоянии от центра тяжести тела, оставалась бы не-
подвижной. Тогда тело А будет иметь одну степень свободы — поворот
вокруг точки Ok. Уравнение собственных колебаний тела А, закрепленно-
го таким образом, будет иметь вид:
где 1О — момент инерции тела относительно точки Ок:
10к-^1с + та\- (2.12)
/(.—-момент инерции тела относительно центра тяжести;
т — масса тела.
277
Коэффициент cOft представляет собой угловую жесткость системы
амортизации при повороте тела А относительно точки Од. Величину cOk
легко определить, если известно положение центра жесткости с0 системы
амортизации, а также ее угловая сч и боковая сг жесткости.
При повороте тела на угол <р относительно точки Ok центр жестко-
сти сместится на величину
z=<p(tzft—е). (2.13)
При этом к телу в центре жесткости будет приложена сила
Pz = czz, направленная влево, и пара сил с моментом M = cv ф, направлен-
ным против часовой стрелки. Момент этих сил относительно точки Ok
M—Pz (a* - е) -J- стср = + сг (ак - е)2] <?.
Откуда получается следующая формула для угловой жесткости cOi _
= — <?)2. (2.14)
Частота собственных колебаний тела с закрепленной точкой Ofe
или
При колебаниях системы в точке Ofe будет возникать сила реакции Р,
зависящая от положения точки Oft. Если бы нам удалось подобрать та-
кую точку закрепления Ok (такое значение аь), для которой /? = 0, то это
означало бы, что такая точка Ок является узлом собственных колебаний
свободной системы с незакрепленной точкой Ok, а соответствующая час-
тота ph являлась бы частотой собственных колебаний свободной системы.
Сила реакции 7? может быть легко определена. При колебаниях
тело Л нагружено силой инерции Ри, приложенной в центре тяжести и па-
раллельной оси Oz,
Рн=— mze = — туа,.,
а также парой сил инерции. Силы от амортизации, приложенные к телу,
также сводятся к горизонтальной силе
Pz = czz=cztp(ak—е)
и паре сил. Поэтому, проектируя все силы, приложенные к телу на ось
ccz, получим
Р = Рг + Ри.
Если
<p = %COS pj,
то
Р=kг тр*ак] <р0 cos р^.
Приравнивая нулю это выражение, получим
278
Отсюда получается следующая формула, связывающая частоту соб-
ственных колебаний системы с положением узла колебаний:
(2.16)
где
Р2г=^- (2-17)
т
Исключая величину рь из уравнений (2.15) и (2.16), получим квад-
ратное уравнение для определения величины а^. Это квадратное урав-
нение всегда имеет два вещественных корня а, и а2, которые соответст-
вуют двум тонам собственных колебаний системы. Для каждого тона по-
лучается определенная частота рл собственных колебаний, которая
при известном аь может быть определена из формулы (2.16) или (2.15).
Для определения частот рь собственных колебаний и соответствую-
щих величин аъ. удобно все формулы привести к безразмерному виду,
введя обозначения:
(2.18)
рй=^; (2.19)
Рг
(2.20)
иге2
(2.21)
сге2
J В таких обозначениях окончательные формулы для определения
ак (6=1, 2) и ри (k—1, 2) можно записать в виде:
z+rVV+‘z- (2.22)
где
у — — (2-23)
?» = ]/1-^-; (при 6 = 1,2). (2.24)
г аР.
а . Для удобства расчета положений узлов собственных колебаний
S первого и второго тона и соответствующих частот колебаний на рис. 3.19
и 3.20 приведены графики, рассчитанные по формулам (2.22), (2,23)
Г и (2,24).
Меньшую из частот pi и р2 будем называть частотой первого тона
J колебаний, а большую — частотой второго тона. Узел колебаний перво-
го тона всегда находится ниже центра тяжести вертолета (ai>0), а узел
колебаний второго тона — выше центра тяжести (а2<0).
На рис. 3. 21 показаны характерные формы колебаний первого и вто-
рого тонов для одновинтового вертолета с пирамидальным шасси.
4. Определение коэффициентов демпфирования
Демпфирование колебаний (т. е. поглощение энергии при колебани-
ях), как правило, мало и для определения частот собственных колебаний
и положений узлов можно им пренебрегать (как это и сделано в п. 3).
279
Рис. 3.19. Графики для определения час-
тот собственных колебаний вертолета
Рис. 3.20. Графики для
определения положения
узлов колебаний
Рис. 3.21. Характерные формы колебаний первой и второго
тона
Р
Рис. 3.22.
Схема ли-
нейного
упругого
элемента с
демпфиро-
ванием
280
Демпфирование колебаний происходит, главным образом, в аморти-
зационных стойках шасси. Демпфирование в пневматиках может в пер-
вом приближении не приниматься во внимание.
Рассмотрим систему, изображенную на рис. 3. 16. Пусть вместо пру-
жин поставлены некоторые линейные упругие элементы с демпфирова-
нием. Такой элемент схематично изображен на рис. 3.22. Пусть сила Р,
действующая на этот элемент, и его смещение s (ход элемента) связаны
соотношением
P=cs-\-k^. (2.25)
Будем называть величины с и k соответственно коэффициентами
жесткости и демпфирования упругого элемента.
Обозначим коэффициент жесткости и демпфирования упругих эле-
ментов в системе, изображенной на рис. 3. 16, соответственно c'z, с , k'zt
k'*. Уравнение колебаний тела А относительно узла может быть запи-
сано аналогично выражению (2.11) в виде;
/ofe? + £o(® + co/P = 0, (2.26)
где величины 10к и cOfe определяются по формулам (2.12) и (2. 14), а ве-
личина kOk по формуле
kok = 2k’a'l-{-2k'z{ak — е)2. (2.27)
Назовем эту величину угловым коэффициентом демпфирования сис-
темы амортизации при вращении тела относительно узла колебаний Од.
Уравнение (2. 26) можно записать в виде:
^4-2«^ + р2?=0, (2.28)
где рь (k=l, 2) частота k-ro тона колебаний, а коэффициент демпфиро-
вания Лд определяется по формуле
(2-29)
Собственные колебания й-го тона вертолета могут быть приближен-
но описаны законом:
cos(/?/-H), (2.30)
где фо — начальный угол отклонения;
ф — фазовый угол.
Частота собственных колебаний ph может приближенно принимать-
ся равной частоте собственных колебаний й-го тона, подсчитанной без
учета демпфирования.
Для того, чтобы вычислить величины k' и k'z для конкретной систе-
мы шасси (см. рис. 3. 17, а и б) надо предварительно рассмотреть дейст-
вие так называемой системы амортизационная стойка — пневматик.
5. Совместное действие системы амортизационная стойка—пневматик
Рассмотрим систему шасси с вертикальными стойками (см. рис.
3.17,6). Система амортизатор — пневматик представляет собой две пру-
жины с жесткостями сам и с^н, соединенные последовательно.
* Как определять коэффициенты kz и ky , будет показано в п. 5 этого параграфа,
а также в пп. 1 и 2 § 3.
281
Рассмотрим работу такой системы в случае, когда амортизатор име-
ет демпфирование. Такая система изображена на рис. 3.23. Пусть амор-
тизатор имеет линейную характеристику, аналогичную выраже-
нию (2.25):
Лм==самзам-1-Лам^
дм ам ам I «и
(2.31)
Составив уравнения движения системы амортизатор — пневматик,
нетрудно показать, что при заданном гармоническом законе изменения ее
общего хода s с частотой р сила Р, действующая на амортизатор, выра-
жается формулой
P=caKBs+kaKS^-t,
(2. 32)
где Сокв и Аэкв — характеристики некоторого эквивалентно линейного
амортизатора обычного типа (рис. 3. 22) и могут быть определены по
стемы амортизационная стойка—пневма-
тик Таким образом, при расчете ко-
лебаний схема шасси с вертикаль-
ными стойками (см. рис. 3. 17, б) может быть заменена схемой, изображен-
ной на рис. 3. 16, в которой характеристики упругости и демпфирования
вертикальных пружин выбираются по формулам (2.33) и (2.34). При
^ам = 0 формула (2.33) дает значение сэкв, равное значению с', получае-
мому по второй из формул (2.6). Таким образом, при наличии демпфи-
рования формула (2. 6), вобще говоря, не верна. Однако для приближен-
ного расчета частот собственных колебании можно пользоваться форму-
лой (2.6) для определения с', так как значение ^экв» определенное по
формуле (2. 33), получается близким к значению су, найденному по фор-
муле (2.6). После того как найдена частота собственных колебаний р,
можно уточнить значение с'у с помощью формулы (2.33), а затем уточ-
нить и расчет частоты р.
Для точного расчета частот собственных колебаний можно пользо-
ваться методом последовательных приближений (практически достаточ-
но упомянутой выше поправки, эквивалентной первому приближению)
или применять следующий прием; задаваясь значениями с в интервале
г»
°ам '"ни
Сам +с^н
находить частоты собственных колебаний, а затем из формулы (2.33) по
заданному сэкв=</ находить соответствующее значение Аам- В результа-
те такого расчета можно построить график зависимости частот собст-
венных колебаний системы от йам. Расчеты показывают, что частоты
и формы собственных колебаний слабо зависят от величины Аам. Поэто-
му практически достаточно делать описанный выше приближенный рас-
чем с последующим однократным уточнением частот.
282
Для расчета коэффициента демпфирования пь (2.29) можно, прене-
брегая демпфированием пневматика, полагать в формуле (2.27):
0 ky ^экв-
В случае пирамидального шасси можно приближенно вычислить
демпфирование колебаний таким же способом, но при вычислении k3KB
в формулу (2. 34) вместо величин сам и kaM подставлять значения так на-
зываемых приведенных к пневматику жесткости и демпфирования амор-
тизатора с”₽ и , определяемых
по формулам:
(2. 35)
где I — расстояние от оси амортиза-
тора до точки А (см.
рис. 3. 18 и 3. 17, а) пересе-
чения осей нижних подко-
сов.
Рассмотрим подробнее зависи-
мость эквивалентного коэффициен-
та демпфирования kэкв системы
Рис. 3. 24. Зависимость эквивалентно-
го демпфирования от демпфирования
амортизатора
амортизатор — пневматик от величины k&n. На рис. 3. 24 показан график
этой зависимости. Как видно из этого графика, величина kaKS увеличи-
вается с увеличением йам лишь до некоторого определенного значения
^ам==^ам^ ПРИ котором достигается наибольшее демпфирование .
При дальнейшем увеличении йам демпфирование системы амортизатор —
пневматик уменьшается.
Из формулы (2. 34) легко получить выражение для оптимального
значения £°р‘:
(2.36)
г
При этом значении £ам формулы (2. 33) и (2.34) дают соответствую-
щие значения с°[В и kf™:
(2.37)
(2. 38)
Из последней формулы видно, что наибольшее значение кото-
рое можно получить, тем больше, чем меньше отношение и чем боль-
спн
ше Спи. Поэтому с точки зрения демпфирования поперечных колебаний
вертолета следует иметь по возможности более жесткий пневматик и как
можно менее жесткий амортизатор. При неправильном выборе характе-
ристик шасси (большей относительной жесткости амортизатора у? мо-
спн
жет случиться, что никаким увеличением демпфирования в амортизато-
ре нельзя устранить земной резонанс.
283
6. Приведение задачи к расчету винта на упругом основании
После того, как выполнен расчет собственных колебаний вертолета
на земле: определены частоты, положения узлов колебаний и коэффици-
енты затухания для обоих тонов собственных колебаний, можно произ-
вести приближенный расчет земного резонанса, сведя задачу к расчету
винта на упругом основании.
Можно было бы производить точный расчет земного резонанса, со-
ставляя уравнения движения лопастей винта и корпуса вертолета подоб-
но тому, как это делалось в § 1 для винта на упругом основании. В этом
случае порядок характеристического уравнения был бы тем выше, чем
больше степеней свободы вертолета на упругом шасси принимается во
внимание. Для каждого случая приходилось бы производить весьма гро-
моздкие вычисления.
Приближенный расчет, основанный на сведении задачи к винту на
упругом основании, позволяет пользоваться готовыми результатами, по-
лученными для винта на упругом основании. Точность такого расчета
вполне достаточна для практики.
Сущность приближенного расчета заключается в следующем; произ-
водится отдельный расчет земного резонанса для каждого тона собст-
венных колебаний вертолета на земле; при этом корпус вертолета рас-
сматривается как тело, имеющее одну степень свободы — поворот вок-
руг соответствующего узла колебаний.
Уравнение движения вертолета с закрепленным узлом колебаний
имеет вид:
+ + (2.39)
Правая часть этого уравнения представляет собой момент силы Р
от колеблющихся лопастей винта относительно узла колебаний рассмат-
риваемого тона. Величина h есть расстояние от плоскости винта до
центра тяжести вертолета.
Введем новую переменную x=tp(/z + afe), представляющую собой ве-
личину смещения центра несущего винта. Тогда уравнение (2.39) мож-
но переписать в виде, аналогичном уравнению (1.2) движения упругого
основания:
< Л + %квх+с^х=Р, (2.40)
где величины с*кв представляют собой массу, демпфирова-
ние и жесткость эквивалентного упругого основания и вычисляются по
формулам:
- /о* . 1с +
экв (а, + Л)2 (ak + Л)2 ’
kk - •
экв (afc + A)= ’
ck с°*
вкв (а» + Л)2'
Таким образом, задача сводится к расчету винта на эквивалентном упру-
гом основании, характеристика которого определяется по формулам
(2.41), (2.42) и (2.43).
Нетрудно убедиться, что при этом для расчета земного резонанса
по формулам § 1 требуются только три характеристики упругого основа-
ния т0 = такв, по = пк [см. (2.29)] и ро = Рк, которые получаются из рас-
чета собственных поперечных колебаний вертолета.
284
(2.41)
(2.42)
(2.43)
Таким образом, для каждого тона собственных колебаний вертолета
на упругом шасси производится приближенный расчет земного резонан-
са по формулам, выведенным для винта на упругом основании (§ 1).
При таком расчете могут быть определены границы зон неустойчивости
и величины коэффициентов демпфирования лопасти и шасси, необходи-
мые для устранения неустойчивости по каждому тону колебаний.
7. Анализ результатов расчета земного резонанса
Результаты расчета земного резонанса удобно представлять в виде
диаграммы безопасных оборотов. На рис. 3.25 показана такая диаграм-
ма для вертолета Ми-4. По оси абсцисс на диаграмме откладываются
числа оборотов в минуту несущего винта, а по оси ординат — сила тяги I
несущего виита.
Частоты колебаний вертолета на земле рассчитываются в двух ва-
риантах:
1) амортизационные стойки шасси работают;
2) амортизационные стойки не работают.
Рис. 3. 25. Диаграмма безопасных оборотов для вертолета Ми-4:
V]—-частота первого тона колебаний с неработающими стойками; л»2—частота второго
тона колебаний с неработающими стойками; и v* —частоты первого и второго
тона с работающими стойками
Это необходимо делать потому, что амортизационные стойки шасси
работают лишь тогда, когда сжимающее усилие на стойке больше так
называемого усилия предварительной затяжки амортизатора. Поэтому
при некотором (критическом) значении тяги Г=7’1(р несущего винта уси-
лие, сжимающее стойку, становится меньше усилия предварительной
затяжки амортизатора и стойка перестает работать. При Т>Ткр аморти-
зационные стойки ведут себя как жесткие стержни, и вертолет может ка-
чаться лишь вследствие упругости пневматиков, практически лишенных
демпфирования. Зоны неустойчивости вертолета с неработающими стой-
ками обычно устранить невозможно и они всегда имеются на диаграмме
безопасных оборотов (на рис. 3.25 эти зоны заштрихованы).
На диаграмме безопасных оборотов наносятся границы зон неустой-
чивости, а также область возможных значений тяги Т и оборотов п несу-
щего винта допустимых системой управления винтом и двигателем (сис-
темой шаг—газ). Если ни одна из возможных комбинаций значений Т
и п не попадает за границы зоны неустойчивости, то это означает, что
устойчивость вертолета обеспечена. При этом всегда желательно (под-
робнее см. § 6) иметь некоторый запас устойчивости, т. е. достаточные
расстояния на диаграмме между границами зон неустойчивости и грани-
цами возможных значений Т и п.
285
Для одновинтового вертолета с обычной конструкцией шасси (пира-
мидальное шасси или шасси с вертикальными стойками, см. рис. 3.17, а
и б) частота первого тона колебаний, как правило, получается ниже ра-
бочих оборотов винта (рис. 3.25), а частота второго тона—-выше рабо-
чих оборотов. Поэтому выбор коэффициентов демпфирования колебаний
должен гарантировать отсутствие зоны неустойчивости первого тона ко-
лебаний с работающими стойками. При этом надо иметь надежный за-
пас демпфирования. Запас устойчивости по отношению ко второму тону
колебаний может быть практически обеспечен лишь «по оборотам винта»,
и его можно характеризовать некоторой величиной tj:
(2.46)
Я шах
где /гшах —максимально возможные обороты винта;
/Zj —обороты, соответствующие нижней границе зоны неустойчиво-
сти второго тона.
§ 3. ХАРАКТЕРИСТИКИ ДЕМПФИРОВАНИЯ
ШАССИ И ЛОПАСТИ.
ИХ ВЛИЯНИЕ НА ЗЕМНОЙ РЕЗОНАНС
1. Определение коэффициента демпфирования амортизатора шасси
При расчете собственных колебаний вертолета мы предполагали, что
амортизаторы шасси имеют линейные характеристики. В действительно-
сти характеристики амортизационной стойки шасси, как правило, нели-
нейны. Однако для расчета малых колебаний вертолета можно (как это
обычно делается в теории нелинейных колебаний) заменять нелинейный
амортизатор некоторым эквивалентным линейным амортизатором, у ко-
торого коэффициенты жесткости и демпфирования зависят от частоты
и амплитуды колебаний. Для приближенного определения жесткости
эквивалентного линейного амортизатора была предложена формула
(2.5). Для определения коэффициента k демпфирования эквивалентного
линейного амортизатора можно также предложить простую формулу.
Эту формулу можно вывести, считая эквивалентным такой линейный
амортизатор, который поглощает за один период колебаний ту же энер-
гию, что и реальный амортизатор при одинаковых частоте и амплитуде
колебаний.
Наиболее распространенные конструкции амортизационных стоек
шасси поглощают энергию вследствие трения в уплотнении и гидравличе-
ского сопротивления при протекании гидросмеси через малые отверстия.
Если считать силу гидравлического сопротивления в такой аморти-
зационной стойке пропорциональной квадрату скорости, то зависимость
силы сопротивления Р стоики от скорости — ее обжатия может быть
di
выражена так:
где Ро — сила трения в уплотнениях, а <Г| и Сг — коэффициенты
лического сопротивления стойки на прямом и обратном ходах.
Пусть шток амортизатора совершает колебания по
, • ds ,
s—sosinpt и, следовательно, $=— = ps0cospz.
(3.1)
гидрав-
закону
286
функция P(t) задана
(3.3)
ds \
— поглощает при
dt /
Вычислим энергию, которую поглощает при этих условиях аморти-
затор за один период колебаний. Эта энергия определяется по формуле
т
A=^P(f)s(t)di-,
о
Вычисляя этот интеграл для случая, когда
уравнениями (3.1),получим:
Л=4Р0з0+-|-а/Л?з,
где
°1 + а2
2
Демпфер с линейным демпфированием {P=k
тех же условиях за один период колебаний энергию Ai=n£/2S0.
Сравнивая выражения для А и Alt получим следующую формулу
для определения коэффициента эквивалентного линейного демпфера:
= (3-4)
п \ps0 3 /
Таким образом, в реальной амортизационной стойке шасси величина
k3KB зависит от амплитуды So и частоты р колебаний, и с этим обстоятель-
ством необходимо считаться при расчете колебаний вертолета.
На рис. 3. 26 приведена зависимость величины ЛЭКв от амплитуды Яд
колебаний. С увеличением амплитуды кол'ебаний величина kaKB умень-
шается, достигает наименьшего значения при некоторой амплиту-
де Яд и при дальнейшем увеличении амплитуды возрастает.
Анализируя выражение (3. 4), нетрудно получить следующие форму-
лы для определения минимального значения и соответствующей
амплитуды $д колебаний штока:
(3. 5)
(3.6)
Из формулы (3.5) видно, что наименьшее демпфирование амортиза-
тора не зависит от частоты и амплитуды колебаний. Поэтому при гру-
бой оценке демпфирующей способности амортизации шасси весьма удоб-
но пользоваться формулой (3.5) и полагать при расчете системы
амортизатор—пневматик = При этом полезно также определить
и величину з* по формуле (3. 6).
В тех случаях, когда имеется возможность провести испытания го-
товых амортизационных стоек на демпфирование, такие испытания сле-
дует обязательно провести, так как предлагаемые формулы дают лишь
приближенные характеристики демпфирования.
Испытания на демпфирование можно проводить одним из двух ме-
тодов:
1) определение зависимости силы гидравлического сопротивления
от скорости движения штока;
2) определение энергии, поглощаемой амортизатором при гармони-
ческих колебаниях штока.
287
вившуюся скорость движения
Рис. 3. 26. Зависимость эквива-
лентного демпфирования для
амортизатора с сухим трением и
квадратичным гидравлическим
сопротивлением от амплитуды ко-
лебаний.
При проведении испытаний любым из этих методов, из амортизаци-
онной стойки должен быть стравлен воздух (или азот), так как при ис-
пытаниях следует определять лишь демпфирующие силы.
Испытания по первому методу можно проводить, измеряя устано-
штока амортизатора под действием по-
стоянной нагрузки при различных ее зна-
чениях.
При втором методе испытаний штоку
амортизатора сообщаются гармонические
колебания на специальном стенде с вра-
щающимся эксцентриком. При различ-
ных значениях амплитуды и частоты
(обороты эксцентрика) колебаний штока
измеряется переменное осевое усилие в
амортизаторе.
Для шасси с вертикальными стойка-
ми (рис. 3.17,6) следует проводить не-
посредственные испытания системы
амортизатор—пневматик. Такие испыта-
ния желательно проводить и для пирами-
дального шасси (см. рис. 3.17, а). При
этом можно испытывать амортизатор,
последовательно соединенный с пневма-
тиком по такой же схеме, как и в случае шасси с вертикальными стой-
ками, но подбирать для испытаний специальный однотипный с приме-
няемым на вертолете пневматик, жесткость которого выше, чем жест-
кость пневматика, соответствующего пирамидального шасси в п раз.
Число п вычисляется по формуле:
где Рам — усилие в амортизаторе при вертикальном усилии Р^н на пнев-
матике.
2. Эффект запирания амортизатора вследствие трения
в уплотнениях и автоколебания вертолета
Сила трения Ро в уплотнениях (манжетах) амортизатора практиче-
ски не зависит от скорости движения штока (3.1). Поэтому эффект тре-
ния в уплотнениях аналогичен эффекту так называемого сухого (или ку-
лонова) трения.
Этот эффект состоит в том, что при малых колебаниях, когда пере-
менное усилие Р<Р0, амортизатор не работает и ведет себя как жесткий
стержень. Поэтому при достаточно малой амплитуде колебаний вертоле-
та амортизаторы не работают и упругими элементами в системе шасси
оказываются лишь пневматики, практически лишенные демпфирования.
Если угловая скорость вращения винта лежит внутри зоны неустой-
чивости вертолета с неработающими амортизаторами, то положение
равновесия вертолета, вообще говоря, всегда неустойчиво и обязательно
возникают малые колебания вертолета с нарастающей амплитудой.
При увеличении амплитуды колебаний растет переменное усилие
в амортизаторе. При некоторой амплитуде колебаний а* усилие в амор-
тизаторе Р становится равным Ро. При больших амплитудах колебаний
а>а* усилие Р>Р0 и (если Т <Ткр) амортизаторы начинают работать.
Если демпфирование амортизации выбрано правильно, в системе
устанавливаются автоколебания с некоторой постоянной малой ампли-
тудой а, большей, чем а*.
288
Таким образом, для всякого вертолета внутри зоны неустойчивости
с неработающими стойками обязательно имеют место автоколебания,
обусловленные эффектом сухого трения в амортизаторах шасси.
Такие автоколебания ни в коем случае не следует смешивать с зем-
ным резонансом в обычном понимании этого термина. Автоколебания
безопасны и могут быть даже тогда, когда запас по земному резонансу
(в больших перемещениях) достаточно велик.
В наиболее распространенных конструкциях амортизаторов (в пнев-
могидравлических амортизаторах) трение в уплотнениях относительно
велико и оказывается, что при расчете амплитуды таких автоколебаний
можно учитывать лишь демпфирование, обусловленное этим трением,
и не учитывать силы гидравлического сопротивления в амортизаторе.
Причем при таком приближенном расчете амплитуда автоколебаний мо-
жет получиться лишь больше действительной.
Рис. 3.27. Схема последовательного соединения пнев-
матика и амортизатора с сухим трением:
1 и 2—пружины,- 5—поршень
Для оценки амплитуды автоколебаний можно получить некоторые
простые формулы.
Рассмотрим систему, состоящую из двух последовательно соеди-
ненных пружин 1 и 2, одна из которых с жесткостью с^н имитирует пнев-
матик, а другая с жесткостью саЛ1—амортизатор (рис. 3.27). Парал-
лельно с пружиной 2 соединен некоторый элемент (поршень 3) с сухим
трением, характеризуемым силой Ро.
.Пусть под действием силы Р(/), меняющейся во времени по некото-
рому закону, система совершает колебания так, что точка А, смещение
которой обозначим через s, совершает гармонические колебания
s = s0cospt. (3.7)
Если амплитуда 50 невелика, то пружина 2 пе работает, а пружина 1
имеет деформацию sl=s, меняющуюся по гармоническому закону (3.7).
При этом сила Р также меняется по гармоническому закону
p = fnH-socosPz-
Но такая работа системы будет лишь при условии Рт.а<^Р0, а следо-
Р Рг>
вательпо, при условии $0<^—При работает пружина 2. При
спн ^пн
этом имеются некоторые промежутки времени, когда пружина 2 рабо-
тает (проскальзывание в элементе 3), и промежутки времени, когда
пружина не работает.
Пусть 6 = s—Si есть деформация пружины 2, которую будем считать
положительной, если пружина 2 сжимается. Тогда зависимость сжимаю-
щей силы Р от величины 6 может быть записана в форме:
р=к>Ж> если ®>°; (3<8)
(сам8 — Ро, если &<0.
При колебательном движении зависимость Р = Р(6) имеет вид петли
гистерезиса (рис. 3. 28).
19 1578 289
Когда величина 6 достигает наибольшего значения а и остается после
этого постоянной (б = а), сила Р может принимать любое значение в ин-
тервале сйма—Р<Р<сыа-\-Р0.
Зависимость б(/) для промежутков времени, соответствующих про-
скальзыванию (д=Н=О), может быть определена из уравнения
(«о cos Р* - а)=сам8 ± Ро,
которое выражает равенство сил на обоих элементах 1 и 2.
Рис. 3.28. Петля гистерезиса
для амортизатора с сухим
трением
Из этого уравнения находим 6(1) для участков проскальзывания:
Ро
8 V) = ?и5° cos pt ± .
спн+ Сам спи + йам
Для участков, где проскальзывание отсутствует, 6 =+а.
На рис. 3.29 изображены графики, показывающие, как меняются
во времени величины s(Z), б(/) и Р(/) для случая сам = с^н и s0 = 2 -у.
епн
Величина амплитуды а колебаний штока амортизатора может быть най-
дена из выражения для б(/), если в нем положить cos pt=l. При этом
получится:
а С *0 - ро
спн + сам
(3.9)
Работа, которую производит при колебаниях сила трения, может
быть определена по формуле
Др0 = 4 Pffl.
Будем сравнивать систему, изображенную на рис. 3.27 с некоторым
эквивалентным линейным амортизатором, который при той же амплиту-
де штока Sq поглощает ту же работу и имеет то же значение наибольшего
УСИЛИЯ Ртах.
Приравнивая выражение работы линейного амортизатора
(4 = лйЭкв P$fy работе силы трения Дополучим следующее выражение
290
для коэффициента демпфирования &экв эквивалентного линейного амор
тизатора:
£
Л
^экв
Р (спн + Сам )
(3. 10)
где т] — некоторый безразмерный коэффициент, зависящий от амплитуды
колебаний s0 и определяемый формулой
1
Л=—
so
4- (ПРИ «о
5 4
(3.11)
(3. 12)
Выражение для жесткости сэкв эквивалентного линейного аморти-
затора получим, сравнивая значения наибольшего усилия для линейного
(Ртах = Сэкв$о) и нелинейного [^тах=с^н(5о—Я)] амортизаторов:
Сам Р 0
С ____пи 0 (3 IS''
экв 1 ПП - • 1 '
Сам -
спн
На рис. 3. 30 изображена зави-
симость величины от безразмер-
ной амплитуды колебаний Sq. Вели-
чина г] достигает наибольшего зна-
чения T]max=Y ПРИ ^о = 2. при
s0>2 демпфирование убывает с ро-
стом амплитуды колебаний.
Наибольшее значение —
Рис. 3. 30. Зависимость безразмерно-
го коэффициента демпфирования т]
от относительной амплитуды колеба-
ний s0
получается равным:
Ьтах 1__________(Сп«)
Э“ я ₽(4 + с«м) ’
(3.14)
Сравнивая это значение с значением , полученным для линейной
системы амортизатор — пневматик [см. формулу (2.38)], видим, что
амортизатор с сухим трением в системе с пневматикой дает при тех же
условиях наибольшее демпфирование, в л/2 раз меньшее, чем линейный
амортизатор.
Таким образом, амплитуда автоколебаний вертолета, обусловленных
трением в уплотнениях амортизаторов, может быть найдена из условия
(3.10):
£пптр =йэкв
(О2
Р (син Т сам )
£
Л
п.
где Апот₽ — демпфирование, потребное для устранения земного ре-
зонанса.
Из этого уравнения определяется соответствующее значение т], а за-
тем по графику на рис. 3. 30 соответствующее значение $0.
19*
291
3. Характеристики демпферов лопасти и их анализ
При изложении методов расчета земного резонанса мы предполага-
ли, что демпферы вертикальных шарниров лопастей имеют линейные ха-
рактеристики, т. е., что момент демпфера М пропорционален угловой
скорости g вращения лопасти относительно вертикального шарнира:
В действительности характеристики демпферов лопасти, как прави-
ло, нелинейны. Употребляются в основном демпферы двух типов:
1) гидравлические демпферы;
2) фрикционные демпферы.
Гидравлические демпферы могут иметь различные характеристики
в зависимости от конструкции. В частности, гидравлический демпфер мо-
жет быть и линейным (так называемый ламинарный демпфер, характе-
ристика а на рис. 3. 31). Однако линейные демпферы применяются край-
не редко, так как имеют серьезные недостатки.
Рис. 3.31. Типовые характеристики демпферов лопасти:
я—линейного демпфера; б—фрикционного демпфера; в—ступенчатого демпфера
Одним из таких недостатков является большая чувствительность
линейных демпферов к температуре, которая объясняется тем, что демп-
фирование в них пропорционально вязкости гидросмеси, сильно завися-
щей от температуры.
Другим недостатком линейных демпферов является то, что момент
такого демпфера пропорционален частоте колебаний лопасти. В самом
деле, если лопасть совершает гармонические колебания относительно
вертикального шарнира g=gosinv?, то момент линейного демпфера при
этом меняется по закону Л1 = ^л§ = т/гл§0 cos vt.
Это обстоятельство приводит к тому, что при поступательном поле-
те вертолета линейные демпферы нагружают комлевую часть лопасти
большими изгибающими моментами, так как частота колебаний лопасти
в полете примерно в четыре раза выше, чем при земном резонансе.
Этот недостаток в значительной степени устранен у наиболее широко
применяемых гидравлических демпферов со ступенчатой характеристи-
кой (см. рис. 3.31, е), а также у фрикционных демпферов (см. рис.
3.31, б). Точка А на характеристике ступенчатого демпфера соответству-
ет моменту открытия специальных клапанов.
Характеристика фрикционного демпфера (см. рис. 3.31,6) может
рассматриваться как частный случай ступенчатой характеристики.
Для расчета земного резонанса вертолета с нелинейными демпфе-
рами лопастей последние могут быть заменены некоторыми «эквивалент-
ными» линейными демпферами, коэффициент демпфирования которых
зависит от амплитуды и частоты колебаний лопасти. Коэффициент Лэкв
такого эквивалентного линейного демпфера может быть определен из
условия поглощения, этим демпфером при данной амплитуде и частоте
гармонических колебаний такой же энергии за один период колебаний.
292
какую поглощает при тех же условиях нелинейный демпфер. Для фрик-
ционного демпфера
^кв=— (3.15)
л vCo
где Мо—момент затяжки демпфера (см. рис. 3.31,6);
£о — амплитуда колебаний лопасти;
v — частота колебаний лопасти.
По этой же формуле можно приближенно определять значение Аэкв
для гидравлических демпферов со ступенчатой характеристикой, если по-
следняя близка к характеристике фрикционного демпфера.
В общем случае величина /?8КВ может быть определена по известной
характеристике нелинейного демпфера с помощью формулы
т
*) = —Ц- fw)^
при
?=^sin vt и /= —.
V
Для готового демпфера величина
/?жв может быть определена также экс-
периментально путем специальных ла-
бораторных испытаний. При таких испы-
таниях штоку демпфера сообщаются
гармонические колебания, и производит-
ся запись на осциллограмму величины
момента демпфера.
Основным недостатком демпферов
со ступенчатой характеристикой и, в
частности, фрикционных демпферов явля-
(3. 16)
Рис. 3.32. Зависимость работы,
поглощаемой за один период ко-
лебаний, от амплитуды для демп-
фера с сухим трением и демпфера
с линейной характеристикой
ется наличие у вертолета с такими демпферами так называемого поро-
га возбуждения. Вертолет, будучи устойчивым при малых амплитудах
колебаний, может стать неустойчивым при больших амплитудах колеба-
ний, превосходящих порог возбуждения.
Рассмотрим это явление на примере фрикционного демпфера. На
рис. 3.32 показаны зависимости работы А, поглощаемой за период коле-
баний фрикционным (кривая а) и линейным (кривая Ь) демпферами от
амплитуды колебаний S,j лопасти (при неизменной частоте колебаний).
Для фрикционного демпфера график A (g0) представляется прямой лини-
ей, а для линейного демпфера параболой. Пусть в результате расчета
земного резонанса было определено значение й™т₽ потребного демпфи-
рования лопасти в случае линейного демпфера и кривая а на рис. 3. 32
соответствует этому значению kn, а кривая b соответствует располагае-
мому демпфированию фрикционного демпфера, фактически имеющегося
па вертолете.
Пусть эти кривые пересекаются в некоторой точке с, соответствую-
щей амплитуде Тогда при колебаниях лопасти с амплитудой £o<g*
демпфирование, обеспечиваемое фрикционным демпфером, будет боль-
ше потребного, а при колебаниях лопасти с амплитудой демпфи-
рование будет недостаточным. Амплитуда колебаний и представляет
собой порог возбуждения. Значение может быть определено из фор-
мулы (3.15):
?* _£.
0 л vA^0TP‘
293
Таким образом, если вертолет получил какое-либо возмущение (тол-
чок), в результате которого начались колебания (и вертолета, и лопас-
тей), то, если амплитуда колебаний лопастей меньше go, движение бу-
дет устойчивым — колебания затухнут. Если же возмущение достаточно
велико > т0 возникнут нарастающие колебания вертолета.
Наличие порога возбуждения у вертолетов с демпферами лопастей,
имеющими ступенчатые характеристики, является серьезным недо-
статком.
На практике было немало случаев, когда на вертолете, уже давно
находящемся в эксплуатации, возникал земной резонанс в результате ка-

кого-либо сильного толчка, чаще
всего в результате грубой посадки с
ударом о землю одним из колес
основного шасси.
Этот основной недостаток не-
Рис, 3.33. Схема элемента, в кото-
ром упругий элемент и демпфер со-
единены последовательно
линейных демпферов может быть
полностью устранен лишь при при-
менении демпферов, обеспечиваю-
щих большое демпфирование при
низких частотах колебаний (земной
резонанс) лопасти и малое демпфирование при частоте колебаний, рав-
ной оборотам несущего винта (и выше). Такой демпфер может быть,
в частности, и линейным. На рис. 3. 33 изображена схема такого линей-
ного демпфера. Демпфер состоит из последовательно соединенных упру-
гого элемента с жесткостью с и собственно демпфера с коэффициентом k.
Характеристики k и с этого демпфера можно выбрать таким обра-
зом, чтобы, обеспечив достаточное демпфирование при земном резонансе,
иметь малые изгибающие моменты на лопасти при поступательном по-
лете вертолета (см. § 6). Для расчета такой элемент может быть заме-
нен некоторым эквивалентным элементом с жесткостью сэкв и коэффи-
циентом демпфирования /гЭКв, определяемыми по формулам
(3. И)
Эти формулы получаются аналогично формулам (2.33) и (2.34).
4. Влияние махового движения винта на земной резонанс
Как уже было сказано, применяемые обычно демпферы лопастей не-
линейны. Основная особенность всякого нелинейного демпфера состоит
в том, что если движение лопасти состоит из двух гармонических состав-
ляющих, то демпфирование одной из этих составляющих зависит от ам-
плитуды и частоты другой гармонической составляющей, в то время как
линейный демпфер поглощает энергию каждой из гармонических состав-
ляющих независимо от величины другой.
Этой особенностью нелинейных демпферов объясняется следующее
важное явление, давно замеченное при испытаниях вертолетов. При ра-
боте вертолета на земле иногда бывает возможно вызвать земной резо-
нанс плавным отклонением ручки управления циклическим шагом от
нейтрального положения. Причем, если затем достаточно быстро убрать
ручку в нейтральное положение, то колебания затухают. Этим явлением
весьма удобно пользоваться при экспериментальной проверке вертолета
294
на земной резонанс. Это явление аналогично эффекту влияния махового
движения на флаттер. Рассмотрим механизм этого явления для случая
фрикционного демпфера (см. рис. 3. 31, б).
Возьмем сначала следующую отвлеченную задачу. Пусть по некото-
рой плите В (см. рис. 3. 34), совершающей в горизонтальном направлении
гармонические колебания по закону r/ = r/osin at, равномерно скользит со
скоростью V некоторое тело А.
Тело А прижато к колеблющейся плите В некоторой нормальной
силой N. Будем считать, что трение между поверхностью тела А и пли-
той В соответствует идеальному закону сухого трения, т. е. сила тре-
ния по величине постоянна и равна Ро — где ц-- коэффициент
трения скольжения.
Направление силы трения за-
висит от направления относительной
скорости тела А относительно пли-
ты В.
Рис. 3.35. Закон изменения во време-
ни относительной скорости и силы
треиия при равномерном движении
тела по вибрирующей плите
у = у0 sin wt
Рис. 3. 34. Схема движения тела по плите,
вибрирующей в горизонтальном направле-
нии.
Будем считать силу Р трения, приложенную к плите, положитель-
ной, если она направлена против абсолютной скорости тела А, т. е. впра-
во. Смещение у плиты В будем считать положительным, если оно на-
правлено влево. Тогда закон трения можно записать так:
р=Нро при V>t/;
I — Ро при V <у.
Для относительной скорости движения плиты имеем выражение:
^отн = У -- У = V - “i'o cos 0)Л
На рис. 3.35 изображен график этой зависимости. Относительная
скорость как функция времени изображается косинусоидой, сдвинутой
на величину V по оси ординат.
Из графика видно, что при Бг<Г<зэг/0 в течение одного периода Т коле-
баний промежуток времени (Т—2Т]), в течение которого Vотн ПОЛОЖИ'
тельна, больше промежутка времени 271], в течение которого Б0Тн отрица-
тельна. Под этим графиком изображен соответствующий график зави-
симости силы трения Р от времени^ В течение одного периода колебаний
на некотором промежутке времени 2Т} сила трения направлена влево
(отрицательна), а на промежутке времени (Г—2TJ, сила трения направ-
лена вправо против движения.
Таким образом, при движении тела А (см. рис. 3.34) по колеблю-
щейся плите В сила трения периодически меняет свое направление, если
только V<^ay0. При этом большую часть времени сила трения направле-
на против движения и, следовательно, в среднем трение оказывает со-
противление движению тела А.
295
I
Для того чтобы осуществлять равномерное движение тела А влево,
к нему нужно прикладывать переменную во времени силу, которая
в каждый момент времени уравновешивала бы силу трения. Вычислим
среднее за период значение Рср этой силы, понимая под этим такую по-
стоянную силу, которая за один период колебаний производит на абсо-
лютном перемещении тела А такую же работу, как и фактическая сила
трения. Если бы масса тела А была бесконечно велика и можно было бы
пренебречь вибрациями тела А, а также считать его движение по виб-
рирующей плите равномерным, то сила Рср представляла бы собой фак-
тическую силу, необходимую для равномерного движения тела А.
Работа осредненной силы за один период колебаний плиты будет
равна;
^ср = РсрРД •
♦
Работа, производимая за один период силой трения, будет равна: ;
Дтр= P0V{T_27’1]-P0V[2T1] = P0V[T-iT{\.
Приравнивая эти два значения работы ЛтриАср, получим следующее 1
выражение для осредненной движущей силы:
т
Для определения значения заметим, что
... v
cos <AJ\ —— .
“>Уо
2тс
Отсюда, учитывая, что Т =— , получаем
й)
7, 1 ( V \
—L=— arc cos ----- .
Т 2rt \ йн/о /
Следовательно,
г> п Гт 2 I V
L Я \o>//0/J
Полученное выражение справедливо лишь при условии, что У-Дсог/0.
Если же Vy>wyo, то сила трения не меняет ни величины, ни знака, оста-
ваясь равной Ро. Учитывая сказанное и вводя безразмерную осреднен-
Др
ную силу Рср= — , получим для последней следующее выражение:
Р о
f. 2 (V \ .
_ р 1-------------arc cos — , если V < »z/0;
р — _5Р — я \иу0/ (3.18)
СР р
(1, если Г>шг,-0.

На рис. 3.36 изображен график зависимости величины Рср от без-
_ v
размерной скорости движения V= — .
и’У(> _
При малой относительной скорости V движения плиты можно поль-
зоваться упрощенной линейной зависимостью РСр(Е), которая получает-
ся, если в разложении arc cos V в ряд по степеням V ограничиться двумя
первыми членами. При этом
р __ 2 V
‘ Ср-------
Я
296
Таким образом, при медленном движении тела по быстро вибрирую-
щей плите осредненную силу трения можно приближенно считать про-
порциональной первой степени скорости:
Рср=ЛквУ, (3.19)
где коэффициент пропорциональности
‘L ро .
Л tof/o
(3.20)
Из сказанного видно, что при рассмотренных условиях сухое трение
в известном смысле эквивалентно линейному вязкому трению, причем
эквивалентный коэффициент демпфирования обратно пропорционален
частоте и амплитуде вибраций плиты. Это важное обстоятельство было
впервые обнаружено Гейнрихом [41] и
проверялось экспериментально Красов-
ским А. А. [14].
Очевидно, что при медленных гармо-
нических колебаниях тела А по быстро
вибрирующей плите В можно также
приближенно вычислять демпфирование
этих колебаний, пользуясь формулами
(3. 19) и (3.20).
Таким образом, если в элементе с
сухим трением относительное движение
Рис. 3. 36. Зависимость относи-
тельной осредненной силы тре-
ния от безразмерной скорости
движения тела по вибрирую-
щей плите
трущихся поверхностей представляет со-
бой сумму двух гармонических колеба-
ний: одного низкочастотного и другого
высокочастотного, то демпфирование
низкочастотных колебаний можно при-
ближенно вычислять, пользуясь форму-
лами (3. 19) и (3.20), понимая под со и r/о соответственно частоту и ам-
плитуду другой (высокочастотной) гармонической составляющей.
Вернемся теперь к рассмотрению колебаний лопасти вертолета,
снабженной фрикционным демпфером, относительно вертикального шар-
нира. При отклонении ручки управления циклическим шагом лопастей
при работе вертолета на земле возникает маховое движение лопастей
винта относительно горизонтальных шарниров. Как известно, при этом
угол р взмаха лопасти меняется во времени по гармоническому закону:
Р = а0 —^cosW —sin и/,
где а0 — угол конусности;
аг и й] — коэффициенты махового движения.
При маховом движении лопасти возникают кориолисовы силы, вы-
зывающие колебания лопасти относительно вертикального шарнира.
Амплитуда первой гармоники gj колебаний лопасти относительно вер-
тикального шарнира может быть определена по известной формуле *:
1— Vq
(3.21)
Как уже было выяснено в § 1 и 3, при земном резонансе (в случае
/2л„=0) лопасти совершают колебания с частотой vqco (vo~O,25), т. е.
в частотой примерно в четыре раза более низкой, чем частота вынужден-
* См„ например, А. Гессоу и Г. Мейерс, Аэродинамика вертолета, Оборон-
гиз, 1964.
297
них колебаний лопасти, вызванных маховым движением. Поэтому в со-
ответствии с изложенным демпфирующий момент, действующий на ло-
пасть при земном резонансе, можно приближенно вычислять по фор-
муле:
= (3.22)
где kSK1~—M±. (3.23)
Величина представляет собой момент затяжди фрикционного
демпфера (см. рис. 3.31,6).
Таким образом, вынужденные колебания в плоскости вращения ло-
пасти с фрикционным демпфером, обусловленные маховым движением
лопасти в плоскости тяги, приводят к эффекту, эквивалентному введению
линейного демпфера в вертикальном шарнире, коэффициент демпфиро-
вания которого (3. 23) обратно пропорционален амплитуде gi вынужден-
ных колебаний лопасти относительно вертикального шарнира. Поэтому
все, что было сказано о пороге возбуждения вертолета с фрикционными
демпферами (п. 3), справедливо лишь в случае, когда отсутствует махо-
вое движение лопастей. Это обычно имеет место при работе винта на ма-
лых оборотах. Следовательно, порог возбуждения следует оценивать для
земного резонанса по первому тону. Формулой же (3.23) следует поль-
зоваться для оценки земного резонанса при наличии махового движения
винта (при рабочих оборотах винта). Это особенно важно при расчете
земного резонанса вертолета на пробеге, которому посвящен § 4.
§ 4. ЗЕМНОЙ РЕЗОНАНС ВЕРТОЛЕТА НА ПРОБЕГЕ
При изложении методов расчета собственных поперечных колеба-
ний вертолета на земле (§ 2) предполагалось, что отсутствует качение
пневматика по поверхности земли.
При качении пневматика его боковая жесткость уменьшается, а вер-
тикальная жесткость остается неизменной. Уменьшение боковой жестко-
сти пневматика при качении, а также некоторое дополнительное демпфи-
рование при боковых смещениях катящегося пневматика могут быть оп-
ределены на основе существующей теории шимми ориентирующихся ко-
лес. В этом разделе дается метод такого расчета.
Уменьшение боковой жесткости пневматика при качении (уменьше-
ние величины ^н,см. рис. 3.17) приводит к снижению частот собственных
колебаний первого и второго тонов, а следовательно, и к снижению гра-
ниц соответствующих зон неустойчивости. Как уже указывалось выше
(§ 2, п. 7), обычно для одновинтовых вертолетов зона неустойчивости, со-
ответствующая второму тону колебаний, находится выше рабочих обо-
ротов винта, причем запас по оборотам винта составляет иногда не более
30%. Снижение зоны неустойчивости при качении пневматика может со-
ставлять величину порядка 20—30%. Поэтому может оказаться, что вер-
толет, устойчивый при работе на месте, становится неустойчивым на
пробеге. В этом случае можно говорить о критической скорости движения
вертолета по земле, при которой движение становится неустойчивым.
1. Жесткость и демпфирование пневматика при качении
Рассмотрим пневматик, который равномерно катится по земле
(рис. 3.37). Пусть при этом колесо совершает поперечные колебания по
гармоническому закону так, что ось вращения колеса остается все время
параллельной своему начальному положению, а расстояние от оси до
земли остается неизменным.
298
Выберем неподвижную прямоугольную систему координат zOs, ле-
жащую на поверхности земли, причем ось Oz направим параллельно оси
колеса. Пусть боковое смещение z диаметральной плоскости колеса из-
меняется во времени по гармоническому закону*:

(4. 1)
где z0 — амплитуда колебаний;
ю—угловая частота колебаний.
Определим боковую силу Pz, приложенную к пневматику со стороны
земли при таком его движении..
Пусть X—боковая деформация пневматика, т. е. расстояние между
диаметральной плоскостью колеса и точкой пневматика, которая была
центром площадки контакта до боковой деформации. Тогда боковая сила
Рг будет равна:
Рг=с™л, (4.2)
где с”я — боковая жесткость пневма-
тика при отсутствии качения.
Пусть далее s — путь, отсчиты-
ваемый по линии качения, а <р—
угловая деформация пневматика,
т. е. угол между линией пересечения
диаметральной плоскости колеса с
поверхностью земли и касательной
к материальной линии, принадлежа-
щей поверхности пневматика и
представляющей собой линию пере-
сечения диаметральной плоскости
колеса с поверхностью недеформи-
рованного пневматика.
Величины z, X и ф связаны так
называемыми условиями качения,
которые в соответствии с гипотезой
М. В. Келдыша [15] имеют вид:
dz .d'K )
—=ч> Н— ;
ds ds
(4.3)
dy
ds
Рис. 3. 37. Вид в плане на площадку
контакта и линию качения пневма-
тика:
<р—угловая деформация пневматика; V-
боковая деформация пневматика («увод»)
Здесь аир некоторые постоянные для данного пневматика величи-
ны, которые могут быть найдены опытным путем.
Переходя к производным по времени t и учитывая, что s=Vt (где
V—скорость движения пневматика в направлении оси Os), получим:
dz , z , dK
dt ‘ 1 dt
(4-4)
Полагая
dt

и
(4.5)

* Имеется в виду, что действительное смещение есть вещественная часть ука-
занного комплексного выражения. Применение комплексных выражений при выводе
основных формул позволяет значительно упростить выкладки.
299
и учитывая (4.1), получим из уравнений (4.4) следующие уравнения для
определения постоянных и <р0:
V 0 =i®z0;
-J- ₽V) <po — «VX0 = 0.
Откуда
X
° aV2
/ш -К ------
(4-6)
Подставляя найденное значение Хо в первую из формул (4, 5), а затем
в (4.2), получим следующее выражение для силы Рг, действующей на
пневматик со стороны земли:
Рг = Рое^, (4.7)
где
1<л 4- рУ
Назовем комплексную величину
D (со) = %-=----------------- (4.8)
za г '
/со 4-------
/со + &V
боковой комплексной динамической жесткостью пневматика при попе-
речных гармонических колебаниях колеса.
Модуль комплексной динамической жесткости представляет собой от-
ношение амплитуды Ро боковой силы к амплитуде колебаний диамет-
ральной плоскости колеса. Аргумент комплексной величины £)(ш) пред-
ставляет собой фазу колебаний силы Рг по отношению к колебаниям z
колеса.
Рассмотрим далее некоторый линейный упругий элемент с демпфи-
рованием (см. рис. 3.22). Сила Р, действующая на этот элемент, и его
деформация s (ход элемента) связаны соотношением (2.25):
, ds
P = CS \-k----
di
Введем понятие комплексной динамической жесткости такого эле-
мента и установим, как оно связано с коэффициентами с и к его жестко-
сти и демпфирования.
Пусть смещение s упругого элемента меняется во времени по гармо-
ническому закону $ = Тогда сила, действующая на этот элемент,
будет меняться также по гармоническому закону:
Р = (с ф- fak)
или
P^poeiat,
где
P0=(c-[-i<»k)s0.
Назовем величину
D (®)=с + fak (4.9)
комплексной динамической жесткостью упругого элемента с демпфиро-
ванием. Как видно из выражения (4.9), вещественная часть комплекс-
ной величины 7D (со) представляет собой коэффициент с жесткости пру-
300
жины, а мнимая — коэффициент k демпфирования элемента, умножен-
ный на о.
Для того чтобы рассчитать собственные колебания вертолета на зем-
ле в соответствии со схемой, изображенной на рис. 3.16, надо правильно
выбрать характеристики упругости и демпфирования элементов с'г и с' .
Очевидно, что для расчета колебаний вертолета на пробеге доста-
точно так подобрать горизонтальные упругие элементы (с™ на рис.
3.17), чтобы их комплексная динамическая жесткость была равна комп-
лексной боковой жесткости пневматика при качении. Коэффициенты
жесткости и демпфирования, подобранного таким образом «эквивалент-
ного» упругого элемента, могут быть определены соответственно как ве-
щественная и мнимая части комплексной величины D(го), которая выра-
жается формулой (4.8).
Отделяя в выражении (4.8) вещественную и мнимую части, по-
лучим:
(4- Ю)
(4.11)
Полученные формулы сравнительно сложны и требуют знания
постоянных пневматика аир.
Формулы для определения сЭКЕ и k3KB мог^т быть значительно упро-
щены, если вместо условий качения М. В. Келдыша воспользоваться так
называемой гипотезой «увода», в соответствии с которой боковая дефор-
мация пневматика /. («увод») связана с угловой деформацией пневмати-
ка <р простым соотношением
(4.12)
В е 1 ,
где т)= —— так называемый коэффициент «увода»,
а
Как показано в работе М. В. Келдыша [15], этот коэффициент при-
ближенно равен радиусу г недеформированного пневматика
Ц—'—
а
(4. 13)
(г—расстояние от оси пневматика до земли при отсутствии обжатия).
При такой гипотезе первое из условий (4.4) дает:
dz V ,। rfX
dt т] dt
Полагая, как и раньше
z — zaeiat\
получим:
1 uq
Р(«>)=^а-=сп=------(4.14)
1+П2
\шп /
301
Рис. 3.38. Зависимость относительных боко-
вой жесткости и бокового демпфирования
пневматика от скорости движения вертолета
по земле м = 18
\ сек
Рис. 3.39. Зависимость относительных боковой жестко-
сти и бокового демпфирования пневматика от безраз-
мерной скорости движения вертолета по земле
302
Отделяя в этом выражении вещественную и мнимую части, получим
следующие выражения для коэффициентов жесткости и демпфирования
эквивалентного упругого элемента:
(4.15)
1 + U
С”)
1+ ~
\П“ /
Упрощенные формулы (4. 15) и (4. 16) более удобны для практиче-
ских расчетов и не требуют знания постоянных пневматика аир. Точ-
ность приближенных формул вполне достаточна для практических целей.
Это иллюстрируется сравнительными графиками на рис. 3.38, которые
получены в результате расчетов, выполненных для колес основного шас-
си вертолета Ми-1 (а=18— соответствует частоте второго тона ко-
сей
лебаний) по теории Келдыша и по теории увода.
Таким образом, при проведении расчетов собственных колебаний
вертолета на пробеге целесообразно применять формулы (4.15) и (4.16).
При этом в формулы вместо со надо подставлять частоту р поперечных
колебаний вертолета. На рис. 3.39 приведены графики зависимости без-
размерных боковой жесткости = сдав'и демпфирования
I с" I
\ z / \cz
от безразмерной относительном скорости 7 = —= — движения. Как вид-
рг
но из графика, боковая жесткость пневматика очень сильно зависит от
скорости движения вертолета. При 7=3 (что для пневматика вертолета
Ми-1 при р= 18 — составляет примерно 50 км1час'\ боковая жесткость
сек
пневматика в 10 раз меньше, чем для неподвижного пневматика.
2. Расчет земного резонанса и его результаты
Расчет земного резонанса на пробеге может быть произведен так же,
как и в обычном случае (§ 2), но значения боковой жесткости с™ пнев-
матика при расчете собственных колебаний должны быть заменены зна-
чениями сэкв, вычисляемыми по формуле (4.15), а при определении ко-
эффициентов демпфирования собственных колебаний (§ 2, п. 4) должно
быть учтено дополнительное демпфирование горизонтальных упругих
элементов (см. рис. 3. 17) в соответствии с формулой (4. 16). При этом
в формулах (4, 15) и (4. 16) вместо значений ® следует подставлять зна-
чения р частоты соответствующего тона колебаний вертолета. Такой при-
ем расчета является вполне оправданным, так как на границах зон не-
устойчивости наблюдаются чисто гармонические (незатухающие) коле-
бания и формулы (4.15) и (4.16) получены именно для случая гармони-
ческих поперечных колебаний пневматика. Цель расчета земного резо-
нанса состоит именно в нахождении границ зон неустойчивости.
При использовании формулы
с3 гв = -----—г (4. 17)
JKB z , V \ 2 X л
1+Ы
в расчете частот собственных колебаний вертолета возникает трудность,
связанная с тем, что для нахождения частоты собственных колебаний р
303
1
на.до знать значение Сэкв? которое в свою очередь зависит от р. Поэтому
расчет собственных колебаний (определение р) следует производить,
задаваясь различными значениями сэкв в интервале 0<[с8КВ<с™ , а затем
после определения р находить-соответствующее значение скорости про-
бега из формулы (4. 17). При этом для определения скорости пробега
получается формула:
/ спн
v=rpV
' сэкв
(4. 18)
В результате такого расчета можно построить график зависимости
границ зон неустойчивости от скорости пробега V. На рис. 3.40 приведе-
Рис. 3.40. Зависимость нижней гра-
ницы зоны неустойчивости от скоро-
сти пробега для вертолета Ми-1:
иКр —критические обороты, соответствую-
щие началу самоиозбуждающихся колеба-
ний; п*—обороты, соответствующие центру
зоны неустойчивости
уменьшаются частоты собственных
ны результаты такого расчета для
вертолета Ми-1. На графике изоб-
ражена зависимость нижней грани-
цы зоны неустойчивости, соответст-
вующей второму тону колебаний от
скорости пробега V.
Как видно из графика, крити-
ческие обороты пкр винта, соответ-
ствующие началу земного резонан-
са, заметно снижаются с ростом
скорости движения вертолета. Если
для неподвижно стоящего вертоле-
та запас по оборотам составляет
36%, то при скорости пробега
60 км/час запас уменьшается до 8%.
Важно отметить, что при увели-
чении скорости V график пКр при-
ближается к некоторой асимптоте.
Это имеет следующий физический
смысл.
При увеличении V боковая
жесткость пневматика, определяе-
мая величиной СЖв [формула
(4. 17)], неограниченно уменьшает-
ся, приближаясь к нулю. При этом
колебаний первого и второго тонов.
причем частота первого тона р стремится к нулю, а частота второго то-
на стремится к значению
/т
(4. 19)
Величина р0 представляет собой частоту собственных поперечных
колебаний вертолета при отсутствии боковой жесткости пневматиков.
Форма колебаний вертолета, соответствующая этой частоте, пред-
ставляет собой вращение корпуса вертолета вокруг главной продольной
оси инерции. Соответствующий узел колебаний (см. § 2, п. 3) совпадает
с центром тяжести вертолета.
Такая же ситуация может возникнуть у вертолета, неподвижно стоя-
щего или движущегося по гладкой поверхности льда, когда можно счи-
тать, что трение между пневматиком и землей отсутствует (при этом так-
же с™ =0).
Из этих рассуждений вытекает возможность упрощенного (оценоч-
ного) расчета земного резонанса на пробеге, когда частота собственных
304
колебаний определяется формулой (4. 19). При этом для массы экви-
валентного упругого основания (§ 2, и. 6) получается формула
= (4-20)
Для коэффициента затухания вертолета получается формула
IcPq I cPs
где: И — расстояние от поверхности земли до центра тяжести вертолета.
Величина &ЭКЕ определяется по формуле
(4. 22)
Величина k.' представляет собой коэффициент демпфирования вер-
тикальных упругих элементов (см. рис. 3. 16), который зависит от демп-
фирующих свойств амортизационных стоек шасси и определяется так
же, как это было показано в п. 5, § 2.
Такой приближенный расчет для вертолета, имеющего зону неустой-
чивости, расположенную выше рабочих оборотов, дает небольшую ошиб-
ку «в запас надежности».
3. О земном резонансе с отрывом пневматикой от поверхности земли
Все изложенные выше методы расчета земного резонанса предпола-
гали линейность характеристик пневматиков. Однако в действительности
характеристику пневматика можно (даже приближенно) считать линей-
ной только, если рассматривать такие си-
туации, при которых пневматик в процес-
се деформации остается прижатым к по-
верхности земли. Вообще же характерис-
тика пневматика имеет вид, изображен-
ный на рис. 3.41.
Если Ру — сила, действующая на
пневматик со стороны земли, a sy—со-
ответствующее смещение, то характерис-
тика пневматика имеет вид:
> ( с А при si/>0;
У ( 0 при Sy<^0.
Рис. 3. 41. Нелинейная зависи-
мость силы, действующей на ппев-
матик со стороны земли, от вер-
тикального смещения оси колеса
Если рассматриваются малые коле-
бания вертолета около положения равно-
весия, соответствующего данной тяге Т
винта, при котором PV = PO и sv = sa, такие,
что точка, изображающая на диаграмме состояние пневматика, нахо-
дится при колебаниях на некотором отрезке АВ, целиком лежащем в ли-
нейной части характеристики, то все методы расчета, основанные на ли-
нейности характеристики пневматика, остаются в силе (для таких ма-
лых колебаний).
Однако при больших амплитудах колебаний может оказаться, что
точка, изображающая состояние пневматика на диаграмме, выходит за
пределы линейности характеристики. Так, очевидно, будет в том случае,
если амплитуда смещения As будет больше, чем величина статического
20 1578
305
обжатия s0- Величина статического обжатия s0, так же, как и сила Ро,
зависит от тяги несущего винта вертолета и уменьшается, когда тяга Т
винта растет, приближаясь к величине веса вертолета G. Если T<^G, то
пневматик прижат к земле, однако амплитуда колебаний вертолета, при
которой пневматики начнут отрываться от поверхности земли, тем мень-
ше, чем ближе величина Т к значению T—G. Поэтому наиболее легко
пневматики отрываются от земли при взлете и посадке вертолета в мо-
менты, когда тяга винта меньше веса вертолета, но достаточно
велика.
Расчет колебаний вертолета с отрывом пневматиков весьма сложен,
однако можно, не производя таких расчетов, сделать некоторые весьма
важные качественные выводы. В самом деле, при колебаниях с отрывом
пневматиков вертолет представляет собой нелинейную колебательную
систему с люфтом. Известно, что частоты собственных колебаний систе-
мы с люфтом зависят от амплитуды колебаний и от величины люфта,
причем, чем больше люфт (при заданной амплитуде), тем ниже частота
собственных колебаний. Это физически понятно, так как наличие люфта
эквивалентно снижению средней (за период колебаний) жесткости упру-
гого элемента.
Следовательно, при колебаниях вертолета с отрывом пневматиков
частоты собственных колебаний снижаются, а вместе с ними снижаются
и границы зон неустойчивости. Поэтому, если зона неустойчивости, соот-
ветствующая второму тону колебаний, находится выше рабочих оборотов
винта, то запас по оборотам до нижней границы зоны неустойчивости
снижается при колебаниях с отрывом пневматиков и может оказаться,
что при достаточно большой амплитуде колебаний нижняя граница зоны
неустойчивости «отпустится» до рабочих оборотов.
Таким образом, вертолет, имеющий при малых колебаниях зону не-
устойчивости, расположенную выше рабочих оборотов, устойчив лишь
при малых амплитудах колебаний, не превосходящих некоторую крити-
ческую амплитуду акр, которую можно назвать порогом возбуждения
при колебаниях с отрывом пневматиков.
Из сказанного выше ясно, что величина порога возбуждения тем
меньше чем,меньше силы, прижимающие пневматики к земле, т. е. чем
ближе величина тяги винта к весу вертолета. Следовательно, наиболее
опасной является ситуация в момент отрыва вертолета от земли и непо-
средственно после приземления. Поэтому в случае возникновения коле-
баний при взлете или посадке необходимо немедленно уменьшить тягу
винта. При этом включаются в работу амортизационные стойки и затруд-
няются колебания с отрывом пневматиков.
Важно отметить, что колебания с отрывом пневматиков представля-
ют опасность лишь в том случае, когда имеется зона неустойчивости,
расположенная выше рабочих оборотов винта. С этой точки зрения пред-
ставляет интерес схема шасси, предложенная фирмой Бристоль (см.
рис. 3.18). Как уже указывалось выше (§ 2, п. 2), в этой схеме шасси
можно выбором значения жесткости специальной пружины спр до-
биться совпадения центра жесткости системы амортизации с центром
тяжести вертолета при удовлетворительных посадочных характеристи-
ках шасси. При этом поперечные поступательные колебания вертолета
и угловые колебания вокруг главной продольной оси инерции фюзеляжа
становятся независимыми.
Расчеты показывают, что в этом случае частота поперечных посту-
пательных колебаний получается примерно такой же (несколько ниже),
что и частота первого тона колебаний вертолета с шасси обычной конст-
рукции, а частота угловых колебаний может быть значительно снижена
по сравнению с частотой второго тона при обычной конструкции шасси
(ее можно в этом случае сделать даже равной частоте первого тона).
306
Таким образом, применение шасси системы «Бристоль» позволяет
получить весьма низкую частоту второго тона колебаний, такую, что со-
ответствующая зона неустойчивости получается расположенной ниже ра-
бочих оборотов винта. У такого вертолета не возможен земной резонанс
с отрывом пневматиков от поверхности земли.
§ 5. ЗЕМНОЙ РЕЗОНАНС ВЕРТОЛЕТОВ ДРУГИХ СХЕМ
1. Общие замечания
Как уже указывалось выше (§ 2, п. 1), для расчета собственных ко-
лебаний вертолета на земле надо рассматривать задачу о колебаниях
твердого тела (если не учитывать упругость фюзеляжа) на упругом ос-
новании. Твердое тело на упругом основании имеет шесть степеней сво-
боды. Соответственно имеются шесть тонов собственных колебаний та-
кой системы, каждому из которых соответствует определенная частота
и форма колебаний. Для одновинтового вертолета, имеющего удлинен-
ный фюзеляж, оказалось возможным приближенно рассматривать лишь
поперечные колебания и при этом не учитывать колебаний рысканья
(§ 2, п. 1).
Для вертолета, у которого моменты инерции фюзеляжа относитель-
но трех главных осей инерции являются величинами одного порядка,
такое упрощение недопустимо. Однако, если имеется плоскость симмет-
рии фюзеляжа, то можно рассматривать продольные и поперечные коле-
бания как независимые. При этом в расчете поперечных колебаний необ-
ходимо рассматривать три степени свободы:
1) поперечное смещение;
2) угол крена;
3) угол рыскания.
При расчете колебаний в плоскости симметрии (продольных коле-
баний) надо рассматривать также три степени свободы:
1) продольное смещение;
2) вертикальное смещение;
3) угол тангажа.
С точки зрения земного резонанса могут представлять опасность
как поперечные, так и продольные колебания.
В этом параграфе даются методы расчета собственных колебаний
вертолета, учитывающие все указанные степени свободы.
Следует отметить, что эти методы приложимы и к одновинтовому
вертолету и позволяют получить результаты более точные, чем резуль-
таты приближенного расчета по методу, изложенному в § 2.
В этом параграфе излагается также метод расчета земного резонан-
са в воздухе, обусловленного упругостью фюзеляжа.
2. Расчет поперечных собственных колебаний
с учетом трех степеней свободы
На рис. 3. 42 изображен вертолет на упругом шасси. Выберем пря-
моугольную неподвижную систему координат cxyz с началом в центре
тяжести вертолета с. Ось сх направим вперед (в плоскости симметрии
фюзеляжа) параллельно поверхности земли, ось су вверх и ось cz впра-
во, если смотреть в направлении оси сх. Пусть z — есть смещение центра
тяжести вертолета в направлении оси cz, а <рх. и <ру — углы поворота фю-
зеляжа соответственно относительно осей сх и су (срх — угол крена,
<ру — угол рыскания),
20*
307
Уравнения поперечных колебаний вертолета могут быть записаны
в виде:
1'хЧх Iхи? и —
' X.U '?х = И ’
mz=Z,
(5. 1)
где /и—масса вертолета:
I х и Jv — моменты инерции фюзеляжа относительно осей сх и су,
/^ — соответствующий центробежный момент инерции;
А!х и Aly —моменты внешних сил, действующих на фюзеляж относительно
осей сх и су,
Z — проекция внешних сил, действующих на фюзеляж на ось cz.
Рис. 3.42. Схема крепления вертолета на упругом шасси
Рассмотрим сначала колебания при отсутствии демпфирования.
В этом случае величины Мх, Му и Z при малых собственных колебаниях
вертолета относительно положения равновесия могут быть линейно вы-
ражены через смещения г, (pv и <ру. Напишем выражения для смещения
центров жесткости амортизации (ц. ж) в сечениях /—/ и //—II фюзе-
ляжа (рис. 3.42), соответствующие переднему и заднему шасси через
величины z, фх, <ру:
1) переднее шасси:
zt = z—<рхеу;
2) заднее шасси:
22 = 2 + фу/2—ф.ге2,
где /j и /2— расстояния плоскостей переднего и заднего шасси от цент-
ра тяжести с;
в] и е2 — расстояния от оси сх до центров жесткости переднего
и заднего шасси.
Зная смещение центра жесткости сечения фюзеляжа z в плоскости
данного шасси, а также поворот этого сечения относительно центра
308
жесткости (который для обоих сечений будет равен ср.т), можно опреде-
лить упругие силы и моменты, действующие на фюзеляж в этом сечении
аналогично тому, как это делалось раньше (§ 2, п. 2) для плоского тела
на упругом основании. Определяя затем величины Л1Л., Му и Z, получим
для них следующие выражения:
=-= - + cez4- Gz; |
— ceftx-\-ctz\ I (5.2)
Z CzZ~Ce^x i ct?V' J
где соответствующие коэффициенты жесткости определяются формулами:
с, = с -4-с ;
z 21 1 2а’
сч = с-.- + с + с, ё, -г с с2;
fl 1 Та 1 21 1 1 2а 2’
С =С Ct —I- С Сп*
Cl~Cz/t—Cil2',
cei = cze.ill-czeJ.<2.
.
Величины c2l, сг2, cTi, с-2 представляют собой коэффициенты боко-
вой и угловой жесткости переднего и заднего шасси.
В первой из формул (5. 2) имеется также член Gz, представляющий
собой момент силы веса вертолета G относительно оси сх, возникающий
при боковом смещении z. *
Подставляя выражения (5.2) в уравнения (5.1), получим оконча-
тельно следующие уравнения малых поперечных колебаний вертолета:
- hv'fy = (G + Z ~ <?х - Сё-у I
ctlzx' (5-4)
mz=- czz + сеЪ. -f- c#y.
Отыскивая решение этой системы в виде;
Z = ZqCOS pt\
?л- = ЙС05/’/;
= cospZ,
где z0, tp°, <р° и р — постоянные, приходим к следующей системе ли-
нейных алгебраических уравнений для определения этих постоянных:
zQ - - с & у = 0;
- (G + се) z0 -1- (с^ - 1яр^ + (си + 1хУр^ - 0;
- + ^ei - Л^2) +(/Gy ~ 1 уР-) = °-
Приравнивая нулю определитель этой системы
(5. 5)
(G-mp2); -се;
-(G + сД
-q;
(G-r - !хР2>,
(^г+Лг/Я;
(4z +W2)
309
и производя несложные преобразования, приходим к следующему харак-
теристическому уравнению для определения частот собственных попе-
речных. колебаний р вертолета:
Ape^Bp^Cp^D=Q, (5.6)
где
A=hxlty— 1; 1
P^P\-hxhyP^Vx-
С = Р\уР2уХ - Р^ + Ply Р} - Pl + Pl} +
+ р1х (^ + ^) + (2«г - 2PlPly + PlyP^hy- (5,7)
D = Р*Р1Л Ply + 2 p'ixp}p} + р1ур2ухр1 -
- PlyP}zPlx - PlPlyP^ ~ PlxPlfi - PlxPljPj
hx=^\ hy — безразмерные коэффициенты.
lx l у
Парциальные частоты рг, р^, pv и
формулами:
величины р^ху, р2уг и т. д. даются

,2-------А.е... • н2 =-?£..
гх т ’ хг 1Х
Уравнение (5. 6) является уравнением третьей степени относительно
величины р2. Можно показать, что его корни р2 (fe=l, 2, 3) всегда ве-
щественны и положительны. Поэтому одним из возможных способов на-
хождения частот собственных колебаний! ру является графический спо-
соб, при котором строится график левой части этого уравнения, рассмат-
риваемой как функция величины р. Точки пересечения этого графика
с осью абсцисс дадут значения частот собственных колебаний
(рис. 3. 43).
Пронумеруем частоты собственных колебаний системы в порядке
возрастания: pi<CP2<Ps- Будем называть величины pi, р2, р3 соответст-
венно частотами первого, второго и третьего тонов собственных попе-
речных колебаний вертолета. Каждой частоте собственных колебаний
соответствует определенная форма колебаний, характеризуемая опреде-
ленным соотношением амплитуд г0, ср°, которое может быть найдено
для данного Pk (k=\, 2, 3) из уравнений (5.5), если в них вместо вели-
чины р подставить ph. При этом получаются выражения:
* \ г°A
(сг тР} (cri + IхуРу) С[Се
(се! +^.»Рй)«г-(с¥г/—
(5.9)
где k— 1, 2, 3.
310
№(p')=flpe+Bp‘,+ CpI+D
Рис. 3.43. Характер графи-
ка Д=Д(р) для определе-
ния частот собственных ко-
лебаний вертолета на упру-
гом шасси
Нетрудно показать, что форма колебаний данного тона характери-
зуется определенной прямой линией, лежащей в плоскости симметрии
фюзеляжа хсу и представляющей собой геометрическое место точек
(принадлежащих фюзеляжу), остающихся неподвижными при колеба-
ниях этого тона.
В самом деле, смещение zA некоторой точки А фюзеляжа, лежащей
в плоскости хсу и имеющей координаты х и у (см. рис, 3.42) может быть,
очевидно, определена по формуле
=z+<p,;y—
При колебаниях к-го тона;
z = £0cos pbt\
'fy = rj?y C0S Рк^‘
Следовательно,
za = (^о + - =Р° *) cos р/ =
=ZO [14- - (=Р°К X] cos pj.
Поэтому условие
1 + — (Ю»Л==,° (5-10)
представляет собой уравнение геометрического места точек в плоскости
хсу, амплитуды колебаний которых равны нулю при колебаниях k-ro
тона. Но это есть уравнение некоторой прямой линии.
Таким образом, форма колебаний ft-го тона может характеризовать-
ся положением некоторой прямой на плоскости хсу. Эту прямую назовем
линией узлов ft-го тона поперечных колебаний. Уравнение линии узлов
(5. 10) легко найти с помощью выражений (5.9) для данного значе-
ния ph.
Рис, 3.44. Характерное расположение линий узлов ко-
лебаний первого, второго и третьего тонов
Результаты расчета собственных поперечных колебаний вертолета
удобно представлять в виде рисунка, на котором изображен вид с боку
на вертолет и нанесены линии узлов всех трех тонов колебаний с указа-
нием соответствующих частот (рис. 3.44).
Приближенный метод расчета собственных поперечных колебаний,
изложенный в § 2 и основанный на предположении о независимости ко-
311
лебаний рыскания, может быть получен как частный случай из выведен-
ных здесь уравнений.
Если оси сх и су есть главные оси инерции (/Ж!/ = 0), а также выпол-
нены условия
ci=yz^i c2J2=0;
то уравнения (5. 4) распадаются на две независимых системы уравнений:
^Ух—^-с^г-с^-,
~~ с^х-
(5. 10')
(5.10")
Уравнение (5.10") определяет независимые колебания рыскания,
а система уравнений (5.10') определяет поперечные колебания, соответ-
ствующие физической картине, изложенной в § 2 (при этом две из линий
узлов параллельны оси сх, а третья совпадает с осью су).
Для реального вертолета условия о=ссг=0 и /жу = 0 в точности ни-
когда не выполняются. Однако для вертолетов с удлиненным фюзеля-
жем, когда угол а между главной осью инерции сх0 и осью сх мал (см.
рис. 3.42), а момент инерции /, мал по сравнению с двумя другими
(/у и Zz), результаты «точного» и приближенного расчетов могут совпа-
дать с достаточной для практики степенью точности.
Для определения коэффициентов демпфирования собственных коле-
баний можно применять приближенный способ, аналогичный изложен-
ному в § 2 (п. 4) для системы с двумя степенями свободы. Для каждого
тона собственных колебаний определяется коэффициент демпфирования
в предположении, что и при наличии демпфирования колебания этого
тона представляют собой также угловые колебания вокруг линии узлов
этого тона. При этом так же, как и раньше (§ 2, п. 4), уравнение собст-
венных угловых колебаний вертолета вокруг линии узлов может быть
записано в виде:
Лт 4-cfftt?==o, (5.11)
где /j —момент инерции вертолета относительно линии узлов А-го
тона;
-угловая жесткость амортизации при повороте относительно
линии узлов £-го тона;
^ — соответствующий коэффициент демпфирования.
Момент инерции вертолета относительно линии узлов может быть
определен по формуле:
4 = ^ + /^cos2Yft+4sin2yz,J-/^siii2Yz., (5. 12)
где hu — расстояние от центра тяжести вертолета до линии узлов;
ук — угол, который составляет линия узлов с осью сх (рис. 3. 44).
Величины hk и ук определяются по формулам:
tgvft=— Ы1; (5.13)
пЛ
312
Коэффициент углового демпфирования определяется выраже-
нием:
+ + + (5-15)
где dllt и d2k — расстояния от линии узлов (рис. 3.45) до линий, соеди-
няющих точки контакта с землей соответственно пнев-
матиков переднего и заднего шасси;
аг и а2 —колея переднего и заднего шасси (рис. 3. 16);
&'у, — коэффициенты демпфирования боковых и вертикаль-
ных пружин (см. рис. 3.16) соответственно переднего
и заднего шасси, имеющие тот же смысл, что и в § 2
(п. 4).
Рис. 3.45. К выводу основных соотношений при ко-
лебаниях вертолета относительно линии узлов fe-ro
тона колебаний
После определения величины kf/i определяется безразмерный коэф-
фициент демпфирования /г-го тона:
'*•»—177—’ vj-
2/kPk
3. Расчет собственных колебаний вертолета в плоскости симметрии
(продольные колебания)
Обратимся к рис. 3. 46. Задача о колебаниях вертолета в плоскости
симметрии сводится к исследованию колебаний плоского упругого за-
крепленного твердого тела в своей плоскости (хОу). Вертикальные пру-
жины с коэффициентами жесткости cVt и сУг имитируют вертикальную
жесткость переднего и заднего шасси, а горизонтальные cXl и сх, жест-
кость переднего и заднего шасси в направлении оси Ох. Если пневма-
тики шасси не заторможены, то сХ1—сх, =0. В случае заторможенных
пневматиков упругость шасси в направлении оси Ох складывается из
упругости пневматика и упругости системы подвески пневматика (на-
пример, упругости на изгиб стоек шасси и т. д.). Продольная жесткость
одного пневматика с™ может быть для ориентировочных расчетов приня-
та равной с™ ~ 1,5с™ .
Пусть точка М (рис. 3.46) с координатами ех и еу представляет со-
бой центр жесткости системы амортизации при продольных колебаниях.
Величина еу представляет собой расстояние центра тяжести вертолета
от поверхности земли, а величина ех определяется из выражения
е . (5. ]7)
+ су<
313
Пусть х и у представляют собой смещения центра тяжести вертолета
в направлении осей Ох и Оу, a <pz угол поворота фюзеляжа относительно
оси Oz. Тогда уравнения малых колебаний вертолета в плоскости хОу
при отсутствии демпфирования имеют вид:
mx=-cxx-^cxey^z-,
ту — Суу Сув^у,
Iг<рг = - (с? - [ схе^ + суе$ Тг + схеуХ - сиеху + Gx,
где
сх=сх,-\-сх,-,
СУ — СУ1 H-fya ’>
с? = Су, (1Л - еху 4- Су, (12 + еху . .
(5. 18)
(5.19)
Рис. 3.46. Схема крепления вертолета на упругом
шасси для расчета колебаний в плоскости симметрии
Введем следующие обозначения:
(5.20)
Введем также вместо <р2 новую переменную
Тогда уравнения (5. 18) можно записать в виде:
х=~ P^ + P^yS;
У=-Р2уУ-Р2уё^;
s^-pls + p^x-p^y.
Отыскивая решение этой системы уравнений в виде
x=x0cosp/; y=y0cospi; s = s0cos pt,
(5.21)
(5. 22)
(5.23)
придем к следующей системе линейных однородных алгебраических
уравнений для определения величины хо, {/о и s0:
(Р2Х - Р2) хо ~ РхО/$о =- °;
(Р2У- Р2}Уо~г P2c'xsq~Q',
ple*x0 4- /?2 ~ехуй -4 (р2 - р2) s0 = 0.
(5. 24)
314
Приравнивая нулю определитель этой системы
получим следующее характеристическое уравнение для определения
частот р собственных колебаний:
ps -j- ар* -f- bp2 с — О,
(5.25)
где
«=^+р^ + р=;
Ь = Р^у + Pffi - р\р2у - Р2Р2 - Р2Р2-,
С = - Р2уР* + Ру 4)-
(5.26)
Это уравнение имеет три вещественных корня р2, которые можно
найти графически, построив график функции Л = Д(р) =ре + ар* + Ьр2 + с,
подобно тому, как это указывалось в § 5 (п. 2) для уравнения (5. 6) (см.
рис. 3.43). Расположим корни уравнения (5.25) в порядке возрастания
Pi<CP2<P3 и будем называть величины рь р2 и р3 соответственно часто-
тами первого, второго и третьего тонов собственных колебаний вертоле-
та в плоскости симметрии или продольных колебаний. Каждому тону
продольных колебаний соответствует своя форма колебаний вертолета,
которую удобно характеризовать положением на плоскости хОу соответ-
ствующего узла колебаний Ок (здесь &=1, 2, 3), т. е. точки фюзеляжа,
которая остается неподвижной при колебаниях этого тона. Координаты
узла колебаний хк и ук могут быть найдены следующим образом: ампли-
туды ах и ау колебаний любой точки фюзеляжа с координатами хк и уь
в направлениях осей Ох и Оу определяются очевидными формулами:
ах=х0—-fayk\
ау=Уо4~?Л>
где <po = SoQ — амплитуда угловых колебаний вертолета.
Координаты хк и ук определяются из условий ах = 0 и ^ = 0, а потому
v __ Уо
xk— '
¥0
So
У к— — „ Q-
То s0
Величины отношений — и
so
уравнений системы (5.24), если
лебаниях k-ro тона получаем:
— могут быть найдены из первых двух
so
известна частота колебаний р. При ко-
у P*~Pk ’
I
'л Ру-Рк
315
Отсюда получаются следующие формулы для определения коорди-
нат узла колебаний:
1
еу
(5.27)
\Рх / J
Укажем две возможности упрощенного расчета собственных колеба-
ний вертолета в плоскости симметрии.
В случае, когда центр жесткости амортизации Af (см. рис. 3.46) ле-
"j (ех = 0), уравнения движения (5.18) упрощаются и при-
жит на оси Оу
нимают вид:
(5.28)
(5. 29)
тУ = —СуУ,
тх = —- cxey®z,
— — c~Oz + -р G) л:.
(5. 28) описывает вертикальные поступательные колеба-
которые не представляют интереса с точки зрения земно-
(5.29) описывают продольные колебания вертолета, ко-
Уравнение
ния вертолета,
го резонанса.
Уравнения
торый в этом случае может рассматриваться как система с двумя сте-
пенями свободы х и <р2. Такая система механически эквивалентна систе-
ме, которая рассматривалась в § 2 (п. 3) и изображена на рис. 3. 16. По-
этому при расчете частот собственных колебаний вертолета в этом слу-
чае (если пренебречь моментом от силы веса С?) можно пользоваться
графиками на рис. 3.19 и 3.20, а также формулами (2.22), (2.23)
и (2. 24), полагая в них
±z__.
теу '
(5. 30)
о C^z _Су/1+Z2
схе2 с,е2
х у х у
Величина — будет представлять собой относительное расстоя-
еУ
ние от узла колебаний fe-ro тона, который в этом случае будет располо-
жен на оси Оу, до центра тяжести вертолета.
У реального вертолета величина ех, как правило, не равна нулю.
Однако она обычно невелика по сравнению с величиной Л-Нг- Прибли-
женный расчет, в котором полагают гж = 0, в большинстве случаев дает
значения частот собственных колебаний, близкие к значениям, получен-
ным путем точного расчета, и может с успехом применяться в качестве
предварительного расчета, когда нужно быстро получить результаты
и нет необходимости в большей точности.
В случае когда производится расчет продольных колебаний при не-
заторможенных пневматиках (сж=0), уравнения движения (5. 18) опять
распадаются на две независимых системы:
(5.31)
тх = 0;
/г<рг = — c^z + G х - суеху.
316
В этом случае при колебаниях можно считать х = 0, так как отсутст-
вует проекция внешних сил на ось Ох. Одна из частот собственных коле-
бании системы равна нулю и соответствует равномерному движению
центра тяжести вертолета вдоль оси Ох. Две другие частоты собствен-
ных колебаний, как и в предыдущем случае, могут быть найдены по гра-
фикам на рис. 3.19 и 3.20 или по формулам (2.22), (2.23) и (2.24), в ко-
торых следует брать:
(5.32)
(5.33)
Величины ак— — будут представлять собой относительные расстоя-
ния от центра тяжести вертолета до узлов колебаний, которые в этом
случае будут лежать на оси Ох.
Наконец, в том случае, когда пневматики не заторможены, а вели-
чина ех = 0, получаются наиболее простые формулы для частот собст-
венных колебаний в плоскости симметрии;
А=--0;
Р2 = Р^]/Г-!>
у т
Рз =/’?==/ 1 2 - .
» Ц
Для определения коэффициентов затухания собственных продоль-
ных колебаний можно опять применять приближенный метод, основан-
ный на предположении, что и при наличии демпфирующих сил, колеба-
ния данного тона есть угловые колебания относительно линии узлов дан-
ного топа, которая в этом случае представляет собой прямую, параллель-
ную оси Oz и пересекающую плоскость хОу в точке с координатами х^
и ук [см. формулы (5. 27)]. Уравнение колебаний данного тока может
быть вновь записано в форме (5.11), только величина Д находится по
формуле:

(5.34)
При определении коэффициента демпфирования k? можно не учи-
тывать демпфирования продольных упругих элементов сЛ, и сх, (см.
рис. 3.46) и учитывать лишь демпфирование вертикальных упругих эле-
ментов с жесткостями и переднего и заднего шасси (см. рис. 3.16).
Соответствующие коэффициенты демпфирования k'y и Д опреде-
ляются так, как это указано в § 2 (пи, 4 и 5).
Вычисляя момент от демпфирующих сил относительно линии узлов,
получим выражение для определения величины к,г ;
Ч=2[*к (А-^+^+х*)2].
Безразмерный коэффициент демпфирования /Д данного тона коле-
баний определяется формулой
Пк М ‘
(5.35)
(5.36)
317
4. Приведение задачи к расчету винта на упругом основании
После того, как найдены частоты и формы собственных колебаний
вертолета на упругом шасси, расчет земного резонанса может быть све-
ден к расчету винта на упругом основании, изложенному в § 1.
Метод расчета, основанный на сведении задачи к винту на упругом
основании, является приближенным и аналогичен методу, изложенному
в § 2 (п. 6) для одновинтового вертолета.
Сущность приближенного метода заключается в следующем: произ-
водится отдельный расчет земного резонанса для каждого тона собст-
венных колебаний; при этом корпус вертолета рассматривается как твер-
дое тело, имеющее одну степень свободы — поворот вокруг линии узлов
данного тона. Конечно, такой приближенный метод оправдан лишь,
в том случае, когда частоты собственных колебаний различных тонов-
достаточно «далеки» друг от друга.
В случае когда имеются две «близкие» частоты собственных коле-
баний, в расчет необходимо вносить некоторые поправки. Метод уточне-
ния расчета в этом случае будет изложен ниже.
Итак, для расчета земного резонанса рассматриваются колебания
вертолета по каждому тону отдельно как угловые колебания фюзеляжа
вокруг некоторой неподвижной прямой — линии узлов данного тона.
Можно показать, что при таком упрощении уравнения движения сис-
темы сводятся к системе уравнений, аналогичной системе (1.16) (§ 1).
При этом все формулы § 1 остаются в силе и можно пользоваться гра-
фиками для определения границ зон неустойчивости (см. рис. 3. 3—3. 12),
однако под величиной по нужно в этом случае понимать безразмерный
коэффициент демпфирования пк данного тона колебаний, определяемый
по формулам (5.16) или (5.36) (§ 5, пп. 2 и 3), а под величиной е вели-
чину gft, вычисляемую для данного тона по формуле:
е»=еи»4' езд+ • (5.37)'
! = 1
где
г=1, 2,..., $;
s — число несущих винтов, а каждая из величин Юь определяется
формулой:
Здесь Ik — момент инерции фюзеляжа (с массами несущих вин-
тов, сосредоточенными в их центрах) относительно
линии узлов &-го тона [см. формулы (5. 12) и (5. 34)];
Ik — расстояние от центра данного i-ro несущего винта
до линии узлов k-ro тона, если рассматриваются по-
перечные колебания, или расстояние от линии узлов
k-ro тона до плоскости вращения данного несущего
винта, если рассматриваются продольные колеба-
ния вертолета;
п — число лопастей данного винта;
Зв.ш и /в ш — соответственно статический момент и момент инер-
ции лопасти винта относительно вертикального шар-
нира.
Несущие винты могут быть различными, однако указанный прием
справедлив лишь в том случае, если все винты имеют одинаковые угло-
вые скорости вращения и одинаковые значения параметра v0 [см. форму-
лу (1.9)].
318
Как уже указывалось выше, изложенный здесь приближенный ме-
тод расчета оправдан лишь тогда, когда частоты колебаний различных
тонов достаточно «далеки» друг от друга: Можно показать, что если име-
ются две близкие частоты собственных поперечных (или продольных) ко-
лебаний, например рп и рт, то расчет границ зон неустойчивости может
быть проведен для одного тона, например, рт, но уточнен введением
в расчет некоторой величины йжи вместо пт (для данного тона, причем
»экв<Пт), которая определяется по формуле:
^экв =«„,---J-----. (5.39)
УКр lit г \ '
1 I 1т
Нп In
Эта формула выведена для случая, когда рп~рт, т. е. когда часто-
ты собственных колебаний двух рассматриваемых тонов в точности сов-
падают. Если же Рп¥=Рт, то формула (5.39) дает заниженное значение
Я-экв-
В случае если имеются две близких частоты собственных колебаний
Рп и рт, причем одна из них, например, рп, является частотой n-го тона
поперечных колебаний, а другая рт частотой щ-го тона продольных ко-
лебаний, то, вообще говоря, необходимо рассматривать винт на упругом
основании с двумя степенями свободы (см. § 1, п. 4). В этом случае мож-
но приближенно (в запас надежности) оценивать потребное демпфиро-
вание по формуле (1.52) для винта на изотропном упругом основании,
подставляя в нее величины п0 и s для того из двух рассматриваемых ТО-
ЛЬ
нов, для которого меньше величина отношения ~ .
Следует отметить, что необходимость такого расчета возникает
лишь в том практически весьма редком случае, когда для обоих рассмат-
риваемых тонов не только близки значения частот рп и рт, но и значения
— и — . Если же величина — для одного из тонов более чем в 2,5—
£Л еЯ2 , —
3 раза больше, чем для другого, например, — = 3- п— , то можно не при-
еЯ2
нимать во внимание колебаний n-го тона, а рассматривать лишь колеба-
ния m-го тона (как независимые).
5. Самовозбуждающиеся колебания в полете вертолета
с упругим фюзеляжем
При полете вертолета в воздухе также возможны самовозбуждаю-
щиеся колебания типа земного резонанса. Фюзеляж реального вертоле-
та представляет собой упругую систему, которая имеет свои частоты
и формы собственных колебаний. Если форма колебаний какого-либо
тона упругого фюзеляжа такова, что центр несущего винта (или центры
несущих винтов) при колебаниях этого тона смещается в плоскости вра-
щения винта, то возможен земной резонанс, при котором фюзеляж будет
совершать колебания с формой этого тона.
Частоты собственных колебаний упругого фюзеляжа обычно высоки
по сравнению с частотами колебаний вертолета на амортизации шасси
и лишь низкие один или два тона собственных колебаний могут пред-
ставлять опасность с точки зрения возможности самовозбуждающихся
колебаний.
Низшие частоты собственных колебаний фюзеляжа соответствуют
обычно колебаниям изгиба фюзеляжа.
319
На рис. 3.47 изображена форма колебаний первого тона изгиба фю-
зеляжа вертолета Ми-4 в горизонтальной плоскости. Форма колебаний
изображается в виде графика упругой линии и=и(х) (и—амплитуда
колебаний точки с коорди-
Рис. 3.47. Форма первого тона колебаний
упругого фюзеляжа вертолета
ляться по формуле:
натой х).
Частоты и формы соб-
ственных колебаний изгиба
фюзеляжа могут быть най-
дены обычными методами,
разработанными для упру-
гих балок переменного по-
перечного сечения (см., на-
пример, гл. 2 настоящей
книги) или определены экс-
периментально (в случае
имеющегося готового верто-
лета) .
Если известна частота
ра и форма и(х) какого-ли-
бо тона колебаний изгиба
фюзеляжа, то расчет само-
возбуждающихся колебаний
с формой этого тона может
быть сведен к расчету винта на упругом основании по формулам § 1 иля
по графикам на рис. 3.3—3. 12. При этом величина е должна опреде-
S —sl+e2 +
(5.40)
где s — число несущих винтов.
Величины er (i = 1, 2, ..., s) определяются по формулам:
<?2
___ п дв,ш .
2
(5-41)
(5.42)
где
(х) =
ц(х) .
и(х;)
— координата центра i-го несущего винта;
0 —погонная масса фюзеляжа (интеграл берется по всей длине фю-
зеляжа).
Величина йг-(х) представляет собой амплитуду колебаний в точке
с координатой х, отнесенную к амплитуде колебаний центра i-го винта.
Величина m3I!E есть наибольшее значение кинетической энергии фюзеля-
жа при колебаниях по форме данного тона с амплитудой колебаний
в центре г-го винта, равной единице, отнесенное к величине р?.
Величина п0 должна быть равна в этом случае безразмерному коэф-
фициенту демпфирования данного тона колебаний фюзеляжа. Она опре-
деляется исключительно потерями на гистерезис в конструкции фюзеля-
жа и составляет обычно 0,02—0,05.
Такое сравнительно малое значение по не позволяет устранить зем-
ной резонанс в полете с помощью демпфера лопасти, и надежность вер-
толета может быть обеспечена лишь при достаточном запасе по оборо-
320
там винта до нижней границы зоны неустойчивости. Поэтому самовоз-
буждающиеся колебания в воздухе представляют опасность, лишь для
вертолетов, имеющих сравни-
тельно низкие частоты собст-
венных колебаний упругого
фюзеляжа. Например, для
вертолета Ми-4 запас по обо-
ротам до нижней границы зо-
ны неустойчивости, соответст-
вующей первому тону колеба-
ний фюзеляжа (см. рис. 3.47),
составляет 28%.
Наибольшую опасность
земной резонас в воздухе пред-
ставляет для вертолетов попе-
речной схемы, имеющих длин-
ное упругое крыло (рис. 3.48).
Опасность самовозбуждаю-
щихся колебаний для таких
Рис. 3. 48. Форма низшего тона колебаний вер-
толета поперечной схемы, наиболее опасная
с точки зрения земного резонанса
вертолетов усугубляется тем, что центры несущих винтов расположены
в пучностях соответствующего тона колебаний, что дает сравнительно
малые значения тЭкв [формула (5. 42)] и, следовательно, относительно
широкоие зоны неустойчивости.
§ 6. ВЫБОР ОСНОВНЫХ ПАРАМЕТРОВ ШАССИ
И ДЕМПФЕРОВ ЛОПАСТЕЙ. РЕКОМЕНДАЦИИ
ПО ПРОЕКТИРОВАНИЮ
Как это видно из общей теории устойчивости винта на упругом осно-
вании, запас устойчивости, вообще говоря, может быть увеличен как пу-
тем увеличения степени демпфирования колебаний лопасти, так и увели-
чением демпфирования колебаний фюзеляжа, т. е. увеличением демпфи-
рующей способности шасси.
Однако возможности увеличения этих обоих видов демпфирования
практически весьма ограничены, так как и демпфер лопасти и шасси вы-
полняют ряд других функций,- не связанных с земным резонансом.
Демпфер лопасти работает при поступательном полете вертолета
и нагружает комлевую часть лопасти переменным изгибающим момен-
том тем большим, чем больше степень его демпфирования. Причем проч-
ность комлевой части лопасти и втулки, а следовательно, и их вес опре-
деляются главным образом именно наличием демпфера.
Чрезмерное увеличение степени демпфирования шасси без примене-
ния специальных устройств приводит к увеличению жесткости аморти-
зации и, следовательно, к увеличению динамических нагрузок при по-
садке вертолета.
С этими особенностями работы демпферов лопасти и шасси прихо-
дится считаться при проектировании вертолета. При этом зачастую не
удается обеспечить достаточный запас по земному резонансу без приме-
нения некоторых специальных конструктивных устройств, иногда в дем-
пфере лопасти, иногда в системе шасси.
Для вертолетов одновинтовой и продольной схемы наиболее опас-
ным обычно оказывается случай земного резонанса на пробеге. Поэтому
данный случай удобно считать расчётным для выбора характеристик
демпфирования лопасти и шасси. При этом для простоты можно счи-
тать, что вертолет качается вокруг горизонтальной оси, проходящей че-
рез его центр тяжести, что достаточно верно при большой скорости про-
бега (см. § 4, п. 2). В этом случае, как мы видели, получаются особенно
21 1578
321
простые расчетные формулы (4.18) — (4.21) и удается наиболее простым
способом определить требуемые характеристики шасси и демпфера ло-
пасти. Однако после того, как характеристики шасси и демпферов лопас-
ти выбраны, необходимо провести полный расчет земного резонанса на
все возможные случаи, включая земной резонанс на пробеге, и построить
диаграмму безопасных оборотов (см. рис. 3.25). После этого в случае
необходимости откорректировать выбранные характеристики шасси
и втулки.
1. Выбор характеристик демпфера лопасти
Главной особенностью работы демпфера лопасти является то об-
стоятельство, что частота собственных колебаний лопасти (характерная
для земного резонанса) всегда примерно в 3—4 раза ниже частоты вы-
нужденных колебаний лопасти при поступательном полете.
В самом деле в полете лопасть совершает вынужденные колебания
относительно горизонтального и вертикального шарниров с частотой и,
равной оборотам несущего винта, в то время как частота собственных
колебаний лопасти рл = то<о. Причем обычно vo = 0,25-?-0,3, а угловая ско-
рость к> вращения винта при земном резонансе, во всяком случае, не мо-
жет быть больше, чем угловая скорость вращения винта в полете.
Этой особенностью объясняется, в частности, нецелесообразность
применения демпферов с линейной характеристикой (§ 3, п. 3), обуслов-
ленная тем, что линейный демпфер при неизменной амплитуде колеба-
ний развивает момент, пропорциональный частоте колебаний.
Наиболее простыми демпферами, дающими момент, не зависящий
от частоты колебаний, являются фрикционные демпферы, а также гид-
равлические демпферы со ступенчатой характеристикой, причем эту ха-
рактеристику следует по возможности приближать к характеристике
фрикционного демпфера (см. рис. 3. 316). Гидравлический демпфер с та-
кой характеристикой целесообразно применять на тяжелых вертолетах,
так как такой демпфер получается более легким, чем соответствующий
фрикционный, причем выигрыш в весе демпфера растет с увеличением
его мощности.
При применении обычных демпферов момент Мо демпфера выби-
рается из соображений прочности лопасти, а его коэффициент демпфиро-
вания определяется по формуле (3.23). Запас демпфирования по земно-
му резонансу может быть обеспечен в этом случае лишь соответствую-
щим выбором характеристик шасси. В тех случаях, когда это не удается,
приходится думать о применении специальных конструкций демпферов
лопасти, которые давали бы большое демпфирование лопасти при низких
частотах колебаний (характерных для земного резонанса) и малое демп-
фирование при частоте колебаний, соответствующих полету вертолета.
Одним из наиболее простых типов такого демпфера является демпфер,
последовательно соединенный с упругим элементом (см. рис. 3.33). На
рис. 3.49 изображен один из возможных вариантов конструкции такого
демпфера. Будем называть такой демпфер пружинным *.
Для того чтобы оценить преимущества пружинного демпфера, срав-
ним его с обычным фрикционным демпфером. Пусть вертолет имеет зем-
ной резонанс на пробеге такой, что центр зоны неустойчивости совпада-
ет с рабочими оборотами винта. Пусть далее наибольший момент в по-
лете, допустимый по соображениям прочности лопасти, равен А1о. Тогда
* Схема пружинного демпфера лопасти для устранения земного резонанса была
предложена инженерами О. П. Баховым, Л. Н. Гродко, И. В. Куровой и М. А, Лей-
ландом. (Авторское свидетельство № 184142).
322
эквивалентный коэффициент демпфирования в случае применения фрик-
ционного демпфера определяется формулой (3. 23):
Ьфрикц —
^ЭКВ — ’ с ’
JT
где — есть амплитуда первой гармоники колебаний лопасти в плоско-
сти вращения.
Рис. 3.49. Демпфер с последовательно соединенным упругим
элементом:
/—упругие элементы (резина): 2—корпус; <3—предохранительный клапан;
4—шток-. 5—регулировочная игла
В случае применения пружинного демпфера соответствующий эк-
вивалентный коэффициент демпфирования определяется формулой
(3.17):
£пруж = £ --?-----
где рл — есть частота колебаний лопасти при земном резонансе, которую
можно считать равной произведению veto.
Pn=,Vo(O.
Момент, который будет давать в полете пружинный демпфер, может
быть определен по формуле
которая при гармонических колебаниях лопасти с частотой <о дает сле-
дующее значение амплитуды момента М (см. формулы (3.17)]:
М = . (6.1)
Поставим теперь следующий вопрос: если выбирать значения с и k
у пружинного демпфера так, чтобы он давал в полете такой же мо-
мент Мо, как и фрикционный, то какое наибольшее значение мож-
но получить, варьируя величинами с и fe? При этом будем считать, что
амплитуда колебаний лопасти по первой гармонике в полете и при
пробеге вертолета по земле одна и та же.
21* 323
Относительное увеличение демпфирования при применении пружин-
ного демпфера удобно характеризовать величиной
, _ СГ _____ Я и£1____k_____ (6. 2)
^KU 2 Мо 1 + ^2'
Подставляя в этой формуле рл=ток> и учитывая условие Л4 = Л4О,
получим
где безразмерная величина
k=—. (6.4)
С
Таким образом, относительное преимущество от применения пру-
жинного демпфера зависит исключительно от выбора значения k. На
рис. 3.50 изображен график зависимости ф(й) для случая vo=0,25. Как
видно из этого графика, при увеличении k величина ф сначала возраста-
ет, а затем убывает, достигая наибольшего значения ф = фтах при неко-
тором значении k = kopt, которое мы назовем оптимальным.
г-г
Приравнивая нулю производную -=• , найдем:
dk
(6.5)
(6.6)
.1. л 1
Углах ~Z~ , г-----5 •
2 V0V 1 — Vq
При vo = O,25, получается &opt =3,74, фтах = 3,24.
Таким образом, применение пружинного демпфера позволяет более
чем в три раза увеличить демпфирование при земном резонансе, сохра-
нив неизменным момент, нагружающий лопасть в полете.
Этим, однако, не исчерпывается преимущество пружинного демпфе-
ра по сравнению с обычным. Дело в том, что пружинный демпфер дает
324
«упругость» в вертикальном шарнире (сЭ1!в), а наличие такой упругости,
как показано в п. 2, § 1, снижает значение потребного демпфирования
[см. формулу (1. 31) и график на рис. 3.13].
Расчеты показывают, что с учетом всего изложенного, запас демп-
фирования при земном резонансе может быть увеличен в 5—6 раз при
сохранении неизменным момента, действующего на лопасть в полете.
Рис. 3.51. Схема втулки винта с межлопа-
стными связями
здних лопастей (71 и £b+i(7).
2. Винт с межлопастными упругими элементами и демпферами
До сих пор мы рассматривали лишь случай, когда упругий элемент
и демпфер в вертикальном шарнире включены между лопастью и кор-
пусом втулки, так что момент, действующий на лопасть, зависит лишь от
движения данной лопасти и не зависит от движения остальных лопастей.
Иногда применяются конструк-
ции втулок с так называемыми
межлопастными связями. Схема
такой втулки изображена на
рис. 3.51. Будем считать, что
каждый такой межлопастный
элемент обладает некоторой же-
сткостью с и демпфированием,
характеризуемым коэффициен-
том k, так что сила Р, действую-
щая на такой элемент, связана с
изменением его длины s соотно-
шением:
p = csLk— .
1 dt
В этом случае момент, дейст-
вующий на данную (й-ю) ло-
пасть со стороны межлопастных
элементов, будет зависеть не
только от движения этой лопасти,
характеризуемого углом £&(/), но
также и от движений двух о
При малых колебаниях лопастей относительно вертикальных шар-
ниров момент, действующий на k-ю лопасть, будет выражаться фор-
мулой:
= Со — ^_]) -|- Со (Ей — ;й+1) -|- k0 (Вй — ?й_[) -f- k0 (?'й — Вй+1),
причем
1
k0 = kh?, J
где h — плечо межлопастного элемента (см. рис. 3.51).
Поэтому уравнения движения лопастей в этом случае имеют следу-
ющий вид [сравни с (1.8)]:
Л.пЛ 4" ^о(^ — ^й-1) 4" (4 ='*+i) Н~
+ со - ^-1) + +г) +
V2/
(6.8)
а
где
£=1,2,3, . . . п.
325
Если вал винта совершает колебания по гармоническоу закону
x=x0cos pt,
то можно найти вынужденные колебания лопастей. Правая часть урав-
нений (6. 8) в этом случае имеет вид:
хо — 4.ш(51пA l^-sin[(/? + «>)/+—А
«ь*В.Ш I |_ и J |_ fl
Уравнения (6. 8) допускают в этом случае решение вида:
(0 = ^01 sin [(/? - ш) t —d 4- £02sin [(/? + ») /+ — k
I n J I n
Подсчитаем упругий момент, действующий на А-ю лопасть со сторо-
ны межлопастных упругих элементов при колебаниях лопасти по какой-
либо одной из этих гармоник, например, гармоники (р—to)=pn. Имеем:
^упр — са (Sft ~ ^4-1) 4" со ('ft ~ ’ft+i)—со (2£ft — — £ft+i)-
Далее:
?4=?oisin (/М —k ) =
B^^sin [рл/-^(А-1)]=В018Щ
?ft+1 = ^oi sb [рл/ - ^(A + 1)] = BM sin ,
где
, 2л ,
<Pft=/M----A.
n
Используя эти выражения, получаем
'Мупр = ^0 {2 sin % - sin - sin .
Учитывая, что
. I , 2л \ . 2л , .2л
sin <рйч--=sin<p.,cos----cos sin—;
\ n / n n
. [ 2л \ 2л .2л
sin ------I =Sin COS-----COS sin-------,
получаем окончательно следующее выражение:
Мупр == 2 с0 [1 - cos Ео sin <рй=
= 2с0 Г 1 — cos—1 Во sin Гр J — — • А
L п J L п
В случае обычных упругих элементов с угловой жесткостью сЭКн,
включенных между лопастью и корпусом втулки, мы бы имели:
^ynp = ^^osin А
Таким образом, межлопастные упругие элементы для данной лопас-
ти эквивалентны одному обычному упругому элементу с жесткостью
с9кв=2г0 [1-cos^-]. (6.9)
326
Точно также можно установить, что межлопастные демпферы для
данной лопасти эквивалентны одному обычному демпферу, включенному
между лопастью и корпусом втулки и имеющему коэффициент демпфи-
рования
£экв=2£0 [1- cos^] . (6.10)
Следовательно, расчет земного резонанса вертолета с межлопастны-
ми упругими связями и демпферами можно производить по обычным
формулам, беря коэффициент демпфера, равный £жв, и коэффициент
жесткости в вертикальном шарнире, равный сЭКЕ.
В табл. 3. 2 приведены значения величины:
£экв = *экв.=з2(1—C0S—'l (6.11)
Со *0 \ п /
для винтов с различным числом
лопастей.
Одним из недостатков винта
с межлопастными демпферами
является то, что при одновремен-
ных отклонениях лопастей отно-
сительно вертикальных шарниров
(все в одну сторону и на один
угол), которые могут случаться на переходных режимах полета, а также
при запуске винта такие демпферы не работают.
На существующих конструкциях втулок этот недостаток иногда
устраняют, применяя комбинированные конструкции, в которых упругие
элементы делаются в виде межлопастных связей, а демпферы делаются
индивидуально для каждой лопасти, т. е. включаются между лопастью
и корпусом втулки.
3. Выбор характеристик жесткости и демпфирования шасси *
После того, как выбраны характеристики демпферов лопасти, мож-
но приступать к выбору основных параметров шасси. Для вертолетов
обычной одновинтовой и продольной схем колею шасси 2а (см. рис. 3.17)
следует выбирать таким образом, что частота рга1 собственных колеба-
ний вертолета на пробеге (вращение вокруг продольной оси, проходящей
через центр тяжести) с неработающими стойками (работают лишь пнев-
матики) была приблизительно на 20% выше рабочих оборотов винта.
Это дает условие (4. 19):
Если шасси четырехколесное, то в этой формуле вместо величины
2<?“на2 надо брать величину a?_r=afl + cfl [см. формулы (5.3)].
Так как пневматики выбираются по стояночной нагрузке, то величи-
ну с в данной формуле можно считать известной, поэтому из нее мож-
но найти соответствующее значение а.
Жесткость амортизаторов и их демпфирование можно выбирать,
полагая, что центр зоны неустойчивости на пробеге (при колебаниях
с работающими стойками) совпадает с рабочими оборотами винта. Та-
кой подход вытекает из следующих соображений: если выбрать жест-
* Излагаемый здесь метод выбора параметров шасси был разработан инж.
Ю. А. Мягковым.
327
кость амортизаторов так, чтобы зона неустойчивости на пробеге была
выше рабочих оборотов, то возникает опасность возникновения земного
резонанса с отрывом пневматиков от поверхности земли (см. § 4, и. 3),
так как при колебаниях вертолета с отрывом пневматиков зона неустой-
чивости может «спуститься» на рабочие обороты. Сделать так, чтобы
зона неустойчивости была ниже рабочих оборотов обычно не удается
(исключение составляет шасси системы Бристоль, конструкция которого,
однако, достаточно сложна), так как для этого требуется неосуществи-
мо низкая жесткость амортизаторов. С другой стороны, если зона не-
устойчивости находится непосредственно на рабочих оборотах и запас
демпфирования достаточен, то земной резонанс с отрывом пневматиков
возникнуть не может, так как при отрыве пневматиков зона неустойчи-
вости будет оказываться ниже рабочих оборотов. Это обстоятельство
было проверено многочисленными расчетами и моделированием на
электронной машине земного резонанса с отрывом пневматиков, которое
было выполнено инженером Ю. А. Мягковым.
Будем считать для простоты, что шасси имеет вертикальные амор-
тизационные стойки (см. рис. 3.17,6). Как было показано в § 2, п. 5,
наибольшее демпфирование системы амортизатор—пневматик, которое
может быть получено при выборе оптимального демпфирования аморти-
затора, зависит от отношения с~ . Если воспользоваться формулами
ру
LnH
(2. 37), (2. 38) и считать, что на пробеге
Р’-У
то можно получить следующую формулу, определяющую наибольший
возможный коэффициент располагаемого демпфирования вертолета на
пробеге:
где
(6.13)
С
Это означает, что наибольший возможный коэффициент демпфиро-
вания, который можно получить на пробеге, варьируя величиной Аам,
зависит исключительно от отношения - . Поэтому, зная демпфирова-
ли
ние, потребное для устранения земного резонанса, нетрудно определить
необходимую жесткость амортизатора Сам- Если известно демпфирова-
ние лопасти, то потребное демпфирование п0 может быть определено
по формуле (1.31):
f«o]noip= ~~-пн°- 2°*Д’ (6. 14)
av0 пл
где п”н—-коэффициент демпфирования лопасти пл, отнесенный к частоте
/?пн собственных колебаний вертолета на пробеге с неработаю-
щими стойками (на одних лишь пневматиках):
Рпн
2с"нд2
(6. 15)
Рпи
328
р* — частота собственных колебаний вертолета с работающими
стойками при оптимальном демпфировании, отнесенная к вели-
чине рпн:
=1/^—2* .
/>пн у 1 + 2х
Пусть требуется обеспечить запас демпфирования
7 ]расп
J^olmax
--------/
LnnJпотр
Пользуясь формулами (6.12), (6.14) и (6.16), получим:
(6. 16)
(6-17)
0,25 8уол”н f 1 +2х 1
У х (1 4- х) е (1 — vo) |/ 2х а
Это соотношение можно переписать
следующим образом:
.<ь-ад
где
(6. 18)
(6. 19)
После выбора характеристик лопа-
сти и пневматика и назначения необхо-
димого запаса демпфирования р левая
часть уравнения (6. 18) величина извест-
ная. Зная величину а, нетрудно найти ве-
личину х из уравнения (6.19), а затем
и необходимую жесткость сам амортиза-
тора. Для удобства определения х на
рис. 3.52 приведен график зависимо-
Рис. 3.52. График зависимости
коэффициента а от х
сти а(х).
Для выбора жесткости сам по указанному методу можно брать т] = 1,
так как в приведенных формулах не учитывается «кинематическое»
демпфирование пневматика на пробеге [см. формулу 4. 21)]. Действитель-
ный запас демпфирования q с учетом этого дополнительного демпфиро-
вания должен получиться не менее 1,5—2 *.
После того, как найдена жесткость амортизатора, его оптимальный
коэффициент демпфирования может быть определен по формуле (2.36),
а именно:

/гоР1_^н+См (6.20)
ам р* ’ ' '
где _____
Так как в действительности характеристика демпфирования амор-
тизатора, как правило, нелинейна (§ 3, п. 1), то под величиной сле-
дует понимать коэффициент демпфирования эквивалентного линейного
амортизатора.
* Следует помнить, что случай, когда отсутствует кинематическое демпфирова-
ние, реализуется при колебаниях вертолета на льду, когда трение между пневматикой
и землей отсутствует (см. § 4, п. 2).
329
4. Некоторые рекомендации по конструированию шасси
Одной из основных трудностей, возникающих при проектировании
шасси, является сложность обеспечения необходимого демпфирования
амортизационной стойки. Если размеры отверстий, через которые проте-
кает гидросмесь при работе амортизатора выбирать из условий земного
резонанса, то, как правило, работа амортизатора при посадке будет не-
Рис. 3.53. Амортизационная стойка с клапаном
удовлетворительной (будут слишком большие усилия при ударе о зем-
лю). Если же выбирать их из условий посадки, то получится слишком
малое демпфирование при поперечных колебаниях вертолета, совершен-
но недостаточное для устранения земного резонанса.
Эту трудность можно преодолеть двумя способами [18]:
1) увеличением демпфирования на обратном ходе амортизатора;
2) установкой специальных клапанов в конструкции амортизатора.
Первый из этих способов является наиболее простым и заключается
в том, что размеры отверстий, через которые протекает гидросмесь на
прямом ходе амортизатора (сжатие), выбираются из условий посадки,
а размеры отверстий, через которые гидросмесь протекает на обратном
ходе амортизатора (растяжение),— из условий земного резонанса. Это
оказывается возможным потому, что при колебаниях вертолета в каж-
дый момент времени одна из амортизационных стоек (правая или ле-
330
вая) работает на обратном ходе. Поэтому, вообще говоря, нужный ко-
эффициент демпфирования вертолета при земном резонансе может быть
обеспечен одним лишь демпфированием на обратном ходе амортиза-
торов.
Однако увеличивать демпфирование на обратном ходе можно лишь
в известных пределах. Чрезмерное увеличение демпфирования на об-
ратном ходе (очень малые отверстия) приводит к очень медленному
«выходу» амортизационных стоек из обжатого состояния после удара
при посадке. Поэтому, если вертолет по условиям эксплуатации должен
совершать посадки с пробегом по неровному грунту, когда после первого
удара о землю могут последовать дальнейшие толчки, такой способ уве-
личения демпфирования может оказаться неприемлемым.
Второй способ не имеет указанного недостатка и заключается в том,
что в амортизаторе устанавливают специальный пружинный клапан, ко-
торый открывается только тогда, когда усилие сжатия в амортизаторе
превосходит (при ударе о землю) некоторое критическое значение
При /’ам<С^’а£ работают отверстия, размеры которых выбраны из усло-
вий земного резонанса, а при P3yi>P"v работают дополнительно отвер-
стия большего диаметра, размеры которых выбираются из условий огра-
ничения перегрузки при посадке. На рис. 3.53 изображены схема конст-
рукции и диаграмма динамического обжатия такого амортизатора.
Другим важным фактором, с которым следует считаться при проек-
тировании шасси, является неизбежное наличие у всякого амортизатора
усилия предварительной затяжки (§ 2, п. 7), т. е. усилия, при котором
амортизатор начинает работать. Для вертолетного шасси желательно
иметь как можно меньшие усилия предварительной затяжки Ро, так как
при большой тяге несущего винта усилия Р на шасси уменьшаются и при
Р<Р0 амортизаторы не работают. При этом может развиваться земной
резонанс с неработающими амортизаторами на упругих пневматиках,
практически лишенных демпфирования. Для вертолетных шасси надо
так выбирать характеристики стойки, чтобы усилие предварительной за-
тяжки составляло не более 10% от стояночной нагрузки на амортизатор
при нулевой тяге несущего винта.
331
ГЛABA 4
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАСЧЕТА ПОДШИПНИКОВ
ОСНОВНЫХ АГРЕГАТОВ ВЕРТОЛЕТА
Срок службы основных агрегатов вертолета во многом зависит от
работоспособности их подшипниковых узлов, поэтому вопросам теории
расчета подшипников качения в вертолетостроении уделяется большое
внимание.
Известно, что долговечность подшипников качения общего назначе-
ния из-за различных факторов металлургического и технологического ха-
рактера может колебаться в широких пределах. В связи с этим необхо-
димая надежность подшипниковых узлов в общем машиностроении до-
стигается за счет введения соответствующих коэффициентов безопасно-
сти, т. е. определенного завышения расчетных нагрузок. Понятно, что
требования к точности расчета подшипников при этом могут быть су-
щественно снижены. Для изделий авиационной техники, где повышение
надежности должно достигаться за счет совершенства конструкции без
увеличения габаритов и веса подшипниковых узлов, такой путь, есте-
ственно, неприемлем. Тем более, что авиационные подшипники изготав-
ливаются из улучшенных материалов, имеют высокую точность и под-
вергаются в производстве особо тщательному контролю, в результате
чего рассеивание долговечности для них заметно уменьшается. Авиаци-
онные подшипники, в том числе и подшипники, применяющиеся в верто-
летах, должны рассчитываться возможно более точно с учетом особен-
ностей их нагружения и эксплуатации.
В последние годы благодаря работам отечественных и зарубежных
исследователей практические методы расчета подшипников качения по-
лучили значительное развитие, но тем не менее они далеко не всегда
обладают необходимой точностью. Это особенно относится к случаям
работы подшипников при сложных комбинациях внешних нагрузок и
при качательном движении с малыми амплитудами, а эти случаи именно
и представляют наибольший интерес для вертолетостроении. Отсутствие
надежных методов расчета подшипников качения, работающих в указан-
ных условиях, затрудняет проектирование редукторов, автоматов пере-
коса, втулок несущих и рулевых винтов вертолетов. Можно привести не-
мало примеров, когда эти жизненно-важные агрегаты выходили из строя
до выработки ресурса из-за разрушения неудачно подобранных подшип-
ников.
В настоящей главе сделана попытка обобщить результаты теорети-
ческих и экспериментальных исследований, выполненных с целью уточ-
нения методов расчета подшипников агрегатов вертолета. Как показала
практика, изложенные ниже методы расчета позволяют более полно ис-
пользовать несущую способность подшипников. Применение этих мето-
дов при конструировании подшипниковых узлов во многих случаях дало
332
возможность создать достаточно компактные и легкие конструкции, спо-
собные надежно работать в течение длительного времени при весьма вы-
соких нагрузках.
§ 1. УРАВНЕНИЯ СТАТИЧЕСКОГО РАВНОВЕСИЯ РАДИАЛЬНЫХ
И РАДИАЛЬНО-УПОРНЫХ шарикоподшипников
ПРИ КОМБИНИРОВАННОЙ НАГРУЗКЕ
Зависимости, используемые при расчетах подшипников, базируются
на результатах исследования распределения внешней нагрузки между
телами качения.
Составим уравнения, с помощью которых могут быть найдены дав-
ления на шарики в общем случае нагружения радиальных и радиально-
упорных шарикоподшипников.
Пусть однорядный шарикоподшипник имеет после посадки на вал
и в корпус при установившемся температурном режиме работы узла ра-
диальный зазор 2А.
Рис. 4.1. Схема перемещений внутреннего кольца
подшипника под действием приложенной к нему про-
извольной внешней нагрузки
Возьмем прямоугольную систему координат xyz с началом в цент-
ре О наружного кольца. Ось х направим по оси вращения этого кольца
(рис. 4. 1) .
При приложении к подшипнику произвольной внешней нагрузки
центр внутреннего кольца перемещается в точку О' с координатами s, I
и и, а его ось вращения х' отклоняется относительно оси х на некоторый
угол Д’, проекции которого на плоскости хОу и xOz соответственно рав-
ны 0’1 и (рис. 4. 1).
Будем считать, что на шарик, центр которого Ош лежит в плоско-
сти П, составляющей с плоскостью xOz угол -ф, действуют нормальные
силы Рф, одинаковые по величине и направленные по общей прямой, про-
ходящей через центры Он и ОЕ сечений желобов наружного и внутренне-
го колец и точку Ош (рис. 4.2). Смещением центра площадки контакта
шарика с внутренним кольцом из плоскости П и касательными силами,
возникающими в точках контакта шарика с кольцами, как это обычно
принято в теории подшипников качения, пренебрегаем.
Согласно известным формулам Герца
Рф=5В3ф/2.
(1.1)
Здесь бф — сближение желобов колец в направлении OSOB за счет упру-
гих деформаций в зонах контакта.
333
Для шарикоподшипников с обычной внутренней геометрией можно
полагать
d1
(1.2)
где v — множитель, зависящий от соотношения между ра-
диусами ги и гв желобов наружного и внутреннего
колец и диаметром шарика dB1;
g = ru-\-ra—<4п — расстояние между точками Он и Ов в момент ка-
сания шарика с кольцами (при бф =0).
Если диаметр с?ш выра-
жен в миллиметрах, а силы
в килограммах, то при моду-
ле упругости материала ко-
лец и шариков £ = 2,08Х
ХЮ6 кгс!см2 коэффициент
Во равен 62.
Множитель v имеет зна-
чения, указанные в табл, 4. 1.
Таблица 4. i
rH 0,510 0,515 0,520
4 0,63 1,00 1,39
Рис. 4.2. Схема сил, действующих иа шарик Из условий статического
равновесия элементов под-
шипника следует, что внешние силы и моменты, приложенные к внутрен-
нему кольцу, могут быть записаны так (см. рис. 4. 2):
А = ^Z\sin
/?,,= — Рф cos ₽ф sin Ф;
= V Рф cos Рф cos ф;
=г0 р* sin cos Ф;
Мг =Г0 Рф Sin РфБШ ф.
(1.3)
Здесь Рф — угол контакта шарика с кольцами;
г0 — радиус, на котором расположены центры шариков.
Знак S распространяется на все нагруженные шарики.
Допустим, что кольца имеют абсолютно правильную геометрическую
форму, не изменяющуюся при приложении нагрузки. В этом случае для
определения сближения желобов бф и угла контакта (Зф могут быть ис-
пользованы формулы
Зф=[(sH-VosinФ+Vo cosф)2-|-(g- —Д —/зтф4-KCos Ф)2]1^ — (1, 4)
g _ arc t * + У0з!Пф + У0созф _ (1.5)
g — Д — t sin Ф + U COS <p
334
Выразив в формулах (1.4) и (1.5) все линейные величины в долях
расстояния g, перепишем их в виде:
84'=[(s+ sin +s2 cos’?)2+(cos -1; (1.6)
^=arctg ,.7+7lSM + ^C0sfr , (L7)
COS Po — t sin + « Cos ф
где ₽0=arccos -—— — так называемый начальный угол контакта (угол
& контакта при чисто осевом смещении колец за
счет рабочего радиального зазора 2Д).
В выражениях (1.6) и (1.7) через и е2 обозначены величины
»! И &, .
g g
Следует иметь в виду, что рабочий осевой люфт подшипника s0 свя-
зан с углом Во следующим соотношением:
2s0 = 2gsinfJ0
или, переходя к относительным величинам,
2s0=2sin fi0. (1.8)
Относительные величины везде обозначаются теми же буквами, что
и абсолютные, с черточками над ними.
Приведенные уравнения описывают условия статического равнове-
сия радиальных и радиально-упорных шарикоподшипников при любых
комбинациях внешних нагрузок. Из них могут быть найдены все пара-
метры, характеризующие распределение усилий между отдельными ша-
риками. Нужно, однако, иметь в виду, что из-за сложности зависимостей,
связывающих величины бф и рф с относительными смещениями колец,
практическое применение этих уравнений сопряжено с большим объемом
вычислений. В связи с этим при инженерных расчетах они обычно заме-
няются теми или иными приближенными соотношениями. Один из наи-
более удобных для практики вариантов таких соотношений, обладающий
достаточно высокой точностью, описан ниже.
Анализ условий работы подшипниковых узлов различных типов по-
казывает, что в большинстве случаев результирующая радиальная сила
R = (Ry 4-А|2)1/з и результирующий момент М= (М^ -(-ЛР)1''2,воспринимае-
мые подшипником, действуют в одной плоскости. В соответствии с этим,
располагая плоскость координат хОг таким образом, чтобы она совпа-
дала с плоскостью действия внешних нагрузок, приложенных к подшип-
нику, можно написать:
^=0;

Как свидетельствуют расчеты, распределение нагрузки мало зави-
сит от углового расположения комплекта шариков. Принимая во внима-
ние это обстоятельство, будем считать, что шарики расположены сим-
метрично относительно плоскости хОг. При этом условии
/=0;
е1 —0;
(1-Ю)
I
I
)
335
Имея в виду равенства (1.10)^ разложим выражение (1.6) в ряд
Маклорена в окрестности и = 0 и 8г = е=0. Ограничиваясь линейными
членами, после несложных преобразований получим
8ф = § + (« cos р 4-в sin p)cos^. (1. 11)
В равенстве (1. И)
l=(s2 + cos2P0)1/2-l (1.12)
И
P=arctg f—. (1.13)
(cos ₽0 /
Величины й и р есть ни что иное, как относительное сближение же-
лобов и угол контакта в сечении ф = 90°.
Как следует из выражения (1.7),
sin О _____________________$ + е1 sjnfr +е2СО^Ф __________________ .
* [(s+71 sin ip + е2 cos'Р)2 + (cos р0 •—/ sin ф-р в cos ф)2]1/2 ’ I
,, cos Ро — Zsinip + ucostb
V [(?+£1 sin ф + е2 c°s Ф)2 + (cos Ро—f sin ф + и cos ф)2]1/2
(1.14)
Поступив с равенствами (1.14) таким же образом, как и с выраже-
нием (1.6), после отбрасывания нелинейных членов и соответствующих
преобразований имеем
sin = sin р Г1 — CQs2 (и — в ctg р) cos Ф
L cospo
cos Рф =)cos р [ 1 4- -S1"-E (и — в ctg р) cos О
L cosPo
Положив
и COS р-ре sin Р_
"8 ~ ’
(1- 15)
(1-16)
представим зависимости (1.11) и (1.15) в виде:
Ц^6(1-|-ксо8<р); (1.17)
sin pd=sin р [1 _.C0S_L/' xs--—1 cos 01;
L COSpQ \ Sinp ) J (J 18)
COS Рф = С05 р Г 1 4~-C°Sj- tg2p I --—cos с-1.
L COS Ро \ sin Р / J
Величина б, определяющая давление на шарик, центр которого на-
ходится в плоскости хОу, может быть выражена через углы р и ро’.
g cos Ро |
COS Р
(1-19)
Зона нагружения подшипника, как известно, находится из условия,
что на ее границах бф=О.
Полагая в равенстве (1.17) бф=О, получаем следующее выражение,
устанавливающее границы зоны нагружения:
'4’"=arccosf--. (1.20)
336
Рис. 4. 3. Зона
нагружения
подшипника
Относительное сближение желобов колец бФ достигает максималь-
ного значения бо в центре зоне£ на гружения, который расположен в се-
чении ,ф = 'фо=О, если Mcos|3 + esinp = 6^>0, и в сечении 1ф=1фо=180°,
если и cos р + е sin р = бл<Т) (рис. 4.3).
В случае Со=О 0<Ф’<180° и ф'=,~ф" а в случае Фо= 180°
180°<Ф” <360° и 'У ==360° — '!/.
Понятно, что выражение (1.20) справедливо только тогда, когда
параметр X по абсолютной величине превосходит единицу. Если
|Х| <1, то зона нагружения состав-
ляет 360°, т. е. в подшипнике несут
нагрузку все шарики, причем вели-
чина б в этом случае всегда поло-
жительна, а знак X совпадает со зна-
ком cos 4’о. Последнее означает, что
для подшипников, у которых нагру-
жены все шарики, при т['О— 0
0<Х< 1 и при 4o=18O° —1<Л<0.
Приняв в равенстве (1. 17)
4=-фо, находим:
80=8(1+Xcos<|’0). (1.21)
С помощью выражений (1.2), (1
S,
= —, приведем формулу (1.1) к ви.
. 17) и (1.21),
вспоминая, что <5ф =
+ X cos ф \3/2
1- Xcos ф0 /
(1.22)
Зависимости (1.19) и (Е21) показывают, что в случае Х = оо, т. е.
при зоне нагружения 180°, 6 = 0 и, следовательно, р = р0 независимо от
уровня нагрузки.
Введем в рассмотрение суммы
= 2(1+^<М)Исо8*-- (1.23)
где
k-= 1, 2, 3.
Здесь, как и во всех предыдущих равенствах, угол 4 может прини-
мать только те дискретные значения, которые определяют угловое поло-
жение нагруженных шариков.
Преобразуем теперь с помощью полученных выражений уравнения
(1.3).
Заменив в этих уравнениях Pi, sin рф и cos « их значениями по
формулам (1. 22) и (1. 18), в соответствии с равенствами (1. 9) и (1. 23),
учитывая зависимость (1.21), получим:
Д cos 3 / 160 г \ 721
[ cos р0 \1 + X cos фо sin р / 7j J ’
7? «73/2. w (1-24)
= W cos,V2X
zva in
X Г1 4- -E21JL tg2 rj f-^0--------L_.
L cos Po \14-Xcosip0 sin p / 72 J
22 1578
337
M
(1.24)
X [ 1 C0SP / ' ''о______г ) А
L cos Ро \1 + X cos фо sin р ) J2
Из зависимостей (1.19) и (1.21) вытекает следующее выражение
для угла р:
cos 80
COS i —------—
80
(1.25)
Равенства (1.24) и (1.25) являются теми соотношениями, которы-
ми могут быть заменены при инженерных расчетах «точные» уравнения
статического равновесия радиальных и радиально-упорных шарикопод-
шипников. Как показывают соответствующие исследования, ошибка
в конечных результатах, обусловленная такой заменой, обычно не пре-
вышает нескольких процентов.
При изменении числа шариков суммы (1-23) изменяются незначи-
тельно. Это позволяет выразить их через интегралы
—Г—TW \ (4 + Xcos %COSф)3/2cos*—14,«'Р, (1.26)
2л (1 + Xcos ipo) •’
являющиеся функцией произведения Kcostpo- Здесь k=l, 2, 3.
Нетрудно убедиться, что при обычных количествах шариков
А^СОз*-Ч0Л.
(1.27)
Значения интегралов Д даны в табл. 4. 2.
Таблица 4. 2
X cos фо 7| Л Уз W X COS фо /1 72 Уз W
0 1,000 0,000 0,500 1,000 3,33 0,323 0,247 0,210 0,612
0,1 0,868 0,065 0,435 0,879 5 0,309 0,242 0,207 0,605
0,2 0,766 0,114 0,385 0,804 10 0,294 0,236 0,203 0,596
о,3 0,686 0,151 0,346 0,757 20 0,286 0,233 0,201 0,59
0,4 0,622 0,180 0,316 0,726 0,279 0,229 0,199 0,587
0,5 0,570 0,202 0,292 0,705 -20 0,271 0,225 0,197 0,583
0,6 0,528 0,220 0,273 0,690 — 10 0,262 0,221 0,194 0,578
0,7 0,494 0,233 0,258 0,678 -5 0,247 0,212 0,188 0,567
0,8 0,466 0,243 0,246 0,670 -3,33 0,229 0,201 0,181 0,556
0,9 0,443 0,250 0,237 0,663 -2,5 0,211 0,189 0,172 0,543
1 0,425 0,255 0,231 0,657 —2 0,192 0,175 0,162 0,528
1,111 0,409 0,257 0,226 0,651 —1,667 0,171 0,159 0,149 0,512
1,25 0,395 0,258 0,223 0,645 -1,429 0,147 0,140 0,133 0,488
1,429 0,380 0,258 0,220 0,639 -1,25 0,120 0,116’ 0,112 0,459
1,667 0,366 0,256 0,218 0,633 -1,111 0,084 0,083 0,080 0,414
2 0,352 0,254 0,215 0,626 —1 0,000 0,000 0,000 0,000
2,5 0,338 0,251 0,212 0,619
338
§ 2. РАСЧЕТ РАДИАЛЬНЫХ И РАДИАЛЬНО-УПОРНЫХ
ШАРИКОПОДШИПНИКОВ ПРИ КОМБИНИРОВАННЫХ
НАГРУЗКАХ В СЛУЧАЕ ОТСУТСТВИЯ ВЗАИМНОГО ПЕРЕКОСА
КОЛЕЦ
1. Давления на шарики
Если расстояние между опорами велико по сравнению с диамет-
ральными размерами подшипников и все детали подшипникового узла
обладают высокой жесткостью, то при вычислении давлений на тела ка-
чения можно пренебрегать взаимным-перекосом колец под нагрузкой
и учитывать только их смещения в радиальном и осевом направлениях.
В формулу (1.22), определяющую давления на шарики в радиаль-
ных и радиально-упорных шарикоподшипниках, входят величины бо и А.
Соотношения (1.24) и (1.25), связывающие эти величины с внеш-
ними нагрузками, приложенными к подшипнику, при отсутствии взаим-
ного перекоса колец, т. е. в случае й- = 0, могут быть представлены
в виде:
Л г, Vq/o о • / 1 cos 3 Д’ 1
---— — Sill 8 /. I I---<-£.--У— ;
cos fo 1 4” Ji J
J (2. 1)
cos P t 2 3 xao _7з \ _
cos fo 1 I- x h I ’
° \
cos 0/2( 1
**аш \
Выражение для момента не выписываем, так как при Й = 0 оно не
играет самостоятельной роли и не используется в расчетах.
Для удобства предполагаем, что направление оси z совпадает с на-
правлением радиальной нагрузки R. При этом условии радиальное сме-
щение и положительно и, следовательно, угол фо равен нулю. Это обсто-
ятельство учтено как и в уравнениях (2. 1) и (2.2), так и во всех после-
дующих зависимостях.
Следует отметить, что случай it —0 является основным в теории
подшипников качения. Обычно, когда не делают особых оговорок о кон-
струкции и особенностях нагружения подшипникового узла, имеют в ви-
ду именно этот случай. Применительно к нему выполнены основные ис-
следования [22], [23], [29], [42], направленные на уточнение методов рас-
чета подшипников качения, работающих при комбинированных на-
грузках.
Статическая нагруженность подшипника характеризуется величи-
ной максимального давления на тело качения.
Согласно формуле (1.22) максимальное давление на шарик
Ро - \ (2.3)
При длительном статическом нагружении невращающегося под-
шипника наибольшее напряжение смятия Отах на дорожке качения внут-
реннего кольца, обусловленное этим давлением, не должно превышать
40 000 кгс[см2. Если статические нагрузки, действующие на невращаю-
щийся подшипник, создают большие контактные напряжения, то на до-
рожках качения появляются заметные следы остаточных деформаций
в виде вмятин от шариков.
Указанное допускаемое значение Птах выбрано из условия, что ве-
личина остаточной деформации дорожки качения составляет не более
22*
339
одного микрона на каждый сантиметр диаметра шарика. В этом случае
не нарушается плавность вращения подшипника и не снижается его
несущая способность.
В расчетных зависимостях, употребляющихся для вычисления сро-
ка службы подшипников, фигурирует величина
/ Фн \1/т
'’•-к-г?*
(2.4)
где т — показатель степени при нагрузке в формулах долговечности.
С помощью равенств (1.22) и (2.3) приведем выражение (2.4)
к виду
P3-=wPa. (2.5)
Коэффициент w здесь равен
----------------------(1 + COS Фо COS <Ж2т i/Ф
2л (1X cos ф0)3/2 J' 1 то ./ Г
< -I
(2-6)
Заметим, что величина Рэ является тем постоянным давлением
/-*+ = const, при котором вероятность усталостного разрушения вращаю-
щегося кольца в данных эксплуатационных условиях та же, что и при
действительном распределении усилий между телами качения. Это дает
основание называть ее эквивалентным давлением на тело качения для
вращающегося кольца.
Нужно иметь в виду, что величину Рэ иногда относят не ко всей дли-
не дорожки качения, как это сделано в выражении (2.4), а только к на-
груженной зоне с" —'V .
При т = 3,33, как это принято в отечественной практике,
1
тг> = 1----------------------
(л (1 + X COS фо)5
—и )
2 \ ‘ 8 /
» / 137 , 607 -j 2 । 1°'3
н \ 60”’Г120 15 /])
(2.7)
При практическом использовании формул (2.6) и (2.7) нужно
помнить, что для выбранного направления оси z угол фо равен нулю.
Углы Фп и ']/ в формуле (2.7) берутся в радианах. Значения коэффи-
циента w, найденные по этой формуле, приведены в табл. 4.2 вместе со
значениями интегралов jh.
Давления Ро и Ра при заданных внешних нагрузках R и А могут
быть вычислены двумя путями.
Первый из них состоит в подсчете этих величин по формулам (2.3)
и (2. 5) с использованием значений <5о и Л, полученных в результате пря-
мого решения уравнений (2. 1) и (2. 2).
Так как уравнения (2. 1) и (2.2) имеют сложную структуру, то этот
путь, естественно, сопряжен с большими трудностями. Они достаточно
велики даже тогда, когда задача решается приближенным образом.
Второй, более приемлемый для практических приложений, путь оп-
ределения давлений Ро и Рэ основан на следующих соображениях.
340
Если бы угол контакта всех шариков был одинаков (Зф =p = constt
то
-Л,—ЗД.Л?Л;
(2.8)
Соотношения (2.8) отличаются от уравнений (2. 1) тем, что в них
отсутствуют члены, учитывающие изменение угла контакта в зависимос-
ти от положения шарика относительно плоскости xOz.
При зоне нагружения 180°, когда в подшипнике работает половина
шариков, Х=±оо и, следовательно, {3= ро, ^ = 0,279, /2 = 0,229 и 10 = 0,587.
Из соотношений (2. 8) для данного случая находим
4=4tg?=i,2i7tgg0,
К Л
при этом
Л =-----— =-4,37----;
?COS{V2 ^COsPo
pg = wpo==2,57
R
^COSfc
Формулы (2. 10) известны в теории подшипни-
ков качения под названием формул Штрибека.
Для случая — #=1,217 tg [30 давления Ро и Р3
R
могут быть представлены в виде
Р,,-4,37 KoF ;
Z COS ро
Рэ = 2,57——----,
Z COS Ро
(2-9)
(2.10)
Рис. 4.4. Резуль-
тирующая сила,
приложенная к
подшипнику
где = Л2)1-'2- результирующая нагрузка на
подшипник (рис. 4.4).
Эта же форма записи может быть сохранена и при учете перемен-
ности угла Рф .
Подставив в выражение (2. 11) значения Ро и Ра из равенств (2.3)
и (2. 5), имеем
Btfin'2 cos Ро
ко ~ —
4,37-------у-
К =----------tfn.
0,587 0
1
I
I
I
(2. 12)
Коэффициенты Ко и к являются своеобразными коэффициентами
приведения, отнесенными к результирующей нагрузке F. Существенно,
что они могут быть найдены из уравнений (2.1) и (2.2) различными
косвенными методами, исключающими необходимость прямого решения
этих уравнений.
Значения коэффициентов ко и к для подшипников с начальными
углами контакта Ро = О, 12, 18 и 36°, полученные из уравнений (2. 1)
и (2.2) графоаналитическим способом [30], приведены в табл. 4.3.
341
Таблица 4. 3
Продолжение
\ а
Л \ 0° 10° 20’ 30" 40° 50° 60° 70° 80° 90° W».' 0° 10° 20° 30" 40° 50° 60° 70° 80° 90°
гуЛш \ Л \
Значения коэффициента к0 fo = 26°
₽о = 1 0,02 1,914 1,815 1,478 0,872 0,692 0,667 0,611 0,594 0,530 0,454
0,02 1,000 1 0,889 1 1,070 1,210 1,308 1,381 1,425 1,428 1,398 1,308 0,04 1,609 1,528 1,321 0,865 0,692 0,665 0,635 0,587 0,523 0,447
0,04 1,000 0,890 0,966 1,091 1,148 1,196 1,212 1,192 1,152 1,080 0,07 1,483 1,415 1,218 0,858 0,692 0,661 0,629 0,577 0,514 0,440
0,07 1,000 0,880 0,924 1,014 1,078 1,116 1,116 1,094 1,056 0,976 0,11 1,389 1,326 1,150 0,850 0,692 0,656 0,621 0,566 0,504 0,431
0,11 1,000 0,920 0,14 1,336 1,279 1,119 0,847 0,692 0,655 0,618 0,560 0,500 0,424
0,880 0,958 1,010 1,034 1,030 1,006 0,956 0,874 0,21 1,249 1,204 1,069 0,845 0,692 0,650 0,611 0,551 0,492 0,413
0,14 1,000 0,926 0,873 0,933 0,974 0,994 0,984 0,952 0,906 0,826 0,35 1,175 1,125 1,011 0,837 0,693 0,647 0,600 0,544 0,480 0,398
0,21 1,000 0,936 0,858 0,898 0,930 0,938 0,916 0,886 0,836 0,750 0,53 1,121 1,078 0,975 0,828 0,696 0,642 0,593 0,535 0,466 0,383
0,35 1,000 0,948 0,858 0,858 0,876 0,872 0,850 0,804 0,746 0,667 0,70 1,087 1,051 0,955 0,826 0,698 0,639 0,589 0,527 0,455 0,373
0,53 1,000 0,956 0,874 0,836 0,842 0,828 0,798 0,75( 0,686 0,602 1,00 1,051 1,016 0,932 0,819 0,701 0,632 0,580 0,515 0,440 0,358
0,70 1,000 0,961 0,882 0,824 0,822 0,802 0,748 0,718 0,648 0,566 В < fo = 36°
1,00 1,000 0,967 0,893 0,818 0,800 0,774 0,734 0,678 0,602 0,526 0,02 2,171 ',051 1,823 1,426 0,795 0,580 0,507 0,455 0,388 0,310
Ж!' 0,04 1,815 1,756 1,574 1,242 0,777 0,575 0,507 0,453 0,388 0,307
fo = 12" 0,07 1,629 1,567 1,403 1,132 0,757 0,574 0,514 0,453 0,385 0,304
0,02 1,399 1,171 0,839 0,897 0,963 0,999 1,005 0,992 0,937 0,877 0,11 1,496 1,425 1,272 1,052 0,746 0,578 0,514 0,451 0,380 0,299
0,04 1,249 1,109 0,842 0,875 0,933 0,959 0,956 0,938 0,883 0,808 J&' 0,14 1,445 1,359 1,205 1,011 0,742 0,578 0,51.4 0,449 0,379 0,299
0,07 1,184 1,077 0,847 0,858 0,902 0,918 0,914 0,879 0,824 0,752 ж 0,21 1,313 1,262 1,144 0,970 0,736 0,578 0,510 0,449 0,375 0,299
0,11 1,136 1,046 0,853 0,841 0,871 0,881 0,870 0,831 0,777 0,705 ж. 0,35 1,207 1,156 1,060 0,913 0,724 0,578 0,510 0,445 0,370 0,291
1,114 1,034 0,53 1,129 1,086 0,999 0,870 0,714 0,578 0,509 0,444 0,364 0,285
0,14 0,860 0,831 0,859 0,862 0,847 0,809 0,754 0,681 Я'| 0,70 1,098 1,053 0,967 0,848 0,707 0,578 0,506 0,440 0,364 0,283
0,21 1,086 1,018 0,870 0,816 0,833 0,833 0,809 0,771 0,713 0,636 / 1,00 1,053 1,006 0,925 0,821 0,696 0,578 0,502 0,434 0,356 0,275
0,35 1,056 1,008 0,889 0,803 0,806 0,799 0,781 0,721 0,655 0,579
0,53 1,038 1,002 0,899 0,802 0,789 0,772 0,734 0,688 0,623 0,538 Значения коэффициента к
1,028 0,995 fo = 0'
0,70 0,908 0,810 0,778 0,754 0,715 0,665 0,601 0,514 Ж'.-1 2,270
1,00 1,020 0,983 0,912 0,813 0,761 0,734 0,694 0,636 0,567 0,479 0,02 1,000 0,995 1,297 1,520 1,710 1,882 2,030 2,150 2,230
0,04 1,000 0,962 1,150 1,350 1,502 1,655 1,758 1,825 1,870 1,900
1 ffi 0,07 1,000 0,950 1,055 1,212 1,355 1,475 1,540 1,608 1,680 1,710
1,628 Р 18° 0,11 1,000 0,968 1,005 1,130 1,232 1,325 1,400 1,452 1,477 1,490
0,02 1,476 1,001 0,785 0,804 0,813 0,804 0,770 0,718 0,647 Ж?: 0,14 1,000 0,966 0,985 1,093 1,190 1,275 1,330 1,375 1,395 1,408
0,04 1,453 1,338 0,981 0,818 0,797 0,799 0,789 0,759 0,697 0,625 0,21 1,000 0,963 0,952 1,045 1,120 1,175 1,225 1,260 1,275 1,283
0,07 1,327 1,238 0,961 0,786 0,780 0,782 0,766 0,727 0,672 0,597 Яь 0,35 1,000 0,970 0,937 0,979 1,041 1,082 1,107 1,122 1,133 1,140
0,11 1,252 1,172 0,951 0,781 0,777 0,770 0,749 0,707 0,649 0,572 0,53 1,000 0,972 0,934 0,944 0,986 1,015 1,025 1,032 1,030 1,029
1,217 1,140 0,948 0,782 0,771 0,761 0,741 0,70 1,000 0,977 0,934 0,928 0,952 0,919 0,973 0,976 0,972 0,968 0,896 0,966 0,890
0,14 0,696 0,637 0,560
1,169 1,108 1,00 1,000 0,982 0,935 0,907 0,926 0,922 0,905
0,21 0,941 0,784 0,763 0,749 0,719 0,675 0,612 0,534 W
0,35 1,108 1,058 0,932 0,789 0,748 0,730 0,694 0,646 0,582 0,496 fo=12 О
0,53 1,073 1,027 0,924 0,789 0,739 0,717 0,671 0,618 0,554 0,466 0,02 1,237 1,090 0,929 1,039 1,191 1,301 1,384 1,438 1,486 1,489
0 70 1,056 1,018 0,926 0,797 0,736 0,707 0,661 0,604 0,536 0,455 0,04 1,125 1,051 0,919 0,991 1,142 1,235 1,29f 1,335 1,369 1,377
1,00 1,035 1,008 0,915 0,806 0,732 0,682 0,647 0,590 0,518 0,429 0,07 1,093 1,034 0,913 0,979 1,082 1,159 1,215 1,251 1,270 1,280
0,11 1,065 1,014 0,913 0,963 1,041 1,101 1,146 1,18 1,188 1,197
343
34 2
Продолжение
х. а ~^г\ \ 0’ 10° 20° 30° 40° 50° 60° 70° 80° 90°
0,14 1,053 1,006 0,914 0,951 1,017 1,071 1,111 1,136 1,149 1,152
0,21 1,037 0,999 0,916 0,921 0,981 1,022 1,051 1,057 1,082 1,077
0,35 1,017 0,994 0,923 0,897 0,937 0,959 0,983 0,986 0,991 0,989
0,53 1,010 0,988 0,929 0,885 0,911 0,927 0,931 0,925 0,918 0,917
0,70 1,006 0,982 0,931 0,883 0,891 0,897 0,892 0,885 0,877 0,869
1,00 1,001 0,976 0,933 0,873 0,870 i0= 18 0,864 0,851 0,834 0,826 0,812
0,02 1,336 1,260 0,972 0,879 0,944 1,003 1,048 1,070 1,091 1,102
0,04 1,231 1,175 0,962 0,873 0,931 0,979 1,008 1,036 1,056 1,062
0,07 1,170 1,115 0,952 0,866 0,915 0,957 0,981 0,999 1,017 1,013
0,11 1,125 1,077 0,941 0,860 0,899 0,933 0,957 0,965 0,973 0,965
0,14 1,104 1,057 0,937 0,856 0,889 0,920 0,942 0,944 0,951 0,942
0,21 1,067 1,033 0,932 0,856 0,872 0,894 0,906 0,906 0,913 0,906
0,35 1,041 1,011 0,935 0,856 0,856 0,865 0,865 0,865 0,858 0,856
0,53 1,024 0,996 0,934 0,856 0,837 0,846 0,836 0,825 0,810 0,808
0,70 1,013 0,986 0,932 0,856 0,830 0,830 0,818 0,799 0,780 0,780
1,00 0,999 0,974 0,929 0,856 0,819 о = 26 0,806 0,789 0,770 0,751 0,737
0,02 1,451 1,411 1,227 0,863 0,775 0,778 0,782 0,778 0,775 0,767
0,04 1,285 1,249 1,132 0,863 0,773 0,776 0,773 0,772 0,767 0,759
0,07 1,215 1,195 1,078 0,859 0,772 0,769 0,764 0,761 0,754 0,747
0,11 1,182 1,159 1,034 0,856 0,769 0,762 0,754 0,749 0,741 0,732
0,14 1,150 1,120 1,011 0,854 0,768 0,758 0,749 0,741 0,732 0,722
0,21 1,096 1,071 0,980 0,850 0,766 0,755 0,741 0,729 0,719 0,705
0,35 1,043 1,021 0,959 0,847 0,764 0,746 0,728 0,707 0,692 0,678
0,53 1.016 0,992 0,936 0,841 0,764 0,737 0,714 0,690 0,668 0,652
0,70 1,005 0,971 0,923 0,836 0,764 0,732 0,705 0,678 0,652 0,634
1,00 0,989 0,953 0,905 0,836 0,764 0 = 36с 0,728 0,701 0,658 0,634 0,615
0,02 1,525 1,480 1,363 1,149 .0,778 0,643 0,603 0,566 0,540 0,526
0,04 1,367 1,333 1,124 1,060 0,769 0,639 0,603 0,566 0,536 0,525
0,07 1,269 1,233 1,141 0,990 0,756 0,638 0,600 0,564 0,534 0,521
0,11 1,195 1,157 1,076 0,942 0,748 0,637 0,599 0,558 0,531 0,518
0,14 1,157 1,120 1,045 0,922 0,746 0,638 0,599 0,557 0,527 0,514
0,21 1,098 1,066 0,996 0,888 0,744 0,639 0,597 0,554 0,520 0,508
0,35 1,035 1,012 0,946 0,858 0,736 0,639 0,592 0,550 0,511 0,498
0,53 0,993 0,970 0,910 0,832 0,728 0,639 0,589 0,544 0,502 0,491
0,70 0,970 0,946 0,890 0,815 0,723 0,639 0,585 0,540 0,500 0,485
1,00 0,945 0,914 0,863 0,798 0,718 0,639 0,582 0,534 0,493 0,473
344
Введение табулированных коэффициентов приведения Ко и к су-
щественно облегчает отыскание давлений Ро и Ра, позволяя использо-
вать для этой цели весьма простые и удобные формулы (2. 11).
г
Коэффициенты Ко и к даны в табл. 4.3 в функции величины -,
характеризующей уровень нагрузки, воспринимаемой подшипником,
и угла а = arc tg , определяющего направление результирующей
силы F *.
2. Приведенные нагрузки
Обозначим через Q радиальную силу, создающую в сочетании с осе-
вым усилием Л = 1,217 tg pflQ при постоянном угле контакта шариков
с кольцами Рф =Po=const такое же эквивалентное давление Рэ, что и
действительная комбинация внешних нагрузок, приложенных к под-
шипнику.
Силу Q принято называть приведенной динамической нагрузкой.
Наряду с понятием приведенной динамической нагрузки в теории
подшипников качения широко используется понятие приведенной ста-
тической нагрузки. Под последней понимается радиальная сила Qo, ко-
торая создает в указанных условиях максимальное давление на шарик
Ро, равное действительному.
Замена действительных нагрузок приведенными нагрузками, опре-
деленными вышеуказанным образом, позволяет использовать при рас-
чете подшипников, работающих при комбинированных нагрузках, дан-
ные каталогов и справочников, относящиеся к радиально нагруженным
подшипникам.
Сопоставляя равенства (2. 10) и (2. 11), видим, что
Q = | 13
CV- лтЛ J
В зарубежной, а в последнее время и в отечественной практике, для
определения приведенных нагрузок часто применяется формула вида
Q = xR-±-yA.
Разные источники дают разные значения коэффициентов приведе-
ния х и у, поэтому приведенные нагрузки, вычисленные для одних и тех
же расчетных случаев, могут существенно отличаться друг от друга.
Так как все применяющиеся на практике методы расчета радиаль-
ных и радиально-упорных шарикоподшипников при комбинированных
нагрузках базируются на одних и тех же исходных уравнениях (1. 1) —
(1.7) и по сути дела отличаются друг от друга только допущениями,
принятыми для упрощения их решения, то одним из главных критериев
совершенства той или иной расчетной методики может служить бли-
зость приведенных нагрузок, подсчитанных на ее основе, к «точным»
значениям этих нагрузок, вытекающим из указанных уравнений.
На рис. 4. 5 сопоставлены приведенные нагрузки, определенные с
помощью коэффициентов табл. 4. 3, с приведенными нагрузками, най-
денными в результате «точного» решения уравнений (1.1) — (1-7). Там
же показаны приведенные нагрузки, подсчитанные по методике между-
* При вычислении величин ------т , а также -----г и ---а- диаметр всегда вы-
zvd],, гч<Рш
ражается в миллиметрах.
345
народной организации по стандартизации (ИСО*), принятой в послед-
нее время за рубежом, а также по методике М. П. Белянчикова [24], ко-
торая рекомендуется сейчас для расчета подшипников общего назна-
чения.
Как видно из рис. 4. 5, приведенные нагрузки, полученные при ис-
пользовании данных табл. 4. 3, наиболее близки к их «точным» зна-
чениям.
Рис. 4. 5. Сравнение различных методов расчета при-
веденных нагрузок на подшипник
Применение методики ИСО дает при определенных условиях завы-
шение приведенных нагрузок на 20—30%, что для подшипниковых уз-
лов авиационных агрегатов, естественно, недопустимо.
При расчете радиально-упорных шарикоподшипников с углами кон-
такта [% >26° по методу М. П, Белянчикова получаются достаточно
точные значения приведенных нагрузок. Однако при меньших углах
контакта точность метода существенно снижается. Так в случае углов
контакта р0= 12-=-18° ошибка в приведенной нагрузке может доходить до
40%. Для углов контакта менее 12° этот метод вообще неприменим.
* Проект рекомендаций но расчету динамической грузоподъемности шариковых
и роликовых подшипников, ИСО, № 278, 1960.
346
3. Статистическая теория динамической грузоподъемности
В расчетах на долговечность обычно используются общие законо-
мерности статистической теории усталости металлов, предполагающей,
что разрушение материала под действием переменных нагрузок являет-
ся случайным процессом накопления усталостных повреждений, облада-
ющим теми или иными вероятностными характеристиками. Такой под-
ход к проблеме долговечности действителен для всех деталей машин,
работающих при переменных напряжениях, в том числе и для подшип-
ников качения, выходящих из строя вследствие усталостного выкраши-
вания дорожек или тел качения.
Статистические представления, лежащие в основе современных мето-
дов определения сроков службы подшипников качения, разработаны
главным образом Вейбуллом [43], Лундбергом и Пальмгреном [44]. Раз-
витию этих представлений для малых вероятностей разрушения посвя-
щены исследования Харриса [45] и других.
Основные положения статистической теории динамической грузо-
подъемности подшипников качения могут быть сформулированы таким
образом.
Пусть с/п— вероятность того, что подшипник, вращающийся с чис-
лом оборотов п в минуту, проработает h часов без признаков усталости.
На основании теоремы математической статистики о произведении
независимых событий, пренебрегая вероятностью разрушения тел каче-
ния в виду ее малости по сравнению с вероятностью разрушения доро-
жек качения, можно написать
?п=?вр9ип, (2. 14)
где qBV и <?нп— соответствующие вероятности, характеризующие надеж-
ность вращающегося и неподвижного колец.
Учитывая особенности напряженного состояния при действии кон-
тактных нагрузок, а также характер первичных усталостных микротре-
щин, образующихся в подшипниках качения, Лундберг и Пальмгрен
ввели следующее распределение, определяющее вероятность F & появле-
ния следов усталости на участке дорожки качения длиной ДА после
перекатывания по нему N тел качения, нагруженных постоянным уси-
лием Р:
5д=-1- ехр ---Д1/ . (2.15)
V 2 /
Здесь Н\ — коэффициент, зависящий от свойств материала, чистоты
обработки и точности изготовления;
то — наибольшее касательное напряжение, действующее в пло-
щадках, параллельных поверхности площадки контактной
деформации;
.г0 — глубина, на которой возникает это напряжение;
ДУ—напряженный объем.
При щ2=0, что имело бы место в случае, когда вероятность разру-
шения, вносимая каждым элементарным объемом, не зависит от его рас-
положения относительно поверхности, распределение (2.15) переходит
в обычное распределение Вейбулла.
Напряжение То и глубина могут быть соответственно выражены
через наибольшее напряжение смятия ор в центре площадки контактной
деформации и малую полуось b этой площадки:
] (2.16)
?о = «26. |
347
Напряженный объем AV в первом приближении можно принимать
равным
AV=2az0AA, (2. 17)
где а — большая полуось площадки контактной деформации.
Как следует из теории контактных напряжений и деформаций, для
радиальных и радиальио-упорных шарикоподшипников
2
1
— Т 1
Ч
а =0,0108 р. / 4-г------- | 3Р3й(ш;
°
\ ч /
JL
Z> = 0,0108v / 4 +-------Р3а^.
I 1 , 6 I
\ —т 1 !
\ Ч '
(2. 18)
В равенствах (2. 18) приняты следующие обозначения:
Л
<Лп cos ро
2г0
Коэффициенты ffj, а, и аг, строго говоря, не являются постоянны-
ми величинами, однако это можно практически не принимать во внима-
ние, так как пределы, в которых меняются их значения (в зависимости
от отношения 6/ц) весьма незначительны.
Нетрудно убедиться, что
ДА cos₽0

(2. 19)
где Аф— центральный угол, соответствующий рассматриваемому участ-
ку дорожек качения.
С помощью равенств (2. 16) — (2. 19) приведем выражение (2. 15)
к виду:
/ рт
Рд = 1 — ехр — /У2 cos ?о —
lNl Дф
“гс 2Л
(2. 20)
.Количество шариков, контактирующих с каждым участком дорожки
качения за h часов работы подшипника, будет
N=30znh(l ±т|).
(2.21)
Подставляя это значение в формулу (2. 20), окончательно получаем
Рд = 1 — ехр
— H,zl cos (nhV -----т- —
з ген ) d^tc 2я
(2.22)
Показатели тис выражаются через показатели mi, т2 и I следую-
щим образом:
т
т1 2 —
31
— 5
ni\+2 —
(2. 23)
348
По данным иностранных подшипниковых фирм, обобщенным в ре-
комендациях ИСО, zn=3 и с= 1,8 (при tZm^25 мм).
Участок дорожки качения неподвижного кольца, расположенный на
азимуте ф, при перекатывании по нему шариков каждый раз нагружа-
ется одним и тем же усилием . Полагая в соответствии с этим в ра-
венстве (2. 22) P = Pt> , для такого участка имеем
Лд=1 - ехр

(2. 24)
Из выражения (2. 24) следует, что вероятность qw, характеризую-
щая надежность неподвижного кольца в целом, равна:
где
'7нп=п(1-^^) = ехр
(2.25)
—//32ZC0S р0(/1Й)г —
О 1 ° 4 7 rftnlc
В течение достаточно большого отрезка времени каждый элемент
дорожки качения вращающегося кольца контактирует с шариками
практически на всех азимутах.
С учетом этого обстоятельства, считая справедливой гипотезу ли-
нейного суммирования повреждаемости, для любого участка дорожки
качения вращающегося кольца из выражения (2. 22) находим
Ft,— 1 — ехр
7^ л,
— H,zl cos 8 (n/i)1 —~
3 ' О V / dmU 2л J
(2.26)
/ Фп
Здесь Р — I —
I 2л J
Вероятность qBP, характеризующая надежность всего вращающегося
кольца в соответствии с выражением (2. 26), будет
т
I —то самое эквивалентное давление, кото-
рое рассматривалось в п. 1.
9ЯР=П(1-Дд7)=ехр
— H?zl cos $0(п1гУ
(2. 27)
э
J'
Коэффициент Н3, фигурирующий в приведенных выше равенствах,
может быть представлен в виде произведения некоторой постоянной Hi
и величины
являющейся функцией т] и 9, т. е. параметров, характеризующих внут-
реннюю геометрию подшипника.
Допустим, что вращается внутреннее кольцо. Для этого случая из
формул (2. 14), (2.25) и (2.27) имеем
1 1 , 1 , , 1
In — — In----Fin — =
Яи <7вр Янп
Г /р \ml 1 р^1
-Н4 Нв\- М Нк ^соз^/гй)2-^-. (2.29)
X / j
349
Индексы «в» и «н», а также верхние и нижние знаки в формулах
(2.18), (2.19), (2.21) и (2.28), соответственно относятся к внутренне-
му и наружному кольцам подшипника.
Пусть при 11 — 0,2, 0 = 0,52 и л-оо
нв+(^уХ=я5.
Введем далее величины Со и /? по формулам:
C0^f’rd‘J'~\ (2.30)
где
(2.31)
Используя формулы (2.30) и (2.31), преобразуем выражение
(2.29) таким образом:
0,39s cos %Рв (nKf =С0(cos ft . (2.32)
Выразив здесь Р% через эквивалентную динамическую нагрузку Q,
получаем:
1 I
Q(nh)m =Cfqm , (2.33)
где
с..с;(со^0)'1-“г1.
Аналогично может быть рассмотрен случай, когда вращающимся
является наружное кольцо.
Объединив формулы долговечности для случаев вращения внутрен-
него и наружного колец, после введения в них коэффициентов кд и к.,
учитывающих влияние на несущую способность характера нагрузки и
температурного режима подшипника, окончательно имеем
1 1
K6KTKKQ(tth) т .
Здесь кк— 1, если вращается внутреннее кольцо, и
(2. 34)
(2. 35)
если вращается наружное кольцо.
350
При конкретных числовых расчетах радиальных и радиально-упор-
ных шарикоподшипников на основе таблиц коэффициентов ко и к зна-
чения кинематического коэффициента кк можно приближенно опреде-
лять в зависимости от величины w = 0,587 — по графику рис. 4. 6.
«о
В зарубежной практике при вычислении коэффициентов работоспо-
собности Со и С коэффициент f' обычно полагают равным 150—200.
Расчеты показывают, что при данном 9
коэффициент f" зависит главным образом
от т]. При т = 3, С=1,8 и I— 1,11, что соот-
ветствует рекомендациям ИСО, он имеет
значения, указанные в табл. 4. 4.
Таблица 4.4
д 0,05 0,10 0,20 0,30 0,40
г 0,77 0,92 1 О,9з|о,81
Для подшипников общего назначения
расчетной считается долговечность й]0, при
которой вероятность разрушения равна 10%.
Так как при ^ = 0,9 fG= 1, то
1
Рис. 4.6. Кинематический
коэффициент Кк
(2.36)
k6ktkkQ (nhw) т—С.
Сопоставляя равенства (2.34) и (2. 36), находим
<г
(2.37)
Из формул (2.37) и (2.31) следует, что средняя долговечность под-
шипников качения определяется выражением:
(2.38)
где Г — гамма-функция аргумента ^1ф- yj •
Отношение медианного значения долговечности /ijn, соответствую-
щего надежности <7 = 0,5, к расчетной долговечности hl0 будет:
/ 1
/ In------
Л.50 | 0.6
(2. 39)
Лю \ . 1
\ 1п ------
\ 0,9/
Соотношения (2. 38) и (2. 39) показывают, что основным парамет-
ром, характеризующим рассеивание долговечности подшипников каче-
ния, является показатель степени I.
В большинстве случаев отношение — колеблется в пределах от
Лю
4,08 до 5. При —-°-=4,08 /— 1,34, а -- = 4,95. Если —^-=5, то /=1,17
Лю Л1о h]0
и ^=6,5.
Л10
351
4’
[10(1-O* +^-
Aw/ Ajo
(2.41)
Как свидетельствуют экспериментальные исследования, приведен-
ные зависимости удовлетворительно описывают рассеивание долговеч-
ности при уп-<0,9. В области же малых вероятностей разрушения наблю-
даются заметные отклонения от них. Эти отклонения можно учесть, если
для этой области выражение (2. 37) заменить следующим:
(2.40)
Лю — "0
Здесь Ло — некоторый порог долговечности, до которого вероятность
разрушения равна нулю.
Так как при 7п<0,9 ff;p^[10(l—^п)]17', то формулу (2.40) можно
окончательно записать в виде
h
А О
h
По данным Харриса [45], для шарикоподшипников °-«0,045. Это
обозначает, что для обеспечения 100-процентной надежности нужно
иметь запас расчетной долговечности порядка 22, что соответствует за-
пасу по нагрузкам 2,8.
Выше были изложены основные положения статистической теории
динамической грузоподъемности радиальных и радиально-упорных ша-
рикоподшипников . Аналогичным образом построены соответствующие
статистические теории динамической грузоподъемности и для подшипни-
ков других типов.
Главные результаты, вытекающие из статистических представлений
о долговечности подшипников качения, нашли отражение как в зарубеж-
ной, так и в отечественной практике. При этом, однако, нужно отметить,
что некоторые зависимости, использованные при составлении отечест-
венных каталогов и справочников, имеют иной вид, чем это принято за
рубежом. Так, например, коэффициенты работоспособности Со и С у
нас подсчитываются не по формулам (2.30) и (2.33), а принимаются
равными:
Со = /- *“* - z
J l+0,02dm
C=C0cos 0О-
Для подшипников общего назначения f=65. Напомним, что в оте-
чественной практике показатель степени т считается равным 3,33.
Долговечность двухрядных подшипников, а также опор качения,
состоящих из нескольких одинаковых подшипников, которые могут рас-
сматриваться как один многорядный подшипник, определяется выраже-
нием:
(2.42)
0,39 л-йл;тг cos (лй10)т = С.
Входящее сюда эквивалентное давление
(2. 43)
.ml
ml
(2.44)
3U
К .
где Рэ и тск —эквивалентная нагрузка и кинематический коэффициент
7 для /'-го подшипника.
Формулы (2.43) и (2.44) непосредственно следуют из приведенных
выше зависимостей для отдельных подшипников.
Если все подшипники нагружены одинаково, то
3v
(2.45)
352
Как показывает анализ значений коэффициентов f", приведенных
в табл. 4. 4, работоспособность подшипников качения заметно зависит
от величины т]. В выражениях (2.42) это важное обстоятельство отра-
жения не нашло, что является их существенным недостатком.
Как известно, для авиационных подшипников, обладающих высо-
кой точностью и изготовленных из особо качественного металла, коэф-
фициенты работоспособности имеют много большие значения, чем те,
которые получаются из формулы (2.42) при f = 65.
Поэтому, используя в расчетах авиационных конструкций данные
машино-строительных каталогов и справочников, можно ожидать, что
в действительности расчетной долговечности Ню будет соответствовать
не 10-процентная вероятность разрушения, а значительно меньшая. При
таком подходе к определению срока службы подшипниковых узлов ави-
ационных агрегатов эту долговечность часто отождествляют с требуе-
мым ресурсом. Практически это достигается тем, что в формулах (2. 36)
и (2. 43) h10 заменяется на Л, и под h понимается долговечность, при ко-
торой обеспечивается необходимый для изделий авиационной техники
уровень надежности подшипников.
4. Влияние осевой нагрузки на работоспособность подшипников
Проследим, как влияет осевая нагрузка на работоспособность ра-
диальных и радиально-упорных шарикоподшипников.
На рис. 4.7 и 4.8 показаны типовые графики зависимости — =
/ _Д \ р
=/—I при -------—=const, построенные по данным расчетов, выполнен-
\Я)
ных при составлении таблиц коэффициентов к0 и к.
Как видно из этих графиков, для каждого уровня нагрузки сущест-
вует диапазон значений — , в котором Его границы приведены
R
в табл. 4. 5.
Таблица 4.5
R Значения А/R при начальных углах контакта р0 град
0 12 18 26 36
0,02 0-0,15 0,26—0,38 0,39—0,56 0,56-0,82 0,84—1,20
0,11 0—0,28 0,25—0,45 0,37—0,60 0,55-0,84 0,76-1,21
0,35 0-0,37 0,22—0,47 0,35—0,63 0,47—0,85 0,38—1,21
1,00 0—0,43 0,04-0,49 0,00-0,65 0,00—0,86 0,00-1,22
При значениях — .указанных в табл. 4. 5, осевая нагрузка не только
R
не снижает несущую способность подшипника, но даже несколько уве-
личивает ее. Правда это увеличение незначительно, так как возможное
уменьшение приведенной динамической -нагрузки составляет несколько
процентов.
В радиально-упорных шарикоподшипниках на шарики действуют
кориолисовы силы, которые стремятся заставить их вращаться вокруг
осей, перпендикулярных поверхностям контакта. Такому «верчению»
шариков препятствуют силы трения, возникающие в точках касания
с кольцами. Если в подшипнике имеется ненагруженная зона, то в этой
зоне силы трения, предотвращающие «верчение» шариков, отсутствуют,
23 1578
353
Рис. 4.7. Графики
Q /Л-
мости — = /|jr
зависи-
при не-
которых постоянных зна-
пениях ----й- и 0о—О
354
и шарики начинают проскальзывать относительно желобов колец, что
при больших скоростях вращения приводит к перегреву и быстрому из-
носу подшипников. Естественно, что при проектировании быстроход-
ных подшипниковых узлов с радиально-упорными шарикоподшипника-
ми нужно всегда стремиться, чтобы нагрузку несли все шарики. Практи-
чески это достигается либо путем установки подшипников с соответству-
ющими углами контакта, либо их некоторой дополнительной осевой
подгрузкой за счет предварительного натяга.
Величина зоны нагружения зависит от соотношения осевой и ради-
альной нагрузок, приложенных к подшипнику. Чем больше отношение
AIR, тем больше эта зона. Как уже указывалось ранее, при фо = О зона
нагружения составляет 360°, если O+XX-l. Значение Х=0 соответствует
случаю осевого нагружения подшипника, при котором давления на ша-
рики одинаковы. Значение Х=1 определяет минимальную величину отно-
шения AjR, при котором нагружены все шарики. Это, в частности, сле-
дует из формулы (1. 22), показывающей, что в случае фо=О и Л.= 1 уси-
лие, воспринимаемое шариком, расположенным на азимуте фо=18О°,
обращается в нуль.
Учитывая, что при X—1 /1 = 0,425, /2 = 0,225 и /з = 0,231, из уравнений
(2. 1) и (2. 2) находим
А
«а,
1,666
— “о
sin2 ₽0+ ё0+ —
COS Ро
1 +0,905
°о
1 — 0,6—^-
2+ 60
Sin2 р0 + 80 + -
cos2 р0
во__
2+ Во
(2.46)
при этом радиальная
нагрузка R определяется
о,51 cos
-g3/2 I Sin2 p0 +
—1 + 0,905
2 + Bq '
выражением
II \
10 + 4 у
cos2p0 2+8о/
(2.47)
а отношение
= 0,5025 •
1 + 0,905
Как видно из равенств (2. 46),
"В2
— sin2pQ + Во + ——
QQ__________________4
2 + Бо cos2 Pg
(2,47) и (2. 48), (величины
(2. 48)
и
угла контакта, так и от уровня на-
— зависят как от начального
\ R Ji-i
грузки, воспринимаемой подшипником.
Для наиболее часто встречающихся начальных углов контакта
— 0, 12, 18, 26 и 36° с помощью равенств (2.46), (2,47) и (2.48) на
рис. 4.9 и 4.10 построены кривые, определяющие значения и
/ Q \ R
— в функции —
\ R h-i zvdui
При малых нагрузках
1.
23*
355
С ростом нагрузки величины j и возрастают. Так напри-
р
мер, для угла ро= 18° при ----?- = 1
zvd*
ш
(4) = 2,6tg₽0 и (4) =1,064.
\ R Л=1 \ R Л-1
Как было показано выше, в случае постоянного угла контакта ша-
риков с кольцами при зоне нагружения 180°, когда параметр Х=±оо,
отношение — = 1,217 tgfjo.
Рис. 4.11.
\ R
Зависимость отношения
от уровня нагрузки
Рис. 4.12. Зависимость отношения
I— от уровня нагрузки
\ R jx= ОО
Значения отношения (— с учетом изменения угла контакта
\R =-оо
в зависимости от положения шарика относительно плоскости xOz могут
быть найдены по кривым, показанным на рис. 4. 11. На рис. 4. 12 изобра-
жены кривые, по которым могут быть определены соответствующие
значения отношения 4)
\R
Графики на рис. 4.11 и 4. 12 построены с помощью формул
) = 1,217 tg Ро--^Р’8228^- ;
\Rh — & ° 1 +0,868 tg^Mo
(-V) =О,229До 83/2 cos ₽0(1 + 0,868 tg^ р080);
\ Ш / X — ОО
m =___________?—
k R h.-~ 1 + 0,868 tg2₽0a0
(2.49)
вытекающих из уравнений (2. 1) и равенств (2. 12) и (2. 13).
Приведенные данные позволяют оценить влияние осевой нагрузки
на несущую способность радиальных и радиально-упорных шарикопод-
шипников. С их помощью может быть установлен оптимальный осевой
предварительный натяг, с которым должны монтироваться подшипники
в узел, и подобраны наиболее рациональные значения начального угла
контакта [Jo для различных сочетаний радиальной и осевой нагрузок.
5. Приближенные решения уравнений (2.1) и (2.2)
Нужно помнить, что угол Ро определяется рабочим радиальным за-
зором 2Д, который, имеется в подшипнике после его посадки на вал и в
корпус при установившемся температурном режиме работы агрегата,
356
а также фактическим расстоянием g между центрами 0н и 0Е сечений
желобов колец [см. рис. 4. 2 и формулу (1. 7)].
Из-за влияния посадочных натягов, неравномерности нагрева от-
дельных элементов узла, а также возможной разницы в величинах ко-
эффициентов линейного расширения вала и корпуса зазор 2А может су-
щественно отличаться от начального радиального зазора в свободном
подшипнике. На величине расстояния g могут заметно сказаться откло-
нения радиусов желобов колец и диаметра шарика. В связи с этим при
расчете высоконагруженных радиальных и радиально-упорных шарико-
подшипников угол Ро не всегда можно заменять номинальным началь-
ным углом контакта, указанным в каталоге. Это обстоятельство нельзя
упускать из виду при проектировании особо ответственных подшип-
никовых узлов агрегатов вертолетов и других летательных аппа-
ратов.
Значения коэффициентов к0 и к для радиальных и радиально-упор-
ных шарикоподшипников с начальными углами контакта [30, отличными
от стандартных, могут быть получены интерполяцией данных, приве-
денных в табл. 4. 3. Вместе с тем есть немало случаев, когда удобнее
не прибегать к этому способу, а решать задачи, связанные с расчетом
таких подшипников, путем прямого определения величин б0 и из урав-
нений (2. 1) и (2.2), используя с этой целью следующие приближенные
методы.
Если t ’ т- е- нагрузку несут все шарики, то интегралы
могут быть найдены из выражений:
У1(1+Х)3/2=1+Ак2.
10
£ \ Ол /
(2. 50)
Правые части равенств (2.50) представляют собой первые члены
степенных рядов, в которые разлагаются произведения /\(1Н-Л,)в/“ при
фо = О и 0-<Х<1. Учитывая быструю сходимость этих рядов в указанной
области, члены, содержащие параметр X в степени выше третьей, здесь
отброшены.
Решая уравнения (2. 1) и (2.2) с учетом равенств (2.50), в резуль-
тате последовательных приближений получаем рабочие формулы:
где
I —
32 2
(2. 52)
357
Коэффициенты Du D2 и D3 соответственно равны:
£>1 = Д2/3
/ А X1''2
sin2fo + 2(—J
1/3 ’
(sln^o + ZP!)1^
2 sin2 ₽0 + 2D] Di \
3 cos2 Ро 1 + L>J
(2.53)
1 - — Dl
32 2
3 ,
I + —
T 16 2
При ——) формула для максимального давления на шарик
R \ R /х=1
может быть представлена в виде
= (2.54)
Из выражений (2.3) и (2.51) следует, что коэффициент к^А) в фор-
муле (2.54) можно полагать равным
(2. 55)
Нетрудно заметить, что в рассматриваемом случае приведенные на
грузки Qo и Q могут быть выражены следующим образом:
Q0 = 0,229«^A> cos ₽ЦД;
Q = 0,390wk^ cos Р0Л.
(2. 56)
Сравнивая равенства (2.56) и (2. 13), для данного случая находим:
к0 = 0,229«<л> cos sin а;
к = 0,390w«<)y|) cosp0sina.
(2. 57)
Если радиальная нагрузка /?=0, то в соответствии с равенствами
(2. 53) _О2 = 0 и D3 = 1. Подставив эти значения в выражение (2. 55), для
случая чисто осевого нагружения имеем
/э* (А) А)
ло л00
(л V'2
sin2fe+2W
1/2
(2. 58)
На рис. 4, 13 приведены графики зависимости Коо*’=коо’ (.4), полу-
ченные из исходных уравнений статического равновесия радиальных и
358
радиально-упорных шарикоподшипников без каких-либо упрощающи:;
предположений. Там же знаком «X» нанесены значения коэффициента
подсчитанные по формуле (2.58), что дает возможность наглядно
убедиться в ее вполне удовлетворительной точности.
Описанный способ определения величин 6о и X может быть применен
только в том случае, когда в подшипнике нет незагруженных шариков.
Пусть теперь зона нагружения составляет менее 360°. При зоне на-
гружения, меньшей 360°, величина X
может колебаться в пределах от оо
до I и от —оо до некоторого отри-
цательного значения X», соответст-
вующего случаю, когда подшипник
воспринимает чисто радиальную на-
грузку. При отсутствии осевой на-
грузки центр площадки контакта
«сползает» на середину желоба и
угол р обращается в нуль. Полагая
в формуле (1. 19) угол р равным
нулю, видим, что при радиальном
нагружении подшипника
8=cosfJ0—1. (2.59)
Введем обозначения
Рис. 4.13. Графики зависимости
Л(А) _ 3(Л) /Т)
коо ~ коо W
р — 1____.
1 (П-Х)7^ ’
Е — — •
Ji
р _ Х /3
2 1 + х ’ if'
Е4=1-^.
h
(2. 60)
Значения величин Е в функции X приведены в табл. 4. 6.
Таблица 4.6
I X £з Л4 1 X £i £2 £з £4
1 1,244 1,125 1,666 0,600 —0,1 —0,304 2,670 1,185 -8,441
0,9 1,173 1,149 1,594 0,697 -0,2 —0,704 3,126 1,164 —4,296
0,8 1,097 1,187 1,532 0,816 -0,3 — 1,248 3,146 1,139 —2,927
0,7 1,017 1,242 1,476 0,968 —0,4 —2,021 4,597 1,115 —2,243
0,6 0,930 1,317 1,430 1,166 —0,5 —3,191 5,899 1,093 -1,829
0,5 0,831 1,409 1,386 1,443 -0,6 —5,111 7,998 1,075 —1,550
0,4 0,717 1,522 1,346 1,857 —0,7 -8,663 11,74 1,051 —1,360
0,3 0,586 1,662 1,309 2,546 -0,8 -16,91 20,23 1,032 -1,210
0,2 0,429 1,836 1,277 3,915 -0,9 —47,49 52,48 1,015 -1,094
0,1 0,238 2,055 1,247 8,021 — 1 — оо OQ 1 —1
0 0 2,321 1,217 оо
и р = 0 второе уравнение (2. 1) может быть пред-
При 6 = COS Ро—1
ставлено так:
^2/3 COS 3q — 1
Bl
(2.61)
л -А..,..
П Bozvd^
где
359
Напомним, что в соответствии с принятым направлением оси z угол
фо=О и, следовательно, Хсозфо = Х и бо = б(1+Х).
Из равенства (2. 62) следует, что %* должно удовлетворять условию
^1(U=££^-1. (2.62)
Для решения уравнений (2. 1) и (2.2) в случае —<(—') поступим
следующим образом. Считая параметр X известным, с помощью метода
итераций найдем из второго уравнения (2. 1) величину <5 = Заменив
14-Л
тригонометрические функции угла £} соответствующими значениями, вы-
текающими из уравнения (2.2), в качестве приближенного
примем
значения 6
(2.63)
где
(2.64)
Нужно иметь в виду, что поскольку выражение (2. 63) является при-
ближенным, значение б, определенное из этого выражения при Х=Х*,
несколько отличается от значения, соответствующего формуле (2.59).
Из уравнений (2. 1) далее имеем
А ___ Ез_______________(sin2 26 + S2) 6 \
R cos p0 sin2flo + 26 + 82 £2 6 ( 4 1 + 6 )
cos2 p0 1 + a
(2.65)
Задаваясь X, строим с помощью формул (2. 63) и (2. 65) график за-
висимости — =F(X) (рис. 4. 14). По этому графику, зная отношение — ,
находим значение X, являющееся приближенным решением уравнений
(2.1) и (2.2). Используя полученное значение X, вычисляем по формуле
(2. 63) действительное значение б и по нему находим 6».
Как показывают числовые расчеты, точность формул (2.63) и
(2. 65), так же как и формул (2. 51) и (2. 52), является вполне достаточ-
ной для инженерных приложений. Отклонения величин бо и X, вычис-
ленных при помощи указанных формул, от соответствующих «точных»
значений, определяемых уравнениями (2.1) и (2.2), при начальных
углах контакта §0<45° составляют, как правило, не более 3—4%.
Руководствуясь выражением (2.63), можно написать
р0=«Х,(1+№й2 с^г.' <2- ев)
COS Ро
360
Вспоминая, что
л \
— 1 находим
/? /Х=1
£) =-----—и А? =------
(1 + Х)?2 В0г^ш
А
, для случая —
R
Здесь

R
Z COS Pg
^>=у-
72
(2. 67)
(2. 68)
Сопоставляя равенства (2. 11) и (2.67), нетрудно убедиться, что ко-
эффициент кд в данном случае может быть выражен так:
«о=О,229«(;?) cos а.
Соответственно
k=0,390wkJr) cos и.
6. Относительные смещения колец
Для некоторых высокоточных быст-
роходных подшипниковых узлов важное
значение имеет правильное определение
относительных смещений колец подшип-
ников под нагрузкой. При воспринятой
радиальными и радиально-упорными ша-
рикоподшипниками комбинированных на-
грузок эта задача решается так.
Как видно из соотношений (1.13) и
ного перекоса колец) e='t> —=0)
Рис. 4. 14.
(2.1)
мень-
Вспомогательный
график для приближенного
решения уравнений
при зоне нагружения,
шей 360?
(1. 16), при отсутствии
взаим-
s=tgPcos ро;
хв
«=------.
cos ,
Используя зависимость (1. 19), находим
s = (sin2 ft) 4-28 + S2)1/2;
- Д8(1 + &)
COS Ро
Пусть. При этом условии, пренебрегая в равенствах
(2.69)
(2. 70)
(2.42) величиной й2 в i 1 . . +
(2. 52) получаем для относительных смещений s и й следующие выра-
жения;
виду ее малости, с помощью формул (2. 51) и

А W2]2/3
1/2
s—
1,41£>з
А \1/2р/3
1,4Юз 7 J
Р2 1+ 16 PLF
c°sPo , „2 \°з /
32
/ A W
sin2йо+ 2 I ----I
™ yl,41£)3y
(2. 71)
361
нии осевой нагрузки
Как изменяются смещения s и й при изменении соотношений ра-
диальной и осевой нагрузок, можно проследить на примере подшипника
36207, для которого на рис. 4. 15 по формулам (2. 71) построены кривые
(р \ / R \
---и s==s (-----“) при постоянном значении осевой нагрузки
**4/ W/.
/—=0,5з\ Для сравнения там же знаком «X» указаны точные значе»
\г^ш /
ния смещений s и и, подсчитанные при помощи уравнений (1.3), (1.6)
и (1. 7) для случаев Х = 0 и %=1, определяющих границы применимости
формул (2.71).
Как следует из приведенных
материалов, уравнение моментов
не входит в систему уравнений,
с помощью которой исследуется
распределение нагрузки в ради-
альных и радиально-упорных ша-
рикоподшипниках, работающих
без перекоса колец. Поэтому
предположение о действии ради-
альной силы и момента в одной
плоскости, использованное при
составлении соотношений (1.24),
не вносит никаких дополнитель-
ных ограничений, суживающих
область применения изложенной
выше методики расчета таких
подшипников.
До сих пор радиальная и осе-
вая нагрузки, действующие на
подшипник, считались заданными.
Радиальные нагрузки на подшипники находятся из уравнений рав-
новесия вала, на котором они смонтированы.
При больших расстояниях между опорами определение этих нагру-
зок не составляет особого труда, так как в этом случае они мало зави-
сят ог моментов, воспринимаемых подшипниками, в связи с чем при их
вычислении последние могут не учитываться.
Что касается осевой нагрузки, то при ее подсчете часто встречаются
значительные трудности. Строго говоря, осевую нагрузку можно считать
известной только в том случае, когда рассматриваемый подшипник вос-
принимает всю осевую силу, приложенную к валу, как это имеет место
Ft подшипниковых узлах с одной фиксированной в осевом направлении
опорой.
Если уравнений равновесия вала не хватает для отыскания нагру-
зок, действующих на его опоры, то изолированно рассчитывать подшип-
ники, смонтированные в отдельных опорах, естественно, нельзя. В по-
добных случаях для определения давлений на шарики приходится сов-
местно решать уравнения равновесия вала с уравнениями статичес-
кого равновесия всех установленных на нем подшипников.
§ 3. НЕКОТОРЫЕ ЗАДАЧИ РАСЧЕТА
РАДИАЛЬНО-УПОРНЫХ ШАРИКОПОДШИПНИКОВ
С УЧЕТОМ ПЕРЕКОСА ИХ КОЛЕЦ ПОД НАГРУЗКОЙ
1. Основные соотношения
В ряде агрегатов вертолета радиально-упорные шарикоподшипни-
ки, расположенные на небольшом расстоянии друг от друга, восприни-
362
моменты при малых рас-
Рис. 4. 16. Схема нагру-
жения двух шарикопод-
шипников радиальной и
осеной силами и момен-
том
мают комбинированные нагрузки, в которых, если не главную, то во
всяком случае значительную роль играет момент. Понятно, что при оп-
ределении параметров, характеризующих работоспособность таких под-
шипников, нельзя пренебрегать взаимным перекосом колец, как это де-
лалось в предыдущем параграфе, в связи с чем их расчет сильно услож-
няется.
Отсутствие надежных методов расчета радиально-упорных шарико-
подшипников, воспринимающих значительные
стояниях между опорами, затрудняет конст-
руирование многих подшипниковых узлов, в
частности, узла тарелки автомата перекоса,
являющегося одним из наиболее нагруженных
и ответственных элементов вертолета.
Рассмотрим некоторые задачи расчета ра-
.диально-упорных шарикоподшипников с уче-
том перекоса их колец под нагрузкой. Резуль-
таты, полученные при решении этих задач, по-
зволяют ответить на главные вопросы, возни-
кающие при проектировании подшипниковых
узлов агрегатов вертолета, предназначенных
для воспринятая-больших моментов.
Пусть подшипниковый узел, состоящий из
двух радиально-упорных шарикоподшипников,
воспринимает комбинированную нагрузку в
виде радиальной силы 7?, приложенной в сере-
дине между опорами, осевой силы А и момен-
та М (рис. 4. 16). Предполагается, что сила Д
и момент М действуют в одной плоскости.
Присвоим индекс 1 тому из подшипников
узла, для которого давления на шарики, обус-
ловленные действием силы R и момента М,
складываются. Все величины, относящиеся к
этому подшипнику, будем записывать с этим
индексом. Второму подшипнику, входящему в состав узла, и всем отно-
сящимся к нему величинам присвоим индекс 2.
Направим оси координат для подшипников 1 и 2 так, как показано
на рис. 4. 16. Легко заметать, что в системе координат Xii/iZj сила R
и момент М всегда имеют положительные значения, а осевая сила А
может быть как положительной, так и отрицательной.
Условия равновесия вала, на котором установлены подшипники,
сводятся к системе уравнений:
А-А,-А2;
/? = /?!-R2;
(3-1)
где L — расстояние между опорами.
Так как моменты A4X и М2 при небольших расстояниях между опо-
рами не только соизмеримы с моментами 7?i — и но и могут значи-
тельно превышать их, то уравнения (3. 1) должны решаться совместно
с уравнениями статического равновесия подшипников 1 и 2.
Допустим, что в нагруженном узле центр пакета внутренних колец
смещен в направлении действия сил А и R на расстояния s и и, а общая
ось вращения этих колец повернута по направлению действия момента
363
Л1 на угол ф. Угол -О' является углом перекоса как для подшипника 1, так
и для подшипника 2.
Относительные смещения *, определяющие положение центров внут-
ренних колец подшипников 1 и 2 в системах координат ЯдГ/iZ! и x2y2Z2,
Рис. 4. 17, Схема перемещений
внутренних колец подшипников
под действием приложенной к
ним произвольной внешней на-
грузки
согласно фиг. 4. 17, равны:
s1=sinp04-An+s; j
== Й —Ь ^=1 I
- - } (3.2)
52 = 8Ш8О4.ДП —S;
«2=^ —J
Здесь Дп —половина осевого предвари-
тельного натяга, с которым
установлены подшипники;
- L
<,=------отношение расстояния ме-
2г 0
жду подшипниками к диа-
метру, на котором располо-
жены шарики; е = & —.
g
Написав для обоих подшипников ра-
венства (1.16) и подставив в них выра-
жения (3.2), после несложных преобра-
зований получим
_________1 ________ (tg fe + С)
2/tgPi + tgfe + A I cospt
(tg + О ^252
COS 32
_______1__________ | X] , X3o2
tg Pl + tg fe A [cos Pl cos p2
(3.3)
I
В подшипниковых узлах рассматриваемого типа обычно применяют-
ся радиально-упорные шарикоподшипники с большими начальными уг-
лами контакта, для которых относительные смещения Si и S2 редко пре-
вышают 0,25 sin2 Ро- При указанных значениях величин Si и 62 равенства
(3. 3) могут быть заменены следующими приближенными соотношения-
ми:
1
2 cos Ро
(XjBi Х2й2);
(3-4)
1
(ХД+Мг)-
2cosp0(tgpo+0 ' 1 1 1 3
При выбранном направлении осей координат угол -фо, определяю-
щий положение наиболее нагруженного шарика в подшипнике 1, всегда
равен нулю. Угол -фаз, характеризующий положение наиболее нагружен-
ного шарика в подшипнике 2, в зависимости от соотношения между ра-
диальной силой 7? и моментом М, может иметь как нулевое значение
(при преобладающем моменте), так и быть равным 180° (при преобла-
дающей радиальной нагрузке).
* Все относительные величины, как и ранее, выражаются в долях расстояния
g — Гн -f тв dm.
364
Имея в виду последнее обстоятельство, с помощью равенств (1.24),
(1.25), (1.21), (К 27) и (3.4), учитывая сделанные замечания о поряд-
ке величин 61 и 6s, представим силы и моменты, воспринимаемые под-
шипниками 1 и 2, таким образом:
4 . -Z?0§oi sin Pq/jj 1 + Aj S02 'j .
1 + X2 cos фоз У
т?1 __ = B$'i2 cos Po/2i | 1 "Г Л1 c2itg2₽o- 02 1 + x2 COS Ф02,
Z?o^oi sin Pq./2i (1-Lb • ®01 -4- c. s°2 1
rozv^u V 1 21 i+*i l+Xg COS Ф02/
^2 ^0^02 Sin rty/12 1 । h . &02'
1 [ ^12 4 , Л . 1-F X2 cos Ф02
л cos Po/22 Фми2^-,—— l+k2cos4>02
(3.5)
-с22^2?о'г5т) cos'!o2;
1 + Aj/
% = 6o®O2Sin S07 22 f 1 Г ^22 ‘ i , X гл j, "Ь C22 1 ) C°S ’^°2’
у 1 + ^2 Cosmos 1 + *!/
В выражениях (3. 5) приняты следующие обозначения:
= Ctg3 Ро + уМ . 9Я 7УЯ ,— - Ф1
71! L sin2p0 (tgrpo + С) J
с —hi____________4_______.
11 Ju' Sin2fo(tg₽o + C) ’
b 2.=ctg2p04-^-[---------1---------ilk,;
Л1 I sin 2p0 (tg p0 + 0 J
c — hi___________h_______.
21 ]2l sin2₽o(tg₽o + 0
&i2=ctg% +Jf- Г -T 1 -1] X2 COS фо2;
712 L sm2p0 (tgp0 -p Q J
ci2 ———;--------—-------со5Ф02;
712 sin 2₽o (tg ₽o 4-C)
^22 = Ctg2₽0 4- Г . 1 - - 11 k2 COS Ф02;
722 LSln2po(tgpo+C) J
C22 = [--------------- . cos Л 1
J22 L Sin2₽0(tg₽0 + C) ,02J
(3-6)
Как следует из формул (3. 2) и (1. 13),
tg ?i + tg ?2=2tg % + •
cosp0 COS₽0
Так как при 8 <0,25 sin2 p0 можно приближенно полагать tgp=
=tgp0-]---—---, то из последнего выражения находим
sin PqCos р0
8i-|~82~—2Дпз1п р0.
365
Используя равенство (1.21), окончательно имеем
601
502
1 Н- X2COS Ф02
= 2Дпзшр0.
(3.7)
Зависимости (3.5), (3.6) и (3.7) совместно с уравнениями (3.1)
позволяют определить все параметры, характеризующие работоспособ-
ность радиально-упорных шарикоподшипников при малых расстояниях
между опорами, когда взаимным перекосом колец под нагрузкой пренеб-
регать нельзя. Как показывают числовые расчеты, точности этих зави-
симостей, полученных в предположении, что величины б[ и бз не превы-
шают 0,25 sin2 Ро, при начальных углах контакта р0^26°, с которыми
обычно приходится сталкиваться в подшипниковых узлах, предназна-
ченных для воспринятая больших моментов, является достаточной.
Разберем основные расчетные случаи, встречающиеся при проекти-
ровании подшипниковых узлов этого типа для агрегатов вертолета.
2. Случай «чистого» момента
Если подшипниковый узел, состоящий из двух одинаковых радиаль-
но-упорных шарикоподшипников, воспринимает «чистый» момент
(рис. 4. 18), то в виду идентичности нагружения обоих подшипников
= А1=Аа и Л4]—Л42. Естественно, что.
в этом случае 1|?о2='Фо1 = О, Xi=%2 и 601 = 602-
Рис. 4.18. Схема нагруже-
ния двух шарикоподшипни-
ков «чистым» моментом
Рис. 4. 19. Влияние предварительного
натяга иа зону нагружения
Как видно из формулы
(3.7), при Ф02 — 0, %i —7.2 и 601 — 602
^=>sin₽04n.
(3.8)
Следовательно, при действии «чистого» момента
6 01 _ J
sin ₽о Дп
(3.9)
Понятно, что отношение----должно быть всегда больше еди-
sin р0 Дп
ницы. Это становится очевидным, если принять во внимание, что произ-
ведение sin р0Дп представляет собой относительное сближение желобов
колец, обусловленное предварительным натягом, т. е. относительное
366
сближение желобов колец, которое имеется до приложения к узлу внеш-
' ней нагрузки.
, Соотношение (3. 9) определяет зону нагружения в зависимости от
t уровня нагрузки и предварительного натяга. Из него, в частности, вид-
>. но, что для того, чтобы нагрузку несли все шарики, подшипники долж-
ны быть смонтированы с относительным предварительным натягом
2ДП>
Sin
Влияние предварительного натяга на зону нагружения показано на
рис. 4. 19.
, Предварительный натяг часто задают не в виде относительного Осе-
S. вого смещения 2 Ап, а в виде соответствующей осевой нагрузки Лп, опре-
деляемой выражением
Лп = гВ0у4д3п'25ш^р0 f 1 И- -^.Д,,). (3. 10)
? k Sinpo /
; Так как при действии «чистого» момента и Д1=Л2, то первые
два уравнения системы (3. 1) удовлетворяются тождественно. Третье
* уравнение этой системы для случая «чистого» момента может быть пре-
’ образовано с помощью зависимостей (3.5), (3.6) и (3.7) следующим
образом:
f.
X f 1 + ctg2 7• (1 + ^1- —tg Po kA -^-1. (3.11)
, _ 1 + C ctg Ро у /21 1 + C ctg /l + ^i
Пользуясь равенствами (2.3), (2.5), (3.9) и (3.11), нетрудно по-
строить графики зависимостей ——ьА и =
^rozvd^’
по которым могут быть найдены максимальное и эквивалентное давле-
ния на шарики. Примером таких графиков могут служить кривые, изо-
браженье на фиг. 4.20. Они получены в предположении, что ₽о—36°,
С—0 и Дп sin Во=0,01.
Представим максимальное давление на шарик Хп в виде:
к(0М)М 4,Ъ1к{0м>М
2/21х_ югог sin р0 (1 + Cctg₽0) Чг^г sin 30 (1 + г ctg р0) ’
Соответственно будем полагать
Рэ1=.-®Р,
2,57к(л1) М
2г0гв!пр0(1-у :ctgp0)
(3.13)
где к№ —rfn
0,587 0 1
Следует отметить, что при действии «чистого» момента Poa = -Poi и
Р#2~Р эь
Нетрудно убедиться, что коэффициент
4Л,=-
721
1 +ctg2 ^'ГГГтМ1 -! Za
1+CctgPo I
1 — Ctgftp \ 801 '
1-KctgPo' ’/I + Zj
(3- И)
367
При нулевом предварительном натяге, когда согласно формуле
(3.9) Л1=оо, из соотношения (3. 14) имеем
к<Л1> =
(3. 15)
Значения коэффициента соответствующие выражению (3. 15)
можно определять по графику на рис. 4.21. Здесь по оси абсцисс от-
— 1 м
ложена величина М =------5-----------------. В качестве параметра
zvd\Sin₽o (1 + С ctgpo) го
принята величина р=| .
Itgfe+d
Графики на рис. 4.22 и 4.23 показывают, как изменяются коэффи-
циенты и в зависимости от предварительного натяга при р0=36°
и £ = 0. Из приведенных кривых видно,
что предварительный натяг целесооб-
разно выбирать таким образом, чтобы
параметр Aj лежал в пределах от 1
до 1,25. При таком выборе предвари-
тельного натяга коэффициент к^м>, а
следовательно, и максимальное давле-
ние на шарик, снижаются на 10—12%.
При этом коэффициент к(Ж), а вместе
Рис. 4.21. Значения коэффициен-
та в зависимости от па-
раметров g и М
р
Рис. 4.20. Значения —и
Рэ1 М
—в зависимости от---------г
rozvd^
при ₽0 = 36°
с ним и эквивалентное давление на шарик, сохраняют примерно ту же
величину, что и в случае, когда предварительный натяг отсутствует.
К аналогичным выводам можно прийти и при рассмотрении других ком-
бинаций величин Ро и
Крайне важно оценить влияние предварительного натяга на угло-
вую жесткость подшипникового узла. Это легко сделать при помощи
второго из соотношений (3.4), которое для случая «чистого» момента
может быть представлено в виде:
г=-------. (з. 16)
cos₽0(tg ₽о + С) 1+%
Формула (3. 16) показывает, что переход от M=oo к Х1 = 1ч-1,25
приводит к уменьшению перекоса колец подшипников в 2,2—2 раза.
Из изложенного ясно, что при установке радиально-упорных шари-
коподшипников с оптимальным предварительным натягом, соответству-
368
ющим значениям параметра ?ч от 1 до 1,2о, условия работы подшипни-
ковых узлов, нагруженных моментом, заметно улучшаются.
Рис. 4.22. Значения коэффициента
в зависимости от предварительного на-
тяга при некоторых постоянных значе-
44
ниях
Предварительный натяг, при котором параметр = 11,25, при
практических расчетах может вычисляться по приближенной формуле:
1 Г (1,96 4-1,94)44 У*/3
(2 4-2,25) sin fo [ 1 -j- Н [(1,96 4- 1,94)Л?]2'3 J !
(3. 17)
где
1
2 4-2,25
ctg2 X Г Хг [1 + (°-905 1 ’°8)
1 "Г t cig Ро |_
1 —Ctgpo 1
1 + С Ctg fo J
Рис. 4.23. Значения коэффициента лг(Л1) в за-
висимости от предварительного натяга при не-
М
которых постоянных значениях -------к-

Н
При этом величины Р01 и Ра1 соответственно равны:
р =_____________________(3,92 4- 3,88)44_________________.
01 2г0г sin fo (1-j-С ctgfo) {1 4-4/[(1,96 4- 1,94)Л4]2/3} ’
Рэ1 = (0,657-4-0,645) Р0!.
(3.18)
24 1578
369
3. Совместное действие момента и осевой силы
При совместном действии момента и осевой силы (рис. 4. 24) усло-
вия нагружения подшипников 1 и 2 неодинаковы, что существенно ус-
ложняет расчеты, связанные с определением давлений на шарики. Для
того, чтобы найти величины Рп, Psi, Роз и РЭ2, в данном случае прихо-
дится строить ряд вспомогательных графиков. Порядок построения этих
графиков нетрудно уяснить на следующем примере.
Пусть начальный угол контакта Ро==36°. Будем для простоты счи-
тать, что относительный предварительный натяг Дц=0 и относительная
база ^0, т. е. рассмотрим случай, имеющий
прямое отношение к расчету подшипников
тарелки автомата перекоса, для которых
в достаточной мере справедливы эти допу-
щения.
Рис. 4.24. Схема нагруже-
ния двух шарикоподшипни-
ков моментом и осевой си-
лой
Рис. 4.25. Типовой график 5Oi=6oi(x, X) при R=Ri~
—Rz—Ь
Согласно уравнениям (3.5) при радиальной нагрузке
величины 801, 802, \ и связаны между собой следующим соотношением:
___/§02.У/2; —Г; ь _; с 1 ^oi ।
J 21 I =^J J 22—l6 ГО 72Ш21 I; I /22622 , , 5 Щ
1 501 / \®01 / 1 T 4
4-tg2 Г/2Л1 1
\»oi / J 1 +
(3.19)
В равенстве (3. 19), как и во всех последующих зависимостях, учте-
но, что при совместном действии момента и осевой силы, как и в случае
действия «чистого» момента, фо2=фсн=0-
Из формулы (3.7) при нулевом предварительном натяге имеем:
< _2о2-_=,О. (3. 20)
I 4- Xj I 4- Х2
Откуда
/01
(3.21)
В дальнейшем отношение будем везде обозначать через х.
soi
_ Используя равенства (3.6), (3. 19), (3.20) и (3.21), строим кривые
бо1 = &о1 (х, Xi), удовлетворяющие условию Z?=/?i—^?2 = 0 (рис. 4. 25). Пе-
370
ресекая полученные кривые линиями 601=const, находим значения к,
соответствующие при данных значениях М (от оо до 0) выбранным зна-
чениям 6о1. Принимая далее Xi в качестве параметра, с помощью урав-
нений (3. 1), (3.5) и упомянутых выше равенств, вычисляем величины
Д Р09 о <п РдО ого ®^9
---— , -----=—, а также отношения ---=х3Ди .
гч<Рш r^zvd^ Р01 P3i tfj
Результаты расчета представляются графически, как это сделано
на рис. 4. 26—4. 28. Рис. 4. 26 позволяет по заданным значениям -—- и
определить величины 60I и Xi, зная которые можно легко под-
считать максимальное и эквивалентное давления Р01 и Рэь Из рис. 4. 27
некоторых постоянных значениях 801 и Aj
и 4. 28 находят отношения ~~ и — и затем вычисляют максимальное
Ли Ai
и эквивалентное давления Аг и Az-
Выше был разобран случай Дп=0 и £=0. При произвольных значе-
ниях этих величин, а также при других начальных углах контакта ро
определение давлений Р9\, Psi, Р02 и Аг производится таким же образом,
как и в рассмотренном примере. Нужно только помнить, что при нали-
чии предварительного натяга величина 601 не может быть менее sin роДц.
Следует отметить, что случай Дп=0 и £=0 характерен не только для
подшипников тарелки автомата перекоса, но и для многих опор качения
больших диаметров, применяющихся в поворотных устройствах совре-
менных машин и механизмов.
Из приведенных материалов видно, что при превалирующем момен-
те, когда Х]>I, наиболее нагруженным чаще всего оказывается подшип-
ник 2, хотя на первый взгляд условия работы подшипника t, в сторону
которого направлена осевая нагрузка А, представляются более тяже-
лыми.
Изложенный способ расчета радиально-упорных шарикоподшипни-
ков при совместном действии момента и осевой силы требует выполне-
ния большого объема вычислений и построений. Поэтому его примене-
ние оправдано только в специальных исследованиях, имеющих целью
вскрытие особенностей распределения нагрузки в подшипниковых уз-
24* 371
лах с малыми расстояниями между опорами, а также для разработки
вспомогательных графиков, с помощью которых могут рассчитываться
отдельные типовые конструкции. Если такие графики заранее не постро-
Рис. 4.27. Зависимость отношения
—— от -— при некоторых ПОСТОЯН-
НО! м
ных значениях 60i
Рис. 4.28. Зависимость отношения
Ра2 1
— от — при некоторых постоян-
на!
ных значениях 80i
ены, то в инженерных расчетах следует пользоваться упрощенной мето-
дикой, основанной на предельных зависимостях, полученных для случая
малых нагрузок, когда усилия распределяются между шариками наибо-
лее неблагоприятным образом.
4. Предельные зависимости от малых нагрузок
При малых нагрузках можно считать, что углы контакта всех ша-
риков примерно одинаковы и равны р0-
Отбросив в уравнениях (3. 5) члены, учитывающие изменение углов
контакта, и введя в них вместо величин 6oi и боа максимальные давления
на шарики и Р02, что более удобно для малых нагрузок, имеем
cos
A^a^sm
A^=r0zP01sinfJ0/21;
^2=zP02 cosft>/’22;
A2=zP02sin ftjJb;
A/2 = r0zP02sinft/22.
Подставив зависимости (3.22) в уравнения (3.1), получим
PzP01 cos ft, (y21 — ^2j22 cos o02);
A =ZP01 Sin ft, (/n — V-3/2/12);
M = razP01 sin ft, (1 + C ctg ft,) (/2] + x3/2/22 cos %2),
(3.22)
(3. 23)
^02
где, как и прежде, .
soi \Pqi/
Так как в данном случае угол Фог может и не быть равен нулю, то
с учетом этого обстоятельства из равенства (3 7) находим
х G + ^i)
л2 COS '/02—
(3. 24)
372
Рассмотрим систему уравнений:
/21+х3;2Л2 _
Л]-Х3',2/2и
Л1 + '1'-3,2./22
(3. 25)
).2cos%2= —
Нетрудно убедиться, что значения Ль Х2 и х при нулевом предвари-
тельном натяге, удовлетворяющие уравнениям (3.25), удовлетворяют
также уравнениям (3.23) и (3.24), если положить:
ппн ro^(i + Cctg3o)tg₽0 b
Л4
т М .
ro.4(l+Cctg₽o) ’
(3. 26)
/о* (1 + С ctgfo) tgfo ,
Л1
_ то/?(1 + СCtg fe) tg > р
Р Л1 ’
«-fig?.;
13'27)
Го R (1 + С Ctg р0) tg Ро ’
Следует иметь в виду, что в первом случае угол ф02 равен нулю, а
во втором 180°.
Если во внешней нагрузке главную роль играет осевая сила, то дав-
ления на шарики обычно записываются в виде
p _ . 4)1 . □ »
z sin

p = 1 • 31 z sin Po ’
k^A FJ KO2 л 1 02 • q » z sin p0 (3.28)
к1д,Д
^32- • г sin ₽0
Если превалирует момент, то, как правило, используется форма
записи, которая уже применялась ранее:
р _ 4,37/^41
*01 —------------—• — ’
2г0г sin 0О( 1 4- Сctg ₽0)
р _ 2,57к{М)М
31 2r0?sin₽0(l-|-Cctg₽0) ’
_ 4,37^’Л!
j 02—---------------------- " i
2r0* sin ₽o(l -I- £ctg?0)
p 2,57«^>M
5,2 2ro*sln₽o(l + Cctg ₽0)
373
Согласно уравнениям (3.23)
2
К(М) — ____________________
01 4,37 (/л + х3,2у22 cos 'Уоз)
1
(3. 30)
д-(Л) _______________
01 , ,3/2, ’
/11—*' /12
к<^)_ 3/2„(И)
^02 —'• /vol •
Что касается коэффициентов к<м\ к[А\ и то они равны:
*1(Л)=-М?); <>=^7 <1>;
Рис. 4.29. Номограммы для приближенного расчета подшипников, нагру-
женных осевой и радиальной силами н моментом
Заметим, что между коэффициентами к<А> и лг<Л,> существует сле-
дующая связь:
м
4л)
4-^Kw
2 МО +Cctg₽0)
(3. 31)
Решение системы (3. 25) может быть представлено в виде графи-
ков, изображенных на рис. 4.29. По этим графикам, зная г и и, нетрудно
отыскать значения х и Xi, по которым вычисляется произведение
374
Л2 cos 1|>02 и затем подсчитываются коэффициенты к^, л:<Л), к$>, к^л> или
«(«), к(М>, «w, После этого определение давлений на шарики не сос-
тавляет особого труда.
Графики на рис. 4. 29 интересны тем, что в них не фигурируют ни
угол р, ни %. Таким образом мы пришли к весьма удобному для прак-
тики приближенному способу расчета радиально-упорных шарикопод-
шипников с большими начальными углами контакта в наиболее общем
случае их нагружения. Предварительный натяг, как мы уже убедились
при рассмотрении подшипниковых узлов, нагруженных «чистым» мо-
ментом, сказывается, главным образом, на жесткости системы, мало ме-
няя расчетные значения максимальных и эквивалентных давлений на
шарики. Поэтому изложенный приближенный метод определения этих
величин, основанный на допущении, что предварительный натяг равен
нулю, может быть использован для решения достаточно широкого кру-
га задач, связанных с расчетом радиально-упорных шарикоподшипни-
ков с большими начальными углами контакта, установленных в под-
шипниковых узлах, имеющих малое расстояние между опорами и вос-
принимающих произвольную комбинированную нагрузку. В более прос-
тых случаях нагружения при рассмотрении предельного распределения
усилий между шариками, соответствующего малым нагрузкам, предва-
рительный натяг при необходимости может быть сравнительно легко
учтен.
Пусть узел нагружен только моментом и осевой силой. При отсутст-
вии радиальной нагрузки, как следует из уравнений (3.23),
/21—х8/а /22 cos фо2=0. Используя это соотношение, приведем выражения
для коэффициентов «М и кГ1) к виду:
К(Ж) = “01 1 4,37./21 vM) — “01 — т . 2Л1
kW = 1 Т_ .
4,37/22 2/22 (3. 32)
Wj ; к<д> = TW1
2,57/2! 2/21
^2 ; к<д) = Т^2
2,57/22 2/22
Соотношения (3.32) действительны и при наличии предваритель-
ного натяга.
Коэффициенты к<м>, и kW, определяемые формулами (3.32),
при нулевом предварительном натяге могут быть найдены по графикам
на рис. 4.30 и 4. 31. Так как при малых значениях отношения — коэффи-
т
циенты и д(М) для подшипника 2 существенно больше, чем для под-
шипника 1, то естественно возникает вопрос, нельзя ли выравнять их
значения за счет соответствующего подбора предварительного натяга.
Не останавливаясь на преобразованиях, связанных с решением этой за-
дачи, поскольку они достаточно очевидны из изложенного выше, приве-
дем сразу окончательное решение. На рис. 4.32 изображены кривые, no-
д., sin 8п
называющие, при каких значениях отношения ——— может быть тео-
601
ретически обеспечена идентичность статического и динамического нагру-
жения подшипников 1 и 2, т. е. равенство коэффициентов к^) и«<£Оили
kWh к<Л1\ Значения этих выравненных коэффициентов пунктирными ли-
ниями нанесены на рис. 4. 30 и 4. 31.
375
Для узлов, которые должны иметь повышенную жесткость, жела-
тельно, чтобы в обоих подшипниках были нагружены все шарики. Эта
задача также легко решается путем подбора предварительного натяга.
1 ак как при совместном действии момента и осевой силы зона нагру-
жения в подшипнике 1 всегда больше, чем в подшипнике 2, то условием
Рис. 4.30. Значения коэффициента
—^для случая совместного
действия момента н осевой силы
Рнс. 4. 31. Значения коэффициента
к^=к(Л1) (—'j для случая сов-
\ т /
местного действия момента и осе-
вой силы
полной загрузки шариков обоих подшипников является неравенство
Хг>1. Значения коэффициентов отношения Д"52п^°,
°01
соответствующие случаю ^2=1, также даны на рис. 4.31 и 4.32.
Рис. 4. 33 показывает, что при наличии предварительного натяга, обес-
печивающего загрузку всех шариков обоих подшипников, угловая жест-
кость узла возрастает более чем в два раза, при этом максимальные и
эквивалентные давления на шарики увеличиваются примерно на 10—
15%.
Рис. 4.32. Значения предваритель-
ного натяга для обеспечения усло-
вий к.('и)=Д'и\ и Х2= 1
1 X UJ их X
Рис. 4.33. Влияние предвари-
тельного натяга (условие Х2=1)
на угловую жесткость узла
Предельные зависимости, полученные для случая малых нагрузок,
весьма удобны для практических расчетов, так как они существенно
уменьшают трудоемкость определения давлений на шарики. Нужно
только иметь в виду, что использование этих предельных зависимостей
приводит к определенному завышению расчетных давлений на шарики.
При контактных напряжениях порядка 20 000 кгс1см2 оно составляет
376
15—25% для угла р0 = 26° и 2—17% для угла Ро = 6О°. Учитывая послед-
нее обстоятельство, при вычислении расчетных нагрузок на подшипнико-
вый узел в случае применения указанных предельных зависимостей
можно принимать меньшие значе-
ния коэффициента безопасности.
Рис. 4.34. Упор-
ный двухрядный
шарикоподшип-
ник, нагруженный
осевой силон и мо-
ментом (эксцент-
рично приложен-
ной осевой силой)
Рис. 4.35. Значения ко-
эффициентов н
в зависимости от т
На основе приведенных выше
зависимостей могут быть определе-
ны давления на шарики эксцентрич-
но нагруженных двухрядных упор-
ных шарикоподшипников. При этом следует помнить, что для начального
угла контакта Ро=9О° при Дп=0 формулы (3.32) дают «точные» значе-
ния коэффициентов, входящих в формулы (3.28) и (3.29). Заметим, что
в данном случае величина г представляет собой относительный эксцент-
риситет — (рис. 4. 34).
го
Если эксцентрично приложенную осевую силу воспринимает одно
рядный упорный шарикоподшипник, то
Р0==4д).Л;
Z
Р=кЩ-,
Z
где Чл>=—, №= — .
° Ji Л
(3. 33)
Значения коэффициентов к^А> и /с<Л) находятся по кривым, представ-
ленным на рис. 4. 35. Эти кривые получены из значений %, соответствую-
/л
щих уравнению — =?, непосредственно вытекающему из условий ста-
J1
тического равновесия.
5. Распределение нагрузки между рядами шариков
двухрядных радиально-упорных шарикоподшипников
Для воспринятия совместно действующих радиальных и осевых на-
грузок в агрегатах веротолета широко применяются радиально-упорные
шарикоподшипники с начальными углами контакта 26 и 36°, имеющие
небольшой предварительный натяг (рис. 4.36).
Попытаемся установить, как распределяется нагрузка между ряда-
ми шариков таких подшипников, работающих в условиях, исключающих
возможность заметного взаимного перекоса их колец.
377
Имея в виду, что небольшой предварительный натяг мало сказы-
вается на величине давлений на шарики, воспользуемся для приближен-
ного решения задачи предельными зависимостями, приведенными в пре-
дыдущем пункте. __ _
Полагая в равенствах (3.4) и (3.7) е = 0 и Лп = 0 и вспоминая, что
6i= ,г'01, и 62= —, находим Хг=М. Индекс «1» присвоен ряду
1+^! 1 + Ajcosfoz
шариков, в сторону которого направлена осевая сила. Так как при на-
Рис. 4.36. Двухрядный
радиально-упорный ша-
рикоподшипник, нагру-
женный радиальной и
осевой силами
Рис. 4. 37. Значения Zi и коэффи-
циентов в зависимости от —
гружении подшипника радиальной и осевой силами угол ф02=180° и, сле-
довательно, со5 1фо2 = — 1, то для рассматриваемого случая из уравнений
(3. 23) имеем
*1 + 1 ’
(3. 34)
Л = zPm sin р0 - (h—2у/2у 12] ;
R=zPm cos Ро р21iy'2/22j.
(3.35)
Зависимости, определяющие давления Р01 и Рщ для двухрядных ра-
диально-упорных шарикоподшипников, могут быть записаны следую-
щим образом:
4,37
г cos ₽0 2
(3.36)
где
-378
Эквивалентные давления для обоих рядов шариков соответствен-
но равны
^sl ^01 ’ 1 /о 074
р —an PI ' ' '
--W2^02- J
Значения параметра и коэффициента в зависимости от вели-
чины —=— ctgp0 могут быть найдены по графикам на рис. 4.37.
т R
Как показывают расчеты, первый ряд всегда является более нагру-
женным. При — 1,67, когда ki^l, он несет всю нагрузку, приложен-
ную к подшипнику. Заметим, что при т = 0,6 отношение - = 1,67 tg Ро-
R
При преобладающих осевых нагрузках, когда работает один ряд
шариков, с целью получения более точных результатов расчет двухряд-
ных радиально-упорных шарикоподшипников всех типов, в том числе
и рассмотренных в данном пункте, следует производить с помощью зави-
симостей § 2.
6. Примеры расчета
Пример 1. Определить расчетный срок службы подшипников тарел-
ки автомата перекоса (рис. 4.38), нагруженных моментов М =
Рис. 4. 38. Автомат перекоса несущего винта вертолета
= 150 кгс • м и вращающихся с числом оборотов 240 в минуту. Подшип-
ники имеют следующие параметры: р0=36°, rfm=9,525 мм, z=42, zo =
= 79 мм.
379
Относительная база £=0,1, предварительный натяг Дп = 0.
Так как подшипник имеет нулевой предварительный натяг, то коэф-
фициенты к^а к<м>, необходимые для вычисления нагрузок на шарики,
определяются с помощью рис. 4. 21.
Подсчитываем величины
I 1—Ctgpp I [ 1-0,1-0,726 |=1 12.
1 tgpo + C I I 0,726 + 0,1 | ’
м=—2----------!-------—.—=
zvd^ sin Ро (1 +Cctg Ро) го
==-------------= о,744.
42-1-9,5252-0,588(1 + 0,1-1,376 ) 0,079
Поскольку ^^ = 0,515, то коэффициент v принят равным единице.
__
Согласно рис. 4.21, полученным значениям q и М соответствует
значение к^Л1) =0,912.
Таким образом, максимальные давления на шарики в обоих под-
шипниках будут
4,37к'ЛпЛ1
р -_р —__________’ ° —
01 02 2 r0zsin ₽o(l+UtgPo)
_________£^.91+150__________=
2-0,079-42-0,588(1 +0,1-1,376)
В рассматриваемом случае ^i = A-2=o°. Следовательно,
P3i==Pa2^w^pm=0,587-134,7 = 79,1 кгс.
Эквивалентное давление Рэу, определяющее долговечность узла,
может быть найдено по формуле (2.44). Учитывая, что при A-i = A,2=oo
кК1 =Кк2= 1,2 (см. рис. 4. 5), из этой формулы находим
= ^1кк1Р31 => 1,21 • 1,2 • 79,1 = 114,8 кгс.
Здесь принято, что /=—.
Для подшипников с указанными размерами согласно формуле
(2. 42) коэффициент работоспособности
С = 65 • ------~----=- 65 • 420’7 ---------=67 794.
l+0,02rfm Ц-0,02-9,525
Как показывают результаты стендовых испытаний, для подшипни-
ков тарелки автомата перекоса произведение коэффициентов КбКт/см=
В соответствии с этим из выражения (2.43), считая, что /г = /г10, по-
лучаем
---------£-------=----------™----------=40,5.
0,39-квКтКыгР9.усО8р0 0,39-1,1-42-114,8-0,809
Откуда
. ООО О-7П Z. 228 370 ГгЛ
/гй = 228370и й —------ss950 час.
240
Пример 2. Вычислить максимальные и эквивалентные давления на
шарики в подшипниках, рассмотренных в примере 1, при воспринятая
ими момента М = 60 кгс м и осевой силы <4 = 500 кгс.
380
Так как относительная база £ мала, то для определения указанных
давлений воспользуемся рис. 4. 26 — 4. 28.
По величинам
М ------------52------=0,1993 кгс1млР
rggvdl, 0,079-42-1-9,5252
И
_Д _ =-------500---=,013]2 кгс! мм?
zvd2w 42-1-9,5252- '
с помощью рис. 4.26 находим: doi = O,O55 и %i = 0,7.
Подсчитываем далее Ан и Раъ Так как fa = 0,7 соответствует значе-
ние w=0,678, то согласно формулам (2.2) и (2.6) имеем:
Р01 = £0^2ш&30/2=62-1 -9,5252-0,0553'2 = 72,5 кгс-,
P3-l = ’wPm — 4^,2 кгс.
По графикам на рис. 4.27 и 4.28 отыскиваем значения P^l^si и
P02/Ai’ Используя эти значения, получаем
PQ2— 1,085Р01 = 78,7 кгс;
Рэ2—0,875Рэ1=43 кгс.
§ 4. РАСЧЕТ КОНИЧЕСКИХ роликоподшипников
ПРИ КОМБИНИРОВАННЫХ НАГРУЗКАХ
1. Расчет однорядных конических роликоподшипников
Выше были изложены методы расчета радиальных и радиалыго-
упорных шарикоподшипников, воспринимающих комбинированные на-
грузки. Рассмотрим теперь особенности расчета конических роликопод-
шипников, работающих в условиях
сложного нагружения.
Прежде всего дадим решейие
задачи об определении усилий, дей-
ствующих на ролики однорядного
конического роликоподшипника,
при заданных значениях приложен-
ных к нему радиальной и осевой на-
грузок (рис. 4.39).
Нормальные усилия Ру и Р^,,
действующие на ролик со стороны
наружного и внутреннего колец,
связаны между собой соотношением
p;=90S<V-V<p (4.1)
cos ут
При обычных значениях углов
Сечение сод углом ф
к плоскости, нагружения хдг
Рис. 4. 39. Схема нагружения кониче-
ского роликоподшипника радиальной
и осевой силами
у и уч практически можно считать,
что
р;=рФ. (4.2)
В соответствии с теорией Герца для случая линейного контакта
можно с достаточной степенью точности полагать
Рф = ^8ф, (4.3)
где бф— сближение колец в сечении, расположенном под углом ф к
плоскости нагружения.
381
При отсутствии взаимного перекоса колец под нагрузкой сближение
определяется выражением
6Ф =ssinfJ+ucospcosi|). (4.4)
Здесь и и s — радиальное и осевое смещения внутреннего кольца отно-
сительно наружного, отсчитываемые от положения, при
котором в подшипнике выбраны зазоры;
Р — угол конуса наружного кольца.
Положив
— ctg^X, (4.5)
из выражений (4. 3) и (4. 4) получаем
РФ = В ssin р(1+Хcost])). (4.6)
Если направление радиальной нагрузки совпадает с положитель-
ным направлением оси z(P>0), то смещение и>0. В этом случае центр
зоны нагружения находится в сечении ,ф = 'фо = О. Если радиальная нагруз-
ка действует в противоположном направлении (7?<0), то смещение
и<^0, при этом центр зоны нагружения располагается в сечении ф=фо=!
= 180°.
Согласно формуле (4. 6) максимальное значение усилия равно
P0 = 5ssin₽(l+^cosi|)o). (4.7)
Используя равенство (4. 7), окончательно имеем
РФ=~1^пТ. •(1+XC°S^ (4' 8)
1 A. COS фо
Как следует из условий статического равновесия,
7? — -——г- Cos ₽ V (1 cos Ф)cos Ф;
1 + Xcos<p0
о „ (4-9)
А=ттЪт-sin ₽ V о+* cos ф).
1 н- A cos Фо
При обычных количествах роликов уравнения (4.9) могут быть за-
менены соотношениями
Здесь
7?=>P0z cos P/2cos<|>0;
A = Pozsin p/р
(4.10)
тн
Ji , ч f (1 + * cos % COS Ф) йГф=
2л (1 +Х cos фо) J ,
1
Л J <' +k с“ “s *)cos =
*н
(4.11)
(2 5[«-«+ s'“ М •
382
Границы зоны нагружения ф' и ф' определяются так же, как и для
радиальных и радиально-упорных шарикоподшипников [см. формулу
(1. 20) и пояснения к ней].
Из соотношений (4. 10), полагая для простоты 7?>0 и, следователь-
но, 0, находим
, _ 1 Л
0— Z-------7.
fa z cos?
(4. 12)
Эквивалентное давление Рэ для конического роликоподшипника может быть представлено в виде: Рэ = даР0, (4.13) где
1 w=- 1 -h X cos Значение величин табл. 4. 7. *н —Л (1 + X cos Фо cos ф)3-33^ 2л J /2 И w в функции АС 0,3 os % приведены в
Таблица 4. 7
k cos ф0 71 72 W X cos фо J1 h W
0 1 0,5 1 2,000 0,405 0,268 0,698
0,1 0,909 0,454 0,913 2,500 0,389 0,267 0,692
0,2 0,833 0,417 0,853 3,333 0,371 0,264 0,686
0,3 0,769 0,385 0,806 5,000 0,354 0,261 0,679
0,4 0,714 0,357 0,773 10,000 0,336 0,256 0,670
0,5 0,667 0,333 0,751 со 0,318 0,250 0,660
0,6 0,625 0,312 0.738 -10,000 0,300 0,242 0,648
0,7 0,588 0,294 0,729 —5,000 0,281 0,234 0,634
0,8 0,555 0,278 0,725 —3,333 0,261 0,222 0,617
0,9 0,526 0,263 0,722 —2,500 0,240 0,210 0,598
1,0 0,500 0,250 0,720 —2,000 0,218 0,196 0,575
1,111 0,479 0,258 0,718 — 1,667 0,194 0,178 0,548
1,250 0,460 0,264 0,714 —1,428 0,167 0,156 0,518
1,428 0,440 0,266 0,708 -1,250 0,136 0,130 0,484
1,667 0,424 0,268 0,704 -1,000 0,000 0,000 0,000
Расчет конических роликоподшипников так же как и радиально-
упорных шарикоподшипников обычно ведется с помощью приведенных
статической и динамической нагрузок. Эти нагрузки находят из условия,
что
Ро — 1______2° 4 Qo .
?2Х_ и 2C0Sp ZCOSjl
Л = —^-=2,64 —2—.
/2х_дагс°8₽ z cos р
(4- 14)
383
Сопоставляя равенства (4.14) с равенствами (4.12) и (4. 13), по-
лучаем (4.15) R=K^R, J
где ° h h ' (4.16) w к (R) —7°’38w . 4=. "° h
В соответствии с соотношениями (4. 10), значения параметра X, не-
обходимые для определения коэффициентов и должны удовлет-
ворять условию
#=4^=т- <4-17)
?! л
Так как при Х=1 — =0,5, то для того, чтобы в однорядном коничес-
ком роликоподшипнике были нагружены все ролики, величина т не дол-
жна превышать 0,5.
При т^0,5 значения коэффициентов и могут быть опреде-
лены по графикам, приведенным на рис. 4. 40. Эти графики построены
на основании равенств (4. 16) и (4.17).
Если т-<0,5 и, следовательно, Х<1, то выражения для интегралов
Л и ]2 принимают вид
1______
2 1 + Л '
Из выражений (4. 17) и (4. 18) находим
4 = 2т;
— = 2 + —.
h т
(4. 19)
Таким образом, при т<0,5, когда нагрузку несут все ролики,
Н*)=^ = 0 54 0125
0 h т
о,76w4-0,38 —.
4.. ° т
Как следует из равенств (4.20), при всех загруженных роликах
Qo = 0,5/?4-0,254 ctg ₽; (4.21)
Q=0,76w/?4-0,38w4 ctgt3. (4.22)
Значения w в функции т удобно определять по кривой, показанной
на рис. 4. 41.
Приведенные зависимости дают ответ на все основные вопросы,
возникающие при расчете конических роликоподшипников, воспринима-
ющих комбинированные нагрузки, при условии, что взаимным переко-
сом их колец можно пренебречь.
384
Как видно из рис. 4.40, в области т~0,6-:-0,8 кривые =к^>(т)и
к<й> = л(й)(т) имеют достаточно ярко выраженный минимум. Это говорит
о том, что соответствующим подбором угла контакта р можно добиться,
чтобы при заданной комбинации
радиальной и осевой нагрузок мак-
симальное и эвивалентное давления
на ролики имели наименьшее зна-
Рис. 4.40. Значения коэффици-
ентов к(7?) в зависимо-
сти от Т
Рис. 4.41. Значения w в зависимо-
сти от т
чсние. Оптимальные углы контакта, при которых выполняются условия
Po=P™in и P:j=P'"hl , определяются графиками, показанными на
рис. 4. 42. Эти графики получены
zPQ /Л\ гРэ Л\
теи И -fAr)
лежащих в диапазоне от 0 до 30°.
в результате исследования зависимос-
построенных для ряда углов контакта,
2. Некоторые замечания к расчету подшипниковых узлов,
состоящих из двух конических роликоподшипников
Если подшипниковый узел, состоящий из двух конических ролико-
подшипников, нагружен моментом, действующим в сочетании с ради-
альной и осевой силами (рис. 4.43), то для его расчета может быть ис-
пользована система уравнений
cos ₽ (/21 -x/22'cos %2);
А = гР013т?(;п —V12);
М = r0zP01 sin ? (1+С ctg ₽) (/2i + -z/22cos Фоа);
4. 23)
аналогичная системе уравнений (3.23) и (3.24). описывающих условия
статического равновесия подшипниковых узлов с двумя радиально-упор-
ными шарикоподшипниками в предположении, что углы контакта всех
шариков одинаковы и равны начальному.
Следует отметить, что уравнения (4.23) являются «точными», по-
скольку в конических роликоподшипниках углы контакта действительно
постоянны и не меняются под нагрузкой, причем эти уравнения действи-
тельны как при наличии, так и при отсутствии взаимного перекоса
колец.
В уравнениях (4.23) вместо величины яЛ2 фигурирует величина х.
Это объясняется тем, что для конических роликоподшипников
Р02 __ 802 _у
Лп ®01
25 1578 385
В случае нулевого предварительного натяга значения X] и н, удов*
летворяющие уравнениям (4.23), находятся по графикам, приведенным
на рис. 4. 44. Величины тип здесь имеют такой же смысл, что и для ра-
диально-упорных шарикоподшипников [см. формулы (3. 26) и (3. 27)].
По найденным значениям Мих подсчитывается величина Мгсозфог-
Рис. 4. 42. Значения оптимального
угла контакта в зависимости от
отношения AIR
Рис. 4.43. Схема нагружения двух
конических роликоподшипников
радиальной и осевой силами и мо-
ментом
Максимальное и эквивалентное давления на ролики
1 и 2 определяются из выражений:
в подшипниках
Здесь
Si

KwA
r0*sinP(l + С ctg р) 2 sin Р к<л>Л
roz sin Р(1 + С ctg Р) 2 sin Р
1,32к[л1>Л4 к[Л)Л
/•0*sinp(l + С ctg Р) 2 sin Р
1,32к^>Л4 4л>л
r02 sin Р(1 + с ctg Р) 2 sin 3
1
; = хлг<л1)
2(/ai + V22 cos ф02) 2 01
/11 —х /12
w1
(4. 24)
(4. 25)
^(ЛО.
'1 0,66 01 ’

2 0,66 02 ’
^Л)=®2^>.
Положив в системе (4. 23)
ниям, описывающим условия
упорных роликоподшипников:
0=90°, приходим к следующим уравне-
статического равновесия двухрядных
— ^01 (Ун Via); 1
М = rozPm (/Л-тV'ss)- J
(4. 26)
Способы решения уравнений (4. 26) ясны из предыдущего, поэтому
останавливаться на них особо не имеет смысла.
386
-f, S.------------------‘-------------------------L_J
0 0,1 0,* 0,6 0,8 1,0 1,1 ±
Рис, 4. 44. Номограммы для расчета подшипников, нагруженных радиаль-
ной и осевой силами и моментом
I
I
I
Рис. 4.45. Значения ко-
эффициентов и
в зависимости от т
23*
387
Если в уравнениях (4.26) принять х=0, то они приобретут вид:
А=гР0Л; |
M = r0zP0J2. J
(4.27)
N 1 Ьь-
Соотношения (4. 27) характеризуют распределение нагрузки в од-
норядных упорных роликоподшипниках.
Значения максимального Ро=к^Л) - и эквивалентного =
и Z
давлений на ролик, удовлетворяющие соотношениям (4.27), удобно на-
ходить с помощью кривых к^Л) =кУ1)(т) и к0)=кИ)(т),приведенных на
рис. 4.45.
При л-<1, когда в подшипнике нагружены все ролики, интегралы /т
и /2 определяются выражениями (4.18).
тт м
Нетрудно убедиться, что в этом случае, имеющем место при т==—
гоЛ
^0,5,
Х = 2т;
1 (4- 28)
к<л>=—=1-Н=1-2т.
Л
§ 5. РАСЧЕТ ПОДШИПНИКОВ, РАБОТАЮЩИХ
ПРИ КАЧАТЕЛЬНОМ ДВИЖЕНИИ
При проектировании вертолетов значительные трудности представ-
ляет правильный выбор подшипников втулок несущего и рулевого вин-
тов. Эти подшипники, как известно, работают в специфических условиях
качательного движения. Они выходят из строя не из-за контактной уста-
лости, а вследствие местного износа дорожек качения, получившего наз-
вание «ложного бринеллирования». Понятно, что обычные методы рас-
чета для таких подшипников неприменимы.
Большое влияние на работоспобность колеблющихся подшипников
оказывают свойства смазки. Практика показала, что надежная работа
многих ответственных подшипниковых узлов вертолета возможна лишь
при применении специальных масел и смазок. Поэтому в вертолетостро-
ении приходится уделять серьезное внимание вопросам подбора смазоч-
ных материалов для подшипников качения. Это прежде всего относится
к подшипникам осевых шарниров втулок несущих и рулевых винтов, вос-
принимающих значительные осевые нагрузки от центробежных сил ло-
пастей.
Сложность расчета подшипников втулок несущего и рулевого вин-
тов заключается и в том, что относительно низкая жесткость их основ-
ных деталей, особенно на тяжелых вертолетах, может приводить к за-
метным деформациям колец, которые трудно учесть при определении
усилий, действующих на тела качения. Разработать общие методы рас-
чета, учитывающие влияние всех факторов, определяющих несущую спо-
собность подшипников втулок несущего и рулевого винтов, пока не уда-
лось. Однако накопленный к настоящему времени экспериментальный
материал позволяет дать определенные рекомендации по выбору допус-
каемых нагрузок и определению долговечности наиболее распространен-
ных видов подшипников, применяющихся в этих сложных и ответствен-
ных агрегатах. Аналогично обстоит дело и с расчетом подшипников
шарниров автоматов перекоса и механизмов управления вертолетов,
которые так же, как и подшипники втулок, работают при качательном
388
движении. Здесь только должно быть дополнительно учтено, что нагруз-
ки, воспринимаемые большинством из этих подшипников, имеют дина-
мический характер.
1. Особенности механизма износа подшипников качения
в условиях качательного движения
Рассмотрим особенности механизма износа подшипников качения
при качательном движении.
При небольших амплитудах колебаний, когда контакт тел качения
с кольцами происходит лишь на отдельных участках дорожек качения,
в подшипниках образуются вмятины в виде лунок от шариков или кана-
вок от роликов, которые по мере выкрашивания их поверхности превра-
щаются в глубокие раковины (рис. 4.46). Разрушение тел качения
в большинстве случаев начинается только после значительного пов-
реждения колец.
Рис. 4. 46. Кольца упорных шарико- и роликоподшипников после дли-
тельной работы при качательном движении с малыми амплитудами
Анализ результатов испытаний показывает, что при качательном
движении износ подшипников в значительной мере определяется окис-
лительными процессами и особыми условиями смазки в зонах контак-
та тел качения с кольцами.
В зонах контакта происходит интенсивная фрикционная коррозия.
Получающиеся при этом продукты окисления железа, смешиваясь со
смазкой, образуют своеобразную полировочную смесь, которая вызыва-
ет быстрый износ дорожек качения. При перекатывании тела качения
перед площадкой контакта образуется «порог» смазки, а за ней —
струйки смазки, стремящиеся заполнить пространство за движущимся
телом качения (рис. 4.47). Если смазка недостаточно подвижна и не ус-
певает сразу же заполнить это пространство, то участок дорожки каче-
ния, непосредственно прилегающий к площадке контакта, окажется по-
крытым лишь тонкой пленкой смазки. Естественно, что в момент измене-
ния направления движения тело качения будет проходить этот плохо сма-
занный участок раньше, чем к нему вновь поступит смазка. Вследствие
этого на границах участков контакта тел качения с кольцами, где про-
исходит изменение направления движения, возникают пики давления,
приводящие к ускорению износа. При очень малых амплитудах колеба-
ний, когда площадки контакта в крайних положениях тела качения пе-
рекрываются, нарушение слоя смазки может оказаться постоянным.
В этом случае пики давлений еще более возрастают и долговечность
389
подшипников заметно уменьшается. Увеличение подвижности смазки
улучшает условия работы колеблющихся подшипников. Тем не менее
даже при применении масел, обладающих высокой подвижностью,
условия их работы существенно отличаются от условий работы подшип-
ников, вращающихся в одном направлении.
Из изложенного ясно, что в подшипниковых узлах, работающих
при качательном движении, во всех случаях, когда это возможно по
конструктивным соображениям, следует применять масла, а не консис-
тентные смазки. При использовании консистентных смазок несущая
способность колеблющихся подшипников заметно снижается.
2. Смазка высоконагруженных колеблющихся подшипников
при малых амплитудах колебаний
смазки.
контакта
Участок пло-
хой смазки
Струнки,
смазки
Рис. 4. 47. Схема смазки при кача-
тельном движении
Поскольку свойства смазки оказывают большое влияние на долго-
вечность колеблющихся подшипников, то говорить о допускаемых на-
грузках для таких подшипников в отрыве от применяемых в них сма-
зочных материалов нет смысла.
Подшипники вертолетов, работающие при качательном движении,
могут быть разделены на две основные группы:
1. Подшипники втулок несущего и рулевого винтов, автоматов пе-
рекоса и некоторых элементов управления, работающие при амплиту-
дах колебаний до 10°. Для этих под-
шипников суммарное число качаний
между двумя капитальными ремон-
тами, при которых производится их
замена, обычно составляет не менее
10 миллионов.
2. Подшипники механизмов уп-
равления, совершающие ограничен-
ное число качаний (до 100000) с ам-
плитудами более 20°. Имеется в виду,
что перекрытие соседних площадок
контакта при этом не происходит.
Практика показала, что подшип-
ники второй группы могут удовлетворительно работать на хороших кон-
систентных смазках. Это объясняется тем, что на дорожках качения
таких подшипников могут быть допущены значительные вмятины от тел
качения, поскольку их работоспособность обычно ограничивается только
величиной допустимого момента трения.
В подшипниках автомата перекоса и элементов управления, при-
надлежащих к первой группе, применение консистентных смазок влечет
за собой заметное снижение несущей способности, однако по конструк-
тивным соображениям с этим приходится мириться и компенсировать
недостаточно высокие смазывающие свойства смазок некоторым умень-
шением допускаемых нагрузок. Что касается подшипников втулок несу-
щих и рулевых винтов, то в виду того, что для них допустимые износы
дорожек качения сравнительно невелики, они могут длительно работать
при высоких контактных напряжениях только в случае применения ма-
сел, обладающих определенным комплексом физико-химических
свойств.
Долговечность колеблющихся подшипников существенно зависит от
качества уплотнения подшипниковых узлов. При плохих уплотнениях,
позволяющих кислороду воздуха проникать внутрь узлов, а также при
малых объемах смазки и больших объемах воздуха долговечность ко-
леблющихся подшипников заметно уменьшается. Весьма эффективным
средством для увеличения срока службы подшипников, работающих
при качательном движении, является подача смазки под давлением и
390
особенно переход на циркуляционную смазку, обеспечивающую непре-
рывное поступление свежего неокисленного масла к зонам контакта
и удаление из них продуктов износа.
Остановимся на вопросах подбора масел для втулок несущих
и рулевых винтов более подробно, так как эти вопросы весьма актуаль-
ны для вертолетостроения.
Масла для осевых шарниров втулок несущего и рулевого винтов.
Как показывают многочисленные эксперименты, подшипники осевых
шарниров, воспринимающие значительные осевые нагрузки от центро-
бежных сил лопастей, особенно чувствительны к физико-химическим
свойствам смазки. Масла для этих узлов, срок службы которых обычно
определяет общий ресурс втулок несущих и рулевых винтов, должны
удовлетворять следующим основным требованиям:
— во-первых, эти масла не должны вызывать усиления окислитель-
ных процессов в зонах контакта;
— во-вторых, они должны сохранять высокую подвижность во всем
диапазоне рабочих температур и обеспечивать достаточную прочность
масляной пленки на всем протяжении участков контакта.
Допустимый уровень вязкости масла ограничивается также допус-
тимой величиной момента трения осевого шарнира. Если исходить из
опыта эксплуатации вертолетов Ми-1 и Ми-4, то можно считать, что при
минимальной рабочей температуре кинематическая вязкость не должна
превышать 90 000 сст. Испытания показывают, что в этом случае не на-
блюдается ни заметного роста моментов трения, ни снижения долговеч-
ности подшипников из-за уменьшения подвижности масла. Следует от-
метить, что масло МС-14, успешно работающее в осевых шарнирах
втулок несущих винтов вертолетов Ми-1 и Ми-4 при температурах до
минус 25° С, имеет указанную кинематическую вязкость при температу-
ре минус 20° С.
В силу специфических условий работы колеблющихся подшипников
масла и смазки для них должны подбираться только по результатам
испытаний при качательном движении. Стандартная методика испыта-
ний масел и смазок на четырехшариковом приборе для этих целей со-
вершенно непригодна. Смазывающие свойства масел и смазок для осе-
вых шарниров втулок несущих и рулевых винтов целесообразно прове-
рять в упорных шарикоподшипниках, так как они работают при более
высоких контактных напряжениях. Эксперименты показывают, что
смазочные материалы, обладающие наивысшей работоспособностью
в таких подшипниках, являются лучшими и для колеблющихся подшип-
ников других типов, в том числе для упорных подшипников с «поверну-
тыми» роликами, которые в настоящее время успешно применяются во
втулках несущих винтов всех серийных отечественных вертолетов, а так-
же для многорядных радиально-упорных шарикоподшипников, уста-
новленных во втулках несущих и рулевых винтов ряда зарубежных
вертолетов. Поскольку в упорных шарикоподшипниках нагрузка рас-
пределяется между шариками равномерно, то при качательном движе-
нии каждый контактирующий участок дорожки качения может рассмат-
риваться как самостоятельный объект испытаний.
Существенным моментом в испытаниях масел и смазок для под-
шипников осевых шарниров втулок несущих и рулевых винтов является
правильная оценка состояния дорожек качения. Даже при самых уме-
ренных контактных напряжениях после непродолжительной работы на
дорожках качения появляются лунки от шариков. Если появление таких
лунок независимо от их глубины считать за начало выхода подшипника
из строя, то придется браковать подшипники, которые могут еще на-
дежно работать в течение длительного времени. Кривые на рис. 4. 48 по-
казывают, как влияет глубина лунок на коэффициент трения упорного
391
шарикоподшипника. При глубине лунок 7—10 мк коэффициент трения
возрастает на 30—40%. Увеличение коэффициента трения в таких пре-
делах обычно не ощущается в эксплуатации. Поэтому состояние упор-
ных шарикоподшипников при глубине лунок до 10 мк следует считать
удовлетворительным. Такую же
глубину лупок можно допускать
и в радиально-упорных шарико-
подшипниках.
Испытаниями установлено,
что масло МС-20 является одним
из лучших для колеблющихся
подшипников. В соответствии с
этим оно может быть принято в
качестве эталона для оценки сма-
зывающих свойств масел и сма-
зок, предназначенных для работы
в осевых шарнирах втулок не-
сущих и рулевых винтов. Резуль-
таты испытаний упорных шарико-
подшипников на масле МС-20
Рис. 4.48. Зависимость коэффициента
трения упорного шарикоподшипника от
глубины лунок на кольцах
представлены на рис. 4. 49 в виде
кривой долговечности сг=сг(л/г), устанавливающей связь между кон-
тактным напряжением о и произведением nh числа колебаний в минуту
на продолжительность работы в часах. Испытания проводились при
амплитуде колебаний подвижного кольца <ро = 4,5°, частоте п =
= 240 кол! мин и температуре масляной ванны 20—40° С.
При значениях контактных напряжений, определяемых кривой дол-
говечности, изображенной на рис. 4. 49, 98% лунок на дорожках качения
имеют глубину, не превышающую 10 мк.
Рис. 4.49. Кривая долговечности a=<s(nh)
для упорных шарикоподшипников
Рис. 4.50. Кривая распределения
дшах
аи
отношения - ср
“и
Следует отметить, что между максимальной А™* и средней глу-
биной лунок имеется определенная статистическая связь. Эта связь Ус'
танавливается экспериментальной кривой распределения F( jотн°’
шения -^-.которая, как видно на рис. 4.50, близка к часто встречаю-
щемуся в технике распределению Максвелла
392
Анализ кривой долговечности на рис. 4.49 позволяет предложить
следующий режим ускоренных отборочных испытаний масел и смазок
для осевых шарниров втулок несущих винтов: продолжительность
100 час, число колебаний 240 в минуту, амплитуда колебаний 4,5°, кон-
тактные напряжения 34 000 кгс!см?. Такой режим позволяет сравнивать
смазывающие свойства испытываемого масла со смазывающими свойст-
вами масла МС-20.
Нужно иметь в виду, что с увеличением продолжительности испы-
таний роль окислительных процессов, протекающих в зонах контакта,
возрастает. Тем не менее предварительные отборочные испытания масел
и смазок для подшипников осевых шарниров могут проводиться по при-
веденной сокращенной программе, так как ускоренные испытания во
многих случаях позволяют сразу же отбраковать значительное число об-
разцов.
Масло МС-20 в условиях качательного движения обладает весьма
высокими смазывающими свойствами. Однако оно может применяться
только в летнее время. Зимой масло МС-20 обычно заменяется маслом
МС-14, смазывающие свойства которого также вполне удовлетворитель-
ны. Так как при температуре минус 30° С масло МС-14 застывает, то
при более низких температурах и его применение оказывается невозмож-
ным, что сильно затрудняет зимнюю эксплуатацию вертолетов. Замена
масла МС-14 низкозастывающими маслами общего назначения не дает
положительных результатов. Испытания показали, что при работе на
обычных низкозастывающих маслах осевые шарниры втулок несущих
винтов, как и при работе на консистентных смазках, быстро выходят из
строя. На этом вопросе нужно остановиться особо, поскольку законо-
мерность такого результата долгое время оспаривалась некоторыми
специалистами в области смазочных материалов, что на длительное
время задержало решение проблемы смазки осевых шарниров втулок
несущих винтов при низких температурах.
Экспериментами установлено, что масла для осевых шарниров вту-
лок несущих и рулевых винтов должны иметь при температуре 100° С
кинематическую вязкость не менее 9—10 сст. При работе на маловязких
маслах наблюдаются повышенные износы дорожек качения, а также вы-
крашивание и разрушение тел качения.
Низкозастывающие масла с высоким уровнем вязкости в области
положительных температур обычно состоят из маловязкой минеральной
или синтетической основы и высокополимерного загустителя. В боль-
шинстве случаев загустители, как и сама основа, обладают низкими
смазывающими свойствами. Поэтому в такие масла добавляют специ-
альные противоизносные присадки, содержащие серу, хлор, фосфор или
определенные комбинации этих химически активных элементов. В зо-
нах высоких контактных температур присадки взаимодействуют с по-
верхностью металла, образуя соответственно пленки сульфидов, хлори-
дов и фосфидов железа, предотвращающие непосредственный контакт
трущихся тел и уменьшающие износ.
По данным стандартного четырехшарикового прибора смазывающие
свойства низкозастывающих загущенных масел с противоизносными
присадками намного превосходят смазывающие свойства масел МС-20
и МС-14. Тем не менее для работы в условиях качательного движения
они совершенно непригодны. Это объясняется тем, что под влиянием
противоизносных присадок усиливаются окислительные процессы в зо-
нах контакта, играющие решающую роль в механизме износа колеблю-
щихся подшипников. При этом также нужно иметь в виду, что большин-
ство высокополимерных соединений, применяющихся в низкозастыва-
ющих маслах, легко разрушается при механическом воздействии с об-
разованием полимеров меньшего молекулярного веса. Деструкция за-
26 1578 393
густителя приводит к уменьшению вязкости масла. В подшипниковых
узлах, работающих при качательном движении, средняя деструкция
масла обычно невелика. Однако поскольку механическому воздействию
подвергаются лишь небольшие объемы масла, непосредственно примы-
кающие к телам качения, местная деструкция, а следовательно и падение
вязкости в зонах контакта, могут достигать значительной величины
и приводить к заметному снижению прочности масляной пленки.
При испытаниях масел с противоизносными присадками нередко
приходится сталкиваться с противоречивыми результатами. Это показы-
вает, что испытания таких масел должны проводиться на достаточно
большом числе образцов и что об их смазывающих свойствах нельзя
судить по единичным положительным результатам.
Из сказанного следует, что масла для осевых шарниров втулок не-
сущих и рулевых винтов не должны иметь ни противоизносных приса-
док, ни деструктирующих загустителей. Это делает понятным неудовлет-
ворительную работу этих узлов на всех обычных низкозастывающих мас-
лах, при создании которых не были учтены указанные обстоятельства.
Руководствуясь приведенными материалами по работоспособности
смазочных материалов в условиях качательного движения, ВНИИ НП
предложил для осевых шарниров втулок несущих и рулевых винтов низ-
козастывающее масло ВНИИ НП-25 [28].
Масло ВНИИ НП-25 содержит маловязкую нефтяную фракцию
с температурой застывания минус 67° С и загущающий высоковязкий
компонент, отличающийся чрезвычайно высокой механической и терми-
ческой стабильностью. Под действием высоких температур трения неф-
тяная фракция в зонах контакта может испаряться, однако соприкосно-
вения тел качения с кольцами не произойдет из-за наличия пленки за-
густителя, обладающего большими адгезионными свойствами. Высокая
термическая и механическая стабильность загущающего компонента
и антиокислительная присадка обеспечивают незначительные изменения
свойств масла ВНИИ НП-25 в процессе эксплуатации.
Основные свойства масла ВНИИ НП-25 приведены в табл. 4. 8.
Таблица 4.8
Темпе- ратура засты- вания °C Вязкость кине- матическая ост Смазывающая способ- ность на четырехша- риковом приборе (</ш=19 мм) Коррозионность в приборе Пинкевича (при темпера- туре + 70° С в течение 50 час)
при + 100° С при —35° С критичес- кая нагруз- ка кге ширина пятна износа мм сталь ЗОХГСА сплав БрАЖМц 10-3-1,5 латунь Л С-59
—56 10,2 23 660 64 0,85 +0,11 -1-0,26 +0,24
Как свидетельствуют результаты испытаний, масло ВНИИ НП-25
по смазывающим свойствам при качательном движении близко к маслу
МС-20.
Подшипники всех типов, работающие на масле ВНИИ НП-25 как
при положительных, так и при отрицательных температурах, имеют не-
большие износы.
Улучшение смазывающих свойств масел может явиться важнейшим
фактором, способным резко увеличить ресурс втулок несущего и рулево-
го винтов вертолетов. Поэтому работы в этом направлении будут при-
нимать все более и более широкий характер. При их проведении долж-
394
ны учитываться описанные выше особенности механизма износа и усло-
вий смазки высоконагруженных колеблющихся подшипников.
Масла для игольчатых подшипников горизонтальных и вертикаль-
ных шарниров. Эти подшипники, как правило, менее нагружены, чем
подшипники осевых шарниров, поэтому они не так чувствительны к свой-
ствам смазки. Подбор смазочных материалов для игольчатых подшип-
ников горизонтальных и вертикальных шарниров втулок несущих винтов
облегчается тем, что застывание в них смазки при неработающем винте
не влечет за собой неприятных последствий. В горизонтальных и верти-
кальных, если они есть, шарнирах рулевых винтов допускать застывание
смазки нельзя, так как повышенные моменты трения в этих узлах могут
вызвать тряску вертолета.
В настоящее время в горизонтальных и вертикальных шарнирах
втулок несущих и рулевых винтов отечественных вертолетов применяет-
ся гипоидное масло. Опыт эксплуатации вертолетов показывает, что ги-
поидное масло несмотря на наличие в нем свободной серы при обычных
удельных давлениях обеспечивает достаточно высокую долговечность
колеблющихся игольчатых подшипников. Для осевых шарниров гипоид-
ное масло, как и другие масла с противоизносными присадками, непри-
годно.
Гипоидное масло обладает весьма высокой липкостью, в связи с
этим оно обеспечивает необходимую смазку контактирующих элементов
даже при неполной герметичности втулок. Замена гипоидного масла
консистентными смазками (к ней иногда приходится прибегать в руле-
вых винтах вертолетов, эксплуатирующихся при особо низких темпера-
турах) существенно снижает срок службы игольчатых подшипников го-
ризонтальных и вертикальных шарниров.
3. Расчет подшипников втулок несущих и рулевых винтов
Подшипники осевых шарниров. На рис. 4. 51 дана типовая конструк-
ция осевых шарниров втулок несущих винтов отечественных вертолетов.
Рис. 4.51. Осевой шарнир втулки несущего винта
При расчете подшипников осевых шарниров втулок несущих винтов
принято учитывать центробежную силу лопасти W и момент в плоскости
вращения Л4Д, создаваемый демпфером.
В осевых шарнирах, выполненных по схеме, показанной на рис. 4.51,
центробежная сила лопасти воспринимается упорным подшипником 1.
Момент демпфера частично воспринимается этим же подшипником, час-
тично — радиальными подшипниками 2 и 3.
Нагрузки в полете на радиальные подшипники 2 и 3 сравнительно
невелики, поэтому они обычно подбираются из статических соображений
но весовому моменту лопасти, передающемуся на них при стоянке вер-
26*
365
толета, когда несущий винт нс вращается и лопасти лежат на ограни-
чителях свеса. Как показывает практика, нагрузки на радиальные под-
шипники осевых шарниров от весового момента лопасти могут доходить
до 100—ПО процентов их статической грузоподъемности, указываемой
Рис. 4. 52. Упорный подшипник с повернутыми
роликами; запись движения сепаратора под
шипника при качательном движении
шарнирах втулок несущих винтов всех
в каталогах.
Долговечность упорных
подшипников осевых шар-
ниров вычисляется на осно-
ве экспериментальных зави-
симостей о = сг(/гЛ), полу-
ченных в результате испыта-
ний соответствующих типов
подшипников в условиях ка-
чательного движения при
чисто осевой нагрузке. Для
упорных шарикоподшипни-
ков кривая долговечности
a=a(nh) была приведена на
рис. 4. 49.
Как уже говорилось, в
настоящее время в осевых
серийных отечественных верто-
летов применяются упорные подшипники с повернутыми роликами.
Принципиальная схема таких подшипников изображена на рис. 4. 52.
Благодаря расположению гнезд сепаратора под углом к радиальному
направлению в подшипниках этого типа сепаратор не только колеблется
вместе с подвижным кольцом, но и непрерывно, хотя и очень медленно,
смещается в одном направлении. Непрерывное смещение сепаратора
предотвращает «бринеллирование» дорожек качения и приводит к су-
щественному увеличению несущей способности подшипника.
В результате испытаний установлено, что долговечность упорных
подшипников с повернутыми роликами в значительной степени зависит
от скорости смещения сепарато-
ра. Эту скорость принято харак-
теризовать временем Тс, в течение
которого сепаратор поворачива-
ется на угол 360°. Оптимальные
значения времени Тс для ампли-
туд и частот колебаний, с которы-
ми работают упорные подшипни-
ки осевых шарниров втулок несу-
щих винтов, составляют 40—
80 мин. При Гс>80 мин возраста-
ет вероятность выхода подшипни-
ка из строя из-за выкрашивания
металла на роликах. Несмотря
Рис. 4.53. Кривая долговечности
а=а(лй) для упорных подшипников
с повернутыми роликами
на непрерывное смещение сепа-
ратора в соприкосновении с кольцами находятся одни и те же участки
поверхности роликов. Поэтому разрушение упорных подшипников с по-
вернутыми роликами в большинстве случаев начинается с повреждения
роликов. Следует отметить, что при 7’с = 2,5-к6 час стойкость роликов
снижается примерно в два раза. При Гс<40 мин заметно увеличиваются
потери на трение и износ дорожек качения.
Кривая долговечности a=a(nh) для упорных подшипников с повер-
нутыми роликами, имеющих оптимальную скорость смещения сепарато-
ра Гс = 40-?-80 мин, показана на рис. 4. 53. Эта кривая построена по ре-
зультатам испытаний нескольких партий таких подшипников на масле
396
МС-20 при амплитуде подвижного кольца <р0 = 4,5° и частоте п =
= 240 кол!мин, т. е. в условиях, аналогичных условиям испытаний, ре-
зультаты которых были использованы при построении зависимости о =
= о(п/г) на рис. 4. 49.
Стендовые испытания и опыт эксплуатации свидетельствуют о том,
что кривые долговечности, изображенные на рис. 4. 49 и 4. 53, могут быть
использованы для определения расчетного срока службы упорных под-
шипников втулок несущих винтов при всех режимах работы этих агре-
гатов, встречающихся в реальных условиях.
Как видно из рис. 4. 49 и 4. 53, уравнения кривых долговечности
о=д(п/г) для колеблющихся подшипников имеют тот же вид, что и для
подшипников, вращающихся в одном направлении:
<зт* («Л) = const, (5.1)
где в случае точечного контакта ш* = 10 и в случае линейного контакта
т * = 6,66.
Возьмем за базу произведение nh= 120 000, что примерно соответ-
ствует 500-часовому ресурсу работы вертолетов типа Ми-1. При nh=
= 120 000 допускаемые контактные напряжения составляют 29 000 кгс/см2
для упорных шарикоподшипников и 18800 кгс/см2 для упорных подшип-
ников с повернутыми роликами. Обозначим через До осевую силу, соз-
дающую в подшипнике при равномерном распределении усилий между
телами качения контактные напряжения, равные допускаемым при
nh= 120000. Тогда в соответствии с формулой (3. 1) допускаемое усилие
на шарик будет:
P0=Jp/J20000 W (5 2)
z \ nh J
Здесь учтено, что д^я шарикоподшипников контактные напряжения
пропорциональны корню кубическому, а для роликоподшипников корню
квадратному из нагрузки.
Специальными экспериментами установлено, что момент, который
нужно принимать во внимание при вычислении срока службы упорного
подшипника осевого шарнира в зависимости от особенностей конструк-
ции узла и зазоров в радиальных подшипниках составляет от 25 до 50
процентов момента демпфера. При этом расчет ведется по мгновенному
максимальному давлению на тело качения, т. е. момент, действующий
на упорный подшипник осевого шарнира, условно считается постоянным
по величине и направлению.
Максимальное давление на тело качения упорного подшипника, на-
груженного осевой силой и моментом, может быть представлено в виде
р0=^4-
Сопоставляя это равенство с равенством (5.2), подучаем следую-
щее выражение, определяющее расчетный срок службы упорных под-
шипников осевых шарниров втулок несущих винтов:
/ У’3- Ло . (5 3)
\ 120000/ k(0A)N ' ' ’ ’
Как следует из §§ 3 и 4, коэффициент к^А} зависит От относительно-
го эксцентриситета приложения осевой силы, который в данном случае
равен
т - (0,25 -е- 0,5) ~л~. (5.4)
r0N
397
При обычных соотношениях между моментом демпфера и центро-
бежной силой т не превышает 0,1, поэтому в упорных подшипниках осе-
вых шарниров всегда нагружены все тела качения. *
Для упорных роликоподшипников, в которых нагрузку несут все
ролики,
к(л> = 1Н-2т.
(5. 5)
При малых значениях т коэффициенты для упорных шариковых
и роликовых подшипников практически совпадают. Это позволяет поль-
зоваться формулой (5. 5) и при расчете упорных шарикоподшипников.
Рис, 4. 54, Осевой шарнир втулки несущего вннта, выполненный па многорядных ради-
ально-упорных подшипниках
Из равенств (5. 4) и (5. 5) окончательно находим
(0,5-н1)-^А. (5.6)
Следует отметить, что расчет радиально-упорных подшипников раз-
личных типов, предназначенных для работы в осевых шарнирах втулок
несущих и рулевых винтов, также может производиться с помощью
формул (5.3) и (5.5), если только предварительно для этих подшипни-
ков определены допустимые осевые нагрузки Ло, соответствующие зна-
чению лЛ=]20 000. При этом предполагается, что моменты, действующие
на подшипники, известны из расчетов или экспериментов.
Нужно иметь в виду, что значения Ло, полученные не по полной кри-
вой долговечности сг=сг(/гЛ), соответствующей определенной вероятнос-
ти выхода подшипников из строя, а путем пересчета, по результатам
экспериментов, проведенных при каком-либо одном значении nh, при не-
достаточно большом числе испытанных образцов могут оказаться непра-
вильными, что, по-видимому, связано со значительным рассеиванием
долговечности, которое трудно выявить при одном уровне нагрузки.
В осевых шарнирах втулок несущих и рулевых винтов некоторых
вертолетов успешно применяются многорядные радиально-упорные ша-
рикоподшипники с углами контакта Рс=45° и уменьшенным отношением
радиуса желоба к диаметру шарика (рис. 4. 54). Обычно в подшипниках
качения это отношение равно 0,515. В указанных многорядных подшип-
" Относительный эксцентриситет, при котором появляются нснагруженныс тела
качения, как известно, составляет 0,5 для упорных роликоподшипников и 0,6 для упор-
ных шарикоподшипников.
398
никах оно уменьшено до 0,510, что приводит к снижению контактных
напряжений примерно на 7% и, следовательно, увеличивает расчетный
срок службы подшипников в 2 раза. Понятно, что такой путь повыше-
ния несущей способности радиально-упорных шарикоподшипников при-
годен главным образом для случая качательного движения, так как
уменьшение отношения радиуса желоба к диаметру шарика увеличива-
ет длину площадки контактной деформации, из-за чего заметно возрас-
тают потери на трение. Результаты испытаний говорят о том, что при ка-
чественном выполнении, обеспечивающем достаточно равномерное рас-
пределение внешней нагрузки между подшипниками комплекта, для
многорядных радиально-упорных шарикоподшипников допустимые кон-
тактные напряжения, исходя из которых нужно подсчитывать осевую
силу, составляют 24 000 кгс!см2.
Достаточно проверенных данных о допустимых контактных напря-
жениях для радиально-упорных роликоподшипников при работе их в
условиях качательного движения еще не имеется.
Приведенные выше значения допустимых контактных напряжений
относятся к случаям работы осевых шарниров втулок несущих и руле-
вых винтов на маслах, не уступающих по смазывающим свойствам мас-
лам МС-20 и МС-14. Если это условие не выполнено, то они должны
быть соответственно снижены.
На допустимые контактные напряжения оказывают заметное влия-
ние размеры тел качения, поэтому при применении подшипников боль-
ших габаритных размеров должна вноситься определенная поправка на
масштабный фактор. Как свидетельствуют результаты испытаний, при-
веденные выше значения допустимых напряжений можно считать дейст-
вительными для подшипников с шариками диаметром до 25 мм и роли-
ками диаметром до 15 мм. При переходе от роликов диаметром 15 мм
к роликам диаметром 24 мм, допустимые контактные напряжения для
упорных подшипников с повернутыми роликами снижаются примерно
на 10%.
Игольчатые подшипники горизонтальных и вертикальных шарниров.
У большинства втулок несущих винтов в горизонтальных и вертикаль-
ных шарнирах применяются игольчатые подшипники.
Работоспособность игольчатых подшипников обычно оценивается
по величине удельного давления на единицу площади проекции дорож-
ки качения внутреннего кольца.
При расчете игольчатых подшипников вертикальных шарниров, как
правило, полагают, что нагрузка равномерно распределена по длине
игл (рис. 4. 55, а). В соответствии с этим удельное давление для под-
шипников принимается равным
где D — диаметр дорожки качения внутреннего кольца;
/в — суммарная рабочая длина игл.
Игольчатые подшипники горизонтальных шарниров помимо цент-
робежной силы лопасти N воспринимают еще некоторый момент М
(рис. 4. 55,6), постояннная часть которого Л1а с достаточной степенью
точности определяется выражением
. (5.8)
\ ^Н.В / ^В.1И
Здесь Мц.в — крутящий момент несущего винта;
Zii.b — число лопастей несущего винта;
399
a— «снос» середины горизонтального шарнира с оси вращения;
/2—’расстояние между горизонтальным и вертикальным шар-
нирами;
/в.ш — «вынос» вертикального шарнира.
Переменная составляющая Mv момента М при расчете игольчатых
подшипников горизонтальных шарниров втулок несущих винтов не учи-
тывается, так как она мало сказывается на их долговечности. Принято
считать, что в горизонтальных шарнирах, выполненных по схеме, пока-
занной на рис. 4. 55,6, нагрузка распределяется по длине подшипников
по закону трапеции. При этом нагруженность подшипников характери
Рис. 4.55. К расчету игольчатых подшипников горизонтальных
и вертикальных шарниров втулок несущих винтов
зуется удельными давлениями qi и <72 на внешних краях колец, обуслов-
ленными совместным действием силы W и момента Л1а. Эти давления
подсчитываются по формуле
N
“71,2
Кб-----
DEft
(5.9)
где В — рабочая ширина комплекта подшипников.
Подставив в формулу (5. 9) значение Л4а, приведем ее к виду:
Qi,i
N
Dls
(5. 10)
Как свидетельствует опыт проектирования, соответствующим под-
бором «сноса» а можно добиться, чтобы на основных режимах моторно-
го полета удельные давления q{ и q^ были бы достаточно близки к сред-
нему удельному давлению f/0 = — . Следует отметить, что «снос» сере-
дины горизонтального шарнира с оси вращения на расстояние а равно-
значен повороту этого шарнира на угол sr.nt = arctg — (см. рис. 4. 55).
Z в.ш
Согласно выражению (5.10) удельные давления q\ и д2 зависят от
центробежной силы N и крутящего момента Л1Н.В. Поэтому их можно
рассматривать как некоторые функции числа оборотов и мощности не-
400
сущего винта. Построив с помощью выражения (5. 10) графики зависи-
мостей = (Мыз) и <72 = <72(Лгн.в) при наиболее характерных оборотах
несущего винта, как это сделано на рис. 4.56, можно легко определить
значения удельных давлений qi и на основных режимах полета вер-
толета, а также оценить правильность
выбора «сноса» а и при необходимости
внести соответствующие коррективы в
конструкцию втулки несущего винта.
Рис. 4.56. Зависимость удель-
ных давлений а, и q2 от числа
оборотов и мощности несущего
винта:
лкР , 2VKP —обороты н мощность не-
п.в н.в
сущего винта на крейсерском режиме;
п , N —обороты и мощность нс-
h.в н.в
сущего винта на режиме крейсерской
скорости; лвзл, №зл — обороты и
н.в и.в
мощность несущего винт на налетном
режиме; обороты и мощ-
ность несущего винта на режиме
авторотации
Рис. 4. 57. К расчету широкоразнесен-
ных игольчатых подшипников гори-
зонтальных шарниров
Если горизонтальные шарниры
выполнены в виде двух самостоятель-
ных опор, расстояние L между кото-
рыми существенно превышает диа-
метр дорожек качения D (рис. 4.57),
то можно считать, что в пределах каж-
дой опоры удельные давления в под-
шипниках постоянны.
В этом случае расчетные удельные давления, определяющие долго-
вечность игольчатых подшипников горизонтальных шарниров, равны
(71.2
N
Dls
„/ Л1„.в \
2 --------— а ) ,
। i * г 2
7 7в,щ
(5.11)
где I а — суммарная длина игл в обоих подшипниках. ,
При применении гипоидного масла допустимые удельные давления в
хорошо уплотненных игольчатых подшипниках, соответствующие долго-
вечности 1000 час при 240 кол/мин, составляют не менее 350 кгс]см2 для
горизонтальных шарниров и 400 mcjcM2 для вертикальных шарниров.
Относительно меньшая величина допустимых удельных давлений в под-
шипниках горизонтальных шарниров в известной степени может быть
объяснена тем, что они работают при амплитудах колебаний от 2 до 6°,
в то время как амплитуда колебаний подшипников вертикальных шарни-
ров обычно не превышает Г. Хотя это и противоречит установившимся
взглядам, практика показывает, что при амплитудах колебаний до 1° дол-
говечность игольчатых подшипников оказывается выше, чем при ампли-
тудах 2—6°. Возможно здесь играет определенную роль и то обстоя-
тельство, что из-за деформации деталей под нагрузкой в известных слу-
чаях фактические удельные давления на краях игольчатых подшипников
горизонтальных шарниров могут превышать расчетные.
401
Л4ноголетний опыт эксплуатации подтверждает, что при выборе раз-
меров игольчатых подшипников горизонтальных и вертикальных шарни-
ров втулок несущих винтов легких и средних вертолетов можно надежно
руководствоваться указанными выше значениями допустимых удельных
давлений. Для тяжелых вертолетов, детали кото-
рых, как правило, имеют относительно меньшую
жесткость, на эти цифры можно ориентироваться
только в том случае, когда приняты специальные
Рис. 4.59. Разрушение игольчатого подшипника из-за
недостаточной жесткости конструкции
где Ма~
МРВ
Рис. 4.58. Влияние Рис. 4.60. К расчету иголь-
жесткости пальца и чатых подшипников втулок
податливости колец хвостовых винтов
на распределение
удельных давлений
по длине игольчатых
подшипников гори-
зонтального шарнира: меры, обеспечивающие равномерность распределе-
б—вчияние^паль 11ИЯ нагРУзки в подшипниках вертикальных шарни-
шенной жесткости; в— ров и приближение эпюры распределения нагрузки
копцо"с ко.™1?даподшш. в горизонтальных шарнирах к трапециедальной
ника (см. эпюру на рис. 4.55,6). Как правило, удовлет-
ворительное распределение нагрузки по длине
игольчатых подшипников горизонтальных и вертикальных шарниров
можно получить путем подбора жесткостей проушин и пальцев, а также
соответствующим увеличением податливости концов колец. Это, в част-
ности, видно из рис. 4.58, на котором показаны экспериментальные
эпюры изменения расстояния между образующими наружного и внут-
реннего колец при трех вариантах конструктивного выполнения гори-
зонтального шарнира втулки несущего винта тяжелого вертолета. Сле-
дует отметить, что недостаточная жесткость проушин и пальцев гори-
зонтальных и вертикальных шарниров может приводить не только к
местному увеличению глубины «бринеллирования» на краях дорожек
качения, но и к выкрашиванию больших участков их поверхности, а
иногда и к поломке игл (рис. 4. 59).
402
Расчет игольчатых подшипников горизонтальных шарниров втулок
рулевых винтов (рис. 4. 60) представляет собой значительно более труд-
ную задачу, чем расчет игольчатых подшипников горизонтальных шар-
ниров втулок несущих винтов, так как они, как правило, воспринимают
значительный переменный момент, которым при оценке их работоспо-
собности пренебрегать нельзя. Этот момент создается переменными аэ-
родинамическими и инерционными (кориолисовыми) силами, действу-
ющими на лопасти рулевого винта в плоскости вращения. При прики-
дочных расчетах нагруженность игольчатых подшипников горизонталь-
ных шарниров рулевых винтов принято характеризовать мгновенным
максимальным удельным давлением, возникающим на краю дорожки
качения. В предположении, что нагрузка распределяется по длине под-
шипников по закону трапеции, это давление равно
(5. 12)
где Л1р в —крутящий момент рулевого винта;
гр в — число лопастей рулевого винта;
Mv — амплитуда переменного момента, нагружающего горизон-
тальный шарнир.
Значения удельного давления <?, вычисленного по формуле (5.12),
для рулевых винтов легких и средних вертолетов на режиме крейсерско-
го полета не должны превышать 300—350 кгс/см2. При этом в случае
применения в горизонтальных шарнирах гипоидного масла можно ожи-
дать, что долговечность подшипников будет не менее 1000 час.
Окончательно долговечность игольчатых подшипников горизонталь-
ных и вертикальных шарниров втулок несущих и рулевых винтов опре-
деляется в результате испытаний этих агрегатов на специальных стен-
дах.
4. Расчет подшипников автоматов перекоса и механизмов управления
Допускаемые нагрузки на подшипники шарниров автомата переко-
са и непосредственно связанных с ними элементов управления обычно
определяются экспериментальным путем. Для этого на специальных,
весьма сложных установках, позволяющих создавать все виды усилий,
действующих на автомат перекоса в полете, проводятся длительные ис-
пытания.
Нагрузки на автомат перекоса носят динамический характер. Это,
в частности, видно из показанных на рис. 4. 61 осциллографических
записей шарнирного момента лопасти Л4Ш и усилий РПрод и РПоп в тягах
продольного и поперечного управления, соединяющих соответствующие
качалки автомата перекоса с гидроусилителями.
Естественно, что при таком сложном характере нагружения, любые
рекомендации по расчету подшипников шарниров автомата перекоса
неизбежно будут носить весьма условный характер. Тем не менее неко-
торые из них могут помочь конструкторам ориентироваться в вопросах
подбора подшипников для этих ответственных агрегатов, в связи с чем
на них следует коротко остановиться.
Если считать, что при подобных конструкциях несущих винтов из-
меняется только абсолютная величина шарнирного момента лопасти,
а соотношение между амплитудами и фазами его отдельных гармоник
остается неизменным, то при подборе подшипников для аналогичных
403
шарниров автомата перекоса, выполненных по одной и той же конст-
руктивной схеме, можно исходить
WW
из максимального значения воспри-
нимаемой ими нагрузки Ртах
(рис. 4. 62).
Для автоматов перекоса, близ-
ких по конструкции к автоматам пе-
рекоса вертолетов Ми-1 и Ми-4 (см.
рис. 4. 38), при цельнометаллических
лопастях несущего винта, имеющих
прямоугольную форму в плане, в
случае применения консистентных
смазок типа ЦИАТИМ-201 допус-
t
Рис. 4.61. Осциллограммы записи
шарнирного момента лопасти и
усилий в тягах продольного и по-
перечного управлений
Рис. 4.62. Нагрузка па подшипники
шарниров автомата перекоса
каемые нагрузки Р™* могут быть определены с помощью табл. 4. 9 Эта
таблица составлена по результатам стендовых испытаний с учетом опы-
та эксплуатации автоматов перекоса.
Таблица 4. 9
Допустимые значения {кгс) для подшипников различных
Место установки шариковые радиаль- ные, ради- ально-упор- ные и упорные шарико- вые сфе- рические ролико- вые сфе- рические роликовые радиально- упорные и упорные иголь- чатые шарнир- ные типа шс
Шарнир ы тарелки, тяги и рычаги пово- рота лопасти Подшипники кар- дана Подшипники кача- лок продольного и поперечного управ- ления Подшипники тяг продольного и попе- речного управления, соединяющие качал- ки с наружным коль- цом кардана Подшипники рыча- га общего шага 0,8 QCT Qct Qct Qct Qct Qct 0,8 QCT 0,8 QCT 0,8 Qcr 2 DI 2 DI 2 DI Db
Qct — допустимая статическая нагрузка на невращающийся подшипник, ука-
зываемая в каталогах и справочниках;
D — диаметр дорожки качения внутреннего кольца игольчатого подшипни-
ка или сферы шарнирного подшипника в .и.и;
b — ширина наружного кольца шарнирного подшипника в мм;
I — рабочая длина игл в мм.
404
Приведенные в табл. 4.9 значения допускаемых нагрузок Р™* при
числе оборотов несущего винта 240 в минуту соответствуют долговеч-
ности 1000—1200 час. При других оборотах долговечность находится из
выражения: . 240 000 , (о. 13) п
где п— номинальные обороты несущего винта.
Если характер нагрузок будет иным, чем для автоматов перекоса
Бертолетов Л1и-1 и Ми-4 при цельнометаллических лопастях несущего
винта, то допустимые значения Р“апх должны быть уточнены в результате
соответствующих стендовых и эксплуатационных испытаний.
До сих пор рассматривались колеблющиеся подшипники, соверша-
ющие в течение расчетного срока службы большое число качаний (свы-
ше 107).
Допустимые нагрузки на подшипники механизмов управления лета-
тельными аппаратами* для которых суммарное число качаний не превы-
шает 100 0001, а амплитуда качаний равна 20° и более, ВНИПП реко-
мендует определять по следующей экспериментальной формуле*:
/<оп = адоп^- (5.14)
Значения коэффициентов адоп для некоторых типов подшипников,
работающих на консистентных смазках, при числах качаний 25 000
и 100 000 приведены в табл. 4. 10.
Таблица 4. 10
Тип подшипника Обозначение подшипника Внутренний диаметр подшипника мм Значения коэффициента адоп
при 25 000 качаний при 100 000 качаний
Шариковый радиальный 7000100 100 200 До 50 5 2
900000 До 9 Свыше 9 5 4 2 1,6
980000 До 9 Свыше 9 5 4 2 1,6
981000 До 9 Свыше 9 2,5 2 2 1,6
Ш ариковый сферический 1000 До 10 ' 4 2,8
1200 До 50 4 2,8
1300 971000 До 50 4,7 3,3
Предполагается, что площадки контакта соседних тел качения ие перекрываются.
405
§ 6. ТЕОРИЯ и ВЫБОР
ОСНОВНЫХ ПАРАМЕТРОВ УПОРНЫХ ПОДШИПНИКОВ
С «ПОВЕРНУТЫМИ» РОЛИКАМИ
Как уже указывалось в предыдущих параграфах, в осевых шарни-
рах втулок несущих винтов отечественных вертолетов успешно применя-
ются упорные подшипники с цилиндрическими роликами, расположен-
ными под углом к радиальному направлению. Высокая несущая способ-
ность таких подшипников, получивших название упорных подшипников
с «повернутыми» роликами, объясняется тем, что в них сепаратор при
качательном движении не только колеблется вместе с подвижным коль-
цом, но и непрерывно смещается в одном направлении. Время поворота
сепаратора Тс на угол 360°, характеризующее скорость этого смещения,,
определяется рядом факторов. Оно зависит от коэффициента трения
скольжения между роликами и кольцами, амплитуды и частоты колеба-
ний подвижного кольца, а также от ряда геометрических параметров,
из которых главную роль играют углы наклона гнезд сепаратора.
Понятно, что эти углы должны быть подобраны таким образом, чтобы
время Тс лежало в оптимальных пределах, обеспечивающих высокую
стойкость роликов при приемлемых износах дорожек качения. Ниже
излагается теория, с помощью которой может быть решена эта задача.
1. Определение времени Тс
В упорных подшипниках с повернутыми роликами отношение угло-
вой скорости сепаратора к угловой скорости подвижного кольца А= —
СО
зависит от направления вращения. Это обусловливает непрерывное сме-
щение сепаратора, наблюдающееся в таких подшипниках при качатель-
ном движении.
Значения отношения А, соответствующие случаям вращения под-
шипника против часовой стрелки и по часовой стрелке, находят следую-
щим образом.
Силы трения скольжения, возникающие в точках контакта ролика
с кольцами, приводятся к результирующим силам Fiy, Flx, F2y, F2x и мо-
ментам Лф, Af2z (рис. 4. 63). При постоянном коэффициенте трения сколь-
жения ц между роликами и кольцами величины этих сил и моментов
с достаточной степенью точности могут быть вычислены по формулам:
г2У=?Р(в10-^в^-,
Л10 + Ап
(6-1)
М1г = ^Р1 [с10 + jx сп -I- С13 (-^.у];
= ~ +С1з(^У]-
Здесь Р — усилие, воспринимаемое рассматриваемым роликом;
Ух и У%— координаты точек контакта, в которых отсутствует про-
скальзывание в направлении, перпендикулярном оси ролика;
г/р — диаметр ролика;
/ — рабочая длина ролика.
406
При выводе формул (6. 1) предполагалось, что нормальные нагруз-
ки q\ и <72 распределяются по длине ролика по закону:
Р 21
где
Такое распределение нормаль-
ных нагрузок обусловлено действи-
др
ем момента (Л„ + ^2„) — > стремя-
у у 2
щегося повернуть ролик вокруг оси
ОрЛ,'. Так как обычная концентрация
нагрузки на краях ролика мало ска-
зывается на времени Тс, то для
упрощения расчетных зависимостей
ее не учитываем. Ввиду малости си-
лы трения (fix—F2х) считаем, что
j qxdy — q2dy — P.
Рис. 4.63. Силы и моменты, дейст-
вующие на «повернутый» ролик
Коэффициенты, входящие в формулы (6. 1), определяются равенст-
вами
где
I
го sin у
(6.3>
Р
407
Из кинематических соотношений и уравнения моментов относитель-
но оси Ору можно получить следующие выражения *:
У\
I
f dv
± р-Ус Ао
ft 21
и
r0 cos у
I
J “Р ,
± №с ,,, Ао
и. 21
Ап
У2 __ Г
I ~~
А Л
А°
Ап
(6.4)
f
Гр cos у
I
/ А .
± Н*с Ао
ц 21
В этих выражениях
Pdp
где /н — коэффициент трения качения;
Л4Р — момент, учитывающий трение по торцам ролика и трение о
смазку;
ре — коэффициент трения между роликами и сепаратором.
Верхние знаки относятся к случаю, когда Fix—F2x>0, а нижние —
к случаю, когда FJX—F2x<^0.
Угол наклона у считается положительным, если ролик может быть
установлен в радиальное положение поворотом вокруг точки Ор против
часовой стрелки. При этом условии положительным значениям сил, вы-
численным по формулам (6. 1), соответствуют направления, указанные
на рис. 4. 63. Знаки углов наклона роликов и направление вращения
определяют при рассмотрении подшипника со стороны подвижного
кольца.
Ролик с углом наклона у создает относительно оси вращения сепа-
ратора момент
-V = (^ix - Лц) rocos V+(Л;, - Р2у) Го sin Y - - М2г).
Как показывают расчеты, сопротивление качению и трение ролика
о сепаратор и смазку практически не сказываются на величине этого
момента. Принимая в соответствии с этим f = pc = O и учитывая, что в ре-
альных конструкциях угол у<(6°, а следовательно, cosy~l, с помощью
выражений (6.1), (6.3) и (6.4) преобразуем последнее равенство так
где
М =^РгйМ,
> = 2|1^--Д10-2411А1(2Л-1).
(6. 5)
В табл. 4. И даны значения коэффициентов Л10 и Ли в зависимости
от величины 1/р.
* Предполагается, что величиной цс(2Л—1) можно пренебречь по сравнению
с единицей. Инерционный момент ролика ие учитывается.
408
Таблица 4. Il
В случае отрицательных значений
тов Лю и Дп могут быть использованы
p для определения коэффициен-
соотношения:
^10 ( Р)— Ао (.Р) 1
и г
Ai (-/>)=Ди (/>)• J
Эти соотношения непосредственно следуют из равенств (6. 3).
При небольших амплитудах колебаний, когда инерционными сила-
ми можно пренебречь, уравнение движения сепаратора подшипника с
«повернутыми» роликами сводится к условию
(6-6)
Л4С—Л4т = 0. (6.7)
Здесь Л1С = 2Л1 — суммарный момент сил трения скольжения, действу-
ющих на ролики со стороны колец подшипника;
Л4Т — момент сопротивления движению.
Допустим, что сепаратор имеет z гнезд, в каждом из которых на-
ходится s роликов. Обозначим углы наклона гнезд сепаратора на сред-
нем радиусе гс через ус,., а углы наклона роликов через YzA- Индекс I
обозначает номер гнезда сепаратора, а индекс k указывает на положе-
ние в нем ролика. Обычно в каждом гнезде помещается по два ролика.
Нагрузка на ролик с рабочей длиной lt равна:
Ч
р _ N
РЧ—г
(6.8)
где /2—суммарная рабочая длина роликов, расположенных в одном
гнезде;
W— осевая сила, приложенная к подшипнику.
Изменение направления вращения подшипника равносильно изме-
нению знаков углов наклона роликов. Имея в виду это обстоятельство,
из равенств (6. 5), (6. 6) и (6. 8) получаем
Z $

AoG%)~
z
.2
(6-9)
и
— значения коэффициентов Д10 и Дп при
1 ъ
Р ^Pl. =------Г------
*
27 1578
409
Для определенности будем считать, что знаки углов наклона роли-
ков даны для случая вращения подшипника против часовой стрелки.
Подставив выражение (6.9) в уравнение (6.7), получаем:
— при вращении против часовой стрелки:
2 rc y-Nr,
1 м.
(6. 10)
— при вращении по часовой стрелке:
Зная величины Л7 и А", нетрудно подсчитать время Тс. Из рис. 4. 52
следует, что за каждый полупериод колебаний сепаратор смещается на
угол Дфс=(Л/—Л") <ро. Следовательно, время поворота сепаратора на
угол 360° будет:
Т 360
с 2 | Л' — Л" | <рол ’
1 «
где п =--------число колебании подвижного кольца в минуту.
тй
Так как момент М? сопротивления движению сепаратора не должен
зависеть от направления вращения, то в соответствии с приведенными
выше соотношениями
180
dp
i-1Л- 1
(6. 12)
Таблица 4. 12
Время Тс (мин) при температуре
масла (град)
+ (20=30) - (30=40) - (45 =55)
63 54 58
Масло ВНИИ НП-25 (ч=10 сспг
при /=+100° С и ч=50 000 ест при
/=—40° С)
Формула (6. 12) является основ-
ной для теории упорного подшипника
с «повернутыми» роликами. Из нее,
в частности, следует, что сопротивле-
ние движению сепаратора не влияет
на время Тс. Этот важный для практи-
ки вывод подтверждается результата-
ми экспериментов по определению вре-
мени Тс при низких температурах,
когда из-за возрастания вязкости мас-
ла момент Мг может достигать замет-
ной величины (табл. 4.12).
410
2. Выбор углов наклона гнезд сепаратора
гнезд, при этом нужно иметь в ви-
углов, но и допуски на изготовле-
Рис. 4.64. Определение величин р
при наличии зазоров между ролика-
ми и сепаратором
Заданную скорость смещения сепаратора обеспечивают соответст-
вующим подбором углов наклона его
ду не только номинальные значения
ние, которые оказывают заметное
влияние на время Тс. Остальные
геометрические параметры под-
шипника, влияющие на время Тс,
.выбираются по конструктивным
соображениям.
Производственные отклоне-
ния углов наклона гнезд сепара-
тора при весьма совершенной тех-
нологии и строгом контроле гото-
вых изделий достигают 7—10'.
Если же не принимать особых
мер при изготовлении подшипни-
ков, то эти отклонения могут до-
ходить до 20—30'.
Время Гс зависит также от
зазоров между роликами и сепа-
ратором. При наличии зазоров
положение роликов в гнездах се-
паратора, а следовательно, и фак-
тические углы наклона роликов
определяются силами трения
скольжения, действующими на
них со стороны колец. Так как в
общем случае определение этих сил затруднительно, то будем считать,
что ролики с равной вероятностью могут занимать любое из двух поло-
жений, показанных на рнс. 4. 64:
— в положении /:
р. -________________________1'л______
life в ' / в- ' ’
rcsitiYc +—L rcsin ус. + —— I
‘2 \ ' 2гс /
— в положении //:
ч ч
-----------—7---------------;Г
гс sill Ус,- — r(. sin ус,—
Из приведенных равенств видно, что влияние зазоров на время Тс
может быть учтено увеличением расчетных отклонений углов наклона
гнезд сепаратора до величины
t__ I t ___ ''rn.'lv
~ “ 2гс ’
где — половина производственного допуска, а етах — максимальный
зазор.
Наиболее общим случаем расположения гнезд сепаратора, пред-
ставляющим практический интерес, является случай, когда в сепараторе
имеется 2, гнезд с углом наклона yi±fe (yi>0) и z2 гнезд с углом накло-
на 0±|.
27*
411
Для упрощения дальнейших выкладок положим, что Zlj;>=/ = const.
Если величина £ такова, что разность А'—А" положительна, то при усло-
вии Ti;, =/=const время Тс может меняться от некоторого
r(fflax)_^ 180 2гс А1(Х)+хА1(/>г) (б 13)
¥onvjx' rfP -410 (/’i)-5 (Р2)
до некоторого
y.fmin) = 180 2гс (fl) + 7.А1 (р2) (6.14)
срдЛУр." Г/р ^10(^1) + Vho(/>2)
Здесь
I_________ , _ _ I _
rcsin(Y1 —£) ’ 2 rcsin£ ’
п I " I
rc sin (Vj + 6) ’ "°2 rc sin Е
Коэффициент о обычно близок к единице (ц=0,98ч-1). Это свиде-
тельствует о том, что время Тс мало зависит от числа роликов s, находя-
щихся в одном гнезде.
В выражениях для Г<тах,и 7'(mln> через ц' и ц" обозначены минималь-
ное и максимальное значение коэффициента трения скольжения ц. При
хорошей смазке ц'~0,05 и ц"=«0,08.
Пусть верхняя и нижняя границы диапазона оптимальных значе.-
ний Гс соответственно равны Tj и Г". Как следует из результатов испы-
таний, для упорных подшипников с повернутыми роликами, работающих
в осевых шарнирах втулок несущих винтов, 7^ = 80 мин и =40 мин.
Установлено, что для обеспечения максимальной стабильности скорости
смещения сепаратора величины yi и % следует подбирать таким образом,
чтобы при данном значении | 7’<шах) было равно Тс'. При Т<1пах> —Т'с ве-
личины Yi, х и g связаны между собой определенным соотношением. По-
лагая в выражении (6.13) 7Ушах, = 7'', представим это соотношение гра-
фически в виде семейства соответствующих кривых*. Из рис. 4.65, на
котором приведено семейство таких кривых, видно, что условие Т(тах>=
налагает известные ограничения на выбор величин yi и |. Так, в слу-
чае Т' =80 мин отношение х не должно превышать 1,28 при £ = 0 и 0,77
при £=15', а угол Yi должен быть не менее некоторого минимального
угла у’™"1» = •»'-|-Е(где у(— значение у1(1В,п)при х = 0и£=0). Диапазон из
менения скоростей смещения сепаратора характеризуется отношением
Т’ (min)
_________
1 j-(max) ’
На рис. 4.66 приведены кривые ц=г|(^) для углов Yi==5° и yi = 30',
построенные в предположении, что 7’(шах) = 7”. Рис. 4. 66 показывает, что
отношение р зависит главным образом от величины £. Угол yi оказывает
* Везде, где не сделано особых оговорок, предполагается, что т\ = 8О мин. При
этом все конкретные числовые значения относятся к случаю rfp = 9 мм, rc — i0 мм,
1=8 мм, v=l, <ро=4,5°, п = 240 кол!мин, ц=0,06.
412
на г| весьма малое влияние. Таким образом, с точки зрения стабильнос-
ти скорости смещения сепаратора различные комбинации углов наклона
гнезд примерно равноценны, если только они обеспечивают выполнение
условия Г <гаах>=7''. Согласно рис. 4. 66 отклонение при котором 7'<mln> =
40
--Т' = 40 мин и, следовательно, i]= — =0,5, составляет около5'. Отсюда
следует, что даже при самом тщательном изготовлении сепараторов не
исключены случаи, когда время Тс будет выходить за пределы оптималь-
ного диапазона.
На практике встречаются два варианта расположения гнезд сепара-
тора. В первом из них все гнезда имеют одинаковый угол наклона, не
превышающий 1°, во втором — несколько гнезд расположены под углом
3—6°, а все остальные гнезда — радиальные. Сравним эти варианты на
следующих примерах.
Рис. 4.65. Кривые Yi=Yi(x) при различных зна-
чениях отклонения g
Рис. 4. 66. Зависимость от-
ношения г] от отклонения g
при различных углах yi
Рассмотрим подшипник, у которого yi=45", х=0, dp=9 мм, гс=
= 40 мм, 1 = 8 мм, еШах=0,2 мм, ^п=7' и 5 = 2; подшипник работает при
<j?o = 4,5° и л=240 кол!мин.
В случае, когда все ролики имеют угол наклона, равный у,
(6. !5)
To'W dp Л10 (/>)
где '
I
Р=----:—•
Ccsin у
На рис. 4.67 приведены кривые Гс = Тс(у), показывающие как ме-
няется время Тс в зависимости от угла у при ц=р'=0,05 и p=p" = 0,08.
Выделим между кривыми Тс=Тс(у) область, ограниченную вертикаль-
ными прямыми у=у1+£п+~^ = 60Л и у=yj—gn—у^ = 3(У. В пределах
этой области должны лежать фактические значения времени Тс. Нетруд-
но заметить, что для такого подшипника Т(гаах> =74 мин и 7(сга1п>=31 мин.
Эти значения достаточно близки к оптимальным. Результаты экспери-
ментов по определению времени Та для нескольких сотен подшипников с
приведенными параметрами показали, что фактические значения Та
практически не выходят за пределы указанного диапазона, группируясь
вокруг средних значений Т<ср> =504-60 мин.
Пусть теперь подшипник имеет следующие параметры; yi = 5°, %=5,
dv = 5 мм, ле = 28 мм, 1 = 4,2 мм, ета1=0,2 мм, £п = 7', s = 2 и работает при
Фо = 4,5° и /г=300 кол!мин.
413
Предположим, что фактические углы наклона радиальных гнезд
равны £. Тогда
•J- __ 180 2гс (Pi) 4- х-Ац (ро)
тЧ№ rfp I j4]0 (Pl) +x^io(z,2) I
(6.16)
где
I I
Pi =—:---- И p2=------—
Гс31Пу| rc sin «
Из рис. 4. 68, на котором приведены кривые ТС = ТС(§), построенные
по формуле (6. 16), видно, что при £ = 0 в зависимости от коэффициента
трения ц время 7^ = 163-4-261 мин. Ес-
ли g~—5', то время Тс будет стре-
миться к бесконечности. Иными сло-
вами, при небольших отрицательных
отклонениях углов наклона радиаль-
ных гнезд возможна остановка сепа-
ратора. Такие случаи неоднократно
наблюдались при испытаниях подшип-
ников с большими значениями %.
При ц = 0,08 и £=^+^=15'
2г с
время Тс = 47 мин. Следовательно, в
рассматриваемом случае время Тс мо-
жет меняться от 78тах) — ос до —
= 47 мин.
Рис. 4. 68. Зависимость времени Тс
от отклонения g
Рис. 4.67. Зависимость времени Тс
от угла наклона гнезд сепаратора Т
Из рассмотренных примеров видно, что только первый вариант рас-
положения гнезд сепаратора обеспечивает работу подшипников в усло-
виях, близких к оптимальным.
При расположении гнезд сепаратора под одинаковыми углами
уменьшаются также потери на трение и неравномерность распределе-
ния нормальной нагрузки вдоль линий контакта.
3. Потери на трение
Потери на трение в упорных подшипниках с «повернутыми» ролика-
ми зависят как от скорости смещения сепаратора, так и от того, как вы-
браны величины Vi и %, обеспечивающие смещение сепаратора с данной
.скоростью.
414
Момент трения подшипника обычно записывается так:
Л/тр=Др^Гс, (6. 17)
где /тр — приведенный коэффициент трения.
Используя зависимости, полученные в предыдущих пунктах, после
ряда преобразований находим
y (6.18)
У тр J К ! J «- I 2jV/* v
Здесь fK — коэффициент трения качения;
fc—коэффициент, характеризующий потери на трение скольже-
ния.
Коэффициент /с может быть представлен в виде (см. работу [27]);
sin Yi [В 10(Pi) - Д1С10(/>!)] +-я— ' — VfoF' л “ 1
° ГС ‘ с Л11'.В1)
A = ij.------------------------------------1(6. 19)
. Ai (Pi) Т с ^io(Pi) .
+ 2 |_ > ‘ (РО
где
у-(0) 180 2гс
<p0MJJLV
С помощью табл. 4. 10 нетрудно убедиться, что при увеличении угла
1Л10(/Ц| х
наклона роликов отношение J вначале быстро возрастает, достигая
при у= arc sin 0,57 //гс значения, равного единице. При дальнейшем уве-
личении угла отношение -- не меняется. Это означает, что величи-
(р)
на Г •'’’представляет собой минимальное время, которое может быть по-
лучено при данном значении коэффициента трения ц [см. формулу 6. 15)].
Из рис. 4. 69 видно, что при одной и той же скорости смещения сепа-
ратора с уменьшением угла уь потери на трение падают. Отсюда следу-
ет, что минимальные потери на трение действительно имеют место при
расположении всех гнезд сепаратора под одинаковыми углами к ради-
альному направлению. При оптимальных скоростях смещения сепарато-
ра( —»0,5j отказ от такого расположения гнезд может привести к уве-
личению потерь на трение скольжения в 1,5 раза.
4. Дополнительные соображения об оптимальной конструкции
упорных подшипников с «повернутыми» роликами
Согласно приведенным выше формулам, коэффициент К, характе-
ризующий неравномерность распределения нагрузки по длине ролика,
равен:
К = 6р d'" (2510 р 1/1 .
‘ 2Z \ 1 r 2Z 11 I )
Так
как |2Вю| j В
то
можно с достаточной точностью
dP
считать, что К=12ц—9|0.
Таким образом, коэффициент К зависит лишь
от угла у. Из кривой К=К(у), приведенной на рис. 4.70, следует, что
при переходе от угла 5° к углу 45', соответствующему расположению
всех гнезд под одинаковыми углами, коэффициент К уменьшается с 0,35
До 0,14.
415
Расположение всех гнезд сепаратора под равными углами предпоч-
тительнее и по следующим соображениям. Если угол наклона гнезд
одинаков, то силы—F?x, прижимающие ролики к их боковым поверх-
ностям, очень малы. В случае 7Ит = 0 и s=l они теоретически вообще
отсутствуют.
При разных углах наклона гнезд, когда «повернутым» роликам
приходится преодолевать сопротивление радиально расположенных ро-
Рис. 4.69. Потери иа трение
скольжения
ликов, силы Fix—Fix могут достигать за-
метной величины (до 0,1рР) и вызывать
износ сепаратора (особенно при боль-
ших х).
Рис. 4. 70. Зависимость коэффициента
К от угла наклона роликов
До сих пор предполагалось, что все ролики имеют одинаковую дли-
ну. Теперь посмотрим, что может дать чередование длинных и коротких
роликов в шахматном порядке.
Из табл. 4. 13 видно, что в последнем случае время Тс и приведен-
ный коэффициент трения fTP изменяются незначительно, а коэффициент
К для коротких роликов возрастает в 3 раза. Это свидетельствует о том,
что в упорных подшипниках с повернутыми роликами целесообразно
применять ролики одинаковой длины.
Таблица 4,13
Влияние распределения длин роликов на величины
Т’с- /тр и К
Вариант распределения длин роликов Тс мин Ар (при /к=0,003) К
Ролики одинаковой длины (71=72=8 мм) 48 0,00616 0,14
Длинные и короткие ролики, че- редующиеся в шахматном порядке (Z1=ll мм; 12=5 мм) 45,7 0,00674 0,43 (для коротких роликов)
При оценке влияния на долговечность подшипника
ти распределения нагрузки, обусловленной действием
, нельзя упускать из виду, что нагрузка в каждой точке контак-
неравномернос-
момента (/'1^+
та не остается постоянной, а меняется при изменении направления вра-
щения. В частности, на концах роликов нормальная нагрузка меняется
по закону:
416
Вследствие этого неравномерность распределения нагрузки, обус-
ловленная действием указанного момента, не должна сильно снижать
срок службы подшипника.
Большее значение имеет обычная концентрация нагрузки на кон-
цах роликов, которую мы не учитывали, полагая, что при у = 0 q=const.
Для уменьшения вредного влияния последней целесообразно применять
ролики с бомбиной.
5. Пример расчета упорного подшипника с «повернутыми» роликами
В заключение приведем пример расчета упорного подшипника с
«повернутыми» роликами.
Осевая нагрузка 1V=2O ООО кгс, амплитуда колебаний подвижного
кольца сро — 4,5°, частота «=180 кол!мин.
Для данных условий подобран подшипник со следующими пара-
метрами: с/р=12 мм, гс = 61 мм, /=10,5 мм (полная длина роликов I'=
= 12 мм), z = 20 и s = 2.
Требуется определить углы наклона гнезд сепаратора, обеспечива-
ющие его смещение е оптимальной скоростью, и срок службы подшип-
ника.
Вычисляем коэффициент v:
Полагаем, что все гнезда имеют одинаковый угол наклона. Подста-
вив в формулу (6.15) ф0=4,5°, «=180 кол!мин, о = 0,99 и ц.=ц.'=0,05,
с помощью табл. 4. И строим кривую 7’с = 7'с (у). По кривой находим зна-
чение у', угла у, при котором 7'с = 7^ = 80 мин. В нашем случае у' = 46'.
Принимая £п = 7' и етах = 0,18 мм, определяем расчетное отклонение
1 = 7= 57,3-60°^ =12'.
1 2-61
Номинальное значение углов наклона гнезд сепаратора
№/+£=46+12 = 58'.
Контактные напряжения в подшипнике
4 = 860-1/ —^— = 8601/-----------------«17000 кгс{см?.
у zs-dpl у 20.2-1,2-1,05 '
Согласно рис. 4. 53, этому значению сг соответствует nh = 27-104. Сле-
довательно, срок службы подшипника
, 27-104
п=-------= 1о00 час.
180
ЛИТЕРАТУРА
1. Риз П. М., Пожал ос тин А. И., «Вибрации и динамическая прочность воз-
душных винтов». Труды ЦАГИ № 609, 1947.
2. Миль М. Л. О динамическом закручивании лопасти ротора автожира в полете
«Техника воздушного флота» № 2, 1937.
3. Баскин В. Э., «Индуктивные скорости воздушного винта, обдуваемого под
углом к его оси», Доклад на Всесоюзном съезде по теоретической и прикладной меха-
нике, Москва, 1960.
4. Некрасов А. В., «Расчет форм и частот собственных колебаний лопастей
воздушных винтов», Труды ЦАГИ № 898, 1964.
5. Некрасов А. В., «Расчет форм и частот собственных изгибно-крутильных
колебаний лопасти вертолета в пустоте», Труды ЦАГИ № 898, 1964.
6. Н е к р а с о в А. В., «Расчет напряжений в лопасти несущего винта вертолета
на больших скоростях полета», Труды ЦАГИ №' 898, 1964.
7. Некрасов А. В., «Расчет изгибных напряжений в лопасти вертолета на ма-
лых и средних скоростях полета», Труды ЦАГИ № 913, 1964.
8. Галкин М. С., «О решении задачи Коши для одного уравнения», АН СССР,
«Прикладная математика и механика», т. XX, вып. 2, 1956-.
9. Липская М. Э., «Определение высоких собственных частот винтовых лопа-
стей и турбинных лопаток». Труды МАП СССР, № 676, 1949
10. Марченко В. М., Сармина Л. А., Вронский Г. В„ «Расчет собствен-
ных колебаний лопастей с помощью интегральных уравнений на быстродействующих
вычислительных машинах», Труды ЦАГИ № 898, 1964.
11. Рыжик И. М. и Градштейн М. С., «Таблицы интегралов, сумм, рядов
и произведений», ГИТТЛ, 1951.
12. Богатырев Б. В., «Статическая и динамическая прочность лопастей рото-
ров винтокрылых аппаратов» АН СССР, 1948.
13. Гуреев Д. И., «Самоколебания лопастей геликоптера», Изд. ВВА им. Жу-
ковского, выпуск 391, 1950.
14. Красовский А. А., «О вибрационном способе линеаризации некоторых
нелинейных систем», «Автоматика и телемеханика», 1948, № 1, т. 9.
15. Келдыш М. В., «Шимми переднего колеса шасси самолета», Труды ЦАГИ,
вып. 564, 1945.
16. Пановко Я. Г., «Внутреннее трение при колебаниях упругих систем»,
Физматгиз, 1960.
17. Гродно Л. Н„ «Вынужденные колебания изгиба стержня при наличии линей-
ного демпфера в шарнирной заделке», Журнал «Прикладная математика и механика»,
АН СССР, том XVII, вып. 5, 1953.
18. Белозеров А. И., Г р о д к о Л. Н., Литваков Б. М., «Способ устра-
нения земного резонанса вертолетов», «Бюллетень изобретений», № 18, 1961, авторское
свидетельство № 141391.
19. Ден-Гартог Дж. П., «Механические колебания», Физматгиз, Москва, 1960.
20. Бабаков И. М., «Теория колебаний», Гостехтеоретиздат, 1958.
21. Беляев И. М., «Сопротивление материалов», Гостехтеоретиздат, 1958.
22. Канторович Л. В., Крылов В. И„ «Приближенные методы высшего
анализа», Гостехтеоретиздат, 1950.
23. Решетов Д. Н., «Совместное действие на шариковые подшипники радиаль-
ной и осевой нагрузки», «Подшипник», 1939, № 10—11.
24. Б ел янчиков М. П., «Новая методика расчета грузоподъемности и долго-
вечности радиально-упорных шарикоподшипников», «Подшипниковая промышленность»,
1960, № 3.
25. Бейз ель май Р. Д., Цыпкин Б. В., «Подшипники качения», Справочник,
Машгиз, 1960.
26. Спицын Н. А., Спришевский А. И., «Подшипники качения». Справоч-
ное пособие, Машгиз, 1961.
418
27. Л е й к а н д М. А., Коросташевский Р. В., «Упорные подшипники повы-
шенной грузоподъемности для 'качательного движения», Труды ВНИПП, 1961, № 4.
28. Л е й к а н д М. А., К У р о в а И. В., К о м и с с а р о в а Т. М., «Смазка под-
шипников качения, работающих при качательном движении», «Подшипниковая про-
мышленность», 1962, № 6.
29. Бочков В. С., «Теоретическое определение смещения центра тяжести ра-
диально-упорных шарикоподшипников при комбинированной нагрузке», Труды ВНИПП,
.№ 4, 1962.
30. Лейканд М. А., «Расчет шарикоподшипников, работающих при комбиниро-
ванных нагрузках», Сборник «Прочность и динамика авиационных двигателей»,
Машгиз, 1966, № 3.
31. Пальмгрен М.. «Шариковые и роликовые подшипники», Машгиз, 1949.
32. М о г г 1 s Т., Т у е W., „The Stressing of Rotor Blades”, Aircraft Enginee-
ring, Vol. X, № 112, 1938.
33. Horvay О., „Stress Analysis of Rotor Blades”, Journal of the
Aeronautical Sciences, Vol. 14, 1947.
34. H о r v a у G., „Chordwise and Beamwise Bending Frequencies of Hinged
Rotor Blades”, Journal of the Aeronautical Sciences, Vol. 15, 1948.
35. Coleman R. P., „Theory of Self Excited Mechanical Oscillations of
Hinged Rotor Blades”, NACA, ARR, July 1942; NACA, ARR, № 3029, 1943.
36. С о 1 c m a n R. P. and F c 1 n g о 1 d A. M., „Theory of Ground Vibrations
of a Two-Blade Helicopter Rotor on Anisotropic Flexible Supports”, NACA, T. N.
№ 1184, 1947.
37. llorvay G., „Vibrations of a Helicopter on the Ground”, Journ, Aero.
Sci., November, 1946, Vol. 13, № 11, pp. 605—619.
38. Ha war th and Jones, „Ground Resonance of the Helicopters,” The
Journal of the Helicopter Association of G. B., April—1954, Vol. 7, № 4.
39. Sibley and Jones, „Some Design Aspects of Tandem Rotor Helicop-
ters*, The Journal of the Helicopter Association of G. B. October, 1959, Vol. 13,
№ 15.
40. G i 11 у I., N о r m a n d Y., „Stability au sol des helicopteres tripales”,
Technique et science aeronautiques, № 6, 1952.
41. Heinrich, „Uber die Kompensation der Reibung durch zusatzliche,
Schwingbewegung”, ZAMM, № 22, pp. 136—142, 1942.
42. Meldau E., „Druckverteilung im Radial Rollen Kugellager”, „Werkstatt
nnd Betrieb”, N 87, 1954.
43. Weibull W., „А Statistical Representation of Fatigue in Solids”, Trans-
actions of Royal Institute of Technology, N 27, 1949.
44. Lundberg G. and Pa Imgren A., „Dynamic Capacity of Roller Bea-
rings”. Acta Polytechnica 96, 1952.
45. H a r r i s A., „Predicting Bearing Reliability”, Machine Design, N 1, 1963.
46. Lariviere J. S., „Calcul de la duree d’utilisation des pales d’helicop-
teres”, Technical note STA/VT, N 165.
47. Selichov A. F., „On the theory of Calculation of Service Life of a
Structure”, Proseeding of the 4 th Congress of JCAS Spartan Press, 1965.
J
ОГЛАВЛЕНИЕ
Стр.
Предисловие....................................................... 3
Введение ........................................................... 5
Глава 1. Упругие колебания и прочность лопасти............................ 15
§ 1. Задачи расчета. Основные допущения и вывод дифференциальных
уравнений изгибных деформаций лопасти................................. 16
1. Конечная цель расчета упругих колебаний лопасти................. 16
2. Расчет лопасти на прочность...................................... 17
3. Режимы полета, опасные для усталостной прочности конструкции . . 18
4. Допущение о равномерном поле индуктивных скоростей.............. 18
5. Допущения, используемые при расчете аэродинамических нагрузок па
профиль лопасти.................................................... 19
6. О связи деформаций при изгибе в двух взаимно перпендикулярных на-
правлениях и принимаемых в связи с этим допущениях в расчетах ... 20
7. Об учете крутильных деформаций лопасти при расчете изгибных коле-
баний ......................................... 21
8. Два этапа расчетов при проектировании лопасти: расчет частот собст-
венных колебаний и расчет напряжений............................... 21
9. Идеализированные модели лопасти, применяемые в расчете.......... 22
10. Вывод дифференциального уравнения изгиба лопасти в поле центро-
бежных сил при колебаниях в плоскости взмаха....................... 23
11. Дифференциальное уравнение изгиба лопасти в плоскости вращения не.
сущего винта....................................................... 24
§ 2. Свободные колебания лопасти невращающегося впита............... 25
1. Метод расчета, приводящий к решению интегрального уравнения коле-
баний лопасти...................................................... 25
2. Расчет форм и частот собственных колебаний модели лопасти с дискрет-
но распределенными параметрами..................................... 26
3. Условие ортогональности и вычисление последующих тонов собственных
колебаний ......................................................... 28
4. Особенности расчета частот и форм собственных колебаний шарнирно
заделанной лопасти ................................................ 29
5. Расчет форм и частот собственных колебаний лопасти как свободной
балки............................................................ 30
§ 3. Приближенный метод определения частот собственных колебаний лопа-
сти в поле центробежных сил......................................... 30
1. Применение метода Б. Г. Галеркина для определения частот собствен-
ных колебаний лопасти ........................................ 30
2. Резонансная диаграмма колебаний лопасти........................ 32
3. Выбор параметров лопасти для исключения резонансов при колебаниях
в плоскости взмаха . .............................................. 32
4. Выбор параметров лопасти для исключения резонансов в плоскости вра-
щения .......................................................... 35
§ 4. Расчет форм и частот собственных колебаний лопасти в поле центро-
бежных сил ......................................................... 37
1. О целях и задачах расчета....................................... 37
2. Пределы применимости методов расчета, сводящихся к решению инте-
грального уравнения колебаний лопасти ............................. 37
3. О возможных методах расчета свободных колебаний лопасти в поле
центробежных сил................................................... 39
4. Метод трех моментов для расчета форм и частот собственных колебаний
лопасти в поле центробежных сил.................................... 40
420
Стр.
5. Определение изгибающих моментов по известным силам.............. 45
6. Определение перемещений по известным изгибающим моментам .... 47
7. Случай жестко закрепленной в комле лопасти...................... 49
8. Возможные упрощения при расчете коэффициентов................... 49
9. Некоторые результаты расчета форм и частот собственных колебаний
лопасти . . . . .................................................... 50
§ 5. Крутильные колебания лопасти . ................................ 56
1. Задачи, решаемые при расчете крутильных колебаний............... 56
2. Дифференциальное уравнение крутильных колебаний лопасти .... 57
3. Определение форм и частот собственных колебаний лопасти на кручение 58
4. Определение форм и частот собственных колебаний несущего винта
в целом............................................................. 62
§ 6. Совместные изгибно-крутильные колебания лопасти................. 63
1. О связи между изгибными и крутильными колебаниями............... 63
2. Методика расчета совместных колебаний........................... 64
3. Влияние связи между изгибом и кручением на частоту собственных ко-
лебаний ............................................................ 68
§ 7. Вынужденные колебания лопасти.................................... 73
1. Применение метода Б. Г. Галеркина для расчета деформаций лопасти.
Определение статических деформаций лопасти ...................... 73
2. Определение деформаций лопасти при периодическом приложении внеш-
ней нагрузки.......................................п................ 75
3. Упрощенный подход к расчету вынужденных колебаний лопасти .... 76
4. Амплитудная диаграмма колебаний лопасти......................... 79
5. Расчет колебаний в случае, когда фаза приложения внешней нагрузки
переменна по длине лопасти ......................................... 79
6. Аэродинамическая нагрузка на жесткую лопасть.................... 80
7. Определение коэффициентов махового движения лопасти............. 84
8. Упрощенный расчет упругих колебаний лопасти..................... 87
§ 8. Расчет изгибных напряжений в лопасти на малых и средних скоростях
полета............................................................... 90
1. Особенности, отличающие режимы полета на малых и средних ско-
ростях ............................................................. 90
2. О методе расчета напряжений......................................... 91
3. О допущениях при определении индуктивных скоростей ........ 91
4. Расчетные формулы для определении поля индуктивных скоростей . . 93
5. Преобразования расчетных формул в частных_случаях................... 95
6. Численное определение величии интегралов J (Рт) и J (Рт)....... 96
7. Допущения, принятые при определении аэродинамических сил .... 99
8. Расчетные формулы . . ............................................. 160
9. О переходе к эквивалентному несущему винту.......................... ЮЗ
10. Основные допущения, используемые при расчете изгибных напряжений ЮЗ
11. Дифференциальное уравнение колебаний лопасти и его решение . . . 104
12. Определение коэффициентов левой части уравнений табл. 1.8 ... . 104
13. Определение коэффициентов правой части уравнений табл. 1.8. . . 107
14. Система уравнений после подстановки формул (8.34) и (8.38) .... Ю8
15. Общая схема расчета ................................................ Ю8
16. Определение коэффициентов деформаций............................... Ю9
17. Программа расчета.................................................... Ш
18. Сравнение расчета с экспериментом на малой скорости полета . . . ИЗ
19. Сравнение расчета с экспериментом на средних скоростях полета . ... 115
20. Возможные пути дальнейшего уточнения результатов расчета........... 116
§ 9. Расчет изгибных напряжений в лопасти с учетом нелинейной зависимо-
сти аэродинамических коэффициентов от угла атаки профиля и чис-
ла М..................................................................... И8
1. Рассматриваемые режимы полета ................................... 118
2. Определение аэродинамических нагрузок............................ 118
3. Метод расчета лопасти как системы, движение которой связано задан-
ными заранее формами колебаний.................................... 120
4. Расчетные формулы для модели лопасти с дискретными параметрами 123
5. Об учете переменного поля индуктивных,скоростей................... 124
6. Особенности численного интегрирования дифференциальных уравнений
упругих колебаний лопасти .......................................... 12°
7. Способ численного интегрирования, предложенный Л. Н. Гродко
и О. П. Баховым..................................................... 138
421
Стр.
8. Последовательность операций при выполнении расчета и практическая
оценка различных шагов интегрирования............................. 133
9. Сравнение результатов расчета по методу численного интегрирования
с методом расчета по гармоникам................................... 136
10. Некоторые результаты расчетов..................................... 136
§ 10, Расчет изгибных колебаний с непосредственным определением траек-
торий движения точек лопасти..................................... 142
1. Сущность метода расчета............................................ 142
2. Определение упругих сил, приложенных к рассматриваемой точке лопа-
сти со стороны смежных участков..................................... 143
3. Особенности численного интегрирования уравнений (10. 1)........... 14&
4. Уравнения движения при рассмотрении многошарнирной членистой мо-
дели лопасти . .................................................... 148.
5. Последовательность операций при расчете упругих колебаний методом
численного интегрирования . . ...................................... 151
6. Метод расчета с обратным порядком определения переменных при чис-
ленном интегрировании............................................. 152.
7. Сравнительная оценка различных методов расчета изгибных колебаний
лопасти............................................................. 155
§ 11. Усталостная прочность и ресурс лопасти .......................... 158
1. Испытания конструкции для определения ее ресурса ................ 158
2. Рассеяние характеристик выносливости при усталостных испытаниях . 158
3. Основные характеристики усталостной прочности конструкции .... 160
4. Напряжения действующие в конструкции лопасти в полете............. 163
5. Гипотеза линейного суммирования повреждаемостей и средняя эквива-
лентная амплитуда переменных напряжений............................. 164
б. Разброс амплитуд переменных напряжений на заданном режиме полета 168.
7. Метод расчета ресурса с использованием коэффициента надежности . 169
8. Метод А. Ф. Селихова для подсчета необходимого запаса надежности
по числу циклов г] ................................................. 172
9. Об определении SIglv с заданной доверительной вероятностью .... 176
10. Разброс в уровнях нагружения различных экземпляров конструкции
и запас надежности по амплитуде переменных напряжений Т]о . . . 177
11. Метод определения запаса надежности предложенный А, Ф. Сели-
ховым ............................................................... 182
12. Пример расчета ресурса . . ....................................... 185
13. Возможные пути определения минимального предела выносливости кон-
струкции ............................................................ 188
14. Преимущества и недостатки различных подходов при определении не-
обходимых запасов надежности и примерная оценка их точности . 191
15. Требования к прочности лопасти при выборе ее конструкции........... 192
16. Прочность лопасти со стальным трубчатым лонжероном................ 193
17. Прочность лопасти с дуралюмииовым лонжероном....................... 197
18. Влияние условий эксплуатации на усталостную прочность лонжеронов 198-
Глава 2. Вибрации вертолета . . . ................................... 200
§ 1. О силах, вызывающих вибрации вертолета.............................. 200
1. Частоты возбуждения................................................. 200
2. Зависимость Спектра частот возбуждающих сил от гармонического соста.
ва колебаний лопасти ............................................ 203
§ 2, Колебания изгиба фюзеляжа как упругой балки......................... 212
1. Расчет вынужденных колебаний упругой балки методом разложения по
собственным формам................................................... 212
2. Динамическая жесткость балки. Резонанс и антирезонанс.............. 217
3. Применение метода динамической жесткости к расчету колебаний вер-
толета поперечной схемы.............................................. 220
4. Метод добавочной массы . . ........................................ 22,3
5. Влияние демпфирующих сил. Колебания при резонансе.............. 224
§ 3. Расчет вибраций с учетом особенностей фюзеляжа................. 228
1. Особенности фюзеляжа. Поперечные и вертикальные колебания .... 228
2. Расчет колебаний фюзеляжа в плоскости симметрии методом остатка . 231
3. Учет влияния деформаций сдвига................................. 238
§ 4. О совместных колебаниях системы фюзеляж—несущий винт........... 239
1. О колебаниях системы фюзеляж—несущий виит......................239
2. Расчет частот собственных колебаний лопастей винта в плоское!и вра-
щения с учетом упругости вала винта и его крепления к фюзеляжу . . 242
422
Стр.
Глава 3. Земной резонанс ................................................. 251
§ 1. Устойчивость винта на упругом основании.......................... 252
1. Постановка задачи и уравнения движения........................... 252
2. Анализ устойчивости и основные результаты........................ 256
3. Физическая картина поведения винта при земном резонансе.......... 267
4. Винт на изотропном упругом основании............................. 271
§ 2. Поперечные колебания одновинтового вертолета..................... 273
1. Предварительные замечания . ..................................... 273
2. Боковая и угловая жесткости шасси. Центр жесткости............... 274
3. Собственные поперечные колебания вертолета....................... 277
4. Определение коэффициентов демпфирования . ....................... 279
5. Совместное действие системы амортизационная стойка — пневматик , . 281
6. Приведение задачи к расчету винта на упругом основании........... 284
7. Анализ результатов расчета земного резонанса .................... 285
§ 3. Характеристики демпфирования шасси и лопасти. Их влияние на земной
резонанс............................................................... 286
1. Определение коэффициента демпфирования амортизатора шасси .... 286
2. Эффект запирания амортизатора вследствие трения в уплотнениях
и автоколебания вертолета ........................................... 288
3. Характеристики демпферов лопасти и их анализ..................... 292
4. Влияние махового движения винта на земной резонанс............... 294
§ 4. Земной резонанс вертолета на пробеге............................. 298
1. Жесткость и демпфирование пневматика при качении................. 298
2. Расчет земного резонанса и его результаты........................ 303
3. О земном резонансе с отрывом пневматиков от поверхности земли . . . 305
§ 5. Земной резонанс вертолетов других схем........................... 307
1. Общие замечания . ............................................... 307
2. Расчет поперечных собственных колебаний с учетом трех степеней сво-
боды ................................................................ 307
3. Расчет собственных колебаний вертолета в плоскости симметрии (1410-
дольные колебания)................................................... 313
4. Приведение задачи к расчету винта на упругом основании........... 318
5. Самовозбуждающиеся колебания в полете вертолета с упругим фюзе-
ляжем ............................................................... 319
§ G. Выбор основных параметров шасси и демпферов лопастей. Рекоменда-
ции по проектированию.............................................. 321
I. Выбор характеристик демпфера лопасти............................ 322
2, Винт е межлопастными упругими элементами и демпферами . . 325
3. Выбор характеристик жесткости и демпфирования шасси.............. 327
4. Некоторые рекомендации по конструированию шасси ................. 330
Глава 4. Теоретические основы расчета подшипников основных агрегатов
вертолета ............................................................. 332
§ 1. Уравнения статического равновесия радиальных и радиально-упорных
шарикоподшипников при комбинированной нагрузке......................... 333
§ 2. Расчет радиальных и радиально-упорных шарикоподшипников при ком-
бинированных нагрузках в случае отсутствия взаимного перекоса колец 339
1. Давления на шарики...............-............................... 339
2. Приведенные нагрузки............................................. 345
3. Статистическая теория динамической грузоподъемности.............. 347
4. Влияние осевой нагрузки на работоспособность подшиппикоп......... 353
5. Приближенные решения уравнений (2. 1) и (2. 2)................... 356
6. Относительные смещения колец.................................... 361
§ 3. Некоторые, задачи расчета радиально-упорных шарикоподшипников
с учетом перекоса их колец под нагрузкой .............................. 362
1. Основные соотношения............................................. 362
2. Случай «чистого» момента......................................... 366
3. Совместное, действие момента и осевой силы....................... 370
4. Предельные зависимости для малых нагрузок........................ 372
5. Распределение нагрузки между рядами шариков двухрядных радпально-
yiiojuiux шарикоподшипников . ...................................... 377
6. Примеры расчета................................................. 379
§ 4. Расчет конических роликоподшипников при комбинированных нагрузках 381
1. Расчет однорядных конических роликоподшипников , ................ 381
423
Стр.
2. Некоторые замечания к расчету подшипниковых узлов, состоящих из
двух конических роликоподшипников ................................ 38,5
§ 5, Расчет подшипников, работающих при качательном движении.......... 388
1. Особенности механизма износа подшипников качения в условиях кача-
тельного движения.................................................. 389
2. Смазка высоконагруженных колеблющихся подшипников при малых
амплитудах колебаний ............................................. 390
3. Расчет подшипников втулок несущих и рулевых винтов............... 395
4. Расчет подшипников автоматов перекоса и механизмов управления . . , 403
§ 6. Теория и выбор основных параметров упорных подшипников с «поверну-
тыми» роликами....................................................... 406
1. Определение времени Тс........................................... 406
2. Выбор углов наклона гнезд сепаратора............................ 411
3. Потери на трение................................................. 414
4. Дополнительные соображения об оптимальной конструкции упорных под-
шипников с «повернутыми» роликами................................... 415
5. Пример расчета упорного подшипника с «повернутыми» роликами . . . 417
Литература........................................................ 418
Михаил Леонтьевич Миль, Андрей Владимирович Некрасов,
Александр Самойлович Браверман, Лев Наумович Гродко,
Матвей Абрамович Лейканд
ВЕРТОЛЕТЫ
(Расчет и проектирование)
Книга вторая. Колебания и динамическая прочность
Редактор Г. И. Калашник Переплет художника Л. А. Витте
Редактор издательства М. С. Аникина Суперобложка худож. А. Г. Другова
Корректор В. Д. Замчевская Технический редактор А. Я. Новик
Г-40029 Слано в набор 31/V I960 г. Подписано в печать 25/1 1967 г.
Формат 70X108/16 псч. л. 29,5 (усл. псч. л. 41,3, в т. ч. 9 вкл.) уч. изд. 30,35 бум. л. 1-1,76
Бумага № 1. Тираж 4800 экз. Заказ 1578/936. Цена 2 р. 28 к. Тем. план 1966 г. № 233
Издательство «Машиностроение», Москва, Б-66, 1-й Басманный пер., 3
Московская типография № 8 Главлолнграфпрома
Комитета по печати при Совете Министров СССР,
Хохловский пер., 7
Таблица J.7
J=0 f Члены, не зависяи2,и.е omjioaqjcpu.- цаентов деформации.
Br, ao a? Sr «2 *2 аз ъз ач , • • • ео С1 c2 cs a3 Сч ^4 Ув ^п fK Jn
i = 0 po = Bo /£ГХ^ ~i ?г*о 1 „г ЧР ' A’'*, Ь2ло> 1 -pre, prtgut (r2+lp2)if>r г ^0 + 3^1
i = 7 !
i-2 cos <j> p< = *7 -!ir xofr2*!?2) р2^в2 Р™, -JP2*, № -firji^ x/r2r^ft2) ry(1)r^ft2fi(,i -jiy(r>+j fir^’) >!ГЖ, -№х1 l/21^ у -(г2ч1р2)ег -ТП . 1 ' rX' +JAS
i = 3 sin ф I = *7 хо(р2+&2) ~Р™о ~2^ ~ЧР2 ~чР2хо -ryO+^fi2^ x,(F2+l/c2) -If2^ '« -2? '31-а- + <ч । РгЧ^Й гвр(рг гХ7 jp7-t
1=0 cos 2tf К = ~Вг ЦТ 'в™, х0(г2+1р2) 2 г2 -for /сгк0 -ip2*' -zfoy^+lfirft^ ^(rl+lft2) 2ry<’> -^y^zf2^ pra^ --^*1 If2^ 5 /ггр, ~l^2?r Р2-2 ~2в^1 ~ ^з)
i=5 sin 2<f p2 ss ^2 ~Уг Г»'! рг -2г2 х'(Гг*з)р2 ~РРхо -fir -ip2 -$Р2*о -lflW> prx. -2ry(,> -^x, -i^x. -х«гел г\2 +-fi(k~ Х?)
i-S cos 3 i> P3 = B3 ~чв2зео ~1р2 & -р™„ *o(r2 + lfl!) Зг2 -jpr ргхй • • • -1^(0 fty^^ftrjB*0 \-flfH, X,(r2^/C2) 3ry fr) - Zfiy^r^ftrfi^ ^x, « • • i/22^
i = 7 sin 3$ =P3 = B3 ?> ргхе ’vf ~3r2 *в(г2+2?г) -firxo • • • ~h2xi ftrx^ -3ry<1> te7(r2+jfc2) -forx1 -2fiy^^firfiw / т,/2-2^ г I" + Jp(kz-t^
t=e COS 4 tji — вч - V Р2*о ~i^2 2 fir -ргх„ Хд(г2Цр2) Чг2 • • • - №*, jpyW+jfirj^'* -ftrn1 X^+jfl2) Чгу2^ • • • Jf2 (^"з~
i=9 sin 4 jf =x *4 - (2г ЧГ ~Чр2*1 2 fir -4F2 xe(rz+ift2) • • • -l^x, t2fiX1 -чгу^^ x,(r2+^fi2) • • •
• ее • • • • ее • • • • • • 1 • • • • • • • • • • • • • • • • • •
Зак. 1578
1
Таблица 1-8
J=0 J=t 2 J=J
Т1 1 -а0 а. bl ьз ач ъч • 1 • -С0 с d2 С7 di Ct d,, ... -еа — ef Ч fl е3 А et л ... А л А £l Зц. S ...
1-0 0 0 Q 3 Т и L К Q 3 7 и 4 К Q 3 7 и L К а 3 7 У 4 к =
f К Q 3 1 7 и 4 1 Я Q 3‘ 7 и 4 Я a 3 7 У 4 я а 3 7 У 4
1 2 23 R ^Q+L з-Л 7 у д К. 2Н Я Q^L S+K 7 У L к 2N я q+L 3+к 7 и L к гз я a-tL S+K 7 У 4 к
3 3 3 7 и д К я-и a-L 3 7 и 4 3 Я-У a-L 3 7 и 4 N я-и а-ч 3 7 У L
2 Ч М н Я гу “Л 7 U д к м N я а 3 7 и L к' ... м 3 я а 3 т У 4 К м 3 я а 3 7 и 4 К
5 гк L м 3 L< у.! 3 7 и 4 2К М N я a 3 7 и L гк 4 л? 3 я a 3 7 У 4 2К L м N я а 8 7 У 4
3 6 L М 3 R VQ У! 7 и ... 4 М Я я Q 3 Т и ... 4 м 3 я 3 3 7 У ... 4 М 3 я а 8 7 У ...
7 К L М 3 3 т ... К L м N Я Q S 7 ... К L м 3 я а 3 7 ... К 4 м 3 я а 3 7 ...
У 8 L м И я Га~ ... L М N Я в 3 ... д м 3 я а 3 ... 4 м 3 я а 3
9 К д М N !л_ л1 ... К 4 М N я Q ... к L м N я а ... К 4 м 3 я а ...
/=/ 0 0 Q S т и L к Q 3 7 и д К Q <7 Т и L К а 3 7 У L К
1 Я 9 3 7 и д Я Q s Т и L Я Q 3 7 и L я а 3 7 и L
1 2 23 € 3+L StK 7 и д К 2N Я IjfL s+tf 7 и L К 23 Я Q+L 3+К Т и 4 К 23 я QtL S-tK 7 и L к
3 3 R-U Q-ч 3 7 и Д N 9-^ 3 7 У L 3 я-и q-L 3 Т У L N я-и а-а 3 7 и L
2 Ч М 3 Я а 3 7 и д к М я я Гв~ ~3~> 7 и 4 к М N Я a 3 7 и 4 к м 3- я а 3 7 и 4 к
S гк L м 3 я я 3 7 и 4 2К L м N 'Л 3 7 и 4 2К 4 М Д' я Q ’7 7 У L 4 м .4 я Т У =
3 6 L м 3 a 3 7 и ... ~Г М я 'Г(Г 7 и ... L 'м N Я a 3 т У ... 4 м N я а 3 7 и ...
7 К L М 3 я G 3 т ... к 4 м я |л Q\ 3 7 ... К 4 м 3 я Q 3 7 ... 4 М 3 я а 3 7 .. .
Ч 8 L м 3 я 0 ... д м Я я Гй~ "J"! ... 4 м 3 Я а 3 ... L м 3 я Q J’
3 К L М 3 Я ц ... к 4 м N Л! ... к 4 м 3 я а ... К 4 М 3 Я а
1-2 0 0 0 3 7 и L К a 3 т £/ д К 3 3 7 и L К а 3 7 У 4 К
1 3 4 S' 7 и Д я Q 3 7 У L Я Q 3 7 и 4 я Q 3 7 У 4
1 г 23 R Q+L S-K 7 и Д К 23 Я QtlAStK 7 и L К 2N Я ’рй- зц 7 и L К 23 Я Q-fL S+к 7 У 4 к
3 3 R-U 3-L 3 7 и д N Я-L/'.C-L 3 7 и 4 3 jf-У у-д 3 7 и 4 3 я-и Q-L 3 7 У L
2 ч М 3 Я a 3 7 и д к тМ N Я a 3 7 и 4 к м 3 я !у" ~'Г 7 У 4 к м N Я а 3 7 и L к
5 2К L М N к Q 3 7 и 4 гк 4 м N я Q 3 Г У 4 гк 4 м 3 пг Q 3 7 У L 2К 4 М 3 я а 3 7 и д
3 6_ L М N Я а 3 7 и ... 4 М N Я Q 3 7 и ... L м N я 'Га~ ~з~‘. 7 У ... 4 М 3 я Q 3 7 и ...
7 К L М 3 R 0 3 7 ... К Д М N Я а 3 7 ... К д М N 3 т ... К 4 м N Я а 3 7 ...
Ч 8 L м я Я Q 3 ... д М N я Q 3 4 М N Я Та~ "У1 ... L м N я а 3 . г .
3 К д М 3 я 0 ... к 4 М N Я Q ... К 4 М 3 iJL ... К 4 м 3 я а ...
>3 0 0 Q з 7 и L к Q 3 т У д К Q 3 7 и 4 К а 7 У L К
/ к Q S 7 и д я а 3 7 У 4 я Q 3 7 У 4 я а 3 7 и 4
1 2 23 Я д-п. 3tK 7 и д К 2N я CtL S+K 7 и ь К гз Я ди з+к 7 и 4 к 2N я ’C+L зз\ 7 и 4 Л'
3 3 я-и a-ч 3 7 и 4 N я-и Q-L 3 7 и 4 3 я-и а-ч 3 7 У 4 3 fi-u <?-д| 3 7 У 4
2 Ч М N я 3 3 7 и 4 к М N Я а 3 7 и 4 К м 3 я в 3 7 У 4 к м 3 я У 7 и д к
5 2К L м 3 Я 0 3 7 и 4 2К L М N к а 3 7 У 4 гк L м N Я Q 3 7 У 4 гк 4 м 3 г«" "al 3 7 У 4
3 6 д M N я Q 3 7 и ... Д М N я Q 3 7 У 4 М N Я а 3 7 У ... 4 м N Я Гу Т] 7 и • • •
7 к д М з я 3 3, 7 ... К 4 М N Я Q 3 7 ... К L м 3 я а 3 7 ... К 4 М 3 lA r?J 3 7 . •.
ч 8 L м N Я Q 3 ... 4 м N Я Q 3 ... 4 м 3 я Q 3 •.. L м 3 Я |у У •. •
3 К д М 3 я 0 ... — К 4 М N Я Q К в м N Я а ... К L м 3 L« _У_1 ...
Зак. 1578

J^1 Таблица, 1.9
1=0 п i -аг 8ft ft. 8, a? 62 !3 b3 d > . . -c0 c^ ...^ ii ft2 ^2 c3 ^3 <4 А-Ч 4 4 4 *n pJL-
0 0 1 гд ^PlX0Cg gpLHl)O ;7wj - P'-^Bq 1^-4^ ~^Р-гв10 pBgSf р^Л^Вд frlpq ФЛ
1
1 2 ~P[joo t fO^in ^Р-^^д-Вдо) pXgBB -‘Г.дСд "'fal'Hoo ~p^10 -эфд+1^1с0) ~oP-(zF;g~Gigj -P^jBg -^Р6к1со ~^P-lPo ~^д+^ргС^Эг ?,*
3 РдЛР ^oc -^(рЦр^о) J-AXo^O p(ZFog-Ggg) fa ' Po fa^o -K^Aq+^/PCq) P^lB0 Yp(iFW~Big) i^P^ho ifP^x^Cq 1 '(Ао+^Р Gg^6j Рг-Цосвсд 2pB? ?fA
2 9- уР(ррРо) JZ d^Bf, 3__ To~ -xpgPpCo) "2 Doo -JXKq Bq faZK0C0 ~2p(pfo~^iej P-^Bq -^i(^O+lpZBg) -ZIPo ~2р(^Ю~^1о) ~pKiBg ipzx\& -1-„ ZH l^P H10 рв^ -1^1 ф^- vz
6 ~ р' Ро -jik0&s 'jpPoo^oo) ZD DO 3__ Tt> PfPPzPty FP^^OO'^Oo) faZPo -y/l KqCq -pKjBo -^pfrltp^.o) ^B>10 -x^Aq+^P lp(3Ffo~Gfo) iplH\o ^РгХ,Сд -pBa^i Ф*
-7 V В I i;J^occ. ^JpHgg -^(гРцрВод) J-L q Bq lP ^1>) ~3DBB %P (ч Po ~ Po) -J'XaBg • « * Gg ip2H’o -^Р^чд+Вю^ px-iB0 -Xj(A0+^Cg) -3Dg iP^-^o) -px^Bo 4 4 4 ^ргСд8г
7 ~~U~Hoo ^/Z XqCq PPP .ррТдрС^ _L_ Го -*o(Ao+№Co) yxgBg I^^Fqo-Gqq) 1 4 • Z U Q “ tЦ/ fft-f Вg ~"z p(^ia+B!0) 3Dj0 -x^Afp^P2^ j PX;\B0 iP^BjQ-C,^ 4 4 4 {p2c<PP
ч 8 ~PZ*PO B^2hoo -fafhpcao) JZ^qBq IL- Го ~^йоо 4 4 4 ^p2X1C0 -цр^Ню --^p(3Fj0+GIQj pXtBg -X^Ap^y. Cgj ~^o • 4 4 фА ‘ <f
9 -yP^oo ^P^XqCq -jppBg ~fa(3Fgg+Gggj ^одд F.- '^О^ц+^-Р ^oj 4 4 4 Ч;Р2н1о tp^c,, ~PX,B3 ~2p(3F10+G1Dj ^10 -X^Ap1lfPCgj 4 4 4
• ♦ • ... • • • 4 4 4 • 4 • « 4 • 4 4 f 444 ♦ 4 4 4 4 4 4 4 4 • • 4 • • 4
1=7 0 0 |М’%> -~РУР 7 V/Z?£^z 4 P^OI J-(pL\ -[IXflf ~ipZHn -pB^, pt^AgB, A^P^P Ф/
1
7 Z ^-1 0^4 -jcJas^cJ -^оГ^Р^О', — у p(ZF<M~Goi) -p*0P fa1^ ~faZHg1 -p^11 -^g+^p.lCf) ^11~l.pZHr! {p^-Gn) {p2^ C1 ~^ргн11 ~(Ay^plcjdz фА
з px0B, ' il{^^or^oi) ^‘01 faZ*sci -Рц-цР^Нц г/лУ~ -^(A1+^p-lCi) j^Xi.B, jp^Fff-Gj^ ip2fi11 1ргхр, -[А^гС^ P^PWl IpBp фА
2 ч- 1 ' ZDB1 lP$3. '3gt) -yyp -l пгН ‘fP' HD1 rP V ? 1 -2D„ IpI'^-4 -p,n1B1 TfP1^^ ~ipl"n pBt e, -jjPcf ф/
S J V* ~lP^op3D^ 2Bgi 4vJA) ^1 2p(3Fgi-frB1) { p2»0C1 " pjK-f В ; ( ~ 2 22),z 1-L-PL\- T-ty y^f px,Br Jpl^Bjf-C^'j ip%i ^pl^Ci -рВ18г ф/
3 6 i 1 I <• /'M? ~ko(*i\p?^ ~3Dgi ^P'l^^or^Ol) -pStgBl 4 4 • ту p 1G ip^if pat^B, -X^pjp^C,) ~3Dji ^p(‘tFfrGn) ~рк1в1 4 4 1 ^рЗс^ ф/
*7 -- iPh,,. 4 ' J 4 p1 XgC. -fiX,S, ;Pfooi+fy)i) 3D№ -^(Apzptp) • ♦ • -^P1*” P p.-H,C1 -j-p^ZF^+Gfjj 3^11 Т(з-А)- Л ’ СУ?/ -iti(Ai+l/llCf) в z Ip^i-g^) 4 4 4 ip2w
8 i i I -I— I I у//гЛ,С7 AP^ ^iP^^tP^Ol) pX0Bf -^01 ' 4 4* ЪРгХ1с1 ifp^n ~jP(3Wi) pj^Bj ip-pp- 'X^A-^ilPCfj -4D,, 4 14 ф^
5 ~1р%1 - /l^XyC] - ~pxgB, ~2p(3F01+G0i) -Хд(Ар^ргСг) • 4 4 1Р%С1 -PK1B1 ~lP(3FfpB„) Tit16"^}- ~^i+lPlci) 4 14 ф^
*• « • I • • t ♦ • • . . . 4 4 4 4 4 4 4 4» • 4 « • • » 4 4 4 • 4 4
Зак. 1578