Избранные труды. Математика. Механика - Яненко Н.Н.

Автор: Яненко Н.Н.
Теги: дифференциальные, интегральные и другие функциональные уравнения конечные разности вариационное исчисление функциональный анализ математика механика
ISBN: 5-02-000243-7
Год: 1991
Похожие
Системы квазилинейных уравнений в газовой динамике
Курс высшей математики и математической физики. Выпуск 7. Дифференциальные уравнения
Методы решения нелинелинейных уравнений математической физики и механики
Разностные методы решения краевых задач
Текст
                    ,^~. -^ч
£ -
sf г: "*
-=а м
^
-^ N~" ^
—.^-^
<, s%
~ ^! - ^ >-
_^ ^ - ч-
-- _, Ч

Н.Н.ЯНЕНКО
Избранные
труды
МАТЕМАТИКА
МЕХАНИКА
МОСКВА
"НАУКА"
1991

УДК 517.9
Яненко Н.Н. Избранные труды. Математика. Механика. - М.: Наука, 199,1. - 416 с.
ISBN 5-02-000243-7
В книгу включены работы известного советского математика и механика академика Н.Н. Яненко
(1921-4984) по геометрии, уравнениям математической физики, механике и вычислительным
методам. Приводятся краткие биографические сведения.
Издание рассчитано на специалистов в области математической физики, вычислительной
математики и механики, а также на студентов и аспирантов.
Yanenko N.N. Selected works. M.: Nauka, 1991. - 416 p.
This book incorporates the works of an outstanding Soviet mathematician and mechanician N.N. Yanenko
(1921-1984) in geometry, equations of mathematical physics, mechanics and computational methods.
Brief biographical data are given.
It is intended for a wide circle of specialists in the field of mathematical physics, computational
mathematics and mechanics, as well as for students and post-graduates.
Редакционная коллегия
академики В.Е. НАКОРЯКОВ (председатель), В.М. МАТРОСОВ,
члены-корреспонденты АН СССР А.Ф.СИДОРОВ, Ю.И. ШОКИН,
доктор физико-математических наук В.М. ФОМИН,
кандидаты физико-математических наук Б.Г. КУЗНЕЦОВ, СВ. МЕЛЕШКО
Рецензенты
доктора физико-математических наук Ю.А. БЕРЕЗИН, Ю.С. ЗАВЬЯЛОВ
1604010000-500 тх , 4_
Я Без объявления © Издательство "Наука", 1991
042 (02)-91
ISBN 5-02-000243-7

ПРЕДИСЛОВИЕ
Публикация избранных трудов членов АН СССР — давняя традиция Академии,
продиктованная естественной заботой о преемственности поколений в науке. Однако
предлагаемые вниманию читателя Избранные труды выдающегося советского
математика и механика, трижды лауреата Государственной премии СССР, Героя
Социалистического Труда, академика Николая Николаевича Яненко не только дань традиции:
высказанные им идеи и предложенные методы не потеряли новизны до настоящего
времени.
Н.Н. Яненко родился 22 мая 1921 года в сибирском городе Каинске (ныне
Куйбышев). В 1939 году после окончания средней школы в Новосибирске поступил на
физико-математический факультет Томского государственного университета, который
окончил с отличием в 1942 году. С ноября 1942 года по май 1945 года находился на фронтах
Великой Отечественной войны (Волховский, Ленинградский, 2-й и 3-й Прибалтийские).
В декабре 1945 года был демобилизован и в феврале 1946 года поступил в аспирантуру
механико-математического факультета Московского Государственного университета.
В 1949 году защитил кандидатскую, в 1954 — докторскую диссертации. В 1966 году
избран в члены-корреспонденты АН СССР, а в 1970 — действительным членом АН СССР
по отделению механики и процессов управления.
Н.Н. Яненко — ученый с очень широким диапазоном научных интересов. Свою
научную деятельность он начинает под руководством известного советского геометра
П.К. Рашевского исследованиями по многомерной дифференциальной геометрии,
посвященными проблеме класса римановой метрики. В этом весьма интересном разделе
геометрии, который привлекает внимание исследователей с 1870 года до настоящего
времени, им были получены основополагающие результаты: для широкого класса
поверхностей даны необходимые и достаточные признаки изгибаемости поверхностей в
эвклидовом пространстве, установлены связи между метрическими и проективными
свойствами поверхностей и даны критерии вложимости соответствующих метрик.
Часть работ этого цикла помещена в предлагаемом собрании Избранных трудов.
С августа 1948 года по июль 1953 года Н.Н. Яненко работает в геофизической
комплексной экспедиции Геофизического института АН СССР, а затем по октябрь 1955 года
в Отделении прикладной математики Математического института АН СССР в группе
Андрея Николаевича Тихонова. Здесь он начал участвовать в решении сложнейших
прикладных задач, имевших важное значение для народного хозяйства страны.
Проведенные им исследования асимптотических свойств и приближенных решений
обобщенной модели Томаса—Ферми были фактически первыми в мире и легли в основу
построения интерполяционных формул уравнения состояния вещества в широком
диапазоне давления и температур. Исследования были удостоены в 1953 году
Государственной премии СССР.
С октября 1955 по ноябрь 1963 года Н.Н. Яненко руководит большим научным
коллективом, занятым решением прикладных задач. В этот период деятельности им
были, в частности, проведены аналитические исследования нелинейных систем
уравнений с частными производными. Созданный им метод нахождения точных решений
нелинейных уравнений (метод дифференциальных связей) получил широкое
признание. Суть метода состоит в том, что к исследуемой системе уравнений добавляются
дополнительные уравнения (дифференциальные связи),. отражающие некоторые
з

задаваемые исследователем свойства решений. Полученная таким образом
переопределенная система уравнений исследуется затем на совместность, что и позволяет
выделить точные решения исходной системы уравнений. На основе этого метода был
найден целый ряд новых точных решений уравнений газовой динамики. Работы этого
направления также можно найти в предлагаемых Избранных трудах.
В это же время Николай Николаевич начинает вплотную заниматься вопросами
численного решения задач механики сплошной среды. Исследования были продолжены в
Сибирском отделении АН СССР сначала в Вычислительном центре, а затем в Институте
теоретической и прикладной механики, директором которого он был назначен в
1976 году. Впервые в стране Н.Н. Яненко предложил, обосновал и применил для
решения различных задач метод расщепления многомерного разностного оператора (метод
дробных шагов). Суть этого метода состоит в том, что многомерный оператор
определенного вида заменяется последовательностью одномерных операторов,
аппроксимирующих исходный многомерный. Возникающие при этом разностные уравнения
могут быть эффективно решены с существенной экономией времени работы ЭВМ.
Разработанные на основе метода дробных шагов алгоритмы легли в основу цикла
прикладных программ, удостоенных в 1972 году Государственной премии СССР.
В последний период жизни Николай Николаевич уделяет большое внимание
вопросам математического моделирования различных процессов, включающего в себя
построение (или усовершенствование) физико-математических моделей,
построение дискретных моделей и алгоритмов, модульный анализ, создание пакетов
прикладных программ и, наконец, численные эксперименты как с целью уточнения
физико-математических моделей, так и более аккуратного истолкования опытных
данных. Так, в 1973 году в связи с вопросами моделирования сложных течений
вязкой жидкости Н.Н. Яненко ввел в рассмотрение новый класс уравнений в частных
производных, характеризующихся тем, что на решении уравнения может происходить
смена направления параболичности. Впоследствии такие уравнения получили
название уравнений переменного типа. Н.Н. Яненко и его учениками были получены
априорные оценки решений для некоторых уравнений этого типа, исследованы
качественные свойства решений, доказаны теоремы существования и единственности
решений регуляризованных задач. Некоторые работы этого направления читатель найдет
в данных Избранных трудах.
Список работ Н.Н. Яненко весьма обширен и поэтому при решении вопроса о том,
какие работы поместить в Избранное, редколлегия руководствовалась
соображением, что в первую очередь следует включать оригинальные материалы, а также труды,
напечатанные в труднодоступных для современного читателя изданиях.
В избранное не включены такие широко известные, переиздававшиеся на
нескольких иностранных языках, монографии как "Метод дробных шагов решения
многомерных задач математической физики" и "Системы квазилинейных уравнений и их
приложения к газовой динамике" (в соавторстве с Б.Л.Рождественским,
удостоенная в 1985 году Государственной премии СССР).
Работы Николая Николаевича Яненко оказали существенное влияние на развитие
ряда областей математики и механики, особенно численных методов решения задач
механики, и получили заслуженное признание как в Советском Союзе, так и за его
пределами. Результаты большинства работ Н.Н. Яненко вошли в учебники и
специальные монографии, стали само собой разумеющейся частью научного багажа
современного ученого — математика, механика, вычислителя. Проблемы, которыми занимался
Николай Николаевич всю свою сознательную жизнь, всегда были актуальны; все они,
за редким исключением, актуальны и сегодня.

ГЕОМЕТРИЯ
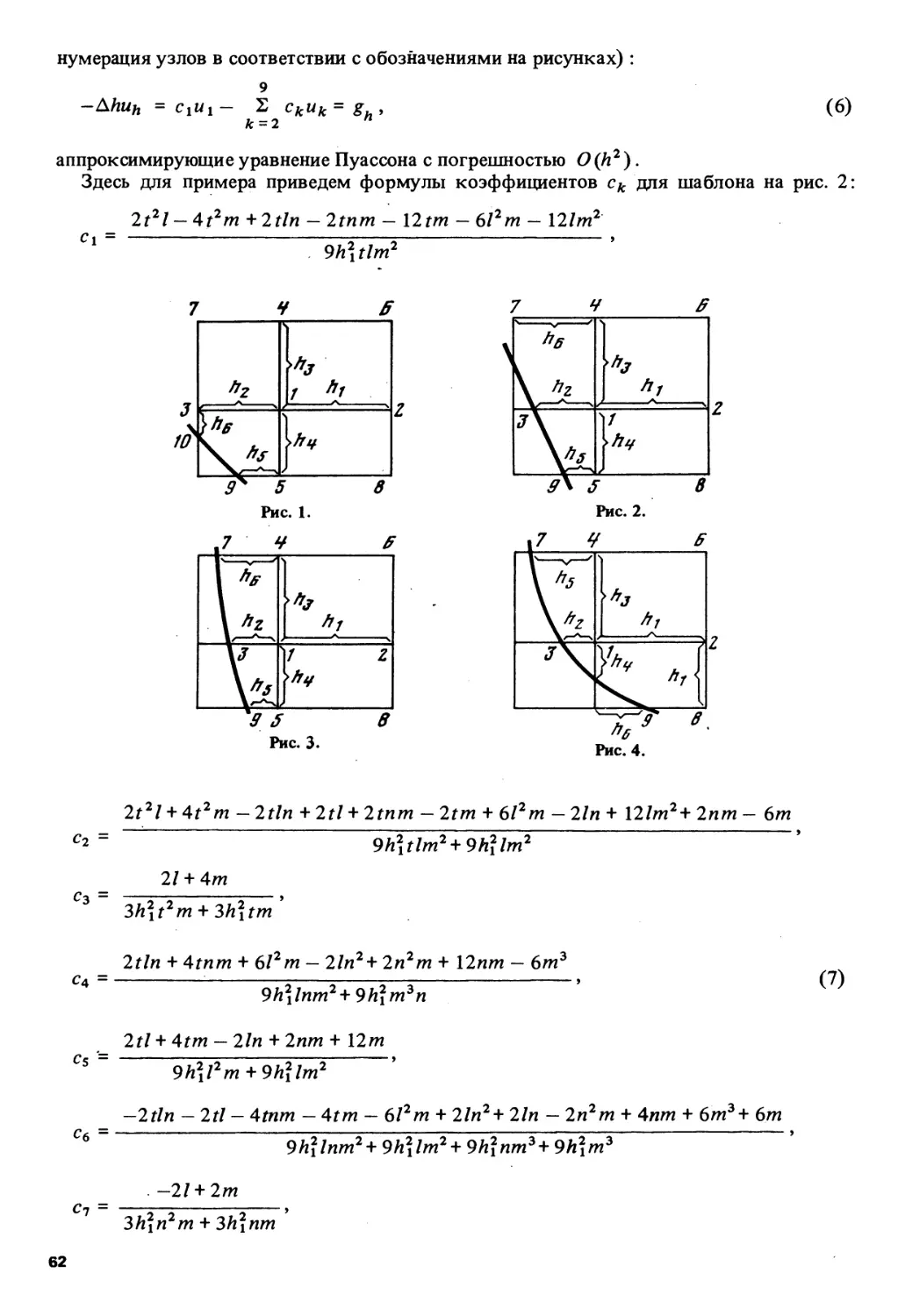
ГЕОМЕТИЧЕСКАЯ СТРУКТУРА
ПОВЕРХНОСТЕЙ МАЛОГО ТИПА*
В 1939 г. Аллендорфер [1], исследуя общие вопросы вложения римановых метрик
в многомерные евклидовы пространства, ввел в рассмотрение некоторый
арифметический инвариант поверхности, называемый типом (t). Этот инвариант играет
большую роль при исследовании вопросов вложения поверхностей в ЕП9 в частности в
вопросе об изгибании поверхностей.
Именно, им доказана следующая теорема, являющаяся обобщением теоремы
Beez'a: поверхность Vm СЕт+д,_дпя которой t(Vm) >2, однозначно определена в
Em + q> т.е. всякая поверхность Vm, изометричная Vm, ей конгруентна. Отсюда, для
того чтобы Vm допускала нетривиальное изгибание, необходимо t(Vm) < 2.
Определение типа, данное Аллендорфером, является чисто аналитическим, и
геометрическая структура поверхностей малого типа (t = 0, 1, 2) остается неясной.
Целью настоящей работы является установление геометрической характеристики
поверхностей малого типа (t - 0,1,2). Предварительно дадим определение типа
поверхности. Будем считать, что поверхность Vm трижды дифференцируема.
Если задать в каждой точке поверхности дважды дифференцируемый
ортогональный единичный репер /i,..., Jm\ Ли+i»-» Лл + g» ГД£ векторы /i,..., Jm
касательные, Jm+\= £i, Jm + q~ %q нормальные, то, как известно, имеют место
деривационные формулы
dr = со'.Л, / = 1, ..., т\
Ыт+Х = ... = и»*** =0;
dJ«= (")£V <*,j3=l,..., m+q;
wjj + "i= °' <*, 0=1,..., m+Q'
Формы coa, со" удовлетворяют условиям интегрируемости
(со*)' = [оАо«] = [со'of], a,j3 = l,..., m + cy, / = 1 m;
(cop' = [соДО], a,j3,7= 1, •••, m + q.
Будем вьщелять, в частности, формы со™ + s = i//*, 5=1, ,.., q9 a = 1, ..., m,
которые будем называть в дальнейшем смешанными.
Формы i//£ при преобразовании векторов Ja (a = 1,..,, т) и %s (s = 1, ..., q)
Ja^A^Jfi9 a, 0=1,..., m,
соответственно
*s=bUt> s,t = l9...9q,
•Докл. АН СССР. 1949. Т. 64, № 5. С 641-644.
5

где ||Л£||, ||fc* || — единичные ортогональные матрицы, преобразуются по закону
Ф'а= АЩ, а,/3=1,..., т, s = l,..., q
или соответственно
К= К К* *>' = 1>..., <7, а=1,..„ га.
Мы рассмотрим два важнейших арифметических инварианта системы форм {\ps },
а именно ранг г и тип Г.
Ранг г системы { ф } = { i//* } есть число линейно независимых форм ф1 ,..., ф£
(&; = 1,..., га). Ясно, что ранг г есть инвариант системы {ф}, т.е. не зависит от
выбора репера /i,..., /m; £i,..., £g и имеет вполне определенный геометрический
смысл. А именно, ранг г равен числу параметров, от которых зависит qr-вектор
нормали Eq - { ti,..., %q }, или, что то же, касательная плоскость Ет = {Jl9..., Jm) .
Мы будем называть ранг форм {ф } рангом поверхности.
Поверхности ранга г, как легко видно, состоят из плоскостей Ет_г, вдоль
которых касательная плоскость Ет постоянна: Vm = °°гЕт_Г9 где вдоль Em_r Eq -
~ { £i»•••> %q } остается постоянной.
Поверхности малого ранга г <т могут рассматриваться как аналоги
развертывающихся поверхностей в Еъ.
Тип t системы {ф} определяется следующим образом.
Составим выражения
1 a J Ofj ... ol
Вообще
h.-vj"[v,....j-Vi....r1]'
где а. = (а1! ... а1), i = 1,..., т+1, суть произвольно фиксированные комбинации
индексов о^ = 1...., га.
Если [^ ] == 0 для любой комбинации д, то тип системы t (ф) = 0.
Если [Ч?а ] Ф 0, но [^fl \1>& ] = 0 для всех а, Ь9 то тип t (ф) = 1, и т.д.
Вообще, если [Чг ... Ч?а ] ф 0, но \ч?а ... Ч?а 1=0 для всех аг, ..., я . ,,
а 1 аГ I ! Г + 1 I Т 1
то тип Г(ф) = т. I J
Данное нами определение типа по существу совпадает, с аллендорферовским
определением, но отличается от него по форме.
Типом поверхности Vm в данной (произвольной) точке называется тип системы
форм {ф} = {ф*а).
Очевидно, тип инвариантен относительно выбора реперов /i,..., Jm, §i, ., %q-
Для случая гиперповерхности тип t совпадает с рангом г, и в этом случае теорема
Аллендорфера вырождается в теорему Beez'a об однозначной определенности
гиперповерхностей ранга > 2.
Для дальнейшего введем еще одно понятие.
Будем называть систему форм { ф } = Кф%\ типа t непростой, если можно образо-
6
г к*^ •••*«,>]'
i«,= 1,
т;

вать такие линейные комбинации <р'а= ^i^5»-»» <?£ = ^P,//S» s = l,..., q, a = l,...,
1<P< 9, °
M x1,
tf KW
m,
rang
= P,
что система форм {V } = {<£« ••• ^ ) имеет тот же тип г. В противном случае систему
{\jjs } будем называть простой.
Тогда имеет место следующая
Теорема алгебраической структуры. Если система форм {\jjsa)
типа t простая, то ранг системы г < N*, где число N*, зависит только от t и q,
но не зависит от т.
Для q =2 удалось найти точные оценки, а именно Nf = 1, Nj = 3, N? = 5,
вообще N{ = It + 1.
Для общего случая q>2 удалось установить только оценки сверху, например:
Л£<<7(<7-1)/2, Л£< 2q2 + q2(q-l) = q3+q2,
N2q< %q(q2+q+2).
В частности, из нашей теоремы следует, что, грубо говоря, простые системы "малого"
типа имеют "малый" ранг.
Непосредственным применением предыдущей теоремы получается
Теорема геометрической структуры. Если VmC Em + q, t{ Vm) =
= *(*£) = t, то
КпсУт + .> rang Vm + S < (Л£ + 1)2^-^^-1, (*)
где s может меняться от О до q — 1, р есть размерность максимальной простой
подсистемы (<р) С (ф) = (ф^ ... ф%), обладающей тем же типом, что и (ф).
Или же, формулируя описательно:
Поверхности малого типа принадлежат поверхностям малого ранга или же суть
сами поверхности малого ранга.
Для случая q = 2 удалось получить точные оценки и тем самым прийти к
эквивалентному геометрическому определению типа.
Именно, имеет место следующая теорема:
Теорема. Поверхность Vm С Ет + 2 типа t (t = 0, 1, 2, ...) удовлетворяет
альтернативе:
1) Vm есть ранга г = 2t или 2t+ 1;
2) Vm принадлежит гиперповерхности Vm + i ранга г = t.
Обратно, если поверхность Vm удовлетворяет альтернативе 1) и 2), она есть
поверхность типа t.
Таким образом, в случае q = 2 альтернатива 1)—2) есть полный геометрический
эквивалент данного нами аналитического определения типа.
Легко видеть, что в случае q - 2 тип поверхности является ее проективным
инвариантом, т.е. проективное преобразование евклидова пространства Еп переводит
Vm в Vm того же типа.
Из теорем геометрической структуры и из теоремы Аллендорфера имеем, в
частности:
Для того чтобы поверхность Vm допускала нетривиальное изгибание,
необходимо, чтобы удовлетворялись условия (*) (в случае q = 2 альтернатива 1) —2)).
Полученные нами теоремы структуры дают возможность сформулировать следую-
7

щие необходимые условия того, чтобы данное риманово пространство Vm класса q
допускало неоднозначно определенное вложение в Ет + q.
Теорема. Для того чтобы вложение Vm С Em + q было неоднозначно
определенное, необходимо, чтобы Vm допускала расслоение на R-параметрическое
семейство метрик Vm_R, каждая из которых класса s < q — 1: Vm = °°RVm-R, класс
Vm_R = s < q — 1, причем R - число, зависящее только от s и q.
Для случая q =2 можно сформулировать более точную теорему.
Теорема. Для того чтобы метрика Vm класса 2 допускала неоднозначно
определенное вложение в Ет + 2, необходимо выполнение одного из условий:
1. Vm допускает расслоение на 5-параметрическое семейство евклидовых метрик:
Ут = оо5£
'm '-'тп — 5 •
2. Vm допускает расслоение на двупараметрическое семейство метрик класса 1:
Vm = °°2Vm_l, где класс Vm_1 =1.
ЛИТЕРАТУРА
1. Allendorfer СВ. // Amer. J. Math. Soc. 1939. Vol. 61. P. 633.
О СВЯЗИ МЕЖДУ МЕТРИЧЕСКИМИ
И ПРОЕКТИВНЫМИ СВОЙСТВАМИ ПОВЕРХНОСТЕЙ*
1. В предыдущих заметках [1, 2] нами были даны определения проективно
инвариантных понятий ранга поверхности и фокальных плоскостей поверхности и в этих
проективно инвариантных терминах сформулирован ряд необходимых признаков
изгибаемых поверхностей.
Как известно jj3 этих заметок, поверхность Vm С Em+qy допускающая собственное
изгибание Vm со Vm, допускает расслоение на °°г плоских образующих Ет_Г9 вдоль ко-
торых ^-нормаль £i ... %q остается постоянной. Удалось установить дальнейший
необходимый признак собственного изгибания, характеризующий инфинитезимальную
структуру пересечений плоских образующих. Именно, справедлива следующая теорема:
Теорема 1. Плоскость Ег 1 Ет _г (Ег + Ет_г = Ет, где Ет - касательная
плоскость к Vm ) может быть представлена в виде
Er=EPi +^2 + ...+£/0р(р1 +р2+...+Рр=г), (1)
причем каждое направление плоскости Ер является фокальным и любая плоскость,
построенная на фокальных направлениях, является фокальной. Этот необходимый
признак также является проектено-инвариантным.
Аналитически этот факт означает наличие репера Jx ... Jr, Jr+1 ... Jm, Jm + i = %\, ...,
Jm+q = %q (удовлетворяющего требованиям Jm +sJa = bm +sa, 5=1,..., q, a = 1,..., m+q),
в котором формы Картана соа, со^ имеют вид
т+* = со<* =0) 5=i, ...,4, а = г+1,...,т;
<х m+s ' ' '^' ' ' '
со' =а[ со' = касо',
i = 1,..., г, а = г + 1,..., m (по / не суммируется),
со? + 1 =П; со7', \* .. =0, Kair Фк^т . (2)
*Докл. АН СССР, 1952. Т. 82, № 5. С. 685-688.
8

Такой репер мы будем называть фокальным. Отличительный его признак состоит в
том, что векторы Jx ... Jr являются фокальными векторами.
Если формы со' являются дифференциалами: со' = du\ то фокальный репер/i ... Jm
будем называть голономным.
Теорема 2, Радиус-вектор г собственно изгибаемой поверхности с голономным
фокальным репером удовлетворяет системе дифференциальных уравнений
Ъг . Ъг Ъг
+ <.—7 +<• —-, i^h a = r+l,...,m;
д2г
ЪиЫи'
д2г
ди'Ьи"
Ъгг
Ч Эй' "ди1 V диа'
, ЪГ а Ъг
=4|£Г'+<5Г'',в1""-г' a=r+1 m; (3)
Ъи°ъие=0'а'*=г+1>-'т-
Обратно, если радиус-вектор г поверхности Vm С Em+q удовлетворяет системе
(3), поверхность Vm есть поверхность ранга г с голономным фокальным репером.
Переходя к тангенциальным координатам, можно дать иную дифференциальную
характеристику изгибаемым поверхностям.
Пусть 7TS есть левая часть уравнения
*s=Jm+s(r-ro) = 0 (4)
касательной гиперплоскости Em+q_l к поверхности Vm в точке М с
радиусом-вектором г0.
Теорема 3. Левые части its уравнения касательных гиперповерхностей к
собственно изгибаемой поверхности с голономным фокальным репером удовлетворяют
системе уравнений
Ъи
'1 = 1,...,Рь h=Pi + 1,...,Рг >-»-'..,'р -Pp-i + l,.»,Pp=r; (5)
где Р1 = 0 - уравнение некоторых гиперплоскостей. Исключая Р*, получаем уравнение
d2^ dirt Этт, т
мыши fttasikilfkt bulk ii asi^f buh +0W/*r;
dns bit* birs dns
= 0, (6)
1дирк+1 Ъир*+2 ■"' Ъир*+1 Эн'*+1
Si,s2,...,s= 1,...,C7, k = 09...,p- 1,
где [ ] = 0 означает линейную зависимость векторов в скобке.
В частности, собственно изгибаемая поверхность с конечным числом фокальных
плоскостей всегда имеет голономный фокальный репер и удовлетворяет системе
уравнений
Ъ2п5 bns diTs
ЪЯТ*** "^7 +ttsft^P~ +ll„"r. *r-l q; t/-l,...,r; /#/; (7)
bns I Ъпт I я
~bi;/K<~-^/K't=^kTsU^s,t,r=l,...,q; /=l,..,r<2*

2. Для того чтобы поверхность Vm CEm+q допускала изгибание, необходимо, чтобы
коэффициенты asiJ-9 к* удовлетворяли некоторым условиям.
В случае q = 2, г = 4, I к1, к1. I Ф 0 можно сформулировать необходимые и достаточ-
к 4\
ные условия собственного изгибания1 поверхности.
Образуем величины
2 2
Ып(о{-о1коа1ок1)
о,= Е к/4 af/=2 к* к Г, /,/=1,...,4,
aifk = 2^ - -—-| + , (8)
/ Э 1пк/\
а<> = 2\а°>--^г) Ъи>
1Ф]'ФкФ1, i,j, Аг, /= 1 4.
Теорема 4. Необходимое и достаточное условие того, чтобы поверхность общего
положения допускала изгибание на °° неконгруентных поверхностей, имеет вид
<*//* = 0, (Ф;Фк, /,/Д=1 4, (9)
dctij/du1 = dctji/duJ = (XjjCLji9 гФ]', i,j= 1, ..., 4.
*
Эти необходимые и достаточные условия являются аналогом формул, полученных
для изгибаемых гиперповерхностей С браном и Картаном.
С поверхностью общего положения можно ассоциировать систему инвариантов sh
удовлетворяющую уравнениям
й bsjbu* = a1.. sf - а\. Xih й Э^/Эн* =а]а si9 (10)
(Sf — Ац) (5/ — Aji) = Сij,
где Аф Су, 2# суть внутренние величины, связанные с метрикой поверхности.
Для того.чтобы поверхность Vm допускала непрерывное изгибание, необходимо и
достаточно, чтобы система (10) допускала бесконечное число решений.
Пусть 5? — инварианты данной поверхности, s — инварианты ей изометричной,
a^l/fo-S?).
Величины а,- удовлетворяют системе уравнений
Эа,/Эив - а*ш o'i = 0, Вц а, + Я//а, = 1,
/,/=1,...,4; а=1,...,/и; /=£а, /=£/. (11)
Из линейности системы (11) сразу следует такое свойство изгибаемых поверхностей:
Если имеются две поверхности Vm, неконг£уентные между собой и с Vm и изомет-
ричные Vm, то существует °° поверхностей Fw <*> Fw, т. е. существует непрерывное
изгибание.
Таким образом, в случае дискретного изгибания существует только одна
поверхность
V Ф V V ™V
3, Для многомерных поверхностей понятие бесконечно малого изгибания можно
сформулировать совершенно аналогично трехмерному случаю как бесконечно малую
1 Поскольку рассматриваемый класс поверхностей определяется неравенствами, мы будем
называть такие поверхности поверхностями общего положения. Можно показать, что поверхности
общего положения допускают только собственное изгибание.
10

деформацию 8г поверхности, удовлетворяющую условию 8dr2 = 0, т. е. сохраняющую
метрику с точностью до бесконечно малых второго порядка. Но, в отличие от
трехмерного, в многомерном пространстве не всякая поверхность допускает бесконечно малое
изгибание. Таким образом, нежесткие поверхности составляют некоторый класс П.
Теорема 5, Класс П является проективно инвариантным, т. е. любое проективное
преобразование переводит нежесткую поверхность в нежесткую же.
Таким образом, наличие бесконечно малого изгибания является максимальной
проективно инвариантной характеристикой непрерывно изгибаемых поверхностей,
составляя естественную грань, разделяющую проективные признаки изгибания от
непроективных. Между бесконечно малыми изгибаниями и конечными изгибаниями
существует определенная связь.
Теорема 6. Если поверхность Vm С Ет+2 общего положения допускает
конечное изгибание и бесконечно малое изгибание, то она допускает и непрерывное
изгибание.
Теорема 1. Всякая нежесткая поверхность общего положения аппроксимируется
дискретно изгибаемыми поверхностями.
Эти результаты проще всего могут быть проиллюстрированы на примере изгибаемых
гиперповерхностей. Согласно классификации Сбрана—Картана, непрерывно изгибаемые
гиперповерхности разделяются на следующие классы: I — гиперплоскости и
развертывающие гиперповерхности (поверхности ранга 0,1) ; II - цилиндрические и конические
поверхности (поверхности ранга 2 с °° фокальных направлений); III - поверхности
ранга 2 с одним кратным фокальным направлением; IV — поверхности ранга 2 с двумя
фокальными направлениями. Эти поверхности удовлетворяют уравнению
Э2ет Зет Зет
—— =а — +0— +77Г, (12)
OU OV OU OV
где я — нормированная левая часть уравнения касательной плоскости поверхности, а
коэффициенты а, /3 удовлетворяют условию
Ъа/Ъи = Ър/дь = оф. (13)
Классы I—III проективно инвариантны, класс IV — нет. Однако если рассмотреть
класс IV нежестких поверхностей ранга 2 с двумя фокальными направлениями, то они
по-прежнему удовлетворяют уравнению (12), коэффициенты а, /3 удовлетворяют
условию Эа/Эы = Э/З/Эи, которое уже является проективно-инвариантным. Таким образом,
класс IV является проективно-инвариантным,
ЛИТЕРАТУРА
1. Яненко Н.Н. И ДАН СССР. 1949. Т. 65, № 4.
2. Яненко НН // Там же. 1950. Т. 72, № 6.
О КЛАССЕ РИМАНОВОЙ МЕТРИКИ*
Как известно, классом m-мерной вещественной римановой метрики ds2 = gtjdulduJ
(i, /=1, ..., m) называется число q такое, что метрика ds2 реализуется в виде т-мерной
поверхности Ущ в (m + q) -мерном вещественном евклидовом пространстве Em+qy
но не реализуется в пространстве меньшей размерности. Условие того, что данная
метрика имеет класс 0, т, е. является евклидовой, имеет вид Rijfki - 0,', h k, I= 1» —> m>
где Rijfki — тензор Римана—Кристофеля,
* Докл. АН СССР. 1952. Т. 83, № 4. С. 533-536.
11

Полная классификация метрик класса I стала возможной в результате работ [1-5].
В настоящей заметке формулируются необходимые и достаточные критерии класса
< q для метрик типа t > 3 (определение типа метрики дается ниже; см. также [6]).
Сформулируем основную теорему существования, с помощью которой получаются
критерии класса метрик.
Теорема 1, Если система линейных дифференциальных форм от дифференциалов
du1, ...,dum:
co/;cow+5 = 05[co1 ...со"1] ^0, /=l,...,m, s=l,...,<r, (1)
co£, a,0=l,...,m+<7,
и симметричная положительно определенная матрица gap (и1, ..., um), Det(gap) Ф 0,
удовлетворяют соотношениям:
(со*)'= [со'* со"], а=1 /fi+flf, /= 1 (2а)
(co))'=[co*co'J 4"p4,J> /,7=1, ...,m, s=l,...,<?; (26)
(а>™+°)'=Щ"™+5] +[«7+fcom;f*]; (2в)
(со'' + У = [со7' ■ со'. ] + [со"1 I* со'' 1 ; (2г)
(^jn +s у = r m +/ m +si + r m +r m +s i (2д)
^ w+Г7 L m+f i J L m+t m+Ti9 v M/
dgaP = b>Zgyft+<<>}gya* (2')
го система дифференциальных уравнений
dr=GJiIi, dIa = G>Plp (3)
w конечных соотношений
g*fi = I*h (4)
вполне интегрируема и определяет с точностью до движения поверхность Vm С Em+q,
для которой уравнения (3) являются деривационными формулами,
В дальнейшем мы ограничимся реперами {/<*}, для которых
Im+sIoc=Zm+sa = bm+sa> S=l9...9q, С* = 1, ..., m + tf. (5)
В таких реперах имеют место соотношения
со
= -g"o>^°, «£««-«£« dgif = a>".gki + o>«gki. (6)
На основании теоремы 1 задача определения класса метрики ds2 =^//со'со/, /, /= 1,...,
т, где со' — линейные формы от du1;..., dum, ставится следующим образом.
Возможно ли к системе форм
co'',cow+5 = 0, /=1,...,т, 5=1,...,?; (7)
со{=ГДсо*, /,/=1,...,т
(Г.£ — неголономные коэффициенты связности метрики) присоединить систему форм
ф? = ы™+5, *=1,...,</, i=i,...,/я;
так, чтобы удовлетворялись условия (2). Если это возможно, то в силу теоремы 1 класс
метрики < q.
Отметим, что условия (cow+*)' = [co'co™**] = ° означают соГ"+* = ^со7, X// = ijh
s= l,... 9q,i,f= l,...,w.
12

Опуская в условиях (26) индекс / с помощью тензора ##, мы можем привести их к
виду
% = ("//)' - [<of со*,] =*//,*/ [du* dul] = I [ф* ф» ]. (9)
s=l '
Для дальнейшего введем несколько понятий чисто алгебраического характера.
Определение \. Системой скалярных произведений называется система чисел
2<*0 = 2ра, получающаяся из некоторой квадратной симметрической матрицы 2ар =
= £ра (а, /3 = 1,..., т) выбрасыванием некоторых ее элементов.
Определение 2. Система скалярных произведений 2а^ = 2^а (а, (3 пробегают
некоторые части сегмента [1 ... п]) имеет класс q, если система уравнений
р
2а0 = 2 // uj = (ма »р) (Ю)
■5=1
разрешима при р = #, но не разрешима при р < q.
Система (2ар) класса q называется жесткой, если уравнения (10) при р = q
допускают единственное решение, и нежесткой в противном случае.
В двух частных случаях алгоритм определения класса довольно прост.
А. В случае, когда система (2ар) есть квадратная симметричная матрица II 2ар II
(а, /3=1,..., т). В этом случае класс (£ар) равен рангу матрицы II 2ар II.
Б. В случае, когда система имеет вид, представленный на рисунке, т, е. состоит из
[т(т — 1)]/2 невырожденных квадратных матриц т/;-, в каждой из которых имеется
q2 элементов Lijst. При этом диагональные квадраты не заполнены. Элементы этой
матрицы образуют систему скалярных произведений (LijSt).
Условие класса q состоит в следующем. Приравниваются нулю определители (q +
+ 1)-го порядка и отсюда явно определяются элементы Ltjst центральных матриц как
рациональные функции величин Lijst. Ранг полученной матрицы должен равняться
q. В этом случае величины Ljfst реализуются как скалярные произведения векторов
4 т т
afS: 2 aisaft = Lijst. Условие вещественности реализации состоит в положительной
Т = 1
определенности полной матрицы Lijst.
Определение 3. Присоединенной системой линейных форм данной системы
косых #-форм
/i,..., iq = l,...,m, a=l,...,m,
где aai _;,• — антисимметрический тензор, называется совокупность линейных форм
m
13

Базисом и рангом системы форм (11) называется, соответственно, базис и ранг
присоединенной системы форм.
Определение 4, Рангом метрики ds2 = #,yCo'co7 называется ранг системы
билинейных косых форм £2# = Ry ki[dukdul]. Из условий (9) легко следует, что для
метрик класса < q формы
Ф«р =[««„], «,0=1,...,«, (12)
являются простыми в любом репере.
Определение 5. Обозначим Uap — базис Фар, га/3 — ранг Uap\ Uaapy — базис
ф<*0> фс*7> Г<*<*07 ~ РЗНГ Uolol^ UocfiyS ~ базис Ф&р„8, га0у8 ~ Р*НГ Uapy8 И Т, Д. Тогда,
по определению, / = 0, 1, если в любо^ репере Фар = О или rap < 2q; t = 2, если Фар Ф О,
rem07 < ^Ъ Г = 3> еСЛИ Г<*<*07 ^ 3?' Г<*075 < 4?' Т' е' [Ф<*0 Ф7« ] = О, И Т. Д.
После этого можно сформулировать следующие теоремы.
Теорема 2, Если тип метрики > 2, то ранг и тип метрики совпадают
соответственно с рангом и типом реализации.
Теорема 3. Если тип метрики > 3, то условия (2г) являются следствиями
условий (26), (2в).
Теорема 4, Если тип метрики t > 4, то условия (2в), (2г), (2д) алгебраически
следуют из условий (26).
Теорема 5. Если тип метрики t > 3, то условия (26), (2в) эквивалентны
условиям
КД...^1 = 0> Ui,...,/<,el, •..,»!, (13)
где
A* = (^)'-[cof^], 4 *=1 m. *=1,...,?. (14)
Теорема 6, Для того чтобы условия (9) выполнялись, необходимо и достаточно
выполнение следующих условий,
А. Система уравнений
[Ф/7- \р{\ = О, / произвольно фиксировано, / = 1,..., m, (15)
где \pt - линейные формы, должна иметь q и только q линейно независимых решений
Ч>\9..., <£? для любого /= 1,..., т, причем [</?! ... <£?<£? ... <£?] =£ 0.
Б.
[щ*1 ...^-1^Г1^...^/^1... ^]
A/sf» О6)
где Z,^ - числа.
В. Алдгс системы скалярных произведений LtjSt равен q.
Легко видеть, что условия А сводятся к оценке ранга некоторой системы линейных
однородных уравнений, *pf находятся как решения системы линейных однородных
уравнений. Следует заметить также, что система Lijst при t > 3 жесткая, формы
^/определяются из (9) однозначно.
Теорема 6 дает условие разрешимости системы уравнений
n,;=Z Г0/0/1. /,/=l,...,m.
ty=Z [*/*/], /,/=1,
Можно указать также алгоритм для определения \jjf. Действительно, из уравнений
я
LiJst=Z aj a* /,/=l,...,m, s, t= l,...,?, (17)
величины а£ определяются с помощью рациональных операций и операции извлечения
14

корня. Тогда ф? определяются с помощью соотношении
' т=1 '* '
Теорема 7. Если тип метрики t>3,To из соотношений (9) следует
*; = Х*.аУ, Ц; = \*г (18)
На основании этих теорем можно сформулировать следующие условия класса.
Теорема 8. Для того чтобы метрика ds2 - gybi'di1 типа t > 4 имела класс,
равный q, необходимо и достаточно выполнение условий А—В теоремы 6,
Теорема 9. Для того чтобы метрика ds2 = g,yCo'W типа t>3 имела класс,
равный q, необходимо и достаточно, чтобы выполнялись, кроме условий А—В теоремы 6,
условия
[А^...^] = 0, /,/!,..., /g = l,...,m, (19)
гдеА*. = (Фр'-[<*>{*)].
Заметим, что мы рассматриваем метрику в репере общего положения, т. е.
предполагаем, что все соотношения типа / Ф 0, которые могут быть получены в результате
преобразования репера, выполняются.
ЛИТЕРАТУРА
1. Sbrana U. // Rend. Ore. Mat. Palermo. 1909. Vol. 27.
2. Cartan E. 11 Bull. Soc. Math. France. 1916. Vol. 44.
3. Weise KM. // Math. Ann. 1934. Vol. 110. P. 522.
4. Thomas W.I. // Acta math. 1936. Vol. 67. P. 169.
5. Розенсон Н.А. 11 Изв. АН СССР. Сер. мат. 1943. Т. 7, № 6. С. 253.
6. Яненко Н.Н. //ДАН СССР. 1949. Т. 64, № 5.
МЕТРИКИ КЛАССА 2*
В заметке [1] нами были даны необходимые и достаточные условия того, что
данная метрика ds2 = g^co'cc?7 (/, / = 1, ..., т, со'— линейные формы от дифференциалов
dul,..., dum) имеет класс, равный q, для случая, когда тип метрики t > 3.
Общая теория применима полностью и к случаю q = 2. Таким образом, подлежат
исследованию метрики типа t < 2. В случае метрик класса 2 можно сформулировать
следующую теорему
Теорема 1. Для того чтобы метрика
ds2 = gijof<J, i, j = 1,..., m,
runat > 2 имела класс < 2, необходимо и достаточно, чтобы существовала система
форм oj™+s = \ps = Xs.cJ\ Xs.. = Xs.., s = 1, 2, i = 1,..., m, удовлетворяющая условиям
Д[^;]=Яу=Я.. kl[o>kc>1]; (1)
[д'оЛ!,]=[д;«;,'0|;[^;>]",д!('*А1"0' <2)
♦Докл. АН СССР. 1952. Т. 83, № 5. С 667-669.
15

где
AJ = (**)' - ЩЦ\, »=1,2, i,j=l,...,m.
(3)
Условия (1) суть условия Гаусса, условия (2) эквивалентны условиям Кодацци-
Риччи.
В дальнейшем рассматриваются метрики типа t = 2 и ранга > 4.
Согласно теореме 2 заметки [1], в случае t > 2 ранг и тип метрики совпадают с
соответствующими инвариантами поверхности, реализующей метрику. Как известно [2],
поверхности типа 2 суть или поверхности ранга г = 4, 5 или, в случае г > 5, подповерх-
ности гиперповерхности ранга 2.
Это означает, что формы co™+s = ф11. должны удовлетворять альтернативе:
1) ранг {ф*}> 5, но зато имеется комбинация ф( = Хф^ + уф2 ранга 2;
2) ранг{1//?}= 5 (случай г- 4исключается из рассмотрения).
В случае 1) можно сформулировать следующую теорему.
Теорема 2. Если t = 2ur>5,TO система уравнений
(4)
[<V]=0>
где
*«р-[п(в1/»,"«,/»,)]
и симметрирование производится по (о^аО, (|3ij32) в отдельности, <р - линейная форма
от со1,..., сот, имеет два и только два линейно независимых решения *р\,*рг.
Это условие проверяется, а формы «^, <р2 находятся с помощью операций линейной
алгебры..
Пусть Д „. 7W — репер, в котором
{со1, со2} «{0lfy2 }, (6)
где значок ^ означает, что формы со1, со2 разлагаются по формам *р1, <р2 и обратно.
Репер {Л ... /w}, формы со', £2/7 и компоненты^- находятся с помощью линейного
алгоритма.
Пусть форма ф((Г) определяется с помощью равенства
0(d) = Д"
«32(4 80
«31(^82)
«32(4 82)
где
k2i2(8i,8a-) «12(82. <0 «12(^80
A=h23(8i,82) £223(82,<f) ft23(4 80
p3i(8i,82) ^31(82,^) fi3i(4«i)
Образуем {m + 1)-мерную метрику
ds^g.M + t^2,
где
П^со' + б'зЛ+Гсо'з.
(7)
(8)
(9)
(10)
Легко видеть, что метрика ds2 есть включающая по отношению к метрике ds2, т.е.
при t = 0ds2 переходит в ds2 = g..(J<J.
Теорема З.Для того чтобы метрика ds2 = gijColcJ типа t = 2 и ранга > 5 имела
класс < 2, необходимо и достаточно, чтобы метрика ds2, построенная вышеуказанным
образом, имела класс < 1.
16

Рассмотрим случай 2), когда ранг метрики равен 5.
Рассмотрим систему
[V«]=0>
(и)
где / произвольно фиксировано,/ меняется от 1 до т (i = 1,..., т).
Теорема 4. Если метрика типа t = 2 имеет ранг 5, то возможны только два
случая:
а) система (11) имеет только два линейно независимых решения </?!, <£2 ;
б) система (11) имеет три линейно независимых решения <£?,<£?, <£..
В случае а), согласно теореме 6 [1], необходимое и достаточное условие
разрешимости системы
П. = £ №Ф'-]> if/=l,...,m
состоит в том, что система скалярных произведений
hu =
'/21
2 Л]
£.
//12
Lij22
[&ijViVj]
ЬрУ§<р}-*}]
имеет класс 2.
Формы ф1. ,ф2 могут быть явно выражены через <р!, <р? [ 1].
В силу теоремы 1, для того, чтобы метрика имела класс 2, необходимо и
достаточно, чтобы определенные таким образом формы $s. удовлетворяли условиям (2).
В случае б) вновь оказывается возможным построить включающую метрику.
Пусть 1Х ... Im — репер, в котором
со1, со2, со3 со ^ , tf, tf
(i произвольно фиксировано),
«41(4 «О «41(4 82)
nA2(d,6x) n42.W82)
1^12(81,82) n12(82,d) £212(£/,б!)
«24(8i,82) «24(8i,82) «24(^8!)
1^41(81,62) £241(62,tf) «41W8O
где
nf = со1'+6i£/r + rcoi.
Тогда для того, чтобы метрика <is2 = gijcj'cj имела класс < 2, необходимо и
достаточно, чтобы ds2 имела класс < 1.
Заметим, что мы рассматриваем метрику в репере общего положения, т.е.
предполагаем, что все соотношения типа / Ф О, которые могут быть получены в результате
преобразования репера выполняются.
ф = Д"
А =
ЛИТЕРАТУРА
1. Яненко Н.Н. И ДАН СССР. 1952. Т. 83, № 4.
2. Яненко Н.Н. // Там же. 1949. Т. 64, № 5.

МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ СВЯЗЕЙ
БЕГУЩИЕ ВОЛНЫ СИСТЕМЫ КВАЗИЛИНЕЙНЫХ УРАВНЕНИЙ*
1. Рассмотрим систему квазилинейных уравнений вида
2aikJ(uu...,um)--— =0, i,j,k=l,...,m. (1)
/, / Эх,
Назовем бегу щей волной 1-го рода (простой волной) решение u£xl9 ...9хт)9 i = 1,...,
га, имеющее общую систему гиперповерхностей уровня.
Таким образом, по определению, должны иметь
Щ=Ш)> i= 1, ...,т, (2)
гдет(Х1, ...9хт) — некоторая функция отх1? ...9хт.
Подставляя (2) в (1), получаем систему уравнений
Ът
ЪА1к- =0, i,*=l,...,/w, (3)
i dxf
где
^ f-
Atk = *atkj(fi..'.fm)TL> i,j,k*l9...9m. (4)
/ от
Для того чтобы система (3) допускала нетривиальное решение, необходимо
условие
Det| 4/jk|=0. (5)
Уравнение (5) есть обыкновенное дифференциальное уравнение 1-го порядка с m
неизвестными функциями и имеет решение, зависящее от га — 1 произвольной
функции одного аргумента.
Тогда из системы (3) будем иметь
дт/дхх дт/дх2 дт/дхт
—а = —л"— = •* = ~~а > (6)
Ai А2 Am
где Al9 ..., Ат — известные миноры (т — 1)-го порядка, являющиеся функциями от г.
Общий интеграл системы (6) имеет вид
Ai (т)*! + ... + Aw(r)xw + Л(г) = 0, (7)
где А(г) — произвольная функция от т.
Рассматриваемая в пространстве (xl9 ...,xw,t) гиперповерхность (7) представляет
собой "линейчатую" гиперповерхность, состоящую из плоских образующих,
параллельных оси т.
Решение (7) системы (3) зависит, таким образом, от га произвольных функций
параметра г (существенно от т — 1 произвольных функций одного параметра).
2. Рассмотрим систему уравнений гидродинамики трехмерного изэнтропического
*Докл. АН СССР. 1956. Т. 109, № 1.
18

движения
1 Эр
Р Эх,
р = а2ру.
= — + 2 wfe
ЭГ fc=l Ъхк
Эр з Э(рц^) _^
ЭГ fc=l Ъхк
Пользуясь соотношениями
с2 = dp/dp = уа2ру~1. (7 — 1 )<ilnp = 2d\nc,
получим систему уравнений
2 dc dtii з bus
с + + 2 ик =0, i=l,2,3;
7—1 Эх/ bt k=i Ъхк
Ъс з Ъик 2
+ 2 с - +
7-1 bt k=i
Ъхк
7—1 к=\
з Ъс
2 и*- =0.
Ъхк
(8)
(9)
(10)
Положим
щ = иг{с).
Тогда уравнения (10) примут вид
# Ъс з
щ — + 2
ЭГ Л;=1
"*И/ +
7-1
сд:
ik
2 Эс 3
+ 2
7-1 ЭГ *== 1
7-1
ик+сик
Ъс
Ъхк
Ъс
Ъхк
= 0,
о;
где точка означает производную по с; 5,^ — символ Кронекера.
Отсюда уравнение для определения функций ик(с) имеет вид
иъ
ихих +
2
7-1
7—1 7—1
"Hi +CWi
W2"2 +
и2й3
2
7-1
"3"l
7-1
Ы2+С"2
С W3"2
"з"з +■
7-1
7-1
иъ +сйъ
Раскрывая определитель (13), получим
"i+"l+"! = (2/(7-l)2,
а уравнение для функции с имеет вид
Ъс/Ъх Ъс/Ъхг Эс/Эхз
Ъс/bt
и2
= 0.
С + ("l"l +U2U2 +"з"з)
7-1
(11)
(12)
(13)
(14)
(15)
3. Нетрудно получить выражение для функций м,(с), удовлетворяющих
уравнению (14).
19

Полагая
2
- с = т, (16)
имеем из (14)
du\ +dul + du\ -dr2 = 0. (17)
Отсюда для W/(r) получаем выражения
"i(r) = /апб(т)со8^(т)£/т, ы20") = /sin^(r)sin^(r)cfr, (18)
И3(т) =/COS0 (т)</т,
где 0(т), v?(r) — произвольные функции т.
Нетрудно видеть, что в пространстве иь ы2, Из, т кривая (18) характеризуется
тем, что касательная к ней составляет постоянный угол со = я/4 с осью г, или, что то
же, с плоскостью и ь и2, иъ.
Таким образом, кривая (18) есть линия равного наклона, лежащая на
цилиндрической поверхности с образующей, параллельной оси т.
Интеграл системы (15) имеет вид
йххх +и2х2 +иъхъ - [(7- \)12^ихих + и2й2 +u3u3]t + A(T)=Q, (19)
где А(г) — произвольная функция от г,
щ = dut/dT. (20)
Таким образом, общий интеграл явно выражен через три произвольных функции
Параметризация (18) может быть преобразована к виду
wi(r) = #/sin(0 + yp)dr + *4Jsin(0 - yp)dr,
u2(r) = *4fcos(0 - <p)dr - u/cos(0 + <p)A\ (21)
w3(r) = fcosddT.
Интеграл (19) явно может быть записан в виде
^ne(r)costp(r)Xi + sinO(T)sin<p(T)x2 + cos0(r)x3 —
- |^-Т + - Tf COS[0(S) + ф) - 0(7) - sf(T)] ds +
I 2 4 r0
+ - / cos[0(s) - *(s) - 0 (r) + *(t)] Л - - / cos [0(s) + tfs) + fl(T) - </*>)] A -
4 r0 4r0
- - / cos [0(s) - *(s) + 0(r) +" <*т)] ds) + A(r) = 0. (22)
4 r0 J
Рассмотрим частный случай двухмерного движения. Тогда уравнения (14) и (15)
примут вид
«+111 = 1, (23)
Ьт/Ьх, = дт/Ьх2 -Ът/dt
их й2 (7- l)r/2 +(wiwx +и2й2У
где ii,- означает dUfldr, т = 2с/(7 — 1)«
20

Из (23) имеем
Mi = cos</?(t), u2 = sin(/?(r), (25)
и i = fcos<p(T)dTf u2 = fsimp(T)dT. (26)
Выбирая в качестве независимого переменного </?, вместо уравнения (24) имеем
Ъу1Ъхх b<p/bx2 -bylbt
= = * , (27)
со&р sin<£ Ф ((/?)
где Ф((/?) — функция от \р, связанная с функцией т(ф) соотношением
Ф(#) = т(ф) + ■/ cos(s - ip)T(s)ds. (28)
2 «^0
Уравнение поверхностей уровня (гиперплоскостей) принимает вид
со&р • х! + sirup • jc^ — Ф(<р)Г = Д<р» (29)
Соответствующие значения функций ulf и2, с имеют вид
и\ ~ fcosy • r'(ip)dip, u2 = fsirup • T'(ip)dip9
7-1 ' ч
c= т(<р). (30)
В простейшем случае одномерного течения (14) принимает вид
(Л/Л)2 =(2/(т-I))2, (31)
откуда интеграл (19) принимает вид
±x-(c±u)t+f(c)=Q, (32)
где Дс) — произвольная функция от с.
Из равенства (31) следует, что в бегущей волне сохраняется или величина г = и +
+ 2с/(у — 1), или величина s = и - 2с/(у — 1) (инварианты Римана), а из равенства
(32) следует известное представление Римана одномерной бегущей волны
c = f\±x-(c±u)t].
О БЕГУЩИХ ВОЛНАХ УРАВНЕНИЙ ГАЗОВОЙ ДИНАМИКИ*
В работе [1] были рассмотрены простые бегущие волны системы квазилинейных
уравнений вида
аук(цг,...,ит)дщ/дхк = 09 Ц,к= l9...9m. (l")
Назовем бегущей волной ранга г решение ut = М/(хь ..., хт) системы (1),
удовлетворяющее т — г функциональным зависимостям фа(ц\, ..., ит) = 0, а = 1, ..., т — г.
В данном определении бегущая волна ранга 1 совпадает с простой бегущей волной
заметки [1].
В настоящей работе на примере уравнений газовой динамики полигропного газа
рассматриваются бегущие волны ранга т — \.
♦Докл. АН СССР. 1958. Т. 119, № 3. (Соавторы Ю.Я. Погодин, В.А. Сучков).
21

Уравнения движения политропного газа
(Ъщ but\ Ър dp Ър Ъик a2py
p[— +uk — )+-:— =0; —— + w/c —— + p—-=0; p=—JL-9 (1')
\ dt Ъхк I dxf dt дхк Ъхк У 7 V }
i, k= I,..., m - 1
в адиабатическом случае в переменных щ, в = а2 ру~ */(7 - 1) принимают вид
Ъщ Ъщ Ъв Ъв Ъв Ъик
В изотермическом случае а2 = RT= const, у = 1,0 = lnp, и вместо (2)
Эй,- Ъи( , Э0 Э0 Э0 3wfc
—— + w* + д2 =0, + ик + — =0. (2')
Эг dx^ Эх,- Эг Ъхк Ъхк
Для простоты мы ограничимся случаем т = 3, хотя метод рассмотрения является
общим и применим не только для случая т = 3, 4, но и к системам типа (1).
Функциональную зависимость ищем в виде в - ^р(и ь и2 ).
Пусть дифференциальное уравнение общих линий уровня функций иь и2, 0 есть
Э/ Э/
dxj/dt = At. Тогда для любой функции /(иь м2, б) справедливо — + Ак —= 0. Поль-
Эг Ъхк
зуясь этим, уравнения (2) записываем в виде
Э^! Ъих Ъи2 Ъи2
(Mi-Ai+^i)- + (w2 -А2) —- +^2—— + 0- 7"=0;
d^i Эдг2 о*! Эх2
Э^! Э^! Эг^2 Ъи2
°' Г" + ^ Г" +("i ~Ai) 7~ + <"2 _A2 +^)т— =0; (3)
Ъхх Ъх2 Ъхх Ъх2
Ъих Ъих Ъи2
[(7-l)^ + </?i("i-Ai)] 7~ +^i("2 -Аг)— +^2("i-Ai)t +
Ъхх Ъхг охх
Ъи2
+ [(т - 1)* + <М"2 - а2)] — = о,
Эх2
где урх = 9v?/3w/, /=1,2.
Потребуем, чтобы для фиксированной функции <£(мь ы2) бегущая волна обладала
произволом двух функций одного аргумента. Для этого необходимо, чтобы ранг
системы (3) равнялся 2.
Отсюда получаем два случая:
а) & = А/ - щ = -д/, i = 1, 2;
б) ацрх +а2у2 = 0, (д2! +д!) [<Л + ^1 — (Т — !)</>] =(7- lM^2i +fPl).
Ограничимся первым случаем, который является основным. Из а) следует, что линии
уровня прямые и А,- = ЭД/Эн/, А = </? + Щи\ + и\). Уравнения (3) принимают вид
Ls=LbUilbxj = 09 /,/,5=1,2; (4)
0ii=<*22=O, ах2 =-а21 = 1, а.. = (у- 1)<^,у - W/> (5)
5/у - символ Кронекера. Из (4), (5) следует, что движение является потенциальным.
Соотношения Э///Эt = О вместе с (5) дают новые условия:
s Ъщ Ъщ Э2А л
4-Аь,—- —- =0, Ак1= . (6)
^ klbXj Ъхк ЪикЪщ
22

Для того чтобы (6) следовало из (4), необходимо и достаточно
ЦЯ>)= [Ь- О*-*!] (*и +l) + 2v»i^3^i3 + [(7- l^-^ilfoa +0=0. (7)
Условия 3*1,73 Г* = 0, * > 1 ничего нового не дают. Отсюда следует.
Теорема 1. Если функция <p(ult u2) удовлетворяет уравнению (7), то бегущая волна
обладает произволом двух функций от одного аргумента.
С помощью преобразования годографа систему (4) можно привести к виду
[(7 - 1)* - <р\] ^ГТ + 2*иЛ - - + [Ь ~ О* - V2] Г1Г = 0. (8>
dX = x:du1 +x2du2.
Ъи 1 Эи2
Эй2,
£>=/?/# \jrf=Cfi
1 #/7 1 /
[ ^ | #/
«2% ~ CZ &
x2=fz(t)
Примыкание двойной волны к простым
Для изотермического движения при а2 = 1 \р, X удовлетворяют уравнениям
(1 -V0(<p22 + 1) + 2<^2</>12 +(1 -^)Ои + 1) = 0;
Э2Х
- д2Х
Ъи2
, Э2Х
+ (1 -<pl) —; =0-
(9)
(10)
Теорема 2. Л случае, когда у = Q + CV/1 + С2м2 — (ц\ + "l)/2, С,- - константы, все
течения конические, т.е. прямые линии уровня сходятся в одной точке (центрированная
бегущая волна ранга 2). Д)|л остальных решений <р уравнения (7) движения, вообще
говоря, не конические, но для любого решения у имеется решение X уравнения (8),
определяющее коническое течение.
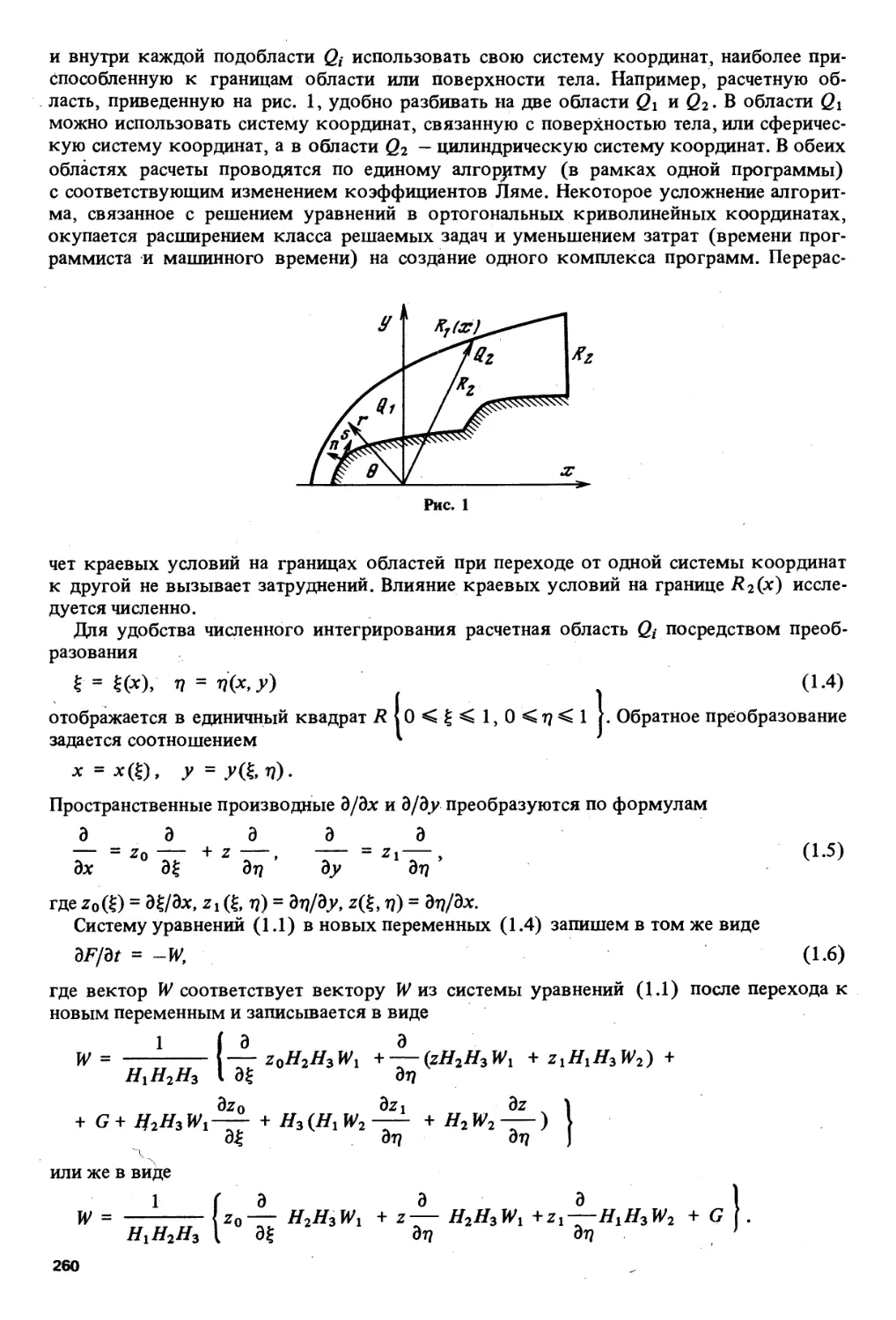
Решим теперь задачу о двух плоских поршнях, ограничившись для простоты
изотермическим случаем, когда решение получается в явном виде.
Пусть плоскости хх = 0, х2 = 0 ограничивают массу политропного газа, заключенного
во внутреннем угле. Начиная с t = 0, плоскости движутся по закону xt =//(0. В каждый
момент времени в плоскости xlf x2 будем иметь следующие области движения
(рисунок) : в области / — покоящийся газ, в областях На, 116 — простые бегущие волны.
В области III будем искать решение в виде бегущей волны ранга 2. Из условия
непрерывности примыкания волны III к волнам Па, 116 следует, что решение уравнения (9)
удовлетворяет краевым условиям
<p(fii,0)= их + Q> , Ф,и2) = и2+0> . С11)
Нетрудно видеть, что уравнению (9) и условиям (11) удовлетворяет функция в =
= *p(ulf и2) = их + и2 + 0. Из уравнения (10) тогда следует, что ut = gfycit t). Нетрудно
видеть, что фронты слабых разрывов будут прямыми, параллельными осям.
Рассуждение сохраняет силу ив случае, когда один или оба фронта являются ударными
волнами, движущимися с постоянной скоростью. Таким образом, решение имеет вид
в области / и i = и2 = 0 (область покоя);
в области Па и i - gx(x ь f), и2 = 0 (простая бегущая волна);
в области Пб их - 0, и2 = g2 (x2, t) (простая бегущая волна);
23

в области III и i =gi(xlf r), и2 =^2(^2, 0 (бегущая волна ранга 2).
Во всех областях в = y(ui> иг) ~ их + и2 + в 0, если нет сильных разрывов. В
противном случае в выражение для в входит аддитивная постоянная, зависящая от области.
Функции gt(xj, t) суть решения уравнений Римана
и/ = */[*/-(и/+1)*].
Ясно при этом, что
fft) = Ft\f0)-{ft*\)t\.
Указанное представление справедливо в следующих случаях.
1. Линии Xj = C[t суть фронты слабого разрыва. Тогда Сх = С2 = 1, функции
fi(t) могут быть произвольны.
2. Линия хх = Cxt есть фронт слабого разрыва, линия х2 - C2t есть фронт ударной
волны. Тогда С2 > 1, /2(г) = и10 > О, СХ = 1, fx(t) произвольна. В Па, III — простые
бегущие волны, в 7, Пб — постоянные движения.
3. Обе линии хх = Cit, х2 = C2t являются фронтами ударных волн. Тогда Сх > 1,
Сг > 1 ,/i = и\ о > 0,/г = "2 о > 0. Во всех областях — постоянные движения.
В адиабатическом случае функция у определяется так же, как и в изотермическом
случае, как решение уравнения (7) с соответствующими краевыми условиями;
например, в случае 1
1
<р(0,и2)-
*("i,0) =
7- 1 L 2
ч-1
их + С0
7-1
и2 +С0
Однако фронты в этом случае искривляются, и краевая задача для функции X
усложняется.
ЛИТЕРАТУРА
1. Яненко Н.Н, Бегущие волны системы квазилинейных уравнений // ДАН СССР. 1956: Т. 109, •
№ 1.С. 44-47.
К ВОПРОСУ О НЕСТАЦИОНАРНЫХ ПЛОСКИХ ТЕЧЕНИЯХ
ПОЛИТРОПНОГО ГАЗА С ПРЯМОЛИНЕЙНЫМИ ХАРАКТЕРИСТИКАМИ
В предлагаемой заметке дается полная классификация неустановившихся
плоских течений политропного газа, имеющих прямолинейные характеристики — общие
линии уровня величин и(9 с в фазовом пространстве хх, х2, t.
Уравнения гидродинамики для нашего случая имеют вид
Ъи, Ъс 2 Эм,
-I+2KC— +2 "*-^=0, i=l, 2; (1)
Ы Ъх( к=\ Ъхк
уравнение неразрывности
(Ъс 2 Ъс
2к[ —+2 и
\ к
\ ot k=l Ъх% i k=i ол^
+ сБ —*=0, (2)
/ к=\ ЪХъ
где к = 1/(7 — 1); у = cp/cv > 1 — показатель адиабаты; с2 = (dp/dp)s; р = a2(s)py; S
энтропия.
* Докл . АН СССР. 1958. Т. 119, № 3. (Соавтор А.Ф. Сидоров.)
24

Уравнения характеристик зададим в виде
Эх, _9x2_3f
(3)
причем, поскольку мы рассматриваем прямолинейные характеристики, функции ui9
е9 А( будем считать зависящими от двух параметров о^, а2, в качестве которых примем
величины
(4)
A-t=d. г = 1 2
Дифференцируя (4) подтай t, найдем выражения для Ъа{/Эхк и да{/bt, а затем,
пользуясь найденными выражениями, перейдем в уравнениях (1), (2) к переменным
ах, <х2. После этого их можно записать в виде
i4f-+f/*, = 0, /=1,2,3,
2
(5)
где
Ъс Ъих Ъих
+ h + h >
7—1 Ъосх Ъосх Ъа2
2 Ъс Ъи2 Ъи2
А2 = +/j — +/2 —,
7—1 Эа2 dct\ Ъа2
А* =
Ъс
*i =
Ъс
h
Ъс Ъих Ъи2
3 1\ т 12 -г -г 9
7—1 Ъосх 7—1 da2 Эо^ Эа2
7-1
2 Ъс Ъих Ъих
Р22 Z ГР21 —+ (*lP22 -hPll): + (?2Pll -/lP2l)—,
7—1 d<*2 oaj Эа2
2 Эс Эы2 Ъи2
В2 =- -Pl2T— + ГРИГ" + (7lP2 2 -/2Р12) — + (72Pll -/lP2l)r-,
7 — 1 Эах 7—1 Эа2 3<Xi Эа2
Эы2
2 Эс 2 Эс Э^! Э^!
#з = '—(!iP22 - /2Р12)—+ г(*гР 11 -'iP2i)—-+Р22;— -Р21— -Р12 г—
7—1 3<Xj 7 — 1 д<*2 3«i Ъа2 оа.\
+ Pi
Эы2
Эа2
P0 = 3Aj/3oy, l^iUj-AJ/c.
Так как Ai\iBi суть функции от аь а2, а уравнения (5) должны выполняться при
любом Г, то должны быть выполнены условия
Af = 0, Я, = 0, /=1,2,3. (6)
Мы получили переопределенную систему уравнений для пяти неизвестных
функций, совместность которой следует исследовать. Вначале будем считать, что их ии2
функционально независимы, т,е.
Ъих/дах Ъих/Ъа2
Ф О
К=
(7)
Ъи2/Ъах Ъи2/Ъа2
Полагая с = с{их, и2 ) и введя функцию
0(и1уи2)=2с(иии2)/(у-11 (8)
систему уравнений (6) можно записать как систему шести уравнений, однородных
относительно производных Ъи^Ъак. Ранг этой системы г <3.
Исследуя эту систему, приходим к еле дующим результатам.
25

1. Случай г = 1 тривиален, он приводит к течениям с с = const.
2. Случай г= 2 дает следующие возможности:
а) конические течения, характеризуемые условиями
р21 =р12 = 0, ри =р22; (9)
б) потенциальные течения, причем уравнения В\ = 0, В2 = 0 выполняются
автоматически, а уравнение В3 =0 дает уравнение второго порядка для функции 0:
%(7-l)fl[(l-fl?)fl22 + 2fl1flafl12+(l -^22)^ii]+%(7-3)(0?+0?) + 2 = O,
Ai связаны с 0 соотношениями
Af = iif. + % (7-l)flflf; (11)
wt и w2 определяются из уравнений А2 = 0, Аъ - 0, а затем как функции хь х2, f
находятся из соотношений (4);
в) в случае у = 2 и только в этом случае существуют вихревые течения,
описываемые уравнениями
2в2=(2и1 +А)2 +(2м2 +В)2 (12)
(Л и В константы) ;
Эа2 3с*! Эа2 Эо^ Эа2 49ai ^ пт>
(х+дО—+*—i-j—=0, х — + 7—- + (* _;,)—= 0, (13)
3j> 3j> Эх dj> Эх Ъх
где 2wt + А = х, 2м2 + i? = j>;
Д. определяются из равенств
'•-«-""'тяятт- <14>
Укажем одно частное точное решение системы (13). Пусть у/х = £. Тогда функции
at = a, lnx + <*1(£), a2 = <h lnx + а^Ш, (15)
где
о (1+t2)2
«i=/-- Т-Т7^ d* + cb
a2=o; a~T?? d*+Ca;
a\, U2> ci, c2 — произвольные постоянные, суть точные решения системы (14), и
соответствующее течение является вообще говоря вихревым и не принадлежит ни к
классу простых волн, ни к классу конических течений.
3. Случай г = 3 приводит лишь к коническим течениям, описываемым
уравнениями A. = 0, i = 1, 2, 3 и условиями (9).
Рассматривая далее случай, когда К = 0 (7), например и2 = /(wi)> и исследуя
систему шести уравнений, однородных относительно Э0/Эа-, 3w1/3af полученную из
системы (6), совершенно аналогично предыдущему случаю можно показать, что в данный
класс течений входят лишь простые волны или конические течения.
Таким образом, исследованы все случаи и можно сформулировать следствие:
В классе нестационарных плоских адиабатических движений газа (7 ^ 2) с
прямолинейными характеристиками не существует вихревых течений, отличных от простых
волн и конических течений.
26

ТЕОРИЯ СОВМЕСТИМОСТИ
И МЕТОДЫ ИНТЕГРИРОВАНИЯ СИСТЕМ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ*
1. Известно, что методы интегрирования нелинейных уравнений в частных
производных, развитые в XVIII—XIX в. (построение решения с помощью метода огибающих
или характеристических полос или метода Лагранжа — Шарпи), по своей природе
являются чисто геометрическими. Однако эти методы имеют резко очерченную
границу применения, будучи годными только для систем уравнения первого порядка с
одной неизвестной функцией. Кроме предложенного Риманом [1] преобразования
годографа, позволяющего сводить однородную квазилинейную систему из двух уравнений
к линейной системе, нам неизвестны какие-либо методы интегрирования систем
нелинейных уравнений. Задача нахождения общего интеграла систем нелинейных
уравнений не поставлена даже в принципе, и мы в нашем докладе не будем ее касаться. Мы
рассмотрим более частную, но, тем не менее, очень трудную задачу о выделении
классов решений произвольной нелинейной системы и об уменьшении размерности
пространства дифференциального уравнения. Задача эта имеет большое теоретическое
и практическое значение.
В связи с этим следует остановиться на двух основных методах выделения
частных решений.
Первый метод — я назову его физическим — состоит в наложении на решение
системы дифференциальных уравнений ряда дополнительных требований типа
начальных данных или краевых условий. На языке физики это означает, что, зная
состояние некоторой материальной системы или поля на данный момент времени, мы должны
определить состояние системы (поля) на все последующие моменты. На
геометрическом языке это означает, что искомая интегральная поверхность S должна проходить
через фиксированную поверхность Z меньшей размерности (задача Коши). Как
правило, задание поверхности Б определяет однозначно S.
Так как общий интеграл отсутствует, то для заданной конкретной поверхности 2
мы можем тем или иным разностным методом определить с какой-то точностью
поверхность S, не зная, правда, ничего о структуре общего решения. Тем самым на
каждый конкретный вопрос дается конкретный ответ, но не больше.
Второй метод выделения решения — я назову его геометрическим — состоит также
в наложении на решение дополнительных требований. Эти требования носят
характер описания каких-то свойств решения, и по этим дополнительным свойствам решения
мы определяем сразу некоторый класс точных решений. Ясно, что выделенный таким
образом класс решений не может удовлетворять предложенным краевым условиям
и начальным данным. Наоборот, приходится иногда по данному классу решений
определять те физические условия, которым он должен удовлетворять.
Поэтому в литературе (см. обзор Неменьи [2]) такой метод называется иногда
обратным. Мы считаем этот термин неудачным, так как он не говорит, каковы
признаки, выделяющие решения, и каковы методы выделения решения.
В настоящее время существуют два четко сформулированных метода выделения
решений.
I . Теоретико-групповая характеристика. Класс решений описывается некоторым
групповым свойством или свойством симметрии. Указывается группа преобразований
переменных, относительно которых инвариантно решение; отыскиваются соответствующие
решения. На такой основе был получен ряд важных решений (так называемые
автомодельные решения). Достаточно упомянуть имена Л.Д. Ландау, Я.Б. Зельдовича, Л.И. Седова,
К.П. Станюковича, Л.В. Овсянникова. Наиболее полно с математической точки зрения
♦Труды ГУ Всесоюз. мат. съезда. Л.: Наука, 1964. Т. 1.
27

этот подход представлен работами Овсянникова. Я не буду останавливаться на этом
вопросе, так как он освещен в докладе Овсянникова [3]. Сделаю только два замечания.
1а. Полученные таким образом точные (автомодельные) решения, как правило,
имеют вполне определенное физическое содержание, Однако большей частью класс
автомодельных решений имеет небольшой произвол. Обычно задача нахождения
автомодельных решений сводится к интегрированию систем обыкновенных дифференциальных
уравнений, что означает константный произвол решения.
2°. Подход, основанный на групповых свойствах решения, имеет отношение ко
второму методу выделений решений, о чем мы скажем несколько позже.
И. Дифференциальная характеристика решения. В наиболее общем виде этот метод
может быть сформулирован так.
К системе дифференциальных уравнений
Ф;1 *,; ик, ~^ 1~°>
1\] к э*/Г*"Э;ф... Ъх^1
i,*,a=l,..., л;/,0=1,...,/и; fa + &+...+ 0т=Р (l)
присоединяется система дополнительных дифференциальных соотношений
F3[xhuk, , ..., —£ 7—1 = 0. w
\ р к Ъхр ЪхЬ ...Э^« /
Требуется найти решение переопределенной системы (1), (1.2). Задаваясь различным
произволом класса решений, получаем различные условия на функции F3.
Соотношения (2) будем называть дифференциальными связями, ^-порядком дифференциальной
связи; решения переопределенной системы (1), (2) определяют класс решений (1)
с дифференцианальной связью или дифференциальной характеристикой. Определение
и исследование класса решений с дифференциальной характеристикой опирается в
основном на анализ совместимости переопределенной системы. Главная особенность
анализа совместимости, в отличие от обычно принятого в геометрии, заключается в
том, что не исследуется заданная переопределенная система и определяется произвол
решения, а напротив, исходя из произвола решения, находятся дифференциальные
связи.
Мы можем придать геометрическую формулировку нашим определениям, пользуясь
понятием продолженной системы. Обозначим
Ъки. (3)
c*i +... + <*„,=*< г, r=max(p,<7).
Для величин Pia a получим систему уравнений
1"<*1 ...<*т _ п (4)
а*,
/в, ...<*s+l .., ап
и конечных соотношении
ф,-(*/ЛЛ> •••> р«е%... ej = о, р, +;.. + -рт = г. (5)
Соотношения (5) получаются из (1) дифференцированием по всем переменным
xl9 .,. 9х до получения производных порядка г Система (3), (4) называется
продолженной. Тогда в пространстве переменная Pia a продолженной системы
дифференциальные связи (2) определяют векторную поверхность а.
Задача ставится следующим образом: определить условия, которым должна
удовлетворять поверхность а, для того чтобы содержать интегральные многообразия
продолженной системы в указанном произволе.
28

Заметим, что дифференциальная связь всегда может быть сделана конечной связью,
лишь бы продолженная система имела достаточно высокий порядок.
Чем больше произвол выделяемого класса, тем большие ограничения
накладываются на дифференциальные связи, тем с большей легкостью они
определяются. В некоторых простых случаях функции Fs определяются из алгебраических
соотношений или из дифференциальных уравнений невысокого порядка в пространстве
меньшей размерности.
Указанные два метода выделения решений — физический и геометрический —
представляют собой два принципиально различных подхода к задаче интегрирования. В
первом методе мы получаем конкретное решение, удовлетворяющее определенным
начальным и краевым условиям, но не имеем представления о структуре решений; во
втором методе, напротив, имея представление о структуре решений, мы не можем,
вообще говоря, удовлетворить заданным краевым условиям, т.е. получаем "формальные"
решения. Имеется ли мостик межДу указанными методами? Можно ли вторым
методом получать не только формальные решения, но и решать задачи с определенным
физическим содержанием?
В этом направлении наиболее обещающими являются исследования типа "бегущих
волн".
Рассмотрим однородную квазилинейную систему
Z flf/*(Mi,..-,Mm)r-z-=0. (6)
/, к ' ОХ к
Назовем бегущей волной решение (6) непрерывно примыкающее к тривиальному
решению
иГигО (7>
через некоторую характеристическую поверхность S.
До сих пор остается открытым вопрос о том, являются ли бегущие волны,
определенные таким образом, решением с дифференциальной характеристикой.
Исследованные до сих пор примеры бегущих волн обладали дифференциальной и, более того,
конечной характеристикой.
Перейдем теперь к обзору исследований по бегущим волнам, имея в виду
приложение их в газовой динамике.
2. Уравнения газовой динамики невязкого нетеплопроводного газа в декартовых
координатах имеют вид системы (6). Так, в случае политропного газа, выбрав в
качестве неизвестных функций компоненты скорости ulf u2, и3 и скорость звука с,
а в качестве независимых переменных — эйлеровы декартовы координаты,
приходим к следующим уравнениям:
oui^l oui 2 Ъс
^7 ?yUT"+ Гс7~=0> *'* = 2'2'3'
ot k=\ oxk 7-1 d*i
Ъс з Ъс \ з Ъии (8)
2 Ъс з Ъс \ з Ъиъ
( +2 ик— +с2 — = 0
7-1\Эг /t = i ' Ъхи к=\Ъхи
y—L\ut к=1 ОХк/ к=10Хк
Мы видим, что коэффициенты уравнений (8) являются функциями от неизвестных
величин Ui,u2,u3 и система (8) принадлежит к типу (6). Пространство
переменных ul9 u2, и3, сбудем называть пространством годографа. Будем говорить, что
решение щ(хк, t) , с (xk,t) имеет вырожденный годограф, если и{(хк, t)9 c(xk, t)
связаны одной или несколькими функциональными зависимостями,
В работе [ 1 ] Риман описал класс бегущих волн в случае одномерного плоского
течения. Ему принадлежит теорема: бегущая волна есть движение с вырожденным
годографом. Величины и9 с связаны соотношением
и±2с/(у- 1) = const. (9)
29

Дальнейшее развитие результатов Римана пошло по пути формального определения,
т.е. рассмотрения движения с вырожденным годографом.
Назовем бегущей волной ранга г решение системы (6) с вырожденным годографом,
•—-
дх,-
равен г. В частности, волны ранга
1 называются простыми, волны ранга 2 — двойными и т. д. Естественно, что сначала
были исследованы волны ранга 1. Этим исследованиям посвящены были работы Майера
[4], Буземана [5], А.А. Никольского [6], Гизе [7], Бондера [8], Бурната [9] и автора
[10]. Этот случай сейчас полностью исследован, и на нем я не буду останавливаться.
!_-
F
Исследование сильно усложняется при переходе к двойным волнам. Анализ
двойных волн не закончен и по настоящее время. К этому направлению относятся работы
А.А. Никольского [11], Гизе [7], О.С. Рыжова [12], Ю.Я. Погодина, В.А. Сучкова, Н.Н.
Яненко [13], А.Ф. Сидорова, Н.Н. Яненко [14, 15], А.Ф. Сидорова [16], Ю. Бондера
[17], Л.В. Комаровского [18]. В наиболее общей форме алгоритм нахождения
бегущих волн сформулирован в работах [13, 14, 17].
3. Перейдем теперь к вопросу о связи между решениями с вырожденным
годографом и бегущими волнами, определенными как решения, граничащие с тривиальными.
Почти все исследованные решения с вырожденным годографом являются бегущими
волнами. Однако утверждать эквивалентность этих понятий пока нет оснований.
Укажем в качестве примеров из гидродинамики следующие течения с вырожденным
годографом, которые являются бегущими волнами.
1°. Простые волны. Эти течения обладают следующим свойством: в фазовом
пространстве хь ...,'xm,t существует однопараметрическое семейство гиперплоскостей,
вдоль которых все величины ul9 ...9um9t постоянны. Ясно, что простые волны
могут граничить с постоянным движением через одну из таких плоскостей.
2°. Двойные волны в задаче о двух поршнях. В работе В.А. Сучкова, Ю.Я.
Погодина, автора [13] была рассмотрена следующая задача.
Покоящийся политропный газ заключен в квадрате х.>0, ? = 1, 2.
Плоскости хг = 0, х2 =0, его ограничивающие, начинают двигаться по закону
т.е. остаются параллельными своему начальному положению. В газе возникает
двойная волна //, которая граничит с областью покоя 0 через простые волны Римана /
(рисунок) .
4. Как видно из предыдущего, определение дифференциальной связи является
первой основной задачей, за которой уже следует задача интегрирования
получившейся системы меньшей размерности. При этом в зависимости от порядка связи и
произвола решения мы можем получать различные классы решений. Здесь, конечно,
возможна и необхошша большая классификационная работа. Однако можно ожидать,
что, даже получая широкие классы решений, мы приходим большей частью к фор-
30

мальным решениям, не связанным с какими-либо задачами физики или газовой
динамики.
Следовательно, выбираемые дифференциальные связи должны быть таковы,
чтобы выделяемые классы решений удовлетворяли каким-то физически определенным
условиям. Ясно, что все краевые задачи мы не можем решать методом
дифференциальной связи. Основной краевой задачей, которая соответствует методу дифференциальных
связей, является задача примыкания.
Пусть D0 есть область, в которой существует некоторое известное уже решение
и0(х), удовлетворяющее дифференциальным связям, Z>i - область, примыкающая
к D0 через характеристическую поверхность s.
Тогда ищется решение Wi(x), непрерывно переходящее вы0(х)через
характеристическое многообразие & Задача о примыкании, выше сформулированная, может
рассматриваться как задача Коши для характеристической поверхности. Как
показывает пример задачи с. двумя поршнями, ей можно придать и другую формулировку:
пусть в областях Di, D2 определены решения ut (х ), и2 (х), удовлетворяющие
дифференциальным связям. В области Z), граничащей cDi9D2 через характеристические
поверхности sb s2, следует определить решение w(x), примыкающее непрерывно к
Mi (*), и2 (х) через соответственно st s2.
В этом случае мы приходим к задаче Гурса. В задаче о примыкании
разграничивающей поверхности s вместо характеристической поверхности может быть ударный фронт.
Тогда соответственно формулируются условия перехода через поверхость s.
Возникающие при этом задачи рассмотрены А.Ф. Сидоровым [19].
Пока нет единого метода решения задачи о примыкании. Однако в случае простых
волн, примыкающих к тривиальному решению, справедлива следующая теорема [20]:
дифференциальные связи,характеризующие простые волны, являются инвариантными.
Как было определено в работе [20], связь (2) называется инвариантной, если для
решений и+(х), и~(х), непрерывно примыкающих одно к другому через
характеристическую поверхность s, справедливо соотношение
4''Mfc'iV •■•:aj#...d*^rF'(*''"i'dV"-' э*?> ...axj- (10)
5. Между методом дифференциальной характеристики и теоретико-групповым
подходом существует определенная связь. Частным видом автомодельных решений
уравнений газовой динамики являются центрированные или конические течения. В
одномерном случае справедлива теорема: огибающая однопараметрического семейства
центрированных течений есть бегущая волна Римана. Известные классы бегущих волн
содержат в себе подклассы центрированных волн [11, 13]. Л.В. Овсянникову [3]
удалось показать, что простые волны можно выделить также групповой
характеристикой. Вопрос об эквивалентности дифференциальной и групповой характеристик в
общем случае остается пока открытым.
6. Заметим, что и другие задачи теории квазилинейных и нелинейных уравнений
сводятся к исследованию совместности переопределенной системы уравнений. Таково,
например, исследование законов сохранения систем квазилинейных уравнений,
проведенное Б.Л. Рождественским [21 ].
7. Трудности аналитического исследования даже в случае простейших
дифференциальных связей велики. Они прогрессивно возрастают при переходе к
дифференциальным связям более высокого порядка и к более сложным дифференциальным
уравнениям. Поэтому возникает, необходимость реализации дифференциального
алгебраического алгорифма на электронных вычислительных машинах. Этому вопросу
посвящена статья В.А. Шурыгина и автора [22].
31

ЛИТЕРАТУРА
\.РиманБ. Сочинения. М.: Гостехтеориздат, 1948.
2.Неменьи // Проблемы механики. М.: Изд-во иностр. лит., 1955. С. 234-257.
З.Овсянников Л.В. II Тр. IV Всесоюз. мат. съезда. Л., 1961.
4.Мёуег Ц Forsch. Ver. Dt. Ing. Berlin, 1908. Bd. 62. S. 531-657.
S.Busemann HJ/ Luftfahrtforschung. 1942. Bd. 19, N 4. S. 137-Л44.
6. Никольский А. А. //Сборник теоретических работ по аэродинамике. М., 1957. С. 34—38.
l.Gize H Quart. Appl. Math. 1951. Vol.9. P. 237-246.
^.Bonder И Arch. mech. stosow. 1956. Vol. 8, N 4. S. 647-670.
9.Burnat И Bull. Acad. pol. sci. Ser. sci. techn. 1959. Vol. 7, N 10.
Ю.Яненко Н.Н. И ДАН СССР. 1956. Т. 109, № 3. С.'44-47.
11.Никольский А.А. И Сборник теоретических работ по аэродинамике. М., 1957. С. 39-42.
П.Рыжов О.С. И ПММ. 1957. Т. 21, вып. 4. С. 564-568.
13.Погодин Ю.Я., Сучков В.А., Яненко Н.Н. // ПММ. 1958. Т. 22, вып. 2.
Ы.Сидоров А. Ф., Яненко Н.Н. // ДАН СССР. 1958. Т. 125, № 5.
15.Сидоров А.Ф., Яненко Н.Н. // Изв. вузов. Математика, 1959. № 1. С. 187-198.
16.Сидоров А.Ф. //ПММ. 1959. Т. 23, вып. 5. С. 940-943.
П.Бондер Ю. И ПММ. 1960. Т. 24, вып. 6. С. 1079-1087.
18.Комаровский Л,В. // ПММ. 1960. Т. 24. Вып. 3. С. 491-495.
19.Сидоров А.Ф. II Тр. IV Всесоюз. мат. съезда. Л., 1961.
Ю.Яненко Н.Н. И Изв. вузов. Математика, 1961. № 3. С. 185-194.
21.Рождественский Б.Л. // ДАН СССР. 1957. Т. 115, № 3. С. 454- 457.
П.Шурыгин В.А., Яненко Н.Н. // Пробл. кибернетики. 1961. № 6. С. 33-43.
/^СВОЙСТВА СИСТЕМ ОДНОМЕРНЫХ УРАВНЕНИЙ ДИНАМИКИ
НЕУПРУГОЙ СПЛОШНОЙ СРЕДЫ*
В последнее время в ряде работ [1—4] предложено довольно-таки общее уравнение
состояния динамических процессов в сплошной среде. Их авторы пытаются
определить вид уравнения состояния с точностью до констант, исходя из физических и
математических предпосылок, а константы определить подбором при сравнении
численных расчетов с экспериментом. В предлагаемой работе изучаются некоторые
математические свойства системы уравнений одномерной неупругой сплошной
среды, при этом получаются ограничения на вид уравнения состояния. Аналогично
могут быть исследованы другие модели механики сплошной среды.
1. Введем ряд определений.
Определение 1. Система дифференциальных уравнений обладает /}-свой-
ством, если система S U D, полученная объединением системы S и системы
дифференциальных связей D [5], совместна и находится в инволюции.
Вид дифференциальных связей можно априори не фиксировать, а находить из
требования, чтобы решение системы обладало заданным произволом. Это
требование в ходе анализа на совместимость системы S U D дает условия на функции,
определяющие вид дифференциальных связей. Обозначим символом D*} »(* [тъ*} кр
j\tji->"*im h f',lp
совокупность условий существования у данной системы S решения, зависящего
от к@ произвольных функций от /р аргументов, |3 = 1,..., р, и характеризуемого [5]
совокупностью ia дифференциальных связей D порядка ja (or = 1, 2, ..., т). Кратко
назовем их £>7г-условиями. В общем случае они являются системой уравнений
в частных производных относительно функций, определяющих вид
дифференциальных связей D
Определение 2. Система S UD, удовлетворяющая D ет-у ел овиям,
называется 1>я-системой.
*Докл. АН СССР. 1974. Т. 215, № 5. (Соавторы В.М. Фомин, В.П. Шапеев.)
32

Определение 3. Решения системы уравнений S, являющиеся решениями
/Эя-системы, называются /Эя-решениями.
Применим понятие D-свойства к системе уравнений динамики одномерной
сплошной среды в безразмерных переменных
Щ = ох, et = vx (1)
с уравнением состояния
ot = А (о, 6) et 4- В (а, б) ех 4- Н (а, е) ох 4- С (о, б), (2)
где а — напряжение, v — скорость перемещения материальной точки, е —
деформация, t — время, х — лагранжева координата, а коэффициенты А(о, б), 5(а, б),
С(а, б ) и Я(а, б ) — пока произвольные функции своих аргументов.
Предварительно' потребуем, чтобы системы (1), (2) имели гри вещественные
характеристики, модули тангенсов углов наклона двух характеристик разных
семейств в точке пересечения были равны, и третье семейство характеристик
совпадало с траекториями частиц среды. Отсюда следует, что уравнение (2) должно иметь
вид
at = a (о, e)et + с (а, б). (3)
К системе (1), (3) присоединим самую общую квазилинейную дифференциальную
связь первого порядка
А (о, б) ох 4- Е(о, б) et 4- F(o, б) ех 4- G (о, б) = 0 (4)
и выпишем D} я?-условия для системы (1), (3), (4). В результате анализа на
совместность устанавливаем, что в общем случае вместо (4) достаточно рассматривать
связь
ох = Е(о, e)et + F (a, e)ex + G(o,e)- (5)
при этом имеют место два случая D \ я\ -систем с решениями
F=0, а=Е2, c = ±c3(l3 +c4c%l4 +c1c%l4e)i/2,
E = c3l, G = ±ll/2 + с/с3 •/, 1 = схо + с2\ (6а)
£ = 0, а=Е, G = cxc(p,e), F = c (f (c3/c2)da + /(б)). (66)
Здесь сь с2, ^3» ^4 — произвольные константы, /(б), с(а, б) - произвольные
функции соответственного одного и двух аргументов.
Теорема 1. Для того чтобы система уравнений (1), (3) имела D\it*-решения,
характеризуемые дифференциальной связью (5), необходимо и достаточно, чтобы
коэффициенты уравнения состояния определялись либо соотношениями (6а) с
произволом в четыре константы, либо соотношениями (66) с произволом в одну функцию
одного аргумента и одну функцию двух аргументов.
К переопределенной системе (1), (3), (5) присоединим вторую самую общую
квазилинейную дифференциальную связь первого порядка и выпишем D2n\-условия
для полученной системы. Анализ на совместность показьюает, что в качестве второй
дифференциальной связи в общем случае достаточно взять связь
et = г (о, е)ех 4-5 (а, б), (7)
при этом Z>i7t1-условия можно привести к системе Коши—Ковалевской первого
порядка относительно четырех функций
se = (hha - c~sa - rhs0)l s, h€ = Qic0 - ch0 4- r2hs0)/s,
re^(T2h0 + hrra -2r3sa)/s + (hc~a -ch0 -2rhh0 + 2rcs0 + r2hsa)/s2,
c€ = -r2c~a +3r3ha - 3r45a +3 (rhc0 -crha -r2hh0 + cr2s0)/s,
h = sD 4- G, a = r2, с = с - as, F = r2 -Dr. (8)
2. Зак. 953

Теорема 2. Для того чтобы система уравнений (1), (3) имела D\n\-решения,
характеризуемые дифференциальными связями (5) и (7), необходимо и достаточно
выполнения условий (8), при этом произвол в определении коэффициентов
уравнения состояния равен четырем функциям одного аргумента.
В результате рассмотрения всех возможных случаев £>7г-решений системы (1),
(3) с функциональным произволом получены следующие результаты:
Решения D\ тт] D\n\ D\*\ D\<n\ D\*\
Условия (6) He в инволю-i Несовмест- (8) Несовместны
ции ны
Здесь можно также выписать такие /Эет-условия, которые одновременно
являются как D\п\-условиями, так и D\ъ\-условиями. При этом в более содержательном
случае D\tt\ П D\я}-условий их можно свести к системе трех уравнений типа Коши—
Ковалевской.
Если уравнение (3) и связь (5) линейны, то для существования D\ n\-решений
уравнение (3) должно быть вида
ot = aet 4- kiO-aki€ + k2,
#i» ^2# a — произвольные константы. Имеют место три различных подслучая:
1). а Ф О, к2 Ф 0; 2) а = 09 ki Ф 0; 3) кх =09а Ф 0, каждый со своей
дифференциальной связью. Для них легко выписать D\ir\ -решения, а также общее решение
системы (1), (3). В первом случае решение системы (1), (3) задается формулами
о = </>+!// + к\ <*е-к*\ v = (ф-у)/аУг +к1ь>£ек**,
е = (#+ф)/а + <»ххек** + к21(акх);
во втором случае
о = а>ек**-к2/ки v = ихек^/кх + /(*),
е = <*1хек*'1к1 +/ir +*(*);
в третьем случае
а = </> + i//, v = (\jj - ф)1а1/г - к2х/а,
е - (Ф + <Р)/я - <*>/а - к2 t/a.
Здесь % = t + xjdh ,т? = t - х/аУ2 ,a функции /, g, у = ^(т?), ф = ф(%) и со =
= со(х) произвольные.
2). Уравнение (3) и связь (5) представляют из себя замкнутую систему. Если
известно ее решение, то v находится как решение вполне интегрируемой системы.
Когда Е, F, G не зависят от а, то лучше сначала выделить из системы (1), (3), (5)
уравнения
vx ■= е„ vt = E(e)et + F(e)ex + G (e) (9)
и исследование вести относительно переменных v и е. При этом в случае б)
D\ъ\-системы коэффициент я в уравнении (3) определяется как а = F = <р'(6 ), где а = <р(е ) —
статическая зависимость (а — е ), а неоднородный член — как функция аргумента
(а — fFde). Если G = 0, то систему (9) полезно линеаризовать преобразованием
годографа. Дополнительно предположим, что (3) распространяется и на статику, т.е.
из et -ot = 0 следует с?(0) = 0, и рассмотрим две связанные между собой задачи
о динамическом деформировании стержня длины / и диаметра d, I > d, один конец
которого жестко закреплен.
34

Сравнение теоретических
расчетов с экспериментальными
данными
1 — экспериментальная
зависимость ст=ст(г, О), 2 — расчет
по нашей модели (2) и 3 — по
модели Соколовского—Мальвер-
на(5)
Задача 1. Найти функции v и е Е с2, удовлетворяющие системе (9) в области
t > 0, х £ [0, / ] начальным е (0, х ) = е 0, v (0, х) = v0, х Е [0, jc] и граничным
условиям и (Г, 0) = О, u(f,/) =м0, * >0.
Задача 2. Найти функцию с(а — <£(е)), если известны а(7, 0) = Fi(t) и решение
задачи 1.
Используя результаты работы [6], устанавливаем, что решение задачи 1
существует и единственно, если F(e ) Е с1. Взяв известную после решения задачи 1 функцию
X(а -</?)= i//"1, обратную к функции \p(t) = Fi(t) - ip(e(t, 0)), решение задачи 2
определяем формулой с =F\ - у • е[ (х,: 0).
С целью получения простого аналитического решения в качестве конкретного
примера было взято уравнение состояния
1
Of =
4(ае+РУ
et + с2
Г1 V °1 12а(ае + 0)3/ J
и проведено сравнение теоретических расчетов с экспериментальными данными,
изложенными в работе [7]. "Результаты приведены на рисунке, где <7= (а — а0)/а* (а0 =
= 10 кг/см2, а* = 8 кг/см2), 7 = (Г - f0)/'o Со =3,4 • 10"3 с). Константы ai =0,69,
а = 0,3 4, 0 = 0,71 выбирались из условия аппроксимации статической зависимости
(а — е ), а константы Ci = 0,38, с2 = 1,42 из требования близости экспериментальной
и теоретической кривых (Г = а(7, 0). Величины ао, t0, a также все другие
необходимые исходные данные взяты из [7].
ЛИТЕРАТУРА
Х.Фомин В.М., Шапеев В.П., Яненко Н.Н. // V Всесоюз. совещ. по аналит. методам газовой
динамики: Тез. докл. М., 1972.
2. Cristescu N. // Int. Struct. 1972. Vol. 8, N 511.
3. Brevet P., Guiraldeng P.H., Gobin P.F. // Mec. Mater. Elec. 1972. N 269.
4.НигматуллинР.И.,ХолинН.Н. // ДАН СССР. 1973. Т. 209, № 1.
5. Яненко Н.Н. // Тр. IV Всесоюз. мат. съезда. Л,, 1961.
6. Соболев С.Л. Уравнения математической физики. М., 1966,
7. Кокошвили СМ., Калнинь П.П. // Механика полимеров. 1970. № 1.
2*
35

ПРИМЕНЕНИЕ МЕТОДА ДИФФЕРЕНЦИАЛЬНЫХ СВЯЗЕЙ
К ОДНОМЕРНЫМ УРАВНЕНИЯМ ГАЗОВОЙ ДИНАМИКИ*
В данной статье изучаются вопросы построения точных решений уравнений
одномерной газовой динамики с помощью метода дифференциальных связей [1—5].
Доказано, что существуют решения с о дно функциональным произволом,
характеризуемые дифференциальной связью специального вида. Приведены примеры
интегралов уравнений одномерной газовой динамики и решения некоторых краевых задач.
Кроме того, показана возможность построения более общих решений с помощью
той же дифференциальной связи. Указанные здесь точные решения можно
использовать в качестве тестов для приближенных методов расчета одномерных неизэнтропи-
ческих течений газа.
1. ПОСТАНОВКА ЗАДАЧИ
Будем исходить из уравнений одномерной газовой динамики в лагранжевых
переменных
Ъи Ър ЪУ Ъи bS
— 4- = 0, =0, = 0, (1.1)
dt Ъх bt Ъх Ъг
где и — скорость, р — давление, V — удельный объем, S — энтропия. Введение
функции / (р, х), которая определяется уравнением состояния V = у (р, S) и
распределением энтропии S =S (x) из соотношения
f2(p,x) = d<p(p,S(x))/dp,
позволяет представить (1.1) в виде
Ъи Ър „ Ър Ъи
— + — = 0, f (р,х) — + — = 0. (1.2)
Ы Ъх Ы Ъх
Из всех решений (1.2) выделим те, которые характеризуются квазилинейной
дифференциальной связью .
Ъи Ър
— 4- А (р, х) 4- 4- В (р, х) = 0, (1.3)
где А (р,х) и*В (р,х) —пока неопределенные функции.
Мы получили неопределенную систему уравнений (1.2), (1.3), которая не всегда
совместна. Дальнейшая задача состоит в исследовании произвола в решении
системы (1.2), (1.3) и определении функций /, А, В.
2. ИССЛЕДОВАНИЕ ПЕРЕОПРЕДЕЛЕННОЙ СИСТЕМЫ УРАВНЕНИЙ
Введя обозначения Эм/Эг =pj> Ъи/Ъх =р\, Ър/bt =pl, Ър/Ъх = р\, запишем (1.2),
(1.3) в виде
ph = -Apl-B, p\ = -fpl pi = Apl + В. (2.1)
Систему уравнений (2.1) исследуем на совместность методом Картана [6]. Из
определения решения этой системы следует, что имеется пять уравнений Пфаффа
du = ph dt 4- р\ dx, dpi = - Adp\ -p\ dA - dB,
dp = p\dt + p\ dx, dp\ = -fdp\ -pldf2, (2.2)
rfp? = Adp% 4- p\dA 4- dB
*Изв. вузов. Сер. Математика. 1974. № 11(150). (Соавторы В.Е. Распопов*, В.П. Шапеев.)
36

относительно шести неизвестных
К Р,>о, Ри pl, Р\ (2-3)
и соответствующие им два коварианта
[dphdt] + [dp\dx] = 0, \dp\dt\ + [dpidx] = О, (2.4)
где квадратные скобки обозначают внешнее произведение. С помощью (2.2)
и параметрического дифференциала
dpi = q°dt + qldx (2.5)
из (2.4) находим
Aql-f2q°+pl(App\+Ax) + Bpp\+Bx-2ffp(plf = О,
ql-Aq«-Ap(plf-Bppl = 0.
Нижние индексы у функций А, В, f обозначают частные производные по
соответствующим аргументам.
Характеры систем (2.2) следующие: sx = 1, s2 = 0; поэтому число Картана 6 = 1-
Для того чтобы уравнения (2.2) были совместны с однофункциональным произволом,
необходимо, чтобы ранг линейной относительно q° и q1 системы уравнений (2.6)
равнялся единице. Назовем это условием (R) . Отсюда получим
A ~±f, (2.7)
± (2fBp + Bfp + fx)p% + (ВВр +ВХ) = 0. (2.8)
Дальнейшее исследование разветвляется в следующих направлениях.
А. Если (2.8) выполняется тождественно по переменным х, t и (2.3), т.е. не
является новым уравнением, то условие (R) является и достаточным для совместности
системы (2.2) с однофункциональным произволом. Исходя из этого, положим
2Bpf + Bfp + /, = 0, ВВр + Вх = 0. (2.9)
Теорема 1. Если выполняются (2.7) и (2.9), то система уравнения (1.2), (1.3)
совместна и ее решение при фиксированных f (р, х) и В (р, х) содержит одну
произвольную функцию одного аргумента; функция f (pt х) определяется с
произволом двух функций одного аргумента.
Замечание. В работе [7] Мартин с помощью специальных переменных сводит
уравнения одномерной газовой динамики к уравнению Монжа—Ампера
ipp%xx-eip + f2(p,x) = 0, f2(p,x) = -dV(p,S(x))ldp,
интегрирование которого ведет затем методом промежуточного интеграла.
Исследования Мартина, Ладфорда и Ю.С Завьялова [7—9] показали, что промежуточный
интеграл существует только для следующих функций / (р, х) :
f(p,x)=F(alP+a2x), f(p,x) = * ч2 f( P ^ ) (2.10)
Нетрудно показать, что при переходе от нашей постановки к постановке Мартина
дифференциальная связь (1.3) преобразуется в дифференциальную связь второго
порядка, в та время как промежуточный интеграл является связью первого порядка.
Как следствие при определении / (р, х) получаем дополнительный произвол в одну
функцию одного аргумента.
Б. Пусть (2.7) и (2.8) справедливы, а (2.9) не выполняются, тогда
BBD+BX
pl = + £ * = +с. (2.11)
2Bpf+Bfp+fx
37

В этом случае из (2.1), (2.7) и (2.11) имеем
ph = fC-B, pi = +С, р\ = ±f2C, p\ = -fC + B. (2.12)
Требование совместности системы уравнений (2.12) дает одно уравнение второго
порядка пдя определения В\
(2BpF + Bfp +Д) (Вхх + 2ВВрх + В 2Врр) - (ВВр + Вх) X
X (2fBpx + IfBBpp + 2fxBp + 2fpBBp +fppB 2 + 2fpxB +fxx) = 0, (2.13)
следовательно, верна
Теорема 2. Если справедливы (2.7) , (2.8) и не выполняется (2.9), то решение
системы уравнений (1.2), (1.3) эквивалентно интегрированию уравнения второго
порядка (2.13) и вполне интегрируемой системы (2.12) . Функция f(p,x) произвольна.
В. Пусть теперь ранг алгебраической системы (2.6) равен двум. Уравнения (2.2)
не могут иметь функционального произвола в решении. Систему (2.2) нужно
продолжить. Из (2.6) найдем q° и ql, подставим в (2.5) и получим систему шести
уравнений Пфаффа (2.2), (2.5) относительно шести неизвестных (2.3). Из условия
вполне интегрируемости этой системы имеем некоторый кубический полином
относительно р I:
Ро (Plf + Pi (Po)2 + PiPl + 0з = 0. (2.14)
Представляются две возможности для дальнейшего исследования. В') требование
тождественного выполнения (2.14) дает переопределенную систему четырех
уравнений относительно функций А и .5. В") из (2.14) можно найти ро, вернуться
к (2.2), (2.4) и вести дальнейшее исследование на совместность. Оба эти случая
опустим ввиду громоздкости выкладок.
3. ПОЛИТРОПНЫЙ ГАЗ
Рассмотрим отдельно уравнения, описывающие одномерное течение политропного
газа (K=e2/7(S)p"1/7; см. [5]):
Ъи Эр , Эр Ъи 1 „ i 7 + 1
— + 7 = °> Фр~к ~+— =0, Ф =~ *2/7(S(*)), *= (3.1)
at ox at Ъх у у
Для уравнений (3.1) дифференциальная связь (1.3), дрпускаяющая решение с одно-
функциональным произволом, существует только в том случае, когда энтропия
распределена по закону
ф = (схх + с2)к~\ (3.?)
где Li, с2 — произвольные постоянные. Отметим, что (3.2) совпадает с функцией
распределения энтропии,полученной Мартином [7].
Дифференциальная связь (1.3) в данном случае принимает вид
ut ± (cxx + c2)kl2-2p-kl2pt + ClP = 0. (3.3)
СхХ+С2
Система уравнений (3.1), (3.3) легко интегрируется и в результате получаем
и = + (clX+c2)k'2-2p^-k)l2 Cj—fpdt+ — , (3.4)
2— к ciX+c2 CiX+c2
\с1Х+с2)к12-*_
(с,х +с2\ , ,
J, ф = (clX+c2)k-<
ркп \ р
Здесь произвольная функция F может быть определена из краевого условия.
38
(3.5)

Задача 1. Пусть масса газа х > х0 с распределением ф(х) = (cix + с2)к~4
ограничена слева поршнем х=х0, который движется по закону и =/ (t),f (0) =0.
Подставим в (3.3) и = / (Г), х = х0 и решение полученного обыкновенного
дифференциального уравнения запишем в виде t = Г (а, с*)1 , а = (схх0 + с2)/р. Для
определения функции F в (3.5) положим х =х0, Г= Г (а, с4), т.е.
F(a) = OLkl2l(cxx0 + с2) + С! Г (а, с4).
Функцию р = Р (f,x) определим из (3.5) после подстановки найденного F (а)
в правую часть и замены а на (cix + с2)/р, а функцию w = w (f, x) — из (3.4).
Константы съ и с4 определяются из условий и(0, дг0) =0, р(0, дг0) = Ро- Причем
неопределенный интеграл в (3.4) следует сделать определенным с нижней границей интегри-
2
рования 0 и верхней Г, а съ = ± (схх0 +c2)kf2~lp£2~k^2.
L—К
Следует отметить, что в данном случае при t = 0 и и р — вполне определенные
функции от х, отличные от констант.
Задача 2. Пусть в плоскости t, x (рисунок) ударная волна GH отделяет
область Вх (за ударной волной), ограниченную характеристикой первого семейства DH
и характеристикой второго семейства DG, от области В2, ограниченной отрезком
оси xEG и характеристикой первого семейства ЕН. Если в одной из этих областей
течение газа описывается решением (3.4), (3.5), то, как это следует из известного
метода характеристик и соотношений на ударной волне [10], течение в другой
области описывается решением, имеющим двухфункциональныи произвол, который
складывается из произвола функции F в (3,5) и закона движения ударной волны
х = X(Г),и при заданных F и X(t) вполне определяется.
Приведем пример, когда функции F и X(t) определяются из условий
примыкания. Пусть газ с параметрами р0 = const, u0 = const, Ро=Ро(*) находится перед
ударной волной, а течение за ударной волной определяется решением (3.4), (3.5).
На заднем фронте из условий Гюгонио известны и = /i(po, Ю> Р =/г(Ро, #)> Р =
= /з(Ро, АО, следовательно, и ф = /4(ро, Ю> гДе N ~ ^(Ро, х) — скорость ударной
волны определяется из соотношения {С\Х + с2)к"4 =/4(р<ь N). Функция р0 = Ро(х)
находится из условия того, что и = /i(po, N{fj0f х)) и р = /2(Ро., М(р0, х)) должны
обратить (3.4) в тождество. (Например, в случае сильной ударной волны и ф = С1Хк~~4,
"о =0, съ = 0 (3.4) переходите соотношение
7
— АС^-Ъ^2\ v(3"37/2 D(7-l)/2/\ + 7 '2 \
+ 1 ' Г , Ро V" (7-4)*/
= 0,
+ /p(o7"1)/2^(1-37)/2^
Л = (7 + 1)^+^2 (7 - I)"7/2 77/2 2"*,
которому удовлетворяют величины
2
Ро = c4xat а = 3- —— .)
(7-1)±т%2%(7-1)%
1 В частности, для к = 3, f=-t
rfa с4> = .4 + с^-'А f1 * + ^ь (1+^ )].
39

Для полного решения задачи о движении газа за ударной волной следует решить
обыкновенное дифференциальное уравнение
dx-/dt = ро (x)N(х)
и тем самым определить х = X(t) — закон движения ударной волны и P(t) = /2 (ро(Х),
N(po(x), X)). Подстановка величины р = P(t) на линии х = X(t) в (3.5) позволит
определить функцию F. Давление р = р (t, х) и скорость и = и (Г, х) находятся
последовательно по формулам (3.5) и (3.4).
вврр +
Уравнение (2.13) в случае политропного газа переходит в следующее:
{-^-вр-1-гвр- _i ф'ф-^вхх + г\в(^вр-* -гвр- -у^'Г1)
+ (ВВр + Вх)]врх +15'( YВр~х -2Вр - -1 ф'ф-1) + 2В(ВВр + Вх )J
+ (BBp+Bx)\(-^Bp-l-2Bp- li Ф'ф-^^-Вр-1 ^Ф'ф-1) +
+ (.— В2р~г + — ф"ф~1 - —ф'2ф-2) \= 0, ф'=-^—. (3.6)
\ 2 2 2/1 dx
Это соотношение можно использовать для построения частных решений системы (3.1).
Например,положим B=prj(x); тогда вместо (3.5) имеем
Ф'Ф~1
[(т-*)--Т]«'^*[(т*7-^-Т*>-'-
^Ит"гМ'-4)*"*-*.+
(— —к= 0-
ф1 ф-2 ф
4
(3.7)
откуда при заданном г\ (х) можно найти ф = Ф(х). При т? = с = const уравнение
(3.7) допускает частное решение ф = с*е 3 , с4 — произвольная константа, а с3 =
= с (к — 2) ± с >/Т"^~~2£. Решение вполне интегрируемой системы, аналогичной
системе (2.12), дает в этом случае
и = ± у-
2с4
2-fc
fcc
L \^7(2±\/4-2А:)
Г + с5
1-2/fc
e * ' + c6,
40

kc
t + cs
V^ (2 ± \A - 2k)
-2/k
съх1к
где с, c3, c4, c5, c6 — производьные постоянные.
В заключение авторы выражают благодарность В.М. Меньшикову за полезную
дискуссию.
ЛИТЕРАТУРА
\. Яненко Н.Н. Теория совместности и методы интегрирования систем нелинейных уравнений
в частных производных // Тр. IV Всесоюз, мат. съезда. Л., 1964. Т. 2.
2. Яненко Н.Н. Бегущие волны системы квазилинейных уравнений // ДАН СССР. 1956. Т. 109,
№ 1.С. 44-47.
3. Погодин Ю.А., Сучков В.А., Яненко Н.Н. О бегущих волнах уравнений газовой динамики //
ПММ. 1958. Т. 22, вып. 2. С. 188-196.
4. Сидоров А.Ф. О некоторых плоских и пространственных задачах газовой динамики: Дис.
... канд. мат. наук. Свердловск, 1969.
5. Рождественский Б.П., Яненко Н.Н. Система квазилинейных уравнений. М.: Наука, 1968.
6. Фиников СП. Метод внешних форм Картана в дифференциальной геометрии. М.; Л.: Гостех-
теоретиздат, 1948. 432 с.
I.Martin M.H. The Monge-Ampere partial differential equation rt - s2 + n2 = 0 // Pacif. J. Math.
1953. Vol. 3, N1. P. 165-187.
8. Ludford G.S.S. Generalized Riemann invariants // Ibid. 1955. Vol. 5, N 3. P. 441-450.
9. Завьялов Ю.С. О некоторых интегралах одномерного движения газа // ДАН СССР. 1955. Т. 103,
№ 5.
10. Кочин НЕ., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. М.: Физматгиз, 1962. Ч. 2.
/СВОЙСТВА СИСТЕМЫ УРАВНЕНИЙ
СИММЕТРИЧНЫХ ТЕЧЕНИЙ ГАЗА*
Применяется метод дифференциальных связей [1] к уравнениям одномерной
газовой динамики. Дана классификация всех D\П\""'-решений (/ = 1, 2, 3) [2], указаны
ОТ-условия и отдельные /Ш-решения. В случае уравнения.состояния частного вида
решена задача об интерференции волны Римана и контактной полосы.
Определение /Ш-систем,/Ш-условий и £>П-решений дано в [2].
1. Уравнения газовой динамики рассмотрим в лагранжевых переменных
, Ъи vuv
+ Axv— + А = 0,
bq х
— +xv— = 0 -^- -xv— - —
dt dq- dt dq X
dx I dS \( dS\l
= o,
dt
(1)
Из [3, 4] следует, что дифференциальные связи первого порядка в данном случае
являются квазилинейными. Полный анализ показывает, что система (1) имеет только
два вида D\ П\ -решений:
a) D\ U\-решения, характеризуемые дифференциальными связями вида
dv , Эр
— +Л"1— =f(p.p,q), (2)
bq oq
где / определяется уравнением
Э/ Э/ . ЪА
— -А — + А-1 /=0;
dv dp dv
* Докл. АН СССР. 1979. Т. 244, № 2. (Соавторы В.Е. Распопов, В.П. Шапеев.)
41

6) Dx П i -решения, характеризуемые дифференциальной связью вида
Ъи _у Ър
— + Л — = Л", p, v, q, t) , (3)
dq dq
где/ определяется системой трех уравнений, А может зависеть только от р. Если /Ф О,
то функция А находится однозначно. Если / = 0, то v = 0 иА = А(р) - произвольная
функция.
Найденные дифференциальные связи позволяют строить D\ Uj -решения системы
(1). Например, при v =0в случае б) положим/= О,А =а2рп; тогда наиболее общее
решение системы имеет вид
2pi-"/2 pi-n
и = ±— — + сь v = + <7i(<7)> G(j>,±q+apn'2t) = 0, (4)
(2-п)а (и-1)д2
где qlt G — произвольные функции, сх, п, а — произвольные константы.
2. Рассматривая вопрос о существовании D\U\-решений, устанавливаем, что
возможны только следующие случаи:
а) существуют Dill}-решения, характеризуемые дифференциальными связями
Эй _ Ър du _у Ър
— + Л-1— =/ifa,p, u,flf,0, "±Л "7" = Ми>Р>»>Я>*)> (5)
Ъq dq Ъq Ъq
и соответствующие Z>f П} -условия представляют собой систему четырех квазилинейных
уравнений относительно Д и/2, которые совместны при определенных видах уравнения
состояния (в случае политропного газа А = ypv"1, у — показатель политропы может
равняться только 3);
б) существуют Dill}-решения, характеризуемые связями
du/dq = Fx (м, р, v, q, t), dp/dq = F2 (w, р, v, q, t) ; (6)
D\ П{ -условия при v = О имеют вид
1 ЭД /2 Э/2 Л ЭД h Э/2 Э/2 Э/2 //Л2 ЪА
+ /2 — + + ( — ) - (7)
Ър Ъq \ А I Ър
А Ы
А
А3
+
dq
~ А Ъи
ЪА
А
- = о,
э/,
+
h
А
Ър
Ър
■ -
+
h
А
э/2
Ъи
Ъи
- /
Э/2 Э/2 Эг2
— + — + — = о,
Ър Ър Ъг
/i ("> Р> Q* 0
^i (и> Р, v, <7, 0 = —~ ■ , Fi (", Р, у, <7, 0 = /2 (н, р, и, ?, 0,
А{р, v)
а при v Ф 0 они представляют собой систему трех уравнений относительно Fx и F2.
Система (7) совместна и произвол в ее решении зависит от вида уравнения состояния.
Рассмотрим здесь при v = 0 политропный газ (А = ypv"1). Имеют место случаи
60 /i = ЯФ, /2 = -(" +сО —— + —- —— ) , (8)
\ у Я» dt /
гдес! - произвольная константа, a &(t) находится из уравнения
7 + 3 7 + 1
f" + f9" + —т- f3 = 0. (9)
У У
Среди решений системы (1), характеризуемых дифференциальными связями (6),
42

(8), (9), содержится решение с функциональным произволом Л.И. Седова [5],
описывающее течение газа с линейным профилем скорости.
б2) функции/i =/i (p, q, i)J2 -f2 (p, q, i) определяются неявно из соотношений
^i(/ip-(7+1)/7, 7Р/Г1 - U Я) = 0, G2(f2, qf2 -p,t) = 0
(где Gx и <72 - произвольные функции), причем они должны удовлетворять еще
одному уравнению)
d/i ЭД Э/2 Э/2
bq dp dp bt
Например, (10) справедливо, если
/i = 7р/(*+*i), /2 = fo(f+ ei)"7+p)/flf; Л = тр/(*+ *i), (11)
/2 = c2(f+ cO"7;
. /1 =c1(t7+c2)-1/V7+1)/7, • /2 =p/(d+c2)9
DJUl-решение системы (1) в случае (6), (11) имеет вид
и =
(г+сО1-7*/^), Р = foflf+^X' + ei)"7, и = £'(?)('+ ci)-
7-1
Так как рассматривается политропный газ
Р = t(S(q))v-4 = t(q)v~\
то должно выполняться соотношение
(PXq))4c3q+c2) = ф(д).
Наконец, выясняя вопрос о существовании у системы (1) />? П?-решений,
характеризуемых дифференциальными связями
dv Ъи Ър
— = Я\ (", Р, vt q, t), — = g2 (и, р, v, q, f), "— = gs (", р, v, q, t) , (12)
bq bq bq
устанавливаем, что D? П? -решения существуют при любом уравнении состояния и
соответствующие D\ П? -условия являются системой Коши-Ковалевской относительно
Q\, Q2 и #з, при этом переопределенная система (1), (12) будет вполне интегрируемой.
3. Система (1) имеет три характеристики 7ь 72 и 7з, которым в каждой точке
области течения газа соответствуют характеристические направления х\ = \[АУ х2 = — \fA
и JC3 =0. Рассматривая вопрос о существовании характеристик у переопределенных
систем [6], приведенных здесь, устанавливаем, что система (1), (2) имеет две
характеристики 7i и 72 ; система (1) , (3) - или 7i и 73, или72 и 7з (при знаке " + " перед вторым
членом во второй дифференциальной связи) ; система (1), (5) — или 7i, или 72;
система (1), (6) — 7з; наконец, система (1), (12) не имеет ни одного характеристического
направления. Рассматривая решения перечисленных систем, можно Х^П?_I-решения
разбить на следующие классы: D\\{\{ylt 72b D\l[\{^lf 7з>, П\Ъ\(Ч2, 7з>, ^in}(7i>,
^1П}(72>, Я?П}(7зЬ/>1П?-решения.
Представителем класса Z>lni(7i, 72)-решений является решение системы (1) с
постоянной энтропией, представителями классов D\П} (7i)- и D\\\\ (72) -решений
являются две волны Римана и представителем класса D\ П} (73) является решение (и = const,
р = const, S = S(q)), называемое контактной полосой. Это рассмотрение указывает
на то, что решения уравнений газовой динамики с точки зрения функционального
произвола и их связей с характеристиками можно разбить на классы К\ (7ь 72 ), К\ (7ь 7з),
К\(Чг> 7з), ^i(7i), ^1(72), ^}(7з)> К°\ , представителями крторых, в свою очередь,
являются соответственно в порядке перечисления указанные D\ Гц "'-решения.
4. В заключение рассмотрим задачу: контактная полоса и = 0, р = р0 = const, S = Si (q)
43

ограничена слева поршнем q = q0, который движется по закону и = C/(t), U(0) = 0.
Определить параметры движущегося газа.
Интегралы (4) перепишем в виде
2р0 _ (13)
U а(п-2) вС«"2)
р1-п
*> = — 7Г + ^ito); (14)
apn,2t-q = q2(p). (15)
Из (13) и условия задачи находим на поршне
_% Й ?ni""/2 9П1""/2
t
\д(и-2) а(л-2) /'
где U l обозначает функцию, обратную к U. Давление р, как функция от q, t,
определяется согласно (15) из соотношения
Л-п/2 2d1-"/2
а(п - 2) а(п -2) /
Для определения u(q, t) следует подставить в (13) найденное p(q, r). Из (14)
определяется v(q, t), где gx (q) = Si (q). Краевое условие на движущемся поршне
удовлетворено по построению. Область покоя от области движения отделяет прямолинейная
характеристика
ap0n,2t - q = q0.
Задача решена.
ЛИТЕРАТУРА
1. Яненко Н.Н. Ц Тр. VI Всесоюз. мат. съезда. Л., 1961. Т. 1.
2. Фомин В.М., Шапеев В.П., Яненко Н.Н. // ДАН СССР. 1974. Т. 215, № 5. С. 1067.
3. Распопов В.Е. // Числ. методы механики сплош. среды. 1975. Т. 6. С. ПО.
4. Жижин А.Е. Ц Там же. 1976. Т. 7. С. 57.
5. Седое Л.И. Методы подобия и размерности в механике. М., 1965.
6. Шапеев В.П. // Там же. 1974. Т. 5, № 4. С. 116.
МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ СВЯЗЕЙ
И ЗАДАЧА О РАСПАДЕ ПРОИЗВОЛЬНОГО РАЗРЫВА*
Методом дифференциальных связей [ 1 ] изучаются квазилинейные системы
дифференциальных уравнений с двумя независимыми переменными. Выписаны необходимые и
достаточные условия существования у них DIl-решений [2]. Приводится теорема о
существовании гладкого решения задачи Коши для переопределенных систем. Примыкая
различные /Ш-решекия через сильный и слабый разрывы, строим решение задачи о
распаде произвольного разрыва.
1. Система квазилинейных дифференциальных уравнений
+ G(u, х, t)ux = f(u, х, г), u = ( UlX f = I y. J ,
(1)
\un/ \jm/
ut = bujbty ux = du/dx
♦Докл. АН СССР. 1980. Т. 254, № 4. (Соавторы СВ. Мелешко, В.П. Шапеев.)
44

с присоединенными к ней ^-дифференциальными связями порядка т
^( Ъ"и \ / ЭФ \
Ф , ..., Wv, и, х, t) = О, rank ( ) = Q (2)
\ Ъхт х J \ д(дти/дхт) I W
может быть записана в виде
S = Lut + ALux - Lf = 0; (3)
Ъти / Ъти \
D = BtL + Ф\В2Ь , ..., ux,u,x,t)= 0,
Ъхт \2 Ъхт х I
(4)
А = LGL~\ (Вх\. = Sio(jy (B2)k/ - 6к+д9оиу
где L = L(u, х, t) — неособая матрица, 1 < i < q, 1 < к < п - q, 1 </<и, 5/у- - символ
Кронекера и о - некоторая подстановка чисел 1, 2,..., п. Обозначим:^ = B2L(dmu/dxm),
Фу = (ЭФ//Эу*), Э*' 1 - формальная производная порядка к + / (к раз по х, I раз по г),
J — джет-расслоение порядка т, I(SD) — множество нулей (SD) в Jm, Iq - (iif i2, ...,
iq), 1 < 1к < п. 1>П-решение, удовлетворяющее (SD), будем называть Dj -решением,
где ik = o(k), 1 < к < q. Здесь через (SD) обозначена система уравнений, состоящая из
системы (3), ее продолжений Э*' S(k + /<m — 1)и системы дифференциальных связей
(4). В дальнейшем, если не оговорено особо, предполагаем, что L £ С71 (У°), A G С"(У0),
/ест(У°),Фес1</1И).
Теорема. 1. Дая того чтобы система (SD) была в инволюции, необходимо и
достаточно выполнение условий
(b°/D + (в, + Фув2)Ав'1д1ф-0п-(в1 +*yB2)b2-0s)\iiSD) = о; . (5)
(В, + ФуВ2)А = (В, +ФуВ2)АВ\(В, +ФУВ2). (6)
Для гиперболической системы (1) в качестве матрицы// может быть взята матрица,
составленная из левых собственных векторов матрицы G. Тогда условия (6) означают,
что в /),• (1 < i < q) коэффициентами при старших производных будут левые
собственные векторы матрицы G, соответствующие только одному значению ^a(i) Ф/ О ^/ ^ л) —
собственные значения матрицы G).
Теорема 2. Если (1) — гиперболическая система и (SD) находится в инволюции,
то существует решение задачи Коши и(х, t) E Cm переопределенной системы (3), (4).
В [3] аналогичная теорема формулируется для строго гиперболических систем со
связями первого порядка и более жесткими ограничениями на гладкость функций.
Наряду с гладкими решениями системы (1) необходимо рассматривать решения со
слабым и сильным разрывами. Путем примыкания различных £>П-решений можно
получить решения с сильным и слабым разрывами [2—6].
2. Полная система дифференциальных уравнений, описывающая одномерное
термомеханическое поведение реологического материала с внутренними изменениями, может
быть записана в виде
vt = аех + Ьвх + саХах, 0t = fox + d, (8)
X? = V°. о = po Ъф/де, a = 1, 2, ..., N, n = N + 3,
где po — плотность, о — компонента первого тензора напряжений Пиолы-Кирхгофа,
v — скорость, б — градиент перемещений, в — температура, ха (<* = 1, 2, ...,А0 -
внутренние переменные, связанные со структурными изменениями и реологическими
эффектами в материале, ф — удельная свободная энергия [7]. Предполагаем, что система
(8) гиперболическая, т.е.
а + bf = h2 и bh/Ъе + fbh/дв < 0.
Пусть начальные данные (t = 0)
и = и+ при х > 0, и =ы_ при х < 0
45

таковы, что система -(8) имеет решение с контактным разрывом ([а] =0, [v] = 0 при
х - 0, условия на начальные данные, при которых имеет место такое решение, можно
получить аналогично уравнениям газовой динамики [8]), и пусть выполнены/Ш-условия
bd
Э/
<£
7Г
э/
Эх*
'W 7эхв/
bd Ы
-Te-fTe-°'
\ Эе
эТ
+ /■
э^а
Э0
э</
Э0
) = 0,
= о,
(9)
dd
ос = 1,2, ..., л;
(имеются примеры решений системы (9)). В случае выполнения (9) задача о распаде
у_, £_, Д-;«г?0 0+, £+, #+,£>+ х
разрыва имеет конфигурацию, приведенную на рисунке. В областяхI, VI — "покой"
(Dfl-решение с константным произволом); в областях II, V - DIl-решения с одно-
функциональным произволом со связями
B[x)Lux = 0, B[2}Lux = 0
соответственно; в областях III и IV — DIl-решения, характеризуемые
дифференциальными связями как в II и V. Решение задачи о распаде произвольного разрыва в
терминах /Ш-решений позволяет свести его к интегрированию систем обыкновенных
дифференциальных уравнений в областях.
Теоремы о примыкании через сильный [5] и слабый разрывы позволяют построить
все конфигурации в задаче о распаде произвольного разрыва для одномерных
уравнений неупругой сплошной среды
p0vt = ax, et = vx
с уравнением состояния [5]
ot = E\e)et + g(a - Е(е))
и уравнений, описывающих одномерное течение газа в поле сил тяжести. Численные
расчеты различных конфигураций распада произвольного разрыва, проведенные для
одномерных уравнений неупругой сплошной среды, совпадают с точными решениями
[5] с точностью до порядка погрешности численного метода.
ЛИТЕРАТУРА
1. ЯненкоН.Н. Ц Тр. IV Всесоюз. мат. съезда. Л., 1961. Т. 1.
2. Фомин В.М., Шапеев В.П., Яненко КН. Ц ДАН СССР. 1974. Т. 215, № 5. С. 1067.
3. ЖижинА.Е. И ДАН СССР. 1978. Т. 238, № 1. С. 15.
4. Распопов В.ЕЧ Шапеев ВЛ.У Яненко КН. Ц ДАН СССР. 1979. Т. 244, № 2. С. 308.
5. Мелешко СВ., Шапеев В.П. // Числ. методы механики сплош. среды. 1979. Т. 10, № 6.
6. Шапеев В.П. // Там же. 1974. Т. 5, № 4.
7. ПэжинаП., Савчук А. // Проблемы теории пластичности и ползучести. М., 1979. С. 94.
8. Рождественский Б.Л., Яненко КН. Системы квазилинейных уравнений и их приложения к
газовой динамике. М.. 1978.

АНАЛИТИЧЕСКИЕ ВЫКЛАДКИ НА ЭВМ
О РЕАЛИЗАЦИИ НА ЭЛЕКТРОННЫХ
ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
АЛГЕБРАЙЧЕСКО-ДИФФЕРЕНЦИАЛЬНЫХ АЛГОРИФМОВ*
ВВЕДЕНИЕ
Основной областью применения быстродействующих электронных вычислительных
машин является осуществление арифметических алгорифмов, т.е. проведение
определенных последовательностей арифметических операций над числами с необходимыми
логическими разветвлениями. Появление электронных вычислительных машин как раз
и связано с большим объемом вычислительной работы во многих арифметических
алгорифмах.
Однако в математике большую роль играют и неарифметические алгорифмы, в
частности алгорифмы, связанные с выкладками в буквах. Научная математическая работа
во многих случаях требует проведения вычислений по таким алгорифмам, но
проведение этих вычислений самим математиком иногда бывает очень утомительным
и зачастую представляется вообще невозможным из-за большого объема
вычислительной работы. Естественно поэтому поставить вопрос об осуществлении и таких
алгорифмов на электронных вычислительных машинах, тем более, что многие из этих
алгорифмов требуют проведения (вообще говоря многократного) небольшого количества
различных типов операций.
Примером такого алгорифма является алгорифм Картана (см. [1]). Он распадается
на следующие сравнительно простые математические операции, проводимые в буквах:
1) алгебраические операции над функциями от нескольких переменных: сложение,
вычитание, умножение;
2) подстановка функции в функцию вместо переменной (суперпозиция функций)1;
3) дифференцирование функций от нескольких переменных по ее аргументам.
Алгорифм Картана первоначально возник как аналитический аппарат исследования
поверхностей, обладающих различными геометрическими свойствами. В настоящее
время он находит применение в другой области математики — в теории аналитических
(точных) решений уравнений в частных производных.
Если рассматривается система уравнений
т п Эы-
2 2 Ч* Т7 = Fi> '=l>2,...,m, (1)
/ = 1 к = 1 Ъхк
где atjk9 Ft есть функции от ulf ..., ит, xlt ..., хп, то наиболее общий метод
получения точных решений системы (1) заключается в присоединении к (1) дополнительного
уравнения
/ = 0, (2)
(/ _ ФУНКЦИЯ ОТ Xi, ..., Хп, Ui, ..., Um И ОТ ЧаСТНЫХ ПРОИЗВОДНЫХ фуНКЦИЙ Uj ПО Хк
порядка от первого до р-го включительно) и рассмотрении условий совместности
получающейся при этом системы.
♦Проблемы кибернетики- 1961. Вып. 6. (Соавтор В.А. Шурыгин.)
1 Операции, представленные в п. 1, можно осуществлять также подстановкой заданных функций
в функции вида х + у, х - у, ху. Поэтому эти операции можно считать частными случаями
подстановок.
47

Накладывая различные требования на произвол решения системы (1) и (2), можно
выделить различные классы решений системы (1).
Ряд работ, в которых находятся аналитические решения уравнений газовой динамики,
ограничивается случаем р = О, т.е. в качестве (2) берется уравнение
f(xu ...,*„, иь .-., ит) = О,
хотя и при этом часто получаются громоздкие выкладки (см. [2—4]). Случаи же, когда
р > 0, зачастую требуют от математики непосильной вычислительной работы. Поэтому
применение электронных вычислительных машин для реализации алгебраическо-диф-
ференциального алгорифма Картана является весьма желательным.
Кроме того, машинизация математических алгорифмов должна найти применение
во многих других областях математики (тензорный анализ, линейная алгебра, алгебра
форм, алгорифмы аналитического интегрирования, разложение в ряды и т.п.).
Предлагаемая алгебраическо-дифференциальная программа АДП позволяет решать
довольно широкий класс задач по определению совместности систем дифференциальных
уравнений в частных производных, а также многие другие задачи на электронной
вычислительной машине "Стрела" (описание и систему команд этой машины можно
найти, например, в [5]).
1. ОПЕРАЦИИ, ОСУЩЕСТВЛЯЕМЫЕ АДП
Описываемая алгебраическо-дифференциальная программа является одной из первых
в СССР программ, осуществляющих буквенные выкладки. Поэтому при ее создании
естественно было ограничиться (как для первых опытов) буквенными выражениями
как можно более простого вида, но в то же время такими, чтобы круг задач, решаемых
с помощью АДП, не был бы слишком узок и программа имела бы хоть какую-то
практическую ценность.
АДП преобразует выражение вида
Р = 2±д,*?1'х?2/ ... x%niy (3)
где я,-, осы — любые числа, каждое из которых может быть записано в одной ячейке
памяти, х^ — буквы, причем если они обозначают переменные величины, то одни из них
могут быть функциями других.
Выражения вида (3) мы будем называть полиномиалами.
Полиномиалы имеют очень простой вид, однако путем введения соответствующих
. обозначений любое буквенное выражение, встречающееся в математической практике,
можно представить в виде полиномиалов. Например, выражение
a sinx + ln(cos>>)
превращается в полиномиал, если обозначить sinx через и, a ln(cos^) — через v.
Выражение
R = ах + у/су2 + Г
dx2 + еу2
можно записать как полиномиал
R = ахи'1 + v^u"1,
где и, v — функции от х и уу имеющие вид полиномиалов
и = dx2 + еу2, v = су2 + 1.
Для ввода в машину полиномиалы кодируются определенным образом числами
(см. разд. 2), кроме того, каждый полиномиал имеет свой номер — какое-нибудь
число в восьмеричной системе от 4000 до 6777, которое можно рассматривать как
числовой код буквы Р в (3).
48

Последовательность операций, которую нужно выполнить над полиномиалами,
задается в виде так называемой псевдопрограммы, по виду напоминающей обычную
программу из машинных команд, причем в ней указываются только номера поли-
номиалов, но не сами полиномиалы. Таким образом, одна и та же псевдопрограмма
может быть иногда использована для решения фактически разных задач.
АДП выполняет две основные операции над полиномиалами.
1. Подстановка полиномиала в полиномиал вместо буквы. Пусть полиномиал Р
содержит букву q, причем только в целых неотрицательных степенях, а полиномиал Q
букву q не содержит. Программа может подставить Q в Р вместо буквы q.
Для более удобного задания операции подстановки сделано следующее. Номер
подставляемого полиномиала Q должен совпадать с кодом буквы q (о кодировании
полиномиалов речь пойдет в разд. 2), если нужно вместо буквы qt подставить
полиномиал £?!, вместо q2 — полиномиал Q2 и т.д. и вместо qn — полиномиал Qn, и коды
букв q% или, что то же самое, номера полиномиалов Qt идут подряд, т.е. код qt + х
равен коду qt плюс единица, то достаточно задать номер полиномиала Р, коды Qx и
Qn (см. таблицу).
При этом не обязательно, чтобы полиномиал Р содержал все буквы от q{ до qn
(в частности, он может их совсем не содержать), и не обязательно, чтобы для каждой
буквы qi от qx до qn, входящей в полиномиал Р, имелся бы соответствующий
полиномиал Qf (в частности, таких полиномиалов может не быть ни для одной буквы из
Подстановкой можно осуществлять алгебраические операции сложения, вычитания
и умножения (см. сноску1).
Операция подстановки сделана двух типов: с приведением подобных членов у
результата и без приведения. Последняя введена для экономии времени, так как приведение
подобных членов в длинных полиномиалах проходит долго и обычно в промежуточных
выкладках не требуется.
Исходный полиномиал Р, в который производилась подстановка, в памяти машины
по окончании подстановки не остается. Результат подстановки — новый полиномиал —
имеет тот же номер р,
2, Дифференцирование полиномиалов. Пусть полиномиал R зависит от величин
Х\, ..,, хПУ tь ,.., tm> причем Xj есть дифференцируемые функции от переменных tk.
Задается таблица производных
Ъх/btk = yikt /= 1, ..., п\ к= 1, ..., ту (4)
с учетом которой АДП может вычислить полиномиал
с ЪК " dR A d*R ...
S = — = 2 —yik + —-> (5)
Otfc /= 1 OXi Otk
расписанный, конечно, в виде (3).
Здесь слева мы написали dR/dtkj так как это при т > 1, вообще говоря, является
частной производной с учетом зависимостей (4) при фиксированных всех остальных
tj(j Ф к). Справа d*R/dtk — частная производная R по tk, входящей в R явно, без
учета зависимостей (4).
Описанных операций подстановки и дифференцирования достаточно для решения
очень многих задач, в частности во многих случаях для реализации алгорифма Картана.
АДП проводит над полиномиалами также операции вспомогательного характера.
1. Присвоение полиномиалам с номерами Р, Р + 1, ..., Р + л, других номеров Q,
Q + 1 * • • •» Q + п соответственно.
2. Дублирование полиномиалов с номерами Р, Р + 1, ..., Р t n, причем новым
полиномиалам присваиваются заданные номера Qy Q+ 1,..., б + л соответственно.
3. Ввод полиномиалов с номерами Р, Р+ 1,..., Р+ п. Перфокарты с набитыми на них
полиномиалами ставятся на читающее устройство машины, причем перед каждым поли-

Таблица
Операции
Подстановка с
приведением подобных
чле„нов
Подстановка без
приведения подобных
членов
Дифференцирование
Присвоение других
номеров
Дублирование
Ввод
Вывод
Стирание
Псевдокоманда
IA
Р
Р
R
Р
Р
0000
Р
Р
ПА
Ci
Ci
tk
п
п
п
п
п
III A
Qn
Qn
S
Q
Q
P
0000
0000
Контрольный
сигнал
1
1
1
1
1
1
1
1
Код операции
05
04
06
10
07
01
02
03
номиалом помещается перфокарта, в первой строке которой в разрядах второго адреса
команд указывается число строк (ячеек памяти), занимаемых полиномиалом,
уменьшенное на единицу, в восьмеричной системе. Эта перфокарта называется справкой
данного полиномиала.
4. Вывод полиномиалов с номерами Р, Р + 1, ..., Р + п. Перед выдачей каждого из
этих полиномиалов выдается его справка.
5. Стирание полиномиалов с номерами Р, Р + 1, ..., Р + п. После осуществления этой
операции место, занимаемое этими полиномиалами, считается свободными и может
быть занято другими полиномиалами.
Во всех этих операциях п может быть равно нулю (когда операция проводится над
одним полиномиалом).
Задаются эти операции в виде строк — псевдокоманд (см. таблицу).
Обозначения в этой таблице те же, что в описании операций выше. Вид операции
задается в тех же разрядах, что и код операции в обычных машинных командах, причем
в 36-м разряде должна стоять единица.
Псевдокоманды располагаются в памяти машины в том порядке, в каком они
должны исполняться, причем они могут чередоваться и с обычными машинными командами,
исключая только команды групповых операций, задаваемые в две строки. Машинные
команды, стоящие в псевдо про грамме, мы также будем называть псевдокомандами.
Они в 36-м разряде должны иметь 0.
Команда условного перехода первого рода (код операции 20), стоящая в
псевдопрограмме, передает управление только на псевдокоманды, при этом нуль по третьему
адресу не заносится. Команда условного перехода второго рода (код операции 27)
передает управление только на подпрограммы из машинных команд, причем эти
подпрограммы могут содержать команды групповых операций.
2. КОДИРОВАНИЕ ПОЛИНОМИАЛОВ
ОСНОВНЫЕ ПРИНЦИПЫ РАБОТЫ ПРОГРАММЫ
Ячейка памяти машины "Стрела" состоит из 43 разрядов, имеющих номера с 0
по 42. Назовем группу разрядов с 0 по 11-й первой клеткой данной ячейки, группу
разрядов с 12 по 23-й — второй клеткой, с 24 по 35-й — третьей клеткой данной ячейки.
Рассмотрим, как кодируются полиномиалы (все указываемые при этом числа —
в восьмеричной системе).
50

Знак плюс кодируется числом 7001, знак минус — числом 7003, буквы — любыми
числами от 4000 до 7000 включительно. Численные коэффициенты и показатели степени
записываются в нормализованном виде в двоичной системе в специально отведенных
для них ячейках, а в строке 3 кодируются номером соответствующей ячейки,
отсчитывая от первой из ячеек, занимаемых полиномиалом, считая ее за нулевую.
В первую клетку первой из ячеек, занимаемых полиномиалом, записывается номер
полиномиала, а в 36-й разряд этой ячейки ставится единица. Со второй клетки этой
ячейки начинается запись самого полиномиала. Кодами символов, из которых состоит
эта запись, заполняется вторая и третья клетки первой ячейки, затем первая, вторая
и третья клетки следующей ячейки и т.д. Коды численных коэффициентов
записываются в начале одночленов, коды показателей степеней — сразу после тех букв, к которым
они относятся.
Буквы в одночленах записываются в порядке возрастания их кодов. За счет этого
ограничения получается большой выигрыш в скорости работы программы.
Знак "+" в начале полиномиала не опускается. Буквы с нулевыми показателями
степени и коды числа 1 не пишутся (кроме случая, когда весь одночлен равен 1).
В конце полиномиала ставится знак 7002.
Числа, относящиеся к полиномиалу, обычно записываются сразу же после ячеек с
закодированным полиномиалом, хотя возможны и другие случаи расположения.
Пример. Полиномиал
Р = 2ххх\ - 1 + х\гхъ
можно закодировать, положив коды д:,- равными соответственно 4001, 4002 и 4003,
номер полиномиала равным 5000, следующим образом:
^дрес ячейки
к
к+1
к + 2
к + 3
к + 4
к + 5
к + 6
к + 1
I клетка
5001
4001
7003
4002
7002
2000
2000
2000
II клетка
7001
4002
0006
0007
0000
0000
0000
0000
III клетка
0005
0005
7001
4003
0000
0000
0000
0000
36-й разряд
1
0
0
0
0
0
0
0
37-42-й
разряды
00
00
00
00
00
02
01
00
Последние три строки таблица — числа 2, 1 и 0,5 в двоичной системе в
нормализованном виде.
Полиномиал, тождественно равный нулю, кодируется так:
Р 7002 0000 1 00
где Р — номер полиномиала.
При выборе способа кодирования полиномиалов приходится считаться с
имеющимися в наличии устройствами для набивки перфокарт и печати с перфокарт на бумагу,
так как эти устройства объединяют двоичные цифры в группы по три или по четыре,
образуя восьмеричные или десятиричные цифры, которые, в свою очередь, разбиваются
на отдельные группы — мантиссу и порядок в числах, адреса и код операции в командах.
Выбранный способ кодирования полиномиалов хотя и не очень экономичен с точки
зрения использования разрядов ячеек памяти, однако удобен при набивке перфокарт
и печати с перфокарт на бумагу. Как показывает опыт, при некотором навыке
кодировать, и читать полиномиалы нетрудно, и ошибок при этом не бывает, однако на повестку
дня необходимо поставить вопрос о создании устройств, позволяющих набивать на
перфокарты информацию, заданную непосредственно для печати буквенных выражений
с перфокарт, на которых они набиты в виде численных кодов. Иначе говоря, требуется
автоматизировать процесс кодирования буквенных выражений, что имеет большое
значение также для автоматизации программирования.

Можно кодировать полиномиалы и другими, более удобными способами, и
специальными программами переводить эти коды к опи'санному здесь виду.
То, что на каждое число отводится целиком ячейка памяти, позволяет использовать
числа в очень широких пределах с большим числом значащих цифр.
Таблица обозначений производных (4) кодируется так:
I клетка
7000
*i
х2
*з
II клетка
0000
'i
U
'э
и так далее
III клетка
0000
Ун
УХ2
У13
36
-й разр.
1
0
0
0
0
37-
-42-й разр.
00
00
00
00
00
Порядок строк произвольный, только в конце должна стоять строка из нулей. Эта
таблица находится в памяти машины на правах полиномиала, имеет номер 7000, ее
можно вводить в машину и выводить с помощью псевдокоманд ввода и вывода как
полиномиал с номером 7000, а также стирать, присваивать ей другой номер и
дублировать ее как обычный полиномиал, только к моменту исполнения операции
дифференцирования она должна иметь номер 7000. Это позволяет иметь несколько различных
таблиц и использовать каждый раз ту, которую нужно, например, в задачах, где
требуется вычислять то полные, то частные производные зависимость каких-нибудь
переменных от других то учитывается, то не учитывается.
Для обработки полиномиалов служит специальный блок программы — блок
просмотра. Чтобы описать его работу, представим себе, что клетки, в которых записан
полиномиал, расположены в одну линию или нанесены на узкую ленту в один ряд.
Пусть по этой ленте может двигаться считывающая и записывающая головка, которая
может делать следующие операции:
1) сдвинуться на одну клетку вправо и выдать символ, записанный в клетке, в
которую сдвинулась головка, в 1 клетку какой-нибудь стандартной ячейки памяти
машины;
2) та же операция, но с движением влево;
3) записать в клетку, в которой находится головка, новый символ, заданный в
1 клетке стандартной ячейки;
4) в любой момент времени можно запомнить, в какой клетке какой ячейки
находится головка, т.е. записать в какую-нибудь ячейку памяти машины адрес ячейки
и номер клетки, где находится головка в данный момент;
5) в любой момент времени можно вернуть головку в клетку, которая была
отмечена по предыдущей операции.
Кроме этой головки пусть имеется вторая головка, которая может двигаться по
ленте только вправо и только считывать символы, но не записывать новые, и третья
головка, которая может только записывать символы и после каждой записи
автоматически сдвигаться на одну клетку вправо.
Если в клетках ленты записаны полиномиалы, то с помощью этих головок можно
над ними проделывать различные операции. При этом удобнее иметь именно три
головки указанного типа.
При подстановке полиномиала в полиномиал первая головка двигается по поли-
номиалу, в который производится подстановка, вторая — по подставляемому поли-
номиалу, а третья головка, получая от первых двух необходимую информацию,
записывает на свободном месте в памяти машины результат подстановки — новый полиномиал.
При приведении подобных членов первая и вторая головки двигаются по различным
одночленам полиномиала. Первая головка при этом стирает ненужные одночлены
и записывает коды новых численных коэффициентов.
Таким образом, операции над полиномиалами можно разбить на элементарные
операции, осуществляемые головками, и на операции сравнения символов, считываемых
52

головками, между собой и с определенными эталонами. Результаты сравнения
определяют последовательность этих элементарных операций.
Блок просмотра имитирует работу описанных головок. Каждая операция,
осуществляемая головкой, задается одной неизменной командой. В большей своей части АДП
состоит из этих команд, команд сравнения и команд условных и безусловных
переходов.
3. РАСПРЕДЕЛЕНИЕ ПАМЯТИ. БЛОК-СХЕМА ПРОГРАММЫ
Память машины распределена следующим образом
АДП
Ячейки с 1 по 714 (включая рабочие ячейки)
Псевдопрограмма
Полиномиалы
Свободное место под новые полиномиалы
Полиномиалы располагаются в памяти машины вплотную один к другому, без
пропусков. Новые полиномиалы, вырабатываемые АДП, записываются на свободное место
вплотную к уже имеющимся.
В начале работы в ячейках 15, 16, 17 должна быть записана следующая информация:
в 1 клетке ячейки 15 — адрес той псевдопрограммы, с которой надо начать работу,
в 1 клетке ячейки 16 — адрес ячейки, с которой начинаются полиномиалы,
в 1 клетке ячейки 17 — адрес ячейки, с которой начинается свободное место под
полиномиалы.
В процессе работы программы информация в ячейках 15 и 17 автоматически
корректируется, причем в ячейке 15 указывается адрес псевдокоманды, которая будет
исполняться следующей.
По функциональным признакам АДП можно разбить на следующие блоки.
1. Блок управления, который выбирает из псевдопрограммы псевдокоманды,
определяет, не являются ли они машинными командами, и, если являются, то исполняет их,
если же они задают операции над полиномиалами, то подготавливает работу нужного
блока и передает на него управление.
2. Блок элементарных подстановок, выполняющий двоякую функцию.
Во-первых, он в заданный полиномиал Р подставляет всюду вместо qm, где q —
заданная буква, полиномиал Q™ ~l, где Q — полиномиал, подставляемый вместо q.
Во-вторых, вырабатывает полиномиалы
ЭД d*R „л
— У1к> — (6)
OXj Otk
для производной (5). Какую из этих функций будет выполнять блок зависит от того,
на какой из двух его входов передано управление.
3. Блок управления подстановкой осуществляет операцию подстановки полиномиа-
лов 6i, ..., Qn в Ртак, как она была описана в разд. 1 путем многократного
обращения к блоку элементарной подстановки.
4. Блок управления дифференцированием выбирает из таблицы производных
величины д>/7-, затем, обращаясь к блоку элементарной подстановки, получает компоненты (6)
и складывает их.
5. Блок приведения подобных членов.
6. Блок ввода, вывода, стирания, присвоения других номеров и дублирования поли-
номиалов.
7. Блок просмотра, имитирующий работу описанных в разд. 2 головок.
Все эти блоки сделаны по возможности независимыми друг от друга, т.е. при
внесении изменений в отдельный блок остальные блоки останутся без существенных
изменений — в них, как правило, изменяется только команды передачи управления на
измененный блок, если они имеются.
53

Ни один блок АДП не использует магнитную ленту, однако при решении больших
задач ее все же стоит использовать, главным образом для того, чтобы при случайном
сбое машины можно было бы начать счет не с самого начала, а с какого-нибудь из
промежуточных этапов. Проще всего для этого, по-видимому, время от времени
записывать на ленту весь внутренний накопитель. Команда записи на ленту или считывания
с ленты может стоять в псевдопрограмме в качестве псевдокоманды, в том числе
команда с кодом операции 60 для обращения к стандартной программе, закоммутиро-
ванной в "Стреле", проводящей операции с лентой с контрольным суммированием.
Ввиду того, что заранее обычно неизвестно, в каких ячейках памяти будет находиться
данный полиномиал, записывать на ленту отдельные полиномиалы в процессе работы
программы очень турдно. Часто бывает целесообразным промежуточные полиномиалы,
занимающие много места в памяти, для уменьшения нехватки памяти на то время, пока
они не нужны, выводить на перфокарты и в памяти машины стирать, а затем, когда
понадобится, снова их вводить с помощью соответствующих псевдокоманд.
Все операции АДП проводит в один просчет. Для организации второго просчета с
целью выявления случайных сбоев машины также удобно использовать ленту. При этом
также можно записывать на ленту весь внутренний накопитель, кроме одной ячейки,
где находится контрольная сумма, чтобы при считывании с ленты она не затиралась.
4. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
С помощью АДП можно решать довольно разнообразные задачи.
Приведем пример одной из таких задач. В работе [6] был указан алгорифм для
получения дифференциального уравнения для функции w = w (и, v) в случае, когда
и, v и w удовлетворяют системе квазилинейных дифференциальных уравнений
Ъи . Ъи Ъи , , bv ^ Эн> Эн> _ ч
*/— + */— + ct— + dt— + et— + //—- = 0(/ =1,2,3),
ох Ъу Ъх Ъу ox Ъу
где я,-, ...,// — функции от и, v и w. В этой же работе этот алгорифм в качестве примера
был применен к конкретной системе
Ъи , -к Ъи л . '
— + wv — = 0, к = const;
Эх Ъу
*L + ^ = 0; ^ = 0.
Ъу Ъх Ъу
Программа смогла повторить выкладки, приведенные в работе, за 12 минут. Было
получено уравнение третьего порядка (в [6] приведено не это уравнение, а уравнение
второго порядка, но АДП уравнения не интегрирует и поэтому сделала несколько
меньше, чем сделано в работе).
Не всегда применение АДП дает нужный эффект. Если задача имеет сложную схему
вычислений и громоздкие исходные полиномиалы, то на подготовку задачи к счету
уходит очень много времени. Однако есть задачи, при решении которых АДП оказывает
неоценимую помощь. Сюда следует прежде всего отнести вычисление определителей,
элементами которых являются буквенные выражения — полиномиалы.
Задачи, в которых требуется вычислять такие определители, иногда встречаются
в некоторых разделах прикладной математики, но вычислить такой определитель,
например четвертого порядка, вручную часто бывает очень утомительно. АДП эту
работу проделывает довольно быстро путем подстановки буквенных выражений в
определитель, расписанный в виде суммы произведений своих элементов — полиномиал,
расписанный раз навсегда. Определители до четвертого порядка включительно
расписываются таким образом в виде сравнительно небольших полиномиалов. Оказалось не
очень трудным расписать и определитель пятого порядка, хотя он занял неполную
54

21 перфокарту. Определители более высокого порядка можно свести к определителям
пятого порядка, причем если исходный определитель имеет много нулей среди своих
элементов, то эта задача сильно упрощается, если же нулей мало, то, как показывает
опыт (да и простые подсчеты), получаются, как правило, настолько громоздкие
выражения, что памяти машины не хватает и решать эту задачу с помощью АДП на
"Стреле" нет возможности.
Применение АДП эффективно при решении большого числа однотипных задач,
имеющих одну и ту же (пусть сложную) псев до про грамму.
До тех пор, пока кодирование полиномиалов не будет автоматизировано, АДП
будет более эффективна в тех случаях, когда исходные данные и нужные результаты
не являются громоздкими, в частности, в задачах, где требуется проверить равенство
нулю каких-нибудь выражений, например определителей в буквах.
Ввиду того, что псевдопрограмма может содержать циклы и может сама себя
изменять в процессе работы, возможности АДП очень большие. С ее помощью, в
частности, можно вести вычисления не только по алгорифмам, всегда приводящим к
определенной цели, но и решать — точнее, пытаться решать — задачи, сводящиеся к поиску
каких-либо выражений и к перебору большого числа различных возможностей,
например к поиску решений дифференциальных уравнений, и т.п. В такого ряда задачах
вопрос о возможности достижения цели обычно перестает быть открытым только
тогда, когда цель бывает уже достигнута, но не раньше.
Описанную программу следует рассматривать прежде всего как инструмент, не-.
посредственно обрабатывающий полиномиалы. При добавлении к ней других блоков,
управляющих ходом выкладок, можно изменить способ задания операций над поли-
номиалами, т.е. от псевдокоманд описанного здесь вида перейти к какому-нибудь
совершенно другому способу. Этим можно упростить подготовку задачи к счету и тем
самым расширить круг задач, решение которых с помощью АДП эффективно. Надо
сказать, что при создании программы вопрос о наиболее рациональном способе задания
операций над полиномиалами не решался, так как все внимание было обращено
непосредственно на техническое осуществление программы. Возможно, этот вопрос имеет
много общего с проблемами, стоящими при автоматизации программирования.
Принятый нами способ кодирования полиномиалов хоть и не очень удобен и
довольно громоздок, все же имеет то достоинство, что программа с большой скоростью
работы. При других способах, предлагавшихся при создании программы, эта скорость
получилась в несколько раз меньше. Как мы уже говорили, можно полиномиалы
кодировать другими способами и специальной программой переводить коды к принятому
нами виду.
При составлении псевдопрограмм можно использовать метод стандартных
программ из псевдокоманд.
В заключение пользуемся случаем выразить благодарность Ю.И. Морозову и особенно
Б.К. Потапкину за ценные предложения по составлению АДП.
ЛИТЕРАТУРА
1. Фиников СИ Метод внешних форм Картана в. дифференциальной геометрии. М.; Л.: Гостех-
теоретиздат, 1948. 432 с.
2. Яненко Н.Н. Бегущие волны системы квазилинейных уравнений // ДАН СССР. 1956. Т. 109,
№ 1.С 44-47.
3. Погодин Ю.Я., Сучков В.А., Яненко Н.Н. О бегущих волнах уравнений газовой динамики // ПММ,
1958. Т. 22, вып. 2. С 188-196.
4. Сидоров А.Ф., Яненко Н.Н. К вопросу о нестационарных плоских течениях политропного газа
с прямолинейными характеристиками // ДАН СССР. 1958. Т. 123, № 5. С 832-834.
5. Китов А.И., Криницкий Н.А. Электронные цифровые машины и программирование. М.: Физматгиз,
1959.
6. Яненко Н.Н. Сведение системы квазилинейных уравнений к одному квазилинейному
уравнению // УМН. Т. 10, вып. 3 (6). С. 173-178.
55

РЕАЛИЗАЦИЯ МЕТОДА ВНЕШНИХ ФОРМ КАРТАНА НА ЭВМ*
В последнее время все большее значение приобретают вопросы реализации
аналитических и численно-аналитических, методов на ЭВМ. Для решения этой важной задачи
разработаны специализированные системы программирования, языки и
вычислительные машины [1—7]. В [1] были исследованы некоторые подходы к разработке про-
грммы символьных преобразований, позволяющей автоматизировать отдельные этапы
метода внешних форм Картана [8] . Предметом настоящего сообщения является
реализация алгоритма Картана на ЭВМ БЭСМ-6 в системе программирования
"Авто-Аналитик" [2].
Исследуется совместность и произвол в решении системы Пфаффа
du* = al (х, и, ф) dua + Ь\ (х, ы, ф) dxT, (1)
/ = 1, 2, ,.., s, a = s + 1,..., г, т = 1, 2, ..,, л,
где и1 — неизвестные функции, хт — независимые переменные, коэффициенты а*а, Ь1т
априори нефиксированы и могут зависеть от некоторых произвольных функций
у\х, и) (/=1,2,..., rri) й параметров.
Помимо прямой задачи анализа совместности конкретной системы (1) решается
обратная задача: какими должны быть функции у1(х, и), чтобы (1) имела заданный
произвол в своем решении.
Метод Картана как алгоритм для ЭВМ был сформулирован в виде
последовательности операций [9].
1. Получение системы уравнений, определяющих наиболее общий интегральный
элемент.
2. Выбор полной, независимой и непротиворечивой подсистемы в системе
определяющих уравнений.
3.Понижение ранга определяющей системы за счет условий на функции $1(х, и).
4. Построение цепи интегральных элементов, вычисление характеров и проверка
критерия Картана.
5. Продолжение системы Пфаффа.
6. Дифференцирование системы конечных соотношений и выбор среди них полной
независимой и непротиворечивой подсистемы.
7. Дополнение системы Пфаффа и проверка непротиворечивости дополненной
системы.
8. Приведение дополненной системы к исходному виду (1).
Алгоритм может работать в режиме /, когда полученные конечные соотношения
присоединяются к исходной системе, или в режиме //, когда конечные соотношения
удовлетворяются за счет выбора функций у1(х, и). П.З включается в работу алгоритма
только в режиме II. Следуя [1], в данной работе решение прямой и обратной задач теории
совместности трактуется как выполнение некоторого
алгебраическо-дифференциального алгоритма. Поэтому программная реализация метода Картана выполнена в виде
пакета операторов, осуществляющих необходимые алгебраические и
дифференциальные преобразования. Перечислим основные операторы пакета.
Оператор "Выделение подсистемы" выбирает из системы уравнений, линейных
относительно заданных букв, независимую полную подсистему. Оператор "Вычисление
ранга" определяет ранг основной и расширенной матриц коэффициентов системы
линейных уравнений. Оператор "Решение системы" находит решение системы линейных
уравнений. Оператор "Понижение ранга" выписывает систему соотношений,
обращающих в нуль все определители заданного порядка в главной и расширенной матрицах
♦Докл. АН СССР. 1974. Т. 214, № 4. (Соавторы Е.А. Арайс, В.П. Шапеев.)
56

коэффициентов. Оператор "Дифференцирование" вычисляет все производные от
заданной сложной функции. Оператор "Внешнее дифференцирование" определяет систему
ковариантов, соответствующую системе Пфаффа. Оператор "Дифференцирование
конечных соотношений" вычисляет полный дифференциал от заданной системы
конечных соотношений.
Кроме перечисленных, при реализации алгоритма Картана использовались различные
модификации операторов подстановки, приведения подобных, проверки на
зависимость и другие.
Функции компилирующей программы выполняет оператор "Картан", который
связывает перечисленные операторы и реализует логику алгоритма. Отметим, что "Авто-
Аналитик" в целом является системой модульного (операторного) программирования,
имеющей специализированный язык написания модулей. Программирование
алгоритма Картана показало следующие преимущества "Авто-Аналитика": а) достигается
значительная экономия оперативной памяти (соответствующая алгоритму программа
занимает около 1000 ячеек памяти, что весьма немного для такого сложного метода) ;
б) упрощается программирование; в) сокращается время отладки; г) наличие
библиотеки операторов позволяет легко реализовать другие алгебраическо-дифференциальные
алгоритмы.
При помощи разработанной программы решен ряд тестовых прямых и обратных
задач теории совместимости. Программа не требует от математика, использующего ее,
знания программирования.
Авторы выражают благодарность А.В.Шутенкову и В.И.Карначуку за оказанную
помощь.
ЛИТЕРАТУРА
1. Шурыгин В.А., Яненко Н.Н. // Пробл. кибернетики. 1961. Вып. 6.
2. Арайс Е.А., Сибиряков Г.В. // Вопросы программирования и автоматизации проектирования.
Томск, 1971. Вып. 1. С. 166.
3. Глушков ВЖ, Бондарчук ВТ. и др. // Кибернетика. 1971. № 3. С. 102.
4. Смирнова Т.Н., Костометова Е.М., Рыбакова Ю.В. // Зап. науч. семинара Ленингр. отд-ния Мат.
ин-та АН СССР. 1971. Т. 23. С 132.
5. Barton D., Fitch J.P. // Commun. ACM. 1971. Vol. 14, N 8. P. 542.
6. Rink R.A., Streifer W.I 11 IEEE Trans. Comput. 1971. Vol. 20, N 8. P. 901.
7. Эпсилон-система автоматизации программирования задач символьной обработки / Под ред.
А.П. Ершова. Новосибирск, 1972.
8. Фиников СП. Метод внешних форм Картана в дифференциальной геометрии. М.; Л.: Гостехтеор-
издат, 1948. 432 с.
9. Шапеев В.П. Комплексы программ математической физики. Новосибирск, 1972.
РЕАЛИЗАЦИЯ НА ЭВМ АЛГОРИТМА ИССЛЕДОВАНИЯ
НА СОВМЕСТНОСТЬ СИСТЕМ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ*
При изучении систем дифференциальных уравнений в различных областях
математики возникает необходимость исследовать эти системы на совместность. Эта
задача связана с громоздкими символьными вычислениями. Одним из методов ее
решения является алгоритм Картана [1, 2]. В [3] показана возможность
использования для этого ЭВМ. Другим методом решения этой задачи является алгоритм,
начальная формулировка которого дана Рикье, Жане, Томасом и Риттом. Современное
изложение его дано в работах Спенсера, Гольдсмита, Кураниши и Поммаре. Среди работ
советских математиков можно упомянуть работы [4—9]. Предметом данного сооб-
* Докл. АН СССР. 1981. Т. 261, № 5. (Соавторы В.Г. Ганжа, СВ. Мелешко, Ф.А. Мурзин, В.П. Шапеев.)
57

щения является реализация на ЭВМ второго алгоритма. Одним из его преимуществ
перед алгоритмом Картана является то, что нет необходимости переходить к внешним
дифференциальным уравнениям. Поэтому он более экономичен, особенно в
использовании памяти ЭВМ, что в данной задаче очень важно. Программы написаны на языке
РЕФАЛ, специально созданном для работы с символьной информацией [10].
Вычисления проводились на ЭВМ БЭСМ-6 в рамках мониторной системы "Дубна".
Для получения ответа на вопрос о совместности заданной системы
дифференциальных уравнений порядка т
Ф^(х,и,р) = 0, /i=l,2,..., s, (S)
где х = (Xi,х2,..., хп), и = (иг, и2 , ..., щ), р — производные до определенного
порядка т от и по переменным х, ра = Э'а 'и /Ъх01, а = ((*!, а2 ,..., а„), по второму
алгоритму необходимо выяснить, находится ли данная система в инволюции, иначе ее
надо продолжить, дополнив дифференциальными следствиями
где djdxi обозначает полную производную по xt.
Система (S) находится в инволюции, если выполнены следующие условия [11]:
1) Сх (S) — инволютивное подпространство;
2) существует окрестность iS С Jm точки Х0 Е S такая, что тройка (P(S) П
П (р^+ *) _1 ($), S П S, p™+1) есть расслоенное многообразие, где S —
многообразие, определенное соотношениями Фд = 0, p(S) — многообразие, определенное
соотношениями Фм = 0, </Фм/Ух/ = 0, Jm — множество всех m-джетов jm, pm+1(fm¥\f)) =
= /Т(/).
Проверка условий 1), 2) на ЭВМ сводится к следующим действиям. Проверяется
равенство
То = Т0 + Ti + ... + Т„,
где it — размерности определенных подпространств в Сх (5), r0 = dim(C£ (P(S))) ,
Xq = рт+1(Х0)- Нахождение Tt сводится к подсчету рангов соответствующих матриц
систем линейных уравнений, определяющих пространство в CX(S) с учетом всех
уравнений системы (S).
Если 1) не выполнено, то одно из ответвлений алгоритма заключается в том, что
делаются невырожденные линейные преобразования независимых переменных. В
реализованном варианте программы это осуществляется математиком при помощи нового
запуска программы после преобразования переменных.
Условие 2) означает, что следствием <2ФДД1^ =0, д = 1, 2, ..., s; / = 1, 2, ...,л не
должно быть соотношение <р(х, и,р) , которое не содержит старших производных
порядка га+1 и не зависит от системы уравнений Фм = 0. Последнее проверяется
подсчетом рангов соответствующих якобианов с учетом всех уравнений системы (S).
В общем случае для автоматической проверки обоих условий требуется, чтобы
исходная система (S) была в разрешенном виде. Два квазилинейных уравнений при
проверке первого условия это требование может быть опущено, что учтено в одном
из вариантов программы, а при проверке второго условия решение системы легко
поручить машине. Кроме того, правильный ответ может получиться и в других случаях,
если система (S) в неразрешенном виде, но при этом часть работы поручается
математику. Если при проверке второго условия возникли непротиворечивые новые,
не зависящие от (S) уравнения, то программа выдает их на печать. Эти соотношения
надо присоединить к системе (S) и сделать новый запуск программы. Если получились
противоречивые соотношения, то система несовместна. Если показано, что при общем
58

невырожденном линейном преобразовании независимых переменных не может быть
выполнено 1), то систему (S) следует продолжить и начать все сначала для
продолженной системы P(S). Программа выполняет продолжение автоматически.
Если условия 1) , 2) выполнены, то программа также заканчивает работу и в
результате выдает т(9 т0. Как известно, через Tf вычисляются характеры системы по
формулам а/ + 1 = Т/-т,+ 1.
Входной информацией для программы являются: а) система дифференциальных
уравнений; б) список неизвестных функций; в) список независимых переменных,
который фиксирует порядок при построении квазирегулярного базиса; г) порядок
системы. В настоящее время программа работает с системой, каждое уравнение
которой в разрешенном виде представляет собой отношение двух полиномов от
независимых переменных, искомых функций, их производных и параметров, являющихся
константами. К этому виду относится довольно таки широкий класс систем
дифференциальных уравнений.
Для реализации данного алгоритма потребовались следующие подпрограммы:
1) сложение, умножение и дифференцирование полиномов [12]; 2) вычисление
рангов матриц с коэффициентами, являющимися полиномами от всех переменных задачи;
3) решение системы линейных алгебраических уравнений.
При помощи этих программ был сосчитан ряд примеров, в том числе исследовались
на совместность двумерные и трехмерные системы уравнений Навье-Стокса, уравнений
теории упругости в смещениях, некоторые переопределенные системы уравнений
динамики неупругого твердого тела и газовой динамики, которые возникают при
применении к ним метода дифференциальных связей [13]. Были сосчитаны также все
примеры из [14], которые можно привести к указанному выше виду. При счете
некоторых рассмотренных примеров возникали матрицы большого порядка. Например, при
исследовании трехмерной системы уравнений Навье-Стокса появляется матрица
размерности 116x32, элементы которой суть полиномы. Она сильно разреженная и
поэтому помещается в оперативной памяти. Однако на практике встречаются системы,
для исследования которых недостаточно оперативной памяти БЭСМ-6. Время счета
названных примеров было в пределах от 10 с до 10 мин,
ЛИТЕРАТУРА
1. Картам Э. Внешние дифференциальные системы и их геометрические приложения. М.: Изд-во
МГУ, 1962.
2. Фиников СП. Метод внешних форм Картанав дифференциальной геометрии. М., Л.: Гостехтеор-
издат, 1948. 432 с.
3. АрайсЕЛ., Шапеев В.П., Яненко Н.Н. // ДАН СССР. 1974. Т. 214, № 4. С. 296.
4. Паламодов В.И Линейные дифференциальные операторы с постоянными коэффициентами. М.:
Наука, 1964.
5. Самбровский СН. // ДиффереНц. уравнения. 1980. Т. 16, № 3. С. 516.
6. ЧеботаревскийБ.Д. //Дифференциальная геометрия многообразий фигур. Калининград, 1979.
№ 10. С. 148.
7. Виноградов A.M., Красильщик И.С., ЛычагинВ.В. Геометрия пространств джетов и
нелинейные уравнения. М., 1977.
8.ЖижинА.Е. //ДАН СССР. 1978. Т. 238, №1. С 15.
9. Мелешко СВ., Шапеев В.П., Яненко Н.Н. // Там же. 1980. Т. 254, № 4. С. 796.
10. Базисный рефал: Описание языка и основные приемы программирования: (Метод,
рекомендации). М., 1974. Вып. V-33.
11. KuranishiM. Lectures on involutive systems of partial equations. Sao Pulo: Publ. Soc. Math., 1967.
12. Резников И.Г., СтеллецкийВ.И., Топунов В.Л. // Тез. Всесоюз. конф. по методам трансляции.
Новосибирск, 1981. С 177.
13. Яненко Н.Н. II Тр. IV Всесоюз. мат. съезда. Л., 1964. Т. 2. С. 247.
14. PommaretJ.F. Systems of partial differential equations and Lie pseudogroups. P.: College de France,
1978.
59

ЗАДАЧА АВТОМАТИЧЕСКОГО ПОСТРОЕНИЯ
И ИССЛЕДОВАНИЯ НА ЭВМ
РАЗНОСТНЫХ СХЕМ В АНАЛИТИЧЕСКОМ ВИДЕ*
Задача построения и исследования разностных схем на ЭВМ в аналитическом виде
изучалась в работах [1—5]. В нашей работе рассматривается разработка
единообразного формализованного алгоритма метода неопределенных коэффициентов для
аппроксимации различных дифференциальных уравнений на разных сеточных шаблонах с
произвольным порядком и реализация этого алгоритма на ЭВМ в целом с помощью
символьных операций. Приводится пример построения в случае задачи Дирихле для
уравнений Пуассона новой монотонной разностной аппроксимации четвертого порядка.
1. Одним из самых общих подходов при построении разностных уравнений на
произвольных сеточных шаблонах является метод неопределенных коэффициентов [6—8],
позволяющий строить аппроксимацию высокого порядка для сложных краевых задач.
Однако его широкому распространению препятствует необходимость громоздких
аналитических выкладок при формировании алгебраической системы уравнений для
разностных коэффициентов, анализа ее разрешимости и нахождения решений с
требуемыми свойствами. Принципиальное решение проблемы в автоматизации этого
алгоритма на ЭВМ в аналитическом виде.
2. Пусть и(х) = u(xi ,х2,..., хп) — функция п независимых переменных,
удовлетворяющая линейному дифференциальному уравнению r-го порядка
£(")= S S а? . \ . =/(*i,*а,-,*i,) (О
<* = 1 il+...+in=a 'i'""1" 3*V... дх1пп
с постоянными коэффициентами а?
Обозначим через Ш (х) шаблон некоторой разностной сетки £lh в окрестности точки
х = { xl9x2,..., хп}9 представляющий собой совокупность N узлов х + Ак, к- 1,2, ...,7V,
на котором задано разностное уравнение
N
Lhuh= 2 ckuh(xi + Aitk) = gh9 А1ук= aiikh9 (2)
аппроксимирующее дифференциальное уравнение (1) с погрешностью порядка р
{Lu(x))h-Lh{u(x)}h-{f(x)}h+gh = 0(h?).
Здесь h — характерный шаг сетки, uh — некоторая определенная на £Lh функция,
{и(х))и — сеточная функция, определенная как совокупность значений и(х) в
узлах Йл.
3. Определим метод неопределенных коэффициентов для построения разностного
оператора Lh следующим образом:
а) раскладываем в окрестности точки (х1} х2,..., хп) все члены выражения
N
Lh{u(x)}h= Г ck{u{xx+bl9k9 ...,*„+ Дя,*)}л (3)
в ряд Тейлора до порядка т включительно; результат разложения обозначим 21э
р> т— г;
б) разрешенное относительно одной (любой) из старших производных исходное
уравнение дифференцируем последовательно по всем независимым переменным до
♦Докл. АН СССР. 1984. Т. 275, № 3. (Соавторы А.Н.Валиуллин, В.Г.Ганжа, В.П.Ильин, В.П.Шапеев.)
60

получения произвольных порядка т9 т.е. выписываются следствия уравнения. Левые
части всех полученных равенств назовем главными производными. В этих равенствах
все главные производные последовательно исключаются из правых частей. Результат
оформляется в виде некоторой таблицы;
в) в S] выделяем все производные,.входящие в исходное дифференциальное
уравнение (1). Обозначая коэффициенты при них через b^ f , приводим Sj к виду
22 = S 2 Ьа . s г-+2з; (4)
<* = i /! + ... + /„=<* »1-»л дх[1...дх}»
г) в 23 с помощью упомянутой таблицы поочередно исключаем все главные
производные в порядке убывания их степеней; полученное выражение обозначим 24.
Целью этого этапа является учет всех следствий исходного дифференциального
уравнения;
д) в Z4 делаем приведение подобных членов относительно одинаковых степеней
h\, h2,..., hn; полученное выражение обозначаем символом Z5:
mm I Ъи Ъи Ъти \
е) в коэффициентах Z5 делаем приведение подобных членов относительно
различных производных. Найденные коэффициенты при различных производных
приравниваются нулю;
ж) коэффициенты Ь? из (4) приравниваются коэффициентам а? .
исходного уравнения (1). Добавляя к ним полученные в п.е) уравнения, приходим к
линейной алгебраической системе относительно неизвестных ск\
з) исследуем вопрос о совместности построенной системы;
и) выводим формулу общего решения (если оно существует) в аналитическом
виде.
В итоге получим выражение для искомых разностных коэффициентов, зачастую
содержащее неопределенные параметры, подбором которых можно добиваться
желаемых свойств системы разностных уравнений.
4. Рассмотренный выше алгоритм реализован на ЭВМ БЭСМ-6 в виде пакета
программ, осуществляющего полную автоматизацию построения разностных
уравнений, аппроксимирующих произвольное линейное дифференциальное уравнение на
произвольном сеточном шаблоне. В пакет включены следующие программы
аналитических вычислений:
а) программы обработки полиномов (сложение, умножение, дифференцирование,
деление, нахождение наибольших общих делителей и наименьших общих кратных
полиномов многих переменных);
б) программа дифференцирования рациональных функций;
в) программа разложения в ряд Тейлора функций от многих переменных;
г) программа исключения одного выражения из другого;
д) программы матричной алгебры (сложение, умножение, нахождение
сопряженной, нахождение обратной, подсчет определителей различных матриц) ;
е) программа тригонометрических преобразований;
ж) программа решения систем линейных алгебраических уравнений.
Все программы пакета написаны на языке РЕФАЛ [9], специально
предназначенном для проведения символьных преобразований на ЭВМ.
5. Для шаблонов на рис. 1—4 с помощью описанного выше пакета программ
построены девятиточечные разностные соотношения вида (ниже используется локальная
61

нумерация узлов в соответствии с обозначениями на рисунках) :
-Ahuh = схих- 2 ckuk=g.,
к = 2
(6)
аппроксимирующие уравнение Пуассона с погрешностью OQi2).
Здесь для примера приведем формулы коэффициентов ск для шаблона на рис. 2:
С\ =
2t2l-4t2m +2tln -2tnm - \2tm -6I2m - \2lm2
9h\tlm2
7 у е
h2
s
V I
г*
Рис. 1.
J ¥
\\hz\
Ш
hi
> * ч|
3 5
Рис. 3.
в
ы
\hj
hi
А *• J
I*
2t2l + 4t2m -2tln +2tl + 2tnm -2tm + 6l2m -2ln + \2lm2+2nm- вт
c2 =
съ =
c4 =■
cs =
c6 =
Cn =
9h\tlm2+9h\lm
2/^2
2/ + 4m
3h\t2m + 3h\tm
2tln + 4tnm + 6I2m - 2ln2+2n2m + \2nm - 6m3
9h2lnm2+9h2m3n
2tl + 4tm - 2ln + 2nm + 12m
9h\l2m + 9h\lm2 '
-2tln - 2tl - 4tnm - 4tm - 6I2m + 2/и2+ 2ln - 2n2m + 4nm + 6m3 + 6m
__
(7)
9h\lnm2 + 9h\lm2 + 9h\nm?4 9/*im
-21 +2m
3h\rCm + 3h\nm
62

-2tl - Atm + 2ln - 2nm + 6m
C8= 9h\l2m + 9h?lm2 ' *9 = °'
где
h3 h4 _ h2 h6 hs
hx hv hi hi hi
Условие положительности ск описывается неравенствами
t<\fbft л>-1 + \/Т, /> л/5/12, т>/, г>л, т< 1. (8)
6. Пусть и — решение уравнения Пуассона
Ъ2и Ъ2и
-Аи=--—-—Г= f(x, у) (9)
Эх2 Э^2
в ограниченной области G, на кусочно-гладкой границе Г которой задано условие
Дирихле ит = <р (х, у). Предполагаем, что форма границы и вид функций /, <р
обеспечивают ограниченность шестых производных искомого решения и.
Для аппроксимации краевой задачи построим покрывающую область G
прямоугольную сетку х,- = x0+ihx, y-= y0+ jhy. Для регулярных узлов сетки (/, /), у
которых все соседние узлы с индексами (/ ± {0 или 1}, /± {0 или 1}) лежат
внутри (7, используем известную девятиточечную аппроксимацию с погрешностью
О (А4) :
/ h2x+hl ' \
-(Д1"а)<,/=|Л*ый + Ауин + -———AxAyuhJ t . =
"^i* Ъ{АхГ)*>1+ W(Ayf)i>r (10)
где AX9 Ay — обычные трехточечные разностные операторы,
(Л*"л)1;/= (l/Ai)(w/-if/-2ii/f/ + ii/+1>/ ).
Если же узел (/, /) лежит вблизи границы, то вместо внешних соседних узлов
используем ближайшие точки пересечения границы с координатными линиями и
выписываем уравнения типа (6).
Выведены условия на геометрические параметры сеточных шаблонов, при
которых уравнения типа (6), записанные для шаблонов на рис. 1—4, являются
"монотонными", т.е. когда все коэффициенты ск положительны и согласно терминологии,
(ci>,i4
используемой в [8], имеют диагональное преобладание I Ci > 2 ск\. Здесь
учитывается, что члены уравнений, содержащие значения функции на границе,
переносятся в правую часть.
Таким образом, вся система уравнений разностной краевой задачи состоит из
"монотонных" уравнений, которые в регулярных узлах имеют погрешность О (Л4),
а в около граничных — OQi2)9 причем в последнем случае они имеют строгое
диагональное преобладание. В соответствии со свойствами такого типа систем
справедлива согласно [8] следующая
Теорема. Решение системы уравнений разностной краевой задачи при условиях
монотонности аппроксимирует с погрешностью 0(h4) решение "и" задачи Дирихле
для уравнения Пуассона (если и имеют ограниченные 6-е производные).
Для проверки полученных разностных уравнений был проведен численный экспе-
63

римент. Результаты расчетов показали, что полученные на ЭВМ формулы имеют
указанную выше погрешность.
7. С помощью описанного пакета программ автоматизированы также следующие
алгоритмы:
а) вывода дифференциальных приближений разностных схем для линейных и
нелинейных дифференциальных уравнений;
б) подсчета порядка аппроксимации разностных схем;
в) исследования устойчивости разностных схем для систем линейных
дифференциальных уравнений.
Все перечисленные алгоритмы реализованы в случае многих независимых
переменных. Отметим, что пакет программ проверен на значительном количестве примеров.
ЛИТЕРАТУРА
1. Keller //., Регеуга V. // Math. Comput. 1978. Vol. 32. P. 955-971.
2. UleryD.L., KhalilHM. // Lect. Notes Comput. Sci. 1979. N 72. P. 177-188.
3. Cloutman L.D., Fullerton L.W. // J. Comput. Phys. 1978. Vol. 29, N 1. P. 141-144.
4. Валиуллин A.H., ГанжаВТ., Мурзин Ф.А. и др. Новосибирск, 1981. (Препр. / ИТПМ СО АН СССР;
№•7).
5. Ефимов Г.Б., Тишкин В.Ф., Шашков М.Ю., Щенков И.Б. (Препр. ИПМ АН СССР; № 20). М., 1982.
6. Березин И.С.,Жидков Н.П. Методы вычислений. М.: Наука, 1966. Т. 1,2.
7. Годунов С.К., Рябенький B.C. Введение в теорию разностных схем. М.: Наука, 1977.
8. Вазов В., Форсайт Дж. Разностные методы решения дифференциальных уравнений в частных
производных. М.: Изд-во иностр. лит. 1963.
9. Базисный рефал: Описание языка и основные приемы программирования: (Метод,
рекомендации). М., 1974. Вып. V-33.

нелинейные уравнения
переменного типа
ОБ ОДНОЙ МОДЕЛИ ЖИДКОСТИ
СО ЗНАКОПЕРЕМЕННЫМ КОЭФФИЦИЕНТОМ ВЯЗКОСТИ*
1. Рассмотрим уравнение
Ъи _ Э Г (Ъи \ Ъи
Ы Ъх[ \Ъх/Ъх
(О
для которого поставлены периодические начальные данные
и(х,0) = ио(х\ 0<х<1, (2)
(О, /) — интервал периодичности на вещественной оси — °° <х < °°.
Если функция v(bu/bx) удовлетворяет условию
v (Ьи/Ьх) > v0 > 0, (3)
то задача Коши (1), (2) корректна. Если, напротив, удовлетворяется условие
v (Ьи/Ьх) < v0 < О, (4)
то задача (1), (2) некорректна.
Представляет интерес рассмотреть случай, когда коэффициент v (Ьи/Ьх) является
знакопеременным. Мы будем предполагать, что коэффициент v(bu/bx) является
асимптотически положительным, т, е, принимает отрицательные значения только в конечной
области изменения переменного р = Ьи/Ьх, а при достаточно больших \р \ положителен
и возрастает достаточно сильно. В случае полиномиальной зависимости
е>0, (5)
v(p) = e
1+2 Pip"*
где щ — натуральные числа, возрастающие с г, для асимптотической положительности
необходимо и достаточно, чтобы
*,>0. (6)
Можно показать, что при условии (6) соответствующим подбором vt можно добиться
знакопеременности Ъ(р), так что при этом достаточно гладкое решение (1), (2) будет
ограничено для всех t, в некоторой норме%к.
2. Рассмотрим сначала случай квадратичного двучлена v(p):
v(p)=l +ViP+ViP2, *>2>0. (7)
Для его знакопеременности необходимо и достаточно
v\ -4v2= 5>0. (8)
Дифференцируя уравнение (1) под:, получим
Ьр Ь2 Ьи
— =—-ы(р\ р = — 9 (9)
bt Ьх2 Ьх
•Численные методы механики сплошной среды. Новосибирск. 1973. Т. 4, № 2. С. 142-147. (Соавтор
В.А. Новиков).
3. Зак. 953
65

где положено
co(p) = pv(p) = p+v1p2 +v2p3. (10)
Для уравнения (9) естественно ставятся начальные данные
p(xt0) = po(x) = duo(x)/dx. (И)
Умножая уравнение (9) на крк~г, интегрируя по х в пределах интервала
периодичности и применяя интегрирование по частям, находим
^fpkdx = -k(k--l)fpk-2cb(^) dx, (12)
at \дх/
где
co(p) = dcj(p)/dp-= l +2vlp + 3v2p2. (13)
Рассмотрим серию равенств (12) при последовательных значениях kt к. + 1, к + 2.
Умножая первое равенство на 1, второе на я, третье на Ь и складывая, получим
э - --©г
— f pkA(p)dx = -k(k-l)fpk-2<b[^-) n(p)dx, (14)
где положено
A(v)=l+ap+bp2% П(р)=1+к1ар+к2Ьр2, (15)
*i=(*+ l)/(* - 1), к2=(к + 2) (А: + 1)/к(к - 1).
Потребуем, чтобы
П(р)=ы(р). (16)
Из (16) следует
a = 2(v1/k1\ Ь = 3(р2/к2). (17)
Потребуем, чтобы при этом
Л(р)>0. (18)
Подбором к, vl9 v2 этому условию можно удовлетворять. Достаточно, например,
положить
к=29 vl-4v2=8>0, v2-2/9v2i>0. (19)
Тогда
А(р)= 1 + 2/з РгР"+ й *>2Р2 > 0, (20)
в то время как v(p\ co(p), со(р) знакопеременньь Равенство (14) принимает вид
•■—,.^®-
ffp2A(p) dx = -2fu2[ —) dx. (21)
Отсюда следует
/р2ЛСр)<£с |^<0. (22)
Обозначим
Ci=minA(p)>0, с2=/р2Л(р)<£с|г=о>0. (23)
Тогда
с, J>2 dx |f </p2 Л(р)<&: lr</p2 Л(/>)<&: l,=0=c2. (24)
Откуда следует оценка
/p2dx = / [Эы(х, t)/dx]2 dx <са/е,. (25)
66

Аналогичным образом можно показать для
v(p)=l -»iP2m +»2Р2п, т<п, vl9v2>0t (26)
что подбором vlyv2tmt n при достаточно больших т, и можно получить оценку
fpkdx<c(m,n,vl9v2)fp%A(po)dx (27)
для сколь угодно больших к, где с не зависит от к. Заметим, что при этом Л(р) будет
четной функцией в отличие от А(р) в рассмотренном примере.
3, Аналогичные оценки можно получить для уравнения
Ъи 'Ъи Ъ Ъи
— +w = — со(р), р = —
bt Ъх Ъх Ъх
(28)
где снова со(р) = v(p) • р = р + v1p2 + v2p3 • Поставим для (28) первую краевую задачу:
и(х, 0) = uo(x)t и(1, г) = и(0,г) = 0. (29)
Умножим уравнение (28) на ut и проинтегрируем по области (0, /) Х^(0, t) = Qt
f ujdxdt+f uux utdx dt = f co(p)utdxdt.
Qt Qt Qt &*
Интегрируя по частям правую часть (30), получим
Э Э ' Э / /1 vt
f —u(p)utdxdt = -f (их +vxu\ + v2ux)—(ux)dx dt = -f—[fp2 - + —-p
Qtbx Qt dt о dt\ \2 3
+ ^p2jdx)dt = -fp2(- +-yP+~7-P2 )dx
Перепишем (30) следующим образом:
/ u2dxdt + fp2\- +"- p+—p2\
Qt L2 3 4 J
(30)
dx
Л = —/ uuxutdxdt.
0 Qt
(31)
(32)
Заметим, что
1 *>i ^2 2
, - + —P+ — P
L2 3 4
>ep\ e>0,
как только
„2
Пусть е таково, что вместе с (33) v\ — Av2 = 5 > 0. Тогда
/ u2dxdt + efp4dx
Qt
t<fp2
1 *>1 *>2 2
- + p+ p2
2 3 4
dx
t=o-f wxUtdxdt.
0 Gr
Далее [1]
/ uuxutdxdt
Qt
<-/ (u2 +u2u2x)dxdt<- f u2dxdt+—f\\p\\* dt
2 Qt 2 Qt 2 о L*
Положим
IP2
- +■—p + —p2
2 3 4
dx \t=Q = c2>0.
(33)
(34)
(35)
(36)
3*
67

Тогда (34) можно переписать
1 С\ *
- f u2tdxdt + efp*dx<c2 +—fWpK dt. (37)
2 Qt 2 о L*
Пусть c3 = min{H, e), c3 > 0. Тогда
f u2tdxdt+fp4dx^- + -^— f \\p И dt. (38)
Qt съ 2съ о L*
Отсюда
Ир II? < —+ — /|рИ Л. • (39)
1/4 c3 2съ о L*
Воспользуемся леммой: t
Лемма. Если y(t) < F(t) + f b(f)y (r) tfr, гдеF(t) - неубывающая неотрицательная
о
функция, ab(t) - неотрицательная суммируемая по t функция, то
t t
y(t)<m
1 +f b(r)dT -expfb(r)dT
о о
t t m t
f b(r)y(j) dr <F(t) f b(r) dt • exp / Ь(т) dt.
О 0 0
В данном случае
F(t) = c2/c3f b(t) = c1/2c3,
то есть
Co Co C\ C\
\\p\\\ <— +— -1 r-exp—-t = c4(t). (40)
L* съ c3 2c ъ 2c ъ
Тогда из (38)
/ u2dxdt+\\p V <cs(t). (41)
Qt la
4. Решения уравнений (1), (28) могут носить осцилляторный характер. Для
некоторых начальных данных и0(х) возможна ситуация, когда и(х, t) не имеет предела при
х фиксированном и t -> °°, в то время как
1 t
u(xr t)= — f u(x, s)ds
t о
такой предел имеет.
В этом случае коэффициент вязкости v меняет знак и может происходить каскад-
Ъи Ъ Ъи
ный процесс, обусловленный не конвективным членом и —, а диффузионным — (у—).
Ъх Ъх Ъх
Зависимость коэффициентов вязкости от градиентов потока может быть принята и
для уравнений вязкой, сжимаемой жидкости. В случае асимптотически
положительных коэффициентов вязкости можно также ожидать осцилляторных решений, что даст
возможность моделировать автоколебательные и турбулентные течения.
ЛИТЕРАТУРА
1. Ладыженская О.А. О новых уравнениях для описания движения вязких несжимаемых жидкостей
и разрешимости в целом для них краевых задач // Тр. МИАН СССР. 1967. Т. .11. С. :85 -104.
68

О НЕКОТОРЫХ УРАВНЕНИЯХ ПЕРЕМЕННОГО ТИПА
ди dv
— + =
dt дх
д
=
дх
ди
р(и) —
L дх J
dv ди
= _ а
dt дх
1. Для описания нелинейной неустойчивости и автоколебательных движений
сплошной среды в последнее время предложены математические модели, основу которых
составляют уравнения в частных производных переменного типа.
В работе [1] проведены численные эксперименты и дан качественный анализ
системы уравнений
Я Г ritJ I Я?) ?\11
a- const, (1)
которая представляет собой упрощенную модель баротропного газа с коэффициентом
искусственной вязкости v(u), зависящим от скорости. Решением системы (1) являются
автоколебания, возникающие в областях пространства скоростей и, где коэффициент
v{u) меняет знак,
2, Система (1) неинвариантна относительно преобразования Галилея. Очевидно, что
содержательные феноменологические модели механики сплошной среды должны быть
инвариантны относительно основной группы преобразований, В связи с этим в работе
[2] предложена математическая модель, являющаяся аналогом одномерного
уравнения Бюргерса, но с коэффициентом вязкости, зависящим от градиента скорости
ди ди
дх L \ дх I дх
Здесь коэффициент вязкости v — асимптотически положительная функция ди/дх,
принимающая отрицательные значения в некоторой конечной области изменения ди/дх.
Рассмотрим сначала уравнение (2) без конвективного члена и(ди/дх) с начальным
условием и(х, 0) = и0(х)9 0<х<1и периодическими граничными условиями. Если
ди /ди\2
i;=1+i;i"ax +l4lx/' "2>°9 Vl-4V2=8>0> (3)
то имеет место следующая априорная оценка решения :
K^l^xfdx<C{v^v2tu0)t (4)
Если v-l — vx {ди/дх)2171 + v2(du/dx)2n, т < п, vx, v2 > 0, v\ — 4v2 > 0, то для
достаточно больших т, п имеет место следующая априорная оценка:
ди\н
дх]
fl—)dx<C(m,n,vl9v2,k,u0).
Для полного уравнения (2) с начальными и граничными условиями и(х, 0) = и0(х)9
ы(0, t) = u(l, t) = 0 получена оценка
fujdxdt + fu* dx<C(yl9v2, u0, t).
Для задачи (2), (3) установлен разностный аналог оценки
tii
f f и2 dxdt + / и% dx < const,
oo о
гарантирующий слабую компактность в соответствующих пространствах решений
разностных уравнений.
Оценим теперь отклонение решения уравнения (2) с коэффициентом вязкости (3)
* Теория кубатурных формул и вычислительной математики. Новосибирск: Наука, 1980. С. 48-54.

от решения уравнения Бюргерса. Начально-краевые условия выберем в виде и \t=0 =
= и(х)9 и(1, г) = и (О, t)\ О < t < Г. Предполагаем, что vt, v2 — малые параметры и что
коэффициент v(p) = vQ + i^p' + v2p2 положителен, а коэффициент */(/?) = vo + -^i/7 +
+ 3^2P2 при второй производной в уравнении (2) знакопеременен. Из этих требований
вытекают следующие условия на коэффициенты:
»1 > 0, v\- 4v0v2 < 0, v\- 2>v0v2 > 0. (5)
Из предположения малости vl9 v2 следует, что для выполнения соотношения (5) при
фиксированном v0 и при изменяющихся малых vx, v2 достаточно, чтобы v2 = kv\ с
некоторой фиксированной постоянной к.
Итак, рассматривается уравнение
Э
ut+uux= —
Ъх
Оо + ^i"* + *"i "i) —
ох
с условиями на коэффициенты
1-4^0<0, 1 - ЗЛг^о >0,
и константа к выбирается по v0.
Пусть и°(х, t) — решение уравнения Бюргерса
ut+uux=vuxx
с указанными выше нечально-краевыми условиями. Запишем решение задачи в виде
и(х, t) = и°(х, t) +R(x, t), Тогда справедлива оценка
\\R\\2<k(Tfu°)vlt
3. В работе [3] рассмотрено уравнение
Ъи Ъи Ъ Г / Ъи\]
— + 2дн— = — Ы —) , (6)
bt Ъх Ъх I \ Ъх)\
где со(£) — гладкая функция, для которой со'(£) > 5 >0, \%\> N > 0, и со'(£) может
принимать отрицательные значения для | £ I <N.
В случае начальных и граничных условий и(х, 0) = и0(х)9 м(0, t) = м(1, f) = 0
априорная оценка в норме С(0,1) имеет следующий вид:
И"Ис(о,1) + K»c(o,i) <C0V> "о, ', ВД), (7)
где К(Т) = sup | и(х, t) |, 0 < t < Г. Если /i = 0, то величина С в (7) не зависит от К.
X, t
В работе [3] получены также теоремы существования обобщенного и гладкого
решений для задач
/ Э4 \ Ъи Ъи Ъ /Ъи\
1 +€-—.) +ы = со! —);
\ Эх4/ Ы Ъх Ъх \Ъх)
Ъи Ъи Ъ (Ъи\ Ъ4и
— +2аш— =— со —1-6—-
bt Ъх Ъх \Ъх/ Ъх4
Ъи Ъи
с условиями и(х, 0) = и0(х), ы(0, i) =—(0, t) = u(l,t)-—(1, t) = 0 и со знакоперемен-
Ъх Ъх
ным коэффициентом со'(£).
Для задачи (6) в работе [4] установлена более сильная оценка типа (7) с константой
С в правой части, не зависящей от К{Т), и оценка
*2,
Д со' -)dxdt + fu2tdxdt<C(N,u0, r).
70

Для гладких решений уравнения (6) с краевыми условиями вида
аих - ф)\х = 0=Рих - Ф(и)\х=1 = О (8)
получена оценка \их | через \и | и sup \\и0\ + \и'0 II, а также априорная оценка \и | для
третьей краевой задачи при дополнительных условиях на рост ip(u), ф(и), со(их).
Для обобщенных решений задачи (6), (8) получена оценка в классе обобщенных
решений, допускающих аппроксимацию в определенном смысле гладкими функциями.
Если коэффициент со'(5) ^ 0 вырождается, то методом конечных разностей ддя
первой и третьей краевых задач при дополнительных ограничениях на рост функций
у(и), ф(и), oj(ux) доказана теорема существования решения задачи (6), (8) из класса
функций, для которых конечно выражение
t \ 1
/ / К2 + (<о'(и*) uxxf ] dxdt + / со(i*x) dx + sup | и | .
0 0 О
В случае знакоперенной величины со'(их) показана слабая компактность приближенных
решений в соответствующих пространствах.
Методом Галеркина доказана теорема существования и единственности
обобщенного решения рассматриваемой задачи из класса И^^вслУчаевЬ1Р°ждающегосякоэффи
циента со'(£) > О (-С0 + Сх | £ \2v < со'(J) <С2 \£ \2Р + С3) и слабая компактность
приближенных решений в случае знакопеременной функции со'(£).
В [6] получены априорные оценки \их | через \и | и \\и0 \\с1 для квазилинейных
уравнений с одной пространственной переменной
ut = а(х, и, их) ихх + Ь(х, и, их) + f(x, и, их, ихх),
где а > а0 > 0, / - финитная функция, а также оценка \их | через \и | и \\и0 llci при
/=/ift х, и, их)ихх +f2(t, x, и, их, ихх)9 где/i, /2 финиты по их, ихх.
4, Следуя работе [4], рассмотрим систему уравнений типа Навье—Стокса
Ъи
з Э Г (Ъи\ ЪиЛ
+ (*.V)h+VP = 2 — \v — 1— ;divH = 0, (9)
где x £ £2 С R3, Q, — ограниченная область с достаточно гладкой границей ЭГ2, и = (ult
"2, "з), 0 <!<«>,
-(
ди\ [ Ъи\2т
Ъи |4т 1
— , v2 > 0, т >. -
Эх ' 2
дх\ \U=i\tef I /
Условие v2 >' 0 означает, что рассматриваются только асимптотически положительные
полиномы v{p).
Ддя уравнения (9) рассмотрим следующие начально-краевые условия:
"'эп = 0' Ч=0="о(*). 0°)
Пусть V - замыкание множества W={v \v G C0°°(^), divu = 0} в норме Щ+^т(Р),
где ^Im+ii^) ~ пространство Соболева. Пусть со, (/" = 1, 2, ..., л, ...) — некоторая
полная в банаховом пространстве V система функций. Будем искать приближенное
71

решение задачи (9)- (10) с помощью метода Галеркина, т. е. в виде
un(t,x)=X С? (О "/(*)■
где коэффициенты C!(t) находятся из уравнения
з / (Ъип\Ъип Эсо.Д
*■:•'»)♦»■"•')" "•">>♦,?,(" fc fe- W)"0, '='-2 "■ (11)
а (,) — скалярное произведение в L2(£l). Начальные условия для системы (11) найдем
из соотношений С?(0) = а?, где of! определяются из условий
н"(0,х) = 2 а,лсо,(х), ww(0,x)->woW (12).
при и -> °° в норме пространства V. Справедлива следующая
Теорема. Пусть и1 (t, х) = С\(t)cji(x) — первое галеркинское приближение задачи
(9), (10), ь>г(х) е V, fcjjdx = 1, и\09 х) = с^со^х). Обозначим \С[ \2m = y(t\a0 =
= 2mvQ f \dojJdx\2dxr ax = -2mvx f \bu1/dx\2m+2dx, a2 = -2mv2 f \bcj1/dx\4m+2dx.
Тогда функция y(t) удовлетворяет уравнению Абеля первого рода
by/dt = a0y + aty2 + а2у3 (13)
и имеют место следующие утверждения:
1) если v0 > 0, то нулевое решение асимптотически устойчиво по Ляпунову при
t -> °°; при v\ — 4vov2<0 не существует других стационарных решений уравнения (13) ;
при v\ — 4v0v2 > 0, vx < 0 существует еще одно асимптотически устойчивое по
Ляпунову при t -> °° положительное решение для некоторых 03x(x) ;
2) если v0 < 0, то для некоторых со1(х) существует только одно положительное
асимптотически устойчивое решение уравнения (13),
5. Для выяснения свойств модельного уравнения (2) со знакопеременным
коэффициентом вязкости (3) было проведено численное решение этого уравнения
конечно-разностным методом [5]. Когда коэффициент вязкости v отрицателен, то задача
становится некорректной и решение может возрастать. Поскольку ожидалось появление
колебаний, связанных с изменением знака коэффициента вязкости, то была
выработана схема, которая на решениях уравнения Бюргерса (ух = v2 = 0, vQ = const > 0).
давала заведомо монотонный профиль. Была изучена эволюция начального распределения
в виде ступеньки, Расчеты позволили установить нестационарные колебания при
стационарном осреднением течении, обнаружить свойство перемежаемости, т, е.
чередование сильных и слабых осцилляции.
6. Рассмотрим задачу о газовом шаре, находящемся под действием сил гравитации
и газокинетического давления. В предположении сферической симметрии исходные
уравнения имеют вид
Ъи _ М(г) 1 Ър_
bt r2 p 3r ' w о
= -G—y - ~ -Т- i M(r) = f47rr'2p(r')dr'; p=p(pf Г), (14)
где и — радиальная скорость; р — плотность; р — давление газа; G — гравитационная
постоянная.
В случае политрогагой зависимости давления газа от плотности р -Ср2 система
уравнений (14) имеет стационарное решение: p(r) = p0sin7rr/7rr (p0 — плотность в центре
шара, радиус которого равен R0 =\/7t/2G— 48,5 м).
Большой интерес представляет решение системы (14) в случае немонотонной
зависимости pip), например типа зависимости Ван-дер-Ваальса, поскольку области, где
dp/dp < 0, являются неустойчивыми. Численное решение исходной системы уравнений
с немонотонной связью между давлением и плотностью показало, что в зависимости
72

от глубины "ямы" на графике р(р) получаются существенно различные
распределения плотности по радиусу шара: либо происходит разделение шара на две области с
заметно различающейся плотностью и резкой границей между этими областями —
режим I, либо имеет место непрерывное изменение плотности — режим II [7].
В режиме I плотности газа справа и слева от разрыва находятся в области, где dp /dp <
< 0. Шар делится на две части потому, что область с dp /dp < 0 неустойчива. С
течением времени плотности и радиус шара испытывают колебания, причем колебания
плотности во внешней части шара существенно меньше, чем во внутренней.
В режиме II также наблюдаются колебания плотности, совпадающие по порядку
величины с колебаниями плотности в режиме I в области, внешней по отношению к
разрыву.
Таким образом, немонотонные уравнения состояния типа Ван-дер-Ваальса могут
определять гидродинамические автоколебательные процессы. Эти особенности
физически связаны с фазовыми переходами и источниками энергии, а математически находят
свое выражение в переменности типа исходных уравнений (гиперболический —
эллиптический) .
7. Интересная система уравнений переменного типа описывает нелинейные альфве-
новские волны, распространяющиеся в разреженной анизотропной плазме вдоль
магнитного поля [8—10]:
Ъи b Г „ bv 1 Эй Э Г 0 Ьи
— + (1- Я2 -В2)Н =0; — +— (1-Я2 -В2)В + —,
bt bz[ bz \ bt bz[ bzl
= 0; (15)
ЪН bu ЪВ _ bv
bt bz bt bz
Здесь Я, В(и, v) — компоненты магнитного поля (скорости) в плоскости,
перпендикулярной основному магнитному полю Н0, направленному по оси z.
Система (15) записана в безразмерном виде. Все коэффициенты, характеризующие
среду, устранены с помощью преобразования масштабов. После линеаризации этой
системы относительно малых возмущений состояния покоя, пропорциональных
expi(kz — co^f), получается дисперсионное уравнение
a>k=k2/2 + iyk, Ук = к(1-к2/4)у\ (16)
где к — волновое число малых возмущений; ук — инкремент их роста.
Из формулы (16) следует, что возмущения с волновыми числами к < 2 неустойчивы.
Гармоники с волновыми числами к > 2 устойчивы, что связано с эффектом
"магнитной вязкости" (математически — с членами bu/bz, bv/bz в первых двух уравнениях
системы (15)). В нелинейном случае рост амплитуды волн ограничивается членами
(Н2 +В2Щ(Н2 +В2)В.
Система уравнений (15) допускает частное решение следующего вида:
H(z, t) = A(t) sin(kz + *p(t))\
B(z, t) = A (t) cos(kz + y(t) ),
где амплитуда волны A(t) удовлетворяет обыкновенному дифференциальному
уравнению
d2A/dt2 -у2А+к2А3-СА-3=0, C= const,
допускающему несложный качественный анализ и запись решения в квадратурах.
Амплитуда волны испытывает с течением времени автоколебания.
73

ЛИТЕРАТУРА
1. Dalv J.B. The stability properties of a coupled pair of non-linear partial difference equations // Math.
Comput. 1963. Vol. 84. P. 346-360.
2. Яненко H.H., Новиков В А. Об одной модели жидкости со знакопеременным коэффициентом
вязкости // Числ. методы механики сплош. среды. 1973. Т. 4, № 2. С. 142-147.
3. Зеленяк Т.И., Новиков ВЛ., Яненко Н.Н О свойствах решения нелинейных уравнений
переменного типа // Там же. 1974. Т. 5, №4. С. 35-47.
4. Зеленяк Т.И. Об одном уравнении со знакопеременным коэффициентом диффузии //
Математические проблемы химии. Новосибирск: Наука, 1975. 4.1.
5. Berczin YuA., Dudnikova G.I., Novikov V.A», Yanenko N.N. Analytical and numerical studies of
equations with sign changing viscosity coefficient // Lect. Notes Math. 1976. N 594. P. 30-38.
6. Белоносов B.C., Зеленяк Т.И. Нелокальные проблемы в теории квазилинейных параболических
уравнений. Новосибирск: Наука, 1975. 155 с.
7. Яненко Н.Н., Березин ЮА„ Криволуцкий B.C. Гравитируюший газовый шар // Числ. методы
механики сплош. среды. 1978. Т. 9. № 4. С. 13.9-145.
8. Березин Ю.А., Сагдеев Р.З. Одномерная нелинейная модель неустойчивости анизотропной ппаз-
мы // ДАН СССР. 1969. Т. 184, № 3. С. 570-573.
9. Березин Ю.А. Нелинейные движения в анизотропной плазме // ЖЭТФ. 1971. Т. 61, вып. 5(11).
С 1877-1881.
10. Berezin Yu.A., Vshivkov V.A. On the firehose instability of alfven waves // J. Comput. Phys. 1976.
Vol. 20: Nl.P. 81-96.
О НЕКОТОРЫХ НОВЫХ КЛАССАХ УРАВНЕНИЙ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ*
Известно, что реальные физические явления с определенной степенью достоверности
можно моделировать уравнениями математической физики [1].
Классическая теория уравнений математической физики имеет дело с тремя типами
уравнений: эллиптическим, параболическим, гиперболическим.
Однако развитие новой технологии, необходимость более детального рассмотрения
природы физических явлений потребовало от математиков и механиков исследования
новых объектов математической физики, прежде всего уравнений переменного типа.
Как правило, это квазилинейные уравнения в частных производных второго порядка,
тип которых зависит от свойств решения, например уравнение Буземана,
описывающее трансзвуковые течения газа:
uxuuxx-uyY = Q. (1)
Оно эллиптично, если их < 0, и гиперболично, если их > 0.
Другой класс уравнений переменного типа был предложен Н.Н. Яненко [2] для
моделирования гидродинамической неустойчивости
ut-(F(ux))x = 0, (2)
где функция F'(ux) может менять знак. Это уравнение в зависимости от знакаF'(ux)
параболично "вперед" или параболично "назад".
Постановка краевых задач для уравнений (1) и (2), исследование их разрешимости
и численный расчет представляются чрезвычайно трудной проблемой.
I. В тесной связи с уравнениями (1), (2) находится уравнение в частных
производных третьего порядка
$utt +ut- (F(ux))x - д(Л(^))х,=/(х, О- (3)
Если /3 = 1, F \их) > 0, Fi(ux) > 0, /i = 1, то уравнение (3) возникает в теории
материалов, обладающих памятью, и его рассмотрели Д. Гринберг, Р. Мак Камм, В, Мизел [3].
Труды конференции по дифференциальным уравнениям и их приложениям. ГДР, 1982. С.: 159—
164. (Соавторы Н.А. Ларькин, В.А. Новиков.)
74

К уравнению вида (3) приводится система уравнений, описывающая
нестационарные одномерные течения вязкого баротропного газа в лагранжевой системе координат
Э(1/р) dv bv Ьр(р) Э
№
= 0, + = д р— ; (4)
ы ъх ы ах ах \ ах / v
отметим, что при немонотонной зависимости давления р от плотности р и при д = 0
система (4) будет системой переменного типа. При ц > 0 разрешимость краевых задач
для системы (4) изучалась А.В. Кажиховым и В.А. Николаевым [4].
А.И. Кожанов, Н.А. Ларькин, Н.Н. Яненкр [5] исследовали разрешимость краевых
задач для общего уравнения (3) в случае, когда производные второго порядка
образуют оператор переменного типа. Основным допущением являлось следующее:
Рг'(их)>8>0, д>0, 0>О, (5)
\F'(ux)\<C(l+Fl(nx))9 O0.
При этих условиях удалось доказать теоремы об однозначной разрешимости в целом
по t начально-краевых задач для уравнения (3), а также задачи Коши,
Более строго справедливо утверждение.
Теорема 1, Пусть F(ux\ F,(ux) G C\R\ Q = (0, 1) X (0, Г); u0(x) G И/|(0, 1) П
П #2(0, 1); Ul(x) G Wl(0, 1 ),/(*, t)GL2(Q) и выполнены неравенства (5), тогда
существует единственная функция и(х, t)
и GLoo (0, Т; И>|(0, 1) П ^(0, 1)), UtGLn (0, Т; ^(0, 1)),
"tt^L2(Q\ uxxteL2(Q),
удовлетворяющая п.в. в Qуравнению (3) и принимающая следующие начальные и
краевые значения:
и(х,0) = ио(х), ut(x,0) = u1(x), и|х=о>1=0.
В этом случае, если функции F(ux), Fx(ux)9f(x, f), и0(х)9 их (х) более гладкие и
согласованы в точках х = 0, 1; t = 0, то полученное решение является более гладким.
Доказательство существования решения проводится в два этапа, 1. Доказывается
существование гладкого решения на достаточно малом промежутке времени. 2,
Получаются априорные оценки гладкого решения, позволяющие продолжить решение по t
на более широкий промежуток времени.
Для получения априорных оценок уравнение (3) умножается сначала на ии затем
на — (Fj(ux))x и результаты преобразуются совместно,
Из этих оценок следует, что в уравнении (3) можно устремлять к нулю параметр /3.
Более того, в некоторых случаях можно отказаться от ограничения Fl(ux) > Ь > 0,
а потребовать только Fl(ux) > 0,
Технические моменты доказательства теоремы 1 имеются в [5]. Указанная
процедура доказательства существования решения обобщается на многомерное уравнение
вида
ии - Г (Ft(uxi))xi - 22 (Ф, (uxi))xit = /(х, t), (6)
рассматриваемое в цилиндре Q= £1 X (0, Г), где £2 — область с достаточно гладкой
границей.
Условия (5) заменяются следующими:
С,(1 + \их)\г-2)<Ф',("хд<С2(1 +\их1\Р~2), (7)
1^1(и*/)12<С(1+Ф;.(и^)), Р>2.
В этом случае удается доказать теорему существования обобщенного решения
первой начально-краевой задачи для уравнения (6) в целом по t
75

В случае задачи Коши второе из условий (7) можно ослабить:
1*>ж,)|<с(1+ф;(их/)).
II. Положив в уравнение (3) /= /3 = jjl = 0, придем к уравнению (2)
ut-(F(ux))x = 0;
отсутствие в этом уравнении в отличие от (3) сильной диссипации (при условии зна-
копеременности функции F\ux)) приводит к ухудшению свойств решений: потере
гладкости, неоднозначности, несуществованию гладких решений у ряда краевых задач.
Будем искать решения уравнения (2), удовлетворяющие начальным и краевым
условиям:
"*Uo="i(0> »x\x = 1="2(t), и(х,0) = ио(х). (8)
Теорема 2. Пусть F(p) = (y0 + v2p2),v0 < 0, v2 > 0; u1(t) = 0,u2(t) = (\vq\I3v2)v\
u0(x) G C~(0, 1); u0(l) = 0, F'(u'o(x)) < 0, u'0(0) = 0, u'0(l) = i\vQ\l3v2)v\ Тогда, если
I^oI'l (0,1) = (I^o 1/10^2) и t* = 15/|^o I» то при t > t* не существует решений задачи
(2), (^^принадлежащих C2(Qt), Qt = (0, 1) X (0, t)\
Доказательство теоремы 2 основано на аналоге принципа максимума для
параболических уравнений. Тем не менее при "хороших" начальных данных уравнение (2)
ведет себя как обычное параболическое уравнение, что утверждает
Теорема 3. Пусть /) F(p): R -> R - достаточно гладкая функция, и существует
р
интервал \рх, р2] CR, на котором F'(p) > 0;//) функция ^(p) = f (F'(rj))V2dri имеет
непрерывную обратную для р G \p t, р2 ]; />/) 0 G \p j, р2 ],
"о ей/| (0,1) П#*(0,1). р1<и'о(х)<р2.
Тогда существует, по крайней мере, одно решение и(х, t)
и G W12(Q)nLQO (0, 77 Wl(0, 1)), Щих) G W\(Q)
задачи (2), (8), удовлетворяющее уравнению (2) п.в. в Q.
Теорема 3 доказывается при помощи монотонного продолжения функции F(p) с
интервала [Pi, P2 ] и рассмотрением вспомогательной задачи
"ef = (^l("ex))x +eUexx> иех\х=0Л =0, U€(x, 0) = UO€(x),
где е > 0, Fi(p) — монотонное продолжение функции F(p).
Для полученной задачи доказываются равномерные по е > 0 априорные оценки,
позволяющие осуществить предельный по е -> 0 переход. Более полное изложение
теорем 2,3 см. в работе В.А. Новикова [6].
Следующий результат говорит о возможности стабилизации решений задачи (2),
(8) (см. [7]). Рассмотрим стационарное уравнение
{П»Х))Х = 1И»2)Х (9)
и его нестационарный вариант
ut+uux = (F(ux))x. (10)
Будем изучать задачу (10), (8) при следующих предположениях:
/) F(p) e С1 (Л), и существует интервал \plf p2] CR такой, что F'(p) > 0, VP ^ \Р\,
Рг\\
ii) sup F(p)<F(p1)<F(p2)< inf F(p);
pe(- -,pl)' p<=(p2,<~)
in) \F(p)p\<C(l + \p\m), C> 0,m > 1.
Теорема 4. Пусть выполнены предположения i) — Hi) и существует обобщенное
решение v(x) уравнения (9) такое, что
p1+€<vf(x)<p2,e>0.
76

Пусть также существует обобщенное решение уравнения (10) с произвольным
начальным условием и0(х) G W^ (0, 1) и краевыми условиями ы(0, t) = u(0), ut(t) = v(l).
Положим Pi>0. Тогда справедлива оценка
ll"-ylli2(o,i)<^6f»"olli2(o,i)'
Утверждения теорем 2—4 характеризуются тем, что начальные условия всегда
задаются при t = 0.
Однако для параболических уравнений с меняющимся направлением времени
предложена постановка краевых задач, когда условия могут задаваться и при некотором
значении t = Т > 0, Линейные задачи такого типа изучались С.А. Терсеновым [8],
нелинейный вариант рассмотрели В.Н. Врагов и Д.Г. Подгаев.
В полосе П = ЛХ(0,Г) заданы уравнения
vt = ((\vnxx-C0\v\)9 (11)
где а > 1, С0 > 0, v — неизвестная функция.
Заданы следующие краевые условия
v(x, 0) = vo(x)>0,x<L;v(x, T) = vT(x)<09x>L. (12)
Неотрицательная при х < L и положительная при х > L ограниченная функция v Е
G (^(П), 7 > 0 называется обобщенным решением задачи (11), (12), если для
произвольных чисел R, Ri > 0 выполняется интегральное тождество
-; ; (vft + \v\afxx-c0w\f)dxdt+f vfdx\*zi-nvFfdt%:* ^o,
где/GС2,1(П),/(Л, t)=f(—Rlf t) = 0 — в остальном произвольна. Имеет место
Теорема 5. Пусть v0(x) =J) при L — hx < x^< L и х < -R2, v0(0) > 0, Ъг > 0;
vT(x) = 0 при L <x <L + h2 <L иприх >R3,vT(L)<0,h2 >0;vO9vTGC1 ;R2fR3 >
> 0. Тогда при достаточно больших Со существует единственное обобщенное решение
задачи (11), (12),
Доказательство теоремы 5 основано на факте локализации возмущений для
нелинейных параболических уравнений.
ЛИТЕРАТУРА
1. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М.: Наука, 1968.
2. Новиков В.А., Яненко Н.Н, Об одной модели жидкости со знакопеременным коэффициентом
вязкости // Числ. методы механики сплош. среды. 1973. Т. .4, № 2. С. 142-147.
3. Greenberg J.M., MacCamy R.C., Mizel V.J. On the existence, uniqueness and stability of solutions of the
equation // J. Math, and Mech. 1968. Vol. 17, N 7.
4. Кажихов А.В., Николаев ВА, К теории уравнений Навье-Стокса вязкого газа с немонотонной
функцией состояния // ДАН СССР. 1979. Т. 246, № 5. С. 1045-1047.
5. Kozanov A.I., Larlcin N,A„ Yanenko NJV. On a regularization of equations of variable type // So v. Math.
Dokl. 1980. Vol. 21, N 3. P. 758-761.
6. Новиков В.А. Теоремы существования и несуществования для одного класса уравнений
переменного типа // ДАН СССР. 1980. Т. 253, № 6.
7. Новиков В.А. Качественные свойства решений одного класса уравнений переменного типа // Тр.
семинара "Численные методы решений уравнений баланса". Берлин, 1980.
8. Терсенов С А. Первая краевая задача для уравнений параболического типа с меняющимся
направлением времени: Препр. СО Ин-та математики АН СССР. Новосибирск. 1978.

ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
МЕХАНИКИ СПЛОШНОЙ СРЕДЫ.
ТЕОРИЯ РАЗНОСТНЫХ СХЕМ
ОБ ОДНОМ РАЗНОСТНОМ МЕТОДЕ СЧЕТА
МНОГОМЕРНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ*
1. В работе [1] был рассмотрен метод приведения многомерных разностных схем к
двумерным в применении к явным схемам, аппроксимирующим гиперболические
системы (такой метод в дальнейшем будем называть методом расщепления). В
настоящей заметке мы покажем на примере уравнения теплопроводности, что метод
расщепления может быть применен для получения простых устойчивых и сходящихся
неявных схем.
Рассмотрим многомерное уравнение теплопроводности
Ъи „ »* Ъ2и
— =Lu = a2 Б —-, (1)
bt i=\ Ъх.
i
для которого в прямоугольной области П, определяемой неравенствами
0<х/<1,0<Г<Г,г=1,...,т, (2)
может быть поставлена смешанная задача
и(*ь ..., хт, 0) = </?(*!,..., хт)\ (3)
u(xi,..., xs_ i, 0,xJ+1,..., xm)=fs(xlf..., xs_ i, xs+i, xm, t), (4)
ti(Xi, ..., Xs_i, 1,XJ+1, ..., Xm) —gs\Xi, ..., Xs_ i, Xs+i, ..., Xm, t).
Задаче (1)—(4) может быть поставлена в соответствие следующая разностная схема:
п + 1 "
7
т
li—lm s=1 s «i—'m
n
" 1
f
— a w+i
a. —
2 «i—«m
hi
1 +a
2
..'s+l-.
.'щ
>
.'7л J
d')
m? . = *, / ; (3')
HW = fw (4')
/|...'s-lO/s+1...i^, ' si,.../,_ 1*1+1..Лт*
где положено
"? / =u(x1,x2,...,xm,t)9 (5)
xs = ishs, t = nr, is = 0, 1, ...,A^ + 1,(JV, + 1)A,= 1.
•Докл. АН СССР. 1959. Т. 125, № 6. С. 1207-1210.
78

При ос = 1 получаем явную схему с временным интегрированием по Эйлеру, при
а = -1, 0 получаем неявные схемы с временным интегрированием по Эйлеру с
опережением и по трапеции соответственно.
Покажем, что схема (l')— (4') аппроксимируется схемой
n+s/m n + (s—\)lm
li—lm li—lm _д
т
0
1 ~a n+s/m 1 +<X n + (s-l)/m
2 'i—'/и 9 h"'lm
О")
n+s/m -n ..
U —f (А Л
*1—*8-1°*з+1—*т «'i•..'s-l«Vfl•»«'m, V ;
W • = If
Ввиду однородности схемы (Г)- (4'), (l")~(4") в дальнейшем обозначаем
"Г'/^="'/т^ = 0»1-..,^. (6)
Уравнения (l')»0") примут вид
Ли1 - Ви° =0, (7)
соответственно
Asu"m-B, u<-l>"»=09s=l9...9m, (8)
где
^s = Е + тду, BS = E + rbs, А=Е + та,В = Е + тЬ\ (9)
я=2я5,Ь = 2 bs,as = —— Л„*, = Л5. (Ю)
s=i s=i 2 2
Нетрудно видеть, что операторы As, As, Bs перестановочны:
[\M = [AsAs'] = [BsBs'] = [AsBsi]=09s,s'=l9...9m. (И)
Умножая первое равенство (8) на А2, второе на Вх и пользуясь перестановочностью
операторов As, Bs>, имеем AгА2и2,т - В1В2и° = 0.
Продолжая аналогично дальше, получаем
Ах...Атих -В1...Вти°=0. (12)
Польузясь представлением (9), (10), уравнение (12) преобразуем к виду:
Аи1 -Bu°+T2[ZaSlaS2ul -VbSlba2u°] +т3[2а,1д,аа,8м1 -
-2^АЛз"°1 ^"^гя[(а1...ат)и1 -(Ьг...Ьт)и°]=0. (13)
Из (13) следует, что схема (l") и эквивалентная ей схема (13) аппроксимирует
уравнение (1) с той же точностью, что и схема (Г). Докажем устойчивость схемы
(l"). Операторы As, Bs с учетом краевых условий (4) имеют собственные функции
vPs = &npsirxs,ps- 1,...,NS. (14)
Операторы А 1г..„ Ат, Blf..., Вт имеют собственные функции
т
VPl..:pm=VPiVP2 -VPm =П ЯПр,7ГХ,. (15)
s=l
Собственными значениями операторов А ХА2 ... Ат, ВХВ2 ... Вт будут
т
XPi...>w=n [1 +2rs(l-a)sin2ps7rhs] (16)
s=l
79

соответственно
т
AtPl...>m = n [1 -2r,(l + a) sin2psnhs], (17)
S— 1
где rs = та2/hi. Полагая
"^^p,...^,"^^^^.;^ (18)
и подставляя (18) в (12), получаем
Ppi..:Pm=a*t*o=Vpl..:Pmlbpl..:pm' (19)
Нетрудно видеть, что при любых г, hs, ps,u — Ка<0
fPp....>«l<1- (20)
Таким образом, схема (1") устойчива.
Учитывая, что при фиксированном г произвольных hlr..., hm и —1 < а < О
|^....>„1>ь <21>
видим, что решение задачи (1") — (4") сходится в среднем к решению задачи (1) —(4) с
порядком интегральной точности 0(т) (см. [2]).
2. Установленный результат остается в силе для операторов L, А (расщепляющиеся
операторы), удовлетворяющих условиям:
1). Операторы L, Л имеют вид
m ps
Z = 2 LS,LS = Z asaD°Ds = d/dxs,s=l9...9m, (22)
s=l ct=0 S
rn ns
Л=Е Л„Л, = Е bsaT», (23)
s=l <x=—ms S
где mSt ns — целые, Ts — оператор сдвига
Tsu(xlt..., xm) = u(xlt..., xs + hs, ..., xm). (24)
Оператор Л аппроксимирует Z, с точностью О (г1 +0f), a > 0.
2). Схема
н"+1_н" i_a _ 1+а
Л,^+1—— Л5и" (25)
г 2
или эквивалентная ей схема
Asun+1-Bsun=0; (26)
As = E + TaS9Bs = E + TbS9as = — As,bs = — As (27)
устойчива.
3) Собственные значения XPs операторов As ограничены по модулю снизу
\\Ps\>k>09ps=l9...9Ns. (28)
При удовлетворении этих условий схема
Ажи**т -Bsu(s-1Vm=0 (29)
будет устойчивой и сходящейся в среднем с интегральной точностью 0(ts) .
ЛИТЕРАТУРА
1. Багриновский КЛ., Годунов СК. // ДАН СССР. 1957. Т. 115, № 3. С. 431.
2. Douglas J. Ц J. Soc. Ind. Appl. Math. 1956. Vol. 4, N 1.
80

НЕЯВНЫЕ СХЕМЫ РАСЩЕПЛЕНИЯ
ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ И СИСТЕМ*
В работе [1] было показано, что система уравнений гиперболического типа
dtii biij
7— =*#*—- + btjUj, i,j = 1,2,..., л, к= 1,2,..., m (1)
Ot OXfr
может быть аппроксимирована одномерными явными разностными схемами.
Получающиеся схемы устойчивы при определенных требованиях на шаг, которые в основном
совпадают с известным критерием Куранта.
В настоящей работе аналогичным методом (в дальнейшем мы его называем методом
расщепления) получается система одномерных неявных схем, аппроксимирующих
гиперболические уравнения и устойчивых для произвольного шага.
Рассмотрим для простоты случай системы линеаризованных уравнений газовой
динамики
ди dp dv dp Ър ди dv
— + —^- = 0, + — = 0, + + = 0, (2)
dt Эх dt ди dt дх ду
которой эквивалентно уравнение
Э2/ _ Э2/ Ъ*1_
д~? э^2 +T^/ (3)
где/ — любая из функций и, v, p.
Предположим для определенности, что краевые условия и начальные данные
формулируются в терминах р, например:
р(х, Г) =/(*, Г), x.tGS; (4)
Ър
р(х, 0) = <р(х), — (*, 0) = Ф(х), (5)
ot
где область П определения функции р(х, t) = p(xlf x2, t) характеризуется
неравенствами
0 < xt < 1, 0 < t < Т, (6)
S есть граница П.
Следуя методу расщепления; аппроксимируем систему (2) следующей неявной
схемой:
(Г/2 - Е)ип + 6Х(*Е + рГл)рп = 0, (7а)
(7* - E)vn = 0, (76)
(ТУ2 - Е)рп + д-г(аЕ + рТ1Л)ип = 0; (7в)
(Т- TV2)vn + 62(аГУз + ($Т)рп= 0, (8а)
(Г - ТУ2)ип = 0, (86)
(Т- ТУ2)рп + o-2(aTV2 + 0T)vn = 0, (8в)
а > 0, 0 > О, а +0 = 1о
Докл. АН СССР. 1959. Т. 128, № 6. С. 1103-1105. (Соавтор Н.Н. Анучина.)
81

Здесь приняты следующие обозначения для операторов:
Д,- Т{ - Е Е - Г/"1
6. = т-г- = т-~ , 8_, = т — ; (9)
h, ht hj
Tfn = fn+it тЪр = /n+% (10)
Tifn{Xi) = /"(x, + A,), 771/"(*,) = /"(*/ - ht).
Используя равенства (76), (86), получаем следующую систему операторных
уравнений относительно и", у", р", р"+":
(Т - Е)и" + 0- v" + aSip" + Ррп+Уг = 0,
6_,(<*£- + рТ)и" + 0- v" - Ер" + Ерп+1А = 0, <11а)
0-ни + (7-£)«/• + №гТрп + аб2р"+% = 0, П1еП
О и" + 8_2(аЕ + PT)v" - Тр" - Ер" +* = 0. К '
Исключая из равенства (11) любые три функции, для четвертой получаем
уравнение
А/ = 0, (12)
где Д есть определитель системы (11). Вычисляя явно определитель Д, получаем для
/ схему 3-го порядка, эквивалентную системе (11):
[(Т - Е)(аЕ + 0Г)2(5,5_, + 828_2) - (Т - Е)3 +
+ (аЕ + рТ)2(а2Е - Р2Г)818_1828_2] f = 0. (13)
Нетрудно видеть, что при любых a,/J она аппроксимирует уравнение
Ъ3и Э / Ъ2и Ъ2и \
^- =v\~^- +-j?) (14)
с точностью до 0(т).
При a = |3 = Vi порядок схемы (13) понижается на единицу, в результате получаем
трехслойную схему
,/1 + 2
и
2ип+1 + ип / А1А_1 А2А_Л/ц" + 2un+l + ип+2 \ _
г2 " \~Й] + hi Л 4 / "
4 Л1Л2
которая аппроксимирует уравнение (3) с точностью до 0(т2).
Нетрудно показать, что схема (15) является спектрально устойчивой и тем самым
сходящейся в среднем к уравнению (3).
Покажем, что схема (7), (8) может быть сведена к одномерным прогонкам
попеременно в направлениях х, у. Действительно, исключая из уравнений (Па) ип,
получаем при a = |3 = Vi уравнение
р"+3А _ p"+i _ р"+У2 + рп AiA.! ( рп+Ъ + рп + 1 + рплУг
^-i(pn+3/2 + Pn + 1 + РпЛУг ■+ Р* \_
г2 Л?
(16)
Аналогично, исключая и" из уравнений (116), находим

Схема (16), (17) спектрально устойчива при любом г, имеет точность 2-го порядка
и, таким образом, решение задачи (16), (17) при соответственно поставленных
начальных и краевых условиях сходится к решению задачи (3) — (5) .
В общем случае многомерного гиперболического уравнения
Ъ2р т Ъ2р
ТТ ~ 2 "ГТ = ° (18)
Эг2 i= 1 дх2
i
соответствующая ("расщепленная") схема имеет вид
n+1+s/m __ n+l + (S-l)/m _ n + s/m + л+ (s-l)/m
_
A^A-s pn+1 + s/m + pn+l + (s-l)/mpn + s/m + n+(s-l)/>
s *
Она аппроксимирует (18), спектрально устойчива и, следовательно, сходится
ЛИТЕРАТУРА
1. Багриновский К.Л., Годунов С.К. // ДАН СССР. 1957. Т. 115, № 3. С. 431.
ОБ ЭКОНОМИЧНЫХ НЕЯВНЫХ СХЕМАХ
(метод дробных шагов) *
1. Рассмотрим систему линейных уравнений, записанную в матричном виде
Ъи/Ъг = P(D)u. (1)
Здесь P(D) — матрица, действующая на вектор и, элементы которой суть полиномы
от символов дифференцирования Д = Э/Эдг, (/■= 1, ..., т). Индексно уравнение (1)
записывается так
" Эй,-
01 ],а
Как известно, однородной разностной схемой называется схема, инвариантная
относительно операторов сдвига. Такая схема может быть записана в виде
А(Т)и = О, (3)
где Л(7) - полином относительно операторов сдвига
Л(Г) = :Еввов1...вт7?оГ1в'... Cw> (4)
а
T^fixo, xlf ..., xm) = f(x0, ..., x( + OLthh ..., xm), x0 = t. (5)
Наиболее общая однородная двухслойная схема, решающая уравнение (1), имеет вид
(ип+1 -ип)1т = Т\х(Т)ип + 1 + П2(7>л, (6)
где
П (Г) ~ P(D), ЩТ) = Пх (Г) + П2(7) (7)
(~ — знак аппроксимации) ,
ип(хи ..., хт) = и(пт, х1у ..., хт). (8)
* Докл. АН СССР. 1960. Т. 134, № 5. С. 1034-1036.
83

Когда П^Г) = 0, схема (6) является явной и алгоритм решения прост и очевиден.
Однако обычно явные схемы условно устойчивы, т.е. устойчивы при достаточно
малых т. Поэтому прибегают к схемам абсолютно устойчивым, которые, как правило,
являются неявными, так что Hi (Т) ^ 0. С увеличением числа m неизвестных и
порядка полинома P(D) растет размерность оператора Пх (Т), что приводит к усложнению
схемы и увеличению числа операций. В этом основной недостаток однородных схем:
решая задачу построения устойчивой и аппроксимирующей схемы сразу на одном
шаге, мы неизбежно и в сильной степени усложняем алгоритм решения.
2. Следовательно, чтобы решить эту задачу без большого усложнения алгоритма,
мы должны решать ее по этапам, вводя вспомогательные, дробные шаги. На каждом
дробном шаге аппроксимация и устойчивость разностного оператора могут не иметь
места, достигаясь только при переходе с целого шага на целый.
В последнее время появился ряд схем, основных на этом принципе [1—6]. Мы
сформулируем общую теорему, позволяющую установить сходимость в общем виде для
всех схем такого типа.
Теорема. Пусть схема с дробными шагами
un+s/p _ un + (s-l)/p
Uls(T)un+s^ +П2Д7>"+(*-1>/'\ 5=1, ..., р (9)
г
удовлетворяет условиям
Пц(Г) ~Pls(D), U2s(T) ~P2s(D\ I (Л, + ^2.) = P (Ю)
s=i
Каждая из двухслойных схем (9) имеет матрицу умножения gs [7], так что
11*1*2 ...gp II = 1 + 0(Т). (И)
Тогда решение (9) сводится к решению (1) в среднем.
Доказательство. Приведем сначала доказательство для случая, когда и
скалярная, а не векторная функция. Запишем уравнения (9) в виде
A&W - Bsun+^-^p = 0. (12)
As = Е - тП1д, Bs = Е + tU2s. (13)
Пользуясь коммутативностью операторов As, BS9 получаем эквивалентную
однородную схему, не содержащую дробных шагов:
Ах • А2 • ... • Apun+l - Вх • В2 • ... • Врип = 0. (14)
Разлагая (14) по степеням т, после несложных преобразований
un+l-un р р р
— = 2 lllsun+1 + £ U2Sun + 0(r) = S (Tlls + Tl2s)un+0(T). (15)
В силу (10) схема (15) и тем самым эквивалентная ей схема (9) аппроксимируют
уравнение (1). В силу (11) схемы (15), (8) устойчивы, что требовалось доказать.
Пусть и - вектор-функция. Продолжим равенства (8), заменив п на и + 1:
un+s/p+l „" + (*-1)/р + 1
= П1,ия+*/*+1+П2,1*я+<*-1>'''+1. (16)
г
Складывая сначала р равенств (8), затем последние р — 1 равенств (8) с первым
(16), последние р - 2 равенств (8) с первыми двумя (16) и продолжая аналогично
84

дальше, получаем равенства
w+j/p+l _ un+s/p s р
= S Illrun+r/p+l + S nlrww+^ + (12')
7 r=l r=.s+l
+ £ n2rww+(r-1)^+1 + I гь^с-1^.
Рассматривая величины un + l/p, un+2fp, ..., ип+р^р как неизвестные функции и",
l>2, ..., и", видим, что разностные уравнения (12) аппроксимируют систему
дифференциальных уравнений
bv( р р
— = S П1гиг + П21ир + Г. ГЬ^.! . (17)
В силу (11) система в разностях (12) и эквивалентная ей (12') устойчивы.
Следовательно, дифференциальная система (17) устойчива, т.е. задача Коши для (17)
корректна. При Vi = v2 = ... = vp = и система (17) переходит в систему (1) и, следовательно,
аппроксимирует последнюю. Отсюда следует, что решение системы (12) сходится к
решению (1), что требовалось доказать.
3. Преимущество описанного метода (дробных шагов) заключается в том, что
размерность операторов Ylls(T), U2s(T) меньше размерности операторов ni(7), П2(Т).
Тем самым неявные схемы, применяемые на дробных шагах, значительно упрощаются
и во многих случаях могут быть сведены к неявным трехточечным схемам, решаемым
с помощью прогонки. Это упрощение неявных схем с избытком окупается увеличение
объема вычислений за счет введения дробных шагов. Ясно, что метод дробных шагов
может быть применен для построения итерационных схем решения некоторых систем
линейных уравнений.
ЛИТЕРАТУРА
1. Douglas J. J. Soc. Ind. Appl. Math. 1955. Vol. 3. P. 42.
2. Douglas J., RachfordH.H. 11 Trans. Amer. Math. Soc. 1956. Vol. 82, N 2. P. 421.
3. Багриновский К.А., Годунов С.К. // ДАН СССР. 1957. Т. 115, № 3. С. 431.
4. Яненко Н.Н. // Там же. 1959. Т. 125, № 6.
5. Анучина Н.Н., Яненко Н.Н. // Там же. Т. 128, № 6. С. 1103.
6. Яненко Н.Н., Сучков В.А., Погодин Ю.Я. // Там же. Т. 125, № 5. С. 903,
7. Lax P.D., Richtmeyer R.D. // Commun. Pure and Appl. Math., 1956. Vol. 9. P. 267.
О СЛАБОЙ АППРОКСИМАЦИИ СИСТЕМ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ*
Рассмотрим задачу Коши в полупространстве |х| < °°, t> 0 для линейной системы
дифференциальных уравнений:
[ди(х, t)}/dt = L(x, t,D)u +/(*, Г), (1)
u(x,0) = uo(x)t (2)
где w(x,r), f(x,t) — векторные функции векторного аргумента, L(x,t,D) —
линейный дифференциальный оператор, коэффициенты которого зависят от х, t.
* Доклады III Сибирской конференции по математике и механике. Томск, 1964. С. 21-24.

Пусть u(x,t) — решение однородной задачи (1), (2), отвечающее некоторой
функции и0 (х). Тогда
u(x,t2) = s(t1,t2)u(x,tl), ti<t2, (3)
Оператор s(t\,t2) из (3) будем называть оператором перехода и считать заданным
в некотором банаховом пространстве В, которому принадлежат и0(х), u(x,t),f(x,t)
при t фиксированном.
Задачу (1), (2) будем называть равномерно корректной в пространстве В, если
115 (f, t + Г) 11= 1+С(Г, Т)-Т, (4)
где \C(t,r)\<M(T) для всех Г, т, г+ т<Т.
Будем предполагать, что система (1) обладает следующим свойством (свойство С):
решение и(х,t) задачи (1), (2) принадлежит Cq, если u0(x),f(x, t) принадлежат Ср иq
достаточно велико прир достаточно большом.
Определение. Семейство некоторых функций FT(x,t) слабо
аппроксимирует по t функцию F(x, r), если
Ч
. / [FT (х, s) - F(x, s)] ds = б(х, f ь t2, г) (5)
tx
и \д(х, Гь t2, r)|->0 при т-*0 и любых Гь Г2, х.
Оператор LT(x,t,D) слабо аппроксимирует оператор L(x,t,D), если каждый его
коэффициент слабо аппроксимирует соответствующий коэффициент оператора
L(x,t,D).
Положим
L=LX+L2 + . . .+£р, (6)
р р
LT= 2a/L/, AT=L-LT= 2 6/L/, (7)
/=i 1=1
o»(r.r)-p. /G {(n+^)r, (» + ^)r).
a,(T.t) = 0, гё|(и + —jr, (n + -jr J,
(8)
e,-= 1 — a,-, L/ — некоторые дифференциальные операторы. Из (7) следует, что
оператор LT слабо аппроксимирует L, Обозначим через S/(tl9t2) оператор перехода системы
1 Ъи
- —=Li(x,t,D)u9 (9)
р bt
через sT(t\, t2) — оператор перехода системы
du/bt=LTu. (10)
Из (6) следует
/ р-\ \ ( р-2 р-\ \
(•■•♦?)
sT(t,t + r) = sp (/ +
. .. Si/r, t+-V (11)
Будем полагать, что каждая система (9) равномерно корректна в пространстве В и
обладает свойством С.
86

Теорема. Пусть u(x9t) есть решение неоднородной задачи Коши (1), (2),
соответствующее достаточно гладкой функции и0(х). Тогда решение иT(x,t) задачи Коши
bu/bt=LTu+f, (Г)
и(х,0) = и0(х) (2')
с теми же функциями f(x, t), и0 (х), что ив (1), (2), сходится в В к решению и (х, t)
задачи (1), (2) при т->0.
Доказательство. В силу равномерной корректности в В операторов s,- (г i, t2 ),
будет равномерно корректен в В и оператор перехода sT(tl9t2). Отсюда следует
справедливость пр^дсгавления Дюгамеля
ит (х, t) = sT \f, Q)u (х, 0) + fsr (t, 6)f(x, 0)d0
(12)
для решения задачи (l'), (2'). Разность v(x, t) = u(x, t) —uT(x, t) есть решение
задачи Коши
Эи/Эг=/,ти + у>, v(x, 0) = 0, (13)
p
y = ATu = S ь(т, t)Vi(x, Г), ъ =LiU(x, r). (14)
1=1
Отсюда при t = nr имеем
t p t
v(x, t)= fsT(t, в)<р(х, d)dd = 2 fsT(t, e)enpjde =
0 1 = 1 0
P n-l (к + 1)т
= 2 2 / sr(t,e)ei(T,0)yi(x,e)de. (15)
/ = i k=o kT
Фиксируем /, положив для определенности i = 1. Тогда, разбивая интервал
интегрирования /ст, (Л: + 1) г на подынтервалы (k + (s - 1)/р)т, (k+s/p)T9 находим
(к+1)т (к+1/р)т
f sr(t,0)e1(T90)<p1(x,0)dO = (l-p) f sTyxdQ +
кт кт
(к + 2/р)т (к+1)т
+ / 5T^!^+...+ / Зтфх(1в =
(к+1/р)т (к+(р-1)/р)т
(kfl/p)T \ 1 Т \ ( т\ 1
= / I St у,0+~ )<рг ^.в+- j -Srftfl)^i(^fl)Jdfl +
<*+1/р)т Г / 2Г \ / 2Г \ I
J [ST {t,e+ — j <px \x,e+—J -ST(f, «)*!(*, fl)l £» + ...
STU 0 + 7 j (^ [x, в + rj - ST(f, 0)^(*, в)
Агт
(к+1/р)т
...+ /
Оценим интеграл
(Ю.
(16)
(*+1/р)т Г / * г \ / т \ ]
f |sTUe + - 1 ^i^.fl + - j -*тМ)*1(*.в)]«Ю =
(*+1/р)г Г / г \ I
= / I sT{t, в + - j -МЛ в) *i(*. в)£/в +
(к+1/р)т
87

(к+1/р)т I T \ \ / T \ 1
= / sTUe + -J• [E-sr[o,o + -J Ul{xtd)de
(к+1/р)т ( T \\ ( T \
+ / sT\t,e + - j ^i^*,fl + - j -<Pi(x,0)
dd. (17)
\ p / J
Но для гладких функций
(Е-зт)у1 = тф19 (18)
где \pi — гладкая функция. Отсюда следует
(к+1/Р)%т (t,&+ ~ \\е - 8т(в,в + - j J M*> WO \ = 0(т2). (19)
Аналогично
</?! (x, 0 + т/р) - </>i (х, в) = TOJt (x, t),
где co-j (x, r) — гладкая функция. Отсюда
| (к+\/р)т / т\ \ / т V
dd
= 0(r2). (20)
II кт \ P i L \ p
Применяя аналогичную оценку к остальным интегралам в равенство (16), получим
/ Mi^N(r2). (21)
Аналогичные оценки получаются для </?2, • • . , Фр- Отсюда следует из (15)
1Ы1=0(т). (22)
Теорема доказана.
Теорема остается справедливой только в случае, когда функции Щ(т, t) имеют
не специальный вид (8), а лишь удовлетворяют условиям
* ^.(т, t) 1 t + r
2—^-^=1, - / а,-(г,0)</0=1. (23)
/=i р т t
РЕШЕНИЕ МНОГОМЕРНОГО КИНЕТИЧЕСКОГО УРАВНЕНИЯ
МЕТОДОМ РАСЩЕПЛЕНИЯ*
Рассмотрим одно скоростное уравнение, описывающее перенос нейтронов в среде
с изотропным рассеянием:
- ■p+nv^ + a^=^-;rfnV(rfn'>o+s(r.aO. (1)
v at 4я
Для уравнения (1) поставим смешанную задачу Коши
<р(г,П, 0 = 0, Пл<0, г, Л, геГ; ,(2)
</>(г,Л,0)=Ф(г,П), r,ft£A (3)
в цилиндрической области П = D X Г основанием D, боковой границей Г = у X Г, 7 =
= D-D,
♦Докл. АН СССР. 1964. Т. 157, № 6. С 1291-1292. (Соавтор Г.И. Марчук.)
88

Наряду с нестационарной задачей (1)—(3) будем рассматривать стационарную задачу
(см. (1))
av<p + a^= —/rfaVfrO')+S(r,fl), (la)
4я
</?(r,ft)=0, Qn<0, г,Пеу. (2а)
Применим для интегрирования задачи (1)—(3) следующую схему (схему
неполного расщепления):
(*>"+* ^^и)/г=Л1(в^ + '4 + fr") + £ (4а)
(<,"+1+*," + *)/г = Л2(<**>п+1+^" + *), (46)
где Л! = — оЕ + (а5/4я)ДЛ'Е, Л2 = —Лб^^ разностные аппроксимации операторов
-оЕ + (os/4ir)fdSl\—&Vip соответственно;S — аппроксимация 5, г = v A f, а > 0, 0> О,
а + 0=1.
Схема (4) реализуется следующим образом. Суммируя (4а) по всем углам Л,
получим
(*>о+У2 -rf)/T=_-oc(yZ+V2 +№ + £>; (5)
</?0 = 2^ДП', S0 = 25ДП', ас = а - а5, (5а)
и, следовательно,
^0 = ~^0 +^0^ (6)
1 +агас
После этого интегрируется уравнение (4а), которое можно переписать в виде
*"*/г ~*"+a(V + * +р„») = ^(в„ГИ +|8^)+5. (4в)
г 4ет v '
Методом, аналогичным [2], можно показать, что схема (4) неполного
расщепления сходится при любом т/Л, если а = 1.
Расщепляя оператор второго дробного шага, получаем схему полного расщепления
(*»+V - *")lT = Л^V+1/™ + ft,») + 5, (7а)
где Л2 =Л21+ . . . + A2w_i; Л2/ - аппроксимации одномерных операторов П/Э/Эх/;
/ = 1, . .. , m — 1; (m — 1) — разномерность пространства. Схема (7) также сходится
при любом т/Л, если a > V2 •
Если областью П задачи (1)—(3) является параллелепипед, реализация краевых
условий (2) в схеме полного расщепления очевидна: на каждом s-м дробном шаге (76)
осуществляется схема бегущего счета вдоль xs в направлении от освещенной грани
(£1п < 0) . В случае произвольной цилиндрической области П0 с основаниемD0
последняя заключается в параллелепипед П, и значения у соответственно доопределяются
в область П — П0.
На рисунке показано, как в двумерном случае доопределяется у в сечении/) -ABCD
параллелепипеда D на момент времени t = (п + 7з ) т.
При проведении первого дробного шага (5=1) из (76) принимается: $п+2/з=0
на АВ; у п + lh = 0 в FBg,gAE.
После этого делается второй дробный шаг (s = 2) из (76) в квадрате ABCD с
начальными данными уп+ 2/з , полученными указанным способом и с краевыми условиями
ifn + 1 на AD. При ос = /3 = х/2 схемы (4), (7) имеют второй порядок точности и могут
применяться как схемы установления (итерационные схемы) для решения стационар-
89

ной задачи (la), (2a). При этом схема (4) неполного расщепления будет сходиться
при любом г, схема (7) требует для сходимости выполнения условия г -*0.
Заметим, что итерационная схема (4) может быть реализована как схема (7) с
внутренними итерациями в (76).
Аналогичным образом в случае неполного расщепления может быть получено
решение задачи (1а), (2а) с помощью уравнения
(Е - тАг)(Е - тА2)<рп +1 = (Е+тАх)(Е + тА2)уп - 2rS. (8)
Эта схема сходится при любом шаге т.
Итерационная схема на установление при ш>2 будет иметь второй порядок точ-
ности по г, если она будет определена следующим образом.
m -1 m - 1 _
(Е-тАг) П (Е-тА2а)*рп+1 = (Е + тАг) П (Е + тА25)уп - 2tS. (8а)
Схемы расщепления целесообразно применять и в одномерном случае.
Изложенные алгоритмы очевидным образом переносятся на случаи произвольной
индикатрисы рассеяния и задачи с энергетической зависимостью.
ЛИТЕРАТУРА
Х.Марчук Г.И. Методы расчета ядерных реакторов. 196-1.
2. Яненко Н.Н. // Журн. вычисл. математики и мат. физики. 1962. Т. 5. С. 933.
ИССЛЕДОВАНИЕ ЗАДАЧИ КОШИ
МЕТОДОМ СЛАБОЙ АППРОКСИМАЦИИ*
В работе [1] исследован вопрос о сходимости метода дробных шагов в
дифференциальной форме при решении корректной задачи Коши в банаховом пространстве.
В настоящей работе этот вопрос рассматривается без предположения корректности
исходной задачи Коши и показывается, что ее корректность есть следствие
равномерной корректности некоторой вспомогательной задачи Коши. В основе предлагаемого
метода исследования лежит идея слабой аппроксимации дифференциальных операторов.
Определение 1. Семейство функций FT(x,t) слабо аппроксимирует по t
функцию F(x91) для 0 < t< Т и xG &, Я С Ет, если
Ч
f[Fr(x,s) -F(x,s)]ds= 6(x,tl9t2, r) (1)
tx
и || 5 || -^0 при т-*0 для любых фиксированных допустимых t\, t2. Семейство ли-
* Докл. АН СССР. 1966. Т. 167, № 6. С 1242-1244. (Соавтор Г.В.Демидов.)
к
\У
я j/f t
sr
X
А
\ "' I
\.У
у
Е/ 0
=».
90

нейных дифференциальных операторов LT (х, t) слабо аппроксимирует по t
оператор L(x,t), если слабая аппроксимация имеет место для коэффициентов.
Интеграл в (1) следует понимать в смысле Римана, кроме случая пространства
Lq (£1), где используется также интеграл Лебега.
Исследуем корректность постановки задачи Коши
bu/bt=Lu, 0< t<T, u\t=sQ= u0, u0G В • (I)
в банаховом пространстве В. Относительно пространства В мы предполагаем:
а) В есть пространство функций т вещественных переменных х\9х2,..., хт,
которые могут параметрически зависеть от t\ б) в В определены операции
дифференцирования по пространственным переменным д/Ъхк и по времени Э/Эг, замкнутые
относительно сильной сходимости; в) достаточно гладкие функции плотны в В.
Пусть оператор L представим в виде суммы
L = Li+ L2 + ... + Lp
линейных операторов вида
*i.«..*w *!•••*« Эх,1... Эх*"1
где агк к — вещественные функции, ограниченные и непрерывные по г в
равномерной топологии. Если функция a(xi,... хт, t) имеет все производные, входящие
в выражение (2), то мы будем говорить, что она имеет производные до порядка L,
если такую процедуру дифференцирования можно повторить / раз, то мы будем
говорить, что a(xi9 ...,xm,t) имеет производные до порядка (L)1. Пусть а* .
/с1 ... кт
имеют производные по пространственным переменным до порядка (Z,)7. Тогда,
формально дифференцируя уравнение и начальные данные задачи (1), мы получим
задачу
du!lbt=L'ui9 0<t< Г; uf\t=0 = 4, (I7)
где Z> = М+ Z,'2 + ...+ Lfp.
Здесь через и1 обозначена вектор-функция, состоящая из и и производных
от и по пространственным переменным до порядка (Z,)7; V. — оператор,
естественно соответствующий оператору Z/, если придерживаться правила
ЪМ\) ЪМ , ., 9i>
v + М
Ъхк Ъхк Ъхк
где v — компонента вектора и7; М — линейный дифференциальный оператор и dv/dxk
понимается как компонента вектора и1. За норму и1 мы выберем евклидову
векторную норму, обозначая через В; множество функций и В, для которых эта норма
конечна.
Пусть параметру 0 поставлено в соответствие семейство задач
du/dt=Lu, 0<6<t<T; u\t = e = u09 u0eB. (3)
Определение 2. Задача (I) равномерно корректна в В при
0< t< Г, если; а) задача (3) однозначно разрешима для множества функций и0,
плотного в В, т.е. u(t) = S(t,0)и0; б) оператор перехода S(t,0) обладает
следующими свойствами:
S(t290) = S(t2,tl)S(tl90)9 О<0< tx<t2< Т; (4)
\\S(t2/tl)\\<ea{t2~ti)9 0<tx< t2< T; (5)
91

\\S(t9e)uo-uo\\t^e-+09 O<0< t< Т. (6)
Если оператор S(t90) удовлетворяет в В условиям (4)—(6), то мы будем также
говорить, что он удовлетворяет условиям равномерной корректности. В терминах
теории полугрупп оператор S(t96)9 удовлетворяющий условиям (4)—(6),
принадлежит классу (С0) [2].
Задаче (1) поставим в соответствие вспомогательную (факторизованную) задачу
buT/dt=LTuT9 0<t<T; uT\t=z0=u0, и0^В9 (IT)
где
LT= £ cc(t9r)L.9
/ = i l l
<p,te [{n +(/-i)/p)r, (л+//р)т],
lO в остальных случаях.
Свойства решений семейства задач (1т) полностью определяются свойствами
решений задач
buf/bt = pL\uj9 0< t < Г; (1j\
и/1*=о=ио' "о^/5 7=0,1,..., и°=и, В0= В.
Нетрудно видеть, что оператор перехода задачи (1т) есть произведение операторов
перехода задач (I?),
ST(t + т,0 = Splt + r, t + т)... Si[r+—>f) при Г = wr.
Теорема 1. Если задачи (I?), (I?), (I?) равномерно корректны, то uT(t)
равномерно по t сходится к функции u(t) = S(t90)uo при т-*0, причем оператор
перехода S(t90) удовлетворяет условиям равномерной корректности.
Теорема 2. Если задачи (I?), (I?), (I?), (I?) равномерно корректны, то
ит (г) ел!есге с производными по хк до порядка L равномерно по t сильно сходится
к функции u(t) при т-*0. Предельная функция u(t) имеет производную по t и
является решением задачи (I).
В терминах теории полугрупп теоремы 1 и 2 дают достаточные условия для того,
чтобы замыкание некоторого сужения суммы производящих операторов полугрупп
класса (С0) также было производящим оператором полугруппы класса (Со).
Первые результаты по выделению класса операторов, являющихся производящими
операторами полугрупп, принадлежат Хилле [3] и Иосида [4]. Дальнейшее развитие этой
теории и ее приложение к изучению абстрактной задачи Коши изложено в
монографии [2]. Полугруппы с зависящим от t производящим оператором и связанную с
ним задачу Коши изучали П. Лаке и Р. Рихтмайер [5]. Обзору исследований по
абстрактно задаче Коши посвящена работа [6].
т
ПустьВ\ — пространство с нормой || /|| = / ||/|| dt.
*е е в
Неоднородной задаче
Эи/Эг = Lu+ /, 0< t < Т\ (l v
"1, = о= "о, и0е В; /€ Bh
92

и параметру в поставим в соответствие семейство неоднородных задач
bu/bt = Xu+f9 0<e<t<T; (?ч
и|, = 0= "о, и0е В; /G В*.
Если при данных и0 и t задача (7) разрешима, что введем обозначение v(t) =
= u(t) — S (Г, 0) и0, где S (Г, в) — оператор перехода задачи (3).
Определение 3. Задача (1н) корректна по правой части при
0< t< Г, если v(t) непрерывно зависит от/.
Пусть u(t) — решение задачи (I) . Справедлива
Теорема 3. Если: а) и(0) = и0 € Вх\ б) Ltu равномерно непрерывны по t\
в) задачи (1°), (I*) равномерно корректны; г) задачи (1?н> корректны по
правой части, то и (t) - единственное решение задачи (I), удовлетворяющее а) и б),
uT(t) сходится к u(t) равномерно по t.
В случае, когда B=Lq (£2) , q > 1, £2 С Em, мы будем считать, что и1 (t)
включает в себя, по крайней мере, все первые производные по пространственным
переменным от u(t). Мы будем говорить, что u(t) гладкая функция, если она имеет все
производные, входящие в уравнение задачи (I), принадлежащие Lq{p,1), 121 =
= Qx (0, Г).
Тоерема 4. Если: а) задачи (I?), (I?) равномерно корректны; б) задачи (1^ )
корректны по правой части, то uT(t) равномерно по t фундаментальна при т-*0
и всякая гладкая предельная функция и (t) является решением задачи (I), в случае
и о Е Lq (12) и (t) — гладкое и единственное решение задачи (1).
Наконец, если m=p9 q=2, Lt = Af(xf t) Э/Эх,-, где At — симметричные
матрицы, непрерывные в 12* вместе с первыми производными по пространственным
переменным, 121 — обычный конус зависимости, имеет место
Теорема 5. Задачи (I), (I?) равномерно корректны. Функция uT(t)
равномерно по t сходится при т-+0 к решению задачи (I).
ЛИТЕРАТУРА
1. ЯненкоН.Н. //Сиб. мат. журн. 1964. Т. 5, №6. С 1431.
2. Хилле Э., Филлипс Р. // Функциональный анализ и полугруппы. М.: Изд-во иностр. лит. 1962.
3. Хилле Э. И Функциональный анализ и полугруппы. М.: Изд-во иностр. лит. 1951.
4. YosidaK. //J. Math. Soc. Jap. 1948. Vol. 1,N 15.
5. Lax P.D., Richtmeyer R.D. // Commun. Pure and Appl. Math. Vol. 9. P. 267.
•6. Красносельский MA., Крейн С.Г. // Тр. IV Всесоюз. мат. съезда. Л., 1964. Т. 2. С 292.
ПРИМЕНЕНИЕ МЕТОДА РАСЩЕПЛЕНИЯ (ДРОБНЫХ ШАГОВ)
ДЛЯ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ*
1. Разностная схема, кроме обычных требований аппроксимации и устойчивости,
должна удовлетворять ряду дополнительных свойств, таких, как экономичность,
повышенная точность, дивергентность и т.д. Поэтому построение разностных схем на
основе обычных однородных аппроксимаций встретило трудности, которые смогли
быть разрешены на основе метода дробных шагов, использующего неоднородную
аппроксимацию.
♦Некоторые вопросы вычисл. и прикл. математики. Новосибирск, 1966. С 5-22. (Соавтор Г.И. Мар-
чук.)
93

Первые результаты в этом направлении были получены в работах Писсмана, Рэк-
форда и Дугласа [1—3] .В дальнейшем эти результаты были развиты и углублены в
ряде работ [4—8].
В основе указанных работ лежат схемы Писсмана, Рэкфорда, Дугласа (метод
попеременных направлений, АДМ и метод стабилизирующей поправки Дугласа—Рэкфорда).
Эти методы предполагают обязательную аппроксимацию дифференциального
уравнения либо на каждом дробном шаге (метод попеременных направлений), либо на
первом дробном шаге с последующей корректировкой устойчивости (метод
стабилизирующей поправки).
Большой цикл работ американских авторов был посвящен проблеме
оптимального выбора параметров итерационных схем [9—11] и получению разностных схем
повышенного порядка точности [12].
В основу работ советских авторов положен метод расщепления сложных
операторов на простейшие. При таком подходе интегрирование данного уравнения
сводится к последовательному интегрированию уравнений более простой структуры. При
этом схемы дробных шагов обязаны удовлетворять условиям аппроксимации и
устойчивости только в окончательном итоге. Это дает возможность гибкого
построения схем по существу для всех основных уравнений математической физики.
Одной из первых в этом направлении была работа по применению метода
расщепления к решению многомерных задач гидродинамики, в которой были использованы
явные схемы расщепления [13].
В работе [14] был предложен метод дробных шагов, основанный на расщеплении
многомерного уравнения теплопроводности на последовательность простейших
одномерных уравнений. Метод дробных шагов в дальнейшем получил развитие в ряде
работ [15-17].
Цикл работ выполнен А.А.Самарским в связи с исследованиями по
локально-одномерным схемам, тесно примыкающим к методу расщепления. Им также рассмотрены
схемы повышенного порядка точности для уравнений теплопроводности. Для
исследования вопросов сходимости автор разработал специальные методы априорных оценок
[18-21].
В работе [22] был указан алгоритм построения неявной системы разностных
уравнений с факторизованной матрицей. В работе [23] указан способ дополнения
локального разностного оператора до факторизованного (приближенная факторизация
разностного оператора).
В работах [24—26] сформулирован метод построения схем с расщепляющимся
(факторизованным) верхним оператором для уравнений параболического и
гиперболического типа. В работах [27—29] предложены методы расщепления для приближенного
интегрирования нерегулярных систем в динамической метеорологии (заддчи прогноза
погоды).
Методы расщепления оказались весьма эффективными при решении многомерных
кинетических уравнений Больцмана [30—31], теории упругости [32—35] и др.
Оказалось возможным метод расщепления трактовать как метод слабой
аппроксимации, что позволило применить его для исследования корректности
задачи Коши [36].
Опыт, накопленный при решении сложных задач математической физики методами
растепления, позволяет сделать вывод об их эффективности и универсальности.
Далее будут обсуждены результаты исследований, в основном полученные
авторами доклада и сотрудниками Вычислительного центра СО АН СССР.
2. Формулировка метода. Пусть
bujbt = Slu + Ef (1)
есть интегро-дифференциальное уравнение с неизвестной вектор-функцией и, Г2 '=
= L(D) + S — пространственные операторы, из которых L — дифференциальный, S —
интегральный, Е — тождественный оператор, / — вектор-функции. Для системы (1)
94

поставлена задача Коши:
и(х90) = ыо(х) (1а)
при соответствующих краевых условиях.
Для задачи (1) , (1а) будем предполагать справедливым принцип Гюйгенса—Адамара.
Тогда равенство
u(x,t2) = S(t2,t1)u(x,t1); tx <t2 < T (2)
определяет оператор перехода S (f 2 , f i).
Задачу Коши будем предполагать равномерно корректной в некотором банаховом
пространстве i?, так что должно выполняться требование
II S(t + T,t) \\в < 1 + const • т, t + т<Т. (3)
Наряду с нестационарной задачей (1) будем рассматривать соответствующую задачу
Пи + / = 0. (4)
Тогда метод дробных шагов в применении к (1) формулируется следующим образом.
Путь Лу, Л,- (/, /=1,..., г) — некоторые пространственные операторы
произвольной структуры, которые, в частности, могут быть разностными или
интегро-дифференциальными. Строится совокупность схем
(un + 1f- ип)/т = А10ип + Л11Мл+1/г+ Л2/,
(ип+21г-ип+1'г)/т = Л20ип + Л2 lUn+l'r + Л22ип+2'г + Л2 /,
(5)
(ии + 1-ил+(г-1)/г)/т = Л пип+ А%ип + 1!г + ... + А ип+1 + А /.
Операторы Л,у должны удовлетворять условию аппроксимации
2Л .~П, 2 Л. ~Е (6)
и устойчивости
|| С || = 1 + const • г, (7)
где С есть оператор перехода от ип к un+l, получаемый из (5) исключением
ип+ 1fr,..., ип+ (^-1)/г. Произвол в выборе операторов Л., позволяет строить точные
устойчивые и экономичные схемы.
Методу дробных шагов может бьтгь придана другая формулировка (метод
приближенной факторизации).
Пусть
(un+l - ип)/т = Агип + г + А0ип+ Fn (8)
есть обычная однородная аппроксимация (1), которая может быть переписана в виде
Aun + l = Вип + TFn; А = Е-тА1'9 В=Е+тА0; (9)
Л1 = Л11+Л12+...+ Л1г; Л0 = Л01 + Л02 +... + Л0г • (Ю)
Схема (10) заменяется без нарушения аппроксимации факторизованной схемой.
Аг...Агип + 1 = Bx...Brun + rFn9 At = Е-тЛи, В( = Е + TAoi. (И)
Схемы интегрирования нестационарной задачи (1) могут трактоваться как
итерационные схемы стационарной задачи (4).
95

Итерационная схема, сходящаяся при любом конечном г, должна удовлетворять
дополнительному условию полной аппроксимации (тождественной относительно г),
которому удовлетворяет не всякая схема интегрирования (1). Поэтому метод
дробных шагов в применении к стационарному уравнению принимает следующую
специфическую форму. Пусть
Ли+/=0 (12)
есть разностный аналог (4). Уравнению (12) может быть поставлена в соответствие
итерационная схема (универсальный алгоритм [37]) :
/ и" + 1 - ип\
В у ) = Аип+ /, (13)
где В есть произвольный оператор. Схема (13) может быть приведена к
нормальному виду
(ип+1-ип)/т = В~1(Аип + /). (14)
Оператор В (будем называть его стабилизирующим) должен обеспечивать быструю
сходимость. Как правило, он должен быть сильно устойчивым, т.е. удовлетворять
требованию
ПСИ = НЯ+т/Г'ЛН < 1-е. (15)
Для простоты реализации В может быть выбран как факторизованный оператор
В = А1-...-Аг. (16)
При этом не обязательно условие
'г E-At
Б - = Л.
1 = 1 7
Для r-слойных итерационных схем можно положить
Вх[Аип1т] + В2[(А/т)2ип] + ...+В, [(Д/т)гиг] = Лип+ /, (17)
где Аип = ип + х - ип, Bf — произвольные операторы. Первые схемы такого рода
были сформулированы в работах [20, 48, 49].
3. Метод дробных шагов дает возможность получения многообразных схем
решения задач математической физики.
Для гиперболических систем
bu/bt + A(bu/dx) = 0 (18)
и для систем с "вязкостью"
to + Atbu\.sv±(Bbu\ (19)
bt \дх/ Ъх \ Ъх)
метод расщепления позволяет, в частности, строить схемы с положительными
коэффициентами или матрицами (мажорантные схемы). Соответствующие неявные схемы
просты в реализации и могут также использоваться как итерационные схемы.
Применяя дополнительно прием предиктор—корректор [39], указанные схемы
можно сделать более точными.
Для уравнений гидродинамики метод дробных шагов применим не только в
декартовых координатах. При введении криволинейной сетки, разбивающей область
интегрирования на сетку криволинейных каналов, следует перейти к контравариантным
компонентам, которые характеризуют скорость в канале. На каждом дробном шаге рассчи-
96

тывается течение в каналах одного семейства с применением простой одномерной
схемы.
Для уравнений упругости схемы интегрирования и итерационные схемы могут быть
построены как на основе уравнения в переменных смещениях
Э2и/Эг2 = ( X + м) grad divu + /iAu = 0, (20a)
так и на основе уравнения для функций Эйри
+ р —
Ъг dt
в __+ р_+ ААф = 0, в>0. (206)
В работе [34] для решения (20а) были применена симметричная неявная схема
приближенной факторизации 2-го порядка точности
(е- ^-\\(е- l!-A2Vuw + 1 + u""1) = Fu"+ T2Ef,
(21)
где операторы Л1э Л2, F определяются равенствами (со — произвольная векторная
функция с компонентами со!, со2)
Aico = [(Х + 2д)Л11со1, дЛцСОгЬ Л2со = [/iA12coi, (Х +2д)Л22со2 ],
F-co = [2со1 + г2(Х + м)Л12со2, 2со2+ г2 (Х + м)Л12со!],
A,A_, (A1+A_1)(A2+A_2)
л« = —г?—; л12 =
Я 1,2
a; 4/i1/i2
(22)
А/ = 7/ -£, A_f=E- Г_/ = E-Tf1.
Для решения стационарной задачи
( X + /i) grad div u + мAu = 0 (23)
в работе [35] была применена итерационная схема стабилизирующей поправки:
= AlUw + ,/2 +Фи", = A2(uw + 1-uw+,/2), (24)
г г v '
где
Л! + Ф ~ ( X + /i) grad div + /iA. (25)
Метод расщепления кинетического уравнения для многомерных областей
сформулирован в работе [30]. В работе [31] дано дальнейшее развитие и обоснование схем
расщепления для различных постановок задач теории переноса. Рассмотрим задачу (4),
для которой
■П = со grad + оЕ - (os/4tt) f tfco' (26)
и удовлетворяются граничные условия
и (г, со) =0, con < 0 на Г, (27)
где Г — внешняя граница области G. Положим
£2=^+^2, n1 = co.grad, П2 = оЕ - — jdu', (28)
4ет
тогда имеет место следующая
4. Зак. 95 3 97

Теорема. При любых и° Е D и т>0 релаксационный процесс
(е+—£12\(е+ —SlA(un + l-un) = -т(Пил+/) (29)
сходится в L2 к единственному решению уравнения (4). Здесь D - некоторое
множество функций, плотное в L2 [40].
Для схем (29) указывается оптимальное значение т.
4. Метод дробных шагов допускает специфическую формулировку для задач, не
принадлежащих классу Коши—Ковалевской (нерегулярных систем [27—29]). Пусть
bujbt = Llu + L2v + /, (30a)
Кхи + K2v+ g = 0 (306)
есть нерегулярная система, для которой
3w/3r=L1w+F, F=L2v + f (31)
есть подсистема, замкнутая и регулярная при заданном F. Здесь и, у, /, g — вектор-
функции. Для интегрирования (30) применяется смешанная релаксационно-нестацио-
нарная схема
(un + lf -ип)/т = А10ип+ A11un + 1frA1Fn,
(ип+У-ип + 1!г)/т = Л20""+ А21ип + 11>' + Л22ип+2!'' +... + A2F", (32a)
(un + l- un+(r-l^r)/r = \r0un+ Arlun + llr + ... + Arrun + l+ ArFn+l.
При решении системы уравнений (32а) на последнем дробном шаге необходимо для
замыкания использовать разностный аналог соотношения (306)
Мхип + 1 + M2vn + l+ gn + l = 0. (326)
Здесь
Fn + 1~ (f+L2v)n + 19 Mt~Kt (i = l,2). (33)
Таким образом интегрируются уравнения динамической метеорологии и
нестационарные уравнения Навье—Стокса.
Для стационарных уравнений Навье—Стокса
Lu = f (34)
также может быть построена нестационарная система
A(bujbt) = Lu- /, (35)
для которой на основании метода дробных шагов, строится итерационная схема
(см.[47]).
5. Метод дробных шагов может быть сформулирован как метод слабой
аппроксимации [36].
Для системы (1) положим
П = П!+ П2 + ... + Яг , (36)
где £ls таковы, что системы
bujbt = £lsu (37)
равномерно-корректны в том же пространстве 2?, что и система (1). Образуем систе-
98

мы с осциллирующими коэффициентами
buT/dt= SlruT + Ef, (38)
П = 2 /,(Г,т)П_, (39)
T s = i s
где
/,(Г,т) = г5./5 г
Г /-1 /
Л + 7, Л + '
L г г
(40)
f(x,t) — та же функция из (1). Поставим для (38) задачу Коши с теми же
начальными данными и0(х)9 что и в (1а). Тогда справедлива теорема [36].
Пусть u(x,t) —решение (1), (1а), соответствующее достаточно гладкой функции
и0 (х). Тогда при сделанных предположениях
\\ur(x, t) - u(x,t) \\B -* 0, т-*0.
При более сильных предположениях относительно системы (38) справедлива
обратная теорема:
Если системы (37) равномерно-корректны каждая вместе со своими
продолженными системами до 3-го порядка включительно, то (38), (1)
равномерно-корректны и ит (х, t) -* и(х, t). Предельная функция и(х, t) есть гладкое решение (1), (1а).
Аналогичная интерпретация схемы расщепления как последовательного
приближенного интегрирования одномерных уравнений была дана в работе [18],
6. Сходимость метода дробных шагов. Примененный впервые в работах [1—3]
метод исключения дробных шагов является эффективным в случае коммутирующих
операторов Л|;-, Л/. В случае некомму тирующих операторов анализ аппроксимации
усложняется.
В работе [43], развивающей идеи [42], сформулирована общая теорема сходимости
метода дробных шагов.
Рассмотрим сначала частный случай двухслойных схем (5), когда Л2о = Л3о =
= Л31 =... = Аг0= Л„._2 = 0.
Двухслойная схема (5) называется корректной, если
\\ср...с1\\в = 1+ L-r,
\lcpep-1...cl\\B<k, / = 2, ..., р, (41)
\\л-1\\в<м
и константы L, К9 М не зависят от п, г, И. Здесь С^ есть операторы перехода схем (5).
В предположении достаточной гладкости решения и(х, t) задачи Коши (1), (1а),
корректности (5) в смысле (41) и аппроксимации (6) решение соответствующей
задачи Коши для схемы (5) сходятся в В к решению задачи Коши (1), (1а).
Соответствующие теоремы формулируются для многослойных схем.
В работах [17, 18, 46] рассматривается сходимость величины, средней по дробным
шагам
й»= r-l(un+ un+1'r+ un+2lr + ...+ un+{r-l)lr). (42)
Во многих случаях применение осредненной величины облегчает анализ сходимости.
Доказательству сходимости схем с дробными шагами методом априорных оценок
посвящены работы [18-21, 24-26, 44-45].
7. Некоторые проблемы метода дробных шагов :
1). Неоднозначность аппроксимации и возникающий в связи с этим набор
свободных параметров делают возможным многообразие схем. Метод дробных шагов дает
4* 99

возможность рационального выбора неопределенных операторов и коэффициентов.
Для отбора схем на основе общих принципов возможно применение ЭВМ.
2). Как известно, метод распараллеливания счета в ЭВМ применим к явным
разностным схемам. Метод дробных шагов делает возможным применение
распараллеливания и для неявных схем, ввиду полного расщепления алгоритма и перерабатываемых
массивов чисел.
3). Оптимизация вычислительных алгоритмов путем построения различных схем
расщепления и выбора итерационных параметров.
ЛИТЕРАТУРА
1. Реасетап D.W., Rachford Н.Н. The numerical solution of parabolic and elliptic differential equations //
J. Soc. Industr. and Appl. Math. 1955. Vol. 3. P. 28-41.
2. Douglas J. On the numerical integration of by implicit methods // Ibid. P. 42-65.
3. Douglas J., Rachford НЯ. On the numerical solution of heat conduction problems in two and three
space variables // Trans. Amer. Math. Soc. 1956. Vol. 82, N 2. P. 421-439.
4. BirkhoffG., Varga R.S. Implicit alternating direction methods // Ibid. 1959. Vol. 92. P. 13-24.
5. Peargy C. On convergence of alternating direction procedures // Numer. Math. 1962. Vol. 4. P. 172-176.
6. Douglas J. (Jr.), Pearcy C. On convergence of alternating direction procedures in the presence of singular
operators// Ibid. 1963. Vol. 5. P. 175-184.
7. Douglas J (Jr.). Alternating direction methods for three space variables // Ibid. 1962. Vol. 4. P. 41-63.
8. Douglas J.(Jr.). Gunn J.E. A general formulation of alternating direction methods. 1. Parabolic and
hyperbolic problems // Ibid. 1964. Vol. 6. P. 428-453.
9. Wachpress E.L., Habetler G.I. An alternating direction implicit iteration technique // J. Soc. Industr.
and Appl. Math. 1960. Vol. 8. P. 403.
10. Wachpress E.L. Optimum alternating direction implicit iteration parameters for a model problem // Ibid.
1962. Vol. 10. P. 339.
11. Wachpress E.L. Extended application of alternating direction implicit iteration model problem theory //
Ibid. 1963. Vol. 11. P. 994.
12. Douglas J. (Jr.), Gunn J.E. Two high order difference analogues for the equation of multidimensional
heat flow // Math. Comput. 1963. Vol. 17, N 81. P. 71-80.
13. Багриновский И.А., Годунов С.К. Разностные методы для многомерных задач // ДАН СССР.
1957. Т. 115, №3. С 431-433.
14. Яненко Н.Н. Об одном разностном методе счета многомерного уравнения теплопроводности //
Там же. 1959. Т. 125, № 6. С. 1207-1210.
15. Яненко Н.Н., Сучков В.А., Погодин ЮЛ. О разностном решении уравнения теплопроводности
в криволинейных координатах // Там же. Т. 128, № 5. С 903-905.
16. Анучина Н.Н., Яненко Н.Н. Неявные схемы расщепления для гиперболических уравнений и
систем // Там же. № 6. С 1103-1106.
11. Яненко Н.Н. Об экономичных неявных схемах: (Метод дробных шагов) //Там же. 1960. Т. 134,
№5. С 1034-1036.
18. Самарский А А. Об одном экономическом разностном методе решения многомерного
параболического уравнения в произвольной области // Журн. вычисл. математики и мат. физики. 1962.
Т. 2, №5. С 787-811.
19. Самарский А А. О сходимости метода дробных шагов для уравнения теплопроводности // Там
же. 1963. Т. 3, № 5. С 812-840.
20. Самарский АА. Схемы повышенного порядка точности для многомерного уравнения
теплопроводности // Там же. С. 812-840.
21. Самарский АА. Об одном экономическом алгоритме численного решения систем
дифференциальных и алгебраических уравнений // Там же. 1964. Т. 4, № 3. С 580-585.
22. Baker GA.fJr.), Oliphaut ТА. An implicit numerical method for solving the two dimensional heat
equation// Quart. Appl. Math. 1960. Vol. 17, N 4. P. 361-373.
23. Яненко Н.Н. О неявных разностных методах счета многомерного уравнения
теплопроводности // Изв. вузов. Математика. 1961. № 4(23). С. 148-157.
24. Дьяконов Е.Г. Разностные схемы с расщепляющимися операторами для многомерных
нестационарных задач // Журн. вычисл. математики и мат. физики. 1962. Т. 2, № 4. С. 549-568.
25. Дьяконов Е.Г. О применении разностных расщепляющихся операторов // Там же. 1963. Т. 3,
№2. С 385-388.
26. Дьяконов Е.Г. Разностные схемы с расщепляющимися операторами для общих параболических
уравнений второго порядка с переменными коэффициентами // Там же. 1964. Т. 4, № 2. С. 278-
291.
27. МарчукГ.И. Теоретическая модель прогноза погоды // ДАН СССР. 1964. Т. 155, № 5.
28. Марчук Г.И. Численный алгоритм решения уравнений прогноза погоды // Там же. Т. 156, № 2.
100

29. Марчук Г.И. Новый подход к численному решению уравнений прогноза псгоды // Симпозиум по
долгосрочным методам прогноза (MWO), США, Боулдер, июль, 1964.
30. Марчук Г.И. t Яненко Н.Н. Решение многомерного кинетического уравнения методом
расщепления //ДАН СССР. 1964. Т. 157, № 6.
31. Марчук Г.И., Султангазин УМ. О сходимости метода расщеплений для уравнений переноса
излучений // Там же. 1965. Т. 161, № 16.
32. Conte S.D., Dames R.T. An alternating direction method for solving the biharmonic equation //
Math. Tab. and Other Aids Comput. 1958. Vol. 12. P. 128-205.
33. Conte S.D. Numerical solution of vibration problems in two space variables // Pacif. J. Math. 1957.
Vol. 7, N4. P. 1535-1544.
34. Коновалов А.Н. Применение метода расщепления к численному решению динамических задач
теории упругости//Журн. вычисл. математики и мат. физики. 1964. Т. 4, №4. С. 760-764.
35. Коновалов А.Н. Об одной итерационной схеме решения статических задач теории
упругости // Там же. № 5. С. 942-943.
36. Яненко Н.Н. О слабой аппроксимации систем дифференциальных уравнений //Сиб. мат. журн.
1964. Т. 5, № 6. С. 1432-1434.
37. Фадеев Л.К., Фадеева В.Н. Вычислительные методы линейной алгебры. М.: Физматгиз, 1960.
38. Douglas J.(Jr.). The application of stability analysis in the numerical solution of quasilinear
parabolic differential equations//Trans. Amer. Math. Soc. 1958. Vol.89. P. 484-518.
39. Годунов С.К., Семендяев K.A. Разностные методы решения задач газовой динамики // Тр.
IV Всесоюз. мат. съезда. Л., 1964. Т. 2.
40. Владимиров B.C. Математические задачи односкоростной теории переноса частиц // Тр. МИАН
СССР. 1961. Т. 11.
41. Яненко Н.Н. Некоторые вопросы теории сходимости разностных схем с постоянными и
переменными коэффициентами // Тр. IV Всесоюз. мат. съезда. Л., 1964. Т. 2. С. 613-621.
42. Яненко Н.Н. О сходимости метода расщепления для уравнения теплопроводности с
переменными коэффициентами // Журн. вычисл. математики и мат. физики. 1962. № 5. С 934-937.
43. Бояринцев Ю.Е. Дис. ... канд. физ.-мат. наук. Новосибирск, 1965.
44. Less M. Alternating direction and semi explicit difference methods for parabolic partial differential
equations // Numer. Math. 1964. Vol. 3, N 5. P. 398-462.
45. Lees M. Alternating direction methods for hiperbolic differential equations // J. Soc. Industr. and Math.
1960. Vol. 10, N 4. P. 610-616.
46. Kellog. Another alternating direction implicit method // Ibid. 1963. Vol. 11, N 4. P. 976-979.
47. Владимирова Н., Кузнецов Б.Г., Яненко Н.Н. Численный расчет симметричного обтекания
пластинки плоским потоком вязкой несжимаемой жидкости // Тр. симпоз. по прикл. и вычисл.
математике. Новосибирск, 1965.
48. Дьяконов Е.Г. О некоторых итерационных методах решения систем разностных уравнений,
возникающих при решении методом сеток уравнений в частных производных эллиптического
типа // Вычислительные методы и программирование. М.: Изд-во МГУ, 1965.
49. Самарский АЛ. О разностных схемах для многомерных дифференциальных уравнений
математической физики // Apl. mat. 1965. Sv. 10, N2. P. 146-163.
ОБ ОДНОЙ АБСОЛЮТНО УСТОЙЧИВОЙ СХЕМЕ
ИНТЕГРИРОВАНИЯ УРАВНЕНИЙ ГИДРОДИНАМИКИ*
1. В 1951 г. Ландау, Мейманом, Халатниковым [1] для интегрирования уравнений
газовой динамики был предложен неявный метод бегущего счета в эйлеровых
координатах, позволяющий произвольно крупный шаг по времени. Однако предложенная
ими схема была недивергентной и различала до- и сверхзвуковой режимы течения,
что ограничивало ее практическое применение. Аналогичная схема в лагранжевых
координатах была предложена в работе [7].
Годунов, Семендяев [2] в докладе на IV Всесоюзном математическом съезде
предложили метод пересчета для явных недивергентных схем, делающий схемы
дивергентными и повышающий их точность (метод предиктор—корректор). Аналогичные схемы
известны и для уравнения теплопроводности [4, 5]. С.К. Годунов [3] получил методом
предиктор—корректор неявную симметричную схему для уравнений газовой динамики.
Эта схема требует матричных прогонок по пространству.
Предлагаемая схема также основана на методе предиктор—корректор, но использует
"Труды МИАН СССР. 1966, № 74. С. 141-146. (Соавтор И.К. Яушев).
101

алгоритм бегущего счета. На первом (промежуточном) шаге расчет ведется в
инвариантах Римана по схеме бегущего счета, которая абсолютно устойчива, но не дивер-
гентна. На втором шаге применяются дивергентные формулы. В результате разностная
схема становится диверген ной, и законы сохранения выполняются. Эта схема
позволяет явно задать ударный Ьронт, который на каждом шаге переходит из точки сетки
в другую; тем самым сетка размечается последовательным движением фронта. Такой
способ построения сетки был предложен М.В. Келдышем. Схема имеет второй порядок
точности на равномерной сетке и не требует матричных прогонок, сводя алгоритм
к двухточечному бегущему счету.
2. Вначале рассмотрим систему линейных уравнений, после чего полученные
результаты будут перенесены на случай уравнений гидродинамики.
Пусть дана система
Ъи „ Ъи Ъи Ъи
а2 =0, — =0, (1)
Ъг Ъх bt Ъх
где
а = const > 0.
Наряду с системой (1) будем рассматривать также эквивалентную ей систему
Ъг Ъг ds ds
_+я_=0; а— = 0, (2)
bt Ъх bt Ъх
которая получается из (1) заменой
г-и - av, s = u+av. (3)
Как известно, переменные г и s называются инвариантами Римана.
Расчет уравнений (1) ведется по схеме
7
т
vn+1
7
-ип
J
-vn
J
упл Уг _ уп+ i/2
7+1 7-1
2h
цп+у2 _ цп+у2
7+1 7- 1
2h
= 0,
(4)
= 0,
где через UP+V2 , K.w+% обозначены вспомогательные величины на промежуточном
слое, которые определяются из уравнений
7
г/2
Sn+V2 _
7
г"
s"
1
т/2
Гп+У2 _ п + Уг
+ а_> izi_ =0)
(5)
если положить
r?=u?-avn, sn=un +av"9 (6)
rn+y2 ^Vn + y2 __aVn+y sn+y2 =£/«+й +дК"+У2. (7)
7 7 7 ' 7 7 7 V '
Таким образом, переход к новому шагу совершается в два этапа: с помощью
абсолютно устойчивой схемы бегущего счета (5) переходим к промежуточному шагу и на
нем по формуле (7) вычисляем вспомогательные величины Un+V2 , у?+У2 , после
чего определяем окончательные значения и? +1, vn + * по формулам (4).
102

Цель вспомогательного шага — получить запас устойчивости, цель окончательного —
внести поправку для повышения порядка точности.
Покажем, что схема (4), (5) абсолютно устойчива. Если ввести двухкомпонентный
вектор и (и, и>), где w = av, то ее можно переписать в виде
AVn+v> =ип, uw + 1=u" +BVn+y> . (8)
Исключив из (8) вспомогательный вектор U"+Vi , получим схему перехода к новому
шагу
ил + 1=Сил, (9)
где С-Е +А~1В — матрица перехода. Фурье-образ матрицы С имеет вид
(10)
2к2 smkh
<*,/«
|0/, а
где
а
= 1 -
1 +4к(1 +K)sin2(A;/i/2) '
2Ksinkh [1 +к(1 -coskh)] _ т
1 +4к(1 + fc)sin2(A;/i/2) ' ^ ^'
Матрица (10) нормальная, и норма ее равна единице. Следовательно, схема (4), (5)
абсолютно устойчива. По схеме (5) организуется бегущий счет; для rn + i/2 — слева
направо, а для s? + V2 — справа налево; при этом такой счет обладает пространственной
устойчивостью, где коэффициентом перехода служит величина к/(1 + к).
3. Пусть задана система уравнений
Ъи Ър bv Ъи
— +—=0, =0 (11)
bt Ъх bt Ъх
одномерного изэнтропического течения в лагранжевых переменных, где р = kv~y,
к, у — постоянные величины. Применение лагранжевых координат позволяет не
различать случаи до- и сверхзвукового течения, как это делалось в работе [ 1 ].
Как и в предыдущем пункте, расчет разбивается на два этапа: на вспомогательном
шаге счет ведется по устойчивой недивергентной схеме 1-го порядка точности (схема
бегущего счета)
(12)
/ l+к '; ' /-1 ' ' 1+к"^ I > ' 1 '
п С"Т dP + 2 2
к =—-—, сг = -v—, г = ы + с, s=u с.
J IxP.h dv 7-1 7-1
Окончательные величины un + l, v? + l вычисляются по дивергентным формулам
„" + !=„"_ JL(p"+* -РГ\*\ v" + *=vn+—(u"+* -U?+*)9 (13)
где вспомогательные величины U?+i/l , Pf+^ связаны с г?+Уг и s?+Vl соотноше-
ниями
рп+ъ _ ((т~1)/4) fr"+1/* _s«+%Wy-i (14)
' /* 42/7-1 *' ' '
103

Таким образом, мы получаем схему расчета (12) —(14), которая обладает
следующими свойствами: 1) имеет 2-й порядок точности на равномерной сетке, 2) абсолютно
устойчива, 3) дивергентна, 4) решение неявных уравнений проводится двухточечным
счетом без прогонок.
При расчете гладких решений счет следует вести на равномерной сетке, выбирая
шаги г, h из соображений точности вычислений. При заданной сетке величина crjlvn
будет иметь разное значение в разных точках. Если потребовать, чтобы счет промежу-
точного слоя следовал характеристикам dx = ±— dt так близко, как это возможно при
Рис.1
заданной сетке, то в точках, где CTJlvh
менять явную схему (рис. 1)
1, вместо неявной схемы (12) следует при-
тп + у2 _ гп
«/"(гГ-Г-.)'
S«+V4 =sn
■Kn(s"t-sn).
(15)
При этом условие устойчивости не нарушается. Полученная явно-неявная схема
бегущего счета аналогична схеме Карлсона [6].
4. При расчете течения с ударным фронтом наиболее простой алгоритм получается,
если г определять из условия
T = h/D(x,t),
(16)
где h фиксирован, D — скорость перемещения ударного фронта; при этом сетка
неравномерная и размечается по оси t последовательным движением фронта,
переходящим на каждом шаге счета из одной точки сетки в другую. Предположим для
определенности, что ударная волна движется вправо (рис. 2).
Счет фронта ударной волны проводится в инвариантах г и s подобно тому, как это
делается в методе характеристик. Условие (16) дает координаты очередной точки
ударного фронта. Из соотношений на разрывах
(и2 -u1)D=p2 -pl9 (v2 -v1)D = -(u2 -ux) (17)
104

исключается величина Д и полученное соотношение записывается в инвариантах г и s:
(7-D2
l(r2- s^/у-1 -(г, - s,)2"'11-1] X
1
1
(r.-s,)2^1 (r,-s2?n-1
-4l(r2 +s2f-(ri +Slf] = 0.
(18)
Значения rx, sl9 r2 приносятся на фронт вдоль соответствующих характеристик
с предыдущего слоя. После этого из (18) определяется s2.
Рис.3
Рис.4
Алгоритм расчета одного вида граничных условий будет дан в следующем пункте
на примере конкретной задачи.
5. Рассмотрим взаимодействие ударного фронта с простыми волнами (волна
разрежения, сжатия). Пусть по некоторому газу, находящемуся в полубесконечном
цилиндре, перемещается вправо ударный фронт. Цилиндр слева закрыт поршнем,
движущимся по закону ир = Up (t), и пусть dup/dt Ф 0. Тогда движение поршня порождает
простую волну, которая взаимодействует с ударным фронтом. Требуется рассчитать
возникающее при этом течение.
Алгоритм решения задачи будет состоять в следующем. Пусть в момент времени
t = t0 ударный фронт находится в некоторой точке сетки. По алгоритму, описанному
в п. 4, рассчитывается очередная точка ударного фронта на промежуточном шаге. Для
повышения точности организуется при этом обычный итерационный процесс. После
того как значение s за фронтом найдено, явно-неявная схема бегущего счета
определяет все s
п+К
/
вплоть до границы. Значение на границе находим из условия
С* =2uVVl
По найденному r% + %
(19)
-П+Уг
W + 1
Vi+1 находится
организуется бегущий счет слева направо по определению всех
гу '* . Найденные rn + 1/l ,sn + V2 определяют вспомогательные величины ип + Ул 9P?+Yi
по формулам (14). Очерёдная точка ударного фронта на основном шаге
рассчитывается аналогично тому, как это было сделано на промежуточном шаге.
Схема (13) определяет величины и ? + *, v? + 1 вплоть до значений и " + *, v" + *. Расчет
границы на основном шаге проводится просто. По известным и\
s" + 1. Asq + 1 определяется по одной из формул
«г1 —k+* +*г* sr1), *г* >i,
1+кГ*
105

Распределение удельного объема и скорости частиц по оси х за ударным фронтом
(через 8 шагов по схеме предиктор—корректор и через 27 шагов
по схеме "Распад произвольного разрыва")
и?
J
предиктор—
корректор
0,6126
0,6351
0,6603
0,6753
0,6953
0,7129
0,7323
0,7492
0,7697
0,7868
0,8056
0,8206
0,8363
0,8481
0,8611
0,8714
0,8845
0,0000
и
точное
0,6126
0,6358
0,6579
0,6789
0,6990
0,7183
0,7368
0,7547
0,7719
0,7886
0,8047
0,8203
0,8355
0,8503
0,8647
0,8787
0,8924
0,0000
Vs.
J
предиктор—
корректор
0,6108
0,5946
0,5865
0,5777
0,5692
0,5621
0,5535
0,5462
0,5380
0,5312
0,5236
0,5180
0,5118
0,5077
0,5026
0,4991
0,4944
1,0000
V
точное
0,6108
0,5999
0,5898
0,5804
0,5716
0,5633
0,5556
0,5483
0,5413
0,5348
0,5285
0,5225
0,5168
0,5114
0,5062
0,5012
0,4964
1,0000
«' \ м
/+1/2
"Распад
разрыва"
0,6536
0,6700
0,6898
0,6904
0,7031
0,7301
0,7621
0,7709
0,7631
0,7831
0,8144
0,8365
0,8588
0,8874
0,8023
0,6118
0,1688
0,0300
и
точное
0,6378
0,6492
0,6712
0,6922
0,7123
0,7315
0,7500
0,7678
0,7850
0,8016
0,8177
0,8333
0,8485
0,8633
0,8776
0,8916
0,0000
0,0000
»* \ „
/+1/2
"Распад
разрыва"
0,5931
0,5919
0,5747
0,5584
0,5552
0,5564
0,5518
0,5432
0,5177
0,5173
0,5246
0,5237
0,5165
0,5060
0,4712
0,6167
0,8449
0,9711
V
точное
0,5990
0,5937
0,5838
0,5745
0,5659
0,5578
0,5502
0,5430
0,5361
0,5297
0,5235
0,5177
0,5121
0,5067
0,5016
0,4966
1,0000
1,0000
Тогда Го+ 1 = 2uq + 1 - 5o + 1. Этим заканчивается счет одного шага. Далее этот процесс
повторяется.
По этой схеме был проведен ряд экспериментальных расчетов. Для примера ниже
приводятся некоторые результаты расчета взаимодействия ударного фронта с волной
разрежения. Для сравнения наряду с точным решением дается решение, полученное
по схеме С.К. Годунова "Распад произвольного разрыва" (см. табл. и рис. 3, 4). На
рис. 3 кривые соответствуют точному решению, а точки — решению по методу
предиктор—корректор. На рис. 4 сплошными линиями дано точное решение, а линиями
с нанесенными на них точками — решение по схеме "Распад произвольного разрыва".
ЛИТЕРАТУРА
1. Ландау Л.Д., Мейман И.Н., Халатников ИМ. Численные методы интегрирования уравнения в
частных производных методом сеток // Тр. III Всесоюз. мат. съезда. М., 1958. Т. 3. С. 92-100.
2. Годунов С.К., Семендяев КЛ. Разностные методы численного решения задач газовой динамики
// Журн. вычисл. математики и мат. физики. 1962. Т. 2, № 1. С. 3-14.
3. Годунов С.К. Разностные методы решения уравнений газовой динамики. Новосибирск, 1962.
4. Douglas J. The application of stability analysis in the numerical solution of quasilinear parabolic
differential equations // Trans. Amer. Math. Soc. 1958. Vol. 89, N 2. P. 484-518.
5. Douglas J., Jones B.F. On predictor-corrector methods for non-linear parabolic differential equations
// J. Soc. Industr. and Appl. Math. 1963. Vol. 11, N 1. P. 195-204.
6. Рихтмайер Р.Д. Разностные методы решения краевых задач. М.: Изд-во иностр. лит. I960.
7. Охоцимский Д.Е., Кондрашева И.Л., Власова З.П., Казакова Р.К. Расчет точечного взрыва с
учетом противодавления // Тр. МИАН СССР. 1957.
106

ЧИСЛЕННЫЙ РАСЧЕТ СИММЕТРИЧНОГО ОБТЕКАНИЯ ПЛАСТИНКИ
ПЛОСКИМ ПОТОКОМ ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ*
В работе с помощью численного эксперимента показывается возможность
использования метода дробных шагов для решения некоторых задач гидродинамики вязкой
несжимаемой жидкости. Указывается разностная схема и приводятся результаты расчета
плоского течения около пластинки конечной ширины.
1. Постановка задачи. Рассматривается следующая задача: найти функции и(х, у),
v(x> У)* Р(х> У)* удовлетворяющие в области D :\х\ < а, 0 < у < b системе уравнений
ъ2л +ъ-
Ъх2 Ъу
и г>( ди Ъи ^ Ър\
- = RI и — + и— + — I
•2 V Ъх Ъу Ъх),
; + z = R[ U
Ъх2 Ъу2 \
Ъх Ъу
Ъу
Ъи Ъи
— + v —
Ъх Ъу
Ър
Ъу
),
п)
при условиях
1. 1*1 = в;
2. \х\<а;
3. |*| <с;
4. с<|х|<а;
5. х = -а;
0<у<Ь;
У = Ь;
У = 0
у = 0
у = 0
и=1
и = \
и = 0
v = 0
v = 0
v = 0
ди/Ъу = 0, o=0
р = 0.
(2)
Здесь и, v — безразмерные компоненты скорости, р — безразмерное давление, R —
число Рейнольдса, х, у — безразмерные координаты.
Если a, b неограничены, задача (1), (2) описывает симметричное обтекание
пластинки шириной 2с потоком вязкой несжимаемой жидкости. Случай конечных, но
достаточно больших a, b можно рассматривать как приближенное решение этой задачи. Задача
(1), (2) решается численно методом установления. Для этого краевая задача (1), (2)
заменяется следующей смешанной задачей.
Найти функции и(х, у, г), v (х, у, г), р(х, у, г), удовлетворяющие в области DT:
Z) X (0 < t <T) системе уравнений
Ъи t Ъи , Ъи Ър
— + и — + v— + —
Ъt Ъх Ъу Ъх
гЪи_
+ м_— +1;^-+^ 1
Ъх
*И + ^ = r(
Ъх2 Ъу2 \
Ъх2 Ъу2 \
bt\ 4 / Элг Ъу
с начальными условиями
t = 0, u=\, v=0, p = 0
),
Эи + дрл
Ъу Ъу t
(3)
(4)
*Некоторые вопросы вычисл. и прикл. математики. Новосибирск, 1966. С. 186—192. (Соавторы
Н. Владимирова, Б.Г. Кузнецов.)
107

и граничными условиями:
1. \х\=а, 0<у< Ь, и=1, и=0;
2. \х\ <д, у = Ь, и=1, и = 0;
3. |*|<д, 7 = 0, $Ъи1Ъу+(£-\)и = ($-\)<1\ и=0, (5)
4. х=-а, у = 09 р = 0.
Здесь d < 1,
1 при с + е<|х|<д,
(х-с + е)/2е при с-е<х<с + е,
(е - х - с)/2е при -с - е < л: < - с + е,
I 0 при |лг| < с - е.
5 =
Нетрудно видеть, что при t -* °°, б -* 0 условия (5) переходят в краевые условия (2),
а решения смешанной задачи (3)—(5), асимптотика которых стационарна, являются
решениями краевой задачи (1), (2).
При малом е Ф 0 условия (5) при t ->• °° будут отличаться от (2) локально в
окрестности переднего и заднего концов пластинки. Предполагается, что такое локальное
изменение краевых условий не окажет существенного влияния на решение задачи
в целом.
2. Разностная схема. Задача (3)—(5) решается методом дробных шагов. Система
уравнений (3) разбивается на две подсистемы. На каждом дробном шаге t = (п + Vl)t
численно решается система
д. /I*U *)=*!" RJL*>+U*J>) = *!>9 (6)
\2 dt Ъх) Ъх2 \2Эг Ъх) Ъх2
1^ + ^=0
2 Эг Ъх
(здесь q=p + w2/2)
при краевых условиях
\х\=а, 0<y<b, £i=l, и = 0. (7)
В качестве начальных условий каждый раз берутся функции и, v, p, сосчитанные на
предыдущем целом шаге. В частности, для начала счета используются начальные условия.
На каждом целом шаге t = пт численно решается система
\2dt Ъу) Ъу2 \2bt Ъу) Ъуг
(8)
2 bt Ъу
при краевых условиях
1. |*|<л, у = 09 H(bulby) + (£-\)u = (%-\)d\ и = 0,
2. |х|<в, У=Ь, . м=1, v = 0,
и начальных условиях, взятых с предыдущего дробного шага.
Кроме того, для обеспечения четвертого условия (5) (которое, кстати, может быть
задано в любой точке потока, не обязательно на границе) на каждом целом шаге из
поля давлений р вычитается значение давления в точке (—а, 0).
(9)
108

Для реализации системы уравнений (6) применялась следующая разностная система
П + Уг
Щк
- + —— \aqik + (1 - a)qik - - j-—-1 [auik + (1 - a)uik ] - 0,
r /ij L J R hj
"fc**-1** + *4 Ыа«Ь + (1 - «)«u+* 1 - £ ^i-1 [«fit + О - Ф?к+ *]=0.
(10)
<?&+*-<& + Д*1 [аипк + (1 _ a)„»fc+%] = о
г Л
(/=i,2,..., /- i,* = o, i *).
Здесь т — шаг по времени, hx — шаг по оси х, А±1 - оператор сдвига по первому
нижнему индексу.
'га
^
ц
А
—"
\
д
\\
\
——
S
=*>*
*—.
и
"^
0J5
*—.
т
/<?
—
z)
А
i—^
и.
/
Ч
/
го
■—«
z
/
f
*
О 10 ZO 30 40 50 60 х
Рис. 1
15
Ml
м
МП
и
/ил
О 11 Z7 47
Рис. 3
U*-5
0
Ч
<:
j
/
z\
п
/
А\
1
йг
1
2#
Л
0,1
0,1
30
Ри<
1
5.2
//7
-*J
деГ
г\
\
\Ш
тч
/
ь
\
ч*
V
^
W
ZO
/5
- 1 1 1 1 1 1 1 1 1
№
N
\ I и \\ 1 \
11 Z7 47
Рис.4
Решение системы (10) проводится в следующем порядке.
Исключая из первого и третьего уравнения (10) qpk+V2, получаем систему
разностных уравнений второго порядка для функции ип + 1/2, которая решается методом
прогонки с использованием условий (7). Второе уравнение (10) также решается методом
прогонки. После этого с помощью третьего уравнения (10) находим q?k+ Уг, а
следовательно, и р"к+ 1/2 во всех точках области D и на ее границе, кроме части границы х = д,
Аналогичным образом решается задача (8), (9). Система (8) заменяется системой
разностных уравнений
, .п' + 1 , .п + Уг д
uik - Щк . „л +Уг ^ + 2[п/1.П +Уг , (л ^4-/1+И
; + vik —7~lauik + U ~<*)Щк J —
т h2
1 A_2A+2
R h\
[au?k+*+(l-a)u?k+l]=Q,
109

т h2 R h\
2
xM+* + (i-<*K*+1l = o, (ii)
ГкП + 1 /^Л+Vi д
^'fc " ^'fc + ^±2 [eW|«+* + (1 _ e)w»+1 j = о
(/=o,i,..., -Л k=i,2,..., K-i)
при условиях
1*0 = 0, & = (A+2/^2)uf0+ ' + (8/ - lKo+' = tti - 1)*(я + 1)T,
"/V1=i, y«+l=o (/=o,i,...,/).
Здесь h2 — шаг по оси у, А±2 — оператор сдвига по второму нижнему индексу.
Системы разностных уравнений (10), (11), как легко показать, по исключении
дробного шага аппроксимируют систему (3) с первым порядком точности по г, h\, h2.
3. Результаты численных расчетов. Для чисто неявной схемы а = 0 получена
экспериментальная сходимость метода. Расчеты проводились при следующих значениях
параметров:
г = 0,1, /=60,
д=1, К=30,
6=1, Л! = 1/30,
с = 0,5, й2 = 1/30,
d = 0,5, 6 = 2/30
при числах Рейнольдса 105; 10; 0,1.
Результаты расчетов приведены на рис. 1—4. На рис. 1 изображено распределение
компоненты скорости и на линиях у = 2h; у = I0h; у = 20 Л при R = 10.
Интересно отметить отсутствие симметрии в характере распределения v
относительно оси у и наличие значительного изменения в окрестности носика и конца
пластинки. На рис. 2 дано распределение компоненты скорости v. На рис. 3, 4 даны эпюры
компоненты скорости v в сечениях х= llhlPx = 27hlt x = 47 hi.
О ПРИМЕНЕНИИ МЕТОДА РАСЩЕПЛЕНИЯ
ДЛЯ ЧИСЛЕННОГО РАСЧЕТА ДВИЖЕНИЯ
ТЕПЛОПРОВОДНОГО ГАЗА В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ*
В настоящей статье предлагается алгоритм численного расчета задачи об осесимметри-
ческом движении с учетом теплопроводности в неоднородных средах, основанный на
применении метода расщепления (дробных шагов) [1—3]. Решение двумерной задачи
сводится к последовательности одномерных расчетов.
В двумерных задачах одним из главных вопросов является выбор способа описания
движения. Широко известны эйлеров и лагранжев методы. В методе Эйлера
определяется распределение параметров состояния движущейся среды для каждой заданной точки
пространства. Для численных расчетов этот метод удобен при наличии неподвижных
♦Изв. СО АН СССР- Сер. техн. наук. 1967. № 8, вып. 2. С 74-82. (Соавторы В.Д. Фролов. В.Е. Не-
уважаев.)
11в

границ и отсутствии границ раздела сред и допускает большие деформации вещества.
В методе Лагранжа определяется движение и состояние для каждой фиксированной
частицы вещества. В численных расчетах этот метод удобен при наличии границ раздела
сред, но не допускает больших смещений частиц относительно друг друга, например
скольжения слоев.
В последнее время появились комбинированные методы, использующие для
численных расчетов достоинства обоих представлений. Так, в работе [4] применяется
подвижная эйлерова сетка. В.Ф. Дьяченко, как известно авторам, использовал в расчетах
эйлерово-лагранжевы координаты, в которых границы раздела сред являются лагранже-
выми линиями.
В предлагаемой работе также применяется смешанный эйлерово-лагранжев способ
описания движения, когда одно семейство координатных линий, совпадающее с
границами раздела, — лагранжево, а другое — эйлерово. Это позволяет следить заграницами
раздела и просто рассчитывать перетекание вещества в слоях. В силу того, что форм?,
границ раздела может быть переменной во времени, для сохранения границ в качестве
координатных линий на каждом шаге расчета с ними связывается новая криволинейная
система координат.
В данной работе реализуются неявные разностные схемы, позволяющие вести расчет
с достаточно крупным шагом по времени.
В п. 1 уравнения, описывающие движение сплошной среды, записываются в
произвольных криволинейных координатах. Это позволяет использовать произвольную
метрику, а на границах, совпадающих с лагранжевым семейством координатных линий,
сохраняет непрерывной соответствующую контравариантную составляющую вектора
скорости, что дает возможность не выделять специально при расчете границы раздела.
Далее, в п. 2 эти уравнения расщепляются на две системы, в каждой из которых
учитываются лишь производные по одному из направлений. В системе, содержащей
производные по координате, отвечающей границам раздела, переходим к лагранжевой
массовой координате. Для каждой из полученных систем в п. 3 пишутся неявные
разностные схемы в основе которых лежит метод последовательной прогонки [5]. Сначала
решается система, описывающая движение в эйлеровой сетке, затем используются
полученные значения и ведется расчет системы в лагранжевых координатах, т.е. решение
задачи сводится к расчету М одномерных задач в эйлеровой сетке и К одномерных
задач в лагранжевой сетке, где М и К — количество счетных интервалов на каждом из
координатных семейств.
В п. 4 приводятся некоторые результаты расчетов, полученных по программе,
реализующей описываемую методику на ЭВМ. Программа составлена В.М. Грибовым,
В.И. Легоньковым и Л.Н. Хохряковой. В разработке методики принимал участие
А.И. Зуев. Авторы благодарят всех товарищей, помогавших им при выполнении
настоящей работы.
1. Основные уравнения. Движение теплопроводного газа описывается следующими
уравнениями:
dp/dt + pdiv\ = О, pdyjdt + gradp = 0, (1.1)
de х d(l/p) 1 А. , ,_ч
— + р = -div(Kgradr).
dt dt p
Здесь р = р(р, Т) — давление, е = е(р, Т) — внутренняя энергия, р — плотность, Т -
температура, v— вектор скорости, к = к(р, Т) — коэффициент теплопроводности.
Пусть ук (к = 1, 2, 3) — декартовы ортогональные координаты, xl (i = 1, 2, 3) -
произвольные криволинейные координаты. Введем обозначения:
gik Т^ 1Гк; 8 =
Эх' ЪхК
11
2 1
31
g\2
g2 2
g3 2
£Чз
£2 3
#3 3
(1.2)
111

ik _ алгебраическое дополнение
* g ~~'
" r Va*' эх* .aW'
V,^ = dvK/dxli + иЛГ^.
Криволинейную систему координат в каждый момент времени t будем выбирать так,
чтобы линии х1 = г = const совпадали с границами раздела слоев, а также чтобы х2 = в
их3=(/), где в и у — соответственно полярное расстояние и долгота. Пусть R = R (/\ в) —
k*t/г
Г/ц Гт ТТЛ-/ ГТ Г0
x-r/z
расстояние от данной точки с координатами г, в до начала координат. Тогда декартовы
координаты уь и криволинейные х1 будут связаны между собой соотношениями
'Ух - R sin0cos<# у2 = R sin0 sin</?; уъ = R cos0.
Выражения (1.2) с учетом (1.3) примут вид
gu = R2r', gi2=RrR$'> gi3 = 0,
gl\=g\2\ g22 = R2 +R2d\ ^23=0,
fti = 0;
Ti i - Rrr/Kr\
П, = 0;
£32 = 0;
g=R*R2 sin2 0;
S33 = /?2sin20,
r?2 = Rr/R; rl,= 2Д„/я
Г22 -
RRr
Здесь индексы гиб означают дифференцирование соответственно по г и в.
Если обозначить
и = и1; и = v2;
Э Э _,_ Э А Э
= + И — +U —
£f dt Ъг Ъв
и применить к системе уравнений (1.1) преобразование (1.3), то получим
Dp + p Ibsfgu + aVjt)\ 0.
— +r[lU2+2r'l2uv+r^v2 =
Dt pR2
1 / Ър Эр\.
+ 2Г!2ии + Г!2и2 =
1 / dp Эр\
(1.3)
(1.4)
(1.5)
112

De p (ду/gu .dy/gv\_ 1 Э my/g ( ЪТ ЪТ\
-+—{ + j " PVgbrRiR2[g22^- '" Ъв)
(1.6)
Dt P\fg\ Ъг Ъв
1 Ъ_ Ksfg j ЪТ ЪТ
ps/gM R2Rl\ gl2dr g11 Ъв
У
Задача ставится следующим образом: определить решение системы (1.6) в некоторой
области D (см. рисунок), ограниченной осью симметрии и некоторой кривой
г = гв; 0< в < тг, (1.7)
если в момент t = t0 известны и(г,в, t0), v(r, ву r0), р(гу в, t0), Т(г, в, t0),a на границе
(1.7) заданы, например, следующие условия:
p = p(9,t); *{ЪТ/Ъп) = f(T), (1.8)
где Ъ/Ъп означает дифференцирование вдоль нормали к кривой (1.7). Заметим, что
поток в (1.8) может быть записан в координатах г к в:
RR
_* / ЪТ ЪТ\ _ ,,_
^1'" * -fta W"/(Г)-
(1.9)
На осях симметрии в = 0; в = я:
Эр = ЪТ = Ьи =
дв Ъв Ъв
0; v=0.
2. Расщепление системы (1.6). Разобьем систему (1.6) на две, по возможности
учитывая в каждой производные только по одному из направлений г и в:
1 Ъи , Ъи -v , 2
+ и— + .Г12ыи + Г22и
2 Эг Э0
2 bt Ъв
L^£ + у?? + JL byfzv = о
2 ЭГ Ъв y/g Ъв
1 I6 + и ^£ + р эУ^и =
2 Эг Э0 p\fg' Ъв
R6
PR2
1
РЛ2
ДгЭ0
Ър =
Э0
=
0;
0;
(2.1)
1 Эй
Ъи
ps/g Ъв R2R
R2 +Rl Ър _
яу/*( R R дТ R*dT\
+ и— + rijt/2 + Г\2ии +
2 Ъг Ъг pR2R
Ъг
= 0;
1 Зи Эи , _,, Re
2 Ы Ъг pR2Rr Ъг
L*£ + и— + — ду^и = о
2Эг Ъг y/g Ъг
Ъу/gu _ 1
Э'=0;
(2.2)
1 Ъе , Эе ^ р
2 Эг Эг pV?
э\/?
(Я2+Я2*)
Эг
Ъг py/g bt R2Rl
Введем замену
U = uRr, H = Re/R
и в системе (2.2) перейдем к лагранжевой массовой координате
dq = pR2Rrdr.
*'«>¥е>
(2.3)
113

Тогда будем иметь
1 Эо
Ъи
2 dt
— + v— + 2
Ъв
Uv
R
+ 2Hv2 +
1 Ър _
pR2 Ъв
-rz= 0;
2 dt Ъв \Ъв } pR Ъв
1 Эр Ър p Ъ . r~ . n
2 Э* Э0 \fgbe
1 Эе Эе р 3
+ и— + -^-p, —
2 Эг Э0 pV? Э0
, r . 1 Э ^VJ / ЪТ _,_ _ ЭГ\
+ Л — £/и + R2 (1 + Я2)^ = 0;
ЭЯ
ЭЛ
2 Эг
2 Эг Ъд
>2иЪР =
£ЭД
2 Ъ1
'Ъд
= У;
1 Э(1/р) эл2£/ _
2 Эг
Ъд
ЪR2U
= 0;
1 Эех
2 Эг Ъд
= ±<*R2
Ъд
R\l+H2)p
ЪТ
Ъд
ЯЭГ
R Ъв
(2.4)
(2.5)
3. Расчетные формулы. Пространственная сетка строится с помощью лучей вк + у2 =
= const, проведенных из некоторого центра, и линий rm = const, причем последние
выбираются так, чтобы границы раздела были координатными линиями (см. рис.).
Величины R, U, v, р, T будем определять в следующих точках:
Я(гт,0*+уь) = Rm, к+Уг\ ^(Гт^к+Уг) = ^т,к\-Уг\
V(rm + у29 вк) = Vm +y2t к\
Р(гт + Уг> Ок + %) = Рт + Уг, к + Уг > Т(гт + Уг$к + Уг)^Тт + Уг, к + Уг
Если необходимо знать эти величины в других точках, то они находятся интерполяцией.
Расчет шага по времени ведется в два этапа: на первом (2.1) аппроксимируется
некоторой разностной схемой на интервале [пт, (п + %)т] и определяются величины
U, и, р, Г; на втором этапе система (2.2) аппроксимируется на интервале [{h + Vl)t,
(я+1)т] схемой (5) и получаются окончательные значения U, и, р, Т при t=tn + 1 =
= (п+ 1)т.
Ниже приводятся разностные уравнения. Система (2.1) расписывается следующим
образом.
Д0*
= 0*
0*-
W± = v±\v | /2; Д0* = вк + % - 0* _ у2
Рк+Уг + —7^ [Рк + Уг ~ Рк-Уг) + Т^ [Рк + '/г ~ *> к - К) +
Д0*
7Pfc + % Л /Гй r,,w+^ ^/^„и+М = л"
114

иГ-Л + .£?£_(,,»♦* _u»+*ij
ДА,
k-Vi
Ав
Р^№\*г-***) + 2r№)" + 2г(Я„*)»
(3.1)
'm +1
_ Rk + 1 — Rk
к + V
Rk + 1 + ^A: A#A: + Vi
DW + % + п(оП + # Tn ) + mn (l)n + V2 пп+Уг) риги n"^ п"+^<^П-
P к + Уг * P \Pk + Vi' 7 A: + %/ + CPa: + *Ь\и* + 1 _ UA: / ' еСЛИ UA: + 1 ~ Vk ^ U>
Pfc + Уг Р\Р* + */2> У Аг + У2У' еСЛи Ufr+1 - UA: ^°>
fc = 0,1, ...., K\
Vo
n + Yt _ ,,w + И _
= У
= 0;
Р-У2 А>У2
nw + Vi _ nw + Уг
Рк-Уг PlC + Уг'
Здесь для простоты записи индекс т + Уъ везде опущен и
т = О, 1, ..., М- 1.
Система (3.1) решается методом прогонки для векторных величин и определяются
значения vn + Уг, рп + Уг. Затем находятся значения Тп + Уг и Un + Уг\
Сп+Уг , Т^к+Уг(^п + Уг Сп+Уг\ .
6к + К + —^ \вк + Уг ~ ек-Уг) +
. 7™к + Уг(гп+Уг -я+%\
ТРк + Уг
АД \«<i-/2 К. туг/ п +Уг л /ТП г АД
Д0к + 1 Х Р* + % V^A: + % Д^ + %
Р* + % V£* + % Д** + %
I L \ >7w + 1 - >7w '-«A: + 1 Д0* + 1
[/тл T« \ tw + 1/2 _ Tw + Х/г 1 1
-(^)г(Гуи+д"Гуи) -<*r)i k+* *-*
\ rm+i ~rm / k A0k J
/о ч« _ ^A: + Va *k - У2 . /r> ч« _ ^w +1 ~ Km .
(Re)k т~й > (Rr)k - — — ,
(3.2)
Гп + Уг _ /г» w + У2
y/J +У2 _ 7W + Vi .
У2 " JK + Уг>
ттп +Уг _ ттп т ™ m, к + xh (ттп + Уг ттп + Уг \
um, к + К " ит,к + Уг Т^ [и т, к + Уг ~ и т, к - Уг)
115

' m
Авк
i, k + Уг (JTn + Уг гтп + Уг \ . тттп ттп п _
\U m,k + */2 ~ ит,к+Уг) + Tnm, к + Уг u m, к + Угит, к + Уг
к + 1
~Т Rm, к + Уг ( — ~ Н2 - 1 )£, к + у2 (Vm, к + Уг f +
ттП —П + Уг jr П + Уг
+ r "»» k + V* Pm> k + 1~ Pm> k •
Рщ,к+ УгКт,к+Уг ^к + %
(ш\п _ (#% + i -я^)т
По найденным £/w + */2, vn + 1/2, р" + */2, Г" + */2 производится расчет этапа, на котором
решается следующая система разностных уравнений:
Pw + % Р т + Уг * w + %
(Mj\ П + Уг ттП + Уг ттП + Уг
оп\ - "т + 1 ~ пт — 1 .
-W + 1 _ ( « + 1 Тп + Уг \ , П + % (ТТП +1 гг/2 + lb
Р m + Уг Р\Рт + Уг> J т + Уг) + сРт + УЦ Um + 1 ~ ит ) ,
если Um + ! - Um < 0;
РГЛ =p(Pm-V Снесли £/т+1 - Um > 0;
f/o" + 1.= 0; pm + Vi = p(0fc + *. r" + 1);
-и + 1
- сп + Уг
" 6т + %
^W + Уг
т [ Г Л" + !
^ + Т I И + Уг /пИ + 1 ч2 Pw + 1 /р2 . r>2 \ W + Уг у
Уг + - „ + % ]вт + 1 ^™ + 1' ~1TT%" * 0 '"» + 1
^W + Уг I L #т + 1
/Tw + 1/2 _ Т" + 1/2 \ 1
у [ т« + 1 т" + ! 1 (п \п + Уг I А к + \ J к 1
Х ( У m + 3/2 " У w + % J - ^в) w + 1 I — /
\ &Vk + Уг ' m + 1 J
aaW + Уг /О « + 1 \2 Рт /г>2 . г,2 ч П + Уг ^W + 1 грп + 1 \
- ®w K^m ) л + и I* +^e)m (Ут + У2 - 1т-Уг)
(r W + Уг _ Т п + Уг \ 1 )
(^ г> \ w + Уг TW + 1 TW + 1
*К I rnW + 1 /р2 , п2ч« + Уг УМ + Уг ~ J M - Уг
не

Здесь для простоты опущен индекс к + Vi, к = 0, 1,..., К — 1.
,./1+1 _ ,.W , Т П?2тт\П + Уг /— = \/2 + 1
Um + Ъ,К " У^ + У*,К + „ + i/2 УК И> m + %, AT I Pm + 1, JC ~ Pm, *)
Qm + У2, tf
4. По описанной методике были проведены методические расчеты, подтвердившие
возможность ведения счета по предлагаемому алгоритму. В качестве примеров
использовались одномерные задачи, решения которых заранее известны: задача (а) о разлете
газового шара в пустоту [6]; задача (б) о сходящейся ударной волне к центру [6].
Расчеты проводились в двумерной сетке, для чего за начало координат выбиралась
точка, на 1/3 радиуса отстоящая от истинного центра. Начальный радиус шара в обоих
случаях был равен R = 1.
Проведенные расчеты показали, что отклонение 5 наружной границы от сферы
составило
в задаче а (при R = 2,555)
в 0,08 1,34 2,91
о,% 2,53 -0,43 2,82
в задаче б (при R = 0,596)
в 0,08 1,81 3,06
а, % -0,54 0,27 1,1
Результаты сравнивались с расчетами, проведенными по программам,
рассчитывающим сферически симметричное движение. Форма ударной волны в задаче б была близка
к сферической, отклонение от сферы — в тех же пределах.
Следует отметить,что Полученная асимметрия вызвана не погрешностями двумерного
счета, а грубостью счетной сетки по R, ибо одномерные расчеты, проведенные с сетками,
эквивалентными двумерным сеткам на лучах в = 0,08; 1,34; 2,91, дали отличия,
сравнимые с отклонениями от симметрии в двумерном счете. Так, в задаче а при AR = 1/22
(в = 2,91) 5 = -3,69, при AR = 1/29 (в = 1,34) 5=0, при &R = 1/45 (в = 0,08) 5 = 2,59.
Сетка как по в, так и по R выбиралась равномерной. По в было взято 20 точек.
ЛИТЕРАТУРА
1. Яненко Н.Н. Об одном разностном методе счета многомерного уравнения теплопроводности //
ДАН СССР. 1959. Т. 128, № 6.
2. Анучина Н.Н., Яненко Н.Н. Неявные схемы расщепления для гиперболических уравнений и
систем // Там же.
3. Яненко Н.Н., Сучков В.А., Погодин Ю.Я. О разностном решении уравнения теплопроводности
в криволинейных координатах // Там же. № 5.
4. Годунов С.К., Забродин А.В., Прокопов Г.П. Разностная схема для двумерных нестационарных
задач газовой динамики и расчет обтекания с отошедшей ударной волной // Журн. вычисл.
математики и мат. физики. 1961. Т. 1. № 6.
5. Яненко Н.Н., Неуважаев В.Е. Один метод расчета газодинамических движений с нелинейной
теплопроводностью // Тр. МИАН СССР. 1966. Т. 74.
6. Станюкович К.П. Неустановившиеся движения сплошных сред. М.: Гостехтеоретиздат, 1955.
117

ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ПОВЫШЕННОЙ ТОЧНОСТИ
ДЛЯ ПОЛИГАРМОНИЧЕСКОГО УРАВНЕНИЯ*
Настоящая работа посвящена алгебраическому методу исследования экономичных
двухслойных разностных схем повышенного порядка точности, а именно четвертого
и шестого порядка точности для гармонического уравнения в р = 2-, 3-, 4-мерных
пространствах, для бигармонического и трижды гармонического уравнений в
двумерном пространстве. Алгебраический метод исследования схем повышенной точности
для двумерного гармонического уравнения рассмотрен в работе [1]. Построению
разностных и экономичных разностных схем повышенной точности посвящены
работы [1-9]. В работе [2], кроме схем четвертого порядка точности, были рассмотрены:
схемы шестого порядка точности для эллиптических уравнений в р = 2-, 3-мерных
пространствах. _
1. Пусть в области G: {О < xt < я} , G = G + Г ищется решение гармонического
уравнения
р Ъ2и
*ТТ=0> (1Л)
/=i Эх;
удовлетворяющее на границе Г условию
wl г =£(*)> x = (xl9...9xp). (1.2)
Для нахождения численного решения задачи (1.1), (1.2) используется разностная
схема
I P h2 \
Ш=[ ЕЛ/ + — 2 Л,Л/)м = 0, (13)
\/=i 6 /<i /
и 1г =*(*), С1-4)
где
л = А|*-/ _ Vt -Е){Е- Т_д _ Т, -2Е+ T_t
T±if = f(xi, ..., xt±h, ..., xp), h - шаг сетки (для простоты положено h( = h) ,u(kxh\ ...,
kph) = Wfcl#..fc , kt = 1, ...,iV; (7V+1)Л = я, / = 1, ...,p; аппроксимирующая (1.1) в классе
достаточно гладких решений до величин порядка 0(h6) прир = 2 и 0(h4) при р = 3,...
Рассмотрим схему
Д( ) = Ф£1ип, (1.5)
которая может послужить основой для построения итерационного процесса при решении
разностной задачи (1.3), (1.4). В схеме (1.5) г - шаг по времени (пт = г, 0 < t < Г,
л = 0, 1, ..., М; М = Г/г), 5иФ - некоторые операторы, перестановочные с операто-
рами Л,-. р л2
Оператор £2=2 Л/ +— 2 Л,-Л; отрицательно определен только дляр < 4. В связи
/=i 6 /</
с этим обстоятельством в дальнейшем везде будет положено р = 2, 3, 4. Собственные
числа операторов Д Ф, £2 обозначим через Ь, </?, со соответственно. Справедливы
следующие теоремы.
Теорема 1. Если:
1) оператор Ф обратим и
2) схема (1.5) сходится, то она сходится к решению системы (1.3), г. е. \imun -и.
п-*<*>
*Изв. СО АН СССР. Сер. техн. наук. 1967. № 13, вып. 3. С. 88-96. (Соавтор А.Н. Валиуллин).
118

Действительно, при выполнении первого условия теоремы 1 схему (1.5) можно
написать в виде
ф-1В((ип+1 -ип)/т) = Пип. (1.6)
В пределе вместо (1.6) будет иметь место (1.3).
Теорема 2. Если:
1) операторы В, Ф положительно определенные и Ф обратимый и
2) их собственные числа удовлетворяют условию
0<ф<2/с. (1.7)
где
с = max
(р \ 8
пах(— г со) = max! Z я,-—а 2 Я/Яу)< ,
л/ в/ \/=1 /</ / 9а
Г- '"£['-57(1-т4 ""77- (18)
4г _ А:
at-—— sin2
1 /22
то схема (1.5) сходится.
Доказательство. Очевидно, для погрешности wn = и — ип имеет место
B((wn+1 -ww)/r) = Ф^ww. (1.9)
Пусть
р
qsk= U sinsjkih, (110)
где
* = (*i,...,*p), s = (sl9...,sp)9 5, = 1,2,...
Тогда
■4 0 kth
Согласно (1.9), рассматривая разложение по собственным функциям
w<°> = Z«,</*, (1.12)
S
нетрудно установить, что
и,(П+1) = Бр«+1~9,) (113)
S
где
\ Ь / /=1 /</
Сходимость будет иметь место, когда
lpl =
1 * -
1 — со
Ь
<1. (1.14)
При выполнении второго условия теоремы 2 соотношение (1.14) выполняется.
Схема (1.5) при указанных выше условиях на операторы В, Ф обладает свойствами
полной аппроксимации, сильной устойчивостих и повышенного порядка точности,
а именно 0(h6) порядка при р = 2 и 0(h4) порядка при р = 3,4.
1 Определение понятий полной аппроксимации и сильной устойчивости дано в работе [1 ].
119

Замечание 1. При доказательстве теоремы 2 мы предполагали, что
и" I г =*(*)■ (1.15)
Замечание 2. Наиболее простым выбором операторов В и Ф является
р
Ф = Е, В= П (Е-arAi), р = 2, 3, 4, (1.16)
7=1
где а — некоторый положительный коэффициент.
Тогда схема (1.5) имеет вид
р un+l -ип ( р h2 \
П(Е-атАЦ =( ZA, + — X А{\Лип. (1.17)
/=1 Г \i = l 6 /'</ /
Достаточным условием сильной устойчивости схемы (1.17) является
а>1/2. (1.18)
Замечание 3. Если для задачи (1.1), (1.2) рассмотреть разностную схему
,1(Л'-^Л?)"=0' (119)
то схема
Р un+l -и" Р I h2 \
П(Е-атЛ,) = 2 Л,-— А2)и" (1.20)
/=1 г /=1\ 12 /
сильно устойчива при ос > 2/3 для любого р. Но при использовании схемы (1.19)
требуется провести анализ краевых условий.
2. Остановимся на одном способе выбора операторов В и Ф, исходя из
двухслойных схем с дробными шагами.
Для задачи (1.1), (1.2) рассмотрим разностную схему
_ / Р h2 h*
Пи=[ 2Л/ + — 2 Л/Л/ + — цх 2 Л,Л/ЛГ +
\/=1 6 /</ 36 /•</</
И2 \
+ —— М2Л1...Л4Ь = 0, (2.1)
216 /
и\г=Я(х), (2.2)
где Цх ,/i2 — некоторые неотрицательные коэффициенты, удовлетворяющие условию
/i2/6<Mi. (2.3)
Нетрудно показать, что оператор £1 отрицательно определен только для/^, д2 из (2.3).
Схема (2.1) шестого порядка точности при р = 2 и четвертого порядка точности при
р = 3, 4 переходит в схему шестого порядка точности при р = 3, 4, если положить /ij =
= 6/s(M2<36/5).
Для решения разностной задачи (2.1), (2.2) рассмотрим схему
ип+т/р _ цп+(т-1)/р / р
= ос1Атип+т/р +[ос2Ат + а3 2Л, + а4т2 Л,Л/ +
г \ /=i /</
+ <*5т2 2 Л|Л/Л,+а6т3Л1Л2Л3лЛ^+(т"1)/Р) w= 1, ...,р(р<4) (2.4)
с неопределенными коэффициентами otq (q = 1, ..., р + 2). Эквивалентная однородная
схема имеет вид
5ww+1=^ww, (2.5)
120

где
В= П (Е-агтАт),
т=1
(2.6)
= П (Ь
т = 1\ . . ,
+ а5т3 2 Л/Л;Лг + а6г4Л1 ... Л4).
А = П (Е + а2тЛт + а3т 2 Л, + а4т2 2 Л,Л; +
Подбирая коэффициенты о^ (q = 1, ..., р + 2) так, чтобы оператор Л — i? делился на
оператор Й (£2 = тЦ), получим необходимые и достаточные условия полной
аппроксимации схемы (2.5):
1) а2 +(*!=£, А: = const > 0, (2.7)
<** +(-1)к-Чк+/?ак+2 ак+2 (1, к = 2,
2)
А;+/?а3
где
к = 2,...,/?(/? = 2, 3,4), а = /г2/6г.
Тогда схема (2.5) приводится к виду
Ф_1Я((н" + 1 -ww)/t) = £2mw,
(2.8)
где
(р- 1) 2Л/ + (р-2)а2т X
/=i
Ф = А: +ра3 +а2а3т
X 2Л|Л/ + (р-3)а1г2 2 AiAjAr\+a23TX
/<i V
f<i
r<j<i
<(■
ACP +«_itt2TS Af + C^^r2
12 +
■alr^ + C3,-^?- S A,W +C>^r3S23.
(2.9)
Из условий полной аппроксимации (2.7) получим две системы значений для
коэффициентов otq:
k = 0, ol2 =—<*!((*!>()), а4 = аа3,. а5 = а2а3, (2.10)
a6 = a3M2«3(M2/6<Mi);
к = а + 2а! (а! > 0), а2 = о + а!, а4 = аа3,
а5 = а2(1 +(^/(7+ а?/а2)а3, а6 = а3(1 + 2aJo + 2а?/а2)а3. (2.11)
Теперь коэффициент а3 подбираем так, чтобы схема (2.5) была сильно устойчива.
Для системы коэффициентов (2.10) дисперсионное соотношение схемы (2.5) имеет
вид ,
р р
р= U рт= П 11 - а3 X
т=1 т=1 I
2 д,- - а 2 a{ai + а2/*! 2 а{а,аг - о3ц2а1 —<**
1 = 1 /</ Г</</
1 +оцат
(2.12)
121

Для того чтобы \рт\ < 1 достаточно, чтобы коэффициент а3 удовлетворял условию
0<a3<2d, (2.13)
где
1 ^а1ат
d = min
ar I P
(2.14)
I 2 a,- - a 2 Я/Д; + a2^j 2 Д/Д;дг — о3ц2а1 -~а4
, M2/6</ii, m=l9...,p (p = 2,3,4).
трудно показать
27a(l+(*!?-) /Л2 \
d> ^^ a = — ,а!>0.
Нетрудно показать, что для d имеет место следующая оценка:
(2.15)
Для системы коэффициентов (2.11) дисперсионное соотношение схемы (2.5) имеет
вид
р р
р = П рт = П X
w =1 т = 1
X I 1 - (а + 2а1)дш + а3( 2 я, - a S Я/Д/ + а2 X
Х(1+7~ ^^Д,,***/*'-^ (2.16)
Для того чтобы \рт\ < 1, достаточно, чтобы коэффициент а3 удовлетворял условию
-fa+ 2ai)di <a3 <tf2,
(2.17)
где
cf1=min|flwX Sfl, —a 2 ataj + (a2 + aja +я2) 2) atajar —
ai [ l /=1 /'</ r<j<i
-o(o2 + 2alo + 2a2l)al...a4 J"1 1 ,
d2 = min | (2 — адш) X S a,- - a S Я/Я/ + (a2 + aj a + a2) 2 a^-a,. -
a/ I L/=l /<i /•</</.
-a(a2 + 2а1а + 2а?)д1...д4 Г1 } .
Нетрудно показать, что для dx и tf2 имеют место следующие оценки:
27ar
(2.18)
ep + CjOWa + a?/*2)] '
£f2 >
9a
2[3 + C^(l+a1/a + a2/a2)]
(2.19)
(2.20)
Полученные результаты можно сформулировать в виде теоремы.
Теорема Ъ.Если неопределенные коэффициенты aq (q = 1,...,..., р + 2)
удовлетворяют условиям (2.7), (2.13), (2.17), то двухслойная однородная схема (2.5)
обладает свойствами полной аппроксимации, сильной устойчивости, повышенного порядка
точности, сходится и реализуется в виде схемы (2.4) .
122

Замечание 1. Схема (2.5) в двумерном случае переходит в схему В.А. Еналь-
ского [6], если положить
<*i = l, а2 = 1+а, а3 = а4 = 0, к = 2 + а; (2.21)
в схему В.А. Енальского [7], если положить
<*i = l, <*2 = -1, а3 = 1+а, а4 = а.(1+а), к = 0; (2.22)
в схему А.А. Самарского [8], если положить
с»! = (1 - а)/2, а2 = (1 + а)/2, а3 = а4 = 0, * = 1. (2.23)
Замечание 2. В случае к = о + 2glx из условий полной аппроксимации для цг и
д2 получены выражения
ai a? а* а?
Mi = 1 + +-г, д2 = 1+2—+ 2— . (2.24)
о oz о о*
При р = 3, 4 схема (2.5) переходит в схему шестого порядка точности, если положить
Mi = 6/5, /i2 = 7/5. (2.25)
Тогда из (2.24) для <*! получим значение
3. В случае бигармонического уравнения
Д2ы = 0, (3.1)
где
Д=Э2/Эх2 + Э2/Э*|,
мы будем рассматривать краевые условия типа
и1г = 0, Аи\г=/г(х)9 x = (xl9x2). (3.2)
Схема
[(А1 + А2)2 + Va^Ai + A2)A! А2]н = 0 (3.3)
аппроксимирует уравнение (3.1) с точностью до величин порядка 0(h4) в классе
достаточно гладких решений.
Она реализуется в виде двухслойной схемы
ип+т/2 _ип+(т—1)/2
+ а1А%1и»+""2 + [а2А?п+аз(А1+А2)2 +
7
+ a4N/r(A1+A2)A1A2]ww+^-1>/2=0, #и=1,2 (3.4)
с некоторыми неопределенными коэффициентами al9 ..., а4. Эквивалентная
однородная схема обладает свойствами полной аппроксимации и сильной устойчивости, если
коэффициенты о^,..., а4 удовлетворяют условиям
а!+а2 = 0, a4 = aa3, 0<а3<2</3, (3.5)
где
,2
( 1+<*!<£ ) 27 о
^3 = min —————I — >_-a2(i+ai7))
at I (Д! +^2X^i +я2 - оаха2) J 64
(3.6)
4>/F , А:,-А
o = h2/3y/r; /,7=1,2.
123

Рассмотрим, наконец, трижды гармоническое уравнение
А3и = 0 (3.7)
с краевыми условиями типа
М|г = 0, Ди|г =/,(*), A2u\r=f3(x), х = (х1,х2). (3.8)
Уравнение (3.7) заменяется разностной схемой
\(А1+А2)3+ — (А1+Л2)2Л1А2\и = 0, (3.9)
которая имеет четвертый порядок аппроксимации в классе достаточно гладких решений
и реализуется в виде схемы
ип +т/2 _ ип + (т -1 )/2
= aiA2, "w + w/2 + [сс2А3т +а3(Л! +Л2)3 +
г
+ a4v9(A1+A2)2A1A2]ww + (w-1>/2, /я =1,2. (3.10)
Эквивалентная однородная схема обладает свойствами полной аппроксимации и
сильной устойчивостью, если неопределенные коэффициенты oti, ..., а4 удовлетворяют
условиям
а!+а2 = 0, а4 = аа3, 0<a3<2tf4, (3.11)
где
1 +аха\
<74 = iTiin{ ; 1 } >— (1 +«!т),
а{ { (а! +а2)2(а1 +а2 - оаха2) ) 32
а = Л2/2^/?; /,7=1,2.
ЛИТЕРАТУРА
1. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск, 1966.
2. Андреев BE. Разностные методы решения некоторых задач для стационарных и нестационарных
уравнений математической физики: Дис.... канд. мат. наук. М., 1966.
3. Bramble LH., Hubbard B.E. On the formulation of finite difference analogues of the Dirichlet problem
for Poisson's equation // Numer. Math. 1962. Vol. 4, N 4. P. 313.
4. Bramble LH. Forth order finite difference analogues of the Dirichlet problem for Poisson's equation in
the three and four dimensions // Math. Comput. 1963. Vol 17, N 83. P. 217.
5. Douglas J.(Jr.), Gunn I.E. Two high correct difference analogues for the equation of multidimensional
heat flow//Ibid. N81. P. 71.
6. Енальский В.А. О двух схемах повышенной точности для решения задачи Дирихле // Тр. МИАН
СССР. 1966. Т. 74.
7. Енальский В.А. Об одном итерационном процессе повышения точности // Докл. III Сиб. конф.
по математике и механике. Томск, 1964.
8. Самарский А.А. Схемы повышенного порядка точности для многомерного уравнения
теплопроводности // Журн. вычисл. математики и мат. физики. 1963. Т. 3, № 5. С. 812.
9. Fairweather G., Gourlay A.R., Mitchell A.K. Some high accuracy difference schemes with a splitting
operator for equations of parabolic and elliptic type // Numer. Math. 1967. Vol. 10, N 1. P. 56.
124

О МЕТОДАХ РАСЧЕТА ЗАДАЧ ГАЗОВОЙ ДИНАМИКИ
С БОЛЬШИМИ ДЕФОРМАЦИЯМИ*
1. Многообразие численных алгоритмов решения задач газовой динамики возникает
из выбора схем расчета и сетки. Подразделяя алгоритмы по выбору сетки, мы имеем
следующие основные группы,
а. Метод характеристик (гладкая область) [1, 4,5].
б. Схемы в эйлеровых координатах (неподвижная сетка) [2, 3, 28].
в. Схемы в лагранжевых координатах [6, 10, 29].
г. Схемы в эйлерово-лагранжевых координатах [7,9, 11].
д. Подвижная эйлерова сетка [12].
е. Метод частиц [8, 13].
Метод частиц в ячейках [8] использует неподвижную эйлерову сетку, сохраняя и
информацию о траекториях частиц.
В данной работе мы остановимся в основном на методе частиц в ячейках и
рассмотрим некоторые вопросы теории разностных схем в эйлеровых и лагранжевых
координатах.
2. Анализ метода частиц в ячейке, идущего от работ Харлоу и его сотрудников [30],
привел нас к выводу, что существует тесная связь между методом частиц в ячейке и
методом расщепления и что, по существу, метод частиц представляет собой
своеобразную и остроумную модификацию метода расщепления. То разделение алгоритма на
два этапа, которое имеется в методе частиц, есть не что иное, как расщепление схемы
на два дробных шага. Интерпретация метода частиц в терминах метода расщепления
облегчает математическую формализацию и анализ такого сложного алгоритма как
метод частиц. Мы будем пользоваться дифференциальной формулировкой метода
расщепления (см, обзор работ в [14]). На самом деле схема расщепления
осуществляется для законов сохранения и лишь для простоты мы используем дифференциальную
форму,
Дифференциальные уравнения, описывающие движение газа в переменных Эйлера
в форме законов сохранения имеют вид
d(prv) Ът Ъп
— - +—+— =0, (1)
dm Ъти bmv bPrv
— + + + =Pvrv~l,
bt Ъг Ъг Ъг
Ъп Ъпи Ъпи ЪРгр
—: + + + = 0,
Эг Ъг Ъг Ъг
ЪЕ ЪЕи ЪЕи Ъ{Ргри) Ъ(Рг%)
— + + + + — =0, P = F(p9e),
Ы Ъг Ъг Ъг Ъг
где р — плотность, Р — давление, е — удельная внутренняя энергия, и, v — компоненты
скорости по направлениям г, г, т = prvu, п = prvv, Е = prv(e + (и2 + и2)/2); v = 0 для
плоского движения, v = \ для движения с осевой симметрией; (г, г) — декартовы или
цилиндрические координаты (в последнем случае ось г направлена по оси симметрии),
t — время. Мы можем уравнения первого и второго дробного шагов (этапов, по Хар-
* Численные методы механики сплошной среды. 1970. Т. 1, № 1. С. 40-62. (Соавторы Н.Н. Анучина,
В.Е. Петренко, Ю.И. Шокин.)
125

лоу) записать в виде
а: б:
Э(рг")(1) Э(рО<2> Эт<2> Эи<2>
= 0, + — + — = О,
Ъг Ъг Ъг Ъг
Ът™ d(Prv)W ' n v л Эт<2> д(ти)Ы Э(ти)<2>
+ =vP<1>rv-l9 + —-—— + —-— =0, (2)
Ъг Ъг Ъг Ъг Ъг К '
Ъп™ d(Prv)W Эи<2> Ъ(пи)Ы Э(ии)<2>
—— +——-—=0, + + —^— =о,
Ъг Ъг Ъг Ъг Ъг
ЪЕ^\ Ъ(Рг»и)(1\ Э(Рг^)(1>_ Э£<2> Ъ(Еи)Ы Ъ(Еу)Ы _
Ъг Ъг Ъг ' Ъг Ъг Ъг
Идея Харлоу заключается в том, что уравнения первого этапа (уравнения первого
дробного шага (2а)), не содержащие конвективных членов, интегрируются в
неподвижной эйлеровой сетке, в то время как уравнения второго дробного шага (26) служат
для определения потоков на основе модели частиц. Потоки определяются дискретным
образом: как только частица пересекает границу эйлеровой ячейки, переходя из
ячейки 1 в ячейку 2, масса, импульс, энергия частицы вычитаются из массы, импульса,
энергии ячейки 1 и прибавляются к массе, импульсу, энергии ячейки 2. Такие скачки
потоков составляют характерную черту метода Харлоу, Они приводят к большим
флуктуациям рассчитываемых величин, особенно плотности, В дальнейшем мы
остановимся на анализе этих флуктуации.
Как известно, первоначальная схема Харлоу [30] обладала недостаточной
устойчивостью, в связи с этим в дальнейших работах [8] были предприняты попытки усилить
устойчивость метода частиц. Оставаясь последовательно на точке зрения расщепления
и применяя неявные схемы, можно сильно повысить устойчивость метода частиц,
Ш. Рассмотрим анализ устойчивости метода частиц. Схема первого этапа легко
может быть представлена как однородная разностная схема. Алгоритм второго этапа
есть некоторая дискретная модель, которая не может быть прямо представлена как
однородная разностная схема. Более точно мы получаем разностную схему с
коэффициентами, зависящими от числа частиц, пересекающих границы ячейки. Если N —
число частиц в ячейке велико, то поток ансамбля частиц может быть осреднен, и мы
приходим к асимптотическому представлению метода частиц в виде некоторой
однородной разностной схемы. Весь анализ аппроксимации, устойчивости и аппроксима-
ционной вязкости проводится в этом приближении, который мы будем называть
асимптотическим.
Рассматривая этапы метода Харлоу как дробные шаги, мы можем записать
соотношение
где S — оператор полного шага, Slf S2 — операторы первого и второго дробного шага
соответственно. Для устойчивости достаточно
11511= над и <1+о(т) (3)
и тем более достаточно, если условию (3) удовлетворяет каждый оператор шага.
Схема интегрирования первого этапа по Харлоу абсолютно неустойчива, т. е. при
любых г, h оператор Sx удовлетворяет условию
1511>1+е9
где б не зависит от г, К Однако на втором этапе, схема которого является условно
126

устойчивой (к < 1/|и|), происходит компенсация неустойчивости первого этапа, и,
в целом, оператор полного шага условно устойчив. В этом случае анализ схемы
полного шага, основанный на локальном критерии но методу Фурье, дает следующее
необходимое условие устойчивости:
к<|н|/(н2+я2),
где
2 Р / 2 P/P2~FP Г
2p2FP ^C FP h '
с - местная скорость звука. Если заменить неустойчивую схему первого этапа по Хар-
лоу условно устойчивой схемой, например, вводя аддитивно в Р линейную вязкость
q = -Bcph Ъи/Ъх, то получим следующую оценку
к ^ к ^
\и\+2Вс [(1 + В) \и\ + с]2
Применение неявной схемы на первом этапе приводит к дальнейшему повышению
устойчивости схемы полного шага:
к<1/\и\.
Нами были использованы различные явные и неявные схемы первого этапа (табл. 1,
где приведены также условия устойчивости указанных схем). Заметим, что анализ
устойчивости производился как локальным методом Фурье, так и методом первого
дифференциального приближения (см. п. VI). Аналогичный анализ был проведен для
схем полного шага.
Пока еще не получены абсолютно устойчивые разностные схемы. Действительно,
если схемы первого этапа абсолютно устойчивы, то схема второго этапа, на котором
прослеживается отдельно траектория каждой частицы, является условно устойчивой,
и, следовательно, условно устойчивой является схема полного шага. Анализ
устойчивости и аппроксимационной вязкости метода частиц приводит к следующим выводам:
а) если разностная схема полного шага в классическом варианте метода частиц
была неустойчивой в области застоя (и -* 0, с Ф 0), то применение на первом этапе
явных условно устойчивых схем делает схему полного шага условно устойчивой;
б) для веществ с большой скоростью звука (слабо сжимаемые среды), когда \u\jc <
< 1 использование на первом этапе явных схем приводит к сильному ограничению на
шаг по времени г, которое может быть ослаблено применением неявных разностных
схем (к < 1/|ы|);
в) аппроксимационная вязкость и условия устойчивости не инвариантны
относительно преобразования Галилея, Это обстоятельство может использоваться для улучшения
устойчивости. В то же время оно имеет отрицательное значение, так как ширина и
профиль разностной ударной волны зависит от скорости потока. Неинвариантность
аппроксимационной вязкости относительно преобразования поворота может приводить к
большим погрешностям при счете сферических сходящихся течений;
г) такая зависимость аппроксимационной вязкости и условий устойчивости от
величины и приводит к автоколебаниям численного решения: в области малых скоростей
схема неустойчива, начинается "разболтка", \и\ растет, схема становится устойчивой, и
принимает вновь малые значения и т. д.
IV. Наряду с неустойчивостью и автоколебаниями имеют место также нефизические
флуктуации рассчитываемых величин. Если первые два явления имеют место и в
асимптотике, т. е. при Af -* °°, то флуктуации связаны с конечным числом частиц в ячейке.
В методе частиц поток вещества через границы ячейки меняется дискретно, что и
приводит к флуктуациям плотности и давления.
Для уменьшения флуктуации были предложены следующие приемы:
127

Схемы
Анализ Неймана
Анализ п.фл.д.п.
Анализ г.ф.п.д.п.
1. Схема Харлоу
DP"
Ък
-Du
Абсолютно неустойчива
\2 <0
К =0
7=е" Du
2. Схема Харлоу
~ *, ак
Z = u" DP"
2
Ък _
2
3. Схема Лакса
ак
u = olMu" Df1
2
Ък
7= Me" Du"
4. Схема Харлоу с линейной вязкостью
q = -Bc0phux
и = и" -aKDM(P"+g)
*€ = е" - bKDM(u) - anDM{qu) + aKuDM(q)
5. В уравнении энергии вязкость
q = -a1c(;hPx
~ ак
и = и" DP"
2 ГГ^
к < -V
С 7-1
1 / 27
С 7-1
1 ГТ~*
к < — >/ (а =
С 7-1
27 Вс0
к <
7-1 С2
1
к <
к < 7 ■
2Вс0
2а1с0
К <0
1 Г
К<-у/ -
С 7-1
к<
2уВс0
(7-D С2
к <
1
2*7,(7- 1)*0
к <
'-/-
с 2(7-1)
(III)
1 Г
к <— V-
С 7-1
1
(III)
к <
2£с„
(И)
е=е Du+aKDM(q)
2
1
к <
2^(7-1)^

."* 6. Схема Лакса-Вендроффа
j? (0 = 0)
Я и = ипакОМ(Рп) + ка*(1+0)^СРя, ип)
ы 2
J = Jn-aK[DM(Pu)n-uDMPn]+—- к2(1+0)Х к < - V \2,\3>0 к < '
2
и*=Мип D.P*
27- 1
к<
2(7-1)
1
с
к< Цс
7
к <
10.
и*=ип-акОМ(Р)п
Е*=Еп- -DM(Pu)n
2
2 с у- I с у-I
X [N(J, P)"+N(Pu, и)" - uN(Pu)n]
7. Видоизмененная схема Лакса-Вендроффа (в Ф 0)
7
к < _ J \2, \3 > 0 к < - У-
С (7-1)(1+0) с (7_1)(1+0)
Схемы типа предиктор-корректор.
Приводится лишь предиктор, корректором везде является схема вида
р = рп, и = ип~акПМ(Р*)
J=jn _ qkDM{Pu)* - uanDM(P)*
8. Схема Годунова
п М^сР)П п .
Р*=МРп Dxun к< к<1/с к<1/с
7 1
к <
2М(сР)" 7-1 с 7-1 с
9. Схема Лакса ,
u*=Mun-aKD,Pn k<-J— К<1У_1_
J*=MJn-bKDxun с 7-1 с 7-1
1 /Т~ /
7 1
С 7- 1 2(7- 1) С

Схемы
11. Неявная схема с весами I
ак +
и*=и" [yxD\P* + (l-yl)DlPn]
2
J*=J" [42D2u* + (1 - y2)D2un]
2
12. Неявная схема с весами II
и*=и" [yxD2P* + (l-yv)D2Pn]
2
Ък
J*=Jn [72Д,и* + (1 - y2)D2un]
2
13. Неявная симметрическая схема
ак
u*=un_—DP*
4
b*
J*=Jn Du*
4
14. Неявная схема бегущего счета в инвариантах
/у - Г кс
кс /у - Г
S*=Sn + —V D,S*
2 у
15. Явная схема в инвариантах
У у — 1 к
Drn
у 2
кс I у— 1*
Анализ Неймана
Анализ п.ф.п.д.п.
Анализ г.ф.п.д.п.
Абсолютно устойчива
Абсолютно устойчива
Абсолютно устойчива
Абсолютно устойчива
ПГ 1
к < 2V -
у - 1 с

-«
Примечания.
Схемы первого этапа. Обозначения:
Du =ul+1-ut_v Ми =(и.+ 1+и._1)/2,
D1un = u".-u4, М1ип = (и",+и'!)12,
D2m =w/-"/_1, M2u ={u. +и._г)/2,
N(f,\lj)=MlfSDi\lJ-M2f-D2\lJ, p = pn
«/ = («/+«")/2, DMun = uni+v*-ull_i/2;
п.ф.п*д.п., г.флдл. — соответственно параболическая и гиперболическая форма первого
дифференциального приближения; \j — собственные значения матриц "вязких" членов.
а) введение параметров формы частицы. "Одномерная" частица трактуется как
тонкий стержень, "двумерная" частица представляет собой прямоугольник или круг.
Такое введение "параметров формы" частицы приводит к ослаблению флуктуации;
б) введение третьего этапа, на котором происходит пересчет плотности по
формулам, аппроксимирующим уравнение неразрывности. Рис. 3, 4 дают представление об
уменьшении флуктуации.
По-видимому, метод частиц сходится при измельчении сетки и фиксированном
числе N частиц в ячейке, хотя конечность TV приводит к флуктуациям. Увеличение N
означает сильное увеличение объема перерабатываемых массивов и требует большой
памяти и быстродействия ЭВМ. По существу, метод частиц увеличивает на единицу
размерность задачи. Следует заметить, что пересчет плотности позволяет получить
удовлетворительные результаты при небольшом числе частиц в ячейке. В некоторых
случаях это позволяет резко сократить объем перерабатываемых массивов и время
счета. .
Заметим, что улучшение устойчивости метода и устранение флуктуации позволяют
распространить данный метод на слабосжимаемые течения жидкости. Например, в
приближении вязкопластического течения были проведены расчеты соударения двух
тел.
V. Флуктуации устраняются, если уравнения второго этапа решать по разностной
схеме на эйлеровой сетке, а частицы использовать только как носители информации
о потоке, траекториях и границах сред, не вводя их в алгоритм расчета. Здесь мы
имеем аналогию с методом маркеров, где схема расчета основана на эйлеровой сетке
и по расчетным скоростям определяются положения частиц и границ. Положение
границ входит в расчет для определения осредненных термодинамических величин в
ячейке. Во внутренних ячейках все потоки определяются без учета частиц по
выбранной (однородной) схеме.
Метод маркеров позволяет применять неявные абсолютно устойчивые схемы и,
следовательно, особенно удобен для расчета течений слабосжимаемых жидкостей.
Авторы провели расчеты методом маркеров с применением неявной схемы в
эйлеровых координатах, например рассматривалась задача о высокоскоростном ударе тела
о преграду.
Неявные абсолютно устойчивые схемы в неподвижной эйлеровой сетке с
расщеплением типа Харлоу на два дробных шага применялись в задачах метеорологии (см.
[22]).
Заметим, что аппроксимируя уравнения второго этапа (26) явной разностной
схемой, в которой пространственные производные аппроксимируются с учетом знака
скорости, мы приходим к уравнениям метода FLIC [36].
VI. Рассмотрены некоторые вопросы теории разностных схем для
гиперболических систем уравнений. Оказалось возможным задачу исследования устойчивости и
аппроксимационной вязкости разностных схем свести к исследованию некоторой
дифференциальной системы уравнений, отличающейся от исходной дифференциаль-
5* 131

нои системы уравнении в случае схем первого порядка точности членами порядка
О (г). Эта вспомогательная система дифференциальных уравнений названа первым
дифференциальным приближением разностной схемы и может быть записана в
двух видах. Определение первого дифференциального приближения дано в работах
[15,16]. Например, в случае разностной схемы
,п+1
(х)= ХВаип(х + т\а)9
(4)
аппроксимирующей гиперболическую систему дифференциальных уравнений в
частных производных
Ъи s Ъи
— = Z Ак — (5)
ЭГ А:=1 Ъхк
гиперболическая и параболическая формы первого дифференциального
приближения имеют, соответственно, вид
т Ъ2и
2
ъе
Ъи
ы
= L Cjk
/,*=i Ъх;Ъхк
+ S Ак
fc = l
ЪАк
Ъхк
Ъи * Ъи
— = X Dk +
Ъи2
s
2 cjk
у, к= 1 Эх7- Эх*.
(6)
(7)
где
<7*
2 а
БХ'ХЧ
с/л = <7*
г
— Л/Ль,
2 '
2 1ЭГ /= 1 Эху
^А: (X 0» ^а (*» 0 _ вещественные тХ т матрицы, х€Д2, t = пт, Ха = (Х^, ..., Х£) -
вектора смещения, и (х, t) — вектор-функция с m компонентами. При этом
предполагается, что разностная схема имеет первый порядок точности и, следовательно,
выполнены следующие условия совместности:
XB0l=I, v^*
Of
/ — единичная матрица.
Систему уравнений (7) назовем неполной параболической в точке (х, t), если при
всех вещественных со i,..., cos сумма квадратов которых равна единице, корни
уравнения
det
- 2 со/ со*: cjk - XI
j,k=i
= 0
имеют неположительные действительные части
ReX7<0 (j= l,...,/w).
Система уравнений (7) отличается от исходной системы уравнений (5) "вязкими"
Ъ2и
ЪХ; Ъхк
Если система дифференциальных уравнений (6) является гиперболической, то для
нее имеет смысл рассматривать характеристики'и область зависимости Q точки (х, t).
132
s
членами Z
/, к = 1

Для разностной схемы (4) мы можем также ввести понятие области зависимости
Q* точки (х, t), как наименьшего замкнутого множества на гиперплоскости t = О
такого, что как только начальное значение и0 (х) равно нулю в открытом множестве,
содержащем Qf9 соответствующее решение разностной схемы в точке (х, t) равно
нулю для всех значений т.
Оказалось, что устойчивость разностных схем определяется неполной параболич-
ностью их первых дифференциальных приближений и характером зависимости
областей QnQf. Ниже приводится ряд теорем, доказательства которых содержатся
в работах [16—18].
Для одномерной гиперболической системы уравнений
ди/dt = А(ди/дх) (8)
рассмотрим две схемы
а) простую схему [15, 16,31]
un + l(x) = S В«и"(х + т\а)9
а= 1
И
б) мажорантную схему [15, 16, 19]
1
ип+1(х) = 2 Bfun(x+jh)9
где
В^кА*, В_1=-кА~, А + >09 А~<09 А=А + +А~.
Справедливы следующие утверждения.
Теорема 1. Если A (х, t) - симметрическая липшиц-непрерывная матрица, то
неполная параболичность системы уравнений первого дифференциального
приближения является необходимым и достаточным условием устойчивости простой
разностной схемы.
Теорема 2. Если А - симметрическая матрица, А*, А~ - липшиц-непрерывные
матрицы, то для устойчивости мажорантной схемы необходимо и достаточно, чтобы
ее первое дифференциальное приближение было неполной параболической системой
уравнений.
Здесь и ниже устойчивость понимается в смысле выполнения неравенства
\\иП + 1 || < [1+0(7)] ||Ы"||,
где || • II означает норму пространства Z,2 •
Рассмотрим схему расщепления
аппроксимирующую систему (5) . Справедливы следующие теоремы:
s Thi
Теорема 3. Пусть £27- = 2 В1 Т. <* (J = 1,..., s), т.е. имеем простую схему рас-
а = 1
щепления. Тогда, если Aj - липшиц-непрерывные симметрические матрицы и система
уравнений первого дифференциального приближения простой схемы расщепления
является неполной параболической, то схема — устойчивая.
Теорема 4. Рассмотрим мажорантную схему расщепления (см. [19, 21])
П, = К;А+ 7) + (I-Kj \Aj \)E-KjA7T_r
A;=A+ + A7, A+>09 A7<09 \A,- | = A)-Aj, к, = т/А,-.
133

Если Aj- симметрические матрицы, A+j,Aj~- липшиц-непрерывные матрицы и
первое дифференциальное приближение мажорантной схемы расщепления является
неполной параболической системой, то схема —устойчивая.
Теорема 5. Если Aj - симметрические матрицы, А) , Af—
липшиц-непрерывные матрицы и Q<Qf, тс мажорантная схема, аппроксимирующая систему
уравнений (6) является устойчивой.
Теорема 6. Если Aj - липшиц-непрерывные симметрические матрицы и Q < Qf,
то разностная схема Фридрихса [32], аппроксимирующая систему (6), является
устойчивой.
Метод первого дифференциального приближения был также применен к
исследованию устойчивости и аппроксимационной вязкости разностных схем,
аппроксимирующих нелинейные уравнения (в частности уравнения газовой динамики), хотя
строгого обоснования этому пока не имеется. В этом случае анализ методом первого
дифференциального приближения дает ограничения на устойчивость, аналогичные случаю
анализа локальным методом Фурье, и позволяет провести качественное сравнение
разностных схем в смысле характера их устойчивости.
Возвращаясь к ранее изложенному, заметим, что система уравнений (6) получается
из разностной схемы (4) разложением в ней функций un + l (х), ип (х + тХа) в ряды
Тейлора и удержанием членов порядка О (г2) включительно, а система уравнений
(7) получается из системы уравнений (6) заменой d2u/dt2 через пространственные
производные с использованием исходной системы уравнений (5). Удерживая в
разложении un + l (x) члены более высокого порядка, чем О (г2), и оперируя с ними
аналогично вышесказанному, в результате получим в матрицах "вязких членов" (с;к)
дополнительные члены, зависящие от градиентов решений. Эти добавочные члены
объясняют неустойчивость некоторых разностных схем, наблюдаемую в расчетах,
которая не улавливается при анализе локальным методом Фурье, ибо он не
учитывает влияния градиентов. Аналогичный подход применен в работе [33] при
исследовании разностных схем для нелинейного уравнения газовой динамики.
VII. При решении задач математической физики разностными методами имеют
место эффекты аппроксимационной вязкости, т.е. вязкости, порождаемой структурой
разностных схем. Численные расчеты показывают, что свойства разностной схемы
особенно сильно проявляются при взаимодействии разрывов. В областях взаимодействия
отмечаются большие отклонения газодинамических параметров от истинных значений.
Эти отклонения ведут себя по-разному в зависимости от диссипативных свойств схемы
и разностной сетки.
В зависимости от диссипативных свойств разностные схемы можно разделить на два
класса. Во-первых, схемы, допускающие контактные разрывы (например, схема Ней-
мана-Рихтмайера [29]) и, во-вторых, схемы, недопускающие контактных разрывов
(например схема Лакса [8]). Изучению диссипативных свойств разностных схем
посвящен целый ряд исследований (см. работы [20, 23, 25, 34, 35], где приведена также
достаточно полная библиография).
Диссипативные свойства схемы тесно связаны со структурой первого
дифференциального приближения. Если система уравнений параболической формы первого
дифференциального приближения является сильно параболической (параболической
по Петровскому), то, как известно, имеет место сильное "размазывание" разрывов
(в случае системы уравнений газовой динамики размазываются не только ударные
волны, но и границы раздела двух сред). Так, например, схема Лакса, которой
соответствует сильно параболическая система уравнений первого дифференциального
приближения, размывает контактные границы и приводит к искусственной диффузии.
Во избежание этого следует потребовать, чтобы аппроксимационная вязкость не
работала на контактной характеристике (^-свойство). В работах [18, 26] с помощью
понятия первого дифференциального приближения исследуются условия, при
выполнении которых разностные схемы обладают свойством К.
134

Для системы уравнений (8) рассмотрим разностную схему первого порядка
точности
ип+\х) = ZBaiin(x+ah)9 (9)
Of
где Ва — постоянные тХ т матрицы, к = т/h = const,
ZBa=I, ЪаВа = кА.
а а
Первое дифференциальное приближение схемы (9) имеет вид
Ъи Ъи Ъ2и
— = А — + С —-,
Ы Ъх Ъх2
где
С= — \?а2Ва-к2А2 .
Пусть матрица А имеет различные вещественные собственные значения £i, ..., £w,
и предположим, что одно из них равно нулю, т.е. существует вектор Xтакой, что ХА = 0.
Определение. Разностная схема (9) обладает свойством К, если из
соотношения ХА = 0 следует, что ХС = 0.
При переходе к системе уравнений газовой динамики получаем, что наличие у
разностной схемы аппроксимационной вязкости, сохраняющей контактный разрыв,
равносильно тому, что схема обладает свойством К.
В работах [18, 26] сформулированы и доказаны необходимые и достаточные
условия того, чтобы разностная схема обладала свойством К. Анализ аппроксимационной
вязкости схем первого порядка точности может быть перенесен и на схемы
повышенного порядка точности.
Сформулированные утверждения были использованы при построении разностных
схем, обладающих свойством сохранения контактных разрывов и
аппроксимирующих систему уравнений газовой динамики как в эйлеровых координатах, так и в
лагранжевых координатах. Метод первого дифференциального приближения
позволяет выбрать из таких схем устойчивые разностные схемы. Разностные схемы
строились так, чтобы аппроксимационная вязкость входила дивергентно в первое
дифференциальное приближение и, кроме того, требовалось, чтобы первое
дифференциальное приближение (а следовательно, и аппроксимационная вязкость) было инвариантно
относительно преобразования Галилея.
VII. Были проведены многочисленные методические расчеты одномерных и
двумерных газодинамических течений с целью получения монотонных схем расчета, улучшения
устойчивости метода частиц в ячейке, устранения нефизических флуктуации, поиска
эффективных операторов сглаживания решения. Анализировалось влияние на точность
расчетов величин шагов сетки по пространству и времени, расположения частиц в
ячейке на начальный момент. Точность расчетов контролировалась сравнением с расчетами,
проведенными по другим двумерным методикам (см., например, рис. 6,6) или же с
одномерными расчетами в тех случаях, где это было возможно.
Рис. 1—5 иллюстрируют влияние некоторых приемов сглаживания численного
решения на примере ряда одномерных течений. Аналитическое решение изображено на
рисунках тонкой сплошной линией. На рис. 1 показан профиль скорости в
стационарной ударной волне при использовании различных искусственных вязкостей:
пунктирная линия — счет по методу PIC без вязкости, тонкая непрерывная линия - линейная
Ъи
вязкость вида q =ас0 • h —, аддитивно входящая в Р\ жирная непрерывная линия —
Ъх
135

и
V
р
А
\
1 1 1 1 1 1 1
\
Рис. 1
р
иг
FY
Z0
т~Л
40 £0
Рис.5
»vv i
ffO i
линейная вязкость q =-*c0 (ЬР/дх), входящая только в уравнение энергии. Следует
заметить, что в расчетах по методу частиц в ячейке давление испытывает наибольшие
флуктуации по сравнению с флуктуациями скорости и удельной внутренней энергии, и
поэтому на рис. 2-5 показаны только профили давления. Рис. 2 иллюстрирует влияние
"параметров" формы частиц в задаче о плоской детонационной волне в случае иници-
рования ВВ у жесткой стенки: пунктирная линия - счет по методу PIC с линейной
вязкостью, жирная непрерывная линия - частицы представляются в виде слоев (при этом
ас0 = 0,2), рис. 3, 4 иллюстрируют влияние пересчета плотности соответственно в
задаче об одностороннем истечении продуктов детонации и задаче о распаде разрыва
скоростей. При этом на рис. 3 при Г«0 число частиц в ячейке равно 2, а ас0 = 0,2.
На рис, 5 показан случай, когда в качестве схемы первого этапа взяты соответственно
схема Годунова [10] и видоизмененная схема Лакса-Вендроффа [27].
136

iififi
iiii li ,
iliifiili! iPiiipi
liiiiiii
»:
m
ff
^.iW/.iilii.'iMiiinibiM,,,,,^'
ii.{»fnii/iiWYiVuv.-.nnV»iV
Рис.6
~h
H-
V
_J I I l_
-I I I L-
Рис. 7
С помощью метода частиц в ячейке был решен ряд двумерных задач, часть из
которых является повторением (с несколько измененными параметрами) расчетов,
описанных в [37—40]. В частности, рассматривались взаимодействие ударной волны с
деформируемым предметом, осесимметричное движение газов под действием
приложенного давления, течение газа в каналах со скачком сечения, задача о
взаимодействии тел при больших скоростях соударения, течения газа с детонационными волнами,
дифракция ударных волн на клине и конусе и задача о тейлеровской неустойчивости.
Кратко опишем результаты некоторых двумерных расчетов. На рис. 6 показано
расположение частиц в разные моменты, а также движение контактной границы и
ударной волны в случае осесимметричного движения двух невязких нетеплопроводных
газов с уравнениями состояния Ра = (уа—1)раеа, 7а = 5/3, а = 1,2 под действием
постоянного давления Р = 1, приложенного на верхнюю и правую границы второго газа.
137

При t = 0 газы холодные покоящиеся и их начальное положение показано на рис. 6,а.
Первый газ, расположенный во внутреннем цилиндре, имеет плотность 0,67,
второй — 11,4. Ячейки сетки-квадраты со стороной 0,05. На рис. 6, б указано положение
внешней границы в момент времени t = 0,774, полученное из расчета по методике,
описанной в [12]. На рис. 7, а—г показаны на различные моменты времени формы
кратера и цилиндра при высокоскоростном соударении цилиндра с толстой
преградой (начальная стадия процесса), а на рис. 7,д — траектории отдельных частиц,
лежащих на лицевой стороне преграды.
ч в
1 дК^ааь***"Т
^s^-
Рис.9
Рис.8
Начальная стадия деформирования стенки цилиндра при набегании детонационной
волны изображена на рис. 8.
На рис. 9 даны траектории отдельных частиц в задаче о дифракции ударной волны
на клине.
ЛИТЕРАТУРА
1. Жуков А.И И Тр. МИАН СССР, 1960. Т. 8.
2. Русанова В.В. // Журн. вычисл. математики и мат. физики. 1961. Т. 1, № 2. С. 267-279.
3. Годунов С.К. Разностные методы ре'шения уравнений газовой динамики. Новосибирск, 1962.
4. Ричардсон Дж. // Вычислительные методы в гидродинамике / Под. ред. Б. Олдера и др. М.: Мир,
1967.
5. Носкин Н.Э. II Там же.
6. Шулъц У.Д. /J Там же.
7. НохВ.Ф. //Там же.
8. Харлоу Ф.Н. И Там же.
9. Франк РЖ, Лазарус Р.Б. // Там же.
10. Годунов С.К. I/ Мат. сб. 1959. Т. 47 (89), № 3. С. 271-306.
11. Яненко Н.Н., Фролов В.Ф., Неуважаев В.Е. // Изв. СО АН СССР. Сер. техн. наук. 1967. № 8,вып.2.
12. Годунов С.К., Забродин А.В., Прокопов Г.П. // Журн. вычисл. математики и мат. физики. 1961.
Т. 1,№6.
13. Дьяченко В.Ф. // Там же. 1965. Т. 5, № 4. С. 680-688.
14. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики. М.:
Наука, 1967.
15. Яненко Н.Н., Шокин Ю.И. // ДАН СССР. 1968. Т. 182, № 4. С. 776-778.
16. Шокин Ю.И., Яненко Н.Н. // Мат. заметки. 1968. Т. 4, № 5. С. 493-502.
17. Шокин Ю.И. II Тр. Всесоюз. семинара по числ. методам механики вязкой жидкости / Под ред.
Н.Н. Яненко. Новосибирск: Наука, 1969.
18. Яненко Н.Н., Шокин Ю.И. Ц Сиб. мат. журн. 1969. Т. 10, № 5.
19. АнучинаНН // Тр. МИАН СССР. 1966. Т. 74. С. 5-15.
20. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М.: Наука, 1968.
21. Яненко Н.Н. // Тр. IV Всесоюз. мат. съезда. Л., 1964. Т. 2.
22. МарчукГ.И. Ц Численные методы в прогнозе погоды. Л., 1967.
23. Рихтмайер Р.Д. Разностные методы решения краевых задач. М.: Изд-во иностр. лит. 1960.
138

24. Куропатенко В.Ф. // Тр. МИАН СССР. 1966. Т. 74. С. 107-137.
25. Русанов В.В. // ДАН СССР. 1968. Т. 180, № 6. С. 1303-1305.
26. Яненко НН, Шокин Ю.И. // Там же. Т. 182, № 2. С. 280-281.
27. Яушев И.К. // Изв. СО АН СССР. Сер. техн. наук. 1967. № 8, вып. 2. С. 190-120.
28. LaxP.D. // Commun. Pure and Appl. Math. 1954. Vol. 7, N l.P. 159-193.
29. Neumann J. von, Richtmyer R.D. // J. Appl. Phys. 1950. Vol. 21. P. 232.
30. Harlow F.H. II J. Assoc. Comput. Math. 1957. N 4. P. 137.
31. Hahn S.G. II Commun. Pure and Appl. Math. 1958. Vol. 11, N 2. P. 243-255.
32. Friedrichs K.P. // Ibid. 1954. Vol. 7, N 2. P. 345-392.
33. Hirt С W. I/ J. Comput. Phys. 1968. Vol. 2, N 4. P. 339-355.
34. KreissH.O. // Commun. Pure and Appl. Math. 1964. Vol. 17, N 3. P. 335-353.
35. LaxP.D., WendroffB. //Ibid. 1960. Vol. 13, N l.P. 217-238.
36. Gentry R.A., Martin R.E., Daly B.J. //J. Comput. Phys. 1966.Vol. 1,N l.P. 87-118.
37. Harlow F.H., Dickman D.O., Harris D.E., Martin R.E. // Los Alamos Sci. Lab. Rep. 1959. N LA-2301.
38. EvansM.W., Harlow F.H, Meixner B.D. // Phys. Fluids. 1962. Vol. 5, N 6.
39. Harlow F.H., Pracht W. //ibid. 1966. Vol. 9, N 10. P. 1951-1959.
40. Riney T.D.// Al A A J. 1965. Vol. 3, N l.P. 52-63.
ВЛИЯНИЕ ВЯЗКОСТИ НА ГЛАДКОСТЬ РЕШЕНИЯ
В НЕПОЛНО-ПАРАБОЛИЧЕСКИХ СИСТЕМАХ*
В работе исследуется вопрос о гладкости двух групп компонент решений системы,
у которых оператор пространственных переменных расщепляется на два:
параболический и гиперболический.
1. Рассмотрим систему дифференциальных уравнений
Ъи m Ъи
— + X В, = ВАи, т>\, (1.1)
Э t /=1 bXj
где и = (иь..., ип) (п > 1) — неизвестная вектор-функция, матрицы Bj, В —
симметрические, матрица i? — не отрицательная, А — оператор Лапласа размерности т.
Системы вида (1.1) описывают колебания среды с учетом влияния
теплопроводности [1]. В работах [2, 3] методом сеток исследовалась задача Коши. Доказана
корректность задачи Коши в некоторой норме, предложены разностные схемы для
нахождения ее решения.
Известно, что для уравнений газовой динамики часть переменных (и, р) непрерывна
на контактной границе, в то время как р разрывно. Это связано со структурой
физической вязкости, не содержащейся в уравнении неразрывности. Мы ставим себе
задачей доказать линейный аналог этого свойства для гиперболических систем (1.1).
Рассмотрим случай, когда матрицы BJr В постоянны. Пусть Xi9 ..., Хр —
положительные собственные числа матрицы В (р> 1), собственные числа Хр + 2, ..., Хп
матрицы В равны нулю. Можно составить такую ортогональную матрицу |3 из собственных
векторов матрицы В, что матрица $В$~1 имеет вид
т~1 =\ о |, (1.2)
0 ""О'
т.е. РВР-1 — диагональная матрица, у которой на диагонали стоят сначала положитель-
*Мат. заметки, 1971. Т. 10, № 1, С. 93-99. (Соавтор Ю.Я. Белов .)
139

ные собственные числа, а затем нули. Умножим систему (1.1) на 0 слева. Получим
— + s fiBjP-1 —=m-1&v, (1.3)
bt j = ! Эх,
где v = f$u9 матрицы /3.S/3~"X симметрические вследствие ортогональности матрицы 0
и симметричности матриц Bj. Таким образом, система (1.1) может быть сведена к
системе вида
Ъи ™ Ъи
— + 2 Af— = М&и, (1.4)
Ъ t / = 1 ЭХу
где Aj — симметрические матрицы, а Л/ имеет вид (1.2).
Рассмотрим задачу Коши для системы (1.4) с начальными данными
н(0,х) = но(х), xGRm. (1.5)
В дальнейшем под периодическими по х функциями с периодом 2я будем понимать
функции периодические с периодом 2 я по каждому хк, к = 1, ..., т.
Пусть <£ (х) — периодическая функция с периодом 2я и </? (x)EL2 (0, 2 я) .
Рассмотрим последовательность периодических функций {фг (х)} , yr (x)GC°°(Rm). Пусть
функциям <рг(х) соответствуют периодические по х решения иг (г, х) задачи (1.4),
(1.5) (ur (t, х)ЕС°° ([О, Т] XRm)). Вследствие симметричности матриц Aj легко
доказать единственность таких решений.
Пусть периодическая по х с периодом 2я функция и (t, x) суммируема с квадратом
в области 2[0Г] ={t, x/te [О, Т\9 х7е(0,2я)}и и (0,х) = </?(х).
Определение. Назовем функцию и (Г, х) обобщенным решением задачи (1.4),
(1.5), если для любой последовательности функций ur (t, x) таких, что
||^(x)-^(x)||L2(O27r)^0, Г+оо, (1.6)
верно
\\«r(t,x)-u(t,x)liLAQi^T])^o, i-~, (1.7)
Единственность обобщенного решения в смысле (1.6), (1.7) задачи (1.4), (1.5) следует
из самого определения.
В классе периодических функций мы построим обобщенное решение задачи (1.4),
(1.5) и исследуем влияние "вязкости" М на его гладкость.
2. В случае одной пространственной переменной (т = 1) система (1.4) примет вид
+ А~ = ^T~f- (2.0
Ъи Ъи Ъ2и
— + А— = М—-
Эг Эх Эх
Пусть
и (0,х) = и0(х), xGR1, uo(x)eL2(09 2 я) , (2.2)
где и0(х) — периодическая вектор-функция с периодом 2я. Ищем решение задачи
(2.1), (2.2) в виде ряда
ul(t,x)= Xulk(t)eikx, I = 1,..., п. (2.3)
X
Подставим (2.3) в (2.1) и для к-й гармоники формально получим систему
обыкновенных дифференциальных уравнений
Ъик (t)ldt + ikAuk (f) = -k2Muk (t) (2.4)
140

с начальными данными
Uk(P) = ck9 (2.5)
где ск = (с\к,..., спк) — коэффициенты Фурье начальных данных
и01(х) = Ъс1ке'кх, /=1,...,и. (2.6)
к
Решение задачи (2.4), (2.5) есть (см. [4])
Uk(t) = e-(ikA+k*M)tCk (27)
Пусть ||i4||i =max 2 \ajk\ (j = 1, ...,и). Так как Re К,- < 0 (j = 1, ..., п) , где X, - собст
/ *=1
венные числа матрицы - ikA - к2М9 то (см. [4] )
\\е-«кА+кЛм>%<ае"<ае€Т. (2.8)
Здесь а> О — некоторая постоянная, зависящая от размерности матрице, Ми вели
чины е>0. Обозначим аееТ = К (Г). Из (2.7), (2.8)
\\uk(t)\\1<K(T)\\ck\\1. (2.9)
Из (2.4) имеем
k2t
\cfk+ik } Z anulke»ik%BdV(t /=1,...,р, (2.10)
i о 1=1 J
м=| 0
о • о,
Пусть w = w + w , где
w1 =(w, wp,0,...,0), w2 =(0,...,0, wp + lf.... wp). (2.11)
Тогда из (2.9) , ^2.10) при / > t0 > 0 получим
II «i (О II < ^lk*Hi/i*|, (2.12)
где TV — постоянная, зависящая от г0, Г, \\А ||ь ||M||i.
Подставим ик (г) (решения задачи (2.4), (2.5)) в (2.3). Из (2.9) следует, что
функциям (г, x)GL2 (G[o г])» если w0 (*)е^2 (0, 2тг),и u(t, x)GC°°([0, Г)] X Л1), если
MoMGC00^1).
Рассмотрим последовательность функций (</v(x)} • Последовательность функций
ur (t, x), полученных указанным выше способом (ur (t, x)GC°° ([0, Т] X Л1)),
является последовательностью решений задачи (2.1), (2.2). Доказательство этого факта
очевидно. Выше было замечено, что гладкое решение единственно. Отсюда и из (2.9)
следует, что функция u (t, х), полученная при и0 (х) = <р(х), есть обобщенное решение
задачи (2.1), (2.2) в смысле (1.6), (1.7). Из (2.12) следует, что функция и1 (Г, х) =
= Z u\(t)eikx имеет обобщенную производную по х при t>to>0. Следовательно,
к К
функция и1 (f, х) абсолютно непрерывна по х при t>t0 >0 (см. [5]). Доказанное
выше сформулируем в виде теоремы.
141

Теорема 1. Пусть и0(х) — периодическая функция с периодом 2я, и0(х) G
EL2(0, 2я). Тогда задача (2.1), (2.2) имеет единственное периодическое обобщенное
решение в смысле (1.6), (1.7), коэффициенты Фурье функции ul(t, x) при t>to>0
удовлетворяют неравенству (2.12), вследствие чего гарантирована абсолютная
непрерывность функции и1 (г, х) по хпри t > t0 > 0.
3. Рассмотрим систему дифференциальных уравнений
Ъи/bt+A (du/dx) = MLru, (зл)
где Lr - д2+4г/дх2+4г - дифференциальный оператор, г > 0 - целое число. Аналогично
п.2, можно доказать существование обобщенного периодического решения задачи
(3.1), (2.2). Из рассмотренного выше легко заметить, что при t > t0 > 0
\\uxk{t)\\x<Nx lk*|li/l*l1+4r, (3.2)
где Nx — постоянная, зависящая лишь от t0, Г и норм матриц А, М. Из (3.2) следует,
что при увеличении г гладкость функции и1 (t,x). по х при t > t0 > 0 увеличивается
(при одних и тех же начальных данных). Например, при г = 1 функция и1 (t, x) имеет
абсолютно непрерывные четвертые производные, если и0 (x)EL2 (0,2я).
4. Рассмотрим случай многих пространственных переменных (т > 1) . Пусть
начальные данные задачи (1.4), (1.5)
и(09х) = <р(х) (4.1)
- периодические с периодом 2я, <р (x)GL2 (0, 2я) и
*(*) = Sc**'**-**, (4.2)
А:
т
где (£• х) = Z АгуЛу — скалярное произведение, k = (klf..., A:w) — m- мерный вектор,
/=i
Лу — целые числа.
Решение задачи (1.4), (4.1) ищем в виде ряда Фурье
u(t,x)= 2 uk(t)ei{kx\ (4.3)
к
Нетрудно доказать неравенства
\\uk{i)\\x<N2 Ik* Hi, (4.4)
II и\ (Г) lit <N3 || с* IU/1 * |, Г > r0 > 0, (4.5)
где \к\ =1. Z A;2) , постоянные N2,N3 зависят соответственно от Г, ЦЛ/Hi, \\М\\Х и
■W-
Г0, Т, \\Aj\\i, ||М|1ь "а: (0 являются решениями системы обыкновенных
дифференциальных уравнений
duk (t) m ,
+ i 2 Аг.Л; uk (Г), = - i к yMuk {f)
dt /=i
с начальными данными м* (0) = c^.
Аналогично одномерному случаю доказывается, что функция и (Г, х) из (4.3) есть
периодическое обобщенное решение задачи (1.4), (4.1). Из оценки (4.5) следует,
что функция и1 (г, х) имеет обобщенные производные по х первого порядка при
t>to>0.
142

5. Рассмотрим систему уравнений
(5.1)
ди
где
Lr-
т Ъи
+ 2 Aj —
/= 1 Эдс/
Э2+4Г
— А.
' дх2+4г
= MLru,
д2+4г
'+ дх2+4г'
г>0
TY А ТТ/"ЧЛ
— целое.
Легко доказать существование обобщенного периодического решения в смысле
(1.6), (1.7) задачи (5.1), (4.1). В этом случае верно неравенство, аналогичное
неравенству (3.3),
KWlli<AUknii/l*l1+4'', t>to>09 (5.2)
где N^ — постоянная, зависящая лишь от t0, Г и норм матриц Aj, M. Из (5.2) следует,
что функция и1 (t, х) имеет обобщенные производные по х до порядка 1 + 4 г.
Применяя теорему вложения С. Л. Соболева, нетрудно установить при t>t0> 0
зависимость между величиной г и порядком гладкости по х функции и1 (t, x).
! ЛИТЕРАТУРА
1. Рихтмайер Р.Д. Звук и теплопроводность // Некоторые вопросы вычислительной и прикладной
математики. Новосибирск, 1966.
2. Новиков О.Б. Задача Коши для системы уравнений в частных производных» содержащей
гиперболический и параболический операторы // Журн. вычисл. математики и мат. физики. 1969.
Т. 9. № 1.С. 122-136.
3. Пяста С. Разностные схемы с расщепляющимся оператором для систем дифференциальных
уравнений смешанного типа // Там же. № 4. С. 884-893.
4. ДемидовичБ.П. Лекции по математической теории устойчивости. М., 1967.
5. Соболев С.Л. Некоторые применения функционального анализа в математической физике.
Новосибирск, 1962.
О СТРУКТУРЕ АБСОЛЮТНО АППРОКСИМИРУЮЩИХ
И АБСОЛЮТНО КОРРЕКТНЫХ РАЗНОСТНЫХ СХЕМ*
Введение. Рассмотрим разностную схему вида
(ип+1(х) - ип(х))/т=А(т, h)u!(x), (1)
где
Л (т, Л) =2 я„,(т,/0Г"(/0. (2)
m
Оператор TQi) называется оператором сдвига и определяется следующим образом:
T(h)f(x)=f(x+h)
для любой функции f{x). В дальнейшем мы для краткости будем писать Т вместо
T(h).
Коэффициенты ят(т, И) — непрерывные функции г и h при г Ф 0 и h Ф 0. Кроме
непрерывной пространственной переменной х, с разностной схемой (1) обычно свя-
*Проблемы прикладной математики и механики. Новосибирск; Наука, 1971. С. 137-144. (Соавтор
Г.В. Демидов.)
143

зывают дискретную временную переменную V.
t = qT, 4 = 0,1, 2,..., и ...
Параметры г и h могут рассматриваться в некоторых утверждениях как комплексные
числа. Будем предполагать, что либо I = п (явная схема) , либо / = п + 1 (чисто неявная
схема). Каждое множество функций {ип(х) } , удовлетворяющее уравнению (1),
называется его решением. Функция ип(х) называется л-м слоем этого решения.
Рассматриваемые нами разностные схемы являются двухслойными, так как в
уравнении (1) участвуют лишь два слоя: л-й и (п + 1)-й. Схемы вида (1), (2), как правило,
возникают при конечноразностной аппроксимации какого-либо дифференциального
уравнения вида
Ъи N Ьки
— = 2 а к —т—
bt * = o ЪхК
с постоянными коэффициентами ак. В теории разностных схем наиболее важными
являются понятия аппроксимации и корректности разностной схемы. Здесь мы
ограничимся определением понятий абсолютной аппроксимации и абсолютной
корректности разностной схемы вида (1) [1].
Определение. 1. Разностная схема вида (1) называется абсолютно
корректной, если для достаточно малых вещественных положительных г и h она эквивалентна
разностной схеме вида
un + l(x) = C(T,h)un(x) (3)
и равномерно по г и h имеет место оценка
II С(т, К) II < 1 + 0(т) (4)
для г2 + h2 < Tq .
Эквивалентность разностных схем (1) и (3) просто означает, что каждое решение
разностной схемы вида (1) является решением схемы (3) и, наоборот, каждое
решение схемы (3) является решением схемы (1).
Будем для простоты рассматривать операторы С(т, h) как операторы,
действующие в одном и том же пространстве [2]. Понятие аппроксимации разностного
оператора обычно связывают с некоторым достаточно широким классом функций U.
Желательно, чтобы этот класс функций U был плотным в одном или нескольких банаховых
или линейных топологических пространствах.
Определение 2 (см. [3]). Разностная схема вида (1) абсолютно
аппроксимирует дифференциальное уравнение
ди/dt -Lu
на классе функций U, если
для каждой u^U.
Это определение связывает разностную схему с заранее заданным
дифференциальным уравнением. Однако можно свойство аппроксимации разностной схемы
определить независимо [4].
Определение 3. Разностная схема вида (1) называется абсолютно
аппроксимирующей на классе функций U, если для каждой и £ U существует
lim A(r, h) и(х) = у(х) . (5)
Заметим, что г и Л в определениях 2 и 3 могут быть комплексными.
Ясно, что если разностная схема вида (1) удовлетворяет определению 2, то она
удовлетворяет и определению 3 с у(х) = Lu(x). Верно и обратное. Если разностная
144

схема вида (1) удовлетворяет определению 3, то соотношение (5) определяет
некоторый линейный оператор Lu(x) = ф(х) .на классе функций U. Таким образом,
определение 3 предполагает существование некоторого оператора L, хотя его
конкретный вид и основные свойства могут быть неизвестны.
Цель нашей работы — изучить структуру простейших разностных схем, которые
удовлетворяют требованиям абсолютной корректности и абсолютной аппроксимации.
1. Рассмотрим оператор А (т, h) вида
м
A(r,h)= 2 am(T,h)Tm9 (6)
m~ — М
где М не зависит от г и Л.
Установим общую структуру коэффициентов ат(т, Л), которая гарантирует, что
схема вида (1), (6) удовлетворяет определению 3 в предположении, что г и h
принимают комплексные значения. В качестве класса функций U возьмем множество
функций вида {elXx) , где X — любое вещественное число. Этот класс функций удобен
тем, что каждая функция elXx является собственной функцией оператора Т и, как
следствие, собственной функцией оператора А(т, И). Кроме того, эти функции
образуют полную систему во многих широко известных пространствах.
Пусть </?(Х; т, h) — собственное число оператора А(т, Н), соответствующее
функции eiKx, т.е.
А (г, h) eiXx = <р(Х; г, К) eiXx. (7)
Требование абсолютной аппроксимации разностной схемы вида (1), (6) в смысле
опеределения 3 в данном случае эквивалентно требованию существования предела
ton <р(Х;т,й) = ^.(Х). (8)
т->0, Л-»-О
Предположим, что коэффициенты ат(т, h) являются однозначными
аналитическими функциями г и Л в окрестности точки г = 0 и h = 0, т.е. представимы в виде
двойного ряда Лорана
эо
(9)
2 /WXKA", (10)
(П)
Условие абсолютной аппроксимации (8) влечет
/WX) = 0, (12)
если ц < 0 либо v < 0. Преобразуя выражение (11), получим
am(T,h) =
На основе (6)
*(Х;т,А) =
где
m
2
и
m
М
2
- ОО
(7)
ОО
2
м
2
V- —
ОО
имеем
ап
м
ОО
2
р = 0
,(т,
в(«)
h)e'
в(«)
H.V-P
r^hv.
Xmh _
(i\mf
р!
oo
2
Р»ЛЪ= 2
P = o p\
M
2 a<w> mP
L m = —M
li,v-p
= 0, (13)
если только д < 0 либо v < 0. Отсюда в силу произвольности X следует
м
2 ма%1-ртР = 0 О4)
m = -М м» и
при каждом р > 0, если выполнено одно из условий: д < 0 или v < 0.
145

В случае ц < 0 фиксированный индекс vx - v — р участвует в условии (14) при
каждом р > 0. Первые 2М + 1 этих условий приводят к системе уравнений
м
2 a<w> mp=09 р = 0,1,...,2М, (15)
определитель которой есть определитель Вандермонда, отличный от нуля. Отсюда
следует, что если ц < 0 и vx любое, то все о£т^ = 0. Таким образом, в разложении
(2) могут участвовать только неотрицательные степени т.
В случае v < 0 фиксированный индекс vx = v — р в условиях (14) встречается лишь
конечное число раз. Так, например, vx = — 1 возможен лишь при р = 0 и ^ = — 1; vx =
= -2 возможен дважды: при ^ = -1,р=г1 и при *> =-2, р = 0. В общем случае при
фиксированном индексе ^условия (14) возникают —vx раз, если ^ отрицателен.
Этих условий нет, если vx > о. Если ^ < — (2Л/+1), то аналогично предыдущему
доказывается, что коэффициенты а£"5* равны нулю при любом д. Если же - 2М<
<^i <-1, то коэффициенты а£^ должны удовлетворять - ^ условиям
абсолютной аппроксимации:
м
2 a<w>-mp=0, p = 0,1,...,-(^1+0. (16)
w = — М
V*vx
Итак, если разностная схема вида (1), (6) удовлетворяет условиям абсолютной
аппроксимации и ее коэффициенты имеют вид (9), то они необходимо представимы
в виде
am(r,h)= £ £ а£я>тмА|\ (17)
и, кроме того, должны быть выполнены условия абсолютной
аппроксимации (16).
Представим коэффициенты ат (г, И) в виде
*т(т,й)=г<&(т,й)+ 2 a^\r)h\ (18)
где^(г,Л),а^>(г) - непрерывные функции. Тогда правую часть равенства (6)
можно записать в виде
м -1 / м \
А(т,И)= 2 a°m(Tth)Tm + 2 ( 2 a(w)(r) Г" )/Л (19)
m--M y=-2M\w = -M У /
Из равенства (16) вытекает, что а^т\т) обращают в нуль первые — v моментов:
м
2 тра(т\т) = 0, р = 0,1, -(|/+ 1). (20)
Условия (20) позволяют представить единственным образом вторую сумму в правой
части (19) в виде
-1 / М \ 2М I M-j \/Д V
2 2 'а<т\т)Тт)к"= 2 2 ^(т>(г)Гт)(— , (21)
v = -2M\m=-M V I /=1 \m=-M J /\ h /
где
Дн(х) = ы(х + Л) - h(x) = (Г- 1)и(х) .
Итак, покажем, что преобразование (21) возможно и что Р^\т) единственным
образом определяются по ог™'(т), где v- — /. Предварительно покажем, что равенства
146

(20) эквивалентны следующим:
2М
2 тра<;т-м\т) = 09 р = 0, 1, ..., -(i/+ 1). (22)
m = О
При р = О это очевидно. Докажем, что они справедливы и для каждого р = к, если
к< -(у+ 1).
Действительно,
2 mka(m-M\r)= Z 2 C"(m -М)пМк~п^т ~м\т) =
m = o v "i=o * = o K v
к 2M
= Z C"Mk~n S (m-7lf)wa(w-M>(r).
w = 0 * w = 0 "
Суммы по m для л < — {у + 1) обращаются в нуль по предположению. Поэтому все
равенства (22) верны.
Покажем,что возможно следующее преобразование:
м м-\
2 ot{m >(т) Тт = 2 7(w }(0 ^ Дэ (23)
т=-М v m=-M v
причем при v < — 1 коэффициенты 7 Чг) удовлетворяют системе условий
2М-1
2 mpy(m ~м\т) = 0, р = 0 1,..., -(|/ + 2). (24)
m = 0
Равенства (23) эквивалентны следующим:
7<-">(r)=-a(-">(r), 7Г-1)(0=«Г)(^
7(«)(г) = й<« +1 )(Г) _ «("• )(Т), m = _м + 1,...,М - 1.
Отсюда получаем два различных выражения для 7^М~1 \т) при п= М
у(М-1){р)=а(М)(т)! y(n-l)(j)=_ "я* e(m)(T)f (25)
wi = —М
которые совместны в силу выполнимости (22) прир =0.
Рассмотрим левую часть равенства (24) с учетом (25):
2М-1 2М-1 m
Z mPy(m-M\T)=- Z mp 2 a(fc-M)(r) =
2M-1 l 2M-1 \
= S af"M>(r) S *p).
A: = 0 ^ V w = A: /
Пусть Sp — сумма р-х степеней первых п чисел натурального ряда, т.е.
Spn = lp +2? + ... + пр,
тогда
2М-1
2 mp=Sp t -Sp л.
m = k 2М~г k~l
Известно, что S% имеет вид
Sp=Ag+Apln + ... + Ap + 1np + \
(26)
147

где Ар. постоянные. Поэтому при фиксированном М
Подставляя (27) в (26), получим
> + 1 ] р + 1 2М
2 В?1*\ = 2 В? 2 *V*-M)(r) = 0
. z = 0 / = 0 fc = 0 V
2M
Z о$*-">(т)
в силу предположения.
По индукции приходит к представлению (21). Из равенств (24) следует, что
р{т \т) единственным образом определяются по a<w >(т) , где ^ = -/.
Введем обозначения
м
Ъ0(т,п)= 2 <Pm(?,h)9 b0=b0 (0,0),
m = -M
M-/
Ьу(т)= 2 0<*>(t), bj = bf(p), j= 1,2,...,2М. (28)
m = —M '
Пусть Г = m\ Благодаря представлению (21) легко доказывается следующая теорема.
Теорема 1. Абсолютно аппроксимирующая разностная схема вида (1), (6)
с аналитическими коэффициентами абсолютно аппроксимирует дифференциальное
уравнение вида
Ъи 2М э'и
— = 2 bj —т. (29)
Замечание. Аналитичность коэффициентов ат(т, К) не является необходимым
условием того, чтобы разностная схема вида (1), обладающая свойством абсолютной
аппроксимации, абсолютно аппроксимировала дифференциальное уравнение вида (29).
Для этого достаточно, в частности, чтобы am(r, h) имели вид
em(T,A) = ailS)(T,A)+ 2 а^>(т)й-"+ 2 a<™ >(/*) т"** +
v-1 М= 1 м
+ 22 a(m)T-»h-v,
m=i *=i м"
где л^^(т, A), o£^(r)» с/™*(А) - непрерывные функции, с^™* — постоянные при
2. Мы показали, что для достаточно широкого класса абсолютно
аппроксимирующих схем вида (1) оператор А (г, К) имеет вид
М 2М ( M-j \ ( Д \/
A(r,h)= 2 a°m(T,h)Tm + 2 2 /^(т) Г" ) (—) , (30)
где д£, (r, A), j3^w ^(r) непрерывны при г = 0, A = 0.
В этом и следующих параграфах мы укажем достаточно широкий класс
разностных схем вида (1), (30), которые удовлетворяют требованию абсолютной
корректности в пространстве Z,2(-°°, °°). Свойство абсолютной корректности будем проверять
спектральным методом на функциях вида егХх (X — вещественное).
Пусть у(\; т, К) и <р(А) введены соотношениями (7) и (8).
Определение 4. Спектром разностного оператора А (г, h) назовем множество
значений функции <р(Х; г, И) при т Ф 0, h Ф 0. Предельным спектром оператора А (г, И)
назовем множество значений функции </?(Х).
148

Теорема 2. Если явная абсолютно аппроксимирующая схема вида (1), (30)
такова, что предельный спектр оператора А(т, И) неограничен, то она не может быть
абсолютно корректной. Другими словами^ если предельный спектр оператора А(т, И)
неограничен, то абсолютно корректные и абсолютно аппроксимирующие схемы могут
быть только в классе неявных схем.
Доказательство. На основе теоремы 1 можно явно выписать функцию </?(Х):
2М
*(Х) = S bj(i\y (31)
Очевидно, что условие неограниченности множества значений функции </?(Х)
эквивалентно требованию, что не все bj равны нулю при / > 1.
Условие равномерной корректности (4) в данном случае эквивалентно требованию
И+ту(Х;т,й)1 <1+0(т), (32)
равномерно по X и Л при г2 + h2 <Tq.
Непосредственные вычисления дают
м 2М / /2sin(X/i/2 V M-j
*(Х;т.й)= Б a°m(j,h)eiXmh + Z ( usmW* z -р(«)(т)^(«+>/2).(33)
m--M /= 1 \ h / m = -M J
Из (32) с необходимостью следует
I <р(Х; г, А)1 < 3/г, т2 + А2 < т£. (34)
Фиксируя г перейдем к пределу при h -> 0 в неравенстве (34). Учитывая обозначения
(28), получим
гм 3
1Ь0(г,0)+ 2 (/X)'Wr)l < - (35)
равномерно по X при т<т0.
Левая часть неравенства (35) есть модуль многочлена по степеням X.
Коэффициенты этого многочлена ЬДт) непрерывно стремятся к bj — коэффициентам многочлена
*(Х)в(31).
Так как при / > 1 существует bj Ф 0, то при достаточно малом т0 существует / > 1
такое, что
&Дт)#0, т<т0. (36)
Отсюда следует, что неравенство (35) не может быть выполнено равномерно по X.
Терорема 2 доказана.
Доказанная теорема была сформулирована в виде гипотезы в монографии [1].
3. В работах [5-7] были предложены некоторые общие методы построения
абсолютно корректных и абсолютно аппроксимирующих разностных схем. Доказываемая
ниже теорема дает простой критерий проверки свойства абсолютной корректности
чисто неявной схемы вида (1), (30).
Теорема 3. Неявная разностная схема вида (1), (30) с непрерывными коэ-
фициентами, аппроксимирующая дифференциальное уравнение (29), абсолютно
корректна, если Re(—l)f^b2M<Q-
Доказательство. Для неявной схемы вида (1), (30) собственное число
оператора С(т, h) (см. формулу (33)) , соответствующее функции егХк9 будет
*(Х;т,А)=1/11-т*(Х;т.А)]. (37)
Условие абсолютной корректности (4). в данном случае эквивалентно требованию
li//(X;r,A)l < 1+0(г) при г2 + А2<т2). (38)
Из (37) следует, что для того, чтобы выполнялось (38), достаточно выполнения
149

условия
Re у(к; r,h)<C при г2 + h2 < r% (39)
равномерно пб X, где С— некоторая постоянная.
Для доказательства неравенства (39) введем вспомогательную переменную ц
Ц= + -. (40)
h
M-j
2 |3(т)(г)е/ХЛ(т+//2)
Подставляя (40) в (33), получим
2М-1
^(Х;г,Л) = Р2М(^;Х,г,Л) = ^>(г)(-1)мм2М+ 2 (/д)''
м
+ 2 лй,(т,А)^ХтЛ. (41)
m = -М
Из представления (41) видно, что </?(Х; г, Л) является многочленом степени 2М
относительно д с ограниченными коэффициентами. Так как
0(2^М)О") *Ъгм,
т-0
то при достаточно малых т<:Т0 будет
Re(-l)M^M)(r)<5<0. (42)
Re </?(X; r, Л) при больших \ц\ отрицательна в силу (42) и, следовательно, неравенство
(39) выполнено. Теорема доказана.
ЛИТЕРАТУРА
1. Яненко ИМ. Метод дробных шагов решения многомерных задач математической физики. М.:
Наука, 1967.
2. Рихтмайер РД, Разностные методы решения краевых задач. М.: Изд-во иностр. лит. 1960.
3. Рождественский .Б.Л^ Яненко Н.Н. Системы квазилинейных уравнений и их приложения к
газовой динамике. М.: Наука, 1968.
4. Яненко НМ, Современные численные методы решения задач механики сплошной среды // Тр.
советских ученых Межд: конгресса математиков в Ницце. 1970. М.: Наука, 1972.
5. Ильин AM^ Устойчивость разностных схем для задачи Коши для систем дифференциальных
уравнений в частных производных // ДАН СССР. 1965. Т. 164, № 3.
6. Birkhoff G., Varga R. Discretization errors for well-set Cauchy problems // J. Math, and Phys. 1965.
Vol. 44, N1.
7. Jhomee V. Generally unconditionally stable difference operators // SIAM J. Numer. Anal. 1967. Vol. 4,
N1.
ЭВОЛЮЦИОННЫЕ ДВУХСЛОЙНЫЕ РАЗНОСТНЫЕ СХЕМЫ*
1. В банаховом пространстве X рассмотрим разностную схему
(un+1 -un)/T=A1(T,h;n)un+1 +A0(T,h;n)un+fn, (l)
где Alf A0 — линейные операторы в X, п — неотрицательное число, h = (hlf ..., hm),T —
параметры разностной схемы (1). С разностной схемой (1) свяжем дискретную
временную переменную t: t = It, I = 0, 1, 2,..., n, ... (ht > 0, r > 0).
Последовательность функций {и1}, / = 0, 1, ..., n, ..., и1 G X, удовлетворяющая
уравнению (1), называется его решением.
* Докл. АН СССР, 1972. Т. 204, № 5. С. 1057-1060. (Соавтор Г.В. Демидов.)
150

Если существуют операторы [/— тАх(т, И;п)] *, то разностная схема (1) приводится
к виду
ип+1=С(т,п;п)ип+т<рп, (2)
где уп = [/ - тА! (г, h; ri)]_1 / п и оператор шага С определяется как
С(т, Л; л) = [/ - тЛ х (г, Л; л)] "2 [/ + тЛ0(т, Л; л)]. (3)
Схемы (1) и (2) эквивалентны, так как они имеют одни и те же решения.
Разностные схемы обычно рассматриваются одновременно для некоторого множества
параметров тик, которое является окрестностью нуля. Множество ft = {x}C^Rm будем
называть окрестностью нуля, если a) xt > О Ух = (х1г ..., xm) G £2, б) О G ft. Будем
говорить, что ft является полной окрестностью нуля, если £2 — окрестность нуля и
т
П ft, G ft,
/=1
где ft/ = {x|0<x/<6/}.
Введем оператор S(t, h; n + /, ri) — оператор перехода со слоя ик слою п + /, / > 0 [3].
S(r, h; n+l, п) = С(т, h;n + / - 1) С(т, h;n + / - 2) ...С(т, h;n). (4)
Очевидно, что оператор перехода обладает следующими свойствами:
S(r, h;n +llfn +l)S(T,h;n+l, ri) = S(r,h;n + llf л), /х >/>0; (5)
S(t, h;n, n) = I(I — тождественный оператор). (6)
Определение 1. Оператор S(r, h; n + /, ri) называется ft-устойчивым в
банаховом пространстве X, если
HS(r, h; n+l,n) \\<M(T) при пт<(п + 1)т<Т (7)
равномерно по (г, Л) G ft, где Л/(Г) — постоянная.
Если ft — полная окрестность нуля, то при выполнении (7) будем говорить, что
оператор S(r, h; n + I, n) абсолютно устойчив, в противном случае ft-устойчивый оператор
будем называть условно устойчивым.
Определение 2. Будем говорить, что разностная схема (1) ft-устойчива в X
(абсолютно устойчива, условно устойчива), если оператор S(r, h; n + /, ri) ft-устойчив
в X (абсолютно устойчив, условно устойчив).
Пусть U ={u(t)) — класс функций со значениями в X, непрерывных по t и
непрерывно дифференцируемых по t при t G [О, Т].
Определение 3. Будем говорить, что разностная схема (1) обладает
свойством ft-агшроксимации на классе функций U, если сильный предел в X
lim
(г,Л)-*0
u(t + r)-u(t)
" -Аг(т, h;n)u(t + r) - A0(t, h;n)u(t)
*-Ш (8)
существует равномерно по t при t G [0, T], t - пт, u G U.
Если ft — полная окрестность нуля, то при выполнении (8) будем говорить, что
схема (1) обладает свойством абсолютной аппроксимации на классе функций U или
является абсолютно аппроксимирующей на классе функций U. Если разностная схема
(1) обладает свойством ft-аппроксимации и не является абсолютно
аппроксимирующей, то будем говорить, что она является условно аппроксимирующей на классе
функций U.
Теорема 1. Пусть разностная схема (1) Sl-устойчива в X, обладает свойством
Q-аппроксимации на классе функций U, и пусть f = fu вычислена с помощью
предельного перехода (8) по некоторой u(t)GU.
151

Если
1) lim и°=и(0), (9)
(т,Л)-+0
ft
2) lim /w =f(t), t = nr равномерно по Г, (10)
(т,л)->о
3) операторы [I - тАх(т, h; n)]~l ограничены равномерно по (г, h) G £2, t = «r < Г,
то решение { ип) разностной схемы (1) сходится, к u(t) равномерно по t при (г, h) -* 0,
Следствие. В условиях теоремы 1 класс функций U является классом
единственности решения задачи Коши:
dv/dt=A(t)v+fu(t)9 0<t<T, v, uGU, (11)
и(0) = и(0), (12)
где оператор А определяется на U следующим образом :
A(t)*p(t) = lim [A0(T,h;n)<p(t)+A1(T,h;n)<p(t + T)]9 (13)
(т,Л)->0
ft
если </?(f) G U.
Рассмотрим решение однородной (/п=0) разностной схемы вида (1)
К+1 ~"? )/T=Al(T,h;n)u" + l +A0(T,h;n)u" , (14)
и* =м(Г0), uetf, kr = t0, n>k, t0, игЕ [0,Г],
t0 — фиксировано.
Будем говорить, что/и" \ равностепенно непрерывно по t, если
i г01
Vlu"+P -и" \\<ewa0<Tp<8(e,to,u(to)), (15)
Г0 Г0
r+lAKSife гв,к(г0)), (т,А)еп.
Лемма 1. Пусть V t0 G [О, Г] множество Ut ={u(t0)\u G U) плотно в X. Если
решения {и") £2-устойчивой разностной схемы (14) равностепенно непрерывны по
t и сходятся при (г, К) -* 0 для каждой м G £/, то операторы перехода S(r, h; n, к), п> к,
пт= t G [0, Г], сильно сходятся в!к операторам S(t, t0), удовлетворяющим
следующим условиям:
\\S(t, r0)II <М(Т), 0<to<t<T'9 (16)
SfrtiYSfrto^SiUto), 0<to<t1<t<T; (17)
115(Г + АГ, t0)u~S(t, t0) и II-*0, VwGI; (18)
Af-*0
S(t,t) = I, Vt<E[0,T]. (19)
Если оператор шага С(т, Л; и) не зависит от и, то операторы S(t, t0) зависят лишь
от разности аргументов t и t0, т, е. S(t, t0) = S(t - t0). В этом случае операторы 5(f)
образуют полугруппу класса (С0) [2].
В условиях леммы можно говорить, что разностная схема порождает корректную
задачу Коши и, в частности, полугруппу [1].
Теорема 2. Пусть разностная схема (1) удовлетворяет условиям теоремы 1,
причем класс функций U = {u(t)} дополнительно удовлетворяет условиям:
1) для каждой u(t) G U соответствующая fu(t), вычисленная по (8), тождественно
равна нулю;
2) множества Uto ={u(t0)\u(t)G U), t0 G [0, 7) плотны в X.
152

Тогда каждая функция u(t)GU представима в виде
u(t) = S(t, t0)u(t0)9 t>t0, t, tQ e [0, T],
где операторы перехода S(t, t0 ) удовлетворяют условиям (16) — (19).
Теорема 3. Пусть разностная схема (1) с оператором A i (r, h; n) = 0 и
оператором шага, не зависящим от пу т. е. С(т, h; n) = С(т, h),удовлетворяет условиям
теоремы 2.
Тогда
1) операторы S(t, t0) образуют полугруппу класса (С0), г. е. S(t, tQ) = S(t - r0),
и выполнены условия (16)—(19);
2) производящий оператор А1 полугруппы S(t) является расширением оператора
Af определяемого равенством (13).
2. Разностные схемы вида (1) могут рассматриваться в общих локально выпуклых
линейных топологических пространствах. Некоторые предпосылки к этому имеются
в работах [4—8]. Свойства аппроксимации и устойчивости налагают существенные
ограничения на класс разностных схем вида (1) даже в относительно слабых
топологиях. Для примера рассмотрим схему (1) с операторами А} вида
А, (г, A; t, х) = z' 4 k (r, h; t, x) f ,*' (A,) ... T^m (Am), / = 0, 1, (20)
где t = пт, ak # ^ — квадратные матрицы порядка г, х, h - r-мерные векторы, числа
Kj конечны и не зависят от Г, х, г, h (условие равномерной финитности), Т{(п{) —
операторы сдвига [3]. Операторы вида (20) допускают представление
Ai(r,h;t,x)=^o b>ki ; km (T,h;t,x)Ak1t...Ak™ ТГ** (A,) ... T~Km(hm), (21)
где Д/ = (Г/(А,)-/)/А,.
Пусть U — множество векторов размерности г, координаты которых либо нули,
либо имеют вид tp° х?1 ... х^т с неотрицательными целыми Pit / = 0, 1,..., т.
Теорема 4, Если разностная схема вида (1), (21) обладает свойством £1-ап-
проксимации на классе функций U в топологии поточечной сходимости (сходимость
в каждой точке (Г, х)), то
а) существуют конечные пределы
ton [b°k . (г, h; t, х) + Ь\ . (г, h; t, x)] = b°k (t, х),
ft
lim rbl .. (j,h;t,x) = b\ (f, x);
(т,Л)-*0 Ki—Km Ki—Km
ft
б) оператор A (f), определенный равенством (13), имеет вид
** •* (Л*) —г—: Г" +bl . (t,x) . .
ki-Km 3XV1 ... Эх*"1 *i—*m dtdXi* ... Эх*"1
1 m x m
Л(0 и s S
fc,=o
Пример. Разностная схема
un+l(x)-u"(x) _ r(h~a) u"(x+h)-un(x)
т ~ t2 + h2 h
ф+а) un+l(x+h)-un+l(x)
m
T2+h*
(22)
абсолютно устойчива в L2(—°°, °°) при о? > О, но является условно аппроксимирующей,
В зависимости от закона предельного перехода она аппроксимирует различные диф-
153

ференциальные уравнения и, следовательно, порождает различные полугруппы.
Предельными дифференциальными уравнениями для схемы (22) будут
Ъи 2к Ъи а. Ъ2и
— = г — + г , ft =<(т, h)\h = кт),
Ы 1+А:2 Ъх 1+к2 ЪтЪх
Ъи Ъ2и
— =а——, ПЩ(т,к)\к=0(т)}.
bt Ъг Ъх
ЛИТЕРАТУРА
1. Ianenko N.N. Methodes numeriques nouvelles en mecanique du continu // Actes Congr. Intern. Math.
1970. Vol. 3.P. 297.
2. ИосидаК. Функциональный анализ. М., 1967.
3. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск: Наука, 1967.
4. Ильин A.M. Ц ДАН СССР. 1965. Т. 164, № 491. .
5. Thomee V. // SIAM J. Numer. Anal. 1967. Vol. 4, N 1.
6. Кузнецов Н.Н. Ц Числ. методы механики сплош. среды. 1970. Т. .4, № 2.
7. Кузнецов Н.Н. // Журн. вычисл. математики и мат. физики. 1971. Т. .11, № 6.
8. Яненко Н.Н., Демидов Г.В. Ц Проблемы прикладной математики и механики: Сб. ст.
Новосибирск: Наука, 1971.
ОБ ОДНОЙ НЕЯВНОЙ СХЕМЕ РАСЧЕТА ТЕЧЕНИЯ
ВЯЗКОГО ТЕПЛОПРОВОДНОГО ГАЗА*
Достаточно подробное изучение задач сверхзвукового обтекания тел должно быть
основано на использовании полной системы уравнений вязкого сжимаемого
теплопроводного газа. Ввиду сложности этих уравнений получение аналитических решений в
настоящее время представляется невозможным, что приводит к необходимости
применения численных методов, которые интенсивно разрабатываются в течение ряда
лет [1-10].
Явные схемы, рассмотренные в [1, 2, 4—6], обладают условной устойчивостью, и
для них существуют сильные ограничения на шаг по времени (или итерационный
параметр в случае стационарных задач) при умеренных и малых числах Рейнольдса. Схема,
предложенная в [7], снимает ограничения на шаг г, связанные с вязкостью, но
ограничения, связанные с обычным условием Куранта для газодинамики без вязкости,
остаются. В этом смысле схема является промежуточной между явными и неявными.
При решении стационарных задач важно иметь абсолютно устойчивую схему,
свободную от ограничений на итерационный параметр, В нашей работе построена одна
из возможных неявных абсолютно устойчивых схем первого порядка точности с
полной аппроксимацией.
1. Постановка задачи, Система уравнений, описывающая течения вязкого
сжимаемого теплопроводного газа, имеет следующий вид:
— +(£2+,4)f=0, (l)
4
где £2 = 2 О/ — дифференциальный матричный оператор,
/=i
*Численные методы механики сплошной среды. 1972. Т. 3, № 4. С. 3-18. Соавторы Ю.А. Березин,
B.M. Ковеня.)
154

«1 =
ft2
Эх
О
О
о
э
и —
О
О
О
а э
-л— о
Эх 3Rep Эх Эх
О
О
О
у -
О
О
Э 1 Э Э
by Rep by by
b 1 Э Э
Эх Rep bx bx
О
О
О
э 4 э а
v ц —
by 3Rep by by
О
О
О
и
О
О
О
bx Pr Rep bx
bx
bv
7 a a
m —
RePrp by by
П3
f =
*i
О
(7
О
P
и
у
€
э
Ту
р— О О
е Э
D-- о
р Эх
о
О (7
О О
О
bx
(7-1)е—0 О
bx
а4 =
О р
О О
а^
о
о
(7-
Л=-
Rep
О О
О О
О ъ
О О
О О
а
Ьх
Ьи
Ьх
bv bit
by bx
2 b
3 bx
by
0 ^3 <P4 0
Э
^2 = -
Эх by
2 Э Э
3 ЬуЦ bx
bv\ b (bit bv\
~ЪугТх + ц\ьу bx)
\ b / bu bv\
Г by *\by* bx)
a
Ту
b_
bx'
Здесь использованы следующие обозначения: х, у — декартовы координаты, t — врет
мя, и, v — проекции вектора скорости на оси х, у; р, е — плотность, внутренняя энергия,
р — коэффициент динамической вязкости, у = cp/cv — отношение теплоемкостей, Рг -
число Прандтля, Re - число Рейнольдса. Система (1)-(3) записана в безразмерных
переменных t = u0l/L; x = x/L, у = y/L, и = и/и0, v = v/u0, е = е/но, Р = р/р<ь М = р/р0 >
Pr = срр0/\0, Re = Рои0Ь/цо (черточки относятся к размерным величинам, индекс 0 —
к величинам в набегающем потоке), Х0 — коэффициенты теплопроводности,/, —длина
тела, и0 — скорость набегающего потока.
Давление газа р исключено из системы (1)—(3) с помощью уравнения состояния
р = (7 — 1)ре, Предполагается, что коэффициенты вязкости ди теплопроводности X
являются степенными функциями внутренней энергии (ср, cv = const).
На поверхности тела ставятся условия прилипания и тепловой изоляции
н = и=0; Эе/Эл = 0. (4)
155

Для нахождения стационарного решения задачи обтекания
(£2+,4)f=0 (5)
используется метод установления.
2. Разностная схема. Введем в цилиндре DH = D X Н (D — прямоугольная область,
в которой ищется численное решение, Н = [О, Т], Г = G X Н — граница) разностную
сетку с коэффициентами
/ к
t=rXn; jcf=S h1(i);yk = 2 h2 (к), и = 0,...,М
/ = 0 ~кх
Здесь г — итерационный параметр, hx(i) и h2(k) — шаги сетки по координатам х и
у. Введем сеточную функцию f^1 (р£/, "&/, v£i9 eki) и разностные операторы Ц?, ЛЛ,
аппроксимирующие исходные дифференциальные матричные операторы с первым
или вторым порядком точности. Разностный оператор граничных условий Iй
аппроксимирует (4) со вторым порядком точности. Поставим в соответствие
дифференциальной задаче (4), (5) разностную задачу:
в цилиндре DH найти решение уравнений
(nh+Ah)fn = 0 (6)
с граничными условиями
/"f„ = 0. (7)
Для решения разностной задачи (6) методом установления предлагается следующая
неявная схема расщепления:
(Е + тх П?) Г+1/4 = -r(nh + Ah) f nh,
№ + т3п5)Г1+вл=Г + а/*, (8)
(£- + г4^)Г+1=Г+3/4,
rw+l =fi j.fcW + 1
где £я+/'/4 (/= 1, 2, 3, 4) — вспомогательный вектор.
Исключение дробных шагов дает схему универсального алгоритма [11], обладающую
свойством полной аппроксимации:
Г/2+1 _ ГП
В =-(Пи +Ah)fnh, (9)
7
4 4
/=i 7 /=1 7
Разностная схема (8) позволяет обойтись без трудоемкой матричной прогонки.
Сходная схема расщепления, но не обладающая полной аппроксимацией, рассматривалась в
[12].
Рассмотрим методом Фурье при т7 = т устойчивость линеаризованной схемы,
соответствующей схеме (9). Выбирая решение в виде fkj = Хп eiu>l,hl +1и>*кнг^ получим
следующее характеристическое уравнение:
[ГоСХ-О + сооЦг^Х-О + со^Ч^СХ-О + сог] + (у - 1) е [tt(\ - 1) + 1] X
Х{[Г0(Х - 1) + со0] [Г2(Х - 1) + 1] (7 - 1) + [Г0(Х - 1) + 1] [Г2(Х - 1) + со2]} X
{(7-1)е^^Г(Х-1) + (^+^)[Г1(Х-1) + со1]} = 0, (10)
где
со0=д + Ь; со! =о;0 +Г! + г2; со2 =со0 +6 (rj +r2);
156

f0 = (l +лХ1 +*); h =(1 +Л+ГОО +ft +r2);
r r
r2 =(1 + tf + 6r1)(l + b +5r2); di =/— sin/*!; d2=i — sinkh2;
hx h2
. 4дг 9 jhx Ацт . АЛ2
T\ = snr —; r2 = г snr — ;
.RepA? 2 RepAl 2
a = 2— |w| sin —+/— и cosjh1;
hx 2 hx
т . fc/*2 г
Ь = 2 — \v\ sin2 + / — v cos fc/i2 .
h2 2 h2
При достаточно больших значениях внутренней энергии е, что соответствует областям
за сильными ударными волнами (при гиперзвуковых течениях), уравнение (10)
принимает вид
[Г1(Х-1) + 1]{[Г0(Х-1) + со0][Г2(Х-1) + 1](7-1)+[Го(Х-1)+1] X
X [г2(Х-1) + со2]} (Х-1) = 0. (10а)
При отсутствии вязкости (/7 = 0) корни (10а) равны
Xi = 1; Х2,з = 1-1/'<>; Х4 = 1-<ооЛо, 00
а в случае малых скоростей Xj = 1; Х2 = 1 — t/t2;
^з,4 = [(27 - l)f2 - ^2 - (7 - О ± %/[Г2 + со2 +(7-1)]2 -47со2Г2] X
Х(27Г2Г1. * " (12)
При малых значениях внутренней энергии е (области сильного разрежения)
характеристическое уравнение
[Г0(Х - 1) + СО0] [fl(X - 1) + СО! ] 2 [f2(X - 1) + С02] = 0
имеет корни
Xj = i-co0Ao; ^2,3 = i-^iAi; х4 = 1-со2д2. (13)
Из формул (11) —(13) следует, что X = max |Х/| < 1, т. е. в рассмотренных
предельных случаях схема (9) является абсолютно устойчивой. Разумеется, проведенный
линейный анализ не является достаточным, поэтому необходима проверка с помощью
методических расчетов. Такая проверка была проведена, и оказалось, что схема
устойчива, по крайней мере, до чисел Куранта К < 10, где
г
К= -Qil |и|+й2 М+с.тах^Лг)).
hth2
Предложенная разностная схема может быть использована и для расчета осесиммет-
ричных течений,
3. Примеры численных расчетов. 1). Обтекание клина. Проведены расчеты плоского
течения вязкого сжимаемого теплопроводного газа около клина длины L по оси х под
произвольным углом атаки. На поверхности тела ставились условия (4), и плотность
определялась из уравнения неразрывности со вторым порядком точности. Вязкость д
определялась по формуле д = (е/е0)ы (со = 0,75). Передняя, верхняя и нижняя
границы расчетной области выбирались так, чтобы на них можно было поставить условия,
соответствующие невозмущенному потоку:
m = h0cosj3; u = -H0sinj3; Р=1, е= 1/(у (у - 1)М2), (14)
где 0 — угол атаки. Оказалось, что достаточно выбирать расстояние от клина до перед-
157

7^ z,0
Рис. 1
и 0,0HI МММ U
0 az 0л0,0 0,0 и *
Рис.3
0 0,3 0,0 0,0 я
Рис.4
У а е 0 0,20*0,5 0,0 г, г
Рис.5
Рис.6
ней границы области порядка L, а до верхней и нижней границ -3-5 1 Задняя
граница области отодвигалась на расстояние X = 5 ч-15 L от клина, и на ней задавалось
граничное условие 3f/3/ - 0, где / - направление набегающего потока. Сравнение
численных решений в сечении х = SL при X = 1L и X = 12L показывает, что их разница не
превышает 1%. г
Шаг согласованной разностной сетки по оси х от 0 до а выбирался равномерным и
равным h{ - Ahx - \\m (m - число точек на клине), при х >а шаг выбирался
неравномерным по формуле ft, = hi_v + Ah,. Шаг по оси у в окрестности клина задавался
формулой Лк - Ah2 = AMg</>, а в остальной части области - формулой hK =hk_x +
+ Ah2. Расчетная область содержала 56 точек по у и 40 точек по х, т. е. всего 2360 точек*
число точек на теле m = 10. В качестве начальных данных во всей области, кроме
границ тела, задавались условия (14). Численные расчеты проводились при различных
значениях итерационного параметра г = 0,03; 0,05; 0,1; 0,2; 0,3, что соответствует
числам Куранта К = 0,5 ч- 8,5. Сравнение установившихся численных решений на
поверхности тела для различных г и Ah показало, что при изменении г имело место
совпадение значении искомых функций с тремя знаками после запятой (т. е. установившееся
решение не зависит от г), а при уменьшении шагов сетки на 60%разница не превышала
158

Таблица 1
м
2
2
2
2
3
3
3
Re
tg*>
*о
е
/0
100
0,3
-
0,606
0,410
250
0,3
0,36
0,591
0,476
500
0,3
0,65
0,550
0,591
1000
0,3
0,9
0,482
0,601
100
0,3
-
0,368
0,273
250
0,3
0,1
0,310
0,427
500
0,3
0,36
0,264
0,519
5 -^6%. Критерием установления являлось выполнение условия
тах|Эр/Эг|<6, (15)
где 5 = 10~3 во всей расчетной области.
Результаты расчета обтекания клина под нулевым углом атаки при у = 1,4, Рг = 0,72
представлены в табл, 1 и на рис. 1—3. Здесь 5с0 — задняя критическая точка (граница
зоны возвратного течения на оси симметрии у = 0), е и р — внутренняя энергия и
плотность на дне клина при у = 0; М, Re — числа .Маха и Рейнольдса невозмущенного
потока. Изменение Зс'о в зависимости от чисел М и Re качественно совпадает с расчетами
[5].
На рис, 1 дано распределение л:-компоненты скорости на оси у = 0 при различных
числах Re (100 -ь 1000) для случая М = 2,0,<£= 16,6°, 0 = 0°. Увеличение числа
Рейнольдса приводит к увеличению области возвратного течения. Проведем оценку счетной
вязкости в ближнем следе за телом. Физическая вязкость Рф = /i/(Rep) непосредственно
за донным срезом имеет порядок ~0,02 (при р « 0,5, д « 1,5, Re » 100 -г 300), а счет-
h
ная, определяемая по формуле vcr ^— |w,|, имеет порядок ~0,001 -г- 0,002 (hx = 0,1,
\ut\ с~ 0,03 -г 0,1, / = 1,2). Таким образом, в ближайшем следе счетная вязкость
значительно меньше физической.
На рис. 2 приведено распределение плотности газа на дне клина при Re = 100, 250,
500, 1000, М = 2, \р = 16,6°. В точках, ближайших к угловой, имеет место падение
плотности до величины, близкой к нулю, С увеличением Re эта зона уменьшалась и при
Re = 1000 вырождалась в одну точку. Указанная особенность течения была отмечена
ранее в [5]. Вдоль образующей клина наблюдается падение плотности от значений в
окрестности носика, близких к прямому скачку, до почти невозмущенных значений.
Внутренняя энергия вдоль образующей близка к постоянной, которая уменьшается с
ростом Re. На рис. 3 даны эпюры дг-компоненты скорости на различных расстояниях
от дна клина вдоль оси симметрии при Re = 1000, М = 2, <£ = 16,6°. Расчеты
показывают, что перед клином образуется присоединенная ударная волна (рис. 4) (Re = 100,
250, 500). С увеличением числа Re (> 250) распределение скорости в ударной волне
почти не меняется, что, по-видимому, можно объяснить влиянием счетной вязкости,
Для более подробного выяснения характера течения в окрестности поиска
необходимы расчеты по схемам высокого порядка точности.
Были проведены расчеты по обтеканию клина под ненулевым углом атаки (/3=11,5°;
М = 2 -5- 3; Re = 100, 500, 1000; \р = 16,6°, 29°). На рис. 5, 6 представлены графики
распределения внутренней энергии и дг-компоненты скорости на различных расстояниях
от клина (М = 2, Re = 500, <р = 16,6°). Из рис, 5 видно, что ось вихрей располагается
вдоль направления набегающего потока. Как известно (см., например, [13]), за
обтекаемым телом существует веер волн разрежения. На рис. 6 хорошо видна зона
пониженной внутренней энергии, соответствующая этим волнам разрежения. Аналогичное
явление отмечалось ив наших расчетах обтекания клина и под нулевым углом атаки.
2), Обтекание пластины. Проведены расчеты течения около пластины длины L = 1
и толщины 5 = Ah2 под различными углами атаки. Расчетная область и шаги сетки вы-
159

Таблица 2
М
Re
Угол
атаки,
град
100
0
200
0
400
0
500
0
1000
0
100
0
200
0
400
0
м
10
Re
Угол
атаки,
град
200
0
400
0
200
0
400
23
1000
23
200
11,5
400
34,5
2000
23
4000
23
Таблица 3
М
Re
Сопротивление
расчетное
Сопротивление
теоретическое
Л = (°f)p ~ (cf*T
A/(£/)r> %
2
2
2
3
3
3
100
200
400
100
200
400
0,1366
0,0926
0,0618
0,1401
0,0940
0,0601
0,1328
0,0940
0,0664
0,1328
0,0940
0,0661
0,0038
-0,0014
-0,0046
-0,0073
-0,0036
-0,0060
2,В6
-1,5
-6,93
-5,5
-3,84
-9,05
бирались так же, как и в случае клина. Типичные расчеты проводились при т = 0,1 "=" 0,2;
Aht = 0,1; Ah2 = 0,03. Для ускорения сходимости в качестве начальных условий
бралось установившееся решение при меньших числах Рейнольдса, что приводило к
уменьшению числа итераций примерно на 30%, Течение считалось установившимся при
выполнении условия (15), Параметры рассчитанных вариантов представлены в табл. 2,
В расчетах по обтеканию пластины под нулевым углом атаки изучалось образование
пограничного слоя в зависимости от чисел Маха и Рейнольдса. Известно (см.,
например, [13]), что толщина пограничного слоя при обтекании тел несжимаемой жидкостью
определяется формулой б ^ Re"1/z с коэффициентом пропорциональности порядка
единицы. В случае сжимаемого газа, как показывают расчеты, качественная
зависимость толщины б от числа Рейнольдса сохраняется (Re =100 (7), 200 (2), 400 (5)
(рис, 7)), но величина б больше; это увеличение толщины б определяется
взаимодействием теплового и пограничного слоев [13]. Характерной особенностью течения
является утолщение пограничного слоя в передней части пластины, где происходит
его слияние с присоединенной ударной волной. Обращает на себя внимание отмеченное
в [13] увеличение толщины пограничного слоя с ростом числа Маха (М = 2, 3, 5, 10)
при Re = 200,0 = 0 (рис, 8).
При М = 10 профиль скорости в зоне развитого Пограничного слоя близок к
линейному. Распределение плотности на пластине слабо зависит от числа Re. Вдоль пластины
наблюдается падение плотности до значений меньших, чем в невозмущенном потоке
(р « 0,75, Ро, М = 2). В передней части пластины наблюдается резкое повышение
плотности, связанное с формированием ударной волны. Распределение внутренней энергии
вдоль пластины почти линейное, лишь в окрестности начала пластины имеется ее скачок,
связанный с ростом энтропии при переходе через ударную волну (так называемый
энтропийный слой). Превышение внутренней энергии на пластине под энергией в
набегающем потоке невелико и уменьшается с ростом числа Рейнольдса,
160

В расчетах вычислялся локальный и полный коэффициент сопротивления пластины
по следующий формулам:
cf =
Re
Ъи
Ту
Ь=о
2 l Ъи
Re о Ъу
dx.
\у=0
(16)
В табл. 3 проведено сравнение коэффициентов сопротивления трения пластины,
вычисленных по формуле (16) и по эмпирической формуле Юнга [13] (со = 0,75):
1 l
cf= -== 0,664 [1 +0,365 (7-l)Mg VpT] ("-O^ cf=2fcfdx.
v Re* о
(17)
Рис. 7
Возрастание отклонения расчетного коэффициента
сопротивления от определяемого по формуле (17)
можно объяснить тем, что формула (17) справедлива
для пограничного слоя, не искаженного влиянием
ударной волны. В наших же расчетах всегда имеет место
взаимодействие пограничного слоя с присоединенной
ударной волной, что приводит к некоторому изменению
профиля скорости вблизи тела. Кроме того, с
увеличением числа Re возрастает относительное влияние счетной
вязкости, приводящее к погрешности вычислений
коэффициента сопротивления. Как и при обтекании клина,
в этих расчетах имеет место искривление ударной волны в передней части пластины
за счет вязкого взаимодействия. Вниз по потоку наклон ударной волны
приближается к ее наклону в невязком газе (для М = 2, Re = 500 угол наклона ударной волны
в невязком газе составляет ~30°, а расчет дает ~32°).
Проводились также расчеты по обтеканию пластины под ненулевым углом атаки.
Внутренняя энергия и плотность на наветренной стороне значительно больше, чем на
подветренной (рис, 9,д) (при /3 = 23°, М = 2, Re = 400). На подветренной стороне
имеется зона разрежения, в которой профили х-компоненты скорости близки к линейным;
течение смещено по направлению потока (рис* 9,5),
При угле атаки /3 = 0,4 проводились расчеты при Re = 1000, 2000 и 4000, М =2.
Предполагалось, что при больших Re будет иметь место образование вихрей, Расчеты
показали, что при Re = 1000 возникает изменение направления скорости в одной точке
над концом пластины; однако дальнейшее увеличение Re не приводило к появлению
вихря. При обтекании пластины не образуется застойных зон, поэтому скорости
течения и, естественно, счетная вязкость в окрестности пластины достаточно велики, чем,
по-видимому, можно объяснить отсутствие вихрей. Для контроля точности расчетов
6. Зак 953
161

f 0,7
и 0 0,Z0J 0,0
Рис.9
проводилась проверка выполнения законов сохранения массы и полной энергии.
Погрешность в сохранении массы не превышала 1,5%, энергии - 0,3%.
В типичных расчетах число итераций до установления составляет ~200 -г 250 для
клина и 150 для пластины, а время счета одного варианта на ЭВМ БЭСМ-6 составляет
16—25 минут.
Выводы
1. Для системы уравнений, описывающей плоское течение вязкого сжимаемого
теплопроводного газа, построена неявная разностная схема расщепления первого
порядка точности по пространственным переменным, обладающая полной
аппроксимацией,
2. Методом Фурье показана абсолютная устойчивость этой схемы в предельных
случаях.
3. Методические расчеты показали, что схема устойчива, по крайней мере, до чисел
Куранта К = 10.
4. Установление течения до е = 10"3 (е = тах|Эр/Эг|) происходит за 150 -г 300
итераций.
5. Схема позволяет проводить расчеты при произвольном задании начальных
условий.
6. Получена картина течения около клина и пластины под различными углами атаки
(присоединенная ударная волна, вихревая зона и зона разрежения);
ЛИТЕРАТУРА
1. Рихтмайер Р. Разностные методы решения краевых задач. М..: Изд-во иностр. лит. 1960.
2. Lax P.D., Wendroff В. Difference schemes for hyperbolic equations with high order of accuracy //
Commun. Pure and Appl. Math. 1964. Vol. 17, N 3.
3. Годунов C.K., Забродин А.В., Прокопов Г.П. Разностная схема для двухмерных
нестационарных задач газовой динамики и расчет обтекания с отошедшей ударной волной // Жур. вычисл.
математики и мат. физики. 1961. № 6.
4. Браиловская И.Ю. Разностная схема для численного решения двумерных нестационарных
уравнений Навье-Стокса для сжимаемого газа//ДАН СССР. 1965. Т. 160, №5.
5. Браиловская И.Ю, Явные разностные методы для расчета отрывных течений вязкого
сжимаемого газа // Некоторые применения метода сеток в газовой динамике. М.: Изд-во МГУ, 1971.
Вып. 4. .
6. Павлов БМ. Численное исследование сверхзвукового обтекания затупленных тел потоком
вязкого газа // Там же.
7. Полежаев В.И. Численное решение системы двумерных нестационарных уравнений Навье-
Стокса для сжимаемого газа в замкнутой области // Изв. АН СССР. МЖГ. 1967. № 2.
8. Любимое А.Н., Русанов В.В. Течение газа около тупых тел. М..: Наука, 1970.
9. Яненко Н.Н., Фролов В.Д., Неуважаев В.Е. О применении метода расщепления для численного
расчета движений теплопроводного газа в криволинейных координатах // Изв. СО АН СССР.
Сер. техн. наук. 1967. № .8, вып. 2..
162

10. Белоцерковский О.М., Давыдов Ю.М. Метод "крупных частиц" для задач газовой динамики //
Числ. методы механики сплош. среды. 19,70. Т. .1. № 3.
11. Марчук Г.И., Яненко Н.Н> Применение метода расщепления (дробных шагов) для решения
задач математической физики // Некоторые вопросы вычислительной и прикладной
математики. Новосибирск: Наука, 1966.
1 2. Ковеня В.М, Численный метод расчета стационарных уравнений Навье-Стокса сжимаемого
газа // Числ. методы механики сплош. среды. 19.70. Т.Д. № 3.
13. Лойцянский Л.Г. Механика жидкости и газа. М..: Наука, 1970.
ОБ ОДНОМ МЕТОДЕ УСКОРЕНИЯ СХОДИМОСТИ
ИТЕРАЦИОННЫХ СХЕМ*
1. В настоящей работе мы покажем как можно построить итерационную схему с
более высокой скоростью сходимости, чем итерационная схема
В(ип+1 - ип)/т = Ли", (1)
где
В = (Е-тАх)(Е - тЛ2) , Л = АХ +Л2 = a2(A1A_1/hj + A2A_2/h22),
являющаяся разностной схемой универсального алгоритма [1].
2. Рассмотрим в прямоугольной области G задачу Дирихле
Ли = 0, (2)
и(*ь х2) = g(xi, х2), (xlf x2) G 7, (3)
где 7 — граница Gy G = { 0 < х( < я, /=1,2}. Наряду с задачей (2), (3) рассмотрим
нестационарную задачу
(ип+*-ип)/т = (1 +fn)A1un+V2 + Л2н", (4)
(ип+1 -ип+У2/т) = (1 +fn)A2un + l - Л2*Л
и0 = и0. (5)
с теми же стационарными краевыми условиями (3). Здесь /„ — некоторая
положительная функция.
В целых шагах разностная схема (4) имеет вид
(£'-т(1+/я)Л1)(£,-т(1 +/„)Л2)[(и" + 1 -un)/T](l+fn)Aun - (6)
- т/„(1+/„)Л1Л2и".
Очевидно, что решение задачи (4), (5), (3) сходится к решению задачи (2), (3),
если /„ -► 0 при п -* °°.
Пусть сделано п итераций. Тогда амплитуда гармоники sinkxhi • smk2h2 умножается
на величину [1,2]
Pfnfri. W = Р/, • ... -Р/я,
где
l+(l+/„)XiX2
Pfn
1 +(1 +/w)(Xi +X2) + (1 +/w)2XiX2
At sin2 (kihi/2)
A, = ьа • * = 1.2.
* Численные методы механики сплошной среды. 1974. Т. 5, № 5. С. 57-62. (Соавторы Ю.Н. Захаров,
Ю.И. Шокин.)
6*
163

Таблица 1
0,
тах|м — и
тах| и - 1|
0,4.10"3
0,4 .10"э
0,4 . Ю-3
0,4. Ю-3
0,4. Ю-3
0,4.10 "3
1
1
1
103
ю5
10*
ю9
10м
ю12
103
ю4
ю12
0
0 1
0 1
0 1
0 1
0 1
0 1
0 1
0 1
L 0
L 0
L 0
L 0
L 0
L 0
L 0
L 0
0
0,7
0,2
0,9
0,9
0,9
0,9
0,8
0,9
0,9
. 10"5
10-ю
10~6
10"11
1(Г10
10-ю
ю-5
1<Г6
10-ю
0,9
0,8
0,9
0,9
0,9
0,9
0,9
0,8
0,8
10~6
10"*
10"6
10"9
10-ю
10-ю
10"5
10"6
10-ю
5
4
3
3
3
3
3
4
3
Таблица 2
01
тах| м — С/|
1
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
5
10
10
10
ю2
10
ю2
ю2
103
103
103
103
103
10*
10*
10*
10*
10*
10*
10*
10*
ю2
ю2
ю2
2
0
1
2
2
4
1
2
2
0
0
0
0
0
0
10
12
0
1
0
8
8
8
10
10
10
0
О
1
1
1
О
ю2
10
10
10
10
10
103
103
о
ю2
ю4
ю2
ю4
106
о
о
10
10
ю2
0,5
0,9
0,1
0,9
0,5
0,4
♦ 0,5
0,4
0,3
0,9
0,5
0,2
0,7
0,7
0,9
0,5
0,5
0,8
0,9
0,8
ю-2
10"3
10"2
10"3
10"2
10"2
ю-2
10"2
10"2
10"2
10"2
10"2
10"2
10"2
10"2
ю-2
ю-2
10"2
ю-2
10"2
19
15
13
14
13
14
14
16
15
18
15
17
15
16
20
16
17
13
11
15
При/„ =0
V 1 +Xj +x2 +XjX2 /
Сравнивая Р^ и Р„, видим, что
Pfn <Pn-
Следовательно, разностная схема, (4) при/„ Ф 0 сходится быстрее, чем с/„ = 0.
3. Расчеты проводились в квадрате со стороной равной единице, и с а2 =
табл. 1-3 приведены результаты с h = 0,02, в табл. 4—6 — с h = 0,1. В табл. 1
164

Таблица 3
max I iv
U\
max| и —U\
5
5
5
5
10
20
1
1
1
0,7. 10"3
0,5 .10"a
0,9 • 10"2
16
18
28
5
5
20
20
2
4
0,4. 10"2
0,5 .10"2
18
16
Таблица 4
0.
7i | 6 j 6, maxlif -u max | и - 1 |
5
5
5
5
5
5
103
103
103
108
10» °
10»5
1
2
4
0
12
0
1
1
1
10
о
1
10
10
10
102
10
0
0 1
0 1
0 1
2 1
0 1
-
L 0,1. 10"5
L 0,1. 10"5
L 0,1-10"5
L 0,1-10"7
L. 0,1. 10"9
0,1.10"»»
0,1 .10"5
0,1 -lO"5
0,1 lO"5
0,1 10"7
0,1 .10"»»
0,3 .10"»»
3
3
3
2
2
2
Таблица 5
0i
max | и -U \
5
5
5
5
5
103
103
103
108
10»°
1
2
4
0
12
1
1
1
10
0
10
10
10
102
0
0
0 1
0 1
2 ]
0 1
L 0,1-10"2
L 0,1. 10"2
L 0,1 .10"2
L 0,1 10 "2
L 0,1. 10"2
13
13
14
15
17
Таблица 6
max \ и -U \
max | и -U\
5
5
5
5
10
10
1
1
2
0,2 -lO"2
0,1 10"2
0,1 .10"2
16
18
16
5
5
15
20
2
4
0,1 • 10"2
0,1 .10"2
18
15
Таблица 7
Область
Методы
Зейделя
ВР
ПВР
ППП
ПТ
дпт
ПТЧУ
ПТМН
Квадрат
50X50
1531
327
190
60
101
61
38
25
Примечания. ВР — метод последовательной верхней релаксации; ПВР — метод прогонки
по строкам с верхней релаксации; ППП — метод продольно-поперечной прогонки (неявный метод
Писсмана—Ракфорда) ; ПТ — попеременно-треугольный метод (явная схема переменных
направлений) ; ДПТ — двухпараметрический попеременно-треугольный метод; ПТЧУ —
попеременно-треугольный метод с чебышевским ускорением; ПТМН — попеременно-треугольный метод с
минимальными невязками.
165

приведены данные с
/„ = *2(0тах| ипц - ип.~х l6/«7 + ^imax| и»"1 - и»"2 l6'/"71^
а в табл. 3,6- с /„ = а2 ехр(]3 - л7) , где 0, Pi, 7, 7i, 5, 61 - некоторые положитель
константы.
Далее приведены типичные графики зависимости (рис. 1, 2)
ег = тах||Л -ип~1\, е2=тах|ы"-Н, е3 = max | к" - 1|
«\/ ' ' »\/ ' • /,/ '
от количества итераций Я , где V — решение, полученное разностной схемой стабши
sz
Z Ч 0 0 W
Рис.1
0
-Z
-ч
-0
г
1 1
\ *
V
1 1 l i I 1
*>2
1 1 i,_i€z_
/0 /V /0 ZZ /Г
Рис. 2
рующей поправки с г = 5 за 68 итераций с точностью е = 10"4. По оси абсцисс
отложено количество итераций, по оси ординат порядок величине! и е2.
Итерации продолжались до тех пор, пока для всех /, / не выполнялось условие
тах|и£ - ип.Гх \ < КГ4.
Приведем также для сравнения табл. 7 данных по числу итераций для различных
методов решения задачи (2), (3) с граничными условиями и | г = 1 и начальной
функцией и° = 0. Для каждого метода приведенные данные соответствуют величинам
итерационных параметров, близких к их оптимальным значениям [3].
ЛИТЕРАТУРА
1. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск: Наука, 1967.
2. Самарский А.А. Введение в теорию разностных схем. М.: Наука, 1971.
3. Ильин В.П. Разностные методы решения эллиптических уравнений. Новосибирск, 1970.
К ТЕОРИИ РАЗНОСТНЫХ СХЕМ ГАЗОВОЙ ДИНАМИКИ*
ВВЕДЕНИЕ
Многообразние применяемых разностных схем для задач газовой динамики делает
необходимым их классификацию в первую очередь по дйссипативным свойствам. В то же
время любые критерии, предъявляемые к разностным схемам для уравнений газовой
динамики, должны носить физически содержательный и, следовательно, инвариантный
характер, что неизбежно приводит нас к групповой теории. Как известно,
неинвариантность разностных схем относительно преобразований переноса и поворота является до-
* Труды симпозиума по механике сплошной среды и родственным проблемам анализа. Новосибирск,
1974. С. 292-306. (Соавтор Ю.И. Шокин.)
166

полнительным источником неточности расчета, что особенно ясно видно на примере
схемы Харлоу в методе "частиц в ячейках" [1].
Метод первого дифференциального приближения [2] позволяет дать групповую
классификацию разностных схем. Действительно, первое дифференциальное приближение,
сохраняя достаточную информацию о разностной схеме, является дифференциальным
уравнением, и к нему может быть целиком применима групповая теория
дифференциальных уравнений [3].
Будем говорить, что разностная схема допускает некоторую группу
преобразований, если эту группу допускает ее первое дифференциальное приближение.
В первом параграфе настоящей работы дается групповая классификация
двухслойных разностных схем для двумерной системы уравнений газовой динамики. Строится
класс устойчивых двухслойных разностных схем, допускающих ту же группу
преобразований, что и исходная система уравнений газовой динамики.
Во втором параграфе исследуется класс разностных схем для системы одномерных
уравнений газовой динамики в лагранжевых координатах, допускающих ту же
группу преобразований, что и переходная система уравнений газовой динамики. Кроме
того, выделяются и исследуются некоторые важные подклассы таких разностных
схем. Приводятся результаты численных расчетов.
1. ГРУППОВАЯ КЛАССИФИКАЦИЯ ДВУХСЛОЙНЫХ РАЗНОСТНЫХ СХЕМ
ДЛЯ ДВУМЕРНОЙ СИСТЕМЫ УРАВНЕНИЙ ГАЗОВОЙ ДИНАМИКИ
1. Рассмотрим систему двумерных уравнений газовой динамики в айлеровых
координатах:
Эи> Э/ dg
+ — + =0, (1.1)
bt Ъх Ъу
где
и> = Р» , /= P«v , g =
р+ри2
puv
ри
риЕ + up
puv
p+pv2
pv
pvE + vp
u, v — компоненты вектора скорости в направлении х иу соответственно, р — давление
газа, р — плотность, Е = е + lA(u + и2), е — удельная внутренняя энергия. Предполагаем,
что уравнение состояния газа имеет вид/? = р(е, р).
Система уравнений (1.1) при произвольном уравнении состояния допускает
пространство операторов с базисом
э
bt
Ъ
L5 = t
by
Э
Ln = t
bt
.+
+
L2
Э
17'
Э
x —
Эх
Э
Ьх'
U =
Э
+ v
by
Ьг =
д
v — ■
дх
>
Э
~э7
э
- х—
Ъу
+
L4 =
д
v —
Ъи
Ъ Ъ
t — + —
Ъх Ъи
Ъ
— и— ,
Эи
(1.2)
которым соответственно отвечают следующие конечные преобразования,
сохраняющие систему уравнений (1.1) : 1) сдвиг по оси г, 2) сдвиг по оси х, 3) сдвиг по оси у,
4) преобразование Галилея вдоль оси х, 5) преобразование Галилея вдоль оси у,
6) преобразование поворота, 7) преобразование геометрии в пространстве х, у, г.
167

2. Аппроксимируем систему уравнений (1.1) следующей разностной схемой:
A0wn(x,y) Тх - Т_х
Г 2»!
+ AJ1 «12(^^(^,2 - r_W2)j + hi1 (Ту,2 - Т_у/2) [h^n21(xfy)(Tx/2 - Г_х/2) +
+ hl1£l22(x,y)(Ty/2-T_y/2)\) [7То+(1-7)Щ w"(x,v),
где hlf h2 — шаги разностной сетки по х и у соответственно, г шаг по оси t, a/hj = const,
Тх — оператор сдвига по оси х, Ту — оператор сдвига по оси у, Е — тождественный
оператор, Т0 — оператор сдвига по оси f, А0 = Т0 - Е, t = пт\ £2# — матрицы
размерности 4 Х4, которые могут зависеть от функции w и ее производных, причем элементы
матрицы £2,у имеют порядок 0(т)\ О < а, Д; у < 1, Г2;7- = Щ (t, х, у) (/, / = 1, 2)9fn(x, у) =
= fW(x,y))9Jt(x,y)=g(yr(x,y)).
Параболическая форма первого дифференциального приближения разностной схемы
(1.3) имеет вид
Эи> Э/ bg Э / Эи> Эи> \ Э / Эи> Эи> \
bt Ъх Ъу Ъх\ Ъх Ъу ) Ъу\ Ъх Ъу /
где
clf = Щ - (т/2) (1-2а)АгА,-9
c2j = П2/ - (r/2)(l-2P)A2Aj (f = 1,2),
A i = df/dw, А 2 = dg/dw.
Систему уравнений (1.4) можно представить в виде
Ъи Ъи Ъи 1 Ър 1 и
Fx = — + и— + v + — Nx + — N3 =0,
bt Ъх Ъу р Ъх р р
Ъи Эи Эй 1 Эр 1 v
F2 = + и + v + —N2 + — N3 =0,
Ы Ъх Ъу Р Ъу р р
Ър Ър Ър Ъу Ъи
F3 = — +w — +t» — + р + р -N3=09
Ъг Ъх Ъу Ъх Ъу
Ър Ър Ър „ Ъи „ Эи и v
F4 = — + и — + v + а2 + а2 + bN3 + Л^ + N2 -
Ъг Ъх Ъу Ъх Ъу рер рер
- — N4 = 0, (1.5)
Е + р(Ъе/Ър) -и2 -v2
р(Эе/Эр)
Mil) + м(2)
ЛГ</> + М$ \ Ъ (лл Ъ ,_,
2х 2у \ = ^(1) + М(2)^
м^Ц +ЖЦ I ax ъу
4х 4y
168

AfV> = CjxWx + CnWy = || AfW lit, / = 1,2,
... ., 3w ., dv ., Эр ., Эр .- Эм .,, Эи
• * У" Эх *2 Эх *3 Эх *4 Эх fcl dv *2 Эу
/2 It /2 j^
"i'l = 'K'l + ""'*4 )• ^2 = P(^2 + ™'L )•
^4=PV^4> '„ = H ^ ||t,
/,/=1,2; /Д=1,2,3,4.
3. В силу нашего определения, разностная схема (1.3) допускает ту же группу
преобразований, что и исходная система уравнений газовой динамики (1.1), тогда и
только тогда, когда выполняются соотношения
LaFk\ = 0,
Fx=Qt F2= О, F3= О, F4= 0
где La — дважды продолженный из La оператор (а = 1, 2, ..., 7) (см. [3]).
Справедлива
Теорема 1. Если в разностной схеме f..3) элементы матриц $2,-7- (/,/=1, 2)
выбраны так, что выполнены следующие условия:
(1.6)
= 0, (1.7)
dt
ЭП& _
э^
9S% _
Эх
Э^_
Чг
™'>, _
Ъф ^
^xt
о,
э^/ _
Э<л
. эп".
Э</>
.9^/
Э<£ .
Nl = uN3 + R1, N2=vN3 + R2,
N4 = %(и2+ v2)N3 + R3 + uRi+ vR2,
(1.8)
— N3=—R = —N3= —R =0 (ли = 1,2,3), (1.9)
Ъи Ъи m dv dv m
l6Ni = N2- vN3, l6N2 = -Nt + uN3i\
l6N3=0, l6N4= uN2-vNlt\
(1.10)
lnNk= Nk (ft = 1,2,3,4), (1.11)
где
Э Э Э Э ч Э
+ p p + p p + (v + и + и ) +
y ьРх p* bPv py dPx p* dPv « *y y*} ъихх

Л 7\ Л
+ (V + V - U ) + (V -U + U ) .+ ... —(v + V ) !
^иух "ху ихх> Зп - ** ** уу ди удс ХУ Ъп
хх ху * у у
Э Э Э Э „ а
/- = и + w + и + ... + р + 2и
х ди у Ъу х dv у Ър хх Ъи
+ 2и
^ Эм У* Эм
ху ух
u,v, р, р,
э
.. + 2р
ууу Ър
fyy
то разностная схема (1.3) допускает пространство операторов с базисом (1.2).
4. Будем говорить, в первом дифференциальном приближении отсутствует
диффузия массы, если N3 = 0.
Можно показать, что N3 — 0, если выполнены равенства
аЦ = d(r-u2 + zv2 + zu2-Ez), Sl\\=dz9
П\\ = du(2-z), a\l = -dvz,
ai\ = dv, ail = du, ail = -duv, a\\ =a\\ = o, (112)
a\\ = qv, a\l = qu, аЦ = —quv,
^?,2i = -gwz, ^32 = ?u(2-z),
аЦ = q(r-v2+ zv2+ zu2-Ez), a\24 = qz, •
где
r r 9p ' 1 Эр
<,= ^-(l-2a), q = -(l-2P)9 r = —, * = -±~r^-
2 2 dp P.de
Справедлива
Теорема 2. /Гели выполнены равенства (1.6), (1.7), (1.11), (1.12), и, кроме
того,
dNJdu=0, bN./dv=0 (/=1,2,3), (1ЛЗ)
N4= иАгг+ vN2+ R, ЭЛ/Эы = ЭЛ/Эи = 0, (1.14)
/6Ari = А'2, l6N2 = -Nl9 /6/V4 = -vN^ uN29 (1.15)
7t) в первом дифференциальном приближенци разностной схемы (1.3) отсутствует
диффузия массы, а сама разностная схема допускает пространство операторов с
базисом (1.2).
Можно показать, что равенства (1.13) выполнены, если имеют место следующие
соотношения:
+ ddj.(u2-v2z) + qd2k(v2-u2z),
П3-' I . = S23-'' { . - f vb\ + u62)n3~>' i +
/ 3-/ / 3-1 V I 1)1 4
+ qh\ (u2 - v2z) + dSj (v2-u2z),
170

a*~f '. = ti3-> ! - (u8l+v8})n3-> i + (q8} + d82) uv(2-z),
II II \ I I ) I 4 \H I I / V '
0*_y 4= П*_, '3 + (**; + «««») (-2«25'-2»262+ m + r) -
-«(0*3., '.-«O*,., /4) -»(о*_/2-Ю0*з_/4)-соП*з_/4,
П?-'4= П3_/Ч + (<7u61 + rfM62H-2u251-2u262 + m + r) -
—(n;-// -«o;-"J - *(n;-"2 - *n;-"4) -wn;-"4,
П{{ = Ojj- (u8) + v82) Щ + 3(du28} + qv282)(l-z),
& i . = Ъ.'. I . - (v8l + u82 ) a" - 3(d8l + q82) uvz,
I 3-/ i 3-1 \ I I I I 4 \ I ^ 1 J
Sl>.'3 = П'.'3 - (du8l + qv82 ) (2м28} + 2v282 - 3r - 3m) -
-«П/4 - (ив/ + v82)[&> - (нв; + v82) П//4] -
(1.16)
3-/
к ' H""k}"j ' \"""k ' *«""*/"
где 5* — символ Кронекера,
АИ = (U2 + О2 - £) Z, Ш= %(U2+ V2),
ъЪ.к! дпк!
iL_ —LL =0,
Ъи dv
(/,*,/= 1.-2; / = 1,2,3,4).
5. Инвариантом системы уравнений (1.1) является энтропия S, которая
удовлетворяет уравнению
as as as
—+и + и — = 0. (1.17)
Эг Эх Э>>
Будем говорить, что разностная схема (1.3) обладает ^-свойством, если
выполнено равенство
32w 32w 32wl
<*n 77 + (C12 + c2i)—-+ c22 77 =0,
Эх2 ЪхЪу дуг J
где AT —вектор, так ой, что ХАХ = иХ, ХА2 = vX.
Можно показать, что если разностная схема (1.3) обладает /^-свойством, то
энтропия S в первом дифференциальном приближении удовлетворяет уравнению (1.17).
6. Устойчивость построенных классов разностных схем проверяется методом
первого дифференциального приближения. Для этого требуется найти условия, при кото-
171

рых система уравнений (1.4) является неполной параболической и область
зависимости гиперболической формы первого дифференциального приближения не
превосходит области зависимости разностной схемы [2, 5].
Заметим, что аналогичный анализ может быть проведен и в случае системы
уравнений газовой динамики в лагранжевых координатах.
2. ОБ ОДНОМ КЛАССЕ РАЗНОСТНЫХ СХЕМ
ДЛЯ СИСТЕМЫ УРАВНЕНИЙ ОДНОМЕРНОЙ ГАЗОВОЙ ДИНАМИКИ
В ЛАГРАНЖЕВЫХ КООРДИНАТАХ
1.Нйже подробно исследуется класс инвариантных разностных схем для системы
уравнений газовой динамики в лагранжевых координатах с одной
пространственной переменной
bw/bt = bf/bx, (2.1)
где
-О- '-(!)■
v — удельный объем (v = 1/р).
Систему уравнений (2.1) аппроксимируем следующей разностной схемой:
A0wn(x) Ai + Д. F +1 ]
г 2ft [tt/ (X) + (1""tt)/J +
+ ^M"(*+i)Ai~"(*~y)^ (2,2)
где £2 = ЦП .И? — квадратная матрица третьего порядка, A_t - Е - T_l9 At =
= Г1-£, 0<а, |3< 1, т/А = к = const.
Параболическая форма первого дифференциального приближения разностной схемы
(2.2) имеет вид
bw bf
+
bt bx
bx \ bx J
где
т о df
С = П--Л2, А = —.
2 dw
Справедлива
Теорема 3. Если вектор N = Cwx такой, что
JLNlx = ^-N2x = 0, -^-N3x= Nlx,
bu bu bu
(u -i-
\ X dux
э э „ „ a
a + »x -r—+ P-r-r + 2Uxx + 2vxx - +
dux dvx dpx bvxx
+ 2P« J^)N.MmN*x («=1.2,3)
172

и, кроме того,
Ы2.. Э£2.. Э£2.. ЬП.. д£1.. дП..
и = _ ij = «/_ _ «;_ = ч_ _ = »/_ _ q
Эг Эх Эмг buxf dufx Ъри
то разностная схема (2.2) инвариантна относительно той же группы преобразований,
что и система уравнений (2.1).
Выделим из рассматриваемого класса разностных схем подкласс схем,
обладающих свойством К [2], которое состоит в том, что при счете контактного разрыва
энтропия не "мажется". Математически свойство К определяется равенством ХоС = 09 где
Х0А = 0.
Устойчивость полученного подкласса разностных схем проверим методом первого
дифференциального приближения. Это приводит нас к неравенствам
(1 -2а) (г/2)а2 < со. < h2/2т (/ = 1, 2, 3), (2.3)
где со/ — собственные числа матрицы £2, а — скорость звука. ~ h2
Заметим, что (2.3) можно при а = 0 записать в виде а2 < — со. < — • Но это
есть условие последовательного включения областей зависимости исходной системы
уравнений газовой динамики (2.1), системы уравнений гиперболической формы
первого дифференциального приближения и разностной схемы. Такая запись условий
(2.3) помогает объяснить тот факт, что наилучшие результаты при счете с помощью
исследуемых схем получаются при таких к = т/п, которые цепочку неравенств (2.3)
приближают к равенствам.
Заметим также, что в выделенный подкласс схем входят многие хорошо
известные разностные схемы, такие, как схема Лакса—Вендроффа, предиктор—корректор,
мажорантная и другие [4].
Введем в рассмотрение еще один подкласс разностных схем, а именно, разностных
схем в первом дифференциальном приближении которых отсутствует диффузия массы,
N2x = 0. Если N2x = 0, то при выполнении свойства К аппроксимационная вязкость входит
в систему первого дифференциального приближения как аддитивная добавка к
давлению, аналогично физической вязкости.
2. Для численных расчетов были выбраны разностные схемы, в которых матрица С
вязких членов имела вид
fJLoh 0 %0h
С =
0 0 0
ufioh 0 u%0h
где до, £о — постоянные или функции, не зависящие от г, х, и и производных по t
от функций и, v,p.
Предварительно рассмотрим задачу о движении стационарной ударной волны,
распространяющейся с постоянной скоростью D, когда все характеристики движения
зависят от переменной s = х - Dt. Переходя в системе уравнений первого
дифференциального приближения к переменной s (при £0 =0, /i0 = const) и интегрируя
полученную систему уравнений с учетом граничных условий
P(+00) = Pi, Р(-°°) = Р<ь u(+°°) = ui, и(-оо) = v0,
и(+°°) = Hi, и(-оо) = но, Nlx(+oo) = N2x(-oo) =0,
получим
.Ul+ V0 V1-V0
v = + ФОО.
173

где
а 0,5 (y+l)DA v
Ф(г) = th —, а = 5, Av=vl—v0.
2 jjL0h
Ширина зоны размазывания выражается формулой
2yiQh ui-uo
As = In (2.5)
Av(y+1)D v.-vo
Отсюда можно заключить, что, меняя д0, можно регулировать ширину зоны
размазывания разрыва в соответствии с формулой (2.5) (см. рис. 3) .
4 Заметим, что для выбора ц0 следует решить задачу на оптимизацию, ибо
уменьшение До ведет к сужению зоны размазывания и к большей устойчивости; в то же
время, уменьшение д0 ограничено тем, что на ударной волне вязкость должна быть
достаточно сильной, в противном случае возникают осцилляции.
3. Для проверки разностной схемы (2.2) с матрицей С вида (2.4) был произведен
ряд расчетов разрывных решений уравнений газовой динамики.
Решалась задача распада разрыва с возникновением слева ударной волны и справа
волны разрежения с начальными данными
х< 0,
х>0,
1 w0,
И! = 0,698, и0 =0, Vi = 2,245, v0 = 2; рх = 3,528, р0 = 0,5714.
Уравнение состояния имеет вид pv = (у — 1) б, у = 1,4. Графики численных расчетов
приведены на рис. 6—10. Расчеты с линейной вязкостью (д0 = const, £0 = 0) показали
ее негибкость (см. рис. 7,8). Для ц0 выбирались другие выражения
_ 1**1 , _ \"х\ , _ \"хРх\
Мо = Мо —T~h, До = Мо Л, До = Мо ; >
a1 v 1 + \ихрх\
где До = const, a — скорость звука. Наиболее точное неосциллирующее решение
получалось в случае
Аы > 0,
Vo =
0,
I их Рх I
Мо ; ' Аи< 0, До = 0,5.
1+KpJ
В этом случае ударная волна размазывается на 2—3 ячейки и за фронтом волны
отсутствуют осцилляции (рис. 4—6).
Улучшение счета ударной волны можно получить, если считать уравнение
неразрывности с третьим порядком точности по г (рис. 9) .
Большинство схем рассматриваемого класса хорошо считает контактный разрыв и
ударную волну, при счете волн разрежения точность относительно ниже. Точность
расчета волн разрежения повышается, если потребовать дополнительное ограничение
на матрицу С, а именно, потребовать, чтобы X_х С = 0, где Х_ХА = —аХ_х. Расчеты
показали, что этот прием существенно повышает точность расчета воли разрежения
(рис. 10).
174

3. ОПИСАНИЕ ГРАФИКОВ
На рис. 1—3 приведены графики решения задачи, описывающей распространение
стационарной ударной волны в политропном газе (7=1,4) с постоянной
скоростью D. Начальное положение разрыва следующее:
ui=l, v0 = 2; Wi=l, u0 = 2; рх = 1,5714; р0 = 0,5714, D=\.
На рис. 1—3 представлены профили скорости и удельного объема и,
рассчитываемые по схеме Лакса—Вендроффа (кривая 7) и по схеме (2.2) с матрицей С вида
(2.4), где ^о =0 (кривая 2) с к = 0,337, д0 = 1- На рис. 3 даны результаты расчета
при к=0,1, до = 1 (кривая7); к=0,4, д0=0,5 (кривая2); к = 0,4, /z0 =0,5
(кривая 3). Решения даны на момент времени t =0,13 (рис. 1), t -■ 0,26 (рис. 2) и
Г =0,16 (рис.3). Везде h =0,01. Везде на рис. 1—3 пунктирная линия изображает
точное решение.
f,o
0,в
o,ff
о,ч
0,2
1 /
яА/
"""тл'
Л|
\
\
1 UX...J
7
.*/
it '
М!
\
\
IL
50
ffO 70
Рис. 1
во
2,Ог
1,0\
f,7
1,5
1,3
't,1
t,0V-
о,в\-
о,оу
ачу
azy
50
j_
60 70
Рис.3
во
У
— ^е^Т
~4J~y3 J*0\
zA
zA
ш
r,j\
, °Л
-
г
[ j
1
J/7
<//7 £/7
Рис.4
ffl
7/7
J 7,7
fftr~'i
-Л 0,7
ai
/ z
: у]
- \
-----§-
JO
w
JO
Рис.5
0/7
7/7
175

-^-\
v_^^
1 1
3,6
3,Z
Z,8
Z,0
f,£
f,Z
0,8
-
-
i
btz
**^Щ
i
i-
30
ЧО 30
Рис.6
55
7/7
Z,0
1,5
1,0
0,8
l
-•
А—т*
17""
Z ЗА
1 Y"f
45 50 50 70
Рис. 9
¥77 577
Рис. 10
На рис. 4—10 представлены графики решения задачи распада разрыва, описанной
в предыдущем пункте. Пунктирная линия на рис. 4—10 изображает точное решение.
На рис. 4—6 приведены распределения удельного объема и, скорости w и давления р,
полученные в результате расчета по схеме Лакса—Вендроффа и по схеме (2.2) с
до = 0,5 и до = До I ихРх | / (1 + | ихрх |) , До = 0,5, £0 =0, изображенные
соответственно кривыми 1,2,3. Всюду к =0,377, h =0,01, m=40,. m — число шагов по
времени.
На рис. 7—8 представлены графики удельного объема и давления по схеме (2.2)
176

с до = 1 и различными к: к =0,1; к =0,337, к = 0,4 (соответственно кривые 1,
2,5), h =0,01, t =0,16.
На рис. 9 приведены профили удельного объема, рассчитываемые по схеме (2.2)
(до=0,5, к = 0,377 и к = 0,4) и по схеме (2.2), когда уравнение неразрывности
аппроксимируется с третьим порядком точности по г при jjl0 = 0,5, к = 0,377, h =
= 0,01, г =0,15. Графики решений обозначены соответственно кривыми 2,3,1.
На рис. 10 представлены профили удельного объема, полученные по схеме (2.2)
с /!0=0>5, к = 0,3 и по схеме (8) с Д0 =0,1, к = 0,3; д0 =0,2, к = 0,377, ц0 =
= До \UxPx\l(l + \uxPx\)> при условии, что Х_1С=0, обозначенные
соответственно кривыми 1, 2, 3\ h = 0,01, Г =0,15.
Авторы выражают благодарность З.И.Федотовой за проведение численных расчетов.
ЛИТЕРАТУРА
1. Вычислительные методы в гидродинамике / Под ред. Б.С. Олдера и др. М.: Мир, 1967.
2. Яненко Н.Н., Шохин Ю.И. О первом дифференциальном приближении разностных схем для
гиперболических уравнений // Сиб. мат. журн. 1969. Т. 10, № 5. С. 1173-1187.
3. Овсянников Л.В. Групповые свойства дифференциальных уравнений. Новосибирск, 1962.
4. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М., 1968.
5. Hirt C.W. Heuristic stability theory for finite difference equations // J. Comput. Phys. 1968. Vol. 2, N 4.
P. 339-353.
О ПОСТРОЕНИИ РАЗНОСТНЫХ СХЕМ
ПОВЫШЕННОГО ПОРЯДКА АППРОКСИМАЦИИ
НА ОСНОВЕ ДИФФЕРЕНЦИАЛЬНЫХ СЛЕДСТВИЙ*
1. В последние годы в связи с появлением высокопроизводительных ЭВМ все
большее применение в практических расчетах находят разностные схемы повышенного
порядка аппроксимации. Исследованию их посвящены работы [1—7], Разностные
схемы, имеющие наперед заданный шаблон, рассмотрены в [1, 2, 5, 6]. В [3, 4] даны
важные критерии устойчивости диссипативных разностных схем. В работе [7]
предложен метод построения разностных схем повышенного порядка аппроксимации на
основе регуляризатора.
Настоящая работа посвящена построению разностных схем повышенного порядка
аппроксимации на основе дифференциальных следствий исходного уравнения.
2. Рассмотрим задачу Коши
Ъи/bt = Lu9 f >0, xe Rl9 (1)
н(х,0) = и0(х), (2)
где L = Ь(д/дх) — некоторый дифференциальный оператор с постоянными
коэффициентами; и0 (х) — достаточно гладкая функция. Будем считать, что задача (1)—(2)
поставлена корректно в некотором банаховом пространстве В.
Аппроксимируем уравнение (1) разностной схемой
W" + 1(x) = Shw"(x) (3)
первого порядка аппроксимации. Здесь Sh = Sh(Ti) — оператор шага схемы; 7\ —
оператор сдвига по оси х, и0 (х) = и (х, 0), t = пт> т/h6 = const, e — порядок
оператора L.
* Некоторые проблемы вычисл. и прикл. математики. Новосибирск: Наука, 1975. С. 184-191.
(Соавторы Л.А.Тушева, Ю.И.Шокин.)
177

Разностная схема первого порядка аппроксимации представляет собой следующее
дифференциальное уравнение:
Ъи/bt = Lu+TRtu + t2R2u + ... ,
где Rf = Rj(d/dx) — некоторый дифференциальный оператор, способ нахождения
которого дан в [8, 9].
Пусть функций fn(x) с точностью 0(т) аппроксимирует величину Riu(nT9x).
Тогда разностная схема
un*1(x) = Shu-(x)-T2fn(x),, (4)
и°(х) = и(х,0) (5)
аппроксимирует уравнение (1) с более высоким порядком.
Так как L — оператор с постоянными коэффициентами, то все производные г(/г) =
= bRu/bxR удовлетворяют уравнению вида (1)
driR)/dt = Lr(Ry
Поэтому f"(x) может быть найдено по разностной схеме вида
fn+1(x)= Shf"(x), (6)
/»(*) = Ди°-(*), (7)
где А — некоторая разностная аппроксимация оператора R j порядка 0(т).
Обозначим через ип(х) и fn(x) решения разностных схем (4), (5) и (6), (7)
соответственно, и(птух) — точное решение дифференциальной задачи (1), (2) на
момент времени г = пт. Имеет место
Т-еорема I. Пусть
а) устойчивая в В разностная схема (3) аппроксимирует с первым порядком
дифференциальную задачу (1) , (2) ;
б) оператор перехода дифференциальной задачи (1), (2) перестановочен с опера-
юром SA;
в) производные решения до некоюрого порядка являются гладкими решениями
уравнения (3).
Тогда
\\ип(х)~ и(пт9х)\\в = 0(т2).
Доказательство. В силу условия б) можно записать
ип(х) -и(пт,х) = nS^-l{Sh-C{r) -т2 А)и°(х) - V S* " ~ 2~* S« ( S„ -
R=0 a=0
'-C(T))2C((n-R-a-2)r)u°(x)9
\\un(x)- и(пт,х)\\ < n\\S£-1 || || (Sh-C(r) -г2 A) u° (x) || +
+ \ \\S*\\ "~2~ ||5Ла|| \\(Sh-C(T))2C«n-R-a-2)T)u°(x)\\.
R=0 <x = 0
Первое слагаемое есть величина пК\0(т3) в силу выбора оператора г2 А и
условия а).
В силу в) функция, определяемая остатком ряда Тейлора, получающегося при
разложении по степеням г, h величины (5Л-С(т)) и (пт, х); принадлежит области
178

определения оператора С(т) и является гладкой функцией. Поскольку эта функция
имеет вид т2Я(д/дх)и (пт>х), то вторая сумма оценивается как п2К20(т4) =
= 0(т2). Тем самым теорема доказана.
2. Из доказательства видно, что ошибка в начальных дднных возрастает не более
чем в п раз. В случае, когда разностную схему (4) можно представить в виде
ип + 1(х) = Фпип(х),
получаем обычную разностную схему, слабоустойчивую в смысле Стрэнга [10].
Пусть, например, в качестве исходной для уравнения
Ъи Ъи
Ъг Ъх
взята схема Лакса, т.е.
кя+1 ка — 1 т
S = тх — Г., к = —= const,
h 2 2 h
устойчивая при ка< 1. Первое дифференциальное приближение этой схемы имеет
вид
Ъи Ъи h2 „ „ Ъ2и
= а— + —(1-kV) —-•
bt Ъх 2т Ъх2
Разностная схема второго порядка аппроксимации имеет вид
un+l(x) = S£+lu°(x) - ?—(l-K2a2)SZ+lA1A_1u0(x)9 (8)
где
AiA-i = Tl~2E+T_l.
Ее можно представить в виде
u" + 4x) = S2+*Rn + 1u°(x),
где
R = Е- -(1-kV)AiA-!.
п 2
Так как
(Rnv, v) > (v,v) .Ул =0,1,-..,
то операторы Rn обратимы, и разностную схему (8) можно записать в виде
ип + 1(х) = Фпип(х),
где
Ф = ShR 4.1Л"1.
Множители усиления имеют вид
п ЛЛ кп+1 кп
где рс и р„ — спектральные образы операторов S. и R соответственно.
*И "п п п
179

X
Тогда
2
""''-'V'^ -(l-wi(.-KV)(l-*-i))
П
Г l+2(A2-H)(l-K2g2)sin2|/2l2
L l+2fl(l-/<V)sin2£/2 J '
где £ = kh9 A; — двойственная переменная, и разностная схема (8) является
слабоустойчивой в L2-
3. Покажем, каким образом, исходя из схемы первого порядка аппроксимации,
можно для уравнения
Ъи Ъи
— = а (9)
dt Ъх
построить схему третьего порядка аппроксимации.
Второе дифференциальное приближение разностной схемы первого порядка
аппроксимации имеет вид
Ъи Ъи Ъ2и Ъ3и
= а + тс2 —х- + т съ г •
Ы Ъх Ъх2 Ъх3
Для построения схемы третьего порядка точности необходимо знать величины
f2n(x) и /"(х), аппроксимирующие Ъ2и(пт,х)/Ъх2 с точностью О (г2) иЪ3и(пт,х)/
Ъх3 с точностью 0(т) соответственно. Они могут быть найдены по схемам
f2"+1(x) = Shf2"(x) -fc2SZ -^i fi(x); /?(*) = ^lV(x);
/3"+1 (*) = Sh f"(x); ft {x) = -^Zi (Al + д_,)uo (*);
2/r
u"(jc) будет находиться по схеме
«n+1 (х) = 5Й и"(х) - i*c2'f?(x) - r3c3ft (х), и°(х) = и (х, 0). (10)
Имеет место
Теорема 2. Дут устойчивая В разностная схема с первым порядком
аппроксимирует дифференциальную задачу (9). Тогда, если выполнены условия теоремы 1,
\\и"(х)-и(пт,х)\\в = 0(г3).
Доказательство.
u"(x)-u(nr,X)=Yo S* ""£%« П"да_3(5й-С(г))3С((„-/?-а-
-0-2)т)и°(*) + wS£-> (5Л - С(т)-к2с2Д,Д_, - У2 k3c3AiA..! (Д, +
+ Д_,)) «° (х) - я (и - 1) Snh~2 (Sh - С(г)) (S„ - С(т) - к2.с2 А, Д_.) и0 (*) +
180

»(« 1) c^2(s C(r)_K2,2AlA_i)2w0(;c))
2
'Л V~/2
и это есть величина 0(т3), если соответствующие производные решения принадлежат
области определения оператора С(т) и имеют необходимую гладкость.
4. Основная идея метода построения схем повышенного порядка аппроксимации
на основе дифференциальных следствий исходного уравнения может быть перенесена
на случай нелинейных уравнений.
Рассмотрим уравнение
^L + u^L = o, t>o, (ii)
Эг Эх
и (х, 0) = и0 (х) , -оо < х < +°°, (12)
где и0 (х) — достаточно гладкая функция.
Дифференциальные следствия уравнения (11) уже не являются уравнениями такого
же типа. Так, например, первая, вторая, третья и четвертая производные решения по х
удовлетворяют соответственно уравнениям
ЭгО)
dt
Эг(2)
dt
Эг(3)
dt
Эг(4)
+
+
+
+
Эг(0
ЭГ(2)
И
Эх
Эг(з)
и
Эх
ЭГ(4)
и
+ '<!>=
-+ Зг(1
+ 4'о)
+ 5г„,
0;
)Г(2)
г(з)
Г/„Ч
=
+
+
0;
Зг2 =
ЮГ^ЧА
0;
9f дх W W W <3'
Рассмотрим разностную схему первого порядка аппроксимации
un + l(x) = Shu"(x)9 (13)
где
Sh= Е-^[(ип(х) ^\ип(х)\)Т^2\ип(х)\Е^(ип(х)^\ип(х)\)Т^]9
устойчивую при условии ка< 1.
Для построения схемы третьего порядка аппроксимации выпишем второе
дифференциальное приближение разностной схемы (13) . Оно имеет вид
х(^У+9^ ^„з^М (^ V]. (14)
\ Эх / Эх Эх2 Эх3/ \Эх / J V
Чтобы построить разностную схему третьего порядка аппроксимации, надо знать
величины и, Ъи/Ъх, Э2и/дх2, Э3«/Эх3 с первым порядком точности и величины
181

и, ди/дх, Ь2и/Ьх2 со вторым. Введем векторы W и Р
и О
W = ' "'(2) >■ P=(-3r(i)r(2)
Г(3) "3^2)-440r(3)"
Г(4) -10Г(2)Г(3)-5Г(1)Г(4)/
Они удовлетворяют уравнению
\V + wW = Р,
решение которого может быть найдено с помощью разностной схемы первого порядка
аппроксимации
W" + 1 = 5ЛУГ+ тР". (15)
Для нахождения величин и, и*, ихх со вторым порядком точности воспользуемся
тем, что вектор
* = '<и (16)
'(2).
удовлетворяет уравнению
Kt+uKx=F,
ё =1 -r\iy | (17)
_ЗГ(1)Г(2)'
Применим для нахождения К разностную схему
Kn+1 = ShKn+ те. (18)
Первое дифференциальное приближение схемы (18) имеет вид
Ъи , Ъи
7+"э7= ^[iftK1-"i«i)'-a-2"M'o)];"
О) 9г(]) А • тг , „ , 1
— + " -дТ" = 2 |М|Г(3)- 2L6MrO)r(2)+M rO)+2r(i)J;
(2) 9Г(2) А Г Г , Л , , "1
— + "^Г= 2l"|rH)-il8Mr(l),'(3)+6"'-(2)+12''(l)'-(2)+M'-(4)J
182

или
дК ^ дК ж( \
Э7 Э7= гФ1М'Г0),Г(2)'г(з)'''(4))-
Разностная схема
K»+l = ShK" + тё"-т*ф(и", г",,-, г-а), г^з) • ?4> )• (19)
где компоненты Ф вычисляются как функции решения разностной схемы (15),
аппроксимирует уравнение (17) со вторым порядком. Решая ее, найдем величины
и, ди/дх> Ъ2и/Ъх2 с точностью. О (г2).
Тогда разностная схема
un+1 = Shu"- k- [|S"|(l-K|M"|)r("2)-2K0(r("2))2]-
^[кЧб«"(^1))Н9(^)2г("1)г(«2)М2")3г("з)-«"(г71))э]
имеет третий порядок аппроксимации! Здесь знаки "*- и « означают, что данная
величина есть решение разностной схемы (15) или (19) соответственно.
Анализ сходимости в линейном случае приводит к разностной схеме (10) и условию
на к, обеспечивающему устойчивость оператора S/,, т.е. к \ и | < 1.
ЛИТЕРАТУРА
1. Strang G. Trigonometric polynomials and difference methods of maximum accuracy // J. Math. Phys.
1962. Vol. 16, N 2. P. 147-154.
2. Strang G. Accurate partial difference methods: Nonlinear problems // Numer. Math. 1964. Vol. 6,N 1.
P. 36-46.
3. Kreiss H.-O. On difference approximations of dissipative type for hyperbolic differential equations //
Commun. Pure and Appi. Math. 1964. Vol. 17, N 3. P. 335-353.
4.Parlett B. Accuracy and dissipations in difference shemes // Ibid. 1966. Vol. 19, N 1. P. 111-123.
5. Русанов В. Разностные схемы третьего порядка точности для сквозного счета разрывных
решений // ДАН СССР. 1968. Т. 180, № 6. С. 1303-1305.
в. Паасонен В.П. Абсолютно устойчивые разностные схемы повышенного порядка точности для
системы гиперболического типа // Числ. методы механики сплош. среды. 1972. Т. 3, № 3.
С. 82-91.
7. Демидов Г.В. Об одном методе построения устойчивых схем высокого порядка
аппроксимации // Там же. 1970. Т 4, № 6. С. 60-69.
8. Яненко Н.Н., Шокин Ю.И. Об аппроксимационной вязкости разностных схем для
гиперболических систем уравнений // ДАН СССР. 1968. Т. 182, № 21. С 280-281.
9. Шокин Ю.И. Некоторые вопросы теории разностных схем для гиперболических систем
уравнений: Дис. ... канд. физ.-мат. наук. Новосибирск, 1969. 80 с.
10. Strang G. Difference methods for mixed boundary problem // Duke Math. J. 1960. Vol. 27, N 2.
P. 221-231.
183

РАЗНОСТНАЯ СХЕМА ДЛЯ РЕШЕНИЯ
МНОГОМЕРНЫХ УРАВНЕНИЙ ГАЗОВОЙ ДИНАМИКИ*
Существующие конечно-разностные схемы для решения уравнений газовой
динамики [1, 3] являются условно устойчивыми. В работах [4, 5] продолжены
абсолютно устойчивые разностные схемы, но не обладающие свойством консервативности.
В настоящей работе для уравнений газовой динамики и уравнений вязкого сжимаемого
теплопроводного газа построены устойчивые разностные схемы, обладающие
свойством консервативности в стационарном случае. Схемы.основаны на расщеплении
исходных уравнений по физическим процессам и пространственным переменным [6].
Одномерный случай. Уравнения газовой динамики с учетом вязкости и
теплопроводности газа могут быть записаны в виде
Э/ dW
— 4- В
dt дх
= О,
(О
где f =
и
е
F =
ри
Е
'■•-(£)
ри
W = l ри1 + р - jjl
дх
дТ
и(Е + р)-\- ^м
Эх
Э
дх
Для замыкания системы уравнений (1) задано уравнение состояния и зависимости
вязкости и теплопроводности от температуры (или внутренней энергии)
р=р(р,е), е = е</>. Т), ц = (ц(Т))", Х = (Х(7-))Ш>.
Исключая давление из исходных уравнений с помощью уравнения состояния,
представим уравнение (1) в виде расщепления по физическим процессам
Э/ 2
— + 2 Sl,f = a,
«i/=
(2)
Яа/Н
('"
|[-
U»
('
1д2
с2
д
дх
Э
дх
д
дх
д
и
дх
д
— Р +
дх
д
и
1
Р
У
Р
ъг
д
дх
д
дх
д
е
дх
дх
\ ,
Г» о =\
I
\
\
=1 о
Р \ дх I
/
*Докл. АН СССР. 1977. Т. 232, № 6. С. 1273-1276. (Соавтор В.М, Ковеня.)
184

a2=— — , b2 = — —> c2 = —-
P bp P be P
Введем в области D, в которой отыскивается численное решение уравнений (1),
разностную сетку DTh с шагами г и Л. Дифференциальные операторы Г2;-
аппроксимируем разностными операторами £2*Л с учетом знака скорости и (знак + (—)
выбираем при unh >0 {цпн <0)) с порядком к (к = 19 2, 3)
р
h
РПнА>ь
о
"а
V,ft = ±Л_1 <ft-ft? i), A\g, = ± 'АЛ"1 (3ft-4ft* ! + ftT2),
A'ft = ± VeA"1 (3ft-6ft, i + 2ft ± , + ft¥ 2), ЛЛ = % h~l (?,+ i -ft_ i),
AaAgj = h-2 [at+yi(gt+ 1 -gi)-ai_Vl (ft-ft-i)], в/±н = Уг (*/+*/± i)-
Аппроксимацию оператора ЭЙ^/Эх выберем согласованной с аппроксимацией
операторов fiy:
/ Л* (ри)Л
П JS ^ = I Л* (ри)\ + Л* р„ - А(л"И Аи„
\ Л* [и(Е + р)]„ _ ЛХ„ ATh - A»"h Au\ /2
Дня численного решения уравнений (1) рассмотрим разностную схему расщепления
(Е + та2П'2И)^" + 1 = $» + *, (3)
f П + 1 _ ftl i I. W + 1
которая в целых шагах эквивалентна схеме универсального алгоритма
C'(f"h + 1-rh)!T = -B"hSlkhW». (4)
.2
Оператор С = П (Я + щSl.h ) назовем согласованным, если в системе уравне-
ний (4) / = к.
Разностная схема (4) аппроксимирует уравнение газовой динамики при jjl = X = О
с погрешностью О (г +■ hk) (к = 1? 2, 3), а с учетом вязкости и теплопроводности
185

с погрешностью О (г + hk + jdh2). Схема реализуется скалярными трехточечными
(/ = 1) или пятиточечными (/ > 1) прогонками, что делает ее экономичной.
При получении стационарного решения методом установления в качестве
стабилизирующего оператора выберем несогласованный оператор С1 (/ = 1). В этом случае
разностная схема (4) аппроксимирует уравнение (1) с погрешностью О (hk + jdh2)
и обладает свойством консервативности (матрица Bnh невырожденная, а
стационарные уравнения записаны в виде выполнения разностных законов сохранения).
Устойчивость разностной схемы (4) исследована для системы линейных
уравнений (2) с постоянными коэффициентами, полученных линеаризацией уравнений (1).
Справедлива следующая
Теорема. Если оператор С1 согласованный, то разностная схема (4) для
системы линейных уравнений устойчива при otj > 1/2. В противном случае схема (4)
устойчива при OLj > 1.
Многомерный случай. Система многомерных уравнений газовой динамики с
учетом эффектов вязкости и теплопроводности газа представима в виде
— + В[ X —Wj) = О, р =р(р,е); (5)
bt \/=i Эху '/
здесь Xj — ортогональные координаты, TV — размерность уравнений, N = 1, 2, 3,
В = (3F/3/)"1, Wj — потоки массы, импульсов и полной энергии.
Исключая давление, перепишем уравнения (5) в виде расщепления по физическим
процессам и пространственным переменным
Э/ 2N
— + 2 П,/= а, (6)
ot j = i
где операторы £2 х,..., £2 N учитывают конвективные и вязкие члены, а £2 N+l,..., £2 2n ~
члены с давлением и свободные члены в уравнениях движения, возникающие
вследствие криволинейно сти координат и члены вида divw в уравнениях неразрьшности
и энергии по каждому направлению Xj. Вектор о содержит смешанные производные.
Для численного решения системы уравнений (6) рассмотрим схему расщепления.
• (7)
ftt+1 _ fYl I £/2+1
Jh J h K
Разностная схема (7) эквивалентна в целых шагах схеме универсального алгоритма
с f\~n --д;(Дп*уд)» (8)
2N
где С1 = .П (Е + TOt.j£ll.h ) при / = 1, 2, 3. Погрешность аппроксимации схемы (8) есть
0(т + hk +дЛ2), где Л =max /ь.
К, j <N
Как и в одномерном случае, разностная схема (7) устойчива при тех же
ограничениях на otj реализуется трехточечными (/ = 1) или пятиточечными (/ > 1) скалярны-
186

ми прогонками. При решении стационарных задач в качестве стабилизирующего
оператб.ра выбирается несогласованный оператор С1. Погрешность аппроксимации
разностной схемы (8) в этом случае О (hk + iih2) (к = 1, 2, 3). Схема обладает
свойством консервативности.
Замечание. Разностная схема (8) может быть представлена в дробных шагах
различными способами, например в виде схемы типа стабилизирующей поправки
г"1 (fhn + ll(2N)-fh")+ оч^[н(ГнП+1К2Ю-Гн")=-Впн[^1П^"н}
г-1 (C+1 -/;♦<*"-'>/(*">) + a2NnlNh(fh"+1 -/;> = о.
Примеры расчетов. Численно изучено течение около цилиндра, обтекаемого со
сверхзвуковой скоростью потоком вязкого теплопроводного газа при числах М = 3,
8, 30 и Re = 45, 200. Использована система координат s, n, связанная с поверхностью
тела. Стационарное решение задачи (5) отыскивалось в области, ограниченной осью
симметрии, поверхностью тела, лучом s = s0 ^ я/2 и верхней границей R(s).
Посредством преобразования £ = 5/5<ь V = n/R(s) расчетная область отображалась
в единичный квадрат. Для решения уравнений . (5) в переменных £ и т? применялась
разностная схема (8) при / = к = 1, а;- = 1.
Расчеты показали, что разностная схема (8) является устойчивой и для системы
нелинейных уравнений (итерационный параметр г изменялся в диапазоне 0,5Л <т <5Л,
где h - max (Л19 h2)). Для получения стационарного решения, т.е. до выполнения
1 Эр
условия max |- 1 < 10 , требовалось 250—350 итераций на разностной сетке
18X20 или 18X30 (в качестве начальных условий в расчетной области задавался
невозмущенный поток, а на поверхности тела условия прилипания и тепловой
изоляции). Результаты расчетов хорошо согласуются с приведенными в работах [2, 5]. Ддя
получения численного решения с той же точностью, что и по не консервативной
схеме [5], число узлов разностной сетки в направлении п может быть уменьшено в 2 раза.
ЛИТЕРАТУРА
1. Рихтмайер Р.Д-, Мортон К. Разностные методы решения краевых задач. М.: Мир, 1972.
2. Павлов Б.М. II Некоторые применения метода сеток в газовой динамике. М.: Изд-во МГУ,
1971. Вып. 4.
3. Численное исследование современных задач газовой динамики / Под ред. 0,М. Белоцерковско-
го. М.: Наука, 1974.
4,Яненко ИМ., Фролов ВЛ, Неуважаев В.Е. Ц Изв. СО АН СССР. Сер, техн. наук. 1967. № 8,
вып. 2.
5. Березина Ю.А., Ковеня В.М., Яненко Н.Н. // Аэромеханика: Сб. ст. М.: Наука, 1976.
в.Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск: Наука, 1967.
187

О РАЗНОСТНЫХ СХЕМАХ В ПРОИЗВОЛЬНОЙ
КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ*
1. В настоящей работе предлагается метод построения разностных схем на
произвольной сетке на основе разностной схемы, заданной на равномерной сетке в той же
системе координат. Исследуется вопрос о сохранении разностной схемой на
произвольной сетке характеристик исходной разностной схемы.
2. Использование криволинейных систем координат при решении задач газовой
динамики конечно-разностным методом позволяет рассчитьшать течения в областях
сложной конфигурации, учитывая поведение особенностей течения. Применение
криволинейных систем координат ставит перед вычислителем задачу построения
разностных схем в таких системах координат. Возникает вопрос о преобразовании
разностных схем (при преобразовании координат), хорошо зарекомендовавших себя в
декартовой системе координат, и, в частности, о преобразовании разностных схем
при невырожденном преобразовании координат.
Пусть Rn — л-мерное евклидово пространство х, у G Rn9 ф : Rn -+Rn (ф(х) = у) —
невырожденное преобразование, В (со) и В (со) — пространства сеточных функций,
определенных на сетках со G Rn и со G Rn соответственно, причем ф(со) = со.
Сужения отображений ф и ф~* на множества со и со соответственно индуцируют
отображения ф\В(со) -^ В (со) и ф"1 :В(со) -* В (до), определяемые равенствами
(ФТ)(х) = Г(Ф(х))> ($~70) =/(Г1 00);
здесьдгЕсо, у G со,/ G В (co),7^G В (со). Поэтому, если Л— оператор,отображающий
В (со) в В (со), то отображение ф: со -* со определяет преобразование этого оператора
в оператор Л, отображающий В (со) в В (со), следующим образом:
л/ = Ф~1[\(Ф7п
Заметим, что в этом случае сетка в "новой" системе координат зависит от "старой"
сетки (25 = ф(со)).
3. Пусть Л ™+1 = {(Г, х): t > 0, xG Rm }, Дискретное множество точек (tn,xn) G
Е R™+1 будем называть сеткой, если существует невырожденное отображение ф:
R™+1 -+R™+1 такое, что точка (f„,х?) является прообразом (при отображении ф)
точки (иг, /1Л1, ..., ]mhm)\ здесь т, п = (Л1} ..., hm) — шаги по соответствующим
осям пространства Д ™+1, / = (/i> ->/m), x™ GRm.
Таким образом, под сеткой понимается прообраз равномерной сетки при
некотором неввгрожденном отображении.
Суть предлагаемого метода состоит в следующем. Пусть В1 — некоторое банахово
пространство функций, определенных на R™+1, L :В' -+ В1 — некоторый оператор.
В системе координат (t, x) зададим на равномерной сетке разностную схему
^тнитн ~ frh'» аппроксимирующую уравнение Lu ='/; и* /» нтЛ,/тЛ е &•
Обозначим через со равномерную сетку в системе координат (/', х1), т — шаг по оси
t , h1 = (h'u ..., h'm), h'k — шаг по оси х'к, к =1.,,.., т. Предположим, что системы
координат (Г, х) и (t\ х') связаны невырожденным преобразованием t' =t,
х = х (t, х), а параметры г, h и г', h1 — гладким преобразованием г = г и W -
= hr (r, h) таким, что якобиан этого преобразования отличен от нуля в точке г = О,
h = 0. Пусть со — прообраз сетки сЗ при отображении (г, х) -> (f', х'). На сетке со по-
*Докл. АН СССР. 1978. Т. 242, № 3. С. 552-555. (Соавторы Ю.И. Шокин. А.И. Урусов.)
188

строим разностную схему
(и \ /'еЯ(со) — банахово пространство сеточных функций), аппроксимирующую с
максимальным порядком задачу AjhuTh =fTh- Здесь под аппроксимацией мы
понимаем существование и равенство нулю предела
lim lSr.h.urh -/'II = О
(т, Л)->0
на решениях uTh задачи \ThuTyl = fTh. Далее по полученной на сетке со разностной
схеме строим разностную схему
?? ~~ "У
Sr'H'U =/
на сетке 23. Очевидно, что последняя является "преобразованной" схемой
Лгл uTh = fTh
и зависит от используемого шаблона в криволинейной системе координат и от
функций т' = ту h' = h' (r, И).
4. Ниже для простоты ограничимся случаем т = г, Л' = Л и невырожденным пре-
образвванием координат V = f, х' = х' (Г, х).
Рассмотрим разностную схему
(ип+1 (х)-ип(х))/т = Л^и" (х), (1)
аппроксимирующую уравнение
Ъи/bt = Аи, 0 < t < Т, (2)
с порядком О(т7 + \h \к) на достаточно гладких решениях и (Г, х) G с7; здесь А —
линейный оператор, А :В ~* В\ U — всюду плотное подмножество в В> причем £/
содержит бесконечно дифференцируемые функции. Под решением уравнения (2)
понимаем однопараметрическое семейство элементов и (Г) Е В, удовлетворяющих
условию
lim \\u(t + At)-u(t))IAt~Au(t)\\ = О, ty t + Ate [0, T].
Рассмотрим также разностную схему
'— '— = £* !>"(*;), (3)
аппроксимирующую (1) с порядком 0(т 1 + | h \ 1) на решениях и (х) G U, т.е.
\ип(х)еи
Uu»tf+1)-u»{xp)lT ~ [АтНип{хр-АтНип{хп^Щв{^ <
< M(w,I)(r/l +I/H*1);
здесь i?(co) — банахово пространство сеточных функций, определенных в узлах
сетки со { (пт,х,г)} 9п> 0,пт<Т, xn ERm, j — мультииндекс.
В этом случае разностная схема (3) аппроксимирует уравнение (2) с порядком
0(т1* +|Л |*2),где /2 =min (/,/i), k2 =min (к,кг).
Имеет место
Теор,ема, Пусть разностная схема (1) аппроксимирует уравнение (2) на
решении и (t, х) из некоторого эталонного класса U С В с порядком О (г 4- \h | ), а
рсЬностная схема (3) аппроксимирует разностную схему (1) на решении и из класса
U с порядком 0(t*i +|/i \kl)t причем 1\ ^ /,Агх ^ к. Тогда:
189

1) разностная схема (3) аппроксимирует уравнение (2) с порядком 0(i* +\h\k);
2) если разностные схемы (1) и (3) устойчивы, то
1"я-у"1ад < С(т1* + |й|*«)
равномерно по t = пт Е [ 0, 7], где { и"} - решение разностной схемы (1) с
начальным условием
и° (х) = и(х) G U,
{vn) - решение разностной схемы (3) с начальным условием
3) диссипация и дисперсия [1] разностных схем (1) и (3) различаются на величи-
Ik
ну О (г 1 + | Л | *) для каждой гармоники.
5. П-формы дифференциальных представлений разностных схем (1) и (3) имеют
соответственно вид [2]
du/dt = г"1 In (Е + тЛ) и, rfu/tff = г"1 In (£ + тЛ) у.
Пусть г/Лу = к7- = const,/ = 1, ..., m (что обычно для случая гиперболических
уравнений), и разностная схема (1) аппроксимирует уравнение (2) с порядком 0(т[),
а разностная схема (3) аппроксимирует уравнение (2) с порядком 0(t1i).
Тогда
атИ = а + е,
где
Qvn (xh) = ЛтЛиЛ(хЛ)-Ли,1(л:Л).
Но
Qun(xn) = (1/т)(Е + тА)[ип (х1+1)-ип (хр] + фп (ип)9
фп (ип) = АтИип (хп)-Аип (хп+1 )-(1/т)[ип (хп+1)-ип (У.)]-
Таким образом, в случае неподвижной сетки
Qun (хп) = i//" (н")>
и, следовательно,для ип£ U
ll<2""llB((J)<c("'')7','
а тогда
tfu _.1п(Я + тЛ)
dt т
' ■=( 5 ^— Л/ + Г1» 5 ("r)/"1 /z1 c'aV1)'-'*-"1©')'-* I »,
1/= 1 / /= 1 / k=0 J J
где Q' = т~1! Q. Отсюда
[ 1п(£ + тЛ) 1п(ЕЧ-тЛ) \ ,
(г - г 1 "=0(Г,)
для достаточно гладких функций из класса U.
Итак, если сетка (пт, х?) неподвижна, r/hj = Ку = const, / = 1, ..., m, kx > l\ >
■> min (/, А:), то первые дифференциальные приближения (п.д.п.) разностных схем
190

(1) и (3) совпадают. Тогда в случае разностных схем нечетного порядка
аппроксимации из корректности п.д.п. разностной схемы (1) следует корректность п.д.п.
разностной схемы (3), что означает выполнение необходимого условия устойчивости
разностной схемы (3). В случае разностных схем четного порядка аппроксимации
это также имеет место, если
h - 1 > min(/, к).
Из совпадения п.д.п. разностных схем (1) и (3) следует преемственность свойств
разностных схем, определяемых через п.д.п. (например, свойства К, свойства М,
свойства инвариантности разностных схем [2, 3]). Используя метод предиктор-
корректор, можно получать консервативные разностные схемы в криволинейных
системах координат.
ЛИТЕРАТУРА
I.IUokuh Ю.И. // Числ. методы механики сплош. среды. 1976. Т. 7, № 7. С. 131.
2. Шокин Ю.И. II Численные методы газовой динамики: Инвариантные разностные схемы.
Новосибирск, 1977.
3. Яненко Н.Н.У Шокин Ю.И. // ДАН СССР. 1968. Т. 182, № 4. С. 776.
УПРОЩЕННЫЕ УРАВНЕНИЯ
ДЛЯ ОПИСАНИЯ ТЕЧЕНИЙ ВЯЗКОГО ГАЗА*
Численное исследование сверхзвукового обтекания тел на основе многомерных
уравнений Навье—Стокса связано со значительными трудностями, вызванными
ограниченностью памяти и быстродействия существующих ЭВМ. Поэтому при исследовании
сверхзвукового обтекания тел потоком вязкого газа широко применяются упрощенные
уравнения [1—6], которые справедливы как во внешнем потоке, так и в пограничном
слое. Эти упрощения связаны с оценкой порядков малости членов в уравнениях Навье—
Стокса и исключением членов порядка 0(1/Re) или 0(1 A/Re).
Упрощенные уравнения имеют эволюционный тип относительно пространственной
переменной, что позволяет решать их как начальнокраевую задачу маршевым методом,
требующим существенно меньших затрат машинного времени и памяти ЭВМ по
сравнению с традиционным методом установления. Известно [3], что краевая задача для
упрощенных уравнений является корректной лишь в сверхзвуковой области
течения. Для численного решения в дозвуковой области используются различные
приближения [3,4], позволяющие корректно сформулировать краевую задачу.
В настоящей работе для численного решения задач обтекания предлагаются
упрощенные уравнения Навье—Стокса, описывающие течения с поперечными вихрями. Для
устранения некорректности в дозвуковой области предложен подход получения
устойчивого решения без понижения точности в сверхзвуковой области.
Исходные уравнения. Рассмотрим систему двумерных упрощенных
уравнений, записанных в цилиндрических (/=1) или декартовых (j =0) координатах
Эр Эр / Ъи 1 Э . \
и — +у + р + — rJv =0,
Ъх Ъг \ Ъх п Ъг J
Ъи Ъи 1 +ф Ър 1 Э . Ъи
v Ъх Ъг р Ъх Rer7p Ъг Ъг
* Докл. АН СССР. 1979. Т. 245,№ 6. С. 1322-1324. (Соавторы В.М. Ковеня, С.Г. Черный.)
191

Эе Эе р Ъи 1 Э . \ 1 1 Э . ЪТ I Ъи \2
и + v + - I — + -т — r'v) = {—.— г'Х + д(-— ) } ,
дх Ъг р \ Ъх г> Ъг ) Rep [ г'Ъг Ъг \Ъг } \
р = р(р,Т), (X = м (Г), X = Х(Г).
В системе уравнений (1) сохранены члены, порядок малости которых 0(1), и один
член в уравнении поперечной компоненты количества движения порядка <?(1/\/r£).
/•'
1
гш/я) ^
I
I
l^L--
*fc
Xf Хг X Г Zp О 0,4 0,8 1и
Рис. 1
Геометрия модели
Распределение плотности р (а) и составляющей скорости и (б)
1 — метод установления (уравнения Навье—Стокса) ; 2—4 — маршевый метод (наши данные (2) ,
данные [4] (3) , данные [3] (4))
щ
Ъх
, а вектор f имеет компо-
Такая модель позволяет описывать поперечные вихри, исключая только возвратные
течения. Функции <р и ^вводятся таким образом, чтобы в сверхзвуковой области члены
Ъи ф Ър
уи — и имели порядок малости 0(1/VRe), а в дозвуковой области задача
Ъх р Ъх
Коши была корректно поставлена:
V? = 6F01, ф = -(5F/(1 +F)f,
где б = 0(1/у/Ш)\ а, 0 — весовые множители; F = 2
ненты/ь /2, /з, Л = Р, w, f, 71. Введение функций у и ф позволяет автоматически
заданием параметров ос и 0 рассчитывать дозвуковые области. Действительно, с
возрастанием колебаний газодинамических функций, вызванных некорректностью задачи,
увеличивается влияние членов 1ри(Ъи/Ъх) и (ф/р)(Ър/Ъх) и краевая задача (1) становится
корректной. При у = 0 и ф = — 1 данный подход совпадает с рассмотренным в [4].
Для удобства численного интегрирования вводится преобразование координат
£ = х, т? = ^-^ — ,. (2)
R(x)-rw(x)
которое переводит расчетную область в единую полосу; здесь rw(x) — поверхность
обтекаемого тела R (х) — внешняя граница.
Примеры расчетов. Для опробования предложенной модели проведены
расчеты обтекания цилиндрического тела с "юбкой" (рис. 1) сверхзвуковым потоком
192

вязкого теплопроводного газа под нулевым углом атаки. Система уравнений (1) в
переменных £ и ц решалась численно по неявной разностной схеме типа Кранка—Николсо-
на. Для повышения точности расчетов использовалась подвижная разностная сетка,
построенная на основе вариационного принципа [7] и сгущающая узлы сетки в
области больших градиентов в поперечном направлении. Координаты узлов сетки
определялись из решения уравнения
Ъг Ъ Ъг
= К (3)
bt Ъц Ъц
при t -*°° со стационарными краевыми условиями, где
К = А +
V| Ъг | /=i J Эт? I /'
Выбором параметров аг и /Зх задавалось необходимое сгущение узлов разностной
сетки. Решение уравнения (3) находилось по неявной разностной схеме, после чего
вычислялись коэффициенты преобразования координат Ъг\[Ъх и Ъц/Ъг. Совместное
решение системы уравнений (1) —(3) в каждом сечении находилось итерациями.
Проведены расчеты обтекания цилиндрического тела с изломом образующей при
следующих параметрах: М = 6; Re = 10а; Рг = 0,72; у - 1,2. Уравнение состояния взято
в виде р = (7 — I) ре. Вязкость и теплопроводность выбраны зависящими от
температуры по степенному закону с со = 0,75. Угол наклона образующей в =15°. В сечении
х = 0 опробовано два типа начальных условий: условия невозмущенного потока и
условия, полученные из решения полных уравнений Навье—Стокса. Головной скачок в
процессе решения не выделялся, на поверхности тела задавались условия прилипания
и тепловой изоляции. Некоторые результаты расчетов приведены на рис. 2, где даны
распределения плотности (а) и составляющей скорости и (б) в сечении* = 0,63. Там же
для сравнения нанесены результаты расчетов, полученные по другим моделям.
На основе приведенных расчетов можно сделать вывод, что предложенная модель
применяется для получения общей картины течения. Для детального описания
структуры течения в дозвуковой области необходимо использовать уравнения Навье—Стокса.
Кроме того, решение, полученное на основе упрощенной модели, может быть взято
в качестве начального для решения полных уравнений Навье—Стокса, что позволяет
значительно уменьшить затраты машинного времени.
ЛИТЕРАТУРА
1. RudmanS., Rubin S.G. // AIAA J. 1968. Vol. 6, N 10. P. 1883.
2. Головачев Ю.П., Попов ФД,. II Журн. вычисл. математики и мат. физики. 1972. Т. 12, № 5.
С. 1292.
3. Байт E.t DemsemM.R. // AIAA J. 1967. Vol. 5, N 7. P. 1224.
4. Lin T.C., Rubin &G. // Comput. and Fluids. 1973. Vol. 1, N 1. P. 37.
5. ВоронкинВ.Г. И Изв. АН СССР. МЖГ. 1974. № 6. С. 99.
6. Hellvwel W.S.r Lubard S. G. 11 Comput. and Fluids. 1975. Vol. 3, N 1. P. 29.
7. Яненко НЖ, Данаев H.T., Лисейкип В.Д. /•/ Числ. методы механики сплош. среды. 1977. Т. 8,
№4. С. 157.
7. Зак. 953
193

О ПРИМЕНЕНИИ ПРИБЛИЖЕННОЙ ФАКТОРИЗАЦИИ
В МЕТОДЕ РИТЦА И В МЕТОДЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ*
В работе [1—4] получил широкое развитие эффективный метод приближенной
факторизации, основанный на аппроксимации исходных дифференциальных уравнений ко-
нечноразностными и позволяющий сводить решение многомерных задач
математической физики к последовательному решению некоторых одномерных разностных
уравнений. Перенесем по аналогии основные представления этого метода на решение
многомерных задач на основе классического метода Ритца или метода конечных элементов.
Последний метод эквивалентен методу Ритца при определенном выборе координатных
(базисных) функций [5].
Рассмотрим использование приближенной факторизации в методе Ритца на примере
решения двумерного нестационарного уравнения теплопроводности:
Ьи Ь2и Ь2и
— =Дм + / = г+ +/ (1)
Ы Ьх2 Ьу2
в области £2 (0 < х < 1,0 <у < 1) для случая третьей краевой задачи, когда на границе
области S задано Ьи/Ьп + ои = 0, где о = const > 0, п — внешняя нормаль к границе
области. В момент времени t = 0 задано в Т2 также некоторое начальное распределение
температуры.
Один из возможных подходов к решению этой задачи на основе метода Ритца
заключается в следующем. Заменяя производную по времени конечноразностным
выражением с точностью 0(т) ^представим (1) в виде
и"+* _ TAun+l = г/ + и",
где г — "шаг" по времени, верхние индексы п и п + 1 обозначают номер слоя по времени.
Таким образом, на каждом временном слое приходим к решению следующего
дифференциального уравнения:
Аи + аи = \р, (2)
где <£ — известная функция; а < 0.
Решение этого дифференциального уравнения при соответствующих граничных
условиях, третьей краевой задачи в области 12 на основе метода Ритца будет экстремаль
следующего функционала:
F(u) = ${VuVu + luy - аи2)ст + fou2dS,
si s
Ь Ь ,
где точка означает скалярное произведение; Д= i —+/ .
Ьх Ьу
Применяя стандартную процедуру метода Ритца или метода конечных элементов
находим решение и, дающее минимум функционала F(u). Как видно, приходится
минимизировать двумерный функционал.
Используя метод приближенной факторизации, уравнение (2) можно представить
в виде системы двух одномерных дифференциальных уравнений
b2v Ь2и
т—г - v = -ту, т-ГТ ~ и = v (3)
Ьх2 Ьи2
с граничными условиями при х = 0, х = 1:
-bv(0yy)/bx + ov(0,y) = 0; bv(l,y)/bx + ov(l,y) = 0,
* Динамика твердого тела. Новосибирск, 1980. Вып. 45. С. 48-57. (Соавтор С.Н.Васильковский).
194

приу = 0,у=1:
-bu(x, 0)/by + ои(х, 0) = 0; ду(х,1)/ду + ои(х, 1) = 0.
Следует заметить, что система уравнений (3) эквивалентна уравнению (2)
приближенно с точностью О (г) в то время, как граничные условия для функции v являются
точными. Для системы (3), с соответствующими ей граничными условиями, можно
дать эквивалентную вариационную формулировку. Тогда функция v находится как
точка минимума следующего одномерного функционала Ix (v)
1 / dv dv \
h (р) = Д т - 2rv<p + v2)dx + таи2(1,у) + rou2(0,v),
0 \ Ъх Ъх I
а искомая функция и находится как точка минимума функционала 12(и)
1 (Ъи Ъи \
1г(ц) = S ( т + 2vu+u2)dy + тои2(х, 1) + той2(х, 0).
о \ Ъу Ъу /
Таким образом, используя приближенную факторизацию в методе Ритца и в методе
конечных элементов при решении многомерных задач, приходится минимизировать
последовательность одномерных функционалов, что является более эффективным при
проведении практических расчетов.
По предложенному здесь нестационарные поля температур в двумерной области со
сложной геометрией, изображенной на рис. 1—3. Заданная область интегрирования в
форме прямоугольника имеет три отверстия: одно (самое большое по размерам) в
центре, на верхней границе которого задано краевое условие третьего рода, т.е. условие
теплообмена кЪи/Ъп + ки~ киср, где к — коэффициент теплообмена между средой
(воздухом) и металлом (в данном случае рассматривалось железо), иср — температура
нагретой среды (воздуха), и два других, меньших по размерам отверстия по краям
области. На внутренних границах этих двух отверстий температура и = 0. Все три
отверстия имеют форму прямоугольников. Температура и = 0 также и на внешней границе
заданной прямоугольной области с внутренними отверстиями. В начальный момент
времени t = 0 температура во всей области интегрирования равна нулю. Поскольку
поставленная задача симметрична относительно вертикальной прямой, проведенной
через середину области, то на рис. 1—3 изображена только левая половина заданной
области
Поставленная задача решалась путем минимизации одномерных функционалов
Ii(v) и /г (и) на основе метода конечных элементов. Рассмотрим типичный отрезок,
на котором приходится минимизировать функционалы Л (и) и /2("), исходя из
поставленной выше краевой задачи для четырех связной области интегрирования. Пусть это
будет -отрезок,параллельный оси *, границы которого для простоты будем обозначать
от 0 до 1. На левом конце этого отрезка по условию поставленной задачи имеем и =0,
на правом конце рассмотрим условие теплообмена Ъи/Ъх + охи- ух(у). Если мы
определим искомую функцию на первом дробном шаге, то граничные условия для нее
соответственно перепишутся на левом конце отрезка v = 0, на правом конце отрезка
Эи/Эх + oxv = Tip"(y) - ^100== Фг'(у) как'и = тЪ2и/Ъу2 —и. Таким образом, типичным
функционалом, который приходится минимизировать в поставленной выше задаче
на отрезке [10, 1], является функционал
lip) = }(rv2+2unv + v2)dx+ т[о^2(1,у)-2фМ19у)}9 (4)
0
учитывая v(0,y) = 0.
Разбиваем отрезок [0, 1] сеткой узлов 0 = х0 <хх < ... <xN = 1. Конечными
элементами считаем /^ = [хк, хк+1 ], где к меняется от 0 до N— 1. Пусть также hk =хк+ г —
7*
195

■хк. На элементе 1к принимаем линейную интерполяцию
..к Хк+1 ~х , ^к+1 *-*к
v(x) = vK^ + и*+1-—^-, (5)
где для краткости введено обозначение vk = v(xk). Подставляя (5) в функционал
(4), имеем
I(v) = 2_1 Г1 (tv2 + 2unv + v2)dx+r[o(uN)-2vN\p] =
*=0 хк Х
N-\\ Т ._,_, . „ ^хк+1 Хк+% -X и^*хк+1 Х-Хк
= 2 — (vk+1 -vk)2+2vk / unJ^ dx + 2vk+1 J -undx +
k=o L hk *£, hk xk hk
+ lhhk(vk+lvk+l +ufe+1/+yV) +т[а1(иЛГ)2 -2iAiM S*V .-..i^).
Необходимыми условиями минимума F(vl,..., t)W) на множестве у* являются
bF/to* = О, *=1,2,...,М
Рассмотрим эти условия для внутренних точек к =1, 2,..., iV— 1:
9F
\ 3 /**_! / L 3 \ftfc_! Ajt /j
— - — }vk+1 +2/ ня*?(х)Л = О,
3 A* / ^дг-1
(6)
где
{(x -хк_г)/ hk_ly x£ /fc_!;
(x*+1 -x)/hkt x<=lk;
0, *^ /fc_i, /*.
Пусть /i* = (^_j + hk)/2, тогда
*A:+1 IIя ^*
/ -тег- Л = Ц»(**)
при Л* -* 0, так как
*k+i фк(х)
f I dx =1.
*fc-l hk .
Таким образом можно представить (6) в виде
- -тг J + —=— » + /з »'
fcfc L hk hk_l J 6й* 6Afc
+ «"(**) = 0>
что, как легко видеть, является разностной аппроксимацией первого уравнения из
(3) при/ но.
Рассмотрим условие минимума dF/bvk при Л = N, тогда
dF 2т ,N .w_n.„ w "„ , . „*jy . „ж-»аг-1 ,.
* + -~vk+i+ (7)
-(1Л-илг-1) + 2т01илг-2тф1+2/ к" АГ"1 dx
+ 2hhN_x^-^-vN-i =0_ (8)
196

Интегральный член в этом уравнении также, как и выше, можно представить в виде
hN_lun{ \,у) при hN_x -* 0. При условииhN_x <тв уравнении (8) можно пренебречь
тремя последними членами и представить его в виде
ivN_vN-l)/hN_i +0iVN = ф^ (9)
что, как нетрудно видеть, является разностной аппроксимацией уравнения Эи(1 ,у)/дх +
+ о1и(1,у) = ф1(у).
Таким образом, используя обычную трехточечную прогонку из уравнений (7) и (9),
можно определить все неизвестные vk (к = 1, ...,N). Тогда функция v(x) определится
■ Г i ' 1 I 1 i i i 1 i | LJ 1 1 1 1 L_
О 0,Z 0,¥ 0,0 0,0 /,0 0 0,Z О,* 0,0 0,0 /,0 0 0.Z 0,4 0,0 0,0 1,0
Рис.1 Рис.2 Рис.3
как
v(x) = vk(xk+i -x)/hk +u*+1(x -**)/** на lk,
к = 0, ..., N — 1 и даст приближенное решение задачи о минимуме функционала (4).
Аналогично минимизируется функционал /2 (и).
На рис. 1—3 представлены некоторые результаты расчетов по предлагаемой
методике. Сетка узлов, на которой ищется решение задачи, была выбрана неравномерной. С
одной стороны, выбор неравномерной сетки диктуется чисто математическим условием
hN-\ < г, с другой — такой выбор определяется физической сущностью задачи, так
как в окрестности нагреваемой границы возникают большие градиенты температуры,
для правильного расчета которых необходимо мельчить "шаг" сетки в окрестности
нагреваемой границы. Выбор неравномерной сетки в исследуемой задаче осуществлялся
по рекомендациям, данным в [6].
На рис. 1—3 изображено распределение изотерм 0 = в/Т0 в заданной области в
различные моменты времени: 7= 7,2 • 10"2 (рис. 1); t = 3,6 • 10"^ (рис. 2); 7 = 7,2 • 10"1
(рис. 3), где безразмерное время t определяется по формуле 7 = kt/pcd2 (к —
коэффициент теплопроводности, р — плотность, с — удельная теплоемкость, d — характерный
линейный размер области). Остальные безразмерные переменные определялись по
формулам: х = x/d, у = yjd, в = в/Т0, где Т0 - начальная температура области. Результаты
расчетов представлены для железа. Коэффициент теплообмена к = 5,84 • 103 кг/град.с3,
197

мср = const = 1500 К. Из приведенных результатов на рис. 1—3 видно, что эффективный
разогрев материала осуществляется в виде "температурной волны",
распространяющейся с некоторой конечной скоростью в двумерной области интегрирования (см., напр.,
[7]).
ЛИТЕРАТУРА
1. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск: Наука, 1967.195 с.
2. Годунов С.К., Рябенький B.C. Разностные схемы. М.: Наука, 1972. 439 с.
3. Самарский АЛ. Теория разностных схем. М., 1976. 552 с.
4. Марчук Г.И. Методы вычислительной математики. Новосибирск: Наука. 1969.455 с.
5. Зенкевич О., Чанг И. Метод конечных элементов в теории сооружений и в механике сплошной
среды. М.: Недра, 1977. 239 с.
6. Васильковский С.Н., Спирков В.Л. Напряженное состояние и инициирование образцов
прямоугольной формы твердого ВВ при локальном тепловом воздействии на границе // Динамика
сплошной среды. Новосибирск, 1977. Вып. 29. С. 20-26.
7. Зельдович Я.Б., Райзер Ю.Я. Физика ударных волн и высокотемпературных гидродинамических
явлений. М.: Наука, 1966.
РАСЧЕТ ГАЗОДИНАМИЧЕСКИХ ТЕЧЕНИЙ
НА ОСНОВЕ МЕТОДА КОНЦЕНТРАЦИИ*
1. Для расчета газодинамических течений в однородной среде с успехом применяются
вычислительные методы, использующие переменные Эйлера (см., напр., [1,2]). Однако
применение этих методов при расчете течений в неоднородной среде наталкивается
на значительные трудности, связанные с выделением границ веществ и
предотвращением счетного размазывания (счетной диффузии) первоначальных скачков
плотности, энергии и других величин. Эта проблема различным образом решается в ряде
методик [3—5].
Особое место занимает метод "частиц в ячейках" [6—8]. Каждому веществу здесь
соответствуют частицы определенного сорта, положение частиц данного сорта
определяет распределение веществ в задаче. Этим методом можно рассчитывать течения
с большими деформациями.
В данной работе излагается другой подход к расчету газодинамических течений
неоднородной среды в переменных Эйлера, использующий массовые концентрации
веществ и специальный алгоритм счета потоков из счетных ячеек, в которых
содержится несколько веществ (метод концентраций). Метод концентраций примыкает
к методам типа частиц в ячейках.
2. В качестве исходных уравнений, описывающих нестационарные осесимметрич-
ные движения газа, принимаются соотношения, выражающие законы сохранения для
неподвижного объема со:
дМ
—— = -fpuds; (1)
dt s
dK
+fPds = - fpu(uds); (2)
dt s s
dE
— + / P div udco = - f epuds. (3)
dt ijj s
Здесь s — поверхность, ограничивающая объем со; М = / pdco — масса, Е = f epdco —
♦Докл. АН СССР. 1981. Т. 257, № 3. С. 566-569. (Соавторы СМ. Бахрах, Ю.П. Глаголева, М.С. Сами-
гулин, В.Д. Фролов, Ю.В. Янилкин.)
198

внутренняя энергия, К = f pudco — количество движения заданного объема со; р —
to
плотность, Р — давление, е — удельная (на единицу массы) внутренняя энергия,
u(v, w) — скорость. Система (1)—(3) замыкается уравнением состояния Р = Р(р, ё).
В области интегрирования £2 задается некоторая счетная сетка, на которой строится
разностная аппроксимация уравнений»(1) — (3) . Используемая нами разностная схема
в случае однородной среды близка к схеме работы [4]. Изменение величин М, К, Е
за счет членов, стоящих в правых частях уравнений (1)—(3), определяется потоками
соответствующих величин через стороны счетных ячеек.
3. В неоднородной среде в дополнение к основным величинам (х, у, v, w, р, e) в
каждой счетной ячейке задаются массовые концентрации веществ
где Mi — масса ьго вещества в ячейке, М — масса ячейки, и удельные (на единицу
массы данного вещества) внутренние энергии е,-. Наличие в системе различных по своим
свойствам веществ приводит к появлению ячеек, содержащих смесь различных
веществ ("смешанные ячейки"). Локализация контактных границ может проводиться
по полю соответствующих концентраций веществ.
При таком подходе возникают две основные проблемы, от решения которых
зависит эффективность вычислительного метода: вычисление давления и плотностей
компонент в смешанной ячейке и счет потоков массы, энергии и других величин из
смешанной ячейки.
4. Первая проблема аналогична соответствующей проблеме для метода частиц в
ячейках. Задача сводится к определению по заданным уравнениям состояния
компонент смеси
и известным Величинам — плотности смеси р, удельным внутренним энергиям е,-
компонент смеси и их массовым концентрациям а,- — известных величин: давления Р и
плотностей Pi веществ. Предполагается аддитивность удельных объемов и равенство
давлений всех веществ в ячейке. Таким образом, приходим к следующей системе
алгебраических уравнений:
1 ** ос{
- = 2 — , P = Pi(Piyei)9 i= 1,2, ...9N, (4)
Р '"=i Pi
где TV—число веществ.
Система (4) разрешима в конечном виде лишь в простейших случаях (например,
когда все вещества <- идеальные газы); в общем случае для ее решения используются
итерационные методы. Определенные из системы (4) плотности р,- используются при
счете потоков массы из смешанной ячейки.
5. Вторая проблема носит более фундаментальный характер. Если не вводить
специальных алгоритмов счета вытекающего потока из смешанной ячейки, то, например,
в одномерном течении с постоянной скоростью число смешанных ячеек будет расти
пропорционально числу счетных шагов (на каждом счетном шаге будет добавляться
одна счетная ячейка, в которую втекает смесь веществ). Другие величины — плотность,
внутренняя энергия — также будут "размазываться" счетным образом.
Для того чтобы предотвратить счетное размазывание, предлагается следующая
простая идея: из смешанной ячейки в чистую вытекает вначале то вещество, которое
содержится в чистой ячейке; тем самым ограничивается счетное размазывание. В общем
случае производится анализ поля концентраций; по полю концентраций
определяется вид-" контактной границы и на этой основе определяется поток из смешанной
ячейки.
В том случае, когда из смешанной ячейки вытекает смесь веществ а и /3, принимается
(в зависимости от вида контактной границы), что скорости иа и ив вытекания веществ
199

различны: эти скорости определяются по скоростям ближайших узлов сетки,
принадлежащих соответствующим чистым ячейкам; т.е. вводится скольжение и появляется
возможность учитывать тангенциальные разрывы. Таким образом определяются
потоки массы и энергии для каждой из компонент.
Для неоднородной среды вместо одного уравнения энергии (3) рассматриваются
соответствующие уравнения для каждой из энергий компонент ег-. При этом возникает
(так же как и в методе частиц в ячейках) проблема вычисления для каждой из
компонент приращения внутренней энергии за счет работы сил давления. Здесь используются
те же подходы, что и в работах [6—8].
Рис. 1 Рис. 2 Рис. 3
6. Построенный на этих принципах вычислительный алгоритм ЭГАК использует
прямоугольную сетку, линии которой параллельны координатным осям (ось Ох ось
симметрии). Разностная схема методики ЭГАК имеет порядок точности, является
условно устойчивой. Ограничение на шаг г интегрирования по времени имеет
следующий вид:
t{\v\ Ay + \w\ £x + cmzx(Ax, Ау))<Ах- Ay/ (5)
где с — скорость звука.
Для расчета течений с ударными волнами используется квадратичная счетная
вязкость
q = kp [(dv/Ъх)2 Ах2 + (dw/Ъу)2 Ау2 ], (6)
которая обеспечивает размазывание ударных волн на практически одинаковое число
счетных точек независимо от направления волны по отношению к линиям сетки.
7. По своим счетным возможностям методика ЭГАК оказалось близкой к методам
частиц в ячейках. По методике проведено большое количество расчетов тестового
характера; совпадение с аналитическими решениями, результатами расчетов,
проведенных по другим методикам, и с экспериментальными данными вполне
удовлетворительное. Вычислительный метод ЭГАК обеспечивает практически локализацию
положения контактных границ с точностью до одной счетной ячейки. Ниже приводятся
примеры расчетов, которые иллюстрируют возможности и особенности методики
ЭГАК.
8. Развитие конечных возмущений контактных границ двух газов после
прохождения ударной волны. Плоская ударная волна (М = D/c0 = 1,44), распространяющаяся
200

по воздуху (вещество 1, рис. 1) (р0 = 1,205 • 10~3 г/см3, у = 1,4, Р0 = 1 атм) выходит
на границу раздела, имеющую форму уступа (см. рис. 1) ; второй газ — фреон-12
(вещество 2; ро = 5,13 • 10"3 г/см3, ?= 1Д39, Р0 = 1 атм). На рис. 1 изображена
полученная в расчетах форма контактной границы на моменты времени t = 0; 185; 314; 505;
634 мкс.
9. Неустойчивость Гельмгольца— Кельвина. В газе (р0 = 1, Ро =0,6, у = 5/3) задан
тангенциальный разрыв скорости Ам = 1. Граница раздела имеет форму синусоиды
с амплитудой а0 = 0,1 и длиной волны X = 1. На рис. 2 изображена полученная в
расчете эволюция возмущения (f = 0; 0,3; 0,7; 1,1; 1,5; 2,1; 2,5).
10. Высокоскоростное соударение. Тело из железа, имеющее форму цилиндра
(R = 1,5, L = 3), со скоростью и =2,5 км/с налетает на алюминиевую пластину
толщиной 2,2 см. Задача считалась в газодинамическом приближении. Уравнения состояния
принимались в форме Ми-Грюнайзена со следующими параметрами: алюминий (р0о =
= 2,7 г/см3, ро = 2,84, с0 = 5,51 км/с, п = 2,5, у =2,33), железо (р00 = 7,8, р0 = 7,8,
с0 = 3,8, п = 5, у = 2,67). На рис. 3 представлены полученные в расчете конфигурации
пластины и ударника на различные моменты времени (t = 0; 5f 10; 20; 25; 30 мкс).
Проведенные расчеты демонстрируют эффективность предлагаемого метода при
расчетах сложных газодинамических течений неоднородной среды.
ЛИТЕРАТУРА
1. Белоцеркобский ОМ.у Давыдов ЮМ. // Числ. методы механики сплош. среды. 1978. Т. 3, № 3.
2. Gentry R., Martin R.E., Daly B.J. // J. Comput. Phys. 1966. Vol. 1, N 1.
3. Годунов С.К., Забродин В.В., Прокопов Г.П. // Журн. вычисл. математики и мат. физики. 1961.
Т. 1,№6.
4. НохВ.Ф. И Вычислительные методы в гидродинамике. М., 1967. С. 128.
5. Hirt C.W., AmsdenAA., Cookl.L. 11 J. Comput. Phys. 1974. Vol. 14, N3.
6. Харлоу Ф.Х. И Вычислительные методы в гидродинамике. М., 1967. С. 316.
7. Яненко Н.Н., Анучина Н.Н., Петренко В.Е., Шокин Ю.И. II Числ. методы механики сплош. среды.
1970. Т. 1, № 1.С. 40.
8. Анучина ИМ. // Там же. № 4. С. 1.

МЕТОД ДИФФЕРЕНЦИАЛЬНОГО
ПРИБЛИЖЕНИЯ
ОБ АППРОКСИМАЦИОННОЙ ВЯЗКОСТИ РАЗНОСТНЫХ СХЕМ*
1. При интегрировании гиперболических систем конечноразностными методами
возникают эффекты так называемой аппроксимационной вязкости, связанные с дис-
сипативным характером разностных схем. В некотором смысле аппроксимационная
вязкость схемы и ее диссипативные свойства определяются первым
дифференциальным приближением, понятие которого приведено ниже. Будут даны два понятия схем,
обладающих аппроксимационной вязкостью в смысле сохранения (не размазывания)
контактных границ, и для ряда схем будут установлены условия, при которых они
обладают этим свойством.
2. Пусть гиперболическая система
dufdt = Adu/dx (1)
аппроксимируется разностной схемой
ип + 1(х)=2 Ваип(х + ah) = П(Т)ип(х). (2)
а
Здесь А — постоянная вещественная m x m-матрица с различными . вещественными
собственными значениями; и(х, t) = \их(х, г), ..., um(xt t)). Ba — постоянные
вещественные т х m-матрицы; Т— оператор сдвига по х\ t = пт.
Ввиду аппроксимации выполнены следующие условия совместности:
^Ba = IfXaB0l = (r/h)Ar
I— единичная матрица.
Разлагая в (2) функции un + l(x)9 un(x + ah) в ряды по параметрам г и Л
относительно точки (jc, t) и отбрасывая члены выше первого порядка по г и Л, имеем
h2
du/bt = A Ъи/Ъх + С д2и/дх2, С= 2 (а-р)2ВаВв. (3)
47Г а,0
Систему (3) будем называть первым дифференциальным приближением
разностной схемы (2). Здесь и в дальнейшем первое дифференциальное приближение рао
сматривается на решении.
3. Гармоника и = u0eOJt+tkx является решением (1), если со и к связаны диспер^
сионным соотношением
det WcoI-ikA 11 = 0. (4)
Если для некоторого семейства со = со (А:) решений (4) со (А:) = 0, то Аи0 =0, и
соответствующий инвариант системы (1) переносится вдоль характеристики без
изменения (контактная граница сохраняется).
Определение 1. Разностная схема (2) обладает аппроксимационной вязкостью,
сохраняющей контактный разрыв (свойство К), если из соотношения Ащ - 0 следует,
что Cuq =0.
♦Докл. АН СССР, 1968. Т. 182, № 2. С. 280-281. (Соавтор,Ю.И. Шокин.)
202

Лемма 1. Если из Аи0 = О следует, что 2 а2Ваи0 = 0> то схема (2) обладает
свойством К. а
Теорема 1. Если
1)C=F-A
или
2) Ха2Ва=Н.А,
или
^)Ba=F0l^A,
где F, Н, Fa - некоторые матричные функции, то схема (2) обладает свойством К.
Теорема 2. Для того чтобы простая разностная схема
2 2 2
un + 1(x)= 2 Ваип(х + т\,)9 2 5a = /, 2 КВа^Л (5)
а=1 а=1 а=1
обладала свойством К, необходимо и достаточно, чтобы выполнялось одно из
следующих условий:
1) Xi =0 (Х2^0)
или
2) Х2=0 (Xi *0).
Теорема 3. Мажорантная схема
1
ип+1(х)= 2 Baun(x + oth),
*!=(t/A)A+, Д_!=-(т/А)Л", В0=1=(В1+В_1), (6)
обладает свойством К.
Рассмотрим схему предиктор—корректор
О!
ип + 1(х) = ип(х) + (г/А) Л [и*(х + А/2) - и*(* - А/2) J, (8)
где (7) — произвольная разностная схема, а (8) — схема "крест".
Теорема 4. Схема предиктор-корректор (7), (8) обладает свойством К.
4. Определение 2. Разностная схема (2) обладает сильным свойством К, если
из соотношения Аи0 = 0 следует, что
[£l(eikh)-I]u0= 0.
Здесь Г2(е'*л) = 2 Baelkah — матрица усиления схемы (2).
а
Теорема 5. Если £l(elkh) — I = F - А, где F- произвольная матричная функция,
то схема (2) обладает сильным свойством К.
Теорема 6. Для того чтобы простая схема (5) обладала сильным свойством К,
необходимо и достаточно, чтобы выполнялось одно из следующих условий: 1) Xi =0
(Х2*0) или 2) X2=0(Xi^0).
Теорема 7. Мажорантная схема (6) обладает сильным свойством К.
Теорема 8. Если ВаА = АВа, то схема предиктор-корректор (7), (8) обладает
сильным свойством К.
Следствие 1. Схема Лакса (простая схема с Xi = А/г, Х2 = -А/г) не обладает
свойством К в обоих случаях.
Следствие 2, Схема Лакса—Венд рофа обладает свойством К в обоих случаях.
203

О КОРРЕКТНОСТИ ПЕРВЫХ
ДИФФЕРЕНЦИАЛЬНЫХ ПРИБЛИЖЕНИЙ
РАЗНОСТНЫХ СХЕМ*
1. Пусть A(t, х, т, h, T) есть разностный оператор, аппроксимирующий
дифференциальный оператор%(ty х, b/bt, b/bx). Здесь х — точка вещественного s-мерного
пространства RS9b/bx=X(b/bxl9 ..., b/bxs)'9 T1 = (Tl9 ..., Ts)9 Г= (Т0, Г1); Т0 - оператор
сдвига по Г; 7) — оператор сдвига по xf9 r,h — сеточные параметры;, h = (hl9 ..., hs).
Имеет место операторное представление:
Разлагая оператор A(t, ху T,h,T) = A(t, x, т, h, eT d/df, eh д!Ъх) в ряд по параметрам
т, А, получим
A(t, х, r,h,T) = Щ, х,т, h, b/bt, b/bx) + Д,
2С(Г, x, т, h, b/bt, Э/Эх)= S5(f, x, b/bt, b/bx) + т°7*1Ра/3(Г, x, Э/Э/, b/bx)9
R = TyhsPy8(t,x,bfbt,bfbx).
Суммирование проводится по повторяющемуся индексу, таИ?Рар(1, х, b/bt, b/bx) -
первые члены разложения (наименьшие по степеням г и И).
Оператор i£(£, х, г, А, З/df, д/Эх) будем называть первым дифференциальным
приближением разностного оператора A(t, х, т, h, 7), а уравнение 95 (Г, х, г, h, b/bt,
b/bx) и = О — первым дифференциальным приближением разностного уравнения A(t, х,
r,h,T)u = 0.
2. Рассмотрим задачу Коши для гиперболической системы уравнений первого
порядка
bu s bu
— = 2 Ак(х, г) — , (1)
и(х,0) = ио(х)9 ( (2)
где м = и(х, t) — вектор*функция с m компонентами; х = (хх, ..., ;Су) — точка
вещественного s-мерного пространства/V, Ак(х, t) — вещественные m х т-матрицы.
Аппроксимируем систему (1) разностной схемой
ип + 1(х)=ХВаип(х + тХа). (3)
Для аппроксимации должны выполняться условия совместности
ZBa = I, 2X^a = 4, А;= !,...,*. (4)
а а
Здесь /— единичная матрица; Ва - m x m — вещественные матрицы; Л^ = (Л^,..., А^) —
вектора смещения.
Первое дифференциальное приближение разностной схемы (3) имеет вид
bu s b2u s bu
— = Б Ск1——— + 2 Dk
bt к, i=i bxkbxi fr=i bxk
Сы=7~ [2\ка\1аВа-АкА,], (5)
2 a
£>fc = >lfc- -
&4fc * ЪА
—- + Ъ At
bt i= l bx,
lf\
♦Докл. АН СССР, 1968. Т. 182, №4. С 776-778. (Соавтор Ю.И. Шокин.)
204

Здесь и в дальнейшем для гиперболических систем первое дифференциальное
приближение рассматривается на решении.
Теорема \„В случае постоянных коэффициентов задача Коши для первого
дифференциального приближения (5) разностной схемы (3), коэффициенты которой
являются симметрическими положительно определенными матрицами, поставлена
корректно.
Корректность понимается в смысле И.Г. Петровского [1]. Заметим, что схема
устойчива ввиду критерия К.О. Фридрихса [2].
Разностная схема (3) называется простой [3], если число векторов смещения равно
числу независимых переменных.
Лемма. Если матрицы Ак — симметрические, то коэффициенты простой схемы —
симметрические матрицы.
3. Аппроксимируем систему
du/dt = A(x,t)bu/dx (6)
простой схемой
2
ип + 1(х)= 2 ^"(х + тХ*). (7)
А{ху t) — вещественная симметрическая m x m-матрица Ее первое
дифференциальное приближение
du/dt=Cd2u[dx2 +Ddu/dx, (8)
^ г Г i 2 Л г \ЪА ЪАЛ
С= - 2 \1ва-А2\у D = A- - +А — .
.2 U=i J 2 L ЭГ Эх J
Теорема 2. Для того чтобы простая разностная схема (7) в случае постоянных
коэффициентов была устойчива, необходимо и достаточно, чтобы задача Коши для
ее первого дифференциального приближения была корректна.
Теорема 3. В случае переменных коэффициентов, если матрица А
Липшиц-непрерывна, то корректность первого дифференциального приближения (8) простой схемы
(7) является достаточным условием устойчивости схемы.
Трехточечную разностную схему, аппроксимирующую систему (6),
ип + 1(х)= 2 B^ix + ah),
а = —I
11
X Ва=1, 2 aBa = rAf г=т/А, (9)
<х = — 1 а = — 1
назовем мажорантной [4,5], если
Вх=гА*, В_!=-гА~, А=А++А~, А+>0, А~ <0.
Первое дифференциальное приближение схемы (9) имеет вид (8), где
С=ф2/2т)(1-В0)В0.
Теорема 4. Для устойчивости мажорантной схемы в случае постоянных
коэффициентов необходимо и достаточно, чтобы ее первое дифференциальное
приближение было корректно.
Теорема 5. В случае переменных коэффициентов, если матрица А липшиц-непре-
рывна, то корректность первого дифференциального приближения мажорантной схемы
является достаточным условием устойчивости схемы.
Теорема 6. Для того чтобы устойчивая трехточечная схема (9) в случае
постоянных коэффициентов была мажорантной, необходимо и достаточно, чтобы ее коэффи-
205

циенты были попарно перестановочные симметрические матрицы uBxB_i = 0. Заметим,
что в случае необходимости устойчивость не обязательна.
Следствие. Если коэффициенты трехточечной разностной схемы (9) в случае
постоянных коэффициентов попарно перестановочные симметрические матрицы и
ВхВ_Л = 0, то для устойчивости схемы необходимо и достаточно, чтобы ее первое
дифференциальное приближение было корректно.
ЛИТЕРАТУРА
1. Петровский И.Г. II Бюл. МГУ. Секция А. 1938. Т. 1, вып. 7, № 1.
2. Friedrichs К.О. // Commun. Pure and Appl. Math. 1954. Vol. 7., N 2. P. 345.
3. Hahn S.C II Ibid. 1958. Vol. 9, N 2. P. 243.
4. Яненко Н.Н. 11 Tp. IV Всесоюз. мат. съезда? Л, 1964. Т. 2.
5. АнучинаНМ. 11 Тр. МИАНСССР. 1966. Т. 74, № 5.
О ГРУППОВОЙ КЛАССИФИКАЦИИ РАЗНОСТНЫХ СХЕМ
ДЛЯ СИСТЕМЫ УРАВНЕНИЙ ГАЗОВОЙ ДИНАМИКИ*
ВВЕДЕНИЕ
Настоящая работа посвящена групповой классификации разностных схем,
аппроксимирующих уравнения газовой динамики. Известно, что уравнения газовой динамики
инвариантны относительно некоторой группы точечных преобразований в пространстве
независимых и зависимых переменных. Эта инвариантность является следствием
инвариантности законов сохранения, из которых вытекают уравнения газовой динамики.
Любая разностная схема реализуется на конкретной сетке, которая сама по себе вносит
неинвариантность в алгоритм расчета. Эта неинвариантность может сказываться,
например, в расчетах особенностей потока, которые движутся под различными углами к
линиям сетки. Переход к разностной схеме затрудняет групповой анализ, поскольку
разностные операторы обладают иными групповыми свойствами, нежели дифференциальные.
Поэтому нам показалось целесообразным проводить групповую классификацию
разностных схем на основе их первого дифференциального приближения.
Понятие. первого дифференциального приближения было введено в работах [1—3]
и оказалось плодотворным для исследования свойств устойчивости и особенно дисси-
пативных свойств разностных схем. Будучи дифференциальным уравнением,
содержащим в своих коэффициентах параметры схемы, первое дифференциальное
приближение занимает промежуточное положение между исходными уравнениями газовой
динамики и аппроксимирующей их разностной схемой, сохраняя информацию об
исходных уравнениях в своей гиперболической части и о разностной схеме — в
параболической части. При этом возникает естественный вопрос: насколько первое
дифференциальное приближение сохраняет групповые свойства уравнений газовой динамики.
В соответствии с этим все схемы могут быть подразделены на два класса: схемы,
сохраняющие групповые свойства, и схемы, не сохраняющие групповые свойства.
В работе формулируются условия, при которых система уравнений параболической
формы первого дифференциального приближения допускала все группы
преобразований [4], которые допускает исходная система уравнений газовой динамики. В случае
одной пространственной переменной система уравнений газовой динамики
рассматривается как в эйлеровых координатах, так и в лагранжевых, в случае же двух
пространственных переменных -в эйлеровых координатах.Кроме того, выделены случаи, когда
в системе лагранжевых уравнений первого дифференциального приближения выполнен
закон сохранения массы и когда этот закон не выполнен. Устойчивость построенных
классов схем проверяется методом первого дифференциального приближения.
♦Труды МИ АН СССР, 1973. Т. 122. С. 85-97. (Соавтор Ю.И. Шокин.)
206

1. СЛУЧАЙ ОДНОЙ ПРОСТРАНСТВЕННОЙ ПЕРЕМЕННОЙ
1. Рассмотрим систему уравнений газовой динамики в эйлеровых координатах в
случае одной пространственной переменной
",=/*, (Ы)
ГД6 / PU\ ( ~P'PU2 \
\ рЕ ) \-puE-up)
и — скорость газа, р — давление, р — плотность, е — удельная внутренняя энергия.
Уравнение состояния газа имеет вид
e=e(pf р).
Аппроксимируем систему уравнений (1.1) следующей разностной схемой:
Apw"(x) A1+A_t ^ ч ft(x + h/lXA./h) - ft(x - h/2)(A_ x/h)
= — fix) + 7 — wn(x), (1.2)
т 2h h
где t = пт,т — шаг по оси t, x — шаг по оси xf wn(x) = w(x, ит), ft = lift.. II? — пока не
известная матрица, причем lift И = 0(т), А0 = Т0 - Е, Ах = Тх - Е, А_г■ = Е - 71 ь Т0 —
оператор сдвига по t, Тх — оператор сдвига по х, Е — тождественный оператор, Т_х =
= 7Т*. Разностная схема (1.2) имеет по крайней мере первый порядок точности.
Гиперболическая и параболическая формы первого дифференциального
приближения разностной схемы (1.2) имеют вид соответственно
(r/2)wu +wf = fx +(Slwx)Xi (1.3)
wt = Fx+(Cwx)Xi (1.4)
где
C= ft - (т/2)А2 = Цу II?, A = df/dw,
Mi l = ^i l - 072) (3w2 + в + zq - 3u2z)9
Mi 2 = &>i 2 + (t/2)u [2u2 - 26 - 3u2z + 3Ez + zr\],
M13 = ^i3 -3kruz, /i21 = ^2 l - (r/2)ii(2 - z),
/la2 = ft22 + (r/2)(«2 - (9 - h2z + Fz), /i2 з = ^2 з -(t/2)z,
Мз 1=Пз1 -ти(Е + <п-и2г)-(т/2)и(0-Ег),
M32 = ^32 + (т/2)[(2н2 +^z)(^ + r?)-(w2 + ^ + r?)^-w2(2w2-^)z],
Мз 3 = ^з 3 - (r/2)w2 (1 + 2z) - (r/2)z(tf + r?),
2 = Pe/P> 1? = /VP> в = Pp> «i/ = *fy(*f ft W, WXf Wf) .
Систему уравнений (1.4) можем записать в виде
wt=fx+Nx, (1.5)
N =
Nk~-
Vfc2
[NA
N2
\N3J
z»kl"x
= Wki
i
= Cwx
+ »k2Px +
+ M*2 +(E
= Cwx,
*>къРх,
+ P^)M
w =
»kl
кг,
fu\
(;)
= P(M
*Ъз =
,C=II^II?,
kl +"МА:з),
ptpVkb.
207

Выражая функции w, / через функцию w, получим, что система уравнений (1.5)
эквивалентна системе уравнений
Fx = щ + иих +р~*рх - P~lN\x + up~lN2x = 0,
Рг = Pt + "Px + Р"х ~ N2x = О,
F3 =pt+upx + а2их + bN2x + (u/pep)Nlx - (\/p€p)N3x = 0, (1.6)
где
а2 =(р- р2ер)/рер, Ъ = (е + рер - Уш2)\рер.
2, Система уравнений (1.1) допускает пространство операторов с базисом |4]
э э э э э э
ii =—, Ь2 = , Z,3 = r— + , Z,4 = f— '+* , (1.7)
bt Ы Ъх - Ъи bt Ъх
которым соответственно отвечают следующие конечные преобразования,
сохраняющие систему уравнений (1.1): 1) перенос по времени; 2) перенос по пространственной
координате; 3) преобразование Галилея; 4) преобразование подобия.
Потребуем, чтобы система уравнений (1.4), или, что то же, (1.6), допускала
пространство операторов с базисом (1.7), что приведет нас к некоторым ограничениям на
выбор матрицы П.
Система уравнений (1.6) допускает пространство операторов с базисом (1.7)
тогда и только тогда, когда выполнены равенства (см. [4])
LaFk\ F^Q F2=Q F3=0 = 0, <* =1, 2, 3, 4; к = 1, 2, 3,
L — оператор, полученный продолжением оператора La последовательно 2 раза.
Например, в рассматриваемом случае имеем (Еа — первое продолжение оператора La)
A =Li =Э/Эг,- L2=L2=b/bx,
ъ ъ э
Ьъ = t — + — - их
Ъх Ъи but
д Ъ Ъ
L^-t — +л: — - ut —
bt Ъх Ъщ
Ъ Ъ
-Рх— -Рх —
bpt Ър
Э Э
-Pt— -Pt~
bpt bpt
ъ ъ ъ
^"7 -Рх— -Рх~ •
Ъих Ърх Ърх
Лемма. Если в разностной схеме (1.2) элементы матрицы £1 не зависят от t их,
то система уравнений (1.6) инвариантна относительно преобразований переноса по
времени и переноса по пространственной координате.
Действительно, при выполнении условий леммы, имеем
« 1 Э и Ъ
р bt р bt
« 1 Э и Ъ
^2^=-- —Nlx + -—N2x = Q,
р ох р ох
LiF2=- — N2x=Q, LiF2*-—N2x = Q,
ot ox
« Э и b I д
LtF3 = Ь —N2x + - —Nlx -N3x =0,
bt pep bt pep ot
208

« Э ид 1 Э
L2F3=b—N2x + — —Ntx- — — *Гъх = Ъ
бх fi€p ах рер ох
так как; независимость элементов матрицы ft от х и t означает также независимость
vtf от jc, г. Лемма доказана.
Теорема 1.1. Если выполнены условия леммы и, кроме того,
Гк *Ч *\
— nif=09. — % = 0,—-£2^ = 0 (/,/=1,2,3), (1.8)
but opt . dpt
гь А '7\
— Nix=N2X,—N2x = 0,—N3x=Nlx, (1.9)
ои ои ои
( Ъ Э Э Э Э Э \
I их — + Р* Т + Р* "Г + 2ихх + 2рхх - + 2рхх XN^ =Nax,
\ ™х °Рх °Рх °ихх °Pxxs дРхх I (НО)
то система уравнений (1.6) первого дифференциального приближения разностной
схемы (1.2) допускает пространство операторов с базисом (1.7).
Доказательство. Из леммы при наших предположениях следует, что
LjF^O, L2Fk = 0, (*= 1,2,3).
Рассмотрим далее оператор L3. Тогда
« 1 ~ и ~ 1 1 ~
L3FX =- -L3Nlx + - L3N2x + - N2x=- - (L3NXx-N2x) +
P P P P
и ^ 1 / Э \ и Э
-L37V2;c = - - ( — Nlx -N2x) + - — N2x = 0,
p p \ Ъи f p ои
« ~ Э
^2 = ~L3N2x = - -г-ЛГ2.х = О,
ом
L3F3=bL3N2x - — 7V2jc + —L3Nlx + tflx - Z37V3;c =
pep pep peP P€p
= —(t-NvX-N2x)+ —(-T-N3x+Nlx)=0.
p€p \Ъи I p€p \ Ъи )
Пусть
Э Э Э Э Э Э
5?4 =Цк "Г + Px ~ + Px~— + 1uxx + 2pxx— + 2pxx— ,
дих брх дрх Ъихх дрхх дрхх
тогда
L*F2 = -pf - upx - pux + X4N2x = - 7V2x + #4^2* = 0,
« 11 w ^
Z^ =-ut-uux - -px + -X47Vlx - - &AN2x =
p p p
1 w 1 ,y, и ^
p p p p
LtF3=b(N2x- XAN2x)- —(X4Nlx-Nlx)+—( XAN3x -N3x) = 0.
pep pep
209

Теорема доказана.
ЪМ2х
Условие = 0 означает, что N2x не зависит явно от функции и. Тогда равенства
Ъи
(1.9) могут быть переписаны в виде
= 0, Nlx = uN2x+Ru N3x = Ku2N2x+uRl+R2i (1.11)
ЪМ2х
Ъи
bRx bR2
= 0, -=0.
Ъи Ъи
Если
^2i = ^2i + 7М(2 ~f)-ulu23 - — z I ,
2
л12 2 ~* 5*<2 2
^2 3 =: ^2 3 >
где _
-ыШ21 -м( П2з --г 1 --w2(2-z)-1/2w2(n23 --z) , (1.12)
■•0 (*= 1,2,3), (1.13)
ди
то
ЭА^2х
= 0.
Ъи
Таким образом, теорема 1.1 остается справедливой, если в ее формулировке
условия (1.9) заменить условиями (1.11)-(1.13).
3. Потребуем, чтобы в первом дифференциальном приближении разностной схемы
(1.2) был выполнен закон сохранения массы, т.е. имело место равенство
и, следовательно,
ft21 = -w(2-z), П22 = - (0 -ez-u2 + u2z)9 J223 = -z. (1.14)
Тогда система уравнений (1.6) примет вид
1 1
Fx =ut + иих + -рх - - Nlx = 0, F2 = pt +upx +pux = 0, (1.15)
Р Р
0 и 1
F3=Pt+upx+azux+ Nlx N3x = 0.
рсР Р€р
Теорема 1.2. Если выполнены условия леммы, равенства (1.8), (1.10), (1.14)
и, кроме того,
bNlx ЭД
—^=0, N3x=(uN1)x+R-uxNli —-=0, (1.16)
Ъи Ъи
то система уравнений (1.15) первого дифференциального приближения разностной
схемы (1.2) допускает пространство операторов с базисом (1.7) ив первом
дифференциальном приближении выполнен закон сохранения массы.
Действительно, из (1.14) получаем, что
v2k = 0 (£=1,2,3),
т.е. N2 = 0, и, следовательно, в первом дифференциальном приближении выполнен
210

закон сохранения массы. Далее, справедливость теоремы 1.2 следует из теоремы 1.1,
так как в этом случае условие (1.9) примет вид
ЭЛЛ <МУз¥
Ъи Ъи
т.е,
ЪЯ
Mix^uN^+R^iuN^+R-iixN^ -—=0. (1.17)
Ъи
Независимость^^ от функции и означает, что коэффициенты vlk (к = 1,2,3) не
зависят от функции и. Полагая
^и -Яц -ий13 +3/2 ти{\ -z),
^12 = ^12 -ийХ1 +V2U2U13 -- и[2и2 -20 -3u2z + 3Ez+r]z], (1.18)
1213 = П13 +3/2rwz, =0 (£= 1,2,3),
Ъи
получим, что
^11 =Р^и --P(0+zt?), ^12 = ^12 +(е + рер)П13, (1.19)
также не зависят от функции и. Таким образом, условие (1.16) в формулировке
теоремы 1.2 может быть заменено условиями (1.17)—(1.18).
4. Следствием системы уравнений (1.11) является уравнение
st+usx=Q,
выражающее сохранение энтропии s вдоль характеристики с наклоном dx/dt = и
(траектории). Формально это уравнение получается умножением уравнения (1.1) слева
на вектор X = 1/р(—иу и2 — Е — т?, 1), являющийся левым собственным вектором
матрицы А и соответствующий собственному значению — м. При этом используется второй
закон термодинамики.
Известно, что наличие физической вязкости, аддитивно входящей в р, приводит
к возрастанию энтропии, т.е. вместо уравнения (1.19) справедливо уравнение
st + usx = \iu\ =4, Я> О-
Если в разностной схеме (1.2) элементы матрицы 12 не зависят от*, t и, кроме того,
выполнены равенства (1.8), (1.10), (1.14), (1.17), (1.18) иЛ = uxNx, то аппроксима-
ционная вязкость входит аддитивно в р в системе уравнений первого
дифференциального приближения, и при условии uxNx > 0 эта вязкость приводит к возрастанию
энтропии.
Действительно, в этом случае система уравнений (1.15) может быть записана в виде
(pu)t +(p+pw2)* = 0, pt + (ри)х = 0, ^ 2ф
(pE)t+(puE + up)x=0,
гцер = р +Ni. Умножая эту систему уравнений слева на вектор X, получим
st + usx = (\lpT)uxNl>0.
В силу теоремы 1.2 система уравнений (1,20) допускает также пространство
операторов с базисо м (1.7 ).
211

Заметим, что если условие R = uxNt не выполнено, то аппроксимационная вязкость
уже не входит аддитивно в р, аналогично физической вязкости, и при этом имеет место
соотношение
Из условий (1.9), или, что то же, (1.16), в частности, следует, что если
аппроксимационная вязкость входит в уравнение движения (Nt Ф 0), то она обязательно входит и
Э
в уравнение энергии (N3 Ф 0). Обратно, если — N3x = 0, то Nlx = 0, но N3x Ф 0, т. е.
Ъи
существует аппроксимационная вязкость, входящая только в уравнение энергии (N3 Ф
Ф 0), но не входящая в уравнение движения (Nt = 0). Разностные схемы с аналогичной
вязкостью используются при численном решении ряда задач газовой динамики [5].
5. В работах [2, 3, 6] определено свойство К разностных схем, аппроксимирующих
гиперболические системы уравнений с постоянными коэффициентами. Введем
аналогичное свойство и в рассматриваемом случае.
Определение. Разностная схема (1,2) обладает свойством К, если справедливо
равенство ХС= 0.
Пусть Af2 = 0, тогда
(Ми Mi2 M13V
0 0 0 I
^31 Мз2 Мзз/
Равенство ХС- 0 означает, что
-uvik + Дз* = 0 (k= 1,2,3)
и, следовательно,
П31 = uSlxl +ти(е + г}-и2 + lAzr} + lAu2z -гЛЕг)9
Q32 =ы£212 +(т/2)и [2и2 -20 -3u2z + 3Ez +zr?] -(r/2)[(2w2 + EzXE + r))-
-{и2+Е)в-пв -u2(2u2 -E)z]9 (1.21)
ft33=wfi13 +(r/2)z(^ + T?) + (r/2)w2(l -z).
Таким образом, если N2 = 0 и выполнены равенства (1.21), то разностная схема
обладает свойством К.
Пусть N2 = 0 и ХС= 0. Тогда
XCwx = XN= р"1 {-uNx + N3) = 0,
т. е.
N3=uNt (1.22)
и, следовательно,
(у31 ~-uvxl)ux +(^32 ~М\г)Рх +(^зз -"^1з)Рх=0.
Последнее равенство будет иметь место при.
V3k=ufilk (£=1,2,3).
и, следовательно, как показано выше, при выполнении равенства (1.21).
Итак, справедлива
Т е о ре м а 13, Если в разностной схеме (1.2) элементы матрицы £1 удовлетворяют
условиям леммы и выполнены равенства (L8), (Ы9), (1.14), (1.17), (1.18), (1,22),
го разностная схема обладает свойством К, в ее первом дифференциальном
приближении выполнен закон сохранения массы и система уравнений первого
дифференциального приближения допускает пространство операторов с базисом (1.7).
212

6. Устойчивость полученного семейства разностных схем исследовалась методом
первого дифференциального приближения, т, е. находились условия, при которых
система уравнений первого дифференциального приближения является неполной
параболической (О 0) и область зависимости системы уравнений гиперболической формы
первого дифференциального приближения
(r/2)wtt + wt = Q,wxx+(A+ax)wx
не превосходит области зависимости разностной схемы, Эти условия приводят к
неравенствам
(т/2)А2<а<(к2/2т)1
которые дают дополнительные ограничения на выбор матрицы Г2 и шагов сетки т, h.
В частности, отсюда следует, что для устойчивости необходимо
r2u2/h2<\9 T2{u±a)2/h2<\~
Аналогично проводится групповая классификация разностных схем для системы
уравнений газовой динамики в лагранжевых координатах, а также неявных
разностных схем.
2. СЛУЧАЙ ДВУХ ПРОСТРАНСТВЕННЫХ ПЕРЕМЕННЫХ
1. Система уравнений газовой динамики в случае двух пространственных переменных
имеет вид
(2,1)
и, v — компоненты вектора скорости в направлении х иу соответственно,/? — давление
газа, р — плотность, Е=е + lA{u2 +i>2), e — удельная внутренняя энергия. Уравнение
состояния газа имеет вид р = р (р, е).
Аппроксимируем систему уравнений (2.1) следующей разностной схемой:
+ fn{*,y)+—— gn(*,y) =
т 2/ix 2h2
I 1 - - 1 - 1 _
= — A1[£l11(x,y)A1] + — A2[Sl22(x,y)A2] + —— A1[Sl12(xty)A2] +
I h\ h2 hxh2
+ -±- A2[n21(xfy)A1]\wn(xty)i (2.2)
где hx, h2 — шаги разностной сетки по х я у соответственно,
A^Tt-E, Д_, = *-77\
Д,= Г/%-Г/-%, Т_^ТГХ (/=1,2),
7\ — оператор сдвига по оси х, Т2 — оператор сдвига по оси у, £2// — пока
неопределенные 4X4 матрицы, причем Ш#8 = 0(г).
Гиперболическая и параболическая формы первого дифференциального приближения
213

разностной схемы (2.2) имеют соответственно вид
г Э Э
-wtt + wt+fx+gy=—(n11wx+n12wy)+—(Sl21wx + £l22wy)9 (2.3)
Э Э
*V+/*+*>= — (Cuwx+C12wy)+ — (C2lwx+C22wy)y (2,4)
Ъх Ъу
где
Сц = ай,-(т/2)А{А, (/,/=1,2),
^41 = df/dw, А 2 = dg/dw.
Систему уравнений (2.4) алгебраическими преобразованиями можно привести к
виду
1 1 4
Fx = ut+uux +vuy +-px - -Мх +-Л3 =0,
Р Р Р
1 1 и
F2 =yf+wux +Wy +- py —Мг + -Лъ =0,
P P P
F3-Pt+ Wx + VPy + P"* + P"j; ~Л3 = О,
F4 =p, + wpx + vpy + fl2wx + fl2y + bSb +
(2.5)
Здесь
a2=(p-p2ep)/p€p, b = (E + pep
М(1)+ЛГ(2)
2x 2y
vO>+W(2)
l Зх 3У I
Uif =
w2)/pep
:7Va)+7V(2> ,
x у
pep
peP
= 0.
4x
4У
N(1'> = Cllwx+C12wy=mkw\\1,
NW = c21wx+c22wy=mvnt,
Nli}="", «*+K\v*+ <\ p*+K\ p*+ vl\ uy+vl\ ь+ i\ py+vll py
"2з=и"*1 +uw« +w*3 +(^ + Pep)^4,
i>'i4=pepa>j>4, Q^llcofJI? ft/=1,2; *.<?= 1, 2,3,4).
2. Наиболее широкая группа Ли точечных преобразований, допускаемая системой
уравнений (2.1), имеет порядок семь. Базис соответствующей алгебры Ли состоит из
операторов [4]
А =
ЭГ
_ э - °
L2- — , L3- — ,
Ъх Ъу
Ъ Ъ Ъ Ъ
L$ — t + , L$ — t + ,
Ъх Ъи Ъу Ъю
Ъ Ъ Ъ Ъ
од: Ъу ои ov
Ъ Ъ Ъ
Ln=t—+х— +у —,
Эг Эл: Ъу
(2.6)
которым отвечают следующие конечные преобразования, соответственно сохраняющие
214

систему уравнений (2Л): 1) перенос повремени; 2) перенос по координате*; 3)
перенос по координате .у; 4) преобразование Галилея по оси л:; 5) преобразование Галилея
по оси .у; 6) преобразование поворота; 7) преобразование подобия.
3. Найдем условия, при которых система уравнений (2.4), или, что то же, (2.5),
допускает преобразования, задаваемые операторами (2.6). Как показано в работе
[4], это будет тогда и только тогда, когда выполнены равенства
^*If,=o,f2=o,f3=o,f4=o =0' «=1,2,3,4,5,6,7; £=1,2,3,4.
В рассматриваемом случае, например,
Lf = Lf = Lf (/=1,2,3),
Э Э Э Э
Z,4 =£4 - их vx — -Рх— -рх —,
out ovt opt opt
Э Э Э Э
L5 =LS - иу — ~ vy — - py — - py — ,
out ovt opt opt
Э Э /Э Э \ /Э Э \
L6=L6+vt— -Щ — + (и*+иу)1- — )+(uy-wx)l-r- +— J+
Э Э Э Э
+ f>y— -Px— +Py— ~Px — >
opx ору Ърх Ъру
.#
^ э э э э э э э э
L7 =L7 - ut — - их — - иу — - vt — - vx — - vy — - pt px — -
but Ъих Ъиу dvt bvx dVy bpt dpx
Э Э Э Э
-Py— -P*— "Px— -Py— .
ору bpt Ърх у dp у
Теорема 2.1. Если в разностной схеме (2.2) элементы матриц £2# не зависят от
t, х, у и, кроме того,
Э
— Г2"=0 (^ = и,и,р,р), (2.7)
^4 = 1/4("2+у2Мз+^1+*+^
Э Э Э Э
—^з=0, —^i=0, —Л2=0, Д = 0,
Ъи Ъи Ъи Ъи
Ъ Э Э Э
—.^з = 0, —^1=0, —^2=0, —Д = 0,
Эи Эи Эи Эи
«C6.^l = J*2 -tU^3, ^6.^2 =ИЛз -М\,
«С 6^3 = 0, «C6^4 = -VMx + HJ£2 ,
InMk^Mk (/,/=1,2; Лг, /= 1,2,3,4),
где
f6=fe+^)— +(^-"x)— +Py— 'Px— +- + ("хх + иху+иух)—- +
Ъих Ьиу ' Ьрх Ъру ' * Ъихх
Ъ
+ ... + (рух + рху)
Ьр
УУ
215

э э а э э э
+... +
<£? = «* — +% — +Рх — + - + Р>> — + 2wx:c --— + 2иху
Ъих Ъиу Ърх Ъру , Ъихх Ъиху
Э
+ 2рУУ ^Г '
ОРуу
то система уравнений (2.5) допускает пространство операторов с базисом (2.6).
Доказательство, При выполнении условий теоремы имеем
1 и
LkF1=--LkjCi +-Zr*j03=O,
Р Р
« ' 1 -и '
£fc^2 = ~ ~ £fc^2 + ~LkM3 = 0,
Р Р
LkF3 = ~Lkjt3=09
« М У 1
LkFb = ЬЬкМъ + Lkjl\+ ЬкМг Z,fc*y#4=0
рер рер рер
для £ = 1, 2, 3. Далее
» 1 ~ 1 ^, и 1^1 у
L4Fi = Z,4J*i +-/,4(«.^з)=- Лъ L^jli =-(у^з -I4Ji) = -^3-
Р Р р Р Р Р
1/ Э Э \ и 1/ Э Э Л
— иТ^"ТРз= -^з -- («—-u—Uuji3 +^x)=0,
р\ дм Эи/ р р\ Эм Эи/
1 - 1 „ w 1 ы 1 / Э
P P p p p P\ Ъи
/ Э Э \
Z4F3 = ~£4 J*3 = -^4 Л*3 = -IW —- -U —)Мъ = О,
\ ou av/
% ~ W И ~ 1 l> ~ 1^
L4F4=bL4Jl3 Лъ + ^4 jf^i + .>0i + £4^2 Z,4J£2=0.
pep pep рбр рбр pep
Аналогично можно показать, что при выполнении условий теоремы
^1^=0^=0^=0^=0 = 0 («=5,6,7; *= 1,2, 3,4).
Теорема доказана.
4. Будем говорить, что в системе уравнений первого дифференциального
приближения разностной схемы (2,2) выполнен закон сохранения массы, если имеет место
равенство
Лз=0. (2,8)
Заметим, что если £212 = &21 = 0, то закон сохранения массы в системе уравнений
первого дифференциального приближения разностной схемы не выполнен,
Действительно, в этом случае можно показать, 4toJ£3 ^ 0 ни при каком выборе матриц Яп,
£22 2'
Легко видеть, что если
Яз1=-и(2-г), fi32=--uz,
2 2
216

ftii= -[-и2 +в+(и2 +и2 -tf)z], J2Si = -zf
П|?= -оэ-"ЯН=-и, ЯЙ =--«">» «34=0, (2.9)
2 2 2
a|i = -w, «12 =-и, «|3 = --«u, afi = o,
2 22
r r
«Ii = uz, Q,ll = -v(2-z}9
аЦ = - [-v2 + в + (и2 + u2 - £>], ПЦ= -z,
где
z=pe/p, в=р/А, n„=ln^It (/,/=1,2),
то имеет место равенство (2.8).
Теорема 2.2, Если в разностной схеме (2,2) элементы матриц £1ц (i, / = 1, 2)
«в зависят от t, xr у и, кроме того, выполнены равенства (2.7), (2,9) и
Э Э
Э# Эй
д#/эы = о, ая/эи = о,
£7^/ = ^/(/=1»2,3,4),
го система уравнений первого дифференциального приближения разностной схемы
допускает пространство операторов с базисом (2.6) и в ней выполнен закон
сохранения массы.
Доказательство проводится аналогично доказательству теоремы 2.1,
ЛИТЕРАТУРА
1. Яненко Н.Н„ Шокин Ю.И. О корректности первых дифференциальных приближений разностных
схем // ДАН СССР. 1968. Т. 182, № 4. С. 776.
2. Яненко Н.Н., Шокин Ю.И. О первом дифференциальном приближении разностных схем для
гиперболических систем уравнений // Сиб. мат. журн. 1969. Т. 10, № 5- С. 1174.
3. Yanenko NJV., Shokin Yu.1. First differential approximation method and approximate viscosity of
difference schemes // Phys. Fluids. 1970. Vol. 12, N 12. P. II-28-II-33.
4. Овсянников Л.В. Групповые свойства дифференциальных уравнений. Новосибирск, 1962.
5. Яненко Н.Н., Анучина Н.Н., Петренко В.Е., Шокин Ю.И. О методах расчета задач газовой
динамики с большими деформациями // Числ. методы механики сплош. среды. 1970. Т. 1,№ 1. С. 40»
6. Яненко Н.Н.% Шокин Ю.И Об аппроксимационной вязкости разностных схем // ДАН СССР. 1968.
Т. 182, №2. С. 280.
217

КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ РАЗНОСТНЫХ СХЕМ
МЕТОДОМ ДИФФЕРЕНЦИАЛЬНОГО ПРИБЛИЖЕНИЯ*
При построении математических моделей прикладных задач, как правило,
осуществляется предельный переход от дискретного к непрерывному. Получаемые
математические модели очень часто являются весьма сложными для непосредственного
изучения, и большое количество практически важных задач поддается изучению только с
помощью численных методов. При построении численных алгоритмов совершается
обратный переход от непрерывного к дискретному. Получаемая таким образом
дискретная модель должна быть максимально близкой по своим свойствам к
исходной непрерывной модели. В настоящее время одним из наиболее широко
применяемых методов перехода от непрерывной математической модели к дискретной является
метод конечных разностей. В этом случае дифференциальные уравнения, описывающие
исходную задачу, заменяются разностной схемой, которая может быть построена
не единственным образом. С учетом вышеизложенного очевидна важность
качественного исследования разностных схем.
При анализе разностных схем для уравнений гиперболического типа широко
используется метод дифференциального приближения [1], который позволяет строить новые
разностные схемы с заранее определенными свойствами, проводить анализ свойств
существующих и вновь создаваемых разностных схем, а также дать классификацию
разностных схем по определенным свойствам.
В данной работе показывается, что с помощью дифференциальных приближений
можно проводить асимптотический анализ разностной схемы, а также доказывается,
что инвариантные разностные схемы ближе к исходной непрерывной математической
модели, чем неинвариантные по отношению к группе непрерывных преобразований,
допускаемой исходным дифференциальным уравнением.
I. Асимптотическое разложение решения разностной задачи Коши.
Асимптотический анализ является одним из важных методов качественного исследования
разностных схем. Возможность исследования асимптотических свойств разностных схем с
помощью дифференциальных приближений изучалась в работах [2—5]. В работе [2]
показана сходимость решений ряда схем в пространстве обобщенных функций к
решению соответствующих дифференциальных приближений при t -+ °° и фиксированном
шаге по времени. В работах [3, 4] изучалось асимптотическое поведение решений
однопараметрического семейства разностных схем и показано, что в некотором тополо
гическом пространстве (при довольно жестких ограничениях на схемы и
дифференциальные приближения) решения задачи Коши для дифференциальных приближений
дают асимптотическое представление решения разностной задачи Коши. Далее, следуя
работе [5], будет показано, что аналогичное утверждение, причем без существенных
ограничений на разностные схемы и дифференциальные приближения, имеет место
в линейном топологическом пространстве обобщенных функций Z'.
1. Для простоты рассмотрим случай одной независимой пространственной
переменной, хотя все результаты справедливы и в многомерном случае. Напомним
некоторые определения и обозначения из теории обобщенных функций, необходимые для
дальнейшего изложения.
Пусть S — пространство быстро убывающих функций вещественного аргумента,
D (R) — пространство финитных функций, носитель которых содержится на
вещественной оси R, Z — пространство целых аналитических функций комплексного
аргумента, удовлетворяющих следующему условию: для всякой функции <p(z)EZ и для
любого к(к> 0) существуют такие постоянные ау Cki что справедливо неравенство
\zky(z)\ < Cfcexp{dr|Imz|}.
* Журн. прикл. механики и техн. физики. 1980. № 5. С. 8-16. (Соавторы А.И. Урусов, Ю.И. Шокин.)
218

Пространства обобщенных функций (т.е. пространства линейных непрерывных
функционалов) над пространствами S, D (R),Z обозначаются соответственно через
S't D' (Д), Z'.
Если / — обобщенная функция, то ее значение на основной функции обозначится
так: (/, ф). Если/(х) — суммируемая функция, то
(/;*) = / f(x)*p(x)dx.
— оо
На рассмотренных выше пространствах основных функций определены
следующие операторы:
FMtt) = +feix*v(x)dx, F-l[<p](S)=^-+f~e-ix*<p{x)dx, (1.1)
£>"V(x) = Ътфхт, Ту<р(х) = <р(х+у),
&*ф) (х) = ?ч>(у)ф (х-у) dy, (р(х) = * (-х),
— оо
которые можно определить в пространствах обобщенных функций таким образом,
чтобы в случае, когда обобщенная функция является основной, соответствующие
операторы действовали на нее так же, как и в пространстве основных функций. Ниже
приводятся определения операторов (1.1) в пространстве обобщенных функций
(через / и g обозначим обобщенные функции, через </? — основную функцию) :
{F\f\9<p) = (f9F[<p])9 {F-l[f]9<p) = (f,F-l[<p])9
(f,*) = (fj), XDmf9tf = {-\r<f.Dm&9
(Tyf, ф) = (f, T_y<p)9 (f**) (x) = (f9 T_J)9
(/*£,>) = &,/*</>).
Через ду будет обозначать обобщенную функцию, которая действует по формуле
(6у,ф) =$(у).
2. Рассмотрим разностную схему
2 ft"1 Г ./я+1 = 2 blT„Jn (1.2)
a. a.hJ в 3hJ к '
l<*|<<7, \0\<Qo
в пространстве обобщенных функций S'. Здесь 0 < q0f Ц\ < °°; Ъ1а, ft? — некоторые
вещественные постоянные; h — параметр. Схему (1.2) можно записать в виде
wrfn+l = w0*fn, (1.3)
где
"w/ = A/60= 2 *'>_«„, / = 0,1.
Всюду в дальнейшем будем предполагать, что выполнены следующие неравенства
F[Wj](x)*0 VxtER, 7 = 0,1. (1.4)
П-формой дифференциального представления разностной схемы (1.2),
удовлетворяющей условиям (1.4), будем называть уравнение
df(t)ldt = г'1 F-'[In F[w0] -lnFlwJWCf). (1.5)
219

Для уравнений (1.2), (1.5) рассмотрим задачу Коши с начальным условием
/°=/(0)=/о- (1.6)
В работе [5] доказано следующее утверждение:
Теорема 1. Пусть /0€S'f тогда задачи Коши (1.2), (1.6) и (1.5), (1.6)
имеют единственное решение в пространстве S'. Кроме того, а) если f{t) —
решение задачи (1.5), (1.6), то \ /"J^q - решение задачи (1.2), (1.6), где fn =/(/ir; б) ее-
AUlfni™=o~ Решение задачи (1.2), (1.6), то существует однопараметрическое семейство
обобщенных функций fit), являющееся решением задачи Коши (1.5), (1.6) и такое,
что /(ит)=/Л.
В работе [5] также показано, что в некотором пространстве обобщенных
функций, зависящем от разностной схемы (1.2), имеет место равенство
F-1[lnF[w/]]*/= S v\hk(iDff, 7 = 0,1. (1.7)*
k = 0
Равенство (1.7) справедливо, вообще говоря, в более слабой топологии, чем
топология пространства S'. В (1.7) через т)*к Aк обозначены коэффициенты разложения
функции InF [wj] (х) в ряд Тейлора в окрестности точки х = 0, т.е. In F [w;] (x) =
= 2 Vjkhkxk.
fc=0
3. Покажем, что правую часть в (1.7) можно понимать как асимптотическое
разложение обобщенной функции F г [InF [Wj] ]*/при А-*0 в топологическом
пространстве S'.
оо
Напомним, что формальный ряд 2 а^кк называется асимптотическим разложе-
к - 0
нием функции sp (А) при А -* 0, если для всякого натурального^ N
Umo у (А) - 2 akhk\ /hN = 0.
Это записывается следующим образом:
оо
*(й)~2 akhk (А + 0).
к'О
Аналогично определяется асимптотическое разложение обобщенных функций, зави-
оо
сящих от параметра: ряд Б fkhk называется асимптотическим разложением однопара-
к = 0
метрического семейства обобщенных функций/(A) (f(h)GS\ fkES'Vk) при А -* 0,
если для любой основной функции ^Е5 справедливо соотношение (/(А), ф) ~
оо
~ Z A*(ffc,<,) (А-0).
fc= о
оо оо
Можно показать, что если /(А) - Б fkhk (А -> 0), то F [/] ~ Б F |/fc] А* (А -> 0).
к = 0 fc = О
Кроме того, для каждого фиксированного xGR (здесь и далее индекс/ опущен)
lnF[w](x)~ 2 nkxkhk (*-0).
fr = 0
Покажем, что для любой основной функции ipGS произведение
tN(h)=\\nF[w](x)-X r}kxkhk)v{x)lhN
I k = 0 J
сходится к нулю при А -► 0 в топологии пространства &
220

oo
Так как 2 rikxkhk сходится к функции In F [w] (х) при \xh \ < г0 для некоторого
к = о
г0 > 0, то
jlnF{w]x- Z Vkxkhk\ < CoWA^IjcI^ при |хЛ]<г0,
А: = О
где С0 (Л) -* 0 при Л -> 0. Далее, при x^R
| InF [wj (х) | <d (1 + | xh ify
для некоторых констант С\ иМ1з следовательно, |ln F [w] (x) \ < C2 \xh\M2 при
\xh\>r0, M2> N, отсюда получаем
\ hi F[w](x)- 2 nkx*h*\ <
CQ{h)hN\x\N, \xh\<r0,
k = 0 *w. i^i , \xh\>r0.
iCQ{h)hN\x
\chM \x\M,
Поэтому V ip (x) £ S
II N \ I
I In F[w] (*)- 2 r\kxkhkU{x)jhN\^0 при /*-►{).
*<=# J \ it = О
Аналогично можно показать, что
Ът х
2\М
sup (1 +|* I )'
Ъх"
" (^лг ^) J -* О при h -* 0.
Таким образом, для любой основной функции <р (*)€£ однопараметрическое
семейство функщш £/у-(й) сходится к нулю в 5 при Л->0. Так как для всякой
обобщенной функции /G5'
0^/» = tf *аг*)-*0 при й^О
то доказано следующее утверждение:
Теорема 2. Для всякой обобщенной функции /G5'
оо
F-^lnFtw]]*/-^ nkhk{iDff (h^O)
k = 0
в пространстве S\
m
Пусть Fjm = P'm(hx) = S rfkhkxk. Уравнение
fc=0
Э//Эг = г"1 F-'IPl-Pi,]*/ (1.8)
будем называть дифференциальным приближением разностной схемы (1.2).
Рассмотрим следующие задачи Коши:
df/bt = т ~lF -1 [InF [w] 3 •/. /J^0 =/0SS'; . (1.9)
df/dt = T-1F~l[Pm]*f, /|,=0=/0eS\ (1.10)
ОО
где Pm = 2 T^jt/i х ; г, Л — параметры; w — конечная линейная комбинация обобщен
* = о
оо
к „к
ных функций 5ЛЙ, удовлетворяющая условию (1.4). В этом случае ряд D цкУгкх
fc = 0
221

сходится к функции InF [w] (hx) в некоторой области S2CR, т.е. при xhEiSl. Пусть
Ят, л(0> &т,т, hit) — разрешающие операторы задач (1.9), (1.10) соответственно.
Видно, что
eT,H(t)f=F-1[(F[w])t'T]*f, «,■,*(*): S'-S' (1.11)
(последнее следует из теоремы 1);
fim.r.ft(0/=^-1[^p'»/T]*/, 'am,r,H(ty.s'+z: (i.i2)
Теорема 3. Пусть fT h(t) — решение задачи (1.9), a fm T h(t) — решение
задачи (\A0).ToedaeZ'fTth(tj-fmtT>h(t) = O(hm) (Л-0).
Доказательство. Необходимо показать, что V yp^Z
ИГЛ (|/г,Л(0-/т,г,Л«],^)/Лт=0. (1.13)
Таккак/г>Л(0 = ^Л(г)/о, /т,т,л(0 = Я#и,т,л(0/о> то из (1.11), (1.12) следует, что
соотношение (1.13) эквивалентно равенству
lim (((FMfT-^?^^O)#w=0 v^D(R), (1.14)
где go =F \f0].Пусть g(h;x) = h~m(elnFlw^~Pm —1) . Тогда для всякого целого
неотрицательного к и любого компакта KDkg(h,x)->0 равномерно на ЯГ при /*-*0и
><pGD(R) g(h,x)y(x)^0 в D (R) при Л -* 0. Так как g0eS\ то (^0, ^) -*0 при
/i->0 >ipGD(R). Последнее означает, что
lim (^m(^nF(w]~Pw_1)^o ^)/Лт =
.= lim ((F [w] -epm)g09<p)lhm=Q.
И-+0
Таким образом, доказано равенство (1.14), а следовательно, и утверждение теоремы.
Используя теоремы г и 3, можно доказать
Следствие. Пусть f0^S\ lf"l™=0 — решение задачи Коши (1.2), (1.6), а
fm,T,h(t) - решение задачи Коши (1.8), (1.6), тогда
/;-/«,г,л(яг)-0(й,я) (й + 0)
в топологическом пространстве Z'.
До сих пор рассматривалось двухпараметрическое семейство разностных схем (1.2)
(зависящих от параметров г и h) и исследовалось поведение решения задачи Коши
при стремлении параметра h к нулю. На практике обычно предполагается некоторая
связь между параметрами г и h. Например, для разностных схем вида (1.2),
аппроксимирующих уравнения гиперболического типа, естественной является связь г = к Л,
к = const. Покажем, что и при наличии связи между параметрами г и h имеет место
утверждение, аналогичное теореме 3.
Пусть т = Kha, 0 < а < /, к = const и в разложении функции In F [w] в ряд Тейлора
в окрестности нуля первые / коэффициентов т?0, ..., Vi-i равны нулю. Тогда
1 1 оо
- lnF[w] (hx) = -ха Б nk(hx)k-a. Так как в D (R) при h^O .
Т К к = 1
11 1 °°
lnF[w] (hx) ха Z VkQtx)*-"
hm-a L Kha К к= i
то справедливо следующее утвержение:
0,
222

Теорема 4. Пусть т = кйа, 0 < а < /, а = const, к = const, т?0 =i?i = ... = t?/-i =
= 0, /л (О - решение задачи (1.9), /w л(г) - решение задачи
df 1 Г m 1
m>/.
тогда fhW-fm^W^OQi*1-") при Л ->0 в Z'.
Используя теоремы 1 и 4, можно доказать
Следствие. Пусть г = кк01, 0< а < /, /0 ££', /" ^=0 - решение задачи Коши
(1.2), (1.6) , a/m h(t) - решение задачи (1.8), (1,6). Пусть h -+0 так, что t = пт = const.
&V -if -Za
fi Sx
Рис.1
Рис.2
Рис.3
Еслит?*-^ =т??-т?1=... = ^_1-т?1/1= 0, то/^-/тЛ(/7г) = 0(/!т-а) при h +0
в Z'.
П. Инвариантные разностные схемы. В работе [6] было введено понятие
инвариантности разностных схем. Численные расчеты, выполненные для различных
модельных задач [1,7—9], показали, что инвариантные разностные схемы лучше, чем
неинвариантные, передают качественную картину решения.
1. Пусть дифференциальное уравнение
ut=Lu (2.1)
(L — линейный дифференциальный оператор с постоянными коэффициентами,
содержащий лишь дифференцирование по пространственной неременной х) допускает группу
преобразований G [10] и Г — оператор из G, который отображает пространство
переменных (t, х, и) в себя, т.е. T(t, х, у) = (*', х\ и), где t' = t' (t, х, и); х' = х' (г, ху и);
и' =и' (t,x,u). Если функция и (г, х) удовлетворяет уравнению (2.1), то функция
и\ рассматриваемая как функция переменных (t',x')9 также удовлетворяет
уравнению (2.1). Таким образом, оператор Г, действующий в конечномерном эвклидовом
пространстве, порождает некоторый оператор Г', определенный на множестве
решений уравнения (2.1) и переводящий одно решение в другое: и' = Т'и.
Пусть для (2.1) поставлены корректно две задачи Коши
'*='.'= *(*)
(2.2)
(2.3)
и пусть </> (х) = v (t, х) | t=u , ф (*') = и' {t\ х') | , >=f >, где v (f, х) - некоторое решение
уравнения (2.1), v = T'v. Тогда в силу корректности задач Коши (2.1), (2.2) и
223

(2.1), (2.3) для решений этих задач будет справедливо равенство
»'-Т'и = 0, (2.4)
где и' (t\ х') - решение задачи (2.1), (2.3), а и {tt х) — решение задачи (2.1), (2.2).
2. Пусть уравнение (2.1) аппроксимируется разностной схемой
ип+1=Аип (2.5)
порядка аппроксимации к. Рассмотрим второе дифференциальное приближение схемы
(2.5)
щ =Lu + hkL±u + hk+(3L2uy Д>0, (2.6)
где Zi и L2 — некоторые дифференциальные операторы с постоянными
коэффициентами.
Для схемы (2.5) и уравнения (2.6) поставим две задачи Коши с начальными
условиями
и°=и(0) = ы (2.7)
и°=и(0)=ф, (2.8)
где функции {риф удовлетворяют сформулированным выше условиям (см. (2.2),
(23)).
Пусть uhruh — решения задачи (2.5), (2.8) и (2.5), (2.7) соответственно, аии.м/-
решения задач (2.6), (2.7) и (2.6), (2.8).
Теорема 5. Вообще говоря, u'h-T'uh= О (hk), но если разностная схема (2.5)
инвариантна относительно группы G [в], то и'ь.— Т'ин. = О (hk+P) .
Доказательство. Пусть v = T'v, тогда функция vr (t\ xr)
удовлетворяет дифференциальному уравнению
bv/dt,=Lv+hk(Ltv + LW) + hk+(*(L2v' +L2v),
где Li nL'2 — некоторые операторы, зависящие от группы G.
Отсюда следует, что в пространстве Z'справедливо равенство w—v'.= О(hk),
если Li ^0, или w-v' = О {hk*P), если L'i&Q (последнее означает, что схема (2.5)
инвариантна относительно группы непрерывных преобразований G). Так как из
теоремы 4 следует, что в Z' urh= w + О (*+^) и uh - и■ + 0(hk+P), то окончательно
получаем следующие равенства:
u'h-ruh =(«;~w) + (w-r'U)+ T'v-T'uh.
Откуда следует, что u'h—T'uh = 0{hk), если/,! *^0 (схема не инвариантна), и u'h-T'uh =
= О (hk+P), еслиЬ'х = О (схема инвариантна) .
3. В работе [9] было проведено сравнение результатов расчета по различным
инвариантным и неинвариантным схемам расщепления для следующей модельной задачи:
Ьи Ъи Ъи
— s <*У— -ЮТ-'* (2'9)
bt Ъх Ъу
I 1 - (1/ио)Р, Р2 = (х-а? + (У-Ъ? <ы\г
»Ф,*,У)= (о, р2>4 (2.10)
Задача (2.9), (2.10) описывает вращение кругового конуса (с высотой, равной 1,
радиусом основания и0) вокруг начала координат с периодом 2 п/а. Уравнение (2.9)
допускает преобразование поворота. Представляется целесообразным провести более
детальное сравнение результатов численного расчета по инвариантной схеме
расщепления 2-го порядка аппроксимации с различными известными схемами 2-го порядка.
В качестве таких схем были выбраны: схема Лакса—Вендроффа (модификация Рихт-
майера [ 11 ]), схема Мак-Кормака [12].
224

Расчеты показали, что инвариантная разностная схема расщепления передает
особенности точного решения более верно. На рис. 1—3 приведены линии уровня
и (А х> У) = с =const (с = 0,2; 0,4; 0,6; 0,8) точного (окружности) и разностного
решений на момент времени г = 3, полученного по инвариантной схеме (рис. 1), по схеме
Мак-Кормака (рис. 2) и схеме Лакса—Вендроффа (рис. 3). Расчеты проводились на
прямоугольной сетке, A t/Ax = 0,01, At/Ay = 0,02, At-, Ax-, А^-шага по времени и
пространству соответственно.
ЛИТЕРАТУРА
1. Шокин ЮМ Метод дифференциального приближения. Новосибирск: Наука, 1979.
2. Шокин ЮМ. Об асимптотическом поведении решений разностных схем // Изв. СО АН СССР.
Сер. техн. наук. 1969. № 3, вып. 1.
3. Кузнецов Н.Н. Слабоустойчивые конечно-разностные аппроксимации дифференциальных
уравнений // Журн. вычисл. математики и мат. физики. 1971. Т. 11, № 6.
4. Кузнецов Н.Н. Асимптотика решений конечно-разностной задачи Коши // Там же. 1972. Т. 12,
№2.
5. Шокин ЮМ, Урусов AM. Дифференциальные представления разностных схем в пространствах
обобщенных функций // Числ. методы механики сплош. среды. 1979. Т. 10: № 4.
6. Яненко ИМ., Шокин ЮМ. О групповой классификации разностных схем для системы
одномерных уравнений газовой динамики // Некоторые проблемы математики и механики. Л.: Наука,
1970.
7. Федотова ЗМ. Инвариантные разностные схемы типа предиктор-корректор для одномерных
уравнений газовой динамики в эйлеровых координатах // Тр. V Всесоюз. семината по числ.
методам механики вязкой жидкости. Новосибирск: ВЦ СО АН СССР, 1975.
8. Федотова ЗМ. Анализ свойств аппроксимационной вязкости некоторых разностных схем для
двумерных уравнений газовой динамики. Новосибирск, 1979. (Препр. ИТПМ СО АН СССР;
№10).
9. Шокин ЮМ., Урусов AM. Об инвариантных разностных схемах расщепления // Тр. IV Всесоюз.
семинара по числ. методам механики вязкой жидкости. Новосибирск: ВЦ СО АН СССР, 1973.
10. Овсянников Л.В, Групповой анализ дифференциальных уравнений. М.: Наука, 1978.
11. Рихтмайер Р., Мортон К Разностные методы решения краевых задач. М.: Мир, 1972.
12. MacCormack R.W., Paullay A.J. The influence of the computatuonal mesh on accuracy for initial value
problems with discontinuous or nonunique solutions // Comput. and Fluids. 1974. Vol. 2, N 3/4.
8. Зак. 95 3

ДИФФЕРЕНЦИАЛЬНЫЕ АНАЛИЗАТОРЫ
ДИФФЕРЕНЦИАЛЬНЫЕ АНАЛИЗАТОРЫ УДАРНЫХ ВОЛН*
Существующие в настоящее время алгоритмы определения положения фронта
ударной волны в газодинамических течениях по максимуму искусственной вязкости не
имеют обоснования. В работе сформулированы и доказаны теоремы, которые
обосновывают практические способы локализации ударных фронтов в расчетной области по
результатам сквозного счета.
1. Введем ряд определений.
Определение 1. Дифференциальный анализатор — алгоритм,
предназначенный для локализации особенностей по результатам сквозного счета задач механики
сплошной среды.
Определение 2. Под дифференциальным анализатором ударной волны будем
понимать алгоритм, позволяющий найти координаты центра конечно-разностной
ударной волны в расчетной ячейке по результатам сквозного счета.
Определение 3. Центром конечно-разностной ударной волны (ц.к.р.у.в)
назовем точку, положение которой не зависит от шага сетки h в системе координат,
связанной с ударной волной.
Рассмотрим задачу о стационарной ударной волне в газе. Следуя работе [1],
запишем уравнения одномерной газовой динамики в эйлеровых переменных при
наличии искусственной вязкости q, аддитивно входящей в давление, в координатной
системе, движущейся с постоянной скоростью ударной волны D:
ри= Ci = m, (p + q) + ти = С2, ^
™(W(P(7-1))+72W2) + (P + ^)" = C3;1
здесь р, н, р — соответственно плотность, скорость и давление газа, у = const,
С\, С2, С3 — постоянные интегрирования. Для определенности предположим, что
ударная волна движется слева направо; тогда D>09 т < 0. Величины,
определяющее состояние за фронтом ударной волны, будем помечать нижним индексом 1,
а перед фронтом — индексом 2; пусть v = 1/р.
Теорема 1. Пусть искусственная вязкость qt входящая в уравнения (1),
имеет вид
[ F(hdu/dx, hdp/dx9 hdp/dx9p, р), du/dx<09
Q = (2)
I 0, du/dx >0
(h - шаг расчетной сетки), и система уравнений (1), (2) однозначно разрешима
относительно dv/dx, так что
dv/dx = f(CuC2,C3,v,h)\ (3)
где f(Q, v,h) положительна в интервале (uls v2}, а функция
ф(С,,1;,/0 = Г—Р— (4)
f(Qv9h)
* Докл. АН СССР. 1976. Т. 227, № 1. С 50-53. (Соавторы Е.В. Ворожцов, В.М. Фомин.)
226

непрерывна по v и меняет знак на (vi,v2); тогда существует единственный центр
конечно-разностной ударной волны.
Доказательство. Рассматривая систему уравнений (1), (2) как систему
трех уравнений относительно четырех функций р, w, p, q, найдем w, p, q как
функции v и подставим в обе части равенства (2), в результате чего получим
обыкновенное дифференциальное уравнение относительно v(x). Используя метод
доказательства П-теоремы [2], нетрудно показать, что функция /(Q, v, И), входящая в (3) ,
имеет структуру
f(Cj,v,h) = h^vupiv/Vi, v2/v1\,
где константы Q. из (1) исключены через uls v2. Следовательно, функция Ф(и,Л)
согласно (4) имеет вид
Ф(и, И) = НФг (v), -Фх (и) = — f dv
Vi ^(u/Ui, V2/Vi)'
Таким образом, решение уравнения (3) выражается формулой
Ф^и) = (x-x0)/h,
где х0 — постоянная интегрирования. В силу того, что Ф\ (у)>Ои функция Ф! (v)
меняет знак в интервале (vi,v2), уравнение Oi (и) = 0 имеет единственный корень
Vo £ (vi,v2). Таким образом, точка х0 по определению является центром
конечно-разностной ударной волны, что и требовалось доказать.
Следствие. Если Ф1 (\/^i * v'2) < 0 [Ф1 (VvTH^) >0], то точка максимума
искусственной вязкости находится левее (правее) ц.к.р.у.в. Если кроме того
удовлетворяется неравенство I Ф1 ( V^i, u2)l ^ В, то точка максимума искусственной
вязкости qr отстоит от ц.к.р.у.в. на расстояние, не превосходящее Bh.
Теорема 2. Пусть вязкость (2) удовлетворяет условиям теоремы 1 и кроме
того имеет место равенство Ф,\{р{х0)) = 0, где х0 — центр конечно-разностной
ударной волны; тогда точка дг0 совпадает с точкой экстремума функций
\du/dx\, dv/dx, \d(p + q)/dx\. (5)
Если, кроме того, O'i"(°(*o)) >0 (Oi"(u(jc0)) < 0), то х0 — точка максимума
(локального минимума) функций (5) .
В табл. сведены результаты исследования существования ц.к.р.у.в. при
использовании некоторых искусственных вязкостей вида (2) в газодинамических расчетах
(1 + т?)2 (7 + 1) \Ьо2-ао\ (т - I)]2- 4т/ [aoh(7 - 1) - 4а2 (у + 1)] X
Х(яа2т-4а2)<0, (6)
a2ohi7~l)< 1, (7)
b>[v~ ^-J {(7-1)[27(т?2- l^It,(l+f?) + ^-t?)J } .
(8)
В неравенствах (6)— (8) а, 0\, о2, Ъ — безразмерные постоянные, r\ = v2\v\.
Теорема 3. Если задан максимум искусственной вязкости q (2) и состояние
среды перед фронтом ударной волны, описанной системой уравнений (1), то
состояние за фронтом ударной волны и ее скорость определяются однозначно.
2. Ширина размазанного фронта конечно-разностной ударной волны зависит не
только от величины искусственной, но и схемной вязкости. Порядок схемной
вязкости определяется выбранной численной аппроксимацией системы уравнений и
8*
227

Таблица
Я
"ffl
du
-ahc0p
dx
и du
dx
«. du I A
-ahp 1 o1 с + a2«
dx \
-hacpl 1 + bcp
I
III _
ffi
dx \)
] du
J dx
Существует ли
ц.к.р.у.вЛ
Да
Лд
Да
Да
при (6) и (7)
Да
при (8)
Практический критерий
нахождений ц.к.р.у.в.
по max
1 du/dx |
при du/dx < 0
по max
\du/dx \
при du/dx < 0
по max q
при du/dx < 0
l<&i(V^)l< 1
no max <7
при du/dx <0
I«M\4»»)I<1
no max #
при rfu/ix < 0
.|Oi(V«i«i)l < 1
Литература
tn
[3]
f4]
f5]
поэтому существенно влияет на положение ц.к.р.у.в. В связи с этим представляется
разумным вопрос о существовании ц.к.р.у.в. исследовать с помощью
дифференциальных приближений разностной схемы [4]. Рассмотрим гиперболическую систему
уравнений
Эи/Эг + Мн)/Эх=0, w=(Wl,...,ww), </>=Oi,...,*>„)• (9)
Прежде чем сформулировать теорему, введем ряд обозначений. Пусть w(x, t) —
вектор-функция, которая в узлах сетки совпадает с решением конечно-разностных
уравнений, аппроксимирующих систему (9), а в остальных точках (х, t)
доопределена из требования существования производных
di+tw(x,t)
К i + / < 3, / > 0, / > О,
Ъх1Ъг>
Т±И> Т±т — операторы сдвига по х и по f такие, что T±hw(x,t) = w(x±h,t);
T±tw(x, t) = w(x, t ± r), r — временной шаг, Е — тождественный оператор.
Теорема 4. Если конечно-разностная схема в целых шагах, аппроксимирующая
систему (9), представима в виде
г-1С\^1{Тг-{^ъТн^^Е^а5Т_н)] + 132[(а6Гл + а7^+а8Г_л) - Г_г ] } X
X w(x,t)+h-1[al{Th-E)+a2{E-TLh)][03TT + №+ p5T.-T]<p{w(x9 *)) =
= ^-1 (^/2- Г-л/2) I A-'nCwCx, г)) (^/2- ^W2) [Р6ГТ+ 07ff +
-Л/2
Л/2"
-Л/2>>
+ АГ_Т] }w(*,f)
и выполнены условия:
228
(10)

а) С - трехточечный оператор такой, что его втрое дифференциальное
приближение С имеет вид
/=i Ъх* Л }
где tf,(w), ft(vv) — матрицы размерности пХп, которые могут зависеть не только
от w, но и от производных функций w(x,t):
б) элементы матрицы £1 есть величины порядка 0(т) + 0(h);
в) а,-, |3/, / = 1, ...,8,- константы такие, что
<*i + a2=l, а3 + а:4+а:5= 1, а6+ат+ав= 1,
01 + 02 = 1, 03+04+05= 1, 06+07+08= 1,
0<а.<1, О<0.<1, /=1,...,8,
то тогда первое и второе дифференциальные приближения разностной схемы (10)
могут быть представлены в дивергентном виде.
Теорема 5. Если постоянные коэффициенты aiy fy в схеме (10) и матрицы
aj(w)9 £l(w) удовлетворяют условиям:
а) 0i (<*з-а5) - 02 (а6-а8) = 0;
dip h dip
б) hDa.iw) +г(0з-05)£ —' (ai-a2) + «(w) = P9(D)E;
dw 2 dw
h2 т
в) e= -—[0i(a3+ a5) - j32(a6+a8)] - -( /32 — /32)£>2 + 09 >0,
2r 2
го ^ен7р конечно-разностной ударной волны для схемы (10) существует и единствен,
ЛИТЕРАТУРА
1. Neumann J.R., Richtmyer Д.//J. Appl. Phys. 1950. Vol. 21, N 2. P. 232.
2. Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1967.
3. ЯненкоН.Н., АнучинаН.Н., ПетренкоВ.Е.,ШокинЮ.И. //Числ. методы механики сплош. среды.
1970. Т. 1,№1.С 40.
4. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М.: Наука, 1968.
5. Ивандаев А.И. // Журн. вычисл. математики и мат. физики. 1975. Т. 15, № 2. С. 523.
К ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ АНАЛИЗАТОРОВ
КОНТАКТНЫХ РАЗРЫВОВ*
В заметке сформулирована теория, имеющая целью обоснование методов
локализации контактных- разрывов в расчетной области по результатам сквозного счета
одномерных задач газовой динамики в переменных Эйлера.
1. Исходную систему уравнений Эйлера невязкого сжимаемого газа запишем в виде
bu/bt + Ъ\р(и)1Ъх = 0; (1)
/р \ (9U \
" = 1 Р" I, У>(") = I Р + Р"2 I, E=e+u2/2;
\ pEJ \ pu+puE/
здесь р — плотность, и — скорость, р — давление, е — удельная внутренняя энергия.
15 Докл. АН СССР. 1979. Т. 247, № 1. С 48-52. (Соавтор Е.В.Ворожцов.)
229

Уравнение состояния берется в форме
€ = /(Р,Р>, (2)
где функция f(p, р) предполагается имеющей производные dmf/dpk Ърт~к {in =
= 1,2,3; т-к>0).
Для системы (1), (2) рассматривается задача о распаде разрыва при следующих
начальных данных:
Pi» х<х0 ^ (3)
со
(Pi, x<xQ
Р2, Х>*0
где w0, Ро> Pi> P2, х0 — постоянные, причем р\ Ф р2- Точное решение задачи (1)—(3)
содержит только контактный разрыв, движущийся со скоростью и0.
Рассмотрим класс разностных схем, аппроксимирующих систему (1) с порядком
точности 0(кг)+0(тг)9 1 < г < 2, и таких, что Г-форма их первого
дифференциального приближения (п.д.п.) [1—3] представима в виде
dw 3(/?(w)
Tw = +
dt Ъх
. . / dw dw dr + 1w \
Z hlTIK.[w9 , _,..., )=o,
U "\ Ъх bt dxkdtr+1~k I
(4)
w = { w,, w2, w3\, wt= p, wf = /;(p, u, p, e(p, p)), /=2,3,
^ = * W^K *"°«1 r + 1«
h — шаг равномерной расчетной сетки на оси, х, г — временной шаг, г = 1 или 2 (для
схем соответственно первого или второго порядка точности). Выразим производные
dmw/bxkdtm~k9 т—к>09 входящие в F,.9 через производные пол, пользуясь
алгоритмом, описанным, например, в [ 1 —3]:
dmw/dxkdtm~k= fm k(w, dw/dx9...,dmwldxm).
В результате получим из (4) П-форму п.д.п.
nw= + rv - S AV5:.(w, aw/Эх,..., Эг+1и>/ЭУ+1) =0; (5)
3r Зл: /,/ lJ
/+/ = /•
^(w, 3w/3x,..., 3r + 1w/3xr + 1) = F„(w8 3w/3x, /1)0(w, 3w/3x),...,
, fr+ltk(w9dwldx9...9dr+lw/bxr + i))9 .
*if l ^ijl9 ^i/2> Л/3 **
Определение 1. Операцией квазилинеаризации L п.д.п. (4) или (5) назовем
операцию
TLw =0, YiLw = 0,
где
Lw= \wl9 Lw29Lw3\9 Lw. = f.(p9 Wo,Po,e(po,p)), / = 2,3,
a «b> Po — постоянные значения скорости и давления, входящие в (3).
230

Пусть
U= jl, w0,0,5t4 + /(Po,p) + P —(Po,p)j.
Определение 2. Первое дифференциальное приближение (4) будем называть
/Г-согласованным, если
[Эр Эр
— + и0
Ъг Ъх
. . / bLw bLw dr + lLw \]
- S hlT3F..ALw9 , ,-,
i,i ljl\ Ъх Ъг 9jt*9fr + 1-*/J
= 0,
i + j =r
т.е.; левые части уравнений системы TL w = 0 различаются лишь скалярным
множителем. Аналогично определяется/^-согласованность П-формы (5) п. д. п.
Заметим, что исходная система уравнений (1), (2) обладает свойством /С-согласо-
ванности. Легко доказать, что из /^-согласованности Г-формы п. д. п. (4) следует
К-согласованность П-формы п.д.п. (5). Из определения 2 вытекает, что
исследование свойств /^-согласованного п.д.п. (5) при начальных условиях (3) сводится к
исследованию одного уравнения
Эр Эр . . / bLw 3r + 1JLw\
— +и0— = Б hlTJF.n[L~w9 ,.., . (6)
Ъг Ъх #,/ lJ1\ Ъх Ъхг + 1 I
/+/=#■
Уравнение (6) изучается в дальнейшем при начальном условии
X *\ Xq ,
, ^ ( Pi» х< х°<
р(х,0) =
{ р2, х> х0,
(7)
и краевых условиях
Ът~1р Эш~1р
lim = lim = 0, #2 = 2,..., r\ (8)
X-++°o ЪХ™"1 X-+-«> fix™"1
налагаемых при г > 2. .
Определение 3. Контактной полосой GKD назовем открытую односвязную
область в плоскости (х, г), содержащую контактный разрыв, всюду в которой при
каждом фиксированном г>0 выполняются условия:
а) sign (Эр/Эх) = sign(p2-pi);
б) pi (г — б) > р > р2 (1 + б), если pi > р2; pi (1 +б) < р< р2 (1 — б), если
Pi < Р2, где б — малое положительное число, р(х, г) — решение задачи (6)— (8).
Определение 4. Центральной линией контактной полосы GKD назовем
линию Lxd с Gkd> на которбй значение функции р (х, г), где р — решение задачи
(6) —(8), не зависит от величин сеточных параметров h9 т.
Обозначим через wh(xK г,Н9 т) вектор-функцию, которая в узлах сетки в
плоскости (х, г) совпадает с решением разностных уравнений, аппроксимирующих задачу
(1) — (3), а в остальных точках (х, г) доопределена с помощью интерполяции.
Определение 5. Контактной полосой GK назовем открытую односвязную
область в плоскости (х, г) , содержащую контактный разрыв, всюду в которой
sign[p^(x+/i,r,/i,r) -ph(x-h9t,h9 r)] = sign (pj-pj).
231

Определение 6. Центральной линией контактной полосы GK назовем линию
Lk c Gj£9 являющуюся геометрическим местом точек пересечения профилей
ри(х, t, hi, тх), ph(xt 7, /*2 , г2) при каждом фиксированном t > О, причем } /?i — /г21 "•"
+ \т1-т2\Ф0.
Определение 7. Под дифференциальным анализатором контактной границы
будем понимать алгоритм, позволяющий найти координаты точек линии Lk в
расчетной области по результатам сквозного счета задач газовой динамики.
Определение 8. Эеличину
X{t9h9r9 и09Ро) = | Pi-p2l/ max |Эр/Эх| (9)
х, х е cKD
назовем толщиной по Прандтлю контактной полосы, где р(х, t) — решение задачи
(6)-(8).
Теорема. Если: i) первое дифференциальное приближение разностной схемы
r-го порядка точности, 1 < г < 2, является К-согласованным, ii) уравнение (6) имеет
вид
Эр/Эг+ и0др/Ъх = (-iy+1fi(h9T9u0,Po)br+1pfdxr + 19 (10)
iii) li{h9T9UQ9Po) >0 при и0>69 р0>0 и значениях величин h9r,
удовлетворяющих условию устойчивости разностной схемы, iv) т = 0(Н)9 то тогда существует
единственная центральная линия LKD контактной полосы, причем эта линия совпадает
с траекторией контактного разрыва.
Доказательство теоремы сводится к получению точного решения задачи (10), (7),
(8) и последующему изучению его свойств; при этом в случае г = 1
р(х, г) = 0,5(Р!+ р2) + 0,5(р2-р1)Ф(5(^, О);
при г = 2
p(x,t)= (2p2 + p1)/3+(p2-p1)fAi(\)d\9 (И)
о
где £(х -х0- u0t)/[(5 —г)цг] 1/<г+1) , ф(£) — интеграл вероятности [4], ^/(Х) -
функция Эйри [5].
2. Для практических расчетов с использованием схем первого и второго порядка
точности, удовлетворяющих условиям теоремы, можно вывести следующие три
алгоритма дифференциального анализатора контактного разрыва.
Алгоритм I. Локализация линии Lg непосредственно на основе определения 6.
Алгоритм II. Определение при каждом t >0 точки линии LK как точки \дгр/дхг\
при xG GK.
Алгоритм III. На линии L^d выполняется свойство p=0,5(Pi + p2) при г=1 и
p = (2p2 + Pi)/3 при г =2. Поэтому при известных значениях р\, р2 можно
приближенно найти абсциссу точки линии LK обращением интерполяции функций ph(x, t9h9r).
В табл. подытожены результаты исследований ряда разностных схем первого и
второго порядка точности. Показано, что выполнение равенства
Э
Эр
t\ f
/(РсьР) + р-МРо,р)
Эр
= 0,
где функция f(p, p) входит в уравнение состояния (2) , является необходимым
условием /^-согласованности первых дифференциальных приближений разностных схем,
принадлежащих широкому классу, включающему разностные схемы, рассмотренные
в табл. Отметим тесную связь, существующую между дисперсионными свойствами
232

Таблица
Метод
Порядок
аппроксимации
Толщина X (9)
Практический
критерий для
нахождения линии Lg
Лакса [1]
Годунова [6]
ELIC [7]
"Крупных"
частиц [8]
/п2\ Н2 г
0iT)+0{v) t-~iu1
\2т/ 2т 2
,«ol(^-^l«ol) То
0(т) + G{h)
Тоже
Лакса-Вендроффа 0(т2 )+ 0{h2 )
одношаг. [9]
Лакса-Вендроффа То же
двухшаг. [9]
Мак-Кормака [10] »
Тоже
Тоже
2(тгмГ)
Уг
\u0\(h2-r2u20) Out)
Уз
Ai(SQ)
£0s -1,01879
^ift0)e 0,53566
По max | Ър/Ъх |
при sign (Эр /Эх) =
= sign(p2-p,)
По max|32p/djc2 |
при sign(dp/dx) =
= sign(p2-p,)
и явлением Гиббса, установленными в [11] для полудискретной аппроксимации
волнового уравнения, и свойствами решения [11].
Результаты многочисленных расчетов задачи (1)—(3) с использованием схем,
перечисленных в табл., качественно и количественно согласуются с полученными в рамках
вышеизложенной теории, в частности подтверждена практическая применимость
алгоритмов I—III для локализации контактного разрыва: при этом положение контактного
разрыва определяется с погрешностью <h9 несмотря на то, что ширина контактной
полосы растет пропорционально tl^r + 1^. На центральной линии LK контактной полосы
численное решение для плотности рп "наиболее слабо" зависит от Л, г. В [12] был указан
вид зависимости толщины контактной полосы от времени t. Изложенная теория дает
способ определения зависимости толщины контактной полосы от параметров разностной
схемы й, т и времени t для каждой конкретной разностной схемы (см. табл.) .
Из проведенного исследования вытекает важный вывод о том, что построение
разностной схемы, сохраняющей постоянной ширину контактной полосы в газе, связано
прежде всего с построением такой схемы для скалярного линейного уравнения.
ЛИТЕРАТУРА
1. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М.: Наука, 1968.
2. Яненко Н.Н., Шокин Ю.И. // ДАН СССР. 1968. Т. 182, № 2. С. 280.
3. Шокин Ю.И. Численные методы газовой динамики: Инвариантные разностные схемы.
Новосибирск, 1977.
4. Тихонов А.Н., Самарский АЛ. Уравнения математической физики. М.: Наука, 1977.
5. Смирное В.И. Курс высшей математики. М.: Наука, 1977. Т. 3, ч. 2.
6. Годунов С.К., Забродин A3*. Прокопов Г.П. // Журн. вычисл. математики и мат. физики. 1961.
Т. 1,№6.С1020.
7. Gentry КЛ.. Martin RJE., Daly В J. //J, Compute Phys. 1966. Vol. 1,NL P. 87.
8. Белоцерковский ОМ., Давыдов ЮЖ // Журн. вычисл. математики и мат. физики. 1971. Т. 11.
9. РихтмайерР., Мортон /С Разностные метода! решения краевых задач. М.: Мир, 1972.
Ю. MacCormackR.W. // AIAA Pap. 1969. N 354.
11. Chin R.C. Y. // J. Comput. Phys. 1975. Vol. 18, N3.
12. Rusanov V. К // Fluid Dyaamics Tians. 1969. Vol 4. P. 285.
233

ДИФФЕРЕНЦИАЛЬНЫЙ АНАЛИЗАТОР ДЛЯ РАЗРЫВОВ РЕШЕНИЙ
НЕОДНОРОДНЫХ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ*
В работах Н.Н. Яненко, В.М. Фомина, Е.В. Ворожцова [1, 2] было дано понятие и
развита теория дифференциального анализатора для ударных волн, являющихся
решениями однородных дифференциальных уравнений гиперболического типа. С такой задачей
приходится иметь дело и при определении положения фронта ударной волны с
примыкающей зоной релаксации. В частности, этот вопрос возникает в неравновесной газовой
динамике, в механике многофазных сред, в механике твердого неупругого тела и т.п.
1. Распространение ударной волны с наличием зоны релаксации будем моделировать
с помощью решения смешанной задачи для неоднородного уравнения
du/dt + Ъф)/Ьх = ф(и), (1)
удовлетворяющего начальным и краевым условиям
и = и0, х < О, и = и+, х > О, t = О,
и -»и0, х-*-°°, и -* иь х -* +°°, t > О, (2)
и0 > и+ > их.
Здесь ip(u) удовлетворяет условиям устойчивости [3] в [м+, и0], т.е.
*>» > 0, <р'(ц0) > D > <р'(и+)9
D = М / [и], И = *(ио) - *(«+)> (3)
и<р'(м) -D^Ов[мь м+],а ф(и) непрерьюна на [и0, их],причем
*(ио) = Ф(Щ) = 0, *'(«!)/(/.("i) - Д) < 0. (4)
Теорема 1. Решение задачи (2) для уравнения (1) существует и единственно
при выполнении условий (3), (4) в классе функций К.
Определение класса функций К дано в работе [3].
Доказательство. Разыскивая решение задачи (1), (2) в классе простых волн
и = и(у),у =х - Dt, получим для определения и (у) уравнение
Ъи/Ъу = ШК*(м)-0). (5)
В силу (3) в [и+, и0] существует единственная точка и-и^ такая, что <р'(м*) - D = 0.
Поэтому непрерывного решения данного уравнения, удовлетворяющего условиям
стационарности при у -> ± °°, нет, но можно сконструировать обобщение, состоящее из двух
интегральных кривых
и = и0, у < 0
и решения и = и (у) краевой задачи
и = "+> ' У = 0, ди/ду -* 0, у -* +°° (6)
для уравнения (5), которое существует и единственно в силу предположений (3), (4).
Определение 1. Решение задачи (I), (2) класса К, представляющее собой
зону постоянного течения, граничащую через разрыве зоной переменного течения,назовем
ударной волной с релаксацией (уз.р.) •
Решим задачу (1), (2) о стационарной у.в.р. методом конечных разностей. Выберем
многопараметрический набор конечно-разностных схем вида
г"1 [Тт - {*ХТН +а2Я+ а3Т_л )] и(х9 t) + h'1 [a4(Th - Е) + а5(Е - Г_л)] <р(и(рс, *)) =
= h~^THi2 ~ г-Л/21 ["Г П(и(^ r))(rV2 - Т-И12)\»&> О, (7)
* Докл. АН СССР, 1980. Т. 254, № 3. С. 554-559. (Соавторы А.В. Федоров, B.M. Фомин.)
234

аппроксимирующих (1) с первым порядком точности при у < у0 = const, причем
£1 = (Л/2)^! (O-i — конечная величина); прочие обозначения общеприняты [3].
Замечание. \.-ф(и) = 0 в области у < у0, так как здесь w=w0.
Определение 2. Центром конечно-разностной у.в.р. (ц.к.р.у.в.р.) назовем
точку в решении задачи (1), (2), полученную с помощью некоторого
конечно-разностного метода, которая не зависит от шага h разностной схемы.
Дальнейший анализ проводим, используя некоторые положения метода
дифференциальных приближений (п.д.п.) разностных схем [4].
П.д.п. разностной схемы (7) при условиях
oti +а2 +а3 = 1, <*! — а3 = 0, а4 + а5 = 1 (8)
имеет вид П- или Г-формы
Ъи д#(и) h 3 Г/ ,2 <*i +а3 \ Ъи t Ъи ди Л
3w <ty?(w) r d2</? /i2 32</?
+ -ri-i = v- + (aj +a3) т - (9)
Ъг Ъх 2 Ъг2 К 2т Ъх2 '
h Ъ2#(и) h Ъ Ъи
- (о* - а5) — '2 + — — ni-T- > ' = Г/Л-
2 3dc 2 Ъх Ъх
Определение 3. Задачей А назовем задачу о склейке решений типа простой,
волны уравнения п.д.п. (8) для (1) и уравнения (1), выполняемого на линии у = у0,
и удовлетворяющих условиям стационарности при у -* ± °° соответственно.
Определение 4. Центром конечно-разностной у.в.р. назовем точку в решении
задачи Л, которая не зависит от шага h разностной схемы.
Теорема 2. Если конечно-разностная схема (7) удовлетворяет условиям (8) и
ц(и) = («! + а3)/г - </(а4 - а5 + пр') + Пг > 0, (10)
а функции \р(и), ф(и) удовлетворяют условиям (3), (4), то центр конечно-разностной
у.в.р. не существует.
Доказательство. Рассмотрим для П-формы (8) и для (1) решения типа
простой волны и = и (у). Уравнение, которому удовлетворяет и(у) после
однократного интегрирования, имеет вид
H(u)du/dy = у(и) - ip(u0) - D(u - и0). (11)
Здесь постоянная интегрирования выбрана из условия стационарности при у -* -°°.
Нетрудно убедиться, что при условиях (3) существует и единственное решение (11),
удовлетворяющее условиям и -* и0, du/dy -* 0 при^ -* -°°, но при этом и -* м+, dw/afy -* О
при у -* +°°. Таким образом, ни в какой конечной точке у мы не можем склеить
решение уравнения (11) с решением уравнения (5), удовлетворяющего соответствующим
краевым условиям (6). Отсюда видно, что построить решение задачи Л и
соответствующую ей в смысле п.д.п. конечно-разностную у.в.р. невозможно.
Пример 1.Из теоремы 2 следует, что схемы "Крест", "Лакса", "Русанова" [3]
не обладают центром конечно-разностной у.в.р.
Замечание. 2. Условие (10) означает в каждой из перечисленнных схем
требование выполнения условия Куранта.
Замечание. 3. Теорема 2 утверждает несуществование центра
конечно-разностной уз.р. Можно отметить, что схемная вязкость данных схем размазывает разрыв
(и0, и+) на бесконечный промежуток, т.е. "смазывает" зону релаксации.
Рассмотрим многопарамётрический набор схем второго порядка точности для реше-
235

ния задачи (1), (2) в виде
t-MPiOV-£) + &(*- Г_т)] и{х, О + А'ЧРэО* -Е) + р4{Е- Т_н)]ф(х, 0) =
= (г/2Л2)[Гй/2 - Т_н/2] [П(и(х, t))(Th/2 - T_h/2)] u(x, 0, (12)
которому при условиях
01 +02-/32-^4 = 0, 03-04= 0,
(13)
*-*-{J: °-{!f ■
ше Г-форму п.
L б - эг3 б ах3 J
поставим в соответствие Г-форму п.д.п. при .у <.у0
Ъи Э<р(м)
+
bt Ъх
-[
Теорема. 3. Если конечно-разностные схемы (12) удовлетворяют условиям
(13), а функции ф(и), ф(и) - условиям (3), (4) и h/т = D, то существует центр
конечно-разностной у.в.р.
Доказательство. Рассмотрим для Г-формы (14) и для (1) решение простой
волны и = и (у). Введем функцию F(u) = <p(w) — Du + С, С - произвольная постоянная,
полученная после одной интеграции уравнения длям(у), имеющего после этого вид
-tid2F/dy2= F, v = h2/6. (15)
Уравнение (15) имеет общее решение
F(u) = dx sin(>/V/x) + d2 cosO/V/I).
Выберем С из условия F{u+) - 0; тогда нетрудно убедиться, что F(u0) = 0, и выберем
dx = 0, a d2 = -max | F(u)\ = —| Р(иф)\ . Здесь иф определяется из уравнения
ие[и+,и0].
<£("*) - D = 0 единственным образом в силу (3). После определения произвольных
постоянных решение уравнения (15), определяющее у.в.р. в соответствующей области,
запишем в виде
ио,у/уД?^-7г/2, (16)
F-l(-\ F+\ cos(v/V5)), -я/2 <-y/yfc< я/2.
Легко видеть, что в точке y/yfii = —я/2 функция и(у), определяемая формулой
(16), непрерывна вместе с первой производной, a dujdy < 0 при(>>/\/Де [—-nil, я/2],
w= (я/2) = w+. Существование F~~l(g) следует в силу однозначности cost на [—я/2, я/2]
и того, что F(«)/|F(w*)|< 1,для we [u+, и0]. Таким образом, у.в.р. будет построена
полностью после определения решения краевой задачи (5), (6) (причем и я и+ при
yl\fi± = я/2), существующего в силу теоремы 1.
Таким образом, конечно-разностная у.в .р. построена в классе функций
непрерывных вместе с первой производной в у/уДх = —я/2 и непрерывных в у/\Д1 = я/2.
Очевидно, что центр конечно-разностной у.в.р. расположен в точке\у = 0, т.е. не зависит от h .
Пример 2. Из теоремы 3 следует, что схемы "Лакса—Вендроффа", "Неймана—
Рихтмайера" [3] без искусственной вязкости обладают ц.к.р.у.в.р.
Пример 3. Пусть у(и} = w2/2. В этом случае решение (16) имеет простой вид
и = f "о, y/>/Ji < - я/2,
\ (и0 + м+)/2 - (и0 - м+)/2 VTsin(y/2VJi), -я/2 < у/у/р < я/2.
Здесь цлс.р. ул.р. расположен в точке у = 0 и распространяется со скоростью D ~
= (w0+w+)/2.
2. Рассмотрим решение задачи при использовании искусственной вязкости q. Так,
система уравнений неравновесной газовой динамики в системе координат, движущейся
236

со скоростью Д представима соотношениями.
ри = т, Р + ри = С2, е+Р/р+и2/2 = С39 (17)
и dH/dy = А:(р, Г, £), е = е(р, Г, £), Р = Р(р, Г, £),
где р, w, Р> Т> е — соответственно плотность, скорость, давление, температура,
внутренняя энергия газа, % — релаксационный параметр; т, С2, С3 — константы, определенные
из начальных условий. Функция источников к(р, Г, £) £ С\ (В) (В — область определения
решения) такая, что к(р0, Г0, £о) = &(Рь Тх, ^ ) = 0; нулем и единицей отмечены
начальная и конечная точки равновесия. Помимо этого, функции к, ey P удовлетворяют
естественным условиям, требуемым для существования уз.р. [15];назовем их условиями С.
Теорема 4. Если и0 > су 0 и е(р, Т, £), к(р, Т, £),Р(р, Г, £) удовлетворяют
условиям С, то система (17) обладает решением типа у.в.р. * [5].
Изучим возможность численного нахождения у.в .р. для системы уравнений
неравновесной газовой динамики, используя искусственную вязкость, добавленную аддитивно
к давлению.
Теорема 5. Если искусственная вязкость определена по формуле
Г ар [hnt2min(du/dx, 0)] 2, и0>и>и+ О8)
q " \ 0, м+ > w, w < г,
где г — число, равное порядку точности разностной схемы, то существует центр
конечно-разностной уз.р., а м+, — величина скорости газа за ударной волной при £ = £0.
До казательство. Используя представление (18) и ограничиваясь для
простоты случаем газа, подчиняющегося закону Клапейрона при £ = £о> нетрудно получить
уравнение для и (у) :
^du 7 , 2hn
li = V ("о -и) (и - w+), Д = та,
dy 7 + 1
7 — показатель адиабаты. Данное уравнение имеет известное решение
f Wo. ^/\/м<-7г/2,
" 1 (w0+w+)/2-[(wo-w+)/2]sin(>/\/?), -ir/2 <J>/V^< ir/2.
Таким образом, уз.р. будет построена после определения решения краевой задачи
(6) для уравнения
du_ _ k(e4+PtV)V
dy c}eT(M) - 1) '
здесь через е%, е?, Р$ обозначены частные производные по соответствующим
переменным, V = р-1, Mf — число Маха, определенное по замороженной скорости звука. В силу
теоремы 4 решение (19), (6) существует. Таким образом, у .в .р. построена. Очевидно,
точка у =0 является центром конечно-разностной у.в.р.
ЛИТЕРАТУРА
1. Яненко Н.Н., Ворожцов Е.В., Фомин ВМ. // ДАН СССР. 1976. Т. 227, № 1. С. 50.
2. Fomin V.M., Vorozhtsov E. V., Yanenko N.N// Comput. and Fluids. 1976. Vol. 4. P. 171.
3. Рождественский Б.Л., Яненко Н.Н. // Системы квазилинейных уравнений и их приложения к
газовой динамике. М.: Наука, 1978. С. 437.
4. Шокин Ю.И. Метод дифференциального приближения. Новосибирск: Наука, 1979.
5. Becker E. Gert Bohme steady one-dimensional flow: Structure of compressible waves in non-equilibrium
flows. N.Y.;L., 1969. Ptl.
Альтернативный вариант Cfo>u0 > ce 0, означающий существование дисперсной ударной
волны, для нашего рассмотрения не представляет интереса и потому опущен из формулировки
теоремы 4; су, се — замороженная и равновесная скорости звука.

ПОСТРОЕНИЕ АДАПТИВНЫХ СЕТОК
МЕТОД ПОДВИЖНЫХ КООРДИНАТ В ГАЗОВОЙ ДИНАМИКЕ*
Уравнения газовой динамики в специальных подвижных координатах
рассматривались в [1—3]. В настоящей работе выводятся уравнения газовой динамики в
подвижных координатах в тензорном виде. Применяется вариационный принцип для
построения подвижных координат.
X, обратное к которому обозна-
(1.1)
1. РАЗДЕЛЕННЫЕ ОТОБРАЖЕНИЯ
Пусть заданы арифметические пространства G = {q°, q1, ..., qn}9 X = {х°, х1, ...9хп)
и взаимно-однозначное гладкое отображение л:: G
чим через q: X-+G. Положим
ЭУ/V = а}9 bqi/dxj = А), А = det II а) II, /,/ = 0,1,..., "•
Имеем
Д"1 =det \\А} II, 44т = б?> (1-2).
где приняты обычные в тензорном анализе суммирования по совпадающим индексам и
(0 аФр
(1 а = 0.
(1.3)
Пусть в пространствах X, G задано разделение на время и пространство т.е. X = \ t, хъ ...,
..., хп), G = {г, q1, ..., qn} . Отображения, сохраняющие это разделение, будем называть
разделенными. Для разделенного отображения х: G -* X матрица II а) II имеет вид
1 Э*7ЭГ, ..., Эл^/Эг !
1411=
о
0
0
/,/=0,1,...,и, к, 1=1,..., п.
(1.4)
Обозначим через а матрицу dj (/, / = 1, ..., п) , а через А — матрицу А) (/, / = 1,..., п).
Матрицы а и А взаимнообратны, и
det II я 11 = A, det IIЛ" II = Д-1. (1.5)
Положим
4=^, 4&=У, /= 1 и. (1.6)
Вектор w = { w1, ..., wn) есть скорость точки, движущейся по траекториих(t, q1,..., qn)
в пространстве X при фиксированном (q1, ..., qr")- Аналогично W = { W1, ..., И>л} -
скорость точки, движущейся в пространстве G по траектории q(t, x1, ...9хп) при
фиксированном (х1, ...,лгл). Имеем
iv' = -fljR/', W'^-Ajw*. (1.7)
♦Численные методы механики сплошной среды. 1976. Т. 7, № 2. С. 75-82. (Соавтор В.Д. Лисейкин.)
238

Далее нам понадобятся формулы тензорного закона сохранения для контравариантно-
го тензора первого ранга А1 и второго ранга ЕгК Согласно [4]
АаА« = - -—АА«9 (1.8а)
АаЕа13= Д (-^rAE"P + AriyEay)-7P- (1-86)
В том случае, когда X — эвклидово пространство с ортонормированным базисом {la}9
а переход к новой системе координат задается отображением х: G - X
г»А-^гаЧА'- (ь9)
Для раздельного отображения х: G -> X вектор {А1) в координатах { tt q1,..., qn) имеет
компоненты
А°=А°, А*=-Ъ*А°+А*9 (1.10)
где w\ AJ - компоненты векторов { w1} , {А1} в пространстве П = {q1,..., (/"}.
Поэтому (1.8а) имеет вид
Н^°)+^[А(2/-^0)ь (1п)
2. ЗАКОНЫ СОХРАНЕНИЯ ГАЗОВОЙ ДИНАМИКИ
В РАЗДЕЛЕННЫХ КООРДИНАТАХ
Законы сохранения газовой динамики Bl = Uu}ft = 0,l,2,3 имеют вид
Эр Ъри1 .
— +—-=0, (2.1.а)
Ъри1 Ъ . .
+ —г [pwV+p5j] = pFf, (2.16)
bt Ъх}
Ър(е+и2/2) Э
г ури*(е + у- + - j] = pFV, (2.1в)
Эг • ЭУ
где е = е(р, р), р - р - у div и, и2 = D'(w')2, F — вектор массовых сил. Уравнение (2.1в)
представляет собой скалярный закон сохранения энергии, и мы можем положить
А0=р(е + и212\ А' = р(е + и2/2)и'+ри*. (2.2)
Поэтому из формулы (1.11) закон сохранения энергии в разделенных координатах
имеет вид
dpA(e+gkmTftri2)
+
| Ар[е + gkm ^J-J & ' й') + Ар и7]
ЭГ Ъс(
= *>8аР°Ъ*> (2.3)
где и' = и!А)9 gkm = a\alm, i,/,k,m=l9293. (2.4)
Теперь рассмотрим уравнения (2.1а, б) как тензорный закон сохранения контрава-
239

lirt
ри3
риантного 4X4 тензора второго ранга 2а^:
р ри1 ри2
ри1 рихих +р~811 риЫ2+рР2 ри1и3 + р613
ри2 pu2ul +P621 ри2и2 + рб~22 ри2и3 +р~823
ри3 ри3и1 + рб"31 ри2и3 + рЪ32 риъи3 + рб~33
где S** = б).
В координатах (t, g1, g2, g3 )
200=p,
где^'=ли4-
Уравнение (2.1а, б) в тензорном виде записывается следующим образом:
bAZ^/bg" + ДГ£7 2?а = Л/*3.
При )3 =0 — это закон сохранения массы
ЭрД Э
or <j£r
При /J > 0 — закон сохранения импульса
-!—Ч — + —7 №&' - #')(5' - и?') + Apg"] + д» -— +
Зг Э^7 Ц of
+ 2 -^- (?'' - w')]aJ + [(v*- &k) (5« - wa) + - irfc<*J Г'кв } = Др/',
i,/, k, a, / = 1, 2, 3.
Заметим, что
V
(Д^) + Др^Г^ = Д^
, Эр
Э<7
7 *
1т •
w = w a
Поэтому (2.9) с учетом (2.10) и (2.11) имеет вид
ЬрА $*-$*) Э
bt
+ —г [pA(vj - wj) (v> - w')J +
bq3
\bwi bwl . . .
+ Ap\-—+-^[2v'-w']+vkviriki+g
*£W'-
(2.5)
(2.6)
(2.7)
(2.8)
(2.9)
(2.10)
(2.11)
(2.12)
3. УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ В ЛАГРАНЖЕВЫХ
И ЭЙЛЕРО-ЛАГРАНЖЕВЫХ КООРДИНАТАХ
Лагранжевые координаты определяются уравнением
5''-w' = 0, i=l,2,3. (3.1)
Поэтому из (2.8) следует, что в лагршжевых координатах закон сохранения массы
имеет вид
6рД/Эг=0. • (3.2)
240

Полагая в начальный момент (р А)0 = 1, получим
рД= 1. (3.3)
Теперь, используя (3.1) и (3.3) в (2.9), (2.3), получим, что законы сохранения
импульса и энергии в лагранжевых координатах будут следующими:
(Ьи1 Д . 1 Эр
Э(е + и2/2) Э
+
Уравнения (3.3), (3.4), (3.5) совпадают с уравнениями, выведенными в [5].
Если в криволинейных координатах одна из координат лагранжева, то такая
координатная система называется эйлеро-лагранжевой. Будем, например, считать лагран-
жевой координату q3, т.е.
u3-iv3=0. (3.6)
Подставив (3.6) в наши законы сохранения (2.3), (2.8), (2.10), получим
соответственно
ЭрД
(.♦^♦^Н.-^)*'-*)-^
Эг \ 2 / dq
+ — [Apv3] = Apq^vav^ (3.7a)
ЭрД Э . .
—— + —т [pA(v> - w')] = 0, (3.76)
at dq'
„ dpAfv1 -w') Э .... ( ЭйИ bw*
- +~1[pA(vl-w,)(v'-w')]+Ap\—- + -Tx
bt dq' { tit aqJ
x [2?/_^/]+^^3+s^/r^+I^ q^=ApJ\ (3.7b)
Э153 bv3 . . bv3 ^4 . _ , 1 (dp ,\ ^q
ЭГ bqJ bq5 p \ Э^г /
*До,Дл= 1,2,3, /,/=1,2.
В статье [2] выводятся уравнения рсесимметричного движения газа в специальных
эйлеро-лагранжевых координатах. Получим эти уравнения из уравнений (3.7).
Координатная система задается соотношениями
х1 =R(r, 0, г) sin 0 cos <р, х2 =R(r96, f) sin 0 sin </>, x3 =R(r, 0, f)cos 0, (3.8)
где г — лагранжева координата, а движение не зависит от ф.
Подставив (3.8) в (3.7),получим
ЭрА/ "q*evavfi\ Э / Я, \ Э Г / qaeVavP \ Л
ЭрД Э д
-1— + ■ (pAve) = 0, (3.96)
Э? Э0
dve д , , 2i?e(iJe)2 1 Г Эр Эр ]
+— (Vе? +—- + —ГЧ \Rr— -*о— =0, (3.9в)
dt Ьв R pR2Rj [ Ъв Ъг \
241

( ЪЪГ bvr' bvr Л al Rer-RaRr\
Rr[—vr— + 2 ve) + Rrr(vr)2+2vrve( вг в r +
dp]
( (RRee -R2 - 2(Re)2v° _1
Ъг
R pR2Rr L
Уравнение (3.9г) совпадает с уравнением (3.5) статьи [2].
(3.9г).
4. ВЫБОР КООРДИНАТ ИЗ ВАРИАЦИОННОГО ПРИНЦИПА
Для численного решения уравнений газовой динамики бывает необходимой такая
координатная система, которая бы не сильно отличалась от лагранжевой и в то же
время не сильно искажалась. Искажение координатной системы определяется девиато-
ром скоростей dlJ [в]
d*' = г- + —т-- - 5 .
с1 к ' \ Ъх* J
дх}
Ъх1
(4Л)
Ограничимся для простоты двумерным случаем. Тогда
bw1 bw2 dw1 dw2
II dli 1-
det lid''II
дх1 Ъх1 Ъх1 Эх1
dw1 dw2 bw2 dw1
! Ъх2 ' дх1 дх2 дх1
=_
7 dw1 bw2 у / dw1
Адх7 ~~ЬхТ' +\дх~2
(4.2)
(4.3)
Заметим, что det II dl/ II равен нулю тогда и только тогда, когда отображение (х1, х2) -*
-* (w1, w2) является конформным.
Рассмотрим функционал
<J>(w,f) = / Fdxldx2 = / [2(У -w')2 - ее2 det \\ dif \\] dx1 dx2 9 (4.4)
где £2f — область движения среды при фиксированном t, с — скорость звука, е —
параметр.
В функционале (4.4) первое слагаемое определяет скорость отклонения координат
от лагранжевых координат, второе слагаемое определяет искажение координат. Будем
искать экстремум этого функционала среди всех wl (i = 1,2), удовлетворяющих на
границе £lt условию
и*-ы* = а, (4.5)
т.е. на границе области координатная система — лагранжева.
Экстремальная поверхность w* удовлетворяет уравнению Эйлера, т.«.
Ъх1
(4.6) — уравнение эллиптического типа.
В тензорном виде (4.6) будет
-. (u'-i?i) + A/o'/ = 0
или
Аф' - w') + —т- До" + До^Г^,
(4.6)
(4.7)
(4.8)
242

где
о" = ее2 [(Д,ЯУ" + A,#V") -Л** *] = ее2
(-5?*" г»"К-д-г'^г] <">
Если в функционале (4.4) положить е = е, I —— + —г I » где £ — лагранжевы коор-
динаты, и1 — компоненты скорости в локальном базисе е1 = Ъх/Ъ%\ то уравнения Эйлера
(4.6) сохраняются и в случае одномерного движения дают лагранжевы координаты.
ЛИТЕРАТУРА
1. Яненко Н.Н., Фролов В.Д., Неуважаев В.Е. О применении метода расщепления для численного
расчета движений теплопроводного газа в криволинейных координатах // Изв. СО АН СССР.
Сер. техн. наук. 1967. № 8, вып. 2. С. 74-82.
2. Неуважаев В.Е.У Фролов ВМ., Яненко HJH. Уравнение движения теплопроводного газа в
смешанных эйлеро-лагранжевых координатах // Числ. методы механики сплош. среды. 1972. Т. 3, № 1.
С. 90-96.
3. Vinocur M. Conservation equations of gasdynamics in curvilinear systems // J. Comput. Phys. 1974.
Vol. 14. P. 105-125.
4. Седое JIM. Механика сплошной среды. М.: Наука, 1973. Т. 1.
5. Кочин Н.Е., Кибель Н.А.У Розе И.В. Теоретическая гидромеханика. М., 1963. Ч. 1, 2.
6. Батчелор Дж. Введение в динамику жидкости. М.: Мир, 1973. № 4.
О МЕТОДЕ ПОДВИЖНЫХ КООРДИНАТ
В ГАЗОВОЙ ДИНАМИКЕ*
Излагается применение вариационных методов для построения подвижных
координат. Выводятся уравнения вязкого газа и уравнения Хопфа в разделенных
координатах. Проведен численный расчет одномерного уравнения Хопфа в специальных
подвижных координатах.
1. ПРИМЕНЕНИЕ ВАРИАЦИОННЫХ ПРИНЦИПОВ
ДЛЯ ПОСТРОЕНИЯ ПОДВИЖНЫХ КООРДИНАТ
Построение разностной сетки для решения численными методами уравнений
газовой динамики можно рассматривать как задачу определения в каждый момент
времени t гладкого невырожденного преобразования некоторой области Gt в физическую
область Xt; х: Gt -+ Xt9 т.е. задание в области Xt некоторой криволинейной системы
координат. Узлы разностной сетки при этом определяются точками пересечения
координат. Разностная сетка должна быть в каком-либо смысле "хорошей", например, не
сильно отличаться от лагранжевой, не очень деформироваться, концентрироваться
в областях с большими градиентами каких-либо физических величин и т.д. Для
формулировки этих условий можно использовать вариационные принципы. Так это делается
в [1], где ищется сетка, которая как можно меньше отличалась бы от лагранжевой
и в то же время не сильно искажалась. Скорость сетки wl (/=1,2), является экстре-
* Проблемы мат. физики и вычисл. математики. М.: Наука, 1977. С. 107-115. (Соавторы Н.Т. Да-
наев, В.Д. Лисейкин.) '
£43

мальной для функционала
*(w/,r)= / [Е(и*-у/)2-€С2дёхе*1]<1х1сЬс29 (1.1)
xt i
где и1 -=- компонента скорости движения среды, е > 0, с — скорость звука, ev — девиатор
скоростей деформации сетки
.. dw( 3W1' .. dwa
Ъх1 дх1 Ъха
В этом равенстве и в последующих формулах одинаковые индексы в выражениях
означают суммирование. На границе области Xt в функционале (1.1) сетка задается
лагранжевой. Ввиду этого условия область Gt не зависит от г. Экстремальная сетка
для функционала (1.1) удовлетворяет уравнению Эйлера
и'-^' + е^Э^'/Эх'^О. (1.2)
Для построения конформных и квазиконформных сеток вариационный принцип
применяется в [2, 3]. Сетка в этих работах является-экстремальной для функционала
4x)=fgafiE°pdqldq2, (1.3)
G
где х: G -+ X — отображение, задающее сетку
Ъх1 Эх1' Й /е О \
7"*0 =
sinl]3(<7
1 (eW&-g^ - cos\p(q2) - а(дг)\\
2)-а(^)1 Ucosl^2)-^1)!^^1)-^') / [3]*
Экстремальная сетка для функционала (1.3) в первом случае будет конформной,
а во втором случае — квазиконформной. В [4] строятся эллиптические сетки для
многосвязных областей. Координаты, определяющие сетку, удовлетворяют
эллиптическому уравнению
здесь рг > 0, ^о равно либо максимуму, либо минимуму ql на границе области. С
помощью р1 и ql осуществляется управление сеткой: ql влияет на наклон координатных
линий, рг заставляет концентрироваться линии в областях с большими градиентами.
Уравнение (1.4) можно тоже получить из вариационного принципа, задав функционал
Ф(#') формулой
Экстремальная поверхность функционала (1.5) удовлетворяет уравнению (1.4).
С помощью вариационного принципа можно также находить координатные сетки,
удовлетворяющие каким-либо дифференциальным условиям. (Для этого нужно
применять метод множителей Лагранжа.) Например, ортогональные сетки, которые
описываются условием g\2 - 0, или координаты, являющиеся изоклинами, что эквива-
Э g\2
лентно уравнению —т — - О (А — определитель отображения х: G -* X).
bq А
Вариационное уравнение 5 Ф = 0 годится для построения эллиптических и
гиперболических сеток. Для получения параболических сеток можно воспользоваться вариа-
244

ционным принципом Л.И. Седова [5], который формулируется следующим образом:
6Ф + 6и> + 6и>* = 0, (1.6)
где 5vv* — некоторый задаваемый функционал, 5vv определяется интегралом на
границе от линейной комбинации вариаций определяющих параметров и их производных
и полностью зависит от Ф и 5vv*. В вариационном принципе (1.6) вариация
функционала Ф равна не нулю, а некоторой величине (5vv + 5vv*). С помощью (1.6) выводятся
уравнения движения вязкого газа, которые имеют параболический тип.
Применим вариационный принцип для построения сеток, которые близки к лагран-
жевым, не сильно деформируются и концентрируются в областях с большими
градиентами. Рассмотрим для простоты двумерный случай. Пусть x*(t, q1, q2) (i = 1, 2) -
отображение, задающее координатную сетку. Обратное к нему обозначим через q'(t,
х1, х2). Будем считать мерой отклонения от лагранжевых координат выражение
2 ~-
2 (и1 — w1)2, где и1, vv1 — скорость соответственно среды и координат в локальном
базисе.е1 * bx/bql. Мерой деформации сетки положим определитель девиатора
деформаций отображения q* (i = 1,2), т.е. (bq^bx1 - bq2/bx2)2 + (bql Ibx2 + bq2/bx1)2.
Мерой концентрации сетки считаем определитель отображения {х1 \ -* \ql \ (/ = 1, 2).
2 -•
Обозначим выражение Б (и1 — и)1)2 через /г, а через Уг — выражение (bq /bx —
/=1
— dq2/dx2)2 + (bq1/bx2 + dq2/dx1)2. Пусть Л — произвольная функция трех аргументов
Л1, /z2, Д. Теперь мы можем сформулировать вариационную задачу: среди всех q\
i = 1, 2, найти такие, которые дают минимум функционалу
fAdx1dx2dt. (1.7)
Экстремальная поверхность удовлетворяет уравнению Эйлера
тг(Лэ^}+^/{Лэ^;'}=0- (L8)
Решая уравнение (1.8) с соответствующими краевыми условиями, получаем некоторую
координатную сетку. Здесь есть аналогия с построением моделей сплошной среды
идеального газа, уравнения движения которого удовлетворяют вариационному
принципу dfAdv = О, где Л зависит от скорости движения среды и от элементов
метрического тензора £•#.
Пусть h — функция, зависящая от градиентов физических величин, например h =
= f[(bul/bx1)2 + (bu2/bx2)2]. Зададим Л формулой
Л = 61Л1+б2Л2+е3/2Аа. (1.9)
При минимизации функционала / [е^1 + e2h2 + e3hAc*]dx1dx2dt первое слагаемое
v
стремится сделать сетку лагранжевой, второе — конформной, а третье — мелкой в
областях с большими градиентами физических величин. Ясно, что сетка, являющаяся
минимальной для функционала fAdx1dx2dt, будет не сильно отличаться от лагран-
v
жевой, от конформной и концентрироваться в областях с большими градиентами.
Выпишем уравнения Эйлера для этой сетки. Так как
с? J -
w
dq* bq(
« U}' -г +
Ьх> bt
то
J M bql\2 f/bq1 bq2\2 /bq1 bq2\2]
i\ bx1 bt J [\bxx bx2/ \bx2 bx1 П У '
245

э ~л .^x_LL^« ^,/^i«! ...,i.A««,
Поэтому (1.8) имеет вид
Ъа* а .. .Л
= 0, (1.11)
сне z j
или в координатах t,ql ,q2
= 0, (1.12)
dt bxJ I bxJ 2
—e1A(iii - w') + r\e1A(ui - w') (ff' - wf) + e2Agij' - 6f.€3h— Да + 1
ЭГ bqJ L ' 2
где Gi; - алгебраическое дополнение к элементу dql/dx},
В [1] выписаны уравнения идеального газа в тензорном виде
ЭДа^/Э^ + ДГ^а^-О. (1.13)
Полагая в (1.12) ех = р, е2 = р, е3 = 0, приходим к замкнутой системе уравнений
идеального газа и подвижных координат
ЭДа"7э<7' = 0? г£<,а°* = 0. (1.14)
В формуле (1.9) отклонение от лагранжевых координат можно положить равным
Z (й1 — w1)2. В этом случае экстремальная координатная сетка удовлетворяет урав-
i
нению
Э Ъха Э [ „ „ /Э^3-1' Э?"
A5.(w"w") + |б,Да(и« - w«)(—— —33J- -
Эг Э?/ Э?" I \ ЭГ Ъх6 а
bqn Ъха \ hot ^ )
-Д— г + Д5>а)+52Д^ш-б? Да + 1 =0. (1Л$)
2. УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОГО ГАЗА
В ПОДВИЖНЫХ КООРДИНАТАХ
В [1] изучены уравнения газовой динамики в подвижных координатах с одной
объемной вязкостью v. Уравнения движения газа с двумя вязкостями р и [А совместно
с уравнением неразрывности в декартовых координатах имеют вид
-^ (Е« +Б?) = PF', i, / = 0,1,2, 3, (2.1)
Ъх'
где
£.оо „ р> £.ро = 0 £-0/ = £.io = ри/> Eoi = £-io = 0j
Е'' = риЧ + Ъ*'р, Е[' = ц(ди*1()х> + Ьи'/дх'),
p=p-vdua/bxa, X° = t,
F0 = 0, F* — массовые силы, ?, /, а =1, 2, 3. Составляющие контравариантного тензора
Е'' в подвижных координатах (t, q1, q2, q3) получены в [1 ] и имеют вид
Е00 = р, Ё°' = Ё{°=р(й'-w1),
Е{' = р(и*-й*)(и>-й>)+РЕ{'. (2.2)
246

Найдем тензор Е'( в подвижных координатах (t, д1, q2, q3) :
,, /dua due\ . .
1 =V + !^F)K 0' *'U % *= l' 2' 3' (2-3)
т.е.
Э<?* Э<Л """ bq* bql\bql bq'
Э?" Эх" Э?' dWa*" Эл^
Тензорный закон сохранения (2.1) в криволинейных координатах имеет вид
A(Eap+Ef) + АГ0ЛЕа'+Е?>) = ApF*3. (2.5)
bq
Подставив (2.2), (2.4) в (2.5), получим, что уравнения движения вязкого газа в новых
координатах записываются следующим образом:
ЭрДм' Э ( ... -Г ,,/ди' Л
+ —j {рД(м' - w')u> + Apg" + An\g"l—г + Г'к1ик) +
+^(^+"кг'к')]}+Ч^"п+г|"и](йгп"т+
Для численного решения уравнения газовой динамики бывает необходимой
дивергентная форма записи уравнений. Дивергентную форму уравнений (2.1) в
криволинейных подвижных координатах получим, если воспользуемся известной формулой
тензорного анализа
dAi 1 ЭЛЛ"1'
VT = T-;T7-> '' = °,1,2,3; . (2.7)
Эх A Э<7
/ Ъ<11
здесь А1 — произвольный вектор, Л* = А1 :. Применяя формулу (2.7) к каждой
строке тензора Е0^ + Zs^, получим
ЭрА bpA(uJ'wJ)
+ —Г1 -я0, (2.8)
ЭГ Э?'
ЭрДм' Э ( .
— + [рАи1{иа - wa) + Ap8lJ +
Эг Э?1 I
/Эк1' Э?"1 Эна Э<7Ш\1 Э?' )
В двумерном случае в (2.8), (2.9) можно избавиться от элементов обратной матрицы
dql/dxi. В самом деле, при п = 2
Э?' .^Элт3"'
Э*> Л > bq3
247
Дт7гя.(-1)'+/тз=г- (21°)

Поэтому (2.8), (2.9) при п = 2 имеют вид
ЭрД л., Э Г Эх3"" 1
bq' L
bt bq' L bq
ЭрД
„3-/
= 0, (2.11)
r"+(-1)/+a"aV{ [pM'("a " wa) + лд5** + ^д (Sr(_1)m+a x
Эх3"* x. Эм<* Эх3"' \1 дх3~а |
3. УРАВНЕНИЯ ХОПФА В ПОДВИЖНЫХ КООРДИНАТАХ
В декартовых координатах уравнения Хопфа имеют вид
Ъи* . Ъи* Э Ъи*
+ м/—-_,_-—— = о, /,/=1,2,3, (3.1)
bt Ъх] Ъх* bxJ
или
Эй' Э /' . ЗиЛ . Эй7'
+ —тМи' - v—j] = »'—т . (3.2)
bt bxJ \ ЪхЧ дх*
Уравнение (3.2) запишем как тензорный закон сохранения контравариантного
тензора а17:
— а* = А', /,/ = 0,1,2,3, (3.3)
дх'
где
к1 = и1Ъи^1Ъх^ h°=0, ■ /,/=1,2,3.
В криволинейных координатах (q°, q1, q2, q3) закон сохранения (3.3) имеет вид
Aj5iJ' = h\ (3.4)
или
ЭДа'^Э?у + ДГ^ав*=ДЛ', /,/ = 0, 1,2,3. (3.5)
Вычислим тензор аа? для разделенных координат (Г, #*, #2, q3) . Имеем
~» ЛЛ bq1 dq>
Эх dxp
Значит, a00 = 0, a0/ = 0, oi0=ut,
.. , . {Ъйг . \ „.
P' = й\й> - SO -Л —r + um Y*mky>,
~. 1 _.ЭДи*
•Лшти1?-^/>0- (3-7)
Подставив (3.7) в (3.5), получим уравнение Хопфа в разделенных подвижных коор-
248

динатах
ЭД
■А { Г^о" а + гф "(к * - tf*3) - /|^ + и* Г" fc U*" ] -
- и'—-г Ди> ( = 0, а, (3, /,'/, Л, те = 1,2, 3,
(3.8)
или
дйг ЭиИ дй' 1 Э Г /Эй'
+ ит + (um-wm)- — v—- Д +
bt bqm dqm Д bq'l \bqm
+ "тгЦ^я/] + ГЦи-и' - р№£ +йрГ™Л\«] = О,
i,f,m,n,p, к = 1,2,3. (3.9)
Другой вид уравнений Хопфа получим, если будем рассматривать (3.2) как
скалярный закон сохранения:
ЪА'/Ъх' = И, /,= 0,1,2,3, (3.10)
где
/VX /и1и{-иЪи11Ъх*\ /и'ди'/дхЛ
А°4 " |И'=( и2и(-иди2/дх( 1 Л = | и2Ъи>1Ъх' V (3.11)
\«у \и3и{-Рди31дхЧ \и3ди'/дх>/
В разделенных координатах (3.10) имеет вид
ЭДД° ЪА(А'-А°й{)
= ДА, (3.12)
Эг Э?'
или с учетом (3.11)
Ъи* ди{ . ^. v Ъ ( ди' Л
+ —r(u'-w')- т[Д—rgk' =0, i,/= 1,2,3. (3.13)
bt dq> A dq>{ dqk J
4. ЧИСЛЕННЫЙ РАСЧЕТ
В качестве применения метода подвижных координат рассматривается численный
расчет уравнения (3.13) в одномерном случае в подвижных координатах (1.15)
с о. = 2, ei = 1, е2 = 0, h =.е + I ди/дх\у. Уравнение Хопфа совместно с уравнением
подвижных координат в этом случае имеет вид
ЭыД Э /V ■ Л_ Э /1 ЭгЛ
Ы bq\2 ~UJ~V dq\A dq)'
Э(«-и>)Д2
» +**Г?\ <4,)
Предполагается, что в начальный момент и на границе сетка лагранжева, т.е. w(q90) =
249

= u0(q) и wl г = u\ г . Начальную функцию и0(х) = и(х9 0) выбираем следующим
образом:
1 при О<*<0,
и0(х) = | 2 - лг/в при в<х<2в9 (4.2)
0 при х>2в.
Кроме того, и (0, t) = 1 для любого t > 0.
Система уравнений (4.1) аппроксимировалась неявной, имеющей второй порядок
аппроксимации относительно пространственной координаты, симметричной
разностной схемой.
Результаты расчетов показывают, что в области больших градиентов координатная
функция сгущается, а значит, профиль функции и в координатах q более пологий.
Управление сгущением осуществляется при помощи параметра у.
ЛИТЕРАТУРА
1. Лисейкин В.Д., Яненко Н.Н Метод подвижных координат в газовой динамике // Числ. методы
механики сплош. среды. 1976. Т. 7, № 2. С. 75- 82.
2. Годунов С.К., Прокопов Р.П. О расчетах конформных отображений и построение разностных
сеток // Журн. вычисл. математики и мат. физики. 1967. Т. 7, № 5. С. 1031-1060.
3. Белинский Н.Н., Годунов С.К., Иванов Ю.Б., Яненко Н.Н. Применение одного класса
квазиконформных отображений для построения разностных сеток в областях с криволинейными
границами // Там же. 1975. Т. 15, № 6. С. 1499-1511.
4. Thompson J.F., Thames R.C., Mastin C.W. Automatic numerical generation of body-fitted curvilinear
coordinate system for field containing any number of arbitrary two-dimensional bodies // J. Comput.
Phys. 1974. Vol. 15, N 2. P. 299-319.
5. Седов Л.И. Математические методы построения новых моделей сплошных сред // УМН. 1965.
Т. 20, вып. 5. С 121-180.
О ВАРИАЦИОННОМ МЕТОДЕ ПОСТРОЕНИЯ СЕТОК*
Применяется вариационный принцип для построения подвижных сеток, зависящих
от потока. Вариационный принцип выбирается, исходя из требований, налагаемых на
сетку: а) сгущение в области высоких градиентов; б) близость к лагранжевым
координатам; в) минимальное искажение сетки. Приводится численный расчет одномерного
уравнения Хопфа и течения Блазиуса на пластине в специальных координатах.
1. Формулировка вариационного принципа для построения сеток. При численном
счете уравнений газовой динамики для увеличения точности решения нужно уметь
строить такие сетки, которые концентрируются в области больших градиентов, мало
искажаются и близки к лагранжевым сеткам. Сетки, зависящие от потока и
концентрирующиеся в области высоких градиентов, строятся в [1] с помощью уравнений
P(ql - q'0) = Aq*. В [2,3] применяется вариационный принцип для построения
квазиконформных сеток, не зависящих от потока. В [4] применяется вариационный принцип
для построения сеток, близких к лагранжевым и зависящих от гидродинамических
величин.
Рассмотрим для простоты двумерный случай. Пусть х = \x\ty q1, q2)} (7=1,2 —
отображение, задающее координатную сетку). Обратное к нему обозначим через q =
= \q\t, x1, х2)] (/=1,2). Будем считать мерой отклонения h1 от лагранжевых коор-
*Численные методы механики сплошной среды. 1977. Т. 8, № 4. С. 157-163. (Соавторы Н.Т. Данаев,
В.Д. Лисейкин.)
250

2 . .
динат выражение Б (и1 - w1)2, где и\ wl — скорости соответственно среды и коор-
1=1
динат л локальном- базисе е1 = дх/dq'. Мерой деформации к1 сетки положим
определитель девиатора деформаций отображения q9 т.е. h2 = (dq1 /дх1 — bq2 lbx2)2 + (bql /дх2 +
+ bq2 /Ъх1)2. Мерой концентрации сетки считаем определитель А отображения х : G^X.
Пусть </? — произвольная функция трех аргументов *p(hl, h2, А). Вариационный
принцип для построения сетки формулируем следующим < оразом: среди всех ql (i =
= 1,2), удовлетворяющих заданным граничным условиям на ЪХ, найти такие, которые
дают экстремум функционалу
Щя'] =fv(h1,h29A)dx1dx2dt. (1.1)
Экстремальная поверхность удовлетворяет уравнению Эйлера
i,bt \+Тт Г**|/8х/ =0 (1'2)
i \ **
или в координатах t, q1, q2
[***» ]*т?[4 (»*•** s- - ■***.)]"0; (13)
Э
bt
положим
<p=€1h1A" + €2h2 +e3AP. (1.4)
Здесь е,- — функции, зависящие от гидродинамических величин и их градиентов. При
минимизации функционала (1.1) первое слагаемое в (1.4) стремится сделать сетку
лагранжевой, второе — конформной и третье — мелкой там, где соответственно е,-
велики. Уравнения Эйлера для данной сетки будут
±1е,А~.<?-*>и-±[
dQ? -&)(й' - w')Aa + 1 -
2
('"Й-
= 0, (1.5)
- б''^ Aa+l 2 (ик - wk)2 + е2 Д {*0 - —■) - д"'е3рА^1
где
* Ъхк дхк' ,, .= /
В [4] выписаны уравнения идеального газа в тензорном виде
Э A#W + Ату?* = 0.. (1.6)
Полагая в (1.4) €i = р, е2 = р, е3 = 0, а = 0, получаем замкнутую систему уравнений
идеального газа и подвижных координат
aAVW-o, гур" = о. (1.7)
Вариационное уравнение 50 = 0 годится для построения эллиптических и
гиперболических сеток. Для построения параболических сеток можно воспользоваться
вариационным принципом Седова [5], который формулируется следующим образом:
60 + 6со + 6со* = О, (1.8)
где бсо* — некоторый задаваемый функционал, б со определяется интегралом на
границе от линейной комбинации вариацией, определяющих параметров и их производ-
251

ных, и полностью зависит от ф и бсо*. С помощью (1.8) выводится уравнение
движения вязкого газа.
2. Численный расчет. В качестве применения метода подвижных координат
рассматривается численный расчет уравнения
Ъи Ъи Ъ2и
(2.1)
— +w
bt Ъх
Ъх1
в координатах (1.5) с а = 2, е1 = 1, е2 = 0, е3 = е + | Ъи/Ъх\ 7, /3 = 2. Уравнения для
м(<7, г) n'x(qf f) аппроксимировались неявной, имеющей второй порядок
аппроксимации относительно пропространственнои координаты q, симметричной разностной
схемой. Результаты расчетов показьюают, что в области ударной волны координатная
u^/qj
цп/х)
п-Ш
л=¥00
л=Ш
0,5
Рис. 1
сетка концентрируется и, значит, в области G ударный переход более широк.
Управление сеткой осуществляется параметром 7- Некоторые данные расчетов приведены на
рис. 1.
Вторым примером применения данной методики построения сеток является расчет
течения Блазиуса на пластине. Метод сеток для расчета обтекания пластины
применялся в [6, 7]. В этих работах производилась замена поперечной координаты у на % =
= у/д(х),д(х) — функция, эквивалентная толщине пограничного слоя. При
фиксированном х = х* в этих методах получается равномерная сетка, т.е. она сгущается не
только там, где высокие градиенты, но и по всей координате у. В нашем расчете сетка
определялась соотношением q1 = x, q2 = q2(xt у, t) и находилась из условия экстремума
функционала (1.1) при
Ар = (е + | Ъи/Ъу\ «) (by/bqy + ег 1пД,
V = (е + | Ъи/Ъу\ ")(du/bqy + ех Д"Л
</> = (е + | Ъи/Ъу\ a)(by/bqy + efi'P + е2 Д7*,
(2.2а)
(2.26)
(2.2в)
где е, €г, е2, а, ]3,7, ?? — некоторые вещественные параметры.
Система уравнений пограничного слоя в координатах t, x, q с введением функции
тока ф имеет вид
Э^//Э(/ = «Д,
Ъи Ъф Ъи
А —+ —
Эг Ъq Ъх
Ъф
Ъх
+ VV
Ъи_
ЪЯ
(2.3)
dq
Ъи
w — скорость сетки.
В численном расчете применялась следующая разностная схема второго порядка
аппроксимации по hx, h2 :
♦«"Vi4*1^'
262

О х 0 ос
Рис 4 Рис.5
где
'/*±*-w,+/v±1). /;•_*,=^/Ч-,/)- ■
Д^/ •= /-^« — /• -» Д /..=/..—/.. - для любой сеточной функции /. ..
Уравнения для координат аппроксимировались неявной трехточечной симметричной
схемой. Вычисления проводились при v= 10~3 -г 10~8.
р= Ю-3
ю-6
ю-8
0,104988
0,060615
0,046952
0,39682
0,034996
0,031655
0,029118.
0,027108
0,025463
0,024086
0,022910
0,105207
0,060225
0,046662
0,039429
0,034761
0,031432
0,028906
0,026907
0,025272
0,23914
0,022769
0,003321
0,002348
0,001917
0,001660
0,001485
0,001355
0,001253
0,001174
0,001107
0,001050
0,001001
0,003297
0,002303
0,001918
0,001687
0,001524
0,001399
0,001299
0,001216
0,001148
0,001092
0,001047
0,000332
0,000235
0,000192
0,000166
0,000148
0,000136
0,000125
0,000117
0,000111
0,000105
0,000100
0,000332
- 0,000235
0,000200
0,000180
0,000170
0,000163
0,000159
0,000155
0,000151
0,000147
0,000144
253

Анализ расчетов показывает, что разностные уравнения (2.4) дают при небольшом
числе узлов (N = 40, М = 15) по поперечной координате удовлетворительную точность
и сетка концентрируется в области пограничного слоя. Для сравнения результатов
взяты напряжения трения по поверхности пластины
т(х) = 1л(Ъи/Ъу)у=0.
В таблице помещены результаты расчетов варианта (2.2а) и значения т(х),
вычисленные по асимптотической формуле Блазиуса. Для наглядности приводим на рис. 2, 3
графики функции и, у в координатах q при v = 1СГ6, на рис. 4, 5 изображены сетки,
соответствующие v=- 1СГ3, 1СГ6.
ЛИТЕРАТУРА
1. Thomson J.F., Thames R.C., Mastin C.W. Automatic numerical generation of body-fitted curvilinear
coordinate system for field containing any number of arbitrary two-dimensional bodies // J. Comput.
Phys. 1974. Vol. 15, N 2. P. 299-319.
2. Годунов С,К,, Прокопов Р.П. О расчетах конформных отображений и построении разностных
сеток // Журн. вычисл. математики и мат. физики. 1967. Т. 7, № 5. С. 1031-1060.
3. Белинский Н.Н., Годунов С.К., Иванов Ю.Б., Яненко И.К. Применение одного класса
квазиконформных отображений для построения разностных сеток в областях с криволинейными
границами // Там же. 1975. Т. 15, № 6. С 1499-1511.
4. Лисейкин В.Д., Яненко ИМ. Метод подвижных координат в газовой динамике // Числ. методы
механики сплош. среды. 1976. Т. 7, № 2. С. 75-82.
5. Седов Л.И. Математические методы построения новых моделей сплошных сред // УМН. 1965.
Т. 20, вып. 5. С. 121-180.
6. Игнатьев ВМ. О схеме повышенного порядка точности для расчета уравнения турбулентного
пограничного слоя // Числ. методы механики сплош. среды. 1972. Т. 3, № 4. С 69-77.
7. Пасконов ВМ. Об одном алгоритме для решения задач пограничного слоя // Вычислительные
методы и программирование. М.: Изд-во МГУ, 1967. Вып. 7. С. 150-155.
О ВЫБОРЕ ОПТИМАЛЬНЫХ РАЗНОСТНЫХ СЕТОК*
Вариационный принцип используется в [1,2] для построения сеток с минимальной
деформацией, в [Зг 4] — для построения сеток с минимальной деформацией потока
в новых координатах. Для решения обыкновенных дифференциальных уравнений
[5,6], приближенного вычисления квадратур [7] и интерполирования [8] сетки
выбираются из условия минимизации функционала погрешности. В данной работе принцип
построения сеток, минимизирующих погрешность, формулируется для уравнений
в частных производных.
Пусть
L<p*u) = 0 (1)
дифференциальное уравнение, и — w-мерная вектор-функция, заданная в /я-мерной
области X,
Д* = (/)?.,.,., if"), а. = {а),...,оГ1),
m k
3fc=1
1 m
а. а.
♦Численные методы механики сплошной среды. 1977. Т. 8, № 7. С. 100-104. (Соавтор В.Д Лисейкин.)
254

и пусть
A(W|) = 0, / = 0V,..., im) (2)
устойчивая разностная схема, аппроксимирующая (1) с точностью 0(На)у где h - норма
сетки. Обозначим через е = е* — погрешность и. Тогда
Л(и, +е,) = йве, + Ав+1ел (3)
где Ла+12* - остаточный член, g - ограниченная функция точки пространства (х, w).
Так как для схемы порядка а, е имеет порядок Ла, то
Л(и, + е,)=Л(и,) + 2Л|<*.е* + h«+xQ2. ^h^Q. + h^Q], (4)
2
где Л fc — частная производная Л по ы*, Q - ограниченная функция. При
аппроксимации (1) схемой (2) мы выражение Dau заменяем комбинацией разностных
выражений
Значит,
Л к= 2 Лкй' Ъа к. (5)
г)" и,т
и,т
Поэтому
2А кек = 2 Б Л -Я" *е\ (6)
* " * »* Da u>muk К }
Du,m u>m
но 1У* кек — разностная аппроксимация /7е*е, а 2Л_ — разностная аппроксимация
и,ти j^ol
L . Таким образом, получаем: (6) — разностная аппроксимация уравнения вариаций
и
системы (1), т.е. уравнения
U Dae=0. (7)
Положим 6 = е/А°\ Из условия устойчивости б — ограничено. Из (4) имеем
2 Л Л^-(2+/|<22. (8)
Устремляя h к нулю, получаем
2Z, .Ef*b = Q. (9)
Таким образом, для. устойчивой схемы порядка а, погрешность е с точностью до
ha+i определяется формулой: е = Лаб, где б — решение уравнения (9) с нулевыми
граничными условиями. Аналогичное утверждение для формулы Рунге—Кутта,
аппроксимирующей обыкновенное дифференциальное уравнение Ъу/Ъх = f(x, у) получено в [5].
В этой работе показано, что ошибка асимптотически удовлетворяет уравнению
beldx=fye + haQ + h«+1Q1. (10)
Перепишем систему (1) в новых координатах ql, ..., qm. Для полученной системы
составим устойчивую разностную схему с погрешностью haQt Q в этом случае будет
зависеть от координат, а значит от координат будет зависеть е и б. Мы определяем но-
255

вые координаты условием: 5 в какой-либо заданной нами норме должно быть
минимальным. Пусть
JA(b)dx (11)
норма 5. Тогда задача построения оптимальной сетки, минимизирующей 115II решается
следующим образом: определяется функционал
Ф(<7,6,Л)=/И(6)+Л(/, a*D«b-Q)}dx (12)
D
и
и ищется экстремум этого функционала.
Рассмотрим данную методику построения сеток на примере уравнения Бюргерса,
моделирующего ударную волну. Уравнение запишем в подвижных координатах г = t,
q = q(t, х)
Ъи ^ ^ Ъи v Ъ I Ъи 1 i
— +(и -Ц — - — =0,
Ът bq A bq \ bq A I
(13)
здесь и, w — скорость среды, соответственно сетки в локальном базисе е = дх/dq, А =
= Ъх/bq. Аппроксимируем (13) схемой первого порядка точности по т и второго
порядка точности по q. Тогда
(2=Кд2и/дт2.
Уравнение (9) в данном случае будет
Hi?- L Ъ*и
" " 2 Ът2 '
Э5 Э5 Ъи
— +и — + 5—-
Ы дх Ъх
Ът2
(14)
где S = e/At. Минимизируем погрешность в норме Ьг. Значит (12) будет
Ф(<?>б,Л1)= /
ъь
Ъ8
Ъи
б2 + At — +и — + 6 — -v
Эг
Ъх
Ъх
Э26
Ъх2
1 Ъ2и
2 Ът2
dxdt.
(15)
Имеем
Э _ Э Э<? Э
Ът Эг Э? Ъх
Положим
Ъи Ъq Ъи
М= -Д—- — .
Эг Эг Эх
Определим новый функционал
(16)
Ф(^,5,Л1,Л2)=/
б2 + Л,
/Э6 Э6 Ъи
! [— +w +5
\ bt Ъх Ъх
Ъ2и
Ъх2
1 Э/1
2 bt
A bq Ъ{1
2 bt Ъх
Ъи
+ Л2 М- — +А —
bq Ъи
Ът
bt Ъх
dxdt.
(17)
Экстремальная поверхность функционала (17) будет экстремальной и для (15).
Уравнения Эйлера для (17) будут
Э2Л!
ЭЛХ ЭЛ1
26 - — - и
.Эг Ъх
Ъх2
= 0,
ЭЛ! Э / Ъи\
2Л2=- — +— [А, А— ,
bt Ъх \ Ът
256

Если в (13) аппроксимируем первое и третье слагаемое со вторым порядком
точности, а второе с первым порядком, то в этом случае
и — w Ь2и
Q=—r--rr-- (19)
bq
Функционал (12) имеет вид
... . /95 Ьи- Э5 Э26 ,li-w Ъ2
'?)}
52+Л|— +5— +«— -v—г--''— ———\\dxdt. (20)
\bt Ъх Ъх Ъх2 2 dq2!l K
Экстремальная поверхность удовлетворяет уравнению Эйлера
ЭЛ ЭЛ Э2Л
25- — +и — -и = 0,
bt Ьх Ъх2
Ъ I Ъ2и\ 9 г ъ2и. ,_ ~ I Ъи b2q Ъ2и\Л
Л — + Ли —- + AA*Xu-w) 3 • -~-2 г +
bt { bq2 J Ъх [ bq2 \ bq Ъх2 Ьх2 J J
Э2 Г „ ^.Эи 1
+ -[AA(M-w)-j=0.
ЛИТЕРАТУРА
1. Годунов С.К., Прокопов Г.П. О расчетах конформных отображений и построении разностных
сеток // Журн. вычисл. математики и мат. физики. 1967. Т. 7, № 5. С 1031-1060.
2. Белинский П.П., Годунов ОС, Иванов Ю.Б., Яненко Н.Н. Применение одного класса
квазиконформных отображений для построения разностных сеток в областях с криволинейными
границами // Там же. 1975. Т. 15, № 6. С. 1499-1511.
3. Лисейкин В.Д-, Яненко Н.Н. Метод подвижных координат в газовой динамике // Числ. методы
механики сплош. среды. 1976. Т. 7, № 2. С. 75-82.
4. Яненко Н.Н., Данаев Н.Т., Лисейкин В Д. О вариационном методе построения сеток // Там же.
1977. Т. 8, №4. С 157-163.
5. Morrison D. Optimal mesh size in the numerical integration of an ordinary differential equation // J.
Assoc. Comput. Mech. 1962. Vol. 9, N 1. P. 98-103.
6. Тихонов AM, Горбунов А.Д Оценки погрешности методов Рунге-Кутта и выбор оптимальных
сеток // Журн. вычисл. математики и мат. физики. 1964. Т. 4, № 2. С 232-242.
7. Гайсарян С.С, Об одном оптимальном алгоритме приближенного вычисления квадратур // Там
же. 1969. Т. 9, № 5. С. 1015-1023.
8. Гребенников А.И. О выборе узлов при аппроксимации функций сплайнами // Там же. 1976.
Т. 16, №1. С 219-223.
РАЗНОСТНАЯ СХЕМА НА ПОДВИЖНЫХ СЕТКАХ
ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ ВЯЗКОГО ГАЗА*
Для численного решения уравнений вязкого сжимаемого теплопроводного газа
записанных в ортогональных координатах, предлагается безусловно устойчивая
разностная схема, основанная на расщеплении уравнений по физическим процессам и
пространственным направлениям. Для повышения точности расчетов используются
подвижные разностные сетки, построенные на основе вариационного принципа.
Для численного решения уравнений, описывающих течения вязкого сжимаемого
♦Журнал вычисл. математики и мат. физики. 1979. Т. 19, № 1. С. 174-188. (Соавтор В.М. Ковеня.)
9. Зак. 953 257

теплопроводного газа, к настоящему времени разработано значительное число
разностных схем (см.напр., [1]). Ограничения, накладываемые на устойчивость явных схем,
требуют значительных затрат машинного времени и делают их в ряде случаев
неэкономичными, например при решении стационарных задач методом установления. Неявные
разностные схемы (см., напр., [2]) имеют более слабые ограничения на устойчивость.
Схема [3] является безусловно устойчивой, но не обладает свойством
консервативности. В [4] предложена неявная безусловно устойчивая разностная схема, основанная на
расщеплении исходных уравнений по физическим процессам и пространственным
переменным и являющаяся консервативной в стационарном случае.
Для повышения точности расчетов обычно используются преобразования координат,
сгущающие узлы разностной сетки в области больших градиентов, т.е. априори
использующие информацию о решении. При решении сложных задач такая информация
зачастую отсутствует, поэтому желательно использовать такие преобразования координат,
которые автоматически подстраивают узлы разностной сетки к решению.
Преобразование, зависящее от вектора скорости, предложено в [5]. Подвижные разностные сетки,
построенные на основе вариационного принципа, рассмотрены в [6].
В настоящей работе для численного решения двумерных уравнений вязкого
сжимаемого теплопроводного газа, записанных в произвольных ортогональных координатах,
предлагается неявная разностная схема типа универсального алгоритма [4],
реализуемая на подвижной разностной сетке [6]. Сочетание безусловно устойчивой разностной
схемы и метода подвижных сеток позволяет существенно повысить точность расчетов.
1. ИСХОДНЫЕ УРАВНЕНИЯ. ПРЕОБРАЗОВАНИЕ КООРДИНАТ
Движение газа около тел, обтекаемых сверхзвуковым потоком под нулевым углом
атаки, будем описывать полными уравнениями газовой динамики с учетом эффектов
вязкости и теплопроводности газа. После перехода к безразмерному виду эти
уравнения в ортогональных криволинейных координатах могут быть представлены в
векторной форме
dF/dt = -W,
(1.1)
где
F =
W
Р
ри
pv
Е
Е = р(е+(и2+У2)/2),
ри
р + ри2
puv
и(Е + р)
н^н2н3 {
д д }
H2H3Wl + —H^HsWt + Gj,
Ъх
by
и/,=
w, =
pv
puv
p+pv2
v(E + p)
G =
0
G,
G2
G3
G} - pvH3d - P±- H2H3 -H2H3 \± ±- H\GXX , GXX (-Л
ЭЯ,
1 9Я,
я2 ~ду~
дх
Hj_ дН2
Hi Ьу
258

G2 = -puH3d - p— HXH3 -НхнЛ—; — HxH2Gxy +-^ — H\Gyy -
by [Hi dx H2 oy
G^dH^ gzz аяэ [ l_^h JL^Mi 1 ЪНЛ
Hx by ~ H3 by + УУ\Н2 Ъу'*Нх by + H3 Э v /
r i ьн2 н2 ънх н2 ънъ li
xy[ нх дх ^ ~ Hi дх + нхн3 dx Jr
Э 'l к ЪТ \ Ъ (к ЪТ \
G3 = Тх ад U" "ST+ иС« + v4 +TyHlHT2V*uGxy*v4
l . f г 2 / эм и аяЛ 2 1 , ]
Re Г L ^ \ Ьх H2 by 3 J I
1 Г Г 2 / du w ЭЯ2 \ 2 1 f 1
G^ = ц —( + I div VI + f'divK
** Re Г I #2 \ 3v Я! to, / 3 J J
1 Г 2 /и ЭЯз у ЭЯ3\ 2 I , 1
Д — / + ) <*iv К + f'div V\
Re I [ H3 \HX dx H2 by ) 3 J i
/x f 3 3 / ЪНХ ЪН2 \\
{— uHx + vH2 - 2( и + v )},
HXH2 [by dx \ by bx J)
Gzz =
xy ReЯ]
1/33 \ ЭЯХ ЪНХ
div V = H2H3u + — HxH3v\, d = и - v-
HXH2H3 \ dx by J by bx
Здесь p — давление; p — плотность; e — внутренняя энергия; Е — температура; w, v -
проекции вектора скорости на оси jc, у; ц и f — первый и второй коэффициенты
вязкости; к — коэффициент теплопроводности; HXtH2fH3 — коэффициенты Ляме.
Для замыкания системы уравнений (1.1) задано уравнение состояния
Р = Р(Р> О, (1-2)
законы зависимости коэффициентов вязкости и теплопроводности от температуры
/i = ц(Т), f = S'(T), к = к{Т) (1.3)
и связь между внутренней энергией и температурой. При переходе к безразмерному
виду скорости и плотность нормированы на их значения в невозмущенном набегающем
потоке 1/ж, Роо. а температура - на С/^.
Течение предполагается симметричным относительно оси симметрии у ~ 0. Решение
уравнений (1.1) —(1.3) отыскивается в одной из плоскостей, проходящих через ось
симметрии и ограниченных осью симметрии, поверхностью тела, верхней границей
Rx(x) и задней границей R2(x). На поверхности обтекаемого тела задаются условия
прилипания и = v = 0 и условие тепловой изоляции ЪТ/Ъп = 0, где п — внешняя нормаль
к поверхности тела, или условие охлаждения Т = Т^(х, у). Верхняя граница Rx(x)
выбирается достаточно далеко от тела таким образом, чтобы возмущения в области между
телом и ударным переходом не достигали R х (х). В предположении затухания
возмущений можно выбирать Rx(x) на расстоянии нескольких калибров тела и задавать на ней
условия невозмущенного потока. На задней границе R2(x) задавались "мягкие
условия" д2//Ъх2 = 0 или непрерывность потоков через границу dWx/dx = 0.
Выбор криволинейных ортогональных координат х, у в качестве исходных
позволяет в рамках одного алгоритма (или программы) изучать обтекание широкого класса
тел. В ряде случаев удобно, а иногда и необходимо расчетную область Q разбивать на
ряд подобластей.
Q = z Qt
9*
259

и внутри каждой подобласти Qt использовать свою систему координат, наиболее
приспособленную к границам области или поверхности тела. Например, расчетную
область, приведенную на рис. 1, удобно разбивать на две области Qx и Q2. В области Qi
можно использовать систему координат, связанную с поверхностью тела, или
сферическую систему координат, а в области Q2 — цилиндрическую систему координат. В обеих
областях расчеты проводятся по единому алгоритму (в рамках одной программы)
с соответствующим изменением коэффициентов Ляме. Некоторое усложнение
алгоритма, связанное с решением уравнений в ортогональных криволинейных координатах,
окупается расширением класса решаемых задач и уменьшением затрат (времени
программиста и машинного времени) на создание одного комплекса программ. Перерас-
г
IWb\
RjtxL^-^^^
s^ptz
A^SSRRRS
*l
I >~
Рис. 1
чет краевых условий на границах областей при переходе от одной системы координат
к другой не вызывает затруднений. Влияние краевых условий на границе R2(x)
исследуется численно.
Для удобства численного интегрирования расчетная область Qt посредством
преобразования
£ = *(*V 1? = ri(x,y) (1.4)
Обратное преобразование
|о<£< 1,0<т?<1 |.
отображается в единичный квадрат R \ О < % < 1
задается соотношением
х = *(£)> у = у&ч).
Пространственные производные Ъ/Ъх и д/ду преобразуются по формулам
3 3 Э 3 3
Эх Э£ Эт?
(1.5)
Ъу * Эт?
гдеz0(£) = Э£/Эх, zx{%, т?) = Ъфу, z($, т?) = Ьфх.
Систему уравнений (1.1) в новых переменных (1.4) запишем в том же виде
dF/bt = -W, (1.6)
где вектор W соответствует вектору W из системы уравнений (1.1) после перехода к
новым переменным и записывается в виде
W
= rrl„ |-^Г^оЯ2ЯзИ/1 +^-(ztf2tf3H'1 ^z1H1H3W2)
HiH2H3 I Э£ Э77
3z0 3zi bz \
+ G+foHsWt-^ + H3(H1W2-T- + H2W2 — ) 1
a«
Э77
9*17
или же в виде
W
260
с в виде
1 Г Э Э Э |
Я,#2#з l Э| Эт? Зт7 '

Выбрав в качестве искомых функций вектор / с компонентами (р, иу v, e),
представим (1.6) в недивергентной форме в виде расщепления по физическим процессам
^пространственным переменным [4].
df/dt = -ЕП,/+ Я (1.7)
Дифференциальные матричные операторы ^ и 122 учитывают члены переноса и
вязкие члены (без учета смешанных производных) в направлении £ и 77 соответственно,
а Г23 и Г24 ~ члены с давлением и свободные члены в уравнениях движения и члены
вида div V в уравнениях неразрывности и энергии по каждому направлению.
Оставшиеся члены уравнений учтены в векторе Я. Пусть Е — единичная матрица. Тогда операторы
Г2Х и Г22 могут быть представлены в виде
(ид z0 Г 3 Э 3 3 1)
it и v \ Э z Г Э
\\ Я, Я2/ Эт? d0 L Эт?
zj Э Э Э Э 1}
+ — — zxq3— + -z1?4—ад j
£?о L Эт? Эт? Эт? Эт? J I
Э 3 3
— + —zq2 — H2H3
Эт? Эт? Эт?
где
<7i
<7з =
Н2Н3(1
Я,
Я,
II °
2
1 1
II ?/Рг
11 0 |
1
2
1| 7/Рг |
Г' - 2М/3
Г' - 2м/3
> <?4 =
я2
1 °
1
0
1 °
0
0
1
0
dx = НхН2НЪу d0 = pdiRe.
Для простоты изложения при записи операторов £2i и ft2 использована зависимость
между температурой и внутренней энергией в виде е = cvT, а коэффициент
теплопроводности выражен через коэффициент вязкости по формуле к = т/^/Рг» где у = с^/су,
Рг — число Прандтля. После исключения давления из исходных уравнений (1.6) с
помощью уравнения состояния (1.2) дифференциальные операторы £23 и £14 представим
в виде
Р 3
—-*о — НгНъи
С?! 3?
Пз/ =
Я! I Э£ Эе J
с2 3
Zq H2H3U
dt 3?
+ dv
261

o>/
z
z H2H3u + zi #i#3i>
Зт?
З77
Эр
+ b2
be
-f
З77
З77
a
z Н2Нъи
Эт7
Эт? J
-1
Эт? J
Э
07}
^Язи]
в2 =
tf = Z1U
1 Зр
P Эр
3#!
Э17
У Z0
p
э#2
э*
Зе
+ z
„2 _
P
эя2
Зт?
Свободные члены, возникшие в уравнениях вследствие выбора криволинейных
координат, учитываются в операторе Г23 • Более естественно было бы учитывать их в
операторах и £23 и Г24, однако это приводило бы к некоторому усложнению при реализации
разностной схемы. Из-за громоздкости выражений для векторов Wи Них виц в новых
переменных не приводится.
Система уравнений (1.6) может быть представлена в виде, разрешенном
относительно вектора /
3//ЗГ = -BW,
(1.8)
где
/ =
Р
и
V
€
В =
3F
~эГ
1
Р
1
—U
—V
О
1
О
О
О
1
-(е +(ы2 +у2)/2 -u -v
Системы уравнений (1.7) и (1.8) в дифференциальном виде эквивалентны. Но при
получении стационарного решения методом установления система (1.8) является
консервативной (матрица В невырожденная, а вектор W записан в дивергентном виде).
Поэтому при построении разностной схемы в качестве исходных уравнений используется
система (1.8).
Обратное преобразование координат X = Jt(£), у = у(%, v) будем находить на основе
вариационного принципа, предложенного в [6].
Потребуем, чтобы в каждый момент времени выполнялось соотношение
(| dq/dy\p + e)dy/dv = const, q = \u\ + | v | + | p | + | e | ,
(1.9)
означающее, что в области)больших градиентов функций в направлении т? градиенты
сетки малы. Выбором коэффициента ]3 задается необходимое сгущение координатных
линий, а параметр е выбирается отличным от нуля во избежание особенности при
Э#/Эт7 = 0. Координату у(%, т?) удобнее находить из решения параболического
уравнения методом установления со стационарными краевыми условиями
Ъу_
bq_
43
+ е
(1.10)
262

Очевидно, обратное преобразование невырожденное. Преобразование координат
£ = £(х) можно задавать линейным или зависящим, например, от формы обтекаемого
тела. По аналогии с (1.9) обратное преобразование х = х(£) может быть найдено из
стационарного решения уравнения
дх Ъ pi дх /1 11Л
= (д\К\ + е)— (1Л1>
bt Э£ Э£
со стационарными краевыми условиями х(0) =0 и л:(1) =х0. Здесь К(х) — продольная
кривизна поверхности тела. После нахождения обратного преобразования х = х(£),
У =>Ч£> V) определяются значения коэффициентов преобразования
Z*«) = (Ъх/Ы-Г1, z,(5f v) = (Эу/Зц)"1. *& V) = -z0zi Ъу№ .
Уравнения (1.10) и (Ы1) решаются на каждом временном шаге.
2. РАЗНОСТНАЯ СХЕМА
Введем в области Rh = R X Н, где R — единичный квадрат, Н = [0, Т], t E#,
разностную сетку с постоянными пространственными шагами hx и h2 (h\ = \\I, h2 = 1/K, I,
К - число узлов разностной сетки в направлении £ и т?) и временным шагом г (или
итерационным шагом при решении уравнений методом установления). Определим в
узлах разностной сетки (п, iif i2) сеточные функции р£, W/J, v%, e". Введем сеточную
вектор-функцию/£ =fh(tn, iihlf i2h2) с компонентами pJJ, и«, t>£, eg.
Первые производные на направлениям £ и г\ аппроксимируем несимметричными
разностными операторами Л * с порядком Л: = 1, 2 или симметричными операторами
Лр второго порядка аппроксимации. Индекс р = 1 (2) соответствует направлению
£(7j). При р = i разностные операторы имеют вид
1 , 1
ЛЬ^ = ±— (g/, -gi^i), Л?^ = ± —<3*'i -4ft,*i ■+*/,«)>
flrA!$. = ?4(flr + |flr |)Aj_ +%(flr-U|)"A*+f At = Й(Л}_ + Л}+).
Аналогично вводятся разностные операторы А2?, Л2. Вторые производные
аппроксимируем симметричными разностными операторами на трехточечном или
девятиточечном шаблоне по формулам
A1aA1gii = hi2[aii+y2(gii + 1 -g^) -aii_y2(gii -g/^-iH,
1
AbbA2gihj2 - [bil + 1 j2 {gix +! ,/2 +! - ft, +1 ,/2 -1) -
*\rl\rl2
b
ix - 1 ,/2 (Ai - 1 ,'a +1 ~ q4 ~ l'.'a ~ 1W
fc
Введем разностные матричные операторы £2.hi аппроксимирующие дифференциаль
ные операторы £2,-, / = 1, 2, 3, 4, с порядком к. С учетом введенных выше обозначений
разностные операторы £2^. представляются в виде
■1н = \<Л,% --^ [Л.С^О^Л, + Кг^яг^АаНгНг)h] E.
a2h = *"Л2* - "Г" [A2(z<7,)2A2 + Л2(2<72)"Л2(Я2Я3) J +
'Ой
+ "Т^ [Л2(21<?3)^Л2 + Л2(21?4)^Л2(Я1Я3)Л] Я,
<2ой i
263

£lk f =
*L3hJh
(р^)^йЛ%(Я2Я3«)й
(zo„/"i)KA*±»* +blAl±eh) +dhvh
-dhUh
KJ„ =
4hJh
* ' ~l*A2*("l"3»)J
|(^A*i) [zhAk2T(H2H3u)h + г^Л^С^Яз^]
Здесь </л = (z1uA2H1)h - vh(z0A1H2 + zA2H2)h, fli = (z0w/#i)^ a2 = (zu/Hx + z^vjH^
doh = Rep^j/,, ^1Л = (НХН2НЪ)Н. Члены с давлением в операторах £lk3h и £2к4И
аппроксимируются по формулам, сопряженным к конвективным членам. Такая
аппроксимация разностных операторов £2*j, и £2^/, позволяет, как показывает анализ устойчивости,
построить безусловно устойчивую разностную схему.
Вектор W уравнений (1.8) аппроксимируем в узлах сетки вектором Wh: вторые
производные аппроксимируем разностными операторами, а векторы W\ и W2 —
несимметричными операторами Wih согласованно с аппроксимацией операторов £lkh. В случае
одномерных уравнений газовой динамики разностная аппроксимация вектора W
подробно рассмотрена в [4].
Для численного решения системы (1.8) рассмотрим разностную схему расщепления
по физическим процессам и пространственным переменным:
(Е+тоцП1^)?*1'*- -rBnh(W"h)k, (£- + ra2n'2ft)^+2/4 = Г+1/4,
(^ + га3П3'й)|я+3/4 = £и+2/4, (2.1)
(Е + та,а'4Н)^+1 = |"+3/4, /й"+1 =/»■ + |"+1.
После исключения дробных шагов в (2.1) получим разностную схему типа
универсального алгоритма
(2.2)
c-ifV -r.yir- -.•<»•>*. с-.п^щ.
Весовые множители ау выбираются из условия устойчивости разностной схемы.
Разностная схема (2.2) или эквивалентная ей (2.1) аппроксимирует систему (1.8) с
порядком 0(т + hl), а при установлении — с порядком 0(hk), где h = max (ft t, h2)9k= 1,2,
/ =1,2.
Стабилизирующий оператор С1 назовем согласованным, если к = /, и
несогласованным в противном случае. На каждом дробном шаге п +//4,/ = 1, 2, 3, 4, разностная
схема (2.1) реализуется трехточечными (/=1) или пятиточечными (/ = 2) скалярными
прогонками.
При получении стационарного решения методом установления в качестве
стабилизирующего оператора выбирается несогласованный оператор С1. Тогда разностная схема
(2.1) реализуется трехточечными прогонками, при установлении имеет погрешность
аппроксимации 0(h) ( к = 1, 2) и обладает свойством консервативности: матрица
Впн невырожденная, а стационарные уравнения (W^)k = 0 записаны в виде выполнения
разностных законов сохранения.
Рассмотрим реализацию схемы на дробных шагах. На первом и втором дробных
шагах все разностные уравнения для компонент вектора % = £(£р, £ы, £и, £€)
относительно верхнего временного слоя могут быть решены независимо один от другого
скалярными прогонками, так как матрицы £21 и £2* имеют ненулевые элементы лишь на
главной диагонали и аппроксимируются на шаблоне из 2/ + 1 точек. На третьем дробном
264

шаге система разностных уравнении
эи ^и
С3'2 = С2/4 + «з^«С3/4>
f„+3/4 ш £+2/4 _" «»"S»<* Л^(Я2Яз)й^+3/4
решается в следующем порядке: исключая £"+3^4, £"+3^4, %п+3^4 из уравнения для
|«+з/4^ поддаем (21 + 1)-точечное разностное уравнение
?П + 3/4+т2а2^Г+3/4_ ^'ой
+ &ЙЛ
? Л'
14 rf,
'lft
™з*2й
я,
1*8ди*г2/4 + *2Au*:+a/4i - ™з<*лп+2/4-
Решая его прогонкой, находим ££*3/4, после чего по известному £"+3/4 определяем
£р+3^4, £"+3^4. £"+3^4. На четвертом дробном шаге система разностных уравнений
решается аналогично третьему дробному шагу: исключив £"+1, £"+1> £"+1 из уравнения
для £"+1, получим относительно £w+1 разностное уравнение на (2/ + 1)-точечном
шаблоне. Найдя £у+1, определим новые значения £р+1, £и+1 и £w+1. Наконец, найдя вектор
£и+1 ,из последнего уравнения (2.1) определим значение всех искомых функций на
слое п + 1. На этом расчет одного шага по времени заканчивается, после чего процедура
вычислений повторяется.
При к = 2 или / = 2 система разностных уравнений (2.1) аппроксимируется на
пятиточечном шаблоне, поэтому возникает необходимость доопределения функций в
фиктивных заграничных точках. Значения функций в фиктивных точках находятся путем
экстраполяции по внутренним узлам по формулам
/_! = з(Л> -/О +/2, fN+1 = 3(fN - fN_t) + fN_29
что соответствует изменению несимметричной аппроксимации в приграничных точках
на симметричную. Введением фиктивных точек достигается однородность разностной
схемы без понижения порядка аппроксимации.
Для реализации краевых условий строится разностная! схема типа основной (2.1).
Рассмотрим для примера аппроксимацию уравнения неразрывности на поверхности
тела 77 = 0. С учетом условий прилипания u* = v* = 'l£ = l£=09 s = n + //4,
разностная схема (2.1) при т? = 0 имеет вид
yti+2/4 = yn+3/4 = £П+1/4
ьр *р ?р
П+1 _ ЛП - fcW+1
рГ* ■ "ft + *
265

Заметим, что свободные члены в (2.1) учитываются неявно на верхнем слоев в
операторе ^з - При учете их на нижнем слое явно разностная схема может оказаться
условно устойчивой.
Для численного решения уравнений для сетки (1.10), (1.11) применялась неявная
разностная схема
(У"+1 -У" )1т = A2bA2y?+l, (x"+l -x" )/т = Л,аЛ,*"+1 (2.3)
со стационарными краевыми условиями. После получения стационарного решения
численно определялись значения коэффициентов преобразования z0, z и Z\ в узлах
сетки со вторым порядком.
Методом Фурье проведено исследование устойчивости разностной схемы (2.2) для
системы линейных уравнений, полученных линеаризацией исходных уравнений (1.6).
Анализ устойчивости показал, что разностная схема (2.2) для системы линейных
уравнений безусловно устойчива в случае согласованного оператора Ск при а, > 1А {]' = 1, 2,
3, 4) и при а; > 1 — для несогласованного оператора. Ввиду громоздкостидоказательст-
во устойчивости не приводится. Численные расчеты, проведенные по схеме (2.2),
показали, что устойчивость сохраняется и при решении системы нелинейных уравнений
(1.6). При численной проверке разностной схемы (2.2) на устойчивость итерационный
параметр г изменялся в широких пределах от h2/2 до 20h2, что соответствовало числам
Куранта К от ^ 1 до ~20. Во всех случаях устойчивость разностной схемы не
нарушалась, однако наиболее быстрая сходимость к стационарному решению (200—350
итераций) была при К ^ 3-г5. В качестве тестовой задачи рассматривалось обтекание
затупленного по сфере цилиндра сверхзвуковым потоком вязкого теплопроводного газа.
При расчетах головной скачок не выделялся. Весовые множители выбирались равными
единице. В случае несогласованного оператора С1 (К = 2) при больших числах Re вслед-
стие сильной немонотонности численного решения наблюдалось нарушение
устойчивости. При введении подвижной сетки, сгущающей координатные линии в зоне ударного
перехода, разностная схема оставалась устойчивой и при больших числах Рейнольдса.
Некоторые результаты расчетов приведены в разд. 4.
3. ОРГАНИЗАЦИЯ ВЫЧИСЛИТЕЛЬНОГО ПРОЦЕССА
При создании программы предусматривалась возможность дальнейшей модификации
алгоритма и расширение класса решаемых задач. С этой целью при написании
программы использовался модульный принцип [7]. Опишем состав расчетных модулей для
рассмотренной выше разностной схемы на примере задачи обтекания. Выделены
основные модули, или блоки.
1. БНД — блок начальных данных. В нем задаются начальные распределения
газодинамических функций, определяются границы области и вводятся необходимые расчетные
параметры (числа Маха, Рейнольдса, Прандтля и т.д.). Заданием параметра
фиксируется выбранная система координат, и вычисляются значения коэффициентов Ламе. В
качестве начальных данных в расчетной области Qt (после преобразования координат
Qi — единичный квадрат) задавался невозмущенный поток, а на теле — краевые
условия; вычислялись начальные значения коэффициентов преобразования и
итерационного параметра Го, равного R/2k, где к — число узлов разностной сетки по т?, a R —
расстояние от поверхности тела до верхней границы при £ = 0.
2. БС — блок сетки. По известному распределению газодинамических функций из
решения уравнений (2.3) определяются новые значения координат х и у,
соответствующие узлам сетки (ilt /2), вычисляются в узлах разностной сетки новые значения
коэффициентов Ламе и коэффициенты преобразования z0, z и zlt При решении задачи (2.2)
на установление разностные уравнения (2.3) на каждом итерационном шаге решаются
как нестационарные и делается одна—две итерации. Важно, чтобы разностные
уравнения для сетки (2.3) и система разностных уравнений (2.2) сходились одновременно.
Это может быть достигнуто выбором итерационного шага в уравнении для сетки. Итера-
266

ционный шаг г для решения разностных уравнений (2.2) выбирался неравномерным,
возрастающим за 50—100 шагов от г = г0 до г = 5-г 8 г0.
3. БПЧ — блок правых частей. В нем производится вычисление значений всех
компонент вектора £"(W^)fc на п-м слое во всех точках расчетной области, включая границы.
При аппроксимации уравнений (2.2) со вторым порядком iio формулам (2.3)
вычисляются значения искомых функций в заграничных точках. Определяются значения
коэффициентов вязкости. Значения компонент вектора Bnh (W^ )k засылаются в
элементы массивов вектора £и+ * /4.
.4. Б О — блок стабилизирующего оператора, служит для нахождения функций на
промежуточных дробных шагах п •+ //4. Разностные уравнения решаются скалярными
прогонками, вычисляются краевые условия для £w+#4, определяются новые значения
искомых функций/""*"1 на (л + 1)-мслое.
5. БВ — блок вывода и обработки информации. В нем на основе заложенного
критерия установления
)(fh+1 -Ф'т < е ~ 10-4-10"3
проверяется выход численного решения на стационарный режим во всех точках
расчетной области. Организуется контроль точности расчетов: проверяется выполнение
законов сохранения в контрольных объемах. По найденным значениям функций
вычисляются требуемые, аэродинамические коэффициенты, организуется процедура вывода
на печать газодинамических полей в удобном виде. При необходимости результаты
расчетов выдаются в виде графиков. Вывод полей газодинамических величин может
осуществляться по счетчику шагов.
6. БСО - блок сегментации. При обтекании тел сложной конфигурации или сильно
удлиненных тел производится разбиение расчетной области на ряд лодобластей. Для
/ > 1 выбирается система координат и вычисляются значения коэффициентов Ламе.
С целью уменьшения влияния приближенных граничных условий в области Q/ сеточные
подобласти Qj и б/+1 имеют общее пересечение. Краевые условия в начальном сечении
х0 подобласти Qi+1 берутся из полученного численного решения в подобласти Q,- при
том же значении х0. Программа предусматривает решение в любой отдельной
подобласти Qj+1. В этом случае граничные условия во входном сечении х0 задаются вводом
необходимых массивов данных. Для получения начальных данных в Подобласти Qi+1
значения функций в сечении х0 продолжаются на всю подобласть.
В зависимости от типа решаемых задач отдельные модули могут быть исключены из
программы (например, БСО или БНД). Обращение к БНД и БСО происходит
однократно или равно числу рассчитываемых подобластей, а к БС, БПЧ, БО — на каждом
итерационном шаге. Обращение к БВ происходит в конце счета или по счетчику шагов. Вся
программа находится в оперативной памяти машины БЭСМ-6 и реализована на языке
АЛЬФА-6.
4. ПРИМЕРЫ ЧИСЛЕННЫХ РАСЧЕТОВ
По рассмотренной выше разностной схеме с использованием подвижной сетки
проведены численные расчеты обтекания осесимметричных тел сверхзвуковым потоком
вязкого теплопроводного газа. Ниже приводятся некоторые результаты расчетов
обтекания затупленного по сфере цилиндра и невыпуклого тела.
В первом случае выбрана "естественная" система координат (х — длина дуги,
отсчитываемая от оси симметрии тела, у — внешняя нормаль к поверхности тела). Внешняя
граница области Ri(x) задавалась по формуле
*i(*) = '**(&-*)*",
где а = 4/з, a, b — расстояние от поверхности тела до внешней границы прих = 0 их = х0у
и на ней задавались условия набегающего потока. По £ было выбрано 19, а по 77— 20 то-
267

Ркс4
ОгвУ
0,6
o,z
0,0
Jt/Ч Jt/Z ЗЖ/Ч S
Рис.3
>
Рис.5
o,z6 0,5 ajfr
Рис. в
чек. Шаг сетки в направлении оси jc выбирался равномерным, а по у — находился из
решения уравнения для сетки (2.3), где Ъ = i и2 + v2 \ м2 +е . Параметр /3 изменялся
от 0,2 до 1,0 за 60—80 шагов, после чего выбиралось 0 = 1,0, а е — порядка h2. На рис. 2
приведено распределение нормальной компоненты скорости и и на оси симметрии для
различных Re («> (0); Ю4 (i); 3 - 103 (2); 103 (3); 5 • 102 (4) у затупленного по
сфере цилиндра при М = 6, со = 0,75, Рг = 0,72, дТ/Ъп = 0. Распределение коэффициента
трения по телу для различных Re (104 (1); 3 103 (2); 103 (3); 5 - 102 (4)) дано на рис. 3
(параметры набегающего потока те же, что и на рис. 2). На рис. 4 Приведена расчетная
сетка, полученная в процессе решения при установлении для М = 25, Рг = 0,72, со = 3Д,
7 = 1,2, Re = 3 - 103. В области затупления происходит резкое сгущение узлов
разностной сетки в зоне ударного перехода и пограничного слоя.
В качестве второго примера рассмотрено обтекание невыпуклого тела (рис. 5).
Затупление образовано гладким сопряжением трех окружностей радиуса 1 с центрами
(а = 1, 0 = 0, а = 1, 0 -2; а = 3, /3 = 2, где а, 0 - декартовы координаты). Для расчетов
268

выбрана сферическая система координат с подвижным центром ]3 = 0, а = 3,262. На
рис. 5 приведена расчетная сетка при обтекании невыпуклого охлаждаемого тела
потоком вязкого газа приМ = 15, у = 1,2, со = 0,5, Re = 3 • 103, Рг = 0,72, Гы =5,4(ГЫ -
температура поверхности). В невыпуклой области образуется отрывное течение с
вихрем. Характеристики течения при в = 43° приведены на рис. 6.
В процессе получения решения методом установления при Re/M?CJ > 103
наблюдалось колебание узлов подвижной разностной сетки и решение не выходило на
стационарный режим. Для получения стационарного решения после 200—250 итерационных
шагов разностная сетка фиксировалась, после чего решение быстро (~50-Н00 шагов)
выходило на стационарный режим. Автоколебательный режим связан, по-видимому,
с сильным искажением координатной сетки либо с приближенным вычислением узлов
разностной сетки. На наш взгляд, для расчета течений в сложных областях
необходимо использовать сгущение по двум направлениям.
Для сравнения были проведены расчеты обтекания указанных выше задач с
фиксированной равномерной разностной сеткой, показавшие сильное размывание областей с
большими градиентами. Например, при обтекании невыпуклого тела вихрь на
равномерной сетке не образуется.
Проведенные расчеты позволяют сделать вывод об эффективности предложенной
неявной разностной схемы и метода подвижных сеток.
ЛИТЕРАТУРА
1. Численное исследование современных задач газовой динамики / Под ред. О.М. Белоцерковского.
М.: Наука, 1974.
2. Полежаев В.И. Численное решение системы одномерных нестационарных уравнений Навье-Сток-
са для сжимаемого газа // Изв. АН СССР. МЖГ. 1966. № 6. С. 34-44.
3. Березин Ю.А., Ковеня В.М., Яненко ИМ. Об одной неявной схеме расчета течения вязкого
теплопроводного газа // Числ. методы механики сплош. среды. 1972. Т. 3, № 4. С. 3-18.
4. Яненко Н.Н., Ковеня В.М. Разностная схема для решения многомерных уравнений газовой
динамики//ДАН СССР. 1977. Т. 232, №6. С. 1273-1276.
5. Толстых А.И. О методе численного решения уравнений Навье-Стокса сжимаемого газа в
широком диапазоне чисел Рейнольдса // Там же. 1973. Т. 210, № 1. С. 48-51.
6. Яненко Н.Н., Данаев Н.Т., Лисейкин В.Д. О вариационном методе построения сеток // Числ.
методы механики сплош. среды. 1977. Т. 8, № 4. С. 157-163.
7. Коновалов А.Н., Яненко НЛ. Модульный принцип построения программ как основа создания
пакета прикладных программ решения задач механики сплошной среды // Комплексы программ
математической физики. Новосибирск, 1972. С. 48-54.
О РЕШЕНИИ НЕСТАЦИОНАРНЫХ ЗАДАЧ ГАЗОВОЙ ДИНАМИКИ
В ПОДВИЖНЫХ СЕТКАХ, ЗАВИСЯЩИХ ОТ ПОТОКА*
В [1—3} представлены результаты расчетов широкого круга стационарных и
нестационарных задач газовой динамики, полученные с помощью подвижных сеток,
зависящих только от геометрии области. В [4—7] сетки, зависящие от потока, применены для
повышения точности решения задач обтекания и некоторых других задач
математической физики. Цель настоящей работы — применить к решению нестационарных задач
газовой динамики подвижные сетки, зависящие от потока, для построения которых
с одной стороны используется вариационный принцип, предложенный в [4], а с
другой стороны — геометрический метод построения, предложенный в [8]. Здесь
показывается эффективность такого подхода к решению задач газовой динамики с большими
градиентами параметров среды и большими деформациями областей.
В качестве основной системы уравнений брались уравнения газовой динамики,
♦Численные методы механики сплошной среды. 1981. Т. 12, № 1. С 131-140. (Соавторы
Ю.П.Мещеряков, В.П. Шапеев.)
269

записанные в форме, предложенной в работе [9]-, В двумерном случае эта система
выглядит следующим образом:
-^-+ — [p(ua-wa) (-iy+aalz?] =0,
dr dq> '
^±+-^ ([pM'(«tt-^) + K](-iv+^:; Ц,
ЭрА(е + |»|2/2) , Э |Г / l«'l2\,- *w *ly
+ \ p [e + I (wa— w ) + pu I X
ЭГ a*> U v 2 / J
dt bq>
X (-l)> + ee*:° =0
/,/,*= 1,2. (1)
Здесь p — плотность, e — удельная внутренняя энергия, р — давление, и1 — проекция
вектора скорости среды на г-ю координатную ось, | и |2 = (w1)2* (w2)2, Г — время,
<77 — криволинейные координаты, л:1 — декартовы координаты, wJ = bxJjbt
—проекция скорости движения криволинейной системы координат на /-ю координатную ось,
а\ = Эх'/Э?7, Д=1)(х1, x2)/D(q\q2)9 81а - символ Кронекера. Система (1)
замыкалась двучленным уравнением состояния для металлов
р = (к-1)ре + (р-РоКо, (2)
где к, ро, Со — некоторые постоянные величины, и соотношениями
*' = *'0Л<Л0> / = i,2, (3)
которые определяют связь декартовых координат с криволинейными.
Для аппроксимации системы (1) использовалась схема Годунова [1]. Для
построения сетки, а тем самым и определения соотношений (3) применялся геометрический
метод [8]. При этом закон расстановки точек на границе был следующий.
Обозначим через 7} отношение длин (У, i + 1) дуги к (/, i — 1). Тогда, очевидно,
зная значения 7} в каждой граничной точке и полную длину границы oL, легко
определить длину каждой (У, i + 1) дуги, а следовательно, и новые координаты граничных
точек. Для вычисления же значений 7} использовалась формула
Г(и,.,1~)(|<,|^-|» _,;
[(i*,.,it«)(i«,*Mi+«)TJ'
где #,- — значение кривизны границы в У-й граничной точке, е, 7 — некоторые
управляющие параметры, и* — значение градиента касательной составляющей скорости
границы в 1-й граничной точке. Вычисление величины kt проводилось по формуле
(*! -*.1 ,)(*.* -2*? + х? J-(x2-x? Л(х* -2^ + х1 ,)
к = ■ (5)
правая часть которой, как легко проверить, аппроксимирует кривизну со вторым
порядком точности. Для аппроксимации градиентов скорости и* использовались
центральные разности. В граничных точках, в которых центральные разности для
аппроксимации градиентов касательной составляющей скорости границы и
кривизны не годились, использовались односторонние разности. Нетрудно убедиться,
270

что вычисление величин 7} по формуле (4) приводит к сгущению граничных точек
в тех участках границы, которые обладают большой кривизной и в которых имеются
большие градиенты касательной составляющей скорости.
Для сгущения узлов сетки в областях с большими градиентами применялась с
некоторыми изменениями методика, использующая комбинированный
вариационный принцип на основе результатов [4, 8] и предложенная в [10]. Внесенные
изменения состоят в замене величины h2 = (^i~l)2, которая является мерой
искажения ячеек сетки на величину h2 = (h1 — /)2, где функция/ в произвольной z-й
точке /-й координатной линии вычислялась по следующему алгоритму. Нумерацию узлов
шаблона будем вести в соответствии с рис. 1.
/-/,/-/
Hie. 1
1. Проводятся нормали к отрезкам, соединяющим узлы с номерами (/—1, /—1),
(7-1,/ + 1) и (7 + 1,/-1), (7 + 1,/+1) через узлы с номерами (7—1,/) и (7 + 1, /)
соответственно.
2. Проводится прямая, параллельная отрезку, соединяющему узлы (7,/+1) и
(/,/— 1), и проходящая через узел с номером (7, /).
3. Находятся координаты точек пересечения А и В нормалей с этой прямой.
4. Находятся координаты точки С, лежащей на середине отрезка АВ.
5. Значение функции / в узле (/, /) вычисляется по формуле
( Si/s2, если 0,1 < Si/s2< Ю,
| ю, если Si/s2 > 10,
I 0,1, если Si/s2 < 0,1,
4 =
где Si, s2 длины отрезков, соединяющих точки С, (7, /+ 1) и С> (7, / — 1).
Окончательно, для согласования с выбором меры концентрации hx полагается
\ f.. в промежутках (£,, ^ ) , где \ы (£, т?) I не
17 { f'1 в промежутках [0,1] /(£ , £ ) , где | м(£,
возрастает,
г?) | не убывает.
Здесь, так же как ив [10], м(£, г?) некоторая газодинамическая величина, J 77 =
= const} — семейство координатных линий, вдоль которых меняются значения /,
| % = const} — семейство координатных линий, вдоль которых меняются значения
индекса /. Такой выбор функции / позволяет лучше удовлетворить требованию,
предъявляемому к сетке — ее близости к ортогональной, и особенно, когда в размерах
ячеек наблюдается большая неравномерность. Повторяя теперь рассуждения,
проведенные в [10], и учитывая внесенные изменения, получим новое уравнение для
нахождения параметров сгущения, которое будет иметь вид
*i'-(ei+e2)*» = /■" ■
е2/.
(6)
Уравнение Эйлера для нахождения дополнительной кривизны к2 [9, 10]
выписывается аналогично.
271

В настоящей работе перестройка сетки делалась на каждом шаге по времени
вслед за смещением границ. Поскольку для расчетов применялась явная схема, то
было необходимо не допустить выхода узлов сетки за один шаг по времени за
границы их шаблонов, имевших место на предыдущем временном шаге. С этой целью
сетка, полученная на новом (и+1)-м шаге, подвергалась перестройке по алгоритму:
1) Определяется квадрант, в который попал узел на новом шаге. Пусть это будет
квадрант МАК (см. рис. 2). ,
2) В этом квадранте выделяется область ADCE, образованная соответствующими
координатными линиями и двумя прямыми, пересекающимися в точке С
диагонали АВ. При этом полагается АС/ВС =1/3, AD/DK = 1/3 и АЕ/ЕМ= 1/3.
ХЛ
В
WWW/.
xzk
1 1 1 111 1 1 1 -*
1
xr
*1
«27
Рис.3
Рис.4
Рис.5
3) Если узел сетки F в новом положении лежит внутри области ADCE, то его
координаты не меняются. В противном случае за координаты узла F принимаются
координаты точки пересечения отрезка AF с границей области ADCE.
Для определения шага по времени, обеспечивающего устойчивость счета, в данной
работе использовался критерий Куранта.
Численные расчеты. Для отладки программы и проверки эффективности
методики решались следующие задачи.
1. Удар металлического стержня о твердую стенку в одномерной постановке.
Для того чтобы обеспечить одномерность течения на плоскости и не вносить
переделок в программу, которая была составлена для решения двумерных задач, были
дополнительно поставлены еще две твердые стенки, как показано на рис.3. В
качестве начальных данных задачи брались: м1 = 0, и2= —1,4, р = 0, р = 0, / = 0, АВ =
= 1,2, ВС = 0,42. На твердых стенках АВ, ВС и CD ставились условия непротекания,
а на свободной границе AD полагалось р =0. В этой и последующих задачах
константы для уравнения состояния (2) принимались к = 4,8, р0 = 1, с0 = 1. Поставленная
задача имеет аналитическое решение в виде ударной волны, движущейся навстречу
свободной поверхности. Для расчета использовалась сетка с количеством ячеек 7x13 =
= 91. Результаты численного расчета сравнивались с аналитическим решением в момент
времени t =0Д5, когда ударная волна еще не достигла свободной поверхности AD.
Сравнение показало, что при параметре сгущения у = 0,7 максимальная ошибка
в расчете течения за фронтом ударной волны составляла 0,3%. Аналогичный расчет
с 7 = 0 (случай равномерной сетки) дает ошибку в 8%, и для достижения той же
точности, как и в случае, когда 7 = 0,7, требуется примерно в 6 раз увеличить
количество узлов по переменной х2. Сравнение по затратам машинного времени
показывает, что достижение одинаковой точности вторым способом требует увеличения
времени счета примерно в 5 раз.
На рис. 4 показана сетка в момент времени t = 0,25 при у = 0,7. Из рисунка
видно, что узлы сетки сгущаются на фронте ударной волны. На рис. 5 приведен график
удельной энергии /. Здесь следует отметить интересную особенность — исчезнове-
272

ние так называемого "энтропийного следа", который возникает при сквозном счете
особенностей. Этот эффект объясняется сглаживанием неправильных значений
плотности и энергии, полученных при "размазывании" ударной волны, за счет увеличения
размеров ячеек после прохождения ударной волны и притока в них среды с более
правильными газодинамическими параметрами.
2. Разгрузка нагруженного металлического стержня в вакуум. Эта задача также
рассматривалась в одномерной постановке и поэтому для ее решения использовался
тот же прием, что и для предыдущей. В той же счетной области ABCD (см. рис. 3)
в качестве начальных данных брались и1 = 0, и2 = 0, р = 6,01, р = 1,48, / = 0,98,
АВ =0,6, ВС =0,4. Постановка граничных условий в данной задаче не отличалась
*z\
1 1 1 И1 1 1 1 ъ
X,
Рис.6
йЛ —'
1 г
3
—J
.S^ss
-3
—
Рис.9
Рис.8
Рис. 10
от их постановки в задаче 1. Для расчета использовалась сетка 7x13=91. Кон-троль
точности велся по скорости разлета свободной границы AD в вакуум. При этом
ошибка при параметре сгущения 7 = 0,9 в момент времени 0,15 (волна разгрузки
еще не дошла до твердой стенки ВС) составляла 1,5%. Сопутствующий расчет в
лагранжевой сетке с тем же количеством ячеек дает ошибку 11%.
На рис. 6 приведена сетка в момент времени 0,15 при у =0,9. В этой задаче
интересно отметить, что практически все узлы сетки расположены в зоне, ограниченной
крайними характеристиками, и разности газодинамических величин в смежных по
оси х2 ячейках примерно равны между собой.
3. Косой удар пластины о твердую преграду. Задача рассматривалась в плоской
постановке. На рис. 7 изображена начальная конфигурация. На свободных границах
АВ, ВС и CD задавалось р = 0. На твердой стенке AD условие непротекания и2 =0.
За начальные Данные брались параметры р=0, р= 1, / = 0, и1 = —1,4 cos а, и2 =
= —1,4 sin а. Длины сторон AD и DC равнялись соответственно 0,2 и 0,4. Сторона
АВ || CD, a BCL CD. Эта задача эквивалентна задаче о соударении двух одинаковых
273

пластин под углом друг к другу в предположении зеркальной симметрии картины
движения относительно оси х1, при этом твердая стенка заменяет условие
симметрии. Задача рассматривалась при углах а от 45° до 18°. Для одного из расчетов
использовалась сетка 13x13 = 169. Несмотря на небольшое количество расчетных
ячеек, удалось выделить кумулятивную струю при этих углах.
На рис. 8 изображена полученная конфигурация с кумулятивной струей при угле
соударения а = 18°. Счет велся до выхода скоростей точек А и D на стационарный
режим. Из рисунка видно, что узлы сетки особенно сильно сгущаются в области
кумулятивной струи. Простой подсчет показывает, что в струе, площадь которой занимает
примерно 2% от всей площади счетной области, сосредоточено около 25% общего
количества расчетных ячеек. Таким образом, для расчета этой задачи на эйлеровой
равномерной сетке, с тем же количеством ячеек в струе, потребовалось бы увеличить общее
число узлов как минимум в 12,5 раз. Отметим также, что расчет этой задачи в лагран-
жевых координатах сопряжен с большими трудностями из-за наличия точки
торможения, в окрестности которой происходит разделение потока и имеются большие
градиенты. Затраты машинного времени для получения конфигурации, изображенной на
рис. 8, составили для машины БЭСМ-6 1 час 15 мин.
На рис. 9 изображен график, который дает представление о распределении
скоростей на оси*1. Для оценки сходимости на том же рисунке штриховыми линиями
представлены результаты расчета, выполненного с 20x20 = 400 ячейками и штрихпунктир-
ными с 30x30 = 900 ячейками. По графику видно, что скорости точек А и D вышли
на стационарный режим, а скорость сходимости разностного решения достаточна для
того, чтобы иметь правильное качественное представление о поведении струи по
результатам расчетов, выполненных на сетке с количеством ячеек 13x13 = 169.
Сравнение с результатами расчетов, проделанных для углов а> 18° показывает, что с
уменьшением угла а скорость кумулятивной струи падает, а точка выхода ударной волны
на свободную поверхность CD сдвигается в направлении точки контакта D9 что
хорошо согласуется с результатами работ [3, 11 — 14]. Следует отметить также, что в
данных расчетах, как ив [12, 13], около оси х1 левее и правее точки торможения
получаются небольшие зоны с отрицательным давлением.
Формулы расчета сетки итерационные, но во многих случаях можно обходиться
без итераций. При этом сетка получается более грубой (см. рис. 8). Включение
итерации при построении сетки, а также увеличение числа узлов улучшают ее качество:
она становится более гладкой и регулярной (рис. 10). Тем не менее на величинах
решения газодинамической задачи итерации формул сетки сказываются в
незначительной мере.
Таким образом, приведенные здесь факты позволяют сделать вывод о
возможности эффективного решения по данной методике нестационарных задач механики
с большими деформациями областей.
ЛИТЕРАТУРА
1. Годунов С.К. Численное решение многомерных задач газовой динамики. М.: Наука, 1976.
2. Godunov S.K., Deribas АЛ., Zabrodin A.V., Kozin N.S. Hydrodynamic effects in colliding solids //
J. Comput. Phys. 1970. Vol. 5, N 3. P. 517-539.
З.Шуршалов Л.В. О расчете кумулятивных струй // Изв. АН СССР. МЖГ. 1975. № 4. С 116-122.
А.Яненко Н.Н., Данаев Н.Т.У Лисейкин В Д. О вариационном методе построения сеток // Числ.
методы механики сплош. среды. 1977. Т. 8, № 4. С 157-163.
5. Данаев Н.Т. Об одном способе построения криволинейных сеток, сгущающихся в области
больших градиентов // Там же. 1979. Т. 10, № 4. С 60-74.
6. Шашкин,А.П.у Волков В.Ф. О выборе расчетной сетки при численных исследованиях обтекания
тел пространственных конфигураций // Там же. № 3. С 142-146.
7. Tompson J.F., Thames R.C., Mastin C.W. Automatic numerical generating of body-fitted curvilinear
coordinate system for field containing any member of abritrary two-dimensional bodies // J. Comput.
Phys. 1974. Vol. 15, N 2..P. 299-319.
8. Мещеряков Ю.П., Шапеев В.П. Некоторые геометрические методы построения разностных сеток
274

в областях с криволинейными границами // Числ. методы механики сплош. среды. 1978. Т. 9.
№2. С. 91-103.
9. Лисейкин В.Д., Яненко Н.Н. Метод подвижных координат с газовой динамике // Там же. 1976.
Т. 7,№1. С. 75-82,
10. Мещеряков Ю.П. К вопросу о построении разностных сеток геометрическим методом // Там же.
1979. Т. 10, №2. С. 105-116.
11. Walsh J., Shreffler R., Wellig F. Limiting conditions for jet formation in high velocity collisions // J.
Appl. Phys. 1953. Vol. 24, N 3. P. 349-359.
12. HarlowF.H., Pracht W.E. Formation and penetration of high-speed .collapse jets // Phys. Fluid.
1966. Vol. 9, N 10. P. 1951-1959.
13. ChouP., CarhoneJ., Karpp R. Criteria for jet formation from impinging shells and plates // J.
Appl. Phys. 1976. Vol. 47, N 10. P. 2975-2981.
14. Петренко B.E., Сапожников Г А. Численное решение задачи о симметричном соударении
металлических пластин//Материалы V науч. конф. по математике и механике. Томск, 1975.
4.2.
О РАВНОМЕРНО<:ХОДЯ1ЦЕМСЯ АЛГОРИТМЕ
ЧИСЛЕННОГО РЕШЕНИЯ ОБЫКНОВЕННОГО
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
С МАЛЫМ ПАРАМЕТРОМ ПРИ СТАРШЕЙ ПРОИЗВОДНОЙ*
Проблема построения равномерно—сходящегося алгоритма численного решения
двухточечной краевой задачи с малым параметром при старшей производной была
поставлена и решена Ильиным A.M. [1] с помощью специальной разностной схемы
с весами на равномерной сетке. В [2—4] метод Ильина распространяется на решение
более сложных (параболических, многомерных) краевых задач. Численный счет на
равномерной сетке плохо описьюает пограничный слой, поскольку при достаточно
малом параметре уже первый узел сетки лежит вне погранслоя. Так как для
практических приложений важно знать структуру погранслоя, то разностную сетку нужно
строить не равномерную, а сгущающуюся в области погранслоя. Для численного
решения уравнения v d2u/dx2 — с (х)и = / (х) алгоритм со сгущающейся
разностной сеткой был предложен Бахваловым Н.С. [5]. В данной работе строится
равномерно сходящийся алгоритм численного решения уравнения v d2u/dx2 +
4- a(x)du/dx - с (х) и = f (х) с помощью специальной координатной функции,
сгущающейся в области погранслоя.
Пусть нужно численно решить краевую задачу
L(u) = vd2u/dx2 +a(x)duldx-c(x)u = /(*), xG[0,l], ^ч
w(0) = /0, и(1) = /ь а(х)>а0>09 с (x) > 0, v>0.
Заметим, что задача, для которой а(х) < а0 < 0 сводится к (1) заменой х на 1-х1.
Введем независимую переменную q с помощью монотонного отображения
х (q) G С3 [0, 1], х (0) = 0, х(\) = 1. Задача (1) относительно переменной q
имеет вид
d2u1 dx Г d2x (dx \ 1
ilW.._+_[.w-1>_j_j j
du'
(2)
M'(0) = /o, «'(!)=/,.
♦Численные методы механики сплошной среды. 1981. Т. 12, № 2. С. 45-56. (Соавтор В.Д. Лисейкин.)
275

Положим
-2
dx Г d2x (dx \" 1 ( dx \ I' dx \
" ' *-l'w~ V ЬгУ J- *"eW I"*-) ' Л -/W(*T
Тогда (2) переходит в
Lt(u)svdiu1/dq1+a1(q}du1/dq-cl(q)u1'»fl(fi), и,(0) = /0, «'(Ot'i- (3)
Аппроксимируем (3) монотонной разностной схемой на равномерной сетке д,- =
= iAq,i=0,l,...,N,Aq = \/N,
«£(") = у п~л + ^О—Г~ сЛядЩ
Щ+1 -2щ+щ_х
(Aq)2 — Aq
= Л (Qi), "о = 'о, "^ = li- (4)
Теорема 1. Пусть монотонное отображение х (q) удовлетворяет следующим
условиям:
а) ax(q) >0,
б) max^ (v/diiq)) <cl9
в) max | dbul/dq* | < цк
для fc < 3, где cl9 цк — константы, не зависящие от и, тогда сеточная функция М/,
являющаяся решением (4), сходится равномерно относительно v к решению задачи (3)
с первым порядком, т.е.
\ui-u\qi)\ = \ui-u{xi)\ < CAq, xt = *(<?/),
где С не зависит от v.
Доказательство. Для схемы (4) выполняется принцип максимума, т.е.,
если £ (и) < 0, м0 > 0, uN > О, то щ >0 [6]. Поэтому для произвольной сеточной
функции о- \ Ojl (г = 0,1, ...,АГ)
|о/| < |а01+ lofr| + max, |-£ (а)/*! Ы |. (5)
Действительно -, для
w = {w1* = \о0 1 + 1а^ | + (1 -qi)maxi\£(o)/a1 (?,) | ± а, } ,
£(w) < 0, wo > 0, wN > 0,
и значит из принципа максимума w,- > 0, т.е. выполняется (5). Обозначим через
R = 1 Rj! погрешность аппроксимации уравнения (3) схемой (4). Тогда для
погрешности схемы (4) в = { е,- = щ - и1 (сц}\ > £ (е) =R> и из (5) следует
|е,-| <maxr- |/?i/ai(4*)|. Очевидно, что
(u \ d3ul , d*ul t 1 аМ d2ul , 1
*-4»{Tl-3r<ti)-*!-<M+-Tiv-«')l-
где
Иэ условий теоремы вытекает \Rf\ < Aq — д3 4- и, значит, |е,-| <
[и ju21 \с\Иъ M2I
/z3 "• 1 < А^г + —I, т.е. получаем равномерную сходи-
3ax(qt) 2 J L 3 2 J
мость с первым порядком точности.
276

Теорема доказана.
Таким образом, чтобы сеточная функция, являющаяся решением (4),
равномерно сходилась к и (Xf), нам нужно построить функцию х (д) со свойствами а, Ь, с.
Для этого нам нужно знать, как ведут себя производные функции и (х), являющиеся
решением задачи (1).
Мы воспользуемся результатами, изложенными в [7]. Если коэффициенты
задачи (1) а(х), с (*),/ (х) £Са [0,1], то из [7] легко следует, что решение
задачи (1) имеет вид
X
и (х) = Ь0 (х) • ехр (- у (x)/v) + d0 (x), где </> (х) f a (£) d%9
о
а функции b0(x), d0(x) имеют равномерно по v ограниченные (р.о.) производные
до а + 1 порядка включительно. Отсюда получаем
dku Ьк (х) -?(*) , . , ч ,,ч
—JT = 1— ехР — + dk (*) (6)
dx v v
для fc<a+l, где bk(x), dk(x) — p.o. функции.
Согласно условию задачи (1), а (х) > а0 > 0, поэтому у(х)>а0х и из (6)
dku | 1 Ък (х) | -а0х
< к е*Р —— + I dk (x) |.
dxk
V
1
Пусть х > mv In— , тогда
dku
dxk
bk\ алт
Vk
+ \dk(x)\.
Отсюда имеем: производные функции и(х) до fc-го порядка включительно равномер-
I
но ограничены вне отреза [0, mv In — ], где т = &Д/0 •
' Мы функцию х(д) определим склейкой двух функций таким образом, чтобы одна
1
функция отображала отрезок [0, 1/2] в [0, mv]n — ] по логарифмическому закону,
а вторую определим многочленом так, чтобы в месте склейки производные совпадали
до к-го порядка включительно. Для удобства записи формул мы полагаем а0 = 3,
т.е. задачу (1) домножаем на 3/а0.
Лемма 1. Пусть х (q) - отображение, задаваемое формулой
где
-3vla[l-2q(l-u*')}, «6 [0, 1/2], (7)
*i fo) + *i ХЯ- 1/2)4 ?е [1/2,1],
Х1 (,) = »1п I + Зри2/з (q - 1/2) + 1 PVA (q - 1/2)2 + р3 (q - 1/2)3
р =2(l-y,/3), Л, = 16[1-х,(1)],
и пусть
а(х), с(х), /(*) £ С2[0, 1], а (л:) > 3,
тогда для
,/. dx v d"x dnul
0 < и /3 < 1/2 — > 0, а, (?)>0 и
dq <*,(<?) dqn dqn
p.o. функции при га<3.
27?

Доказательство. Из (7) имеем
x1(l)=uln(l/u) + 3(l-ul/,)uVl+ 3/2(1-у1/з)2у1/з+(1-1)1/з)3.
Функция g (v) =x1 (1) при О < v < 1/2 возрастающая, и поэтому для v < 2
JC!(1) <£(l/8) = 3/81п2 + 3/8 + 3/16 + 1/8 <1.
Отсюда ki = 16 [1 — *i(l)] > 0, и из (7) легко следует, что dx/dq > 0, т.е.
отображение х (q) — монотонное.
При q > 1/2 х (q) > v\n(l/v). Согласно (6)
dnu bn(x) -</>(*)
77 =-^Г * exP —» + dn(x), n < 39
dxn v v
где bn(x), dn(x) — р.о. функции. Так как dy/dx =a(x)> 3, то <р(х) > Зх9 и значит
dnu
. I K (x) | -3*
< n eXP ~~T + \<*П-(Х) |,
а для x > v In (1/u)
|Л/^Й| < |.6и|и3-я + [tfw(*)|>
dnu
и значит для g > 1/2, /7 < 3, —— (д) — р.о. функция. Очевидно из (7), что при
dx
q > 111, n < 3, dnx/dqn — также р.о. функция и поэтому dnuxjdqn при # ^ 1/2,
и < 3 - р.о. функция. Теперь пусть q Е [0, 1/2], тогда х (д) <uln (1/у), но при
л: < i>ln(l/i>) q(x) = p~l (l - exp (-х/Зи)) и поэтому
dx 1 х 2/3 d2x 2x
— = —— = Зриехр — < 3pvf , —r = p2v-exp —
dq dq/dx 3v dq- 3v
d3x/dq3 = 6p3vexp(x/v) < 6p3. (8)
Имеем
du1 du dx d2ux d2u (dx \ du d2x
+
dq dx dq dq2 dx2 \dq J dx dq2
d3ul d3u ( dx \3 d2u d2x dx du d3x
= / + 3 + -' • (9)
dq3 dx3 { dq J dx2 dq2 dq dx dq3
Подставив в (9) значение dnu/dxn из (6) и dnx/dqn из (8), получаем для q E
[О, 1/2]
du1 I Г Ifci I -Зх 1 х -8х
-— < ■—— • ехр —— + \dx I \3pv • exp — < 3 | bi \p • exp —— +
dq \ I v ^ v J 3V Зу
+ 3 |^i \рю2/ъ < ml9
d2u1 t Г 1*2 I -3jc . .1 Л Л 2х Г l*i I -3x
Г I b2 I -3x 1 , , 2x Г | *! I
—;— exp •- 1<^21 I 9p2v2 • exp \r • exp
L v v J 3.v L v
+ | dt I Зр2 и • exp -^- < exp ^—- [9p21 ij I ] + 3p2 |ft» I] + 9p2 | rf2 I и/з +
J ■ 3u ' 3u
+ 3p2|d,lu'/3<m2,
278

+ \d2\
I 63 I -3x
—- • exp +
v
9p3v2* exp — +
,1 , , о x \ \b2\
\d3\ J33pVvexp- +3 [ ^-r-
\di\\6p3v
-3x
exp
I*! I -3;
exp —
V V
X
exp — <
< p3 • exp
—jt33
l&3l + 33|62l +3 |6^l] +
+ 3 V! d3 I u2 + 3 VI rf2 I v + 6p31 £/! I < m3.
Таким образом, производные функции ux(q) — р.о. функции до третьего порядка
включительно.
Теперь докажем, что
v v
di to) dx
dq
a(x) — v
d2x
dx
dq2 \ dq
также р.о. функция. Для q G [0, 1/2] из (8) ai(q) = 3pv
v
a (x) -
1
3\
ЧИТ
exp(—Jt/3u) 11
-r < Пусть q> 1/2, тогда из (7)
-'3 8
exp— »и зна-
3v
а\(Я) Зр a(x)
dx/dq = Зри/з + 3p2vfi (q - 1/2) + 3p3(q - 1/2)2 + nkx(q - 1/2)3
d2x/dq2 = 3pV/s +6p3 й- 1/2)+ 12*!(?- 1/2)?.
(10)
Из (10)
d2x ./dx
-2
Зр2 ц4/з Зр3 to - 1 /2) и 12*! to - 1 /2)2 и
d<72 \ ^7 9p2-u> 18p3to- l/2)u to*/<*7)2
1 12*! to- 1/2)V
2 to*M7)2
Для q — 1/2 = 1/, r< 1/3 имеем
12*ito - 1/2)2у 12*ito ~ 1/2)2у
(dx/dq)2
24k1pv/3(q-l/2)3
У,**-'
< 1/2.
Пусть
(7-1/2 = ur, r > 1/3,
тогда
12*!to- l/2)2u
12*!to--l/2)2u
(d*M?)2
V.
9р2ц4/з + \%p3v to ~ 1/2) + 18p V/a to - 1/2)2
12.16и/э 32
< <
45
15-
Поэтому
a (x) — v
d2x / dx
dq2 \ dq
-2
> 3
2
32
11
~30~
279

v . vh v и,/з-30 1
Очевидно, что при а> 1/2 < и значит < <
dx/dq Ър ax(q) Ър ■ 11 2
Лемма доказана.
Из леммы 1 и теоремы 1 получаем очевидное
Следствие. Пусть а (х), с (х), /(х)ЕС2[0, 1], а0 >3, и'3 < 1/2, тогда сеточная
функция wl5 являющаяся решением задачи (4) при х (q) из (7), сходится
равномерно к решению задачи (1) на разностной сетке х,- =x(qt) с первым порядком
точности, т.е. |и,--и (х,-) I < CAq. ди
В практических приложениях, кроме и (jc,-), нужно знать величину v (■*/)> физи-
dx
чески имеющую смысл силы трения. Мы определим искомую силу трения/ (jc,-)
формулой
/(*/) = ~^J— (^)K+[VF]-"|][V^], если i+ [Vn~]<N,
П*д = <b/dq Ш К'° + lV^3 " "'"oHV^b если i + [y/N] >N9 (11)
где /о — максимальное /, для которого i + [х/Л^] < JV.
Теорема 2. #j>crb
«(*), с (jc), f{x) G C2[0, 1], a (x) > 3, i//s < 1/2, x (q) j
du
— функция, определенная формулой (7), тогда с / (jc,-) сходится к и (х/) с
порядком 1 /2, т.е.
du i/
• !/(*/)-" —(*/) I < CAq/2.
dx
Доказательство. Пусть / 4- [\/N] < N. Согласно следствию из теоремы 1
имеем
€, = И, -И. (*,) = Pj/JV, | р,- | < С! .
Поэтому
["#+-[4/37i-M/HV^] = f"W^ + [v^]-"(^)][\^] + ^ [л/^1 <
cfo1 rfV , 1 2сх du1 l/a
<*7 Л?2 [VAT] у/N dQ
где с2 — р.о. функция, а отсюда следует
du v i/
dx dx
— (<?/)
dq
Так как v/(dx/dq) - р.о. функция, то
du »Л
f(Xi)-v—• (X;) = с3Д<Г ,
dx
где с3 — Р-о. функция.
Таким образом, для значений i таких, что /4- [у/N] <N, теорема доказана.
280

Пусть ./ + [л/N] > N, тогда
du1 du1 d2u1 , i-i0
dq x l/ dij v '0/ dq2 ^l' N
du v f . du2 \
v I — du1 d2ul л i-i0\
где с4 - p.o. функция.
Теорема доказана.
Схема (4) имеет первый порядок точности. Если мы хотим применять
монотонные схемы второго порядка точности, то для доказательства сходимости нам
потребуется равномерная ограниченность d*ul\dq*. Поэтому для численного
решения (3) с помощью монотонных схем второго порядка отображение х (q) зададим
следующим образом:
( -4vln[l-2q(\-v/4)]9q ^ [О, 1/2],
( *ifo) + M<7-l/2)5 Q е [1/2, 1],
ГД6 1 4
Xl(q) = v\n — + 4pvU(q- 1/2) + 2р2 vU (q - 1/2)2 + - p3vU(q - 1/2)3 +
+ p*(q-l/2)\
kx = 32 [I-*! (1)1, p2= 2 [1 -VA], i/A< 1/2.
Отображение x (q) — невырожденное и аналогично, как в лемме 1 доказывается,
что
ax{q) > 0, v/at(ql dnx/dqn
— p.o. функция при п < 4. Если а (х)9 с(х)9 f (x) Е с3[09 1], то в этом случае
% dnu Ья(дс).ехр(-^(х)/1л) , ^,ч
—7Г = '„ + dn(*)>
dx vn
где bn(x)9 dn(x) — p.o. функции, и<4. Поэтому и dnu /dqn — p.o. функции при
n < 4, a (x) > 4.
Аппроксимируем (З) схемой А.А. Самарского [6]
ui+1 -2ui + ui_l ui+1 -u(
(Aq)2 Aq
vi l ■ ,A \2 — + ui(Qi)-J—A L -Ci(.Qi)Ui = fi(qt), (13)
v2
ui = —Г7Т 7T"' u° = l°> un =/i-
|; + 0,5А^в!(^)
Теорема 3. Пусть а(х)9 с (x)9 f (x) G C?[0,1], я (x) > 4, i//4 < 1/2, тогда
при x(q)9 заданном формулой (12), сеточная функция uiy являющаяся решением
(13), сходится к решению задачи (3), и имеет место оценка
\щ- и (х() \< c(v) (Aq)2t \щ - и (xt) | < сх Aq,
где xi = х (qt).
281

Доказательство. Схема (13) удовлетворяет принципу максимума, из
которого следует \е(\ < max,- \R(/аi (</,•)!. Из (13) имеем
d*ux d'u1
^
<V
^^V)
8 [w + 0,5A? •«!(«,)]
/Я„1
rf2M' , d2ul
r«/)+-T4-tti-i)
6 <fy
Л/
<*?'
, f;€[ft+1].
(14)
Так как v/dx(q)9 dnu1/dqn — равномерно ограниченные функции, то из (14)
получаем 15,-j < C(Aqf +■
Cli&qfaM
т.е. верно утверждение теоремы.
Теорема доказана.
Очевидно, что и для схемы (13) мы имеем равномерную сходимость силы тре-
. du
ния, определенной формулой (11) с порядком 1/2, т.е.
/(*/)!
\v — (*,)
dx
< с 'Aq . Н.Т. Данаевым, которому авторы выражают глубокую благодарность,
был проведен численный расчет краевой задачи
d2u du
v +
dx2
dx
= x.
и (0) = м (1) = 0.
(15)
Точное решение (15) и (х) = [(и - 0,5)/(1 -e'lfv)] (1 - *Гх/и ) - и* + *2/2. Расчет
проводился по схеме (4). Функция х (q) определялась по формуле (7). Некоторые
du
данные для погрешностей е = max,- \ut-u (х() | и е2 = max,-1 /(*/) - v (х,-) | приве-
dx
дены в таблице. В данной работе нами рассмотрена задача с одним погранслоем возле
границы отрезка. В случае задачи с двумя граничными или внутренними погранслоями
функция x{q) для построения равномерно сходящегося алгоритма определяется аналогично
склейкой логарифмических функций и многочленов. Многочлен задается вне,
логарифмическая функция — внутри погранслоя.
В заключение авторы выражают глубокую благодарность А.Г. Слепцову,
просмотревшему рукопись и сделавшему ряд полезных замечаний.
V
N= 50
е1
е2
N=20
е1
е2
1(Г
ю-
ю-
0,05209
0,07626703
0,07743196
0,12455
0,16886477
0,17178133
0,11951363
0,17028446
0,17225575
0,24191173
0,30576587
0,30926993
ЛИТЕРАТУРА
1. Ильин AM. Разностная схема для дифференциального уравнения с малым параметром при
старшей производной //Мат. заметки. 1969. Т. 6, вып. 2. С. 237-248.
2. Титов В.А., Шишкин Г.И. О численном решении параболического уравнения с малыми
параметрами при производных по пространственным переменным // Разностные методы решения
краевых задач с малым параметром и разрывными краевыми условиями. Свердловск, 1976.
3. Емельянов Н.В. Разностная схема для трехмерного эллиптического уравнения с малым
параметром при старших производных // Краевые задачи для уравнений математической физики.
Свердловск, 1973. С. 30-42.
4. Шишкин Г.И. Численное решение эллиптических уравнений с малым параметром при
старших производных//Числ. методы механики сплош. среды. 1979. Т. 10, №4. С. 107-124.
5. Бахвалов Н.С. К оптимизации методов решения краевых задач при наличии пограничного
слоя // Журн. вычисл. математики и мат. физики. 1969. Т. 9, № 4. С. 841-869.
6. Самарский АЛ., Андреев В.В. Разностные методы для эллиптических уравнений. М.: Наука, 1976.,
1. Васильева А.Б., Бутузов В.Ф. Асимптотические разложения решений сингулярно возмущенных
уравнений. М.: Наука, 1973.

МАТЕМАТИЧЕСКАЯ ТЕХНОЛОГИЯ
МОДУЛЬНЫЙ ПРИНЦИП ПОСТРОЕНИЯ ПРОГРАММ
КАК ОСНОВА СОЗДАНИЯ ПАКЕТА ПРИКЛАДНЫХ ПРОГРАММ
РЕШЕНИЯ ЗАДАЧ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ*
1. Задачи механики сплошной среды представляют благоприятные возможности
для создания универсальных программ. Эти задачи описываются, в основном,
единообразной системой уравнений, выражающих законы сохранения в той или иной
форме. Различия в этих задачах в подавляющем большинстве случаев могут быть сведены
к различию в выборе:
а) модели среды (уравнений состояния);
б) исходной системы координат и искомых функций;
в) области, в которой ищется решение задачи;
г) предельных условий задачи.
2. Благоприятные возможности для построения единообразных универсальных
программ создают и современные методы численного решения задач механики
сплошной среды (методы расщепления и т.п.). С точки зрения этих методов "любая
сложная" задача механики сплошной среды может быть сведена к последовательному
решению более простых задач, а традиционно различные задачи трактуются с единой точки
зрения:
а) расщепление по размерности делает возможным сведение многомерной задачи к
последовательности одномерных;
б) расщепление по физическим процессам делает возможным сведение задачи
"сложной физики" к задачам "простой физики". Уточнение модели в такой схеме происходит
без существенного изменения первоначальной модели;
в) метод установления позволяет трактовать с единой точки зрения эволюционные
и неэволюционные задачи. В ряде случаев этот метод допускает и физическую
интерпретацию: выход на стационарный режим, введение малой сжимаемости и т.п.;
г) метод сведения сложной краевой задачи к задаче Дирихле позволяет разделить
оператор шага исходной задачи на два: "стандартный" оператор решения задачи
Дирихле, "стандартный" оператор решения задачи Коши, с помощью которого
исправляются краевые условия;
д) методы типа предиктор—корректор позволяют использовать каждый этап и для
решения конкретной задачи.
3. При реализации различных задач механики сплошной среды на ЭВМ используется,
как правило, один и тот же набор так называемых сервисных программ:
а) программы РНД, построение сетки, классификация узлов сетки и т.п.;
б) различные программы интерполяции как самих величин, так и их производных
с различной степенью гладкости;
в) различные программы выдачи и обработки результатов: выдачи разрезов,
изолиний, положения разрывов (дифференциальный анализатор); выдача на график и т.п.;
г) программы вычисления контрольных балансовых соотношений,
характеризующих интегральную точность расчета;
д) стандартная программа отладки.
♦Комплексы программ мат. физики. Новосибирск, 1972. С. 48-54. (Соавтор А.Н.Коновалов.)
283

4. Различные задачи механики сплошной среды, как правило, предъявляют
повышенные требования к общему числу расчетных точек. Поэтому все большее
распространение в качестве сервисных программ получают программы:
а) стыковки, сегментации программ;
б) упаковки и распаковки (для счета с пониженной точностью);
в) транспонирования матрицы как специфического способа подготовки числовых
массивов для применения метода расщепления;
г) сегментация числовых массивов для оптимальной организации обмена с внешней
памятью ЭВМ.
5. В настоящее время имеется возможность для создания эффективной системы
тестов проверки численных методов решения целых классов задач механики сплошной
среды.
6. По существу, в настоящее время уже имеются все предпосылки для
качественно новой организации программ решения задач механики сплошной среды, т.е.
создания пакета прикладных программ решений задач механики сплошной среды.
Независимо от класса задач механики сплошной среды, решаемого с помощью пакета,
последний непременно включает в себя библиотеку так называемых модулей, управляющую
программу и входной язык.
7. В нашем понимании библиотека модулей — это тот набор "неделимых"
кирпичиков, с помощью которых может быть построен любой допустимый алгоритм
решения задачи, входящей в класс исходных и, следовательно, любая допустимая
реализация этого алгоритма на ЭВМ. Тем самым мы должны попытаться дать определение
модуля. Прежде всего перечислим те его свойства, которые, по нашему мнению,
являются определяющими:
а) модуль есть содержательная часть вычислительного алгоритма;
б) функции, которые выполняет модуль, не зависят от реально применяемой ЭВМ;
в) модуль всегда имеет вход и выход, тем самым он определяется вместе с
входной и выходной информацией;
г) алгоритмический размер модуля должен способствовать наиболее
экономичному представлению как можно большего числа алгоритмов рассматриваемого
класса.
Перечисленным свойствам удовлетворяют все сервисные программы,
перечисленные в п. 3—4, а также стандартные программы типа In х9 cos х и т.п., если только
дать расширенное определение вычислительного алгоритма как реализацию его в
виде программы.
8. При решении различных задач механики сплошной среды метод прогонки
решения трехточечных разностных уравнений является одним из основных элементов
вычислительного алгоритма (в узком смысле). Имеет ли смысл считать прогонку
модулем и на этом основании включать в библиотеку модулей для задач механики
сплошной среды? Несложные рассуждения показывают, что метод прогонки
нецелесообразно считать вычислительным модулем, ибо не будет выполнено свойство г)
п. 7. В самом деле, при вычислении прогоночных коэффициентов х, у мы решаем
методом Эйлера задачу Коши для обыкновенного дифференциального уравнения
первого порядка (прямой ход). Та же задача и тем же методом решается и при
определении искомой функции (обратный ход). Нетрудно заметить, что и неявные
схемы бегущего счета при решении гиперболических уравнений можно трактовать
как метод Эйлера решения обыкновенного дифференциального уравнения первого
порядка.
В рассмотренном примере напрашивается определение вычислительного модуля
как решения задачи Коши для обыкновенного дифференциального уравнения
первого порядка.
9. Необходимо пронести анализ модульной структуры вычислительных алгорит-
284

мов (в узком и широком смысле), применяемых при решении задач механики
сплошной среды.
10. Такой анализ можно, например, провести следующим образом. Пусть в
заданной фиксированной области ищется решение корректно поставленной
дифференциальной задачи. Для упрощения будем считать, что расчетная область остается
неизменной в течение всего времени расчета. Дабы не связывать себя в дальнейшем
вопросом построения сетки, будем считать, что заданная область приведена к
стандартной (прямоугольник, прямоугольный параллелепипед), например, методом
фиктивных областей. Численное решение дифференциальной задачи будем осуществлять
с помощью методов, перечисленных в п. 2:
а) метод расщепления по физическим процессам сведет исходную задачу к серии
последовательных задач, каждая из которых учитывает только одну сторону
реального физического процесса. Например, в задаче о конвективном теплообмене с
учетом теплопроводности мы получим задачу "чистого" конвективного теплообмена и
задачу "чистой" теплопроводности. Число таких примеров легко продолжить.
б) метод расщепления по пространственным переменным сводит решение
многомерной задачи к последовательному решению только одномерных задач.
В теоретическом плане обоснование методов типа а) и б) зачастую сводится к
обоснованию метода слабой аппроксимации для задачи рассматриваемого класса.
в) метод установления для стационарной задачи вводит "фиктивный" физический
процесс, после чего возможно применение методов типа а), б). Аналогичная
ситуация возникает и при введении малой сжимаемости и т.п.
г) методы типа предиктор—корректор (их назначение мбжет быть самым
различным: обеспечение полной консервативности, повышение порядка точности,
избавление от итераций по нелинейности и т~п.) также сводят исходную задачу к
последовательному решению некоторых задач, каждая из которых имеет и самостоятельное
значение.
Схематически каждый этап описанного процесса можно представить себе
следующим образом:
Мсхяёная
/га pi/jitvtt/u/M
лг П^ПЪ
Лт
^ 1 \
\*тг\
u^iH
Ятз
Метг?0 расще/гле-
»ия ля npffc/n/Hi//cm\
0МЮ/М/7£р*Ме//#АМ
Ятк
z
*тМ
ffmkZ
МгтяЗ
/Г/7£0ЦКЛ70р-
Тем самым, решение исходной задачи свелось к последовательному решению
простых вспомогательных задач Dmkl. Эти задачи естественно назвать базисом, а
последовательность решения этих задач, обеспечивающих решение исходной —
представлением исходной задачи в данном базисе.
11. Основанием для такого определения базиса служит то обстоятельство, что в
рамках некоторого фиксированного базиса может быть представлен довольно
широкий класс различных задач. С другой стороны, восполнение класса
рассматриваемых задач может быть произведено за счет незначительного расширения базиса.
285

12. Источником пополнения базиса может служить и так называемое понятие
замыкание вычислительного алгоритма (С .Л. Соболев). Однако такое пополнение требует
соответствующего анализа алгоритма решения каждой из базисных задач (см. также
п. 8).
13. Соответствующий анализ можно провести и при реализации в виде программы
каждой из базисных задач.
НЕКОТОРЫЕ ПРОБЛЕМЫ РАЗВИТИЯ ПАКЕТОВ ПРОГРАММ
ДЛЯ РЕШЕНИЯ ЗАДАЧ АЭРОДИНАМИКИ*
Расширение парка ЭВМ различной конфигурации, увеличение их быстродействия,
оперативной и внешней памяти и развитие математического обеспечения позволяют
в настоящее время ставить и успешно решать широкий класс задач математической
физики и, в частности, задач внешней и внутренней аэродинамики. Информация,
полученная с помощью численных расчетов, не только позволяет правильно осмыслить
и понять физические эффекты, полученные, например, на экспериментальных
установках, но, в ряде случаев, и заменить физический или натурный эксперимент машинным,
как более дешевым. Кроме того, машинный эксперимент является иногда и
единственно возможным.
Разработкой методов расчета и, особенно, созданием программ и комплексов
программ для решения аэродинамических задач занято большее число исследователей.
Ввиду разнообразия задач при создании программ даже по одному алгоритму или
численному методу неизбежен параллелизм в работе, когда различные исследователи
при создании программы вынуждены проделать всю работу от начала до конца, что
приводит к неоправданным затратам как людских ресурсов, так и машинного
времени на создание и отладку программ. А также замедляется и сам процесс
исследований. Эти обстоятельства приводят к необходимости перехода на другой путь при
создании- программ, а именно, на путь создания пакетов программ,
ориентированных на решение целых задач. Однако, возникающие при этом технологические
проблемы, являются настолько трудными, что задача их преодоления сама стала задачей
науки.
Некоторые подходы к разрешению этих проблем рассмотрены в обзорной работе
[1]. Вопросам разработки и эксплуатации пакетов программ посвящено
значительное число работ [2—4].
В настоящей работе рассматриваются вопросы, возникающие при создании пакета
программ решения задач аэродинамики в широком диапазоне изменения
определяющих параметров, таких как числа Маха, Рейнольдса, а также геометрий
рассчитываемых областей.
Создание пакета программ для решения задач аэродинамики затрудняется
следующими обстоятельствами:
а) отсутствием адекватных физико-математических моделей для описания течений
в сложных ситуациях и областях;
б) отсутствием достаточно эффективных универсальных алгоритмов для решения
уравнений в частных производных, описывающих те или иные физические модели;
в) отсутствием модульного анализа задач аэродинамики, позволяющего представить
исходную задачу в виде более простых задач, каждая из которых может быть
эффективно решена;
г) трудностями при комплексации простых задач;
д) большими затратами машинного времени на решение задач и большими объемами
перерабатываемой информации.
♦Численные методы механики сплошной среды. 1979. Т. 10, № 3. С. 89-99. (Соавтор В.М. Ковеня.)
286

Требования на пакет программ для решения задач аэродинамики можно
сформулировать следующим образом:
1. Открытость пакета, позволяющая путем наращивания модулей расширить классы
решаемых задач
а) за счет усложнения физико-математических моделей,
б) модификации или изменения методов численного решения уравнений,
описывающих те или иные физико-математические модели,
в) изменением геометрий расчетных областей.
2. Возможность доступа к пакету программ широкого класса пользователей.
3. Адаптацией пакета на существующие или вновь создаваемые классы ЭВМ.
4. Экономичность и эффективность применяемых методов.
5. Надежность и достаточная точность полученных численных расчетов.
1. ФИЗИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Укажем наиболее общую форму уравнений для описания решения задач
аэродинамики в эйлеровых координатах
—- + -^— Б = 9- '. (1.1)
bt Ъха
При записи системы уравнений (1.1) сделано предположение, что исходные
уравнения, описывающие задачи аэродинамики, могут быть представлены в форме
классических уравнений газовой динамики с учетом эффектов сжимаемости и диссипатив-
ных процессов (теплопроводности и вязкости, причем коэффициенты вязкости и
теплопроводности зависят от инвариантных величин). Система уравнений (1.1)
является нелинейной и ее тип определяется самим решением, т.е. параметрами потока.
Для замыкания системы уравнений (1.1) необходимо дополнительно определить
следующие зависимости:
а) давления или внутренней энергии, как функции плотности и температуры, т.е.
задавать уравнение состояния
р=р(р,Г), е=е(р,Г); (1.2)
б) коэффициентов вязкости и теплопроводности от газодинамических величин
М = МСР,П> Х=Х(р,Г)> к=к(р9Т). (1.3)
Функции (1.2)—(1.3) могут, вообще говоря, зависеть также от градиентов
термодинамических параметров или инвариантных функций градиентов скоростей^ При
учете физико-химических превращений зависимости (1.2)—(1.3) определяются из
решения системы уравнений в частных производных для концентраций компонент
газа;
в) если математическая модель является многоскоростной, то к исходным
уравнениям добавляются коэффициенты импульсного обмена 3* q^iPi — vk) ;
г) в выражениях для коэффициентов вязкости /х и X необходимо вводить
критические параметры или функции, отделяющие ламинарный режим течения от
турбулентного, отрывные течения от безотрывных, свободную турбулентность от
пристенной и так далее. В идеальном случае следует иметь универсальные выражения для
коэффициентов д и X, включающие минимальное количество экспериментально
определяемых величин и справедливых для всех режимов течения.
Для получения детальной структуры течения при решении уравнений используются
подвижные и неравномерные сетки. В общем случае для решения исходных
уравнений может быть рассмотрена модель, учитывающая совокупность системы
уравнений с уравнениями управления сеткой.
Разнообразие сингулярностей в потоке диктует наряду с разнообразием моделей
287

и разнообразие применяемых сеток. Учитывая возможность применения сеток
разнообразной структуры и их неаналитического примыкания, различные аналитические
представления, интерполяцию и стыковку сеток, будем говорить об
информационной среде.
В связи со сложностью проблемы целесообразно создание пакета различного уровня,
идя от более простых моделей к более сложным. Так, например, пакет первого уровня
может включать следующие модели:
1. Уравнения газовой динамики идеального газа для двумерных и
пространственных течений.
2. Упрощенные уравнения, описывающие течения вязкого газа в следующих
приближениях: пограничного слоя, вязкого ударного слоя, приближение Прандтля и другие.
3. Полные уравнения Навье—Стокса для сжимаемого газа без учета
физико-химических превращений (для фиксированных геометрий расчетных областей).
2. ЧИСЛЕННЫЕ АЛГОРИТМЫ
Уравнения, описывающие решение задач аэродинамики, могут принадлежать к
гиперболическому, эллиптическому, параболическому или смешанному типам. Разнообразие
типов уравнений приводит к необходимости применения и различных методов,
наиболее приспособленных к решению данного класса уравнений, а разнообразие конфигу-
рагдай расчетных областей — к необходимости использования различных систем
координат.
Рассмотрим вопрос о выборе исходной системы координат. Использование
различных исходных систем координат, каждая из которых наиболее приспособлена для
решения уравнений в компактной геометрии расчетной области, представляется
неоправданным ввиду большого объема программирования и большого числа получаемых
программ или блоков. Кроме того, затрудняется сегментация расчетных областей. Более
целесообразным представляется использование в качестве базисных цилиндрической
(для двумерных плоских или осесимметричных течений) или декартовой (для
пространственных течений) систем координат. Введением общего невырожденного
преобразования координат расчетная область может быть отображена в стандартную
область, например, единичный квадрат или куб. Такой подход позволяет упростить
задачу создания пакета программ и уменьшить объем программирования.
В случае невозможности построения невырожденного преобразования расчетная
область может быть разбита (сегментирована) на ряд отдельных подобластей, для
которых невырожденное преобразование существует. В зависимости от выбранной
модели уравнения аэродинамики могут быть представлены в виде
LW = f, /W = f>, (2.1)
если рассматривается стационарная модель, или в виде
Э\У/Эг + 1У1( = f, /W = f (2.2)
для нестационарной модели. Здесь W — вектор искомых функций (или их
комбинация), a L или bjbt + L — дифференциальные матричные операторы одного из
указанных типов, / — оператор краевых условий. В общем случае система уравнений (2.1)
или (2.2) дополняется уравнениями для сетки
Ду=*,
где D — алгебраический или дифференциальный оператор, вообще говоря,
нелинейный, определяемый из дополнительных требований на сетку и численное решение.
Система уравнений (2Л) может иметь тип гиперболический или параболический,
и тогда одна из координат выбирается в качестве аналога времени. В случае
эллиптичности системы уравнений (2.1) необходимо рассматривать ее решение, как
предельное решение уравнений (2.2) со стационарными и краевыми условиями. При учете
диссипативных эффектов в качестве исходных рассматривается система (2.2).
288

Семейство разностных схем, аппроксимирующих систему уравнений (2.2),
представим в каноническом виде
B{bYHbt)h = -(LhV1h-ihy, Вл<Ъ\*1Ъг)н=-(1нУ<н-Ч>нУ, (2.3)
где LhYfh— %н и Ih^h—Vh — разностная аппроксимация соответствующих
дифференциальных операторов, OW/Эг)^ — аппроксимация производной по времени
двухслойными или трехслойными разностными схемами. Стабилизирующие операторы
В и Вх выбираются из условия устойчивости разностных схем на основе принципа
приближенной факторизации, а в случае нестационарных уравнений — из условия
аппроксимации.
Для численного решения стационарных уравнений (2.1) семейство итерационных
разностных схем может быть представлено в виде (2.3), если стационарное решение
находится методом установления. Если в качестве аналога временной переменной
выбрана одна из пространственных переменных у*9 то схемы вида (2.3) могут
использоваться для решения стационарных уравнений.
Невырожденное преобразование координат
УГ= Ф«>*')> ' ч *0, 1,7=1,.., ЛГ (2.4)
строится таким образом, чтобы разностная сетка в исходной расчетной области обладала
заданными свойствами.
Представление разностных схем в канонической форме (2.3) позволяет упростить
модульный анализ вычислительного алгоритма. Все семейство разностных схем можно
разделить на два класса — явные и неявные разностные схемы, или их комбинацию.
Характерно, что временной (или итерационный) шаг не может быть произвольным,
он связан с пространственными шагами условием типа (для явных схем)
г * Ch (2.5)
(h = max (hj), r, h — временной и пространственный шаги сетки) для систем урав-
нений гиперболического типа, или условиями
г * C2h2 (2.6)
для уравнения параболического типа. Для неявных схем характерна относительная
независимость шага г от пространственных шагов сетки. При решении
параболических уравнений условие (2.6) делает практически невозможным применение явных
схем из-за больших затрат машинного времени. Поэтому при создании пакета
программ необходимо ориентироваться на применение неявных схем. Применение метода
факторизации [5] позволяет построить экономичные разностные схемы, сводящие
решение многомерных задач к набору их одномерных аналогов.
Вопросы оценки времени счета задач матфизики рассмотрены в работе [6].
3. МОДУЛЬНЫЙ АНАЛИЗ ЗАДАЧ АЭРОДИНАМИКИ
В основу модульного анализа положено представление исходной задачи в виде
комплекса или последовательности простых задач и базовых модулей. В основу
определения простой задачи должна быть положена однородность а) физико-математической
модели, б) сетки, в) памяти ЭВМ (вместимости в оперативную память). К этому
добавляются требования устойчивости, точности, эффективности алгоритма в
рассматриваемом классе однородных схем.
Простая задача допускает расщепление на элементарные (базовые) модули, кото-
10. Зак.953
289

рые, являясь ее частями, удовлетворяют всем требованиям, предъявляемым к простой
задаче, и обеспечивают однородность алгоритма и его устойчивость.
Однородность модели означает, что простая задача должна быть "физическим"
модулем, т.е. описывать однородный физический процесс. Однородность сетки определяется
однозначностью отображения области интегрирования на стандантную область, внутри
которой строится стандартная сетка. Однородность памяти означает, что алгоритм,
реализующий простую задачу, исключает переброску массивов между различными
неоднородными видами памяти.
Алгоритм, реализующий простую задачу, должен быть универсальным и включать
в себя максимально возможное число произвольных параметров или функций,
соответствующих свободным параметрам и функциям в исходной системе уравнений,
геометрию и граничные условия задачи.
Однородность алгоритма означает его независимость от выбора конкретного набора
функций и параметров из класса однородности.
Таким образом, простая задача есть многофункциональная задача или однородный
класс задач, отличающихся друг от друга только производными параметрами или
функциями, и не влияющими на тип алгоритма, сетки и так далее.
Введем понятие автономности или неавтономности простой задачи. В случае
автономной задачи на границах рассчитываемой области ставятся' заданные краевые
условия, в соответствии с которыми определяется решение. В случае неавтономной задачи
краевые условия не заданы явно и могут быть определены с помощью модуля обмена
краевыми условиями. Этот модуль обмена может быть простым модулем переноса
массивов (в случае явных схем) или модулем стыковки (в случае неявных схем).
Таким образом, в случае применения неявных схем независимая задача становится
задачей с параметрическими краевыми условиями и должна решаться как
параметрическая. В качестве примера простых задач можно рассматривать задачи,
получающиеся при расщеплении исходной задачи по физическим процессам и (или)
пространственным переменным. Каждый дробный шаг в этом случае можно рассматривать
как простую задачу.
Прежде чем приступить к описанию модулей пакета, следует дать общее описание
структуры аэродинамического пакета.
Аэродинамический пакет есть предметно ориентированный пакет программ, т.е.
совокупность программ (модулей), связанных общностью описания технического
объекта — конструкции летательного аппарата (ЛА), и его действия — в физических,
химических, механических процессах, происходящих в Л А и в контрольном объеме
атмосферы. Совокупность конструкции и контрольного объема атмосферы назовем
обобщенной конструкцией (ОК). При системном анализе действия конструкции
мы производим декомпозицию ОК на части (обобщенные подконструкции).
4. КЛАССИФИКАЦИЯ МОДУЛЕЙ
В соответствии с данным выше определением простой задачи на начальном этапе
создания пакета программ производится разбиение обобщенной конструкции на
простые задачи. Этот элемент разбиения назовем модулем разбиения или сегментации.
Каждая простая задача (или некоторые из них) содержит модуль геометрии
расчетной области. Наиболее простое описание геометрии расчетной области задается в
декартовых или цилиндрических координатах. Эта форма удобна для широкого
класса задач, хотя и не является наиболее экономичной. Например, для уравнений
пограничного слоя или при обтекании выпуклых тел более предпочтительной
является система координат, связанная с поверхностью тела. Поэтому путем
преобразования координат целесообразно от исходной декартовой или цилиндрической перейти
к системе координат, наиболее приспособленной к расчетной области. Это может
быть достигнуто введением модуля преобразования координат, посредством
которого расчетная область отображается в стандартную. В зависимости от требований
290

на расчетную сетку преобразование задается различными способами. Эти способы
целесообразно выделять в модули сетки. В зависимости от принципов построения
сетки создается библиотека модулей сетки. По окончании работы модуля сетки
вычисляются коэффициенты преобразования, которые являются известными
функциями для решения исходных уравнений в преобразованных координатах на новом
шаге. Таким образом, коэффициенты уравнения учитываются явно на нижнем слое,
что приемлемо для решения стационарных задач методом установления. При решении
нестационарных задач для получения решения необходимо проводить совместные
итерации исходных уравнений и уравнений для сетки.
Модули решения строятся в зависимости от используемых физико-математических
моделей и применяемых методов решения. В частности, пакет программ должен
включать модули решения: а) уравнений газовой динамики б) упрощенных уравнений
вязкого газа; в) полных уравнений Навье—Стокса; г) упрощенных уравнений вязкого
газа и уравнений газовой динамики, решаемых маршевым методом.
В соответствии с представлением исходного семейства разностных схем в
канонической форме (2.3) для выбранной физико-математической модели можно выделить
модуль правой части и модули решения операторов В и Вг. Тем самым, все
используемые численные методы будут описываться модулем стабилизирующего оператора
без изменения модуля правой части.
Учет физико-химических превращений (ФХП) в газе и на поверхности тела задается
модулем ФХП, а в случае турбулентных течений — модулем турбулентности.
В зависимости от применяемого метода реализация граничных условий производится
в модулях граничных условий. В случае неавтономных задач эти модули включают
модули стыковки или модули обмена. Для представления результатов расчетов в
требуемой форме вводятся модули вывода и обработки информации, а для контроля
точности — модули тестов.
Управляющий модуль определяет последовательность обращения к различным
модулям, решающим в совокупности как отдельную простую задачу, так и
обобщенную конструкцию в целом. Создание данного модуля является одной из наиболее
сложных задач создания пакета программ и задач системного программирования. При
создании отдельных модулей общие их части могут оформляться в виде микромодулей или
отдельных блоков.
В заключение отметим, что при создании пакета программ для решения задач
аэродинамики необходимо объединение исследователей по всем трем направлениям:
1) физико-математическим моделям, 2) численным алгоритмам, 3) системному
программированию.
Следует заметить, что в случае аэродинамики хорошие физико-математические
модели могут быть получены лишь при сопоставлении экспериментальных и численных
исследований.
ЛИТЕРАТУРА
1. Яненко Н.Н., Карначук В.И., Коновалов А.Н. Проблемы математической технологии // Числ.
методы механики сплош. среды. 1977. Т. 8, № 3. С. 129-157.
2. Легонькое В.И., Петров А А. Некоторые общие вопросы разработки и эксплуатации больших
программ для счета задач математической физики // Комплексы программ математической
физики. Новосибирск, 1972. С. 58-64.
3. Schrem Е. Computer implementation of finite-element procedure // Numerical and computer methods
in structural mechanics. N.Y.; L.: Acad, press, 1973. <
4. Яненко Н.Н. Численное решение задач механики жидкости // Тр. III Всесоюз. семинара по
моделям механики сплош. среды. Новосибирск, 1976. С. 177-199.
5. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск: Наук а, 1967. 197 с.
6. Софронов ИД. Оценка параметров вычислительной машины, предназначенной для решения
задач механики сплошной среды // Числ. методы механики сплош. среды. 1975. Т. 6, № 3.
С 98-147.
10*
291

ВОПРОСЫ МОДУЛЬНОГО АНАЛИЗА
И ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ
В ЗАДАЧАХ МАТЕМАТИЧЕСКОЙ ФИЗИКИ*
К настоящему времени при решении на ЭВМ задач математической физики сложи-
ласть вполне определенная технологическая цепочка [1]: объект исследования
-►математическая модель -* физическая модель -* численный алгоритм -* программа -* расчет
на ЭВМ. Объектом математической технологии здесь является вычислительная часть
этой цепочки: математическая модель -* численный алгоритм -* программа -* расчет на
ЭВМ, которую в дальнейшем будем называть просто вычислительной цепочкой.
Структура ее такова, что допускается цикличность как- для всей цепочки в целом, так и меж-
ду ее отдельными звеньями, т.е. является нелинейной.
В силу этого основная задача математической технологии — оптимизация
вычислительной цепочки — должна рассматриваться как задача глобальной оптимизации.
Примером существенной нелинейной цепочки может служить влияние на ее
структуру применения многопроцессорных ЭВМ. Действительно, их специфика
приводит не только к определенному пересмотру численных алгоритмов, но и вносит в
вычислительную цепочку новое звено — структуру ЭВМ, под которой здесь следует
понимать совокупность технических и системных средств, допускающих взаимодействие
с остальными звеньями цепочки. Тогда вычислительная цепочка приобретает вид:
математическая модель -* численный алгоритм -* программа -*• структура ЭВМ -*
->• расчет. Практика вычислений позволяет утверждать, что структура алгоритма и
программы выдвигает ряд требований, предъявляемых к структуре ЭВМ. Как
следствие, может оказаться целесообразным создание специализированных вычислительных
комплексов для решения задач математической физики. Так, например, в настоящее
время уже назрела проблема создания процессоров и соответствующих структур
оперативной и внешней памяти, специально приспособленных для работы с большими
разреженными матрицами, столь часто встречающихся в задачах математической физики,
поскольку эффективность здесь универсальных ЭВМ крайне низка.
Появление многопроцессорных ЭВМ позволяет решить очень важную проблему -
проблему сокращения существующего разрыва между требованиями по
быстродействию, предъявляемыми к ЭВМ этими задачами, и техническими возможностями
существующих (однопроцессорных) ЭВМ. Так, по оценкам американских специалистов (см.
также [2]) для решения задач пространственного обтекания тел в широком диапазоне
изменения числа Маха набегающего потока для детального учета структуры течения
(ламинарный, переходный, турбулентный участки) требуется ЭВМ с быстродействием
порядка 1С10 оп/с. Очевидно, что вплотную подойти к решению таких задач можно
только с помощью ЭВМ параллельного действия, имеющих достаточно большое число
процессоров. В связи с этим вопрос организации параллельных вычислений,
затрагивающий все звенья вычислительной цепочки, приобретает сейчас принципиальное
значение.
Построение пакета прикладных программ для класса задач математической физики
начинается с модульного анализа вычислительного алгоритма [1,3—7]. Если в основу
алгоритма положены методы расщепления по физическим процессам и
пространственным переменным [8], то решение исходной задачи из рассматриваемого класса
сводится к последовательному решению более простых задач [3]. Расммотрение и учет
условий, накладываемых на программную реализацию таких задач конкретной
структурой ЭВМ, проведенное в работе [9] для задач аэродинамики, привело к
формированию понятия "простая задача". Она была определена как краевая задача с однородной
физико-математической моделью, однородной разностной сеткой и целиком
вкладывающаяся в однородную (оперативную) память ЭВМ. Проводя сегментацию области
♦Комплексы программ математической физики: (Матер. VI Всесоюзн. семинара по комплексам
программ мат. физики). Новосибирск; 1980, С. 3-12.
292

решения исходной задачи на ряд подобластей, в каждой из которых определена простая
задача, мы решаем одновременно проблему перераспределения памяти ЭВМ между
ее неоднородными компонентами и получаем возможность организации
параллельного решения задачи в целом. Для стыковки решения на сложных границах подобластей
используется введенное в [7] понятие обменных краевых условий. Еще одно
преимущество такого подхода заключается в том, что в рамках каждой простой задачи
существенно облегчается задача построения хорошо обусловленной сетки, правда, появляется
задача стыковки решения на разных сетках, но это уже отдельный, впрочем вполне
разрешимый, вопрос.
Определенная выше простая задача может рассматриваться как определение модуля
в смысле [3], сведение же конкретной задачи к последовательности таких "простых
задач" является модульной декомпозицией задачи. Дать определение "простой задачи"
вообще (как, впрочем, и модуля) пока не представляется возможным и поэтому мы
попытаемся указать лишь общий способ ее определения для различных классов задач
математической физики. Опыт решения больших задач показывает, что конечной
устойчивостью (устойчивость при конкретных расчетах, в отличие от теоретической)
чаще всего обладают программы, реализующие однородные алгоритмы и
математические модели в однородной информационной среде. Тогда наложением ряда
независимых требований по однородности на рассматриваемый класс задач (каких именно
определяется как самим классом задач, так и методами их решения и способами
реализации) можно определить "простую задачу". Все конкретные задачи из этого класса
будут представлены конкретной же совокупностью этих "простых задач",
определенная последовательность решения которых и даст решение исходной задачи. Так, для
задач механики сплошной среды "простая задача" должна удовлетворять следующим
требованиям. ч
1. Однородность математической модели. Под этим требованием понимается
единство структуры математического описания физической модели исследуемого явления.
Если, например, для описания используется система дифференциальных уравнений,
то она не должна менять своей структуры, т.е. набора определяющих членов в области
определения "простой задачи", Тип ее может и меняться на решении или от решения
к решению, лишь бы алгоритм решения был единым. Примером здесь может служить
применение метода установления для решения стационарных уравнений Эйлера в
газовой динамике. Однородность математической модели позволяет применять
апробированные, конечно-устойчивые алгоритмы, существенно упрощает тестирование задачи в
целом. Практически однородность модели достигается чаще всего применением
метода расщепления по физическим процессам.
2. Однородность постановки задачи. Включает в себя: а) однородность
математической модели, б) алгоритмическую однородность начальных и краевых условий.
Последнее означает, что заданный набор краевых условий не приводит к изменению
алгоритма решения задачи. Сам этот набор, естественно, зависит от алгоритма.
Например, для уравнения Лапласа Аи= 0 в случае задач Дирихле и Неймана алгоритмы
решения различны. Тогда в случае разнородных условий, когда на одной части границы
области (7) заданы условия и \у =а (уг) , а на другой (ди/Ъп) \Уг = Ъ (7?),
требованиям однородности можно удовлетворить, если* применять алгоритм, допускающий
единую реализацию условий вида а (7) и +13 (7) Ъи/Ъп = g(y), где а (у), Р (у) могут
обращаться в нуль на у или любой ее части.
3. Однородность алгоритма. Здесь наряду с обычными, традиционными
требованиями однородности, предъявляемыми к алгоритмам, цамо понятие однородности
трактуется в более широком аспекте. Прежде всего сюда включено требование модель
ности алгоритма. Модельность алгоритма есть требование аппроксимации корректно
поставленной континуальной задачи. Это означает, что алгоритм не должен содержать
наборов различного рода малых параметров, не связанных с существом задачи и с
дискретизацией континуальной модели, влияние которых на само решение трудно
контролировать. Так, например, для нелинейных неявных разностных схем исполь-
293

зование различного рода итераций по нелинейности может привести к потере модель-
ности. В целом этот вопрос в настоящее время почти не исследован и конкретных
рекомендаций практически нет.
Другим важным требованием, связанным с модельностью и применением методов
аналитического расщепления алгоритма, является требование одноступенчатости
алгоритма. Это означает, что сам алгоритм решения "простой задачи" должен
представлять собой последовательность простых, одноступенчатых алгоритмов. В качестве
примера можно указать на двухшаг овые схемы типа Рунге-Кутта и ряд других.
Такой одноступенчатый алгоритм уже не будет содержать, например, итераций по
нелинейности. По отношению к нему они оказываются внешними, увеличивая лишь
пошаговую дробность всего алгоритма в целом.
Расчетная схема тогда будет следующей. В каждой "простой задаче"
одноступенчатый алгоритм продвигает решение на один шаг. Далее, если нужно, рассчитываются
краевые условия и осуществляется стыковка решений на границах областей
определения "простых задач", и процесс повторяется.
Таким образом, алгоритм решения "простой задачи" может быть только
алгоритмом одного глобального шага.
4. Однородность информационной среды. Под информационной средой в задачах ма:
тематической физики здесь понимается дискретное представление области
определения задачи вместе с формальной структурой аналитического представления решения
(способ дискретизации, шаблон, аппроксимация на этом шаблоне и т.д.).
Информационная среда неотделима от метода решения и определяется самим методом. Так, в
случае применения конечно-разностных методов это будет разностная сетка, для
конечного элемента - упорядоченное множество, определяемое способом
триангуляции области решения и т.д. Требование однородности информационной среды
заключается в том, чтобы в пределах "простой задачи" она не вносила элементов
неоднородности в алгоритм решения. Например, это означает, что разностная сетка должна быть
регулярной, т.е. переход от обработки одного ее узла к другому не должен приводить
к перестройке алгоритма решения. Стыковка различных сеток, не согласованных
между собой, должна осуществляться только на границах областей решения "простых
задач".
Аналитическое представление решения также должно быть однородным, т.е. должно
быть единство способа и порядка аппроксимации решения при переходе от
континуального его представления к.дискретному.
5. Однородность памяти. Это есть требование вложения простой задачи в
оперативную память ЭВМ. Тогда вопрос о перераспределении памяти ЭВМ между внешней и
оперативной для всей задачи в целом решается путем сегментации области решения на
подобласти таким образом, чтобы каждая из них была областью определения "простой
задачи". Для стыковки решения между ними на границах этих подобластей
используются обменные краевые условия [7].
6. Хорошая обусловленность. Под этим требованием понимается, кроме обычного
требования хорошей обусловленности краевой задачи, еще и требование
определенности областей изменения параметров однородного алгоритма, при которых
гарантируется его надежная реализация на ЭВМ.
7. Функциональная и алгоритмическая полнота. Это требование означает, что
алгоритм, реализующий простую задачу, должен быть достаточно универсальным и должен
включать в себя максимально возможное число произвольных параметров и функций,
которые соответствуют свободным параметрам и функциям в исходной системе
уравнений, начальных и краевых условиях, описаниях области решения. В частности,
алгоритм должен быть рассчитан на его применение в достаточно произвольных
областях и допускать достаточно произвольную сетку, основным требованием,
предъявляемым к которой, является требование ее реальной невырожденности.
8. Автономность, неавтономность. "Простая задача" называется автономной, если
ее область определения совпадает с областью решения исходной задачи. Краевые усло-
294

вия для нее заданыГ а ее решение не зависит от решения других "простых задач". Для
больших задач математической физики эта ситуация является исключительной.
Как правило, область решения исходной задачи требуется сегментировать (см. п. 4),
и уже тогда для каждой "простой задачи", определенной на сегменте, на каждой
сопредельной границе должны быть заданы краевые условия, обеспечивающие стыковку
решений этих "простых задач". Такие краевые условия называются обменными [7,9],
а "простая задача" становится неавтономной, так как ее решение зависит от решения
других "простых задач". Реализация обменных краевых условий определяется самим
алгоритмом решения. Так, для конечно-разностных методов в случае явных схем это
может быть просто переброска массивов, в случае неявных приходится рассматривать
параметрические краевые условия и неавтономная "простая задача" должна уже
решаться как параметрическая. .
Рассмотрим теперь какую роль играет "простая задача" в организации параллельных
вычислений в задачах математической физики. Прежде всего заметим, что при редукции
исходной задачи к последовательности "простых задач" (модульная декомпозиция),
как правило, возникает иерархическая структура. В этой структуре сегментация
области решения приводит к стыковкам "простых задач" по пространству только
через обменные краевые условия, что образует горизонтальный уровень. Требование
однородности математической модели (обычно расщепление по физическим
процессам) образует вертикальный уровень, когда строго последовательно решение одной
"простой задачи" передается следующей в качестве исходных значений. Нетрудно
видеть, что горизонтальный уровень этой структуры естественным образом
приспособлен для распараллеливания вычислений. Таким образом, модульная декомпозиция
задачи По существу решает проблему распараллеливания вычислений. В качестве
примера рассмотрим смешанную задачу Коши для уравнения теплопроводности
Ъи 2 э / Ъи У
—= 2 "Г ат 00 Г Ь йт 00 > О,
*t m = 1 Ъхт\ Ъхт]
и(м,о) = </>00, м^А uQi'.t) = VQi',t)9 /i'ey. (l)
Для простоты положим D = \0<хт < 1} , тогда y-D-D. Пусть далее г > 0,
Nmhm = 1 (обозначения см. в [10]). В случае применения здесь явной разностной
схемы можно, например, провести сегментацию области D на прямоугольные
подобласти Di(UDt = D) и определить на Dt простую задачу:
Vy= (£+г(Л1+Л2))«^/,
причем на границах 7/ будут определены обычные и (или) обменные краевые
условия. Для реализации последних достаточно ввести примыкающие к границам
фиктивные узлы разностной сетки и организовать переброску в них значений искомой
функции из соседних подобластей. Однако гораздо целесообразнее воспользоваться
расщеплением по пространственным переменным
«у17* = (я+тл,)«;;,, (2)
''«^1 = (£ + тл2)и-;1/2. (з)
Тогда простой задачей в D( будет решение одномерного уравнения теплопроводности.
Реализация обменных краевых условий здесь существенно проще, а при переходе от
(2) к (3) достаточно выполнить только операцию транспонирования.
Распараллеливание здесь очевидно: в (2) счет по индексу i можно выполнять одновременно для
всех у, а в (3) наоборот. Кроме того, внутри простой задачи также допускается
распараллеливание, дробность которого ограничена только шаблоном разностной схемы.
Такая приспособленность явных схем к распараллеливанию породила ряд необосно-
295

ванных высказываний об усилении их роли в связи с появлением'многопроцессорных
ЭВМ. Однако это совершенно не так. Еще в работе 1965 г. Г.И. Марчука и Н.Н. Яненко
[8] было указано на возможность параллельной реализации неявных схем
расщепления. Это высказывание позднее было повторено Д. Дугласом в дискуссии по большим
компьютерам. Покажем, как для (1) организовать распараллеливание в случае
применения неявных схем.
Будем использовать неявную схему расщепления с весами
(Е-таЛ1)и%112=(Д + тРА1)и?>г (4)
; «В+1/а1ж = о.1=<*-гЛ*)*', + 1. /=1,2,...,ЛГа-1,
(£--г7Л2)М^+1=(^ + г5Л2)М^+1/2, (5)
«n+1ix = o,i=*"+1> /=1,2,...,ЛГ,-1.
Здесь, как и прежде, (4), (5) есть простые задачи, допускающие параллельный счет
по / в (4) и по/ в (5). При сегментации на 25,- реализация обменных краевых
условий осуществляется с помощью параметрической прогонки [11, 12]. Кроме того,
имеется возможности распараллеливания вычислений и в самой простой задаче путем
распараллеливания прогонки [11].
Ряд других примеров, подтверждающих эффективность применения неявных схем
при распараллеливании вычислений, приведен в работе [13]. В заключение отметим,
что модульный анализ и параллельные вычисления органически связаны между собой и
дальнейшее совместное развитие этих вопросов позволит существенно повысить
эффективность решения задач математической физики на ЭВМ.
ЛИТЕРАТУРА
1. Яненко Н.Н., Коновалов А.Н. Технологические аспекты численных методов математической
физики // Acta Univ. carol, math. Phys. 1974. N 1/2. P. 47-53.
2. Софронов И. Д. Оценка параметров вычислительной машины, предназначенной для решения
задач механики сплошной среды // Числ. методы механики сплош. среды. 1975. Т. 6, № 3. С. 98-
147.
3. Коновалов А.Н., Яненко НН Модульный принцип построения программ как основа создания
пакета прикладных программ решения задач механики сплошной среды // Комплексы программ
математической физики. Новосибирск, 1972. С. 48-54.
4. Коновалов А.Н Модульный анализ вычислительного алгоритма в задаче планового вытеснения
нефти водой // Тр. III семинара по комплексам программ мат. физики. Новосибирск, 1973.
С. 81-94.
5. Коновалов А.Н. О принципах построения пакета программ для решения задач математической
физики // Acta Politechn. Pr. CVUT. 1975. Vol. 4. P. 37-49. v
6. Коновалов A.H., Карначук В.И. О пакете прикладных программ математической физики /■/
Структура и организация пакетов программ: Междунар. конф.: (Тез. докл.). Тбилиси: Мец-
ниереба, 1976. С. 51-52.
7. Яненко НН, Карначук В.И., Коновалов А.Н Проблемы математической технологии // Числ.
методы механики сплош. среды. 1977. Т. 8, № 3. С. f 29-157.
8. Яненко НИ. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск: Наука, 1967. 197 с.
9. Ковеня В.М., Яненко Н.Н Некоторые проблемы развития пакетов программ для решения задач
аэродинамики // Числ. методы механики сплош. среды. 1979. Т. 10, № 3. С. 89-99.
10. Самарский А.А. Введение в теорию разностных схем. М.: Наука, 1971.
11. Яненко Н.Н, Коновалов А.Н, Бугров А.Н., Шустов Г.В. Об организации параллельных
вычислений и "распараллеливание" прогонки // Числ. методы механики сплош. среды. 1978. Т. 9,
№7. С. 139-146.
12. Воеводин А.Ф. Метод прогонки для разностных уравнений, определенных на комплексе // Журн.
вычисл. математики и мат. физики. 1*973. Т. 13, № 2. С. 494-497.
13. Яненко Н.Н, Коновалов А.Н Некоторые вопросы теории модульного анализа и параллельного
программирования для задач математической физики и механики сплошной среды //
Современные проблемы математической физики и вычислительной математики. М.: Наука, 1982.
296

МОДУЛЬНАЯ СТРУКТУРА АЛГОРИТМОВ И ПРОГРАММ
В ЗАДАЧАХ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ И СТРУКТУРА ЭВМ*
Производительность современных многопроцессорных ЭВМ, позволяющих за счет
параллельных вычислений достигать скоростей сотен миллионов операций в секунду
(ILLIAC-IV, STAR-100, CRAY-1 и др.), существенно зависит от класса решаемых
задач и алгоритмов их решения. Так, скорости вычислений на "удобных" и
"неудобных" задачах могут отличаться в десятки и даже сотни раз [1], что свидетельствует о
наличии сильной связи между структурой алгоритма и задачи (но не программы!) и
структурой ЭВМ. Выходом здесь может быть создание узкоспециализированных ЭВМ,
как это предложено, например, для решения уравнений Навье—Стокса [2], но тогда
потребуется очень широкий спектр таких машин, массовое производство которых,
по крайней мере в настоящее время, невозможно из-за их высокой стоимости.
Тем не менее успехи современной микроэлектроники позволяют надеяться на
создание мощных многопроцессорных ЭВМ, структура которых может подстраиваться
под структуру алгоритмов конкретных задач [3]. Все это говорит о том, что в
настоящее время уже назрела необходимость проведения структурного анализа не только
самих задач, решаемых на ЭВМ, но и всех основных звеньев технологической
вычислительной цепочки: постановка задачи -* алгоритм -► программа. Конечным
результатом такого анализа должна быть формулировка требований, предъявляемых к
структуре ЭВМ тем или иным классом задач, что является уже по сути переходом к
глобальной оптимизации всей нелинейной технологической вычислительной цепочки.
В данной работе предпринята попытка провести подобный анализ для задач механики
сплошной, среды на основе модульного принципа построения алгоритмов и программ
[4—6] и описать общую структуру ЭВМ, предназначенную для решения этого класса
задач.
В работе [6] для достаточно широкого класса задач было дано определение
"простой задачи", как вычислимой (практически реализуемой на ЭВМ) задачи,
получающейся в результате пересечения ряда независимых требований по однородности,
накладываемых на данный класс задач. Покажем, как для задач механики сплошной среды этот
методологический подход позволяет последовательно проводить модульную
декомпозицию для всех звеньев вычислительной технологической цепочки, т.е. сводить
решение конкретной задачи к определенной последовательности "простых задач".
Этап постановки задачи. Здесь "простая задача" определяется как задача с
однородной физической и математической моделью. Однородность физической модели обычно
достигается разбиением области, в которой исследуется сложное физическое явление,
на подобласти с однородными физическими процессами. Связь между этими
подобластями осуществляется через соответствующие краевые условия. Например, в задачах
аэродинамики при обтекании затупленных тел сверхзвуковым стационарным
потоком газа (рис. 1) можно выделить ряд таких подобластей: вязкое течение
(пограничный слой (///)), течение в ближнем следе {V) и невязкое (области /, //, IV)
течение, для стыковки которых используются только граничные условия. Следует отме-
* Актуальные гцгоблешл прикладной математики и математического моделирования, Новосибирск:
Наука, 1982. С 20-26, ICoam&p А.Д. Агесов.)
297

тить, что разбиение на такие подобласти является традиционным подходом в механике
сплошной среды. Однако тот факт, что к нему же приводит и модульный анализ
задачи, придает этому подходу вполне определенную методологическую основу.
Однородность математической модели есть единство структуры математического и
алгоритмического описаниями достигается обычно применением метода расщепления
по физическим процессам. Единство структуры состоит в том, что система
дифференциальных уравнений, например, не должна менять своих определяющих членов в
области определения "простой задачи", хотя тип ее может меняться в процессе
решения или от решения к решению. Но в любом случае алгоритм решения должен быть
единым. На рис. 1 в областях дозвукового (/) и сверхзвукового (II) течений опре-
! Wr
делены разные "простые задачи", когда алгоритмы их решения различны. Однако,
если для расчета течения используется метод установления, то тогда "простая задача'
будет определена уже на совокупности этих-областей; Таким, образом, уже на этапе
постановки задачи модульная декомпозиция позволяет не только сконструировать
исходную задачу, но и определить связи между отдельными структурными
элементами, ка основе которых для них могут быть построены графы по управлению и
информации.
Этап описания алгоритма. Алгоритм решения "простой задачи" должен
удовлетворять следующим требованиям однородности [6]: однородности математической
модели и краевых условий, однородности информационной среды (однородности
разностной сетки, шабдона, способа аппроксимации на нем и т.д.), однородности
самого алгоритма (пошаговости, модельности, одноступенчатости). Кроме того,
алгоритм должен допускать реализацию обменных краевых условий [5, 6], с помощью
которых осуществляется стыковка решений неавтономных "простых задач".
Напомним, что неавтономной называется "простая задача", областью определения которой
является часть области определения исходной задачи (сегмент) . Тогда на сопредельных
границах соседних сегментов и задаются обменные краевые условия, обеспечивающие
стыковку решений "простых задач".
С помощью сегментации обычно и удается удовлетворить требованиям
однородности, например тогда, когда в области решения исходной задачи применяются разные
сетки, разные алгоритмы и т.п. Однако сегментацию можно применять и в самой
простой задаче, что позволяет организовать в ней параллельные вычисления. Алгоритм
решения "простой задачи", удовлетворяющий описанным требованиям однородности,
всегда допускает расщепление по пространственным переменным, что позволяет
эффективно решать многомерные задачи механики сплошной среды на многопроцессорных
ЭВМ в случае как явных, так и неявных разностных схем.
Этап программирования. Для программной реализации на ЭВМ "простой задачи"
298
Модуль
м2
м3
Mff0ffJTet£
БМг
ЯМ*
5МЛ
т
-Л
—'5
I»
T-—^=f
'#**
's1^
1
It
i
'0f//77(7J7trf/&/U t/fipfof/fi
Рис.2

e
Mam
заёачи
W
W
( Ma ни тор Л
V М000ЛЯJ
Уровень
M0ty;7eu
ypvffewr
0азисю/я
маЯулеи
существенное значение имеет требование однородности памяти [6], т.е. вложения
"простой задачи" в оперативную память ЭВМ. Тогда все вопросы перераспределения
памяти ЭВМ между оперативной и внешней и организации параллельных вычислений,
когда в оперативной памяти могут находиться одновременно несколько "простых
задач", решаются путем сегментации области решения исходной задачи.
Программная реализация "простых задач" дает набор программных объектов
(базисных модулей), имеющих вполне определенные наборы входных и выходных
величин и наборы входов и выходов по управлению, что и составляет основу модульного
программирования. Внутри "простой задачи" на уровне ее программной реализации
возможно и дальнейшее структурирование [7,8], но это уже будет структурирование
программ, не затрагивающее
алгоритмическую структуру задачи в целом, и нами
здесь не рассматривается.
Описанный принцип модульной
декомпозиции задач механики сплошной среды
приводит к следующей иерархической
структуре (рис. 2). На этапе постановки
исходная задача приводится к
определенной совокупности однородных
физических задач, связанных между собой только
через краевые условия. Такие
однородные задачи будем называть модулями, а
реализацию связей между ними по
управлению и информации — сборкой модулей.
Каждый модуль, в свою очередь, строится
(генерируется) из базисных модулей
(БМ), т. е. "простых задач", образующих
два уровня — вертикальный (расщепление
по физическим процессам), когда БМ работают строго последовательно, и
горизонтальный, возникающий при сегментации области определения модуля. На этом уровне связь
между БМ осуществляется только через обменные краевые условия, что позволяет им
работать параллельно. Такая структура, в частности, положена в основу модульной
системы СПРУТ [9, 10], предназначенной для решения прикладных задач газовой
динамики.
Рассмотрим теперь, каким образом в рамках этой иерархической структуры могут
быть организованы параллельные вычисления и какая структура ЭВМ может быть здесь
наиболее эффективной. На уровне сборки модулей их параллельное исполнение
возможно, но оно является нерегулярным, так как определяется в основном графом
информационных связей между модулями. В пределах самого модуля
распараллеливание всегда возможно на каждом из горизонтальных уровней и именно здесь,
особенно в случае многомерных задач, применение многопроцессорных ЭВМ дает
наибольший эффект. Действительно, сегментация на "простые задачи" образует первый
уровень распараллеливания. Далее, внутри каждой "простой задачи" однородность
алгоритма и однородность вычислительной среды позволяют путем расщепления по
пространственным переменным сводить многомерные задачи к совокупности
одномерных. Возможность их независимого решения образует второй, внутренний уровень
распараллеливания.
Теперь о структуре самой ЭВМ. В настоящее время наиболее быстродействующие
многопроцессорные ЭВМ имеют в основном два типа синхронных процессоров -
матричный (ILLIAC-IV) и векторный (STAR-100, CRAY-1). Если под эффективностью
понимать степень загрузки, то использование матричного процессора, управляемого
одним потоком команд, для описанной модульной структуры неэффективно, по
крайней мере, по двум причинам. Во-первых, круг "удобных" задач (алгоритмов)
Рис.3
299

механики сплошной среды, где его эффективность наибольшая, ограничен в основном
классом сравнительно простых явных разностных схем. Во-вторых, использование
расщепления по пространственным переменным переводит его в режим работы
векторного процессора, причем эффективность работы существенно зависит от длины
вектора входных величин и числа элементарных процессоров, входящих в состав
матричного процессора. Эффективность векторного процессора, построенного на
конвейерном принципе [11] (STAR-100, CRAY-1), практически не зависит от длины
вектора, что дает ему значительное преимущество перед матричным для данной
модульной структуры. Однако один векторный процессор не позволяет реализовать
распараллеливание на горизонтальном уровне.
В итоге ЭВМ должна иметь набор универсальных асинхронных центральных
процессоров (ЦП) и набор векторных процессоров (ВП), причем между ЦП и ВП не
предполагается наличия жестких связей, т.е. каждый ЦП может запускать один или
несколько любых ВП. Функциональная схема такой ЭВМ приведена на рис. 3. Монитор задачи
анализирует межмодульные управляющий и информационный графы и определяет,
какие модули могут выполняться параллельно. Каждый такой модуль обрабатывается
своим ЦП. Далее, в самом модуле также имеется свой монитор, реализующий
распараллеливание на горизонтальном уровне для базисных модулей. Как правило, здесь
используется набор ЦП, обслуживающий первый уровень внутримодульного
распараллеливания и набор ВП для второго уровня распараллеливания. Однако возможен и
выход ЦП модуля непосредственно на ВП. Все процессоры работают на общую
оперативную память, объем которой должен позволять разместить в ней как можно больше
БМ модуля (желательно все). Это позволяет упростить реализацию и ускорить счет
обменных краевых условий, а также выполнение операций транспонирования,
связанных с применением расщепления по пространственным переменным.
ЛИТЕРАТУРА
1. Королев Л.Н. Структура ЭВМ н их математическое обеспечение. М.: Наука, 1978.
2. Grutton Е.С. et al. Feasibility of a special-purpose computer to solve the Navier-Stokes equations.
74 p. (RAND Сотр.; R-2183-RC).
3. Каляев А.В. Многопроцессорные системы с распределенной памятью, универсальной
коммутацией и программируемой структурой // Электрон, моделирование. 1979. № 1. С. 8-13.
4. Яненко Н.Н., Коновалов А.Н. Модульный принцип построения программ как основа создания
пакета прикладных программ решения задач механики сплошной среды // Комплексы программ
математической физики. Новосибирск, 1972. С. 48-54.
5. Яненко Н.Н., Карначук В.И., Коновалов А.Н. Проблемы математической технологии // Числ.
методы механики сплош. среды. 1977. Т. 8, № 3. С. 129-157.
6. Яненко Н.Н. Вопросы модульного анализа и параллельных вычислений в задачах
математической физики // Комплексы программ математической физики. Новосибирск, 1980. С. 3-12.
7. Дал У., Дейкстра Э., Хоор К. Структурное программирование. М.: Мир, 1975.
8. Dennis J.B., Modularity // Lect. Notes Comput. Sci. 1975. N 3. P> 128-182.
9. Лымарев АЛ, Рынков А.Д., Яненко НН Опытная версия Модульной системы для решения
прикладных задач газовой динамики // Комплексы программ математической физики.
Новосибирск, 1978. С. 59-65.
10. Лымарев А.П., Рынков А .Д.* Яненко Н.Н Об одной реализации модульной системы для
решения прикладных задач газовой динамики // Там же. 1980. С. 46-59.
11. Жиров В.Ф. Математическое обеспечение и проектирование структур ЭВМ. М.: Наука, 1979.
300

ПЕРСПЕКТИВЫ РАЗВИТИЯ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
НА ОСНОВЕ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ*
1. Сближение математики в целом и вычислительной техники является несомненным
фактом. Традиционно математика является поставщиком задач, методов, алгоритмов
для вычислительной техники. Обратно, развитие вычислительной техники,
обусловленное не только возрастающим потоком задач, но и достижениями техники, оказывает
воздействие на структуру математики, способствует появлению новых идей и
направлений. Возникла и успешно разивается новая научная дисциплина — математическая
технология, которой, несомненно, принадлежит большое будущее.
В теоретической математике влияние вычислительной техники пока заметно слабее,
чем в вычислительной математике, но уже и сейчас оно проявляется достаточно
ощутимо. С помощью ЭВМ в настоящее время доказываются многие теоремы. Так,
например, в ВЦ СО АН СССР (Иркутск) член-корр. В.М. Матросовым с сотрудниками
созданы и реализованы на ЭВМ алгоритмы доказательства теорем из области теории
устойчивости по Ляпунову. В ИТПМ СО АН СССР канд. физ.-мат. наук В.П. Шапеевым с
сотрудниками успешно реализован на ЭВМ метод внешних форм Картана. За рубежом
решена проблема о четырех красках.
Применяя ЭВМ в качестве рабочего инструмента для символьных выкладок,
теоретическая математика может существенно ускорить темпы своего развития.
2. Развитие вычислительной техники дало новые эвристические средства
математическому мышлению, которые с введением математического эксперимента теряют
свой чисто дедуктивный характер. Все более важной задачей математики становится
поиск новых алгоритмов и математических моделей, которые должны реализовывать-
ся на ЭВМ, что придает им определенную специфику и структуру.
История математики свидетельствует о том, что математика в целом всегда
ориентировалась на определенную технологию. Вначале преобладали геометрические методы,
затем они уступили первенство арифметике и алгебре, особенно с появлением
дифференциального и интегрального исчисления и арифмометра. Сейчас, когда мы вступаем
в эпоху мощных ЭВМ, на первое место должны ставиться алгоритм и математические
модели как средство познания и источник новых математических теорий,
3. Основная задача науки вообще и математики в частности — добывание новой
информации об окружающем нас мире. Без новой научной информации немыслимо
развитие науки, техники, народного хозяйства. Однако уже сейчас объем информации
настолько возрос, что ее получение, переработка и передача становится предметом
науки, техники, отраслью промышленности. Первый источник информации —
физический эксперимент, где экспериментальная физика играет решающую роль. Здесь
необходимо использовать ЭВМ для ускорения обработки результатов, поскольку
индивидуальные события современного эксперимента имеют временные интервалы,
лежащие в диапазоне микро- и наносекунд, и без быстрой обработки информации на
. ЭВМ просто не могут быть осмыслены. Поэтому система автоматизации научных
исследований и, в частности, научного эксперимента приобретает большое значение. Но
этот источник информации сам по себе еще недостаточен. Техника не может
поглощать в прямом виде физические данные. Они должны быть воплощены в
математических моделях, которые входят составной частью в пакеты прикладных программ.
Поэтому техника в своей деятельности по созданию новых конструкций использует
два вида информации: первый — физическая информация, которая является
результатом эксперимента, второй — алгоритм, построенный на математических моделях.
Все это воплощено в новом продукте математики — пакетах прикладных программ,
которые содержат и хранят в себе результаты эксперимента, математические модели
*ЭВМ. Перспективы и гипотезы: (Препр. Ин-та теорет. и прикл. механики СО АН СССР № 46).
Новосибирск, 1981. С. 3-6.
301

и алгоритмы. Поэтому проблемы систем автоматизации проектирования (САПР) тесно
связаны как с технической информацией, так и с математикой, как с результатами
эксперимента, так и с математической моделью, которая строится на основе этих
экспериментов,
4. Основная проблема, которая сейчас стоит перед наукой и техникой, — разработка
и производство мощных ЭВМ. Какие ЭВМ нужны технике? Известно, что для
создания хорошего самолета нужны большие наземные эксперименты, Установки для них
становятся все более и бодее дорогими. Поэтому внимание конструкторов все больше
направляется в сторону математического эксперимента, который уже сейчас дополняет,
а вскоре в существенно л мере может и заменить физический — лабораторный или
натурный — эксперимент. Аэродинамические явления, возникающие при полете
современных сверхзвуковых самолетов, чрезвычайно сложны. Их отличительной чертой
является наличие в поле течения особенностей типа ударных волн, пограничных слоев,
зон отрыва и т, п., положение которой заранее, как правило, неизвестно. Поэтому
численное моделирование должно опираться на хорошую теорию и мощные ЭВМ.
Оценки экспертов показывают, что для полного описания аэродинамической задачи
требуется ЭВМ на 10 млрд,оп/с. Задачи экологии, метеорологии, биомеханики требуют еще
большего быстродействия ЭВМ, Повышение быстродействия достигается следующими
направлениями развития вычислительной техники»
1) Улучшение физико-технических свойств элементов и информационных каналов
ЭВМ путем
— повышения быстродействия элементов,
— уменьшения расстояний информационных передач,
— проектирования ЭВМ на основе БИС.
2) Улучшение эффективности действия и структуры ЭВМ на уровне
микроопераций и арифметических операций
— организация виртуальной памяти,
— декомпозиция арифметических действий (конвейерная система),
— оптимизация логических элементов в Б ИСах.
3) Использование векторных и матричных процессоров для синхронной
декомпозиции алгоритма,
Направление 1) является, в основном, технологическим и связано с развитием
элементной базы ЭВМ, направления 2) и 3) связаны с улучшением организации ЭВМ
при данной элементной базе, направление 3) связано с модульным анализом и
распараллеливанием алгоритмов.
На изложенных выше принципах уже построены мощные ЭВМ, достигающие
быстродействия порядка 200 млн,оп/с (Cray-1, Cyber-205 и др.), Дальнейшее повышение
быстродействия может происходить как за счет новой элементной базы (применение
сверхпроводимости, криогенной техники и т, д,), так и за счет создания проблемноориенти-
рованных, специализированных ЭВМ. В последнем случае эффективность реализации
параллельных алгоритмов может значительно возрасти. Именно на этом пути уже в
1985 г. в США могут быть созданы ЭВМ на 1 млрд,рп/с, а в конце этого столетия до
10 млр.оп/с и выше.
Чем шире класс задач, охватываемый специализированной машиной, тем сложнее
ее структура, и как наиболее совершенную форму ЭВМ следует рассматривать ЭВМ
с перестраиваемой структурой. Теоретические основы таких ЭВМ разрабатывались в
ИМ СО АН СССР под руководством д,т«н, Э.П. Евреинова, В настоящее время
создаются опытные образцы. В Институтах физики полупроводников и автоматики и
телеметрии СО АН СССР ведутся глубокие исследования по физике, технологии и структуре
элементов и схем ЭВМ. Все это говорит о том, что СО АН СССР вносит свой вклад в
дело развития современной вычислительной техники.
302

ПАКЕТЫ ПРИКЛАДНЫХ ПРОГРАММ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
И МЕХАНИКИ СПЛОШНОЙ СРЕДЫ*
Пакетная тематика — сравнительно новая многоплановая научнотехническая
проблема, возникновение которой связано с рядом объективных причин. На наш взгляд,
таких причин четыре.
Во-первых, это переход машиностроительных отраслей народного хозяйства на
математические методы проектирования изделий. При этом быстро наступило насыщение
отраслевых фондов большим количеством отдельных прикладных программ и
возникла потребность в качественно новом программном продукте — в пакетах прикладных
программ. Во-вторых, это возрастающая роль в научных исследованиях численного
эксперимента, существенно дополняющего, а нередко и заменяющего натурный,
физический эксперимент. В-третьих, это совершенствование математического обеспечения
ЭВМ БЭСМ-6, реализация проекта ЕС ЭВМ, работы по созданию сетей ЭВМ,
многомашинных и многопроцессорных комплексов. Наконец, в-четвертых, это постоянное
увеличение в общей стоимости современных вычислительных систем доли прикладного
программного обеспечения, что заставляет разработчиков изыскивать более
экономичные способы создания прикладных программ, в том числе и промышленного
назначения,
КЛАССИФИКАЦИЯ ПАКЕТОВ
За минувший десятилетний период создано большое число пакетов прикладных
программ математической физики и механики сплошной среды (в дальнейшем только
о таких пакетах и будет идти речь), значительная часть которых так или иначе попала
в сферу деятельности Секции пакетов прикладных программ (председатель Секции
академик Н,Н, Яненко), Анализ накопленного как отечественного, так и зарубежного
опыта по созданию таких пакетов позволил провести их некоторую классификацию
и дать общее определение пакета [1] как совокупности программ, объединенных
общностью описания физического объекта или же логическим единством
описываемого математического объекта.
Классификация пакетов может быть проведена по ряду "ортогональных"
признаков, в качестве которых были выбраны два, на наш взгляд, наиболее существенных
по назначению пакетов и по принципам их организации. По первому признаку
оказалось целесообразным выделить четыре класса пакетов в порядке увеличения степени
сложности решаемых задач.
Пакеты для решения "простых" задач (ППЗ).
Под "простой" задачей [2] понимается корректная конечно-устойчивая краевая
задача математической физики, обладающая максимальным набором независимых
однородных свойств:
— однородность физической и математической моделей,
— однородность постановки,задачи, т. е, алгоритмическая однородность начальных
и краевых условий,
— однородность алгоритма,
— однородность информационной среды, под которой понимается дискретное
представление области определения задачи вместе с формальной структурой
аналитического представления решения (способ дискретизации, шаблон, аппроксимация на
шаблоне и т. д.),
— однородность памяти, т, е, вложенность простой задачи в оперативную память
ЭВМ,
*Комплексы программ математической физики. Новосибирск, 1982. С. 3-15. (Соавторы В.И. Кар-
начук, А.Д. Рычков, В.М. Фомин.)
303

— хорошая обусловленность,
— автономность, неавтономность.
Простая задача называется автономной, если ее область определения совпадает с
областью решения исходной задачи, Обычно это не так, и область решения приходит*
ся разрезать на сегменты, выставляя на сопредельных границах таких сегментов
обменные краевые условия [1]. Тогда простая задача, определенная на сегменте, будет
неавтономной, ее решение зависит от соседних простых задач. Как правило, простые
задачи есть результат применения принципа модульной декомпозиции к реальным
задачам математической физики и механики сплошной среды. Именно они, по
нашему убеждению, и могут составить основу тех базисных модулей, в рамках которых
может быть представлен достаточно широкий класс различных задач математической
физики [1]. Отдельные компоненты ППЗ присутствуют во многих пакетах, но работа
по созданию ППЗ только еще начинается.
Аналитические пакеты (АП). АП — есть совокупность программ, объединенных
логическим единством описываемого математического объекта. АП может содержать
совокупность методов для решения одной задачи (проблемно-ориентированный пакет)
или одан достаточно универсальный метод, приемлемый для решения класса задач
(методо-ориентированный пакет). К представителям первого вида АП можно отнести
пакеты программ линейной алгебры [3, 4], пакеты для решения систем уравнений
эллиптического и параболического типов [5—7] и ряд других. Ко второму виду
относится семейство пакетов ПОЛЕ [8, 9] для расчета различных физических полей в
областях сложных форм на основе метода Я-функций, АП имеют собственный входной
язык, представляющий пользователю возможность записи на "естественном" для него
языке систем уравнений, граничных и начальных условий, области решения и т. д. Из
зарубежных АП можно отметить пакет PDEL [10] для решения смешанных краевых
задач, пакеты [11] для решения двумерных эллиптических уравнений и DCJ [12] для
решения параболических и эллиптических уравнений.
Физико-инженерные пакеты (ФИП) - есть совокупность программ, объединенных
общностью описания физического объекта. Они предназначены для решения приклад*
ных задач, связанных с проектированием технической конструкции или с
моделированием сложного физического явления, Характерной особенностью ФИП является
неоднородная физико-математическая модель и реальная сложная геометрия. Структурно
ФИП состоит из двух основных частей — системной части и функционального
наполнения. Функциональное наполнение или библиотека функциональных модулей
определяет класс решаемых задач. Модулями обычно являются отдельные
самостоятельные программы, предназначенные для решения какой-либо конкретной физической
задачи, системная же часть пакета позволяет объединять модули в комплексы программ
для решения достаточно больших и сложных задач. Одним из примеров ИФП является
пакет РАМОК-3 [13] для расчета широкого класса оболочечных конструкций,
модулями которого являются процедуры языка PL/1. Для решения задач газовой динамики
разработаны пакеты ГАММА [14], СПРУТ [15], АРГОЛА [16] и ряд других. Весьма
характерным для многих ФИП является независимость системной части пакета от его
функционального наполнения. Это позволяет в рамках того же пакета решать и другие
классы задач, меняя наборы библиотек функциональных модулей [17].
Среди крупнейших зарубежных ИФП отметим пакет MODULEF. [18], созданный
усилиями ряда стран для решения инженерных задач методом конечного элемента, а также
американский пакет NASTRAN [19] и пакет ФРГ ASCA [.20].
Системы автоматизации проектирования (САПР). Применяются при
проектировании я эксплуаяацда конкретных технических конструкций или целых классов
конструкций, В основе таких пакетов лежат некоторая численная модель конструкции,
которая создается, постоянно поддерживается и модифицируется с помощью банка
данных. Главной особенностью этого класса пакетов является учет традиционных приемов
развития проекта, которые связаны и с характерными «особенностями конструкции.
Пакеты САПР должны иметь развитый сервис, не требующий от пользователя знания
304

физико-математической модели и численных методов, обладать эффективными
средствами ввода-вывода информации, иметь высокую степень автоматизации.
По принципам .организации пакетов можно выделить также четыре основных класса
пакетов,
1. Комплексы программ. Это достаточно распространенный способ объединения
программ, характерной особенностью которого является жесткая связь между
элементами системной части (обычно достаточно проста) и элементами функционального
наполнения. Их существенным недостатком является замкнутость, трудность
включения новых элементов в функциональное наполнение, достоинством — простота
эксплуатации и малые "накладные" расходы, связанные с межмодульным интерфейсом.
Комплексы программ есть по сути вырожденный тип пакета. Элементы их
функционального наполнения не удовлетворяют принципам межмодульности, поскольку не
являются перемещаемыми и замещаемыми. Системная часть "растворена" в
функциональном наполнении и зачастую неотделима от него.
2. Пакеты библиотечного типа. Наиболее простая форма организации пакета, когда
функциональное наполнение организовано в виде библиотеки отдельных готовых
программ, оформленных в виде процедур, а системная часть полностью входит в
базовое математическое обеспечение ЭВМ. Примером пакетов этого типа являются пакет
КРУЧА [21 ], а также пакеты [22, 23].
3. Пакеты-комплексаторы. Пакеты этого класса имеют системную часть и
функциональное наполнение в виде библиотек модулей. Модулями обычно являются
замкнутые программы конкретного физического или математического содержания. Имеется
собственный входной язык, транслятор с которого входит в системную часть пакета.
Взаимодействие системной части с функциональным наполнением может быть
одноразовым [10, 15, 24], производится в несколько этапов [11] или осуществляется в
режиме интерпретации [14, 16]. В первом случае обычно пакет выдает программу на
алгоритмическом языке (точнее, комплекс программ) и транслятор играет, таким
образом, роль препроцессора [15]. Характерной особенностью этого класса пакетов
является независимость или слабая зависимость системной части от функционального
наполнения, что дает принципиальную возможность в рамках одного пакета решать
несколько классов задач [17].
4. Пакеты-генераторы. Это наиболее сложный способ организации пакетов. Пакет
этого класса не содержит никакую вычислительную программу в готовом виде, но
способен создать ее из отдельных, заранее подготовленных программных элементов.
Автоматически собранная программа может затем многократно использоваться
отдельно от пакета. Функциональное наполнение пакетов-генераторов есть библиотека
программных элементов, вид которых в значительной мере определяется системной
частью пакета. Пакет имеет свой входной специализированный язык, близкий к
"естественному" языку пользователя в соответствующей прикладной области. Типичными
примерами таких пакетов являются пакет DCJ [12] для решения эллиптических и
параболических уравнений и пакет [25], разрабатываемый в ИТПМ СО АН СССР.
ИНСТРУМЕНТАЛЬНЫЕ СИСТЕМЫ
ДЛЯ СОЗДАНИЯ ПАКЕТОВ ПРОГРАММ
Набор инструментальных средств, применяемый при создании пакетов и их
компонент, находится в широком диапазоне: от универсальных подсистем, входящих в
базовое математическое обеспечение ЭВМ, до специализированных средств,
предназначенных для разработки пакетов определенного класса. Некоторые типы пакетов
прикладных программ сами могут являться инструментальными системами. Так,
вычислительные программы, срздаваемые пакетами-генераторами, могут использоваться для
создания функционального наполнения других типов пакетов, пакеты-комплексаторы
могут генерировать комплексы программ.
305

Языковые средства. Для разработки функционального наполнения обычно
используются универсальные алгоритмические языки высокого уровня (АЛГОЛ, ФОРТРАН),
системные же части пишутся на машинно-ориентированных языках, типа ассемблера.
В настоящее время достаточно распространенным является мнение, что с точки
зрения системного программирования проблемы пакетов нет. Действительно,
операционные системы, трансляторы и т.п. есть не что иное, как большие и достаточно сложные
пакеты программ, организующие работу ЭВМ. Поэтому системными программистами
уже разработаны и созданы практически все средства, необходимые для организации
и ведения баз данных, организации межмодульных связей по информации и
управлению и т. д. Трудность заключается в отсутствие соответствующих эффективных
языковых средств в алгоритмических языках высокого уровня. Их наличие позволило бы
писать системные части пакетов на машинно-независимых языках, что существенно
упрощает решение проблемы транспортабельности пакетов прикладных программ.
Весьма перспективной разработкой в этом направлении следует признать разработку
языка ADA [26]. Этот язык сочетает в себе свойства языков высокого уровня, на
котором пишется функциональное наполнение, со средствами, необходимыми для
создания системных частей пакетов :
— независимость точности вычислений от разрядности ЭВМ,
— макрогенерация,
— условная компиляция,
— построение баз данных,
— организация пакета как множества родственных объектов подпрограмм, общих
наборов данных, описаний типов, внутреннее устройство которых скрыто и защищено
от пользователя.
Метасистемы. Системные части достаточно развитых пакетов прикладных программ
имеют свой входной язык. Разработка трансляторов с такого языка является хотя и
простой, но достаточно трудоемкой задачей и здесь очень эффективным может быть
использование метасистем. В качестве примера укажем систему DEPOT [24],
разработанную в Дрезденском техническом университете. Входным языком этой системы
является метаязык MS, на котором может быть описан синтаксис
проблемно-ориентированного языка и алгоритм трансляции программ на этом языке в один из
универсальных алгоритмических языков (АЛГОЛ, ФОРТРАН, PL/1). По этой метапрограмме
DEPOT автоматически создает транслятор с данного проблемно-ориентированного
языка. По оценкам авторов этой системы ее применение экономит до 90% труда при
разработке трансляторов>
Инструментальные комплексы. Это средства, предназначенные для разработки и
поддержки пакетов программ, С их помощью создаются и ведутся базы данных,
межмодульный интерфейс. Существенным недостатком комплексов является то, что все
они машинно-ориентированны, что создает большие трудности при перенесении пакетов
на другие ЭВМ. Достаточно развитыми инструментальными комплексами являются
системы СОК [27] для БЭСМ-6 и АПРОП [28] для ЕС ЭВМ.
В ИТПМ СО АН СССР разработана инструментальная система ИСТОК [29],
предназначенная для организации, эксплуатации и ведения пакетов на базе готовых программ.
На базе этой системы в ИТПМ СО АН СССР созданы три инженерно-физических пакета
прикладных программ. Свойствами инструментальных систем могут обладать также
пакеты-генераторы и пакеты-комплексаторы, К числу таких относятся генераторы
программ ПОЛЕ [8] и разработанный в ИТПМ СО АН СССР пакет СПРУТ [15, 17],
допускающий генерацию из модулей и включение их в систему. Достаточно широкий
набор инструментальных возможностей содержит система САФРА [30], с помощью
которой был разработан целый ряд пакетов прикладных программ.
306

МАТЕМАТИЧЕСКАЯ ТЕХНОЛОГИЯ РАЗРАБОТКИ ПАКЕТОВ
Основной задачей математической технологии является глобальная оптимизация
всей нелинейной вычислительной технологической цепочки: объект,исследования
-►физическая модель -► математическая модель-► численный алгоритм-►
программа-►структура ЭВМ -* расчет, Структура этой цепочки такова, что допускается цикличность как
для всей цепочки в целом, так и между ее отдельными звеньями, что должно
учитываться при ее реализации. Так, при разработках физических и математических моделей
следует учитывать как структуру численных алгоритмов и программ, так и структуру
самой ЭВМ, на которой в конечном итоге и реализуются эти модели. При выборе или
разработке численного алгоритма должна учитываться особенность его программной
реализации, структура ЭВМ, конфигурация ее математического и аппаратного
обеспечения, Структура алгоритма должна быть и не только хорошо приспособленной к
структуре ЭВМ, но может и сама определять ее структуру, если, например, алгоритм
реализуется на ЭВМ переменной структуры или проектируется специализированная
ЭВМ [31].
Таким образом, необходимо структурировать все звенья вычислительной
технологической цепочки, установить определенные соотношения между элементами этих
структур и на их основе провести глобальную оптимизацию всей вычислительной
цепочки. Это уже есть переход к новой технологии производства программ, которую
можно назвать глобальным программированием в отличие от традиционного,
локального. Для структурирования звеньев вычислительной цепочки на уровнях постановки
задачи и алгоритмических уровнях можно воспользоваться методологическим
подходом, положенным в основу понятия "простой" задачи [2] наложением ряда
независимых требований однородности и общими принципами модульной декомпозиции. На
этапе программирования следует использовать методы и подходы структурного
программирования [32].
Анализ результатов применения этой технологии к задачам механики сплошной
среды [31] показал, что в итоге возникает определенная иерархическая структура,
которая может быть положена в основу принципа построения пакетов прикладных
программ, В общих чертах такой пакет может иметь три уровня. Первый, высший
уровень предназначен для генерации из специальных текстовых заготовок
(шаблоны разностных схем, сами схемы) "простых" задач. Второй уровень из "простых"
задач собирает содержательные однородные физические задачи с нужной геометрией
области определения. Третий уровень из однородных физических задач собирает
комплексы программ для решения задач, уже допускающих разнородность
физико-математических моделей в различных областях ее решения. Модули такого пакета также
образуют некоторую иерархическую структуру (алгоритмические модули,
программные модули стыковки, текстовые заготовки для генерации "простых" задач и т. д.).
Сгенерированные "простые" задачи представлены в виде текста на языке высокого
уровня и сами являются модулями для третьего уровня. Они не зависят от
системной части пакета и могут выступать в роли абстрактных модулей, которыми могут
обмениваться различные пакеты, построенные по такому же принципу, Системная
часть такого пакета имеет тоже несколько независимых, последовательно
работающих уровней и включает в себя все классы организации пакетов: генерация, комплек-
сация, ведение библиотек "простых" задач. Каждому уровню соответствует свой
входной язык, Результатом работы пакета является генерация комплекса программ,
исполнение которого происходит уже независимо от пакета и может быть многоразовым.
Изложенный подход к построению пакетов положен в основу развиваемой в
настоящее время в ИТПМ СО АН СССР модульной системы СПРУТ, частичная реализация
которой изложена в [15, 17]. Особого внимания заслуживает проблема создания
пакетов прикладных программ для многопроцессорных ЭВМ. Работа здесь только
начинается и в настоящее время сосредоточена в основном на вопросах распараллеливания
алгоритмов и на разработке общих принципов построения таких пакетов. Применение
307

здесь описанных выше принципов глобального программирования приводит к
интересному результату — хорошо модульно представленный алгоритм почти автоматически
распараллеливается, т. е. модульная декомпозиция задачи по существу решает
проблему распараллеливания вычислений, разумеется, на алгоритмическом уровне. Более
того, такой алгоритм может и сам определять структуру ЭВМ, на которой он может
быть наиболее эффективно реализован. Так, для задач механики сплошной среды
наиболее эффективной оказывается ЭВМ, имеющая набор асинхронных центральных
и набор векторных процессоров [31]. Большие перспективы здесь открывает
появление многопроцессорных ЭВМ с переменной структурой [33] и вычислительных систем
[34].
В заключение коснемся очень важного вопроса пакетной тематики —
транспортабельности пакетов прикладных программ. Поскольку функциональное наполнение пакетов
пишется на алгоритмических языках высокого уровня машинно-независимых, то
здесь основная трудность заключается в различной точности представления
вещественных чисел на разных ЭВМ. Для ее преодоления можно, как это предложено рабочей
группой 2.5 IFIP, ввести в эти языки соответствующие средства, в частности для языка
ФОРТРАН предлагается использовать в качестве параметров программы векторные
"машинные константы" — и набор стандартных функций на их основе, управляющий
точностью представления чисел. Для системной части пакетов проблему
транспортабельности можно решить только переходом к написанию их на машинно-независимых
языках.
ЛИТЕРАТУРА
1. Яненко Н.Н., Карначук В.И., Коновалов AM. Проблемы математической технологии // Числ.
методы механики сплош. среды. 1977. Т. 8, № 3. С. .129-157.
2. Яненко ИМ. Вопросы модульного анализа и параллельных вычислений в задачах
математической физики // Комплексы программ математической физики. Новосибирск, 1980. С. .3 — 11.
3. Молчанов ИМ. Пакет задач линейной алгебры. Киев, 1979.
4. Библиотека численного анализа НИВЦ МГУ. М.: Изд-во МГУ, 1979.
5. Новещенко Ю.А., Попков Ю.П. ТЕКОН-пакет программ для решения тепловых задач. М., 1978.
(Препр. / ИПМ АН СССР; № 65) .
6. Иванов В.Я. Автоматизация машинного проектирования приборов электроники. Новосибирск,.
1977. (Препр. / ВЦ СО АН СССР; № 40).
7. Горбенко Н.И., Ильин В.П., Попова Г.С., Свешников В.М. Пакет прикладных программ ЭРА
для автоматизации электрических расчетов // Численные методы решения задач электронной
оптики. Новосибирск, 1979.
8. Рвачев В.Л., Манько Г.П., Мацевитый A.M. Генератор программ ПОЛЕ для расчета физических
полей в объектах произвольной формы // Комплексы программ математической физики.
Новосибирск, 1978. С. 100-106.
9. Рвачев В.Л., Шевченко AM. Автоматизация построения пакетов программ для расчета
физических полей методом /^-функций // Там же. 1978. С. .10,7-120.
10. Cardenas A.F.y Karplus W.I. PDEL - a language for partial differential equations // С ACM.
1970. Vol. 13, N3. P. 13-21.
11. RiceJ.R. ELLPACK 78 user's guide - preliminary version. Prude, 1979.
12. Ehgquist В., Swedsaams T. DCJ user's guide. Rep. N 83. Uppsala, 1979.
13. Мальцев В.П., Мяченков В.И. Пакеты программ расчета на ЕС ЭВМ многосвязных
подкрепленных оболочечных конструкций // Комплексы программ математической физики. Новосибирск,
1979. С. 29.
14. Пасконов В.М.У Росляков Г.С. Организация пакета программ для научных исследований в
области аэрогидродинамики // Там же. 1978. С. 88-99.
15. Лымарев А.П.У Рычков А.Д., Яненко ИМ. Об одной реализации модульной системы для
решения прикладных задач газовой динамики // Там же. 1980. С. 39-51.
16. Михайлов ЮА.у Юмашев В.Л. Один способ управления комплексом программ (на примере
гиперзвукового обтекания) // Там же. 1978. С. 74-87.
17. Рычков А.Д.У Лымарев А.П. Структура системной части ППП СПРУТ // Числ. методы механики
сплош. среды. 19.81. Т.; 12, № 3. С.: 105-113.
18. An international pool of user's of numerical analysis applied to man and nature: INTERCOMP / Ed.
O. Perroneau. 1978.
19. MacNeal R.H. NASTRAN theoretical manuel. Wash. (D.C.), 1972. (Sci. and techn. inform, office; NASA
SP-221).
308

20. Fuchs G„ Roy J.R. Solution of the stiffness matrix equations in ASKA. Stuttgart, 1968. (Inst. Statik
und Dynamik der Luft- und Raumfahrtkonstruktionen. Rep.; N 50).
21. Давыдов Ю.М. Пакет прикладных программ КРУЧА для задач аэродинамики // Комплексы
программ математической физики. Новосибирск, 1979. С. 48.
22. Угодников А.Г., Хуторянский ИМ., Турилов В,В, Комплекс программ решения осесимметрич-
ных и плоских начально-краевых задач для скалярного волнового уравнения на основе метода
запаздывающих потенциалов и граничных интегральных уравнений // Там же. С. .41.
23. Carver М.В. FORSIM: FORTRAN package for the automated solution of coupled partial and 3 or
ordinary differential equation systems. 1974. (User's manual; AECL-4844).
24. Lotsch J. DEPOT-formal definition of syntax and semantics of specialized languages for automatic
implementation // Отчет РГ 04 KHBBT: Определение и реализация специализированных языков.
Дрезден, 1979. Ч. 1. С. 116-149.
25. Карначук В.И., Коновалов А.Н. О применении модульного принципа к созданию пакета
прикладных программ математической физики // Комплексы программ математической физики.
Новосибирск, 1978. С. 179.
26. Preliminary ADA reference manual // ACM Sigplan Notices. 1979. Vol. 19, N 6.
27. Воронков А.В. .Система обеспечения комплексов программ математической физики. Препр.
ИПМ АН СССР № 49. М., 1979.
28. Система автоматизации производства программы (АПРОН). Киев, 1976.
29. Яненко Н.Н., Фомин В.М. Современное состояние, пути дальнейшего развития разработки
пакетов и архитектура системы ИСТОК для организации, эксплуатации пакетов прикладных
программ // Автоматизированные системы вычислений. Новосибирск, 1981. С. 3-79.
30. Горбунов-Посадов М.М. Пакет прикладных программ САФРА: Системное наполнение. Препр.
ИПМ АН СССР № 85. М., 1977.
31. Яненко Н.Н., Рынков А.Д. Модульная структура алгоритмов и программ в задачах механики
сплошной среды и структура ЭВМ // Числ. методы механики сплош. среды. 1981. Т. 12, №4.
С. 64-73.
32. Дзержинский Ф.Л., Тер-Сааков AM. Технология программирования - структурный подход.
1978.
33. Каляев А.В. Многопроцессорные системы с распределенной памятью универсальной
коммутацией и программируемой структурой // Электрон, моделирование. 1979. № 1. С. .7-34.
34. Евреинов Э.В., Хорошевский В.Г. Однородные вычислительные системы. Новосибирск: Наука,
1978.
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ МОДУЛЬНОГО АНАЛИЗА
И ПАРАЛЛЕЛЬНОГО ПРОГРАММИРОВАНИЯ
ДЛЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
И МЕХАНИКИ СПЛОШНОЙ СРЕДЫ*
Математические и технологические проблемы создания пакетов прикладных
программ классов задач приобрели в настоящее время особое значение. Не касаясь
здесь всех аспектов этих проблем (достаточно полное изложение идей и взглядов
авторов на эти проблемы можно найти в [1—6]), остановимся на вопросе организации
параллельных вычислений в алгоритмах математической физики и механики сплошной
среды. Этот вопрос приобрел сейчас принципиальное значение.
Рассмотрим идеальную в каком-то смысле ситуацию, когда в технологической
цепочке современной вычислительной математики [3, 4] континуальная
физико-математическая модель рассматриваемого класса явлений известна и неизменна. Как правило,
численные алгоритмы являются дискретными аппроксимациями континуальных
моделей и вносят малые параметры г = At, h ={ ht\. Численный алгоритм является
отображением континуального процесса математической физики в дискретный процесс. В свою
очередь программа отображает этот дискретный процесс в процесс смены дискретных
состояний ЭВМ. В целом эта цепочка отображений представляет итог достижений
современного естествознания в области физики, математики, техники.
♦Современные проблемы мат. физики и вычисл. математики. Новосибирск: Наука, 1982. С. 200-
207. (Соавтор А.Н. Коновалов.)
309

Не будем здесь останавливаться на алгоритмах, связанных с аналоговыми ЭВМ,
а также на ко эффштентно-дискретных алгоритмах, связанных с представлением
функции в виде конечного отрезка бесконечного ряда. Рассмотрим алгоритмы,
являющиеся дискретной аппроксимацией континуальной модели механики сплошной
среды (законы сохранения механики сплошной среды) и опирающиеся на
пространственно-временную сетку: четырехмерную или семимерную (уравнение Больцмана).
Если в случае уравнения Больцмана в каждой точке (ячейке) семимерной сетки
подлежит определению одна неизвестная скалярная функция - функция распределения,
то в случае уравнений механики сплошной среды в каждой точке четырехмерной сетки
подлежат определению, как минимум, пять величин: плотность, внутренняя энергия,
три компоненты вектора скорости. При усложненных физико-математических моделях
число определяемых величин увеличивается и может достигать внушиительной цифры
в несколько десятков (простейший тому пример — многофазные течения). Поэтому
если даже совершенно условно принять, что рассматриваются явления, для полного
описания которых достаточно 102 временных шагов, а требуемая точность вычислений
гарантируется при том же числе пространственных точек по каждому направлению,
то при решении подобной дискретной задачи ЭВМ должна переработать 109-1010
чисел. И это лишь в случае одного варианта смешанной задачи Коши для уравнений
механики сплошной среды! Применение экономичных методов (напомним, что метод
называется экономичным, если число арифметических действий для нахождения одного
неизвестного не зависит или слабо зависит от общего числа неизвестных) при
фактическом решении подобной дискретной задачи требует порядка 1011—1012 операций
на ЭВМ.
Неудивительно, что для решения сложных пространственных задач аэродинамики,
таких, например, как обтекание трехмерных тел потоком в широком диапазоне
изменения числа Маха и с детальным учетом структуры потока (ламинарный, переходный,
турбулентный участки), по расчетам американских специалистов (см. также [7]),
требуются ЭВМ с быстродействием порядка 1010 оп/с. Ныне всеобщее мнение
заключается в том, что проблема повышения быстродействия ЭВМ должна решаться путем
использования параллельно действующих компьютеров (процессоров).
Построение пакета программ для класса задач начинается с модульного анализа ,
вычислительного алгоритма. Если вычислительные алгоритмы решения класса задач
построены на методах расщепления по физическим процессам и пространственным
переменным, то решение каждой исходной задачи из рассматриваемого класса
сводится к последовательному решению более простых задач. Программная реализация
простой задачи и есть модуль в смысле определений из [1-6].
Последовательное по времени решение в ЭВМ простых задач связано не с
модульной декомбинацией алгоритма и программы, а с последовательной структурой
современных ЭВМ. Модульная декомпозиция алгоритма существенно облегчает его
распараллеливание. Хорошо модульно представленный алгоритм почти автоматически
параллелизуется. Ранее, в 1965 г., Г.И. Марчуком и Н.Н. Яненко было указано на
возможность параллельной реализации неявных схем расщепления. Это высказывание
было повторено Д. Дугласом в дискуссии по большим компьютерам. Модульный анализ
и распараллеливание явных схем довольно очевидны [7], и это составляет их известное
преимущество. Мы покажем На простых примерах, как можно параллелизовать
употребляемые в современных вычислениях алгоритмы расщепления и прогонки.
Рассмотрим смешанную задачу Коши для уравнения теплопроводности:
Ъи 2 Э / Ъи \
— = Л - (ат(М) - ),ат(М)>0,
bt m = l Ъхт \ . 0Хт /
и(М,0) = <р(М), MeD, и(М\ Т)=ф(М*, г), ^е7^ (1)
Ддя упрощения дальнейших рассуждений положим D = {0 < хт < 1\ , тогда у = D - D.
310

Пусть далее г > О, Nmhm = 1 (относительно других неразъясняемых обозначений, см.
[8]). Для решения задачи (1) применим неявную схему расщепления с весами.
Переход от utl к ип+1 в этой схеме совершается в два этапа. На первом этапе при
каждом фиксированном/ = 1,2, ...,jV2 - 1 определяется ип.У/г :
(Е-таЛх)ип+*'■ =(Е^трАг)и1г <* + 0= 1, <х,0>О. (2)
К (2) следует добавить краевые условия, например,
""^О.!-^-^)*"1. (3)
На втором этапе при каждом фиксированном г = 1,..., Nt - 1, и"+ г определяется
(Е - гуЛ2)и£+1 = (Е + тдА2)и1+У2 , т + 8 = 1, % 8 > 0. (4)
К (4) добавляются краевые условия
«" + 1l,ro.i-*"+1- (5)
Кроме того, по определению, и0.. = <р°.
Если при проведении этапа (2) мы предпишем хранение массива ип.. по строкам
(/ = const), а при проведении этапа (4) — хранение массива и"+Уг по столбцам (7 =
= const), то становится совершенно очевидной возможность распараллеливания
неявного алгоритма (2) —(5) на каждом из этапов (2), (4). Примерно та же
ситуация возникает, если для решения задачи (1) применяются другие схемы переменных
направлений: схема стабилизирующей поправки, схема универсального алгоритма
[8,9].
Укажем на характерную особенность схемы расщепления, выгодно выделяющую
ее из других вариантов метода дробных шагов (метод стабилизирующей поправки,
метод продольно-поперечной прогонки и др.). В двухслойной схеме расщепления
(2) —(5) при решении каждой f-й одномерной задачи привлекается только один
одномерный массив индекса с предыдущего временного слоя. В то же время в друг.их
методах привлекается большее число массивов и, следовательно, структура
соответствующего программного модуля усложняется, равно как и межмодульный интерфейс.
Таким образом, схема расщепления сводится к полной декомпозиции обобщенного
алгоритма, включая переброски массивов. Модуль стыковки сводится к
транспонированию матрицы двумерного массива. Ситуация переносится на многомерный случай
на схему универсального алгоритма, построенного на основе схемы расщепления.
Итак, алгоритмы метода дробных шагов, алгебраически эквивалентные [9], становятся
алгоритмически и программно неэквивалентными. Схема расщепления является
максимально экономичной в смысле программного исполнения в классе алгебраически
эквивалентных схем.
Существует принципиальная возможность организации параллельных вычислений
и на уровне каждой фиксированной одномерной задачи типа (2), (4). Решение каждой
из одномерных задач типа (2), (4) находится методом прогонки. При изложении
этого вопроса мы в основном следуем [10]. Перепишем задачу типа (2), (4) в таком
виде:
Ai// = //f u0=a, uN = b, i= 1,2,...,ЛГ- 1. (6)
Наряду с (6) рассмотрим следующие задачи:
Ли,—0, Мо = 1, uN= 0;
Ли,-= 0, и0 = 0, uN= 1;
(7)
(8)
(9)
311

Пусть и10 — решение задачи (7), и01 - решение задачи (8), и00 - решение задачи
(9) и и - решение задачи (6). Тогда (принцип суперпозиции)
и = аи10 +bu0l +и00. (10)
Пусть теперь 0 < ix < ... < ik <N — узлы распараллеливания, ат _ г = uim, т = 1, ..., к —
значения искомого решения задачи (6) в узлах распараллеливания, ит — решение
исходной задачи на подынтервале (im _ х, im ). Тогда по принципу суперпозиции
Запишем разностное уравнение (6) для узла imy а для значений (ит). ■ ,
1гп *
(ww + 1). , воспользуемся (10'). Тогда для определения ат будем иметь
Ат<Хт-1+Втат+Стат + 1 = Фт,
ао=а, uk = b. (11)
Если, например, задача (6) записана в индексной форме
Ajut_! + BfUi + С{щ+ г = fu
то
Am=Aim(uTo)im_1, Сга=Сга«+1)(и+1,
Фт=/. +А. (ит0). -С, (^o+I), + 1-
Можно показать, что, как правило, условия устойчивости задачи (6) являются
достаточными и для устойчивости задачи (11). В этом смысле предлагаемый алгоритм
распараллеливания прогонки является устойчивым. Существенно, что задача (11) того же
типа, что и задачи (6) — (9).
Алгоритм распараллеливания задачи (6) заключается в следующем. На р-параллель-
ных процессорах для каждого подынтервала решаются задачи (7) —(9). Затем решается
задача (11), после чего, опять-таки на р-параллельных процессорах, решаются задачи
Лм,- = //, im<i<im+i, ™=1,.., К
Щт = *т„и »im+1=<*m- (12)
Вместо решения задач (12) можно просто воспользоваться представлением (10').
Простой подсчет показывает, что указанный алгоритм распараллеливания выгоден уже
прир>4.
Распараллеливание алгоритма допускают и неявные методы бегущего счета, столь
часто применяемые в задачах газовой динамики [11]. Здесь для простоты изложения
мы ограничимся акустическим приближением. Рассмотрим смешанную задачу Коши
для уравнений акустики
bu/bt - а2 bv/Ьх = 0, bv/bt - Ъи/Ъх = 0, а = const > О,
w(jc, 0) = </>(х), ц(х,0) =i//(x), 0<*<1,. *
K(0,f) = Ml(0, ы(1,г) = д2(0, Г>0. (13)
312

Переход к инвариантам
r-u-av, s = u+av (14)
дает
Ъг/Ъг +аЪг/дх = 0, ds/bt - ads/Ъх = О,
г(х90}=ч)(х)-аф(х)9 5(х90) = ф) + аф(х), ,15)
r(0,f) + s.(0,./)=?Mi(r), г(1,г) + «(1,0=2д2(0.
Неявная схема бегущего счета для задачи (15) выглядит следующим образом:
ОТ1 - >?)/' +fl(^+1 -rt\ )/*=°>(<+1 - <)/r -*(d! - 5Г+1)/Л = °>
>f = Vi - a$u *? = W + e^i, (16)
Из (16) имеем
Определение r?+1 происходит слева направо в порядке возрастания индекса i,
определение s?+1 — справа налево в порядке убывания индекса /. Основная проблема при
реализации алгоритма (17) заключается в том, что при i = О, N9 сами значения r%+1,
s^+1 не заданы, а заданы некоторые комбинации инвариантов. Для удовлетворения
краевых условий применяются различные способы, например определяются r0, sN
по явным формулам с последующим пересчетом и линейной интерполяцией [11] и т.п.
Эти способы не очень удобны для распараллеливания алгоритма бегущего счета.
Поэтому здесь мы предварительно изложим такой способ удовлетворения краевым
условиям в алгоритме бегущего счета, при котором распараллеливание допускается
достаточно просто.
Из (17) имеем
где
Л = к/(1+к); 5= 1/(1+к);
c"N = B[(A)N- V? +(A)N-2r? + ... *А^_Х +/£];
irN=B[(A)N-1snN_l+(A)N-2s"N_2 + ...+As'i+sZ].
К (18) добавим краевые условия
■j8+1+rg+1=2/i7+1f 5^+1+^+1=2мГ1. (19)
Из (18), (19) через известные величины однозначно (это гарантируется условием
А< 1) определяютсяr%+1, *£+1> и задача (16) распадается на две независимые задачи:
313

#1 = (Am^-^+Db-ivr1 . (20)
(A)2N-1
(Л)лг(2МГ1-^) + 4-2мГ1
s"+1 = - - . (21)
N (A)2N-\
Алгоритм бегущего счета распараллелен, ибо каждую из задач (20), (21) можно
считать независимо. Более того, можно распараллелить и каждую из задач (20), (21),
Например, для задачи (20) в узлах распараллеливания im имеем
r"+1 =(А)1т - - + cf ,
lm v (A)2N - 1 т
и на каждом из интегралов распараллеливания (/w, im+i) r"+l может определяться
независимо.
Нетрудно понять, что предложенный здесь алгоритм распараллеливания неявных схем
бегущего счета может применяться и при других краевых условиях, чем в (13).
Отметим также, что алгоритмы бегущего счета в виде (20), (21) рассматривались в [12]
при численном решении динамических задач теории упругости в
скоростях-напряжениях.
Приведем еще один пример неявного экономичного алгоритма, допускающего
распараллеливание. Рассмотрим двумерную задачу Дирихле для уравнения Лапласа
Дм = 0, мед u\y = g(M'l Afey. (22)
В качестве D выберем единичный квадрат, так что D = {0 < хп < 1}, у = D — D. Пусть,
далее, Nh = 1, и тогда
Ahuh=09 uheDh9 Ал = Лл+Л22, uh\yh=gh. (23)
Для нахождения uh применим итерационную схему из [8]
(F + co/^O^ + co^)^1 -^)/г-ДЛ^ = 0,
где
Л,/= А.-1 (/_+/_ ); R2f=-h-1(fx +fx);
к — номер итерации; Ef = f, а итерационные параметры со, г выбираются в соответствии
с общей теорией сходимости из [8].
Определение и*+1 из (24) осуществляется следующим образом. По ик, определяется
Zh '
(£ + co*o4+1=V£> (25)
затем
(E + b>R2)vkh+l=zkh+l (26)
и, наконец,
М^+1=4+гУ*+1. (27)
314

Одним из способов распараллеливания первого этапа (25) является следующий: из
(25) определяем z?l\ после этого возможно независимое определение zn+l (/ = 2,....,
N - I) и z"jl (j = 2, ..., N - 1); далее можно определить z"2* и затем независимо z"2+1
(1 = 3, ..., N - 1) и z"*1 (/•= 3, -., ^ - 1) и т.д. На втором этапе (26) аналогичное
распараллеливание заключается в расчете v^ N_x из (26), затем в независимом
определении '1$+1_х (/ = W-2, ..., 1) и^+_11,/(/ = ^-2,..., 1) и. ак далее. Третий этап (27)
допускает любое распараллеливание. Заметим, что экономичная схема типа (24),
например шахматная схема В.К. Саульева, может применяться и для расчета смешанной
задачи Копти для уравнения теплопроводности, однако аппроксимация в этом случае
будет иметь условный характер.
Заметим, что получивший в последнее время известность метод подконструкций
(Аргирис и др.), а также метод решения сеточных уравнений на графах [13—15]
допускают распараллеливание.
Эффективность экономичных неявных схем, основанных на методах расщепления,
в настоящее время не вызывает сомнений. В сложных задачах механики сплошной
среды эти схемы находят все большее применение. Эта тенденция не меняется и с
появлением более мощных (по быстродействию и памяти) ЭВМ. Однако появление ЭВМ
с параллельными процессорами или даже появление проектов таких ЭВМ не могло
не вызвать стремления к сравнительному анализу эффективности явных и неявных
схем для таких машин. Появились, например, утверждения [7] о том, что наличие
ЭВМ с параллельными процессорами делает неявные схемы малоэффективными в силу
невозможности их распараллеливания. Приведенный выше анализ достаточно
типичных неявных схем показывает, что это не так и что распараллеливание возможно и для
неявных схем. Следовательно, и для ЭВМ с параллельными процессорами в
приведенных примерах сохраняется эффективность неявных схем по сравнению с явными.
Однако в целом вопрос о возможности распараллеливания вычислительных
алгоритмов для задач механики сплошной среды становится в повестку дня современной
вычислительной математики. И к вычислительному алгоритму наряду с обычными
требованиями, такими, как точность, устойчивость, экономичность, следует уже сейчас
предъявлять и требование параллелизуемости, т.е. возможности распараллеливания
вычислительного алгоритма.
ЛИТЕРАТУРА
1. Коновалов А.Н., Яненко Н.Н Модульный принцип построения программы как основа создания
пакета прикладных программ решения задач механики сплошной среды // Комплексы программ
математической физики. Новосибирск, 1972. С. 48-54.
2. Коновалов А.Н. Модульный анализ вычислительного алгоритма в задаче планового вытеснения
нефти водой // Тр. III семинара по комплексам программ мат. физики. Новосибирск, 1973.
С. 81-94.
3. Яненко Н.Н, Коновалов А.Н. Технологические аспекты численных методов математической
физики // Acta Univ. carol. Math. Phys. 1974. N 1. P. 47-53.
А.Коновалов А.Н. О принципах построения пакета программ для решения задач математической
физики // Acta Politechn. Pi. CVUTV. 1975. Vol. 4. P. 37-49.
5. Коновалов А.Н., Каршчук В.И. О пакете прикладных программ математической физики //
Структура и организация пакетов программ: Междунар. конф. (Тез. докл.). Тбилиси: Мецние-
реба, 1976. С. 51-52.
6. Яненко Н.Н, Карначук В.И., Коновалов А.Н. Проблемы математической технологии // Числ.
методы механики сплош. среды. 1977. Т. 8, № 3. С. 129-157.
7. Сафронов И.Д. Оценка параметров вычислительной машины, предназначенной для решения
задач механики сплошной среды // Там же. 1975. Т. 6, № 3. С. 98-147.
8. Самарский АЛ. Введение в теорию разностных схем. М.: Наука, 1971. 552 с.
9. Яненко НН. Метод дробных шагов решения многомерных задач математической физики.
Новосибирск: Наука, 1966. 225 с.
315

10. Яненко Н.Н., Коновалов А.Н., Бугров A.M., Шустов Г.В. Об организации параллельных
вычислений и "распара ллелизации" прогонки // Числ. методы механики сплош. среды. 1978. Т. 9, № 7.
С. 139-146.
11. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М.: Наука, 1968. 592 с.
12. Горский И.М., Коновалов А.Н. О разностных методах решения динамических задач теории
упругости // Тр. III Всесоюз. конф, по числ. методам решения задач теории упругости и пластичности.
Новосибирск, 1974. Ч. 1. С. 68-84.
13. Воеводин А.Ф. О применении метода прогонки для численного интегрирования гиперболических
уравнений, определенных на комплексе // Динамика сплошной среды. Новосибирск: Наука,
1969. Вып. 3. С. 91-110.
14. Воеводин А.Ф. Метод прогонки для разностных уравнений, определенных на комплексе // Журн.
вычисл. математики и мат. физики. 1973. Т. 13, № 2. С. 494-497.
15. Фрязинов И.В. Алгоритм решения разностных задач на графах //Там же. 1970. Т. 10, № 2. С. 474-
477.

УРАВНЕНИЯ СОСТОЯНИЯ ВЕЩЕСТВА
АСИМПТОТИЧЕСКИЕ И ПРИБЛИЖЕННЫЕ ФОРМУЛЫ
ДЛЯ ДАВЛЕНИЯ И ВНУТРЕННЕЙ ЭНЕРГИИ ВЕЩЕСТВА
В ОБОБЩЕННОЙ МОДЕЛИ АТОМА ТОМАСА-ФЕРМИ*
ВВЕДЕНИЕ
Задачей настоящей работы является получение асимптотических и приближенных
выражений для давления и внутренней энергии одноатомного вещества на основе
обобщенной модели атома Томаса—Ферми [1]. Как известно, термодинамическое
состояние вещества определяется двумя термодинамическими параметрами, например
плотностью р и температурой Т.
Остальные параметры, в частности внутренняя энергия 1 см3 вещества Е и
давление Р9 являются функциями от р и Т
Е = Е(р,Т)9 (В.1)
Р = Р(:Р,Т). (В.2)
Соотношения (В.1), (В.2) называются уравнениями состояния.
В случае идеального одноатомного газа, подчиняющегося статистике Больцмана
(невырожденный газ), уравнения состояния имеют простой вид
Е=3/г—ркТ9 (В.З)
А
P=(N/A)pkT9 (B.4)
где Аг = 6,023 • 1023 — число Авогадро, к = 1,38 • 1СГ16 эрг/град — постоянная
Больцмана, Т — определяется в градусах по абсолютной шкале.
В частности, справедливо соотношение вириала
Е=3/2Р. (В.5)
В случае идеального нерелятивистского газа, подчиняющегося статистике
Бозе—Эйнштейна или статистике Ферми— Дирака (вырожденный газ), выражения (В.З), (В.4)
усложняются, но соотношение вириала (В.5) остается в силе1.
При определении энергии и давления одноатомного газа следует учитывать не только
энергию и давление ядер, но также и соответствующий вклад электронов атома.
Статистическая модель атома Томаса—Ферми позволяет приближенно оценить этот вклад
электронов в общую энергию и получить уточненные уравнения состояния.
В настоящей работе дается асимптотическое исследование уравнений состояния,
основанных на обобщенной модели атома Томаса—Ферми, а также получаются
приближенные выражения для Е и Р. Результаты настоящей работы были получены в 1952 г.
и доложены на семинаре математического сектора ГеоФИАН СССР, руководимого
членом-корреспондентом АН СССР профессором А.Н. Тихоновым.
Автор выражает благодарность за ряд критических замечаний, высказанных при
обсуждении этой работы на семинаре, руководителю семинара профессору А.Н.
Тихонову и членам семинара А.А. Самарскому, В.Я. Гольдину и Б.Л. Рождественскому.
♦Сборник научных работ кафедры математики. М.: Атомиздат, 1958. С. 144-195.
*Если скорости частиц газа сравнимы со скоростью света (релятивистский газ), то соотношение
(В.5) теряет силу.
317

1. СТАТИСТИЧЕСКАЯ МОДЕЛЬ АТОМА ТОМАСА-ФЕРМИ
1. Задача о распределении электронов в поле ядра в атоме представляет собой весьма
сложную задачу квантовой теории атома, не решенную полностью и до сих пор.
Различные приближения квантово-механической модели атома делались неоднократно.
Исторически первым и наиболее простым приближением является статистическая
модель атома Томаса—Ферми, выдвинутая в работах [1,2] и дающая, несмотря на
свою простоту, хорошие результаты во многих применениях. В основе этой модели
лежат следующие предположения:
1). Атом, т.е. система ядро + Z электронов, рассматривается как электрически
нейтральная система, заключенная в некоторый объем ("ячейку" или элементарный
полиэдр). Ячейка является конечной в случае атома, находящегося в веществе
конечной плотности, и бесконечной в случае вещества нулевой плотности (свободный атом).
Из соображений симметрии следует, что потенциал V электростатического поля,
создаваемого атомами в веществе, становится стационарным на границе ячейки, т.е.
дУ/Ъг^О (1.1)
на границе атома. Это и является выражением нейтральности атома.
2). Совокупность электронов в атоме-ячейке рассматривается как электронный
газ, находящийся в поле ядра и поле электронных зарядов. Распределение электронов
по скоростям в каждом элементе объема атомной ячейки удовлетворяет статистике
Ферми, что означает, что в одном квантовом состоянии находятся максимум два
электрона (различающихся спинами). Электронный газ считается находящимся в
термодинамическом равновесии. Отсюда, в частности, вытекает, что химический
потенциал электронного газа постоянен в атоме.
3). Потенциал поля зарядов атома удовлетворяет уравнению Пуассона
А¥=4тгре-е. (1.2)
Здесь е — заряд электрона, ре — объемная плотность электронных зарядов, которая
нормируется по числу Z электронов в атоме:
fpedV = Z9 (1.3)
где интегрирование производится по объему атома.
Потенциал зарядов атома имеет в центре атома особенность вида
Zjr. (1.4)
4). Электронный газ атома рассматривается как газ при нулевой температуре, т.е.
низшие квантовые уровни полностью заняты.
Исходя из этого Томас и Ферми получили соотношение между объемной плотностью
электронов ре и потенциальной энергией е • V. Если обозначить через Е0
максимальную полную энергию электрона (из условия термодинамического равновесия следует,
что Е0 одна и та же во всех точках) и через eV его потенциальную энергию, то должны
иметь место соотношения
Pmaxl2m-eV = E09 (1.5)
гдертах (максимальный импульс электрона) связан с ре соотношением
(8тг/3/|3)*4ах=ре, (1.6)
которое означает, что все нижние уровни заняты и что фазовый объем радиусом pmSLX
полностью заполнен.
Отсюда получается соотношение между ре и V
pe = (8ir/3h3)[2m(E0+eV)]3/2. (1.7)
Теперь из (1.2), (1.7) получаем для V следующее уравнение (в предположении сфери-
318

ческой симметрии):
1 d2{Vr) 32тг2е 3/
АК=- ~^- =—-г [2m(E0+eV)]^ (1.8)
г dr ЗА
с краевыми условиями
Vr^Ze, г-* О, (1.9)
ЭК/Эг = 0, г = г0, (ЫО)
где г0 — радиус атома.
Подход Томаса—Ферми был с успехом применен к различным проблемам атомной
физики и, в частности, для нахождения уравнений состояния вещества.
В 1949 г. в работе [3] метод Томаса—Ферми был обобщен на случай произвольной
температуры. Предположение 1)—3) оставались в силе, предположение 4) было
отброшено. Электронный газ рассматривался как находящийся при определенной
температуре Г, которая в силу предположения о термодинамическом равновесии была
постоянна в атоме и равнялась температуре ядерного газа.
В этих предположениях, в соответствии со статистикой Ферми—Дирака, вероятность
заполнения состояния с импульсом р, а отсюда и с энергией р2 /2m - eV, равна
Г / p2/2m-eV YI1
[l+cxp( ^ +,)] , (1.11)
где ц - —цкТ — химический потенциал электронного газа, V — потенциал поля зарядов
в атоме.
Исходя из того, что число возможных состояний для электрона с импульсом р равно
(2/h3)4<np2dp9 (1.12)
для ре получаем выражение
°° Snp2dp/h3 4тг з/ /eV \
Ре = / . ,„2/_, _„ ч = — (2ткТ)Ъ iJ— -п\ ^ (1.13)
\ А3
V)
о /p2/2m-eV ч иЪ
1+ехр("Тг
где
«> xkdx
^'iT^Ti- (114)
Подставляя выражение для ре в уравнение Пуассона
1 d2(Vr)
AV= ~-~=47Г^-е> (1.15)
г dr
получаем уравнение
1 d2(Vr) 16тг2
г
dr2
"45-')
e(2mkT)V2 М —-*?) (1Л6>
с краевыми условиями
bV/dr = 0 при г = а9 (1.17)
где а — радиус атома,
Vr~*Ze при г->0. (Ы8)
319

Радиус атома а, точнее радиус атомной ячейки, определяется из соотношения
/4 6,023-1023 V* , ч
где р — плотность вещества, А — его атомный вес.
Соотношение (1.19) выражает отсутствие "межатомных" промежутков. V —
нормируется условием
F(e) = 0 (1.20)
(потенциал равен нулю на границе).
Для удобства аналитического исследования и численных расчетов можно перейти
к новым переменным, взяв за единицу длины
Г h3 /1*
C~[32ir2e2m(2mkTf2l
и введя в качестве независимой переменной
s = r/c (1.22)
и в качестве неизвестной функции
p=[eV/kT-n] -s. . (1.23)
Тогда уравнения (1Л6), (1.17), (1.18) примут вид
J3 = |За при 5 = 0, dp/ds = 0/s при s = b9 (l .25)
где
Po=Ze1/ckT=clfT*:9 (1.26)
и а 1 (А N \-*/з _ 7*/4 / С2 уь
с с \3 А / р1/3 \pj3b ' '
4тге3(2т)3/4
ci = уЭ| уЭ|- Z> с* =Ci?L О-27)
d2p/ds2=slvtf/s)9 (1.24)
47r(2w)3/4eA:^
<2== ^^~
/4 Ч-'/з ,
I-ttTVJ Л+1/з.
2. Следуя [3], рассмотрим теперь, как выражаются термодинамические параметры
вещества: внутренняя энергия 1 см3 вещества/Г, давление Р, энтропия 1 г вещества S,
свободная энергия 1 г вещества F в функции от электронной плотности ре.
Введем обозначения: Ve(r) — потенциал поля электронов в точке г, VN(r) —
потенциал поля ядра в точке г, V(r) — потенциал поля зарядов атома в точке г, Ек(г) —
объемная плотность кинетической энергии электронного газа в точке г, Р(г) —
давление электронного газа в точке г, Еее — потенциальная энергия взаимодействия
электронов атома, EeN — потенциальная энергия электронов атома в поле ядра или, что то же
самое, потенциальная энергия ядра в поле электронов, Ер — потенциальная энергия
зарядов атома, Ек — кинетическая энергия электронов атома, Et — полная энергия
зарядов в атоме (в координатной системе, связанной с ядром), Se — энтропия
электронного газа атома, Fe — свободная энергия электронного газа атома, v = 4тга3 /3 —
объем атома.
Тогда справедливы следующие соотношения:
VN = Ze/r, (1.28)
V=Ve + VN=Ve+Ze/r, (1.29)
320

Ep=Eee+EeN> (1.30)
1 a
Eee = - -ef peVedT, dT = 47rr2dr, (1.31)
2 о
EeN=-ef PeVNdr, (1.32)
о
b
EeN = - ZkT- f /y2 (fi/s) sds. (1.33)
о
Соотношение (1.33) следует из (1.28)—(1.32) после перехода к новым
переменным с помощью соотношений (1.21) — (1.27)
-ef p€VdT = 2Eee+EeN. (1.34)
о
Соотношение (1.34) следует из (1.29)-(1.32)
Соотношение (1.35) следует из (1.21)—(1.27)
а Ъ Й
f (eV + n)pedT = ZkTf —IvA-)sds. (1.35)
/ (eV + n)pedT= -2Еее -EeN +Z -ц=-2Ер +EeN +Z . д. (1.36)
о
Соотношение (1.36) следует из (1.3) и (1.34)
Ер = -3/2ZkT.M9 (1.37)
где
M-i[f*-№+|)'*-'.
(1.38)
Соотношение (1.37) следует из (1.33), (1.35) и (1.36)
Ек (г) = / _^J ' F F/ , (1.40)
о 1 + exp ((р2/2т - eV)/kT+r])
(p2/3m)S7Tp2dp/h5
P(r)=f — ——— . (1.41)
о 1 +exp((p2/2m-eV)/kT + r))
Соотношения (1.40), (1.41) следуют из кинетической теории идеальных газов,
подчиняющихся статистике Ферми-Дирака. После перехода к переменным j3, s (см.
(1.21)—(1.27) ) получаем выражение
4ir(2mkT)5/2'. / 0 \
*.«-"'''«--15р-Ы7)- (Ы2>
в 3
EK=f EK(r)dr= - ZkT-J, (1.43)
о 2
где
/=1 дГо'Мт)'*" (L44)
П.Зак. 953 321

Объединяя формулы (1,37), (1.44), получаем выражение для Et:
Et=3!2ZkT.e9 (1.45)
где
e=j-M. (1.46)
Давление Р вещества определяется как давление электронного газа на границе атома.
Так как на границе V(r) = 0, то из (1.41), (1.42) имеем
p.v = ZkT-L9 (1.47)
где
2 Ъъ
*-?-А„« 048)
Докажем теперь, что нейтральность атомной ячейки (Зи/Эг = 0, г = а) имеет другую
эквивалентную формулировку
fpedT = Z,
т.е. чго условие (1.3) вытекает из уравнения Пуассона (1.8) для V(f) и краевых
условий (1.9), (1.10).
Переходя к переменным 0, s, преобразуем (1.3) к виду
0о=/ s2IV2W/s)ds. (1.49)
о
Принимая во внимание уравнение (1.24) и краевые условия (1.25) и интегрируя по
частям, имеем
ъ /0 \ * d2$ ь d& dp ' b
f s2Iu - \ds= fs —— ds = f sd — = s —
о \ s J о dsz о ds ds
ь dp /dpy
"' T = Чт~ -0o+0o=0o-
о ds \ds I b
Соотношение (1.49) доказано.
Из уравнения (1.24) сразу же следует
о \ « / \ds ) b \ds / о \ds J о
Выведем теперь соотношение вириала. Докажем предварительно ряд соотношений:
*(£■)''■-^-'«'(т)'* <151)
Соотношение (1.51) получается интегрированием по частям с последующей заменой
d2p/ds2 на s/jiCP/s)
F(S) = /s— Lh (:-)*=- — • (1-52)
ds \ s i 2 \ ds I
Соотношение (1.52) следует непосредственно из (1.24)
T'f 4l)*4NfV/M*(lH- (153)
Соотношение (1.53) получается интегрированием по частям с помощью соотноше-
322

ний (1.51), (1.52) и краевых условий (1.25)
ь dQ ( Р\ ь 1 /dp \2 \b 1 b /dfi \2
2-\Л/ь 2 \ds) о 2° ^s' 2L \ <fc /
+ i/%/1/2(-)s^|.
Принимая во внимание соотношение /^(т?) = klk_1(ri) (см. разд. 2, п. 1) и
предыдущие тождества, можно вывести соотношение вириала.
Рассмотрим интеграл
fs2I3/2(P/s)ds.
о
Интегрируя по частям, имеем
ь /R \ 1 ь (В \ dQ 1 ъ ( Р \
f s2I3/J- )*=V3 b3I3/2(f) - - f s2Iv\-) —ds+-f sIvA-)pds.
о \ s / 2 о \s ' ds 2o 4/
Принимая во внимание соотношения (1.53) и (1.50), получаем
Сопоставляя (1.38), (1.44), (1.48), имеем
/=2, + *Ш (1.55)
или, принимая во внимание (1.37), (1.43), (1.47)
EK^3/2Pv=~1/2Ep. (1.56)
Равенство (1.56) представляет собой соотношение вириала.
Заметим, что в каждой точке г соотношение вириала для электронного газа имеет
вид
Ек(г)-2/3Р(г) = 0.
Выведем теперь выражение для энтропии2 электронного газа в атомной ячейке.
Как известно, химический потенциал ц выражается следующим образом:
Ц = (Е - TS + РК)частица = >
Ре
где Е(г) — полная энергия электронного газа в 1 см3 в точке г. Отсюда получаем
равенство
/ »pedr = / [E(f) - TS(r) + P(r)] dr = J h(r) - TS(r) + - EK(r)]dr =
oo о L 3 J
2 a
= E-TS+ - EK=nf pedr = ZkTf. (1.57)
3 о
2 Впервые это выражение получено Брахманом в [4], однако формула выведена сложным образом.
Мы даем упрощенный вывод.
323

a
Здесь Е = f E(r) dr. Ясно (см. (1.34) ), что
о
E = EK+2Eee+EeN. (1.58)
Отсюда (1.57) принимает вид
5/з #к + 2Ёее + EeN - ZkTf
Se= -L1-JS - — -. (1.59)
Это и есть искомое выражение для энтропии Se.
Для Fe получаем выражение
Fe=Et- TSe = - 2/з #к + ZkTf (1.60)
Fe = V3(EK-Po) + EeN+ZkTf9 (1.61)
или, пользуясь соотношением вириала
или
^е = 4/з(£к -Pu) + ZkT(dp/ds)0. (1.62)
Сделаем еще замечание о вырождении газа. Критерий вырождения электронного
газа в атомной ячейке в точке г = cs имеет вид (см. (1.11))
exp fa - eV/kT) = exp (-j3/s) < 1. (1.63)
Отсюда следует, что в окрестности начала газ всегда вырожден, если 0О Ф0.
Вблизи границы вырождение газа характеризуется величиной
exp(-j3/s)b = exp-/.
Если / — большое отрицательное, то газ на периферии атомной ячейки будет
невырожденным, т.е. близким к идеальному. В разд. 3 будет показано, что тогда и в
целом газ в атомной ячейке будет близким к идеальному, так как вклад окрестности
центра мал. Если/— положительное, то газ будет всюду вырожденным.
При расчете полной энергии и давления газа учитывается кинетическая энергия
и импульс ядерного газа. Так как ядерный газ является невырожденным, то для него
справедливы формулы идеального газа
En = 3/2(N/A)pkT9 (1.64)
Pn = (N/A)pkT9 (1.65)
где Еп, Рп указывают соответственно энергию и давление ядерного газа.
Объединяя формулы (1.45), (1.47), (1.64), (1.65), получаем выражение для Е и Р
Е= 2/з (N/A)ZpkT [в + 1/Z], (1.66)
Р = (N/A)ZpkT[L + 1/Z]. (1.67)
Формулы (1.66), (1.67) и представляют искомые уравнения состояния в
обобщенной теории Томаса—Ферми.
Главная задача состоит в определении функционалов L, J от электронной
плотности ре.
Задача эта неизбежно приводит к интегрированию уравнения (1.29) с краевыми
условиями (1.25) и последующему определению L, J.
В последующих разделах мы дадим асимптотическое исследование функционалов
L, / и на основании этого построим достаточно точные приближенные формулы для
Ей Р.
324

2. АСИМПТОТИЧЕСКИЕ СВОЙСТВА ФУНКЦИЙ
xkdx
о
1. Установим некоторые свойства 1к (у) :
1) функция Ik (у) определена для всех значений у в интервале —°° < у < °° и для
всех значений к в интервале — 1 < к < °°;
2) h (У) — монотонно возрастающая функция у в интервале —°° < у < °°;
3) Ik 0>) — монотонно возрастающая функция к в интервале -1 < к < °°;
4)4W = ^-iW.
Действительно, (2.1)
/*О0 =7iK*-;0**Acf *(*-;>) = -^—: >
о ех у + 1
h(y) = !Фу(х-у)хк<1х = -]\px(x-y)xkdx =
0 0
= -}хк(1ф(х-у) = -ф(х-у)хкГ +к]ф(х-у)хк~1с!х = к1к_г(у)9
о f о
что и требовалось доказать;
5)/оО0 -^ + 1п(1+*-*). (2.2)
2. Установим асимптотику 1к (у) при у -> — °°. Пусть —j> = я > 1. Тогда
/*О0 = 7-4^4 = Л/-^Ас = Ле*7е-***А: = Л*Т(* + 1), (2.3)
о е* + fl + 1 о е о
где А — число, близкое к единице: \А — 1\~ еу.
Таким образом, первый асимптотический член 1к (у) при у больших отрицательных
имеет вид
ЫУ) ~еуГ(к + 1). (2.4)
Отсюда, как следствие, имеем
h(y)lh - iO0 - Г(* + 1)/Г(*) = *, у ~> —. (2.5)
Заметим, что Ik (у) -* 0 тогда и только тогда, когда у -* —°°.
Перейдем теперь к асимптотике 1к(у) при^ больших положительных (jy > 1).
Рассмотрим предварительно некоторые соотношения и оценки.
3. Докажем в первую очередь, что
tk
Действительно,
„ ,fc m
' -ттт <*' < / -ft-: dt> m-W+i,-
J_p_ = /^g--r dt sJtme-t £ (_l)»e~«dr
у el + l у \ + e т у i = o
= 2 (-\y+1 ftme-stdt.. (2.7)
s = 1 у K '
325

Перестановка знаков / и S возможна в силу равномерной сходимости ряда
2 (-l)s + 1e~st на интервале у < t < °°
Jtme"stdt = ^гт/rwe-rdr, Л = ^s. (2.8)
У S l A
Интегрируя по частям, получаем
/ Tme-Tdr = е~А. Ат \\ + - + т(т - l)i- + ... + — ] =
л L А А2 АтУ
= e-ysymsmPm(l/ys). (2.9)
Отсюда
tmt>-stJt = *-^Z
m
ftme'sldt = e-**i- />m
( —) (2Л0)
/J_^= 2 (_i)» + i f_pm(_L (2.Ц)
Так как члены знакопеременного ряда (2.11) монотонно убывают по абсолютной
величине, то
/-^7 <е-^га(1) (2.12)
v ег + 1 ■ \v/.
Отсюда
t*dt
v € + 1
что и требовалось доказать.
4. Введем в рассмотрение функцию
Ф*(0 = Z (-l)^1^-. (2.13)
Ф^ (г) определена (в случае вещественных к) для к в интервале 0 < к < °°, так как
при таких значениях к ряд справа сходится равномерно по t в интервале от 0 до °°.
Следовательно, ряд Ф^ (г) можно интегрировать почленно. Интегрируя ФЛ(г),
получаем
/Ф*(Г)Л = /2(-l)*+1^rff = - S (-1)* + 1-^ = -Ф* + 1«.- (2.14)
Итак,
/ФИО* = -Ф* + i(0, ** + i(0= ~<М0- (215)
В частности, рассмотрим функцию Ф0(0
Ф0(Г) = £ (-1)* + l e~st = 1/(1 + е'). (2.16)
Последнее равенство справедливо при t > 0. Интегрируя равенство (2.16) в интервале
е < Г < °°, получим
* Заметим, что Ф^ (0) связана с функцией £ (к) Римана соотношением (2.17)
Ф*(0) = (1 - ~ТП^
326

*i(0 = -/Фо(0*/ d'
При этом проинтегрированное равенство справедливо при t в пределах 0 < t <°° в силу
равномерной сходимости ряда Ф\(?) в интервале О < t < °°.
И для Ofc (0 справедлива оценка
О < Фк(г) < е-', (2.18)
следующая из знакопеременности ряда и монотонного убывания его членов по величине.
5. Установим асимптотику интеграла
у (t + v)k
I+^flL-yLdt. (2.19)
о е< + 1
Пользуясь соотношениями п. 4, интеграл (2.19) можно представить в виде
о
Интегрируя последовательно по частям, получим
Ut+y)kd4>l(j) = -|(г+^)*Ф,(г)к - *J(r+^)*-^,(Odf} =
О . I О '
" -Н'+У)**^) + k(t+y)k-^2(t) + ... + /fc(fc-l)...(fr-m + 2)X
X</ +7)fc -m + *Фт(г) J\yo + k(k-l) ...(k-m + 1) J Фт0)(r +7)* ~ mdr, (2.20)
где m = [k + 1] есть целая часть числа &+ 1.
Оценим интеграл-остаток
f*m(t)(t+y)*-mdt = f ■%*&*, а = т-к>0,
о о (t+y)a
У ф (Л \ У 1 У 1 _ --.V *■ ' '
Итак, остаток имеет порядок 1/^а, а > 0.
Для того чтобы точно вычислить первый член остатка, нужно продолжить
интегрирование по частям. Тогда получим
f(t+y)k-^—t = - ((г+;и)*Ф1(0 + ... + *(*-!) ... (*-тя+2)(г+^)
о 1+ег I
>J|* - *(*-!) ... (к-т + 1)(г+у)к-тФт + 1(0\У0 +
fc - #И + 1
X
хфш(0
>>
+ *(*.-!) ... (*-1я)/(г+д/Г-|Я-1Фт+1(г)Л. (2.22)
327

Если отбросить часть порядка е у, которую дает подстановка верхнего предела, то
получим
f(t+y)k -^-7 = yk*i(0) + кук'1Фгф) + ... ■+ *(*-1) ...
о 1 + ет
... (к-т + 2)ук~т + 1Фт(0) + Rk(t), (2.23)
где Rk (г) имеет вид (с точностью до членов порядка е~у)
Rk(t) = к(к-1) ... (к-т + 1)ук -тФт(0) + к(к- \) ...
■^-^КФт:^!к- (2-24)
о (f+jO *
При этом интегральный член имеет порядок
1/ym + l-k = 1/у1 +в> (225)
первый член остатка имеет порядок
1/ут -к = 1[уа> а > о. (2.26)
Таким образом, асимптотическая часть интеграла
о 1 +ет
имеет вид
.у^Ф^О) + кук ~ 42(0) + ... + *(*- 1)... (k-m+2)yk ~т+1Фш(0), (2.27)
первый член остатка имеет вид
к{к-\) ... (*-/я + 1);и* "тФт + 1(0). (2.28)
6. Найдем асимптотическое выражение для интеграла
у {у - t)k ■ ч
/_ = / l% ; rff. (2.29)
о е г + 1
Применяя аналогично интегрирование по частям, получим
/_ = 1-(у-0кФг(г) + *Cv-r)*-42(r)+'... (-\)mk(k-\) ...
... (A:-m+2)(^-r)fc ~т + 1Фт(0 1 Г + (~l)w *(* - 1) ...
... (k-m + l)f(y-t)k -m<bm(t)dt. (2.30)
о
Дня того чтобы получить остаточный член, непосредственное интегрирование по частям
уже непригодно, так как получается расходящийся интеграл
}(y-t)k :m-^m + 1(t)dt. (2.3i)
о
Поэтому предварительно рассматриваем интеграл
/_ (е) - У J S (у - t)k " * Фт (t)dt, (2.32)
О
к которому уже можно применить интегрирование но частям.
При этом в получающемся интеграле меняем подынтегральное выражение так, чтобы
при переходе к пределу при е -* 0 получался сходящийся интеграл ("выгоняем" особен-
328

ность из-под знака интеграла). Выделенная особенность гасится особенностью
проинтегрированного выражения, давая конечную величину.
Выкладка выглядит следующим образом:
/-(е)=-
(y-tT
у-е
о
\. ayJ'*m.+ i(t)dt = Фт + ЛО
у-е
dt
*m+l(0
(7 - О"
Г" + Фт + 1О0(тЬг
у-е
О
(y-t)a + 1
= Ф>и-и(0) ~ Фт +lO) _ Фт+lQ-e) ~ Фщ + lOO +
уа еа
У~е Фт + 1(р - Фт + 1(У)
Переходя к пределу при е -* 0 , получим
/ (У - 0* -m*m«)dt = »т+1(Р)-»т*1(У) +
(233)
]Фт+1(»-ФT + i(y)dt>
так как
lim
Фт +lO) - ^m + lO;-<0
lime1 "аФ^ + 1Ы = 0.
(2.34)
(2.35)
Таким образом, получаем
о е +1 I
к - т + 1
Ф«(0
(2.36)
(2.37)
.+ (-1)т _1Л:(Л-1) ••• (Л: - т + 2)(j - 0
где остаток i? fc имеет вид
Я* = -(-1)т*(*-1) ••• (к-т + 1)ук~тФт(0\Уо +■
+ (-1)тк(к-1) ... (k-m + l)f Фт+ l(0 " *от+ + ff dt.
Учитывая, что члены, получающиеся от верхнего предела, имеют порядок е~у, можно
написать
/_ - укФ1(0) - кук ~1Ф2(0) + ... (-1)т~ 1к(к- 1) ...
... (к-т+2)ук 'т+1Фт(0) +Rk, (2.38)
где
Rk = i-l)mk(k~\) ... (к-т + 1)у* ~тФт(0) + (-lY"k(k-l) ...
■■■№ —.)/ «^'У"-1^*.
(2.39)
329

7. Дадим теперь асимптотическое выражение для интеграла
у хк
Iic(y) = / dx.
Преобразуем интеграл Ik (у) следующим образом:
o^'^ + l -у ег + 1 -у ег + 1
о е
+ / Ц^- (2.40)
У £ + 1
Из рассмотрений п. 3 следует
]^l)ldt = 0(e-y). (2.41)
у е + 1
* fr + V)*
Преобразуем интеграл / ч ■ i/f:
-у ег + 1
-у -у 1+е* к + 1 0 1+е* о 1 +е
vfc + *
= У _ + /+ _ /_ (2.42)
*+1
Используя формулы п. 5 и 6, получим
-у е* + 1 к + 1
где s - нечетные числа,
с, = 2кФ2(0),
с3 = 2*(*-1)(Л-2)Ф4(0), (2.43)
с, = 2*(*-1) ... (*^в + 1)Ф,+ 1(0),
а первый член остатка есть первый член ряда с отрицательной степенью .V.
В частном случае интеграла 1<&(у) имеем
Ы?)= V2 y'U + Ф2(0)у-у>. (2.44)
3. НЕКОТОРЫЕ АСИМПТОТИЧЕСКИЕ СООТНОШЕНИЯ ДЛЯ РЕШЕНИЙ
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ФЕРМИ-ДИРАКА
1. Рассмотрим дифференциальное уравнение второго порядка
d2fi/ds2 = sIV2(P/s)- (3.1)
Будем рассматривать решения уравнения (3.1), удовлетворяющие краевым условиям
Р = j30 при 5 = 0, (3.2а)
dp/ds = 0/s при s = b. (3.26)
Мы ставим себе задачей исследовать вид решений и некоторых функций от них при
330

следующих предельных случаях:
I. 0О -* 0 Ъ -* °°,
П. 0О = 0(1), b^O,
III. 0с
0,
IV. 0о = О(1), Z> "►<*>,
Заметим, что параметры 0О, -Ъ связаны с физическими параметрами р, Г
соотношениями (1.26) и (1.27)
0о = cx/fby
Рис. 1
I.
п.
III.
IV.
Р = 0(1)
Т = 0(1)
Р = 0(1)
Г = O(l)
Таким образом, случаи I, II, III и IV соответствуют следующим физическим
случаям:
Т -* ооэ
р -* °°,
Т -* О,
р -» 0.
Сделаем предварительно несколько общих замечаний. Из положительности функции
Iy2(P/s) вытекает,что
d2p/ds2 > 0. (3.3)
Интегральные кривые всюду обращены выпуклостью вниз и могут достигать своего
максимума только на границах.
Из (3.3) следует, кроме того, что d(3/ds всюду на промежутке (О, Ь) является
монотонно возрастающей функцией. Условия (3.2а) и (3.26) на границе s = Ъ имеют
следующий геометрический смысл: касательная к кривой в точке s = Ъ проходит через начало.
Таким образом, кривые 0(s) могут иметь примерно такой вид, как на рис. 1.
Отсюда легко следуют соотношения
0тах >Р> А (3.4а)
0О + fs > 0 > ft, (3.46)
0о +■
fb-t°s>P>fs,
(3.4в)
где
/ = (dp/ds)b = pb/b.
В силу монотонности функции /y2(0/s) имеем
/у2(0тахА) >/%(РД) >/%(/).
(3.5)
(3.6а)
331

Iу, (ft, /» + /) > 'и GV») >/%(/), (3-66)
'■л(0оЛ + / - А>/*) > /й(Р/«) > /%(/)• (з.бв)
Предполагая конечной производную dfi/ds при s = 0, можно придать краевому условию
(3.26) несколько иной вид.
Рассмотрим интеграл
/ s2 L/2(P/s)ds. (3.7)
О
Пользуясь уравнением (В. 1), получим
Ъг гг ($\j ? 2 d2p , *d$ dp
fs4r/2[^)ds = fs2—^ds = fsd-f-= s-f-
n V s * о ds о ds ds
b br dp , _ dp
— / —^-ds = s ——
Пользуясь краевым условием (3.26) и условием (dp/ds)0 Ф- -°°, приходим к формуле
/52/Л^Ц = 0о. (3.8)
Интегральное соотношение (3.8) является эквивалентом условия (3.26)
Из уравнения (3.1) сразу же следует
Ы>-'-($.-
Соотношения (3.8), (3.9) являются основными для дальнейших выкладок.
Геометрическая сущность аппроксимаций, применяемых в дальнейшем,
заключается в следующем: и в случае I и в случаях II, IV левый конец кривой Р = j3(s) является
либо фиксированным (случаи II, IV), либо стремится к точке 0 (случай I), правый же
конец устремляется в бесконечность или по оси 5 (I, IV случаи) или вверх (II случай).
Так как при этом касательная в правом конце все время проходит через начало, а
кривая обращена выпуклостью к касательной, то кривая асимптотически спрямляется,
и с большой степенью точности на большом промежутке можно заменить
Pis на (p/s)b
Правда, в окрестности начала p/s имеет крутой ход, однако на значении интеграла
'»(?)'
это существенно не сказывается, так как подынтегральная функция имеет в нуле
порядок SVl .
2. Рассмотрим первый предельный случай
j30 -> О, Ъ -> оо (ЗЛО)
Докажем в первую очередь, что
/ < 0, а следовательно, Рь < 0. (3.11)
Из соотношения (3.8) и из неравенств
p/s>ft ЫР/з)>Ы/) (ЗЛ2)
следует
Ро>1уг(Г)(Ь313); (3.13)
332

откуда, принимая во внимание (3.10), имеем
/%(0-*ОприР0-*0. (ЗЛ4>
Из замечания в конце п. 2 следует, что /< 0 при ft, достаточно малых.
Так как функция dfijds монотонно возрастающая, то из d(3/ds < 0 при s = Ъ
следует, что
dp/ds<0 для 0<s<Z>, (3.15)
т.е. фукнция ]3(s) будет монотонно убывать.
В частности,
00= Umax- (ЗЛ6)
Оценим интегралы
}lV2(-)sds и fIV2(-)s2ds. (3.17)
О \5 ' О XS '
Пользуясь неравенствами (3.4), (3.6), получаем
fhJ-)sds<fb/l(-+f)sds=ft //%(-+/ rrfr =
о \s / о ^s . ' о ч т '
= «//%(-+/)rdT + flg / /* -+/ rtfr, т=—. (3.18)
Имеет место очевидное при/< 0 неравенство
/%0/r+/)</y20/O прит>1. (3.19)
1У2 (1/г +/)</% (1 +Л =^/+1^ (3.20)
с близко к Г (3/2). Отсюда
fIy2[ — }sds<PlfIV2[-)TdT + ce1+fPl S rdr<
< 0S J/% (") rdr+C-e 1+f& < cfil (3.21)
о \r / 2
где ^ — некоторая константа.
Заметим, что интеграл
//1/2(-)rrfr (3.22)
сходится, так как подынтегральное выражение Ьд (l/r)dr имеет в нуле порядок т~Уг.
Таким образом > имеют место оценки
0< }туг(-)х2<18 < //и (-) sds < eft. (3.23)
С другой стороны,
J/% ^— jsds < J/* ^— Js2ds < fIVz (—J s2rfs = 0O. (3.24)
Отсюда имеем
fdfi\ /d0\
l~\ds)0
333
(d$\ rd$\ * r fr\
V as A \ ds / о о V s /

В силу монотонности (dP/ds) 0<а< 1 + е, е-*0, Р0 -*0.
(dp/ds)b -dP/ds<aP0, dP/ds =/-^(s)j30, 0< 0<я. (3.26)
Интегрируя соотношение (3.26), получим
P-Po=fs-P0fe(s)ds=f.s-K(s)PoS9 0<к<я, (3.27)
о
откуда
0/s=/ + M1/*-k). (3-28)
Ясно, что например, при s > 1 и достаточно малом 0о будем иметь
1-е<(р/«)/-1<1+е (3.28)
о ■ Vv '
гдеЛ,£,£>-*1 при /30^0.
Отсюда имеем
(3.29)
соответственно
(1 -6)/% со <л* ovo < о+в)л* со,
6-*0 при/30-*0.
Отсюда
//% (—^2Л = 0о - ^о = Л fly2 (f)s2ds =ALA (/) ——-, (3.30)
1 \s ' ' i ■ 3
где А близко к 1,0 < d < ~с.
Отсюда следует, что при Р0 -* О
Л4(Л-ЗА,/&3. (3.31)
Ясно, что (см. разд. п. 2)
1*1й(Г)-+91гРо1Ъ39 (3.32)
L=2l9(b3/Po)h/7(f)^U Ро-+0. (3.33)
Найдем теперь асимптотическое значение интеграла
J/a(-W (3.34)
Как было показано,
Р
0 xs
Рассмотрим интеграл
ъ (Р\ ъ Г0о 1 ь
//% - «fr = fly2\ — + /- К0О s^S = AfIy2 (f)sdS =
1 \s J 1 L s J 1
= 4/%(f)(*a -l)!2 = ttBIy2(f)b2=3l2Dp0b-l9 (3.35)
J/%.(- sJs =3/2— + O(|8o). (3.36)
b (P\ Po
0 \s ' b
Пользуясь соотношением
pb3=c2TPo, (3.37)
334

имеем
flJ-)sds~U—) \\ (3.39)
Ь=(с2/рУ/*Ро~1/\ (3.38)
W
Рассмотрим, нак онец, выражение
*-i[b(f)&+i)--4 i3A0)
Преобразуем его следующим образом:
■^BTf-^ + ^(")^+T"^(-)fodil- (3*41)
3 L О Ч5У Р00 V S ' J
Рассмотрим последний интеграл
/7*(-)*Л =//%(-)-5аЛ. (3.42)
О \ S ' 0\5/5
Пользуясь для /fys выражением (3.28), получаем
fly2 (-)/Ы* =fln (")[/+— -кPo]s2ds =
=///% (-ИЛ+^о//%(- *<**-*&//% — Ь2л= (з.4з)
о \s / о >s / о \s /
ъ /0\
О V S /
Подставляя это выражение в (3.41) , получим
Af=-[2J/%(-)srfs-X0o]. (3.44)
Отсюда следует, что
М=0(Ро)- (3.45)
Рассмотрим выражение
2 1 * /Р\ ■
3 р0о \ s '
Легко видеть, что
J^l~it4(f)"L- (3-47)
Рассматривая величину О =J — М, получаем
в = Ь+О(Р0). (3.48)
Эти результаты будут в дальнейшем использованы в п. 3 разд. 4 для получения
асимптотических членов величин Р9Е.
3. Рассмотрим второй предельный случай
0о=0(1), Ь^О.
335

Докажем,что в этом случае
Предположим, что Р0 = 0тах • Тогда
00 =//%( - W < J/% (—b2rfs. (3.50)
о \ s / о \ s J
Так как 0О = #0) * а & мало, j30/s — велико. *
Применяя асимптотическую формулу (1.45) , получим
Po<-A&rs*d8 = -Ati,*bah. (3.51)
3 о 9
где А->1 при &-*0. При достаточно малых Ъ неравенство (3.51) приведет к
противоречию.
Итак, при Ъ ->0 должны иметь &тах = Р0*чю и требовалось доказать.
Оценим теперь порядок величин j, Pb = fb.
Из неравенств
fibls=fbls>fi/s>f. (3.52)
s2ds>P0>fIV2(f)s2ds. (3.53)
Ч-)
переходя к асимптотике, имеем
AShf^b3 >/30 >A22/9f4*b\ (3.54)
гдеЛьЛ2 "*"! при£ -*0.
Отсюда следует, что
f~\\b\ fb-ЦЬ. (3.55)
Оценим теперь интеграл / Iy2 (($/s)sds:
о
fld-)sds<flJ—)sds=B1-f'l*b2~-4 Вл+1. (3.56)
O^S' О \ S / 3 Ъ
Таким образом,
(dP/ds)b - (dp/ds)o =F- (dp/ds)<> < const/Z>. (3.57)
Отсюда следует, что
(dfilds)0~llb2. (3.58)
Таким образом, как и в предыдущем случае, разность производных на концах
меньшего порядка по сравнению с самими производными на концах.
Для дальнейшего целесообразно перейти к новым переменным а, f, изменив
масштабы:
<* = ££, Oo'=0oft. c*ie/b\ (3.59)
t = sjb, f0=0, tx = L
Тогда
dotldt = b2dPjds♦ ф = *2#j. (3.60)
Ясно,что справедливы неравенства
a1jt>alt>at. (3.61)
336

Действительно, умножая неравенства
fb/s =Pb/s>P/s>f
на b2, имеем
fb3/s>b2p/s>Pb2.
Переходя к новым переменным, получаем (3.61). Следовательно,
(da/dt)о~ (da/dt) г =аг~ 1; (3.62)
(daldt) t - (da/dt) 0~-b.
Найдем выражение для da/dt на интервале 0 < t < 1.
Из (3.62) имеем силу монотонности da/dt (с - некоторая ограниченная
положительная функция)
da/dt =ax-cb. (3.63)
Интегрируя (3.63), получим
ф=аг *b(P0lt-d)4 (3.64)
где d — ограниченная функция.
Рассматривая интеграл
Po=flJ-)s2ds
о \ s '
в новых переменных, получаем
0о 1. / 1 а
Ь3 6
1 / 1 а\ п
S1* Т5Г" )tdu <3-65>
о \Ь2 11
Разобьем интеграл (3.65) на две части
/= / + / ; а0=йР0. (3.66)
Оценим первый интеграл
^"о / 1 <*\ о ^"° ( 1 аЛ о ai3/2 з/ Я
/ /й(^7.)^ < J !*{-; 7Y*t -A—afi -^, (3.67)
В то же время
(З.60)
где с — близко к единице.
Это следует из
Ьфо/t - d) < constyjb при t > sfaQ =y/F0\/F. (3.69)
Отсюда
1 ( l0L\ <, 2 <*lk Г 3/1
jk.M'i'T)'"-'»-?-!1—*]• (зло)
Таким образом, равенство (3.65) принимает вид
337

Умножая на б3 и переходя к пределу при Ъ -*■ О, получим
а, = (9/2/30),/з. (3-72)
Отсюда
Л* (Я = 2/з/3/* =2/з«1%6-3 =ЗР0§/с2; (3.73)
/з/2(/)=2/5/5/2=2А«15/^-5; (3.74)
1 = ($/Г)Р%, (3.75)
где
6=4/45(9/2)5/з^2/зсЛ (3.76)
Рассмотрим интеграл
о \s /
В переменных а, Г он имеет вид
stfs=- fat^dt. (3.77)
3 Z> о
Применяя к последнему интегралу интегрирование по частям и заменяя в интеграле
da/dt на а^ , получим
/af-%tff =2af*| -2/— t^dt^-ot^ (3.78)
о о о dt 3
Таким образом,
//% -W^-flo^T-. (3.79)
о \ 5 / 9 Z>
Принимая во внимание равенства (3.72), (1.26) и (1.27), получим
Оценим после этого величины
Ч-)
о \s j
о
o-Kimw-
"ЧН'^тХ^Н <3-81)
2 * /0\ ,
/= --//з/2 (-)s2ds; 0=J-M. •
3/30 о '2 V s i
Преобразуем интеграл в выражении для М
о \s/\/30 / о v s ' Poo s / s
= //у2(- Ы* + —//% (-—+/-- \s2ds =
о \ s / р0 о \ s ' L s Z> J
ь' (Р\ d S 3, at d
= 2/7^-5^+/--=-^-7 + /--; (3.82)
о \s ' 6 9 Z> Z>
d =0(1).
338

Отсюда
М=— jS0%*i- - —, (3.83)
27 Ъ ЪЪ
или
М=Лр1/з, (3.84)
где А — конечная величина.
Рассмотрим теперь выражение для /
/= Ьйи^~УЛг=Wf)b3 -L =тр5/з- (3-85)
Отсюда
в = / _ м = (б/Г) р2/з - А р1/з, (3.86)
ПрИР^о°
e^L = (Ь/Т)р2/\ (3.87)
4. Рассмотрим теперь предельный случай
0о ^°°; Ь3=а/Р0^0; а = с2/р. (3.88)
Докажем, что при достаточно малых а (достаточно больших р)
0т« = 0». (3-89)
Предположим,что 0тах = /30. Тогда
00 <fI*(Pols)s2ds ~2hPohfsV2ds =*/9Po/2b3l2.
о о
Отсюда
1 < *19Р?ЬЧ* =4/9ч^при 0тах =0О. (3.90)
Таким образом, если
у/7< 9/4, т.е. Р> 16с2/81, (3.91)
ТО
0т.х=0». (3-92)
Рассмотрим этот случай. Применим обычные неравенства
Ртшх/s =fbls>P/s>f. (3-93)
/*</ft/S)>/y2(0/S) >/*(/). (3.94)
Интегрируя (3.94), получим
fb\2ds>fi0fln(f)s2ds, (3.95)
о
о V s /
так как
№>/з0; /^>/з0; />0о4/зАЛ (3.96)
то можно применить асимптотические формулы. Таким образом, получим:
*l9f*,2b3>Po>2l9f3kb3. (3.97)
Отсюда сразу же определяется точный порядок /
(9/4я)2Ч4/з < / < (9Ца)2/>№ (3.98)
33£

или
/ = АА4/з; (9/4я)2/з < к < (9/2я)2/з. (3.99)
Перейдем к новым переменным а, Г с помощью формул
а = /3//Зо, t=s/b. (3.100)
Тогда справедливы соотношения
а _ Ъ 0 da __ Ъ d& d2P _ 0О d2a
t ~~ Po' T' dt ~ Po ds ' ds2 " b2 dt2 '
a(0) = <*0 = 1; <*(1) = au (3.101)
и асимптотическое уравнение
d2P/ds2 = 2/303V/2 (3.102)
с краевыми условиями
0(0) =00, (dp/ds)\s=b=f$blb (3.103)
переходит в
d2a/dt2 =21зу/аакТ-у\ a0 = l, (da/dt)\t = 1 = a. (3.104)
Интегральное соотношение
0о =11уг(~)s2ds =- yftU42sV2ds
о ^ s ' Зч о
переидет в
l=2h\/afOL44lAdt. (3.105)
о
Можно также перейти к переменным
tyco = ay, 7 = 4/9fl = 4/9<VP, (3.106)
после чего переходим к уравнениям
d24dt2=(Jkr*\
<^ = У при Г=0; do>ldt=u> при f = 1. (3.107)
Интегральное соотношение (3.105) примет вид
7 = /«*Г%Л. (3.108)
о
Так как в уравнения и краевые условия (3.107) входит только один параметр у =
= ^h(c2/P), то и решения (3.104), (3.107) будут зависеть только от 7» t. Таким
образом, решение (3.104) есть
<* = <*(с2/Р,0, (ЗЛ09)
решение (3.107) есть
" = o>(c2fP,t)> (3.110)
Решение задачи (3.102) принимает вид
0 = 0oa(7,r) = (0o/7)^(7,O. (З.П1)
Оценим теперь функцию ctt = ссг (у). Из равенства (3,99) легко следует ,
а, = (*/0о)/ = *(с3/р)^ (3.112)
340

Отсюда следует, что функция at (с2/р) заключена в пределах
(9/4)*(р/са)* < сц (с2/р) < (9/2)2/з(Р/с2)1/з. (3.113)
Таким образом, имеем
L=<p(c2/p)T-\' (3.114)
где
tf(c2/p) =4l*sc14/*'(c2lP)1/*a1s/K (3.115)
Отсюда нетрудно показать, пользуясь соотношением вириала, что
ffBBW£i)J_. *-^с>(^)%Гв1*-1/«*г-^Л. (З.П6)
V р ' Г . 45 ^ р ' L 3 о J
5. Рассмотрим предельный случай
0О=0(1), б^оо.
Из интегрального соотношения
ъ р
jVy2(-)s2rfs=/30
OS
вновь следует, что при достаточно больших
fl/s<0. f = P0/b<Oy f^-oo приЬ~+оо. (3.117)
Отсюда следует, что
0max=/V (ЗЛ18)
Легко показать, что на интервале (О, Ъ) величина f1 afi/ds заключена в пределах
Kf-^'-dp/dsK 1+е, е-*0 при й->~. (3.119)
Соответственно величина p/s на большей части интервала также заключена в довольно
узких пределах.
Действительно,
< //J-Jsrfe + A,=$ //%l-)/rff + P0=O0). (3-120)
О ^ О ^
В силу неравенств
(dp/ds)0<dP/ds<f (3.121)
утверждение (3.119) с легкостью следует из (3.118) и (3.120).
Интегрируя (5.119), получим
/(l+e)s<H<A (3.122)
P/s = PQ/s+f(l + 6), 6->0, 2>->°°. (3.123)
Рассмотрим теперь равенство
341

Разобьем интеграл на две части
?/й(^),»Л-//й(^).»Л + ;/й(?.),9Л (3.124)
Рассмотрим первый интеграл
/ I^(P-) s2ds = } 11/г [у + /(1 + 5)] s2ds =
Чр» Г1 1 s
= 0?> / /,/2 - +/0+8) t2dt, t = -. (3.125)
о L' J 0о
При /-»• — °° этот интеграл должен стремиться к нулю.
Действительно, подынтегральное выражение в нуле имеет порядок tVl, на конце
интервала t- 1/0о имеет порядок e-f (1+6). При j/| достаточно большом подыинтеграль-
ная функция будет иметь на интервале (е, 1/0о) порядок е^(е-*- 0 при /-*■—°°).
Применяя во втором интеграле (3.124) представление (3.123), получим
Po=AIy2(f)b3/3, А^\ приЬ-+°°. (3.126)
Отсюда
1у (f)= I1A(f)= -?-, L= VIA ■* 1 при 6 +°°. (3.127)
3 1 9 ft,
2 Л Л 2 Ь
Рассмотрим выражение для
/= //„ -)s2ds.
3 0о о /2 v *
Вновь разбивая интеграл/ на две части, получим
2 */А> г 1 1 , 2 ь • 0 \ ,
/=-0§ //,/ - + /(1+8) \t2dt + —r /Л/ - Ь2*. (3.128)
3 о /з L' J 3 0o i /г Vs '
Подынтегральное выражение в первом интеграле имеет порядок
t~Vl при t =0 и ^<1+6> при Г=1/0О.
При |/| достаточно большом оно будет иметь порядок е' в интервале (е, 1/0о),
(е-*-0 при |/| -*•<»). Отсюда вновь получаем
/ = Л(2/3 0о)/й(/)63/3=ЛА А-+1 при 6^°°. (3.129)
Пользуясь соотношением вириала, получим
6-*£.-+1. (3.130)
4. ПОЛУЧЕНИЕ ИНТЕРПОЛЯЦИОННЫХ ФОРМУЛ
1. Анализ асимптотических соотношений, рассмотренных в разд. 2, показывает
1). В случаях I, II, IV справедлива асимптотическая формула
/./2(0 = 3 0о/Ь3. (4.1)
Это обстоятельство не является случайным.
Действительно, во всех случаях правый конец (Z>, (3b) кривой 0 = j3(s) удалялся от
левого (0, j30) или в силу роста Ъ (случаи I, IV), или в силу роста $ъ (случай II).
342

Так как кривая j3(s) всегда является выпуклой, и касательная в ее правом конце
проходит через начало, то во всех трех случаях это приводит к спрямлению кривой,
так что величина (1//) (d(3/ds) заключается в узких пределах на всем интервале (О, Ь).
Соответственно величина /З/s представляется в виде
РА = А,А+/(1+8),8-^0,(й,|8ь)^оо. (4.2)
Учитывая порядок s^ функции Iy2 (0/s) s2 при s = О, легко приходим к формуле
(4.1).
2). Таким образом, соотношение (4.1) являетря устойчивым относительно
перехода от одной асимптотической области к другой. Есть основание поэтому полагать,
Рис.2
что с внесением соответствующих поправок оно может дать хорошее приближение
в широкой области переменных р, Т.
3). Случаи I, IV (Т/р -►<») сходны по своей асимптотике. И в том и в другом
случае имеем
L.0-M. (4.2)
Таким образом, в случае Т/р -+ °° имеем переход к идеальному газу.
Случаи II, III приводят к различной асимптотике. Однако общим для них является
представление
L.T = f(p)', в.Т =*(р). (4.4)
Отсюда следует, что в случае Т/р -+ 0 давление Р и внутренняя энергия Е 1 см3
асимптотически становятся функциями от одного р 3.
2. Для уточнения формулы (4.1) необходимо перейти от аппроксимации кривой
Р = Р (s) с помощью касательной к аппроксимации с помощью хорды. Характер обеих
аппроксимаций ясно виден на рис. 2.
Если в соотношении
0о =//%(-У * (4.5)
о v« }
положить в подыинтегральном выражении
P/s=f (аппроксимация касательной) , (4.6)
то получим значение 0О с недостатком
/30=/*<У)*3/3. (4.7)
Если положить
P/s = ft) /s + /Г T-f—Polb (аппроксимация хордой), (4.8)
3Речь идет только о вкладе в энергию и давление электронного газа.
343

то получим значение j30 с избытком
0о = / /* Г— +/1 s2ds = Й / IV2 Г- + /] Г2А; (4.9)
t = i/Uo.
Истинное значение j30 будет лежать где-то между значениями (4.8) и (4.9).
Оценим интеграл (4.9). Применяя интегрирование по частям, находим
; Lh Г- Л t2dt2 =VaT iV2 Г- +/1 dt3 =
0 L t 1 0 L f J
= У3*% (/) + Vi2/ /_./2[- +/W =
о L ^ J
= 7з *%(/) + lli2k2I-^if)^U22kI_V2(f)^Rt (4.10)
где
^=Vi2/f/_y2(~+7)-/_1/2(f)]^>0. (4.11)
о L 4/
С большой степенью точности в большой области переменных проинтегрированную
часть можно заменить через
7з'-л(Ш*3+(* + *2)/2]. (4.12)
Таким образом, аппроксимация по хорде приводит к следующему выражению для
0о=1/з^3^(/)[1+((е + е2)/2) + 5]; e = ft>/Z>. (4.13)
Первый член выражения (4.13) дает аппроксимацию по касательной, остальные члены
положительны. Отбрасывая 5 > 0, получаем некоторую аппроксимацию, заключенную
между аппроксимацией по хорде и аппроксимацией по касательной. Она дается
формулой
0о = 7з*3/%<Ш1+((е + е2)/2)]; е = р0/Ь. (4.14)
Так как истинное значение также заключено между этими аппроксимациями, то
можно ожидать, что формула (4.14) дает хорошее приближение в широкой области
переменных. Отсюда для L получается выражение
L=2/9 [b3/Mb/2(f)> (4.15)
где / определяется из (4.14).
С большой степенью точности можно также положить
/,= 1/(1+а). (4.16)
Что касается в , то в этом параграфе выражение для в мы получим из
термодинамического соотношения
ЪЕ2 ЪР
—— = Р — -Р, (4.17)
Э(1/Р) ЪТ
344

которое в наших переменных L, в принимает вид
3 Э0 Ы
= рТ . (4.18)
2 Э(1/р) ЪТ
Пользуясь выражением (4.16) для L и представлением j30, Ъ через р, Г, получим
Э0 2 да/ЪТ 2 1/2 е + е2 е + е2
= рт =- — а = (4 19)
Э(1/р) 3 (1+<*)2 3 (1+б/2+б2/2)2 ' 2 V*
Переходя к переменному е получим
Э0 1+2е
Эе (1 + е/2 + е2/2)2 '
Интегрируя (4.20), находим
(4.20)
е + е2
0 = 1-2- 5-+*(Г), (4.21)
2 + е + е2
где \р (7) — произвольная функция Т, причем
^(Г) -*0 при Г-*«>.. (4.22)
</? (Г) интерполируется по просчитанным вариантам.
3. Дадим теперь асимптотические выражения для физических величине (давление)
и Е (внутренняя энергия 1 см3 вещества). *
Как известно, Р и Е выражаются через величины L, 0 следующим образом:
P = cZ/ApT(L + llZ), (4.23)
E=3/2c(Z/A)pT(e-l/Z)9 (4.24)
где А — атомный вес вещества, Z — заряд ядра атома (порядковый номер) ,с = N0 • R,
N0 = 6,023 •1023 — число Авогадро, к = 1,38- 10"16 эрг/град - постоянная Больцмана.
Г измеряется в градусах, Р, Е, р измеряются в системе CGS.
Таким образом, получаем дляР иЕ следующие выражения.
Асимптотический случай I (р = О (1), Т -► °°)
P = epr(l + 1/Z), E=*/2apT(l + l/Z)9 a = cZ/A. (4.25)
Асимптотический случай II (Т = О (1), р -* °°)
L = (8/T)p2/\ O^L, (4.26)
где б — некоторая функция от A, Z. Соответственно этому получаем
Р = ^.5.р5/з, Е=3/2Р (4.27)
Асимптотический случай III (р = О (1), Г-* 0) (р достаточно велико)
£=</>(А Z, р).Г, (4.28)
где <р - некоторая функция р, Л, Z (см. (3.114) — (3.116) :
0 = ф(4,г,р)(1/Т). (4.29)
Отсюда
P = fl-V?(p), Е=3/2аф(р). (4.30)
Асимптртический случай IV (Г = О (1); р -* 0)
L = 0 = 1; P = apT; Е=2/3арТ. (4.31)
345

5. ПРИБЛИЖЕННАЯ ФОРМУЛА ДЛЯ ВНУТРЕННЕЙ ЭНЕРГИИ 1 см3
1. В разд. 4 была получена приближенная формула для L в функции от0о, Ь,
основанная на асимптотическом исследовании решений уравнения Ферми-Дирака и дающая
среднюю точность 1,7% в довольно широкой области переменных j30, b. В настоящем
разделе мы ставим задачей получить соответствующую формулу для внутренней
энергии 1 см3 вещества.
Формула основывается на тех же аппроксимационных соображениях, что и
формула для L, т.е. на замене кривой 0 = j3 (s) касательной и хордой. В данном случае
приходится прибегать к различным аппроксимациям на различных участках интервала
hie. 3
(О, Ь). Так как выражение для L получено, то в силу соотношения вириала
достаточно знать М или /, чтобы определить 0.
Из аналитических соображений удобнее определять J.
Рассмотрим выражение для /
J =
2 ъ
/ /з
30о о '
о
s2ds.
(5.1)
Аппроксимация интеграла по касательной является здесь более грубой, чем в случае
интеграла
ь
о
()
s2ds.
(5.2)
так как порядок обращения в бесконечность подынтегральной i функции в s = 0
увеличивается на 1: с sVl до s~1/2, поэтому аппроксимирующая кривая должна
обязательно проходить через точку (0, 0О) • Такой аппроксимацией является, например,
хорда или ломаная (рис. 3).
Аппроксимация хордой является, однако, слишком грубой, аппроксимация
ломаной приводит к большим аналитическим трудностям. Поэтому мы аппроксимируем
кривую 0 = 0 (s) на некотором участке (0, с) с помощью хорды, на участке (с, Ъ) —
с помощью касательной. Последнее возможно, так как на участке, достаточно
удаленном от начала, аппроксимация касательной является достаточно хорошей. В качестве
точки с мы выберем точку s = 0О.
Аппроксимируя 0 = j3(s) по касательной, имеем
0=/-*, (5.3)
аппроксимируя по хорде, получаем
0 = 0о +/Ч /=/-е, е = Ро/Ь.
Для/ получаем следующее выражение:
2 ь
30о о 1г
(;)
s2ds =
Но / р\ . 2
3 А, о /з
()
s2ds +
s * 3 0о р
ъ
(?)
s2ds.
(5.4)
(5.5)
346

Аппроксимируя в первом интервале по хорде, во втором — по касательной, получаем
(5.5')
/ = ~fi> f /»Д Г- + /] t2dt + L (1-е3).
3 о **'
Таким образом, для J получается следующее выражение:
I. / = £(1-е3) + Ф</)Р§,
где
2 1 П ~1 ,
Ф(0 = -х S hi \-+f\t2dt.
(5-6)
(5.7)
Применяя интегрирование по частям, находим
2 1 Г1 ^\dt3
//3,1 -'
J о
Г1 ~Л.
*(0—//v,L7+/J"
1 1
= -/зЛ(Г+1) + -//1Л(- + ?)^ = -КЛ(?:+1) +
1 ~ 11 (\ ~\
+ -/%(Г+1)+—//_%(- + /)*.
6 12 о \t '
Таким образом, для Ф (/) получаются дополнительно следующие выражения:
* ю=- /./, (7+1)+- / /% (- +./W
(5.8)
(5.9)
(5.10)
Аипроксимационная формула (5.6) может быть варьируема различным образом
путем изменения аппроксимирующих отрезков на соответствующих участках.
Заменяя на участке (0, 0) прямую с наклоном J прямой с наклоном/-1, получим
формулу
И. / = £(1-е3) + Ф(У-1). (5.11)
Различие между аппроксимациями I и II видно на рис. 4 и 5.
В первом случае аппроксимирует ломаная ABCD, во втором — ломаная ACD. Ясно,
что аппроксимация с помощью CD — с недостатком. Наконец, аппроксимация на
(j30, b) может быть улучшена введением поправки, приближающей аппроксимацию
касательной CD к аппроксимации хордой BD.
347

3. Вычисление функции
21 /1 \,
(5.12)
Непосредственное вычисление Ф (а) с помощью формул численного
интегрирования затруднительно ввиду наличия особенности типа t~х/г в 0.
Выделяя особенность в подынтегральном выражении (5.12), получаем
8 2 1
Ф(а)= — + -ff(t,<*)dt,
15 30
/ft а) =Ь/г (1/г + a) t2 -0,4/f*.
(5.13)
(5.14)
-Л/7 -£# -£# -t,0 i
Рис.6
Аналогично из выражений (5.9) и (5.10) находим
2 4 11
ф (а) = _ ь, (а + 1) + - + - fg (r, а) tff,
9 ,2 9 3 о
^(Г,а) = /^(1/Г + а)Г-0,6667/г1/2;
12 1 1
3 9 /2 6 о
Л (Г, а) = /_
(Н-1
(5.15)
(5.16)
(5.17)
(5.18)
Функции/(Г, а), g (г, а), Л (г, а) уже не обладают особенностями.
Интегралы от /(f, a), g (г, а), Л (г, а) вычислялись по формуле Гаусса с восемью
точками. При этом для Ф (а) получились три значения, отличающиеся в среднем друг
от друга на 0,5%.
В качестве Ф (а) бралось среднее арифметическое вычисленных трех значений.
Ф (а) вычислялось в восьми узловых точках на интервале —10 < а< —1. При этом уже
линейная интерполяция для промежуточных а обеспечивает точность 0,1%. Это
объясняется тем, что Ф является функцией с положительной монотонно возрастающей
производной и имеет очень плавный ход (рис. 6). '
С табулированными Ф (а) / определялось по формулам /:
/ = /,(1-е3) + Ф(/-е)/^ (аппроксимация I), (5.19)
J = L (1-е3) + Ф (f-1) Pi (аппроксимация II). (5.20)
После этого вычислялось в по формуле
d=2L-J. (5.21)
348

Затем вычислялся процент ошибки в определении величин /, 0, вычисляемых по
формуле сравнительно с просчитанными вариантами:
Д в % =— • 100; Д в % = —^ • 100.
•'сч ^сч
Результаты сравнения сведены в таблицу; они показали в весьма широкой области
следующий средний процент ошибки по 12 просчитанным вариантам:
аппроксимация I J 2,9%, аппроксимация II J 3,0%,
аппроксимация I 0 4,1%, аппроксимация II 0 3,7%.
4. Оценка точности аппроксимационных формул. Аналитическое исследование
величины ошибки затруднительно. Таким образом, ошибка определяется сравнением с
просчитанными вариантами. Однако для оценки ошибки можно применять и
полуэмпирический метод, основывающийся на сравнении с одним ("наихудшим") вариантом
и свойствах монотонности ошибки.
Аппроксимационная формула
J = L(l-€3) + <b(f-€)p20 (5.22)
носит асимптотический характер (случаи I, IV) и поэтому тем точнее, чем ближе ]30, Ь
примыкают к асимптотической области.
Действительно, в случае I j30 -* 0, Ъ -* 0, е -* 0, в случае IV 0О = О (1), Ъ -* °°, е -> 0.
Заметим, что область применения формулы (5.22) меньше сравнительно с
формулой L, полученной в разд. 3:
L = 2!9(b3/p0)h/2(f)9 (5.23)
где
fSo=(l+<*){b3/3)IV2(f); a = (e + e2)/2, (5.24)
и справедливой для асимптотических областей I, II, IV.
Формула (5.22) для асимптотической области II (0О ~*°°, Ь -> 0) уже неприменима,
так как она выведена в предположении, что ]30 < b, в то время как в случае IIР0/Ь ->°°.
Попытаемся определить степень точности аппроксимационной формулы (5.22)
(аппроксимация I), пользуясь некоторыми геометрическими соотношениями (см.
рис. 4, 5) и соотношениями (1.26), (1.27.). .
Предположим, что для некоторых значений р0, То, которым соответствуют
значения j300, Ь0, мы добились точности
А "~ 1гсч~~^апр)/,'сч-
Вообще говоря, для значений параметров ]30, b0i f$0 < ]300 точность должна увеличиться.
Это следует из того, что при фиксированном Ь0 и уменьшающемся j30 и кривая, и
хорда приближаются к касательной, что увеличивает точность как на участке (0, 0О)
(аппроксимация хордой), так и на участке (]30, b0) (аппроксимация касательной).
Аналогично, если j30 фиксировано, a b возрастает, то точность возрастает. Это следует
из таких же геометрических соображений.
Обозначая через Д (j30, b) функцию относительной ошибки
A(p0,b) = (JC4-Janp)!JC4,
получим таким образом неравенство
|Д(0оо,&о)1 > |A(j3o,Ml, 0оо>0(ь
| Д fa, bo) I > I А (0о, Ь) |, Ь > bo. . (5.25)
Рассуждения являются не вполне строгими, поэтому неравенства (5.25) отражают
только основную тенденцию роста Д, но больших отклонений от нее, очевидно, не долж-
349

Таблица значений Д
1,545
1,545
1,998
2,074
2,159
2,492
21,78
18,605
17,11
15,125
14,31
13,78
13,005
12,005
10,35
9,245
8,405
2,2
-2,2
4,8
-4,9
0,7
-0,9
4,1
-4,6
0,7
-0,5
0,5
-0,5
4,6
-5,8
3,7
-4,0
0,5
-0,4
3,7
-7,7
-1,1
1,1
2,6
-3,2
но быть. Таблица подтверждает это. Заметим, что аппроксимация II не обладает таким
свойством монотонности ошибки.
Рассмотрим теперь Д (j30, b) как функцию параметров р, Г, пользуясь
соотношениями (1.26) и (1.27).
При фиксированном р и возрастающем Т j30 уменьшается, а Ъ увеличивается,
следовательно, точность увеличивается. При фиксированном Т и уменьшающемся р, Ъ
увеличивается и точность увеличивается.
Таким образом, будем иметь
|Д(р, 7\)| < |Д(Р, Г2)|, Т1>Т2,
|Д(рьГ)1<|Д(р2,Г)|, Рг<р2.
(5.26)
Таким образом, выбирая rmin, Pmax> можем получить верхнюю оценку для ошибки
Д(р, Г) в области p<pmax T>Tmin.
Таблица показывает ход ошибки по переменным (30,Ь. Из таблицы видно, что
аппроксимация I, соответствующая рис. 2 (Г=/—б), удовлетворяет в основном этому
требованию монотонности в отличие от аппроксимации И, которая дает тот же средний
процент ошибки, но не обладает свойством монотонности и не улучшает точности при
переходе в асимптотику.
В случае монотонной аппроксимации ошибку можно было бы оценивать сравнением
с наихудшим вариантом.
5. Окончательные формулы. Переходя к переменным р, Г, получаем следующие
выражения для L, в в функции от р, Т
350 /

2,518
2,942
2,946
3,165
3,252
3,587
3,952
-2,7 0,7
3,1 -0,9
-0,8 2,5
1,0 -2,6
1Д -3,7
1,4 -5,0
3,1 -1,7
3,9 2,1
-9,7 -4
16,1 6,1
7,8
11,9
-1,0
1,6
-9,2
15
-2,9
4,8
h/2 {f) - ax (p/T3/> ) (1 + 0,5 a2 p'*lT + *2 p^/T2yl. (5.27)
Это уравнение служит для определения величины /, которая входит в дальнейшие
формулы.
Для довольно широкой области р, Т для/ можно дать явное выражение
/=ln(2/V<) + lna:1 +lnp-3/2 1пГ- [1 + 0,5 а2 р1/*/Т+а2 р2/з/Г2],
которое легко следует из асимптотики/^ (/):
L = (2/3 ах) (Г^/р)/зЛ(Г),
или
1 = (1+0,5а2р'/з/Г + а2р7з/Г2)-1 к(/)>
где
(5.28)
(5.29)
(5.30)
(5.31)
К(/) = 7з/з/2(/)//й(/)
при f<0 к -М. Поэтому в этом случае для Z, можно пользоваться более грубой, но
достаточно точной формулой
L= [I +0,5a2 (р1/з/Г+а2 р^/Г2)]"1. (5.32)
Для У, в получаем выражение
/ = £ [1-а|р/Г3] +с\Т-3/*Ф(/-а2р/*/Т)9 (5.33)
351

0=Z [1 + 4p/T3]-c\T-3/> Ф (f-a2 p^/T). (534>
Отсюда Р, Е выражаются следующим образом:
P = c- p(L + l/Z)9 (5.35)
E=3/2c.p(e + l/Z). (5.36)
Константы ai9 cit c2, с имеют следующие значения (см. (1.26) и (1.27)) :
c=NkT(Z/A)9
4тге3(2т)/4 _ 4п (2 тп)^ • е- к^ /4
С\
4-п(2т)'* • е- к1* (4 \ ч х,
hU-^U ' tfU \з
c2=cic|; (5.37)
«i =3cl/c2; а2 =с?73.
6. Приложения. Результаты счета сведены в таблицу, в которой показана Д
(относительная ошибка) в функции от ]30, Ъ. В каждой клетке расположены четыре величины
в следующем порядке:
hi
0т
е
и
где значок I относится к первой аппроксимации, значок II - ко второй.
На графике (рис. 6) представлена функция
21 /1 \ о
Ф(а) = - //3/ - + а )t2dt.
ЛИТЕРАТУРА
1. Thomas. // Ргос. Cambridge Philos. Soc. 1927. Vol. 23, pt 5.
2. Ferm/ F. // Atti Accad. Lincei. Rend. CI. fis. mat. 1927. Vol. 6. P. 602; Ztschr. Phys. 1928. Bd. 48.
S.73.
3. Feynman R.P., MetropolisN.E., Teller // Phys. Rev. 1949. Vol. 75. P. 1561.
4. Brachman. // Ibid. 1951. Vol. 84. P. 1263.
УРАВНЕНИЕ СОСТОЯНИЯ А-е ФАЗЫ КОРЫ ПУЛЬСАРА
С УЧЕТОМ ДЕЙСТВИЯ СВЕРХСИЛЬНОГО МАГНИТНОГО ПОЛЯ*
Проведен расчет уравнения состояния вещества (железа) в характерном для
пульсаров магнитном поле* порядка 1012 Гс, для давления 103 -=- I08 а.е, Давление 108 а.е.
соответствует расстоянию порядка нескольких десятков метров от поверхности
пульсара. Расчет проведен на основании модифицированной модели Томаса—Ферми. В
модели полагается, что электроны заполняют состояние с определенным номером уровня
Ландау, проекций спина и импульса на направление поля. Уравнение состояния
обладает рядом аномальных свойств. Так, например, скорость звука может падать с ростом
давления, вклад теплового давления ядер в давление может быть отрицательным.
Интерес к свойствам вещества в сверхсильном магнитном поле обусловлен
возможностью существования полей порядка 1012 Гс [1] в пульсарах, В полях1 В^В0 =
•Астрофизика. 1981. Т. 17, вып. 4. (Соавторы Г.В. Гадияк, М.С. Обрехт.)
1 Ниже все величины будем выражать в атомных единицах е = Ь = т - 1, атомная единица давления
составляет 294 Мбар, магнитное поле в единицах В0.
352

= m2e3ch~3 = 2,35 • 109 Гс взаимодействие электронов вещества с внешним
магнитным полем может превышать кулоновское взаимодействие [2, 3]. Говоря на языке
статистической модели, магнитное поле существенно перестраивает электронную
структуру вещества, если энергия взаимодействия электрона вещества с внешним
магнитным полем ем — В сравнима со средней энергией Ферми FF электронного распределения
(чертой сверху обозначаем усреднение по объему элементарной ячейки кристалла).
Для достаточно сильно сжатого вещества в рамках статистической модели справедливо
соотношение ер ^Ъг /з, при этом давление Р ~ns /з. Отсюда следует, что условие В ^ёр
выполняется при Р ^Рм ~В5 U. Таким образом, при Р > Рм мы приходим к обычной
модели Томаса—Ферми, а при Р 4>Рм магнитное поле может сильно изменить свойства
вещества. Так, например, тонкий поверхностный слой коры пульсара, толщиной
порядка 50 -г 100 м (где давление Р ^ Рм)> как показывает расчет, состоит из прослоек с
различным характером зависимости скорости звука от давления: в одних прослойках
скорость звука растет с давлением (глубиной), а в соседних, наоборот, падает.
Подобная аномалия может приводить, в частности, к отрицательному вкладу в полное
давление от ядер, в такой среде могут формироваться ударные волны сжатия и разрежения.
В настоящей работе исследуется уравнение состояния вещества в сверхсильном
магнитном поле в рамках модифицированной модели Томаса—Ферми, описанной в разд. 1.
Последняя является обобщением модели [4] на случай обоих возможных направлений
спинов электронов вещества, при наличии произвольной температуры и давления, В
работах [2, 4—9] и многих других исследовались свойства изолированных атомов при
нулевой температуре. Первый расчет уравнения состояния холодного вещества в
сверхсильном магнитном поле представлен в [10, 11] (заметим, что термодинамика
однородного электронного газа рассматривалась ранее неоднократно [12, 13]).
Исследование [10], проведенное на основе интерполяционной статистической модели, позволило
сделать вывод о ряде особенностей уравнения состояния вещества в сверхсильном
магнитном поле. В [10] было, в частности, отмечено, что сжимаемость вещества резко
падает при наличии сверхсильного магнитного поля. Вследствие этого сжимаемость
вещества в поверхностном слое коры пульсара (порядка нескольких метров) у
магнитного полюса и у экватора могут значительно различаться. В результате расчетов
[10] выяснилось также, что скорость звука имеет аномальную область зависимости
от давления, в которой она падает с ростом последнего. Настоящая работа явилась
естественным продолжением работы [10] и качественно подтвердила ее выводы.
В разд, 2 обсуждается возможность использования выражений для электронной
плотности и плотности энергии однородного электронного газа для описания
неоднородных систем в случае наличия сверхсильного магнитного поля.
Анализ результатов численных расчетов проводится в разд. 3: обсуждается
уравнение состояния, особо подчеркивается аномальный (осцилляторный) характер
зависимости ряда величин от удельного объема (так, например, скорости звука,
электронной теплоемкости и др.).
1, Модифицированная модель Томаса—Ферми, Как известно, спектр электрона в
однородном внешнем магнитном поле имеет вид
ek = (k + 1A+s)B+q2/2. (1)
Здесь к = 0, 1, ... — номер уровня Ландау, s и q — соответственно проекции спина и
импульса электрона на направление поля. В предлагаемой модифицированной
модели Томаса—Ферми полагается, что электроны заполняют состояния с определенными
к, s,.q. Тогда, используя функцию распределения Ферми—Дирака
/(*, s, q) = 1/(1 + ехр((е* - eF)/T)), (2)
можно получить выражение для плотности электронов и плотности
магнитно-кинетической энергии прямым суммированием по всем возможным одноэлектронным со-
12. Зак.953
353

стояниям:
n(eF, T) = Б / ^- f(k, s, q) = аГ* Z /_% (у,. *); (3)
S, к — «> Z7T .У, fc
ем.к. (^ Т) = 2 f е*/(*. s, (jr) ^- = «Г3 /« Л (/1/2 (у,,*) + ("^ -
-ys,k)l_V2b>s,k)) (4)
а = В/{2уД7г2); ys>k = (k + 1A^s)B/T.
Здесь члены рядов являются функциями Ферми—Дирака, определяемыми соотноше-
tkdt
нием Ik(x) = / : . Суммирование в (3), (4) и всюду ниже ведется по всем
о 1 + ехр(? - х)
возможным к = 0, 1, ... °° и s = ± 1/2. Значение ер связано с самосогласованным
потенциалом </?(г) соотношением eF = </?(г) — <р0, где </?(r) = (U(r) + </?e(r))> ^(r) ~ внешний
потенциал (суммарный потенциал ядер), <&,(r) ~ потенциал, создаваемый электронами
вещества, </?0 — химпотенциал, определяемый из условия нормировки / п(ер9 T)dr = z
(К0 — объем элементарной ячейки кристалла, z — атомный номер вещества).
Полная энергия электронов в ячейке легко вычисляется в приближении Вигнера—
Зейтца: каждая ячейка V0 заменяется сферой V равного объема с ядром в центре;
тогда, если пренебречь мультипольными моментами (несимметричностью плотности
электронов в ячейке), задача сводится к рассмотрению независимых
электронейтральных сферически симметричных ячеек, при этом выражение для энергии электронов
в расчете на одну ячейку примет вид
^Т = ^М.К. + Еее+Еея> (5)
где
1 Z
Ям.к.^/ем.к.^г; Еее = - Sve(r)n(eF, T)dr\ Еея=$ - n(eF, T)dr.
2 г
Здесь и всюду ниже интегралы берутся (если не оговаривается противное) по объему
сферизованной ячейки V и предполагается, что фе(г) и п(ер9 Т) зависят только от г
(расстояния до ядра). Справедливость приближения Вигнера—Зейтца для вещества
в отсутствие магнитного поля многократно обсуждалась в литературе (см., например,
[14]). Дополнительная несимметрия, вызванная влиянием внешнего сверхсильного
поля, невелика вплоть до полей порядка z3 для несжатого вещества [2], а с
увеличением давления — даже для больших В. Роль этой несимметрии будет обсуждена
подробнее в разд. 2. Мы ограничим свое рассмотрение областью, где влиянием последней
можно пренебречь.
Выражение для электронной энтропии Se в расчете на одну ячейку легко получить
в одноэлектронном приближении (см., например, [15]), используя равновесные числа
заполнения (2) :
Se = aTV2X (31V2(ys,k)-ys,kI_V2(ys,k))-
s,k /г /г .
Исходя из этого соотношения, выпишем выражение для электронной свободной
энергии в расчете на одну ячейку
F=E -TSe = FUtKt+Eee+EeRi (6)
где
^м.к.=<*Г3/> 2 (^I_V2(ys,k)-2IlA(yStk)).
s,k v I '
354

Прямым дифференцированием свободной энергии (6) по объему ячейки V
нетрудно получить локальную формулу для давления
Р=-(Ш = 2«T*U* '*(*.*)> (7>
КЪУГГ s,k V1
которая связывает давление с химпотенциалом системы.
Заметим, что все полученные выражения справедливы, строго говоря, лишь для
медленно меняющейся электронной плотности (в противном случае велики
градиентные поправки).
2. Область применимости модели. Обсудим характер используемых приближений.
Первое из них — приближение сильного поля [2], в котором предполагается, что
движение электрона в плоскости, перпендикулярной полю, определяется магнитным полем,
кулоновское взаимодействие определяет движение электронов вдоль поля. Оно
справедливо, если выполнено соотношение [2]
z/R<B, . (8)
т. е. когда для большинства электронов в ячейке выполнено условие малости
кулонов ского потенциала, 7р ~~ z/R по сравнению с расстоянием между уровнями Ландау
BiR = (3V/4ity/t.
Статистическое описание системы возможно, если велико число заполненных
состояний. В приближении сильного поля, в силу нормировки, справедливо соотношение
NXN2 = z, где Ni и N2 — число заполненных состояний, для движения вдоль и поперек
поля соответственно, следовательно, условие применимости модели Nlf N2 ^ 1.
Поскольку [16] N2 ~ BR2 (если заполнено небольшое число уровней Ландау), то
условие Ni ^ 1 справедливо при z/N2 > 1, т. е. BR2 <z. Таким образом, модель
справедлива при
KBR2 <z. (9)
Для изолированного атома, подставив значение радиуса атома из [2] в (8) и (9),
имеем z4/3 <В <z3 в соответствии с [2]. В этом случае все электроны в атоме
находятся на нижнем уровне Ландау со спршом, направленным против поля (конечно,
если температура Т < В), в суммах (3) и (4) остается по одному числу, и наша
модель совпадает с моделью [2], но с учетом конечной температуры.
Ограничение (9) можно получить также из условия малости градиентных поправок
к электронной плотности и к плотности кинетической энергии. Действительно,
анализируя уравнение Томаса—Ферми с поправкой на неоднородность и выражение для
плотности кинетической энергии, полученные в [17], получим, что вклад
градиентных членов мал при выполнении условий BR2 > 1; и \ip0\R2 > 1/12; но Nt ~~ \$0\V2R,
т. е. мы снова приходим к неравенству Nlt N2 > 1. Заметим, что малость градиентных
поправок позволяет использовать для неоднородного электронного газа выражения
(3) и (4) для плотности электронов и плотности энергии, выражающиеся через
значение самосогласованного потенциала в данной точке. Как было впервые отмечено в
[2] и позже строго доказано в [7], подобная локальная связь приводит к сферической
симметрии электронного распределения в атоме.
3. Результаты расчета. Полученное модифицированное уравнение Томаса—Ферми
Ауе = -4тт(у-у0, Т)
решали численно, способом, подробно описанным в [10]. Были рассчитаны для
железа в поле В = (10* 30) • z4/3 (что составляет соответственно 1,8 • 1012 и 5,4 • 1012 Гс)
кривые изотермического сжатия при значениях Т = 1, 10, 100, 300. Так, на рис. 1
представлены изотермы Т= 10, 300, рассчитанные в настоящей работе в сравнении с
интерполяционной кривой холодного сжатия [10] для железа в поле В = 10 • z4/3 . Видно,
что ход интерполяционной кривой качественно согласуется с изотермой Т= 10, в част-
12*
355

IgO.
/,ZlgV
8S
p
eu
j
V
\
— \
<54«-^»
"l
——— f
Z
\ 3
s^4^^^^^:^^ y
х/^^ч^-ч
1 1 1 >
-Z,0 -Z,4 -ZM -US ~r,Zl$V
Рис. 1. Зависимость давления Р от удельного объема V для железа в поле В = 10 • z
• 1013 Гс) для нескольких значений температуры Т
Т=Ю(1); 300 (2), О (5) из [10]
4/3
(или 1,8
Рис. 2. Зависимость скорости звука а в железе от удельного объема V для нескольких значений
температуры Т и поля В (скорость звука в см/с):
1 _ т= 10; В = 10 • z4/3; 2 - Т= 300, В = 10 -z4/3; 3 - Т = 300, В = 30 • z ' ; 5- Г = 300,
В = 30 z4/3; 4- Т=0, В = 10 z4^3 (кривая взята из [10])
-*,* -£* -£# -/,/*•
Рис. 3. Зависимости температуры Дебая в решетки Суув = 1/УТ(ЪЕ/ЪТ) уУв железа (а) и
электронной теплоемкости (б) от удельного объема V для нескольких значений температуры Т и поля В
1 - Т= 10, В = 10- z4/3; 2 - Г= 100, В = 10-:4/3; 5 - Г= 300, В = 10 • z4/3; 4 - !Г = 300,
B = 30z4/3
ности, на обеих кривых существуют участки (b*P/bV2) < 0. С ростом давления все
кривые выходят на одну асимптотику — на Томас—Ферми зависимость P(V) для
вырожденного однородного электронного газа.
На рис. 2 изображен ход зависимости скорости звука от объема, приходящегося на
атом2. Сравнивая кривую холодного сжатия в интерполяционной модели [10] и
изотерму Т = 10, приходим к выводу, что интерполяционная модель качественно
передает аномальный рост скорости звука с ростом удельного объема в области
заполнения первого уровня Ландау. На изотермах, рассчитанных в настоящей работе, видно,
что заполнение каждого уровня Ландау приводит к аномальной зависимости скорости
звука от удельного объема, но для не слишком высоких (см. также [11]) температур.
Так, для Т= 300 (т. е. Т — В/2) осцилляционный характер зависимости скорости звука
от удельного объема исчезает. Последнее естественно, поскольку при Т ~ В
дискретность уровней Ландау становится несущественной.
Кроме скорости звука, характерной осцилляционной зависимостью обладает целый
ряд других величин. Так, на рис. 3,я изображена зависимость температуры Дебая 0
решетки железа (для упрощения решетка предполагалась кубической) в зависимости от
удельного объема. Температура Дебая определялась по формуле в = я/Л(97г/4)Уз .
2Скорость звука а находили численным дифференцированием по формуле а2 = -V2 {bP/bV)^/Mpe
(Мр — масса ядра железа).
356

Заметим, что аномальный рост в с удельным объемом приводит к отрицательному
вкладу в давление от ядер (фононов). Действительно, исходя (см., например, [15])
из Гя = ~7г4 Т4/10в3, нетрудно получить
P* = -(dFJW)T = -yi0(7rT/e)4de/dV; Ря<0, (dd/dV)<0.
Отметим также, что если электронный газ сильно вырожден, то температурная
поправка к давлению обусловлена давлением ядер РЯ9 и, как нетрудно видеть, тогда
ХЬР/ЪТ)у — (ЪРя1ЪТ)у < 0. Как известно из термодинамики [15], это в свою очередь
приводит к отрицательности коэффициента теплового расширения (ЪУ/ЪТ)р < 0 (как
у воды при Г<4°С).
В качестве еще одной иллюстрации приведем зависимость электронной
теплоемкости от удельного объема (рис. 3,6). Кроме характерной периодичности с ростом
удельного объема при Т = 100, в поле 5=10- zAU и при Г= 300; в поле В = 30 • z 4/з,
необходимо отметить существенное различие в кривых (1) и (2). Максимумы кривой (Г =
= 100) соответствуют минимумам более низкотемпературной (Г= 10). Это связано с
тем, что при низких температурах фактор вырождения (Т/ер) < 1, что приводит к
падению теплоемкости вырожденного газа с ростом вр при Т ~ 10.
Вернемся теперь к обсуждению влияния квантовых поправок. Как было показано
в [18], они приводят к изменению характера заполнения одноэлектронных состояний
в импульсном пространстве, а именно, ступенчатое распределение электронов
размывается, как при действии некоторой эффективной температуры. Если провести оценку
этой эффективной температуры в нашем случае, мы получим ГЭфф ~ (z1/2/R)ip3/4.
Понятно, что подобное размытие электронного распределения должно дополнительно
сглаживать осцилляции в зависимостях a(V)9 S(V) и др. Характерная величина ГЭфф в нашем
случае порядка 200, т. е. введение столь большой температуры может убрать
осцилляции, но, с другой стороны, для больших полей мы опять получим осцилляции в
скорости звука и в других величинах.
Авторы выражают благодарность за обсуждение результатов и высказанные ценные
замечания Д.А. Киржницу, Н.Н. Калиткину и Ю.Е. Лозовйку.
ЛИТЕРАТУРА
1. Гинзбург В.Л. И УФН. 19.71. Т. 103. С. 393,
2. Кадомцев Б.Б. // ЖЭТФ. 1970. Т 58. С. 1765.
3. Кадомцев Б.Б., Кудрявцев B.C. // ЖЭТФ. 1972. Т. 62. С. 144.
4. Tomishima Y.t Yonei К. // Progr. Theor. Phys. 1978. Vol. 59. P. 683.
5. Labzowsky L.N., Lozovik Y.E. // Phys. Lett. A. 1972. Vol. 40. P. 281.
6. Banerjee В., Constantinescu D.H., RehakP. // Phys. Rev. D. 1974. Vol. 10. P. 2384.
7. Mueller R.O., RauA.R.P., Spruch L. // Phys. Rev. Lett. 1971. Vol. 26. P. 1136.
8. Gadiyak G. V., Lozovik Y.E. 11 J. Phys. B. 1980. Vol. 13. P. 1531.
9. Гадияк Г.В., Лозовик Ю.Е. 11 Сб. тр. HI Всесоюз. семинара по моделям механики сплош. среды.
Новосибирск, 1976. С. 211.
10. Гадияк Г.В., Обрехт М.С., Яненко НЛ. // Числ. методы механики сплош. среды. 1980. Т. 11.
С 27.
11. Gadiyak G. V.t ObrechtM.S., Yanenko N.N. 11 Phys. Lett. A. 1980. Vol. 80. P. 191.
12. Румер Ю.Б. И ЖЭТФ. 1948. Т. 18. С. 1081.
13. Sondheimer E.H., Wilson A.H. 11 Proc. Roy. Soc. London A. 1951. Vol. 210. P. 173.
14. Ruderman M.A., MowersE. Y., Lee J. et al. // Ap. J, 1977. Vol. 215. P. 291.
15. Ландау Л.Д., Лифшиц ЕМ. Статистическая физика. М.: Наука, 1964.
16. Ландау Л.Д., Лифшиц ЕМ. Квантовая механика. М.: Наука, 1974.
17. Tomishima Y., Shinjo К. Ц Progr. Theor. Phys. 1979. Vol. 92. P. 853.
18. Киржниц Д.А. И ЖЭТФ. 1958. Т. 34. С. 1625.

ГИДРОДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ
И ТУРБУЛЕНТНОСТЬ
ОБ ОДНОЙ МОДЕЛИ ЦИРКУЛЯЦИИ АТМОСФЕРЫ
С ЛОКАЛЬНЫМ ЗНАКОПЕРЕМЕННЫМ КОЭФФИЦИЕНТОМ ТУРБУЛЕНТНОСТИ*
ВВЕДЕНИЕ
Как известно, теплообмен между полюсом и экватором осуществляется
нерегулярными движениями в атмосфере, которые можно трактовать как турбулентность
планетарных масштабов.
Роль макротурбулентности заключается не только в теплопередаче;
макротурбулентность есть существенный динамический фактор формирования общей циркуляции
атмосферы. С одной стороны, возможна трансформация энергии регулярных течений
общей циркуляции в энергию макротурбулентности, с другой стороны, за счет энергии
нерегулярных движений могут возникать регулярные течения общей циркуляции.
Макротурбулентность также играет существенную роль в формировании зонального
углового момента. Турбулентные течения описываются системой уравнений Рейнольдса:
р(Эй,/ЭО + pd(Uillf)ldXj = -bp/bXi- pb{u\uf)lbxh dufidxf = 0.
Эта система не замкнута, так как содержит неизвестные напряжения Рейнольдса.
Попытка замкнуть систему, используя некоторые дополнительные связи между
напряжениями и осредненными гидродинамическими полями, предпринималась Буссинеском
(1897), Прандтлем (1925), Тейлором (1932) и Карманом (1930). Обычно
используется предположение о линейной связи между тензорами напряжений Рейнольдса тц
и средними скоростями деформации Фа(3 = bujdxp + Ъи$1Ъха [1, 2]. Это выражается
формулами тц = рКц£1Фар, Kjjap — тензор четвертого ранга, компоненты которого
носят название коэффициентов турбулентной вязкости. Принимается гипотеза об
изотопности тензоров K^f^ = К^н{biQLb^ + d^dJ0L)t Возможны следующие подходы
к определению коэффициента турбулентной вязкости: следуя идее Колмогорова (1942),
считается, что К полностью определяется двумя основными характеристиками
турбулентности — средней энергией пульсаций Ъ2 и средним пространственным
масштабом пульсаций /. Из анализа размерностей находится
КМН ~Ь1ИЛИ КМН _ /2 (ф^ фо0)%
К такому же виду для коэффициента Кмн приводит гипотеза Гейзенберга [1]
о-спектральном переносе энергии, которая была использована Смагоринским [3] в задаче
об общей циркуляции.
В физике атмосферы, теории общей циркуляции определяющими для процессов
формирования и эволюции погоды являются крупномасштабные движения. Отметим
две характерные особенности крупномасштабных движений. Первая состоит в том,
что отношение вертикального масштаба Н к горизонтальному масштабу L мало (Я «
« 10-12 км, L = 3000 км, H/L « 0,003). Вторая особенность состоит в
приблизительной бездивергентности крупномасштабных масс воздуха. Следовательно,
крупномасштабные движения весьма близки к движениям двумерной несжимаемой жидкости.
♦Численные методы механики сплошной среды. 1976. Т. 7, № 1. С. 137-153. (Соавторы Г.П. Кур-
баткин, В.Н. Крупчатников, М.Ш. Эйхер.) '
358

Наиболее существенной характеристикой крупномасштабных атмосферных
процессов является их энергетический спектр. Знание особенностей перераспределения
энергии по спектру позволяет конструировать эмпирические зависимости,
учитывающие макротурбулентный обмен, а также строить модели турбулентности, например,
такие как "цепочки" Обухова [4]. К особенностям двумерной турбулентности следует
отнести [5—7] существование инерционного интервала с "законом 5/3", где перенос
энергии происходит от более высоких к более низким волновым числам, что является
примером эффекта "отрицательной вязкости" [7].
Обуховым была предложена модель нелинейных взаимодействий в потоке
несжимаемой жидкости с помощью цепочек триплетов с "двойным зацеплением". В [4]
показано, что в этом случае существуют два стационарных режима: каскадный
перенос энергии и каскадный перенос квадрата вихря, причем в первом случае каскад
происходит в сторону меньших волновых чисел. Поэтому в конструировании модели
турбулентности двумерной несжимаемой жидкости с применением полуэмпирических
теорий должен быть взят за основу знакопеременный, нелинейный механизм
"турбулентной вязкости".
В статье [8] для описания движения вязкой жидкости было предложено следующее
уравнение:
Ъи Ъи 3 Г (Ьи\ Ъи Л
— +и— =—Ы— — , (В.1)
Ы , Ъх Ъх\- \Ъх1 Ъх J
причем коэффициент и(Ъи/Ъх) является знакопеременным. В предположении о
полиноминальной зависимости v от Ъи/Ъх были получены некоторые априорные оценки
решения уравнения (ВЛ). В работе [9] были получены априорные оценки для
многомерного аналога уравнения (ВЛ), а также доказаны теоремы существования для
некоторых вспомогательных задач. Решение уравнения (ВЛ) может иметь
автоколебательный режим, а само уравнение может служить моделью неустойчивых осциллирующих
и турбулентных течений вязкой жидкости. В данной работе будут получены априорные
оценки для решения уравнения баротропного вихря со знакопеременной
"турбулентной вязкостью", которые являются равномерными относительно t. Употребление
термина знакопеременная "турбулентная вязкость" требует пояснения. Величина v(ux)
строго не может быть названа коэффициентом турбулентной вязкости, однако можно
говорить об эффективном коэффициенте v(ux) = К, где черта означает осреднение
по времени, причем К > 0. В дальнейшем мы будем употреблять термин локальная
знакопеременная турбулентна» вязкость. Подход к моделированию турбулентности,
предложенный в [8], тесно связан с подходом, основанным на теории
гидродинамической неустойчивости, в частности, с теорией, предложенной Л.Д. Ландау (1944).
Уравнения, описывающие движения однородной среды в общем случае, могут быть
записаны в виде
dW/dt = divT, (B.2)
где Т = (TiK) — симметрический тензор напряжений. При выполнении постулатов
Стокса определяющее соотношение имеет вид
G(D,T) = T-aE-PD-yD2, (B.3)
где D = (DiK) — скалярные функции от главных инвариантов тензора D = (Рж). В
данной работе рассматриваются одноуровенные модели атмосферы, т.е. у = 0. Для
движения атмосферы определяющее соотношение может иметь более общий вид
' g[ 8 T,D,f) = 0. (B.4)
\t-tT *
Явная зависимость G от F указывает на влияние стационарных (климатических)
359

t
источников [11]. Обозначение 5 Т указывает на то, что значение тензора напряжений
t-tT
в момент времени t зависит от его значения в момент t — tT.
Работа посвящена исследованию экспериментальных, нелинейных механизмов
горизонтальной "турбулентной вязкости" в задаче параметризации подсеточных процессов.
Как показано в [11], подсеточные движения в моделях долгосрочного фонового
прогноза могут параметризоваться: 1) климатическими источниками, 2) механизмами
турбулентной вязкости, 3) некоторыми механизмами, связывающими подсеточные
процессы с прогнозируемыми планетарными движениями в прошлые несколько дней.
Для воспроизведения реальных планетарных волн использовались полные уравнения
с учетом 2) однородного слоя жидкости, а также фильтрованные (квазисоленоидаль-
ные) с учетом 1) -3), т.е. климатическими источниками и эффектом инерции [11].
1. АПРИОРНЫЕ ОЦЕНКИ
Рассмотрим уравнение баротропного вихря в сферической системе координат
A. 3V2^/ar+/n(V2^+/,^) = Fn (1.1)
с начально-краевыми условиями ФI ^=0 = О,
где
Ч-1ГЭ/Г* 3Fxcos*"|
Fn=(*cos*) |_-__J,
Fa = {a cos*)-1 [±-(KMHDT) + a-1 JL(KMHDS)],
L3X Э* J
Fv = (acosv»)"1 [-£-(KMHDS) -a"1 -?-{KMHDT)\
i-Эл Э* J
_АЪи Ъ Л
DT = (acos*) 4— - — (ucos*) ,
1 о A oA J
i ГЭу э 1
Ds = (acosy) —- +— (hcos*) , (1.3)
LdX Э* J
£мя = (я cos*AX)2(^0 - vx cos*Z> + y2(cos*Z>)2),
D = (D2T+D2s)1/29 v\>AvQv2i u = -a"x , v = (acos*) * .
э* эх
Для начально-краевой задачи выводится априорная оценка
1 t
/ / Ф\ + D2T)2cosydodt < const, (l .4)
t - t0 t0 a
где a — поверхность полусферы. Нетрудно показать, что
fFn *do = a~2f (D2T + D2s)KMHdo,
тогда
t t
Ex -E°<p1f f D3 cos3 ydodt - v2f fD*cos4ydtdo,
a tn о tn
360

где Ег = lAf(V&)2da9 далее, применяя неравенство Гельдера, получим
о
t t
Et -Е° < viU f(D cosy)4 dtdof4 [mesa(f - f0)] % - v2f f (D cosy)4 dodt.
о t0 a t0
Так как E* > О, то 0 <E0/(t - t0) + dZ*A -v2Z,
где
1 *
Cx = meso%p1, Z = / / (D cosy)4 do dt,
to - t tQa
откуда следует (1.4) .
Б. Аналогичная оценка получается также для уравнения
bV2V/bt+In=Fn +кдЕп/Ы..
Заметим, что присутствие члена к bFn/dt означает локальный эффект "инерции".
В. Рассмотрим линеаризованное уравнение баротропного вихря в ^-плоскости,
однородное по у
ЭД2Ф ЭД2^ Э^
+ U +0— = v0V4V(t) + v1V4*(t'-to) (1.5)
bt Ъх Ъх
с начально-краевыми условиями
*(x + 2irf0 = *(x,f), *lre-w<r<re=*o(^0. (1.6)
Предположим, что Ф0 Е С1 (со; L2 [0, 2тг]). Будем искать решение в виде ряда
Ъау sin7* + by cosyx.
Переходя к уравнениям для коэффициентов Фурье, имеем
iy*(U-y-&ly)by(t)-vQy2ay(
dy*(U-y- p/y)by(t) - v0y2ay(t) - vx y2a(t - со),
by = (U- у - P/y)aJt) - vQy2by(t) - vxyby(t - со). (1.7)
В матричном виде (1.7),запишется так
Xy=A-'Xy+B-Xy(t-to), X7=( J.
Ъу
(1.8)
Матрица Л положительно определена, если vQy > \(3/у2 — U\ ? однако мы потребуем
несколько больше vQy > v1y + \Р/у2 — U\. Введем функционал G(X) = (X, X) -
t
- f (AX, X)dr. Можно доказать: 1) IIXll < G(X), 2) ^(Ху) < 0. Следовательно,
II Ху IK G(Xy) < G(X^), и мы приходим к следующей оценке:
1№ II С1 ([0,71; L2[0,2n])< const.
Рассмотрим уравнение (В.1) с начально-краевыми условиями
u(0,x) = ef(x), и(г,0) = ы(г, 1), /(0)=/(1), (1.9)
/'(0)=/'(П, //(*) = 0.
о
Будем искать первое приближение решения уравнения в виде самовозбуждающейся
волны
иЩ,х)=а(гЖх). (1.10)
361

С учетом краевых условий легко получить уравнение для квадрата амплитуды волны
\а\2 = -2аоГ0 \а\2 + 2ахгх \а\3 - 2а2г2 |я|4, (1.11)
где
f\f'\i+2dx
о
П =
f\f\2dx ■
о
с начальным условием I a\ 211=0 = е2. При а0 < 0, ol\ = О, а2 > 0 мы приходим к
известному уравнению Л.Д. Ландау, описывающему возникновение турбулентности при
Re>ReKpHT.
2. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ СО ЗНАКОПЕРЕМЕННОЙ
НЕЛИНЕЙНОЙ ВЯЗКОСТЬЮ ДЛЯ ПРИМИТИВНЫХ УРАВНЕНИЙ
ОДНОРОДНОЙ ЖИДКОСТИ
Предлагается спектральная модель для примитивных уравнений со
знакопеременным, нелинейным механизмом вязкости
aUt = (l-n2yl[-UUx- F(l-/z2)tfM] +ma»V-gZx+Fx,
aVt = (\-ix2Yl [-UVX - V{\ -M2)KM - (C/2 + V%] - 2Sla»V - g{\ - M2)ZM + F„, (2.1)
aZt = (1 - м2)-1 [^-UZX - V(l - m2)Zm - Z(UX + (1 - Д2) FM)],
где ц. = sin<p, U = и - cos</?, V - v • cosip. В качестве начальных данных было задано поле
функции тока неустойчивой волны Россби—Гаурвица:
А
^ = -co/i+ cosm\Pmn(n), со = 0/784810-5Д2, (2.2)
и(и + 1)
и = 9, m = 8, Л = 0,608...
На рис. 1 показаны амплитуды гармоник (8.9) и (8.11) вихря скорости А,
вычисленные на 2 суток по данной модели для четырех вариантов: 1) модель без
вязкости с высоким разрешением (16,19); 2) "усеченная" модель без вязкости с
разрешением (8, 7); 3) "усеченная" модель с линейным механизмом вязкости; 4)
усеченная модель с нелинейным знакопеременным механизмом вязкости. Близость
кривой 4 к кривой 1 ("точному" решению) демонстрирует меру способности нелинейного
знакопеременного механизма воспроизводить "подсеточные" короткие волны.
На рис. 2 показана функция Кмн(р) и интервалы изменений D, рассчитанные как
по реальным (2), так и по варианту IV (3) модельной задачи (2.1), (2.2) (K(D) =
= (v0 - vxD + v2D2) (i)). Приведем энергетическую оценку качества нелинейных
знакопеременных механизмов. Для трех вариантов, перечисленных выше, вычисляется
величина б2 = S(Е% — Е'к)2/'ЕЕЪ • 100%. Е — кинетическая энергия "точного" решения,
к к
взятого на интервале суток через каждые 6 часов; Е — кинетическая характеристика
для усеченной модели. Для вариантов: 2) 5 = 6,4%, 3) б = 4,2%, 4) б = 3,1%.
3. ДИАГНОСТИЧЕСКИЕ ОЦЕНКИ КОЭФФИЦИЕНТОВ МЕХАНИЗМА
НЕЛИНЕЙНОЙ ЗНАКОПЕРЕМЕННОЙ ВЯЗКОСТИ
Так как решается задача о параметризации подсеточных процессов для задач
долгосрочного фонового прогноза, то мы должны ориентироваться на "сглаженные" поля,
но при осреднении метеорологических полей теряется энергия крупномасштабных
неустойчивых процессов, поэтому механизмы нелинейного турбулентного обмена
362

должны быть способны не только диссипировать, но и поддерживать развивающиеся
волны. Решение модельной задачи, рассмотренной в разд. 2, показало целесообразность
использования для этих целей нелинейных знакопеременных механизмов.
Как уже отмечалось во введении, для воспроизведения реальных планетарных волн
было взято баротропное уравнение вихря
bV2*/bt+In = F(k9v)+F"(k9<p9t-tT)9
(3.1)
где F(X, ф) — климатический источник, F" (X, </?, t — tr) — взятое в момент времени
t - tT (для поддержания эффекта "инерции", обусловленной подсеточными
процессами) отклонение от климатического значения члена F. Для нахождения оптимального
[-
1
z
/-f-^>~-\ /
/^ \-&к3
/f \V
^s*'s ч
I I I I I . I I I I
КШ)
Рис. 1
Рис.2
времени запаздывания была решена обратная задача, и tT находилось из уравнения
9^/dr+V:2(/n)^=e^a^/ar (3.2)
методом наименьших квадратов. Причем, считая левую часть уравнения (3.2) в
момент времени t9 правая считалась в моменты времени t — jAt9 где / = 0, 1, ..., 6. При
этом были использованы реальные полусферические поля геопотенциала Ф на 500 мб.
с интервалом по времени At = 1 сут, Ав = 5°, АХ = 10°, с 1 по 25 декабря 1964-1968 гг.
Коэффициенты e™t были вычислены для 81 сферических гармоник. Поле
геопотенциала аппроксимировалось конечным рядом разложения по шаровым функциям
Ф(*,Х,г)= S S Ф*(г)Г;?(*,Х),
т - —М п = </>(т)
(3.3)
где
утя =„im Kp
1 п ^ гт,п
(sin*/?), </>(0) = 2, у(т Ф 0) = I m I.
Функция тока вычислялась по линейному уравнению баланса. Результаты расчетов
e™t по мгновенным и охлажденным полям представлены на рис. 3,4 [т = 0, п = 2 (а),
т = 0, п = 4 (б), т = 0, и = 6 (в), /я = 1, п = 3 (г), /я. = 1, п = 5 (д), т = 1, п = 1 (е),
т = 2, и = 4 (ж), т = 2, п = 6 (з)9 т = 2, и = 8 (и)], где сглаженные поля
получаются из реальных полей геопотенциала после действия на них временного фильтра
С((Ф)э)э)э,
(Ф)з = (Фа;_1 +2Ф*+Ф* + 1)/4 дляй-годня. (3.4)
363

Слагаемое е™ t Ъ^^/dt призвано статистически подправлять частоты. А
выявившиеся минимумы значений коэффициентов е™д t .у, как функций индекса/, и смещение
этих минимумов в сторону возрастания / при осреденении по времени полей
геопотенциала могут быть объяснены тем, что картина фиксированного в данный момент
вихревого ("подсеточного") переноса количества движения совсем не определяется
картиной планетарного течения в тот же момент [11]. Вычисления установили
следующее время запаздывания tT на 500 мб: для мгновенных полей 1—2 суток, для
сглаженных полей 2—4 суток. После нахождения tT была решена обратная задача
одновременного нахождения параметров р0, vx. v2 методом наименьших квадратов. кмн было
КЗ
а г /
I I \У\
ff
Ь4^- К±Х~ fc^
ntr*
tffV
Г /
,i i i
- J
i i i i
\i i i hiii Г\1 i j
/
Г ё
I I I I
- U
Рис.3
Рис.4
выбрано как
Кмн = (flAXcos^Vo + *>i cos</?Z> + v2(cos#D)2), (3.5)
причем знаки коэффициентов не закреплялись заранее. Для сравнения рассматривался
также линейный механизм горизонтальной турбулентной вязкости: F" = 1лп/а2 -v4^".
Аналогичные расчеты были выполнены по реальным полям геопотенциала после
действия на них временного фильтра (((Ф)з)з)з- Ниже приведены вычисленные
значения параметров и оценки для фильтрованных полей: tT = 2 суткам,
vo = 1,8ю5 м2/с, V\ = — l,76ipio м2, v2 = 0,5510is м2/с,
5 = 1—0,01 (для нелинейного механизма),
Мп = 1>2ю5 м2/с, 5 = 1—0,25ю-2 (для линейного механизма);
для мгновенных полей iT = 1 сутки.
vo = ОД юб м2/с, *>i = -5,1109 м2, v2 = 6,0581О1з м2/с,
5 = 1—0,610-2 (для нелинейного механизма),
An =0>910s м2/с, б = 1—0,2ю"2 (для линейного механизма).
Вышеприведенные вычисления и оптимизация проводились по 81 гармонике, где
2(r-F")21
5 =
2 (Г)2
к
Г =
bt
V2*"+/«-F,
364

O'^SEO'^y;
_ 2 я 7г/2
()= / / ()cosyd\dip.
На рис. 5, 6 показаны соответственно для мгновенных и сглаженных полей (по
данным декабря 1967 г.) как функции времени следующие энергетические
характеристики: — L Ф (вверху) сплошная линия; — F"ty (внизу, увеличенные в 100 раз) —
пунктир для нелинейного механизма, пунктир с точкой — для линейного механизма.
Сделаем два замечания: 1) оценка 5 = 1—0,01 приблизительно эквивалентна тому,
что слагаемое F" составляет около 10% от веса адвективного члена в уравнении (3.1);
2) именно осредненные по полусфере энергетические характеристики на рис. 5, 6 до-
L Ч? 2
3
Рис.5
Рис.6
статочно выгодно отличают способность нелинейного знакопеременного механизма
(3.9) описывать нестационарную природу макротурбулентности свободной атмосферы
в сравнении с линейным механизмом дп I^V4^". Наиболее устойчивые результаты
получаются при оптимизации коэффициентов р0> р19 р2 по первым 15 гармоникам.
Вычисления дали следующие результаты: для мгновенных полей для нелинейного
механизма^ = 0,610б м2/с, Р\ =—0,3310и м-2, р\ = 0,4110is м2/с, 6 = 0,987;
для линейного механизма
An = 0,610< м2/с, 6=0,994;
для фильтрованных полей с нелинейным механизмом
i>o = 0,15107 м2/с, i>i =-0,76k)11 м2, *2 = 0,9410" м/с, 6 = 0,973;
для фильтрованных полей с линейным механизмом
An = 0,551О< м2/с, 5 = 0,990.
Уже из этих экспериментов видно, что вес нелинейных знакопеременных
механизмов увеличивается на сглаженных полях, в то время как вес линейного механизма
мал. С этими оптимизированными коэффициентами была дана серия прогнозов по
уравнению (3.1). Интегрирование по времени проводилось по схеме Адамса—Башфорта
с At = 2 часов. Для сравнения эта же серия прогнозов была выполнена с линейным
механизмом диссипации /in/fl2V4^". Введение нелинейных, знакопеременных
механизмов давали систематическое улучшение прогнозов среднем на 2-4% по сравнению
с линейным.
Следующий вопрос, который мы попытались разобрать, был об изучении
эффективности параметризации подсеточных движений с помощью используемых механизмов.
365

Причем исследовался как полный спектр — 81 гармоника, так и длинноволновой
участок спектра (первые 15 гармоник). При вычислении вклада в эти 15 гармоник
учитывалось взаимодействие 81 гармоники. Введем следующие обозначения: (f)3 —
означает осреднение функционала, вычисленного по мгновенным полям, оператор
(f)s означает вычисление функционала по предварительно осредненным полям.
Очевидно, что для линейных функционалов величины (/)3 и (/)3 тождественны, а для
нелинейных
(Я3=/((*)э,(*)з) + /(*\*Г
\/\ / '
- —/
—г.
- —J
—н
\ а
1 Г Т *""П
/ V
t
тогда
ЭФ" 3
= (/")3+/"(*V)3 + F"3, (3.6)
3(»Vw-(Os + (A.
(3.7)
в
Ясно, что для того, чтобы уравнения (3.6)
и (3.7) выполнялись с одинаковой точностью,
необходимо, чтобы (F")3 включали в себя
точное параметрическое описание члена /"(V, фу.
Так как мы проверяли эффективность
параметризации на баротропном уравнении вихря, то
высказанное выше утверждение эквивалентно
тому, что, если
2
W Z0
Рис. 7
хъЛ\ьг )
(3.8)
но
d (iv2*+/-)
< S ((((— У2*"+/„)з)з)з)2
'Эн Of
> Е ((( Д- V2*2 +/„ - F")3)3)3) 2,
(3.9)
то параметризация проведена достаточно хорошо.
На рис. 7 приведены результаты расчетов по проверке эффективности
параметризации подсеточных движений нелинейными знакопеременными механизмами. Графики
на этом рисунке приведены за временной отрезок с 1-го по 23-е декабря 1965 г.
Показаны следующие характеристики:
*Г (рис. 7, а, 7),
/ N п\
I — 2 *&L j/N, где N- количество дней, по которым ведется осреднение (рис. 7,д, 2),
VF" (рис. 7, б),
366

S (L" r 7аз - F" . з \2\IN (рис. 7, e, 2),
* = t( 4.—-V33 \—»з'3 f !
Ф
11 • гз3
\ Ф
r" 2
' Ф
2Г2г=-з№ (рис. 7,в, 7),
IN (рис. 7,в, J),
Причем нижний график начинается с 10-го декабря. Из анализа этих графиков видно,
что, во-первых, вес нелинейных механизмов на сглаженных полях растет, во-вторых,
на участке с 20-го по 23-е декабря уже выполняется неравенство (3.9), но вес
механизмов горизонтальной турбулентной вязкости мал, так как средняя ошибка к этому
моменту мала, что видно из верхнего графика на рис. 7. На отрезке с 1-го по 5-е
декабря вес механизмов достаточно велик, но неравенство (3.9) все же не выполняется.
Чтобы не усложнять чертеж, на рис. 7 не приводятся характеристики линейного
механизма Mn/a2V4^> H0 необходимо заметить, что все характеристики этого механизма
значительно уступают соответствующим характеристикам механизма (3.5).
ЛИТЕРАТУРА
1. Монин А.С., Яглом А.М. Статистическая гидродинамика. 1965. Ч. 1, 2.
2. Монин А.С., Зилитинкевич С.С. Труды симпозиума по численному прогнозу погоды. Токио,
1968.
3. Smagorinsky /. General circulation experiments with the primitive equations: The basic experiment //
Month. Weather Rev. 1963. Vol. 91, N 3.
4. Обухов AM, и др.'Нелинейные системы гидродинамического типа. 1974.
5. Kraichmn R. II Phys. Fluids. 1967. N 7.
6. Leith С. И J. Atmos. Sci. 1971. Vol. 28, N 2.
7. Старр В* Физика явлений с отрицательной вязкостью. М.: Мир, 1971.
8. Яненко Н.Н., Новиков В.А. Об одной модели жидкости со знакопеременным коэффициентом
вязкости // Числ. методы механики сплош. среды. 1973. Т. 4, № 2.
9. Зеленяк Т.И., Новиков ВЛ., Яненко Н.Н. О свойствах решения нелинейных уравнений
переменного типа // Там же. 1974. Т. 5, № 4.
10. Kurbatkin G.P. Ultralong atmospheric waves and a long range forecasting // Tellu. 1972. Vol. 24, N 6.
1 f. Курбаткин Г.П. Гидродинамическая модель долгосрочного прогноза с априорными средне-
квадратическими ограничениями и избыточными степенями свободы: Тр. симпоз. Новосибирск,
1973.
ИНВАРИАНТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ ТЕЧЕНИЙ
СЖИМАЕМОЙ ЖИДКОСТИ*
В связи с математическим моделированием условий обтекания сложных
поверхностей вопрос о быстром определении режима обтекания на основе локальных свойств
среды является актуальным. В теоретическом плане задача возникновения
турбулентности также далека от разрешения. Некоторые успехи ее основной части — линейной
теории устойчивости — не могут удовлетворить ни практиков, ни теоретиков.
Использование до настоящего времени числа Рейнольдса Re в качестве критерия устойчивости
*Докл. АН СССР. 1981. Т. 259, №5. С. 1056-1059. (Соавтор С.А. Талонов.)
367

и перехода не помогает понять физическую природу неустойчивости: критическое
значение Re оказывается различным для разных типов течения. Например, для свободных
струй оно составляет величину порядка 10, в то время как для профиля с
отсасыванием ~105. Число Рейнольдса зависит от скорости внешнего обтекания и глобальных
масштабов неоднородности. Масштабы возмущений меньше геометрических размеров
стационарного поля течения. Неустойчивость связана с наличием неоднородности
течения, и абсолютное значение скорости желательно исключить из рассмотрения в
пользу ее градиентов.
1. Линеаризованные уравнения устойчивости плоскопараллельного потока
относительно возмущений типа q = q(y)exp[i(ooc + j3r - act)] имеют вид [1]
pia(u-c)f + pity у = -iccn + iid2f/dy2,
piot(u - c)h = -/07Г •♦ fid2h/dy2, pia(u - c)y = - dn/dy,
d^p
ia(u - c)r + pyv + p( /a/+ i&h + — ) = 0, (1)
dy
cvpia(u -c)& + pcvTyy=-P( ia/-+ ifjh + dy/dy) +
+ \d2d/dy2, ir/P=r/p + $/T.
Здесь и, p, T, P — соответственно скорость, плотность, температура, давление
основного потока ид, X, Су — коэффициенты динамической вязкости, теплопроводности и
удельной теплоемкости при постоянном объеме. Индекс "у" означает
дифференцирование; /, h, у, 7Г, гу # — амплитуды возмущений соответственно продольной, боковой
и нормальной скоростей, давления, плотности и температуры.
Многочисленные расчеты и эксперименты по устойчивости плоскопараллельных
течений показывают, что наиболее интенсивные колебания параметров потока
(скорости, температуры, плотности) наблюдаются вблизи критического слоя {и = с).
Поэтому можно предположить, что решение системы (1) в сильной степени определяется
локальными свойствами среды в окрестности этой точки. Вблизи критического слоя
можно принять и - с- иу(ус) (у - ус), а другие параметры основного потока равными
их локальным значениям.
Система уравнений восьмого порядка (1) приводится к эквивалентной, состоящей
из системы шестого и второго порядков [1], если воспользоваться заменой
af + (Уг = af, оир = онр9 атг=атг9 аг=аг, а& = ад-9 (*)
где Ъ? - а2 + ]32, cosx = <*/а.
Используя замену (*) и исключая давление из уравнения (1), в окрестности
критической точки для построения решения можно использовать систему дифференциальных
уравнений шестого порядка
KlV d2f l rf3/i
IT
rjtfj + — spx +Л = -— -^ , (2)
o K2 7-1 ^i d2/i
i 7 iRgr drf ioR*r dt)
где 7^ показатель адиабаты, о - число Прандтля, т? = а(у - ус)9 /i = foijuy9 \px =1ра/иу9
#х = #/Т, а коэффициенты имеют вид
2 „„Л,
dh
drj
Ki
*l,"
Ко
d2h
drj2
«;„ dn3 '
1 (fy>.
/ drj
1 d2d
8 \ ца2 J Шу or P ap
368

Таким образом, возмущения зависят от двух переменных: у и т? (медленный и
быстрый масштабы) ; зависимость от у параметрическая. Можно предположить, что
локальная неустойчивость будет развиваться при условии достижения одним из Kt и Rgr своего
критического значения. При этом можно говорить о трех типах неустойчивости в
зависимости от преобладающей роли одного из Kt (/ = 1, 2, 3). По наибольшему из них
можно определить характерное волновое число, соответствующее наиболее опасному
типу неустойчивости. При изменении у роль каждого Kt меняется. К сожалению,
введенные коэффициенты не охватывают всех типов неустойчивости. Например, для
течений несжимаемой жидкости (М = 0) без теплообмена 6j = е = 0, и при иуу = 0 (если это
имеет место) а = 0, a Rgr = °°. Это означает, что плоскопараллельный поток
несжимаемой жидкости с точкой перегиба в профиле скорости неустойчив при любых скоростях
течения.
Следует, однако, иметь в виду, что известные течения сточкой перегиба не являются
плоскопараллельными. При этом на жидкие частицы действует неоднородное поле
ускорения а, которое рассматривалось в [2]. В качестве одного из характерных
волновых чисел там принималось а ~ ау/а.
С учетом изложенного предлагается следующий критерий устойчивости:
Rgr = max [puy/fia2 j % , (5)
у
где
а = max {| иуу/иу\ , ех | uycosx(p/P) I , e21 PylP) > езI ciyla\\ .
j;=const
Выбор постоянных е, может быть сделан на основе сопоставления данных по
устойчивости, например в [2] получено, что е3 ** 1/36. Аналогичным образом для сжимаемых
течений можно определить ех и е2. Однако это требует специального рассмотрения,
которое отсутствует в данной работе из-за недостатка систематических данных по
устойчивости гиперзвуковых скоростей.
2. Приближенный анализ проведен на основе данных по устойчивости
сверхзвукового пограничного слоя на теплоизолированной поверхности. Для этого градиентное
число Рейнольдса записывалось в виде
Rg^Re^^puy/ila2)1^ =Ке*/*К,
где все параметры безразмерные, отнесенные к значениям на внешней границе
пограничного слоя и его толщине.
Расчеты параметра К* (максимальное значение К внутри пограничного слоя)
проведены для случаев: 1) температура на внешней границе пограничного слоя постоянна
при всех числах Маха (7^ = 50 К); 2) температура торможения постоянна (Г0 =
= 300 К). Закон вязкости от температуры принимался по Саттерленду, а число
Прандтля о = 0,72.
На рис. 1 кривые 1 и 2 получены в предположении 6j = е2 - 0; кривые 3 и 4 — ех =
= 0, е2 = 1/30; кривая 5 — е2. = 0, х = 0, ег = 1/30. В случае учета всех членов в (6)
значение К* будет определяться при М < 3,5 либо кривой 7, либо кривой 2 в
зависимости от условий эксперимента или полета, а при М >3,5 — кривой 5. Если учесть
трехмерность, то очевидно, что кривая 5 будет подниматься с изменением х> а К*
определится границей, обозначенной кривыми 1 и 3, либо кривыми 2 (М ^ 6) и 4 (М ^ 6).
Следует отметить, что для принятого значения е2 кривая 3 не пересекает кривую 1
в рассчитанной области чисел Маха (М < 10); тем самым К* определяется только
кривой 7. Важно также отметить, что если истинное значение е2 меньше принятого,
кривая 5 может пересечь кривую 4 при некотором М = М*. В этом случае потеря
устойчивости в области М > М* может быть определена на основе рассмотрения двумерных
возмущений (х = 0), так как трехмерность отражена только коэффициентомK0i
который перестает играть существенную роль. Это не противоречит данным [3] об ослабе-
369

вающеи роли трехмерных возмущений в потере устойчивости при высоких числах
Маха в отличие от случая умеренных значений М.
Градиентные числа Рейнольдса R*r, полученные на основе данных рис. 1 (кривая 1)
и критических чисел Рейнольдса (кривая 2 на рис. 2 — результаты А.А. Маслова, см.
[4]) приведены на риб. 2, кривая 1. Видна универсальность R* для М < 4. Значение
R* при М > 4 трудно-рассчитать из-за отсутствия систематических данных по
критическим числам Рейнольдса.
Качественное поведение зависимости критического числа Рейнольдса потери
устойчивости показано на рис. 3. Результаты получены на основе кривой 1 рис. 1 в
предположении, что R*r = 30.
К gr
,7/7
Zff
u*iw
■Г —i
\
1
/
1
Рис. 1
Z УМ
Рис.2
300 Р
zoo
wo
Приведенные данные согласуются с экспериментальными результатами по
переходу, подтверждающими наличие минимума в окрестности М = 4 и стабилизирующее
влияние числа Маха при М > 5. Кроме того, они находятся в хорошем соответствии
с расчетами Мака [3], в которых было получено, что максимальная степень
нарастания возмущений наблюдается при М « 5. Тем самым подтверждается основная
гипотеза о постоянстве или слабом изменении критического значения градиентного числа
Рейнольдса. Для течений несжимаемой жидкости этот результат был получен в [2].
ЛИТЕРАТУРА
1. Dunn DM, Lin CC .// J. Aeron. Sci. 1955. Vol. 22. P. 455.
2.Яненко Н.Н., Гапонов С.А. // Числ. методы механики сплош. среды. 1979. Т. 10, № 3.
3. Mack LM Boundary-layer stability theory. 1969. (Prepr. JPL; 900).
4. Левченко В.Я„ Володин А.Г., Гапонов С.А. Характеристики устойчивости пограничных слоев.
Новосибирск: Наука, 1975.
370

О МОДЕЛИРОВАНИИ ЭФФЕКТОВ ОТРИЦАТЕЛЬНОГО ПОРОЖДЕНИЯ
ИНТЕНСИВНОСТИ ПУЛЬСАЦИЙ ТЕМПЕРАТУРЫ
В ТУРБУЛЕНТНОМ СЛОЕ СМЕШЕНИЯ*
В целом ряде экспериментальных исследований классических течений механики
турбулентности таких, как струи, следы, слои смешения, течения в каналах [1-4],
обнаруживается нарушение локальных феноменологических соотношений для
турбулентных потоков типа градиентной диффузии (типа Буссинеска), т.е. в виде
градиентов от средних величин. Точки, в которых обращаются в нуль турбулентный поток
(например, - < uv > = О или - < vT) = О в случае плоского течения) и средний градиент
(dU/ду = О или Э0/Эу = 0 соответственно), оказываются смещенными одна
относительно другой: образуется так называемая зона смещения, внутри которой
турбулентный поток и средний градиент имеют одинаковый знак. Это означает, что в пределах
зоны смещения перенос тепла (или импульса) идет в направлении градиента, т.е. в
направлении, противоположном направлению переноса под действием среднего градиента.
Исходя из градиентного механизма переноса в духе феноменологического закона
Буссинеска такая ситуация отвечала бы отрицательному коэффициенту турубулентного
обмена. Зона смещения возникает как в потоках с асимметричными средними
профилями [1, 4], так и в потоках с симметричными средними профилями [2,3] тех или
иных статистических свойств турбулентного течения. Согласно прямым измерениям
[1,4] в зонах смещения порождение турбулентности (&> 0 = — (u'v)dU/dy) или
порождение интенсивности флуктуации скалярного поля (3d i = - (иТ*)дв/ду) отрицательно.
Все феноменологические соотношения типа градиентной диффузии, привлекаемые
для моделирования механизма турбулентного переноса, имеют в физической основе
аналогию с кинетической теорией газов. Проводя эту аналогию несколько глубже,
можно полагать, что турбулентный перенос крупными вихрями, ответственный, в
частности, за возникновение локальных зон отрицательного порождения, есть с позиций
кинетической теории перенос при большой длине свободного пробега (перенос с
большим масштабом корреляций в турбулентном потоке). В кинетической теории газов
при описании переноса с большой длиной свободного пробега тензор напряжений —
зависимая переменная [6], удовлетворяющая некоторому дифференциальному
уравнению сохранения. Зависимой переменной является при этом и поток тепла. Такой
подход к описанию турбулентного переноса уже получил известное развитие й успешно
был применен и к расчету турбулентных течений с наличием зон смещения [7, 8].
Приближенная система уравнений турбулентного переноса статистических свойств
поля скорости и скалярного поля (температуры, концентрации) приведена в [9, 10].
В данной работе, как ив [4], рассматривается развитие плоского турбулентного
течения — слоя смешения, возникающего на краю слегка нагретой плоской струи,
истекающей в затопленное пространство, с одной стороны, и однородный поток, движущийся
со скоростью, равной скорости струи, с другой стороны. Согласно данным опытов
[4] температура рассматривается как пассивная "примесь" (плавучесть не оказьюает
существенного влияния на движение среды), а распределение средней температуры,
наложенное в этом течении на поле скорости, носит асимметричный характер.
Система уравнений для моментов поля скорости в приближении тонкого сдвигового
слоя для плоского развитого свободного турбулентного потока в пренебрежении
эффектами молекулярной вязкости имеет вид
bU bU Ъ(и'и')
U — + V — + = 0,
Ъх Ъу Ьу
*Докл. АН СССР. 1982. Т. 262, № 2. С. 301-305. (Соавтор А.Ф. Курбацкий.)
371

(1)
3<iiV> d(u'v') э Г / , , d-<i/2>
U +V -Mi— r(<«V> +
ax ъу by L \ by
+ 2<u'2> ) + <u'2>— + — <«'«/>= 0,
by Jl ду т
3<i/2> 3<u'2> Э Г / ,_ 9<y'2> \1
C/ +K -/i, rl3<y'2> — +
э* эу э>> L \ эу /J • ■
ТТЪЕ ЪЕ Ъ Г / Э£ , , 3<nV>
С/ — +F— -/хг r(<i/2>— +<nV> +
Эх Эу Ъу I \ Ъу Ъу
п э<у'2> М , , dU a ■
+ <и'2> ) + <nV> — +~ #=0.
Ъу /J Ъу т
В системе (1) U — средняя продольная скорость, V — средняя (взвешенная по массе)
поперечная скорость течения, (u'v) — напряжения Рейнольдса, г = ALE~Vz —
характерный масштаб времени турбулентного движения, Е = 1А((и2> + <i/2 > + <н>'2 >) - средняя
плотность (на ед. массы) кинетической энергии турбулентности, и, v — турбулентные
пульсации скорости в продольном и поперечном к слою смешения направлении
соответственно, w' — турбулентная пульсация скорости в трансверсальном направлении;
L - интегральный масштаб турбулентности, А ^ 4, vx ~ ^, я ~ 1 - эмпирические
постоянные, численные значения которых найдены из решения ряда простейших задач
турбулентного переноса.
Система уравнений турбулентного переноса (1) записана (относительно моментов)
в замкнутом виде; процессы турбулентной диффузии (третьи одноточечные моменты),
появляющиеся в уравнениях для вторых моментов системы (1), заменены
приближенно через вторые моменты с использованием гипотезы четвертых моментов так,
как это было сделано, например, в [7], т.е. с помощью следующего анизотропного
соотношения для третьих моментов:
<„ж>-ft,[(,x,!l^i ♦ Ч4>'^ +<^>!££- ],
1 Эх£ охк ' Ъхк J
где ц1 — численная константа, значение которой принято равным 0,11. Это значение,
найденное путем численной оптимизации, использовалось в различных работах при
моделировании турбулентного переноса.
Выражение для масштаба турбулентности L (масштаба корреляции, в пределах
которого элемент жидкости совершает коррелированное пульсационное перемещение
в среде) взято в алгебраическом виде, согласующемся с автомодельным характером
его изменения в направлении вниз по потоку: L ~~ (х — х0). Такой закон изменения
масштаба в дальней области слоя смешения соответствует экспериментально
наблюдаемому (х0 — виртуальное начало слоя смешения). Используется одна величина
масштаба турбулентности, перемежаемость в потоке не учитывается. Ради удобства
сопоставления с опытными данными выражение для масштаба L определено по некоторой
характерной условной ширине слоя смещения /0, за которую принято расстояние между
точками у = 70,5 и у = у09 (у — поперечная координата), в которых V - lAU0 и U -
= 0,9 U0 соответственно: L = k- /0 (где & = 0,5 — эмпирическая константа).
Система (1) записана в безразмерном виде с использованием в качестве масштаба
скорости U0 (скорости однородного потока на нижней его границе), а в качестве
характерного масштаба длины высоты щели d, из которой истекала нагретая струя. При со-
372

поставлении же вычисленных распределений средних величин и моментов с опытными
данными используется автомодельная переменная ц = (у — ^o,s)/^o- Средневзвешенную
поперечную скорость течения V представлялось удобным находить из выражения V =
= - jf (d'U/dx)dy.
— оо
Уравнения турбулентного переноса статистических свойств поля температуры в том
же приближении тонкого сдвигового слоя в пренебрежении эффектами молекулярной
теплопроводности имеют вид [10]
Э0 Э© Ъ(и'Г)
U — + V — + = 0,
Ъх Ъу Ъу (2)
3<wT> ЪЫТ) а Г / „ Э<и'7">
U +V -ц2 r(2<i/2> +
Ьх Ъу ■ Ъу L V Ъу
, , Э<и'2> \1 ,. Э0 * <и'7">
+ <i/7"> I + <i/2> — +(i>, + v2+3b0A) =0;
Ъу /J Ъу . т
Э<Г'2> Э<Г2> Ъ<Г2и) . . Эв 6Ь0А ■
U + V + +2<v'T')— + <7y2>=0,
Ъх Ъу Ъу Ъу т
3<7*V> Ъ(Г2и) . „ 30 „ Ъ(Г2)
(3)
Ъх Ъу Ъу Ъу
^ , Ъ<и'Т') <r'V>
+ 2< Ги > + (уг +2v2 + 6b0A) = 0.
Ъу т
В (2), (3) 0 — средняя температура в слое смешения, Ь0 — эмпирическая константа
в слагаемом, описывающем скалярную диссипацию интенсивности турбулентных
пульсаций температуры {Т2). Численное значение постоянной Ь0 = 0,05 найдено из решения
задачи о нахождении распределения интенсивности пульсаций температуры в тепловом
турбулентном слое смешения, образующемся за частично нагретой решеткой в
однородном турбулентном потоке. Значение постоянной v2 принято равным единице. За
характерный масштаб средней температуры принята разность между максимальной
температурой в слое смешения и температурой окружающей среды 0О — ®i.
Для сопоставления с опытными данными [4] найденные из решения систем (2),
(3) средние величины и моменты поля температуры представлялись через
автомодельную координату Wi = (у - Уо)11\ (уо — координата точки максимума профиля средней
температуры, а 1Х — масштаб, характеризующий ширину распределения средней
температуры в некотором сечении слоя смешения; расстояние между точками, в которых
значение средней температуры равно половине ее максимального значения, принято,
следуя [14], равным 21х
Как и для поля скорости, замкнутый вид системы уравнений (2) получен с
использованием приближенного анизотропного замыкающего соотношения для третьего
смешанного момента скорости и температуры и обобщенной гипотезы четвертых
моментов :
<«;^г>=-д2г
<"Л>—*—
Ъхк
+ {ики >—^ +ЫкГ) «L-EL
... ах* ъхк
где ц2 = 0,2 — константа, определяемая путем численной оптимизации. Замкнутый вид
373

системы (3) получен при использовании обобщенной гипотезы четвертых моментов:
<и^'2)=<и,ки,а)(Г2) + 2(и'кТ')(и,01Г).
Примечательная особенность уравнений для моментов поля температуры (2) и (3)
состоит в том, что система (3) принадлежит к вполне гиперболическому типу (или
гиперболической по Петровскому квазилинейной системе уравнений в частных
производных первого порядка). Система имеет два действительных характеристических
корня X (= dx : dy) = U(V ± V< v2) )/(V2 - <i/2>), хотя и содержит физический
необратимый'механизм скалярной диссипации для функций (J*2) и < 7*2v). Система (2)
0-ff-
-<v'T'>
i<T'z>'/(90-Bi)
0,6
J&i
^7Wi,r's
0,008
0,00V \-
имеет двухкратную "погранслойную" характеристику \х 2 = 0 (х - const);
порождаемую уравнением параболического типа для турбулентного потока тепла, и одну
действительную (отличную от тривиальной) характеристику Х3 = U/Y (dx : dy - U/V),
совпадающую с линией тока и порождаемую уравнением для средней температуры 0.
Для численного интегрирования систем уравнений (1), (2) и (3) применен метод
конечных разностей. Использована простейшая (не самая, конечно, эффективная)
неявная разностная схема, обладающая свойством безусловной вычислительной
устойчивости (последнее установлено экспериментальным путем). В работе одного из
авторов [9] можно детально ознакомиться с соответствующими конечно-разностными
аппроксимациями дифференциальных операторов второго порядка уравнений (1) —(3).
Разностная схема эффективно реализуется методом векторной прогонки (на
прямоугольной эйлеровой сетке). Расстояние по продольной координате х, которое
достигнуто в численном решении, соответствовало сечению x/d ^ 15. (О достижении в
численном решении этого сечения можно было судить, например, по величине
характерного поперечного масштаба поля температуры (в сечении x/d ^15 масштаб /j ^ 1,1;
374

см. рис. 7 в [4]) ). Изменение масштабов /0 и 1Х в расчете было линейным относительно
продольной координаты, как и в опытах [4].
На рис. 1 нанесено распределение средней температуры поперек слоя смешения:
сплошная линия - расчет; опытные данные [4]: x/d = 10 (2); x/d = 20 (2);x/d = 30 (3).
Расчетный профиль средний температуры имеет асимметричный вид: градиент
несколько круче на высокоскоростной стороне слоя смешения (г1г < 0). На этом же рисунке
нанесено и распределение поперек слоя смешения поперечной составляющей
турбулентного потока тепла < v'T). Заштрихованные участки на рис. 1 и 2 — зона смешения
(зона контрградиентного переноса). При сравнении с рис. 12 работы [4] можно видеть,
что ширина зоны смешения, полученная в расчете, близка к экспериментальной,
указывая на хорошую "разрешающую способность" как модели турбулентного переноса,
так и численного алгоритма.
На рис. 2 приведен второй основной результат данной работы — распределение
поперек слоя смешения поперечной составляющей порождения интенсивности
турбулентных пульсаций температуры. Из сравнения расчетной кривой & х = - < иТ*)д®/ду с
кривой этой функции, найденной прямыми измерениями (см. рис. 14 в [4]), видно, что
зона отрицательного порождения предвычисляется моделью турбулентности, адекватной
опытным данным, как по ее расположению в поперечном к слою смешения
направлении, так и по абсолютной величине максимума функции порождения #> г. И, наконец,
на рис. 3 показана интенсивность пульсаций температуры в слое смешения. И для этого
распределения сравнение с рис: 11 из [4] показьшает, что использование системы
уравнений для функции < 7У2> и < T2v) позволяет получить правильный вид кривой
дисперсии температурных флуктуации с наличием двух характерных максимумов.
Расчетные данные по статистическим характеристикам поля скорости, описываемым
системой уравнения (1), имеются в [9].
ЛИТЕРАТУРА
1. Bequier С, Giralt F., Fulachier L., KefferJ.F. 11 Led. Notes Phys. 1978. Vol. 76. P. 22-35.
2. Batchelor G.K. 11 J. Aeron. Sci. 1950. Vol. 17. P. 7.
3. Fabris G. // Turbulent shear flow: Selected pap. I Intern, symp. 1977. P. 55-70.
4. Bequier C, Fulachier L., KefferJ.F. // J. Fluid Mech; 1978. Vol. 89, N 3.
5. Таунсенд А. Структура турбулентного потока с поперечным сдвигом, М.: Изд-во иностр. лит.,1959.
6. Грэд Г. И Механика, 1952. № 4; 1952. № 5.
7. Hanjattc К., Launder В.Е. // J. Fluid Mech. 1972. Vol. 52, N 4.
8. Курбацкий А.Ф., Онуфриев А.Т. // ПМТФ. 1979. № 6.
9. Курбацкий А.Ф, //ПМТФ. 1975. № 3.
10. Курбацкий А.Ф, II Там же. № 6.
ГАМИЛЬТОНОВЫ ВИХРЕВЫЕ МОДЕЛИ
В ТЕОРИИ ТУРБУЛЕНТНОСТИ*
В работе методом неравновесной статистической механики исследуются вопросы
моделирования турбулентности на основе динамических систем точечных вихрей
в идеальной жидкости. В рамках развиваемого подхода получен ряд известных
результатов теорий турбулентности — знакопеременность вихревой вязкости в плоском
случае, закон "—5/3" и др.
В последние годы в работах ряда авторов [1—7] в качестве статистической
модели двумерной гидродинамической турбулентности рассматривалась система
прямолинейных вихревых нитей, аппроксимирующих мгновенное случайное поле за-
♦Численные методы механики сплошной среды. 1982. Т. 13, № 3. С. 13-28. (Соавторы Ю.Н.
Григорьев, В.Б. Левинский.)
375

вихренности. Возможность такого подхода была впервые указана Онзагером [1].
Он представляет собой альтернативу распространенным в теории турбулентности
спектральным моделям. Можно считать, что в пределе больших чисел Рейнольдса,
когда области завихренности относительно малы и носят характер случайных
вкраплений в потенциальный поток, такая модель в общих чертах правильно отражает
картину турбулентной жидкости.
Динамика вихревых линий допускает описание в гамильтоновом формализме,
что позволяет применить к статистическому ансамблю вихрей методы кинетической
теории. На этом пути был получен ряд результатов, подтверждающих
содержательность данной модели. Так, в работах [3, 5] на основе численного моделирования
была показана врзможность реализации в системе прямолинейных вихревых нитей
каскадов энергии и энстрофии. В серии работ А. Чорина с сотрудниками (см. библиогр.
в [8]) система вихревых нитей успешно использовалась для моделирования плоских
течений несжимаемой жидкости при больших числах Рейнольдса.
Полученные результаты стимулируют инетерс к дальнейшему изучению модели
прямолинейных вихревых нитей, а также к разработке рациональной модели
точечных вихрей для трехмерного случая.
В данной работе, исходя из уравнения Лиувилля для ансамбля прямолинейных
вихревых нитей с использованием диаграммной техники Пригожина—Балеску,
выведено замкнутое эволюционное уравнение для функции распределения
завихренности и исследованы качественные свойства его решений. Получены также некоторые
результаты для статистической модели трехмерной турбулентности, в основу
которой положена введенная в [9, 10] динамическая система малых пространственных
вихрей в идеальной жидкости.
1. Уравнения движения системы N прямолинейных вихревых нитей одинаковой
интенсивности циркуляции к имеют вид [11] '
bFj/bt = -He~XVfHNf i= 1,...,W,
N (1.1)
Hf, = - 2 Vil9 Vif = \n\n-Fj\,
i<j
Ft = {xityt) — радиус-вектор /-го вихря, v,- = d/dFit F — единичный орт нормали
к плоскости движения вихрей.
Эквивалентное (1.1) статистическое описание движения системы дается [12]
уравнением Лиувилля
bfN ^ * N
-f- = -*ё X Z Vf У;; (V/ - Vj)fN = -* S LnfN = -#LfN, (1.2)
ot i<j i<j
где fN (Fx,..., FNt t) — плотность вероятности совместного распределения N
вихрей с условием нормировки
JdFi ... dFNfN = 1. (1.3)
Гамильтониан HN в (1.1) содержит только члены вида К/у, и система вихревых
нитей является сильно взаимодействующей. Это исключает прямое применение
к (1.2) обычных методов статистической механики [12, 13].
Воспользуемся модификацией метода Пригожина-Балеску [14] в варианте
формализма резольвенты [13]. Система обозначений совпадает с принятой в [13].
Исходным аппаратом является Фурье-анализ в классе функций, периодических в
квадрате площади 12. Для функции совместного распределения N вихрей/# и потенциала
межвихрёвого взаимодействия Уц разложения в ряд Фурье представим в виде
Лг(Гь....^О = П-лг|ро + -^- S' Sfp(F, t)е**П + ...], (1.4).
376

V(\~rm-rj\) = 4тг2П-1 SK(|/ \)eilCrm-ri\ (1.5)
kj = 27гГ2" 2 /Ту, й~у — целочисленные векторы.
Условие нормировки (1.3) дает р0 = 1. Фурье-коэффициенты в разложении (1.4)
связаны с приведенными функциями распределения
N1
fs(Tu...,rs>t) =— — fdrs+1 ...drNfN,
(N - s)!
В частности,
W, П "► «>
С использованием (1.4), (1.5) можно получить Фурье-представление формального
решения уравнения Лиувилля (1.2) в виде ряда теории возмущений:
/ 4тг2 \ v'~v
p(Ul,f) = {2*rl-§dze-ixt X (-к)" 2 (——) < Uil^)
* = 0 jfc'J \ ft / (16)
[Z,*o(z)Pl U'j >p( {A:'} , 0). (16)
Матричные элементы в (1.6) определены по базису плоских волн. В частности,
< |jfcl \L\ \k'\ > = Z U*i |2,я«| f *'1 >,
< U ! |£я/| \к'\ > = 47r2n-1^X/(*w- £„)Х
ХУ(\к'п-кп\)1(к^-кп)6-, + Р..е г. • П Sp jf . ■ (1.7)
Матричный элемент невозмущенной резльвенты Ro(z) в данном случае тривиален
<!*П*о(*)1 l^'i> = -^-5ui lis-'} • О-8)
Структура (1.6), (1.7), (1.8) позволяет использовать для их графического
представления те же диаграммы, что и в [13]. Из выражения (1.7) для матричного
элемента оператора взаимодействия следует, что в данном случае (ср. [13]) имеются
три нетривиальных одновершинных диаграммы, представленные на рис. 1.
Соответствующие им матричные элементы имеют вид:
C. <кп, к} \Lnj \k^> = 4тг2ё i(k'n -k„) V( | k'n-kn\ )&'HS-,,__.
D. (k„\Lnl\ k'„, k} > = 4тг2П-'? X
Xi(k'n-k„)V(\k'n-kn\)i(k'n-k'j)8- -, - ;
Кn + Kj Kn
E. {kn, k,\LH,\:k'H, kj> = 4тг2П"1ё X
Xi(k'n-kn)V(\k'n-k„\)i(kn-k'j)8- p - -.
K n + Kj Kn ~ Kj
В силу этих соотношений и представления (1.6) топологические индексы вершин С,
' D, Е равны соответственно 0, 1, 0 [18].
Рассмотрим характерные времена для данной модели. Так как моделируется
двумерная турбулентность, в качестве характеристик процессов хаотизации можно
взять интенсивности е и г] в каскадах энергии и энстрофии [15]. Комбинация
параметров к, с, е и?) дает безразмерный комплекс Г = с^17"^е^. При этом величины,
377
к п Кп — kj

имеющие размерность времени, представимы в виде
Тт =б%2ст?Г1/2Гт. (1.9)
При т = -1 из (1.9) имеем т/ = (кс)"1, а при in =0 тг = (к2с)~Уг€ У2г)~1/г. Время т/
есть период обращения пары вихрей на среднем расстоянии с"У2 друг от друга
и естественно отождествляются с характерным временем взаимодействия.
Время тг, содержащее интенсивности каскадных процессов, можно рассматривать
как характерное время релаксации. Характер зависимости г,-, тг от к и с используем
для отбора из (1.6) взаимодействий, определяющих конвективный перенос и
релаксацию.
Рис.2
Рис.3
Рис.4
^^О^ос
Рассмотрим всевозможные вклады в p(k9 t) порядка (кс)п(к2с)т (п, т =
= 0, 1, ...). Соответствующее диаграммное представление имеет вид, приведенный
на рис. 2. Здесь прямоугольники обозначают бесконечные суммы всевозможных
продолжений, составленных из вершин типа D и "псев до диагональных" фрагментов
[13] (рис.3).
Во второй и третьей группах вкладов внешние суммы берутся по всевозможным
"головным" диаграммам. Было показано, что при т = 0 вклады в p(k9 t)9
существенные на временах г/, изображаются всевозможными диаграммами, составленными
из вершин типа D. Их суммирование приводит к уравнению Гельмгольца для
завихренности, которое описывает ее обратимую во времени эволюцию. Прямое
суммирование вкладов рис. 2 методами [13, 16], также приводит к обратимому во
времени уравнению, которое не описьшает процесса релаксации к стационарному
состоянию и содержит расходящиеся члены порядка О (t) при Г -* °°. Появление
расходимости связано с попыткой описать сильно взаимодействующую систему
последовательностью разделенных во времени бинарных процессов. Расходимость
можно подавить, если учесть коллективный характер взаимодействия вихрей.
Это можно сделать путем перенормировки функции распространения (пропагатора)
[14], для которой при этом возникает замкнутое уравнение.
Рассмотрим следующее диаграммное представление перенормированного
пропагатора, представленное на рис. 4. Здесь учтены вклады всевозможных диагональных
фрагментов, соединенных в произвольном числе, которые образованы введением
элементарных диаграмм рис. 3, а, б между вершинами типа D и С.
378

Соответствующее рис. 4 аналитическое выражение операторного ряда имеет вид
1
G(k,t) = (2 я)-1 #&«-"'
G (к, 0) = /,
где / — тождественный оператор
iz п= о
Ф(к,г)
1
-iz
G(k,Q),
(1.10)
Ф(Л,2)= 2 (-к)2(т+1><А: |£D[/?0(z)i)2m/?o(z)i>c|A:>.
т = О
После дифференцирования (1.10) по времени с использованием представления
пропагатора (1.10) и теоремы о свертке для преобразования Лапласа, получим
bG(k,t) t ., _ 1
— - = (27Г)-1 fdze-lz^(k,z)
Ы
t _ _
= / dez(k,t-6)G(kt6).
о
-iz п = о
Ф(к,г)
1
— iz J
G(k,0) =
(1.11)
z(k9i) = (27Г)"1 ф<Ье-шФ(к;г). (1.12)
С помощью факторизационной теоремы Резибуа [17] операторный ряд (1.12)
можно представить в виде
_ N _ _____ _
z{kht) = _ Б(-к)2 {ki\Lij\ki-ljJj)G(ki-litt)G{lj>t)X
/ = i i
X {ki-liJj\Lij\ki).
В результате, после перехода к "термодинамическому" пределу N^>°°9 Г2 -►oo,7V/£2 ->с
получаем уравнение для перенормированного пропагатора
3G (А:, Г)
-4тг2к2с f d6P(k,t-e)G(k,6),
(1.13)
Р(к,в)= fdT[ёТ[к - 2T) V2 (\T \)ёТ к ]G (к -Tt в) G (Tt в).
После аналогичных преобразований соответствующее рис. 2 уравнение для р(к\ t)
принимает вид
bp(k>t)
Ы
= 4тг2к2сё idkxi{kx -k)V(\k -kx \)i(2kx -k)p(kltt)X
_ _ f _ _ t _
Xp{k -kut)- 4тг2 кV / <Ш> (fc, Г) p(ktt-6)~- 4тг2 к2с fddfdki X
о о
(1.14)
X Л {k>kl)d)p{kl)t-d)p{k -kl9t-0),
Px(k9kud) = fdTe TV(\T\)(k -2T)G(k -Tt 0)X
X G(7~, 0)? (k-T)Vi\k1-T\)(2k1 -k).
Уравнения (1.13), (1.14) имеют немарковский характер и дают замкнутое
описание эволюции вихрей на временах t *~ тг.
Будем полагать \к\ ~~ \ I |, т.е. характерный размер неоднородностей и
эффективная длина их взаимодействия близки, что соответствует представлениям
феноменологической теории турбулентности. Считая, что G (к, t) = G(akt)9 заменим в (1.13)
G (/, 0) —^ G (к, 0), G (к —1,6) ^ I. При этом (1.13) преобразуется к уравнению
с интегралом типа "свертки", решая которое с помощью преобразования Лапласа
379

можно получить
G (к, Г) = (a \к\ tylJx {2a\k \ t\ а2 = Лтг2к2са2,
- о - о - - - о о 0-15)
д* = fdl yl (| / | ) [J _ CQS2(A:> /. ) | / f, д* >0.
/i (x) - функция Бесселя первого рода первого порядка.
Теперь можно обычным образом [16] перейти к марковской форме (1.14).
При этом с учетом (1.15) вклад произведения пропагаторов есть
fd6G(k-Tfe)G(Tte) ~ (а I/"!)"1. (1.16)
о
Возвращаясь к исходным переменным с помощью обратного преобразования
Фурье
fdkeik7 p(ktt) = с'1 \f(r,t)-c] = /i(7,0,
для одночастичной функции распределения завихренности в плоском случае
получаем уравнение
3/(7, t)/dt + U (7, Г) V/(7, t) = (/c201/2^i^_1A/(7, t) +
+ {к2с)х/2а-1 f d7xn (7, t)B (7 - rY): VV (7, 0 -
- {K2cta-ln{rt t)S4rxB (7 -7j): ViVi/(7b О, (Ы7)
где£(7—7i) — тензор второго ранга, В ="ё ~E\r~ —T\Xe ДК(|7—7J),
С/(7, Г) = ксёХ Д/с?71К(|7 -7! I)w(7, Г) -
средняя гидродинамическая скорость, индуцированная локально
некомпенсированной завихренностью; двоеточие —символ скалярного произведения тензоров; а.\
определено аналогично а в (1.15), отличаясь от него лишь дополнительным множителем
| /1""1 в подынтегральном выражении. _
Подставновка в alt а обобщенного Фурье-образа потенциала V( | / I) =
= -(27г| /12)"1 приводит к расходящимся интегралам. Для устранения этих расхо-
димостей можно применить способы из теории кулоновской плазмы [13]. Так как
явные выражения а, ах здесь не нужны, будем полагать их просто ограниченными.
Рассмотрим некоторые качественные свойства полученного уравнения,
Очевидно, что левая часть (1.17) есть оператор Гельмгольца для поля завихренности в
плоском случае. Так как я, а.\ > 0, то первый член в правой части (1.17), содержащий
оператор Лапласа, определяет положительную диффузию распределения
завихренности. Квадратичная форма, образуемая компонентами тензора В (f~— 7i), имеет вид
= _ Э |7-7! I ЭК(|7 -7Х I)
(*?.*) = eik ejn —К— £■ &Ь , (1.18)
где 7 = (xb х2)9 eik — антисимметричный тензор (е12 =-е2Х = 1; ец - е22 = 0)
и подразумевается суммирование от 1 до 2 по повторяющимся индексам.
Непосредственно проверяется, что форма (1.18) неотрицательна. Используя структуру (1.18)
и ее неотрицательность для непрерывных п (F, t), можно показать, что первый и
второй члены в правой части (1.17) определяют эллиптический оператор второго
порядка, знак которого зависит от распределения / (7, t) и может быть различным в
разных точках области течения. Знак последнего члена определяется локальным
значением п (F, О- Это означает, что (1.17) способно описывать локальные процессы
разрушения (положительная диффузия) и возникновения (отрицательная диффузия)
крупных вихревых структур. Как известно [18], последний эффект
отождествляется с явлением отрицательной вязкости.
380

Рассмотрим производство информационной энтропии
S(t) = -fdFf(F,t)\nf(Ftt) (1.19)
в процессе эволюции распределения. Будем предполагать, что / (Г, t) при | 7\ -+°°
убывает достаточно быстро вместе с производными. Умножим (1.17) на -(1 + In/ (7% О)
и проинтегрируем по всему пространству. После ряда преобразований уравнение
баланса энтропии приводится к виду
bS/dt = /dr AU(Ft t)f(F, t) + к2c)x/2axa-1 f dr \f(F, Г)[-1 [Vf(F,t)]2 +
+ 72 {£cf2a-1 ffdFdF, VV'.B (F - Fx) [ln/(F, t) - ln/(Fb t)]X
X \f(r,t)-f(rut)] + (^cfa-1 ffdFdr, X (1.20)
x'J (F - Ft) :V i f(Ft, t)V г/^, t)\f(F, 0]-Ы (F, t) +
+ {K2cta7x ffdFdF1 V V : В (Г - Fx)f(Fu t)n(F, t).
В силу несжимаемости жидкости V • U (r, t) = 0 и конвективный член дает
нулевой вклад в производство энтропии. Положительность вклада второго члена в
правой части (1.20) очевидна. Третий также положительно определен, так как
VV'B (F -FO = IF-Fi I"3 >0, (1#21)
и имеет место неравенство
[1п/(лО-1п/(Гь 01 1/(^0-/(^1.0] > 0.
В силу положительной определенности (1.18), (1.21) знак последних двух
интегралов в (1.20) зависит только от поведения функции п (F, t). При условии, что
полный момент равен нулю
fdrn(F, t) = 0,
оценки показывают, что отрицательный вклад в эти интегралы будет набираться
в основном с периферии области течения, где другие части ^подынтегральных
выражений стремятся к нулю достаточно быстро. Отсюда вытекает, что полный
вклад этих интегралов в производство энтропии будет либо неотрицательным, либо,
по крайней мере, близким к нулю по модулю.
Таким образом, в процессе эволюции / (F, 0, удовлетворяющей (1.17),
энтропия (1.19) монотонно (в широком смысле) возрастает. С другой стороны, из
сходимости интеграла
/ drf(r, 0 <°° .
легко получить, что функционал (1.13) ограничен. Это позволяет сделать вывод,
что в процессе эволюции решение (1.17) стремится к некоторому стационарному
распределению.
Анализ результатов численных экспериментов [4, 6], условия которых близки
к использованным здесь предположениям, показывает, что уравнение (1.17)
правильно отражает характер эволюции больших систем точечных вихрей на плоскости.
Это можно использовать для оценки диссипативных (дисперсионных) свойств
алгоритмов типа [8], как это делается при анализе свойств разностных схем с
помощью дифференциальных приближений [19].
2. Построение динамической модели точечных вихрей в трехмерном случае
затруднено существенно более сложным поведением вихревых полей в пространственных
потоках [11]. В частности, это проявляется в отсутствии в трехмерном случае
универсального точечного носителя завихренности, каким для плоского случая
является прямолинейная вихревая нить.
В [9] и независимо в [10] динамику системы малых вихрей в трехмерном
381

случае было предложено описывать в канонических переменных (,г,-, р,-),
сопряженных относительно гамильтониана
N N _ N
Н = 2 Т(р{) + Б У(п)р{ + е Б Ф1Л-
i-i i=i /</ (21)
Ф*/ = -(4*)"1 [P/Py/l^l'-J^ryXp/F^VIr,,!2]-
Здесь г^ — физические координаты вихрей, р; — их импульсы Лэмба [11], T(pt) —
энергия уединенных вихрей, V (F) — поле скорости внешнего потенциального
потенциального потока, Ф/у — энергия взаимодействия отдельных вихрей,
взаимодействующих как диполи с переменными дипольными моментами.
N
Как следует из [10], Б р1. не является интегралом системы (2.1), и предлагае-
мая модель содержит существенный в трехмерном случае эффект растяжения
вихревых нитей. Известно [11], что энергия уединенного вихря и его скорость сложным
образом зависят от топологии вихревых нитей внутри него. Чтобы упростить
задачу, мы будем использовать для Т модельное представление вида
Т(р)=А \р\^к. (2.2)
Зависимость (2.2) получена аппроксимацией численных результатов [20] для
однопараметрического семейства вихрей. Показатель к £ [5/7, 2] и монотонно
зависит от параметра. При этом к = 5/7 соответствует сферическому вихрю Хилла,
а к = 2 — пределу тонких колец [11]. .
Если принять отношение характерного размера вихрей к среднему расстоянию
между ними пропорциональным отношению микромасштаба турбулентности к ее
интегральному масштабу, то в (2.1) е < 1 и к модели применимы методы
статистических систем со слабым взаимодействием. При этом одночастичная функция
распределения вихрей по импульсам и координатам f(p, r~, t) удовлетворяет
кинетическому уравнению
Э/ _ Э/ / 3/ Э \
bt Ъг \ Ър Ъг )
Здесь й = ЪТ/Ър, v~ (F) — скорость внешнего потенциального потока,
w(Flf г) = fdF2dp2 (ЪФ12/Ърг)/(р2ш Г2, Г)
— скорость, индуцированная в точке распределением вихрей.
г,*ъ Э с a- [pX^"i2][PiX^12]
Эрг 87TZ?o I «12 I
\ bps bpr I
f(p)fWi) (2.4)"
- интеграл столкновений в форме Ландау [21], по повторяющимся индексам
подразумевается суммирование.
Наметим связь между моментными уравнениями, которые можно получить из
(2.3), и уравнениями Рейнольдса для осредненных величин феноменологической
теории турбулентности. В рамках 10-моментного приближения аппроксимируем
функцию распределения как
, /<Р, г, 0 = ехр(-Г(р)/<Г>)[в0(Г, 0 + ?iii"+S2 :йй], (2.5)
где экспоненциальный множитель обращает в нуль интеграл столкновений (2.4),
угловые скобки означают усреднение по f(p, F, t).
382

Коэффициенты в (2.5) можно выразить через следующие осредненные величины:
п (Г, 0 = / dpf (p,F7t), <р> = тГ1 f dppf(p, F, t),
<м > = и-1 / dpuf(p, F, t), (p > = n'1 / dpupf(p, F, t).
Для компонент <р> и <р> получается следующая система уравнений:
-~- + -— [п (<ft/ > + <£/,> <й>] + л </>,> ; =0,
at oXi aXf
Ьпфи) Ьп{ри) 3fc+l
i-iL- + <£/*> t-U— + X
ЭГ 9*fe 5£
f Э Э Э
x 5» <P><«*> + <P><«/> + <?><«/> +
I ' Ъхк дх( bXj
Последний член во втором уравнении (2.6) получен при. интегрировании интеграла
столкновений.
Полагая формально Т малым параметром, в первом приближении из уравнения
для {ру> можно получить
1 / ч /3<tf/> d<U,) \
Если определить осредненную завихренность как
<Г2> = rot<w"> = rotvv = xotnip),
то из последних соотношений видно, что взятие операции rot OTjiepBoro уравнения
(2.6) и подстановка в него (2.7) приводят к уравнению для Ш > в простейшем
приближении скалярной турбулентной вязкости.
Покажем теперь, что в рамках данной модели возможен каскад Колмогорова-
Ричардсона. Так как модель точечная, необходимо получить связь между
импульсом и размером вихрей. Из инвариантности уравнений движения с гамильтонианом
(2.1) относительно растяжения пространства импульсов имеем
р ~г3/2"А 0 = 1/Jfc. (2.8)
Видно, что в предельных случаях тонких колец и вихря Хилла (2.8) точно
воспроизводит искомую зависимость.
В силу физического содержания модели каскадный процесс возникает здесь не
на основе дробления вихрей (трехволновые процессы [22]), а при их растяжении
в процессе парного (четырехволнового) взаимодействия.
В [23] было построено стационарное решение кинетических уравнений с четырех-
волновыми взаимодействиями
f(p) = B\p\s, s =-V2(3<f + /fi), (2.9)
которое соответствует постоянному потоку энергии . по пространству импульсов.
Здесь d — размерность пространства импульсов, тп — показатель однородности
функции рассеяния U(plt р2, Ръ> Рл) в интеграле столкновений.
Записав для функции рассеяния тождество вида
fdou12 = fdp3dp4U(p1,p2,p3tp4)8(p1 +Д2-Рз-Р4)Х
Xb[T(pt)+T(p2)-T(p3)-T(p4)]
и выполнив в нем масштабное преобразование р,- -*Хр/ с учетом (2.8), в нашем слу-
383

чае получаем
и=-8/з+4/зА « = - — (19+418). (2.10)
Используя (2.9), (2.10) и переходя к волновым векторам, для спектра энергии
можно записать
Е(к) -~T(k)f(k)p2(k)\dp/dk\ ~fc-l3/2<2-0)l; к =\к\9
__5/3
откуда следует, что Е(к) ~~ к при j30 = 11/10, j30 G [ 1/2, 7/5]. Было показано, что
при 0=0о интеграл столкновений (2.4) сходится на решении (2.9)-(2.10).
Авторы надеются, что дальнейшие исследования рассмотренных в работе моделей
методами неравновесной статистической механики позволят получить новые
структурные соотношения для процессов турбулентного переноса. Модель вихрей с диполь-
ным взаимодействием может быть также полезна для обобщения на
пространственный случай бессеточных алгоритмов типа [8].
ЛИТЕРАТУРА
1. Onsager L. Statistical hydrodynamics // Nuovo cim. Ser. 9. 1949. Vol. 6. P. 279-287.
2.Новиков E.A. Динамика и статистика системы вихрей // ЖЭТФ. 1975. Т. 68, № 5. С. 1868-1882.
3. Седов Ю.Б. Эволюция системы вихрей // Изв. АН СССР. МЖГ. 1976. № 6. С. 43-48.
4.Pointin Y.B., Lungren T.S. Statistical mechanics of two-dimensional vortices in a bounded container //
Phys. Fluids. 1976. Vol. 19, N 10. P. 1459-1470.
S.Pointin Y.B., Lungren T.S. Statistical mechanics of two-dimensional vortices // J. Stat. Phys. 1977.
Vol. 17, N5. P. 323-355.
e.Kida S. Statistics of the system of line vortices // J. Phys. Soc. Soc. Jap. 1975. Vol. 39, N 5.
P. 1395-1404.
I.Joyce C, Montgomery D. Negative temperature states for the two-dimensional quiding-center
plasma//J. Plasma Phys. 1973. Vol. 10. P. 107-121.
S.Chorin A.J. Vortex models and boundary instability // SIAM J. Sci. Stat. Comput. 1980. Vol. 1, N 1.
P. 1-21.
9. Roberts P.H. A Hamiltonian theory for weakly interacting vortices // Mathematica. 1972. Vol. 19.
P. 169-179.
10. Яненко Н.Н., Веретенцев А.Н., Григорьев Ю.Н. Гамильтонов формализм для
пространственной системы малых вихрей в идеальной жидкости // Числ. методы механики сплош. среды.
1979. Т. 10, №5. С. 144-149.
11. ЛамбГ. Гидродинамика. М.: Гостехтеоретиздат, 1947.
12.Боголюбов Н.Н. Проблемы динамической теории в статистической физике // Избр. тр. Киев:
Наук, думка, 1970. Т. 2.
ХЪ.Балеску Р. Статистическая механика заряженных частиц. М.: Мир, 1967.
14. Balescu R., Senatorski A. A new approach to the theory of fully developed turbulence // Ann. Phys.
1970. Vol. 58, N 2. P. 587-624.
15. Kraichnan R.H. Statistical dynamics of two-dimensional flow // J. Fluid Mech. 1975. Vol. 67, N 1..
P. 155-175.
16. Пригожий И. Неравновесная статистическая механика. М.: Мир, 1964.
ll.Resibois P. New approach to irreversible transport phenomena in plasma dynamics // Phys. Fluids.
1963. Vol. 6. P. 817-823.
IS.CrappB. Физика явлений с отрицательной вязкостью. M.: Мир, 1971.
19. Шокин Ю.И., Яненко Н.Н О первом дифференциальном приближении разностных схем для
гиперболических систем уравнений // Сиб. мат. журн. 1969. Т. 10, № 5. С. 1173-1187.
20.Norbury J. A family of steady vortex rings J/ J. Fluid Mech. 1973. Vol. 57, N 3. P. 417-433.
21. Ладиков-Роев. Статистическая теория вихревых течений в идеальной жидкости // Зап. ОГПИ.
1971. Вып. 10. С. 55-82.
22. Кадомцев Б.Б. Коллективные явления в плазме. М.: Наука, 1976.
23. Кац- А.В., Канторович ВМ.У Моисеев С.С., Новиков В.Е. Точные степенные решения
критических уравнений для частиц // ЖЭТФ. 1976. Т. 71, № 1. С. 177-192.
384

ОБРАЗОВАНИЕ КОГЕРЕНТНЫХ СТРУКТУР
В ТУРБУЛЕНТНОМ СЛЕДЕ ПРИ АКУСТИЧЕСКОМ ВОЗДЕЙСТВИИ*
Хорошо известно, что акустическое поле оказывает существенное влияние на пуль-
сационные и средние характеристики турбулентных течений со сдвигом. Это влияние
связывают обычно с порождением звуковым полем вихревых возмущений
(когерентных структур), которые в значительной мере и определяют развитие такого рода
течений [1]. Под когерентными структурами в турбулентных течениях понимаются долго-
живущие упорядоченные крупномасштабные образования на фоне мелкомасштабной
турбулентности, характерные масштабы которых сравнимы с поперечными размерами
сдвигового слоя. Эксперименты показывают, что большая часть турбулентной энергии
во многих случаях сосредоточена в этих крупномасштабных структурах [2], что
обусловливает их существенный вклад в турбулентный тепло- и массоперенос в данных
потоках.
В настоящей работе ставилась задача изучения преобразования акустических
возмущений в вихревые, т.е. в когерентные структуры в турбулентном следе за тонкой
пластинкой с острой задней кромкой.
Эксперименты проводились в дозвуковой аэродинамической трубе ИТПМ СО АН
СССР МТ-324 с размерами рабочей части 0,2 х 0,2 м2 при скорости потока £/«> = 10 м/с.
След образовывался за пластинкой длиной 300 мм с острыми задней и передней
кромками и максимальной толщиной 3 мм. Для реализации на теле и в следе развитого
турбулентного течения применялся специальный турбулизатор. Акустические
возмущения задавались от звукового генератора с помощью громкоговорителя,
установленного в стенке рабочей части аэродинамической трубы. Пульсационные
характеристики и параметры среднего течения регистрировались и обрабатывались
комплексом термоанемометрической аппаратуры "DISA" и частотным анализатором
"FAT-Г'. Фазовые измерения проводились на двухлучевом осциллографе с
использованием анализатора в режиме фильтрации в полосе спектра А/= 4 Гц.
Синхронизация осуществлялась от опорного сигнала звукового генератора.
На рис. 1 приведены профили средней скорости в ближнем следе за тонкой
пластинкой. Хорошо видно, что течение в этой области характеризуется сильной
пространственной неоднородностью и наличием в профилях точек перегиба.
При включении акустического поля в спектре сигнала от датчика, расположенного
в следе, возникает четко выраженный пик на частоте акустического возмущения. На
рис. 2 приведены результаты измерения в следе продольной составляющей
пульсаций скорости Uf/Uoo, вырезанной в полосе Д/=4 Гц, без акустического воздействия
и с наложенным звуковым полем частотой / = 518 Гц и интенсивностью 101 дб. Для
сравнения на этом же рисунке показано распределение интегральной по спектру
интенсивности пульсаций продольной составляющей скорости w'/£/«>. Можно отметить
качественное совпадение данного распределения и возникшей под воздействием
звукового поля структуры.
Фазовые измерения на частоте звука при акустическом воздействии показали, что
фаза возмущений случайна во времени в турбулентном пограничном слое и только
в следе, вблизи х ~ 0, она приобретает определенное значение (рис. 3), что связано
с возрастанием детерминированной составляющей в спектре возмущений. Закон
нарастания в этой области примерно линейный, и обработка полученных результатов
показывает, что фазовая скорость распространения этих возмущений сильно
отличается от скорости распространения звуковых колебаний и составляет ~0,9 от скорости
набегающего потока, являясь характерной для вихревых возмущений.
На рис. 4 представлены распределение амплитуды Uf/Uoo возникшего возмущения
(учтен вклад турбулентного фона в величину u'f/Uco) в полосе 4 Гц и типичное распре-
*Докл. АН СССР. 1984. Т. 274, № 1. С. 50-53. (Соавторы СП. Бардаханов, В.В. Козлов.)
13. Зак. 953

у, мм
0
-5Y
у,мм
№ 03
7'7JuCp/v~
of
©J
10
*u'f/Uoo,°U
-10
Рис. 1. Профили средней скорости в следе за тонкой пластинкой
х=1мм (7), 10 (2), 30 (5)
Рис. 2. Распределение интенсивности пульсаций скорости в следе л: = 5 мм
1 — интегральная по спектру интенсивность пульсаций, 2 — вырезанная в полосе 4 Гц без
акустики, 3 — вырезанная в полосе 4 Гц с акустикой
!/>
u'f/Uco,Blo~f О
\-0,5
-1,0
0 20 х,м/1 -5t0^
Рис. 3. Нарастание фазы возмущения в следе (/=518 Гц)
Рис. 4. Распределение амплитуды возмущения и фазы по поперечной координате при / = 518 Гц
деление фазы в зависимости от поперечной координаты. Можно отметить: в области
у = 0 фаза претерпевает скачок, близкий к 180°, что согласуется с распределением
амплитуды возмущений в этой области (минимум в области у - 0). Это означает, что
возникшее вихревое возмущение практически антисимметрично. Таким образом,
эти распределения амплитуды и фазы возмущения дают представление о когерентной
структуре, возникшей и развивающейся в турбулентном следе.
В целом эти исследования показали, что звуковые колебания интенсивно
преобразуются в вихревые возмущения в турбулентном следе за пластиной, аналогично
тому, как это происходит в ламинарных течениях со сдвигом [3, 4]. Таким образом,,
и в турбулентных течениях может быть поставлена, с одной стороны, проблема
восприимчивости потока к внешним возмущениям, с другой стороны, — задача о развитии
возникших когерентных структур вниз по потоку, требующие своего математического
решения.
386

ЛИТЕРАТУРА
1. Гиневский А.С., Власов Е.В., Колесников А.В. Аэроакустические взаимодействия. М.:
Машиностроение, 1978.
2. Structure and mechanism of turbulence, 1,2// Lect. Notes. Phys. 1978. Vol. 75/76. P. 295-406.
3. Качанов Ю.С.? Козлов В.В., Левченко В.Я. Возникновение турбулентности в пограничном слое.
Новосибирск: Наука, 1982.
4. Sato Я. // J. Fluid Mech. 1970. Vol. 44, N 4. P. 741-765.
ОБ ОДНОЙ МОДИФИКАЦИИ УРАВНЕНИЙ ДВИЖЕНИЯ
ВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ*
Некоторые явления, наблюдаемые в течениях вязкой жидкости, трудно объяснимы
на основе уравнений Навье—Стокса. Например, потеря устойчивости течения между
цилиндрами при вращении только внешнего цилиндра [1], неединственность
вторичных режимов в течениях между вращающимися сферами и цилиндрами [2]. Как
правило, эти явления имеют место при больших градиентах скоростей потока. В данной
работе предполагается, что при больших градиентах скоростей вязкая жидкость
проявляет свойство упругости. В результате эффективная вязкость становится переменной
величиной и может принимать отрицательные значения. Различные модели жидкости
со знакопеременной вязкостью предложены в работах [3—5].
Предположим, что выделенный объем жидкости претерпевает заданную конечную
деформацию. Используя условия равновесия в форме Лагранжа, можно получить [6],
что силы внутренних напряжений выражаются через обобщенный тензор напряжений
7/fc. В начальной декартовой системе координат Tik имеет вид
Tik = T?l(8lk + duk/dxl), (1)
где Jfk — симметричный тензор множителей Лагранжа, щ — компоненты вектора
перемещений. Несимметричность тензора обусловлена нелинейностью тензора
деформаций. При малых деформациях в (1) можно пренебречь величиной buklbxt. Поэтому
Tfk является симметричным тензором напряжений вязкой несжимаемой жидкости,
T?k=p8ik+nDik, (2)
р — давление, Dik — тензор скоростей деформации. Как следует из формул (1), (2),
при конечных деформациях в жидкости возникают упругие напряжения с модулями
упругости, зависящими от градиента скорости.
Будем считать, что основные эффекты упругости могут быть учтены с помощью
переменной вязкости, и рассмотрим уравнения движения следующего вида:
dvi dvi 1 Ър д bVi
— + *>/ — =- - Т— + — [ Щ) Щ + Y(t) [Г,/]] + /,; —- = 0;
Ot OXi О OX j- OXj OXi
777 (3)
Щ = —L + —l, Tu =—-—!■;
dxj dXj bxj bxt
Г = а11П2+аа1Д12,
1П2= Z (Г/у)2, \D\2= 2 (A7)2,
i>j i>j
где непрерывно дифференцируемые функции W($)9 F(f) удовлетворяют условиям
W(0)=i>>0, Г(0) = 0. (О
*Докл. АН СССР. 1984. Т. 275, № 3. С. 576-579. (Соавтор Б.Ю. Скобелев.)
13* 387

Исследуем задачу об устойчивости течения между вращающимися
концентрическими цилиндрами. Пусть rt, ^Zj — радиус и угловая скорость вращения внутреннего
цилиндра, г2, £12 — радиус и угловая" скорость внешнего цилиндра. Известно, что
стационарное ламинарное течение имеет отличной от нуля только азимутальную
составляющую скорости — Vo (f):
v0(r) = Ar + B/r,
(4)
_ П2г2 - £lxr\ _ (fli - £l2)r2r2
А^ А-А " * = А-А '
Запишем уравнения (3) в ft = 0 в цилиндрической системе координат и будем искать
решения вида
vr = vz = 0, и^ = v(r).
Получим
v2 1 dp
г р dr
\ dWr/dv~\2 7M21 * dY (do v\2}
\ dS \dr . r J d$Wdr J \r / J J rfr \ dr г /
d / d 1 \ _
Lv = — —+ — )v .
dr \ dr r )
Потребуем, чтобы выполнялось равенство ~v(г) = v0(r). Тогда, как нетрудно показать,
нужно положить а2 = 0> т.е. функции W($), F(J") должны зависеть лишь от
завихренности течения. Для удобства проведения выкладок положим с^ = 1/8. Пусть
vr = и (г, z, f ), v^ = v0(г) + v'(r, z,t), vz= q'(r, z,t),
p = p0(r)+p'(z,z, Г), и = u(r)cos XzeGt>
v = v(r)cos Xzeat, q =■ q(f) sin Xzeat.
Линеаризованная относительно возмущений скорости система (3) эквивалентна
системе уравнений для безразмерных функций и и и
(L - X2 )2и - д(Ь - X2 ) и = ТАсо0и, (5)
где
со0=Л+Я/г2, Л = (1-^?2)/(1-т?2), Л=03- 1)т72/(1 -г?2), Р=П!/П2,
^л2 <*г0
Х= ж;ч,2 ~^Т> ^o = ^(fo), ^о = ^(Г0)э
17 = Г!/гаэ *ф = 1?2/(1+8*)2э 5 = 1-7?, в =
Jv0 + /о «Г
$0 = 1ASllA2i X=X5, o = R062o> v=282R0Av>
Ro=n2rll{W0+Y0), T=4R206*X29 Г=-^(4-+ 7^77)•
388

2
+
у Функции u(g), i7(£) должны удовлетворять граничным условиям вида
и = du/dt = v = 0 при % = - 1, 0. (6)
В случае, когда зазор между цилиндрами 5 является малой величиной, можно
показать, что спектр задачи (5), (6) лежит в полубесконечной полосе
Rea<const, \Im д\ < const • 5. (7)
Из требования корректности задачи Коши для возмущений скорости и оценки (7)
вытекает ограничение на вид функций WnY
W+Y>0. (ii)
После несложных выкладок можно получить следующее выражение для Re a:
г о /I d2u I2 ~ | du i2 _ л
L-i \| c#jz I I ^5 I '
Г ° I ^u 12 ~„ ° , , „ П Г ° / I du
+ Mcoo[/i(l+er.W)| — I dt+X» /^и1^][/Д| —
+ X2lwl2)^ + 7>lcoo / Ы2^]"1 +0(6), (8)
ojq — среднее значение со0 •
Из уравнений Навье—Стокса следует [7] устойчивость течения Куэтта при А > О
(j3 < I/772). В нашем случае, как показывает формула (8), нарастающие возмущения
могут существовать и при положительных значениях А, если х — 0 > 1- Этот вывод
подтверждается численными расчетами собственных значений задачи (5), (6) при
фиксированных х и в.
Зададимся конкретным видом функций W(g)y У($) и построим диаграмму
устойчивости в плоскости (RlfR2):
R1=r21n1/u9 R2=r2Sl2/v
Пусть W($) имеет вид
W(f) — безразмерная функция.
При этом
Будем считать, что безразмерные параметры "vx, F2 не_зависят от #j и^2-
1. Рассмотрим случай, когда W($) > 0 при всех J". Тогда можно положить У($") = 0.
Получим
ЛЯ 1 £/Й? - 4R2264\2
Обозначим через /30,- значения 0, соответствующие точке минимума функции W($0).
В этой точке х меняет знак:
001 =rf2[l -(1 -V2)(pJV2)A] <if2,
0О2=Т?-2[1 +(1 -Т?2)^/^)*] >Т?-2.
В области Ri > R2 (/J > I/772) граница устойчивости ламинарного течения качественно
совпадает с границей Тейлора и имеет вид, приведенный на рисунке, кривая 1. При
Ri <R2 возможны три различных случая расположения области неустойчивости.
а) Пусть 1 < 00 1 < I/772. Область неустойчивости лежит внутри кривой2 (см. рис.).
389

Прямые LltL2y задаются уравнениями
б) 0 < 0о 1 < 1 • Качестве! но область неустойчивости имеет тот же вид, что и в случае а),
только меняются уравненш для прямых Lx, L2:
fihx = h 0Il2=0oi.
в) Если j30i < 0, то граница устойчивости определяется кривой 3 (рис.), а прямая
Ьъ задается уравнением
01* =1.
A Ri-Rz/
/ Lw
1 / ys
V^Y/ ^' ь&
U^n £ ^
2. Предположим, что H^f) может принимать отрицательные значения. Тогда в силу
условия (и) Y(£)^0. Если положить
Y=vY($)=v(k1T-k2Y2), к19к2>0,
то коэффициенты Ц, fy можно выбрать так, что при 0 < 1 течение Куэтта будет иметь
две нейтральные кривые, аналогичные кривым 2 и 3 на рисунке 1.
Как показано, уравнения движения (3) позволяют объяснить неустойчивость
течения Куэтта при R2 > R\ > 0, наблюдавшуюся в экспериментах [1]. Положение области
неустойчивости в плоскости (Rlf R2) определяется видом функции вязкости. В
частности, для неустойчивости течения при неподвижном внутреннем цилиндре необходимо,
чтобы функция W(£) имела участки с отрицательной производной. Если W(£) —
знакопеременная функция, то могут существовать две области неустойчивости. Вполне
возможно, что неединственность границы устойчивости, которая наблюдалась в зоне
гистерезиса перехода [1], связана с наличием двух нейтральных кривых.
ЛИТЕРАТУРА
1. Coles D. И J. Fluid Mech. 1965. Vol. 21. P. 385-425.
2. RoesnerK.G. 11 Lect. Notes Phys. 1979. Vol. 90. P. 1-25.
3. Яненко ИМ., Новиков В.А. // Числ. методы механики сплош. среды. 1973. Т. 4, № 2.
4. Зеленяк ТЖ, Новиков ВЛ., Яненко Н.Н. // Там же. 1974. Т. 5, №4.
5. Яненко НМ. // Там же. 1976. Т. 7, № 1.
6. Работное Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1979. 744 с.
7. Линь ЦМ. Теория гидродинамической устойчивости. М.: Изд-во иностр. лит., 1958.192 с.
390

РАСЧЕТ МОДЕЛЕЙ НЕЙТРОННЫХ ЗВЕЗД
С ПИОННОЙ КОНДЕНСАЦИЕЙ*
По современным представлениям нейтронные звезды — это остатки сверхновых
звезд с массой приблизительно от 0,5 до 2 Л/©, радиусом порядка 10 км и плотностью
в центре рс *** 2 • 1014 -^4 • 1015 г/см3. Теоретическое исследование строения и
внутренних процессов в таких небесных телах существенным образом зависит от связи между
давлением и плотностью вещества, т. е. от уравнения состояния.
Согласно работе Мигдала -(1978), в сверхплотном веществе возможны фазовые
переходы с образованием пионных конденсатов. Плотность энергии нейтронного
вещества в этом случае равна е(п) = eN(n) + ея(и), где п — число нуклонов в единице
объема, е^ — плотность энергии нуклонов, еп — плотность энергии, связанной с
появлением пионного конденсата. Давление р и сжимаемость вещества К связаны с
плотностью энергии формулами
d d2e
р = п2—(е/п)9 К = п-—. (1)
dn dnz
Мигдал (1978) предложил следующую интерполяционную формулу:
(eN{n)-y2p(n)(n-n*)2, п>пт9 (2)
[eN(n)9 п<п*9
где п* — некоторая критическая плотность, (3(п) = а + Ь(п*/п) + с(п*/п)2 \а,Ъ,с —
параметры, зависящие от и*. Сжимаемость вещества К имеет при п = п* разрыв.
Действительно, при п < п^ сжимаемость К = KN = nd2e^jdn2 положительна; по мере
приближения плотности к критическому значению п* со стороны больших плотностей
сжимаемость К -► KN — (а + b + c) = KN — 0о. Если Р0 > К при п = п*9 то при плотностях
выше критической сжимаемость отрицательна и состояние системы будет
неустойчивым. Давление вещества определяется по формулам (1), (2) и равно
p(n) = pN(n) - Уг п2 {[а +Ь(п*п) + c(njn2)] (1 - пЦп2) - (njn)(l - njnf X
X[b+2c(nJn)]}e(n-nJ9 (3)
ч J1' п>п*>
в(п ~flj= 1л
v *' 10, п<п*.
Пионная конденсация смягчает уравнение состояния, а при некоторых наборах
параметров и#, я, Ъус уравнение состояния р = р(п) может стать немонотонным (типа
Ван-дер-Ваальса). Область, где dpjdn < 0, неустойчива, поэтому можно ожидать
возникновения скачка плотности и существенной перестройки структуры нейтронных звезд.
Настоящая работа посвящена численному изучению нестационарных
газодинамических процессов в сферически-симметричных нейтронных звездах с немонотонными
уравнениями состояния (3). Исходные уравнения в массовых лагранжевых
координатах имеют следующий вид
Ъи/bt = -4-пг2 bp/bq - Gq/r2, br/bt = и,
br/bq = (4тгрг2Г\ р=р(р)9 (4)
г
где p=rnnn — массовая плотность, q(r) = / 4яр(г')г'2^г'.
о
Начальное распределение плотности выбиралось в виде
p(r,0) = p°c[l-(r/Roy],s = 3[(M0/M)-l]-1
где р% — начальная плотность в центре звезды, R0 — начальный радиус, М0 = (47г/3)р°/?о,
*Письма в астрон. журн. 1952. Т. 8, № 2. С. 86-89. (Соавторы Ю.А. Березин, О.Е. Дмитриева.)
391

f>,WrJ2/CM3
2,0\-
Щ /Ц,/*—' *-^^N/"^—^
D Z V ff f/p 0 0%5 1
Рис. 1. Уравнение состояния нейтронного вещества с пионной конденсацией
1,5 £,МС
Рис.2. Зависимость плотности от времени в лагранжевых точках q0 =0 (1), q30 = 0,5М (2),
q54=0,90M (3), qi5 =0,91 М (4)
0 0,Z 0,V 0f6 0,ff q/м
^определение плотности по Mai
Рис. 4. Зависимость от времени радиуса звезды и радиуса ядра для случая М = 1,4М&
,i I I I 1
J,Jt,MC 3,7
Рис. 3. Распределение плотности по массовой лагранжевой координате в различные моменты
времени
М — масса звезды. Начальные значения эйлеровой координаты r°(q) определялись
итерационным методом из уравнения dr°/dq = [4ттр(г, О)^0)2]""1. Граничные условия
задавались стандартным образом:
'11(0,0=0, Ко, 0 = о, р(л/,о = о.
Метод решения системы (4) изложен в работе Яненко и др. (1979). Расчеты были
выполнены для следующих параметров р°с = 3 • 1014 г/см3; М = 0,45; 1,0; 1,4; 1,85;
2,0Л/©;Л0 = 13 -г 18 км. В качестве монотонной частиРн(р) уравнения состояния (3)
были взяты уравнения состояния Бейма и др. (1971) (область плотностей 1,05 • 104 ■=■
-г 7,7 • 1013 г/см3) и Пандхарипанди (1971) для нейтронного вещества (область
плотностей 8,4 • 1013 т 1,26 • 1016 г/см3). Немонотонная часть р(р) задавалась
параметрами п„ = 0,69, я = 0,9, Z> = -0,23, с = 0,14 (в пионных единицах); в системе единиц СГС
критическая плотность равна р# « 4,1 • 1014 г/см3. На рис. 1 представлено
использованное в расчетах уравнение состояния в пионных единицах.
Рассмотрим результаты расчетов. В начальный момент времени вся звезда находится
в области монотонной зависимости давления от плотности, так как р^<рт. Начальные
конфигурации не являются равновесными, возникают скорости к центру, и с течением
времени звезда "входит" в область немонотонной зависимости давления от плотности.
Во всех вариантах расчета при временах< 1 мс возникает и постепенно устанавливается
разрыв плотности при непрерывном давлении. На рис. 2 представлена зависимость плот-
392

£,MJJ3pz
/г
JL
/?,щ ^
О 0,5 J J,Jt,McJJ U 0,5 I Г,мс
Рис. 5. Зависимость от времени различных видов энергии для звезды с массой М - 1,4М
Рис. 6. Зависимость от времени эйлеровых координат для звезды с массой М = 0,45М&
Цифры на кривых — величина соответствующих лагранжевых координат q/M
ности от времени в ряде лагранжевых координат (кривые 7 и 2 соответствуют
координатам q = 0 — центра звезды и q = 0,5Л/, а кривые 3 и 4 — массовым координатам
разрыва; М= 1,4 М@). Перепад плотности происходит на одном шаге Aq лагранжевой сетки
независимо от величины этого шага. Положение разрыва плотности q = q^ по
лагранжевой координате быстро устанавливается. На рис. 3 приведены распределения плотности
для звезды с М = 1,4 М® в зависимости от лагранжевой координаты в момент времени
t = 0 (кривая 1) и t = 3,7 мс (кривая 2), пунктиром обозначен разрыв плотности.
Результаты расчетов показывают, таким образом, что в случае немонотонного уравнения
состояния (3) формируется плотное ядро звезды и менее плотная оболочка. На рис. 4
представлена зависимость от времени в случае М = 1,4М0 радиуса звезды R(t) и
радиуса ядра R* (t), который соответствует радиусу разрыва плотности. При временах ^0,5 мс
эти радиусы испытывают небольшие колебания около средних значений R = 9,1 км,
R* = 7,7 км. Ниже даны средние значения радиуса звезды и радиуса ядра для различных
масс нейтронных звезд:
м/м@
Я км
^*км
0,45
8,40
5,15
1.0
8,65
6,95
1,4
9,10
7,70
1,85
9,50
8,30
2,0
9,55
8,55
Расчеты с другими начальными конфигурациями показали, что при
квазиустановлении радиусы и плотности в центре звезды и на разрыве определяются только массой
звезды М и не зависят от начальных условий. На рис. 5 приведена для случая Л/= 1,4 М&
зависимость от времени различных видов энергии — кинетической
м м
Екин =f (l/2)u2dq, гравитационной Етх> = —/ (Gq/r)dq
о о
и внутренней 2^,,, связанной с работой сил давления. Полная энергия во всех
вариантах сохранялась с точностью не хуже, чем 0,5%. Указанные расчеты выполнялись на
сетке с Aq=M/6Q.
В работе Мигдала и др. (1979) была высказана гипотеза, что при образовании пион-
ного конденсата может произойти сброс оболочки нейтронной звезды. Для изучения
этого вопроса нами на сетке с измельчающимися от центра к периферии шагами Aq =
= 5 • 10~2 -5- 10~5 М были проведены расчеты начальной конфигурации сМ = 0,4 М0,
р£ = 4 • 1014 г/см3, R0 = 26 км. На рис. 6 представлена зависимость от времени
радиусов, соответствующих различным значениям массовой лагранжевой координаты. В
этом случае масса оболочки равна 0,32 М, а отлетает приблизительно 0,015 М; энергия
отлетающей части оболочки меньше 1050 эрг. Аналогичные расчеты для звезд с масса-

ми 1,4М0 и 1,85 М® показали, что возможен отлет части массы значительно меньшей,
чем 10"5 М (массы оболочек равны соответственно 0,083 М и 0,067 М).
Анализ результатов этих расчетов позволяет сделать вывод, что сброс очень малой
части массы не связан с образованием плотного ядра и разрыва плотности.
Авторы благодарят B.C. Имшенника и Д.К. Надежина за полезные обсуждения.
ЛИТЕРАТУРА
1, Ваут G, Pethick С, Sutherland Р. // Astrophys. J. 1971. Vol. 170. P. 299.
2, Мигдал А. // Rev. Mod. Phys. 1978. Vol. 50. P. 107.
3, MigdalA.B., Chernoutsan A.Ly Mishustin IJSf. 11 Phys. Lett, B. 1979. Vol. 83. P. 158.
4, Pandharipande V.R. // Nucl. Phys. A. 1971. Vol. 178. P. 2123.
5, Яненко Н.Н., Березин ЮА„ Дмитриева О.Е. //Числ. методы механики сплош. среды. 1979. Т..10.
С 150.

СПИСОК ТРУДОВ Н.Н. ЯНЕНКО1
1948
О некоторых необходимых признаках изгибаемых поверхностей в л-мерном эвклидовом
пространстве: Дис.... канд. физ.-мат. наук. М..: Изд-во МГУ, 1948. 150 с.
1949
Геометрическая структура поверхностей малого типа // ДАН СССР. 1949. Т. 64, № 5. С. 641-649.
О некоторых необходимых критериях изгибаемости поверхностей в многомерном эвклидовом
пространстве // Там же. Т. 65, № 6. С. 449-452.
1950
О некоторых проективно-инвариантных свойствах изгибаемых поверхностей многомерного
эвклидова пространства // ДАН СССР. 1950. Т. 72, № 6. С. 1025-1028.
Структура изгибаемых поверхностей в многомерном эвклидовом пространстве // Там же. № 5.
С. 857-859.
1951
О сходимости разностной схемы для одного интегро-дифференциального уравнения: Отчет Геофиз.
ин-та АН СССР, 1951. - Соавт.: Тихонов А.Н.
1952
*Метрики класса 2 // ДАН СССР. 1952. Т. 83, № 5. С. 667-669.
Некоторые необходимые признаки изгибаемых поверхностей Vm в (т + q) -мерном эвклидовом
пространстве // Тр. семинара по векторному и тензорному анализу. М.? 1952. Вып. 9. С. 236-287.
*0 классе римановой метрики // ДАН СССР. 1952. Т. 83, № 4, С. 523-536.
*0 связи между метрическими и проектированными свойствами поверхностей // Докл. АН СССР.
1952. Т. 82, №5. С. 685-688.
1953
Некоторые вопросы теории вложения римановых метрик в эвклидовы пространства // Усп. мат.
наук, 1953. Т.8,вып. 1 (53). С. 2J-100.
1954
К теории вложения поверхностей в многомерном эвклидовом пространстве // Тр. Моск. мат. о-ва.
1954. Т. З.С. 89-180.
К теории вложения римановых метрик в многомерное эвклидово пространство: Дис. ... д-ра физ.-
мат. наук. М., Изд-во МГУ. 1954. 170 с.
1955
О разрывах в решениях квазилинейных уравнений //Усп. мат. наук. 1955. Т. 10, вып. 2 (64). С. 195-
202.
Сведение системы квазилинейных уравнений к одному квазилинейному уравнению // Там же.
Вып. 3(65). С. 174-178.
1 Звездочкой отмечены труды, вошедшие в наст. изд.
395

1956
*Бегущие волны системы квазилинейных уравнений // ДАН СССР. 1956. Т. 109, № 1. С. 44-47.
К теории класса римановых пространств // Тр. семинара по векторному и тензорному анализу.
М., 1956. Вып. 10. С. 139-191.
О взаимодействии ударных волн с бегущими волнами // ДАН СССР. 1956. Т. 109, № 4. С. 713-716. -
Соавт.: Арсенин В. Я.
Приближенные формулы для давления и внутренней энергии газа в обобщенной статистической
модели атома Томаса-Ферми // Там же. № 5. С. 916^918.
1958
* Асимптотические и приближенные формулы для давления и внутренней энергии вещества в
обобщенной модели атома Томаса-Ферми // G6. науч. работ кафедры математики. М.: Атомиздат,
1958. С. 144-195.
Введение в теорию разностных схем уравнений математической физики: Курс лекций на физ.-мат.
фак. Урал. гос. ун-та. 1958. 150 с.
*К вопросу о нестационарных плоских течениях политропного газа с прямолинейными
характеристиками // ДАН СССР. 1958. Т. 123, № 5. С. 832-834. - Соавт.: Сидоров А.Ф.
О бегущих волнах уравнений газовой динамики // ДАН СССР. 1958. Т.. 119, № 3. С. 443-445. -
Соавт.: Погодин Ю.Я., Сучков В.А.
*0 бегущих волнах уравнений газовой динамики // Журн. прикл. математики и механики. 1958.
Т. 22, № 2. С. 188-196. - Соавт.: Погодин Ю.Я., Сучков В.А.
О распространении разрывов в идеальных газах // Сб. науч. работ кафедры математики. NL:
Атомиздат, 1958. С. 20-79. - Соавт.: Арсенин В.Я.
1959
Асимптотические формулы для функционалов решений уравнений Томаса-Ферми // Тр. III. Всесоюз.
мат. съезда (Москва, июнь-июль 1956 г.). М.: Изд-во АН СССР, 1959. Т. 1. С. 226-227.
* Неустановившиеся плоские течения политропного газа с прямолинейной образующей // Изв. вузов.
Сер. Математика. 1959. №1 (8). С. 187-198. - Соавт.: Сидоров А.Ф.
*Неявные схемы расщепления для гиперболических уравнений и систем // ДАН СССР. 1959. Т. 128,
№ 6. С. 1103-1105. - Соавт.: Анучина Н.Н.
О разностном решении уравнения теплопроводности в криволинейных координатах // ДАН СССР.
1959. Т. 128, № 5. С. 903-905. - Соавт.: Сучков В.А., Погодин Ю.Я.
О разрывах в решениях квазилинейных уравнений // Тр. III Всесоюз. мат. съезда (Москва, июнь-
июль 1956 г.). М.: Изд-во АН СССР, 1959. Т. 4. С. 42-43.
О сведении системы квазилинейных уравнений к одному квазилинейному уравнению // Тр. III
Всесоюз. мат. съезда (Москва, июнь-июль 1956 г.). М.: Изд-во АН СССР, 1959. Т. .4. С. .43.
*Об одном разностном методе счета многомерного уравнения теплопроводности // ДАН СССР.
1959. Т. 125, №6. С. 1207-1210.
Проблемы вложения римановых метрик в эвклидовы пространства // Тр. III Всесоюз. мат. съезда
(Москва, июнь-июль 1956 г.). М.: Изд-во АН СССР, 1959. Т.Д. С. 177-178.
Решения уравнений газовой динамики с вырожденным годографом (бегущие волны) // Там же.
Т. 2. С. 160.
1960
*Об экономичных неявных схемах (метод дробных шагов) // ДАН СССР. 1960. Т. 134.
№5. С. 1034-1036.
1961
О неявных разностных методах счета многомерного уравнения теплопроводности // Изв. вузов.
Сер. Математика. 1961, №4(23). С. 148-157.
*0 реализации на электронно-вычислительных машинах алгебраическо-дифференциальных
алгоритмов // Пробл. кибернетики. 1961. Вып. 6. С. 33-43. - Соавт.: Щурыгин В.А.
О сходимости разностных схем для уравнений теплопроводности с переменными
коэффициентами // ДАН СССР. 1961. Т. 139, № 6. С. 1322-1324. - Соавт.: Бояринцев Ю.Е.
Об инвариантных дифференциальных связях для гиперболических систем квазилинейных
уравнений // Изв. вузов. Сер. Математика. 1961, № 3 (22). С. 185-194.
1962
О сходимости метода расщепления для уравнения теплопроводности с переменным
коэффициентом // Журн. вычисл. математики и мат. физики. 1962. Вып. 5. С. .933-937.
396

1964
Некоторые вопросы теории сходимости разностных схем с постоянными и переменными
коэффициентами // Тр. IV Всесоюз. мат. съезда (Ленинград, 3-12 июля 1961 г.). Л.: Наука. 1964. Т..2.
С. 513-621.
*0 слабой аппроксимации систем дифференциальных уравнений // Сиб. мат. журн. 1964. Т..5, № 6.
С, 1431-1434.
О слабой аппроксимации систем дифференциальных уравнений // Тр. III Сиб. конф. по математике
и механике. Томск, 1964. С. 2 ] - 24.
*Решение многомерного кинетического уравнения методом расщепления // ДАН СССР. 1964. Т. .157,
№6. С. 1291-1292. - Соавт.: Марчук Г.И.
Теория совместности и методы интегрирования систем нелинейных уравнений в частных
производных // Тр. IV Всесоюз. мат. съезда (Ленинград, 3-12 июля 1961 г.). Л.: Наука. 1964. Т..2.
С. 247-259.
1966
•*Исследование задачи Коши методом слабой аппроксимации // ДАН СССР. 1966. Т. 167,
№6. С. 1242-1244. - Соавт.: Демидов Г.В.
Исследование задачи Коши методом слабой аппроксимации // Тез. крат. науч. сообщ. Междунар.
конгресса математиков. Секция 14. Вычисл. математика. М„ 1966. С. 53-54. - Соавт.:
Демидов Г.В.
Метод дробных шагов решения многомерных задач математической физики: Лекции для студентов
Новосиб. гос. ун-та. Новосибирск: Изд-во Новосиб. гос. ун-та, 1966. 255 с.
Метод слабой аппроксимации как конструктивный метод построения решения задачи Коши //
Некоторые вопросы вычисл. и прикл. математики. Новосибирск: Наука, 1966. С. 60-83.
*Об одной абсолютно устойчивой схеме интегрирования уравнений гидродинамики //Труды МИАН
СССР. 1966. Т. 74, ч. 1. С. 141-182. - Соавт.: Яушев И.К.
Один метод расчета газодинамических движений с нелинейной теплопроводностью // Там же. С. 138—
140. - Соавт.: Неуважаев В.Е.
*Применение метода расщепления (дробных шагов) для решения задач математической физики //
Некоторые вопросы вычисл. и прикл. математики. Новосибирск: Наука, 1966. С..5-22. - Соавт.:
Марчук Г.И.
Численный расчет водослива // Там же. С. 193-201. - Соавт.: Антонцев СП., Васильев О.Ф.,
Кузнецов Б. Г.
* Численный расчет симметричного обтекания пластинки плоским потоком вязкой несжимаемой
жидкости // Там же. С. 186-192. - Соавт.: Владимирова Н„ Кузнецов Б.Г.
1967
Метод дробных шагов решения многомерных задач математической физики. Новосибирск: Наука,
1967. 195 с.
*0 применении метода расщепления для численного расчета движений теплбпроводного газа в
криволинейных координатах // Изв. Сиб. отд-ния АН СССР. Сер. техн. наук. 1967. Вып. 2,№ 8.
С. 74-82. - Соавт.: Фролов В.Д., Неуважаев В.Е.
Расчет формы каверны в поле тяготения с учетом поверхностного натяжения // Там же. Вып. 3,
№ 13. С 58-61. - Соавт.: Кузнецов Б.Г., Шепеленко В.Н.
* Экономичные разностные схемы повышенной точности для полигармонического уравнения //
Там же. С. 88-96. - Соавт.: Валиуллин А.В.
1968
Введение в разностные методы математической физики: Лекции для студентов Новосиб. гос. ун-та.
Новосибирск: Изд-во Новосиб. гос. ун-та, 1968. Ч. 1. 192 с.
Введение в разностные методы математической физики: Лекции для студентов Новосиб. гос. ун^га.
Новосибирск: Изд-во Новосиб. гос. ун-та. 1968. Ч. 2. С. 197-385.
Метод слабой аппроксимации для произвольного расщепления // Apl. Mat. 1968. Vol. 13, № 2. РЛ48-
151.
*0 корректности первых дифференциальных приближений разностных схем // ДАН СССР. 1968.
Т. 182, №4. С. 776-778. - Соавт.: Шокин Ю.И.
О связи корректности первых дифференциальных приближений и устойчивости разностных схем
для гиперболических систем уравнений // Мат. заметки. 1968. Т. 4, № 5. С. 493-502. - Соавт.:
Шокин Ю.И.
*Об аппроксимационной вязкости разностных схем // ДАН СССР. 1963. Т. 182. № 2. С. 280-281. -
Соавт.: Шокин Ю.И.
397

Расчет характеристик ламинарного пограничного слоя на телах вращения. Новосибирск: Наука,
1968. 219 с. - Соавт.: Алексеева Г.Е., Громов В.П., Дмитриева А.Ф. и др.
Системы квазилинейных уравнений и их приложения к газовой динамике. М..: Наука, 1968. 592 с. -
Соавт.: Рождественский Б.Л»
Methode a pas fractionnaires. Resolutions de problemes polydimensionels de physique mathematique.
Paris: Librairie Armand Colin, 1968. 205 p.
1969
A.c. 251259 (СССР). Устройство для решения дифференциальных уравнений / Заявл. 06.05.1967;
Опубл. 26.08.69. - Соавт.: Лукьянов А.Т. :
Итерационные процессы для точного решения разностной задачи Дирихле повышенного порядка
точности // Тр. конф. по численным методам решения задач теории упругости и пластичности
(Новосибирск, 11-14 февраля 1969 г.) Новосибирск, 1969. С. 129-142. -Соавт.: Валиул-
лин А.Н., Квасов Б.И. .
О первом дифференциальном приближении разностных схем для гиперболических систем
уравнений // Сиб. мат. журн. 1969. Т. 10, №5. С. 1173-1187. - Соавт.: Шокин Ю.И.
О точном решении разностного аналога задачи Дирихле повышенной точности для
полигармонического уравнения // Тр. симпозиума "Вопросы точности и эффективности вычислительных
алгоритмов". Киев, 1969. С. 269—282. - Соавт.: Шокин Ю.И.
Об аппроксимационной вязкости разностных схем для гиперболических систем уравнений // Тр.Все-
союз. семинара по численным методам механики вязкой жидкости. Новосибирск: Наука, 196"»
С 269- 282. - Соавт.: Шокин Ю.И.
Computation of the cavity form in a gravity field with account being taken of surface tension // Fluid
Dynamics Trans. 1969. № 4. C. 739-744. Соавт.: Кузнецов Б.Г., Шепеленко В.Н.
Die Zwischenschriftmethode zur Losung mehrdimensional Probleme der mathematischen Physik. Berlin;
Heidelberg; New York: Springer-Verlag, 1969. 194 p. (Lect. Notes Math. Vol. 91.).
First differential approximation method and approximation viscosity of difference scheme // Phys. Fluids.
Suppl. 2: Intern. Symp. on High Comput. in Fluid Dynamics. 1969. P. 28-33. - Соавт.: Шокин Ю.И.
О zagadnieniu lepkosci aproksymacyjnej w schematsch roznicowych // Metody numery czue w mechanice
plynow. Wroclaw-Warszawa-Krakow, 1969. P. 192-219. - Соавт.: Шокин Ю.И.
The method of fractional steps for numerical solution of the problems of mechanics of continuous media //
Fluid Dynamics Trans. 1969. Vol. 4. P. 135-147.
1970
Итерационный метод построения поликубических сплайн-функций // ДАН СССР. 1970. Т. 195,
№ 5. С. 1055-1057. - Соавт.: Квасов Б.И.
* Итерационный метод построения поликубических сплайн—функций // Численные методы механики
сплошной среды. Новосибирск. 1970. Т..1, № 3. С. 84-86. - Соавт. Квасов Б.И.
Метод дробных шагов решения задач механики сплошной среды // Дифференциальные уравнения
с частными производными: Тр. симпоз., посвящ. 60-летию С.Л. Соболева. М.: Наука, 1970.
С23;9-248.
О групповой классификации разностных схем для системы одномерных уравнений газовой
динамики // Некоторые проблемы математики и механики. Л.: Наука, 1970. С. 277-283. -Соавт. :
Шокин Ю.И.
*0 методах расчета задач газовой динамики с большими деформациями // Численные методы
механики сплошной среды. 1970. Т. 1,.№ 1. С.г 40-63. -:Соавт.: Анучина Н.Н., Петренко В.Е.,
Шокин Ю.И.
Methodes nume'riques nouvelles en mecanique du continu // Actes, Congr. Intern. Math. 1970. Vol. 3.
P. 297-309.
1971
* Влияние вязкости на гладкость решения в неполно-параболических системах // Мат. заметки.
1971. Т. .10, № 7. С. 93- 99. - Соавт.: Белов Ю.Я.
Групповая классификация неявных разностных схем для системы уравнений газовой динамики //
Численные методы механики сплошной среды. 19.71. Т.. 2, № 2. С. 85-92. -Соавт.: Шокин Ю.И.
К теории разностных схем газовой динамики // Симпозиум по механике сплошной среды и
родственным проблемам анализа (Тбилиси, 23-29 сентября 1971 г.) : Тез. докл. Тбилиси, 1971. С. .52-
55. - Соавт.: Шокин Ю.И.
О методах расчета течений сжимаемой жидкости с большими деформациями и аппроксимационной
вязкости разностных схем // Тр. II Междунар. коллоквиума по газодинамике взрыва и
реагирующих систем (Новосибирск, 19-23 августа 1969 г.). М.: ВЦ АН СССР. 1971. С..159-187. - Соавт.:
Анучина Н.Н.,.Петренко В.Е., Шокин Ю.И.
398

*0 структуре абсолютно аппроксимирующих и абсолютно корректных схем // Проблемы
прикладной математики и механики. М.; Наука, 1971. С. .137-144. - Соавт.: Демидов Г.В.
Применение метода дифференциальных связей к однородным уравнениям газовой динамики //
Численные методы механики сплошной среды. 1971. Т..2, № 5. С. 3-11. - Соавт»: Распопов В.Е.,
Шапеев В. П.
Численный расчет непотенциальных течений идеальной жидкости в плоских каналах // Там же. № 1.
С. 3-16. - Соавт.: Гуров Б.Г., Яушев И.К.
On numerical methods of solving gas dynamical problems with large deformations // Fluid Dynamic Trans.
1971. N 5. Pt 1. P. 9-32. - Соавт.: Анучина Н.Н., Петренко B.E., Шокин Ю.И.
On the group classification of difference schemes for systems of equations in gas dynamics// Lect. Notes
Phys. 1971. N8. P. 3-17.
The method of fractional steps. The Solution of Problems of Mathematical physics in Several Variavles.
Berlin; Heidelberg; New York; Springer-Verlag, 1971.
1972
Введение в математический анализ. Новосибирск: Изд-во Новосиб. гос. ун-та, 1972. Ч..1. 33.1 с. -
Соавт.: Шокин Ю.И.
* Модульный принцип построения программ как основа создания пакета прикладных программ
решения задач механики сплошной среды // Комапексы программ математической физики.
Новосибирск, 1972. С. 48-54. - Соавт.: Ковеня В.М.
*Об одной неявной схеме расчета течения вязкого теплопроводного газа // Численные методы
механики сплошной среды. 1972. Т. 3, №4. С. 3-18. - Соавт.: Березин Ю.А., Ковеня В.М.
Применение инвариантных разностных методов к задачам газовой динамики // XIII Междунар.
конгресс по теоретической и прикладной механике (Москва, 21-26 августа 1972 г.): Тез. докл.
М., 1972. С. 111-112. - Соавт.: Шокин Ю.И.
Современные численные методы решения задач механики сплошной среды // Междунар. конгресс
математиков в Ницце. 1970: Докл. сов. математиков. М.;: Наука, 1972. С. .345-351.
Уравнения движения теплопроводного газа в смешанных эйлерово-лагранжевых координатах //
Численные методы механики сплошной среды. 1972. Т. 3,. № 1. С. 90-95. -Соавт.: Неуважа-
ев В.Е., Фролов В.Д.
*Эволюционные двухслойные разностные схемы // Там же. №.5. С. 95-114. - Соавт.: Демидов Г.В.,
Кантор С. А.
Эволюционные двухслойные разностные схемы // ДАН СССР. 1972. Т. .204, № 5. С. 95 — 114. - Соавт.:
Демидов Г.В., Кантор С.А.
Splitting methods for partial differential equations// Intern. Federation on Inform. Proces. 71.1972. Vol. 2.
P. 1206-1213.
1973
Выполнимость основных термодинамических соотношений для электронного газа в обобщенной
модели Томаса-Ферми произвольной конфигурации атомной ячейки // Численные методы
механики сплошной среды. 1973. Т. .4, № 3. С. 56-61. - Соавт.: Гадияк Г.В., Максимов А.Ф.
*0 групповой классификации разностных схем для системы уравнений газовой динамики // Тр.
МИАН СССР. 1973. Т. |22. С. .85.-97. - Соавт.: Шокин Ю.И.
*Об одной модели жидкости со знакопеременным коэффициентом вязкости // Численные методы
механики сплошной среды. 1973. Т. 4, № 2. С. 142-147. - Соавт.: Новиков В.А.
Применение метода дифференциальных связей к построению замкнутых математических моделей,
описывающих одномерные динамические процессы в сплошной среде // Там же. №3. С. .39-47. -
Соавт.: Фомин В.М., Шапеев В.П.
Расчет сверхзвукового обтекания тел // Тез. III Всесоюз. конференции по прикладной
аэродинамике. Киев, 1973. С. 21. - Соавт.: Ковеня В.М., Березин Ю.А.
On some problems of the difference schemes // Proc. Equadiff. 1973. Vol. 3. P. 43-50.
Schemes numeriqucs invariants de groupe pour les equations de la dynamiquede gas // Lect. Notes Phys.
1973. Vol. 18. P. 179-181. - Соавт,: Шокин Ю.И.
1974
Введение в математический анализ. Ч. II (гл. 6, 7). Новосибирск: Изд-во Новосиб. гос. ун-та, 1974.
181 с. - Соавт.: Шокин Ю.И.
Гиперболического типа уравнений в частных производных способы решения // Энциклопедия
кибернетики АН УССР. Киев, 1974. С. 226-239. - Соавт.: Шокин Ю.И.
*2)-свойства систем одномерных уравнений динамики неупругой сплошной среды // ДАН СССР.
1974. Т. 215, № 5. С. 1067-1070. - Соавт.: Фомин В.М., Шапеев В.П.
399

*К теории разностных схем газовой динамики // Тр. симпозиума по механике сплошной среды и
родственным проблемам анализа. Тбилиси, 1974. Т. 2. С. 292-306. - Соавт.: Шокин Ю.И.'
Конечноразностные методы // Энциклопедия кибернетики АН УССР. Киев, 1974. С. 481.
Краевых задач способы решения // Там же. С. 506-509.
О свойствах решения нелинейных уравнений переменного типа // Численные методы механики
сплошной среды. Новосибирск, 1974. Т. 5, № 4. С. 35-46. - Соавт.: Зеленяк Т.И.
Об одном методе построения схем повышенного порядка аппроксимации // Избранные проблемы
прикладной механики. М.: ВИНИТИ, 1974. С. 681-688. - Соавт.: Тушева Л.А., Шокин Ю.И.
*Об одном методе ускорения сходимости итерационных схем // Численные методы механики
сплошной среды. 1974. Т. 5, № 5. С. 57-62. - Соавт.: Захаров Ю.Н., Шокин Ю.И.
* Применение метода дифференциальных связей к одномерным уравнениям газовой динамики //
Изв. вузов. Сер.Математика. 1974.№ 11. С. 69-74. - Соавт.: Распопов В.Е., Шапеев В.П.
* Реализация метода внешних форм Картана на ЭВМ // ДАН СССР. 1974. Т. 214, № 4. С. 737-738. -
Соавт.: Шапеев В.П., Арайс Е.А.
Технологические аспекты численных методов математической физики // Тр. Карлова университета.
Прага = Acta Universitatis Carolinae. Math, et phys. 1974. N 1-2. P. 47-53.
Численные методы // Энциклопедия кибернетики АН УССР. Киев. 1974. С. 530-532.
1975
О модульном анализе одного комплекса программ / Численные методы механики сплошной среды.
Новосибирск, 1975. Т. 6, № 4. С. 123-138. - Соавт.: Сафин Р.И., Савченко Я.Ф., Боднарь Т.А. и др.
*0 построении разностных схем повышенного порядка аппроксимации на основе
дифференциальных следствий // Некоторые проблемы вычислительной и прикладной математики. Новосибирск:
Наука, 1975. С. 184-190. - Соавт.: Тушева Л.А., Шокин Ю.И.
Об одной консервативной схеме для решения стационарных уравнений газовой динамики // Тез. IV
Всесоюз. конф. по динамике разреженного газа и молекулярной газовой динамике (Москва,
1975 г.). М., 1975. - Соавт.: Ковеня В.М.
Структура волн сжатия в неупругих средах // Изв. АН СССР. Сер. Механика твердрго тела. 1975,
№ 5. С. 92-98. - Соавт.: Гулидов А.И., Фомин В.М.
Implicit numerical method for blunt-body problem in supersonic flows // Comput. and Fluids. 1975. Vol. 3.
N 13. P. 271-281, - Соавт.: Березин Ю.А., Ковеня В.М.
Numerical solution of the problems of the MHD flow around the bodies // Lect. Notes Phys. 1975. N 35.
P. 131-136. - Соавт.: Березин Ю.А., Ковеня В.М.
On the theory of difference schemes for gas dynamics, equations // Ibid. P. 293-303. - Соавт.: Паасо-
нен В.И., Шокин Ю.И.
1976
* Дифференциальные анализаторы ударных волн // ДАН СССР. 1976. Т. 227, № 1. С. 50-53. - Соавт.:
Ворожцов Е.В.
Дифференциальные анализаторы ударных волн. Применение теории // Численные методы механики
сплошной среды. 1976. Т. 7, № 6. С. 8-11. - Соавт.: Фомин В.М., Ворожцов Е.В.
♦Метод подвижных координат в газовой динамике // Там же. № 3. С. 75-82. - Соавт.: Лисейкин В Д.
*Об одной модели циркуляции атмосферы с локальным знакопеременным коэффициентом
турбулентности // Там же. № 7. С. 137-152. - Соавт.: Курбаткий ГЛ., Крупчатников В.Н., Эйхер М.Ш.
Разностный метод решения задач обтекания в "естественных" координатах // Аэромеханика.
Новосибирск: Наука, 1976. С. 253-259. - Соавт.: Березин Ю.А., Ковеня В.М.
Численное решение задач механики жидкости // Тр. III семинара по моделям механики сплошной
среды. Новосибирск, 1976. С. 177-199.
Differential analysers of shock waves theory // Comput. and Fluids. 1976. Vol. 4. P. 171-183. - Соавт.:
Ворожцов E.B., Фомин В.М.
Methods for the construction of moving grids for problems of fluid dynamics with big deformations // Lect.
Notes Phys. 1976. Vol. 59. P. 454-459. - Соавт.: Крошко Е.А., Лисейкин В.Д., Фомин В.М. и др.
Modeles numeriques en mecanique des milieux continus // Ibid. Vol. 58. P. 114—132.
Numerische Lbsung strbmungsmechanischer Probleme // Ztschr. Angewandte Math. Mechanik. 1976. Vol. 56.
N 10. S. 420-428.
The method of fractional steps for the solution of problems in continuum mechanics // Amer. Math. Soc.
Transl. 1976. Vol. 105. P. 333-346.
1977
Газовой динамики уравнения // Математическая энциклопедия. М.: Сов. энциклопедия, 1977. Т. 1.
С. 833-836. - Соавт.: Шокин Ю.И.
Газовой динамики численные методы // Математическая энциклопедия. М.: Сов. энциклопедия,
Там же. С. 836-840. - Соавт.: Шокин Ю.И.
400

Гиперболического типа уравнения численные методы решения // Там же. С. 994-99$. - Соавт.:
Шокин Ю.И.
Метод дифференциальных связей для уравнений одномерной газовой динамики // Численные
методы механики сплошной среды. 1977. Т. 8, № 2. С. 100-108. - Соавт.: Распопов В.Е., Шапеев В.П.
*0 вариационном методе построения сеток // Там же. № 4. С. 157-163. - Соавт.: Данаев Н.Т., Ли-
сейкин В.Д.
*0 выборе оптимальных разностных сеток // Там же. № 7. С. 100-104. - Соавт.: Лисейкин В.Д.
О методе подвижных координат в газовой динамике // Проблемы математической физики и
вычислительной математики. М.: Наука, 1977. С. 107-115. ~ Соавт.: Лисейкин В.Д., Данаев Н.Т.
Проблемы математической технологии // Численные методы механики сплошной среды. 1977.
Т. 8, № 3. С. 129-157. - Соавт.: Коновалов А.Н., Карначук В.И.
♦Разностная схема для решения многомерных уравнений газовой динамики // ДАН СССР. 1977.
Т. 232, № 6. С. 1273-1276. - Соавт.: Ковеня В.М.
Тенденции развития современной математики // Методологические проблемы научного познания.
Новосибирск: Наука, 1977. С. 64-72.
Analytical and numerical studies on equations with sign changing viscosity cofficient//Lect. Notes Math.
1977. Vol. 594. P. 30-38. - Соавт.: Березин Ю.А., Дудникова Г.И., Новиков В.А.
1978
Аналитические и численные исследования уравнений со знакопеременным коэффициентом при
старшей производной: Препр. Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 15.
1978. 37 с. - Соавт.: Березин Ю.А., Дудникова Г.И., Новиков В.А.
Гравитирующий газовый шар // Численные методы механики сплошной среды. 1978. Т. 9, № 4.
С. 139-145. - Соавт.: Березин Ю.А., Криволуцкий B.C.
Дифференциальные анализаторы ударных волн в схемах сквозного счета задач газодинамики: Препр.
Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 7. Новосибирск, 1978. 20 с. - Соавт.:
Фомин В.М., Ворожцов Е.В.
Искусственное инициирование Г-слоя в потоке плазмы, взаимодействующей с магнитным полем //
Численные методы механики сплошной среды. 1978. Т. 9, № 5. С. 146-168. -Соавт.: Кацнель-
сон С.С., Керкис А.Ю., Поздняков Г.А.
Локальные критерии гидродинамической устойчивости: Препр. Ин-та теорет. и прикл. механики
АН СССР (Сиб. отд-ние) № 21. Новосибирск, 1978. 19 с. - Соавт.: Гапонов С.А.
Математическая технология // Фундаментальные и прикладные исследования в условиях НТР.
Новосибирск: Наука, 1978. С. 10-37. - Соавт.: Карначук В.И., Коновалов А.Н.
Неявная разностная схема на подвижных сетках для численного решения уравнений Навье—Стокса
сжимаемого газа: Препр. Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 8.
Новосибирск, 1978. 20 с. - Соавт.: Ковеня В.М.
О двух итерационных схемах для решения стационарной системы уравнений Навье-Стокса //
Комплексный анализ и его приложения. М.: Наука, 1978. С. 266-280. - Соавт.: Окунцов В.А.,
Захаров Ю.Н., Шокин Ю.И., Паничкин А.В.
О методике дифференциальных связей // Тез. Междунар. симпозиума по теоретико-групповым
методам в механике. Новосибирск, 1978. С. 24. - Соавт.: Жижин А.Е., Распопов В.Е., Шапеев В.П.
О некоторых методах численного моделирования течений сложной структуры // Сб. докл. VI
Междунар. конф. по численным методам в гидродинамике (Тбилиси, 20-25 июня 1978 г.). Тбилиси,
1978. Т. 3. С. 211-224. - Соавт.: Ковеня В.М., Лисейкин В.Д., Фомин В.М., Ворожцов Е.В.
*0 разностных схемах в произвольной криволинейной системе координат // ДАН СССР. 1978.
Т. 242, № 3. С. 525-555. - Соавт.: Шокин Ю.И., Урусов А.И.
Об одной консервативной разностной схеме для решения стационарных уравнений газовой
динамики // Математические модели течений жидкости: Тр. VI Всесоюз. семинара по числ. методам
механики вязкой жидкости (Кунгур, Перм. обл., осень 1976 г.). Новосибирск, 1978. С. 4-20. -
Соавт.: Ковеня В.М., Борисов А.В.
Об организации параллельных вычислений и "распараллеливании" прогонки // Численные методы
механики сплошной среды. Новосибирск, 1978. Т. 9, № 7. С. 139-146. - Соавт.: Коновалов АН,
Бугров А.Н., Шустов Г.В.
Об уравнениях со знакопеременным коэффициентом диффузии // Вычислительные методы в
математической физике, геофизике и оптимальном управлении. Новосибирск: Наука, 1978. С. 29-33.
Обзор работ по численному моделированию динамики сплошной среды // Тез. VI Междунар. конф.
по численным методам в гидродинамике (Тбилиси, 20-25 июня 1978 г.). Тбилиси, 1978. С. 25-
26. - Соавт.: Фомин В.М., Шокин Ю.И., Ковеня В.М. и др.
Системы квазилинейных уравнений и их приложения к газовой динамике. М.: Наука, 1978. 687 с. -
Соавт.: Рождественский Б.Л.
Структура ударных волн в конденсированных средах // Тр. польско-советского симпозиума
"Механика твердого тела". Варшава, 1978. С. 41-46. - Соавт.: Фомин В.М.
401

Численное моделирование задач высокоскоростного взаимодействия тел // Нелинейные волны
деформации. Таллин, 1978. С. 179-182. - Соавт.: Фомин В.М.
On some methods for the numerical simulation of flows with complex structure // Lect. Notes Phys. 1978.
Vol. 90. P. 565-578. - Соавт.: Ковеня B.M., Лисейкин В.Д.
1979
Гамильтонов формализм для пространственной системы малых вихрей в идеальной жидкости //
Численные методы механики сплошной среды. 1979. Т. 10, № 5. С. 144-149. - Соавт.:
Григорьев Ю.Н., Веретенцев А.Н.
/>свойствэ системы уравнений симметричных течений газа // ДАН СССР. 1979. Т. 244, № 2. С. 308-
311.- Соавт.: Распопов В.Е., Шапеев В.П.
К теории дифференциальных анализаторов контактных разрывов // Там же. Т. 247, № 1. С. 48-52. -
Соавт.: Ворожцов Е.В.
Локальные критерии гидродинамической устойчивости // Численные методы механики сплошной
среды. 1979. Т. 10, № 3. С. 151-155. - Соавт.: Гапонов С.А.
Некоторые модельные уравнения активных волновых систем и их свойства: Препр. Ин-та теорет. и
прикл. механики АН СССР (Сиб. отд-ние), № 11. Новосибирск, 1979. 21 с. Соавт.: Соловьев АС.
♦Некоторые проблемы развития пакетов программ для решения задач аэродинамики // Численные
методы механики сплошной среды. 1979. Т. 10, № 3. С. 89-100. - Соавт.: Ковеня В.М.
Нелокальное нелинейное дифференциальное уравнение в банаховом пространстве // Там же. № 6.
С. 5-26. - Соавт.: Белов Ю.Я.
Нелокальные уравнения вязкой жидкости // Там же. № 4. С. 5-22. - Соавт.: Белов Ю.Я.
О влиянии эффектов памяти и нелокальности на процессы переноса в газах и жидкостях: Препр.
Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние), № 4. Новосибирск, 1979. 19 с. - Соавт.:
Рудяк В.Я.
О соотношении индуктивного и дедуктивного методов в математике // Методологические
проблемы современной науки. М.: Политиздат, 1979. С. 56—73.
Об одной регуляризации уравнения Бюргерса// ДАН СССР. 1979. Т. 246, № 3. С. 521-524. - Соавт.:
Белов Ю.Я.
♦Разностная схема на подвижных сетках для решения уравнений вязкого газа // Журн. вычисл.
математики и мат. физики. 1979. Т. 19, № 1. С. 174-188. - Соавт.: Ковеня В.М.
* Упрощенные уравнения для описания течений вязкого газа // ДАН СССР. 1979- Т. 245, № 6.
С. 1322-1324. - Соавт.: Ковеня В.М., Черный С.Г.
On a regularization of Burgers' equation // Sov. Math. Dokl. 1979. Vol. 20, N 3. P. 476-479 - Соавт.:
Белов Ю.Я,
On some methods for the numerical simulation of flows with complex structure // Comput. Meth. Appl.
Mech. and Engineering. 1979. Vol. 17/18. P. 659-671. -Соавт.: Ворожцов Е.В., Ковеня В.М.,
Лисейкин В.Д., Фомин В.М.
On some methods for the numerical simulation of flows with complex structure // Lect. Notes Phys. 1979.
Vol. 90. P. 565-578. - Соавт.: 1^овеня В.М., Ворожцов Е.В., Лисейкин В.Д., Фомин В.М.
On the non-linear acceleration of iterative schemes // Colloque Intern, sur les Methodes de calcul scienti-
fique et Technique (Versailles, 1979). 1979.- Соавт.: Шокин Ю.И., Захаров Ю.Н.
On the properties of curvilinear shock waves "smearing" in calculations by the particle-in-cell method //
Comput. and Fluids. 1979. Vol. 7. P. 109-121. - Соавт.: Фомин В.М., Ворожцов Е.В.
On the theory of differential analyzers of contact discontinuities // Sov. Math. Dokl. 1979. Vol. 20, N 4.
P. 670-675.
The method of the solution of gas dynamical problems in moving meshes // Lect. Notes Phys. 1979. Vol. 91.
P. 48-61. - Соавт.: Ковеня В.М., Лисейкин В.Д.
1980
Вариационное неравенство в моделях теории плазмы: Препр. Ин-та теорет. и прикл. механики
АН СССР. (Сиб. отд-ние), № 3. Новосибирск, 1980. 10 с. - Соавт.: Крепкий В.М.
* Вопросы модульного анализа и параллельных вычислений в задачах математической физики //
Комплексы программ математической физики: Материалы VI Всесоюз. семинара по
комплексам программ мат. физики (Днепропетровск, 4-7 ноября 1979 г.). Новосибирск, 1980.
С. 3-12.
* Дифференциальный анализатор для разрывов решений неоднородных гиперболических
уравнений // ДАН СССР. 1980. Т. 254, № 3. С. 554-559. - Соавт.: Федоров А.В., Фомин В.М.
Задача Коши для псевдопараболического уравнения в банаховом пространстве // Численные
методы механики сплошной среды. 1980. Т. 11, № 7. С. 12-22. - Соавт.: Белов Ю.Я.
Законы сохранения систем уравнений двухфазных сред // ДАН СССР. 1980. Т. 254, № 2. С. 288-
293. - Соавт.: Рождественский Б.Л., Руев Г.А., Фомин В.М.
К теории дифференциальных анализаторов контактных разрывов // ДАН СССР. 1980. Т. 247, № 1.
С. 48-52. - Соавт.: Ворожцов Е.В.
402

Качественное исследование разностных схем методом дифференциального приближения // Журн.
прикл. механики и техн. физики. 1980, № 5. С. 8—16. - Соавт.: Шокин Ю.И., Урусов А.И.
* Классификация разностных схем одномерной газовой динамики методом дифференциального
приближения // Численные методы механики сплошной среды. 1980. Т. 11. № 2. С. 123-159. -
Соавт.: Шокин Ю.И., Тушева Л.А., Федотова З.И.
Кластерная модель для построения уравнения состояния кристаллического тела при изотропном
сжатии // Там же. 1980. Т. 11, № 6. С. 36-46. - Соавт.: Гадияк Г.В., Чернов СВ.
* Метод дифференциальных связей и задача о распаде произвольного разрыва // ДАН СССР. 1980.
Т. 254, № 4. С. 796-798. - Соавт.: Мелешко СВ., Шапеев В.П.
Неявная разностная схема для численного решения пространственных уравнений газовой
динамики // Журн. вычисл. математики и мат. физики. 1980. Т. 20, № 6. С 1465-1482. - Соавт.:
Ковеня В.М., Тарнавский Г.А.
О влиянии эффектов нелокальности и памяти на процессы переноса //Численные методы механики
сплошной среды. 1980. Т. 11, № 3. С 132-140. - Соавт.: Рудяк В.Я.
О некоторых уравнениях переменного типа // Теория кубатурных формул и вычислительная
математика: Тр. конф. по дифференц. уравнениям и вычисл. математике (Новосибирск, 1978 г.).
Новосибирск: Наука, 1980. С. 48-55.
О нелинейных уравнениях переменного типа // Краевые задачи математической физики и смежные
вопросы теории функций. Л.: Наука, 1980. С 294-300. (Записки науч. семинаров ЛОМИ. Т. 96).
*0 применении приближенной факторизации в методе Ритца и в методе конечных элементов //
Динамика сплошной среды. 1980. Вып. 45. С. 48-57. - Соавт.: Васильковский С.Н.
О принципах построения пакета интервальных операций // Численные методы механики сплошной
среды. 1980. Т. И, № 5. С Н7-153. - Соавт.: Шокин Ю.И., Рогалев А.Н.
О свойствах осредненного движения упругой одномерной решетки и движении мезообъектов: Препр.
Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние), № 14. Новосибирск, 1980. 18 с. Соавт.:
Франк A.M.
О структуре пакета программ для решения задач аэродинамики // Комплексы программ
математической физики: Матер. VI Всесоюз. семинара по комплексам программ мат. физики
(Днепропетровск, 4-7 ноября 1979 г.). Новосибирск, 1980. С. 89-106. - Соавт.: Ковеня В.М.
О численном решении задачи обтекания тела вращения вязким теплопроводным газом на
криволинейной подвижной сетке // Численные методы механики сплошной среды. 1980. Т. 11, № 1.
С. 51-61. - Соавт.: Данаев Н.Т., Лисейкин В.Д.
Об автоколебаниях в некоторых одномерных волновых системах // Там же. 1980. Т. 11, № 7. С. 128-
140. - Соавт.: Соловьев А.С
Об одной реализации модульной системы для решения прикладных задач газовой динамики //
Комплексы программ математической физики: Матер. VI Всесоюз. семинара по комплексам
программ мат. физики (Днепропетровск, 4-7 сентября 1979 г.). Новосибирск, 1980. С. 39-51.
Соавт.: Лымарев А.П., Рычков А.Д.
Об одной регуляризации уравнений переменного типа // ДАН СССР. 1980. Т. 252, № 3. С 525-527. -
Соавт.: Кожанов А.И., Ларькин Н.А.
% Об одном классе нелокальных нелинейных дифференциальных уравнений в банаховом
пространстве // Там же. № 6. С. 1292-1296. - Соавт.: Белов Ю.Я.
Сверхзвуковые двухфазные течения в условиях скоростной неравновесности частиц. Новосибирск:
Наука, 1980. 159 с. - Соавт.: Солоухин Р.И., Папырин А.Н.., Фомин В.М.
Смешанная задача для некоторых классов уравнений третьего порядка: Препр. Ин-та теорет. и
прикл. механики АН СССР (Сиб. отд-ние) № 5. Новосибирск, 1980. 36 с. - Соавт.: Кожанов А.И.,
Ларькин Н.А.
Численный анализ. Теория приближенных функций: Учеб. пособие. Новосибирск: Изд-во Новосиб.
гос. ун-та. 1980. 83 с. - Соавт.: Шокин Ю.И.
Численное моделирование атома в сверхсильном магнитном поле // Численные методы механики
сплошной среды. 1980. Т. 11, № 3. С. 27-46. - Соавт.: Гадияк Г.В., Обрехт М.С
Численное решение упрощенных и полных уравнений Навье-Стокса в приложении к анализу
химически неравновесных и лазерных течений // Матер. VI Всесоюз. симпозиума по горению и взрыву
"Химическая физика процессов горения и взрыва" (Черноголовка, 1980 г.). М., 1980. С. 3-7. -
Соавт.: Головичев В.И.
Anomalous acoustic velocity at a high pressure of condensed matter in a superstrong magnetic field // Phys.
Lett. 1980. Vol. 80A, N 2-3. P. 191-192. - Соавт.: Гадияк Г.В., Обрехт М.С
Conservation laws for systems of equations for two-phase media // Sov. Math. Dokl. 1980. Vol. 22. N 2.
P. 352-357. - Соавт.: Руев Т.Д., Рождественский Б.Л., Фомин В.М.
Differential analyzer for discontinuities of solution of nonhomogeneous hyperbolic equations // Sov. Math.
Dokl. 1980. Vol. 22, N 2. P. 416. - Соавт.: Федоров А.В., Фрмин В.М.
Economical methods of solving the problems of gas dynamics // VII Intern. Conf. on Numerical Methods
in Fluid Dynamics. Stanford, 1980. P. 61-62. - Соавт.: Ковеня В.М., Тарнавский Г.А., Черный СГ.
Local criteria of Hydrodynamic stability // Laminar-Turbulent Transition: IUTAM Symposium Stuttgart,
Germany, September 16-21, 1979. Berlin: Springer-Verlag, 1980. P.. 96-101. Соавт.: Талонов С.А.
403

Numerical method for solving the viscous gas equations on moving grids // Comput. Fluids. 1980. Vol. 8
N 1. P. 59-70. - Соавт.: Ковеня В.М.
Numerical simulation of rarefied gas flows // VII Intern. Conf. on Numerical Methods od Fluid Dynamics.
Stanford, 1980. P. 119-120. - Соавт.: Григорьев Ю.Н., Иванов М.С.
On some algorithms for shock wave recognition by shock-capturing computational results //Comput. and
Fluids. 1980. Vol. 8, N 3. P. 313-328. - Соавт.: Ворожцов Е.В.
On the theory of differential analysers of contact discontinuities in one-dimensional flows I-II // Ibid.
1980. Vol. 9, N 1. P. 1-32. - Соавт.: Ворожцов Е.В.
The implicit difference schemes for numerical solving the Navier-Stokes equations // Lect. Notes Math.
1980. Vol. 771. P. 299-312. - Соавт.: Ковеня В.М.
The solution of nonhomogeneous thermal problems and the Stefan single-phase problem in arbitrary
domains // Comput. Methods in Appl. Mech. and Engineering. 1980. Vol. 22. P. 259-271. - Соавт.:
Ковалев О.Б., Ларькин Н.А., Фомин В.М.
1981
Вариационное неравенство в моделях теории плазмы // Численные методы механики сплошной
среды. 1981. Т. 12, № 1. С. 69-77. - Соавт.: Крепкий В.М.
Изменение волновой структуры при обтекании тел сверхзвуковым двухфазным потоком // ДАН
СССР. 1981. Т. 260, № 4. С. 821-825. - Соавт.: Алхимов А.П., Нестерович Н.И., Папырин А.Н.
♦Инвариантные критерии устойчивости течений сжимаемой жидкости // Там же. Т. 259,№ 5.
С. 1056-1059. - Соавт.: Талонов С.А.
Метод расщепления в задачах газовой динамики. Новосибирск: Наука, 1981. 304 с. - Соавт.:
Ковеня В.М.
Метод расщепления в задачах газовой динамики // Проблемы вязких течений. Новосибирск, 1981.
С. 104-116.
Методологические проблемы современной математики // Вопр. философии. 1981. № 8. С. 60-68.
* Модульная структура алгоритмов и программ в задачах механики сплошной среды и структура
ЭВМ // Численные методы механики сплошной среды. 1981. Т. 12, № 5. С. 166-172. - Соавт.:
Рычков А.Д.
Нестационарные процессы в нейтронных звездах: Препр. Ин-та теорет. и прикл. механики АН СССР
Сиб. отд-ние) № 15. Новосибирск, 1981. 36 с. - Соавт.: Березин Ю.А., Дмитриева О.Е.
О работе секции пакетов прикладных программ за 1975-1980 гг.: Препр. Ин-та теорет. и прикл.
механики АН СССР (Сиб. отд-ние) № 20. Новосибирск, 1981. 20 с.
*0 равномерно-сходящемся алгоритме численного решения обыкновенного дифференциального
уравнения второго порядка с малым параметром при старшей производной // Численные методы
механики сплошной среды. 1981. Т. 12, № 2. С. 45-56. - Соавт.: Лисейкин В.Д.
*0 решении нестационарных задач газовой динамики в подвижных сетках, зависящих от потока //
, Там же. № 1. С. 131-140. - Соавт.: Мещеряков Ю.П., Шапеев В.П.
О свойстве ^-согласованности разностных схем газодинамики// ДАН СССР. 1981. Т. 259, № 1.
С. 18-24. - Соавт.: Ворожцов Б.В.
Одномерная теория контактной полосы: Препр. Ин-та теорет. и прикл. механики АН СССР (Сиб.
отд-ние) № 45. Новосибирск, 1981. 46 с.
Пакет программ для научных исследований в области аэродинамики и гидродинамики // Вопросы
разработки и эксплуатации пакетов прикладных программ. Новосибирск, 1981. С. 3—32. —
Соавт.: Колобов Б.П., Кузнецов Б.Г., Попков А.Н., Шепеленко В.Н.
* Перспективы развития вычислительной математики на основе вычислительных систем: Препр.
Ин-та теорет. и прикл. механики. АН СССР (Сиб. отд-ние) № 46. Новосибирск, 1981. С. 3-6.
Представление спектральных мер квантово-механических операторов в стохастическом фазовом
пространстве: Препр. Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 38.
Новосибирск, 1981. 8 с. - Соавт.: Крепкий В.М.
♦Расчет газодинамических течений на основе метода концентраций // ДАН СССР. 1981. Т. 257,
№ 3. С. 566-569. - Соавт.: Бахрах СМ., Глаголева Ю.П., Самигулин М.С. и др.
♦Реализация на ЭВМ алгоритма исследования на совместность системы уравнений в частных
производных // Там же. Т. 261, № 5. С. 1044-1046. - Соавт.: Ганжа В.Г., Мелешко СВ., Мурзин Ф.А.,
Шапеев В.П.
Слабая устойчивость и преобразование разностных схем // Численные методы механики сплошной
среды. 1981. Т. 12, № 4. С 64-71. - Соавт.: Коробицын В.А.
Смешанная задача для одного класса уравнений третьего порядка // Сиб. мат. журн. 1981. Т. 22,
№ 6. С. 81-86. - Соавт.: Кожанов А.И., Ларькин Н.А.
Современное состояние, пути дальнейшего развития разработки пакетов и архитектура системы
"Исток" для организации, эксплуатации ППП // Принципы организации пакетов прикладных
программ. Новосибирск, 1981. С. 3-80. - Соавт.: Фомин В.М., Чернышева Р.Т., и др.
Структура ударной волны в смеси газов // ДАН СССР. 1981. Т. 261, № 2. С. 285-371. - Соавт.:
Фомин В.М., Руев Г.А.
404

Ill Всесоюзная школа-семинар по механике реагирующих сред // Физика горения и взрьюа. 1981,
№ 3. С. 152-155. - Соавт.: Игнатенко Е.М.
♦Уравнение состояния А-е фазы коры пульсара с учетом действия сверхсильного магнитного поля //
Астрофизика. 1981. Т. 17,вып. 4. С. 765-774. - Соавт.: Гадияк Г.В., Обрехт М.С.
Differential analysers of strong discontinuities in one-dimensional gas flow // Comput. Techn. in Transient
and Turbulent. Flow. 1981. Vol.2. P.59-96.- Соавт.: Ворожцов Е.В.
Economical methods for solving the problems of gas dynamics // Led. Notes Phys. 1981. \ ol. 141.
p 448-453. - Соавт.: Тарновский Г.А., Ковеня В.М., Черный С.Г.
Ham'iltonian vortex models in the theory of turbulence // XV Symposium on Advanced Problems and
Methods in Fluid Mechanics (Jachranka, Poland, September, 1981). Warszawa, 1981. P. 57-58. - Соавт.:
Григорьев Ю.Н.
Invariant criteria of hydrodynamic stability // VII Canadian Congr. of Appl. Mechanics. 1981. P. 671-672. -
Соявт * Талонов С А»
Numericai'simulation of the rarefied gas flows // Lect. Notes Phys. 1981. Vol. 141. P. 454-460. - Соавт.:
Григорьев Ю.Н., Иванов М.С. „.,«///-.*
On the theory of differential analysers of contact discontinuities in one-dimensional flows // Comput.
and Fluids. 1981. Vol. 9, N 1. P. 1-32. - Соавт.: Ворожцов Е.В.
Realization on a computer of an algorithm for studying the consistency of systems of partial differential
equations // Sov. Math. Dokl. 1981. Vol. 24, N 3. P. 638-640. - Соавт.: Ганжа ВТ., Мелешко СВ.,
Мурзин Ф.А., Шапеев В.П.
1982
Анализ на совместность систем дифференциальных уравнений на ЭВМ: Препр. Ин-та теорет. и прикл.
механики АН СССР (Сиб. отд-ние) № 20. Новосибирск, 1982. 28 с. - Соавт.: Ганжа В.Г.,
Мелешко СВ., Мурзин Ф.А., Шапеев В.П.
Вариационный метод построения дискретных вихревых модулей: Препр. Йн-та теорет. и прикл.
механики АН СССР (Сиб. отд-ние) № 29. Новосибирск, 1982. 15 с. - Соавт.: Веретенцев А.Н.,
Рудяк В.Я.
* Гамильтоновы вихревые модели в теории турбулентности // Численные методы механики
сплошной среды. 1982. Т. 13, № 3. С. 13-28. - Соавт.: Григорьев Ю.Н., Левинский В.Б.
Кинетическое уравнение умеренно плотного газа // ДАН СССР. 1982. Т. 264, № 6. 1336-1339. -
Соавт.: Рудяк В.Я.
Классификация разностных схем двумерной газовой динамики методом дифференциального
приближения: Препр. Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 19. Новосибирск,
1982. 53 с. - Соавт.; Шокин Ю.И., Компаниец Л.А., Федотова З.И.
Математические модели и вычислительные алгоритмы для течений вязкой жидкости //
Кибернетика. 1982. № 6. С. 17-22.
Моделирование газодинамических процессов в нейтронном вешестве: Препр. Ин-та теорет. и прикл.
механики АН СССР (Сиб. отд-ние) № 24. Новосибирск, 1982. 39 с. - Соавт.: Березин Ю.А.,
Дмитриева О.Е., Муканова Б.Г.
♦Некоторые вопросы теории модульного анализа и параллельного программирования для задач
математической физики и механики сплошной среды // Современные проблемы
математической физики и вычислительной математики. М.: Наука, 1982."С. 200-207. - Соавт.:
Коновалов А.Н.
Неравновесная статистическая механика систем точечных вихрей в идеальной жидкости и ее
приложения к моделированию турбулентности: Препр. Ин-та теорет. и прикл. механики АН СССР
№ 22. Новосибирск, 1982. 37 с. - Соавт.: Григорьев Ю.Н., Левинский В.Б., Шавалиев М.Ш.
♦О моделировании эффектов отрицательного порождения интенсивности пульсации температуры
в турбулентном слое смешения // ДАН СССР. 1982. Т. 262, № 2. С. 301-305. - Соавт.: Курбац-
кий А.Ф.
*0 некоторых новых классах уравнений математической физики // Teubner-Texte zur Mathematik.
1982. Bd. 47. P. 159-164. - Соавт.: Ларькин Н.А., Новиков В.А.
Об одной задаче о распаде произвольного разрьюа // Численные методы механики сплошной среды.
1982. Т. 13, № 6. С. 77-84. - Соавт.: Мелешко СВ., Шепеев В.П.
Об одной системе дифференциальных уравнений в банаховом пространстве // ДАН СССР. 1982.
Т. 263, № 3. С. 526-529. - Соавт.: Белов Ю.Я.
Об опыте применения пакетной технологии для решения задач внешнего обтекания // Задачи
аэродинамики тел пространственной конфигурации. Новосибирск, 1982. С. 3-17. - Соавт.:
Волков В.Ф., Жибинов СБ., Колобов Б.П., Чернышева Р.Т.
* Пакеты прикладных программ математической физики и механики сплошной среды //
Комплексы программ математической физики: Матер. VII Всесоюз. семинара по комплексам программ
мат. физики -(Горький, 8-11 сентября 1981 г.). Новосибирск, 1982, С. 3-15. - Соавт.: Карна-
чук В.И., Рычков А.Д., Фомин В.М.
Преобразование акустических возмущений в вихревые в турбулентных потоках // Неустойчивость
до- и сверхзвуковых течений. Новосибирск, 1982. С. 93-106. - Соавт.: Бардаханов СП.,
Козлов В.В.
405

Применение численной оптимизации в методе наименьших квадратов // Численные методы
механики сплошной среды. 1982. Т. 13, № 5. С. 85-92. - Соавт.: Аульченко СМ., Латыпов А.Ф.
Разностная схема как самостоятельная математическая модель // Сиб. мат. журн. 1982. Т. 23, № 6.
С. 185-186.
Расчет моделей нейтронных звезд с пионной конденсацией // Письма в "Астрон. журн.". 1982. Т. 8,
№ 2. С. 86-89. - Соавт.: Березин Ю.А., Дмитриева О.Е.
Решение модельной задачи кумуляции в подвижных сетках // Матер. VII Всесоюз. конференции по
численным методам решения задач теории упругости и пластичности. Новосибирск, 1982. С. 193-
198. - Соавт.: шапеев В.П., Мещеряков ЮЛ.
Решение смешанной задачи для волнового уравнения // ДАН СССР. 1982. Т. 262, № 3. С. 549-553. -
Соавт.: Федосов В.П.
Символьные преобразования в методах решения задач математической физики // Комплексы
программ математической физики: Матер. VII Всесоюз. семинара по комплексам программ мат.
физики (Горький, 8-11 сентября 1981 г,). Новосибирск, 1982. С. 123-129. - Соавт.: Валиул-
лин А.Н., Ганжа В.Г., Мелешко СВ. и др.
Устойчивость плоского течения Куэтта жидкости со знакопеременной вязкостью // Численные
методы механики сплошной среды. 1982. Т. 13, № 6. С 95-103..- Соавт.: Молородов Ю.И.,
Скобелев Б.Ю.
Устойчивость стационарных течений жидкости со знакопеременной вязкостью //Там же. № 5. С. 61-
72. — Соавт.: Скобелев Б.Ю.
Hamiltonian vortex models in the theory of turbulence // Arch, of Mech. 1982. Vol. 34, N 5-6, P. 621 -
631. - Соавт.: Григорьев Ю.Н.
Kinetic equations of high nonequilibrium dense gas // XIII Intern. Symposium on Rarefied Gas Dynamics
(Novosibirsk, July 5-9, 1982). Vol. 1. P. 34-36. - Соавт.: Рудяк В .Я.
Les Manipulations symboliques dans methodes de physique de Mathematique // Symposium des Mathema-
tiques de rinformatique (Paris, 16-18 Mais, 1982) 1982. P. 431-438. - Соавт.: Валиуллин А.Н.,
Ганжа В.Г., Мелешко СВ. и др.
Methods of statistical modelling and direct numerical integration of kinetic equations of gas theory // ХШ
Intern. Symposium on Rarefied Gas Dynamics (Novosibirsk, July 5-9, 1982). Vol. 1. P. 196-198. -
Соавт.: Григорьев Ю.Н., Иванов М.С и др.
Modelling of Continuum Mechanics Problems with large deformations // Comput. Methods in Appl. Mech.
and Engineering. 1982. Vol. 32. P. 157-197. - Соавт.: Фомин В.М., Шапеев В.П.
Modelling of Gasdynamic processes in neutron stars with phase transitions // Lect. Notes Phys. 1982. Vol.
170. P. 138-141. - Соавт.: Березин Ю.А., Дмитриева О.Е.
On a system of differential equations in Banach space // Sov. Math. Dokl. 1982. Vol. 25, N 2. P. 365-
369. - Соавт.: Белов Ю.Я.
On the ^-consistence property of difference schemes of gas dynamics-I // Comput. and Fluids. 1982. Vol.
10, N 3. P. 181-204. - Соавт/ Ворожцов Е.В.
On the ^-consistence property of difference schemes of gas dynamics-II // Ibid. P. 205—222. — Соавт.:
Ворожцов Е.В. х
1983
A.C 1029114 (СССР) . Способ возбуждения сейсмических волн. Опубл. в Б.И., 1983, № 26. - Соавт.:
Дулов ВТ., Глазнев В.Н.
Архитектура инженерно-физических пакетов прикладных программ на основе системы
параллельного действия // Тез. докл. Всесоюз. семинара по распараллеливанию обработки информации.
Львов, 1983. Ч. 1. С 4-9. - Соавт.: Булышева Л.А., Фомин В.М., Чернышева Р.Т.
Газодинамические процессы в сверхплотном нейтронном веществе // Модели механики сплошной
среды. Новосибирск, 1983. С. 203-209. - Соавт.: Березин Ю.А.
Дисковый МГД-генератор с неоднородным по производимое™ потоком // Тр. Междунар. конф. по
МГД-преобразованию энергии. М., 1983. Т. 4. С 160-163. - Соавт.: Гриднев Н.П., Кацнель-
сон С.С., Поздняков Г.А. и др.
Математические модели и численные методы расчета полупроводниковых устройств - I: Препр.
Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 32. - Новосибирск, 1983. 47 с.
Соавт.: Березин Ю.А., Вшивков В.А., Головнев И.Ф.
Нелинейные уравнения переменного типа. Новосибирск: Наука, 1983. 269 с. - Соавт.: Ларькин Н.А.,
Новиков В. А.
Об использовании ЭВМ для анализа на совместность систем дифференциальных уравнений //
Аналитические вычисления на ЭВМ и их применение в теоретической физике. Дубна, 1983. С. 125—
131. - Соавт.: Ганжа В.Г., Мелешко СВ., Мурзин Ф. А. ,\ шапеев В.П.
Об эволюции уединенной волны в одной неконсервативной системе с дисперсией: Препр. Ин-та
теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 3. Новосибирск, 1983. 13 с. - Соавт.:
Кудрявцев А.Н., Соловьев А.С
Откольные явления при плоском соударении металлических пластин равной толщины // ДАН СССР.
1983. Т. 272, № 6. С. 1331-1335. - Соавт.: Дерибас А.А., Захаренко И.Д., Фомин В.М., Хаки-
мов Э.М.
406

Применение ЭВМ для исследования и построения разностных схем // Аналитические вычисления
на ЭВМ и их применение в теоретической физике. Дубна, 1983. С. 85-96.- Соавт.: Валиуллин А.Н.,
Ганжа В.Г., Мазурик СИ. и др.
Проблемы вычислительной механики // Численные методы динамики вязкой жидкости: Тр. IX
Всесоюз. школы-семинара. Новосибирск, 1983. С. 3-13.
Уравнения неклассических типов и их приложения в механике сплошных сред // Актуальные
проблемы вычислительной и прикладной математики. Новосибирск: Наука, 1983. С. 22-27. - Соавт.:
Ларькин И. А., Новиков В. А.
Численное изучение волновых явлений в нелинейных средах с дисперсией. Препр. Ин-та теорет.
и прикл. механики АН СССР (Сиб. отд-ние) № 25. Новосибирск, 1983. 25 с. - Соавт.:
Игумнов А. Б.з Соловьев А.С.
Численное моделирование влияния иижекции топлива на структуру ограниченного блюкнего следа //
ДАН СССР. 1983. Т. 272, № 3. С. 542-546. - Соавт.: Головичев В.И.
Численное моделирование проникания тел в упругопластическом приближении // Проблемы
математики и механики. Новосибирск: Наука, 1983. С. 71-81. - Соавт.: Гулидов А.И., Фомин В.М.
Classification of difference schemes of gas dynamics by the method of differential approximation-1 // Com-
put. and Fluids. 1983. Vol. 11, N 3. P. 187-206. - Соавт.: Федотова 3-Й., Тушева Л.А., Шокин Ю.И.
Efficiency of the numerical algorithms and the decomposition principle for modern computers //
Numerical Solutions of Non-Linear Problems: France-Italy-USSR 6-th joint symposium (Rocquencourt,
December, 19-21,1983). Rocquencourt, 1983. P. 93-126.
Gasdynamics processes in superdense neutron matter // Ibid. P. 185-190. - Соавт.: Березин Ю.А.
Numerical modelling of MNOS structures // NASECODE HI: Proo. of the Third Intern. Conf. on the
Numerical Analysis of Semiconductor Devices and Integrated Circuits (Ireland, Galway, 1983). 1983. P. 134-
139. - Соавт.: Гадияк Г.В., Обрехт M.C.
On the construction of K-consistence difference schemes of gas dynamics // Comput. and Fluids. 1983.
Vol. 11, N 3. P. 231-249. - Соавт.: Ворожцов EJB.
On the modelling of effects of negative production of temperature-fluctuation intensity in the turbulent
mixing layer // J. Fluid Mech. 1983. Vol. 130. P. 453-462. - Соавт.: Курбацкий А.Ф.
Symbolic manipulations and their applications to constructing new exact solutions and difference
schemes // Numerical Solutions of Non-Linear Problems: France-Italy-USSR 6-th joint symp.
(Rocquencourt, December, 19-21, 1983). Rocquencourt, 1983. P. 314-329. - Соавт.: Валиуллин А.Н.,
Ганжа В.Г., Мазурик СИ. и др.
Systems of quasilinear equations and their applications to gas dynamics. 1983. 676 p. (Amer. Math. Soc.
Trans, of Mathematics Monograph. Vol. 55). - Соавт.: Рождественский Б Л.
1984
Анализ и построение разностных схем с помощью аналитических выкладок на ЭВМ // Системы
для аналитических преобразований в механике: Тез. докл. Горький. 1984. С. 12-13. - Соавт.:
Ганжа ВТ., Мазурик СИ., Шапеев В.П.
*3адача автоматического построения и исследования на ЭВМ разностных схем в аналитическом
виде // ДАН СССР. 1984. Т. 275, № 3. С. 528-532. - Соавт.: Валиуллин А.Н., Ганжа В.Г.,
Ильин В.П., Шапеев В.П.
Кинетическая теория реальных газов и жидкостей: Препр. Ин-та теорет. и прикл. механики АН
СССР (Сиб. отд-ние) № 1. Новосибирск, 1984. 17 с. - Соавт.: Рудяк В.Я.
Комплекс программ для реализации в символьном виде методов построения и исследования
разностных схем // Комплексы программ математической физики: Матер. VIII Всесоюз. семинара
по комплексам программ мат. физики. (Ташкент, 20-23 сентября 1983 г.). Новосибирск, 1984.
С. 18-23. - Соавт.: Валиуллин А„Н., Ганжа В.Г., Шапеев В.П.
Математическое моделирование явлений отрицательной вязкости в неоднородной турбулентности//
Физическая механика неоднородных сред. Новосибирск. 1984. С. 27-36. - Соавт.:
Курбацкий А.Ф., Скобелев Б.Ю.
Метод дифференциальных связей // Там же. С. 3-13. - Соавт.: Мелешко СВ., Шапеев В.П.
Метод дифференциальных связей и его приложение в газовой динамике. Новосибирск: Наука,
1984. 272 с. - Соавт.: Сидоров А.Ф., Шапеев В.П.
Некоторые автомодельные решения для одного класса уравнений гидродинамики со
знакопеременной вязкостью // ДАН СССР. 1984. Т. 277, № 2. С. 295-299. - Соавт.: Маслова Н.Н.,
Новиков В. А.
*Об одной модификации уравнений движения вязкой несжимаемой жидкости // Там же. Т. 275,
№ 3. С. 576-580. -- Соавт.: Скобелев Б.Ю.
Об устойчивости автомодельных решений в модели жидкости со знакопеременной вязкостью //
Численные методы механики сплошной среды. Новосибирск, 1984. Т. 18, № 2, С. 98-120. -
Соавт,: Маслова Н.Н., Новиков В. А.
♦Образование когерентных структур в турбулентном следе при акустическом воздействии // ДАН
СССР. 1984. Т. 274 Р № 2. С. 50-53. - Соавт.: Бардаханов СП., Козлов В.В.
Пакет прикладных программ для внешних задач аэродинамики Арфа // Комплексы программ
407

математической физики: Матер. VIII Всесоюз. семинара по комплексам программ мат. физики
(Ташкент, 20-23 сентября 1983 г.). Новосибирск, 1984. С. 213-215. - Соавт.: Беккер А.Н.,
Боковиков Ю.Г., Булышева Л. А. и др.
Преобразование акустических возмущений в когерентные структуры в турбулентном следе за
профилем // Инж-физ. журн. 1984. Т. 17, №4. С. 533-536. - Соавт.: Бардаханов СП., Козлов В.В.
Проблема редукции к идеальной трубе в экспериментальной аэродинамике // ДАН СССР. 1984.
Т. 274, № 6. С. 1309-1312. - Соавт.: Воскобойников Ю.Е., Преображенский Н.Г.
Решение смешанных краевых задач для волнового уравнения в угловых областях // Там же. Т. 275,
№4. С. 852-857. - Соавт.: Федосов В.П.
Уравнения в частных производных полуцелой степени // Там же. Т. 276, № 4. С. 804-808. - Соавт.:
Федосов В.П.
Устойчивость течения Куэтта между цилиндрами жидкости с переменной вязкостью // Численные
методы механики сплошной среды. 1984. Т. 15, № 1. С. 124-142. - Соавт.: Скобелев Б.Ю., Жи-
рилкасинов А.
Численный анализ сверхзвукового реагирующего течения в ближнем следе за обратным уступом //
Физика горения и взрыва, 1984. №4. С. 52-56. - Соавт.: Головичев В.И.
Эффективная неравномерная сетка для уравнения Орра-Зоммерфельда и спектр течения Пуазейля.
Препр. Ин-та теорет. и прикл. механики АН СССР (Сиб. отд-ние) № 21. Новосибирск, 1984. 36 с. -
Соавт.: Жирилкасинов А., Скобелев Б.Ю.
Эффективность алгоритмов и принципы их декомпозиции для современных ЭВМ // Комплексы
программ математической физики: Матер. VIII Всесоюз. семинара по комплексам программ
мат. физики. (Ташкент, 20-23 сентября 1983 г.). Новосибирск, 1984. С. 3-17.
Classification of difference schemes of gas dynamics by the method of differential approximation-II //
Comput. and Fluids. 1984. Vol. 12, N 2. P. 93-121. - Соавт.: Федотова З.И., Компанией Л. А.,
ШокинЮ.И.
Efficiency of the numerical algorithms and the decomposition principle for modern computers // PDE
Software: Modules Interfaces and Systems: Proc. of the IFIPTC2 Working Conf. (Sbderkoping,
Sweden, 22-26 August 1983). North-Holland, Amsterdam, 1984. P. 291-308.
Numerical methods of computing the problems of semiconductor physics // Finite Element Programming
with Special Emphasis on Semiconductor Device and Process Modelling. Ireland: Galway, 1983. P. 82-91.
On some optimization procedures for shock localization // Intern. J. for Numerical Methods in Fluids.
1984. Vol. 4. P. 477-496. - Соавт.: Ворожцов Е.В.
On the approximation of the Navier-Stokes equations for an incompressible fluid by evolutionary type
equations // Numerical Methods in Fluid Dynamics. M.: Mir, 1984. P. 290-313. - Соавт.: Кузне-'
цов Б.Г., Смагулов Ш.
On the numerical solution of equations with interior and exterior boundary layers on a nonuniform mesh //
BAIL III: Proc. of the III Intern. Conf. on Boundary and Interior Layers (Ireland, Dublin, 1984). 1984.
P. 68-80. - Соавт.: Лисейкин В.Д.
The splitting method for the numerical solution of problems in gas dynamics // Numerical Methods in Fluid
Dynamics. M.: Mir, 1984. P. 40-61. - Соавт.: Ковеня В.М.
Towards a theory of variable type nonlinear equations // Ibid. P. 315-335. - Соавт.: Ларькин Н.А.,
Новиков В. А.
Transformation of acoustic oscillations into the ones in turbulent flows // Turbulence and Chaotic
Phenomena in Fluids: Proc. Intern. Symp. (Japan, Kyoto, 5-10 September, 1983). Amsterdam, 1984. P. 427-
432. - Соавт.: Бардаханов СП., Козлов В.В.
1985
К теории дифференциальных анализаторов контактовых разрывов и ударных волн // ДАН СССР.
1985. Т. 281, № 1. С. 28-32. - Соавт.: Федоров А.В., Фомин В.М.
Метод дифференциального приближения. Применение к газовой динамике. Новосибирск: Наука,
1985. 364 с. - Соавт.: Шокин Ю.И.
Методы локализации при численном решении задач газодинамики. Новосибирск: Наука, 1985.
224 с. - Соавт.: Ворожцов Е.В.
О численном методе изучения волновых явлений в нелинейных средах с дисперсией // Численные
методы механики сплошной среды. 1985. Т. 16, № 1. С. 49-66. - Соавт.: Игумнов А.Б.,
Соловьев А.С.
Об учете межмолекулярных сил притяжения при выводе кинетических уравнений // Теорет. и мат.
физика. 1985. Т. 64, № 2. С. 277-286. - Соавт.: Рудяк В.Я.
Применение проекционного метода для построения контура тела минимального сопротивления //
Изв. АН СССР. Сер. Механика жидкости и газа. 1985, № 2. С. 108-113. - Соавт.: Аульченко СМ.,
Латыпов А.Ф.
Численный метод решения уравнений вязкого газа на подвижных сетках // ЭВМ в аэродинамике.
М.: Машиностроение, 1985. С. 77-90. - Соавт.: Ковеня В.М.
Stability of finite-amplitude autooscillations in Poiseuille flow // Laminar-Turbulent Transition: IUTAM
408

Symp. (Novosibirsk, 1984). В.: Springer-Verlag, 1985. P. 199-206. - Соавт.: Скобелев Б.Ю., Жирил-
касинов А.
Tie study of shear layer stability by the method of vortex particles // Laminar-Turbulent Transition: IUTAM
Symp. (Novosibirsk, 1984). Berlin: Springer-Verlag, 1985. P. 367-374. - Соавт.: Рудяк В.Я.,
Веретенцев А.Н.
1986
Методологические проблемы математической физики. Новосибирск: Наука, 1986. 296 с. — Соавт.:
Преображенский Н.Г., Разумовский О.С.
1987
Численное решение многомерных задач обтекания на основе метода расщепления // Современные
проблемы аэромеханики. М.: Машиностроение, 1987. С. 59-73. - Соавт.: Ковеня В.М., Тарнав-
ский Г. А., Черный С.Г.

СОДЕРЖАНИЕ
Предисловие 3
ГЕОМЕТРИЯ
Геометрическая структура поверхностей малого типа 5
О связи между метрическими и проективными свойствами поверхностей 8
О классе римановой метрики * 11
Метрики класса 2 15
МЕТОД ДИФФЕРЕНЦИАЛЬНЫХ СВЯЗЕЙ
Бегущие волны системы квазилинейных уравнений 18
О бегущих волнах уравнений газовой динамики , 21
К вопросу о нестационарных плоских течениях политропного газа с прямолинейными
характеристиками 24
Теория совместимости и методы интегрирования систем нелинейных уравнений в частных
производных 27
Л-свойства систем одномерных уравнений динамики неупругой сплошной среды 32
Применение метода дифференциальных связей к одномерным уравнениям газовой динамики . 36
D-свойства системы уравнений симметричных течений газа 41
Метод дифференциальных связей и задача о распаде произвольного разрыва 44
АНАЛИТИЧЕСКИЕ ВЫКЛАДКИ НА ЭВМ
О реализации на электронно-вычислительных машинах алгебраическо-дифференциальных
алгоритмов 47
Реализация метода внешних форм Картанана ЭВМ 56
Реализация на ЭВМ алгоритма исследования на совместность. систем уравнений в частных
производных 57
Задача автоматического построения и исследования на ЭВМ разностных схем в аналитическом
виде . . . 60
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРЕМЕННОГО ТИПА
Об одной модели жидкости со знакопеременным коэффициентом вязкости 65
О некоторых уравнениях переменного типа 69
О некоторых новых классах уравнений математической физики 74
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ.
ТЕОРИЯ РАЗНОСТНЫХ СХЕМ
Об одном разностном методе счета многомерного уравнения теплопроводности 78
Неявные схемы расщепления для гиперболических уравнений и систем 81
Об экономичных неявных схемах (метод дробных шагов) 83
О слабой аппроксимации систем дифференциальных уравнений 85
Решение многомерного кинетического уравнения методом расщепления 88
410

Исследование задачи Коши методом слабой аппроксимации 90
Применение метода расщепления (дробных шагов) для решения задач математической
физики 93
Об одной абсолютно устойчивой схеме интегрирования уравнений гиродинамики 101
Численный расчет симметричного обтекания пластинки плоским потоком вязкой
несжимаемой жидкости 107
О применении метода расщепления для численного расчета движения теплопроводного газа
в криволинейных координатах ПО
Экономичные разностные схемы повышенной точности для полигармонического
уравнения 118
О методах расчета задач газовой динамики с большими деформациями 125
Влияние вязкости на гладкость решения в нецолнопараболических системах 139
О структуре абсолютно аппроксимирующих и абсолютно корректных разностных схем 143
Эволюционные двухслойные разностные схемы 150
Об одной неявной схеме расчета течения вязкого теплопроводного газа 154
Об одном методе ускорения сходимости итерационных схем 163
К теории разностных схем газовой динамики 166
О построении разностных схем повышенного порядка аппроксимации на основе
дифференциальных следствий 177
Разностная схема для решения одномерных уравнений газовой динамики 184
О разностных схемах в произвольной криволинейной системе координат 188
Упрощенные уравнения для описания течения вязкого газа 191
О применении приближенной факторизации в методе Ритца и в методе конечных элементов . . 194
Расчет газодинамических течений на основе метода концентраций 198
МЕТОД ДИФФЕРЕНЦИАЛЬНОГО ПРИБЛИЖЕНИЯ
Об аппроксимационной вязкости разностных схем « 202
О корректности первых дифференциальных приближений разностных схем 204
О групповой классификации разностных схем для систем одномерных уравнений газовой
динамики 206
Качественное исследование разностных схем методом дифференциального приближения .... 218
ДИФФЕРЕНЦИАЛЬНЫЕ АНАЛИЗАТОРЫ
Дифференциальные анализаторы ударных волн 226
К теории дифференциальных анализаторов контактных разрывов 229
Дифференциальный анализатор для разрыва решений неоднородных гиперболических
уравнений 234
ПОСТРОЕНИЕ АДАПТИВНЫХ СЕТОК
Метод подвижных координат в газовой динамике 238
О методе подвижных координат в газовой динамике 243
О вариационном методе построения сеток 250
О выборе оптимальных разностных сеток 254
Разностная схема на подвижных сетках для решения уравнений вязкого газа 257
О решении нестационарных задач газовой динамики в подвижных сетках, зависящих от потока 269
О равномерно-сходящемся алгоритме численного решения обыкновенного
дифференциального уравнения второго порядка с малым параметром при старшей производной 275
МАТЕМАТИЧЕСКАЯ ТЕХНОЛОГИЯ
Модульный принцип построения программ как основа создания пакета прикладных программ
решения задач механики сплошной среды 283
411

Некоторые проблемы развития пакетов программ для решения задач аэродинамики 286
Вопросы модульного анализа и параллельных вычислений в задачах математической физики . . 292
Модульная структура алгоритмов и программ в задачах механики сплошной среды и
структура ЭВМ. . . . 297
Перспективы развития вычислительной математики на основе вычислительных систем 301
Пакеты прикладных программ математической физики и механики сплошной среды 303
Некоторые вопросы теории модульного анализа и параллельного программирования для
задач математической физики и механики сплошной среды 309
УРАВНЕНИЯ СОСТОЯНИЯ ВЕЩЕСТВА
Асимптотические и приближенные формулы для давления и внутренней энергии вещества
в обобщенной модели атома Томаса-Ферми 317
Уравнение состояния А-е фазы коры пульсара с учетом действия сверхсильного
магнитного поля 352
ГИДРОДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ И ТУРБУЛЕНТНОСТЬ
Об одной модели циркуляции атмосферы с локальным знакопеременным коэффициентом
турбулентности 358
Инвариантные критерии устойчивости течений сжимаемой жидкости 367
О моделировании эффектов отрицательного порождения интенсивности пульсаций
температуры в турбулентном слое смешения 371
Гамильтоновы вихревые модели в теории турбулентности 375
Образование когерентных структур в турбулентном следе при акустическом воздействии. ... 385
Об одной модификации уравнений движения вязкой несжимаемой жидкости. 387
Расчет моделей нейтронных звезде пионной конденсацией 391
Список трудов Н.Н. Яненко 395

CONTENTS
Preface 3
GEOMETRY
Geometrical structure of small type surfaces 5
On relationship between metric and projective properties of surfaces 8
On class of the Rieman metric 11
Metrics of the class 2 15
METHOD OF DIFFERENTIAL CONSTRAINTS
Travelling waves of a system of quasilinear equations 18
On travelling waves of gas dynamics equations 21
The theory of compatibility and the methods of integrating the systems of nonlinear equations in
partial derivatives 27
The D-properties of systems of one-dimensional equations of nonelastic continuum dynamics 32
Application of the method of differential constraints to onedimensional equations of gas dynamics . . 36
The Z)-properties of a system of equations of symmetric gas flows 41
The method of differential constraints and the problem on decomposition of arbitrary discontinuity 44
ANALYTICAL COMPUTATION ON COMPUTERS
On implementation of algebraic-differential algorithms on a computer 47
Implementation of the external form method on a computer 56
Implementation of the algorithm of study on the compatibility of systems of equations in partial
derivatives 57
The problem of automatic construction and the study of difference schemes in analytic form on
a computer 60
NONLINEAR EQUATIONS OF A VARIABLE TYPE
On one model of a fluid with a sign-changing viscosity coefficient 65
On some equations of a variable type 69
On some new classes of equations of mathematical physics 74
COMPUTATIONAL METHODS OF CONTINUUM MECHANICS
On one difference method of computation of multidimensional heat equation 78
Implicit splitting up schemes for hyperbolic equations and systems 81
On economical implicit schemes (the method of fractional steps) 83
On weak approximation of systems of differential equations 85
Solution of multidimensional kinetic equation by the splitting up method 88
The study of the Cauchy problem by the method^of weak approximation 90
Application of the splitting up method (the method of fractional steps) for solving the problems
of mathematical physics ', 93
On one absolutely stable scheme of integrating the hydrodynamics equations 101
413

Numerical calculation of symmetric flow about a plate by a plane stream of a viscous incompressible
fluid 107
On application of the splitting up method for numerical calculation of heat-conducting gas motion
in curvilinear coordinates 110
Economical difference schemes of higher accuracy for polyharmonic equation 118
On methods of calculation of gas dynamics problems with large deformations 125
The influence of viscosity on the solution smoothness in incomplete-parabolic solutions 139
On structure of absolutely approximating arid absolutely correct schemes 143
Evolutional two-layer difference schemes 150
On one implicit schemes of calculation of a viscous heat-conducting gas flow 154
On one method of convergence acceleration of iterative schemes 163
On the theory of difference schemes of gas dynamics 166
On construction of difference schemes of higher approximation order on the basis of differential
corollaries 177
Difference schemes for solving one-dimensional equations of gas dynamics 184
On difference schemes in arbitrary curvilinear system of coordinates 188
Simplified equations for description of a viscous gas flow 191
On application of approximate factorization in the Ritz method and in the finite element method ... 194
Calculation of gasdynamic flows on the basis of the method of concentrations 198
THE METHOD OF DIFFERENTIAL APPROXIMATION
On approximation viscosity of difference schemes 202
On correctness of the first differential approximations of difference schemes 204
On group classification of difference schemes for a system of one-dimensional gas dynamics equations 206
Qualitative study of difference schemes by the method of differential approximation 218
DIFFERENTIAL ANALYZERS
Differential analyzers of shock waves 226
On theory of differential analyzers bf contact discontinuities 229
Differential analyzer for discontinuity solutions of nonuniform hyperbolic equations 234
CONSTRUCTION OF ADAPTIVE GRIDS
The method of moving coordinates in gas dynamics 238
On the method of moving coordinates in gas dynamics 243
On the variational method of constructing grids 250
On the choice of optimum difference grids 254
Difference scheme on moving grids for solving the viscous gas equations , 257
On solution of nonstationary problems of gas dynamics in moving grids depending on the flow 269
On uniform-converging algorithm for numerical solution of ordinary differential equations of the
second order with a small parameter by higher derivative 275
MATHEMATICAL TECHNOLOGY
Modular principle of constructing programs as the basis of developing the package of applied
programs for solving the continuum mechanics problems 283
Some problems of developing the program packages for solving the aerodynamics problems 286
Questions of modular analysis and parallel computations in problems of mathematical physics 292
Modular structure of algorithms and programs in problems of continuum mechanics and the computer
structure 297
414

Prospects of computational mathematics development on the basis of computational systems 301
Packages of applied programs of mathematical physics and continuum mechanics 303
Some questions of the theory of modular analysis and parallel programming for problems of
mathematical physics and continuum mechanics . 309
EQUATION OF THE SUBSTANCE STATE
Asymptotic and approximate formulae for pressure and substance internal energy in a generalized
Thomas—Fermi atom model 317
Equation of state of the A-e phase of the pulsar crust with regard for actioivof superstrong magnetic
field 352
HYDRODYNAMIC STABILITY AND TURBULENCE
On one model of atmosphere circulation with local sign-changing turbulence coefficient 358
Invariant criteria of compressible fluid flow stability 367
On simulation of effects of negative intensity generation of temperature pulsations in turbulent
mixing layer 371
Hamiltonian vortex models in the theory of turbulence 375
Formation of coherent structures in turbulent wake by acoustic action 385
On one modification of equations of viscous incompressible fluid motion 387
Calculation of models of neutron stars with pion condensation 391
Bibliography of N.N. Yanneko's works 395

Научное издание
ЯНЕНКО Николай Николаевич
Избранные труды
Утверждено к печати
Институтом теоретической
и прикладной механики
СО АН СССР
Редактор ИМ. Столярова
Художественный редактор В.Ю. Яковлев
Технический редактор Г.И. Астахова
Корректор Р.Г. Ухина
Набор выполнен в издательстве
на наборно-печатающих автоматах
Н/К
Подписано к печати 26.12.90
Формат 70 X 100 1/16. Бумага офсетная № 1
Гарнитура Пресс-Роман. Печать офсетная
Усл.печ.л. 33,8 + 0,1 вкл. Усл.кр»-отт» 35,2
Уч.издл. 34,0. Тираж 1000 экз. Тип, зак. 953
Цена 7 р. 10 к. Заказное
Ордена Трудового Красного Знамени
издательство "Наука"
117864 ГСП-7, Москва В-485, Профсоюзная ул., 90
2-я типография издательства "Наука"
121099, Москва Г-99
Шубинский пер., 6