МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
М.В.КАПРАНОВ, В.К.СНЕДКОВА, Н.Н.УДАЛОВ
РАДИОТЕХНИЧЕСКИЕ СИСТЕМЫ
С ЧАСТОТНЫМ И ФАЗОВЫМ
УПРАВЛЕНИЕМ
КОНСПЕКТ ЛЕКЦИЙ
по курсу
„УСТРОЙСТВА ФОРМИРОВАНИЯ СИГНАЛОВ”
Под редакцией М.В. Капранова
Москва
Издательство МЭИ
1998
УДК
621.396
К205
УДК: 621.396(075.8)
Утверждено учебным управлением МЭИ в качестве учебного пособия для студентов
Подготовлено кафедрой формирования колебаний и сигналов
Рецензенты'.
канд. тех. наук ст. научн. сотр. В.Н. Кочемасов, инженер М.В.Ларионова
Капранов М.В., Снедкова В.К., Удалов Н.Н.
Радиотехнические системы с частотным и фазовым управлением: Конспект
лекций /Под ред. М.В. Капранова. - М.: Изд-во МЭИ, 1998 - 48 с.
ISBN 5-7046-0405-6
Излагаются принципы действия и элементы теории двух типовых
радиотехнических систем с частотным (ЧАП) и фазовым (ФАП) управлением частотой
колебаний автогенераторов
Для облегчения усвоения материала его рассмотрение ведется в сопоставлении
процессов в обеих системах, а необходимые сведения из общей теории нелинейных
колебаний даются по ходу изложения.
Пособие предназначено для студентов старших курсов радиотехнического факультета.
Учебное издание
Капранов Михаил Владимирович, Снедкова Вера Константиновна,
Удалов Николай Николаевич
Радиотехнические системы с частотным и фазовым управлением
КОНСПЕКТ ЛЕКЦИЙ
по курсу
УСТРОЙСТВА ФОРМИРОВАНИЯ СИГНАЛОВ'’
Редактор	Н.Л. Черныш
ЛР №020528 от 05.06.97
Темплан издания МЭИ 1997, учебн. Подписано к печати 02.12.98
Формат 60x84/8 Печ. л. 3,0 Тираж 100 Изд. №40 Заказ 20 Цена 4руб.
Издательство МЭИ, 111250, Москва, ул. Красноказарменная, д. 14
Отпечатано в типографии ЦНИИ “Электроника44,
117415, Москва, проспект Вернадского, д. 39
IBSN 5-7046-0405-6
© Московский энергетический институт,
1998
3
ОГЛАВЛЕНИЕ
Введение...................................................... 4
1.	Основные определения....................................... 5
2.	Сопоставительное изложение элементов теории ЧАП и ФАП...... 11
2.1.	Структурные схемы ФАП и ЧАП.................................. 11
2.2.	Составление общих уравнений систем ЧАП и ФАП................. 13
2.2.1.	Уравнение подстраиваемого генератора.................... 13
2.2.2.	Характеристики фазового и частотного дискриминаторов.... 13
2.2.3.	Цепь управления......................................... 17
2.2.4.	Дифференциальные уравнения систем ФАП и ЧАП............. 18
2.3.	Анализ основных режимов систем ЧАП и ФАП..................... 21
3.	Линейные модели ФАП и ЧАП...................................... 26
3.1.	Линейная модель системы ФАП.................................. 26
3.2.	Локальная устойчивость стационарного синхронного режима..	28
4.	Нелинейная теория ФАП и ЧАП.................................... 31
4.1.	Глобальная динамика систем с ЧФУ первого порядка......... 31
4.2.	Системы ФАП второго порядка.................................. 36
4.2.1 .Фазовое пространство ФАП второго порядка................. 36
4.2.2. Расчет полосы захвата в системе ФАП с однозвенным RC фильтром. 44
Литература........................................................ 48
4
ВВЕДЕНИЕ
В задачах современной физики, техники и, особенно, радиоэлек-
троники широко используются и играют универсальную роль периодиче-
ские колебания с чрезвычайно высокой стабильностью их основных пара-
метров - частоты и фазы (требуемая нестабильность частоты порядка
10’9 - 10 12 и меньше). Эти же параметры радиосигналов большей частью
используются и качестве информационных, поэтому формирование колеба-
ний и сигналов с прецизионной и управляемой частотой и фазой представ-
ляют одну из актуальных задач инженерной практики.
Для ее решения в последние годы с большим успехом применяют
различные системы частотной (ЧАП) и фазовой (ФАП) автоподстройки
колебаний подстраиваемых автогенераторов, а в качестве опорных сигна-
лов используются высокоэталонные колебания кварцевых или квантовых
стандартов частоты.
Наряду с ФАП встречается непосредственная фазовая синхронизация
автогенератора путем прямого воздействия эталонного колебания на эле-
менты его электрической схемы.
Кроме того, в усилителях и передающих трактах удается снизить
влияние дестабилизирующих факторов с помощью систем автоподстройки
фазового набега (АПФ).
Хотя в настоящее время общие принципы различных систем с час-
тотным и фазовым управлением - ЧАП, ФАП, АПФ и их комбинации - ши-
роко используются в самых различных областях радиоэлектроники, изуче-
ние их свойств обычно ведется индивидуально по отношению к каждой из
названных систем.
В данном пособии, которое планируется выпустить в нескольких
частях, предпринята попытка дать по возможности сопоставительное из-
ложение параллельных мест общей теории систем ЧАП, ФАП и АПФ.
Первый выпуск пособия включает в себя описание принципов дей-
ствия, главных структурных звеньев и элементы теории детерминирован-
ных систем ЧАП и ФАП. При этом обстоятельно рассматриваются более
сложные процессы в системе ФАП, а сходные явления в ЧАП затронуты в
меньшей степени.
5
1.	Основные определения
Дадим вначале краткую сводку определений используемых далее основ-
ных терминов.
Система. Под физической системой понимают совокупность взаимодей-
ствующих между собой материальных объектов.
Для теоретических исследований систему представляют в форме матема-
тической модели, имеющей определенное количественное описание. В качестве
описания удобно принять так называемый вектор состояния системы
.т.е. некоторый набор выбранных величин различной размерности, отра-
жающих существо изучаемого явления. По традиции, идущей из аналити-
ческой механики ( от Лагранжа ), компоненты х.(г) вектора состояния часто
называют обобщенными координатами.
В общей теории систем описание теоретической модели считают пол-
ным, если изменение его состояния dx(t) за малый интервал времени dt
определяется лишь самим состоянием , взятым в текущий момент вре-
мени t. Такую систему называют динамической, ее математическую модель
( “полное описание 44) можно дать, например, с помощью системы нели-
нейных обыкновенных дифференциальных уравнений, записанной в кано-
нической форме Коши:
^ = Дх(г)]; t = 0: Я(0).	(1.1)
Здесь f - заданная ( выбором модели ) нелинейная вектор -
функция.
Зная начальное состояние динамической системы х(о) в момент t = 0,
с помощью “полного описания44 (1.1) в принципе можно вычислить состоя-
ние x(t) в любой последующий момент времени t > 0, Если представить
гипотетически, что значение х(о) можно задавать с неограниченной точ-
ностью, то на основании записи (1.1) говорят о так называемом 44 де-
терминизме Ньютона - Лапласа 44.
6
Если состояние некоторой системы наблюдается не непрерывно, а
лишь в дискретные моменты времени (например, с равноотстоящими ин-
тервалами т, так что возникает дискретное время tn-nT), то взамен обыкно-
венных дифференциальных уравнений (1.1) получаем полное описание с по-
мощью разностных уравнений:
п=0:Хо.	(1.2)
Как и в (1.1) , конкретная реализация динамического процесса хп в дис-
кретном времени tn=nT определяется заданием вектора х0 в начальный мо-
мент п=0 . Вообще, процессы в динамических системах с дискретным
временем (1.2) отличаются от процессов в системах с непрерывным вре-
менем (1.1) гораздо большим разнообразием и богатством [8] (несмотря
на кажущуюся их предельную простоту!).
В устройствах цифровой техники некоторые из компонентов векто-
ра состояния х(г) принимают не все возможные значения непрерывно, а
реализуются лишь с четко фиксированными уровнями (например, два
логических уровня “ 0 “ и “ 1 “ в устройствах с двоичной логикой). Та-
кое “квантование по уровню “ возможно в динамических системах как с
непрерывным, так и с дискретным временем.
В радиотехнике при описании процессов большей частью интересуются
не мгновенными значениями физических величин (зарядов, токов, напряже-
ний и т.п.), а рассматривают в качестве компонентов вектора состояния
такие параметры квазигармонических колебаний, как их амплитуда £/(/), час-
тота co(t), фаза <p(t), поляризация электромагнитной волны и др. По ряду
причин особо выделяют системы, использующие информацию , заложенную в
изменениях частоты a>(t) и фазы (p(t) радиосигналов (будем называть их
далее системами с частотным и фазовым управлением , сокращенно -
системы с ЧФУ).
При математическом описании систем с ЧФУ имеют дело не
только с частотой или фазой квазипериодического сигнала, но и с
производными или интегралами от этих величин, поэтому важно их опреде-
ление.
7
Частота. При определении частоты необходимо указать, частота какого
именно события и в каком конкретном пространстве нас интересует. Например,
регулярное появление телеграфных столбив в окне равномерно движущегося
поезда - частота повторения данного события в единицу времени. Если взять от-
резок прямолинейного пути, то частота события - количество столбов на
единицу длины.
Определим понятие частоты f появления некоторого события на шкале
времени для строго периодических процессов ufy = u(t + Т), где Т - период по-
вторения события (рис. 1.1, кривая 1). В этом случае частота его повторения:
1/Т. Если периоду Т сопоставить поворот вектора гармонического колеба-
ния u(t) = U • sin(cor + 0) на 2л радиан, то говорят о круговой частоте,- а> -2лf.
Ясно, что строго периодических процессов в природе не бывает. “ Все в
природе периодично, но ничто не повторяется в точности “ К. Э. Циолков-
ский. Можно ли и для непериодических процессов определенно говорить о часто-
те? Для этого теперь мы должны указать точное событие, относительно кото-
рого вводится понятие частоты его появления. Например, за событие можно
принять прохождение непериодического процесса u(t} через нуль. Отрезки вре-
мени между “нулями” в этом случае будут разные, но можно оценить среднее (на
интервале наблюдений) значение частоты пересечения процессом u(t) нулевого
уровня. При уменьшении интервала наблюдения вводится понятие мгновенной
частоты /T(t).
Если процесс полностью случайный, то вводить понятие “частоты” не-
конструктивно, следует говорить о “ выбросах” случайного процесса [9].
На рис. 1.1 изображены два совершенно разных процесса, причем
непериодический процесс 2 эквивалентен строго периодическому процессу 1
в смысле только одного события - прохождения через нуль. Если использовать для
сравнения этих процессов пороговое устройство не с нулевым уровнем, то частоты
процессов 1 и 2 , очевидно, будут разные.
8
Фаза (состояние, лат.). Для определения понятия “ фаза” выберем
вначале определенный ( например, строго гармонический ) периодический про-
цесс в виде
w(z) = U • sin(cor + 0),	(1.3)
тогда аргумент синуса ф = со/+0 - текущая фаза периодического процесса w(z),
форма которого нами заранее предопределена в виде синусоидальной
функции времени.
Если процесс u(t) - квазигармонический, то дискомфорта при введении для
него такого понятия текущей фазы нет. Если процесс полностью случайный - по-
нятие фазы теряет смысл.
Рис. 1. 2. К определеню понятия " разность фаз"
Разность фаз. Предположим, что мы имеем два строго периодических про-
цесса ц(0 и ^(г) с одинаковым периодом Т, но разной формы (см. рис. 1.2). Под
их разностью фаз (р = (р2 - (рх (в смысле определенного события, например про-
хождения через ноль) понимается разность соответствующих аргументов этих
процессов, форма которых заранее известна.
9
Связь понятий “ частоты” и “ фазы.” Для случая строго периодического
синусоидального процесса с периодом Т=2л/а) из формулы (1.3) находим его час-
тоту
<Уср
(1-4)
Таким образом, частота - производная текущей фазы строго периодическо-
го процесса известной формы. Примем далее, что у квазигармонических процес-
сов такое утверждение справедливо для мгновенной частоты:
(1.Я
v 7 dt
Синхронизация ( syn - приставка в греческом языке, означающая
“соединение”, chronos - время ). Под синхронизацией двух (или нескольких) явле-
ний будем понимать, согласно этимологии этого термина, согласованное во време-
ни их поведение. Например, полное повторение процессом ufy процесса w,(z) с
фиксированным запаздыванием на время т, так что	= w, (t - т).
Явление синхронизации чрезвычайно распространено в живой природе, не-
бесной механике, технике ; его организующая роль огромна. Использованию явле-
ния синхронизации в технике посвящена обширная литература [2].
Фазовая синхронизация - означает согласованное во времени изменение те-
кущих фаз и (p2(t) двух квазипериодических процессов известной формы.
Например, два синусоидальных колебания = Ux(t)sm(px(t) и Uy(t) = t72(r)sin^2(r)
находятся в состоянии фазового синхронизма, если разность их текущих фаз
cp(t) = (px(t)~ (p2(t) = const, причем сам закон изменения фаз во времени при этом
может быть любым ( т.е. мгновенная частота обоих колебаний меняется строго
одинаково ). Заметим, что фазовый синхронизм может строго сохраняться, не-
смотря на произвольное рассогласование изменения амплитуд.
В хронометрии задача фазовой синхронизации возникает в случае, так на-
зываемого, “размножения часов”. На практике для множества разных служб не-
обходимо создать строгую шкалу времени. В этом случае в качестве синхронизи-
рующих источников колебаний используются квантовые генераторы с чрезвы-
чайно высокой стабильностью частоты (нестабильность =. 1О9 ч- 10-12 ) .
У обычных часов несколько шкал: часовая, минутная, секундная. Для их
создания в механике применяются шестеренки. В радиотехнике можно выбрать
10
нужную гармонику п/э эталонного колебания с частотой f3 и получить такую ста-
бильность ее частоты,как у сигнала основной частоты. Таким образом, можно
сделать точную шкалу времени или, другими словами, сформировать эталонную
сетку высоко стабильных частот.
Помимо хронометрии в современной физике и технике часто требуется ог-
ромная точность ( с ошибкой не более 10~10-=-1012 ) при измерении самых различ-
ных физических величин ( перемещение и скорость объектов, температура, давле-
ние и многое другое), причем, обычно не существует подходящего измерительного
прибора с высокоточной шкалой в широком диапазоне измерений. На практике
можно с помощью датчиков преобразовать любые физические величины в измере-
ния частоты ( или фазы) колебаний какого-либо процесса, а затем с помощью си-
стем с ЧФУ сопоставлять эти измерения с высокоэталонными одноименными па-
раметрами колебаний сетки стабильных частот.
Поэтому изучение свойств различных систем с ЧФУ приобретает важное
значение, однако процессы в них очень сложны и требуют глубоких знаний в об-
ласти нелинейной теории колебаний.
Наша цель - дать здесь весьма краткое изложение простейших основ теории
двух наиболее распространенных радиотехнических систем - с частотным
(частотная автоподстройка - ЧАП) и фазовым ( фазовая автоподстройка - ФАП)
управлением соответствующими параметрами колебаний произвольного автоге-
нератора. Для углубления понимания мы дадим общие части теории систем ЧАП
и ФАП автогенератора в сопоставительном изложении.
Помимо автогенераторов, на практике важно управлять процессами уста-
новления частоты и фазы колебаний при прохождении радиосигналов через уси-
лительные каскады и тракты передачи [6]. Основные соотношения в усилителях с
автоподстройкой фазового набега (АПФ) будут изложены в отдельном разделе.
11
2.	Сопоставительное изложение элементов теории ЧАП и ФАП
Несмотря на ряд специфических особенностей, системы ФАП и ЧАП
являются примером типовых радиотехнических систем управления. В качестве
управляемых величин здесь выступают текущие параметры
квазипериодического радиоколебания - мгновенные частота или фаза.
2.1.	Структурные схемы ФАП и ЧАП
Любая система управления автоподстройки содержит три основных
блока:
-	управляемый объект;
-	измерительный элемент;
-	управитель.
(Осе
Рис. 2.1.Структурная схема системы ФАП
Структурная схема системы ФАП изображена на рис.2.1, где: ФД -
фазовый дискриминатор; ПГ - подстраиваемый автогенератор; ЦУ - цепь
управления ; Ur(t) - амплитуда напряжения генератора; (рг (t)- фаза генератора;
й)св - свободная частота генератора; Uc(t) - амплитуда напряжения сигнала; g(t)
- сигнал управления (если сигнал управления равен нулю, то а>г =а>свУ, e(t) -
напряжение ошибки, несущее информацию о расхождении фаз; n(t) - внешние
помехи; %(t) - внутренние помехи.
(Осе
Рис. 2.2.Структурная схема системы ЧАП
12
Структурная схема системы ЧАП изображена на рис.2.2 , где ЧД -
частотный дискриминатор; ПГ - подстраиваемый автогенератор; ЦУ - цепь
управления ; Ur(t) - амплитуда напряжения генератора; o)p(i) - частота
генератора; а)св - свободная частота генератора; Uc(t) - амплитуда напряжения
сигнала; g(t) - сигнал управления (если сигнал управления равен нулю, то а>г
=а>св); e(t) - напряжение ошибки, несущее информацию о расхождении частот;
n(t) - внешние помехи; %(t) - внутренние помехи.
Действие внешнего шума n(t) проявится в сигнале ошибки e(t), но
поскольку рассогласование подстраиваемых координат меняется медленно, то в
ЦУ можно поставить цепи обработки текущих рассогласований и подавления
помехи.
Внутренние дестабилизирующие факторы %(t) возникают из-за
несовершенства условий эксплуатации (вибрации, нестабильности температуры
и т.д.).
Для нормальной работы систем автоподстройки выдвигается ряд общих
требований, среди которых:
нужная динамика (точность подстройки, быстродействие,
характеристики переходных процессов и т. д.);
подавление внутренних помех;
подавление внешних помех.
Так как все эти требования противоречивы, оптимальный вариант
обычно выбирается по минимизации некоторого выбранного гргтерия
качества. Эту задачу решает теория оптимальной линейной и нелинейной
фильтрации. Оказалось, что система ФАП - оптимальный приемник,
позволяющий оптимальным образом выделить информацию из смеси сигнала и
шума [ 10 ].
При сравнении систем ЧАП и ФАП обязательно нужно учесть
нелинейный характер их динамики. Оказывается, что нелинейность
дискриминационной характеристики измерительного органа может разрушить
все оценки, полученные из оптимального синтеза. Поэтому реально синтез
получается секвентным ( т.е. делается несколько последовательных
подходов).
13
2.2.	Составление общих уравнений систем ЧАП и ФАП
Уравнения систем ФАП и ЧАП целесообразно представить в наиболее
общем виде, чтобы, поменяв параметры или характеристику схем, не нужно
было бы их составлять заново. Для составления уравнений необходимо связать
текущие координаты на входах и выходах основных структурных элементов
систем. Напишем уравнения для каждого блока системы ФАП.
2.2.1.	Уравнение подстраиваемого генератора
У ПГ входным является сигнал управления g(t). В момент замыкания
цепи управления мгновенная частота генератора a>r(i) меняется в результате
воздействия напряжения g(t) на вход управляющего элемента ПГ. Пренебрегая
переходными процессами в подстраиваемом генераторе и полагая
характеристику управителя линейной, запишем уравнение для текущей частоты
подстраиваемого автогенератора в виде
сог= a)ce-Sg(t),	(2.1)
где 5 - крутизна характеристики управителя.
2.2.2.	Характеристики фазового и частотного дискриминаторов
Типичные характеристики дискриминаторов ФАП (а) и ЧАП (б)
представлены на рис.2.3. По оси абсцисс отложена разность фаз (р (разность
частот со ), а по оси ординат - напряжение ошибки е.
Рис.2.3. Характеристики дискриминаторов ФАП (а) и ЧАП (б)
При реализации схемы дискриминатора желательно получить возможно
большую крутизну его характеристики в рабочей области (для повышения
чувствительности) и большую ее апертуру (для увеличения диапазона
перестройки). Необходимо также обеспечивать стабильность нуля
дискриминационной характеристики. В силу ряда обстоятельств (старение,
14
влияние изменений температуры и влажности среды и т.п. ), хороший
дискриминатор сделать весьма трудно.
У ФД характеристика 2яг-периодическая, а у ЧД - нарастающий участок
сменяется падающим (рис.2.3.). При правильной работе системы происходят
лишь небольшие отклонения вблизи начала координат, поэтому можно
записать уравнение для линейного участка в виде
еЛинФАП=Зфд((рг~ (рс),	(2.2)
еПин 4An=Sчд(а>г- сос).	(2.3)
Запишем нелинейные уравнения дискриминаторов в виде
еФД=ЕР((р),	(2.4)
ечд^ЕФ(а)Г сос),	(2.5)
где <р =(рг~(рс f (о ~й)г~ сос , Е - наибольшее выходное напряжение, а Е,Ф -
нелинейные характеристики дискриминаторов, нормированные к единице.
(Например, для ФАП F((p)=sin((p)^
Самое главное в характеристиках дискриминаторов - наличие
неустранимой нелинейности (для больших отклонений регулируемых
координат).
Схемы ЧАП и ФАП содержат ряд инерционных элементов (диоды,
конденсаторы), поэтому при отклике на скачок частоты или фазы в схемах ЧД и
ФД будут наблюдаться переходные процессы, что в данном уравнении не
учитывается.
Рассмотрим простейшие варианты схем дискриминаторов и их
характеристики.
Балансный фазовый дискриминатор. (Суммарно-разностное вектормерное
устройство.) Схема балансного ФД и его векторная диаграмма изображены на
рис.2.4.
15
a)	.	б)
Рис. 2.4. Балансный ФД: а) схема ФД, б) векторная диаграмма
Используя тригонометрические соотношения векторной диаграммы
(рис.2.4 б), можно показать [3], что если ис«иг (или иг«ис), то
нормированная характеристика ФД с высокой степенью точности равна
F((p)=sin((p).
Фазовый дискриминатор по схеме перемножителя. Эта схема (рис.2.5 )
очень популярна в системах фазовой автоподстройки, так как она реализуется в
различных частотных диапазонах и позволяет легко пересчитать шумы, идущие
извне, на выход дискриминатора .
n(t)
Uc( t)
ПГ
е( t) = jiuc(t)ur(i)
Рис. 2.5. Схема перемножения мгновенных значений напряжений сигнала и ПГ
Запишем
uc(t)= \Jc(t)cos(pc(t),	(2.6)
ur(t)=Ur(t)s\n(pr(t).
Произведение этих сигналов имеет вид
(fj/2)Uc(t)Ur(t)[sm((pr-(pc)+^га((рг•	(2.7)
Колебание с удвоенной частотой сигнала ( синус суммы фаз генератора и
сигнала) будет отсеяно низкочастотным фильтром в цепи управления. Таким
образом^ получим характеристику фазового детектора по схеме перемножителя
16
e=(/j/2)UcU]b\n(p	(2.8)
Схема ЧД с расстроенными контурами (резонаторами). На рис.2.6 а
изображена блок схема, а также пример реализации данной модели.
6УС
Рис.2.6 а. Блок-схема ЧД с расстроенными контурами и смесителем и пример реализации
Рис.2.6 б . Характеристика ЧД
Рис. 2.6 б поясняет принцип работы схемы и формирование
характеристики ЧД с расстроенными контурами и смесителем ( е = е/ - ej ).
Такой дискриминатор можно сделать в любом диапазоне частот.
Дискриминатор на линии задержки (рис.2.7 ) также достаточно прост по
своему принципу действия.
17
T
Ul( t-т) =U2
ui(t)
e=/Ll U1U2
Рис. 2.7. Частотный дискриминатор с линией задержки и идеальным перемножителем
Здесь перемножаются мгновенные значения незадержанного ui(t) и
задержанного напряжений. Если на входе перемножителя действуют два
гармонических напряжения, то запаздывание между ними приводит к
смещению фазы напряжения uj(t) относительно фазы uj(t) на угол буг, в
результате чего на выходе перемножителя мы получим 2тг- периодичную
характеристику или набор характеристик дискриминатора, смещенных на 2тг;
е=ц U2U, = (ft/2)U2 cos(a> г).	(2.9)
2.2.3.	Цепь управления
Для описания линейных ЦУ составляется их коэффициент передачи в
символической записи. При составлении уравнений в символической записи
учитывается, что символ р =	, ]э = и т.д. Например, простая RC-
цепочка (рис. 2.8).
R
e(t) | с I g(t)
Рис. 2.8. Схема однозвенного RC - фильтра
Ее коэффициент передачи записывается в виде
яъ,)=^) = —,	(2.Ю)
v ' е(с) 7>+1	v ’
где Т =RC- постоянная времени фильтра.
Таким образом, символическое дифференциальное уравнение цепи
управления имеет вид
18
(7>+l)^(z) = <0’
Раскрывая процедуру р = % , получим дифференциальное уравнение ЦУ
(RC-цепочки)
Tj + g(r) = e(0-	(2.Н)
Таким образом, описаны характеристики всех трех основных блоков систем
фазовой и частотной автоподстройки. Выпишем полученные уравнения отдельных
звеньев.
ФАП	ЧАП
Характеристика ПГ	
®г = рсрг - ©св- S g	й)г = СОсв- S g
Характеристика дискриминатора	
е = Е F(<pr-q>c)	е = Е(©г-сос)
Дифференциальное уравнение L	,У (в символической записи)
	g(t)=K(p)e(t)			
В реальной схеме все эти блоки соединены в кольцо Чтобы получить обшее
уравнение системы с ЧФУ, надо подставить одно выражение в другое.
2.2.4.	Дифференциальные уравнения систем ФАП и ЧАП
Получим такое выражение вначале для системы ФАП. Очевидно, что под-
становка уравнений дискриминатора и ЦУ в выражение характеристики ПГ про-
ще, чем другие варианты. Вычитая из левой и правой частей уравнения рус, полу-
чим, что текущая разность частот (р(рг - pcpj равна исходной разности частот
а>св~Р<Рс за вычетом корректирующей расстройки:
Р(рг ~Р(рс = а>св-р(рс-S K(p)EF((рг - (рс) .	<2.12)
Обозначим:
Q - ES - наибольшая корректирующая расстройка, вырабатываемая упра-
вителем частоты ( напомним, что Е - наибольшее напряжение на выходе фазового
дискриминатора. Величину Е можно вывести из под оператора фильтра К(р), если
считать, что Е=const. (Такое возможно при Uc и Ur не меняющихся во времени);
19
(р=фГ- (рс - текущая разность фаз;
у =(й)св~Р(рс)/^- исходная безразмерная разность частот.
Тогда, поделив обе части уравнения (2.12) на Q, получим, что текущая
безразмерная разность частот равна исходной безразмерной разности частот,
скорректированной на величину ошибки:
^ + Х(рМ>) = /.	(2.13)
Выведем теперь уравнение для системы ЧАП. По аналогии, подставим
уравнения ЦУ и дискриминатора в уравнение ПГ, вычтем из левой и правой
частей уравнения номинальную частоту сигнала а> = (а>с+а> д) и обозначим
Таким образом, получим, что текущая разность частот генератора и
сигнала у равна исходному расхождению частот у за вычетом корректирующей
расстройки:
у + К(р)ф(у) = У .	(2.15)
Примечание. Корректирующая расстройка в системе ФАП
вырабатывается за счет изменения разности фаз, а в системе ЧАП-за счет
изменения разности частот, при этом частоты могут быть равны, а фазы не
совпадать. Таким образом, в ЧАП потеряна связь с текущей разностью фаз
сигнала.
Полученные уравнения ФАП (2.13) и ЧАП (2.15) имеют простой вид.
Они также достаточно общие, что позволяет использовать разные
характеристики ФД, ЧД и любые характеристики ЦУ.
Можно выделить три наиболее интересные схемы цепей управления (за
пределами безынерционной цепи К(р)=1):
1.	Дифференцирующая цепочка (рис. 2.9 )
С
i—||_тг7
e(t) I R У |g(t)
Рис.2.9. Схема дифференцирующей цепочки
20
Ее коэффициент передачи в операторном виде
к(р)=-2р_
v ' Тр+1
(2.16)
2.	Инерционное звено (так называемая “интегрирующая” цепочка); ее
схема дана на рис. 2.8, а оператор ЦУ с таким звеном равен
<2'°>
Комбинация этих двух цепочек дает так называемое “пропорционально-
интегрирующее звено”, схема которого приведена на рис.2.10, а коэффициент
передачи имеет вид
к(р) = ~^Т ’
(2.17)
где 0 < q < 1 - коэффициент включения.
qR
e(t) |
Рис. 2.10. Схема пропорционально-интегрирующего фильтра
3.	Идеальный интегратор
К(р) = ^г-	(2.18)
Тр
При комбинировании 1 и 3 получаем “ идеальное пропорционально-
интегрирующее звено”:
=	0<<7<1.	(2.19)
Тр
Отметим, что исходная безразмерная разность частот у в (2.13) и (2.15), в
общем случае является функцией времени. Если же у = уо = const (не зависит от
времени), то такое дифференциальное уравнение (с постоянной правой частью)
называется автономным. Кроме того, величина наибольшей корректирующей
расстройки Q = SE также может меняться, так как величина Е =E(Uc,Ur)
зависит от амплитуды сигнала Uc и генератора Ur.
21
Из-за существенной нелинейности характеристик ФД и ЧД,
инерционности ЦУ нахождение решения усложняется, так как получаются
нелинейные дифференциальные уравнения (2.13) или (2.15) высокого порядка.
Подбирая степень полинома в знаменателе К(р), можно погасить эффект
полиномиального воздействия y(t) в правой части уравнения. Таким образом,
порядок уравнения может увеличиваться с повышением степени полинома y(t).
Например, в режиме линейного слежения за частотой сигнала, когда у =yo+at,
дня ликвидации частотной ошибки следует в ЦУ добавить интегратор, при
наличии ещё одного члена Д t2 - два интегратора и т.д.
2.3. Анализ основных режимов систем ЧАП и ФАП
Рассмотрим стационарный режим, то есть режим, который
устанавливается через значительное время после включения (все переходные
процессы к этому времени закончились).
Выделим важный случай, когда при t—> разность фаз и разность
частот
имеют конечные значения (состояние равновесия):
ФАП:	lim<p0 = ф° = const',	(2.20)
ЧАП:	= yQ = const.
Такие режимы могут получаться, например, если у - полином, а чгобы
его погасить - надо включить в 7<(Д)необходимое число интеграторов. Но мы
рассмотрим более простой случай, когда у = уо = const.
а)Уравнение стационарного синхронного режима для ФАП имеет
вид
£(O)f(<p°) = y°.	(2.21)
Рассмотрим данное уравнение для трех ранее рассмотренных схем ЦУ
0
К(0) =  1	(2.22)
00
22
При А”(0)=1 и К(0)=оо система работает и дает решение (р °= const. При
К(0)=0 кольцо не работает в синхронном режиме, так как через ЦУ постоянное
напряжение не проходит. К(0) = оо возможность получить нулевое
рассогласование по фазе (р 0 = 0.
Выберем ЦУ так, чтобы А/0)=1, тогда уравнение стационарного режима
ФАП упрощается:
4Н=Го-	(2-23)
Решим полученное уравнение ФД графически. Для этого совместим на
одном рисунке график характеристики ФД и /о (рис.2.11).
Рис. 2.11. Графическое решение уравнения стационарного режима ФАП
Решениями (2.23) будут точки пересечения графиков. Из рис. 2.11 видно,
что таких точек при / у °/ < 1 может быть две . В этих точках крутизна
характеристики ФД имеет разный знак, из-за этого меняется знак управления.
Таким образом, только одна из этих точек устойчива. Очевидно, неустойчива
точка (pi . Заметим, что у0 можно менять от +1 до -1. При у°=1 обе точки
сольются и получим сложную точку равновесия. Если же у 0 >1, точки
пересечения исчезают, т.е. синхронный режим оказывается невозможным.
Следовательно, чтобы система ФАП могла находиться в синхронном режиме,
необходимо выполнение следующего условия
-1 ’ т-е- ' (2-24)
Величину /2 называют полосой синхронизма или удержания. Для
увеличения полосы удержания (/2 = SE) можно увеличить напряжение Е, но оно
ограничено уровнем сигнала Uc. Для увеличения крутизны управителя 5 можно
23
поставить усилитель постоянного тока, но в УПТ может возникнуть дрейф нуля,
что в свою очередь, приведет к нестабильности работы ФАП.
Кольцо ФАП может дать синхронизацию либо с фиксированной, но ненуле-
вой разностью фаз, либо даже с разностью фаз равной нулю. Для этого необхо-
димо включить в цепь идеальный интегратор К(0)=оо, однако включение интегра-
тора может нарушить устойчивость. Так как в системе ФАП измеряется разность
фаз на ФД, а сигнал ошибки используется для управления частотой, которая яв-
ляется производной от фазы, то при этом внутри ФАП процесс интегрирования
происходит сам собой.
Построим регулировочную характеристику синхронного режима ФАП при
7<(0J = l (рис.2.12). На рисунке прерывистой линией показан график работы си-
стемы в свободном состоянии, а сплошной линией - в замкнутом состоянии коль-
ца ФАП.
Обычно, асинхронный режим считается аварийным. Но из графика видно,
что при / °, приближающихся к режиму синхронизма, происходит "подтягивание”
средней частоты генератора к частоте сигнала. Если же рассматривать очень
большие расстройки, то разницы между поведением системы в разомкнутом со-
стоянии и асинхронным режимом нет.
Рис. 2.12 Регулировочная характеристика ФАП
б) Уравнение стационарного режима для системы ЧАП:
/+7С(0)ф(/) = У').
(2.25)
24
При Л"(0)=0 система не работает, так как на постоянном токе она
разомкнута. При К(0)= оо и /^0 получаем , Ф(у)=0, что дает возможность
получить нулевую разность частоту ° =0, но разность фаз может быть любая.
Решим графически уравнение ЧАП (2.25), полагая Л(0)=1.
Рис. 2.13. Графическое решение уравнения с/ационарного режима ЧАП
Для этого совместим на одном графике у °+Ф(у °) и у 0 (рис.2.13).
Выберем расстройку у 0 таким образом, чтобы получилось три точки
пересечения (три решения данного уравнения). Далее покажем, что точка
пересечения у2° всегда неустойчива, точки у? и у ° могут быть устойчивы. Точка
У1° - остаточная разность частот в работающем кольце, она много меньше
значения у0, следовательно, получим эффективную подстройку:
v°
(2.26)
1+А
Здесь A=S произведение крутизны характеристик ЧД и управителя
частоты ПГ.
Для хорошей автоподстройки эту величину делают много больше
единицы (А »1). В теории авторегулирования ее называют коэффициентом
регулирования системы.
Точка уз° находится недалеко от линии начальной расстройки,
следовательно, получим не эффективную подстройку:у3°~ у °.
Если увеличивать у °, точки у ° и у2° сближаются и затем соединяются.
Далее остается только точка уз° . Следовательно, это граница эффективной
автоподстройки. Значение у °, соответствующее этой границе, называется
полосой удержания.
25
При уменьшении у 0 сливаются точки у2° и уз° и получается сложная
неустойчивая точка. При дальнейшем уменьшении у 0 всегда получим
эффективный режим у °. Величина у °, при которой сливаются точки у2° и уз°,
называется полосой схватывания. Полоса схватывания является рабочим
диапазоном ЧАП, поэтому ее необходимо сделать возможно шире, чтобы
внутри ее оказались возможные нестабильности собственной частоты ПГ.
26
3.	Линейные модели ФАП и ЧАП
Чтобы выяснить влияние параметров системы на ее динамическое
поведение, нужно обратиться уже не к алгебраическим уравнениям стационарных
режимов ФАП и ЧАП, а к дифференциальным. Рассмотрим вначале линейные
модели ФАП и ЧАП, справедливые для малых возмущений фазы ПГ (или его
частоты) относительно состояния равновесия ^?°(или у0).
3.1.	Линейная модель системы ФАП
Рассмотрим линейную модель системы ФАП. Полагаем, что за счет
вариации фазы сигнала vc(t) фаза колебаний ПГ также получает вариацию vr(t)
относительно его фазы в стационарном режиме. Используя разложение в ряд
Тейлора функции F(ф) в случае малых вариаций vc(t) и vr(t) и учитывая уравнение
стационарного режима (2.21), из уравнения (2.13) получим линейное
дифференциальное уравнение для вариаций:
[	+ ЛШ(ф,°) ]vr = K(p)F^)v .	(3.1)
Отсюда получается математическая модель ФАП для вариаций фаз vr и vC)
которая показана на рис. 3.1.
а)	б)
Рис. 3.1. Представление системы ФАП для вариаций фаз сигнала и ПГ (а);
математическая модель (б)
Коэффициент передачи такой системы равен
’ (3-2)
с 1 +	- -
где т =------•/—дт	- постоянная времени системы ФАП.
пг'ф(ф?)
Перепишем уравнение (3.2) в виде
27
[тр+К(р)]уг(г) = /С(р)ус(г).	(3.3)
С помощью соотношения (3.3) можно решить ряд важных практических
вопросов. Задавая законы изменения vc(t) и подбирая К(р), можно добиться
желаемого отклика vr(t)- Это можно назвать задачей слежения.
Если воздействие vc=Vccoscot, то стационарный отклик vr = VrCOs((Dt+(p).
Модуль коэффициента передачи (3.2) в этом случае определяет АЧХ системы
FF,(co) = vr(co)/vc.
Существуют приемы, позволяющие быстро приближенно построить
АЧХ. Возьмем, например, в качестве фильтра ПИФ (пропорционально-
интегрирующий фильтр) с коэффициентом передачи К(р) :
к(Р)=^£Д.
Тогда коэффициент передачи системы ФАП в символической записи
будет иметь вид
qTp+i
Ттр2 +(x + qT^p+\
(3.4)
Рассмотрим, что будет с АЧХ, если зафиксировать параметр q, а
постоянную времени фильтра Т неограниченно увеличивать.
Запишем предельные выражения при Д —> 0 :
lim Wl(p) =---— = —
Тр-+ю v 7 Tip+qTp 2
x=const
q=const	Я
(3.5)
Иными
характеристику
словами, если величину Т сделать большой, получим
с постоянной времени т/q. Отсюда следует, что предельная
совпадает с АЧХ безфильтровой ФАП , но с постоянной
характеристика
времени т, как бы увеличенной в Uq раз.
Другой способ построения АЧХ (логарифмическая АЧХ) применяется,
когда схема очень сложная (очень много параметров). Взамен сот = £ пишем
log£, а вместо Wj(Q -	Рассмотрим, к примеру, дробно-рациональную
функцию: 1/£ 2 - параболу 2-й степени. Если взять log//^2 , то получим
log/ - 21og£ (рис. 3.2 ).
28
3.2.	Локальная устойчивость стационарного синхронного режима
Ранее было получено уравнение линейной модели ФАП (3.3). Свободные
колебания будут существовать при ус = 0. Таким образом, из (3.3) можно
получить также и уравнение свободных колебаний
[zp+K(p)]vr(t)=0.	(3.6)
Подставим вместо К(р), например коэффициент передачи ЯС-цепочки,
получим
(Ттр2+тр +l)vr(t)=0 .	(3.7)
Рассмотрим, как будет себя вести решение vr во времени. Частное
решение линейного уравнения (3.7) имеет вид
уг=С^‘ .	(3.8)
Подставляя (3.8) в дифференциальное уравнение (3.7), приходим к
характеристическому уравнению
А,2+25А. + С0о =0,	(3.9)
1	2	1
где 25=---затухание, а»о =----собственная частота. Корни уравнения (3.9)
Т	Тх
в общем случае комплексные: Л/,2 =&Re .
Таким образом, получаем общее решение
vr(z) = C/1'+C2?!'.	*	(3.10)
Если рассматривать ФНЧ более высокого порядка, то труднее получать
информацию, так как в решении (3.10) будет очень много экспонент.
При рассмотрении, локальной устойчивости системы можно выбрать
один из двух возможных путей.
29
а	) Алгебраический критерий ( во временной области) применяется, если
имеем невысокий порядок уравнения (3.3).
б	) Частотный критерий (Найквиста) более простым путем дает ответ о
локальной устойчивости. Заменим в (3.6) р на jot, получим
j(OT+K(j(o)=0.	(3.11)
Фактически это не одно равенство, а два; их можно записать в двух формах:
7	форма - выделяем в K(jco) действительную и мнимую части:
K(ja>)=KR,,(ja>) ^jK^ja)).
Тогда из условия (3.6) получаем
ARe =0
/ х	(3.12)
(ОТ + A'im(^y) = о
2 форма выделяем в K(ja>) модуль и фазу:	) =	, и полагаем
Л
+J-
усох = соте 2. Тогда самовозоуждение наступает, если выполнены условия:
сот= К(со) - баланс амплитуд;	(3.13)
0 (со)——л /2	- баланс фаз.	(3.14)
Очевидно, что система уравнений (3.12) и система уравнений (3.13), (3.14),
несмотря на разную форму, описывают один и тот же процесс свободных
колебаний в системе ФАП. Однако чаще всего используется форма 2, так как
физически более понятна и наглядна.
Частота, на которой выполняются оба условия (3.13) и (3.14), называется
граничной частотой corp или частотой самовозбуждения. Как видно из уравнения
баланса фаз (3.14), на частоте самовозбуждения со = ©гр обязателен сдвиг фаз 90°.
Пример. Рассмотрим и-звенный АС-фильтр с коэффициентом передачи
30
Дадим на "частотном языке" ответ на вопрос о том, при каких условиях
произойдет потеря устойчивости.
Баланс амплитуд
Баланс фаз
0.рТ =	(3.16)
2»
Получили простое выражение, которое имеет наглядный физический
смысл. Согласно (3.14), на граничной частоте общий сдвиг фаз в и-звенном
фильтре составляет -л/2. Очевидно, нужно, чтобы каждая цепочка сдвигала в п
раз меньше. При п=1 граничная частота ©гр -> оо, т.е. в системе с однозвенным
фильтром устойчивость всегда гарантирована, так как баланс фаз выполняется
только на бесконечно большой частоте, где модуль К(оо)=0. При п=2 получим
согрТ=\, следовательно, при Т/т =2 произойдет самовозбуждение. Таким
образом, стоит только перейти к двухзвенному фильтру, как ‘ получаем
возможную потерю устойчивости при Т > 2 т.
После того, как рассмотрели систему ФАП в линейном приближении,
учтем особенности нелинейности системы.
31
4.	Нелинейная теория ФАП и ЧАП
Рассмотрим динамику системы ФАП первого и второго порядков (для
системы ЧАП то же самое можно сделать по аналогии).
На рис. 4.1. показана структурная схема ФАП без действия
возмущающих факторов.
Рис.4.1. Структурная схема ФАП без возмущений
Напомним символическую запись автономного дифференциального
уравнения системы ФАП:
+ К (p)F(y) = у0 = const,	(4.1)
б	X	Юсв-РФс
где р - —, (р = (р[ (рс .. текущая фаза, у =	-•- нормированная
dt	Q
начальная расстройка.
Вся неприятность глобального анализа состоит в том, что в уравнении (4.1)
соединились нелинейность F((p) и инерционность (из-за К(р)).
4.1.	Глобальная динамика систем с ЧФУ первого порядка
Сопоставим нелинейные системы ФАП и ЧАП, ограничившись вначале
анализом дифференциальных уравнений первого порядка.
ФАП
^ + K(p)F(p) = y
Рис. 4.2. Характеристика ФД
Каким должен быть вид оператора К(р), чтобы получить уравнение ФАП
первого порядка? Так как в уравнении уже имеется один символ
дифференцирования то, следовательно, достаточно взять К(р) = \. Тогда
получаем дифференциальное уравнение ФАЛ 1-го порядка:
=	(4.2)
32
ЧАП
Рис. 4.3. Характеристика ЧД
Для того, чтобы получить уравнение 1-го порядка для системы ЧАП,
можно использовать:
а) интегрирующий фильтр
Он приводит к уравнению
б) интегратор

Уравнение ЧАП с идеальным интегратором:
Проиллюстрируем подходы к анализу динамики систем с ЧФУ на
примере ФАП первого порядка. Обратимся к дифференциальному уравнению
безфильтровой ФАП (4.2). Выберем начальное условие t = 0 ; <р(0).
Есть несколько путей для анализа.
Первый путь: Поиск временных решений.
Конкретное решение cp(t) уравнения (4.2) определяется тем , в каком
положении находилась система в начальный момент времени (t=0 ). Разделим
переменные в уравнении (4.2) и проинтегрируем :
QZ= f	.
(4.3)
Возьмем для примера Ff^=sin^ тогда
Q/= Г—.	(4.4)
simp
Из таблиц интегралов для этого уравнения легко увидеть, что даже при
простых видах характеристики ФД выражения получаются громоздкими. Если
ее вид сложный, то для вычисления интеграла (4.3) надо применять ЭВМ.
Чтобы выяснить, как будут влиять начальные условия на характер
решения (p(t), необходимо менять у и (р(0) в широких пределах. В результате
получим очень большой набор графиков решений, который трудно охватить в
совокупности, чтобы получить ответы на поставленные вопросы.
33
Второй путь: Будем искать решения в фазовом пространстве.
Информацию о динамике системы ФАП можно
получить
непосредственно из дифференциального
уравнения (4.2), специально записанного в
форме Коши.
За фазовое пространство выберем
поверхность кругового цилиндра (рис.
4.4.). Так поступаем потому, что при
замене у на у ± 2л уравнение (4.2) не
меняется.
Тогда положение точки на
Рис. 4.4. Положение изображающей
точки на поверхности цилиндра
поверхности цилиндра определяет текущее
состояние системы, она называется
изображающей. (Положение точки на
цилиндре задается у и dy/dt). Таким
образом, начальные условия учитываются автоматически. Меняется положение
точки - меняется у и dy/dt. Развернем цилиндр, получим карту цилиндра (рис.
4.5.)
Будем рисовать фазовую траекторию - путь изображающей точки в
фазовом пространстве. Чтобы получить фазовую траекторию, необходимо
указать, в какую сторону будет двигаться система с изменением времени.
В верхней полуплоскости ( dy/ dt > 0) движение происходит слева
направо, в нижней (dy/dt < 0)- справа налево. В точках у® , у2 скорость
равняется нулю, здесь выполняется соотношение:
F(4>1.1) = /.
Видим, что это уравнение стационарного синхронного режима, здесь
разность фаз постоянна (т.е частота подстраиваемого генератора и частота
сигнала совпадают).
Очевидно, точка неустойчива, достаточно дать ей малое возмущение
в положительную сторону и эта точка постепенно перейдет в т. у^+2л. Точка
у? устойчива в пределах от у1-2л до у2* (этот интервал называется областью
притяжения УСТОЙЧИВОГО СОСТОЯНИЯ ТОЧКИ ^7°).
При изменении / от 0 до 1 график на рис.4.5, будет перемещаться вверх
или вниз. Те точки , которые расположены на участке характеристики
дискриминатора с положительной крутизной - устойчивы. Таким образом,
используя фазовую траекторию и задав на ней начальное условие t = 0 , у(0),
34
можно увидеть, что будет происходить с системой дальше. Заметим, что чем
выше точка по оси d(p/dt, тем ее скорость движения по фазовой траектории
больше.
Для второго примера рассмотрим фазовый портрет ЧАП с идеальным
интегратором.
т % = -Ф(у) 	(4.5)
dt
Фазовый портрет этой системы показан на рис. 4.6.
Здесь имеется только одна устойчивая стационарная точка у=0.
Очевидно, что этот режим устойчив при любых начальных условиях у(0).
Однако, если у(0) велико, скорость у'(0) оказывается малой, в результате
движение (как, например, из точки 1) будет медленным. Следовательно, в
нелинейных системах ФАП и ЧАП время установления зависит от начальных
условий .
Вернемся к системе ФАП , когда у> 1 (рис. 4.7).
Выберем любое начальное условие (p(ty, при этом изображающая точка
будет двигаться по траектории вправо. Скорость везде будет положительной,
следовательно, разность фаз постоянно будет нарастать. Фазовая траектория
разомкнутой ФАП совпадает с пунктирной прямой. Области, где F((p)
положительная - области подтягивания частоты подстраиваемого генератора ,
где F((p) отрицательная - отталкивания. Очень важно убедиться
(самостоятельно), что время движения по траектории замкнутой системы
35
больше, чем по траектории разомкнутой системы. При / стремящейся к
единице период асинхронных колебаний, т.е. время, за которое набегает
разность фаз 2л, стремится к бесконечности.
Период асинхронных автоколебаний ( Тас ) может быть найден из
уравнения:
= 1”тл •	(4-6)
-Л-ПФ)
Для простоты вычислений примем форму характеристики ФД
прямоугольной, показанной на рис. 4.8.
Рис. 4.8. Прямоугольная характеристика ФД
В этом случае
ст - °г ^ф . f _ 2л7
-Л-Ь1) Л-1 7 -1
О у — 1	2л
Таким образом, —— =---, где Qac =--частота асинхронных
Я 7
(4.7)
колебаний.
Рис. 4.9. Регулировочная характеристика ФАП
На рис. 4.9 показана зависимость частоты асинхронных колебаний от
начальной расстройки. В области у < 1 в системе ФАП наблюдается
синхронный режим. При у > 1 в системе ФАП устанавливается асинхронный
режим, однако в области расстроек, близких к единице, происходит
подтягивание частоты ПГ к частоте сигнала.
Графики разности фаз ф(/) и напряжения е(7) на выходе ФД для системы
ФАП с прямоугольной характеристикой ФД представлены на рис. 4.10.
36
Рис. 4.10. Временные решения в асинхронном режиме (у > 1)
В разомкнутой системе фаза будет расти линейно (пунктирная линия),
форма напряжения на выходе ФД будет повторять форму рис. 4.8., постоянная
составляющая такого колебания равна нулю. В замкнутой системе ФАП участки
от 0 до л и от л до 2л проходятся за разные промежутки времени. Из графика
напряжения e(t) видно , что получается некоторое среднее значение во Таким
образом, подтягивание частоты автогенератора к частоте сигнала в
асинхронном режиме происходит из-за того, что на выходе ФД появляется
некоторое среднее значение напряжения .
4.2.	Системы ФАП второго порядка
4.2.1.	Фазовое пространство ФАП второго порядка
Уравнение второго порядка получается в тех случаях, когда в цепи
управления ставим какой-либо фильтр первого порядка (это следует из
уравнения (4.1)).
Рассмотрим наиболее популярный пример - систему ФАП с
интегрирующим фильтром:
кЬ)=—!—.	Д.
v ' Тр+1	°	1—1	г
где Г =ЛС-постоянная времени фильтра.	е I	С
(4.8)
Так как у = const, имеем дело с автономным
дифференциальным уравнением , поэтому из (4.1) Рис-41L Схема RC -фильтра
получаем
£^+1^+F(<p)=y .
Q dt1 Q dt w
Это уравнение можно преобразовать двумя способами:
1 вариант
Обозначим 7 = Q.t:

37
nT^+^+F(v)=y.
2 вариант
Обозначим
d 2(р
di2
1 d(p
yJCl T di
+ F(<p)= у
или в более удобном виде
ф + 28ф + +7?(^) = у .	(4.9)
При рассмотрении линейной модели ФАП было установлено , что
система ФАП с большой постоянной времени эквивалентна узкополосному
колебательному контору , что позволяет вырезать мешающие спектры помех .
Таким образом для реализации фильтрующих свойств будем рассматривать
случаи, когда постоянная времени фильтра большая, поэтому удобнее
использовать второй вариант (4.9). В этом уравнении коэффициент 28 играет
роль затухания, если Т велико, то 8-~» 0.
Поставим перед собой задачу изучить все возможные движения в этой
системе при произвольном соотношении параметров. Для решения уравнения
(4.9) есть два пути .
1-й путь: нахождение временных решений <р^,28,у,<р.,ф.\
2-й путь: рассмотрение фазовых траекторий в пространстве состояний
(на поверхности кругового цилиндра). При исследовании систем с ЧФУ
воспользуемся этим способом, как наиболее простым, наглядным и
результативным.
Перепишем уравнение (4.9) в канонической форме Коши. Для этого одно
уравнение второго порядка (4.9) представим в виде системы двух уравнений
первого порядка.
^ = У
(4.Ю)
Это сделано для того, чтобы из уравнения (4.9) исключить время и
рассмотреть решения на цилиндрической фазовой поверхности. Разделив одно
уравнение на другое получим "сопровождающее уравнение" :
_у-28^-^(ф) = /2(ф,у)
У Л(<р,.у)
Порядок уравнения (4.11) понизился на единицу, т.к. интервал dt
исключен.
Сопровождающее уравнение соответствует системе уравнений (4.10),
записанных во временной области, но оно уже не содержит времени .
Сопровождающее уравнение дает поле касательных к фазовой траектории, в
каждой точке которой из (4.11) можно найти	С помощью
сопровождающего уравнения, задав в момент t=0, унач и (рнач можно начертить
фазовую траекторию (рис.4.12.).
38
Рис. 4.12. Элемент фазовой траектории и касательная к ней
Перейдя по касательной в соседнюю точку, взяв ее координаты, снова
находим величину - углового коэффициента к фазовой траектории и т. д.
С помощью сопровождающего уравнения можно установить
характерные точки фазового портрета - особые точки.
Всегда ли сопровождающее уравнение дает однозначный ответ о
величине углового коэффициента ? Этот вопрос тесно связан с состоянием
равновесия, т.е. с особыми точками .
В особых точках, для которых
/(<р°,/)=о|
/2(<р°,/)=о]
угловой коэффициент теряет однозначное определение. Поэтому нельзя
сказать, сколько фазовых траекторий проходит через состояние равновесия -
одна, бесконечное множество, или не одной.
Перейдем к исследованию фазовых траекторий в окрестностях особых
точек.
Стационарный синхронный режим (t -+ об):
limcpf/) = <р° = const:
Как видно из рис. 4.13, при |у| <1 имеем две точки состояния равновесия
о о
Ф1 И ф2 .
Линеаризуем исходное дифференциальное уравнение в окрестности этих
точек. Даем приращения: ^ф-ф^. Считая их малыми, линеаризуем
характеристику ФД в окрестности каждой из точек:
^(ф)=^(ф°2+lj)»^^1+^'(ф“2)^+...
Получаем линейные дифференциальные уравнения для окрестностей
каждой из особых точек.
Точкаф,0:	+ 2^ + ^^,°)? = 0	(4.12)
39
Точкафг0	+	+	= 0 ,	(4.13)
где f;(<p?)>0, г;(ф;)<о.
В первом уравнении оба коэффициента 28 иположительны,
следовательно, точка <pi° устойчива. Для второго уравнения < 0 , точка
ф2° неустойчива.
Нарисуем несколько картин, которые показывают характер фазовых
траекторий в зависимости от вида корней характеристического уравнения
( корни могут быть действительными или комплексно-сопряженными ).
Если корни отрицательные (рис. 4.14.), то каждое решение £,(t) будет
убывающим во времени.
jA, 1
Л, 2 X 1
Рис. 4.14. Отрицательные
вещественные корни
Будем искать решение £,(/) в виде =	+А2ек2‘. Фазовый портрет
для этого случая показан на рис. 4.15.
Такая особая точка называется устойчивым узлом (устойчивое состояние
равновесия, движение во времени апериодическое).
Если оба корня положительные и действительные, то получается
неустойчивый узел (апериодические нарастающие движения).
Рис. 4.15. Фазовые траектории типа устойчивого узла
В случае, когда корни комплексно сопряженные с отрицательной
действительной частью (рис. 4.16), реализуется затухающий колебательный
процесс.
Рис. 4.16. Комплексно-сопряженные корни характеристического уравнения
40
Фазовый портрет для этого случая (устойчивый фокус) и
соответствующее ему временное решение показаны на рис. 4.17. и 4.18.
Рис. 4.18. Временное решение, соответствующее устойчивому фокусу
Если корни Xi и Л<2 на рис. 4.16 переходят в правую
полуплоскость, то будем иметь неустойчивый фокус.
Если корни лежат на мнимой оси (рис. 4.19), то особая точка
- центр (рис. 4.20).
Рис. 4.20. Фазовая траектория типа
центр
Рис. 4.19. Чисто мнимые
характеристические корни
Если корни действительные, но разных знаков (рис. 4.21), то особая
точка - седловая (рис. 4.23).
Рис.4.21. Характеристические корни для
седловой точки
Рис. 4.22. Временное решение для
седловой точки
41
В окрестности седла все траектории приближаются к особой траектории
С2 и отталкиваются от Сь Эти особые траектории, т.е. сепаратрисы Ci и С2,
разделяют фазовую плоскость на области притяжений.
В окрестности седла все траектории приближаются к особой траектории
С2 и отталкиваются от Сь Эти особые траектории, т.е. сепаратрисы Ci и С2,
разделяют фазовую плоскость на области притяжений.
Рис. 4.23. Фазовые траектории в окрестности седла (выбрано Xi=-X2)
Вернемся к дифференциальным уравнениям (4.12.) и (4.13.) . Мы
выяснили , что решения будут определяться корнями соответствующих им
характеристических уравнений.
Особые точки, где крутизна характеристики ФД положительная,
являются либо узлом, либо фокусом . Если крутизна характеристики ФД
отрицательная, то особая точка всегда седло. Особая точка будет являться
фокусом , когда затухание 28 мало. Величина его равна 25 = 1/-JQ.T .
Так как на практике постоянную времени фильтра Т берут большой, то
особая точка на участке характеристики ФД с положительной крутизной
обычно оказывается фокусом.
Нарисуем полный фазовый портрет системы ФАП с интегрирующим
фильтром (рис. 4.24.). Характеристика ФД F((p)= sm$?.
На рис. 4.24. точки (p\Q , (pi - особые, причем точка ^°- седло, так как
крутизна F'(p ((Р2) <0.
Из (4.11) находим уравнение горизонтальной изоклины (dy/a<p = 0) :
28y = y-F((p)	(4.14)
Уравнение изоклины с вертикальной касательной (dy/dcp = 00):
у - 0.	(4.15)
Каков физический смысл фазового портрета? Он показывает, каково
глобальное (при любых начальных отклонениях) поведение системы ФАП. Для
портрета рис. 4.24 все траектории стекаются к устойчивой точке равновесия ^°.
Поэтому куда бы в начальный момент времени систему не забросили, она в
конце концов придет в точку устойчивого стационарного синхронного режима.
Если начальные условия таковы, что разность частот велика, то изображающая
точка несколько раз обернется по цилиндру и все равно придет в фокус. Таким
образом, фазовый портрет (рис. 4.24) демонстрирует глобальную устойчивость
ФАЛ ( т.е. устойчивость при любых начальных условиях ).
42
Рис. 4.24. Полный фазовый портрет ФАП с интегрирующим фильтром
(глобальная устойчивость)
Выясним влияние параметров 28 и у на характер векторного поля
фазовых траекторий. Что будет с угловым коэффициентом dy/d(p, если увеличим
начальную расстройку у ? Из (4.11) следует, что величина станет меньше,
т.е. векторное поле повернется против часовой стрелки в каждой точке,
сепаратриса С1 на рис. 4.24 поднимется , а сепаратриса С2 опустится.
Если Т увеличивается, то 23 уменьшается и, согласно (4.11),
увеличивается, следовательно, векторное поле вращается против часовой
стрелки (рис. 4.25.). Здесь Ci проходит выше С2 и образуется петля из входящих
полусепаратрис седла.
Заштрихованная область - область притяжения устойчивой особой точки
равновесия, в эту область система может попасть не при всех начальных
условиях.
Рис. 4.25. Образование петли сепаратрисы, охватывающей устойчивое состояние
равновесия cpi°
43
Поскольку сепаратрисса Ci идет выше С2, то в верхней полуплоскости
возникает зредельный цикл 2-го рода у(ф)- 2я периодическая траектория
(притягивающая):
у(ф) = у(ф±2л)
Таким образом, существует два центра притяжения (аттрактора).
Устойчивый предельный цикл второго рода -2л периодическая траектория
у(ф). Если начальные условия выберем в незаштрихованной области, то все
траектории придут к предельному циклу у(ф), устанавливается асинхронный
режим, фаза (p(t) все время возрастает. Если находимся в заштрихованной
области, то будет синхронный режим, так как траектории придут в точку ф1°.
Следовательно, характер стационарного режима существенно зависит от
начальных условий.
Нарисуем фазовый портрет, граничный между двумя выше
рассмотренными. Он определяется тем, что входящая сепаратриса С2 и
выходящая С1 сомкнулись (рис. 4.26).
Произошло рождение полуустойчивого сепаратрисного предельного
цикла второго рода. Заметим, что движение по сепаратрисной линии из точки
ф2° к точке ф2°+2тг занимает бесконечное время. При каких соотношениях у и 8
будет такая
Рис. 4 26. Смыкание сепаратрисе и образование полуустойчивого предельного цикла 2-
го рода
ситуация и как это проявляется? Ясно, что расчет соотношения между у и
5 для граничной картины рис. 4.26 имеет принципиальное значение, так как он
дает границу глобальной устойчивости ФАП. Зависимость Угр(5) можно найти,
потребовав смыкания Ci и С2 ( как на рис. 4.26). Оказывается, эта граница
соответствует левой на рис. 4.27 б границе гистерезисной зоны в
регулировочной характеристике ФАП. Ее называют полосой захвата Угр=у3 [3].
44
Рис. 4.27. Регулировочные характеристики ФАП
При наличии большой инерционности фильтра зона глобальной
устойчивости сузилась в пределах 2уз (в этой области при любых начальных
условиях устанавливается синхронный режим).
Задача расчета полосы захвата сводится к следующему: необходимо
связать параметры системы у и 6 таким образом , чтобы произошло смыкание
сепаратрис на фазовой плоскости.
4.2.2.	Расчет полосы захвата в системе ФАП с однозвенным RC
фильтром
Дифференциальное уравнение системы с однозвенным RC фильтром
имеет вид (4.9.)
ф + 26ф + F(p) = у,
где 28 = 1/757.
Рассматриваем автономные системы ФАП, следовательно, у = const.
Для произвольной характеристики ФД при 0 < у < 1 существует значение
параметра 26, при котором на фазовом цилиндре возникает сепаратрисный
предельный цикл >>(ф) (из-за смыкания сепаратрис) эта ситуация соответствует
границе глобальной устойчивости ФАП, а величина у = у3 (рис. 4.26).
Следовательно, чтобы получить выражение , связывающее полосу захвата у3 с
затуханием 26, необходимо получить выражение сепаратрис, т.е. фазовых
траекторий ФАП . Однако для произвольной характеристики F((p) из
сопровождающего уравнения (4.11) не удается найти их аналитического
выражения.
Поэтому представим (4.11.) в другой форме:
у dy + 25у <Уф + ^(ф^ф = у<Уф.	(4.16)
Это уравнение справедливо для всех фазовых траекторий .
В задаче о нахождении полосы захвата рассматриваются только 2 л
периодические по (р решения:
7(ф) = ?(ф ±2д) •
45
Подставляя любое такое решение в уравнение (4.16) и интегрируя от -л до л,
получим следующее соотношение ( его впервые записал Трикоми) :
jydy + 28 fyd<p + |г(ф)<Уф = у р/ф .	(4.17)
-л	-л	-л	-л
В силу периодичности решения у(ф) здесь обращаются в нуль 1-е и 3- е
слагаемые в левой части. Тогда остается:
fy(<p)rf<p = ^.	(4.18)
Z7C *	ZO
-я
Оказалось, что отношение параметров у 3 /28 однозначно определяется средним
значением 5>(ф),т.е.
(?(<₽)) = Ь-.	(4-19)
2о
где скобки ( ) означают среднее значение функции.
Если бы выражение сепаратрисного цикла т(ф) было известно точно , то
подставляя его в соотношение Трикоми (4.17), мы получили бы точное
выражение полосы захвата, но оно неизвестно. Однако мы можем получить
выражение полосы захвата в асимптотическом приближении у—>0, 25^0.
Заметим, что отношение этих параметров, согласно (4.19), является конечным.
Чтобы найти асимптотические периодические решения З/Дф) возьмем вначале
26 =0 , /=0. Тогда взамен (4.17) получим:
j^ + F(^) = O,	(4.20)
о
Это - уравнение консервативной системы. Его можно проинтегрировать,
получив, так называемый, “первый интеграл”:
+ \е(х')Лх = С,	(4.21)
о о
Здесь постоянная интегрирования С играет роль полной энергии системы, а
уравнению (4.21) можно придать смысл закона сохранения энергии в системе
ФАП.
ч>
Тогда функция /7(ф)=	- потенциальная энергия, и закон
о
сохранения энергии приобретает вид
^- + 77(Ф) = С .	(4.22)
Задавая значения константы С, получим точные выражения фазовых траекторий
Уас (ф ) = ± 72[С “ 77 (ф)]	(4.23)
Ценность выражения (4.23) в том, что легко записать для выбранной F((p)
потенциальную энергию П((р) и из (4.23) иметь выражения уас(<р), не прибегая
к интегрированию дифференциального уравнения.
Из (4.23) следует, что при С< max П((р) получаются замкнутые траектории, не
охватывающие фазовый цилиндр, при С > шах П((р) возникают периодические
46
по (р траектории, охватывающие цилиндр. Следовательно, граничная
траектория У рр (ф) получается при С = max П((р) ( это асимптотическая форма
сепаратрисного предельного цикла, он идет из седловой точки ф2° = -л в точку
фз ~ л )• Для примера найдем выражение сепаратрисного предельного цикла в
асимптотическом приближении и построим фазовый портрет для
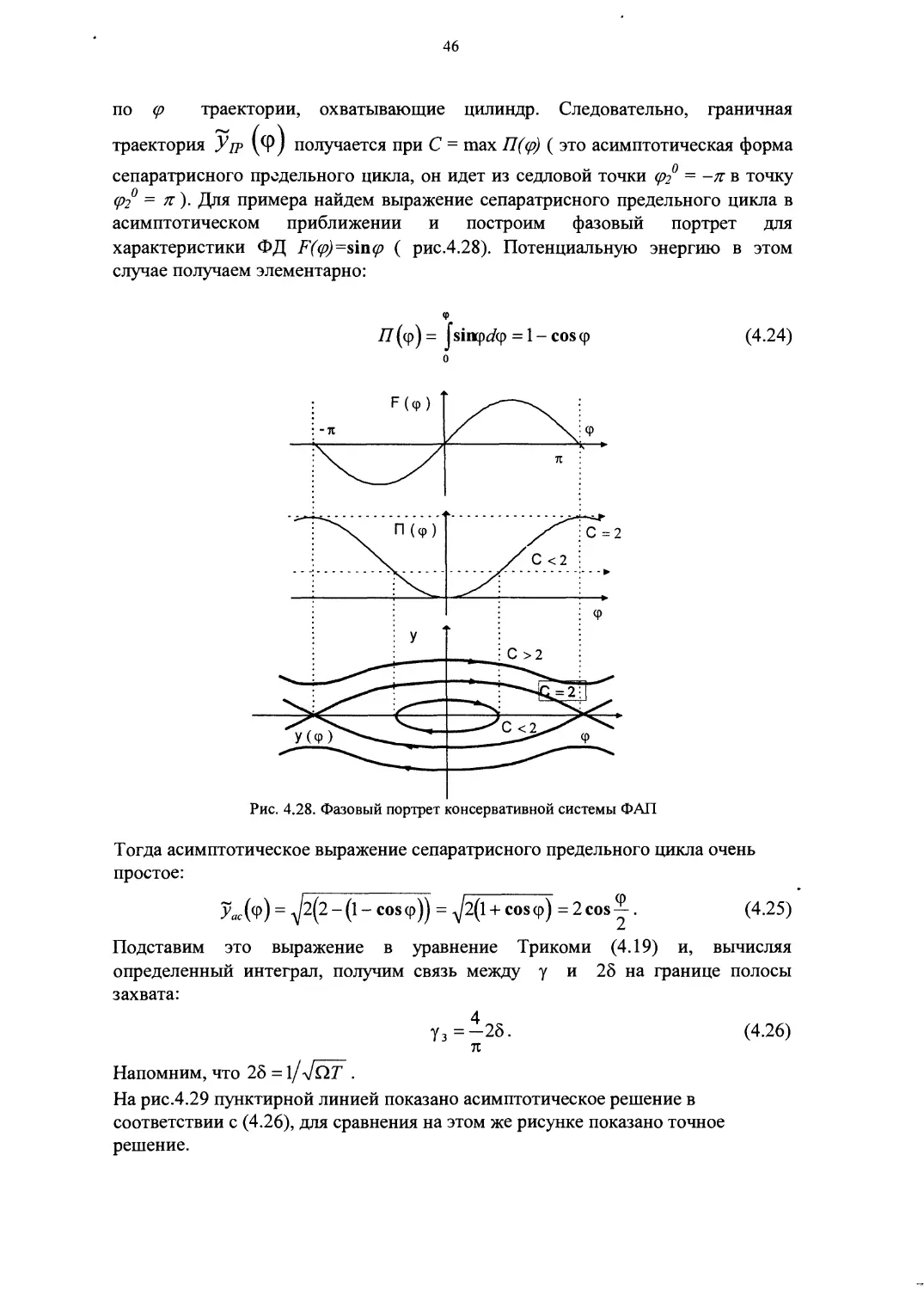
характеристики ФД F((p)=s\n(p ( рис.4.28). Потенциальную энергию в этом
случае получаем элементарно:
ф
77(ср) = jsiiipdcp =1-coscp
о
(4.24)
Рис. 4.28. Фазовый портрет консервативной системы ФАП
Тогда асимптотическое выражение сепаратрисного предельного цикла очень
простое:
Лс(ф) = -^2^2-(1- cos ср)) = ^2(1 + cos ср) = 2 cos у.	(4.25)
Подставим это выражение в уравнение Трикоми (4.19) и, вычисляя
определенный интеграл, получим связь между у и 25 на границе полосы
захвата:
у3 =—25.	(4.26)
71
Напомним, что 25 = 1/ JciT .
На рис.4.29 пунктирной линией показано асимптотическое решение в
соответствии с (4.26), для сравнения на этом же рисунке показано точное
решение.
47
Чтобы уменьшить затухание 2Д надо увеличить Т, следовательно у3 будет
уменьшаться. Таким образом, возникает противоречие между желанием
получить большое Т ( для фильтрации помех) и желанием получить большую
полосу захвата у3 (чтобы гарантировать глобальную устойчивость).
Точные уравнения для фазовых траекторий можно получить при кусочно-
линейной аппроксимации характеристики ФД [ 3.]. Рассмотрим, для примера,
систему ФАП с треугольной характеристикой ФД (рис. 4.30).
Рис. 4.30. Треугольная характеристика ФД
Поведение системы на отдельных интервалах описывается линейными
дифференциальными уравнениями, следовательно, можно получить точные их
аналитические решения. Производя затем "сшивание" траекторий на границах
интервалов, получим точное выражение для уз (&Г).
1-у, к/Д + 1 -1	(~л + arctgVA2 -1
—‘-+ = ==^—ехр ----------1=^=-----
1 + Уз Va + 1+i V Va-1
А Т	1
где Л = —; т =----= —.
т	£!F'((p) 2Q
Подробно процедура сшивания и расчета полосы захвата изложена в
пособии [ 3 ] и книге [ 7 ].
(4-27)
48
Литература
1.	Капранов М.В., Кулешов В.Н., Уткин Г.М. Теория колебаний в
радиотехнике. М.: Наука, 1984. 320 с.
2.	Линдсей В. Системы синхронизации в связи и управлении / Под ред.
Ю.Н. Бакаева и М.В. Капранова. М.: Сов. Радио, 1978. 600 с.
3.	Капранов М.В. Метод сшивания фазовых траекторий в теории
динамических систем с периодической нелинейностью. М.: Моск, энерг. ин-т,
1980. 92 с.
4.	Фазовая синхронизация /В.В. Шахгильдян, Л.Н. Белюстина, М.В.
Капранов и др. / Под ред. В.В.Шахгильдяна, Л.Н. Белюстиной. М.: Связь, 1975.
288 с.
5.	Системы фазовой синхронизации /В.Н. Акимов, Л.Н. Белюстина,
В.Н. Белых и др. / Под ред. В.В. Шахгильдяна, Л.Н. Белюстиной. М.: Радио и
связь, 1982. 288 с.
6.	Автоматическая подстройка фазового набега в усилителях / Г.М.
Уткин, М.В. Капранов, Л.А. Белов и др. / Под ред. М.В. Капранова М.: Сов.
Радио, 1972. 176 с.
7.	Шахтарин Б.И. Анализ кусочно-линейных систем с фазовым
регулированием. М.: Машиностроение, 1991. 192 с.
8.	Шарковский А.Н., Майстренко Ю.Л., Романенко Е.Ю. Разностные
уравнения и их приложения. Киев: Наукова Думка, 1986. 280 с.
9.	Тихонов В.И. Выбросы случайных процессов. М.: Наука, 1970. 392 с.
10.	Тихонов В.И., Харисов В.Н. Статистический анализ и синтез
радиотехнических устройств и систем : Учебное пособие для вузов. М.: Радио и
Связь, 1991. 608 с.