Автор: Черняк В.Г.
Теги: общая механика механика твердых и жидких тел гидромеханика механика жидкостей и газа механика физика газовая динамика гидродинамика
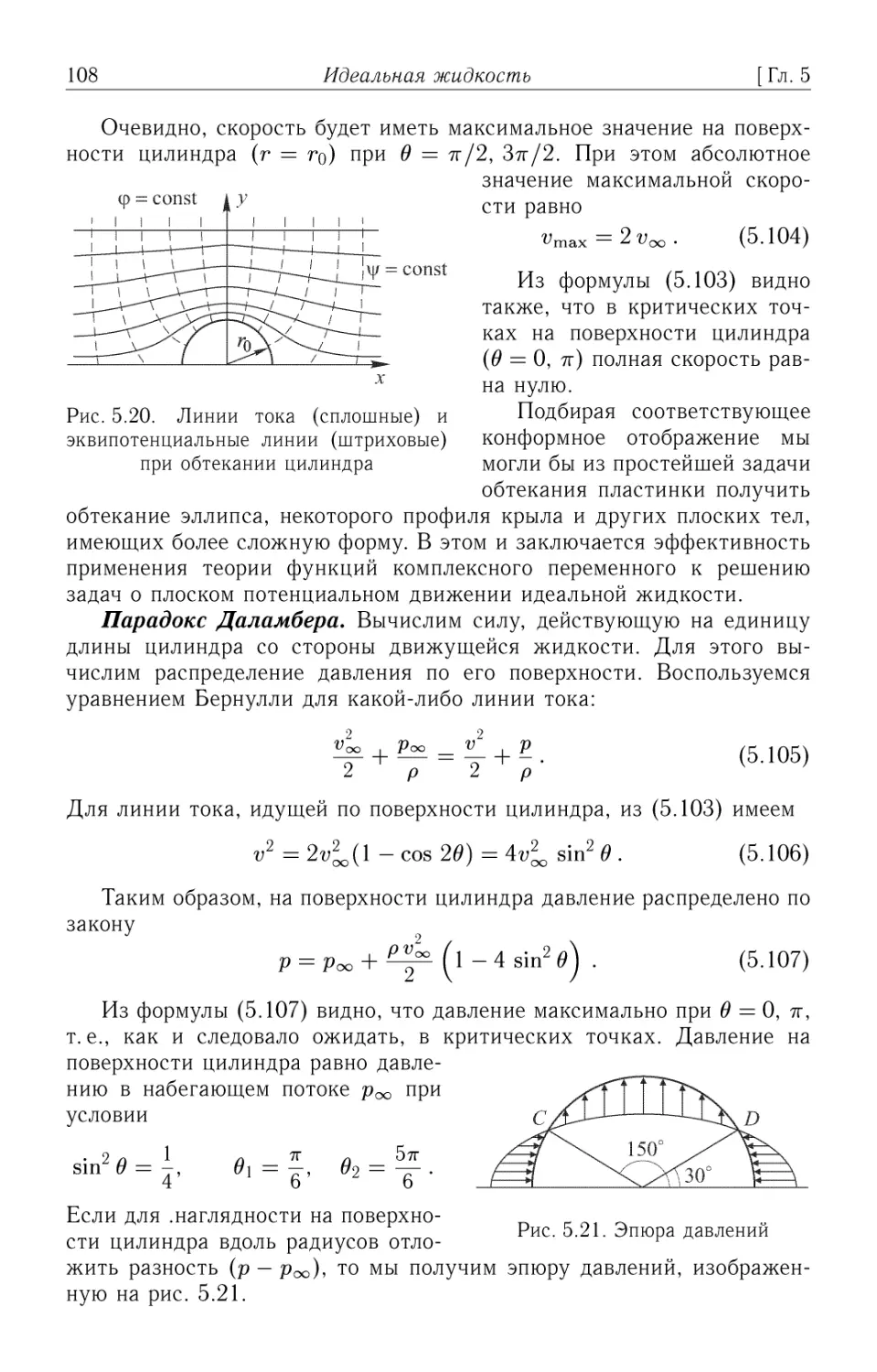
ISBN: 5-9221-0714-3
Год: 2006
УДК 531+532
ББК 22.25
4 49
Черняк В. Г., СуетинП. Е. Механика сплошных сред: Учеб. пособ.:
Для вузов. - М.: ФИЗМАТЛИТ, 2006. - 352 с. - ISBN 5-9221-0714-3.
Излагаются фундаментальные физические концепции кинематики и дина-
динамики сплошной среды, рассматриваются ее различные модели (твердое те-
тело, жидкость и газ). Большая часть учебного пособия посвящена вопросам
гидродинамики идеальной и вязкой жидкости. Включены элементы теории
упругости, газодинамики и магнитной гидродинамики. Показывается, как тео-
теоретические положения используются для решения инженерных задач и для
объяснения некоторых явлений природы.
Вопросы для самоконтроля и примеры решения задач, приведенные в конце
каждой главы, помогут читателю лучше разобраться в теории, приобрести
навыки самостоятельного решения задач механики сплошной среды.
Допущено Министерством образования и науки Российской Федерации
в качестве учебного пособия для студентов высших учебных заведений, обуча-
обучающихся по направлению подготовки бакалавров «Физика».
Учебное издание
ЧЕРНЯК Владимир Григорьевич
СУЕТИН Паригорий Евстафьевич
МЕХАНИКА СПЛОШНЫХ СРЕД
Редактор ДА. Миртова
Оригинал-макет: В.В. Затекин
Оформление переплета: А.Ю. Алехина
Подписано в печать 30.06.06. Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 22. Уч.-изд. л. 25,0. Тираж 1500 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3
Тел.: (8172) 72-55-31, 72-61-75, факс: (8172) 72-60-72
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv
ISBN 5-9221-0714-3
78592207143
ISBN 5-9221-0714-3
© ФИЗМАТЛИТ, 2006
© В. Г. Черняк, П. Е. Суетин, 2006
ОГЛАВЛЕНИЕ
Предисловие 8
ГЛАВА 1. Модель сплошной среды 9
1.1. Модели механического движения 9
1.2. Бесконечно малые в модели сплошной среды 10
1.2.1. Бесконечно малый элемент объема A0). 1.2.2. Бесконечно
малый промежуток времени A2).
1.3. Примеры решения задач 13
ГЛАВА 2. Кинематика сплошной среды 15
2.1. Деформация 15
2.2. Тензор поворота 17
2.3. Тензор деформации 18
2.3.1. Изменение объема тела при деформации A9). 2.3.2. Геомет-
Геометрические свойства линейных деформаций B0). 2.3.3. Эллипсоид
деформации B1).
2.4. Температурная деформация 21
2.5. Теорема Коши-Гельмгольца 23
ГЛАВА 3. Уравнения теории упругости 24
3.1. Тензор напряжений 24
3.1.1. Силы массовые, объемные и поверхностные B4). 3.1.2. Тен-
Тензор напряжений B5). 3.1.3. Результирующая поверхностная сила,
действующая на единицу объема тела B7).
3.2. Термодинамика деформирования 29
3.2.1. Работа внутренних сил B9). 3.2.2. Основное термодинами-
термодинамическое равенство C0).
3.3. Закон Гука 31
3.3.1. Свободная энергия деформируемого тела C1). 3.3.2. Закон
Гука C2).
3.4. Однородная деформация 34
3.4.1. Модуль Юнга и коэффициент Пуассона C5). 3.4.2. Диаграм-
Диаграмма растяжения C6).
3.5. Неизотермическое деформирование 38
3.5.1. Адиабатические и изотермические модули C9).
3.6. Уравнение равновесия изотропных тел 41
3.6.1. Граничные условия D2).
Оглавление
ГЛАВА 4. Фундаментальная система уравнений движения сплош-
сплошной среды 44
4.1. Тензор скоростей деформации 44
4.2. Дифференцирование по времени интеграла по подвижному объему 45
4.3. Уравнение непрерывности 45
4.3.1. Интегральная и дифференциальная форма уравнения непре-
непрерывности D8).
4.4. Уравнение движения сплошной среды 49
4.4.1. Субстанциональное и локальное описание движения сплош-
сплошной среды E0).
4.5. Уравнение момента импульса сплошной среды 53
4.6. Тензор плотности потока импульса 56
4.7. Уравнение сохранения внутренней энергии 57
4.8. Вектор плотности потока полной энергии. Вектор Умова 61
4.9. Замкнутая система уравнений движения сплошной среды 63
4.10. Уравнение теплопроводности изотропных сред 64
4.11. Тензор вязких напряжений 65
4.12. Модели сплошных сред 67
4.13. Упругие волны 69
4.14. Примеры решения задач 73
ГЛАВА 5. Идеальная жидкость 81
5.1. Уравнения движения идеальной жидкости 81
5.1.1. Изэнтропическое движение (82). 5.1.2. Граничные и началь-
начальные условия (84).
5.2. Уравнение Бернулли 84
5.2.1. Линии тока и траектории. Трубка тока (85).
5.3. Применение уравнения Бернулли 87
5.3.1. Скорость истечения идеальной несжимаемой жидкости из
сосуда (87). 5.3.2. Распределение давления в трубе переменного
сечения (88). 5.3.3. Кавитация (89). 5.3.4. Трубка Пито (90).
5.4. Влияние сжимаемости среды 91
5.5. Вихревое движение 94
5.5.1. Теорема Томсона (94). 5.5.2. Теорема Гельмгольца (96).
5.5.3. Одиночная вихревая прямолинейная нить (97). 5.5.4. При-
Примеры вихревых движений (99).
5.6. Потенциальное движение 101
5.6.1. Потенциал скорости A01). 5.6.2. Идеальная несжимаемая
жидкость A02). 5.6.3. Функция тока A03).
5.7. Методы описания движения идеальной жидкости 104
5.7.1. Метод конформных отображений A04). 5.7.2. Метод супер-
суперпозиции потенциальных потоков (ПО). 5.7.3. Графоаналитический
метод A14). 5.7.4. Непосредственное решение уравнений движе-
движения A16).
5.8. Примеры решения задач 121
Оглавление
ГЛАВА 6. Вязкая жидкость 129
6.1. Замкнутая система уравнений движения вязкой жидкости. Уравне-
Уравнение Навье-Стокса 129
6.1.1. Граничные и начальные условия A30). 6.1.2. Вихревое дви-
движение вязкой жидкости A31).
6.2. Диссипация кинетической энергии несжимаемой вязкой жидкости 132
6.3. Точные решения уравнения Навье-Стокса 134
6.3.1. Течение Куэтта A35). 6.3.2. Плоское течение Пуазей-
ля A37). 6.3.3. Цилиндрическое течение Пуазейля A39).
6.3.4. Движение жидкости между двумя вращающимися цилин-
цилиндрами A41).
6.4. Медленное обтекание шара 144
6.5. Примеры решения задач 150
ГЛАВА 7. Методы подобия и размерности 160
7.1. Подобие гидродинамических движений 160
7.1.1. Безразмерные уравнения движения A60). 7.1.2. Сила со-
сопротивления. Коэффициенты сопротивления A63). 7.1.3. Модели-
Моделирование A64). 7.1.4. Аэродинамические трубы. Бассейны A67).
7.1.5. Аналитические коэффициенты сопротивления A67).
7.2. Метод размерностей физических величин 169
7.2.1. Основные и производные величины A69). 7.2.2. Определя-
Определяющие параметры A70). 7.2.3. Выбор определяющих параметров и
основных величин A75).
7.3. Примеры решения задач 176
ГЛАВА 8. Турбулентность 184
8.1. Ламинарное и турбулентное течение 184
8.2. Устойчивость стационарного движения жидкости 187
8.3. Устойчивость движения жидкости между коаксиальными цилин-
цилиндрами 189
8.4. Устойчивость движения в канале 192
8.5. Сценарии зарождения турбулентности 196
8.5.1. Понятия аттрактора и бифуркации A97). 8.5.2. Сцена-
Сценарий Ландау-Хопфа B03). 8.5.3. Сценарий Рюэля-Такенса B05).
8.5.4. Сценарий Фейгенбаума B07).
8.6. Уравнения Рейнольдса 211
8.7. Теории Прандтля, Кармана и Дайслера 214
8.8. Цепочка уравнений Фридмана 217
8.9. Турбулентное движение жидкости в трубах 218
8.9.1. Гладкие трубы B19). 8.9.2. Шероховатые трубы B21).
8.10. Развитая турбулентность 223
8.11. Примеры решения задач 227
Оглавление
ГЛАВА 9. Пограничный слой 232
9.1. Понятие пограничного слоя 232
9.2. Уравнения Прандтля 233
9.2.1. Безразмерный вид уравнений Прандтля B34).
9.3. Обтекание полубесконечной пластины 235
9.3.1. Толщина вытеснения B37). 9.3.2. Разгонный участок B37).
9.4. Интегральное соотношение Кармана 238
9.4.1. Обтекание полубесконечной пластинки B40).
9.5. Отрыв пограничного слоя 242
9.6. Турбулентный пограничный слой 243
9.7. Примеры решения задач 245
ГЛАВА 10. Газовая динамика 250
10.1. Скорость звука 250
10.2. Параметры газа в заторможенном потоке 251
10.2.1. Температура торможения B52).
10.3. Стационарный одномерный поток сжимаемого газа 253
10.3.1. Сопло Лаваля B55).
10.4. Истечение газа из резервуара через сужающийся насадок 256
10.5. Ударные волны и скачки уплотнения 259
10.5.1. Конус Маха B59). 10.5.2. Поверхности разрыва B60).
10.6. Ударная адиабата (адиабата Гюгонио) 262
10.6.1. Прямая ударная волна в идеальном газе B63).
10.7. Ударные волны слабой интенсивности 265
10.7.1. Образование ударных волн B67). 10.7.2. Ударная волна при
взрыве B68).
10.8. Косая ударная волна 270
10.8.1. Максимальный угол поворота потока B72). 10.8.2. Обте-
Обтекание клина B75).
10.9. Волна разрежения 277
10.9.1. Обтекание тупого угла сверхзвуковым потоком B77).
10.9.2. Максимальный угол поворота потока B80).
10.10. Пересечение ударных волн и волн разрежения 284
10.10.1. Отражение ударной волны от стенки B84). 10.10.2. Пе-
Пересечение двух ударных волн B86). 10.10.3. Пересечение ударной
волны с тангенциальным разрывом B87). 10.10.4. Истечение газа
из сужающегося насадка B87). 10.10.5. Сопло Лаваля в нерасчет-
нерасчетном режиме B88). 10.10.6. Обтекание пластинки сверхзвуковым
потоком под малым углом атаки B89).
10.11. Примеры решения задач 290
ГЛАВА 11. Магнитная гидродинамика 297
Введение 297
11.1. Уравнения Максвелла 298
11.2. Модель среды 299
Оглавление
11.3. Уравнения движения проводящей жидкости в электромагнитном
поле 301
11.3.1. Электромагнитные массовые силы C01). 11.3.2. Тензоры
электрических и магнитных напряжений C02). 11.3.3. Уравнение
движения C03). 11.3.4. Уравнение сохранения внутренней энер-
энергии C05). 11.3.5. Замкнутая система уравнений движения C05).
11.3.6. Граничные условия C07). 11.3.7. Плотности потоков им-
импульса и энергии C07).
11.4. Критерии подобия в магнитной гидродинамике 308
11.5. «Вмороженность» магнитных силовых линий 311
11.6. Диффузия магнитного поля 316
11.7. Волны Альвена 318
11.8. Задача Гартмана 320
11.9. Задача Стокса 324
11.10. Магнитогидродинамические машины 325
11.10.1. Электромагнитные насосы C25). 11.10.2. Магнитогид-
родинамический генератор C28). 11.10.3. Плазменные двигате-
двигатели C30).
11.11. Турбулентное динамо 331
11.12. Одномерное движение проводящей жидкости в поперечном магнит-
магнитном поле 333
11.12.1. Уравнение Бернулли в магнитной гидродинамике C35).
11.13. Ударные волны в магнитной гидродинамике 336
11.14. Примеры решения задач 339
Приложения 346
П. 1. Дифференциальные операторы в криволинейных координатах .... 346
П.2. Компоненты тензора деформаций в криволинейных координатах . . 347
П.З. Компоненты тензора напряжений в криволинейных координатах . . 347
П.4. Уравнения движения в криволинейных координатах 348
П.5. Перевод электромагнитных величин из гауссовой системы в СИ и
обратно 349
Список рекомендуемой литературы 350
Предметный указатель 351
y Учителя w сюттмфа
Предисловие
Учебное пособие написано на основе курса лекций, прочитанных авто-
авторами в разные годы студентам физико-технического факультета Уральского
политехнического института (ныне Уральский государственный технический
университет) и физического факультета Уральского государственного универ-
университета. Основная цель пособия состоит в том, чтобы дать студентам общее
представление об основных моделях и методах описания движений сплошной
среды.
Часть материала курса была издана Уральским государственным универ-
университетом около четверти века назад в виде отдельных брошюр:
П.Е. Суетин. Механика деформируемых сред. — Свердловск, 1981.
П.Е. Суетин. Механика жидкости. — Свердловск, 1983.
П.Е. Суетин. Турбулентность. Пограничный слой. — Свердловск, 1984.
П.Е. Суетин. Газовая динамика. — Свердловск, 1984.
П.Е. Суетин. Магнитная гидродинамика. — Свердловск, 1984.
Для данного учебного пособия этот материал существенно переработан и
дополнен с учетом достижений последних десятилетий. Особенно это касается
теории гидродинамической устойчивости и перехода к турбулентному режиму
течения жидкости. Практическое применение всех теоретических положений и
математических моделей иллюстрируется примерами решения задач, которые
приведены в конце каждой главы.
Механика сплошных сред является базовым курсом для подготовки физи-
физиков. Он включает элементы теории упругости, гидродинамики, газодинамики
и магнитной гидродинамики. Материал отобран так, чтобы курс можно было
изучить в течение одного семестра (около 80 часов аудиторных занятий) и
при этом заложить основу для изучения таких дисциплин как теплофизика,
термодинамика необратимых процессов, кинетическая теория газов, физика
атмосферы и др.
Для успешного усвоения материала достаточно знания курсов общей фи-
физики и высшей математики в объеме, предусмотренном стандартной вузовской
программой.
Рассчитано на студентов старших курсов, обучающихся на физических и
механико-математических специальностях университетов, а также на некото-
некоторых инженерных специальностях. Часть материала доступна студентам млад-
младших курсов и может быть использована при изучении соответствующих раз-
разделов общей физики. Учебное пособие будет полезно также магистрантам и
аспирантам, желающим освоить или освежить в памяти методы механики
сплошных сред.
Сложилось так, что работу над учебным пособием мне пришлось за-
заканчивать одному. Я старался придерживаться тех же критериев, которыми
мы руководствовались при отборе и изложении материала, работая вместе с
Паригорием Евстафьевичем. Основной критерий — доступность для студентов,
впервые изучающих механику сплошных сред, в том числе самостоятельно.
Буду признателен за любые замечания, способствующие устранению воз-
возможных ошибок и улучшению содержания учебного пособия.
2006 г. ВТ. Черняк
ГЛАВА 1
МОДЕЛЬ СПЛОШНОЙ СРЕДЫ
Механика сплошных сред (МСС) - раздел механики, основным
содержанием которого является изучение движения газов, жидкостей
и твердых деформируемых тел. Все вещества независимо от их агре-
агрегатного состояния объединены понятием «среда».
1.1. Модели механического движения
Механика сплошных сред по сравнению с механикой материальной
точки и механикой абсолютно твердого тела является дальнейшим
усложнением модели движения тела, модели, приближающей нас к
изучению движения реальных физических тел и объектов. В действи-
действительности реальные физические тела не являются ни точечными, ни
абсолютно твердыми, однако изучение таких абстрактных тел было
необходимо для выявления наиболее характерных и общих законов
движения реальных объектов.
В развитии физики модели изучаемых явлений играют определя-
определяющую роль. Обычно любое исследование начинается с того, что при-
принимается наиболее простая модель изучаемого явления, позволяющая
описать это явление математически и изучить основные характерные
для него свойства. Сравнение теории с опытом подтверждает или, нао-
наоборот, отвергает адекватность построенной модели изучаемому явлению.
Точнее говоря, сравнение теоретической модели с экспериментом поз-
позволяет определить границы применимости теории. В дальнейшем мо-
модель усложняется, что позволяет расширить границы ее применимости.
Так, изучение механического движения тел начинается с простей-
простейшей модели — модели материальной точки. Предполагается, что ос-
основные свойства реальных тел можно изучать, не принимая во вни-
внимание их протяженность и деформируемость. При этом физическое
состояние тела характеризуется только его массой, а положение в про-
пространстве только тремя координатами. На основе такой простой модели
установлены фундаментальные законы движения, например, законы
сохранения импульса и момента импульса, закон сохранения механи-
механической энергии. Это позволило изучить законы свободного падения тел
и движения небесных объектов.
Однако существует достаточно много практических задач, которые
не могут быть решены при помощи модели, игнорирующей размеры ре-
10 Модель сплошной среды [ Гл. 1
альных тел, например, движение волчков, гироскопов и т.д. Для такого
рода задач создана модель абсолютно твердого тела. Предполага-
Предполагается, что тело имеет реальные размеры и расстояние между любыми
двумя точками внутри него не изменяется в процессе движения. В
этом случае физическое состояние тела характеризуется не только его
массой, но и тремя моментами инерции относительно трех взаимно
перпендикулярных осей. Положение тела в пространстве определяется
шестью обобщенными координатами: тремя декартовыми координатами
какой-либо точки тела и тремя углами Эйлера, характеризующими
ориентацию тела относительно выбранной системы координат.
В то же время существует множество явлений, которые не могут
быть поняты и в рамках модели абсолютно твердого тела. Например,
движение жидкостей, газов и упругих тел, при котором расстояния
между двумя точками среды в процессе движения существенно изме-
изменяются.
Таким образом, мы приходим к модели движения деформируемого
тела, являющегося предметом изучения механики сплошных сред.
Усложнение модели абсолютно твердого тела состоит в том, что в про-
процессе движения расстояния между любыми точками тела могут изме-
изменяться — тело деформируется. Разумеется, для такой модели суще-
существенно усложняется используемый математический аппарат. В общем
случае к имеющимся характеристикам движения абсолютно твердого
тела для описания деформации необходимо добавить еще девять, а
само тело должно характеризоваться еще тремя величинами, опреде-
определяющими степень и характер деформации под действием внешних сил.
1.2. Бесконечно малые в модели сплошной среды
Понятие «сплошная среда» также является некоторой физической
моделью реальных тел. Несмотря на то что все физические тела состо-
состоят из отдельных молекул и атомов, масса которых сосредоточена в их
ядрах, так что подавляющая часть пространства внутри тела «пустая»,
будем предполагать, что вещество распределено непрерывно по всему
объему тела и плотность среды является непрерывной функцией коор-
координат и времени. Будем полагать, что и другие физические величины
также являются непрерывными функциями координат и времени.
Такая модель позволяет нам воспользоваться математическим ап-
аппаратом дифференциального и интегрального исчисления. Однако при
этом необходимо определить, что следует понимать под бесконечно
малыми физическими величинами.
1.2.1. Бесконечно малый элемент объема. Рассматривая движе-
движение сплошной среды, будем мыслено разбивать ее на некоторые малые
части, в пределах которых все физические величины можно считать
примерно однородными. Значения физических величин в любой фик-
фиксированный момент времени изменяются лишь при переходе от одной
малой части среды к другой соседней части, и это изменение происхо-
1.2] Бесконечно малые в модели сплошной среды 11
дит непрерывно в зависимости от координат элементарных объемов. В
любом фиксированном элементе объема значения физических величин
могут непрерывно изменяться с течением времени.
Ясно, что малую часть среды следует рассматривать как физи-
физически бесконечно малый элемент объема 0. Это означает, с одной
стороны, что элемент объема AV должен быть много меньше всего
объема системы V с тем, чтобы можно было воспользоваться методами
дифференциального и интегрального исчисления. С другой стороны,
этот элемент объема должен быть достаточно большим, содержащим
большое число молекул для того, чтобы его состояние можно было оха-
охарактеризовать макроскопическими физическими величинами, такими
как давление и температура. Действительно, если бы элемент объема
AV не содержал достаточно большого числа молекул, то флуктуации
макроскопических величин в результате хаотического движения моле-
молекул были бы столь велики, что невозможно было что-либо сказать о
значениях этих величин в данный момент времени.
Пусть п — число молекул в единице объема среды, т.е. п~х - объем,
приходящийся в среднем на одну молекулу. Тогда требование, предъ-
предъявляемое к физически бесконечно малому элементу объема, можно
записать в следующем виде:
n~l < AV< V. A.1)
Очевидно, что понятие бесконечно малого объема в МСС является
понятием относительным. Например, плотность межзвездного газа со-
составляет примерно одну частицу (атомарный водород) на 1см3. Если
попытаться описывать методами МСС движение космического аппара-
аппарата объемом V « 1 м3 в межзвездном газе, то необходимо считать за
элемент объема, по крайней мере, 1см3, т.е. AV/V « 10~6. Однако
в таком элементе объема в среднем содержится лишь одна молекула.
Поэтому термодинамические величины для него не имеют физического
смысла. Методы МСС в данном случае применять нельзя.
С другой стороны, если рассматривать движение Земли в меж-
межзвездном газе, то нам удастся удовлетворить соотношению A.1). Дей-
Действительно, объем Земли составляет около 1012км3. Выбирая элемент
объема 1 км3, нетрудно удовлетворить условию AV <С V. Такой выбор
AV в какой-то мере удовлетворяет и левой части неравенства A.1),
так как элемент объема будет содержать около 1015 молекул, что до-
достаточно для определения макроскопических величин. Следовательно,
задачу о движении Земли в межзвездном газе можно было бы решить
методами МСС, но при этом необходимо уточнить условие A.1) для
случая газовой среды.
В жидкостях и твердых телах среднее расстояние между атома-
атомами и молекулами всегда порядка размера самих молекул. Поэтому
требование достаточно большого числа молекул в элементе объема
0 Впервые этот термин предложил Х.Л. Лоренц
12 Модель сплошной среды [Гл.1
подразумевает, что молекулы непрерывно взаимодействуют между со-
собой. Именно взаимодействие между молекулами является механизмом,
который обеспечивает осреднение физических величин по всему эле-
элементу объема среды.
В газах молекулы большую часть времени двигаются свободно
с различными скоростями. Среднее расстояние /, проходимое отдель-
отдельной молекулой между двумя последовательными столкновениями, на-
называют средней длиной свободного пробега. Если d — эффективный
диаметр молекул (d ~ 10~10 м), an- число молекул в единице объема,
то /~ (nd2)-1.
Следовательно, физически бесконечно малый элемент объема для
газовой среды должен удовлетворять условию
/3< AV< V . A.2)
Это неравенство гарантирует, что в элементе объема будет находиться
достаточно большое число взаимодействующих молекул.
Если снова обратиться к примеру о движению Земли в межзвезд-
межзвездном газе, то нетрудно видеть, что левая часть неравенства A.2) не
выполняется, так как / « 1011 км. Это означает, что в ранее выбранном
элементе объема молекулы не сталкиваются и формальное усреднение
их характеристик даст некоторые макроскопические величины, значе-
значения которых будут испытывать сильные флуктуации. Объем порядка
/3 значительно превышает объем самой Земли и сравним с объемом
Солнечной системы. Поэтому задача не может быть решена в рам-
рамках механики сплошных сред. Необходимо использовать кинетическую
теорию газов.
1.2.2. Бесконечно малый промежуток времени. Для того чтобы
можно было использовать дифференциальное и интегральное исчисле-
исчисление, физически бесконечно малый промежуток времени At, с одной
стороны, должен быть мал по сравнению с характерным временем
задачи тр. (Для периодических движений тр имеет смысл периода, для
неустановившихся движений — времени установления стационарного
состояния или времени релаксации системы.)
С другой стороны, физически бесконечно малый промежуток вре-
времени должен быть много больше характерного времени молекулярного
движения тм. В этом случае выделенный элемент объема в любой фик-
фиксированный момент времени можно охарактеризовать некоторым набо-
набором макроскопических величин, зависящих от его координат. Только
в результате многих межмолекулярных взаимодействий может произой-
произойти выравнивание любой физической величины по всему выделенному
элементу объема.
Для газов тм имеет смысл среднего времени свободного пробега
молекул, для жидкостей — времени локализации молекулы в данной
точке, для твердых тел — периода колебаний молекул или атомов кри-
кристаллической решетки.
1.3] Примеры решения задач 13
Таким образом, физически бесконечно малый промежуток времени
в механике сплошных сред должен удовлетворять следующему условию:
тм<Дг<тр. A.3)
Левая часть неравенства должна выполняться еще и потому, что пере-
передача взаимодействия между соседними элементами среды может осу-
осуществляться только через движение молекул, находящихся на границе
этих элементов. Следовательно, при временах, меньших или порядка
тм, не существует взаимодействия между соседними частями среды,
т. е. отсутствует механизм, при помощи которого непрерывно изменя-
изменяются макроскопические величины.
Контрольные вопросы
1. В чем состоит основная идея метода МСС? Его достоинства и недостатки.
2. Поясните смысл предположения сплошности среды.
3. Как в МСС определяются физически бесконечно малые, элемент объема
и промежуток времени?
4. В чем особенность выбора малого элемента объема в газовой среде?
1.3. Примеры решения задач
Задача 1
При экспериментальном изучении явлений переноса в газах часто
используется метод «двух объемов». Представим себе эксперименталь-
экспериментальную ячейку в виде двух камер, объединенных узким капилляром.
Можно ли моделировать газ как сплошную среду, если среднее дав-
давление в ячейке равно р = 8кПа, радиус капилляра а = 10~3м, длина
L = 0,05 м, объемы камер V = 10~3 м3, время установления стационар-
стационарного состояния г = 60 с. Ячейка заполнена аргоном при температуре
Т = 293К. Газ считать идеальным, а молекулы аргона - твердыми
сферами с эффективным диаметром d = 3,42 • 10~10 м. Молярная масса
аргона М = 0,0399 кг/моль.
Решение. Оценим среднюю длину свободного пробега газовых
молекул при заданных условиях. Как известно из курса общей физики,
для молекул, моделируемых твердыми шариками, имеем
I = -1 . = J*1 . « Ю-6 м, р = пкТ, A.4)
V2 d2 V2d2
где к = 1,38 • 10~23 Дж/К — постоянная Больцмана.
Из макроскопических размеров экспериментальной ячейки, дан-
данных в условии задачи, выберем наименьший, радиус капилляра. Если
неравенство A.2) будет выполняться для этого параметра, то для
других элементов ячейки оно тем более будет выполнено. Поскольку
/3 « 10~18м3, а3 = 10~9м3, то всегда можно выбрать такой элемент
объема AV, чтобы выполнялось неравенство A.2).
14 Модель сплошной среды [ Гл. 1
Среднее время свободного пробега молекул можно оценить по фор-
формуле
тм = = =2,5- 10 ус, V = W__ A.5)
v у ^^
где ^ — средняя скорость теплового движения молекул, R =
= 8,31 Дж/(К • моль) — молярная газовая постоянная.
Характерное макроскопическое время по условию задачи равно
тр = 60 с. Следовательно, можно выбрать такой физически бесконечно
малый промежуток времени At, чтобы выполнялось неравенство A.3).
Таким образом, в данных экспериментальных условиях газ можно
моделировать как сплошную среду.
Задача 2
При движении тел в газе или жидкости имеет место сопротивление
трения. Применим ли метод механики сплошных сред для вычисления
силы сопротивления искусственного спутника Земли, двигающегося по
эллиптической орбите с перигеем h\ = 100 км и апогеем h^ = 300 км?
Диаметр спутника d = 1 м, температура среды Т = 300 К, молярная
масса газа М = 0,029 кг/моль, эффективный диаметр молекул d = Зх
х 10~10м, число молекул в единице объема около поверхности Земли
щ = 2,7 • 1025м-3.
Решение. Для оценки числа молекул в единице объема на высо-
высоте h воспользуемся барометрической формулой:
/ Mghh\ ( Ro \2 n а.
п = п0 ехр (—§г) , gh = (ЖТ1) g. A.6)
Здесь Ro = 6,37 • 106 м — средний радиус Земли, g (= 9,81 м/с2) и gh —
ускорения свободного падения на поверхности Земли и на высоте h.
Ускорение свободного падения и плотность молекул: в перигее — g\ =
= 9,51 м/с2, щ = 3,24 • 1020 м-3; в апогее - g2 = 8,95 м/с2, п2 = 7,43х
х 10пм-3.
Длины свободного пробега вычисляются по формуле A.4): 1\ = 7,7х
х 10-3м, /2 = 3,4- 106м.
Поскольку объем спутника составляет V « 1 м3, то очевидно, что
условие A.2) выполняется лишь вблизи перигея. Следовательно, метод
механики сплошных сред может быть использован для вычисления
силы сопротивления спутника только на части орбиты, близкой к
перигею.
ГЛАВА 2
КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
2.1. Деформация
Деформацией называют изменение формы и объема твердого
тела под действием внешних сил или при изменении его темпера-
температуры.
Рассмотрим в декартовой системе координат некоторое деформиру-
деформируемое тело (рис. 2.1). Обозначим оси координат через Х{, г = 1,2,3. Вы-
Выделим бесконечно малый элемент объема тела, включающий точку Р.
Положение этой точки задается вектором г с координатами х\,Х2,х%.
Пусть тело неподвижно относительно выбранной системы коор-
координат. После приложения внешней силы в целом неподвижное тело
деформируется и точка Р перейдет в другую точку пространства Р',
характеризуемую вектором г' с компонентами x[,xf2,x'3. Смещение
точки Р, равное
и(г)=Г/-Г, Щ(Г) = X't - Xi , B.1)
называется деформацией, или вектором смещения, или просто сме-
смещением. Деформация является функцией координат точки Р, так как
в других точках тела она может быть
и другой. Задание вектора и как
функции г полностью определяет де-
деформацию тела во всех точках.
Теперь рассмотрим деформацию
в точке Q, лежащей около точки Р
в дифференциальной окрестности пер-
первого порядка и имеющей координату
г + dr (рис. 2.1). После деформации
точка Q перейдет в точку Q'. В общем
случае деформация точки Q не будет
совпадать с деформацией точки Р. Из
рис. 2.1 видно, что деформации двух
точек связаны между собой следую-
следующим соотношением:
о
Рис. 2.1. Деформация элемента
объема
u(r + dr) = u(r) + du, щ(г + dr) = щ(г)
B.2)
16 Кинематика сплошной среды [Гл.2
Вектор du называют вектором относительного смещения или
просто относительным смещением.
Разложим функцию щ(г + dr) в ряд Тейлора. Ограничившись ли-
линейными по dxi членами, получим
Fill
^ .... B.3)
Во втором слагаемом правой части по повторяющемуся индексу к,
принимающему значения 1,2,3, подразумевается суммирование 0.
Если деформации тела во всех его точках удовлетворяют соотно-
соотношению B.3), оно называется телом однородной линейной деформации.
Учет нелинейных членов разложения B.3) необходим лишь при боль-
больших деформациях.
Мы будем рассматривать только малые деформации, которые на-
называют упругими. При упругих деформациях после прекращения дей-
действия внешних сил тело полностью восстанавливает свою форму и
объем.
Сравнивая выражения B.2) и B.3) для компонент вектора относи-
относительного смещения получаем
ди ди
^dxk = Aikdxk, Aik = —^. B.4)
OX
dui = dxk = Aikdxk, Aik =
OXk OXk
Тензор Aik второго ранга, третьей мерности (г, к = 1,2,3) назы-
называется тензором относительной деформации. Он характеризует де-
деформацию точки Q относительно деформации точки Р в выделенном
элементе объема. Компоненты Aik являются функциями координат и
времени. При малых деформациях компоненты тензора относительной
деформации малы, т.е. Aik <С 1.
Представим А{к в виде суммы симметричной и антисимметричной
части
Aik = - {Aik + Aki) + - {Aik - Aki) = eik + <pik • B.5)
Симметричная часть А{к называется тензором деформации
Sik = Up. + p), ?ik = ski. B.6)
2 \oxk dxi J
BJ)
Антисимметричная часть А{к называется тензором поворота
ui дик\
) 9 = №
0 В дальнейшем по повторяющимся индексам, обозначающим тензорную
размерность физических величин, всегда подразумевается суммирование, а
знак суммы для простоты не пишется.
9 91
Тензор поворота
П
Компоненты тензора <^& образуют матрицу
2.2. Тензор поворота
Рассмотрим физический смысл тензора поворота. Предположим, что
все компоненты тензора деформаций равны нулю. Тогда в соответствии
с выражениями B.4), B.5) вектор относительного смещения определя-
определяется только тензором поворота, т. е.
B.8)
B.9)
Поскольку еры — антисимметричный тензор, то он включает только
три независимых компоненты. Введем следующие обозначения
/О 1 Г\\
Тогда компоненты вектора du запишутся следующим образом:
B.11)
Если ввести вектор поворота ^ с проекциями на координатные оси
(^ь ^2» ^з)> то выражения B.11) можно записать в векторном виде О
du =
Как известно из механики, именно так записы-
записывается вектор малого поворота на угол р абсолютно
твердого тела.
Таким образом, возвращаясь к рис. 2.1, видим,
что выражение B.12) описывает вектор малого по-
поворота элемента объема, содержащего точку Q, от-
относительно точки Р на малый угол (р как абсолютно
твердого тела (рис. 2.2).
Следовательно, компоненты тензора поворота
описывают не деформацию элемента объема те-
тела в данной точке в собственном смысле этого
слова, а лишь его поворот как абсолютно твер-
твердого тела.
B.12)
Рис. 2.2. Поворот
элемента объема
О Векторные произведения двух векторов а и b будем обозначать квадрат-
квадратными скобками [ab], а скалярные — круглыми (ab).
18 Кинематика сплошной среды [Гл.2
Нетрудно видеть, что
1 /ди\ дщ\ 1
2 \дх2 дх\) 2
I, B.13)
jtZO су \ о о у г 1 су
1 /<9-и3 #гм\ 1
9^31 = ~~ I — ) = —9^2 = — rot2 и •
В векторном виде эти соотношения можно записать следующим образом:
ср = i rot u. B.14)
Таким образом, компоненты тензора поворота есть компоненты ро-
ротора смещений.
2.3. Тензор деформации
Пусть компоненты тензора поворота равны нулю. В этом случае от-
относительное смещение полностью определяется тензором деформации:
B.15)
0
0
0
^22
0
0
0
0
Тензор деформации, как всякий симметричный тензор, можно при-
привести к главным осям. Это означает, что существует такая система
координат ж}, #2> Ж3' в К0Т0Р°й тензор деформации имеет диагональ-
диагональный вид
(ей 0 0 ^
B.16)
Координатные оси х® называют главными осями, а диагональные
элементы е^, е\2, е^ —главными значениями тензора деформации.
Из выражений B.15), B.16) следует, что деформации в главных осях
запишутся в виде
du\ = e°n dx°{ , du°2 = s°22 dx\ , du\ = s°33 dx°3 . B.17)
Здесь du® есть деформация отрезка dx\. Все деформации на-
направлены по главным осям. Отсюда видно, что главные деформации
описывают локальное растяжение или сжатие элемента объема в
направлении главных осей. Растяжение или сжатие по трем взаимно
перпендикулярным направлениям называется чистой деформацией.
Если все компоненты тензора поворота равны нулю, то всегда в эле-
элементе объема, лежащего около точки Р (рис. 2.1), можно определить
главные оси деформации, в которых этот элемент объема испытывает
чистую деформацию. Если же компоненты тензора <^/с не равны нулю,
то они описывают поворот этих главных осей вокруг точки Р на малый
угол (р. Таким образом, деформация некоторого элемента объема
2.3] Тензор деформации 19
тела в общем случае сводится к его чистой деформации, т. е.
растяжению или сжатию по главным осям деформации, и повороту
главных осей деформации на малый угол (р, поскольку этот поворот
происходит как поворот абсолютно твердого тела.
2.3.1. Изменение объема тела при деформации. Компоненты
тензора (pik описывают поворот элемента объема как абсолютно твер-
твердого тела и, следовательно, не определяют изменение объема тела
при деформации. Поэтому рассмотрим чистую деформацию в главных
осях, которая единственно приводит к изменению величины элемента
объема.
Выделим в теле элемент объема для простоты в виде прямоуголь-
прямоугольного параллелепипеда. Его величина до деформации в главных осях
определяется выражением
AVb = Ах^ Ах°2 Ах°3. B.18)
После деформации ребра элементарного параллелепипеда получат
приращения, их длины примут значения
Ах°/ = Ax^ + dvPi, i= 1,2,3. B.19)
В силу линейности деформаций растяжение или сжатие любого
отрезка Ах® (не обязательно бесконечно малого) в соответствии с
выражениями B.17) равно du® = ?%Ах®. Тогда элемент объема после
деформации будет иметь величину
AVtf = A + е?,)A + 4г)A + 4$) Avo ¦ B-20)
Поскольку рассматриваются малые деформации, \е®к\ <С 1, то, пре-
пренебрегая членами второго порядка малости и выше, запишем выраже-
выражение B.20) в виде
ДVtf = 0 + *ii + 4 + 4) ДМ, • B.21)
Для относительного изменения элемента объема при чистой дефор-
деформации получаем
ДУо - AVb о ,-0 , о _ -0 /9 о<л
7
Очевидно, что величина относительного изменения объема тела при
деформации не зависит от выбора системы координат. Таким образом,
след тензора деформаций, т. е. сумма его диагональных элементов,
инвариантен по отношению к выбору системы координат, т. е.
е^ = вц. Поэтому для нахождения относительного изменения элемента
объема тела при деформации нет необходимости приводить тензор
деформации к главным осям.
Соотношение B.22) с учетом B.6) можно записать в следующем
^^ ^ |* B.23)
20 Кинематика сплошной среды [ Гл. 2
Таким образом, изменение величины элемента объема тела при
деформации описывается диагональными компонентами тензора
?ik, а недиагональные компоненты этого тензора описывают де-
деформацию сдвига, т. е. изменение формы рассматриваемого элемен-
элемента объема.
2.3.2. Геометрические свойства линейных деформаций.
1. Точки элемента объема тела, находящиеся до деформации в
одной плоскости, после линейной деформации также расположатся
в одной плоскости.
Действительно, уравнение плоскости в главных осях имеет вид
ax°l+bx02 + cx°3 + d = 0. B.24)
После деформации новые координаты точек плоскости будут связа-
связаны со старыми координатами соотношениями
х\' = х\ + е°и х? , х°2' = х02 + е022х°2, х°3 = х°3 + г°33 х°3. B.25)
Тогда координаты точек после деформации будут удовлетворять
уравнению
« ж?'+ Ъ хо>+ с xo' + d = O) B26)
т. е. новые координаты точек после деформации также будут удовле-
удовлетворять уравнению некоторой, в общем случае другой плоскости. Этот
результат справедлив в любой системе координат и не только для чи-
чистой деформации, которую мы рассматривали для доказательства. Это
обобщение является следствием того, что поворот элемента объема,
содержащего некоторую плоскость, как абсолютно твердого тела не
может сместить точки тела из этой плоскости.
2. Точки, лежащие на одной прямой в элементе объема до де-
деформации, после деформации также расположатся на некоторой
прямой.
Это следует из первого свойства, так как прямая является геомет-
геометрическим местом точек пересечения двух плоскостей. Таким образом,
влияние линейной деформации на точки, расположенные на некотором
отрезке прямой, проявляется, во-первых, в повороте прямой на некото-
некоторый малый угол, и, во-вторых, в растяжении или сжатии этого отрезка.
3. Две параллельные до деформации плоскости в элементе объе-
объема останутся параллельными и после деформации.
Действительно, пусть имеем две параллельные плоскости в элемен-
элементе объема. В главных осях их уравнения имеют вид
Ax\ + Bxl + Cxl = 0, ax\ + bxl + cxl = 0. B.27)
Плоскости параллельны, если выполняются соотношения
- = ^ = - . B.28)
а о с
2.4] Температурная деформация 21
После деформации координаты точек элемента объема примут зна-
значения B.25). Соответственно изменятся и уравнения плоскостей
1 + Е\\ 1+^22
§
B 29)
Нетрудно видеть, что условие B.28) параллельности плоскостей вы-
выполняется и после деформации.
4. Две параллельные прямые, проведенные в элементе объема до
деформации, останутся параллельными и после деформации.
Это следует из свойства 3 сохранения параллельности двух плоско-
плоскостей при деформации.
Повторяя рассуждения свойства 1, можно утверждать, что свойства
параллельности прямых и плоскостей сохраняются при произвольной
линейной деформации.
2.3.3. Эллипсоид деформации. Рассмотрим в элементе объема
сферу единичного радиуса, центр которой находится в начале коорди-
координат. Уравнение сферы в главных осях имеет вид
После деформации точки сферы будут иметь координаты B.25) и
окажутся на поверхности, описываемой следующим уравнением:
т. е. уравнение сферы переходит в уравнение эллипсоида, если все
главные значения тензора деформации различны.
Снова этот результат справедлив не только в главных осях, но и
при произвольной линейной деформации, так как поворот элемента
объема как абсолютно твердого тела не изменит формы поверхности,
расположенной внутри этого объема.
Если все главные значения тензора деформации равны между со-
собой, то, как следует из уравнения B.31), сфера переходит в сферу
большего или меньшего радиуса. Если е®± = е^ ф ^зз' то сФеРа пере-
переходит в эллипсоид вращения.
2.4. Температурная деформация
Деформация тела может происходить не только вследствие прило-
приложения к нему внешних сил, но и в результате изменения его тем-
температуры. В пределах выделенного элемента объема будем считать
температуру однородной, т. е. одинаковой во всех точках. Пусть в на-
начальный момент времени температура элемента объема равнялась То, а
после нагревания или охлаждения тела стала равной Т, т. е. изменение
22 Кинематика сплошной среды [ Гл. 2
температуры равно AT = Т — Tq. При этом внутри элемента объема
в силу однородности его температуры напряжения не возникают, а
происходит лишь тепловое расширение или сжатие этого элемента
объема. В том случае, когда относительное изменение температуры
мало, т.е. |ДТ/ТЬ| <С 1, деформацию элемента объема можно считать
пропорциональной изменению температуры:
duj = ejkdxk, eJk = aikAT. B.32)
В этом выражении роль тензора относительной деформации игра-
играет ejk, называемый тензором теплового расширения] симметричный
тензор второго ранга aik — коэффициенты линейного теплового рас-
расширения. Следовательно, температурная деформация элемента объема
тела происходит без его поворота и заключается в расширении или
сжатии по трем взаимно перпендикулярным главным осям.
В главных осях тензор aik имеет вид
B.33)
Очевидно, при температурной деформации сфера внутри элемента
объема тела переходит в эллипсоид. По аналогии с B.31) имеем
(*?? (*ГJ (*ГJ = ! B 34)
0
0
0
0
0
0
<*зз
Если тело изотропно, т. е. его физические свойства одинаковы во
всех направлениях, то а\х = оР22 = оР^ = а и сфера деформируется
в сферу. Если оРп = а^2 ф с^зз' то сФеРа деформируется в эллипсоид
вращения.
Для изотропного тела тензор теплового расширения записывается
в виде Т /9л,,
eik = aoik /\1 . (/.до)
Здесь 8ik — символ Кронекера — единичный тензор второго ранга,
определяемый так, что 8ik = 1 при i = k и 5ik = 0 при г Ф к\ след
тензора 5ц = 3.
В этом случае для компонент вектора относительной деформации
получаем dUi = aATdXi, *= 1,2,3. B.36)
Так как dui есть приращение отрезка dx{ вследствие температурных
деформаций, то в силу линейности и изотропности деформаций для
приращения любого отрезка / при однородном нагревании тела имеем
А1 = аАТ1. B.37)
Относительное изменение объема при температурной деформации
по аналогии с B.23) определяется следующим выражением:
= 4 = а5цАТ = ЗаАТ . B.38)
2.5 ] Теорема Коши-Гелъмгольца 23
Это соотношение для физически бесконечно малых температурных
деформаций можно записать в дифференциальной форме:
Величину C = За называют коэффициентом объемного теплового
расширения тела. Производная в последнем выражении взята при
постоянном давлении, так как при однородном нагревании тела в отсут-
отсутствие внешних сил внутри него не возникает каких-либо напряжений.
2.5. Теорема Коши-Гельмгольца
При рассмотрении деформаций мы предполагали, что тело в целом
покоится относительно выбранной системы координат. Если же под
действием внешних сил тело перемещается в пространстве, то будет
перемещаться и точка Р (рис. 2.1). Поэтому, рассматривая смещение
произвольного элемента объема в общем случае, мы можем сформули-
сформулировать теорему Коши-Гельмгольца.
Наиболее общее перемещение точки Q элемента объема деформи-
деформируемого тела, содержащего точку Р, может быть представлено в виде
суммы:
1) поступательного перемещения точки Р как полюса,
2) вращения вместе с элементом объема как абсолютно твердого
тела вокруг точки Р на малый угол (р,
3) собственно деформационного перемещения вследствие растяже-
растяжения или сжатия по трем взаимно перпендикулярным осям (глав-
(главным осям деформации).
Таким образом, в соответствии с теоремой Коши-Гельмгольца мож-
можно записать
щ(г + dr) = щ(г) + (fik dxk + ?ik dxk . B.40)
Если температура тела изменяется, то в правой части необходимо
добавить еще один член, учитывающий температурную деформацию
duj = aikAT dxk .
Контрольные вопросы
1. Какие деформации называются упругими?
2. Что характеризует относительная деформация?
3. В чем физический смысл тензора поворота?
4. Что характеризуют диагональные и недиагональные компоненты тензора
деформации?
5. Как определяется относительное изменение объема при деформации?
6. Докажите 4 основных свойства упругих деформаций.
7. Что называют температурной деформацией?
8. Справедливы ли свойства упругих деформаций для температурных де-
деформаций?
ГЛАВА 3
УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
3.1. Тензор напряжений
3.1.1. Силы массовые, объемные и поверхностные. При дей-
действии внешних сил тело деформируется, т. е. происходит смещение
частиц внутри тела. В результате изменения взаимного расположения
частиц происходит не только изменение формы и объема тела, но
возникают силы упругости (напряжения), стремящиеся восстановить
первоначальную конфигурацию частиц, а значит форму и объем тела.
Силы эти действуют внутри деформируемого тела на границах между
его частями.
Таким образом, все силы, действующие на элемент объема дефор-
деформируемого тела, можно разделить на две категории: силы массовые
(или объемные) и силы поверхностные.
Массовые силы. Массовые силы — это силы, пропорциональные
массе элемента объема тела. Если масса элемента объема AV равна
Am, то массовая сила, действующая на этот элемент объема, равна
C.1)
Здесь f — напряженность или плотность массовой силы, характе-
характеризует массовую силу, действующую на элемент объема единичной
массы. В общем случае напряженность массовой силы может зависеть
от координат и изменяться с течением времени, f = f(r, t).
Введем плотность среды р как предел отношения элемента массы
Am к его объему AV при AV, стремящемся к нулю:
р = hm —— . C.2)
да/^о AV
В пределах однородного элемента объема имеем
Am = pAV, AF = pfAV. C.3)
По аналогии произведение pf можно назвать напряженностью или
плотностью объемной силы.
Типичным представителем массовых сил является сила тяжести.
Силы поверхностные. Если внутри деформируемого тела мысленно
выделить некоторый объем, то на его поверхность со стороны осталь-
остальной части тела будут действовать некоторые силы вследствие дефор-
3.1
Тензор напряжений
25
мации, т. е. смещения одних участков тела по отношению к другим.
Поскольку взаимодействие между соседними участками тела может
осуществляться в конечном счете только молекулярными силами с
радиусом действия порядка размера молекул (~ 10~9м), то передача
силового взаимодействия от одного элемента объема к соседнему мо-
может осуществляться практически лишь через разделяющую их поверх-
поверхность. Поэтому нерассматриваемая часть тела действует на выделен-
выделенный элемент объема только через его поверхность, и это воздействие
может быть заменено некоторыми поверхностными силами.
Таким образом, поверхностные силы — это внутренние силы в
деформируемом теле, которые действуют на граничных поверхно-
поверхностях между соседними частями тела. Если на тело не действуют
внешние силы и оно однородно нагрето, то эти внутренние силы
отсутствуют, и все его части находятся в механическом и термодина-
термодинамическом равновесии.
Существенное отличие поверхност-
ных сил от массовых состоит в том, что
они зависят не только от координат и
времени, но и от ориентации площадки,
на которую они действуют.
Рассмотрим некоторый выделенный
объем тела (рис. 3.1). Действие осталь-
остальной части тела на этот выделенный объ-
объем можно заменить некоторыми силами,
действующими на его поверхность. Вы-
делим на этой поверхности элемент пло-
плорис зл. Поверхностные снлы
щади dS. Пусть п — нормаль к элементарной площадке dS. Нормаль
будем считать положительной, если она направлена вне выделенного
объема тела.
Пусть на элемент поверхности действует поверхностная сила dF^n\
Причем сила не обязательно направлена по нормали к элементу по-
поверхности. Верхний индекс (п) указывает на ориентацию площадки.
Тогда можно записать
dF(n) = a{n) dS ^ ^3.4)
Поверхностную силу а^п\ действующую на единицу площади, на-
называют напряженностью или плотностью поверхностных сил или
просто напряжением.
3.1.2. Тензор напряжений. Покажем, что напряжение сг^п\ дей-
действующее на площадку с произвольной ориентацией нормали п, можно
выразить через напряжения, действующие на три взаимно перпендику-
перпендикулярные площадки, в частности, имеющие направления координатных
осей 0.
0 Под направлением площадки здесь и далее подразумевается направление
нормали к этой площадке.
26
Уравнения теории упругости
[Гл. 3
¦A)
Для доказательства рассмотрим элемент объема AV, имеющий
форму тетраэдра ЛВС О (рис. 3.2). Оси декартовой системы координат
направлены вдоль ребер тетраэдра,
как показано на рис. 3.2. Заметим,
что форма элемента объема выбра-
выбрана для простоты доказательства и не
влияет на общность конечного ре-
результата.
Составим уравнение движения
бесконечно малого тетраэдра под дей-
действием массовых и поверхностных
сил.
Если р — плотность тела, то
рАV — масса тетраэдра. Пусть dS —
площадь грани ABC, dSi — пло-
площадь грани, перпендикулярной г-й
координатной оси, сг^ — напряжение
на площадке dSi, f — напряженность
массовых сил, v — скорость движения тетраэдра. Тогда в соответствии
со вторым законом Ньютона уравнение движения запишется следую-
следующим образом:
Рис. 3.2.
Напряжения на гранях
тетраэдра
рАV ^ = pfdV
at
dS
dS\ + <тB) dS2
C.5)
Если п(г) — нормаль к площадке dSi, направленная против направ-
направления г-й координатной оси, то имеем
dSi = (nn^)dS = -mdS, i= 1,2,3.
Здесь rii — проекция нормали п на координатную ось Х{. Знак минус в
последнем равенстве отражает тот факт, что нормаль к площадке dSi
и ось Х{ противонаправлены.
При уменьшении объема тетраэдра в уравнении движения C.5)
левая часть и первое слагаемое правой части уменьшаются пропорцио-
пропорционально кубу линейных размеров элемента объема, а остальные члены —
пропорционально их квадрату. Пренебрегая в уравнении C.5) членами
более высокого порядка малости, получаем
¦ О-C) 713 =
C.6)
Если верхние индексы опустить вниз, то проекции этого векторного
уравнения на оси координат запишутся в виде
0"l =
02 —
О =
СГ22П2
з.г
Тензор напряжений
27
Эти равенства можно записать в эквивалентном виде
а™ = aikUk • C.8)
Трехмерный тензор второго ранга а^ называется тензором напря-
напряжений.
Полученное равенство дает выражение для напряжения, действую-
действующего на произвольно ориентированную площадку, через напряжения,
действующие на три площадки, пер-
перпендикулярные координатным осям.
По физическому смыслу любая
компонента тензора aik представ-
представляет собой силу, действующую в на-
направлении оси г на единичную пло-
площадку, перпендикулярную оси к.
На рис. 3.3 показаны все ком-
компоненты тензора напряжений, кото-
которые действуют на гранях элемента
объема, имеющего форму прямоуголь-
прямоугольного параллелепипеда. Диагональные
компоненты тензора aik называют-
называются нормальными напряжениями, а
недиагональные — касательными на-
напряжениями.
В дальнейшем мы покажем (см. §4.5), что aik — симметричный
тензор, т. е. имеет лишь шесть независимых компонент. Как симмет-
симметричный тензор, он может быть приведен к главным осям и будет иметь
следующий вид:
СУ31'
/
<У21
х2
хг
Рис. 3.3. Напряжения на гранях
элемента объема
В общем случае отличные от нуля диагональные компоненты называют
главными значениями тензора напряжений. Если а®п = а\2 = а\ъ =
= -р, то это означает, что элемент объема испытывает всестороннее
равномерное сжатие. В этом случае тензор напряжений можно запи-
записать в виде
Vik = -$ikP- C.9)
3.1.3. Результирующая поверхностная сила, действующая на
единицу объема тела. Рассмотрим некоторый выделенный объем
деформируемого тела. Напряжения, действующие внутри него, не мо-
могут дать вклад в результирующую силу, так как по закону равенства
действия и противодействия силы взаимодействия между внутренними
частями выделенного объема взаимно компенсируются. Следовательно,
результирующая сила может быть составлена лишь из сил, действу-
действующих на поверхности выделенного объема со стороны исключенной
части тела.
28 Уравнения теории упругости [ Гл. 3
Пусть F — результирующая сила, действующая на единицу объема.
На элемент объема dV действует сила FdV. Результирующая сила,
действующая на объем V, будет равна результирующей поверхностной
силе. С учетом выражений C.4), C.8) имеем
[ F dV = I dF(n) = <? <т(п) dS , C.10)
V S S
\
dS = 1 aiknk dS.
S
Здесь интегрирование ведется по объему V и ограничивающей его
поверхности S. Если для элементарной площадки dS определить на-
направление нормали к ней, то можно ввести вектор dS = ndS такой,
что его модуль равен величине площадки dS, а направление совпадает
с направлением нормали п к этой площадке. Тогда имеем
C.11)
По теореме Гаусса-Остроградского 0 получаем
V. C.12)
Так как выражение C.12) справедливо для произвольного объе-
объема V, то для результирующей силы, действующей на единицу объема
деформируемого тела, имеем
% C.13)
Таким образом, зная зависимость компонент тензора напряжений
от координат и времени, по формуле C.13) можно вычислить силу,
действующую на единицу объема или элемент объема в любой точке
деформируемого тела в любой момент времени, а следовательно, соста-
составить уравнения движения этих элементов.
О Если S — замкнутая поверхность, ограничивающая объем V, то интеграл
от произвольного вектора а по этой поверхности равен интегралу от диверген-
дивергенции а по объему V
ldidS = lakdSk= \dw8LdV= l^dV.
J J J J dxk
S S V v
Для произвольного тензора второго ранга Aik по аналогии имеем
Aik dSk = f ^ dV .
J дхк
v
3.2 ] Термодинамика деформирования 29
3.2. Термодинамика деформирования
3.2.1. Работа внутренних сил. Определим работу, производимую
силами внутренних напряжений при деформировании.
Пусть dAv — работа, производимая силами внутренних напряжений
в единице объема тела, a F — результирующая сила, действующая на
этот единичный объем. Тогда работа силы F на перемещении du с
учетом C.13) равна
dAv = Fi dm = ^ dm . C.14)
OXk
Работа, производимая силами внутренних напряжений внутри неко-
некоторого объема тела, равна
Av = \dAvdV = \ ^- dui dV . C.15)
J J oxk
v v
Интеграл в правой части можно записать в следующем виде:
Av = J ^Ы dm) dV - J aik (^- dm) dV . C.16)
v v
Применяя теорему Гаусса-Остроградского (см. с. 28) к вектору
aik dui в первом интеграле правой части, получаем
(^j dV. C.17)
S V
Рассматривая большой (в пределе бесконечный) объем и полагая,
что его границы недеформированы, т. е. на поверхности сг^ = 0, полу-
получим, что первый интеграл в правой части по бесконечной поверхности
S равен нулю. Второй интеграл с учетом симметрии тензора напряже-
напряжений можно записать в виде
(t)\\?ikdv- (ЗЛ8)
Поскольку выражение C.18) справедливо для произвольного объе-
объема V, то работа внутренних напряжений в единице объема деформи-
деформируемого тела равна
Av = -aikdeik. C.19)
Если после прекращения действия внешних сил тело полностью
возвращается в исходное недеформированное состояние (восстанавли-
(восстанавливает объем и форму), то такие деформации называют упругими. Если
после снятия внешних сил тело не возвращается в исходное состояние,
то такие деформации называют неупругими или пластическими. Ма-
Малые деформации при кратковременном действии внешних сил всегда
являются упругими.
30 Уравнения теории упругости [ Гл. 3
3.2.2. Основное термодинамическое равенство. Если упругая
деформация совершается достаточно медленно, то в каждый момент
времени в элементе объема деформируемого тела успевает установить-
установиться состояние термодинамического равновесия, соответствующее тем
внешним условиям, в которых тело в данный момент находится. Такой
процесс будет термодинамически обратимым. В этом случае первое
начало термодинамики можно сформулировать следующим образом.
Приращение внутренней энергии единицы объема тела dEBH рав-
равно разности полученного извне тепла dQv и производимой силами
внутренних напряжений работы dAv:
dEBH = dQv + aik deik . C.20)
Условимся все величины относить к единице объема недеформиро-
ванного тела, так как при деформации тела его объем может изме-
изменяться.
Равенство C.20) является основным термодинамическим тожде-
тождеством для деформируемых тел.
При обратимом процессе количество теплоты равно Т dSv, где Т —
температура, a Sv — энтропия единицы объема недеформированного
тела. Тогда соотношение C.20) примет вид
dEBH = TdSv + aikdeik. C.21)
В случае всестороннего равномерного сжатия (газы, жидкости)
тензор напряжений равен
Тогда равенство C.21) преобразовывается к известному в традицион-
традиционной термодинамике соотношению. Действительно
dEBH = Т dSv — pSik deik = Т dSv — р den = Т dSv — р d—r— .
Так как все величины отнесены к единице объема недеформированного
тела, т.е. V = 1, то получаем известное в термодинамике равенство:
dEBH = TdSv-pdV.
Получим выражение для свободной энергии энергии Fv единицы объ-
объема деформируемого тела. Известно, что Fv = Евн — TSV. Тогда
dFv = dEBH — Т dSv — Sv dT .
С учетом C.21) имеем
dFv = -Sv dT + (Jikdsik . C.22)
Заметим, что независимыми переменными являются в выражении
C.21) Sv, eik, а в выражении C.22) — Т, е^. Поэтому компоненты
3.3] Закон Гука 31
тензора напряжений можно получить из C.21) дифференцированием
внутренней энергии по компонентам тензора деформаций при постоян-
постоянной энтропии или из C.22) дифференцированием свободной энергии
по компонентам тензора деформации при постоянной температуре
(dFv
1 =(
3.3. Закон Гука
(dFv\ ( ,
=(д—) • F.26)
v \O?ik/ Т
3.3.1. Свободная энергия деформируемого тела. Для решения
задач теории упругости необходимо установить связь между компо-
компонентами тензора деформаций и компонентами тензора напряжений.
Это можно было бы сделать, используя соотношение C.23), если бы
удалось найти явную зависимость, например, свободной энергии от
компонент тензора деформаций.
Будем рассматривать лишь малые деформации при постоянной
вдоль всего тела температуре. Кроме того, для простоты будем рас-
рассматривать лишь изотропные тела Ч.
В силу малости деформаций (\eik\ <С 1) можно представить свобод-
свободную энергию в виде степенного ряда по компонентам тензора деформа-
деформаций.
Поскольку свободная энергия является скаляром, инвариантным по
отношению к преобразованию координат, то и каждый член разложе-
разложения также должен быть скаляром, инвариантным к преобразованию
координат. Из компонент симметричного тензора sik можно составить
три таких независимых скаляра:
1) сумма диагональных элементов (линейный инвариант) вц — от-
относительное изменение элемента объема деформируемого тела,
2) сумма парных произведений (квадратичный инвариант) е\к =
= ?ik?ik,
3) определитель матрицы е^ (кубический инвариант),
Учтем также, что при упругой деформации после прекращения
действия внешней силы, вызывающей эту деформацию, тело должно
возвратиться в исходное состояние, в котором все компоненты тензоров
?ik и &{к равны нулю.
Другими словами, имеем сг^ = 0 в том случае, если е^ = 0. Тогда
из соотношения C.23) следует, что в разложении свободной энергии,
Fv по степеням тензора деформаций должны отсутствовать линейные
по Sik члены. В противном случае при е^ = 0 мы получили бы aik ф 0,
что противоречит определению упругой деформации.
О Для неизотропных тел (например, монокристаллов)используются анало-
аналогичные рассуждения. При этом основные физические параметры имеют более
высокую тензорную размерность, что позволяет учесть неизотропность дефор-
деформируемых тел.
32 Уравнения теории упругости [ Гл. 3
В силу малости деформаций, ограничиваясь лишь квадратичными
членами разложения, свободную энергию можно представить в виде
Здесь Л, 11 — некоторые коэффициенты пропорциональности, называе-
называемые коэффициентами Ламэ; Fq — свободная энергия единицы объема
недеформированного тела.
Любую деформацию в произвольных координатных осях можно
представить в виде суммы деформации чистого сдвига, происходящего
без изменения объема, и деформации всестороннего сжатия или растя-
растяжения, связанной с изменением объема деформируемого элемента. Для
этого тензор деформаций следует записать в виде
= [eik - - 5ik?ii) + з sik?u • C-25)
Действительно, след тензора в круглых скобках выражения C.25)
равен нулю, следовательно, он представляет собой тензор сдвига, а
второй член является тензором всестороннего сжатия или растяжения,
поскольку его след определяет относительное изменение элемента объ-
объема деформируемого тела.
С учетом C.25) выражение C.24) для свободной энергии удобно
привести к следующему виду:
Fv = F0 + v [eik - l- Siksu^j + | 4
где
eik - l- Siksu^j + | 4, C.26)
C-27)
При выводе выражения C.26) учтено, что
1
( ?ik — x Sik?u) Sik = 0.
Коэффициенты к и \± называются соответственно модулем всесто-
всестороннего сжатия и модулем сдвига.
В состоянии термодинамического равновесия (недеформированное
состояние) свободная энергия минимальна. Это значит, что (Fv —
— Fo) — всегда неотрицательная величина, равная нулю только в неде-
формированном состоянии. Тогда из выражения C.26) следует, что
оба модуля \i и к являются каждый в отдельности положительными,
поскольку деформация может быть сдвигом без всестороннего сжатия
или всесторонним сжатием без сдвига. Таким образом, /i > 0, к > 0.
3.3.2. Закон Гука. Для установления связи между тензором на-
напряжений и тензором деформаций найдем дифференциал свободной
энергии. Из выражения C.26) получаем
dFv = ken den + 2/х \eik - ^ Sik?iiJ deik • C.28)
3.3 ] Закон Гука 33
Если dsa записать в виде
dsu = d(Sik?ik) = Sikdsik,
то для дифференциала свободной энергии имеем
dFv = \k5iksu + 2/i [eik - - 5ikeu)\ deik . C.29)
С учетом соотношения C.23) для тензора напряжений получаем
oik = k5iksu + 2/i [eik - - 5iksu^ . C.30)
Выражение C.30) устанавливает линейную связь между компонен-
компонентами тензора напряжений и компонентами тензора деформаций для
изотропного тела при малых изотермических деформациях.
Можно получить и обратную связь, т. е. выразить компоненты тен-
тензора деформаций через компоненты тензора напряжений.
След тензора напряжений равен
аи = кдцбц = Зкец; ?ц = -— ац .
Тогда, подставляя полученное соотношение в C.30), получим
1 х ^0 2 1 Л
Отсюда определяем Е{к
— (aik - - 5ikaiij . C.31)
Полученное выражение называют законом Гука.
Хотя закон Гука получен для малых деформаций, он справедлив во
всей области упругих деформаций.
Из C.31) следует, что относительное изменение объема при де-
деформации определяется только диагональными элементами тензора
напряжений. Действительно,
AV 1
Т" = ?ii = зк аи'
При всестороннем равномерном сжатии
&ik = -pSik] аи = -Зр.
Поэтому при всестороннем равномерном сжатии относительное изме-
изменение объема равно
AV _ р
V ~ к'
Если деформации малы, а температура остается неизменной, и нор-
нормальные напряжения изменяются на малую величину от 0 до р,
2 В.Г. Черняк, П.Е. Суетин
34 Уравнения теории упругости [ Гл. 3
т. е. Ар = р — О, то последнее соотношение можно записать в диффе-
дифференциальной форме
--{-f)- C32)
Величина \/к называется коэффициентом всестороннего сжа-
сжатия.
Поскольку изменение свободной энергии, AF = Fv — Fq, при де-
деформации единицы объема, определяемое выражением C.26), есть
квадратичная однородная функция компонент тензора деформаций, то
из теоремы Эйлера 0 об однородных функциях следует:
eik(^-) =2AF. C.33)
Принимая во внимание выражение C.23), имеем
AF = l-aikeik . C.34)
Мы получили выражение, определяющее изменение свободной
энергии (упругой энергии) единицы объема тела при малых изотерми-
изотермических деформациях.
3.4. Однородная деформация
Деформация тела называется однородной, если все компоненты
тензора деформации постоянны по всему объему тела, т. е. не
зависят от координат.
Рассмотрим однородную деформацию на примере растяжения
стержня. Пусть один конец стержня закреплен, а на другой действует
некоторая растягивающая сила F вдоль оси
X2, совпадающей с продольной осью стержня
(рис. 3.4). Если S - площадь поперечного
^. сечения стержня, то р = F/S — нормальное
л2 к S напряжение.
Поскольку рассматривается однородная
деформация, то компоненты тензора дефор-
jra^in^cnnc Мации постоянны вдоль стержня, в том числе
р rp r± j~\ -\Tf TJ ГГ А
н и на его поверхности. Следовательно, компо-
компоненты тензора деформации можно определить из граничных условий.
О Если f(x\, X2,...) — некоторая однородная функция переменных
х\,Х2,..., то для произвольного числа а имеем
f(ax\, ax2, ...) = апf(x\,X2, ...).
Здесь п — степень неоднородности.
Эйлер показал, что для таких функций справедливо соотношение
х\ Ь х2 Ь ... = nf(xux2,...).
ОХ\ ОХ2
3.4 ] Однородная деформация 35
На боковую поверхность стержня не действуют внешние силы. Это
означает, что поверхностная сила на боковой поверхности стержня
равна нулю. С учетом выражения C.8) имеем
(п)
где пк — проекция нормали п к боковой поверхности стержня на ко-
координатную ось Xk- Очевидно, нормаль п имеет лишь две отличные
от нуля проекции (ri2 = 0). Тогда компоненты тензора напряжений
удовлетворяют следующим уравнениям:
(Т\\П\ + СГ13П3 = 0, СГ21П1 + СГ2ЗП3 = 0, СГ31П1 + СГ33П3 = 0 .
При произвольных п\ и щ полученная система уравнений непротиво-
непротиворечива только тогда, когда все компоненты тензора напряжений, входя-
входящих в нее, равны нулю, т. е. а\\ = 0, сгзз = 0, а^\ = сг12 = 0, а^ъ = я2 =
= 0. Следовательно, единственной компонентой тензора напряжений,
которая может быть отличной от нуля, является компонента <Т22- Ее
величину можно определить из граничного условия на торце стержня,
где приложена растягивающая сила:
&2кПк = Р,
где rik — проекция нормали п к торцу стержня на координатную
ось Xk- Так как на торце п\ = щ = 0, п^ = 1, получаем
Если вспомнить, что по своему физическому смыслу компонента СГ22
определяет силу, действующую в направлении оси Х2 на единичную
площадку, перпендикулярную оси Х2, то полученный результат очеви-
очевиден из самой постановки задачи.
Теперь можно найти компоненты тензора деформаций, используя
закон Гука. Из выражения C.31) следует, что все недиагональные
компоненты тензора деформаций равны нулю, поскольку единственная
отличная от нуля компонента тензора напряжений это сг22- Для диаго-
диагональных компонент тензора деформаций, используя закон Гука C.31),
получаем
1 ( 1 1\ 1 / 1 , 1 Л ,о о^
еп = ?33 = - о о ТГ ]Р> ?22=о[- + Тт]Р- C.35)
3 yz/i бк) 3 \fi бкJ
3.4.1. Модуль Юнга и коэффициент Пуассона. Компонента ?22
определяет относительное удлинение стержня вдоль оси Х2, а обратная
величина коэффициента при р в выражении C.35) для ?22 называется
модулем Юнга (Е):
Е = ^- . C.36)
Видно, что модуль Юнга имеет размерность давления. Компонен-
Компоненты тензора деформаций ец и ?зз определяют относительное сжатие
36 Уравнения теории упругости [ Гл. 3
стержня в поперечном сечении. Отношение поперечного сжатия к
продольному растяжению а называют коэффициентом Пуассона:
ей 1 Зк - 2/х (qo7\
а = = о^ТГ^ • C.37)
Очевидно, что а — безразмерный коэффициент.
Поскольку, как показано выше, к > О и \± > О, то из выражения
C.37) следует, что коэффициент Пуассона может изменяться в преде-
пределах от —1 при деформации чистого сдвига (к = 0) до 1/2 при чистой
деформации (/i = 0). В действительности же, как показывает опыт,
коэффициент Пуассона не может принимать отрицательные значения.
В природе не известны тела, в которых при растяжении увеличивались
бы их поперечные размеры. Таким образом, для реальных тел
Коэффициент Пуассона, близкий к 1/2, наблюдается у тел типа резины,
у которых модуль сдвига мал.
Пользуясь формулами C.27), C.36) и C.37) можно выразить модуль
всестороннего сжатия к, модуль сдвига /i и коэффициент Ламэ Л через
модуль Юнга и коэффициент Пуассона
i Е Е , сгЕ уъ <э?ч
fe~3(l-2a)' ^ - 2A+ 2ог) ' Л-A
Очевидно, что закон Гука C.31) можно записать с использованием
модуля Юнга и коэффициента Пуассона. Целесообразность введения
новых феноменологических параметров — модуля Юнга и коэффициен-
коэффициента Пуассона — оправдана простотой опыта, из которого они могут быть
определены. Как мы видели выше, это могут быть опыты по растя-
растяжению стержней. Достаточно измерить лишь изменение продольных и
поперечных размеров стержня при растяжении.
Относительное изменение объема стержня при однородном растя-
растяжении с учетом соотношений C.35) равно
AV _ _\_ р
V ~ il ~ 3 к '
Таким образом, при однородном растяжении относительное изме-
изменение объема в три раза меньше, чем при всестороннем равномерном
растяжении или сжатии.
Изменение свободной (упругой) энергии единицы объема стержня
при растяжении, согласно C.34), будет равно
3.4.2. Диаграмма растяжения. Важной характеристикой меха-
механических свойств твердых тел является зависимость напряжения от
относительного удлинения стержня. Графическое изображение этой
3.4]
Однородная деформация
37
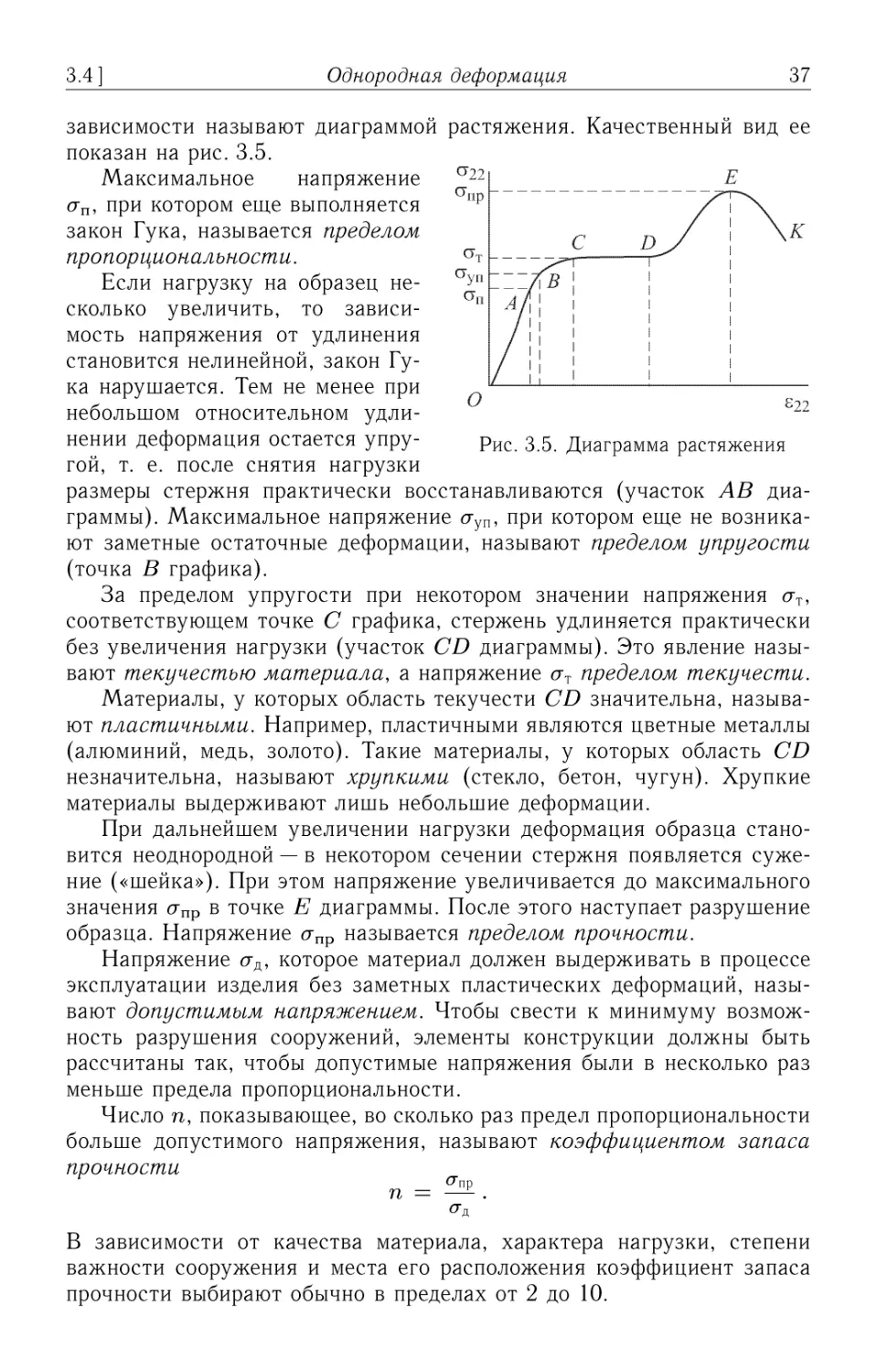
зависимости называют диаграммой растяжения. Качественный вид ее
показан на рис. 3.5.
Максимальное напряжение
<тп, при котором еще выполняется
закон Гука, называется пределом
пропорциональности.
Если нагрузку на образец не-
несколько увеличить, то зависи-
зависимость напряжения от удлинения
становится нелинейной, закон Гу-
Гука нарушается. Тем не менее при
небольшом относительном удли-
удлинении деформация остается упру-
упругой, т. е. после снятия нагрузки
О
Рис. 3.5. Диаграмма растяжения
размеры стержня практически восстанавливаются (участок АВ диа-
диаграммы). Максимальное напряжение <туп, при котором еще не возника-
возникают заметные остаточные деформации, называют пределом упругости
(точка В графика).
За пределом упругости при некотором значении напряжения <тт,
соответствующем точке С графика, стержень удлиняется практически
без увеличения нагрузки (участок CD диаграммы). Это явление назы-
называют текучестью материала, а напряжение аТ пределом текучести.
Материалы, у которых область текучести CD значительна, называ-
называют пластичными. Например, пластичными являются цветные металлы
(алюминий, медь, золото). Такие материалы, у которых область CD
незначительна, называют хрупкими (стекло, бетон, чугун). Хрупкие
материалы выдерживают лишь небольшие деформации.
При дальнейшем увеличении нагрузки деформация образца стано-
становится неоднородной — в некотором сечении стержня появляется суже-
сужение («шейка»). При этом напряжение увеличивается до максимального
значения апр в точке Е диаграммы. После этого наступает разрушение
образца. Напряжение апр называется пределом прочности.
Напряжение <тд, которое материал должен выдерживать в процессе
эксплуатации изделия без заметных пластических деформаций, назы-
называют допустимым напряжением. Чтобы свести к минимуму возмож-
возможность разрушения сооружений, элементы конструкции должны быть
рассчитаны так, чтобы допустимые напряжения были в несколько раз
меньше предела пропорциональности.
Число п, показывающее, во сколько раз предел пропорциональности
больше допустимого напряжения, называют коэффициентом запаса
прочности
п = —- .
В зависимости от качества материала, характера нагрузки, степени
важности сооружения и места его расположения коэффициент запаса
прочности выбирают обычно в пределах от 2 до 10.
38 Уравнения теории упругости [ Гл. 3
3.5. Неизотермическое деформирование
Мы получили выражение C.26) для свободной энергии единицы
объема деформированного тела при изотермическом деформировании.
Теперь рассмотрим свободную энергию единицы объема тела при де-
деформациях, сопровождающихся изменением его температуры. Темпера-
Температура тела может изменяться как вследствие подвода или отвода тепла
при помощи внешних источников, так и в результате самого процесса
деформирования.
Пусть в недеформированном состоянии температура рассматривае-
рассматриваемого элемента объема тела равна То. При изменении температуры этот
элемент объема претерпевает температурную деформацию, даже если
внешние силы отсутствуют. Поэтому в разложение свободной энергии
по степеням тензора деформаций теперь необходимо включить линей-
линейный член (линейный инвариант ец), который должен исчезать при
Т = То. Если изменение температуры мало, т. е. AT = (Т - То) <С То,
то температурную деформацию можно можно считать пропорциональ-
пропорциональной самому изменению температуры.
Для простоты рассмотрим изотропное тело, характеризуемое одним
коэффициентом линейного теплового расширения а. Так как свободная
энергия — скаляр, то дополнительный член в выражении для свободной
энергии должен иметь вид
где А — некоторый коэффициент, не зависящий в первом приближении
от температуры. Тогда для свободной энергии имеем
F = F(TQ)-A(T- T0)eikdik + fi (sik - l- Sike,i) + \ e\. C.39)
Дифференцируя это выражение по компонентам тензора деформа-
деформаций, с учетом C.30) для тензора напряжений получаем
°ik = -А(Т - T0Nik + k6ikeu + 2/i (eik - l- 6ikei^ . C.40)
Для выражения коэффициента А через известные величины вос-
воспользуемся тем фактом, что при свободном однородном тепловом рас-
расширении тела (при отсутствии внешних сил) внутренние напряжения
должны отсутствовать, т. е. сг^ = 0. Тогда из C.40) получим
?ik = ^~ \ -z-Sik?u — к5{к?ц + А(Т — ToNik .
Отсюда с учетом B.38) следует
ец = ^(Т - То) = ej{ = ^- = За(Т - То); А = Зак .
3.5 ] Неизотермическое деформирование 39
Таким образом, тензор напряжений при неизотермическом дефор-
деформировании имеет вид
(Tik = -3ak(T - ToMik + kSikeii + 2/i (eik - - 5ik?iij . C.41)
Здесь первый член описывает напряжения, связанные с изменением
температуры тела.
Повторяя вывод закона Гука, для тензора деформаций получим
eik = а(Т - T0)Sik + ^ 8ikau + i- (aik - l- 5ika^ . C.42)
3.5.1. Адиабатические и изотермические модули. При постоян-
постоянной температуре свободная энергия единицы объема деформируемого
тела определяется выражением C.26). Поэтому модули к и /i в выраже-
выражении C.26) называют изотермическими модулями. Однако деформация
может совершаться и адиабатически, без теплообмена рассматриваемо-
рассматриваемого элемента объема тела с внешней средой и соседними элементами,
т.е. при постоянной энтропии. Если скорость процесса настолько вели-
велика, что за время деформирования элемент объема не успевает получить
или отдать тепло, то такое деформирование будет адиабатическим.
В этом случае модули к и /i, называют адиабатическими модулями
всестороннего сжатия и сдвига. Адиабатические модули обозначим
через ка и /ia. Заметим, что при малых деформациях адиабатические
значения модулей мало отличаются от их изотермических значений.
Вычислим изменение температуры тела при адиабатическом де-
деформировании. Из соотношения C.22) для энтропии единицы объема
имеем /я/
Sv~ y~
Дифференцируя выражение C.39) по температуре, получим с точно-
точностью до членов первого порядка по компонентам тензора деформации
следующее соотношение:
Здесь SV(T) — энтропия единицы объема при температуре Т после
деформации, Sq(T) — энтропия единицы объема тела при температуре
Т в недеформированном состоянии. Следовательно, Sq(T) получено
дифференцированием свободной энергии по температуре при ец = О,
т. е. при постоянном объеме. При адиабатическом деформировании
энтропия единицы объема должна остаться неизменной:
Здесь Sq(Tq) — энтропия единицы объема при температуре То.
Разлагая Sq(T) в ряд Тейлора по температуре относительно То и
ограничиваясь линейными по (Т - То) членами, получим
S0(T) - So(To) = (Т - То) (|^) + ... = {Т-Т0)^-, C.43)
40 Уравнения теории упругости [ Гл. 3
где Cv — теплоемкость единицы объема деформируемого тела при по-
постоянном объеме. Сравнивая два последних выражения, получаем, что
изменение температуры элемента объема при адиабатическом дефор-
деформировании равно
Т-Т0 = -^е«. C.44)
Подставляя это выражение в C.41), для тензора напряжений с
адиабатическим модулем всестороннего сжатия получим
= ka5ik?n + 2/i \eik - ^SikSn) • C.45)
Из сравнения с выражением C.41) видим, что адиабатический и
изотермический модули сжатия связаны между собой следующим со-
соотношением: 9 9
_ 9а2к2Т
гьа — 7^ ~г К •
Но по определению О
V\dP)T к' V\dp)s ka' К С,,' ^-'
Так как Ср > Cv, то ка > к. Тогда из последнего выражения следует,
что относительное изменение объема при адиабатическом деформиро-
деформировании меньше, чем при изотермическом.
Установим еще одну связь между адиабатическим и изотермиче-
изотермическим модулями всестороннего сжатия. Для этого воспользуемся из-
известным термодинамическим соотношением:
"". C.47)
Отсюда с учетом выражений B.39) и C.46) получаем
Пользуясь формулами C.38) и C.48), можно получить соотношения
между адиабатическим и изотермическим модулями Юнга и коэффи-
коэффициентами Пуассона.
Наконец, из выражения C.45) выразим компоненты тензора
деформаций в адиабатическом процессе через компоненты тензора
напряжений. Повторяя рассуждения п. 3.3.2, получим закон Гука при
О Действительно, пользуясь известным правилом преобразования термоди-
термодинамических величин, имеем
' dV\ f®S\ I (dS\ IdV\ I' dT\ I (dT\
~ ~ \dpjv/ \dV)P' \dp)T ~ ~ \dpjy/ \dV)p '
Деля первое равенство на второе, получим
'dV\ /fdV\ _ (dS\ (дТ\ /fdS\ (дТ\ _ Cv _ к
~др) т ~ ~ \др) у \дУ)Р/ \дУ)р \др)у ~ ~Ср~ ~ка'
3.6] Уравнение равновесия изотропных тел 41
адиабатическом деформировании в следующем виде:
eik = -^ 6ik*u + ± (aik - \ 6ik*u) , C.49)
т. е. формально вид закона Гука тот же, что и в изотермическом
процессе, но с другим модулем всестороннего сжатия.
3.6. Уравнение равновесия изотропных тел
Получим уравнение равновесия единицы объема изотропного де-
деформированного тела. Результирующая поверхностная сила, действу-
действующая на единицу объема тела определяется выражением C.13). Если
pf — напряженность объемной силы, то условие равновесия рассматри-
рассматриваемого элемента объема в соответствии с первым законом Ньютона
имеет вид
^i*+p/. =0, k,i = 1,2,3. C.50)
охк
Выражение C.41) для тензора напряжений перепишем, заменив
модули сдвига и всестороннего сжатия на коэффициент Пуассона и
модуль Юнга. С использованием соотношений C.38) имеем
Ь (?ik
Подставляя C.51) в уравнение C.50), получаем
аЕ дТ Е dsik Ест дед f - с\
1 -2а~дх~ 1 + сг дхк A + сг)A -2а)~дх~ Р^~
Используя определение B.6) тензора деформаций е^ через компоненты
вектора деформаций щ, получим
д2щ 1 д2щ о 1+сг дТ 2A+ сг) , /о соч
о 1 = ^& PJi • (O.OZ)
dxt 1 ~~ 2сг oxiOXi 1 — 2сг аа?г ?/
Уравнение C.52) удобно переписать в векторных обозначениях:
А и + ^— grad div u = 2а ?- grad T ^ °' р f . C.53)
1 — Za I — Za h
При решении конкретных задач теории упругости полезна еще
одна форма уравнения равновесия. Используя известное из векторного
анализа соотношение
grad div u = A u + rot rot u,
преобразуем уравнение C.53) к следующему виду:
grad div u — — rot rot u = a grad T — p f . C.54)
1 + a 2A + a) h
Уравнения C.53) и C.54) называют уравнениями равновесия еди-
единицы объема изотропного деформированного тела.
42 Уравнения теории упругости [ Гл. 3
3.6.1. Граничные условия. Уравнение равновесия C.54) —это
векторное уравнение, имеющее три проекции на координатные оси.
Каждое из трех скалярных уравнений представляет собой линейное
дифференциальное уравнение второго порядка, включающее производ-
производные от компонент вектора деформаций по пространственным коорди-
координатам. Поэтому для получения однозначного решения этих уравнений
в общем случае необходимо задать шесть граничных условий. В про-
простейшем случае одномерной деформации, когда отлична от нуля только
одна компонента вектора и, зависящая лишь от одной координаты,
из C.54) следует одно скалярное уравнение равновесия. Разумеется,
в этом случае достаточно двух граничных условий для определе-
определения двух постоянных интегрирования. В уравнении равновесия C.54)
член, содержащий градиент температуры, считается известным. Если
же условие задачи таково, что температура деформированного тела
неизвестна, но ее следует определить, то это делается независимо из
решения уравнения теплопроводности (см. следующую главу).
Обычно используют два способа задания граничных условий.
1. Граничное условие первого рода состоит в задании компонент
вектора деформаций на поверхности деформированного тела, т. е.
Щз = Ui(x\a, X2s, XSs) , C.55)
где индекс s обозначает поверхность тела.
Итак, задача сводится к определению функций щ(х\,Х2,хз), удов-
удовлетворяющих внутри тела уравнениям равновесия и принимающих на
границе заданные значения Щ.
В частном случае щ3 = Ui = const, т. е. деформация во всех точках
поверхности тела одинакова (однородные граничные условия первого
рода). Это может быть осуществлено при деформации изотропных тел
правильной геометрической формы под действием объемных сил, не
зависящих от координат точек поверхности.
К граничным условиям первого рода следует отнести очевидное
условие ограниченности деформаций в любой точке деформированного
тела, т. е.
щ(х\, Х2, Жз) < ОО . C.56)
Заметим, что граничные условия первого рода на практике могут
быть заданы лишь в редких случаях, поскольку обычно деформация
поверхности тела является искомой величиной.
2. Граничное условие второго рода представляет собой баланс сил
в каждой точке поверхности деформированного тела.
На поверхности тела рассмотрим единичную площадку с норма-
нормалью п. Пусть на эту площадку действует внешняя результирующая
сила Р. Так как выделенный элемент поверхности находится в рав-
равновесии и неподвижен относительно других частей деформированного
тела, то в соответствии с первым законом Ньютона напряженность по-
поверхностной силы crj компенсируется плотностью внешней силы Pi.
3.6] Уравнение равновесия изотропных тел 43
С учетом выражения C.8)для любой единичной площадки поверхности
тела можно записать , Л
Pi, C.57)
где rik — проекция нормали п на координатную ось х\~.
Заметим, что такое граничное условие уже было использовано ра-
ранее в задаче об однородном растяжении стержня.
Граничное условие C.57) с учетом выражений C.51) и B.6) в
случае изотермических деформаций преобразуется к следующему виду:
+ ^ + T^Sikd^Jnk = Pi' C'58)
где индекс S обозначает поверхность тела.
В общем случае плотность внешних сил Р{ зависит от координат
точек поверхности (x\s, %2s, X3s)- Если Pi = const, т.е. внешняя сила
действует одинаково по всей границе тела, то C.58) представляет собой
однородное граничное условие второго рода.
Таким образом, задача состоит в отыскании таких функций гц,
которые внутри деформированного тела удовлетворяют уравнениям
равновесия, а их первые производные по координатам на поверхности
тела удовлетворяют условиям C.58).
В одномерном случае при отсутствии внешних сил выражение
C.58) существенно упрощается. Например, если деформация проис-
происходит только в направлении оси у и единственная отличная от нуля
компонента вектора деформаций иу зависит лишь от одной координа-
координаты х, то при отсутствии внешней силы выражение C.58) принимает
простой вид
duy
dx
Контрольные вопросы
1. Какие силы называют объемными и какие поверхностными?
2. Каков физический смысл компонент тензора напряжений?
3. Как записывается тензор напряжений при всестороннем равномерном
сжатии?
4. Какие силы дают вклад в результирующую силу, действующую на
выделенный объем деформируемого тела?
5. Для каких деформаций справедлив первый закон термодинамики C.20)?
6. Почему в разложении свободной энергии по степеням тензора деформа-
деформаций исключен линейный инвариант еи?
7. Почему модули всестороннего сжатия и сдвига неотрицательны?
8. Что устанавливает закон Гука? Каковы пределы его применимости?
9. Почему коэффициент Пуассона для реальных тел не может быть отри-
отрицательным?
10. В каком процессе модуль всестороннего сжатия больше, в изотермиче-
изотермическом или адиабатическом? Обоснуйте.
11. Что представляют собой граничные условия первого и второго рода к
уравнению равновесия изотропного деформированного тела?
ГЛАВА 4
ФУНДАМЕНТАЛЬНАЯ СИСТЕМА УРАВНЕНИЙ
ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Перейдем к выводу замкнутой системы уравнений, определяющих
законы сохранения при движении сплошной среды.
4.1. Тензор скоростей деформации
Из теоремы КошиТельмгольца B.40) следует, что общее смещение
некоторой точки Q, находящейся в дифференциально малой окрестно-
окрестности dr точки Р с радиус-вектором г может быть представлено в виде
ui(y + dr) = Ui(r) + (pik dxk + eik dxk . D.1)
Если это перемещение происходит за физически малый промежуток
времени At, то, разделив выражение D.1) на At, в пределе At —> 0
будем иметь
Щ = voi + фгк dxk + sik dxk . D.2)
Здесь Vi — г-компонента скорости смещения точки, находящейся в
дифференциальной окрестности первого порядка около точки Р, vqi —
г-компонента скорости точки Р как полюса;
. 1 fdvi dvk
В D.3) величины (pik и iik называют тензорами скоростей по-
поворота и скоростей деформации соответственно. Как компоненты
тензора (fik определяют вектор поворота на некоторый угол <р, так
и компоненты ф^к определяют вектор скорости поворота и (угловую
скорость).
Из выражений B.14) и B.23) нетрудно получить следующие соот-
соотношения: 1 1 „г
ш = - rot v, — — = div v . D.4)
В векторном виде равенство D.1) можно записать так:
v = v0 + [ш dr] + ^деф . D.5)
Если в процессе деформирования изменяется температура тела, то
деформационная часть скорости должна включать и скорость деформа-
деформации вследствие изменения температуры, пропорциональную dT/dt.
4.3 ] Уравнение непрерывности 45
4.2. Дифференцирование по времени
интеграла по подвижному объему
В механике сплошных сред часто используется понятие индивиду-
индивидуальный объем — объем, состоящий из одних и тех же частиц среды,
т. е. поток вещества через ограничивающую этот объем поверхность
равен нулю. В процессе движения среды индивидуальный объем может
изменять как свою форму, так и величину.
Пусть /(г, t) — произвольная функция координат и времени. По-
Получим формулу дифференцирования по времени интеграла от этой
функции по некоторому изменяющемуся со временем объему V(t).
Рассмотрим выражение
±\{v,t)dV. D.6)
V
Полная производная по времени определяет скорость изменения
интеграла не только вследствие изменения с течением времени подин-
тегральной функции, но также и вследствие изменения самого объема
V V
Учитывая, что в декартовой системе координат dV = dx\
преобразуем второе слагаемое в подынтегральном выражении
d 7Т, jdx\ j j jdxo j j jdx?. ,
— dV = d—— dx^dx^ + d—— dx\ dxo, + d—— dx\
at at dt at
= dv\ dx2 dx^ + dv2 dx\ dx% + dv% dx\
0v\ dv2 dv%
LHJu \ \JjJb2 ULJu? \^ ~ xJjJb \ \JbJu2 ЬЬгЪ^ \^ _ LHJb \
= —— dV = div v^V .
Тогда выражение D.7) запишется в следующем виде:
^ J /(r, t) dV = J (J + / div v) dV . D.8)
Формула D.8) определяет правило дифференцирования по времени
интеграла по подвижному объему.
4.3. Уравнение непрерывности
Уравнение непрерывности выражает закон сохранения массы лю-
любого индивидуального объема среды. В движущейся среде выделим
некоторый индивидуальный объем V, масса вещества в котором равна
М= [ pdV , D.9)
v
где р — плотность вещества.
46 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Очевидно, что масса вещества индивидуального объема с течением
времени не изменяется (нет потока вещества через ограничивающую
поверхность)
V
Используя формулу D.8), получаем
) dV = 0. D.11)
Поскольку это равенство должно выполняться для произвольного
индивидуального объема, то для его выполнения необходимо равенство
нулю подынтегрального выражения, т. е.
4^ + pdiv v = 0. D.12)
at
Уравнение D.12) называют уравнением непрерывности.
Если координаты х\,Х2,хъ рассматривать как координаты инди-
индивидуальной частицы сплошной среды, то в общем случае плотность
р(х\, Х2, жз, t) зависит от времени как явно, так и неявно через ме-
меняющиеся координаты индивидуальных частиц среды. Тогда полную
производную по времени от плотности можно записать следующим
образом:
% = w + ir-%r = i& + v*ir-- < = 1'2'3- DЛЗ)
dt at oxi at at axi
Последнее выражение в векторном виде будет иметь вид
Итак оператор полной производной по времени можно записать в
следующем виде:
l = l+vV- <4-15>
С учетом выражения D.14) уравнение непрерывности D.12) прини-
принимает вид
g 0. D.16)
Уравнения непрерывности D.12) и D.16) —это две формы зако-
закона сохранения массы среды. Однако физический смысл слагаемых
этих уравнений различен. Если первое слагаемое уравнения D.12)
характеризует скорость изменения массы движущейся индивидуальной
частицы единичного объема, то в уравнении D.16) первое слагаемое
определяет изменение массы единицы объема за единицу времени в
фиксированной точке пространства, через которую с течением времени
проходят разные индивидуальные частицы среды.
4.3 ] Уравнение непрерывности 47
Выясним физический смысл вектора pv, стоящего под знаком ди-
дивергенции в уравнении D.16). Для этого рассмотрим элементарную
площадку AS с нормалью п (рис. 4.1).
Очевидно, за малый промежуток времени
At выделенную площадку пересекут лишь те
индивидуальные частицы среды, которые в \ \ д/
начальный момент времени находились в ко-
косом цилиндре объемом |уп|Д?Д5\ Посколь-
Поскольку единица объема среды имеет массу р,
то величина p\vn\AtAS характеризует массу
среды, проходящую через площадку AS за ^ „in
^ ^ J д. /- Рис. 4.1. Плотность по-
промежуток времени At. Следовательно, pv т(жа
есть плотность потока массы. Модуль этого
вектора определяет массу вещества, пересекающего за единицу време-
времени единичную площадку, ориентированную перпендикулярно потоку.
Таким образом, из уравнения непрерывности в форме D.16) следу-
следует, что изменение массы единицы объема среды за единицу времени
происходит за счет пространственной неоднородности плотности пото-
потока массы вещества.
Уравнение непрерывности можно вывести и другим путем. Рассмот-
Рассмотрим некоторый фиксированный, т. е. неподвижный и неизменяющийся
со временем, объем сплошной среды. Масса вещества в этом объеме
определяется выражением D.9). Изменение массы вещества в этом
объеме может происходить только вследствие потока вещества через
поверхность, ограничивающую выделенный объем. Если pv — вектор
плотности потока массы вещества, то масса вещества, втекающего или
вытекающего из объема за единицу времени, будет равна
ct pv dS .
s
Здесь интеграл берется по неподвижной замкнутой поверхности S,
ограничивающей выделенный объем V; dS = ndS, где п —нормаль к
элементарной площадке dS, направленная вне объема.
Изменение массы вещества в выделенном объеме за единицу вре-
времени должно равняться потоку массы через границы объема, т. е.
^ J p dV = J ^ dV = - j pv dS . D.17)
V V S
Так как объем фиксированный, то в выражении D.17) берется частная
производная по времени, причем производная от интеграла может быть
записана как интеграл от производной подынтегральной функции. Знак
минус перед интегралом в правой части равенства обусловлен выбором
направления нормали п. Поскольку вектор нормали к элементу гра-
граничной поверхности направлен вне выделенного объема, то скалярное
произведение в подынтегральном выражении будет отрицательным,
48 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
если поток вещества направлен извне внутрь объема, и положительным
в противном случае. Тогда знак минус перед интегралом учитывает тот
факт, что масса вещества в объеме убывает, если вектор плотности
потока сонаправлен нормали.
Применяя теорему Гаусса-Остроградского (см. с. 28) к правой ча-
части выражения D.17), получим
J (l?
v
Так как последнее равенство должно выполняться для любого непо-
неподвижного объема, то подынтегральное выражение должно быть равно
нулю, т.е. снова получаем уравнение непрерывности в форме D.16).
4.3.1. Интегральная и дифференциальная форма уравнения
непрерывности. Уравнение непрерывности не изменит свой вид и
в том случае, если под р понимать не массовую плотность среды, а
количество вещества (количество молей или число молекул в единице
объема). Но это будет лишь в том случае, когда отсутствуют источни-
источники и стоки вещества внутри рассматриваемых объемов. Если внутри
фиксированного объема имеется п источников или стоков мощностью
Qi, то уравнение непрерывности в интегральной форме будет иметь
вид п
V S i=l
Здесь второе слагаемое в правой части есть алгебраическая сумма
мощностей источников и стоков. Мощность источника или стока Qi
определяет количество вещества, поставляемого источником или от-
отводимого стоком в единицу времени. При этом мощности источников
положительны (Qi > 0), а стоков отрицательны (Qi < 0).
Источники или стоки могут быть распределены в пространстве
непрерывно с объемной плотностью v. Например, уравнение непрерыв-
непрерывности для числа нейтронов в делящемся материале можно записать в
интегральной форме:
А [ р dV = -1 pv dS + [ v dV . D.20)
ut J J J
V S V
Здесь р — число нейтронов в единице объема, v — их скорость диффу-
диффузии, v — разность числа нейтронов, рождающихся и поглощающихся в
единице объема среды за единицу времени.
Нетрудно видеть, что уравнение непрерывности D.20) можно запи-
записать и в дифференциальной форме. Однако это нельзя сделать в случае
дискретного распределения источников и стоков. Поэтому уравнение
непрерывности в дифференциальной форме D.16) справедливо во всех
точках пространства, кроме точек, в которых расположены источники
или стоки. Интегральная форма уравнения непрерывности является
более общей, поскольку справедлива для всех точек среды.
4.4 ] Уравнение движения сплошной среды 49
Для стационарного случая, когда плотность вещества в любой
фиксированной точке пространства не изменяется с течением времени,
хотя может зависеть от координат, имеем
^=0, divpv = 0. D.21)
at
Для несжимаемой среды плотность вещества не зависит ни от
координат, ни от времени, т. е.
%=0. D.22)
at
Тогда из D.12) имеем, что для всех точек пространства, занимаемого
несжимаемой средой (кроме точек пространства, в которых расположе-
расположены источники и стоки), справедливо выражение:
div v = 0 . D.23)
Заметим, что этот результат следует также из выражения D.4)
\ dV Л. п
v^ = dlvv = 0'
т. е. в несжимаемой среде любой индивидуальный объем не изменяется
по величине в процессе движения.
4.4. Уравнение движения сплошной среды
Уравнение движения выражает закон сохранения импульса спло-
сплошной среды.
Рассмотрим некоторый индивидуальный объем V в движущейся
со скоростью v сплошной среде. Очевидно, pv — импульс единицы
объема. Тогда импульс всего выделенного объема равен
П = f pv dV , U{= i
V V
Пусть F = F(v) + F^) — результирующая сила, действующая на ин-
индивидуальный объем, которая складывается из результирующей объ-
объемных (F^) и результирующей поверхностных (F^) сил. Тогда в
соответствии со вторым законом Ньютона изменение в единицу вре-
времени полного импульса индивидуального объема должно равняться
результирующей всех сил, действующих на этот объем:
dn = F(v) + F(s)f dY}± = F(v) + F(S) ^ ^ 24^
Преобразуем каждый член уравнения D.24) отдельно. Учитывая
правило дифференцирования по времени интеграла по подвижному
50 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
объему D.8), для левой части уравнения D.24) получим
V V
Выражение в круглых скобках представляет собой уравнение непре-
непрерывности D.12) и поэтому равно нулю. Тогда имеем
dt
v
Если f — напряженность массовых сил, то для результирующей
объемных сил можно записать
= J pfi dV. D.26)
v
Результирующую поверхностную силу, действующую на единицу
объема, мы определили выражением C.13). Тогда результирующая по-
поверхностных сил, действующих на весь индивидуальный объем, равна
F(s)= t*pkdVa D.27)
J охк
v
Подставляя выражения D.25)-D.27) в уравнение D.24) и собирая
все члены в левую часть, получим
Г fp^i - pf. - ^h\ dV = О . D.28)
v
Это равенство должно выполняться для любого индивидуального
объема. Следовательно, должно равняться нулю подынтегральное вы-
выражение
Полученное уравнение называют уравнением движения сплошной
среды. Оно представляет собой второй закон Ньютона для единичного
объема сплошной среды. Слева в D.29) стоит произведение массы ин-
индивидуальной частицы единичного объема на ее ускорение, а справа —
результирующая массовых и поверхностных сил, действующих на эту
индивидуальную частицу сплошной среды.
4.4.1. Субстанциональное и локальное описание движения
сплошной среды. Уравнение движения D.29) формально представля-
представляет собой дифференциальное уравнение второго порядка относительно
координаты индивидуальной частицы сплошной среды. Зная коорди-
координаты и компоненты вектора скорости некоторой частицы в начальный
момент времени, из решения уравнения D.29) можно найти ее коор-
координаты и скорость в любой момент времени. Зная траектории всех
индивидуальных частиц данного вещества, можно составить представ-
представление о характере движения сплошной среды в целом. Такой подход
4.4]
Уравнение движения сплошной среды
51
к описанию движения сплошной среды называется субстанциональ-
субстанциональным или описанием в представлении Лагранжа.
Субстанциональное описание движения сплошной среды не всегда
удобно. Для составления полного представления о характере движе-
движения сплошной среды достаточно было бы знать, как изменяется со
временем скорость в любой фиксированной точке пространства, через
которую с течением времени будут проходить, вообще говоря, различ-
различные индивидуальные частицы сплошной среды. Вместе со сведениями
о таких изменениях в различных точках пространства мы получили бы
достаточно полное представление о характере движения. Такое описа-
описание движения называется локальным или представлением Эйлера.
Чтобы перейти от субстанционального описания к локальному, вос-
воспользуемся выражением D.15), устанавливающим связь между полной
и частной производной по времени
Т77 = ^Г + vk 7Г1 ' D-3°)
at dt dxk
Здесь первое слагаемое правой части представляет собой изменение
скорости среды в фиксированной точке пространства с течением вре-
времени. Второе слагаемое характеризует различие значений скорости в
различных точках пространства в фиксированный момент времени,
т.е является как бы мгновенной фотографией скоростей всех частиц
сплошной среды.
С учетом D.30) уравнение движения D.29) примет следующий вид:
_ 1
zdxk ~
dvi dvi I dcjik . _р
dt dx p dx
p dxk
D.31)
Уравнение D.31) называют уравнением движения сплошной среды
в представлении Эйлера.
Физический смысл этого уравнения в целом и каждого члена ста-
становится более очевидным, если рассмотреть не индивидуальный, а
фиксированный элемент объема сплошной среды (рис. 4.2).
Рис. 4.2. Фиксированный элемент объема сплошной среды (к выводу уравнения
движения)
52 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Запишем баланс импульса для фиксированного элемента объема
AV = Дж1Дж2Дж3 (рис. 4.2) в виде соотношения
Скорость
накопления
количества
движения
Скорость
поступления
количества
движения
Скорость
отвода
количества
движения
Сумма сил,
действующих
на элемент
объема
Уравнение движения, имеющее смысл закон сохранения импульса,
является векторным и может быть записано покомпонентно для всех
трех координатных осей х\, х2 и ж3. Получим х\-компоненту этого
уравнения; х2- и ж3-компоненты могут быть записаны по аналогии.
Существуют два механизма переноса импульса: посредством кон-
конвекции (движения среды) и в результате пространственной неоднород-
неоднородности внутренних напряжений.
Скорость накопления х\ -компоненты импульса среды в элементе
объема определяется выражением
Скорости поступления х\-компоненты импульса среды в элемент объ-
объема AV за счет конвекции через грани с координатами х\, Х2 и ж3
соответственно равны
(pv\v\)\xi Аж2Аж3 , (pv\v2)\X2 Ах\Аж3 , (/™1^з)Ц Дж1 Дж2 •
Перенос г-компоненты импульса среды за единицу времени через еди-
единичную площадку, перпендикулярную координатной оси к, характери-
характеризуют компонентами тензора напряжений aik. Скорости поступления
ж 1-компоненты импульса среды в рассматриваемый элемент объема за
счет внутренних напряжений через грани с координатами х\, х2 и ж3
соответственно равны
Скорости отвода х\ -компоненты импульса среды из элемента объема
через грани с координатами х\ + Джь ж2 + Аж2 и ж3 + Аж3 соответ-
соответственно равны:
за счет конвекции
за счет внутренних напряжений
Результирующая внешняя сила, действующая на сплошную среду в
рассматриваемом элементе объема в направлении оси х\ равна
где вектор f — плотность или напряженность массовых сил.
4.5 ] Уравнение момента импульса сплошной среды 53
Соотношение баланса х\ -компоненты импульса в рассматриваемом
элементе объема запишется в следующем виде:
[{pv\vi)\xi - {pv\vi)\xi+Axi + <тп\Х1 ~
Разделим это выражение на AV и перейдем к пределу, устремив
размеры элемента объема к нулю. В результате получим следующее
уравнение:
| ^^ D.32)
С учетом уравнения непрерывности D.16) получим
*l + VhgL = -L%l± + fl. D.33)
dt дхк р дхк
Выражения, аналогичные D.33), могут быть получены для х^- и
жз-компоненты импульса. Обобщая, вновь получим уравнение движе-
движения в эйлеровой форме D.31)
dvi dvi I ddik , j. (A О/1ч
-РГГ + vk-— = -— h fi • D.34)
at oxk p oxk
4.5. Уравнение момента импульса сплошной среды
Рассмотрим в сплошной среде индивидуальную частицу единичного
объема, положение которой определяется радиус-вектором г, проведен-
проведенным из начала координат, и которая движется со скоростью v. Момент
импульса этой частицы относительно начала координат, очевидно, ра-
равен [rpv]. Тогда полный момент импульса некоторого индивидуального
объема V определится следующим выражением:
М
= f[rpv]dV. D.35)
Пусть К = K.(v^ + КE) — момент всех сил, действующих на инди-
индивидуальные частицы выделенного объема, относительно начала коор-
координат, который составлен из момента объемных К.^ и поверхностных
K.W сил.
Как известно из механики, изменение за единицу времени момента
импульса индивидуального объема относительно неподвижной точки О
О По отношению к некоторой инерциальной системе отсчета.
54 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
равно моменту относительно той же точки всех сил, приложенных
к этому объему:
^ = K = K<K> + K(s>. D.36)
CLT
Преобразуем каждый член этого уравнения. Учитывая правило диф-
дифференцирования по времени интеграла по подвижному объему D.8) и
выражение D.35), левую часть уравнения D.36) запишем в следующем
виде:
= \ Vi [rv] + Mg + P div v)] dV. D.37)
dM
dt
Выражение в круглых скобках представляет собой уравнение непре-
непрерывности D.12) и, следовательно, равно нулю. Кроме того, учтем, что
_^
~di
Тогда выражение D.37) будет иметь вид
dM г Г dvl „, {АЩ
dt
v
Это выражение в компонентах можно записать следующим образом:
^ pdV . D.39)
= J
Здесь Eiki — символ Леви-Чивита, единичный антисимметричный тен-
тензор третьего ранга. Его свойства: Siki = 0 — если среди индексов г, к, I
есть хотя бы два одинаковых; e^i = 1 — если упорядоченная система
индексов 1,2,3 получается четным числом перестановок; еш = — 1 —
если упорядоченная система индексов 1,2,3 получается нечетным чис-
числом перестановок.
С помощью символа Леви-Чивита проекции векторного произведе-
произведения любых двух векторов А и В можно записать в следующем виде:
[АВ]( = ешАкВ,; rot< A = [V А], = ?
Справедливо также следующее соотношение:
Теперь рассмотрим момент объемных сил, действующих на выделен-
выделенный индивидуальный объем,
К\У) = \eiklxkflPdV . D.40)
v
4.5 ] Уравнение момента импульса сплошной среды 55
Для момента поверхностных сил имеем
гМ] dS; K\S) = § eiklxka\n) dS . D.41)
С учетом выражения C.8) для поверхностных напряжений, исполь-
используя теорему Гаусса-Остроградского (см. с. 28), получим
J\^ = (D ?iklxk(Jlmnm "'Э = Ф ^ikl^k^lm "^m =
V V m m
= [ (хк^Р^ + a/m4m) dK D.42)
v
Здесь учтено, что
дхк _ г
UXfYi
где 8km — символ Кронекера.
Подставляя выражения D.39), D.40) и D.42) в уравнение момента
импульса D.36), точнее в проекцию этого уравнения на координатную
ось Х{, получим
d?_f }_дрпЛ_ Sm\dv = Om D.43)
dt p OXm / J
Выражение в круглых скобках представляет собой уравнение движения
D.29) и, следовательно, равно нулю. Из остальной части подынтеграль-
подынтегрального выражения следует:
Поскольку индексы т и / — немые, имеем
Тогда можно записать следующее равенство:
Поскольку по свойству символа Леви-Чивита ецш = -?{Ш1, имеем
timli^lm — & ml) = 0.
Отсюда следует:
(Tim = <Jml . D.44)
Таким образом, показано, что тензор напряжений — симметричный
тензор. Этот вывод следует из уравнения момента количества движе-
движения сплошной среды.
56 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
4.6. Тензор плотности потока импульса
Найдем плотность потока импульса в некоторой фиксированной
точке пространства. Для этого рассмотрим некоторый фиксированный
объем V и вычислим изменение за единицу времени импульса среды
в этом объеме. Очевидно, импульс среды в рассматриваемом объеме
равен:
I pv dV.
v
Рассмотрим изменение со временем г-компоненты вектора импульса
среды в фиксированном объеме. Это изменение будет равно потоку
импульса через поверхность, ограничивающую этот объем. Учтем, что
плотность потока некоторого скаляра является вектором. Например,
в уравнении непрерывности pv есть плотность потока скаляра р.
Соответственно плотность потока вектора является тензором второго
ранга. Пусть П^ есть поток г-компоненты импульса через единичную
площадку, перпендикулярную оси к. Тогда можно записать
D.45)
v s
Знак минус в правой части этого равенства обусловлен той же причи-
причиной, что и в выражении D.17)при выводе уравнения непрерывности.
Определим вид тензора плотности потока импульса П^ в отсут-
отсутствие массовых или объемных сил. Для этого преобразуем левую часть
выражения D.45):
Выражая производные по времени от плотности и скорости из урав-
уравнений непрерывности D.16) и движения D.31), в отсутствие массовых
сил получаем
Г/ dpV dv d(J\ т, (Л ,7ч
\ ( JL )V. D.47)
V V
Первые два члена в правой части можно записать в виде диверген-
дивергенции тензора pviVk- Переходя от интегрирования по объему к интегри-
интегрированию по поверхности, ограничивающей этот объем, имеем
— J pvi dV = -1 (pvivk - (jik) dSk . D.48)
v s
Сравнивая выражения D.45) и D.48), получаем
Пг/, = pViVk ~ (Jik • D.49)
Видно, что Yiik — симметричный тензор.
4.7 ] Уравнение сохранения внутренней энергии 57
Уравнение движения D.31) можно записать в следующем виде:
РЛ- D.50)
dUik
dt
Из уравнения D.50) следует, что изменение импульса единицы объ-
объема среды в заданной точке пространства происходит как вследствие
поступления импульса от соседних частей среды, так и вследствие
действия внешних массовых сил.
4.7. Уравнение сохранения внутренней энергии
Рассмотрим индивидуальный единичный объем сплошной среды.
Для него справедливо термодинамическое равенство (см. C.20)):
dEBH = dQv + aik deik . D.51)
Если изменение внутренней энергии происходит за малый проме-
промежуток времени At, то разделив выражение D.51) на At и переходя
к пределу, получим
dEBH dQv . ,. гсу\
-dT = ^r + aik?ik- D-52)
Второе слагаемое правой части, содержащее тензор скоростей де-
деформаций, может быть преобразовано следующим образом:
1 / dvi dvk\ dvi ,л -Q4
Oik ?ik = ^ik о ( Ъ 1" я— ) = aik ^—• D.53)
2 \oxk uXi) ox
В выражении D.53) учтена симметрия тензора напряжений.
Введем внутреннюю энергию единицы массы ?вн:
Евн = р?вн. D.54)
Изменение за единицу времени внутренней энергии некоторого
индивидуального объема V равно
^ J EBH dV = ± J peBH dV . D.55)
v v
Используя правило дифференцирования по времени интеграла по
подвижному объему D.8), получим
div vldv ¦ D-56)
v v
С учетом уравнения непрерывности D.12) имеем
Выражение D.53) определяет работу внутренних напряжений, со-
совершаемую за единицу времени в единице объема. Тогда работа, со-
58 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
вершаемая внутренними напряжениями за единицу времени во всем
индивидуальном объеме, равна
\±V. D.58)
Рассмотрим количество теплоты, поступающей в единицу времени
в индивидуальный объем от внешних источников. Если внутри объема
нет источников или стоков тепла, то тепло может поступать внутрь
объема только через его поверхность. Пусть q — вектор плотности
теплового потока (рис. 4.3).
Величина |nq| характеризует энергию, пере-
переносимую за единицу времени через единичную
площадку с нормалью п за счет теплопроводно-
теплопроводности среды. В СИ величина q измеряется в Вт/м2.
Тогда уравнение баланса тепла в выделенном
объеме с учетом теоремы Гаусса-Остроградского
(см. с. 28) можно записать в следующем виде:
Рис. 4.3. Плотность -^ [ Qv dV = - <? qdS = - [ div qdV . D.59)
теплового потока v s v
Таким образом, из выражений D.52)-D.59) для скорости изменения
внутренней энергии индивидуального объема имеем
V = O. D.60)
Так как это уравнение записано для произвольного индивидуально-
индивидуального объема, подынтегральное выражение также равно нулю:
" = dlvq + ^ D61)
В эйлеровом представлении D.15) имеем
Из этого уравнения следует, что внутренняя энергия единицы
объема изменяется вследствие притока тепла и работы внутренних
напряжений.
При всестороннем равномерном сжатии основное термодинамиче-
термодинамическое равенство для единицы массы сплошной среды записывается в
виде
deBH = TdS -pdV = TdS -pd(l/p) . D.63)
Тогда уравнение сохранения внутренней энергии будет иметь вид
т dS d I 1 \ .. ,. /л п ,ч
pi —— = рр —-[ — ]— div q — р div v , D.54)
at at \p I
4.7]
Уравнение сохранения внутренней энергии
59
или с учетом уравнения непрерывности D.12) в эйлеровом представле-
представлении
D.65)
РТ (^7
Очевидно, уравнение D.62) более общее, так как оно справедливо
для любой деформации.
Вновь получим уравнение сохранения внутренней энергии D.62),
рассмотрев фиксированный элемент объема сплошной среды.
Баланс энергии в выделенном элементе объема AV = Д
(рис. 4.4) может быть представлен следующим соотношением:
Скорость
накопления
энергии
Скорость конвек-
конвективного подвода
энергии
Скорость конвек-
конвективного отвода
энергии
Скорость подвода
энергии за счет
теплопроводности
Скорость отвода
энергии за счет
теплопроводности
Работа внутренних
напряжении за еди-
единицу времени
Энергию единицы объема сплошной среды запишем в виде суммы
внутренней и кинетической энергий:
Еу = р?вн + - pV2 ,
где евн — внутренняя энергия единицы массы.
(v3Ev) I х3+Ат3 ^3 I x3+Ax3
D.66)
Рис. 4.4. Фиксированный элемент объема сплошной среды (к выводу уравнения
сохранения внутренней энергии)
Тогда скорость накопления энергии в выделенном элементе объема
равна
60 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Скорость конвективного подвода энергии через грань, перпендикуляр-
перпендикулярную оси х\ (рис. 4.4), равна
(v\Ev)\ = Аж2Аж3 U (ревн + ^p
L \ Z
Скорости конвективного подвода энергии через грани, перпендикуляр-
перпендикулярные осям х2 и жз записываются аналогично:
Скорости конвективного отвода энергии через грани х\ + Ах\, х2
+ Аж2 и жз + Ажз соответственно равны
Ax2Ax3(viEv)\X[+Axi, AxiAx3(v2Ev)\X2+Ax2, AxiAx2(v3Ev)\X3+Ax3.
Скорости подвода энергии за счет теплопроводности среды в выде-
выделенный элемент объема через грани х\ ,х2 и х% соответственно равны
Аж2Аж3 (q\)Xl , Дж1 Ах3 (q2)X2 , A^i Аж2 (q3)X3 .
Скорости отвода энергии за счет теплопроводности среды из элемента
объема через грани х\ + Ах\, х2 + Ах2 и жз + Ажз соответственно
равны
Аж1 Аж3 (<72)
Работа, совершаемая выделенным элементом объема над внешней сре-
средой, состоит из двух частей: работы против объемных сил (например,
против силы тяжести) и работы против поверхностных сил, характе-
характеризуемых компонентами тензора напряжений aik. Работа может быть
представлена как произведение силы на перемещение. Тогда скорость
совершения работы определится произведением силы на скорость дви-
движения среды.
Работа, совершаемая выделенным элементом объема против объем-
объемных сил f, равна
В этом выражении знак минус учитывает тот факт, что работа системы
против внешних сил равна по величине и противоположна по знаку
работе внешних сил над системой.
Работа поверхностных сил, совершаемая в единицу времени на
шести гранях рассматриваемого элемента объема, записывается сле-
следующим образом:
После подстановки записанных выражений в соотношение баланса
энергии, разделив на AV и перейдя к пределу бесконечно малых
4.8] Вектор Умо в а 61
размеров выделенного элемента объема, получим
= -^ ^Ev) -д^-дГ {щагк) + pVifi ¦ D-67)
дЕу
С учетом выражения D.66) для энергии единицы объема сплошной
среды, уравнений непрерывности D.16) и сохранения импульса D.31)
уравнение D.67) преобразуется к виду D.62). Мы вновь получили
уравнение баланса внутренней энергии в эйлеровом представлении.
4.8. Вектор плотности потока полной энергии.
Вектор Умова
Пусть Е и е — полная энергия соответственно единицы объема и
единицы массы сплошной среды. Тогда можно записать
Е = ре = p(sBH + ?кин + ?ПОт), D.68)
где евн, ?Кин и ?Пот — соответственно внутренняя, кинетическая и по-
потенциальная энергии единицы массы сплошной среды.
Рассмотрим некоторый фиксированный объем V. Баланс полной
энергии вещества в этом объеме при отсутствии источников и стоков
энергии можно записать в виде уравнения непрерывности:
D.69)
V S S
Здесь S — поверхность, ограничивающая рассматриваемый объем V;
I — вектор плотности потока полной энергии, вектор Умова. Его про-
проекция, //,, на координатную ось х^ характеризует полную энергию,
которая переносится за единицу времени через единичную площад-
площадку, перпендикулярную этой оси. В СИ вектор Умова имеет размер-
размерность Вт/м2.
С другой стороны из соотношения D.68) имеем
)]п'- D7О)
Полагаем, что потенциальная энергия единицы массы сплошной
среды не изменяется со временем. Скорость изменения внутренней
энергии в любой фиксированной точке среды определяется уравнением
D.62):
д^пот п девя деви dqk . dvi (A 7П
— =0, р ——- = -pvk Ь (Tik д— • D.71)
at at axk axk axk
=0, р
at at
Кинетическая энергия единицы массы сплошной среды, движущей-
движущейся со скоростью v равна
?кин = i = ™. D72)
62 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Изменение кинетической энергии за единицу времени определяется
уравнением сохранения импульса D.31)
^ D.73)
р дх )
Известно, что сила, действующая на единицу массы сплошной
среды во внешнем поле, связана с градиентом потенциальной энергии
следующим соотношением:
При этом учтем, что
dvi д
Подставляя уравнения D.71)—D.75) в выражение D.70) и приводя
подобные члены, с учетом D.68) получаем
^ J E dV = - J ^- (qk + pvke - Vi*ik) dV . D.76)
V V
Применяя к правой части теорему Гаусса-Остроградского, имеем
^ J E dV = - § (qk + pvke - Vi*ik) dSk . D.77)
V S
Сравнивая выражения D.69) и D.77), для компонент вектора Умова
получаем
h = Чк + pvk? ~ Viaik . D.78)
Это выражение можно условно записать в векторном виде:
I = q + pvs - va, (vcr)k = Viaik . D.79)
Первый член в правой части полученного выражения есть вектор
плотности потока тепла. В изотропной среде его направление зависит
только от направления градиента температуры D.88). Эта составляю-
составляющая вектора Умова отлична от нуля и в покоящейся среде.
Второй член описывает перенос полной энергии самой движущейся
средой — конвективный перенос энергии. Его направление совпадает
с направлением движения среды.
Наконец, третий член есть вектор плотности потока энергии, свя-
связанный с работой внутренних напряжений в единице объема среды. Он
также существует лишь в движущейся среде, хотя его направление не
совпадает с направлением скорости движения среды.
Можно получить уравнение сохранения полной энергии для еди-
единицы объема среды, которое имеет тот же вид, что и уравнение
непрерывности D.16):
^+divI = 0. D.80)
4.9] Замкнутая система уравнений движения сплошной среды 63
Однако в таком общем виде уравнение сохранения энергии приме-
применяется сравнительно редко, так как при решении конкретных задач
оказывается проще рассматривать различные виды энергии в отдель-
отдельности.
4.9. Замкнутая система уравнений
движения сплошной среды
Запишем систему уравнений сохранения, описывающих движение
сплошной среды.
1. Уравнение непрерывности (см. D.16))
|f+div(pv) = 0. D.81)
2. Уравнение движения (см. D.31))
dvi dvi , 1 dajk (Л й9ч
-^г + и*.-— = fi + --^— • D.82)
at oxk p ox
3. Уравнение сохранения внутренней энергии (см. D.62))
D-83)
Чтобы подсчитать количество независимых физических величин в
этих уравнениях, вспомним связь между компонентами тензора напря-
напряжений, тензора деформаций и вектора смещений C.41), B.6):
<rik = -3ak(T - T0Mik + kSikeu + 2/x [eik - l- 5ikei^ . D.84)
1 (dui duk\ dm (A Q[-4
?ik = о ( я •" ~7Г~ ) ' Vi = ~17 ' D.85)
2 \oxk oxi) at
Нетрудно видеть, что пять скалярных уравнений D.81)—D.83) со-
содержат восемь независимых физических величин
р, щ, ?вн, 4i\ г = 1,2,3.
Таким образом, система уравнений сохранения D.81)—D.83) не
замкнута. Необходимы дополнительные уравнения.
Термическое уравнение состояния устанавливает связь между дав-
давлением, плотностью и температурой
Р = Р(Р,Т). D.86)
Например, для одного моля идеального газа, как известно, имеем: р =
= pRT, где R — газовая постоянная.
Калорическое уравнение состояния устанавливает связь между
внутренней энергией, давлением и температурой
?вн = ?вн (р, Т). D.87)
64 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Феноменологический закон теплопроводности Фурье устанавли-
устанавливает линейную зависимость плотности теплового потока от градиента
температуры среды
q = -AVT, qi = -X^L, D.88)
где Л — коэффициент теплопроводности вещества среды.
Таким образом, система уравнений D.81)—D.88) замкнута.
Очевидно, что для решения этих уравнений необходимо задать кра-
краевые условия, т. е. для получения единственного решения необходимо
в начальный момент времени задать все искомые физические величины
на некоторой поверхности. В частности, в случае стационарных процес-
процессов, зная граничные условия, из решения системы уравнений движения
сплошной среды можно определить значения физических величин в
любой точке объема, занимаемого средой.
Вообще говоря, было бы необходимо доказать теорему существо-
существования и единственности решения фундаментальной системы уравне-
уравнений. Однако в силу существенной сложности уравнений эта теорема
в общем случае не доказана. Доказательство можно получить лишь
для простейших случаев. Поэтому нам придется принять на веру, что
решение системы уравнений движения сплошной среды существует и
при заданных краевых условиях оно единственно.
Все феноменологические параметры, входящие в систему, в общем
случае могут зависеть от термодинамических переменных, например,
от давления и температуры. Разумеется, эта зависимость должна быть
известна из опыта или определена из молекулярно-кинетической тео-
теории.
4.10. Уравнение теплопроводности изотропных сред
Уравнением теплопроводности среды принято называть дифферен-
дифференциальное уравнение, описывающее скорость изменения температуры
в любой фиксированной точке среды и пространственную неоднород-
неоднородность температуры в любой фиксированный момент времени в зависи-
зависимости от теплофизических свойств среды.
Вывод уравнения теплопроводности проведем на основе уравнения
сохранения внутренней энергии D.61). Для простоты рассмотрим изо-
изотропную среду, которая характеризуется единственным коэффициен-
коэффициентом теплопроводности Л.
Тогда с учетом закона теплопроводности Фурье D.88) первое сла-
слагаемое правой части уравнения D.61) записывается в следующем виде:
- divq = div(AVT). D.89)
Изменение за единицу времени внутренней энергии индивидуаль-
индивидуальной частицы среды единичной массы в соответствии с уравнениями
4.11 ] Тензор вязких напряжений 65
D.52) и D.53) равно
d^ dgid^ D90)
Индекс т в первом слагаемом правой части отмечает тот факт, что
рассматривается единица массы среды. Преобразуем это слагаемое
следующим образом:
dQm _ dQm dT _ dT (AQ\\
~dT ~ ~dr~ It ~c~di' [ }
где с = dQm/dT — удельная теплоемкость вещества сплошной среды.
Подставляя выражения D.89)-D.91) в уравнение сохранения внут-
внутренней энергии D.61) и переходя к локальному описанию, получаем
ср (^ + v V т) = div (Л V Т). D.92)
Если пренебречь зависимостью коэффициента теплопроводности от
координат, то для покоящейся среды (v=0) имеем
f = aAT. D.93)
Здесь величина
л
а = —
ср
называется коэффициентом температуропроводности.
Если начальные и граничные условия заданы, то решение уравне-
уравнения теплопроводности D.93) однозначно определяет температуру среды
в любой точке в любой момент времени.
4.11. Тензор вязких напряжений
Упругие напряжения возникают в сплошной среде вследствие сме-
смещений под действием внешних сил одних участков среды по отноше-
отношению к другим.
Опыт показывает, что напряжения могут возникать и вследствие
различной скорости смещений соседних элементов среды. В этом легко
убедиться на следующем мысленном эксперименте.
Представим себе тонкую пластинку, плавающую на поверхности
жидкости (рис. 4.5).
Если сдвинуть пластинку в новое положение вдоль поверхности
жидкости, то она останется неподвижной в новом положении, т. е.
упругая сила, возвращающая ее в прежнее положение, отсутствует. Од-
Однако для того чтобы сдвинуть пластинку, необходимо приложить неко-
некоторую силу. Если передвигать пластинку вдоль поверхности жидкости
прямолинейно и равномерно, то в соответствии с первым законом Нью-
Ньютона действующая на пластинку результирующая сила равна нулю. Это
означает, что со стороны жидкости на пластинку действует сила со-
3 В.Г. Черняк, П.Е. Суетин
66 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
противления, равная по величине и противоположная по направлению
внешней силе. Причем эта сила сопротивления существует лишь тогда,
когда пластинка движется. Чтобы в рам-
^ v ках механики сплошных сред, т.е. игно-
игнорируя молекулярное строение жидкости,
понять механизм возникновения силы со-
сопротивления, разделим мысленно весь
объем жидкости на тонкие слои, парал-
параллельные ее свободной поверхности. Слой,
прилегающий непосредственно к пластин-
пластинке, как бы «прилипает» к ней и увле-
увлекается в движение с той же скоростью.
Следующий слой жидкости с одной сто-
стороны увлекается верхним слоем, а с дру-
другой — тормозится нижним, т. е. скорость
его движения меньше. По мере удаления
от пластинки в глубь жидкости скорость
ее движения непрерывно уменьшается и на достаточно большом рас-
расстоянии жидкость покоится. Качественная зависимость скорости дви-
движения жидкости вдоль оси х\ от нормальной координаты ж 2 показана
на рис. 4.5.
Таким образом, сила сопротивления возникает тогда, когда есть
нормальный пластинке градиент скорости движения жидкости. Этот
экспериментальный факт Ньютон записал в виде формулы
Рис. 4.5. Распределение ско-
скорости движения жидкости
при стационарном движении
тонкой пластинки вдоль сво-
свободной поверхности
= rj
D.94)
Здесь (Ji2 — сила, действующая в направлении оси х\ на единицу пло-
площади пластинки; г) — феноменологический коэффициент, называемый
коэффициентом сдвиговой вязкости.
Таким образом, в сплошной среде при деформации могут возни-
возникать напряжения, пропорциональные не самой деформации, а скорости
деформации. Обобщая результат D.94), мы можем по аналогии с тензо-
тензором упругих напряжений сг^, зависящем от деформации C.30), ввести
тензор ац~, зависящий от скорости деформации:
2r/ (eik -
1
D.95)
Тензор <Jik называют тензором вязких напряжений, ? — коэффици-
коэффициент объемной вязкости, rj — коэффициент сдвиговой вязкости или
просто коэффициент вязкости. Очевидно, что в механике сплошных
сред, оба коэффициента вязкости, так же как модули всестороннего
сжатия и сдвига, являются феноменологическими коэффициентами. Их
значения для любых веществ и при любых температурах должны быть
известны из эксперимента или рассчитаны на основе молекулярно-
кинетической теории.
4.12] Модели сплошных сред 67
Выражение D.95) с учетом формулы D.3) для тензора скоростей
деформации может быть преобразовано к следующему виду:
?« = t6ikp- + v(^ + ^- Ьгкр-) . D.96)
OXi \OXk OXi 3 OXiJ
Тензор вязких напряжений — также симметричный тензор. Линей-
Линейная зависимость тензора напряжений от тензора деформаций выражает
закон Гука.
Линейная зависимость тензора вязких напряжений от тензора ско-
скоростей деформаций называется законом Навье-Стокса.
4.12. Модели сплошных сред
В общем случае движения сплошной среды возникающие в ней
внутренние напряжения должны складываться из упругих и вязких
напряжений. Общий тензор напряжений будет иметь вид
- T0Mik + k5ik?ii +
fc—+ ^(—+ —--^fc—) . D.97)
Таким образом, в самом общем случае среда характеризуется (с ки-
кинематической точки зрения) пятью феноменологическими коэффициен-
коэффициентами.
При решении фундаментальной системы уравнений движения
сплошной среды необходимо учитывать все члены выражения D.97).
Однако в такой общей постановке ни одна задача еще не была решена
в силу ее чрезвычайной математической сложности. Для каждой
конкретной задачи или класса задач приходится делать разумные
упрощающие предположения.
Опыт подсказывает нам, что все сплошные среды можно разделить
на три существенно отличающихся друг от друга класса: твердые тела,
жидкости и газы. Не касаясь различий в характере молекулярного дви-
движения в этих средах, определим эти различия с феноменологической
точки зрения.
Твердое тело. В большинстве задач твердое тело можно характе-
характеризовать как среду, в которой деформации подчиняются закону Гука,
а скорости деформации малы, т.е. можно пренебречь вязкими напря-
напряжениями:
кфО, м/0, ? = 0, 77 = 0.
Эти задачи составляют предмет теории упругости (растяжение, изгиб,
кручение стержней, пластинок, оболочек и т.д.).
Второй характерной особенностью твердого тела в обычном понима-
понимании является то, что твердое тело может быть подвергнуто как сжатию,
так и растяжению, т. е. сгц ^ 0. Относительное изменение объема при
деформации мало: | бц |^С 1.
68 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Если возникает необходимость в учете вязкостных свойств твердого
тела, то нужно сохранять в общем тензоре напряжений члены, завися-
зависящие от скоростей деформаций. Это — предмет науки реологии, которая
включает такие разделы как теории пластичности и ползучести
(деформирование за пределами упругости — прокатка, штамповка
и т.д.).
Жидкость. Наиболее характерное физическое свойство сплошной
среды, которую называют жидкостью, заключается в легком изменении
ее формы. Вода, налитая в сосуд, принимает форму сосуда. Наклоняя
сосуд, мы вновь наблюдаем изменение формы жидкости, происходящее
без видимых усилий. Следовательно, такая среда обладает малым
сопротивлением формы, т. е. ее модуль сдвига мал или вообще равен
нулю.
Таким образом, для жидкости имеем
Отметим, что жидкость, как и твердое тело, может быть как сжата,
так и растянута. Однако ее прочность на растяжение, как правило,
значительно меньше прочности твердых тел и в большинстве задач
предполагается а < 0, т. е. жидкость может быть только сжата, но не
растянута. Относительное изменение объема при сжатии, как и для
твердых тел, невелико: | ец |<С 1.
Газ. Газы, как и жидкости, легко изменяют свою форму, поэто-
поэтому могут рассматриваться как среда с исчезающе малым модулем
сдвига:
кфО, /i = 0, f^O, т/^0.
В отличие от жидкостей газы принципиально не могут быть растянуты,
поэтому для газов ац < 0. Другое отличие от жидкостей и твердых тел
состоит в том, что газы сильно изменяют свой объем при изменении
давления 0, ец < 1. Твердые тела и жидкости при решении многих
практических задач можно считать несжимаемыми (ец = 0).
Как для газов, так и для жидкостей при неизменной температуре
тензор упругих напряжений имеет вид
AV г>
Oik = k5ik?u, ец = — = -р aik = -p5ik , D.98)
т. е. в жидкостях и газах давление изотропно.
Релаксация напряжений. Приведенное деление сплошных сред на
твердые тела и жидкости весьма условно. Критерии такого деления в
существенной мере зависят от соотношения между временем действия
внешних сил, прилагаемых к среде твн и временем релаксации внут-
внутренних напряжений тр.
О В соответствии с уравнением Клапейрона-Менделеева для одного моля
идеального газа имеем: pV = RT, т.е. объем, занимаемый одним молем иде-
идеального газа, в изотермических условиях обратно пропорционален давлению.
4.13] Упругие волны 69
После деформации среды возникающие внутри нее напряжения
релаксируют, т. е. исчезают за некоторый характерный для данной
среды и при данных условиях промежуток времени тр. Релаксация
сопровождается некоторым необратимым изменением в среде (измене-
(изменение объема, остаточные деформации и т.д.). После снятия внешних
сил и релаксации внутренних напряжений среда, вообще говоря, не
возвращается в исходное недеформированное состояние.
Если время релаксации внутренних напряжений много больше вре-
времени действия внешних сил, тр ^> твн, то любая среда ведет себя как
твердое тело. Например, вода при быстром воздействии на нее внешних
сил может рассматриваться как твердое тело (удар о воду), обладающее
определенным модулем сдвига.
Если же время релаксации внутренних напряжений много мень-
меньше времени внешнего воздействия, тр <С твн, то любая среда может
рассматриваться как маловязкая жидкость с модулем сдвига, равным
нулю. Изучение движения таких жидкостей составляет предмет гидро-
гидродинамики. Такие жидкости еще называются ньютоновскими жидко-
жидкостями.
Например, битум или смола при быстром воздействии внешней
силы ведут себя как твердое тело (рассыпаются при ударе), а при
длительном действии внешних сил растекаются по поверхности или
принимают форму сосуда, в который были положены, т. е. ведут се-
себя как жидкость. Даже стальной стержень при растяжении силой,
вызывающей в нем заведомо только упругие деформации, с течением
времени течет и необратимо удлиняется, особенно при повышенных
температурах (ползучесть).
Таким образом, выбор модели сплошной среды при решении кон-
конкретной задачи определяется не только агрегатным состоянием веще-
вещества, но и зависит от соотношения между временем внешнего воз-
воздействия, вызывающего деформацию среды, и временем релаксации
внутренних напряжений. Одна и та же среда в различных задачах
может рассматриваться и как твердое тело, и как жидкость.
Подводя итог, запишем выражение для полного тензора напряжений
для ньютоновских жидкостей и газов:
г> я I с я dvi I (dvi dvk 2 - dvi\ (. QQ,
Pik = -P5ik + tSik — + „(_ + _- -Sik—) . D.99)
4.13. Упругие волны
Рассмотрим распространение в упругой среде малых деформаций.
Поскольку распространение любых возмущений в среде, как мы уви-
увидим, происходит достаточно быстро, в виде некоторого волнового про-
процесса, то можно полагать, что деформации в каждом элементе объе-
объема среды совершаются адиабатически, без теплообмена с соседними
частицами среды. Тогда модули сдвига и всестороннего сжатия в
последующих формулах нужно полагать адиабатическими.
70 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Запишем уравнение движения упругой (не вязкой) среды при от-
отсутствии массовых сил:
%p L°p D.100)
р дх
Будем полагать, что скорости частиц среды, возбуждаемые про-
проходящей волной, малы по сравнению со скоростью самого волнового
процесса. На этом основании можно пренебречь вторым слагаемым
левой части уравнения D.100), как членом более высокого порядка
малости.
Для простоты рассмотрим плоскую волну, т. е. волну, при распро-
распространении которой деформации точек среды зависят только от одной
координаты х\ и времени t,
/ ,\ dv,i
u = u(xut), Vi = —.
Тогда уравнение движения для проекции деформации на ось х\ будет
иметь вид 2
0ш±0* DШ1)
dt P дхк
Выражение C.30) для тензора упругих напряжений может быть
записано в следующем виде:
иЯ дщ _l ( dui _l дик 2 Я дщ\ (А \Ю\
°ik = kOik д h li I д h ^ x Oik ^— ) • D.102)
OXi \OXk OXi 3 OXi J
Подставляя это выражение в уравнение D.101), получаем
dt2 ' дх\
гле
D.103)
2 1 Л 4 \ ЕA-а) (А 1А/1Ч
ci = ~ (к+ оМ = п ^ U1 9 ч • D.104)
р \ 3 / рA + сг)A - 2а)
р \ 3 / рA + сг)A - 2а)
Для проекции деформации на оси ж2 и жз получаем идентичные
уравнения
w = *b- w = *b- <4105)
Таким образом, мы получили обычные волновые уравнения для
распространения малых деформационных возмущений в виде плоской
волны. Из уравнений следует, что волна представляет собой, по су-
существу, две независимо распространяющиеся волны. Очевидно, с/ -
скорость распространения продольной волны (смещение точек среды щ
происходит вдоль оси х\), ct — скорость распространения поперечной
волны (смещения и^ и щ перпендикулярны оси х\).
4.13] Упругие волны 71
Поперечные волны при прохождении через частицы среды не из-
изменяют их объем и называются поэтому еще сдвиговыми волнами.
Действительно, если щ = 0, то в соответствии с B.23) имеем
—— = div u = 0 .
Прохождение продольной волны сопровождается адиабатическим изме-
изменением объема, и потому продольная волна называется иначе волной
сжатия. Если щ = щ = О, то
AV = дих
V dxi^
Отношение скоростей распространения волн равно
Поскольку коэффициент Пуассона принимает значения в интервале 0 ^
^ а ^ 1/2, то отношение скоростей изменяется в пределах
V2 ^*<оо.
Ct
Это свойство распространения упругих возмущений используется в
гравитационной разведке и сейсмологии. Действительно, пусть две сей-
сейсмических станции приняли сигналы прохождения продольной волны,
а затем поперечной. Пусть промежуток времени между сигналами на
первой станции равен At\. Тогда его можно определить следующим
образом. Если землетрясение или взрыв произошли на расстоянии 1\
от этой станции, то времена прохождения продольной и поперечной
волн равны
, h , h
41 = —, Н\ = — .
ci ct
Измеряемый промежуток времени между сигналами на первой станции
равен
/ 1 1 \
Ati =tti-tn=li .
V Ct CiJ
Отсюда можно определить расстояние от первой станции до места
землетрясения или взрыва
, Atictci
ч = •
ci - ct
На второй станции, измеряя промежуток времени Д^2 между сигна-
сигналами прихода продольной и поперечной волн, получим расстояние, на
котором произошел взрыв или землетрясение от второй станции
ci - ct
Проведя окружности радиусами 1\ и 1% вокруг станций, в точках пе-
пересечения получим координаты места взрыва или землетрясения. Для
72 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
того чтобы уточнить, в какой именно из двух точек произошел взрыв,
необходимы данные, по крайней мере, еще одной станции.
Ясно, что для таких расчетов нужно знать упругие свойства зем-
земной коры. Эти данные предоставляются специальными геофизическими
исследованиями при помощи, например, взрывов, когда расстояния
заведомо известны.
На этом же принципе основаны гравитационные методы разведки.
Измеряя скорости прохождения волн, создаваемых искусственными
взрывами, можно определить среднюю плотность вещества, в котором
они распространяются или от которого они отражаются, а также полу-
получить информацию об упругих свойствах среды. Опыты по измерению
скорости распространения продольных и поперечных волн могут также
служить способом определения упругих констант различных материа-
материалов при различных условиях.
Для жидкостей и газов с исчезающе малым модулем сдвига мала и
скорость распространения сдвиговых (поперечных) волн. Если /i = О,
то с учетом выражения C.46) скорость распространения продольных
волн сжатия равна:
В заключение приведем таблицу примерных значений констант
некоторых веществ.
Материал
Сталь
Алюминий
Стекло
Каучук
Я,10пПа
2,1
0,70
0,56
0,00008
11, 10ю Па
8,3
2,6
2,2
0,000
а
0,25
0,34
0,25
0,47
ci, м/с
5700
6300
5200
720
ct, м/с
3300
3100
2900
27
Контрольные вопросы
1. Что характеризует след тензора скоростей деформации?
2. В чем отличие между индивидуальным и фиксированным объемами
сплошной среды?
3. Какой физический смысл имеет уравнение непрерывности?
4. В чем принципиальное отличие между субстанциональным и локальным
описанием движения сплошной среды?
5. Из какого фундаментального закона следует симметрия тензора напря-
напряжений?
6. Что характеризует величина вектора плотности теплового потока?
7. В каком случае вектор Умова равен вектору плотности теплового по-
потока?
4.14] Примеры решения задач 73
8. Перечислите уравнения, составляющие замкнутую систему уравнений
движения сплошной среды.
9. При каком условии в среде возникают вязкие напряжения?
10. В чем отличие между тензорами упругих и вязких напряжений?
11. Какое значение имеет модуль сдвига для ньютоновских жидкостей и
газов?
12. Каким критерием руководствуются при выборе модели сплошной среды
(жидкость или твердое тело) при нестационарных процессах?
13. Распространяются ли поперечные волны в объеме ньютоновской жидко-
жидкости или газа? Обоснуйте ответ.
4.14. Примеры решения задач
Общие рекомендации. Очевидно, что каждая задача теории упру-
упругости имеет свою специфику, которая определяется физической приро-
природой действующих сил, геометрическими размерами и формой деформи-
деформируемого тела, характером деформации и т. д. От этих факторов зависит
вид дифференциального уравнения равновесия и граничных условий, и
они в существенной степени определяют выбор того или иного матема-
математического метода решения полученных уравнений. Поэтому невозмож-
невозможно дать какие-либо конкретные рекомендации к решению любых задач
теории упругости. Вместе с тем можно попытаться выявить общее,
характерное для самого подхода решения этих задач.
Общий алгоритм, последовательность действий, состоит в следую-
следующем.
1. Решение задачи следует начинать с анализа всех сил, действу-
действующих на тело. Необходимо выявить природу этих сил, точку приложе-
приложения, направление действия и зависимость от координат.
2. Далее следует проанализировать топологию задачи, т. е. гео-
геометрическую форму тела и свойства симметрии. Отсюда выбирается
удобная система координат, такая, в которой компоненты уравнения
равновесия и граничные условия будут иметь наиболее простой вид.
Для наглядности полезно сделать рисунок.
3. С учетом топологии задачи и направления действия сил опре-
определить направления деформации и от каких координат зависят компо-
компоненты вектора смещения.
4. Записать уравнения равновесия для тех компонент вектора сме-
смещения, которые необходимо определить. При этом следует учесть свой-
свойства симметрии задачи и сделать сравнительную оценку членов по-
полученных уравнений. Решение может существенно упроститься, если
пренебречь членами более высокого порядка малости.
5. Задать граничные условия с учетом симметрии задачи, действу-
действующих объемных сил и вызываемых ими внутренних напряжений.
6. Выбрать метод решения полученных дифференциальных урав-
уравнений точный или приближенный с требуемой точностью.
74 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
7. Проанализировать полученный результат, т. е. рассмотреть пред-
представляющие интерес частные случаи, выявить физические следствия,
найти известные аналогии в механике, сравнить с экспериментом,
оценить прикладное значение и т. д.
из опыта, принципиальная схема ко-
коЗадача 1
Определите модуль сдвига
торого показана на рис. 4.6.
Решение. В рассматриваемом опыте заданы сила F, действующая
на верхнюю грань бруска вдоль оси z, расстояние d от шкалы до бо-
боковой (зеркальной) грани и площадь S
поперечного сечения испытуемого брус-
бруска. Измеряется смещение 5 отражен-
отраженного при деформации светового луча.
Поскольку сила F обусловливает
деформацию чистого сдвига, то по су-
существу задача сводится к определению
компонент тензора деформаций.
Повторяя рассуждения, использо-
использованные при решении задачи об одно-
однородном растяжении стержня (см. с. 34)
можно показать, что единственная от-
отличная от нуля компонента тензора на-
напряжений равна
*** = ?• D.109)
Рис. 4.6. Схема опыта: / — ис-
источник света, 2 — шкала, 3 —
зеркальный торец бруска, 4 —
испытуемый брусок с площадью
основания S; d — расстояние от
зеркала до шкалы, S — смеще-
смещение отраженного луча при де-
деформации бруска
Так как смещение любой точки бруска происходит только вдоль оси
z (смещением вдоль оси х при малой деформации можно пренебречь),
то из рисунка видно, что вектор деформации имеет следующие компо-
компоненты
их = иу = 0, uz = х • tg (p & х - (р . D.110)
Здесь учтено, что угол (р мал.
Из соотношения B.6) следует:
&XZ п.
1 duz 1
D.111)
С другой стороны из закона Гука C.31) с учетом выражения D.109)
получаем
D.112)
2/i
J_ F_
2/1^
Как видно из рис. 4.6,
Тогда из выражений D.111) и D.112) для модуля сдвига получим
о Fd
S5
D.113)
4.14] Примеры решения задач 75
Задача 2
Определите деформацию шара радиуса R и плотностью р под
влиянием собственного гравитационного поля. Ускорение свободного
падения g на поверхности шара известно.
Решение. Выберем сферическую систе-
систему координат (г, в, (р), начало которой сов-
совмещено с центром шара (рис. 4.7). Сила
тяготения, действующая на единицу массы
шара в точке с радиусом-вектором г равна
f = —gr/R. Знак минус означает, что сила
направлена противоположно радиусу-вектору.
Очевидно, если шар представляет собой
изотропное тело, то задача является сфериче-
сферически симметричной и одномерной. Деформация
представляет собой смещение точек шара в . . . д ф р
радиальном направлении. Таким образом, уг-
угловые компоненты вектора смещения равны нулю {uq = и^ = 0), а
отличная от нуля радиальная компонента зависит только от координа-
координаты г, т. е. иг = и(г).
При этих условиях уравнение равновесия C.54) будет иметь сле-
следующий вид:
d f 2 Л л г л A+ <т)A - 2а) ,л П/|,
Для получения однозначного решения этого уравнения следует
задать два граничных условия. Первое констатирует конечную дефор-
деформацию в центре шара, т.е., согласно выражению C.56), имеем
г*(г = 0)<оо. D.115)
Второе граничное условие учитывает тот факт, что на поверхности
шара внешних сил нет и, следовательно, в состоянии равновесия нор-
нормальные напряжения равны нулю, т. е.
arr(r = R) =0. D.116)
Общее решение уравнения равновесия D.114) имеет вид
и(г) = А-?- + С{^ + С2\, D.117)
где С\, Съ — постоянные интегрирования.
Из условия D.115) следует, что С2 = 0. Для определения другой
постоянной С\ необходимо предварительно определить компоненту агг
тензора напряжений.
Из выражения C.51) следует:
- 2сг) ^ a>?rr + а(?вв + ?(р(р^ ' D.118)
76 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Компоненты тензора деформаций вычисляем по формулам (П.4)
приложения с учетом выражения D.117):
с гг —
диг _ 3Arz C]_ _
10R 3 ' ?" ~
Агг
дг 10Д ' 3 ' ^™ ^ г 10Я 3 '
Из граничного условия D.116) при г = R получаем
^ _ _3_ л ^ 3 - G
1 ~ 10
D.119)
D.120)
Таким образом, смещение точек шара в радиальном направлении
равно
, ч ЛЯ /3-сг г^
^W = —[q-^
D.121)
Относительная деформация вдоль радиуса шара определяется сле-
следующим выражением:
AR
10
3-сг
1+сг
D.122)
Отсюда следует, что внутри шара существует недеформированная
(srr = 0) в радиальном направлении сферическая поверхность радиуса
ro = R
3-сг
3A +сг
Поверхностный сферический слой при г > го оказывается растянутым
(егг > 0), а ядро шара при г < го сжато (егг < 0).
Задача 3
Определите деформацию полой цилиндрической трубы с внутрен-
внутренним радиусом R\ и внешним R%, заполненной жидкостью или газом
при давлении р. Давление снаружи отсутствует. Силой тяжести прене-
пренебречь.
Решение. Удобно использовать цилиндриче-
цилиндрические координаты (г, <р, z) с осью z, направленной
вдоль оси цилиндра (рис. 4.8).
В соответствии с законом Паскаля давление жид-
жидкости (или газа) в трубе изотропно, т. е. действует
во всех направлениях одинаково. Поскольку силой
тяжести пренебрегаем, то деформация стенок трубы
происходит только в радиальном направлении, при-
причем радиальная компонента вектора смещения зави-
зависит только от координаты г.
Таким образом, для компонент вектора смещения
имеем
Рис. 4.8. Полый
цилиндр
= uz = 0,
иг = и(г) .
4.14] Примеры решения задач 77
В этом случае rot u = 0. Так как массовых сил нет (fi = 0), то
уравнение равновесия C.54) принимает следующий вид:
grad div u = 0, D.123)
или в цилиндрических координатах с учетом топологии задачи:
= 0. D.124)
dr ir
На внешнюю поверхность трубы силы не действуют, а на внутрен-
внутреннюю действует давление р. Тогда два граничных условия будут иметь
вид
arr(r = Ri) = -p, arr(r = R2)=0. D.125)
Общее решение уравнения D.124) имеет вид
и(г) = ^С{г + С2^, D.126)
где С\ и С2 — постоянные интегрирования.
Диагональные компоненты тензора деформаций равны
Нормальное напряжение в радиальном направлении в соответствии
с выражением C.51) равно
агг = п ^U1 _0^ [A - ст)егг + а(е^ + ezz)] =
Е '^i_(i_ 2G)^1 . D.128)
Теперь из граничных условий D.125) вычисляем постоянные инте-
интегрирования:
С[= 2PR2 A + <г)A-2<г) с2=р ^^ 1 + СГ. D129)
Подставляя эти значения в выражение D.126), получим
D.130)
^ R% — R\
В инженерной практике часто возникает необходимость провести
расчет конструкции на прочность. Для этого необходимо вычислить
компоненты тензора напряжений
_ РЧ / 1 R2
&гг = —* о I 1 о"
Г
О О \ А I 0 1» ^ ZZ ^Н О О
r\-r\ V г2 J r\-r\
78 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Если окажется, что при данном давлении наибольшее из напря-
напряжений превысит предел прочности 0 материала трубы, то следует ис-
использовать трубы из другого более прочного материала или с другими
внутренним и внешним радиусами.
Задача 4
Определите деформацию сплошного цилиндра радиуса R, равно-
равномерно вращающегося вокруг своей оси с угловой скоростью ио. Силой
тяжести пренебречь.
Решение. Цилиндрическую систему координат выберем так, что-
чтобы ось z совпадала с осью вращения цилиндра.
На единицу массы цилиндра в точке с ра-
радиусом-вектором г действует центробежная сила
f = ou2r. Поскольку силой тяжести пренебрегаем,
то деформация цилиндра происходит под действием
центробежной силы только в радиальном направле-
направлении, т. е.
U(p = uz = 0, иг = и{г).
Тогда уравнение равновесия C.54) принимает сле-
следующий вид:
Рис. 4.9. Вращаю- d Г1 d , \\ _ 2 A + <х)A — 2<т) /
щийся цилиндр ~^р [^ ~dr^rU'\ ~ ~PU r д(\ _ а^ ' ^
При постановке граничных условий учтем конечную деформацию на
оси цилиндра и отсутствие внешних сил на его боковой поверхности,
т.е.
u(r = 0)<oo, arr(r = R) =0. D.133)
Общее решение уравнения равновесия D.132) имеет вид
D.134)
где С\, С<} — постоянные интегрирования.
Из первого условия D.133) следует, что С^ = 0. Для определения
другой постоянной С\ поступаем как и в предыдущей задаче. Вначале
вычисляем диагональные компоненты тензора деформаций:
du 3 2 2 A + сг)A -2а)
Е(\ -¦
Cj_
2
?zz = 0,
и
г
,2Г2 A+а)A-2с
Е{\-а)
D.135)
х) Пределом прочности называется напряжение, соответствующее наиболь-
наибольшей нагрузке, выдерживаемой телом перед разрушением. Значения этой вели-
величины для различных материалов табулированы.
4.14]
Примеры решения задач
79
Компоненту <jrr тензора напряжений вычисляем из выражений C.51)
и D.135):
<Jrr =
—^к1-*)*'
ezz)] =
E
Из второго граничного условия D.133) получаем
Ci--W Д C-2^)—^—^—.
. DЛ36)
D.137)
Таким образом, деформация цилиндра определится следующим вы-
выражением:
и{г) = рш2
[C - 2а) Д
2 - г2
D.138)
Задача 5
В теплообменнике, представляющем собой алюминиевую сферу с
внутренним радиусом R\ и внешним R2, находится пар при тем-
температуре Т\. Снаружи сфера обтекается водой при температуре Т2.
Вычислите деформацию сферы, если Т\ =
= 500 К, Т2 = 300 К, Rx = 0,50 м, R2 = 0,52 м.
Радиусы даны при температуре То = 293 К.
Коэффициент теплового линейного расширения
алюминия а = 2,29 • 10~5 К.Коэффициент
Пуассона а = 0,34. Температуру поверхности
теплообменника примите равной температуре
окружающей среды.
Решение. Сферическую систему коорди-
координат (г, 0, <р) поместим в центр теплообменника.
Распределение температуры в сферическом
слое определится из решения уравнения теп-
теплопроводности D.93). В стационарных условиях температура зависит
только от радиальной координаты
Рис. 4.10. Полая сфера
а
г
D.139)
где
R2-Ri
Силой тяжести будем пренебрегать. Тогда деформация теплообменника
изотропна и уравнение равновесия C.54) запишется в виде
dr
1 +сг dT
3A -a) ~dr
D.140)
80 Фундаментальная система уравнений движения сплошной среды [ Гл. 4
Для простоты давлением пара и воды на стенки теплообменника
пренебрегаем. Тогда граничные условия для напряжений имеют сле-
следующий вид:
<тгг=0, r = Ru r = R2, D.141)
общее решение уравнения D.140) с учетом выражения D.139)
Постоянные интегрирования С\ и С2 определяются из граничных
условий D.141). Используя соотношение D.118), получаем
з з D.143)
R\R\
~ l
Результат численного расчета деформации теплообменника дает
u(Ri) = 6,76см, u(R2) = 6,86см.
Таким образом, толщина стенки увеличилась на 1 мм.
ГЛАВА 5
ИДЕАЛЬНАЯ ЖИДКОСТЬ
Гидродинамика 0 - раздел механики сплошных сред, в котором
изучается движение жидкостей и газов со скоростями, меньшими ско-
скорости звука. Это позволяет во многих задачах считать и жидкость,
и газ несжимаемыми средами, что существенно упрощает теорию.
Прикладные задачи гидродинамики связаны, как правило, с изучением
взаимодействия движущейся жидкости с твердыми телами.
Обычно в гидродинамике термин «жидкость» обозначает как ка-
капельную жидкость, так и газ. Случаи, когда речь идет именно о газах,
будем специально оговаривать.
Идеальная жидкость является наиболее простой механической мо-
моделью движущейся сплошной среды. Предполагается, что жидкость не
обладает диссипативными свойствами, т. е. лишена вязкости и тепло-
теплопроводности. При этом она остается ньютоновской жидкостью, модуль
сдвига которой равен нулю. Несмотря на то, что это весьма идеали-
идеализированная модель, многие характерные черты движения жидкости и
газа как сплошных сред могут быть изучены при помощи этой простей-
простейшей модели, по крайней мере вдали от поверхности обтекаемых тел.
5.1. Уравнения движения идеальной жидкости
При изотермическом движении идеальной жидкости полный тензор
напряжений определяется только гидродинамическим давлением р и
имеет вид
Pik = -pSik. E.1)
Тогда уравнение движения запишем в виде
*? + ** i «? +
E.2)
? + ,, = + ,,.
at oxk p oxi
Здесь Vi — г-я компонента скорости движения жидкости, fi —
г-компонента вектора массовой силы. Уравнение E.2) носит название
уравнения Эйлера.
Уравнение непрерывности как уравнение сохранения массы будет
иметь прежний вид:
^ 0. E.3)
х) В переводе с греческого hydor — вода и динамика.
82 Идеальная жидкость [ Гл. 5
Уравнение для внутренней энергии единицы массы жидкости евн
можно записать следующим образом:
-^ + vV?BH) = -p div v E.4)
ИЛИ / я С \
E.5)
где S — энтропия единицы массы жидкости.
Из последнего уравнения получаем физически очевидный результат:
^=0. E.6)
at
То есть энтропия единицы массы идеальной жидкости сохраняется
в процессе движения. Этот результат очевиден, так как мы лишили
жидкость механизмов возрастания энтропии. В силу отсутствия теп-
теплопроводности в элемент объема жидкости тепло не может поступать
извне, так же как и покидать его. Полагая равной нулю вязкость жид-
жидкости, мы устранили источник возрастания энтропии внутри элемента
объема вследствие диссипации механической энергии движения.
Система уравнений движения идеальной жидкости включает пять
независимых уравнений: E.2), E.3), E.4) или E.5). Если внешние си-
силы заданы, то неизвестных искомых функций шесть:
Щ, Р, Р, ?вн-
Для замыкания системы уравнений, очевидно, необходимо доба-
добавить калорическое уравнение состояния, устанавливающее зависимость
внутренней энергии единицы массы жидкости от давления и темпера-
температуры
?вн = / (р, Р) • E.7)
5.1.1. Изэнтропическое движение. Рассмотрим случай, когда
энтропия одинакова во всех точках движущейся жидкости и не изме-
изменяется с течением времени, т. е.
S = So = const. E.8)
Такие движения идеальной жидкости называются изэнтр(эпическими.
В этом случае уравнения E.4)-E.6) оказываются ненужными и мы
имеем лишь четыре скалярных уравнения E.2), E.3), которые вместе
с уравнением состояния образуют замкнутую систему уравнений иде-
идеальной жидкости.
Для изэнтропических движений уравнению движения идеальной
жидкости E.2) можно придать другой вид. Для этого воспользуемся
известным термодинамическим соотношением
h = ?BH+PV, dh= -dp + TdS, E.9)
Р
где h — энтальпия единицы массы.
5.1 ] Уравнения движения идеальной жидкости 83
Так как для изэнтропического движения dS = 0, то имеем
dh = -dp, Vft = -Vp. E.10)
Р Р
Предположим, что поле внешних сил потенциально, т. е.
f =-V?noT, E.11)
где ?ПОт — потенциальная энергия единицы массы жидкости в поле
внешних сил. Тогда уравнение движения будет иметь вид
^ ( ?n0T). E.12)
Воспользуемся известной формулой векторного анализа
vVv= i Vv2 - [v, rot v]. E.13)
Подставляя в уравнение E.12), получим
^ - [v, rot v] = -V (д + h + еП0Л . E.14)
Взяв операцию rot от обеих частей последнего уравнения и учитывая,
что rot V = 0, имеем
/-)
—- rot v = rot [v, rot v]. E.15)
0 T
Последнее уравнение называется уравнением Эйлера в форме Гро-
мека. Замечательно то, что оно содержит только скорости. Таким
образом, в случае изэнтропических течений идеальной жидкости, если
массовые силы имеют потенциал, то скорости могут быть найдены
независимо от других переменных течения. При заданных граничных
и начальных условиях это решение существует и оно единственно, т.е.
задача становится чисто кинематической. Для отыскания других пере-
переменных характеристик течения необходимо, зная скорость, вернуться
к исходной форме уравнений. Например, плотность жидкости может
быть найдена из уравнения непрерывности, а давление — из уравнения
движения.
Если ввести аксиальный вектор 0 ш, называемый вихревой скоро-
скоростью, соотношением
ш = - rot v, E.16)
то уравнение Громека можно записать в виде
f^ = rot[v,w]. E.17)
О Аксиальными векторами или псевдовекторами называют векторы, ко-
которые изменяют свое направление на противоположное при переходе от правой
системы координат к левой(отражение). В отличие от них обычные векторы
называют полярными.
84 Идеальная жидкость [ Гл. 5
5.1.2. Граничные и начальные условия. Поскольку идеальная
жидкость не имеет вязкости, то соседние слои жидкости могут иметь
какие угодно относительные скорости. Так, например, жидкость может
двигаться вдоль обтекаемой твердой поверхности с любой скоростью.
Поэтому единственным физическим ограничени-
ограничением для скорости жидкости на некоторой твердой по-
поверхности, есть условие непротекания. Это усло-
условие ограничивает лишь нормальную к поверхности
тела компоненту скорости жидкости.
На неподвижной поверхности нормальная ком-
компонента скорости жидкости должна быть равна
Рис. 5.1. Гранич- нулю _
ное условие vn = ^п = 0. E.18)
На поверхности, движущейся со скоростью и, нормальные компо-
компоненты скорости поверхности и жидкости должны быть равны (рис. 5.1)
vn = un. E.19)
В качестве начальных условий необходимо задать значения всех
искомых функций в некоторый момент времени в рассматриваемой
области движения жидкости или на поверхности, ограничивающей эту
область.
5.2. Уравнение Бернулли
Движение жидкости, при котором во всем пространстве, заня-
занятом движущейся жидкостью, rot v = 0, называется потенциаль-
потенциальным.
Рассмотрим стационарное движение идеальной жидкости, т. е.
Тогда для стационарного потенциального изэнтропического движе-
движения идеальной жидкости из уравнения E.14) будем иметь
О = V (у + h + еП0Л . E.20)
В любой точке потока последнее равенство может выполняться
только тогда, когда выражение в скобках равно некоторой постоянной
во всей области течения жидкости:
v2
— + h + ?ПОт = const. E.21)
Уравнение E.21) есть первый интеграл уравнения движения Эйлера
и называется уравнением Бернулли. Уравнение Бернулли, очевидно,
является уравнением сохранения полной энергии единицы массы жид-
жидкости. Действительно, первое слагаемое левой части — кинетическая
5.2 ] Уравнение Бернулли 85
энергия единицы массы жидкости, второе — внутренняя энергия плюс
работа сил давления и третье слагаемое — потенциальная энергия еди-
единицы массы жидкости.
Для несжимаемой жидкости (р = const) при изэнтропическом дви-
движении . .
dh= -dp = d ( ? ) . E.22)
Р \Р)
Рассмотрим движение идеальной жидкости в поле силы тяжести.
Если ось z направлена противоположно направлению вектора ускоре-
ускорения силы тяжести, то
?Пот = gZ, f = -УбГпот, f = -g • E.23)
Тогда для несжимаемой жидкости, движущейся в поле силы тяже-
тяжести, уравнение Бернулли запишется в следующем виде:
v— + Е + gz = const. E.24)
5.2.1. Линии тока и траектории. Трубка тока. Линия тока —
это линия, касательная к которой дает направление скорости движе-
движения жидкости в точке касания в данный момент времени (рис. 5.2).
Траектория — это воображаемая линия, описываемая индивидуальной
частицей жидкости при движении. При стационарном движении линии
тока и траектории совпадают. При нестационар-
нестационарном движении это, вообще говоря, разные линии.
Для визуализации течения экспериментаторы
вводят в движущуюся жидкость мелкие частицы,
которые при соответствующем освещении ярко
светятся.
Если теперь сфотографировать поле течения с Рис. 5.2. Линия тока
небольшой выдержкой, то мы получим на фото-
фотографии множество коротких черточек, «прочерчиваемых» за короткое
время экспозиции на фотопластинке множеством светящихся частиц
порошка. Подбирая кривые, касательные к некоторому последователь-
последовательному ряду черточек, получим линии тока в жидкости в данный момент
времени. В другой момент времени нестационарного движения линии
тока могут быть другими.
Если же значительно увеличить время экспозиции, то каждая ча-
частица «прочертит» на фотопластинке непрерывную линию через все
поле течения, охватываемое объективом. Эти линии, очевидно, и явля-
являются траекториями частиц жидкости.
Касательные к линии тока в различных ее точках дают направление
скорости разных индивидуальных частиц в один и тот же момент
времени. Касательные к траектории в различных ее точках дают на-
направление скорости одной и той же индивидуальной частицы в разные
моменты времени.
86 Идеальная жидкость [ Гл. 5
Если в жидкости взять некоторый замкнутый контур и через все
его точки провести линии тока, то они составят некоторую трубку,
называемую трубкой тока (рис. 5.3). Замеча-
Замечательное свойство трубки тока состоит в том,
что по определению линий тока через ее бо-
боковую поверхность нет потока жидкости. Жид-
Жидкость в трубку тока может поступать только
через ее торцы.
Рассмотрим на линии тока две любые близ-
Рис 5 3 Трубка тока кие точки- Тогда дифференциально малое при-
приращение радиуса-вектора dr, разделяющего эти
точки и имеющего координаты (dx, dy, dz), можно считать колли-
неарным вектору скорости v. Поэтому векторное произведение этих
векторов равно нулю
[v, dr}=0. E.25)
Отсюда получаем уравнение линий тока
vx vy vz
Уравнение Бернулли может быть получено и для непотенциального
движения (rot v ф 0), однако требование изэнтропичности и стацио-
стационарности движения жидкости в поле потенциальных сил должно со-
сохраниться. В этом случае уравнение E.14) запишется в виде
E.27)
Спроецируем это уравнение на линию тока. Для этого умножим
скалярно правую и левую части на единичный вектор касательной к
линии тока 1:
2
([v, rot v], 1) = (V(у + h + ?пот), l) . E.28)
Но первый множитель в левой части представляет собой вектор, пер-
перпендикулярный вектору скорости v, а следовательно, и 1. Поэтому их
скалярное произведение равно нулю. Тогда имеем
)=0. E.29)
dl V 2
Следовательно, для данной линии тока можно записать
2
— + /г + ?ПОт = const. E.30)
Уравнение E.30) отличается от уравнения E.21) только тем, что
в случае потенциального движения константа в правой части уравне-
уравнения E.21) одинакова во всем объеме, занятом движущейся жидкостью,
тогда как константа в правой части уравнения E.30) сохраняет свое
5.3]
Применение уравнения Бернулли
87
значение лишь для данной линии тока и может иметь другое значение
для другой линии тока.
Заметим, что мы можем получить уравнение Бернулли всегда, когда
нам удается выразить Vp/p в виде градиента некоторой функции Р:
-Vp = VP. E.31)
Р
Так, для изэнтропического движения Vp/p = V/i, для несжимаемой
жидкости Vp/p = V(p/p). Очевидно, что это можно сделать и при
изотермическом движении.
Движения идеальной жидкости, для которых выполняется соотно-
соотношение E.31), называются баротропными, а функция Р называется
баротропным потенциалом.
Для баротропных движений уравнение Бернулли имеет вид
2
— + Р + ?ПОт =
E.32)
5.3. Применение уравнения Бернулли
Рассмотрим, как с использованием уравнения Бернулли можно ре-
решать задачи и объяснять интересные явления, наблюдаемые в природе
и часто встречающиеся в инженерной практике. Рассмотрим несколько
примеров.
5.3.1. Скорость истечения идеальной несжимаемой жидкости
из сосуда. В качестве первого примера рассмотрим стационарное
истечение идеальной несжимаемой жидкости из отверстия в боковой
стенке сосуда (рис. 5.4).
Если полагать, что сосуд достаточно ве-
велик, а отверстие мало, то можно считать,
что по истечении уровень жидкости в сосуде
не изменяется заметно в течение достаточ-
достаточно продолжительного промежутка времени.
Пусть на поверхность жидкости в сосуде дей-
действует давление ро (например, атмосферное).
Будем также полагать, что струя вытекает
в пространство, где внешнее давление также
равно ро. Обобщение на различные давления
не составляет труда.
Проведем некоторую гипотетическую ли-
линию тока и выберем на ней две точки — одну
на поверхности жидкости в сосуде (точка /),
другую внутри отверстия (точка 2). Тогда
для этой линии тока можно записать уравне-
уравнение Бернулли:
vl , РО , V2 , РО - /г qq\
-тг + — + ez\ = it + + #Z2 • E.33)
ч
i
ч
V
1
\
1 =
\
\
0
2
Po
Рис. 5.4. Истечение жид-
жидкости
Идеальная жидкость
[Гл.5
Поскольку поверхность жидкости в сосуде предполагается неподвиж-
неподвижной (v\ = 0), из последнего равенства получаем
v2 =
E.34)
Заметим, что такую же скорость приобретает тело, падающее в пу-
пустоте с высоты Н.
5.3.2. Распределение давления в трубе переменного сечения.
Рассмотрим стационарное движение идеальной несжимаемой жидкости
в трубе переменного сечения. Действием силы тяжести можно прене-
пренебречь, если труба расположена горизонтально. Выберем какую-либо
линию тока (рис. 5.5). На этой линии тока рассмотрим две произволь-
произвольные точки. Тогда для этих точек на выбранной линии тока в случае не-
несжимаемой жидкости можно записать
E.35)
Рис. 5.5. Давление движущей-
движущейся жидкости в трубке перемен-
переменного сечения
V\ p\ _ V2 P2
Из последнего соотношения видно,
что в той точке линии тока, где ско-
скорость больше, гидростатическое давле-
давление меньше и наоборот.
Непрерывность движения жидкости
в трубе требует выполнения следующе-
следующего условия:
VlSx =v2S2. E.36)
Из этого условия следует, что скорость несжимаемой жидкости тем
больше, чем меньше сечение трубы, и, очевидно, максимальна в самом
узком месте трубы.
Следовательно, в самом узком месте трубы давление минимально.
Если некоторые участки трубы соединить с манометрическими трубка-
трубками, то жидкость в них установится на разных уровнях. Самый низкий
уровень манометрической жидкости, следовательно, будет в самом
узком сечении трубы.
В качестве примеров, которые могут быть просто объяснены при
помощи установленного вывода, можно привести следующие.
Запрещается сближение судов, идущих Wn=Q рп
параллельным курсом. Действительно, при
этом вода между двумя судами приобретает
некоторую скорость, давление между судами
оказывается меньшим давления воды на про-
противоположный борт. В результате возникает
сила, стремящаяся сблизить суда, что может
привести к их столкновению (рис. 5.6).
Хорошо известен экспериментальный факт, что если продувать
воздух между двумя параллельными листками бумаги, то они будут
стремиться сблизиться (рис. 5.7).
<
Рис. 5.6
5.3]
Применение уравнения Бернулли
89
Действие пульверизатора также легко понять на основании по-
полученного вывода. Если вначале жидкость в трубочке и флаконе с
жидкостью была на одном уровне, то при продувании воздуха около
верхнего торца трубочки давление воздуха в ней уменьшается. Тогда
первоначальное атмосферное давление внутри флакона будет выталки-
выталкивать жидкость вверх по трубочке и жидкость будет разбрызгиваться
потоком воздуха (рис. 5.8).
Рг<Р0
Рис. 5.7
Рис. 5.8
Рис. 5.9
При сильных и порывистых ветрах иногда наблюдается необычное,
на первый взгляд, явление. Крыша дома вместе с верхним венцом бре-
бревен поднимается вверх, а затем уже опрокидывается ветром. Нетрудно
понять, почему это происходит. Если перед порывом ветра давление
снаружи крыши и на чердаке дома уравниваются, то при резком порыве
ветра над крышей создается меньшее давление, чем на чердаке, и
если эта разность давлений не успевает выравниваться через щели,
то крышу поднимет создавшейся значительной результирующей силой,
направленной вверх, а затем ветром сбросит с дома (рис. 5.9).
5.3.3. Кавитация. Если увеличивать скорость движения жидко-
жидкости по трубе (см. рис. 5.5) или при том же самом расходе жидкости
уменьшить самое узкое сечение трубы, то можно в этом сечении полу-
получить отрицательное давление. Действительно, из уравнения Бернулли
имеем 2 2
+ -— . E.37)
2 ' р 2
С учетом уравнения непрерывности
имеем
in = Р\
E.38)
E.39)
Из последнего соотношения нетрудно видеть, что если второй член
в правой части полученного соотношения по абсолютной величине
будет больше, чем р\, то минимальное давление окажется отрицатель-
отрицательным, т. е. частицы жидкости, проходящие сечение трубы с отрица-
отрицательным давлением, будут подвергаться растяжению. Однако мы уже
упоминали о том, что жидкость не может находиться в растянутом
состоянии длительное время. Она или вскипит, или сплошность ее
90
Идеальная жидкость
[Гл.5
нарушится в результате выделения пузырьков растворенного в ней
газа. Так или иначе при падении давления до отрицательных значе-
значений в жидкости выделяются пузырьки, заполненные паром жидкости
или газом, растворенным в ней, или тем и другим в той или иной
концентрации. Возникает так называемая кавитация, т.е. нарушение
сплошности движущейся среды.
Явление кавитации играет важную роль в инженерной практике.
Дело в том, что пузырьки, проходя самое узкое сечение, попадают
далее в область более высокого давления и схлопываются. Если такой
пузырек попадает на поверхность трубы, то при схлопывании пузырь-
пузырьков возникают довольно значительные локальные давления, которые
в свою очередь приводят к эррозии, т. е. разрушению материала поверх-
поверхности. Аналогичные явления возникают при быстром движении тел
в жидкости, например, при вращении гребных винтов пароходов или
лопаток гидротурбин. При этом также образуются области растянутой
жидкости, в которых выделяются пузырьки. Кавитация приводит к
чрезвычайно быстрому износу тел и выходу их из строя. Проблема
кавитации и по настоящее время является предметом интенсивного
изучения.
Практически кавитация возникает тогда, когда в жидкости давле-
давление падает до давления насыщенных паров при данной температуре:
Рп
Рн
5.3.4. Трубка Пито. При обтека-
обтекании тупого тела идеальной жидкостью
на нем всегда можно указать точку,
в которой скорость жидкости равна
нулю (рис. 5.10, т. А). Проведем в эту
точку линию тока, которая начинается
вдали от тела и кончается в точке А.
Точка А называется критической точ-
точкой. Для соответствующей линии тока можно записать уравнение
Бернулли, которое для несжимаемой жидкости имеет вид
Рис. 5.10. Критическая точка
^oo Poo _ РО
2 р ~ р
Из последнего соотношения получим
2
РО = Poo H ^ , ^сх) =
E.40)
E.41)
Отсюда видно, что давление в критической точке равно давлению
в набегающем потоке плюс некоторая добавка, обязанная своим воз-
возникновением торможению жидкости в критической точке. Эта добавка
называется скоростным напором. Последнюю формулу в E.41) можно
использовать для измерения скорости движения жидкости или скоро-
скорости движения тела в неподвижной несжимаемой жидкости.
5.4]
Влияние сжимаемости среды
91
Прибор, при помощи которого производятся измерения скорости
потока, называется трубкой Пито или трубкой Прандтля (рис. 5.11).
3d
Рис. 5.11. Трубка Пито
Очевидно, разность давлений р$ — р^ уравновешивается давлением
столба манометрической жидкости — p^gh. Тогда имеем формулу
E.42)
Здесь g — ускорение свободного падения, /?ж — плотность манометри-
манометрической жидкости, р — плотность жидкости, скорость которой измеря-
измеряется. В частности, это может быть и плотность газа.
Таким образом, помещая трубку Пито в поток движущейся жид-
жидкости или газа и измеряя создаваемый перепад давления каким-либо
манометром, можно довольно просто измерить их скорость. В ре-
результате длительного экспериментального и теоретического изучения
в настоящее время выработан определенный стандарт, гарантирующий
процентную точность в оптимальном диапазоне измерений. Рекоменда-
Рекомендации этого стандарта приведены на рис. 5.11.
Как видно из рисунка, давление в отверстии на боковой поверхно-
поверхности трубки будет равно давлению вдали от трубки в невозмущенном
потоке лишь на расстояний 3d от носика трубки. Любое другое рас-
расположение отверстия не гарантирует стандартную точность. Причины
этого будут поняты при последующем изучении движений идеальной
жидкости.
Помещая трубку Пито на самолете, можно измерить скорость поле-
полета самолета.
5.4. Влияние сжимаемости среды
Приближение несжимаемой жидкости заметно упрощает решение
задач гидродинамики. Однако использовать это приближение следует
весьма осмотрительно. Оно выполняется с высокой точностью в случае
капельных жидкостей ввиду малых изменений плотности при значи-
значительных изменениях давления. Так, например, если воду поместить
в цилиндр с подвижным поршнем и увеличить давление от одной
до двух атмосфер, то это уменьшит объем воды только в отношении
1:20000.
92 Идеальная жидкость [ Гл. 5
С другой стороны, такое повышение давления в случае воздуха при
неизменной температуре вызывает уменьшение объема в соотношении
1 :2, как это следует из закона Бойля-Мариотта. Однако многолет-
многолетние исследования воздушных потоков в бесконечной массе воздуха
показывают, что изменение давления лишь в исключительных случаях
вызывает заметное изменение плотности. Объяснение этого экспери-
экспериментального факта состоит в следующем. Если бы изменение давления
газа, вызванное движущимся телом, привело к изменению плотности,
то в газе возник бы волновой процесс, выравнивающий плотность газа
по всему объему со скоростью звука (в воздухе около 340 м/с). Поэто-
Поэтому при обтекании тела газом или движении тела в газе со скоростью,
много меньшей скорости звука, плотность газа не успевает изменяться.
В случае же, когда скорость течения или скорость тел, движущихся
в газе, приближается к скорости звука, изменение давления вызывает
заметное изменение плотности газа. Так как гидродинамика изучает
дозвуковые течения жидкостей, то упрощающее предположение о по-
постоянной плотности жидкости является приемлемым приближением.
Получим количественный критерий сжимаемости среды. Как видно
из соотношения E.41), давление в критической точке больше, чем
давление в жидкости вдали от тела, на величину pv^/2, называемую
скоростным напором. Таким образом, индивидуальная частица газа или
жидкости при движении по критической линии тока подвергается сжа-
сжатию. При этом ее плотность увеличивается. Это явление (изменение
плотности) будет наблюдаться и для частиц, движущихся по другим
линиям тока. Однако наиболее значительное изменение, очевидно, бу-
будет наблюдаться для частиц критической линии тока. Поэтому если
учесть сжимаемость, то давление в критической точке должно иметь
некоторое другое значение, учитывающее, что плотности жидкости
вдали от тела и в критической точке не равны, как это нами пред-
предполагалось при выводе формулы E.41). Оценим влияние сжимаемости
среды на давление в критической точке. Если жидкость несжимаема,
то давление в критической точке равно E.41)
2
Ро = Роо + роо^о° , ро = роо= const. E.43)
Для сжимаемой жидкости в той же ситуации имеем
E.44)
Будем полагать, что сжатие индивидуальных частиц, движущихся
по критической линии тока, происходит адиабатически. Тогда имеем
-^ = const, dh = — , h = — = const • 7 p7~2 dp . E.45)
p p ) p J
5.4 ] Влияние сжимаемости среды 93
Интегрируя с точностью до несущественной произвольной постоян-
постоянной, получим
h = —!— ? . E.46)
7 - 1 Р
Подставляя в уравнение Бернулли E.44), имеем
7 Ро
7 - 1 ро 7 - 1 Роо 2
Из последнего соотношения следует:
РО _ Роо Л , 7 - 1 Poovl
E.47)
РО Роо V 27 Ро
Нетрудно видеть, что полученное выражение можно представить
в виде
1/7 / , 2 \ 7/G-1)
р. "•¦- '-" • ¦ <549)
Полагая, что второе слагаемое в скобках мало по сравнению с
единицей, и разлагая в ряд 0, получим
E.50)
Сравнивая полученное выражение с формулой E.41), можно сде-
сделать следующее заключение. Если справедливо соотношение
^j E51)
47 Роо
то формула E.50) переходит в формулу E.41) для несжимаемой жид-
жидкости. Следовательно, при выполнении неравенства E.51) мы можем
полагать жидкость (газ) несжимаемой.
Как мы видели, скорость распространения продольных волн сжатия
равна
Для идеального газа в адиабатическом процессе
PV^ = const. E.53)
Тогда получим
cj = 7 ~р ¦ E.54)
О Биномиальный ряд при х <С 1 имеет вид
94 Идеальная жидкость [ Гл. 5
Скорость с/ называется скоростью звука, т. е. скорость звука явля-
является скоростью распространения волн сжатия в газе. (Напомним, что
сдвиговые волны в газе невозможны).
Теперь неравенство E.51) можно записать в следующем виде:
^f « 1. E.55)
Таким образом, если скорость движения жидкости значительно
меньше скорости звука в ней, то ее можно рассматривать как несжи-
несжимаемую жидкость. Например, если воздух (с/ « 330 м/с) движется
со скоростью Vvq & 70 м/с, то максимальная поправка к давлению
в критической точке составит не более одного процента, что можно не
учитывать в большинстве инженерных и научных расчетов.
5.5. Вихревое движение
Движение жидкости, при котором ее индивидуальные частицы
перемещаются не только поступательно, но и вращаются около
некоторой мгновенной оси, проходящей через эти частицы, назы-
называют вихревым движением. Это — непотенциальное движение жидко-
жидкости, которое характеризуется отличной от нуля вихревой скоростью ш
(см. E.16)).
В природе вихревые движения наблюдаются в виде смерчей, круго-
круговоротов, циклонов и др.
5.5.1. Теорема Томсона. Циркуляцией вектора скорости v по
замкнутому контуру / называется выражение
E.56)
где d\ — элемент контура интегрирования, dr — разность радиусов-век-
радиусов-векторов двух близких точек контура.
Рассмотрим изменение во времени циркуляции скорости движения
идеальной жидкости по некоторому индивидуальному контуру, состо-
состоящему из одних и тех же частиц жидкости:
dY d Г j /r г—ч
— = — ф v dr . E.57)
dt dt] v ;
i
В процессе движения контур может деформироваться, т. е. изме-
изменять свою форму и длину. Поэтому вектор dr изменяется с течением
времени. Движение жидкости будем полагать баротропным, а внешние
силы — потенциальными. Тогда, дифференцируя подынтегральное вы-
выражение, получим
_^
dt
5.5 ] Вихревое движение 95
Интеграл по замкнутому контуру от полного дифференциала некоторой
функции равен нулю. Полную производную от скорости по времени,
используя уравнение Эйлера, можно записать в следующем виде:
5L- = -ф V(P + ?U0T)dr = - rot [V (Р + ?ПОт)] dS = 0 . E.59)
at J J
I (S)
Здесь использована формула Стокса преобразования интеграла по за-
замкнутому контуру в интеграл по поверхности, опирающейся на этот
контур, а также известное соотношение rot V = 0.
Таким образом, имеем результат, представляющий содержание тео-
теоремы Томсона:
— = 0 , Г = to v dr = const, E.60)
at J
циркуляция скорости движения идеальной жидкости вдоль замкну-
замкнутого контура, состоящего из одних и тех же частиц, в поле потен-
потенциальных сил при баротропных движениях сохраняется. Постоянная
в последнем выражении не зависит ни от координат, ни от времени.
Из уравнения E.60) с учетом теоремы Стокса и выражения E.16)
для вихревой скорости следует
r = (?vdr= [rotvdS = 2 [ ш dS = const. E.61)
I (S) (S)
Рассмотрим любую линию тока. В некоторой ее точке построим ма-
малый индивидуальный контур площадью dS, охватывающий эту линию
тока. Очевидно, при стационарном движении жидкости контур будет
всегда охватывать эту линию тока. Предположим, что в какой-то ее
точке ш = 0. Тогда, согласно теореме Томсона, вихревая скорость будет
равна нулю и во всех последующих точках линии тока, поскольку по
определению линий тока такой контур не может быть при своем дви-
движении сжат в точку dS Ф 0, а произведение u; dS должно сохраняться,
т.е. равняться нулю при любой ориентации площадки dS.
Если движение жидкости нестационарно, то предыдущее рассуж-
рассуждение справедливо для траекторий индивидуальных частиц жидко-
жидкости. Тогда полученный вывод можно продолжить. А именно: если
в какой-то области движение жидкости потенциально, т. е. ш = 0, то
оно будет потенциальным и во всех последующих областях движения.
Так,например, если мы имеем обтекание некоторого тела однородным
вдали от тела потоком (ш = 0), то и вблизи тела и после него движение
жидкости также останется потенциальным. Более того, если движение
идеальной жидкости в некоторый момент времени потенциально, на-
например начинается из состояния покоя, то оно будет потенциальным и
во все последующие моменты времени.
Однако эти рассуждения имеют ограниченную применимость даже
и для идеальной жидкости. Они, очевидно, неприменимы для линий
96 Идеальная жидкость [ Гл. 5
тока, проходящих в непосредственной близости к поверхности обте-
обтекаемого тела, хотя бы потому, что для такой линии тока невозможно
провести охватывающий ее замкнутый контур, который при своем
движении не пересекал бы поверхность тела.
Скорость движения идеальной жидкости на поверхности обтекаемо-
обтекаемого тела, а также на некоторых поверхностях в жидкости за ним может
претерпевать разрыв, что означает появление на этих поверхностях
вихревого движения, несмотря на то, что набегающий поток может
быть и потенциальным.
Для реальных жидкостей, обладающих вязкостью, теорема Томсона
не имеет места в силу непотенциальности вязких сил, действующих
в жидкости. И если вдали от тела действие этих сил может практиче-
практически не проявляться, то вблизи поверхности обтекаемого тела они будут
играть существенную роль. Поэтому если в жидкости образуются вих-
вихри, то они образуются прежде всего вблизи поверхности обтекаемых тел.
5.5.2. Теорема Гельмгольца. Аналогично линии тока можно вве-
ввести понятие вихревой линии. Вихревая линия —линия, касательная
к которой в данной точке дает направление вихревой скорости
жидкости в этой точке. Очевидно,уравнение вихревой линии имеет
вид
dx_ _dy_ _dz_ E 62)
Аналогично трубке тока можно построить вихревую трубку. Рас-
Рассмотрим некоторый контур, охватывающий малую площадку AS. Че-
Через каждую точку этого контура проведем вихревую линию. Тогда
совокупность этих линий образует вихре-
вихревую трубку (рис. 5.12).
Произведение u;AS называется интен-
интенсивностью вихревой трубки. Здесь AS —
вектор, модуль которого равен величине
площадки AS, а направление совпадает с
направлением нормали п к этой площадке,
т.е. AS = ASn.
Теорема Гельмгольца утверждает, что
интенсивность вихревой трубки неиз-
Рис. 5.12. Вихревая трубка менна по ее длине и на зависит от вре-
времени.
Вычислим поток вектора вихревой скорости о; через замкнутую
поверхность S, ограничивающую некоторый объем V вихревой трубки:
г г
(S) (V)
Здесь мы воспользовались формулой Гаусса-Остроградского преобра-
преобразования интеграла по замкнутой поверхности в интеграл по объему,
ограниченному этой поверхностью, а также соотношением divrot = 0.
5.5 ] Вихревое движение 97
Разобьем интеграл по поверхности на две части — интеграл по боко-
боковой поверхности вихревой трубки и интеграл по торцевым площадкам
AS. По определению вихревой трубки интеграл по боковой поверх-
поверхности равен нулю. Интеграл по элементарным торцевым площадкам
в случае узкой вихревой трубки можно записать в виде суммы двух
членов:
шх ASi +u;2AS2 =0. E.64)
Если элементарные площадки перпендикулярны векторам вихревой
скорости, то, принимая во внимание направление нормалей к площад-
площадкам, получим
AS ASE.65)
Можно было бы вдоль трубки построить не две, а несколько пло-
площадок. Следовательно, можно записать
uj\ AS\ = UJ2 Д#2 = • • • = шп ASn = const. E.66)
Из последнего соотношения следует, что интенсивность вихревой
трубки постоянна вдоль трубки. В силу же теоремы Томсона E.60) и
выражения E.61) для элементарной вихревой трубки имеем
-^(u;AS)=0, ш AS = const. E.67)
CLT
То есть интенсивность вихревой трубки сохраняется и с течением
времени. Если в начальный момент времени интенсивность вихревой
трубки была равна нулю, то она будут равна нулю и во все по-
последующие моменты времени. Если же в начальный момент времени
интенсивность вихревой трубки не равна нулю, то она сохранится и во
все последующие моменты времени. То есть вихревое движение в иде-
идеальной жидкости не возникает и не уничто-
уничтожается, что и составляет содержание теоремы
Гельмгольца.
Следовательно, вихревые трубки не могут
начинаться и кончаться внутри жидкости. Они
должны быть или замкнутыми или начинаться и
кончаться на поверхности твердых тел или сво-
свободной поверхности жидкости (рис. 5.13). Так
как теорема Томсона справедлива лишь для ба-
ротропных движений и потенциальных сил, то Ьихревые
источником возникновения вихревых движений тру
жидкости очевидно могут быть или непотенциальные силы вязкости,
или небаротропность движения.
5.5.3. Одиночная вихревая прямолинейная нить. Вихревой ни-
нитью будем называть бесконечно узкую вихревую трубку. Ее интенсив-
интенсивность, очевидно, равна
lim (u; AS). E.68)
AS^O
4 В.Г. Черняк, П.Е. Суетин
98 Идеальная жидкость [ Гл. 5
Рассмотрим прямолинейную вихревую нить, перпендикулярную
плоскости рисунка (рис. 5.14). Наличие вихря приводит к появлению
некоторого поля скоростей жидкости вокруг нити.
Для неограниченно длинной прямолинейной нити поле скоро-
скоростей, очевидно, будет обладать цилиндрической симметрией. Движение
жидкости будет одинаково во всех плоско-
плоскостях, перпендикулярных нити. В этих плос-
плоскостях индивидуальные частицы жидкости
движутся по окружностям, центром которых
является след нити. На плоскости нетрудно
получить закон изменения скорости частиц
в зависимости от их расстояния до нити.
Введем цилиндрическую систему коорди-
координат (г, (р, z) так, что ось z совпадает с нитью
ис. . . ихревая нить (перпендикулярна плоскости рисунка). Если
иметь в виду, что в стационарном случае отличной от нуля будет лишь
одна компонента скорости жидкости v^, которая зависит только от
радиальной координаты г, то для циркуляции получаем
Г = i> v dr = 2тггу(р = const. E.69)
i
Следовательно, имеем
? E.70)
Из E.70) видно, что движение имеет особенность в точке г = 0.
Однако не следует отождествлять вихревое движение с движением
частиц по окружности. Не всякое движение по окружности является
вихревым и не всякое вихревое движение есть движение по окруж-
окружности.
Напомним, движение безвихревое (потенциальное) только тогда,
когда индивидуальные частицы движутся без вращения относительно
некоторых осей, проходящих через сами частицы. В противном слу-
случае—движение вихревое (непотенциальное).
Действительно, в вышеприведенном примере плоского вихря,
несмотря на то, что частицы движутся по окружностям, движение
безвихревое во всех точках, кроме оси вихря. При плоском движении
жидкости около одиночной вихревой нити (рис. 5.14) существует лишь
компонента ротора скорости, перпендикулярная плоскости рисунка
(ось z). В цилиндрической системе координат z-компонента ротора
скорости имеет вид
1 д , ч 1 dvr /c „1Ч
rot^ v = - — (v<pr) ---?—• E.71)
г or ^ г д(р
Так как по определению vr = 0, a v^ определена выражением E.70),
то имеем rotz v = 0, т. е. движение потенциально во всех точках дви-
движущейся жидкости, кроме оси.
5.5 ] Вихревое движение 99
Если бы жидкость вращалась около оси z как твердое тело, то
v^ = ujr (cj -угловая скорость вращения), a rotz v = 2со, т.е. такое
движение непотенциально.
В первом случае, хотя движение жидкости происходит по окруж-
окружности, частицы не вращаются относительно осей, проходящих через
сами частицы (рис. 5.15). Во втором случае частица, делая один оборот
вокруг оси z, в то же время делает также один оборот вокруг оси,
проходящей через саму частицу (рис. 5.16).
Рис. 5.15. Потенци- Рис. 5.16. Вихревое
альное движение движение
Если частицы движутся прямолинейно, но существует некоторый
градиент скорости, то можно утверждать, что такое движение обяза-
обязательно вихревое, т. е. непотенциальное.
5.5.4. Примеры вихревых движений. Вихревое движение инте-
интересно наблюдать на вихревых кольцах. Чаще всего это демонстрирует-
демонстрируется при помощи ящика, в передней стенке которого имеется отверстие,
а задняя стенка достаточно гибкая. Наполняя ящик дымом и ударяя
по задней стенке рукой, можно наблюдать как из отверстия вслед за
ударом вылетают вихревые кольца, которые благодаря частичкам дыма
хорошо видны.
Такие кольца обладают любопытными свойствами. Они могут от-
отталкиваться друг от друга, притягиваться, отражаться от твердой стен-
стенки, попеременно обгонять друг друга и т.д. Эти свойства объясняются
движением, которое такие кольца стимулируют в окружающем воз-
воздухе. Ясно, что если встречаются два кольца, у которых внутренние
потоки направлены навстречу друг другу (например, из разных ящи-
ящиков), то такие кольца должны отталкиваться. Если же при одинаковом
направлении движения более быстро движущееся кольцо нагоняет
впереди идущее, то оно будет втянуто в него, пройдет внутри него
и даже ускорится внутренним потоком предыдущего кольца. В свою
очередь, предыдущее кольцо получит от последующего некоторую «за-
«закрутку», которая заставит его двигаться быстрее. Впоследствии оно
может догнать обогнавшее кольцо и кольца поменяются ролями.
С течением времени вихри затухают вследствие вязкости любой
реальной жидкости. Энергия вихревого движения в конечном счете
переходит в тепло.
100 Идеальная жидкость [ Гл. 5
Зеркальное отражение колец от твердой стенки также можно по-
понять, рассматривая взаимодействие внутреннего движения воздуха
в кольце с твердой поверхностью. В свое время Томсон пытался постро-
построить модель электрона в виде вихревого кольца некоторой субстанции.
Действительно, такая модель обладает некоторыми свойствами заря-
заряженных частиц (притяжение разноименных зарядов и отталкивание
одноименных).
В природе вихревые движения наиболее часто наблюдаются в виде
смерчей. Смерч возникает вдали от поверхности земли в результате
интенсивных встречных вертикальных движений воздуха. Нисходя-
Нисходящие потоки воздуха образуются под грозовыми тучами вследствие
охлаждения его дождем или градом. Если такая туча надвигается
на сильно прогретую местность с интенсивными восходящими пото-
потоками нагретого воздуха, то возникает вязкое взаимодействие этих
резко разграниченных потоков. В результате на фронте тучи возникает
вихрь, концы которого в полном соответствии с теоремой Гельмгольца,
должны затем опуститься на землю. На земле эти вихри наносят
большие разрушения в силу локализации воздействия — разрушаются
постройки, валится лес, ложатся посевы и т. д. Если смотреть сверху,
то в левой ветви смерча на земле воздух будет вращаться по часовой
стрелке, тогда как в правой ветви — против часовой стрелки. Расстоя-
Расстояние между концами вихря на земле иногда достигает десятков и сотен
километров. Поэтому наблюдателю виден чаще всего лишь один его
конец, который кажется сошедшим с неба. Однако, как следует из
теоремы Гельмгольца, на земле на некотором расстоянии обязатель-
обязательно существует и второй его конец. Так, если мы в каком-то месте
обнаруживаем поваленный по часовой стрелке лес, то обязательно (в
лесистых районах) существует место, где лес повален против часовой
стрелки.
Ясно, что при вихревом движении внутри вихря в результате дей-
действия центробежных сил образуется область пониженного давления,
в которую по поверхности воды или земли может интенсивно всасы-
всасываться воздух и перемещаться дальше по оси вихря. Поэтому мелкие
легкие предметы, захваченные этим потоком (листья, белье, щепки и
т. д.) могут быть перенесены по оси вихря, как по трубе, на значитель-
значительные расстояния и для местного наблюдателя, следовательно, «упасть
с неба». История знает немало таких «чудес», когда «с неба» падали
лягушки, рыбы и даже монеты.
Естественно, что вихревое движение в смерчах с течением времени
должно затухать и исчезать вследствие диссипации энергии, так как
реальная жидкость всегда обладает определенной вязкостью. Таким
образом, вихревое движение в природе возникает (непотенциальные
силы вязкости) и исчезает (диссипация энергии движения) вследствие
вязкости реальных жидкостей. Однако модель идеальной жидкости
позволила нам изучить основные законы вихревого движения и понять
роль вязкости в вихревом движении реальных жидкостей.
5.6] Потенциальное движение 101
5.6. Потенциальное движение
Движение идеальной жидкости называется потенциальным,
т. е. безвихревым, если каждая индивидуальная частица деформи-
деформируется и перемещается поступательно, но не вращается относи-
относительно некоторой оси, проходящей через саму частицу.
При потенциальном движении в любой точке пространства, занято-
занятого движущейся жидкостью, rot v = 0.
5.6.1. Потенциал скорости. Из самого определения потенциаль-
потенциального движения жидкости следует, что скорость может быть представ-
представлена в виде градиента некоторой скалярной функции (р, называемой
потенциалом скорости:
v = V^, vx = ^, vy = ^, vz = fz. E.72)
Действительно, если скорость может быть представлена в виде
градиента скалярной функции, то движение потенциально, так как
rot v = rot V <р = 0 . E.73)
Для потенциального движения циркуляция по любому замкнутому
(индивидуальному или неиндивидуальному) контуру в односвязной об-
области течения равна нулю
Г = <? v dv = [ rot v dS = 0 . E.74)
i s
Это означает, что при потенциальном движении не может быть замкну-
замкнутых линий тока, так как в противном случае (линия тока совпадает
с замкнутым контуром интегрирования) циркуляция скорости была бы
отлична от нуля.
Для баротропного потенциального нестационарного движения урав-
уравнение Эйлера записывается в следующем виде:
^-[v,rotv] = V(y + P + ?n0TJ . E.75)
С учетом выражений E.72) и E.73) получаем
v(^ + ^ + P + ?nOT)=0. E.76)
Отсюда имеем
E.77)
Постоянная в правой части уравнения E.77) при нестационарном дви-
движении может зависеть от времени, однако в любой фиксированный
момент времени она одинакова для всех точек пространства, занятого
жидкостью.
102 Идеальная жидкость [ Гл. 5
Поскольку нашей конечной целью является нахождение скорости
движения жидкости, а скорость определяется производными от по-
потенциала по координатам, то любая функция времени, добавленная к
потенциалу, не изменит результата вычисления скорости. После замены
получим в правой части уравнения E.77) нуль. Поэтому без ограниче-
ограничения общности рассмотрения можно в уравнении E.77) функцию f(t)
положить равной нулю.
Таким образом, мы получили уравнение Бернулли для баротроп-
ного потенциального нестационарного движения идеальной жидкости.
В случае стационарного движения первое слагаемое в левой части
уравнения E.77) равно нулю и мы имеем обычное уравнение Бернулли
с постоянной в правой части, независящей ни от координат, ни от
времени.
5.6.2. Идеальная несжимаемая жидкость. Для несжимаемой
идеальной жидкости потенциал скорости должен удовлетворять урав-
уравнению Лапласа
diw = 0, v = V<p, divV(^ = A^ = 0. E.78)
Таким образом, при потенциальном движении несжимаемой жидко-
жидкости нам необходимо найти лишь одну скалярную функцию. Поскольку
при нестационарном движении потенциал скорости должен быть функ-
функцией не только координат, но и времени, а уравнение Лапласа содержит
лишь производные по координатам, то отсюда следует, что время может
быть введено только через граничные условия.
Граничные условия для идеальной жидкости в каждой точке по-
поверхности обтекаемого тела имеют вид (см. E.19))
vn = un. E.79)
Здесь vn — нормальная к поверхности обтекаемого тела компонента
скорости жидкости, ип — нормальная компонента скорости движения
элемента поверхности тела, которая должна быть задана как функция
координат и времени.
Для потенциального движения граничные условия можно записать
в виде
vn = nv = nV^ = P , j? = un. E.80)
on on
Таким образом, потенциал в любой точке несжимаемой жидкости
зависит от времени так же, как и потенциал на поверхности обтекаемо-
обтекаемого тела. Если при движении тела в идеальной несжимаемой жидкости
создаваемое им движение жидкости является потенциальным, то в ка-
каждый момент времени потенциал во всех точках жидкости зависит
лишь от скорости (ип) движения тела в тот же момент времени.
Физически это можно понять, если принять во внимание, что возму-
5.6] Потенциальное движение 103
щение, а следовательно и взаимодействие между различными частями
несжимаемой жидкости, распространяется с бесконечной скоростью
(с/ = оо). Поэтому изменение скорости в какой-либо точке потока ведет
к мгновенному изменению скоростей во всех точках потока идеальной
несжимаемой жидкости.
5.6.3. Функция тока. Рассмотрим плоское движение идеальной
несжимаемой жидкости, т. е. такое движение, при котором все его ха-
характеристики зависят только от двух координат, например х, у. Иначе,
плоское движение — это такое движение, при котором во всех плоско-
плоскостях, параллельных координатной плоскости хОу, его характеристики
одинаковы.
В теории плоского потенциального движения идеальной несжимае-
несжимаемой жидкости удобно ввести понятие функции тока ф в соответствии
со следующими уравнениями:
дф дф {г пП
vx = — , Vy = — — . (o.olj
Для потенциала скорости имели место соотношения E.72) и E.78).
Из E.81) видно, что функция тока условию несжимаемости удовле-
удовлетворяет автоматически по ее определению:
dvx dvy _ ~ д дф д дф _ ^ ,г ооч
дх ду ' дх ду ду дх
Нетрудно видеть, что при потенциальном движении функция тока
так же, как и потенциал, должна удовлетворять двумерному уравнению
Лапласа. Для плоского движения имеем
дх ду ' дх дх ду ду
Таким образом, при плоском потенциальном движении несжимае-
несжимаемой идеальной жидкости как потенциал, так и функция тока должны
удовлетворять уравнению Лапласа, т. е. должны быть гармоническими
функциями. При непотенциальном движении функция тока должна
удовлетворять уравнению, которое можно получить, подставляя E.81)
в уравнение Громека. Очевидно, что функция тока может быть введена
только для плоского движения жидкости.
Свойства функции тока. Функция тока обладает рядом свойств,
которые оправдывают ее введение.
1. Линии тока — это линии, удовлетворяющие уравнению
ф = const. E.84)
Действительно, из уравнения линий тока имеем
dx dy , , ^ дф , дф , ^
= > Vydx — vxdy = U , - ах — — ay = U ,
vx Vy dx dy E.85)
dф = 0, ф = const,
что и требовалось доказать.
104
Идеальная жидкость
[Гл.5
?2
2. Если на плоскости хОу между двумя точками на двух различ-
различных линиях тока провести некоторую произвольную кривую, то поток
жидкости Q через эту кривую (масса
жидкости, протекающей через кривую
за единицу времени) будет определять-
определяться разностью значений функции тока
в этих точках.
Действительно, расход жидкости че-
через линию 1-2 (рис. 5.17) равен
2 2
Q = р \vndl = р \(nxvx + riyVy) dl,
J J
1 ' E.86)
dx
Рис. 5.17. Расход жидкости
между линиями тока
пх = sin V = -у,
at
пу = - cos U = - -
Подставляя соотношения E.86) в фор-
формулу для расхода и используя определение функции тока, получим
2 2
ГЛ [ ( ЭФ „/ , ЗФ „/ \ Г „/ / / / I \ /С О7\
Q — Р ( тг^ dy + "тг2- dx J = p dф = р (ф2 — ф\) • E.87)
1 1
3. Линии тока (ф = const) и линии равного потенциала {ip = const)
взаимно ортогональны в каждой точке течения. Направления нормалей
к этим линиям определяются соотношениями
, n^ = . E.88)
Рассмотрим их скалярное произведение
V^
Vip
у = 0 ,
,/, = 0.
E.89)
Таким образом, каждая кривая семейства (р = const составляет
прямой угол с линиями ф = const в точке пересечения.
5.7. Методы описания движения идеальной жидкости
Для решения задач о движении идеальной жидкости разработаны
специальные методы. Рассмотрим некоторые из них на конкретных
примерах.
5.7.1. Метод конформных отображений. Этот метод весьма эф-
эффективен, но может быть использован только для плоского потенци-
потенциального движения идеальной несжимаемой жидкости, для которого
потенциал скорости и функция тока связаны следующими соотноше-
соотношениями: ^ о / ^ о /
_д^_
дх " ду '
ду
дх
E.90)
5.7]
Методы описания движения идеальной жидкости
105
Но соотношения E.90) совпадают с известными в теории функций
комплексного переменного условиями Коши-Римана, которые гаранти-
гарантируют, что комплексное выражение
C =
E.91)
где г = \/~Т — мнимая единица, является аналитической функцией
комплексного аргумента z = х + гу. Это в свою очередь означает, что
функция /3(z) имеет в каждой точке производную
дх
дх
E.92)
Функция j3(z) называется комплексным потенциалом, а производная
d/31 dz — комплексной скоростью.
Таким образом, пользуясь теорией функций комплексного перемен-
переменного, получаем возможность иметь дело не с двумя функциями (риф
от двух аргументов х и у, а лишь с одной комплексной функцией C от
одной комплексной переменной z.
Кроме того, начиная с решения какой-либо тривиальной задачи,
методами конформных отображений можно получить решение целого
ряда более сложных задач, прямое решение которых часто бывает
затруднительно.
Обтекание бесконечного цилиндра. Рассмотрим потенциальное
обтекание бесконечного цилиндра однородным потоком идеальной
несжимаемой жидкости, перпендикулярным оси цилиндра. Очевидно,
картина обтекания будет идентична во всех плоскостях, перпендику-
перпендикулярных оси цилиндра. Поэто-
Поэтому мы можем рассматривать
движение жидкости как плос-
плоское.
Прежде чем рассматри-
рассматривать обтекание цилиндра,
рассмотрим обтекание беско-
бесконечно тонкой пластинки одно-
однородным плоскопараллельным
потоком жидкости (рис. 5.18).
Пусть пластинка длиной
4го расположена вдоль оси е.
Пусть далее скорость набегающего на пластинку потока вдали от нее
постоянна и направлена вдоль оси е. Картина обтекания в данном
случае очевидна.
Действительно, так как идеальная жидкость может беспрепят-
беспрепятственно скользить вдоль поверхности пластинки, то пластинка во-
вообще не окажет никакого действия на поток. То есть однородный
плоско-параллельный набегающий поток останется таковым и вблизи
пластинки, и после нее. Тогда линии тока будут параллельны оси е, а
^-
ф =
cons
t
\f/ = const
-2г0 О +2r0
Рис. 5.18. Обтекание пластинки
106 Идеальная жидкость [ Гл. 5
линии равного потенциала перпендикулярны к ним. Поэтому имеем
д<р дф
E.93)
Из второго равенства следует очевидный факт, что (р не за-
зависит от rj, а ф не зависит от е. Из первого равенства
имеем
ip = Voqs + const, ^ = г^^ + const. E.94)
Постоянные в последних выражениях несущественны, так как опре-
определяются лишь началом отсчета функций (риф, поэтому мы можем
положить их равными нулю.
Составим комплексный потенциал
C = (р + ъф = ^оох, х = ? + гт7. E.95)
Здесь х — комплексная переменная в плоскости еОг\.
Далее используем следующее конформное отображение точек плос-
плоскости еОг) в точки плоскости хОу:
X +, + y
Предварительно рассмотрим, как преобразуется область
rj > 0, -2г0 ^ е ^ +2г0
E.96)
плоскости eOrj в плоскости хОу. Нетрудно видеть, что она преобразу-
преобразуется во внешнюю область окружности радиуса г$. Действительно, из
E.96) имеем
гу=
E.97)
(e + irj)± у
Пластинка в плоскости еОг] имеет уравнение
г/ = 0, -2г0 ^ е ^ +2г^
Тогда из последнего уравнения E.97) получаем
у = ±^rl - ^ . E.98)
Для уравнения пластинки в плоскости хОу имеем
х2 + У2 = rl
Мы получили уравнение окружности радиусом го, причем точки плос-
плоскости sOrj, соответствующие rj > 0, как нетрудно видеть, попадают вне
круга.
5.7] Методы описания движения идеальной жидкости 107
Таким образом, если в плоскости еОг] мы имеем обтекание пластинки
однородным плоскопараллельным потоком жидкости, то в плоскости хОу
при помощи конформного отображения
E.96) получаем обтекание бесконечно-
го цилиндра. Причем общие свойства
конформных отображений гарантируют
нам, что в точках, удаленных на беско- v
нечность, сохраняется направление ли-
линий тока и равного потенциала и их
ортогональность в любой точке.
Рассмотрим картину обтекания ци- __ с 1П „ .
r A jZ о Рис. 5.19. Обтекание цилиндра
линдра в плоскости хОу. Комплексный г
потенциал E.95) с учетом выражения E.96) в полярных координатах
(рис. 5.19) запишется в следующем виде:
+ ^) = Voo \rcosO + irsmO + Г° . . 1. E.99)
Умножая числитель и знаменатель последнего слагаемого в скобках на
выражение, комплексно-сопряженное знаменателю, получим
/5 = vj\r cos 0 + ir sin 6 + Ц(г cos в - i r sin 0I =(р + 1ф. E.100)
Из последнего выражения имеем следующие формулы для потенци-
потенциала и функции тока:
- -± ) rs'mO. E.101)
Из любого выражения E.101) можно вычислить компоненты векто-
вектора скорости
E.102)
Полученное решение удовлетворяет граничным условиям для идеаль-
идеальной жидкости: при г = го имеем г?г = 0.
Пользуясь выражениями E.102), нетрудно построить линии тока
(<ф = const) и линии равного потенциала — эквипотенциальные линии
(ip = const). Изменяя постоянную в уравнении ф = const на некоторую
заданную величину (определяющую расход жидкости между двумя
соседними линиями тока), можно последовательно построить все ли-
линии тока. Аналогично можно построить и эквипотенциальные линии,
ортогональные линиям тока в любой точке пересечения. На рис. 5.20
изображена примерная картина расположений линий тока.
Величина скорости жидкости может быть определена из формулы:
4-24 cos 20^ . E.103)
г г )
108
Идеальная жидкость
[Гл.5
Очевидно, скорость будет иметь максимальное значение на поверх-
поверхности цилиндра (г = го) при в = тг/2, Зтг/2. При этом абсолютное
значение максимальной скоро-
Ф = const
сти равно
ах = 2 Vo
E.104)
\Ц! = COnSt
Рис. 5.20. Линии тока (сплошные) и
эквипотенциальные линии (штриховые)
при обтекании цилиндра
Из формулы E.103) видно
также, что в критических точ-
точках на поверхности цилиндра
[0 = 0, тг) полная скорость рав-
равна нулю.
Подбирая соответствующее
конформное отображение мы
могли бы из простейшей задачи
обтекания пластинки получить
обтекание эллипса, некоторого профиля крыла и других плоских тел,
имеющих более сложную форму. В этом и заключается эффективность
применения теории функций комплексного переменного к решению
задач о плоском потенциальном движении идеальной жидкости.
Парадокс Даламбера. Вычислим силу, действующую на единицу
длины цилиндра со стороны движущейся жидкости. Для этого вы-
вычислим распределение давления по его поверхности. Воспользуемся
уравнением Бернулли для какой-либо линии тока:
E.105)
Vqo , Poo _ V_ , P
2 p ~ 2 p
Для линии тока, идущей по поверхности цилиндра, из E.103) имеем
v2 = 2*4,A - cos 2(9) = 4^ sin2 0 . E.106)
Таким образом, на поверхности цилиндра давление распределено по
закону
I Р ^ОО (л Л • 2 Л I /С 1 Г\г7\
р = р^ -\- -—— М — 4 sin 0 ] . E.107)
Из формулы E.107) видно, что давление максимально при в = 0, тг,
т.е., как и следовало ожидать, в критических точках. Давление на
поверхности цилиндра равно давле-
давлению в набегающем потоке
условии
при
D
sin2 0 = 1,
'¦-
§¦
Рис. 5.21. Эпюра давлений
Если для .наглядности на поверхно-
поверхности цилиндра вдоль радиусов отло-
отложить разность (р — Роо), то мы получим эпюру давлений, изображен-
изображенную на рис. 5.21.
5.7] Методы описания движения идеальной жидкости 109
Очевидно, что силы давления, действующие на поверхность цилин-
цилиндра, стремятся деформировать (растянуть) его вдоль оси, перпенди-
перпендикулярной набегающему потоку. Если бы мы решили воспользоваться
цилиндром вместо трубки Пито, то отверстие, которое должно воспри-
воспринимать давление в набегающем потоке вдали от тела, должно быть
сделано в одной из точек С или D.
Вычислим силу, с которой поток жидкости действует на единицу
длины цилиндра в направлении скорости набегающего потока (сила
лобового сопротивления). Для этого достаточно проинтегрировать си-
силы давления E.107), действующие на элементы поверхности цилиндра:
(n) dS, Fi=§ Р/П) dS = j Piknk dS = - j рщ dS,
2f E.108)
Pik = -P$ik', Fx = - \ P cos 0 r0 dO = 0 .
о
Полученный результат и составляет содержание парадокса Даламбера.
Вывод справедлив не только для цилиндра, но и для тела произволь-
произвольной формы. При потенциальном обтекании тела идеальной несжи-
несжимаемой жидкостью сила лобового сопротивления равна нулю. Из
симметрии движения очевидно, что и подъемная сила Fy тоже будет
равна нулю:
Fy = - | psm0r0d0 = 0. E.109)
о
Этот удивительный результат был предметом длительной дискуссии
Даламбера и Эйлера. Парадокс (перевод с греческого — неожиданный)
в науке — неожиданное явление, не соответствующее обычным пред-
представлениям. Даламбер говорил: «Странный парадокс, объяснение ко-
которого предоставляю математикам» A744 г.). Объясняя этот парадокс,
Эйлер предполагал, что реальная жидкость не похожа на идеальную.
Эйлер писал: «Если некоторые люди увлекутся и будут думать, что
можно продвигать тела через жидкость, не встречая сопротивления,
так как сила, с которой жидкость действует на переднюю часть тела
будет уничтожаться действием такой же силы на заднюю часть, что
не имеет места при движении действительных жидкостей, то такой
вывод будет неправилен» A755 г.). Уже в то время Эйлер отмечал
влияние трения реальных жидкостей на происхождение сопротивления
тел. Таким образом, парадокс Даламбера не должен иметь места для
движений реальных, хотя бы и маловязких жидкостей.
Вообще говоря, мы могли бы «организовать» силу сопротивления
движению тела и в идеальной жидкости, рассматривая движения с
разрывом скоростей на некоторых поверхностях, отходящих от поверх-
поверхности обтекаемого тела.
Так, при обтекании цилиндра модель идеальной жидкости допус-
допускает существование за телом некоторой застойной зоны неподвиж-
по
Идеальная жидкость
[Гл.5
В
D
Рис. 5.22. Отрыв потока
ной жидкости, ограниченной линиями разрыва скорости АВ и CD
(рис. 5.22).
Очевидно, что для существования застойной зоны давление в ней
должно быть однородным и равным неизменному вдоль линий разрыва
давлению. Тогда давление в застой-
застойной зоне должно быть равно давле-
давлению на поверхности тела в точке воз-
возникновения разрыва (А или С). Но
мы видели, что давление в некоторой
точке А или С меньше, чем давление
в любой точке передней части обте-
обтекаемого тела. Поэтому сила, с кото-
которой жидкость действует на переднюю
часть тела, будет больше, чем сила,
действующая на его заднюю часть,
т.е. возникает некоторая сила сопротивления. Этот прием, т.е. рас-
рассмотрение некоторых разрывных течений идеальной жидкости, исполь-
используется при вычислении подъемной силы и силы сопротивления крыла
самолета, а также в других задачах.
Парадокс Даламбера не имеет места и при таких движениях тела,
при которых образуются волны в жидкости. Например, движение ча-
частично погруженного тела вдоль поверхности жидкости, находящейся
в поле тяжести (судно, лодка). В этом случае существует так называ-
называемое волновое сопротивление. Парадокс отсутствует и при движении
тела со сверхзвуковыми скоростями в сжимаемой идеальной жидкости,
когда в жидкости образуются ударные волны.
5.7.2. Метод суперпозиции потенциальных потоков. При дви-
движении идеальной несжимаемой жидкости потенциал скорости должен
удовлетворять уравнению Лапласа
Д<р = 0. E.110)
Это линейное однородное уравнение. Следовательно, сумма любых его
решений также является его решением. Поэтому, суммируя известные
простейшие решения уравнения Лапласа, мы можем получить реше-
решения, имеющие во многих случаях вполне реальный смысл и практиче-
практическое значение.
Пусть (р\ и ц>2 — потенциалы скоростей «простых» течений иде-
идеальной жидкости, являющиеся решениями уравнения E.110). Очевид-
Очевидно, сумма этих потенциалов также удовлетворяет уравнению Лапласа
E.110) и, следовательно, соответствует некоторому «сложному» движе-
движению жидкости, представляющему собой суперпозицию двух «простых».
Действительно, если
то
А(р\ = 0,
= 0, (р = ф
= 0,
V =
V2 .
E.111)
5.7] Методы описания движения идеальной жидкости 111
То есть скорости «сложного» движения векторно складываются из ско-
скоростей «простых» движений. В этом и состоит принцип суперпозиции.
Обтекание бесконечного цилиндра с циркуляцией. Наложим на
полученное потенциальное движение жидкости при обтекании цилин-
цилиндра плоский вихрь интенсивностью Г , вращающийся против часовой
стрелки. Компоненты скорости движения жидкости, стимулируемого
плоским вихрем, равны (см. E.70))
v8\ = -—, vr\ =0.
Атгг
Складывая со скоростями E.102), получим движение, компоненты ско-
скоростей которого имеют вид
vr = voo (l-4) cos6>' Vs = -Vo
Очевидно, картина обтекания будет теперь симметричной только
относительно оси у. Для изображения линий тока найдем положение
критических точек на поверхности цилиндра.
В критических точках на поверхности цилиндра должны обращать-
обращаться в нуль как vr , так и vs. Радиальная компонента скорости на
поверхности цилиндра в любой точке равна нулю. Касательная же
компонента скорости равна нулю в критических точках, определяемых
из E.112) соотношениями
р
г = го , vs = 0, sin Оъ. = • E.113)
4тгг>П
Если Г = 0 (обтекание цилиндра без циркуляции), то имеем преж-
прежний результат
0к = 0, тг.
Если Г < 4тгг;00го, то критические точки, очевидно, находятся на
верхней половине поверхности цилиндра. Если Г = 4тгг;00го, то обе
точки сливаются в одну при Ok = тг/2. При Г > 4тгг;00го критических
точек на поверхности цилиндра не существует, они могут быть распо-
расположены только где-то внутри жидкости.
Теперь мы можем нарисовать примерную картину линий тока при
обтекании цилиндра с циркуляцией (см. рис. 5.23).
Эффект Магнуса. Вычислим результирующие силы, действующие
со стороны жидкости на единицу длины цилиндра. Для этого найдем
распределение давления по поверхности цилиндра. Из уравнения Бер-
нулли E.105) имеем
E.114)
Подставляя в последнее выражение значение скорости vs на поверхно-
поверхности цилиндра E.112), получим
^) E.115)
112
Идеальная жидкость
[Гл.5
Сила сопротивления Fx и подъемная сила Fy могут быть вы-
вычислены по формулам E.108) и E.109). Нетрудно видеть, что при
подстановке в эти формулы выражения E.115) после интегрирования
получаем
Fx=0, Fy = -pvooF. E.116)
Как и прежде, для силы лобового сопротивления имеем парадокс
Даламбера, однако циркуляция стимулирует возникновение подъемной
силы, направленной противоположно оси у (рис. 5.23).
Г = 4nvwr0
Рис. 5.23. Линии тока при обтекании цилиндра с циркуляцией
Возникновение подъемной силы при обтекании цилиндра с цир-
циркуляцией называется эффектом Магнуса. Эффект Магнуса является
частным случаем общей теоремы Жуковского о подъемной силе крыла.
Согласно теореме Жуковского для вычисления подъемной силы
крыла при обтекании его идеальной жидкостью необходимо вычислить
лишь циркуляцию скорости вокруг крыла. Н.Е. Жуковским, а затем
С.А. Чаплыгиным были разработаны специальные методы вычисления
такой циркуляции при разрывных течениях жидкости около крыла.
Причину возникновения подъемной силы при обтекании цилиндра с
циркуляцией нетрудно понять, если обратиться к уравнению Бернулли.
Как видно из рис. 5.23, в верхней половине течения скорость обте-
обтекания и циркуляционная скорость вычитаются, а в нижней половине
течения — складываются. Таким образом, результирующая скорость
суммарного движения в верхней половине оказывается меньше, чем
в нижней. Из уравнения Бернулли при этом следует, что давление,
действующее на верхнюю половину цилиндра, больше, чем на ниж-
нижнюю. В результате возникает результирующая сила, направленная вниз
(рис. 5.23).
5.7]
Методы описания движения идеальной жидкости
113
0; N
О;
Рис. 5.24. Эффект Магнуса
Приведем несколько примеров, демонстрирующих эффект Магнуса.
Если легкий бумажный цилиндрик скатывается со стола, то его вра-
вращение при падении со стола существенно изменяет траекторию. Без
вращения траектория цилиндрика описыва-
описывается верхней кривой (рис. 5.24), вращение
же делает траекторию более крутой, так
как возникающая при этом гидродинами-
гидродинамическая сила направлена к столу. Вращаю-
Вращающийся цилиндрик вследствие вязкости ре-
реального воздуха стимулирует вокруг себя
циркуляционное движение, что и является
причиной возникновения «подъемной» силы.
Всем известно, что хорошо закручен-
закрученный шарик пинг-понга описывает довольно
сложную траекторию. Так, например, если
мы хотим, чтобы его траектория над столом была круче, то при подаче
мы должны закрутить его по часовой стрелке. В этом случае возни-
возникает сила, направленная вниз. Того же самого эффекта добиваются и
волейболисты, подавая крученый мяч.
В 1924 г. Флетчером было предложено и построено роторное судно,
использующее рассматриваемый эффект (рис. 5.25). На судне были
установлены два легких, обтянутых пару-
парусиной цилиндра, которые приводились во
вращение моторами. Диаметр цилиндров
был равен 2,8м, высота— 18м.
Такое судно развивало скорость около
15 км/ч. Причем естественно, что макси-
максимальная скорость развивалась при боко-
боковом ветре, когда «подъемная» сила была
Ветер
1
Рис. 5.25. Корабль Флетчера
направлена вдоль корпуса судна. Однако это изобретение не получило
своего дальнейшего развития в связи с быстрым развитием паровых и
дизельных двигателей.
Эффект Магнуса является также одной из причин отклонения тра-
траектории снаряда от вертикальной плоскости, проходящей через ось
ствола орудия (деривация).
Снова обратим внимание на то, что в идеальной жидкости, лишен-
лишенной трения, мы не могли бы, вращая цилиндр, создать в жидкости
вращательное движение. Только благодаря вязкости вращающийся ци-
цилиндр создает вокруг себя вращательное движение жидкости, которое
вдали от тела можно считать потенциальным. Отвлекаясь же от при-
причин, создавших вращательное потенциальное движение жидкости, нам
удалось в рамках модели идеальной жидкости рассмотреть и объяснить
многие явления, наблюдаемые в реальных жидкостях.
Вязкость воздуха приводит к его циркуляции вокруг крыла само-
самолета. Профили крыльев имеют острую заднюю кромку (рис. 5.26).
114
Идеальная жидкость
[Гл.5
Рис. 5.26. Обтекание крыла
Вблизи этой кромки возникают вихри, в которых воздух вращается
против часовой стрелки. Вихри увеличиваются, отрываются от крыла
и уносятся набегающим потоком воздуха.
При этом вблизи крыла возникает циркуля-
циркуляция остальной массы воздуха, направлен-
направленная по часовой стрелке. Циркуляционный
поток, складываясь с набегающим, ускоря-
ускоряет движение воздуха над крылом. Согласно
уравнению Бернулли давление над крылом
понижается, а под крылом повышается, возникает подъемная сила.
Примерная картина обтекания крыла показана на рис. 5.26.
Рассмотренный метод суперпозиции потенциальных потоков, как и
метод конформных отображений, позволяет составлять из известных
простейших движений идеальной жидкости такие движения, которые
были бы близки по своим свойствам к движениям жидкости в некото-
некоторых реальных задачах, имеющих практический интерес.
5.7.3. Графоаналитический метод. Суперпозицию плоских по-
потенциальных потоков можно осуществлять и графически. Представим
себе, что на плоскости нанесены линии тока каких-либо двух плоских
потоков (рис. 5.27). Можно в точках пересечения линий тока построить
в одинаковом масштабе скорости движений жидкости в обоих пото-
потоках. Очевидно, скорость результирующего движения в этих точках
изобразится диагональю параллелограмма, построенного на векторах,
изображающих скорости отдельных движений. Причем такое построе-
построение будет тем точнее, чем чаще будут нанесены линии тока «простых»
потоков.
v|/2 = const
= const AA2
f -
(
7.
!
9*-
Рис. 5.27. Суперпозиция двух потоков
Рассмотрим вопрос о масштабах изображения слагаемых потоков.
Для этого обратимся к рис. 5.27. В пределах малых участков линий
тока их можно полагать прямыми.
Для того чтобы отрезки А1\ и А/2 изображали скорости vi и V2
в одинаковых масштабах, очевидно, необходимо выполнить следующее
условие:
E.117)
Ah
V2
А/2
5.7]
Методы описания движения идеальной жидкости
115
Из подобия прямоугольных треугольников получаем
А/ц _ Ah_
A/i2 ~~ A/2 '
E.118)
Но Ah2V\ равно расходу жидкости между двумя соседними лини-
линиями тока первого потока, а произведение Ah\V2 — расходу жидкости
между двумя соседними линиями тока второго потока. Поэтому для
того чтобы масштабы изображений складываемых потоков были оди-
одинаковы, необходимо, чтобы расходы жидкости между двумя соседними
линиями тока в обоих движениях были равны
AQi=AQ2, A^i=A^2. E.119)
Рассмотрим в качестве примера наложе-
наложение двух потоков — прямолинейного поступа-
поступательного потока и плоского источника. Для
начала рассмотрим движение жидкости, со-
создаваемое плоским источником или стоком.
Очевидно, что в плоском источнике линии
тока будут представлены радиусами, прове-
проведенными из точки, в которой расположен ис-
источник (рис. 5.28).
Тогда эквипотенциальные линии — окружности с центром в источ-
источнике. Если мощность источника равна Q, то, принимая во внимание,
что в таком движении скорость жидкости в любой точке направлена
вдоль радиусов, проведенных из центра источника, будем иметь
Рис. 5.28. Плоский ис-
источник
Q =
v =
E.120)
Будем предполагать, что оба потока изображены в одном масштабе,
т. е. расход жидкости между двумя соседними линиями тока прямоли-
прямолинейного поступательного потока ра-
равен расходу жидкости между сосед-
соседними лучами линий тока плоского
источника.
Рассмотрим линию тока О\О пер-
первого потока, проходящую через ис-
источник (рис. 5.29). Так как скорость
прямолинейного поступательного по-
потока постоянна, а скорость вдоль
линии тока источника возрастает
неограниченно с приближением к ис-
источнику, то на линии О\О всегда
найдется точка, в которой результи-
результирующая скорость будет равна нулю.
Обозначим эту точку через А. Проводя далее диагонали в построенной
сетке линий, получим линии тока результирующего потока (рис. 5.29).
Рис. 5.29. Линии тока
116 Идеальная жидкость [Гл.5
Рассмотрим линию тока CAB. Эта линия разграничивает жид-
жидкость, вытекающую из источника, от набегающего потока жидкости.
Так как при обтекании идеальной жидкостью поверхность тела также
является линией тока, через которую жидкость не проникает, то мы
можем полагать линию CAB линией, описывающей контур некото-
некоторой твердой поверхности, обтекаемой прямолинейным поступательным
потоком. Зная скорости отдельных движений в каждой точке, можно
найти скорость в каждой точке для результирующего движения. Вос-
Воспользовавшись формулой Бернулли, нетрудно рассчитать и давление
в каждой точке потока, в том числе и на поверхности обтекаемо-
обтекаемого тела, изображаемой на плоскости линией CAB. Суммируя силы
давления, действующие на элементы поверхности тела, можно найти
результирующую силу, действующую на тело. Если линия АВ пред-
представляет собой контур некоторой горы, обтекаемой ветром, то можно
в каждой точке найти вертикальную составляющую скорости воздуха,
что важно, например, при метеорологических расчетах или при оценке
дальности или продолжительности полета планера при планировании
в предгорьях.
Комбинация плоскопараллельного поступательного потока с источ-
источником и стоком дает картину обтекания некоторого замкнутого кон-
контура, форма которого может быть довольно сложной в зависимости
от интенсивности отдельных слагаемых движений. Добавление еще
нескольких источников и стоков позволит представить картину обтека-
обтекания тела практически любой формы. Конечно, все операции сложения
потенциальных потоков можно провести и аналитически. Однако во
многих случаях графический метод может дать достаточно точный,
а главное наглядный результат, необходимый для решения некоторой
конкретной практической задачи.
5.7.4. Непосредственное решение уравнений движения. При
решении задач о движении идеальной жидкости можно обратиться
непосредственно к уравнениям, описывающим это движение с соответ-
соответствующими граничными условиями. В качестве примера рассмотрим
движение бесконечного цилиндра в идеальной несжимаемой жидкости.
Движение бесконечного цилиндра в идеальной несжимаемой
жидкости. Снова отметим, что такое движение можно рассматри-
рассматривать как плоское. Будем также полагать, что движение жидкости,
вызываемое движением в ней цилиндра, является потенциальным.
Существенное отличие от задачи обтекания неподвижного цилиндра
плоскопараллельным поступательным потоком жидкости заключается
в том, что это движение не является стационарным. Действительно, по
мере продвижения цилиндра в неподвижной жидкости скорость в каж-
каждой фиксированной точке пространства будет изменяться с течением
времени. На бесконечности будем полагать жидкость неподвижной.
Несмотря на то, что задача нестационарна, потенциал скорости
должен удовлетворять уравнению Лапласа E.78), не содержащему
времени явно.
5.7]
Методы описания движения идеальной жидкости
117
У
Выберем систему координат, как показано на рис. 5.30.
Так как на бесконечности v = 0, то производные по координатам от
потенциала (р должны на бесконечности обратиться в нуль. Известно,
что такими производными для цилиндриче-
цилиндрических задач являются производные от In r по
координатам, начиная с первого порядка и
выше. Так как (р — скалярная функция, а
Vlnr — вектор, то общее выражение для ис-
искомого потенциала должно иметь вид
А _, An r /с Ю1\
(р = А\7тг= , n=-. (o.lzl)
г г
Здесь А — некоторый, независящий от
координат вектор, который должен быть свя-
связан с единственным, имеющимся в нашем
распоряжении вектором, от которого может
зависеть решение, вектором скорости движе-
движения цилиндра — и. Очевидно, эта связь может быть установлена из
граничных условий на поверхности цилиндра (см. E.80))
nV(p = nu. E.122)
Из E.121) имеем
Рис. 5.30. Движение ци-
цилиндра
An o An An
= —2— 2 —г- = 5" = nu •
г г г
E.123)
На поверхности цилиндра (г — го), следовательно, из последнего
соотношения получаем
A=-rgu,
v = Ц [2(un)n - и].
E.124)
Г Г
Из полученного выражения можно найти компоненты скорости
в подвижной системе координат, движущейся вместе с цилиндром:
г
= -| и cos в ,
г
= -^ и sin в .
г
E.125)
Таким образом, в каждый момент времени распределение скоростей
вокруг движущегося цилиндра удовлетворяет уравнениям E.125), так
что с точки зрения наблюдателя, движущегося вместе о цилиндром,
картина движения жидкости около цилиндра стационарна. Нетрудно
видеть, что из полученного решения мы можем получить обтекание
неподвижного цилиндра, если на движение, описываемое формулами
E.125), наложим движение всей жидкости вместе с цилиндром с по-
постоянной скоростью и, направленной справа налево. Тогда будем иметь
обтекание неподвижного цилиндра плоскопараллельным поступатель-
поступательным потоком со скоростью и, направленной справа налево. Распределе-
Распределение скоростей такого движения будет описываться полученными выше
формулами E.102), если в них изменить знак скорости набегающего
потока.
118 Идеальная жидкость [Гл.5
Найдем распределение давления по поверхности цилиндра. Для
этого воспользуемся уравнением Бернулли (см. E.77)):
dt + 2 +р" UJoo+ 2°+ р ' UJoo' V°°-0'
E.126)
Давление в любой точке жидкости равно
PV ®P (К 1О7\
V = Voo ^ Р ~7Г~ • (O.lZ/j
Из E.124) следует, что потенциал зависит от скорости цилиндра и
и радиуса-вектора г. То есть если потенциал и зависит от времени,
то неявно — через зависимость от времени скорости движения цилин-
цилиндра и. Потенциал скорости жидкости в некоторый момент времени
определяется значением скорости движения цилиндра в этот момент
времени. Формула E.124) описывает зависимость потенциала и от
координаты точки около цилиндра в тот же момент времени. Но
в нестационарной задаче вся стационарная картина обтекания движет-
движется вместе с цилиндром со скоростью и. Поэтому
dr _
Дифференцируя потенциал по времени как сложную функцию, полу-
ЧИМ dip dip du , dip dr ,- 1OQ4
—— = — 1 . (o.lzo)
Нетрудно убедиться, что для слагаемых в правой части E.128) имеем
^du = _r|rdu) ^*=uV^ = u4[2(un)n-u], E.129)
на поверхности цилиндра
^ = -rln6^ + u2B cos20- 1), v2 = u2 . E.130)
ot at
Подставляя полученные выражения в E.127), получим для распре-
распределения давления по поверхности цилиндра следующую формулу:
р = Роо + Р^- pro^ cos6-2pu2 cos20. E.131)
Присоединенная масса. Найдем силу лобового сопротивления,
которую испытывает единица длины цилиндра при своем движении
в жидкости:
Fx = - [ p cos 0r0 dO . E.132)
о
Используя формулу E.131), получим
~^. E-133)
5.7] Методы описания движения идеальной жидкости 119
Направление силы сопротивления, как видно из формулы, зависит
от знака ускорения du/dt. Если цилиндр движется слева направо с
положительным ускорением (см. рис. 5.30), то сила сопротивления
направлена справа налево, т. е. препятствует движению. Если при
движении в том же направлении цилиндр движется с отрицательным
ускорением, то сила сопротивления действует в сторону движения
цилиндра, т. е. стремится ускорить его. При равномерном движении
цилиндра имеем парадокс Даламбера. Таким образом, парадокс Далам-
бера не имеет места и при движении цилиндра с ускорением.
В силу симметрии движения очевидно, что подъемная сила равна
нулю. В этом нетрудно убедиться и аналитически. Запишем уравне-
уравнение движения цилиндра в проекции на ось х, направленную вдоль
скорости и. Пусть на цилиндр единичной длины действует некоторая
внешняя сила F, вызывающая его движение в жидкости и направлен-
направленная также вдоль оси х. Если М — масса единицы длины цилиндра, то
с учетом E.133) уравнение движения будет иметь вид
, , du ,-, 9 du (л /г 9 \ du ,-, /г 1 гл Л\
М- = F-pvrt-, (M + vrlp)- = F. E.134)
Из E.134) видно, что уравнение движения выглядит так же, как
если бы никакой силы сопротивления не было, а масса тела увели-
увеличилась бы на величину тгг^р = Мп. Эта добавка называется присо-
присоединенной массой. Присоединенная масса зависит от формы тела и
его ориентации по отношению к набегающему потоку. В частности,
для единицы длины цилиндра и для шара присоединенные массы
соответственно равны
Mn = nrlp = PV, Мп = \ъг\р=\рУ. E.135)
В случае тела произвольной формы приведенная масса имеет тен-
тензорный характер и может быть вычислена для тела любой геометриче-
геометрической формы. Присоединенная масса — геометрическая характеристика
формы тела, обтекаемого жидкостью, и его ориентации в набегающем
потоке.
Если присоединенная масса значительно меньше массы тела, то
ею можно пренебречь и рассматривать обычное уравнение движения,
например, движение тяжелых тел в воздухе, плотность которого при
атмосферном давлении на несколько порядков меньше, чем плотность
обычного твердого тела. Однако в некоторых случаях это не так и
в уравнениях движения следует учитывать присоединенную массу, на-
например, при движении подводной лодки, масса которой приблизительно
равна присоединенной массе, или при движении воздушных шаров и
дирижаблей.
В качестве числового примера рассмотрим движение воздушного
шара, освободившегося от удерживающих его канатов. Пусть масса
воздушного шара вместе с находящимся в нем газом, оболочкой и
гондолой равна М. Пусть далее масса вытесненного им воздуха рав-
120 Идеальная жидкость [Гл.5
на Mq. Тогда без учета присоединенной массы уравнение движения
будет иметь вид
Ма = Mog- Mg. E.136)
Уравнение движение шара с учетом присоединенной массы запи-
запишется в следующем виде:
^ E.137)
Тогда отношение ускорений в том и другом случае будет равно
Если положить Mq & М, то получим, что с учетом присоединенной
массы ускорение воздушного шара будет в полтора раза меньше, чем
без ее учета.
Капитаны подводных лодок и надводных кораблей также должны
учитывать эффект присоединенной массы. При торможении судна на
него будет действовать гидродинамическая сила, препятствующая тор-
торможению, стремящаяся двигать судно в прежнем направлении.
Даже при движении тяжелых тел в воздухе в некоторых случаях
необходимо учитывать присоединенную массу. Часы со сферическим
маятником в воздухе по сравнению с их движением в вакууме будут
отставать на несколько секунд в сутки вследствие эффекта присоеди-
присоединенной массы.
Действительно, из обычного уравнения движения математического
маятника период его колебаний, как известно, равен
Juo = K, Т = 2тгх^— . E.139)
у Mgl
Здесь uj — угловое ускорение маятника, М — действительная масса ма-
маятника, / — его длина, g — ускорение свободного падения, J — момент
инерции маятника, К — момент внешних сил {Mg). С учетом присое-
присоединенной массы момент инерции равен
J = (М + МпI2 .
Подставляя в формулу для периода и учитывая, что (Мп/М) <С 1,
получим
В последнем выражении То — период колебаний маятника в вакууме,
рв — плотность воздуха, р — плотность вещества, из которого изготов-
изготовлен шар маятника объемом V.
Теперь нетрудно оценить отставание секундного (То = 1 с) маятни-
маятника, изготовленного из меди (р « 8,9 • 103 кг/м3), за сутки (^ 105 с):
At = (T-T0)- 105 = Т0^^ 1 Ь?^ . 105с^З,6с.
V J 4р 4-8,9-103
5.8] Примеры решения задач 121
При большем периоде колебаний маятника отставание будет еще боль-
больше. Ясно, что это отставание будет зависеть от атмосферного давления,
так как плотность воздуха зависит от давления. Поэтому особо точные
маятниковые часы должны помещаться в вакуум.
Контрольные вопросы
1. Что представляет собой модель идеальной жидкости? Какова область
применимости этой модели?
2. Перечислите уравнения, составляющие замкнутую систему уравнений
движения идеальной жидкости.
3. В чем состоит граничное условие к уравнению Эйлера?
4. Какое движение жидкости называют изэнтропическим? Согласно урав-
уравнению E.6) энтропия индивидуальных частиц идеальной жидкости не изменя-
изменяется с течением времени. Значит ли это, что движение идеальной жидкости
всегда изэнтропическое?
5. Какую жидкость называют несжимаемой? В чем состоит критерий
несжимаемости?
6. Какое движение идеальной жидкости называют потенциальным?
7. Что такое линия тока и траектория?
8. Что называют трубкой тока? В чем состоит ее замечательное свойство?
9. В чем отличие уравнения Бернулли для потенциальных и непотенциаль-
непотенциальных движений идеальной жидкости?
10. Что такое кавитация? Объясните это явление на основе уравнения
Бернулли.
11. Какое движение идеальной жидкости называют баротропным? Приведи-
Приведите примеры.
12. Сформулируйте теорему Томсона о сохранении циркуляции скорости
жидкости. Укажите область ее применимости.
13. Что такое вихревая линия и вихревая трубка?
14. Сформулируйте теорему Гельмгольца об интенсивности вихревой трубки
и ее следствие.
15. Чему равна циркуляция скорости при потенциальном движении идеаль-
идеальной жидкости?
16. Что такое лобовое сопротивление и подъемная сила?
17. В чем состоит парадокс Даламбера?
18. В чем состоит эффект Магнуса? Объясните на основе уравнения Бер-
Бернулли.
19. Что такое присоединенная масса при движении тел в идеальной жидко-
жидкости?
5.8. Примеры решения задач
Задача 1
Определите форму сосуда, используемого для водяных часов. Тре-
Требование: высота уровня жидкости в верхней части должна умень-
уменьшаться равномерно со скоростью v\. Жидкость считать идеальной и
несжимаемой.
122
Идеальная жидкость
[Гл.5
Решение. Пусть S\ — площадь поверхности верхнего уровня
жидкости, $2 — площадь самого узкого сечения сосуда, v2 — скорость
жидкости в самом узком сечении S2.
Выберем систему координат, как показано на
рис. 5.31. Ось z направлена вдоль продольной оси
симметрии сосуда, а ось х проходит через самое узкое
сечение. Тогда площадь поверхности верхнего уровня
жидкости равна
1
с
о у
1
—-^
3)
У
5К
_—-^
)
X
\
S] = 7ГЖ .
E.141)
Воспользуемся уравнением непрерывности в инте-
интегральной форме
^ \
E.142)
Рис. 5.31. Во- у s
дяные часы
где V — объем жидкости в верхней половине сосуда,
S — замкнутая поверхность, ограничивающая объем V и состоящая из
площадок S\, #2 и боковой стенки сосуда.
Поскольку жидкость несжимаема, имеем
pvdS = 0,
=v2S2.
E.143)
Из уравнения Бернулли, записанного вдоль линии тока для сечений
S\ и $2, получаем
^2 = ^2^, E.144)
где g — ускорение свободного падения.
Из выражений E.141), E.143) и E.144) имеем
Отсюда
z = ax ,
E.145)
E.146)
Эта формула и определяет форму сосуда водяных часов как тела
вращения.
Задача 2
Жидкость вытекает из цилиндрического сосуда через небольшое
отверстие в дне сосуда. Покажите, что время, необходимое для исте-
истечения жидкости, вдвое больше того времени, которое потребовалось
бы для истечения того же количества жидкости, если ее уровень
поддерживается постоянным.
Решение. Пусть So и S\ —площади сечения сосуда и отверстия
соответственно, Н — высота жидкости в сосуде.
5.8]
Примеры решения задач
123
На линии тока выберем точки 0 и 1 (рис. 5.32). Из уравнения
Бернулли имеем
р
E.147)
Поскольку z\ = 0, ро = р\, vo = О, то v\ = \j2gz§ .
Рассмотрим два случая.
1. Уровень жидкости в сосуде поддерживается постоянным. Тогда
скорость истечения равна г>1 = \j2gH.
Если t\ — время, в течение которого из
сосуда вытечет объем жидкости ?о//, то из
уравнения непрерывности имеем
S\v\t\ =
t\ =
E.148)
2. Уровень жидкости в сосуде изменяется
со временем. Тогда скорость истечения равна
h
0
y
Уравнение непрерывности запишется в ви-
виде
dz
Siy/2gz =~So^.
E.149)
1
Рис. 5.32. Сосуд с жид-
жидкостью
Знак минус в правой части учитывает, что с течением времени
уровень жидкости в сосуде уменьшается. Если t^ — время истечения
всей жидкости из сосуда, то из уравнения E.149) получаем
2S0H
о
E.150)
Сравнивая E.148) и E.150), видим: t^ = 2ti, что и требовалось
доказать.
Задача 3
Ангар полуцилиндрической формы длиной L = 70 м и радиусом R =
= 10м подвергается действию ветра, скорость которого на бесконеч-
бесконечности Voo = 72 км/ч строго перпендику-
перпендикулярна оси ангара.
Какая сила будет действовать на ан-
ангар, если дверь на участке Л (рис. 5.33)
открыта? Плотность воздуха р = 1,2кг/м3.
Потенциал скорости задан следующей
функцией: (р = Voq (I + R2/r2)rcos0.
Давление внутри амбара считать везде
одинаковым и равным давлению на входе.
Рис. 5.33. Ангар
124 Идеальная жидкость [Гл.5
Решение. Определим нормальную и касательную составляющие
скорости ветра:
E.151)
На поверхности ангара имеем
vr = 0, vs = ^VvoSmO, v2 = 4v2oosm26 . E.152)
Поскольку дверь А открыта, давление внутри ангара равно давле-
давлению ро в точке торможения. Уравнение Бернулли позволяет вычислить
это давление: 2 2
^0 , РО _ ^оо , Роо /г 1 го\
У+ 7~^ Т' [ }
где Роо— давление воздуха вдали от амбара. Если скорость около
входа в амбар приближенно считать равной нулю (vq =0), то давление
внутри амбара равно
Ро = Роо + ^. E.154)
Давление в любой точке наружной поверхности амбара также опре-
определяется из уравнения Бернулли, записанного для прилегающей к этой
поверхности линии тока
^ ^() E.155)
Перепад давлений внутри и снаружи равен
Ро-р = 2pv2oo sin2 0 . E.156)
Проекции на оси координат вектора силы, действующей на амбар
со стороны движущегося воздуха, определяются следующими выраже-
выражениями:
Fx = L Up-p0)Rcos0d0, Fy = -L Up - p0)Rsm0 dO . E.157)
о о
Сила лобового сопротивления Fx равна нулю, что соответствует
парадоксу Даламбера. Подъемная сила равна
Fy = bhpv^R sin3 0d0 = ^npv^LR, Fy = 2,8bl06H. E.158)
о
Сила направлена вверх, т. е. стремится поднять амбар.
Задача 4
В теориях кипения жидкости и кавитации представляет интерес
время схлопывания образовавшегося воздушного пузырька в объеме
жидкости. Пусть начальный радиус пузырька равен Rq. Давление жид-
5.8]
Примеры решения задач
125
кости на бесконечности равно ро. Определите время т, в течение ко-
которого образовавшаяся сферическая полость заполняется жидкостью.
Никаких других сил к жидкости не приложено. Жидкость считать
несжимаемой. Давлением газа в пузырьке пренебречь.
Решение. Воспользуемся сферической системой координат
(г,6,(р), начало которой поместим в центр пузырька (рис. 5.34).
После образования полости движение жид-
жидкости будет радиальным, т. е. v = (vr,0,0). Для
радиальной скорости vr = v уравнение Эйлера
запишется в виде
dv , dv I dp /c л гП\
^7+^^- = — IT- E.159)
dt дг р дг
Поскольку жидкость несжимаема, то из
уравнения непрерывности имеем
2
,. 1 дг v A 2 т-1(л.\
diw = -^ —— = 0, rzv = F(t) .
г or
E.160)
Рис. 5.34. Воздушный
пузырь в жидкости
Здесь F(i) — неизвестная функция времени. Подставив ее в урав-
уравнение E.159), получим
я \9 >^--7Г' F =Чг- E161)
дг \ 2 / р дг dt
Проинтегрируем это уравнение по радиальной координате в преде-
пределах от оо до текущего радиуса пузырька R(t):
Так как давлением газа в пузырьке по условию задачи можно
пренебречь [p(r = R) = 0], то
E.163)
E.164)
Тогда уравнение E.162) примет следующий вид:
dR
Я
— i^L ? у —
dt '
где V — скорость жидкости на поверхности полости. С другой стороны
из уравнения E.160) следует, что на поверхности пузырька
E.165)
E.166)
= R2(t)V(t).
Продифференцировав это выражение по времени, получим
F' = 2RV2 + R2V
dV
dR
126 Идеальная жидкость [Гл.5
Тогда уравнение E.164) запишется в виде
З2^ Р0 E167)
2 dR p
После разделения переменных имеем
f^ = -^. E.168)
3V2 + 2p0/p ^
В начальный момент времени размер пузырька фиксирован, R =
= Ro, а жидкость неподвижна, V(t = 0) = 0. С учетом этого уравнение
E.168) можно записать в интегральной форме:
^. E.169)
Отсюда получаем
dt у Зр [\ R)
Если т — время схлопывания пузырька, то R(t = т) = 0. Тогда
_ "г _ Л3р~ г dR _ _ Г$р~ Г~^> ГE/6)
E.171)
где Г(ж) — гамма-функция или эйлеров интеграл второго рода.
Окончательно получаем
г = 0,915 Roif^- • E.172)
Сделаем численные оценки. Пусть Rq = 10~3 м, р = 103 кг/м3, ро =
= 105 Па. При этих условиях расчет по формуле E.172) дает г « 10~4 с.
Задача 5
Определите форму, которую имеет свободная поверхность полого
вихря с интенсивностью Г в идеальной
z| _ жидкости в поле силы тяжести. Движение
. [11 жидкости потенциальное. Внешнее давле-
"~ ,ч I ., '' ние равно ро-
\ | / Решение. Для потенциального движе-
\ | / ния жидкости в любой точке справедливо
_j;_y уравнение Бернулли
2
V X)
тл с ос гт « -- + - +erz = const. E.173)
Рис. 5.35. Полый вихрь 2 р
5.8]
Примеры решения задач
127
Скорость движения жидкости в поле вихря равна
Г
v =
2тгг
Запишем уравнение E.173) вдоль свободной поверхности:
E.174)
E.175)
Здесь учтено, что при z = 0 жидкость неподвижна. С учетом урав-
уравнения E.174) имеем
+
8ttV
= О.
Тогда уравнение свободной поверхности вихря имеет вид
-^=0.
E.176)
E.177)
Задача 6
Определите силу, действующую на шар радиуса R, закрепленный
на горизонтальной оси в круглом отверстии в стенке плоского сосуда,
заполненного жидкостью (рис. 5.36). Расстоя-
Расстояние от оси шара до поверхности жидкости в
сосуде равно Н, внешнее давление — ро- Тре-
Трения нет. Будет ли шар вращаться вокруг оси?
Решение. Систему координат хОу выбе-
выберем, как показано на рис. E.36). Ось у направ-
направлена вдоль оси шара перпендикулярно плос-
плоскости рисунка, начало координат совпадает с
центром шара.
В неподвижной тяжелой жидкости распре-
распределение давления по высоте задается законом
Паскаля:
V = Ро + pg(H - z) .
E.178)
Рис. 5.36. Шар в стен-
стенке сосуда
В выбранной системе координат сила F, действующая на полусферу
в жидкости, определяется двумя компонентами:
Fx = [ pcosOdS, Fz = - [ psmOdS, E.179)
где S — площадь полусферы в жидкости, dS = тгЯ2 sin в dO — элемен-
элементарная площадка, z = RcosO.
Подставляя выражение E.178) в E.179), после интегрирования
получаем
Fx = l iT2HR2pg , Fz = -\ тг R3pg . E.180)
128
Идеальная жидкость
[Гл.5
Сила направлена вдоль вертикальной оси шара, а ее величина равна
F = y/Fi + Fi = nR2pg^1д2 + ^Я2 . E.181)
Шар не вращается вокруг оси, так как момент силы равен нулю.
Задача 7
Определите вид течения, которое задано комплексным потенциалом
/3 = az3 (a > 0). Какой объем жидкости Qv протекает каждую секун-
секунду через отрезок прямой, соединяющей две точки zi(l,0) и ^A, 1)?
Решение. В комплексном потенциале выделим вещественную и
мнимую части:
C = а(х + iyf = ах(х2 - Зу2) + гау{3х2 - у2) . E.182)
Отсюда определяются потенциал скорости и функция тока
Ч> = ах(х2 - Зу2), ф = ауCх2 - у2) . E.183)
Линии тока задаются уравнениями: ф = const. Положим ф = 0.
Тогда из выражения ауCх2 - у2) = 0 получаем у\ =0, у^ = л/3 ж.
Эти линии тока образуют угол
tga=^ = y/3, a=^. E.184)
X О
Таким образом, комплексный потенциал
E.182) задает движение жидкости внутри
угла с раствором 60° (рис. 5.37).
Компоненты скорости
= -?- = Зах(х2 - у2),
Рис. 5.37. Обтекание угла
E.185)
v _ ^ _ _
Заметим, что vx = 0 при у = х. На линии у = х жидкость движется
так, что проекции ее скоростей при а > тг/4 и а < тг/4 взаимно
скомпенсированы.
Для вычисления объемного расхода воспользуемся свойством функ-
функции тока
Qv =tl>(z2)-rl>(zi)=2a. E.186)
Нетрудно видеть, что функция тока удовлетворяет однородному
уравнению Лапласа:
Аф = бау -6ау = 0.
Следовательно, движение потенциальное.
E.187)
ГЛАВА 6
ВЯЗКАЯ ЖИДКОСТЬ
Более реалистичной по сравнению с моделью идеальной жидкости
является модель вязкой ньютоновской жидкости. В этой модели учи-
учитывается вязкость жидкости и ее теплопроводность, но модуль сдвига
равен нулю.
6.1. Замкнутая система уравнений движения
вязкой жидкости. Уравнение Навье-Стокса
Уравнение движения сплошной среды имеет вид
dvi dvi I dPik _ n
+V=f + FЛ)
В случае вязкой однородной ньютоновской жидкости тензор напря-
напряжений, как было показано ранее D.99), запишется в виде
®Vk 2^ dVi\ {a Оч
W- 3««^J • F-2)
Подставляя выражение F.2) в F.1) и полагая коэффициенты вяз-
вязкости постоянными, получим уравнение движения вязкой жидкости
i 1 dp , г] d2Vi 1 /. 1 \ д dvi . /с оч
3 / dx dx
at дхк р oxi р дхк Р V 3 / dxi dxt
Или в векторном виде
^ + (vV)v = -- Vp + г/Av + - f^ + iry) grad div v + f . F.4)
ot p p \ 6 J
Уравнения F.3), F.4) называются уравнениями Навье-Стокса. Ве-
Величина v = rj/p называется коэффициентом кинематической вязко-
вязкости. Для несжимаемой жидкости div v = 0, и уравнение Навье-Стокса
принимает вид
^ + (vA)v = -- Vp + г/Av + f . F.5)
ot p
Видно, что уравнение Навье-Стокса отличается от уравнения Эйле-
Эйлера дополнительными членами в правой части, учитывающими вязкость
жидкости.
5 В.Г. Черняк, П.Е. Суетин
130 Вязкая жидкость [ Гл. 6
Замкнутая система уравнений движения вязкой жидкости содер-
содержит, разумеется, еще уравнение непрерывности и уравнение баланса
внутренней энергии. Полная система уравнений движения имеет вид
^ + (vA)v = -- Vp + г/Av + - (% + \г]) graddivv + f, F.6)
ut p p \ о '
Уравнения F.6) вместе с уравнениями Фурье, калорическим и термиче-
термическим уравнениями состояния образуют замкнутую систему уравнений
движения вязкой жидкости. Предполагается, что решение этой систе-
системы существует и при заданных начальных и граничных условиях оно
единственно.
6.1.1. Граничные и начальные условия. Прямыми и косвен-
косвенными экспериментами показано, что вязкая жидкость «прилипает» к
поверхности обтекаемого тела. Силы взаимодействия между поверх-
поверхностными атомами тела и прилегающими к ним молекулами жидкости
оказываются достаточными, чтобы последние двигались неразрывно
с поверхностью тела. Поэтому на межфазной границе тело-вязкая
жидкость в каждой точке поверхности должны быть равны не только
нормальные компоненты скорости жидкости v и тела и, но также и
касательные компоненты. Следовательно, на поверхности обтекаемого
тела в каждой точке должно выполняться векторное равенство
v = u. F.7)
Сила, действующая на единицу поверхности тела, определяется
компонентами . л
\] F.8)
где rik — проекция на ось к нормали п, внешней по отношению к телу.
Если мы имеем движение двух несмешивающихся жидкостей, то,
очевидно,на поверхности раздела этих жидкостей скорости их в каж-
каждой точке поверхности раздела должны быть равны:
VI = V2 . F.9)
Для любого элемента поверхности раздела двух несмешивающихся
жидкостей силы, с которыми жидкости действуют друг на друга, равны
по величине и обратны по направлению (третий закон Ньютона). Сила,
действующая в г-м направлении на единицу площади жидкости 1 со
стороны жидкости 2, равна Р\к пк , где пк — проекция нормали,
внешней по отношению жидкости 1. Сила, действующая в том же
направлении на жидкость 2 со стороны жидкости 1, равна Р\к пк , где
пк — проекция нормали, внешней по отношению жидкости 2. Оче-
Очевидно, пк = —пк. Тогда в соответствии с третьим законом Ньютона
6.1] Уравнение Навъе-Стокса 131
можно записать
p(iyi) _ _pB)nB) pWJV - Р{2)п{{) РA) - РB) F 10)
На свободной поверхности жидкости, граничащей с вакуумом, дол-
должно выполняться условие
Piknk=0. F.11)
Условие F.7) не имеет места при движении разреженного газа,
когда длина свободного пробега молекул газа сравнима с размерами
обтекаемого тела. В этом случае газ «скользит» вдоль его поверхности.
При этом на поверхности тела испытывает скачок и температура. Одна-
Однако рассмотрение этих явлений выходит за рамки механики сплошных
сред и является предметом изучения кинетической теории газов.
В граничные условия входит также задание давления и температуры
(или потока тепла) на некоторых поверхностях в жидкости.
Начальные условия необходимы при решении нестационарных за-
задач и заключаются в задании в некоторый начальный момент времени
пространственных распределений скоростей, давлений и температур
в объеме жидкости.
6.1.2. Вихревое движение вязкой жидкости. Рассмотрим урав-
уравнения движения несжимаемой жидкости. Если объемные силы имеют
потенциал E.11), то, воспользовавшись известной формулой векторно-
векторного анализа E.13), уравнение F.5) можно переписать в виде
^ - [v, rot v] = -V(y + V- + ?П0Т) + z/Av . F.12)
Применяя операцию ротора к обеим частям уравнения и принимая
во внимание, что rot V = О, rotv = 2ш, где ш — вихревая скорость
жидкости, получим
— rot[v, ш] = vАи;. F.13)
ОТ
Если v = 0, то из F.13) имеем уравнение Громека для баротропного
движения идеальной жидкости E.17).
Для простоты рассмотрим плоское движение одиночного вихря (см.
рис. 5.14). Очевидно, частицы жидкости в любой момент времени будут
двигаться по окружностям с центром на оси вихря. Тогда нетрудно
видеть, что второй член слева в уравнении F.13) будет равен нулю.
Действительно, вектор [v, ш] в каждой точке направлен по радиусу,
проведенному из центра вихря, а его величина в данной точке зависит
только от времени и расстояния этой точки до центра вихря. Поэтому
ротор такого вектора равен нулю. Тогда из F.13) получаем уравнение
§^ = ^Д". F.14)
В цилиндрической системе координат г, (р, z с учетом топологии дви-
движения жидкости (uor = uj^ = 0, ujz = о;(г, t)) имеем
ди 1 д (дш\ {а 1КЧ
Ж = 1/г д~г Ы- FЛ5)
132 Вязкая жидкость [ Гл. 6
Уравнение F.15) имеет вид уравнения теплопроводности и, как
всякое уравнение параболического типа, описывает некоторый необра-
необратимый процесс (первая производная по времени).
Пусть в начальный момент времени вихревое движение было ста-
стационарным и поддерживалось некоторым постоянным источником (на-
(например вращением тонкого металлического цилиндра). При этом дви-
движение в любой точке, кроме оси вихря, будет, как мы увидим далее,
потенциальным. Траекториями частиц будут окружности с центром на
оси вихря. Скорости частиц определяются формулой E.70):
v = P-- F-16)
Если в начальный момент времени интенсивность вихревого движе-
движения определялась величиной Го, то в последующие моменты времени
после выключения источника вихревого движения движение жидкости
будет описываться известным решением уравнения F.15):
Го -' ш)- <617>
Из F.17) видно, что интенсивность вихревого движения в центре
вихря (г = 0) убывает обратно пропорционально времени. В некоторой
фиксированной точке пространства г = а > 0 интенсивность с течени-
течением времени проходит через максимум при t = о?/Аи, а затем падает до
нуля. При t —> оо интенсивность вихревого движения в любой точке
жидкости стремится к нулю. Таким образом, в отличие от вихревого
движения в идеальной жидкости, которое сохраняется с течением
времени, вихревое движение в вязкой жидкости с течением времени
захватывает все большие области пространства, занятого жидкостью
(диффундирует) и затухает с течением времени вследствие диссипации
энергии механического движения из-за вязкости жидкости. В конечном
счете эта энергия механического движения переходит в тепло. После
выключения источника вихревого движения в любой точке жидкости
rot v ф 0, т. е. движение не потенциально во все последующие моменты
движения.
6.2. Диссипация кинетической энергии
несжимаемой вязкой жидкости
Определим скорость, с которой механическая энергия движения
несжимаемой жидкости вследствие ее вязкости диссипируется в тепло.
Рассмотрим некоторый неподвижный в пространстве объем V, за-
заполненный движущейся жидкостью. Кинетическая энергия жидкости
в этом объеме равна
"^-dV. F.18)
6.2] Диссипация кинетической энергии 133
Найдем изменение кинетической энергии жидкости в этом объеме
в единицу времени
дЕк
=Щ€К <619)
dt
V
Произведем необходимые преобразования под знаком интеграла.
Для этого воспользуемся уравнением движения вязкой несжимаемой
жидкости, пренебрегая действием массовых сил:
F.20)
Слагаемые в правой части можно записать в виде
dvi д ( ViVi\ д ( v
pVV (pv) pv
= (pvk^) = ^ pvk^r , F.21)
дхк дхк \ 2 / дхк \ 2 у
др д р р друк dp (a ооч
-тг~ = «— pvfc- - - ^^ = -— pvk- , F.22)
OXi OXk p p OXk OXk Р
F-23)
В выражениях F.21) и F.22) использовано уравнение непрерывности
для несжимаемой жидкости
q
дхк
С учетом полученных выражений имеем
^^ = - -^— \pvk Иг + - - ^o-ifc UV- cri/c —- dV . F.24)
at } dxk [ \2 pj J J a^fc
v v
Первый интеграл в правой части может быть преобразован в ин-
интеграл по поверхности, ограничивающей рассматриваемый объем.
Нетрудно видеть, что выражение в квадратных скобках F.24) пред-
представляет собой вектор плотности потока энергии (вектор Умова)
в несжимаемой, изотермической жидкости в отсутствие объемных сил.
Полагая, что на бесконечно удаленной поверхности жидкость покоится
или объем ограничен неподвижной твердой поверхностью, на которой
жидкость также неподвижна, убеждаемся, что первый интеграл в пра-
правой части F.24) равен нулю. Тогда второй интеграл в F.24) определяет
изменение кинетической энергии жидкости в единицу времени в рас-
рассматриваемом объеме
дЕк Г ~ dvi , (а 0-.
-w = -]<rikd^hdv- F-25)
V
Для несжимаемой жидкости тензор вязких напряжений имеет вид
134 Вязкая жидкость [ Гл. 6
Тогда выражение F.25) можно записать в виде
V
Так как кинетическая энергия жидкости вследствие необратимой
диссипации из-за вязкости может только уменьшаться с течением
времени, то из F.27) следует, что коэффициент вязкости г\ всегда
положителен.
6.3. Точные решения уравнения Навье-Стокса
Уравнение Навье-Стокса по сравнению с уравнением Эйлера со-
содержит наряду с первыми и вторые производные по координатам. Но
основная трудность решения уравнений движения вязкой жидкости
заключается не в дополнительных членах, учитывающих силы вязко-
вязкости, а в нелинейности этих уравнений, обусловленной членом (vV)v.
В теории движения идеальной жидкости мы обходили эту трудность,
полагая движение потенциальным. Но если для идеальной жидкости
предположение о потенциальности движения не противоречило меха-
механический модели жидкости, то движение вязкой жидкости в общем
случае не является потенциальным: можно назвать лишь несколько
частных случаев, когда движение вязкой жидкости потенциально. Так,
например, движение в любой точке, кроме оси плоского вихря посто-
постоянной интенсивности, является потенциальным вне зависимости от мо-
модели жидкости. Поэтому существует мало точных решений уравнения
Навье-Стокса. Эти точные решения могут быть получены в том случае,
когда удается тем или иным способом избавиться от нелинейного члена
(vV)v.
В чисто математическом смысле краевые задачи теоретической гид-
гидродинамики чрезвычайно трудны. Поэтому успешное развитие теории
во многом связано с различными правдоподобными интуитивными
гипотезами. Известный математик Г.Биркгоф, анализируя положение
в теоретической гидродинамике, называет семь таких гипотез. Мы
укажем только две наиболее употребительные гипотезы.
1. Определяя, какие физические компоненты уравнений движения
необходимо рассматривать, можно полагаться на интуицию. (Интуиция
может быть подкреплена оценкой важности членов рассматриваемых
уравнений).
2. Топологию течения также можно определить интуитивно, пола-
полагая, в частности, что симметричное воздействие вызывает симметрич-
симметричный эффект.
Конечно, с точки зрения чистой математики, такие гипотезы не
имеют права на существование в строгой теории. Но, как мы увидим
далее, они значительно упрощают решение и приводят к результатам,
хорошо согласующимся с опытными данными, что и является конечной
целью теоретического исследования.
6.3] Точные решения уравнения Навье-Стокса 135
Таким образом, решения, полученные на основании таких гипотез,
необходимо проверять экспериментально. В случае адекватности пред-
предполагаемого на основании гипотез движения действительному, наблю-
наблюдаемому в опыте, полученные решения можно считать точными.
6.3.1. Течение Куэтта. Рассмотрим вязкую несжимаемую жид-
жидкость, расположенную между двумя параллельными бесконечными
плоскостями. Верхняя плоскость в некоторый момент времени начинает
двигаться с постоянной скоростью и па-
параллельно нижней неподвижной плоскости I1'
(рис. 6.1).
Спустя некоторое время установится
некоторое стационарное движение вязкой 1
жидкости между плоскостями. Определим |
это установившееся движение. Так как плос- Рис бл течение Куэтта
кости в направлении оси z бесконечны, мы
можем рассматривать движение как плоское. Если ускорение свобод-
свободного падения направлено по оси у, а расстояние h между плоскостями
невелико, то можно пренебречь влиянием силы тяжести на движение
жидкости в зазоре. Здесь мы использовали первую гипотезу.
Далее интуитивно полагаем, что скорость частиц жидкости в любой
точке зазора направлена только вдоль оси х и зависит только от
координаты у в силу бесконечности пластин в направлении х. Здесь
использована вторая гипотеза об интуитивном определении топологии
течения, основанная на предположении о симметрии эффекта при
симметричном воздействии. Так как воздействие (движущаяся верхняя
плоскость) симметрично относительно оси у, то и эффект (движение
частиц жидкости) также будет симметричным относительно оси у, т. е.
скорости частиц будут направлены только вдоль оси х.
Движение жидкости будем полагать изотермическим. В этом слу-
случае нет необходимости рассматривать уравнения баланса энергии. Та-
Таким образом, необходимо решить уравнения движения при следующих
условиях:
—- = 0, f = 0, vx = vx(y), vy = vz = 0, p = const. F.28)
Нетрудно видеть, что при заданной топологии движения жидкости
нелинейный член (vV)v из уравнений движения исчезает, а уравнение
непрерывности удовлетворяется тождественно.
С учетом условий F.28) уравнение движения в компонентах будет
иметь следующий вид:
? ^ |Р, |Р=0. F.29)
dz
? = г/^, |=0, |=0.
дх ду2 ду dz
Отсюда приходим к выводу, что давление не зависит ни от у , ни
от z, а может быть функцией только координаты х.
136 Вязкая жидкость [Гл. 6
Обратимся к первому уравнению системы F.29). Так как справа в
уравнении стоит функция только у, а слева — функция только х, то
равенство возможно только тогда, когда правая и левая части равны
некоторой постоянной величине, не зависящей от координат. Тогда
имеем о
—— = const, p = const • х + рг\. F.30)
дх
Здесь нам снова приходится обращаться к правдоподобной гипотезе
о симметрии эффекта. Из F.30) следует, что мы имели бы бесконечное
давление на бесконечности. Но это трудно понять физически, так
как движение жидкости в любой точке начиналось из одного и того
же состояния, не зависящего от координаты х. Поэтому постоянную
в уравнении F.30) мы будем полагать равной нулю. Кроме того, в со-
соотношении F.30) ро — некоторое постоянное давление, которое можно
обозначить через р.
Тогда для нахождения распределения скоростей в зазоре имеем
уравнение
^L=0, vx = ay + b. F.31)
ду
Граничные условия к уравнению F.31) имеют вид
vx(y = 0) =0, Vx(y = h) = u. F.32)
Используя граничные условия, имеем
vx = и Ц- . F.33)
h
На (рис. 6.2) изображено распределение скоростей частиц жидко-
жидкости в зазоре согласно формуле F.33).
Найдем силы, действующие на едини-
u цу площади поверхностей. Рассмотрим силу,
действующую в направлении оси х на едини-
, > цу площади нижней поверхности. Имеем
т-> г о т-> У- = ГчЬПь', Пх = U, Пу = 1, Tlz = U.
Рис. 6.2. Распределение 1 1К *' х ' у (& ъл\
скоростей (O.O4J
Следовательно, для силы получим сле-
следующее выражение, установленное еще Ньютоном:
р{п) _ р _ ~ — п (®Vx 1 — и и (?> W
\ У / у=0
Проекциями нормали к верхней пластине будут пх =0, пу =
= -1, nz = 0. Тогда сила, действующая на верхнюю поверхность
в направления оси х, равна
Р^ = ~Р*у = -**у = -V {^А =~Vt- <6-36)
6.3]
Точные решения уравнения Навье-Стокса
137
Как и следовало ожидать, силы оказались равными по величине, но
противоположно направленными.
Сила, действующая на единицу площади нижней поверхности в на-
направлении оси у, равна
Р^п) = Руу = -Р + °уу(У = 0) = -р. F.37)
Нетрудно убедиться, что на единицу поверхности верхней плоско-
плоскости в направлении оси у действует сила, равная давлению жидкости р.
Можно показать, что, хотя все частицы жидкости движутся прямо-
прямолинейно вдоль оси х, движение непотенциально. Действительно,
rotz v =
dvv
dvx
dvx
F.38)
дх ду
Таким образом, индивидуальные частицы жидкости, двигаясь по-
поступательно как целое, одновременно вращаются вокруг некоторой
оси, проходящей через сами частицы, что объясняется действием сил
вязкости.
Полученное точное решение задачи Куэтта может быть использо-
использовано для экспериментального определения феноменологического коэф-
коэффициента вязкости rj. Для этого нужно измерить силу, действующую
на единицу площади верхней или нижней поверхности. Тогда, измеряя
расстояние между плоскостями и воспользовавшись формулой F.35),
можем определить коэффициент вязкости. Однако с точки зрения
экспериментальной техники это не самый простой способ измерения
вязкости жидкости.
6.3.2. Плоское течение Пуазейля. Рассмотрим две бесконечные
параллельные неподвижные плоскости, расстояние между которыми
равно h.
Пусть между плоскостями изотермически движется вязкая несжи-
несжимаемая жидкость под действием градиента давления, направленного
вдоль оси х (рис. 6.3). Можно показать,
что, хотя все частицы жидкости движут-
движутся прямолинейно вдоль оси х, движение
непотенциально.
Снова будем предполагать, что если
ускорение свободного падения направлено
вдоль оси у, то сила тяжести не должна
влиять на движение жидкости в зазоре
между плоскостями.
Пусть градиент давления создан
некоторым внешним источником (насос,
компрессор). Будем полагать, что движе-
движение плоское и стационарное. Используя
вторую гипотезу, предположим, что скорость частиц жидкости в за-
зазоре направлена только вдоль оси х и зависит только от попереч-
поперечной координаты у. Таким образом, мы должны решить уравнение
h
Рис. 6.3. Плоское течение
Пуазейля
138 Вязкая жидкость [ Гл. 6
Навье-Стокса при следующих условиях:
— =0, f = 0, vx = vx(y), vy = vz = 0, p = const. F.39)
При сделанных предположениях уравнение движения в компонен-
компонентах будет иметь следующий вид:
§? = ^, |Е = 0> 5е=0. F.40)
Уравнение неразрывности удовлетворяется тождественно.
Из второго и третьего уравнений в F.40) следует, что давление не
зависит ни от у , ни от z, а может быть функцией только х. Тогда из
первого уравнения имеем
р. = А = ^. F.41)
дх ду
Отсюда следует, что давление есть линейная функция х, а скорость
жидкости равна
vx = ^y2 + ay + b. F.42)
Постоянные а и b могут быть определены из граничных условий
vx{y = 0)=0, Vx{y = h)=O. F.43)
Подставляя граничные условия F.43) в выражение для скорости,
имеем
a = ~h, 6 = 0. F.44)
Применяя эти условия к выражению F.42) для скорости жидкости,
получим
I dp
Согласно F.45) эпюра скоростей (см. рис. 6.3) представлена пара-
параболой.
Из формулы F.45) для максимальной и средней скорости течения
жидкости в зазоре нетрудно получить
2 ^2
( i /on h dp _ 1 f 7 h dp (n лгх
^max = vx(y = /г/2) = -— —-, V = - \vxdy = -—— — . F.46)
8r] dx h ) \2r\ dx
0
Знак скорости определяется знаком градиента давления. Если дав-
давление уменьшается вдоль оси х, то (dp/dx) < 0, a vx > 0, т. е. скорость
направлена в сторону уменьшения давления.
6.3] Точные решения уравнения Навье-Стокса 139
Найдем силу, действующую на единицу площади нижней поверх-
поверхности в направлении оси х:
р{п) _ р _~ _ I dv^\ F 47)
°У J
Дифференцируя выражение F.45), получим
Р(П) = _h dp _
х z dx
Точно такое же выражение получим и для силы, действующей на
единицу площади верхней поверхности в направлении оси х. Знак силы
так же определяется знаком градиента давления. Если (dp/dx) < О, то
силы, действующие на плоскости, направлены в ту же сторону, что и
ось х.
Объемный и массовый расходы жидкости, через любое сечение
(единичной ширины), перпендикулярное оси х, равны соответственно
Qv = hv=->tb Qm = phv = -??* F.49)
\2г) dx \2г) dx
6.3.3. Цилиндрическое течение Пуазейля. Рассмотрим устано-
установившееся изотермическое движение вязкой несжимаемой жидкости
в цилиндрической бесконечной трубке, поперечное сечение которой
представляет собой окружность радиуса го. Движение жидкости вы-
вызвано постоянным градиентом давления, направленным вдоль оси труб-
трубки. Для решения задачи естественно воспользоваться цилиндрической
системой координат г, (р, z, где ось z направлена вдоль оси симметрии
трубки.
Уравнение Навье-Стокса, уравнение неразрывности для несжимае-
несжимаемой жидкости, а также компоненты тензора напряжений в цилиндри-
цилиндрической системе координат приведены в приложении.
Если труба расположена горизонтально, то сила тяжести не влияет
на движение жидкости в трубе. Будем также полагать, используя ги-
гипотезу 2, что скорости частиц жидкости в трубе имеют единственную
компоненту, направленную вдоль оси трубы и зависящую только от ра-
радиальной координаты г. Следовательно, необходимо решить уравнение
Навье-Стокса при следующих условиях:
— =0, f = 0, vz = vz(r), vip = vr = 0, p = const. F.50)
При этих условиях уравнение неразрывности удовлетворяется тож-
тождественно, а уравнение Навье-Стокса в проекциях будет иметь сле-
следующий вид:
Из первого и второго уравнений системы F.51) следует, что при
заданной топологии течения давление не должно зависеть ни от г, ни
140 Вязкая жидкость [ Гл. 6
от (р, а может быть функцией только z. Поскольку vz зависит только
от г, то левая и правая части третьего уравнения представляют собой
некоторую постоянную. Обозначив эту постоянную через А, имеем
dp , 1 d ( dvz \ /r ro4
-JL = A = r}-— [r—- ) . F.52)
dz r dr \ dr )
Интегрируя, получим
Vz = 4^Г +alnr + 6' F53)
где a, b — постоянные интегрирования.
Поскольку на оси трубы не может быть бесконечной скорости, то
постоянную интегрирования а следует положить равной нулю. Посто-
Постоянную b найдем из граничных условий
vz(r = r0)=0, b=-^r20. F.54)
Подставляя F.54) в выражение для скорости F.53), имеем
Vz = -^^ (i-4V (е-55)
4?7 dz \ r^J
Теперь можно вычислить максимальную и среднюю скорости дви-
движения жидкости по трубе
9 * г° 2 н
vz ' 2тгг dr = — . F.56)
'"" о
Таким образом, vm3iX/U = 2. Направления скоростей определяются
направлением градиента давления.
Для объемного и массового расхода жидкости через поперечное
сечение трубы получаем формулу Пуазейля:
^ 9_ ТГГп dp ^ ^ РТГ^О ^Р /г г\
Ц/д/ = 7ТГг)У = — , Qm = pQv = о Г" • (Ь.О/)
о?7 а;г: о?7 dz
Найдем силу, действующую на единицу площади поверхности тру-
трубы в направлении оси z:
P{zn) = Pzknk = -azr = -rj №) . F.58)
V dr J r=r0
Здесь учтено, что nz = n^ = 0, nr = — 1. Используя формулу F.55),
имеем ,
r*f?T-) 0 dp /r- ricW
* ~2dz' ^ ^
Вычислим силу трения, действующую на кольцевой элемент поверх-
поверхности трубы длиной Az в направлении оси z:
2/
AF = 2тгг0Дг (^ ^) = тгг20Ар . F.60)
6.3]
Точные решения уравнения Навье-Стокса
141
1
3
Из последнего соотношения видно, что разность сил, действующих
на жидкость, в двух любых сечениях трубы, разделенных расстоянием
Az, равна силе трения жидкости о стенку трубы, действующей на
боковую поверхность рассматриваемого элемента объема жидкости.
Очевидно, это следует из закона Ньютона, т. е. лишь при равенстве сил
рассматриваемый элемент объема жидкости будет находиться в состо-
состоянии покоя или равномерного прямолинейного движения относительно
трубки.
Формула Пуазейля может быть использована для измерения вяз-
вязкости жидкости. Согласно формуле F.57) для измерения вязкости
жидкости необходимо измерить ее массовый или объемный расход.
Тогда, зная радиус трубы и градиент давления, можно вычислить вяз-
вязкость жидкости. Например, можно поставить опыт следующим обра-
образом. Пусть в сосуде / (рис. 6.4) налита
жидкость, вязкость которой необходимо из-
измерить. Эта жидкость может вытекать из
сосуда через тонкий капилляр 2 в сосуд 3.
Тогда, если пренебречь изменением уров-
уровня жидкости в сосуде /, перепад давления
на концах капилляра будет равен гидро-
гидростатическому давлению жидкости на входе
в капилляр. Если это давление разделить
на длину капилляра, то получим dp/dz.
Далее, зная время (по секундомеру) и объ-
объем жидкости, поступившей за это время
в сосуд 3, найдем расход. Измеряя радиус
капилляра и используя формулу Пуазейля
F.57), найдем вязкость жидкости.
Отметим, что в данном эксперименте радиус капилляра следует
измерять довольно точно, так как расход жидкости пропорционален Tq,
т.е. ошибка измерения радиуса учетверяется. Если объем исследуемой
жидкости ограничен, то нетрудно при решении задачи учесть измене-
изменение уровня жидкости в сосуде /.
При не слишком точных относительных измерениях вязкости ка-
капельных жидкостей сосуды и капилляр располагают по вертикали (вис-
(вискозиметр Энглера). Тогда вязкости эталонной и исследуемой жидкостей
будут относиться, как их расходы. Зная вязкость эталонной жидкости
из каких-либо других более точных измерений, можно определить
вязкость исследуемой жидкости.
6.3.4. Движение жидкости между двумя вращающимися ци-
цилиндрами. Рассмотрим установившееся движение несжимаемой вяз-
вязкой жидкости между двумя коаксиальными вращающимися цилин-
цилиндрами. Будем полагать цилиндры бесконечными, так что краевыми
эффектами можно пренебречь. Пренебрежем также действием силы
тяжести.
Рис. 6.4. Измерение вязко-
вязкости жидкости: / — сосуд с
жидкостью, 2 — капилляр,
3 — сосуд для сбора жид-
жидкости
142 Вязкая жидкость [ Гл. 6
Пусть цилиндры с радиусами R\ и R2 (R2 > R\) вращаются с уг-
угловыми скоростями ш\ и UJ2 соответственно (рис. 6.5). При решении
задачи естественно воспользоваться цилин-
цилиндрической системой координат с осью z, на-
направленной по оси цилиндров. Тогда имеем
Vp = V(p(r), p = p(r), p = const.
^/ Уравнения движения в цилиндрических
координатах при заданной топологии задачи
запишутся в следующем виде:
Рис. 6.5. Жидкость 2
между вращающимися *V _ J_ dp d ?V , J_ d?jy _ ?V _ q
цилиндрами г ~~ о dr ' Лг2 г dr r2 ~~
F.61)
z-проекция уравнения Навье-Стокса, а также уравнение непре-
непрерывности выполняются тождественно. Заметим, что второе уравнение
в F.61) для определения скорости не содержит вязкость.
Используя подстановку v^ = Arn, найдем решение второго уравне-
уравнения: ,
v =аг+-. F.62)
^ г
Граничные условия для определения постоянных интегрирования
a, b можно записать следующим образом:
Vy(r = R\) = uo\R\ , v^{r = R2) = 002R2 • F.63)
Отсюда получаем
2 2 / 2 2
а = ——| 1—^ , 6 = -^—g—^4—~ • F.64)
Так как распределение скорости жидкости в зазоре между цилин-
цилиндрами не зависит от вязкости, то такое распределение может иметь и
идеальная жидкость, не обладающая вязкостью по определению.
Проанализируем полученное решение. Если ш\ = UJ2 = и, то жид-
жидкость в зазоре вращается как абсолютно твердое тело с постоянной
угловой скоростью, равной скорости вращения цилиндров.
Если имеется только внутренний цилиндр, вращающийся в беско-
бесконечной жидкости, то из F.62), F.64) получаем потенциальное дви-
движение. При этом циркуляция скорости по любому контуру, охватыва-
охватывающему цилиндр, равна Г = 2тгR\uo\. Таким образом, установившееся
движение вязкой несжимаемой жидкости, покоящейся на бесконеч-
бесконечности, вызываемое вращающимся бесконечным цилиндром, является
потенциальным во всех точках объема вне цилиндра. Очевидно, во
всех плоскостях, перпендикулярных оси цилиндра, движение жидкости
одинаково и может считаться плоским. Как определено выше, такое
движение называется плоским вихрем.
6.3] Точные решения уравнения Навье-Стокса 143
При не слишком большой скорости набегающего потока и угло-
угловой скорости цилиндра подъемная сила, возникающая при обтекании
цилиндра с циркуляцией, согласно теореме Жуковского, может быть
определена следующим образом E.116):
Fy = -pvooF = -pvoo • 2-kR\uj\ . F.65)
Направление подъемной силы и ее величина определяются как
величиной, так и направлением скоростей набегающего потока и вра-
вращения цилиндра. При прочих равных условиях величина подъемной
силы пропорциональна квадрату радиуса цилиндра.
Распределение давления в зазоре между цилиндрами можно опре-
определить из первого уравнения системы F.61):
г 2 / « , 2 \
р = —- dr = р ( - а2г1 + 2ab In г ^ 1 + с . F.66)
Постоянная с может быть определена из граничного условия
p(r = R\) =р\ . F.67)
Если оо\ = 0J2 = oj, то Vp = иг. Тогда распределение давления
в зазоре будет иметь вид
p = pi + l^2(r2_ r\). F.68)
Если в зазоре между цилиндрами находится газ, то при одно-
однородной температуре с учетом уравнения состояния идеального газа
Менделеева-Клапейрона имеем
2 2
up v^ RT dp л iiu) 9 ,п пг,^
— J-1— —z- — — in ^ — и ^ _|_ с ^ (Ь.Ь9)
r RT' r № dr' ^ 2RT
где 11 — молярная масса газа, R — молярная газовая постоянная, Т —
температура; плотность р зависит от координат так же, как давление р.
Определив постоянную интегрирования с из граничного условия
F.67), получим
Г 2 "I Г 2 "I
P = Pi exP wiL (г2 - R\) ' P = Pi exP wiL (r2 - r2)\ • F-7°)
Определим момент сил трения, действующих на единицу длины
внутреннего цилиндра:
(^^) F.71)
dr r J r=Rx
Подставляя значение v^ и дифференцируя, получим
~ ( о ч 26 2(ш2 — u)\)R2
СГ^г(г = ДО = -V -г = ^ ^2 ^И •
144
Вязкая жидкость
[Гл. 6
Тогда для момента сил трения имеем формулу
F.73)
Очевидно, на единицу длины внешнего цилиндра будет действовать
такой же момент сил трения, но с обратным знаком.
На основе полученного точного решения можно провести опыт,
позволяющий определить коэффициент вязкости жидкости (рис. 6.6).
Если между цилиндрами поместить исследуемую
жидкость и вращать только внешний цилиндр, то на
внутренний неподвижный цилиндр будет действо-
действовать момент вязких сил, определяемый формулой
F.73). Если внутренний цилиндр подвешен на упру-
упругой нити, то нить будет закручиваться, что можно
зафиксировать при помощи закрепленного на ней
зеркальца.
Определяя момент сил трения по углу закру-
закручивания нити /, на которой подвешен внутренний
цилиндр 2, по формуле F.73) можно определить
коэффициент вязкости жидкости. При этом геомет-
геометрические размеры цилиндров и угловая скорость
вращения внешнего цилиндра должны быть извест-
известны. Существенную конструктивную трудность такой
установки представляет устранение влияния торцов цилиндров, так как
точное решение, полученное выше, справедливо лишь для бесконечных
цилиндров.
1
2
е
со
Рис. 6.6. Опреде-
Определение вязкости
6.4. Медленное обтекание шара
Пусть неподвижный шар радиусом го обтекается вязкой несжима-
несжимаемой жидкостью со скоростью и на бесконечности. Движение будем
полагать изотермическим. Задача стационарна, уравнения движения
имеют вид
(vV)v = -- Vp + ^/Av, divv = 0. F.74)
Оценим порядок членов уравнения. Скорость набегающего потока
падает до нуля на поверхности шара на расстоянии, равном приблизи-
приблизительно диаметру шара. Поэтому имеем
(vV)v ~ —-,
а
Г) U
Р d
(vV)v pud
7]
= Re.
F.75)
Если безразмерный параметр Re будет значительно меньше едини-
единицы, то в уравнении движения членом (vV)v можно пренебречь по
сравнению с остальными членами. Этот безразмерный параметр назы-
называется числом Рейнолъдса. Очевидно, число Рейнольдса показывает,
во сколько раз инерционные силы в жидкости больше вязких.
6.4] Медленное обтекание шара 145
Таким образом, если Re ^С 1, то уравнения движения имеют вид
-Vp = 0, divv = 0. F.76)
Применим операцию rot к обеим частям уравнения движения, по-
получим
Arotv = 0, divv = O. F.77)
Разложим скорость движения частиц жидкости на две составляю-
составляющие
v = u + v/. F.78)
Очевидно, добавка v' характеризует возмущение скорости жидко-
жидкости вблизи шара и потому должна обращаться в нуль на бесконечно-
бесконечности. Далее из уравнения непрерывности имеем
divv = div(u + v/) =0, divu = 0, divv/ = 0. F.79)
Следовательно, v' может быть представлена в виде ротора некото-
некоторого вектора А:
v' = rotA, divv' = divrotA = 0, v = u + rotA. F.80)
По-видимому, вектор А должен быть функцией координат г и ско-
скорости набегающего потока и. Так как v — вектор полярный (см. сноску
на с. 83), то А должен быть аксиальным вектором. Из имеющихся
в нашем распоряжении векторов (г, и) можно составить единственный
аксиальный вектор — их векторное произведение. Таким образом,
вектор А должен иметь вид
A = /(r)[n,u], n=-. F.81)
Здесь /(г) — некоторая скалярная функция радиальной координа-
координаты г, п —внешняя нормаль.
Последнее соотношение можно записать следующим образом:
]. F.82)
Подставляя это в уравнение движения F.77), имеем
v' = rot[V/, u], A rot rot[V/, u] = 0 . F.83)
Операция rot rot может быть записана следующим образом:
rot rot = grad div - A , F.84)
и уравнение для определения функции /(г) будет иметь вид
A (grad div -A) [V/, и] = 0 . F.85)
Нетрудно доказать следующее равенство:
[V/,u] =rot/u. F.86)
146 Вязкая жидкость [ Гл. 6
Тогда с учетом того, что divrot = 0, уравнение F.83) можно запи-
записать в следующем виде:
A2[V/, u] = 0, A2[V/, и] = [V А2/, и]. F.87)
При произвольной ориентации вектора V/ уравнение F.87) может
выполняться только тогда, когда
A2[V/,u] = VA2/ = 0. F.88)
После первого интегрирования имеем
Д2/ = const. F.89)
Очевидно, постоянную в правой части последнего уравнения сле-
следует положить равной нулю. Действительно, конечной целью решения
является определение скорости v' как функции координат. Но v' опре-
определяется в соответствии с выражением F.83) вторыми производными
от функции / по координатам, тогда как для нахождения /, согласно
уравнению F.89), необходимо проинтегрировать по координатам че-
четыре раза. Поэтому если постоянную не полагать равной нулю, то
скорость v7 не обратится в нуль на бесконечности, что должно быть
по ее определению.
В сферических координатах уравнение F.89) будет иметь вид
<690)
Интегрируя, получим
d а р 2а А „ 2а ,~ г\л\
—А/ = - —, А/ = —+ с. F.91)
dr rz r
По вышеприведенным соображениям постоянную с также следует
положить равной нулю. Следующее интегрирование приводит к резуль-
результату:
1 d ( d \ 2а
При последнем интегрировании постоянная интегрирования опуще-
опущена, так как скорость v7 определяется производными по координатам и
поэтому постоянная интегрирования не существенна.
Используя определение скорости движения частиц жидкости, име-
имеем
v = u + v/ = u + rot[V/, u] = u + rot rot /u = u + (grad div —A)/u .
F.93)
Поскольку и — постоянный вектор, то, используя F.92), имеем
A/u = uA/ = и2^, div /u = uV/ = un (a - ±Л . F.94)
6.4]
Медленное обтекание шара
147
Продолжая вычисления, получаем
V div f u = и ( т
V т г
Группируя члены, в результате имеем
u+(un)n , , 3(un)n — u
v = u- a ^ '- h 6— -o •
\ i a , 36
ur) "^ + -
n.
F.95)
F.96)
Постоянные а и b должны быть определены из граничных условий
на поверхности шара:
v(r = ro) = O. F.97)
Так как вектор скорости жидкости должен быть равным нулю
в любой точке на поверхности шара, т. е. при любой ориентации нор-
нормали п, то, следовательно, должны обращаться в нуль в отдельности
коэффициенты при векторах и и п в вы-
выражении F.96). Тогда получим
а = 4 Го '
F.98)
Очевидно, картина обтекания шара
(рис. 6.7) имеет цилиндрическую сим-
симметрию, поэтому Vp = 0. Компоненты
скорости жидкости vr и ve могут быть
найдены из выражений F.96) и F.98)
. . 3 го 1 го
vr = [ 1 - hx^
Z, / Zi т»
Рис. 6.7. Обтекание шара
4 г
F.99)
Для определения силы, действующей на шар со стороны движущейся
жидкости, возвратимся к исходному уравнению движения F.76):
Vp = 7/Av, Vp = rj A(rot rot /u) = rj A(graddiv — A)/u . F.100)
Принимая во внимание уравнение F.89), имеем
Vp = 77 A grad div /u = grad[?7 A div(/u)] . F.101)
Интегрируя, получим следующее выражение:
div(/u) = ро + v A (u V/) = ро + rj и V (А /). F.102)
Здесь ро — давление в набегающем потоке вдали от шара. Принимая
во внимание, что А/ = 2а/г, получим
/ \ 3 го
= Po~V (un) - -г .
F.103)
На поверхности шара (г = го) распределение давления имеет вид
F.104)
р = ро - - — и cos 0 .
2 го
148 Вязкая жидкость [ Гл. 6
Сила, действующая на шар со стороны движущейся жидкости,
может быть вычислена следующим образом:
F = j P(n) dS, Fi=§ Рг(п) dS = § Piknk dS, F.105)
РггПг + Pi^n^ + Pieno) dS.
Выберем направление действия силы, совпадающее с направлением
скорости набегающего потока. В этом случае проекции нормали к
произвольному элементу поверхности шара будут иметь значения (см.
рис. 6.7)
nr = cos#, п^ = 0, пе = — smO . F.106)
Подставляя эти значения в выражение для силы сопротивления,
получаем
F = <t [(-р + arr) cos в - агв sin в] dS . F.107)
Вычислим значения соответствующих компонент тензора вязких
напряжений на поверхности шара (г = го), пользуясь их выражениями
в сферической системе координат и полученными формулами для ком-
компонент скоростей F.99)
arr = 2 rj —— = 0 , агв = rj ( —— = - - — sin в .
\ дг ) г=г0 V дг ) г=г0 2 г0
F.108)
Подставляя выражения F.104) и F.108) в F.107), получаем
F = 67rr0rju. F.109)
Формула F.109) описывает силу сопротивления при медленном
(Re ^C 1) обтекании шара вязкой несжимаемой жидкостью и называется
формулой Стокса.
Формула Стокса имеет широкое применение. Она использовалась
Милликеном при определении величины заряда электрона, использу-
используется для измерения вязкости жидкостей по методу падающего шарика,
часто используется при изучении движения мелких пылинок или ка-
капель жидкости в атмосфере и т. д.
Более точное решение задачи Стокса с приближенным учетом нели-
нелинейного члена ((vV)v) в уравнении движения было получено Осееном:
, Re< 1. F.110)
Как показывает опыт, формула Осеена справедлива до чисел Рей-
нольдса порядка единицы. При дальнейшем увеличении числа Рей-
нольдса картина обтекания шара существенно изменяется (образование
застойной зоны за шаром, возникновение турбулентности) и вышепри-
вышеприведенное рассмотрение не справедливо.
При малых числах Рейнольдса аналогичную задачу можно решить
для произвольного эллипсоида и диска. Так, для диска, расположен-
6.4]
Медленное обтекание шара
149
ного перпендикулярно и параллельно скорости набегающего потока,
соответственно получено
F=\6r0r]u, F=^ror]u. F.111)
о
Ниже в таблице приведены значения динамической и кинематиче-
кинематической вязкостей некоторых жидкостей:
Жидкость
Вода
Воздух
Спирт
Глицерин
Ртуть
г], КГ'кгДм-с)
0,010
1,8- Ю-4
0,018
8,5
0,0156
v, 10м2/с
0,010
0,150
0,0122
6,8
0,0012
Следует отметить, что коэффициент динамической вязкости как
плотных газов, так и жидкостей слабо зависит от давления. Динами-
Динамическая вязкость газов с увеличением температуры увеличивается
0,5 < п < 1,5.
F.112)
Динамическая вязкость жидкостей с увеличением температуры
уменьшается. Экспериментальные данные по температурной зависимо-
зависимости коэффициентов динамической вязкости жидкостей хорошо описы-
описываются формулой о
Л^. F.113)
Здесь А и В — некоторые эмпирические коэффициенты.
Контрольные вопросы
1. Перечислите уравнения, составляющие замкнутую систему уравнений
движения вязкой жидкости?
2. В чем состоят граничные условия к уравнению Навье-Стокса? Рас-
Рассмотрите поверхность твердого тела, границу раздела двух несмешивающихся
жидкостей и свободную поверхность жидкости.
3. Что такое диссипация кинетической энергии вязкой жидкости? В какой
области движущейся жидкости диссипация энергии наиболее существенна?
4. Покажите на графике качественную зависимость интенсивности плос-
плоского вихря от времени.
5. Что такое массовый и объемный расход жидкости?
6. Как измерить коэффициент вязкости, используя закон Пуазейля о дви-
движении жидкости в трубке? То же, используя закон Стокса о движении шарика
в жидкости.
7. Как коэффициент вязкости газов и жидкостей зависит от температуры?
8. Что такое число Рейнольдса? Запишите формулу и поясните физический
смысл.
150 Вязкая жидкость [ Гл. 6
9. В каком случае можно пренебречь нелинейным членом (vV)v в уравне-
уравнении Навье-Стокса?
10. Покажите, что если линии тока параллельны, то (vV)v = 0.
11. Шарик равномерно движется в жидкости вдоль направления силы тя-
тяжести. Как скорость шарика зависит от его радиуса и вязкости жидкости?
12. Какие жидкости называют ньютоновскими?
6.5. Примеры решения задач
Задача 1
Дно широкого бассейна покрыто тонким слоем воды. На поверх-
поверхности воды плавает тонкая деревянная доска, нижняя поверхность
которой находится на расстоянии d от дна бассейна. Все остальные
размеры доски во много раз больше d. Доска движется горизонтально
с малой скоростью и. Чему равна скорость диссипации энергии в еди-
единице объема воды вблизи середины доски? Воду считать несжимаемой
жидкостью.
Решение. Выберем декартову систему координат, как показано
на рис. 6.8. Распределение скоростей жидкости вдали от краев доски
определяется решением задачи о плос-
плоском течении Куэтта F.33):
Ук
d\ =^w vm = 1y. F.114)
О х Сила трения, действующая на едини-
единицу поверхности доски равна
Рис. 6.8. Движение пластинки
вдоль свободной поверхности р _ ^ ®v* = <п — F 115)
жидкости ху ду d
При этом работа на преодоление силы трения, совершаемая в еди-
единицу времени и отнесенная к единице площади поверхности доски,
равна 2
Е = Pxz'U = rj^-. F.116)
d
Искомая скорость диссипации энергии в единице объема жидкости
определяется следующим выражением:
? _ и?
~d ~
. F.117)
Заметим, что этот результат может быть получен непосредственно
из выражения F.27).
Задача 2
Определите диссипацию энергии при движении воздуха в плоском
канале (рис. 6.9) со средней скоростью U = 20 м/с. Вязкость воздуха
и размеры канала заданы: rj = 1,8 • 10~4 г/(см • с), h = 1 мм, d = 0,5 м,
6.5] Примеры решения задач 151
/ = 1 м. Оцените разность температур воздуха на входе и выходе из
канала за счет диссипации энергии.
Решение. Из решения задачи о у к
плоском течении Пуазейля F.45) извест- Т У/ !
ны компоненты вектора скорости движе- J > ^/\
ния воздуха в канале:
vx = 0, vy = 0 ,
F 11Я) ^ис' ^'^' Движение В03ДУха
„, _ i а,- — ьп,\ -!- в плоском канале
uz —
Тогда из выражения F.27) для скорости диссипации энергии воз-
воздуха в канале получим
v
Средняя по сечению скорость равна F.46)
v = —— ^. F.120)
Отсюда имеем о
/ j~~\ Z л л л „^
v2. F.121)
Выражение F.119) для скорости диссипации энергии принимает
следующий вид: яр 19
?Jl = - Ц vVv2, F.122)
где V = Idh — объем щели.
Численный расчет дает
f = -43,2 Вт. F.123)
В соответствии с первым началом термодинамики уменьшение внут-
внутренней энергии воздуха в случае постоянного объема равно количеству
выделенной теплоты. С другой стороны количество выделенного тепла
пропорционально изменению температуры воздуха
= — = — су pV — , F.124)
где су — удельная теплоемкость при постоянном объеме, р - плотность
воздуха.
Из выражения F.124) получаем
®* ^ l±T ^ I QQ /g 125)
dt ~ At ~ cvpV dt ' v • ;
Среднее время, в течение которого воздух пройдет через весь канал,
равно ,
At= = =0,05с. F.126)
V
152 Вязкая жидкость [ Гл. 6
За это время температура воздуха изменится на величину
ДТ ^—*—^=3,4К. F.127)
cppVv dt
Таким образом, при прохождении воздуха через канал его темпера-
температура повысится на 3,4 К за счет работы сил вязкости.
Задача 3
Слой жидкости толщиной h ограничен сверху свободной поверхно-
поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом а к
горизонту (рис. 6.10). Определите движение жидкости под влиянием
силы тяжести. Слой жидкости считать бес-
бесконечно тонким по сравнению с размерами
наклонной плоскости.
Изучение таких тонких слоев жидкости
связано с работой колонн с орошаемой стен-
стенкой при испарении, а также с нанесением
краски на бумажную ленту.
Рис. 6.10. Движение слоя Решение. Выберем систему координат
жидкости как пока3ано на рис. 6.10. Рассмотрим уча-
участок пленки жидкости, удаленный от концов пластинки настолько, что-
чтобы можно было не учитывать краевые искажения потока. В этом слу-
случае гидродинамические переменные зависят только от координаты z.
Из топологии течения очевидно, что отличной от нуля будет только
ж-компонента скорости: vy = vz = 0, vx = v(z). Проекции уравнения
Навье-Стокса на оси х и z в поле силы тяжести запишутся в виде
d v , ~ 1 dp ~ /п * ооч
v —т- + g- sin а = 0, f- — g cos a = 0 . F.128)
dz P dz
На свободной поверхности при z = h, если пренебречь вязкостью
воздуха по сравнению с вязкостью жидкости, должны выполняться
условия
Pzz = ~Р = -Ро, Pxz = rj—=O, F.129)
где ро — атмосферное давление.
На стенке при z = 0 выполняется условие прилипания: vz = 0.
Удовлетворяющее этим условиям решение есть
Р = Ро + Pg{h - z)cosa, v = z (h —-) . F.130)
Секундный расход жидкости через поперечное сечение слоя (отне-
(отнесенный к единице длины вдоль оси у) равен
h з
Q = p\vdz = ^—sin a ; F.131)
6.5] Примеры решения задач 153
в случае вертикальной плоской стенки
F.132)
Задача 4
Цилиндр радиуса R\ движется стационарно со скоростью и внутри
коаксиального с ним цилиндра радиуса R^ параллельно своей оси
(рис. 6.11). Определите скорость движения жидкости, заполняющей
пространство между цилиндрами, объемный расход жидкости и силу,
действующую на единицу длины движу-
движущегося цилиндра. ^?
Такие задачи возникают при описа- 1}
нии движения плунжеров 0, откатных ^^
устройств в артиллерии, работы устройств Рис б п Течение жидко_
при нанесении на проволоку различных по- сти в кольцевом канале
крытий.
Решение. Выберем цилиндрические координаты с осью z, на-
направленной вдоль оси цилиндров (рис. 6.11). На участке, удаленном
от торцов внешнего цилиндра жидкость движется только вдоль оси z.
Скорость движения жидкости и давление зависят только от радиальной
координаты г:
vr = v(f=0, vz = v(r), р = p(r). F.133)
Уравнение Навье-Стокса в цилиндрических координатах принимает
вид
г dr V dr
Заметим, что конвективный член (vV)v = vdv/dz тождественно равен
нулю. На поверхностях внутреннего и внешнего цилиндров выполня-
выполняются условия прилипания
(r = R2)=0. F.135)
Решение имеет вид
* = ищжтщ- FЛ36)
Объемный расход жидкости в кольцевом зазоре между цилиндрами
1) Плунжер — это длинный подвижный поршень, используемый в специаль-
специальных (плунжерных) насосах и гидравлических прессах.
154
Вязкая жидкость
[Гл. 6
Сила трения, действующая на единицу поверхности движущегося
цилиндра, определяется касательными напряжениями
Zr\r=R,
dv
~dr
r\u
lx Ri\n(Ri/R2)'
при этом сила, действующая на единицу длины цилиндра, равна
F.138)
F —
zr\r=Rx
F.139)
\n{Rx/R2) '
Такая же сила действует на единицу длины внешнего цилиндра.
Задача 5
В опытах по абсорбции поток вязкой жидкости поднимается вверх
по трубке и затем стекает по наружной стенке радиуса R\ вниз
(рис. 6.12). Определите скорость движения жидкости в пленке вдали
от концов стенки и объемный расход жидкости в пленке.
Решение. Воспользуемся цилиндрической системой координат
с осью z, направленной вдоль оси цилиндра (рис. 6.12). Пусть радиус
свободной поверхности пленки известен и равен R2.
На участке, удаленном от торцов трубки, жидкость
движется параллельно оси z. Скорость движения жид-
жидкости зависит только от радиальной координаты г:
vr = Vp = 0 , vz = v(r). F.140)
В этом случае уравнение непрерывности удовлетво-
удовлетворяется тождественно. Поскольку жидкая пленка стека-
стекает под действием силы тяжести, то z-компонента урав-
уравнения Навье-Стокса в цилиндрических координатах за-
записывается в виде
Рис. 6.12 r dr у drJ v
На стенке трубки выполняется условие прилипания жидкости
v(r = Я1) =0. F.142)
На свободной поверхности трение жидкой пленки о внешнюю среду
(например, о воздух) отсутствует, т. е.
г-» i dv
= 0.
r=R2
F.143)
При таких граничных условиях решение задачи имеет вид
^^A-4+2^|1п^). F.144)
Объемный расход жидкости в пленке
Qv =
~Rl П ~R~i
). F.145)
6.5] Примеры решения задач 155
Формула F.145) описывает объемный расход жидкости в пленке
при отсутствии абсорбции. Отклонение измеренного расхода от теоре-
теоретического определяет величину абсорбции жидкости стенкой.
Задача 6
Оцените максимальный диаметр сферических частиц катализатора,
которые могут уноситься с топочным газом. Направленная вертикаль-
вертикально вверх скорость газа на оси дымовой трубы равна v = 30,5 см/с,
динамическая вязкость газа rj = 2,6 • 10~4П (пуаз), плотность газа
рт = 7,2 • 10~4г/см3, плотность частицы катализатора рк = 1,2 г/см3.
Решение. В вертикальном направлении на частицу катализатора
действуют сила тяжести FT, выталкивающая архимедова сила Fa и
сила сопротивления Fc (сила Стокса).
Чтобы частица двигалась вместе с газом вдоль трубы
равномерно и прямолинейно, векторная сумма всех сил,
действующих на частицу, должна быть равна нулю
FT + FA + Fc = 0 .
Проекция этого уравнения на ось z (рис. 6.5) дает
FT = FA + FC. F.146)
В задаче задана скорость газа v на оси дымовой
трубы. Согласно закону Пуазейля это — максимальная Рис. 6.13
скорость газа в трубе. Поэтому самые большие частицы
будут уноситься на оси трубы. Пусть Rm — радиус самых крупных
частиц, которые могут быть унесены газом через дымовую трубу.
Объем такой частицы равен: V = 4тгЯ^/3. Тогда уравнение баланса
сил F.146) запишется в виде
^ d3 Ц}<~> I d. TD I (X 1 Л П\
— 7Т гС Рк§ = ~ ТГ^Ь Рг?> ~г 07TTJ rCrnV . (D.14/)
3 3
Отсюда имеем
Ч Г 9 11/2
Rm = ? /^ , , Rm « 55 МКМ. F.148)
Проверим, можно ли применять закон Стокса для таких частиц.
Для этого оценим число Рейнольдса
Re= ^?«0,46. F.149)
V
Поскольку Re < 1, то закон Стокса применен правильно.
Задача 7
Две параллельные плоские пластинки радиуса R расположены одна
над другой на малом расстоянии h друг от друга (рис. 6.14). Простран-
Пространство между ними заполнено жидкостью. Пластинки сближаются друг
156 Вязкая жидкость [Гл. 6
с другом с постоянной скоростью и, вытесняя жидкость. Определите
испытываемое пластинками сопротивление (задача Рейнольдса).
Решение. Выберем цилиндрические
координаты с началом в центре нижней
пластинки и осью z, направленной перпен-
перпендикулярно пластинкам (рис. 6.14).
Движение жидкости осесимметричное и
вдали от конца пластин радиальное (h <С
<С R). Поэтому vz <С vr причем dvr/dr <С
<С dvr/dz. В этом приближении уравнение
Рис. 6.14. Течение между непрерывности имеет вид
дисками 1 q/ \ q
1^1 ^. F.150)
^ + ^
г or dz
Запишем уравнения Навье-Стокса:
F.151)
dz dr dz
и граничные условия
z = 0, vr = vz = 0, z = h, vr = 0, vz = — и, г = R, p = ро> F.152)
где ро — внешнее давление.
Из уравнения движения F.151) находим
vr = ^-(z-h)^. F.153)
2rj dr
Интегрируя уравнение непрерывности F.150) по координате z, по-
получаем
1 d Г , h d ( dp\ /n лгл\
и= -—\rvrdz = - -—— — (г -f- . F.154)
г dr ] Izrjr dr \ dr J
0
Отсюда давление жидкости в зазоре равно
р = Р0 + ^(Я2-г2). F.155)
h
Сила, действующая на пластинки со стороны жидкости
я 4
F = 2тг \(р — Po)r dr = —-Ц— . F.156)
J 2i гь
О
Заметим, что при сближении пластин (уменьшение К) сила сопро-
сопротивления увеличивается и F^oo в пределе h —> 0. Возможно, этот
«парадокс» связан со следующим. Во-первых, как видно из уравнения
F.154), скорость сближения пластин зависит от /г, т.е при малых
значениях h нарушается стационарность движения жидкости, заданная
условием задачи. Во-вторых, при h —> 0 уравнение движения не может
быть использовано, так как для тонкого пристеночного слоя жидкости
должны выполняться условия прилипания, заданные граничными усло-
условиями F.152).
6.5] Примеры решения задач 157
Задача 8
Несжимаемая вязкая жидкость занимает полупространство у > О
и соприкасается со стенкой у = 0 (рис. 6.15). В начальный мо-
момент времени жидкость и стенка покоились. Затем стенка начина-
начинает двигаться с постоянной скоростью и вдоль оси х. Определите
возникающее при этом движение жидкости.
Решение. Тонкий пристеночный слой ШШШШ
жидкости «прилипает» к стенке и начинает ШШШШ
двигаться вместе с ней вдоль оси х. Силы ШШШШ
внутреннего трения (силы вязкости) приводят Z.
в движение следующий слой. Так с течением
времени в движение вовлекается все больший рис 5.15
объем жидкости. Рассматриваем ламинарное
(слоистое) движение, при котором частицы жидкости движутся только
вдоль оси х. Скорость движения жидкости изменяется с течением вре-
времени и зависит от координаты у, т. е. имеем vy = vz = 0, vx = v(t, у).
Кроме того, давление жидкости не зависит от координаты х. В этом
случае уравнение непрерывности удовлетворяется тождественно, а
ж-компонента уравнения Навье-Стокса принимает следующий вид:
dv д v
FЛ57)
В начальный момент времени жидкость неподвижна во всей обла-
области у > 0. На бесконечном удалении от стенки и на ее поверхности
жидкость неподвижна в любой момент времени. Поэтому начальные и
граничные условия записываются в виде
v(y,t = 0)=0, v(y = 0,t>O) = u, v(y ->> оо,*) =0. F.158)
Заметим, что уравнение движения F.157) и условия F.158) инва-
инвариантны относительно группы афинных преобразований
yf = ay, tf = a2t, F.159)
где а — произвольная постоянная.
Отсюда следует, что если v(y, t) — решение задачи, то v(y',t') —
также ее решение. В силу единственности решения имеем
F = v(yf, tf) - v(y, t)=0 F.160)
для любого а.
Тогда из условия
^ =0, F.161)
оа а=\
получаем
2/?+2*?7=0- F162)
158 Вязкая жидкость [ Гл. 6
Подставляя производную по времени из F.162) в уравнение движе-
движения F.157), имеем
-I |^ = „^. F.163)
2? ду ду2
Общее решение этого уравнения
в
v = Ci [exp(-s2) ds + С2 , в = -}L= , F.164)
где постоянные интегрирования С\ и Сч определяются из условий
F.158). Окончательно имеем
9 ? \
-^ \exp(-s2)ds) =u(\ -erf (9), F.165)
где erf 0 — интеграл вероятности.
Профили скорости жидкости в различные моменты времени (t\ <
< to,) представлены на рис. 6.16.
37! Интеграл вероятности является монотонно
возрастающей функцией в. Он изменяется в диа-
диапазоне от 0 до 1 и достигает значения 0,99 при-
примерно при 0 = 2. Если ввести понятие толщины
пограничного слоя 5 как такое расстояние у, на
котором значение скорости жидкости v уменыиа-
0 и v ется до 0,0Ы, то нетрудно найти, что 5 =
п ЛП „ . Характерно, что толщина пограничного слоя уве-
Рис. 6.16. Профили f f ' ^ г j
личивается пропорционально квадратному корню
из времени.
Таким образом, с течением времени стенка вовлекает в движе-
движение все большее количество жидкости. Через достаточно большой
промежуток времени, в пределе бесконечный, наступит стационарное
состояние, когда вся жидкость будет двигаться со скоростью стенки и.
Задача 9
Несжимаемая вязкая жидкость соприкасается с твердой плоской
стенкой, совершающей в своей плоскости гармоническое колебательное
движение с частотой со и амплитудой А. Определите возникающее при
этом движение жидкости и силу трения, действующую на единицу
площади стенки.
Решение. Выберем систему координат так, что ось х совпадает
с прямой, вдоль которой происходят колебания стенки, а ось у направ-
направлена перпендикулярно плоскости колебаний.
По условию задачи смещение точек стенки описывается гармониче-
гармоническим законом
х = Asm cot, F.166)
6.5] Примеры решения задач 159
мгновенная скорость стенки при этом равна
и = ит cos cot, um = Аи , F.167)
где иш — амплитудное значение скорости стенки.
Движение жидкости таково, что vy = vz = 0, vx = v(t,y). При
этом скорость, как и в предыдущей задаче, описывается уравнением
F.157).
Граничные условия
v(y = 0,t) = u, v{y^oo,t)=0. F.168)
Воспользуемся методом разделения переменных и решение уравне-
уравнения движения F.157) будем искать в виде
v(y, t) = ^ (ф+е1шЬ + ф-е-™*) , F.169)
где ф± — неизвестные функции координаты у.
Подставляя выражение F.169) в уравнение F.157), получим
,_1_ A2ф+ . ._ A2ф~ (а 17АЧ
гооф^ = v—-^-, -гсоф = v—-^- . F.170)
Общее решение уравнений F.170) имеет вид
~ау , ф~ = С3 е?у + С4 е~^у , F.171)
где Cj — постоянные интегрирования.
С учетом граничных условий F.168) для скорости движения жид-
жидкости получим
v(y, t) = иш ехр у-у-^ У) cos (у |^ У ~ utj . F.172)
Полученное решение представляет собой поперечную волну, рас-
распространяющуюся в направлении, перпендикулярном плоскости коле-
колебаний. Благодаря силам вязкости, работа которых приводит к диссипа-
диссипации механической энергии колебаний жидкости, волна быстро затухает
по мере удаления от источника. Амплитуда волны с увеличением
расстояния у уменьшается по экспоненциальному закону.
Таким образом, в вязкой жидкости могут существовать поперечные
волны, которые быстро затухают при удалении от источника колебаний.
Вычислим силу трения, действующую на единицу площади колеб-
колеблющейся стенки
_ my/fp COS
^ + U)t) . F.173)
Видно, что между скоростью стенки и силой трения имеется сдвиг
фаз на тг/4.
Выражение F.173) может быть использовано для эксперименталь-
экспериментального определения вязкости жидкости.
ГЛАВА 7
МЕТОДЫ ПОДОБИЯ И РАЗМЕРНОСТИ
7.1. Подобие гидродинамических движений
В механике жидкости есть несколько известных точных решений
уравнений движения вязкой жидкости. Можно было бы указать еще
несколько примеров и тем самым исчерпать весь список имеющих-
имеющихся точных решений. Однако практика настоятельно требует решения
задач, которые, в силу математических трудностей, не могут быть
решены аналитически точно. В этих многочисленных случаях нам
необходимо обращаться непосредственно к эксперименту. Но и экспе-
экспериментальные данные не всегда возможно получить на тех объектах,
для которых решается данная задача.
Например, мы хотели бы знать силу сопротивления, которую испы-
испытывает новая, проектируемая конструкция самолета при движении его
с заданной скоростью на определенной высоте. Зная силу сопротив-
сопротивления, мы могли бы выбрать двигатель, обеспечивающий требуемые
характеристики полета. Вообще говоря, можно изготовить полностью
такой самолет, поставить на него некоторый двигатель и, поднявшись
на заданную высоту, измерить скорость. Но ведь установленный дви-
двигатель может и не развить заданную скорость, а в распоряжении
конструктора сегодня может и не оказаться подходящего двигателя.
В принципе методом проб и ошибок можно было бы каким-либо ком-
компромиссным способом проблему все же решить, однако такой путь
связан с большими материальными и временными затратами. То же
самое можно было бы сказать о проблемах проектирования больших
турбин, судов, ракет и т.д.
Поэтому, конечно, было бы заманчивым проводить опыты на
небольших моделях реальных объектов в условиях, полностью под-
подчиняющихся и контролируемых экспериментатором. Однако возникает
существенный вопрос, в какой мере, когда и как возможно результаты,
полученные на моделях, применять к натурным объектам. На этот
вопрос отвечает теория подобия гидродинамических движений.
7.1.1. Безразмерные уравнения движения. Рассмотрим уравне-
уравнение Навье-Стокса. В качестве объемной силы рассмотрим силу тяжести:
^ + (vV)v Vp+Av+ (f + ^graddivv + g. G.1)
ot о р о \ 6 J
7.1 ] Подобие гидродинамических движений 161
Для не очень быстрых движений объемная вязкость несущественна
и мы будем полагать ее равной нулю. Кроме того, для простоты будем
полагать движение изотермическим, тогда уравнение баланса внутрен-
внутренней энергии можно не рассматривать.
Приведем уравнения движения к безразмерному виду. Для этого
выберем некоторые характерные размерные величины. Пусть L — неко-
некоторый характерный размер обтекаемого тела (диаметр шара, трубы,
большая ось эллипса, хорда профиля крыла и т.д.). Тогда размерные
декартовы координаты можно записать в виде
х = x*L, y = y*L, z = z*L. G.2)
Здесь ж*, у*, z* — некоторые безразмерные координаты. Нетрудно ви-
видеть, что при переходе к безразмерным координатам с использовани-
использованием вышеприведенных соотношений, мы просто переходим к другому
масштабу измерений расстояний — все расстояния измеряются в долях
расстояния L, которое принято за единицу измерения.
Пусть далее v^ — некоторая характерная скорость движения жид-
жидкости, например, скорость набегающего потока, или скорость движе-
движения жидкости в центре трубы и т. д. Тогда для размерной скорости
жидкости в любой точке потока можно записать
v = v*Uoo , G.3)
где v* — безразмерная скорость движения жидкости.
Для нестационарных задач выберем также некоторое характерное
время т, которое может быть или периодом движения для периоди-
периодических движений, или временем релаксации потока к стационарному
движению, или просто временем прохождения выбранного расстояния /
с выбранной безразмерной скоростью v^. Переход к безразмерному
времени аналогичен
t = Ur. G.4)
Принимая за характерное давление и плотность, например, давле-
давление и плотность в набегающем потоке, имеем
V = Р*Роо , Р = Р*Роо • G.5)
Наконец, измеряя ускорение свободного падения в долях ускорения
силы тяжести на поверхности земли go, примем
g = g*#o • G.6)
Тогда каждый член уравнения G.1) можно записать в следующем
безразмерном виде:
Ж = -Ж' (W)v = 41 (v.V.)v., ЗДу=^^-Д.у.,
ot r at* L P pooL P*
G.7)
Vp Poo V*p* TJ , ,. TjVoo 1 , ,.
= J graddivv = — к — grad* div* v*.
ЗЬ P
P PooL p* Зр
б В.Г. Черняк, П.Е. Суетин
162 Методы подобия и размерности [ Гл. 7
Подставляя полученные соотношения в уравнение Навье-Стокса G.1)
и деля на коэффициент при конвективном члене (vV)v, получим
— I? + <v*v*)v* = -JEssr - v*p* +
TVoo Ot* PooVoo P*
+ —?Цг — (A*v* + i grad, div* v*) + ^ g* • G.8)
Аналогично можно записать уравнение неразрывности в безразмерном
виде я
|^ + ^div»(p*v»)=0. G.9)
При изотермическом движении уравнение состояния для идеально-
идеального газа (закон Бойля-Мариотта) будет иметь вид
^= const*. G.10)
Р*
Обозначим безразмерные коэффициенты уравнений G.8), G.9) сле-
следующим образом:
L Poo ^
Тогда любое решение системы уравнений G.8)—G.10) независимо
от формы движения жидкости будет иметь вид
v#i=*- = /(st, M, Re, Fr, х*, у*, z*, U). G.12)
Аналогичные выражения можно записать для безразмерных вели-
величин давления и плотности.
Из G.12) следует, что в двух потоках жидкости, для которых одина-
одинаковы безразмерные коэффициенты St, M, Re, Fr, в сходственных точках
(одинаковые ж*, у*, z*) в сходственные моменты времени (одинаковые
t*) безразмерные скорости, давления и плотности будут равны. Такие
потоки называются динамически подобными.
Поэтому два изотермических потока жидкости будут динами-
динамически подобны, если выполняются, прежде всего, следующие равен-
равенства:
Sti=St2, Mi = M2, Rei = Re2, Fri = Fr2 . G.13)
Эти безразмерные коэффициенты называются критериями или чи-
числами динамического подобия потоков:
St — число Струхала , Re — число Рейнольдса,
М — число Маха (Маиевского), Fr — числе Фруда.
Нетрудно видеть, что динамически подобными могут быть лишь
потоки, обтекающие геометрически подобные тела, одинаково располо-
расположенные к направлению набегающего потока. Геометрически подобные
тела — это такие тела, для любых сходственных точек поверхности
которых их безразмерные координаты одинаковы, если за характерный
7.1 ] Подобие гидродинамических движений 163
размер L принят один и тот же сходственный размер (например,
большая ось эллипсоида). Или иначе — для геометрически подобных
тел уравнения их поверхностей в безразмерных координатах полностью
совпадают, если за характерный размер принят один и тот же сход-
сходственный размер.
Действительно, из граничных условий следует, что на поверхности
некоторого неподвижного обтекаемого тела скорость должна быть рав-
равна нулю. Следовательно, она будет равна нулю на поверхности другого
тела только в том случае, согласно G.12), если безразмерные коорди-
координаты сходственных точек его поверхности будут равны безразмерным
координатам первого тела, т. е. если тела будут геометрически подобны.
Требование одинаковости сходственного размера и одинаковости рас-
расположения тела по отношению к набегающему потоку также очевидны
из необходимости удовлетворения граничных условий.
Таким образом, два изотермических потока жидкости будут
динамически подобными, если они обтекают геометрически подоб-
подобные тела, одинаково расположенные по отношению к набегающему
потоку, и равны их критерии подобия Струхала, Рейнолъдса, Маха
и Фру да.
Динамическое же подобие означает, что в сходственных точках по-
потока (одинаковые безразмерные координаты) в сходственные моменты
времени (одинаковые безразмерные времена) безразмерные скорости,
плотность и давление будут одинаковы.
Для простоты рассмотрено динамическое подобие лишь изотер-
изотермических потоков. В более общем случае нам необходимо было бы
рассмотреть также уравнение баланса внутренней энергии, что приве-
привело бы к введению еще некоторых критериев подобия, которые необ-
необходимо было бы учитывать при определении динамически подобных
потоков.
7.1.2. Сила сопротивления. Коэффициенты сопротивления.
Рассмотрим обтекание некоторого неподвижного тела. Вычислим
силы, действующие со стороны жидкости на обтекаемое тело.
Сила, действующая в направлении оси г на единичную площадку
поверхности тела с нормалью п, направленной вне тела, равна
= (-PooP*Sik +V^T °*)
V ' G.14)
Тогда силу, действующую в г-м направлении на всю поверхность
тела, можно записать в следующем виде:
Fi = L (-PooP*Sik + V "^ ?*г/с) Пк dS . G.15)
Пусть S — некоторая характерная площадь обтекаемого тела (пло-
(площадь поверхности тела, площадь наибольшего сечения тела плоскостью,
перпендикулярной набегающему потоку (миделево сечение) и т.д.).
Умножая и деля полученное выражение на некоторую постоянную
164 Методы подобия и размерности [ Гл. 7
величину pvoV^S/2, получим
( 2P6ik 2 ^ dSk G Iftt
GЛ6)
Из G.12) следует, что и р*, и 5^/с являются функциями лишь без-
безразмерных критериев подобия, безразмерных координат и безразмерно-
безразмерного времени. При вычислении силы, действующей на обтекаемое тело,
в формуле G.16) нужно подставить значения р* и 5*^ на поверхности
тела, для которой безразмерные координаты есть просто некоторые
числа. Поэтому результат интегрирования будет зависеть только от
безразмерных критериев подобия и безразмерного времени.
Рассмотрим для простоты стационарное движение. Пусть скорость
набегающего потока направлена вдоль оси х, а ось у — вертикально
вверх. Тогда на основании соотношения G.16) имеем
G.17)
Безразмерные коэффициенты Сх, Су, Cz называются, коэффициента-
коэффициентами лобового сопротивления, подъемной и боковой силы соответ-
соответственно.
7.1.3. Моделирование. Теперь можно перейти к решению задачи,
поставленной в самом начале, каким образом опыты на моделях могут
помочь в решении задачи об обтекании реальных (натурных) объектов?
Очевидно, что, во-первых, модель реального тела и само тело или
натура должны быть геометрически подобны. Во-вторых, критерии
подобия в потоках, обтекающих модель и натуру, должны быть одина-
одинаковы.
Тогда, измеряя скорости, давления и плотности жидкости, движу-
движущейся около модели, а также силу сопротивления (а следовательно,
коэффициенты сопротивления) модели, получим простым пересчетом
скорости, давления и плотности в сходственных точках около натуры
и силу сопротивления натуры.
На практике в большинстве случаев нет нужды удовлетворять
равенству всех критериев подобия. Так, очевидно, при стационарных
движениях нам нет необходимости рассматривать число Струхала. Во
многих случаях движения газов влияние силы тяжести несущественно
и можно игнорировать число Фруда. Однако если эти ограничения
числа необходимых критериев вытекают из самой постановки задачи
или условий движения, то имеется более существенное ограничение,
заключающееся в том, что требования удовлетворения равенств сразу
нескольких критериев часто бывают противоречивыми.
7.1 ] Подобие гидродинамических движений 165
Для примера рассмотрим требования, которые вытекают из необхо-
необходимости удовлетворить равенствам чисел Маха и Рейнольдса в натур-
натурных и модельных движениях.
Для числа Маха имеем
(P^L) (P^L) . G.18)
Если речь идет о движении одной и той же жидкости для модели и
натуры, то, деля предыдущее соотношение на показатель адиабаты 7,
получим 2 2
М*=М*, ^ = ^l, G.19)
см сн
где см, сн — скорости звука в набегающем потоке в модельном и натур-
натурном движении соответственно.
Таким образом, необходимо удовлетворить равенствам
^оом ^оон PooVoomLim Роо^оон^н G OCW
2~ — 2~ ' ~~ ' V/ZU/
Если модель в десять раз меньше натуры, т.е. LH/LM = 10, то
при скорости обтекания натуры воздухом, равной 100 м/с (воздух еще
можно считать несжимаемым при одинаковых плотностях р^м и р^н
и вязкостях, согласно второму равенству G.20)), необходимо обдувать
модель со скоростью 1000 м/с. Но при такой скорости движения
воздух нельзя считать несжимаемым и движение его около тела имеет
весьма специфический характер (ударные волны, скачки, уплотнения).
Но самое главное, что это противоречит и первому равенству G.20),
из которого следует, что скорости набегающих потоков на натуре и
модели должны быть одинаковыми, так как скорость звука в одном и
том же газе зависит лишь от его температуры, и если газ в модельном
опыте не подогревать специально, то скорости звука в обоих случаях
будут равны.
В таком случае имеется лишь два выхода. Или осуществить лишь
частичное подобие по одному какому-либо критерию, а влияние дру-
другого учитывать приближенно при помощи каких-то дополнительных
опытов или расчетов. Или менять в модельном эксперименте параметры
газа (давление, плотность, температуру) или даже сменить сам газ на
газ, обладающий другой вязкостью или скоростью звука. К сожале-
сожалению, вязкости наиболее употребительных газов отличаются менее чем
в 4 раза и зависят от температуры лишь как корень квадратный от
абсолютной температуры. Поэтому более перспективным в этом отно-
отношении является изменение давления или плотности газа в модельном
эксперименте.
Пример. Пусть необходимо знать силу лобового сопротивления
некоторой новой конструкции самолета при скорости его полета в ниж-
нижних слоях атмосферы — 720 км/ч (^200 м/с). Предположим, что
изготовлена точная копия этого самолета — модель — в десять раз
166 Методы подобия и размерности [ Гл. 7
меньшая. Если модель обдувается также воздухом при той же самой
температуре, то скорость набегающего на модель потока должна быть
равна
Dp _ Dp ?, _ Г)м Lnpoo^ — 10 Роои у G 9П
Кем — Кен, ^оом — 7 ^оон — 1и ^оон • V/Z1/
^7н -L'mPoom Роом
Если плотности газа в набегающих потоках оставить одинаковыми,
то, как показано выше, моделирование невозможно, так как будут
различными числа Маха, Мм ф Мн. Для обеспечения равенства чисел
Маха необходимо при одинаковых температурах увеличить плотность
воздуха в модельном эксперименте также в 10 раз. В этом случае мы
добились бы полного динамического подобия модельного и натурного
потоков и результаты измерений на модели могли бы без каких-либо
поправок перенести на натуру простым пересчетом.
Предположим, что можно увеличить плотность модельного потока
по сравнению с натурной плотностью только в восемь раз. Тогда
скорость набегающего на модель потока должна быть равной примерно
250 м/с и можно приближенно считать, что модельный и натурный
потоки динамически подобны, так как числа Маха будут отличаться
незначительно, а скорость набегающего на модель потока остается
дозвуковой.
Если каким-либо способом измерить силу лобового сопротивления
модели, то по формуле G.17) можно определить коэффициент лобового
сопротивления, который будет одинаковым как у модели, так и у
натуры, так как в данном случае предполагается, что он зависит только
от числа Рейнольдса, а оно для модельного и натурного движения по
условию G.21) одинаково. Тогда нетрудно рассчитать силу лобового
сопротивления натуры
f4 f4 ^ЖМ f ЖН
°м - Он - 2 ^Г — 2 W '
Роом^оом^м Роон^оон^н
2к)\
хн = ^™ 2—ZT=qI^J >ши^™, G.22)
я г2
^L — i^L F — F
Ьм LM
Зная экспериментальное значение силы лобового сопротивления моде-
модели, можно вычислить лобовое сопротивление натуры, а следовательно,
и выбрать двигатель для обеспечения заданной скорости полета созда-
создаваемой конструкции самолета.
В действительности в аэродинамических лабораториях снимают
серии зависимостей d = /(Re, M), которые позволяют конструкторам
оптимизировать данную конструкцию самолета и сделать выбор двига-
двигателя.
Если необходимо определить скорость воздуха, например, над каби-
кабиной летчика на расстоянии половины размаха крыла (L — характерный
размер — размах крыла), то достаточно измерить ее на модели в той
7.1 ] Подобие гидродинамических движений 167
же сходственной точке. Тогда из G.12) следует
^*н = ^*м , = , ^н = vM = -vM. G.23)
^оом 'Уоон ^оом О
Измеряя скорости движения газа около модели в различных точках,
можно указать скорости движения газа во всех сходственных точках
натуры.
7.1.4. Аэродинамические трубы. Бассейны. Опыты на моделях
проводят для летательных аппаратов в аэродинамических трубах, а
для судов, турбин и других подобных устройств — в бассейнах. Совре-
Современные аэродинамические трубы — это гигантские сооружения, по-
потребляющие мощности в десятки тысяч киловатт. Увеличение размеров
современных аэродинамических труб диктуется следующими обстоя-
обстоятельствами.
Во-первых, если бы было возможно создание аэродинамических
труб, позволяющих испытывать натурные объекты, то, конечно, точ-
точность научных прогнозов значительно бы увеличилась, поскольку мо-
моделирование во многих случаях могло быть полным.
Во-вторых, трудно создать очень маленькую модель, являющуюся
в точности геометрически подобной натуре вплоть до шероховатостей
поверхности модели, заклепок и других тонких, но немаловажных
деталей.
В-третьих, как видно из примера, даже для частичного приближен-
приближенного подобия пришлось плотность, а следовательно, и давление модель-
модельного потока газа увеличить в восемь раз. В этом случае трудно обес-
обеспечить механическую прочность трубы. Если же увеличить модель, то
не нужно так сильно увеличивать давление в аэродинамической трубе
или вместо воздуха использовать другой дорогостоящий газ.
Эти три обстоятельства и заставляют идти по линии увеличения
габаритов современных аэродинамических труб, которые в настоящее
время наряду с крупными ускорителями элементарных частиц яв-
являются уникальными сооружениями, имеющимися лишь у наиболее
крупных, технически развитых стран.
В заключение отметим, что вышеуказанные соображения о дина-
динамическом подобии справедливы и для турбулентных потоков, строгого
математического анализа которых не существует в настоящее время,
и в этом случае их моделирование является единственным способом
решения практических задач. Однако в силу того, что моделирование
носит почти всегда частичный характер, дальнейшее развитие анали-
аналитических методов решения остается важной проблемой современной
гидроаэродинамики.
7.1.5. Аналитические коэффициенты сопротивления. Во всех
случаях, когда сила сопротивления может быть вычислена аналитиче-
аналитически, предоставляется возможность аналитически вычислить и коэффи-
коэффициенты сопротивления.
168 Методы подобия и размерности [ Гл. 7
Рассмотрим движение вязкой несжимаемой жидкости в круглой
цилиндрической трубе. Воспользуемся общей формулой G.17) для вы-
вычисления коэффициентов сопротивления:
Fx = j; PoovioSC* (Re). G.24)
z
В данном случае плотность жидкости постоянна, поэтому р^ = р.
В качестве характерной скорости v^ можно выбрать среднюю скорость
движения жидкости по трубе V. За характерную площадь S можно
принять площадь «трущейся» боковой поверхности трубы радиусом
го и длиной /. Кроме того, учтем, что сила, действующая на рас-
рассматриваемый участок трубы со стороны жидкости, как мы видели,
равна разности давлений на этом участке, умноженной на площадь
поперечного сечения трубы:
pv2TrrllCx№, v=-^ = ^. G.25)
Подставляя Ар в первую формулу G.25), получим
Cx = J!L=™t Re = ^. G.26)
ropv Re 77
Из последнего соотношения видно, что коэффициент сопротивления
является действительно функцией только числа Рейнольдса. Тогда фор-
формулу для силы сопротивления, или для разности давлений на участке
трубы длиной / можно записать в следующем виде:
Ар = ?йл' А = 4С- = ё- G-27)
Коэффициентом сопротивления трубы принято называть не Сх,
а Л. Формула G.27) является универсальной и позволяет вычислять
сопротивление трубы (Ар), если известен коэффициент сопротивления
Л при любом характере движения жидкости в трубе. Коэффициенты
сопротивления участков трубы, имеющих некоторые особенности (рас-
(расширение, сужение, кран, задвижка, поворот и т.д.), измерены экспери-
экспериментально и вычисляются как функции числа Рейнольдса в трубе по
графикам или эмпирическим формулам.
Нетрудно вычислить коэффициент сопротивления шара при мед-
медленном его обтекании вязкой несжимаемой жидкостью. По формуле
Стокса имеем 2
Fx = б7гг]гои, Fx = ^- SCX . G.28)
Возьмем в качестве характерной площади площадь максимального
поперечного сечения шара плоскостью, перпендикулярной к набегаю-
набегающему потоку (площадь миделева сечения). Тогда из G.28) имеем
= ^ , Re = ^. G.29)
Re г]
7.2] Метод размерностей физических величин 169
Аналогично можно вычислить коэффициент сопротивления цилин-
цилиндра и т.д. Следует еще раз подчеркнуть, что удобство введения
некоторых безразмерных коэффициентов сопротивления заключается
в том, что они являются функциями только безразмерных критериев
подобия в любом режиме движения жидкости, как в ламинарном, так
и в турбулентном. Они могут быть вычислены аналитически только
для некоторых простейших ламинарных движений. Во всех же дру-
других случаях для их определения необходимо обращаться к опыту, и
функциональная зависимость их от безразмерных критериев подобия
устанавливается на основании опытных данных, представляемых в ви-
виде таблиц, графиков или эмпирических формул.
7.2. Метод размерностей физических величин
Многие физические явления в силу своей сложности не могут
быть исследованы теоретически на основе обоснованного решения
определяющих уравнений. Поэтому при изучении таких явлений было
бы весьма полезно из тех или иных соображений построить явную
зависимость исследуемой физической величины хотя бы от некото-
некоторых определяющих ее параметров. Целесообразность таких построе-
построений диктуется прежде всего тем, что, во-первых, это заметно сужает
класс возможных исследуемых функций и, во-вторых, часто позволяет
выявить универсальные функции геометрии и параметров состояния,
которые характеризуют данное явление. Последнее обстоятельство осо-
особенно важно. Действительно, однажды определив такую универсаль-
универсальную функцию из некоторого, отдельного эксперимента, можно дать
качественную и количественную оценку интересующего нас явления
для большого спектра параметров состояния и исходных геометриче-
геометрических условий. Знание явной функциональной зависимости исследуе-
исследуемой физической величины от некоторых определяющих ее параметров
может быть получено на основе теории размерностей. Тем самым
анализ размерностей физических величин способствует рациональной
постановке эксперимента.
7.2.1. Основные и производные величины. Между всеми физи-
физическими величинами (сила, скорость, длина и т. д.) существует каче-
качественное и количественное различие (две различные длины, скорости
и т.д.). Подразумевается, что каждая физическая величина может
быть измерена. Мерой физической величины является некоторое число,
которое характеризует ее в количественном отношении в сравнении
с аналогичной величиной, принятой за единицу измерения. Масштаб
меры может быть любым в зависимости от используемой системы
единиц измерения. Например, длина может быть выражена в метрах,
сантиметрах, миллиметрах и т. д.
Все физические величины можно разбить на две категории — ос-
основные и производные. Физическая величина, мера которой не зависит
от масштаба измерения других величин, называется основной. Едини-
170 Методы подобия и размерности [ Гл. 7
цы измерения основных величин вводятся при помощи эталонов или
специальных опытов. Величины, единицы измерения которых зависят
от единиц измерения основных величин, называются производными.
Так, в механике за основные величины принимаются —масса, длина,
время. Их единицы измерения в СИ — килограмм, метр, секунда.
Все остальные производные единицы могут быть выражены через них.
Число основных единиц может быть и больше трех. Так в задачах
гидродинамики, связанных с теплообменом, используются градус и
джоуль (иногда калория). В магнитной гидродинамике вводятся еще
некоторые основные единицы.
Для простоты выберем лишь три основные величины: массу, длину
и время. Обозначим их размерность соответственно: М, L, Т.
Рассмотрим размерность некоторой производной физической вели-
величины Р, которая может быть выражена через размерность основных
величин. Предположим, что при изменении масштабов, в которых изме-
измеряются основные величины М, L, Т, их числовые значения изменяются
в а, C, 7 раз соответственно. Пусть мера исследуемой величины Р
изменилась при этом в тг раз. Тогда если
тг = ат/ЗУ , G.30)
где т, I, t — показатели размерностей — некоторые целые или дробные
вещественные числа, то говорят, что величина Р имеет размерность
ддт^/гр* относительно величин М, L, Т. Это записывают в виде сте-
степенного одночлена:
[Р] = MmL/Tt, G.31)
где символом [Р] обозначена размерность величины Р.
Формула G.31) показывает, как мера величины Р зависит от мер
основных величин М, L, Т, и называется формулой размерности.
Физическая величина нулевой размерности называется безразмерной
величиной. Безразмерная величина инварианта по отношению к изме-
изменениям масштаба измерения основных величин.
7.2.2. Определяющие параметры. Пусть некоторая физическая
величина А, имеющая размерность [А], является функцией ряда опре-
определяющих параметров
2,...on). G.32)
Определяющие параметры а\, а^, • • • ап — это некоторые размерные
физические величины, от которых может зависеть величина А, в том
числе и основные величины. Среди определяющих параметров могут
быть параметры с независимыми и зависимыми размерностями. Раз-
Размерность определяющего параметра является независимой в данном на-
наборе, если она не может быть представлена в виде степенного одночле-
одночлена размерностей остальных определяющих параметров. Например, раз-
размерности L, LT, ML2T~2 независимы, размерности Ь,ЬТ-1,ЬТ~2 —
зависимы. Очевидно, что число параметров с независимыми размерно-
7.2] Метод размерностей физических величин 171
стями не может быть больше числа основных величин (в рассматрива-
рассматриваемом случае не может быть больше трех).
Равенство G.32), выражающее некоторый физический закон дол-
должно быть справедливо для любых масштабов или единиц измерения
основных величин. Следовательно, размерность величины А должна
быть равна размерности функции /
[A] = [f(aua2,...an)}. G.33)
Рассмотрим сначала простейший пример. Пусть определяющими
параметрами будут основные величины, причем, их число равно числу
основных величин
[ai] = M, [a2] = L, [a3] = T. G.34)
Тогда размерность производной величины А может быть записана
следующим единственным образом:
[А] = MmL*T*. G.35)
Приравнивая показатели степеней основных величин в правой и
левой частях уравнения размерности G.35), получим три уравнения
для нахождения трех неизвестных показателей га, Int. Тогда функци-
функциональная зависимость G.32) будет иметь единственный вид
А = ка^а\а\ . G.36)
Здесь к — некоторый постоянный безразмерный коэффициент. Очевид-
Очевидно, что мы можем поступить аналогично и в том случае, когда в ка-
качестве определяющих параметров выступают три параметра, имеющие
произвольные, но независимые размерности. В этом случае уравнение
размерностей должно иметь вид
[А] = ЫаЫ0Ы'у. G.37)
Снова, приравнивая показатели трех основных величин в правой и
левой частях уравнения G.37), можно из трех уравнений определить
неизвестные показатели а, /3, 7- Тогда функциональная зависимость
величины А от определяющих параметров а\, а2, и аз будет иметь вид
А = ка?а%а] . G.38)
Для иллюстрации теории размерностей рассмотрим простой при-
пример.
Период колебаний маятника. Определим функциональную зави-
зависимость периода колебаний математического маятника г от опреде-
определяющих параметров. Предполагаем, что определяющими параметрами
в данном случае будут / — длина маятника, га — масса маятника и g —
ускорение свободного падения. Имеем три определяющих параметра
с независимыми размерностями:
[га] = М, [/] = L, [g} = LT-\ r = f(l,m,g). G.39)
172 Методы подобия и размерности [ Гл. 7
Следуя формуле G.37) имеем
[г] = Т, Т = Mal/(LT~2O . G.40)
Приравнивая показатели степени при одинаковых основных вели-
величинах, имеем
а = 0, /3 + 7 = 0, 1 = -27. G.41)
Из полученных уравнений следует
" = 0, /3 = ±, 1 = ~\- G-42)
Тогда искомая функциональная зависимость периода колебаний ма-
маятника от определяющих параметров, согласно уравнению G.38), имеет
вид
т = k]/i . G.43)
Безразмерная постоянная к, конечно, не может быть определена
этим методом. Напомним, что в соответствии с формулой Гюйгенса
к = 2тг.
Если число определяющих параметров больше трех, то можно вы-
выбрать из них три с независимыми размерностями, тогда размерно-
размерности остальных определяющих параметров могут быть выражены через
независимые размерности выбранных трех параметров в виде степен-
степенных одночленов. Ясно, что в этом случае система размерных уравнений
вида G.38) становится неопределенной, а следовательно, исключена
возможность установления однозначной функциональной зависимости
вида G.38).
Разумеется, что в случае трех определяющих параметров с неза-
независимыми размерностями, из них невозможно организовать ни одной
безразмерной комбинации.
Если число определяющих параметров равно четырем, причем из
них только три имеют независимые размерности, то нетрудно видеть,
что из имеющихся четырех параметров можно составить лишь одну
одночленную степенную комбинацию, не имеющую размерности. Если
имеется пять определяющих параметров, то таких безразмерных ком-
комбинаций можно составить только две, если предыдущая безразмерная
комбинация рассматривается как некоторый четвертый определяющий
параметр и т. д. Если величина А имеет п определяющих параметров,
то из них можно составить п — 3 безразмерных комбинаций. В этом
случае функциональная зависимость G.36) может быть записана в сле-
следующем виде:
А = а? 4 ... a%kf{h ,h- Зп-з). G.44)
Здесь произвольная функция / от независимых безразмерных комбина-
комбинаций 5\, #2 • • • ^п-з остается неопределенной. Показатели степеней дол-
должны выбираться при помощи каких-то дополнительных соображений.
Сказанное выше лучше всего иллюстрировать примером.
7.2] Метод размерностей физических величин 173
Сила сопротивления шара. Найти функциональную зависимость
силы сопротивления F шара , обтекаемого вязкой несжимаемой жид-
жидкостью, от определяющих параметров. Очевидно, определяющими па-
параметрами будут: р — плотность жидкости, v — скорость набегающего
потока, го — радиус шара, v — кинематическая вязкость. Запишем раз-
размерности определяемой величины и параметров
[F] = MLT, [р] = ML, [v] = LT , G.45)
[ro] = L, [i/] = L2T-1.
В данной задаче число определяющих параметров равно четырем. Из
них первые три могут быть приняты за основные, так как они имеют
независимые размерности. Найдем безразмерную комбинацию парамет-
параметров. Очевидно, для этого достаточно составить следующее уравнение
размерности:
А0 = (ML-3)a(LT-1)/3L^(L2T-1)? . G.46)
Приравнивая степени одинаковых основных величин, получим урав-
уравнения для показателей степени
0 = а, 0 =-За +/3 + 7 + 25, 0 = -/3 - е . G.47)
Решение системы имеет вид
а = 0, /3 = 7 = -е. G.48)
Следовательно, показатели /3, 7» ? могут быть любыми одинако-
одинаковыми целыми или дробными вещественными числами. Безразмерная
комбинация параметров имеет вид
5 = (^.у = (Ref = /(Re). G.49)
В последней формуле показатель степени /3 остается неопределен-
неопределенным, поэтому заменим степенную формулу некоторой функцией от
числа Рейнольдса. Тогда общий вид формулы для силы сопротивления
будет иметь вид
F = pOLv^r1^u?kf{Re). G.50)
Поскольку, приравнивая показатели степеней правой и левой частей
уравнения размерности G.44), мы получим лишь три уравнения для
четырех показателей, задача становится неопределенной. Мы можем
их определить лишь в двух предельных случаях движения.
Рассмотрим сначала случай движения при малых числах Рей-
Рейнольдса. Движение жидкости при малых числах Рейнольдса можно
рассматривать как движение жидкости, обладающей очень большой
вязкостью. В этом случае, очевидно, плотность жидкости не должна
играть существенной роли и ее можно исключить из числа определяю-
174 Методы подобия и размерности [ Гл. 7
щих параметров. Тогда определяющими параметрами будут v, ro, rj,
имеющие независимые размерности:
[F] = MLT~2, [v] = LT~1,[r0] = L, [rj] = ML-lT~l . G.51)
Уравнение размерностей имеет вид
MLT~2 = (ЫУЬ^МЬ^Г1O . G.52)
Естественно, что никаких безразмерных комбинаций из этих трех
параметров составить нельзя. Для нахождения показателей степеней
имеем уравнения:
1=7, i = QJ + )g_7> _2 = -а_7. G.53)
Из системы уравнений находим
7 = 1 , а = 1 , /3=1. G.54)
Следовательно, функциональная зависимость силы сопротивления
будет иметь вид
F = krjrov . G.55)
Таким образом, мы получили формулу Стокса с неопределенным
безразмерным численным коэффициентом к. Аналитическое решение,
как мы видели, показывает, что к = бтг.
Рассмотрим другой предельный случай обтекания шара — обтека-
обтекание при очень больших числах Рейнольдса (Re ^> 1). В этом случае
движение жидкости можно рассматривать как движение маловязкой
жидкости. Тогда из определяющих параметров можно исключить вяз-
вязкость. Размерности остальных определяющих параметров р, v, го неза-
независимы, и из них нельзя образовать некоторую безразмерную комби-
комбинацию. Уравнение размерностей имеет вид
MLT~2 = (ML~3)a(LT-1)/3L7 . G.56)
Для показателей степени имеем уравнения:
1=а, 1 = -За + /3 + 7, -2 = -/3. G.57)
Решая полученную систему, получим
а=\, C = 2, 7 = 2. G.58)
Тогда сила сопротивления должна зависеть от определяющих пара-
параметров следующим образом:
F = pv2r\k . G.59)
Таким образом, сила сопротивления шара при больших числах
Рейнольдса (в том числе и при турбулентном движении) должна быть
пропорциональна квадрату скорости, а не первой степени, как в преды-
предыдущем случае (Re <C 1). Неизвестный безразмерный коэффициент к
может быть определен из опыта.
7.2] Метод размерностей физических величин 175
При промежуточных числах Рейнольдса метод размерностей не мо-
может однозначно определить функциональную зависимость силы сопро-
сопротивления от всех определяющих параметров. Однако и в этом случае
метод размерностей может быть весьма полезен.
Действительно, при любых числах Рейнольдса уравнение размерно-
размерности имеет вид
MLT-2 = (ML)a(LT-y L^L2!1N . G.60)
Система уравнений для нахождения показателей степеней содержит
три уравнения для нахождения четырех неизвестных:
1 = а, 1 = -За + /3 + 7 + 25, -2 = -0-е. G.61)
Решение системы неоднозначно. Если положить /3 = 1, то получим
a = 1 , /3=1, 7=1» г = 1 ¦ G-62)
Тогда функциональная зависимость силы сопротивления от опреде-
определяющих параметров должна иметь вид
F = pvroiskf(Re). G.63)
Если положить /3 = 2, то 7 = 2, е = 0 и аналогичное выражение
нужно записать в следующем виде:
F = pv2r2okf{Re). G.64)
К сожалению, теория размерностей не может нам указать, какая
из этих формул является правильной. Но во всяком случае теперь
мы имеем дело лишь с двумя функциональными зависимостями и
дело экспериментатора определить неизвестные коэффициенты, функ-
функциональную зависимость от безразмерных комбинаций определяющих
параметров, а также пределы применимости той или иной формулы.
Это обстоятельство значительно сокращает объем необходимой экспе-
экспериментальной работы и является направляющей идеей для рациональ-
рационального планирования эксперимента.
7.2.3. Выбор определяющих параметров и основных величин.
Если известна математическая постановка задачи, то выбор определяю-
определяющих параметров следует из уравнений движения и граничных условий.
В этом случае определяющие параметры — это все данные, которые
необходимо задать для вычисления искомых физических величин. Если
же уравнения, управляющие данным явлением, неизвестны, то оста-
остается, полагаясь на физическую интуицию и предварительные экспе-
экспериментальные данные, испытать несколько гипотез о предполагаемой
системе определяющих параметров.
Здесь рассмотрены лишь три основные величины — масса, длина и
время. Поэтому для нахождения показателей степеней имелось всегда
только три уравнения, и, если число определяющих параметров было
больше трех, это ставило нас в затруднительное, но не всегда без-
176 Методы подобия и размерности [ Гл. 7
выходное положение. Введение некоторых дополнительных основных
единиц измерения могло бы помочь в некоторых случаях решить зада-
задачу однозначно, хотя вряд ли это было бы полезно в методологическом
отношении.
В заключение отметим, что полезность теории размерности со-
состоит в том, что она без решения уравнений движения определяет
точный вид функциональной зависимости (если число независимых
определяющих параметров меньше или равно числу основных вели-
величин) или предоставляет некоторые альтернативные функциональные
зависимости (если число определяющих параметров больше, чем чи-
число основных величин) и тем самым помогает целенаправленно по-
поставить эксперимент, значительно сокращая объем экспериментальной
работы.
Контрольные вопросы
1. Что представляет собой моделирование? Каковы его цели?
2. Каково назначение аэродинамической трубы? Какие основные требова-
требования предъявляются к аэродинамическим трубам?
3. В чем состоит предназначение метода подобия в гидроаэродинамике?
4. Какие потоки называют подобными?
5. Как выводятся критерии подобия течений вязкой жидкости?
6. Поясните физический смысл чисел Маха, Рейнольдса, Фруда и Струха-
ла.
7. Что такое геометрическое и динамическое подобие двух потоков жидко-
жидкости?
8. Обязательно ли динамически подобные потоки должны быть геометри-
геометрически подобными и наоборот?
9. Какие тела называются геометрически подобными?
10. Что дает анализ размерностей физических явлений?
11. Что такое мера физической величины? Чем определяется масштаб меры?
12. Какие физические величины называют основными и производными?
13. Что называют размерностью физической величины?
14. Какие величины являются основными в гидродинамике?
15. Что такое определяющие параметры?
16. Сколько безразмерных комбинаций можно составить из N определяю-
определяющих параметров, если п из них являются основными?
17. Как построить уравнение размерности?
18. Как получить уравнения для показателей размерностей?
19. Как выбрать определяющие параметры и основные величины?
7.3. Примеры решения задач
Задача 1
Определите буксировочное усилие, требуемое для буксировки в на-
натуре тела, имеющего форму эллипсоида вращения. Длина тела 1,5 м,
и его предполагается буксировать глубоко погруженным в воду при
температуре 15 °С со скоростью 3 м/с. Геометрически подобная модель
7.3] Примеры решения задач 177
испытывается в аэродинамической трубе с регулярным давлением и
скоростью движения воздуха 30 м/с при температуре 15 °С. Плотность
воды равна 1000кг/м3. Отношение коэффициентов вязкости для воз-
воздуха и воды при заданной температуре равно 0,016.
Решение. Поскольку число Маха мало (М <С 1) сжимаемостью
среды можно пренебречь. Влиянием силы тяжести также пренебре-
пренебрегаем. Поскольку движение стационарное, то единственным критерием
подобия является число Re.
Из равенства чисел Рейнольдса для натуры и модели имеем
pMvMLM _ pHvHLH ,- ^гч
Отсюда
Рм = ru VuLu_ ^ Рм = 0 ош ш 3J_5 = Q 0()8 G 66)
рн щ vMLM рн 30-0,3
Чтобы это соотношение выполнялось, плотность воздуха должна
быть равна
рм = рн . 0,008 кг/м = 8 кг/м .
Поскольку плотность атмосферного воздуха при температуре 15 °С
равна 1,33 кг/м3, то для обеспечения требуемой плотности давление
воздуха в аэродинамической трубе должно быть около батм « 6х
х 105Па.
Пусть в этих условиях измеренная сила сопротивления модели
оказалась равной FXM = 2,95 Н. Тогда из равенства коэффициентов
сопротивления имеем
FXM Jj^, G.67)
PuVMSM puVuSu
где SM и SH — площади поверхности модели и натуры. Условие геомет-
геометрического подобия записывается в виде
2 . G.68)
Тогда сила, которую следует приложить для буксировки тела в на-
натуре, равна
FXH = FXH * (^lJ = 92,2 Н . G.69)
р \vLJ
м \vMLM
Задача 2
В химических технологических процессах часто используют боль-
большие резервуары, в которых осуществляется гидродинамическое пе-
перемешивание вещества (рис. 7.1). Необходимо найти глубину цен-
центральной воронки при стационарном движении жидкости в резервуаре
как функцию угловой скорости мешалки П. Диаметры резервуара и
мешалки велики и равны D и d соответственно. Предполагается по-
178
Методы подобия и размерности
[Гл.7
:_ Vl =щ
ставить модельные опыты в геометрически подобном сосуде меньших
размеров. Необходимо определить условия, при которых следует про-
проводить модельное испытания, чтобы пра-
правильно предсказать результаты для натуры.
Решение. Скорость движения жидко-
жидкости мала по сравнению со скоростью звука,
т. е. М "С 1. Поэтому жидкость можно счи-
считать несжимаемой и число Маха не прини-
мать во внимание. Поскольку по условию
задачи движение жидкости стационарно,
то и число Струхала также можно не рас-
рассматривать.
В качестве характерного размера вы-
выберем диаметр турбинной мешалки d, a
в качестве характерной скорости — линей-
линейную скорость мешалки ftd. Тогда числа
2' i
D
\
d
/
I
Рис. 7.1. Центральная во-
воронка в сосуде с мешалкой
Рейнольдса и Фруда определятся следующими выражениями:
Re = ^^ , Fr = — . G.70)
Из условия равенства чисел Fr для модели и натуры находим
Условие равенства чисел Re дает
dMuMpM _ d
С учетом выражения G.71) имеем
G.71)
G.72)
3/2
v , , • G.73)
рм рн \ «н /
Полученное выражение свидетельствует о том, что динамическое по-
подобие (в данном случае подобие центральных воронок) не может быть
достигнуто, если в натурном и модельном сосудах используется одна
и та же жидкость. В модельном сосуде должна использоваться менее
вязкая жидкость. Если размер модельной мешалки в два раза меньше
размера натурной мешалки (dM/dH = 1/2), то кинематическая вязкость
жидкости в модельном аппарате должна быть равна кинематической
вязкости жидкости в натурном аппарате, умноженной на 1 /л/8.
Задача 3
Поток идеальной несжимаемой жидкости обтекает шар радиуса R
со скоростью v. Давление жидкости вдали от шара равно нулю, а
давление в критической точке равно р. Используя анализ размерностей,
7.3] Примеры решения задач 179
исследовать зависимость давления р от скорости v и определить силу
лобового сопротивления F.
Решение. Поскольку жидкость идеальна, то определяющими па-
параметрами будут плотность р, скорость v и, возможно, радиус шара R.
Таким образом, представляет интерес функциональная зависимость
p = f(p,v,R). G.74)
Запишем уравнение размерностей:
[р] = [p]a[vf[Ry , L-'MT-2 = (ML-3)a(Lry^ . G.75)
Отсюда для показателей размерностей получим
-l = -3a + /3 + 7, 1 = <*, -2 = -/3, а = 1, /3 = 2, 7 = 0. G.76)
Для давления получаем следующее выражение:
р = kpv2, G.77)
где к — некоторый безразмерный коэффициент.
Если учесть статическое давление жидкости р$ вдали от шара, то
можно записать
р = Ро + kpv2. G.78)
Заметим, что давление жидкости в критической точке не зависит от
радиуса шара.
Определим силу лобового сопротивления
F = f(p,v,R). G.79)
Запишем уравнение размерностей
[F] = [p]x[v]y[R]z , LMT-2 = (ML-3)sr(LT-1)Lz . G.80)
Отсюда для показателей размерности получаем
х=\, у = 2, z = 2. G.81)
Для силы сопротивления имеем
F = Apv2R2, G.82)
где А — безразмерная постоянная.
Поскольку сила зависит от квадрата скорости, то F(—v) = F(v).
С другой стороны ясно, что при изменении направления движения
жидкости должен измениться и знак силы F(—v) = —F(v). Это про-
противоречие исчезает лишь при F = 0 или, что то же самое, при А = 0.
Напомним, что отсутствие лобового сопротивления при движении тел
в идеальной жидкости называют парадоксом Даламбера.
Задача 4
В теориях кипения жидкости и кавитации представляет интерес
время схлопывания образовавшегося воздушного пузырька в объеме
жидкости. Пусть начальный радиус пузырька равен Rq. Давление жид-
180 Методы подобия и размерности [ Гл. 7
кости на бесконечности равно ро- Определите время т, в течение ко-
которого образовавшаяся сферическая полость заполняется жидкостью.
Никаких других сил к жидкости не приложено. Жидкость считать
несжимаемой. Давлением газа в пузырьке пренебречь.
Решение. Поскольку жидкость идеальна, то определяющими па-
параметрами времени захлопывания полости г являются начальный ра-
радиус полости Rq, плотность жидкости р и давление ро, т.е.
T = f(p,Po,Ro). G.83)
Уравнение размерностей
М = [Ro]x[p]y[Po}z , Т = L^ML-^tL^MT-2)* . G.84)
Отсюда для показателей размерностей получим
0 = x-3y-z, 0 = y + z, 1 = -2z;
1 1 G.85)
х=1, У=2> z = ~2'
Тогда время захлопывания пузырька равно
G.86)
Из точного решения этой задачи для безразмерного коэффициента
получено значение к = 0,915.
Задача 5
Методом анализа размерностей определить скорость звука в упру-
упругой среде как функцию плотности р и модуля Юнга Е.
Решение. Поскольку скорость звука является функцией плотно-
плотности упругой среды и модуля Юнга, то уравнение размерностей запи-
запишется в виде
[v] = \p]a[Ef. G.87)
Напомним, что модуль Юнга имеет размерность давления. Поэтому
из G.87) имеем
LT = (ML~3)a(L-1MT-2)/3, G.88)
Отсюда показатели размерностей равны
а = -
Для скорости звука получим
\, Р=\. G.89)
G.90)
Безразмерная постоянная к может быть определена из эксперимента
или рассчитана из решения волнового уравнения.
7.3] Примеры решения задач 181
Задача 6
Газовый пузырь, образовавшийся в результате глубинного подвод-
подводного взрыва, осцилирует с периодом т. Методом анализа размерностей
определить зависимость периода осциляции от статического давле-
давления р, плотности воды р и полной энергии взрыва е.
Решение. Физические величины, составляющие задачу, имеют
следующие размерности:
[т]=Т, [p] = L-1MT~2, [p] = ML~3, [e] = ML2T-2. G.91)
Из уравнения размерностей
[т] = \р\а [pf [еГ G.92)
определяем показатели
0 = а + /3 + 7, 0 = а + 3/3-27, -1=2а + 27, G.93)
Следовательно, для периода осциляции получим
/ 3 2 4 1/6
т = к (*-!-] . G.94)
Таким образом, чем больше мощность взрыва, тем больше период
осциляции.
Задача 7
Установившееся движение несжимаемой вязкой жидкости в трубе
радиуса R и длины / обусловлено постоянным перепадом давления
вдоль трубы Ар = р\ — Р2- Используя анализ размерностей, определить
объемный расход Q и среднюю по сечению трубы скорость v жидкости.
Рассмотреть случай ламинарного медленного течения.
Решение. Очевидно, имеем четыре определяющих параметра:
плотность жидкости р, коэффициент вязкости г], радиус трубы R и
перепад давлений на единицу длины цилиндра Ар/1.
Размерности физических величин
[Ар/1] = L-2MT~2, [р] = ML, [rj] = ML-'T-1 , G.95)
Поскольку из четырех определяющих параметров три имеют незави-
независимые размерности, то можно построить только одну безразмерную
комбинацию 5:
[AP/l]a[p]0[T,]i[RY = l,
1
182 Методы подобия и размерности [ Гл. 7
Отсюда определяются показатели размерностей
2а-3/3-7 + ? = 0, а + /3 + 7 = 0, -2а -7 = 0, G.97)
о е 2
О/ — I) — — «"у — — — f
М о ' / о
О О
Безразмерный параметр имеет вид
х pR Ар /7 OQ4
д = —g р • G.У8)
ту /
Выражения для расхода и средней скорости жидкости в общем
случае имеют вид
Q = Fl(S)(Ap/l)nipn2rjn3RnA,
G.99)
v = F2(S)(Ap/l)rn'prn2rjrn3Rrn4,
где F\(S) и F2(S) — неизвестные функции безразмерного параметра S;
rii, mi — показатели размерностей.
При медленном движении жидкости расход и скорость должны
линейно зависеть от перепада давлений. Поэтому
FX=C\5, F2 = C25, m =mi=0. G.100)
Здесь С\ и С2 — некоторые безразмерные постоянные.
Тогда формулы размерностей запишутся в виде
[Q] = \рГ Ыпз [ЩПА, [v] = [рГПлГ3 [Щт4 ¦ G.Ю1)
Отсюда определяем показатели размерностей
п2 = — 1 , щ = щ = 1 , т2 = — 1 , тз = 1 , rri4 = — 1 . G.102)
Следовательно, выражения G.99) запишутся в следующем виде:
q = Ci^^, v = c2^^. G.103)
Очевидно, что расход и скорость жидкости связаны между собой:
Q = ttR2v. Отсюда С\ = кС2.
Из решения уравнений Стокса известно, что С\ = тг/8.
Задача 8
Рассмотрим струйное движение идеальной жидкости через водо-
водослив, который представляет собой вертикальную стенку с отверстием
треугольной формы с углом а (а) и прямоугольной формы с шириной
канала b (б). Высота уровня жидкости над основанием канала равна h.
Требуется определить массовый расход жидкости Qm через отверстие
водослива. Движение жидкости считать установившимся.
Решение, а) Сечение канала имеет треугольную форму с углом
при основании а. Определяющими параметрами будут плотность жид-
7.3] Примеры решения задач 183
кости р, ускорение свободного падения g, и высота уровня жидкости
в канале h. Размерности этих величин, а также массового расхода:
[р] = ML , [g] = LT-2 , [ft] = L , [Qm] = МГ1 . G.104)
Уравнение размерностей имеет вид
Qm = Срх gy hz , МГ1 = (ML)* (LT-2)*' Lz . G.105)
Отсюда получим показатели размерностей
х=1, у =1/2, z = 5/2. G.106)
Для массового расхода имеем
Qm = C(a)Pgl'2h5'2. G.107)
Значение безразмерной постоянной С зависит от угла а.
б) Сечение канала имеет форму прямоугольника с шириной основа-
основания Ь. В этом случае будет четыре определяющих параметра: р, g, b, h.
Из них можно составить одну безразмерную комбинацию — h/b. Тогда
решение будет иметь вид
Qm = f(h/b)pgl/2h5'2. G.108)
Функцию f(h/b) можно определить опытным путем, наблюдая те-
течение через водослив различной ширины Ь, но с постоянным уровнем
жидкости h. Определив таким способом функцию f(h/b), полученную
формулу можно применять для любых значений безразмерного пара-
параметра h/b.
ГЛАВА 8
ТУРБУЛЕНТНОСТЬ
8.1. Ламинарное и турбулентное течение
Известно, что медленные течения жидкостей или течения сильно
вязких жидкостей являются упорядоченными, плавными, слоистыми.
Такие течения называют ламинарными (от латинского lamina — пла-
пластинка, полоска). Ламинарным является течение воды в спокойных
реках, газа в узких капиллярах, смазки в подшипниках.
При увеличении скорости упорядоченный слоистый характер тече-
течения жидкости нарушается. Оно становится беспорядочным, сопровож-
сопровождается перемешиванием различных слоев жидкости и образованием
завихрений. Такие течения называют турбулентными (от латинского
turbulentus — бурный, беспорядочный). Примерами турбулентного те-
течения являются движение воздушных масс в атмосфере, воды в бурных
реках, дыма из труб и так далее.
Все сценарии зарождения турбулентности основаны на факте воз-
возникновения первичных возмущений ламинарного течения. В природе
и технике возмущения появляются при обтекании различных препят-
препятствий. Турбулентность атмосферы связана с возмущениями воздушного
потока при движении вблизи неоднородностей земной поверхности
(овраги, лес, горы, строения и так далее) или при взаимодействии
с другими потоками. Турбулизация воды в реках обусловлена неров-
неровностями речного дна, порогами, выступами и тому подобное. При
течении в трубопроводах возмущения возникают на входном участке
трубы, в местах резкого изменения площади сечения трубопровода.
При обтекании тел смена режимов течения может происходить непо-
непосредственно вблизи поверхности этих тел или уже за телом образуется
турбулентный след.
Иногда говорят, что турбулентное движение жидкости в отличие
от ламинарного является вихревым. Турбулентное движение жидко-
жидкости, действительно, всегда является вихревым. Но и большинство
ламинарных течений также являются вихревыми, т. е. движениями,
для которых ротор скорости в каждой точке пространства, занятого
движущейся жидкостью, не равен нулю.
Отметим следующие особенности турбулентных течений.
1. Турбулентное движение можно представить суперпозицией вих-
вихрей различных размеров и завихренностей. Верхний предел размера
8.1 ] Ламинарное и турбулентное течение 185
вихрей определяется масштабом течения, т. е. размером устройства,
в котором движется жидкость. Нижний предел зависит от вязкости
жидкости и уменьшается с увеличением скорости осредненного пото-
потока. Внутри наименьших вихрей движение жидкости перестает быть
турбулентным и определяющую роль играет вязкость. В связи с этим
следует иметь в виду, что минимальный масштаб вихрей должен быть
макроскопическим. Это означает, что минимальный размер вихрей дол-
должен быть много больше средней длины свободного пробега молекул.
Известно, например, что при скорости воздушного потока до 100 м/с
минимальный размер атмосферного вихря составляет около 10~3м.
Средняя длина свободного пробега молекул в воздухе при нормальных
условиях составляет 10~7м, что на четыре порядка меньше размера
минимального вихря.
2. Физические величины, характеризующие турбулентное движе-
движение (скорость, давление, плотность, температура и т.д.), изменяются
хаотически как во времени, так и в пространстве. Действительно,
индивидуальная частица жидкости может двигаться неупорядочено
относительно неподвижного наблюдателя и упорядочено по отношению
к наблюдателю, движущемуся вместе с частицей. В любой фиксиро-
фиксированной точке пространства физические величины претерпевают хаоти-
хаотические изменения с течением времени.
3. Если ламинарное движение может быть как установившимся,
так и неустановившимся, то турбулентное движение всегда неустано-
неустановившееся, так как мгновенные скорости частиц жидкости в данной
точке пространства все время изменяются как по направлению, так и
по величине.
4. Турбулентное движение можно назвать квазипериодическим, по-
поскольку через некоторый неопределенный промежуток времени в дан-
данной точке пространства скорость снова может принять прежнее мгно-
мгновенное значение. В некоторый фиксированный момент времени весь-
весьма схожие картины течения повторяются более или менее регулярно
в пространстве.
Если во всех областях поля течения турбулентность имеет каче-
качественно одну и ту же структуру, то такую турбулентность называют од-
однородной. Пульсационные характеристики однородной турбулентности
в среднем не зависят от координат. Если же пульсационные величины
в среднем не зависят от направления, то такую турбулентность называ-
называют изотропной. При изотропной турбулентности пульсации в различ-
различных точках течения в общем случае разные. Разумеется, изотропная
турбулентность может быть и однородной, а однородная — изотропной.
Первые экспериментальные исследования ламинарно-турбулентного
перехода провел Осборн Рейнольде A883). Опыты заключались в сле-
следующем. В трубу с движущейся жидкостью вводилась тонкая трубоч-
трубочка, из которой в жидкость поступало красящее вещество (рис. 8.1).
При малых скоростях движения жидкости краска распространялась
вдоль трубы в виде тоненькой прямолинейной ниточки, простираю-
186 Турбулентность [Гл.8
щийся от носика трубки с красящим веществом до конца основной
трубы (верхний рис. 8.1). При постепенном увеличении скорости дви-
движения жидкости наступает момент, когда струйка красящего вещества
начинает произвольно изгибаться и затем раз-
,_, мываться, окрашивая равномерно всю жидкость
^^^^—^^^^— в трубе (нижний рисунок). Очевидно, что до
^^^^_^^^^ этого момента частицы жидкости двигались па-
"Л- OfW) раллельно оси трубы, т.е. движение имело сло-
истый (ламинарный) характер. При некотором
„ о 1 ^ т^ « значении скорости, которая называется крити-
Рис. 8.1. Опыт Реи- г > г г
и^пип^о ческой, ламинарное течение жидкости перехо-
дит в турбулентное.
Рейнольде, проводя опыты с различными жидкостями в трубах раз-
различных диаметров, установил, что переход от ламинарного движения
к турбулентному наступает всегда, когда число Рейнольдса, достигает
некоторого определенного значения.
Следовательно, переход ламинарного движения жидкости в трубе
в турбулентное происходит всегда при одном и том же числе Рей-
Рейнольдса, называемом критическим — ReKp. Поэтому число Рейнольдса
играет важную роль не только в динамическом подобии потоков вязкой
несжимаемой жидкости, но и является управляющим параметром их
движения.
Если не принимать специальных мер к сглаживанию условий входа
жидкости в трубу, а также специальному устранению шероховатостей
стенок трубы, то ReKp « 2300. В этом случае, если Re < 2300, то
случайные возмущения, возникающие в потоке, будут затухать вниз по
течению и движение жидкости сохраняет свой ламинарный характер.
Если же Re > 2300, то возмущения, не передаваясь вверх по пото-
потоку, разрастаются вниз по течению жидкости. Вообще сглаживанием
условий входа в трубу и устранением шероховатостей стенок трубы
можно существенно сдвинуть переход ламинарного течения в турбу-
турбулентное. В таких случаях можно наблюдать ламинарное движение при
Re = 60000 и более.
Опыт показывает, что ReKp = 2300 не является универсальным
значением и характерно только для цилиндрической трубы кругло-
круглого поперечного сечения. Так, в расширяющейся трубе ReKp < 2300,
в сужающейся трубе ReKp > 2300. При внешнем обтекании цилиндра
плоскопараллельным потоком жидкости, перпендикулярным оси ци-
цилиндра, ReKp = 34.
Таким образом, для каждой геометрии течения имеется свое кри-
критическое число Рейнольдса.
Из опытов Рейнольдса следует вывод о том, что переход к турбу-
турбулентности связан с потерей устойчивости течения жидкости. Поэтому
для определения критериев, определяющих характер течения, необхо-
необходимо исследовать проблему устойчивости этого течения.
8.2] Устойчивость стационарного движения жидкости 187
8.2. Устойчивость стационарного движения жидкости
В курсе элементарной физики понятие устойчивости обычно объ-
объясняют на примере шарика, находящегося на различных поверхностях
(рис. 8.2). Пусть шарик покоится на дне вогнутой полости. Если немно-
немного сместить шарик из равновесия, а затем отпустить, то он обязательно
возвратится в положение равновесия. Это
происходит потому, что сила тяжести и
реакция стенки не уравновешиваются,
а равнодействующая этих сил всегда
направлена противоположно смещению. _ n ^ _
о * Рис. 8.2. Равновесие: а —
В этом случае положение шарика абсо- „ ^
J „ г устойчивое, б — неустоичи-
лютно устойчиво. вое? в _ асимптотичеСки
Теперь пусть шарик находится в по- устойчивое, г - безразличное
ложении равновесия на выпуклой по-
поверхности. Сколь угодно малое отклонение приводит к возникновению
результирующей силы, перемещающей шарик еще дальше от положе-
положения равновесия. Такое равновесие называют абсолютно неустойчи-
неустойчивым.
В третьем случае состояние шарика устойчиво при малых откло-
отклонениях от равновесия и неустойчиво при больших отклонениях. Такие
состояния называют асимптотически устойчивыми.
Если смещать шарик на гладкой горизонтальной поверхности, то
он останется в равновесии. Такое равновесие, сохраняющееся при всех
смещениях, называют безразличным.
Таким образом, для исследования устойчивости течения жидкости
можно воспользоваться методом малых возмущений. Для простоты
рассмотрим лишь принципиальную схему этого метода в случае стацио-
стационарного движения несжимаемой жидкости при отсутствии массовых сил.
Пусть vo, Po есть скорость и давление жидкости, зависящие
от координат и удовлетворяющие стационарному уравнению Навье-
Стокса и уравнению непрерывности
(v0V)v0 = -- Vpo + ^ Av0, divvo = O. (8.1)
Запишем эти уравнения в безразмерном виде. Для этого введем
безразмерные величины и дифференциальные операторы, обозначенные
символами со звездочкой:
где V и L — характерные скорость и линейный размер течения соответ-
соответственно. Подставляя эти величины в уравнения (8.1) и для простоты
опуская звездочки, получим
(voV)v0 = - Vp0 + ^ Av0 , div v0 = 0, Re = ^ . (8.2)
188 Турбулентность [Гл.8
Как мы выясним ниже, именно значение числа Рейнольдса опреде-
определяет переход от ламинарного режима течения к турбулентному.
Пусть по каким-то причинам произошло возмущение течения. Поля
скорости и давления представим в виде сумм стационарных решений и
возмущений:
v(x, у, z, t) = щ(х, у, z) + vf(x, у, z, t),
р(х, у, z, t) = po(x, у, z) + pf(x, у, z,t) .
Заметим, что возмущения скорости и давления зависят не только
от координат, но изменяются с течением времени.
В рамках линейной теории устойчивости рассматриваются только
малые возмущения, т. е.
Дальнейшая задача состоит в анализе эволюции малых возмущений.
Необходимо выявить условия, при которых возмущения будут с те-
течением времени либо исчезать, либо увеличиваться. В первом случае
течение будет устойчивым, а во втором — неустойчивым. Важно опре-
определить критические значения параметров (в частности, критическое
число Re), при которых стационарное течение начинает разрушаться.
Очевидно, возмущенное течение жидкости описывается нестацио-
нестационарным уравнением Навье-Стокса:
^ + (vV)v = - Vp + ^ Av , div v = 0 . (8.4)
Подставляя выражения (8.3) в уравнения (8.4), пренебрегая члена-
ми второго порядка малости (~ v' ) и учитывая стационарное уравне-
уравнение движения (8.2), получим
^ + (voV)v' + (v'V)v0 = -Vp' + J- Av', div v' = 0 . (8.5)
ut Re
Полученные уравнения необходимо дополнить граничными услови-
условиями. Предположим, что для возмущений также выполняются условия
непротекания, т. е. на неподвижных границах они равны нулю
v'(x0, уо, zo, t) = 0, (х0, уо, z0) e S, (8.6)
где S — граничная поверхность.
Таким образом, эволюция возмущения скорости течения описывает-
описывается дифференциальным уравнением (8.5) с коэффициентами, зависящи-
зависящими только от координат. Общее решение такого уравнения можно пред-
представить в виде суперпозиции гармонических колебаний с различными
частотами Uk, зависящими от числа Re, и амплитудами Д, зависящими
только от координат
у[(х, у, z,t) = J2 fik{x, у, z) exp(-iukt) . (8.7)
8.3]
Устойчивость движения между цилиндрами
189
Частоты ujk в общем случае являются комплексными величинами
Поэтому можем записать
v[(x,y,z,t) =
(8.8)
Очевидно, что если в спектре частот uj^ окажется хотя бы одна,
мнимая часть которой положительна (Ьк = Im ujk > 0), то возмуще-
возмущение скорости v[ с течением времени будет неограниченно расти, т. е.
первоначальное стационарное течение будет абсолютно неустойчиво.
Для того чтобы стационарное течение было устойчивым к малым
возмущениям, необходимо, чтобы мнимые части всех частот были
отрицательны. Тогда все малые возмущения с течением времени будут
затухать.
Рис. 8.3. Эволюция возмущения: а — затухание, б —рост
Как показывают исследования, стационарные течения с невысокими
скоростями (при малых числах Re) являются устойчивыми. С увели-
увеличением скорости (числа Re) потока в спектре частот появляется такая
частота, мнимая часть которой оказывается равной нулю. Соответству-
Соответствующее число Рейнольдса определяет границу устойчивости стационар-
стационарного течения и называется критическим числом Рейнольдса — ReKp.
При дальнейшем увеличении числа Re появляется все больше частот
с положительной мнимой частью, движение становится абсолютно
неустойчивым.
8.3. Устойчивость движения жидкости
между коаксиальными цилиндрами
Рассмотрим качественно проблему устойчивости движения вязкой
несжимаемой жидкости между двумя вращающимися коаксиальными
цилиндрами (Рэлей, 1916). Идея исследования заключается в следу-
следующем. Мысленно сместим какую-либо индивидуальную частицу жид-
жидкости с ее стационарной траектории в некоторое соседнее положение.
Если при этом возникают силы, стремящиеся возвратить ее в исходное
190 Турбулентность [Гл.8
положение, то такое движение является устойчивым. В противополож-
противоположном случае, если возникающие силы стремятся сместить частицу еще
дальше от установившейся траектории, движение будет неустойчивым.
Распределение скоростей частиц жидкости между цилиндрами не
зависит от вязкости жидкости, поэтому мы можем рассматривать такое
движение как движение идеальной жидкости. Пусть
для определенности Я2 > R\ (рис. 8.4).
Рассмотрим силы, действующие на некоторую ин-
индивидуальную частицу жидкости массы т, враща-
вращающуюся по окружности радиусом го с угловой ско-
скоростью оио. В стационарном состоянии на частицу
действует центробежная сила тии^го, стремящаяся
сдвинуть частицу от оси вращения вдоль радиуса,
и равная ей, но противоположно направленная си-
сила, обусловленная радиальным градиентом давления
Рис. 8.4 в зазоре между цилиндрами. При стационарном дви-
движении обе силы взаимно скомпенсированы, следо-
следовательно, частица вращается по некоторой стационарной траектории.
Центробежная и градиентная силы, действующие на частицу, могут
быть выражены через момент импульса частицы /л:
[л = mnujr1, muj^ro = -—^ , /io = тоо^г^ . (8.9)
Теперь мысленно сдвинем частицу вдоль радиуса в некоторое новое
положение на расстояние г от оси вращения (см. рис. 8.4). Так как
рассматривается движение идеальной жидкости, то при таком переме-
перемещении частицы должен сохраниться ее момент импульса. Следователь-
Следовательно, на частицу в новом положении будет действовать центробежная
сила, равная /j^/mr3. Для того чтобы частица стремилась возвратиться
в исходное положение, эта центробежная сила должна быть меньше ее
равновесного значения /22/гтгг3, которое на расстоянии г равно силе,
вызванной градиентом давления. Таким образом, для устойчивости
движения жидкости должно быть выполнено следующее условие:
М2 - Мо > 0 •
Считая смещение малым, момент импульса можно разложить в ряд
и, ограничиваясь членами первого порядка малости по Аг = г — го,
имеем /Я
(
Учитывая, что Аг > 0, условие устойчивости примет вид
М^>0. (8.10)
Точное решение стационарной задачи дает для скорости частиц
жидкости в зазоре следующую формулу (см. п. 6.3.4):
v = аг -\— , \i = moor2 = mrv = m(ar2 + Ь) . (8.11)
8.3]
Устойчивость движения между цилиндрами
191
Подставляя это выражение в условие устойчивости (8.10), имеем
m(ar2 + bJamr > 0, 2т2аг3со>0. (8.12)
Полученное соотношение, обеспечивающее устойчивость движения,
будет выполняться, если асо > 0. Подставляя постоянную а из точного
решения задачи, имеем
U2R2 —
СО > \) .
R2 — R\
При R<2 > R\ движение жидкости между двумя вращающимися коак-
коаксиальными цилиндрами будет устойчивым, если в любой точке зазора
выполняется неравенство
>0.
(8.13)
Проанализируем полученное неравенство. Для этого рассмотрим
несколько частных случаев.
1. Цилиндры вращаются в разные стороны, т.е. со\ и со2 имеют
разные знаки. Нетрудно видеть, что движение в этом случае будет
неустойчивым при любых значениях со\ и со2, так как внутри зазора
угловая скорость жидкости со изменяет знак и, следовательно, нера-
неравенство (8.3) не может быть выполнено ни в одной точке зазора.
2. Цилиндры вращаются в одну и ту же сторону. Если это направле-
направление вращения цилиндров считать положительным, то угловая скорость
жидкости также положительна в любой точке зазора, со > 0. Поэтому
условие устойчивости в этом случае будет иметь вид
uJRl>w\R2\- (8-14)
3. Вращается только внешний цилиндр. Тогда со\ = 0, со2 > 0, со > 0
и, следовательно, движение устойчиво при любых скоростях вращения
внешнего цилиндра.
4. Вращается только внутренний ци-
цилиндр. Тогда со\ > 0, со2 = 0, со > 0 и, сле-
следовательно, движение жидкости неустой-
неустойчиво при любых скоростях вращения внут-
внутреннего цилиндра.
Все сказанное выше можно изобразить
графически (рис. 8.5).
Нетрудно видеть, что рисунок отражает
все рассмотренные выше случаи. Однако
некоторые утверждения с физической точ-
точки зрения кажутся сомнительными. На-
Например, утверждение, что движение бу-
будет всегда неустойчивым, если вращается
только внутренний цилиндр, вряд ли справедливо при достаточно мед-
медленном вращении внутреннего цилиндра.
Область неустойчивого
движения
1
го2
Рис. 8.5. Граница устойчи-
устойчивости — прямая / (соответ-
(соответствует уравнению uo\R\ =
2
192
Турбулентность
[Гл.8
Анализ устойчивости с учетом вязкости жидкости, сделанный
Тейлором A924) с использованием описанного выше метода спектра
частот, приводит к результатам, изобра-
изображенным на рис. 8.6.
Исследование удалось провести до кон-
конца только в случае малых зазоров, т. е. при
выполнении следующего условия:
h <С Я, h = R2 - R\ , ~R = —^—- .
Рис. 8.6. Граница устойчи-
устойчивости — штриховая линия
Из рис. 8.6 действительно видно, что
если вращается только внутренний ци-
цилиндр (со2 =0), то существует некоторая
критическая скорость его вращения. Если
скорость вращения внутреннего цилиндра меньше критической со\кр,
то движение жидкости в зазоре остается устойчивым. Точное решение
дает для критической скорости следующее выражение:
41,3*/
hVhR
Как видно из предыдущего рассмотрения, оригинальный и простой
метод Рэлея дает правильную оценку устойчивости некоторых случаев
движения жидкости в зазоре.
Действительно, он правильно определил асимптоту точного реше-
решения uo\R\ = ио^Щ и верно предсказал устойчивость движения в том
случае, если вращается только внешний цилиндр.
Теория Тейлора обнаруживает поразительное совпадение с опытом
и является классическим примером исследования устойчивости движе-
движения вязкой несжимаемой жидкости.
После потери устойчивости в зазоре образуются локальные ячеи-
ячеистые вихревые движения, которые затем по мере углубления в область
неустойчивого движения переходят в беспорядочное турбулентное дви-
движение.
8.4. Устойчивость движения в канале
Рассмотрим устойчивость стационарного движения жидкости в ка-
канале на примере плоского течения Пуазейля. Напомним, что скорость
стационарного течения vo зависит только от поперечной координаты у
и направлена вдоль оси канала х, т.е.
vo = (г>0ж,0,0), v0x = vo-
Для упрощения предположим, что существуют только плоские воз-
возмущения: v' = (v'x,vy,Q):
' = г* f? , (v'V)vo = v'y^.
8.4] Устойчивость движения в канале 193
Уравнения (8.5) в проекциях на координатные оси запишутся в этом
случае в следующем виде:
dt + ° дх ^ у ду дх + Re
$? дж <9у ^е
^4 ^i =n
(8Л5)
+
дх ^ ду
Для плоского возмущения несжимаемой жидкости можно ввести
функцию тока ф:
/ дф t дф /о 1СЧ
w* = -^> w» = ef- (8Л6)
Из уравнений (8.15) получаем
_д_дг^_ д2ф дф dv0 _ dp' I . ^^
~di~dy Щ дхду ~дх~ ~ду ~ ~дх~ Re ~fry' /Q174
9 , (О. 1 / )
д_ ch^ д2ф _ dp 1 д дф
dt дх Щ дх2 ~ ду Re дх'
Заметим, что уравнение непрерывности выполняется тождественно
и потому в (8.17) не приведено.
Чтобы исключить возмущение давления, из второго уравнения
в (8.17), продифференцированного по координате х, вычтем первое
уравнение, продифференцированное по координате у. Учитывая, что
скорость стационарного течения жидкости vq зависит только от попе-
поперечной координаты у, получим
Граничные условия (8.6) предполагают, что на пластинах, располо-
расположенных в у = 0 и у = 1 (напомним, что у — безразмерная координата),
функция тока удовлетворяет следующим условиям:
^ = ?^ = 0, у = 0,1. (8.19)
ду дх
Принципиальная трудность решения задачи (8.18), (8.19) состоит
в том, что неизвестен вид начального возмущения. Если бы оно было
известно, то дальнейшая эволюция возмущения стационарного течения
однозначно описывалась бы уравнениями (8.18), (8.19).
Обычно в теории устойчивости течения жидкости в трубах рассмат-
рассматривают нормальные возмущения в виде бегущей вдоль трубы волны:
ф(х, у, t) = Ч?(у) exp[z(cjt - kx)}, (8.20)
где к — волновое число, Ф(у) — амплитуда возмущения, зависящая
только от поперечной координаты у.
7 В.Г. Черняк, П.Е. Суетин
194 Турбулентность [Гл.8
Выражение (8.20) соответствует возмущениям, которые изменяются
с течением времени и периодически зависят от продольной коорди-
координаты х. Таким образом, в теории появился дополнительный пара-
параметр—волновое число к, или, что тоже самое, длина волны возмуще-
возмущения Л = 2тг/к. Поэтому граница перехода от устойчивого течения к
неустойчивому будет определяться двумя параметрами — числом Рей-
нольдса Re и волновым числом к.
Подставим выражение (8.20) в уравнение (8.18) и учтем значения
производных:
дф , дф .. . дф iTf/ ф
дх2 ду2 V ) Ф
/у - 2кЧ" + к
Здесь штрихами обозначены производные по координате у. После под-
подстановки в (8.18) и деления на гк получаем
/У~2кЧ"+ ^4ф) • (821)
Это дифференциальное уравнение четвертого порядка называют
уравнением Орра-Зомерфелъда A937).
Граничные условия (8.19) принимают следующий вид:
Ф(у = 0, 1) =0, Ф/(г/ = О, 1)=0. (8.22)
Поскольку разрушение стационарного течения наблюдается при
больших числах Рейнольдса, то в первом приближении было бы це-
целесообразно исследовать эволюцию невязких возмущений. Действи-
Действительно, отсутствие вязкости эквивалентно бесконечно большому чи-
числу Рейнольдса (Re —> об). При этом правая часть уравнения (8.21)
становится пренебрежимо малой, математические преобразования су-
существенно упрощаются. Такая модель исследования устойчивости те-
течения впервые была использована Джоном Уильямом Рэлеем. Важ-
Важнейшим результатом этого исследования является установление связи
между профилем скорости стационарного движения жидкости и его
устойчивостью. В частности, Рэлей показал, что необходимым усло-
условием потери устойчивости течения в канале является наличие точки
перегиба профиля скорости, т. е. такой точки, в которой обращает-
обращается в нуль вторая производная скорости по поперечной координате.
Например, плоское течение Пуазейля характеризуется параболическим
профилем скорости, на котором отсутствуют точки перегиба, и потому
в приближении идеальной жидкости является устойчивым. Если по
каким-то причинам, например, под действием силы тяжести, профиль
Пуазейля деформируется, то течение в канале оказывается неустой-
неустойчивым.
8.4] Устойчивость движения в канале 195
Теория Рэлея породила так называемый парадокс гидродинамиче-
гидродинамической устойчивости, суть которого в следующем. Так как малые воз-
возмущения течения Пуазейля исчезают с течением времени без учета
вязкости, то с учетом вязкости, казалось бы, они должны исчезать
тем более. Ведь вязкость определяет диссипативные свойства жидко-
жидкости, играет стабилизирующую роль. Напрашивается следующий вывод:
если удается доказать устойчивость стационарного течения без учета
вязкости, то дальнейший анализ с учетом вязкости может изменить
только количественные значения определяющих параметров, но не по-
повлияет на качественный вывод об устойчивости движения жидкости.
Однако эксперимент и теория показывают, что учет вязкости приводит
к качественно новым результатам, позволяет определить границу пере-
перехода от устойчивого течения к неустойчивому.
После Рэлея исследование устойчивости течения жидкости в ка-
канале продолжил В. Гейзенберг A924). Он рассмотрел течение при
больших, но конечных числах Рейнольдса. Решение уравнения (8.21)
отыскивалось в виде разложения амплитуды возмущения Ф в степен-
степенной ряд по малому параметру е = 1/ Re. Позднее, в 1945 г., результаты
Гейзенберга были уточнены и обобще-
обобщены американским математиком Линь Re i
Цзя-Цзяо. С тех пор теория носит на-
название Гейзенберга и Линя.
Основной результат теории Гейзен-
берга-Линя состоит в обнаружении су-
существования так называемой нейтраль- 6rp
ной кривой на плоскости k — Re для
течения Пуазейля (рис. 8.7). Каждая
точка этой кривой соответствует кри- ^ф к
тическому значению числа Рейнольдса Рис 8 7 Нейтральная кривая
для возмущения с данным волновым
числом. Область неустойчивости внутри петли заштрихована, за пре-
пределами петли — область устойчивости.
Таким образом, точки кривой разделяют две области, определяют
границу устойчивости и потому являются нейтральными. Точка мини-
минимума кривой, соответствует критическим значениям числа Рейнольдса
(ReKp) и волнового числа (/гкр). Здесь ReKp — это наименьшее значение
числа Рейнольдса, при котором начинается рост возмущений. Как
показывают расчет и эксперимент для плоского течения Пуазейля,
ReKp = 5772, kKp = 1,02.
В теории к — безразмерное волновое число, связанное с длиной волны,
обезразмеренной по отношению к расстоянию между пластинами h.
Если Л — размерная длина волны, то к = 2тг/г/Л. Поскольку кК? « 1, то
это означает, что наиболее опасными являются возмущения с длиной
волны, превышающей высоту канала приблизительно в 2тт раз.
196 Турбулентность [Гл.8
При Re < ReKp возмущения с любыми волновыми числами являются
затухающими, т.е. движение устойчиво. Если Re > ReKp, то движе-
движение жидкости будет устойчивым только для точек плоскости к - Re,
лежащих слева и справа от петли, а для точек внутри петли — неустой-
неустойчивым. Справа от нейтральной кривой при некоторых значениях вол-
волнового числа в область неустойчивости можно попасть, уменьшая
число Рейнольдса. В этом случае вязкость играет дестабилизирующую
роль. Однако в области больших к (т.е. коротковолновых возмущений)
движение всегда устойчиво при любых числах Рейнольдса, даже при
Re —> оо. В этом случае коротковолновые возмущения подавляются
вязкостью жидкости.
Экспериментальная проверка теории Гейзенберга-Линя осложня-
осложнялась тем, что ожидание появления возмущений с различными зна-
значениями волнового числа и измерение соответствующих критических
чисел Рейнольдса требует больших затрат времени. В 1947 г. для
проверки теории была разработана оригинальная экспериментальная
методика, в которой стало возможным искусственно возбуждать воз-
возмущения. Узкая лента вводилась в жидкость перпендикулярно течению
и с помощью электромагнитного генератора приводилась в попереч-
поперечные колебания. От ленты вниз по потоку распространялись волны,
затухая или усиливаясь. Частота колебаний подбиралась так, чтобы
при заданном значении числа Рейнольдса волны не затухали и не
усиливались. Так определялись нейтральные точки. Существование
нейтральной кривой, предсказанное теорией Гейзенберга-Линя, полу-
получило экспериментальное подтверждение. Экспериментальные значения
критических параметров в области минимума кривой совпали с теоре-
теоретическими с точностью до погрешности измерений.
8.5. Сценарии зарождения турбулентности
Мы провели анализ устойчивости стационарных течений для двух
частных наиболее простых случаев — цилиндрического течения Куэтта
и течения Пуазейля в канале.
Вот уже второе столетие, начиная с первых работ Рейнольдса,
не ослабевает интерес физиков, математиков, инженеров к явлению
турбулентности. Настойчивые попытки хотя бы понять возможные ме-
механизмы разрушения стационарных течений жидкости пока не привели
к созданию общей теории гидродинамической устойчивости, справед-
справедливой для любых типов течений.
До недавнего времени существовали только линейные по возму-
возмущениям теории-гипотезы. Появление мощных компьютеров, развитие
качественной теории дифференциальных уравнений (теории динамиче-
динамических систем) положили начало численным исследованиям нелинейных
моделей перехода ламинарных течений в турбулентные.
Детальное изучение существующих моделей гидродинамической
устойчивости выходит за рамки данного курса, так как требует введе-
8.5] Сценарии зарождения турбулентности 197
ния новых понятий и определений, дополнительных знаний по некото-
некоторым разделам физики и математики.
Поэтому ограничимся обсуждением этих моделей лишь в общих
чертах. Но даже в этом случае полезно иметь представление о том, что
такое аттрактор и бифуркация.
8.5.1. Понятия аттрактора и бифуркации. Проще всего пояс-
пояснить смысл этих терминов можно на примере колебаний математиче-
математического маятника. Пусть маленький шарик массы т подвешен на невесо-
невесомой нерастяжимой нити длиной /, закрепленной в точке О (рис. 8.8).
Под действием сил тяжести и натяжения
нити шарик приобретает центростремительное
ускорение 10, где в — угол отклонения подве-
подвеса от положения равновесия, а верхними точ-
точками обозначено дифференцирование по вре-
времени. Если на шарик действует также сила
трения, обусловленная вязкостью среды и рав-
равная —2jml6, где 7 ~~ коэффициент трения,
то уравнение движения маятника запишется
в следующем виде:
в + 2j6 + ujI sin 0 = 0 , (8.23)
9,1 ^ » Рис- 8.8. Математиче-
где u;g = el1 — квадрат собственной цикличе- ский маятник
ской частоты колебаний.
В линейном приближении (при малых углах #, т.е. sin# « в) это
уравнение легко интегрируется при заданных начальных условиях.
Результат хорошо известен
в = в0 exp(-7?) sin(ujt + <р0) • (8.24)
Здесь #о — начальная амплитуда колебаний, uj =
лическая частота, (ро — начальная фаза колебаний, определяемая на-
начальными условиями.
При отсутствии трения G = 0) полученное решение описывает
незатухающие гармонические колебания. Такой маятник представляет
собой консервативную систему 0. При наличии сил трения G ф 0) ма-
маятник является диссипативной системой. Его свободные гармонические
колебания затухают, величина амплитуды уменьшается с течением вре-
времени по экспоненциальному закону с декрементом затухания j. В этом
случае энергия механических колебаний, пропорциональная квадрату
амплитуды, уменьшается за счет работы сил трения и рассеивается
(диссипируется) в окружающую среду в виде теплоты.
О Системы, в которых действуют только консервативные силы, т. е. силы,
работа которых не зависит от траектории движения тела, а определяется
только начальным и конечным положением этого тела, называются консерва-
консервативными. В противном случае, например при наличии неконсервативных сил
трения, системы называют диссипативными.
198 Турбулентность [Гл.8
Если отвлечься от физического объекта, для которого получено
уравнение (8.23), и обратиться к свойствам этого уравнения, то можно
рассмотреть случай 7 < 0. Тогда из решения (8.24) следует, что даже
при малом отклонении от положения равновесия энергия системы будет
неограниченно возрастать с течением времени по экспоненциальному
закону. Такое равновесие неустойчиво.
Часто необходимо исследовать такие физические системы и процес-
процессы, для которых не удается получить аналитические решения соответ-
соответствующих дифференциальных уравнений. В таких случаях используют
специально разработанную качественную теорию дифференциальных
уравнений. Основу этой теории составляет фазовое пространство
или, как часто говорят, пространство состояний, в котором осями
координат служат определяющие физические величины. Состоянию
системы в некоторый фиксированный момент времени в фазовом про-
пространстве соответствует одна точка — фазовая точка. При временной
эволюции системы эта точка движется в фазовом пространстве вдоль
некоторой кривой, которая называется фазовой траекторией. Сово-
Совокупность фазовых траекторий образует фазовый портрет системы,
дающий качественное представление о ее эволюции при различных
значениях управляющих параметров.
Вновь обратимся к уравнению (8.23). Только теперь вместо его
интегрирования представим решение на фазовой плоскости (в, в).
Полная механическая энергия маятника определяется суммой его
кинетической и потенциальной энергий
Е= ^т12в2 + mgl(l -cos6>). (8.25)
Отсюда скорость изменения энергии определится следующим выра-
выражением:
Ё 2 1)в. (8.26)
Сравнивая (8.26) с уравнением (8.23), получаем
Ё = -27ш/2 в2. (8.27)
Рассмотрим консервативную систему, для которой 7 = 0. В этом
случае Ё = 0, т. е. механическая энергия колебаний с течением вре-
времени не изменяется, Е = const. Тогда в линейном приближении
A - cos0 « в2/2) из уравнения (8.25) имеем
4+ -^-2 = 1, Л2 = ^^. (8.28)
A (Aujq) ml u0
Здесь учтено, что в любом случае энергия не может быть отрицатель-
отрицательной, Е ^ 0.
Таким образом, при отсутствии трения фазовой траекторией гармо-
гармонических колебаний на плоскости (в, в) является эллипс с полуосями
А и Aouq. При различных значениях энергии Е получим фазовый порт-
8.5]
Сценарии зарождения турбулентности
199
рет в виде семейства замкнутых кривых (эллипсов), охватывающих
точку равновесия 0 = 0 = 0 (рис. 8.9).
Из уравнения (8.27) видно, что скорость
изменения энергии колебаний пропорцио-
пропорциональна кинетической энергии
Е = -47ЕК,
1
2 л2
Ек = "- mlz О
(8.29)
Поскольку кинетическая энергия осцил-
осциллирует, то диссипация полной энергии в те-
течение периода колебаний Т = 2тт/со проис-
происходит неравномерно. Нас интересует среднее
изменение энергии за период
Е = -47#к
(8.30)
Рис. 8.9. Фазовый порт-
портрет незатухающих малых
колебаний для двух зна-
значений энергии, Еч > Е\
Известно, что для незатухающих гармонических колебаний средние
за период кинетическая и потенциальная энергии равны между собой.
Ввиду малости затухания колебаний за один период (|7| <С ио) можно
считать, что средняя кинетическая энергия равна половине полной
энергии, Ек = Е/2. Тогда имеем
Е = -2-уЕ.
(8.31)
Таким образом, усредненная за период колебаний скорость измене-
изменения энергии пропорциональна самой энергии. Если начальная механи-
механическая энергия равна Eq, to решением уравнения (8.31) будет
Е = #оехр(-27*).
(8.32)
Энергия колебаний пропорциональна квадрату амплитуды, Е ~ в2ш.
Поэтому изменение амплитуды колебаний в среднем за период описы-
описывается выражением
0 0G*), (8-33)
где #о — начальная амплитуда колебаний.
При малом коэффициенте затухания (|7| <С со) осциляции угла 0
близки к гармоническим при 7 = 0, т. е.
0 & 0ш s'm((jut + (fo), 0 « 0ти) cos((jut + ipo).
Отсюда фазовая траектория на плоскости @, 0) имеет вид
(8.34)
в в
¦V + ~^-^ = 1 • (8-35)
Мы получили уравнение спирали, закручивающейся G > 0) к точке
равновесия 0 = 0 = 0 или раскручивающейся G < 0) от нее. При
7 = 0 фазовой траекторией будет замкнутая кривая. Эти три случая
схематически показаны на рис. 8.10.
200
Турбулентность
[Гл.8
Основной вывод полученного результата состоит в следующем. При
7 < 0 положение равновесия неустойчиво, так как при малом откло-
отклонении от него действующие силы уводят систему еще дальше от рав-
новесия(фазовые траектории раскручиваются). При 7 = 0 положение
равновесия обладает нейтральной устойчивостью, поскольку смещения
у <0 у=0 у >0
Рис. 8.10. Фазовые траектории вблизи равновесия [3]
не усиливаются и не затухают со временем. В случае 7 > 0 лю-
любые смещения затухают с течением времени, все фазовые траектории
заканчиваются в начале координат фазовой плоскости. Поэтому при
7 > 0 точку фазовой плоскости 0 = 0 = 0 называют притягивающей
точкой или аттрактором (attraction в переводе с английского означа-
означает притяжение). В рассмотренном примере и в других случаях точеч-
точечный аттрактор соответствует стационарному равновесному состоянию
системы.
Мы рассмотрели собственные колебания, которые в реальных усло-
условиях при наличии трения с течением времени затухают. Для под-
поддержания колебаний необходимо внешнее воздействие силой, работа
которой компенсировала бы диссипацию энергии колебаний. При на-
наличии вынуждающей силы уравнение (8.23), описывающее свободные
колебания, должно быть модернизировано.
Действие постоянной внешней силы приводит лишь к смещению
положения равновесия. Например, действие силы тяжести на груз,
подвешенный на пружине, приводит к растяжению пружины, но не
может поддерживать колебания пружинного маятника. Поэтому вы-
вынуждающая сила должна быть переменной во времени.
Рассмотрим простой случай вынужденных колебаний математиче-
математического маятника под действием внешней силы, пропорциональной угло-
угловой скорости в. Кроме того, учтем, что вынуждающая сила подавляет
любые возмущения колебаний за конечный промежуток времени. Если
в результате каких-то возмущений энергия колебаний уменьшается
в некоторый момент времени, то работа внешней силы компенсирует
это уменьшение энергии. При случайном увеличении энергии маят-
маятника внешняя сила совершает отрицательную работу, восстанавливая
начальную величину энергии. Таким образом, любые возмущения ко-
колебательной системы не могут возрастать до бесконечности, как это
следует из уравнения (8.23). По этому принципу работает часовой
механизм, электрический колебательный контур и т.д.
8.5] Сценарии зарождения турбулентности 201
Дифференциальное уравнение колебаний, соответствующее таким
условиям, может быть формально получено из уравнения (8.23), если
величину 7 представить в виде
7 = -70 1 - ~2 , (8.36)
где 7о > 0, #о — начальная амплитуда. В этом случае имеем
7 < 0 при 02 < 0q, 7 > 0 при О2 > 01.
С учетом выражения (8.36) уравнение (8.23) для малых колебаний
(sin 0^0) будет иметь следующий вид:
в - 27о (l - 4 V + 0 = ° • (8-37)
Запишем это уравнение в безразмерном виде, выбирая
за единицу амплитуды и 1/оио — за единицу времени
0-(е-02H + 0 = О, (8.38)
где е = 270/^0 — безразмерный параметр.
Уравнение (8.38), известное как уравнение Ван дер Поля A922 г.),
имеет следующую замечательную особенность. Поскольку параметр е
положителен, то при малых отклонениях от равновесия О2 <С е это
уравнение описывает колебания, амплитуды которых увеличиваются
с течением времени по экспоненциальному закону. В плоскости @, 0)
фазовые траектории таких колебаний в окрестности начала координат
расходятся по спирали (см. рис. 8.10 при j < 0). В другом случае
при в2 ^> е уравнение Ван дер Поля описывает затухающие колебания,
фазовые траектории которых вдали от начала координат закручиваются
по спирали к началу координат (см. рис. 8.10 при j > 0). Численный
анализ показывает, что для каждого значения параметра е существует
единственное устойчивое решение уравнения Ван дер Поля. В плоско-
плоскости @, 0) этому решению соответствует замкнутая фазовая траекто-
траектория, к которой асимптотически стремятся другие фазовые траектории.
Таким образом, замкнутая фазовая траектория представляет собой
аттрактор, который А. Пуанкаре назвал предельным циклом.
В биологии ярким примером предельного цикла является дина-
динамика популяций. В частности, периодические колебания численности
рыб обусловлены существованием оптимального соотношения между
рыбами-хищниками и рыбами-жертвами, условно — между щуками и
карасями. Если щуки поедают слишком много карасей, то числен-
численность карасей падает, что приводит к сокращению щук. Сокращение
количества щук способствует увеличению числа карасей. Имеют место
циклические изменения численности видов.
На рис. 8.11 схематически показан фазовый портрет уравнения
Ван дер Поля. Решение, изображаемое замкнутой кривой представля-
202
Турбулентность
[Гл.8
Предельный
цикл
Рис. 8.11. Фазовый портрет
уравнения Ван дер Поля
ет собой предельный цикл, т. е. циклический аттрактор, к которому
стремятся все фазовые траектории. Обе кривые, одна из которых начи-
начинается вне предельного цикла, а другая внутри него, асимптотически
сходятся к предельному циклу с двух
сторон.
Заметим, что форма предельного
цикла существенно зависит от числово-
числового значения параметра е уравнения Ван
дер Поля.
Продолжим анализ уравнения (8.38),
полагая, что безразмерный параметр е
может быть как положительным, так и
отрицательным. При е < 0 начало коор-
координат фазовой плоскости 9 = 0 = 0 ха-
характеризует устойчивое равновесие, т. е.
является точечным аттрактором. При
е > 0, как мы видели, точка начала координат становится неустойчивой
и переходит в другой аттрактор — предельный цикл. Следовательно,
при е = 0 происходит качественное изменение решения уравнения
(8.38). Физически это соответствует качественной перестройке колеба-
колебательного движения при плавном изменении внешних условий.
Обобщая этот результат введем еще одно понятие, имеющее фун-
фундаментальное значение в теории сильно неравновесных систем и,
в частности, в теории турбулентности. Качественное изменение ре-
решения дифференциального уравнения при некотором фиксированном
значении параметра этого уравнения называется бифуркацией (bifur-
(bifurcation в переводе с английского означает раздвоение, разветвление).
Соответствующее значение параметра называется критическим, так
как при этом значении имеется несколько ветвей решения, устойчивых
или неустойчивых. Для уравнения
Ван дер Поля, как мы видели, кри-
критическим значением параметра е бу-
будет е = ек = 0. График зависимо-
зависимости свойства решения от параметра
уравнения называют бифуркационной
диаграммой. На рис. 8.12 показана
типичная бифуркационная диаграмма,
демонстрирующая качественную зави-
зависимость свойств решения уравнения
(8.38) для максимальной амплитуды
колебаний вт от параметра е.
При значениях е < ек устойчивое
решение соответствует точечному ат-
аттрактору. Напомним, что для уравнения (8.38) этой точкой на фазовой
плоскости (в, в) является начало координат, так как ек = 0. При
е = ек решение претерпевает качественное изменение: точечный ат-
Предельный
цикл
Неустойчивая
неподвижная точка
Точечный\
аттрактор
Рис. 8.12. Бифуркационная диа-
диаграмма уравнения Ван дер Поля
8.5 ] Сценарии зарождения турбулентности 203
трактор сменяется предельным циклом, а неподвижная точка фазового
пространства, которая была аттрактором, соответствует неустойчивому
решению (штриховая часть оси е на бифуркационной диаграмме).
Явление возникновения предельного цикла при некотором фикси-
фиксированном значении параметра е = ек называется бифуркацией Хопфа
(Hopf E., 1942). Предельный цикл в окрестности бифуркации Хопфа
обладает важным свойством. В частном случае уравнения Ван дер
Поля амплитуда предельного цикла вблизи точки ветвления пропор-
пропорциональна квадратному корню из параметра е, а в общем случае —
(е - екI/2. Это означает, что при плавном росте параметра е > ек,
начиная от точки бифуркации амплитуда растет как (е — екI/2. Это
составляет основу возможного сценария разрушения стационарного
ламинарного течения жидкости и зарождения турбулентности.
8.5.2. Сценарий Ландау-Хопфа. Основу сценария турбулизации
течения, предложенного Л. Ландау A944 г.) и независимо Е. Хопфом
A948), составляет гипотеза непрерывного перехода к турбулентности
через бесконечный каскад бифуркаций.
Ландау исходил из того, что уравнения Навье-Стокса и непре-
непрерывности всегда имеют стационарное решение, устойчивое при малых
числах Рейнольдса. Пусть этим решением для скорости течения будет
vo(r). Заметим, что скорость зависит только от радиуса-вектора г, но
не зависит от времени t.
Если в жидкости возникает возмущение, то скорость течения может
быть представлена в виде суммы скорости стационарного течения и
возмущения v(r, t) = vo(r) + vi(r, t). Как было показано, возмущение
vi описывается уравнением (8.5) и удовлетворяет стационарному гра-
граничному условию (8.6). Решение имеет вид
vi (r, t) = fo(r) exp(-ic^) . (8.39)
Подставляя это выражение в уравнение (8.5), можно определить
комплексные собственные частоты uj = а + Ы. Если все комплекс-
комплексные частоты имеют отрицательные мнимые части (Ь < 0), то малые
возмущения затухают и решение vo устойчиво. Если же при увели-
увеличении числа Re до некоторого критического значения Rei появится
одна собственная частота ш\ = а\ + b\i, мнимая часть которой равна
нулю (Ь\ = 0), то возникает состояние нейтрального равновесия, когда
возмущение не исчезает, но и не растет. При этом течение жидко-
жидкости становится периодическим по времени с частотой ш\ и периодом
Т\ =2tt/o;i.
Таким образом, значение управляющего параметра Re = Rei явля-
является первой точкой бифуркации решения уравнения (8.5).
Как поведет себя жидкость при дальнейшем увеличении чис-
числа Рейнольдса? Отвечая на этот вопрос, Ландау выдвигает гипо-
гипотезу о том, что существует такое значение Re = Re2, при котором
в жидкости возникает второе периодическое движение с частотой
UJ2, которое накладывается на первое с частотой uj\. Таким обра-
204
Турбулентность
[Гл.8
зом, течение жидкости становится квазипериодическим со скоростью
v(r, t) = vo(r) + vi (r, t) + V2(r, t), причем возмущение второго порядка
определяется следующим выражением:
= fi (r, i) exp(—i
(8.40)
Здесь амплитуда fi (r, i) — периодическая функция времени с периодом
Т\ основного колебательного движения. В соответствии с гипотезой
Ландау частоты колебаний uj\ и UJ2 должны быть несоизмеримы, т. е. их
отношение шъ/шх является иррациональным числом. Это существенно,
так как состояния, фазы которых отличаются на целое кратное 2тг
физически тождественны.
Значение Re = Re2 > Rei является второй точкой бифуркации ре-
решения уравнения (8.5). При дальнейшем увеличении числа Рейнольдса
и достижения им величины Re3 > Re2 возникает третье периодиче-
периодическое по времени движение с частотой cj3 и т.д. Следовательно, при
плавном увеличении числа Рейнольдса появляются точки бифурка-
бифуркации Rei, Re2, Re3,... и соответствующий спектр частот ш\, со2, <^з>
Сценарий Ландау предполагает, что с увеличением числа Рейнольдса
интервалы между точками бифуркации быстро сокращаются. Вновь
появляющиеся периодические движения жидкости имеют все более
мелкие масштабы. Наконец, число Рейнольдса достигает значение
ReKp, при котором точки бифурка-
бифуркации сливаются и решение уравнения
Навье-Стокса становится неустой-
неустойчивым. Таким образом, нерегуляр-
нерегулярное (турбулентное) течение возника-
возникает в результате бесконечного каскада
бифуркаций.
На рис. 8.13 показана бифур-
бифуркационная диаграмма перехода от
ламинарного течения при Re < Rei к
турбулентному при Re < ReKp через
бесконечный каскад бифуркаций Хоп-
фа. При плавном увеличении числа
Рейнольдса в каждой точке бифур-
бифуркации происходит рождение нового
предельного цикла. При этом ампли-
амплитуда / предельного цикла уменьша-
уменьшается с увеличением значения Re,
т. е. вновь рождающиеся возмущения
имеют все более мелкие масштабы. Течение жидкости приобретает
все более сложный и запутанный характер. Наконец при некотором
критическом значении Re = ReKp поток полностью турбулизуется.
Как изменяются фазовые траектории системы в пространстве состо-
состояний, в котором осями координат служат амплитуды фурье-компонент
скорости течения? При появлении первой частоты uj\ движение жид-
Re
Рис. 8.13. Бифуркационная диа-
диаграмма турбулизации течения по
сценарию Ландау-Хопфа; / — ам-
амплитуда возмущений; затемнен-
затемненная область при Re > ReKp соот-
соответствует турбулентному потоку
8.5]
Сценарии зарождения турбулентности
205
Рис. 8.14. Фазовая тра-
траектория при квази-
квазипериодическом движе-
движении в виде спиральной
кривой на поверхности
тора
кости становится устойчиво-периодическим. В пространстве состоя-
состояний точечный аттрактор превращается в предельный цикл, фазовые
траектории представляют собой замкнутые кривые. При увеличении
числа Рейнольдса, когда появляется второе периодическое движение
с частотой U2, течение становится квазипериодическим. В трехмерном
пространстве состояний двоякопериодическому
движению соответствует фазовая траектория
в виде незамкнутой намотки на двумерный
тор 0 (рис. 8.14).
Фазовая траектория квазипериодического
движения формируется наложением двух кри-
кривых. Основная частота ш\ соответствует вра-
вращению по образующей тора, частота uj^ — вра-
вращению на поверхности тора.
При дальнейшем увеличении числа Рей-
Рейнольдса появляется третья частота оо^. Резуль-
Результирующему движению жидкости в простран-
пространстве состояний соответствует фазовая траек-
траектория в виде незамкнутой кривой, намотанной на трехмерный тор.
Поскольку сценарий Ландау-Хопфа предполагает переход к нерегуляр-
нерегулярному течению через каскад конечного, но большого числа бифуркаций,
то геометрическим образом турбулентного потока в пространстве со-
состояний будет многомерный тор.
В настоящее время теория Ландау-Хопфа подвергается критике.
Основным аргументом являются ссылки на эксперименты, из которых
следует, что турбулизация потока происходит значительно быстрее, чем
это предсказывает теория.
8.5.3. Сценарий Рюэля-Такенса. В сценарии Д. Рюэля и
Ф. Такенса A971) турбулизация течения связывается с возникнове-
возникновением странного аттрактора после трех бифуркаций. Хаотическим
или странным аттрактором в физике называют ограниченный объем
пространства состояний диссипативной си-
системы, куда фазовые траектории только вхо-
входят, образуя внутри него неустойчивые цик-
циклы и незамкнутые блуждающие траектории.
Это своего рода «черная дыра», затягиваю-
затягивающая в себя все фазовые траектории и не вы-
выпускающая их наружу. На рис. 8.15 показан
один из известных странных аттракторов —
так называемый аттрактор Лоренца, харак-
Рис. 8.15. Странный ат- теризующий динамическое поведение жидко-
трактор Лоренца сти в условиях конвекции. Это первый стран-
0 Имеется ввиду поверхность «бублика» без заключенного в ней объема.
В данном случае речь идет о двумерной поверхности в трехмерном простран-
пространстве.
206
Турбулентность
[Гл.8
Рис. 8.16. Расхождение
первоначально близких
фазовых траекторий [3]
ный аттрактор, который был открыт (Э. Лоренц, 1963) и исследован.
Видно, что он представляет собой «клубок» непересекающихся фазо-
фазовых траекторий в элементе объема трехмерного пространства состоя-
состояний.
В отличие от обычных аттракторов (предельная точка, устойчивый
предельный цикл) странный аттрактор обладает замечательным свой-
свойством—чувствительной зависимостью от начальных условий (ЧЗНУ).
Физически это означает, что характер течения существенно зависит
от значений возмущений в момент их возникновения. С точки зрения
математического описания эволюции возмущений решения уравнений
гидродинамики сильно зависят от начальных условий. Если движение
устойчиво, то малая неточность в граничных
условиях приведет к такой же неточности
в конечном результате. Если же движение
неустойчиво, то эта неточность в начальных
условиях растет с течением времени и реше-
решение не предсказывает дальнейший характер
течения жидкости.
Вследствие ЧЗНУ две любые близкие
в начальный момент фазовые траектории на
странном аттракторе с течением времени рас-
расходятся (рис. 8.16).
Кажущееся противоречие между нашим представлением об ат-
аттракторе как объекте, притягивающем фазовые траектории, и ЧЗНУ,
приводящей к расхождению этих траекторий, свидетельствует лишь
о существовании нижней границы размерности аттрактора. На дву-
двумерной поверхности возникновение странного аттрактора невозможно.
Это связано с тем, что фазовые траектории не пересекаются. В про-
противном случае точка пересечения порождала бы две траектории, т. е.
существовало бы такое состояние, из которого
система ведет себя неопределенным образом.
Следовательно, разрушение двумерного тора и
превращение его в странный аттрактор невоз-
невозможно. Размерность тора, который может пе-
перейти в странный аттрактор должна быть не
меньше трех.
Для примера рассмотрим трехмерное фазо-
фазовое пространство. На рис. 8.17 показано пове-
поведение фазовых траекторий, которое в принципе
не может быть реализовано на двумерном торе.
Две первоначально близкие траектории расхо-
расходятся на плоскости по спирали, затем выходят
из плоскости и вновь возвращаются в центр
спирали. Бесконечное повторение этого процесса приводит к возник-
возникновению странного аттрактора как элемента фазового объема, внут-
Рис. 8.17. Расхождение
первоначально близ-
близких траекторий в трех-
трехмерном пространстве
состояний [3]
8.5 ] Сценарии зарождения турбулентности 207
ри которого эволюционирует притягивающее множество неустойчивых
траекторий.
Еще раз подчеркнем, что в соответствии со сценарием Рюэля-
Такенса течение может стать турбулентным уже после третьей бифур-
бифуркации. Напомним, что по теории Ландау переход к турбулентности
происходит через каскад бесконечного числа бифуркаций.
8.5.4. Сценарий Фейгенбаума. Сценарий Фейгенбаума
(M.J. Feigenbaum, 1978) представляет непрерывный переход к
турбулентности через бесконечный каскад бифуркаций с удвоением
периода. Эта идея родилась после анализа итерационного уравнения
жп+1 = гхп(\ - хп), (8.41)
где г — некоторая постоянная, принимающая значения в диапазоне
0 < г ^ 4; переменная хп принадлежит единичному интервалу [0, 1].
Видно, что значение хп+\ также принадлежит единичному интервалу
[0, 1]. Если считать, что индексы п и п + 1 относятся к настоящему
и последующему моментам времени, то уравнение (8.41) описывает
некоторый эволюционный процесс.
Решение, для которого хп+\ = хп, называют неподвижной точкой
(последующее решение равно предыдущему). При всех значениях г
существует неподвижная точка х = 0, и при г > 1 есть еще одна непо-
неподвижная точка х = 1 — 1/г. Пусть 1 < г < 3, тогда линейный анализ
показывает, что при любом начальном значении xq > 0 итерационный
процесс по уравнению (8.41) в пределе п —> оо приводит к решению
хп = 1 — 1/г. Таким образом, при 1 < г < 3 точка х = 1 — 1/г является
аттрактором. Если один шаг итерации принять за единицу времени, то
можно утверждать, что мы получили аттрактор с периодом 1. Действи-
Действительно, при хп = 1 — 1/г получаем жп+1 = 1 — 1/г, т.е. за один шаг
мы получили то же самое решение.
Ситуация принципиально изменяется при г > 3. Неподвижная точ-
точка х = 1 — 1/г в этом случае оказывается неустойчивой. Если на-
начальное значение xq как угодно мало отклоняется от этой точки,
то итерационный процесс (8.41) уводит решение еще дальше от нее.
Неподвижная точка х = 1 — 1/г уже не является аттрактором. Зато
при 3 < г ^ 3,45 появляются две такие особые точки с абсциссами х\
и х\, что
х\ = гх\{\ — ж*), х\ = гх\{\ — х%) .
Итерации попеременно совпадают то с одной из них, то с другой.
Начав с любой из этих точек, мы через два шага вновь вернемся
в нее. Следовательно, точки х\ и х\ образуют аттрактор с перио-
периодом 2, т. е. происходит удвоение периода. При дальнейшем увеличении
параметра г, т. е. при г > 3,45 появляется решение периода 4, а
решение периода 2 хотя и не исчезает, но теряет устойчивость. Плавное
увеличение параметра г до значения г^ « 3,56998 приводит к тому,
что устойчивые решения с периодом 2к последовательно заменяются
208 Турбулентность [ Гл. 8
устойчивыми решениями с периодом 2/с+1. Чем больше значение к,
тем меньше интервал значений г, при которых решение периода 2к
устойчиво. При г = Гоо итерации (8.41) становятся неустойчивыми,
наступает хаос. Если параметр г отождествить с числом Рейнольд-
са, то очевидна аналогия итераций (8.41) с теорией турбулентности
Ландау. Фейгенбаум также заметил, что значения параметра г, со-
соответствующие каждому удвоению периода, сходятся к значению г^
как геометрическая прогрессия со знаменателем 6 « 4,6692 Число 6
носит название постоянной Фейгенбаума.
Качественно проиллюстрируем сценарий Фейгенбаума примени-
применительно к уравнению Навье-Стокса:
^ + (vV)v = -- Vp + v Av . (8.42)
ОТ р
Если L и v — характерный размер и величина скорости течения
соответственно, то второе слагаемое в левой части уравнения (8.42)
имеет порядок v2/L, а второе слагаемое правой части можно оценить
как vvIL2. С учетом этих оценок уравнение (8.42) запишем качествен-
качественно в виде
^ = av2 + b + cv, (8.43)
где все коэффициенты не изменяются с течением времени.
Пусть в жидкости имеется некоторое характерное периодическое
течение с периодом Т. Тогда левую часть можно приближенно пред-
представить как л /* , гпч и\
dv v(t + T)-v(t) {R ,
Перепишем уравнение (8.43) для скорости жидкости в разностной
форме
v(t + Т) = av(i) + Cv2(t) + 7 , (8.45)
где а, /3, 7 — некоторые новые постоянные. Линейный член в правой
части уравнения (8.45) может быть исключен, если перейти в другую
систему отсчета, движущуюся относительно исходной с некоторой по-
постоянной скоростью V. Тогда уравнение (8.45) можно записать в виде
v(t + T) = v0 + \ ^, (8.46)
где vo — некоторая характерная скорость течения, например, скорость
тела, движущегося в жидкости, Л — безразмерная постоянная. Эта
постоянная может быть качественно идентифицирована с числом Рей-
нольдса, Re. Действительно, из приведенных выше оценок следует, что
отношение квадратичного члена уравнения Навье-Стокса к «вязкому»
имеет порядок vLjv = Re.
Разностное уравнение принимает следующий вид:
v(t + Т) = v0 - Re ^-^ . (8.47)
8.5 ] Сценарии зарождения турбулентности 209
Знак минус перед квадратичным членом выбран из тех соображений,
что в противном случае при vo > 0 скорость v неограниченно увели-
увеличивается при повторении периодов времени Т. Полученное уравнение
(8.47), качественно сохраняющее основные черты уравнения движения
Навье-Стокса, формально похоже на итерационное уравнение (8.41),
которое исследовал Фейгенбаум. Роль управляющего параметра играет
число Рейнольдса.
Строго периодическое решение означает, что v\(t + T) = v\(t). То-
Тогда из (8.47) получаем квадратное уравнение
vl=v0- Re ^^ , (8.48)
v0
решением которого будет
л/1 4- 4 Re — 1
2 Re
Для определенности мы взяли только положительный корень (8.48).
Рассмотрим малое возмущение этого периодического решения v =
= v\ + Av. Подставляя это в (8.47) и ограничиваясь членами первого
порядка малости по возмущению Av, получим
Av(t + Т) = -2 Re vi ^^ . (8.50)
Если выполняется неравенство 2Re^i < vq, to из уравнения (8.50)
следует: \Av(t + T)\ < \Av(t)\. Это означает, что возмущение периоди-
периодического решения со временем уменьшается, т. е. периодическое реше-
решение является устойчивым. Если же 2Rei?i > vq, to течение неустойчи-
неустойчиво, так как возмущение нарастает со временем. Потеря устойчивости
происходит в нейтральной точке при значениях Re = Rei и v\ = v*,
которые связаны между собой следующим соотношением:
2Rei^ = ?;o- (8.51)
Подставляя Re = Rei и v\ = v* в (8.49), а затем с учетом соотноше-
соотношения (8.51) исключая v*, получим
V^Rei+l =2, Rei =3/4. (8.52)
Таким образом, Re = Rei —точка бифуркации. Периодическое те-
течение со скоростью v\ устойчиво при Re < Rei и неустойчиво при
Re > Reb
В точке бифуркации Re = Rei, согласно (8.50), имеем Дг>(? + Т) =
= —Av(t) и, следовательно,
Av(t + 2Т) = -Av(t + Т) = Av(t).
Таким образом, течение со скоростью v\ + Av тоже периодично
с периодом 2Т, т. е. с удвоенным периодом исходного периодического
течения.
210 Турбулентность [Гл.8
Найдем условие потери устойчивости нового периодического тече-
течения с периодом 2Т. Для этого проитерируем уравнение (8.47) через
один период. Это дает
v(t + 2Т) = Vo(l - Re) + 2 Re2 ^ - Re3 ^ . (8.53)
^о vq
Поскольку v < vo, последним слагаемым правой части можно прене-
пренебречь как членом более высокого порядка малости. Введем обозначения
v(t) = v{t){\ -Re), A = 2Re2(Re-l). (8.54)
Тогда упрощенное уравнение (8.53) примет вид
v(t + 2T) = vo-\ ^ . (8.55)
Vo
Это уравнение формально совпадает с (8.47), если произвести за-
замену v —> v и Re —> А. Поэтому повторяя проведенный выше ана-
анализ, согласно (8.52), получим, что потеря устойчивости периодическим
течением с периодом 2Т происходит при Л = Л2 = 3/4. Тогда из
(8.54) находим, что соответствующее значение числа Рейнольдса равно
Re = Re2 = 1,23. Это вторая точка бифуркации.
Следовательно, периодическое течение с периодом 2Т устойчиво
при Re < Re2 и неустойчиво при Re > Re2.
Результат следующей итерации уравнения (8.47) еще на один пе-
период даст условие устойчивости течения с периодом 4Т. Очевидно
потеря устойчивости этого периодического течения будет происходить
при II = 3/4 fjL = 2А2(А - 1). Отсюда А = А3 « 1,23 и Re3 « 1,34. Мы
получили третью точку бифуркации.
Следующее число Рейнольдса, при котором происходит потеря
устойчивости периодического течения с периодом 8Т, равно Re = Re4 ~
w 1,36.
Повторяя итерационную процедуру мысленно бесконечное число
раз, получим, что полная потеря устойчивости течений со всеми пе-
периодами имеет место при достижении критического числа Рейнольдса
ReKp. В соответствии с (8.54) это число определяется из уравнения
ReKp = 2Re2p(ReKp-l). (8.56)
Отсюда получаем
( /)/ 1,37.
Область Re > ReKp соответствует возникновению турбулентности.
Отметим быстрое сближение чисел Рейнольдса Ren с ростом номе-
номера п, соответствующего потери устойчивости периодического течения
с периодом 2П~1Т. Из проведенных оценок следует, что уже при
Re « Re4 возникающие вихревые потоки быстро разрушаются и течение
становится турбулентным. Это качественно согласуется со сценарием
Рюэля-Такенса.
8.6] Уравнения Рейнольд с а 211
8.6. Уравнения Рейнольдса
Свойства турбулентного движения очень сложны и известны глав-
главным образом из экспериментов. Опыты показывают, что при установив-
установившемся турбулентном движении скорость в данной точке пространства
все время изменяется как по величине, так и по направлению. Также
изменяется и давление. Если измерить изменение мгновенной продоль-
продольной компоненты скорости в данной точке трубы с течением времени,
то получим примерный график, изобра-
изображенный на рис. 8.18.
Из рисунка видно, что при устано-
установившемся движении компонента скоро- {vx)
сти вдоль оси трубы (ось х) пульсиру-
пульсирует около некоторого среднего значения,
определяющего расход жидкости в трубе.
Если использовать более чувствительный
и менее инерционный прибор, то обна-
ружилось бы, что при увеличении чис- Рис'8Л8' n^cau™ скор°-
ла Рейнольдса каждый кажущийся более
или менее прямолинейным участок кривой (рис. 8.18) на самом деле
представляет собой также некоторую зигзагообразную ломаную линию.
Очевидно, поперечная составляющая скорости будет пульсировать око-
около среднего значения, равного нулю.
Средние значения некоторой компоненты скорости и давления мо-
могут быть получены следующим образом:
Г
= ± \pdt. (8.57)
Здесь Т — промежуток времени, достаточно большой по сравне-
сравнению с «периодом» основных пульсаций скорости, но в то же время
достаточно малый по сравнению с характерным временем медленного
изменения основного нестационарного течения (осредненное по случай-
случайным пульсациям движение может быть и нестационарным). При этом
условии начало отсчета промежутка времени Т произвольно и может
быть принято за нуль.
Очевидно, что с точки зрения теории в выборе пульсаций, по
которым необходимо усреднять, существует определенный произвол.
Однако на практике этот выбор очевиден.
Тогда мгновенное значение скорости или давления в любой момент
времени можно представить следующим образом:
Vi = (vi) + v'it p=(p)+pf. (8.58)
Здесь v[ и р' — пульсационные скорость и давление соответ-
соответственно.
212 Турбулентность [Гл.8
Будем полагать, что турбулентное движение содержится в точных
решениях уравнения Навье-Стокса. Рассмотрим несжимаемую жид-
жидкость и усредним каждый член уравнения движения.
Определим правила усреднения. Пусть f(x, у, z, t) — некоторая
пульсирующая характеристика движения, мгновенное значение
которой в данной точке пространства можно в любой момент времени
представить в виде
т
/ = </> + /', </} = ^ \fdt. (8.59)
о
Очевидно, по определении (/') = 0 . Среднее значение суммы равно
сумме средних
</l+/2) = </l} + (/2>. (8.60)
Среднее значение произведения двух величин, из которых лишь
одна испытывает пульсации, равно произведению средних
<(/!> • /2> = </>>¦ </2> , ((/.) • /2> = </1> • </2> = 0 • (8.61)
Среднее значение двух независимых пульсирующих величин не
равно произведению средних
(/i • /2> = (/!>• (Н) + (/,' • П), (/,' • П) ф 0. (8.62)
Среднее значение производной от пульсирующей характеристики
равно производной от среднего значения
/df\ d(f) /df\ d(f) ,Rfi,.
Ш/ = -дГ' fe/ = ^7' (8-63)
Заметим, что, согласно интегральной формуле осреднения по вре-
времени Т, два последних соотношения выполняются лишь приближенно.
Далее, невозможно осреднить все характеристики движения одина-
одинаковым образом, не нарушая вида основных физических законов. На-
Например, если в уравнении состояния идеального газа мы одинаковым
образом усредним давление р, плотность р и температуру Т , то,
согласно принятым правилам, получим
I <"> <т> + 1л <"'т'> •
Но тогда закон Клапейрона-Менделеева не будет справедлив для сред-
средних величин, что, по-видимому, физически некорректно.
Поэтому в различных теориях турбулентности применяют различ-
различные правила для осреднения различных величин, характеризующих
движение.
По вышеприведенным правилам проведем осреднение уравнений
Навье-Стокса для несжимаемой жидкости (р = (р) = const). Для этого
8.6] Уравнения Рейнольд с а 213
коэффициент кинематической вязкости и будем считать постоянным О
и примем во внимание, что
/dvkvi\ / dvk\ д , х
= \-в^Г/ - \Vid^k/ = Ъ^к {vkVi) =
к <^>+к <« <> S+ ^ <« • (8-64)
= к
Здесь учтено уравнение неразрывности для несжимаемой жидко-
жидкости dvk/dxk = 0. Тогда при отсутствии массовых сил уравнения
Навье-Стокса и неразрывности после осреднения будут иметь вид
ЁЫ + {Vk) вЫ = ЛЁШ + „#Ы-Л- ,vw.) ЁМ. = о
at +{к> дхк р дхг + дх\ дх„Кк%'' дхк
(8.65)
Первые два члена в правой части можно записать через осреднен-
ный тензор напряжений (Pjfe) = —{p)&ik + (&ik) B виде
+
Р OXi дхк Р
Теперь осредненные уравнения Навье-Стокса можно представить
следующим образом:
Таким образом, уравнения движения для средних величин имеют
тот же самый вид, что и для мгновенных величин, но при этом со-
содержат дополнительный член —р(У}У'к), — турбулентные напряжения
или напряжения Рейнольдса. Тензор турбулентных напряжений — это
симметричный тензор второго ранга
Tik = -р(у№) • (8-68)
При турбулентном движении общий тензор напряжений включает
в себя давление жидкости, вязкие и турбулентные напряжения
+ (Zik) + Tik • (8.69)
Уравнения (8.67) называются уравнениями Рейнолъдса для осред-
ненного турбулентного движения вязкой несжимаемой жидкости.
Происхождение дополнительных напряжений при турбулентном
движении физически очевидно. Вязкие напряжения возникают вслед-
вследствие направленного переноса импульса молекулами из слоя жидкости,
движущегося с большей макроскопической скоростью к соседнему мед-
медленно движущемуся слою. При турбулентном движении перенос им-
0 Это строго справедливо только для разреженных газов при постоянной
плотности и неизменной температуре. В случае плотных газов и жидкостей
коэффициент вязкости зависит от давления и, следовательно, изменяется при
изменениях давления.
214 Турбулентность [Гл.8
пульса от одного слоя жидкости к другому, соседнему, происходит не
молекулами, а индивидуальными макроскопическими частицами жид-
жидкости, движущимися с осцилирующими относительно среднего значе-
значения скоростями. Поэтому иногда турбулентно движущуюся жидкость
рассматривают как жидкость, обладающую некоторой дополнительной
турбулентной вязкостью, и записывают по аналогии с молекулярной
вязкостью несжимаемой жидкости (Т.В. Буссинеск, 1877)
Tik = r,J^+ °J2±>) , (8.70)
\ dx dx J
где 77т — коэффициент турбулентной вязкости.
В этом случае при исследовании турбулентного движения акцент
переносится на изучение турбулентной вязкости, а уравнение Рей-
нольдса можно записать в виде
at ' x Kl dxk p dxi p v' ' ll> dx\ ' dxk
(8.71)
Однако достигнутое упрощение проблемы только кажущееся, так
как турбулентная вязкость в отличие от молекулярной не является
консервативным параметром, характеризующим только саму жидкость,
а зависит от свойств и геометрии течения, в частности, от числа
Рейнольдса. Причем при больших числах Рейнольдса коэффициент
турбулентной вязкости значительно больше коэффициента молекуляр-
молекулярной вязкости.
Таким образом, для определения осредненного движения несжима-
несжимаемой жидкости имеем четыре уравнения (8.67). К числу неизвестных
добавилось еще шесть неизвестных компонент симметричного тензора
турбулентных напряжений. В результате система уравнений гидроди-
гидродинамики оказалась незамкнутой. Для замыкания системы уравнений
имеется два пути. Необходимо или каким-то образом выразить компо-
компоненты тензора турбулентных напряжений через осредненные скорости
и их производные (Прандтль, Карман) или дополнить систему урав-
уравнений (8.67) какими-либо уравнениями, которые устанавливают связь
между средними и пульсационными скоростями или их моментами
(Фридман). К сожалению, ни тот, ни другой путь сегодня не привел
к созданию удовлетворительной количественной теории турбулентного
движения.
8.7. Теории Прандтля, Кармана и Дайслера
Теория Прандтля A925) турбулентного движения жидкости осно-
основывается на аналогии с молекулярным движением в газе. Применяется
в основном к одномерным течениям (пограничные слои, каналы, тру-
трубы). Рассмотрим плоское турбулентное движение несжимаемой жидко-
жидкости вдоль бесконечной стенки (рис. 8.19).
8.7] Теории Прандтля, Кармана и Дайслера 215
Выберем два слоя, параллельных оси х. Среднюю скорость дви-
движения частиц жидкости в них обозначим через (vx) = и и и + du.
Из топологии течения очевидно, что средняя скорость зависит только
от поперечной координаты, и = и(у), а средняя поперечная скорость,
представляющей собой поперечные осциляции скорости около нулевого
значения, равна нулю, (vy) = 0.
Пусть расстояние между слоями равно V.
Прандтль по аналогии с кинетической теорией
газов предполагает, что V — некоторый аналог
средней длины свободного пробега молекул
в газе. Тогда частицы жидкости могут пере-
переходить из слоя в слой лишь благодаря сво-
3
4 u + du
f
u
им поперечным пульсационным скоростям vy.
Причем импульсы таких частиц сохраняются х
при прохождении длины V. Частица жидко- рис g 19 к теории
сти, попадающая из нижнего слоя в верхний, ' ' прандтля
имеет среднюю скорость и, отличающуюся от
средней скорости и + du верхнего слоя на du. Очевидно, «сталкиваясь»
в верхнем слое с его частицами, она может изменять скорость послед-
последних также на величину порядка du. Это изменение создает пульсацию
v'x порядка du. Таким образом, полагаем
v'~ du~lf — . (8.72)
dy
Полагая далее турбулентность изотропной (по крайней мере вдали
от стенки), v'x ~ v'y, для тензора турбулентных напряжений получим
\Txy\ = p(v'xv'y) = kp((l'f)(^\ =P12(^) , I2 = k((l'f).
I—г (873)
Величина / = у к{A') ) называется длиной пути перемешивания,
которая может зависеть от поперечной координаты у.
Далее Прандтль предполагает, что вблизи границы длина пути
перемешивания прямо пропорциональна расстоянию от стенки
1 = ?у- (8.74)
Здесь ? — некоторый безразмерный коэффициент пропорциональности.
Предположение (8.74) можно подкрепить рассуждением о том, что
стенка препятствует развитию поперечных пульсационных скоростей
и, очевидно, на самой стенке длина пути перемешивания должна быть
равна нулю.
Очевидно, турбулентное напряжение при стационарном движении
вдоль бесконечной стенки не должно зависеть от у и должно рав-
равняться его значению то на самой стенке. Действительно, рассмотрим
в плоскости хОу некоторую частицу жидкости в виде прямоугольника
(рис. 8.19). При прямолинейном и равномерном движении в соответ-
216 Турбулентность [Гл.8
ствии с первым законом динамики на нее не должна действовать
какая-либо сила. Поскольку давление вдоль оси х постоянно, то силы
давления, действующие на грани 1-2 и 3-4, равны между собой по
величине и противоположны по направлению. Следовательно, должны
быть равны и противонаправлены силы трения, действующие на грани
1-4 и 2-3. Таким образом, в поперечном направлении пристеночной
области течения тензор турбулентных напряжений одинаков, Тху = то.
Тогда для определения средней скорости имеем уравнение:
t2 2 (du\ du 1 [tq 1 /Q ryrx
то = pi у [ ~г ) ' т~ = 7 \ — ~ • (8.75)
\dyJ dy ? у р у
Решение имеет вид
1 HZ
(8.76)
Таким образом, из (8.76) следует, что средняя скорость турбулент-
турбулентного движения вязкой несжимаемой жидкости вдоль бесконечной стен-
стенки распределена по логарифмическому закону. Величина \Ао/р имеет
размерность скорости и обычно обозначается следующим образом:
Формулу (8.76) удобно записать в безразмерном виде. Для этого соста-
составим безразмерную комбинацию из величин у, v, v*. Такой комбинаци-
комбинацией является выражение yv*/v. Тогда формулу (8.76) можно записать
в виде
Л 11п!^ + С1. (8.77)
Очевидно, что и при турбулентном движении жидкости на по-
поверхности обтекаемого тела вследствие условий прилипания всегда
существует тонкий пристеночный слой, в котором преобладают силы
вязкости и жидкость движется ламинарно. Этот слой называется «вяз-
«вязким подслоем». Ясно, что формула (8.77) справедлива лишь вне вязкого
подслоя. Постоянная с\ должна быть определена экспериментально.
Другую формулу для турбулентных напряжений, исходя из сообра-
соображений размерности, получил Т. фон Карман A930):
Тху — —рк2
(du/dy)
(d u/dy )
du
dy
(8.78)
Здесь &2 — универсальная постоянная, экспериментальное значение
которой по данным разных авторов составляет 0,36-0,40.
Формулы Прандтля и Кармана неприменимы в области течения,
непосредственно прилегающей к стенке, так как здесь существенна
8.8] Цепочка уравнений Фридмана 217
молекулярная вязкость. Для этой области следующую эмпирическую
формулу предложил Р.Г. Дайслер A955):
^)]^y, (8.79)
где п — эмпирическая постоянная. Измеряя распределение скоростей
турбулентных потоков в трубах, Дайслер нашел, что п = 0,124.
8.8. Цепочка уравнений Фридмана
Альтернативный метод замыкания уравнений гидродинамики тур-
турбулентного течения разработал А.А. Фридман. Этот метод состоит в
построении из уравнения Навье-Стокса цепочки эволюционных урав-
уравнений для моментов пульсаций скорости. Моментом п-го порядка для
пульсаций будем называть тензор п-го ранга в трехмерном простран-
пространстве т
Щ (« <) }
о (8.80)
Например, для первых моментов имеем
M°=l, Mli=(v/i}=0, M2ik = {v'iv'k) = --Tik. (8.81)
Моменты высших порядков не имеют физического смысла. Тем не
менее для каждого из них можно построить эволюционное уравнение.
Покажем схему вывода такого уравнения для момента второго порядка
(для турбулентных напряжений).
Как и ранее полагаем, что турбулентное течение может быть описа-
описано уравнением Навье-Стокса. Для несжимаемой жидкости при отсут-
отсутствии массовых сил оно имеет вид
^± + v.^ = -Ll^ + l/^i. (8.82)
3 H г OXj
Умножая это уравнение на vk, получим
Лл' Л- 1 dp d2Vi ,яя^
— — Ь wk 2~ • (о.оо)
Р хг OXj
Далее умножим уравнение Навье-Стокса для к-и компоненты ско-
скорости на Vi. Соответствующее выражение можно формально получить
из (8.83) после замены г —ь к, к —> i:
V.^ + V.V.^--V.LJ^ + vv. t^ (8 84)
dt ^ dxj p dxk dx)
Складывая уравнения (8.83) и (8.84), получаем
— I Hi. — 1- П- — I -I- Vlli.
dXj p \ dXi dxk) dx1. dx1.
(8.85)
218 Турбулентность [Гл.8
Подставим мгновенные скорости и давление в виде (8.58) и про-
проведем осреднение по правилам (8.58)-(8.63). В результате получим
следующее уравнение для момента второго порядка:
+{V) {VV} {VV} {VVV)
dt +{Vj) dXj {ViVi} dXj {VkVi} dXj
Мы получили уравнение эволюции тензора турбулентных напря-
напряжений. Видим, что оно включает новые моменты второго порядка,
описывающие корреляции пульсаций компонент скорости с градиентом
давления и скорости с лапласианом скорости, и момент третьего по-
порядка. Для этих новых моментов также можно вывести эволюционные
уравнения и т.д. Система уравнений для моментов все возрастаю-
возрастающих порядков называется цепочкой уравнений Фридмана. Уравнение
Рейнольдса (8.67) и уравнение (8.86)— два первых уравнения этой
цепочки. Но при этом центральная проблема теории турбулентности,
получение замкнутой системы уравнений для турбулентных течений,
остается нерешенной, так как цепочка не замкнута. Действительно,
эволюционное уравнение для момента п-го порядка содержит момент
(п + 1)-го порядка.
В настоящее время не разработаны обоснованные критерии обры-
обрыва цепочки уравнений Фридмана. Обрыв осуществляют произвольно,
выражая моменты высших порядков через моменты низших порядков.
При этом используют различные полуэмпирические модели, основан-
основанные на интуиции и экспериментальных данных. В основе простейших
моделей лежит теория Прандтля. В предыдущем параграфе эта теория
позволила выразить момент второго порядка (тензор турбулентных
напряжений) через производные по координатам от компонент средней
скорости. Точно также, используя понятие длины пути перемешивания,
можно выразить момент третьего порядка через моменты второго по-
порядка или момент четвертого порядка через моменты третьего порядка
и так далее. Очевидно, что появляющиеся при этом феноменологиче-
феноменологические коэффициенты должны быть определены из эксперимента.
8.9. Турбулентное движение жидкости в трубах
Движение жидкости в трубах, как очень важное для практики,
интенсивно изучается на протяжении многих лет, начиная с работ
Пуазейля A840-1842) и Рейнольдса A876-1883). Более ранние опыты
в существенной мере оказались бесполезными для науки, так как
исследователи не имели представления о подобии движений и зачастую
в экспериментах изучали зависимости от некоторых отдельных пара-
параметров, характеризующих движение (диаметр трубы, плотность жидко-
жидкости, скорость движения и т.д.). Возможность правильной постановки
8.9] Турбулентное движение жидкости в трубах 219
опытов и обобщения их результатов появилась лишь после открытия
критерия динамического подобия потоков — числа Рейнольдса.
8.9.1. Гладкие трубы. Блазиусом A911) в основу обобщения
экспериментальных результатов было положено число Рейнольдса, что
позволило ему эмпирически найти формулу для коэффициента сопро-
сопротивления труб при турбулентном движении, пригодную для любых
жидкостей в широком диапазоне изменения скорости и диаметров труб:
A=rfA^ = 03164 Re=pvd шз Re 10s (8g7)
L Pv2/2 Re1/4 V
Здесь U — средняя по сечению трубы осредненная скорость движе-
движения жидкости; р, rj — плотность и вязкость жидкости; d, L — диаметр
и длина трубы; Ар — перепад давления на концах трубы.
Таким образом, формулы для расчета сопротивления гладких, круг-
круглых цилиндрических труб в соответствии с G.27) имеют общий вид
Ар=ф\к, A = A(Re), Re = ^. (8.88)
Блазиус установил, что для турбулентных течений коэффициент
сопротивления определяется выражением (8.87), а для ламинарного
движения
А = jg . (8.89)
Из формул (8.87)-(8.89) видно, что сопротивление труб при лами-
ламинарном движении пропорционально первой степени средней скорости,
тогда как при турбулентном движении оно пропорционально т;7/4 или
приблизительно квадрату скорости.
Из закона сопротивления трубы для турбулентного течения при
некоторых предположениях можно вывести закон распределения ско-
скорости по сечению трубы.
Предположим, что при турбулентном движении жидкости в трубе
обеспечивается кинематическое подобие при изменении скорости и
радиуса трубы. Это означает, что если в какой-то точке трубы ско-
скорость изменилась в некоторое число раз, то во всех точках трубы
она изменится, во столько же раз. Если за характерную скорость
выбрать скорость на оси трубы г?тах , то это условие можно записать
следующим образом: / ч
v = vmaxf (^) . (8.90)
Здесь у — расстояние от стенки, го — радиус трубы. Из формулы
(8.90) следует, что средняя по сечению скорость и пропорциональна
скорости на оси трубы и что коэффициент пропорциональности не
зависит ни от г>тах, ни от радиуса трубы. Действительно,
ГО 1
v = ^r\f (-Jтг(г0 -y)dy = 2?w \f(y-\(l-JL\d]L = ^max,
ТГГп J V Го / J \rO/\ 7*0/ r0
0 ° (8.91)
где к — некоторая постоянная.
220 Турбулентность [ Гл. 8
Кроме того, из формулы (8.90) следует, что местная скорость v
зависит только от отношения у/го и не должна зависеть от радиуса
трубы как-то иначе.
Выразим сопротивление трубы Ар через силу трения го, действую-
действующую на единицу площади стенки. Рассматривая осредненное по вре-
времени движение жидкости в трубе как равномерное и прямолинейное,
можем записать
Ар ^- = TrdLro , Ар = 4т0^ . (8.92)
4 а
Используя (8.76), (8.87) и (8.92), имеем
pv2
, L pv2 L 0,3164 _ ,1/7 1/7 /о по\
4т0 — = ^- — гут , v ~ d4' ~ ту . (8.93)
d 2 d (pvd/r])l/4 °
Из выражений (8.90) и (8.91) следует:
1
(8.94)
к \ то /
Поскольку v ~ г0' , как это установлено в (8.93), из гидродинамиче-
гидродинамического подобия движения жидкости следует, что
Здесь учтено, что на оси трубы скорость движения жидкости макси-
максимальна и поэтому при у = го, согласно (8.90), должно выполняться
условие /A) = 1.
Следовательно, для распределения по сечению трубы осредненной
по времени скорости при турбулентном движении имеем
г ч 1/7
--J , (8.96)
где г = (го — у) — расстояние до оси трубы.
Из формулы (8.96), используя (8.91), нетрудно получить следующее
соотношение: QR
^=^^ах. (8.97)
Таким образом, при турбулентном движении средняя скорость дви-
движения жидкости по трубе мало отличается от максимальной, в отличие
от ламинарного движения, при котором v =
= ^max/2.
На рис. 8.20 представлены примерные
эпюры скоростей при ламинарном и турбу-
турбулентном движении жидкости в трубе.
Впоследствии турбулентное движение
жидкости в трубах изучалось многими
Рис. 8.20. Профили скоро- исследователями. Для коэффициента со-
стей при ламинарном (/) и противления трубы в настоящее время су-
турбулентном B) течениях ществует более десятка различных эмпири-
8.9]
Турбулентное движение жидкости в трубах
221
ческих формул. Так, в 1932 г. Никурадзе, обработав свои эксперимен-
экспериментальные результаты в духе теории турбулентности Прандтля (8.77),
получил для распределения скоростей следующую эмпирическую фор-
формулу:
J J
1
— =2,50 In
,5.
(8.98)
Здесь у — расстояние от стенки трубы. Формула (8.98) хорошо опи-
описывает экспериментальные результаты во всех точках сечения трубы,
кроме, конечно, тонкого ламинарного подслоя, примыкающего непо-
непосредственно к стенке. Из этой формулы можно получить закон сопро-
сопротивления (коэффициент сопротивления) трубы
-U =0,880 In (Re VX) - 1,01, 4 • 103 ^ Re ^ 32 • 105.
л/А V /
Re «2300
In Re
Рис. 8.21. Коэффициент со-
сопротивления при ламинар-
ламинарном (/) и турбулентном B)
течениях
(8.99)
Формула Никурадзе (8.98) справедлива в более широком диапа-
диапазоне изменения чисел Рейнольдса, но более сложна для практического
использования, чем формула Блазиуса
(8.87). График качественной зависимо-
зависимости коэффициента сопротивления гладких
труб от числа Рейнольдса изображен на
рис. 8.21.
Как видно из рис. 8.21, при пере-
переходе от ламинарного режима течения к
турбулентному коэффициент сопротивле-
сопротивления трубы возрастает скачком. Тщатель-
Тщательные опыты Никурадзе показывают, что по-
показатель степени в формуле (8.96) для
распределения скорости по сечению трубы
непрерывно убывает от 1/6 при Re = 4х
х 103 до 1/10 при Re = 32 • 105. Это соот-
соответствует тому, что сопротивление трубы (Ар) с увеличением числа
Рейнольдса приближается к квадратичному закону в зависимости от
средней по сечению скорости движения.
8.9.2. Шероховатые трубы. Выше рассмотрено турбулентное
движение жидкости в гладких трубах. Опыт показывает, что степень
шероховатости внутренней поверхности трубы существенным образом
сказывается на ее сопротивлении, причем тем сильнее, чем больше
число Рейнольдеа. Так, трубы после длительной эксплуатации (вслед-
(вследствие коррозии) увеличивают коэффициент сопротивления более чем
в два раза. Очевидно, формулы для распределения скоростей и для
коэффициента сопротивления каким-то образом должны учитывать
шероховатость труб. Это тем более очевидно, что шероховатость труб
является геометрическим параметром, необходимым для динамическо-
динамического подобия потоков.
На рис. 8.22 приведены опытные кривые Никурадзе. Обозначим
среднюю высоту бугорков шероховатостей на стенках трубы через h.
222
Турбулентность
[Гл.8
пк
Ламинарный
I
Re я 2300
In Re
В опытах Никурадзе шероховатость создавалась искусственно прикле-
приклеиванием к стенкам трубы песка, имеющего некоторый средний размер
зерен h.
Очевидно, что трубы будут гео-
геометрически, а потоки динамически
подобны, если для них сохраняет-
сохраняется отношение h/ro. Следователь-
Следовательно, и формулы для распределения
скоростей и коэффициента сопро-
сопротивления шероховатых труб долж-
должны быть некоторыми функциями от
относительной шероховатости h/ro.
На рис. 8.22 показаны эксперимен-
экспериментальные кривые при различных зна-
значениях относительной шероховато-
шероховатости h/ro.
Обрабатывая многочисленный
экспериментальный материал, Ни-
Никурадзе получил результаты, приве-
приведенные на рис. 8.22. График 8.22
можно разбить на три области чисел
Рейнодьдса — область ламинарного движения I, переходная область II
и область III, в которой Л не зависит от числа Рейнольдса. Очевидно,
что экспериментальные кривые трудно описать некоторой единой
формулой. Однако для больших чисел Рейнольдса (область III),
в которой, как видно из графика, ко-
коэффициент сопротивления не зависит от
числа Рейнольдса, а зависит лишь от от-
относительной шероховатости, Никурадзе
приводит следующие эмпирические фор-
формулы:
Рис. 8.22. Зависимость коэффи-
коэффициента сопротивления от чис-
числа Re при турбулентном тече-
течении в трубах различной шерохо-
шероховатости; h — средняя высота ше-
шероховатостей, го — радиус трубы;
(h/ro)i < (h/roJ < (h/roK <
< (h/ro)A
— =2,50 In f + 8,48,
г>* h
-U=0,87 In ^ + 1,74,
/X h
(8.100)
In — >4,25.
Вышеприведенное условие примени-
применимости формул (8.100) на практике почти
всегда выполняется.
Сложный характер кривых можно
истолковать физически следующим об-
образом (рис. 8.23).
При ламинарном движении (область а), если шероховатости не
загромождают сечение трубы, их влияние никак не сказывается на
Рис. 8.23. Влияние шерохова-
шероховатости стенки на турбулизацию
течения
8.10] Развитая турбулентность 223
сопротивление трубы. При этом, очевидно, бугорки шероховатостей
погружены в неподвижную между ними жидкость, играющую роль
смазки (рис. 8.23а). Даже при турбулентном движении основного
потока около стенки всегда существует ламинарный подслой, который
прикрывает бугорки шероховатостей.
При дальнейшем увеличении числа Рейнольдса (область б) вер-
вершины бугорков начинают обнажаться и с них срываются вихри, что
создает дополнительную турбулизацию потока, а следовательно, уве-
увеличение сопротивления (рис. 8.23 6). Причем это произойдет при тем
больших числах Рейнольдса, чем меньше относительная шероховатость
трубы. Наконец, при больших числах Рейнольдса (область в) бугорки
шероховатостей полностью обнажаются (рис. 8.23 в) и степень турбу-
лизации потока полностью определяется вихрями, срывающимися с их
вершин, а следовательно, коэффициент сопротивления не зависит от
числа Рейнольдса, характеризующего основное движение в трубе.
8.10. Развитая турбулентность
Рассмотрим свойства турбулентного движения, пользуясь методом
анализа размерностей физических величин.
После потери устойчивости движения в жидкости сначала появ-
появляются крупные вихри, создающие крупные нерегулярные пульсации
скорости. При этом частицы жидкости движутся по сравнительно
плавным траекториям, хотя сами траектории сильно перепутаны. По
мере дальнейшего увеличения числа Рейнольдса траектории частиц
становятся менее плавными, появляются более мелкие вихри. На фоне
плавных траекторий появляются более мелкие искривления, а скорость
частиц приобретает более мелкие нерегулярные пульсации. При боль-
больших числах Рейнольдса турбулентное движение содержит вихри от
самых крупных до самых мелких, в которых частицы жидкости уже
движутся как целое с одинаковыми скоростями — развитое турбулент-
турбулентное движение.
Очевидно, турбулентное движение можно рассматривать как ре-
результат наложения движений различных масштабов. Под масштабом
движения будем понимать порядок тех расстояний, на которых ско-
скорость частиц жидкости изменяется существенно.
При закритических числах Рейнольдса, появляются сначала круп-
крупномасштабные пульсации. Масштаб крупномасштабных движений по-
порядка размеров самой области движения / (для трубы — порядка
диаметра трубы). На меньших расстояниях изменение скорости незна-
незначительно. Крупномасштабные движения обладают и наибольшей ам-
амплитудой пульсаций. Их скорости по порядку величины сравнимы
с изменением средней скорости Аи на расстоянии /.
При увеличении числа Рейнольдса появляются все более и более
мелкомасштабные пульсации вплоть до пульсаций самого мелкого мас-
масштаба Aq. Области жидкости размером Ао движутся при заданном чис-
224 Турбулентность [ Гл. 8
ле Рейнольдса как целое, внутри них частицы движутся с одинаковыми
скоростями.
На больших расстояниях порядка / изменение скорости определя-
определяется в основном крупномасштабными пульсациями и по порядку вели-
величины равно Аи. На малых же расстояниях изменение скорости опреде-
определяется мелкомасштабными пульсациями, так как в крупномасштабных
движениях участки жидкости более мелких масштабов движутся как
целое.
Наряду с числом Рейнольдса Re = pvl/rj, характеризующим тур-
турбулентное движение в целом, а также крупномасштабное движение,
можно ввести числа Рейнольдса, характеризующие движение в любых
масштабах от самого крупного до самого мелкого
x (
V
В формуле (8.101) Л — масштаб движения, v\ — порядок величины
скорости пульсационного движения масштаба Л.
При больших числах Рейнольдса движения в целом велики и числа
Рейнольдса крупномасштабных движений. Движение жидкости при
больших числах Рейнольдса мы можем рассматривать как движение
маловязкой (в пределе — идеальной) жидкости. Поэтому крупномас-
крупномасштабное движение, которое определяет и движение жидкости в целом,
мы можем рассматривать как движение идеальной жидкости, подчиня-
подчиняющееся уравнению Эйлера. Отсюда следует, что в крупномасштабных
движениях не должно происходить заметной диссипации энергии дви-
движения.
С уменьшением масштаба движения Л уменьшается и величина
v\ и тем более ReA. Поэтому при уменьшении масштаба движения
вязкость играет все большую роль вплоть до самого мелкого масштаба
Ао. Именно в наиболее мелкомасштабных движениях масштаба До,
происходит основная диссипация энергии турбулентного движения.
Таким образом, мы приходим к следующей схеме диссипации энер-
энергии механического движения жидкости при турбулентном движении.
Почти вся энергия турбулентного движения содержится в крупно-
крупномасштабных движениях. Эта энергия передается в движения самых
мелких масштабов порядка До, в которых и происходит ее диссипация
в тепло, т. е. существует направленный поток энергии от крупномас-
крупномасштабных к мелкомасштабным движениям, причем этот поток, проходя
промежуточные масштабы, остается почти неизменным.
Определим порядок величины диссипируемой энергии в единицу
времени в единице массы жидкости — е. Как установлено, эта энер-
энергия определяется крупномасштабным движением, хотя ее диссипация
происходит в самых мелких масштабах. Поскольку крупномасштабное
движение можно рассматривать как движение идеальной жидкости
G7 = 0), то параметрами, определяющими это движение, будут р, Аи, I.
8.10] Развитая турбулентность 225
Из этих определяющих параметров можно образовать единственную
комбинацию, имеющую размерность е
^. (8.102)
Формула (8.102) определяет порядок величины диссипируемой
энергии при турбулентном движении.
Как уже отмечалось, турбулентно движущуюся жидкость можно
рассматривать как жидкость, обладающую некоторой турбулентной
ВЯЗКОСТЬЮ 77т-
Очевидно, что турбулентная вязкость также должна определяться
крупномасштабным движением, т. е. теми же определяющими парамет-
параметрами р, Аи, I, поскольку характер осредненного движения в основ-
основном определяется крупномасштабными пульсациями. Из них можно
образовать лишь одну комбинацию, имеющую размерность вязкости —
pAul. Поэтому порядок величины турбулентной вязкости определяется
выражением
Al (8.103)
Деля правую и левую части на молекулярную динамическую вяз-
вязкость rj, получим
*«^«Re. (8.104)
Г] Г]
В формуле (8.104), вообще говоря, может стоять значительный по
величине безразмерный числовой коэффициент. Очевидно, что этот
числовой коэффициент будет значительно ближе к единице, если мы
поделим правую часть на критическое число Рейнольдса (8.104) ReKp.
Тогда при Re « ReKp имеем rjT « rj, что и следует из физических
соображений:
!^«-!^-. (8.105)
г] ReKp v ;
Из соотношений (8.102) и (8.104) величина диссипируемой энергии
может быть определена следующим образом:
t } ¦ (8.106)
Интересно сравнить полученное выражение с аналогичным выраже-
выражением для ламинарного движения. Для диссипации энергии за единицу
времени в единице массы ламинарно движущейся несжимаемой жид-
жидкости имеем F.27)
2
1 dE 77 / dvi , dvk\ ri fAu\ /o 1Г^Ч
^ = -T7T7 = -^- б—+ ^— ~- \-r) • (8.107)
Из (8.106) и (8.107) видно, что формулы, определяющие порядок
величины диссипируемой энергии при турбулентном и ламинарном
движениях идентичны при замене г] на 7/т.
8 В.Г. Черняк, П.Е. Суетин
226 Турбулентность [ Гл. 8
Рассмотрим движение в промежуточных масштабах Ло < Л < /.
В соответствии с принятым предположением передача энергии от
крупномасштабных вихрей вихрям меньшего масштаба происходит без
потери энергии вплоть до самых мелких масштабов, где энергия дви-
движения диссипируется в тепло. Пусть е — поток энергии через иерархию
вихрей от самых крупных к самым мелким. Очевидно, в качестве
параметров, определяющих движение в промежуточных масштабах,
можно выбрать р, Л и е. По-видимому, вязкость для движений в про-
промежуточных масштабах еще не играет заметной роли.
Оценим порядок v\, т.е. величину изменения скорости на концах
отрезка порядка Л. Из вышеуказанных параметров можно образовать
лишь одну величину с размерностью скорости — (ёЛI/3. Таким обра-
образом, имеем
уI 3 • (8.108)
(у
Из (8.108) видно, что изменение скорости на расстояниях порядка
Л пропорционально кубическому корню из этого расстояния. Соотно-
Соотношение (8.108) называется законом Колмогорова-Обухова.
Перейдем, наконец, к рассмотрению самых мелких масштабов дви-
движения Ло, в которых и происходит диссипация энергии турбулентного
движения вследствие вязкости жидкости. Оценим порядок величины
самых мелких масштабов движения Ло. Рассмотрим число Рейнольдса
масштаба Л:
ReA =
(у)' • (8.109)
Очевидно, для самых мелких масштабов движения, когда вязкость
играет определяющую роль ReA0 = 1. Тогда из (8.109) имеем
^ (8.110)
Формулу (8.110) можно получить, рассматривая в качестве опреде-
определяющих параметров для движения в масштабах Ло параметры р, е и rj.
Формулой (8.110) определяется размер областей жидкости, которые
при заданном числе Рейнольдса движутся как целое. Чем больше число
Рейнольдса, тем меньше размер этих областей.
Контрольные вопросы
1. Каковы особенности ламинарного и турбулентного течения?
2. В чем причины турбулизации течения?
3. Что такое критическая скорость и критическое число Рейнольдса?
4. Что такое однородная турбулентность?
5. Что такое изотропная турбулентность?
6. Какое равновесие называют устойчивым, неустойчивым, асимптотически
устойчивым и безразличным? Приведите примеры.
8.11 ] Примеры решения задач 227
7. Что является критерием устойчивости течения жидкости в линейной
теории возмущений?
8. В каких случаях цилиндрическое течение Куэтта будет устойчивым и
неустойчивым: а — цилиндры вращаются в разные стороны, б — цилиндры
вращаются в одну сторону, в — вращается только внешний цилиндр, г —
вращается только внутренний цилиндр?
9. Жидкость находится между соосными цилиндрами с радиусами R\ и
R,2, вращающимися в одну сторону. Угловая скорость внутреннего цилиндра
равна ал. При какой угловой скорости внешнего цилиндра U2 произойдет
потеря устойчивости течения Куэтта?
10. В чем смысл нейтральной кривой на плоскости к — Re для течения
Пуазейля?
11. Что такое фазовое пространство? Фазовая точка? Фазовая траектория?
Фазовый портрет? Поясните на примере колебаний математического маятника.
12. Что такое аттрактор? Какому состоянию системы соответствует точеч-
точечный аттрактор?
13. Какой процесс описывает уравнение Ван дер Поля?
14. Какое состояние системы описывается аттрактором, который называют
предельным циклом?
15. Что называют бифуркацией? Что такое бифуркация Хопфа?
16. В чем состоит основная идея перехода к турбулентности по сценарию
Ландау-Хопфа?
17. Что такое странный аттрактор? Приведите пример.
18. В чем суть сценария Рюэля-Такенса?
19. В чем суть сценария Фейгенбаума?
20. Что характеризуют осредненные и пульсационные гидродинамические
величины?
21. В чем отличие уравнения Рейнольдса от уравнения Навье-Стокса?
22. Как вводится турбулентная вязкость? Как оценивается ее величина
относительно молекулярной вязкости?
23. В чем состоит модель Прандтля для турбулентных напряжений? Что
такое длина пути перемешивания?
24. Как строится цепочка моментных уравнений по методу Фридмана? В чем
состоит проблема замыкания этой системы уравнений?
25. Что такое развитая турбулентность?
26. Что понимают под масштабом пульсаций?
27. Как происходит диссипация энергии жидкости в режиме развитой тур-
турбулентности?
28. В чем состоит закон Колмогорова-Обухова?
29. Как оценить масштаб самых мелких пульсаций?
8.11. Примеры решения задач
Задача 1
Имеется установившееся равномерное турбулентное течение жид-
жидкости в направлении оси х между параллельными горизонтальными
стенками, перпендикулярными оси у. Определите: а) распределение
осредненного давления в плоскости, перпендикулярной направлению
течения; б) турбулентные касательные напряжения Тху.
228 Турбулентность [ Гл. 8
Решение. Согласно условию задачи с учетом топологии течения
имеем а/ х а/ х
^М=0, ^=0, Ы = («,>=0. (8.111)
Все производные по координате х, за исключением д(р)/дх, также
равны нулю.
Тогда проекции уравнения Рейнольдса на оси координат запишутся
в следующем виде:
d\vx) djvWy)
** * в" (8.112)
_д(р> д(^ о = 3(Р)
ду Р ду ' dz '
Из второго уравнения следует:
(р) + Р«2) = const. (8.113)
Таким образом, распределение давления в плоскости, перпендику-
перпендикулярной направлению течения, превышает гидростатическое давление
на величину p{v'y). Обычно это малая величина, но в некоторых
случаях она может играть важную роль.
При больших числах Рейнольдса в первом уравнении можно прене-
пренебречь членом с молекулярной вязкостью. Тогда это уравнение примет
ЁШ = -рЩ&. (8.114)
дх ду
Поскольку левая часть этого уравнения не зависит от координаты у,
то после интегрирования получим
Txy = -P(v'xv'y) = y^-, (8.115)
т. е. турбулентное напряжение, также как и вязкое напряжение при
ламинарном течении, изменяется по линейному закону в зависимости
от расстояния до стенки.
Задача 2
Найдите осредненное по времени распределение скоростей для
турбулентного потока в длинной трубе (вдали от стенки), используя
гипотезу Прандтля и понятие длины пути перемешивания. Радиус и
длина трубы соответственно равны R и L.
Решение. Обозначим через s = R — г расстояние от стенки трубы
и, следуя гипотезе Прандтля (8.74), примем, что путь перемешивания
равен / = ?s, где ? — некоторый феноменологический коэффициент.
Пусть ось z совпадает с осью симметрии трубы. Тогда по формуле
Прандтля (8.73) имеем
te*)\ (8.116)
8.11 ] Примеры решения задач 229
Топология осредненного течения такова, что (vr) = (v^) =
= 0, (vz) = (vz(r)). Если продольный градиент осредненного
давления приближенно записать через разность давлений на концах
трубки, d(p)/dz « —Ap/L, то проекция уравнения Рейнольдса на
ось z будет иметь вид
где Prz = arz + Trz — полное касательное напряжение.
Из симметрии задачи следует, что на оси трубы касательных напря-
напряжений нет, т. е. Prz(r = 0) = 0. При этом условии решением уравнения
(8.117) будет
^Др_^Л М (8Л18)
где го = Prz{s = 0) = RAp/BL) — касательное напряжение на стенке
трубы.
В турбулентном ядре потока, т. е. в основной области изменения
координаты s, вклад молекулярного напряжения arz пренебрежимо мал
по сравнению с вкладом турбулентного напряжения Trz. Другими сло-
словами, в объеме жидкости перенос количества движения осуществля-
осуществляется главным образом турбулентными вихрями. Поэтому приближенно
можно записать, что Prz « Trz. Тогда из выражений (8.116) и (8.118)
имеем х 2
v(^)() <8Л19>
Прандтль рассматривал движение жидкости при условии s <С R,
полагая правую часть уравнения (8.119) равной то. Это упрощение вно-
вносит некоторую погрешность, но существенно упрощает математические
выкладки. Следуя Прандтлю, из последнего уравнения получаем
(8.120)
р
Очевидно, что физический смысл имеет только знак +, так как
осредненная скорость при удалении от стенок трубы (координата s
увеличивается) должна возрастать.
Если уравнение (8.120)проинтегрировать, начиная с некоторого рас-
расстояния от стенки трубы si до произвольного значения s, то получим
(vz)-(vzi) = ^ In-, s>si. (8.121)
s sl
В безразмерных переменных v+ = (vz)/v* и s+ = sv^p/r] это выраже-
выражение запишется в виде
V+-V+ = i ln^p, s+>s+. (8.122)
Таким образом, скорость турбулентного потока в трубе на некото-
некотором удалении от стенок распределена по логарифмическому закону.
230 Турбулентность [ Гл. 8
На основании опытных данных Дайслер установил, что ? = 0,36. Он
же предложил использовать значение s+ = 26, при котором v+ = 12,85.
При этом из выражения (8.122) имеем
v+ = _L in 5+ + 3,8 , s+ ^ 26. (8.123)
0,36
Многочисленные исследования показали, что логарифмическое рас-
распределение (8.123) хорошо описывает профили скоростей в турбу-
турбулентных потоках с числами Рейнольдса Re ^ 20000 за исключением,
разумеется, узкого пристеночного слоя жидкости, в котором течение
становится ламинарным.
Задача 3
Применяя эмпирическую формулу Дайслера (8.79), рассчитайте
профиль скорости в ламинарном подслое и в буферной области при
турбулентном течении несжимаемой жидкости в трубе.
Решение. В пристеночном слое жидкости действуют как вязкие
так и турбулентные напряжения. Тогда полное касательное напряже-
напряжение, используя закон Навье-Стокса для вязких напряжений и формулу
Дайслера (8.79) для турбулентных напряжений, можно записать в сле-
следующем виде:
и d(v*) 2/ wd \|"i ( n2{vz)(R-r)
Prz = -rj -±-L - pn (vz)(R - r) [1 - exp( ^ J-
pn (vz)(R r) [1 exp(^^) j .
(8.124)
Воспользовавшись выражением (8.118) и заменяя разность 1 — s/R
единицей (вблизи стенки трубы s ^C R), получим
d(vz) . 2 / \ Г-1 ( п (vz)s\~\ d(vz) /o 1ОП
то = г] -^ +pnz(vz)s\l -ехр —^)\^г^- (8.125)
as L \ и / \ as
Это уравнение проинтегрируем в пределах от s = 0 до произвольно-
произвольного значения s. В безразмерных переменных такой интеграл имеет вид
9 , , ds 9 , , , O^s+^26. (8.126)
l+nVs+[l-exp(-nVs+)]
0
Здесь использованы те же безразмерные величины, что и в преды-
предыдущей задаче. Эмпирический параметр п для длинных гладких труб
равен 0,124.
Для решения нелинейного интегрального уравнения (8.126) можно
воспользоваться, например, итерационным методом. При малых значе-
значениях s+ второе слагаемое в знаменателе подынтегрального выражения
мало (порядка s+ ) и в первом приближении может быть проигнориро-
проигнорировано. В этом случае получаем
?;+ = s+. (8.127)
Полученная формула удовлетворительно описывает опытные дан-
данные при 0 ^ 5+ ^ 5.
8.11 ] Примеры решения задач 231
Задача 4
Определите соотношение между молекулярной и турбулентной вяз-
костями в точке г = 0,5R при турбулентном течении воды с по-
постоянной скоростью в длинной гладкой трубе радиуса R = 7,62 см.
Касательное напряжение на стенке трубы равно го = 1,63- 104 Па,
плотность воды р = 103 кг/м3, кинематическая вязкость воды v =
= Ю-6 м2/с
Решение. Удобно использовать цилиндрическую систему коорди-
координат, в которой полярная ось z совпадает с продольной осью трубы, а
г — радиальная координата в плоскости сечения трубы. Полное каса-
касательное напряжение может быть записано в виде
Prz = - (v + Vt) d^i = (v + Vt) ^^, s = R-r. (8.128)
Отсюда отношение вязкостей равно
5i = I _?fL—- 1 . (8.129)
77 77 d(vz)/ds
Подставляя тензор напряжений из выражения (8.118), получим
ттт = J_ тоA-*/Д) _ j = l-s/R _ j .g 130)
77 77 d(vz)/ds dv+ /ds+
где использованы безразмерные величины, введенные в задаче 2. При
s = 0,5Я имеем
77 2т7
Используя формулу (8.123), вычислим производную от безразмер-
безразмерной скорости
Подставляя в выражение (8.130), получим
^ = 86, (8.133)
77
Этот результат соответствует теоретическому положению о том, что
при турбулентном течении вдали от стенки молекулярным переносом
количества движения можно пренебречь по сравнению с турбулентным.
ГЛАВА 9
ПОГРАНИЧНЫЙ СЛОЙ
9.1. Понятие пограничного слоя
Как упоминалось выше, движение вязкой жидкости при больших
числах Рейнольдса можно рассматривать как движение идеальной
жидкости, подчиняющейся уравнениям Эйлера. Однако такое рассмот-
рассмотрение будет заведомо неверным вблизи поверхности обтекаемого тела.
Скорость вязкой жидкости, обтекающей неподвижное тело, падает до
нуля на его поверхности в тонком пристеночном слое, называемом
пограничным слоем. Его поперечная толщина мала по сравнению
с продольными размерами. Пограничный слой характеризуется боль-
большими градиентами скоростей, перпендикулярными к поверхности тела,
что свидетельствует о больших силах вязкости, определяющих движе-
движение жидкости в этом слое.
Таким образом, всю область движения жидкости, обтекающей тело,
можно разбить на две области: область тонкого пристеночного погра-
пограничного слоя, в которой движение, в основном, определяется вязкостью
жидкости, и вся остальная область движения вне пограничного слоя,
в которой жидкость движется как идеальная. Скорости движения жид-
жидкости в двух областях «сшиваются» между собой на внешней границе
пограничного слоя.
Режим течения жидкости в пограничном слое зависит от значения
числа Рейнольдса и может быть ламинарным или турбулентным. При
ламинарном режиме траектории движения индивидуальных частиц
жидкости имеют форму, близкую к форме обтекаемого тела. Лами-
Ламинарный пограничный слой формируется в области перед обтекаемым
телом. При турбулентном пограничном слое на осредненное движение
накладывается пульсационное движение индивидуальных частиц жид-
жидкости.
Турбулентный пограничный слой формируется в области за обте-
обтекаемым телом и непосредственно граничит с общим турбулентным
потоком жидкости за телом. Значение критического числа Рейнольдса,
при котором ламинарный режим течения жидкости в пограничном слое
переходит в турбулентный, зависит не только от скорости движения
и вязкости жидкости, но и от степени шероховатости поверхности
обтекаемого тела.
dvx dvx I dp , (d2vx d2vx\
-^ h vy —— = — + i/ ( 2" H Y '
dx y dy p dx V дх dy >
9.2 ] Уравнения Прандтля 233
9.2. Уравнения Прандтля
Поскольку пограничный слой предполагается тонким, т. е. его тол-
толщина 5 значительно меньше линейных размеров обтекаемого тела /,
то движение жидкости в пограничном слое можно рассматривать как
плоское движение. Рассмотрим стационарное изотермическое движе-
движение вязкой несжимаемой жидкости в пограничном слое. Выберем си-
систему координат хОу так, что ось х направлена вдоль поверхности
обтекаемого тела. Тогда уравнения движения вязкой несжимаемой
жидкости запишутся в виде
dy p dx V дх dy
Vx dx +Vy dy - p ду+"\дх* + ду2)'
dvx dvy_ _ ^
dx dy
Оценим порядок членов уравнений (9.1) в пограничном слое. Очевидно,
скорость vx внутри пограничного слоя порядка скорости набегающего
потока г^:
Vx Voo> dx I ' (*'Z)
Из уравнения непрерывности имеем
X + у = 0. «» ~ «оо у • (9.3)
Поскольку 5 <& I, то из последнего соотношения следует, что vy <^
^С vx. Остальные члены уравнений (9.1) имеют порядок
Подставляя эти оценки в уравнения (9.1), получим
9 ^^ о ~Г '
lz lz p Vy \ I3
1 S ' (9.4)
Сравним прежде всего члены в скобках в правой части первого из
уравнений (9.1) о t o
dxz I dy1
Поэтому первым членом в скобках первого уравнения (9.1) можно
пренебречь. Далее оценим отношение поперечного градиента давления
к продольному
dp I dp vice I <5 ,
dy dx /
2
234 Пограничный слой [ Гл. 9
Такого же порядка 5/1 отношение любых соответствующих членов
уравнений (9.4). Поэтому мы можем не рассматривать второе урав-
уравнение (9.4) вообще, полагая др/ду = 0 , что свидетельствует о том,
что давление поперек пограничного слоя постоянно и не зависит от у.
Тогда система уравнений (9.1) примет вид
dvx dvx _ I dp d vx
дх у ду р дх ду2 ' /g 5)
ду дх ду
Обозначим скорость жидкости вне пограничного слоя, зависящую от
продольной координаты х, через и(х). Рассмотрим линию тока, огра-
ограничивающую пограничный слой. Мы можем полагать, что с внешней
стороны эта линия находится в идеальной жидкости и для нее спра-
справедливо уравнение Бернулли:
Р , и j. I dp du /n c\
- + — = const, - -у- = -и — . (9.6)
р 2 р dx dx
Тогда уравнения движения вязкой несжимаемой жидкости в погра-
пограничном слое будут иметь вид
дх у ду dx ду2 ' /g j\
®Р_=г) dvx . dvy _ 0
ду ' дх ^ ду
Система уравнений (9.7) называется уравнениями Прандтля для по-
пограничного слоя.
Таким образом, задача об обтекании тела вязкой несжимаемой
жидкостью при больших числах Рейнольдса распадается на две задачи.
Прежде всего необходимо рассмотреть обтекание тела несжимаемой
идеальной жидкостью. Причем, так как пограничный слой тонок
E ^С /), можно и не увеличивать размер тела на толщину погранич-
пограничного слоя, а рассматривать обтекание реального тела. Если первая
задача решена, то известна скорость и(х). Подставляя и(х) в уравне-
уравнения Прандтля (9.7), найдем компоненты скорости жидкости vx и vy
в пограничном слое как функции координат, а следовательно, и силы,
действующие на поверхность тела со стороны движущейся жидкости.
9.2.1. Безразмерный вид уравнений Прандтля. Приведем урав-
уравнения Прандтля к безразмерному виду. Для этого воспользуемся следу-
следующими соотношениями для безразмерных величин (обозначены звез-
звездочкой): .
, (9.8)
vy = —= vy* , и = ^oofi* , Re = .
Здесь / — характерный размер обтекаемого тела, Voo — характерная
скорость набегающего потока.
9.3 ] Обтекание полубесконечной пластины 235
Подставляя соотношения (9.8) в уравнения Прандтля (9.7), получим
dvx* dvx* _ du* д vx*
дх* у* ду* * dx* dyl ' т д\
dvx* dvy* _ ^ dp _ ^
Видно, что безразмерные уравнения не содержат вязкости жидкости.
Не содержат вязкости и граничные условия
у*=0, г>ж*=0, г>у*=0; у* = 5, vx* = г^* . (9.10)
Поэтому общее решение системы (9.9) имеет вид
^ж* = /i(a*,2/*), vy* = /2(ж*, г/*) • (9.11)
Из вида общих решений (9.11) следует, что при увеличении числа
Рейнольдса картина движения в пограничном слое подвергается по-
подобному преобразованию, причем продольные скорости и координаты
остаются неизменными, а поперечные скорости и координаты умень-
уменьшаются в л/Re раз, поскольку функции f\ и /2 от числа Рейнольдса
не зависят и в сходственных точках (одинаковые ж* и у*) будут равны
при любом числе Рейнольдса.
Очевидно, где-то в середине пограничного слоя безразмерные ко-
координаты будут порядка единицы (ж* = 1 и у* = 1). Тогда при помо-
помощи соотношений (9.8) можно оценить порядок толщины пограничного
слоя:
у ~5, ?/*~1, 5~-}=. (9.12)
Re
9.3. Обтекание полубесконечной пластины
В качестве примера рассмотрим стационарное обтекание вязкой
несжимаемой жидкостью полубесконечной тонкой пластинки (рис. 9.1).
Пусть пластинка расположена вдоль набегающего потока. Решение
первой части задачи нам известно. При обтекании пластинки иде-
идеальной жидкостью она вообще не оказывает
никакого влияния на набегающий поток, т.е. »
однородный поток остается однородным около Z^
пластинки и после нее. Следовательно, 1
и = Voo = const, — = 0 . Рис- 9л- Обтекание пла-
dx стинки
Тогда для определения движения жидкости внутри пограничного слоя
имеем следующие уравнения Прандтля:
Я^Н^ = ^, dv^ д^ = 0 (913)
дх у ду ду дх ду
236
Пограничный слой
[Гл.9
Граничные условия имеют вид
у = 0, х ^ 0 , vx = 0, vy = О; у = 5 , vx = г^ .
Из безразмерных уравнений Прандтля следует, что решение можно
записать в следующем виде:
vx* = — = fi(x*,y*), Uj,* = л/Re — =/2(ж*,2/*).
Однако в силу бесконечности пластинки решение не должно зависеть
от характерного размера /. Это значит, что функции f\ и /2 должны
зависеть от таких комбинаций ж* и у*, которые не содержали бы
размер /. Нетрудно видеть, что такой комбинацией является
= 2/1
(9.14)
Точно так же должен отсутствовать размер / и в определении vy.
Это возможно только тогда, когда множитель перед функцией /2 будет
иметь следующее значение:
/2(ж*, 2/*) =
h {
, у*
Таким образом, искомые функции должны иметь вид
J— ) , vy = J1^- /2 (yJ— ) •
М vx J y V x \ V vx )
(9.15)
При помощи уравнения непрерывности можно выразить f\ через /2
или наоборот. Тогда, используя первое уравнение Прандтля, получим
нелинейное дифференциальное уравнение второго порядка для неиз-
неизвестной функции /i или /2. Полученное уравнение с использованием
вышеприведенных граничных условий может быть решено только чис-
численно и приводит к следующим результатам. Дифференцируя vx по
координате у и умножая на коэффициент вязкости, для касательного
напряжения получим
Pxy=V
dvx
ду
у=0
= 7?
у=0
= к
(9.16)
Коэффициент к = /{ определен численно и равен к = 0,332.
у=0
Интегрируя вдоль пограничного слоя по х от 0 до /, получим силу,
действующую на обе стороны пластинки единичной ширины:
F = 1,328л
(9.17)
Толщину пограничного слоя на пластинке можно оценить следую-
следующим образом. На верхней границе пограничного слоя у ~ д, a vx « v^.
Тогда функция f\ должна быть порядка единицы. Это в свою очередь
будет тогда, когда безразмерный аргумент функции f\ будет равен
9.3]
Обтекание полу бесконечной пластины
237
некоторому числу, постоянному для всего пограничного слоя. Тогда
имеем
[^ = const, 5 = const •<—. (9.18)
Из (9.18) видно, что толщина пограничного слоя растет вдоль
пластинки пропорционально корню квадратному из расстояния от пе-
передней кромки пластинки.
Можно оценить толщину пограничного слоя и следующим образом.
Согласно (9.12) имеем
5
I
Однако это выражение не должно содержать характерной длины /.
Это возможно только тогда, когда умножим правую часть последнего
выражения на некоторое безразмерное число ->/х^. Тогда получим
/ж*
Re
5 = const •
(9.19)
9.3.1. Толщина вытеснения. Вообще толщина пограничного
слоя — величина неопределенная. Скорость жидкости в пограничном
слое плавно переходит в скорость вне пограничного слоя. Никакой
резкой границы между двумя областями дви-
движения в действительности, конечно, не су-
существует. Для определенности при сравнении
результатов различных расчетов пользуются
понятием толщины вытеснения 5*.
Определение толщины вытеснения очевид- (
но из рис. 9.2. Приравнивая площадь S^v^
и площадь, заключенную между асимптотой
vx = г^оо и кривой vx(y), получим
= — | (vqo -vx) dy .
Woo J
0
(9.20)
Рис- 9.2. Толщина вы-
вытеснения
oo характеризует
расхода за счет торможения жидкости
Согласно выражению (9.20) произведение
уменьшение объемного
в пограничном слое.
В задаче обтекания полубесконечной пластины потоком вязкой
несжимаемой жидкости для толщины вытеснения в результате числен-
численного расчета получим
E* = 1,72,/— . (9.21)
9.3.2. Разгонный участок. Интересно применить идею о погра-
пограничном слое к оценке длины разгонного участка в трубе диаметром d.
Пусть из некоторого резервуара жидкость поступает в трубу, имея
на входе почти однородное по сечению трубы распределение скоростей.
238
Пограничный слой
[Гл.9
d
По мере продвижения вдоль трубы профиль скорости становится все
более вытянутым и, наконец, после прохождения некоторого участка
трубы длиной Lp профиль скорости становится параболическим, соот-
соответствующим точному решению задачи об установившемся ламинарном
движении жидкости в трубе (рис. 9.3).
Мы можем рассматривать такую задачу
следующим образом.
Очевидно, в начале трубы на ее
стенке образуется пограничный слой,
тогда как внутри трубы жидкость дви-
Рис. 9.3. Разгонный участок жется с одинаковой скоростью. По ме-
мере продвижения вдоль трубы толщина
пограничного слоя растет, и после того, как она становится равной
радиусу трубы, можно полагать, что профиль скорости становится па-
параболическим. Тогда, используя вышеприведенные формулы, получим
Re
Re =
vd
(9.22)
где v — средняя по сечению трубы скорость жидкости.
Так, при числе Рейнольдса, равном 600, разгонный участок ра-
равен 50 d. Это означает, что лишь после прохождения вдоль трубы
расстояния, равного пятидесяти диаметрам, движение в трубе будет
подчиняться теоретическим формулам, полученным для ламинарного
движения в бесконечной трубе.
Точное, аналитическое решение задачи о длине разгонного участка
приводит к следующему результату:
т Re j
9.4. Интегральное соотношение Кармана
От дифференциальных уравнений Прандтля можно перейти к одно-
одному интегральному соотношению. Для этого проинтегрируем эти урав-
уравнения по толщине пограничного слоя.
Напомним, что движение вязкой жидкости в пограничном слое
описывается уравнениями (9.7):
dvx
dvx
du
—
dx
(9.23)
ду ох ду
Воспользуемся следующей формулой дифференцирования интегра-
интеграла с переменными пределами:
Ъ(х) Ъ(х)
— [ f{x,y)dy= [ — dy + f{x,b) — - f{x,a) — . (9.24)
а{х) а(х)
9.4 ] Интегральное соотношение Кармана 239
Проинтегрируем первое уравнение (9.23) по координате у в преде-
пределах от 0 до 5(х). Сделаем это почленно. Используя (9.24), для первого
члена левой части имеем
s s s
J^) ^J^-2^^'^^- (9-25)
Интегрирование по частям второго члена левой части уравнения
(9.23) дает
Г ovx , ° Г ovy , / г\ / г\ , Г ovx ,
\Vy ~д^ У = VxVy о ~ J Vx ~ду У = Vx^Xj >Vy(Xj S' + J Vx~fac~ У =
0 0 0
8
= vx(x, 5)vy(x, ^ + Hc\^dy-l-vl(x,S)^. (9.26)
0
При выводе соотношения (9.26) мы воспользовались уравнением
непрерывности и тем, что на граничной поверхности (при у = 0) ком-
компоненты вектора скорости должны быть равны нулю.
Проинтегрируем по у уравнение непрерывности
. (9.27)
Подставляя полученное соотношение (9.27) в выражение (9.26),
получим
8 8 8
dvx f -v д [ , 1 д 1 ^
0 0 0
(9.28)
Интегрирование остальных членов уравнения Прандтля очевидно
Г du , du г. f a vx , avx wx /п опч
\ u— dy = и — о , \v ^ dy = is —— = -v —— . (9.29)
J dx y dx ' ) dv2 dy *"¦
8
dvx
у=0
В первом соотношении учтено, что скорость жидкости вне погранич-
пограничного слоя не зависит от координаты у. Во втором соотношении пред-
предполагается, что профиль скорости vx в зависимости от координаты у
плавно переходит при у = S в скорость и вне пограничного слоя, так
что производная от vx по у при у = 5 равна нулю.
Принимая во внимание, что на границе пограничного слоя
vx(x, 6) = и(х), и подставляя полученные соотношения в уравнение
Прандтля, получим интегральное соотношение Кармана для устано-
240 Пограничный слой [ Гл. 9
вившегося движения вязкой несжимаемой жидкости в пограничном
слое:
s s
д Г 2 i д Г , , <9?;ж
— \vxdy-u — \vxdy + v ——
ox j ox J a?/
= и ^ 5. (9.30)
ах
п ах
у=0
0 0
Интегральное соотношение Кармана может быть использовано при
решении задач о движении несжимаемой жидкости в пограничном слое
следующим образом. Как и ранее, прежде всего необходимо решить
задачу об обтекании рассматриваемого тела несжимаемой идеальной
жидкостью. В результате этого решения определяется функция и{х).
Можно представить скорость движения жидкости в пограничном слое
vx в виде полинома по степеням координаты у. Коэффициенты этого
полинома могут быть найдены из граничных условий и окажутся за-
зависящими от толщины 5 пограничного слоя как от параметра. Если
теперь подставить vx в интегральное соотношение Кармана, то полу-
получим некоторое дифференциальное уравнение относительно S. Решая
это уравнение, находим S(x). Подставляя найденное выражение для
5(х) в формулу для vx, получим окончательное выражение для vx.
И, наконец, дифференцируя vx по координатам, находим силы, дей-
действующие на обтекаемое тело.
9.4.1. Обтекание полубесконечной пластинки. Проиллюстри-
Проиллюстрируем вышеописанный алгоритм на задаче обтекания плоской полубес-
полубесконечной пластинки потоком вязкой несжимаемой жидкости (рис. 9.1).
Решение этой задачи для идеальной жидкости получено нами ранее:
. du A
и = г^оо = const, -—=[).
dx
Будем искать решение для vx в виде полинома третьей степени по
переменной у
vx = a0 + а\у + а2у2 + а3у3 . (9.31)
Как указывалось, коэффициенты сц должны быть найдены из гра-
граничных условий и будут зависеть от S как от параметра. Рассмотрим
следующие граничные условия:
vx=0, —f = 0,
ду
y = S, vx = voot -^=°-
Равенство нулю первой производной скорости принимается исходя
из предположения, что скорость vx плавно переходит в Voo на внешней
границе пограничного слоя. Равенство нулю второй производной
скорости следует из дифференциального уравнения Прандтля, так как
при у = 0 все его члены для плоской пластинки равны нулю, а следова-
следовательно, равен нулю и член, содержащий вторую производную скорости
vx по координате у. Из первого граничного условия следует, что ао = 0,
из второго условия — а2 = 0. Третье и четвертое граничные условия
9.4] Интегральное соотношение Кармана 241
приводят к уравнениям для коэффициентов а\ и аз:
8 0 = а\ + За^б
O = ai
Отсюда получаем
_ Voo _ 3 Vo
Тогда для скорости vx имеем выражение
1
vx = ^
Подставим полученное выражение для скорости г>ж в интегральное
соотношение Кармана (9.30). После интегрирования по у получим
дифференциальное уравнение для толщины пограничного слоя 5
T^voo^ = j- (9.33)
140 dx 6
Общее решение этого уравнения имеет вид
§2 _ 280 у
Постоянную интегрирования с, очевидно, следует положить равной
нулю, так как 5 = 0 при х = 0. Тогда имеем
(9.34)
Найдем силу, действующую на единицу площади пластинки
dvx
Рху ~ '' ду
(9.35)
у=0
Напомним, что в точном решении числовой коэффициент равен
0,332. Интегрируя вдоль длины пластинки, найдем силу, действующую
на обе стороны пластинки единичной ширины длиной /:
и оо •
В точном решении числовой коэффициент равен 1,328.
Найдем толщину вытеснения
8
1г 3
°° о
Подставляя в последнее выражение 5 из (9.34), получим
(9.36)
(9.37)
Точное решение дает коэффициент 1,72 вместо 1,74.
242 Пограничный слой [ Гл. 9
Таким образом, интегральное соотношение Кармана позволяет до-
довольно просто получить решение поставленной задачи, практически не
отличающееся от ее точного решения.
9.5. Отрыв пограничного слоя
Из опыта известно, что при обтекании выпуклых тел при увеличе-
увеличении числа Рейнольдса происходит отрыв потока от поверхности обтека-
обтекаемого тела и образование зоны вихревого турбулентного движения за
кормой тела, что приводит к резкому возрастанию силы сопротивления.
С физической точки зрения это явление можно объяснить следующим
образом.
Рассмотрим обтекание некоторого выпуклого тела (рис. 9.4). Мак-
Максимальная площадь сечения тела плоскостью, перпендикулярной набе-
набегающему потока, называется площадью миделева сечения. Рассмотрим
линию тока, прилегающую к погранично-
7pmin му слою. Можно полагать, что она прохо-
^Т дит в области «идеальной» жидкости и к
ней применимо уравнение Бернулли.
Опираясь на точные решения, можно
утверждать, что до миделева сечения ско-
Рис. 9.4. Обтекание выпук- Рость потока возрастает вниз по потоку
лого тела от скорости набегающего потока до неко-
некоторой максимальной скорости в миделе-
вом сечении. Следовательно, согласно уравнению Бернулли, давление
при этом уменьшается от давления в набегающем потоке до минималь-
минимального давления в миделевом сечении. После миделева сечения картина
изменяется на обратную: скорость вниз по потоку падает, а давление
возрастает. Поскольку давление поперек пограничного не изменяется
и определяется давлением на его внешней границе, то и внутри погра-
пограничного слоя давление после миделева сечения будет возрастать, вниз
по потоку.
Таким образом, жидкость в пограничном слое за миделевым сече-
сечением тормозится не только вследствие вязкости жидкости, но и вслед-
вследствие противодавления, препятствующего
ее движению. В результате может оказать-
оказаться, что в некоторой точке поверхности тела
скорость движения жидкости внутри по-
пограничного слоя окажется равной нулю не
только на поверхности тела, но и в близ-
близких к поверхности тела участках жидкости „ л r „
, л с\ т? Рис- 9.5. Скорость в погра-
(рис. 9.5). Более того, в точках, лежащих ничном слое
еще ниже по потоку, жидкость в погранич-
пограничном слое может двигаться навстречу движению жидкости вне погра-
пограничного слоя.
9.6 ] Турбулентный пограничный слой 243
На рис. 9.5 изображены приблизительные эпюры скоростей внутри
пограничного слоя за миделевым сечением. Ясно, что такое встречное
движение стимулирует образование завихренности потока в кормовой
части тела. Пограничный слой как бы подмывается встречными дви-
движениями и отрывается от поверхности тела в виде крупных нерегу-
нерегулярных вихрей. Это приводит к резкому увеличению сопротивления
тела. Очевидно, с математической точки зрения возможный отрыв
пограничного слоя произойдет не раньше чем будет равна нулю про-
производная (dvx/ду) при у = О (точка А на рис. 9.5). Только в области
ниже по потоку относительно точки А, в которой (dvx/ду) = 0, мо-
может существовать встречное движение жидкости в пограничном слое,
а следовательно, и отрыв пограничного слоя.
Таким образом, для уменьшения сопротивления обтекаемых тел
необходимо, если это возможно, или предотвратить отрыв погранич-
пограничного слоя, или, если это невозможно, стремиться к тому, чтобы его
отрыв произошел как можно ближе к задней кромке обтекаемого тела.
В последнем случае размер области спутного турбулентного движения
будет меньше, а следовательно, будет меньше и сопротивление тела.
Поэтому хорошо обтекаемые тела должны иметь каплевидную форму
с плавной, постепенно сужающейся кормовой частью. Поверхности
хорошо обтекаемых тел должны быть гладкими, лишенными даже
незначительных выступов и шероховатостей. Такую форму имеют про-
профили крыльев и фюзеляжей современных дозвуковых самолетов.
Иногда для предотвращения отрыва пограничного слоя впереди
крыла ставят предкрылки, в которых воздух разгоняется и «продувает»
пограничный слой до конца профиля.
Одним из способов предотвращения отрыва пограничного слоя яв-
является отсос воздуха внутрь обтекаемого тела. При этом пограничный
слой как бы прижимается к поверхности. Дополнительные энергетиче-
энергетические затраты на отсос воздуха могут окупиться уменьшением сопро-
сопротивления тела. Для хорошо обтекаемых тел основной вклад в силу
сопротивления дает не отрыв пограничного слоя, а вязкие силы трения
жидкости на обтекаемой поверхности.
9.6. Турбулентный пограничный слой
Ламинарное движение жидкости в пограничном слое при больших
числах Рейнольдса становится неустойчивым и движение в погранич-
пограничном слое будет турбулентным. Действительно, можно провести анало-
аналогию между движением в пограничном слое и движением в плоском
канале. Средняя скорость внутри пограничного слоя порядка скорости
набегающего потока г^. Вместо расстояния между плоскостями ка-
канала можно рассматривать толщину пограничного слоя. Тогда можно
записать число Рейнольдса для движения жидкости в пограничном
слое: Re = v^S/is. При достижении в пограничном слое некоторо-
некоторого критического значения числа Рейнольдса движение в нем будет
244 Пограничный слой [ Гл. 9
турбулентным. Очевидно, в направлении движения жидкости число
Рейнольдса в пограничном слое будет увеличиваться как
Re ~ 5, 5 ~ у/х , Re ~ \/ж .
Поскольку толщина пограничного слоя пропорциональна у/х, то, сле-
следовательно, и число Рейнольдса также будет пропорционально у/х.
Это означает, что если в некоторой точке с координатой х число
Рейнольдса достигнет своего критического значения, то пограничный
слой будет состоять из двух частей: ламинарной передней части и по-
последующей части турбулентного движения. Расчет турбулентного дви-
движения в пограничном слое основан на теории турбулентности Прандт-
ля, предсказывающей логарифмический профиль скорости жидкости
в пограничном слое с некоторыми эмпирическими коэффициентами.
Как показывает опыт, толщина турбулентного пограничного слоя про-
пропорциональна х, а не у/х, как для ламинарного слоя, т.е. толщина
турбулентного пограничного слоя растет вниз
МС по потоку быстрее, чем ламинарного.
Рассмотрим изменение коэффициента со-
сопротивления шара при обтекании его вязкой
несжимаемой жидкостью в зависимости от
числа Рейнольдса.
Экспериментальный график имеет вид,
приведенный на рис. 9.6.
11 е При малых числах Рейнольдса коэффи-
Рис. 9.6. Зависимость циент сопротивления определяется формулой
коэффициента сопро- Стокса (область I)
тивления шара от числа 9Д ,
Рейнольдса С = — , Re = ^^ .
Re v
При дальнейшем увеличении числа Рейнольдса падение коэффициента
сопротивления несколько замедляется, а в дальнейшем даже возрас-
возрастает (область II). Возрастание связано с тем, что при этих числах
Рейнольдса происходит отрыв ламинарного пограничного слоя и за
шаром образуется большая область турбулентного движения, размер
которой в основном и определяет сопротивление шара.
Далее, в довольно широком интервале изменения чисел Рейнольдса
коэффициент сопротивления остается практически неизменным. Дей-
Действительно, как следует из безразмерных уравнений Прандтля, карти-
картина движения в ламинарном пограничном слое при увеличении числа
Рейнольдса подвергается подобному преобразованию. При этом все
продольные координаты и скорости остаются неизменными, а попереч-
поперечные уменьшаются обратно пропорционально л/Re. Следовательно, и
продольная координата точки отрыва пограничного слоя не изменяется
при увеличении числа Рейнольдса, поэтому не изменяется и размер
турбулентной области за шаром, а стало быть, и коэффициент сопро-
сопротивления должен оставаться приблизительно постоянным.
9.7 ] Примеры решения задач 245
При числах Рейнольдса B-3) • 105 (область III) наступает резкое
уменьшение коэффициента сопротивления, причем настолько резкое,
что уменьшается не только коэффициент сопротивления, но и сама
сила сопротивления шара. Это явление называется кризисом сопро-
сопротивления. Кризис сопротивления обязан своим возникновением турбу-
лизации пограничного слоя на шаре. Турбулентный пограничный слой
лучше «связан» с основным потоком жидкости за счет поперечных
турбулентных пульсаций, что и смещает точку отрыва пограничного
слоя в кормовую часть шара. Это в свою очередь приводит к уменьше-
уменьшению области турбулентного движения за шаром, а следовательно, и к
уменьшению его сопротивления.
Контрольные вопросы
1. Какое свойство жидкости определяет ее течение в пограничном слое?
2. Что является критерием при определении положения верхней границы
пограничного слоя?
3. Каковы причины турбулизации пограничного слоя?
4. Как изменяется толщина пограничного слоя при увеличении числа Рей-
Рейнольдса?
5. Во сколько раз увеличится или уменьшится сила, действующая на
пластинку со стороны жидкости, которая движется вдоль поверхности этой
пластинки, если скорость жидкости увеличить в 4 раза?
6. Как различается толщина пограничного слоя на полубесконечной пла-
пластинке в точках с координатами ж = 1 см и ж = 4 см?
7. Что называют толщиной вытеснения? В чем смысл этой величины?
8. Как изменится длина разгонного участка, если скорость течения жид-
жидкости в трубе увеличить в два раза?
9. В двух одинаковых трубках с одинаковыми скоростями движутся жид-
жидкости с разными вязкостями, причем коэффициент вязкости жидкости в первой
трубке больше. В какой трубке больше длина разгонного участка?
10. Что такое миделево сечение?
11. Как изменяются скорость и давление жидкости в пограничном слое вниз
по потоку до миделева сечения и после него?
12. Какой критерий используют для определения точки отрыва погранично-
пограничного слоя?
13. Как изменяется число Рейнольдса вниз по течению жидкости вдоль
плоского пограничного слоя?
14. Как изменяется сила сопротивления при отрыве пограничного слоя?
15. Что называют кризисом сопротивления?
9.7. Примеры решения задач
Задача 1
Определите динамику нарастания толщины пограничного слоя
вблизи бесконечной пластинки, которая внезапно приведена в движе-
движение со скоростью v в плоскости расположения пластинки. Вычислите
246
Пограничный слой
[Гл.9
силу, действующую на единицу площади пластинки со стороны вязкой
жидкости, и толщину вытеснения.
Решение. Лабораторную систему координат хОу выберем так,
что ось х направлена в сторону движения пластины, а начало коорди-
координаты у совместим с поверхностью пластины (рис. 9.7). Время начинаем
отсчитывать с того момента, когда пласти-
пластина начинает двигаться.
Внезапное движение пластины с по-
постоянной скоростью v, благодаря прилипа-
прилипанию жидкости к поверхности пластины и
силам внутреннего трения (вязкости), вы-
вызывает течение жидкости. Толщина слоя
жидкости, вовлекаемой пластиной в дви-
движение, будет расти с течением времени,
т.е. S(t\) < 6fa) < 6fa) (рис. 9.7), причем
на большом удалении от пластины жид-
жидкость остается неподвижной.
Таким образом, течение жидкости бу-
будет происходить в пристеночной области
О < у < S(t), где 5(t) — растущая со временем толщина пограничного
слоя. Предположим далее, что профили скорости с течением времени
остаются подобными, т. е.
у (9.38)
О х
Рис. 9.7. Рост толщины по-
пограничного слоя с течением
времени
причем неизвестная функция р(у*) определяется профилем скорости
течения.
Обратимся к интегральному соотношению Кармана (9.30). Посколь-
Поскольку мы рассматриваем нестационарное течение жидкости, то к левой
части уравнения (9.30) следует добавить член
S{t)
Г dvx
Ot
dy.
Прежде всего учтем, что вне пограничного слоя жидкость неподвижна,
т. е. и = 0. Кроме того, скорость vx не зависит от продольной коорди-
координаты х. Тогда интегральное соотношение Кармана запишется в виде
Гdvx , dvx
= 0.
(9.39)
у=0
Вычислим производные, входящие в это уравнение:
dvx _____ _
dt '
dt
ду
у=0
У=0
где штрих означает дифференцирование по
9.7 ] Примеры решения задач 247
Подставляя полученные выражения в уравнение (9.39), после интег-
интегрирования по у* получим
М6 S = ^' <9-40)
at
где
М = - ^'у* dy* = \(р dy* , N = - (р'\ =0 .
о о
В выражении для величины М учтены граничные условия
р(у^ = 0) = 1, (р(у* = 1) = 0 . (9.41)
Интегрирование уравнения (9.39) по времени с учетом начального
условия 5 = 0 при t = 0 приводит к следующему выражению:
(9.42)
Таким образом, толщина пограничного слоя растет пропорциональ-
пропорционально корню квадратному из времени.
Чтобы рассчитать величины М и N, определенные выражениями
(9.40), необходимо знать распределение скоростей в пограничном слое,
т.е. функцию (р. Можно было бы воспользоваться точным выражением
для функции (р, которое было получено ранее (см. решение задачи 8
в гл. 9, выражение F.165)). Но мы поступим иначе и будем при-
придерживаться того алгоритма приближенного решения задачи, который
приняли в этой главе.
Будем искать решение для функции ip в виде полинома третьей
степени по переменной у*\
^^ ^^ 2 i^ 3 /Q Л О\
Неизвестные коэффициенты сц найдем из граничных условий (9.41)
и двух соотношений
9
у = 0, 5?_^.= о, у = 5, ^=0. (9.44)
Обоснование этих соотношение приведено на с. 240 при решении зада-
задачи обтекания полубесконечной пластины потоком вязкой несжимаемой
жидкости.
В приближении полинома третьей степени для функции (р получим
следующее выражение:
4>=l-\v* + \vl> (К j/* ^ 1 . (9.45)
Используя это выражение для вычисления величин М и N, имеем
S(t) = 2\[ЪЛ . (9.46)
248 Пограничный слой [ Гл. 9
Найдем силу, действующую на единицу площади пластинки:
Рху =
dvx
ду
= rj
v dtp
у=0
S ду*
у=0
3 v _ 3 rjv
2 ^ ~6 ~ 4 ~JbJi
Следовательно, действующая на пластинку сила направлена проти-
противоположно направлению движения пластинки и уменьшается обратно
пропорционально корню квадратному из времени.
Теперь вычислим толщину вытеснения:
8 1
S* = l \(v - vx) dy = д J(l - ф) dy* = | 5 = \VbJt . (9.47)
о о
Разумеется, толщина вытеснения растет со временем так же, как и
толщина пограничного слоя.
Задача 2
Оцените толщину пограничного слоя вблизи критической точки у
обтекаемого вязкой жидкостью кругового цилиндра радиуса R. Ско-
Скорость набегающего потока равна v^.
Решение. Обозначим через х = R — г расстояние от критической
точки. Следуя решению задачи об обтекании цилиндра идеальной
жидкостью, вблизи критической точки вне пограничного слоя для
радиальной скорости имеем E.102)
1 - 4) - (9-48)
г )
Поскольку мы рассматриваем расстояния, малые по сравнению с ра-
радиусом цилиндра, т.е. x/R <C 1, то выражение (9.48) преобразуется к
виду
и « 2Voo ^ . (9.49)
Не повторяя рассуждений § 9.3, напомним, что оценка толщины
пограничного слоя при обтекании с большими числами Рейнольдса
полубесконечной пластины дает (9.18)
г I их
V и
где v — кинематическая вязкость жидкости, под и следует понимать
скорость идеальной жидкости вне пограничного слоя. В данном случае
оценкой для скорости и является выражение (9.49). Тогда для толщины
пограничного слоя вблизи критической точки получим
(9.50)
Таким образом, вблизи критической точки толщина пограничного
слоя остается неизменной независящей от координат.
9.7 ] Примеры решения задач 249
Задача 3
В задаче обтекания полубесконечной пластины (п. 9.4.1) исполь-
используйте вместо кубической (9.31) линейную аппроксимацию продольной
скорости движения жидкости в пограничном слое и рассчитайте тол-
толщину пограничного слоя, толщину вытеснения и силу, действующую со
стороны жидкости на часть пластинки единичной ширины и длиной /.
Решение. По условию задачи продольная скорость жидкости
имеет вид
vx = ao + aiy . (9.51)
Для определения коэффициентов clq и а\ воспользуемся гранич-
граничными условиями для скорости на пластине и на верхней границе
пограничного слоя:
vx(y = 0) = 0, vx(y = 6) = voo, (9.52)
где Voq — скорость набегающего потока. Отсюда получаем
а0 = 0, а\ = Voq/5 .
Тогда интегральное соотношение Кармана запишется в виде
о ах о
Решение этого уравнения имеет вид
/^ (9.54)
Полученное выражение отличается от (9.34) только числовым ко-
коэффициентом.
Сила, действующая на единицу площади пластинки, равна
РХу=Г]
dvx
ду
(9.55)
После интегрирования по ж в пределах от 0 до / найдем силу, дей-
действующую на обе стороны пластинки единичной ширины и длиной /:
F = 1,156^7//^ . (9.56)
Найдем толщину вытеснения
s
S* = — Uvoo -vx)dy=l-5= 1,73./— . (9.57)
о
Заметим, что числовой коэффициент в выражении (9.57) мало от-
отличается от полученного ранее (9.37), 1,74, и от точного расчета, 1,72.
ГЛАВА 10
ГАЗОВАЯ ДИНАМИКА
Движение газа можно рассматривать как движение несжимаемой
жидкости лишь при скоростях, существенно меньших скорости распро-
распространения в газе малых возмущений (скорость звука). При скоростях,
равных или больших скорости звука, движение газа настолько спе-
специфично, что оно является предметом изучения специального раздела
механики сплошной среды — газовой динамики.
Движение газа при больших скоростях будем рассматривать как
движение идеальной жидкости.
10.1. Скорость звука
Известно, что скорость распространения малых возмущений
в сплошной среде или скорость звука определяется следующим
соотношением:
Для идеального газа с учетом уравнения состояния Клапейрона-
Менделеева имеем
др\ р RT Ср Г^р I RT /1ПО\
7Г =7-= 7 > 7 = 7^' С=\П = V 7 • A0-2)
op IQ р ц Cv Vpvm
В формулах A0.2) 7 ~~ показатель адиабаты Пуассона; Ср , Су — теп-
теплоемкости при постоянном давлении и объеме соответственно; \i — мо-
молярная масса газа; R = 8,314 ДжДмоль • К) —универсальная газовая
постоянная.
Для показателя адиабаты элементарная молекулярно-кинетическая
теория дает следующее соотношение:
N + 2
где N — число степеней свободы молекулы газа. Так, для одноатомного
газа N = 3 ,7 = 5/3 « 1,67, для двухатомного — N = 5 ,7 = 7/5 « 1,4
и т.д.
Сравнивая скорость звука со средней тепловой скоростью молекул,
vT = (бЯТ/тг/iI/2, видим, что они примерно равны. Этого и следовало
ожидать, поскольку всякое взаимодействие между двумя соседними
10.2] Параметры газа в заторможенном потоке 251
макроскопическими частицами газа происходит только через столкно-
столкновения молекул. Следовательно, скорость распространения такого взаи-
взаимодействия (скорость распространения малых возмущений) будет про-
происходить со средней скоростью движения самих молекул. Из элемен-
элементарной молекулярно-кинетической теории идеального газа следует, что
величина 7 и теплоемкости не зависят от температуры и давления газа.
Хотя эксперимент показывает слабую зависимость величин 7 > Ср , Су
от температуры и давления, в большинстве газодинамических задач их
можно считать постоянными.
Поскольку скорость звука в газе зависит только от температуры,
то во всех термодинамических формулах и соотношениях мы можем
температуру заменить скоростью звука.
Из основного термодинамического равенства для единицы массы
газа имеем
dQ = dem+pdV, cv=(|^)v=(^)v, sm=cvT, A0.3)
где су , ср — удельные теплоемкости при постоянном объеме и давле-
давлении соответственно.
Далее, для энтальпии единицы массы газа имеем
h = eBH+pV = cvT+ — = cpT, A0.4)
В выражении A0.4) использована формула Р. Майера и уравнение
состояния для единицы массы идеального газа
R л/ RT
ср - су = — , pV = .
Отсюда получаем следующую формулу:
ср R 7 РУ
2 р
с =1-=
cv , с 1
Из соотношений A0.3)—A0.5) имеем следующие выражения для
внутренней энергии, энтальпии и энтропии единицы массы идеального
газа
вн = СуТ =
pV _ с
V1 7GГ (Ю.6)
= cpT = ^- = -?— , Sro = cv In 4 •
и 7 — 1 7 — 1 Р
10.2. Параметры газа в заторможенном потоке
При больших скоростях движение газа вне тонкого пограничного
слоя можно рассматривать как движение идеальной жидкости, лишен-
лишенной вязкости и теплопроводности. Тогда движение каждой индивиду-
252 Газовая динамика [Гл. 10
альной частицы газа будет совершаться адиабатически и для любой
линии тока справедливо уравнение Бернулли
v2
— + h = const.
Найдем плотность, давление и температуру газа в критической точке
на обтекаемом теле. Если индексом «оо» обозначить значения физиче-
физических величин в набегающем потоке, а индексом «0» — в критической
точке, то для критической линии тока можно записать
Voo , U U ^оо , 7 Роо 7 Р0 ПП7\
2 2 7 - 1 Роо 7 - 1 Ро
Отсюда имеем
Ж^ 21Р 1 + 7^1ф1 (ю 8)
2 ^
Poo P0 27 °° Роо 2 с^
Обозначим отношение v/c через М . Здесь v — скорость газа в неко-
некоторой точке потока, с — скорость звука в этой же точке. Безразмерная
величина М, характеризующая отношение скорости движения газа к
скорости звука, называется числом Маха. Для адиабатического дви-
движения газа, используя уравнение Пуассона, получим
Р0 Роо Роо (РоЛ 7 _Р0_ Л , 7~ 1 М2 \7/G~1}
U ' V + 2
Нетрудно получить аналогичную формулу для плотности:
Роо
Воспользовавшись уравнением Клапейрона для единицы массы га-
газа,
имеем
Ро =
R
— Tqo
0, Роо
_ R
То ро Роо
Роо , 7^~ = •
Too Роо РО
Тогда из соотношения A0.8) получаем
7^ = 1 + ^ М^ . A0.11)
J- оо ^
10.2.1. Температура торможения. Температура газа То в крити-
критической точке на обтекаемом теле называется температурой торможе-
торможения. При больших скоростях движения температура торможения может
оказаться значительной. Так, например, если спутник при торможении
входит в атмосферу со скоростью ~ 4000 м/с, то число Маха равно
примерно 10. Тогда по формуле A0.11) имеем в критической точке
температуру, равную
7=1,4, Т0
10.3] Стационарный одномерный поток сжимаемого газа 253
Если Too = 300 К, то температура торможения равна примерно 6000 К.
При такой температуре поверхность спутника оплавляется и если он
не сгорает, то только благодаря краткосрочности воздействия и теп-
теплообмена с окружающей средой. Причем такая температура будет не
только в критической точке, но и на всей поверхности обтекаемого
тела, так как скорость вязкого газа на поверхности неподвижного тела
тоже равна нулю. Для сохранения спутника применяются специальные
защитные конусы, которые сгорают в атмосфере, забирая все тепло,
выделяющееся при торможении.
Температура стенок аэродинамической трубы будет равна темпера-
температуре неподвижного газа на входе в трубу, так как в обеих точках ско-
скорость газа равна нулю. Газ, входя в трубу, расширяясь, охлаждается,
но при торможении на стенках трубы снова нагревается до первона-
первоначальной температуры.
При обтекании выпуклого тела скорость в миделевом сечении будет
максимальна, а, следовательно, температура газа минимальна:
2 2
у + h = у + срТ = const.
Этим можно объяснить образование пелены за самолетом при полете
в воздухе, достаточно насыщенном влагой. Если температура воздуха
несколько больше температуры конденсации, то понижение темпера-
температуры, создаваемое движением самолета, может оказаться достаточным
для конденсации и образования за ним характерной пелены.
Термометр, погруженный в движущийся газ, не покажет температу-
температуру газа, а покажет температуру торможения. Так, например, термометр,
помещенный в воздух, движущийся со скоростью 70 м/с, покажет
температуру
1+0,2 (^) J «1,008 Тж.
Если температура газа Т^ равна 300 К, то термометр покажет тем-
температуру на 2,4 К большую, чем температура газа, или температура,
которую он показал бы, если бы двигался вместе с газом со скоростью
70 м/с.
10.3. Стационарный одномерный поток
сжимаемого газа
Рассмотрим линию тока, которая начинается в неподвижном газе,
например, в некотором сосуде, содержащем неподвижный газ, вытека-
вытекающий из этого сосуда в окружающее пространство. Для такой линии
тока можно на основании уравнения Бернулли записать
v = y/2(ho - ft) , A0.12)
254
Газовая динамика
[Гл. 10
где /го — энтальпия единицы массы неподвижного газа. Скорость дви-
движения газа будет максимальной при h = 0. Поскольку h = cpT, то это,
в свою очередь, возможно только тогда, когда абсолютная температура
газа станет равной нулю:
О013)
Из вывода видно, что г>тах — это максимальная скорость направ-
направленного движения, которая может быть получена при истечении газа
из сосуда. Характерно, что она зависит только от температуры газа
в сосуде, но не зависит от давления в нем. При этом абсолютная
температура вытекающего газа должна равняться нулю.
Далее рассмотрим некоторую линию тока. Из уравнения Бернулли
следует, что при увеличении скорости вдоль линии тока температура
газа уменьшается, а следовательно, уменьшается и скорость звука.
Может оказаться, что в какой-то точке рассматриваемой линии тока
скорость движения газа станет равной скорости звука в этой точке.
Скорость движения газа, равная местной скорости звука, называется
критической скоростью с*. Критическая скорость может быть найдена
из соотношения
2
51*
2
7+1
27-1 7-1 2
Отсюда с учетом A0.13) имеем
7-1 '2G-1)"
= V
A0Л4)
Из A0.12) и A0.13) видно что и максимальная и критическая
скорости могут быть выражены через скорость звука в неподвижном
газе и зависят лишь от температуры неподвижного газа.
Рассмотрим изменение плотности потока pv вдоль линии тока
d(pv) = pdv + vdp ,
d(pv) dv dp
pv v p
v
— + h = const,
Sm = const,
vdv + dh = O, dh = TdSm + Vdp,
dh =
= —
vdv -\—- = 0 .
Учитывая определение скорости звука, имеем
2
с =
др
—-
, 2т i , 2 dp n
dp = с dp , vdv + с — = 0 ,
Р
Подставляя в предыдущее соотношение, получим
d(pv) dv v j
v } = 9 dv .
pv v cz
dp
Р
vdv
10.3] Стационарный одномерный поток сжимаемого газа 255
Окончательно имеем
Рассмотрим некоторую трубку тока с переменной площадью попе-
поперечного сечения S. По определению во всех сечениях трубки тока
расход несжимаемой жидкости одинаков. Поэтому
pvS = const, pvdS + Sd(pv)=O, d[pv^ = _dS ^ (ю.16)
pv Ь
Из последнего соотношения видно, что изменение плотности по-
потока газа противоположно изменению площади сечения трубки тока.
Поэтому при дозвуковом течении (М < 1) при увеличении скорости
(dv > 0) растет и плотность потока, а трубка тока сужается. В случае
сверхзвукового движения (М > 1) при увеличении скорости (dv > 0)
плотность потока уменьшается, а, следовательно, трубка тока расши-
расширяется. Поэтому при сверхзвуковом течении с увеличением скорости
плотность потока уменьшается (за счет уменьшения плотности газа),
а сечение трубки тока должно увеличиваться.
Таким образом, при дозвуковом движении газа с увеличением его
скорости вдоль трубки тока ее сечение должно уменьшаться, а плот-
плотность потока возрастает. При этом, как следует из уравнения Бернул-
ли, температура газа вдоль трубки тока уменьшается, следовательно,
уменьшается и местная скорость звука. Также уменьшаются вдоль
трубки тока плотность и давление:
2 2 2
— = const, p = const • p1, — + cpT = — H =
+ cpT = H
7l=^ + ^_constl/7
2 71
= + = ^ + const =^ +
2 7 —\ p 2 7—1 2 7—1
При сверхзвуковом движении с увеличением скорости газа вдоль
трубки тока сечение трубки должно увеличиваться, а плотность по-
потока уменьшается. Так же, как и в дозвуковом потоке, уменьшаются
температура, скорость звука, плотность и давление.
10.3.1. Сопло Лаваля. Из вышесказанного следует, что в сужаю-
сужающейся трубке не может быть достигнута сверхзвуковая скорость. Ско-
Скорость движения газа может стать сверхзвуковой только в расширяю-
расширяющейся трубке тока. Для разгона газа до звуковой скорости он должен
двигаться в сужающейся трубке тока. При одномерном движении иде-
идеального газа в реальной трубе ее стенки мож-
можно рассматривать как боковую поверхность
трубки тока. Поэтому труба, плавно перево-
переводящая дозвуковое движение газа в сверхзву-
сверхзвуковое, должна иметь сужающуюся дозвуко-
дозвуковую часть и расширяющуюся сверхзвуковую ^ л. л _
/ 1А1\^г s Рис 10.1. Сопло Лаваля
(рис. 10.1). 1акая труба называется соплом
256 Газовая динамика [Гл. 10
Лаваля. Очевидно, что местная скорость звука будет достигнута в са-
самой узкой части сопла Лаваля. В самом узком сечении сопла скорость
газа будет равна местной (в этом сечении) скорости звука.
Нетрудно найти форму сопла Лаваля, т. е. зависимость числа Маха
от размера сечения сопла. Из соотношений A0.15), A0.16) имеем
dS _ /1 iui2\ dv кд _ v dM _ dv dc
S ^ ' v ' с ' M v с
Из уравнения Бернулли получим
2 , п dv 2 с dc 2 I dc
d U
, , 2 , п
vdv H cdc = U, ^ ^
7—1 v 7 ~ U с 1 — 1 М с
Из предыдущих соотношений следует:
dM _ dv , М2 7 — 1 dv dv _ dM 2
M v 2 v ' v M 2 + G - 1) M2
Тогда имеем следующее дифференциальное уравнение:
_d# _ 2A -М2) dM
S ~ м[2 + G- 1)М2] '
Интегрируя, получим
м ¦ • <10-17)
Здесь Sm\n — минимальное сечение сопла Лаваля, в котором число
Маха равно единице. Формула A0.17) дает связь между площадью
сечения сопла и числом Маха в этом сечении.
Выше приведен приближенный расчет сопла Лаваля, в котором
не учитывалась вязкость газа. Очевидно, что, несмотря на формулу
A0.17), не следует делать слишком резких изменений сечения в сверх-
сверхзвуковой части, так как поток газа может и не следовать за стенкой, а
оторваться от нее с образованием между стенкой и основным потоком
газа некоторой застойной зоны в сверхзвуковой части сопла. Точного
расчета сопла Лаваля с учетом вязкости в настоящее время не суще-
существует, и чаще всего конструктор производит расчет методом проб и
ошибок.
10.4. Истечение газа из резервуара
через сужающийся насадок
Рассмотрим истечение газа из некоторого большого резервуара че-
через сужающийся насадок (рис. 10.2). Будем полагать, что параметры
газа в сосуде при истечении остаются неизменными, а скорость газа
в сосуде равна нулю.
Для нахождения параметров газа на срезе сопла очевидно мож-
можно, обратив задачу, воспользоваться формулами A0.9)-A0.11), полу-
10.4]
Истечение газа через сужающийся насадок
257
ченными нами для нахождения давления, плотности и температуры
в критической точке на обтекаемом теле. В прежнем обозначении это
будут poo , poo , Too. Будем постепенно уменьшать
давление газа на выходе из сопла, оставляя дав-
давление в резервуаре прежним. Очевидно, с умень-
уменьшением давления на выходе будет увеличивать-
увеличиваться скорость на срезе сопла, причем она будет
максимальной в самом узком сечении сопла, т. е.
на его срезе. При дальнейшем уменьшении дав-
давления на срезе сопла может быть достигнута
скорость движения газа, равная местной скоро-
скорости звука, т.е. критической скорости газа с*.
При этом М = 1, а параметры газа будут иметь
соответствующее критическое значение 0 A0.9)—A0.11):
Ро
Ро
то
Рис.
ры
10.2.
газа
Р
Т
-^"^ v
Парамет-
в насадке
р* =
= Р0
-1\7/A-7)
)
Р* =Роо =Р0
= ТОО = То
A0.18)
При дальнейшем уменьшении давления на выходе из сопла давле-
давление, плотность и температура газа на срезе сопла будут неизменными,
зависящими только от давления, плотности и температуры газа в ре-
резервуаре. Скорость же, равная критической скорости, будет зависеть
только от температуры газа в резервуаре:
Из формул A0.18) следует, что критическая скорость на срезе сопла
будет достигнута для воздуха G = 1,4) при следующем отношении
давлений:
V ( <v-l\7/(l-7) / 2 \7/G} v
— =A + X^i) =(^=-г) ' ^=0,53. A0.19)
PoV 2 / у 7 + 1 / Ро
Физически это понятно, так как после достижения на срезе сопла
критической скорости, равной местной скорости звука, газ внутри ре-
резервуара и сопла не «чувствует» изменения параметров вне сопла, так
как возмущения, распространяющиеся со скоростью звука, не могут
проникнуть внутрь сопла. При этом расход газа через сопло достигает
О Следует различать параметры газа в критической точке на обтекаемом
теле, в которой скорость газа равна нулю, ро, ро, То, и параметры газа в той
точке линии тока, в которой скорость газа равна местной скорости звука,
9 В.Г. Черняк, П.Е. Суетин
258 Газовая динамика [Гл. 10
своего максимального значения, которое не зависит от дальнейшего
уменьшения противодавления на срезе сопла.
При помощи имеющихся в нашем распоряжении формул можно
вычислить максимальный массовый расход газа через сопло:
/ 2 \VG-i)
= P*C*Smln = [)
G+0/BG-1))
Максимальный объемный расход можно вычислить по формуле
nin = СО '
Ро о / 27
= От\п\
7+lpo V7+1 М
Из A0.20), A0.21) видно, что расход зависит только от состояния
газа внутри сосуда и не зависит от его параметров вне сосуда. Не
трудно получить формулу для скорости истечения газа из резервуара
при промежуточных противодавлениях. Пользуясь формулой Бернулли
и прежними обозначениями, получим
^РЛ РРЛ A0.22)
2 7 - 1 Роо 7 - 1 Ро 7 - 1 Ро V Р Ро
Для адиабатического течения имеем
Р 1 V Ро
-Чу = const, -Чт = Чг .
Р7 Р7 Ро
Подставляя эти значения в предыдущее равенство, получим формулу
Сен-Венана и Вантцеля:
Из формулы A0.23) видно, что при р = ро скорость истечения равна
нулю, а при критическом перепаде давления (см. A0.19)) р = р* имеем
2 27 роЛ 2 \ 27 ро
\ 7 ро 2 /
= ^т =со—гт» ^°° = сол/—г~г =с*
/ 7+1р0 7 + 1 V7+1
^оо = —Ч- I1 гт = ^т =со—гт»
00 7 — 1 ро V 7 + 1 / 7+1р0 7 + 1
Таким образом, скорость движения газа на срезе сопла равна кри-
критической скорости, т. е. местной скорости звука.
Если же р = 0, то скорость истечения равна
v =
10.5] Ударные волны и скачки уплотнения 259
Таким образом, максимальная скорость истечения может быть до-
достигнута лишь при истечении в вакуум (р = 0) при абсолютной темпе-
температуре вытекающего газа, равной нулю.
Приведем некоторые оценочные расчеты для воздуха G = 1,4) при
Т = 288К, /i = 0,029 кг/м3:
I Г)ГТ1 I 2
со = 4/7 =340 м/с, vma^ = c0\ г =756 м/с,
Тот факт, что расход газа через сужающийся насадок не зависит
от противодавления при уменьшении последнего меньше критического
на срезе сопла (при р < р*), используется в технике для стабилизации
расхода газа в различных технологических и лабораторных устрой-
устройствах. Сужающийся насадок чаще всего выполняется в виде тонкой
диафрагмы с отверстием, называемой звуковой диафрагмой. Если дав-
давление за звуковой диафрагмой (для воздуха) будет меньше чем 0,53
давления перед диафрагмой, то дальнейшее уменьшение давления за
диафрагмой или его колебания не изменит расхода газа через нее.
10.5. Ударные волны и скачки уплотнения
Физически сверхзвуковое движение газа отличается от дозвукового
характером распространения малых возмущений в потоке.
10.5.1. Конус Маха. Рассмотрим, как распространяются в дви-
движущемся потоке газа малые возмущения. Предположим, что в неко-
некоторой точке дозвукового течения газа возникло возмущение плотности
газа. Это возмущение будет сноситься вниз по потоку и распростра-
распространяться со скоростью звука во все стороны, и если газ однороден,
то поверхность одинаковой фазы распространения возмущения будет
представлять собой поверхность шара, расширяющегося со скоростью
звука (рис. 10.3 а). При этом возмущение при дозвуковом движении
газа распространяется как вниз, так и вверх по потоку.
При сверхзвуковом движении газа возмущения, распространяющи-
распространяющиеся со скоростью звука, не могут проникнуть в область течения вверх
по потоку (рис. 10.3 6), а сносятся потоком вниз по течению.
Поверхность, ограничивающая область возмущенного потока, будет
представлять конус, называемый конусом Маха,. Если движение газа
прямолинейное, а газ однороден, то конус Маха будет прямым круго-
круговым конусом. Из рис. 10.3 6 очевидно, что угол конуса равен
sina =- = -"-. A0.24)
v M
Угол а называется углом Маха. Поверхность конуса Маха называ-
называется еще характеристической поверхностью, а линии пересечения ее
260
Газовая динамика
[Гл. 10
с плоскостью, проходящей через ось конуса, называются характери-
характеристиками.
v<c
v>c
vt2* °\
Щ
С?2\( \
O3 J
Рис. 10.3. Область распространения возмущений
Из рассмотрения рис. 10.3 очевидно, что сверхзвуковой поток на-
набегает на обтекаемое тело (являющееся, в частности, источником воз-
возмущения) «слепо». Сверхзвуковой поток не предчувствует обтекаемое
тело, в то время как в дозвуковом потоке влияние тела сказывается и
вверх по течению, т. е. дозвуковой поток «чувствует» обтекаемое тело
значительно раньше, чем его достигнет.
10.5.2. Поверхности разрыва. Ранее рассматривались движения
газа, при которых все скорости и термодинамические параметры изме-
изменялись непрерывно, т. е. были непрерывными функциями координат и
времени.
Однако оказывается возможны движения, при которых термоди-
термодинамические параметры и скорости могут претерпевать разрыв непре-
непрерывности. Скорости и термодинамические параметры могут изменяться
скачком вдоль некоторых поверхностей. Эти поверхности называются
поверхностями разрыва.
При нестационарных движениях поверхно-
поверхности разрыва сами могут двигаться в газе, од-
однако скорость их движения не имеет ничего
общего со скоростью движения индивидуаль-
индивидуальных частиц газа, которые могут при своем
движении пересекать поверхности разрыва.
Рассмотрим некоторую поверхность разры-
разрыва и свяжем с ней оси координат. Тогда в этой
системе координат поверхность разрыва будет
покоиться.
Рассмотрим малый участок поверхности
разрыва, который приблизительно можно счи-
считать плоским. Направим ось х по нормали к
рассматриваемому участку поверхности разрыва (рис. 10.4). На по-
поверхности разрыва должны соблюдаться определенные граничные усло-
условия.
A
Ti
Pi
vi
Pi
/ »
1 ^ .
Рис.
10.4. Поверхность
разрыва
10.5] Ударные волны и скачки уплотнения 261
1. На поверхности разрыва должна быть непрерывна нормальная
компонента плотности потока вещества (закон сохранения вещества)
P\V\x = P2V2x • A0.25)
2. На поверхности разрыва должен быть непрерывен поток энергии
(закон сохранения энергии). Плотность потока энергии определяется
вектором Умова
+ ?пот + g VJ + Як ~
где ?вн , еПОТ — внутренняя и потенциальная энергия единицы массы
газа, qk — /^-компонента вектора плотности теплового потока, Р^/с —
тензор напряжений. Пренебрегая потенциальной энергией, для идеаль-
идеального (невязкого и нетеплопроводного) газа имеем
h = ( + У + 2) [h +
Здесь /г — энтальпия единицы массы газа.
Непрерывность нормальной компоненты плотности потока энергии
на поверхности разрыва приводит к следующему соотношению:
hx = hx , P\v\x \h\ + g vi) = Р2^2Ж (^2 + 2 V " (Ю-26)
Соотношение A0.26) с учетом равенства A0.25) дает
hi + \v\ = h2 + \vl. A0.27)
3. На поверхности разрыва должен выполняться закон сохранения
количества движения. Это означает, что плотность потока импульса
с обеих сторон поверхности разрыва должна быть одинакова, в против-
противном случае на поверхность разрыва будет действовать некоторая сила,
которая должна вызывать движение этой, по определению неподвиж-
неподвижной, поверхности в выбранной системе координат. Имеем
[П^ = [Uik]2 , Ylik = p5ik + pvivk - &ik •
Для идеального (невязкого) газа aik = 0. Если ось г есть ось х, то
равенство плотностей потока импульса в направлении оси х приводит
к соотношению
Равенство плотностей потоков импульсов в направлении осей у и z
дает следующие равенства:
PlV{xViy = p2V2xV2y , P\V\XV\Z = p2^2x^2z • A0.29)
Последние два соотношения с учетом A0.25) дают
V\y = V2y, V\Z=V2Z. A0.30)
262 Газовая динамика [Гл. 10
Соотношения A0.30) свидетельствуют о том, что на поверхности
разрыва должны быть непрерывны касательные к ней скорости движе-
движения газа.
Рассмотрим движение газа, при котором линии тока до поверхности
разрыва перпендикулярны поверхности разрыва. Такая поверхность
разрыва называется прямой ударной волной, если она перемещается
по отношению к обтекаемому телу. Если же поверхность разрыва
неподвижна по отношению к обтекаемому телу, то она называется
прямым скачком уплотнения.
Из A0.25)-( 10.28) следует, что в прямой ударной волне или пря-
прямом скачке уплотнения скорости газа и термодинамические параметры
должны удовлетворять следующим соотношениям:
2 2
P\V\x = P2V2x , ftl + у = h2 + у , Р\ + p\v\x = Р2
A0.31)
10.6. Ударная адиабата (адиабата Гюгонио)
По определению прямой ударной волны v\y = v\z = 0. Равенство
A0.30) свидетельствует о том, что и V2y = V2Z — 0. Следовательно,
если линия тока до прямой ударной волны перпендикулярна поверхно-
поверхности разрыва, то она останется перпендикулярной и после поверхности
разрыва, т. е. линия тока при прохождении прямой ударной волны не
испытывает излома. Поэтому в равенствах A0.31) v\x = v\ ,V2X = Щ,
и их можно записать в окончательном виде:
2 2
p\V\ = P2V2 , h\ + —^ = /l2 + -у , Р\ + p\v\ = Р2 + Р2^| • (Ю.32)
Установим соотношение между термодинамическими параметрами
и скоростями в прямой ударной волне.
Введем следующие обозначения:
p\V\ = P2V2 = J , V\ = JV\ , V2 = JV2 •
Здесь V\ и V2 — объемы единицы массы газа до и после ударной волны
соответственно. Из третьего уравнения A0.32), получим
P, + j2vi=p2 + jV2, J2 = f^f- (ю.зз)
Далее имеем для разности скоростей:
v2-v{ = J(Vi - V2) = [(Vi - V2)(p2 - Pi)]42 ¦ A0.34)
Используя, наконец, второе уравнение A0.32), получим следующее
соотношение:
hi-h2 = ± J2(V22 - V?), hx-h2={-{Px- p2)(V{ + V2).
10.6]
Ударная адиабата (адиабата Гюгонио)
263
Последнее соотношение называется ударной адиабатой или адиаба-
адиабатой Гюгонио:
h =
Из A0.35) следует, что уравнение ударной
адиабаты дает связь между р% и V2, если из-
известны р\ и V\. При заданных р\ и V\ кривая
Рг(^2) имеет вид, изображенный на рис. 10.5.
Из уравнения A0.35) видно, что кривая
Рг(^2) обязательно проходит через точку р2 =
= р\ и V2 = V\, так как при этом уравнение
удовлетворяется тождественно.
Из рис. 10.5 следует:
7
7-1
pV.
A0.35)
-\p?J
; \
1
of
1
P\J\
V—-
1 Vrj
1 ^
tga =
- V2
= JZ.
A0.36)
Рис. 10.5. Адиабата Гю-
Гюгонио
10.6.1. Прямая ударная волна в идеальном газе. Рассмотрим
полученные соотношения для термодинамически идеального газа. За-
Запишем уравнения A0.35) в следующем виде:
h =
7
pV,
7
- P2V2) + I
7-1 VJ
Разделив это выражение на V\ и разрешив относительно V2/V1, полу-
получим
V2 = piG+ 1)+Р2G- 1) _ 7+ 1 + (P2/pi) G-
V^i pi G — 1) Н~ Р2 G ~
A0.37)
РгG + 1) 7 — 1 + (P2/pi) G+1)
Из последнего равенства с учетом уравнения состояния идеального
газа имеем
= — P2V2 = — — = — = Plll
fi fi ' Тх рхУ\ Pi 7
(P2/pi) G ~
(Р2/Р1) G+1) "
A0.38)
Из соотношения A0.37) видно, что отношение объемов в зависимо-
зависимости от отношения давлений является
/р ' равнобочной гиперболой (рис. 10.6) с
асимптотами
V<2 7 — 1 Р2 7 — 1
V\ 7 + 1 ' Pi 7 + 1
Предельное отношение температур
V2/Vi
Рис. 10.6. Зависимость отно-
отношения удельных объемов га-
газа после и до прямой ударной
волны от отношения давлений
при (p2/pi) -> 00 равно
Т\ = 7-1 Р2
Тх 7 + 1 Pi '
Таким образом, при бесконечном
скачке давления скачок температуры в
ударной волне может быть как угодно
264 Газовая динамика [Гл. 10
большим. Однако отношение плотностей стремится к некоторому по-
постоянному пределу. Для воздуха G = 1,4) этот предел равен
Р1 = 04 = I
Р2 2,4 б '
Для скоростей можно получить следующие соотношения:
• (Ю.39)
Аналогичное выражение можно получить для г>2:
7_
Для разности скоростей имеем
Критические скорости до и после ударной волны определяются
следующим образом:
? ? ? 7+1
2
2
2
2
+
+
7
7
с?
-
2
С2
—
1
1
си
2
2
^2*
2
+
+
cl
7 - 1
2
^2*
7 - 1
С1*
- г2
С2*
Г^ — П '
, A0-42)
7+ 1
2G- 1) "
Поскольку левые части соотношений A0.42) в ударной волне со-
сохраняются, то имеем
I 2
ci* = с2* = с* = coa/^ty ' A0.43)
Нетрудно видеть, что в ударной волне сохраняются и температуры
торможения:
у + срТх = срТю , Ц- + срТ2 = срТ20 , Т10 = Т20 . A0.44)
Пользуясь вышеприведенными формулами, можно доказать следу-
следующее соотношение:
l A0.45)
Интересующие нас соотношения можно выразить через число Ма-
Маха. Так, из формулы A0.39) можно получить соотношение
P*=JTLM?-7_^1 A046)
pi 7+1 7+1
10.7] Ударные волны слабой интенсивности 265
В свою очередь М2 можно выразить через Mi, пользуясь форму-
формулами A0.39), A0.40) и A0.46). Произведя необходимые вычисления,
получим
м!=2 + ^-1>М'. A0.47)
2 27М?-G-1)
Для отношения скоростей из A0.39), A0.40) и A0.46) следует
формула
!?* = 2-hG-l)MJa
vi G+1) М?
Наконец, пользуясь формулой A0.45), из последнего соотношения
имеем
A0.49)
10.7. Ударные волны слабой интенсивности
Для определения характера изменения термодинамических величин
и скоростей в ударной волне рассмотрим ударные волны слабой ин-
интенсивности, т. е. будем полагать, что, например, изменение давления
в ударной волне незначительно (р2 — р\)/р\ <С 1. Здесь и в дальнейшем
индексом 1 будем обозначать величины до ударной волны, а индек-
индексом 2 — после ударной волны.
Рассмотрим изменение энтропии газа, прошедшего через ударную
волну слабой интенсивности. Учтем, что энтальпия и объем единицы
массы газа зависят от давления и энтропии:
h = h{p,S), V = V(p,S).
Разложим энтальпию в ряд около ее значения в состоянии 1 (до
ударной волны). Тогда для энтальпии после ударной волны получим
(и-")" + -- <1а50)
В дальнейшем будет видно, что изменение энтропии пропорци-
пропорционально (р2 - PiK- Поэтому, ограничиваясь в разложении члена-
членами третьего порядка малости по (p2~Pi)> B последующих выраже-
выражениях можно пренебречь членами, пропорциональными (S^ — S\J и
E2-5i)(p2-pi).
266 Газовая динамика [Гл. 10
Аналогично для объема имеем
В этом разложении мы ограничились членом второго порядка ма-
малости по (р2 — р\). Это связано с тем, что выражение A0.51) будет
использовано в уравнении ударной адиабаты, которое уже содержит в
качестве множителя малую величину (р2 —р\).
Используем следующие термодинамические соотношения:
ар Js \aSJp
Подставляя A0.50)—A0.52) в уравнение ударной адиабаты A0.35),
получим
1 / С\ь Л Г \
A0.53)
1 f д2У
Из A0.53) следует, что скачок энтропии в ударной волне имеет
третий порядок малости по отношению к скачку давления. Соотно-
Соотношение A0.53) замечательно тем, что оно указывает на изменение
энтропии в ударной волне в идеальной жидкости, лишенной вязкости
и теплопроводности.
Следовательно, ударные волны являются еще одним механизмом
(наряду с трением и теплопроводностью) возрастания энтропии в дви-
движущихся жидкостях.
Можно показать, что производная (d2V/dp2) s всегда положитель-
положительна. В частности, для идеального газа (d2V/dp2}s = G + l)/(p2p/y2).
Поскольку энтропия может лишь возрастать (#2 > S\), то из соотно-
соотношения A0.53) следует:
Р2 > Р\ •
Из соотношения A0.33), J2 = (p2 —p\)/(V\ — V2), можно сделать вы-
вывод
Vi > V2 •
Из соотношения для скоростей v\/v2 = P2/P1 = V1/V2 можно заклю-
заключить:
V2 < V\ .
Из уравнения ударной адиабаты или уравнения Бернулли можно прий-
прийти к следующему выводу:
/i2 > h{, T2>T\.
Поскольку скорость звука зависит только от температуры, то
С2 > С\ .
10.7] Ударные волны слабой интенсивности 267
Из определения скорости звука следует:
Скорости движения газа в ударной волне могут быть определены
по формулам A0.33) и A0.36)
)
A0.55)
Рассматривая график ударной адиабаты Р2{У2) (см. рис. 10.5) и
сравнивая соотношения A0.54) и A0.55), приходим к заключению:
Следовательно, для образования ударной волны необходимо, чтобы
газ до ударной волны двигался со сверхзвуковой скоростью. Движение
же газа после прямой ударной волны всегда происходит с дозвуковой
скоростью. В газе, прошедшем прямую ударную волну, не могут суще-
существовать новые ударные волны.
Таким образом, в прямой ударной волне выполняются следующие
неравенства:
Р2 > Р\ , V\ > V2 , Р2 > Р\ , Т2>ТХ,
С2 > С\ , V\ > С\ , V2 < С2 , V2 < V\ ,
Си = С2* , Т10 = Т2о •
В газе, прошедшем прямую ударную волну, возрастает энтропия,
давление, плотность и температура, уменьшается лишь скорость дви-
движения газа, становясь дозвуковой.
Выше рассмотрена неподвижная прямая ударная волна или скачок
уплотнения. Если на рассматриваемое движение наложить скорость
v\, направленную справа налево (рис. 10.7), то
газ в области / окажется неподвижным относи-
относительно наблюдателя, ударная волна будет дви- 1
гаться справа налево со скоростью v\, а газ vx
за ударной волной в области 2 будет двигать-
ся справа налево со скоростью v\ - V2 = vcu —
скоростью спутного потока. Из формулы A0.41) щ
следует, что скорость движения плоской ударной -^
волны тем больше, чем интенсивнее волна, т. е. рис jq у
чем больше отношение Р2/р\-
10.7.1. Образование ударных волн. Образование прямой удар-
ударной волны можно понять, рассматривая следующий опыт. Пусть име-
имеется некоторая бесконечная труба с газом, на одном конце которой
имеется подвижный поршень (рис. 10.8).
268 Газовая динамика [Гл. 10
Пусть поршень внезапно начинает двигаться с некоторой скоро-
скоростью, а дальше продолжает двигаться со скоростью спутного потока.
Тогда в первоначальный момент времени перед поршнем образуется
уплотнение газа. Примерный график изменения плотности в трубе
в этот момент показан на рис. 10.8.
Разобьем этот уплотненный участок
газа на тонкие элементарные слои.
Поскольку более интенсивное уплот-
уплотнение распространяется в газе и
с большей скоростью, то в процессе
движения более плотные задние слои
будут догонять менее плотные перед-
передние слои и в последующий момент t\
график р(х) будет иметь более крутой
вид. При дальнейшем движении кру-
Рис. 10.8. Формирование ударной тизна увеличивается и в конце концов
волны в тру е будем иметь разрыв, имеющий очень
малую толщину и двигающийся слева направо со скоростью v\,—
ударную волну. За ударной волной газ будет двигаться со скоростью
спутного потока v\ — V2. Таким образом, ударные волны являются
самоформирующимися образованиями в газе. Не очень резко ограни-
ограниченное уплотнение в газе по мере движения автоматически переходит
в резко ограниченную ударную волну. Очевидно, толщина поверхности
разрыва термодинамических параметров и скоростей в прямой удар-
ударной волне должна быть порядка средней длины свободного пробега
молекул газа. При последующем движении ударной волны в реальном
газе ударная волна «размывается» и исчезает вследствие вязкости и
теплопроводности реального газа.
Если поршень резко сместить влево, то в начальный момент време-
времени перед ним возникает разрежение. Это разрежение будет в дальней-
дальнейшем распространяться вправо. Однако те же рассуждения показывают,
что в этом случае не происходит самоформирования резкого перехо-
перехода между невозмущенным газом и областью разрежения. Наоборот,
более или менее резкое возмущение в начале движения поршня при
дальнейшем движении расползается, занимая постепенно все большую
и большую область пространства трубы. Это значит, что ударные
волны разрежения, т. е. резкие переходы, при которых в газе после их
прохождения давление уменьшается, существовать не могут.
То же самое можно показать, пользуясь уравнением ударной адиа-
адиабаты. Точки ударной адиабаты (см. рис. 10.5) правее точки (p\,V\),
которые соответствовали бы ударной волне разрежения (р2 < р\), не
реальны, так как они соответствуют такому процессу, при котором
энтропия уменьшалась бы (см. A0.53)).
10.7.2. Ударная волна при взрыве. Рассмотрим числовой при-
пример. При взрыве атомной бомбы образуется сферическая или полусфе-
полусферическая ударная волна. Вдали от эпицентра взрыва участок сфериче-
10.7] Ударные волны слабой интенсивности 269
ской ударной волны можно приближенно рассматривать как плоский и
для расчетов пользоваться полученными выше формулами для плоской
ударной волны. Интенсивность волны будем характеризовать отноше-
отношением давлений р^/рх-
Эксперимент показывает, что при взрыве мегатонной бомбы на
расстоянии 2,5 -=- Зкм от эпицентра взрыва р2/р\ ~ 2. Пусть скорость
звука в неподвижном воздухе будет равна 340 м/с. Вычислим скорость
движения ударной волны v\.
Из формулы A0.39) имеем
Таким образом, скорость распространения ударной волны почти
в полтора раза больше, чем скорость звука в неподвижном газе. Поэто-
Поэтому наблюдатель сначала обнаружит ударную волну, а уж затем услы-
услышит звук взрыва. Причем скорость распространения ударной волны
тем больше, чем больше ее интенсивность, т. е. чем больше отношение
Найдем скорость V2, необходимую для вычисления скорости спут-
ного движения воздуха за ударной волной A0.40):
v2 = Cl 7+l + (P2/Pi)G-l) = 0,84С1 .
{2[1 + (/)(+1)]}1/2
Скорость спутного потока газа за ударной волной равна
vcn = v\ — V2 ~ 0,5 с\ & 170 м/с.
Таким образом, воздух за ударной волной движется с ураганной ско-
скоростью, производя большие разрушения.
Найдем температуру воздуха за ударной волной, если температура
неподвижного воздуха Т = 300 К A0.38):
Zl = ?2 V| = Р2«2 й j 25 т 375К.
Т\ р\ V\ р\ V{
Таким образом, наряду с излучением объекты, подвергающиеся
воздействию ударной волны, не только испытывают резкий перепад
давления при ее прохождении (рг/pi ~ 2), воспринимаемый как удар,
но также могут разрушаться и возгораться под воздействием горячего
(~ 100 °С) ураганного ветра (~ 170 м/с), создаваемого спутным пото-
потоком, движущимся вслед за ударной волной.
Разбегающийся с большой скоростью от эпицентра взрыва воздух
создает около него область весьма низкого давления. Поэтому спустя
некоторое время после прохождения ударной волны воздух устремля-
устремляется по поверхности земли обратно к эпицентру, неся с собой много
пыли.
Этот запыленный нагретый воздух, устремляясь вверх, и создает
тот «гриб», который характерен для наземных ядерных взрывов.
270
Газовая динамика
[Гл. 10
10.8. Косая ударная волна
Рассмотрим более общий случай, когда линии тока в набегающем
потоке не перпендикулярны ударной волне (рис. 10.9). Направим ось х
по линии тока в набегающем потоке. Разложим скорость набегающего
потока на перпендикулярную и каса-
касательную к ударной волне компоненты
скорости.
Так как тангенциальная компонен-
компонента скорости движения газа в ударной
волне непрерывна, а нормальная компо-
компонента после прохождения ударной вол-
волны (прямая ударная волна) уменьшает-
уменьшается, то, следовательно, линия тока после
прохождения ударной волны поворачи-
поворачивает, приближаясь к ударной волне.
Очевидно, для нормальных компо-
компонент скорости справедливы те соотно-
соотношения, которые получены для прямой
ударной волны. Обозначим угол между осью х и ударной волной
через (р, а угол поворота потока через %. Тогда можно записать сле-
следующие соотношения.
Из условия непрерывности тангенциальной компоненты скорости
имеем
v\t = V2t, v\ cos <p = V2X cos (p + v^y sin <p , ctg(p= v
Рис. 10.9. Параметры газа в
косой ударной волне
V\ -
A0.56)
A0.57)
По аналогии с прямой ударной волной A0.48) для отношения нор-
нормальных компонент скорости можно записать
У2п _ 2+ G - l)Min |у| _ У\п
vin (т+1)М?п ' ci
Из рис. 10.9 имеем следующие соотношения:
V\n = V\ Sin (f , V2n = V2X sin ^ — V2y cos <? •
Подставляя в A0.57), получаем
— V2y COS (p
2C\
7 — 1
sin <p =
1
Последнее выражение можно записать в следующем виде:
У2х - V2y Ctg (р _ 2с\{\ +Ctg2 (f) 7 - 1
ctgz <p = -
G +
7-1
7+1
7+
v\ — г
v\
-1
A0.58)
10.S
Косая ударная волна
271
В уравнении A0.58) для V2y использовано соотношение A0.56).
Умножая числитель и знаменатель правой части A0.58) на v\, а также
вычитая и прибавляя в числителе v\, получим следующую формулу:
ctg2 р = {-^J = [^ («, - |) - (t,, - t*.)] x
cT
7+ 1
-1
Таким образом, окончательно имеем уравнение
= (Vl- v2xJ
I
Щ . (Ю.59)
^ 7+1«1
Уравнение A0.59) называется уравнением ударной поляры. Оно
дает связь между v2y и V2X, если заданы v\ и с\.
Введем в уравнение ударной поляры вместо с\ критическую ско-
скорость с*. По определению критическая скорость может быть получена
из первого уравнения A0.42):
27+1 2
После подстановки A0.60) в A0.59) получим
2 / \2 V\V2x - el
V2y = \vl ~ V2x) ~Y~
с* - v2xv\ +2^1/G + 1)
A0.60)
A0.61)
При заданных v\ и с* функция v^y = f{v2x) представляет собой
уравнение строфоиды и имеет вид, изображенный на рис. 10.10.
/ с,
^¦^~~~
V2y
^<
о
//
А
У2
У
т
\/
ч
>чУс X /!
v2 |ф\\ "fr
F^ /
^ S
v
Рис. 10.10. Кинематические величины ударной поляры
272 Газовая динамика [Гл. 10
Обозначим точки пересечения строфоиды с осью V2X через А и В.
Очевидно, что радиус-вектор, проведенный из начала координат в лю-
любую точку С строфоиды представит скорость V2. Угол, составляемый
этим вектором и осью V2X, будет углом поворота потока, х- Длина
отрезка OD соответствует касательным составляющим скоростей до и
после ударной волны, v\t = v^t- Координаты точек А и В могут быть
определены из условия V2y = 0.
Приравнивая к нулю левую часть уравнения, для координат точек
А и В получим следующие значения.
Двойная точка пересечения В, очевидно, имеет координаты
{v2x)B = vi .
Координаты точки А следуют из равенства нулю числителя дроби
A0.61)
Таким образом, точки А и В ударной поляры определяют скорости
в прямой ударной волне. Точки строфоиды за точкой В нереальны, так
как соответствовали бы условиям в прямой ударной волне, при которых
V2 > v\, что невозможно.
Проведем прямую через точки В и С и опустим перпендикуляр из
начала координат на эту прямую. Обозначим угол DOB через /3, тогда
из рис. 10.10 следует:
ctg/3 = —^—=ctg(p, P = <p.
v\ - Щх
Следовательно, угол /3 равен углу наклона ударной волны к скорости
набегающего потока.
Далее из рисунков 10.9 и 10.10 имеем
OD = v\ cos (p = v\t = V2t, BD = v\ sin (p = v\n ,
DC = V2 Sin(<p - X) = V2n •
Если из начала координат провести касательные к ударной поляре,
то точки касания Е практически будут совпадать с точками пересече-
пересечения окружности V2 = с* с ударной полярой.
10.8.1. Максимальный угол поворота потока. При увеличении
числа Маха Mi , за счет увеличения скорости набегающего потока
v\ точка В будет передвигаться вправо, а точка А влево, так как
V[V2 = С*.
Поэтому ударные поляры для меньших Mi будут лежать внутри
ударных поляр, построенных для больших Мь
Найдем уравнение ударной поляры в предельном случае Mi —> оо.
При этом критическое число Маха будет иметь следующее предельное
10.S
Косая ударная волна
273
значение A0.49):
м?.
= (-У
= G+l)Mf
2+ G-1) Mi
_ 7+ 1
Mi-
7 ¦
1 '
A0.62)
v\ = с
2 7+1
= V
1 max '
7-1
Подставляя эти значения в уравнение ударной поляры A0.61), по-
получим
/ FT, ! Г" \ / ГГ. Г" \
A0.63)
Уравнение A0.63) представляет собой окружность (рис. 10.11) ра-
радиусом
/7+1 _ /т — 1 Л
7-1 V 7+ 1 У
в точках А и В, имеющих координаты
1
Окружность пересекает ось
соответственно
{Пх)А = С*
7+ 1
Касательная, проведенная к окружности из начала координат, имеет
угол с осью V2X, определяемый соотноше-
соотношением
sin xm
R
1
7
с R + OA
По определению угол хтах является макси-
максимально возможным углом поворота потока
в косой ударной волне, достигаемый только
при бесконечном числе Маха в набегающем
потоке. Для воздуха G = 1,4)
_ I _ _L
W
45°.
Рис. 10.11. Максимальный
угол поворота потока в ко-
косой ударной волне
Таким образом, для воздуха поток, прошедший косую ударную
волну, не может повернуть на угол, больший чем 45°.
Рассмотрим изменение скорости за косой ударной волной при за-
заданном Mi и изменении угла \ (рис. 10.12). Если точка С прибли-
приближается к точке В, то при этом v^x стремится к v\. Скачок скорости
уменьшается, и ударная волна в пределе переходит в слабый разрыв —
в слабую ударную звуковую волну. Однако при этом угол (р имеет
конечное значение.
Это значение можно определить из уравнения ударной поляры. При
v\ —> V2X из A0.59) имеем
1 1*11
Sin (f С\
1
sin (р = —- = sin a ,
Mi
<р = а ,
274
Газовая динамика
[Гл. 10
Таким образом, слабая ударная волна (звуковая волна), как и сле-
следовало ожидать, распространяется под углом а (угол Маха).
Рис. 10.12. Строфоида
При перемещении точки С к точке А скорость V2 за ударной волной
уменьшается и после прохождения точки Е становится дозвуковой.
При этом угол (р монотонно увеличивается и, наконец, в точке А
становится равным 90°, что соответствует прямой ударной волне. Из
соотношения A0.59) при щх -^^в этом случае немедленно следует
формула A0.48), полученная для прямой ударной волны
V2 _ 2 +G- 1) Mf
V\
G+l)Mf
Из рис. 10.12 видно, что если угол (р при перемещении точки С от
точки В к точке А растет монотонно, то угол х достигает некоторого
максимального значения в точке Е (v2 = с*), а затем начинает убывать.
Точка Е делит ударную поляру на две части: часть BE, для которой
V2 > с*, и часть ЕА, в точках которой V2 < с*. Причем, как отмеча-
отмечалось выше, точка Е почти совпадает с точкой касания касательной,
проведенной к поляре из начала координат. Следовательно, для точек
поляры BE скорость газа, прошедшего косую ударную волну, остается
сверхзвуковой, для точек ЕА скорость газа после косой ударной волны
становится дозвуковой.
Точки части поляры BE называются точками слабого семейства,
а точки поляры ЕА — точками сильного семейства ударных волн. За-
Заданному углу х на ударной поляре всегда (кроме точки Е) соответ-
соответствуют две точки, из которых одна принадлежит слабому, а другая
сильному семейству. Опыт показывает, что в действительности реа-
реализуются лишь точки слабого семейства. Точки сильного семейства
никогда не реализуются, кроме как в прямой ударной волне (точка А).
По-видимому, ударные волны, соответствующие точкам сильного се-
семейства, кроме точки А (прямая ударная волна), неустойчивы. Поэтому
за косой ударной волной скорость движения газа остается сверхзвуко-
сверхзвуковой (v2 > с*), и в нем могут возникнуть еще косые или прямые ударные
волны.
10.S
Косая ударная волна
275
10.8.2. Обтекание клина. Рассмотрим обтекание сверхзвуковым
потоком газа плоского клина (рис. 10.13).
Пусть заданы величины v\ и Mi. Для практических расчетов су-
существуют номограммы, которые представляют собой ударные поляры,
вычисленные для различных Mi. Они изображены в виде строфоид,
вложенных одна в другую. Причем стро-
строфоида, построенная для меньшего Мь ле-
лежит внутри строфоиды, построенной для
большего Mi. В данном случае нам из-
известны v\ и Mi, а также угол поворота
потока х, так как поток должен повернуть
вдоль поверхности клина.
Проводя из начала координат
(рис. 10.14) прямую под углом х, получим
две точки пересечения этой прямой
с ударной полярой, построенной для заданного Mi. Выбираем точку
слабого семейства — точку С. Отрезок ОС определяет скорость за
косой ударной волной — г^. Проводя секущую через точки В и С и
опуская на нее перпендикуляр из начала координат, получим угол
(р — угол наклона косой ударной волны к набегающему потоку (см.
рис. 10.10).
Рис. 10.13. Обтекание клина
Рис. 10.14. Ударные поляры
В прямой ударной волне для отношения давлений имели формулу
A0.46)
^ = -=2- М? -^—- . A0.46а)
7+ 1
7+ 1
Для косой ударной волны, следуя формуле A0.57), аналогичная фор-
формула будет иметь вид
р\
^_^sin2^_l^l=^_
7+1 с? 7+1 7+1
7+1
A0.64)
Отношение остальных термодинамических величин может быть по-
построено из полученных выше формул A0.37), A0.38).
276 Газовая динамика [Гл. 10
Из сравнения формул видно, что при заданном Mi скачок давления
в косой ударной волне всегда меньше, чем скачок давления в прямой
ударной волне. Также меньше скачки и других термодинамических ве-
величин, в том числе и энтропии. Скорость газа за косой ударной волной
также изменяется меньше, чем в прямой, оставаясь сверхзвуковой.
Если при заданном Mi будем увеличивать угол раствора клина, то
может оказаться, что прямая, проведенная из начала координат под
углом х> не пересекается с ударной полярой, по-
построенной для Mi. При этом, как показывает опыт,
перед клином образуется отсоединенная ударная
волна (рис. 10.15).
Если увеличить число Mi, то состояние газа за
косой ударной волной будет изображаться ударной
полярой, соответствующей М2 > Mi. Прямая, про-
^ ЛГл лг ^ веденная под углом у, может пересечься с этой
Рис. 10.15. Отсое- о \ ^ ^ ^
диненная ударная УДаРН0И полярой. Это означает, что косая ударная
волна волна снова будет «посажена» на носик клина. Если
при заданном М2 снова увеличить угол раствора
клина х> то снова может оказаться, что прямая, проведенная под новым
углом х не пересечется с ударной полярой М2. В этом случае косая
ударная волна снова отойдет от носика клина, т. е. снова образуется
отсоединенная ударная волна. И так далее. По-видимому, это рассуж-
рассуждение можно продолжать до тех пор, пока угол раствора клина не
достигнет максимального значения
1
Sin Xmax = - •
Для клина, имеющего угол раствора х > Xmax, даже при бесконечном
числе Маха ударная волна будет отсоединенной. Для воздуха xmax ~
& 45°. Для тупого тела ударная волна будет всегда отсоединенной.
Если из каких-либо источников нам известно направление косой
ударной волны и угол х клина, то всегда можно подобрать ударную
поляру, удовлетворяющую обоим углам. А это означает, что, зная (р
и х, можно определить Mi. Если известна температура газа, то зная
Mi, можно определить скорость движения газа или скорость движения
клина. А если скорость движения клина известна, то можно опреде-
определить температуру газа. На практике иногда пользуются этим методом
определения температуры газа, в котором движется ракета, так как
скорость ее движения может быть определена очень точно другими
радиофизическими методами.
Отсоединенную ударную волну можно рассматривать как волну,
содержащую участки прямой и последовательной серии косых ударных
волн. Так, участок отсоединенной ударной волны перед самым носиком
клина можно рассматривать как прямую ударную волну. Поскольку
скачок давления в прямой ударной волне при заданном Mi больше, чем
в косой, то и лобовое сопротивление клина будет больше, чем оно было
10.9] Волна разрежения 277
бы при косой присоединенной ударной волне. Поэтому для снижения
сопротивления тел в сверхзвуковом потоке необходимо стремиться к
тому, чтобы перед обтекаемым телом не образовывалось отсоединен-
отсоединенных ударных волн. При заданном числе Mi это можно сделать только
уменьшением угла раствора клина. Таким образом, хорошо обтекаемые
тела в сверхзвуковом потоке должны иметь острую переднюю кромку.
С образованием ударных волн связан и так называемый звуковой
барьер. При достижении самолетом скорости, равной скорости звука,
на передних кромках обтекаемых частей самолета образуются ударные
волны, что связано с резким увеличением сопротивления, что в свою
очередь резко увеличивает нагрузки на различные элементы самолета.
Увеличение сопротивления ведет к снижению скорости самолета до до-
дозвуковой и, следовательно, к снижению сопротивления. Самолет снова
разгоняется и достигает звуковой скорости и т.д., т.е. самолет, уве-
увеличивая скорость, как бы постоянно натыкается на некоторый барьер,
для преодоления которого необходимы мощные двигатели и достаточно
прочная конструкция самолета.
С той же целью уменьшения сопро-
сопротивления крылья современных самолетов
делаются стреловидными (рис. 10.16).
Действительно, при заданной скорости
полета скорость потока, набегающего на
крыло, можно разложить на касательную
и нормальную составляющую к передней
кромке крыла. При этом нормальная со-
составляющая, ответственная за образова-
образование ударной волны на крыле, окажется, рис jq ^
конечно, меньше скорости набегающего
потока. Поэтому если самолет дозвуковой, то он может двигаться
с большей скоростью без образования на плоскостях ударных волн.
Если же самолет сверхзвуковой, то при этом отсоединенный скачок
появится при большей скорости, а косой скачок будет менее интенсив-
интенсивным.
Теория трубки Пито в сверхзвуковом потоке непременно должна
учитывать образование перед ней отсоединенной ударной волны, так
как по необходимости передний носик трубки Пито является тупым.
10.9. Волна разрежения
10.9.1. Обтекание тупого угла сверхзвуковым потоком. Рас-
Рассмотрим обтекание сверхзвуковым потоком тупого угла (рис. 10.17).
Линию АОВ можно рассматривать как одну из двух стенок плоского
расширяющего насадка.
Пусть газ движется вдоль АО с постоянной сверхзвуковой скоро-
скоростью v\ > c\ и вытекает в пространство, в котором давление меньше,
чем давление в набегающем потоке. Газ будем полагать идеальным
278 Газовая динамика [Гл. 10
(т. е. коэффициенты динамической и объемной вязкости равны нулю,
7/ = 0, ? = 0), а движение установившимся. В данной задаче, очевидно,
удобно воспользоваться полярной систе-
>1,/?1 \ср =0 мой координат. Если плоское сопло очень
широкое, то движение газа можно рас-
рассматривать как плоское, в котором все
термодинамические величины и скорости
зависят только от угла (р полярной си-
системы координат с началом в точке О и
не зависят от радиальной координаты г.
Рис. 10.17. Обтекание тупого Пусть линия (р = 0 определяет начало от-
Угла счета углов (р.
Принимая во внимание вышесказанное, из уравнения Эйлера в ци-
цилиндрической системе координат получаем следующую систему:
v^p dvr v<p _ r\ @vr _
г ' др ^'
г д(р г ' д(р
dip r rp uip V Oip I p
+ ^=0, °P=-JL,Vr +
toA=_±%L, (Ю.65)
dip J p dip
r dip r ' dip Vy у dip
Произведем следующие преобразования:
dp _ I dp\ dp _ 2 dp I dV(p\ _ с
Таким образом, имеем следующее уравнение:
°- A066)
Уравнение A0.66) имеет два решения. Первое решение
vr + -^ = 0 .
dip
Принимая во внимание уравнения A0.65), получим ряд последователь-
последовательных выводов
vr + -^- = 0 , -J- = 0 , р = const, d/i = TdS H— (ip ,
dip dip p
S = const, t— = - -7-^-, h = c^T = const, T = const.
dip p dip
Из уравнения Бернулли следует, что в этом случае и скорость газа
постоянна, v = const.
Далее можно показать, что при этом и направление потока не изме-
изменяется. Действительно, рассмотрим направление скорости в какой-либо
точке потока (рис. 10.18).
10.9] Волна разрежения 279
Пусть угол (р полярной системы координат и угол %, опреде-
определяющий направление скорости в любой точке потока по отношению
к выбранному постоянному направлению
(линия АО), отсчитываются, как показа- Vr/s
но на рис. 10.18. - ч ¦**
Из рисунка следует
^Р — Х~ ^ — X ~ arcctg — .
Дифференцируя по <р, имеем
2 / \
\ — ^Х_ _|_ V(p ( _L °Vr _ Vr °v<p j m Рис. 10.18. Обтекание тупо-
^ v\ + vr \v<p dip v2^ dip J го угла
Принимая во внимание равенства A0.65) и решение уравнения A0.66),
vr = -dv^/dip, получим
dy
-А = 0 , v = const.
dip
Следовательно, в этом случае не изменяется и направление потока.
Значит, первое решение описывает случай плоскопараллельного
поступательного потока вдоль АО.
Второе решение уравнения A0.66)
v +^=0, v(p = c. A0.67)
Уф
Тогда из уравнения непрерывности (пятое уравнение системы 10.65)
имеем
d{pc) A0.68)
dip J pvr J pvr
Скорость vr может быть определена следующим образом:
2 2 1 2
9 99 99 9 99^ С 7+1 С*
vz = vl + vl = vl + c2, v2r = v2-c2, T + _T = X_^.
Из последнего соотношения видно, что vr может быть определена через
сие*:
/7+1 B 2\
Далее можно сделать следующие преобразования:
с = 7 — , — = const, с = const • 7Р7 >
_Р Р 2/G-1) Р1 _ Р« _ Р2 A0-69)
о — consx * с , ^ — ~^т — ~^т .
Р\ Р* Р2
Подставляя полученные соотношения в A0.68), получим
/7+ 1 Г dc /7 + 1 с ,
(р = —\ А . — \\ arccos Ь const.
V 7 - 1 J Jcl - с2 V 7 - 1 с*
280 Газовая динамика [Гл. 10
Постоянная интегрирования связана с началом отсчета углов, и ее мож-
можно положить равной нулю, а начало отсчета углов найти из физических
соображений. Таким образом, имеем
v<p = c = c# cosW^pj <p, vr = c*^LA sinj-^- (p. A0.70)
Из соотношений A0.69) следует
\p*s *> — A071)
2/G-0 / / г \ 27/G-0
COS ч / (f I , р =
Движение газа, описываемое соотношениями A0.70) и A0.71), на-
называется волной разрежения.
Из полученных соотношений видно, что с увеличением угла (р все
термодинамические величины и скорости изменяются непрерывно,
причем с увеличением угла (р плотность, давление и скорость звука,
а следовательно, температура газа, убывают. Скорость же движе-
движения газа, как это следует из уравнения Бернулли, возрастает. Та-
Таким образом, изменение всех термодинамических величин и скоростей
в волне разрежения прямо противоположно их изменению в ударной
волне
pi, pi, Ti, ci, vt-
Следует еще раз подчеркнуть, что если в ударной волне все термоди-
термодинамические параметры и скорости изменяются скачком, то в волне раз-
разрежения они изменяются непрерывно. Следовательно, волна разреже-
разрежения занимает определенную область пространства в движущемся газе.
10.9.2. Максимальный угол поворота потока. Из физических
соображений следует, что поток, движущийся вдоль АО, должен по-
повернуть вдоль стороны угла ОВ. Если теперь углы <р и х отсчиты-
отсчитывать по направлению потока, то очевидно, что компонента v^ пол-
полной скорости должна быть всегда положительна (v^ > 0). В области
возмущенного движения положительной должна быть и компонента
скорости vr (vr > 0), так как возмущения, вызываемые вершиной
угла, распространяются вдоль прямых (характеристик), исходящих из
вершины угла в положительном направлении.
Тогда из формул A0.70) следует, что v^ и vr могут быть одновре-
одновременно положительны только в первой четверти изменения их аргумен-
аргумента. Поэтому (р может изменяться только в следующих пределах:
п п h -1 ^
<р = 0, ^min=0, ^_ ч> = -
Поэтому волна разрежения не может занимать сектор с вершиной
в точке О, больший, чем сектор, ограниченный прямыми, исходящими
10.9]
Волна разрежения
281
из точки О с углом раствора
A0.72)
Для воздуха G = 1,4) А<^тах = 219°.
Рассмотрим,как изменяется угол поворота потока х (рис. 10.19)
при изменении угла (р. Отсчет обоих углов будем вести по потоку от
некоторого начального направления <р = 0.
Из рис. 10.19 следует:
i I
/7-1
X = <р + arctg ^ = (р + arctg
v
A0.73)
Угол х» очевидно, будет изменяться от его значения хо при
до значения хтах при (р = <^тах. Подставляя в A0.73), получим
= 0
Х0 — су ' Хтах — fy-^max — су
тах — Х
A0.74)
Таким образом, из A0.74) следует, что поток в волне разрежения
не может повернуть на угол, больший , чем угол Ахтах- Для воздуха
имеем Ахтах ~ 130°.
Из формул A0.70), A0.71) следует, что при (р = ^тах имеем
= 0,
vr = с*
V = Vn
Следовательно, линия (р = <^тах есть линия, граничащая с вакуумом,
когда абсолютная температура вытекающего газа становится равной
нулю. Только в этом случае возможен
поворот потока воздуха на угол 130°.
Для построения картины обтекания
тупого угла необходимо найти начало от-
отсчета углов (р и х • Ранее при интегри-
интегрировании постоянная интегрирования, ко-
которая определяет начало отсчета углов,
положена равной нулю. Для нахожде-
нахождения начала отсчета углов можно восполь-
воспользоваться физическими соображениями.
Действительно, вершина обтекаемого уг-
угла является источником возмущений.
Возмущения же распространяются в движущемся газе под углом а.
Поэтому начало возмущенного потока или начало волны разрежения
определяется линией, проведенной из вершины угла под углом а к
направлению набегающего потока или к направлению стороны уг-
угла АО. Эта линия, очевидно, является первой характеристикой, огра-
Рис. 10.19. Угол поворота по-
потока х
282
Газовая динамика
[Гл. 10
ничивающей волну разрежения слева, т. е. со стороны невозмущенного
набегающего потока.
Очевидно, этой начальной характеристике нужно приписать угол (р
который следует из соотношений A0.70) при v^ = с\, где с\ — скорость
в набегающем невозмущенном потоке. Таким образом, первой характе-
характеристике необходимо приписать угол
Ч>\ =
A0.75)
7-1
Откладывая угол ip\ от линии, проведенной под известным (при
заданном числе Маха Mi, sin a = I/ Mi) углом а влево, получим начало
отсчета угла (р.
В свою очередь, угол хь очевидно, может быть определен по
формуле A0.73) при подстановке в нее угла (р = <р\.
Последнюю характеристику, ограничивающую волну разрежения
справа, можно найти, используя следующие соображения.
Пусть поток после прохождения вершины угла поворачивает и дви-
движется вдоль стороны угла ОВ. Тогда известен угол поворота потока
Ах- Причем из рис. 10.20 следует
Ах = Х2 ~ XI = 180° - C , Х2 = A80° - /3) + XI • A0.76)
Поскольку известны углы х и Р> то известен и угол Х2- Тогда,
подставляя в формулу A0.73) х = Х2> можно определить и угол <р2,
отсчитываемый от вычисленного вы-
выше начала отсчета углов и опреде-
определяющий характеристику, ограничи-
ограничивающую волну разрежения справа.
На рис. 10.20 построена волна
разрежения, образующаяся при об-
обтекании тупого угла. Прежде всего,
зная Mi, определим угол а и отло-
отложим его от направления АО. Линия
ОС является первой характеристи-
характеристикой, ограничивающей волну разре-
разрежения слева. По формуле A0.75)
ю=0
Рис. 10.20. Волна разрежения
найдем угол (р\, и отложим его от линии ОС влево. Тогда линия OD
определит начало отсчета углов. Подставляя <р\ в A0.73), получим хь
Зная углы xi и /5» по формуле A0.76) найдем угол \2> а по
формуле A0.73) найдем угол <?>2, отсчитываемый от начала отсчета
углов (линия OD).
Линия ОЕ определит характеристику, ограничивающую волну раз-
разрежения справа. Из рассмотрения видно, что все термодинамические
параметры и скорости изменяются непрерывно только внутри сектора,
ограниченного характеристиками ОС и ОЕ. Вне этого сектора все тер-
термодинамические величины постоянны, постоянны также направление
и скорость газа.
10.9]
Волна разрежения
283
Таким образом, если провести линию тока, то она будет параллель-
параллельна линии АО вплоть до пересечения с первой характеристикой. После
первой характеристики линия тока поворачивает в волне разрежения
до пересечения со второй характеристикой. После второй характери-
характеристики линия тока будет параллельна стороне угла ОВ.
Вообще характер движения газа при обтекании тупого угла сверх-
сверхзвуковым потоком в существенной мере зависит от противодавления р%
(рис. 10.17), т.е. давления, которое встречает поток газа, движущийся
вдоль стороны угла АО. При заданном Mi и угле /3, как показано
выше, можно рассчитать противодавление (р2)теор> ПРИ котором поток
в волне разрежения в точности повернет вдоль стороны ОВ. Для этого
необходимо определить начало отсчета углов <р\ по формуле A0.75),
найти xi по формуле A0.73), вычислить Х2 по формуле A0.76), опре-
определить (f2 по формуле A0.73) и, наконец, по формуле A0.71), зная р\
и р\, найти (р2)теор- Если р2 > (р2)теор> то газ при заданных параметрах
набегающего потока и C не будет двигаться вдоль стороны угла ОВ.
Между стороной О В и крайней линией тока образуется застойная зона
покоящегося газа (рис. 10.21). В застойной зоне вследствие вязкости
реальных газов будут образовываться крупные нерегулярные вихри.
Если уменьшать давление р2, то при достижении р2 = (р2)теор по-
поток будет полностью прилегать к стороне угла О В без образования
застойной зоны. Если дальше уменьшить давление р2 < (р2)теор> то
поток будет продолжать двигаться вдоль стороны угла ОВ. Если
при р2 = (р2)теор уменьшить угол /3, то газ снова не будет следо-
следовать вдоль ОВ и снова в газе должен образоваться тангенциальный
разрыв скоростей ОС на линии тока, граничащей с неподвижным
газом, который будет в действительности (в силу вязкости реальных
жидкостей) размываться в зону вихревого турбулентного движения.
2 = 0, р2 = 0
Рис. 10.21
Рис. 10.22
Если при уменьшении угла /3 уменьшить и противодавление, то можно
добиться давления р2, при котором газ снова будет двигаться вдоль
О В без образования застойной зоны и т.д.
Очевидно, при р2 = 0 угол /3 будет минимален, а угол поворота
потока максимальным (для воздуха Axmax ~ 130°). При этом крайняя
линия тока, как указывалось выше, должна граничить с вакуумом,
абсолютная температура газа должна быть равна нулю, а компоненты
скорости газа равны v^ = 0, vr = г?тах (рис. 10.22). Если теперь угол /3
284
Газовая динамика
[Гл. 10
еще уменьшить, то газ не будет следовать вдоль стороны угла О В и
между стороной О В и крайней линией тока будет зона вакуума.
Рассмотрим движение, при котором противодавление р^ больше,
чем давление в набегающем потоке р\ (р2 > р\). Очевидно, что в этом
случае должна образоваться косая ударная волна, исходящая из вер-
вершины О обтекаемого угла ЛОВ. Зная р\ , Mi , и р% по формуле A0.64),
можно определить угол (р — угол наклона косой ударной волны к
направлению набегающего потока (рис. 10.23). Зная Mi и угол <р, по
ударной поляре можно найти V2 и \- При этом должен образовать-
образоваться тангенциальный разрыв скорости ОС, разграничивающий область
движущейся жидкости от застойной зоны хаотического турбулентного
движения.
Рис. 10.23
Рис. 10.24
При дальнейшем увеличении р^ может оказаться, что sin <p, опреде-
определяемый по формуле A0.64), окажется больше единицы. Это означает,
что в движущемся газе должна образоваться отсоединенная ударная
волна (рис. 10.24).
10.10. Пересечение ударных волн и волн разрежения
Ударные волны и волны разрежения в движущемся газе могут,
встречаясь, пересекаться или, падая на твердую стенку, ограничиваю-
ограничивающую движение, отражаться от нее, или, встречая тангенциальный раз-
разрыв, испытывать отражение или преломление. Рассмотрим качественно
отражение или пересечение ударных волн и волн разрежения.
10.10.1. Отражение ударной волны от стенки. Пусть на твер-
твердую стенку падает косая ударная волна (рис. 10.25).
Представим , что где-то вдали от стен-
стенки в сверхзвуковой поток помещен клин,
от которого отошла рассматриваемая удар-
ударная волна. Для определения движения га-
газа за падающей ударной волной восполь-
воспользуемся ударной полярой (рис. 10.26).
Выберем на номограмме поляру, соот-
соответствующую заданному числу М. Прове-
Проведем из начала координат прямую под из-
М
V
Рис. 10.25. «Правильное»
отражение
10.10]
Пересечение ударных волн и волн разрежения
285
Рис. 10.26
вестным углом ip\. Из точки В\ опустим на эту прямую перпендикуляр.
Тогда, как известно, пересечение этого перпендикуляра с ударной поля-
полярой определит отрезок ОС\, характеризующий скорость за падающей
ударной волной, а также угол по-
поворота потока х- Зная Mi и <рь по
формулам A0.47), A0.56), A0.57)
определим М2 — число Маха за па-
падающей косой ударной волной. Оче-
Очевидно, М2 < Mi. Поэтому ударная
поляра, соответствующая М2, будет
лежать внутри ударной поляры, со-
соответствующей Mi.
На рис. 10.25 можно провести
линию тока за падающей ударной
волной. Но газ за падающей удар-
ударной волной должен двигаться вдоль твердой стенки. Это значит, что
от точки пересечения падающей ударной волны со стенкой (точка О)
должна отойти также косая ударная волна, в которой газ должен
повернуть на тот же самый угол %, направив поток газа вдоль стенки.
Скорость за отраженной ударной волной может быть найдена, если
определена точка С2 — точка пересечения линии ОС\ с ударной поля-
полярой, соответствующей М2.
Если теперь из точки Б2 провести через точку С2 линию, а на нее
из начала координат опустить перпендикуляр, то линия OD2 определит
угол (f2 — угол отражения падающей ударной волны. Снова, зная М2
и (f2, можно определить число Маха за отраженной волной. Очевид-
Очевидно, Мз < М2. Поскольку М2 < Mi, то </?2 > (р\. Пользуясь формулами
A0.47), A0.56), A0.57), это можно показать и аналитически.
Таким образом, падающая на твердую стенку косая ударная волна
отражается от нее также в виде косой ударной волны, причем угол
отражения всегда больше угла падения (рис. 10.25). Только очень сла-
слабые (звуковые) ударные волны, М2 « Mi, будут отражаться от твердой
стенки «зеркально» (</?2 « (р\).
Если падающая ударная волна очень
интенсивная, то может оказаться, что
линия ОС2 (рис. 10.26) не пересечет
ударную поляру, соответствующую М2.
В этом случае отражение будет непра-
неправильным (рис. 10.27). Между стенкой
и точкой отражения возникает участок
прямой ударной волны О\О. Вообще
скорость газа, прошедшего через отра-
отраженную волну, может быть и не равна скорости газа, прошедшего
прямую ударную волну. Это значит, что от точки О\ может отойти
тангенциальный разрыв (на рис. 10.27 показан штриховой линией),
т. е. линия, на которой все термодинамические параметры непрерыв-
О
7
1
Рис. 10.27. «Неправильное» от-
отражение
286
Газовая динамика
[Гл. 10
ны, нормальные компоненты скорости равны нулю, а тангенциальная
к поверхности разрыва скорость газа делает скачок. Ударная волна
сильного надземного взрыва будет отражаться неправильно, и вдоль
поверхности земли будет двигаться прямая ударная волна.
10.10.2. Пересечение двух ударных волн. Рассмотрим пересе-
пересечение в газе двух ударных волн. Снова можно представить, что они
образовались от двух клиньев, обтекаемых сверхзвуковым потоком
газа (рис. 10.28). Если ударные волны одинаковой интенсивности (оди-
(одинаковые клинья), то линия тока, проходящая через точку пересечения
(точку О), не должна претерпевать каких-либо изменений, ее можно
рассматривать, как твердую стенку и воспользоваться предыдущим
рассмотрением отражения падающей ударной волны от твердой стенки.
Линию ОВ можно теперь рассматривать или как пересеченную
волну 01 или как отраженную волну ОН.
Рис. 10.28. Пересечение двух
ударных волн
II
Рис. 10.29. Пересечение двух
ударных волн
V -, < V ,
Если пересекаются волны различной интенсивности, то скорость
газа, прошедшего разные волны, может быть различной, но после пере-
пересечения она должна повернуть на один и тот же угол. Поэтому резуль-
результат пересечения волн различной интенсивности должен быть таким,
каким он изображен на рис. 10.29.
Т\ у Л Vj Следовательно, от точки пересечения
(точка О) может отойти тангенциаль-
тангенциальный разрыв (пунктирная линия), повер-
повернутый относительно направления скорости
до ударных волн на некоторый угол. Ясно,
что если ОН — волна большей интенсив-
интенсивности, то скорость за ней будет меньше,
чем за волной 01, и поток будет прибли-
приближаться к более интенсивной волне.
Из предыдущего рассмотрения ясно,
что волны большой интенсивности будут пересекаться «неправильно»
(рис. 10.30), т.е. с образованием вилок и участка прямой ударной
волны. Также от точек пересечения могут исходить тангенциальные
разрывы (штриховые линии).
IF" ^B *з
Рис. 10.30. «Неправильное»
пересечение двух ударных
волн
10.10]
Пересечение ударных волн и волн разрежения
287
В<
Ръ/
10.10.3. Пересечение ударной волны с тангенциальным раз-
разрывом. Рассмотрим пересечение ударной волны с тангенциальным
разрывом. Пусть имеется тангенциальный разрыв, на котором все
термодинамические параметры непрерывны, нормальные компоненты
скорости равны нулю, а тангенциальная
компонента скорости делает скачок —
линия АОВ (рис. 10.31).
Определим качественно результат
пересечения с тангенциальным раз-
разрывом косой ударной волны. Так как
газ, прошедший косую ударную волну,
должен повернуть на некоторый угол, то
и тангенциальный разрыв тоже должен
повернуть на тот же угол. Кроме того,
поскольку давление за косой ударной
волной растет, а на тангенциальном раз-
разрыве давление должно остаться равным
давлению до косой ударной волны, то это возможно только в том слу-
случае, если от точки пересечения отойдет волна разрежения, в которой
повышенное давление за косой ударной волной упадет до давления перед
ней, а тангенциальный разрыв повернет поток еще на некоторый угол,
соответствующий повороту в волне разрежения.
Таким образом, приходим к выводу,
что ударная волна, падающая на тан-
тангенциальный разрыв, отражается от него
в виде волны разрежения.
Аналогичное рассмотрение пересече-
пересечения волны разрежения с тангенциальным
разрывом приведет нас к заключению, что
волна разрежения, падающая на танген-
тангенциальный разрыв, отражается от него в
виде косой ударной волны (рис. 10.32).
Рис. 10.31. Пересечение удар-
ударной волны с тангенциальным
разрывом
Р\ < Ро
Рис. 10.32. Пересечение вол-
волны разрежения с тангенци-
тангенциальным разрывом
10.10.4. Истечение газа из сужающегося насадка. В заключе-
заключение качественно рассмотрим истечение газа из сужающегося насадка
в неподвижный газ. Выше уже отмечалось, что при достижении на вы-
выходе сопла некоторого давления, равного его критическому значению,
скорость газа на срезе сопла достигает скорости звука с*. Однако вне
сопла давление может оказаться и больше и меньше этого критическо-
критического значения.
Рассмотрим случай, когда давление вне сопла больше критического
давления, и нарисуем качественную картину движения газа вне сопла.
Будем полагать для простоты, что сопло плоское. Тогда край сопла
можно рассматривать как источник возмущения (рис. 10.33). Газ вне
сопла неподвижен, газ, выходящий из сопла, имеет скорость, равную
скорости звука на срезе сопла. Тогда от края сопла должен отойти
тангенциальный разрыв. Для того чтобы давление в выходящем газе
288
Газовая динамика
[Гл. 10
Рис. 10.33. Пересечение волны
разрежения с тангенциальным
разрывом
повысилось от давления р* до давления ро > Р* необходимо, чтобы от
края сопла отошла ударная волна. Ударные волны, отошедшие от обеих
кромок сопла, пересекутся по известному закону, а затем упадут на
тангенциальный разрыв, от которого
они отразятся в виде волн разрежения.
В свою очередь волны разрежения по-
после пересечения отразятся от танген-
тангенциального разрыва в виде ударных
волн и т.д. Газ, проходящий удар-
ударные волны, тормозится, давление в нем
возрастает, а газ, прошедший вол-
волны разрежения, ускоряется и давление
в нем падает. Это чередование ударных
волн и волн разрежения будет происходить до тех пор, пока в силу
вязкости и теплопроводности кинетическая энергия движения не дис-
сипирует настолько, что скорость движения газа не станет дозвуковой.
Если давление газа вне сопла ро меньше р*, то от кромок соп-
сопла прежде всего отойдут волны разрежения, которые отразятся от
тангенциального разрыва в виде косых ударных волн. Далее вниз по
течению картина повторяется до тех пор, пока скорость газа не станет
дозвуковой. При р > р* вне сопла движение газа будет происходить
без образования ударных волн или волн разрежения.
10.10.5. Сопло Лаваля в нерасчетном режиме. Режим дви-
движения газа в сопле Лаваля также в существенной мере зависит от
противодавления. Рассмотрим качественно, как будет происходить дви-
движение внутри сопла Лаваля по мере уменьшения противодавления.
На рис. 10.34 представлен график
изменения давления вдоль сопла
в зависимости от противодавления.
Если pout = ро, то, очевидно, дви-
движение газа внутри сопла отсутству-
отсутствует и давление будет одинаковым
в любом сечении сопла (прямая /).
По мере уменьшения выходного дав-
давления газ начнет двигаться вдоль
сопла и распределение давления
вдоль сопла представится некоторой
кривой 2. Очевидно, минимальное
давление всегда будет в самом уз-
узком сечении сопла. При дальнейшем
Р*
Рис. 10.34. Изменение давления
газа вдоль сопла в зависимости от
противодавления
уменьшении роп\ в минимальном сечении скорость газа может достиг-
достигнуть скорости звука в этом критическом сечении, а давление будет
равно р*. При этом возникает альтернатива. Или дальше, за критиче-
критическим сечением, газ будет двигаться дозвуковым образом, а давление
вниз по потоку будет возрастать от р* до pfoui (кривая 3), или газ будет
двигаться далее сверхзвуковым образом, а давление будет продолжать
10.10] Пересечение ударных волн и волн разрежения 289
падать до p"ut (кривая 4). Очевидно, что эта альтернатива разрешается
величиной противодавления. Давление p"ut можно рассчитать следу-
следующим образом. Ранее была получена формула A0.17), связывающая
величину поперечного сечения сверхзвуковой части сопла Лаваля с чи-
числом Маха Q
Поэтому, зная Sm-in, можно рассчитать число Маха в любом сечении
сверхзвуковой части сопла и, в частности, число Маха в выходном
сечении. Далее, воспользовавшись формулой для давления в критиче-
критической точке (на обтекаемом теле) A0.9), можно вычислить расчетное
значение p»t /A_т)
Pout = Ро (l + ^у1 1С)
Таким образом, если выходное давление будет равно p"ui, рассчи-
рассчитанному по приведенной формуле, то газ будет двигаться за критиче-
критическим сечением (Sm\n) сверхзвуковым образом. Если давление на вы-
выходе из сопла будет меньше расчетного p"ut, то дальнейшее ускорение
потока и падение давления будет происходить вне сопла.
Если же давление на выходе сопла будет больше расчетного pfmi, то
движение газа внутри сопла за критическим сечением не может быть
везде сверхзвуковым. В этом случае внутри сопла образуется прямая
ударная волна, переводящая в этом сечении давление до ударной волны
в давление рт\ > р"п{. По мере увеличения давления от p"ut до р'оп{
ударная волна проникает все глубже и глубже внутрь сопла (рис. 10.34,
кривые 5, 6, 7).
И, наконец, при рт{ = р'т{ ударная волна достигает критического
сечения и переводит весь поток внутри сопла в дозвуковой.
10.10.6. Обтекание пластинки сверхзвуковым потоком под ма-
малым углом атаки. Рассмотрим обтекание плоской пластинки, рас-
расположенной к набегающему сверхзвуковому потоку под малым углом
атаки а (рис. 10.35).
I/ /II
Рис. 10.35. Сверхзвуковое обтекание пластинки под углом а
Проведем линию тока, оканчивающуюся на передней кромке пла-
пластинки (точка А). Тогда движение газа выше этой линий тока, очевид-
очевидно, можно рассматривать как движение при обтекании тупого угла /3.
10 В.Г. Черняк, П.Е. Суетин
290 Газовая динамика [Гл. 10
А это значит, что из точки А должна исходить волна разрежения,
ограниченная характеристиками I, II. Движение же газа ниже этой
линии тока можно рассматривать как движение при обтекании клина,
поворачивающего поток на угол \ — а-
Контрольные вопросы
1. Что называют температурой торможения газового потока?
2. При каком условии скорость истечения газа из сосуда будет максималь-
максимальной?
3. Какую скорость движения газа называют критической?
4. Как изменяются максимальная и критическая скорости при изменении
температуры газа?
5. Как изменяются площадь сечения трубки тока и плотность потока при
увеличении скорости газа в случае: а) дозвукового движения газа? б) сверх-
сверхзвукового движения газа?
6. Что представляет собой устройство, называемое соплом Лаваля? Каково
назначение сопла?
7. Как будут изменяться давление, плотность и температура газа на срезе
сужающегося насадка в случае уменьшения давления на выходе при истечении
газа из большого резервуара через этот насадок?
8. Что характеризует угол Маха? Как его величина зависит от числа Маха?
9. Что такое поверхность разрыва?
10. Что называют прямой ударной волной и прямым скачком уплотнения?
11. Как изменяются скорость, энтропия, давление, плотность и температура
в газе, прошедшем прямую ударную волну?
12. В каком случае ударные волны называют косыми?
13. Какие величины связывает между собой уравнение ударной поляры,
если скорость движения газа и скорость звука до ударной волны заданы?
14. При каком условии угол поворота потока в косой ударной волне будет
максимальным?
15. При каком условии образуется отсоединенная ударная волна (на приме-
примере обтекания клина)?
16. Как изменяются давление, плотность, температура, скорость звука и
скорость движения газа в волне разрежения?
17. Проанализируйте качественно характер движения газа при обтекании
тупого угла сверхзвуковым потоком.
18. Как соотносятся между собой углы отражения и падения при отражении
косой ударной волны от стенки?
19. Что происходит с ударной волной и волной разрежения после отражения
от тангенциального разрыва?
10.11. Примеры решения задач
Задача 1
Вычислите скорость звука в воздухе G = 1,4) при температуре
О °С, —50 °С и +15 °С. Удельная теплоемкость воздуха при постоянном
давлении равна ср = 1,006- 103 Дж/(кг-К).
10.11] Примеры решения задач 291
Решение. Из второго уравнения в A0.6) имеем
h = cpT = ^-j , с2 = G - 1)срТ. A0.77)
Расчет по этой формуле дает следующие значения скорости звука:
Т = 273К, с = 331,2 м/с, Т = 223К, с = 299,4 м/с,
Т = 288 К , с = 340,2 м/с .
Задача 2
Тело с затупленным носом летит в воздухе G = 1,4) со скоростью,
равной 1,5 с ; 2,0 с ; 3,0 с ; 5,0 с и 10 с, где с —скорость звука. Перед
головной частью тела образуется отсоединенная ударная волна. Давле-
Давление и температура воздуха равны р = 1 • 105 Па, Т = 288 К.
1. Вычислите давление и температуру торможения невозмущенного
потока.
2. Какие значения имеют давление и температура на оси симметрии
непосредственно за головной волной при заданном числе М набегаю-
набегающего потока?
3. Вычислите давление и температуру в передней критической точ-
точке.
4. Какое давление измеряет трубка Пито, находящаяся в потоке
перед головной волной?
Решение. Индексом 1 будем отмечать величины, относящиеся
к набегающему (невозмущенному) потоку. По условию задачи число
Маха набегающего потока (Mi) может принимать следующие значения:
Mi = — = 1,5; 2,0; 3,0; 5,0; 10.
с
При таких числах Маха (Mi > 1) перед головной частью движущегося
тупого тела всегда возникает отсоединенная ударная волна. Величины,
характеризующие движение газа после ударной волны, будем отмечать
индексом 2.
1. Температура торможения Тю и давление торможения рю в случае
невозмущенного ударной волной потока газа определяются формулами
A0.11) и A0.9) соответственно
9\
f)
7/G-!)
/ у _ 9 у — 1 9\/()
Тю = Т, (l + ^ Mf) , рю =Pi A + X^"L Mf) -(Ю.78)
2. На оси симметрии переход через поверхность разрыва можно
рассматривать как переход через прямой скачок уплотнения. Тогда
скачки давления и температуры описываются формулами A0.46) и
A0.38) соответственно
_т_ М2 _7цЛ l = pl 7+ + (p2/pi) G-
7+1/' Тх pi 7- l + (P2/pi) G+1) '
A0.79)
10*
292
Газовая динамика
[Гл. 10
3. Из уравнения Бернулли следует, что температура торможения не
изменяется в ударной волне, т.е. Т20 = Тю (см. уравнение A0.44)).
Давления газа после ударной волны р2ив критической точке р2о
связаны между собой соотношением A0.9)):
Р20 _
Р2
7/G-1)
A0.80)
Число Маха после ударной волны, М2, выразим через Mi по форму-
формуле A0.47)). Тогда получим
Р2
G-0/7
Р2
Р\
7+1
М
A0.81)
Подставляя сюда отношение давлений из формулы A0.46), получа-
получаем для давления торможения следующее выражение:
Р20 = Р\
7+1
М?)
27
7+1
м -
7-1
7+1
-1/G-0
A0.82)
4. Перед носиком трубки Пито также возникает отсоединенная
ударная волна. Трубка измеряет давление у>2 за ударной волной.
Результаты расчета искомых величин по формулам A0.78), A0.79)
и A0.82) при различных значениях Mi представлены в таблице.
Mi
1,5
2,0
3,0
5,0
10,0
Т10, К
418
518
806
1728
6048
Рю, Ю5, Па
3,67
7,83
36,7
529
42439
Р2, Ю5, Па
2,46
4,50
10,3
29,0
117
т2, к
380
486
772
1670
5872
Р20, Ю5, Па
3,41
5,64
12,1
32,7
129
Задача 3
Самолет летит на высоте 1000 м, где температура воздуха 8,5 °С,
и на высоте 10000 м, где температура воздуха -50,0 °С, со скоростью
1000 км/ч. Чему равна температура в критической точке на носу са-
самолета? На сколько повысится эта температура при скорости самолета
2000 км/ч? Молярная масса и показатель адиабаты воздуха имеют
соответственно следующие значения: /i = 0,029 кг/моль, 7 = 1,4.
Решение. Поскольку температуры на разных высотах различны,
то различны и скорости звука. Поэтому при фиксированной скорости
полета самолета числа Маха на разных высотах будут разными.
10.11
Примеры решения задач
293
Скорость звука при разных температурах вычислим по формуле
A0.2):
/ r>rj-i
A0.83)
Число Маха набегающего потока определится отношением М = v/c.
Чем ниже температура, тем меньше скорость звука и при v = const
больше число М. Напомним, что от давления газа скорость звука не
зависит.
Температуру торможения То на носу самолета вычислим по формуле
A0.11):
То = Т П + ^у-^ M2J . A0.84)
Результаты расчета приведены в таблице.
h, км
1
10
т, к
281,5
223,0
1000,
М
0,8259
0,9279
км/ч
То, К
319,9
261,4
2000,
М
1,652
1,856
км/ч
То, К
435,2
376,6
Заметим, что при скорости 1000 км/ч движение самолета было
дозвуковым, а при скорости 2000 км/ч — стало сверхзвуковым. Обра-
Образование ударной волны не влияет на температуру торможения (см.
задачу 2), поэтому в обоих случаях используется одна и та же формула
A0.84).
Задача 4
Параметры газа до ударной волны р\, р\, v\, Т\ и после ударной
волны р2, Р2, Щ, T<i заданы. Определите скорость распространения
ударной волны и.
Решение. В системе координат, движущейся со скоростью и,
ударная волна неподвижна и является как бы прямым скачком. Ско-
Скорости газа до и после скачка относительно этой системы координат
соответственно равны v\ - и и V2 - и. Тогда на ударной волне в соот-
соответствии с A0.31) можно записать следующие условия:
p\{v\ - и) = p2(v2 -и),
(vi - иJ/2 = h2 + (v2 - иJ/2,
A0.85)
Считая газ идеальным и используя соответствующее выражение для
энтальпии, запишем второе уравнение из A0.85) в следующем виде:
7 Pi
7 - 1 Pi
_ 7 Р2 | (^2 — и)
~ Т^Т^ 2
A0.86)
294
Газовая динамика
[Гл. 10
Исключая скорости, получим адиабату Гюгонио:
№ = G+ l)P2/pi ~ G~ 1)
A0.87)
Третье уравнение A0.85) с учетом первого уравнения и выражения
для скорости звука с2 = 7Р/Р преобразуем к следующему виду:
V2 — V\ =
с\
7(^2 -
с\
Уравнение A0.86) запишем так:
2 / ч2
С\ [V\ — U)
7-1 2 = 7-1 ^ 2 '
Исключая из двух последних уравнений с2, получим
(г*, — v2J — ^—-— (г^1 — v2)(u — v2) — с\ = 0.
A0.88)
A0.89)
A0.90)
Отсюда для скорости распространения ударной волны имеем
и = v2 + ^—— (v\ — v2) + ( ^—— ) (v\ — v2) + с2\ . A0.91)
Перед корнем взят только знак плюс, так как скорость ударной
волны должна быть положительной. Из полученного выражения видно,
что скорость распространения ударной волны больше скорости звука,
и > с2. При малых скоростях газа и —> с2, т. е. при малых возмущениях,
ударная волна переходит в звуковую волну.
Задача 5
В закрытом с одного конца цилиндре находится газ. С другого
конца цилиндра начинает двигаться поршень со скоростью U, сжимая
газ (рис. 10.36). В момент начала движения впереди поршня через по-
покоящийся газ с параметрами р2, р2, v2 = 0 перемещается ударная волна
со скоростью и (рис. 10.36а). Скорость газа в области между поршнем
и ударной волной можно считать равной скорости поршня, т. е. v\ = U.
U
а б
Рис. 10.36. Ударная волна в цилиндре при движении поршня
Определите параметры газа до ударной волны р\, р\, скорость прямой
ударной волны и, скорость отраженной ударной волны г^з и давление
газа на стенку от падающей ударной волны рз (рис. 10.36 6).
1
Р\
Pi
щ
И Р2
-*"- Р2
v2=0
и
I
Р\
Pi
щ
щ
1
Рз
Рз
3 =0
10.11] Примеры решения задач 295
Решение. Из первого и третьего уравнений A0.85) и A0.91)
получим следующие выражения для рь р\, и:
Pi =P2 + P2UU , р\ =
u-U '
A0.92)
Дойдя до стенки, прямая волна отразится от нее и по среде с пара-
параметрами р\, р\, v\ будет распространяться отраженная ударная волна
со скоростью щ в направлении, противоположном направлению скоро-
скорости v\ движущегося газа (рис. 10.36 6). Между стенкой и отраженной
ударной волной газ будет заторможен. Параметры газа в этой области
обозначим через рз, /?з, ^з- Заменяя в уравнениях A0.85) и A0.91)
р\, р\, v\ соответственно на рз, /?з, г?з = 0, а р2, Р2, щ — на pi, p\, —v\
и и на щ, получим для определения р$, р$, щ следующие уравнения:
= (рз -Pi),
Из выражения A0.87) для отраженной волны имеем
Pi _ G+ Qpi/рз + G ~ О
Рз G+ О + G - l)pi/P3 '
С другой стороны, из первых двух уравнений A0.93) получим
A0.94)
Рз Рз - Р\
Из уравнений A0.85) при v^ = 0 имеем
A0.95)
. A0.96)
Р2 Pi — Р2
Подставив в последнее уравнение значение р\/р2 из адиабаты Гю-
гонио в форме A0.87), получим
Pmi = 2(l-p2/pi) A0 97)
Р1-Р2 G+ 1)Р2/Р1 + G - О '
Отсюда уравнение A0.95) запишется в следующем виде:
Pi = I Pi -Р2 2A -p2/pi) A0 98)
Рз Рз-Pi G+l)P2/pi + G-О '
С учетом выражения A0.94), получим квадратное уравнение для
определения отношения рз/рь
9 9
Р1.Л EL A±± + рА = (р1-Л A±±Р1 + Л . (Ю.99)
Pi / Р2 V7-1 Р2/ \Р2 I \7-lpi /
296 Газовая динамика [Гл. 10
Решение этого уравнения имеет вид
Рз = 1 + _2т Pi/P2- 1 A0 100)
Pi 7+1 Pi/P2 + G+l)/G- О '
Из полученного выражения следует, что в случае слабой ударной
волны, т.е. при е = (р\ ~Р2)/Р2 <^С 1, в линейном приближении по
малому параметру е имеем
')l+2e. (ШЛО.)
Таким образом, давление газа у стенки в два раза больше давления
на фронте падающей волны.
В случае сильной ударной волны, т.е. при р\/р2 > 1
WRJ1 + _2TL = 37^1> A0Ю2)
р2 7-1 7-1
Для воздуха G = 1,4) давление у стенки в 8 раз превышает давле-
давление газа на фронте падающей волны.
ГЛАВА 11
МАГНИТНАЯ ГИДРОДИНАМИКА
Введение
За последние десятилетия получил большое развитие раздел меха-
механики сплошных сред, называемый магнитной гидродинамикой. Предме-
Предметом магнитной гидродинамики является изучение движения электро-
электропроводящей жидкости и газов в присутствии магнитного поля. Основы
этого раздела механики были заложены в 1940-х годах шведским
физиком X. Альвеном. В дальнейшем мощным стимулом к развитию
магнитной гидродинамики послужила, с одной стороны, практическая
потребность создания электромагнитных насосов для атомной промыш-
промышленности и магнитогидродинамических генераторов для энергетики,
плазменных двигателей для ракет, с другой стороны, интенсивное
развитие термоядерных исследований и астрофизики.
Электропроводящими являются ионизированные газы, жидкие ме-
металлы, жидкие электролиты, различные суспензии и так далее. Во всех
случаях, как правило, будем использовать единый термин — жидкость.
Как и ранее, принимаем гипотезу сплошности. При этом считаем, что
не только масса непрерывно распределена по объему жидкости, но
также и электрический заряд.
Если проводящая жидкость движется в магнитном поле, то в ней
индуцируются электрические токи, которые в свою очередь создают
магнитные поля. Взаимодействие последних с основным (внешним)
полем оказывает существенное влияние на движение самой жидкости.
Действительно, на электропроводящую жидкость в электрическом и
магнитном полях действует объемная сила. Эта, так называемая, пон-
деромоторная сила может оказывать существенное влияние на дина-
динамику жидкости и должна быть учтена в уравнении движения. Кроме
того, возникающие в жидкости токи приводят к выделению джоулева
тепла, что должно быть учтено в уравнении сохранения внутренней
энергии. Таким образом, полное описание сложной картины движения
и взаимодействия проводящей жидкости с магнитным полем должно
основываться на совместном рассмотрении механических и электроди-
электродинамических уравнений (уравнений Максвелла).
Трудность понимания процессов, происходящих в проводящей жид-
жидкости, движущейся в магнитном поле, заключается в том, что здесь
298 Магнитная гидродинамика [Гл.11
нарушаются причинные связи, известные нам из лабораторной прак-
практики. В обычной лабораторной практике причинная связь явлений
заключается в том, что некоторая электродвижущая сила определяет
электрический ток, ток создает магнитное поле, которое воздействует
на рассматриваемое тело. В магнитной гидродинамике причинная связь
чаще следующая. Движущаяся жидкость изменяет внешнее магнитное
поле. Изменение магнитного поля, согласно уравнениям Максвелла,
вызывает электрическое поле, определяющее ток, который, в свою
очередь, создает магнитное поле, влияющее на движение жидкости
через взаимодействие с внешним магнитным полем.
11.1. Уравнения Максвелла
Электромагнитное поле в вакууме характеризуется напряженностью
электрического поля Е и индукцией магнитного поля В. Эти векторные
величины определяют силы, действующие со стороны поля на электри-
электрические заряды и токи. Распределение зарядов и токов в пространстве
задается объемной плотностью заряда ре (величина электрического
заряда в единице объема) и плотностью электрического тока j.
Для характеристики электромагнитного поля в материальной среде
дополнительно вводятся вектор электрической индукции D и вектор
напряженности магнитного поля Н, которые учитывают электрические
и магнитные свойства среды.
Уравнения макроскопической электродинамики, определяющие зна-
значения векторов Е, В, D, Н в любой точке пространства в любой мо-
момент времени в зависимости от распределения заряда ре и тока j в сре-
среде были сформулированы Дж. Максвеллом в результате обобщения
эмпирических законов электромагнетизма. Максвелл выдвинул гипоте-
гипотезу о том, что магнитное поле может возникать не только в результате
движения электрических зарядов, но также порождается переменным
электрическим полем. Величину, пропорциональную скорости изме-
изменения электрической индукции, Максвелл назвал током смещения.
Полный ток определяется суммой токов проводимости и смещения.
Макроскопические уравнения электродинамики, называемые обыч-
обычно уравнениями Максвелла, для изотропных сред относительно непо-
неподвижной системы координат записываются в следующем виде О
гоШ= - —+ —j, rotE = — — ,
с at с с at
divB = 0,
j = <тгЕ, D = s~E, В =
О Уравнения A1.1) записаны в гауссовой системе единиц, которая обычно
принята в электродинамике. В приложении приведена таблица, устанавливаю-
устанавливающая связь основных электродинамических величин в системах единиц Гаусса
и СИ.
11.2] Модель среды 299
Здесь е и \± — диэлектрическая и магнитная проницаемости среды со-
соответственно, <тг — удельная электропроводимость среды, с — скорость
света.
Первое уравнение в системе A1.1) является обобщением на пере-
переменные поля закона Био-Савара-Лапласа о возбуждение магнитного
поля электрическим током. В правой части этого уравнения первое
слагаемое связано с током смещения, а второе —с током проводимо-
проводимости. Второе уравнение выражает закон электромагнитной индукции
Фарадея. Третье уравнение утверждает отсутствие магнитных зарядов,
аналогичных электрическим, что вытекает из замкнутости магнитных
силовых линий. Следующее уравнение выражает тот факт, что источ-
источниками электрического поля являются электрические заряды (обобще-
(обобщение теоремы Гаусса на переменные поля). Пятое уравнение представ-
представляет собой закон Ома. И последние два уравнения, устанавливающие
связь между векторами напряженности и индукции полей, учитыва-
учитывают электромагнитные свойства среды и называются материальными
уравнениями изотропной среды.
Если среда движется со скоростью v, то напряженность электриче-
электрического поля относительно движущейся системы координат равна
Е' = Е + - [v, H] .
В этом случае закон Ома записывается в виде
A1.2)
11.2. Модель среды
Магнитная гидродинамика обычно рассматривает лишь такие сре-
среды, для которых с большой точностью можно положить
е= 1, 11= 1.
Несмотря на это ограничение, набор сред магнитной гидродинамики,
имеющих практический интерес, достаточно велик. Это проводящие
жидкости, расплавленные металлы, ионизированные газы, плазма.
В магнитной гидродинамике обычно рассматриваются лишь изо-
изотропные среды. Если для е и /j, это ограничение достаточно определен-
определенно, то требование изотропности проводимости аг необходимо рассмот-
рассмотреть более подробно на микроскопическом уровне. В магнитном поле
электрические заряды, обусловливающие ток проводимости, движутся
по сложным винтовым траекториям. Так, частица, имеющая заряд е
и массу га, влетая в однородное магнитное поле напряженностью Н,
перпендикулярное скорости частицы, будет вращаться вокруг силовой
линии с угловой частотой Лармора со = еН/тс. В то же время заря-
заряженная частица, движущаяся вдоль силовой линии магнитного поля,
не испытывает со стороны этого поля никакого влияния. Поэтому
300 Магнитная гидродинамика [Гл.11
проводимость среды в магнитном поле может быть существенно ани-
анизотропной. Проводимость вдоль магнитного поля будет значительно
больше, чем поперек.
Сравним период ларморовой прецессии — ?л и среднее время сво-
свободного пробега молекул в газе — tM. Очевидно,
t _ тс f _ 1
еН vT
Здесь vT — средняя тепловая скорость частиц, / — средняя длина сво-
свободного пробега. Нетрудно понять, что проводимость газа можно счи-
считать изотропной, если выполняется следующее условие:
*м<*л, /<^т- (П.З)
В этом случае частые столкновения частиц не позволяют им описы-
описывать замкнутые траектории в поперечном магнитном поле. Траектории
на малой длине свободного пробега будут почти прямолинейными, а на
макроскопическом масштабе они будут определяться столкновениями,
а не действием магнитного поля. Следовательно, проводимость будет
изотропной, не зависящей от направления магнитного поля. Заметим,
что электропроводимость капельных жидкостей с высокой точностью
можно считать изотропной.
В задачах магнитной гидродинамики обычно пренебрегают токами
смещения по сравнению с токами проводимости, т. е. предполагается,
что выполняется неравенство
^«1- (П.4)
3 ot
Так, если среда находится в периодическом электрическом поле
Е = Eq smut, то отношение амплитуд тока смещения и тока проводи-
проводимости будет равно
D = eE, j = arE, - — = —.
j dt ar
Поэтому для того чтобы пренебречь токами смещения по сравнению
с токами проводимости, необходимо выполнение следующего неравен-
неравенства:
— «1. A1.5)
аг
Неравенство A1.5) означает, что при заданной проводимости маг-
магнитная гидродинамика не рассматривает слишком быстропеременных
электромагнитных процессов, при которых ток смещения играл бы су-
существенную или определяющую роль (электромагнитные волны). Напри-
Например, проводимость меди равна 5 • 1017 ед. СГСЭ, проводимость солнеч-
солнечной короны 1 • 1015, проводимость земной ионосферы 1 • 1010 ед. СГСЭ.
Из формулы A1.5) следует, что ограничение по скорости изменения
электродинамических и механических величин в магнитной гидродина-
11.3] Уравнения движения проводящей жидкости 301
мике не слишком сильное. Поскольку рассматриваются сравнительно
медленные движения сплошной среды, включая и ударные волны, то
и вызываемые ими скорости изменения электрических и магнитных
величин практически всегда удовлетворяют неравенству A1.5).
Физически пренебрежение токами смещения означает, что между
изменениями напряженностей электрического и магнитного полей нет
запаздывания. Значения Н в некоторый момент времени определяются
значениями Е в тот же момент времени. Таким образом, уравнения
Максвелла в магнитной гидродинамике имеют вид
rot H = — j , rot Е = — , div H = 0 ,
с dt (П6)
div Е = Атгре , j = <тг [е + - [v, H]l .
11.3. Уравнения движения проводящей жидкости
в электромагнитном поле
Уравнение движения сплошной проводящей среды может быть за-
записано в виде
ovi avi I aPik . . /11 7\
at охи р охи
В уравнении A1.7) вектор f представляет результирующую плотность
массовых сил. Составляющими этого вектора являются электрическая
f# и магнитная fH силы, действующие на единицу массы жидкости, а
также массовая сила не электромагнитной природы fg (например, сила
тяжести). Таким образом, имеем
/г = /^ + /яг + /0г- (П-8)
11.3.1. Электромагнитные массовые силы. Сила, действующая
на единицу объема проводящей жидкости с объемной плотностью элек-
электрического заряда ре со стороны электрического и магнитного полей,
очевидно, равна
F = peE+i[j,H]. A1.9)
В выражении A1.9) первое слагаемое представляет кулоновскую силу,
действующую на единицу объема жидкости в электрическом поле.
Второе слагаемое представляет силу Ампера, действующую на единицу
объема проводящей жидкости, по которой протекает электрический ток
плотностью j.
Если ро — импульс единицы объема жидкости, то уравнение дви-
движения при отсутствии массовых сил не электромагнитной природы
запишется в виде
^ 1 И,Н]. A1.10)
302 Магнитная гидродинамика [Гл.11
Выражая j и ре из системы уравнений A1.1), при е = 1, /х = 1
имеем dpo = J
dt 4-
Для симметризации этого уравнения добавим к его правой части рав-
равное нулю выражение
1 г/ 1
4тг L V с
Равенство нулю этого выражения следует непосредственно из уравне-
уравнений Максвелла A1.1). В результате получим
= ±- (EdivE- [E,rotE] +HdivH- [H,rotH]) . A1.11)
Второе слагаемое в круглых скобках левой части уравнения A1.11)
^^>Н1- (ПЛ2)
представляет собой импульс единицы объема (плотность импульса)
электромагнитного поля. Левая часть уравнения A1.11) описывает ско-
скорость изменения полного импульса единицы объема среды, состоящей
из жидкости и поля. Очевидно, правая часть уравнения A1.11) пред-
представляет векторную сумму плотности объемных электрических pf# и
магнитных р$н сил. Таким образом, имеем
f ! (Е div Е - [Е , rot E]) ,
A1.13)
fo = ^~(Н divH- [H,rotH]) .
Полученные силы должны быть учтены в уравнении движения
проводящей среды A1.7), находящейся в электромагнитном поле.
Если на жидкость действует только электрическое поле (Н =
= 0, rotE = 0), то плотность массовой электрической силы равна
fE = ^PeE. A1.14)
11.3.2. Тензоры электрических и магнитных напряжений. Из
векторного анализа известно, что для любой функции А справедливо
следующее равенство:
[А, rot A] = i VA2 - (AV) А .
Тогда выражения A1.13) в проекции на г-ю координатную ось запи-
запишутся в виде
fEi = J- -*- (ElEk - i ЕЧгк) ,
i a) i 2 \ AM5)
/яг = -л— д— [HiHk — - H Sik
4ттр дхк \ 2 )
11.3] Уравнения движения проводящей жидкости 303
С другой стороны, плотности массовых сил связаны с напряжениями
в среде известными соотношениями (см. C.13)):
• A1.1b)
d<rik j, I daik
ag
jEi = ^, jHi = ?•
Р oxk р oxk
Из сравнения выражений A1.15) и A1.16) получаем
g = -L (ElEk - I Е%Л ,
**} J { A1.17)
ofk = ± [HtHk - i H4ik) .
Тензоры <jfk и <jfk называют максвелловскими тензорами на-
напряжений электрического и магнитного полей соответственно. Они
характеризуют силы, действующие со стороны электрического и маг-
магнитного полей в направлении оси г на единичную площадку, перпенди-
перпендикулярную оси к. Если в среде мысленно выделить единичный элемент
объема в виде кубика, грани которого перпендикулярны координатным
осям, то диагональные элементы тензоров afk и afk определяют силы,
действующие по нормали к граням. Величина рм, определяемая как
среднее арифметическое диагональных элементов максвелловского тен-
тензора напряжений магнитного поля, называется магнитным давлением
Ри = \°й = -^Н2. A1.18)
Знак минус в правой части выражения A1.18) констатирует, что маг-
магнитное давление направлено во вне выделенного единичного объема.
Обычно интересует модуль давления и знак минус не пишут.
Недиагональные элементы тензора напряжений представляют каса-
касательные силы, действующие на гранях рассматриваемого единичного
объема. Пусть постоянное магнитное поле направлено вдоль оси х%.
В этом случае недиагональные элементы тензора напряжений а^к рав-
равны нулю, а для диагональных имеем
Я,=0, #2 = 0, Щ = Н, <т» = а& = -±-Н2, <т» = ?н2.
Представим, что элементарные кубики проводящей жидкости нани-
нанизаны на соседние магнитные силовые линии. Тогда взаимодействие
магнитного поля с веществом можно, согласно Максвеллу, представить
в виде отталкивания друг от друга магнитных силовых линий с силой
рм = Я2/8тг и их натяжения с силой 2рм = Я2/4тг. Таким образом,
если пользоваться наглядным представлением об отталкивании магнит-
магнитных силовых линий и их натяжении, то можно сказать, что магнитные
силовые линии всегда стремятся выпрямиться или сжаться (если они
замкнутые) вследствие их натяжения, а их распределение в веществе
стремится стать однородным вследствие их взаимного отталкивания.
11.3.3. Уравнение движения. Уравнение движения проводящей
жидкости при наличии внешнего электромагнитного поля формально
будет иметь вид A1.7), если под fi понимать плотность массовых сил
304 Магнитная гидродинамика [Гл.11
не электромагнитной природы, а тензор напряжений представить в виде
Ргк = -pSik + *ik + <T?k + °fh ' О 119)
где aik — тензор вязких напряжений.
Нетрудно показать, что в хорошо проводящей жидкости не мо-
может быть значительных по величине сторонних зарядов, если заряды
разных знаков не разделяются какими-либо внешними постоянны-
постоянными факторами (градиент давления, градиент концентрации вещества).
Электрические микроскопические поля, возникающие при разделении
зарядов, столь велики, что немедленно приводят к их возвращению
в положение, обеспечивающее нейтральность малого элемента объема
проводящей жидкости.
Действительно, возьмем дивергенцию от первого уравнения из си-
системы A1.1) (при е = 1 ,/i = 1). Тогда с учетом четвертого уравнения
из A1.1) получим
^ A1.20)
Уравнение A1.20) представляет собой уравнение непрерывности
для сторонних зарядов. В неподвижной среде, используя четвертое и
пятое уравнения из A1.1), а также уравнение A1.20), имеем
^ е. A1.21)
Из последнего уравнения следует
Ре = Ре0ехр(
Очевидно, что даже для ионосферы Земли плотность сторонних
зарядов исчезает за времена порядка 10~10 с. Как указывалось выше,
магнитная гидродинамика не рассматривает столь быстропеременные
процессы. Если пренебречь токами смещения, то аналогичное рассмот-
рассмотрение первого и пятого уравнений A1.1) приводит непосредственно к
выводу ре = 0, а следовательно, divE = 0.
Было бы неправильно полагать, что если ре = 0, то и Е = 0.
В движущейся в магнитном поле проводящей жидкости напряженность
электрического поля возникает не вследствие объемных зарядов, а
вследствие закона электромагнитной индукции, представленного вто-
вторым уравнением системы A1.6).
Вследствие медленного изменения магнитного поля член [Е,rot E]
в выражении A1.13) для f# мал и им можно пренебречь. Таким об-
образом, в магнитной гидродинамике предполагается, что электрические
массовые силы отсутствуют.
Вообще говоря, в выражении тока проводимости в проводящей
среде, движущейся со скоростью v, в формулу для j (см. A1.6)) необ-
необходимо было бы добавить член pev — конвективный перенос заряда
самой движущейся жидкостью. Этот член в выражении A1.6) опущен
также из-за отсутствия в проводящей жидкости сколько-нибудь значи-
значительных объемных зарядов.
11.3] Уравнения движения проводящей жидкости 305
Таким образом, уравнение движения проводящей жидкости при
наличии внешнего магнитного поля будет представлять собой уравне-
уравнение Навье-Стокса, которое в качестве аддитивной добавки включает
магнитную силу:
т;—Н (vV)v = Vp + vAv H— f ? + - 77J grad div v
ot p p \ 6 J
--^[H,rotH]+f. A1.22)
4тгр
В этом уравнении f — плотность массовых сил не электрической природы.
11.3.4. Уравнение сохранения внутренней энергии. Из урав-
уравнения сохранения внутренней энергии для непроводящей жидкости
следует, что внутренняя энергия единицы объема жидкости изменяется
вследствие притока тепла извне в этот единичный объем, а также
вследствие его сжатия и диссипации в нем механической энергии из-за
вязкости жидкости.
В проводящей жидкости при наличии магнитного поля появляется
еще один источник изменения внутренней энергии единицы объе-
объема жидкости — выделение джоулева тепла. По закону Джоуля-Ленца
в единице объема проводящей жидкости, в которой протекает электри-
электрический ток плотностью j, за единицу времени выделяется количество
тепла, равное j2/crr. С учетом первого уравнения из системы A1.6)
объемная плотность выделившегося джоулева тепла равна
Qd = —V" (rotHJ. A1.23)
1бтг а г
Уравнение сохранения внутренней энергии проводящей жидкости
во внешнем магнитном поле запишется в виде
ds^ = _di +р dgi+ c (rotHJ, A1.24)
dt OXk 1бтг crr
где Pik — тензор напряжений при отсутствии электромагнитного поля.
11.3.5. Замкнутая система уравнений движения. Запишем за-
замкнутую систему уравнений движения проводящей жидкости в маг-
магнитном поле. Очевидно, уравнение непрерывности как уравнение со-
сохранения массы не изменяет свой вид. Тогда имеем
^V / ,_.ч 1 _ . 1 / . 1 \ _ _.
Ь (vV) v = — vp + vAv H— [?, ~\— V ) grad div v —
dt p p \ 3 /
- -A- [H, rot H] + f,
dp . Anp
—— + div pv = 0 ,
A1.25)
, тт 4тг . 4тгсгг / 1 г ТТ-Д
rot H = — j = Е + - v, H J ,
с с \ с L V
306 Магнитная гидродинамика [Гл.11
Система A1.25) содержит 11 скалярных уравнений для нахождения
16 неизвестных — v, E, H, q, р, р, T, евн. Вместе с калорическим и
термическим уравнениями состояния
SBH = SBH{P, Т), р = р(р,Т)
и уравнением теплопроводности фурье
q = -AVT
система A1.25) полностью определяет механические, электромагнит-
электромагнитные и термодинамические характеристики проводящей жидкости, дви-
движущейся в магнитном поле. Эта система включает четыре феномено-
феноменологических коэффициента (г/, ? — коэффициенты сдвиговой и объем-
объемной вязкости, Л — коэффициент теплопроводности и аг — проводимость
жидкости), которые считаются известными. Решения системы должны
удовлетворять двум дополнительным условиям
divE = 0, divH = 0. A1.26)
Из четвертого и пятого уравнений системы A1.25) можно исклю-
исключить напряженность электрического поля Е. Для этого возьмем опера-
операцию rot от обеих частей четвертого уравнения
rot rot H = ^^ (rot E + - rotfv , Hi) .
с \ с J
Используя известное векторное равенство
rot rot = grad div —A ,
с учетом пятого уравнения из A1.25) и второго уравнения из A1.26)
получим
^ = rot[v,H] + -^- АН. A1.27)
ot 4тгсгг
Если не интересоваться напряженностью электрического поля, то
тогда полная система уравнений будет состоять из первых трех урав-
уравнений системы A1.25) и уравнения A1.27). В этом случае будем иметь
лишь 13 уравнений с 13 неизвестными. Если из этой системы найдена
напряженность магнитного поля как функция координат и времени,
то напряженность электрического поля при необходимости может быть
найдена из пятого уравнения системы A1.25).
Для несжимаемой жидкости уравнения системы A1.25) упрощают-
упрощаются. В частности уравнение движения принимает вид
** \ Л . Х /ТТГ7\ТТ П (]] ОЯ\
dt р \ Sn J 4тгр
Здесь использовано векторное равенство
[H,rotH] = i VH2-(HV)H.
11.3] Уравнения движения проводящей жидкости 307
11.3.6. Граничные условия. Запишем наиболее характерные гра-
граничные условия к уравнениям магнитной гидродинамики A1.25).
1. На неподвижной твердой поверхности выполняются условия
«прилипания», т.е. скорость движения жидкости на поверхности равна
нулю
v = 0. A1.29)
Если система координат выбрана так, что тело движется в жидкости со
скоростью и, то в каждой точке поверхности тела должно выполняться
условие
V = U.
2. Пусть п и t — нормальный и касательный единичные векторы
в некоторой точке поверхности жидкости. Тогда на границе раздела
двух несмешивающихся проводящих жидкостей для проекций векторов
напряженностей электрического и магнитного полей имеем
En = E2t, Я1п = Н2п , Ни - H2t = ^ jo • (П-30)
В последнем выражении j0 — плотность поверхностного тока на грани-
границе жидкостей.
11.3.7. Плотности потоков импульса и энергии. Напомним, что
тензор плотности потока импульса П^ определяет поток г-компоненты
импульса через единичную площадку, перпендикулярную оси к. Обоб-
Обобщение полученного ранее выражения для непроводящей среды на слу-
случай проводящей жидкости в магнитном поле очевидно: к полученному
ранее выражению следует добавить тензор магнитных напряжений
Пг/г = pViVk - (Pik + afk) = pvivk + p5ik - aik -
1Ч) A1.31)
Здесь Ъ{к — тензор вязких напряжений; тензор электрических напря-
напряжений опущен, поскольку, как указывалось выше, в проводящей жид-
жидкости не может быть сколько-нибудь значительных электрических по-
полей.
Вектор плотности потока энергии — вектор Умова — был получен
ранее для непроводящей среды
h = Як + pvk? -ViPik .
В этом выражении е — полная энергия единицы массы непроводящей
среды, qk — проекция вектора плотности потока тепла на ось к, V{ —
проекция вектора скорости движения жидкости на ось г, Р\к — тензор
напряжений непроводящей среды.
В магнитной гидродинамике следует учесть плотность потока элек-
электромагнитной энергии S — вектор Пойнтинга.
Для нахождения энергии электромагнитного поля воспользуемся
уравнениями Максвелла A1.1). Умножим второе уравнение этой си-
308 Магнитная гидродинамика [Гл.11
стемы скалярно на Н, а первое уравнение — на Е. Вычитая одно из
другого, с учетом соотношений для D и В из A1.1) получим
^+j E = -divS, A1.32)
где w — объемная плотность энергии поля,
вектор Пойнтинга
S = /- [Е,Н]. A1.33)
При выводе уравнения A1.32) учтено векторное равенство
div[E , Н] = Н rot Е - Е rot H .
Уравнение A1.32) представляет закон сохранения энергии электромаг-
электромагнитного поля. Величина вектора S определяет энергию поля, пере-
переносимую за единицу времени через единичную площадку, лежащую
в плоскости векторов Е и Н.
В результате вектор плотности потока энергии для проводящей
жидкости в магнитном поле запишется в виде
h = Qk + pvk? -ViPik + Sk • A1.34)
Поскольку объемная плотность энергии поля равна w, то полная
энергия единицы объема в магнитной гидродинамике будет равна
ps + w .
Поэтому закон сохранения полной энергии среды запишется в виде
lj-(pe + w) = -dWI. A1.35)
где вектор I определен выражением A1.34).
11.4. Критерии подобия в магнитной гидродинамике
Рассмотрим несжимаемую проводящую жидкость в поле силы тя-
тяжести в присутствии внешнего магнитного поля. Ее движение описы-
описывается уравнением A1.28), в котором роль плотности массовых сил
играет вектор ускорения свободного падения (f = g). Приведем это
уравнение к безразмерному виду.
Пусть / — характерный размер течения; to ~~ характерное время за-
задачи; ро, ро, щ, Hq — значения плотности жидкости, давления, скоро-
скорости, и напряженности магнитного поля в некоторой характерной точке
потока. Введем безразмерные величины (отмечены звездочкой)
t = t0U, V = yV*, А = ^А*, р = роР*, (Ц36)
Р = POP*, g = g-g*, Н = #0Н*, Е =
11.4] Критерии подобия в магнитной гидродинамике 309
Безразмерное уравнение движения A1.28) имеет вид
1 Йлг 11 1 су А
_L 41^ + (v*V)v* = —\ — V*p* + — A*v* + 5и - _ [Н*, rot* Н*].
М Р* е р* (ii37)
Здесь
с. _ ^о*о М2 _
Р° „2 ' (П-38)
Fr = ^ , А^ =
Безразмерные критерии Струхаля (St), Маха (М), Рейнольдса (Re)
и Фруда (Fr) были введены ранее как критерии подобия движения
непроводящей жидкости. В магнитной гидродинамике появился новый
критерий А, называемый числом Алъвена. Число А характеризует
отношение магнитной и кинетической энергий единицы объема.
Согласно закону Ома (см. A1.6)) плотность тока, индуцированного
магнитным полем, равна
Из четвертого уравнения системы A1.25) следует
rotH= —j = ^ [v,H]. A1.39)
с С
Тогда слагаемое уравнения движения (см. A1.25)), содержащее напря-
напряженность магнитного поля, можно представить в виде
4
с р
Переходя к безразмерным величинам, согласно соотношениям A1.36),
получим
, rot HJ -
Разделив это выражение на Uq/1, как это было сделано при выводе
безразмерного уравнения движения A1.37), получим еще один безраз-
безразмерный критерий подобия магнитной гидродинамики
So = ^. A1.40)
с
Критерий So называют параметром магнитогидродинамического
взаимодействия или числом Стюарта. Он характеризует отношение
магнитной силы от индуцированных токов к силе инерции.
Запишем уравнение A1.27) в безразмерном виде, используя обозна-
обозначения A1.36):
^=r0t*[v*,H,] + J-A,H*. A1.41)
310 Магнитная гидродинамика [Гл.11
Здесь введено так называемое магнитное число Рейнолъдса
4тг
Rem = — аг1щ. A1.42)
с
Понять физический смысл числа Rem нетрудно из анализа уравнения
A1.39). Пусть Hi и Не — величины напряженностей магнитных полей
от индуцированных токов и внешних источников соответственно. Эти
напряженности связаны между собой уравнением A1.39)
| rot Hi | = —$- |[v,He]|.
Отсюда следует:
Hiq сггщНео HiQ 4тг
аг1щ = Rem .
I С2 ' Яе0 С2
Таким образом, магнитное число Рейнольдса характеризует отно-
отношение напряженности магнитного поля от индуцированных токов к
напряженности внешнего магнитного поля.
Аналогия между гидродинамическим и магнитным числами Рей-
Рейнольдса очевидна
, m , m
Величина i/m имеет ту же размерность, что и кинематическая вяз-
вязкость v и называется магнитной вязкостью. Иногда пользуются маг-
магнитным числом Прандтля, которое определяют отношением магнит-
магнитного числа Рейнольдса к гидродинамическому
р _ Rem _ v ... до\
Из выражений A1.38), A1.40) и A1.42) следует связь между пара-
параметром магнитогидродинамического взаимодействия, числом Альвена
и магнитным числом Рейнольдса
So = А2 ¦ Re,
Произведение
С 7]
где rj = рои — коэффициент динамической вязкости, характеризует от-
отношение магнитной силы от индуцированного магнитным полем тока
к силе вязкости. Обычно вводят корень квадратный из этой величины
На= VSo • Re = - Hol xl^ . A1.44)
с у г)
Безразмерный критерий На называется числом Гартмана.
В модельных экспериментах, чтобы сохранить динамическое подо-
подобие модели и натурного объекта в проводящей жидкости при наличии
11.5]
«Вмороженность» магнитных силовых линий
311
внешнего магнитного поля, необходимо обеспечить равенство всех
независимых критериев подобия для модели и натуры.
Характер течений электропроводной жидкости во внешнем маг-
магнитном поле определяется значениями критериев подобия. В таблице
приведена классификация течений в зависимости от значений чисел
Re, На и Rem. Здесь же приведены порядки предельных значений
магнитного числа Прандтля Prm и числа Стюарта Sq.
Re
0-2000
2000-4000
2000-4000
0-2000
0-2000
На
0-10
0-10
10-100
0-10
10-100
Rem
0-1
0-1
0-1
1-10
1-10
Prm
ю-3
ю-4
ю-3
ю-2
ю-2
So
ю-2
ю-2
1
ю-1
10
Характер течения
Ламинарное течение
Турбулентное течение
Течение с турбулентностью, подав-
подавленной магнитным полем
Течение сильно влияет на магнит-
магнитное поле; магнитное поле слабо
влияет на течение
Течение сильно влияет на магнит-
магнитное поле; магнитное поле сильно
влияет на течение
11.5. «Вмороженность» магнитных силовых линий
Рассмотрим принцип, формулировка и доказательство которого при-
принадлежат Альвену. Этот принцип играет большую роль в создании
тех немногих образных представлений, которые возможны в магнитной
гидродинамике.
Рассмотрим уравнение A1.27) или его безразмерный вид A1.41).
При больших магнитных числах Рейнольдса (Rem ^ 1), что соответ-
соответствует высокой электропроводности жидкости, вторым членом в правой
части этого уравнения можно прене-
пренебречь. Тогда получим
Ш
dt
= rot[v,H].
A1.45)
Это уравнение выражает сохранение
магнитного потока через индивидуальный
замкнутый контур, т.е. через контур, рис ц j
состоящий из одних и тех же частиц
жидкости. Действительно, рассмотрим индивидуальный замкнутый
контур /. Частицы жидкости, составляющие этот контур, движутся
с локальной скоростью v. Рассмотрим некоторый элемент контура d\
(рис. 11.1).
Очевидно, за малый промежуток времени dt в процессе движения
он изменяет площадь S, охватываемую контуром, на dS = [cQ,v] dt.
312 Магнитная гидродинамика [Гл.11
Изменение магнитного потока <1Ф через контур за рассматриваемый
промежуток времени обусловлено, во-первых, изменением напряженно-
напряженности магнитного поля: ятт
d&x = dt\ ^ dS, A1.46)
s
и, во-вторых, изменением площади, охватываемой контуром:
[dl,v] H. (П.47)
i
Используя теорему Стокса, запишем уравнение A1.47) в виде
d<S>2 = dtl [H,v] d\ = -dti [v,H] d\= -dt f rot[v,H] dS . A1.48)
i i s
Таким образом, скорость изменения магнитного потока через по-
поверхность, опирающуюся на индивидуальный замкнутый контур иде-
идеально проводящей жидкости (аг —> оо), определится следующим выра-
выражением:
S
С учетом уравнения A1.45) получаем
f=0. A1.50)
Из полученного уравнения A1.50) следует, что магнитный поток
через любую поверхность, опирающуюся на индивидуальный замкну-
замкнутый контур, в идеально проводящей жидкости (аг —> оо) не изменя-
изменяется с течением времени. Физически это означает, что при сжатии
контура сближаются линии магнитной индукции, т. е. напряженность
поля увеличивается. И наоборот, при расширении сверхпроводящего
индивидуального контура линии магнитной индукции «разбегаются»,
т.е. напряженность поля уменьшается. Таким образом, при движении
жидкости поперек магнитного поля вместе с ней перемещается и
магнитное поле. Образно говоря, магнитные силовые линии как бы
«вморожены» в жидкость. «Вмороженность» магнитных линий связана
с тем, что при изменении потока вектора напряженности магнитного
поля через проводящий контур в нем индуцируются электрические
токи, поле которых препятствуют изменению этого потока. Заметим,
что движение жидкости вдоль силовых линий не влияет на внешнее
магнитное поле.
Явление «вмороженности» магнитных силовых линий в жидкость
наглядно иллюстрируется теоремой Валена, которая может быть сфор-
сформулирована так: Если индивидуальные частицы идеально проводя-
проводящей жидкости в некоторый начальный момент времени находились
на одной магнитной силовой линии, то они и останутся на ней во
все последующие моменты времени.
11.5] «Вмороженность» магнитных силовых линий 313
Для доказательства этой теоремы вновь обратимся к уравнению
A1.45). Преобразуем его. Запишем г-компоненту ротора векторного
произведения [v, Н] через тензор Леви-Чивита:
t; [V , Н] =
— I =
dvi dHj dvk
= Vi — h Hk Vk -^ Hi -— .
OXk OXk OXk OXk
Получено векторное соотношение
rot[v , H] = v div H + (HV)v - (vV)H - H div v .
Поскольку divH = 0, то уравнение A1.45) запишется в виде
^ = (HV)v- (vV)H-H divv. A1.51)
ОТ
Из уравнения непрерывности имеем
4
Подставляя последнее выражение в A1.51), получим
^ = (HV)v - (W)H + ^ (|f + (W)p) . (И.52)
Рассмотрим выражение
/ д ^\ Н 1 <9Н Н др 1 . . Н
kr+vV - = -^- 2^7 + ~ (vV)H 2
\dt J p p dt pz dt p v ' pz
Комбинируя A1.53) и A1.52), получим
Ьт + vV - =— Vv, — — = — V v. A1.54)
\dt ) р \ р ) dt р \р )
Обсудим смысл полученного выражения. Пусть в жидкости имеется
некоторая индивидуальная линия, т. е. линия, состоящая из одних и
тех же частиц жидкости.
Рассмотрим малый участок 51 этой линии жидкости (рис. 11.2). Так
как скорости концов участка линии различны, то она будет растяги-
растягиваться или сжиматься. Найдем изменение длины выделенного участка
E1 с течением времени. Очевидно, что за время dt участок 51 получит
приращение
^ = 5lnVvdt,
где п — единичный вектор вдоль отрезка dl. Так как 51 = 51п, то можно
записать
d(Sl) = {6W)vdt.
314 Магнитная гидродинамика [Гл.11
Или в векторном виде
e A1.55)
at
Сравнивая уравнения A1.54) и A1.55), приходим к заключению,
что величины Н/р и 51 описываются одним и тем же уравнением.
Если при этом начальные и граничные условия к
v/ +(ov//01H1 обоим уравнениям идентичны, то и решения будут
также идентичны.
§1 У^ *"" Отсюда можно сделать следующие заключения:
1) Если в некоторый начальный момент времени
векторы Н/р и E1 параллельны, то они остаются
параллельными и во все последующие моменты вре-
времени, а их величины будут изменяться пропорци-
пропорционально. Это в свою очередь означает, что если
Рис. 11.2. Линия дВе близкие частицы жидкости находятся на одной
из одних и тех же магнитной линии, то они остаются на ней во все
частиц жидкости
последующие моменты времени.
2) Если расстояние между двумя частицами жидкости увеличива-
увеличивается, то соответственно увеличивается и величина Н/р.
Таким образом, если перейти к конечным расстояниям между оди-
одинаковыми частицами жидкости, то можно прийти к выводу, что если
вещество с бесконечной проводимостью перемещается в магнитном
поле, то вместе с ним перемещается и само магнитное поле. Ин-
Индивидуальные частицы жидкости при движении не могут пересекать
магнитные силовые линии, которые, в свою очередь, не могут опе-
опережать или отставать от движущихся частиц. Но в этом и состоит
явление «вмороженности» магнитных силовых линий в жидкость. Если
жидкость несжимаема (р = const), то вследствие растяжения жидкой
линии напряженность магнитного поля вдоль нее будет увеличиваться
и наоборот.
Рассмотрим теперь некоторый индивидуальный контур жидко-
жидкости, перпендикулярный напряженности магнитного поля. Если теперь
каким-либо образом стянуть этот контур, то в силу «вмороженности»
магнитных силовых линий стянется и магнитное поле. Поскольку поток
напряженности магнитного поля через этот контур останется посто-
постоянным, то при сокращении контура напряженность поля внутри его
увеличивается. Это явление используется при создании сверхсильных
импульсных магнитных полей. Вещество сжимается взрывом, в резуль-
результате чего магнитное поле на короткое время в некоторой ограниченной
области достигает сотен тысяч эрстед.
Явлением «вмороженности» магнитных силовых линий объясняют
происхождение магнитного поля звезд. Как известно, звезды образуют-
образуются в результате гравитационного сжатия галактических туманностей —
космической пыли и межзвездного газа. В начальной стадии рождения
протозвезды существующие потоки заряженных частиц создают слабое
магнитное поле. В процессе сжатия газопылевого скопления начальное
11.5] «Вмороженность» магнитных силовых линий 315
поле значительно усиливается, превращаясь в магнитное поле сформи-
сформировавшейся звезды (или планеты).
На этом же принципе основано устройство сверхпроводящих экра-
экранов. Если есть необходимость какую-то часть экспериментальной уста-
установки защитить от воздействия внешних магнитных полей, то она
окружается оболочкой из сверхпроводника, охлаждаемого жидким ге-
гелием. И в этом случае магнитные силовые линии внешних магнитных
полей, «приклеенные» к сверхпроводящей оболочке, не могут проник-
проникнуть внутрь экспериментального объема.
Эта идея используется и в термоядерных устройствах для удержа-
удержания и сжатия плазмы. Пусть в плазме, организованной в виде тонкого
шнура, течет ток, который вызван некоторым сторонним источником
(рис. 11.3). Вокруг этого шнура с током об-
образуется соленоидальное магнитное поле. /~\ ^
Под действием максвелловского натяжения I
магнитные силовые линии соленоидально- \у ^у ^у ^у
го магнитного поля также стремятся со-
сократиться. Действительно, натяжение маг- рис цз. Сжатие плазмы
нитной силовой линии можно определить,
пользуясь тензором магнитных напряжений. Если магнитное поле на-
направлено вдоль оси х, то магнитная сила, действующая в направлении
магнитного поля на единичную площадку, перпендикулярную оси х,
равна
н Hi
а™ = 8^ •
Но в силу «вмороженности» магнитных силовых линий, сокращаясь,
они увлекают за собой и вещество, сжимая его в еще более тонкий
шнур. Это сжатие будет происходить до тех пор, пока все увеличи-
увеличивающееся термодинамическое давление в плазме шнура не будет равно
магнитному давлению.
Если в предыдущем примере магнитное поле создается электри-
электрическим током в сжимаемом веществе, то можно себе представить и
устройства, в которых сжатие вещества происходит
некоторым независимым внешним магнитным по-
полем (магнитные «бутылки», «ловушки») (рис. 11.4).
Система встречных магнитных полей создается
неподвижными прямолинейными проводниками, по
которым в разных направлениях течет электриче-
электрический ток. В этом случае плазма помещается меж-
между проводниками в нарастающее магнитное поле,
р ... ^ которое, адиабатически сжимая ее, одновременно
мГмагнитной ло- увеличивает ее плотность и температуру.
вушки Одним из возможных источников сильных маг-
магнитных полей в космическом пространстве являет-
является столкновение двух областей межзвездного газа, обладающих до
столкновения в силу некоторого направленного движения заряженных
316 Магнитная гидродинамика [Гл.11
частиц или по другим причинам слабыми магнитными полями. В этом
случае сжатие межзвездного газа в результате столкновения приведет
также к концентрации магнитного поля в сравнительно небольших
областях, а значит, и к увеличению в них напряженности магнитного
поля.
Опираясь на принцип «вмороженности» магнитного поля в веще-
вещество, нетрудно понять и запаздывание частиц, приходящих на Землю
вследствие взрывов на Солнце. Наблюдения показывают, что после
взрыва на Солнце на Землю спустя примерно 20 часов обрушивается
поток заряженных частиц. Сами индивидуальные частицы движутся со
скоростями, достаточными для прохождения расстояния от Солнца до
Земли за несколько десятков минут. По-видимому, во время взрывов от
Солнца отрываются большие куски плазмы вместе с магнитным полем.
Магнитное поле удерживает частицы как в «мешке», который движется
к Земле с некоторой гидродинамической коллективной скоростью (око-
(около 1500 км/с), значительно меньшей, чем скорость индивидуальных
частиц в «мешке». Подходя к Земле и нарушая ее магнитное поле,
заряженные частицы «высыпаются» на Землю, инициируя магнитные
бури и полярные сияния.
11.6. Диффузия магнитного поля
Принцип «вмороженности» магнитных силовых линий следует из
общих уравнений электродинамики в том случае, когда среда имеет
бесконечную проводимость. Однако реальные среды в обычных услови-
условиях (не слишком низкие температуры) имеют конечную проводимость.
Такая реальная среда будет просачиваться, диффундировать через
магнитное поле или, наоборот, магнитное поле будет диффундировать
в проводящей среде.
Рассмотрим случай малых магнитных чисел Рейнольдса (Rem <C 1).
При этом уравнение A1.27) с учетом оценки его членов по безразмер-
безразмерной форме A1.41) записывается в виде
^М = -^- АН. A1.56)
dt 4тг<тг
Уравнение A1.56) формально имеет тот же вид, что и уравнение
диффузии, описывает диффузию магнитного поля в слабо проводящей
или неподвижной среде. Величина
^ A1.57)
называется магнитным коэффициентом диффузии. Коэффициент
Dm тем меньше, чем больше проводимость среды, при бесконечной
проводимости он равен нулю, что и следует из принципа «вмороженно-
«вмороженности» магнитных силовых линий.
11.6] Диффузия магнитного поля 317
Рассмотрим в качестве примера диффузию магнитного поля в про-
проводящее полупространство. Пусть проводящая среда, занимающая об-
область х > 0, отделена экраном S, от области х < 0, в которой создано
постоянное магнитное поле напряженностью Но
(рис. 11.5). В некоторый момент времени экран xl\
убирают и магнитное поле проникает в прово-
проводящую среду. Эта задача имеет гидродинами- ^—^—
ческую аналогию, которая известна как задача т д
Рэлея, в которой течение вязкой жидкости вы- *
зывается внезапным движением пластинки с по- ри ^ г т\иа,а,
стоянной скоростью вдоль ее собственной плос- магнитного поля
кости.
Выберем систему координат таким образом, чтобы ось z находилась
в плоскости х = 0 и совпадала с направлением вектора напряженности
магнитного поля Hq. Ограничимся плоским одномерным случаем, когда
вектор напряженности в любой момент времени имеет только одну
отличную от нуля z-компоненту, т.е. Н = (О,О, HZ). При этом Hz
зависит от времени t и только от одной координаты х. Тогда уравнение
диффузии A1.56) запишется в виде
^ = Dm^^. A1.58)
Зададим значения Hz на поверхности х = 0 и на бесконечности
(х —> оо). Вид граничных условий очевиден
О для t < О,
Начальное условие выражает тот факт, что в начальный момент
времени магнитное поле в проводящей среде отсутствует
Hz(x,0)=0 для 0<ж<оо. A1.60)
Решение задачи A1.58)—A1.60) имеет вид
/ т \
Hz(x,t) = Но I I -erf , A1.61)
где erf и — интеграл вероятности.
Интеграл вероятности монотонно возрастает с увеличением рассто-
расстояния х, принимая значения от 0 до 1. Это позволяет ввести понятие
глубины проникновения магнитного поля в проводящую среду как та-
такого расстояния х = 5, на котором напряженность Hz уменьшается до
0,01 Hq. Отсюда следует, что 5 = A^Dmt. Проникновение магнитного
поля в проводящую среду на ограниченное расстояние в физической
электронике называют скин-эффектом. Он возникает вследствие того,
что изменение магнитного поля индуцирует ЭДС и, следовательно,
индуцирует ток, магнитное поле которого, согласно закону Ленца,
препятствует изменению начального магнитного поля.
318 Магнитная гидродинамика [Гл.11
Очевидно, характерное время диффузии магнитного поля в прово-
проводящей среде определяется следующим выражением:
2 2
1р ~ лп — 2 ' [11.OZ)
^1-/т С
Например, время релаксации магнитного поля в медном шаре ради-
радиусом 100 см составит около 15 с. Для космических объектов это время
очень велико. Если считать, что ядро Земли состоит из расплавленного
железа и в нем возникло магнитное поле, то время затухания земного
поля оценивается в 15000 лет. Время затухания магнитного поля в сол-
солнечных пятнах — около 300 лет, а магнитного поля Солнца — 1010 лет.
11.7. Волны Альвена
Пусть при стационарном движении проводящей жидкости в по-
поле постоянного однородного магнитного поля напряженностью Но в
ней по каким-то причинам возникает некоторое возмущение, кото-
которое передается и магнитному полю. Очевидно, внезапно возникающие
возмущения будут распространяться в жидкости в виде магнито-
гидродинамических волн. Эти волны классифицируют в зависимости
от направления распространения по отношению к внешнему магнит-
магнитному полю, характера и частоты колебаний индивидуальных частиц
проводящей среды. Например, в плазме различают несколько типов
магнитогидродинамических волн, распространяющихся в направлении
вектора напряженности внешнего магнитного поля: продольные волны
(ленгмюровские волны) и два типа поперечных волн, которые раз-
различаются между собой диапазоном частот (альвеновские и быстрые
магнитозвуковые волны).
Механизм возникновения ленгмюровских волн связан с дально-
действующими кулоновскими силами в плазме, которые придают ей
электродинамическую упругость. При смещении группы электронов от
их равновесного положения возникает электростатическая сила, стре-
стремящаяся вернуть электроны обратно в положение равновесия. В ре-
результате начинаются колебания, которые распространяются в плазме в
виде волны. Заметим, что ленгмюровские волны могут возникать и при
отсутствии внешнего магнитного поля.
Поперечные колебания в жидкостях и газах невозможны при от-
отсутствии внешнего магнитного поля, так как жидкости и газы не
обладают упругостью формы (модуль сдвига равен нулю). Природа
возникновения поперечных колебаний в проводящей среде связана
с принципом «вмороженности» силовых линий внешнего магнитного
поля в эту среду. Поперечное к линиям напряженности магнитного по-
поля смещение индивидуальных частиц проводящей жидкости вызывает
соответствующее поперечное смещение силовых линий, растягивая их
вследствие «вмороженности» в жидкость. Магнитные силовые линии,
подверженные растяжению, стремятся сократить свою длину. Таким
11.7] Волны Алъвена 319
образом, линии напряженности магнитного поля совершают попереч-
поперечные колебания подобно струнам музыкального инструмента. При этом
они увлекают в колебательное движение проводящую жидкость, в ко-
которую частично или полностью вморожены.
Для сплошной среды характерны низкочастотные алъвеновские
волны — поперечные магнитогидродинамические волны низкой ча-
частоты, распространяющиеся вдоль вектора напряженности маг-
магнитного поля Но. Действительно, если частота волны uj сравнима или
больше ионной циклотронной частоты uj^i = eHo/rriiC (га^ — масса
иона), то поведение ионов и свободных электронов среды будет различ-
различным, т.е будет нарушаться сплошность среды. Для альвеновских волн,
как отмечалось ранее, характерно поперечное возмущение внешнего
магнитного поля. В магнитозвуковых волнах при со ^ coHi возмущения
магнитного поля, перпендикулярные Но, отсутствуют.
Рассмотрим явление распространения альвеновских волн в невяз-
невязкой несжимаемой идеально проводящей (Rem ^> 1) жидкости. Пусть
на внешнее однородное магнитное поле Но наложено малое попе-
поперечное возмущение h. Результирующее поле, взаимодействующее со
средой, определяется суперпозицией основного поля и возмущения:
Н = Но + h.
При больших магнитных числах Рейнольдса, когда силовые линии
«вморожены» в жидкость, полная напряженность магнитного поля удо-
удовлетворяет уравнению A1.45)
^=rot[v,H]. A1.63)
Выберем систему координат так, чтобы координатная ось х была
направлена вдоль вектора напряженности Но, а ось z — вдоль возму-
возмущения h. Волна распространяется вдоль оси х. Таким образом, имеем
Но = (#0,0,0), h = @,0, h(x, t)), v = @,0, v(x, t)) и уравнение
A1.63) записывается в виде
§ = "о?- A1.64)
dt дх
Из уравнения движения A1.28) для идеальной несжимаемой жид-
жидкости, пренебрегая конвективным членом (vV)v как членом более вы-
высокого порядка малости (скорость газа много меньше фазовой скорости
волны), а также квадратичным по возмущению членом ~ h2, имеем
dt 4тгр дх
Дифференцируя уравнение A1.64) по t, уравнение A1.65) по х, а
затем наоборот, получим уравнения для скорости среды v и возмуще-
возмущения напряженности поля h:
d2h 2 d2h d2v 2 d2v Ho пл аа,
—к- = a —x, —к = a —x, a = —== . A1.bo)
dt2 дх2 dt2 дх2 JA^p
320
Магнитная гидродинамика
[Гл. 11
Уравнения A1.66) описывают волновые процессы, причем возмуще-
возмущения среды и поля распространяются вдоль вектора напряженности Но
с одинаковой скоростью а = Но/^/Аттр. Это соответствует принципу
«вмороженности». Заметим, что скорость альвеновских волн не зависит
от частоты, а определяется напряженностью внешнего магнитного поля
и плотностью среды. Решения уравнений A1.66) для волн, распростра-
распространяющихся в положительном направлении оси х, имеют вид
h =
— kx)\,
v =
-кх)}, A1.67)
где uj — частота колебаний, к = и /a — волновое число. Амплитуды
колебаний связаны между собой соотношением, которое следует из
уравнения A1.64)
ho = -
Поскольку мы рассматривали идеально проводящую среду (аг —>
—> оо), решения A1.67) описывают незатухающие колебания. Реальные
среды обладают некоторым электрическим сопротивлением. С учетом
этого мы вновь получили бы волновой процесс, в котором амплитуды
колебаний уменьшались бы вдоль направления распространения волны
по экспоненциальному закону (~ехр(—ах)). Коэффициент затухания
а зависит от частоты колебаний и, проводимости среды аг и альвенов-
ской скорости а. Величина а~х характеризует глубину проникновения
волны, т. е. расстояние, на котором амплитуда колебаний уменьшается
в е раз — магнитогидр о динамический поверхностный скин-эффект.
11.8. Задача Гартмана
Рассмотрим установившееся движение проводящей несжимаемой
жидкости между двумя параллельными бесконечными пластинами
в перпендикулярном магнитном поле напряженностью Hq. Будем по-
полагать, что движение вызывается градиентом давления, направленным
вдоль пластин по оси х (рис. 11.6). Пусть
расстояние между пластинками равно 2а.
Движение жидкости должно подчиняться
следующим уравнениям:
Рис. 11.6. К задаче Гарт-
Гартмана
(vV)v = —
Р
rot[v,H
4тгсгг
div v = 0 ,
4тгр
АН = 0,
divH = 0.
[H,rotH],
A1.68)
Скорость жидкости направлена вдоль пластин и зависит лишь от
поперечной координаты z, т. е.
vx = vx(z), vy = 0, vz = 0 .
11.8] Задача Гартмана 321
В силу бесконечности пластин в направлении осей х и у очевидно,
что напряженность магнитного поля также может зависеть только от
координаты z. Тогда задача может рассматриваться как плоская
Нх = Hx(z), Hy=0, Hz = Hz(z).
Из векторного анализа известны следующие соотношения
rot; [v, Н] = (HV)«i - (vV)#; - Я; divv + v{ divH =
Проекции уравнений A1.68) на координатные оси с учетом топологии
задачи записываются в виде
®v. - „ t^± + JL и ®1Ll ЁЕ-п
dx~V Qz2 4тг z Oz ' ду~ '
8z 4тг x 8z '
dv c2 9>H AL69)
Атгсгг dz2 '
dz2 ' dz
Из последнего уравнения A1.69) имеем
Hz = const = Яо. A1.70)
Тогда предыдущее уравнение A1.69) удовлетворяется тождественно.
Из второго уравнения следует, что давление р зависит только от
координаты х.
Из третьего уравнения получаем, что сумма гидродинамического и
магнитного давлений не зависит от координаты z, а может зависеть
только от координаты х, т.е. имеем
Продифференцируем первое уравнение системы A1.69) по коорди-
координате z, с учетом выражения A1.70) и четвертого уравнения системы
получим уравнение для скорости движения жидкости:
d\x 1 dvx _ 0 д _ с Гп
где На —число Гартмана.
Решение уравнения A1.72) ищем в виде
vx = A exp(rz).
11 В.Г. Черняк, П.Е. Суетин
322 Магнитная гидродинамика [Гл.11
Характеристическое уравнение для параметра г
з 1 а а 1 1
г -->г = 0, п=0, г2 = -, гз = -д.
Таким образом, общее решение уравнения A1.72) имеет вид
A1.73)
Постоянные интегрирования А\, А^ А^ должны быть определены
из граничных условий. Поскольку стенки канала неподвижны, то ско-
скорость жидкости на их поверхностях равна нулю. Из симметрии задачи
следует, что на оси канала скорость течения жидкости максимальна и
равна г>тах. Тогда граничные условия имеют вид
z = ±a, vx=0; 2 = 0, vx = г>тах. A1.74)
Отсюда получаем
Д _ ^max ch(Ha) Д Д ^тах (] 1 7^
Лх~ l-ch(Ha) ' Л2"Лз[1-сЬ(На)]' [П^}
Таким образом, скорость течения проводящей жидкости в канале
определяется следующим выражением:
Величина продольной составляющей напряженности магнитного по-
поля Нх определяется интегрированием четвертого уравнения системы
A1.69)
А=
Г _ ch CHa ?\1
L V а/ \
= Щ А=
oz с1 с1 ch(Ha) — 1
A1.77)
В выражении A1.77) постоянная А не зависит от z. Но так как Нх
не зависит от х, то А не должна зависеть и от координаты х, т.е.
постоянная А не зависит от координат. Обозначая выражение перед
квадратными скобками в A1.77) через а, в результате интегрирования
имеем
-^ sh (hla ^)] + Az + В . A1.78)
Поскольку на границе нет никаких поверхностных токов проводи-
проводимости, то при z = ± а должна быть непрерывна тангенциальная со-
составляющая напряженности магнитного поля. Поскольку вне жидкости
имеется лишь поперечное магнитное поле Hz = Но, то для продольной
составляющей напряженности Нх можно записать следующие гранич-
граничные условия:
z = ±a, Hx=0. A1.79)
Из этих условий для постоянных интегрирования получим:
В = 0, А = -- Lch(Ha) - -5- sh(Ha)l .
а I На J
11.8] Задача Гартмана 323
Тогда выражение A1.78) запишется в виде
_ 4тг(тгЯо a {z/a) sh(Ha) - sh(Ha z/a) m йт
П ЦТ ^ i ^llOUJ
2
С
На max ch(Ha) - 1
Скорость жидкости на оси канала может быть определена из пер-
первого уравнения системы A1.69). Дважды дифференцируя A1.76) по z
и используя выражение A1.80) для Нх, получим
_ _а ch(Ha) - 1 dp л 1 ЯП
<W-"- Hash(Ha) ~дх~ ' ( j
Обычный гидродинамический результат из A1.81) можно получить
в том случае, когда жидкость не взаимодействует с магнитным полем.
Это будет тогда, когда или отсутствует магнитное поле или когда про-
проводимость жидкости равна нулю (На —>• 0). В этом пределе, раскрывая
неопределенность в A1.81) по правилу Лопиталя, получаем известный
результат для плоского течения Пуазейля:
_ а др
тах 2г\ дх
Точно так же из формулы A1.76) при На —>• 0 снова имеем результат
обычной гидродинамики
а"
Из формул A1.71) и A1.80) следует, что только при z = ± а и
z = 0 давление в жидкости равно гидростатическому давлению. Во
всех остальных точках поперечного сечения плоского канала остается
неизменной лишь сумма гидростатического и магнитного давлений
Следовательно, в этих точках недостаток гидростатического давле-
давления восполняется магнитным давлением так, что сумма их остается
постоянной в данном сечении.
При На <С 1, разлагая в ряд числи- | | { Щ
тель и знаменатель A1.81) с точностью
до На2, получим н| f f Н^О )н = 0
^тах = -|
Из последнего выражения видно, Рис. 11.7. Профили скорости
что при заданном градиенте гидроста- (справа от штриховой линии) и
тического давления с увеличением Но линии напряженности (слева)
или аг скорость уменьшается, т. е. маг-
магнитное поле препятствует движению проводящей жидкости, и это
сопротивление тем больше, чем больше проводимость жидкости и
напряженность магнитного поля. Профиль скорости становится более
плоским, как при турбулентном движении (рис. 11.7), а магнитные
силовые линии изгибаются (натягиваются) в направлении движения
жидкости.
324 Магнитная гидродинамика [Гл.11
При больших значениях На скорость жидкости становится постоян-
постоянной почти по всему сечению канала, и только вблизи стенок имеются
так называемые гартмановские слои с большими градиентами скорости.
В первом приближении безразмерная толщина этих слоев пропорцио-
пропорциональна На~ .
Объемный расход жидкости в канале с учетом выражения A1.76)
для скорости равен
^ = Ьdz=dlS^r ИНа> - i shH • AL83)
— a
Средняя скорость определится следующим выражением:
11.9. Задача Стокса
Рассмотрим стационарное медленное (Re <С 1) обтекание непрово-
непроводящего шара плоскопараллельным потоком несжимаемой проводящей
жидкости в присутствии внешнего магнитного поля. Пусть вектор
скорости набегающего потока v^ направлен
вдоль оси х и составляет угол а с вектором
напряженности магнитного поля Но в невоз-
невозмущенной области (рис. 11.8). Радиус шара
равен а.
Для определения поля скоростей и на-
напряженности магнитного поля необходимо ре-
решить систему уравнений A1.68). Граничные
Рис. 11.8. Стоксово об- уСЛовия задаются для скорости жидкости и
текание шара
^ напряженности поля на поверхности шара и
на бесконечном удалении от него в невозмущенной области течения.
Поскольку поверхностных токов на непроводящей сфере нет, имеем
г = у/х2 + y2 + z2 =а : v = 0, H = 0; A1.85)
r^oo: v = Voo, H = H0. A1.86)
Приближенное решение задачи удалось получить только при малых
и больших числах Гартмана. Опуская громоздкие вычисления, приве-
приведем результаты для силы, действующей на шар со стороны жидкости.
При На <С 1 сила лобового сопротивления равна
|к = 1 + ! (l + I sin2 a) Ha+O(Ha2). A1.87)
Здесь Fq = ^TrrjaVoo — сила Стокса при отсутствии магнитного поля.
Таким образом, наличие магнитного поля при На ^С 1 увеличивает
сопротивление на величину порядка На. Очевидно, это связано с явле-
явлениями натяжения и «вмороженности» магнитных силовых линий, уси-
11.10] Магнитогидродинамические машины 325
ливающими асимметрию поля течения относительно оси z. По этой же
причине возникает подъемная сила, лежащая в плоскости, образуемой
векторами скорости v^ и напряженности Но:
^ = J- Hasin2a + O(Ha2). A1.88)
Только в том случае, когда угол между векторами v^ и Но равен
а = 0 или а = тг/2, поле течения симметрично относительно оси х, и
подъемная сила отсутствует.
Заметим, что выражения A1.87) и A1.88) не изменятся и в случае
проводящего шара. Вклад в силу сопротивления и подъемную силу
взаимодействия тока внутри проводящего шара с магнитным полем
проявляется в членах порядка На2 и выше.
При На > 1 получено решение лишь в случае продольного магнит-
магнитного поля при а = 0
^ = |на. A1.89)
Таким образом, при больших числах Гартмана сила лобового сопро-
сопротивления может увеличиваться в десятки раз.
11.10. Магнитогидродинамические машины
11.10.1. Электромагнитные насосы. В последние годы широко
используются для перекачки проводящих жидкостей электромагнит-
электромагнитные насосы. Они оказались особенно необходимыми в атомных реакто-
реакторах с жидкими металлическими теплоносителями типа калия, натрия
и их смесей. Преимуществами электромагнитных насосов, которые
обеспечили их широкое применение, являются следующие.
1. Чрезвычайная простота конструкции и простота регулировки их
производительности как по величине, так и по направлению.
2. Абсолютная герметичность насоса, что очень важно при пере-
перекачке вредных агрессивных или взрывоопасных веществ. Так, утечка
жидкого натрия из контура охлаждения создает большую пожарную
опасность, так как при соединении с водой (например, находящейся
в теплообменнике) реакция идет со взрывом.
3. Простота монтажа насоса в магистральном трубопроводе без
создания дополнительных гидравлических сопротивлений.
Все электромагнитные насосы можно разделить на два класса — ин-
индукционные насосы и насосы прямого действия (фарадеевского типа).
Принцип действия индукционного насоса можно понять следующим
образом (рис. 11.9). Представим себе, что вдоль трубопровода с прово-
проводящей жидкостью специальные индукторы создают бегущее магнитное
поле. Это можно осуществить по тому же принципу, что вращающееся
магнитное поле в статоре асинхронного двигателя, которое индукцион-
но увлекает ротор. Бегущее магнитное поле также индукционно увле-
увлекает проводящую жидкость, прокачивая ее по трубопроводу в том или
326
Магнитная гидродинамика
[Гл. 11
ином направлении в зависимости от направления «бега» магнитного
поля. Для увеличения производительности насоса индукторы бегущего
магнитного поля обычно помещают в начале и в конце трубопровода.
ШШ
1Ш
=ff:=:
1
3
Рис. 11.9. Схема индукционного насоса: /, 3 — индуктор бегущего магнитного
поля, 2 — трубопровод
Ясно, что часть трубопровода, находящаяся между индукторами маг-
магнитного поля, должна быть сделана из немагнитного материала с малой
электропроводностью (например, тонкая нержавеющая сталь).
Индукционный насос можно осуществить и следующим образом.
Если в статор асинхронного двигателя поставить стакан с ртутью,
то при включении статора его вращающееся магнитное поле будет
увлекать ртуть в стакане и придаст ей вращательное движение. Те-
Теперь можно представить, что статор надет на трубопровод, а внутри
трубопровода находится винт (рис. 11.10). Тогда вращающаяся про-
проводящая жидкость будет «ввинчиваться» вдоль оси трубы, создавая
поступательное движение жидкости в трубопроводе. К сожалению,
КПД индукционных насосов очень мал и составляет 2-^3%, так как
велики потери в стенках трубопрово-
у///////////^/////А 2 да и самой жидкости на ее нагрев.
U
Н
/ууууууу\
Рис. 11.10. Индукционный
насос: / — статор, 2 — тру-
труба, 3 — винт
Рис. 11.11. Схема электро-
электромагнитного насоса прямого
действия
Принцип действия электромагнитных насосов прямого действия
ясен из рис. 11.11. В насосе прямого действия магнитное поле по-
постоянно и создается или электромагнитом, или постоянным магнитом.
Между полюсами расположен прямоугольный участок трубопровода
с проводящей жидкостью. Перпендикулярно магнитному полю через
боковую поверхность трубопровода, а следовательно, перпендикулярно
и скорости жидкости, течет ток плотностью j, создаваемый также неза-
независимым источником тока. Если постоянное магнитное поле создается
электромагнитом, то ток j и ток электромагнита могут создаваться
одним и тем же источником тока. Ясно, что боковые поверхности пря-
11.10] Магнитогидродинамические машины 327
моугольной трубы должны быть изготовлены из хорошо проводящего
немагнитного материала, в то время как поверхности, перпендикуляр-
перпендикулярные магнитному полю — из немагнитного материала, обладающего пло-
плохой проводимостью. Коэффициент полезного действия насосов прямого
действия значительно выше,чем индукционных насосов, и составля-
составляет 25-^30%. Причем в этот КПД входит и КПД выпрямительных
устройств источников питания.
Сделаем грубый, ориентировочный расчет насоса прямого действия
при следующих приближениях.
1. Будем полагать, что магнитное поле постоянно, однородно в объе-
объеме аЫ (рис. 11.11) и определяется только полем постоянного магнита.
Магнитное поле индукционных токов мало и слабо влияет на магнит-
магнитное поле постоянного магнита.
2. Будем также полагать, что ширина канала много больше его
высоты (Ь ^> а), тогда задачу о движении жидкости в прямоугольном
канале можно рассматривать как плоскую, как задачу о движении
проводящей жидкости между двумя параллельными бесконечными
плоскостями (рис. 11.12).
3. Пусть в трубопроводе нет градиен-
градиента гидростатического давления неэлектро-
неэлектромагнитного происхождения. Тогда в стацио-
стационарном случае имеем следующее уравнение
движения для несжимаемой жидкости:
I ;
I j
Но
J
{ J
' qz2 ~ с ' Рис. 11.12. Плоский канал
Заметим, что уравнение A1.90), если заменить правую часть про-
продольным градиентом давления, формально совпадает с уравнением,
использованным в задаче о плоском течении Пуазейля. Поэтому можно
воспользоваться известным решением, заменив градиент давления на
Hoj/с. Следовательно, объемный расход проводящей жидкости через
трубопровод шириной b (пренебрегая торможением жидкости боковыми
поверхностями трубы) будет равен
Сделаем примерный расчет насоса, прокачивающего смесь Na-K
E6%-ный натрий + 44%-ный калий), применяемую в качестве тепло-
теплоносителя атомных реакторов. Приведем исходные данные:
Яо = 103 Э, / = 200 А, г/B50 °С) = 0,00346 Па • с,
а = 2см, 6= 10см, / = 40см.
Плотность тока равна
j = J- А/см2 = /¦ • 3 • 109 ед. СГСЭ/см2.
la ' la '
328 Магнитная гидродинамика [Гл.11
Подставляя значения величин, входящих в формулу A1.91), для объ-
объемного расхода получаем
/гЛ а ЬН$1 -3-10 г л ^л з /
Qv = Tjz—j « 5 • 104 см7с .
\2r]lac
Средняя по сечению канала скорость жидкости
v = Ц^ъ 25м/с.
Ьа
Конечно, приведенный расчет претендует лишь на порядок величин,
так как мы не учитывали магнитного поля, создаваемого самим током,
что существенно будет снижать расход.
При расчете реальной гидравлической системы разумеется необхо-
необходимо знать ее гидравлическое сопротивление, которое в существенной
мере будет определять расход жидкости.
11.10.2. Магнитогидродинамический генератор. Магнитогид-
родинамический генератор (МГД-генератор) — машина для непосред-
непосредственного преобразования тепловой энергии в электрическую. Принцип
работы МГД-генератора тот же, что и у электромагнитного насоса
прямого действия (см. рис. 11.11).
Если по каналу (рис. 11.11) при помощи некоторой не электромаг-
электромагнитной силы двигать проводящую жидкость, то на боковых поверхно-
поверхностях канала возникнет разность потенциалов. Если теперь эти боко-
боковые поверхности соединить с внешним сопротивлением, то через него
потечет ток. В этом случае устройство будет работать как генератор
электрической энергии. Преимущество МГД-генераторов перед суще-
существующими генераторами очевидно. В них нет движущихся частей, нет
паровых турбин, и, как показывают расчеты, КПД магнитогидродина-
мического генератора большой мощности может достигать 60 % против
40% на существующих электростанциях. Поэтому проблема создания
МГД-генераторов большой мощности в настоящее время интенсивно
разрабатывается как у нас, так и за рубежом.
Оценим мощность магнитогидродинамического генератора.
В устройстве (рис. 11.11) без внешней цепи ток не течет. При этом
напряженность электрического поля будет равна
=0, E = ^vH0. A1.92)
Если боковые поверхности трубы соединить с внешней нагрузкой
сопротивлением Явнеш , то в электрической цепи потечет ток, равный
/ - U
Мощность, потребляемая во внешней цепи, будет равна
w = /2явнеш = , и Двнеш .о •
11.10] Магнитогидродинамические машины 329
Внутреннее сопротивление генератора определяется проводимостью
столба газа (проводящей жидкости) площадью la и длиной Ь. Поэтому
сопротивление RBH равно
- Ь
аг1а
Если RBH = ЯВнеш (при заданном U максимальная мощность W), то
с учетом A1.92) имеем
W = °rUHoV v = labm AL93)
Ac
Электрическая энергия может быть получена только за счет тор-
торможения и сжатия вещества. Так, если внутри трубы постоянного
сечения двигалась бы проводящая несжимаемая жидкость (например,
ртуть), то в силу несжимаемости жидкости и непрерывности расхода
(постоянства скорости движения жидкости) такое устройство не могло
бы служить генератором электрической энергии. Поэтому рабочим
веществом в МГД может служить только газ.
Как следует из формулы A1.93), рабочий газ должен обладать
определенной проводимостью. Следовательно, это должен быть иони-
ионизированный газ.
Достаточную ионизацию газа можно получить, или нагревая его до
высоких температур C -S- 6) • 103 К, или добавляя к нему легко иони-
ионизирующиеся присадки. В качестве присадок могут служить вещества
с малым потенциалом ионизации, например пары цезия. Для сравне-
сравнения: потенциал ионизации азота равен 14,5эВ, кислорода— 13,5эВ,
цезия — 3,88 эВ. Из всех элементов цезий имеет наименьший потенци-
потенциал ионизации. Достаточная ионизация воздуха, а следовательно, его
достаточная проводимость может быть достигнута только при очень
высоких температурах порядка E -S- 6) • 103 К. Но в настоящее время не
существует конструкционных материалов, которые бы длительное вре-
время выдерживали столь высокую температуру. Именно с целью сниже-
снижения температуры газа для обеспечения его достаточной проводимости
и необходимо делать легко ионизирующиеся присадки. Но поскольку
цезий дорогой материал, то очевидно, что газ с присадкой должен
циркулировать в некотором замкнутом контуре, обеспечивающем со-
сохранность присадки.
Сделаем некоторый ориентировочный расчет. Пусть МГД-генератор
имеет следующие характеристики:
#о=1О4Э, v=105cm/c, crr=1012c-1,
а = 10 см, Ь= 100 см, /= 100 см.
Тогда напряжение на боковых пластинах МГД будет равно
= ^ [ед. СГСЭ] = 1000В.
о
330 Магнитная гидродинамика [Гл.11
Мощность генератора
W = 2,5- 1013 эрг/с = 2,5 МВт.
Из формулы A1.93) следует, что наряду с увеличением проводимости
рабочего газа необходимо увеличивать его скорость и напряженность
магнитного поля. В настоящее время конструкторы стремятся исполь-
использовать явление сверхпроводимости для создания сильных постоянных
магнитных полей.
Формула A1.93) может использоваться только для грубых оценок,
так как при ее выводе мы не учитывали много факторов, сильно
влияющих на эффективность работы МГД (магнитное поле тока в элек-
электродном промежутке, торможение газа и т.д.).
Реальные магнитогидродинамические генераторы состоят из камеры
сгорания или нагрева рабочего газа с присоединенным к ней соплом
Лаваля, в котором газ ускоряется. Сопло Лаваля помещено в попе-
поперечное постоянное магнитное поле. Внутри сопла также смонтированы
токоприемные пластины, к которым и подключается внешняя электри-
электрическая нагрузка.
11.10.3. Плазменные двигатели. Тяга, создаваемая реактивным
двигателем, равна Mv , где М — масса вещества, выбрасываемая дви-
двигателем в lc, v — скорость, с которой эта масса выбрасывается. Сле-
Следовательно, для создания максимальной тяги при заданном количестве
вещества должна быть максимальной скорость выброса этого вещества
двигателем. Если воспользоваться газодинамическим способом ускоре-
ускорения газового потока, то скорость вытекающего газа из сопла двигателя
не может быть больше максимальной скорости
г W7 Г , A1.94)
V 7 - 1 V М 7 - !
где со — скорость звука, 7 ~~ показатель адиабаты, R — молярная газо-
газовая постоянная, То — температура газа, \± — молярная масса газа.
Из формулы A1.94) видно, что для увеличения скорости истечения
газа необходимо увеличивать его температуру То и использовать газ
с малой молярной массой. Формула приведена лишь затем, чтобы пока-
показать, что существует предел увеличения скорости газодинамическими
средствами. В действительности известно, что скорость г?тах может
быть достигнута при истечении газа в вакуум, где абсолютная темпера-
температура равна нулю. При этом поток должен повернуть на определенный
угол так, что направленная вдоль двигателя реактивная тяга некоторой
части струи будет равна нулю или даже отрицательной.
Однако существует возможность увеличить скорость отбрасыва-
отбрасываемого вещества электромагнитными способами. Это можно сделать
в устройстве типа электромагнитного насоса прямого действия, если
газ является достаточно хорошо проводящей плазмой. Если же в двига-
двигателе каким-либо способом организовать источник ионов, то их можно
разогнать в электростатическом поле практически до субсветовых ско-
11.11] Турбулентное динамо 331
ростей. Конечно, как в том, так и в другом случае на борту космическо-
космического корабля должен быть достаточно мощный источник электрической
энергии.
11.11. Турбулентное динамо
Из принципа «вмороженности» магнитных силовых линий в веще-
вещество следует, что магнитное поле будет препятствовать возникновению
турбулентного режима течения проводящей жидкости. Так, если поле
направлено вдоль трубы, по которой движется проводящая жидкость,
то, очевидно, что возникновение поперечных составляющих скорости
вследствие натяжения при этом магнитных силовых линий будет за-
затруднено, а следовательно, переход от ламинарного режима течения
к турбулентному будет происходить при больших числах Рейнольдса,
нежели в непроводящей жидкости или в проводящей жидкости, но без
магнитного поля. Точно так же магнитное поле, направленное вдоль
тангенциального разрыва в проводящей жидкости, увеличивает его
устойчивость.
Турбулентное движение проводящей жидкости обладает интерес-
интересным свойством самопроизвольного возникновения в нем сравнительно
больших магнитных полей. Это явление называют турбулентным ди-
динамо.
В проводящей жидкости всегда существуют эффекты, приводящие
к возникновению слабых магнитных полей, например механомагнит-
ный эффект или флуктуации электрического заряда.
Рассмотрим, как будет вести себя в дальнейшем раз возникшее сла-
слабое магнитное поле при турбулентном движении проводящей жидко-
жидкости. Для этого, очевидно, мы должны рассмотреть два конкурирующих
эффекта.
1. При движении проводящей жидкости в возникшем слабом маг-
магнитном поле в ней, с одной стороны, будут наводиться индукционные
токи, а следовательно, будет происходить диссипация электрической
энергии из-за джоулевых потерь, что в конечном счете должно умень-
уменьшать спонтанно возникшее магнитное поле.
2. С другой стороны, поле будет стремиться увеличиться в силу
принципа «вмороженности» магнитных силовых линий, поскольку на-
напряженность поля пропорциональна расстоянию между двумя близки-
близкими жидкими частицами, а это расстояние при турбулентном движении
в среднем всегда увеличивается с течением времени.
Очевидно, что при некоторых условиях обе тенденции могут ока-
оказаться равносильными и в турбулентной жидкости возникает магнит-
магнитное поле определенной напряженности. Для оценки величины этой
напряженности рассмотрим уравнения движения.
До тех пор пока напряженность магнитного поля мала в урав-
уравнении движения Навье-Стокса для несжимаемой жидкости можно
пренебречь магнитной массовой силой как квадратичной по малой
332 Магнитная гидродинамика [Гл.11
величине Н. Тогда уравнение Навье-Стокса после применения к нему
операции rot можно записать в следующем виде:
—— = rot[v, ш] + v Аш, u? = -rotv. A1.95)
0 l A
В магнитной гидродинамике для напряженности магнитного поля
имеем следующее уравнение A1.27):
f t[H] + ^
f =rot[v,H] + ^AH. A1.96)
Сравнивая два последних уравнения, обнаруживаем, что они совер-
совершенно идентичны. Следовательно, решения этих уравнений должны
быть пропорциональными
и> = const • Н .
В этом случае, очевидно, при постоянной завихренности может суще-
существовать и стационарное магнитное поле. При этом ни завихренность,
ни магнитное поле не увеличиваются и не убывают.
Сама величина этого стационарного (в турбулентном смысле) поля
может быть определена лишь из решения уравнений A1.95) и A1.96).
Однако, очевидно, можно сделать и следующее заключение. Если
аг > с2/Dтг1у), то диссипация магнитного поля через индукционные
токи (Qd = j /ar) будет меньше и магнитное поле может возрастать
дальше благодаря растяжению магнитных силовых линий. Если же
аг < с2/(Атпу), то напряженность магнитного поля должна убывать.
Таким образом, для того чтобы напряженность спонтанного магнит-
магнитного поля при турбулентном движении проводящей жидкости возрас-
возрастала, необходимо, чтобы выполнялось условие
^>1. A1.97)
с
Возрастание напряженности магнитного поля, конечно, не мо-
может быть беспредельным, так как сильное магнитное поле в свою
очередь будет подавлять механическое турбулентное движение, и
наше рассмотрение будет несправедливым, поскольку в уравнении
Навье-Стокса уже нельзя будет пренебрегать магнитной массовой си-
силой.
Из общих физических соображений ясно, что максимальная на-
напряженность магнитного поля не должна превышать величину, при
которой энергия единицы объема магнитного поля примерно равна
кинетической энергии единицы объема движущейся жидкости
Ятах ^ 1 2
~bT~2pV '
Рассмотренный механизм позволяет объяснить возникновение зна-
значительных магнитных полей во Вселенной, и в частности, на Солнце.
11.12] Одномерное движение проводящей жидкости 333
К сожалению, проверить сделанные выше выводы в земных усло-
условиях довольно затруднительно, так как, например, для ртути (<тг =
= 1016 1/с, v = 0,001 см2/с) имеем
с2
10
7
Однако во Вселенной в достаточно разреженных (малая плотность)
сильно ионизированных (большая проводимость) газовых скоплениях
условие A1.97) может выполняться, и в этом случае в газовых скоп-
скоплениях и на поверхности Солнца могут существовать значительные
магнитные поля напряженностью в десятки и сотни эрстед.
11.12. Одномерное движение проводящей жидкости
в поперечном магнитном поле
Рассмотрим одномерное движение проводящей сжимаемой жидко-
жидкости в поперечном магнитном поле. Направим ось х вдоль линии тока, а
ось z — перпендикулярно к ней. Пусть напряженность магнитного поля
имеет единственную компоненту, перпендикулярную линии тока и,
следовательно, оси х. Таким образом, топология движения определена
следующим образом
vx = vx(x), vy=0, vz=0, Hx=0, Hy=0, Hz = Hz(x).
Будем полагать, что жидкость имеет бесконечную проводимость
и является идеальной в гидродинамическом смысле (отсутствует вяз-
вязкость). В такой жидкости не может происходить никаких диссипа-
тивных процессов ни вследствие вязкости жидкости, ни вследствие
джоулевых потерь.
Уравнения движения такой жидкости имеют вид
A1.98)
Как было показано (см. A1.54)), из двух последних уравнений
системы A1.98) следует:
^ h = /hv\ (П99)
dt р \Р J
Проецируя на ось х первое уравнение из A1.98) и уравнение A1.99),
получим
dvx dvx _ 1 dp 1 „ dHz
~dt х~д^~~~р~дх~~^Гр zlT
A1.100)
dt ~~
334 Магнитная гидродинамика [Гл.11
Из второго уравнения системы A1.100) следует
ТТ
—- = const = b , Hz = bp .
P
Тогда первое уравнение системы A1.100) можно записать в виде
dt 2 дх р дх 8тгр дх р дх у 8тг
Из уравнения A1.101) нетрудно видеть, что оно не содержит магнит-
магнитного поля и имеет обычный гидродинамический вид, если в качестве
давления взять следующее соотношение:
Очевидно, и все решения уравнения A1.101) можно получить из
решений обычного гидродинамического уравнения, если в них вместо
давления р подставить Р. Этот результат почти очевиден, поскольку Р
представляет собой полное давление, равное сумме гидростатического
давления р и магнитного давления Я|/8тг.
В частности, скорость звука или скорость распространения малых
возмущений вдоль оси х, представляющих собой продольные волны
сжатия, может быть определена по известной формуле:
= 4/(^1 =4/(^1 + ^(^4 =a/C2+2^2
8тг
A1.103)
Из A1.103) следует, что скорость распространения малых возмущений
в идеально проводящей жидкости (аг —> оо) перпендикулярно магнит-
магнитному полю возрастает на величину а, равную
а = HzXP- . A1.104)
у 4тгр v '
Из сравнения с A1.66) видно, что а — скорость волн Альвена. По-
Полученный результат физически понятен. Скорость распространения
упругих продольных волн в проводящей жидкости в поперечном маг-
магнитном поле возрастает, так как в силу натяжения магнитных силовых
линий упругость проводящей среды как бы возрастает, что и ведет к
увеличению скорости звука.
Хотя ртуть имеет конечную проводимость, по формуле A1.104)
можно оценить порядок скорости волн Альвена. При Н = 1000 Э,
р = 13 г/см3 получаем а = 75 см/с. Для скорости звука в ртути добавка
мала, однако для разреженного вещества (ионосфера Земли, солнечная
корона) скорость волн Альвена может оказаться сравнимой со скоро-
скоростью звука. Очевидно, на скорость распространения продольных коле-
колебаний, направленных вдоль магнитного поля, последнее не оказывает
никакого влияния.
11.12] Одномерное движение проводящей жидкости 335
Замечательно то, что в проводящей жидкости в магнитном поле
могут распространяться и поперечные волны. Если первоначальное
возмущение перпендикулярно магнитным силовым линиям, то это воз-
возмущение распространяется вдоль силовой линии как по резиновому
натянутому шнуру, что приведет (в силу «вмороженности» магнитных
силовых линий) к распространению поперечных колебаний и в мало-
маловязкой проводящей среде.
Для вычисления скорости распространения поперечных колебаний
воспользуемся аналогией.
Уравнение поперечных колебаний в направлении оси х струны,
расположенной вдоль оси z, как известно, имеет вид
д их , д их /1 1 1 Аг\
т 7T = k f. A1.105)
dt2 dz2
Здесь их — смещение точек струны в направлении оси х, т — масса
струны на единицу длины, к — натяжение струны. По общему свойству
волнового уравнения скорость поперечной волны равна
ct = \ — • A1.106)
у т
Рассмотрим вещество, находящееся около магнитной силовой ли-
линии в прямоугольном параллелепипеде с поперечным сечением (пер-
(перпендикулярно силовой линии), равным 1 см2. Тогда в формуле A1.106)
т = р, а к — натяжение на единицу площади, т.е. к = Я|/4тг. Поэтому
скорость распространения поперечных колебаний проводящей жидко-
жидкости в магнитном поле равна
f^ A1.107)
В отличие от скорости распространения продольных колебаний,
которая складывается из обычной скорости звука и скорости волн Аль-
вена, скорость распространения поперечных колебаний, определяемая
формулой A1.107), в невязкой жидкости с бесконечной проводимостью
является единственно возможной.
11.12.1. Уравнение Бернулли в магнитной гидродинамике.
Уравнение A1.101) представляет проекцию уравнения движения
в магнитной гидродинамике на ось х или на линию тока, совпадающую
с осью х. Для стационарного движения из A1.101) имеем
( ,
2 дх р дх 8тгр дх р дх
Поскольку ось х совпадает с линией тока, то скорость жидкости
имеет единственную компоненту vx, т.е. vx = v2. По определению на-
напряженность магнитного поля также имеет единственную компоненту,
перпендикулярную линии тока. Следовательно, Н\ = Я2.
336 Магнитная гидродинамика [Гл.11
В обычной термодинамике изменение энтальпии единицы массы
равно
dhT = TdS+-dp.
Р
В идеальной жидкости, имеющей бесконечную проводимость, энтропия
каждого индивидуального объема постоянна. Поэтому имеем
д , 1 дР
—- пТ = - тт- •
ох р ох
Тогда уравнение A1.108) примет вид
V
<1U09>
В уравнении A1.109) постоянная не зависит от координаты х, т.е она
постоянна для рассматриваемой линии тока. Уравнение A1.109) и есть
уравнение Бернулли в магнитной гидродинамике.
Последнее уравнение можно получить другим путем, если в каче-
качестве давления в выражении для энтальпии взять полное давление Р
Р _ р Н2
р р 8тгр
Таким образом, энтальпия в магнитной гидродинамике вследствие
изменения внутренней энергии на величину Н2 /8тгр имеет вид
Отсюда из обычного гидродинамического уравнения Бернулли
2
V
— + h = const
вновь получаем уравнение A1.109).
Уравнение Бернулли в виде A1.109) представляет уравнение сохра-
сохранения энергии индивидуальной частицы жидкости единичной массы
вдоль линии тока.
11.13. Ударные волны в магнитной гидродинамике
Для простоты рассмотрим прямую ударную волну в проводящей
сжимаемой жидкости при отсутствии вязкости и при бесконечной про-
проводимости. Рассмотрим лишь случай, когда напряженность магнитного
поля направлена параллельно линии разрыва или перпендикулярно
линии тока вещества.
Индексами 1 и 2 будем отмечать гидродинамические и термоди-
термодинамические величины до и после ударной волны соответственно. На
прямой ударной волне должны быть непрерывны следующие величины:
плотность потока вещества
A1.110)
11.13] Ударные волны в магнитной гидродинамике 337
плотность потока импульса
2^ l ^-; A1.111)
О7Г
плотность потока энергии
+ /г1т+ = + /г2т+ (ПЛ12)
Кроме того, в силу «вмороженности» магнитных силовых линий
имеет место соотношение
— = const, — = —. A1.113)
Р Pi P2
Таким образом, из полученной системы уравнений следует, что
полученные в обычной газовой динамике формулы будут справедливы
и в магнитной газодинамике, если в них сделать замену
В частности, уравнение ударной адиабаты будет иметь вид
^ {H\VX - H22V2) + \{Vx + V2)(p2 - pi) +
^ 2-H2l)=0. A1.114)
В уравнении A1.114) при помощи соотношения A1.113) везде мож-
можно заменить Я2 на Н\р2/'р\.
Таким образом, уравнение будет зависеть лишь от Н\, которое
предполагается заданным. После некоторых преобразований можно
получить уравнение ударной адиабаты в магнитной гидродинамике
в следующем виде:
Не решая уравнений, можно сделать некоторые качественные вы-
выводы. Так как плотность газа за ударной волной растет, то из A1.113)
следует, что за ударной волной возрастает и напряженность магнитного
поля. Поскольку магнитное давление препятствует сжатию вещества,
то, очевидно, скачок плотности на прямой ударной волне в магнитном
поле будет меньше, чем без него.
Следовательно, меньше будет и скачок температуры и энтропии, так
как кинетическая энергия газа переходит не только в тепловую, но и
в энергию поля.
В косой ударной волне, если магнитные силовые линии пересекают
поверхность разрыва, то, как и в обычной газодинамической косой
ударной волне, они преломляются на ней, приближаясь к поверхности
разрыва. При этом на поверхности косой ударной волны испытывают
скачок не только нормальные составляющие скорости движения газа,
338 Магнитная гидродинамика [Гл.11
но и тангенциальные, что невозможно без поля. В этом случае поле
влияет меньше на сжатие и нагрев газа, чем в прямой ударной волне,
параллельной полю.
Контрольные вопросы
1. В каком направлении электропроводимость среды больше — вдоль сило-
силовых линий магнитного поля или поперек них? При каком условии проводимость
среды можно считать изотропной?
2. При каком условии можно пренебречь током смещения по сравнению
с током проводимости?
3. Какой физический смысл имеют компоненты максвелловских тензоров
напряжений электрического и магнитного полей? Как определяется магнитное
давление?
4. Перечислите источники изменения внутренней энергии единицы объема
проводящей жидкости в присутствии магнитного поля.
5. Что представляют собой граничные условия для векторов напряженно-
стей электрического и магнитного полей?
6. Что характеризуют число Альвена, число Стюарта, магнитное число
Рейнольдса, число Гартмана? Как вводится магнитная вязкость?
7. В чем состоит явление «вмороженности» магнитных силовых линий
в проводящей жидкости? Сформулируйте теорему Валена. На основе явления
«вмороженности» объясните формирование магнитного поля звезд, сжатие
плазмы и принцип магнитной ловушки.
8. В чем состоит скин-эффект при диффузии магнитного поля в проводя-
проводящей среде?
9. Поясните механизм возникновения продольных (ленгмюровских) и по-
поперечных (альвеновских и магнитозвуковых) волн в проводящей среде. Как
скорость альвеновских волн зависит от частоты изменения магнитного поля,
амплитуды напряженности и плотности жидкости?
10. Как профиль скорости движения проводящей жидкости в канале в по-
поперечном магнитном поле изменяется при увеличении числа На?
11. В каком случае расход проводящей жидкости в канале будет больше —
при наличии поперечного магнитного поля или без него?
12. Как изменится сила лобового сопротивления при медленном обтекании
шара проводящей жидкостью в магнитном поле? Обоснуйте ответ.
13. В каком случае не возникает подъемная сила при медленном обтекании
шара проводящей жидкостью в магнитном поле?
14. Объясните причину того, что магнитное поле подавляет возникновение
турбулентности в проводящей жидкости.
15. Что такое турбулентное динамо? При каком условии напряженность
спонтанного магнитного поля, возникающего при турбулентном движении про-
проводящей жидкости, будет возрастать?
16. В чем принципиальное отличие скоростей распространения продольных
и поперечных колебаний в проводящей жидкости при наличии магнитного
поля?
17. Как изменяется напряженность магнитного поля в ударной волне? В ка-
каком случае скачок плотности, температуры и энтропии ионизированного газа
в прямой ударной волне будет больше — при наличии магнитного поля или без
него?
11.14] Примеры решения задач 339
11.14. Примеры решения задач
Задача 1
Вычислите скорость установившегося течения несжимаемой
проводящей жидкости между бесконечными параллельными пла-
пластинами в перпендикулярном магнитном поле напряженностью Hq
(см. рис. 11.6). Течение вызвано движением пластин, расположенных
в плоскостях z = ± а, в разные стороны со скоростями vo
(магнитогидродинамическое течение Куэтта).
Решение. Принципиальное отличие этого течения жидкости от
задачи Гартмана состоит лишь в том, что течение жидкости обусловле-
обусловлено движением стенок канала, а не продольным градиентом давления.
Поэтому воспользуемся общим решением уравнения движения, полу-
полученным в задаче Гартмана A1.73):
vx = Ах + Л2ехр ^ + А3ехр(--^) . A1.116)
Постоянные интегрирования А\, А2, А3 должны быть определены
из граничных условий. На стенках канала следует учесть «прилипа-
«прилипание» жидкости к их поверхностям. Кроме того, из симметрии задачи
следует, что на оси канала скорость течения жидкости равна нулю.
Тогда граничные условия имеют вид
z = ±a, vx = ±v0; z = 0, vx=0. A1.117)
Отсюда получаем
vo = A\ + A2 exp ^ + A3 exp y~^J
0 = Ai + A2 + A3.
Из уравнений A1.118) имеем
v°
"•""' ~*- ^-2sh(Ha)'
Тогда скорость движения жидкости между пластинами равна
_ sh(Ha г/а) ,п lig.
При малых числах На из A1.119) по-
получаем известное в обычной гидродина-
гидродинамике выражение для скорости течения
Куэтта: ^
а
тт 11 ю л. Рис- П-13. Профили скорости
На рис. 11.13 показаны профили r ^ r
скорости при малых и больших числах На. Чем больше На, тем меньше
изменяется скорость в сечении канала. Большие градиенты скорости
+а
-а
Hi»
о{
3
На»0
V
X
340 Магнитная гидродинамика [Гл.11
имеют место лишь в пристеночном слое (гартмановский слой), толщина
которого тем меньше, чем больше На.
Задача 2
Определите скорость течения проводящей вязкой жидкости вдоль
бесконечной пластины в поперечном магнитном поле напряженно-
напряженностью Hq. Скорость невозмущенного потока вдали от пластины рав-
равна Vvq. Вычислите силу трения, действующую на единицу площади
пластины, и напряженность магнитного поля.
Решение. Систему координат выберем так, чтобы ось х лежала
в плоскости пластины и была направлена вдоль скорости v^, а ось z
направлена перпендикулярно пластине вдоль вектора напряженности
магнитного поля Но (рис. 11.14 ). Вновь воспользуемся общим реше-
решением уравнения движения, полученным для течения Гартмана A1.73)
или A1.116).
Граничные условия состоят в том, что скорость течения жидкости
вдали от стенки равна скорости невозмущенного потока v^, а на
поверхности пластины она равна нулю:
z = oo, vx = Voo; z = 0, vx=0. A1.120)
Отсюда для постоянных интегрирования получим
A{=voo, A2 = 0, A3 = -voo.
Следовательно, скорость течения жидкости вдоль пластины равна
A1.121)
Геометрия этой задачи такова, что в ней нет характерного размера.
Выберем в качестве характерной длины величину ^/(рг^), где rj —
динамическая вязкость жидкости, р - плотность. В этом случае введем
число На и безразмерную координату следующим образом:
^ (
С pVoo Г)
В этом случае выражение A1.121) запишется в виде
vx = voo [I -exp(-Haz*)]. A1.123)
При На = 0 задача о стационарном течении жидкости вдоль бес-
бесконечной пластины не имеет решения. Физически это означает, что
бесконечная пластина в начале своего движения увлекает за собой
все большую массу вязкой жидкости, и при достижении стационарного
состояния пластина должна была бы вовлечь в движение бесконечную
массу жидкости в полупространстве z > 0.
При На ^> 1 профиль скорости всюду однороден, за исключением
тонкого гартмановского слоя у поверхности пластины. Чем больше
На, тем больше градиент скорости вблизи стенки (рис. 11.14). Этот
результат аналогичен тому, который получен в задаче о течении прово-
11.14]
Примеры решения задач
341
дящей жидкости в плоском канале. Различие состоит лишь в том, что
в рассматриваемой задаче отсутствует градиент давления.
Найдем силу трения, действующую в направлении оси х на единицу
площади поверхности пластины. Очевидно, она определяется тензором
вязких напряжений:
Fx =
Рис. 11.14. Течение вдоль пла-
пластины
A1.124)
т. е. сила сопротивления пропорциональ-
пропорциональна числу Гартмана.
Для того чтобы вычислить напряжен-
напряженность магнитного поля, вновь обратим-
обратимся к решению задачи Гартмана. Установлено A1.70), что поперечная
составляющая напряженности неизменна во всей области течения и
равна
Hz = const = Но .
Для продольной составляющей напряженности получено следующее
уравнение A1.77):
дНх
где А — некоторая постоянная, определяемая из граничных условий.
Интегрируя это уравнение с учетом выражения A1.121) для скорости,
получим
Их = g— ^оо z + А ехр l——\\+Az + B, A1.125)
где В — постоянная интегрирования.
Поскольку на пластине нет поверхностных токов проводимости,
то при z = 0 должна быть непрерывна тангенциальная составляющая
напряженности магнитного поля. Кроме того, на большом удалении
от пластины величина напряженности магнитного поля должна быть
ограничена.
Таким образом, граничные условия имеют вид
z = 0, #ж=0; z-^oo, Нх < оо.
Отсюда определим постоянные интегрирования
A1.126)
Окончательно получим
- ехр
-—JJ
A1.127)
Следовательно, движущаяся проводящая жидкость растягивает маг-
магнитные силовые линии в направлении своего движения. Из выражения
342 Магнитная гидродинамика [Гл.11
A1.127) получим, что вдали от поверхности (в невозмущенной области
течения) это растяжение равно
Задача 3
Бесконечная пластина совершает гармонические колебания в своей
плоскости вдоль оси х. Скорость колебаний изменяется по закону
и = U exp(i(jut), где U — амплитуда, (^ — циклическая частота. Полу-
Полупространство над пластиной (z > 0) заполнено несжимаемой прово-
проводящей жидкостью. Жидкость находится в постоянном магнитном по-
поле, напряженность которого Но направлена перпендикулярно пластине
вдоль оси z.
Определите скорость жидкости, считая ее движение ламинарным,
напряженность магнитного поля и скорость распространения коле-
колебательного движения в жидкости. Вычисления проведите для двух
частных случаев:
1) идеальная (невязкая) жидкость,
2) идеально проводящая жидкость (аг —> оо).
Коэффициент поглощения (мнимая часть комплексного волнового
числа) много меньше волнового числа (действительная часть комплекс-
комплексного волнового числа)
Решение. Вначале рассмотрим общий случай вязкой проводящей
жидкости. Градиента давления в жидкости нет. Поэтому система урав-
уравнений движения жидкости и напряженности магнитного поля имеет
вид
^ + (vV)v = isAv - ^i- [H , rot H],
^ <1U28>
divv = 0, divH = 0.
На любом расстоянии z от пластины частицы жидкости совершают
колебания параллельно оси х. Топология задачи такова, что
vx = vx(t, z), vz = vy=0, HX = Hx(t, z), Hy = 0, HZ = Hz(t, z) ,
В этом случае уравнения A1.128) в проекциях на оси координат
запишутся в следующем виде:
dvx d2vx , 1 ТТ дНх
dt dz2 4тгр z Oz '
^ = Hz^ + Dm *Щ?- , A1.129)
dHz _ d2Hz dHz л
— J-Jn
dt ~Um a,2 ' dz
11.14] Примеры решения задач 343
Здесь Dm — магнитный коэффициент диффузии, определенный выра-
выражением A1.57)
4тг<тг
Из последних двух уравнений системы A1.129) следует, что попе-
поперечная составляющая напряженности не зависит ни от координат, ни
от времени:
Hz = const = Яо. A1.130)
Очевидно, распространение колебаний в жидкости представляет
собой поперечную волну. Поэтому решение первых двух уравнений
будем искать в виде плоских волн, бегущих вдоль оси z:
vx = Aexp[i(ojt-\-kz)], Нх = В exp[i(ojt-\-kz)], A1.131)
где к — волновое число.
Подставляя выражения A1.131) в эти уравнения, получим два
алгебраических уравнения для неизвестных амплитуд:
A1.132)
Hoik A - {ш + Dmk2) В = 0 .
Приравняв к нулю определитель, составленный из коэффициентов
при амплитудах, получим дисперсионное уравнение для волнового чи-
числа и частоты:
vDmkA + \iw{v + Dm) + а2] к2 -и2 = 0, A1.133)
где использовано обозначение
а = —±- .
4тгр
Рассмотрим частные случаи, указанные в условии задачи.
1. Идеальная жидкость {у = 0).
Дисперсионное уравнение A1.133) упрощается и принимает сле-
следующий вид:
( a2} к2 -и2 =0, A1.134)
Решение уравнения A1.134) ищем в виде
k = a + if3, /3/а<1. A1.135)
Здесь а — действительное волновое число, C — коэффициент поглоще-
поглощения. Подставляя A1.135) в A1.134), пренебрегая членами порядка
(/3/аJ и разделяя вещественные и мнимые части, получим
о о о A1.1.30)
а2а2 2Df3 2
а2а2 - 2ujDmaf3 = ио2 .
344 Магнитная гидродинамика [Гл.11
Решение уравнений A1.136) имеет вид
«1,2 = ± , . °" , А.2 = Т. /""" ¦ (П-137)
¦2О.
Волновые числа а\ и а^ описывают волны, распространяющиеся
против и вдоль направления оси z соответственно. В данной задаче а\
не имеет физического смысла и следует выбрать только волновое число
с^2, т. е. а = — |oi21 -
Величина C\ описывает колебания жидкости, амплитуда которых
растет при удалении от пластины, что противоречит закону сохранения
энергии. Величина /?2 соответствует затухающим колебаниям. Поэтому
коэффициент затухания равен /3 = /32.
Таким образом, имеем
vx = Ae~^zexp[i(Ljt-az)]9 Hx = Be~^z exp[i(ut - az)]. A1.138)
Амплитуду колебаний скорости определим из граничного условия
«прилипания» жидкости к поверхности пластины
vx(z = 0) = u. A1.139)
Отсюда получим
A = U. A1.140)
Из уравнений A1.132) при v = 0 определим амплитуду напряжен-
напряженности магнитного поля
Окончательно имеем
vx = Ue~Pz exp[i(oot — az)} ,
TT _$z rv . Л] A1.142)
Ue pz exp[i(out - az)\ .
Знак минус в выражении для напряженности означает, что фаза
колебаний напряженности совпадает с фазой колебаний координаты
и отстает на тг/2 от фазы колебаний скорости. Это соответствует
принципу «вмороженности» магнитных силовых линий в жидкость.
Фазовая скорость волны определяется отношением циклической
частоты к волновому числу:
^ ^ A1.143)
Заметим, что фазовая скорость волны зависит от частоты колеба-
колебаний, т.е. имеет место дисперсия скорости.
Величину поверхностного скин-эффекта можно определить как рас-
расстояние z = 6, на котором амплитуда колебаний уменьшается в е раз
^- 2„ „^ т. A1.144)
11.14] Примеры решения задач 345
При низких частотах и большой проводимости жидкости выполня-
выполняется неравенство
В этом случае получаем
2 2
уф = а=-^=, /3= ш С р2 , 5 = Р~1, В = -д/4^р- A1-145)
у4тгр 2агНоа
Как и следовало ожидать, при низких частотах скорость распро-
распространения поперечной волны равна скорости волн Альвена, и ампли-
амплитуда напряженности зависит только от плотности жидкости.
2. Вязкая идеально проводящая жидкость (Dm = 0).
Поскольку коэффициенты вязкости и магнитной диффузии входят
в дисперсионное уравнение симметрично, формально решение A1.142)
не изменится и в этом случае. Изменятся только выражения для
волнового числа и коэффициента поглощения, которые могут быть
получены из A1.137) заменой коэффициента магнитной диффузии на
коэффициент кинематической вязкости
2
auo n uo v /111 лп\
а= / ^=, Р = , (П.146)
V а4 + uo2v2 2а\/а4 + uo2v2
Фазовая скорость волны равна
уф = - = -Va4 + u;2iy2 . (П.147)
а а
При низких частотах, когда выполняется неравенство оои/о? ^С I,
получим
а=-, Р = —Т, V& = а = ^— . (П.148)
а 2а у/4тгр
Как и в предыдущем случае идеальной жидкости, при низких частотах
скорость распространения волны равна скорости волн Альвена. Отме-
Отметим также, что для коэффициента поглощения получено выражение,
которое с точностью до множителя 4/3 формально совпадает с извест-
известной формулой Стокса-Кирхгофа 0.
О В формуле Стокса-Кирхгофа а — обычная скорость звука в газах и жид-
жидкостях.
ПРИЛОЖЕНИЯ
П.1. Дифференциальные операторы
в криволинейных координатах
1. Цилиндрические координаты (г, сру z). Пусть и и v — про-
произвольные скалярная и векторная функции координат; er, e^, ez —
единичные базисные векторы. Тогда
_ л ди 1 ди ди
\/и = grad и = — ег Н— ^— е^ + — ez;
л. 1 d(rvr) , 1 dvm , dvz
div v = H — H ;
г dip dz (пл)
rot v = I - — . ~r , .
r av? a^: / V a2;
( 1 fl(rty) 1
r dr V dr) ' r2 ^(^2 dz1'
2. Сферические координаты (г, ср, в). er, e^, e$ — единичные ба-
базисные векторы.
, ди 1 ^г^ 1 ди
grad г* = —- er H ^— —- е^ + - -— е^;
dr rsm 9 д(р ^ г д9
,. 1 <9(r2vr) I ^vv I afv^sin в)
div v = ^7 — Н Н ^5
r2 ^r r sin 9 dip r sin 0 дв
(П.2)
1 /0(tVsin0) ^Л ¦ ! (d{rve) dvr ,
rot v = . ,, ( yo/> ^ - -^— I er + - [ \ - -^- ) e^ +
Ou
rsin в dip r or
д _ J_ d_ ( 2 <b\ , 1 а2г^ J_ dju ctg 6> ^u
П.З] Компоненты тензора напряжений 347
П.2. Компоненты тензора деформаций
в криволинейных координатах
1. Цилиндрические координаты (т% (р, z).
_ dur _ 1 du^ ur _ duz
dr ^ r dip r zz dz
2 _ J_ duz duy 2? — ®Ur _i_ ®Uz m 34
^z r dip dz ' rz dz dr
г» $г^ u<p 1 ^itr
V Qr r r Q^p
2. Сферические координаты (г, 0, ip).
dur 1 c^y, ur ue , q 1 $i?0 i^r
^r ' ^ rsin ^ ^y? r r r $# r
2?й - i (Ё*р _ t Л , 1 9«в m 4)
^ r \ dO ^ J rsin б' dip
q ^ifc^ г^^ 1 dur (-v 1 ^itr ^ity, u<p
or r r ou rsin и oip or r
П.З. Компоненты тензора напряжений
в криволинейных координатах
1. Цилиндрические координаты (г, сру z).
Prr = -р~\
dr '
/ 1 Я«, Я«, \
(П.5)
Y2 I и иг и иz \ г) / w U(P и<Р 1 UVr
dr r r dip
2. Сферические координаты (г, ср, в).
тэ I о ®vr тэ . о / 1 dvv vr ve ,
Prr = -p + Zrj ——, P^p = -p + Zrj —^— —^ H 1 ctg
п o /1 dve , vr\ п /^v^ ^6» . 1 dvr\
„ ч (П.6)
- 5
r \ dO sin t/ a<^ у
348 Приложения
П.4. Уравнения движения
в криволинейных координатах
1. Цилиндрические координаты (т% (р, z).
Уравнение непрерывности для несжимаемой жидкости:
1 d(rvr) \ dv^ dv^ n
r dr ^ r dip dz
Компоненты уравнения Навье-Стокса
dvr , / _ч vv \ dp .
4^V (П.8)
dip J
dt y ' ^ r rp dip \ r• r'
dvz , ^ч 1 dp Л
где операторы (vV) и А определяются следующими выражениями:
2. Сферические координаты (г, у?, 0).
Уравнение непрерывности для несжимаемой жидкости:
dt
dv6
dt
dt
1 d(rvr)
r dr r i
Компоненты уравнения
p dr [
r
1 dp \a
rp d6 [
? I /WW I VrVv i vv
\ у V V J V\n \ \
r
1 dp +v \t
rp dip
1 ^(sin^v^
0 i
sin# de
Навье-Стокса:
Г r2 r2
r
2 dvr
,vlctg в
r
2
r sin e
2
sin21
ve
sin
dip
1 <9?v
rsin# ^(/?
d(vesme)
) de
2 cos e
e r2 sin2 6>
r2 sin2 6> ^
2
r
4>
(W
2 dv
sin6> dip
¦1 m,
J'
r sin 0
П.5] Перевод электромагнитных величин из гауссовой системы в СИ 349
где операторы (vV) и А определяются следующими выражениями
2 df
df
d2f
r2 sin2 в д<р2 '
П.5. Перевод электромагнитных величин
из гауссовой системы в СИ и обратно
Переводные коэффициенты приведены по книге Е.А. Памятных и
Е.А. Турова 0.
Величина
Скорость света
Напряженность электрического поля,
потенциал
Заряд, плотность заряда, ток, плотность
тока
Магнитная индукция, магнитный поток
Напряженность магнитного поля
Удельная электрическая проводимость
сгс
с
Е, <р
q, Ре, 1,3
В, Ф
Н
аг
СИ
1
л/Атгео (Е, (р)
(q, ре, 1,3)
V4^Mo H
Значения электрической и магнитной постоянных:
?0 = 8,854 • 1(Г12 Ф/м , /i0 = 4тг • 1(Г7 Гн/м .
Для уравнений Максвелла и силы Лоренца:
divD =
rotH =
div В =
rotE =
F = eE
СГС
Апре
1 5D 4тг .
с dt с 3
0
1 dB
с ~dt
+ f [v.B]
divD
rotH
div В
СИ
= Ре
_ dr>
~ ~dt
= 0
_ ^E
F = eE + e
+ j
\
v,B]
0 Е.А. Памятных, Е.А. Туров. Основы электродинамики материальных
сред в переменных и неоднородных полях. — М.: Физматлит, 2000.
Список рекомендуемой литературы
1. Абрамович Г.П. Прикладная газовая динамика. — М.: Наука, 1976.
2. Берд Р., Стъюарт В., Лайтфут Е. Явления переноса. — М.: Химия, 1974.
3. Берже Я., Помо П., Видалъ К. Порядок в хаосе. О детерминированном
подходе к турбулентности. — М.: Мир, 1991.
4. Брановер Г.Г., Циновер А.Б. Магнитная гидродинамика несжимаемых
сред. — М.: Наука, 1970.
5. Гершуни Г.З. Гидродинамическая неустойчивость. Изотермические тече-
течения // Соросовский обр. ж. 1997. № 2. С. 99.
6. Гидродинамические неустойчивости и переход к турбулентности / Под ред.
Суинни X., Голлаба Дж. — М.: Мир, 1984.
7. Гинзбург И.П. Аэрогазодинамика. — М.: Высш. школа, 1966.
8. Каулинг Т. Магнитная гидродинамика. — М.: Наука, 1959.
9. Кирко И.М., Кирко Г.Е. Магнитная гидродинамика несжимаемых сред.—
Пермь: Изд-во ПГУ, 1980.
10. Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. — М.:
Физматгиз, 1963, Т. 1,2.
11. Крайнов В.П. Качественные методы в физической кинетике и гидрогазоди-
гидрогазодинамике. — М.: Высш. школа, 1989.
12. Ландау Л.Д., Лифшиц Е.М. Теория упругости. — М.: Физматлит, 2006.
13. Ландау Л.Д., Лившиц Е.М. Гидродинамика. — М.: Физматлит, 2006.
14. Ландау Л.Д., Лившиц Е.М. Электродинамика сплошных сред. — М.:
Физматлит, 2005.
15. Лойцянский Л.Г. Механика жидкости и газа. — М.: Наука, 1987.
16. Милн-Томсон Л.М. Теоретическая гидродинамика. — М.: Мир, 1964.
17. Осватич К., Шварценбергер Р. Сборник задач и упражнений по газовой
динамике. — М.: Мир, 1967.
18. Пикельнер СБ. Основы космической электродинамики. — М.: Наука, 1966.
19. Породное Б.Т., Флягин А.Г., Черняк В.Г. Механика сплошных сред.—
Свердловск: Изд-во УПИ, 1989.
20. Прандтль Л. Гидроаэромеханика. — Ижевск: НИЦ «РХД», 2000.
21. Седов Л.И. Механика сплошной среды. —М.: Наука, 1994, т. 1.
22. Седов Л.И. Методы подобия и размерности в механике. — М.: Физматлит,
1999.
23. Суетин П.Е. Механика деформируемых сред. — Свердловск: Изд-во УрГУ,
1981.
24. Суетин П.Е. Механика жидкости. — Свердловск: Изд-во УрГУ, 1983.
25. Суетин П.Е. Турбулентность. Пограничный слой. — Свердловск: Изд-во
УрГУ, 1984.
26. Суетин П.Е. Газовая динамика. — Свердловск: Изд-во УрГУ, 1984.
27. Суетин П.Е. Магнитная гидродинамика. — Свердловск: Изд-во УрГУ, 1984.
28. Трубецков Д.И. Турбулентность и детерминированный хаос // Соросовский
обр. ж. 1998. № 1. С. 77.
29. Фабрикант П.Я. Аэродинамика. — М.: Наука, 1964.
30. Фрик П.Г. Турбулентность: модели и подходы. Курс лекций. Часть 1.—
Пермь: Изд-во ПГТУ, 1998.
31. Хинце О.И. Турбулентность, ее механизм и теория. — М.: Физматгиз, 1963.
32. Шерклиф Дж. Курс магнитной гидродинамики. — М.: Мир, 1967.
Предметный указатель
Адиабата Гюгонио, 263
Аттрактор, 197
— Лоренца, 205
— странный, 205
— точечный, 200
— циклический, 202
Бифуркация, 197
— Хопфа, 203
Вектор Пойнтинга, 308
— Умова, 62, 261, 308
— теплового потока, 58
Волна разрежения, 280
— ударная косая, 270
прямая, 262
Волны альвеновские, 319
— ленгмюровские, 318
— магнитогидродинамические, 318
Вязкость кинематическая, 129
— турбулентная, 214
Давление магнитное, 303
Движение баротропное, 87
— вихревое, 94
— плоское, 103
— потенциальное, 101
Деформации пластические, 29
— упругие, 16
Деформация температурная, 21
Диаграмма бифуркационная, 202
— растяжения, 37
Длина пути перемешивания, 215
Закон Гука, 33
Кавитация, 90
Конус Маха, 259
Коэффициент Пуассона, 36
— всестороннего сжатия, 34
— вязкости
магнитной, 310
объемной, 66
Коэффициент вязкости сдвиговой, 66
— запаса прочности, 37
— магнитной диффузии, 316
— сопротивления, 219
— температуропроводности, 65
— теплопроводности, 64
Коэффициенты Ламэ, 32
Кризис сопротивления, 245
Масса присоединенная, 119
Модуль Юнга, 35
— всестороннего сжатия, 32
— сдвига, 32
Нить вихревая, 97
Парадокс Даламбера, 109
Поверхность разрыва, 260
Пограничный слой ламинарный, 232
— турбулентный, 232
Подобие геометрическое, 163
— динамическое, 163
Потенциал баротропный, 87
— комплексный, 105
— скорости, 101
Предел пропорциональности, 37
— прочности, 37
— текучести, 37
— упругости, 37
Предельный цикл, 201
Пространство состояний, 198
— фазовое , 198
Равновесие безразличное, 187
— асимптотически устойчивое, 187
— неустойчивое, 187
— устойчивое, 187
Расход массовый, 139
— объемный, 139
Скин-эффект, 317
Скорость вихревая, 83
— волны поперечной, 70
352
Предметный указатель
Скорость волны продольной, 70
— комплексная, 105
— критическая, 186, 254
Смещение, 15
— относительное, 16
Температура торможения, 252
Тензор вязких напряжений, 66
— деформации, 16
— напряжений, 27
магнитного поля, 303
электрического поля, 303
— относительной деформации, 16
— плотности потока импульса, 56
— поворота, 16
— теплового расширения, 22
Теорема Валена, 312
— Гельмгольца, 96
— Жуковского, 112
— Томсона, 95
Теория Гейзенберга-Линя, 195
— Дайслера, 217
— Кармана, 216
— Ландау-Хопфа, 203
— Прандтля, 214
— Фейгенбаума, 207
Течение ламинарное, 184
— турбулентное, 184
— Куэтта
плоское, 135
цилиндрическое, 141
— Пуазейля
плоское, 137
цилиндрическое, 139
Толщина вытеснения, 237
Трубка Пито, 91
— вихревая, 96
— тока, 86
Турбулентность изотропная, 185
— однородная, 185
— развитая, 223
Турбулентные напряжения, 213
Угол Маха, 259
Уравнение Орра-Зомерфельда, 194
— Бернулли, 84
нестационарное, 101
— Ван дер Поля, 201
— Громека, 83
Уравнение Кармана, 240
— Прандтля, 234
— Пуассона, 252
— Рейнольдса, 213
— Фурье, 64
— Эйлера, 81
— внутренней энергии, 58
— волновое, 70
— движения, 50, 51
— непрерывности, 46
— строфоиды, 271
— теплопроводности, 65
— ударной поляры, 271
Условие Коши-Римана, 104
— непротекания, 84
— прилипания, 130
Участок разгонный, 238
Фазовая точка, 198
Фазовая траектория, 198
Фазовый портрет, 198
Формула Блазиуса, 219
— Гюйгенса, 172
— Колмогорова-Обухова, 226
— Никурадзе, 221
— Осеена, 148
— Пуазейля, 140
— Сен-Венана, 258
— Стокса, 148, 174
Функция тока, 103
Циркуляция скорости, 94
Число Альвена, 309
— Гартмана, 310
— Маиевского, 252
— Маха, 162, 252
— Прандтля
магнитное, 310
— Рейнольдса, 162, 186, 187
критическое, 186
магнитное, 310
— Струхала, 162
— Стюарта, 309
— Фейгенбаума, 208
— Фруда, 162
Эллипсоид деформации, 21
Энтальпия, 82
Эффект Магнуса, 112