Текст
Жопилярнъге лекции
ПО МАТЕМАТИКЕ
Ю. И.ЛЮБИЧ И Л. А. ШОР
КИНЕМАТИЧЕСКИЙ
МЕТОД
Б ГЕОМЕТРИЧЕСКИХ
3'*'ЧАХ
щ
ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
, ВЫПУСК 42
Ю. И. ЛЮБИЧ и Л. А. ШОР
КИНЕМАТИЧЕСКИЙ
МЕТОД
В ГЕОМЕТРИЧЕСКИХ
ЗАДАЧАХ
Издание второе,
исправленное
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1978
513
Л 93
УДК 513.0
АННОТАЦИЯ
Решая геометрическую задачу, полезно пред-
представить себе, что будет происходить с элементами
рассматриваемой фигуры, если некоторые ее точки
начнут двигаться. Зависимость одних элементов от
других может стать при этом наглядно очевидной,
и решение задачи бросится в глаза.
Связи между величинами отрезков, углов и
т. п. в геометрических фигурах обычно являются
более сложными, чем связи между скоростями из-
изменения этих величин в процессах деформации
фигур. Поэтому для решения геометрических задач
может быть полезной «теория скоростей» — кине-
кинематика.
В этой брошюре на нескольких примерах де-
демонстрируется применение кинематики к задачам
элементарной геометрии и приводится некоторое
количество задач для самостоятельного упражне-
упражнения. Необходимые общие сведения из кинематики
(и векторной алгебры) излагаются предварительно.
Брошюра написана на* основе лекций, прочи-
прочитанных- в школьном математическом кружке при
Харьковском государственном университете им.
А. М. Горького. Оиа рассчитана на учащихся 9—
10 классов,
© Главная редакция
20202—038 физико-математической литературы
Л „co/Am is 85-76 издательства «Наука», 1976,
Орд (О/)-/О с изменениями,
ВВЕДЕНИЕ
Однажды в серьезной математической книге *) нам
встретилась задача, которая, казалось, попала туда из
еочинений Конан-Дойля или Стивенсона. В ней шла
речь об отыскании клада. Одному человеку было извест-
известно, чго в той местности, где зарыт клад, растут только
три дерева: дуб, сосна и береза. Для того чтобы найти
кла«, надо стать под березой (рис. 1, на котором она
обозначена точкой Б) ли-
лицом к прямой линии, прохо-
проходящей через дуб и сосну (на
рис. 1 это точки Д и С).
При этом дуб должен ока-
оказаться справа, а сосна слева.
Затем надо пойти к дубу,
считая шаги. Дойдя до дуба,
повернуть под прямым уг- Г"
лом направо и пройти столь- г
ко же шагов, сколько было
пройдено от березы до дуба.
В этом месте остановиться и поставить вешку (на рис. 1
это точка Si). Затем следует вернуться к березе и пой-
пойти от нее к сосне, считая шаги. Дойдя до сосны, повер-
повернуть под прямым углом налево и пройти столько же
шагов, сколько было пройдено от березы до сосны.
В этом месте остановиться и поставить вешку (на рис. 1
это точка В2). Клад зарыт точно посредине между веш-
вешками (на рис. 1 это точка К).
При такой подробной инструкции отыскание клада
не могло вызвать затруднений. Однако они все-таки
Рис. 1.
*) Т. С а а т и, Математические методы исследования операций,
Воеииздат, 1963,
возникли. Дело в том, что когда кладоискатель попал
в указанную местность, он обнаружил там только дуб
и сосну. Березы же не было и в помине. И. все же он на-
нашел клад. Спрашивается, как ему это удалось?
Поскольку задача была приведена в Серьезной
Математической книге, следовало ожидать, что дело
здесь не просто в удаче. И, ?
действительно, задача име- \
ет математическое решение, /
кстати вполне доступное >
школьнику. )
Опустим из точек Si, В^
Б я К перпендикуляры на
прямую ДС (см. рис. 2).
Основания их обозначим
через В\, В'г, Б' и А' со-
рис 2 ответственно. Отметим ра-
равенство следующих пар пря-
прямоугольных треугольников (по стороне и острому
углу):
'2 = АСББ'.
Из равенства треугольников следует, что В\В[—ДБ',
ДВ'\ = ББ' и В2В'2 = СБ', СВ'2 = ББ'. Так как точка
К — середина отрезка ВХВ2, то КК' — средняя линия тра-
трапеции В1ВШ2В2 и поэтому
КК' = -j (BiBi + В2В'2) = y ЩБ' + Б'С) = j ДС
Далее, точка К' — середина отрезка В'\В2 и так как
ДВ'\ = СВ2{=ББ'), то К' — середина отрезка ДС.
Таким образом, положение точки К не зависит от поло-
положения точки Б. Чтобы найти точку К, достаточно к от-
отрезку ДС восставить перпендикуляр в его середине и
отложить на этом перпендикуляре отрезок, равный
-<гДС, в такую сторону, чтобы точка Д оказалась спра«
ва, а точка С — слева.
Хотя приведенное решение безупречно, оно все-та-
все-таки оставляет чувство некоторой неудовлетворенно-
неудовлетворенности. Основная идея — опустить перпендикуляры из
точек Si, В2, Б и К на прямую ДС — никак не свя-
связана с постановкой задачи и, на наш взгляд, явля-
ется весьма- искусственной*). Гораздо более естест-
естественно выяснить, как зависит положение точки К о г
положения точки Б, или, иначе, как будет двигаться
точка К при движении точки Б. Эта идея подсказы-
подсказывается, кстати, и самой фабулой задачи. Легко себа
представить, что, не увидев березы, кладоискатель
начинает бродить по местности в поисках ее остат-
остатков и при этом рассуждает: «Если бы береза была
здесь, то клад должен был бы быть там, а если береза
была бы здесь, то ...». И тут он мог бы заметить, что
положение клада не зависит от положения березы. За-
Заметив это, он взялся бы за заступ, отложив поиски
доказательства до лучших времен. Нас же, в отличие
от него интересует как раз вопрос о том, как, рассу-
рассуждая таким образом, не только заметить, но и дока-'
зать, что положение точки К (клада) не зависит от по-
положения точки Б (березы).
Представим себе, что точка Б начала двигаться.
Пусть v — вектор ее мгновенной скорости. Так как отре-
отрезок Д??1 получается из отрезка ДБ поворотом на угол-j»
то точка Si будет двигаться согласованно с точкой Б,
а именно так, что вектор vt ее скорости будет полу-
получаться из вектора v поворотом на угол -^. Анало-
Аналогично, вектор v2 скорости точки В2 будет получаться
из v поворотом на угол**) —у. Поэтому v2 =—v\.
И значит, точка К как середина отрезка BiB2 имеет
скорость
и = -^ (»i + v2) = 0.
Но если скорость точки все время равна нулю, то
эта точка неподвижна! Итак, при произвольном
движении точки Б точка К остается неподвижной.
*) Подобные «искусственности» очень часто встречаются в ре-
решениях геометрических задач. Это дало повод известному француз-
французскому математику Ж. Фавару сказать, что для многих людей «гео-
«геометрия остается искусством доказывать какое-нибудь свойство, рас-
рассматривая коварно выбранный круг и удачно соединяя старательно
разобщенные точки».
**) Напомним, что угол поворота считается положительным,
если поворот происходит против часовой стрелки, и отрицательным,
если поворот происходит по часовой стрелке,
Следовательно, положение точки К не зависит от
положения точки Б.
Чтобы найти теперь положение точки К, доста-
достаточно выбрать одно какое-нибудь положение точки Б.
Пожалуй, проще всего совместить точку Б с точкой С
и применить построение,
известное кладоискателю
(рис. 3).
Это решение, основан-
основанное на кинематических со-
соображениях, при всей его
естественности, может по-
показаться трудным школь-
школьнику ввиду' недостаточного
знакомства его со свойства-
рнс з. ми векторов и скоростей.
Поэтому в книжке, по-
посвященной применению ки-
кинематического метода к геометрическим задачам, нам
пришлось довольно много рассказать о векторах и
о скоростях. Эти понятий играет важную роль в ряде
разделов математики и физики. Поэтому ознакомление
с ними полезно и само по себе.
В §§ 1—2 многое не доказывается, а лишь поясня-
поясняется. Но, обращаясь к чертежам и размышляя само-
самостоятельно, читатель сможет без особого труда прийти
к достаточно полным доказательствам. Сведущий чита-
читатель может ограничиться беглым ознакомлением с ма-
материалом этих параграфов.
Параграф 3 — основной в этой книге. Там разобрано
некоторое число задач на применение кинематического
метода и сформулированы задачи для самостоятельного
упражнения.
§ 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
п° 1. Векторами называются направленные отрез*
ки. На чертеже векторы изображаются отрезками,
снабженными стрелками, указывающими направление
(см. рис. 4). Начало вектора называется также его
точкой приложения. Вектор с_началом А и концом В
обозначается АВ (но не ВА\ ВА обозначает век-
вектор с началом В и концом А). Часто для обозначе-
обозначения вектора применяют одну букву, например, АВ = а.
Эту букву принято печатать жирным шрифтом, чтобы
сразу дать понять, что речь идет о векторе, а не о числе.
Если вектор обозначен, например, через а, то его длина
обозначается \а\, подобно абсолютной величине чис-
числа*). Длина вектора часто также называется абсолют-
абсолютной величиной.
Равенство двух векторов понимается не как полная
тождественность, а несколько шире. Именно, два век-
Рис. 4.
Рис. 5.
тора называются равными, если их длины равны, а
направления одинаковы. Таким образом, равные век-
векторы обязательно параллельны или лежат на одной
прямой (короче говорят: «коллинеарны»). На рис. 5
Из определения равенства_ вытекает, что при па*
раллельном переносе вектор не изменяется.
Для дальнейшего важно рассматривать точку как
отрезок, начало и конец которого совпадают. Такой
«вырожденный» отрезок тоже считается вектором,
но ему не приписывается никакого определенного
направления**). Он называется нулевым вектором и
обозначается 0. Его длина равна нулю: |0| = 0.
п°2. Суммой векторов а и Ь называется вектор
с = а + Ь, идущий из начала вектора а в конец век-
вектора Ъ (рис. 6), при условии, что начало вектора Ъ
совмещено с концом вектора а (этого всегда можно
добиться параллельным переносом вектора 6).
*) Длина вектора АВ часто обозначается просто АВ.
**) То есть любое направление считается направлением этого
вектора.
Сложение векторов, как и сложение чисел, подчи-
подчиняется переместительному и сочетательному законам.
Переместитёльный закон выражается формулой
а + Ь = Ь + а. A)
Его справедливость усматривается из рис. 7, на
котором векторы а и Ь приложены в одной точке
и служат сторонами параллелограмма. Диагональ
этого параллелограмма, идущая из
общего начала векторов, а и 6, рав-
равна (как вектор) с одной стороны
сумме a -f Ь, с другой стороны —
сумме Ъ -\- а.
Сочетательный закон выражает-
выражается формулой
{а + Ь) + с = а + (Ь + с), . B)
справедливость которой усматривается из рис. 8.
Благодаря переместительному и сочетательному за-
законам можно при сложении векторов так же, как и при
сложении чисел, не обращать внимания ни на порядок
слагаемых, ни на их группировку. В частности, можно
писать просто а -\- Ъ -\- с, опуская скобки.
с=а+Ь
Рис. 6.
(a+b)+c=a+(b+c)
Рис. 8.
Сложение нескольких векторов поясняется на рис. 9,
на котором векторы аи а2, аз, #4, последовательно при-
приложенные друг к другу, образуют ломаную, «замыкае-
«замыкаемую» вектором-суммой а^ -\- а2 + а3 -\- а4.
Очевидно, сумма нескольких векторов равна нулю
тогда и только тогда, когда образованная ими ломаная
замкнута, т. е. конец последнего слагаемого вектора
совпадает с началом первого (см. рис. 10).
Пусть, например,
а + 6 = 0.
3
Тогда длина вектора Ь должна быть равна длине век-
вектора а, а направление прямо противоположно направ-
направлению вектора а. Определенный таким образом век-
вектор Ь называется противоположным вектору а и обозна-
обозначается —а.
Формулы
с + 0 = а, а + (- а) = 0, C)
непосредственно вытекающие из определений, играют
важную роль в векторной алгебре. В частности, с их
а,\
Рис. 9.
помощью можно исследовать операцию вычитания век--
торов, обратную к операции сложения.
п° 3. Разностью а — Ь векторов а и Ь называется
такой вектор с, что
Ь + с = а. D)
Способ построения разности указан на рис. 11, а.
Вместе с тем вычитание можно свести к сложению сле-
следующим образом. Прибавим к обеим частям равен-
равенства D) вектор —Ь:
а + (- Ь) = F + с) + (- Ь).
В силу сочетательного и переместительного законов
получаем:
откуда в силу формул C)
а + (— Ь) = с + О = с.
Таким образом,
а- 6 = а + (-6).
2 Ю, И. Любич, Л. А. Шор
E)
9
Это дает еще один способ построения разности, указан-
указанный на рис. 11,6.
Отметим еще формулы
а — 0 = а, 0 — а = — а, а — а = 0. F)
Между прочим, поскольку согласно определению разно-
разности равенства
а — 6 = с, а = Ъ + с
означают одно и то же, то вектор можно переносить
из одной части равенства в другую с противоположным
знаком.
п° 4. Нам понадобится одно важное неравенство,
которое называется неравенством треугольника.
Рис. 12.
Обратимся к рис. 6 (стр. 8). Согласно известной геомет-
геометрической теореме имеет место неравенство
|о + 6|<|о| + |Ы. G)
Здесь знак равенства достигается тогда и только тогда,
когда векторы одинаково направлены.
Можно указать еще несколько неравенств, аналогич-
аналогичных неравенству треугольника, например,
|о-Ы<|о|+|Ы; \а-Ь\>\а\-\Ь\. (8)
п° 5. Произведением Ха вектора а на вещественное
число X называется вектор с, определяемый следующими
условиями.
1) |с| = |А,|-|а| (\Х\—абсолютная величина чис-
числа X);
2) с коллинеарен вектору а;
3) при X > 0 направление вектора с совпадает
с направлением вектора а, при % < 0 эти направле-
направления противоположны. На рис. 12 представлены случаи
10
L—JL и pl = _A# Очевидно,
a = 1 • a, a + a = 2a, a-f-a-f-a = 3a, ...
i
— a = (— 1)-a, (—a)+ (—«)== (—2). a;
Перечислим основные законы, которым подчиняется
умножение вектора на число.
1) Сочетательный закон
'9)
иллюстрируется рис. 13, на котором представлены
случаи Л>0, ц>0иЛ>0, ц<0.
2) Распределительный закон относительно числового
множителя
1{а + Ь) = Ха + ХЬ A0)
2* П
иллюстрируется на рис. 14, на котором представлены
случаи % > 0 и % < 0.
3) Распределительный закон относительно векторно~
го множителя
(I + ц) а — Ха + ца A1)
иллюстрируется рис. 15,
случаи Л>0, ц > 0 и
на котором представлены
А, > 0, ц < 0, Л^цХ),
а)
ю
К>0,
Рис. 15.
Обратим еще внимание читателя на очевидные равен-
равенства:
0-а = 0, Л,- 0 = 0. A2)
Можно ввести и деление вектора на число. Частным
от деления вектора а на число % Ф 0 называется произ-
произведение вектора а на число, обратное к К:
х=4-в- A3)
Итак, мы видим, что рассмотренные действия век-
векторной алгебры подчиняются тем же основным законам,
что и соответствующие действия над числами. Поэтому
в векторной алгебре справедливы все логические след-
следствия этих законов, что позволяет оперировать с векто-
векторами так же, как с числами. Например, в выражении
(Л + р.) (а + Ъ) можно обычным образом раскрыть
скобки, в результате чего получим Ка -f- Xb -f-, |д,а -(- цЬ
(это следует из распределительных законов).
п° 6. Начиная с этого места, мы будем считать, что
все векторы лежат в одной плоскости*), т. е. будем
заниматься только планиметрией.
*) Читатель, не знакомый со стереометрией, по-видимому, с са-
самого начала так и считал. Он не потерял при этом ничего сущест-
существенного,
12
Пусть а и Ъ — два неколлинеарных вектора н
с—какой-нибудь третий вектор. Если вектор с колли-
неарен одному из векторов а или Ъ, например, векто-
вектору а, то найдется такое число X, что
с = Ка.
A4)
В общем случае приложим все три вектора в од-
одной точке О (рис. 16) и после этого проведем через
конец С вектора с прямые,
параллельные векторам а и
Ъ. Они пересекутся с пря-
прямыми, на которых лежат а
и Ъ, в точках А я В соответ-
соответственно.
Очевидно,
' "• __ - Рис. 16.
Но так как векторы ОА
и а коллинеарны, то найдется такое число А,, что
Аналогично найдется такое число (д., что
OB==\ib.
Следовательно,
c = Xa-±-\ib. A5)
Представление вектора с в виде A5) называется
разложением этого вектора по векторам а и Ъ. Любой
вектор с можно разложить по двум неколлинеарным
векторам а и Ъ. Коэффициенты Лиц при этом опреде-
определены единственным образом.
Отметим, что равенство A4) записывается в виде
A5) с коэффициентом ц = 0.
п° 7. Пусть А, В, С —три точки, лежащие на одной
прямой. Говорят, что точка С делит отрезок АВ в отно-
отношении т : п, если *)
A6)
*) Числа т, п — любые вещественные, не равные нулю одновре-
одновременно. Если m = 0, то точка С совпадает с точкой А; если п = 0,
то С совпадает с В,
13
Очевидно, абсолютная величина отношения т: п
равна отношению длин АС:СВ. Отношение т:п поло-
положительно, если точка С лежит внутри отрезка АВ, и
отрицательно, если она лежит вне отрезка (рис. 17).
Теорема. Пусть точка С делит отрезок АВ в отно-
отношении m : п и пусть О — произвольная точка плоскости
(рис. 18). Тогда
~Т; пОА + тОВ
Обратно, если для какой-нибудь точки О выполнено
равенство A7), то точка С делит отрезок в отноше-
отношении пг ; п.
Рис. 18.
Доказательство. Пусть выполняется A6). Так
как
~АС = ОС-О~А, С~В = ОВ-ОС,
то
п (ОС — ОА) = пг (ОБ — ОС).
Решая это уравнение относительно ОС, приходим к
A7).
Аналогично из A7) получается A6).
п° 8. Как известно, осью называется прямая, снаб-
снабженная «положительным» направлением.
Пусть / — некоторая ось и АВ — некоторый вектор
(рис. 19). Обозначим через А\ и В\ проекции точек А
и В на ось / (т. е. основания перпендикуляров к /, про-
проведенных через А и В). Рассмотрим число, равное длине
отрезка А{Ви взятой со знаком плюс, если направление
вектора А\В^ совпадает с направлением оси /, и взятой
со знаком минус'в противоположном случае. Это число
называется проекцией векгора АВ на ось / и обозна-
обозначается
14
Пусть ф — угол между вектором а и осью /, заклю-
заключенный между 0 и я (рис. 20). Очевидно,
прг а = \ а | • cos<p. A8)
В частности, если а перпендикулярен к /, то пр/а = 0,
Рис. 19.
Отметим еще два свойства проекций (рис. 21, 22):
1) прг (а + Ь) = пр(а -t^npfft,
2) прг(Ха) = % пр;й (К — любое число).
Эти свойства принято выражать следующими сло-
словами: «проектирование вектора на ось является линей'
С
Рис. 21.
Рис. 22.
ной операцией над векторами». Последовательно приме-
применяя свойства 1) и 2), можно написать вообще:
пр, (М. + КЩ. + ¦ ¦ • + М») =
= ^пр(а, + А,2прга2+ ••• +А,„пР/а„ A9)
для любых векторов «ь а2> • • • > «п и любых чисел %п
15
Между прочим, умножение вектора на число X тоже
есть линейная операция (см. (9), A0)).
п° 9. Еще один важный пример линейной опера-
операции дает операция поворота вектора на заданный
угол а (положительный, отрицательный или нуле-
нулевой—безразлично). Эту операцию мы будем обозна*
чать через Ua, а результат ее применения к вектору а —
tz<0
Рис. 23.
через Uaa. Таким образом, вектор Uaa получается
из вектора а поворотом на угол а. При этом, оче-
очевидно,
\Uaa\ = \a\ B0)
(рис. 23).
Очевидно, Uoa — а, т. е. операция Uo не меняет век-
вектора. Операция, не меняющая вектора, называется
тождественной операцией.
Заметим еще, что
Una = — a, U2na = a. B1)
Как было уже сказано, операция поворота Ua линейна:
1) иа(а + Ь)=иаа+иаЬ (рис. 24),
2) Ua(Ka) = Waa, где Я — любое число (рис.25).
Следовательно, подобно A9),
= А,,?/аа, + X2Uaa2 + ... + XnUaan. B2)
п° 10. Пусть 5, Т — две операции над векторами
(например, S — проектирование вектора на некото-
некоторую ось /, Т — поворот вектора на прямой угол).
Результат последовательного выполнения двух опе-
операций называется произведением операций. При этом,
вообще говоря, важен порядок, в котором выпол-
выполняются операции. Если в приведенном выше примере
16
пары операций 5, Т взять лежащий на оси / вектор
а Ф 0 и применить к нему сначала Т, а затем 5, то
получается 0; если же к а применить сначала 5, то
получится число, а к числу попросту нельзя приме-
применить операцию Т (операция Т применяется только
к векторам).
'Ла
Рис. 25.
Рис. 26.
Если сначала выполняется операция Т, а затем one*
рация 5, то произведение записывается в виде ST.
Таким образом, по определению
\О 1 ) п О ^ 1 и) \^^)
для любого вектора а.
Рис. 26 показывает, что U$Uaa = Ua+$a для любого
вектора а, т. е. короче*):
= tW B4)
?/а?/ = UJUa, B5)
хотя, вообще говоря, ST Ф TS.
Если ST = TS, то говорят, что операции S и Т пере-
перестановочны. Таким образом, любые два поворота пере-
перестановочны. Любой поворот перестановочен также с
умножением на число (свойство 2 операции Ua).
Из формулы B4) следует
Отсюда видно, что
т. е. U-aUaa = а для любого вектора а.
*) Две операции Т\, Т2 над векторами считаются равными, если
= Т^а для всех векторов а.
17
Свойства поворотов и других геометрических преоб-
преобразований могут быть с успехом использованы для
решения разнообразных задач (см. книгу И. М. Яглом,
Геометрические преобразования, I, II, Гостехиздат,
1955—1956).
§ 2. ЭЛЕМЕНТЫ КИНЕМАТИКИ
п° 1. Возьмем на плоскости какую-нибудь точку О —
полюс. Для произвольной точки М вектор г = ОМ
(рис. 27) называется ее радиусом-вектором относительно
полюса О. Точка и ее радиус-вектор взаимно опреде-
определяют друг друга.
М
-ОМ
1-'ис. 27.
Рис. 28.
Если точка движется, описывая некоторую траекто-
траекторию (рис. 28), то ее радиус-вектор изменяется в зависи-
зависимости от времени; он является функцией от времени.
Это обозначается так:
г — г (t) (t — время). A)
Слово «изменяется» нельзя понимать здесь слишком
буквально. Важным частным случаем движения являет-
является покой. Если точка покоится, то ее радиус-вектор во
все моменты времени будет одним и тем же. Как функ-
функция от времени он является постоянной, «константой».
Это записывается так:
г — const. B)
Когда говорят, что, например, г есть функция от t,
имеют в виду только тот факт, что при каждом значе-
значении t вектор г является вполне определенным: если t
фиксировано, то г уже не может меняться,
18
¦ n° 2. Рассмотрим какой-нибудь промежуток времени
[^о, ^i] (^1 > А)), начинающийся в момент to и кончаю-
кончающийся в момент ti. Длительность этого промежутка
равна *)
M = t1 — tQ. C
Если в момент ^о радиус-вектор движущейся точки М
равен г0 (г0 = r(t0)), а в момент t\ он равен rt (г, =
= г(U)), то вектор J
Д
показывает перемещение точ-
точки М за промежуток времени
[to,ti] (рис.29).
Мы хотим теперь ввести
важнейшее понятие скорости
движения. Грубо говоря, ско-
скорость — это перемещение за
единицу времени. При этом " РйС 2д
скорость должна описывать как
абсолютную величину перемещения за единицу вре-
времени, так и направление этого перемещения, т. е.
скорость должна быть вектором.
Если мы знаем, что за промежуток времени [to, tt]
точка М испытала перемещение Аг, то чтобы получить
перемещение за единицу времени, естественно разделить
Дг на длительность промежутка времени. При этом по-
получится вектор, который называется средней скоростью
точки за данный промежуток времени:
*ср = -^. D)
Этот вектор направлен так же, как вектор переме-
перемещения Аг, но его абсолютная величина равна расстоя-
расстоянию MqM], деленному на At, т. е. говоря грубо, — пути,
проходимому точкой за единицу времени.
Что мы хотим подчеркнуть словами «грубо гово-
говоря»? Дело в том, что точка М в течение промежутка
времени [^о, ti] движется, как правило, неравномерно,
т. е. за равные части этого промежутка времени
*) Значок Д употребляется для обозначения приращения какой-
нибудь величины, т. е. для обозначения того, на сколько изменилась
величина,
.19
она проходит неравные пути. К тому же она дви-
движется, как правило, не по прямой MaMi, а по кривой,
соединяющей те же точки. Вектор перемещения Аг
характеризует лишь итог этого движения, но не его
промежуточные стадии. То же относится и к векто-
вектору средней скорости, и
это подчеркивается сло-
словом «средняя».
Легко понять, одна-
однако, что средняя скорость
будет достаточно точной
... л характеристикой движе-
' ния, если длительность
промежутка времени
весьма мала. Поэтому
О Для получения идеально
рис. зо. точной характеристики
нужно устремить время
А^ к нулю, т. е. фиксируя начало ^о промежутка време-
времени, устремить ti к t0. При этом средняя скорость vcv бу->
дет, вообще говоря, стремиться к некоторому пределу V.
v = lim »cp = lim ~r.
E)
В какой-то степени это иллюстрируется рис. 30.
Вектор v называется (мгновенной) скоростью дви-
движения в момент t0. Его направление является предель-
предельным для направлений векторов средних скоростей.
Вектор средней скорости за промежуток [^о, ^i] ле-
лежит на секущей MQMi. Если ^ стремится к tQ, то точ-
точка Mi стремится к точке /Ио, двигаясь по траектории.
При этом секущая MqMi, поворачиваясь, стремится
к некоторому предельному положению MqT. Прямая,
предельная для секущей МйМи называется касатель-
касательной к траектории в точке Мо *). Вектор скорости в
момент ^о лежит на касательной к траектории в точ-
точке Мо.
Недостаточно подготовленного читателя могут
смутить слова «стремится», «предел», «предельное
*) Читателю рекомендуется сопоставить это общее определение
касательной с обычным «школьным» определением касательной к
окружности,
20
положение». К тому же мы употребляем эти слова
в применении к переменным векторам (и даже к пе-
переменным прямым), а не только числам. Для пере-
переменных чисел смысл этих слов должен быть читате-
читателю известен из школьного курса математики, где
излагаются элементы теории пределов. Но нам нуж-
нужна более общая теория, которую мы сейчас вкратце
изложим.
п°3. Пусть р (s) — функция числового аргумента s,
принимающая числовые значения*). Напомним чита*
телю точный смысл равенства
lim p (s) = 0 F)
0
и соответствующей фразы: «функция p(s) стремится
к нулю при s, стремящемся к нулю». Они означают, что
каким бы малым ни было число 8 > 0, найдется столь
малое число б > 0, что неравенство
| р (s) К в
будет выполняться при всех \s\ <C б.
Пусть теперь fl(s) — векторная функция аргумента s.
Вектор Ъ называется пределом для a(s) при s, стремя-
стремящемся к нулю (запись: b = \ima(s)), если скалярная
функция
стремится к нулю при s, стремящемся к нулю.
Основные теоремы теории пределов для векторных
функций аналогичны известным читателю теоремам для
скалярных функций.
Теорема 1. Двух различных пределов у одной и
той же функции быть не может **).
Доказательство. Пусть
Ъх = lim a (s) и &2 = lim a (s).
0 0
*) Такие функции называют скалярными в противоположность
векторным.
**) Но может не быть, нн одного: предел может не существо-
существовать, но, если он существует, то он единствен,
2!
Очевидно,
6.-62 = [61-a(s)] + [a(s)-62].
Отсюда согласно неравенству треугольника
\bl~b2\^\b1~a(s)\-\-\a(s)-b2\.
Так как оба слагаемых в правой части последнего нера-
неравенства стремятся к нулю при s->0, а левая часть
неравенства не зависит от s, то она не может быть по-
положительной:
Но она не может быть и отрицательной (длина вектора
всегда неотрицательна). Следовательно,
Это означает, что Ъ\ — Ь2 = 0, т. е. Ь\ = Ь2.
Теорема 2. Если
lim a, (s) = 6,, lim a2(s) = b2,
s-»0 s-»0
TO
lim (<*! (s) + a2 (s)) = 6, -f 62
S-»0
(«предел суммы равен сумме пределов»*).
Теорема 3. Если
lima(s) = 6,
o
го лры любом фиксированном числе Л
lim Xa(s) — Xb
S-»0
(«предел произведения на число равен произведению
предела на это число»).
Доказательство теорем 2 и 3 предоставляется чи-
читателю *).
Теорема 4. Если
lim a (s) = b,
s-»o
*) При доказательстве теоремы 2 следует воспользоваться не-
неравенством треугольника,
22
то для любого фиксированного угла а будет
s-»0
Доказательство. Имеем (см. § 1, формулу
B0)):
| Uaa (s)-Uab\ = \Ua(a(s)-b)\ = \a(s)-b\.
aa
Так как по условию
lim | a (s) — Ь | = О,
то и
lim \ Uaa (s) — UаЬ \ = {
s-»0
т. е.
lim Uaa (s) = Uab.
s-»0
n°4. Теперь мы в состоянии изложить в нужном нам
виде теорию скоростей.
Скорость точки определяется равенством E) *).
Физически очевидна следующая
Теорема 5. Скорость неподвижной точки все вре-
время**) равна нулю.
Доказательство. Действительно, если точка не-
неподвижна, то для любого промежутка времени вектор
ее перемещения равен нулю, т. е. Дг = 0.
Следовательно, vcp = -rj- = 0. Но тогда и v = lim bcp=
— 0 в каждый момент времени.
Сформулируем обратную теорему.
Теорема 5'. Если скорость точки все время (в те-
течение которого рассматривается движение этой точки)
равна нулю, то точка остается неподвижной.
*) Читатель, знакомый с дифференцированием, может сказать:
«скорость точки есть производная от ее радиуса-вектора по времени».
Дифференцирование является одной из важнейших операций в мате-
математике. Доступное школьнику изложение дифференцирования содер-
содержится в брошюре В. Г. Болтянского «Что такое дифференцирова-
дифференцирование?» (Гостехиздат, 1955).
**') Разумеется, в течение которого эта точка неподвижна,
23
При всей своей физической очевидности эта теорема
с математической точки зрения не так проста. Дабы не
заходить слишком далеко в сторону, мы опускаем ее
доказательство.
Теоремы 5 и 5' говорят о том, что равенство
г = const
равносильно равенству v = 0.
Теорема 6. Пусть п — fi(t), r2 = rz(t), r = r(t) —
радиусы-векторы точек Mi, M2, M соответственно. Если
точки движутся так, что все время
г = г, + га,
то их скорости связаны аналогичным соотношением:
t> = t>,+t>2- @
Доказательство. Вектор перемещения точки М
за промежуток времени [t, t -\- At] равен
Аг = г (t + АО - г (t) = [r, (t + АО + r2(t + АО] - [г, @ +
+ г2 @] = [г, (/ + АО - г, (/)] + [г2 (/ + АО - г2 @] =
= Аг! + Аг2.
Отсюда
Wcp ~" д! ~~ КГ + ТГ ~ °1ср
и по теореме 2
»= lim »ср= lim »lcp+ lim »2ср = », + v2
Д(>0 Д*^0 Д*>0
что и требовалось доказать.
Аналогичная теорема справедлива для разности.
Теорема 6'. Если скорости точек Mit M2, M все
время связаны соотношением G), то все время
г = г, + r2 + const. (8)
Доказательство. Рассмотрим вспомогательную
точку Р, радиус-вектор которой все время равен
ОР = г - (г, + га). (9)
Но тогда скорость точки Р равна, по доказанному ра-
ранее, v— (»i + v%), .т. е. равна нулю. Следовательно, точ-
точка Р неподвижна, т. е. OP = const. Отсюда и из (9)
непосредственно вытекает (8),
24
Аналогично теоремам б и 6' могут быть доказаны
(с помощью теорем 3, 4) следующие пары теорем.
Теорема 7. Пусть п = гх(г), rz = МО— радиусы-
векторы точек Mi и М2 соответственно. Если точки дви-
движутся так, что все время
где % — постоянное число, то их
скорости связаны аналогичным со-
соотношением
v2 = KVi. A0)
Теорема 7''. Если скорости то-
точек Mi, Мг все время связаны со-
соотношением A0), то все время
га = Лг, +const. Рис-зк
Теорема 8. Пусть п = г^), r2 = rz(t) — радиусы-
векторы точек М\ и М<2 соответственно. Если точки дви-
движутся так, что все время
где ос — постоянный угол, то их скорости связаны ана-
аналогичным соотношением
v2 = Uav]. A1)
Теорема 8'. Если скорости точек Ми М2 все время
связаны соотношением A1), то все время
r2 = Uar] + const.
п°5. Пусть r=r(t) — радиус-вектор движущейся
точки М. Рассмотрим перемещение MaMi = tsr точки
за некоторый промежуток времени [to, ti] (рис. 31).
Проведем дугу окружности с центром в полюсе О и
радиусом OMq. Она пересечет луч ОМ] в точке М*.
Очевидно,
Аг = ЛЩ = М0М* + ЛГМ,. A2)
Перемещение МйМ* не изменяет расстояния движу-,
щейся точки М от полюса О и связано только с поворо»
том луча ОМ. Перемещение M*Mi связано только о
изменением расстояния точки М от полюса,
Деля обе части равенства A2) на А/ = tt — to и пе-
переходя к пределу при А/ -> 0, получим:
.. мм* , ,. M*Mt /1Q\
v= hm ~jj-+ lim —л-1- A3)
Первый из пределов, стоящих в равенстве A3) справа,
называется трансверсальной скоростью точки М и обо-
ir значается vx, второй — называет-
^1\ ся радиальной скоростью точки
4 Ми обозначается v0.
Итак,
v — vx-\-v . A4)
Ч>
Формула A4) дает разложение
вектора скорости на радиальную
и трансверсальную составляю-
составляющие (рис. 32). Эти составляющие
взаимно перпендикулярны.
Рис. 32". Радиальная скорость есть
скорость изменения расстояния
точки М от полюса О или, что то
же самое, — скорость изменения длины радиуса-вектора
ОМ. Она направлена вдоль этого вектора, если ОМ
возрастает, и в противоположную сторону, если ОМ
убывает.
Обозначим проекцию вектора скорости точки М
на ось, определяемую вектором ОМ, через vp. Оче-
Очевидно,
где плюс берется в случае возрастания ОМ, а минус —
в случае убывания.
Если точка М движется по окружности с центром
в полюсе, то ее полная скорость совпадает с трансвер-
трансверсальной:
Если же точка движется по лучу, исходящему из
полюса, то ее полная скорость совпадает с радиаль-
радиальной:
п° 6. Рассмотрим вращение луча ОМ вокруг его
начальной точки О. Пусть за промежуток времени
26
[/, t + А/] луч повернулся на угол*) Аф. Средней угло-
угловой скоростью луча за промежуток времени [t, t -\- At]
называется отношение
Предел средней угловой скорости юор при Д^-> 0 назы-
называется (мгновенной) угловой скоростью луча и обозна-
обозначается просто со:
со = lim <oco = lim ¦—.
Угловая скорость — это не вектор, а число**). Она
положительна, если вращение луча происходит в поло-
положительном направлении, и отрицательна, если луч вра-
вращается в отрицательном направлении.
Для угловых скоростей справедливы следующие
теоремы, аналогичные теоремам о скоростях точек.
Теорема 9. Угловая скорость луча все время рав-
равна нулю тогда и только тогда, когда луч все время не-
неподвижен.
Теорема 10. Угловые скорости двух лучей***) OiM
и О2М все время равны тогда и только тогда, когда
угол между лучами остается постоянным.
§ 3. КИНЕМАТИЧЕСКИЙ МЕТОД
В ГЕОМЕТРИЧЕСКИХ ЗАДАЧАХ
Теперь мы можем во всеоружии приступить к реше-
решению геометрических задач. Прежде всего мы рекомен-
рекомендуем повторно проанализировать кинематическое реше-
решение «задачи кладоискателя», указанное во введении.
При этом необходимо проследить, как используется
материал §§ 1—2, с тем чтобы лучше подготовиться
к дальнейшим задачам.
Задача 1****). На сторонах произвольного тре-
треугольника ABC построены вне него равносторонние
*) Этот угол может иметь любой знак.
**) Для неплоских движений угловая скорость вводится более
сложным образом и там она оказывается векторной величиной.
***) Oi, O2 — любые две (может быть, и совпадающие) непо-
неподвижные точки.
****) Эта задача, так же как и большинство приведенных ниже
задач, заимствована из серии книг «Библиотека математического
кружка» И. М. Яглома и др. Некоторые задачи взяты из книги
Ж. Адамара «Элементарная геометрия», т, 1 (Учпедгиз, 1948),
27
треугольники ABC, ВСА' и АСВ' (рис. 33)". Доказать,
что центры Оь 02 и 03 этих треугольников сами явля*
ются вершинами равностороннего треугольника.
Решение. Закрепим вершины А я В треуголь-
треугольника ABC и будем двигать вершину С. Пусть Vc.~-'
ее скорость. При этом тре-
треугольник ABC будет оста-
оставаться неизменным, а вер-
вершины А' и В' равносторон-
равносторонних треугольников А'ВС и
АВ'С будут каким-то опре-
определенным образом двигать-
двигаться 1_Рассмотрим векторы АС
и АОг. Очевидно,
Кроме того, угол между век-
векторами АС и АО2 равен -g-.
Поэтому, если мы повернем вектор АС на угол -g- (при
этом длина его не изменится) и умножим полученный
вектор на —т-
Уз
записать так:
=¦, то получим вектор АО2. Это можно
3
По теореме 8
э2 — скорость точки О2). ¦
Аналогично
1
Отсюда
Следовательно,
V L
28
6 6
Примем теперь неподвижную точку Ог за полюс. Тогда
из равенстваA) согласно теореме 8' получится
где вектор R = const, т. е. R не зависит от положения
подвижной точки С. Вектор R
неизвестен, но его можно най-
ти, выбирая одно какое-ни-
будь положение точки С, ко-
которое мы будем кратко назы-
называть в дальнейшем определя-
определяющим положением. Если ока-
окажется, что в определяющем
положении точки С вектор R
равен нулю, то, будучи посто-
постоянным, он равен нулю всегда,
т. е. всегда
сЩ=^яОА. B)
з
Но это как раз и означает, что треугольник О4О2Оз
всегда является равносторонним!
Действительно, в B) написано, что отрезок OiO2
получается из отрезка OiO3 поворотом на угол, рав-
„ п
НЫИ "о" •
Остается найти подходящее определяющее положе-
положение точки С. Его целесообразно выбирать так, чтобы
вся конфигурация была как можно более про-
простой. В данной задаче конфигурация выглядит весь-
весьма просто (рис. 34), если точка С занимает такое
положение, при котором треугольник ABC— равно-
равносторонний. Здесь имеет место симметрия: конфигу-
конфигурация совмещается сама с собой при повороте на
угол -о я вокруг центра треугольника ABC. Поэтому
треугольник O1O2O3 оказывается равносторонним, и
следовательно,
т. е. в этом положении действительно R = 0.
Упражнения. 1. Доказать, что утверждение задачи 1 спра-
справедливо, если треугольники ABC, ВСА', АСВ' заменить треугольни-
треугольниками ABC", ВСА", АСВ", симметричными им относительно сторон
треугольника ABC (рис. 35).
2. На сторонах произвольного треугольника ABC построены рав-
равносторонние треугольники ВСА', АСВ', ABC, так что вершины А' и
Рис. 35.
Рис. 36.
А, В' и В расположены соответственно по разные стороны от ВС и
АС, а С' и С по одну сторону от АВ (рис. 36). Доказать, что если
точка М есть центр треугольника ABC, то треугольник А'МВ' рав-
нобедренныи и угол при его вершине М равен -^ я.
О
3. На сторонах произвольного треугольника ABC вне него по-
построены равнобедренные треугольники ВСА', АСВ' и ABC с углами
при вершинах А', В' и С', соответственно равными а, р и у (рис. 37),
Доказать, что если
а + Р + Y = 2ft,
то углы треугольника А'В'С равны "о"> "§"' 2 ' т- е- не зависят
от формы треугольника ABC. Один частный случай этого утвержде-
утверждения известен как «задача Наполеона» (см. журнал «Кванг», 1972,
N° 6, стр. 29).
Задача 2. Дан четырехугольник ABCD. На сто-
сторонах его снаружи построены равнобедренные прямо-
прямоугольные треугольники ABM, BCP, CDQ и DAS
30
(рис. 38). Доказать, что отрезки MQ и SP равны и пер-
перпендикулярны.
Решение. Закрепим вершины А, В и D и начнем
двигать вершину С. Так как
RP = —LuaBC,
V2 т
ТО
/2 7
Аналогично
Перейдя от соотношения между скоростями к соотноше-
соотношению между радиусами-векторами, получим:
SP — UaSQ -j- const.
~2
Так как SQ = SM + MQ и SM = const, то
где R == const.
Выберем определяющее положение вершины С.
Например, совместим ее с вершиной А. Четырех-
Четырехугольник ABCD превратится
при этом в две пары слившихся
отрезков АВ = СВ и AD = CD
(рис. 39). Треугольники АВМ и
СВР образуют квадрат, по-
построенный на АВ как на диаго-
диагонали. Аналогично, треугольники
ADS и CDQ образуют квадрат
с диагональю AD. Отсюда сле-
п
на y
дует, что поворотом
треугольник ASP совмещается
с треугольником AQM (при этом
точка 5 совмещается с точкой -Q, а точка Р с точ-
точкой М). Поэтому для рассматриваемого положения
точки С
31
Таким образом здесь, а значит, и всегда
т. е. всегда
SP =
Но это равенство говорит о том, что отрезок SP
всегда получается из отрезка
MQ поворотом на прямой угол.
Следовательно,
SP=MQ, SPJLMQ.
Задача 3. На сторонах
произвольного параллелограмм
ма ABCD вне него построены
квадраты. Доказать, что их
центры М, Р, Q и S сами яв-
являются вершинами квадрата
(рис.40).
Решение. Закрепим точ-
точки А и D и будем двигать от-
отрезок ВС параллельно самому
себе. При этом точки В и С будут двигаться с одной и
той же скоростью. Эту же скорость будет иметь точка
Q — центр квадрата*), построенного на отрезке ВС.
Подсчитаем скорость точки S — центра квадрата,
построенного на отрезке CD. Так как
Рис. 40.
-4=-с/я
V2 -у
ТО
Аналогично,
Так как
vB = vc = vQ,
*) Весь квадрат будет двигаться, как говорят, поступательно,
32
то
Следовательно,
где
V2 4 V2 -7
i?i = const, Лг^ const.
В качестве определяющего возьмем то положение
отрезка ВС, в котором четырехугольник ABCD является
квадратом. Тогда окажется
Таким образом, уже не только в этом положении,
но и всегда
~ -j=UnMQ, MP = -^U „MQ,
четырехугольник
а эти равенства означают, что
MPQS — квадрат.
Упражнения. 4. Доказать, что утверждение задачи 3 сохра-
сохранится, если все квадраты заменить симметричными им относительно
сторон параллелограмма ABCD.
5. Дан четырех) гольник ABCD. Доказать, что если вершины Р
и S равнобедренных прямоугольных треугольников АВР и CDS сов-
совпадают Между собой, то совпадают так-
также и вершины Q и Т равнобедренных '
прямоугольных треугольников BCQ и
DAT (рис. 41). Все треугольники строятся
внутри четырехугольника ABCD.
В
Рис. 41.
6. Дан четырехугольник ABCD. На сторонах ВС и DA снаружи
и на сторонах АВ и CD внутри четырехугольника построены равно-
равнобедренные прямоугольные треугольники АВР, BCQ, CDS, DAT
33
(рис. 42). Доказать, что если вершины Р и 5 совпадают, то отрезок
QT проходит через них и делится ими пополам.
7. Доказать, что в задаче 1 отрезки АА', ВВ' и СС равны и,
2
пересекаясь в одной точке, образуют углы, равные -=- п.
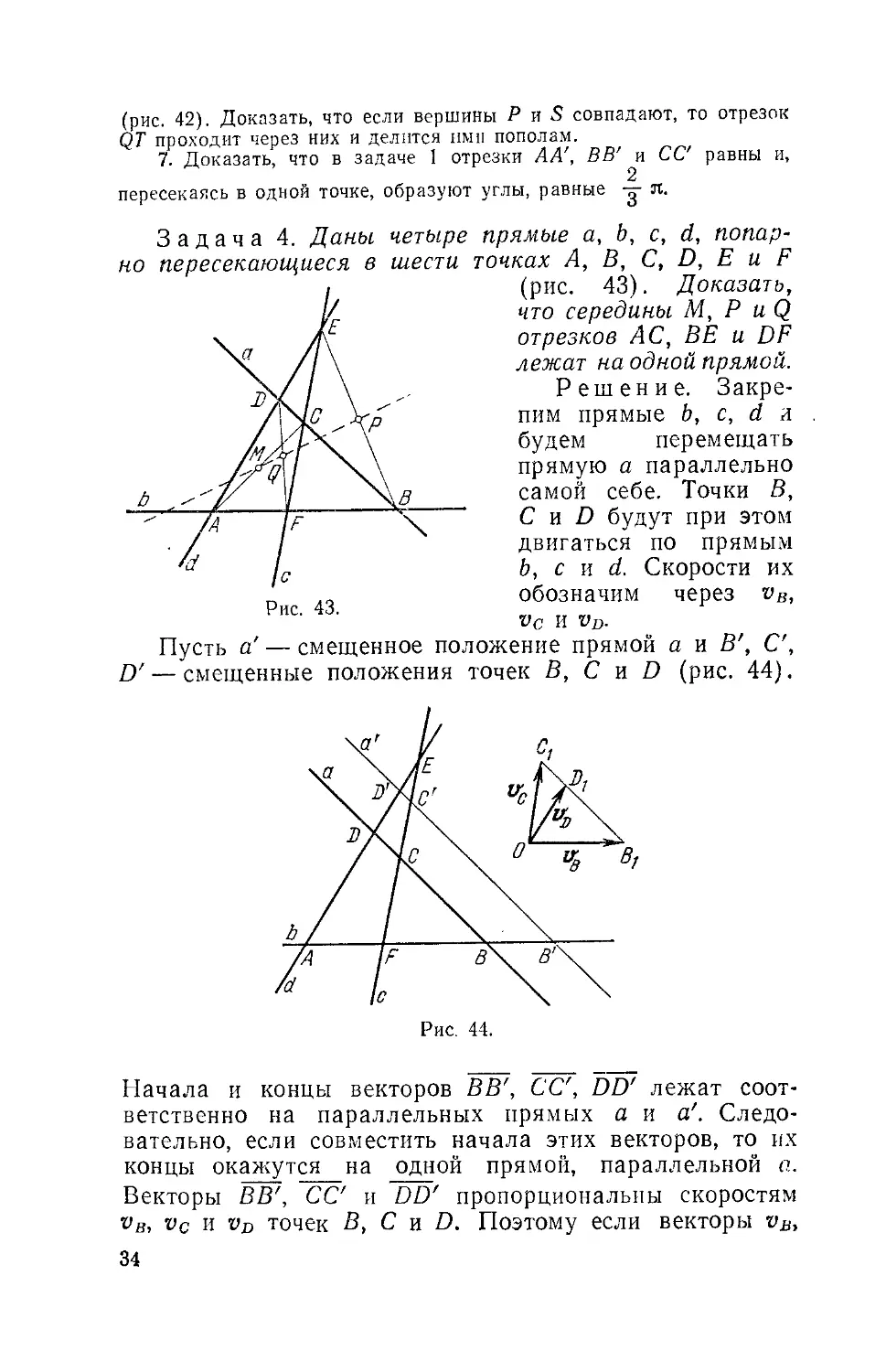
Задача 4. Даны четыре прямые а, Ь, с, d, попар-
попарно пересекающиеся в шести точках А, В, С, D, Е и F
i (рис. 43). Доказать,
что середины М, Р и Q
отрезков AC, BE и DF
лежат на одной прямой.
Решение. Закре-
Закрепим прямые Ь, с, d a
будем перемещать
прямую а параллельно
самой себе. Точки В,
С и D будут при этом
двигаться по прямым
Ь, с и d. Скорости их
„ ло обозначим через vB,
Hue. 4j. 1
VC И VD.
Пусть а' — смещенное положение прямой а и В', С,
D' — смещенные положения точек В, С и D (рис. 44).
Рис. 44.
Начала и концы векторов ВВ', СС, DD' лежат соот-
соответственно на параллельных прямых а и а'. Следо-
Следовательно, если совместить начала этих векторов, то их
концы окажутся на одной прямой, параллельной а.
Векторы ВВ', СС и DD' пропорциональны скоростям
vB, vc и vD точек В, С и D. Поэтому если векторы vB,
34
Vc и vD отложить из некоторой точки О, то их концы
В\, Cj и D, будут лежать на одной прямой (параллель-
(параллельной прямой а). Отсюда согласно теореме из § 1, п° 7
следует, что существуют такие постоянные числа ш
и п, что
C)
т + «
Точка М (см. рис. 43) является серединой отрез-
отрезАС, т. е. АМ = --А
то отсюда следует, что
ка АС, т. е. АМ = --АС. Так как точка А неподвижна,
1
Аналогично получаем равенства
D)
E)
В силу C) —E)
mvM + nv,
Q
т + п
Примем теперь неподвижную точку Е за полюс.
Рис. 45.
Тогда, последовательно, применяя теоремы 6' и 7', бу-
будем иметь:
тЁМ +пЩ
ЕР
¦ + R, R = const.
F)
35
Пусть прямая а в определяющем положении
проходит через точку Е (рис. 45). В этом положении
точки D и С совмещаются с точкой Е. Точки М, Q
и Р оказываются серединами отрезков АЕ, FE и BE.
Так как точки A, F и В лежат на одной прямой, то
точки М, Q и Р будут также лежать на одной пря-
прямой (параллельной Ь), Треугольники PEQ и В\С\О по-
подобны (стороны одного
параллельны сторонам
другого: РЕ\\а\\ВхСг<
PQ\\b\\OB,- EQWcWOCx).
Аналогично подобны
треугольники РЕМ и
BiDiO. Из подобия тре-
треугольников следует
PE
PQ'
Рис. 46.
OB i МР
Отсюда
МР __
PQ ~
OBi
т. е. точки Р и В\ делят соответственно отрезки MQ и
CtDt в одном и том же отношении. Но для точки Bi оно
равно т : п. Следовательно, и для точки Р оно равно
т : п, откуда
7Г75 тЁ1л + nE~Q
т + п
G)
Сравнивая равенства F) и G), видим, что в опреде-
определяющем положении R = 0. Но так как R = const, то
R = 0 всегда. Значит, всегда имеет место равенство
G) и точки М, Р, Q всегда лежат на одной прямой.
Упражнение 8. Доказать, что точки пересечения высот че-
четырех треугольников BCD, ABE, DEF, ACF, образованных четырьмя
попарно пересекающимися прямыми а, Ъ, с, d, лежат на одной пря-
прямой (рис. 46),
Задача 5. Пусть точка Р лежит на окружности
К., описанной вокруг треугольника ABC, и Pit Р2, Рз —
проекции точки Р на стороны ААВС (рис. 47). Дока-
Доказать, что точки Pi, P2, Рз лежат на одной прямой
(это — так называемая прямая Симпсона, соответствую-
соответствующая точке Р и треугольнику ABC),
36
Решение. Будем вращать стороны АС и ВС во«
круг точек А и В с одной и той же угловой скоро-
скоростью и. Точка С при этом перемещается по окруж-
окружности *) К- Так как углы PPiA и РР2А прямые, то
точка Р% движется по окружности Ки проходящей
через неподвижные точки А, Р, Рь При этом луч
РРг, будучи все время перпендикулярен к лучу АС,
Р(С,Рг,Р3)
Рис. 48.
вращается вокруг точки Р с той же угловой скоростью
со (согласно теореме 10 § 2). Поскольку лучи РР2 и
Р1Р2 вращаются так, что точка Р2 их пересечения дви-
движется по окружности Ки то угол между ними остается
постоянным. Следовательно, по теореме 10 их угловые
скорости равны. Поэтому угловая скорость луча PiP2
равна со. Аналогично равна со угловая скорость лу-
луча Р4Р3.
Итак, лучи Р1Р2 и Р1Р3 вращаются с одной и той
же угловой скоростью. Поэтому угол между ними
постоянен. Чтобы обнаружить, что он равен нулю
(и тем самым закончить доказательство), рассмотрим
положение, в котором точка С совпадает с точкой Р
(рис. 48). В этом положении Р2 совпадает с Р3 (и с Р
и С) и рассматриваемый угол равен нулю. Значит, он
равен нулю всегда.
Упражнения. 9. Пусть точки Р и Q лежат на окружности
К, описанной вокруг треугольника ABC. Доказать, что точка
*) В самом деле, так как угловые скорости лучей АС н ВС рав-
равны между собой, то согласно теореме 10 угол АСВ остается все
время постоянным и, следовательно, точка С движется по дуге ок-
окружности К-
37
пересечения соответствующих прямых Симпсона р и q (рис. 49)
описывает окружность К' при движении точки С по окружности К
(точки А. В, Р и Q считаются неподвижными),
10. Пусть точка Р лежит на окружности К, описанной вокруг
треугольника ABC, и Ри Рг, Рг — точки, симметричные с точкой Р.
Рис. 50.
относительно сторон треугольника ABC. Доказать, что точки Рь Р2
и Ръ лежат на одной прямой, проходящей через точку пересечения
высот треугольника ABC (рис. 50).
Задача 6. Доказать, что четыре окружности Ки
Кг, Кз и Ki, описанные вокруг четырех треугольников
ABD, BFC, CED и AFE, образо-
образованных четырьмя попарно пере-
пересекающимися прямыми а, Ь, с, d,
проходят через одну точку
(рис. 51).
Решение. Так как окружно-
окружности /Ci и Кг имеют общую точку
В, то они имеют еще одну общую
точку*). Обозначим ее через М.
Докажем, что М принадлежит
также Кз и Ki.
Закрепим точки В, С я
D и начнем вращать вокруг
них прямые Ь, с и d с одной
и той же угловой скоростью со. Так как угол BAD ос-
остается при этом постоянным (см. теорему 10 § 2), то
*) Если бы точка В была точкой касания окружностей К\ и К%
то треугольники ABD и BFC были бы подобны. При этом прямые
AD и FC должны были бы быть параллельны, что противоречит ^ус-
^условию, - -
38
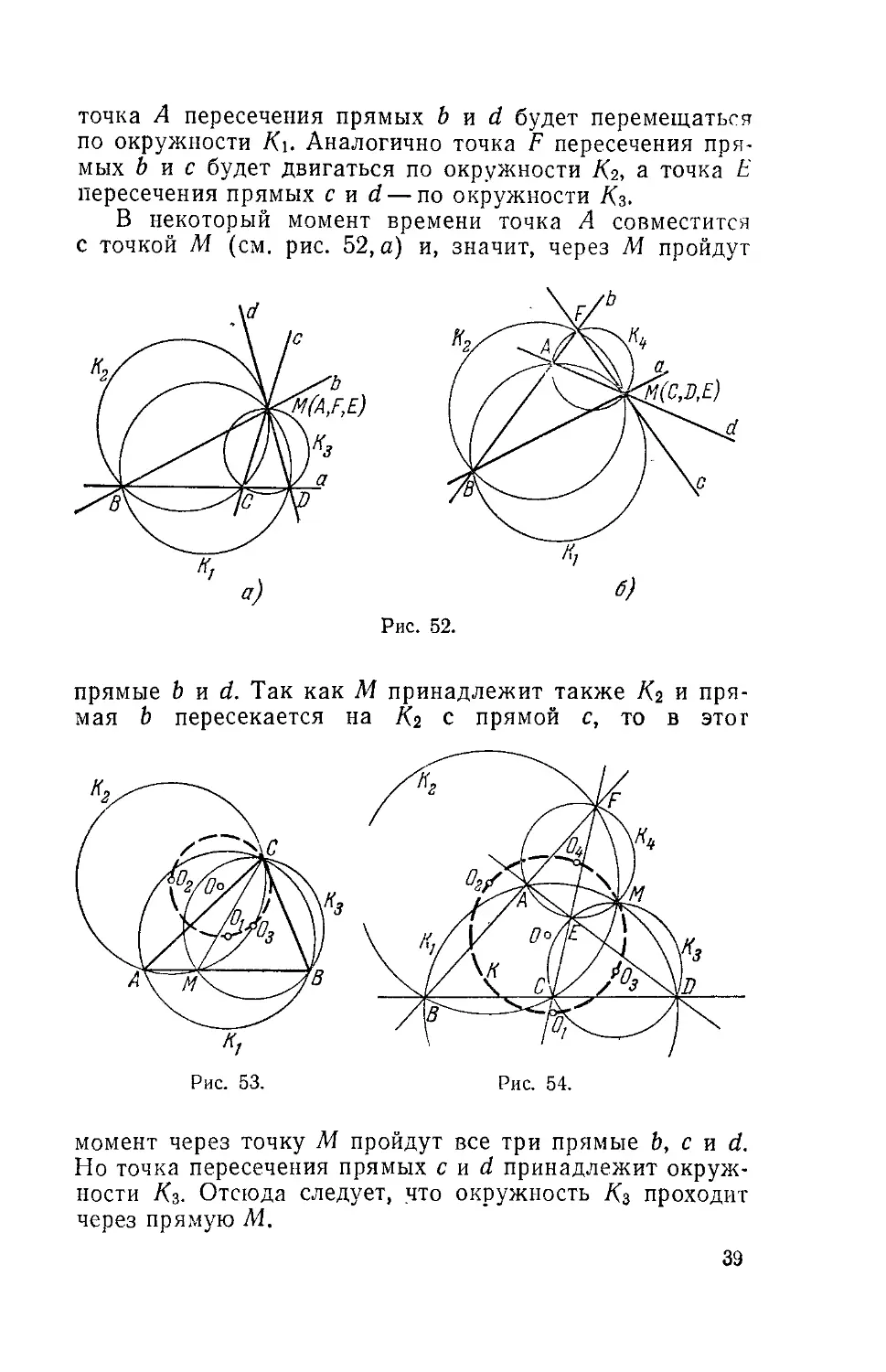
Рис. 51.
точка А пересечения прямых bud будет перемещаться
по окружности К\. Аналогично точка F пересечения пря-
прямых бис будет двигаться по окружности Яг, а точка Е
пересечения прямых cud— по окружности Яз.
В некоторый момент времени точка А совместится
с точкой М (см. рис. 52, а) и, значит, через М пройдут
Рис. 52.
прямые bud. Так как М принадлежит также Яг и пря-
прямая b пересекается на К2 с прямой с, то в этот
Рис. 53.
Рис. 54.
момент через точку М пройдут все три прямые Ь, с и d.
Но точка пересечения прямых cud принадлежит окруж-
окружности Яз. Отсюда следует, что окружность Яз проходит
через прямую М.
39
Чтобы доказать, что через точку М проходит так-
также окружность Ki, закрепим точки Д, А и F и бу-
будем вращать вокруг них прямые a, d и с с одной и
той же угловой скоростью (рис. 52,6). Аналогично
предыдущему докажем, что в некоторый момент все
три прямые a, d и с пройдут через точку М. Значит,
через точку М проходит
и 0КРУЖН0СТЬ -^4, на ко-
торой пересекаются пря-
прямые end.
Упражнения. 11. На
стороне АВ треугольника ABC
взята произвольная точка М.
Доказать, что центры Oi, O2 и
Оз окружностей, описанных во-
круг треугольников ABC, AMC
и ВМС, лежат на окружно-
сти, проходящей через точку С
(рис.53).
12. Теорема Штейнера. До-
Доказать, что центры окружностей
Ki, Кг, Кг, К\ (см. условие за-
дачи 6) лежат на одной окруж-
окружности. Эта окружность прохо-
проходит также через точку пересечения окружностей К\, Кг, Кз и Kt
(рис. 54).
Задача 7. Даны две окружности Ki и Kz (рис. 55),
пересекающиеся в точках А и В. Точка М, движущаяся
по окружности Ki, соединена с точками А и В. Пусть
N и Р — точки пересечения прямых МА и MB с окруж-
окружностью /<2. Доказать, что центр О окружности К, описан*
ной вокруг треугольника MNP, описывает окружность.
Решение. При движении точки М по окружно-
окружности Ki лучи AN и ВР вращаются вокруг точек А
и В с одной и той же угловой скоростью со. Угло-
Угловые скорости радиусов O2N и О2Р, проведенных из
центра О2 окружности Ki в точки N и Р, равны *) 2со.
Отсюда следует, что угол PO2N остается постоян-
постоянным и треугольник PO2N движется, оставаясь неиз-
неизменным. Так как длина хорды PN и угол PMN
Рис. 5э.
*) Действительно, пусть за промежуток времени [t, t + At] луч
AN повернется на некоторый угол NAN'. За этот же промежуток
времени радиус O2N повернется на угол NO2N', который как цен-
центральный равен удвоенному вписанному углу NAN'. Так как соот-
соотношение ZNO2N' = 2ZNAN' имеет место при любом At, то угловая
скорость радиуса O2N равна удвоенной угловой скорости луча AN.
40
Рис. 56.
постоянны, то окружность К, описанная вокруг тре-
треугольника MNP, движется, оставаясь неизменной.
Вместе с ее центром О и хордой PN движется, оста-
оставаясь неизменным, и треугольник PON. Отсюда сле-
следует, что движется, не изменяясь, и треугольник O2ON.
Так как его вершина О2 неподвижна, то точка О
описывает окружность.
Покажем, что радиус
этой окружности равен
радиусу окружности /Ci.
Для этого совместим точ-
точку М с точкой В (рис.
56). При этом секущая
МБР превратится в каса-
тельную к окружности К\
в точке В (см. п°2 § 2).
Хорда МА совпадет с
хордой АВ и точка N сов-
совместится с точкой В. Треугольник MNP «выродится»
в отрезок ВР (дважды покрытый). Центр О описанной
вокруг него окружности лежит в точке пересечения
перпендикуляра к хорде ВР, проведенного через ее се-
середину, и перпендикуляра к хорде АВ, проведенного
через точку В *). Отсюда следует, что четырехугольник
О%ОгОВ — параллелограмм и*О2О = Rt.
Итак, точка О описывает окружность с центром в
точке О2 и радиусом Ri.
Упражнения. 13. Доказать, что сторона PN треугольника
MNP (см. условие задачи 7) касается некоторой фиксированной
окружности.
14. Доказать, что точка пересечения высот треугольника MNP,
построенного в задаче 7, описывает окружность при движении
точки М. /
В заключение рассмотрим некоторые свойства
эллипса, гиперболы и параболы. Определения этих кри-
кривых будут даны ниже.
Эллипсом называется кривая, состоящая из веек
точек, сумма расстояний которых от двух заданных
точек Ft и Fz равна заданной постоянной величине
(рис. 57). Точки Fi и F2 называются фокусами эллипса.
*) Сторона МЛ' треугольника MNP выродилась в точку, но на-
направление этой вырожденной стороны определяется при переходе к
пределу и совпадает с направлением хорды АВ.
41
Задача 8. Доказать, что касательная к эллипсу
образует с радиусами-векторами, идущими из фокусов в
точку касания, равные углы. Обратно, если касательная
к кривой в каждой точке образует равные углы с радиу-
радиусами-векторами, идущими из двух фиксированных точек
Fi и F2 в точку касания, то эта кривая есть эллипс с фо-
фокусами в точках Fi и F2 (или дуга указанного эллипса).
М
Рис. 57.
Рис. 58.
Решение. Пусть точка М движется по эллипсу со
скоростью v. Проекции вектора v на радиусы-векторы *)
rl = FlM и r2 = F2M (рис. 58) соответственно равны
о, = npr v = — v cos a, i>2 = прГз v — v cos р, (8)
где аир — углы между ги г2 и касательной. Так .как
по определению эллипса |/"i| + |/|= const, то**)
Щ + Щ = 0.
Подставив сюда выражения длч vt и v2 из (8), полу-
получим:
v cos a — v cos p = 0,
или
cos а = cos p,
откуда а = р, так как аир — острые углы.
*) То есть на оси, направленные вдоль этих векторов.
**) Так как сумма |ri| + |г2| есть величина постоянная, то при-
приращения длин векторов ri и Га равны по абсолютной величине и
противоположны по знаку. Следовательно, и скорости изменения
длин вектор ri я Гз равны по абсолютной величине и противополож-
противоположны по знаку, Согласно п" 5 § 2 эти скорости как раз и есть vi и сг,
42
Обратно, пусть касательная к кривой L образует
с радиусами-векторами, идущими в точку касания
из фиксированных точек F4 и F2, равные углы. Про-
Проектируя скорость v точки, движущейся по кривой L,
Рис. 59-.
Рис. 60.
на радиусы-векторы Г\ и г2 этой точки, получимз
с»! = npn v = — v cos a, v2 = прг v = v cos а,
где а — угол между касательной и радиусами-вектора-
радиусами-векторами. Складывая эти равенства, получим:
откуда следует, что сумма длин радиусов-векторов rt
и г2 есть величина постоянная, т. е. кривая L является
эллипсом.
Гиперболой называется кривая, состоящая из всех
точек, разность расстояний которых от двух даннык
точек Ft и F2, называемых фокусами, есть величина по-
постоянная (рис. 59).
Упражнение. 15. Доказать, что касательная к гиперболе
является биссектрисой угла между радиусами-векторами, проведен-
проведенными из фокусов в точку касания (рис. 60).
Обратно, если касательная к кривой в каждой точке является
биссектрисой угла, образованного радиусами-векторами, идущими
из двух фиксированных точек Fi и F2 в точку касания, то кривая L
является гиперболой с фокусами в точках Ft и F2 (или дугой этой
гиперболы).
Параболой называется кривая, состоящая из всех то-
точек, расстояния которых от данной точки F, называемом
43
фокусом, и данной прямой d, называемой директрисой,
.равны между собой (рис. 61).
Упражнение. 16. Доказать, что касательная к параболе яв-
является биссектрисой угла между радиусом-вектором, проведенным из
фокуса F в точку касания, и перпендикуляром, опущенным из точки
касания на директрису d (рис. 62),
Рис. 61.
Рис. 62.
Обратно, пусть касательная к кривой в каждой точке является
биссектрисой угла, образованного радиусом-вектором, идущим из
фиксированной точки F в точку касания, и перпендикуляром, опу-
опущенным из точки касания на фиксированную прямую d. Тогда эта
кривая есть парабола с фокусом F и директрисой, параллельной d
(или дуга этой параболы).
В качестве дополнительных упражнений рекомен-
рекомендуем читателям решить кинематическим методом сле-
следующие задачи из журнала «Квант»: 1) 1970, № 4,
стр. 27, задача М18 (а); 2) 1971, № 4, стр. 33, зада-
задача М79; 3) 1973, № 4, стр. 43, задача М198; 4) 1974,
№ 11, стр. 40, задача М291; 5) 1974, № 12, стр. 44, за-
задача М297,
УКАЗАНИЯ К УПРАЖНЕНИЯМ
1. Решение аналогично решению задачи 1. Нужно заметить, что
теперь для равностороннего треугольника ABC точки Ои О2, О3
совместятся (треугольник O1O2O3 «выродится» в точку), и векторы
'O1O2 и О\О3 обратятся в нуль. Тем самым из равенства
получится, что R = 0.
2. Закрепить точки А, В и двигать точку С. Проследить при
этом за скоростями точек А', В'. В определяющем положении сов-
совместить точку С с точкой С.
3. Решение аналогично решению задачи 1. В определяющем по-
положении точку С совместить с одной из точек А или В.
4. Решение аналогично решению задачи 3.
5. Закрепить точки А и В и двигать точки С и D. При этом
движение точек С и D должно быть согласованным так, чтобы тре-
треугольник CSD с неподвижной вершиной S оставался равнобедрен-
равнобедренным треугольником. Показать, что Vq = vT.
6. Аналогично предыдущему упражнению показать, что vq =
= —Яг.
7. Аналогично задаче 1 доказать, что
АА' = U „СУС, Ш7 = илС7С.
~ Т 1
Отсюда вывести, что прямые АА', ВВ\ СС попарно пересекаются
на окружности, описанной вокруг треугольника ABC.
8. Закрепить прямые 6, с и d и двигать прямую а параллельно
самой себе с постоянной скоростью. Далее доказать, что
где Я = const, ц = const. Равенство нулю констант Ri и R2 устано-
установить, рассматривая два (!) определяющих положения: а проходит
через точку А, а проходит через точку В. Воспользоваться тем, что
вектор, коллинеарный одновременно двум пересекающимся прямым,
равен нулю.
9. При движении точки' С угловая скорость вращения прямых
Симпсона р и q равна угловой скорости вращения лучей АС и ВС.
10. Используя результат задачи 5, сначала доказать, что точки
Л> Яг, Рз лежат на одной прямой. Затем, закрепив точки Л, В и
45
Р, вращать вокруг точек А и В прямые АС и ВС с одной и той же
угловой скоростью. Рассмотреть угловые скорости прямых РЛ^з
и P\G. Определяющее Положение выбрать так же, как и в за-
задаче 5.
11. Закрепить точки А а С и вращать вокруг них прямые АВ,
СМ и СВ с одной и той же угловой скоростью. Проследить за дви-
движением точек Oj, Оа и Оз. Рассмотреть положение, в котором прямые
АС и АВ сливаются.
12. Закрепить точки В, С и D и вращать вокруг них прямые
BF, CF и DA с одной и той же угловой скоростью до тех пор,
пока они не пройдут через точку М. Далее использовать результат
предыдущего упражнения.
13. Воспользоваться тем, что длина хорды PN остается постоян-
постоянной (см. решение задачи 7).
14. Предварительно доказать, что расстояние от вершины тре-
треугольника до точки пересечения высот равно удвоенному расстоя-
расстоянию от центра окружности, описанной вокруг треугольника, до со-
соответствующей стороны. Это легко сделать без кинематики. Далее
воспользоваться тем, что при движении точек М, N и Р прямые О\М
и NP остаются перпендикулярными одна к другой, а расстояние ог
точки О до прямой NP — постоянным.
15. Решение аналогично решению задачи 8.
16. Решение аналогично решению задачи 8, но вместо скорости
изменения длины второго радиуса-вектора следует рассмотреть ско-
скорость изменения расстояния движущейся точки от директрисы.
СОДЕРЖАНИЕ
Введение it ......... 3
§ 1. Элементы векторной алгебры 6
§ 2, Элементы кинематики .......... 18
§ 3. Кинематический метод в геометрических задачах « 27
Указания к упражнениям ......' 45
Юрий Ильич Любич
и Леонид Абрамович Шор
КИНЕМАТИЧЕСКИЙ МЕТОД В ГЕОМЕТРИЧЕСКИХ
ЗАДАЧАХ
(Серия: «Популярные лекции по математике»)
-М.г 1976 г., 48 стр. с илл.
Редакторы Ф. И. Кизнер, В. В. Донченко
Техн. редактор Е. В. Морозова
Корректор Л. С. Сомова
Сдано в набор 11/VI11 1975 г.
Подписано к печати 19/11 1976 г.
Бумага тип. № 3 84Х108'/32- Физ. печ. л. 1,5.
Условн. печ. л. 2,52. Уч.-изд. л. 2,14.
Тираж 1ОЭООЭ экз. Цена 6 коп.
Заказ 859
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 2
имени Евгении Соколовой Союзполиграфпрома
при Государственном комитете Совета Министров
СССР по делам издательств, полиграфии
и книжной торговли.
198052, Ленинград, Л-52, Измайловский проспект, 29,
Цена 6 п.
ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
Вып. I. А. И. Маркушеаич. Возвратные последовательности.
Вып. 2. И. П. Натансон. Простевшие задачи на максиму и машшуш.
Вып. 3. И. С. Сомияскнй. Метод математической индукции.
Вып. 4. А. И. Маркушевич. Замечательные кривые.
Выи. 5. П. П. Коровкин. Неравенства.
Вып. 6. Н. Н. Воробьев. Числа Фибоначчи.
Выя. 7. А. Г. Курош. Алгебраические уравнения произвольных стеиеяея.
Вып. 8. А. О. Гельфоид. Решение уравнений в целых числах.
Вып. 9. А. И. Маркушевич. Площади н логарифмы.
Вып. 10. А. С. Смогоржеаский. Метод координат.
Выл. II. Я- С. Дубнов. Ошибки в геометрических доказательствах.
Вып. 12. И. Л. Натансон. Суммирование бесконечно малых величин.
Вып. 13. А. И. Маркушевич. Комплексные числа и конформные отобра-
отображения.
Вып. 14. А. И. Фетисов. О доказательствах в геометрии.
Вып. 15. И. Р. Шафаревич. О решении уравнений аысших степеней.
Вып. 16. В. Г. Шераатов. Гиперболические функции.
Вып. 17. В. Г. Болтянский. Что такое дифференцирование?
Выи. 18. Г. AL Мнракьян. Примой круговой цилиндр.
Выл. 19. Л. А. Люстериик. Кратчайшие линии.
Вып. 20. А. М. Лопшнц. Вычисление площадей ориентированных фигур.
Вып. 21. Л. И. Головина и И. М. Яглон. Индукция в геометрии.
Вьш. 22. В. Г. Болтянский. Равновеликие и равиосоставленкые фигуры.
Вып. 23. А. С. Смогоржевскнй, О геометрии Лобачевского.
Вып. 24. Б. И. Аргуиоа я Л. А. Скорнвков. Конфигурационные теоремы.
Вып. 2S А. С. Смогоржевскнй. Линейка в геометрически * построениях.
Вып. 26. Б. А. Трахтенброт. Алгоритмы и машинное решение задач.
Вып. 27. В. А. Успенский. Некоторые приложения механики к матема-
математике.
Вып. 28. Н. А. Архангельский н Б. И. Зайцев. Автоматические цифровые
машины.
Вып. 29. А. Н. Костовский. Геометрические построения одним циркулем
Вып. 30. Г. Е. Шилов. Как строить графики.
Вып. 31. А. Г. Дорфмаи. Оптика конических сечений.
Вып. 32. Е. С. Вентцель. Элементы теории игр.
Вып. 33. А. С. Барсов. Что такое линейное программирование.
Вып. 34. Б. Е. Маргулис. Системы линейных уравнений.
Вып. 35. Н. Я. Вилеикни. Метод последовательных приближения
Вып. 36. В. Г. Болтянский. Огибающая.
Вып. 37. Г. Е. Шнлоа. Простая гамма (устройство ыуэыкалыюА шкальи
Вып. 38. Ю. А. Шрейдер. Что такое расстояние?
Вып. 39. И. Н. Воробьев. Признаки делимости.
Вып. 40. С. В. Фомин. Системы счисления.
Вып. 41. Б. Ю. Коган. Приложение механики к геометрии.
Вып. 42. Ю. И. ЛюОич н Л. А. Шор. Кинематический метод в геометри-
геометрических задачах.
Вып. 43. В. А. Успенский. Треугольники Паскаля.
Вып. 44. И. Я. Бакельмаи. Инверсия.
Вып. 45. И. М. Яглом. Необыкновенная алгебра.
Вып. 46. И. М. Соболь. Метод Монте-Карло.
Вып. 47. Л. А. Калужнии. Основная теорема арнфметнк|.
Вып. 48. А. С. Солодовников. Системы линейных неравенств.
Вып. 49. Г. Е. Шилов. Математический анализ в области рациональных
функций.
Вып. SO. В. Г. Болтянский. И. Ц. Гохберг. Разбиение фигур иа меньшие
части.
Вып. 51. И. М. Бескин. Изображения пространственных фигур.
Вшп 52. И М. Веский. Явление отрезка в данном отпошенни.
Вьш. 33. Б. А. Розенфельд и Н. Д. Сергеева, Стереографическая про-
проекция.