Ф. Д. ГАХОВ
КРАЕВЫЕ ЗАДАЧИ
ИЗДАНИЕ ТРЕТЬЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1977

517.2
Г 25
УДК 517.11
Краевые задачи. Ф. Д. Гахов Изд. 3-е.
Главная редакция физико-математической литературы
издательства «Наука», 1977.
В настоящей книге рассматриваются краевые
задачи теории аналитических функций и
дифференциальных уравнений эллиптического типа и их
приложения к особым (сингулярным) интегральным
уравнениям с ядрами Коши, Гильберта, степенными,
логарифмическими и некоторыми другими.
Изложение ограничивается линейными задачами для одной
неизвестной функции.
В настоящем издании книга значительно
дополнена. Заново написан ряд новых параграфов.
Дополнения ориентированы на новые работы, появившиеся
за время между вторым и третьим изданиями.
Илл. 18, библ. 366.
Федор Дмитриевич Гахов
КРАЕВЫЕ ЗАДАЧИ
М., 1977 г. 640 стр. с илл.
Редактор И. Е. Морозова
Техн. редактор И. Ш. Аксельрод Корректор В. П. Сорокина
Сдано в набор 10. 09. 76. Подписано к печати 18. 02 77. Бумага 60X90!/ie тип. № 1.Физ. печ.
л. 40. Условн. печ. л. 40. Уч.-изд. л. 42,49. Тираж 7 000 экз. Т-04117. Цена книги 2 р. 94 к.
Заказ № 305
Издательство «Наука»
Главная редакция физико-математи-юской литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 2 имени Евгении
Соколовой Союзполиграфпрома при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли. 198052, Ленинград, Л-52,
Измайловский пр , 29
20203—043 © Главная редакция
Г Пго/ло\ 77 39-76 физико-математической литературы
Uoo(Uz)-// издательства «Наука», 1977, с изменениями.

ОГЛАВЛЕНИЕ
Предисловие к третьему изданию 9
Из предисловия к первому изданию 11
Введение 13
Глава I. Интеграл типа Коши 15
§ 1. Определение интеграла типа Коши и примеры 15
§ 2. Функции, удовлетворяющие условию Гёльдера 19
2.1. Определения и свойства ( 19 ). 2.2. Функции многих переменных. ( 21 ).
§ 3. Главное значение интеграла типа Коши 22
3.1. Несобственный интеграл ( 22 ). 3.2. Главное значение особого
интеграла ( 23 ). 3.3. О многозначных функциях ( 24 ). 3.4. Главное значение
особого криволинейного интеграла ( 27 ). 3.5. Свойства особого интеграла ( 30 ).
§ 4. Предельные значения интеграла типа Коши. Интегралы по
действительной оси 33
4.1. Основная лемма ( 33 ). 4.2. Формулы Сохоцкого ( 37 ). 4.3. Условие того,
что произвольная комплексная функция есть краевое значение
аналитической в области функции ( 39 ). 4.4. Предельные значения производных.
Производные предельных значений и дифференцирование особого
интеграла ( 42 ). 4.5. Формулы Сохоцкого для угловых точек контура ( 44 ).
4.6. Интегралы типа Коши по действительной оси ( 44 ). 4.7. Формулы
Коши ( 49 ).
§ 5. Свойства предельных значений интеграла типа Коши 52
5.1. Предельные значения удовлетворяют условию Гёльдера ( 52 ).
5.2. Расширение предположений ( 55 ). 5.3. Интеграл типа Коши в
классах Lp ( 57 ).
§ 6. Формулы Гильберта для предельных значений действительной
и мнимой частей аналитической функции 58
6.1. Ядро Коши и ядро Шварца ( 58 ). 6.2. Формулы Гильберта ( 59 ).
§ 7. Перестановка порядка интегрирования в повторном особом
интеграле 60
7.1. Случай, когда один интеграл обыкновенный ( 60 ). 7.2. Формула
перестановки ( 62 ). 7.3. Обращение особого интеграла с ядром Коши для
замкнутого контура ( 65 ).
§ 8. Поведение интеграла типа Коши на концах контура
интегрирования и в точках разрыва плотности 66
8.1. Случай плотности, удовлетворяющей условию Гёльдера вплоть до
концов ( 66 ). 8.2. Случай разрыва первого рода ( 67 ). 8.3. Частный случай
особенности степенного характера ( 68 ). 8.4. Общий случай особенности
степенного порядка ( 72 ). 8.5. Особенность логарифмического типа ( 74 ).
8.6. Особенность степенно-логарифмического типа ( 75 ). 8.7. Интеграл типа
Коши по сложному контуру ( 76 ).
§ 9. Предельные значения обобщенных интегралов и двойных
интегралов типа Коши 78
9.1. Постановка вопроса ( 78 ). 9.2. Формулы, аналогичные формулам
Сохоцкого для интеграла типа Коши ( 78 ). 9.3. Формула перестановки по-

4
ОГЛАВЛЕНИЕ
рядка интегрирования ( 80 ). 9.4. Кратные интегралы типа Коши.
Постановка вопроса ( 81 ). 9.5. Особый двойной интеграл Формула Пуанкаре —
Бертрана ( 81 ). Формулы Сохоцкого ( 82 ).
§ 10. Интеграл типа Коши и потенциалы 84
§11. Исторические сведения 86
Задачи к главе I 87
Глава И. Краевая задача Римана 95
§ 12. Некоторые вспомогательные теоремы 95
12.1. Принцип непрерывности. Продолжение по симметрии ( 95 ). 12.2.
Принцип аргумента. Обобщенная теорема Лиувилля ( 99 ).
§ 13. Индекс 101
13.1. Определение и основные свойства ( 101 ). 13.2. Вычисление индекса ( 102 ).
13.3. Частичные индексы функции двух переменных ( 105 ).
§ 14. Задача Римана для односвязной области 106
14.1. Постановка задачи ( 106 ). 14.2. Отыскание кусочно-аналитической
функции по заданному скачку ( 106 ). 14.3. Каноническая функция ( 107 ). 14.4.
Решение однородной задачи ( 109 ). 14.5. Решение неоднородной
задачи ( 111 ). 14.6. Примеры ( 113 ). 14.7. Задача Римана для
полуплоскости ( 118 ). 14.8. Двумерная задача о скачке ( 121 ). 14.9. Постановка задачи
Римана для бицилиндрических областей ( 123 ). 14.10. Некоторые результаты,
относящиеся к многомерной задаче Римана ( 129 ).
§ 15. Исключительные случаи задачи Римана 130
15.1 Однородная задача ( 131 ). 15.2. Неоднородная задача ( 133 ). 15.3. О
корректности постановки краевой задачи Римана ( 138 ).
§ 16. Задача Римана для многосвязной области. Некоторые новые
результаты 139
16.1. Постановка задачи ( 139 ). 16.2. Решение задачи ( 141 ) 16.3. Некоторые
другие результаты ( 144 ).
§ 17. Краевая задача Римана со сдвигом 146
17.1. Постановка задачи и общие замечания ( 146 ). 17.2. Задача с нулевым
скачком ( 147 ). 17.3. Задача с заданным скачком ( 150 ). 17.4. Однородная
задача с нулевым индексом ( 152 ). 17.5. О сведении задачи со сдвигом
к обыкновенной задаче Римана ( 153 ).
§ 18. Другие обобщенные задачи 157
18.1. Постановка задач ( 157 ). 18.2. Краевая задача Гильберта со
сдвигом ( 158 ). 18.3. Краевая задача Карлемана ( 163 ).
§ 19. Исторические сведения 166
Задачи к главе II 167
Глава III. Особые интегральные уравнения с ядром Коши 171
§ 20. Основные понятия и обозначения 171
20.1. Особое интегральное уравнение ( 171 ). 20.2. Основные результаты
теории интегральных уравнений Фредгольма ( 173 ).
§ 21. Характеристическое уравнение 176
21.1. Сведение к краевой задаче Римана ( 176 ). 21.2. Решение
характеристического уравнения ( 178 ). 21.3. Решение уравнения, союзного
характеристическому ( 181 ). 21.4. Примеры ( 182 ). 21.5. Полные особые уравнения,
разрешаемые в замкнутой форме ( 183 ). 21.6. Уравнение на действительной оси.
Исчезающие на бесконечности решения ( 188 ). 21.7. Уравнение на
действительной оси. Решение в классе ограниченных на бесконечности
Функций ( 190 ). 21.8. Случай а (оо)=#=0 ( 191 ). 21.9. Случай а (оо)е=0 ( 192 ). 21.10
Уравнение, аналогичное характеристическому ( 194 ). 21.11. Приближенное
решение ( 194 ). 21.12. Поведение решения п угловых точках ( 196 )
§ 22. Регуляризация полного уравнения 198
22.1. Композиция особых операторов ( 198 ). 22.2. Регуляризующий
оператор ( 201 ). 22.3. Способы регуляризации ( 203 ). 22.4. Связь между
решениями особого и регуляризованного уравнений ( 204 ).

ОГЛАВЛЕНИЕ
5
§ 23. Основные свойства особых уравнений 206
23.1. Некоторые свойства союзных операторов ( 206 ). 23.2 Основные
теоремы об особых интегральных уравнениях (теоремы Нётера ) ( 208 ). 23.3
Некоторые следствия ( 212 ). 23.4. Общая теория нётеровых операторов ( 214 ).
23 5 Особые интегральные уравнения со сдвигом Карлемана ( 215 ).
23.6. Особые интегральные уравнения, содержащие комплексно
сопряженную неизвестную функцию ( 219 ). 23.7 Бисингулярное уравнение ( 220 ).
§ 24. Равносильная регуляризация. Третий способ регуляризации . . 222
24.1. Постановка вопроса Различные толкования понятия равносильной
регуляризации ( 222 ). 24.2. Равносильная регуляризация оператора ( 223 ).
24.3. Равносильная регуляризация слева особого уравнения.
Необходимое условие ( 224 ). 24.4. Сопряженное уравнение. Другая форма условий
разрешимости неоднородного уравнения ( 225 ). 24.5. Теорема о
равносильной регуляризации уравнения. Сингулярная резольвента. Сингулярное
решение ( 228 ). 24-6. Регуляризация решением характеристического
уравнения (способ Карлемана —Векуа ) ( 232 ). 24.7. Пример ( 236 ).
§ 25. Исключительные случаи особых интегральных уравнений ... 241
25.1. Решение характеристического уравнения ( 242 ). 25.2. Регуляризация
полного уравнения ( 244 ). 25.3. О сведении исключительного случая
особых интегральных уравнений с ядром Коши к уравнениям нормального
типа ( 246 ). 25.4. Вырожденные случаи ( 249 ).
§ 26. Исторические сведения 257
Задачи к главе III 259
Глава IV. Краевая задача Гильберта и особые интегральные
уравнения с ядром Гильберта 264
§ 27. Постановка задачи Гильберта и некоторые вспомогательные
формулы 264
27.1. Постановка задачи Гильберта ( 264 ). 27.2. Оператор Шварца для одно-
связной области ( 265 ). 27.3. Определение аналитической функции,
имеющей полюс, по значениям ее действительной части на контург
(задача А ) ( 269 ). 27.4. Обобщенная задача А0 ( 271 ).
§ 28. Регуляризующий множитель 273
28.1. Определение регуляризующего множителя ( 273 ). 28.2.
Действительный регуляризующий множитель ( 275 ). 28.3. Регуляризующий множитель
с постоянным модулем ( 277 ). 28.4. Другие виды регуляризующего
множителя ( 278 ).
§ 29. Краевая задача Гильберта для односвязной области 280
29.1. Однородная задача ( 280 ). 29.2. Неоднородная задача ( 281 ). 29.3.
Задача для единичного круга и полуплоскости ( 282 ). 29.4. Задача
Гильберта для внешней области ( 285 ). 29.5. Примеры ( 287 ).
§ 30. Связь краевых задач Гильберта и Римана 289
30.1. Постановка вопроса ( 289 ). 30.2. Связь между краевыми
условиями ( 290 ). 30.3. О задаче Гильберта для бикруга ( 291 ).
§ 31. Особое интегральное уравнение с ядром Гильберта 292
31.1. Связь характеристического уравнения с краевой задачей
Гильберта ( 292 ). 31.2. Решение уравнения ( 293 ). 31.3. Уравнения с постоянными
коэффициентами ( 296 ). 31.4. Полное уравнение ( 298 ).
§ 32. Краевые задачи для полигармонических и полианалитических
функций, приводимые к краевым задачам Гильберта и Римана 300
32.1. Представление полигармонических и полианалитических функций
через аналитические ( 300 ). 32.2. Постановка краевых задач Гильберта для
полнаналитических функций ( 303 ). 32.3. Краевые задачи для круга ( 305 ).
32.4. Краевые задачи для областей, отображающихся на круг
рациональными функциями ( 310 ). 32.5. Решение основной задачи теории упругости
для области, ограниченной улиткой Паскаля ( 312 ). 32.6. Краевые задачи
Римана ( 316 ).
§ 33. Обратная краевая задача аналитических функций 319
33.1. Постановка задачи ( 320 ). 33 2 Решение внутренней задачи ( 321 ).
33.3. Другие способы задания ( 324 ). 33 4. Решение внешней задачи ( 324 ).
13.5. О числе решений внешней задачи ( 327 ). 33.6. О задаче Шварца с ло-

6
ОГЛАВЛЕНИЕ
гарифмической особенностью на контуре ( 329 ). 33.7. Особые точки
контура ( 331 ). 33 8. Об однолистности решения ( 333 ). 33.9. Некоторые
дополнительные вопросы ( 336 ).
§ 34. Исторические сведения 338
Задачи к главе IV 340
Глава V. Различные обобщенные краевые задачи 344
§ 35. Краевая задача типа задачи Гильберта с краевым условием,
содержащим производные 344
35.1. Постановка задачи и различные формы краевого условия ( 344 ).
35.2. Представление аналитической функции интегралом типа Коши с
действительной плотностью ( 347 ). 35.3. Интеграл типа Коши, плотность
которого есть произведение заданной комплексной функции на
некоторую действительную ( 350 ). 35.4. Интегральное представление
аналитической функции, т-я производная которой представляется интегралом
типа Коши ( 354 ). 35.5. Сведение краевой задачи к интегральному
уравнению Фредгольма ( 357 ). 35.6. Вопросы разрешимости краевой задачи ( 359 ).
35.7. Другие методы исследования ( 363 ).
§ 36. Краевая задача типа задачи Римана с краевым условием,
содержащим производные 365
36.1. Интегральное представление для кусочно аналитических
функций ( 366 ). 36.2. Решение краевой задачи ( 368 ). 36 3. Новый способ
решения задачи ( 372 ). 36.4. Особое интегро-дифференциальное уравнение ( 374 ).
§ 37. Краевая задача Гильберта для многосвязной области 375
37.1. Задача Дирихле для многосвязной области ( 376 ). 37.2. Оператор
Шварца для многосвязной области ( 381 ). 37.3. Различные формы
постановки краевой задачи Гильберта для многосвязной области ( 385 ).
37.4. Метод регуляризующего множителя в случае многосвязной
области ( 386 ). 37.5. О нахождении регуляризующего множителя в случае
многосвязной области ( 390 ). 37.6. Интегральное уравнение задачи
Гильберта ( 392 ). 37.7. Союзное интегральное уравнение и союзная задача
Гильберта ( 393 ). 37.8. Исследование вопросов разрешимости ( 396 ). 37.9.
Исследование случаев *с=*0 и и=гт—1 ( 399 ). 37.10. Связь с отображением
на плоскость с разрезами ( 403 ). 37.11. Заключительные замечания ( 406 ).
37.12. Некоторые новые результаты ( 407 ).
§ 38. Обратная краевая задача для многосвязной области 408
38.1. Постановка задачи ( 408 ). 38.2. Решение внутренней задачи ( 409 ).
38.3. Условия разрешимости ( 410 ).
§ 39. Краевая задача типа задачи Римана для многосвязной области
и краевые задачи со сдвигом и сопряжением 412
39.1. Интегральное представление ( 412 ). 39.2. Краевая задача и интегро-
дифференциальное уравнение ( 415 ). 39.3. Краевая задача с
сопряжением ( 416 )« 39.4. Дальнейшие обобщения ( 419 ).
§ 40. Исторические сведения 422
Задачи к главе V 423
Глава VI. Краевые задачи и особые интегральные уравнения с
разрывными коэффициентами и с разомкнутыми контурами 427
§ 41. Решение задачи Римана с разрывными коэффициентами
приведением к задаче с непрерывными коэффициентами 428
41.1. Постановка задачи и определение функции по скачку ( 428 ). 41.2.
Фундаментальные вспомогательные функции ( 430 ). 41.3. Приведение к задаче
с непрерывными коэффициентами. Простейший случай ( 431 ). 41.4.
Решение однородной задачи ( 433 ). 41.5. Решение неоднородной задачи ( 435 ).
§ 42. Краевая задача Римана для разомкнутых контуров 439
42.1. Постановка и решение задачи ( 439 ). 42.2. Пример ( 442 ). 42.3.
Обращение интеграла типа Коши ( 444 ).
§ 43. Непосредственное решение задачи Римана 447
43.1. Задача для разомкнутого контура ( 447 ). 43.2. Задача с разрывными
коэффициентами ( 448 ). 43.3. Примеры ( 449 ). 43.4. Краевая задача Карле-
мана. Продолжение ( 452 ). 43.5. Заключительные замечания ( 454 ).

ОГЛАВЛЕНИЕ
7
§ 44. Задача Римана для сложного контура. Исключительные случаи 455
44.1. Постановка задачи ( 455 ). 44.2. Новый метод решения задачи Римана
для замкнутой кривой ( 456 ). 44.3. Общий случай ( 457 ). 44.4. Случай
совпадения концов ( 460 ). 44.5. Исключительные точки на концах контура ( 461 ).
§ 45. Краевая задача Гильберта для кусочно аналитической функции 462
45.1. Постановка задачи ( 462 ). 45.2. Отыскание решения ( 463 ). 45.3.
Исследование разрешимости ( 465 ).
§ 46. Краевая задача Гильберта с разрывными коэффициентами . . 466
46.1. Задача Гильберта для полуплоскости ( 467 ). 46.2. Пример ( 469 ).
46.3. Смешанная краевая задача аналитических функций ( 472 ). 46.4.
Задача Дирихле и ее видоизменения для плоскости со щелями ( 474 ).
§ 47. Характеристическое уравнение для разомкнутых контуров . . . 480
47.1. Основные понятия и обозначения ( 480 ). 47.2. Решение
характеристического уравнения ( 482 ). 47.3. Решение уравнения, союзного с
характеристическим ( 487 ). 47.4. Примеры ( 488 ). 47.5. Уравнение на
действительной полуоси ( 489 ). 47.6 О методе неполной факторизации ( 491 ). 47.7.
Характеристическое уравнение в банаховых пространствах ( 496 ).
§ 48. Полное уравнение для разомкнутых контуров и разрывных
коэффициентов 496
48.1. Регуляризация решением характеристического уравнения ( 497 ).
48.2. Исследование регуляризованного уравнения ( 498 ). 48.3.
Характеристическое уравнение на сложном контуре и с разрывными
коэффициентами ( 500 ). 48.4. Регуляризация полного особого уравнения ( 504 ).
48.5. Основные свойства особого уравнения ( 508 ). 48.6. Теория Нётера
особых уравнений со сдвигом Карлемана на разомкнутом контуре ( 509 ).
§ 49. Краевая задача Римана с бесконечным индексом 510
49.1. Некоторые сведения из теории функций ( 510 ). 49.2. Однородная
задача с бесконечным индексом степенного порядка в случае
одностороннего завихрения ( 512 ). 49.3. Неоднородная задача с бесконечным
индексом степенного порядка для одностороннего завихрения ( 517 ).
49.4. Задача с бесконечным индексом логарифмического порядка для
одностороннего завихрения ( 518 ). 49.5. Случай двустороннего
завихрения ( 520 ). 49.6. Задача на счетном множестве контуров ( 522 ).
§ 50. Исторические сведения 523
Задачи к главе VI 525
Глава VII. Интегральные уравнения, разрешимые в замкнутой форме 532
§ 51. Уравнения с автоморфными ядрами с конечной группой .... 533
51.1. Некоторые сведения о конечных группах дробно-линейных
преобразований и об автоморфных функциях ( 534 ). 51.2. Приведение одного
полного особого интегрального уравнения к краевой задаче ( 537 ). 51.3.
Решение краевой задачи ( 540 ). 51.4. Решение интегрального уравнения ( 543 ).
51.5. Пример ( 544 ). 51.6. Случай, когда вспомогательная аналитическая
функция не обращается на бесконечности в нуль ( 546 ). 51.7.
Дополнительные замечания ( 549 ).
§ 52. Уравнения с автоморфными ядрами с бесконечной группой . . 550
52.1. Краевая задача Римана ( 550 ). 52.2. Особое интегральное
уравнение ( 553 ). 52.3. Некоторые приложения ( 554 ). 52.4. Интегральное
уравнение с неосновной автоморфной функцией ( 560 ). 52.5. Пример ( 562 ).
§ 53 Краевые задачи на римановых поверхностях 564
53.1. Некоторые сведения о римановых поверхностях ( 564 ). 53.2. Краевая
задача Римана ( 567 ). 53.3. Краевая задача Гильберта ( 568 ). 53.4.
Различные обобщенные задачи ( 569 ). 53.5. Принцип локально-конформного
склеивания ( 570 ). 53.6. Симметрия относительно алгебраической кривой ( 571 ).
§ 54 Интегральные уравнения со степенным ядром 572
54.1. Интегральное уравнение Абеля ( 572 ). 54.2. Связь особого интеграла
с ядром Коши с интегралами со степенным ядром ( 573 ). 54.3.
Обобщенное уравнение Абеля с внешними коэффициентами ( 575 ). 54.4.
Обобщенное уравнение Абеля с внутренними коэффициентами ( 577 ). 54.5. Случай
постоянных коэффициентов ( 578 ). 54.6. Полные уравнения со степенным
ядром ( 580 ). 54.7. Уравнения со степенным ядром на бесконечной
прямой ( 582 ). 54.8. Некоторые другие результаты ( 584 ).

8
ОГЛАВЛЕНИЕ
§ 55. Интегральные уравнения с логарифмическим ядром 585
55.1. Характеристическое уравнение с логарифмическим ядром ( 585 ).
55.2 Уравнение с логарифмической особенностью в правой части ( 588 ).
55.3. Обобщенное уравнение Карлемана ( 589 ). 55.4. Некоторые другие
типы интегральных уравнений с логарифмическим ядром ( 593 ).
§ 56. Исторические сведения 596
Задачи к главе VII 597
Приложение I. Индекс как гомотопический инвариант 604
Приложение II. Оператор с полярно-логарифмическим ядром . . . . 606
Приложение III. Использование краевых задач в теории
приближения функций 609
Приложение IV. Применение краевой задачи Римана в теории
массового обслуживания 615
Литература 624
Предметный указатель 639

Светлой памяти
Николая Ивановича
МУСХЕЛИШВИЛИ
посвящается
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
За 13 лет, прошедших со времени второго издания,
излагаемые здесь теории интенсивно развивались. Опубликованы сотни
оригинальных работ, ряд обзоров. Некоторые разделы
(например, краевые задачи со сдвигом и сопряжением, различные типы
особых интегральных уравнений, разрешаемых в замкнутой
форме), прежде состоявшие лишь из разрозненных эпизодических
исследований, не только пополнялись новыми важными
результатами, но в значительной степени приняли стройный, близкий
к завершению вид. Возникли новые, принципиально важные и
имеющие перспективу дальнейшего развития дисциплины:
теория краевых задач с бесконечным индексом, теория краевых
задач для функций многих переменных и др.
Обогатились связи с прикладным знанием. Кроме ставших
уже традиционными приложений к механике сплошной среды
или к некоторым другим разделам математической физики
(электродинамике, теории дисперсионных соотношений и др.),
установлены связи с новыми прикладными дисциплинами:
теорией массового обслуживания, теорией игр и др.
Усложнился используемый математический аппарат. В
значительных объемах используются теории алгебраических и ав-
томорфных функций, римановых поверхностей, целых и меро-
морфных функций, функционального анализа, топологии и др.
Кроме того, возникло обратное взаимодействие: теория краевых
задач аналитических функций плодотворно используется для
решения задач других математических дисциплин. В первую
очередь можно указать на работы Ю. А. Казьмина по теории
приближения функций (см. приложение III), а также решение
Н. В. Говоровым задачи Винера — Пэйли теории целых
функций и Э. И. Зверовичем классической проблемы обращения
Якоби.
В связи со сказанным, книга подверглась серьезной
переработке. Наибольшие изменения претерпели главы II, III, VI, VII.
Написаны дополнения I—IV. Кроме того, в разных частях
книги внесено большое число небольших дополнений и
значительно переработан весь прежний текст.

10 ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Автор старался сохранить доступность книги широкому
кругу читателей: в основном материале сохранен элементарный
характер изложения. Вопросы, опирающиеся на более сложный
аппарат, даны в виде дополнений к основному тексту.
При подготовке настоящего издания мне оказали ценную
помощь В. А. Какичев, А. А. Килбас, С. Г. Самко и многие
другие мои ученики. Всем им я выражаю глубокую
признательность.
Автор

ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Настоящая книга имеет в своей основе курс лекций,
читанных автором, начиная с 1947 г., студентам сначала Казанского,
а затем Ростовского университетов. Имея перед собой в течение
ряда лет живую аудиторию, за которой можно было следить во
время лекции и впоследствии на экзаменах, автор, понятно,
уделял много внимания вопросам ясности и доступности
изложения, отдавая им часто предпочтение перед вопросами
строгости, общности и безупречной последовательности. Иногда
изложение начинается не с самой общей постановки задачи, а с
рассмотрения простого случая, чтобы наиболее ясно оттенить
принципиальную сторону вопроса; при этом изложение ведется
достаточно подробно. При переходе же к общей задаче автор
ограничивался только указанием на существенно новые
моменты и приведением формул. Примеров такого изложения много;
укажем на два характерных: изложение краевой задачи Римана
начинается с простейшего случая односвязной области (гл. II),
а теории интегральных представлений аналитических функций —
с интеграла типа Коши с действительной плотностью (§ 34).
Кроме соображений педагогической целесообразности,
учитывалось, что имеется круг читателей, которым для их целей ничего,
кроме простейшего случая, не понадобится. Поэтому начинать
изложение с общей постановки задач было бы вдвойне
неоправданно.
Как правило, подобному изложению вопроса предшествуют
краткие замечания наводящего характера. В наиболее важных
случаях имеются еще и заключительные параграфы. Это ведет
иногда к повторениям, которых при другом способе изложения
можно было бы избежать.
Принятый здесь способ изложения может вызвать осуждение,
поэтому, желая пояснить свою точку зрения по этому вопросу,
приведем высказывание известного математика и педагога
Ф. Клейна*): «...Всегда находятся люди, которые по примеру
средневековых схоластиков начинают свое преподавание с самых
общих идей и защищают этот метод как якобы единственно
научный. А между тем и это основание неправильно: научно
обучать значит научать человека научно думать, а не оглушать его с
самого начала холодной, научно напряженной систематикой».
*) Ф. Клейн, Элементарная математика с точки зрения высшей,
ОНТИ, 1935, т. 1, стр. 426.

12
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
В той же связи автор старался, где только можно, избегать
специальной символики, заменяя ее описательными оборотами.
Всякая специальная символика, сокращая формулировки,
представляет большие удобства для лиц, хорошо освоившихся с ней,
т. е. лиц, постоянно имеющих дело с подобного рода вопросами.
Однако она оказывается препятствием и часто серьезным для
широкого круга людей, не специалистов в данной области,
желающих ознакомиться с ней. Приведу высказывание по этому
поводу одного из проникновенных математиков нашей эпохи
Н. Г. Чеботарева: «...Если бы наука (какая угодно) не
принимала особых мер для своей недоступности (научная
терминология, предъявляемые к сочинениям специальные требования
относительно цитат и т. п.), а, наоборот, стремилась бы путем
популярных сочинений стать ближе к широким слоям
населения, то она продвигалась бы несравненно быстрее. Мы,
математики, в этом деле грешим меньше других» *).
В излагаемой теории главным является возможность
качественного исследования. Многие практически важные задачи
(например, смешанная задача для аналитических функций, задача
Дирихле для плоскости со щелями и т. п.) были решены
различными частными приемами задолго до возникновения общей
теории. Но только общая теория, давшая простые зависимости
числа решений и условий разрешимости от индекса и последнего
от допускаемого класса функций, внесла в вопрос ясность.
В тех случаях, когда решение дается в замкнутой форме,
соответствующие формулы приводятся полностью, но когда
задача приводится к решению интегральных уравнений, ядра
последних, как правило, не выписываются. Устанавливается лишь
факт сводимости задачи к уравнению и указывается процесс
получения последнего. Читатель, усвоивший принципы теории,
при решении практических задач легко составит
соответствующее уравнение сам.
В тех случаях, когда имеется несколько различных путей
доказательства, автор старался выбрать самый простой, другие
же, если они имели теоретический интерес, предлагались в
качестве задач, приложенных к каждой главе. Некоторые задачи
сформулированы так, чтобы читатель, не решающий их
самостоятельно, мог пользоваться ими как дополнительным
теоретическим материалом. Наиболее трудные задачи отмечены
звездочками.
Все главы заканчиваются историческими очерками, которые
в совокупности дают представление об истории вопроса.
Автор
*) Н. Г. Чеботарев, Математическая автобиография, УМН III, вып. 4
B6), 1948, стр. 65.

ВВЕДЕНИЕ
Предметом настоящей книги является теория краевых задач
аналитических функций и ее приложения к решению особых
интегральных уравнений с ядрами Коши и Гильберта. Мы
ограничиваемся линейными задачами для одной неизвестной
функции.
Излагаемые теории зародились в начале настоящего
столетия в трудах классиков математики Гильберта и Пуанкаре; они
были существенно продвинуты в начале 20-х годов трудами
Нётера и Карлемана и переживают период бурного развития в
течение последних 40 лет.
Этот период почти целиком связан с трудами советских
математиков, среди которых в первую очередь следует назвать:
И. Н. Векуа, Н. П. Векуа, Д. А. Квеселава, В. Д. Купрадзе,
Л. Г. Магнарадзе, С. Г. Михлина, Н. И. Мусхелишвили,
И. И. Привалова, Б. В. Хведелидзе, Д. И. Шермана.
Укажем на некоторые особенности употребляемой
терминологии.
Вместо терминов «сингулярные» (уравнения),
«эквивалентная» (регуляризация) приняты соответственно «особые»,
«равносильная».
В отношении аналитических функций совершенно не
употребляются такие термины, как «голоморфность» и
«регулярность», а принят один лишь термин «аналитичность».
За основу берется аналитичность в точке, т. е. разложимость
функции в окрестности точки в степенной ряд. Под функцией,
аналитической в области, понимается функция, аналитическая
в каждой точке области. Она может быть получена
аналитическим продолжением из какого-нибудь одного ее элемента.

14
ВВЕДЕНИЕ
В случае многосвязной области функция может оказаться
многозначной. Однозначность рассматривается как
дополнительное условие. В случае, если у аналитической функции
допускаются какие-либо особенности, то это каждый раз специально
оговаривается с точным указанием того, какие именно
особенности допускаются.

ГЛАВА I
ИНТЕГРАЛ ТИПА КОШИ
Из курса уравнений математической физики хорошо
известно, что основные краевые задачи для уравнения Лапласа —
задачи Дирихле и Неймана — решаются с помощью так
называемых потенциалов простого и двойного слоев.
При решении краевых задач, относяш.ихся к другим
дифференциальным уравнениям, применяются различного рода обоб-
ш^енные потенциалы. Для решения краевых задач теории
аналитических функций комплексного переменного аналогичным
аппаратом являются интеграл типа Коши и различные его
обобщения.
Прежде чем непосредственно перейти к решению краевых
задач, необходимо предварительно изучить свойства
математического аппарата, применяемого для их решения.
Настоящая глава является вспомогательной. Материал ее
будет использоваться не весь сразу, а постепенно; поэтому,
чтобы быстрее перейти к основному материалу книги, мы
рекомендуем читателю изучать эту главу по частям. Сначала нужно
усвоить содержание первых пяти параграфов, после чего можно
приступить к изучению главы П, посвященной краевой задаче
Римана. Прежде чем перейти к главе П1, содержащей теорию
особых интегральных уравнений, нужно изучить § 7 о
перестановке порядка интегрирования в повторных особых интегралах.
Для понимания главы IV потребуется знание § 6, а для главы
V — § 10. Лишь после этого целесообразно изучать остальные
параграфы этой главы.
§ 1. Определение интеграла типа Коши и примеры
Пусть L — некоторый гладкий замкнутый контур*)
плоскости комплексного переменного z. Область, лежащую внутри кон-
*) Под гладким контуром мы здесь и в дальнейшем подразумеваем
простую (т. е. без точек самопересечения) замкнутую или незамкнутую линию
с непрерывно меняющейся касательной и не имеющую точек возврата
(заострения).

16 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
тура L, будем называть внутренней и обозначать />¦*", а
дополнительную к D^ + L область, содержащую бесконечно
удаленную точку, будем называть внешней и обозначать D.
Если f{z)—функция, аналитическая в D"^ и непрерывная
в D'^ + L, то согласно известной из теории функций
комплексного переменного формуле Коши
^S^"-!"* '^^*- (...)
2ш JX Z ( о, г е D".
Если же /(г) аналитична в области D и непрерывна в D" + L,
то
2», J, . |_f(^) + f(oo). zmD-.
За положительное направление обхода контура L, как обычно,
будем принимать то, при котором область D'^ остается слева.
Формула Коши дает возможность вычислить значения
функции в любой точке области, если известны ее значения на
границе области; коротко это обстоятельство выражают словами:
формула Коши решает краевую задачу для аналитических
функций. Интеграл, стоящий в левой части формул A.1) и A.2),
называется интегралом Коши.
Пусть теперь L — гладкий замкнутый или незамкнутый
контур, целиком расположенный в конечной части плоскости; т —
комплексная координата его точек и ф(т)~ непрерывная
функция точек контура. Тогда интеграл
L
построенный так же, как и интеграл Коши, называется
интегралом типа Коши. Функция ф(т) называется его плотностью, а
-— ядром.
Легко видеть, что интеграл типа Коши представляет собой
функцию, аналитическую во всей плоскости комплексного
переменного, за исключением точек самого контура L.
Доказательство аналитичности Ф(г) заключается в установлении
возможности дифференцирования по переменной z (параметру) под
знаком интеграла и приводится во всех учебниках теории
функций комплексного переменного.
Мы проведем аналогичное рассуждение для несколько более
общего случая, который нам встретится в дальнейшем. Из него
аналитичность интеграла типа Коши будет вытекать как
частный случай.

§ I] ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА ТИПА КОШИ И ПРИМЕРЫ 17
Теорема. Пусть L — гладкий контур {замкнутый или
незамкнутый) , f (т, z) — функция, непрерывная по переменной
t е L, аналитическая по z в некоторой области D для всех
значений x^L и ограниченная постояннойМпри всех x^L и z^D.
Тогда функция, представленная криволинейным интегралом
F{z)=\f(T,z)dx, A.4)
есть аналитическая функция переменной z.
Доказательство*). Выберем круг радиуса R с центром
в точке Z, ограниченный окружностью С, целиком лежащей в D.
Тогда, представляя аналитическую по z функцию f{x,z)
интегралом Коши, интеграл A.4) можно записать так:
L С
Используя тождество
1 г 1 [_] _ 1 ^ ^z
^z\.t-z-^z /-2J {t-zY (t-zy{t-Z'-'^z) *
получим равенство
F(z-^^z)-F (Z) 1_ f ^^ f f (т, t) dt _
/ = ¦
Аг 2я/ J J (/ — 2J
^\ i(r.t)dt
^z)
~ 2я/ J "^ J (t-zYit-z-.
L С
Пусть / — длина кривой L. Легко найдем оценку
При достаточно малом |Az| величину |/| можно сделать
меньше любого заданного числа е > 0. Следовательно, функция
F{z) имеет производную, равную
L С
С Другой стороны, еще раз используя формулу Коши и
дифференцируя ее, будем иметь
д\ (т, Z) \ [ ( (т, /) dt
^ 1 С мт, /:
2ш J (/-;
dz 2ш J (t-z)
*) Доказательство этой теоремы взято из книги Э. Гурса «Курс
математического анализа», т. II, ч. I, ОНТИ, 1936,

18 ИНТЕГРАЛ ТИПА КОШИ |ГЛ. I
Отсюда и из A.5) следует
дг
rB) = JiLi|b^rfT.
Таким образом, F{z) есть функция, аналитическая по z
всюду в области аналитичности f{x,z). Те значения z, при
которых функция /(т, г) перестает быть аналитической, будут
особыми точками функции F{z).
Для интеграла типа Коши с непрерывной плотностью ф(т)
единственными точками, где подынтегральная функция
перестает быть аналитической относительно г, являются точки
линии интегрирования L. Последняя является особой линией для
функции Ф(г) A.3). Важные вопросы о поведении интеграла
типа Коши при приближении точки z к контуру L, а также на
самом контуре будут изложены позже, в §§ 4 и 5.
Если L — незамкнутый контур, то Ф{z) будет функцией,
аналитической во всей плоскости с линией особенностей L. Пусть
теперь L — замкнутый контур. Тогда Ф{z) распадается на две
самостоятельные функции: Ф+(г), определенную в области D+,
и Ф~{z), определенную для точек области D-. Функции эти,
вообще говоря, не являются аналитическим продолжением друг
друга.
Аналитическую функцию Ф(^), определяемую в двух
дополняющих друг друга до полной плоскости областях D+, D- двумя
самостоятельными выражениями Ф^{z), ф-B), будем в
дальнейшем часто называть кусочно аналитической функцией.
Отметим одно важное свойство интеграла типа Коши.
Функция Ф{z), представленная интегралом типа Коши A.3), б
бесконечно удаленной точке обращается в нуль,
В самом деле, разложим Ф{z) в окрестности бесконечно
удаленной точки в ряд по степеням —. Так как
% — Z Z z^ ' ' ' z^ ' * •'
то, умножая на -^—^ и интегрируя почленно, получим
где

§2] ФУНКЦИИ. УДОВЛЕТВОРЯЮЩИЕ УСЛОВИЮ ГЁЛЬДЕРА 19
В разложении отсутствует нулевая степень, откуда и следует,
что функция, представимая интегралом типа Коши, необходимо
удовлетворяет условию
ф-(с5о) = 0. A.6)
В дальнейшем (пп. 4.2 и 4.6) покажем, что при соблюдении
некоторых дополнительных функциональных ограничений это
условие является также и достаточным для представимости
кусочно аналитической функции интегралом типа Коши.
Пример. Вычислим интеграл типа Коши, взятый по единичной окруж-
2
кости I 2 I = 1, с плотностью ф (т) = —-,——оГ' '^' ^*
Ф(,) = _LC_J ^1 L.[1.^L.
2jii J т — 2 X — z 2я/ J т X — z *
L L
Функция ——^ аналитична в D"^, a — аналитична в D" и обращается на
бесконечности в нуль. Первый интеграл по формуле A.1) равен —^-^ для
z^D^ и равен нулю для z ^ D^. Второй интеграл по формуле A.2) для
z^D" равен , а для г е D"*" равен нулю. Отсюда
§ 2. Функции, удовлетворяющие условию Гёльдера
2.1. Определение и свойства. Прежде чем перейти к
основному вопросу — изучению поведения интеграла типа Коши на
самой линии интегрирования, рассмотрим вспомогательный
вопрос о классах функций.
Пусть ф{/) —некоторая функция, причем аргумент / и
функция ф(/) могут быть как действительными, так и комплексными.
Непрерывность функции, как известно, заключается в том, что
1ф(^2) — ф(^1) I может быть сделан сколь угодно малым, когда
1^2 — ti\ достаточно мал, т. е. приращения аргумента и функции
одновременно стремятся к нулю.
Вопрос о порядке малости приращения функции по
отношению к приращению аргумента при этом не рассматривается; этот
порядок может быть каким угодно. Однако многие свойства
функции, например разложение ее в различного рода ряды и
быстрота сходимости этих рядов, представление интегралами
и т. п., тесным образом связаны с порядком малости модуля
непрерывности *) функции. Поэтому оказывается целесообразным
*) Модулем непрерывности функции ф (/) называется функция со (б) =
= sup I ф (to) — Ф (/i) I, где точки /i и /г принадлежат L и \t2 — ti\ <, 6.

20 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. 1
разбить обширное множество непрерывных функций на классы
в зависимости от порядка малости модуля непрерывности.
Весьма важным является класс функций, для которых
модуль непрерывности есть степенная функция от приращения
аргумента. К рассмотрению этого наиболее интересного для нас
класса мы и переходим.
Пусть L — гладкая кривая и ц>{1)—функция точек этой
кривой. Говорят, что функция ф(/) удовлетворяет на кривой
условию Гёльдера {условию Я), если для любых двух точек
этой кривой
\^{t2)-^{tx)\<A\t,-t,\\ B.1)
где А и X — положительные числа. А называется постоянной
Гёльдера, а К —показателем Гёльдера. Если бы К было больше
единицы, то из условия B.1) вытекало бы, что производная (^^{t)
всюду равна нулю и функция ф(^) была бы тождественно равна
постоянной. Поэтому мы будем считать, что
Если Я= 1, то условие Гёльдера совпадает с известным
условием Липшица, (Заметим, что во многих руководствах условие
Гёльдера называется условием Липшица порядка %,)
Если t\, t2 достаточно близки друг к другу и условие
Гёльдера выполняется для некоторого показателя Ки то оно будет,
очевидно, выполняться и для всякого показателя К < Х\.
Обратное, вообще говоря, несправедливо. Таким образом,
меньшему К соответствует более широкий класс функций. Наиболее
узким классом будет класс функций, удовлетворяющих условию
Липшица.
На основании последнего свойства легко установить, что если
функции ф1@» ф2@ удовлетворяют условию Гёльдера
соответственно с показателями Хь ^2, то их сумма, произведение, а
также частное при условии, что знаменатель не обращается в
нуль, удовлетворяют условию Гёльдера с показателем X =
= min(A,i, Хг).
Если ф@ дифференцируема и имеет конечную производную,
то она удовлетворяет условию Липшица. Это следует из
теоремы о конечном приращении. Обратное, вообще говоря,
неверно, что показывает хотя бы следующий пример функции,
заданной на действительной оси:
ф(л:) = |а:|.
Функция (р{х) удовлетворяет условию Липшица, но в начале
координат не имеет производной, так как правая и левая
производные равны +1 и —1<

§ 2) ФУНКЦИИ, УДОВЛЕТВОРЯЮЩИЕ УСЛОВИЮ ГЁЛЬДЕРА 21
Для сложной функции, когда происходит наложение
функциональных зависимостей с различными показателями Гёль-
дера, результирующая функция будет удовлетворять условию
Гёльдера с показателем, равным произведению показателей
Гёльдера всех звеньев цепи. У нас часто будут встречаться
аналитические функции от функций, удовлетворяющих условию
Гёльдера. Такие функции удовлетворяют условию Гёльдера с
тем же показателем. Доказательство получается
непосредственной проверкой с учетом того, что аналитическая функция
удовлетворяет условию Липшица. Если функция в некоторой точке
обращается в бесконечность порядка а, то ее определенный
интеграл удовлетворяет в этой точке условию Гёльдера с
показателем I — а. Доказательство следует из непосредственной
оценки интеграла. Укажем еще, что удовлетворение
периодической функции условию Гёльдера является достаточным условием
для разложимости ее в равномерно сходящийся ряд Фурье.
Приведем два примера.
1. Функция ф(а;) = Л^а: удовлетворяет условию Н с показателем А.= 1/2
на любом интервале действительной оси; если же интервал не содержит
начала координат, то эта функция на нем аналитична и, следовательно,
удовлетворяет условию Липшица.
2. Пусть функция ф (х) = -j для О < д: ^ — и ф @) = 0. Легко
видеть, что эта функция непрерывна на всем замкнутом интервале (отрезке)
О ^ дс ^ 1/2. Но так как Птл: 1па: = 0 для любого Я > О, то каковы бы
ч\\ были Л и Л, можно указать такое значение х, что | Ф (а:) — ф @)| =
= -^j > Л;с . Следовательно, функция ф(л;) на рассматриваемом
отрезке не удовлетворяет условию Гёльдера.
В дальнейшем нам придется рассматривать случаи, когда
условие Гёльдера выполняется всюду на контуре, за
исключением отдельных заданных точек. Это мы будем понимать в том
смысле, что условие Гёльдера выполняется на всякой
замкнутой части контура, не включающей указанных точек. В том же
смысле понимается выполнение этого условия на разомкнутом
контуре, если исключительными точками являются его концы.
Во втором из приведенных примеров функция Ц){х)
удовлетворяет условию Гёльдера на полуоткрытом интервале ^ <Сх ^ -к
и не удовлетворяет ему на отрезке О ^ л: ^ Y •
2.2. Функции многих переменных. Понятие условия Гёльдера
может быть распространено на функции любого числа
переменных. Рассмотрим для определенности случай функции двух
переменных. Говорят, что функция ф(/, т) удовлетворяет условию

22 ИНТЕГРАЛ ТИПА КОПШ [ГЛ. I
Гёльдера, если для любых пар значений ti, /2; ti, Т2,
принадлежащих заданным множествам,
|ф(^2, Т2)~ф(/ь x,)\<A\t,^Ur + B\x^^T,\\
где А, В, jn, v — положительные постоянные, |ы^ 1, v^ 1.
Если X — наименьшее из чисел \х, v, то можно подыскать
такую постоянную С, чтобы выполнялось неравенство
I Ф (^2, 1^2) — Ф (^1, Ti) i < С [ I ^2 — ^1 1^ + Из — Ti t\
Очевидно, что если ф(^т) удовлетворяет условию Гёльдера
по совокупности переменных /, т, то она удовлетворяет условию
Гёльдера по переменной t равномерно относительно т и по т
равномерно относительно t.
§ 3. Главное значение интеграла типа Коши
3.1. Несобственный интеграл. Рассмотрим определенный
интеграл от действительной функции. По первоначальному
определению как предела суммы он имеет смысл только для функций
ограниченных. Если подынтегральная функция обращается в
бесконечность в некоторой точке с на отрезке интегрирования
а ^ с ^ Ь, то интегралу от такой функции придается смысл
посредством второго перехода к пределу. Именно, вырезается
окрестность точки с, берется интеграл по оставшейся части, а затем
переходят к пределу, когда длина вырезанного интервала
стремится к нулю. Пусть с — внутренняя точка интервала. Предел
h
[с-8, Ь -1
5 f(x)dx+ 5 fWdJc ,
81 ^ - .
если он существует, называется несобственным интегралом от
неограниченной функции f{x) по интервалу (а, 6).
В этом определении существенным является то, что
вырезанная окрестность берется совершенно произвольно при
соблюдении условия, что размеры ее стремятся к нулю.
Следовательно, ei и 62 стремятся к нулю по любому закону независимо друг
от друга.
В курсе анализа доказывается, что несобственный интеграл
существует, если порядок бесконечности f{x) меньше единицы,
т. е.
Если f(x) обращается в бесконечность первого порядка или
более высокого, то несобственный интеграл не существует или,
как говорят, расходится.

§ 31 ГЛАВНОЕ ЗНАЧЕНИЕ ИНТЕГРАЛА ТИПА КОШИ 23
3.2. Главное значение особого интеграла. Рассмотрим
интеграл
b
X— с
а
{а<с< Ь),
Вычисляя его как несобственный, получим
i х-с е^о J с-х ^ J х — с\
= 1п-^^=^+ limln-^. C.1)
Предел последнего выражения зависит, очевидно, от способа
стремления ei и ег к нулю. Следовательно, интеграл,
понимаемый как несобственный, не существует. Его называют особым
{сингулярным) интегралом. Можно, однако, ему придать смысл,
если установить некоторую зависимость между ei и 82- Полагая,
что вырезаемый интервал расположен симметрично
относительно точки Су т. е.
8j = 82 = 8, C.2)
МЫ приходим к понятию главного значения особого интеграла
по Коши.
Определение. Главным значением по Коши особого
интеграла
[
4h {a<c<b)
называется
-С-8 b
с .JJL.+ \ _^|.
J х — с J л: —с
а с+в -¦
Учитывая формулу C.1) и условие C.2), будем иметь
b
\
" 'ni^. C.3)
X — С с — а
а
Рассмотрим теперь более общий интеграл
b
^ х — с
dx.

24 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. 1
где (р{х)—некоторая функция, удовлетворяющая в интервале
(а, Ь) условию Гёльдера. Этот интеграл аналогично
рассмотренному выше будем понимать в смысле главного значения,
которое определим следующим образом:
Г (^{x)dx ^ij^l f Ц>(х)йх ¦ f ц>(х)с1х\
J х — с e^oV J ^~^ J ^""^ У
a ^ a c+8 ^
Записывая тождество
b b b
5.^1^=5114^^ ^.+Ф(с) 5
c?;c
a
замечаем, что первый интеграл в правой части сходится как
несобственный, поскольку в силу условия Гёльдера
I ф(г:)-ф(с)
<
х-с\^-^
I X — с
а второй интеграл совпадает с C.3).
b
Таким образом, получаем: особый интеграл \ ^^ dx, где
J X ~— с
а
ф(х) удовлетворяет условию Гёльдера, суи^ествует в смысле
главного значения по Коши и равен
b b
\^JA.aX==\ <Р^-ф(^)^;,+ <р(,Iп.Ь1^..
Jjc — С J X — с »Y\/ с — а
а а
Для обозначения особого интеграла, некоторые авторы
употребляют специальные символы, например \ или v. р. \ (valeur
principale). Однако в этом нет особой необходимости, потому
b
что, с одной стороны, если интеграл \ ^_ dx существует как
а
обыкновенный или как несобственный, то он существует и в
смысле главного значения, причем их значения совпадают, с
другой же стороны, особый интеграл мы всегда будем понимать
в смысле главного значения. Поэтому особый интеграл мы
будем обозначать обычным знаком интеграла.
Заметим, что понятие главного значения в некоторых
случаях применимо и при особенностях подынтегральной функции
порядка выше первого (см. задачи 2, 3 в конце главы).
3.3. О многозначных функциях. В дальнейшем нам много
раз придется иметь дело с двумя элементарными многозначными

§ 31 ГЛАВНОЕ ЗНАЧЕНИЕ ИНТЕГРАЛА ТИПА КОШИ 25
аналитическими функциями — степенной и логарифмической.
Использование этих функций представляет немалые трудности
для начинающих и ему уделяется недостаточно внимания в
распространенных курсах теории функций, поэтому целесообразно
привести здесь основное из того, что понадобится далее.
В задании комплексного числа z = ре^*^ модуль р
определяется однозначно, аргумент же 9 с точностью до слагаемого,
кратного 2я. Последнее обстоятельство не приводит к
многозначности представления числа в силу того, что аргумент входит
в это представление через посредство функции е^^, имеющей
период 2я. Но если аналитическая функция такова, что в ее
выражение аргумент (угол) входит посредством функции не
периодической, то она окажется многозначной. Среди
элементарных функций к таким принадлежат логарифм и степенная с
нецелым показателем. Рассмотрим их параллельно:
In (г — го) = In I 2 — го I + / arg {г — го) = In р -f /в,
(^-^,)V = pY^'VB_ C.4)
= р« [cos (р In р) + / sin (р In р)] e'Ye^**2"*v (y == а + /р).
Во всех рассуждениях под логарифмом модуля комплексного
числа всегда понимается его действительное значение согласно
обычному определению,
принятому в курсе математического ана- !1\
лиза. Общее представление
аргумента в имеет вид
e = 9-f 2А:я,
/
/
/
/
\
\
\
\
^^с"
где k может принимать любые
целые значения (^ = 0, ±1,
±2, ...), а 9 — наименьшее по
абсолютной величине значение
аргумента (рис. 1).
Каждому выбранному
значению k будет соответствовать
определенная ветвь многозначной ^"^" ^*
функции. У логарифмической
функции число ветвей бесконечно; у степенной при
иррациональном или комплексном показателе также бесконечно. Если же
показатель рациональный, у ="^» то степенная функция имеет
q ветвей. Ветви логарифма отличаются друг от друга на
слагаемое вида 2тя/, а ветви степенной функции на множитель
Q2myni (щ —целое число). Для задания многозначной функции,
очевидно, необходимо указать выбранную ветвь. Однако, в
отличие от функций действительного переменного, этого еще

26 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
недостаточно для полного определения многозначной функции
комплексного переменного. Для последних существуют на
плоскости точки, обладающие тем свойством, что, когда
переменное, изменяясь по замкнутому контуру, окружающему эту
точку, возвращается к начальному значению, выбранная ветвь
функции не остается неизменной, а переходит в некоторую
другую ветвь. Такие точки называются точками ветвления
многозначной функции. Для рассматриваемых нами функций
точками ветвления будут Zo и бесконечно удаленная. Если
переменное описывает контур, окружающий точку zq (на рис. 1 указан
пунктиром) в положительном (отрицательном) направлении, то
аргумент G изменяется на 2я (на —2л).
При этом логарифм получает слагаемое 2т {—2я0» ^
степенная функция множитель е^'^^^ {е~^^^^). Следовательно, ветвь,
соответствующая выбранному значению k = п, переходит в
соседнюю ветвь, соответствующую значению й=/г+1 {k = п — 1).
Исследование в бесконечно удаленной точке производится, как
обычно, путем подстановки 2 = у и исследования в точке ^ = 0.
Сохранить выбранную ветвь функции удастся лишь в том
случае, если сделать невозможным обходы вокруг точек
ветвления. Последнее достигается проведением в плоскости разрезов,
соединяющих точки ветвления. В рассматриваемых нами
случаях логарифмической и степенной функции нужно провести
разрез вдоль некоторой линии, исходящей из точки Zq и
удаляющейся в бесконечность. Для указанной цели — закрепления
выбранной ветви — форма разреза безразлична. Однако если
приходится учитывать еще и другие обстоятельства, то иногда
форма разреза оказывается предписанной заранее. Если нет
каких-либо особых соображений, то разрез выбирается
наиболее простым, а именно прямолинейным (предпочтительнее
параллельным оси абсцисс или радиальным). Многозначную
функцию можно считать вполне определенной, если выбрана ее
ветвь и задан разрез.
Границы изменения аргумента в определяются положением
разреза. Если, например, разрез проведен по лучу,
образующему с осью абсцисс угол Эо, то для главной ветви *) {k = 0)
9,о^в^6о + 2я. В частности, для разреза, направленного по
положительной полуоси абсцисс, О ^ 0 ^ 2я, по отрицательной
полуоси, —п ^ в ^ я. Если разрез криволинейный, то границы
изменения аргумента будут функциями точки. Начальное
значение аргумента соответствует левому (если смотреть от точки
го) берегу разреза, конечное — правому. Обозначим значение
*) Если, по условию, берега разреза исключаются из плоскости, го знаки
равенства нужно отбросить.

3]
ГЛАВНОЕ ЗНАЧЕНИЕ ИНТЕГРАЛА ТИПА КОШИ
27
аргумента на левом и правом берегах разреза соответственно
0+ и 6". Тогда
0""~0^ = 2я.
Разрез для выбранной ветви будет линией разрыва. На берегах
разреза выполняются соотношения (рис. 2)
In B- - zo) = In (г+ - zo) + 2я/, {z- - го)^ = е''^"^ (г+ - Zo)\
Свойство разрывности ветвей многозначных функций на
берегах разреза широко используется при решении краевых задач
с разрывными
граничными условиями. Логарифм yi
используется в том
случае, когда разрывная
функция входит в краевое
условие в качестве
слагаемого, степенная
функция, — если множителем
(см. пп. 41.2, 41.3).
Таким образом,
каждая ветвь многозначной
функции на разрезанной
соответствующим
образом плоскости будет
однозначной и разрывной.
Сохранение
непрерывности возможно лишь в том
случае, если аргумент многозначной функции считать
изменяющимся на многолистной плоскости — римановой
поверхности, число -листов которой равно числу ветвей многозначной
функции и листы скреплены по берегам разрезов таким образом,
чтобы переход с одного листа на другой строго соответствовал
замене ветвей при обходе точек ветвления*). Этот вопрос еще
будет затронут в п. 53.1.
3.4. Главное значение особого криволинейного интеграла.
Пусть L — гладкий контур; т, / — комплексные координаты его
точек. Рассмотрим криволинейный особый интеграл
Рис. 2.
ф(т)
dx.
*) Для первоначального ознакомления со сложной теорией изображения
многозначных функций на римановых поверхностях можно рекомендовать
весьма доступное изложение В. Ф. Кагана в дополнении к т. I книги Ф,
Клейна «Элементарная математика с точки зрения высшей».

28
ИНТЕГРАЛ ТИПА КОШИ
[ГЛ. I
Если а, S — длины дуг, отсчитываемые от начальной точки
интегрирования до точек т, /, и т = т(а)— уравнение контура в
комплексной форме, то, подставляя в интеграл т = т(а), / = /E),
dT = T^(a)da, мы привели бы его к двум действительным
особым интегралам, как это и будет сделано в § 10. После этого
можно было бы
целиком воспользоваться
результатами п. 3.2, не
прибегая к новым
рассмотрениям. Однако, так
как в дальнейшем мы
будем постоянно решать
задачи непосредственно
в комплексных
переменных, не переходя к
действительным,
целесообразно рассмотреть особый
интеграл как функцию
комплексного
переменного самостоятельно.
Проведем из точки /
контура, как из центра,
окружность радиуса р, и
пусть t\, /2 —точки
пересечения этой окружности
с кривой (рис. 3). Радиус
будем считать настолько
малым, чтобы окружность
не имела с кривой L
других точек пересечения, кроме t\, /2. Обозначим часть контура L,
вырезаемую окружностью, / и возьмем интеграл по оставшейся
дуге
Ф W
Рис. 3.
L-1
X-t
dx.
Определение. Предел интеграла \ -^^rt^'^ "Р^ р-^0
L-l
называется главным значением особого интеграла
$•
/
Начнем рассмотрение вопроса о существовании особого
интеграла с простейшего случая \ -^-zrj Подынтегральная функ-

ГЛАВНОЕ ЗНАЧЕНИЕ ИНТЕГРАЛА ТИПА КОШИ
29
ция допускает первообразную 1п(т — t), поэтому исследование
может быть произведено так же, как и в п. 3.2. Затруднение
представляет лишь то обстоятельство, что первообразная есть
многозначная функция. Будем считать, что 1п(т—t) есть
контурное значение аналитической функции In (г—/), однозначной
в плоскости, разрезанной вдоль некоторой кривой, соединяющей
точки разветвления / и оо. Условимся для определенности, что
разрез проходит справа от кривой (см. рис. 3). Тогда
dT
= 1п(т-0 +1п(т-0
= 1П-
L-/
t.
где а и b — начальная и конечная точки контура L. Но
In
t2-t
In
t2-t
+ /[arg(/,~/)-arg(/2-01.
По определению, |/2 —^| = |^i — t\, следовательно, первое
слагаемое обращается в нуль. В силу выбора разреза
выражение в квадрантных скобках равно тому из двух углов между
векторами ttu tt2y который расположен слева от кривой (рис. 3).
Обозначим а (О ^ а ^ 2я) предельное значение этого угла при
р-^0. Очевидно, что а есть угол, отсчитываемый от правого
касательного вектора *) к левому против часовой стрелки. В
частности, а = я во всех точках гладкости. В угловых точках
а =7^ я и а = О или а ^ 2я в случае точки возврата. Таким
образом,
и тогда
limln-r^—7 =/а,
р->0 *2— *
dT I b — t . .
C.5)
Если t — точка гладкости, то последний интеграл можно
представить в виде
C.6)
(выбирая ветвь логарифмической функции In z так, что
1п(—1)=:я/).
Если контур L замкнут, то, полагая a=zb, видим, что
первый член правой части формулы C.5) обращается в нуль и
*) Под правым касательным вектором понимается преде.1ьное положение
секущей, направленной от точки / в сторону положительного обхода.

30 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
интеграл имеет простое выражение:
\-^ = in, C.7)
L
если / точка гладкости, и
\-:^-i-, C.70
если t — угловая точка.
Рассмотрим теперь особый интеграл
J т—/
где ф{т) удовлетворяет условию Гёльдера.
Представляя его в виде
\^dr=\^^^dr-^,it)\^ C.8)
L L L
И рассуждая так же, как в п. 3.3, получим, что особый интеграл
\ ^__ , dx для функции ф(т), удовлетворяюи{ей условию Гель-
L
дера, суи{ествует в смысле главного значения по Коти.
Во всех точках гладкости его можно представить в двух
видах:
J^,,^jMli^|^,, + ,W[,„i^ + „.], ,3.9)
L L
\^dx^\^^^l-Jt^'^ dr + ^mn^. C.10)
L L
В частности, для замкнутого контура, полагая в C.9) а = 6,
получим
\^dr = \^^'lZf^ й.Л-1щ{Ц C.11)
L L
Всюду В дальнейшем, говоря об особом интеграле, будем
понимать под этим его главное значение.
3.5. Свойства особого интеграла. Совершенно очевидно, что
особый интеграл обладает обычными свойствами интеграла:
интеграл от суммы равен сумме интегралов и постоянный
множитель можно выносить за знак интеграла. Прежде чем перейти

§ 3] ГЛАВНОЕ ЗНАЧЕНИЕ ИНТЕГРАЛА ТИПА КОШИ 31
К выводу менее тривиальных свойств — правила замены
переменной и интегрирования по частям, сделаем одно важное
замечание.
При введении понятия главного значения подчеркивалось
как самый существенный пункт, что вырезаемая окрестность
берется симметрично относительно исследуемой точки. Но если
подвергнуть определение главного значения более точному
исследованию, то окажется, что в строгой симметрии нет
необходимости. В самом деле, в п. 3.2 существенным является не
требование 81 = 82, а условие lim—^ = 1. Точно так же в п. 3.4
8,->0 ^2
82->'0
существенно не то, что точки tu ^2 лежат на одной окружности
(I^2 — ^I = Ui — ^I), а условие
iim
= 1. C.12)
Таким образом, если мы отбросим условие симметрии и
сохраним только условие C.12), то особый интеграл, определенный
с такой более общей точки зрения, будет совпадать с
введенным ранее главным его значением.
Теорема (правило замены переменной). Если функция
х=а(^) имеет непрерывную первую производную а^(С), нигде
не обращающуюся в нуль, и преобразует контур L взаимно
однозначно в контур и, а ф(л:) удовлетворяет условию Гель-
дера, то
еде
^ = a(g).
Доказательство. Интеграл, стоящий справа в C.13),
существует в смысле главного значения. Вырежем из контура
и достаточно малой окружностью с центром в точке ^ дугу 1\
Пусть ее концы |i и ^2, а /i и /2 — соответствующие им точки
контура L, тогда
С ф[а(?)]«М^) .._ .. f Ф[аШ]аЧ?) .^
Сделав подстановку ^= Р(т), где Р(т) —функция, обратная для
а(^) (в силу условия теоремы обратная функция существует и
однозначна), убедимся, что правая часть равенства совпадает с
f Ф(т]
J т—-
Iim \ -^dx.

32 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
Точки ti И ^2 расположены на L уже не симметрично
относительно точки /, но они, как мы сейчас докажем, удовлетворяют
условию C.12).
Разлагая функцию а (С) в точке g в ряд Тейлора и
ограничиваясь двумя первыми членами, получим
to = а (У = t+W il) + 62 (^2, Ш ih - l\
ti=a (I,)=i + w (I)+8i (lu m ih - I),
где в силу предположенной непрерывности а'(^), Si и 82
стремятся к нулю при gi, |2~^^
Тогда
\t2-t
\ tl — t
НО,
lim 7^
=
-/ 1
а' а) + 62 1
a'(l) + ei 1
= lim I
1 ^
S2 —
I
Ui-g
2-1
1-g
И, следовательно,
I / у I 16 t I
В силу замечания, сделанного в начале пункта, теорема
доказана.
Условие взаимной однозначности преобразования
существенно, хотя, впрочем, нет нужды его особенно подчеркивать, так
как оно является существенным и для обыкновенного интеграла.
Теорема (интегрирование по частям). Если (р(х) —
непрерывно дифференцируемая функция и точка t не совпадает с
концами гладкого контура L{a и Ь), то справедлива следующая
формула интегрирования по частям:
^^dx = i7t(f{t) + фF) 1пF - О ~ф(а) In (а - О
-^(p'{x)\n{T-t)dx. C.14)
Напомним, что однозначная ветвь 1п(т—t) в соответствии
с п. 3.4 выделяется с помощью разреза, соединяющего точку /
с бесконечно удаленной точкой, справа от L. Если этот разрез
будет проведен слева от L, то в первом члене правой части
формулы C.14) надо взять знак минус.
При доказательстве *) исходим из интеграла правой части
J ф' (т) In (т -1) dx,
L
Последний имеет смысл как несобственный. Для его
определения можно вырезать окрестность точки / любым способом.
*) Здесь мы в основном следуем статье [15].

§ 4] ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 33
Сделаем это так, как при определении главного значения
5ф'(тIп(т —OrfT = lim J ф'(тIп(т-0^т+5ф'(тIп(т-/)йт .
Произведя интегрирование по частям в обыкновенных
интегралах, стоящих в квадратных скобках, будем иметь
f, b
5 ф' (т) In (т ~ о dT + J ф' (т) In (т -1) dx =
а t2
= (f{b)\n{b — t) — (f{a)\nia — t) + (f{ti)lniti-t)-
t. ь
-^it,)\nif,-t)-\^dx-\^dx.
a ti
Переходя к пределу при р->0, находим, что первые два члена
остаются неизменными; последние два в сумме дадут интеграл
Ф W
L
rfr.
понимаемый как главное значение. Для нахождения предела
остальных слагаемых сделаем следующее преобразование:
Ф (/,) In iU - О - Ф (^2) 1п [h - О = Ф (О [In (/i - /) - In (/2 -1)\ +
+ [ф (^i) - Ф @1 In (^i - 0 - [Ф (У - Ф @1 In (/2 - 0.
Функция ф@» как непрерывно дифференцируемая,
удовлетворяет условию Липшица. Отсюда на основании того, что
Итл:1пА: = 0, получим, чго пределы последних двух слагаемых
предыдущего выражения будут равны нулю.
Предел ln(/i — t)—In (^2 — t) уже рассматривался в п. 3.4.
Он будет равен in. Теорема доказана.
Если L замкнутый контур (а = &), то формула C.14)
упрощается:
\ TTTf dx = 1щ (t) - J ф' (т) In (т - t) dx. C.15)
L L
§ 4. Предельные значения интеграла типа Коши.
Интегралы по действительной оси
4.1. Основная лемма. Как уже указывалось ранее, для
аналитической функции, определяемой интегралом типа Коши, сам
контур интегрирования является особой линией. Сейчас мы
приступаем к рассмотрению важнейшего вопроса — исследованию

34 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
поведения интеграла типа Коши на самом контуре
интегрирования. Основной результат, который далее будет получен,
состоит в том, что интеграл типа Коши с плотностью,
удовлетворяющей условию Гёльдера, ведет себя так же, как потенциал
двойного слоя с непрерывной плотностью, т. е. имеет
непрерывные предельные значения при приближении к контуру с каждой
его стороны, но эти предельные значения различны, так что при
переходе через контур происходит скачок.
Основная лемма. Если плотность ф(т) удовлетворяет
условию Гёльдера и точка t не совпадает с концами гладкого
контура L, то функция
L
ведет себя при переходе через точку z = t контура как функция
непрерывная, т. е, она имеет определенное предельное значение
при приближении z к t с любой стороны контура по любому
пути:
Доказательство. Оценим разность
Допустим сначала, что стремление z к t происходит по
некасательному к L пути, т. е. нетупой угол между отрезком zt
и соответствующей касательной к L в ^ не меньше некоторого
острого угла шо > 0. Разобьем оцениваемый интеграл на два
слагаемых: /i — по участку L^ контура L, лежащему внутри
круга радиуса б с центром в точке /, и h — по остальной части
L — L^ (рис. 4). При этом число б выберем настолько малым,
что острый угол, образованный вектором /т, где xeL^, с одним
из касательных векторов в точке /, был бы меньше 0о/2.
Применяя к треугольнику zh теорему синусов, получим
I ^ -• И ^ sin р ^ 1 ^ у .
|т —г1 sin© "~^ . ©о \^-^/
sin —
где К — некоторое положительное число.
Согласно условию Гёльдера имеем
где г = I т — Л

§4]
ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ
35
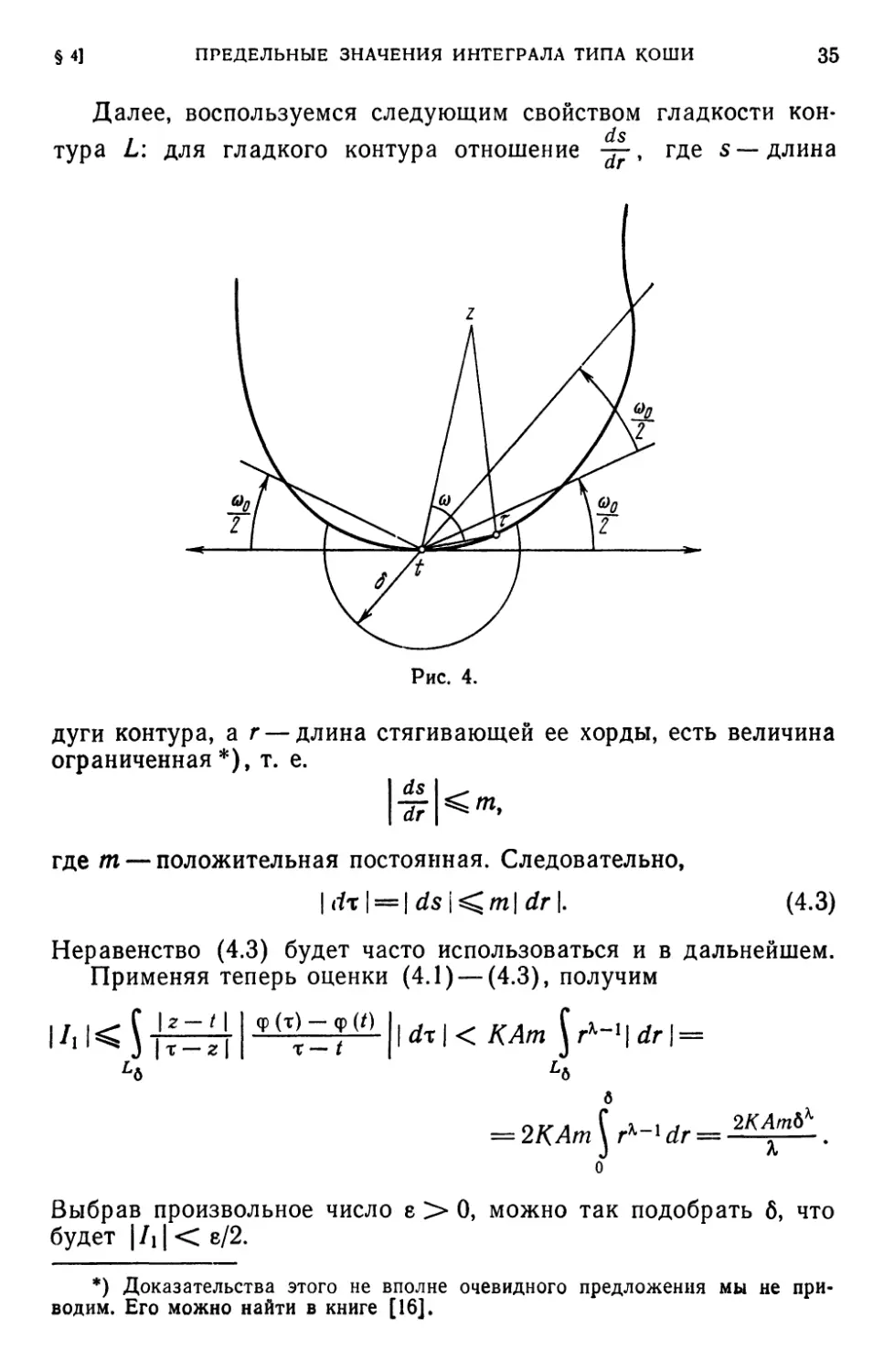
Далее, воспользуемся следующим свойством гладкости кон-
/ ds
тура L: для гладкого контура отношение -j-, где s —длина
Рис. 4.
дуги контура, а г — длина стягивающей ее хорды, есть величина
ограниченная*), т. е.
где т — положительная постоянная. Следовательно,
\dx\ = \ds\^m\ dr\.
D.3)
Неравенство D.3) будет часто использоваться и в дальнейшем.
Применяя теперь оценки D.1) — D.3), получим
\h\<\^\\''^''\Zf'\\dr\<KAm\r^-^\dr\ =
= 2КАт
2КАт6^
Выбрав произвольное число 8 > О, можно так подобрать б, что
будет |/i|<e/2.
*) Доказательства этого не вполне очевидного предложения мы не
приводим. Его можно найти в книге [16].

36 ИНТЕГРАЛ ТИПА КОШИ 1ГЛ. 1
Теперь, когда б уже выбрано, перейдем к оценке интеграла
/г. На участке контура L — L^ будет хф1, поэтому интеграл /г
в точке / является непрерывной функцией от z. В силу
непрерывности для достаточно малых \z —1\ будет выполняться
неравенство
|/21<|
равномерно по t при указанном стремлении z к t. Поэтому
|t|)B:)-a|)(OI<|/il + |/2l<8.
Остается еще освободиться от условия, что z стремится к
/ по пути, не касательному к контуру.
Предварительно заметим, что оценка разности \'^(z) — ^{t)\
была произведена независимо от t, следовательно, стремление
г|)B) к своему пределу происходит равномерно. Отсюда
вытекает, что предельное значение функции г|р(г) на контуре L —
функция 1|)(/)—непрерывна. В самом деле, если tyt\—две точки
контура L, то
|гК/)-г|)(/01<1г|)@-г|)B:)| + И(г)--гКО1.
В силу равномерности стремления ^(z) к пределу оба
слагаемых в правой части неравенства могут быть сделаны сколь
угодно малыми при достаточной
близости точек t, ti и z друг
к другу.
Допустим теперь, что z
стремится к ^ по некоторой кривой Y,
касательной к L. Возьмем на
кривой Y точку 2, достаточно
близкую к /, и проведем через нее
какую-нибудь кривую yi так,
чтобы она пересекала контур Lb
некоторой точке /ь достаточно
близкой к /, и была не
касательной к контуру L. Линию yi всегда
можно взять так, чтобы длины
^"^- ^- хорд zt и zti были одновременно
сколь угодно малы (рис. 5).
Применяя сначала доказанное выше утверждение о
существовании предела по некасательному пути, а затем свойство
непрерывности предельных значений, будем иметь, что
сколь угодно малы, а отсюда и

§ 4] ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 37
будет сколь угодно мал. Этим устанавливается существование
предела по любому пути.
Заметим, что существование предела функции \|)(г) есть
свойство локальное, т. е. справедливость его в данной точке /
вытекает из свойств плотности ф(т) в окрестности данной точки.
В самом деле, при доказательстве мы непосредственно
оценивали интеграл, взятый по сколь угодно малой дуге контура,
окружающей точку /, для чего использовалось условие Гёльдера.
Для непрерывности в точке / функции г|)B) не потребуется,
чтобы ф(т) и на остальной части контура удовлетворяла условию
Гёльдера, она может быть там просто непрерывной и даже
иметь разрывы при соблюдении условия интегрируемости.
4.2. Формулы Сохоцкого. Теперь уже можно рассмотреть
основной вопрос о существовании предельных значений
интеграла типа Коши на контуре интегрирования, а также
установить связь между ними и особым интегралом.
Пусть
L
где ф(т) удовлетворяет условию Гёльдера.
Будем считать контур L замкнутым и гладким. В случае,
если контур окажется незамкнутым, мы дополним его какой-
нибудь кривой до замкнутого, положив на этой дополнительной
кривой ф(т) = 0.
Для исследования предельных значений 0{z) в некоторой
точке t контура возьмем изученную в п. 4.1 функцию
*И-^5^П^«т. D.5)
L
Обозначим Ф+@» ^"^@ предельные значения аналитических
функций ФB), \|?(г) при стремлении точки z изнутри L к точке
t контура, а Ф~(/), t|)'"@—при стремлении извне. (Для
незамкнутого контура это соответствует предельным значениям слева
и справа.) Чтобы подчеркнуть направление перехода к пределу,
будем писать соответственно 2:->/+ или z->/- Значения
соответствующих функций в точке / контура будем обозначать
просто Ф@» ^@» причем Ф@ будет обозначать особый интеграл
1 Г Ф(т)
2я/ J т-^
dx, понимаемый в смысле главного значения.
Исходя из равенств
f 2ш, Z е D"^,
5т^= О, ^^^^ D.6)

38 Р1ЫТЕГРАЛ ТИПА КОШИ [ГЛ. I
будем иметь
z>^^ L L L J
^^i I L L J
Так как по основной лемме функция \|)(/) непрерывна, то
правые части написанных равенств совпадают, т. е.
Ф+ (О - Ф (/) = Ф- (t) = Ф (О - у Ф it). D.7)
Отсюда окончательно получаем
L
D.8)
причем особый интеграл \ ^_ ^ dx понимается в смысле глав-
L
ного значения.
Формулы D.8), полученные впервые в 1873 г. русским
математиком Ю. В. Сохоцким [24], будем называть формулами
Сохоцкого. Они являются основными для всего дальнейшего.
Сформулируем полученный результат.
Теорема. Пусть L — гладкий контур {замкнутый или
незамкнутый) и ф(т) — функция точек контура, удовлетворяющая
условию Гёльдера. Тогда интеграл типа Коти
*и-1к$шл
имеет предельные значения Ф+@» Ф~@ ^^ ^^^^ точках контура
L, не совпадающих с его концами, при приближении к контуру
слева или справа по любому пути, и эти предельные значения
выражаются через плотность интеграла ф@ и особый интеграл
Ф@ по формулам Сохоцкого D.8).

§ 4] ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 39
Вычитая и складывая формулы D.8), получим пару
равносильных им формул
Ф+@-ф-(/) = ф@. D.9)
Ф+ (О + ф- (О = ^ 5 -fill- dx, D.10)
L
которыми в дальнейшем часто будем пользоваться.
В § 1 было показано, что условие
ф-(сх)) = 0
является необходимым для представления кусочно
аналитической функции интегралом типа Коши. Легко вывести, что оно
является также и достаточным. В самом деле, пусть Ф±(/) —
краевые значения кусочно аналитической функции,
удовлетворяющие условию Гёльдера. Тогда, взяв плотность интеграла
типа Коши в виде ф(/) = Ф+(/)—Ф~(/), на основании формул
Коши A.1), A.2) с учетом A.6) будем иметь
L ( Ф (г), z^D .
4.3. Условие того, что произвольная комплексная функция
есть краевое значение аналитической в области функции. Пусть
на гладком замкнутом контуре L задана некоторая непрерывная
комплексная функция ф(/) точек контура, и пусть t^t(s) =
= t\{s) +it2(s) — уравнение контура в комплексной форме, где
t{s) есть функция дуги s, отсчитываемой от какой-либо точки
контура.
Подставляя в выражение функции ф(/) комплексную
координату, отделяем действительную и мнимую части:
ф (/) = ф [/ (s)] = ф1 E) + /ф2 E).
Легко показать, что на вопрос, существует ли такая
аналитическая в области D+(D-) функция, для которой заданная
комплексная функция ф(/) является ее предельным значением
на контуре, нужно ответить, вообще говоря, отрицательно. В
самом деле, по значениям действительной части ф1E) можно
построить гармоническую в области D+ (или D-) функцию и{х,у),
предельные значения которой на контуре совпадают с заданной
функцией ф1E) (задача Дирихле). По функции и{х,у) можно
определить сопряженную с ней гармоническую функцию v{x,y)
с точностью до произвольного постоянного слагаемого. Таким
образом, получим аналитическую функцию f{z)=:u{x,y)-\'
+ iv(x,y), для которой (p\{s) является краевым значением

40 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
действительной части. Если теперь взять предельное
значение мнимой части v{Xyy), то оно, вообще говоря, не будет
совпадать с заданной функцией ф2E) и, следовательно, заданная
комплексная функция ф(/) не будет предельным значением
функции, аналитической в области D+ (или D-). Как
показывает рассуждение, произвольно можно задавать лишь значения
одной составляющей — действительной или мнимой, вторая же
составляющая определится тогда с точностью до постоянного
слагаемого.
Таким образом, данная комплексная функция будет
предельным значением аналитической функции лишь при
удовлетворении некоторым соотношениям. Переходим к выводу этих
соотношений.
В дальнейшем будем считать ф(/) удовлетворяющей
условию Гёльдера.
Рассмотрим интеграл типа Коши с плотностью ф(/)
L
Если 2:eD+ и (p{t)—краевое значение аналитической в D+
функции, то
ф-^(г) = фB);
если z^D- и ф(/) — краевое значение аналитической в D-
функции, то по формуле Коши для бесконечной области
Ф""B:) = --фB:) + ф(оо).
Беря теперь предельные значения на контуре L и используя
формулы Сохоцкого D.8), получим
L
если ф(г)—аналитическая в D+, и
-ф@ + Ф(оо) = -1ф(/) + ^5|^ЙТ.
если ф(г)—аналитическая в D- Отсюда
L
T<PW+2irS-r?r^^-r = 0 (Г = Ф(оо)). D.12)

^ 4) ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 41
Приведенными рассуждениями устанавливается
необходимость условий D.11), D.12), чтобы функция ф(/) была краевым
значением аналитической функции соответственно в областях
D+ и D- Нетрудно показать, что они являются также и
достаточными.
В самом деле, пусть, например, ф(^) удовлетворяет условию
D.11). Для интеграла типа Коши
*<-)=iirS^'"
согласно формулам Сохоцкого D.8) это означает, что Ф""@ = 0.
Но отсюда из формулы D.9)
Ф@ = ф-'@-Ф"@ = Ф''@.
Сформулируем полученный результат.
Теорема. Пусть на гладком замкнутом контуре L задана
комплексная функция ф@» удовлетворяющая условию Гель-
дера. Чтобы эта функция была краевым значением функции,
аналитической во внутренней области D+, необходимо и
достаточно выполнение условия D.11); чтобы ф(/) была краевым
значением функции, аналитической во внешней области D- и
обраи^аюш^ейся на бесконечности в заданное число Г,
необходимо и достаточно выполнение условия D.12).
Можно поставить более общую задачу: вывести условие
того, что заданная на контуре комплексная функция есть
краевое значение функции, аналитической в области, за
исключением отдельных точек, где она имеет заданные особенности.
Для дальнейшего имеет интерес случай, когда ф(/)
представляет собой краевое значение функции, аналитической в области
/)", за исключением бесконечно удаленной точки, где она имеет
полюс порядка п с заданной главной частью:
у(г) = а^г"' + а^г^-^+ ... -]гa^-xZ + а,,.
Рассуждая аналогично предыдущему, легко показать, что
условие будет иметь совершенно тот же вид, что и D.12), с той
лишь разницей, что постоянная Г заменится выражением
y(t), т. е.
y^(^) + iST^^^-V@ = 0. D.13)
L
Иногда равенства D.11), D.12) называют условием
аналитической продолжимости (распространимости) комплексной
функции, заданной на контуре, в область. Однако термин

42 ИНТЕГРАЛ ТИПА КОШЬ [ГЛ. Г
аналитическая продолжимость часто применяется не только к
функциям, аналитическим во всех точках области, но и к таким,
которые имеют в этой области особенности в некоторых точках.
Для таких функций условия D.11), D.12) надо заменить более
сложными (см. задачу 12 в конце главы).
Формулами D.11), D.12) можно пользоваться для
вычисления особых интегралов в случае, когда плотность интеграла
есть краевое значение аналитической функции (см. задачу 10).
4.4. Предельные значения производных. Производные
предельных значений и дифференцирование особого интеграла.
1°. Пусть ф(/) —функция точек замкнутого контура L, т-я
производная которой удовлетворяет условию Гёльдера.
Покажем, что у производной т-го порядка функции Ф(г),
определяемой интегралом типа Коши
L
существуют предельные значения на контуре и что эти
предельные значения удовлетворяют соотношениям, аналогичным
формулам Сохоцкого D.8):
ф(«)+@ = 1ф('»>(/) + ^ 5 ^^rfT. D.14)
L
ф(т)-(^) = _|ф(«)(/) + _1_^ф!!!11).^Т. D.15)
L
Производная т-го порядка интеграла типа Коши, как это
следует из A.3), выразится формулой
2ni J (т-гГ-^^
Проинтегрируем интеграл правой части т раз по частям.
Вследствие замкнутости контура проинтегрированная часть
каждый раз будет обращаться в нуль. Поэтому
^"'w=iS^''-
Применяя к полученному интегралу типа Коши формулы
Сохоцкого D.8), придем к формулам D.14), D.15).
2°. Покажем теперь, что в формулах D.14), D.15) операции
дифференцирования и перехода к пределу на контур перемести-
тельны, т. е. что предельные значения на контуре производных

§ 4) ПОНЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА tHHA КОШИ 43
интеграла типа Коши совпадают с производными от его
предельных значений:
[Ф*(оГ'=[Ф""'(/)]".
если плотность ф(^)(^) удовлетворяет условию Гёльдера.
Ограничимся рассмотрением случая первой производной.
Покажем вначале, что
По формуле C.15) имеем
Продифференцируем интегральное слагаемое (используя
обозначения п. 4.1), тогда
¦j^W{x)\n{x-t)dT=-\im-^ J ф'(т)In(т-/)dt =
= lim Г - \ ^ dx + ф' ih) In (т -1,) - ф' {^,) In (t - h)\ =
-\
^ dx + lim [ф' (t^) - ф' т In (т - ^2) +
+ lim ф' (/i) [In (т - /г) - In (т -1^)]. D.17)
б>0
Так как ф'(/) удовлетворяет условию Гёльдера, то первый
из оставшихся пределов равен нулю, а второй вычислен ранее
в пп. 3.4—3.5 и равен 7ii(p'{t). Поэтому из D.17) получаем
L
ЧТО и доказывает D.16).
Равенства [O^it)}^ = [0^{t)Y следуют теперь из D.16)
непосредственным применением формул Сохоцкого.
В D.17) мы не обосновывали возможности перестановки
дифференцирования и предельного перехода. Доказательство с
полным обоснованием можно найти в работе Ю. М. Крикунова
4), которой мы в основном следовали при доказательстве
формулы D.16). Укажем также, что формула D.16) без
доказательства приведена в заметке Р. С. Исаханова 1). Этими

44 ИНТЕГРАЛ ТИПА КОШИ (ГЛ. 1
авторами формула была дана и для случая разомкнутого
контура.
4.5. Формулы Сохоцкого для угловых точек контура. В
исследованиях п. 4.1 свойство контура, которое фактически было
использовано, можно сформулировать следующим образом:
отношение малой дуги контура к стягивающей ее хорде есть
величина ограниченная. Однако это свойство справедливо не
только для контуров с непрерывно меняющейся касательной, но
и для контуров, имеющих угловые точки. Таким образом, все
рассуждения п. 4.1 справедливы и в том случае, когда
исследуемая точка есть угловая точка контура.
В этом случае вместо значения интеграла D.6) при z^L
надо воспользоваться интегралом C.7'):
f dx
J Т-/
L
где а — угол между правым и левым касательными векторами
к L в угловой точке t.
Равенства D.7) примут вид
Ф+(/)-ф(/) = ф-@ = Ф@--|^Ф@,
откуда получим выражения для Ф'^(/) и Ф" {t)\
L
ф-@ = -^Ф@ + ^$|^^т. D.19)
L
Полученный результат можно сформулировать следующим
образом.
Теорема. Если интеграл типа Kouiu берется по контуру,
имеющему конечное число угловых точек, то предельные
значения интеграла существуют, причем для неугловых точек
остаются в силе обычные формулы Сохоцкого D.8), а для
угловых точек имеют место формулы D.18), D.19).
Проведенное доказательство не может быть непосредственно
перенесено на точки возврата. Однако при помощи
дополнительных рассуждений можно показать, что формулы D.18),
D.19) остаются справедливыми и в этом случае. В них следует
только положить а = О или а = 2я, смотря по тому, направлено
острие вправо или влево от контура. Доказательство этого
можно найти в [16].
4.6. Интегралы типа Коши по действительной оси. Пусть
ф(т) — комплексная функция действительного переменного т,

§ 4] ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 45
удовлетворяющая условию Гёльдера при всех конечных т
и стремящихся к определенному пределу ф(оо) при т->±оо.
Потребуем, чтобы для больших т было справедливо
неравенство
|ф(т)-ф(сх>)|<-^ (|х>0, Л>0). D.20)
Рассмотрим интеграл типа Коши
— с»
считая Z не лежащим на действительной оси.
Если ф(оо)=7«^0, то несобственный интеграл D.21) будет
расходящимся, т. е. выражение
f Ф(т)
J X — Z
dx
не будет стремиться к пределу, когда Л^' и N'' стремятся
соответственно к —оо и к +00 независимо друг от друга.
Действительно,
N"
В первом интеграле правой части подынтегральная функция
в силу D.20) при больших |т| имеет порядок |т|~^~^ так что
соответствующий интеграл с бесконечными пределами будет
сходящимся на основании известного признака сходимости
несобственных интегралов.
Второй интеграл нетрудно вычислить:
J ^ = 1п(Л^''-г)~1п(Г-г) = 1п-!^;^±/а.
Здесь а — угол между прямыми, соединяющими точку z с
точками Л^' и Л^'^; второй член нужно брать со знаком плюс, если z
лежит в верхней полуплоскости, и со знаком минус, если в
нижней (читателю рекомендуется сделать чертеж).
Если Л^' и Л^'' стремятся (независимо друг от друга) соответ-
ственно к —сх> и к +оо, то а стремится к я, но ^^\Jp г не

46 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
стремится ни к какому пределу, откуда следует, что не
стремится к пределу и левая часть равенства D.22).
Будем теперь считать, что пределы интегрирования Л^' и iV
стремятся к бесконечности симметрично, т. е. —Л^' = Л^'^ = Л^.
Тогда
lim In , '^дГ^' =1п1=0,
и мы получим
— iV -оо
где знак выбирается указанным выше способом.
Выражение, стоящее в левой части, называется главным
значением интеграла D.21), взятого между бесконечными
пределами. В дальнейшем под интегралами с бесконечными
пределами будем всегда подразумевать их главные значения. Если
соответствующий интеграл существует как несобственный, то,
очевидно, главное значение будет совпадать с его значением
как несобственного.
Итак, мы установили существование главного значения
интеграла D.21), причем
2л
-S^^-iS^^^f^-h^T^M. М-23)
где в правой части — интеграл в обычном смысле. Если
ф(оо) = 0, то интеграл D.21) сходящийся.
Так как интеграл
оо
г ф (т) dx
J (T-z)«
— ОО
сходится абсолютно для любого г, не лежащего на
действительной оси, то интеграл D.21) можно дифференцировать по
параметру Z и, следовательно, Ф(г) будет функцией, аналитической
в верхней и нижней полуплоскостях. Функции эти будем
обозначать соответственно Ф+B:), Ф~(г).
Предположим теперь, что 1тг = 0, т. е. точка z=^t
расположена на линии интегрирования. Тогда под интегралом
оо
\^dx D.24)

§ 4) ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 47
будем понимать его главное значение, определенное следующим
образом:
-оо g^O --^ ^+S
В частности,
-00 e^O '• -Af <+e ' e->0
Пользуясь этим равенством, можно записать
оо • /—8 yV X
ф(т) ~ф(оо) ^^_|_ J ^^^^ — Ф^(оо) ^^ I _-
-oo 8-»oo ^ _;\^ /4.g У
^ —00 t+B ^
причем оба последних интеграла сходятся в обычном смысле.
Для доказательства существования предела при 8->0 можно
повторить рассуждения п. 3.4. То обстоятельство, что в
рассматриваемом случае длина контура интегрирования
бесконечна, не имеет существенного значения, так как можно
вернуться к случаю конечного контура, применив преобразование
t-e оо / t—A оо ч t-B t+A
-00 f+e ^-oo t + A'^ t-A t+B
Интегралы в скобках не зависят от е, а предел суммы двух
других интегралов, как было установлено в п. 3.3, существует.
Итак, если ф(т) удовлетворяет сформулированным выше
условиям, то существует главное значение интеграла D.24).
Повторяя рассуждения п. 4.2, можно доказать
справедливость формул Сохоцкого для бесконечной прямой
оо
D.25)
ф-@ = -|ф@ + ^5^^х.

48 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
Здесь Ф+@ и Ф""@—пределы Ф(г) при стремлении z к /
соответственно из верхней (нижней) полуплоскости.
Изучим еще поведение функции 0{z) в окрестности
бесконечно удаленной точки, которая теперь является граничной
точкой. С этой целью произведем замену переменной
1
Когда точка z = x пробегает действительную ось в
положительном направлении, соответствующая ей точка а = —1/т также
пробегает действительную ось и в том же направлении.
Производя в интеграле D.21) замену переменных и вводя
обозначения
ФB) = ф(-|) = Ф*(а Ф(т) = (р(-|) = <Р*(а).
получаем
^ ^^' 2ш- J a{a-i)
— ОО
оо оо
L { Ф* (t^) '^g 1 { ф1(?)^ог. (.оК\
— оо
все предыдущие интегралы понимаются в смысле главных
значений. Второй интеграл правой части D.26) есть величина
постоянная, и поэтому изучение функции ФB) вблизи точки
2 = оо сводится к изучению интеграла
оо
1 f ф* (а) d(y
2ni J а — S
— оо
вблизи точки ^ = о, т. е. к знакомому нам вопросу.
Предположим, что функция ф*(а) удовлетворяет условию Гёльдера
в окрестности точки а = О, т. е.
|ф*(ст2)-Ф*(ог,I<В|а2-а1Г @<^1<1).
Для функции ф(т) имеем тогда
I Ф(Т2) - Ф(Т1) К SI^ - -- Г (О < ^ < I). D.27)
Легко заметить, что из последнего неравенства следует
условие D.20).

§ 41 ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 49
Если Z уходит в бесконечность по любому пути, оставаясь
в верхней или нижней полуплоскости, то ^->0, оставаясь также
в верхней или нижней полуплоскости. Поэтому, применяя к
первому интегралу правой части D.26) первую из формул D.25),
получаем
ф+(оо) = Ф*+@) =
оо оо
' „,*^m_L ^ С Ф* (О') ^<^ 1 С ф' (а) do _ 1 , .
—оо —оо
Проведя еще такое же рассуждение для Ф", получим
ф+ (оо) = 1 ф (оо), ф- (оо) = -1 ф (оо). D.28)
Отсюда и из D.25) следует
ф+(оо) + Ф"(оо) = 0, D.29)
оо
lim \ i^dT = 0. D.30)
f->oo J Т^ — *
— 00
Нами показано, что функция, представимая интегралом
типа Коши на действительной оси, необходимо удовлетворяет
условию D.29). В п. 4.7 мы покажем, что это условие является
также и достаточным для представления кусочно аналитической
в верхней и нижней полуплоскостях функции интегралом по
действительной оси.
Подобное исследование можно провести для интеграла типа
Коши, взятого по произвольной гладкой кривой, уходящей в
бесконечность.
Заметим, что заменой переменных
можно было бы изучение интеграла типа Коши, взятого по
действительной оси, свести к изучению интеграла, взятого по
единичной окружности плоскости ^.
В частности, отсюда без дополнительных исследований
можно установить, что если плотность интеграла удовлетворяет
условию Гёльдера, то этому же условию удовлетворяют
предельные значения интеграла.
4.7. Формулы Коши.
Теорема. Если аналитическая в верхней полуплоскости
функция непрерывна в замкнутой полуплоскости и в окрестно-

50 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
ста бесконечно удаленной точки удовлетворяет условию D.20),
то
-« I —2 ' 1т<г<0.
Доказательство. Построим в верхней полуплоскости
полукруг, ограниченный полуокружностью Cr радиуса R
с центром в начале и отрезком [—/?, R]. Выберем R настолько
большим, чтобы точка лежала внутри полукруга.
В силу формулы Коши A.1) и теоремы Коши
1
J x — z
f ф (Т) — ф (ОО) - , I г ф (Т) — ф (оо) ,
] Т^ГТ—^^ + ^ ] —ГГ1 dx =
1
Ф B) — ф (сх>), Im 2 > о,
D.32)
ч
О, Im г < 0.
Согласно D.20) при возрастании R подынтегральная
функция стремится к нулю порядка 1//?^+**, а длина контура растет
пропорционально Ry следовательно, интеграл по Cr стремится
к нулю. Переходя к пределу при /?->оо, получим
2ni
f Ф(г)-ф(оо) . _/ф(г)-фМ, 1т2>0,
3 "^^^ "^^ о, 1тг<0. ^^•'*^'
Отсюда на основании формулы D.23) придем к D.31).
Так же доказывается формула
если ф(т) удовлетворяет аналогичным условиям в нижней
полуплоскости. Можно показать, что для справедливости формул
D.31), D.34) достаточно, чтобы условие D.20) для больших
|т| удовлетворялось не во всей окрестности бесконечно
удаленной точки, а лишь на действительной оси.
Выше было доказано, что кусочно, аналитическая функция,
представленная интегралом типа Коши D.21), необходимо

§ 4] ПРЕДЕЛЬНЫЕ 3^1АЧЕНИЯ ИНТЕГРАЛА ТИПА КОШИ 51
удовлетворяет равенству D.29). Покажем, что это условие
является также достаточным для представимости кусочно
аналитической функции таким интегралом. В самом деле, пусть
теперь ФB), заданная в верхней и нижней полуплоскостях,
кусочно аналитическая функция и Ф+(т), Ф~(т)—ее предельные
значения, удовлетворяющие на действительной оси условиям
D.29) и D.20).
Положив ф (т) = Ф^ (т) — Ф~ (т), из D.31) и D.34) получим
2ш ]^x-z '^ 1ф"(г), lmz<0,
т. е.
— ОО
Таким образом, выполнение условия D.29) необходимо и
достаточно для представимости кусочно аналитической функции
рассматриваемого класса интегралом типа Коши. Оно заменяет
здесь выведенное ранее для конечного контура условие
ф-(оо) = 0. A.6)
Подобное исследование можно провести для интеграла типа
Коши, взятого по произвольной гладкой кривой, уходящей
в бесконечность. При этом остаются в силе все приведенные
результаты.
В случае, когда ветви кривой уходят в бесконечность по
разным асимптотическим направлениям, бесконечно удаленная
точка является угловой. (Подробности исследования этого
случая можно найти в работе А. С. Моткина 1).)
Сравнивая пары формул A.1), D.31) и A.2), D.34),
замечаем, что формулы Коши для конечного контура и контура,
простирающегося в ОО, совпадают только при ф(оо) = 0.
Рассмотрим еще несколько более сложный интеграл,
который будет использован в дальнейшем,
1 [ (г-го)ц>{х)с1т: _ 1 f ф (т) ^^ 1 f Ф (т) . ,. о^ч
2я/ J (т - го) (т - г) "" 2ni J т - г ^^ 2я/ J т - го ^^' ^^'^^^
L L L
где го^?^" ^ — произвольный гладкий замкнутый контур,
конечный или простирающийся в бесконечность; ф(т)
удовлетворяет на L условию Гёльдера. Из формул A.1) и D.31) вытекает
2./i(.-.„)(x-.)^- 1 О, z^D-, ^^ ^

52 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
если ф(т) есть краевое значение функции, аналитической в D-^.
Если же ф(т) аналитична в D-, непрерывна в D- + L и
удовлетворяет на L условию Я, то из A.2) и D.34) следует
1 f (г-2о)ф(т) ^^_ ( фBо), z^D^,
2я/
Таким образом, при условии, что ф(оо) заменяется на ф(го),
для интеграла D.35) формулы Коши имеют тот же вид, что
и формулы Коши A.1), A.2) для конечного контура.
Укажем еще на одно видоизменение интеграла типа Коши,
полезное в случаях, когда плотность интеграла — растущая на
бесконечности функция. Выделим из ядра Коши ^_^
некоторый отрезок начальных членов его разложения в окрестности
начала координат и будем вместо ядра Коши пользоваться
остатком
г^-П 2^ 1
Тогда интеграл
+ 00
'^i') = 4r S ^{^а? (^-38)
имеет смысл (как главное значение) даже в том случае, когда
плотность интеграла ф(т) на бесконечности растет как |т|^
(так что ф(т)т~^ удовлетворяет условию Гёльдера на
бесконечности) при условии, что ф(т) обращается при т = 0 в нуль
порядка q. В то же время этот интеграл сохраняет основные
свойства интеграла типа Коши. Главное, для него справедливы
аналоги формул Сохоцкого, а формула для скачка имеет тот же
вид, что и для интеграла типа Коши.
§ 5. Свойства предельных значений интеграла
типа Коши
5.1. Предельные значения удовлетворяют условию Гёльдера.
В п. 4.1 было установлено, что предельные значения интеграла
типа Коши, функции Ф+@ и Ф~(/), непрерывны на контуре L.
Оказывается, однако, что эти функции обладают более глубоким
свойством, чем непрерывность, а именно, они сами
удовлетворяют условию Гёльдера.
Это устанавливается в следующей теореме.

§ 51 СВОЙСТВА ПРЕДЕЛЬНЫХ ЗНАЧЕНИЙ 53
Теорема. Если L — гладкий замкнутый контур и ф (О
удовлетворяет на L условию Гёльдера с показателем X, то
предельные значения интеграла типа Коти Ф+@ " Ф~@ также
удовлетворяют этому условию, причем с тем же показателем,
если Ж 1, W с показателем, сколь угодно мало отличаюи{имся
от X, если i = 1.
Из равенства C.11) видно, что сформулированную теорему
достаточно доказать для функции
^^-М'Ч^^^-
Для этого оценим
ш>^-ш)\=Ш{^Щ^^-^^^>^Е^}<1^
E.1)
для двух произвольных достаточно близких точек ti и /г- Из
точки t\ опишем окружность радиуса б так, чтобы она
пересекалась с L в двух точках, которые обозначим а и Ь. Часть
контура L, лежащую внутри этой окружности, обозначим /. Пусть
^2 — произвольная фиксированная точка дуги /, отличная от
точек а и Ь, Положим 8 = k\t2 — /i|. Очевидно, что k>l.
Обозначим 5 = s(/,t) длину меньшей из двух дуг контура L
с концами / и т.
Из свойства D.3) гладкости контура L следует, что для
любых двух точек ti и ^2 можно написать
s{tut2)<m\t2-t,l E.2)
где т — положительная постоянная.
Представим интересующий нас интеграл E.1) следующим
образом:
, 1 f i ф(т)~ф(/2) ф(т)-ф(/1) 1 ^^_
'^ 2ш J I Т-./2 т-/, J«^ —
L-l
_ 1 с ф(т)~ф(/2) . 1 С ф(т)-ф(/1) ^^ ,
--Ш]—7^^2—^^"'ьа]—Т^^г—^^ +
I 1 Г Ф(^1)~Ф(М . , 1 С [ф(т)-ф(/2)](/2-/1) ^^
Li I Z. —*

54
ИНТЕГРАЛ ТИПА КОШИ
[ГЛ. 1
Рассуждая, как в п. 4.1, получим оценку для интеграла
<
о
Здесь, а также и в дальнейшем все числовые коэффициенты —
некоторые положительные постоянные.
Совершенно аналогично
|/lK^2|/2~^ll'.
Интеграл /з оценим так:
dx_
. ^^
U-/ I и-/
Последний интеграл вычисляется непосредственно, а именно:
. J i_ |ф(^1)-ф(Ы1 I С dT \^ A\t2-U)!' I С dx
L-/
Следовательно, он ограничен при всяком t\ на L. Поэтому
имеем оценку
Перейдем к оценке наиболее сложного интеграла /4.
Используя условие Гёльдера и неравенство D.3), получим
Т-/,
А так как
L-1
r-h
1-Л.
dx[.
то
*|T-/2l>*[|T-/i|-Ui-/2l]>(^-l)|t-/,|
и, следовательно,
\h\<A"(^y~\t^-t,\\r^-4r,
R
где
R = max I т — /11.

§ 51 свойства предельных значений 55
Если Я<1, то, вычислив последний интеграл, найдем
Если Л=1, то таким же способом получим оценку
Принимая во внимание, что |1пл:| при х-^О растет медленнее
любой отрицательной степени | х Г® (е < 0), получим
Сопоставляя оценки для /i, /2, /3 и /4 и замечая, что при
Я, = 1 в оценках /ь /2, h показатель X можно заменить на 1 — е,
убеждаемся в справедливости утверждения теоремы.
Доказательство проведено для замкнутого контура. Однако
из замечания п. 4.2 о переходе от разомкнутого контура к
замкнутому, очевидно, вытекает, что теорема справедлива и для
разомкнутого контура, исключая его концы.
Из доказательства теоремы о свойстве предельных значений
интеграла типа Коши непосредственно вытекает следующее
свойство интеграла в смысле главного значения Коши:
Если q)(t) на гладком замкнутом контуре L удовлетворяв!
условию Гёльдера с показателем X, то
ф('>=^5^^
также удовлетворяет этому условию, причем с тем же
показателем, если А,<; 1, и с показателем 1—е, где е — сколь угодно
малое положительное число, если Х= 1.
Это утверждение, равно как и предыдущая теорема, легко
обобщается (см. [16], стр. 57) на случай, когда плотность
интеграла ф(т, С) зависит от некоторого параметра ^, причем по ^
она также удовлетворяет условию Гёльдера. В частности,
может оказаться, что ? == /.
5.2. Расширение предположений Как уже указывалось, основные
предположения, при которых выводились свойства предельных значений интеграла
типа Коши (§§ 4, 5)—гладкость контура и условие Гёльдера для плотности,
являются лишь достаточными, но не необходимыми.
В п. 4.5 было, например, произведено обобщение формул Сохоцкого на
случай контура с конечным числом угловых точек. Укажем коротко на другие
возможные обобщения.
Расширение условий, налагаемых на контур и плотноегь, может
производиться в двух направлениях: 1) в направлении, при котором сохраняется
свойство равномерного стремления к пределу во всех точках контура при
приближении по любым путям и, как следствие этого, сохранение условия,
что предельные значения являются функциями, непрерывными на контуре, и
2) в направлении, при котором предельные значения существуют лишь почти

56 ИНТЕГРАЛ ТИПА КОШИ [ГЛ I
всюду (за исключением множества точек контура меры нуль) и лишь по
путям, не касательным к контуру.
Рассмотрим сначала обобщения первого типа, при которых мы остаемся
в рамках классического определения интеграла Римана. Вопрос, как мы
видели, сводится к исследованию интеграла
Г
Обозначим длину дуги контура L между точками ti и /2 через s(/i,/г) и
длину стягивающей эту дугу хорды через r(/i, ^2) = Id — tz].
Если сохранить условие, что отношение длины дуги к хорде есть
величина ограниченная (класс кривых, удовлетворяющих этому условию,
включает в себя класс кусочно гладких кривых), то для того чтобы выражение
Ф(т) — ф@ ^ ^
' 7^ было интегрируемым, достаточно потребовать, как это мы и де-
т — t
лали, чтобы функция ф@ удовлетворяла условию Гёльдера.
Условие интегрируемости будет выполнено и в том случае, если на
функцию ф@ наложить более слабые ограничения: например, потребовать, чтобы
имело место неравенство
|ф(т)-ф(/)|<,,„,/_^(), (р>1)
или еще более общее условие
Ф (т) - ф (О I <
^ 11п|т-^|||1п|1п|т-/||| ... |1п|1п ... |1п|т-/|| ... И/' ^Р>^^'
Величины, стоящие в правых частях последних неравенств, стремятся к нулю
при \t—t\-^0 медленнее, чем |т —^|\ поэтому класс функций,
удовлетворяющих последним условиям, включает в себя класс функций,
удовлетворяющих условию Гёльдера. Наиболее общим среди условий интегрируемости
является условие Дини
С @(s)
ds<+со (О < а < -f со),
где О)(s)—модуль непрерывности функции ф@ (см. сноску к п. 4.1).
Если расширять класс рассматриваемых контуров, то придется
соответственно сужать класс допустимых функций (pit). Наглядным подтверждением
этого положения служит следующая теорема*).
I) Вели контур, представляющий собой жорданову спрямляемую кривую^
и плотность интеграла типа Коши удовлетворяют условиям
s(/i,/2)<С|/,-^зГ @<а<1),
|ф(/1)-ф(^2)|<Ли,-^2|^ A-а<р<П,
то интеграл типа Коши имеет непрерывные предельные значения на контуре
всюду, кроме, быть может, концов.
*) См., например, [18], стр. 197.

§ 5] СВОЙСТВА ПРЕДЕЛЬНЫХ ЗНАЧЕНИЙ 57
2) Если контур L есть жорданова спрямляемая кривая и если плотность
ф(/) удовлетворяет условию Липшица
|ф(/1)-Ф(/2I< ли,-/jI,
то интеграл типа Коши имеет непрерывные предельные значения на
контуре L, за исключением, быть может, концов.
Обобщения второго типа, связанные с привлечением к рассмотрению
интегралов Лебега и Стилтьеса и еще более общих, имеют в настоящее время
в основном теоретический интерес и пока что мало связаны с практическими
приложениями.
Не вдаваясь в подробности, сформулируем один наиболее общий
результат, принадлежащий И. И. Привалову*).
Теорема. Пусть L — замкнутая жорданова спрямляемая кривая
длины /, 6 — угол между положительным направлением оси абсцисс и
касательной к L, а F(s)—комплексная функция дуги s с ограниченным изменением
на сегменте [О, /]. Тогда интеграл типа Коши — Стилтьеса
I
e'^^^'^dFjo)
о
имеет конечные предельные значения по всем некасательным путям почти
всюду на контуре L и эти значения удовлетворяют соотношениям
0^(t)^±i-r(s) +
2 ' ' ' 2я/ J т (а) - / *
L
где интеграл в правой части определен как особый.
В частности, если F(s) абсолютно непрерывна, то интеграл типа Коши —
Стилтьеса обращается в интеграл типа Коши — Лебега rr-r \ dx,
2ш J т — Z
1 С Ф(т)
J Т —5
где Ф (О *= Ф R (s)] = F' (s) почти всюду на L, а предыдущие формулы —
в обычные формулы Сохоцкого D.8).
5.3. Интеграл типа Коши в классах Lp. Наибольший интерес с точки
зрения приложений к краевым задачам здесь представляют работы Б. В. X в е-
д е л и д 3 е [30] по теории интеграла типа Коши с плотностью из класса Lp,
р > 1 (интегрируемых в степени р по Лебегу). Формулируем два основных
результата, которые будут использованы в дальнейшем (п. 16.3).
1. Если (p(t)^Lp, то и особый интеграл
L
принадлежит тому же классу Lp. Предельные значения интеграла типа Коши
по всем некасательным путям существуют почти всюду, и для них
справедливы формулы Сохоцкого D.8).
2. Особый оператор 5 в норме пространства Lp (/^ > 1) есть оператор
ограниченный, т. е.
*) См. [18], гл. III.

58 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
где Мр — постоянная, не зависящая от ф. Контур L считается кривой
Ляпунова (угол a(s), образованный касательной к контуру с осью абцисс,
удовлетворяет условию Гёльдера).
Доказательство основано на использовании соответствующего результата
Рисса для интеграла с ядром Гильберта и исследования интеграла
\<f{'^)[-^-cis^do],
в котором при сделанных относительно контура предположениях
подынтегральная функция будет иметь особенность порядка меньше единицы.
§ 6. Формулы Гильберта для предельных значений
действительной и мнимой частей аналитической функции
6.1. Ядро Коши и ядро Шварца. Пусть f{z) = и{х,у)+
+ iv{Xyy) есть функция, аналитическая в единичном круге.
Обозначим S и о длины дуг окружности, отсчитываемых от точки
пересечения ее с положительным направлением оси абсцисс.
Пусть, далее, непрерывная функция u{s) есть предельное
значение действительной части функции f{z) на контуре круга.
Тогда, как известно (см. конец п. 27.2), формула Шварца
дает возможность выразить аналитическую в круге |2|<1
функцию f{z) через значения ее действительной части на
окружности с точностью до постоянного мнимого слагаемого Ivq.
Полагая в F.1) 2 = О и пользуясь теоремой о среднем, найдем, что
2я
t;o = i;@, 0) = ±^v{a)da. F.2)
о
Выражение ^^ называется ядром Шварца. Между
ядрами Шварца и Коши имеется простое соотношение. Обозначая
т комплексную координату точки окружности (т = е^^), получим
^+^do
е'"
= (-l-\--W^)do = --^ da. F.3)
Отсюда следует, что
2л 2Л
2я
и

§ 6] ФОРМУЛЫ ГИЛЬБЕРТА 59
Последняя формула, устанавливающая связь между
интегралом Шварца и интегралом типа Коши с действительной
плотностью, взятым по контуру единичного круга, будет
использована в следующем пункте.
6.2. Формулы Гильберта. Выведем соотношения между
предельными значениями на контуре действительной и мнимой
частей аналитической в единичном круге функции.
Перейдем в формулах F.1), F.4) к пределу, когда z
стремится к точке единичной окружности t = е^^, и воспользуемся
формулой Сохоцкого D.8). Получим
u{s) + iv E) = у2иE) +-2JJ7 J Т=Т^^ ^llr J " (^^ ^^ + ^"^0-
L О
Произведя сокращение и объединяя оба интеграла правой
части, будем иметь
2Я
2я/ ^
о
_. a+s
Умножая в ядре интеграла числитель и знаменатель на е ^
получим
g'a + ^/s е ^ +е ^ 1 , <y-^s
e ^ —e
Следовательно,
2Я
o(s) = -^J«(a)ctg-^rfa+Oo. F.6)
0
Эта формула дает выражение краевого значения мнимой части
аналитической функции через действительную.
Чтобы выразить u{s) через v{s), заметим, что для функции
— // (г) = t; •— ш
действительной частью является у, а мнимой — и. Применяя
формулу F.6) к последней функции, получим
2я
«(S) = ^ J f {о) ctg -^ do + щ («о = и (О, 0)). F.7)
О
Симметричные формулы F.6), F.7) носят название формул
обращения Гильберта, а выражение ctg—^^ называется ядром
Гильберта.

\u{a)cig^^da==c{s)
60 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. J
При а = 5 ядро обращается в бесконечность первого
порядка, так что интегралы, входящие в формулы Гильберта,
являются особыми и их нужно понимать в смысле главного
значения. Формулы обращения F.6), F.7) можно истолковать как
решение интегрального уравнения
1
2я
о
(см. п. 31.3).
Мы не останавливаемся на сложном вопросе о том, каким
наименее ограничительным условиям нужно подчинить
функции u{s) и v{s) для того, чтобы формулы F.6) и F.7) имели
место. Ограничимся очевидным утверждением, что для этого
достаточно, чтобы они удовлетворяли условию Гёльдера.
Дополнением к настоящему параграфу являются задачи 14,
16, 23, 25, 29 в конце главы.
§ 7. Перестановка порядка интегрирования
в повторном особом интеграле
7.1. Случай, когда один интеграл обыкновенный. Прежде чем
произвести исследование вопроса о перестановке порядка
интегрирования в повторных особых интегралах, рассмотрим
предварительно более простой случай, когда в повторном интеграле
лишь один интеграл особый, другой же обыкновенный.
Рассмотрим повторный интеграл
/=J<D(T, 2)dT5-?i^rfT, G.1)
L L
и интеграл, получившийся после изменения порядка
интегрирования,
/' = SdT,5^ib^^^ipidt. G.2)
L L
Лемма. Пусть функция ф (т, ti) удовлетворяет условию
Гёльдера по обеим переменным, а (о(т, г) удовлетворяет по т
условию Гёльдера при каждом фиксированном значении z из
рассматриваемого множества^ L — гладкий контур.
Тогда интеграл G.1) допускает перестановку порядка
интегрирования*), т. е.
Ja(T/2)dt5^|b^dT, = 5rfT,5^ib|)±lpidT. G.
3)
*) Результат справедлив и при более слабых предположениях
относительно ф(Т,Т1).

^ 7] ПЕРЕСТАНОВКА ПОРЯДКА ИНТЕГРИРОВАНИЯ 61
Для доказательства разобьем контур интегрирования в
интеграле / по переменной ti на две части: дугу /, вырезанную из
L окружностью радиуса 6, проведенной из точки ti = т как из
центра, и на дугу L — /. Для интеграла Г проделаем то же
самое, взяв центр окружности в точке т = ть
Обозначим
где
L L-t
Аналогичным образом разобьем и интеграл /':
В повторных интегралах /о, /о все интегралы являются
обыкновенными. В них допустима перестановка порядка
интегрирования*), т. е.
/о = /5.
Поэтому
|/~П = |/б-/И<|/б1 + 1/^|.
Оценим последние два интеграла.
Во внутреннем интеграле повторного интеграла
L I
произведем обычное преобразование
1
Т
Первый из интегралов правой части уже рассматривался в
п. 4.1. При достаточно малом б его модуль может быть сделан
*) Равенство станет особенно наглядным, если будем определять
положение точек т и Ti контура L дуговыми абсциссами s и 5i @^5^/,
О ^ si ^ /, где / — длина контура L) и рассматривать их как прямоугольные
координаты точки на вспомогательной плоскости Ossi. Тогда в обоих
интегралах /о и /q областью интегрирования будет квадрат со стороной / с
выключенной вдоль диагонали узкой полоской.

62
ИНТЕГРАЛ ТИПА КОШИ
ГГЛ I
меньше положительного числа г/4М, где
М = тах
\ со (т, z)
dx
Далее, обозначая концы дуги I через х\ х" и применяя формулу
C.6), получим
где а — угол между секущими (рис. 6).
При достаточно малом б в силу гладкости кривой этот угол
может быть сделан сколь угодно малым. Следовательно, можно
добиться оценки
Тогда
\h\<'^iM\\^{:^,z)dx
Аналогичными рассуждениями можно
получить оценку
откуда
Рис. 6.
\П\<^.
|/-Г|<е.
Но, с другой стороны, разность / —/', очевидно, не зависит от
величины б, следовательно,
что и требовалось доказать.
7.2. Формула перестановки. Рассмотрим пару повторных
особых интегралов, отличающихся порядком интегрирования:
L L
М« = ^)л,^г^^„2^Л. G.5)
Оба интеграла имеют смысл. В самом деле, первый из них
1 С X(x)dx
я/ J т —/ •

§ 7) ПЕРЕСТАНОВКА ПОРЯДКА ИНТЕГРИРОВАНИЯ 63
где
xw-ilrj^!^'"..
существует в смысле главного значения Коши, так как
плотность х(т) на основании п. 5.1 удовлетворяет условию Гёльдера.
Во втором интеграле проделаем следующие преобразования.
Разложим функцию . ^t)(T: — т) "^ простые дроби:
^[т^т-Т:^]- G.6)
(т - t) (Ti - т)
Тогда, обозначая
L
будем иметь
, ^ J_ f 0(/, Ti)~u)(Ti, Ti) ^^
' я/ J Ti--t ^ •
L
По теореме п. 5.1 a)(S,Ti) удовлетворяет условию Гёльдера,
следовательно, интеграл /i существует как несобственный.
Проведенное рассуждение справедливо для всех точек /, не
являющихся концами контура. Для последних нужно было бы
провести дополнительное исследование. На этом, однако, мы
не останавливаемся.
Хотя интегралы / и /i отличаются лишь порядком
интегрирования, но они не равны, что показывает следующая формула
перестановки Пуанкаре—Бертрана:
1 f dT 1 f ф(т, Ti) , _
ni ] x-t ni ] T, - T "^J ~
L L
L L
Для доказательства образуем функции /(г), /1B), заменив
в интегралах !{(), I\{t) переменную t переменной г,
изменяющейся во всей плоскости:
j(^) = ±[-^-L\^Sl,Iildxu G.8)
L L
/^ (г) = л f dT, л [ , "^^У^ , dx. G.9)
* ^ ^ я/ J ' я/ J (т — г) (Ti — т) ^ '

64 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
Для всех г, не лежащих на L, на основании предыдущей
леммы можно переставить порядок интегрирования. Поэтому
/B) = 7,B).
Обозначая предельные значения этих функций как обычно,
будем иметь
Л@ = /Г@, /-(/) =/г (/).
Но по формуле D.10)
I{t) = Ul'{t) + r{t)l
или, используя предыдущие равенства,
/@ = у[/1'@ + /Г(/)]. G.10)
Воспользовавшись разложением G.6), представим /i(^)
в виде
^^ ^ яО Ti — Z ш I J т — г J т — Ti I
^Л^Г1|>(..т.)
Ш J Ti — 2 ^
L
Последнее выражение показывает, что Ii{z) есть интеграл
типа Коши с плотностью
зависящей от параметра z.
Найдем по формулам Сохоцкого D.7), D.8) значения
it {t) и IT {t)y учитывая, что в качестве значения плотности
^(г,/) в точке t нужно брать lim^(e, О, равный yp+{tj), когда
z-^t, оставаясь слева от L, и ^~{tj) при z->t справа от L*).
Таким образом,
/Г«=**(',0 + ^5^^л„
L
*) Обоснование применимости формул Сохоцкого к случаю, когда
плотность интеграла типа Коши зависит от г, мы не приводим (см. [16],
стр. 128).

§ 7) ПЕРЕСТАНОВКА ПОРЯДКА ИНТЕГРИРОВАНИЯ 65
откуда
у[/Г{0 . -^ WJ-2
т т (t)+IT @] =ii^ut,t)-r it, 0]+
1
2я/
J VL(Liii_ttiiiLld^,. G.11)
Ho согласно формулам D.9), D.10)
2
i-[a|j-^(/, /)-г|?-(/./)] = ф(/,0.
L L
с/ J (T-0(T-T,) "^•
Вставляя последние выражения в формулу G.11) и
используя G.10), получаем требуемую формулу G.7).
Формулу перестановки G.7) можно записать еще в таком
виде:
L L
L L
Изложенное здесь доказательство дано И. И. Мусхели-
швили [16]. Имеется и другой вывод формулы перестановки
(см. задачи 27, 28 в конце главы).
7.3. Обращение особого интеграла с ядром Коши для
замкнутого контура. Дадим приложение формулы перестановки
G.7) к выводу формулы обращения особого интеграла с ядром
Коши для замкнутого контура.
Пусть дан особый интеграл
L
Поставим задачу: выразить плотность ф(/) через значение
самого интеграла, т. е. через функцию 'ij)@. Заменим в обеих
частях переменную t на ть умножим на —г ^ ^'
проинтегрируем по контуру L и переставим по формуле G.7) порядок

66 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
интегрирования. Получим
L L L
Ho
J (Ti -/) (T - Ti) T~/ [J T,-/ Jti-tJ
= r (in — /я) = 0.
Таким образом, имеем
L
Последняя формула есть формула обращения особого
интеграла; она взаимна с формулой G.12).
Если обозначить S оператор особого интегрирования
I >5ф = —г \ ^^"^^^ \ а / — единичный оператор (/ф^ф), то
соотношения G.12), G.13) в операторной форме выразятся так:
S2 = /.
Заметим, что формулы G.12), G.13) родственны с
формулами обращения Гильберта F.6), F.7). Последние нетрудно
получить из формул обращения G.12), G.13) особого
интеграла Коши, используя связь ядер Коши и Гильберта (см. § 6),
и их можно рассматривать как формулы обращения особого
интеграла с ядром Гильберта ctg —-^— (см. п. 6.2).
§ 8. Поведение интеграла типа Коши
на концах контура интегрирования
и в точках разрыва плотности
8.1. Случай плотности, удовлетворяющей условию Гёльдера
вплоть до концов. При исследовании в § 5 поведения
предельных значений интеграла типа Коши на контуре все время
исключались из рассмотрения концы контура. То, что конец яв*
ляется исключительной точкой, видно хотя бы из того, что его
нельзя заключить в двусторонний интервал и, следовательно,
нельзя определить особый интеграл как его главное значение.

§ 8] ПОВЕДЕНИЕ ИНТЕГРАЛА ТИПА КОШИ 67
Перейдем к изучению поведения интеграла типа Коши на
концах контура.
Пусть L —разомкнутый контур с концами а и & и ф(/)
удовлетворяет условию Гёльдера на всей кривой, включая
концы.
Рассмотрим интеграл типа Коши
L
Поступая как в п. 3.4, представим Ф(г) в виде
L L
= ^ In 1п? +-L f ±(lL=fiU ^т,
2л1 а — Z * 2ш J х — г »
L
где t — любая точка контура L.
При Z = / последний интеграл существует как
несобственный. Поэтому он представляет собой функцию, ограниченную
и стремящуюся к определенному пределу при приближении
точки Z ко всякой точке контура, включая концы (см. п. 4.1).
Главную особенность для Ф(г) на концах дает первый член.
Полагая в последнем выражении последовательно / = а,
t = b, получим
(8 I)
где Ф\(г), ФгС-г) — функции, ограниченные в окрестности
соответствующих концов и стремящиеся к определенным пределам,
когда Z стремится соответственно к а или Ь.
Таким образом, на концах контура интеграл типа Коши
имеет особенности логарифмического характера, полностью
определяемые значениями ф(а) и ф(&).
8.2. Случай разрыва первого рода. Рассмотрим теперь
родственный вопрос о поведении интеграла типа Коши в точках,
где плотность имеет разрыв первого рода. Пусть с — точка
разрыва. Будем считать точки, предшествующие точке с при
движении по контуру в положительном направлении, левой
окрестностью точки с, а точки, следующие за с, — правой. Пределы
ф@ справа и слева будем обозначать, как обычно, ф(с:±0).

68 ИНТЕГРАЛ ТИПА КОШИ 1ГЛ. I
Разобьем интеграл по контуру аЬ на два интеграла по
участкам ас и сЬ:
HS + S-
аЬ ас сЬ
Тогда с является соответственно правым и левым концом
частичных контуров, причем в первом интеграле нужно считать
ф (с) = ф (с — 0), а во втором ф (с) = ф (с + 0).
Применяя формулы (8.1), получим представление
ф (^) _ Ф(.-0)-^Ф(с + 0) ,„ (^ _ ^) ^ ф^ (^)^ (8.2)
где Фо(<2:) в окрестности точки с обладает теми же свойствами,
что и функции Ф1(г), ФгС^) в формулах (8.1).
Формулы (8.1)— (8.2) будут существенно использованы
далее.
8.3. Частный случай особенности степенного характера.
Прежде чем перейти к общему исследованию поведения
интеграла типа Коши в точках, где плотность обращается в
бесконечность степенного порядка, рассмотрим интеграл типа Коши
частного вида
ао
где и — некоторая определенная точка контура.
При рассмотрении этого интеграла возникают специфические
трудности, вытекающие из многозначности как
подынтегральной функции, так и самого интеграла. Необходимо внимательно
следить за тем, при помощи какого разреза в плоскости
комплексного переменного выделяются однозначные ветви
рассматриваемых функций. Такого рода вопросы уже встречались
в пп. 3.4, 3.5 и еще встретятся в гл. VI.
Будем исследовать интеграл Q{z) при различных
положениях точки ^0.
Г. Точка ^0 совпадает с левым концом (/о = а).
Многозначную функцию (/ —a)-Y примем за контурное
значение аналитической функции (г —а)-\ Последнюю же будем
рассматривать как однозначную в плоскости, разрезанной вдоль
какой-нибудь линии, соединяющей точки разветвления а и оо.
Условимся разрез проводить через контур L. Выберем на левой
стороне разреза какую-нибудь ветвь этой функции, примем ее
за значение (/ —a)-Y на контуре интегрирования и возьмем в
качестве плотности интеграла (8.3); таким образом, по
определению,

§8]
ПОВЕДЕНИЕ ИНТЕГРАЛА ТИПА КОШИ
69
Значение же ее на правой стороне контура будем получать
путем обхода около точки а в положительном направлении
(рис. 7), учитывая, что при этом степенная функция (/ —a)-Y
приобретает множитель е"я/7.
Для произвольной точки контура
t будем иметь
= (l_g-2mY)(/_a)-\ (8.4)
Покажем, что в окрестности
точки 2 = а функция Q (z) имеет
следующее представление:
(8.5) __
Рис. 7.
2/ sin YJi
где йо (г)— функция, аналитическая
в окрестности точки а.
Для доказательства заметим прежде всего, что по формуле
Сохоцкого
Положим
J"^(/)-Q"(/) = (/-a)"\
(8.6)
(й(г) =
Jyn
I - e-2"^Y 2/ sin уя
B—a)
-Y
и рассмотрим функцию fi(z)—а)(г).
Учитывая (8.5) и (8.6), будем иметь
[Q@-co(/)]-^ = [Q@-CD@]^
(8.7)
Покажем теперь, что функция йB:) —соB) вблизи точки а
удовлетворяет неравенству
|а(г)-со(гЖ^^22±^, (8.8)
где V — действительное число, удовлетворяющее условиям
0<a<v< 1.
Обозначая 2 — а = ре^^, найдем, что
I 2 - а 1^ *
Функция л (г) ограничена при 2->а и, следовательно,
С,
|со(гЖ
и-аГ
@<а<1),

70 ИНТБГРАЛ ТИПА КОШИ [ГЛ. I
Перейдем к оценке | Q {г) |. Полагая |т — а| = г HO<a<v<l,
будем иметь
^ ' р^ L 2я/ Д г" (т - 2) ^ 2я/ Д т - г J
Убедимся в ограниченности интегралов /] и I^. Учитывая
неравенства *)
|р-г|- ||2-а|-|т-а||<|2-т|,
|р^-г^1<|р-гГ<|2-тГ
и ограниченность Л(т), получим
ао
Последний интеграл при всех значениях р существует как
несобственный и, следовательно, ограничен. Ограниченность
интеграла /г следует из того факта, что функция r'^-^h{x)
удовлетворяет условию Гёльдера с показателем v — а. Таким образом
Р I г - а I
Заметим, что равенство (8.5), доказываемое ниже, дает точную
оценку (v = a). Однако для получения последней нам придется
использовать только что полученную более грубую оценку.
Неравенство (8.8) следует из оценок для |й)B)| и |QB)|.
Равенство (8.7) показывает, что функции [йB:)—©(г)]+,
[Q(z) —о)B)]~ аналитически продолжимы через контур аЬ и
образуют, следовательно, единую во всей плоскости
аналитическую функцию Q (г) — © (г). Эта функция может иметь только
изолированную особенность в точке а. В силу оценки (8.8)
точка а является устранимой особенностью*^). Следовательно,
й(г)—(о(г) аналитична в окрестности точки а, что и приводит
к представлению (8.5).
*) Неравенство | р^ — г*^ I < I р — г Г устанавливается определением
максимума функции /(jc) = (l — х^)(\ — jc)""*^ @<jc< 1), где jc=8-?. (xz=^L.\^
если г > р (г < р).
**) См., например, М. А. Евграфов, Аналитические функции, «Наука»,
1968, гл. II, теорема 2.1.

ПОВЕДЕНИЕ ИНТЕГРАЛА ТИПА КОШИ
71
Для получения значения Q{z) на контуре вновь применяем
формулу Сохоцкого D.10):
и получаем
¦-\—
dx
2ni J (т-
a)Y(T-0
= -i[Q-^@ + Q"@]
Q@ = ^(^-«nctgY« + Qo@,
(8.9)
где Qo(О"-функция, аналитическая в окрестности точки а.
2°. Точка /о совпадает с правым концом (/о=Ь),
В этом случае при условии, что для функции (г —6)~y разрез,
соединяющий точку Ь с оо, проходит через контур L, при
помощи аналогичных рассуждений получим
'"'"" .B-6)-'+0,B).
(8.10)
QB) = .
Q@ =
2/ sin ук
Отметим, в частности, что если у === 1/2 и,
следовательно, ctgYn = 0, формулы (8.9), (8.10) дают
Q@ = Q,@ (/ = 0, 1),
т. е. особый интеграл (8.3) является функцией,
ограниченной вблизи концов.
3°. Точка ^0 есть некоторая
внутренняя точка контура (/о™ с).
dx
аЬ ^
(т-с)^(т-г)
Рис 8.
Будем считать, что разрез для функции (г —c)~y от точки с
до оо проходит через участок сЬ контура (рис. 8).
Разбивая интеграл на два
S-S+5.
аЬ ас сЬ
МЫ сведем исследование к случаю, когда точка разветвления с
совпадает с концами контура интегрирования. Второй интеграл
может быть непосредственно вычислен по формулам (8.5),
(8.9). Для вычисления первого интеграла понадобятся
добавочные рассуждения, вызванные тем, что, в отличие от 1°, кон-
тур ас не является линией разреза. Поэтому функция (г —с)"*^
изменяется при переходе через контур ас непрерывно:
[(^
С)
.-vn+
] =[(/-с)~^]" на ас.
(8.11)

72 ИНТЕГРАЛ ТИПА КОШИ (ГЛ. I
С другой стороны, по формуле Сохоцкого
Q"^@-Q"@ = (^-^)"^ на L (8.12)
Из последних формул можно заключить:
1. В представлении функции ?2(г) в окрестности точки с
участвует функция (г —с)-v.
2. На разных сторонах контура Q{z) представляется
различными аналитическими выражениями.
Будем искать представление первого слагаемого функции
Q(z) в окрестности точки с в следующем виде:
\ = Л (а: — с)"'^ + Q2 (^) на левой стороне контура,
ас
\ = В B — с?)-'^ + Q2 B) на правой стороне контура,
ас
где А и в — неопределенные коэффициенты, а Q2{z) — функция,
аналитическая в окрестности точки с. Из формул (8.11) и (8.12)
следует
Л-В=1. (8.13)
Для получения второго соотношения, связывающего Л и 5,
dx
рая из формул (8.10) независимо от способа выбора ветви
функции (г —c)-Y. Снова применяя формулу D.10), получим
Л + В = --ус1ёуя. (8.14)
Из (8.13) и (8.14) имеем
заметим, что для интеграла \ ~ справедлива вто-
J (т — с^ " ^^
ас
21 sin уя * 2/ sin ул
Следовательно, Й(г) в окрестности точки с имеет такое
представление:
Q(z) = {z—c)'"^+ Q^{z) слева от L, (8.15)
QB) = Q4(^) справа от L, (8.16)
Q (/) = 1 (/ ^ с)"^ + Q5 (О на L. (8.160
Все й/(г) есть функции, аналитические в окрестности точки с,
8.4. Общий случай особенности степенного порядка. Пусть ф*
(т)—функция, удовлетворяющая условию Гёльдера на замкнутой дуге аЬ с
показателем Л.

ПОВЕДЕНИЕ ИНТЕГРАЛА ТИПА КОШИ
73
Рассмотрим интеграл
2П1 Ux- c)Y (т - z)
ab
(Y = a + /p, 0<а<1) (8.17)
и запишем его в следующем виде:
dx
(т— с)'^(т —г)
2ш J (т-с)^(т-г) 2я/ J (т-с)^
— ф* {с) dx
(8.18)
Первое слагаемое есть интеграл, исследованный в п. 8.3. Приступим
к исследованию поведения второго интеграла при г->с. Функция
(t^C)^^:
,/piin|f-c|+/el,
' [cos (р In I / - с I) + / sin (р In I ^ - с I)]
в точке с будет разрывной, но ограниченной. Учитывая это, можно показать
(на чем мы не останавливаемся), что функция (t — с)^^^^ при а > О
удовлетворяет условию Гёльдера с показателем а.
Тогда
Ф*@-Ф*(с)
Если ав=0, то имеет место оценка
Ф* (t) - Ф* {с)
<A\t-c
\K-Q.
~ г\^^
(t-c)
<A\t-c\
К-г
(8.19)
(8.19')
где е — сколь угодно малое положительное число.
Из последних оценок вытекает:
1. Если а < А. (в том числе а = 0), то подынтегральная функция
второго интеграла в формуле (8.18) удовлетворяет в силу (8.19) условию
Гёльдера и, следовательно, сам интеграл представляет функцию Фо(г),
ограниченную и стремящуюся к определенному пределу, когда z-^c.
2. Если а ^ Я, то ФоB) представляет функцию, неограниченную в
окрестности точки с, но имеющую порядок бесконечности ниже а.
Полное доказательство приведенных утверждений сопряжено с довольно
громоздкими выкладками, которые мы не приводим. Подробное изложение
читатель может найти в книге [16].
Не вдаваясь в подробности, рассмотрим случай, когда функция ф*@
имеет в точке с разрыв первого рода. Если разбить контур L на два участка
ас и с6, то ф*@ на каждой из замкнутых дуг удовлетворяет условию
Гёльдера.
Разобьем интеграл (8.17) на два интеграла по участкам ас, сЬ. К
каждому из полученных интегралов применим преобразование, приводящее к виду
(8.18). К интегралам
Ф*(с~0)
2я/
1-
dx
Ф* (с + 0)
c)Y (х — z)* 2я/
h'-
dx
(т — с)'^ (т — z)
применим рассуждения п. 8.3, а при рассмотрении остальных интегралов
воспользуемся приведенными выше свойствами I, 2.

74
ИНТЕГРАЛ ТИПА КОШИ
1ГЛ. I
Окончательно получим, что функция Ф(г) вблизи точки с имеет
следующее представление:
ф (.) ^ -^"Ч' (^ + 0)- ^-^"'Ф- (о - 0) (, - ,)-У +
^ ' 2/ Sin Y« V / I
+ Фо (г) слева от L,
g^* (g + 0) - g^* (g - 0)
2/ sin Y^
+ Фо (г) справа от L, J
причем Фо(г) вблизи точки с допускает оценку
с
\ (8.20)
Ф(г).
(г-с)-^ +
|Фо(г)|<
2 — с
1»»
(оо < а).
(8.21)
В частности, если показатель Гёльдера Я > а, то Фо (z) ограничена.
Для значения интеграла (8.17) на контуре будем иметь представления
+ Ф* (О на ас, (8.22)
ф (О=[^ Ф-(с+0) - ^^^ji:;!^ Ф-(с - 0)] (/- o-v+
+ Ф* (О на сЬ. (8.23)
причем Ф* (/) допускает оценку (8.21).
8,5, Особенность логарифмического типа. Рассмотрим интеграл типа
Коши
аЪ
(8.24)
(8.25)
где р — целое положительное число.
Чтобы выделить главную часть разложения Q(z) вблизи точки д, вводим
функции сор B, а) следующими рекуррентными соотношениями:
®1 (г, а) = - -^ In (г - а),
©2 (г, а) « - -^ 1п2 (г - а) + Y in (г - а),
р-1 ^
»р (^'«) — 2^ •"' (^ -") - Z ^*-. ттг %-* <^' -"^ <">'>•
где С* I — биномиальные коэффициенты.
Будем считать, что контур аЬ совпадает с линией разреза для функции
©i {г, а), так что
cd/'(/, а) —of (/, а) —1.
Непосредственными вычислениями можно показать, что функции (йр{г,а) при
любом р удовлетворяют соотношениям
а^^ {и а)- у {U а)^\п^^^ {t - а).
(8.26)

§ 81 ПОВЕДЕНИЕ ИНТЕГРАЛА ТИПА КОШИ 75
Опираясь на эти соотношения и формулы Сохоцкого для Q(z) и
рассуждая аналогично тому, как это делалось в п. 8.3, получим
Q (г) = (Ор (г, а) + Qo (г), (8.27)
где Qo {^) — функция, аналитическая в точке а.
Для точек контура вблизи точки а имеем
Приведем в заключение несколько более общие формулы. Пусть
^ 2ш J т —аг
(8.28)
(8.29)
где ф* (т) — функция, удовлетворяющая условию Гёльдера.
Тогда вблизи точки а справедливо представление
Ф (z) -X ф» (а) ©р (г, а) + Фо (г), (8.30)
Ф (О - Y Ф* (а) [@^ (^ а) + (oj (/, а)] + Фо @. (8.31)
Если в выражении для плотности интеграла (8.29) заменить а на ^, то
представление Ф (г) в окрестности точки b будет иметь вид (8,30), (8.31) с
заменой ф* (а) на ф* (Ь) и функций ©р (г, а) на функции ©*;
©1B, г^) = ^5^1п(г--^;),
^2 (^' ^) = i ^"' (^ - ^) + 4 ^" (^ - ^)' (8.32)
ft-l
Формулы для точек, лежащих внутри контура а6, оказываются довольно
сложными, и мы их не приводим.
8.6. Особенность степенно-логарифмического типа. Обобщая результаты
пп. 8.4 и 8.5, рассмотрим интеграл
0(,)._L U-(T)ln^(T-a)^^^ (833)
2ш J (т —a)Y(T —2)
Введем функции
So B, а) = .^гД (Z - a)-Y,
^ 2f sin уя ^
Sp (г. а) = -^?^ '""^^"^^ + -f^ У С* BяО^ 5р_, (г. а) (8.34)
2t sin ул (г — ау 2i sm У^ f^.
(p=l,2, ...).

76 ИНТЕГРАЛ ТИПА КОШИ (ГЛ. I
S+(/, а) - S; (/, а) = "'^/' ^7 (Р = 0» Ь2, ...),
Нетрудно показать, что функции Sp (г, а) удовлетворяют условиям
откуда и будет следовать, что в окрестности точки а функция Ф (г) имеет
представление
Ф (г) = ф* (а) Sp (г, а) + Ф* (г), (8.35)
Ф (О = Y Ф* (а) [S+ (^ а) + S; (/, а)] + Ф* {t\ (8.36)
где Ф* {г) — аналитическая на разрезанной по контуру аЬ плоскости функция,
для которой в окрестности точки а справедлива оценка
\^*(^)\< . "^ .а.> «o<ReY.
Аналогично для интеграла
ф _L f fl(l)ln?(x^:i) ,, (8.37)
2я/ J (т - 6)^ (т - г)
ао
В окрестности конца b получим представление того же типа, в которое будут
входить функции
s>.b)—;:"' 'f'-/' --^^|:с^,-1)>Bд/)'5;_.(..».
'^ 2f sin Y^ (г — by 2t sin vn f-',
(8.38)
Материал пп. 8.5 и 8.6 изложен по работе И. М. Мельника 2).
П. Г. Юров 1), 2) с помощью теории уравнений в конечных разностях дал
выражения для главной части интегралов (8.24) и (8.33) в явной (а не
рекуррентной) форме через многочлены Бернулли и Эйлера. Для понимания
работы требуется знание элементов теории целых функций.
8.7. Интеграл типа Коши по сложному контуру. До сих пор для простоты
предполагалось, что интеграл типа Коши берется по контуру, состоящему из
одной простой кривой, замкнутой или незамкнутой. Однако ничто не мешает
все полученные результаты распространить на сл>'чай, когда контур
интегрирования состоит из конечного числа кривых, совершенно раздельных или же
имеющих некоторое число точек пересечения. Заметим сразу, что, не
ограничивая общности, можно считать все кривые простыми, так как если бы какая-
нибудь кривая оказалась самопересекающейся, то можно было бы разбить ее
на отдельные участки без самопересечения и считать эти участки
самостоятельными кривыми.
Итак, пусть дан интеграл типа Коши
L
ВЗЯТЫЙ ПО контуру I, состоящему из конечного числа простых кривых La;
L = Li + L2+ ... +Lm.

§ 8] ПОВЕДЕНИЕ ИНТЕГРАЛА ТИПА КОШИ 77
Среди кривых Lk могут быть как замкнутые, так и незамкнутые. Очевидно,
Ф(г) можно представить в виде суммы
Каждый из членов суммы есть интеграл типа Коши, взятый по простой
кривой, и, следовательно, к нему, применимы выводы всей предшествующей
теории. Отсюда непосредственно вытекает следующая георема.
Теорема. Интеграл типа Коши (8.39), взятый по сложному контуру L,
представляет функцию^ аналитическую во всей плоскости комплексного
переменного, за исключением точек контура L, и обращающуюся в нуль на
бесконечности.
Рассмотрим предельные значения интеграла. Пусть точка z приближается
к некоторой точке t контура, лежащей на какой-нибудь кривой Lj и не
являющейся точкой пересечения кривых Lk. Все члены суммы (8.40), кроме /-го,
будут функциями аналитическими и, следовательно, непрерывными в точке t
Интеграл же, взятый по контуру Lj, подчиняется всем условиям, при которых
были получены результаты предшествующей
теории. Отсюда вытекает, что вся эта теория прило-
жима и к рассматриваемому здесь случаю
сложного контура. Таким образом, во всех теоремах
о предельных значениях, включая формулы Сохоц-
кого, формулы перестановки порядка
интегрирования и т. п., можно считать контур L сложным,
т. е. составленным из конечного числа простых
кривых, при условии, что точка t, в которой
исследуются предельные значения, не является точкой
пересечения простых контуров Lk.
Для точки пересечения простых контуров дело
обстоит значительно сложнее. Здесь несколько
членов суммы (8.40) одновременно испытывают
разрывы. Простые кривые, пересекающиеся в точке /, по
разбивают плоскость на секторы, и предельное зна- ^^^- "•
чение интеграла (8.39) будет зависеть от того, в
каком из этих секторов лежит путь у» по которому приближаемся к точке t
(рис. 9). Исследование предельных значений в точке пересечения простых
кривых представляет серьезные трудности, если исследовать интеграл, взятый по
всему пучку простых кривых, исходящих из данной точки (так это делал
впервые рассматривавший этот вопрос Тшицинский [Trjizinsky 1)]). Однако
трудности совершенно исчезают, если, как это предложил Д. А. К в е с е-
лава 3), предельное значение в точке пересечения кривых взять как сумму
предельных значений всех членов, входящих в сумму (8.40). Если задан
сектор, в котором лежит путь у» то для каждого из интегралов по кривым La,
пересекающимся в точке /, можно точно определить сторону (правая или
левая), с которой происходит стремление к пределу, и, следовагельно,
указать ту из формул Сохоцкого D.7), D.8), которая соответствует выбранному
пути перехода к пределу.
Условимся в дальнейшем не придавать интегралу (8.39) в точке
пересечения никакого определенного значения. Предельные же значения будем
определять для каждого пути стремления к пределу, исходя из
сформулированного выше принципа разбиения интеграла на сумму интегралов, взятых по
простым кривым. При таком способе исследования случай, когда точка
пересечения является концом кривой, проходящей через эту точку, не
представляет никаких затруднений, так как изучение поведения интеграла
производится обычным приемом п. 8.2.

78 ИНТЕГРАЛ ТИПА КОШИ 1ГЛ. I
§ 9. Предельные значения обобщенных интегралов
и двойных интегралов типа Коши
Распространим часть результатов, изложенных выше, на обобщенные
интегралы (пп. 9.1—9.3) и на двойные интегралы типа Коши (пп. 9.4—9.6).
9.1. Постановка вопроса*). Пусть L — гладкий замкнутый или
незамкнутый контур. Рассмотрим криволинейный интеграл
при следующих предположениях относительно функций Р и Q:
\. Р и Q — целые аналитические функции относительно комплексного
переменного Z для всех значений т е L.
2. Р удовлетворяет по переменной т условию Гёльдера.
3. Q имеет непрерывную производную по т, удовлетворяющую условию
Гёльдера.
4. В точках, где Q(t, 2)=0, Q^(t, г) и Q^(r,z) отличны от нуля.
Согласно § 1 интеграл (9.1) представляет собой функцию, аналитическую
во всей плоскости, за исключением значений 2, удовлетворяющих уравнению
Q (т, г) = О (т S L), (9.2)
и, может быть, бесконечно удаленной точки.
Поведение 4^B) на бесконечности может быть исследовано лишь в том
случае, если наложить определенные условия на поведение целых функций Р
и Q на бесконечности. Вопрос этот мы оставим в стороне.
Уравнение (9.2) определяет конечное или бесконечное число кривых Г.
Решая это уравнение относительно z и беря значение t из уравнения
контура L: X = t(a), получим уравнения кривых Г в параметрической форме.
В силу условий 3 и 4 уравнение (9.2) определяет взаимно однозначное и
непрерывное соответствие между контуром L и каждой из кривых Г.
Следовательно, все кривые Г будут одновременно замкнутыми или незамкнутыми
в зависимости от того, будет замкнут или не замкнут контур L В
дальнейшем для определенности будем считать контур L замкнутым.
Кривые Г будут особыми линиями для функции ^(z).
Оказывается, что при условиях 1—4, наложенных на функции Р и Q,
функция ^(z) ведет себя на особых линиях Г так же, как интеграл типа
Коши на контуре интегрирования, т. е. имеет непрерывные предельные
значения при приближении с каждой стороны контура; эти значения не
совпадают, так что кривые Г являются для функции 4^B) линиями скачков.
Метод исследования заключается в сведении рассматриваемого сложного
интеграла, взятого по контуру L, к интегралу типа Коши по кривой Г. Не
проводя все исследование подробно, ограничимся лишь указанием
принципиальных моментов.
9.2. Формулы, аналогичные формулам Сохоцкого для интеграла типа Коши.
Выберем некоторую определенную кривую Г и обозначим ^ комплексные
координаты ее точек, так что
Q(T, S) = 0. (9.2')
Пусть
? = гКт) (9.3)
*) Вопросы пп. 9.1—9.3 не строго и не вполне точно были рассмотрены
впервые в работе Л. Г. Михайлова 1). Изложение, данное здесь,
заимствовано из работы И. М. Мельника 1).

§ 9) ОБОБЩЕННЫЕ И ДВОЙНЫЕ ИНТЕГРАЛЫ 79
есть уравнение кривой Г, полученное решением уравнения (9 2')
относительно J.
Согласно теореме Вейерштрасса аналитическая функция Q(t, г) двух
комплексных переменных т, г, удовлетворяющая условию -^ФО, может быть
представлена в виде
Q (т, Z) = [г|) (т) - 2] Q (т, г), (9.4)
где \f) (т), Q (т, z) — аналитические функции своих переменных, причем
Q(r,z)^0 в 01 рестности исследуемых точек.
В рассматриваемом случае Q(t, 2) не аналитична относительно т, однако
простые рассуждения показывают, что и в эгом случае справедливо
разложение (9.4) с тем лишь различием, что ^т и Q будут не аналитическими
относительно т, а функциями того же характера, что и сама функция Q (условие 3).
Легко заметить, что функция i|)(t), входящая в разложение (9.4), есть
правая часть уравнения (9.3).
Учитывая разложение (9.4), интеграл (9.1) представим в виде
Желая привести интегрирование по контуру L к интегрированию по
исследуемой кривой Г, сделаем подстановку (9.3). Обозначая w функцию,
обратную tf:
т == (О (S),
и вводя функцию
сведем исследуемый интеграл к следующему:
г
Интеграл (9.7) отличается от обычного интеграла типа Коши лишь тем,
что в нем плотность ф(?, 2) сама зависит от переменной z. Однако это
обстоятельство не вносит никаких изменений в поведение интеграла вблизи
контура Г. Известно (см. сноску к п. 7.2), что для этого интеграла
справедливы обычные формулы Сохоцкого.
Следовательно, будем иметь
L
Полагая (o{w)==^t и учитывая, что со' (w) = "т-ттг, "ф' (/) Q (/, w) = Q!^ (/, а>),
получим
1тг±/ ч 1 Р(Л ш) , 1 г Р(т, ш) .
W* (оу) = ± г Н \ —-^—г dXy (9.8)
где последний интеграл понимается в смысле главного значения

80 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
9.3. Формула перестановки порядка интегрирования. Для двойного
особого интеграла рассмотренного типа справедлива формула перестановки
порядка интегрирования, аналогичная формуле G.7) (Пуанкаре — Бертрана).
В основе вывода лежит следующее предложение.
Лемма. Пусть на контуре L задана функция ф(/, т), удовлетворяющая
условиям:
1. Она непрерывна по обеим переменным и имеет пзрвую производную
по т, удовлетворяющую условию Гёльдера по х и t.
2. ф (^, 0 = 0, но ф!^ (/, /)=7^0. Тогда ф (/, т) представима в виде
Ф(Лт) = (т-0 5(^т), (9.9)
где S (/, т) удовлетворяет условию Гёльдера и s (/, t) = ф-j (/, i).
При доказательстве исходим из очевидного равенства
т
Ф (^ т) - ф (/, О = ^ Фх (^ «) du.
t
Учитывая, что ф (/, О == 0> и производя подстановку
м = / + у(т-0, (9.10)
получим требуемое представление (9.9), в котором
S (и x)=\(9x\f,t + v(x-' /)] dv,
и
и интеграл берется по дуге U (с концами О, 1), в которую подстановка
(9.10) взаимно однозначно и непрерывно отображает дугу tx контура L.
Доказательство того, что s(/, т) удовлетворяет условию Гёльдера и что
S (/, t) = ф<^ (/, t)y производится прямым подсчетом и мы его не приводим.
Перейдем теперь к выводу формулы перестановки. Пусть
П функция Р(т, а), заданная на L, удовлетворяет условию Гёльдера;
2) функция со(т, а) удовлетворяет условиям леммы;
3)Q(t,и;)—функция, удовлетворяющая условиям 3, 4 п. 9.1, причем w —
произвольная точка кривой Г.
При этих условиях имеет место следующая формула перестановки;
J Q (т, ш) J 0 (т, а)
L L
^i^^a =
0;(/,ш)(о;(^/) J J Q(T,^)co(T,a)
Доказательство проводится сведением к интегралам типа Коши. На основании
леммы
(О (т, а) = (а — т) 5 (т, а). (9.9')
Так как а> = -ф (О, то функция Q (т, а;) = Q [т, ф @1 удовлетворяет условиям
леммы, следовательно,
Q[T,a|)(/)] = (T-0 5i(T,/). (9.9'0
Отсюда
f dx
J Q (т, w)
\ PJ^ do=[^[ ^(b^ da. (9.12)
J CO (T, a) J T — / J a — t ^ ^

§ 9] ОБОБЩЕННЫЕ И ДВОЙНЫЕ ИНТЕГРАЛЫ 81
где функция
Ф (т, а, о = • -
Si (т, о S (т, а)
удовлетворяет условию Гёльдера по т и а при / е L. Применяя к интегралу
(9.12) формулу перестановки G.7') и учитывая, что
5(/, о=со;(/. О, 5^(/,/)=q;(/, ш),
т. е.
Р (и t)
^(t.t.t) =
Q[(t,t)(i>'^(tJ)'
придем к требуемой формуле (9.11).
9.4. Кратные интегралы типа Кошм. Постановка вопроса *). Пусть в
плоскости комплексного переменного Zk (/г = 1, 2, ..., п) дан простой гладкий
замкнутый контур Lk, делящий ее на две части: внутреннюю D^ и
внешнюю D^. В этом случае топологические произведения
называют регулярными полицилиндрическими областями*'^). Границы всех
этих областей имеют общую часть, а именно L = Li X ^2 X . • • X ^п,
которая называется остовом границ соответствующих областей (просто остовом).
Интеграл
Ф(гь ...,^;,)~^2^^j (Т1-гО...(Т;,-г„) '
(9.13)
плотность которого ф(Т1, ..., Тп)—непрерывная функция точек остова L,
называется кратным интегралом типа Коши.
Ниже будет дано изложение некоторых вопросов, относящихся к таким
интегралам, причем ради простоты рассматривается случай двух переменных.
Будет показано, что интеграл (9.13) обладает в основном свойствами,
аналогичными соответствующим свойствам обычного однократного интеграла типа
Коши.
9.5. Особый двойной интеграл. Формула Пуанкаре — Бертрана. Пусть на
остове L = LiX^2 задана функция ф(^1,/г), удовлетворяющая условию
Гёльдера с показателями Xi и А,2, короче, феЯ(Я1, ^.г). Введем обозначения:
Ф, = Ф (Ть /з) — Ф (^1, t2)y Ф2 = ф (^ь Тз) - ф (tu /2),
Ф12 = ф (f ь Тг) — Ф (Ti, /2) — ф (^1, Т2) + ф(/1, /г).
На основании результатов п. 2.2 найдем, что
I Ф1 I < Л1 |Ti - /, 1^', I ф2 I < ^2 I Т2 - /2 |Ч
I Ф,2 к 2Ai |Ti - /1 1^', IФ121 < 2^ I Т2 - /2 |Ч
(9.14)
*) Изложение пп. 9.4—9.6 следует в основном статьям Б. А. К а к и ч е-
ва 1) и 2). О формулах Сохоцкого см также М. Б. Гагу а 1), Л. Битт-
н е р [L. Bittner] 1) н А. Г. Д ж в а р ш е и ш в и л и 1).
**) Точка Bi, ..., 2„) принадлежит топологическому произведению
PtX^2X..-X^n множеств Dk (Л = 1, 2, .,., п), если г^еЬ/^.

82 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. I
Из последних двух неравенств имеем
|ф12|<Л,2|т1-^,Г^Чт2-/2|^^-^^^^ @<а<1). (9.15)
Отметим еще такое тождество:
ф (Ti, Т2) = Ф1 + Ф2 + Ф12 + ф (^1, ^2). (9.16)
Рассмотрим особые интегралы
L\ L2
- с ^ if 'P(Ti, T2)rfTidT2
Очевидно, интегралы 51ф и 52ф существуют в смысле главного значения (см.
п. 3.4).
В плоскости Zk с центром в точке tk е La опишем окружность
|2а —^fc|= р и часть контура Lft, лежащую внутри этой окружности,
обозначим /а. Главное значение особого интеграла Si2(p определим как предел
Нт [ Ф(Т1, T2NfTifi?T2 .J.
Р->о J (т, - ^,) (Т2 -/2) • ^''
(L,-/0X(L2-/2)
Если ф^Я(Х1, А-г), то, заменяя в (9.17) ф(Г1, Тг) правой частью
тождества (9.16) и учитывая неравенства (9.14), (9.15) и равенство D.6), можно
показать (аналогично тому, как это сделано в п. 3.4, что интеграл 512ф также
существует в смысле главного значения.
Отметим еще такие операторные равенства, либо доказанные выше, либо
легко доказуемые:
^[^2 "^ "^г"^! "^ *^12» ^j "^ "^0» ^i^o ^^ ^o^i "^ ^i (/ "^ ^» 2), (9.18)
где So — тождественный оператор, т. е. 5оф = ф.
Далее, применяя схему доказательства формулы Пуанкаре — Бертрана,
предложенную В. Д. Купрадзе*), получим соответствующую формулу
Пуанкаре — Бертрана для случая двух переменных, которую в операторной форме
можно записать так:
5i2 (аф12) — Si2 (ф512) =
= аф + 5i$i + 52Ф2 + 512Ф12 — Si (ф1а1 + $2012) — S2 (ф252 + Ф1а12)»
где a{tut2)y ф(/1,/2)—функции точек остова L, удовлетворяющие на нем
условию Гёльдера.
Из этой формулы при а s 1 следует формула композиции оператора S12:
512Ф = 5i2$i2 = Ф»
из которой в свою очередь вытекают следующие формулы обращения: если
t|? = 512ф и ф е Я, то ф = Si2\|?, и наоборот.
9.6. Формулы Сохоцкого. Если ф(^:, t2)^H(Xu Я2), то, рассуждая как и
при доказательстве леммы п. 4.1, можно показать, что при переходе через
*) См. Купрадзе В. Д., Граничные задачи теории колебаний и
интегральные уравнения, Гостехиздат, 1950.

§ 91 ОБОБЩЕННЫЕ И ДВОЙНЫЕ ИНТЕГРАЛЫ ИЗ
контуры Z.1, ^2 и ОСТОВ L интегралы
^ 1 Г ф1 ^Ti ^ 1 Г ф2^Т2
^* 2я/ J т, - г, ' ^^ 2я/ J Т2 - 22 '
, j_ f у 12 ^Т| Д?Т2
L
ведут себя как непрерывные функции.
Обозначим Ф* * (/i, /2) предельные значения интеграла (9.13), когда точка
{zu Z2) е D* ^ стремится к точке (tu ^2) ^ ^.
Из очевидного равенства
JEl с Д^Т| _ ф(/ь /2) f t/Ti Д?Т2
2ш- J т, - 21 4я2 J (Ti - z{) (Т2 •
+ ¦
L. L - ''^
при помощи рассуждений, аналогичных проведенным в п. 4.2 при выводе
формул Сохоцкого для одномерного интеграла типа Коши, будем иметь
± ^хф dh 52ф + 512ф),
фЧ=51ф±52ф + 522ф).
Отсюда
ф++±ф+-±ф-+ + ф—= f ^12Ф,
I Ф,
Ф++ =р ф+- ± ф-+ _ ф— = I
(9.19)
5,ф,
52ф.
(9.20)
Формулы Сохоцкого (9.19) можно компактно записать в виде одной формулы
следующим образом:
4Ф=*=± = {(± 5о + Si) (± So + 52)} ф,
где сначала надо по формулам (9.18) найти соответствующие операторы, а
затем применить их к функции ф(/1,/г).
В случае произвольного п формулы Сохоцкого имеют следующий вид:
2«ф±± ... ± _ {(± 5о + 5i) (± 5о + 52} ... (± 5о + 5„)} ф.
Применяя неравенства (9.14) и неравенство (9.15) при а = еА2 или
а = 8Д|, получим, что если ф(/1,/2) ^ ^(^i» ^г). то 51ф е Я (^i, Я2 — е),
^гф е fiC^i — 8, Л2), где 8 -— сколь угодно малое положительное число.
Поэтому особый интеграл 512ф, а также предельные значения Ф^* (^ь ^г)
принадлежат классу Н (Я| — е, Яг —• е).

84
ИНТЕГРАЛ ТИПА КОШИ
1ГЛ 1
§ 10. Интеграл типа Коши и потенциалы
Как уже указывалось ранее, между интегралом типа Коши
и потенциалами (логарифмическими) существует тесная связь.
Дадим явное выражение этой связи.
Будем считать контур L замкнутым и положим
^{z) = u(x,y)^-iv{x,y) = ^\^dx.
L
Для простоты будем считать, что плотность ф (т) — функция
действительная. Если бы она была комплексной, то нужно было
бы разбить интеграл типа Коши на два, выделив у плотности
действительную и мнимую
^j- части. Обозначим (рис. 10)
т — 2 = г^^®, г = I т — г I,
0 = arg(T~-2). A0.1)
Тогда
= d(lnr + /e) =
yk
= -y- + ide. A0.2)
Поэтому
u{x,y)'\-iv{x,y) =
1 С ^e , i [ dr
L L
A0.3)
Согласно уравнениям Коши — Римана, примененным к функции
1п(т —2:) = 1пг + ^'0, имеем
Рис. 10.
ds
д\пг
дп
д , 1
дп г
Следовательно,
L L
1 г COS (г, п) J ,-^ J.K
L

§ \0] ИНТЕГРАЛ ТИПА КОШИ И ПОТЕНЦИАЛЫ 85
Формула A0.4) показывает, что действительная часть
интеграла типа Коши есть логарифмический потенциал двойного
слоя.
Чтобы выразить правую часть формулы A0.5) через
потенциалы, допустим, что плотность ф(/) есть дифференцируемая
функция. Произведя в последней формуле интегрирование по
частям и замечая, что проинтегрированная часть в силу
замкнутости контура равна нулю, получим
L L
Сравнивая последнее выражение с потенциалом простого
слоя в обычной записи
^li{s)ln yds,
L
видим, ЧТО мнимая часть интеграла типа Kouiu есть
логарифмический потенциал простого слоя с плотностью
Так как полный заряд (масса) потенциала
m = 5nE)rfs=--l-5-g-rfs = 0, A0.7)
то формула A0.6) представляет собой потенциал не совсем
общего вида, а лишь при условии, что полный заряд равен нулю.
Заметим, что если даже не предполагать плотность ф(/)
дифференцируемой, можно было бы провести интегрирование
по частям, только получившийся интеграл \ 1п—^ф нужно по-
L
нимать как интеграл в смысле Стилтьеса.
Используя представление интеграла типа Коши через
потенциалы, можно получить формулы Сохоцкого для его предельных
значений. Первое слагаемое — потенциал двойного слоя —
представляет функцию, разрывную при переходе через контур L,
Предельные значения даются выражением
±1-4)+ ^ J Ф^^^. A0.8)
L
Потенциал простого слоя ведет себя при переходе через контур
как функция непрерывная, причем интеграл A0.6) нужно пони-

86 Интеграл типа коши 1ГЛ. i
мать в смысле главного значения. Суммируя оба члена,
получим формулы Сохоцкого. Заметим, что для кривых,
удовлетворяющих условию Ляпунова (п. 5.3), вывод формул Сохоцкого
указанным способом не представляет никаких трудностей (при
условии, что уже выведены формулы A0.8) для предельных
значений потенциала двойного слоя). Однако для случая любого
гладкого контура встретились бы серьезные затруднения, связан-
ные с вопросом о существовании интеграла \ ф -^ ds на контуре.
§ 11. Исторические сведения
Трудно назвать автора, впервые указавшего на интеграл типа Коши, т. е.
предложившего в интеграле Коши рассматривать в качестве плотности
произвольную функцию. Однако можно совершенно точно указать время и
автора, впервые давшего важнейшее исследование по теории этого интеграла.
В 1873 г. в своей докторской диссертации Ю. В. Сохоцкий [24] исследовал
поведение интеграла типа Коши на контуре и вывел формулы D.7), D.8)
при тех же условиях (условие Гёльдера), как это изложено в § 4.
Замечательно, что там же, в [24], рассмотрены и случаи разрыва плотности.
Эти исследования не строги с современной точки зрения, но вполне
соответствуют требованиям строгости своего времени. Фундаментальные
исследования Сохоцкого были, однако, незаслуженно забыты и не оказали
влияния на дальнейшее развитие теории*).
Следующее по времени исследование предельных значений интеграла
типа Коши было сделано Гарнаком [Нагпас 1)] в 1885 г. Этот автор
разлагает интеграл типа Коши на сумму двух потенциалов (см. § 10) и выводит
формулы Сохоцкого, опираясь на формулы для предельных значений
потенциала двойного слоя. На плотность и контур накладываются жесткие
ограничения. Работа Гарнака также не оказала значительного влияния на
последующие исследования: они пошли, хотя и независимо от работ Сохоцкого,
по пути, намеченному им, — рассмотрения интеграла типа Коши как единой
комплексной функции.
Большое значение имеют две работы Племели [Plemelj 1), 2)]. Здесь
были вновь выведены формулы Сохоцкого при тех же условиях Гёльдера, но
уже достаточно строго. Схематически была доказана основная теорема о
поведении предельных значений интеграла типа Коши (см. п. 5.1). Но, самое
главное, здесь впервые интеграл типа Коши был использован как
математический аппарат для решения конкретной краевой задачи теории аналитических
функций. Следует упомянуть также работы Пуанкаре [Poincare [20]] и
Бертрана [Bertrand 1)], где была получена формула перестановки повторных
особых интегралов.
Дальнейшее развитие теории и приложений интеграла типа Коши в
основном связано с именами советских математиков И. И. Привалова и
Н. И. Мусхелишвили. В работах первого, начало которых относится к 1918 г.,
формулы Сохоцкого для функций, удовлетворяющих условию Гёльдера, были
выведены с наибольшей полнотой и строгостью и затем произведены далеко
идущие обобщения в отношении плотности интеграла и контура
интегрирования. Некоторые сведения об этих обобщениях приведены в п. 5.2. В работах
Н. И. Мусхелишвили, начиная с 1922 г., интеграл типа Коши систематически
применяется к решению задач теории упругости.
*) На роль работ Ю. В. Сохоцкого в теории интеграла типа Коши
впервые указал А. И. Маркушевич.

ЗАДАЧИ К ГЛАВЕ I 87
Эти работы, ставшие широко известными благодаря его книге [17],
сыграли огромную роль во внедрении интеграла типа Коши как
математического аппарата в различные отрасли теоретической и прикладной математики.
В 1941 г. появилась работа Н. И. Мусхелишвили 1), в которой дано глубокое
исследование поведения интеграла типа Коши на концах контура ингегриро-
вания и в точках разрыва плотности. Работа эта сразу нашла широкое
применение в теории краевых задач и особых интегральных уравнений.
Из дальнейших работ по теории интеграла типа Коши упомянем в
первую очередь работы Л. Г. Магнарадзе 1), С. Г. Михлина и Б. В. Хведелидзе.
В работе [15] интеграл типа Коши рассмотрен как оператор в пространстве
функций с интегрируемым квадратом. Это дает возможность использовать в
некоторых случаях в качестве аппарата исследования функциональный
анализ. Аналогичное исследование проведено Б. В. Хведелидзе 2) для функций,
интегрируемых в степени р '> \ с некоторым весом. О дальнейших
обобщениях интеграла типа Коши будет сказано в исторических сведениях к гл. VI.
Наиболее полное изложение теории интеграла Коши при классических
условиях, обеспечивающих существование непрерывных предельных значений
всюду на контуре, дано в книге Н. И. Мусхелишвили [16]. Последнее
положено в основу изложения многих разделов настоящей главы (§§ 4, 7,
пп. 8.3, 8.4).
Задачи к главе I
b
1. Вычислить особый интеграл \ —^j—, определяя его как
а
-с-8 b
г4-Ьр. -¦
b
lim
е->0 L
*- а c+ke
2. Показать, что если /г > О — нечетное число, то особый интеграл
dx
_ тгг > определенный как главное значение, существует.
а
3. Показать, что если п — нечетное число и ф (х) удовлетворяет условию
b
I Ф (jt) — ф (с) к л I д: — с |\ где Л > л — 1, то интеграл \ , ^ .^ dx суще-
J \^ ^)
а
ствует.
4, Показать, что если особый интеграл \ ——г- определить условием
L
lim ^ "" == k (обозначения п. 3.4), то предельные значения интеграла
Коши Ф (г) = ¦^—г \ __ dx выразятся формулами
типа

88 ИНТЕГРАЛ ТИПА КОШИ 1ГЛ. I
5*. Доказать, что если ф (t) удовлетворяет условию Н (Я), то для
производной интеграла типа Коши Ф (г) = -^"^ \ __ dx в точках контура
L
будет справедлива оценка
|Ф'(г)|<Л|2-/|^~^ при Я<1,
|Ф'(г)|< Л1п|г-/| при Л=1.
(Н. И. Мусхелишвили [16], § 20.)
1 f т2
6. Вычислить особый интеграл —г \ з _ i ^'^'
|т| = 1
Ответ. 1.
7. Пусть L — простой замкнутый контур, делящий плоскость на области
D+ и D-. Доказать, пользуясь теоремой и формулой Коши, чго если
плотность интеграла типа Коши Ф (г) = ¦^—г \ ^ dx может быгь представле-
L
на в виде
Ф (т) == Ф+ (т) + ф- (т),
где ф+ и ф~ — краевые значения функций, аналитических соответственно в
областях D+ и D-, то справедливы формулы
ф+ {z) = ф"*" (г) + ф" (со), ф- (г) = - ф- (г) + ф~ (оо).
Вывести то же из формул Сохоцкого.
8. Пользуясь результатом предыдущей задачи, вычислить интеграл типа
Коши для случаев:
а) ф@—краевое значение функции, аналитической в D+, за исключением
конечного числа точек ла, где она имеет полюсы;
б) ф@—функция такого же типа в D-.
Ответ:
а) ф^.) = ф(.)--2],,(_!_), ф-(.) = --^,^(_1_);
где gkiz), ^(г)-—многочлены, представляющие главные части разложения
ф(/) соответственно в окрестности конечных полюсов и бесконечно удаленной
точки (^л@)= 0).
9. Вычислить интеграл типа Коши
л/ч 1 f тЧ-^ч-т-4г , "V-a
1
-2 Т, , 1
' + sin -
Т2-Ы
: - 3 ' т - 1
I т*--Зт2-4 "^ т2.
L
где L — окружность | г | = 3/2.
dx
Т —2

ЗАДАЧИ К ГЛАВЕ I
89
Ответ.
Ф"*" B) =
2+ 1П
2-2
+ sin
22-4
Ф- B) =
2-1
22+1
10. Пользуясь формулами D.11), D.12), вычислить особый интеграл
1
я/ J
т^ + /т2 + т — 4i
In
т-2
• + sin
1
т* - 3x2 - 4
т-1
где L —контур задачи 9.
/-2
/ + 1п
Отрет.
/-3
т2-4
в + sin ¦
т2+1
dx
T-t '
— I
i^-4
+
/2+1
II*. Вывести формулу для разности предельных значений интеграла типа
Коши ф+(/)—ф-(/)== ф(^), не требуя от ф@ удовлетворения условию
Гёльдера, а допуская только ее непрерывность. (И. И. Мусхелишвили [16],
§ 17.)
12. Доказать, что если ф(/) есть краевое значение на контуре L
функции ФB), аналитической в области D+, за исключением конечного числа
точек, где она имеет полюсы, причем сумма главных частей разложения ФB)
в окрестностях полюсов есть R(z), то она должна удовлегворять условию
уф@ +
1 с Ф(т)
2ni J т —/
dx + R(t)=-^0.
13. Вывести формулы для предельных значений производной т-го
порядка интеграла типа Коши
ФB) =
.JLfjPiZ
' 2ni J т —
т)
dx,
считая контур L незамкнутым с концами а, Ь, Плотность ф(/) предполагается
дифференцируемой требуемое число раз.
14. Вычислить особые интегралы с ядрами Гильберта:
2я
а) -^5 cos/zectg^4^^e;
9 —ф
2
о
2Я
б) --^5 sinnectg-^^^G;
о
2Я
ч ^ f 1 о I • в I i в-ф
3) _J inoL.n_l.. Ф
siny ctg- 2
dQ.

90 ИНТЕГРАЛ ТИПА КОШИ (ГЛ, 1
Ответ, а) — sin Пф; б) cos Лф; в)
2
2л
Замечание. Из а) при л = О получим \ ctg —^-^ dQ = 0. Получить
о
этот результат непосредственным вычислением особого интеграла как
главного значения.
15. Вычислить особые интегралы:
1
" _J Vl - Т2 (Т - О
. J_ Г \n\x — T\dT
и е. Сделать :
cos е-cos ф 2 8Шф L ^ 2 ^^^
-1
Указание. Сделать замену переменных т = cos9, / = cosф, учесть
тождество
J !^Г* Ф + 6 , , Ф —6]
и воспользоваться результатом предыдущего примера.
Ответ.
ч р (arccos t — п) + а arccos /
а) -i-^ / ;
f{\ arccos / — я8 (jc — /)
°> Vl^F '
где 0(jc—0= 1 при jc > / и 0(д: —/) = О при х < t.
16. Доказать, что если фE) —периодическая дифференцируемая функция,
то для особого интеграла с ядром Гильберта справедлива следующая
формула интегрирования по частям:
п п
1
2я
-я —я
17. Вычислить интеграл типа Коши
«w-iS-r^"'-
L
если начало координат принадлежит D+, а In / определяется условием
О < Im 1п / < 2jt.
Указание. Применить теорему Коши или формулу Коши к интегралу,
взятому по контуру, состоящему из кривой L, берегов разреза, соединяющего
точку ^0 с началом координат, и малой окружности около начала.
Ответ. Ф"^ (г) = In B -/о), Ф" (г) = In Г] —^V

ЗАДАЧИ К ГЛАВЕ I
91
18. Пусть L = ^ L/fe — контур, состоящий из т простых разомкнутых
кривых, не имеющих общих концов. Координаты концов, взятые в
каком-нибудь порядке, обозначим Си ^2, ..., сгт. Пусть р — некоторое целое число
О ^ /э ^ 2т и Р(г)—некоторый многочлен.
Вычислить особый интеграл
L 1ЦХ-С,Г
Указание. Рассмотреть интеграл типа Коши
di.
, г П('-«.)"' „,,
2m
dx,
г п i^-^-^r
взятый по совокупности петель, охватывающих кривые La. Перейти к пределу,
когда петли переходят в разрезы по кривым La, и воспользоваться формулой
Сохоцкого / = Ф+ + Ф-.
Ответ. /@=—Р*@» где P*{z) есть многочлен, представляющий собой
главную часть разложения плотности интеграла типа Коши в окрестности
бесконечно удаленной точки, т. е. многочлен, удовлетворяющий условию
lim
Z->oo
2m
P {z) - P* (z)
= 0.
19. Пользуясь результатом предыдущей задачи, вычислить следующие
особые интегралы:
-I
а
б) — \ , (п > О, целое);
—а
Ъ
, 1 Г тз - 2x2 4- Зт -f 1 ^^
в) —\—, .
ni J V(t — a){x — b) X — t
Ответ.
a) — л:^ + jc - 3,5;

92 ИНТЕГРАЛ ТИПА КОШИ {ГЛ. 1
m
^) ^''"' + Z ^l.'V/^Al'^^ a^^;c'^-2*-^ где m = | - 1 при п четном,
при п нечетном;
2
в) - ^2 + 4- D - а - ^) / + 4" (ва + 86 - 2а6 - За2 - Зб^).
2 о
20. Вычислить особые интегралы:
b Г. г-аУ
dx
Р^' я^ J V(T - а) (т -
а
V(T - а) (т - 6) -^ - ^ '
dx
(р — целое неотрицательное число).
Ответ.
а) /,W = -I
k
р Г In"-* 4^ 1
Lj р^ LV«-a)(<-6) P-*"J
Л ""I
/о @=0;
Р+1 Р + 1 -1
где Cp — биномиальные коэффициенты.
a
21. Показать, что фB) = -^—г \ v (О cth (^ — г) rf/ является периодиче-
ской с периодом я/ функцией, аналитической вне отрезков — а^х^а,
y=^kni (Aj = 0, ±1, ±2, ...).
22. Показать, что для функции Ф (z) из предыдущей задачи имеет место
соотношение
th а th а
ф-(.) + ф-(.) = ±- \ v.(s)^+± J v.(s)-
1-S2
-tha -tha
где Vi (s) = V (arth s), a = th j; {— a < x < a),
23*. Пусть L есть гладкий замкнутый контур с длиной дуги / и G"*" (г, 5),
G"" (г, S) — функции Грина задачи Неймана соответственно для областей D^ ,D~

ЗАДАЧИ К ГЛАВЕ I 93
Доказать, что имеют место следующие формулы обращения Гильберта:
О о
О о
t'- E) = - у j ~—-и- (а) do +jy- (а) da,
о о
, , if дО~ {s,a) / ч . , 1 f / ч .
и- E) = — j 5~—^ V- (а) do + '^^u- (or) da,
о о
где 0"^ (s, a) = cig'j' (s — а) + регулярная функция. (Hilbert [10], стр. 84—88.)
Указание. Воспользоваться выражением для решения задачи Неймана
через функцию Грина, уравнениями Коши — Римана в форме -^— =
dv dv ди
= ^, -^ = -т— и интегрированием по частям.
24*. Доказать, что необходимым и достаточным условием того, что
^¦^(s)= a{s)+ib(s) есть краевое значение функции, аналитической в
области Ь+, является выполнение равенства
О о
Соответственно для области D- условие имеет вид
о о
(Hilbert [10]).
Указание. Воспользоваться формулами из 23*.
25. Пусть fB:)= м(д^, (/)+/у(д:, (/)—функция, аналитическая в верхней
полуплоскости. Обозначим через и{х), v(x) предельные значения ее
действительной и мнимой части на действительной оси. Показать, что имеют место
формулы обращения Гильберта
— оо —оо
где Мво, Уоо — значения действительной и мнимой части на бесконечности.
26. а) Вычислить интеграл типа Коши
'^^'^-4и\^'-

94 ИНТЕГРАЛ ТИПА КОШИ [ГЛ. 1
если Ф (т) == ф+(т) + Ф"" (т), где ф='=(т) удовлетворяют условию Гёльдера
всюду на оси и суть краевые значения функций, аналитических
соответственно в верхней и нижней полуплоскостях.
Ответ.
Ф+ (г) = ф+ (г) ~ 1 ф+ @0) + 1 ф- (со),
Ф- (г) = - ф- (г) -1 ф+ (со) +1 ф- @0).
Замечание. Можно по желанию принять
ф+ (со) ==ф (со), ф-(СО)=0 или ф- (со) = ф (со), ф+(оо)==гО.
б) Вычислить, пользуясь решением п. а), интеграл типа Коши
Ф(,) = Л t^ir —
Z
Ответ. Ф'*'(г) = —^-г, Ф" (г) = 2^.
27*. Показать, что
аЬ аЬ
(В. Д. Купрадзе, см. сноску на стр. 82).
28*. Вывести формулу перестановки G.7) при помощи преобразования
\
Т
(В. Д. Купрадзе, см. сноску на стр. 82).
Указание. Произвести перестановку порядка интегрирования в
интегралах, где лишь один интеграл является особым, и воспользоваться
результатом предыдущего примера.
29. Получить формулы обращения F.6), F.7), используя тождество
2-^^id(s + cig^^da, где / = Л т = е^
и необходимое и достаточное условие D.11).
Аналогично, с помощью необходимого и достаточного условия D.12),
показать, что для функции аналитической в области |г|> 1, формулы
обращения F.6), F.7) принимают вид
2я
u(s) = —j u(G)c{g^-^do + v(co\
о
2Я
иE) = --25^ j v{sj)cig^^^dG + u(co),

ГЛАВА II
КРАЕВАЯ ЗАДАЧА РИМАНА
В настоящей главе будет рассмотрен центральный вопрос
теории краевых задач аналитических функций — краевая
задача Римана. Вокруг этого вопроса группируется весь материал,
и к нему мы будем неоднократно возвращаться в дальнейшем
в связи с различного рода обобщениями и приложениями.
Начнем с вспомогательных предложений.
§ 12. Некоторые вспомогательные теоремы
Приведем здесь четыре наиболее часто используемые далее
теоремы теории аналитических функций. Все они излагаются
в руководствах по этой теории, поэтому мы в основном
ограничиваемся лишь формулировками и разъяснением
терминологии. Лишь в случаях принципов симметрии и аргумента, где
приходится, приспосабливая материал к нуждам теории краевых
задач, обобщать результат или изменять его формулировку,
дается более подробное изложение.
12.1. Принцип непрерывности. Продолжение по симметрии.
Г. Теорема об аналитическом продолжении
в соприкасающихся областях (принцип
непрерывности). Пусть две области Dx и Ог граничат вдоль некоторой
гладкой кривой L; в областях Dx и D2 заданы аналитические
функции fx{z) и /г (-2^). Предположим, что при стремлении точки
Z к кривой L обе функции стремятся к предельным значениям,
непрерывным на кривой L, причем эти предельные значения
равны между собой. При этих условиях функции fx{z), f2(z)
будут аналитическим продолжением друг друга,
2°. Доопределение функции по симметрии.
Точками, симметричными относительно прямой, будем, как обычно,
называть точки, являющиеся зеркальным отображением друг
друга относительно прямой, т. е. точки, лежащие на одном пер-
пендикуляре к прямой, на равных расстояниях от нее по
разные стороны. Если прямая — действительная ось и координаты
точки z = х + iy, то координаты симметричной ей точки будут

96 КРАЕВАЯ ЗАДАЧА РИЛ\АНА [ГЛ. II
z* = z = X'-iy. Точками, симметричными относительно
окружности, называются точки, являющиеся инверсией друг друга
относительно этой окружности. Если данная точка лежит на
расстоянии г от центра окружности радиуса /?, то симметричная
ей точка лежит на том же радиусе на расстоянии р = R^/r от
центра. Если окружность единичная и данная точка имеет
координату г, то симметричная ей точка имеет координату г* = — .
Здесь и в дальнейшем мы будем использовать ряд
обозначений. Приведем их:
а) f(z), как обычно, функция, сопряженная с данной;
б) f (i) — функция, получаемая из f(z) путем замены в ней z
на г, т. е. у на —у;
в) f (г) — функция, определяемая условием f{z)=^f(z).
Заменив в последнем равенстве z на г, получим f{z) = f{z).
Если, например, f (z) за'дана рядом f {z) = J^ Cnz"', то
TW)--ZcnZ\ f{z) = ZcnZ^ f{z) = ZcnZ''.
Если f{z) = u (a:, y) + iv (a:, y), то
Ш) = и{х, y)-iv{x, у), f{z) = ti{x, -y) + iv{x, -y\
f{z) = u{x, -y) — iv{x, -y).
Для функции, представленной интегралом типа Коши
L
будем иметь
Т7Т\_^__ J С Ф(Т)^ ./-ч 1 { ф(т)г/Т
i^^^— 2ш ] X-Z ' ' ^^^ ~" 2ni J т-2' '
L
Z
Заметим, что если функция удовлетворяет условию ]{z) = f{z),
то для вещественных значений z она принимает чисто
действительные значения. Справедливо также и обратное предложение.
Продолжение аналитической функции по симметрии
является в теории аналитических функций простым и
эффективным средством аналитического продолжения. В таком виде оно
под названием принципа симметрии и излагается в
руководствах по этой теории. В приложениях к теории краевых задач
условия аналитической продолжимости часто не выполняются

§ 12] НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ТЕОРЕМЫ 97
И метод доопределения функции по симметрии служит не для
аналитического продолжения, а для образования кусочно
аналитической функции.
А. Аналитическое доопределение по
симметрии. Пусть Dz — некоторая область плоскости 2, Lz — прямая
или окружность, имеющие с контуром области Dz некоторую
общую часть. Множество точек, симметричных относительно Lz
всем точкам Dz, образуют область, которую обозначим Dz и
назовем областью, симметричной Dz относительно L^. Пусть,
далее, w = f{z) — функция, аналитическая в Dz, отображающая
ее на некоторую область Dw\ Lw — произвольная прямая или
окружность в плоскости W и Do;—область, симметричная D^o
относительно Lyj, Определим в Dz функцию w = \*{z), ставя
в соответствие точкам 2*, симметричным г, значения ш*,
симметричные значениям w = f{z)\ в частности, если L^ и L«; —
действительные оси, то
r{z)=W)=Hz).
Лемма. Функция w = f*{z) аналитична в области Z)^.
Приведем здесь доказательство, основанное на свойствах
интеграла типа Коши — основного математического аппарата
этой книги*).
Пользуясь круговым свойством дробно-линейных
преобразований, производим в плоскостях Z vi W дробно-линейные
преобразования такие, что Lz, Ьго переходят соответственно в
отрезки действительных осей г и ш. В силу свойства
инвариантности симметричных точек при дробно-линейном преобразовании
точки, симметричные относительно L^, L^, перейдут в точки,
симметричные относительно действительных осей плоскостей z
и ш. Таким образом, дело сводится к случаю, когда парами
симметричных точек будут г, z\ w, w. Для доказательства
аналитичности /*(z) воспользуемся интегралом Коши. Имеем
По определению
Z
rff.
Заменим под знаком интеграла т на f и f (т) на f*{x). При
этом контур Lz перейдет в L^, проходимый в отрицательном
направлении.
*) Другие способы доказательства можно найти в различных
руководствах по теории аналитических функций.

98 КРАЕВАЯ ЗАДАЧА РИМЛНА [ГЛ, II
Получим
Т. е. /*(г) представляется интегралом Коши, следовательно,
аналитична.
Функция
г/(г), z^D,,
является кусочно аналитической в совокупности областей
В. Перейдем теперь к установлению принципа симметрии
в обычной формулировке.
Теорема (принцип симметрии). Пусть функция w:=f{z)
аналитична в области Dz, имеющей частью своей границы
отрезок прямой или дугу окружности, и отображает область D^ в
некоторую область Dw так, что указанные отрезок или дуга снова
переходят в отрезок прямой или дугу окружности. Тогда
функция f*(z), определенная по симметрии в области Dz, будет
аналитическим продолжением функции f{z) в область Dz-
Рассуждая, как при доказательстве леммы, можно свести
рассмотрение к случаю, когда отрезок действительной оси
плоскости Z отображается на отрезок действительной оси
плоскости W. в силу леммы f*{z) аналитична в Dz- Когда z стремится
к точке действительной оси, то и симметричная ей точка z
стремится к той же точке оси. По определению симметрии и условию
теоремы w и w стремятся к одной и той же точке
действительной оси плоскости W. Следовательно, граничные значения f{z)
и /*(г) совпадают. Условия принципа непрерывности
выполнены, и теорема доказана.
Понятие симметрии может быть значительно обобщено.
Пусть L — аналитическая кривая, определяемая
параметрически: л: = ф(^), у = \|)(/), где ф, -ф — аналитические функции
действительного параметра t. Равенство z = (р (t) + iy^ (t) при t
действительном определяет точку кривой L, при комплексном
же t оно задает некоторую точку комплексной плоскости, не
принадлежащую L. Заменив t на ?, получим точку г* = ф(?) +
+ ^'ф(?), симметричную по определению*) точке z относительно
L Возьмем в последнем выражении сопряженное значение и
*) Смысл этого определения заключается в зеркальном отражении в
бесконечно малом с последующим аналитическим продолжением.

S 1?! НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ТЕОРЕМЫ 99
присоединим к нему выражение для z. Решая систему, получим
Если уравнение кривой L задано в неявной форме
уравнением /(^,f/)=0, то для определения точки г*, симметричной z
относительно кривой L, получим уравнение
/[у(г* + 2), ^. B*-г)] = 0.
Для произвольной аналитической кривой алгоритм
построения симметричных точек не изучен. Для более частного случая
алгебраической кривой он разработан и в некоторых случаях
может быть осуществлен эффективно (см. п. 53.6).
12.2. Принцип аргумента. Обобщенная теорема Лиувилля.
1°. Принцип аргумента. Пусть в области D,
ограниченной контуром L, функция /(г) аналитична, за исключением
конечного числа точек, где она может иметь полюсы. Выпишем
разложение в ряд в окрестности некоторой точки z^\
/(г) = сЛ2:-^оГ + ^.+1B-^оГ'"Ч ... =B-^оГ/1D
Число п называется порядком функции в точке Zq. Если
м > О, то порядок функции есть порядок ее нуля, если п < О,
то порядок ее есть порядок полюса с противоположным знаком.
Если порядок функции в ^0 есть нуль, то в такой точке функция
принимает конечное, отличное от нуля, значение. При
рассмотрении бесконечно удаленной точки бином z — Zq нужно заменить
на —. Если точка го лежит на контуре L, то порядком функции
будем считать число n/2.
Пусть Nd, Pd\ A^l, Pl соответственно числа нулей и полюсов
в области и на контуре, причем каждый из них берется столько
раз, какова его кратность. Символом [w]l обозначим
приращение величины W при обходе контура в положительном
направлении*). Сформулируем теорему, называемую принципом
аргумента, в том виде, в каком она будет использоваться далее
(п. 36.4).
Принцип аргумента. Пусть f(z) есть функция,
аналитическая и однозначная в многосвязной области D,
ограниченной гладким контуром L = Ц-\- Li-{- ... + L^, за
исключением конечного числа точек, где она может иметь полюсы,
непрерывная в замкнутой области D -^ L и имеет на контуре не
*) Положительным обходом, как всегда, считается тот, при котором
рассматриваемая область остается слева.

100 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
более чем конечное число нулей целого порядка. Тогда
справедлива формула
Мп-'Ро+^ {Nl -Pl)^-^ [arg f (г)]^.
Доказательство этой теоремы *) мы не приводим. Его
можно найти в работе Ф. Д. Г ахов а, Э. И. Зверовича,
С. Г. Сам ко 1). В ней дано далеко идущее обобщение
принципа аргумента. Для упрощения
^ формулировки этого обобщения
^ ограничимся здесь случаем одно-
связной области, ограниченной
простым кусочно гладким
контуром.
Обобщенный принцип
аргумента. Пусть f(z)
аналитична в D, за исключением конечного
Рис. 11. числа точек, где она имеет полюсы,
и непрерывно продолжима на
контур всюду, кроме точек th в окрестности которых она предста-
вима в виде
f(z) = fk(z){z-ФIn^^(г-4) {k = \,2, ..., n\
где fk {z) Ф 0, Л;^, у,^ — некоторые, вообще говоря, комплексные
постоянные.
Тогда
A^z)-^d + yE «^Re^^ = i-[arg/(e)]b
где ah — У^ол между касательными векторами в угловой точке
(см. рис. 11 и п. 3.4).
2°. Теорема Лиувилля (обобщенная). Пусть функция
f{z) аналитична во всей плоскости комплексного переменного,
за исключением точек ао = оо, ah (^ = 1,2,..., п), где она
имеет полюсы, причем главные части разложений функции f{z)
в окрестности полюсов имеют вид
Gq (г) = c\z + c^z^ -f ... + cl^z"^^ в точке «о,
Gbl = h  То + ... + ^-zr- в точках аь.
*) Для случая Ml = Pl = О доказательство можно найти во всех
руководствах по теории аналитических функций.

§ 131 ИНДЕКС 101
Тогда функция f{z) есть рациональная функция и может
быть представлена формулой
п
f{z) = c + Go{z) + Y.GJj^)
В частности, если единственная особенность функции f{z)
есть полюс порядка т в бесконечно удаленной точке, то f{z)
есть многочлен степени т:
т
f{z) = Co + c^z+ ... +c^z'
§ 13. Индекс
13.1. Определение и основные свойства. Пусть L — гладкий
замкнутый контур и G{i) — заданная на нем непрерывная
функция, не обращающаяся в нуль.
Определение. Индексом к функции G{t) по контуру L
называется разделенное на 2я приращение ее аргумента при
обходе кривой L в положительном направлении:
x=IndG@==^[argG@]L. A3.1)
Так как In G(/) = ln|G(/) | +larg G(/) и после обхода
контура L функция |G@| возвращается к своему начальному
значению, то [1п G(^)]l =/[argG(if)]ь и следовательно,
x = -2^[lnG@k. A3.2)
Индекс можно представить в виде интеграла
H = lndG{t) = ^\dlnG{t) = -^\dargG{t). A3.3)
При ЭТОМ, если G{t) не дифференцируема, но имеет
ограниченную вариацию, то интеграл понимается в смысле Стилтьеса.
В силу непрерывности G{t) образ Г замкнутого контура L
будет также замкнутым контуром и приращение аргумента G(t)
при обходе контура L будет кратным 2я; следовательно:
1. Индекс функции, непрерывной на замкнутом контуре и
нигде не обраи{ающейся в нуль, есть целое число или нуль.
Из определения индекса непосредственно получаем:
2. Индекс произведения функций равен сумме индексов
сомножителей. Индекс частного равен разности индексов
делимого и делителя.

102 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
Пусть теперь G{t) дифференцируема и представляет собой
краевое значение аналитической внутри или вне контура L
функции. Тогда
n = ^\d\nGit) = ^\^dt A3.4)
L L
оказывается равным логарифмическому вычету функции G{t),
Из принципа аргумента вытекают следующие свойства индекса:
3. Если G{t) есть краевое значение функции, аналитической
внутри или вне контура, то индекс ее равен числу нулей внутри
контура или соответственно числу нулей вне контура, взятому
со знаком минус.
4. Если функция G(z) аналитична внутри контура, за
исключением конечного числа точек, где она может иметь полюсы,
то число нулей нужно заменить на разность числа нулей и числа
полюсов.
Нули и полюсы считаются при этом столько раз, какова их
кратность.
Заметим еще, что индексы комплексно сопряженных
функций обратны по знаку.
13.2. Вычисление индекса. Пусть
t = t^{s) + it2{s) @<S</)
— уравнение контура L. Подставляя выражение комплексной
координаты t в функцию G(t), получим
G{t) = G [t, is) + It, (s)] =Ш + Щ is). A3.5)
Будем рассматривать |, г\ как декартовы координаты. Тогда
представляет собой параметрическое уравнение некоторой
кривой Г. В силу непрерывности функции G{t) и замкнутости
контура L кривая Г будет замкнутой.
Число витков кривой г вокруг начала координат, т. е. число
полных оборотов радиуса-вектора, когда переменная s
изменяется от О до Z, и будет, очевидно, индексом функции G(t),
Число это иногда называют порядком кривой Г относительно
начала координат.
Если кривую Г удается построить, то число витков
усматривается непосредственно. Можно привести много примеров, когда
индекс может быть определен по виду кривой Г. Например,
если G{t) — действительная или чисто минимая функция, не
обращающаяся в нуль, то Г есть отрезок прямой (проходимый
четное число раз) и индекс G(t) равен нулю. Если
действительная часть l{s) или мнимая t|(s) не меняет знака, то индекс,

§ 13] ИНДЕКС 103
очевидно, также равен нулю и т. п. Если функцию G{t) можно
представить в виде произведения или частного функций,
являющихся предельными значениями аналитических внутри или вне
контура функций, то индекс вычисляется на основании свойств
2, 3, 4.
В общем случае вычисление индекса может быть
произведено по формуле A3.3). Полагая в ней на основании формулы
A3.5)
dargG{t) = daTctg^
и предполагая I и ц дифференцируемыми, получим
г о
в некоторых простых случаях можно дать алгебраический
алгоритм для вычисления индекса (см. задачи 1, 2, 3 в конце
главы).
Понятие индекса может быть распространено на случай
незамкнутого контура L, а также на случаи, когда G{t) имеет
разрывы (см. пп. 41.2 и 42.1).
Замечание. Если G{t) есть краевое значение
аналитической функции, то контур L можно менять в широких пределах,
не меняя величины индекса. Очевидно, индекс будет меняться
всякий раз, когда контур, деформируясь, переходит через нуль
или полюс G{z).
Пример. Вычислить индекс G (t) = t^ по любому кон*
туру L, окружающему начало координат.
1-й способ. Функция t^ есть краевое значение функции z'^,
имеющей один нуль порядка п внутри контура. Следовательно,
X = Ind t"^ = п.
2-й способ. Если аргумент / есть ф, то аргумент t^ равей
/1ф. Когда точка ^ обойдя контур L, возвращается к начальному
значению, ф получает приращение 2я. Следовательно,
Вычисление индекса может быть проведено численными
методами на быстродействующих вычислительных машинах.
Очевидно, что в силу целочисленности значений индекса
приближенное значение его, найденное с погрешностью, меньшей 1/2,
и округленное до ближайшего целого числа, даст точное
значение.

104 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
Приведем один из численных методов вычисления индекса. Разобьем
промежуток [О, /] изменения параметра s, определяющего уравнение
контура L, на п равных частей точками so = О, Si, S2, ..., Sa = /. В результате
сам контур L и кривая Г, являющаяся отображением L с помощью функции
С (О, разобьются на п дуг. Пусть Y/ — одна из таких дуг кривой Г, а
(|;_1, ^i_i)» {li^ Л/) — координаты ее концов. Здесь 1^ = 1^{з1 т]. =-q^ (s).
Обозначим Дф^ угол между радиусами-векторами концов дуги уи Тогда по
формуле A3.1)
п
Для достаточно большого п имеем
Дф^. « sin Дф^ =
Vii-.+4?->Vi?+ni'
и поэтому
где Rn — погрешность.
Легко можно было бы показать, что если функции ti{s) и ^2E), входящие
в уравнение контура L, удовлетворяют условию Гёльдера с показателем а,
а функция G{t)—этому же условию с показателем р, то
где С — постоянная.
Отсюда при ар > 1/3 и л ~> со имеем Rn -^ 0. Таким образом, получили
расчетную формулу
п
з< «
.y-J^i^lZ^l^===r, A3.7)
которая легко программируется для вычислительных машин.
Приведем пример вычисления по формуле A3.7), выполненного на
электронной вычислительной машине «Стрела)^. Для индекса функции, не продол-
жимой аналитически в область,
w = u+iv = sin^{x + y)- 8(^.^ Д^)^; +1{х-у),
на единичной окружности получено с округлением до третьего знака:
при л = 32 « « — 0,949,
при /г = 64 X ж — 0,983.
Следовательно, >с = — 1.
Как показывает пример, для достижения этого результата достаточно
было бы взять п значительно меньшим.

§ 131 ИНДЕКС 105
Действительная и мнимая части рассматриваемой функции заданы
аналитическими функциями и их аналитически можно продолжить внутрь круга.
Продолженная функция w{x,y) имеет нуль в точке A/2, 1/2) и обращается
в бесконечность на окружности {х + \/2У-{-у^ = 1/8. Из примера видно, что
для неаналитических комплексных функций какой-либо простой зависимости
индекса от нулей и бесконечностей функции в области не существует.
Последний материал заимствован из работы Л. А. Чикина 4).
13.3. Частичные индексы функции двух переменных*).
Рассмотрим функцию G{tut2) переменных ti и ^2, непрерывную и
отличную от нуля в точках остова L = Li X ^2 некоторой бици-
линдрической области (см. п. 9.4).
По аналогии с 13.1 индекс такой функции вдоль любой
непрерывной замкнутой кривой FczL, задаваемой уравнениями
t, = t,{s\ h^U{s) @<5<Г),
определим как изменение ее аргумента при обходе Г в
направлении возрастания параметра 5:
Хр = Indp G = -^ [arg G {tu /sWr =
т
= ^ \d\nG(tu t,) = -^\d\nG{t,{s), t2{s)).
Г о
в частности, получим
Li Li
И заметим, что интеграл хь являясь непрерывной функцией
переменного ^2 ^ ^2 и одновременно целым числом, в силу этого
не зависит от ^2- Точно так же Х2 не зависит от t[.
С помощью топологических соображений нетрудно показать,
что справедливо соотношение
Хр = mjXj + ^2^2» ^1» ^2 ""* ВДлые.
Отсюда, если 'х^ = к^ = 0, то >Ср = 0, а если Хр = 0 для всякого
замкнутого контура FciL, то одновременно и Xi = X2 = 0.
Целые числа Xi=Ki{G) и X2 = X2(G) будем называть
частичными"^*) индексами функции G(/i, 1<^фО и непрерывной на L.
*) Изложенные здесь понятия взяты из работ И. Б. Симоненко 4)
и В. А. Какичева 3).
**) В оригинальных работах используется название частные индексы. Мы
изменили термин, чтобы не смешивать его с термином того же наименования
в теории краевых задач со многими искомыми функциями, где он имеет
другой смысл.

106 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
Частичные индексы функции двух переменных обладают
теми же свойствами, что и индекс функции одного переменного.
Например,
ху {GF) = к J (G) + ху {FI ху (-I-) = ху (G) - х/ (f),
а если функция 0B:1,2:2) аналитична в бицилиндрической
области Di XD2 и непрерывна в ее замыкании, то равенства щ =
= Х2 = О равносильны тому, что G{zuZ2) не обращается в нуль
в замыкании Di X ^2.
§ 14. Задача Римана для односвязной области
14.1. Постановка задачи. Даны простой гладкий замкнутый
контур L, делящий плоскость комплексного переменного на
внутреннюю область Z)+ и внешнюю D- и две функции точек
контура G{t) и g{t), удовлетворяющие условию Гёльдера,
причем G{t) не обращается в нуль.
Задача Римана. Найти две функции*):
Ф+(г)—аналитическую в области /)+, и ф-{г) —аналитическую в области D'^у
включая г = оо, удовлетворяющие на контуре L линейному
соотношению
ф+(^)=з:С(ОФ~@ (однородная задача) A4.1)
или
ф+(/)=:0(/)ф~(/) + ^(/) (неоднородная задача). A4.2)
Функцию G{t) будем называть коэффициентом задачи
Римана, а функцию g{t)—ее свободным членом.
14.2. Отыскание кусочно аналитической функции по
заданному скачку. Рассмотрим предварительно задачу Римана
частного вида. Пусть на замкнутом контуре L дана функция ф@,
удовлетворяющая условию Гёльдера. Требуется найти кусочно
аналитическую функцию Ф(г) (Ф(г) = Ф+(г) при ге/)+
ФB)=ф-B:) при eeD"), исчезающую на бесконечности и
испытывающую при переходе через контур L скачок ф@, т. е.
удовлетворяющую условию
ф-'(/)-ф-(/) = ф@. A4.3)
Функция
L
*) Употребляя терминологию § 1, можно говорить об одной кусочно
аналитической функции.

§ 141 ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 107
на основании формулы D.9), очевидно, дает решение этой
задачи. Легко показать единственность полученного решения.
В самом деле, допуская существование двух решений и
рассматривая их разность, получим, что для этой разности скачок
на линии L равен нулю; следовательно, это будет функция,
аналитическая во всей плоскости и обращающаяся в нуль на
бесконечности. Отсюда по теореме Лиувилля следует, что эта
разность тождественно равна нулю.
Решению рассмотренной задачи можно дать еще следующую
формулировку:
Заданную на замкнутом контуре произвольную функцию
ф@» удовлетворяюи^ую условию Гёльдера, можно
единственным образом представить в виде разности функций Ф+(/),
ф-(<), являющихся краевыми значениями аналитических
функций Ф+B), Ф""B:), при дополнительном условии ф-(оо) = 0.
Если отбросить дополнительное условие ф-(оо)=0, то
решение задачи, как легко видеть, будет даваться формулой
^(^) = iSTS^^ + ^°"^t. D.40
14.3. Каноническая функция. Начнем с нахождения
некоторой вспомогательной функции, через которую, как будет
показано далее, выражается общее решение как однородной, так
и неодцородной краевых задач. Будем искать частное решение
однородной задачи A4.1) в классе функций, не обращающихся
на контуре в нуль. Пусть Л^+, Л^- — число нулей искомых
функций соответственно в областях /)+, D". Взяв индекс обеих
частей равенства A4.1), на основании свойств 2 и 3 п. 13.1
получим
N+ + N^ = Ind G (О = X. A4.4)
Индекс X коэффициента задачи Римана будем называть
индексом задачи.
Пусть X = 0. При этом условии ]nG{t) будет однозначной
функцией. Из A4.4) следует Л^^. = iV_ = О, т. е. решение не
имеет нулей во всей плоскости. Функции 1пФ±(г) будут
поэтому аналитическими в своих областях и, следовательно,
однозначными вместе со своими краевыми значениями 1пФ='=(/).
Логарифмируя краевое условие A4.1), получим
1п Ф+ (О - In Ф" (О = In G @. A4.30
Для 1пО(/) можно брать любую ветвь. Окончательный
результат, как легко проверить, не зависит от выбора ветви.
Мы пришли к задаче отыскания кусочно аналитической
функции 1пФ(г) по заданному на L скачку. Решение ее при

10Й К^^АЁВАЯ ЗАДАЧА РИМАНА [ГЛ, II
дополнительном условии 1пф-(оо) = 0 дается формулой
Обозначим для краткости
^|11?<11„=ги. A4.6)
L
Решениями краевой задачи A4.1)» удовлетворяю1Цими
условию Ф''(оо)=1, будут, как это непосредственно вытекает из
формул Сохоцкого, функции
ф+ (Z) = /"^ ''\ Ф- (г) = /" ^Ч A4.7)
Если отбросить дополнительное условие ф-*(оо)==1, то в
формуле A4.5) нужно добавить произвольное постоянное
слагаемое и решение задачи будет иметь вид
ф+ (г) = л/"" ^'\ Ф- (Z) = л/"" ^^\ A4.8)
где А — произвольная постоянная. Так как Г~(оо) = 0, то А
представляет собой значение Ф"(г) на бесконечности.
Таким образом, в случае х = О и при произвольном
ф-(оо)=7^0 решение содержит одну произвольную постоянную,
следовательно, имеется одно линейно независимое решение.
Если ф-(оо) = 0, то Л = О и задача имеет только тривиальное
решение — тождественный нуль, что естественно в силу Л^_ = 0.
Отсюда можно получить важное следствие. Заданную на
контуре L произвольную функцию С{1)фО, удовлетворяюи^ую
условию Гёльдера и имеющую индекс нуль, можно представить
в виде отношения функций Ф+@ и Ф~@» являющихся крае-
выми значениями функций, аналитических в областях /)+, D"
и не имеющих в этих областях нулей*). Функции эти
определяются с точностью до произвольного постоянного множителя
и даются формулами A4.8).
Переходя теперь к общему случаю, будем искать кусочно
аналитическую функцию, удовлетворяющую однородному
краевому условию A4.1) и имеющую нулевой порядок во всей
плоскости, кроме одной исключительной точки, где ее порядок
равен индексу задачи. За такую точку можно принять любую
точку плоскости. В дальнейшем всюду, где не будет
оговариваться противное, в качестве исключительной будем брать
бесконечно удаленную точку.
*) Это же справедливо и для более широкого класса функций, что будет
следовать из результатов п. 16.3.

§ 14] ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 109
Определение. Канонической функцией Х(г) будем
называть функцию, удовлетворяющую краевому условию A4.1) и
кусочно аналитическую всюду в плоскости, за исключением
бесконечно удаленной точки, где порядок ее равен индексу задачи.
Эту функцию можно построить приведением к случаю
нулевого индекса. Запишем краевое условие в виде
ф+(/) = /^О@Ф~@.
Представляя имеющую нулевой индекс функцию t-'^G{t) как
отношение краевых значений аналитических функций
легко получим выражение для канонической функции:
Х+(г) = /"'^^\ X-(e) = 2-V"*^^\ A4.10)
Из Х+@= G{t)X-{t) следует, что коэффициент задачи Римана
может быть представлен в виде отношения канонических
функций:
G@ = -^^^. A4.11)
Иногда вместо X~{z) берут —::— (порядок при этом ме-
X (г)
няет знак на противоположный) и получают представление
коэффициента в виде произведения G(/) = Х+(/)Х-(/). Такое
представление называют факторизацией. Однако при этом
окончательные формулы решения теряют симметрию. В дальнейшем
мы всюду будем пользоваться представлением A4.11).
При X ^ О каноническая функция, имея на бесконечности
нуль порядка х, является одним из частных решений краевой
задачи A4.1). При х<0 каноническая функция имеет на
бесконечности полюс порядка |х| и уже не является решением, но
она и в этом случае используется в качестве вспомогательной
функции при решении неоднородной задачи.
14.4. Решение однородной задачи. Пусть x = IndG(/) есть
любое целое число. Представляя G{t) по формуле A4.11),
приведем краевое условие A4.1) к виду
Ф"^ (t) ^ Ф~ it)
Х^ (/) Х- (/) •
В левой части последнего равенства стоит краевое значение
функции, аналитической в D+; в правой — краевое значение

по Kt^AEBAH ЗАДАЧА РИМЛНА 1ТЛ. II
функции, имеющей на бесконечности порядок не ниже —х
(Х(г) имеет, по определению, порядок х). По принципу
непрерывности (п. 12.1) функции левой и правой частей являются
аналитическим продолжением друг друга на всю плоскость, за
исключением разве что бесконечно удаленной точки, где в
случае X > О возможен полюс порядка не выше х. Отсюда, при
X > О по обобщенной теореме Лиувилля эта единая
аналитическая функция является многочленом степени х с произвольными
коэффициентами. Если х << О, то по обычной теореме Лиувилля
функция есть постоянная. Но так как на бесконечности она
должна обратиться в нуль, то отсюда следует, что она есть
тождественный нуль. Следовательно, получаем: при х < О
однородная задача имеет только тривиальное решение —
тождественный нуль. Здесь и в дальнейшем мы будем называть не-
разрешимыми, задачи, не имеющие других решений, кроме
тривиального нулевого. Таким образом, однородная задача A4.1)
при отрицательном индексе неразрешима.
При X > О, обозначая многочлен степени х с произвольными
коэффициентами Py^iz), получим решение в виде
ФB) = Р^(г)Х(г),
или
ф+ B) = Р^ (z) /"" ^'\ Ф" (z) = z'^'P^ (z) /" ^'\ A4.12)
где T{z) определяется формулой A4.9). Рассмотренный в
п. 14.3 случай X = О входит сюда как частный: Р^^ (z) здесь
вырождается в постоянную.
Резюмируем результат.
Теорема. Если индекс х краевой задачи Римана
неотрицателен, то однородная задача A4.1) имеет х+ 1 линейно
независимых решений
фt(z)=zV''^'\ Ф1{2)=г^-^^'' {k = 0, 1, ..., х). A4.13)
Оби^ее решение содержит х + 1 произвольных постоянных и
определяется формулой A4.12). При отрицательном индексе
задача A4.1) неразрешима.
Многочлен Р^ (z) имеет в комплексной плоскости точно х
нулей. Из формул A4.12) следует, что число всех нулей
решения однородной краевой задачи Римана точно равно индексу х.
В зависимости от подбора коэффициентов многочлена эти нули
могут попасть в любую из областей D^, а также и на контур.
Обозначая, как и ранее, N± число нулей решения в областях
D±, а No число нулей на контуре L, получим, что в общем
случае (без ограничения отсутствия нулей на контуре) формула
A4.4) примет вид
N+i-N^ + No^yi. A4.40

§ 14] ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ Щ
14.5. Решение неоднородной задачи. Заменяя коэффициент
G{t) краевого условия
Ф'¦{t)=G{t)ф-{t) + g{t) A4.2)
отношением краевых значений канонической функции однород-
Х^ (t)
ной задачи G{t)= _^ , приведем A4.2) к виду
X (t)
ФUt) _ ф-ц) , g{t)
х+ (/) х- (О х+ (О •
Согласно п. 5.1 функция ^ удовлетворяет условию
Гёльдера. Заменим ее согласно п. 14.2 разностью краевых
значений аналитических функций:
_^ = 4'+@-W-(/),
где
г)
'^(^) = T^SlF7T-^^- A4.14)
2nt J X (т) X — 2
L
Тогда краевое условие можно будет записать в виде
Х+(/) ^ ^^^~Х-(/) ^ ^^^•
Заметим, что при х ^ О функция —::г^ будет иметь на беско-
X (z)
нечности полюс, а при х < О нуль порядка х.
Рассуждая совершенно так же, как это делалось в п. 14.4
при решении однородной задачи, получим следующие
результаты:
Г. X ^ 0. Тогда
^IW ^ хр+(^) = Ф1(^ ^ ^{г-(^) = р^ (^).
х+(/) ^^ х-(О ^^ ""^^
Отсюда имеем решение
Ф(г) = Х(г)[^(г) + Рк(^)], A4.15)
причем ХB), ^(z) выражаются формулами A4.10), A4.14),
а Р^ — многочлен степени х с произвольными коэффициентами.
Легко видеть, что формула A4.15) дает общее решение
неоднородной задачи, так как оно содержит в качестве
слагаемого общее решение однородной задачи X.{z)Py^{z),

112 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
2°. X < 0. В этом случае —:~^ равно нулю на бескенечно-
X (г)
сти и
откуда
х+@ ^^ х-@
Ф(г) = ХB)Ч^(г). A4.16)
В выражении функции ф-B:) первый множитель на основа-
НИИ формулы A4.10) имеет на бесконечности полюс порядка
—X, а второй, как интеграл типа Коши A4.14), имеет на
бесконечности в общем случае нуль первого порядка. Следовательно,
Ф~(г) имеет на бесконечности полюс порядка не выше чем
—X—1. Таким образом, если х<—1, неоднородная задача,
вообще говоря, неразрешима. Она будет разрешима лишь тогда,
когда свободный член удовлетворяет некоторым
дополнительным условиям. Для получения их разложим в ряд интеграл
типа Коши A4.14) в окрестности бесконечно удаленной точки
(см. § 1)
где
(т)
Для аналитичности ф-{г) в бесконечно удаленной точке
нужно, чтобы первые —х— 1 коэффициентов разложения ^-(г)
обратились в нуль. Отсюда получаем, что для разрешимости
неоднородной задачи в случае отрицательного индекса (х <—1)
необходимо и достаточно, чтобы удовлетворялись следующие
—X— 1 условий:
^-li^^k^idx^O (Aj=1,2, ..., -х~1). A4.17)
J Х-(т)
В итоге исследования может быть сформулирован
следующий вывод.
Теорема. В случае х ^ О неоднородная задача Римана
разрешима при любом свободном члене и ее общее решение
дается формулой

§ 14) ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ ЦЗ
где каноническая функция Х(г) определяется из A4.10),
а Pyiiz)—полином степени к с произвольными комплексными
коэффициентами. Если х = —1, то неоднородная задача также
разрешима и имеет единственное решение.
В случае >с <—1 неоднородная задача, вооби{е говоря,
неразрешима. Для того чтобы она была разрешима, необходимо
и достаточно, чтобы свободный член задачи удовлетворял
—к — 1 условиям A4.17). При выполнении последних
единственное решение задачи дается формулой A4.18), где нужно
положить Ру^ (г) ^ 0.
Важные применения в дальнейшем (гл. III) будет иметь
решение с дополнительным требованием, чтобы оно обращалось
в нуль в бесконечно удаленной точке. В этом случае вместо
многочлена степени х нужно взять многочлен степени %—1,
Для разрешимости задачи в случае отрицательного индекса
придется потребовать обращения в нуль также и
коэффициента с^.
Следовательно, при условии ф-(сх)) = 0 решение будет
задаваться при X ^ О формулой
0{z)^X{z)[W{z) + P^^dz)] A4.180
(при X = о нужно положить Py,^\(z) = 0).
Если X < О, то решение по-прежнему будет выражаться
формулой A4.18'), где P'^^-\{z)^b, при соблюдении —х условий
разрешимости:
SlF7T^'~'^^=^-0 (^=1,2,..., -X). A4.19)
J X (т)
Таким образом, теорема о разрешимости неоднородной задачи
принимает более симметричный вид.
При X ^ О общее решение неоднородной задачи линейно
зависит от X произвольных постоянных.
При X < О число условий разрешимости равно —х.
Заметим, что здесь при х = О неоднородная задача
безусловно разрешима и притом единственным образом.
14.6. Примеры. На основании изложенного решение краевой
задачи Римана сводится в основном к двум операциям:
1. Представление произвольной функции, заданной на
контуре, в виде разности краевых значений функций,
аналитических в областях D+ и D-. (Задача о скачке.)
2. Представление пеисчезающей функции в виде отношения
краевых значений аналитических функций. (Факторизация.)

114 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
При этом вторая операция может быть сведена к первой
путем логарифмирования. Некоторые осложнения при ненулевом
индексе вносит только неоднозначность логарифма. Первая
операция для произвольной функции равносильна вычислению
интеграла типа Коши. В связи с этим решение задачи по
формулам A4.10), A4.14) —A4.16) выражается явно (или, как
принято выражаться, в замкнутой форме) через интегралы типа
Коши.
В общем случае нет простого алгоритма для вычисления
таких интегралов. Нужно применять какой-нибудь из приемов
приближенного вычисления интегралов, что сопряжено с весьма
трудоемкими вычислениями. Мы здесь ограничимся случаем,
когда коэффициент и свободный член задачи аналитически про-
должимы с контура в плоскость комплексного переменного.
Тогда операции 1 и 2 могут быть выполнены элементарно. Если
при этом варьировать контур интегрирования L, то решение
будет меняться только при изменении положения относительно
контура нулей и особых точек коэффициента G{z),
Заметим, что значение излагаемого здесь способа решения
задачи с рациональными коэффициентами выходит за рамки
иллюстрирующего примера, так как произвольная непрерывная
(а тем более удовлетворяющая условию Гёльдера) функция
может быть с любой точностью приближена рациональными
и решение задачи с рациональными коэффициентами может
стать основой ее приближенного решения в общем случае (см.
ниже, п. 16.3,6°).
Для иллюстрации решим краевую задачу Римана с
контуром, состоящим из конечного числа простых кривых,
коэффициент G{t) которой есть рациональная функция, не имеющая
нулей и полюсов на контуре:
^*ii) = j^'^~ii) + S{t)- A4.20)
Разложим многочлены р(г), q{z) в произведение
р {г) = р^ {г) р^ {z\ q {z) == q^ {z) q^ (г), A4.21)
где /7+(г), q+{z)—многочлены, корни которых лежат в D+
а p-{z), q-{z)—многочлены с корнями в D- Из свойства 4
индекса (п. 13.1) легко получить, что х = т+ —az+, где т+, п+ —
числа нулей многочленов /7+(г), ?+(г).
Ввиду того, что коэффициент задачи есть функция,
аналитически продолжимая в области D±, здесь
целесообразнее не пользоваться общими формулами решения, а
получить последнее непосредственно, пользуясь аналитическим

141
ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ
115
продолжением *). Представляя краевое условие в виде
P_W
<7+W
p-{t)
(каноническими функциями здесь являются X = —, X =
q,
=^^), на основании тех же соображений, что и в п. 14.5,
получим решение в виде
Ф~B) = ^^[ЧЧ2) + Рх-,B)],
dx
(ф-(оо) = 0).
A4.22)
Если индекс окажется отрицательным, то нужно положить
f^_i^O и добавить условия разрешимости:
S^S'(T)t*-'rfT = 0 (fe=I,2, .... -х). A4.23)
Полученное выражение согласуется с общими формулами
A4.14), A4.15), если учесть, что каноническая функция здесь
будет иметь вид X = —, X = —. Последнее можно полу-
чить, исходя из определения канонической функции (п. 14.3).
Заметим, что и в общем случае при практическом
решении задачи Римана выгодно бывает коэффициент представ-
лять в виде G = —^—Gi, где Gi — функция с нулевым ин-
дексом, а многочлены р±, q± подбираются, исходя из вида
*) При этом следует учитывать, что роль стандартной функции t^,
используемой для сведения индекса к нулевому, способно играть произведение
X
JJ (/ — аХ где Лр ..., ci -- любые точки области D+.
/-1

Иб
КРАЕВАЯ ЗАДАЧА РИМАНА
1ГЛ. II
коэффициента. При целесообразном подборе этих многочленов
решение может быть получено наиболее простым путем.
В качестве примера решим задачу Римана
Ф+(/)--
Ф~@ +
/3-/
Рис. 12.
при условии, что ф-(оо) = о и L —
произвольный гладкий замкнутый контур следующего
вида:
а) контур L содержит внутри себя
точку zi = О и не содержит точек Z2 =» 1,
2з = —1;
б) контур L содержит внутри себя
точки zi = О, 22= \ и не содержит точки
гз==—1;
в) контур L содержит внутри себя точки
21 = 0, Z2= 1, гз== —1;
г) контур L содержит внутри себя точки
22 = 1, 23 == —1 и не содержит точки Z\ = 0.
Для решения используем указанный выше
прием.
а) В данном случае (рис. 12)
P^(t)=^t, р_ (/) = !, m^ = I,
Записываем краевое условие в виде
(/2 - I) Ф+(/) -/Ф~ (/) = 1 (/^ -/2 + О (/+ 1).
Отсюда
1
1 Г ^_ (т) dr 1 Г тз - т + I 1 f Т
L L L
И, значит, в силу формул A.1) и A.2) имеем
iF"^ B) = 2^ - z + 1, 1! {г) = - —.
Z
Общее решение задачи содержит одно произвольное постоянное. По формуле
A4.22) находим
•2+1
22-1
1 '
где с — произвольное постоянное. Заменяя с на c — l, можно решению
придать еще и такую форму:
Ф+B) = г +
22-1 *
Ф B) = ~ —V- + -Г

§ 14] ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 117
б) Здесь
т+1
z^ + z при z^D^,
z+l
ЦТ (z) = -rr-T \ ¦— dx + -jr—г \ —^ dx =
^ ^ 2я/ J т —2 2ш J X — Z
L L
"i-f^ZTiJ при ^^0~-
Задача имеет единственное решение:
Р+(^) 2 \ 2B—1)/ 22
в) В данном случае
1
^ ' 2я^ J Т — 2 ' 2я/ J Т — 2
L L
2 При 2eD"^,
1
-I
2B-1)
при z^D .
Решение задачи существует лишь при выполнении условий разрешимости
A4.23) или, в данном случае, одного условия:
f q-(r)
J Р-(т)
L
Вычисляя этот интеграл, находим
g(x)dx^=0.
L L L L
Условие разрешимости, таким образом, выполняется, и единственным
решением задачи будет
Ф+B) = 2, ф-B)==-^±1.
г) в этом случае
P+(t)^l P^{t) = t; q_^(t)^i^-^l ^-,@ = 1;
X = m+ — /z+ = — 2 < 0.

118 К1раевАя задача РИМАНА tfjl. п
Для разрешимости задачи необходимо выполнение двух условий:
J Р-(т)
д(т)т^'^ di^O (А: =1,2).
Вычисляя этот интеграл при ^ = 1, находим
L L
Таким образом, условие разрешимости не выполнено, и потому задача не
имеет решения.
Заметим, что если формально вычислить функцию ФB), то она будет
иметь полюс в бесконечно удаленной точке и, следовательно, не может
являться решением задачи.
Когда контур L конечен и, следовательно, область D+ ограничена,
указанный способ решения применим также и в том случае, когда p{t), q{t) не
многочлены, а целые функции. Пусть р+@» ^+@ — многочлены, имеющие
в D+ своими корнями нули соответственно функций p{t), q(t) с теми же
кратностями. Тогда, представляя р и q ъ виде
Р it) = Р+ (О Р+ (О, я (О = я+ (О Q+ @>
получим краевое условие в виде
Далее можно поступить как в предыдущем.
14.7. Задача Римана для полуплоскости. Пусть контур L есть
действительная ось. Как и ранее, задача Римана заключается
в том, чтобы найти две ограниченные аналитические
соответственно в верхней и нижней полуплоскостях функции Ф+(г),
ф-(г) (кусочно аналитическую функцию ФB)), предельные
значения которых на контуре удовлетворяют краевому условию
ф+ (/) = G (/)Ф- (О + g{t) {-oo<t< оо). A4.24)
Заданные функции G{t) и g{t) удовлетворяют условию
Гёльдера как в конечных точках, так и в окрестности бесконечно
удаленной точки контура (см. условия D.20), D.27)). Считаем
также, что 0{1)Ф 0.
Решение будем проводить по тому же плану, что и для
конечного контура. Главное отличие от рассмотренного ранее
случая аднечной кривой состоит в том, что здесь бесконечно
удаленная точка и начало координат лежат на самом контуре и
потому не могут быть приняты в качестве исключительной
точки, где для канонической функции допустим ненулевой
порядок. Вместо употреблявшейся в предыдущем
вспомогательной функции /, имеющей по L индекс, равный единице, здесь

§ 141 ЗАДАЧА РИМ АН А ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 119
будет введена обладающая тем же свойством на
действительной оси дробно-линейная функция
/- i
t + i
Аргумент этой функции
argT^rj = ^^ё р ¦!¦ 1 = 2 arg (/ ~ i)
изменяется на 2я, когда / пробегает действительную ось в
положительном направлении. Таким образом,
ind4^=i.
Если IndG@ = >c, то функция
имеет индекс, равный нулю. Ее логарифм будет на
действительной оси функцией однозначной.
Строим каноническую функцию, для которой
исключительной точкой будет точка —i:
Х*(г) = Г» X-D = (f^)""/-«, A4.25)
Пользуясь предельными значениями этой функции, преобразуем
краевое условие A4.24) к виду
Ф+(/) _ Ф-(/) . g{t)
X^it) Х-it) Х+(/)
Далее, вводя аналитическую функцию
оо
2nt J X (т) т — г
— оо
представим краевое условие в виде
Х'^(/) ^^ х-(/) ^^
Заметим, что, в отличие от случая конечного контура, здесь,
цообще говоря, W""(oo)=7«^'0. Применяя теорему об аналитиче-

120 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
СКОМ продолжении и учитывая, что единственной особенностью
рассматриваемой функции может быть лишь полюс в точке
2 = —i порядка не выше к (при х>0), на основании
обобщенной теоремы Лиувилля будем иметь
х+@ ^^ х-(/) ^^ (^ + 0''
где Py^it)—многочлен степени не выше х с произвольными
коэффициентами. Отсюда получаем общее решение задачи
0{z) = X{z)[w{z) + -^^] при х>0, A4.27)
0{z) = X{z)[V{z) + C] при х<0. A4.28)
При X < О функция X{z) имеет в точке z = —i полюс порядка
—X, поэтому для разрешимости задачи нужно положить С =
|=—Ч^~(—/). При х<—1, кроме того, должны выполняться
еще следующие условия:
оо
с _?A) ^^=0 {k = 2, ..., -к). A4.29)
Таким образом, получены результаты, аналогичные тем,
которые имели место в случае конечного контура.
Теорема. При х ^ О однородная и неоднородная краевые
задачи Римана для полуплоскости безусловно разреилимы и
решение их зависит линейно or х + 1 произвольных постоянных.
При X < О однородная задача неразреилима. Неоднородная
задача при X < О разрешима однозначно, причем в случае х =
= —1 безусловно у а при х < —1 лишь при выполнении —х— 1
условий A4.29).
До сих пор мы искали решения задачи Римана, которые
были просто ограничены на бесконечности. Сейчас специально
остановимся на случае исчезающих на бесконечности решений.
Подставляя в краевое условие ф+(сх)) = ф-(оо) = О,
получим gr(oo)=0. Следовательно, чтобы задача Римана имела
решение, исчезающее на бесконечности, свободный член краевого
условия должен на бесконечности обращаться в нуль. Будем
считать это условие выполненным. Для получения решения в
рассматриваемом случае нужно в A4.27) вместо Р^ взять
Р^_,, а в A4.28) постоянную С приравнять нулю. Таким
образом,
Ф (г) = X B) [Ч^,(г) + ^g^] ¦ A4.30)

§ 141 ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 121
При х^О в этой формуле нужно положить P^_i^O. К
условиям разрешимости A4.29) добавится еще одно: Ч^(—/) = 0.
Таким образом, эти условия примут вид
\^i;fw=° ''-' -"'• <"•'"
— оо
Теперь при х > О будем иметь решение, зависящее от х
произвольных постоянных, при X ^ О решение единственно,
причем при X < О для его существования необходимо и достаточно
выполнения —х условий.
Для произвольного гладкого замыкающего на бесконечности
контура L решение краевой задачи Римана можно проводить
так же, как и для действительной прямой. Отличие состоит
лишь в том, что вместо имеющей на действительной оси индекс,
равный единице, вспомогательной функции jx^ здесь вводится
обладающая тем же свойством на L функция " , где Zq е
eD"*", Zx ^D^, Исключительной точкой является zi,
14.8. Двумерная задача о скачке*). Каждой функции ф(/1,/2),
удовлетворяющей условию Гёльдера на общем остове L =
1= Li Х^2 четырех бицилиндрических областейD"*" "^ = Df X^f,
сопоставим интеграл типа Коши
Ф (....,)=ш (..,..)=-^ S (:/!;'Xl1:) . A4.32)
определяющий четыре функции
Ф"" ^ (^1, ^2) = (^Ф) (^1, ^2) при Bь 22) е D * "=,
аналитические в D±=t, причем Ф-'''(-г1,г2) и ф-~(<г1,-г2)
исчезают во всех бесконечно удаленных точках областей Z)±=f и D—
соответственно.
В силу второй из (9.20) формулы Сохоцкого на L имеет
место равенство
ф+^^tu /2)-Ф"^(^Ь ^2)-Ф'""(^1, ^2) + Ф"(^Ь ^2) = Ф(^1, ^2). A4.33)
Двумерная задача о скачке заключается в нахождении четырех
функций Ф-=*^(г1,г2), аналитических соответственно в областях
D±± удовлетворяющих условию A4.33) с заданной функцией
Ф класса Я.
*) При написании пп. 14.8 и 14.9 нами использован материал из оабо|
В. А. К а к и ч е в а 3) и 4).

122 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. 11
Приступая к решению двумерной задачи о скачке, сделаем
одно замечание общего характера. Если функция двух
переменных в силу некоторых соображений играет роль постоянной
относительно одной из переменных, то она является
произвольной функцией от другой переменной.
Пусть сначала ф(/1,/2)^0; тогда, переписывая A4.33) в
виде равенства
и применяя к нему теорему Лиувилля по переменному tu
убедимся, что каждая часть равенства является произвольной
функцией класса Н только переменного ^2, которую обозначим
Отсюда следует, что
Ф^^ {tu к) - Ь^ (У = 0=*=^ (^ь h) - b' ih) = а* (/О,
где a±(/i) также произвольные функции соответствующих
классов.
Таким образом, общее решение двумерной однородной
задачи о нулевом скачке имеет вид
Ф'='=(^ь^2) = ^'=(^1) + Ь'=Ы A4.34)
где a^{zi) и 6-B2) — произвольные функции, аналитические
соответственно в Dt и Df и имеющие предельные значения
класса Я.
Для единственности решения двумерной задачи о скачке*)
удобно задать дополнительные условия в таком виде:
Ф*=(г1, oo) = a='(ei), Zi^Dt,
—^ ^ -t. A4.оо)
ф-^(оо, г2) = &='Ы, Z2^Df,
где a'^izi) и 6-(г2) наперед заданные функции, обладающие
перечисленными выше свойствами.
Точно так же, как при условии Ф""(оо) = 0, интеграл
D.4) определял единственное решение задачи A4.3), интеграл
A4.32) определяет единственное решение задачи A4.33) при
*) Отметим полезную (и далеко идущую) аналогию: если и'(л;)=0, то
« — произвольная постоянная, а если и^у(Хуу)='0, то и(х,у)= а(х)+^(у),
где а и Р — произвольные функции своих аргументов. Однако уравнение
м^^ = 0 вместе с соответствующими условиями Коши имеет единственное
решение.

§ 14] ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 123
дополнительных условиях:
Ф~~(^ь ^)==0 при Zi^Dff
Ф=^ (оо, гг) = О при Z2 е Df.
В общем случае единственное решение задачи A4.33) при
дополнительных условиях A4.35) является суммой интеграла
A4.32) и соответствующей суммы из A4.34).
Отметим два полезных следствия, вытекающих
непосредственно из решения задачи о скачке и формул Сохоцкого (9.19).
1. Всякая функция ф е Я единственным образом предста-
вима в виде суммы ф'^"'^ — ф""*" — ф"^""+ ф предельных
значений Ф'*''^(/1, /г) функций Ф'^'^B:1 ^г), аналитических в D"^"^
и такиху что ф-"(г1, сх>) = 0 при Zi^Dt и Ф"*(оо, г2) = 0
при Z2 е Dt-
2. Для того чтобы функция ф е Я была представима в виде
одной из сумм
1) ф±± _ ф+- _ ф-+, 2) Ф"^^ - Ф^"^ + Ф""",
3) ф^^ - ф=^^, 4) Ф-'^ - Ф'^"', 5) Ф^"* - Ф^'^,
где Ф^=*= обладают теми же свойствами, что и в \, необходимо
и достаточно, чтобы она удовлетворяла соответственно
условиям:
1) ф =F 51Ф =F 52ф + 512ф = 4Ф^'^ = О,
2) - Ф ± 51ф =F 52ф + 512ф = 4Ф'^=*^ = О,
3) Ф =F 51ф = 2 (Ф^'^ - ф=^=^) = О,
4) Ф =F 52ф = 2 (Ф^'^ - Ф^'') = О,
5) =F ф ± 512Ф = 2 (ф+'= + Ф^'^) = 0.
14.9. Постановка задачи Римана для бицилиндрических
областей. Задачу Римана для функций, аналитических в
бицилиндрических областях, можно сформулировать следующим
образом.
Пусть Л, В, С, D и f — заданные функции, удовлетворяющие
на общем остове L четырех бицилиндрических областей Z3±±
условию Гёльдера. Требуется по краевому условию
A{tu ^2)Ф'''"(^1, t2)-B{tu /2)Ф"''(^1, h)-
- С {tu к) Ф^- {tu h) + D {tu h) Ф" (^1, к) = f {tu hi A4.36)

124 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
заданному на L, определить четыре функции Ф=^*(г1,г2),
аналитические в D±± и удовлетворяющие дополнительным
условиям
,^ 1 A4.37)
Ф-±(СХ), г2)==0, 22 ^^2^=.
Теория двумерных задач A4.36) —A4.37) существенно
отличается*) от теории одномерной задачи A4.2), а ее решение
в замкнутом виде в настоящее время еще не получено. Для
выяснения некоторых особенностей этой задачи обратимся к
примеру.
Пример. Пусть L\ и L2 — единичные окружности,
/(/ь/2)^0и
Л=1, B = t[ti\ C = tT't2\ D = tTt^\ A4.38)
где /i, /2, т\у m2, пи ^2 — некоторые целые числа. Эта задача,
назовем ее двумерной однородной элементарной задачей,
аналогична одномерной элементарной задаче Ф+(/) =/^ф-(/),
имеющей при х > О и дополнительном ¦ условии Ф~(оо) = О
точно X линейно независимых решений и неразрешимой при
X ^ 0. В отличие от этой задачи, как будет сейчас
показано, двумерная однородная элементарная задача может иметь
решение, зависящее от конечного числа функций одного
переменного.
Мы еще более упростим задачу, отыскивая сначала только
те ее решения, в которых любые две из четырех искомых
функций тождественно равны нулю.
Пусть сначала 1) Ф^=(гь2:2) = 0; тогда рассматриваемая
задача принимает вид
Ф'"^(^1, ^2) = ^^2^Ф"^(^Ь а Ф""''@0, ^2) = 0, 32^02^ A4.39)
Аналитически продолжая краевое условие A4.39) по
переменному Z2 в область D2 и сопоставляя его с условием
соответствующей одномерной задачи, убедимся, что задача A4.39)
в действительности является задачей Римана только по
переменному tu Si 22^. D2 входит в ее условие как параметр.
Следовательно, задача A4.39) разрешима лишь при
выполнении условия /i > 0. Пусть /i > 0; тогда, в соответствии с
*) В некотором смысле различие в двумерных и одномерных задачах
Римана такое же, как между линейными дифференциальными уравнениями
с постоянными коэффициентами в частных производных и обыкновенными.

§ 141 ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОИ ОБЛАСТИ 125
формулами A4.12), общее решение задачи A4.39) имеет вид
0^^{zuZ2)^Zct{z2)zl A4.40)
zi'O-^'izu Z2) = zT'^ Z ct{z2)zl A4.400
Если /г ^ 0, TO в этих формулах c+(г) —произвольные
функции, аналитические в ^г" и удовлетворяющие условию Гёль-
дера на L2; если же h > О, то такой должна быть каждая из
функций
Отвлекаясь пока от исходной задачи A4.36) — A4.38),
приведем одну из возможных формулировок дополнительных
условий, при которых задача A4.39) с /i > О имеет единственное
решение. Для простоты предположим, что I2 = 0. Пусть с^ {z^,
k = Qy 1, ..., /1 —1, наперед заданные функции, аналитические
в dJ и удовлетворяющие условию Гёльдера на L2; тогда
краевая задача A4.39) имеет единственное решение,
удовлетворяющее дополнительным условиям:
Гг?ф-+ (гь Z2) ~ Z cU^i {Z2) z{'] I = cUh B:2),
Z2^Dt> fe=l, 2, ..., /i.
Рассуждая как и при решении задачи A4.39), убедимся, что
исходная задача имеет решения, зависящие от конечного числа
функций одного переменного и такие, что
2) Ф*+B„ Z2)^0, 3) Ф+*B„ 22)^0, 4) Ф=*(гь Z2)^0,
тогда и только тогда, когда соответственно
2) A2i > Шь 3) «2 > /2, 4) /Пз > 0.
Отыскивая еще решения задачи, в которых
5) O^=^(^b^2) = 0,
получим задачу
Ф-'^^Ь ^2) + /Г'/2"Ф"(/1, ^2) = 0, ^^^^^^
A4.41)
Ф (оо, 2:2) = 0, 22^02, Ф B^1, оо) = 0, Zi^Di.

126 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
Применяя теорему Лиувилля к задаче A4.41) сначала по
переменному tu а затем по переменному /г, найдем, что она
разрешима тогда и только тогда, когда одновременно пх > О и П2 > 0.
Если /ti > О и Ai2 > О, то решение задачи A4.41) описывается
с помощью произвольного полинома, содержащего П1П2
произвольных постоянных:
/1,-1 /1,-1
Аналогичные рассуждения показывают, что исходная задача
имеет решения, зависящие от конечного числа произвольных
постоянных и такие, что
&)Ф''^{ги 22)^0
лишь в том случае, когда li> т\ и Шг > k.
Разрешимая двумерная однородная элементарная задача,
как показывают непосредственные вычисления, всегда имеет
бесконечное число линейно независимых решений таких, что
либо только одна из четырех искомых функций тождественно
равна нулю, либо все они отличны от нуля.
Анализ всех случаев показывает, что двумерная однородная
элементарная задача разрешима при выполнении одного из
следующих необходимых и достаточных условий на показатели
мономов A4.38):
1) 1, > О, 2) п, > Ши 3) «2 > /2, 4) тз > О,
5) 1х> Шх и т2> ky 6) П1 > О и AZ2 > 0. ^ * '
Она имеет общее решение, зависящее от конечного числа
произвольных постоянных, тогда и только тогда, когда
Щ = 1^и к~^2у 1\ = т2 = 0 и /21^2 >0. A4.43)
Если задача разрешима, а ее общее решение зависит от
произвольных аналитических функций одного переменного, то
заданием не более чем /i + m2 + (AZi — mi) + (/22 —/г)
дополнительных функциональных условий можно добиться того, что
решение такой задачи будет зависеть уже только от конечного числа
произвольных постоянных.
Переходя к рассмотрению двумерной неоднородной задачи
A4.36) — A4.38), отметим, что она, в отличие от одномерной,
может быть неразрешима даже в том случае, когда разрешима
соответствующая ей однородная задача. Это на первый взгляд
неожиданное явление объясняется, во-первых, тем фактом, что

§ 14) ЗАДАЧА РИМ AHA ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 127
В формулу Сохоцкого A4.33) входит четыре слагаемых, а не
два, как в одномерном случае, и, во-вторых, влиянием
показателей мономов A4.38), что аналогично влиянию индекса
одномерной задачи.
Первое явление хорошо иллюстрируется следствием 2 в
конце п. 14.8, а для демонстрации второго рассмотрим один
простой пример. Пусть в A4.38) А = 1, /г = mi = тг = Aii =
= П2 = 0; тогда однородная задача, в силу первого неравенства
из A4.42), разрешима и ее общее решение имеет вид
ф-^+ (^ь Z2) = а" iZ2), Ф""+ {Zu Z2) = zT'd^ (Z2\ Ф^= {Zu Z2) = О,
где a+(z2)—произвольная аналитическая в Dt функция. С
другой стороны, применяя формулу Сохоцкого A4.33) к интегралу
типа Коши F{zuZ2)=^{Kf){zuZ2) и используя следствие 1 из
п. 14.8, получим следующие равенства:
ф++(/,, t,)^t,ф-^{tu t2) = F''-^{tu t2)-F-^{tu /2),
O^'izu Z2)-=-'F~(Zu Z2\ z^Ф'^^{zu 32) = F + "B:b 2:2),
последнее из которых возможно лишь в том случае, когда
F'^' (О, 22) == О при Z2 е D^.
Если это выполняется, то для получения частного решения
Фо''*'B:1, Z2J неоднородной задачи достаточно положить
^^''(zu 22) = F^^Bi, 22), Ф^^(г,, z2) = zT'F^^{zu 22).
Для получения условий разрешимости неоднородной
элементарной задачи в общем случае надо разложить заданную
функцию в двойной ряд Лорана
И приравнять нулю те ее коэффициенты f^^, которые
отсутствуют в разложениях в ряды Лорана функций
Ф^''(/1, /2), (Ы^Ф-^ {tu t2\ tT^rO-^' {tu t2\ tTtTO"{tut2\
где Ф'*'~(г1,22) —произвольные функции своих классов,
удовлетворяющие условиям A4.37).
Если, например,
1) ni>Zi>0, П2>т2>0, /2<0, mi < О,
2) mi = rti, k^n2, Zi = m2 = 0, AZin2<0 (ср. с A4.43)),
3) /i = ni>0«0), m2 = M2<0(>0), mi = /2 = 0,
TO неоднородная элементарная задача соответственно

l^g КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
1) безусловно разрешима;
2) разрешима при выполнении конечного числа
необходимых и достаточных условий разрешимости;
3) разрешима при выполнении счетного множества
необходимых и достаточных условий разрешимости.
Разрешимая двумерная неоднородная элементарная задача
имеет, вообще говоря, бесконечно много различных частных
решений. Наиболее простой способ нахождения частного решения
состоит в следующем. Положим Фо""^ Bi, Z2) = F'^'^ {z\, гг) и,
исходя из этого, потребуем выполнения равенств
в которых надо определить функции U'^'^y U , F""^, V ,
W^^^^y W~~ и тем самым функции Ф'^"^ и Фо"", входящие в
частное решение задачи. В силу этих равенств в рядах Лорана,
например, для функций U'", 1/"", W'" только часть
коэффициентов может быть отличной от нуля. Обозначим множества таких
коэффициентов соответственно Za~, Z7~» Zw^, тогда
объединение этих множеств совпадает со множеством тех
коэффициентов ряда Лорана функции F~~, которые не входят в
необходимые и достаточные условия разрешимости. Потребуем теперь,
чтобы коэффициенты функции t/"~, входящие в Zc/",
совпадали с соответствующими коэффициентами функции F'". Затем
коэффициенты функции V~", входящие в множество Zu~ — Zi7",
приравняем нулю, а входящие в множество Z^ ~-—Zf/" к
соответствующим коэффициентам функции f""". И, наконец,
положим равным нулю коэффициенты функции W , входящие в
множество Z^~ — (Z^" + Z^""), а остальные приравняем к
соответствующим коэффициентам функции F~~. Аналогичным
образом определим и оставшиеся функции и"^"^, У""^ и W~^,
В заключение введем следующие обозначения: X — число
линейно независимых решений однородной задачи A4.36) —
A4.37), [А — число линейно независимых необходимых и
достаточных условий разрешимости соответствующей неоднородной
задачи. Как это следует из рассмотренного примера, возможны

§ 14] ЗАДАЧА РИМАНА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 129
следующие четыре случая: а) Ж+оо, j^t <+оо, конечную
разность х = Я — \1 такой задачи называют ее индексом,
б) X = +00, |1<+00, в) Ж +00, JX = +00, г) ^=+СХ),
jx = -|-oo. Все эти случаи в действительности реализуются,
в чем и состоит основное отличие двумерной задачи Римана от
одномерной, для которой при рассматриваемых здесь
предположениях возможен только один случай а).
14.10. Некоторые результаты, относящиеся к многомерной задаче Римана.
Г. Решение в замкнутой форме общей задачи A4.36) —A4.37), как уже было
сказано ранее, в настоящее время неизвестно. В пп. 14.8 и 14.9
рассматривались два простейших случая решения задачи Римана в замкнутой форме.
Отметим ряд других таких случаев.
Используя методику решения одномерных задач, можно дать (В. А. К а-
к и ч е в 3)) решение шести «вырожденных» задач Римана, получающихся из
условия A4.36), если в нем положить:
1)Л = Б = 0, 2) Л==С==0, 3) B = D = 0,
4)C = D = 0, 5) Л = ^ = 0, 6)В = С = 0.
Методом, аналогичным методу разделения переменных, используемому в
уравнениях математической физики, В. Д Какичев 4) решает два типа задач,
равносильных конечному числу элементарных и вырожденных задач. Методом
последовательного исключения предельных значений, приводящим к
вырожденным задачам, им дано решение ряда других задач, в частности задачи
с коэффициентами Л, В, С, D, допускающими представление
Этот метод был использован Ю. И. Черским, а затем В. С. Р а б и н о в и*
чем 1).
В. А. Малышев 1), 2) привел задачу о блужданиях в четверть*
плоскости к решению задачи Римана, в которой L — единичный тор,
/J^/^Л (^р /g)"~ многочлен и В = С = —D == I. Такая задача при
специальных дополнительных условиях сведена им к решению одномерной задачи
Римана на некоторой римановой поверхности (см. п. 53.2).
2^ Двумерная мультипликативная задача (задача о факторизации),
аналогичная задаче, рассмотренной в 1° п. 14.3, состоит в представлении функции
G (tu t2)?^ О н удовлетворяющей условию Гёльдера на L в виде произведения
четырех функций 0^=*=(/i, ^г), являющихся предельными значениями функций
Ф±±B1,22), аналитических.в /)=*==*=.
Так же, как и одномерная задача, она тесно связана с задачей о скачке
и при Xi(G) = K2(G) =0 и дополнительных условиях вида A4.35) имеет
единственное решение. При |xi| + |>«2|>0 положение дел существенно
усложняется (см. В. А. Какичев 5)).
3^ Так как решение задачи Римана в замкнутой форме неизвестно, то в
изучении ее возрастает роль качественных методов. И. Б. Симоненко 4),
5), используя разработанный им локальный метод исследования линейных
операторов, изложение которого выходит за рамки настоящей книги, указал
необходимые и достаточные условия, выделяющие класс задач Римана с
конечным индексом (см. случай а) в конце п. 14 9). Сформулируем эту важную
теорему И. Б. Симоненко с обобщением ее, полученным В. С. Пилиди 1).

130 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
Теорема. Пусть А, В, С, D и f суммируемы со степенью р >> \ на
остове L, образованном простыми замкнутыми кривыми Ляпунова. Тогда
условия:
а) Л=?^0, ВФО, С ФО, D=?^0 на L;
б) yci (Л) = XI (В), xi (С) = Ki (D),
Х2 (Л) = Х2 (С ), К2 (В) = >С2 (D)
необходимы и достаточны для того, чтобы задача A4.36) — A4.37) имела
конечный индекс.
4°. Задача Римана для биполуплоскостей заключается в нахождении
четырех функций Ф±^(г1, гг), аналитических соответственно в биполуплоскостях
Imzi^O и 1тг2^0, по условиям A4.36) —A4.37), в которых теперь L
является плоскостью: Im Zi = О, Im гг = 0. Эта задача изучалась в работах
И. Б. Симоненко 3) и В. С. Рабиновича 1) в предположении, что
функции А, В, С, D и f непрерывны на множестве Й^, полученном
замыканием плоскости L одной бесконечно удаленной точкой. В этом случае вдоль
любой замкнутой кривой Г d R^ индекс функции, непрерывной на R^y всегда
равен нулю.
Поэтому при выполнении только одного условия а) из теоремы в п. 3°
индекс задачи Римана для биполуплоскостей оказывается равным нулю.
Такая задача при В = С = —D = 1 и когда Ли/ — функции
специального вида, имеет многочисленные приложения: в односкоростной теории
переноса частиц (см., например, А. Leonard 1)), в теории дифракции
электромагнитных волн (Е. А. Kraut, G. W. Lehman 1)) и др.
5°. Задача Римана для гиперконуса \zi\ -f \z2\ < 1 изучалась учениками
А. А. Т е м л я к о в а. Обзор полученных результатов дан в статье Г. Л. Л у-
к а н к и н а 1).
6°. Многомерная задача Римана для радиальных трубчатых областей
поставлена и изучена в статье В. С. Владимирова 1), являющейся
исторически первой из работ по этой тематике. Радиальной трубчатой областью
называется множество Г^ точек z==(zu ..., Zn) таких, что Re2==jc =
= (^1, ..., Xn)^R'^y а lmz = y= (уи ..., Уп) принадлежит конусу V±.
Конусы У+ и V~ = —F+ предполагаются выпуклыми, не содержащими
целиком прямой с общей вершиной в начале координат. В задаче Римана надо
определить пару функций Ф^(г), аналитических в Г^, по краевому условию
ф+ (х) = G {х) Ф- (х) + g {х\ X е R"", A4.44)
в котором G(x) и g(x)—известные функции из некоторых классов, а Ф^'^ (л:) —
предельные значения функций O'^(z) при у-^0 и г/ е У=^.
Задача A4 44) исследована В. С. Владимировым 1), когда
предельные значения Ф-{х) являются а) непрерывными функциями, представимыми
интегралами Фурье, б) обобщенными функциями медленного роста.
Задача A4.44) является, в известном смысле, обобщением знаменитой
теоремы об «острие клина» Н. Н. Боголюбова, которая возникла в теории
дисперсионных соотношений квантовой механики (см. В. С.
Владимиров 2)).
§ 15. Исключительные случаи задачи Римана
В постановке краевой задачи Римана (п. 14.1) требовалось,
чтобы коэффициент G{t) удовлетворял условию Гёльдера, что
исключало возможность обращения его в бесконечность, и
нигде не обращался в нуль. Ограничения эти, как было видно из

§ 151 ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ ЗАДАЧИ РИМАНА 131
хода решения (использование \nG(t)), существенны. Здесь мы
проведем исследование задачи, отказавшись от этих
ограничений, т. е. допуская, что функция G(t) в отдельных точках
контура обращается в нуль или бесконечность целых порядков.
Для простоты будем предполагать, что контур L состоит из
одной замкнутой кривой.
15.1. Однородная задача. Запишем краевое условие
однородной задачи Римана в виде
П ('-«.г*
Ф+Ц) = ^ С,(Оф-(/). A5.1)
Здесь ан (й = 1,2,... ,fx), Pj (/= 1,2,..., v) — некоторые точки
контура; т^, pj — целые положительные числа;
Gi(/)—функция, удовлетворяющая условию Гёльдера и не обращающаяся
в нуль. Точки ak будут нулями функции G{t). Точки Pj будем
называть ее полюсами*). Обозначим
Решение будем искать в классе функций, ограниченных на
контуре**).
Пусть Х(г) есть каноническая функция задачи Римана с ко-
Х+ и)
эффициентом G\{t). Подставим в A5.1) Gi (/) = _ и запи-
X (/)
шем краевое условие в виде
Ф+ (t) Ф- (/)
/г-1 / = 1
A5.2)
Применим к последнему равенству теорему об
аналитическом продолжении и обобщенную теорему Лиувилля (ср. п. 14.4,
случай х>0). Точки а^, Pj не могут быть особыми точками
единой аналитической функции, так как это противоречило бы
*) Так как функция G(t) неаналитическая, то применение термина
«полюс» не вполне законно. Мы будем употреблять этот термин для краткости,
понимая под этим точку, где функция (неаналитическая) обращается в
бесконечность целого порядка.
**) Легко установить, что существенным является лишь требование
интегрируемости, т. е. ограничение, что допустимо обращение в бесконечность
лишь порядка ниже первого. Отсюда уже вытекает и ограниченность (см.
задачу 12 в конце главы).

132 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
предположению об ограниченности Ф+@ или Ф"@-
Следовательно, единственной возможной особенностью является
бесконечно удаленная точка. Порядок на бесконечности X-{z) есть
V
X, а порядок 11(г —Ру)''/ равен —р. Отсюда порядок на
бесконечности функции :^-^ есть —к + р. При х—р^О
Х--(г)П(^~Р/)'/
/-1
согласно обобщенной теореме Лиувилля
Х+(г)П(г-аХ* Х" (г) П (г - р//
ft-i /-1
откуда
Ф+ (г) = Х+ B) й B - а^Г" Р^-р B),
ф- {Z) = х- B) П {Z - Р;)''/ Р^^, {Z).
A5.3)
Если X —р<0, то нужно положить Py^^p{z)^0 и,
следовательно, задача не имеет решений.
Назовем краевую задачу с коэффициентами Gi@
приведенной задачей. Индекс приведенной задачи х назовем вместе с тем
и индексом данной задачи. Формулы A5.3) показывают, что
степень многочлена ^(-г) на р единиц меньше индекса задачи х.
Отсюда следует, что число решений задачи A5.1) в классе
функций, ограниченных на контуре, не изменяется от наличия
нулей у коэффициента задачи и уменьшается на суммарный
порядок всех полюсов. В частности, если индекс оказывается
меньше суммарного порядка полюсов, то задача неразрешима.
Если задача разрешима, то ее решение дается формулами
A5.3), в которых каноническая функция приведенной задачи
X{z) находится по формулам A4.9), A4.10), причем в них
G{t) нужно заменить на G\(t). Если наложено дополнительное
условие ф-(оо) = 0, то число решений уменьшается на единицу
и многочлен P{z) нужно взять степени х — р— 1.
Расширим теперь класс решений, допуская, что одна из
искомых функций (Ф+(г) или Q>-{z)) может обращаться на
контуре в некоторых точках в бесконечность целого порядка, в то
время как другая в этих точках остается ограниченной. Легко
усмотреть, что такое допущение не повлечет никаких изменений
в неисключительных точках. Здесь ограниченность одной из
функций автоматически влечет за собой ограниченность другой.

§ 18J ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ ЗАДАЧИ РИМАНА 133
Иначе обстоит дело в исключительных точках. Запишем
краевое условие A5.1) в виде
Рассуждая аналогично предыдущему и учитывая, что правая
часть имеет на бесконечности полюс порядка х + т, получим
общее решение в виде
Ф+ B) = Х+ B) П (Z - а*)-"* Р^+ш (г),
Ф- (г) = Х- (г) П B - Р/)-"/ Ях+т (.г).
/-1
A5.30
Последнее показывает, что в классе решений с допустимой
полярной особенностью у одной из функций число решений по
сравнению с классом ограниченных на контуре функций
увеличивается (при X > 0) на суммарный порядок всех нулей и
полюсов коэффициента.
15.2. Неоднородная задача. Запишем краевое условие в
форме
Ф^ (О = '-Т Gi (О Ф"" (О + g @. A5.4)
/-1
Легко видеть, что краевое условие не может быть
удовлетворено конечными Ф+(/), O~@i если допустить, что g{t) имеет
полюсы в точках, отличных от pj, или если в последних точках
порядки полюсов g{t) превышают pj. Исходя из этого, примем
как условие, что g{t) может иметь полюсы только в точках Pj
и порядки их не превышают pj.
Для применимости дальнейшей теории нужно потребовать,
V
чтобы функции G\{t) и П (^ — Р/)^^ й^ (О в исключительных точ-
/-1
ках были дифференцируемы достаточное число раз. Порядок
требуемой высшей производной определяется в дальнейшем.
Заменим, как и в однородной задаче, Gi{t) отношением
канонических функций jfz-У- и запишем краевое условие A5.4)

134 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. V
В виде*)
П» - р/' 1^=П <' -«.)"' 1^+Пс - W' Mi ¦
A5.4')
V
функция Д (^ —• Р/)^^ x+it) ^У^^'^ интегрируемой. Заменив ее
разностью краевых значений аналитических функций
где
приведем краевое условие к виду
П (^ - р/' 1^ - ^^^)=П (^ - «*)'"* 1^ - ^" @.
*) Нельзя преобразовывать краевое условие, как это делалось при реше-
V
НИИ однородной задачи (формула A5.2)), оставляя на месте П(^ —Ру) ^ и
/-1
деля на JJ (t — а^) ^ , так как свободный член стал бы неинтегрируемым.
Наоборот, переписывая условие A5.2) в виде A5.4'), мы получили бы
решение
Ф"" (г) = П (^ - Р/)"""^ ^^ (^) ^н+т (г),
ф" W = П (^ - «^)"'"^ ^" (^) ^><+т (^)-
Условие конечности Ф (/), Ф~ (i) заставило бы нас взять многочлен в виде
P.+ n^ (^) = П (^ - %f' П (^ - Р/)"' Р^-р (^).
что привело бы к полученному ранее решению A5.3),

§ 1Й ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ ЗАДАЧИ РИМАНА 135
Применяя, как обычно (п. 14.4), теорему об аналитическом
продолжении и обобщенную теорему Лиувилля, получим
ф+ B) = ^^^^'^ [4^+ (г) + Р,^^ (г)],
ф- B) = ^ ^ <"> [W- B) + Р,+„ B)].
Последние формулы дадут решения, которые, вообще говоря,
будут обращаться в бесконечность в точках а^, Pj. Для того,
чтобы решение было ограниченным, необходимо, чтобы функция
4^-^{z)-\-Py^+m{z) имела нули порядков pj в точках Pj, а
функция 4f^{zL' Pyi+m{z) — нули порядков ш^ В точках ak. Эти
требования наложат т-\-р условий на коэффициенты многочлена
Py^\-m{z). Если коэффициенты многочлена Р^+т(-г) подберем
согласно наложенным условиям, то формулы A5.6) дадут
решение неоднородной задачи A5.4) в классе ограниченных функций.
Указанный способ решения представляет неудобства как
в практическом отношении (трудности решения системы
уравнений), так и в теоретическом: необходимость доказательства
совместности и независимости уравнений, вытекающих из
условия конечности решения в точках а^, Pj, к которым могут
добавиться еще условия конечности решения в бесконечно
удаленной точке.
Чтобы избежать этих затруднений, Л. А. Чикин 1)
предложил строить специальное частное решение, названное им
канонической функцией неоднородной задачи.
Определение. Канонической функцией Y{z)
неоднородной задачи A5.4) называется кусочно аналитическая функция,
удовлетворяющая краевому условию A5.4), имеющая всюду
в конечной части плоскости (включая и точки a/i, Pj) нулевой
порядок и обладающая на бесконечности наивысшим
возможным порядком.
При построении канонической функции будем исходить из
решения, даваемого формулами A5.6). Построим многочлен
Q{z) так, чтобы он удовлетворял следующим условиям:
Q<"(P/) = 4'+<"(P/) (/ = 0, 1, .... р,-\; i=\, 2, ..., V),
Q"'(aft) = ?-<"(aft) (/ = 0, 1, ..., m,-l; k=\, 2, ..., ц),
где 4'+<'')(Pj), Ч'"-<')(ал)—значения производных 1-го и /-го

136 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
порядков В соответствующих точках*). Таким образом, Q{z)
есть интерполяционный многочлен Эрмита для функции
, - (г) в точках 6,,
{z) в точках ak
с узлами интерполяции Pj, а^ кратностей соответственно Pj, тд.
Известно**), что такой многочлен определяется
единственным образом и его степень р равна
Р == /7Z + р — 1.
Каноническая функция неоднородной задачи выражается через
интерполяционный многочлен следующим образом:
y^(.) = X-W^:'"-"'"', Г(.)-Х-(.)П<2Ь5»<51.„5.7)
Пр-р/' П(»-».Г*
Для построения общего решения неоднородной задачи
A5.4) воспользуемся тем, что это общее решение складывается
из некоторого частного решения неоднородной задачи и общего
решения однородной. Используя формулы A5.3) и A5.7),
получим
ф+ (г) = ?"¦ {Z) + Х^ {Z) П B - a,f' Р^^, {z\
A5.8)
Ф- {Z) = у- {Z) + Х- {Z) П (^ - Р/)'^ Р^-р {г).
В случае, если х — р < О, нужно положить P^^p{z)^0.
Пользуясь формулой A5.7), нетрудно подсчитать, что порядок
у-(г) на бесконечности равен к — р+1. Если х<р—I, то
Y-{z) имеет в бесконечно удаленной точке полюс и
каноническая функция перестает быть решением неоднородной задачи.
Однако, подчиняя свободный член g{t) р — х—1 условиям,
можно добиться повышения порядка на бесконечности функции
Y{z) на р — X—1 единиц и тем самым вновь сделать
каноническую функцию Y{z) решением неоднородной задачи. Для
*) Существование этих производных будет обеспечено, если на функции
V
IX (^"~ Р/) ^ ^ W» ^1 (^) наложить условие, чтобы в точках ал, Pj они имели
/-1
производные порядков тл, pj, удовлетворяющие условию Гёльдера.
**) См., например, Гончаров В. Л., Теория интерполирования и
приближения функций, Гостехиздат, 1954, § 14.

§ lai ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ ЗАДАЧИ РИМАНА 137
этого, очевидно, необходимо и достаточно, чтобы в разложении
функции 4^B)—Ор(г) в окрестности бесконечно удаленной
точки первые р — х—1 коэффициентов обращались в нуль. Это
и даст р — X—1 условий разрешимости задачи в этом случае.
Выясним характер этих условий. Разложение Ч^(г)—Qp{z)
можно представить в виде
Ч^{z) - Qp (г) = - c,z^ - Cp-ieP-J - ...
... — Co+^-i2-' + C-22:-^+ ... +С-;^2:-^+ ...,
где Со, С\, ..., Ср — коэффициенты многочлена Qp{z), а c^k —
коэффициенты разложения функции Ч^(г), вычисляемые, как
легко показать, по формуле
^"¦* 2ш J Х+(т) ^^•
L
Вышеуказанные условия разрешимости будут иметь вид
^p^^p-i^' •••
=^р-р+н+2довели на решение наложено дополнительное условие
ф-(оо)=0, то при X — р>0 в формулах A5.8) нужно взять
многочлен Pj^_p_i(z), а при х — р < О понадобится
удовлетворить /7 — X условиям.
Замечание. Метод построения канонической функции
неоднородной задачи может быть применен и в других случаях,
когда требуется построить решение, удовлетворяющее
некоторым заданным условиям (см. задачу 13 в конце главы).
Легко усмотреть, как изменятся рассуждения и результаты,
если искать решения в указанном в п. 15.1 классе функций с
полярной особенностью на контуре у одной из них. Формулы
A5.6) как раз представляют собой решения в этом классе, для
которого, следовательно, отпада^от все последующие
рассуждения о нулях функций Ч^±(г) + Р^+тB:). Таким образом,
допущение в исключительных точках у одной функции решения
полярной особенности уменьшает число условий разрешимости.
Предположение о том, что нули и полюсы — целого порядка,
несущественно. Метод применим и в более общих случаях.
Исследование, в предположении любого степенного порядка нулей
и полюсов, дано в [6]. Еще более общий случай, когда
G{t)^'\l{t-cj4n'Ht^Ck)Q,{t\
исследован в [30].

138 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
15.3. О корректности постановки краевой задачи Римана. Под корректной
постановкой краевой задачи обычно понимается такая ее постановка, когда
задача безусловно и однозначно разрешима и ее решение устойчиво по
отношению к малым изменениям коэффициентов или контура.
Устойчивость по отношению к изменению коэффициентов краевого
условия непосредственно вытекает из того, что: 1) решение задачи дается в явном
виде через интегралы типа Коши, 2) интеграл типа Коши есть оператор
ограниченный и, следовательно, при малых изменениях плотности (в
рассматриваемом классе Я) получает малые приращения. Более сложный вопрос об
устойчивости по отношению к изменению контура исследовал Л. А. Ч и к и н
2), 3). Он доказал, что для G и g, удовлетворяющих условию Гёльдера,
необходимым и достаточным условием для устойчивости является 0(()Ф 0.
Таким образом, в неисключительных случаях краевая задача Римана устойчива.
Но первое условие корректности, вообще говоря, не выполняется. В
зависимости от величины индекса может нарушаться или однозначность, или
разрешимость задачи. Рассмотрим, как следует изменить постановку задачи,
чтобы она стала корректной. Для достижения большей симметрии в
результатах условимся искать решение в классе функций, исчезающих на
бесконечности ф-(оо) = 0.
1°. Ind (?(/)= X > 0. В этом случае решение краевой задачи содержит
произвольные постоянные, поэтому для достижения однозначности на
решение придется наложить дополнительные условия.
Пусть cci, ..., am; Рь ... ,Рп — произвольно выбранные точки, лежащие
соответственно в областях D+, D- Потребуем, чтобы решения неоднородной
краевой задачи Римана A4.2) удо.. 1Створяли следующим х условиям:
Ф'^^^^(а.) = а[ (/=1,2,..., т; / = 0,1, ..., р,. - 1), A5.9')
Ф"^'^(М = ^1 (А: = 1,2, ..., п; / = 0,1,...,^^-!), A5.9'')
где а[, Ь^^ — произвольные числа, /, / •— порядки производных,
т п
llPi+Z4=-''^ A5.10)
f-i fe-i
и пусть P{z)—многочлен Эрмита с узлами интерполяции A5.9'), а — QB:) —
такой же многочлен по степеням — с узлами A5.9''). Будем искать решение
краевой задачи A4,2) в виде
тп
Ф+ (Z) = Р (г) + П (г - a^f^ Ф+ Bг),
/=-1
п A5.11)
Ф- B) = -1 Q (г) + Д A - ^У ФГ (г) (ФГ (со) = о).
Легко видеть, что так определенные функции автоматически
удовлетворяют условиям A5.9). Вставляя их выражения в краевое условие A4.2),
получим для Ф^ (z) новую краевую задачу
Ot{t) = G,{tH^{t) + g^{t). A5.12^
Для (?1, ^1 легко получить явное выражение и показать, что в силу
A5.10) Ind (?i(/)= 0. Следовательно, задача A8.12) разрешима безусловно

§ 161 ЗАДАЧА РИМАНА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ J39
И однозначно. Отсюда получаем, что исходная краевая задача Римана с
дополнительными условиями A5.9'), A5.9'') поставлена корректно
2°. X < 0. Здесь задача Римана разрешима лишь при выполнении
дополнительных условий. Чтобы получить задачу безусловно разрешимую,
возможны два пути: 1) ввести в свободный член краевого условия некоторые
произвольные элементы, 2) расширить класс решений, считая допустимыми в
некотором числе точек полярные особенности. Начнем изложение с первого
способа.
—7- — много-
член по степеням -—, коэффициенты которого совпадают с начальными
членами разложения 4^B) по степеням—. Тогда, если в краевом условии A4.2)
свободный член взять в виде суммы g (t) + Х+ (О Q ( -г ) > то для
единственного решения задачи условия разрешимости будут выполняться
автоматически.
Следовательно, если в краевом условии A4 2) к свободному члену
добавить слагаемое вида Х+ (t) Qy-r)* то задача Римана будет поставлена
корректно.
Укажем еще второй способ корректной постановки при х < 0.
Предположим, что у искомого решения допускаются в Z)+ полюсы порядков г,- в
некоторых точках у и а в Z)- полюсы порядков Sj в некоторых точках 6j
(/= 1, ..., m; /= 1 п)\
т п
Е^+Е^/"!"!- A5.13)
Отыскивая решение в виде
+ Фо" (Z) Фо~ (г)
Ф*^=^;Г-^ . ^-(')= п / , S,' A5-14)
придем к краевой задаче
Ф+ (/) = G2 (/) Ф2" (О + ^2 @. A5.15)
Индекс нового коэффициента есть нуль, и поэтому задача A5.15)
безусловно и однозначно разрешима. Следовательно, задача Римана с индексом
к < О в классе функций с допустимыми в некотором конечном числе точек
полюсами будет поставлена корректно, если суммарный порядок полюсов
равен \п\,
§ 16. Задача Римана для многосвязной области.
Некоторые новые результаты
16.1. Постановка задачи. Пусть L = Lo + Li + ... -\-Lm —
совокупность т -f 1 непересекающихся контуров, причем контур
Z-c содержит внутри себя все остальные (рис. 13). D+ назовем

140
КРАЕВАЯ ЗАДАЧА РИМАНА
[ГЛ. И
(т + 1)-связную область, лежащую внутри контура Lo и вне
контуров Li, ..., Lm. Обозначим D- дополнение D+ + L до
полной плоскости. Для определенности будем считать начало
координат расположенным в области D+. Положительным
обходом контура L считается тот, который
оставляет область D+ слева, т. е. кон*
тур Lo нужно обходить против
часовой стрелки, а контуры L\, ..., Lm — по
часовой.
Прежде всего укажем, что задача
о скачке
Ф+(/)-ф-@ = ёг(/)
решается той же формулой
L
ЧТО и В случае односвязной области.
Это вытекает из формул Сохоцкого,
которые, как показано в п. 8.7, имеют для
многосвязной области тот же вид, что
и для односвязной.
Задача Римана (однородная и
неоднородная) формулируется совершен-
Рис. 13. но так же, как это делалось в п. 14.1
для односвязной области.
Обозначим >Ck= 2^ [arg G{t)]^ (все контуры обходятся в
только что установленном положительном направлении).
Индексом задачи назовем величину
m
« = Z «ft-
ft-O
A6.1)
Если Tik (/г = 1,2,...,m) для внутренних контуров равны
нулю, то решение задачи, как легко видеть, имеет совершенно
тот же вид, что и для односвязной области.
Для приведения общего случая к простейшему вводим
функцию
т
где Zk — некоторые точки, лежащие внутри контуров L^
(ft=l,2, ..., m).

16] ЗАДАЧА РИМАНА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 141
Учитывая, что [arg {t — Zk)]Lf = О, если кф],и [arg (/ — Zj)]ij =
= —2л;, легко получим
(/=1, 2, ..., m).
Отсюда
{arg[G@n«-2,r*]J^ =.0 (/=1. 2 m).
m
Вычислим изменение аргумента функции G{t)Yl{t —ZkT^
ft-i
no контуру Lq:
= 4r t^^S^ ^ (^^1^0 + i" Z t^^ ^^2 ^^ ~" ^^)l/:o = XO + 2 >«Л = X.
Так как начало координат лежит в области /)**", то
[arg t]^^ = 0 (Л = 1, 2, ..., m), [arg t]^^ = 2я.
Поэтому
{ arg [/-^ ft (^ - z,r^ a (/)] j^ = 0. A6.2)
16.2. Решение задачи.
P. Однородная задача. Запишем краевое условие
ф+(/) = 0(^)ф-(/) A4.1)
в виде
^' (^)=^й-^fГ" П (^ - ^*)''* G w] ф" (О- ^^'-'^
m
Функцию f^Jlit — Zk)^^ о {t), как имеющую на каждом из
контуров Lft (^ = О, 1, ...» fn) индекс нуль, можно представить

142 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
В виде отношения
^ Г+ (i)
г" П(^'- ^кГ''ОЦ)=^^—, A6.4)
где
г(-) = W J П-г ^-- A6.5)
Каноническая функция (п. 14.3) задачи будет даваться
формулами
т
Х+ {z) = ll{z-Zkr''^e^^^'\ Х-(г) = 2->^еГ-(^). A6.6)
k -1
Теперь краевому условию A6.3) придадим вид
Ф"^ (t) _ Ф- (О
Х+ (О Х- (О •
Применяя, как обычно, теорему об аналитическом
продолжении и обобщенную теорему Лиувилля, получим
т
Ф"" B) = П B - 2,)-"* ег+ (-)Р^ B),
ft-1 A6.7)
ф-(г) = г-«/-<^'Р,(г).
Решение, как видим, отличается от полученного ранее
решения задачи для односвязнои области лишь наличием у функции
m
Ф+B) множителя Yli^ — ^k)~^^'
При дополнительном условии ф-(оо) = 0 в формулах A6.7)
нужно брать многочлен Py-i{z),
В дальнейшем (п. 21.2) нам понадобятся формулы для
предельных значений на контуре канонической функции ХB).
Беря в формуле A6.5) предельные значения, по формулам Со-
хоцкого будем иметь
Г^ (О = + у 1п [Г'^П (О G (/)] + Г (О,
где Г@ есть главное значение интеграла A6.5) и
т
п@ = П{^-2*)'**.
/г«1

§ 16] ЗАДАЧА РИМАНА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 143
Переходя теперь в формулах A6.6) к пределу при z-^t,
получим
Х^@=д/-^^^в^^^ Х"@= > ^ е^^'\ A6.8)
V /""П (t) V^ П {t) G (t)
Знак корня определяется выбором ветви функции 1п[/-'^П(/)С(/)],
которая может быть взята произвольно (см. п. 14.3).
2°. Неоднородная задача. Рассуждая совершенно
аналогично тому, как это делалось в п. 14.5, представим
краевое условие
Ф+@ = С(/)ф-@ + ^@ A4.2)
в виде
х+(/) ^ ^^^ Х-(О ^ ^^^'
гдеЧ^(<г) определяется формулой A4.14).
Отсюда получаем общее решение
Ф{г) = Х{г)[Ц^{г) + Р^г)] A6.9)
или
0{z) = X{z)[W{z) + P,-,{z)l A6.10)
если на решение наложено условие ф-(оо) = 0.
При X < О неоднородная задача разрешима тогда и только
тогда, когда выполнены условия
f ^(^^ tk-idt = 0^ A6.11)
J Х+ (t)
где k принимает значения от 1 до —х—1, если ищутся
решения, ограниченные на бесконечности, и от 1 до —х, если
считать, что ф-(оо) = 0.
При выполнении условий A6.11) решение можно получить
из формул A6.9) или A6.10), полагая в них Р^(г)^0.
Покажем, как следует видоизменить решение задачи, если
отсутствует внешний контур Lq и область D+ представляет
собой плоскость с дырами. Заметим, что теперь бесконечно
удаленная точка содержится в D+, а не в Z)-, как ранее. Поэтому
нужно учитывать поведение на бесконечности уже функции
Ф+(г), а не O'iz).
Главное отличие от предыдущего случая состоит в том, что
теперь нулевой индекс относительно всех контуров L/j (k=l,
т
2, ...,m) имеет функция П (/—г/^)'^^ G (/), в которую не входит

144 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
множитель ^-^ Поэтому для получения решения задачи
достаточно повторить все прежние рассуждения, опустив этот
множитель.
16.3 Некоторые другие результаты. Более поздние работы по краевой
задаче Римана направлены главным образом на расширение класса заданных
и искомых функций. Здесь мы изложим основные из полученных в этом
направлении результатов.
1**. Б. В. Хведелидзе во многих работах, сводное изложение
которых дано в статье [30], исследовал задачу Римана в предположении, что
G{i), как обычно, удовлетворяет условию Гёльдера*), а g(t)^Lp
(интегрируема в степени р по Лебегу). На основе теории интеграла типа Коши в
соответствующем классе (см. п. 5.3) получено полное решение краевой
задачи. Полученные результаты (и в качественном отношении — подсчет числа
решений и условий разрешимости в зависимости от индекса, — и
алгоритмически — вид формул, дающих решение в замкнутой форме) — такие же, как
и в случае g(t), удовлетворяющего условию Гёльдера. Различие лишь в том,
что здесь, как и всюду, где приходится иметь дело с интегрированием по
Лебегу, соответствующие предельные значения на контуре существуют лишь
почти везде (за исключением множества меры нуль) и лишь по путям,
некасательным к контуру.
2^ Освободиться от ограничения, что коэффициент удовлетворяет условию
Гёльдера, сохраняя лишь естественное условие непрерывности, удалось
недавно. Вопрос этот настолько назрел, что его решение было дано
одновременно и независимо несколькими авторами. Вначале мы приведем решение
И. Б. Симоненко 1).
В основе лежит следующая простая идея. В случае G{t) ^ 1 имеем
задачу о скачке, которая безусловно и однозначно разрешима в классе Lp.
Оказывается, что малые отклонения коэффициента не меняют характера
решения. Переход к общему случаю производится путем приближения
непрерывной функции функциями, удовлетворяющими условию Гёльдера.
Пусть в краевом условии задачи Римана
Ф^(t)^G(t)Ф'{t) + git)
G{t) есть непрерывная функция, а g{t)^Lp, Решение схематически можно
разбить на четыре этапа.
1. На основе результатов Б. В. Хведелидзе для интеграла типа Коши
в классе Lp (см. п. 5.3) выводится оценка
||Ф*(/)|| = ||±-2-ф+2-5ф||< ^11ф||.
где Мр — норма оператора S j 5ф = — \ ^_\ di j.
2. Опираясь на принцип сжатых отображений (метод последовательных
приближений), автор доказывает, что задача Римана, коэффициент которой
есть измеримая функция, удовлетворяющая условию
|О@-11<
имеет единственное решение.
*) О возможности разрывов в отдельных точках см. п, 41.6.

S 16] ЗАДАЧА РИМАНА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 145
3. В случае нулевого индекса доказывается однозначная разрешимость
задачи следующим образом. Берется функция Gi{t), удовлетворяющая
условию Гёльдера, не обращающаяся нигде в нуль и достаточно близкая к G{t):
\G(t)GTHt)-l\<-^
для нее осуществляется каноническое представление
о,=хМхг)"
и вводятся новые неизвестные функции Ф^ = Ф^ (Xf) •
Задача A4.2) при переходе к этим неизвестным преобразуется в задачу
с коэффициентом GG^K
4. Случай любого индекса исследуется сведением его к нулевому.
Применяемый для этого способ мало отличается от изложенного здесь (пп. lo.l,
16.2).
Полученные результаты совершенно те же, что и у Б. В. Хведелидзе
для G, удовлетворяющего условию Гёльдера. Таким образом, показано, что
расширение класса коэффициента G до функций просто непрерывных не
приводит к сужению класса решений, он по-прежнему совпадает с классом Lp
свободного члена.
3^ Решение той же задачи, данное В. В. Ивановым 3) и Б. В.
Хведелидзе 2), основывается на теореме В. И. Смирнова, дающей оценку
порядка роста особого интеграла типа Коши с непрерывной плотностью. Этот
интеграл, вообще говоря, не будет ограниченным, но если он бесконечно
растет, то лишь очень медленно, так что не только сам 5ф, но и е^^^ е L^
при любом г > О *).
Пусть x = IndG@=0, g{t)^Lp. На основании сказанного канониче-
illnG+isinC
екая функция задачи Римана X* (/) = е ^ е L^. Приводим,
как обычно, краевое условие к виду задачи о скачке:
Ф+ (i) __ Ф- (О g(t)
х+ (О х- (/) '^ х+ (О •
На основании так называемого неравенства Гёльдера**) правая часть будет
принадлежать классу Lp-g, где е — любое сколь угодно малое положительное
число. Решение задачи, краевые значения которого определяются формулой
принадлежит тому же классу Lp-e- Последний результат менее точен, чем
полученный выше по методу И. Б. Симоненко; там установлено, что можно
положить 8 = 0.
Изложенное показывает, что хотя при переходе от коэффициента гёль-
дерова класса к классу непрерывных функций качественные результаты
*) Согласно результатам п. 8.2 в случае разрыва первого рода 5ф имеет
логарифмическую особенность, следовательно, е^^ имеет степенную
особенность; можно подобрать величину скачка так, чтобы порядок роста был
сколь угодно высоким.
**) См., например. Хард и, Литтльвуд и Полна, Неравенства,
ИЛ, М., 1948, стр. 169.

146 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. П
(число линейно независимых решений или условий разрешимости) остаются
неизменными, но существенно меняется характер решения: из непрерывного
оно может стать всюду разрывным. Простая по своей постановке проблема:
в каком максимально широком классе можно взять коэффициент G, чтобы
решение краевой задачи Римана осталось непрерывным, до сих пор остается
нерешенной.
4°. Ю. И. Черский 1) рассмотрел краевую задачу Римана в
абстрактном пространстве, считая, что в краевом условии
А есть линейный оператор, а Ф+, ф-, g — элементы пространства Банаха.
Аксиоматически определяется сингулярный оператор 5. Основным
определяющим свойством является S^ = I [I — единичный оператор] при условии
5 =5^ dz/ (см. п. 7.3). Элементы ф=ь образуются из произвольного элемента ф
по формулам Ф^ =-о-(± Ф + 5ф). Индекс определяется через некоторый
оператор. Дано полное решение задачи в такой постановке.
Основной особенностью этой работы является единство исследования
вопросов существования решения и построения алгоритма для его фактического
получения. Это единство проистекает из того, что абстрактная теория
построена на основе изложенного выше (§§ 14—17) эффективного решения
задачи Римана путем замены в нем конкретных операторов и функций
абстрактными операторами и элементами абстрактного пространства. Краевая
задача рассматривается в связи с решением особых интегральных уравнений
(см. п. 21.1).
б*'. В качестве одной из реализаций абстрактной теории Ю. И. Ч е р-
с к и й 2) дал решение задачи Римана в обобщенных функциях
(функционалах над некоторым пространством основных функций).
В дальнейшем эту проблему с разных точек зрения изучал В. С.
Рогожин. Из большого числа опубликованных им по этому вопросу работ
укажем на три главные: 6), 7), 8).
6°. Вопросы приближенного решения краевой задачи Римана
рассматривались в работе А. В. Б а ты рев а 1). Им указаны два способа. Оба они
основаны на приближении коэффициента краевого условия рациональной
функцией. В первом способе коэффициент G(t) приближается функцией
п
г (t) = ^ uf^t^. Однородная задача с коэффициентом Гп (t) решается по
fe=» —/г
способу п. 14.6. Во втором способе логарифмированием однородная задача
сводится к задаче о скачке, а затем той же функцией rn(t) приближается
\nG(t). Приведена оценка погрешности.
Другие работы, посвященные этому вопросу, связаны с рассмотрением
особого интегрального уравнения. Они будут изложены в п. 21.11.
§ 17. Краевая задача Римана со сдвигом
17.1. Постановка задачи и общие замечания. Дан простой
замкнутый контур L, делящий плоскость на внутреннюю область
/)+ и внешнюю D-. На нем заданы функции G(t), g{t),
удовлетворяющие условию Гёльдера, и функция а@» отображающая
контур L взаимно однозначно на себя с сохранением
направления и имеющая производную a^{t), удовлетворяющую условию
Гёльдера и не обращающуюся в нуль; а(/) будем называть
функцией сдвига,

§ 17] КРАЕВАЯ ЗАДАЧА РИМАНА СО СДВИГОМ 147
Требуется определить функцию Ф"^(г), аналитическую в
области D+, и функцию Ф~(г), аналитическую в области D-,
предельные значения которых на контуре непрерывны и
удовлетворяют линейному соотношению
ф+[а(/)] = а(/)Ф~@ (однородная задача) A7.1)
или
Ф"^ [а (/)] = G (/) Ф" (t) + g (t) (неоднородная задача). A7.2)
Сформулированная задача представляет собой обобщение
краевой задачи Римана. В частном случае, когда a{t) есть
краевое значение аналитической в области D+ функции, задача
может быть сведена к задаче Римана. Для этого достаточно
ввести новую искомую кусочно аналитическую функцию
Oi (г) = Ф^ [а {Z)], ФГ {Z) = Ф- B).
Задача со сдвигом в обидем случае также может быть сведена
к обыкновенной краевой задаче Римана. Однако
предварительно нужно дать решение задачи о скачке:
ф+[а@]~ф-(/) = я@. A7.3)
Последнее основывается на исследовании простейшей
задачи о нулевом скачке:
Ф+[а@]~-Ф"@ = 0. A7.30
В основе решения обыкновенной задачи Римана лежит
подобная же задача
Ф+@-Ф"'(/) = 0,
но последняя решается непосредственно на основании теоремы
об аналитическом продолжении и теоремы Лиувилля. В отличие
от этого, задача A7.30 решается не элементарно, и
рассмотрение ее требует привлечения теории интегральных уравнений
Фредгольма.
17.2. Задача с нулевым скачком. Требуется определить
кусочно аналитическую функцию Ф(г), удовлетворяющую на
контуре краевому условию
Ф+[а@]-Ф""(/) = 0 A7.4)
и дополнительному условию ф-(оо)= 0.
Составим интегральное уравнение задачи, использовав
условия D.11), D.12) того, что Ф-(/) являются краевыми
значениями аналитических в соответствующих областях функций.
Имея в виду исследование разрешимости получаемого
уравнения, введем две новые аналитические функции, взяв искомые

148 КРАЕВАЯ ЗАДАЧА РИМАНА ТГЛ II
функции за плотности интегралов типа Коши:
V^M-wS^^"'. *"<^) = 1НГ$^Л. A7.5,
L L
На основании формул Сохоцкого и условий D.11), D.12) будем
иметь на контуре:
L
>F-@ = -4o+@+iJ-^^rft = 0. A7.7)
L
Правая часть равенств будет справедлива тогда и только тогда,
когда Ф^(/) будут краевыми значениями аналитических в Z)±
функций.
Составим уравнение относительно Ф'"@> Для чего образуем
выражение
W+ (О ^ W- [а (/)] = 4 {Ф" (О + Ф-*- [а (/)]} +
L L
Исключим теперь из последнего равенства при помощи
краевого условия A7.4) функцию Ф+ Для этого во втором
интеграле сделаем подстановку T = a(Ti), затем переменную ti
снова обозначим т. В результате получим для определения
ф-(/) интегральное уравнение
Чг+(^)_>р-[а@1-^
Покажем, что ядро уравнения
к-а г'\ — "' ('^^ 1
^^^' ^^~а(т)~.а(/) "" Т-/
имеет в точке x = t особенность порядка ниже первого.
Вычитая друг из друга очевидные равенства
t
а (О — а (т) = \ а' {и) du,
X
t
а'(т)(/-т)=5а'(т)^и,

§ 17] КРАЕВАЯ ЗАДАЧА РИМАНА СО СДВИГОМ 149
получим
а (О - а (т) - а' (т) (/ - т) = J [а' (и) - а' (т)] du.
X
Для оценки последнего интеграла обозначим | «-— т | = г
и воспользуемся неравенством D.3) п. 4.1 \du\ = \ds\< mdr.
Учтя условие Гёльдера | а' (и) — а' (т) | < Аг^, будем иметь
|а(/)-а(т)~аЧт)(/~т)|<
о
где р —некоторое достаточно малое число. Отсюда
|iC(/, т)|<Лl|/~т|'-^
где М — некоторая постоянная.
Таким образом, интегральное уравнение A7.9) есть
уравнение Фредгольма *). Легко видеть, что функция Ф''@>
удовлетворяющая краевому условию A7.4) и условию аналитичности
A7.6), удовлетворяет интегральному уравнению A7.9). Это
вытекает из самого способа образования этого уравнения. Вопрос
о том, является ли всякое решение интегрального уравнения
решением краевой задачи, мы оставим пока в стороне.
Установим основной для рассматриваемого вопроса
результат.
Лемма I. Обобщенная задача с нулевым скачком при
дополнительном условии ф-(сх))= О неразрешима**).
Допустим обратное, т. е. что эта задача разрешима. Пусть
кусочно аналитическая функция Ф{г) является ее решением.
Из вида краевого условия A7.4) сразу заключаем, что
решениями задачи являются также и функции
Ф,B) = [ФB)]*
*) Так как от функций Ф='=@ мы не требовали, чтобы они
удовлетворяли условию Гёльдера, то нельзя утверждать, что формулы Сохоцкого для
предельных значений будут справедливы всюду на контуре; они будут
справедливы только почти всюду. Но в уравнении A7.9) и первый член есть
функция непрерывная, и второй член, в силу доказанного свойства ядра,
будет также функцией непрерывной. Если же равенство, в котором все члены
непрерывны, удовлетворяются почти всюду, то оно удовлетворяется везде.
Таким образом, уравнениеA7.9) справедливо для всего контура.
**) Однородную краевую задачу или однородное интегральное уравнение
будем, как и ранее, называть неразрешимыми, если они не имеют другого
решения, кроме тривиального нулевого.

150 КРАЕВАЯ ЗАДАЧА РИМАНА (ГЛ. И
при любом целом положительном k (нетрудно было бы
доказать, что и вообще при любом к). Все эти функции, очевидно,
линейно независимы. Как было указано выше, функции ФГ@
удовлетворяют интегральному уравнению A7.9), которое имеет,
следовательно, бесконечное множество решений. Так как
интегральное уравнение Фредгольма может иметь лишь конечное
число решений, то полученное противоречие и доказывает
лемму.
Из доказанной леммы еще нельзя сделать вывод, что
уравнение A7.9) также неразрешимо, поскольку мы еще не
доказали, что всякое решение этого уравнения является решением
краевой задачи. Займемся этим вопросом.
Лемма П. Однородное интегральное уравнение Фредгольма
A7.9) неразрешимо.
Допустим, что однородное интегральное уравнение
Фредгольма A7.9) имеет отличное от нуля решение Ф~@- По этому
решению построим новую функцию Ф'^(/) = Ф^[Р@]» где р(/)
есть функция, обратная a{t) {^[a{t)]^t). Затем построим по
формулам A7.5) две аналитические функции Ч^+(г), Ч^~(г).
Из интегрального уравнения A7.9) следует
гр+@ = ?~[а@]
или
4^+[p(/)] = >F-(^) A7.10)
при дополнительном условии Ч^-(с5о) = 0.
Функция р(/), так же как и а(/), отображает контур на
себя. Поэтому задача A7.10) того же типа, что и задача A7.4),
и, следовательно, в силу леммы I Ч^+(г) = ^-(z) ^ 0.
На основании формул A7.6), A7.7) из последнего следует,
что Ф'^@' Ф~@ суть краевые значения функций,
аналитических соответственно в областях D+, D-. Отсюда вытекает, что
функции Ф+(-г), ф-(г) являются решением краевой задачи
A7.4) и опять-таки по лемме I тождественно равны нулю.
Следовательно, ф-(/)^ О, что и требовалось.
17.3. Задача с заданным скачком. Рассмотрим теперь
краевую задачу
Ф+[а(/)]-ф-@ = я(/). A7.3)
Имея в виду дальнейшие приложения, несколько обобщим
постановку задачи, отыскивая ее решение в классе функций,
допускающих на бесконечности полюс заданного порядка /г.

S 17] КРАЕВАЯ ЗАДАЧА РИМАНА СО СДВИГОМ 151
На основании формул D.11) —D.13) условия аналитичности
В этом случае запишутся в виде
-W^'^ + M^o^'O.
L
где Pn{z) = €0 + ciz+ ... + ^п-г^ — многочлен, представляю-
щий собой главную часть функции Ф"(г) на бесконечности.
Вводя подобно предыдущему кусочно аналитическую
функцию
L
запишем условия A7.11) в виде двойных равенств:
^ л + A7.13)
L
Поступая так же, как в п. 17.2, придем к неоднородному
уравнению Фредгольма относительно Ф~(/):
W^@-^F-[a(/)]s
L
L
Соответствующее однородное уравнение совпадает с
уравнением A7.9), которое, согласно лемме II, неразрешимо.
Следовательно, уравнение A7.14) разрешимо при любой правой
части (см. далее, п. 20.2).
Пусть /?(/,т) есть резольвента уравнения A7.14). Тогда,
как известно, его решение может быть представлено в виде
Ф' (О = gi (О + Pn{t)+\R it. т) [g, (т) + Рп (т)] dt, A7.15)
I'

152 КРАЕВАЯ ЗАДАЧА РИМАНА {ТЛ. II
где
8,«)=-^«@ + ^5^Й?^Л. A7.16)
L
Нетрудно доказать, что для g(t), удовлетворяющей условию
Гёльдера, решение уравнения A7.14) также удовлетворяет
этому условию. Действительно, резольвента R{tyX) уравнения,
как известно, может быть представлена в виде суммы
итеративных ядер. Итерация неособых ядер улучшает их свойства,
следовательно, функциональные свойства резольвенты такие же,
как и у ядра. В § 5 было доказано, что особый интеграл
с ядром Коши переводит функции, удовлетворяющие условию
Гёльдера, в себя. Это тем более справедливо для интеграла со
слабой особенностью*).
Рассуждая так же, как при доказательстве леммы II,
получим, что решение уравнения A7.14) является решением
краевой задачи A7.3). Из краевого условия A7.3) определим
краевое значение Ф+@-
Ф-^ (О = Ф" [р @] + г [р it)] (Р [а (t)] ^ t\ A7.17)
после чего по формуле Коши построим функции Ф+B:), Ф"(г).
Таким образом, получена следующая теорема.
Теорема. Задача о скачке A7.3) в классе функций,
имеющих на бесконечности заданную главную часть, разрешима
безусловно и однозначно.
Легко можно было бы доказать, что если считать
коэффициенты многочлена Рп{^) произвольными, то уравнение имело
бы Ai+ I линейно независимых решений **).
17.4. Однородная задача с нулевым индексом. Пусть
Ф^ [а @] = G it) Ф- (О (G (t) Ф 0). A7.1)
Будем искать решение, удовлетворяющее условию ф-(оо)= 1.
Поступая как в п. 14.3, можно показать, что в случае х = О
ненулевое решение Ф=^^(г) нигде не обращается в нуль, так что
функции 1пФ*(г) будут аналитическими и однозначными.
Логарифмируя поэтому соотношение A7.1), получим
In Ф^ [а Щ - In Ф" (О = In G @.
Для кусочно аналитической функции Г(г) = 1пФ(г)
получим краевое условие типа A7.3) с дополнительным условием
Г(оо) = 0.
*) Фактически ядра такого типа улучшают свойства функции.
**) Если решать задачу со сдвигом непосредственно без сведения ее к
задаче Римана, то этот факт кладется в основу подсчета числа линейно
независимых решений задачи.

§ 17J КРАЕВАЯ ЗАДАЧА РИМАНА СО СДВИГОМ 153
Явное выражение функций Г^@ дается формулами A7.15),
A7.17), в которых нужно положить g(t) z=: \п G(t) и Pn{t)^0,
Следовательно, задача имеет единственное решение,
определяемое формулами
Ф(.) = /^^>; r-(e) = iJ-^dT, A7.18)
r^@ = r-[p@] + lnG[p@],
A7.19)
где g\{t) определяется формулой A7.16) при g{t)=lnG{t),
а /?(/, т) — резольвента интегрального уравнения A7.14).
Решим одну частную задачу, которая нам понадобится
далее. Определить кусочно аналитическую функцию y^{z)
(у-"(оо)= 1) по краевому условию
YMa@1=-^Y-@. A7.20)
Докажем, что а'(/) имеет нулевой индекс. Рассмотрим
отношение ^ lZ.t * ^Р^ обходе точкой т контура L числитель
и знаменатель получают одинаковое приращение я.
Приращение аргумента дроби равно нулю при любых
неравных друг другу t и X, Переходя к пределу при т->/, получим
искомое. Кроме того, известно, что а'(/)=7^0. Следовательно,
задача A7.20) безусловно и однозначно разрешима.
17.5. О сведении задачи со сдвигом к обыкновенной задаче
Римана*). Глубокая аналогия между задачей со сдвигом и
обыкновенной краевой задачей Римана наводит на мысль о
наличии между ними прямой связи. Оказывается, что такую связь
действительно можно установить. Для этого достаточно
произвести конформное взаимно однозначное отображение областей
D± на две новые разделенные общим контуром и взаимно
дополняющие друг друга до полной плоскости области Z)f так,
чтобы точки t и a(t) исходного контура L перешли в одну и ту
же точку нового контура Li. После этого можно простой
заменой переменных свести задачу со сдвигом к обыкновенной
задаче Римана. Обоснование этого удается сделать на основе
произведенного выше решения задачи о скачке и однородной
задачи с нулевым индексом.
*) Способ сведения задачи со сдвигом к краевой задаче Римана указан
Г. Ф. Манджавидзе и Б. В. Хведелидзе в кратком замечании к
работе 1). На a(t) накладывалось условие существования второй производной
класса Гёльдера. Обоснование излагаемого здесь способа заимствовано из
работы И. Б. Симоненко 3).

154 Краевая задача римана 1гл. It
Начнем с отыскания упомянутого выше конформного
отображения.
Решим вспомогательную задачу с нулевым скачком
0+[а(/)]-(о-(О = О A7.40
при условии, что (О"" (г) имеет на бесконечности простой полюс:
^-{z) = z+Co + ^+ ... A7.21)
Составим интегральное уравнение задачи. Полагая в A7.14)
g(t) = 0, Pn{t) = t и Ф"(/) = а)~@, получим безусловно и
однозначно разрешимое уравнение
--^'^-ш\[тF^-T^У(-)dr = t A7.22)
L
Определив отсюда со"" (/), а из краевого условия A7.40 ©"^@==
= (о~[р@], по формуле Коши получим искомые функции ©^(г).
Пусть а@-—функция, обратная со* (О (со-[а@]^0- Заменяя
в A7.40 t на а (О, будем иметь тождественно
CD+{а [а (/)]} = /. A7.23)
Введем кусочно аналитическую функцию Ф1 (г) равенствами
ф+ (г) =г ф^ [со-^ {z)l Ф" (z) = ФГ [@^ {z)l A7.24)
В новых функциях краевое условие задачи со сдвигом A7.2)
запишется в виде
Ф!"^ {со^ [а (/)]} = G (t) ФГ [(о~ @] + g (/).
Вставляя здесь ^ = a(/i), будем иметь
фГ {со^ [а (а (^,))]} = G[a {U)] ФГ (/i) + g [а (h)].
Учитывая тождество A7.23) и обозначая Gi = G, gi=g^
получим краевую задачу Римана
Ot{t) = G,{tH;{t) + g^{t), A7.25)
Таким образом, краевая задача со сдвигом сведена к
обыкновенной краевой задаче Римана. Для полного решения
вопроса нужно еще доказать равносильность обеих задач, т. е.
что каждому решению задачи со сдвигом A7.2) соотношения
A7.24) ставят в соответствие определенное решение задачи
Римана A7.25), и наоборот.
Пусть аналитические в области D± функции (o-{z)
отображают их на области Z)f, ограниченные соответственно
контурами Lf. Установим следующее:

§ 17] КРАЕВАЯ ЗАДАЧА РИМАНА СО СДВИГОМ 155
1°. Области Dt не имеют общих внутренних точек и
разделены общей границей Li, дополняя друг друга до полной
плоскости.
2°. Соответствие областей D~, Df взаимно однозначное.
Доказательство. Контуры Lf задаются соответственно
уравнениями
^ = (о+@, ^ = со-@ (t^L),
Но, в силу краевого условия,
o)-(/) = (o+[a(/)] = co+(/i).
Когда / обходит однократно контур L, t\ = a{t) также
обходит его однократно и в том же направлении. Следовательно,
контур Lf совпадает с 1^. Будем обозначать его просто Li.
Для установления взаимно однозначного соответствия
областей достаточно установить, что это свойство справедливо для
контуров; тогда, в силу общих свойств конформного
отображения*), то же будет справедливо и для областей.
Предварительно установим, что контурные значения
решения краевой задачи A7.4') имеют производную,
удовлетворяющую условию Гёльдера. Рассмотрим равенство, получаемое
формальным дифференцированием **) краевого условия A7.4^):
a'{t)y^[a{t)]^y-{t) • (yB) = 47). 07.26)
Краевую задачу A7.26), в силу равенства A7.21), нужно
решать при условии Y~(oo)= 1. Последняя задача, по существу,
совпадает с решенной в п. 17.4 задачей A7.20). Поэтому
решение ее существует и y-it) удовлетворяют условию Гёльдера.
К решению исходной задачи A7.V) перейдем
интегрированием. Нужно только еще убедиться, что интегрирование не
введет логарифмического члена, поэтому следует доказать, что
вычет относительно бесконечно удаленной точки равен нулю.
Действительно,
5 Y- (О dt=\a' it) Y+ [а {t)] dt=\y^ {t,) dt, = 0.
L L L
Интегрируя y{z) и подбирая соответственным образом
произвольную постоянную, придем к решению задачи A7.4'),
которое, следовательно, согласно доказанному будет иметь на
контуре производную, удовлетворяющую условию Гёльдера.
*) См., например, [22], т. 3, ч. 2.
**) В обосновании законности дифференцирования нет необходимости,
так как последнее является лишь наводящим рассуждением. Все рассуждение
можно вести, рассматривая A7.26) как исходное.

156 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ, II
Перейдем теперь к основной части доказательства.
Допустим противное, т. е. что для /i Ф U
со- (/i) = со- (У = ©0.
Рассмотрим разности ©1'= (z) == 0=*= (г) — со^. Функции со^* {z)
удовлетворяют краевому условию A7.40, и для них будут
справедливы равенства
«>г (^)=«т (Q=«i^ [«(^.)]"" «>;' [«(^2)]=о-
Введем функции, не обращающиеся на контуре в нуль:
<0Г(^)=(г-1')У-/з)- <(^)=[.-a(/!i][?-a(/.)]- A7.27)
Выражая в краевом условии A7.4') функции cuj'=@ через (о|'(/),
придем к следующему краевому условию:
<l°Wl=|.„0-al/.HL)"--WI "»-<"•
Так как индекс коэффициента равен нулю*) и в силу A7.27)
(й"(оо) = 0, то согласно п. 17.4 (о|=(<г)^0. Отсюда ©=*= (г) = со^ =
= const, что невозможно, так как (о" (z) на бесконечности должна
иметь полюс. Однозначность отображения полностью доказана.
Установленная сводимость задачи со сдвигом к задаче Ри-
мана позволяет сформулировать результат.
Теорема. Однородная задача со сдвигом при х ^ О имеет
к + 1 линейно независимых решений. Неоднородная задача
безусловно разрешима, и ее решение зависит линейно от х + 1
произвольных постоянных. При х^—1 однородная задача
неразрешима, а для разрешимости неоднородной требуется
выполнение —X — 1 условий.
Отметим принципиальную важность доказанного факта, что
краевые значения решения задачи A7.4^ имеют производные,
удовлетворяющие условию Гёльдера. Отсюда вытекает, что если
в исходной задаче со сдвигом контур L был кривой Ляпунова,
то при сведении ее к обыкновенной задаче Римана контур L\
последней будет того же класса. Исходя из этого, можно
перенести без дополнительного обоснования все результаты,
касающиеся расширения класса коэффициентов, известные для
задачи Римана (см. п. 16.3), на задачу со сдвигом.
Использованный здесь метод, сводящий с помощью
конформного отображения краевое условие, связывающее
предельные значения искомых функций в разных точках контура (за-
*) См. рассуждение в конце п. 17.4.

§ 18] ДРУГИЕ ОБОБЩЕННЫЕ ЗАДАЧИ 157
дача со сдвигом), к краевому условию, связывающему
предельные значения в одной общей точке (задача Римана), носит
название принципа конформного склеивания (см. далее, п. 53.5).
§ 18. Другие обобщенные задачи
18.1. Постановка задач. Рассмотренная в § 17 задача
допускает простое обобщение. Вместо требования, чтобы функция
а (О отображала контур L на себя, можно допустить, что она
отображает L на некоторый другой контур L\. Изложенная
теория с незначительными изменениями может быть перенесена
и на этот случай. Он может быть сведен также к уже
рассмотренному случаю при помощи конформного отображения
(Л. И. Чибрикова и В. С. Рогожин 1)).
Наряду с предельными значениями самих аналитических
функций можно вводить в краевое условие их сопряженные
значения. Заметим, что задачи, когда в краевые условия
входят функции, сопряженные аналитическим, часто возникают
в вопросах прикладного характера. Рассматриваются также
задачи с условием, что функция а(/) отображает контур L на
себя с изменением направления обхода на нем.
Сформулируем пять краевых задач указанного типа,
предполагая, что L — простой замкнутый контур Ляпунова, G{t)
и g{t) — функции, удовлетворяющие тем же условиям, что
и в § 17.
Задача I. Найти функцию Ф+(г), аналитическую в Z)+,
и функцию Ф"(г), аналитическую в Ь- по заданному на L
краевому условию
0'-[a{t)] = G{tH^) + g{t\
где a{t) изменяет направление обхода.
Задача П. Найти функции Ф^U) и Ф2'(^), аналитические
в области D+, удовлетворяющие на L краевому условию
OU^(t)] = G{t)OUt) + g{t).
причем а (О изменяет направление обхода.
Задача III. Найти функции ФГ(г) и Ф2*B:), аналитические
в области D+ удовлетворяющие на L краевому условию
Ot[a{t)] = G{t)Or(t) + g(t),
где а(/) сохраняет направление обхода.
Задача IV. Найти функцию Ф+B:), аналитическую в
области D+, удовлетворяющую на L краевому условию

158 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
причем а (О изменяет направление обхода и подчиняется
условию a[a(t)]^ t (задача Карлемана).
Задача V. Найти функцию Ф+B:), аналитическую в
области D+, удовлетворяющую на L краевому условию
0'-[a{t)]=G{t)OUt) + g{t\
где а (О сохраняет направление обхода и подчиняется условию
а[а(/)] = / (задача Гильберта со сдвигом).
Задачи I—III можно привести к задаче, рассмотренной в
§ 17, конформным отображением области Z)+ на единичный
круг с последующей заменой неизвестных функций и
переменных (Л. И. Чибрикова и В. С. Рогожин 1)). Задачи IV
и V будут рассмотрены в пп. 18.2 и 18.3.
Заметим, что при решении задач I—V существенное
значение имеет направление, устанавливаемое на контуре L функцией
а(/). Если допустить, что в краевых условиях этих задач a(t)
устанавливает на L ориентацию, противоположную указанной,
то возникают существенно новые задачи, которые могут иметь
бесконечное множество линейно независимых решений.
Примером может служить задача Ф+(—/) = Ф+(/), |/|= 1, решением
которой является произвольная четная аналитическая функция
в 1^:1 < 1. Это краевое условие не принадлежит к типу IV, так
как функция а@ = —i сохраняет направление обхода на
1^1= 1. В общем случае задачи такого вида можно привести
к интегральным уравнениям Фредгольма первого рода
(Э. И. Зверович и Г. С. Литвинчук 1)).
Более сложные задачи со сдвигом, в краевых условиях
которых сопрягается более двух предельных значений искомых
функций, будут изучены в гл. V.
18.2. Краевая задача Гильберта со сдвигом *). Рассмотрим
краевую задачу V:
Ф+[а@] = С(ОФ^@ + ^@, A8.1)
a{t) сохраняет направление обхода контура и удовлетворяет
условию
а [а (/)]=/ (условие Карлемана). A8.2)
Предполагаем, что а(/) не обращается тождественно в t.
Заменим в краевом условии t на а(/) и, учитывая A8.2),
перейдем к комплексно сопряженным значениям. Исключая из
*) Этот пункт написан по работе Э. Г. Хасабова 2). Заметим, что
оправдание термина «Задача Гильберта со сдвигом» будет даяо в §§ 29, 30,
где рассмотренная здесь задача будет решена при a(t)^t. Этот случай
здесь исключался из рассмотрения,

§ 18) ДРУГИЕ ОБОБЩЕННЫЕ ЗАДЛЧИ 159
полученного равенства и A8.1) Ф+[а(/)], придем к соотношению
[G{t) G [а{t)] - 1] Ф-^ (/) + G [а @] g{t) + g [а{t)] = 0. A8.3)
Оно будет удовлетворяться в двух случаях:
14 т) G[a{t)]'gTr) + g[a{t)]
1) Выражение ^ ' ^—-—11- есть краевое значение
аналитической в D+ функции. В этом случае сама искомая
функция сразу определится по своему краевому значению
интегралом Коши.
2) Соотношение A8.3) вырождается в тождество.
Следовательно,
G [а@] G(/)= 1, GR)Igr(/) +7Й0] =0. A8.4)
В дальнейшем будем решать задачу A8.1) в предположении,
что условия A8.4) выполнены.
При решении будем опираться на далеко идущую аналогию
с данным в § 17 решением краевой задачи со сдвигом. С
помощью конформного преобразования отобразим предварительно
область D+ на единичный круг. Таким образом, не ограничивая
общности задачи, можем считать, что D+ есть единичный круг.
Как и в § 17, начнем с решения задачи о нулевом скачке.
Лемма. Обидим реигением задач
ф-^[а@]±Ф+@ = 0 A8.5)
является произвольная постоянная, действительная при нижнем
знаке и чисто мнимая при верхнем.
В самом деле, =РФ+(<) можно рассматривать как краевое
значение аналитических в D" функций Ч^~ (<г) = =F Ф"^ Г—j
(доопределение по симметрии (п. 12.1)). Следовательно, задачи
A8.5) можно рассматривать как задачу A7.4) без
дополнительного условия обращения на бесконечности в нуль. Отсюда
следует результат леммы.
Далее рассмотрим задачу с заданным скачком
Ф+[а@]~Ф^@ = г@. A8.6)
В этом случае (G(/)^l) первое из условий разрешимости
A8.4) обратится в тождество, а второе даст необходимое
условие разрешимости задачи A8.6):
ёЫт + Ш) = 0. A8.40
Покажем, что оно является также и достаточным. Будем
искать решение в виде интеграла типа Коши
^^^)-l^\^T^dr, A8.7)

160 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
плотность которого удовлетворяет условию
ф[а@] + ^) = 0. A8.8)
Переходя по формулам Сохоцкого в A8.7) к предельным
значениям на контуре и учитывая A8.8), придем от A8.6) к
интегральному уравнению
Ядро уравнения можно представить в виде
^'^<^\-1Т^—Ч\ + \^-Щ\- A8.10)
L а (т) — а (О X — t А L т — / х — t J
На единичной окружности т = е^^, т^ = /т, т=1/т, i=l/t,
поэтому второе слагаемое есть постоянная, равная /, первое же
слагаемое, согласно результатам п. 17.2, есть фредгольмово
ядро; следовательно, уравнение A8.9) есть фредгольмово.
Доказывается, что однородное уравнение, соответствующее
A8.9), неразрешимо и, следовательно, неоднородное A8.9)
разрешимо безусловно и однозначно. Далее устанавливается, что
все решения удовлетворяют условию A8.8). Рассуждения
близки к проведенным в пп. 17.2, 17.3; мы их не приводим.
Отсюда с учетом леммы I получается следующая
Теорема. Общее решение задачи о скачке A8.6) дает
формула
^i^) = ^\^^dr + a„ A8.11)
L
где ф@ ^сть реигение интегрального уравнения A8.9), а а^ —
действительная постоянная.
Следующим этапом является решение задачи о скачке
A8.6) в классе функций, имеющих полюс некоторого порядка т
в центре круга. Отыскиваем функцию в виде
ф+B) = ^ ^2fe-i + ^^2fe +4^^ (г). A8.12)
Вставляя последнее выражение в A8.6) и обозначая
^2Л-1-р ^,^^^у П2Н- р--^^
получим для определения Ч^+(г) следующее краевое условие:
2т
V+ [а @1 - ^+ it) = g{t)+Z a,h, (/).

§ 1Й) ДРУГИЕ ОБОБЩЕННЫЕ ЗАДАЧИ 1в1
Пусть ф(/) —решение интегрального уравнения A8.9),
а ф2л~1@» ф2й@ — решения того же уравнения с правыми
частями соответственно Лгл-ь 1^2к\ тогда по формулам A8.11),
A8.12) решения краевой задачи представляются в виде
Общее решение определяется формулой
2Х
fe-0
Перейдем к решению однородной задачи
ф+[а(/)] = О(/)Ф+@. A8.14)
Здесь должно удовлетворяться условие разрешимости
G[a(/)].G@ = 1. A8.4'0
Если x = IndG(/) = 0, то в рассуждении имеется полная
аналогия с п. 17.4. Взяв индекс обеих частей краевого условия,
с помощью обобщенного принципа аргумента A2.2)
убеждаемся, что решение нигде в плоскости не имеет нулей. Проло-
гарифмируем A8.14) и обозначим 1пФ+(г) = Г+(г). Учитывая,
что In Ф = In Ф, получим задачу о скачке
Г+[а@]-Г+(/) = 1пО(/), A8.15)
решение которой дается формулой A8.11). Отсюда общее
решение задачи A8.14) представится формулой Ф"^ (г) == се^"*" <^^ где
с — действительная постоянная.
Переходя к случаю любого индекса, покажем сначала с
помощью условия A8.4^'), что индекс задачи есть, необходимо,
число четное.
Пусть ti — произвольная точка окружности L, и пусть /г =
= a(/i). Эти точки разбивают окружность на две части Li (от
ti к /г) и L2 (от /2 к /i), обладающие тем свойством, что когда
точка t пробегает Lu точка а(/) пробегает L2, и наоборот. Из
равенства A8.4'^ следует, что
arg О [а @1 ~ arg G (t) = 2ят, A8.4^^0

162 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. II
так ЧТО argG[a@] и arg G{t) отличаются на постоянную и
поэтому
[argG[a@]]^=[argG(/)]^_
или, что то же,
[argG(/)]^^ = [argG(/)]^_.
Прибавляя [argG@]?^ к обеим частям последнего равенства,
получим
jxx = [argG(/)]^^,
где K=lndG{t). С другой стороны, из A8.4''0 вытекает, что
[arg G (t)]^^ = arg G (/2) — arg G (/j) = 2ят и тогда x = 2m — четное
число.
Представляем G{t) в виде G@ = -^^—^Go@. Очевидно,
IndGo(/) = 0. Используем полученное выше решение задачи
с нулевым индексом
Хо [a{t)] = Go (О Хо (t), Хо (z) = е^' (->,
Функция X (г) = г ^ Хо (г), очевидно, удовлетворяет краевому
10ВИЮ A8.14), поэтому будем иметь G(
условие A8.14) можно представить в виде
условию A8.14), поэтому будем иметь G(t)= и краевое
X (/)
Фр^Ж = (^). A8.140
Х+[а(/)] VX+@/ ^ '
Рассмотрим два возможных случая:
Ф+ B)
1) X ^ 0. Здесь ^ имеет полюс порядка не выше к/2
в начале координат. Используя решение A8.13) задачи о скачке
в классе функций с полярной особенностью (при g{t)^0,
ф(^)вО), получим решение задачи A8.14) в виде
Следовательно, задача имеет х + 1 линейно независимых
решений.

§ 18] ДРУГИЕ ОБОБЩЕННЫЕ ЗАДАЧИ 163
2) X < 0. В ЭТОМ случае, очевидно, однородная задача
A8.14) не имеет отличных от нуля решений.
Переходим к решению первоначально поставленной
неоднородной задачи A8.1). Считаем условия разрешимости A8.4)
выполненными. Решение совершенно аналогично изложенному
в § 14 решению краевой задачи Римана; поэтому не будем
останавливаться на подробностях.
С помоихью канонической функции представим краевое
условие в виде
Ф-^ [« @1 _ ( Ф^ (t) Л ^
Х+ [а (t)] \ Х+ (t) )
g(t)
[а (t)] \ Х+ (t) ) Х+ [а @1
Используя, далее, решение задачи о скачке в классе
функций с полярной особенностью, получим решение в виде
ф+ (г) = Х+ {Z) r^F+ (z) + Z c^(b^{z)\. A8.16)
если x>0, и
ФB) = ХB)[Ч^(г) + ао], A8.18)
если X < О и свободный член удовлетворяет условиям
разрешимости:
. ' A8.19)
j9[a(T)]T-^dT = 0 (fe = 2, 3, ..., -х),
L
где ф(/)-—решение уравнения Гф = —~-^-!—.
18.3. Краевая задача Карлемана*). В качестве еще одного
примера рассмотрим краевую задачу Карлемана на простом
замкнутом контуре Ляпунова L (см. п. 18.1, задача IV):
Ф+ [а (/)] = G it) Ф^ (О + Я (О, A8.20)
где a{t) изменяет направление обхода контура и a[a{t)]^ t.
*) Материал этого пункта, а также п. 43.4, где завершается
исследование задачи, написан по работе В. А. Чернецкого 1).

164 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
Рассуждая аналогично п. 18.2, приходим к выводу, что интерес
представляет тот случай, когда выполнены условия
G [а@1 G @=1, G{t)g[a{t)]-^g{t) = 0. A8.21)
Покажем, что путем применения метода конформного
склеивания, близкого к описанному в п. 17.5, краевая задача A8.20)
сводится к задаче Римана на разомкнутой дуге Ляпунова.
Приведем лишь схему исследования, не останавливаясь на
подробностях.
Прежде всего устанавливаем таким же способом, как и
в § 17, утверждение, аналогичное лемме I из § 17.
Лемма. Краевые задачи
Ф+[а@] = ЯФ+@, Я=±1,
не имеют других решений, кроме произвольной постоянной,
равной нулю при X == —1.
Далее решаем вспомогательную задачу с нулевым скачком
(о+[а@]-со+@ = 0 A8.22)
в классе функций, имеющих простой полюс в некоторой точке
го е /)+, т. е. в классе функций вида
Ч^+(г)—аналитическая функция в D+. В силу A8.23) получим
для Ч^+B:) следующее краевое условие:
W- [а @1 - WMO = 7^ - ^(ТуЬ: • A8.24)
Решение краевой задачи A8.24) будем искать в виде интеграла
типа Коши
^'(^) = wj^'^^. A8-26)
плотность которого удовлетворяет соотношению
а|)@ + ^[а(/)] = 0. A8.26)
Вычисляя Ч^''"[а@] и '^'^{t) по формуле Сохоцкого и
используя условие A8.26), получим для определения y^{t)
интегральное уравнение
^(^)+2^S[tJt-«w-«(o]^(^^^^^«@-^o~7^'
а 8.27)

% 18] ДРУГИЕ ОБОБЩЕННЫЕ ЗАДАЧИ 1в6
ядро которого имеет в точке х == t особенность порядка меньше
единицы (см. п. 17.2) и является поэтому уравнением Фред-
гольма; при этом любое интегрируемое решение этого
уравнения удовлетворяет условию Гёльдера.
Методами, близкими к использованным в пп. 17.3, 18.1,
доказывается, что однородное интегральное уравнение,
соответствующее A8.27), неразрешимо (и, следовательно,
неоднородное разрешимо безусловно и однозначно), а также, что это
решение удовлетворяет условию A8.26). Отсюда по формулам
A8.25) и A8.23) получаем решение краевой задачи A8.22).
Функция а(/), очевидно, имеет две неподвижные точки t=A
и / == 5, делящие контур L на две неналегающие дуги L+ =
= (Л,В), L- = E,i4). Функция ©+B:), являющаяся решением
задачи A8.22) с условием A8.23), отображает область Z)+ на
плоскость с разрезом Lu который задается уравнением w ==
= (о+(/), /eL, и имеет своими концами образы а==со+(Л)
и Ь = 0+(В) неподвижных точек функции a{t). Рассуждая
аналогично п. 17.5, можно установить, что Li является кривой
Ляпунова, а конформное отображение, осуществляемое функцией
W = (о+(г), взаимно однозначно.
Примем за положительное направление на Li то, которое
ведет от а к Ь. Тогда для функции z{w), обратной к w =
¦в (й+(г), имеем
г+(ш) = ^ 2-(ш) = а@, wmLu t^L-^, A8.28)
или, что то же самое (в.силу условия a[a{t)] = /)»
z^{w) = a{t), z''{w)^t, ше11, t^L''. A8.29)
Используя A8.28), для / е L+ перепишем краевое условие
A8.20) в виде
ф+ [г- (ш)] = G [2+ (w)] Ф+ [2+ {w)] + g [z+ {w)l
Вводя новую функцию
Oy{w) = 0^[z{w)l A8.30)
аналитическую в плоскости с разрезом Li, получим краевое
условие задачи Римана:
ФГ (w) = G [z^ (w)] ФГ (w) + g [2^ {w)l A8.31)
Если же воспользоваться формулами A8.29), то получим
ф+ (w) = G [z" (ш)] ФГ (w) + g [z- {w)l A8.32)
Краевые условия A8.31) и A8.32) совпадают, так как из
условий A8.21) и соотношений A8.28) следует, что
G [2+ (ш)] G [Z- (ш)] = 1, G [г+ (ш)] g [z" {w)] + g [г+ {w)\ = 0.

166 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
Таким образом, задача Карлемана A8.20) на замкнутом
контуре L сведена к равносильной ей задаче Римана A8.32) на
разомкнутом контуре Li. Задачи этого рода будут изучаться
в гл. VI, поэтому окончание исследования рассматриваемой
задачи мы переносим в п. 43.4.
Изложенный способ применим и для решения задачи в
многосвязной области при условии, что функция сдвига а@
отображает взаимно однозначно каждую из кривых L^ контура на
себя. В самом общем случае, когда a{t) переводит весь контур
на себя, но так, что отдельные кривые контура могут
переходить друг в друга, метод конформного склеивания оказывается
недостаточным. Используется так называемый принцип
локально конформного склеивания, В этом случае для исследования
приходится привлекать теорию краевых задач на римановых
поверхностях. (Несколько подробнее об этом • будет сказано
в п. 53.5.)
§ 19. Исторические сведения
Краевая задача A4.1), называемая здесь задачей Римана*), впервые
встречается в работе Римана о дифференциальных уравнениях с
алгебраическими коэффициентами ([21], стр. 177). Задача (однородная) формулируется
им для случая п пар искомых функций в связи с задачей отыскания
дифференциального уравнения, интегралы которого при обходе около особых точек
претерпевают заданную линейную подстановку (уравнение с заданной
группой монодромии). Эта тема выходит за пределы настоящей книги, и мы не
будем ее касаться; читателей, интересующихся этим вопросом, можно
отослать к работе [7].
Риман не сделал никаких попыток решить поставленную им задачу.
Первое решение однородной краевой задачи A4.1) дал Гильберт. Пользуясь
условиями того, что произвольная комплексная функция является краевым
значением аналитической функции (см. задачу 24*, гл. I), Гильберт составил
интегральное уравнение Фредгольма, которому удовлетворяет решение задачи.
Анализируя это уравнение, он доказал альтернативу: одна из двух задач с
коэффициентом G(t) или G(t) разрешима. В дальнейшем авторы,
рассматривавшие общий случай краевой задачи (Пикар [19], Привалов 1)), шли потому
же пути сведения задачи к интегральному уравнению, используя в качестве
аппарата интегралы типа Коши. Вместо альтернативы Гильберта здесь
получалась альтернатива для коэффициентов G(t) и ртттч- Метод этот до сих пор
применяется при решении задачи Римана со многими неизвестными функциями.
Особняком стоят две работы, где рассматривалось решение задачи в
замкнутой форме. Племель [Plemelj 1)] мимоходом показывает, что в случае
однозначного 1пС@ решение однородной задачи может быть получено явно
в интегралах типа Коши. Карлеман [Carleman 1)] при решении особого
интегрального уравнения с ядром Коши (см. гл. III) попутно решает
неоднородную задачу Римана с постоянным коэффициентом G(t) для случая, когда
контур есть отрезок действительной оси [О, 1]. Способы решения Племель и
Карлемана, в сущности, те же, что и изложенные в настоящей главе, но при-
*) Для этой же задачи употребляют еще следующие названия: «задача
Гильберта», «задача линейного сопряжения», «задача сопряжения», «задача
Гильберта -- Привалова», «задача Римана — Привалова».

ЗАДАЧИ К ГЛАВЕ П 167
менимы они к весьма частным случаям, где характерные черты задачи не
выявляются. В них прежде всего не вводится понятие индекса, который, как
уже знает читатель, изучивший главу, является основной характеристикой
как для самой задачи Римана, так и для ее обобщений.
Следует упомянуть еще о работе Винера и Хопфа [Wiener und Hopf I)],
посвященной решению особых интегральных уравнений типа свертки. Работа
эта никогда ранее не упоминалась в связи с задачей Римана, однако тесно с
ней связана. Решение упомянутых интегральных уравнений приводится к
задаче того же типа, что и краевая задача Римана, но с тем различием, что
соотношение между аналитическими функциями задается не на контуре, а в
точках целой области (полоса, ограниченная двумя прямыми, параллельными
оси абсцисс). Метод решения отличается от метода решения краевой задачи
Римана лишь несущественными подробностями. Понятие индекса здесь также
отсутствует.
Полное решение задачи Римана для односвязной области примерно в
том же виде, как оно здесь изложено *), дано автором в 1936 г. в 1). В 1941 г.
Б. В. Хведелидзе 1) обобщил это решение на многосвязную область.
Исключительные случаи задачи Римана (§ 15) были рассмотрены впервые в работах
автора 2), [6], а затем в более общем виде в работе Л. А. Чикина 1).
Задача Римана со сдвигом (§ 17) встречается впервые у Газемана [Hase-
man 1)]. Он сводит ее способом, аналогичным тому, который применил
Гильберт для решения задачи Римана, к интегральному уравнению Фредгольма и
получает ту же альтернативу, что и Гильберт для задачи Римана.
Полное решение задачи Римана со сдвигом, некоторых ее видоизменений
и задачи Карлемана дано Д. А. Квеселава, первая работа которого 1)
относится к 1946 г., обзорное изложение материала дано в работе 2).
Сведение задач I—III к задаче Римана со сдвигом дано в работе
Л. И. Чибриковой и В. С. Рогожина 1). В последние полтора десятка лет
теория краевых задач со сдвигом интенсивно разрабатывается. Опубликовано
весьма большое количество оригинальных работ различных авторов, в первую
очередь Н. П. Векуа, Э. И. Зверовича, Г. С. Литвинчука, Э. Г. Хасабова,
Р. А. Кордзадзе и др., в которых эта теория существенно продвинута вперед.
Исторические сведения о возникновении и развитии теории краевой
задачи Римана в многомерных областях давались в тексте.
Дальнейшие сведения о задаче Римана и задачах со сдвигом будут даны
в главах V, VI в связи с различными их обобщениями.
Задачи к главе II
1*. Доказать, что индекс функции | (s) + ir\ (s) (О < 5 < /) (g (s + /) =«
= g (s), Ti E -f /) == Ti {s)) равен полуразности числа случаев, когда функция
-~j-r- обращается в бесконечность, переходя от положительных значений к
отрицательным, и числа случаев, когда она обращается в бесконечность,
переходя от отрицательных значений к положительным.
Замечание. Коши, введя понятие индекса, определил его как разности
числа случаев перехода функции через бесконечность от положительных
значений к отрицательным и от отрицательных к положительным. Следовательно,
индекс в смысле Коши равен удвоенному индексу в смысле данного нами
определения. Понятие индекса Коши применимо и для непериодических функ*
ций. При этом, по условию,
отбрасывается.
*) Понятие канош1ческой функции дано И. И. Мусхелишвили»

168 КРАЕВАЯ ЗАДАЧА РИМАНА [ГЛ. II
2*. Пусть 5 (О» Л (О " многочлены относительно / (a^t^b). Образуем
последовательность
% ?, - Г„ - Г2, . . ., - Гп^и ~ Гп, A)
где Г] — остаток от деления Т1 на g, Гг — остаток от деления | на Г] и т. д.
Доказать, что индекс функции % (s) + /ti (s) равен полуразности числа
перемен знаков в последовательности A).
3*. Пусть Ф (Ху у), ф (х, у)у i|) (Ху у) — три функции двух независимых
переменных х, у, имеющие непрерывные частные производные.
Предполагается: 1) функции Ф, ф, -ф не обращаются одновременно в нуль, 2) их
якобиан также не обращается в нуль и 3) кривые Ф==0, ф = 0, \|) = 0
замкнуты. Точки плоскости, для которых ф, -ф < О, назовем внутренними, а точки,
где ф, -ф > О, — внешними. Переход из внешней области во внутреннюю
назовем входом а обратный переход выходом.
Характеристикой функций Ф, ф, -ф — х (Ф' Ф. '^) Кронекер называл
полуразность числа точек входа и выхода кривой Ф (х, t/) = 0 через кривую
Ф (^' ^) = 0 или, что все равно, ч^рез кривую ф (д:, у) = 0. Показать, что:
1) характеристика % (Ф, ф, г))) совпадает с индексом функции G (х + iy) =
=* Ф (Ху у) + /-ф (Ху у) по кривой Ф {Ху у) = 0:
2) характеристика не меняется от круговой перестановки функции Ф, ф,
1|) и меняет знак при перестановке двух из них. (И. Г Ч е т а е в,
Характеристики Кронекера, Уч. зап. Казанск. ун-та, т. 98, кн. 9, 1938.)
Примечание. Кронекер определил понятие характеристики для
общего случая п + 1 функций от п переменных.
Всюду в дальнейшем контур L есть простая замкнутая кривая, делящая
плоскость на две области: внутреннюю D+ и внешнюю D-; а обозначают
произвйльные постоянные.
4. Решить краевую задачу Римана
^ (^)=^(/ + /)(/ + 2/)^ (^)+(/+/J(^ + 2/)(/-.Г
считая, что точки /, 21 принадлежат области D"*". а точки — /, — 2/ —
области D",
Ответ.
ф-(г) =
(z+iy{z + 2i) ^ {z + i){z + 2i)'
1 Cq + CiZ + CzS'^
(z - if (z - 2i) "^ (г - /) (z - 2i)
6. При каком значении параметра а будет разрешимой краевая задача
Римана
+ а - о (t - 20 2t(f- 21) {at + 1)
если контур L оставляет точку — / в области D , а точки /, 2/, — 2/ в D"" ?
Решить задачу при найденном значении а.
л , >»v+/ ч —2iz(z — 2i) ^-/ ч л
Ответ, а —~/, Ф^B:)= ^^.—^, Ф (а:)-0.
^ Решить краевую задачу Римана
1
ф+ (/) — Ц— ф" (t) + sint + Д, Ф" @0) — О
для контура I, 99Тдвляющего точки О, 1 в области D'^.

ЗАДАЧИ К ГЛАВЕ II 1в9
Ответ, ф"*" (г) = sin z + Со + c^z,
Ф-«_1л,„(,.1)-(^+,),„(,_1).
7. Решить краевую задачу Римана
ф+(/) = (^-.1)ф-(/) + /2_1
при следующих предположениях:
а) точка 1 принадлежит D"^;
б) точка 1 принадлежит D";
в) точка 1 принадлежит L,
Ответ.
а) Ф"*" (z)='Z^-\+Co + c,z, Ъ- (z) = (г - 1)-^ (Со + c,z)\
б), в) Ф"^ B) = 2^ - 1 + Со B-1), Ф- (г) = Со.
8. Решить краевую задачу Римана
Ф+ (/) = (/ - 1)-^ф- (t) + t + (t^ 1)-»
при тех же предположениях, что и в предыдущей задаче.
Ответ.
а, в) Ф"*'B)«г, ф-(г) = -1;
б) Ф"*" (г) = B - П'Чг^ - 2 + 1 + Со), Ф- (z) « Со.
9. Показать, что задача Римана
^-3
при условии, что точки о, 3 принадлежат D"^, а точки 1, 2 лежат на
контуре L, разрешима лишь при а = I. Дать решение в этом случае.
Ответ. Ф+(г)-г+1, ф-(г)-:3 ^""^^^^^^^ ^
10« Решить краевую задачу Римана
^' (h + \)t-i^ ^'^ (h+\)t-i
(А — действительная, отличная от ±1, — со < / < со).
Ответ. При А < — 1
д,+ ,.л а I 6(А+1) + аЛ . , с
^ ^^'~2(А + 1) "^ (А+1) [(А+ 1J-»] "^ "''" (A+l)z-i'
^-/ ч_ (^ + ^)z —«' Г_ д ¦ I g 1
* ^^^~ (Л-1J + 3/L 2(А + 1) ¦*¦''° ¦+¦ (A+lJ-/J'
при - К А < 1
•^^(^)=2(АТТТ+'''
^-/-^¦¦_ (A + lJ-f Г а az + b . Л.
•^ (»)-(А-1J + 3/[т^АТ1Т~('^4-1)г-,-+''Р

170 КРАЕВАЯ ЗАДАЧА РИМАНА 1ГЛ. И
При h > 1
^^^ 4Л + 2
^^^ Ah+ 2
II, Решить краевую задачу Римана
(Л — действительная, отличная от0и2, --оо<^< с»).
Ответ. При /г < О
при О < Л < 2
При А > 2
г + (/г-2)/ ^ ° ^ 2 + B-Л)/'
-,_ , , г + (/г — 2) / г , с 1
ф (-)^ t:r^-b+ z + (h-2)i\
12*. Доказать, что если в качестве решения допускать функции,
обращающиеся на контуре в бесконечность интегрируемого порядка, то такое
допущение не расширяет класса решений. Класс решений, для которого
допустимы на контуре указанные особенности, совпадает с найденным в § 14
решением, непрерывным вплоть до контура. (Ф. Д. Гахов [6].)
13*. Дать решение задачи Римана со сдвигом в исключительном случае,
когда коэффициент задачи может обращаться в нуль или бесконечность
целого порядка,
ф+ [а (/)] = Щ G, (О Ф- (/).
V
Показать, что число решений равно Ind Gj (/) — ^ р., (Л. И. Чибрикова 1).)
/=1
Указание. Представить краевое условие в форме
ф''[«@] _тт г ^-^^fe Т^г. и^ ф"(О
-И Г ^"^^^ Т
Ml. ^ li I am-а, I -^(^)" V
Рассмотреть аналогичный случай неоднородной задачи.
14. Применяя принцип симметрии к единичной окружности, показать, что
формула Шварца для функции, аналитической в области |2:|> 1, имеет вид
2я
О ^ ^

ГЛАВА III
ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ
КОШИ
В настоящей главе будет дано одно из важнейших
теоретических приложений краевой задачи Римана — исследование
особых интегральных уравнений с ядром Коши. В соответствии
с тем, что краевая задача Римана рассматривалась пока лишь
для замкнутых контуров, будем исследовать интегральные
уравнения с интегралами, взятыми по таким же контурам.
В дальнейшем в связи с обобщениями в постановке задачи
Римана соответственно будут изучены и другие типы
интегральных уравнений.
§ 20. Основные понятия и обозначения
20.1. Особое интегральное уравнение*). Если в линейном
интегральном уравнении
ф@+5/С(/, т)ф(т)йт = /@
L
ядро имеет вид
^(^.'^) = fzi^ @<а<1).
где М(/,т)—непрерывная функция, то, как известно, при
помощи итерации его можно привести к интегральному
уравнению с непрерывным ядром. Такое уравнение обладает всеми
свойствами уравнения Фредгольма и называется квазифред-
гольмовым или иногда просто фредгольмовым.
Если а= 1, то интеграл становится особым (сингулярным)
и указанный способ приведения уравнения к фредгольмову
теряет силу. Для таких уравнений нужно строить специальную
теорию.
*) Напомним, что в литературе, посвященной теории рассматриваемых
здесь уравнений, они часто называются сингулярными (см. Введение).

172 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ У1»АВНЕНИЯ С ЯД1*ОМ КОШЙ {ГЛ. П1
Мы здесь будем рассматривать уравнения с ядром Коши
типа
Кф = а(/)ф(/) + -1-$-^^^^ B0.1)
Интеграл, понимаемый в смысле главного значения, берется
по контуру L, состоящему в общем случае из m + 1 замкнутых
гладких кривых L = Lq 4" ^i + • • • + ^m, расположенных, как
указано на рис. 13 (п. 16.1). Заданные на L функции а(/), /(/),
M{t,x) будем считать удовлетворяющими условию Гёльдера,
причем последнюю по обеим переменным.
Буква К (каппа) — это символ операции, производимой над
функцией ф(^) в левой части уравнения.
Совершив над ядром преобразование
M{t, т) ^ M{t, T)-M{t, t) , M(t, t)
x-t ^ x-t "*" x-t
и обозначив
M{t,t)^b{t), l^M^^^tzJ^^k{t,x\ B0.2)
запишем уравнение B0.1) в виде
Кф = а(Оф@+4^$-:^^т + 5м^т)ф(т)^т = /@. B0.3)
L L
Из формул B0.2) следует, что функция b{t) удовлетворяет
условию Гёльдера на всем контуре L, а k{t,x) всюду, кроме
точек т = ^, где для нее справедлива оценка
1М^, t)i<-|^37iT=5^ (о<;^<1).
Уравнение B0.3) будем называть полным особым
интегральным уравнением. Если \{t) не нуль, будем иметь неоднородное,
в противном случае — однородное уравнение.
Выражение
КОф ^a{t)^f{t)-^^\^dx B0.4)
L
называется характеристической, а член \ k (/, т) ф (т) dx — регу-
лярной частью. Уравнение
К»ф^а(Оф@ + -^$^^т = /@ B0.5)

^ 20] ОСНОВНЫЕ ПОНЯТИЯ и ОБОЗНАЧЕНИЯ 173
будем называть характеристическим уравнением,
соответствующим полному уравнению B0.3), а оператор К° —
характеристическим оператором.
Вводя для регулярной части уравнения обозначение
k^^\k (/, т) ф (т) dx,
L
ное уравнение в виде
Кф = К\ + А?ф = /(/).
L
можем записать полное уравнение в виде
Уравнение
K^^^a{f)^{t)^^\^^^di:+\k{x,t)^{x)dx = Q, B0.30
L L
получаемое из однородного уравнения Кф = О перестановкой
(транспозицией) переменных в ядре, называется союзным или
транспонированным. Оператор К' называется союзным
(транспонированным) оператору К.
В частности, уравнение
К°Ч^а(/) 1|)@-^ J4^^(т)Л = О B0.50
будет уравнением, союзным характеристическому уравнению
B0.5). Заметим здесь же, что оператор К°', союзный
характеристическому оператору К°, не совпадает с оператором К',
характеристическим для союзного. Последний определяется *)
формулой
К'Ч ^ а (О tD (/) —^ S ^ dx. B0.6)
L
Всюду в дальнейшем будем искать решения особых
уравнений, удовлетворяющие условию Гёльдера.
20.2. Основные результаты теории интегральных уравнений
Фредгольма. Приведем для справок основные факты теории
линейных интегральных уравнений Фредгольма 2-го рода
а@ф@ + ^5/С(^ т)ф(т)^т=/@;
L
некоторыми из них мы уже пользовались в п. 17.3.
*) в формуле B0.30 нужно произвести преобразование:
L L L
И первый интеграл отнести к регулярной части.

174 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
Предполагая a{t) не обращающимся в нуль, можно без
ограничения общности считать a{t)^l. Поэтому в
дальнейшем будем рассматривать уравнения Фредгольма вида
(f{t) + l[K{t, т)ф(т)dx = f(t) (неоднородное) B0.7)
L
И
(p(t) + x\^K {t, т) ф (т) rfx = О (однородное). B0.8)
L
Определение. Если при некотором значении параметра
Х = Хо однородное уравнение Фредгольма имеет нетривиальное
решение, то ко называется собственным значением, а сами
решения (линейно независимые) ф1 (О» • • •» фп (О — собственными
функциями ядра K{t,x) или, что все равно, однородного
уравнения B0.8).
1°. Теоремы Фредгольма. Следующие три теоремы
называют соответственно первой, второй и третьей теоремами
Фредгольма.
Теорема I. Если Я = Ло не является собственным
значением ядра, т. е. если однородное уравнение B0.8)
неразрешимо'^), то неоднородное уравнение B0.7) разрешимо при
любой правой части f{t).
Общее решение дается формулой
Ф@ = /@-5^(/, т)/(т)йт, B0.9)
L
где функция RityX) — резольвента уравнения — определенным
образом выражается через ядро К{(,%).
Теорема П. Если ^ = Яо является собственным значением
однородного уравнения B0.8), то оно является собственным
значением также и для союзного уравнения'^*)
^{t) + l\K (т, t) а|) (т) dx = О, B0.70
L
причем оба уравнения имеют одинаковое число линейно
независимых решений (собственных функций, принадлежаи{их
собственному значению Яо).
*) Однородное уравнение называем неразрешимым, если оно не имеет
других решений, кроме тривиального нулевого.
**) Вместо уравнения B0.7') союзным уравнением часто называют
уравнение -ф (О + Я \ К (т, /) ф (т) т'(а) йГа = О (т = т (а)). Простыми преобразо-
L
ваниями легко показать, что последнее уравнение имеет столько же решений,
что и уравнение B0.70 (см. п. 24.4),

§ 20] ОСНОВНЫЕ ПОНЯТИЯ и ОБОЗНАЧЕНИЯ 175
Общее решение однородного уравнения представляется
в виде
п
где ф1@» •••» фп@ — полная система линейно независимых
собственных функций, принадлежащих собственному значению
Хо, а Ck — произвольные постоянные.
Теорема III. Если однородное уравнение разрешимо, то
неоднородное уравнение, вооби{е говоря, неразрешимо. Оно
будет разрешимо тогда и только тогда, когда выполнены условия
f{t)^t)dt = 0, B0.10)
где ypkit) {k== 1,2,... ,п) есть полная система собственных
функций союзного уравнения B0.7'), принадлежаи^их данному
собственному значению Хо-
Если условия B0.10) выполнены, то общее решение
неоднородного уравнения дается формулой
п
Ф (О = f (О - 5 я (/, т) / (т) dx + Y, с,ф, @. B0.11)
п
где Н{1,х) — обоби^енная резольвента, а 2 с^^ф^ (/) —общее ре-
шение соответствующего однородного уравнения.
2°. Спектр уравнения.
Определение. Множество собственных значений
параметра Х интегрального уравнения называется его спектром.
Приведем две теоремы, характеризующие спектр уравнения
Фредгольма.
Теорема IV. Множество собственных значений
интегрального уравнения Фредгольма не имеет предельных точек на
конечном расстоянии. Если множество собственных значений
бесконечно, то его предельной точкой является бесконечно
удаленная точка.
Иначе говоря, спектр интегрального уравнения Фредгольма
есть множество изолированное (дискретное). Это следует из
того, что собственные значения Х^ интегрального уравнения
Фредгольма являются корнями аналитической функции,
которая в частном случае, когда ядро уравнения вырождено
[K{t, т)= X] a/(OP/(t)), обращается в многочлен, а в
остальных случаях является целой трансцендентной.

176 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ И!
Теорема V. Каждому собственному значению
принадлежит конечное число собственных функций.
Последнее свойство уже использовалось в теореме III.
§ 21. Характеристическое уравнение
21.1. Сведение к краевой задаче Римана. Рассмотрим
простейший тип особого интегрального
уравнения—-характеристическое уравнение B0.5):
K''^^a(t),f{t)-\--^\-^dx = f{t). B1.1)
L
В ЭТОМ случае решение уравнения можно свести к решению
краевой задачи Римана (гл. II) и дать решение уравнения в
замкнутой форме.
Введем кусочно аналитическую функцию, заданную
интегралом типа Коши, плотностью которого служит искомое
решение характеристического уравнения
Согласно формулам Сохоцкого D.9) и D.10)
Ф@ = Ф^0-Ф"@,
т) + B1.3)
^^ Л = ф+(/) + Ф'"@.
1 С Ф(т
t
Внося значения ф@, —г \ ^_^ dt в уравнение B1.1) и решая
L
его относительно Ф"^ (/), получим, что кусочно аналитическая
функция Ф (г) должна являться решением краевой задачи Римана
0^it) = G{iH'{t) + g{t\ B1.4)
где
В силу того, что искомая функция Ф(г) представлена
интегралом типа Коши, она должна удовлетворять
дополнительному условию
ф-(оо) = 0. B1.6)
Индекс коэффициента ^ \1 Т и L! задачи Римана B1.4)
будем называть индексом интегрального уравнения B1.1).

§ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 177
Решив краевую задачу B1.4), по формуле B1.3) найдем
решение уравнения B1.1).
Итак, интегральное уравнение B1.1) свелось к краевой
задаче Римана B1.4). Чтобы установить равносильность
уравнения и краевой задачи, нужно доказать, что и, обратно, ф@»
найденная указанным образом из решения краевой задачи,
удовлетворяет уравнению B1.1). Для этого нужно установить,
что справедлива и вторая из формул B1.3). Докажем это.
Если решение задачи B1.4) представлено интегралом типа
Коши B1.2), то будут справедливы обе формулы B1.3) и от
краевой задачи можно однозначно прийти к исходному
уравнению. Допустим теперь, что имеется другая функция Ф1(-г),
удовлетворяющая тем же условиям. Тогда для разности Фг =
= ф — Oi будет справедливо равенство
Ф2^(/)-Ф2"@ = 0.
По теореме об аналитическом продолжении и теореме Лиу-
вилля (с учетом B1.6)) Ф2B)^0. Следовательно, Ф1(г) =
= ФB), что и требовалось.
Рассмотрим сначала нормальный (не исключительный)
случай, когда коэффициент G{t) задачи Римана B1.4) не
обращается в нуль или бесконечность, что соответствует для
уравнения B1.1) условию
a{t)±b{t)^0. {21 Г)
Для упрощения дальнейших формул разделим предварительно
все уравнение B1.1) на л/а^(t) — Ь^(t) (нормируем), т. е. будем
считать, что коэффициенты этого уравнения удовлетворяют
условию
a^@-b4t)=l, B1.7)
Исключительные случаи будут рассмотрены в конце главы
(§ 25).
Заметим еще, что и, обратно, легко составить особое
интегральное уравнение, соответствующее заданной краевой задаче
B1.4). Подставляя в краевое условие B1.4) предельные
значения интеграла типа Коши, по формулам D.8) получим
характеристическое особое интегральное уравнение
1[1+О@]ф(/) + -Щ^$^^т = ^@. B1.8)
L
Из решений последнего уравнения по формуле B1.2)
получим решение краевой задачи Римана. Поскольку нет способа
решения характеристического уравнения, независимого от
решения задачи Римана, то на уравнение B1.8) нужно смотреть
не как на новый способ решения задачи Римана, а просто как

178 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
на формулу, по которой можно быстро построить
характеристическое особое интегральное уравнение, соответствующее
заданной краевой задаче Римана.
21.2. Решение характеристического уравнения. Выпишем по
формулам A6.10), A6.8) решение краевой задачи Римана
B1.4), считая х ^ О, и вычислим по формулам Сохоцкого
предельные значения соответствующих функций
ФМ') = х*«)[{^ + ч'«)-1р.-,(«].
где Т@-—особый интеграл, получаемый заменой в формуле
A4.14) Z на i. Произвольный многочлен взят в форме
— yPx-iCO для удобства дальнейших обозначений.
Отсюда по формуле B1.3)
^«-7[' + ff]^«
+
+ ^*<'>['-|^]['^<'>-Т''"-<'>]'
На основании краевого условия заменяем ¦ .^ ^ = .
^ ^ Х+ (О G (t) *
а функцию 4^{t) ее выражением по формуле A4.14). Тогда
L 0(/)]|_2я/ J Х+(т) T-t 2 '^¦'J
Подставляя, наконец, вместо Х+(/) ее выражение из
формулы A6.8) и значения G{t) и g(t) из B1.5), имеем
ф(/) = а@/(/)--^^^ 5-^:^4-й@ 2@Рн-,@. B1.9)
L
где
г (О
Z (t) = \а [t) + b (/)] Х+ (О = [а (О - b @1 Х" @= /
r(/) = -L. = -L aT) + &(T)J
m
n@=S(^-2ft)'** B1.11)

§ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 179
и коэффициенты а(/), b{t) удовлетворяют условию B1.7^).
Здесь П(/)^1 в случае, когда L — простой контур,
охватывающий односвязную область. Так как функции а(/), b{t),
f{t) удовлетворяют условию Гёльдера, то на основании свойств
предельных значений интеграла типа Коши функция ф(/)
также будет удовлетворять условию Гёльдера.
Последний член формулы B1.9) представляет собой общее
решение однородного уравнения (/(/)^0), а первые два
члена —некоторое частное решение неоднородного уравнения.
Сравнивая формулу B1.9) с формулой B0.11), видим, что
, b{t)z (t)
функция /2 (т) (т --1) ^'^^ характеристического уравнения
играет роль резольвенты, а его собственными функциями будут
щ(()= b(t)Z{t)t^~^ (/г = 1,2,... ,х). Частное решение
уравнения B1.1) можно записать как /?/, где R — оператор*),
определяемый равенством
' \ / / V / д; J 2 (Т) Т — /
L
Тогда общее решение уравнения B1.1) примет вид
4>{t) = Rf+tckCp,{ty B1.12)
Заметим, что в тех случаях, когда задача Римана B1.4)
может быть решена непосредственно путем аналитического
продолжения (см. п. 14.6), удобнее искать решение
характеристического уравнения не по формуле B1.9), а непосредственно
по формуле B1.3).
Если X < О, то, как мы знаем, задача Римана B1.4), вообще
говоря, неразрешима. Условия ее разрешимости
Sl^^'""'^^ = 0 (^ = 1,2, ..., -х) A6.11)
L
будут вместе с тем и условиями разрешимости уравнения B1.1).
Заменяя ^(т) и Х+(т) их выражениями B1.5) и B1.10),
можно записать условия разрешимости в виде
$-Ш-^'~'^^==0 (fe=l, 2, ..., -х). B1.13)
L
Если условия разрешимости соблюдены, то решение
неоднородного уравнения B1.4) дается формулой B1.9) при
*) Оператор R обратен оператору К' в том смысле, что оператор К*
функцию ф переводит в функцию f, а оператор R обратно / в ф.

180 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
Сформулируем результаты исследования.
Г. Если X > О, то однородное уравнение К°ф = О имеет х
линейно независимых решений
^{t) = b{t)Z{t)t''-' (^=1, 2, ..., х).
2°. Если X ^ О, то однородное уравнение неразрешимо,
(Тривиальное нулевое решение в расчет не принимается.)
3°. Если X ^ О, то неоднородное уравнение разрешимо при
любой правой части f{t) и его оби^ее решение линейно
зависит от X произвольных постоянных.
4°. Если X < О, то неоднородное уравнение разрешимо
тогда и только тогда, когда его правая часть f удовлетворяет
—X условиям:
\^k{t)f{t)dt = 0, B1.14)
где i^,{t)^-J^t'-\
Сравнивая перечисленные свойства характеристического
особого интегрального уравнения со свойствами интегрального
уравнения Фредгольма (п. 20.2), можно усмотреть между ними
существенные различия. Для уравнения Фредгольма в случае
разрешимости однородного уравнения неоднородное, вообще
говоря, неразрешимо и, наоборот, в случае неразрешимости
первого второе безусловно разрешимо. Для особого же
уравнения при разрешимости однородного безусловно разрешимо и
неоднородное, при неразрешимости же первого, вообще говоря,
неразрешимо и второе.
Введем аналогично уравнению Фредгольма в ядро
характеристического уравнения параметр к и рассмотрим уравнение
к1ф^а@ф(<) + ^5-^йт = 0.
L
Как было показано, последнее уравнение разрешимо, если
^==ind-';;;-f,i;;>o.
а (t) + Ab (t)
Индекс непрерывной функции (п. 12.3) изменяется
скачкообразно, причем только для таких значений Я, для которых
a{tL^Xb{t) = 0. Если в комплексной плоскости X = Я,1 + йг
провести кривые X = ±-^jjy, то они разделят плоскость на
области, в каждой из которых индекс будет постоянным.
Таким образом, собственные значения характеристического
особого интегрального уравнения заполняют целые области, еле-

§ 2ll ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 181
довательно, спектр его, в отличие от спектра уравнения Фред-
гольма, является не дискретным, а сплошным.
21.3. Решение уравнения, союзного характеристическому.
Уравнение
K'>'^^am(t)—^\^^^^dx^h{t), B1.15)
L
союзное с характеристическим уравнением К°ф = /, само не
является характеристическим. Однако путем подстановки
6(Ог|?(/) = 0(О B1.16)
оно превращается в характеристическое уравнение
относительно функции о)(^):
a{t)^{t)-±^\^dx=^b{t)h{t). B1.17)
L
Определив из последнего уравнения (^(t) по формуле
получающейся сложением равенств B1.15) и B1.16), найдем
искомую функцию \|?@-
Вводя кусочно аналитическую функцию
тем же путем, что и в п. 21.2, придем к краевой задаче Римана
" U) — a{t)^b (t) " ^^^ -^ a(t)-^b (t) • ^^^'^^f
Коэффициент последней задачи есть величина, обратная
коэффициенту задачи Римана B1.4), соответствующей уравнению
К°ф = /. Следовательно,
г/-ТпН ci{t)-^b(t) _ Tr.fl ^W-^(^) - V то(\\
^ -^^^'a(t)^b(t)-^^'^^ a{t) + b(t) -~^- B^-20)
Вспоминая формулу A4.10), определяющую каноническую
функцию однородной задачи Римана, замечаем, что
канонические функции \'{z) для уравнения B1.19) и Х(г) для B1.4)
будут обратны по величине:
x'(.)=xir-

182 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
Поступая так же, как и в п. 21.2, получим решение особого
интегрального уравнения B1.15) при х^ = —х ^ О в виде
^it) = ait)h(t) + -^\ ИтJ(х)/.(х)^^^_1_^^^_^^^^^ ^^^^^^
L
где Z{t) задается формулой B1.10), Qx^-i (О — многочлен
степени х^—1 с произвольными коэффициентами. (Если х'= О,
то Q{t) = Q,)
Если х'= —X < О, то для разрешимости уравнения B1.15)
необходимо и достаточно выполнение условий
[b{t)Z{t)h{t)t^''^ dt = 0 (А;=1,2, ..., -к'\ B1.22)
при соблюдении которых решение дается формулой B1.21),
где нужно положить Qx'-i @^0.
Заметим, что условия разрешимости B1.13) и B1.22)
имеют такой вид, какой требуется третьей теоремой Фредголь-
ма. В дальнейшем мы покажем, что это же имеет место и в
общем случае для полного особого интегрального уравнения.
Результаты одновременного исследования
характеристического и союзного уравнений показывают новое существенное
отступление от свойств уравнения Фредгольма. Вопреки второй
теореме Фредгольма, союзные однородные особые
характеристические уравнения никогда не бывают одновременно
разрешимы. Они или оба неразрешимы (х = 0), или, при ненулевом
индексе, разрешимо то из них, которое имеет положительный
индекс.
Разность чисел решений характеристического и союзного
однородных уравнений равна индексу х. Это свойство,
справедливое, как будет показано ниже, и для полных уравнений,
является характернейшим для особых интегральных уравнений.
Утверждения Г, 2° и 3°, 4°, сформулированные в п. 21.2,
называются первой и второй теоремой Нётера для
характеристического уравнения, а отмеченная здесь связь индекса
уравнения с количеством решений однородных уравнений К°ф = О
и K°'\|) = О — г/7^гбей теоремой Нётера, В дальнейшем (п. 23.2)
они будут распространены на полное особое уравнение.
21.4. Примеры. Как уже отмечалось, основная трудность
практического решения задачи Римана, а следовательно, и
характеристического особого интегрального уравнения
заключается в вычислении особых интегралов, входящих в формулу
B1.9). Вычисление это в общем случае может быть
произведено применением приближенных методов интегрирования. При
этом чаще предпочитают не пользоваться окончательной фор-

§ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 183
мулой B1.9), а применять приближенные методы
непосредственно к самому уравнению B1.1) (см. ниже, п. 21.11).
Здесь ограничимся примером, когда решение краевой задачи
Римана B1.4), соответствующей интегральному уравнению,
было найдено элементарно, путем аналитического продолжения
(п. 14.6). Решение самого интегрального уравнения получим
непосредственно по формулам Сохоцкого B1.3).
Пусть дано интегральное уравнение
L
Здесь
Г(Л~- a(t)-b{t) t__ ..^ f(t) _P^t^ + \
^^^^~ a{t) + b(t) ~ f'-l ' ^^^^ a(t) + b(t)~ t^-^-t
И, следовательно, краевое условие B1.4) примет вид
Ф" (О = 7^ Ф" it) + ''~/_V-
Решение этой краевой задачи, удовлетворяющее условию
ф-(оо)= О, было получено в п. 14.6 для различных контуров L,
Г. Если L — контур из примера а) п. 14.6, то
Ф"'B) = г+^^, ф-{г) = -^ + ^
И решением заданного интегрального уравнения будет функция
cf(t) = 0Ut)-0-{t)^^^±^ + c^^.
2°. Если L — контур из примера в), то индекс равен —1;
условие разрешимости задачи Римана, как было показано,
выполняется, и
ф+B) = 2, ф-(г) = -^.
Решение интегрального уравнения дается формулой
Ф@ = Ф+@-Ф"@=-Ц^.
Разбор всех остальных случаев расположения контура
предоставляем читателю.
21.5. Полные особые уравнения, разрешаемые в замкнутой
форме*). В предыдущих пунктах исследовалось
характеристическое уравнение и союзное с ним и было показано, что они
решаются в замкнутой форме. Полное особое уравнение, в
отличие от них, не решается, вообще говоря, в замкнутой форме
*) Изложение этого пункта дано в основном по статье С. Г. Самко 1).

184 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
и В общем случае будет сведено к уравнению Фредгольма.
Однако имеется ряд случаев, когда и полное уравнение может
быть также решено в замкнутой форме. Рассмотрим сейчас
некоторые из таких случаев. Позже (в § 51) будут изучены и
другие типы полных уравнений, решаемых в замкнутой форме
с помощью более сложных теорий.
Решая полное уравнение
а(Оф@ + ^^^^^Ф^^^ = ^^' B1.23)
L
будем основываться на некоторых аналитических свойствах
функции Л1(^,т).
Лемма 1. Пусть функция Л1(/, т), гёльдеровская по обеим
переменным на контуре L, аналитически продолжима в область
D+ по каждой переменной. Если M(tyt)^ 1, то решение
уравнения
l.'^M_^,p^r)d'c^f{t) B1.24)
L
дается формулой обраи{ения, аналогичной G.13):
Действительно, применяя формулу перестановки G.7)
Пуанкаре— Бертрана, получим
nt J 1 — t яг J Ti — т ' ^ ^^ ^
L L
L L
-'^^^ + niLr:^\lu) T^t ^^-
L *- L
_1^«„.0*|(,..),1 ,,,,3j
L J
Так как функция M(^, т) аналитически продолжима в D+ по
каждой переменной, то согласно условию D.11)
J_J МК^^Ш^^^^^^^^ т,)М(^0 = Ма.т,).
L
4

^ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 185
Следовательно, выражение в квадратных скобках в B1.25)
равно нулю, что и доказывает лемму.
Уравнение B1.24) можно решить и не ограничивая функцию
M(tyT) условием M{t,t)^L Именно, пусть функция M{t,x)
аналитически продол>кима в D+ по каждой переменной, и пусть
М(г, z)=7^0 для z^D+, Тогда решение уравнения B1.24) дается
формулой
^^^^ ni M(t, /) J Af(T, т) x-t ' {^1.^0}
L
Рассмотрим теперь уравнение B1.23). Запишем его в виде
^^Ф^ + т5-ГГ7^^ + ^^(^ т)ф(т)йт = /@, B1.27)
где, очевидно, b{t) = M{t, t).
Покажем, что уравнение B1.27) решается в замкнутой
форме, если a{t) и b{t) постоянны, а /С(/, т) — любая функция,
аналитически продолжимая в область D+ по каждой переменной.
Уравнение B1.27) при указанных предположениях имеет вид
аф@ + -^5^^^^Ф(т)^т = /@, B1.28)
где M{t,x)=zb + ni{x—t)K{t,x), так что Л1 (/,/) = 6 = const.
Пусть 6 =7^ 0. Обозначим
Согласно лемме 1 функция ф(/) выражается через г|?@ точно
так же, как y^{t) через ф@. Уравнение B1.28) записываем в
виде
acs>{t) + by^{t) = f{t). B1.30)
Применяя к обеим частям операцию B1.29), получим
a^{t) + bif{t) = g{t\ B1.31)
где обозначено
L
Решая систему уравнений B1.30) —B1.31), находим ф(/):
ф@ = ^г^[«/@--^75^т5гГ-/^^^] B1.32)
при условии, что а ^ ±,Ь,

186 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ТЛ. Ш
Таким образом, при а ф ±Ъ и аналитически продолжимом
ядре K{t,%) уравнение B1.28) разрешимо и имеет единственное
решение, даваемое формулой B1.32).
Уравнение B1.27) рассматривалось при b Ф 0. Это
предположение естественно ввиду того, что при b ^ О уравнение
B1.27) перестает быть особым. Покажем, однако, что и
получаемое при b = О фредгольмово уравнение
аф
{t)+\K (/, т) ф (т) dx = / (О, а = const, B1.33)
разрешимо в замкнутой форме при аналитически продолжимом
ядре K(tyX), Применим следующую лемму, которая
понадобится и в дальнейшем.
Лемма 2. Пусть функция K(t, х) аналитически продолжима
в область D+ по каждой переменной и непрерывна при t,x^ L
Тогда 1) функция
0+(/)=JiC(/, т)ф(т)йт
аналитически продолжима в область D+ для любой гёльдеров-
ской функции ф(/);
2) если гёльдеровская функция ф+@ аналитически
продолжима в область ?)+, то
J/C(^ т)ф+(т)йт = 0. B1.34)
L
Утверждение 1) леммы получается непосредственной
проверкой условия D.11), а утверждение 2) вытекает из
интегральной теоремы Коши.
В силу леммы 2
^K{t, x)dx J/C(t, x,)(p{x^)dx, = 0 B1.35)
L L
для любой (гёльдеровской) функции ф@. Поэтому из B1.33)
находим, что
a\K{t, т)ф(т)йт= J/C(^ x)f{x)dx
и тогда
Ф (О = ^ [а/ (О - S /С (^ х) f (т) dx j. B1.36)
Следовательно, если ядро /С(/, т) аналитично в области D+
по каждой переменной и непрерывно при t^x^L, то уравнение

§ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 187
B1.33) разрешимо при любой правой части и его решение
дается формулой B1.36).
Перейдем, наконец, к общему случаю разрешимости
уравнения B1.27) в замкнутой форме, когда функция ' ' ^^
a(t) + b(t)
аналитична по х и мероморфна по t в области D+.
Обозначим для краткости
Кф= J/C(/, т)ф(т)^т
и заметим, что
Кф+=0 B1.37)
для всякой функции ф+@» аналитически продолжимой в
область D+ Полагая, согласно A4.3), ф@==Ф"^@—Ф""@>
приводим с учетом B1.37) уравнение B1.27) к соотношению типа
задачи Римана
ф-" (О - а it) lb (t) ^^"" = ^ (^) Ф"^ ^^^ + g -^^> B1-3^^
где, как обычно,
^^^> а (О+ 6 (О' ^^' a{t) + b{t)-
По предположению имеем
К (t, т) _ /1+ (/, т)
a(i) + b{t) 11+it)
n''{t) = l[it-z,ri^, B1.39)
fe = l
где Zh^D+, nth — целые положительные числа, а функция
Л+(/, т) аналитична по / и по т в D+.
Соотношение B1.38) принимает вид
П^ (О Ф^ (О + Л-^ф- = П^ (О [G (О Ф- (/) + g (/)], B1.40)
где Л+—интегральный оператор с ядром Л+(^, т). Так как
функция Л+ф- аналитична в D+ (см. лемму 2), то последнее
соотношение представляет собой обычную задачу Римана,
из которой в замкнутой форме определяются функции
П+(/)ф+(/) + ^"^Ф~ и ф-@» 2 следовательно, и ф(/). Именно,
Х+ (Л
записывая G{t) в виде G@ = —i—, где Х±(г)—канониче-
X {t)
екая функция задачи Римана, и приводя соотношение B1.40)
к виду, допускающему применение теоремы Лиувилля, придем
п
к многочлену степени >^ — 1 + 2] ^jfe с произвольными коэффи-

188 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. III
п
циентами (в случае х+Х^а>0)- Однако наличие множи-
теля П+(/) перед ф+@» обращающегося в О в D+ с суммарным
п
порядком нулей Yj f^ky очевидно, уменьшит число произволь-
ных постоянных в общем решении. (Соответствующие выкладки
предоставляются читателю.)
Заметим в заключение, что аналогично может быть
рассмотрен случай, когда ядро K{t,x) мероморфно и по т. Тогда
уравнение B1.27) можно свести к задаче Римана типа B1.38) и
некоторой линейной алгебраической системе.
Примеры. Рассмотрим уравнения
1. Яф(/) + ^5^^^^^ф(т)йт = /@.
L
2. \ц> (О + ^ j %%Р Ф (т) dx = f it).
L
Замечаем, что функции M(/, т) = cos(t — t) и Л1(^, т) ==
= —^^^ обладают свойством M(t,t)^ 1. Поэтому остается
воспользоваться формулой B1.32), так что соответственно для
1 и 2 имеем
Здесь L — произвольный замкнутый контур и Л^±1.
3. Уравнение
Pit)^(t) + ^\-^dt + \^<f{x)dr = f(t),
L L
где P{t), Q@» ^@ и p{t,x)—многочлены, относится к
рассматриваемому случаю и, следовательно, решается в замкнутой
форме для любого замкнутого контура L, не проходящего через
нули многочлена /?@-
21.6. Уравнение на действительной оси. Исчезающие на
бесконечности решения*). Построенная в гл. I теория интеграла
типа Коши показывает, что если плотность интеграла типа Ко-
ши, взятого по бесконечной кривой, равна нулю на бесконечно-
*) Материал пп. 21.6—21.10 взят из работ А. С. Мотки на 1), 2) и
других его статей.

§ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 189
сти, ТО свойства интеграла в случаях конечного и бесконечного
контуров во всем суш.ественном совпадают. В полном
соответствии с этим, как будет далее показано, теория особого
интегрального уравнения на бесконечном контуре в классе
исчезающих на бесконечности решений совпадет с изложенной выше
теорией уравнения на конечном контуре. В случае же ф(сю)=7^0
условия представимости кусочно аналитической функции для
конечного и бесконечного контуров (A.6) и D.29)
соответственно) различны. Это, как увидим ниже, ведет к далеко идущему
различию в теории особых интегральных уравнений на
бесконечном и конечном контурах.
Так же, как в случае конечного контура, особое
интегральное уравнение
оо
a{t)cf{t) + ^ \-^dx = f{t) B1.41)
— оо
с помощью интеграла типа Коши
оо
-^оо
и формул B1.3) сводим к краевой задаче Римана
^"'(^) = 7{f^^~W + 7G5TW (--<^<-)- B1.43)
Из формул B1.3) условие равносильности особого
уравнения и краевой задачи можно представить в виде
ОС
i S ^^4^Р^йт = Ф-@ + ф-@. B1.44)
— оо
Оно имеет тот же вид, что и в случае конечного контура, и
автоматически удовлетворяется, если решение представимо
интегралом типа Коши. Условием такой представимости является,
как показано в п. 4.6, выполнение равенства D.29).
Следовательно, соотношение D.29), т. е.
Ф+(оо) + Ф'-(сх)) = 0,
является условием равносильности интегрального уравнения
B1.41) и краевой задачи B1.43). Здесь оно заменяет
аналогичное условие A.6):
ф-(оо) = 0,
справедливое для конечного контура.

190 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
Если D.29) выполнено, то из решения краевой задачи
B1.43) по формуле
ф(^) = ф+(/)~ф-(/) B1.45)
получим решение уравнения B1.41).
Для упрощения дальнейших формул будем считать
выполненным условие
a4t)-bHt)=l, B1.46)
Обозначим x = Ind ^L T^L • Сначала будем искать решение
уравнения в классе исчезающих на бесконечности функций.
Полагая в уравнении B1.41) t = оо и учитывая D.30) и
равенство ф(оо)=0, получим, что необходимо должно
выполняться условие f(oo) = 0. Из D.28) следует, что ф+(оо)=:
= ф-(оо) = 0. Следовательно, условие D.29) автоматически
выполняется (здесь оно совпадает с условием A,6) для
конечного контура).
Используя формулы A4.25) — A4.30) решения задачи Ри-
мана для полуплоскости и поступая так же, как и в п. 21.2 для
конечного контура, получим при х ^ О решение интегрального
уравнения
оо
^it) = a{t)fit)—^^^ \^^^^b(t)Z(t)^ff^. B1.47)
-оо U "Г О
В случае х ^ О нужно положить Px-i {t)^0 и потребовать
при X < О выполнения условий разрешимости
оо
[ fix) dx_^Q (;^_1^ 2, ..., ~х). B1.48)
Z{r) (x+i)
Можно так же, как это делается в п. 21.3, доказать
справедливость теорем Нётера.
Как видим, результаты здесь совершенно аналогичны
полученным для уравнения на конечном контуре.
21.7. Уравнение на действительной оси. Решение в классе
ограниченных на бесконечности функций. Исследуем прежде
всего выполнимость условия равносильности D.29). Вычислим,
используя формулы D.28), предельные значения решения
A4.27), A4.28) задачи Римана B1.43) в бесконечно удаленной
точке. После некоторых выкладок получим
f(oo)
ф+ (оо) = 1^^ + '-
ф- (СХ>) = -/ (оо) -(^)-^Ь(оо) ^ ^ ^^ (^) ^ ^^ (^)j^

§ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 191
Здесь с — коэффициент при старшем члене многочлена Py.{z)y
если X ^ О, и
--^ \
^ ^, если к<0. B1.49)
— оо
Х"^ (Т) Т + / '
Отсюда Ф+(оо) + Ф"'(оо) = 2а(оо)-с — f(oo)»b(oo), и условие
D.29) равносильности интегрального уравнения B1.41) и
задачи Римана B1.43) примет вид
2a(oo).c==f(oo).6(oo). B1.50)
Из приведенных рассуждений следует
Теорема. Особое уравнение B1.41) и задача Римана для
действительной оси с дополнительным условием B1.50)
равносильны в следующем смысле: если Ф(г) есть общее решение
краевой задачи B1.43), удовлетворяющее условию B1.50), где
с — коэффициент при старшей степени многочлена Py,(z) при
оо
3<>0, и C='-';r-r \ -^^ z при X < 0, TO
^ ' 2я^ J [a (t) + Ъ (t)] X+ (t) t + / '^
— oo
функция B1.45) есть решение уравнения B1.41); обратно, если
((>{t) —общее решение уравнения B1.41), то интеграл типа
оо
Коши ФB:) = у^ \ ^_ dx есть решение задачи Римана
— оо
B1.43), удовлетворяющее условию B1.50).
Следует различать два существенно различных случая:
а{оо)фО^ а(оо) = 0.
21.8. Случай а(оо)^0. Здесь из условия B1.50) с
определяется единственным образом. Для однородного уравнения
(/ ^ 0) с = 0. Общее решение однородного уравнения при
х>0 содержит произвольный многочлен Px-i@» и,
следовательно, уравнение имеет х линейно независимых решений. При
X ^ О однородное уравнение неразрешимо.
Для неоднородного уравнения из условия B1.50)
/(оо).б(оо)
с = -
2а (оо)
Решение уравнения можно получить по формуле ф@==
= Ф+@ — Ф"@» ^сли при х^О в решении краевой задачи
Римана A4.27) положить старший коэффициент многочлена
равным
f(oo)'bicc)
2а (оо)

192 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. И!
а при X < о к условиям разрешимости задачи Римана
прибавить дополнительное условие
оо
1 с /(т) dx _ /(оо).б(оо) /2151)
Ji' J [о (т) + 6 (т)] Х+(т) x + i а(оо)
— ОО
Можно показать, что третья теорема Нётера о разности
чисел решений транспонированных уравнений {п — п^ = к)
остается справедливой; вторая же теорема о разрешимости
неоднородного уравнения будет верна, как следует из равенства
B1.51), лишь при f{oo)'b{oo) = 0. В этом состоит отличие
теории интегрального уравнения по бесконечному контуру от
теории на конечном.
21,9. Случай а(оо) ^0. Для однородного уравнения (f ^ 0)
условие равносильности B1.50) удовлетворяется автоматически
для произвольных значений с. Общее решение однородного
уравнения при х^О содержит произвольный многочлен Рк@>
и, следовательно, однородное уравнение имеет к + 1 линейно
независимых решений. При х < О однородное уравнение
неразрешимо.
Учитывая, что на основании B1.46) Ь{оо)=±:1фО, для
существования решений краевой задачи, удовлетворяющих
неоднородному уравнению B1.41), и, следовательно, для
разрешимости неоднородного уравнения необходимо должно
удовлетворяться равенство
f(oo) = 0. B1.52)
Последнее условие разрешимости можно получить
непосредственно, полагая в обеих частях уравнения C1.41) t = оо. Если
это условие не выполнено, то неоднородное уравнение B1.41)
неразрешимо, каков бы ни был его индекс.
Допустим, что условие B1.52) удовлетворено. Тогда условие
B1.50) выполняется для произвольного с\ следовательно,
решение неоднородного уравнения при х^—1 зависит линейно
от х+ 1 произвольных постоянных. При X < —1, кроме B1.52),
должны удовлетворяться —х—1 условий разрешимости:
оо
\
_ш-^=° '*-' -"'¦ <^'-='>
транспонированное к B1.41) однородное уравнение
со
а@^'@-^ 5^^^^dT = 0 B1.64)

I 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ Ш
обычным способом сводится К краевой задаче Римана
^''@-;{,^}lfe{iJ4^~@- B1.55)
Если индекс исходного уравнения есть х, то индекс
транспонированного будет х' = —X. Обозначим /, Г числа линейно
независимых решений соответственно у данного и
транспонированного уравнений. Тогда:
Если х = 0, то х' = 0, / = Г=1, / —Г = 0.
Если X > О, то х' < О, / = X + 1, Г = О, / — Г = х + 1.
Если х<0, то х'>0, 1 = 0, Г = --х+ 1, Z —Г = х— 1.
Следовательно, в случае а(оо) = 0 лишь при нулевом
индексе соблюдается третья теорема Нётера. В остальных
случаях наблюдается отклонение, причем различное в случае
положительного и отрицательного индексов.
Естественно поставить вопрос, в чем заключается причина
такого большого отличия теории особого интегрального
уравнения на бесконечном контуре от подобной теории на
конечном контуре. Полное решение этого вопроса довольно сложно
и опирается на теорию абстрактных нётеровых операторов
(см. далее, п. 23.4). Не входя в подробности, все же укажем
главное.
Так как значения на бесконечности заданных и искомых
функций влияют на число решений и условий разрешимости,
то рассматриваемое особое интегральное уравнение B1.41) в
классе решений, не исчезающих на бесконечности, не является
аналогом такого же точно по форме уравнения на конечном
контуре. Оно представляет собой аналог полного уравнения.
Чтобы убедиться в этом, нужно рассматриваемые функции
разбить на две составляющие: функцию, исчезающую на
бесконечности, и постоянную, равную значению функции на
бесконечности (ф@== Фо@ + ф(°^) и т. п.). Соответственно этому
уравнение превратится в пару уравнений: особое интегральное
относительно (ро@ и числовое соотношение на бесконечности.
Уравнение сопряженное будет также представлять собою
совокупность особого интегрального уравнения относительно г|)о@
и числового соотношения на бесконечности. Скалярное
произведение функций будет составляться по правилу скалярного
произведения векторов (ф, if) = (фо,'фо) + ф(оо) • г|?(оо).
При таком построении теории оказываются справедливыми
все теоремы Нётера и теория особого интегрального уравнения
на бесконечном контуре составляет часть общей теории так
называемых нётеровых операторов (см, п. 23.4).

194 ОСОБЫЕ Интегральные уравнения с ядром коши [ГЛ. iti
21.10. Уравнение, аналогичное характеристическому. На
действительной оси аналогом характеристического уравнения
будет уравнение вида
—оо
где го —точка, не лежащая на контуре; для него будут
справедливы все качественные результаты и формулы, полученные
в пп. 21.1—21.2 для характеристического уравнения на
замкнутом конечном контуре. В частности, оказываются
справедливыми формулы обращения интеграла типа Коши, аналогичные
формулам G.12), G.13) для конечного контура*):
оо оо
—оо —00
в заключение отметим, что все приведенные в пп. 21.6—
21.10 результаты переносятся безо всяких изменений на случай
произвольного гладкого контура, уходящего в бесконечность с
одним общим асимптотическим направлением. Действительная
ось была взята лишь для упрощения формулировок. Если
контур уходит в бесконечность с двумя различными
асимптотическими направлениями, то следует внести поправку на то, что
бесконечно удаленная точка будет угловой точкой контура.
21.11. Приближенное решение. Решение характеристического особого
интегрального уравнения равносильно отысканию контурных значений решения
краевой задачи Римана. Поэтому любой способ решения краевой задачи (см.,
например, п. 16.3, 6°) представляет собой одновременно и способ решения
интегрального уравнения. Однако отыскание одних лишь контурных
значений может быть произведено проще, чем отыскание всего решения
краевой задачи. На этом основаны специальные методы решения
характеристического уравнения. Приведем здесь схематически два таких метода, указанные
В. В. Ивановым 1), 2).
Пусть
a(t)<^(i) + ^\^dx^nt) B1.1)
Y
— заданное уравнение и
Ф+@-0(ОФ-@ = §{0 {g = T+T> ^ = 74т) <21-4)
*) д. Пшеворска-Ролевич в работе Sur Tintegrale de Cauchy
pour un arc ferme a I'infini. Ann. Polon. Math., 8, 1960 приводит формулы
обращения в том же виде, что и для конечного контура. Но это не так, что
можно показать на простом примере.

§ 21] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 195
— соответствующая ему краевая задача Римана. Будем считать, что контур у
есть окружность и что
x=Ind -Ц^>0.
а + b
1. Метод моментов. Формула A4.18') показывает, что существует я
линейно независимых решений задачи Римана, имеющих на бесконечности
соответственно порядки 1, 2, ..., х. Для определенности будем искать
решение, имеющее на бесконечности наивысший возможный порядок.
Приближенное решение ищем в виде
ф^(о = 1]^/, ф"(о= Ё ^/"^ B1.56)
Подставляя B1.56) в B1.4), затем умножая последовательно на ?•'+*
(/ = 0, ±1, ..., dtn) и интегрируя по у, получим для определения
постоянных Са 2/1 + 1 уравнений *)
Опираясь на общие методы приближенных вычислений (Л. В.
Канторович, Г. П. Акилов, Функциональный анализ в нормированных
пространствах, Физматгиз, М., 1959, гл. XIV), можно доказать, что при достаточно
большом п система B1.57) безусловно и однозначно разрешима.
2. Смешанный метод. Здесь также решение ищется в форме B1.56),
ко уравнения для определения постоянных ск выводятся не приравниванием
моментов, а из интерполяционного требования совпадения левой и правой
частей B1.4) в 2/г + 1 точках окружности. Их для простоты можно брать
С-^-^О
равноотстоящими V//= е "''^'^ ) . Система запишется в виде
t "k^l - G С/) t-r ~t "ki) = 8 {t,). B1.58)
Можно доказать, что при достаточно большом п система безусловно и
однозначно разрешима.
Решение уравнения B1.1) определится формулой
ф@ = Ф'^(/)-Ф~(/) = |;с/- 2 V^"**- B1-59)
В случае >« < О, если условия разрешимости A6.11) выполнены, решение
уравнения можно искать в виде
Те же методы с небольшими видоизменениями применимы и к решению
полного уравнения B0.3).
*) Это есть приравнивание «моментов» левой и правой частей B1.4).
Отсюда название метода.

196 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ 1ГЛ. П1
Изложение используемых ныне методов приближенного решения особых
интегральных уравнений дано в довольно полном виде в монографии [11].
21.12. Поведение решения в угловых точках. Из формул Сохоцкого для
угловых точек D.18), D.19) получим пару равносильных им формул:
Ф@ = Ф"*'@-Ф''(а B1.61)
L
Проанализировав внимательно решение краевой задачи Римана, можно
обнаружить, что в нем используется лишь одна из формул Сохоцкого, а
именно B1.61). Но эта формула имеет для угловой точки совершенно
тот же вид, что и для точки гладкости контура. Отсюда следует, что решение
задачи Римана от наличия на контуре угловых точек не изменяется и все
полученное для этой задачи на гладком контуре остается без изменения и
для контура с угловыми точками*).
Посмотрим теперь, как обстоит дело с решением характеристического
уравнения
а (/) Ф W + -^ J -^ dx = / @. B1.1)
L
В точке гладкости контура (а == я) для особого интеграла справед-
л С i \
лива формула —г \ __ . f/т ==» Ф @ + Ф~ (О- Для изолированной угловой
точки его предельные значения слева и справа будут выражаться той же
формулой. Но само значение особого интеграла в угловой точке должно
вычисляться по формул§ B1.62). Следовательно, угловая точка для особого
интеграла будет точкой устранимого разрыва. Отсюда легко вывести, что
уравнение B1.1), вообще говоря, не может в угловой точке /о иметь непрерывного
решения. В самом деле, если допустить, что 6(/о)'#'0 и ф(^о) непрерывна,
получим противоречие, так как в уравнении один член будет разрывным, а
остальные непрерывными.
Будем искать решение уравнения в виде
Ф@==Ф1@ + иО. B1.63)
где ф1 (О—функция, удовлетворяющая условию Гёльдера, \(t) равна нулю
всюду, кроме угловых точек. Вставляя B1.63) в уравнение и замечая, что
\ \J. dx s О, получим
L
а (t) Ф1 (О + -^ J -^ dx = / (t) - а (/) I (/). B1.64)
L
Здесь ф1 и 5 нужно подобрать так, чтобы уравнение удовлетворялось.
Вводя интеграл типа Коши Ф (г) = -—г \ -^-^— dx и учитывая, что во
всех неугловых точках для его предельных значений должны выполняться
обычные формулы Сохсщкого и g@=0, получим, что для точек гладкости
*) Пака имеется в виду лишь конечное число угловых точек.

§ 2!] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 197
уравнение B1.1) сводится к обычной краевой задаче Римана, которую
запишем в форме
[а (О + b (/)] Ф+ (/) - [а it) - b it)] Ф- (/) = / (/). B1.65)
В последнем равенстве все члены — непрерывные функции, поэтому оно,
выполняясь почти везде, необходимо выполняется везде*). Следовательно,
краевое условие B1.65) справедливо для всего контура, не исключая и угловых
точек. Но, с другой стороны, для угловых точек справедливы формулы Сохоц-
кого B1.61), B1.62) (в которых ф нужно заменить на ф1). Поэтому из
B1.64) получаем, что для угловых точек контура краевое условие будет иметь
вид
[а (t) + ^b (/)] Ф+ (О ~ [а (t) - B - -^) /^ (/)] Ф- (О = / (О - а (/) I (/).
B1.66)
Исключая отсюда f{i) с помощью B1.65), полу-чим для l(t) следующее
выражение:
^ (') "-Щ- (' - ?) '^^^ ('^ - '^" (')^- B'-^^)
При этом предполагается, что в угловой точке аA)Ф 0. Случай a{t)= О
является исключительным.
Таким образом, для всех неугловых точек решение особого уравнения
получается из решения краевой задачи Римана B1.65) по обычной формуле
Ф@ = Ф1(/) = ф-^@~Ф"(а
для угловых же точек нужно к решению прибавить еще выражение B1.67).
Рассматривая угол между левым и правым касательными векторами
контура как функцию точки а = а(/) (для точек гладкости а (О == я), можно
записать решение уравнения для всего контура в виде одной формулы **)
Ф (О = Ф1 (О + МО = { 1 + -^ [l - ^\ ] [Ф+ (О - Ф- (/)], B1.68)
где Ф±@ —решение краевой задачи B1.65).
До сих пор предполагали на контуре лишь конечное число угловых точек.
В этом случае вопрос полностью разрешается при помощи одних лишь
элементарных соображений. Естественно поставить вопрос, для какого наиболее
широкого класса контуров указанные рассуждения остаются в силе?
Рассмотрение этого вопроса требует привлечения аппарата теории функций
действительного переменного. Формулируем результат, полученный А. Д.
Алексеевым 1), 2).
Если контур L есть замкнутая кривая, в каждой точке которой
существует левая и правая касательные, непрерывные сооответственно слева и
справа, то для решения уравнения B1.1) остается справедливой формула
B1.68). Укажем, что рассматриваемые контуры (А. Д. Алексеев назвал их
кривыми класса R) могут иметь счетное множество угловых точек. Но при
*) Проведенное в § 5 рассуждение о характере предельных значений»
интеграла типа Коши остается в силе и для контура с угловыми точками.
**\ Этот результат иным способом был получен Д. А. К в е с е л а в а 3)«

198 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
ЭТОМ ЧИСЛО угловых точек, для которых скачок угла касательной с осью
абсцисс превышает заданное число е > О, всегда лишь конечно. Контуры
класса R включают в себя как часть введенный И. Радоном класс кривых с
ограниченным вращением*).
§ 22. Регуляризация полного уравнения
22.1. Композиция особых операторов. Как было показано в
§ 21, некоторые простейшие особые интегральные уравнения
решаются в замкнутой форме. В дальнейшем (гл. VII) будут
выделены некоторые частные типы полных особых
интегральных уравнений, которые также могут быть разрешены в
замкнутой форме. В обш,ем же случае решение особых интегральных
уравнений производится приведением их к интегральному
уравнению Фредгольма.
Процесс приведения особого (сингулярного) интегрального
уравнения к уравнению Фредгольма (регулярному) называется
регуляризацией. Ниже будут изложены различные способы
регуляризации, важнейшие из которых состоят в применении к
особому оператору другого, специально подобранного, особого
оператора.
Пусть КьКг — особые операторы:
L
К2(о=02 @«) (О + i S ^^7^ «(^) ^^- B2.2)
L
Оператор К = К2Кь определяемый формулой Кф = К2(К1ф),
будем называть композицией или произведением операторов
К] и Кг (в указанном порядке: произведение операторов,
вообще говоря, не переместительно).
Составим выражение для оператора К:
Кф = К^К.ф = а, it) [а, it) Ф (О + ^ J -^7^ ^ W ^-^J +
+ iS^T#7^[-^(^)^W + i5 B2.3)
¦) См. «Успехи матем. наук», т. I, эып. 3—4, 1946, стр. 96—124.

§22) РЕГУЛЯРИЗАЦИЯ ПОЛНОГО УРАВНЕНИЯ 19^
И выделим его характеристическую часть. Для этого проделаем
следующие преобразования:
J ^1/ Ф(-г)^т^ = All (^ О J ^^'^ + J ^^^ Ф(-^)^-г,
——^ ф (т) dt =
L
^adt)M,(t, О j ^dT + S °' ^"^""'^'' '-iIГ ^'^^'^'' '^ Ф(т) rfr,
Z, L
B2.4)
Л^См.(^т) _1^ГЛ1.(г,т,)
=MAt, t)MAt, оф(о+^5ф(х.)^т.± 5 ^;f^^;^!:;;^ ^т.
L L
(В последней строке мы воспользовались формулой
перестановки порядка интегрирования G.7).)
Легко усмотреть, что все ядра интегралов в последних
слагаемых правых частей формул B2.4) в точке х = t имеют
особенность порядка не выше
|т-/|^-1 (Л<1).
Для первых двух ядер, если учесть, что функции ai(/),
Ali(/,т), M2{tyT) удовлетворяют условию Гёльдера, это
очевидно. В последнем ядре, вводя обозначение M2{t,x)Mi(xyX\) =
= M{tuXyXi)y сделаем преобразование:
_ 01 (/, Т|) --аJ(/, Ti)
xi-t
где
,, ч f Af(/, т, Ti) * /2 \ { М(/, т, Ti) ,
^1 i^> Ti) = J \Jt dx, ©2{t> b) = J ^^^/ dx.
L L
Ha основании п. 5.1 функции a)i(f, xi), co2(/, ti) удовлетворяют
условию Гёльдера и, кроме того, (Oi(/, О = «2(^, О» поэтому
последнее ядро также имеет при т = t особенность не выше
|т—/|^~^ Обозначая, как в п. 20.1,
M,{tJ) = b,{t\ MAtyt)==bAt\ B2.5)

^ОО ОСОБЫЕ интегральный уравнения с ядром КОШИ [ГЛ. 1П
получим, что характеристический оператор К** композиции
"(произведения) К двух особых операторов Ki и Кг выражается
формулой
К°ф = (К2К1Г Ф = [^2 (О а, it) + b, (t) b, @1Ф (О +
^ fl2@^i@ + ^2@fli@ f Ф(т) ^^ ,22 6)
L
Запишем операторы Кь Кг в форме B0.3) с явно
выделенной характеристической частью:
К1Ф=а1(/)ф@ + -^5^^т+5/^1(/,т)ф(т)^т, B2.7)
L L
К2(о^а2@ (О(О + -^ 5 ^dT + \ k,{t, т)со(т) dx. B2.8)
L L
Таким образом, коэффициенты a{t), b(t)
характеристической части произведения операторов К2К1 выражаются
формулами
a{t) = a,{t)a,{t) + b,{t)b,{t)^
b{t) = aAt)bAt) + bAt)a,{t).) ^ -^^
Эти формулы не содержат регулярных ядер ku ^2 и они
симметричны относительно индексов 1 и 2. Отсюда заключаем:
Г. Характеристическая часть произведения особых опера-
торов не зависит от их регулярной части и не зависит от
порядка следования этих операторов в произведении.
Таким образом, изменение порядка операторов, а также
изменение их регулярной части оказывает влияние только на
регулярную часть произведения операторов, не затрагивая ее
характеристической части.
Вычислим коэффициент задачи Римана, соответствующей
характеристическому оператору (K2Ki)°. По формулам B1.5),
B2.9) имеем
^@- a(t) + b(t)-[a,{t) + b,(t)]laAt) + b,(t)]-^^^^^^^^^f^ B2.10)
где
обозначены коэффициенты задач Римана, соответствующих
операторам К?, Кг. Из этого вытекает важное заключение:
2°. Коэффициент задачи Римана оператора (K2Ki)° равен
произведению коэффициентов задач Римана операторов К? и
Кг, Uy следовательно, индекс произведения особых операторов
равен сумме индексов перемножаемых операторов:
>с = }<1+>С2. B2.12)

§ 22] РЕГУЛЯРИЗАЦИЯ ПОЛНОГО УРАВНЕНИЯ 201
В ПОЛНОМ виде оператор К2К1 будет определяться
выражением
L L
где a{t)y b{t) определяются формулами B2.9). Для
регулярного ядра k{t,x) на основании формул B2.4) легко выписать
явное выражение, но так как в дальнейшем нигде этим
выражением не будем пользоваться, то его и не приводим.
22.2. Регуляризующий оператор. Если особый оператор Кг
таков, что оператор К2К1 является регулярным (фредгольмо-
вым), т. е. в нем отсутствует особый интеграл (b(/)sO), то Кг
называется регуляризующим оператором по отношению к
особому оператору Ki или, коротко, его регуляризатором.
Заметим, что если Кг является регуляризатором, то в силу
свойства Р композиции операторов регулярным будет и
оператор KiKz.
Найдем общий вид регуляризующего оператора.
По определению, должно выполняться равенство
b (t) = а2 (t) 61 (/) + 62 (О cii{t) = О, B2.13)
из которого следует, что
«2 (t) = и (t) а, (/), б2 {t) = -u (О Ь, (О, B2.14)
где u{t)—произвольная неисчезающая функция,
удовлетворяющая условию Гёльдера.
Следовательно, если К — особый оператор:
Кф = а@ф@ + -^$-^^^т+5^(^т)ф(т)йт, B2.15)
то общий ВИД его регуляризатора, который будем обозначать К,
таков:
K(i>^u{t)a{t)(o{t)- ""^^1^^^^^ ^~j^dT + ^fe(^T)(o(T)rfT, B2.16)
L L
где k{tyX) — произвольное фредгольмово ядро, а
u{t)—произвольная функция, удовлетворяющая условию Гёльдера.
Так как индекс регулярного оператора F(^)^0), очевидно,
равен нулю, то из свойства 2° произведения операторов
вытекает, что индекс регуляризующего оператора равен по
абсолютной величине и обратен по знаку индексу регуляризуемого
оператора. Это же заключение можно сделать непосредственно

202 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
ПО виду регуляризующего оператора B2.16), исходя из того,
что
G(t)= ^(^)-И0 _^ a{t) + b{t) ^ 1
a{i) + b{t) a(t)^b{t) G(t)'
Таким образом, для любого особого оператора с ядром Ко-
ши B2.15) нормального типа {a{t)dz b(t)^ 0) существует
бесчисленное множество регуляризующих операторов B2.16) с
характеристической частью, зависящей от произвольной функции
u{t), и содержащих произвольное регулярное ядро й(/,т).
Произвольными элементами м(/),й(^,т) можно, при случае,
распорядиться так, чтобы регуляризующий оператор
удовлетворял некоторым дополнительным условиям. Можно, например,
добиться в регуляризованном уравнении нормирования
коэффициента при ф, сделав его равным единице. Для этого нужно
положить и= 1/(а2 — Ь^). Если никаких условий не налагается,
то естественно воспользоваться простейшими регуляризаторами.
Мы получим их, если в формуле B2.16) положим:
Г. w(/)^l, й(^, т)^0, после чего регуляризатор будет
иметь вид
К(о = К^°0 ^a{t)(o (О - -^ 5 -^ dx; B2.17)
L
Т. «@ = 1, fe(/,T) = -i.^i4^' ™^ла
Ко = К°'(о = а (О (О (О - -jjf S ^^^^^^^^ dx. B2.18)
L
Простейшие операторы К'° и К°' употребляются в качестве
регуляризаторов наиболее часто.
Так как перемножение операторов не переместительно, то
следует различать два вида регуляризации: регуляризацию
слева, когда в результате получается оператор КК, и
регуляризацию справа, когда она приводит к оператору КК.
На основании сделанного выше замечания регуляризатор
справа является одновременно и регуляризатором слева, и наоборот.
Таким образом, операция регуляризации переместительна.
Из свойства 1° п. 22.1 вытекает, что эта операция взаимна,
т. е. если оператор К является регуляризующим для оператора
К, то и обратно, оператор К является регуляризатором для
оператора К.
Операторы К1К2 и К2К1 могут отличаться друг от друга
лишь регулярной частью. Если обозначить регулярный (фред-
^ольмов) оператор Г, то символически связь между произведе-

§ 22) РЕГУЛЯРИЗАЦИЯ ПОЛНОГО УРАВНЕНИЯ 203
ниями особых операторов, отличающимися порядком
следования множителей, будет записываться так:
К|К.2 — К-2"^! ^^^^ ^*
22.3. Способы регуляризации. Пусть дано полное особое
интегральное уравнение
^^^a{t)^{t)+^\^dx + \k{t,T)^{x)dx = f{t). B2.19)
L L
Как уже указывалось, решение (а также и теоретическое
исследование) такого уравнения производится путем
регуляризации*). Употребительны три способа регуляризации. Первые два
основаны на композиции данного сингулярного оператора и его
регуляризатора (регуляризация слева и справа). Третий способ
существенно отличается от первых двух, здесь устранение
особого интеграла производится путем решения соответствующего
характеристического уравнения.
При построении теории сингулярного уравнения (теоремы
Нётера) нами будут использованы только первые два способа
регуляризации, поэтому изложим в первую очередь их, а
изложение третьего способа, чтобы не прерывать логическую связь,
отнесем на конец § 24.
Г. Регуляризация слева. Возьмем регуляризующий
оператор B2.16)
К© = W (О а (t) о (О - -^^^^1^ \ -^ dx + \k (/, т) со (т) dr. B2.20)
L L
Подставляя в Ко вместо функции со выражение Кф — /,
придем к интегральному уравнению
ККф = К/. B2.21)
По определению (К — регуляризатор) оператор КК фредголь-
мов, следовательно, уравнение B2.21) есть уравнение Фред-
гольма. Таким образом, мы преобразовали особое интегральное
уравнение B2.19) в интегральное уравнение Фредгольма
B2.21) относительно той же неизвестной функции ф(/).
В этом состоит первый способ регуляризации —
регуляризации слева. Заметим, что этот метод употреблялся еще
основоположниками теории особых интегральных уравнений
Гильбертом и Пуанкаре (см. исторические сведения).
*) Методы непосредственного решения (в общем случае приближенного)
полного особого уравнения до настоящего времени недостаточно разработаны.
В последнее время выполняется много работ, посвященных разработке этих
методов (см. [11]).

204 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ (ГЛ. П1
2°. Регуляризация справа. Подставив в уравнение
B2.19) вместо искомой функции выражение B2.20):
ф(/) = К(о, B2.22)
где (о@—некоторая новая неизвестная функция, придем к
интегральному уравнению
ККсо = /, B2.23)
которое также является фредгольмовым. Таким образом, от
особого интегрального уравнения B2.19) относительно неизвестной
функции ф(^) мы перешли к интегральному уравнению Фред-
гольма относительно новой неизвестной функции (о@.
Решив уравнение Фредгольма B2.23), по формуле B2.22)
найдем решение исходного уравнения B2.19). Применение
формулы B2.22) требует только вычисления квадратур (один
интеграл обыкновенный и один особый). В этом состоит второй
способ регуляризации — регуляризации справа.
22.4. Связь между решениями особого и регуляризованного
уравнений. В процессе приведения особого интегрального
уравнения к регулярному над уравнением производили некоторое
функциональное преобразование. Это преобразование может,
вообще говоря, или внести посторонние решения, не
удовлетворяющие исходному уравнению, или вызвать потерю некоторых из
них. Поэтому получаемое уравнение, вообще говоря, не
равносильно исходному. Займемся установлением связи между
решениями этих уравнений.
1°. Регуляризация слева. Пусть
Кф = / B2.24)
— заданное особое уравнение и
ККф = К/ B2.25)
— соответствующее ему регулярное. Запишем B2.25) в форме
К(Кф-/) = 0. B2.250
Так как оператор К однородный, то всякое решение
исходного уравнения B2.24) (функция, обращающая выражение
Кф —/ в нуль) удовлетворяет также и уравнению B2.25^.
Следовательно, регуляризация слева не приводит к потере решений.
Поставим теперь обратный вопрос: всякое ли решение
регуляризованного уравнения является решением исходного? Легко
показать, что это не всегда так.
Рассмотрим особое интегральное уравнение, соответствующее
регуляризующему оператору
Ка) = 0. B2.26)

§ 22] РЕГУЛЯРИЗАЦИЯ ПОЛНОГО УРАВНЕНИЯ 205
Пусть 0I (О» •••» сор@—его полная система решений, т. е.
совокупность всех линейно независимых собственных функций ре-
гуляризующего оператора К.
Рассматривая уравнение B2.25^) как особое уравнение вида
B2.26) с искомой функцией со = Кф — /, будем иметь
Кф-Г=ЕауСОу, B2.27)
где aj — некоторые постоянные.
Таким образом, регуляризованное уравнение равносильно не
исходному уравнению B2.24), а уравнению B2.27).
Если применить к уравнению B2.27) оператор К, то придем
к уравнению B2.25) при произвольных aj. Отсюда как будто
можно сделать заключение, что уравнение B2.25) равносильно
уравнению B2.27) при произвольных а^. (Начинающий
неизменно приходит к такому ошибочному заключению.) На самом
деле это будет лишь в том случае, когда уравнение B2.27) раз-
решимо при произвольных aj. Если же для его разрешимости
свободный член должен удовлетворять некоторым условиям, то,
вставляя в условия разрешимости выражение f + Zj «/®/,
получим для величин «j некоторую систему уравнений. Может
оказаться, что эти уравнения удовлетворятся при произвольных
значениях aj, может быть из них определится лишь часть
постоянных, а остальные останутся произвольными, а может
оказаться, что все aj примут определенные вначения. Нетрудно
построить примеры, в которых будет осуществляться любая из
перечисленных возможностей. Следовательно, уравнение B2.25)
равносильно уравнению B2.27), в котором aj — произвольные
или определенные постоянные. Может оказаться, что уравнение
B2.27) разрешимо только при условии, что все aj = 0. В этом
случае уравнение B2.25) будет равносильно исходному
уравнению B2.24), и регуляризатор будет равносильным. В частности,
если регуляризатор не имеет собственных функций, то правая
часть уравнения B2.27) тождественно равна нулю, и он
обязательно является равносильным. Такой оператор заведомо
существует при X ^ 0; например, им может быть регуляризатор K'^
не имеющий в этом случае собственных функций *).
Вопросы равносильной регуляризации в общем случае будут
рассмотрены позже.
2°. Регуляризация справа. Пусть
Кф = / B2.24)
*) Это следует из выводов п. 21.2, так как индекс регуляризатора К'*
(характеристического) равен —к ^ 0.

йо^ ОСОБЫЕ Интегральные уравнения с яд^'ом коши 1гл. m
— исходное особое уравнение и
KK(o = f B2.28)
— регуляризованное уравнение, полученное подстановкой
К0 = ф. B2.29)
Если (Oj есть какое-нибудь решение уравнения B2.28), то из
формулы B2.29) получаем соответствующее ему решение исходного
уравнения
Фу «=» к©/.
Следовательно, регуляризация справа не может привести к
посторонним решениям.
Пусть, наоборот, щ есть некоторое решение исходного
уравнения. Тогда решение регуляризованного уравнения B2.28)
может быть получено как решение неоднородного особого
уравнения
Ксй = ф;^,
которое, однако, может оказаться неразрешимым.
Таким образом, регуляризация справа может привести
к потере решений. Такой потери не произойдет, когда уравнение
B2.29) разрешимо при любой правой части. В этом случае
оператор К будет равносильным регуляризатором справа.
Замечание. Имея в виду использование этих результатов
в дальнейшем материале книги, мы говорили о связи решений
исходного особого уравнения и уравнения, полученного из него
посредством регуляризации. Но сами результаты имеют более
широкое значение. Везде, где говорилось о регуляризованном
уравнении, можно говорить об уравнении, полученном из
данного путем умножения на некоторый оператор слева или справа.
Полученные здесь соотношения между решениями исходного и
преобразованного уравнений справедливы для преобразующего
(слева или справа) оператора любого вида.
§ 23. Основные свойства особых уравнений
23.1. Некоторые свойства союзных операторов. В
дальнейшем будем использовать два свойства союзных операторов.
Свойства эти не являются характерными для особых операторов,
а присущи всем линейным операторам. Для удобства читателя
мы дадим вывод этих свойств. Так как наличие особого
интеграла не вносит осложнений в доказательства, то будем
обозначать для простоты особое ядро просто /С(/, т).

§ 23) ОСНОВНЫЕ СВОЙСТВА ОСОБЫХ УРАВНЕНИЙ 207
Пусть К —особый оператор:
Кф=а(Оф@+J/C(/, т)ф(т)^т;
1С — его союзный оператор:
K'i|) = а (/) It (О + 5/С (т,/) г|) (т) dr.
L
1-е свойство. Для любых функций (p{t) wip(t),
удовлетворяющих условию Гёльдера, справедливо тождество
^^K(fdt=^(pK'^dt. B3.1)
Доказательство. Имеем*)
5 а|)Кфй/= J гКО Га (/)ф@ +\к(и т)ф(т)^т1 Л =
= \^(t)a{t)^{t)dt+\^{x)\\K{t,x)^{t)dt\dx.
L L Vl J
Обозначая в двойном интеграле переменную т через ty а t
через т и группируя члены соответствующим образом, получим
искомое равенство B3.1).
Заметим, что тождество B3.1) полностью характеризует
союзный оператор и его иногда принимают за определение этого
оператора.
2-е свойство. Имеет место тождество
(К2К,)' = К;К^. B3.2)
Доказательство. Составив, как в п. 22.1, композицию
особых операторов B2.3) и произведя несложные
преобразования, в числе которых применение формулы перестановки порядка
интегрирования G.7), найдем
К2К1Ф = [а, (О «2 it) + b, it) &2 it)] Ф (О +
. 1 Г ai (т) Л/2 (/, т) + Q2 (О Afi (^ т) ^ ,^^ ^^ ,
+ 1и] T^t Ф(т)^т +
+
*) Напомним, что согласно лемме п. 7.1 перестановка порядка
интегрирования в двойном интеграле, в котором лишь один интеграл особый,
допустима.

+
208 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. Ш
Отсюда по определению союзного оператора (п. 20.1)
(KjK,)' t = [а, it) а, (t) + 6, (/) b2 it)] ^ it) -
1 Г g, @ Mi (T, i) + 02 (t) Mi (t, t) ,. ^^
I.
lw)[l^J (T,-0(T-T,) ^^.JtWrft.
Совершив теперь композицию операторов
И сравнив полученные результаты, убедимся в справедливости
B3.2).
23.2. Основные теоремы об особых интегральных уравнениях
(теоремы Нётера). Основные свойства интегральных уравнений
Фредгольма характеризуются тремя теоремами, известными под
названием теорем Фредгольма (п. 20.2). Рассматривая в § 21
простейшие особые интегральные уравнения —
характеристические,— мы заметили, что некоторые из этих свойств (условия
разрешимости неоднородного уравнения) совпадали со
свойствами уравнения Фредгольма, другие же (например, зависимость
между числами решений двух союзных уравнений) существенно
отличались. Тогда уже отмечалось, что основные свойства
характеристических уравнений справедливы и для общего случая
полного уравнения. Докажем это и, таким образом, установим
основные свойства особых уравнений рассматриваемого типа.
Пусть дано полное особое интегральное уравнение
Кф = /. B3.3)
Известно, что число решений интегрального уравнения
Фредгольма (число собственных функций, принадлежащих данному
собственному значению) конечно. Легко установить, что это же
свойство справедливо и для особых уравнений.
Теорема I. Число решений особого интегрального
уравнения B3.3) конечно.
Доказательство непосредственно вытекает из возможности
регуляризации особого уравнения. Как было установлено
(п. 22.4), регуляризация слева не дает потери решений.
Следовательно, число решений особого уравнения B3.3) не больше

§ 23] ОСНОВНЫЕ СВОЙСТВА ОСОБЫХ УРАВНЕНИЙ 209
числа решений уравнения Фредгольма ККф = К/. Отсюда и
вытекает утверждение теоремы, что полностью согласуется с
теоремой V (п. 20.2).
Докажем, что условия разрешимости особого уравнения
имеют тот же вид, что и для уравнений Фредгольма (третья
теорема Фредгольма).
Теорема II. Необходимым и достаточным условием
разрешимости особого уравнения B3.3) является выполнение
равенств*)
\f{t)Mp,it)dt==0 (/=1,2...., пО. B3.4)
L
где \|)i@» •••» ^5п'@ — полная система линейно независимых
решений союзного однородного уравнения K'tp = 0.
Необходимость условий B3.4) является простым следствием
тождества B3.1). В самом деле, полагая в интеграле B3.4)
/(^) = Кф и используя тождество B3.1) и тот факт, что K'i|)j = О,
получим равенства B3.4):
\f{t) y^f{t)di=^\ г|),Кф Л= 5 ^K%dt^O (/= 1, 2, ..., AzO.
L L L
Доказательство достаточности распадается на два случая.
1. X ^ 0. Регуляризующие операторы имеют индекс —к ^ О,
поэтому из множества этих операторов всегда можно выбрать
такой оператор К, который не имеет собственных функций
(например, К'°). Поэтому уравнение Фредгольма
ККф = К/ B3.5)
равносильно исходному уравнению B3.3) и, следовательно,
уравнения B3.5) и B3.3) одновременно разрешимы или
неразрешимы.
Выпишем условия разрешимости уравнения B3.5):
5xyKfd/ = 0, B3.6)
L
где Xi@ — решения уравнения
К'Г5С = 0, B3.50
союзного в силу тождества B3.2) с уравнением B3.5).
*) Так как рассматриваемые функции комплексные, то условие B3 4)
нельзя истолковать как условие ортогональности функций /(/), ibj(/) (см.
п. 24.4).

210 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
Применив тождество B3.1), придадим условию B3.6) вид
J/K'x/d/=0. B3.60
L
Рассматривая уравнение B3.50 как особое интегральное
уравнение с оператором К' и искомой функцией К'х, видим, что
функция К'х. является собственной функцией оператора К^
Обозначая ее \|)j@> придем к условию B3.4).
2. X < 0. Применим регуляризацию справа*). Произведя
подстановку
Ф = К°Ч B3.7)
придем к уравнению Фредгольма
КК^'со = /, B3.8)
равносильному исходному уравнению B3.3) в том смысле, что
они одновременно разрешимы или неразрешимы и что каждому
решению уравнения B3.8) формула B3.7) ставит в соответствие
определенное решение уравнения B3.3) и наоборот — каждому
решению уравнения B3.3) по формуле B3.7) соответствуют
некоторые решения уравнения B3.8) (см. п. 22.4).
Выпишем условия разрешимости уравнения B3.8):
5/@Х/@Л = 0,
где Xi@—полная система решений уравнения
К°Гх = 0, B3.80
союзного с уравнением B3.8).
Рассматриваем уравнение B3.80 как особое с оператором
К° и искомой функцией К^х- Оператор К°, как
характеристический с отрицательным индексом, не имеет собственных функций,
поэтому
К'х = 0.
Последнее означает, что Xj@ является собственной функцией
оператора К'. Обозначая ее \^j(/), снова придем к условиям
B3.4).
Теорема доказана полностью.
Перейдем к доказательству теоремы, являющейся
центральным пунктом в теории особого уравнения с ядром Коши.
Согласно второй теореме Фредгольма, союзные уравнения Фред-
*) В этом случае регуляризатор слева без собственных функций не
существует (см. п. 23.3, следствие 2°).

§ 23] ОСНОВНЫЕ СВОЙСТВА ОСОБЫХ УРАВНЕНИЙ 2t 1
гольма имеют одинаковое число решений. В противоположность
этому, числа решений союзных особых уравнений, вообще
говоря, не совпадают. Следующая теорема устанавливает точную
зависимость между ними.
Теорема III. Разность числа п линейно независимых
решений особого уравнения Кф = О « числа п^ линейно
независимых решений союзного уравнения К^г|) = О зависит лишь от
характеристической части оператора К и равна его индексу, т. е.
п — п' = ус. B3.9)
Доказательство. Пусть х ^ 0. Возьмем в качестве регу-
ляризующего оператора К°'. Тогда фредгольмово уравнение
К'^'Кф = 0 будет равносильно исходному уравнению Кф = О
и, следовательно, тоже будет иметь п решений. В силу второй
теоремы Фредгольма союзное ему уравнение
К^КЧ = 0 B3.10)
будет иметь также п решений. Последнее уравнение равносильно
(см. п. 22.4, Г) следующему характеристическому:
К°г|) = а1'ф1+ ... +а„4п'. B3.11)
Так как х ^ О, то, в силу результатов п. 21.2, последнее
уравнение разрешимо при любой правой части и, следовательно, все
постоянные olj в нем будут произвольными. Уравнение B3.11)
будет иметь столько же решений (т. е. п), что и B3.10). Но
оно есть неоднородное характеристическое с индексом х ^ О,
и по формуле B1.12) его решение имеет вид
гКО = Еа//?фу+Е^/Ф/@.
Нетрудно доказать, что п^ + % функций, стоящих в правой части
последнего равенства, линейно независимы. Действительно,
допустим, что выполняется соотношение
п' X
Za//?ilv+ Ес;ф/@ = 0
хотя бы при одном aj, отличном от нуля. Это ведет к
противоречию, так как левая часть последнего выражения есть решение
неоднородного уравнения К°ф = 2«/'Ф/ и, следовательно, не
может быть нулем. Равенство 2^/Ф/@^0 также может удов-

212 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. 1П
летворяться лишь при всех Cj, равных нулю, в силу того, что
функции ф^(/) линейно независимы по определению*).
Следовательно, уравнение B3.10) имеет п^-\-к линейно
независимых решений. Отсюда п = п^ + Ку что и приводит к B3.9).
Для случая X < О не требуется отдельного доказательства.
Так как свойство операторов быть союзными взаимно, то в
качестве исходного возьмем союзный оператор К', имеющий
индекс х' = —X > 0.
На основании доказанного будем иметь
/г' — п = — X,
откуда опять приходим к равенству B3.9). Теорема доказана.
Три теоремы, доказанные в настоящем пункте, обычно
называются теоремами Нётера (см. Исторические сведения).
23.3. Некоторые следствия. Теорема III Нётера, выражающая
собой, как уже подчеркивалось ранее, характернейшее свойство
особого уравнения с ядром Коши, дает возможность вывести
некоторые важные следствия, часто используемые в приложениях
этих уравнений.
Г. Все теоремы Фредгольма в той формулировке, в какой
они обычно даются (п. 20.2), оказываются для особого
уравнения несправедливыми и должны быть заменены только что
установленными теоремами Нётера. Однако различие это
проявляется не в одинаковой мере. Вторая теорема Фредгольма,
утверждающая равенство чисел решений союзных уравнений,
решительно противоречит теореме III Нётера и должна быть
заменена ею. Первая же и вторая теоремы Фредгольма не
переносятся на особые уравнения только в силу той специфической
формулировки, которая им придана. Можно так изменить ее,
чтобы они, оставаясь справедливыми для уравнения Фредгольма,
оказались пригодными также и для особых уравнений. Для
этого нужно только в формулировке этих теорем заменить
данное однородное уравнение на союзное.
Теоремы I и III Фредгольма (объединенные и
видоизмененные).
Если однородное уравнение, союзное данному, неразрешимо,
то неоднородное безусловно разрешимо. Если же союзное
однородное уравнение разрешимо, то неоднородное разрешимо только
¦) Результат рассуждения может быть сформулирован так: если правая
часть уравнения содержит линейную комбинацию rv линейно независимых
функций с произвольными коэффициентами, а соответствующее однородное
уравнение имеет х линейно независимых решений, то неоднородное уравнение
имеет п' + X линейно независимых решений. Этим результатом нередко
приходится пользоваться при различных рассуждениях.

§ 23] ОСНОВНЫЕ СВОЙСТВА ОСОВЫХ УРАВНЕНИЙ 213
при выполнении условий
[f{t)^t)dt = 0,
где ^k{t) — полная система собственных функций союзного
оператора.
Если индекс оператора >с = О, то теорема III Нётера
совпадает со второй теоремой Фредгольма. В этом случае теоремы I
и III Фредгольма пригодны для особого уравнения в той же
формулировке, в какой они были даны для уравнения Фредгольма.
Таким образом, для особого уравнения с нулевым индексом
оказываются справедливыми все теоремы Фредгольма. Это дало
повод Н. И. Мусхел ишвил и ([16], стр. 236) назвать особые
интегральные уравнения с нулевым индексом квазифредголь-
мовыми*).
2°. Из теоремы III Нётера можно вывести важное
Следствие. Из всех особых уравнений, имеющих данный
индекс X, наименьигее число реилений имеют характеристические.
Действительно, число решений характеристического
уравнения равно точно X при х > О и равно нулю при х ^ 0. Так как
число решений п' союзного уравнения неотрицательно, то
rt = X + п' ^ X,
где п — число решений данного особого уравнения.
Таким образом, никаким подбором регулярной части ядра
в полном уравнении нельзя уменьшить число его решений по
сравнению с характеристическим. Наоборот, без труда можно
доказать, что подходящим подбором регулярной части можно
добиться того, чтобы полное уравнение имело любое заданное
число решений, большее х (см. задачу 15 в конце главы).
Однако, как будет показано ниже (п. 24.6), случаи, когда числа
решений полного уравнения и соответствующего ему
характеристического не совпадают, являются лишь исключительными. Как
правило, полное уравнение имеет столько же решений, сколько
и его характеристическое.
Из доказанного следует, что у оператора К с отрицательным
индексом не существует регуляризующего оператора К без
собственных функций.
Это непосредственно вытекает из того факта, что индекс ре-
гуляризатора обратен по знаку индексу самого оператора, и из
установленного выше следствия.
*) В абстрактной теории линейных операторов (см. п. 23.4), строящейся
в функциональном анализе, оператор с нулевым индексом причисляется к
фредгольмовым операторам.

2l4 ОСОБЫЕ ИнТЕГ|>АЛЬЙЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
23.4. Общая теория нётеровых операторов. На основе
изложенной теории интегральных операторов с ядром Коши
возникла абстрактная теория линейных операторов, для которых
справедливы теоремы Нётера. В ней предметом исследования
являются абстрактные линейные операторы в банаховых
пространствах и операторами Нётера по определению называются
те линейные операторы, для которых справедливы основные
свойства особых (сингулярных) операторов, полученные нами
под названием теорем Нётера. При этом основная в теории
сингулярных (нётеровых) операторов теорема III, отличающая их
от теории фредгольмовых операторов, служит аксиомой, так что
индекс сразу определяется как разность чисел нулей самого
оператора и ему сопряженного.
Сформулируем используемые в дальнейшем результаты этой
теории.
Теорема А. Произведение двух операторов Нётера также
является оператором Нётера, причем индекс произведения
операторов равен сумме их индексов:
Ind (Л^1. N2) = Ind Nx + Ind N2^
Теорема Б. Если N — нётеров оператор, а Т — некоторый
вполне непрерывный оператор, то М + Т — оператор Нётера и
lnd{N + T) = lndN.
Теорема В. Для всякого нётерового оператора N суи^е-
ствует такое число е > О, что для всех линейных операторов V,
для которых \\V\\<Z 8, оператор Л^ + ^ является оператором
Нётера и
lnu(N + V) = lndN.
Говорят, что линейный оператор Л^ допускает левую
(правую) регуляризацию, если существует такой линейный
ограниченный оператор N, что R-N (N-N) является фредгольмовым
оператором. Оператор Я в этом случае называется левым
(правым) регуляризатором оператора N.
Теорема Г. Для того, чтобы линейный оператор N был
нётеров, необходимо и достаточно, чтобы он допускал левую
и правую регуляризации.
Сравнительно доступное изложение основ абстрактной
теории можно найти в книге: И. И. Д а н и л ю к, Лекции по краевым
задачам аналитических функций и сингулярным интегральным
уравнениям, изд-во Новосибирск, ун-та, 1964.

§ 23] ОСНОВНЫЕ свойства ОСОБЫХ УРАВНЕНИЙ 215
23.5. Особые интегральные уравнения со сдвигом Карлема-
на*). В § 17 была рассмотрена обобщенная краевая задача Ри-
мана
0''la{t)]^G{tH-{t) + g{t) B3.12)
со сдвигом а(/), отображающим контур взаимно однозначно на
себя с сохранением направления. К краевой задаче B3.12)
приводится особое интегральное уравнение со сдвигом (см. задачу
16 к гл. III).
Рассмотрим более общее уравнение
Л^Ф^а(/)ф(/) + й@ф[а@1 + ^$^^т +
L
L L
где й(/,т) —регулярное ядро, предполагая, что функция сдвига
а (О имеет производную а'(О, удовлетворяющую условию Гёль-
дера и не обращающуюся в нуль. При этом сдвиг а(/) может
как сохранять, так и изменять направление на контуре.
Если на сдвиг а (О не налагать дополнительных условий, то
изучение уравнения B3.13) представляет большие трудности
и вопрос о полном исследовании уравнения B3.13) остается
открытым до сих пор. Если функция сдвига a(t) удовлетворяет
дополнительному условию
а [а @1=/, B3.14)
уравнение B3.13) допускает относительно простое
исследование. Сдвиг а (О, удовлетворяющий условию B3.14), называется
сдвигом Карлемана, Покажем, что исследование уравнения
B3.13) в случае B3.14) может быть сведено к исследованию
уже изученного особого уравнения без сдвига. Это позволит
получить для уравнения B3.13) теоремы Нётера, аналогичные
теоремам п. 23.2. Сведение уравнения B3.13) к уравнению без
сдвига основано на том, что композиция особых операторов
B3.13) с карлемановским сдвигом является снова особым
оператором такого же вида. Именно, пусть A^i и N2 — операторы
вида B3.13):
N, = а,1 + b,Q + c,S + d,QS + Ки
N2 = «2/ + 62Q + ^2^ + d2QS + /С2,
*) Изложение этого пункта дано в основном по работе Н. К. К а р а п е-
тянца и С. Г. Сам ко 1). Относительно теорем Нётера для краевых задач
со сдвигом см. п. 37.4.

216 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
где для простоты обозначено
дф = ф[а@].
5ф = Л(-^^т.
Ki и /Сг — интегральные операторы с регулярными ядрами.
Составление композиции N2N1 осуществляется по-разному в
зависимости от того, сохраняет или изменяет направление на
контуре функция a{t).
Случай I. Сдвиг a{t) сохраняет направление на контуре.
Составим композицию Л^гЛ^ь используя следующие свойства
особого оператора 5 и оператора сдвига Q: 1) S^ = I согласно
п. 7.3; 2) Q2 = / в силу B3.14); 3) в силу равенства
iSQ-QS)<p = ±\[:^-^?^]<f{.)dx B3.15)
операторы S и Q перестановочны с точностью до слагаемого
с регулярным ядром.
Имеем
Л^2Л^1Ф = m (О Ф (О + p{t)Qcp + n {t) 5ф + G (О QS(p + /Сф, B3.16)
где /С —оператор с регулярным ядром и
т (О = а, (О «2 (О + Ь, (t) &2 [а (/)] + с, (t) с^ (О + d, [Ы^ [а (/)],
p@ = ai@62@ + 6i@a2la(/)] + Ci@d2@ + rfi@^2[a@1,
п (О = а, {t) с, (О + Ь, (О d, [а (/)] + с, (t) а, {t) + d, {t)b,[a@], ^^"^^ ^^
qit) = a, it) rf2@ + b, it) C2 [a{t)] + c, (t)b^(t) + d, {t)a,[a{t)].
(Мы не приводим выкладок, читатель может сделать их
самостоятельно.)
Напомним, что в § 22 регуляризация особого оператора Ki
основывалась на возможности подобрать особый оператор Кг
так, чтобы композиция К2К1 была фредгольмовым оператором.
Естественно возникает вопрос, можно ли для данного оператора
Ni со сдвигом так подобрать оператор Л^2, чтобы их композиция
B3.16) была просто особым оператором, не содержащим сдвига,
т. е. чтобы в B3.16)
p{t) = q{t)^0.
Оказывается, это всегда возможно. Именно, если N = Ni —
оператор B3.13), то в качестве N2 можно взять оператор
Л/ф = а [а (/)] ф (О - 6 (О Ф [а (t)] + с [а (/)] Eф) (/) - d @Eф)[а(/)].

§ 231 ОСНОВНЫЕ СВОЙСТВА ОСОБЫХ УРАВНЕНИЙ 217
Тогда В соответствии с B3.16)
NNcp = m{t)q> (t) + п {t) {Sq>) {t) + T^(p B3.18)
и аналогично
NNq> = m{t)(^ (t) + n (t) (Sep) (t) + Г2Ф, B3.19)
где Ti и T2 — операторы с регулярными ядрами, а коэффициенты
m{t) и n{t) имеют согласно B3.17) следующий вид:
m{t) = a it)а [а(/)] + c{t)c [а(/)] -b(t)b [а{t)] -d{t)d [а(/)],
n{t) = a it) с [а it)] + c{t)a [а (t)] -b{t)d [a (t)] -d{t)b [a {t)l
Поскольку особое уравнение с ядром Коши может быть
сведено к уравнению Фредгольма, то в силу B3.18) — B3.19) и
уравнение B3ЛЗ) со сдвигом может быть сведено к фредгольмову.
Вопрос о равносильности такого сведения представляет
значительные трудности и до настоящего времени не исследован.
Обозначим Ai@ = ^@~~^@» А2@= ^@+^@ и будем
считать, что А1(/)=й=0, Д2@=7^'0. Тогда имеет место следующая
Теорема 1. Для уравнения B3.13) справедливы все три
теоремы Нётера, и его индекс вычисляется по формуле *)
«(^^) = Tl"dAf- B3.20)
Чтобы получить утверждения теоремы, удобно
воспользоваться общими теоремами п. 23.4, хотя этого можно было бы
достичь и без обращения к общей теории линейных операторов.
Справедливость теорем Нётера для уравнения B3,13) следует
из теоремы Г п. 23.4 о регуляризаторе, поскольку из равенств
B3.18) — B3.19) вытекает, что оператор Л^ допускает и левую
и правую регуляризацию. Из B3.18) — B3.19) вытекает также
в силу теоремы А п. 23.4, что
Поэтому ДЛЯ доказательства формулы B3.20) достаточно
показать, что %{N) = ус{Щ. Для этого введем операторы
Лф = а (/) ф (/) 4- ^ (t) 5ф, Лф = а [а (/)] Ф (О + ^ [а (t)] Sep
и обозначим и оператор умножения на функцию
u{t) = a{t)-t.
*) Заметим, что правая часть в B3.20)—целое число, так как индекс
функции д^ . . , не изменяющейся при замене / на а (О, четен.

218 ОСОБЫЕ Интегральные уравнения с ядром коши 1ГЛ. ш
Так как сдвиг сохраняет направление на контуре, то из условия
B3.14) вытекает, что а(^) не имеет неподвижных точек на
контуре*). Следовательно, u(t)^0. Непосредственной проверкой
можно убедиться в справедливости равенства
UANq) = NAUcp + Г3Ф, B3.21)
где Гз — оператор с регулярным ядром. Если а^{t)-'с^(t) Ф'О,
то операторы А и А нормального типа и х(Л) = х(Д). Из B3.21)
в силу теоремы Б п. 23.4 следует, что
7i{UAN) = K{NAU),
откуда k{N)=:h{N), что и требовалось. Если же условие
a^it) —c^{t)^0 не выполнено, то поступим следующим
образом. Приблизим функции a{t), c(t) близкими функциями ае@»
Ce{t) так, чтобы а|@ —с|(/L^0. Тогда согласно предыдущему
х(Л^е) = х(^е), т. е. равны индексы соответствующих
операторов Л^е, Л^е, если 8 достаточно мало. В силу устойчивости индекса
при малых: изменениях (теорема В п. 23.4) получаем, что
и x{N) = x{N). Последнее окончательно доказывает формулу
B3.20).
Случай П. Сдвиг a{t) изменяет направление на контуре.
Здесь композиция N2N1 операторов со сдвигом составляется
аналогично, только, в отличие от B3.15), регулярное ядро имеет
оператор SQ + QS, Оператор Я следует взять в виде
ууф = а [а it)] ф (О - fe (О Ф [а @] - с [а (t)] Eф) (/) - d (/) Eф) [а (/)].
Рассуждая по той же схеме, что и выше, придем к следующей
теореме.
Теорема 2. Пусть
А (О = {а [а @1 + с [а [t)]} [с {t) - а (t)] -
- [b it) + d (t)] {d [a it)] - b [a (/)]} Ф 0.
Тогда для уравнения B3.13) справедливы все три теоремы Не-
тера, и его индекс равен
>c = IndA@.
Доказательство теоремы 2 аналогично доказательству
теоремы 1 с той лишь разницей, что в равенстве B3.21) вместо
оператора U следует взять оператор S.
*) Действительно, предположим противное, что а(/о)=/о для некоторой
точки ^0, лежащей на контуре. Возьмем какую-нибудь другую точку iu
такую, что a{ti)^ti. Тройка точек ^о, tu a(/i) задает направление обхода на
контуре. Их образы а (/о), a(^i), a[a(/i)], т. е. точки /о, a(/i), /1, определяют
противоположное направление на контуре, что противоречит тому, что а(/)
сохраняет направление на контуре.

§ 23) ОСНОВНЫЕ СВОЙСТВА ОСОБЫХ УРАВНЕНИЙ 219
23.6. Особые интегральные уравнения, содержащие
комплексно сопряженную неизвестную функцию *). Рассмотрим
особое уравнение вида
+'1Ш^^+^тМ^В^^+
+ \k{t,x)q> (т) dx+\l {t, т) ф (т) dx = f (О, B3.22)
L L
где k{t,x) и /(/,т)—регулярные ядра. Такое уравнение, как
увидим далее, во многом аналогично уравнению со сдвигом
Карлемана, изменяющим направление на контуре.
Так же, как и в п. 23.5, можно свести уравнение B3.22)
к особому уравнению без комплексного сопряжения и
непосредственной проверкой убедиться в том, что композиция двух
операторов вида B3.22) снова является таким же оператором.
Именно, если
N\^ = CL\^ + bx^ + CxS(^ -f- dxS(^ + K\^ + /^19,
Л^2ф = ^2Ф "Ь ^2Ф "f" ^2'^Ф + ^2»5ф "Ь ^2Ф "Ь ^2Ф»
где Ки ^ь ^2, /^2 ~" операторы с регулярными ядрами, то
Nr,Nx^ = тф + РФ + п5ф + G5ф + Гф + V>, B3.23)
где Г и F — операторы с регулярными ядрами, а
т it) = а, (О а2 (t) + b, (t) b^ (t) + с, (t) c^ (t) - d, (t) d, (/),
p @ = b, (t) a2 (t) + a, (t) &2 @ - d, (t) C2 @ + c, (t) d^ (/),
B3.24)
n (t) = c, (t) a2 it) + d, (t) Й2 (t) + a, it) C2 (t) - b, (t) d^ @,
q it) = d, (t) «2 (t) + FJf) b2 it) - b, it) C2 (t) + MO ^2 @.
Подберем коэффициенты оператора N2 так, чтобы уравнение
B3.23) не содержало сопряжения в своей главной части, т. е.
Р@^0, q{t)^0.
Для этого достаточно взять
chit)==^_ b2{t) = -b,{t\
с, it) с, it), d2{t) = -dAty
*) Этот пункт написан по работам Н. К. Карапетянца и С. Г. Самко.
О нётеровости некоторых краевых задач, содержащих комплексно
сопряженные неизвестные функции, см. пп. 37.3^ 37.4.

220 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
Таким образом, если Л^ — произвольный оператор вида B3.22),
то, положив
N(^ = a{t)(f{t)-b{t)q>(t)-c{t)S(p--d{t)Sq>,
будем иметь
Л^Л^ф =т(/)ф (О + п@5ф + Г1ф + 17;ф
и аналогично
NNq> = m{t)q>(t) + n{t) 5ф + ?'2Ф + V^,
где операторы Ти У^ Гг, V2 имеют регулярные ядра и в
соответствии с B3.24)
m@ = |a@P~|6@l^k@P + |rf(/)|2, _
п (О =7{t) c{t)-'a {t)T{t) +Щ d{t)-b (t) d it).
Таким образом, как и в п. 23.5, пришли к особому уравнению
с ядром Коши. Поступая аналогично рассуждениям п. 23.5,
получим для уравнения B3.22) теоремы Нётера и формулу для
индекса. Не останавливаясь на этом подробно, сформулируем
окончательный результат. Предварительно заметим, что при
рассмотрении линейной независимости решений однородного
уравнения, соответствующего B3.22), и при составлении его общего
решения используются только действительные постоянные.
Поэтому индекс уравнения B3.22) окажется удвоенным (см.
формулу B3.25)).
Теорема. Пусть
т {t) - n{t) = [a{t) - с@] [Щ+Щ] - [b{t) + d{t)M) - Щ1)]Ф0.
Тогда для уравнения B3.22) справедливы теоремы Нётера, его
индекс равен
X = 2 Ind [т (О - п (/)] B3.25)
и условия разрешимости имеют вид
Rejf@t/@rf^ = 0,
где \|)j@ — полная система решений сопряженного уравнения,
23.7. Бисингулярное уравнение, l^ Характеристическое би-
сингулярное уравнение
Х^'ф = аоФ + а151ф + ^^2^29 + ax2Sx2^ = g, B3.26)
где Si, S2 и Si2 —операторы, введенные в п. 9.5, ао, clu ^2, ^12,
g — функции, удовлетворяющие условию Гёльдера на остове
L^=LiXL2y равносильно краевой задаче Римана A4.36)—

§ 231 ОСНОВНЫЕ СВОЙСТВА ОСОБЫХ УРАВНЕНИЙ 221
A4.37), в которой
А\ D\
^ } = ao±ai±a2 + ajg, „ | = Gq ^ «i ± ^2 — ^i2-
Решение характеристического уравнения B3.26) в
замкнутой форме может быть получено для всех тех случаев, когда
в такой же форме будет получено решение соответствующей
ему задачи Римана.
Оператору
S4 = ^оФ - S, (a.ip) - S2 (азф) + 5,2 (а,2^^),
союзному к оператору S^ соответствует краевая задача
(АЧ^)^^ - (ВЯ""*" - (CW)-*"" + {DW' == h.
Ее структура существенно отличается от структуры задачи
A4.36) — A4.37). В этом и состоит одно из отличий двумерного
характеристического оператора от одномерного. Второе
отличие в том, что разность 5^5^ —S^S« композиций двух
характеристических операторов S^ и S^ не является регулярным
оператором, как это было в одномерном случае. Она, помимо
регулярной части, содержит еще операторы вида K1S2, где
К1ф = J ^1 (/1, /2, Ti) ф (ть /2) dxi
— оператор, имеющий ядро со слабой особенностью. (О
сказанном выше см. Ф. Д. Г ахов, В. А. К а кич ев 1) и В. А. Ка-
кичев 6), 7).) В работе 7) В. А. Какичева, кроме этого,
указаны достаточные условия того, чтобы разность двух
различных композиций полных двумерных сингулярных
операторов была регулярной. Эти условия сводятся к разрешимости
двух систем полных сингулярных уравнений, каждая из
которых содержит две искомые функции и зависит от второго
переменного как от параметра.
2°. Нётеровость бисингулярных операторов
и краевых задач. Рассмотрим бисингулярный оператор
Кф ^ feo (^1, /2) Ф(^1, h) + S ^'^il'1%^'^ Ф (Ti, /2) dx, +
+ 5 r,-t, «f (^b T2) dx, + ] (^^_^^)(^^_^^) Ф (T,, To) dx, dx„
B3.27)
естественным образом обобщающий оператор B0.1). Если L —
тор, а функции ^, ku /^2, ^12 удовлетворяют условию Гёльдера

222 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
по всем переменным, то оператор B3.27) будет нётеровым
в пространстве функций, суммируемых с квадратом, тогда
и только тогда, когда обратимы четыре оператора, имеющие
ту же структуру, что и оператор B0.1), но зависящие еще от
одного переменного как от параметра. Этот результат,
принадлежащий И. Б. Симоненко 5), распространен В. С. Пи-
лиди 2) на функции, суммируемые со степенью р>1 на
LiX^2, где Lj — простые гладкие замкнутые кривые
Ляпунова. Этими же авторами вычислен индекс нётерова оператора
B3,27), а также индекс задачи A4.36) — A4.37), условия нё-
теровости которой даны в теореме из 3° п. 14.10.
В заключение заметим, что исследование на нётеровость
бисингулярных операторов основано на использовании
локального метода изучения линейных операторов, разработанного
И. Б. Симоненко 6).
§ 24. Равносильная регуляризация. Третий способ
регуляризации
24.1. Постановка вопроса. Различные толкования понятия
равносильной регуляризации. В п. 22.4 уже указывалось, что
операция регуляризации приводит к уравнению, вообще говоря,
не равносильному исходному. Может произойти как появление
посторонних решений (при регуляризации слева), так и потеря
решений (при регуляризации справа). Представляет
значительный интерес, теоретический и практический, решение вопроса,
при каких условиях и как особое уравнение может быть
приведено к равносильному фредгольмову, т. е. такому, которое
содержит все решения исходного уравнения, с одной стороны, и
все решения которого удовлетворяют исходному, — с другой.
К вопросу можно подходить с разных точек зрения, и
постановка его нуждается в уточнении.
Можно требовать равносильности данного и регуляризован-
ного уравнений при любой правой части. В этом случае речь
идет о равносильной регуляризации не индивидуально взятого
уравнения с определенной правой частью, а всего класса
уравнений с заданным особым оператором К. Таким образом, в
сущности, здесь решается вопрос о равносильной регуляризации
оператора К. Можно тот же вопрос ставить для некоторого
определенного уравнения с заданной правой частью. Здесь уже
будут учитываться и свойства правой части и возможно такое
положение, когда уравнение с одним и тем же оператором
допускает равносильную регуляризацию при одной правой части
и не допускает ее при другой.
Решение поставленного вопроса существенно зависит также
и от того, требовать или нет, чтобы регуляризованное уравне-

$ 24) РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 223
ние содержало ту же искомую функцию, что и исходное, или
же допускается составление регулярного уравнения
относительно новой функции. Применительно к способам
регуляризации это означает, требуем ли мы обязательно регуляризации
слева или же допускаем также и регуляризацию справа.
Сначала решим более простой вопрос о равносильной
регуляризации оператора.
24.2. Равносильная регуляризация оператора. Г. Будем
считать допустимой только регуляризацию слева.
Лемма. Для того чтобы оператор К был равносильным ре-
гуляризатором для особого уравнения Кф = / при любой
правой части /, необходимо и достаточно, чтобы он не имел
собственных функций.
Доказательство. Если условие выполнено, то из
К(Кф —f) = 0 сразу вытекает Кф--/ = 0, что и
устанавливает достаточность его.
Докажем теперь необходимость.
По условию существует оператор К, равносильно регуляри-
зующий уравнение Кф = / при любом f. Допустим, вопреки
условию леммы, что оператор К имеет собственную функцию
(О, и положим f = ©. Тогда, по условию, уравнения Кф = со
и ККф = Ксо = О будут равносильны. Но последнее, а
следовательно, и первое уравнения имеют нулевое решение. Отсюда
необходимо @^0, что и требовалось доказать.
Как доказано в § 23, оператор с неотрицательным индексом
имеет регуляризатор, не имеющий собственных функций, а
оператор с отрицательным индексом такого регуляризатора не
имеет. Из соединения этого результата с доказанной леммой
вытекает следующий вывод.
Теорема. Для того чтобы особое интегральное уравнение
Кф = f допускало равносильную регуляризацию при любой
правой части f, необходимо и достаточно, чтобы индекс
оператора К был неотрицательным.
Установленная теорема полностью разрешает вопрос о
равносильной регуляризации оператора слева.
Требование применять регуляризацию только слева делает
невозможной, как показывает полученный результат,
равносильную регуляризацию всего класса операторов, имеющих
отрицательный индекс.
2°. Будем считать теперь допустимой регуляризацию как
слева, так и справа. Условимся регуляризацию справа считать
равносильной, если каждому решению ф исходного уравнения
Кф = / по формуле подстановки Ко = ф соответствует
определенное решение ш регуляризованного уравнения ККсо = /,

224 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
и наоборот, в таком случае, как легко показать, всякие
ограничения отпадают и становится возможной равносильная
регуляризация всего класса особых операторов.
Все необходимое для обоснования этого утверждения
содержится в п. 22^4, приведем лишь окончательные выводы.
Оператор К = К^° является при любом индексе
равносильным регуляризатором, причем
при X ^ О нужно применять регуляризацию слева,
при к^О — регуляризацию справа,
В последнем случае получается уравнение относительно
новой функции 0), но знание ее позволяет найти все решения
исходного уравнения квадратурами, причем по свойству
регуляризации справа не может возникнуть посторонних решений.
Таким образом, при отсутствии ограничения на способ
регуляризации и обобщении понятия равносильности всякий особый
оператор можно регуляризовать равносильно. Этот факт мы
уже использовали, не формулируя его как особое свойство, при
доказательстве теорем Нётера.
24.3. Равносильная регуляризация слева особого уравнения.
Необходимое условие. Поставим такой практически важный
вопрос. Дано особое уравнение
Кф = / B4.1)
с определенным образом заданной правой частью. Требуется
установить, при каких условиях для него существует регуляри-
затор слева К, приводящий его к равносильному уравнению
Фредгольма:
ККф = К/, B4.2)
и в случае существования такого оператора К построить его.
Когда индекс >с ^ О, существует, как мы знаем, оператор,
не имеющий собственных функций (например, К'°). Он,
очевидно, будет равносильным регуляризатором слева при любом /.
Интерес поэтому представляет случай х < О, когда не
существует регуляризатора без собственных функций.
Легко найти необходимое условие существования у данного
уравнения равносильного регуляризатора. Как было
установлено в п. 22.4,1°, уравнение B4.2) будет равносильно
уравнению
п
Кф = /+Еа/а>/, B4.3)
где 0I, «2, ..., (Ор — полная система собственных функций
оператора К; аь ..., ар — некоторые постоянные, которые
могут быть или произвольными или определенными.

§ 241 РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 225
По определению, уравнение B4.2) будет равносильным
исходному уравнению B4.1) тогда и только тогда, когда все aj
окажутся равными нулю. Посмотрим, как это может
произойти.
Пусть ipi, \|J, ..., t|)g — полная система собственных функции
союзного оператора К'. Умножая уравнение B4.3)
последовательно на фь 1|?2, ..., \|)д и интегрируя по контуру L, получим,
учитывая тождества \K9i|)/d/ = 0, систему уравнений
tauai = -fi (/=1,2, ..., G), B4.4)
где
«// = 3 Ф/со, Л, fi = J fyi>i
dt.
Очевидно, система B4.4) может удовлетворяться нулевыми
значениями а^ лишь в том случае, если все Д- = 0. Но
последние равенства являются условиями разрешимости уравнения
B4.1). Отсюда имеем следующий результат:
Если регуляризующий оператор имеет отличные от нуля
собственные функции, то для того чтобы данное особое инте-
гральное уравнение B4.1) могло быть приведено к
равносильному уравнению Фредгольма B4.2), необходимо, чтобы оно
было разрешимым.
Является ли это условие достаточным? Ответ на этот
вопрос утвердительный, однако доказать это не просто. Нужны
вспомогательные сведения, к изложению которых мы и
переходим.
24.4. Сопряженное уравнение. Другая форма условий
разрешимости неоднородного уравнения. Введенное в п. 20.1 понятие
союзного оператора отлично от аналогичного ему понятия
сопряженного оператора, употребляемого в теории линейных
комплексных операторов. В связи с этим и условие разрешимости
получило другую форму. Мы, например, нигде не могли
сформулировать его как условие ортогональности свободного члена
к решению сопряженного уравнения. Сейчас введем понятие
сопряженного оператора и дадим новую форму условий
разрешимости неоднородного уравнения.
По тем же соображениям, что и в п. 23.1, не будем явно
выделять особенность ядра.
Пусть К —особый оператор, определяемый формулой
Кф ^ а (О (f{t)+\K (/, т) ф (т) rfr, B4.5)

22fi ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. И1
и пусть
т = т(а) @<а</) B4.6)
— уравнение контура L, где а — дуговая абсцисса. Когда а
принимает частное значение s, то соответствующую
комплексную координату / будем обозначать t{s).
Условимся обозначать функции действительных переменных
5, а, получаемые заменой переменных B4.6), теми же буквами,
что и исходные функции комплексных переменных /, т.
Например,
(p(t) = (p[t(s)]^(p{s),
Kit, x) = K[t{s\ x(g)]^K{s, a) и т. п.
Тогда оператор B4.5) можно записать в виде
Kq> = a (s) (f){s)+\K E, а) х' (а) ф (а) da.
о
Назовем оператор К*, определенный формулой
К*я|)* ^ ^ г|)* (s) + 5 К (о, s)f(s) Г (а) da, B4.7)
о
сопряженным оператору К.
Уравнения Кф = О и К*г|)* = О будем называть
сопряженными. Очевидно, сопряженный оператор удовлетворяет условию
(кт = к.
Назовем выражение
(ф, i|5)= 5фE)^^5 B4.Я)
о
скалярным произведением двух функций ф и '\\\
Очевидно,
(Ф, ф) = 5 Фis)ФE) ds = (ф, г|)).
о
Если (ф, \|?) = О, то функции ф и \|5 называются ортогональными.
Аналогично п. 23.1 можно доказать тождество
(Кф, г|)) = (ф, КЧ). B4.9)
Установим связь между решениями союзного уравнения
КЧ ^a(t)y^(t)+^K (т, t) t (т) dx = 0 B4.10)

§ 241 РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 227
И сопряженного уравнения
КЧ* ^^ г|)* (s) + 5 K{a,s)f{s) г|5* (а) da = 0. B4.11)
о
Переходя к комплексно сопряженным величинам и
употребляя обозначения п. 18.1, получим
K^-^f (s)[a@^+JiC(T, t)Щ¦dx'j = 0. B4.110
Сравнение уравнений B4.10) и B4.1 К) показывает, что
решения союзного и сопряженного уравнений связаны зависимостью
r(t)
Щ' = ^И) или r{t) = f{s)^{t). B4.12)
Отсюда, между прочим, следует, что уравнения,
сопряженное и союзное данному, имеют одно и то же число решений.
Пользуясь формулами B4.12), условию разрешимости
неоднородного особого уравнения B4.1)
Кф = /
можно придать другую форму.
Из B3.4) имеем
\f{t)^fit)f{s)ds = 0.
О
Отсюда, учитывая B4.12), получаем
I
(f. t;)=5f@W)'^« = 0 (/=1.2. .... п'). B4.13)
П
Условия разрешимости B4.13) можно сформулировать в
следующем виде:
Для того чтобы особое неоднородное уравнение B4.1) было
разрешимым, необходимо и достаточно, чтобы свободный член
уравнения был ортогонален всем решениям сопряженного
однородного уравнения B4.11).
Выведем еще одно вспомогательное тождество
I
(К*Ка), ю) = (К0, К©) = 51 Ксо р ds. B4.14)
о
Рассматривая функцию К*К(о как результат применения
оператора К* к функции Ко), первую часть равенства получим из

228 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. III
тождества B4.9), а вторую — согласно определению
скалярного произведения B4.8).
Теперь вернемся к вопросу о равносильной регуляризации
уравнения.
24.5. Теорема о равносильной регуляризации уравнения.
Сингулярная резольвента. Сингулярное решение.
1°. Лемма. Пусть неоднородное особое интегральное
уравнение
Кф = / B4.1)
разрешимо. Тогда оно равносильно уравнению
К*Кф = К7. B4.15)
По условию теоремы существует функция ф1@»
удовлетворяющая уравнению B4.1). Она же является, в силу
однородности оператора К*, также решением уравнения B4.15).
Докажем, что всякая другая функция ф2@> удовлетворяющая
уравнению B4.15), будет удовлетворять и уравнению B4.1).
Имеем
гкф1 = к7,
к*Кф2=к7.
Вычитая первое равенство из второго, получим, что
функция со = ф2 — ф1 является решением однородного уравнения
К*Ка) = 0.
Образуем теперь скалярное произведение функций К*Ксо
и @. Пользуясь последним равенством и тождеством B4.14),
получим
0 = (К*Ксо, (o)=5|K(dNs.
о
Отсюда Ко) «= О или
Кф2 = Кф1.
Но Кф1 = /, следовательно,
Кф2 = Л
что и требовалось доказать.
Теперь можно перейти к выводу основного результата.
Легко прямым подсчетом показать, что оператор К*,
вообще говоря, не является регуляризующим для оператора К
(он будет регуляризатором только в том случае, если оператор
К действительный). Следовательно, уравнение B4.15) не будет
фредгольмовым. Индекс сопряженного оператора К* будет сов-

§ 24] РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 229
падать с индексом союзного оператора К^ следовательно, он
равен индексу данного оператора К с обратным знаком. Так
как индекс композиции двух операторов равен сумме индексов
составляющих операторов (п. 22.1), то, следовательно,
уравнение B4.15) есть особое интегральное уравнение с индексом,
равным нулю. Но такое уравнение, как мы знаем (п. 22.4),
имеет регуляризатор без собственных функций, хотя бы,
например, оператор (К*К)^°.
Таким образом, установлен следующий основной результат
о равносильной регуляризации уравнения.
Теорема. Если в особом уравнении
Кф«=/ B4.1)
правая часть f{t) такова, что оно разрешимо, то суи^ествует
регуляризуюи^ий оператор слева, приводяи{ий его к
равносильному уравнению Фредгольма.
Согласно проведенному выше доказательству, в качестве
такого эквивалентного регуляризатора может быть взят
оператор
К = (К*К)'°К*, B4.16)
где К* — сопряженный оператор, определяемый формулой
B4.7), а (К*К)^'' —характеристический оператор, определяемый
по оператору К*К формулой B0.6).
Следовательно, хотя при х < О и не существует (как
показано в п. 24.2) оператора, производящего регуляризацию при
любой правой части, однако при свободном члене /,
удовлетворяющем условию разрешимости особого уравнения Кф = /, для
него существует и эффективно может быть построен
равносильный регуляризующий оператор. При этом замечательно, что вид
этого оператора не зависит от правой части, так что для всех
разрешимых уравнений с заданным оператором К можно брать
один и тот же равносильный регуляризатор.
Равносильный регуляризатор, определяемый формулой
B4.16), является отнюдь не единственным, обладающим
таким свойством. Произведение двух фредгольмовых операторов
является, очевидно, оператором Фредгольма. Отсюда следует,
что, умножая равносильный регуляризатор B4.16) на
произвольный фредгольмов оператор без собственных функций, снова
получим равносильный регуляризатор. Следовательно, для
любого разрешимого особого интегрального уравнения можно
построить бесконечное множество регуляризаторов слева,
приводящих его к равносильному уравнению Фредгольма.
2°. Сингулярная резольвента. Пусть
Кф = / B0.3)

230 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
— данное разрешимое особое интегральное уравнение и К —
один из его равносильных регуляризаторов. Тогда ККф =
= Kf — фредгольмово уравнение, равносильное исходному
уравнению B0.3). Решая его по формуле B0.11), получим
п
Ф(/)=к/+5я(/, т)кмт+j; с,ф,(о.
L fe-l
Согласно рассуждениям п. 22.2 оператор К определяется
формулой B2.16). В целях нормирования возьмем в ней и= 2_/,2
и обозначим
В.
q2 _ ^,2 ^*, д2 _ 1,2
Тогда будем иметь
fe-I
где y(^t^)-~ некоторое вполне определенное фредгольмово ядро.
Запишем последнюю формулу в виде
л
Ф@ = Л (Of (/)+ S Г(/, T)/(T)rfT + 2 cm(t). B4.17)
L fe-1
Ядро
Г(^т) = -^^^АЙ_4.^(/.г)
называется сингулярной {особой) резольвентой особого
интегрального уравнения B0.3). Из сравнения формулы B4.17)
с формулой B0.11) следует, что ядро Г(/,т) при решении
особого интегрального уравнения играет такую же роль, как и
резольвента уравнения ФредгоЛьма.
Л. Берг 1), 2), получивший впервые (более сложным, чем
здесь изложено, путем) сингулярную резольвенту, установил
ряд ее свойств, аналогичных свойствам фредгольмовой
резольвенты; в частности, он вывел два интегральных уравнения,
связывающих сингулярную резольвенту с ядром особого
уравнения и вполне аналогичных соответственным уравнениям в
теории фредгольмовой резольвенты.
3°. Сингулярное решение. Одним из важных
приложений сингулярной резольвенты, данным Л. Бергом 2),
является установление условий существования так называемых
сингулярных решений.

§ 241 РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 231
Изложенная в этой главе теория особых интегральных
уравнений с коэффициентами класса Гёльдера позволяет
получить все их решения гёльдерова класса. Допущение в
качестве 'решений более широкого класса функций с
интегрируемыми особенностями в действительности не расширяет класс
решений. Интегрируемые решения особых интегральных
уравнений с коэффициентами класса Гёльдера необходимо сами
принадлежат классу Гёльдера.
Естественно поставить вопрос, нельзя ли получить новые
решения, допуская неинтегрируемые особенности. Считая
допустимыми только особенности, при которых сохраняется
интегрируемость в смысле главного значения, будем иметь
решение в виде
где /i — точка контура, m{tJi) удовлетворяет условию
Гёльдера.
Вставляя ф в уравнение B0.3) и учитывая, что правая часть
есть функция ограниченная, а интегральный член на основании
рассуждений п. 7.2 будет в точке ti иметь особенность порядка
меньше единицы, получим, что для того чтобы ф(/)
удовлетворяло уравнению, необходимо, чтобы
a(/i) = 0.
Таким образом, сингулярные решения могут порождать только
такие точки tu которые являются корнями коэффициента a(t).
Легко получить второе необходимое условие разрешимости.
Вставим ф(/) в интегральное уравнение B0.3), а затем
умножим обе части на решения \|?j транспонированного уравнения
К'г|) = О и проинтегрируем. Произведя в повторном особом
интеграле перестановку порядка интегрирования по формуле
Пуанкаре—Бертрана G.7) и учитывая тождество B3.1),
придем к равенствам
b(t,)т{tu t,)Hpf{t,) +\f{t)г|),(/)dt = 0,
которые должны выполняться для полной системы решений
транспонированного уравнения К^гр = 0.
Используя сингулярную резольвенту, Л. Берг 2) показал,
что последнее условие вместе с равенством a{t\)=0 является
также достаточным для существования сингулярного
решения ф@-

232 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. III
В связи С изложенным остановимся на различии между
интегральными уравнениями первого и второго рода. Для фред-
гольмовых уравнений, как известно, свойства этих двух типов
уравнений существенно различны. Причина этого состоит в том,
что для ядер Фредгольма оператор \/г(/, т)ф(т)йт переводит
функцию ф(/) в функцию более узкого класса; поэтому для
выполнения равенства \ ^(/, т)ф{т)^т = /(/) (уравнение пер-
вого рода) правая часть должна браться из более узкого
класса, что приводит к дополнительным условиям для функции
/(О (условия Пикара). В особом уравнении функция ф(/) и
особый интеграл от нее принадлежат к одному и тому же
классу, и, следовательно, отсутствие в уравнении члена с
самой функцией не меняет класса левой части; поэтому при
отыскании обыкновенных решений свойства уравнений первого
и второго рода неразличимы.
При нахождении же сингулярных решений дело обстоит
иначе. Для уравнения первого рода а(/)^0, поэтому
необходимое условие удовлетворяется тождественно и, следовательно,
любая точка t\ контура может стать источником особого
решения. , Например, простейшее уравнение первого рода
\ x--t ^'^^^^ (а = /? = /== О, Ь=\) удовлетворяется функ-
Ци^й ^_^ при любом t\ (см. п. 7.3). Следовательно, это
уравнение имеет континуум сингулярных решений.
24.6. Регуляризация решением характеристического
уравнения (способ Карлемана—Векуа). В построенной выше теории
особого уравнения использовалась только регуляризация,
основанная на композиции особых операторов; упомянутый в
п. 22.3 третий способ регуляризации, заключающийся в
использовании явного решения характеристического уравнения,
оставался пока в стороне.
Изложим теперь этот важный в теоретическом и
практическом отношении способ.
Перенося регулярный член особого уравнения в правую
часть, запишем его в следующем виде:
a[t)^{t) + -^\^dx = f {t)^\k{t, т)ф(т)йт B4.18)
L L
или, в символической форме,
К> = /-/еф. B4.180

§ 24J РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 233
Решим последнее уравнение как характеристическое,
рассматривая временно правую часть как известную функцию*).
Применяя формулу B1.9), получим
B4.19)
при х^О следует положить Px-i@ —О- Меняя в двойном
интеграле порядок интегрирования, запишем выражение в
последних квадратных скобках следующим образом:
Так как Z{t) удовлетворяет условию Гёльдера (следовательно,
ограничена) и не обращается в нуль, а ^(тьт) вблизи х\ = х
имеет оценку \k(xi, т)|<-—-—г-, то легко видеть, что и весь
I Tl - т Г
интеграл
[ kjxux) .
J Z{x,)(x,^t) ^^^
L
имеет ту же оценку, что и k(xux). Следовательно, ядро
/((/, x) = Rtk(t,x) =
= aV)k V. ,) - Щ^ 5 _±A^ ,„ ,24.20)
является фредгольмовым. Перенося все члены, содержащие
ф(/), в левую часть, получим
(i>(t)+\K(t, x)cp(x)dx = fAt), B4.21)
*) Идея, заложенная в последнем способе регуляризации, часто
применяется в теории уравнений математической физики для приведения краевых
задач к интегральным уравнениям (см., например, приведение к
интегральному уравнению задачи Штурма — Лиувилля или приведение к
интегральному или интегро-дифференциальному уравнениям краевой задачи уравнения
эллиптического типа).

234 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
где K{t,x)—фредгольмово ядро, определяемое формулой
B4.20), а /i(/) — свободный член, имеющий вид
h (О = a{t)f (t) - ^^^ J Т7^ Т^ + ИО Z (О Р«-, (/). B4.22)
Если индекс уравнения B4.19) х < О, то, согласно п. 21.2,
формула B1.9), в которой нужно положить Px-i@^0» имеет
место только при соблюдении условий B1.13). В
рассматриваемом случае в последнем условии f(t) нужно заменить на
f{t)-\k{t,T)cp{T)dx.
L
Следовательно, при х < О наряду с уравнением Фредгольма
B4.21) функция должна будет удовлетворять соогношениям
(А;=1,2, ..., -х).
Сформулируем полученный результат.
Если X ^ О, то решение полного особого интегрального
уравнения B4.18) приводится к реигению интегрального
уравнения Фредгольма B4.21). Если х < О, то уравнение B4.18)
приводится к уравнению B4.21) {где нужно положить
Px-i(O^O) совместно с функциональными условиями B4.23),
которые можно записать в форме
9k (т) Ф (т) dx = /, (А> = 1, 2, ..., - х), B4.24)
где р/^(т)=\ ^'У t^"^ dt—известные функции ufk=\ ^щ'^"^ ^^—
L L
известные числа.
Равенства B4.24) есть условия разрешимости регуляризо-
ванного уравнения B4.21). Однако не все они являются
условиями разрешимости исходного сингулярного интегрального
уравнения B4.18); часть их может оказаться условиями
равносильности этих двух уравнений. Разделим условия
указанных двух типов.
Пусть среди функций р^ имеется h линейно независимых.
Можем выбрать нумерацию так, чтобы это были pi, р2, ..., р^.
Тогда будем иметь
\
р, (О ф (О л = /ft (Л = 1, 2, ..., Л). B4.240

§ 241 РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 235
Кроме того, будут выполняться v = |x|--Л независимых
линейных соотношений
«/iPi+ ••• +«/|х,Р|х, = 0 {/=1,2, ..., V).
Умножим равенства B4.24) последовательно на а^, ..., алх|
и сложим. Учитывая последние равенства и вводя обозначение
yfPi{t) = [Z{t)r^ Z aд/^-^ получим
5 / (О ^,(t)dt = 0 (/=1,2...., V). B4.24")
L
Эти равенства, не содержащие искомой функции ф, будут
условиями разрешимости, которым необходимо должен
удовлетворять свободный член / для того, чтобы исходное
сингулярное уравнение и его регуляризованное были разрешимы.
Равенства B4.24') будут условиями равносильности уравнений
исходного особого и регуляризованного. Из решений фредголь-
мова уравнения B4.21) данному особому уравнению B4.18)
будут удовлетворять лишь те, которые удовлетворяют
условиям B4.240.
Таким образом, при к ^ О регуляризованное уравнение
B4.21) равносильно исходному особому. При х<0 исходное
уравнение будет равносильно регуляризованному (вместе с
общими для них условиями разрешимости B4.24^')) и условиям
B4.240.
И. Н. В е к у а 2) указал линейную подстановку такую, что
для новой искомой функции условия B4.24') выполняются
автоматически. Регуляризованное уравнение с такой функцией
уже будет полностью равносильно исходному.
На основе указанного способа регуляризации можно
построить полную теорию сингулярного интегрального уравнения
(см. И. Н. Векуа 2)).
Возвратимся, в заключение, к уже затрагивавшемуся в
конце п. 23.3 вопросу о соотношении между числами решений
полного уравнения и соответствующего ему характеристического.
Введем, аналогично тому как это делалось в теории уравнений
Фредгольма, в регулярную часть ядра сингулярного
интегрального уравнения в качестве множителя произвольный параметр
К, Тогда уравнение B4.18') запишется в форме
К°ф = /-Л*ф, B4.18'0
а после регуляризации соответствующее уравнение Фредгольма
примет вид
Ф (О + ^ S Kit, т) ф (т) dT = f, (/), B4.210

236 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
где /с и /i определяются, как и ранее, формулами B4.20),
B4.22) (предполагаем к^О). Так как правая часть содержит
X независимых произвольных постоянных, то в случае, когда X
не есть собственное значение ядра /С, уравнение B4.2Г), а
следовательно, в силу равносильности и исходное уравнение
B4.18''), имеют х решений, которые будут линейно независимы
(см. рассуждения в конце п. 23.2). Следовательно, число
решений полного уравнения может превышать число решений
соответствующего характеристического лишь на множестве
собственных значений параметра Я, являющемся дискретным.
Таким образом, из двумерного континуума значений, которое
может принимать параметр X, лишь на дискретном множестве его
значений с единственной возможной предельной точкой на
бесконечности числа реигений уравнений полного и
характеристического могут не совпадать. Это доказывает утверждение конца
п. 23.3, что случаи несовпадения являются исключительными.
24.7. Пример. В качестве примера для иллюстрации
изложенной теории произведем различными способами
регуляризацию следующего особого интегрального уравнения:
Кф^(^ + Г0ф@ +
L L
где L — единичная окружность.
Регулярная часть ядра является вырожденной, поэтому тем
же способом, который применяется при решении уравнений
Фредгольма с вырожденным ядром, уравнение может быть
сведено к совокупности характеристического уравнения и
линейного алгебраического уравнения и, следовательно, решено в
замкнутой форме. Таким образом, здесь нет необходимости в
регуляризации. Однако рассматриваемое уравнение удобно для
иллюстрации на нем общих методов, так как здесь все
выкладки могут быть проведены до конца.
Для удобства дальнейших рассуждений предварительно
решим данное уравнение. Обозначая
1
2я/
J (т + т- О Ф (т) rfr = Л, B4.26)
запишем его в форме характеристического:
0 + г')ф@ + -4р-5^^т=2/ЧлО + г').

§ 24] И^АВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 237
Для соответствующей краевой задачи Римана
А_
2
ф+ (t) = Г'Ф- (О + / + 4 A + Г') B4.27)
индекс к = —2 и условия разрешимости (см. п. 21.2) будут
выполняться только при Л = 0. При этом
ф+B) = г, Ф"B) = 0.
Отсюда получим решение уравнения B4.25)
Ф (О = Ф^(/)-ф-(/) = /.
Подставляя последнее выражение в равенство B4.26),
убеждаемся в том, что оно удовлетворяется при Л = 0.
Следовательно, данное уравнение разрешимо и имеет единственное
решение
Ф (/) = /.
Г. Регуляризация слева. Так как индекс уравнения
X = —2 < О, то любой его регуляризующий оператор будет
иметь собственные функции (не менее двух), поэтому
регуляризация слева приводит, вообще говоря, к уравнению, не
равносильному исходному.
Рассмотрим сначала регуляризацию слева при помощи
простейшего регуляризатора К'°. Найдем собственные функции
уравнения
K'°«>-(/ + r')co@--4p-S-^iT = 0.
Соответствующая краевая задача Римана
ф+(/) = /2ф-(/)
имеет теперь индекс х = 2. Находя по формулам п. 21.2
собственные функции оператора К'°, получим
На основании общей теории (п. 22.4, 1°) регулярное
уравнение К'°Кф = К'7 будет равносильно особому:
Кф = / + «iO>i + а202, B4.28)
где аь аг — некоторые постоянные, которые могут оказаться
или произвольными или определенными. Учитывая B4.26),

238 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. Ш
запишем уравнение B4.28) в форме характеристического:
L
= 2/^ + Л О + /" О + ai (I - Г^) + а2 (/ - Г О-
Соответствующая ему краевая задача Римана будет такова:
Ее решение формально представляется в виде
Ф^(г) = 2 + 1л + 1а2,
ф- (г) = \i Wz-^ + (а2 - Л) г-'~ а^г"^].
Условия разрешимости дадут
«1 = 0, а2 = Л.
Решение уравнения B4.28) определится тогда формулой
ф(/) = ф-*-@-Ф"@ = ^ + Л.
Подставляя найденное значение ф в равенство B4.26), получим
тождество А-=^ А, Следовательно, постоянная аг = Л остается
произвольной, и регуляризованное уравнение равносильно не
исходному уравнению, а уравнению
Кф = f + «2@2,
имеющему решение ф@=^ + Л, где Л — произвольная
постоянная. Последнее решение удовлетворяет исходному
уравнению только при Л = 0.
Приступим теперь к нахождению равносильного регуляриза-
тора слева. Поскольку данное уравнение разрешимо, такой
регуляризатор для него существует и может быть эффективно
построен по теореме п. 24 5.
Построим прежде всего сопряженный оператор К*. По
определению,
2я
я/ J г — т
о
2Я
Учитывая, что

§ 24] РАВНОСИЛЬНАЯ РЕГУЛЯРИЗАЦИЯ 239
получим
KV = (/ + r')V@-
-^S(^-^"')r?l^^-iSO+^"H+--')V(T)rfT. B4.29)
L L
Согласно лемме п. 24.5 уравнение К*Кф = К*/ будет
равносильным исходному, но, вообще говоря, не будет регулярным.
Роль преобразования оператором К* сводится в общем случае
к приведению данного разрешимого особого уравнения к
другому, равносильному ему особому уравнению с нулевым
индексом; последнее окончательно регуляризуется. Однако в
рассматриваемом случае характеристическая часть оператора К*
совпадает с оператором К^°, который, как известно, является
регуляризатором для оператора К. Поэтому уравнение К*Кф =
= К*/ будет фредгольмовым.
Выполняя все выкладки (советуем читателю, пользуясь
общей схемой п. 24.3, проделать их), получим следующее
уравнение Фредгольма:
^(^)+-4^7$(^^~^-'^"')^^^^ = '- B4.30)
L
Равносильность последнего уравнения исходному вытекает из леммы
п. 24.5 и поэтому не нуждается в каком-либо дополнительном обосновании.
Укажем, однако, имея в виду другие аналогичные случаи, где такое
обоснование может читателю понадобиться, как это сделать здесь, не опираясь на
указанную лемму.
Поскольку уравнение B4.30) имеет вырожденное ядро, то самое
простое — решить это уравнение. Окажется, что оно, так же как и исходное
особое уравнение, имеет единственное решение ф@ =/. Более общий прием —
это использование того метода, которым ранее нами была установлена
неравносильность уравнения К'°Кф = К'7 исходному. Проведем схематически
это исследование.
Решая уравнение К*г|)* = О, найдем собственные функции оператора К*:
Решая затем особое уравнение с вырожденным регулярным ядром
равносильное уравнению Фредгольма B4.30), получим, что оно разрешимо
только при ai = аг = О Этим доказательство равносильности заканчивается.
2°. Регуляризация справа. В качестве регуляриза-
тора справа возьмем простейший оператор К'°. Полагая
Ф (О = К'°(о ^ (/ + г о (О (О - -Ц^ \ т=Т ^^' B4.31)

240 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
получим (советуем читателю самому проделать необходимые
выкладки) уравнение Фредгольма относительно функции ©(/):
КК''(о^(о@~
-¦i S t^ (^^- I + ^") + 2т-^ + ГЧт^ + 3 + т-^) - 2ГV^] X
X(o(T)dT = -J. B4.32)
Решая последнее уравнение как вырожденное, будем иметь
0(O = Y + a(/-rO + p(l~r^),
где а, р — произвольные постоянные.
Таким образом, регуляризованное уравнение имеет
относительно (О(О два линейно независимых решения, тогда как
исходное уравнение B4.25) решалось однозначно. Подставляя
найденное значение (о@ в формулу B4.31), получим
Ф@ = К'°[4 + аО-ГО + рA-Г^)] = /
— решение исходного особого уравнения. Результат согласуется
с общей теорией, так как при отрицательном индексе
регуляризация справа является равносильной.
3°. Регуляризация решением
характеристического уравнения. Этот способ регуляризации проводится
по формулам B4.19) — B4.22). Однако нужно помнить, что эти
формулы применимы к уравнению, для которого выполняется
условие а^ — &2 = 1; поэтому предварительно нужно разделить
уравнение B4.25) на 2.
Тогда будем иметь
Z@ = (a + 6)X^=/,
L
Rtk{t,x)^-^{t-\-r')-^it+r'){x + x-')-V
«-Г')<(т + т-') Г т, + тГ' dT, ^ I _

§ 251 ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 241
Регуляризованное уравнение имеет вид
<f(t)-'^\{r + x-')q>{x)dx = L B4.33)
[
К нему нужно добавить еще условия B4.24) для fe= 1, 2.
Решая его как вырожденное, найдем общее решение ф(/) = f +Л,
где А — произвольная постоянная. Выпишем условия B4.24^),
B4.24^0. Здесь
L L
Р,(Т) = 0, Р2(Т) 1(т+4).
L L
Функции pi, p2 линейно зависимы. Зависимость a/iPi + . •.
... + ay|^,p,j^, = 0 (см. п. 24.6) имеет вид
aiPi+0-p2=0.
Отсюда условие разрешимости B4.24'') выполняется
тождественно. Условие равносильности B4.24')
5р2(т)ф(т)йт = -15(т+1)(т + Л)^т = 0
L L
удовлетворяется лишь при /4 = 0. Следовательно, из
множества решений регуляризованного уравнения ф(/)=/ +Л
исходному особому удовлетворяет лишь функция ф(/) = /.
Рассмотренное уравнение было использовано И. Н. В е-
куа 2) для иллюстрации метода регуляризации решением
характеристического уравнения.
§ 25. Исключительные случаи особых интегральных уравнений
При исследовании особых интегральных уравнений
исключались случаи, когда функции a{t)±:b{t) обращались на
контуре L в нуль. Это вызывалось тем, что коэффициент
G{t)= д(аТ^(/) задачи Римана, к которой приводится
характеристическое особое уравнение, имеет в этих случаях на
контуре нули и полюсы, и, следовательно, такая задача не
подчиняется общей теории. Опираясь на результаты § 15, проведем
отдельное исследование указанных исключительных случаев.

242 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. III
Будем предполагать, что коэффициенты исследуемых особых
уравнений таковы, что обеспечивается выполнение
дополнительного требования дифференцируемости функций, которое
предъявлялось в § 15 при рассмотрении исключительных случаев
задачи Римана,
25.1. Решение характеристического уравнения. Рассмотрим
характеристическое уравнение B1.1)
К°Ф-а(Оф@ + ^$^^ = /@. B5.1)
L
В Предположении, что функции a{t)—b(t) и a{t)-\'b{t) имеют
на контуре нули соответственно в точках аьаг, ..., а^ и
Pi, Рг, ..., Pv целых порядков и, следовательно, представимы
в виде
а@~&@ = П(<~сх/^Г^/-@,
a(t) + b{t) = fl{t^^jY!s(t\
/-1
где r{t) и s{t) нигде не обращаются в нуль. Все а^, Pj
предполагаются различными.
Удобно разделить обе части уравнения B5.1) на ^JTЩ7^f)
и в дальнейшем считать, что коэффициенты его удовлетворяют
соотношению
а^ if) - b' (О = ft (< - а,)"** flit- ф = По. B5.2)
Л=1 /-1
Уравнение B5.1) тем же путем, что и в п. 21.1, приводится
к задаче Римана
П (/ - a^j.)'"/^
<l>''{t) = ^ GAtH'it)'h- ^-^ , B5.3)
/-1 /-1
где Gi{t) = r{t)/s{t). Решение этой задачи в классе функций,
удовлетворяющих условию ф(оо)=0, определяется формулами
A5.7) и A5.8). Применяя их, находим
ф-ь (^) = -.^^^ [xi;+ (г) ~ Q, (г) + Ho^x-p-i (z)l
Ф" iz) = -т-^-^ [}V- {Z) - Qp (г) + ПоР,-р., {z)l
П i^-^kf'
/г-1

§ 25J ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 243
где
xV{z) = ^[ '-Ц ^, B5.5)
2я/ J S (т) Х^ (т) т - Z
а Qq{z)—интерполяционный многочлен для функции 4^(z)
степени р = m + Р— 1 с узлами в точках а^ и Р; соответственно
кратностей т^ и pj, где m = Х т^^ а p = T,pf.
Условимся многочлен Qp{z) рассматривать как оператор,
ставящий в соответствие свободному члену f{t) уравнения
B5.1) многочлен, интерполирующий указанным образом
интеграл типа Коши B5.5). Обозначим этот оператор
YTf = Q,iz). B6.6)
Коэффициент 1/2 здесь взят для удобства дальнейших
преобразований.
Поступая далее, как в п. 21.2, из B5.4) найдем
ф+и)= Х+@ г1 f(<) . 1 Г /(т) dx
ГГ(<_р)Р/ 1^ ^(')^''W 2я< J s(T)X+(T) x-t
/-1
-jTf{t)-±IkP^.,.y{t)l
ф-(л_ X-@ г 1 lit) . 1 Г f(x) dx
f\(t-a\'"k\. 2 «WX''@ 2я/ J s(T)X+(T) T-<
Л-1
Г/@-уПоЯ.-р-1@].
Коэффициент —1/2 в последних слагаемых этих формул взят
в силу произвольности коэффициентов многочлена Px-p-i@-
Следовательно,
Ф@==Ф*'@-Ф'@ =
Х^@ \ f(t) .
П с-«.)"')
П-ПоР^-р-,(о). B5.7)
"^(т) Т-/

244 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. III
Введем обозначение
Z{t) = s (t) Х-^ (t) = г (t) X' {ty B5.8)
Используя это обозначение, а также соотношение B5.2),
представим формулу B5.7) в виде
+ b{t)Z{t)P^-,.^{t).
Вводя оператор Rf формулой
j^f^^[a(t)f{t)-±S!m!}.\^ iir! x'-f +bit)Z{t)Tf], B5.9)
окончательно получим
cp{t) = Rf + b (t) Z (t) P^-,-, (t). B5.10)
Формула B5.10) дает решение уравнения B5.1) при
X — р > О, которое линейно зависит от х — р произвольных
постоянных. Если к — р < О, то решение существует лишь при
выполнении р — х специальных условий разрешимости,
налагаемых на свободный член f{t) и вытекающих из условий
разрешимости соответствующей этому случаю задачи Римана
B5.3). Выписывать явно эти условия не будем.
С. Г. Самко 2), обобщив работу Ю. И. Черского 1) (см. п. 16.3, 4°),
исследовал общее сингулярное уравнение
(Л, + AoS) ф = /
в исключительном случае, когда операторы Л1±Л2 не обязательно обратимы.
Был рассмотрен случай, аналогичный обращению коэффициента G{i) задачи
Римана в нуль или бесконечность целого порядка. В операторной форме это
г
соответствует представлению вида Л] + ^2 = JJ F^ — Я//)^/Л', где Л' —
/-1
уже обратимый оператор, Xj принадлежит спектру оператора U, «j —целые
положительные числа. Решение уравнения найдено в явном виде; при этом
использовался некоторый аналог интерполяции элементов банахова
пространства.
25.2. Регуляризация полного уравнения. Рассмотрим полное
особое уравнение
Kcp^a{t)cp{t) + ^\-^dx+\k{t, т)ф(т)йт = /@ B5.11)
при тех же предположениях относительно функций a{t)dbb{t),
что и в п. 25.1

§ 25] ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 245
Представив его в виде
K'(p = f{t)-\k{t, т)ф(т)йт,
применим метод регуляризации решением характеристического
уравнения. По формуле B5.10) получаем уравнение
Ф (О = /? Г/ (t) - 5 ^(/, т) ф (т) dxl + b{t)Z it) P^_,_i (/),
или
Ф(О + /? П ^ (^ т)ф(т) dxl = Rf + b{t)Zit)Р,,-,-, (/). B5.12)
Покажем, что в выражении /?Г\ fe(f, т)ф(т)^т 1 операция R
по переменной t и операция интегрирования по т
перестановочны.
Развернем это выражение по формуле B5.9):
R\\k{t, т)ф(т)йт1 =
^ L L L
+ b{t)Z{t)T\\^k{t, т)ф(т)йт1|. B5.13)
Во втором слагаемом правой части B5.13) допустима
перестановка порядка интегрирования (п. 7.1). Совершив ее и
изменив обозначение переменных интегрирования t на а и а на т,
получим
в третьем слагаемом оператор гГ\/г(/, т)ф(т)^т1,
согласно его определению в п. 25.1 (формулы B5.5), B5.6)), дает
многочлен, интерполирующий функцию
¦h \ Z (х)% _ ,) ^ Мт, а) ф (а) da = ^ Ф (т) dx ^ \ ^^^^(о-г) ¦

246 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ ГГЛ. П1
Из возможности перестановки порядка интегрирования
можно заключить, что
T\[k{t,x)(p(т)dx] = \ Ф(т)Tt [k(t, т)] dx.
l\k{t, x)(f{x)dx'] = \q>
Индекс t у символа оператора Tf указывает, что операция
B5.6) производится по переменной t.
Теперь равенство B5.13) можно преобразовать так:
R\\k{t, т)ф(т)йт1 =
{ / \ ^ ( /л ии \ b(t)Z(t) [ k (а, т) do ,
+ b{t)Z it) Tt [k (/, т)] \dx=\RAk (/, т)] ф (т) dx.
Перестановочность операций доказана.
Возвращаясь к уравнению B5.12), придадим ему вид
Ф (О + J Rt [k (^ т)] ф (т) dx = Rf + b (t) Z it) Рн-р-1 (/). B5.14)
L
Так как оператор R ограниченный, то полученное интегральное
уравнение B5.14) является уравнением Фредгольма и,
следовательно, задача регуляризации особого уравнения B5.11)
решена.
Из общей теории регуляризации (п. 24.6) следует, что при
к — р^О уравнение B5.11) равносильно уравнению B5.14), а
при X — р < о — уравнению B5.14) и системе некоторых
функциональных уравнений.
В заключение заметим, что для рассмотренных случаев
особых интегральных уравнений теоремы Нётера оказываются,
вообще говоря, несправедливыми.
25.3. О сведении исключительного случая особых
интегральных уравнений с ядром Коши к уравнениям нормального типа.
Используем теперь для исследования особого интегрального
уравнения способ композиции особых операторов, аналогичный
регуляризации слева. При этом будем допускать у функций
а ±6 и общие нули. Задано уравнение
Кф^а(/)ф@ + -^5|^^т+5/(/, т)ф(т)йт = /(/), B5.15)

^ 25] ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 247
У которого
a(t)-b it) = П (^ - yiP tit- а,)'"^ г (О,
a{t) + b it) = П(/ - у,Г flit- ^jYf s(О,
t-i /-1
где r{t) и s{t) нигде на L не обращаются в нуль; а^, Pj, уг —
точки контура L. Некоторые точки Vi могут совпадать с а^ или
с Pj; rtunikyPj — целые положительные числа.
Совершим равносильное преобразование уравнения B5.15)
с помощью композиции слева с так подобранным оператором
Л^, чтобы все исключительные точки а^, Р;, уг стали общими
нулями новых коэффициентов характеристической части. С
помощью формул B2.9) композиции операторов нетрудно
подсчитать, что для этого достаточно взять
L
так, чтобы его коэффициенты удовлетворяли условию
«1 it)-b,it) = Uit-^j)'^, «1 it) + b,(t) == П (^-oikT^.
Здесь индекс xi = О и число полюсов Pi = 2^/^ = ^, по-
этому xi — /?! < о и из результатов п. 25.1 вытекает, что
оператор Л^ не имеет собственных функций. Следовательно (п. 22.4),
уравнение Л^Кф = Nf равносильно исходному уравнению B5.15).
Преобразованное уравнение запишется в виде
NKc^^Ait)^it) + -^\^dx+\kit,x)^ix)dx = Fif).
L L
B5.16)
Здесь, согласно формулам B2.9) для композиции особых
операторов,
/г-1 /-1 i~\
ft=i /=i i-i

248 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
Выражение для регулярного ядра k{tyX) ввиду его
громоздкости явно не выписываем.
В преобразованном уравнении исключительные точки а^, pj,
Yi играют одинаковую роль. Для упрощения последующих
формул условимся единообразно обозначать их gj с
последовательными номерами /=1, ..., ji; |и+1, ..., р,-+-v; pi + v+1, ...
..., [А + V -f- X, а кратности нулей т^, pj, tii через Sj с теми же
последовательными номерами. Будем считать, что в окрестности
точек Oj функции F{t)y k{t,x) имеют производные по / порядков
Sj, удовлетворяющие условию Гёльдера.
Из вида уравнения B5.16) вытекает, что для его
разрешимости функция F (/)— \ ^(/, т)ф(т)йт должна в исключитель-
L
ных точках Gj обращаться в нуль порядков Sj. Отсюда следует,
что в разложениях по формуле Тейлора в окрестности точек gj
должны обращаться в нуль Sj последовательных начальных
членов разложения. После этого все уравнение можно сократить
на Е (/-oг^)^
В результате исследования может быть сформулирована
Теорема. При сделанных предположениях уравнение
B5.16) равносильно уравнению нормального типа
L L
B5.17)
совместно с функциональными соотношениями
L
0'=1, .... n + v + Я,; V/ = 0, 1, ..., s,-l).
B5.18)
где
л,(о=-^Ш^. BAt)-=^^^^^^
Vy-0
^i(^)= E —4^ f(/)-. J]f(v/)(a,)
Vy — U
V/I

§ 25J ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 249
Qsi-\{t) — многочлены степени Sy—l, определяемые из равенства
П ('-«^,/' '-' ('-^'^'
/-1
Действительно, из предыдущего рассуждения вытекает, что
всякое решение уравнения B5.16) будет удовлетворять
уравнению B5.17) и функциональным соотношениям B5.18). С
другой стороны, умножая равенства B5.18) соответственно на
(Vi\)-^{t —oj) ^Qs,-\{t) и складывая их почленно с равенством
B5.17), придем к исходному уравнению B5.16). Следовательно,
всякая функция, удовлетворяющая одновременно равенствам
B5.17) и B5.18), удовлетворяет также и уравнению B5.16).
Исходному уравнению будут удовлетворять только те
решения уравнения B5.17), которые удовлетворяют соотношениям
B5.18); поэтому последние для уравнения B5.16) играют роль
условий разрешимости-равносильности. Совершенно аналогично
тому, как это делалось в п. 24.6, можно разделить условия
B5.18) на условия равносильности и условия разрешимости.
Далее, как уже упоминалось в п. 24.6 (И. Н. Веку а 2)),
можно подобрать такую линейную замену искомой функции, что
условия равносильности удовлетворятся тождественно. Таким
образом, оказывается справедливой
Теорема. Особое интегральное уравнение в
исключительном случае может быть приведено к равносильному ему
нормальному особому интегральному уравнению и некоторому
числу условий разрешимости.
Если исходное уравнение разрешимо безусловно, то условия
разрешимости удовлетворятся тождественно и уравнение в
исключительном случае приведется к равносильному нормальному
уравнению.
Изложенный здесь способ решения был указан А. И.
Тузиком 1), 2). Уравнения рассматриваемого типа на отрезке
[О, 1] в случае,' когда а±Ь имеют только общие нули (порядка
меньше единицы) на концах отрезка, встречаются в теории
краевых задач для вырождающегося гиперболического
уравнения и исследовались в связи с этим X. Г. Бжихатловым
(Дифф. ур. 7, № 1, 1971). Исследование исключительных
случаев методами функционального анализа имеется в ряде работ.
Обзор результатов содержится в работе S. Prossdorf 1).
25.4. Вырожденные случаи *). В заключение рассмотрим
случаи, когда а + й или а — b обращаются в нуль тождественно.
*) Настоящий пункт написан по работе автора 9).

250 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
Будем называть эти случаи вырожденными. В предположении,
что b{t) не обращается в нуль*), можно записать уравнение
в виде
Кф^ + 1ф@ + ^$^йт+5/^(/, т)ф(т)^т = /@. B5.19)
L L
1°. Формальные соотношения. Начнем с вывода
некоторых простых зависимостей. Пусть, как в п. 16.3, 4°, / и S —
операторы, тождественный и особого интегрирования, и введем
операторы
M''^-j{±I + S). B5.20)
Тогда для кусочно аналитической функции, представленной
интегралом типа Коши ф^ (z) = уу \ _ ^ dr, формулы Сохоц-
L
кого примут вид
ф'=@ = ^(±/ + 5)ф=МЧ B5.21)
Для функции двух переменных fe(/, т), употребляя
обозначения MtMxk{t, x) = k'^~{t, т) и аналогичные, будем иметь
очевидные формулы
k{t^ x) = kt -kT = kt -kx=k'^^ -k^' -k"^ ^-k" B5.22)
(cm. аналоги в п. 9.6).
Если учесть равенство S^ = I (п. 7.3) и очевидные
соотношения Я = /, /5 = S/ = S, легко получить следующие свойства
операторов ЛГ±:
М-^М^ = М"^, М'М' = - М~, М+М" = М"М^ = 0. B5.23)
Последнее соотношение можно было бы также легко
получить не формальным путем, а из интегральных теоремы и
формулы Коши. Кроме того, справедливы легко проверяемые
соотношения
{М''У = -М^. B5.24)
2°. Характеристическое уравнение. В новых
обозначениях уравнение B5.19) может быть записано так:
Кф = Л1*Ф + /гф = /, B5.190
*) Допущение у b{t) нулей в отдельных точках привело бы к
уравнению, ядро которого имеет неподвижные полярные особенности Это
специальный вопрос, аналогичный встретившемуся в п 25.3, и здесь он не
рассматривается.

§ 251 ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 251
а его характеристическое уравнение —
К-ф^М^Ф = /. B5Л9'0
Коэффициент соответствующей характеристическому уравнению
краевой задачи Римана обратится тождественно в нуль (в
случае оператора М+) или в бесконечность (для М-), Сама
краевая задача будет иметь вид
Ф*{0 = /@ (неоднородная задача), B5.25)
Ф*(/) = 0 (однородная задача). B5.25")
Общим решением однородной задачи будет, очевидно,
f Ф'*'B) = 0, 1 ф-^{г) = ФТ(г),
< или \
{ ф-B:) = ФГ(г) I ф-B) = 0,
где Ф*(г)— произвольные аналитические в D+ или в D-
функции. Из вида краевого условия B5.25) вытекает, что
неоднородная краевая задача B5.25) будет разрешима тогда и только
тогда, когда правая часть имеет вид /=•=(/), т. е. в том случае,
когда выполняются условия
Г @ = 0. B5.26)
Если оно выполнено, то общее решение неоднородной краевой
задачи запишется в виде
ф+ (г) = /+ (г), Ф- B) = ФГ (г) B5.27)
для верхнего значка и
ф+ >2) = Oi (г), Ф" (z) = Г (г) B5.270
для нижнего значка.
Условие разрешимости B5.26) краевой задачи будет
одновременно и условием разрешимости характеристического
уравнения B5.19^0» и в случае его выполнения общее решение
последнего по формуле Сохоцкого представится выражением
Ф (/) = ф+ (/) - ф- (/) = /+ (t) - ФГ (Л B5.28)
для верхнего значка и
Ф@ = Ф?'@-Г@ B5.280
для нижнего значка.
Полученные результаты позволяют сделать заключения по
эопросу о выполнимости для вырожденного случая теорем

252 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. HI
Нётера. Произвольная аналитическая функция зависит от
бесконечного множества параметров. Отсюда вытекает, что уже
первая теорема Нётера оказывается несправедливой. В отличие
от исследованных ранее нормального и исключительного
случаев, теперь число решений может стать бесконечным.
Легко решить вопрос относительно третьей теоремы. Как
уже указывалось, коэффициент краевой задачи Римана равен
здесь нулю или бесконечности, следовательно, само понятие
индекса теряет смысл. Можно это же заключение вывести и из
других соображений. Было установлено, что число решений
однородного уравнения бесконечно. Число решений
транспонированного уравнения, которое, как легко показать, совпадает
с числом условий разрешимости B5.26), также бесконечно.
Следовательно, формула B3.9), дающая выражение индекса,
принимает неопределенный вид: х = оо — оо.
Можно было бы показать, что вторая теорема Нётера для
характеристического уравнения остается справедливой. Но на
обосновании этого факта, не имеющего для общей теории
принципиального значения, не останавливаемся.
3^ Полное уравнение. Регуляризация слева.
Из общего вида регуляризатора B2.16) следует, что
простейшим регуляризатором (слева и справа) для уравнения B5.19')
будет оператор М"^, Произведя композицию, получим
М'^Кф^М"^ kcp^^kf(/, т)ф(т)dr = Г@. B5.29)
В отличие от случаев нормального и исключительного, регу-
ляризованное уравнение будет уже не уравнением второго, а
уравнением первого рода. Это обстоятельство, как увидим
далее, вносит в теорию новые черты. Уравнение B5.29), вообще
говоря, не будет равносильным исходному; оно может содержать
посторонние решения. Возьмем от уравнения B5. 19')
композицию на оператор Af± слева. Учитывая B5.23), получим
Л1=*=Кф = ± M^q) + kt(p = f *. B5.30)
Вычитая из B5.29) равенство B5.30), придем к равенству
B5.19'). Следовательно, особое интегральное уравнение в
вырожденном случае равносильно совокупности двух уравнений
B5.29) и B5.30), из которых одно фредгольмово первого рода,
а второе снова особое вырожденное, но более частного вида.
Из сформулированного свойства уже можно было бы
сделать некоторые теоретические выводы, но удобнее сделать их
с помощью другого способа регуляризации.

% 25) ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 253
4°. Регуляризация решением
характеристического уравнения. Для упрощения записи будем брать
лишь верхний значек. Перенесем в уравнении B5.19') член йф
в правую часть и используем формулы B5.28) и B5.26),
заменяя в них / на / — k(p. Получим
(f{t)+\kt{t, т)ф(т)^т = /^@-ФГ@, B5.31)
кГ (/, т) (p{x)dx = r @. B5.32)
S
L
Таким образом, полное вырожденное особое интегральное
уравнение оказывается равносильным совокупности
интегрального уравнения Фредгольма второго рода B5.31), правая часть
которого содержит бесконечное множество произвольных
параметров (произвольную функцию ФГ@)» и уравнение
Фредгольма первого рода B5.32). Последнее будет представлять собою
совокупность условий разрешимости-равносильности.
Записывая с помощью резольвенты решение уравнения B5.31) в явном
виде и вставляя его в уравнение B5.32), получим в общем
случае бесконечную систему уравнений относительно
бесконечной совокупности произвольных параметров. С помощью
рассуждений, аналогичных проведенным в п. 24.6, можно отделить
уравнения, не содержащие произвольных параметров. Они
будут чистыми условиями разрешимости одновременно
исходного и регуляризованного уравнений. Из остальных уравнений
произвольные параметры определяются так, чтобы решения
преобразованного уравнения удовлетворяли исходному особому
уравнению.
Вопрос о том, какое число параметров останется
произвольным и войдет линейно в общее решение, зависит от ранга
соответствующей матрицы и в общем случае не решается; то же
справедливо и для числа условий разрешимости. На примере,
который далее будет рассмотрен, можно показать, что
реализуются две возможности: оба эти числа могут быть
одновременно или конечными, или бесконечными.
Остался еще открытым вопрос о месте второй теоремы
Нётера. Нетрудно показать, что необходимость условия
\f{t)'\\-){t)dt = 0 сохраняется. Действительно, оно является про-
L
стым следствием тождества \ Кфф rf/= \ фК'г|) rf/, а последнее
L L
основано на возможности перестановки порядка
интегрирования, которая, очевидно, в одинаковой мере справедлива для
всех случаев: нормального, исключительного и вырожденного.

254 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. III
Однако условие, накладываемое этой теоремой, перестает быть
достаточным. В самом деле, предположим, что в уравнении
B5.32) все функции принадлежат классу L2 и что ядро kt {t, т)
симметрично*). Согласно теореме Пикара (см.
Привалов И. И., Интегральные уравнения, М., ОНТИ, 1935)
должны выполняться необходимые и достаточные условия
разрешимости
где Xk — собственные значения ядра кГ (t, х). Это — условие
существенно нового типа. Наглядную иллюстрацию сказанному
дает следующий
Пример. Пусть на единичной окружности задано
уравнение
Кф = Лф@ +
+ ^ $ T^dr+^ J I; с„^ф(т)йт = /@. B5.33)
|т|-1 |Т|«1/1--«>
Постоянный коэффициент Х будем пока считать
неопределенным. Вырожденным случаям будут соответствовать значения
Х= ±1. Все входящие в уравнение функции будем считать
принадлежащими классу L2 и, следовательно, разложения
П—-00 /1-.-0О П"--оо
B5.34)
считать сходящимися в смысле среднего квадратичного, а
коэффициенты удовлетворяющими условиям
Е 1/«Р<оо, Z \СпГ<оо^ Z 1ФпР<оо.
Будем решать уравнение непосредственно с помощью рядов.
Вставим ряды B5.34) в уравнение и вычислим соответствующие
*) Предположение о симметричности ядраА?^ (/,т) сделано для простоты.
В общем случае можно воспользоваться обобщением 3. Шмидта на
несимметричные ядра условий Пикара, приведенным в книге: Э. Г у р с а, Курс
математического анализа, т. HI, ч. 2, стр. 142 (см. также статью Б. Н.
Бабкина 1)).

^ 251 ИСКЛЮЧИТЕЛЬНЫЕ СЛУЧАИ 255
интегралы
1x1 = 1
sign /г = j _
Л = 0 П— — 1 п'^-оо
1 для Д ^ О,
1 ДЛЯ п < О,
ОО JL
1x1 = 1 fe = -«>
ОО ОО ОО
=i- Е «р» Е ^*^' 3 T-*-'+«dT= х; ф„с„л
«=-оо fe=-oo |Х|=»1 rt=-oo
Вставляя ф, / и значения полученных интегралов в уравнение
и приравнивая коэффициенты при одинаковых степенях /,
получим для определения коэффициентов фп бесконечную систему
равенств
(Pn{^ + signn + Cn) = fn {п = 0, ±1,...). B5.35)
В случае однородного уравнения (f(/)^0) последняя система
будет также однородной. Тем значениям индекса п, для
которых выполняются равенства
к + sign п + Сп = 0, B5.36)
будут соответствовать линейно независимые решения t'^
однородного уравнения B5.33). Для разрешимости неоднородного
уравнения должны соответственно выполняться условия fn = 0.
В интегральной форме они имеют вид
J f(/)r""'rf/ = 0. B5.37)
|t|-i
Нетрудно простым подсчетом показать, что функции 'Фл = /~'*~^
будут линейно независимыми решениями транспонированного
уравнения К'\|) = О, соответствующими тем значениям Спу для
которых выполняется условие B5.36), т. е. тем Сп, для которых
f^ является собственной функцией оператора Кф = 0. Таким
образом, при X произвольном (соответствующем как
невырожденному, так и вырожденному случаям) условия B5.37),
вытекающие из второй теоремы Нётера, должны выполняться.
Допустим, что они удовлетворены. Тогда из равенств B5.35)

256 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ ГГЛ. Ill
могут быть определены коэффициенты фп. Для принадлежности
решения к классу Lg необходимо и достаточно выполнение
условий
Если Я#±1, то при п->оо K + signn + Cn ^J^ +sign пФ о,
поэтому условие B5.38) равносильно условию 2 I /л i^ < ^»
которое в силу / е L2 заведомо выполняется. Таким образом, для
невырожденного случая условия B5.37) являются
необходимыми и достаточными условиями разрешимости; это можно
было получить и из общей теории.
Пусть теперь имеем вырожденный случай. Положим для
определенности Л= 1. Тогда условие B5.38) примет вид
I
+ EfeF<-- B5.39)
^ \2 + Сп\
Так как с„—^0, то коэффициенты fn при отрицательном п
rt->oo
должны стремиться к нулю быстрее, чем это следует из
принадлежности /(/) классу ^2. Следовательно, в вырожденном случае
составляющая /""(О правой части уравнения должна
принадлежать к более узкому классу, чем L2. При Я.= — 1 аналогичному
условию должна удовлетворять /+(/). Таким образом, условия
B5.37) второй теоремы Нётера здесь уже не являются
достаточными для разрешимости уравнения B5.33).
Полученные заключения можно было бы вывести и из
условия равносильности-разрешимости B5.32), записываемого здесь
(при X = 1) в виде
1
2ш
оо
|t|-ln-l
Остановимся в заключение на вопросе о числе линейно
независимых решений однородного уравнения и числе условий
разрешимости неоднородного. Однородное интегральное уравнение
будет иметь собственные функции t^ для тех /г, для которых
выполняется равенство B5.36). Так как с^—^0, то при КФ±1
/г*>оо
может существовать лишь конечное число собственных функций
/^, что соответствует первой теореме Нётера. Для вырожденного
случая К = 1 собственная функция /^ будет соответствовать
любому л<0, для которого Сп = 0. Таким образом, при Хс»1,
выбирая равными нулю конечное число коэффициентов Сп (п <
<0), получим однородное интегральное уравнение B5.33) с ко-

§ 26] ИСТОРИЧЕСКИЕ СВЕДЕНИЯ 25?
нечным числом собственных функций Г^; бесконечному числу
исчезающих Сп {п < 0) будет соответствовать бесконечное
множество собственных функций. Каждой собственной функции V^
данного однородного уравнения будет соответствовать
собственная функция /-^-^ транспонированного уравнения. Таким
образом, реализуются два случая: или оба транспонированных
уравнения имеют одинаковое конечное число линейно независимых
решений, или оба имеют бесконечное число решений. Если
отвлечься от возможности бесконечного числа решений, то дело
обстоит так же, как и в случае альтернативы Фредгольма.
Найти пример реализации третьей возможности для особых
уравнений, когда два взаимно транспонированных уравнения
имели бы одно конечное, а другое бесконечное число решений,
нам не удалось.
§ 26. Исторические сведения
Теория особых интегральных уравнений с интегралом в смысле главного
значения начала разрабатываться почти одновременно с теорией уравнений
Фредгольма. В первых работах (Poincare [20], Hilbert 1) 1903—1904 гг.)
рассматривались интегральные уравнения с ядром ctg —-— (см. § 31).
В указанной работе Гильберта допущены ошибки, разобранные в работе ав-
G — S\
тора [5]. Общая теория особого уравнения (также с ядром ctg—-—j
была разработана впервые в работе Нётера [Noether 1)] в 1921 г. Здесь были
установлены общие свойства особых уравнений, известные теперь под
названием теорем Нётера. Следует заметить, что аппарат, которым пользовался
Нётер (решение задачи Гильберта, см. гл. IV), не позволяет вывести эти
теоремы для комплексных уравнений с ядром Коши. Работа Нётера написана
очень тяжело и трудна для понимания.
Вскоре появилась работа Карлемана [Carleman 1)], о которой уже
говорилось в предыдущей главе. В ней было дано решение характеристического
уравнения с ядром Коши в частном случае, когда коэффициенты его
постоянные и контур есть отрезок оси абсцисс [О, 1]. Здесь же был указан
способ регуляризации решением характеристического уравнения. Общая
теория особых уравнений в работе Карлемана не затрагивалась.
После появления в 1937 г. работы автора 1) к исследованию особых
уравнений стало применяться данное в ней решение краевой задачи Римана.
Первые шаги в этом направлении были сделаны С. Г. Михлиным 2) в 1939 г.
Затем И. Н. Векуа в 1940 г. в работе 1) дал исчерпывающее решение
характеристического уравнения и начало общей теории особого уравнения.
Эта теория была развита им в ряде последовавших вскоре работ A941—
1943 гг.), из которых укажем важнейшие: 2), 3). Особенно тщательно им
был разработан метод регуляризации решением характеристического
уравнения 2) (Н. И. Мусхелишвили назвал его методом Карлемана —Векуа). Им
же впервые был введен метод регуляризации справа, который также был
использован для разработки общей теории. Простое доказательство второй
теоремы Нётера, приведенное в п. 23.2, принадлежит И. Н. Векуа 3).
Одновременно (начиная с 1941 г.) появился ряд работ В. Д. Купрадзе,
из них упомянем две важнейшие: 1), 2), в которых также разрабатывалась
общая теория особого уравнения. Пользуясь исключительно классическим
методом регуляризации — регуляризацией слева, он дал в нескольких вариантах

258 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. Ill
доказательство основных свойств особых уравнений — теорем Нётера и
теоремы равносильной регуляризации. Доказательство теоремы III Нётера,
приведенное нами в п. 23.2, дано в работе В. Д. Купрадзе 2).
Исключительные случаи особых интегральных уравнений путем
использования исследований для соответствующего случая краевой задачи Римана
(§ 15) были схематически рассмотрены автором в 1941 г. в его диссертации 2)
(см. также [6]). В 1952 г. этот вопрос тем же методом был обстоятельно
исследован Л. А. Чикиным 1). В 1948 г. Д. И. Шерман 2) независимо от
работы автора другим методом дал исследование исключительных случаев
систем особых интегральных уравнений; в частности, там содержится
решение для рассматриваемого случая.
Вопросы равносильной регуляризации начали разрабатываться С. Г. Мих-
линым 1) в 1938 г. Но в этой работе и во всех последующих он ограничился
постановкой вопроса о равносильной регуляризации при любой правой части
(см. п. 24.1). Несмотря на то, что в первых работах им применялись
тяжеловесные методы (например, метод последовательного приближения 1)),
следует отметить их важность как первых работ по данному вопросу,
привлекших внимание исследователей к вопросам равносильной регуляризации.
Теорема о равносильной регуляризации уравнения в том виде, как она нами
сформулирована здесь (п. 24.5), была высказана впервые автором книги
в 1941 г. в диссертации 2).
Доказательство этой теоремы вскоре было дано вначале В. Д.
Купрадзе 2), а затем другим способом И. Н. Векуа 3). Приведенное нами
доказательство (см. п. 24.5) по существу совпадает с доказательством Векуа, хотя
по форме значительно от него отличается. Оно воспроизводит с некоторыми
изменениями доказательство, данное С. Г. Михлиным [15].
Следует заметить, что разработка теории равносильной регуляризации
оказалась наиболее трудной и здесь в разное время в публикациях
различных авторов был допущен ряд ошибок.
Полное и сравнительно простое решение вопроса о равносильной
регуляризации, основанное на упомянутых выше работах, изложенное в настоящей
книге, принадлежит к числу важнейших достижений теории особых
интегральных уравнений.
Следует указать еще на работы Д. И. Шермана 1)~4), которые хотя
прямо не относятся к регуляризации, но тесно связаны с ней. Им разработан
метод, позволяющий при помощи специальных интегральных представлений
аналитических функций сводить краевые задачи непосредственно к
уравнениям Фредгольма, минуя особые уравнения как промежуточный этап.
(Подробно об этом см. § 34.)
Разработка основных вопросов теории особых интегральных уравнений
с ядром Коши (включая и случаи разрывных коэффициентов и незамкнутого
контура (см. гл. VI)), базирующаяся на решении краевой задачи Римана,
была произведена в 1940—1944 гг. в основном трудами грузинских
математиков. Чтобы в полной мере оценить прогресс, достигнутый в этой области,
читателю следует сравнить приведенное в настоящей книге изложение
вопроса с изложением в работе Нётера [Noether 1)] или хотя бы в работе
С. Г. Михлнна 1), выполненной в 1938 г., когда разработка этой теории
только начиналась.
Дальнейшая разработка велась в направлении различных обобщений.
Имеется значительное число работ грузинских математиков, в которых дается
обобщение теории особых уравнений на основе идей теории функций
действительного переменного — использования интегралов в смысле Лебега
(Л. Г. Магнарадзе, Б. В. Хведелидзе, И. Н. Карцивадзе) и более общих
А-у В', Ф- и ^-интегралов (А. Г. Джваршейшвили, Г. А. Хускивадзе). Мы
не касались этих вопросов, так как они выходят за пределы настоящей книги.
П ряде работ теория особых уравнений связывается с идеями
функционального анализа. В первую очередь здесь следует отметить статью С. Г. Мих-

ЗАДАЧИ К ГЛАВЕ III 259
лина [15]. В работе Ф. В. Аткинсона 1), посвященной абстрактным
операторам в банаховом пространстве, было показано, что условие регуляризуемости
(слева и справа) является необходимым и достаточным для того, чтобы
оператор подчинялся теории Нётера (см. п. 23.4). 3. И. Халиловым [29] и
Ю. И. Черским 1) была построена основанная на аксиоматическом подходе
абстрактная теория операторов, аналогичная теории особого оператора с
ядром Коши (см. п. 16.3). В близком направлении велись исследования в
работах Д. Пшеворской-Ролевич [D. Przeworska-Rolewicz 1), 2)]. В работе
И. Ц. Гохберга 1) был предложен некоторый другой абстрактный подход
к исследованию сингулярных операторов, основанный на методах теории
нормированных колец*).
Теоремы Нётера для рассмотренных в п. 23.5 особых интегральных
уравнений со сдвигом Карлемана были впервые получены Г. С. Литвинчуком 6).
Характеристическая часть этих уравнений соответствует краевым задачам со
сдвигом, исследуемым в гл. V. Теоремы Нётера для особых уравнений,
содержащих комплексно сопряженную неизвестную функцию (п. 23.6), были
получены в работе Л. Г. Михайлова [14] (см. также Г. Ф. Манджавидзе 1),
Р. С. Исаханов 2)), а для общих уравнений, содержащих члены как с
комплексным сопряжением, так и со сдвигом Карлемана, — в работе Г. С. Лит-
винчука 1).
Задачи к главе III
Всюду в задачах контур L есть простая замкнутая кривая, делящая
плоскость на две области: внутреннюю D+ и внешнюю D-, буквы си ^2, ...
обозначают произвольные постоянные.
1. Решить характеристическое особое интегральное уравнение
. /. оч /.ч , ^^ - 6/ + 8 f ф (т) ^ 1
L
считая, что точка г = О принадлежит области D+, а точка 2 = 2 —
области D".
гч /л - /^ + 6/ - 4
Ответ. ф@= st{t--2y '
Указание. При решении задач 2—8 следует соответственно
использовать результаты задач 4—8, 10, 11 гл. II.
2. Решить характеристическое особое интегральное уравнение
it'
считая, что точки г, 2i принадлежат области D+, а точки —f, —2i —
области D"*.
Ответ ф(Л = -^^1^1:^^1—+. '(^° + ^-^>
итвет. Фи;— {*2 л. ^\2 /i2 \ л\ *
(^2+1J(^2 + 4) ^ (/2+1) (/2 + 4) •
3. Показать, что уравнение
{Р -- 2)ф (О + -|- ^-^dx===2t (t - 2/) A + at)
*) См. также И. Ц. Г о х б е р г и И. А. Фельдман, Уравнения в
свертках и проекционные методы их решения, М., «Наука>, 1971.

260 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. П1
при условии, ЧТО точка —/ принадлежит D+, а точки t, 2/, —2i
принадлежат D-, разрешимо лишь при а = —L Дать решение уравнения для этого
значения параметра.
^ ,,, - 2И (t - 2/)
Ответ, ф(/) = T+2i •
4. Решить уравнение
L
==2lny-^(sin/ + e^)
для контура L, оставляющего точки О, 1 в области D+.
Ответ.
ф@=5Ш/-j^^ In (l~l)+(Co + ClO[l+ jln (^-~Т)]'
5. Решить уравнение
L
при следующих предположениях:
а) точка I принадлежит D+;
б) точка 1 принадлежит D~;
в) точка 1 принадлежит L.
Ответ, а) ф (/) = ^2 _ | +^^_^.Z^. g) и в) ф@==/2_ |^
6. Решить уравнение
L
при тех же предположениях, что и в предыдущей задаче.
1
О т в е т. а) и в) Уравнение неразрешимо; б) ф (^) = / + . _ .
7. Решить уравнение при указанных значениях постоянной h
(ht
CXJ
(/i — действительная, отличная от ±1, — со < / < со).
Ответ. При h < — \
at + b , a{h- I) (/-2/) ,
Ф@ =
(h + \)t'-i ' h(h+\)[(h-'\)t + 3i] '
1
'^4(h+\)t-i (/г-1)/ + з/]'

ЗАДАЧИ К ГЛАВЕ III 261
при О < I Л К 1
/ ,4 а , /?6 — ai
ф(^) = т- + -
h ^ /г[(/г-1)/ + з/] '
при А = 0
При выполнении условия разрешимости а == 0;
при h > I
ф(/) = -6/
при выполнении условия разрешимости а = — 6А/.
8. Решить уравнение
il-H),it) + ^\-^<ir = f
{h — действительная, отличная от О и 2, — со < / < со)
а) в классе функций, удовлетворяющих условию
|ф(/)|<Л|/Г" (а>0) при больших | /1;
б) в классе функций, удовлетворяющих условию
|ф1 (О —Ф1 («>I < ^МГ" (а>0) при больших | /1.
Ответ, а) При h<0 ф(/)=0 и лишь при выполнении условия
разрешимости / = О,
при О < Л < 2
при л > 2
б) при Л < О
ф1 @~ j _,^>
при О < Л < 2
Ф1(/) = Ф(/) + ^7?^,
при л > 2
Ф1 (О = Ф (/) + go ^ Zifi '
9. Показать, что дая уравнения
Кф ^ A + О Ф (О + i^ 5 ^^^ ^т + ^ 5 е^Ч (т) ^^
L L
при условии, что начало координат принадлежит области D+, оператор К'°
является равносильным регуляризатором слева. Построить регуляризованное
уравнение.
Ответ. Ф@ + -45^ 5(б''^-|- + 2)ч{т)йГт = /.

262 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ КОШИ [ГЛ. Ill
Равносильность вытекает из того, что оператор К' , как
характеристический с отрицательным индексом, не имеет собственных функций.
10. Для уравнения
|т1=-1 Itf-l
показать, что:
а) простейший регуляризатор К'** не является равносильным регуляри-
затором слева;
б) сопряженный оператор К* есть равносильный регуляризатор слева.
Построить регуляризованное интегральное уравнение К*Кф = K*f.
Ответ, а) Уравнение Фредгольма К'°Кф = К'7 равносильно уравнению
Кф = 2/ + а(^1-^-^)
при произвольном а;
б) Ф+^ 5 l^f(x)dx = t.
lTl=-l
11. Показать, что для уравнения
Кф=(<Чг2)ф@ +
L L
оператор К' является равносильным регуляризатором слева, если начало
координат лежит в D"*". Построить уравнение Фредгольма К'°Кф = К'7.
Ответ, ф (/) - ^ "^^^. \ (т + т-^) ф (т) dx =» t^,
12. Для уравнения
ИИ1 |т|=1
а) построить равносильный регуляризатор слева
К = (К*К)'°К*;
б) показать, что характеристический оператор /С'° является также
равносильным регулйризатором слева. Составить регуляризованное уравнение
К^°Кф = К'7.
Ответ.
а)(КК) Кф=A_202(/_2)*(^)"" A-20^-^ J "Г:^ ^^ +
1т|-1
+ 1а \ ^(^-2И1 -2/) (^ +Т) + (^- 2) A -2041 -2т)]* (^^ ^^^
1т|-1

ЗАДАЧИ К ГЛАВЕ III 263
13. Вывести формулу обраш.ения особого интеграла типа Коши
L
(п. 7.3) из формулы решения характеристического уравнения B1.9).
14. Вывести основные свойства особых интегральных уравнений (теоремы
Нётера п. 23.2), основываясь на регуляризации решением характеристического
уравнения. (И. Н. Векуа 2).)
15. Пусть
Кф^а(Оф(/) + -^^5-^^^^+5/г(/,т)ф(т)^т = /
(/)
— некоторое особое интегральное уравнение (разрешимое или неразрешимое).
Доказать, что можно, не меняя характеристической части, так изменить
регулярную часть ядра k(t,x), чтобы уравнение
L L
имело не менее чем некоторое заданное число решений.
16. Показать, что обобщенное особое интегральное уравнение
L L
Приводится к обобщенной краевой задаче Римана
Ф+[а(/)]=О(/)ф-@ + ^(/),
где
L
(Д. A. Квеселава 2)).
17. Показать, что решение особого интегрального уравнения
П
регулярное ядро которого k {f, т) = У а, (t) р, (т) вырождено, может быть
/ -1 ' '
сведено к решению системы линейных алгебраических уравнений. Провести
исследование указанного уравнения, основываясь на теоремах о
разрешимости систем линейных алгебраических уравнений.
18*. Доказать, что разность чисел решений союзных уравнений не зависит
от регулярной части ядра, не пользуясь решением задачи Римана. (Noe-
ther 1), Н. И. Мусхелишвили [16], § 53.)

ГЛАВА IV
КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА
И ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
С ЯДРОМ ГИЛЬБЕРТА
В этой главе мы рассмотрим вторую основную краевую
задачу теории аналитических функций, так называемую задачу
Гильберта, а также тесно связанные с ней особые интегральные
уравнения с ядром Гильберта. Кроме того, будет рассмотрен
ряд вопросов, являющихся вспомогательными для решения этой
задачи (оператор Шварца, регуляризующий множитель). В
заключение будет дано приложение задачи Гильберта к решению
краевых задач для полигармонических и полианалитических
функций.
В отличие от задачи Римана, где случаи односвязной и
многосвязной области не отличаются существенно друг от друга,
для задачи Гильберта переход от односвязных к многосвязным
областям вносит серьезные трудности. Поэтому здесь будут
рассматриваться только односвязные области. Задачи Гильберта для
многосвязных областей будет рассмотрена в следующей главе.
§ 27. Постановка задачи Гильберта
и некоторые вспомогательные формулы
27.1. Постановка задачи Гильберта. Дан простой гладкий
замкнутый контур L и действительные функции дуги 5 контура
a{s), b{s), сE), удовлетворяющие условию Гёльдера.
Краевой задачей Гильберта будем называть следующую
задачу. Найти аналитическую в области D+ и непрерывную на
контуре функцию
f{z) = u{x, y) + iv{x, у\
предельные значения действительной и мнимой части которой
удовлетворяют на контуре линейному соотноиьению *)
а (s) u{s) + b (s) v{s) = c E). B7.1)
*) Всюду в дальнейшем функции, полученные заменой координат
функциями дуги .9, будем для простоты обозначать той же буквой: например,
u[x{s), y(s)] = u{s) и т. п.

§ 27] ПОСТАНОВКА ЗАДАЧИ ГИЛЬБЕРТА 265
При c{s) ^0 будем иметь однородную задачу и при c(s),
отличной от нуля, — неоднородную. (Аналогичная «внешняя»
задача будет рассмотрена в п. 29.4.)
Для решения поставленной задачи потребуются некоторые
вспомогательные формулы, к рассмотрению которых мы
переходим.
27.2, Оператор Шварца для односвязной области. Часто
приходится решать задачу об определении аналитической в области
функции F{z) =:U-{-iv по заданной на границе области ее
действительной части u(s). В дальнейшем будем эту задачу для
краткости называть задачей Шварца. В существенном она
сводится к задаче Дирихле*). По u{s) определяется
гармоническая в области функция и(х,у), а по ней интегрированием
полного дифференциала (уравнения Коши — Римана) с точностью
до произвольного слагаемого находится сопряженная
гармоническая функция v(x,y). Таким образом, задача Шварца
решается с точностью до произвольного постоянного слагаемого.
Решение будет вполне определенным, если задать в какой-либо
точке области значение мнимой части искомой аналитической
функции. Для решения задачи Шварца введем понятие
оператора Шварца. Пользование им упрощает формулировку многих
результатов.
Под оператором Шварца будем понимать оператор,
восстанавливающий аналитическую функцию по граничным значениям
ее действительной части. Точнее, это можно формулировать так.
Пусть на гладком контуре задана некоторая действительная
функция u(s), удовлетворяющая условию Гёльдера. Оператором
Шварца S будем называть оператор, который определяет
аналитическую функцию F{z), предельное значение действительной
части которой на контуре совпадает с функцией u{s), а мнимая
часть в заданной точке Zq обращается в нуль.
Символически это будем записывать так:
F{z) = u {х, у) + iv (л:, у) = Su,
Если контур L есть единичная окружность, то оператор
Шварца совпадает с известным интегралом Шварца; если L —
действительная ось, оператор Шварца есть удвоенный интеграл
типа Коши (см. B7.5)). Для произвольного контура можно дать
явное выражение оператора Шварца через функцию Грина.
Пусть
G(x, у\ I, y\) = \nj + g{x, у\ I, т))
— функция Грина оператора Лапласа для области D+, причем
г = ^J{x — If + {у — л)^ а ^(л:, у\ g, т]) — гармоническая функ-
*) В случае многосвязной области имеется существенное отличие (см.
п. 36 2).

266 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА {ГЛ. IV
ция обеих пар переменных х, у и 1^ т], принимающая значение
In г, когда одна из точек {х,у), (|, г]) оказывается лежащей на
контуре.
Будем рассматривать G{x,y; l,r\) как функцию двух
комплексных переменных Zz=zX-\-iy, ^ = |-|-ir], изменяющихся
каждая в области D+ и обозначать ее далее G{z, ^).
Известно из теории гармонических функций, что решение
первой краевой задачи гармонических функций — задачи
Дирихле—дается формулой
" (^. г/) = -^ J ^^fe^ «(^) ^''. B7-2)
о
где т = т(а)—комплексная координата точки контура, п —
внутренняя нормаль.
Пусть H{z,t,)—гармоническая функция, сопряженная
функции 0B,^) по переменной z. Она определяется на основании
уравнений Коши — Римана формулой
Z
где Zq — фиксированная точка области D+.
Так как область D+ односвязна, то функция Н определяется
однозначно, причем на основании формулы B7,3)
удовлетворяет условию
H{Zo^)^0,
Функция
M{z^) = G{z, 0 + iH{z, О
называется комплексной функцией Грина области /)+*). Она
будет аналитической по переменной z всюду, кроме точки г = ^,
где она имеет логарифмическую особенность.
В силу равенств B7.2) и B7.3) формула
о
дает гармоническую функцию v{x,y), сопряженную функции
и{х,у).
Отсюда равенство
*) Термин введен С. Г. М и х л и и ы м [15].

§27] ПОСТАНОВКА ЗАДАЧИ ГИЛЬБЕРТА 267
определяет аналитическую функцию, действительная часть
которой на контуре равна заданной функции и(о),
удовлетворяющую дополнительному условию v{zo) =0.
Следовательно, оператор Шварца задается формулой
^"-iri^^^"»-')'"'- B7.4)
О
Если отбросить условие v (zq) = О, то
Р{г) = 8и + фо. B7.6)
где Ро — произвольная постоянная, равная v{zo).
Функция Т (г, т) = —^г~ называется ядром Шварца для
контура L. При конформном отображении области D+ на
единичный круг оно переходит в ядро Шварца для круга Т (г, т) =
= ^(см. п. 6.1).
Комплексная функция Грина и оператор Шварца тесно
связаны с конформным отображением области на круг. Пусть
w = F{z,0 = {z-OFAz^)
есть функция, конформно отображающая область D+ плоскости
г, ограниченную контуром L, на единичный круг плоскости w
и переводящая некоторую точку g области в начало координат.
В силу взаимной однозначности отображения никакая другая
точка области не переходит в начало, поэтому f i (г, g) Ф 0.
Теорема. Л1 (г, ^) = G + /Я = —In F (г, Ь) есть
комплексная функция Грина области D+.
Для доказательства достаточно установить, что
действительная часть G есть обыкновенная функция Грина области D"*-.
В самом деле,
Q{zЛ) = -Я^\nFizЛ)=--\n\F{zЛ)\ = \nJJ4r^-'\n\F,{zЛ)l
Последний член правой части есть функция гармоническая,
поэтому G имеет в области /)+ единственную особенность In —.
Когда точка z обходит контур L, соответствующая ей точка w
обходит единичную окружность, поэтому на Z, |f (г, ^) 1 = 1,
откуда
Gk = 0.
Теорема доказана.
Напоминаем, что в формуле B7.4) z является параметром,
а переменная, по которой производится дифференцирование и
интегрирование, есть g. Поэтому при вычислении ядра Шварца

268 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА (ГЛ. IV
дМ
-^нужно взять производную по нормали к контуру, считая, что
g есть комплексная координата контура. Можно получить явное
выражение оператора Шварца для любой области, для которой
известна в явном виде огображающая функция.
В качестве иллюстрации вычислим комплексную функцию
Грина и ядро Шварца для полуплоскости и круга.
1. Функцию, конформно отображающую верхнюю
полуплоскость на круг, можно взять в виде
w = F(z,0 = ^^ (^ = | + /Л, ri>0).
Комплексная функция Грина М(г, ^) = —In F{z, t,) =
=—InB: — ^)+InB — ^). Обычная функция Грина G{z,l)=:
= —In I f B,^I = In
Ha контуре (действительной оси)
положительное направление нормали совпадает с
положительным направлением мнимой оси г\:
дх\
_ Г 1 . ^ L_ .^11 ^
т]-о L^-g д'х\ 2-е ^лЛп^о
Чг-! ^ 2-iJ- I-;
Решение задачи Шварца
/ (г) = и + iv = Su =
+00 +00
= 1fS "(^)Нт^^+'-^о = ^-$ fS^dl + iv, B7.50
+ 00
Решение задачи Дирихле и{х, у) = —] и (|) ^^ _ J!^^ _^ ^^ dl (см.
— оо
еще задачу 2 в конце главы).
2. Функция, отображающая круг с центром в начале
координат радиуса R на единичный круг, переводящая точку ^ в
начало, имеет вид
w = F{z^) = R^"^^^
AfB, ^) = -1п^ = ~1п(г~Й + 1п(г^-/?^)~1п/?.
Положительное направление нормали здесь совпадает с
отрицательным направлением радиуса-вектора, поэтому вычисление

§ 27] ПОСТАНОВКА ЗАДАЧИ ГИЛЬБЕРТА 2б9
ядра Шварца целесообразно проводить в полярных координатах:
R' = ll Т{2Л) = -^
dR
OR . ^'dR ^
L г - ? 2S - /?-
Учитывая, что дуга 5 = 7?ф, получим решение задачи Шварца
2я
f(e) = w + /u = ^^ i^(ф) |±?с/ф +/%
о
Полагая z = ге^^ и отделяя в последнем равенстве
действительную часть, получим решение задачи Дирихле для круга в виде
интеграла Пуассона:
2л
О
27.3. Определение аналитической функции, имеющей полюс,
по значениям ее действительной части на контуре (задача А).
В предыдущем пункте определялась аналитическая в области
функция по действительной части на контуре. В дальнейшем нам
понадобится решение более обнхей задачи, когда для искомой
аналитической функции в некоторой точке области допустим
полюс. Задачу эту в дальнейшем будем именовать задачей А.
Дадим ее точную формулировку.
Дан простой гладкий замкнутый контур L, ограничиваюи^ий
внутреннюю область D+. Требуется определить функцию F{z),
аналитическую в области D+, за исключением точки го, где для
нее допустим полюс порядка не выиле п и действительная часть
которой на контуре L обраш^ается в заданную функцию u{s).
Соответствующую однородную задачу {u{s)^Q) назовем
задачей Ао. Решение ее будем обозначать Q{z),
Дадим сначала решение задачи Ао для случая, когда контур
L есть единичная окружность и го = 0.
Выпишем разложение искомой функции в окрестности
начала координат:
QB)= Е ^а2^

270 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
По условию
Re Z сИ' = 0.
k = — n
Обозначая С/^ = а;^ + ^'Рл, получим
оо
^ {akCOskS'-'^kSinks) = 0.
в силу единственности разложения в ряд Фурье будем иметь
ао = 0, a^k= — (^-ky P-/fe = Pb *=1, 2, ..., а?,
а;^==Рл = 0, k> п.
Отсюда
^о = ^'Ро, c-k = — Ck (^=1, 2, ..., п), Ck = 0 {k>n).
Следовательно, искомая функция Q{z) имеет вид
Q (г) = /Ро + Е (с,г^ ~ с,г-^). B7.6)
Замечание. Если в формулировке задачи Ао для
единичного круга заменить область Ь+, внутреннюю для единичной
окружности, на область D-, внешнюю для нее, то как
рассуждения, так и окончательный результат останутся неизменными
и, следовательно, формула B7.6) дает решение задачи Ао также
и для области D- внешней по отношению к единичной
окружности с полюсом на бесконечности.
Решение задачи Ао для произвольной области, а также для
единичного круга, но с полюсом в точке го, может быть получено
из найденного решения при помощи конформного отображения.
Пусть
ш==(о(г) B7.7)
есть функция, конформно отображающая область D+ плоскости
Z на единичный круг плоскости w так, что некоторая точка Zq
переходит в начало координат со (го) = О и со^(го) > 0.
Тогда формула
Q {Z) = /Ро + Z W [со {z)f - Ck [(О (г)] -') B7.8)
дает, как это легко проверить, решение задачи Ао для
произвольной области D+ с полюсом порядка п в точке 2о.
Если под (о(г) понимать функцию, отображающую
конформно область Ь- на область, внешнюю для единичной окружности
и переводящую бесконечно удаленную точку в бесконечно уда-

§ 27] ПОСТАНОВКА ЗАДАЧИ ГИЛЬБЕРТА 271
ленную, причем а)'(оо)>0, то формула B7.8) даст решение
задачи Ао для области D-.
Теперь мы подготовлены к тому, чтобы решить задачу А.
По определению оператора Шварца, Su есть аналитическая
в области /)+ функция, действительная часть которой на контуре
равна u{s). Разность F{z) —Su будет, очевидно, функцией,
удовлетворяющей условиям задачи Ао. Следовательно,
F{z)-Su = Q(z\
откуда
F{z) = Su + Q(z), B7.9)
где оператор Шварца Su определяется формулой B7.4), а
решение Q{z) однородной задачи Ао — формулой B7.8).
Как показывают формулы B7.8), B7.9), в решения задач Ао
и А входят линейно 2п -j- 1 произвольных действительных
постоянных
Ро, «ь Рь А==1, 2, ..., Az {Ck = ak'\'i^ky
В частности, когда полюс отсутствует (м = 0), формула B7.9)
обращается в формулу B7.5).
Для построения обладающей перечисленными выше
свойствами функции F{z) по предельным значениям на контуре ее
мнимой части v{s) достаточно заметить, что
Im/'@ = Re[~-/F@] = t;(s),
откуда
-iF{z) = Sv + Q{z\
т. е.
F{z) = iSv + iQ{z). B7.10)
27.4. Обобщенная задача До. В п. 27.3 у решения задачи Ао
допускалась единственная и простейшая особенность — полюс в
начале координат. Здесь будут допускаться особенности любого
характера с заданной главной частью.
Определение 1. Главной частью функции 0B) на
множестве 2 называется функция /(г), аналитическая во всей
плоскости, за исключением точек множества 2, и такая, что
разность 0\{z) =ФB:)—f{z) аналитична на множестве 2.
Следствие. Если Ф{z) аналитична в области D, за
исключением множества ее точек 2, то разность Ф1(г)=ФB) —
— f{z) аналитична в D.
Определение 2. Обобщенной задачей Ао будем называть
задачу определения функции Q{z)y аналитической в круге у
радиуса R с центром в начале координат, кроме множества его
точек 2, где она имеет некоторые особенности с заданной
главной частью /(г), при условии, что действительная часть Q(z) Н9

272 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
контуре круга Lz равна нулю:
ReQ(e)l^^ = 0. B7.11)
Для решения воспользуемся принципом симметрии. Краевое
условие B7.11) геометрически означает, что функция Q{z)
отображает окружность Lz плоскости Z на мнимую ось плоскости
Wz=Q{z). Таким образом, условия, при которых доказывался
принцип симметрии, выполнимы (п. 12.1).
Точками, симметричными относительно мнимой оси, будут
точки W и w^ = —W.
Функцию Q{z) представим в виде
Q{z) = QAz) + f{z\ B7.12)
где Qi(z)—неизвестная пока функция, аналитическая в круге
у. Продолжим теперь функцию Q{z) на внешность окружности
Lz по симметрии, т. е. поставим в соответствие точкам z и
D2
2:* = -т-, симметричным относительно окружности Lz, точки w
и W* := —W, симметричные относительно мнимой оси плоскости
W, Тогда согласно принципу симметрии (п. 12.1) функции
w = Q(z) = QAz) + f{z)
и
W
—0(f)—a(f)-Kf)
будут аналитическим продолжением друг друга. На контуре Lz
их значения равны
или
[ft^ + /-(f)]^=[-M.)-Q-,(f)]^.
в левой части стоит функция, аналитическая в круге у.
Согласно свойствам продолжения по симметрии правая часть есть
функция, аналитическая вне у. Согласно принципу
непрерывности (п. 12.1) они являются аналитическими продолжениями друг
друга; поэтому они составляют функцию, аналитическую во всей
плоскости, являющуюся по теореме Лиувилля постоянной. В силу
краевого условия B7.11) эта постоянная будет чисто мнимой.
Следовательно, будем иметь
QiB) + fD^) = /p,
где tp — чисто мнимая произвольная постоянная. Отсюда

§ 28] РЕГУЛЯРИЗУЮЩИЙ МНОЖИТЕЛЬ 273
Вставляя последнее в выражение B7.12), получим решение
обобщенной задачи Ао
Q{z) = f{z)^f[^)+^. B7.13)
Если окружность единичная и допускается единственная
особенность— полюс порядка п в начале координат, то, взяв глав-
—, получим формулу B7.6).
k=\ ^
Формула B7.13) позволяет решать задачи значительно большей
общности: множество особых точек 2 может состоять как из
изолированных точек (полюсы и существенно особые точки в любом
количестве), так и содержать целые континуумы особенностей.
Пример 1. Пусть множество особенностей состоит из точек
бесконечной последовательности Zk = -j== (^==1 2 ) ко-
торые являются простыми полюсами с вычетом единица, и ее
предельной точки г = О, которая, очевидно, будет существенно
особой точкой.
Легко проверить, что главная часть может быть представлена
в виде /B^) = ";i7ir—J-- Отсюда /(-7")= g^W_i '
Решение обобщенной задачи Ао дает функция
^ (^) == e^lz^ - I "" ?w—Г + ^'Р-
Пример 2. Множество 2 есть линия разрыва С со скачком
ф(^). Главная часть представляется интегралом типа Коши
fW=li7 5fS^-
с
Решением задачи является функция
С с Z
Идея использованного метода дана в работе Якоба [С. Jacob,
1)], где она используется для решения других задач.
§ 28. Регуляризующий множитель
28.1. Определение регуляризующего множителя. Пусть L—
простой гладкий замкнутый контур, ограничивающий
внутреннюю область D+, и
G(t) = G[t{s)] = a{s) + ib{s)

274 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 1ГЛ. IV
— заданная на нем комплексная функция, удовлетворяющая
условию Гёльдера и не обращающаяся в нуль. Произвольная
функция G{t), как это уже указывалось в п. 4.3, вообще говоря,
не является краевым значением функции, аналитической в
области Z3+
Выясним, можно ли определить такую удовлетворяющую
условию Гёльдера функцию точек контура R(t), умножив на
которую функцию G{t), получим краевое значение функции Ф+{г),
аналитической в области D+, т. е,
О@/?@ = Ф^@. B8.1)
Функцию R{t)y обладающую указанным свойством, назовем
регуляризуюи^им множителем.
Можно еще несколько обобщить постановку задачи, допуская
у функции Ф+B:) в некоторых точках области D+ особенности
заданного характера.
Задача в такой постановке не является определенной, так как
если она допускает какое-нибудь одно решение, то она, очевидно,
допускает и бесчисленное множество других решений,
получаемых из данного путем умножения его на краевое значение
любой функции, аналитической в D+. Поэтому постановка задачи
нуждается в уточнении. Чтобы задача стала определенной, на
регуляризующий множитель нужно наложить некоторые
дополнительные условия; последние могут быть весьма
разнообразными.
С одним случаем отыскания регуляризующего множителя мы
уже имели дело при решении однородной краевой задачи Ри-
мана. В самом деле, записав краевое условие этой задачи в виде
О(/)Ф-@ = Ф^@,
видим, что оно является равенством типа B8.1), причем R{t) =
t=0-(t). Таким образом, краевую задачу Римана можно ?ас-
сматривать как задачу отыскания регуляризующего множителя,
на который наложено дополнительное условие, что он является
краевым значением функции, аналитической во внешней области
D". Решение задачи Римана устанавливает существование
такого множителя для х ^ 0.
Кроме указанного, в практике встречаются еще два вида ре-
гуляризующих множителей:
1) с постоянным аргументом;
2) с постоянным модулем;
Без ограничения общности можно в первом случае постоян
ный аргумент принять равным нулю и считать, следовательно,
множитель действительным положительным, а во втором считать
модуль равным единице. Отысканием регуляризующих
множителей указанных типов мы займемся в следующих двух пунктах.

§ 28} РЕГУЛЯРИЗУЮЩИЙ МНОЖИТЕЛЬ 275
28.2. Действительный регуляризующий множитель.
Потребуем, чтобы регуляризующий множитель R{t) был
действительной функцией; обозначая его в этом случае p{s), имеем
p{s)[a{s) + ib{s)]=0-'{ty B8.2)
Беря индекс обеих частей и учитывая, что индекс p{s)
равен нулю, получим
X = Ind [а (s) + ib (s)] = Ind Ф+ (/).
Вспоминая свойства индекса (п. 12.1), будем иметь:
1. При х = 0 функция Ф+(г) не может иметь нулей в
области D+.
2. При н > О функция Ф+(г) должна иметь в D+ х нулей.
3. При х<0 функция Ф+(г) не может быть аналитической
в D+, она должна иметь там не менее —к полюсов.
Желая обеспечить разрешимость, и притом однозначную,
задачи отыскания регуляризующего множителя рассматриваемого
типа при любом индексе, дадим этому понятию несколько иное
определение, при котором у искомой аналитической функции
допускается полюс в области Z)+.
Для простоты записи будем считать, что начало координат
лежит в области D+.
Определение. Регуляризующим множителем комплексной
функции a(s)+/6(s), заданной на контуре L, будем называть
такую действительную положительную функцию точек контура
p{s), что произведение p(s) [a{s) +ib{s)] есть краевое значение
функции x^iz), аналитической и имеющей нулевой порядок
всюду в области ?)+, за исключением разве что начала
координат, где ее порядок равен индексу к функции a(s) -\-ib{s).
(Определение порядка см. в п. 12.2.)
Докажем существование регуляризующего множителя и
выведем формулы для его определения.
Г. X = 0. Функцию x^iz), как не имеющую в области /)+
нулей, можно представить в виде показательной функции
Х+ (г) = е^У (-), y{z) = (o (л:, у) + 1щ {х, у), B8.3)
(Множитель ( в показателе вводится для удобства дальнейших
выкладок.)
По определению регуляризующего множителя будем иметь *)
р is) [а (s) + ib (s)] = e'Y it) = e-^ ^'W^ ^'l B8.4)
Приравнивая модули и аргументы обеих частей последнего
равенства, получим
p{s)^/aЦs) + bЦs) = e-<'^^'\ 0E) = arctg|||. B8.5)
*) Мы применяем упрощенные обозначения (см. сноску на стр. 264).

276 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
Последняя формула определяет краевое значение гармонической
функции со (л:, г/). Сама функция (х){х,у) определяется решением
задачи Дирихле. Затем из уравнений Коши — Римана
определяется сопряженная гармоническая функция coi (х, г/), через
краевое значение которой выражается искомый регуляризующий
множитель p{s).
Проще всего выразить результаты при помощи оператора
Шварца.
Согласно B7.5) и B8.5) будем иметь
Y (г) = со (л:, у) + 1щ (а;, у) = S arctg -^, B8.6)
где на y{z) для определенности наложено условие
ImY(^o) = coi(eo) = 0. B8.7)
Регуляризующий множитель определяется формулой
p-(ii is)
р (s) = —7====-. B8.8)
Рассмотрим вопрос о единственности регуляризующего
множителя. Допустим, что существуют два различных множителя
p{s) и p\{s). Будем иметь равенства
р is) [а (s) + ib (s)] = х" {s\ р, {s) [а {s) + ib {s)] = %+ E).
Деля последние равенства почленно и обозначая
1
= a|)(e), получаем
p(s) ^ ^ ^
Мнимая часть функции \\i{z) на контуре равна нулю.
Поэтому в силу единственности решения задачи Дирихле Im г|)(г) =
= 0 всюду в области D+. Отсюда г|р(г) = const.
Следовательно, регуляризующий множитель определяется с
точностью до постоянного множителя. Условие B8.7) определяет
этот постоянный множитель.
Таким образом, доказаны существование и единственность
регуляризующего множителя в случае к тт О при дополнительном
условии B8.7).
2° X =7«^ 0. По определению будем иметь
р E) [а (S) + ib (s)] = tV' *'* = fe-''- ^V <^». B8.9)
Беря модули и аргументы обеих частей, получим
^ ^^^ Va2 (s) + b'' (s) '
CD E) = arg {/-^ [a 0 + ib (s)]) = arctg— — xarg/.
B8.10)

§ 28) РЕГУЛЯРЙЗУЮЩИЙ МПОЖИТГЛЬ 277
Отсюда
YB) = s[arctg-^-xarg/]. B8.11)
Регуляризующий множитель определится формулой B8.10).
Единственность решения вытекает из предшествующего, так как,
согласно равенству B8.9), задача сводится к отысканию регуля-
ризующего множителя от функции t'-'^[ct{s)-{' ib{s)], индекс
которой равен нулю.
Таким образом, доказана
Теорема. Произвольная функция точек контура^
удовлетворяющая на нем условию Гёльдера и не обращающаяся в нуль,
имеет действительный регуляризующий множитель, который при
дополнительном условии B8.7) определяется формулами B8.6),
B8.8), B8.10), B8.11) единственным образом.
Отыскание регуляризующего множителя в виде
действительной функции, как показывает исследование, равносильно
отысканию аналитической функции по заданным на контуре значениям
ее аргумента, что в свою очередь приводит к решению задачи
Шварца.
28.3. Регуляризующий множитель с постоянным модулем.
Будем теперь отыскивать регуляризующий множитель в виде
j^{t) = e^ns)^ B8.12)
Представим заданную комплексную функцию также в
полярных координатах а + ift = ге^*« По определению имеем:
г^^*(«+«)==ф+(/). B8.13)
Будем искать функцию 9(s) при условии, что при обходе
контура L она приобретает приращение 2kv, где v — заданное целое
число. Взяв индекс обеих частей последнего равенства, получим
x + v = n, B8.14)
где п есть число нулей функции Ф+B) в области Z)+, зависящее,
таким образом, не только от индекса заданной функции а + ib,
но и от индекса самого регуляризуюи^его множителя, который,
в отличие от предыдущего, не обязательно равен нулю.
Наложим на искомую функцию Ф+B) условие, что она имеет
порядок п в начале координат, считая его принадлежащим
области D+. Представляя искомую функцию Ф+(г) в виде z'^e'^^'^\
будем иметь
ге^ (в+а) = /V (О = fe"^ ^^^^'^' ^'К B8.15)
Приравнивая в последнем равенстве модули и аргументы,
получим
со = In (г |/Г"), B8.16)
0J = 0 + а — п а rg ^ B8.17)

278 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
Следовательно, краевое значение действительной части со
искомой аналитической функции y{z) известно. Решив задачу
Дирихле, найдем гармоническую функцию со (л:, у). Отыскав затем
сопряженную гармоническую функцию o)i, определим функцию
в (по формуле B8.17)), через которую по формуле B8.12)
выражается сам регуляризующий множитель.
Результат легко записать с помощью оператора Шварца
Y (г) = (О {X, у) + ш, {X, y) = Slnir\t Г\ B8.18)
причем для определенности принято
ImYCo) = 0. B8.19)
Регуляризующий множитель определяется формулой
/?(f) = eM@.-a+nargO. B8.20)
Формулы B8.18) — B8.20) определяют регуляризующий
множитель требуемого вида однозначно.
Как показывает решение, определение регуляризующего
множителя с постоянным модулем равносильно отысканию
аналитической функции по краевым значениям ее модуля, что в
конечном счете сводится к решению задачи Шварца.
28.4. другие виды регуляризующего множителя. Общее определение
регуляризующего множителя, данное в п. 28.1, дает широкий простор для выбора
различных видов этого множителя. Можно усмотреть большое сходство
определения регуляризующего множителя с определением известного в теории
дифференциальных уравнений интегрирующего множителя. Для обоих этих
множителей допустим большой произвол в выборе и задача отыскания их
становится определенной только тогда, когда отказываемся от общей
постановки и ищем множитель определенного вида.
В пп. 28.2, 28.3 рассматривались простейшие виды регуляризующего
множителя, когда модуль или аргумент его постоянны. Случаи эти допускают
геометрическое истолкование.
Будем рассматривать задание комплексной функции a{s)+ ib(s)=: ге^^
как задание кривой Г, параметрическое уравнение которой в полярных
координатах имеет вид
г=:^г (s), а = а (s).
Умножая функцию re ^ на действительный положительный
регуляризующий множитель p(s), мы совершаем над точками кривой Г преобразование,
заключающееся в том, что радиусы-векторы кривой Г, оставаясь неизменными
по направлению, изменяются по величине в отношении p(s), т. е. совершаем
преобразование растяжения (с переменным модулем растяжения). Решаемая
задача заключается в том, чтобы так подобрать переменный, непрерывно
изменяющийся модуль растяжения, чтобы преобразованная кривая Fi,
уравнение которой ri = p(s)r(s), ai = a(s), давала геометрическое изображение
(в указанном выше смысле) комплексной функции Ф+@» являющейся
краевым значением некоторой аналитической в области D+ функции.
Умножение комплексной функции ге^^ на множитель вида е^^^^^
геометрически можно истолковать как поворот радиусов-векторов кривой Г на
некоторый переменный, непрерывно изменяющийся угол G(s), причем угол этот
подбирается так, чтобы преобразованная кривая с уравнением ri = r(s).

§ 28] РЕГУЛЯРИЗУЮЩИЙ МНОЖИТЕЛЬ 279
ai tea а (s) + 0 E) представляла собой геометрическое изображение краевого
значения функции, аналитической (за исключением разве что полюса в
начале координат) в области D+.
Если по примеру предыдущего строить геометрическое изображение
самого регуляризующего множителя, то в первом случае он будет задаваться
уравнением р = p(s), ф = О и геометрически изображаться отрезком
положительной полуоси, проходимым дважды .или, вообще, четное число раз. Во
втором случае он имеет уравнение р = 1, ф = 0(s) и, следовательно,
геометрически изображается в виде единичной окружности, проходимой п — >с раз
(см. B8.14)).
Обобщая естественным образом постановку вопроса, можно искать
регуляризующий множитель, геометрическим изображением которого служит
наперед заданная кривая.
Пусть на контуре L задана некоторая комплексная функция
a{s)+ ib(s)= ге^^, геометрическим изображением которой служит кривая Г.
Зададим еще некоторую кривую С, полярное уравнение которой р = fF).
Для функции a{s)+ib{s) требуется найти регуляризующий множитель
R(t)= p(s)e^^^^\ молуль и аргумент которого связаны такой зависимостью
р = /@), что геометрическим изображением R{t) служит данная кривая С.
Принимая изменение a(s)-f0(s) при обходе контура L равным 2я/г,
условимся искомую аналитическую функцию Ф+B) считать имеющей
порядок п в начале координат.
По определению будем иметь
р (S) г (S) е^ 1« ^^)+® <^^1 = /V ^%^^^ <^>. B8.21)
Выражая из последнего равенства p(s) и G(s) и используя уравнение
кривой С, получим
г (s)! [(Oi (s) - а (s) + л arg /] == I ^ |« в® ^'\ B8.22)
Последнее соотношение есть краевое условие, связывающее
действительную (со) и мнимую @i) части аналитической функции у (г). Таким образом,
общая постановка задачи об отыскании регуляризующего множителя
приводит, вообш,е говоря, к нелинейным краевым задачам. Для задач такого рода
известны способы решения лишь в некоторых простейших случаях. Поэтому
решение краевой задачи B8.21), как правило, остается неосуществимым.
Однако можно указать отдельные случаи, когда задача становится
линейной и допускает решение. Например, если кривая С есть логарифмическая
спираль, уравнение которой р = е , то краевое условие B8.22) превратится
в линейное типа задачи Гильберта
0J — 0 = а — In г + л In I /1 — AI arg /.
Записав последнее в форме
- Re [A + /) Y it)] = а (s) - In г E) + « In I / (s) I - л arg t (s),
легко получим функцию y(^)= со + tcoi, a no ней решение всей задачи.
Заметим, что можно было бы взять за основу задание кривой С в
декартовых координатах.
Изложенные рассуждения, опирающиеся на установление некоторой
зависимости между модулем и аргументом или действительной и мнимой частью
регуляризующего множителя, указывают лишь на один из возможных путей
его построения. Можно искать множитель, исходя из совершенно других
соображений, что показывает, хотя бы, пример множителя, возникающего при
решении задачи Римана, на что указывалось в начале параграфа.
Представляется заслуживающим внимания проведение исследований в
направлении поисков регуляризующих множителей, подчиненных тем или

280 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 1ГЛ. IV
другим условиям, аналогично тому, как это делается в теории интегрирующего
множителя. Может быть, удалось бы прийти к таким случаям, когда регу-
ляризующий множитель, с одной стороны, оказался бы пригодным для
решения какой-нибудь практически используемой задачи, а, с другой стороны,
отыскание его производилось бы при помощи некоторого практически
осуществимого алгоритма.
§ 29. Краевая задача Гильберта для односвязной области
29.1. Однородная задача. Приступим, наконец, к основному
предмету главы — решению краевой задачи Гильберта. Выпишем
краевое условие однородной задачи
a(s)u{s) + b{s)v{s) = 0. B9.1)
Будем считать, что коэффициенты a{s) и b{s) не обращаются
одновременно в нуль. Поделив краевое условие на л/а^{8) + 6^E),
приведем его к такому случаю, когда коэффициенты
удовлетворяют условию
аЦ8) + ЬЦ8)=1. B9.2)
Всюду в дальнейшем будем считать, что условие B9.2)
выполняется.
Имеем
^1] !^ = (а — ib) {и + iv) — au + bv + i (av -— bu).
Поэтому краевое условие B9.1) можно записать в двух
равносильных формах:
^Ч-5Т7Г} = 0^ B9.3)
Re{{a-ib)F{t)} = 0, B9.30
где
F{z) = u{x,y) + iv{x,y) B9.4)
— искомая функция.
Индекс к функции a(s) -{- ib{s) будем называть индексом
задачи Гильберта.
Деля обе части равенства B9.3) на регуляризующий
множитель функции a + ib (формулы B8.9), B8.10)), приведем его
к виду
Рассмотрим отдельные случаи.
Г. X = 0. В этом случае краевое условие B9.5) есть условие
задачи Шварца. В силу единственности решения этой задачи

§29] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ ОДПОСВЯЗНОЙ ОБЛАСТИ 281
будем иметь в области D+
откуда
f (г)=:/ро^'>(г)^ B9.6)
где Ро — произвольная постоянная.
2°. к > 0. Краевое условие B9.5) есть условие задачи Aq. На
основании результатов п. 27.3 получим
f B) = 2VY(^)QC), B9.7)
где Q{z) определяется формулами B7.7), B7.8). Следовательно,
задача имеет 2х + 1 линейно независимых решений.
3°. X < 0. Решения задачи в аналитических функциях не
существует. Задача имела бы решение, если в качестве
допустимых брать функции, имеющие в области D+ не менее —х
полюсов.
29.2. Неоднородная задача. Запишем краевое условие B7.1)
в виде
R«[7(irrW] = ^(^)- B9.8)
Аналогично тому, как это делалось для однородной задачи,
разделим обе части краевого условия на регуляризующий
множитель функции а (s) + ib (s):
Re
Рассмотрим отдельные случаи.
1^ X = 0. Краевое условие B9.9) есть условие задачи
Дирихле. Взяв от обеих частей оператор Шварца и выражая F(z),
получим
F (z) = е^У (^) [5 (е^^ (^) с (s)) + /Ро]. B9.10)
2°. X > 0. Краевое условие B9.9) есть условие задачи А, и на
основании результатов п. 27.3
F (z) = z^e^y <^) [S (I /1-^^^' ^^)с E)) + Q B)]. B9.11)
Так как формулы B9.10) и B9.11) содержат в качестве
слагаемых общие решения соответствующих однородных задач, то
ясно, что они дают общее решение неоднородной задачи.
3°. X < 0. Поступая аналогично предыдущему, получим
F B) = 2Vy (^) [S (| t Г"" ef^ ^'"^с (s)) -f /с]. B9.12)
Ввиду наличия множителя z"^ функция F{z), определяемая
последней формулой, может иметь полюс порядка —х. Чтобы

282 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
получить аналитическое решение, нужно потребовать, чтобы
функция
S(|/r^^i(^)c(s)) + /C
имела нуль порядка —х в начале координат. Это даст, как
можно показать прямыми выкладками, —2к—1 условий, которым
должен удовлетворять свободный член для того, чтобы решение
задачи было возможно. Не имея явного выражения оператора
Шварца для произвольного контура, нет возможности выписать
эти условия разрешимости в общем случае. В тех случаях, когда
такое выражение известно, можно выписать эти условия явно.
(В следующем пункте мы сделаем это для единичного круга.)
Сформулируем полученные результаты.
Теорема. Если индекс комплексной функции a{s) + ib{s)
х^О, то однородная краевая задана Гильберта B9.1) и
неоднородная B9.8) безусловно разреилимы. Однородная задача
имеет 2х + 1 линейно независимых решений, линейная
комбинация которых входит слагаемым в оби^ее решение.
Если X < О, то однородная задача неразрешима.
Неоднородная задача разрешима тогда и только тогда, когда свободный
член удовлетворяет —2х — 1 условиям разрешимости.
Изложенная теория показывает, что решение задачи
Гильберта в основном сводится к решению трех задач Дирихле.
Первая задача решается при отыскании регуляризующего
множителя, вторая — при нахождении частного решения неоднородной
задачи и, наконец, отыскание функции Q{z) для произвольной
области сводится к нахождению функции, конформно
отображающей область на круг, что в свою очередь равносильно
решению задачи Дирихле.
29.3. Задача для единичного круга и полуплоскости. Для
единичного круга оператор Шварца совпадает с интегралом
Шварца. Обозначим
f (г) = «(л:, y)^iv{x, у\
2Я
Y B) = (й {х, у) + /©1 {х, у), B9.13)
Q (г) = /Ро + Z {CkZ^ - CkZ-^). B9.14)
Учитывая, что |/|==1 на контуре, получим, что решение
задачи Гильберта
а (s) u{s)-{- b (s) v{s) = c {s)
представится следующими формулами:

§ 29] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ ОДНОСВЯЗНОИ ОБЛАСТИ 283
Г. При х = 0
F (г) = е^У (-) у^ 5 е^^ io) с {о)^^ da + /PoJ • B9.15)
2^ При X > О
F {z) = z-^e^y А^\ е^ ^^^ с (а) ^^ da+Q{z)\, B9.16)
3°. При X < О
F [г) = z'^e^y <^) ^ J е«' (<^) с (а) -^^^ da. B9.17)
В последнем случае для разрешимости задачи функция
2л
2П 2Я
= "^ S ^'^' ^^^^(с^)^^ + ^ S б^ ^'^с{а) ^ ^^J^_,, B9.18)
должна иметь нуль порядка —х в начале координат. Разлагая
ее в степенной ряд в окрестности начала и приравнивая нулю
первые —X коэффициентов, получим
2Я
J e«^^>c(a)e-'^^rfa = 0 {k = 0, 1, ..., ~х-1) B9.19)
о
или, в действительной форме,
2Я 2Я
f ^©^ (а) ^ (or) COS ka da = 0, [ e^' ^^^ с (a) sin kada = 0 B9.20)
0 0
(/^ = 0, 1,2, ..., -x-1).
Формулы B9.20) дают —2x— 1 условий разрешимости, которым
должен удовлетворять свободный член, чтобы неоднородная
задача Гильберта с отрицательным индексом была разрешима.
Приведем, не останавливаясь на подробностях, еще решение
задачи Гильберта для полуплоскости. Оператор Шварца здесь
совпадает с интегралом типа Коши (см. формулу B7.5')). Беря

284 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
функцию, конформно отображающую полуплоскость на круг,
в виде
(О B) = г-г ,
для решения задачи Ао по формуле B7.8) будем иметь
выражение
QB) = /Po + j;[c,(f^)'-c,(-2±i)*]. B9.14')
Вместо примененной выше для приведения индекса
коэффициента к нулевому функции t здесь можно использовать "Г \ (см.
* "г *
П. 14.7).
Употребляя те же, что и в предыдущем, обозначения, с
помощью аналогичных рассуждений получим для неоднородной
краевой задачи Гильберта в верхней полуплоскости следующее
решение:
Г. При х = 0
j_ J ^^!!sp_dt + ^\ B9.150
—оо -*
2°. При X > О
[+00 -.
2.\^^l^dt + QiA B9.160
—оо -¦
3°. при X < О
+ 00
Р(^) = ШТе^'^'^^ \ ^^dt B9.170
— оо
при соблюдении условий разрешимости
+ 00
S ¦^^5Г-^^ = 0 (Aj = 0, I, ..., -х-1). B9.190
Последние условия можно представить в виде —2х — 1
действительных.
Здесь Q{z) определяется формулой B9.14'), а y{z)
представляется в виде
Ц-по
Y B) = со {X, у) + т, {х,у) = ^\^ dt, B9.130

§ 29] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 285
где
0(O = arg[(-^)"'(aH-/6)] = arctg^ + 2>carctgl.
29.4. Задача Гильберта для внешней области. Покажем
коротко, как нужно изменить проведенные рассуждения, чтобы
получить решение задачи Гильберта для бесконечной области D"".
внешней по отношению к некоторому простому гладкому
контуру L.
Имея в виду дальнейшие приложения, будем, так же как и
в случае внутренней области Ь+, брать (при определении
индекса) положительный обход контура L против часовой
стрелки*). Определим для интересующего нас случая регуляризую-
щий множитель. Условимся считать начало координат
принадлежащим области D+
Пусть
Ind [а (s) + ib (s)] = х.
Будем называть регуляризующим множителем для заданной
на контуре L комплексной функции a{s) -{• ib{s) по отношению
к внешней области D- такую действительную
знакоположительную функцию p(s), чтобы произведение p(s)[a(s) +/&(s)] было
краевым значением функции, аналитической и имеющей нулевой
порядок всюду в D-, кроме разве бесконечно удаленной точки,
где порядок ее равен индексу, взятому с обратным знаком (—х).
Следовательно, по определению (см. п. 28.2), будем иметь
р is) \а (s) + ib E)] = /V^ ^'\ B9.21)
где y{z) =0) (л:, у) + Ш\ (л:, у) — функция, аналитическая всюду
в D", включая и бесконечно удаленную точку.
Рассуждая аналогично тому, как это делалось в п. 28.2,
получим
YB) = s[arctg4->carg/], Р(^)- v'a^s)+^м1Г' ^^^'^^^
где S — оператор Шварца для области D- с исчезающей на
бесконечности мнимой частью.
Перейдем теперь к задаче Гильберта.
Считая, так же как и ранее, что выполнено условие
а2E) + б2E) = 1,
можем записать краевое условие задачи Гильберта в виде
*) То есть в положительном направлении относительно области D+ и
отрицательном относительно D-.

286 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 1ГЛ. IV
После деления на регуляризующий множитель получим
Рассуждая как в п. 29.2, с той лишь разницей, что вместо
начала координат исключительной точкой здесь является
бесконечно удаленная, будем иметь:
Г. При X < О
F (z) = z^'e^y <^) [S (l t I'^'e^^ <^) с {s)) + Q (г)], B9.25)
где Q{z) есть функция, аналитическая в D- всюду, за
исключением бесконечно удаленной точки, где она имеет полюс
порядка не выше —х, и ее действительная часть на контуре равна
нулю. Легко видеть, что определенная формулой B7.6) для
единичного круга функция Q{z) будет пригодна также и для
внешности единичного круга. Удобнее взять выражение для Q{z)
в несколько ином виде, заменив в формуле B7.6) г на —.
Таким образом, функцию Q(z) для области, внешней по
отношению к единичной окружности, можно записать в виде
-X
Q B) = фо + Е (с^-' - hz"). B9.26)
Для произвольной области D- она будет иметь вид
Q {Z) = /ро + Е {ck [<о {z)r' - с, [со {zt}. B9.27)
где а)B)—функция, конформно отображающая область D- на
область, внешнюю по отношению к единичной окружности, и
переводящая бесконечно удаленную точку в бесконечно
удаленную. В частности, для х = 0 функция Q{z) обращается в
произвольную чисто мнимую постоянную фо.
2°. X > 0. Решение может быть получено из формулы B9.25)
при Q{z) ^0. Функция, определяемая формулой B9.25), будет
иметь полюс порядка к в бесконечно удаленной точке. Поэтому
однородная задача Гильберта оказывается неразрешимой, а
неоднородная разрешима лишь при выполнении некоторых
условий, которые можно получить, разлагая в ряд функцию
S (I М'* ^® ^^^ с (s)) в окрестности бесконечно удаленной точки и
приравнивая нулю первые х коэффициентов разложения.
В случае области, внешней по отношению к единичной
окружности, как известно*), оператор Шварца равен интегралу Швар-
*) См., например, Л. В. Канторович и В. И. Крылов,
Приближенные методы высшего анализа, М., Физматгиз, 1962, стр. 594.

§ 291 ЗАДАЧА ГИЛЬБЕРТА ДЛЯ ОДНОСВЯЗНОЙ ОБЛАСТИ 28?
ца со знаком минус. Разлагая интеграл Шварца в ряд по
степеням — и приравнивая нулю первые х коэффициентов,
получим, что 2х—I условий разрешимости задачи Гильберта для
внешности единичной окружности будут определяться теми же
формулами B9.20), что и для единичного круга.
Окончательно сформулируем полученные результаты.
Теорема. В случае х^О однородная задача Гильберта
имеет —2х + 1 линейно независимых решений, а неоднородная
безусловно разрешима и ее решение линейно зависит от —2н + 1
произвольных действительных постоянных, (Решение дается
формулой B9.25).)
В случае х > О однородная задача Гильберта неразрешима,
а неоднородная разрешима лишь при выполнении 2х — 1 условий
и имеет тогда единственное решение.
Легко видеть, что сформулированная теорема может быть
получена из соответствующей теоремы п. 29.2 для области /)+,
если в последней х заменить на —х. Если бы при определении
индекса был взят обход контура не против часовой стрелки, а,
что более естественно для области D~, по часовой стрелке, то
только что полученный результат совпал бы с соответствующей
теоремой для области D+
29.5, примеры. 1. Решить краевую задачу Гильберта
fcos 2s — cos 5 + -г-) и (s) + (sin 25 — sin s) v (s) =
«=(-7- —cos s J (cos2s + ^i COSS +Лг),
где hu Л2 — некоторые постоянные, для единичного круга.
Запишем краевое условие в виде B9.3').'
Rej (coss —yJ — sin^s— / • 2 sins fcoss — yj (м + /y) I =
= f-^ —cossj (cos 2s + Л| COS s + Л2).
Выполнив преобразование
a (s) — ib (s) == f cos s — g- J — sin^ s — 2/ sin s f cos s —^ J =
ear 1 1 rnS S 1 / sin S 1 5= - ^ ^
«Mcoss J isiriij 12—~?—
'¦^ [(coss-i-J + /sinsJ (f-
представим его так:
Г ^ it) 1
^^ 1  1~Г9 1 = cos 2s + ^1 cos S + ^2.
• cos s J
4Г

288 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА (ГЛ iV
Слева jctoht краевое значение функции, аналитической в единичном круге,
исключая точку 2 = 1/2, где возможен полюс второго порядка. При общих
рассуждениях краевое условие предварительным преобразованием
приводилось к такому виду, чтобы возможный полюс находился в начале координат.
Однако при решении конкретных примеров, когда регуляризующий
множитель находится простым путем при помощи аналитического продолжения и
где заранее известно положение точки с ненулевым порядком решения, можно
обойтись без такого преобразования. (В данном случае оно потребовало бы
сложных вычислений.) Рассуждая совершенно так же, как в общем случае»
получим
F (г) = (z - -i-) [S (cos 2s + A, cos s + A2) + Qi (г)],
где Qi(z) есть функция, аналитическая в единичном круге, кроме точки
г = 1/2, где она имеет полюс второго порядка и действительная часть
которой на единичной окружности обращается в нуль. Эта функция может быть
определена по формуле
Qi (z) =- Q (со (г)),
где (О B) есть функция, конформно отображающая единичный круг на себя
так, чтобы точка z = 1/2 перешла в начало координат. В качестве (о(г)
можно взять
___1^
со(,) = .^_ = __.
Так как при z = е'^
cos 2s + hi cos s + Л2 = Re [z^ + h^z + ^2],
TO в силу единственности аналитической функции, определяемой интегралом
Шварца, будем иметь
5 (cos 2s -f hi cos s + Л2) = 2:2 + f^^^ + f^^
Учитывая формулу B9.14) для функции Q, окончательно получим
f (г) = (г-i-)"[2^ + Л:2 + А, +/р + с, ^5l +
в силу безусловной разрешимости задачи (х = 2 > 0) постоянные /ii и hi
могут быть любыми.
2. Решить краевую задачу Гильберта
( cos 2s — cos S -f -J ) « ^ (sin 2s — sin s) 0 = cos 2s + hi cos 5 + ^2
для единичного круга.
Так как индекс задачи х = —2 < О, то задача, вообще говоря,
неразрешима. Она окажется разрешимой лишь при специальном подборе
постоянных hi и hz.
Преобразованиями, аналогичными проведенным в предыдущей задаче,
приведем краевое условие к виду
Re Ut - у) /" @1 = cos 2s + Ла cos s + Л2.

$ Щ связь КРАЕВЫХ ЗАДАЧ ГИЛЬБЕРТА И РИМАНА 289
Отсюда
-2
^(г)=(г~1) (г2 + Л,2 + А2).
При произвольных hi и Лг функция, определяемая последней формулой, имеет
полюс второго порядка в точке 2 = 1/2. Для устранения полюса постоянные
нужно положить равными hi = —1, Л2 = 1/4.
Если это выполнено, то задача имеет единственное решение.
§ 30. Связь краевых задач Гильберта и Римана
ЗОЛ. Постановка вопроса. Сравнивая только что полученное
решение краевой задачи Гильберта с решением задачи Римана
(гл. II), можно усмотреть между ними сходство. Это наводит
на мысль, что имеется связь и между самими задачами,
несмотря на различие в их постановке. Для простейших контуров
(прямая и окружность), для которых существует простая связь
оператора Шварца с интегралом типа Коши, может быть
установлена прямая сводимость задачи Гильберта к задаче Римана.
Для других контуров такой непосредственной связи не
существует, но она может быть установлена при помощи конформного
отображения соответствующих областей на круг или
полуплоскость.
Имеется два способа такого сведения. Первый (указанный
автором) состоит в установлении факта, что «внутренняя»
функция Ф+(г) решения краевой задачи Римана
Ф+ /.ч _ а is) + ib Ш ф- /.ч , 2с (s) ,0^ ..
при подходящем подборе произвольных постоянных дает
решение краевой задачи Гильберта
а E) u{s) + b (s) v{s) = c (s). C0.2)
Доказательство опирается на имеющиеся в замкнутой форме
решения обеих краевых задач и заключается в прямом
преобразовании формул решения краевой задачи Римана из гл. II
в формулы решения задачи Гильберта п. 29.3.
Второй способ (указанный Н. И, Мусхелишвили) сведения
краевого условия задачи Гильберта C0.2) к краевому условию
задачи Римана C0.1) путем доопределения по способу
симметрии в дополнительную область решения задачи Гильберта мы
далее рассмотрим подробно. Этот метод интересен тем, что он
сам независимо от изложенного в § 29 метода регуляривующего
множителя может служить источником решения задачи
Гильберта. Кроме того, этот метод применим и при исследовании
некоторых других задач.

29d КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА {ГЛ. IV
30.2. Связь между краевыми условиями. По-прежнему будем
считать, что контур L есть прямая или окружность.
Различие в постановках краевых задач Римана и Гильберта
заключается прежде всего в том, что в первой задаче
отыскивается кусочно аналитическая функция, определенная во всей
плоскости, тогда как в последней ищется функция,
определенная только в области D+, а дополнительная область D"
совершенно не затрагивается. Поэтому, чтобы установить связь
между указанными краевыми задачами, исходя из самой их
постановки, прежде всего нужно найти целесообразный способ
доопределения аналитической функции Ф+(г) (являющейся
решением задачи Гильберта) в область D- так, чтобы получить
кусочно аналитическую функцию, определенную во всей
плоскости.
Так как контур L, по условию, прямая или окружность, то
такое доопределение может быть произведено, как показывает
дальнейшее исследование, путем продолжения по симметрии
совершенно так же, как это делается в принципе симметрии.
Различие будет заключаться лишь в том, что поскольку могут
не выполняться условия этого принципа (отрезок прямой или
дугу окружности функция должна отображать в отрезок
прямой или дугу окружности), то и полученное продолжение,
вообще говоря, не будет аналитическим. Это нам и не требуется,
так как речь идет только о построении в области D- некоторой
новой функции Ф~(-г), которая была бы так связана с функцией
ф+{г), определенной из краевой задачи Гильберта, что краевое
условие последней задачи стало бы равносильным краевому
условию задачи Римана, связывающему функции Ф+(г) и
ф-{г),
В дальнейшем будем пользоваться обозначениями п. 18.1.
Продолжим по симметрии заданную в области /)+
(единичном круге или верхней полуплоскости) функцию Ф+(г) в
область D- (внешность единичного круга или нижняя
полуплоскость), считая, что в точках, симметричных относительно
контура, функции принимают сопряженные значения, т. е.
ф- (z) = ф'+A) = ф+B) C0.3)
в случае действительной оси,
ф-(г) = Ф^(|) = Ф^D) C0.4)
в случае единичного круга.
Определенная таким образом функция ф-(г) будет
аналитической в области D- (п. 12.1).
Совокупность функций Ф+(г) и ф-B) можно рассматривать
как одну кусочно аналитическую функцию.

§ 30] связь КРАЕВЫХ ЗАДАЧ ГИЛЬБЕРТА И РИМАНА 291
Когда точка z из области D+ стремится к точке t контура,
симметричная ей точка в /)~ стремится к той же точке t.
Поэтому
ф- (/) = ф+(^)== ф+ (О, C0.5)
ф- (/) = ф+ Ш = ф+ it). C0.6)
Таким образом, предельные значения функций Ф+B) и
Ф~(г) на контуре комплексно сопряжены друг другу.
Следовательно, заданную на контуре функцию Ф+(^) можно
рассматривать как предельное значение функции Ф~(/).
Теперь уже можно доказать сводимость задачи Гильберта
к задаче Римана.
Запишем краевое условие задачи Гильберта
Re \(а —• ib) {и + iv)] = с
в такой форме:
{а ~ ib) Ф"^ (О + {а + ib) Ф+ (/) = 2с. C0.7)
Заменяя на основании изложенного выше Ф+@ на Ф~@»
из C0.7) получим краевое условие задачи Римана
»"<'>=-^±lt*-W+7i^^. C0.8)
Следовательно, решение краевой задачи Гильберта C0.2)
равносильно отысканию функции Ф+(<г) из решения краевой
задачи Римана C0.8) при условии, что для всякого -г, не
лежащего на контуре.
ф-(г) = ф+(г,). C0.9)
Способ сведения задачи Гильберта к задаче Римана,
изложенный в настоящем пункте, имеет то преимущество перед
первым способом, что он не опирается на явное решение этих
задач. Поэтому способ этот может быть использован и в том
случае, когда таких явных решений не существует, например,
в соответствующих задачах со многими неизвестными
функциями (см., например, [3], стр. 172). Кроме того, можно было бы
не давать отдельного решения задачи Гильберта, а
использовать для этой цели решение задачи Римана, что и сделано в [16].
30.3. о задаче Гильберта для бикруга. Пусть a{t\j2)j b{t\,t2)
и c{tut2) — действительные функции, удовлетворяющие на
единичном торе L ^z= Li X Li условию Гёльдера, g = а + ib и
a^-]-b^=l. По аналогии с п. 27.1 и пп. 29.1—29.2 двумерную
задачу Гильберта для бикруга D = D++ сформулируем так.

292 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 1ГЛ. IV
Найти функцию F{zuZ2)='u{zuZ2)+iv{z\,Z2)y аналитическую
в D и непрерывную на L по краевому условию
Re {gF) == Re [{а - ib) F]=au + bv = с, C0.10)
заданному на L.
При g^l задача C0.10) превращается в двумерную
задачу Дирихле, которая, как известно, разрешима при
выполнении счетного множества необходимых и достаточных условий
разрешимости
\c{tu t2)tr'tr4t,dt2 = 0 {Пи П2=1, 2, ...).
L
М. А. Бородин 1) свел задачу Гильберта C0.10) к
последовательному решению двух задач Дирихле и элементарной
задачи
Re[/r72-"-'f(/b^2)] = 0,
где Щ = XI (g) и К2 = K2{g) .
Если обе такие задачи Дирихле разрешимы и xi ^ О, хг ^ О,
то общее решение задачи C0.10) зависит от Bxi + 1)Bх2+ 1)
произвольных действительных постоянных и представимо
двумерным интегралом Шварца (ср. с п. 29.3).
Решение задачи Гильберта для бикруга может быть
получено с помощью регуляризующего множителя, а также
сведением к двумерной вырожденной задаче Римана
ЖЛ)Р^''Ии t2) + g{tiy k)F~{tu t2) = 2c{tu /2),
аналогично тому, как это сделано в одномерном случае
соответственно в п. 29.2 и в п. 30.2 (см. В. А. Какичев 8), 9)).
§ 31. Особое интегральное уравнение с ядром Гильберта
31.1. Связь характеристического уравнения с краевой
задачей Гильберта. Ядром Гильберта, как уже указывалось в п. 6.2,
называется функция ctg—j-^. Особое интегральное уравнение
вида
ais)u(s)--^\ u{a)dg^da=c{s), C1.1)
О
где a(s), 6E), с E) —заданные функции, удовлетворяющие
условию Гёльдера, называется характеристическим *) особым
*) Термин возник исторически и с современной точки зрения не вполне
оправдан (см. далее, п. 52.3).

2я
y(a)rf(T = 0, C1.3)
§ 311 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ ГИЛЬБЕРТА 293
уравнением с ядром Гильберта. Если c(s) = 0, оно называется
однородным, в противчом случае неоднородным. Решение будем
искать в классе функций, удовлетворяющих условию Гёльдера.
Как характеристическое особое интегральное уравнение с
ядром Коши связано с краевой задачей Римана, так и
характеристическое уравнение C1.1) с ядром Гильберта еще более
непосредственно связано с задачей Гильберта. Покажем это.
Будем считать функцию u{s), являющуюся решением
уравнения C1.1), краевым значением гармонической в единичном
круге функции и(х,у). Ввиду безусловной разрешимости задачи
Дирихле для произвольного непрерывного краевого значения
такое предположение законно. Тогда в силу формулы F.6)
будем иметь
2Я 2Я
v{s) = --^\u{a) ctg ^ da + \v (о) da. C1.2)
о о
Положив
S
о
придем от особого уравнения C1.1) к краевой задаче Гильберта
а is) uis) + b is) v{s)=-c (s) C1.4)
для аналитической в единичном круге функции F{z)= и{х,у) +
'+ш(х,(/). Таким образом, установлен следующий факт.
Теорема. Характеристическое особое уравнение с ядром
Гильберта C1.1) равносильно задаче Гильберта C1.4) для
круга с дополнительным условием C1.3) в том смысле, что если
F{z) есть решение краевой задачи C1.4), удовлетворяющее
условию C1.3), то граничное значение его действительной части
есть решение уравнения C1.1), и обратно, имея u(s) — решение
уравнения C1.1), используя оператор Шварца и условие C1.3),
получим решение задачи Гильберта C1.4).
В дальнейшем для решения характеристического уравнения
C1.1) будет использовано полученное в § 29 решение задачи
Гильберта.
Из свойств гармонических функций следует, что условие
C1.3) означает равенство нулю гармонической функции v(x,y)
в начале координат.
31.2. Решение уравнения. Будем называть индекс функции
дE) + /ЬE) индексом характеристического уравнения C1.1).
Рассмотрим подробно случай нулевого индекса, имеющего
особенности по сравнению с соответствующим случаем уравнений
с ядром Коши: X = Ind[a(s) +/ftE)] = 0. Рассмотрим сначала

294 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 1ГЛ. IV
однородное уравнение, положив в C1.1) c(s):=0. Решением
соответствующей однородной задачи Гильберта будет функция
f (г) =/po^'Y B)^ где у(г) определяется формулой B9.13), Ро —
произвольная действительная постоянная.
На контуре t = е^^ и
F{t) = u (s) + iv (s) = /po^^'Y ^^^.
Положим
,VY(^)=|(s) + /n(s). C1.5)
Тогда
и {s) = foolish t;(s) = Po^(s).
Условие разрешимости уравнения C1.3) принимает вид
Jn((y)da = 0. C1.6)
о
Таким образом, при нулевом индексе возможны два случая:
1) Если условие C1.6) выполняется, то однородное
характеристическое уравнение C1.1) имеет решение*)
u{s) = U{sy C1.7)
2л
2) Если \ т] (or) da Ф О, то уравнение решения не имеет.
о
Перейдем к неоднородному уравнению. Решение задачи
Гильберта, согласно формуле B9.15), имеет вид
-^\с{а) е^' (^) ~J^ da + /ро . C1.8)
Положим
2Я
iei^ {z) = ^^ly^^ — U (а) е^^ <^) -ф^ da = W B).
2я J е — Z
о
На основании свойств интеграла Шварца на контуре будем
иметь
ReW@ = c(s)e^'(^),
2Я
ImWit)^ -^\с (а) ««•¦ (<') ctg -^ da.
C1.9)
*) Этим уравнение с ядром Гильберта отличается от уравнения с ядром
Коши, которое в соответственном случае всегда неразрешимо.

§ 31) ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ ГИЛЬБЕРТА ^95
Беря в формуле C1.8) предельные значения и учитывая
формулы C1.9), получим
2л
и E) = Ро^ (s) + Т1 (S) С 'S) e^^'^^l's)^^c (а) е^ (^» ctg ^-=^ da,
о
2л
V 's) = РоЛ (s -lis с (s) е^^'^-ц{8)'^^с а) е^ '^' ctg -^^ da,
C1.10)
На основании C1.3) должно иметь место условие разрешимости
2л 2я
Ро j Л E) ^5 — ^ I (si С (s е'' ^'^ ds —
2п 2я
5 Л E) rf5~^ J С а) е^ (^^ ctg-5^ da =0.
и о
Переставляя в двойном интеграле порядок интегрирования
и учитывая, что согласно формуле Гильберта F.7)
2я 2Л
ir\'^'<s)''4^ds^l{o)--^\l a)da,
О О
получим
2я 2я 2л
^о\^{(У) da+^c{a)e''''^a^^l a)da = 0, C1.11)
о и и
2я 2я
Заметим, что интегралы -g— \ I (а) da, ^ \ л [о) da дают
и о
значения действительной и мнимой части функции ie^^^^^ =
= 5(^1 ?/) +^л(^»^) в начале координат, а потому не могут
одновременно обращаться в нуль.
Возможны два случая:
2Я
1) Если \r\{a)da Ф О, т. е. соответствующее однородное
о
уравнение неразрешимо, то условие C1.11) дает возможность
определить произвольную постоянную ро и, следовательно,
неоднородное уравнение C1.1) имеет единственное решение
C1.10).

296 Краевая задача гильберта 1гл. iV
2) Если \ Т1 (сг) da = О, т. е. соответствующее однородное
о
уравнение разрешимо, то неоднородное уравнение, вообще го-
воря, неразрешимо. Учитывая, что \ |(а) da =5^ О, из C1.11) по-
0
лучим условие его разрешимости
2Я
\^с{а)^^^Ыо = 0. C1.12)
о
В случаях ненулевого индекса ограничимся формулировкой
результатов.
Как показывает исследование, при хт^'О условие C1.3)
не может выродиться в тождество, поэтому по сравнению с
задачей Гильберта оно при х > О уменьшает на единицу число
линейно независимых решений, а при х < О на столько же
увеличивает число условий разрешимости. Точные результаты
дает следующая
Теорема. При х > О однородное уравнение C1.1)
{с {$) ЯЕ 0) имеет 2х линейно независимых решений, а
неоднородное безусловно разрешимо и зависит линейно от 2х
действительных постоянных.
При X < О однородное уравнение неразрешимо, а
неоднородное разрешимо лишь при выполнении —2х действительных
условий разрешимости.
Решения уравнения и условия разрешимости могут быть
получены из формулы п. 29.3 при соблюдении условия C1.3).
Учитывая, что комплексный параметр содержит два
действительных, а комплексное условие разрешимости равносильно
двум действительным, заключаем, что при кф О качественные
результаты исследования характеристического уравнения с
ядром Гильберта полностью совпадают с соответствующими
результатами (п. 21.2) для характеристического уравнения с
ядром Коши.
31.3. Уравнения с постоянными коэффициентами. Рассмотрим
часто встречающийся на практике частный случай, когда коэф-
фициенты а, b — постоянные числа. Будем считать, что деление
на л/а^ -f b^ уже произведено, так что удовлетворяется условие
1®. В случае однородного уравнения
a'^is)--^'\u{a)dg^da^O C1.1°)
о

§ 311 ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УВАВНЕНИЯ С ЯДРОМ ГИЛЬБЕРТА 297
непосредственно получим решение соответствующей однородной
задачи Гильберта
F{z) = u + iv = /Po^^'v (г) = /р^ (а + ib).
Отсюда
g E) = — 6, Т1 E) = а, в®' <^) = I.
Условие разрешимости C1.6) запишется в виде
\ У] (а) do = а ' 2я = О,
о
Следовательно, при афО однородное уравнение не имеет
отличных от тривиального решений.
При а = О уравнение
2я
\ и (а) ctg ^^^ rfa = О
о
имеет в качестве решения произвольную постоянную u{s)=f^.
2°. Неоднородное уравнение
2Я
аи {s} - -Jf J «(о^) ctg -^^ da = с (s) C1. Г)
о
при а =7^ о в силу предыдущего безусловно разрешимо.
Согласно C1.11)
2Я
2яаро~6 \c{a)da = 0.
о
Подставляя отсюда значение ро в формулу C1.10), получим
решение уравнения C1.Г) в виде
2я 2л
u{s) = ac {s) + -^у{а) dg^^ da - -^
о о
Если а = О, то для разрешимости уравнения
2я
-^]ti{o) ctg^^da=c (s),
о
согласно C1.11), должно выполняться условие
2Я
Jc(a da = 0. C1.13)

298 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
Если ОНО выполнено, то, положив в C1.10) т)E) = 0, ^E) =
= —b = 1, получим решение в виде
u(s) = --^\c{a)dg^da + C, C1.14)
о
где С — произвольная постоянная.
Последнее решение можно было бы получить из формул
обращения Гильберта (п. 6.2). Полагая в формуле F.7) Щ) = 0
и рассматривая в ней u{s) как заданную, а v(s) как искомую
функцию, получим, что формула F.6) дает решение уравнения
F.5), совпадающее с C1.2). Условие
2л
= ^5a(a)da-0
о
совпадает с C1.13).
31,4. Полное уравнение. Полным особым интегральным
уравнением с ядром Гильберта называется уравнение вида
Кф ^ а (s) ф (s) —
2я 2Я
-^\<p(a)cig^da+\K{s, a)cfia)da = f{s), C1.15)
О О
где аE), 6(s), f{s)y /С(s, а) —действительные функции, причем
а E), b{s), f(s) удовлетворяют условию Гёльдера, а ядро
K{SyO) удовлетворяет условию Гёльдера всюду, кроме, может
быть, точек а = S, где для него справедлива оценка
Интеграл
1^E, о)\<—^ @<А<1).
2л
К (s, а ф (а) da
о
называется регулярной частью уравнения.
Для уравнения C1.15) можно было бы провести все
исследования, которые проведены в §§ 23 и 24 для уравнения с
ядром Коши, с тем лишь различием, что вместо используемого
там решения краевой задачи Римана здесь пришлось бы
использовать полученное в § 30 решение задачи Гильберта, В силу
вещественности рассматриваемого здесь уравнения многие
рассуждения упростились бы. Можно доказать, например, что
оператор K^ союзный данному, является для него равносильным
регуляризатором (см. задачу 18 в конце главы) —свойство, кр-

§ 31) ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЯДРОМ ГИЛЬБЕРТА 299
торое уже несправедливо для комплексных операторов.
Заметим, что основные свойства особых уравнений (теоремы Нёте-
ра), были впервые выведены Нётером [Noether 1)] именно
для уравнений вида C1.15) путем использования решения
задачи Гильберта и лишь 20 лет спустя были получены для
комплексных уравнений с ядром Коши путем использования
решения задачи Римана (см. Исторические сведения к гл. III и IV).
Однако в самостоятельном выводе свойств
рассматриваемого здесь уравнения нет нужды. Проще будет установить
сводимость уравнения C1,15) к уравнению с ядром типа Коши,
в связи с чем вся теория последнего может быть
непосредственно перенесена на это уравнение. Так как регулярные части
у обоих типов уравнений имеют одинаковый характер, то
достаточно установить соотношение между ядром Гильберта ctg—^
dx
и ядром Коши ^___ ^ , что делается так же, как в п. 6.1.
Пусть контур интегрирования есть единичная окружность.
Тогда
и
dx /е^^ do
т: _ t е'"" - е^'
Умножая числитель и знаменатель последнего выражения на
. оЛ-s
е 2 и пользуясь формулами Эйлера, получим
dx ^ ^ I ^У — S . i \ .
или
I , а — S , dx \ dx /т лп\
yctg-^-da = :^^--y —. C1,16)
Заменяя в уравнении C1.15) ядро Гильберта последним
выражением и подставляя 5 =-г In ^, а = -г-1пт, da = -—^,
приведем уравнение C1.15) к уравнению с ядром Коши:
aAt)<fxii)-^\^dx + \kAt, x)dx = f,{t). C1.17)
L L
Коэффициент задачи Римана, соответствующий уравнению
C1.17), имеет вид
п /А _ Qi (О + ibx (t) _ fl (s) + ib (s) .г.. .Q.
^\^)- a,(t)--ib,(t) - a(s)^ib(s) ' ^^^'^^)

300 К^>АЕВАЯ ЗАДАЧА ГИЛЬВЕРТА [ТЛ, IV
Следовательно,
Ind G (О = 2 Ind [а {s) + ib (s)]. C1.19)
Из последнего равенства видно, что если стремиться к тому,
чтобы свойства уравнения C1.15) выражать с помощью его
собственного индекса*) х= Ind[a + i*H то во всех результатах
§§ 23, 24 нужно X заменить на 2х.
Например, теорема III Нётера будет формулироваться так:
Разность чисел линейно независимых решений уравнения
Кф = О C1.15) и его союзного К'г|? = О равна 2к, еде х =
^ Ind [а{s)+ib{s)].
При этом линейная зависимость или независимость
понимается с действительными коэффициентами или, как
выражаются в алгебре, над полем действительных чисел.
§ 32. Краевые задачи для полигармонических
и полианалитических функций, приводимые
к краевым задачам Гильберта и Римана
32.1. Представление полигармонических и
полианалитических функций через аналитические. Дадим прежде всего
определение полигармонической функции.
Определение. Полигармоничвской порядка п функцией
U{x,y) называется всякий интеграл полигармонического
уравнения
A"f/ = 0, C2.1)
где Д ==-j-y + ут •*" оператор Лапласа, а показатель п
означает, что оператор Л применяется последовательно п раз.
Полигармоническая функция называется регулярной в
данной области D, если она в этой области непрерывна вместе со
своими производными до порядка 2/г.
В дальнейшем будем постоянно предполагать, что
рассматриваемые полигармонические функции регулярны.
Для простоты будем рассматривать лишь односвязные
области.
Дадим краткий вывод представления полигармонической
функции через аналитические.
Кратчайшим путем для вывода искомого представления
является переход от действительных переменных х,у к комплекс-
*) Н. и. Мусхелишвили [16] называет индексом уравнения C1.15),
так же как и задачи Гильберта, индекс G(t), Поэтому индекс в его
определении равен удвоенному индексу в нашем определении.

$ 32] ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 301
ным переменным *):
z = x -}- iy^ z = x — iy.
Будем считать z и z независимыми переменными. Тогда по
правилу дифференцирования сложной функции имеем
дх dz ^ дг ' ду dz dz ^ ^
Отсюда легко получим
Следовательно,
Д = -5-+-|^=4^- C2.3)
dz'^dz'^ •
И полигармоническое уравнение можно представить в виде
44^-0. C2.4)
Записывая последнее в форме
\дг'^-^дг'^-W
д"
dzdz
И Применяя хорошо известный способ интегрирования уравне-
"^^ 'Шу""^* получим
^ , ^ , = Ф B) + Ф* (г),
где фB:) и ф*B)—аналитические функции своих аргументов.
Так как левая часть последнего равенства есть величина
действительная, то функции ф(г) и ф*B) должны быть комплексно
сопряжены. Поэтому будем иметь
dz^-^ dz^"' -^ Ф и + Ф (^) = 2 R^ Ф (^)-
Если считать полигармоническую функцию известной, то, как
показывает последняя формула, единственным образом опреде-
*) Переход к комплексным переменным закономерен вследствие хорошо
известного факта аналитичности решения уравнения эллиптического типа с
аналитическими коэффициентами. Несколько различных доказательств
аналитичности решений уравнений эллиптического типа читатель может найти
в т. VIII A940) журнала «Успехи матем. наук». Подробное исследование
вопроса о комплексных представлениях решений полигармонического
уравнения дано в книге [1], стр. 170.

302 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
ляется действительная часть ф(г). Сама функция фB:),
следовательно, определится с точностью до произвольного мнимого
слагаемого.
Считая начало координат принадлежащим области регуляр-
оо
ности полианалитической функции и полагая Ф B^) = 2 ^/г^;*,
можем записать
л ^ оо оо
дг^'^дг"
Интегрируя обе части по г, а затем по г, получим
= 2Re[zz<fi{z) + yff{z)],
где
«P'^^^^Zirr^*
k=0
единственным способом определяется через ф(-г), а
\|)(г)—новая аналитическая функция, которая, так же как и фB:),
определяется через и с точностью до чисто мнимого слагаемого.
Повторяя процесс, примененный выше, еще п — 2 раз,
придем к искомому представлению полигармонической функции
U(x,y) = 4eZz'z^4>p{zl C2.5)
где все (pp{z)—аналитические функции, выражающие через
U{x,y) с точностью до чисто мнимого слагаемого.
Функцию
V(x, у) = 1т Zz^'z^cfpiz), C2.6)
р=0
которая, очевидно, также будет интегралом
полигармонического уравнения, назовем полигармонической функцией,
сопряженной с U{x,y),
Определение. Если U и V — две сопряженные
полигармонические функции, то функция
F{z,z) = U{x,y) + iV{x,y) C2.7)
называется полианалитической.
Полианалитическая функция, очевидно, является, так же
как и полигармоническая, интегралом полигармонического

§ 32] ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 303
уравнения и на основании определения будет иметь следующее
представление:
F (г, Z) = Е гП\, {Z) = 2 z'f, (г). C2.8)
Имеются представления полигармонических и
полианалитических функций, отличающиеся от приведенных здесь по
форме*), но нам они не понадобятся, поэтому мы их не
выписываем.
При п = 2 уравнение A^U = О называется бигармоническим,
а решение его — бигармоническими функциями. Решения би-
гармонического уравнения имеют тесную связь с основными
величинами, изучаемыми в теории упругости (напряжения и
смещения), и интегрирование бигармонического уравнения
составляет одну из основных задач теории упругости. Заметим
еще, что представление бигармонической функции через
аналитические чаще берется в виде
и(х, y) = Re[zq>{z) + y\}iz)]. (Формула Гурса.)
32.2. Постановка краевых задач Гильберта для
полианалитических функций. Сначала условимся в обозначениях и
установим некоторые вспомогательные соотношения.
Пусть
t = x{s) + iy (s)
есть уравнение контура L в комплексной форме. Тогда
ds (is ' ds '
Обозначая, как всегда, i = x{s) — iy{s) и учитывая, что
\ dt \ . ^
—- = 1 будем иметь
\ ds \ ' -^
/'=-!- =-г- C2.9)
Если W{z,z) есть некоторая, достаточное число раз
дифференцируемая функция, то для производной по дуге контура
получим выражение
I^ = ^t' + ^-f. C2.10)
ds dt dt ^ ^
Считая, что нормаль направлена внутрь области, т. е.
касательная и нормаль расположены соответственно так, как оси
*) См., например, [1], § 32, формулы C2.18), C2.19), C2.22).

304 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
абсцисс И ординат, будем иметь
Отсюда получим
дх ду дх ду
дз дп ' дп ds
дп ^^' дп ^^'
d^'W
после чего выражению для —г- можно придать вид
дп'^
d^W
m-O
C2.11)
Перейдем теперь к формулировке основных краевых задач
для полианалитических функций.
Как и решение всякого уравнения 2а1-го порядка
эллиптического типа, полигармоническая функция определяется
заданием п независимых краевых условий. Условия эти могут быть
даны в очень разнообразных формах. Приведем четыре
наиболее часто встречающиеся краевые условия, формулируя их
сразу для полианалитических функций.
Пусть L — простой замкнутый контур, уравнение которого
допускает производные до Bп + 2)-го порядка,
удовлетворяющие условию Гёльдера. Требуется определить в области D+
полианалитическую функцию /г-го порядка:
F{z,z) = U{x,y) + iV{x,y\
непрерывную на контуре области по следующим краевым
условиям:
Задача I.
aAs)t^^U+bk{s)ls!'V = Ck{s) {k = 0, 1, ..., n-1). C2.12)
Задача П.
а, (s) Ы^и + Ь, {S) ^^V = Ck E),
(k = 0, 1, ..., V^—J» причем в случае п нечетного
отбрасывается последнее условие).
Задача П1.
<^*(^)^ + ^*(«)^ = '^*Н (^^ = 0» I. "м «-!), C2.14)

I 82J ЗАДАЧИ. ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 305
Задача IV.
^k {s) , . % , + bk {s) —\\ , = Ck E) C2.15)
(/e=l, 2, ..., n\
где Uf^ E), бд, (s), a^ (s), ft;^ (s) — заданные на L действительные
функции длины дуги, удовлетворяющие условию Гёльдера
вместе со своими производными до Bп —/г-—2)-го порядка*),
причем al{s) + bl{s)^0, [a[{s)f + [bl{s)f Ф 0. Будем также
считать, что
cil{s) + bl(s)=l [aiis)f + [bi{s)f=L C2.16)
Если с помощью представления C2.8) вычислить левые
части краевых условий, то придем к краевым задачам
относительно аналитических функций ц>р{г). При этом краевые
условия будут, вообще говоря, содержать все функции фр, а также
и их производные. Решение таких краевых задач представляет
вопрос весьма сложный. Мы ограничимся здесь случаем
простейших контуров (окружность и прямая), когда каждую из
краевых задач I—IV можно свести к совокупности краевых
задач Гильберта, любая из которых содержит лишь одну
неизвестную функцию. На основании теории, данной в § 29, решение
всех перечисленных задач дается в замкнутой форме.
При 6ft(s) = 0, ak{s)=l рассматриваемые краевые задачи
полианалитических функций переходят в задачи для функций
полигармонических.
32.3. Краевые задачи для круга**). Краевые условия C1.12)
задачи I, учитывая C2.16), можно записать в следующем виде:
Re [(а,{S) - ib„(s))^'F (t, i)] = Ck{s) (/^ = 0, 1, ..., n - 1).
C2.17)
Пользуясь представлением C2.8) полианалитических
функций, простыми вычислениями получим
^'F {Z, z) = A'Y,jf^zP-HzP%{z)f\ C2.18)
*) В краевые условия входят производные до B/г —2)-го порядка
искомых функций. Поэтому на коэффициенты краевых условий нужно наложить
ограничения, достаточные для существования у этой высшей производной
предельных значений на контуре, удовлетворяющих условию Гёльдера.
Настоящее ограничение обеспечивает это для всех рассматриваемых краевых
задач.
**) Результаты данного и следующего пунктов взяты из работы
В. С. Рогожина 1) и работ М. П. Г а н и н а 1) и 2).

306 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 1ГЛ. IV
Трудность сведения краевых задач для полианалитических
функций к краевым задачам для аналитических заключается
в том, что в их представление входит неаналитическая
функция г. Основная задача состоит в том, чтобы краевое значение
этой функции выразить через краевое значение некоторой
аналитической функции, что очень легко сделать для
рассматриваемых нами простейших случаев.
Пусть область D+ есть единичный круг. Тогда для точек
окружности i = 1//. Учитывая это, введем новые
аналитические функции
ф^ (г) = У — ^ ^^'/ . C2.19)
На окружности будем иметь
Поэтому краевые условия C2.17) можно записать так:
Re Г ^"^'^l ,.Л = 7Г^^(^) (* = 0, 1, ..., /г~1).
L Ч (S) + ibj, (S) J 4"
Получили п краевых задач Гильберта для определения
аналитических функций Фк{^)-
По формулам п. 29.3 найдем решения этих задач:
[2Я -
О -¦
причем если для некоторых k индекс Кк < О, то нужно
положить Qii(z)^0 и потребовать выполнения следующих условий
разрешимости:
2я
Jcfe(a)A^^^^-''"^"rfa = 0 (m, = 0, 1, ..., -х,-1). C2.20)
о
Если хоть одно из этих условий не выполняется, задача
решений не имеет.
Пусть все условия разрешимости выполняются. Тогда все
функции Фй(г) можно считать известными. Чтобы получить
искомую полианалитическую функцию, остается выразить
аналитические функции фр(г), входящие в ее представление, через
найденные функции Фк{г),
Прик = п—1 из C2.19) имеем

^ 32] ЗАДАЧИ. ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 307
Интегрируя это равенство п— 1 раз, получим функцию срп-\{^)-
Заметим, что так как функция z^-^(pn-\i^) и ее производные до
(п — 2)-го порядка обращаются в нуль при г = О, то все
произвольные постоянные интегрирования этим условием определятся
и функция фп-1 (z) определится через функцию Фп-i (z)
единственным образом.
Полагая k = n — 2, будем иметь
(z^ ^Фп-2 (^)) = i;^—2ji L^«-2 (^^ i 2 J •
Правая часть есть известная функция. Отсюда интегрированием
определяется Фп-гС-^^)-
Пусть, вообще, определены функции (pk^^iz), Фая-2(^), ...
•••, Фп-1 (-2^)- Тогда из равенства C2.19) получим
п-1
(p-k)\ z^-^
{z\k{z)t ^ = -vp Ф, B) - > ТгЧтГ Z^k = ^k {z\
C2.21)
где ш^^ (г) —известная функция.
Отсюда /г-кратным интегрированием находим
Z
о
Вставляя в формулу C2.8), получим решение задачи
п-\ _ ^
F (г, г) = Шо(г) + J] Tp^TljT J (^ " ^У ^^ W ^^- C2.22)
р=1 о
Если все индексы щ неотрицательны, то задача безусловно
разрешима и ее решение зависит от
произвольных действительных постоянных.
В общем случае, когда
хо<0, xi <0, ..., х^<0; х^+1>0, ..., х^.^^О,
решение существует только при выполнении
S(-2>c,-l)

308 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
условий разрешимости типа C2.20), и если эти условия
выполнены, ТО решение зависит от
произвольных действительных постоянных.
Рассмотрим схематически еще задачу IV. Краевые условия задачи
C2.15) можно записать в виде
Re[(a,(s)-,-6,E))-g^J^] = c,E) (k = \,2 п). C2.23)
Пользуясь выражениями C2.2), будем иметь
-^ \dz dzj \dz dzj
n—k k-\ ^
n—k k-\
откуда на основании представления C2.8)
а^ 'F{z,z) _ .fe-i у V(-nPc« С^ Y
X Z G=:T=rp)T^''-"-^(-4W/"-"-'-". C2.24)
Желая свести краевые условия C2.23) к совокупности краевых задач
Гильберта, введем новые аналитические функции, получаемые путем замены
в последнем выражении z на 1/z и умножения на г^-^ (последнее делается,
чтобы избежать полюса в начале координат).
Итак, положим
а-О Р-0
X S (р-;'-р)!^""''"°^^"'(^Ч(^))'""°"^-" C2.25)
р-а+Р
(Aj=1, 2, ..., л).
На контуре будем иметь
Q^n-k^yk-i - ^n-i ^ПО.

§ 35J] ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 309
Поэтому краевые условия C2.23) можно записать в виде
Получили п задач Гильберта для определения аналитических функций Фк(г).
Не останавливаясь на решении этих задач, допустим, что функции Фа (г)
уже определены. Покажем теперь, как по известным функциям Фк(г)
определить функции фрB), входящие в представление полианалитической
функции. При Э'^ом приходится пользоваться тремя фактами:
1. Производные от F по х, у легко выражаются через функции Фа (г).
2. Производные от F по z, z могут быть выражены через производные
по V, у.
3. Функции фрB) на основании интегрального представления
полианалитической функции выражаются через производные от f по z и ?
Имеем:
z
-{[Tte-'i)r[K^+'ir><-'U=
z
(n~k k-\ \
= 2"-' \L L^ ^>^ ^^n-k^k-X „_,_v-,, ,+v f
n-ft fe-I
z
Введем для краткости обозначение
л-1
G=.0 v-=0
p^k-X
,_1ТгКфр(^)Г -^^(^)-
Не останавливаясь на условиях разрешимости, возникающих в результате
требования, чтобы обе части последнего равенства имели одинаковый
порядок в начале координат, будем считать, что все эти условия выполнены.
Тогда, полагая в последнем равенстве последовательно ^ == п, п—1, ..., I,
определим все функции фр(г).
Полный подсчет числа линейно независимых решений возможен, но для
этого понадобились бы более подробные исследования. Укажем только, что
кроме произвольных постоянных, возникающих в результате решения задач
Гильберта с положительными индексами, возникают еще дополнительные
постоянные из-за того, что краевые условия содержат производные.

310 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
Задачи II и III могут быть решены аналогичными приемами. Отметим
лишь, что, так же как и в рассмотренных задачах I, IV, удается ввести такие
вспомогательные аналитические функции, что краевая задача для
полианалитических функций превращается в п краевых задач Гильберта относительно
этих функций. Затем функции фрB:), входящие в представление искомой
полианалитической функции, определяются через найденные вспомогательные
аналитические функции.
Если область D+ есть верхняя полуплоскость, то задача
решается совершенно так же, как в рассмотренном случае круга.
Различие будет лишь в том, что вместо использованного в п. 39.2
условия i = l/t здесь придется пользоваться условием ? = /.
Поэтому при построении вспомогательных функций вместо
замены г на 1/г здесь z нужно будет заменить просто на 2.
Относительно решения задач Гильберта для полуплоскости
см. задачи в конце главы.
32.4. Краевые задачи для областей, отображающихся на
круг рациональными функциями. Данное в предыдущем пункте
решение в захмкнутом виде краевых задач полианалитических
функций для круга переносится путем небольшого
видоизменения метода также и на области, отображаемые на круг при
помощи рациональных функций.
Этот факт хорошо известен для основных задач теории
упругости*), т. е. для краевых задач бигармонического уравнения
д2^ = О, и основан на том, что ядра интегральных уравнений,
к которым приводятся указанные задачи, оказываются
вырожденными. Пользуясь этим методом (приведение к
интегральному уравнению с вырожденным ядром), П. К. Зерагия 1) дал
решение в замкнутой форме краевой задачи
полигармонического уравнения (задача IV при aft = 1, 6^ = 0).
Пусть D — конечная или бесконечная область в плоскости
комплексного переменного 2, ограниченная простым достаточно
гладким замкнутым контуром L, и пусть рациональная функция
^ = (о(Й
конформно отображает круг |^| < I на область D. Обратную
ей функцию обозначим 1 = у(г). Тогда все формулированные
в п. 32.2 краевые задачи могут быть решены для области D
в замкнутой форме **).
Рассмотрим в качестве примера краевую задачу IV. На
основании C2.23), C2.24) краевое условие задачи на контуре L
*) См. [17], стр. 304.
**) Излагаемые далее результаты получены М. П. Ганиным.

§32] ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 311
может быть записано в виде
Re L, - lb,) /*-'!; CI., j;'(- \f CU X
^ a-O p-0
X E (p^'a-^W ^"'"'"^(^4@)^'"""^"^^ \ = cu{t). C2.26)
Подставляя в последнем равенстве /==:со(т), преобразуем
краевое условие, заданное на контуре L, в краевое условие,
заданное на окружности |т| = 1.
Введем п новых функций:
n—k k—\
а=>0 3=0
п-Х
X Z (, - : - р), ^°—^ (т) (^'Ф^ (^)Г.У""• C2-27)
р=а+3
Эти функции В Круге | ? I < 1 могут иметь особенности только
в тех точках, где имеет особенность функция ^ (т") • Выделим
эти особенности.
Пусть
со(?) =
a^g^ + a^,ig^~^ + ,.. +ао
РгГ +Рг-1Г"Ч ... +Ро
Тогда
Положим для определенности г > q и обозначим
f (S) = (роГ + Pi^"' + ... + Рг)'"'. C2.28)
Функции
f(S)Фdo)(?)]
будут аналитическими в единичном круге. Обозначим
ФИсо(^)] = Фи?).
Относительно новых функций краевое условие на единичной
окружности может быть записано в виде
^ f «ь [to (т)] — ib. [со (т)] г fc_i« 1 i)
Re{ ' ц,^ ' [i' 7(т)ф1 (т)]\ = с,[<,(т)] C2.29)
(^ = 0, 1,..., п-1),

312 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
после чего получим п краевых задач Гильберта для
определения аналитических в единичном круге функций /(^)Ф1(^).
Допустим, что мы решили все краевые задачи C2.29) и,
следовательно, определили все функции ФкЦ)- Тогда можно
считать известными и функции Ф^^(г) = Ф1 [yB)]. Остается
определить функции фрB:), входящие в представление
полианалитической функции. Это делается вполне аналогично тому, как это
делалось в предыдущем пункте при решении той же задачи для
круга. Поэтому, не останавливаясь на подробностях, приведем
лишь основное равенство, соответствующее равенствам 1), 2)
предыдущего пункта:
Е (р-;'-1),^''-^-(^''Фр(^)Iг.^;„ =
n-k k-l
Подставляя в последние равенства последовательно k = п,
п—1, ..., 1, определим все функции (pp(z).
На вопросах подсчета числа решений и условий
разрешимости мы не останавливаемся. Укажем только, что этот подсчет
можно произвести совершенно точно.
При a/i == 1, 6/^ = О получим решение рассмотренной П. К. 3 е-
рагия I) краевой задачи для полигармонических функций.
32.5. Решение основной задачи теории упругости для области,
ограниченной улиткой Паскаля. Рассмотрим в качестве примера основную краевую
задачу теории упругости для области Dj, ограниченной улиткой Паскаля L,
которая в параметрической форме задается следующими уравнениями:
х=: R (cos 6 + m COS 26), у = R (sin Q + msln 29)
{R>Q, 0<m<\/2, 0<е<2я).
Известно (см., например, [17], стр. 141), что основная задача теории
упругости сводится к отысканию бигармонической функции U{x,y) по двум
условиям на контуре L:
1^-^@. I^-AW. C2.30)
где g(t), h(t) —заданные действительные функции координат точек контура t,
удовлетворяющие условию Гёльдера.
Для бигармонической функции, исходя из общего представления
полигармонических функций C2.5), имеем
и (х, у) = Re [zzcp (z) + ф (г)], (82.3J)
где (f(z)^ г|)B)—произвольные аналитические функциц.

§ 32] ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 313
С помощью этого выражения на оаношаиия формул C2.2) краевые увлв-
вия можно записать в виде
Re {i [/ф (/)]' + г|)' (/) + /ф it)} = g (/), ^^^ ^^^
Re {/ [t (/ф @)' + Г (/) - /Ф @1} = h it).
Функция со (S), конформно отображающая область D^ на внутренность D^
единичной окружности Г комплексной плоскости g и удовлетворяющая
условиям со @) = О, со' @) > О, равна
г = со (?) = /? (? + т?2).
Обратная функция
S = Y(^) = -i+Vl^ + -^
Z
т
Ветвь корня определяется условием у (О)" О- ^^ единичной окружности Г
будем иметь
Rd + m)
? = (О (I) = /? (I + тр) ^ р
C2.33)
поэтому краевые условия запишутся так:
Re { ^^^^"^^ ф, (I) + ф, (I) + R(l + mV) ф [о (I)] } = ^ [0 AI
Re { i [-^^^^^^ ф, (I) + Ь (I) -/?(! + /^1^) Ф [со (I)]]} = /г [со (|)],
где
ф1 (S) = [гф W]z-(D(t)» ^» (^) "" *' (*)г«(д(С)-
Каждое из краевых условий C2.33) является условием задачи А для
единичного круга (при /г = 2), рассмотренной в п. 27.3. Применяя формулу
B7.9) и заменяя в ней оператор Шварца на интеграл Шварца (см. п. 6.1),
получим
^^'У ""'^ Ф1 (S) + *1 (S) + R(i+ mV) Ф [со (?)] =
^ C2.34)
= |._IS3 + |_5s+,a+i5.[co(|)]i±if,
г
/1 ^^? + ^) <р, (?) + ф, (S) - Л (S + /п$2) ф [(О (?)] } =
где Л, В, С, D "^ комплексные, а а и р ^ действительные произвольные
постоянные.

314 Краевая задача гильберга 1ГЛ. iv
Умножим второе равенство на i и сложим с первым. Так как функция
ф[(о(^)] аналитична в единичном круге, то коэффициенты при ?"^ и S"*
обратятся в нуль, и, заменив ? на y(z), придем к соотношениям
2гф (г) = - (А + iC) у^ (z) - (В + Ш) у (z) + /а - р +
Л + /С = О, В + Ю = 0. C2.36)
Полагая в C2.35) z = О и учитывая, что у@)= 0. дополнительно найдем, что
y'{t)
У it)
а + /Р = 2^ 5 [^ (О + /Л @1 ^Ш- dt. C2.37)
Для определения я|)(г) вставим в любое из уравнений C2.34) значения
ф[^(?)] и ф1(С), взятые из формулы C4.25) и равенства, полученного ее
дифференцированием.
Учитывая C2.36), будем иметь
+ ^v-wivw+^i p,,,,)^,_^.|,,,,,^.,,,,,__m_p,,-|.
C2.38)
Приравняем (в силу аналитичности функции ф' (z)) коэффициенты при
отрицательных степенях у (z) к нулю. Для этого заметим, что
оо
И
En {у
После несложных преобразований получим систему уравнений для отыска*
ния Л и J5:
A+mB=:-^\[g(t) + ih{t)\J^dt,
2я/ J
2mJ+B + (l~2m^M= ^ ^^^^' ^ [g(/) +//^@]-^lllL rf/+
L
C2.39)
+5Si««+"">i^'"-

§ 32] ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 315
Система C2.39) имеет решения лишь при условии
= Re I 2^ J [gf (О + ih @1 rf71 = 0. C2.40)
Ho последнее условие есть условие равенства нулю главного момента
внешних сил и должно необходимо выполняться из механических
соображений.
Полагая Л = aj +ia2, В = bi -h ib2 и преобразовывая систему C2.39),
получим три уравнения:
ai + m^, = Ref^5{^[0(g)] + //i[co(|)]}-|| j,
2та, + b, = -^^[gW (Ш + ih [со (|)]} [^ + |^] ^|, C2.41)
г
«2 - тб2 - Im I -^ 5 {g [со Ш + ih [(О (Ш) -||- I.
При решении системы C2 41) одну из величин, а^ или Ьг, можно взять
произвольно.
Подставляя в формулу C2.31) значения z(^{z) и i|)(e), полученные
интегрированием равенства C2.38), найдем искомую бигармоническую функцию
, zy(z) f U(t) + ih(t)]dt
¦^ 2nRi J Y@[l+2mY(/)l[Y@-
L
z
YB)l
I ' C^r^ [g(t)-ih(t)\4t
"*" 2я;?/ J ""^ J [1 + 2mY @1 [Y @ - Y (Т
I ^
+ 2R{A + тВ) Y (г) - ^ ^^y'J"^)"'^^ + 2^? Bma, + 6,) In у (г) -
1 f [Y(T) + m]rfT Г g«) + //i(<) fД I rr
2лШ J Y' (T) [1 + 2mY (т)] J [1 + 2mY @1 (Y @ - Y (т)]^ '^Ч + «•
о z, -*
Легко проверить, пользуясь равенствами C2.39) или C2.41), что функция
U(x,y) аналитична в начале координат.
Решение содержит одну произвольную постоянную К, что соответствует
тому факту, что величины, характеризующие напряженное состояние, зависят
от производных бигармонической функции U{x,y) и, следовательно,
наличие Л не оказывает влияния на напряженное состояние.

316 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 1ГЛ IV
Задача разрешима лишь при условии, что заданные функции g{t), h(t)
удовлетворяют условию C2.40). Заметим, что условие C2.40), имеющее ука.
занный выше механический смысл, вытекает также из математического
условия — отсутствия в начале координат логарифмической особенности.
32.6. Краевые задачи Римана*). Пусть контур L (п. 32.2)
делит плоскость на конечную область D+ и область, содержащую
бесконечно удаленную точку D~. Функции, полианалитические
в D± (кусочно полианалитическую функцию), можно
представить в виде
F"- (г, Z) = Z г^г>; iz) = Z г'Щг), C2.8')
F-(z, г) = ф„-B)+Е ^VP~V(^) = "^'2%-B), C2.8'0
р-1 "^ р=-0
где ф=*=B:), f^(z)—функции, аналитические соответственно в
областях D±, связанные соотношениями
А;(^) = С(г), %{z) = f;{z\ z-'^'cp;{z) = f;{z). C2.42)
Из последних вытекает, что порядок fp{z) в начале координат
не ниже р; порядок f^ (г), р^1, в бесконечно удаленной точке
не меньше /?-f 1, а /"(г)-— не меньше нуля.
Можно сформулировать четыре краевые задачи, находящиеся
к задачам п. 32.2 в таком же отношении, как решенная в §§ 14,
15 краевая задача Римана к исследованной в § 29 краевой
задаче Гильберта. Дадим точную формулировку задачи I.
Задача I. Найти кусочно полианалитическую порядка п
функцию F^{z,z), непрерывную по z вместе со своими npouQ-
водными —7—7- до (п — 1) -го порядка, ограниченную на бес-
конечности и удовлетворяющую на контуре L п краевым
условиям:
^'F^ а, t) = G, (t) AV- {t, t) + 4'g, (t) C2.43)
{k = 0, 1, ..., /г-1),
где Gk{t), gk{t) удовлетворяют условиям Гёльдера, О^ЩФО.
Множитель 4^^ введен для удобства дальнейших обозначений.
В целях достижения большей симметрии результатов задачу
будем решать в классе функций, исчезающих на бесконечности.
*) Материал настоящего пункта написан по работам И. А. Соколова
1)-4).

§ 32] ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ ГИЛЬБЕРТА И РИМАНА 317
Из формул C2.80, C2.8'0 дифференцированием (см.
формулу C2.18)) получим
^'FUz, z) = /Y,j^z''-'ff\z). C2.180
1^ Рассмотрим сначала более простой случай, когда контур
L есть окружность. Исходя из тех же соображений, что и в
п. 32.3, введем вспомогательные аналитические функции
Ф*(^)= Е -(^^*"%*'*'(^)- C9.190
Через них краевые условия C2.43) запишутся в виде
^t W = G,(t)ф;(t) + g^{t) (Aj = о, 1, ..., n- 1). C2.44)
Таким образом, краевая задача Римана (I) для
полианалитических функций свелась к совокупности п краевых задач Римаиа
для кусочно аналитических функций Of (г). Подсчитаем порядки
этих функций соответственно в нуле и бесконечности.
Функции fp{z) в силу C2.42) имеют в нуле порядки р,
fp {^) ¦— порядки р — k, а of (z) согласно C2.19) — нулевые
порядки. Функции fp (z) в силу C2.42) имеют порядки р + 1 + Л,
а Ok{z) по C2.190 —порядки 2fe+l- Следовательно, задачи
Римана C2.44) нужно решать в классе функций, обращающихся
в нуль порядков 2/г + 1 на бесконечности.
Пусть IndGft@=>«ft. Из теории краевой задачи Римана
(п. 15.3) следует, что решение задачи с заданным нулем
{2k + l)-T0 порядка равносильно решению задачи с простым
нулем и индексом, уменьшенным на 2k.
Назовем Xfe=x/i — 2k приведенным индексом
соответствующей задачи Римана. Если кк > О, то соответствующая
однородная краевая задача имеет й^ линейно независимых решений;
если Xft :^ О, то решение однородной задачи есть тождественный
нуль. Обозначим й+ сумму положительных приведенных
индексов. Тогда общее число линейно независимых решений всей
совокупности краевых задач Римана C2.44) равно й+. При этом
все решения могут быть выписаны явно по формулам § 14.
По найденным Ф^ функции /^, а отсюда и ф^ могут быть
определены с помощью интегрирования, вполне аналогично тому,
как это делалось в п. 32.3. При этом никаких дополнительных
произвольных постоянных не появляется. Таким образом, может
быть сформулирована

318 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
Теорема I. Однородная краевая задача C2.43) для поли-
аналитических функций, исчезающих на бесконечности, имеетк+
линейно независимых решений, гдек^ — сумма всех
положительных приведенных индексов. Все решения выражаются в явном
виде через коэффициенты Gk{t) по формулам § 14.
Рассмотрим теперь неоднородную задачу. Ее исследование
производится на основе результатов § 15. Отличие от
предыдущего будет в том, что при й/t < О потребуется удовлетворить
—х/1 условиям разрешимости. При этом произвольные
постоянные, возникающие при решении задач с положительными
приведенными индексами, в силу независимости краевых задач не
могут быть использованы для удовлетворения условий
разрешимости. Не останавливаясь на подробностях, сформулируем
результат. Пусть х+ —сумма положительных приведенных индексов и
й- — сумма абсолютных величин отрицательных приведенных
индексов. Справедлива
Теорема П. При выполнении й- условий разрешимости
неоднородная краевая задача C2.43) имеет решение, исчезающее
на бесконечности, зависящее линейно от й+ произвольных
постоянных. Условия разрешимости и сами решения могут быть
выражены в квадратурах через коэффициенты Gk{t), gk{t)
краевых условий.
Способом, близким к использованному выше, на основе
результатов § 17 может быть решена задача со сдвигом
AV+ [а it), Щ] = G, (О F- [t, t) + g it). C2.45)
В качественном отношении результаты вполне аналогичны
сформулированным выше.
2^ Рассмотрим схематически задачу на произвольном контуре. Отметим
сразу же существенное отличие этого случая от только что рассмотренного
случая окружности. Там, опираясь на свойство t = 1//, удалось построить
такие комбинации искомых функций Фа (г), что краевая задача для
полианалитической функции распалась на п независимых краевых задач Римана
для аналитических функций. Для каждой из них самостоятельно велся
подсчет линейно независимых решений или условий разрешимости. В силу этого
оба эти числа точно выразились через индексы заданных коэффициентов Gk
и свободные члены gk-
В случае произвольного контура удается свести задачу
полианалитическую к п последовательным краевым задачам Римана, каждая из которых
содержит лишь одну пару искомых функций, последовательно/^_1, .. .,/о^.
Но лишь одна из них (относительно /^_i) независима от других; у
остальных же в свободные члены входят решения задач с предыдущими номерами.
Из-за этого точные результаты можно получить лишь в случаях
приведенных индексов одного знака; при всех неотрицательных приведенных индексах
число линейно независимых решений равно их сумме, при всех
неположительных число условий разрешимости равно сумме их абсолютных величин.
При наличии приведенных индексов разного знака условия разрешимости,
соответствующие отрицательным приведенным индексам, дают системы линей-

§ 33J ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕСКИХ ФУНКЦИЙ 3l9
ных алгебраических уравнений относительно параметров, возникающих в
задачах с положительными приведенными индексами. В этих случаях число
решений и условий разрешимости зависит не только от приведенных индексов,
но и от ранга некоторых матриц. При этом на примерах удается показать,
что последняя зависимость существенна и при одних и тех же индексах
ранги, а следовательно, и число решений или условий разрешимости задач могут
оказаться различными.
Но точно так же, как и в случае окружности, при произвольном контуре
решения и условия разрешимости могут быть выражены в квадратурах через
данные задачи.
3°. Исследована также краевая задача типа II на окружности.
Определить кусочно полианалитическую функцию F^B, г) по краевым условиям
A*F+«, F) = Ofc«)A*f-«, F) + g^@ (* = 0, I,.... т, '« = [-^^]).
C2.46)
Исследование здесь значительно сложнее, чем в задаче 1. Даже в случае
окружности совершенно точных результатов получить не удается. Изложим
схематически основные результаты.
Удается построить такую систему п вспомогательных кусочно
аналитических функций Ф^^ (г), Ф^ (г), довольно сложно выражающихся через искомые
функции /а(г), что краевая задача C2.46) распадается на п раздельных
краевых задач Римана. Таким образом, для вспомогательных аналитических
функций оказывается возможным точно подсчитать число линейно
независимых решений и условий разрешимости и представить решения в
квадратурах.
Отыскание искомых функций /^ (г) по известным Ф^^, Ф^ сводится к
решению системы линейных дифференциальных уравнений. Ее тоже удается
решить в квадратурах. Но оказывается, что найденные функции /^ {z) должны
иметь нули некоторого определенного порядка на бесконечности. Это в общем
случае приводит к решению систем линейных алгебраических уравнений
относительно входящих в решение параметров. В силу этого, аналогично тому, что
выше говорилось относительно задачи I для произвольного контура, точные
результаты удается получить лишь в случаях всех неотрицательных и
положительных приведенных индексов. Если индексы разных знаков, число
решений и условий разрешимости выражается через ранг некоторой матрицы.
Укажем, что исследование задачи II связано с весьма громоздкими
выкладками. Остальные две краевые задачи (III, IV) до настоящего времени не
исследованы.
§ 33. Обратная краевая задача аналитических функций
Под обратными краевыми задачами понимаются задачи
отыскания контура области по некоторым величинам, заданным на
нем. Обычная постановка таких задач заключается в том, что
в искомой области ищется функция, принадлежащая заданному
классу (аналитическая или являющаяся решением какого-либо
заданного уравнения), причем на контуре независимых условий
задается на единицу больше, чем их требуется для решения
обычной (при заданной области) для данного класса функций

320 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ. IV
краевой задачи. Излишнее краевое условие используется для
отыскания контура области. Имеется значительное число
различных постановок обратных краевых задач. Здесь мы
рассматриваем задачу аналитических функций, которая грубо может
быть формулирована как задача отыскания контура
по заданным на нем краевым значениям
аналитической функции.
33.1. Постановка задачи. Даны две функции параметра
S (О < 5 < О:
u==u{s), v=^v{s), C3.1)
периодические с периодом /, имеющие первые производные,
удовлетворяющие условию Гёльдера, не обращающиеся
одновременно в нуль и удовлетворяющие условию: при двух значениях
параметра Si Ф S2
Уравнения C3.1) определяют в плоскости комплексного
переменного W Bszu + iv простую замкнутую кривую Ляпунова,
делящую плоскость на области: внутреннюю D^ и внешнюю Dw*
«Внутренняя» задача. Определить в плоскости z
кривую Lz, ограничиваюи^ую конечную область Dt {eoo6uie говоря,
многолистную) так, чтобы, считая параметр s длиной дуги
кривой Lz, выражение w{s) = u{s) -^ iv{s) было краевым
значением аналитической функции, конформно отображающей
область Dt на область Dw или Dw-
«Внешняя» задача. Определить в плоскости z кривую Lz,
ограничивающую область Dz {содержащую бесконечно
удаленную точку и, вообще говоря, многосвязную) так, чтобы, считая
параметр s длиной дуги кривой Lz, выражение w{s) =«(s) +
•\-iv{s) было краевым значением аналитической функции,
конформно отображающей область Dz на область Dw или DZ*
Если бы мы имели дело с обычной краевой задачей (при
заданном контуре), то для определения аналитической в области
функции (с точностью до постоянного слагаемого) достаточно
было бы задать лишь одну из функций {u{s) или v{s)).
Задание второй функции позволяет определить неизвестный
контур Lz.
Комбинируя области Dz, Dw9 можно получить всего четыре
задачи. Но легко видеть, что существенно различными являются
лишь те, которые отличаются знаками областей Dz, так как
область Dw можно предварительно конформно отобразить на
некоторую область типа D+. Для определенности будем считать,
что с самого начала задана область Dw» В дальнейшем символ +

§ 331 ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕСКИХ ФУНКЦИЙ 321
У области Dw будем опускать и обозначать ее просто Dw. В
плоскости г, где контур Lz является искомым, нельзя внешнюю
область свести к внутренней и задачи, отличающиеся знаками
области Dz, приходится решать каждую самостоятельно.
Будем считать, что положительные направления контуров
данного Lyj и искомого Lz выбраны так, чтобы при их обходе
области Di, Dw оставались слева. Тогда на основании свойств
конформного отображения получим как необходимое условие
разрешимости требование, чтобы при возрастании s от О до /
для внутренней задачи контур Lw обходился в положительном
направлении, а для внешней — в отрицательном. В дальнейшем
будем считать, что эти условия выполнены.
33.2. Решение внутренней задачи. Будем исходить из хорошо
известного свойства конформных отображений, что отношение
длин линейных элементов, соответствуюид^их друг другу при
отображении, равно модулю производной отображающей функции.
Длина элемента дуги контура Lz уже задана, это дифференциал
параметра ds. Из уравнений C3.1) по формулам
дифференциальной геометрии легко определяется длина элемента
кривой Lyj
do = ^Ju'\s) + v'\s) ds.
Отсюда
dw
dz
= ^ = ^u'\s)+v'\s).
Таким образом, нам известен модуль производной функции
w=:w(z), конформно отображающей область Dt на Dw, как
функция дуги 5. Поскольку контур Lz неизвестен, полученная
формула еще не может служить источником решения задачи.
Для получения такой формулы перейдем к обратной функции
z = z{w) и будем рассматривать в качестве носителя данных
заданный контур Lw.
S
Равенство а=\уи' + у' ds определит а как монотонно
о
возрастающую функцию от s. Путем обращения последней
получим S = s{g). Тогда будем иметь
"'^ \^z -^ C3 2)
^^1 ^/u^'ls(cJ)] + v^Us{a)]'
Следовательно, на контуре Lw известен модуль производной
dz
-^ функции, конформно отображающей область Dw на
область Dt-

322 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА ГГЛ IV
Таким образом, пришли к следующей задаче, которую
назовем фундаментальной в теории обратных краевых
задач.
Определить функцию, аналитическую в области Dyj и не об-
ращающуюся там в нуль*), по заданным на контуре
значениям ее модуля.
Эту задачу легко свести к задаче Шварца. Логарифм
модуля функции, аналитической и не обращающейся в области
в нуль, есть функция гармоническая, являющаяся
действительной частью логарифма самой аналитической функции.
Следовательно,
'" ?- = ~ У ^'" ^"'' ^' (^)] + ^'' 1^ <^^]^ + ^'«' C3.3)
где 5 — оператор Шварца для области D^;, а — произвольная
действительная постоянная.
Потенцируя, а затем интегрируя, получим саму функцию
z{w). Таким образом можно получить законченное решение
задачи. Однако на практике удобнее иметь дело с такой
областью, для которой известно явное выражение оператора
Шварца, поэтому предварительно от области Dyj переходят
к некоторой стандартной области. Изложим подробно этот путь
решения, выбрав в качестве стандартной области единичный
круг.
Пусть w = w{t,) есть аналитическая функция, конформно
отображающая единичный круг у плоскости t, на область 0^»
Переходя на контур, будем иметь равенство
и (s) + iv [s) = w {e^^).
В силу взаимно однозначного соответствия между точками
контуров 1г/, и Y из последнсго равенства можно определить s
как однозначную функцию полярного угла 0
5 = (о(в). C3.4)
Теперь можно оставить плоскость w и решать обратную
краевую задачу, рассматривая соответствие между плоскостью
Z и вспомогательной плоскостью ^. Учитывая, что полярный
угол численно равен длине дуги единичного круга, на
основании уже использованного свойства конформных отображений
будем иметь
^ dz\_ds _ , .д
dz
Беря от обеих сторон логарифм, для функции 1п-^ снова
приходим к задаче Шварца. Последняя разрешается теперь
*) Последнее вытекает из требования конформности отображения.

§ 33) ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕГКИХ ФУНКТТИЙ 323
интегралом Шварца
ас, 2я J е — g
Потенцируя, получим
откуда
z = f@ = e'^\e^^^4l + C, C3.5)
где С — произвольная комплексная постоянная.
Вставляя в выражение для функции f{t) значения
аргумента ^ = е^^, получим параметрическое уравнение искомого
контура в комплексной форме
Как показывает формула C3.5), искомая область Dt
определяется с точностью до движения (параметр а определяет
поворот, а С—параллельный перенос). Произвол,
заключающийся в возможности движения, является естественным и
вытекает из постановки задачи. Поэтому решения, отличающиеся
лишь положением области, будем считать одним решением.
Для установления того, что движение есть единственный
произвол, допускаемый решением задачи, необходимо сначала
условиться о том, как понимать, что два различных искомых
контура носят на себе одинаковые данные. Примем как
определение следующее:
Считаем, что два контура Lz и L^, носят на себе
одинаковые данные w{s), W\(s\), если при конформном отображении
областей, ограниченных этими контурами, для точек,
соответствующих друг другу при отображении, значения заданных
функций и их производных равны, т. е.
W [s) = Wx E,), w' (s) = W\ {S\).
Допустим теперь, что два контура Lz и L^ являются
решением обратной задачи и пусть Z\ = Zi{z) есть функция,
осуществляющая конформное отображение областей, ограниченных
этими контурами.
Дифференцируя первое равенство по 5, имеем w^{s) =
ds
= w\{s\)'-j^. Отсюда, принимая во внимание равенство произ
водных, будем иметь
dz
_ dsx _ .
^ ds ~^

324 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА ГГЛ IV
И, далее,
In
dZ]
dz
= 0, ln-^=/a, 2, =^'«г + С.
Следовательно, контур Lz может быть получен из L?
движением, что и требовалось.
33.3. Другие способы задания. В рассмотренной задаче
краевые значения аналитической функции задавались как функции
длины дуги искомого контура. Этим определялся способ
решения (отыскание логарифма модуля производной). Если в
качестве параметра, связывающего заданные краевые значения
и, V с искомым контуром, взять другие геометрические
величины, например абсциссу или ординату искомого контура, его
радиус-вектор, полярный угол и т. п., то способы решения
будут изменяться. За исходную функцию придется брать уже не
логарифм производной, а аналитическую функцию, теснее всего
связанную с выбранным параметром.
Пусть, например, параметр есть абсцисса х,
и = и {х), v = v {х).
Производя отображение Dyj на круг |?|< 1 и рассуждая, как
и выше, определим абсциссу как функцию полярного угла 6
X = x{Q), Учитывая, что л: = Rez, получим
Контур Lz здесь определяется с точностью до сдвига по мнимой
оси. Аналогично решается задача, если параметр есть
ордината у. Если параметр есть радиус-вектор р или полярный
угол 9, то в качестве исходной функции нужно будет взять In 2.
Мы здесь не останавливаемся на вопросе о преод)лении
трудностей, связанных с возможной неоднозначностью
представления и, V через указанные параметры*).
33.4. Решение внешней задачи. В этом случае некоторая
точка области D^ должна перейти в бесконечно удааенную,
следовательно, отображающая функция z{w) должна в области
Dw иметь полюс. В силу требования конформности
отображения этот полюс должен быть простым. Таким образом, в
отличие от предыдущего, здесь нужно искать функцию,
аналитическую в Dw, за исключением одной точки**), где она имеет
простой полюс. Так же как и в предыдущем, будем считать, что
*) См. М. Т. Нужин 1).
**) при этом дополнительно предполагаем, что область D~ в окрестности
бесконечно удаленней точки однолистна.

^ -^31 ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕСКИХ ФУНК1ПТП 325
произведено отображение области D^, на единичный круг
вспомогательной плоскости I и вычислили S как функцию
полярного угла 9
5 = @(9).
Пусть F(l) — функция, производящая конформное
отображение круга I!; I < 1 на D7, и ^о — точка, переходящая в
бесконечно удаленную. Тогда
Функция F^{t) будет иметь в точке go полюс второго
порядка. Сведем отыскание F'{t) к уже рассмотренному ранее
случаю аналитической функции, используя хорошо известный
в теории функций комплексного переменного прием устранения
нулей и полюсов.
Функция -^—^ при произвольном go производит отобра-
жение круга самого на себя, поэтому на контуре круга модуль
ее равен единице.
Следовательно,
\2
*®-(TffrP'<"
будет аналитической в единичном круге и иметь на контуре
круга тот же модуль, что и F^{t). Отсюда, употребляя те же
обозначения и используя те же рассуждения, что и в п. 33.3,
будем иметь
Ф (g) = е^аех (?), z = F{0 = е'^ \ {^JIT^^^ ^^^ ^i + С. C3.6)
Последняя формула определяет функцию, которая в точке
go, кроме простого полюса, имеет, вообще говоря, еще
логарифмическую особенность. Полученная функция будет являться
решением поставленной задачи лишь в том случае, если такая
особенность отсутствует. Для этого необходимо и достаточно,
о _ ° J ф(С) относительно точки go
был равен нулю. Вычислим этот вычет.
Беря разложения в окрестности точки go функций
(l~gog)^ = (lgol^~I)^ + 2go(|gol^-l)(g-go) + go(g-go)^
ф(g) = ф(go) + фЧgo)(g-go)+ ...
и перемножая их, получим, что искомый вычет, равный
коэффициенту при первой степени (g — go) этого произведения,
будет выражаться так:
С-1 = A go I'- 1) |2goФ (go) + (I go 1'~ l)Ф^go)].

326 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ IV
Приравнивая этот коэффициент нулю, найдем, что для
разрешимости внешней задачи комплексная координата полюса ^о
должна удовлетворять уравнению
ф' (Со) __ 2Ёо
C3.7)
Ф (So) 1 - I So |2 •
Разрешимость внешней задачи будет доказана, если будет
установлена разрешимость последнего уравнения. Приступим
к этому доказательству. Рассуждения, используемые для этой
цели, имеют несколько искусственный характер. Укажем для
ориентировки читателя, что первая половина выкладок близка
к тем, которые употребляются в теории однолистных
аналитических функций при доказательстве так называемых теорем
искажения.
Обозначим |5о| = г. Умножив обе части равенства C3.7)
на ^0 и воспользовавшись тождеством*) ''"^ = ^0-^,
придадим исследуемому уравнению форму
а In ф _ 2г'^
^ дг ~" I - г2
или
Цель дальнейших рассуждений заключается в том, чтобы
привести исследуемое комплексное уравнение к системе двух
действительных уравнений, являющихся условиями экстремума
некоторой действительной функции.
Воспользовавшись одним из условий Коши — Римана в
полярных координатах "л^^^УЖ ^ приняв во внимание, что
|,1пA-г^) = ^. ^1пA-г^) = 0.
приведем исследуемое уравнение к виду
|г1п[A-г2)|ф|]-/-1^1п[A-г2)|ф|] = 0;
последнее равносильно системе двух действительных уравнений:
^1п[A-г2)|ф|] = 0, ^1п[A-г2Iф|]=0, C3.8)
представляющей необходимое условие экстремума поверхности
/ = ф(г,9)==1п[A-г2)|ф(г,в)|].
*) Исходим ИЗ t,o = ге и учитываем, что при переходе от
дифференцирования по г к дифференцированию по ^о аргумент 6 нужно считать
постоянным.

§ 33] ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АН^\ЛИТИЧЕСКИХ ФУНКЦИЙ 327
Таким образом, чтобы доказать разрешимость уравнения
C5.7), достаточно установить, что функция Ф(г, 9) достигает
экстремума внутри единичного круга. Это сделать нетрудно.
В самом деле, так как u^{s), v^{s) по условию принадлежат
к классу Я, то легко заключить, что и a)^(s), а следовательно,
и ln(o'(s) также удовлетворяют условию Гёльдера. Отсюда
в силу свойств интеграла Шварца граничные значения ф(^)
будут также удовлетворять условию Я и, следовательно, будут
ограниченными. Отсюда
ИтA-г2)|ф| = 0, Ит1п[A-г2)|ф|] = -оо.
На окружности радиуса г = 1 — е при достаточно малом е
Ф(г, 6) будет принимать сколь угодно большие по абсолютной
величине отрицательные значения. Так как внутри круга
Ф(г, 6) ограничена, то ее верхняя грань, которая в замкнутом
круге достигается, не может быть достигнута на контуре.
Следовательно, эта верхняя грань, являющ^аяся максимумом
функции, достигается внутри круга. Отсюда следует, что уравнения
C3.8), а следовательно, и исходное уравнение C3.7)
удовлетворяются, что и требовалось доказать.
33.5. О числе решений внешней задачи. Если ^о — корень
уравнения C3.7)—есть определенное число, то, как
показывает формула C3,6), внешняя задача допускает тот же
произвол в виде движения, что задача внутренняя, т. е. согласно
принятому условию будет иметь единственное решение.
Следовательно, вопрос о числе решений внешней задачи сводится
к исследованию количества решений уравнения C3.7).
Последнее является, вообще говоря, трансцендентным, и полное
исследование его в общем случае провести не удается. Однако
установлен фундаментальный факт, что его решение может быть
не единственным. Это показано В. С. Р о г о ж и н ы м 4) путем
построения следующего примера.
Пусть область Dw есть единичный круг, заданный
уравнениями
t/ = cose, t; = sin9, 6 = 6E), 0<5</, 0<6EХ2я,
причем функция 6(s) задается дифференциальным уравнением
sin 29
¦W = ' ' ' 0<а<1.
Здесь область Ого сама является стандартной, так что можно
сразу решать задачу для нее, не прибегая к вспомогательному
отображению.

328 КРАЕВАЯ ЗАДАЧА ГИЛЬБРРТА [ГЛ IV
Пусть z = F{w) есть функция, производящая конформное
отображение круга Dw на область DJ. Тогда будем иметь
, ^ __ sin 20
\F'{w)\ = \
Отсюда
1п|ф(ш) | = 1п Г-
1 dz
\ dw
W —
h
Wq
WqW
ds
"dd"'
.)V.
= e
(Ш)
sin 26
Правая сторона есть краевое значение действительной части
функции / —. Следовательно,
iw*
Отсюда по формуле C3.6)
z = F{w) = е'^ \ ( ^J^'Jl ) е~ dw + С. C3.60
Прообраз бесконечно удаленной точки Wq определится из
уравнения C3.7), которое примет вид
. Wq_ Wq
Полагая 1<Уо = ге*^, придем к системе двух уравнений:
r(I-r2)cos2p = 0,
r[(l~r2)sin2p + a] = 0.
Последняя удовлетворяется тремя значениями W(^, лежащими
внутри круга:
il^ jLi
ауо = 0, WQ = ^J\'-ae ^ , wl* = '-^J\—ae ^
Л i
(корни ¦±.^/\-\-ae^ отбрасываем).
Подставляя эти значения Wq в формулу C3.6), получим три
решения задачи, которые обозначим соответственно f, f*, f**.
Теперь остается установить, что эти решения существенно
различны. Уже упоминалось, что контуры, отличающиеся лишь
положением в плоскости, соответствуют одному решению
обратной краевой задачи. Кроме того, очевидно, конформное
преобразование круга |ш|<;1 самого в себя также не меняет
решения.
Докажем, что f, F* не могут удовлетворять тождеству
ги=..эу.(^) + с.

§331 ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АН А ППТИЧГГКИХ ФУНКЦИЙ 329
Дифференцируя последнее и учитывая C3.6') и то, что Wo = О,
получим
^а \\-bwJ _
A -bwY
ИЛИ
\ 1 — Шпгг; / \ч ш —6 / A —
2 •
A -bw)
Так как слева стоит трансцендентная функция, а справа —
рациональная, то ни при каком выборе b (|&|< 1) для
фиксированного а @<;«<I) последнее тождество не может
выполняться. Аналогично можно доказать существенное отличие от
двух рассмотренных третьего решения. Таким образом, в
рассмотренном примере внешняя обратная краевая задача имеет
три существенно различных решения. Следовательно, решение
этой задачи может оказаться не единственным.
33.6. О задаче Шварца с логарифмической особенностью на
контуре. При решении задачи Шварца предполагалось, что
заданная на контуре действительная часть удовлетворяет
условию Гёльдера. В дальнейшем встретится случай, когда у нее
могут оказаться особенности логарифмического характера.
Начнем с исследования частного случая. Рассмотрим краевое
значение аналитической в единичном круге |^|< 1 функции
ф(^) = 1п(^-^о) = 1п(С-^^*Ч
Будем иметь
= ln[/^'^.2sin-^]-ln|2sin^^
+ /Y.
где
^±Ц±^ при e>0o,
^ + ^° + '^ при eoo.
Отсюда следует, что решением задачи Шварца в классе
функций, имеющих логарифмические особенности на контуре,
когда краевое значение действительной части есть w(9) =

330
КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА
[ГЛ IV
= 1П
2 sin
е-00
, является функция
Ф@ = 1п(?-?о) + т.
Установление единственности полученного решения в
рассматриваемом классе сводится к доказательству отсутствия
решений, отличных от мнимой постоянной, у следующей
однородной задачи:
Определить аналитическую в единичном круге функцию
{возможны логарифмические особенности на контуре),
действительная часть которой на контуре равна нулю.
Искомая функция отображает единичную окружность в
мнимую ось. Следовательно, здесь применим принцип симметрии.
Продолжив по симметрии искомую функцию во внешность
круга, получим функцию, аналитическую во всей плоскости,
кроме отдельных изолированных точек, где возможны
логарифмические особенности. В силу требования однозначности
функции у нее необходимо должны быть разрезы, соединяющие
предполагаемые логарифмические точки ветвления. Но в силу
аналитичности (а следовательно, и непрерывности) разрезы
невозможны, поэтому предполагаемые особенности являются
устранимыми. Функция аналитична во всей плоскости; в силу
теоремы Лиувилля она есть постоянная, которая, очевидно,
будет чисто мнимой. Этим единственность установлена*).
Если действительная часть искомой функции задана в виде
суммы
t^(e)-ln|2sin^^| + t/o(9),
где Uq{Q) — функция, удовлетворяющая условию Гёльдера, то,
вычитая из искомой функции интеграл Шварца с плотностью
«о(9), придем к рассмотренному случаю.
Учитывая, что функция
е~0о
1-ео
In
2 sin
- In I е - Во
In
2 sin
е-бо
*) Это рассуждение останется справедливым и в том случае, если вместо
логарифмических особенностей считать допустимыми степенные особенности
порядка, меньшего единицы, а также произведение степени порядка,
меньшего единицы, на логарифм. Но дальнейшее обобщение невозможно Если
допустить на контуре полярные особенности, то существуют функции,
отличные от нуля, действительная часть которых на контуре обращается в нуль.
2
Примером этого может служить функция! , аналитическая внутри
окружности, заданной уравнением х^ + у'^ — 2х = 0.

« 33] ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕСКИХ ФУНКЦИЙ 331
В окрестности точки e^^o аналитична и, следовательно,
удовлетворяет условию Гёльдера, получим, что если краевое значение
действительной части искомой аналитической функции
представлено в виде суммы 1п|9 — 6о| + ^о(В), то решение
запишется в виде*) In ll — ^о) + Фо@, где фо ограничена в go-
33.7. Особые точки контура. Условия, наложенные на
задаваемые функции u{s), v{s): 1) принадлежность w'(s), v'(s)
классу Гёльдера; 2) отсутствие у них общих нулей обеспечивают
гладкость искомого контура Lz (более точно, принадлежность
его классу кривых Ляпунова). Несоблюдение какого-либо из
этих условий повлечет за собой нарушение гладкости, т. е.
контур Lzy вообще говоря, будет иметь особенности. Исследуем их
характер, предполагая нарушенным второе условие. Будем
предполагать, что заданные функции в окрестности исследуемой
точки разлагаются по формуле Тейлора.
Пусть Uj V заданы следующими разложениями:
u = {s — 8оУ [uo + E — So) а {s)l
с; = E — So)'' [Vo + E — So) b (S)],
C3.9)
где uoy Vo — постоянные, не обращающиеся одновременно
в нуль, a{s), b{s) имеют производные, удовлетворяющие
условию Гёльдера.
Из дифференциальной геометрии известно, что если р —
нечетное, то начало координат (s = So) есть обыкновенная точка
контура Lw] если же р — четное, то будем иметь точку
возврата. В последнем случае приходится различать две
возможности, когда угол равен нулю или 2я. Рассмотрим схематически
все случаи.
1. Обыкновенная точка контура Ly,, Пусть функция
w = w{t,) конформно отображает круг |^|<1 на область Ь^,
причем значению So соответствует значение угла Эо(^о == ^^^0-
В окрестности go отображающая функция имеет вид
W (?) = (С - Zo) W, (О, W, (Со) Ф 0. C3.10)
Из соотношения на контуре | м (s) + iv (s) | == | ш {е^^) |, учитывая
C3.9) и C3.10), получим
|5-5оГфE)=|е~ео|г|)(е), ф(so)>o, ^{%)>q
или, извлекая корень,
р ±_ Р
|5-5о1л/фE)=|в-ео1'' V^(9).
*) Используя конформное отображение, можно перенести результат на
случай любого замкнутого контура.

332 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ IV
Применяя теорию неявных функций, можно получить
следующее соотношение:
^=ie-eoii(e), Ф,(во)>о.
где 1|3|F) удовлетворяет условию Гёльдера. Отсюда
In
dz
='^n^ = [-^-l)\n\Q-%\ + ylpAQ).
Согласно результатам п. 33.6 будем иметь
'"if ^(^""О'^^^-^^^^ + ^^^^-
Отсюда
Из последнего выражения и свойств конформного отображения
вытекает, что контур Lz при 6 = Эо имеет угловую точку с
углом, равным nip,
2. Точка возврата с углом 2я. Функция,
отображающая единичный круг на область Dw, в окрестности ^о имеет вид
ш=соа) = (^-Ы^оI@ (а),(^о)?=0). Отсюда
а>(^^в) = (е-еоJг|)(е), (г|)(ео)^0).
Операциями, аналогичными примененным в предыдущем
случае, получим
ii = ie-eoi'^"'/(8) (/(ео)>о).
Из последнего следует, что исследуемая точка контура Lz есть
угловая точка с углом 2л/р. Если, в частности, р = 2, то
угловая точка превращается в обыкновенную.
3. Точка возврата с нулевым углом.
Отображающая функция имеет вид
соа) =
1п(?-?о) + ^о + ф(|) •
Не приводя исследования, которое здесь значительно сложнее,
чем в двух рассмотренных случаях, укажем, что искомый
контур Lz в исследуемой точке имеет точку возврата. Подробности
читатель может найти в работе Ф. Д. Г ахов а и И. М.
Мельника 1). Там же исследованы случаи, когда заданная
функция имеет некоторые особенности элементарного характера.

§ 331 ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕСКИХ ФУНКЦИЙ 333
Пример.
и = u(s) = а cos S A + cos s),
• iT 0<5<2я.
V = t; (s) = a sin s A + cos s),
Контур L^ есть кардиоида.
Имеем и' (п) = v' (л) = 0. Разложение в окрестности 5 = я имеет вид
и (S) = (S - яJ [- -J + а (S)], с; (s) = (s - я)^ р (s).
Здесь р = 2. Начало координат (s = я) есть точка возврата с углом 2я *).
Искомый контур Lz будет иметь здесь угловую точку с углом — =
= -^г- ^ я, т. е. обыкновенную точку.
Искомый контур Lz может быть найден элементарными рассуждениями.
Функция о; = ш (S) = — (^ + 1J отображает единичный круг на внутренность
кардиоиды. На границе будем иметь
u{s)-
Отсюда получим
и is) + iv (s) = w {e'% ae'' A + coss) = y (e^® + l)^
s = e,
dz
ds . , dz ia
г = г(г) = е'«? + С.
Последнее преобразование есть движение. Следовательно, контур Lz также
есть единичная окружность.
33.8. Об однолистности решения. Наложенное в постановке
задачи требование конформности отображения области Dz на
Dto исключает нули производной отображающей функции и,
следовательно, исключает точки ветвления. Но оно не влечет
за собою однолистности отображения. По условию, контур Lw
простой и область 0^ однолистная, но функция z{w),
получаемая в результате решения обратной краевой задачи, может
оказаться неоднолистной; в последнем случае контур Lz будет
не простым, а самопересекающимся.
Поясним это на примере. В его основу будет положено
известное отображение, осуществляемое показательной функцией
z = е"^.
Пусть в плоскости W задан круг
u = acosQ, v = asmQ,
где 9 = 9(s) задается уравнением
^_l^-acose (е@) = 0).
*) Последнее можно было бы установить путем анализа разложения
u(s), v(s) в окрестности 5 = я (Ф. Д. Гахов и И. М. Мельник 1)).

334 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ IV
Имеем
In
I dz
I dw
dz
dw
ds 1 ds ^^^cA
г = />fl COS о
do a dQ ^
= acos0 = Rew.
Отсюда
'""ёг = ^ + ^*«' -ёг=^'"^''» 2=^^V- + C.
Расположим в плоскости z оси координат так, чтобы а = О,
С = 0. Тогда функция, отображающая Dw на Ь^, примет вид
Z = е"^. Положив в последнем w = а cos 6 + ia sin 0, получим
параметрическое уравнение искомого контура L^ в декартовых
координатах
л: = в« cos е cos [а sin 9), у = е'^ ^^^ ^ sin (а sin 9), О < 9 < 2я.
Параметрическое уравнение той же кривой в полярных
координатах может быть записано в виде
р _ ^а cos е^ Ф = а sin 9.
Построение контура легче производить по последнему
уравнению. Вид кривой Lz будет существенно зависеть от величины
а — радиуса, задаваемого в плоскости w круга. Если а < я, то
функция 2 = е^ отображает круг однолистно и контур Lz будет
простым; при а > я отображение хмноголистно и Lz будет
иметь самопересечение; в пограничном случае а = п контур
Lz имеет точку соприкосновения*). На рис. 14 изображен кон-
3 3
тур Lz для трех случаев радиуса а=-т-я, я, уя. Читателю
рекомендуется произвести это построение.
Во всех известных приложениях обратных краевых задач
требуются контуры без самопересечения. В связи с этим
возникает важная задача: указать признаки однолистности
отображения, по возможности более просто выражающиеся через
заданные функции u{s), v{s). Решение этой задачи опирается
на теорию однолистности конформного отображения, лежащую
в стороне от интересов данной книги, поэтому мы не входим
в подробности этого важного вопроса. Приведем лишь
некоторые результаты.
*) Этот результат можно вывести из хорошо известных геометрических
свойств функции е^. Она однолистно отображает полосу —я < Im ш < я
на плоскость с разрезом по отрицательной действительной полуоси. Если
область Dw целиком лежит внутри указанной полосы, отображение однолистно
и контур Lz простой, в противном случае отображение многолистное и L,
имеет самопересечения.

331
ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕСКИХ ФУНКЦИЙ
335
Имеющиеся в настоящее время признаки однолистности
решения обратных краевых задач относятся не к
первоначально заданным функциям u{s), v{s), а к «приведенной»
dz
функции Р(9) = 1п-^. В предположении, что последняя
удовлетворяет условию Липшица |P(9i)—P{Q2)\< N\Qi —
62I,указываются допустимые границы постоянной Л^.
Первый достаточный признак однолистности был указан
И. С. Красновидовой и В. С. Рогожин ым 1):
Для того чтобы решение внутренней обратной краевой
задачи было однолистным, достаточно, чтобы выполнялось ус-
п
4 In 2
ловие N^
В дальнейшем многие авторы (Ф. Г. Авхадиев, Л. А. Ак-
сентьев, В. Н. Гайдук, С. Н. Кудряшов, В. С. Рогожин),
используя различные признаки однолистности конформного
отображения, дали в разных формах признаки однолистности
решений внутренней и внешней обратных краевых задач.
Был поставлен вопрос о нахождении такой постоянной Nt
в условии Липшица, что при N < Nt решение внутренней
(внешней) обратной краевой задачи однолистно, а при N ^ No
имеется по крайней мере одна функция, такая, что решение
неоднолистно. В настоящее время получены следующие
оценки *):
1,73
0,88
= V3 < N^ < 2,69 .,
'^^"^ < Л^о"<1,30
л;
*) Левая оценка для внутренней задачи дана Ф. Г. Авхадиевым и
В. Н. Гайдуком 1), правая — В. Н. Гайдуком 1). Для внешней задачи
левая и правая оценки указаны соответственно Л. А. А к с е н т ь е в ы м,
Ф. Г. А в X а д и е в ы м 1) н С. Н. К у д р я ш о в ы м 1).

336 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА (ГЛ IV
Вопрос О степени точности оценок пока не решен. Кроме
того, нужно иметь в виду, что здесь, как это вообще бывает
в случае оценок, пригодных для всего класса функций в целом,
даже абсолютно точная оценка может оказаться грубой, когда
она применяется для отдельного представителя класса.
Для ряда прикладных задач указаны специальные, более
точные, чем получаемые из общей теории, признаки
однолистности.
33.9. Некоторые дополнительные вопросы. Изложим обзорно еще три
важных вопроса рассматриваемой теории.
1°. Приложения. Теория обратных краевых задач используется для
построения контуров, обладающих некоторыми наперед заданными
свойствами. Известные в настоящее время приложения относятся главным образом
к гидромеханике. Основная задача здесь — построение контура по заданному
на нем распределению скорости обтекающего потока идеальной жидкости.
Главное техническое приложение — определение формы авиационного профиля
по заданному на нем распределению давления.
По величине скорости можно путем интегрирования определить потенциал
потока фE). Обтекаемый профиль является линией тока, поэтому на нем
функция тока постоянная г|? = const (эту постоянную можно принять равной
нулю). Следовательно, на искомом контуре известно краевое значение
характеристической функции потока ш = ф + ^'Ф- Контуром L„, здесь всегда
является отрезок оси абсцисс. Отображая плоскость, разрезанную вдоль этого
отрезка^ на внешность единичного круга, приходят к обратной краевой задаче
типа Dly Dz.
Реально существующие течения являются вихревыми. Поэтому
соответствующая указанной механической задаче обратная краевая задача в ее
математической постановке заключается в о рысканий аналитической в Dt,
функции, имеющей в бесконечно удаленной точке логарифмическую
особенность. Это вносит существенные осложнения в исследования. Для указанной
частной задачи все трудности удается преодолеть и получить полное решение.
Дальнейшее усложнение постановки (допущение в потоке или на искомом
контуре источников или вихрей) приводит к самой общей постановке
обратной краевой задачи. Стоящие здесь теоретические трудности очень велики и
в настоящее время не преодолены (см. ниже).
Мы не касаемся здесь других приложений. Читатели, интересующиеся
ими, могут обратиться к книге [27], в которой освещены все встретившиеся
приложения обратных краевых задач. Там же можно найти обширную
библиографию вопроса.
2. Обобщения функционального характера.
Рассмотренная выше постановка обратной краевой задачи обеспечивала существование
непрерывных вплоть до контура решений (допускаемые в п. 33.7 особенности
исследовались каждая отдельно). Естественно поставить вопрос, при каких
наиболее широких предположениях относительно задаваемых функцией u(s),
v(s) остается в силе постановка задачи и использованная схема решения.
Исследование опирается на методы теории функции действительного
переменного Приведем результаты.
Теория конформного отображения дает, что наиболее общий класс w(s),
v{s), для которого возможна постановка задачи в смысле п. 33.1, есть класс
абсолютно непрерывных функций. Для применимости используемого при
решении задачи математического аппарата приходится накладывать еще два
дополнительных ограничения: I) tt'(s), v'{s) имеют почти везде ограниченные
производные; 2) множество точек, где w'(s), v'(s) одновременно обращаются

§ 33] ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА АНАЛИТИЧЕСКИХ ФУНКЦИЙ 337
в нуль, имеет меру нуль. Указанные условия являются достаточными для
доказательства разрешимости обратной краевой задачи.
При указанной широкой постановке задачи приходится учитывать тот
факт, что в состав решения может входить дополнительный множитель е^^^*
где
2я J в'" — г
i|?(9) есть так называемая сингулярная функция (невозрастающая, с
производной, почти всюду равной нулю). Поэтому без дополнительных
ограничений на искомый контур Lz доказанная в п. 33.1 теорема единственности
внутренней обратной краевой задачи оказывается здесь уже несправедливой.
Единственность можно сохранить, если ограничить класс искомых контуров
кривыми В. И. Смирнова*).
Читатель, интересующийся обобщениями функционального характера,
может найти подробности в работах Ф. Д. Г ахов а 3), 4), откуда взяты
сформулированные результаты (см. также С. И. Андрианов 1)).
3°. Об общей постановке обратной краевой задачи.
Данная в п. 33.1 постановка задачи, когда требуется отыскать функцию,
дающую конформное отображение областей, и, следовательно, полностью
исключаются точки ветвления, а из особенностей допустимым может быть лишь
один простой полюс (в случае внешней задачи), является простейшей.
Практика выдвигает задачи большей сложности. Обратная задача гидромеханики,
как указывалось выше, в самом своем простейшем случае приводит к
отысканию функции с логарифмической особенностью в области. Ее обобщенные
постановки потребуют решения в классе функций с любым числом
логарифмических и полярных особых точек. Топологическая теория функций
комплексного переменного показывает, что аналитическая функция, имеющая в
области определенное число логарифмических и полярных особенностей,
краевые значения которой заданы, имеет в области точно определенное число
точек ветвления. Соответствующие формулы получены в работе Ф. Д. Г а-
хова иЮ. М. Крикунова1).От задаваемого контура L^o в этом случае
уже нельзя требовать, чтобы он был простым. Область Dw будет
располагаться на некоторой римановой поверхности, и контур Ly, будет простым на
этой поверхности; проекция же его на плоскость будет, вообще говоря,
самопересекающейся.
Сформулируем теперь обратную краевую задачу в общем виде**). Даны
2v функций параметра s
tt = w^^(s), v^v^(s), 0<s</^^ (A; = l, 2, ..., v),
определяющих в плоскости комплексного переменного w v кривых Lkw
(вообще говоря, самопересекающихся). Определить в плоскости комплексного
переменного z v замкнутых кривых Lkz» ограничивающих некоторую конечную
область dJ, вообще говоря, многолистную, но без точек ветвления, так, чтобы,
считая параметр s длиной дуги искомого контура Lz = Liz + Lzz + ... + Z-vz»
выражение Wk(s)= Uh{s)-\-ivh{s) было краевым значением на контуре Lkz
*) Кривая Смирнова — кривая, у которой логарифм модуля производной
функции, конформно отображающей ограниченную ею область на круг,
представим интегралом Пуассона через свои граничные значения (см [18],
стр. 250).
^'') О решении обратной краевой задачи для многосвязной области см.
§ 38.

338 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ IV
функции W = f{z), аналитической в области Dj", за исключением отдельных
точек, где она может иметь особенности заданного типа (логарифмические
или полярные) с заданной главной частью.
Число прообразов точек ветвления (точки, где /'(г)=0), как
указывалось выше, определяется по формулам, доставляемым топологической теорией,
и поэтому тоже должно считаться известным.
Решения сформулированной общей задачи в настоящее время нет.
Отдельные частные случаи, встретившиеся в приложениях, решались на
основании механических соображений без математического обоснования. Сведения
об этом можно получить из упоминавшейся книги [27].
Укажем схематически на основные теоретические проблемы, стоящие на
пути решения общей задачи.
Основная проблема — конструирование той римановой поверхности, на
которой контуры, задаваемые уравнениями « = флE), v = ^k(s), определяют
область, подобную однолистной, т. е. такую, которая может быть взаимно
однозначно и всюду, за исключением точек ветвления, конформно
отображена на некоторую стандартную однолистную область, например плоскость
с прямолинейными разрезами или с выключенными кругами. Даны контур,
определяемый краевыми значениями искомой функции, число и характер
особенностей, число точек ветвления с их кратностями. На пути решения стоят
следующие трудности: 1) определение числа и характера задаваемых
особенностей (и соответственно числа точек ветвления), допустимых при заданных
краевых значениях; 2) допустимое расположение особенностей и точек
ветвления, при которых заданный контур Iw может стать контуром области,
подобной однолистной; 3) число существенно различных областей,
возникающих при различных способах скрепления листов. Последнее связано с
числом решений обратной краевой задачи.
§ 34. Исторические сведения
Краевая задача Гильберта, принадлежащая наряду с рассмотренной в
гл. II задачей Римана к числу основных краевых задач аналитических
функций, является самой старой из задач этого типа. Это относится и ко времени
первой постановки, и ко времени первой разработки, и ко времени получения
полного решения. То же можно сказать и о времени первых прилол<ений
(теоретических —- к исследованию особых интегральных уравнений и
практических— к решению задач гидродинамики), и о начале различных обобщений.
Началом постановки задачи Гильберта можно считать работу Римана [21]
«Основы общей теории функций» A851). В разделе XIX, говоря о
возможных способах задания аналитической в области функции, он указывает, что
вместо задания на контуре действительной части ее (что приводит к решению
задачи Дирихле) можно задать некоторое соотношение между
действительной и мнимой частями. Это есть наиболее общая постановка краевой задачи
такого типа.
В оправдание тому, почему рассмотренная в настоящей главе
задача B7.7) (Гильберта) менее связывается с именем Римана*), чем
задача A4.1) гл. II (Римана), нужно ясно указать, что вопрос о фактическом
отыскании аналитической функции по заданному на контуре соотношению
между ее действительной и мнимой частями ни в коем случае не выдвигался
Риманом как практическая задача для решения. Речь шла только о способах
задания функции. При этом Риман не приводит никаких формул: замечание
о возможности определения функции указанным краевым соотношением он
делает попутно с другими еще более общими рассуждениями, например с
возможностью задания функции соотношением, связывающим значения действи-
*) Некоторые авторы называют ее задачей Римана — Гильберта.

§ 341 ИСТОРИЧЕСКИЕ СВЕДЕНИЯ 339
тельной и мнимой частей в п различных точках контура. (Заметим, что
задачи такого рода до сих пор еще не рассматривались). В противоположность
этому, краевая задача A4.1) (Римана) была выдвинута Риманом как
практическая задача для решения. Сделано это было, правда, не с целью
рассмотрения ее как самостоятельной краевой задачи аналитических функций,
а в связи с решением задачи совсем другого характера (см. Исторические
сведения к гл. И, § 19). Таким образом, связывание краевой задачи A4.1)
с именем Римана исторически более оправдано, чем краевой задачи,
рассмотренной в настоящей главе.
Отчетливая формулировка краевой задачи Гильберта*) B7.1), так же
как и попытки ее решения, сделана впервые, по-видимому, в работе Воль-
терра [Volterra 1)] в 1883 г. Однако работа эта почему-то оказалась
изолированной от других работ и не оказала существенного влияния на последующие
исследования. Отметим как странное явление, объяснение которому трудно
дать, что эта важная работа не цитируется ни в одной работе по теории
краевых задач, кроме работы автора [6].
Полное решение рассматриваемой краевой задачи дал Гильберт (Hilbert
[10]) в 1905 г. Однако это решение было получено не сразу. Первое решение
этой задачи, данное им в 1904 г. в докладе третьему Международному
конгрессу математиков в Гейдельберге, основанное на сведении к особому
интегральному уравнению с ядром ctg —^—, было ошибочным (разбор этого
см. в работе [6]), Окончательное решение Гильберта [10], хотя и не
разработанное в подробностях, легло в основу всех дальнейших исследований по
этому вопросу. Из последующих работ наиболее важна работа Нётера [Noe-
ther 1)], затем следует отметить еще работу С. Л. Соболева 1). В них задача
Гильберта разработана во всех подробностях.
В работе Нётера, кроме того, был сделан новый важный принципиальный
шаг. Если ранее исследователи пытались получить решение краевых задач
(Гильберта и Римана) из интегральных уравнений, здесь, наоборот, решение
краевой задачи (Гильберта) было использовано для исследования особых ин-
тегральных уравнений (с ядром ctg—^—)• Результаты, полученные таким
способом, оказались исключительно плодотворными; они привели к
установлению основных свойств особых уравнений (теоремы Нётера) и оказали
большое влияние на последующие исследования (см. Исторические сведения
к гл. HI, § 26).
Решение задачи Гильберта, изложенное в настоящей главе, опирающееся
на понятие регуляризующего множителя, впервые дано автором в 1941 г. в его
докторской диссертации 2) (см. также [6]). Решение это отличается от
данных ранее только методическим подходом, являющимся, как кажется автору,
наиболее естественным для данной задачи. В связи с решением задачи
Гильберта следует еще упомянуть работу И. Н. Векуа 4), в которой дано
обстоятельное изложение вопроса.
Полное изложение решения задачи Гильберта для единичного круга дано
в курсе [22]. Общее понятие регуляризующего множителя введено впервые
автором в указанных выше работах. Понятие это оказалось полезным при
решении задачи Гильберта, а также в решении обратных краевых задач.
Вопрос о возможности других применений регуляризующего множителя пока
остается открытым.
о — 5
Особые интегральные уравнения с ядром Гильберта ctg —^— впервые
встречаются в работе Гильберта**) [Hilbert 1)]. Это были, по-видимому.
*) Термин «задача Гильберта» введен впервые Пикаром (Picard [19]).
**) Одновременно в работе Пуанкаре (Poincare [20]).

340 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА [ГЛ IV
первые особые уравнения, ставшие известными математикам. Полную теорию
уравнения с ядром Гильберта дал, как на это уже указывалось, Нётер в
многократно цитированной работе. Теория характеристического уравнения с
ядром Гильберта в более простой, чем у Нётера, форме излагалась автором
в работе [6].
Методы сведения краевых задач для полигармонических и
полианалитических функций в случае простейших контуров (прямая и окружность)
к краевой задаче Гильберта были указаны впервые В. С. Рогожиным 1).
Подробную разработку вопроса произвел М. П. Ганин, часть результатов
которого опубликована в работах 1), 2). Изложение § 32 произведено в
основном по работам М. П. Ганина.
Обратная краевая задача была сформулирована Рябушинским [Riabou-
chinsky 1)] как задача гармонических функций: определить контур по
заданным на нем значениям гармонической в области функции и ее нормальной
производной. Задачу в такой постановке решал Демченко [Demtchenko I)].
Так как в этой постановке нет контура носителя данных, то Демченко
пришлось ввести в качестве определения, что носителем является некоторый
вспомогательный круг. Постановку и решение задачи, рассмотренной в § 33,
дал М. Т. Нужин 1). Существенным вкладом, внесенным последней работой,
является введение естественного носителя данных — контура Lwy
определяемого самими данными задачи. Доказательство существования решения
внешней задачи (п. 33.4) дано в работе Ф. Д. Гахова 4). Большое число
технических приложений дано в работах казанских механиков. Изложение этих
работ и полная их библиография до 1957 г. дана в работе Г. Г. Тумашева и
М. Т. Нужина [27]. На некоторые другие математические работы по обратным
краевым задачам указывалось в тексте.
Задачи к главе IV
1. Показать, что общее выражение оператора Шварца для верхней
полуплоскости имеет вид
оо
где С(I)—произвольная действительная функция действительной
переменной g. Отсюда вывести два различных выражения для оператора Шварца:
'>^"-iSf^«^»^«-i 5 ««>-т^т1
2
2. Доказать, что функция QB), являющаяся решением задачи Ло
(п. 27.3) для верхней полуплоскости, может быть взята в виде
в<^'-ЕЬ(Ш)*-'.(Й7)>*-
3. Вывести выражение для функции QiB), обладающей следующими
свойствами:
1. Она аналитична в единичном круге, кроме заданных точек Zu Zz, ...
..., Zmy где она имеет простые полюсы.

.ЗАДАЧИ К ГЛАВЕ IV 341
2. На единичной окружности действительная часть Qi(z) обращается
в нуль.
Ответ. Q,(z) = ^o + Y,[c,^^-c,-j^].
k= I
4. Обобщить результаты предыдущей задачи на случай, когда полюсы
кратные, кратностей соответственно pi, рг» •••! Рт-
Ответ. Q.(-)='Po+f;;^[^/(^^y-^/(-f^)'].
5. Решить задачи Гильберта для единичного круга:
а) е'^^" 2^ cos (cos 2s) и (s) - е~^^" ^^ sin (cos 2s) v (s) = e^°^ ^ cos (sin s);
б) Tcos s + y) " (s) + (sin s — у j t; (s) ==
1/49 2 \
= У V'36 + ^^^ ^ """ "з" s^" ^ J In E — 4 cos s).
Ответ, a) F (г) = e"'*^' (e^ + /Po);
6) FB) =
/" J 1 1 Л Ti / ox . ft . 62 + 3-2/ _ 6 + C + 2/) 21
(Po-—действительный, с — комплексный произвольные параметры).
6. Показать, что задача Гильберта для единичного круга
cos S • м (s) — I sin S + -о" ) ^ (^) = cos 2s + Л
разрешима лишь при значении параметра h = 1/4. Дать решение задачи для
этого случая.
Ответ: F (z) = z ^ i.
7. Показать, что однородное особое интегральное уравнение с нулевым
индексом
(cos S + 2) а (s) — \ и (а) ctg —г— da = sin s
о
безусловно разрешимо. Дать его решение.
Ответ. « (s) =-г-sin S.
8. Показать, что неоднородное интегральное уравнение с нулевым
индексом
2я
^ , sins + 2 f / ч X 0^ —s . /г . ^ . ч/ , IS
и (s) cos s ^ \ и (а) ctg —'— fifa = E + 4 sin s) (cos s + h)
0

342 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА (ГЛ. IV
разрешимо лишь при значении параметра Л = 0. Дать решение уравнения
для этого случая.
Ответ: w (s) = cos 2s — 2 sin s — Po (sm s + 2).
9. Показать, что для заданной на контуре L комплексной функции
a(s)+ib{s) определение регуляризующего множителя /?(/)= а(s)-f ip(s),
изображением которого служит кривая Г, заданная уравнением р = да),
можно свести к решению краевой задачи
bu-ao^-(a^ + b^)f{^^).
где и + iv — аналитическая функция, определенная равенством
R (t) [а (s) + ib (s)] = u{s) + iv (s),
10. Пусть G(t) = a(s) + ib(s) —заданная на контуре L функция с
индексом X и R(t)—ее регуляризующий множитель, индекс которого по условию
есть V. Пусть, далее, Ф+B)—функция, удовлетворяющая на L условию
R{t)G{t)^= Ф'^СО» аналитическая в области D+, за исключением, может быть,
заданных точек zi, Z2, ..., Zmy где она имеет порядки «i, Мг, .... «т, причем
т
все tik одного знака и J] ^/fe ~ ^ "f" '^*
Показать, что функция Ф+@ и регуляризующий множитель R{t)
определяются с точностью до множителя, являющегося краевым значением
функции, аналитической в D+ и имеющей там нулевой порядок.
11*. Дать решение краевой задачи Гильберта для полуплоскости.
Указание. Воспользоваться результатами задач 2 и 3.
12. Дать решение краевой задачи Гильберта для области, внешней по
отношению к единичной окружности.
13. Пусть D~ — область, ограниченная простым контуром L. Показать,
что общим решением краевой задачи Гильберта
Re[rF-@] = 0,
где
/'-^
является функция
где й)B)—функция, отображающая конформно область D- на внешность
единичного круга. (И. Н. Векуа [2], стр. 272.)
14. Каким условиям должна удовлетворять функция c(s) для того, чтобы
задача Гильберта
Re[t'{s)F^{t)]^c{s)
была разрешима?
15. Показать, что особое интегральное уравнение
a(s)u{s)+^^u(a)^^^^^^da = c^s) (а^ + Ь^ = \),
L
где G и / означают то же, что в задаче 23 гл. I, сводится к краевой задаче
Гильберта
Re [—гЙг?Тт1 = ^ (^)
L а (s) dh lb (s)J

ЗАДАЧИ К ГЛАВЕ IV 343
с дополнительным условием \v~(a)da = 0 для области соответственно Z)"^
L
или D-, [Hilbert 1).]
16. Пользуясь связью между ядром Гильберта и ядром Коши, свести
решение характеристического особого уравнения с ядром Гильберта к
решению краевой задачи Римана. Получить отсюда полное исследование
указанного уравнения.
17*. Вывести теоремы Нётера непосредственно для уравнения с ядром
Гильберта. [Noether 1).]
18*. Показать, что для особого интегрального оператора
2я 2я
K{u)^a{s)u(s)--^^ u{a)c\g-^^da+ J К (s. о) и (а) do
о о
сопряженный оператор
2л 2Я
K'l^a{s)l(s) + -^^ b(G)l(a)cig -^^rfa+J Л: (a, s)l(a)do
0 0
является равносильным регуляризатором. (В. Д. Купрадзе 3).)
19*. Пользуясь методом п. 32.3, дать решение краевых задач И, П1
полианалитических функций (п. 32.2) для круга.
20*. Дать решение краевых задач I—IV полианалитических функций для
полуплоскости.
21*. Решить основную задачу теории упругости (п. 32.5) для области D-,
Х^ у/2
ограниченной эллипсом "T' + 'tr^^^' пользуясь тем, что область D- отобра»
жается конформно на внутренность единичного круга функций г = ©(Й =
=—/?fg-f-z-J,a на внешность единичного круга функцией z = rI^ + —j,
где
R^l{a-\-b\ Rm^^{a-b).
22*. Показать, что краевая задача I полианалитических функций для
произвольного контура может быть сведена к п задачам Гильберта и,
следовательно, решена в замкнутой форме. (М. П. Ганин 1).)

ГЛАВА V
РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ*)
Основные краевые задачи Римана и Гильберта допускают
обобщения в различных направлениях. В настоящей главе
будут рассмотрены следующие обобщения:
1. Допущение в краевых условиях (задач типов Гильберта
и Римана) наряду со значениями функций значений ее
производных, а также членов интегрального характера.
2. Рассмотрение многосвязных областей.
3. Постановка краевых задач для функций более общего
вида, которые включают в себя гармонические и аналитические
как частный случай, например, для решений уравнений эллип-
1ического типа, а также систем такого типа **).
Заметим, что обобщение краевой задачи Римана на
случай многосвязной области уже было рассмотрено ранее. Для
задачи же Гильберта переход от односвязной области к
многосвязной представляет принципиальные трудности и приближает
ее и по применяемому способу решения и по результатам,
которые удается получить, к задачам этой главы.
Возможности обобщений, понятно, не ограничиваются
перечисленными. Так, например, в следующей главе будет изучен
вопрос о расширении класса допустимых коэффициентов и
контуров (разрывные коэффициенты и разомкнутые контуры).
Естественным является обобщение в смысле увеличения
числа искомых функций, задаваемых системой совокупных краевых
условий, однако этих вопросов здесь касаться не будем.
§ 35. Краевая задача типа задачи Гильберта
с краевым условием, содержащим производные
35.1. Постановка задачи и различные формы краевого
условия. Различные авторы, решавшие задачу, брали краевое
условие в различных формах, хотя и отличающихся друг от друга
*) Так как основное содержание гл. VI и VII не зависит от материала
настоящей главы, то читатель может, пропустив ее, перейти в случае
надобности к гл. VI и VII и вернуться к настоящей главе после изучения последних.
**) Последний материал в настоящем издании исключен.

§ 351 КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 345
ПО внешнему виду, но, по существу, равносильных. Чтобы
ориентировать читателя в этих формах краевого условия,
приведем их.
Автор книги, впервые рассмотревший задачу в работе [5],
опубликованной в 1938 г., формулировал ее так:
Определить функцию Ф{г)= и (л:, у) + iv (х, у),
аналитическую в области D+, ограниченной простым гладким контуром
L, удовлетворяющую на контуре краевому условию
Zh(^)l7- + ^*(^)li-] = /(^). C5-1)
fe=0
где коэффициенты а^(з), bh{s), f{s) — действительные
непрерывные функции; из них am{s)y bm{s)y f{s) удовлетворяют
условию Гёльдера.
И. Н. Веку а 4) рассматривал краевое условие в форме
Re Х; [а, (О Ф(^) (О + \ h, iU т) Ф^^^ (т) аЛ = / (О, C5.2)
где ak{t)y hh{t,x) — комплексные, а f{t)—действительная
функции такого же характера, что и коэффициенты краевого
условия C5.1); hh{t,x) — фредгольмовы ядра. Под Ф<'^)(^)
понимается граничное значение производной k-го порядка
функции Ф(г).
Д. И. Шерман 1) формулировал ту же, в сущности,
задачу как задачу гармонических функций.
Определить гармоническую в области D+ функцию и{х,у)у
удовлетворяющую краевому условию
т k
to /Го ^^' ^^У^
где коэффициенты akj{s), f{s) того же характера, что и выше.
Из трех выписанных краевых условий наиболее общим
является условие C5.2) ввиду наличия в нем интегральных
членов. Внеинтегральные члены в условиях C5.1) и C5.2)
идентичны; в условиях C5.3) отсутствует член с v{s), т. е. если
преобразовать это краевое условие к виду C5.1), то окажется,
что bo(s)^ 0.
В принципиальном отношении краевые задачи C5.1) — C5.3)
равносильны как в отношении методов, которые могут быть
применены для решения любой из них, так и в отношении
результатов, которые при этом получаются. Дело заключается
в том, что, как будет видно из дальнейшего, исследование

346 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ V
ведется только по совокупности внеинтегральных членов,
содержащих высшие производные, которые образуют
характеристическую часть получаемого особого интегрального уравнения
(см. п. C5.6)). Изменение же остальных членов приводит лишь
к изменению регулярной части ядра, что не меняет положения
дела, поскольку последняя все равно содержит произвольно
задаваемые функции — коэффициенты краевого условия.
Так как мы будем решать краевую задачу преимущественно
в форме C5.2), то покажем, каким образом привести к ней два
остальных краевых условия. Совсем просто это делается для
C5.3). Достаточно использовать соотношения
дх ~ dt* ду ~^ dt *
вытекающие из правила дифференцирования сложной функции
(/ = д: -|- iy). Будем иметь
k
Обозначая X ^*^^л/через ak{t)y придем к форме C5.2).
У-о
Для перехода от краевого условия C5.1) к C5.2) выразим
производные по дуге 5 через производные по комплексной
координате контура t:
^ = Ф'И)Г, -^ = -^ [Ф' (О П = Ф" (О f' + Ф' it) t",
-^-^ = ф('п) (/) f + члены, содержащие производные
функции Ф(/) порядка </п.
Тогда
= Re I f; (а, - ib,) ^\ = Re \_f^ {а^ - ibj ф(-) (/)] + члены,
содержащие производные Ф низшего порядка. C5.2')

§ 35) КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 347
Аналогичным путем легко осуществить переход от любой
из трех рассматриваемых форм краевого условия к двум
другим.
Покажем на частном примере, как от формы C5.1) перейти к формам
C5.2), C5.3).
Пусть дано уравнение вида C5.1):
sin S -т- + B — cos s) -т 2tt (s) = • (s).
as as
Преобразуя его при помощи приведенных выше формул, получим
Re {[sin 5 - / B - cos s)] t' (s) Ф' (/) - 2Ф (/)} = f (s).
T. e. краевое условие в форме И. Н. Векуа, если считать, что s выражено
через t при помощи уравнения контура. Наконец, полагая t'(s)=x^(s)+iy'{s),
придем к условию в форме Д. И. Шермана:
W (S) sin S + у' (S) B - cos S)] -g- +
+ W is) sin s - x' (s) B - cos s)I |~ - 2t/ (s) = / (s).
Укажем здесь же, что частный случай рассматриваемой
задачи при т = 1 был исследован Пуанкаре в связи с теорией
приливов еще в 1902 г. Именно эта задача побудила
выдающегося математика заняться теорией особых интегральных
уравнений (см. Исторические сведения к гл. III, § 26).
В дальнейшем (пп. 35.3—35.6) будет изложен способ
решения Д. И. Шермана 4), который приводит краевую задачу
непосредственно к интегральному уравнению Фредгольма,
минуя особое*).
35.2. Представление аналитической функции интегралом
типа Коши с действительной плотностью. Хорошо известно,
какую большую роль при решении краевых задач
математической физики играют представления решений дифференциальных
уравнений различного рода потенциалами. С помощью таких
представлений краевые задачи для функций, являющихся
решениями дифференциальных уравнений исследуемого вида,
приводятся к интегральным уравнениям относительно
плотности потенциала. Простейшими из потенциалов являются
обычные логарифмические потенциалы простого и двойного слоя,
применяемые при решении краевых задач гармонических
функций **).
*) при этом оказывается, что ядра получаемых уравнений выражаются
через элементарные функции (не содержащие квадратур), что представляет
известные удобства при численных методах решения.
**) Кроме них хорошо изучены также тепловые и волновые потенциалы.
К этому же кругу идей относится также операционный метод, сводящийся
к представлению искомых функций интегралами Лапласа, Фурье и
различными их обобщениями.

348 РАЗЛИЧНЫЕ ОБОВЩРННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ V
Учитывая тесную связь между интегралами типа Коши и
потенциалами (§ 10), естественно ожидать, что в теории краевых
задач аналитических функций важную роль будет играть
представление аналитических функций интегралами типа Коши и
их обобщениями.
Начнем с рассмотрения простейшего случая, чтобы затем
перейти к более сложным.
Пусть Ф+(г)—аналитическая функция, заданная в области
D+, ограниченной простым контуром L. Поставим вопрос
о представлении ее интегралом типа Коши:
L
на плотность которого \i(o) не накладывается никаких
дополнительных условий, кроме выполнения равенства C5.4).
Возможно ли такое представление и в какой мере определена
функция \х по заданной функции Ф+(г)?
Как известно, формула C5.4) определяет одновременно две
аналитические функции: заданную функцию Ф+(г) для eeD+
и, кроме того, некоторую другую функцию Ф~(г) для z^D-.
Применяя обычные обозначения для предельных значений
функций на контуре L, по формуле Сохоцкого D.9) получим
li(t) = 0'^{t)-0^(t). C5.5)
Последняя формула показывает, что плотность интеграла
типа Коши Jul (О определяется по заданной функции Ф+(г)
с точностью до слагаемого, являющегося краевым значением
аналитической в области D- функции, подчиненной
единственному ограничению ф-(оо)=0. Обратно, если подставить в
формулу C5.4) значение C5.5), то на основании теоремы
Коши и формулы Коши ползучим для 2eD+ данную
функцию Ф+B:).
Чтобы задача представления заданной аналитической
функции интегралом типа Коши стала определенной, на плотность
|Li(a) нужно наложить некоторые дополнительные условия. Эти
условия могут быть весьма разнообразными*). Мы рассмотрим
сначала простейшее условие: потребуем, чтобы |Li(a) была
действительной функцией.
Здесь так же, как и в гл. IV, рассматриваемые величины
будем задавать или как функции комплексных координат точек
t, т, или как функции действительных переменных (дуговых
*) В этом вопросе много аналогии с задачей определения регуляризую-
щего множителя.

§ 351 КРАЕВАЯ ЗАДАЧА ТИПА 34ДАЧИ ГИЛЬБЕРТА 349
абсцисс) S, а. Они связаны уравнением контура t = t{s).
Таким образом, |Li@= IlaI^C^)] = ii{s).
Возвращаясь к рассматриваемой задаче, исключим в C5.5)
искомую функцию |х(/), взяв мнимые части. Получим
1тФ"{0 = 1тФ'"@.
Правая часть последнего равенства есть известная функция.
Для определения функции 0~{z) получим задачу Шварца для
области D- с дополнительным условием Ф"(оо) = 0, которое
делает задачу, вообще говоря, неразрешимой. Поэтому
представление произвольной функции ф-^{2) интегралом типа Коши
с действительной плотностью, вообще говоря, невозможно.
Чтобы сделать представление возможным, введем в правую
часть C5.4) пока произвольное чисто мнимое слагаемое, т. е.
будем искать представление в виде
Ф(^)=2йг5т^^^ + '^- C5.6)
L
Здесь и всюду в дальнейшем при рассмотрении
интегральных представлений под функцией Ф(г), определенной в
дополнительной области, будем понимать функцию, задаваемую
одним только интегралом типа Коши без дополнительных
членов, входящих в интегральное представление. Например, в
рассматриваемом случае
L
Запишем формулу C5.6) в виде
L
И применим к интегралу типа Коши формулу Сохоцкого.
Получим
^ (/) = [ф+ (/) - /С] - Ф~ {t). C5.7^
Отсюда
1т[Ф"(/) + /С] = 1тФ^(/).
Теперь мы пришли к задаче Шварца для внешней области
без всяких ограничений; эта задача разрешима единственным
образом. Пусть
\т[ф-{z) + iC'\ = v(x,yl

350 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ V
Тогда из условия 1тФ~(оо)=0 единственным образом
определяется постоянная С. Действительная часть Ф~B) по
уравнению Коши — Римана определяется с точностью до
постоянного слагаемого. Последнее находится из условия
Кеф-(оо) = 0. Таким образом, и действительная часть ф-B)
также определится точно. Следовательно, плотность |п(/) по
формуле C5.7) определяется единственным образом.
Итак, получаем следующий результат:
Представление произвольной аналитической в области D+
функции Ф^{г) в форме C5.6) возможно, причем С и \л{а)
определяются по Ф+(г) единственным образом.
Пусть теперь Ф{г)—функция, аналитическая в D". Тогда,
учитывая, что интеграл типа Коши исчезает на бесконечности,
ищем представление в виде
Ф(^) = 1Ь-$Т^^^ + Ф(°°)- C5.8)
L
Рассуждая аналогично предыдущему, придем для
определения \i{t) к равенству
^х {f) = Ф+ (О - [ф- {t) - Ф (оо)]. C5.9)
Отсюда для определения мнимой части Ф+(г) придем к
однозначно разрешимой задаче Шварца
Im Ф+ (t) = Im [ф- {t) - Ф (оо)].
Сама функция Ф+(г) определяется с точностью до
действительного слагаемого, после чего плотность \i{t) находится по
формуле C5.9) также с точностью до действительного ела-
гаемого.
35.3. Интеграл типа Коши, плотность которого есть
произведение заданной комплексной функции на некоторую
действительную. Перейдем к рассмотрению более общего
представления аналитических функций интегралами типа Коши, когда
плотность есть произведение заданной функции, которую будем
писать в форме '^тпгГ/мТГ' "^ некоторую искомую
действительную функцию \i{s).
Итак, будем искать представление аналитической функции
Ф(г) в виде
*М = ^$м;Ш^7^- C5.10)
Будем предполагать, что а + 1Ьф{), Без ограничения
общности можно считать а^ -{- Ь^ = 1.

§ 35] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 351
Рассмотрим случай z е D+, т. е. будем считать функцию
0"'-(z) заданной, а ф-(г) — произвольной. Выше было
показано, что вопрос о представимости аналитической функции
в форме интеграла типа Коши с действительной плотностью
сводится к решению задачи Шварца для дополнительной
области. Аналогично этому вопрос о представимости в форме
C5.10) сводится к решению задачи Гильберта. Так как
последнее существенно зависит от индекса, рассмотрим
отдельные случаи.
Г. X = Ind(a-b/Ь) > 0. Аналогично предыдущему имеем
цE) ==ф+(^)__ф-(/). C5.11)
а (S) + ьЬ (S)
Освобождаясь от знаменателя и беря мнимые части,
получим
Im { [а (S) + ib E)] Ф- (/)} = Im { [а (s) + ib (s)] Ф"' (t)).
Полученное равенство есть краевое условие задачи
Гильберта для внешней области D- (см. п. 29.4), с той лишь
разницей, что множитель ¦ , .. заменен на a + ift*) (см. еще
конец п. 27.3).
Умножая обе части последнего равенства на регуляризую-
щий множитель p{s) (для области D-) функции a-\-ib и
обозначая
рEIт[(а + /6)ф-'@] = /E),
придем к равенству
1т[/У^^^^ф-@] = /E).
Используя результаты п. 29.4 и формулу B7.10), получим
ф- {Z) = 2-^е-''^^"^ [/S/ + /Q B)]. C5.1 Г)
По формуле C5,11) определим затем функцию \x{s). Так как
ф-(оо)=0, то функция Q(z), определяемая формулой B9.27),
содержит только 2х — 1 произвольных действительных
постоянных. Следовательно, при х > О представление C5.10) возможно
и функция \i{s) зависит от 2к— 1 произвольных действительных
постоянных.
2°. X ^ 0. При неположительном индексе, беря
представление в форме C5.10), мы пришли бы к задаче Гильберта, вообще
говоря, неразрешимой. Желая обеспечить разрешимость, введем
*) Указанное изменение приводит к тому, что результаты настоящего
пункта отличаются от результатов п. 29.4 знаком индекса.

352 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ (ГЛ V
в Представление дополнительный многочлен и будем искать
функцию Ф{г) в виде
где Ck — пока произвольные коэффициенты.
Поступая совершенно аналогично предыдущему, получим
сначала
Vi is) = [а (s) + ib (s)\ [ф+ (О - Ф" {t) - Z с А , C5.13)
а затем придем к задаче
решение которой дается в виде
-X
k
ф- B) = г-^в-'^^'^ [/5/ + ао] - Е Ck:^
fe=0
Разложим правую часть в ряд в окрестности г = сх), обозначая
2-x^-.Y(^)[/sf + ao]= Ё AkzK
Й= - оо
По условию, должны иметь
ф-(оо) = 0.
Последнее будет выполнено, если положить
Ck=^Ak (^ = 0, 1, ..., -х).
Коэффициенты Со, ^ь ..., C-x-i определяются из последних
равенств единственным образом. Ввиду того, что коэффициент Л_н
содержит в себе произвольную действительную величину ао,
равенство с-у^ = А-^ не определяет полностью комплексный
коэффициент с_х, а дает два действительных уравнения с тремя
действительными неизвестными. Рассмотрим эти уравнения
подробнее.
Пусть
/Sf+ аи = ао4-/ро + —+ ...,

§ 351 К^^АЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 353
— разложения соответствующих функций в окрестности 2 = сю,
причем
щ = е«1 М cos со (оо), Pi = e'^^ ^°°^ sin со (оо).
Тогда из равенства
с_, = с% + ic% = {а,% + Р.Ро) + '¦ («iPo - Pi«o)
Для трех произвольных величин с!1к, ^-х» ао получим два
уравнения:
«i«o + Mo = ^^i^x» «iPo-Pi«o = ^^l- C5.14)
Известные коэффициенты аь Pi не могут одновременно
обращаться в нуль. Если они оба отличны от нуля, то системе
C5.14) можно удовлетворить, положив одну из постоянных
^'ix» ^-х равной нулю, т. е. взяв с_х действительным или чисто
мнимым (безразлично). Если же одно из чисел аь Pi обращается
в нуль (т.е. cosco(oo)=0 или smco(oo)=0), то С-^ можно
взять действительным при Pi т^ О и чисто мнимым при ai ф 0.
Таким образом, во всех случаях С-у^ можно считать
действительным или чисто мнимым.
Следовательно, при х ^ О представление C5.12) возможно,
причем коэффициенты Cq, сь ..., c_^_i — некоторые комплексные
постоянные, а с_х — действительное или чисто мнимое число.
Таким образом, представление C5.12) содержит —2х + 1
действительных параметров, которые необходимо ввести для того,
чтобы представление стало возможным.
Аналогично решается вопрос и для случая, когда функция
Ф(г) задана в области Z)-. Здесь вопрос о представимости Ф~(г)
в указанном виде приводится к решению задачи Гильберта для
внутренней области D+. Не излагая подробностей, приведем
результаты.
1°. X = Ind(a + ib)^ 0. Аналитическая в области D-
функция Ф(г) в этом случае может быть представлена в виде
Ф(^) = 1^Г]Т(#ГЬГТ% + ФМ. C5.15)
причем ii{s) содержит —2х + 1 действительных произвольных
постоянных.
2°. X > 0. В этом случае представление может быть дано
в виде
X
I с и(а) dr v-< Сь
фЫ = \ i-i- 1.ф(ооL-У i-^. C5.16)
L к—1

354 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
где Zo — некоторая фиксированная в D+ точка, Ck — некоторые
постоянные, однозначно определяемые через Ф(г), причем Cy^
может быть взято или действительным или чисто мнимым.
35.4. Интегральное представление аналитической функции,
т-я производная которой представляется интегралом типа Коши.
При решении краевых задач типа C5.1) — C5.3) полезно иметь
интегральное представление аналитических функций, в котором
высшая производная, входящая в краевое условие,
представляется интегралом типа Коши рассмотренного в предыдущем
пункте вида.
Ядро такого интегрального представления можно получить,
очевидно, путем т-кратного интегрирования ядра Коши —з~-
Однако для простоты изложения мы ограничимся проверкой
результата т-кратным дифференцированием *).
Докажем справедливость тождества
J^J^[„_,r-.,„(,-|)] = _±_. C5.17,
Доказательство можно провести непосредственным
применением формулы Лейбница для дифференцирования произведения.
Однако, имея в виду рассмотреть в дальнейшем более сложный
случай, где применение формулы Лейбница затруднительно,
докажем тождество C5.17) методом математической индукции,
учитывая, что при т = 1 оно, очевидно, справедливо. При т =
= п + 1 имеем
Так как на основании индуктивного предположения
^[(,_.Г.,„(,_л)],
(п-1)! 1
(-1)'* Т-2
а у«-(т^ —^Г" =0, то тождество C5.17) доказано.
Перейдем теперь к выводу интегрального представления.
Вид его будет зависеть от величины Ind(a + f&)=x, как это
было и в простейшем случае, рассмотренном в п. 35.3. Кроме
того, оно будет зависеть от порядка производной т. Форма
представления будет изменяться в зависимости от того, будет
ли т> % или т ^к.
*) Мы не интересуемся возникающими при интегрировании
дополнительными слагаемыми, так как нам достаточно иметь какое-либо одно
выражение для ядра.

§ 35] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 355
Г. m > X. Докажем, что в этом случае функция Ф+{г)
может быть представлена в виде
т-х
+ 2с,г*. C5.18)
Jfe-0
где для логарифма берется ветвь, исчезающая при г = 0. При
доказательстве придется рассматривать два отдельных случая
в зависимости от знака к.
а) X ^ 0. Дифференцируя т раз равенство C5.18), получим
фС"^^) = J^ [ !LH ^ +
^ ^'^^ 2т J а (or) + ib (о) x-z^
m-x
+ 2]^(^j^l) ... {k-m+\)CkZ^-"'. C5.19)
Для функции ф(^)B:) мы пришли к представлению C5.12)
(если заменить ^ — m на ^ и (^+/п) (Л+т — 1) ... (Л + 1)^^+,^
на Cft). На основании исследования п. 35.3 представление C5.19)
возможно, причем коэффициенты Ст, Суп+и ..., Cm-yi-\ являются
определенными комплексными постоянными, а Сщ-ц можно взять
или действительным или чисто мнимым. Функция |li(s)
определяется единственным образом.
Для определения первых т коэффициентов суммы сравним
первые т членов разложения обеих частей формулы C5.18)
в ряд Тейлора. (Остальные члены будут тождественными в силу
равенства C5.19).) Будем иметь
L
ik = 0, I, ..., m-l),
где коэффициенты ай, получаемые перемножением рядов для
(т — z)"^-^ и 1пП — —). имеют определенные выражения
1 С'п,-, . . i-lf-'^"-'
«0 = ^, «fe — -7- — . _ , +
k k-l ^ "' ^ 1
(^=1,2, ..., m-l).
При этом учитываем, что ii{s)—функция уже известная.

356 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Из равенств C5.20) коэффициенты Cq, с\, ..., Ст-\
определяются единственным образом. Таким образом, представление
C5.18) доказано. При этом установлено, что входящая в C5.18)
сумма содержит 2{т — х)+ 1 действительных параметров,
б) X > 0. Дифференцируя C5.18), придем к равенству
Для ф(^^)(г) имеем представление типа C5.10). На
основании исследования п. 35.3 представление C5.21) в
рассматриваемом случае возможно, причем [i(s) будет зависеть, согласно
формулам C5.11) и C5.1Г), от 2к—1 произвольных
действительных постоянных.
Приравнивая аналогично случаю х ^ О первые т членов
разложения обеих частей равенства C5.18) в окрестности начала,
снова получим равенства C5.20), в которых нужно положить
т комплексных уравнений C4.20) (следовательно, 2т
действительных) будут содержать всего
2 (т ~ X + 1) + 2% - 1 = 2т + 1 C5.22)
действительных параметров. Можно доказать, на чем мы не
останавливаемся, что все эти уравнения будут совместными и
независимыми. Из них можно полностью определить
коэффициенты Со, С\, ..., Ст-ус-1 и произвольные постоянные, входящие
в выражение для [i{s)\ с^-^ можно взять действительным или
чисто мнимым.
Таким образом, и для этого случая доказано представление
C5.18), причем установлено, что и здесь представление
содержит 2{т — х) + 1 действительных параметров, а плотность \i{s)
определяется при заданной функции Ф+B:) единственным
образом.
Рассмотрим, наконец, последний случай.
2°. m ^ X. Теперь можно было бы ожидать, что внеинтег-
ральная сумма в представлении C5.18) будет вовсе
отсутствовать, но тогда, учитывая выбранную ветвь Infl —;^J, получим,
что функция, представляемая интегралом, будет обращаться в
нуль при 2 = 0. Поэтому, чтобы представить произвольную
функцию ФB), нужно сохранить в сумме постоянное слагаемое Со,

§ 35) КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 357
Т. е. искать представление в виде
Ф(г) =
-J^ir\TiiTh)(^-^r-'^n{l -^)^г + Со. C5.23)
где
Со = Ф{0). C5.24)
Доказательство проводится совершенно аналогично
предыдущему. Сначала устанавливаем, что jli(s) определяется через
Ф<'^)B) и содержит линейно 2х— 1 действительных постоянных.
(Нужно помнить, что здесь обязательно к > 0.) Далее, из
разложения в окрестности начала координат получаем равенство
C5.24) и еще т — 1 комплексных уравнений, которые
удовлетворяются из-за наличия постоянных в \i{s). Эти уравнения
дают возможность определить не все постоянные, а лишь
2(т— 1) из них; остальные остаются произвольными, и,
следовательно, функция \i{s) по заданной функции Ф+(г)
определяется не единственным образом, а с точностью до выражения,
линейно зависящего от
2х - I -- 2 (ш - 1) = 2 (>< ~ т) + 1 C5.25)
произвольных действительных постоянных.
35.5. Сведение краевой задачи к интегральному уравнению
Фредгольма. Возьмем краевое условие в форме C5.2):
Re Y, Uk it) Ф^^' (О + \ h [t, т) Ф^'^(т) dr] = f (s). C5.26)
Считаем, что ашЩфО, Кроме того, чтобы сделать
возможным применение разработанного в п. 35.4 интегрального
представления, наложим на контур L дополнительное условие, что
он является кривой Ляпунова (см. п. 18.1).
Применим для решения задачи интегральное представление
C5.18), причем в качестве заданной функции a-^-ib, входящей
в это представление, возьмем коэффициент при старшей
производной краевого условия am{t)\
^ ^ {т— 1I 2я/ J а^ (т) ^ ^ V т / '
т-х
+ Y, ^kz'. C5.27)
L
fe=0
Дифференцируя последнюю формулу последовательно т раз,
получим интегральное представление всех производных Ф(г)

358 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
ДО т-го порядка. При этом ядра представлений самой функции
и ее производных до (т — 2)-го порядка включительно будут
функциями, непрерывными вплоть до контура, и их предельные
значения можно получить путем непосредственной подстановки
вместо переменной z ее контурного значения t. Ядро (т— 1)-й
производной будет иметь на контуре особенность
логарифмического характера и будет фредгольмовым; его предельное
значение на контуре также получается путем замены z на t. Лишь
т-я производная, представляющаяся интегралом типа Коши
C5.19), при переходе к краевым значениям даст по формуле
Сохоцкого особое ядро Коши.
Рассмотрим подробнее член, содержащий высшую
производную, и покажем, что при выбранном нами интегральном
представлении (a + t6 = ain@) особый интеграл превращается
в обыкновенный:
Re[a,WO'"'@]-Ra[i.(s) + i]tf^''']-
Преобразуем последний интеграл:
\^,^,^^- \ tV-O HW^t+S^-it. C5.28)
L L L
В силу того, ЧТО am{t) удовлетворяет условию Гёльдера, первый
интеграл — обыкновенный. Вопрос, следовательно, сводится
к рассмотрению интеграла
Re
{Ц^'Л
Вспомним данное в § 10 разложение интеграла типа Коши
на сумму двух потенциалов. На основании формул A0.3),
A0.4)
R4wS-^^^l=iSMe = iS.(a)^i^.a. C5.29)
L L л L L
где все обозначения взяты согласно § 10.
При условиях, наложенных на контур L (кривая Ляпунова),
потенциал двойного слоя, стоящий в правой части последнего
равенства, представляет собой обыкновенный интеграл, т. е. ядро
cos (г, п) ^
^ ^ есть ядро Фредгольма.
Перейдем затем к действительным переменным, заменив
t, X функциями дуги S, а. В результате для определения ^i(s)

§ 35) КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 359
получим интегральное уравнение фредгольма:
Ii{s) + \k E, о) li (а) da = 2/ {s) - Re J] с,щ {s\ C5.30)
где /C(s, a)—ядро Фредгольма, которое можно выписать явно
(мы этого не делаем, так как явное выражение нигде нам не
понадобится); спи (s) — некоторые определенные комплексные
функции, получающиеся в результате подстановки в краевое
условие суммы 2 ^k^^ и ее производных и группировки чле-
нов, содержащих одну и ту же постоянную с^. При m ^ х
в сумме нужно сохранить один член Сощ(8).
Решив интегральное уравнение и применив формулу C5.27),
получим решение исходной краевой задачи C5.26).
Следовательно, изучение вопросов разрешимости краевой задачи
сводится к исследованию разрешимости интегрального уравнения
C5.30).
Прежде чем приступить к исследованию интегрального
уравнения, отметим двойственную роль, которую играют постоянные
Ck при выводе интегрального представления, с одной стороны, и
при исследовании интегрального уравнения — с другой.
При выводе интегрального представления функция Ф{г)
считалась заданной, поэтому постоянные Ck, входящие в
представление и определяемые через эту функцию, тоже считались
известными. В противоположность этому, при использовании
интегрального представления для решения краевых задач функция
Ф{г) является неизвестной, подлежащей определению. В связи
с этим постоянные, входящие в интегральное представление,
также нужно считать неизвестными величинами, и,
следовательно, при изучении вопросов разрешимости их нужно
рассматривать как произвольные параметры.
Таким образом, дело сводится к исследованию
разрешимости интегрального уравнения Фредгольма, правая часть
которого содержит некоторое число произвольных параметров.
35.6. Вопросы разрешимости краевой задачи. Вводя в
рассмотрение действительные и мнимые части параметров Ck и
функций a)ft(s) и учитывая, что Ст-х действительное или чисто
мнимое, запишем интегральное уравнение C5.30) в форме
2/П-2Х+1
liis) + ]K{s,o)ii{a)da = 2f{s)+ J] a,g,{s), C5.31)
где ak — произвольные действительные параметры, а gft(sl—
определенные действительные функции.

360 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Прежде чем перейти к исследованию, сделаем некоторые
замечания общего характера о решении краевых задач методом
интегральных уравнений.
Исследование краевых задач методом интегральных
уравнений можно считать полным тогда, когда, не решая самого
интегрального уравнения, удается подсчитать число его линейно
независимых решений и выразить этот результат через
некоторую величину, характеризуюндую краевую задачу. Исследование
такого рода может быть произведено в двух случаях:
1. Когда ядро уравнения есть вполне определенная функция,
не зависяи;ая от произвольных функций, входящих в краевое
условие. Такого рода случай встречается, например, при
решении краевых задач Дирихле и Неймана, где ядра уравнений
являются соответственно ядром потенциала двойного слоя и
нормальной производной потенциала простого слоя.
2. Когда ядро хотя и содержит произвольные функции, но
в силу каких-либо дополнительных соображений физического,
геометрического или аналитического характера, вытекающих из
смысла исследуемой краевой задачи, можно доказать
единственность решения (неразрешимость однородной задачи).
Такое положение имеет место, например, в краевых задачах
гидродинамики и теории упругости, где исследование производится
на основе доказанной предварительно единственности решения
соответственных механических задач. Со случаем подобного рода
мы встречались в § 17, где ядро, хотя и содержало
произвольную функцию а(/), но из аналитических соображений удалось
заранее доказать неразрешимость задачи с нулевым скачком
(п. 17.2).
В рассматриваемом нами случае ядро уравнения /C(s, а)
содержит в себе коэффициенты краевого условия, являющиеся
произвольно задаваемыми функциями. С другой стороны, ввиду
большой общности рассматриваемой краевой задачи нет
возможности сделать заключение о числе решений непосредственно
по краевому условию. Поэтому здесь речь идет не о полном
исследовании краевой задачи с подсчетом числа решений, а лишь
о том, чтобы, не решая интегрального уравнения, дать
некоторые заключения о ее разрешимости.
Г. Рассмотрим подробно случай m > х, который, как
показывают результаты п. 35.3, характеризуется тем, что плотность
[i{s) и коэффициенты Ck (а следовательно, и а^) выражаются
единственным образом через функцию Ф{г), и притом
однородно, т. е. при ФB)=0 также и [1 = 0, а^ = 0. Обратное,
очевидно, вытекает из вида интегрального представления
C5.27).
Из этого свойства легко получить, что если решения краевой
задачи Ф1(г), 02B:) линейно независимы, то нельзя подобрать

§ 35] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 361
постоянных ри Р2у отличных ОТ нуля, чтобы ВЫПОЛНЯЛИСЬ
равенства
Pil^i + Р2\'2 ^ 0. Pi«y^ + Р2< = о C5.32)
{k=\, 2, ..., 2(m~x)+l).
Чтобы исследовать интегральное уравнение C5.31),
воспользуемся третьей теоремой Фредгольма (п. 20.2). Предположим,
что однородное уравнение, соответствующее данному уравнению
C5.31), имеет q решений. Тогда уравнение
V (s) + 5 ^ [о, s) V (а) do = О,
союзное с данным, также имеет q решений. Пусть
ViE), V2E), ..., v^(s)
— полная система этих решений.
Для разрешимости уравнения C5.31) необходимо и
достаточно, чтобы выполнялись условия
^2/E)+ Y. <^kgk{s)Ui{s)ds = 0 (/ = 1,2,....?). C5.33)
Обозначая
2 5 / (s) V/ is) ds = ^ fj, \ g, is) Vf E) ds = gj,, C5.34)
получим, что разрешимость данного уравнения равносильна
разрешимости следующей системы линейных алгебраических
уравнений относительно произвольных постоянных (Xk*
2(m-x)+l
Z gjkOik = fi (/=1,2,...,^). C5.35)
Рассмотрим сначала однородную краевую задачу {f{s)^ 0).
Тогда все /j = О и система C5.35) обращается также в
однородную. Обозначим ранг матрицы || gjk II системы, т. е. число
линейно независимых уравнений, входящих в нее, г. Очевидно,
г ^ min {9, 2 (m — х) -{- 1}. Однородная система алгебраических
уравнений, как известно, всегда разрешима. Поэтому
однородная система C5.35) безусловно разрешима и имеет 2(т — х) +
-^1 — г линейно независимых решений.

862 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Выписывая при помопхи резольвенты общее решение
интегрального уравнения C5.31) (для f{s) ^ 0)
2{m->c)+l <7
fi(S) = Y. Oft \g,is)+\R{s, a)gu(or)da] + J] р,ц,(s) C5.36)
(где последняя сумма представляет собой общее решение
однородного уравнения C5.31)), видим, что это решение зависит от
2{т — х)-|-1—/* + ? линейно независимых параметров.
Вставляя это значение [х в интегральное представление C5.27),
найдем, что решение краевой задачи будет содержать столько же
параметров. Учитывая, что г ^ 9» получим следующее:
При m > X однородная задача безусловно разрешима и
имеет не менее 2 (т — х) + 1 {точно 2{т — х) + 1 + q — г) ре-
тений.
Перейдем к неоднородной краевой задаче (/E)# 0). Из
линейной алгебры известно, что если ранг расширенной матрицы,
получаемой присоединением столбца свободных членов, есть
тоже г, то неоднородная система C5.35) разрешима. Отсюда
можно получить такой вывод.
Теорема. Для того чтобы неоднородная краевая задача
C5.26) была разрешима, необходимо и достаточно, чтобы ранг
г матрицы II gjk II системы C5.35) не повышался от
присоединения к матрице столбца свободных членов.
Если это условие выполнено, т. е. неоднородная задача
разрешима, то решение линейно зависит от 2{т — >с)+ I +^ —''
действительных постоянных.
2°. Пусть теперь т ^ к. Особенность этого случая по
сравнению с рассмотренным заключается в том, что в интегральном
представлении выражение [i(s) через Ф(-г) содержит
произвольные постоянные, число которых на основании формулы C5.25)
равно 2 (к — т)+ 1. Поэтому существуют такие ненулевые
решения интегрального уравнения, которым соответствуют
нулевые решения краевой задачи. Отсюда легко вывести, что число
решений краевой задачи на 2(х — т)+ 1 меньше числа
решений интегрального уравнения. С учетом этого обстоятельства
исследование происходит совершенно аналогично предыдущему
случаю. Мы не останавливаемся на подробностях.
Приведенное рассуждение является типичным для многих
вопросов. Оно применяется во всех краевых задачах общего типа,
рассматриваемых в настоящей главе, а кроме того, во многих
других вопросах (например, в теории фредгольмовых интегро-
дифференциальных уравнений, по которым существует
обширная литература). Схематически это рассуждение выглядит так.
Для решения задачи составляется интегральное уравнение,
правая часть которого зависит линейно от некоторого числа па-

§ 35] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ ГИЛЬБЕРТА 363
раметров. Делается некоторое предположение о числе решений
СОЮЗНОГО интегрального уравнения и составляются на
основании третьей теоремы Фредгольма условия разрешимости.
Получается система линейных алгебраических уравнений
относительно параметров. Делая предположения о ее ранге, получают
заключение о разрешимости и числе решений исходной задачи.
Таким образом, исследование ведется по схеме «если...,
то ,..» без возможности точно указать в общ.ем случае, когда
именно выполняется это «если». Точные результаты удается
получить только в отдельных частных случаях. Один результат об-
ш.его характера мы укажем в следующем пункте.
35.7. Другие методы исследования. Уже упоминалось в
начале параграфа о других способах решения рассматриваемой
задачи, данных И. Н. Векуа и Ф. Д. Гаховым. Способ И. Н.
Векуа заключается в использовании разработанного им в связи
с решением данной задачи интегрального представления,
которое в наших обозначениях может быть записано в виде
Ф(^) = -(^ПуГ^]»^(<^)A-тГ'>"A-т)^<^ + ^о. C5.37)
Легко видеть, что представление это может быть получено из
интегрального представления Д. И. Шермана C5.23), если
положить
a + ib^x^-W.
Индекс последнего выражения есть т, что и соответствует как
раз формуле C5^3). Пользуясь этим представлением*),
И. Н. Векуа сводит краевую задачу к особому интегральному
уравнению с ядром Коши (еще проще было бы получить ядро
Гильберта), индекс которого равен 2(т — к), где х = Ind am{t).
Применив к последнему теорию особых интегральных
уравнений, он установил результаты, которые были получены в
предыдущем пункте**).
Способ решения Ф. Д. Гахова заключается в использовании
формул Гильберта, связывающих краевые значения
действительной и мнимой части аналитической функции. Для круга эти
формулы, имеющие очень простой вид, были выведены в п. 6.2.
*) представление И. Н. Векуа было дано раньше, чем представление
Д. И. Шермана.
**) И. Н. Векуа формулирует условия разрешимости еще в другом виде
при помощи понятия полноты ядра. Фактическое установление полноты или
неполноты ядра может быть произведено решением соответствующего
интегрального уравнения. Поэтому точные результаты, приводимые И. И. Векуа,
относятся только к тем случаям, когда ядро не содержит произвольных
функций (задача Дирихле и задача Гильберта).

364 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Для произвольного контура формулы имеют более сложный вид
(см. задачу 23 к гл. I) и требуют привлечения функции Грина.
Этот способ приводит к интегральным уравнениям с более
сложными ядрами, чем два указанных выше, что влечет за
собой трудности при практическом решении задачи. Однако
в принципиальном отношении, в смысле исследования вопросов
разрешимости, этот способ имеет преимущество перед другими,
так как здесь не приходится преодолевать трудностей,
связанных с разработкой интегральных представлений, и, кроме того,
истолкование полученных результатов прош.е, потому что
неизвестной интегрального уравнения является сама искомая
функция краевой задачи, а не вспомогательная функция (плотность
интегрального представления), как в других способах.
В целях экономии места мы не входим в подробности других
методов решения (см. предыдущие издания).
Назовем приравненную нулю совокупность внеинтегральных
членов, содержащих производные высшего порядка, главной
частью краевой задачи. Остальные члены краевого условия
будем называть его дополнительной частью. Главная часть будет
иметь вид
«mE)-jpr + bm(s) -j^ = 0 (в форме Ф. Д. Гахова), C5.38)
Не[^т(ОФ^'"ЧО] = 0 (в форме И. Н. Векуа). C5.39)
Если проанализировать полученные результаты, то придем
к заключению, что, в сущности, они сводятся к двум
следующим:
1) Задача может быть приведена к линейному
интегральному уравнению Фредгольма. (Особые уравнения, получаемые
способами Ф. Д. Гахова и И. Н. Векуа, являются лишь
промежуточным этапом.)
2) При X ^ О число решений краевой задачи не меньше
числа решений ее главной части *).
Возникает естественный вопрос: когда число решений
общей задачи больше (при х ^ 0) числа решений ее главной
части, т. е. когда дополнительные члены изменяют число решений?
Относительно каждой индивидуальной задачи ничего
определенного сказать нельзя, но можно получить интересное заключение
для всего множества задач с общей главной частью.
Если краевое условие C5.2) одним из указанных в
настоящем пункте способов свести к равносильному особому
интегральному уравнению, то, как легко подсчитать, характеристи-
*) При X < О этот результат может оказаться неверным, так как
простейшая задача имеет т решений Фа (г) =2* (/г = О, 1, ,,,, т—1), а
общая задача может их совсем не иметь.

§ 36] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАНА 365
ческая часть уравнения будет зависеть только от главной части
краевой задачи. Если в дополнительную часть ввести
множителем произвольный параметр Я, то такой краевой задаче будет
соответствовать особое интегральное уравнение, регулярный
член которого будет содержать множителем параметр X. Как
вытекает из исследований п. 24.6, число его решений
превышает число решений соответствующего характеристического
уравнения лишь для множества значений параметра К,
являющихся собственными значениями фредгольмова ядра;
следовательно, лишь для дискретного множества значений X с
предельной точкой на бесконечности.
Так как множество всех возможных значений X есть
континуум, то можно сделать вывод: число решений оби^ей краевой
задачи C5.1) — C5.3), вообще говоря, совпадает с числом ре-
шений ее главной части. Случаи отклонения являются
исключительными и осуществляются лишь на дискретном множестве
значений параметра X, (См. еще п. 36.2.)
§ 36. Краевая задача типа задачи Римана
с краевым условием, содержащим производные
Краевая задача Римана может быть обобщена в том же
направлении, в каком это было сделано в предыдущем параграфе
для задачи Гильберта. Обобщенную задачу будем
формулировать так:
Дан простой гладкий замкнутый контур L, делящий
плоскость на две области D+, D^, Определить две функции Ф+(г),
ф-B), аналитические соответственно в областях D+, D" (одну
кусочно аналитическую функцию Ф(-г)), удовлетворяющие на
контуре следующему краевому условию:
-I Ы<)^^+\влкт)^^л1=по, C6.1)
fe-0 L L J
где ah{t)f bk{t)—заданные непрерывные функции, причем an{t),
bp{t) удовлетворяют условию Гёлъдера и не обращаются в нуль;
Ak{t, т), Bk(t, т)— фредгольмовы ядра.
Метод решения сформулированной краевой задачи, как и
задачи, решенной в § 35, заключается в сведении ее к
интегральному уравнению, что было впервые сделано Л. Г. М а г н а-
радзе 2). Мы изложим более простой способ решения,
опираясь на специальное интегральное представление, данное
Ю. М. Крикуновым 1).

366 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
36.1. Интегральное представление для кусочно
аналитических функций. Цель интегрального представления,
разрабатываемого ниже, заключается в том, чтобы выразить искомые
функции и все их производные, входящие в краевое условие
C6.1), через одну неизвестную функцию. Кроме того, ядро
интегрального представления подбирается так, чтобы высшие
производные выражались интегралом типа Коши.
Будем предполагать, что предельные значения на контуре
производной порядка п функции Ф+(г) и производной порядка/?
функции ф-(г) удовлетворяют на L условию Гёльдера. Для
определенности будем считать начало координат
принадлежащим области /)+.
Докажем, что функции Ф+(-г), ф-(г) могут быть
представлены следуюи^ими формулами:
L ft-0
C6.2)
+ Y, f^k-^'^'^'z' Idx + O" (oo), C6.3)
где \i (t) — комплексная функция, удовлетворяюи^ая условию
Гёльдера; с^ ¦— комплексные постоянные, причем \х. (т) и Cf^
определяются по Ф"^ (г) и Ф~ {z) единственным образом;
Рл= 1 + 2 + ••• + р-^-1
(Cpli, C)it\, ..., сpZ\ — биномиальные коэффициенты). Под
Infl—-^J понимается ветвь, исчезающая при г = 0, а под
Infl —^Л —ветвь, исчезающая при г = оо.
Доказательство. При выводе представления,
удовлетворяющего поставленным вначале условиям, необходимо
помнить, что производная порядка р от аналитической функции
обращается на бесконечности в нуль порядка р + 1. Учитывая это
обстоятельство, при выводе формул C6.2), C6.3) будем исхо-
rf'^O^ (г) ^+
дить из того, что функция —-j^—, аналитическая в D , и
р е1^Ф~ iz) г.
функция Z —. р , аналитическая в ?)- и исчезающая на

§ 36] КРАЕВАЯ ЗАДАЧА ТИПА 5АДАЧИ РИМАНА 367
бесконечности, могут быть представлены интегралом типа Коши
с одной и той же плотностью (п. 14.2):
^"Ф+ iz)
L
гШ^^. C6.4)
а^Ф- iz)
-l^S^''- №5)
dzP
Плотность \x{t) определяется через функции Ф+(г), Ф"-B)
по формуле Сохоцкого:
\^{П==—jjn 1 —j^p—. C6.6)
Представления для функций Ф+(г), Ф""B) получаются из
равенств C6.4), C6.5) путем соответственно п- и р-кратного
интегрирования по г.
Из установленного в п. 35.4 тождества C5.17):
следует, что результат п-кратного интегрирования по z обеих
частей равенства C6.4) может быть представлен в виде C6.2).
Произвольные постоянные интегрирования си могут быть
определены из разложения обеих частей равенства C6.2) в ряд
в окрестности начала координат:
ж [Ф* @)]"'=- т^ ^ $ i- W '"-'-' ¦*'+1. (зв.т)
где
«0-0, а^-у-Х1ГГ + -Г=Т" '•• + 1
(^=1, 2, ..., /2—1); ср. с равенствами C5.20).
Из равенств C6.7) все постоянные определяются.
Следовательно, представление C6.2) доказано. Вставляя в равенство
C6.2) значения коэффициентов, определяемые из уравнений
C6.7), можно дать представлению Ф+(г) еще другую форму:
ф-*"(г) =
(-1)'* 1
(/г— 1I 2л/
1л
5^х(т)Г(т~-2)'^-МпA-f) +JI а,т-^-^гЛйт +

368 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Последней формулой удобно пользоваться в том случае,
когда значения Ф+@), [Ф+@)Г, ..., [Ф+@)](^-^) задаются
заранее. Тогда представление C6.8) не будет содержать никаких
произвольных постоянных. Если начальные значения функции
и производных заранее неизвестны, то удобнее пользоваться
представлением в форме C6.2).
Применяя аналогично тому, как это делалось при выводе
тождества C5.17), метод полной индукции, получим следующее
тождество:
t^'-'^[('--)'-'|"('-t)]-W=1)- (*»'
Исходя из этого, найдем, что результат р-кратного
интегрирования обеих частей равенства C6.5) будет иметь вид
L
+ Y,dkz'. C6.10)
л=о
Для определения постоянных интегрирования dk
воспользуемся разложением обеих частей последнего равенства в
окрестности г = оо. Учитывая, что разложение аналитической в D"
функции ф-(г) не содержит положительных степеней, будем
иметь
L
(p-l)llfrS^W^"'"^^^ (й = 1,2, ..., Р-.2),
dp-, = 0.
При этом Pfe задаются формулами
h= Z
i-k •
Подставляя найденные значения dk в формулу C6.10),
получим формулу C6.3).
Таким образом, интегральные представления C6.2), C6.3)
полностью доказаны.
36.2. Решение краевой задачи. Для решения краевой
задачи C6.1) воспользуемся только что установленными
интегральными представлениями C6.2) и C6.3).

§ 36] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАНА 369
Дифференцируя последовательно равенство C6.2) п раз,
а равенство C6.3) р раз, получим интегральные представления
для всех производных функций Ф+(г), Ф~{г) до
соответствующих порядков. Ядра этих производных при г, стремящемся
к точке контура /, ведут себя так же, как ядра производных
интегрального представления C5.27), т.е. ядра производных
соответственно до {п—1)-го и (р—1)-го порядка
включительно являются фредгольмовыми; производные же высших
порядков (пир соответственно) выразятся интегралами типа
Коши C6.4), C6.5), и их предельные значения по формулам
Сохоцкого имеют вид
Подставляя краевые значения функций Ф'*'(/), Ф"@ и их
производных в краевое условие C6.1), получим для определения
функции ii{t) особое интегральное уравнение
a(t)vi{t) + -^'\i^dx+ \kit,x)ii{x)dx =
L L
=Ht)-Y^Ck^{t), C6.11)
где
a(t) = ^Un{t) + rX{t)l 6(/) = 4к(/)-Г^&р(/)], C6.12)
k{t, t)—вполне определенное фредгольмово ядро, а a)/i(/) —
функции, которые получаются путем группировки членов,
содержащих одну и ту же постоянную с^.
Так как
а(/) + 6@ = «Л0=^0 и a{t)~^b{t) = r'b,{t)^0,
то уравнение C6.11) есть особое интегральное уравнение с
ядром Коши нормального типа и к нему применима общая теория
этих уравнений (гл. III).
Исследование вопросов разрешимости может быть проведено
по тому же плану, что и в § 35. При этом можно производить
исследование непосредственно особого уравнения, используя
теоремы Нётера, как это делал И. И. Векуа, либо можно сначала
произвести регуляризацию и затем уже воспользоваться теоре-

370 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
мами Фредгольма, как это было сделано в п. 35.6. Не вдаваясь
в подробности, укажем на основные результаты исследования.
Коэффициент задачи Римана, соответствующей уравнению
C6.11), по формуле B1.5) выразится так:
^W— a(t) + b(t) —^ TJi)' ^^^'^^^
Обозначим
Ind -^^ = Ind bp (/) ^ Ind an {t) = щ C6.14)
и назовем его индексом краевой задачи C6.1). Тогда индекс
особого интегрального уравнения определяется формулой
x = Xi —р. C6.15)
Учитывая наличие в правой части уравнения п произвольных
параметров и свойство полного особого интегрального
уравнения (п. 23.3), что число его решений не меньше числа решений
соответствующего характеристического уравнения, получим
следующее заключение: число линейно независимых решений
краевой задачи C6.1) не меньше чем кх — р + п, где щ — индекс
задачи, п — наивысший порядок производной от функции Ф+(г),
входяш^ей в краевое условие, р — соответствуюи^ий порядок
производной от функции ф-{г).
Это — результат, который можно получить, не решая самого
уравнения (или, что все равно, его союзного).
Аналогично п. 35*7, назовем приравненную нулю
совокупность внеинтегральных членов, содержащих высшие
производные, главной частью краевой задачи, а остальные члены
краевого условия его дополнительной частью. Главная часть здесь
запишется в виде
an it) [Ф^ {t)T - h (О [Ф" @]^" = О C6.16)
ИЛИ
\^''it)T=^\^-it)T'
Результаты исследования, получаемые без решения
уравнения, сводятся к двум следующим:
1. Краевая задача C6.1) может быть сведена к линейному
интегральному уравнению {сначала особому, а затем фредголь-
мову).
2. При X ^ О число решений задачи не меньше числа
решений ее главной части *).
*) См. сноску на стр. 364.

§ 36] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАНА 371
Первый результат очевиден, поясним второй. Рассмотрим
главную часть C6.16). Считая [Ф"^B:)]", [Ф~ (а:)] искомыми
функциями, можно рассматривать последнюю краевую задачу
как обыкновенную задачу Римана. То обстоятельство, что
«внутренней» искомой функцией является производная
аналитической в области D+ функции, не накладывает на эту функцию
никаких дополнительных условий. Условием же того, что
«внешняя» функция есть р-я производная от аналитической в D""
функции, является обращение ее на бесконечности в нуль
(Р + 1)-го порядка.
Следовательно, краевую задачу Римана C6.16) нужно
решать в классе функций, обращающихся на бесконечности в нуль
{р + 1)-го порядка.
Число таких решений будет, как легко видеть, щ — р, где,
т А ^Р^^^ ГТ
как и ранее, щ = Ind —77т— индекс задачи. При интегрирова-
НИИ «внутренней» функции возникнут п новых произвольных
постоянных; интегрирование «внешней» функции не даст новых
произвольных постоянных, так как все получающиеся в
результате интегрирования функции должны на бесконечности
обращаться в нуль. Следовательно, задача C6.16) имеет щ — р 4" ^
решений, что согласуется с полученным ранее результатом.
Читателю рекомендуется самому провести исследование по схеме
п. 34.6, опираясь в данном случае не на теоремы Фредгольма,
а на теоремы Нётера.
Рассмотрим в заключение вопрос о том, когда число
решений общей краевой задачи окажется больше числа решений ее
главной части (см. п. 35.7). Выделим в краевом условии C6.1)
главную часть C6.16), а в дополнительную часть введем в
качестве множителя произвольный параметр Я. Поступая так же,
как в предыдущем, придем вместо C6.11) к особому
интегральному уравнению
L L
/1-1
=/(о-х;с/. C6.110
Опираясь на результаты п. 24.6, с помощью рассуждений,
аналогичных проведенным в п. 35,7, придем к заключению, что
при X ^ О число линейно независимых решений полной
краевой задачи C6.1) может превышать число решений его главной
части C6.16) лишь для дискретного множества значений
параметра Я, имеющего предельную точку на бесконечности.
Следовательно, число решений общей задачи, вообще говоря, совпа-

372 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
дает с числом решений его главной части. Случаи отступления
от этого правила являются исключительными.
36.3. Новый способ решения задачи. В. С. Рогожин
3) получил новое интегральное представление, позволяющее
свести краевую задачу C6.1), минуя особое интегральное
уравнение, непосредственно к уравнению Фредгольма, аналогично
тому, как это было сделано в пп. 35.3—35.6 для обобщенной
краевой задачи типа задачи Гильберта. Это достигается путем
введения в плотность интегрального представления C6.2)
дополнительного множителя, который затем соответствующим
образом подбирается.
Устанавливается следующее:
Пусть c{t)—заданная на L функция, удовлетворяющая
условию Гёлъдера и не обращающаяся в нуль. Если п'^ к =
= Ind c{t), то для кусочно аналитической функции Ф-{г), у
которой предельные значения производных Ф+<^)@, Ф~^^ЧО ^^
контуре удовлетворяют условию Гёльдера, справедливо
интегральное представление
/г-х-1
+ Е Skz\ C6.17)
L
fe=0
р-2 -1
+ Е ^kt^''^'^^^ dt + Ф" (ос), C6.18)
где |i(t)—комплексная функция, удовлетворяющая условию
Гёльдера, g^ —постоянные, определяемые по Ф=^@» ^ Pft ^^'
даются выражениями
р.= Z
/-Л+1
Если п = X, то в формуле C6.17) нужно Y^g^z^ заменить на
го = Ф+@).
При доказательстве, аналогично п. 35.4, приходится
рассматривать три подслучая. Приведем рассуждения для одного из
них: п > X > 0. Продифференцировав формулы C6.17), C6.18)

§ 36] КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАНА 373
соответственно п п р раз и введя упрощенные обозначения
ф+(^^) B) _р+ (^)^ 2Рф-(Р) (^) == /г- (^у
придем к равенствам
f+B) = JLCiii4_^l_, C6.19)
L
^"(^) = ж5т:?1^- C6.20)
L
Обозначив функции, определяемые интегралами в
дополнительных областях, соответственно Ч''"(г), W+(z)y по формулам Со-
хоцкого будем иметь
F^{f) + ^-it) = ^, ?+@-f-@ = ^@. C6.21)
Исключая \i{t)y для определения Ч^=*=(г) придем к задаче Ри-
мана
W+ (О = с (О ч^- (О + ^ (О /="" (О + /^" (О, C6.22)
которую нужно решать при условии Ч^~(оо) = 0. Свободный член
ее обраш^ается в нуль только тогда, когда F{z)^0. В самом
деле, приравнивая его нулю, мы получили бы однородную
краевую задачу Римана с коэффициентом т^т-, имеющим
отрицательный индекс. Отсюда получили бы F{z)=0. Согласно
п. 14.5 задача C6.22) решается безусловно и решение ее
(формула A4.18')) содержит линейно к произвольных постоянных.
Входящие в интегральное представление постоянные gkj Рл,
а также входящие в \x{t) к произвольных постоянных
определяются путем приравнивания начальных п членов разложения
обеих сторон C6.17) в окрестности начала координат и первых
р членов C6.18) в окрестности бесконечно удаленной точки.
Эту операцию мы уже проделывали в предыдущем пункте,
а также в п. 35.4, так что здесь на этом не будем
останавливаться.
Случай X < О отличается тем, что при доказательстве
представления приходится решать задачу Римана с отрицательным
индексом. Оставшиеся после дифференцирования C6.17) |х|
произвольных постоянных подбираются так, чтобы эта задача
была разрешимой. Остальное делается примерно так же, как
и в предыдущем случае.
Используя полученное интегральное представление, можно
свести краевую задачу C6.1) к интегральному уравнению. Если

374 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
при этом выбрать с (t) = ^^ ... , то легко подсчитать, что
члены, содержащие высшие производные, дадут интеграл с
ядром
ViPan(T) tPan(t)\ т-1
и, следовательно, интегральное уравнение будет фредгольмовым.
Исследование интегрального уравнения можно провести
совершенно аналогично тому, как это сделано в п. 35.6.
36.4. Особое интегро-дифференциальное уравнение. С краевой
задачей C6.1) тесно связано интегро-дифференциальное
уравнение с ядром Коши следующего вида:
j; а, it) v<*> (О + X i S ^Т=Т- ^'" (^) ^^ = ^ (')' C6.23)
fe=0 fe=0 L
где aft (О, f@» Яа(/,т) —заданные функции, удовлетворяющие
условию Гёльдера, а v(^)—искомая функция, отыскиваемая
в классе функций, производная г-го порядка которых (г =
= тах(р, q)) удовлетворяет условию Гёльдера.
Запишем уравнение C6.23) в форме с явно выделенной
характеристической частью:
р
-a.@v«@+Z^5^''^ +
+ 2 \ Q* (^. -") ^'*' (^) ^^ = ^ (О, C6.24)
А;«0 L
где положено Р,@ = П(^ О, QH^ '^) = i * "^^^Ц^Т^^^-
Очевидно, Pj5.@ удовлетворяют условию Гёльдера, а Qk{t, т) —
фредгольмовы ядра.
Будем также предполагать, что величины ap{t) при p>q,
р^@ при q>py ap{t)±^g{t) при p^q нигде не обращаются
в нуль.
Вводим аналитическую функцию посредством интеграла типа
Коши, плотностью которого является искомое решение интегро-
дифференциального уравнения
^(-) = iS7^^-- C6.25)

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 375
Согласно формулам Сохоцкого D.14), D.15) будем иметь
I f v^^) (T) , ^^Ф+ @ , d^O" (t) {Ъ&.2&)
J x-t
Tti ^ x — t dt^ dt^
Подставляя выражения C6.26) в уравнение C6.24), получим
A-oL L ах ^
где
ak{t) = ci,{t) + Mt\ b,{t) = a,{t)^f^,{t) (^==0, 1, ..., г),
причем нужно считать ak{t) ^ О для k > р при р <. q, Рл@ ^^ О
для й > q' при р > д-
Краевая задача C5.27) есть, очевидно, частный случай
рассмотренной выше задачи C5.1), и рассуждений, связанных с ее
решением, можно не приводить.
Найдя решение задачи C5.27), по формуле Сохоцкого
v@ = O'*"@-O"@
получим решение исходного интегродифференциального
уравнения C6.23).
§ 37. Краевая задача Гильберта
для многосвязной области
Особенностью аналитической функции, определенной в
многосвязной области, является то, что она, оставаясь
аналитической в области, т. е. допуская в окрестности каждой точки
области разложение в ряд Тейлора, может быть неоднозначной. Для
задачи Римана, где краевое условие задается в комплексной
форме, это обстоятельство не оказывает существенного влияния
на решение. Однозначное задание краевого условия приводило
там необходимым образом к однозначному решению. Иначе
обстоит дело в том случае, когда аналитическая функция
отыскивается по краевому условию, задаваемому в действительной
форме, как это имеет место в задаче Гильберта. Здесь порядок
связности области существенно влияет на разрешимость
краевой задачи и на число ее решений.
Наше изложение будет состоять из трех самостоятельных
частей. В первой части к задаче Гильберта будет применен метод

376 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
регуляризующего множителя (см. § 29) с изменениями,
вызванными многосвязностью области. Основное внимание здесь
уделяется исследованию возможности эффективного решения
задачи Гильберта в операторах Шварца. Во второй части краевая
задача Гильберта исследуется методом интегральных уравнений.
Третья часть посвящена исследованию особых случаев
однородной задачи Гильберта, не поддающихся изучению методом
интегральных уравнений.
Аналогично тому, как это делалось в гл. IV, начнем
изложение со вспомогательных вопросов.
37.1. Задача Дирихле для многосвязной области. Пусть D
есть (т + 1)-связная область, ограниченная простыми
непересекающимися гладкими кривыми Lo, Li, ..., Lm, из которых Lo
охватывает остальные. На контуры наложим дополнительное
условие, что они являются кривыми Ляпунова (см. п. 18.1).
Классическую задачу Дирихле можно сформулировать так:
Задача Дирихле. Найти функцию и (л:, у),
гармоническую в D+ и непрерывную в Z)+ + L, по краевому условию
u = f{s\ C7.1)
где f(s)— заданная на контуре непрерывная функция,
В случае, если контур Lo отсутствует и, следовательно,
область D+ — бесконечная, накладывается еще условие, чтобы
функция и была ограниченной на бесконечности.
Для случая односвязной области мы уже многократно
пользовались тем, что задача Дирихле разрешима, и притом
единственным образом. Это же справедливо и для
сформулированного случая многосвязной области, если только на искомую
функцию не накладывать дополнительных условий. В некоторых
приложениях (в том числе и для наших дальнейших
исследований) требуется, чтобы искомая функция была не просто
гармонической, но, кроме того, была действительной частью
однозначной аналитической функции. (Вообще говоря, она является
действительной частью неоднозначной аналитической функции.)
При этом дополнительном условии задача Дирихле оказывается
в общем случае неразрешимой. Чтобы сделать ее разрешимой,
нужно в задание функции на контуре ввести некоторые
произвольные элементы, что приводит к так называемой
видоизмененной задаче Дирихле*). Дадим ее точную формулировку.
Видоизмененная задача Дирихле. Найти функцию
и{х, у) у являюш^уюся действительной частью некоторой функции
ф(г), аналитической и однозначной в области D+, непрерывную
вплоть до контура, по краевому условию
u = f{s) + h{s\ C7.2)
*) Этот термин введен Н. И. Мусхелишвили.

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 377
где h{s) принимает на контурах Lj произвольные постоянные
значения hj, не задаваемые заранее.
Постоянные hj определяются, как показывает исследование,
условиями задачи (требование однозначности ФB:)), если
задать одну из них. В дальнейшем мы будем считать Ло = 0.
Единственность решения классической задачи Дирихле
вытекает из хорошо известного предложения, что гармоническая
функция, отличная от постоянной, достигает минимума и
максимума на контуре.
Для доказательства единственности решения видоизмененной
задачи достаточно установить, что однородная задача (/(s)^0)
имеет только нулевое решение.
Исходим из хорошо известной в теории гармонических
функций формулы
Применяя уравнение Коши — Римана *) и краевые данные, имеем
так как функция v по условию однозначна. Отсюда -^ = -Ji =
=0. Следовательно, и = const. Но так как на Lq и = О, то и
всюду и{х, у)== 0.
Если отбросить условие Ао = О, то решением однородной
задачи является постоянная Ло и два решения видоизмененной
задачи могут отличаться на постоянную величину.
Дадим решение видоизмененной задачи Дирихле при
помощи потенциала двойного слоя. Заданную функцию f{s)
будем считать удовлетворяюихей условию Гёльдера **).
Аналитическую функцию Ф(г) будем искать в виде
интеграла типа Коши
ф{г) = и{х, y) + iv{x, y) = -^\^dx + iC C7.3)
*) Мы не останавливаемся на обосновании справедливости этих
соотношений на контуре.
**) В дальнейшем можно было бы освободиться от требования, что
функция f(s) удовлетворяет условию Гёльдера, и доказать, что полученное
решение имеет место и в том случае, когда f{s) просто непрерывна. Мы не
будем проводить соответствующего рассуждения. (См. Н. И. М у с х е л и-
ш в и л и [16], § 61.)

3?8 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
с искомой действительной плотностью |яE), которую будем
считать удовлетворяющей условию Гёльдера.
Беря по формуле Сохоцкого предельное значение на
контуре, отделяя действительную часть (см. § 10) и вставляя
в краевое условие C7.2), придем к интегральному уравнению
Фредгольма
и (S) + i 5 ц (а) -^^i^ da = 2 и (s) + h {s)]. C7.4)
L
Однородное интегральное уравнение
t* (s) + -^ J IX {о) ^^^ da = О C7.40
имеет следующие решения:
ci при t^Li (/==1, 2, ..., m),
О на остальных контурах.
Докажем это.
Уравнение C7.4^) можно записать в виде
v^i E) = I
C7.5)
Re lim rJ-,CjiM.dJ=o.
Если |i = fXj, TO интеграл no L сводится к интегралу по L;.
Учитывая, что \-~-^^т = 0 для z, лежащего вне L^, полу-
ч
чим, ЧТО функции C7.5) действительно удовлетворяют
уравнению C7.40.
Других решений уравнение иметь не может на основании
следующих соображений. Согласно свойству интеграла типа
Коши, если функция piE) есть решение уравнения C7.4^, то
она есть краевое значение функции, аналитической в D^, Но
\i{s) действительна. Следовательно, краевое значение мнимой
части аналитической в D" функции равно нулю. Но тогда вся
аналитическая функция \л{г) есть постоянная в Z)-. При этом
в каждой связной области Do", D{, ..., Dm допустимы
различные значения этой постоянной. В области Do" ее значение равно
нулю. Таким образом, решениями уравнения C7.4^ могут быть
только такие |лE), которые принимают на каждом из контуров
Lj некоторые постоянные значения. Чтобы удовлетворились
равенства C7.4^, необходимо положить на контуре Lq постоянную
равной нулю. Беря всевозможные комбинации постоянных,
придем к решениям C7.5).

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 379
Общее решение уравнения C7.4^) является линейной
комбинацией следующих т линейно независимых решений:
{1 при /е L, (/= 1, 2, ..., т),
О на остальных кривых.
Согласно теоремам Фредгольма, однородное уравнение,
союзное с C7.40:
а E) - 1 5 а (а) ^^^^ da = О C7.4^0
также имеет т решений, а неоднородное уравнение C7.4)
разрешимо лишь при выполнении т условий ортогональности:
S[fE) + AE)]a;E)d5 = 0 (/ = 1, 2, ..., m), C7.6)
L
где aj{s)—линейно независимые решения уравнения C7.4'').
Вводя обозначение
Bik = S а/ is) ds (/, & = 1, 2, ..., m), C7.60
перепишем равенства C6.6) в виде системы линейных
уравнений относительно постоянных Л^:
m
Y,Bikhk=-\f{s)^i{s)ds (/=1, 2, ..., m). C7.6-)
Это система однозначно разрешима. Последнее вытекает из того,
что однородная система C7.6'0 имеет только тривиальное
решение. (Если бы это было не так, то задача Дирихле при / = О
имела бы ненулевое решение.) Таким образом, видоизмененная
задача Дирихле разрешима. При этом все постоянные h^
приобретают вполне определенные значения.
Из установленной разрешимости видоизмененной задачи
Дирихле можно заключить, что гармоническая функция,
являющаяся действительной частью аналитической и однозначной
функции Ф{г), может быть единственным образом представлена
в виде потенциала двойного слоя:
«(^, у) = Re
[Ц^'^\
Отсюда можно вывести важное для нас
Следствие. Аналитическая и однозначная в конечной мно-
еосвязной области D+ функция Ф(г) может быть представлена

380 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
интегралом типа Коши с действительной плотностью
^(^^ = ш\т^d^¦^^C^ C7.7)
L
где С — произвольная действительная постоянная,
В случае, если кривая Lq отсутствует и, следовательно,
область становится бесконечной, можно доказать справедливость
представления
Плотность [i{s) определяется по заданной функции Ф(г)
с точностью до произвольной постоянной на каждом внутреннем
контуре Lj (формула C7.5)), Это будут те значения jj,, при
которых интеграл типа Коши для z ^ D+ обращается в нуль.
Итак, для многосвязной области справедливы те же
представления аналитических функций интегралами типа Коши,
которые были выведены в п. 35.2 для случая односвязной области
{формулы C5.6), C5.8)) с тем, однако, различием, что
плотность [х определяется по функции Ф(г) неоднозначно.
На основе проведенного исследования видоизмененной
задачи Дирихле легко указать способ решения классической
задачи Дирихле.
Будем искать решение последней задачи в форме
т
и{х, y) = U(x, y)+Y,Ak\n\z-Zkl C7.9)
где и (х, у)—действительная часть однозначной аналитической
функции, Zh — некоторые произвольно закрепленные точки в
областях Df, D2y ..., Z)m» а y4ft —пока неопределенные
постоянные.
Функция U{x, у) должна будет удовлетворять краевому
условию
m
U = !{s)-YA,\n\t^Zk\.
Умножая это равенство на полную систему aj(/) решений
уравнения C7.4'0, получим
т
о = 5 / (s) а/ (s) ds - J] Ла 5 In I / - z„ |а; (s) ds C7.10)
L k-l L
{/=1, 2, .... m).

§ 371 ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 381
Здесь в левой части стоит нуль за счет того, что U{x, у) должна
быть действительной частью однозначной функции. CncTeivia
C7.10) однозначно разрешима относительно постоянных
Ль ^2, ..., Am, так как в силу единственности решения задачи
Дирихле соответствуюихая ей однородная система имеет только
тривиальное решение.
Вставляя найденные значения U{x, у) и Aj в выражение
C7.9), получим решение задачи Дирихле.
Если кривая Lq отсутствует, то доказанная теорема остается
в силе с тем только изменением, что постоянные Ak нужно
подчинить условию
т
Ел,=о.
Условие это вытекает из требования ограниченности решения
в бесконечно удаленной точке.
Д. И. Ш е р м а н 5) показал, что задача Дирихле для многосвязной
области может быть решена и иным способом, не связанным с решением
видоизмененной задачи. Функция и(х,у) отыскивается им в виде
^ /г
И (^, ^) = — j V (s) —^ ds + Y^B^ In г J, ^/ = J "v (s) ds,
L y = l Ly
где плотность v(s) действительна и rj=\z — Zj\, Интегральное уравнение
для v(s) (оно составляется так же, как и уравнение C7.4)) оказывается
при этом всегда однозначно разрешимым. При таком способе отпадает
необходимость составления и решения системы C7.10).
37.2. Оператор Шварца для многосвязной области. Оператор
Шварца для многосвязной области определяется совершенно
так же, как это было сделано в п. 27.2 для случая односвязной
области; мы будем пользоваться понятиями и обозначениями
этого пункта.
Пусть
G(e, t,) = \n-y + g{x, у\ I, Ti)
— функция Грина. Отыскание ее, как известно, сводится к
решению частного случая задачи Дирихле, что и устанавливает ее
существование.
Пусть Я (г, ^)— сопряженная с G гармоническая функция по
переменному z и
M{z, l) = G + iH
— комплексная функция Грина.
Всюду в дальнейшем положительное направление обхода
контура будем брать относительно области D+. Это означает, что

382 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
контур Lo будет обходиться против, а контуры Lj (/= 1,2,...
..., m)—по часовой стрелке. Положительное направление
нормали берется внутрь области D+. Таким образом,
положительные направления касательной и нормали на любой кривой
контура расположены так, как оси абсцисс и ординат.
Если и + iv — аналитическая функция и если под -j-, -^
на контуре понимать предельные значения производных по
соответствующим направлениям в области, то на контуре будут
выполняться уравнения Коши —Римана
ди дУ ди ду П7 1П
ds ~ дп' дп ~ ds • KO(AV)
Заметим еще, что под знаком интеграла ds всегда означает
величину положительную.
Вернемся к комплексной функции Грина и выясним ее
аналитический характер.
Функция М{г, I) будет многозначна по двум причинам: во-
первых, она содержит слагаемое — ln(g — г), во-вторых, в силу
многосвязности области она, вообще говоря, при обходе в
области D+ около любой внутренней кривой Lj получает некоторое
приращение. Функция Грина 0(г, ^), по определению,
однозначна. Обозначим приращение H{z, ^) при обходе некоторого
внутреннего контура L^ против часовой стрелки 2яР;(^).
Согласно равенству C7.11) эти величины выразятся формулами
М) = -4^Щл^ = 4;;Щл^. C7.12)
ч ч
причем здесь ? — внутренняя точка области D+, а г — точка
контура. Функция Л1(г, g) при обходе контуров L^ против
часовой стрелки приобретает приращение /2nPj(^). Такое же
приращение имеет функция Pj (g) In {z — z^), где Zj — некоторая
точка внутри Ly Следовательно, комплексная функция Грина
имеет следующее представление:
М {Z, I) = М, (Z, О - In (g - г) + Е р/ (О In {Z - zj\
где Mq{z, Q—аналитическая и однозначная функция
переменного Z.
Выясним характер функций Pj. Перепишем формулу C7.12),
изменяя названия переменных. Учитывая симметричность
функции Грина относительно переменных г, ^, будем иметь
Р/й-^ S^^^"- C7.13)

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 383
Так как функция -^ гармонична по г, то последняя формула
определяет ^j(z) как гармонические в D+ функции. Сравнение
формулы C7.13) с формулой B7.2), дающей в замкнутой форме
решение задачи Дирихле посредством функции Грина,
показывает, что на контуре она принимает следующие значения*):
P,(x) = {i'
если X ^ Li (/=1,2,..., m),
^ ' ' ' ' C7Л4)
на остальных кривых.
Они совпадают с функциями C7.5), образующими полную
систему решений интегрального уравнения C7.4').
Образуем теперь ядро Шварца, взяв производную от М по
положительному направлению нормали:
т
-г /- ^ч _ дМ (г, i) _ дМо {г, Q 1 ^Z ."^ г. if\]n {^ ¦у \
i-i
C7.15)
где
а/(?) = -^|г-. C7.140
На основании тех же соображений, что и в п. 27.2, получим,
что формула
определяет аналитическую (но, вообще говоря, неоднозначную)
функцию, действительная часть которой принимает на контуре
заданное значение u{s).
Следовательно, так же как и в п. 27.2, оператор Шварца
определяется формулой
Sti^^\T{z,x)u{o)do. C7.17)
Аналитическая функция F{z), определяемая оператором
Шварца
F{z) = Su + iVQ,
*) В теории гармонических функций функции Р;(г) называются
гармонической мерой кривой Lj относительно области D+,

384 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
имеет следующий характер:
т
F (г) = Fo{z) + Y.^ •" (^ - ^/)» C7.18)
/-1
где
„ , ч iff дМо (г, т) , 1 ^т 1 , ч ,
L
— однозначная аналитическая функция, а
Vj=^u{o)af{x)da C7.19)
L
— определенные постоянные.
Из формулы C7.18) легко усмотреть, что постоянные Vj
равны приращению функции F(z) при обходе контуров Lj.
Чтобы оператор Шварца определял однозначную функцию,
очевидно, нужно потребовать, чтобы все Vj обращались в нуль.
Отсюда вытекает важный результат:
Для того чтобы произвольная функция w(s), заданная на
контуре, могла быть действительной частью аналитической и
однозначной в области функции, необходимо и достаточно, чтобы
она удовлетворяла т соотноилениям
JwE)a/(/)d5 = 0 (/=1, 2, ..., m). C7.20)
L
Сравнивая эти соотношения с условиями разрешимости
C7.6), заключаем, что функции C7.14^) образуют полную
систему решений интегрального уравнения C7.4^').
В случае бесконечной области D+, когда контур Lq
отсутствует, все выписанные формулы останутся справедливыми,
только условие ограниченности на бесконечности дает для Pj и
OLj условия
т т
Ер/(?)=!, Zay(S)-0. C7.21)
Для кругового кольца комплексная функция Грина может
быть выражена через известную в теории эллиптических
функций функцию Оь а ядро Шварца через ^-функцию Вейер-
штрасса *).
*) Необходимые формулы читатель может найти, например, в книге:
Н. И. А X и е 3 е р, Элементы теории эллиптических функций, Гостехиздат,
1948, стр. 221-229.

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 385
Для произвольной многосвязной области Э. И. Зверович
2) построил новое выражение для оператора Шварца, выразив
ядро Шварца в явном виде через т-кратный 0-ряд и
гармонические функции Р;(г), граничные значения которых даются
формулами C7.14).
37.3. Различные формы постановки краевой задачи
Гильберта для многосвязной области. Пусть на границе L области D"**
заданы действительные функции дуги: аE), &(s), c(s),
удовлетворяющие условию Гёльдера. Краевой задачей Гильберта
будем называть следуюн^ую задачу:
Найти все функции f{z) = u{Xyy)-}-iv{x,y), однозначные и
аналитические в области Z)+, непрерывно продолжимые на
границу L области D+ где должно выполняться линейное
соотношение *)
а E) u{s) + b is) v{s)=^c (s). C7.22)
При c{s)^ О будем иметь однородную задачу, а при с{8)Ф О —
неоднородную.
Будем считать, что коэффициенты a{s) и b{s) не обращаются
одновременно в нуль. Поделив краевое условие C7.22) па
л/а^ {s) + b^ (s), приведем его к такому виду, когда
a^s) + b^s)^L C7.23)
Считая условие C7.23) выполненным и полагая a{s)+ ib{s)^=^
= X[/(s)], можно переписать краевое условие C7.22) в
следующих равносильных формах:
Re {{а -Jb) f (/)} = с (/), C7.24)
Re{W)f{t)}^c{t\ C7.25)
причем |Я(/)|^ 1. Функцию X{t) будем называть
коэффициентом задачи Гильберта,
Обозначим
i{argA(/)}jr^ = x, (/ = 0, 1, ..., m),
причем все кривые Lj обходятся в положительном направлении
относительно области D+ (внутренние кривые по часовой
стрелке, наружная — против). Величину
т
назовем индексом коэффициента X{t) задачи C7.25).
*) См. сноску к п. 27. L

386 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Функция {t — Zf)~^'l (/=1, 2, ..., т) имеет вдоль кривой
Lj при Zj, лежащем внутри Lj, то же изменение аргумента, что
m
И K{t), Поэтому функция X{t)Yl(t — Zf)^i имеет на всех
внутренних кривых изменение аргумента, равное нулю. Производя
в C7.25) замену неизвестной функции
получим
фB) = /(г)ПB-2:,Г/,
Re| ^ 1 = ^@.
Разделив, наконец, обе части последнего равенства на
( т I
|я (t) П (^ -^ Zj)^^ L получим, ЧТО новый коэффициент будет иметь
единичный модуль. Таким образом, не ограничивая общности,
можно считать, что в задаче C7.25) |Л(/)|^1, а функция
2iVgX{t) имеет вдоль всех внутренних кривых нулевое
приращение, а вдоль кривой Lq — приращение к.
37.4. Метод регуляризующего множителя в случае
многосвязной области. Будем предполагать, что начало координат
находится в области D+. В случае односвязной области D+ задачу
Гильберта можно свести к задаче А, т. е. к виду B9.9), деля
ее краевое условие на специально подобранный положительный
регуляризующий множитель p{t). Его существование обеспечено
тем, что в случае односвязной области задача Шварца всегда
имеет однозначное решение. Поскольку этот последний факт для
многосвязных областей не имеет места, то в этом случае,
вообще говоря, не существует положительного регуляризующего
множителя /?(/), позволяющего свести задачу C7.25) к виду B9.9).
Чтобы обеспечить существование регуляризующего
множителя p{t) для многосвязной области D+, изменим его
определение по сравнению со случаем односвязной области, вводя
некоторые произвольные элементы. Будем искать положительную
функцию p{t) и точки Zu 2:2, ..., Zm, лежащие строго внутри
области Z)+, так, чтобы имело место равенство
т
Р (О >^ (О = f"-"" П fe -1) б'^ '\ t е L, C7.26)
где y{z)— однозначная аналитическая в D+ функция.
Оставляя вопрос о нахождении всех величин, входящих
в C7.26) (см. далее, п. 37.5), предположим, что они уже

37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОИ ОБЛАСТИ 387
найдены. Деля краевое условие C7.25) на pit), получим
с it)
p{t)
Щ ^"':"'"" 1-4^. '-i- C7.27)
"-'"П(-.-'
/г = 1
Вводя здесь новую неизвестную функцию Ф (г) =6~''y B)^B),
получаем, что задачу Гильберта для многосвязной области можно
свести к задаче Гильберта с рациональным коэффициентом:
Re( V^ l=f|f. t^L C7.270
Обозначая выражение, стоящее в фигурных скобках, f (/),
получаем задачу А:
R^^W = 7@"' (^^-^^^'^
где неизвестная функция F{z) аналитична в D+, кроме полюсов
в точках Zu Z2y ..., z^-a е Z)+ и точки г = О, где она допускает
полюс порядка не выше х — т при у.'^ т\ при к <. т функция
F{z) должна иметь в точке 2 = 0 нуль порядка не ниже т — х.
При c{t)^0 задачу C7.27^^ будем называть задачей Aq.
Ее общее решение обозначим Q{z). Для односвязной области
(т = 0) задачи А и Ао решаются элементарно, если известен
оператор Шварца области D+ (см. § 27). Например, решение
задачи Ао для односвязной области, даваемое формулой B7.8),
в терминах оператора Шварца имеет вид
Q B) = /Ро + Е {if - 5 (не ^) }. B7.80
где S — оператор Шварца, а Ро, [ih — произвольные постоянные.
Аналогичные результаты имеют место для многосвязных
областей:
Если известен регуляризующий множитель p{t)y связанный
с коэффициентом X{i) формулой C7.26), то решение задачи
Гильберта для многосвязной области можно построить
элементарно в операторах Шварца,
В самом деле, если известен регуляризующий множитель, то
задачу Гильберта C7.25) можно свести к равносильной задаче А
C7.27^'). Таким образом, вопрос сводится к построению
решения задачи А. Ограничимся пока случаем, когда х ^ т, а все
точки z\y Z2, ..., г,п, входящие в C7.26), попарно различны.

388 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Peiuewie задачи C7.27^0 ищем в виде
х-т т
F (г) = ^(г) + /Ро + Х; ^ + j; -^, C7.28)
где 4^B)—новая неизвестная аналитическая в D+ функция,
ро — произвольная действительная постоянная, \ih,^h —
неопределенные комплексные постоянные. Подставляя выражение для
F{z) из C7.28) в C7.27"^, получим краевую задачу Шварца
для функции ^{z)\
x-m т
Re^(f) = iAi- у Rei^-V Re-^, / s L. C7.29)
Ее решение, согласно постановке исходной задачи, должно быть
однозначным в Z)+, поэтому для правой части равенства C7.29)
должны выполняться условия C7.20):
^Sfw"/^^^'^'' (/=1, 2, .... m). C7.30)
А-1 L k'-X L
L
Полученные равенства образуют систему уравнений*),
линейных относительно Re \лк, Im jift, Re v^, Im va. Подставляя
решение задачи C7.29) в C7.30), получим искомое общее решение
задачи А:
л — г/г т
,-, ^^ ^x'-^k
j,s{^-Y^^4-t^^-^- C7.31)
Функция F{z) однозначна, если \ih и v^ связаны равецствами
C7.30). При c(t)=0 формула C7.31) дает решение Q{2)
задачи Ао. Если, кроме того, т = 0 (область D+ односвязна), то
все Xk и (Lift —нули, система C7.30) отсутствует, а C7.31)
переходит в B7.80 •
*) Здесь мы не исследуем разрешимость системы C7.30). Ниже (п. 37.8)
будет показано, что при х ^ m число решений задачи Гильберта / =»
= 2у- —ш + 1. Отсюда будет следовать, что ранг матрицы системы C7.32)
равен т, т. е. числу уравнений.

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 389
Сравнивая C7.27) и C7.27''), находим общее решение f{z)
задачи Гильберта C7.25):
т
f (г) = z^-^ II {Z, - z) е^У (^^F (г), C7.32)
где в случае с(/)^ О следует заменить F{z) на Q{z).
Формула C7.32) обобщает на случай многосвязной области
формулу B9.11), дающую общее решение задачи Гильберта для
односвязной области.
Опираясь на существование регуляризующего множителя,
докажем в заключение этого пункта один важный результат,
используемый в дальнейшем:
При X < О однородная задача Гильберта
Re (МО/(/)} = О C7.33)
не имеет нетривиальных решений.
Допустим, что задача C7.33) при х < О имеет нетривиальное
решение /(г). Установим прежде вСего с помощью принципа
симметрии, что это решение необходимо имеет конечное число
нулей и все эти нули имеют целые конечные кратности. В самом
деле, разделив краевое условие C7.33) на регуляризующий
множитель p{t), можем свести задачу C7.33) к задаче Aq:
Re Q @ = 0. C7.330
Так как p{t)> О, то утверждение о нулях достаточно доказать
аля функции Q{z). Пусть t = t(t)—предельное значение
функции Z = t{w)y взаимно однозначно и конформно отображающей
область G+, ограниченную окружностями, на область D+
Подставляя t = t(i) в C7.33'), получим
ReQ[/(S)] = 0.
Из последнего вытекает, что Q{z) отображает окружности на
мнимую ось. Следовательно, функцию Q[t{w)] можно по
принципу симметрии аналитически продолжить через граничные
окружности. Поэтому Q[t{w)], а значит, и Q{z) имеют конечное
число нулей и эти нули имеют целые конечные кратности.
Таким образом, утверждение о нулях решения задачи C7.33)
доказано.
Пусть N+ и No — числа нулей (с учетом кратностей)
некоторого решения задачи C7.33) в D+ и на L соответственно.
Перепишем равенство C7.33) в виде
W)f{t)~^X{t)fJ).

890 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ 1ГЛ. V
Беря индекс обеих частей последнего равенства и опираясь на
принцип аргумента (п. 12.2), получим
- X + yV+ + Л^о/2 = X ~ Л^+ - yVo/2.
Отсюда
x=A^+ + yVo/2>0,
что противоречит предположению х •< 0. Предложение
доказано.
37.5. О нахождении регуляризующего множителя в случае
многосвязной области. Если область D+ односвязна (т = 0), то
регуляризующий множитель p{t) функции 'k{t)^= а + ib
определяется формулами B8.9) — B8.11). Его нахождение сводится
в этом случае к решению задачи Шварца для области D+
Последнее утверждение становится, вообще говоря,
неверным, если область D+ многосвязна (т > 0). В самом деле,
исходя из определения, данного в п. 28.2, легко показать, что
регуляризующий множитель при m > О, вообще говоря, не
существует. Если же исходить из более общего определения
регуляризующего множителя, данного в п. 37.4 (формула C7.26)), то
регуляризующий множитель хотя и существует, но его
вычисление уже значительно сложнее, чем для случая односвязной
области.
Переходя к рассмотрению вопроса, предположим, что в
задаче Гильберта C7,25) функция kit) приведена к такому виду,
когда |Х@|^ 1, а индекс функции X{t) вдоль каждой из
внутренних кривых Li, L2y ,.. у Lm равен нулю. Будем искать
положительный регуляризующий множитель p(t), исходя из
равенства
т
p{t)k{t) = t''-"'l[{^k-t)e'y^'\ t^L C7.26)
Регуляризующий множитель p{t) будет найден, если будут
определены лежащие в области D+ точки Z\, гг, ..., г^ и
однозначная аналитическая в D+ функция y{z).
Для нахождения упомянутых величин выделим аргументы
обеих частей равенства C7.26). На внешней кривой Lq контура
L имеем
т
arg X (О = (х - /п) arg / + Z arg {z^ - О + Re y (О, i ^ U C7.34')
Здесь под аргументами понимаются произвольно
зафиксированные ветви, непрерывно изменяющиеся и имеющие разрыв в
некоторой лежащей на Lq точке, принятой за начальную точку
обхода. На каждой из внутренних кривых Li, L2, . • •, ^m контура
I. можно выделить непрерывные ветви аргументов Sivgi{t), arg/,

§ 3f\ ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 391
arg(/ — Zh). Они могут быть выбраны независимо одна от
другой. Таким образом, на внутренней кривой Ly контура L из
C7.26) получим
т
2irgX{t) = {K'-m)argt+ Xi ^rg{zk — t) +
+ Re Y (t) + 2nAZv, t^Ly (v = 1, 2, ..., m), C7.34'0
где Mv — некоторое целое число, свое для каждой кривой Ly.
Числа Пу возникают от того, что функция Кеу@ определена
с точностью до постоянной, одной и той же для всех кривых
контура L. Эта постоянная однозначно определяется равенством
C7.34^. Таким образом, входящая в C7.34^^) функция Rev (О
не содержит произвольных элементов. Поскольку ветви argX(t),
arg/, eirg(Zk — t) фиксируются произвольно на каждой кривой
Lv контура L, то без слагаемого йлпу равенство C7.34^') будет,
вообще говоря, неверным. Используя функции
( 1, если t^Ly, (v = 1, 2, ..., m);
р^ (/) = {' ' ' ' '' C7.14)
^ ^ (, О на остальных кривых, ^
равенства C7.34') и C7.34'^) можно объединить в одно
равенство, справедливое на всем контуре L:
т
argA,(О == (х — т) arg/ + 2 argiZk — t) + Re y@ +
fc-i
+ 2я1;луру@, t^L C7.34)
v-l
Входящая в это равенство функция Re у (О должна быть
действительной частью однозначной аналитической функции y{z).
Поэтому для Rev (О должны выполняться условия C7.20).
Учитывая это, умножим C7.34) на aj{t) и проинтегрируем вдоль L
Получим
V \ arg {Zk — t) а/ (/) ^5 + 2я V AZv \ Pv (О ^i (О ds =
= 5 argЯ@а;(Оd5- (х-тM argta; {t)ds C7.35)
L L
(/=1,2, ..., m).
В полученной системе уравнений неизвестными являются целые
числа Пи П2у ... у ПтП точки гь ^2, ..., г^. Э. и. 3 в е р о в и ч 5),
[9] доказал, что система C7.35) имеет решение и указал

892 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ 1ГЛ. V
алгоритм, позволяющий с помощью аппарата 0-функции
построить это решение. Однако рассуждения основаны на
сложной теории, поэтому их не приводим.
Предполол<им, что система C7.35) решена. Подставляя ее
решение в C7.34), находим функцию Rey{t), которая в силу
C7.35) является действительной частью предельного значения
однозначной аналитической функции у (г):
[т m "I
argA (О - (х - m)arg/ - Ц агд(г^ - /) - 2я 2 /^vPv (О •
Здесь S — оператор Шварца.
Подставляя найденные значения Zu г2, ..., ^щ и у('2^) в ра-
венство C7.26) и беря модули обеих частей этого равенства,
находим искомый регуляризующий множитель
т
p{t)^\tr"'Ti\Zk-t\e-^^^^^\ C7.350
Некоторые результаты, полученные с использованием этого
множителя, уже изложены в п. 37.4. Следует отметить, что
использование метода регуляризующего множителя позволяет решить
задачу Гильберта и в том случае, когда граница L области D+
не является гладкой.
Вычисление числа решений и условий разрешимости задачи
Гильберта с помощью метода регуляризующего множителя
требует привлечения аппарата теории функций на римановых
поверхностях. Чтобы избежать этого, мы переходим к
исследованию задачи Гильберта методом интегральных уравнений. Метод
интегральных уравнений позволяет получить картину
разрешимости задачи Гильберта сравнительно простыми средствами, но
его обоснование требует, чтобы граница области Z)+ состояла из
кривых Ляпунова.
37.6. Интегральное уравнение задачи Гильберта. Будем
искать решение задачи Гильберта
Re {[а E) - ib {s)\ F {t)) == с {s) C7.36)
в виде интеграла типа Коши с действительной плотностью
П^)-М^^^'^' C7.37)
L
Согласно исследованиям п. 37Л (формула C7.7)) такое
представление возможно, причем С определяется по функции F{z)
однозначно, а плотность \k{s)— с точностью до постоянного ела*
гаемого на каждом внутреннем контуре.

<^ 37] ЗАДАЧА ГИЛЬБЕРТ:А ДЛЯ многосвязной ОБЛАСТИ 893
Чтобы упростить дальнейшее исследование, представим
слагаемое С в виде интеграла от плотности jn. Выделим
какой-нибудь из внутренних контуров, например L^, и аддитивную
постоянную, с точностью до которой определена плотность |uiE)
на Lm, определим условием, чтобы выполнялось равенство
С = \\1{(у) da.
Подставляя это выражение для С в формулу C7.37), получим
^ (^) = i S T:?F ^^ + ^* S ^^(^) ^^' C7.370
причем плотность |i вполне определена на контуре L^, а на
остальных KOHTypaJc определяется с точностью до слагаемого
вида
где Cj — произвольные действительные постоянные, а
(\ при /sL/ (у=1, 2, ..., т— 1),
р (s) = j^ ^ ^ ^ ' ' ' ^' C7.38)
^^ ^ ^ (, О на остальных кривых. ^ ^
Беря по формуле Сохоцкого предельное значение функции
C7.370 и подставляя в краевое условие C7.36), получим для
определения ii(s) интегральное уравнение
a{s)^.{s) + R.[^^'^-f^'^\-^d.^
+
+ 26 E) J ^1 (а) da = 2с (s), C7.39)
которое будет исследовано позже (п. 37.8).
37.7. Союзное интегральное уравнение и союзная задача
Гильберта. Для исследования вопросов разрешимости
интегрального уравнения C7.39) составим союзное ему уравнение.
Для этого перейдем к действительным переменным, полагая
t = t (s), т = т (а), dx = т' (а) da,
и представим последний интеграл левой части уравнения C7.39)
в виде
2 ^b{s)f^^{a)ix{a)da.

394 РАЗЛИЧНЫЕ OБOБlДEIiHЫE КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Однородное уравнение, союзное уравнению C7.39), можно
записать тогда так:
a(s)v(.)-Re{il[flJ^iHL^
= -2f^rn{s)\b{a)v{o)da. C7.390
L
Интегральное уравнение C7.39^ будем рассматривать как
составленное для решения некоторой задачи Гильберта, подобно
тому, как для решения задачи C7.36) было составлено
уравнение C7.39).
т
Рассмотрим интеграл типа Коши, определенный в J] ^Г,
L
Тогда на основании формул Сохоцкого, примененных к каждой
из областей D/", уравнение C7,39^ можно записать в виде
Re [f is) Ф it)] = - 2^^ (s) J 6 (a) V (a) da. C7.41)
L
По условию функция Ф{г)у заданная формулой C7.40),
определена в дополнительной по отношению к D+ области.
Следовательно, равенства C7.41) представляют собой краевые условия
задач Гильберта для т + 1 односвязных областей: Df, ДГ, . •.
..., Dm, лежащих внутри кривых Li, ..., L,n, и Do",лежащей вне
кривой Lq. Из них задачи для областей Df, ..., Dm-\ будут
внутренними однородными, для области Dm внутренней
неоднородной и для области Do" внешней однородной.
Покажем, что все краевые задачи C7.41) могут иметь только
нулевое решение. Рассмотрим интегралы
г
Ч^У (г) = 5 Ф(т)dr, z^DJ (/ = 0,1,..., m), C7.4Г)
и
где ФB:)—решение задачи C7.41), а путь интегрирования не
выходит за пределы DJ + L/. При z-= t ^L-^ (/ = 1» 2, ...
,.., m—-1), предполагая путь интегрирования взятым по L^

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МИОГОСВЯЗНОЙ ОБЛАСТИ 395
С учетом краевого условия C7.41), будем иметь
t t
Re4^^0= \ Не[Ф(т)тЧа)] da^^Q - do-=0. C7.41^0
Ч Ч
Из последних равенств следует, что Ч^/ (г) ^ О (/ = 1, 2, ..., w — 1),
поэтому Ф (г) ^ О при z^iDJ (/ = 1, 2, ..., m — 1).
В случае j = т из C7.41) и из C7.4Г) имеем
t
Re Ч^^ (t) = J Re [Ф (т) х' (а)] da = - 2 J 6 (а) v (а) da • дл. дуги /у/.
^/ ^
Левая часть последнего равенства есть функция однозначная,
в правой же части дуга может меняться в зависимости от числа
обходов по кривой Lj, поэтому последнее равенство возможно
только при выполнении условия
J&(a)v(a)da = 0. C7.42)
Таким образом, Re ^m{t) =0, t ^ L^, и, следовательно,
Wm{z) = ic. Подставляя в C7.4Г) и дифференцируя, получим
Ф(г)= О при Z е D^.
Перейдем, наконец, к области Do , Разлагая интеграл C7.40)
в ряд в окрестности бесконечно удаленной точки и учитывая
равенство C7.42), получим
^(^)==ii\^(<')''i<')do'Y+ ••• C7.43)
L
Отсюда по теореме о вычетах
^0{t)dt = -2^a{o)v{a)da,
откуда
ImJ O{t)dt = 0.
и
Но из равенства C7.4 Г^) при / = О следует, что Re \ ф(<)Л =
= 0; следовательно, \ Ф (/) d/= 0. Последнее равенство доказы-
и
вает однозначность функции ^q{z), определенной равенством
C7.4Г) в Do, Поскольку ReVo@= О при t ^ Ц, то ФB:)^ О
в Do".

396 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Таким образом, мы доказали, что ф(г)^ О для любой точки
дополнения D+ до полной плоскости. Отсюда следует, что
плотность интеграла типа Коши C7.40) есть краевое значение
некоторой функции ф+(г), аналитической в D+, т. е.
Исключая отсюда vE), получим
Re {if (s) [а is) + ib {s)] ф+ (t)} = 0. C7.44)
Последнее равенство есть краевое условие задачи Гильберта
относительно функции ф+('г). Эту задачу будем называть
союзной по отношению к данной задаче Гильберта C7.36).
37.8, Исследование вопросов разрешимости. Решив
интегральное уравнение C7.39), мы по формуле C7.37^) найдем
все решения краевой задачи Гильберта C7.36). Поэтому
исследование вопросов разрешимости краевой задачи сводится в
первую очередь к исследованию разрешимости интегрального
уравнения и затем к выяснению вопроса, всякому ли решению
интегрального уравнения соответствует решение (ненулевое)
краевой задачи.
Рассмотрим однородное интегральное уравнение
a{s)Yi{s) +
+
ReUa{s)-ib{s)]-^\^dx\ + 2b{s)\ |x(a)da = 0, C7.45)
соответствующее однородной краевой задаче Гильберта (сE)=н
^0). Прежде всего покажем, что уравнение C7.45) имеет
т — 1 ненулевых решений, которым соответствуют нулевые
(F{z)^ 0) решения краевой задачи.
В самом деле, уравнение C7.45) можно записать в виде
ИтКе|[аE)--/И5)]Г2^7$1^ n(a)daj| = 0.
Рассуждая совершенно так же, как в п. 37.1 при решении
уравнения C7.4^), придем к тому, что функции
п„р„ <..,«=., 2 ж-а
^^ ^ (^0 на остальных кривых
являются решениями уравнения C7.45).
При этих значениях ii{s) формула C7.37') дает функцию
F(z)y тождественно равную нулю. Отсюда следует, что число

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 397
решений краевой задачи Гильберта на т — 1 меньше числа
решений соответствуюш^его интегрального уравнения.
Пусть k — число решений интегрального уравнения C7.45)
и / — число решений соответствующей (однородной) задачи
Гильберта. На основании только что сказанного
k--l = m-\. C7.46)
Обозначим k\ Г соответствующие числа для союзных
интегрального уравнения и задачи Гильберта. Согласно равенству
(*) каждому решению союзного интегрального уравнения
C7.39^) соответствует определенное (ненулевое) решение
союзной краевой задачи Гильберта. Следовательно, будем иметь
k' = V. C7.47)
Подсчитаем индекс интегрального уравнения C7.45). Для
этого выделим его характеристическую часть. Так как (см. § 10)
ТО интегральное уравнение C7.45) можно записать в виде
a{s)y.{s)^^\v.{a)^+^\y.{o)dQ + 2b{s)\ fi(a)da = 0.
Интеграл \ [x(a)d9 представляет собой потенциал двойного
L
СЛОЯ и при сделанном предположении относительно контура
(кривые Ляпунова) не является особым. Особый интеграл даст
член \\i{o)-^. Можно было бы, исходя из геометрических
соображений, доказать, что — = -2^^g—^ + фредгольмово
ядро, и таким образом свести уравнение C7.45) к уравнению
с ядром Гильберта (действительному). Однако проще выделить
характеристическую часть с ядром Коши. Для этого вычтем и
прибавим член
L
Получим
/ \ / \ b(s) [ \к(а) , , а E) + ib is) { / ч ^л i
a{s)\i{s) ^37^^^+ п j^M^9 +
L L
-f 26E) 5 ^(а)йГа = 0.

398 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗЛДЛЧИ [ГЛ. V
Коэффициент соответствующей задачи Римана имеет вид
(п. 21.1)
Р (f\ _ fl {s) + ib (s)
^ ^^^ "" a (s) - ib (s) •
Следовательно, индекс уравнения будет равен
¦"Ofi^-^x. C7.48)
Вычислим еще индекс у/ союзной задачи Гильберта C7,44);
у! = Ind {V [а (s) - ib (s)]} = - Ind f - x.
Как уже указывалось, f =:-^ = е^^, где а — угол, образованный
касательной к контуру с осью абсцисс. Когда точка / обходит
в положительном направлении внешний контур, аргумент f
получает приращение 2я, а когда внутренний контур, —2я; поэтому
Ind t^ = I — m и, следовательно,
>«' = -x + m-l. C7.49)
Определение. Ind/^, т.е. число полных оборотов
касательной к контуру при обходе контура в положительном
направлении, назовем угловым порядком области.
Угловой порядок рассматриваемой здесь области равен
1 — т.
Соотношение C7.49) можно формулировать так: индекс
союзной задачи Гильберта равен сумме индекса данной задачи
Гильберта и углового порядка области, взятых с обратными
знаками.
На основании третьей теоремы Нётера (п. 23.2) будем иметь
Учитывая соотношения C7.46), C7.47), C7.49), получим
/-r = fe-/^'-(m-l) = 2x-(m-l) = x~K', C7.50)
т. е. разность числа реигений союзных задач Гильберта равна
разности их индексов.
Это — основной результат, который может быть получен из
теории интегральных уравнений.
Используем теперь еще результат, полученный в п. 37.4 при
непосредственном изучении самой краевой задачи:-
Краевая задача с отрицательным индексом неразреилима,
т, е. I =^ О при X < О, а Г = О при у! < 0.
Отсюда имеем, что при х < О неразрешима данная
однородная задача Гильберта, а при х > m — 1 неразрешимой будет

* 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 399
союзная задача (а следовательно, и союзное особое
интегральное уравнение).
Используя еще вторую теорему Нётера о разрешимости
неоднородного особого уравнения, получим следующий результат.
Теорем а. Разность между числом решений однородных
задач Гильберта C7.24) и C7.44) равна
/~-Г = 2к-т + 1. C7.50')
Если X < О или X > m — 1, то
/ = тах@, 2х-т+1}. C7.51)
Для разрешимости неоднородной задачи Гильберта C7.24)
необходимо и достаточно, чтобы выполнялись равенства
\c{s)[a{s) + ib{s)U-^{t)dt = Q (/=1, 2, ..., Г),
L
где ф^ (О -~ линейно независимые решения союзной однородной
задачи Гильберта C7.44).
Содержащийся в формуле C7.51) результат может быть
сформулирован так:
Если индекс задачи больше углового порядка области с
обратным знаком, то число решений задачи равно сумме
удвоенного индекса задачи и порядка области.
Полученный в гл. IV результат о числе решений ,задачи
Гильберта для односвязной области (т = 0) входит в
сформулированный выше результат как частный случай.
Таким образом, полностью исследованы случаи х < О и х >
> m — 1. Остаются еще не изученными случаи *) О ^ х ^
^ m — 1, к которым мы и переходим.
37.9. Исследование случаев х = 0 и х = т-~1. Здесь
придется видоизменить примененные ранее методы. Заметим прежде
всего следующее. В п. 37.4 (формула C7.32)) было показано,
что в случае Ind(a + ib)'^ О существование однозначного регу-
ляризующегб множителя является достаточным условием
разрешимости однородной задачи Гильберта Re[(a —/6)F(/)] = 0.
Легко усмотреть, что при Ind(a + ib)= О существование такого
множителя является также необходимым условием
разрешимости этой задачи. Действительно, если такого множителя не
существует, то левая часть краевого условия не может быть
представлена как действительная часть однозначной аналитической
в области функции и, следовательно, решение задачи Гильберта
в однозначных аналитических функциях невозможно.
*) И- Н. Век у а назвал эти случаи особыми (см. [2]).

400 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ 1ГЛ. V
Лемма. Кро^е^ия задача Гильберта
Re[e^^(^)f @] = 0, C7.52)
где
h{s)==0 на Lq, л(s) = Лу = const на Lj (/== 1, 2, ..., m),
C7.53)
причем
-у<Л/<у C7.54)
разрешима тогда и только тогда, когда h{s) ^ 0.
Доказательство. Пусть р{s) есть регуляризующий
множитель задачи, так что выполняется равенство
p(s)e^ftE) = e^*Y@.
Согласно рассуждениям п. 37.5 отыскание регуляризующего
множителя равносильно отысканию аналитической и однозначной
функции y(z) по краевому условию Rey{t)^= h{s). На
основании теоремы единственности видоизмененной задачи Дирихле
(п. 37.1) Кеу(^)^ 0. Отсюда и h(s)^ О, что и требовалось
доказать.
Заметим, что путем изменения в случае надобности знака
в краевом условии C7.52), что равносильно умножению
равенства на е~^\ всегда можно достигнуть того, чтобы hj
удовлетворяли условию C7.54).
Перейдем теперь к рассмотрению основного вопроса.
А. Пусть X = Ind[aE) +;6(s)] = 0. Будем искать
регуляризующий множитель в классе однозначных функций. Отыскание
множителя, как известно, равносильно отысканию аналитической
функции у (г) по краевому значению ее действительной части
(o(s). Так как решение этой задачи в классе однозначных
функций, вообще говоря, невозможно, то сведем вопрос к
видоизмененной задаче Дирихле.
Положим
а (s) + ib (s) = е'^ ^'^ = ^-^^ ^'У ^^ (^)+л (^П,
где h{s) определяется выражениями C7.53). Согласно
исследованиям п. 37.1 можно найти однозначную аналитическую
функцию y('^)» действительная часть которой на контуре принимает
значение o)(s)+ftE) {hj не задаются заранее). На основании
этого краевое условие однородной задачи Гильберта можно
привести к виду
Re W^ ^'^е-^У (^)F (t)] = О, C7.55)
причем все hj однозначно определяются и удовлетворяют
условию C7.54).

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 401
Если В последнем выражении A(s)^0, то будем говорить,
чт# удовлетворяются условия однозначности. Если же хотя бы
одна hj отлична от нуля, то будем считать условия
однозначности невыполненными. Рассмотрим эти случаи.
1. Условия однозначности не выполнены
(Л(/)#0). В силу леммы однородная задача Гильберта не
имеет решений, т. е. / = 0. Отсюда по формуле C7.50) V =
= k^ =: т— 1. Следовательно, в этом случае неоднородная
задача разрешима тогда и только тогда, когда выполнены т — 1
условий ортогональности.
2. Условия однозначности выполнены (/г(/)^0).
Тогда однородная краевая задача имеет одно решение, Z = L
Отсюда Г = &' = т. Следовательно, неоднородная задача
разрешима при выполнении т условий.
Б. Пусть теперь х = т—1. Тогда на основании формулы
C7.49) х' = 0.
Проведем рассуждение, аналогичное предыдущему, по
отношению к союзной задаче Гильберта.
Здесь снова будут иметь место два случая.
1. Для союзной задачи условия однозначности не
выполнены. Тогда Г == fe' = О, I = т — 1. В этом случае однородная
и неоднородная задачи Гильберта будут безусловно разрешимы
и первая будет иметь т — 1 линейно независимых решений.
2. Условия однозначности для союзной задачи выполнены.
Тогда Г = fe' = 1, / = т. Здесь однородная задача Гильберта
имеет т решений. Для разрешимости неоднородной задачи
необходимо и достаточно выполнения одного условия
ортогональности.
Чтобы правильно оценить результаты, полученные в
настоящем пункте, нужно учесть, что вопрос о том, выполнены или нет
условия однозначности, может быть решен независимо от ин*
тегральных уравнений. Поясним это подробнее.
Равенство всех hj нулю означает, что заданная функция
coE) = arctg—Ш- есть краевое значение действительной части
функции yiz), аналитической и однозначной в Z)+. Если
отыскивать функцию y{z) с помощью оператора Шварца, то в силу
единственности получим ту же функцию, что была получена из
решения видоизмененной задачи Дирихле. При этом должны
выполняться условия однозначности C7.30). Выполнение
последних, очевидно, равносильно равенству нулю всех hj.
Функции aj{s)y входящие в условия C7.30), не зависят от условий
краевой задачи, а зависят только от вида контура L (см.
формулы C7.13) и C7.14')) и могут быть поэтому определены без
решения интегральных уравнений задачи.
Поясним сказанное примером.

402 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ (ГЛ. V
Пусть заданная область D+ есть кольцо между двумя концентрическими
окружностями q <, \z\ < 1. Заметим, что всякая двусвязная область может
быть приведена к этому частному случаю конформным отображением (при
соответствующем подборе q) *).
Рассмотрим краевую задачу Гильберта
Re [(а - ib) F (/)] = с
с нулевым индексом.
Определим сначала функции ^j(z) согласно условиям C7.14). Здесь
m = 1. Непосредственная проверка показывает, что гармоническая в кольце
функция р1, обращающаяся в единицу на внутренней окружности и в нуль на
внешней, может быть определена в полярных координатах равенством
Pi(r,e)=:-i^Inr.
\_
\nq*
, имеем
на Lo а, A, 6) = -^
на L, а.(<?,е) = -^
5Р> 1
Г-1 ^^ 1
Г-д or |^_1
q\nq'
Выпишем теперь условие однозначности C7.30). Тогда da = dQ на Lo и
интегрирование ведется от О до 2я, а на Li а = Bп — d)q, da = ¦— q dB
с пределами интегрирования Bя, 0). Переставляя в последнем интеграле
пределы интегрирования и обозначая значения arctg —^^ на Lq и Lj
соответственно ©о F) и ©1 F), получим
2л 2Я
_5_Lcoo(e)de + 5^1co.(e),rfe = o
О О
или
2Я 2Я
о
Учитывая, что последние величины дают начальные коэффициенты
a^Q\ а^^^ разложения соответствующих функций в ряды Фурье, получим
следующий результат:
Если в разложениях функции arctg—^ на окружностях \z\= \ и
\z\ = q в ряды Фурье начальные коэффициенты a{f\ а^^ разложений
совпадают, то обе однородные союзные задачи Гильберта имеют по одному
решению-, неоднородные же задачи разрешимы при выполнении одного условия.
Если эти коэффициенты различны, то однородные союзные задачи
неразрешимы, а неоднородные разрешимы безусловно и однозначно.
Сформулируем еще результаты для случая трехсвязной области m = 2,
/ —/'= 2х—1.
I. X < 0. Однородная задача неразрешима. Неоднородная задача
разрешима при выполнении 1 — 2>с условий.
*) См., например, М. В. Келдыш 1).

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 403
II. X > 1. Однородная задача имеет 2х — 1 решении. Неоднородная
задача безусловно разрешима.
III. х = 0, / —Г = —1.
1) Условия однозначности для функции а + ib выполнены.
Однородная задача имеет одно решение, неоднородная разрешима при
выполнении двух условий.
2) Условия однозначности для функции а + ib не выполнены.
Однородная задача неразрешима, неоднородная разрешима при
выполнении одного условия.
IV. х= 1, / —Г = 1.
1) Условия однозначности для функции Г(а — ib) выполнены.
Однородная задача имеет два решения, неоднородная разрешима при
выполнении одного условия.
2) Условия однозначности для V{a — ib) не выполнены.
Однородная задача имеет одно решение, неоднородная безусловно
разрешима.
Таким образом, для двусвязных и трехсвязных областей исследование
задачи Гильберта можно считать законченным. Для m > 2 остаются
неисследованными т — 2 случаев 1 ^ х ^ m — 2.
37.10. Связь с отображением на плоскость с разрезами.
Изложим теперь некоторые соображения относительно
разрешимости задачи Гильберта для оставшихся неисследованными
случаев О < X < т— 1.
Пусть индекс задачи равен единице и для функции а + ib
выполнены условия однозначности. Тогда краевое условие
однородной задачи может быть приведено к виду
Re[^] = a C7.56)
Эта задача имеет очевидное решение f (г)= iCz. Но существует
F iz)
ли такое решение задачи, что—--^ф const? Если такое решение
существует, то в силу условия C7.56) функция со B:) = —^ на
контуре L принимает чисто мнимые значения. Геометрически
это означает, что в этом случае существует аналитическая
однозначная функция О)(г), отображающая область Z), ограниченную
данным контуром L, на плоскость с прямолинейными разрезами,
расположенными вдоль мнимой оси, и имеющая простой полюс
в начале координат.
Обратно, если существует функция со (г), производящая
указанное отображение, то задача Гильберта C7.56) имеет t5oлee
одного решения. Таким образом, вопрос о числе решений
рассматриваемой краевой задачи оказывается тесно связанным
с геометрическими свойствами области.
Известно *) из теории конформного отображения, что
существует функция, отображающая конформно любую многосвязную
область на плоскость с прямолинейными разрезами, параллель-
*) См., например, М. В. Келдыш 1).

404 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
ными некоторой прямой; но эти разрезы, вообще говоря, не
лежат на одной прямой.
Определение. Если многосвязная область D
отображается аналитической однозначной функцией, имеющей простой
полюс в начале, на плоскость с разрезами, лежащими на одной
прямой, то будем говорить, что D есть область типа D^. В
противном случае D не будет областью типа D^.
Легко показать, что существуют области типа Z)° любой
конечной связности. Например, если область имеет ось симметрии,
разбивающую ее на две односвязные области, то она типа Z)°.
В этом легко убедиться, отображая часть области, лежащую по
одну сторону оси симметрии, на полуплоскость и пользуясь
принципом симметрии. Известно*), что двусвязные и трехсвязные
области принадлежат типу D^. Это можно легко получить из
высказанного выше соображения, так как всякую двусвязную и
трехсвязную область можно отобразить на круговую область,
имеющую ось симметрии.
Для областей типа D^ можно вывести следующий точный
результат о числе решений задачи Гильберта.
Теорема. Если область типа D^ и выполняются условия
однозначности C7.30), то однородная краевая задача Гильберта
с индексом О ^ к ^ т имеет / = х + 1 линейно независимых
решений.
Доказательство. На основании предыдущего в
рассматриваемом случае краевое условие можно привести к
следующему виду:
Re[r^F@] = 0. C7.57)
Задачу, выражаемую последним краевым условием, можно
сформулировать так: определить функцию Q(z), однозначную в Z) и
аналитическую в ней, кроме начала координат, где допустим
полюс порядка не выше х, действительная часть которой на
контуре равна нулю. Это — задача, которую мы в п. 37.4 называли
задачей Ао, но с дополнительным ограничением об
однозначности решения. Оказывается, что для областей типа D^ функцию
Q (г) легко построить.
Пусть (i)(z)= и + iv отображает область D на плоскость
с прямолинейными разрезами вдоль действительной оси, причем
нуль переходит в бесконечно удаленную точку. Для
однозначной определенности потребуем еще, чтобы контур Lq
отображался в отрезок оси между точками О и 1.
Тогда функции
Wu {2) - / [со (zt (й = О, 1, ..., х) C7.58)
*) См. С. А. Чаплыгин, К теории триплана, Собр. соч., т. II, 1948.

§ 37] ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 405
будут являться решением задачи. В самом деле, эти функции
будут иметь в начале координат полюс порядка не выше х и,
кроме того, на контуре в силу свойства функции со (г) будет
Im (О (О = V (/) == 0. Поэтому
Re [Wk it)] = Re {/ [и (/) + iv {tt} = Re {/ [u {t)]'} = 0.
Заметим сразу же, что в силу постановки задачи C7.57), если
некоторая функция Ф(^) является ее решением для некоторого
к = хо, то она будет решением также при любом к > хо.
Докажем теперь, что, кроме полученных х + 1 решений,
которые, очевидно, будут линейно независимыми, нет других
решений. Допустим противное, что при некотором хо (О ^ хо ^ пг)
существует еще одно решение Ф(г). Тогда в силу сделанного
выше замечания оно будет решением также и для к = т. От-
сюда следует, что задача при к ^= т имеет m + 2 линейно не-
зависимых решений
Го (г), W,{z), ..., Wmiz), Ф{г).
Но это противоречит установленному ранее (п. 37.8) факту, что
при к = т задача имеет 2т—(т— 1)= m + 1 решений.
Теорема доказана.
Общее решение Q (z) будет иметь вид
Q{z) = it h(^4z\ C7.59)
где Pft — произвольные действительные постоянные.
По формуле C7.50) будем иметь
Г == / — 2х + (т — 1) = /п — X.
Следовательно, неоднородная задача Гильберта в
рассматриваемом случае будет разрешима при соблюдении т — х условий.
Выскажем некоторые общие соображения по поводу
полученных результатов.
Было установлено, что для значений х<:0 и х>т — 1
вопросы разрешимости задачи Гильберта зависят только от
величины этого индекса. В случаях х = 0 и х = т — 1 дело обстоит
сложнее и для исследования разрешимости приходится
привлекать еще другую характеристику — условие однозначности. Для
каждого из рассматриваемых двух случаев возможны два под-
случая в зависимости от того, выполняются или не выполняются
условия однозначности.
Обе величины, характеризующие разрешимость (индекс и
условие однозначности), сами зависят от вида контура, и
поэтому вопросы разрешимости задачи Гильберта так или иначе
связаны с геометрическими свойствами области. Но при х :^ О

406 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРЛЕВРЛЕ ЗАДЛЧИ [ГЛ. V
И К ^ т — 1 оказывают влияние лишь те свойства области,
которые определяют индекс а + ib и значения Vj (формулы
C7.19)).
Иначе обстоит дело в случаях О < к << т—1. Здесь, как
показано в настоящем пункте, в исследовании разрешимости
задачи Гильберта участвует еще третья характеристика —
принадлежность или непринадлежность области к типу D°. Для
областей Z)° в случае соблюдения условий однозначности вопросы
разрешимости были решены исчерпывающим образом.
Для О < X < m — 1 остались неисследованными еще три
случая.
I. Область не принадлежит к типу D®:
а) Условия однозначности выполняются.
б) Условия однозначности не выполняются.
II. Область принадлежит к типу D°:
Условия однозначности не выполняются.
Остается пока не ясным, является ли принадлежность или
непринадлежность области к типу D^ единственной
дополнительной геометрической характеристикой, оказывающей влияние
на разрешимость задачи Гильберта, или же имеются еще и
другие характеристики. Полученные для двусвязных и трехсвязных
областей законченные результаты показывают, что для этих
областей принадлежность их к типу D^ играет решающую роль.
37.11. Заключительные замечания. Читатель, знающий из
гл. IV, какой законченный вид имеет решение задачи Гильберта
для односвязной области, испытает после чтения настоящего
параграфа некоторое разочарование. Различные методы
исследования и наличие неисследованных случаев О < х < m — 1
показывают на незавершенность решения.
Может возникнуть вопрос, идет ли здесь речь о
незаконченности исследования, или о невозможности дать более
определенные результаты. В несравненно большей степени
неопределенными были результаты, относящиеся к обобщенным задачам,
рассмотренным в первых параграфах главы, но там мы считали
такое положение соответствующим природе вопроса. Не обстоит
ли и здесь дело таким же образом? Я думаю, что это не так.
Между вопросами, изложенными в первых параграфах главы, и
предметом настоящего параграфа имеется принципиальное
различие. Оно заключается в том, что для краевых задач общего
типа именно из-за их большой общности нет других методов
исследования (в общем случае), кроме сведения их к
интегральным уравнениям. Полученные там результаты содержат все, что
может быть выведено этим методом; поэтому такие результаты,
несмотря на большую их неопределенность, следует считать
законченными. Дальнейшее их усовершенствование возможно
только при рассмотрении отдельных частных случаев. Для прак-

371 ЗАДАЧА ГИЛЬБЕРТА ДЛЯ МНОГОСВЯЗНОЙ ОБЛАСТИ 407
тики ЭТО может оказаться даже очень важным, что, однако, не
меняет характера нашего общего высказывания.
Иначе обстоит дело для задачи Гильберта. Она принадлежит
к числу простейших и имеет в случае односвязной области
законченное решение методом, не связанным с интегральными
уравнениями. В случае многосвязной области этот метод тоже
применим, но в связи с возможностью многозначных решений он
не дает исчерпывающих результатов. Однако и в этом случае
первый законченный результат (неразрешимость задачи с
отрицательным индексом) получен таким методом. Дальнейшие
законченные результаты (х = О, >« ^ m — 1) получены путем
комбинирования этого метода с методом интегральных уравнений.
Существование указанного метода, независимого от
интегральных уравнений, и дает основание предполагать, что
неопределенность результатов для О < х < m — 1 вытекает не из
природы вопроса, а от незавершенности исследования, и
позволяет надеяться, что дальнейшие изыскания дадут полное
решение задачи.
37.12. Некоторые новые результаты. В последнее время исследование
случаев индекса О < х < m — 1 продвинуто вперед работами И. Н. Векуа и
Б. В. Боярского. Не имея возможности входить в подробности, приведем
основные факты, заимствуя их из книги И. Н. Векуа [2]. (Там же
помещено добавление Б. В. Боярского по рассматриваемому вопросу.)
Г. В п. 37.10 было показано, что в случае, когда условия однозначности
выполняются, при росте индекса число линейно независимых решений
однородной задачи не может убывать, т. е. 1у^^ | ^ /j^. Теперь установлено, что
этот факт имеет место в общем случае. Доказательство несложно. Оно
вытекает из того, что число решений краевой задачи Re[e'^^^^ F(t)] = 0
в классе функций с допустимым полюсом порядка х + 1, во всяком случае, не
меньше чем это число при допустимом полюсе порядка к. Но, с другой
стороны, рост числа решений не может происходить слишком быстро. Нетрудно
показать, что при увеличении индекса на единицу может прибавиться не
более чем два новых независимых решения, именно те, у которых главные части
начинаются с членов l/2^'^^ i/z^'^K Следовательно, для числа решений
получаем оценку
/х</>с+1</х + 2. C7.60)
2°. Указана точная верхняя граница числа решений
/х<х+1. C7.61)
Она получена Б. В. Боярским при помощи несложного, но остроумного
приема, заключающегося в подсчете числа решений краевой задачи, получаемой
перемножением краевых условий двух взаимно сопряженных краевых задач.
Сначала выводится неравенство /^^+ /^< /п+ Ь откуда затем на основании
C7.50) следует C7.61).
Точность оценки вытекает из наличия примеров, в которых она
достигается. Одним из таких примеров является теорема п. 37.10.
3°. Исследование разрешимости краевой задачи можно свести к
исследованию разрешимости некоторой системы р линейных алгебраических
уравнений с 2к неизвестными. Это было показано еще Д. А, К в е с ел ав а 4). Таким
образом, подсчет числа решений краевой задачи равносилен установлению

408 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
ранга соответствующей матрицы. В тех случаях, когда этот ранг
оказывается равным 2>с, число решений задачи подсчитывается по формуле
C7.51) /х= шах@, 2х —т+1), справедливой для неисключительных
случаев индекса (п. 37.8). Б. В. Боярский установил, что сумма квадратов
модулей миноров порядка 2к исследуемой матрицы есть аналитическая функция
постоянных /ii, ..., Лт и ТОЧКИ ^о, В которой допустим полюс решения (у нас
этот полюс брался в начале координат). Таким образом, ранг матрицы
оказывается отличным от 2х лишь на множестве нулей некоторой аналитической
функции. Отсюда следует, что нарушение нормальной формы C7.51) для
числа решений происходит лишь в исключительных случаях.
4°. Подобно тому как в п. 37.10 для случая выполнения условий
однозначности была установлена связь с отображением на плоскость с разрезами
по действительной оси, в общем случае устанавливается связь с
отображениями на плоскость с радиальными разрезами.
§ 38. Обратная краевая задача для многосвязной области *)
Рассмотрим задачу, отличающуюся от рассмотренной в § 33
лишь тем, что задаваемая в плоскости w область будет
многосвязной. Соответственно этому и искомая область будет также
многосвязной.
Схема решения остается той же, что и ранее (п. 33.2), с тем
лишь различием, что здесь, в общем случае, нет канонической
области, для которой было бы известно явное выражение
оператора Шварца; поэтому задачу Шварца приходится решать
непосредственно в заданной области D^,, преодолевая трудности,
вытекающие из возможной многозначности решения.
38.1. Постановка задачи. Даны п+1 пар функций
параметра S
u = Uk{s\ v = Vk{sl O^s^k {k = 0, 1, ..., /г), C8.1)
периодических с периодами k и имеющих производные,
удовлетворяющие условию Гёльдера и не обращающиеся в нуль.
Уравнения C8.1) определяют в плоскости w = u-\-iv п+1
замкнутых кривых Lo^wy Liyjy ..., Lnw Будем считать функции «^(s),
Vhis) такими, что кривые Lkw не самопересекающиеся, а также
не пересекают друг друга. Они определяют (п + 1)-связную
область Dw в плоскости W, являясь контуром области {Lw =
Внутренняя задача. Определить в плоскости z контур
Lz, состоящий г/3 П + 1 кривых Lozy L\zy ..., Lnz {Lz = Lqz +
+ Liz+ ... +Lnz)y ограничивающих конечную область Dt
(вообще говоря, многолистную) так, чтобы, считая s длиной дуг
кривых Lkwy комплексные функции Wk{s) = Uk{s)+ivh{s) были
краевым значением аналитической функции w = w (z),
конформно отображающей область Dt на область D^j.
*) Настоящий параграф написан по работам Ф. Д. Г а х о в а 5) ц
Д^. Т. Нужина 2).

§ 38] ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА ' 409
Внешняя задача. Если в предыдущей формулировке
конечную область Dt заменить на DJ, содержащую бесконечно
удаленную точку, получим постановку внешней обратной задачи.
Будем считать для определенности, что область Dw —
конечная и что контур Lou; охватывает все остальные. Если бы
первоначально заданная область была бесконечной, лежащей вне
контуров Lft, то, взяв точку woy лежащую внутри контура Lowy
и произведя преобразование w = -^^—, пришли бы к
сформулированному случаю.
38.2. Решение внутренней задачи. Для длины дуги о
контура Lw будем иметь выражение
S
o = o{s)=^ ^/u'^{s) + v'^{s) ds. C8.2)
о
функция g{s) и ее обратная s{o) будут монотонными,
положительными и иметь производную, удовлетворяющую условию
Гёльдера.
Для функции z = z{w), производящей конформное
отображение области Da, на dJ, в силу геометрических свойств
отображения на контуре L^ будет справедливо соотношение
"^^l "^^ ^ =со(а). C8.3)
dw
^°^ ^/u'^[s(a)] + v''[s(a)]
Таким образом, решение обратной задачи свелось к решению
следующей прямой краевой задачи:
Найти аналитическую и однозначную в многосвязной обла-
dz
сти Dw функцию -^, не имеюи{ую в этой области нулей^ если ее
модуль на контуре равен данной положительной и удовлетво-
Idz
1—
гармоническая, является действительной частью аналитической
dz
функции 1п-^. Выясним характер последней в области D^.
dz dz
В силу отсутствия у -^ нулей In -^— будет аналитической
в области Dw функцией, но она не обязательно должна быть
однозначной. При обходе в области D^ по замкнутому контуру,
окружающему какой-либо внутренний контур Lkw> она может
получить приращение, кратное 2яг.
Следовательно, In -^ может быть представлена в виде
п
In -g- = Q (ш) + J] т; In (ш - шД C8.4)
/-1

4l0 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
где Q{w)—функция, аналитическая и однозначная в Dy^, nij —
целые числа, Wj — некоторые фиксированные точки внутри
контуров Ljyj.
Таким образом, задача свелась к следующей:
dz
Определить функцию 1п-^—, имеюи^ую в области D^
аналитический характер, определяемый формулой C8.4),
действительная часть которой на контуре области равна заданной функции
In co(s).
Эта задача решается с помощью оператора Шварца S (см.
п. 37.2)
п
dz Y~^ Pi
Постоянные р^ определяются формулами C7.19):
р/ = \ а/ (а) 1п 0(а) da\ C8.6)
L
y(w)— аналитическая однозначная функция.
38.3. Условия разрешимости. Сравнивая выражения C8.4) и
C8.5), видим, что формула C8.5) определяет решение
поставленной задачи только тогда, когда постоянные pj будут
кратными 2я. Следовательно, доказана
Теорема 1, Для того чтобы обратная краевая задача
в случае многосвязной области была разрешима, необходимо,
чтобы были выполнены условия
S
а J (а) In со (а) do = 2пт, {j= I, 2, ..., п\ C8.7)
L
где ntj — некоторые целые числа {положительные или
отрицательные) .
Исследуем, опираясь на геометрический смысл
рассматриваемых функций, вопрос о допустимых значениях целых
чисел nij.
Обозначим Qwy Qz углы, образуемые с осью абсцисс
касательными к контурам Ljg,, L^ и 02' — значения аргумента -^ на
контуре. Из геометрического смысла производной аналитической
функции следует равенство
9г = бку + 02'
Возьмем определенную кривую Lj^, и пусть Lkz —
соответствующая ей искомая кривая в плоскости z. Рассмотрим в последнем
равенстве изменение аргумента, когда w обходит в
положительном (относительно области D^) направлении кривую Ljw Из ра-

§ 38] ОБРАТНАЯ КРАЕВАЯ ЗАДАЧА 411
венства C8.4) в силу однозначности Q{z) следует, что
изменение аргумента [Qz']^ равно — 2jim/. Следовательно, будет
справедливо равенство
[Qzh,^ = Ю,^^ - 2ят/ (/ = 1, 2, ..., п). C8.8)
Так как все точки Wj лежат также и внутри Lo, то
[в.Ь =[ej, +2ntmj. C8.9)
По определению
[ej^ =2я, [ej. =-2я (/=1, 2, ..., /г). C8.10)
Будем искать решение рассматриваемой обратной краевой
задачи в классе однолистных функций и, следовательно, будем
считать, что искомый контур L^ лежит в одной плоскости. Тогда
для кривых Lkz будут справедливы соотношения, аналогичные
C8.10). Пусть теперь искомая функция z{w) преобразует
внешнюю кривую Lom; снова во внешнюю кривую Lqz и, следовательно,
все внутренние кривые Ljw снова переходят во внутренние. Тогда
из равенств C8.8) вытекает, что все ntj = 0. Если же Lo^
переходит в одну из внутренних кривых L^z, а поэтому одна из
внутренних кривых Lj^ переходит в Lqz, то из равенств C8.8) —
C8.10) будет следовать, что для некоторого /о будет
выполняться равенство 2я = —2я — 2ят/„, откуда следует m/g==
= — 2. Все остальные ntj равны нулю.
Таким образом, для однолистных решений обратной краевой
задачи (искомый контур без самопересечения) возможны лишь
два случая: 1) все кривые контура при отображении сохраняют
направление обхода — все ntj равны 0; 2) внешний контур
переходит во внутренний, а один из внутренних переходит во
внешний — одно trij равно —2, остальные равны нулю.
Перейдем снова к общему случаю. Потенцируя равенство
C8.5) и затем интегрируя, будем иметь
п
г = е^^^ J eY(«') Jliw- w^Tidw + с. C8.11)
/-1
В силу многосвязности области Du^ последняя функция может
оказаться многозначной. Необходимым и достаточным условием
однозначности является выполнение равенств
п
J еУ(«')Д(гг,_ау;)'"/(^ш = 0 (/=1,2, .... п).

412 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ 1ГЛ. V
Уравнение искомого контура получим, переходя в формуле
C8.11) к контурным значениям.
Пример. Пусть область Dvj есть круговое кольцо q <. \w\<. 1.
Рассуждая совершенно так же, как в примере п. 37.9, придем к следующему
условию:
^ J In шо (9) dQ-^ynwi @) ie = m In 1
или
о
Cq — fltj = — m In <7»
где Oq, aj —начальные члены разложения в ряд Фурье функции \nw{Q)
соответственно на окружностях \w\= 1, |м;| = q.
§ 39. Краевая задача типа задачи Римана
для многосвязной области и краевые задачи
со сдвигом и сопряжением
Сначала распространим решение общей краевой задачи C6.1) на случай
многосвязной области, а затем (пп. 39.3, 39.4) опишем некоторые результаты,
относящиеся к обобщенным задачам Римана и Гильберта, содержащим
операции сопряжения над искомыми функциями, или сдвиги, или и то и другое
одновременно.
39.1. Интегральное представление. Аппаратом решения общей краевой
задачи для случая многосвязной области также является интегральное
представление искомой кусочно аналитической функции, которое строится из тех
же принципов, что и в п. 36.1. Но здесь, как и вообще в задачах,
относящихся к многосвязным областям, возникают осложнения из-за возможной
многозначности аналитических функций, определяемых интегральными
представлениями.
Чтобы несколько объяснить и оправдать сложность применяемых в
дальнейшем интегральных представлений, рассмотрим сначала один простой
пример.
Пусть в двусвязной области /)+, ограниченной внешним контуром Lo и
внутренним Lu производная аналитической функции задана интегралом типа
Коши
^ 2я/ J т — г
L
Взяв интеграл от О до г, получим для самой функции выражение
Ф"" W = - 2^Г 5 JX (т) In (l - -|) dx + Ф+ @). C9.1)
L
Формула C9.1) определяет функцию, вообще говоря, многозначную.
Многозначность возникает за счет интеграла, взятого по внутреннему контуру,
потому что для функции, определяемой этим интегралом, всякий замкнутый
контур, проведенный в области D+ и окружающий контур Lu разделяет две
точки разветвления ядра г ¦• т и г «« оо. Установим многозначность прямым
подсчетом. Пусть 2ri —некоторая точка, принадлежащая D[". Выражение C9.1)

§ 39] ОБЩАЯ КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАИА 413
МОЖНО представить в виде
и L
- In B - г,) -^ J ^1 (т) ^т + "У^ J [i (т) In (- т) dx + Ф+ @).
Все члены правой части, кроме третьего, однозначны. Отсюда следует, что
для однозначности интегрального представления C9.1) от плотности ц(т)
нужно потребовать, чтобы \ \л (т) dx = 0.
Lx
Рассмотренный простой пример показывает, что нельзя добиться
однозначности представляемой аналитической функции, если точно следовать тому
пути, которым были получены представления C6.2), C6.3).
Перейдем теперь к общему случаю (т + 1)-связной области (рис. 13,
стр. 140). D+ — связная область, а D" = Dq + D^ + ... + D~ — сумма
раздельных областей, которую для краткости будем именовать также
областью.
Найдем интегральное представление кусочно аналитической и
однозначной в областях D+, D- функции Ф(г) =» {Ф+(г), ф-(г)}, если известны
[Ф+B)](^), [Ф-B)](р).
Соображения, которые выходят за рамки нашего изложения, показывают,
что требуемое представление для ФB) может быть достигнуто, если
исходить из следующего представления для производных:
р+тп , ,
-^ [ф-(.)]"'^=
П(^-^/)"
где Ц @ — искомая комплексная функция, г. — некоторые закрепленные точки
из областей DJ.
По заданным \0>^ (г)] ", [ф~ (г)\'' плотность ц (/) из формул Сохоцкого
определяется следующим образом:
,, р+тп
Ц (О - [Ф"" И)Г - -fir f*^~ ^'" (' ^ ^»)' C9.4)
{р+тп \
[ф*(оГ-пг^ [«-(оГ!
Д('-,)" 1
р (О _ ((- г,г\ [Ф* тГ - V [ф- «I'"Ч да«
(/е Lg] gr — 1, 2, ..., m).

414 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
Представления для самих функций Ф+B)[, ф-B) находятся путем
интегрирования формул C9.2), C9.3). Воспользуемся разложением ядер
П
1 ~1
'Л + у ^
{Z - Zjf (т - г) (т - г^)'^ (г - т) ^^ (^ - г^)«-^+1 (г - г^)* '
Беря п-кратный интеграл от обеих частей равенства C9.2) от О до 2,
после довольно громоздких выкладок получим
где г n—i (z)—многочлен степени п—1, коэффициенты которого можно
вычислить путем сравнения первых п членов разложения в степенной ряд обеих
частей равенства C9.6).
/ г\ ( T-^/\
Под In II I, In I 1 —— J здесь понимаются ветви,
обращающиеся в нуль соответственно для z = О, z = оо. Так как все члены правой
части формулы C9.6) однозначны, когда z изменяется в D+, то,
следовательно, функция 0+(z) будет в области D+ аналитической и однозначной.
Для функции 0~(z) получим два различных представления в
зависимости от того, будет ли z находиться в одной из конечных областей D~ или же
в бесконечной области D^. Не приводя выкладок, дадим окончательные
результаты р-кратного интегрирования равенства C9.3) по z в пределах от Zj
до Z.
Для zeD~ (^7 = 1, 2, ..., т) будем иметь
т
/=1 i/ ^ L /J
m
+ JzJJi, J-Lir) '-\~2^ (r - .)P- in (l -±),r +
(p — 1 I 2л/ J T V T/
(p-l)l 2ш J
bo
+ J] Л^г* In 2 + ^ -^ + 2] rf<,fez* C9.7)
*-0 ft-l ^ ft-Q

§ 39] ОБЩАЯ КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАНА 4l5
где штрих у произведения означает, что нужно пропустить множитель,
соответствующий k = /. Постоянные Л л, Вн выражаются определенным образом
через функцию |я(т), dqk — постоянные, вычисляемые разложением обеих
частей равенства C9.7) в степенной ряд в окрестности точки z = Zq.
Для z^D~ представление Ф^ (z) можно дать в виде
ф-(г) =
т
тп
S
/г=-1
р-1
f+z
/5*0
Здесь штрих у произведения означает, что для т е Lj (/= 1, 2, ..., т)
нужно пропустить множитель при k = /. Постоянные В^ те же, что и в
формуле C9.7), а постоянные doh определяются путем разложения обеих частей
равенства C9.8) в ряд в окрестности 2 = оо.
39.2. Краевая задача и интегродифференциальное уравнение.
Сформулируем краевую задачу:
Требуется определить две функции: Ф+(г), аналитическую и однозначную
в {т-\- \)-связной области D+, и Ф~B), аналитическую'^) в области D-,
удовлетворяющие на контуре краевому условию
п
U,(/)-^^+jAf.(/,T)-^-^^TU
А-1 L L J
где ak(t), bk(t), M/i(/,т), Nk(tут)—функции того же типа, что и в краевой
задаче C6.1).
На основании интегральных представлений C9.6), C9.7), C9.8) можно
выразить все неизвестные функции, входящие в краевое условие, через
плотность представлений \i{t). При этом все производные до (п—1)-го и
(р—1).го порядков соответственно выразятся интегралами, в которых можно
переходить к краевым значениям путем прямой замены z на t. Высшие
производные выразятся интегралами типа ^ши по формулам C9.2), C9.3).
*) Здесь аналитичность обязательно означает и однозначность.

416 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ТЛ,_ V
Переходя в этих формулах к краевым значениям, будем иметь
[Ф+ {1)Г = у (^ - 2^)-'^ fi (О + Ф (О, C9.10)
' [Ф- @]"" = - т (^ - ^/)"" МО + I' it)
т _
(<eL/, /=1, 2, .... т),
[<i>+wr = |t* (О+ *(/). C9.11)
-^ [ф-(ОГ' = -уЦ(') + Ф@ ('е?о),
Д('--/)"
где i|)@ означает правую часть формул C9.2), C9.3) при замене в них г
на t.
После замены всех неизвестных функций их выражениями через fi@
краевое условие C9.9) приведется к особому интегральному уравнению с
ядром Коши вида
а (t) ^^ (О + -~р 5 -^^ dx+^K (U т) ^1 (т) ^т = gr (/), C9.12)
L L
где
— — Р^.
a{t)=^an(t) + t ^ '""ПС^-^/Г^Р^'
^1' C9.13)
b (t) = an (t) - Г^""^"" П (^ - ^/Г ^Р W>
/-1
а /С(^т)—вполне определенное фредгольмово ядро; ^(/)—функция,
выражающаяся через заданные функции и постоянные интегрального
представления.
Дальнейшее исследование должно производиться по обычной схеме, о
которой подробно говорилось в §§ 35, 36.
Особое интегродифференциальное уравнение типа C6.23), заданное на
контуре L== Lq + L\ + ... + Lm, тем же приемом, что и в п. 36.3, может
быть сведено к краевой задаче C7.9).
Краевая задача типа задачи Гильберта общего вида, подобная задаче
C5.2), здесь не рассматривается. Решение ее получено Д. И. Шерма-
ном 1). Развернутое и упрощенное изложение имеется в работе Э. Г. X а с а-
т
б о в а 1). Упрощение достигается введением множителя JJ {t — zS^k^ сво-
дящего индексы по внутренним контурам к нулю.
39.3. Краевая задача с сопряжением. Пусть D+, D- —те же области, что
и в предыдущем, а L — контур, составленный из кривых Ляпунова.
Рассмотрим задачу отыскания кусочно аналитической функции 0B),
удовлетворяющей краевому условию
Ф+ (О = Gi (/) Ф- (О + С?2 (О Ф- (О + 8 (th C9.14)

§ 39] ОБЩАЯ КРАЕВАЯ 3 \ДАЧА ТИПА ЗАДАЧИ РИМЛПА 4l7
Заданные функции Gi, G2, g б\дег»1 считать \довлетворя10щими условию
Гёльдера и будем требовать выполнения условия Gi@?= О
Одним из возможных способов исследования поставленной краевой
задачи является многократно использованный в настоящей главе метод
интегральных уравнений. Отыскивая решение в виде интеграла типа Коши с
искомой плотностью, можно свести краевую задачу C9 14) к равносильному ей
особому интегральному уравнению Различные авторы, исследовавшие задачу
(Н П. Векуа, Б. В. Боярский, Л. Г. Михайлов), вводили искомую плотность
интеграла типа Коши в разных формах. По этой причине и получаемые
интегральные уравнения также несколько различались. Но в конечном счете
исследование с помощью теорем Нётера приводит к следующим результатам.
Назовем х = -г—[arg Gi (/)]д индексом задачи C9.14), а краевую задачу
Gi (/) г|)+ (/) + G, (/) ?'2 г|)-^ (/) == ф" (/) C9.14')
ее сопряженной задачей. Справедливы следующие две теоремы (Нётера):
I. Для разрешимости задачи C9.14) в классе исчезающих на
бесконечности функций необходимо и достаточно, чтобы для полной системы ^);@ Р^'
шений однородной сопряженной задачи C9.14') выполнялись условия
Re \e(t)^-^{t)dt=^0 (/=:.l, 2. ..., Г). C9.15)
L
П. Разность чисел линейно независимых (с действительными
коэффициентами) решений /, /' сопряженных задач равна удвоенному индексу
задачи:
/~Г = 2х. C9.16)
Укажем, что сформулированные утверждения можно получить из общей
теоремы п. 23.6.
Более точные качественные результаты о разрешимости задачи удается
получить лишь при некоторых дополнительных частных предположениях
относительно коэффициентов краевого условия и контура. Исследованию
поддаются случаи:
I Gi (О [> I G2 (О I — эллиптический, C9.17)
I G, (О I = I Go (О I — параболический. C9.18)
В эллиптическом случае краевая задача ведет себя особенно просто.
Оказывается, что в качественном отношении дело обстоит совершенно так же,
как и в обыкновенной краевой задаче Римана (G2@^0) (см. §§ 14, 15),
т. е. при X > О краевые задачи, однородная и неоднородная, имеют решения,
зависящие линейно от 2х произвольных действительных постоянных (/ = 2х,
/' = 0). Если X ^ О, однородная задача не имеет отличных от нуля решений,
а неоднородная разрешима при выполнении Г = 2|х| условий C9.15).
Б. В. Боярский 1) получил впервые этот результат с помощью
введения новых искомых функций. Краевое условие для введенных им новых
функций упрощается до обычной задачи Дирихле, но зато усложняется их
класс; из сопряженных гармонических функций (решений системы Коши —
Римана) они превращаются в решения общей системы уравнений
эллиптического типа. Опираясь на теорию таких систем, ему удалось сначала доказать
неразрешимость однородной задачи при х < О, а затем на основе
приведенных выше двух теорем установить точные качественные результаты.
Однако необходимость использования сложной теории эллиптических
систем вынуждает автора накладывать на коэффициенты краевого условия
жесткие ограничения (удовлетворение условию Гёльдера с показателем, сколь
угодно близким к единице).

418 {РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ (ГЛ. V
Л. Г. Михайлов упростил решение, использовав предложенный И Б. С и-
моненко 1) метод решения краевой задачи Римана с непрерывным
коэффициентом. Рассуждения Л. Г. Михайлова проходят точно по схеме,
изложенной в п. 16.3, 2°. Наряду с упрощением исследования задача получила
полное решение при минимальных ограничениях на коэффициенты
(непрерывность Gi, измеримость G2).
В случае круговой области и функции Gz, удовлетворяющей условию
Гёльдера, И. X. Сабитов 1), 2) показал, что общий случай может быть
сведен к эллиптическому.
N N
Пусть ^ с^е^^^=^ ^ с^^/^ — отрезок ряда Фурье функции OgC/),
\0-2(t)- t '/
< I Gj (/) |, и пусть
для которого удовлетворяется условие
с_^--первый из коэффициентов с_д^, с_^_^у ..., не обращающийся в нуль.
Умножим краевое условие на / и продолжим по симметрии Ф"~ (/) в D^
с помощью функции Ф]*" (г) = Ф~ 1 — J. Тогда при обозначениях
Ыл-п
G\^eG,. G'.^t-G,^ Y. М'"""' s' = ^'s,
JV+rt
^+B) = г'^Ф^-(г) + Y, Cf^z^'^^'O^ (г)
краевая задача C9.14) сведется к задаче
^+ (О = G\ (/) Ф- (О + 0^ (/) Ф- (О + g' (О,
для которой условия эллиптичности выполнены. Число линейно независимых
решений и число условий разрешимости точно выражаются через x = IndGi@
и номер п аппроксимирующего отрезка ряда Фурье.
В параболическом случае, как показал Л. Г. Михайлов [14],
рассматриваемая краевая задача сводится к последовательности двух обыкновенных
краевых задач Гильберта (см. § 29). На основе их анализа может быть
подсчитано число линейно независимых решений или условий разрешимости.
Для случая круговой области оригинальный метод исследования
рассматриваемой краевой задачи предложил Г. С. Литвинчук 2). Он опирается
на теорию краевой задачи Римана со многими парами искомых функций
(кусочно аналитического вектора). Мы остановимся на изложении лишь
схемы этого исследования.
Присоединим к краевому условию C9.14) условие, полученное из него
переходом к комплексно сопряженным значениям. Пусть теперь Of (г) =
•' Ф^ (г) — искомая пара функций и Ф* (z) = Ф^ ( ~~ ) "" полученная
из
них доопределением по симметрии в дополнительную область другая пара.
Тогда краевая задача C9.14) оказывается в определенном смысле
равносильной краевой задаче Римана с двумя парами искомых функций Ф^ (г), Ф|^ B)
(двумерного кусочно аналитического вектора) с заданными матрицей
коэффициентов и вектором свободных членов.
В общем случае из теории краевой задачи Римана для кусочно
аналитического вектора можно получить формулированные выше две теоремы Нё-
тера, установленные Б. В. Боярским. Эллиптический случай исследуемой
краевой задачи соответствует случаю устойчивости так называемых частных ин-

§ 39] ОБЩАЯ КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАПА 419
дексов полученной задачи для двух пар функций. Здесь удается вычислить
оба частных индекса (оба они оказываются равными индексу
коэффициента Gi). Отсюда вытекают все приводимые выше для эллиптического случая
результаты.
В параболическом случае матрица коэффициентов полученной краевой
задачи оказывается треугольной, т. е. задача распадается на
последовательность двух краевых задач Римана, каждая из которых содержит лишь одну
пару искомых функций. На основе анализа этих задач удается не только
найти все полученные Л. Г. Михайловым из анализа двух краевых задач
Гильберта результаты, но и уточнить их. Оказывается, что если k =
= Ind(/2@^0, то частные индексы устойчивы и числа линейно
независимых решений и условий разрешимости (/, р) те же, что и в эллиптическом
случае. Если ^ < О, то частные индексы неустойчивы, а (/, р) зависят как
от X, так и от k.
Укажем еще, что если краевое условие C9.14) разбить на два
действительных, то его геометрически можно рассматривать как линейное
преобразование переменных w", v- в м+, v^. Б. В. Боярский 1) показал, что
эллиптический случай соответствует преобразованию со знакоположительным
якобианом.
39.4. Дальнейшие обобщения. Рассмотренная в предыдущем пункте
краевая задача допускает обобщения в различных направлениях. Простейшим
из них является дополнение краевого условия C9.14) членом Ф+(/).
Исследование проведено Л. Г. Михайловым, а затем уточнено Г. С. Литвинчуком.
Окончательные результаты, естественно, значительно усложняются. Наиболее
общая задача подобного типа
а (О Ф^ (О + b (t) ф-@ + с Ц)Ф'^Ц) + d (t) ф-(/) = ^@
соответствует особому уравнению с комплексным сопряжением (теория Нё-
тера для этого случая была изложена в п. 23.6).
Более существенным обобщением является наличие в краевом условии,
наряду с сопряжением, сдвига. В этом направлении краевая задача
Ф+ [а @1 = G, (О Ф~ it) + G2 (ОФ"" (О + S (О, C9.19)
где сдвиг а (О сохраняет направление обхода на L, непосредственно
обобщает задачу C9.14) так же, как рассмотренная в п. 18.1 задача со сдвигом
обобщает задачу Римана. При выполнении условия d (/) =й О, а также
условий C9.17) или C9.18) для задачи C9 19) Л. Г. Михайловым [14]
получены точно такие же результаты для индекса, числа решений и числа
условий разрешимости, что и для задачи C9.14). Аналогично исследуется случай,
если в C9.19) сдвиг a(t) изменяет направление обхода.
Все другие обобщения задачи C9.14) в указанном направлении
составляют более трудные проблемы, и их исследование можно довести до уровня
исследований задач C9.14) и C9.19) лишь при дополнительных
предположениях о сдвиге a(t). При этом, в отличие от задачи C9.19), как условия
разрешимости, так и окончательные результаты, по существу, зависят от
сдвига а(/).
В том случае, когда сохраняющий или изменяющий направление обхода
на L сдвиг a{t) удовлетворяет так называемому условию Карлемана
а [а (/)] = и C9.20)
Г. С. Литвинчук 1) получил теоремы Нётера I и II для самой общей
задачи
а (О Ф"^ (О + Ь (О Ф"** [а (/)] + с (О Ф- (О + d (t) ф- [а (/)] +
+ а, (/) Ф+ (О + Ьх (О ф-*- [а @1 + сг (О Ф- (О + d, {t) Ф" [а (/)] = g (t),
C9.21)

420 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
В частности, для краевой задачи
а (/) Ф+ (О + b (t) Ф+ [а @1 + с it) Ф- (/) + d (t) Ф- [а (/)] = g (t), C9.22)
которая при условиях C9.20) и ф-(оо)=0, очевидно, равносильна
характеристической части особого интегрального уравнения со сдвигом Карлемана,
полученные Г. С. Литвинчуком теоремы были изложены в п. 23.5. Г. С. Л и т-
винчук 3), 4), 5) (см. также Э. И. Зверович, Г. С. Литвинчук [9])
рассмотрел для задачи C9.22) аналоги эллиптического и параболического
случаев задачи C9.14). Результаты здесь сильно усложняются, и их
формулировка заняла бы слишком много места.
Аналогичные результаты для задачи C9.21) в случае b(i) = d(t) =
= fli(t) = Ci(t) = 0 были получены в работе Г. С. Литвинчука и
Э. Г. Хасабова 4).
Наибольшие трудности для исследования доставляют краевые задачи со
сдвигом и сопряжением для одной функции, аналитической в области D+
(или D-). Хотя краевые условия этих задач формально являются частными
случаями условия C9 21), теоремы Нётера I и II и дальнейшие результаты,
в отличие от задачи C9.22), не следуют из соответствующих теорем,
установленных Г. С. Литвинчуком для общей задачи C9.21). К настоящему
времени наиболее полно исследованы так называемая обобщенная краевая
задача Гильберта со сдвигом
Re {а (/) ф-^ (/) + b (t) Ф+ [а {t)]} = g (t) C9.23)
и краевая задача
Ф+ [а @1 = G, (О Ф"" it) + G2 И) Ф^ (О + g (О, C9.24)
которая при а (О, сохраняющем направление обхода на L, естественным
образом обобщает задачу Гильберта со сдвигом (см. п. 18.2), а при а (О,
изменяющем направление, обобщает задачу Карлемана (см. п. 18.3).
Задача C9.23) изучена в работах Г. С. Литвинчука и Э. Г.
Хасабова 1), 2). Используя представление аналитической функции Ф+B)
интегралом типа Коши с действительной плотностью (см. п. 34.2), эти авторы
привели задачу C9.23) к особому интегральному уравнению со сдвигом
Карлемана (см. п. 23.5) и, основываясь на теории последнего, а также используя
построенную ими сопряженную для C9.23) задачу, получили для задачи
C9.23) теоремы Нётера I и II.
Краевая задача C9.24) была поставлена Н. П. Веку а 1)*), который
свел эту задачу к интегральному уравнению фредгольмова типа, указал
необходимые условия ее разрешимости, обобщающие соответственно тождества
A8.4) и A8.21), и построил сопряженую задачу. Теоремы Нётера I и II для
задачи C9.24) были доказаны Г. С. Литвинчуком и А. П.
Нечаевым 1), 2), причем оказалось, что / — Г = х+1, где x = IndG2@ или
х = —lndai@, смотря по тому, сохраняет или изменяет направление
обхода на L сдвиг Карлемана a(t). Соответственно этому же в случае
1^2@1 >|Gi(/)| C9.25)
при сохраняющем направление сдвиге и в случае
I Gi (О I > I G2 (/) I C9.26)
при (x{t), изменяющем направление, в статьях Г. С. Литвинчука и
А. П. Нечаева 1), 2) вычислены сами числа / и Г. Кроме того, исходя из
необходимых условий разрешимости, было показано, что на всем контуре L
*) Н П Векуа предполагал, что a(t) удовлетворяет условию Карлемана
и изменяет направление обхода на L,

§ 39] ОБЩАЯ КРАЕВАЯ ЗАДАЧА ТИПА ЗАДАЧИ РИМАНА 421
обязательно должно выполняться либо условие C9.25), либо условие C9.26).
В случае а(/), изменяющего направление обхода, указанные результаты
можно получить, сводя задачу C9.24) к задаче C9.14) на разомкнутом
контуре методом, изложенным в п. 18.3. Это сделано в работе В. А. Чернец-
кого 2).
Дальнейшим обобщением является рассмотренный впервые Н. П. Векуа
случай, когда а(/) удовлетворяет так называемому обобщенному условию
Карлемана
ctm (О = а [«m-i (t)\ ^ t (а, (t) s а @), C9.27)
где т (т "> 1)—любое натуральное число, являющееся порядком конечной
циклической группы, порожденной итерациями сдвига a(t). В этом случае
Г. С. Литвинчук 1) доказал теоремы Нётера и вычислил индекс краевой
задачи
т-\
Z Kw^'"KW] + ^,(oo4«^w] +
л«о
+ Cf^ И) Ф- [а^ (/)] + df^ it) Ф- [а^^ (/)]} = g it). C9.28)
естественным образом обобщающей на случай m > 2 задачу C9.21). Был
применен метод приведения задачи C9.28) к системе 2т особых
интегральных уравнений с ядрами типа Коши без сдвига относительно 2т неизвестных
функций. Оказалось, что индекс краевой задачи C9.28) равен поделенному на
2т индексу упомянутой системы особых интегральных уравнений. Для т=2*
аналогичный результат независимо был получен Р. А. Кордзадзе 1).
Вопрос о вычислении чисел / и Г для задачи C9.28) пока остается открытым.
Еще более общие задачи возникают, если в краевое условие входит не
один, а несколько различных сдвигов. В работах А. С. Сосунов а 1), 2),
П. Г. Башкарева и А. П. Нечаева 1) получены теоремы Нётера I и II
для случая, когда краевое условие зависит от двух сдвигов a{t) и Р(/),
удовлетворяющих условию Карлемана и условию коммутативности а[Р(/)] =
= Р[а(/)]. Эти сдвиги, очевидно, порождают конечную (но уже не
циклическую) коммутативную группу итераций. Индекс краевой задачи в этом
случае, как и в случае задачи C9.28), получается делением на порядок
упомянутой группы индекса некоторой системы особых интегральных уравнений
без сдвига (или делением индекса системы на удвоенный порядок группы,
если в краевое условие входят корлплексно сопряженные значения
неизвестной функции).
Как видно из работы А. Б. Антоневича 1), 2), эта закономерность
сохраняется и в общем случае любой (вообще говоря, некоммутативной)
конечной группы сдвигов. Однако вопрос о теоремах Нётера I и II, не говоря
уже о дальнейших результатах, для указанного общего случая пока еще
нельзя считать решенным. В указанной работе задача с любой конечной
группой сдвигов рассматривается в очень общей постановке (для так называемых
псевдодифференциальных операторов), но зато предполагается бесконечная
гладкость контура и коэффициентов. Индекс задачи выражается через
характеристики, фактическое вычисление которых представляется весьма
затруднительным.
В последнее время в работах В. Г. Кравченко 1), 2) начато изучение
того случая, когда сдвиг а (О, входящий в краевое условие задачи C9.22),
порождает бесконечную группу итераций, т. е. на контуре L всегда найдется
такая точка /о, что am(io)?=to при любом т. Этот сдвиг иногда называют
некарлемановским. Если, используя формулы Сохоцкого, от задачи C9.22)
перейти к соответствующему особому интегральному уравнению со сдвигом,
то с помощью метода регуляризации (понимаемого несколько шире, чем

422 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
В § 22) удается показать следующее. В случае сдвига а (О, сохраняющего
направление, для упомянутого интегрального уравнения справедливы теоремы
Нётера I и II, если каждое из функциональных уравнений
а it) Ф [а (/)] + МО Ф it) = gi (/), C9.29)
с (t) t [а (/)] + d(t)^ (t) = ^2 (О C9.30)
имеет единственное решение, удовлетворяющее условию Гёльдера, при любых
функциях gi{t) и ^2@ из этого же класса. Условия существования таких
решений уравнений C9.29) и C9.30) зависят, прежде всего, от того, имеет ли
сдвиг неподвижные точки или нет. Если a(t) имеет конечное число
неподвижных точек на L, то эти условия носят альтернативный характер: 1) значения
коэффициентов a(t) и b(t) (соответственно c(t) и d(t)) во всех неподвижных
точках tj сдвига a(t) должны удовлетворять одному и тому же из двух
неравенств некоторого вида; 2) в зависимости от того, какое из этих двух
неравенств выполнено во всех tj, требуется еще, чтобы один из
коэффициентов a{t) или b(t) (соответственно c(t) или d(t)) был отличен от нуля всюду
на L. При выполнении этих условий оказывается, что индекс задачи C9.22)
равен либо индексу одной из задач Римана
а@ф+@ + МОф-(О = 0
или
б(ОФ+@ + ^(/)ф-@ = о,
либо индексу одной из задач Римана со сдвигом (см. п. 18.1)
а@ф+[а@1 + ^@ф-@ = 0
или
МОФ+[а@1 + с(Оф-@ = о.
Краевая задача C9.22) с некарлемановским сдвигом а(/), изменяющим
направление, приводится к предыдущему случаю, а именно к задаче со сдвигом
ai@"= а[а@]. который уже сохраняет направление и обязательно имеет
неподвижные точки, так как такие точки в этом случае всегда имеет сдвиг
a(t).
Имеется много публикаций, в которых краевые задачи со сдвигом и
сопряжением изучаются для случая многосвязной области, а также на
конечных римановых поверхностях. В последнем направлении наиболее полные
результаты получил Э. И. Зверович 2), 3), 6), разработавший метод
локально-конформного склеивания, обобщающий теоремы склеивания,
изложенные в пп. 18.1 и 18.3 (см. еще п. 53.5).
§ 40. Исторические сведения
Исторические замечания по поводу общей краевой задачи, рассмотренной
в § 35, были даны при изложении самой задачи, и мы не будем здесь этого
вопроса касаться.
Обобщенная краевая задача типа задачи Римана (§ 36) была
рассмотрена впервые Л. Г. Магнарадзе 2). Решение, данное этим автором (оно
опубликовано только в виде сводки формул без указания способа их
получения), неполно и очень сложно. Решение, изложенное нами в § 36, дано
Ю. М. Крикуновым 1), 2). Более подробная разработка вопроса дана тем же
автором в 3). Обобщение этой задачи на случай многосвязнон области
произведено М. П. Ганиным 4), 5). Им поставлена задача в весьма общем виде
сразу для многих неизвестных функций и в предположении, что предельные
значения изнутри и извне контура берутся в разных точках контура.
Аппаратом для решения этой общей задачи служит то же интегральное
представление C9.6)—C9.8), которое использовано нами для решения рассмотренного

ЗАДАЧИ К ГЛАВЕ V 423
в § 39 случая. Подробное изложение вопроса дано в диссертации М. П.
Танина 5). Краевая задача C9.14) с комплексным сопряжением впервые была
рассмотрена А. И. Маркушевичем 1). Дальнейшие исторические сведения
о задачах с сопряжением, а также со сдвигом (пп. 393, 39.4) давались в
тексте.
Задачу Гильберта для многосвязной области впервые рассмотрел
Д. А. Квеселава 4). Пользуясь интегральным представлением C7.37), он свел
задачу к особому интегральному уравнению и дал исследование его примерно
в том плане, как это изложено в п. 35.6 для обобщенной задачи. Самым
важным результатом Д. А. Квеселава является установление неразрешимости
задачи для отрицательного индекса. Этот законченный результат лег в
основу дальнейших исследований. Союзной краевой задачи Д. А. Квеселава
не рассматривал.
Исследование, приведенное в п. 37.7, изложено по работе И. Н. Векуа [2],
где оно прилагается к более общему случаю. Исследование пограничных
случаев к == О и к = /п — 1 и установление связи с конформным отображением
даны в совместной работе Ф. Д. Гахова и Э. Г. Хасабова 1). Регуляризую-
щий множитель (п. 37.5) нашел Э. И. Зверович 5). Дополнительные
исследования (п. 37.12) провел Б. В. Боярский (см. дополнение к книге И. И.
Векуа [2]).
Задачи к главе V
1. Решить обобщенную краевую задачу Гильберта
sin S —г cos S --:—h cos su (s) + sin sv (s) = cos 3s (cos 5 — 1)
для единичного круга.
Ответ. FBr) = tt + /У = —-g-^s + -—2* -- — г^ + Az^ + Bz + A где
A, В — произвольные постоянные.
2. Показать, что обобщенная краевая задача Гильберта
sin S -^—h B — cos s) -^ 2w (s) = 2 (cos 2s + Л cos s)
для единичного круга разрешима лишь при значении параметра Л = —I.
Дать решение для этого случая.
Ответ. F(z) = u +iv=^z^ + ia +A(z^ Y)» ^^^ Л — комплексный,
a — действительный параметры.
3. Решить обобщенную краевую задачу Гильберта
sin S -^—h B — cos s) -^ 2 cos su (s) — 2 sin sv (s) =
3 1
= 2 cos 3s — 3 cos 2s -{- Y cos s — -j
ДЛЯ единичного круга.
1 / I \2
Ответ. F {z) = и + iv =^ ai {z — \) + -^ z \z — -^ \ •
4. Показать, что если коэффициенты краевой задачи
du , . dv , , .
fli — + 6, -^ -f aott + М = с

424 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. V
удовлетворяют условию
то решение задачи может быть сведено к решению задачи Гильберта и,
следовательно, дано в замкнутой форме (Ф. Д. Гахов [5].)
5. Решить обобщенную краевую задачу Гильберта
cos 2s cos 5 —;—I- sin 2s cos s—;—|- ("" 2 sin 2s cos s + cos 2s sin s) u +
ds ds * ' '
+ B cos 2s cos s + sin 2s sin s) t; = cos^ s (sin 2s — 3 sin s)
для единичного круга.
Указание. Воспользоваться результатами предыдущей задачи.
Ответ,
f B) = 12«~125 + (л2+уJ4 + (л,+а~-~)гЗ + /рг2-Л^^
6. Решить обобщенную краевую задачу Гильберта
du dv
cos xs —z sin HS -r; X sin xsw — H COS xsy = — 2 sin 2s
ds ds
для единичного круга (к — целое число).
Ответ. При н ^ О
F{2)==u+iv = z-''[z^ + c+Q (z)l
где Q(z) определено формулой B7.6), при О < х < 2 f (г) = г2-х, при
к > 2 задача неразрешима.
7. Доказать, что однородная краевая задача Пуанкаре
^+Bis)^ + cis)u=l(s),
коэффициенты которой удовлетворяют условию
1b'(s)-c(s)>0,
однозначно разрешима. (Б. В. Хведелидзе 1).)
8. Показать, что краевая задача Гильберта
Re [(а - ib) F (t)] = аи + bv = с
при помощи интегрального представления
^^^^ 2ш J a{a)-ib(o) т - 2 ^ ^ ^^^'
где IX(а) —действительная функция, а P(z)—соответствующим образом
подобранный многочлен, может быть сведена к интегральному уравнению Фред-
гольма. На основе этого дать исследование разрешимости задачи Гильберта.
(Д. И. Шерман 4).)

ЗАДАЧИ К ГЛАВЕ V 425
9. Решить обобщенную краевую задачу Римана
ф- (oo) = О,
в следующих предположениях:
а) точки /, — / е D"^, точка О е /)"";
б) точки /, ¦— /, О е D"*".
Ответ, а) ф+(г) = г + 4г + '^> Ф"(^) = Т-Г-^+ ^' '
б) Ф+B) = г, ф-(г) = у-р^+ j^^^.
10. Найти решение интегро-дифференциального уравнения
L
L L
при тех же предположениях относительно контура, что и в предыдущей
задаче.
Ответ, а) ф@'
\^t2 -^ t ^ i^ ' 1 + ^
2 »
б)ф@—p^ + TTF-
11, Показать, что краевая задача
/ (^ - I) [Ф^ @]Ч B/- I) Ф"^ (О =
= (/ + 1) [Ф" @1' + 2Ф- (О + 2 ^^' ~ f ~ ^ , Ф~ (со) = О,
где точки О, 1 е D+, разрешима лишь при а = 2. Найти решение в этом
случае.
Ответ. Ф'*"B)=2, ф-B) = J-.
12. Показать, что интегро-дифференциальное уравнение
(t'+\H'it) + {2t + \H{t) +
_^l-:.2^^f Ф^
L L
где L — контур тот же, что и в предыдущей задаче, разрешимо лишь при
а = 2. Дать решение в этом случае.
Ответ. Ф (О = ji—.

426 РАЗЛИЧНЫЕ ОБОБЩЕННЫЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ, V
13. Решить краевую задачу
у [Ф^ {t)r - -jr [Ф" @1' = t' [Ф- it)r + 6/2 [Ф- (/)]' + 6/ф- (t) +
+ 2 G+TJ2 ' Ф @0) = О,
в случаях:
а) точка —1 е D**", точки О, I е О";
б) точки —1, OsD"*", точка 1 е D~.
Ответ, а) Задача неразрешима.
б) ф+ (г) = 2^ + 4ciz^ + C2Z^ -2z + Cg,
_ _ , . -, In B + 1) , - _i ^ In 2 , -Of
Ф B) = 2—4з—^+6^12 ^-2—^+CiZ ^ + c^z
14. Решить интегро-дифференциальное уравнение
L
6/^ + 1 1 Г ФЧт) ^^ 6/ Г Ф(т) ^^^^ 4/3 + 8/2 + 4/+1
/2 л/ J т — / я/ J т — / <
/2 л/ J Т-/ Ш J Т-/ (/+1J
L L
При тех же предположениях относительно контура, что и в предыдущей
задаче.
Ответ, а) Решения нет.
к^л.u^ /^-21п(/+1) ,^ 2/*~3 , ., . » In / - /^ ,
б) Ф(/) = ^3^^ - + 2ci '^ + С2/2 + 2 р +
+ сз - С4/-2 - cg/-^
15. Решить краевые задачи Гильберта для кругового кольца — < | 2| < 1:
а) cos Qu (9) + sin бо (9) = sin 6 на | 21 = 1.
2 cos9а (9) + 2 sin Bv (9) = cos29 на | 2 | ^-g-'
б) cos Qu (9) + sin 9о (9) =» 1 на | 21 = 1,
cosr9 + -~)tt(9) + sinr9+j)o(9) = sin9 на
Ответ.
а) FB) = M+/0 = -^23-i./22+/p2-~/+-j|.2-^
6)FB) = {i-^/V3- + -l,[(io + ,6V3).-^^-f^^]}2.
Замечание. В случае а) выполнены условия однозначности. Поэтому
однородная задача имеет решение фB)=/С2, а неоднородная задача
разрешима при выполнении одного условия, которое оказывается выполненным.
В случае б) однородная задача неразрешима, а неоднородная разрешима
безусловно и однозначно.
|.|=|.

ГЛАВА VI
КРАЕВЫЕ ЗАДАЧИ
И ОСОБЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ
И С РАЗОМКНУТЫМИ КОНТУРАМИ
Во всех задачах, с которыми мы до сих пор имели дело,
коэффициенты краевых условий считались непрерывными
функциями *) и предполагалось, что контур области состоит из
замкнутых кривых. В связи с этим решениями являлись только
функции, непрерывные вплоть до контура. При этом
непрерывность решения на контуре вытекала не из специальных
ограничений, накладываемых на решения, а из самой постановки
задач. Если провести анализ исследования основных краевых
задач (гл. II, IV), то выяснится, что существенным ограничением,
накладываемым на решение, являлось требование
интегрируемости его краевых значений. При этом условии непрерывность
решения будет вытекать автоматически из условий
непрерывности, наложенных на коэффициенты (см., например, задачу 12
к гл. II).
В настоящей главе мы расширим постановку задач, допуская,
что коэффициенты краевых условий могут иметь разрывы 1-го
рода в отдельных точках, а контур может состоять как из
замкнутых, так и из разомкнутых кривых. В связи с этим придется
расширить класс допустимых в качестве решения функций.
Мы сохраним требование интегрируемости. Необходимость
этого вытекает из разных соображений. Прежде всего в
практических приложениях оказывается пригодным только этот класс
функций. С теоретической точки зрения это условие придает
постановке задачи определенность. Если допускать решения,
обращающиеся на контуре в бесконечность сколь угодно высокого
порядка, то простое рассуждение покажет, что для любой из
рассмотренных краевых задач существует сколь угодно много
линейно независимых решений.
*) Рассмотренные в § 15 исключительные случаи, где допускалось
обращение коэффициента в бесконечность, не характерны, так как исследование
их примыкало к случаю непрерывных коэффициентов.

42d КРАЕВЫЕ ЗАДАЧИ [ГЛ. Vl
Отметим сразу, что производимое здесь расширение
постановки задач имеет большое практическое значение, так как к
задачам с разрывными коэффициентами сводится много важных
задач с так называемыми «смешанными» краевыми условиями.
Прежде чем приступать к дальнейшему чтению, читателю
следует возобновить в памяти пп. 8.1 — 8.4 и § 14.
§ 41. Решение задачи Римана
с разрывными коэффициентами приведением к задаче
с непрерывными коэффициентами
41.1. Постановка задачи и определение функции по скачку.
Будем сначала рассматривать простейший случай, когда контур
состоит из одной простой замкнутой кривой. Пусть функции
0(t), g{t) в краевом условии задачи Римана
0^{t) = G(tH-(t) + g{t) D1.1)
всюду на L удовлетворяют условию Гёльдера, за исключением
точек t\, t2, ..., tmy где они имеют разрывы 1-го рода. Точки,
предшествующие точке 4 при положительном обходе контура,
будем считать левой окрестностью этой точки, а точки,
следующие за ней, — правой. Левый и правый пределы в точке 4
будем обозначать, как обычно, GD — 0) и GD+0) (GD — 0)=^
Ф G{tk + 0)). Будем предполагать, что никакое из предельных
значений не обращается в нуль и что краевое условие
выполняется всюду, кроме точек разрыва, где оно теряет смысл.
Решение задачи будем искать в классе функций,
интегрируемых на контуре. Отсюда будет вытекать, что решение будет
непрерывно в смысле Гёльдера всюду, кроме разве что точек 4-
В последних точках имеются разные возможности.
1. Можно потребовать ограниченности во всех точках
разрыва, отыскивая, следовательно, решение всюду ограниченное.
2. Можно потребовать, чтобы решение было ограниченным
в некоторых точках разрыва, допуская интегрируемую
бесконечность в остальных точках разрыва.
3. Можно допустить обращение решения в бесконечность
интегрируемого порядка во всех точках, где это допускается
условиями задачи *).
Первый класс решений является наиболее узким. Второй
класс получается из первого путем допущения бесконечности
в некоторых точках и является более широким. Самым широким
является последний класс. Число решений, как это будет
показано в дальнейшем, зависит от того класса, в каком отыски-
*) Как мы увидим далее, существуют такие точки разрыва, где
интегрируемость автоматически влечет за собой ограниченность.

§ 41) РЕШЕНИЕ ЗАДАЧИ РИМАНА 429
вается решение, и может оказаться, что задача, разрешимая
в более широком классе, будет неразрешимой в более узком.
Аналогично тому как это делалось в § 14, начнем рассмотрение
задачи с простейшего случая определения кусочно
аналитической функции по ее скачку. Положим в D1.1) G{t)= 1 и будем
отыскивать аналитические функции Ф+(-г), ф-(г) по краевому
условию
Ф^@-ф-@ = ё^@, D1.2)
причем g{t) может в отдельных точках иметь разрывы 1-го рода
или же особенность вида
g@ = -/^ (ReY<I). D1.3)
где g*@ удовлетворяет условию Гёльдера.
Решение иш,ется в классе функций, допускающих на контуре
оценку
|Ф*@|< ,/, ,« (а<1) D1.4)
П "^ Ч I
И обращающихся в нуль на бесконечности.
На основании формул Сохоцкого решением задачи является
функция
Ф(^) = ^$^^-. D1.5)
L
причем согласно исследованиям пп. 8.1 —8.4 эта функция имеет
в точках разрыва 1-го рода функции g{t) логарифмическую
особенность, а в точках, где g{t) имеет вид D1.3),— особенность
того же характера.
Покажем, что других решений в том же классе функций
задача D1.2) иметь не может. Как это всегда бывает в линейных
задачах, исследование единственности сводится к вопросу о
разрешимости однородной задачи. В рассматриваемом случае она
имеет вид
Ф'"@~Ф^@=0. D1.20
Рассуждая как и в Г п. 8.3 и используя оценку D1.4),
найдем, что в рассматриваемом классе задача D1.2^ имеет только
нулевое решение и, следовательно, решение D1.5) задачи D1.2)
единственно.
Заметим, что на таком же рассуждении основано
утверждение, что в случае непрерывности коэффициента G{t) допущение
у решения интегрируемой особенности на контуре не расширяет
класс решений.

430 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Если искать решение задачи D1.2) в классе функций,
имеющих на бесконечности полюс некоторого порядка х, то
решением, как легко показать, опираясь, как и в § 14, на
обобщенную теорему Лиувилля, будет функция
L
где Ру,{г) —многочлен степени х с произвольными
коэффициентами.
Метод решения общей задачи D1.1), излагаемый в
настоящем параграфе, заключается в сведении ее к задаче,
рассмотренной ранее в § 14. Для этого строятся специальные функции,
имеющие в точках h те же разрывы, что и G(/), и такие, чтобы,
считая их коэффициентами задачи Римана, можно было для
них решить эту задачу. Вводя затем с их помощью новые
неизвестные функции, мы придем к задаче Римана уже с
непрерывными коэффициентами.
Сейчас мы приступим к построению упомянутых выше
вспомогательных функций.
41.2. Фундаментальные вспомогательные функции. Идея
построения таких функций заключается в возможности
рассматривать многозначную аналитическую функцию в соответствующим
образом разрезанной плоскости как однозначную разрывную.
Введем две аналитические функции:
(г-го)\ (а:-/0\
где го — некоторая точка в области /)+, U — точка на контуре,
Y = а + ф — некоторое комплексное число. Точки разветвления
этих функций будут соответственно го, оо, и t\, оо. Проведем
в плоскости г разрез из точки го через точку t\ до бесконечности.
В разрезанной таким образом плоскости обе функции будут
однозначными, причем разрез будет для них линией разрыва.
Условимся, что участок разреза го/i лежит целиком в D+, и
рассмотрим функции
<оМг) = (г-^Г. (о-(г) = (-|^)\ D1.7)
При выбранном способе разреза функция о)+(г) будет
аналитической в D+, а (о~(г)—в D". На контуре обе функции будут
непрерывны (даже аналитичны) всюду, кроме, может быть,
точки t\. Поведение этих функций в точке ^i будет зависеть от
величины Y- Оставим этот вопрос пока в стороне и рассмотрим
отношение их краевых значений. Для всех точек контура,
отличных от tu очевидно,
^(^)=|т|f = (^-'гor• D1.8)

§ 41] РЕШЕНИЕ ЗАДАЧИ РИМАНА 431
В точке /i функция Q{t) неопределенна; найдем сейчас
отношение ее левого и правого пределов, совпадающих с
соответствующими пределами функции (/ — го)'-^.
Так как левая и правая окрестности точки ti лежат по
разные стороны разреза для функции (z — 2o)y, то по свойству
степенной функции
Q(/,+0) ^ • ^^^'^^
Исследуем теперь поведение функций 0+B:), со" (г) в
окрестности точки t\. Для этого достаточно исследовать функцию
@+B) = (Z-/i)Y.
Обозначая z — t\ = re^^y будем иметь
B-/0'^ = ^'^'"^'"''^ = rV^V^P^"^-^«^ D1.10)
Из D1.10) следует, что при аФ Q порядок функции (г — /i)y
зависит только от а. При а > О она имеет нуль порядка а, при
а < О — бесконечность порядка —а и, наконец, при а = О эта
величина остается ограниченной, но не стремится при
приближении к /д ни к какому пределу. При —1 < а < О функции
(о+B:), со~"B:) будут иметь в точке t\ бесконечность
интегрируемого порядка.
41.3. Приведение к задаче с непрерывными коэффициентами.
Простейший случай. Рассмотрим сначала однородную задачу
ф-^(/) = О@Ф"@, D1.10
предполагая, что коэффициент G{t) имеет лишь одну точку
разрыва t\.
Полагая
1 t G(tx —0) .,. - .V
(выбором ветви логарифма мы займемся позже в зависимости
от допускаемого класса решений), по формулам D1.7) построим
функции со+(г) и со"(г).
Введем новые неизвестные функции ФT{z), положив
ф=^B) = а)'=(г)ФгB). D1.12)
Краевое условие D1. Г) переходит теперь в условие
ФГ@ = 01(ОФГ@, D1.13)
где

432 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Вводя те же обозначения, что и в п. 41.2, получим
Gi(/) = Q(/)G@ = (<-eo)"^C@. D1.14)
Новый коэффициент Gi(t) является уже всюду непрерывной
на L функцией, включая и точку ti. Действительно, применяя
формулы D1.9) и D1.11), находим
Qi(^i-O) _ Q it, - 0) G (U - 0) ^ ,^i^ G it, - 0) ^ .
C, (/, + 0) — Q {t, + 0) G (/, + 0) ^ G (/, + 0)
T. e. G\ (/i — 0) = Gi {ti + 0), что и означает непрерывность Gi (/)
в точке t\. Итак, задача D1.Г) с разрывным коэффициентом
G{t) сведена к задаче D1.13) с непрерывным коэффициентом
Gi(/), изученной в § 14.
Займемся исследованием вопроса об индексе задачи.
Поведение решения задачи D1.Г) вблизи точки разрыва ^ь как это
видно из формулы D1.12), зависит от поведения функций (о+(г)
и о)~B:). В предыдущем пункте было показано, что последнее
определяется величиной а = Re y, т. е., в конечном счете
выбором ветви логарифма в формуле D1.11). Этот выбор надлежит
производить в зависимости от допустимого класса решений,
а именно: нужно требовать, чтобы выполнялось условие
0<ReY<l, D1.15)
если допускаются решения, ограниченные вблизи точки tu и
условие
-l<ReY<0, D1.16)
если отыскиваются решения, имеющие в точке /i бесконечность
интегрируемого порядка*). Посмотрим, что означают эти
требования для коэффициента G{t) исходной задачи D1.Г).
Обозначим Э приращение какой-нибудь ветви аргумента G{t)
при обходе контура L. Заметим сразу же, что 0 можно
рассматривать как скачок аргумента G{t) в точке разрыва, взятый
с противоположным знаком. Поэтому можно положить
-^-^h:=^ = oe^^ D1 17)
Тогда по формуле D1.11)
1 I G(/,-0) е . inp /., юч
У=^^'' Git, + 6) "г^е-'^-^^-гГ- D1.18)
*) Условие Re Y >—1 немедленно вытекает из требования
интегрируемости. Смысл правой части неравенств D1.15) и D1.16) заключается в том,
чтобы не накладывать на решение лишних условий. Нарушение неравенств
сопровождалось бы потерей допустимых решений.

§ 41] РЕШЕНИЕ ЗАДАЧИ РИМАНА 433
где целое число к нужно выбирать в соответствии с условиями
D1.15) и D1.16), которые принимают вид
0<-|--х<1, D1.150
2я
е
2я
-~1<^-х<0. D1.160
Отсюда следуют формулы:
для класса ограниченных решений
« = [-1^]; D1.19)
ДЛЯ класса неограниченных вблизи точки ti решений
« = Ш+1. D1.20)
Символ [х] — «антье х» — означает, как это принято в теории
чисел, наибольшее целое число, не превосходящее х.
Подсчитаем теперь индекс задачи D1.13). Учитывая
формулы D1.14), D1.17) и D1.18) (последняя определяет выбор
ветви логарифма), находим
^"dG,(/) = i{InG.(/)k = J^ln(|i^e-^v) =
Эту величину мы и назовем индексом данной задачи D1.10.
Индекс определяется, таким образом, формулой D1.19) или
D1.20) и зависит от выбранного класса решений, причем
индекс задачи в классе неограниченных решений на единицу
больше индекса в классе ограниченных решений.
Если 0/2я есть целое число, то из двух условий D1.150 и
D1.160 может выполняться только первое при к = 6/2я.
Точку разрыва ti в таком случае будем называть точкой
автоматической ограниченности. Решение задачи D1.10, оставаясь
ограниченным вблизи этой точки, не стремится при
приближении к /i ни к какому пределу (см. конец п. 41.2).
Выяснив принципиальную сторону дела в рассмотренном
простейшем случае, перейдем к решению задачи в общем виде.
41.4. Решение однородной задачи. Пусть коэффициент G{t)
имеет разрывы 1-го рода в точках tu ^2, •.., ti. Разобьем
контур L на участки между 4 и 4+i точками разрыва и будем
определять в каждой начальной точке участка ветвь arg G{tk + 0)
произвольно; в конечной же точке участка arg G(tk+\—0)
будем получать из выбранной ветви arg G{th + 0) путем
непрерывного изменения.

434 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Обозначим, как и раньше,
где 9ft есть скачок аргумента в точке разрыва 4, взятый с
обратным знаком.
Положим
1.-6. In р.
у, = _1пЛ,=-2^-х.-/-^ D1.21)
(целые числа Xk определяются формулой D1.19) или D1.20)),
Ф+(г) = П(г-4Г*ФГB), Ф~{^) = '[[(^У''ФГ{г), D1.22)
причем разрезы для функций B — 2:0)^^ проходят через точку 4
контура. Подставляя в уравнение D1.Г), придем к краевому
условию
Ф^ it) = U{t- ZoV'^ G it) ФГ @, D1.23)
в котором, по определению, функция (/ — 2оУ^^ испытывает
скачок при переходе через точку /ft.
Рассуждая аналогично рассмотренному выше случаю одного
разрыва, убеждаемся, что коэффициент Gi{t) = YL (^ — ^о)"^^ G (/)
есть функция непрерывная. Следовательно, мы снова пришли
к решению задачи с непрерывным коэффициентом. Нетрудно
вычислить индекс коэффициента Gi(/). Беря приращение
аргумента G\{t) по всему контуру L как сумму приращений по
участкам между точками разрыва и учитывая, что каждый бином
(/ — го)^* удовлетворяет в точке tk условию
(tk — O — gp)^* ^ ^2я/Y^fe
(/fe + 0-гоЛ
получим
Ind G, (О = i {In G, it)}, = ^ j; (In G, (/)};*+¦ =
Последнюю величину будем называть индексом исходной
задачи D1.1').

§ 41) РЕШЕНИЕ ЗАДАЧИ РИМАНА 435
Как уже отмечено выше,
если решение ищется в классе ограниченных функций, и
для класса неограниченных интегрируемых функций.
Отсюда видно, что индекс задачи в классе функций, имеющих
в данной точке разрыва бесконечность интегрируемого порядка,
на единицу больше, чем индекс в классе функций, ограниченных
в данной точке.
Пусть требуется найти решение, имеющее интегрируемую
бесконечность в некоторых р точках разрыва и ограниченное
в / — р остальных таких точках. (Все точки автоматической
ограниченности, очевидно, войдут во вторую группу.) Согласно
предыдущим рассуждениям индекс задачи в указанном классе
выразится формулой
« = Е[ж] + /'- D1.25)
Можно было бы выразить индекс через приращение аргумента
G{t). Однако здесь не получится такой простой формулы, как
это было в случае одной точки разрыва, и потому этого
выражения мы не приводим. При решении конкретных задач индекс
вполне определяется последними формулами.
Для получения общего решения поставленной задачи нужно
найти по правилам § 14 общее решение Ф\{г) задачи D1.23)
с непрерывным коэффициентом, тогда формулы D1.22) дадут
общее решение исходной задачи. Мы здесь не будем выписывать
соответствующих формул, а перейдем к решению неоднородной
задачи. В состав общего решения этой последней задачи входит,
как известно, и общее решение однородной задачи; в п. 41.5 мы
приведем формулы полностью.
41.5. Решение неоднородной задачи. Рассмотрим
неоднородную задачу
Ф+(/) = О(/)ф-(/) + г@.
Относительно G{t) будем исходить из тех же
предположений, что и в предыдущем пункте, а g{t) будем пока считать
удовлетворяющей условию Гёльдера.
Вводя новые функции Ф1**(г), ФТ {z) подстановками D1.22),
приведем краевое условие задачи к виду
Ф1^ (О = П (^ - ^о)"'^ G (О ФГ (О + П (^ - hr""' g (/).

436 КРАЕВЫЕ ЗАДАЧИ (ГЛ. VI
/
Заменяя непрерывный коэффициент Г1(^ —2:о) ^G{t) отно-
шением канонических функций (см. п. 14.3), придадим краевому
условию форму
х+(/) Xf(o х+(о
Последняя задача есть задача D1.2) определения
аналитической функции по заданному скачку, причем на бесконечности
ФГ (^)
функция •—: имеет порядок —к. Согласно равенству D1.6)
Xj (z)
решение ее дается формулой *)
ФЫ 1 flic-'•)'"«<'> ,
При X < О нужно положить Pyi(z) ^ 0.
На основании формул D1.22) решение поставленной задачи
имеет вид
Ф*" {Z) = П C - hr^ Xt (z) [Чг^ (г) + Рх {z)l
/5-1
где
D1.27)
/fe-i
Xi^ (г) = е^"- <^'. ХГ (г) = (г - го)"" /' '^'.
L
D1.28)
Легко установить, что решение, определяемое последними
формулами, принадлежит заданному классу.
*) Теперь ясно, что Rey/i должно быть меньше единицы (см. замечание
ва стр. 432, а также п. 8.4).

§ 4lJ РЕШЕНИЕ ЗАДАЧИ РЙМАНА 437
Пусть, например, ReY/>0. Тогда, в силу формул (8.20),
функция 4^{z) вблизи точки tf будет иметь порядок роста
{z — tiY^I и, следовательно, в силу наличия множителя {z — tf^ff
Ф(г) будет ограниченной.
Если ReY/<0, то 4^{z) будет в точке tj ограниченной,
а Ф (г) будет обращаться в бесконечность порядка Re у/.
Если на решение наложить дополнительное условие
ф-(оо) = 0, D1.29)
то в формуле D1.27) нужно заменить Py^iz) на P'n^i(z).
Результат исследования может быть сформулирован в виде
теоремы, которая будет почти дословным повторением теоремы
п. 14.5.
Теорема. Если индекс к задачи Римана в заданном классе
положителен, то общее реисение неоднородной задачи линейно
зависит от X +1 произвольных постоянных и определяется
формулой D1.27), где при дополнительном условии ф-(оо) = 0
Pj^ следует заменить на Px-i-
При X ^ О однородная задача в заданном классе
неразрешима, а неоднородная задача разрешима тогда и только тогда,
когда выполняются —х условий
\'°' у+,, T/-'rfT = 0 (/=1, 2 -к). D1.30)
^ -^1 (Т)
Если эти условия выполнены, то неоднородная задача имеет
единственное решение, которое получается из D1.27) при
Напомним, что индекс задачи в данном классе, совпадающий
с индексом задачи D1.23) с непрерывным коэффициентом,
определяется формулой D1.25).
Замечание. Несмотря на то, что в формулы D1.27) явно
входит произвольно выбранная точка го, легко показать
(предоставляем это читателю), что общее решение не зависит от
выбора этой точки.
Рассмотрим теперь, какие изменения нужно внести в
полученное решение, если допустить, что g{t) имеет разрывы в
конечном числе точек.
Пусть в окрестности точек /i, /2, ..., ^г g (О имеет
представление
g(^)==/'?4vl (y; = «; + 'K. 0<а;<1), D1.31)

438 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
где g^{t) удовлетворяет условию Гёльдера, а в точках /и
/2, ..., t's имеет разрывы 1-го рода g {Ц + 0)Ф g {й — 0).
Рассмотрим отдельно два случая.
Г. Все точки разрыва свободного члена
отличны от концов*). Рассуждения, с помощью которых было
получено решение, в предположении, что свободный член
удовлетворяет условию Гёльдера, полностью останутся в силе и для
рассматриваемого случая, и мы снова придем к формулам
D1.27), D1.28). Различие будет лишь в том, что теперь
решения, кроме особенностей на концах, определяемых выбранным
классом решений, будут иметь особенности в точках разрыва
функции g{t). В силу свойств интеграла типа Коши (пп. 8.2,
8.4), решение будет иметь особенность вида
0(f)=.(/-i^)-v^O*(/)
в точках t\, /2, • • •, ^г и особенности логарифмического
характера в точках f\, /2, •••, t's*
При этом, в отличие от концов, где поведение решения в
какой-то степени зависит от некоторого произвола (выбор класса),
в точках разрыва свободного члена поведение решения целиком
определяется характером разрыва.
2°. Некоторые точки разрыва g{t) совпадают
с концами. Для точек разрыва g(t), не совпадающих с
концами, очевидно, остается в силе предыдущее рассуждение.
Далее, легко усмотреть, что совпадение с концами точек разрыва
g{t) 1-го рода не вносит ничего нового по сравнению с
рассмотренным случаем свободного члена, удовлетворяющего условию
Гёльдера, так как поведение функции -^^ -^ , являю-
Xj (т)
щейся плотностью интеграла типа Коши, будет одинаковым как
для функции g{t), удовлетворяющей условию Гёльдера, так и
в случае, когда она имеет разрыв 1-го рода.
Для точек tk, совпадающих с концами, может произойти
сложение особенностей, поэтому этот случай нужно рассмотреть
подробнее.
Пусть tk = tk. Вставляя в формулы D1.28) вместо функции
g{t) ее выражение D1.31), получим, что в точке 4 плотность
соответствующего интеграла типа Коши будет иметь вид
(/ —- tk)' (^^¦*'^^) ф1 (О (ф1 {t) удовлетворяет условию Гёльдера),
т. е. будет иметь порядок — (а^^ + «^).
По определению а^^О, число же а^ будет равно нулю для
особенного конца, а в случае неособенного конца будет
положительным, если отыскивается решение, ограниченное на конце
*) Концами мы называем точки разрыва коэффициента G(/).

§ 42] КРАЕВАЯ ЗАДАЧА РИМАНА ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 439
tk, И отрицательным в противном случае. В гл. I было дано
исследование интеграла типа Коши с плотностью, обращающейся
в бесконечность, только для случая бесконечности порядка
меньше единицы. Если отыскиваются решения, не ограниченные
в точке th, то а;^ + а^<1 и применимость теории обеспечена.
Простой подсчет даст, что в этом случае решение будет иметь
в точке tk порядок не ниже, чем min (а;^, — а^).
Для решений, отыскиваемых в классе ограниченных функций
в случае, когда а^ + «& < 1, теория также применима, но только
решение в исследуемой точке фактически окажется
неограниченным (исключая случай ajfe = 0); его порядок будет равен — а^.
Если a^fe + ttfe > 1, то потребуется дополнительное исследование.
§ 42. Краевая задача Римана для разомкнутых контуров
42.1. Постановка и решение задачи. Пусть контур L состоит
из совокупности т простых гладких непересекающихся кривых
Li, L2, ..., Lmy концы которых ak и бд (положительный обход
производится от Qh к 6ft), и пусть 0{t)y g{t) — заданные на L
функции, удовлетворяющие условию Гёльдера, причем всюду
G@?=0.
Требуется определить функцию ФB), аналитическую на всей
плоскости, кроме точек контура L, граничные значения Ф+(/),
ф-(/) которой при приближении к L слева и справа суть
интегрируемые функции, удовлетворяющие краевому условию
Ф+@ = о(Оф-@ + г@. D2.1)
Задача Римана для разомкнутого контура, как видно из
постановки, принципиально отличается от задачи для замкнутого
контура тем, что вся плоскость с
разрезом по кривой L составляет одну
область и приходится отыскивать не Л'
две самостоятельные аналитические \?
функции Ф-^iz), Ф(г), а одну
аналитическую функцию Ф(г), для которой
контур L является линией скачков.
Сформулированную задачу можно
свести к рассмотренной в § 41 задаче
для замкнутого контура с разрывными Рис. 15.
коэффициентами следующим
формальным приемом*). Дополним контур L т произвольными
кривыми Li, L2, ..., Lm так, чтобы образовалась одна замкнутая
кривая С (Li -f Li + ... + ^-m + ^^m = О без самопересечений
(рис. 15).
*) Идея, заложенная в этом приеме, была устно высказана впервые
Н. Ц. Л^ейманом.

D2.4)
440 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
На дополняющих кривых, очевидно, Ф+(/)=ф-@.
Учитывая это, задачу D2.1) можно рассматривать как задачу на
замкнутом контуре
Ф^@ = 0,(/)Ф-@+^1@, D2.2)
причем
Gi @ = 0@, gi{t)=g{t) на L,,
Gi(/)=1, ^i@ = 0 на U (^=1, 2, ..., m). ^^^'"^^
Дальнейшее решение представляет собою пример на
применение теории предыдущего параграфа. Положим G (а^^) = pj^e'^^
" G (bi^) = p'f^e (^k'^^k)^ где д^^ обозначено изменение arg G (t)
на L/fe. Тогда
Gi (а, - 0) = 1, G, {а, + 0) = G (а,) = р,е'\
O,F,-0) = GF,)=^p;.'(^^^4 G,F, + 0)=I;
(^i(«. + ^) p/ ' ^i(^;^ + 0) ^' • J
Значение аргумента Qk *) в начальной точке uk контура
условимся брать в пределах
~2я<еА<0, D2.5)
если ищется решение, ограниченное в точке ад, и в пределах
О < е^ < 2я, D2.6)
если искомое решение не ограничено в точке а^.
Условия эти накладываются только для упрощения
следующих формул и не оказывают влияния на окончательные
результаты.
Положим (см. формулу D1.21))
1 е^л , ' D2.7)
^k 2т ^" VPfe^ ; 2ji ^^ ^ 2я '
где Xfe — целые числа, которые на основании формул D1.16),
D1.18) определяются как
«* = [ТГ^] D2-8)
*) Следует иметь в виду, что теперь 0л означает просто скачок
аргумента функции Gi(t) в точке ад, а 0л + Да —скачок в точке бд, взятый по-
прежнему с обратным знаком.

§ 42] КРАЕВАЯ ЗАДАЧА РИМАНА ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 441
ДЛЯ решений, ограниченных в точке Ь^, и как
«* = [^] + 1 D2.9)
ДЛЯ решений, не ограниченных на этом конце.
Индекс задачи представляется формулой
т
fe-i
где Xft определяется формулой D2.8) или D2.9) в зависимости
от того, ограниченным или неограниченным должно быть
решение в конце bh. В свою очередь начальное значение аргумента
в точках uk должно удовлетворять условию D2.5) для
ограниченного и условию D2.6) для не ограниченного в точке а^
решения.
Легко видеть, что допущение неограниченности решения на
любом из концов повышает индекс на единицу. Это является
простым следствием соответствующего свойства для точек
разрыва.
Концы, на которых G{t) есть действительное положительное
число (аргумент кратен 2я), будем называть концами автомата-
ческой ограниченности (особенными). Если таким концом
является начальная точка а^, то нужно положить Э^ = О, а если
^k + Ч
конечная точка й^, то к^ = 2к *
Вводя новые функции подстановкой
т г
Ф"" B) = П B - а*)"* B - bS^<^\ B).
"т . .«. , . .V'. D2.10)
^-й=ПЙ^)(^) ^гй,
придем к задаче с непрерывным коэффициентом G на
замкнутом контуре С:
т f
ФГ (/) = П (^ ~ ^о)~'^ {t - ^о)""^ Gi (О ФГ (/) +
ft-i
+ П (< - а*)"'* {t - h)-'" g, @. D2.11)
Дальше решение производится обычным способом, и нет
нужды специально его излагать. Легко доказать (см. задачу 1
в конце главы), что решение не зависит от вида замыкающей
кривой L\

442 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
42.2. Пример. В качестве примера изложенной теории
рассмотрим задачу (встречающуюся во многих приложениях), на
которую в дальнейшем будем неоднократно ссылаться.
Пусть на контуре L, состоящем из т разомкнутых кривых»
G(/) = —1, т. е. краевое условие задано в виде
Ф"'@ = -Ф'@ + ё^@. D2.12)
Выпишем краевое условие для замкнутого контура:
Ф^(/) = е,@Ф~(/) + г1(/); D2.120
Gi@ = -I, gi{t) = g{t) на L,
Gi@=l, giit) = 0 на L\
Будем сначала искать решение в наиболее широком классе
функций, не ограниченных вблизи всех концов. В этом случае
получим
Gi(a,~0)=l; Gi(a, + 0) = -l=^^«;
АК-^)_.-/я.
G, (Ьь4-0)=1' ^i(^fe-"Q) ^ in.
Так как Q^ = n и A^^ = 0, то x^ = [y]+l = l, y;; = -1/2.
Следовательно,
m
^=Ys y^k^rn. D2.13)
Согласно подстановке D2.10) задача на замкнутом контуре С
с непрерывным коэффициентом запишется в виде
"* 1 ±
фТit)^liit-zoni-гоJ G,(/)ФГ(О +
m 2 i
+ n(/-«/^)M^-W2fi^i@. D2.14)
Функция Gi (/) меняет знак в точках ад, fe^. По определению,
в каждой из этих точек меняет знак один из биномов (/ — Zq)\

§ 42] КРАЕВАЯ ЗАДАЧА РИМАНА ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 443
Поэтому МОЖНО положить *)
т 1 1
Hit- ZoY it - го) 2 G, (О = {/ - гоГ.
Для краткости условимся употреблять в дальнейшем такие
обозначения:
"^ 1 1
I[{2-a,)^{z-b,y=Riz),
m '"'i т 1 D2.15)
Uiz-a.y^RAz), 'n.{z-b,y=Rb{z).
Тогда условие D2.14) примет вид
Фt{t) = (t-z,)'"Ф;it) + R{t)g^^t). D2.16)
Так как индекс задачи к = т, то по формулам D1.28)
найдем **)
Xi{z)=l, ХГB) = (г-го)-'".
Согласно D1.27) решение исходной задачи, не ограниченное на
всех концах, определится формулой
где
Ф+ (Z) = Ф- B) = ф B) = ^ [VF B) + Рт(г)], D2.17)
^(^) = W$^^^^- D2-18)
В приложениях часто приходится иметь дело с решением,
удовлетворяющим дополнительному условию
Ф(с») = 0. D2.19)
В этом случае нужно в формуле D2.17) Рт{г) заменить на
Pm-i{z), (Все дальнейшие формулы приведем для решения,
удовлетворяющего условию D2.19).)
Если на каких-либо концах а^, bj потребовать
ограниченности решения, то нужно взять соответствующие показатели у^, Y/
равными 1/2. Требование ограниченности на любом конце, как
уже указывалось в общем случае, понижает индекс на единицу.
*) На этом примере читатель может наглядно проследить механизм
устранения разрыва.
**) Разумеется, и в этом случае и во всех последующих функции Х^ (г)
могут быть найдены непосредственно.

444 КРАЕВЫЕ ЗАДАЧИ 1ГЛ VI
Решение, ограниченное в начальных точках ак и не
ограниченное в конечных точках &й, имеет вид
(Индекс X здесь равен нулю.)
Решение, ограниченное на всех концах, определяется
формулой
причем, так как здесь х = —т, решение существует только
в том случае, когда выполнены т условий разрешимости
St(|^'"'^^==0 (/=1,2, ..., m). D2.22)
L
Выпишем, наконец, решение в самом общем случае.
Обозначим все концы единообразно буквами Си Сг, ..., С2т- Пусть на
каких-нибудь концах Си ^2, ¦ • •, Ср решение ограничено, а на
всех остальных концах ^р+ь ..., С2т допускается интегрируемая
бесконечность. Концы автоматической ограниченности, как легко
видеть, здесь отсутствуют. Обозначим
V"p / 2m
ПB-с,), /?2(г)-Д/ П B-Cft). D2.23)
Индекс равен m — /?, и решение будет иметь вид
Если р ^ т, то Pm-v-\ ^ о» причем в случае р > т решение
существует только при соблюдении условий разрешимости
S^^(T)t/-^dT = 0 (/=1,2, ..., p-m). D2.25)
L
42.3. Обращение интеграла типа Коши. Рассмотрим
практически важную задачу обращения интеграла типа Коши
±5^rf, = ^@. D2.26)
L
Контур L будем считать таким же, как и в п. 42.2.

§ 421 КРАЕВАЯ ЗАДАЧА РИМАНА ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 445
Уравнение D2.26) есть частный случай особых интегральных
уравнений с ядром Коши, теория которых для замкнутых
контуров излагалась в гл. III, а для разомкнутых контуров будет
рассматриваться в §§47 — 48. Здесь мы решим это уравнение, не
опираясь на общую теорию, но применяя метод, на котором эта
теория основана.
Вводим аналитическую функцию (ср. п. 21.1)
^(-) = iST:?F^- D2.27)
L
На основании формулы Сохоцкого D.10)
L
Подставляя последнее в уравнение D2.26), придем к краевой
задаче
ф-^ (О = -ф-@-^7@, D2.28)
рассмотренной в предыдущем пункте {g{t)= —if{t)), при
условии D2.19).
Решение уравнения D2.26) может быть получено из решения
краевой задачи по формуле Сохоцкого D.9):
Ф@ = Ф"'@-Ф~@.
1°. Решение, не ограниченное вблизи всех
концов. Чтобы в формуле D2.17) перейти к краевым значениям,
определим точнее ветви многозначных функций, входящих в эту
формулу. В качестве R{t) выберем какую-нибудь определенную
ветвь этой функции. Ветвь R{z) выберем, например, так, чтобы
при приближении к контуру слева краевое значение /?+@ этой
функции совпадало с выбранной ветвью R{t), Тогда будет
справедливо равенство
R-{t) = -R^{t) = -R{t).
Учитывая это, по формулам Сохоцкого получим

446 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Отсюда
BP;;t-i снова обозначаем Pm-i)-
Легко видеть, что второй член правой части D2.29)
представляет собой общее решение однородного уравнения D2.26)
(/@ = 0).
Аналогичными рассуждениями получим следующие
результаты.
2°. Решение, ограниченное на концах а^ и не
ограниченное на концахbfti
* (^^ -"" тш т ] та^ т^ ^^- ("^2-^^)
3°. Решение, ограниченное на всех концах:
<p@ = -;?(O^J^-^. D2.31)
L
При условии, ЧТО свободный член /(/) удовлетворяет условиям
5^^^""'^^ = 0 (/=!' 2, ..., т). D2.32)
Исходя из формулы D2.24), читатель может легко выписать
решения в общем случае.
Приведем еще решение важного для приложений случая,
когда кривая L есть отрезок действительной оси а ^ / ^ 6,
причем представим функцию R(t) так, чтобы иметь дело только
с действительными величинами.
1. Решение, не ограниченное на обоих концах:
а -*
2. Решение, ограниченное на конце а и не ограниченное на
конце Ь\
а
3. Решение, ограниченное на обоих концах:
b
^(t)^-^{t-a)[b-t)^\-—f^^'> '^\, D2.310

§ 43] НЕПОСРЕДСТВЕННОЕ РЕШЕНИЕ ЗАДАЧИ РИМАНА 447
при условии
Ъ
Г f{x)dT ,^Q ^42.320
Решению рассмотренной задачи различными частными
приемами посвящено много работ. Библиография этих работ
приводится в книге Н. И. Мусхелишвили [16].
§ 43. Непосредственное решение задачи Римана
Для задачи Римана с разрывными коэффициентами и с
разомкнутым контуром, кроме изложенного в предыдущих
параграфах способа, опирающегося на сведение ее к ранее решенной
задаче с непрерывными коэффициентами, известен еще другой
способ, заключающийся в непосредственном применении метода
решения задачи с непрерывными коэффициентами. Здесь
удобнее начинать со случая разомкнутого контура.
43.1. Задача для разомкнутого контура. Начнем с
однородной задачи
ф+(/) = С(ОФ"'@. D3.1)
Рассуждениями, аналогичными тем, которые применялись
в п. 14.3, установим *), что функция
фB) = ^г(г)^ Y(z) = -^\^^^dx D3.2)
L
удовлетворяет краевому условию D3.1) всюду, исключая, может
быть, концы. Изучим поведение Ф{г) на концах. На основании
формул (8.1), (8.2)
{аь\ Оу 1прь
/^^^ D3.3)
/^^'\ D3.4)
где Tk{z) и Г1 (г) — функции, ограниченные соответственно
в окрестности точек а^, &л. Условимся значение аргумента G(t)
в начальных точках а^ брать согласно D2.5) или D2.6) и
введем целые числа х^, удовлетворяющие условию D2.8) или
D2.9). Рассмотрим функцию
пг
ХB) = ПB-&*Г*е^'''. D3.5)
gViz),
еГ(г),
= (г
= B
— ОкУ
1
In 0(aj)
Ш /* (г)
^^/;-=
= (г
¦.{Z-
2л
InpJ
2л
*) arg G[t) по-прежнему считаем непрерывно изменяющимся на каждой
из дуг.

448 КРАЕВЫЕ ЗАДАЧИ [ГЛ. V'l
Очевидно, она будет также удовлетворять краевому условию и
вместе с тем будет принадлежать на концах заданному классу
решений.
Функцию Х(г) назовем канонической функцией задачи. Так
как Г(оо)= О, то, очевидно, порядок Х(г) на бесконечности
будет равен
m
7i=Z ^k- D3.6)
X^ (t)
обычным способом. Представляя G {t)= ^ , запишем крае-
Число X будет индексом задачи. Дальше решение производится
обычным способом
вое условие в виде
откуда при X ^ О
^llfI=^фlШ. D37)
Ф(г) = ХB)РЛг). D3.8)
Если требуется, чтобы ф(оо)=0, то Р^ нужно заменить на Р^-и
Обычным приемом находим решение неоднородной задачи (при
ф(оо) = 0):
Ф B) = X (г) [W (г) + Рн-1 BI. D3.9)
где
W(z) = -^\-^-^^, D3.10)
^ 2я« J Х+ (т) Т - 2 ^ ^
причем при X < О должны выполняться условия разрешимости
\
lSlL^l-idx = 0 (/-1, 2, ..., -X). D3Л1)
L ^ (^^
43.2. Задача с разрывными коэффициентами. Разбивая
контур L на участки между точками разрыва коэффициента G{t) и
рассматривая эти участки как самостоятельные кривые, можно
решать предложенную задачу как задачу на разомкнутом
контуре. Своеобразие задачи состоит в том, что концы кривых *)
попарно совпадают. Покажем описательно, как видоизменить
решение задачи из п. 43.1, чтобы получить решение
рассматриваемой задачи.
Выбираем некоторую точку разрыва /i за начальную и
определяем в ней arg G(/i+0) t= 01 выбором какой-нибудь опре-
*) В дальнейшем термин концы мы будем применять не трлько к концам
кривой, но и по отношению к точкам разрыва.

§ 43] НЕГ!0СРЕДСТВЕНН0Ё РЕШЕНИЕ ЗАДАЧИ РЙМАНА 443
деленной ветви. Путем непрерывного изменения определяется
arg G (^2 — 0) = 01 + Ль Величина arg G (^2 + 0) = 62
определяется так, чтобы
- 2я < arg G (/2 - 0) - argG (/2 + 0)< О, D3.12)
если ищутся решения, не ограниченные в точке /2, и
О < arg G (/2 - 0) - arg G (/2 + 0)< 2jt, D3.13)
если ищутся решения, ограниченные в этой точке *).
Аналогичным образом поступаем во всех остальных точках
разрыва (/з, ..., ^п). В точке t\ определяем целое число х,
удовлетворяющее одному из условий:
— 2я < arg G (^1 — 0) — arg G (^i + 0) — 2хя < О, D3.14)
О < arg G (/1 — 0) — arg G (/1 + 0) — 2хя < 2я, D3.15)
в зависимости от того, неограниченным или ограниченным
должно быть решение вблизи точки t\. Число х и есть индекс
задачи. Тогда
Х(г) = B-^,Г/'^>. Г(г)=2^г$^7^^^ D3.16)
L
будет канонической функцией однородной задачи.
Решение неоднородной задачи дается формулами D3.9) —
D3.11).
43.3. Примеры. 1. В качестве первого примера на применение метода,
изложенного в настоящем параграфе, рассмотрим задачу, встретившуюся при
решении одной конкретной механической проблемы.
Пусть контур L есть отрезок действительной оси (О, /). Рассмотрим
краевую задачу
"^^ (') =ТТ77ГТЙГ^" W + ^ (')• D3.17)
a-f- tyao-f- ait)
где а, Ооу ai —некоторые заданные действительные постоянные, g(t)
-—заданная функция, удовлетворяющая условию Гёльдера. Ищется решение, обра*
щающееся на бесконечности в нуль.
Так как |G(Ol= 1, то
In G (t) = 2/ arg [а - / (uo + aiOl = ~ 2/arctg ^^+^'^ = 2/9. D3.18)
Точки с аффиксами a — i(ao + ait) геометрически будут изображаться от-
езком прямой, параллельной оси ординат между точками ?i == а — Шо и
12 = а — 1(^0 + ail); поэтому А = {9}l < я.
*) Предполагается, что /г не есть точка автоматической ограниченности.
Если она принадлежит к последнему классу, то в левой части формулы
D3.13) нужно взять знак равенства.

450
КРАЕВЫЕ ЗАДАЧИ
1ГЛ. VI
Возьмем для определенности а > 0. Всего могут представиться четыре
различных случая:
1) Sii ?2~обе в I четверти;
2) ^1. ^2— обе в IV четверти;
3) ^1 — в I, ?2 — в IV четверти;
4) ti — в IV, ^2 — в I четверти.
Будем для определенности искать решение, ограниченное в начале
координат и не ограниченное на другом конце. Разберем подробно 4-й случай
(рис. 16).
Согласно D2.5) для 20i нужно взять ветвь, удовлетворяющую условию
—2я < 201 < О, причем это неравенство определяется только выбранным
,,, А V п классом решений. Тогда О < 202 = 2@i + Д) < 2я.
^1 ^ч'Ыа^'^а^Ь) По формуле D2.9)
«=[i±i]+,-,.
Каноническим решением задачи будет функция
ХB) = B-0-'е1'Ч
Г (г)
=-iS
arctg -^ —
Т —2
'^т, D3.19)
а общим решением
Ф(г)-ХB)[1^(г) + Со],
D3.20)
Рис. 16.
где
4r(.) = -LD^
2ni J Х+ (т)
dx
-, а Со —
произвольная постоянная.
Для остальных случаев, не входя в подробности, укажем основные
характеристики.
1-й случай:
-2я<2е2 = 2(е1 + Д)<0, -l<-^^-t^<0, х = Г^^ "^^1+1=0.
эх L л J
2-й случай:
3-й
случаи:
- 2я<2е2 =* 2 (91 + Д)< О, X = 0.
4я< 202 = 2 @1 + Д)< - 2я, X = - 1.
Во всех этих случаях однородная задача неразрешима, а неоднородная
задача разрешима единственным образом, причем в последнем случае лишь
при соблюдении одного дополнительного условия.
Читателю рекомендуется в качестве упражнения самому исследовать
решение в остальных трех возможных классах функций.
Полученное решение будет использовано нами в п. 47.4 при решении
особых интегральных уравнений.
Сделаем некоторые замечания к решению задач. В практическом
отношении, когда требуется довести решение до окончательного результата, главную
трудность составляет вычисление соответствующих интегралов. В теоретиче*

§ 43] НЕПОСРЕДСТВЕННОЕ РЕШЕНИЕ ЗАДАЧИ РИМАНА 151
ском отношении (определение числа решений), как читатель мог убедиться из
разобранного примера, дело сводится к тому, чтобы правильно выбрать
начальное значение аргумента (в зависимости от требуемого класса решений) и
проследить за тем, чтобы его конечное значение получалось из начального
путем непрерывного изменения.
2. Для лучшего усвоения техники решения задач рассмотрим еще пример,
в котором данные подобраны так, чтобы решение выражалось в
элементарных функциях.
Пусть L — единичная окружность и Li и L2 — соответственно ее правая
и левая полуокружности. Решим краевую задачу Римана:
Ф- (О = G (О Ф- (О + i^ii^i^ (^)"'^ A а I < ,). D3.21)
где
-{
Многозначная функция ( . j задана некоторой определенной ветвью.
Будем сначала искать решение в самом широком классе функций,
имеющих интегрируемые особенности в обеих точках разрыва ±i. Пользуясь
формулами D3.16), найдем сначала каноническую функцию однородной задачи:
Г(г)
1 f 1п G (т) , я Г т . , 2я f т
2ш J т — г 2nt J т — 2 2л1 j х — z
JL L,\ Li
2яг J T — 2 2/ J T — 2 2i ) X— z 2i z — i
L i L
Применяя к интегралу для z ^ D формулу Коши, а для z е D" теорему
Коши, получим
Тиг) = лг-1+^1п^, r-(.) = -l+^lnf±j.
Отсюда
х*,.,_...-.(Л-)"«, х-«..-.(^)-.
Легко проверить непосредственной подстановкой значений ±/, что в этих
точках X{z) ведет себя как (г —i)~^^^, (z + 1)~^^^,т. е, принадлежит
заданному классу. Следовательно, дополнительные множители {z ± i) ^ не
требуются, т. е. индекс задачи х = 0. Для полной определенности канонической
функции, а затем и самого решения задачи нужно указать еще способ
задания многозначной функции со (г) = ( —-г--г ] , что сводится к заданию
разреза, соединяющего точки ветвления ±i, и заданию ветви. Вставляя X
в однородное краевое условие, получим
( @~ (/) на Li,
"""(') = { л-W на и
Последнее означает, что разрез должен быть проведен по левой
полуокружности L2, причем значение а)~@ на правой (внешней) стороне получается из

462 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
значения сй+{0 на левой (внутренней) умножением на е~"^ Если ©бвйти
вокруг- одной из точек ветвления (например, i), то как раз и возникает мно-
жите.1ь e^"* ^'^/^^ = 6""^^ В дальнейшем предельные значения на L изнутри
мы будем обозначать одним и тем же выражением q+ (/) = f J ;
такими же должны браться значения со-(О на Li; значения же (и (t) на Li
должны умножаться на ^~" . Изложенные здесь соображения очень важны
в приложениях краевых задач к решению особых интегральных уравнений
(см. п. 48.6).
Ветвь (О (г) выберем так, чтобы о)+@ совпадала с соответствующей
функцией, входящей в g{t).
Найдем теперь ^{z). По формуле D3.10)
^C) = -LC_iIi1^^-=-^( (т^ + 1)Dт + /:
2я/ 3 х"^ (т) (т - z) 2ш } т2 + а2
)-"^ dx
Пользуясь теорией вычетов, после всех выкладок получим
"^ (^) = ' ^2 + ^2 [ 1 ''" «^ ~ (^ + 4^) (cos ап'-е «^ -jTT^ J J'
т (г) =» е "д ^ sin an — {i + Az) cos ая .
По формуле D3.9), в которой нужно взять не Рх-ь а Ру,, окончательно
будем иметь
«*м-(-Й7)""«"'-'!''*«+л
Советуем читателю самому решить задачу в предположении, что в точке i
допускается интегрируемая бесконечность, А всюду в остальной плоскости
решение ограничено.
Для справок приводим ответы:
«¦*<«-^"(т^)""?т^[""'""(т-^-+")+
+ COS an {Siz + 4а^ - l) + е""^ {4z^ _ з/г + 1I,
ф- (^) = {тггУ^" -FTP" h "^ (i - ^'' -^ ^ +
+ со8аяC/« +4а2 — 1I
43.4. Краевая задача Карлемана. Продолжение. Приведем
здесь заключительную часть решения краевой задачи
Карлемана A8.20). В п. 18.3 оно было приведено к решению задачи
Римана
Ф+ {w) = Gj (w) Ф; (w) + gj И A8.32)
D3.23)

§43]
НЕПОСРЕДСТВЕННОЕ РЕШЕНИЕ ЗАДАЧИ РИМАНА
453
на разомкнутом контуре Li с концами а = (о+(Л), b = (о+E).
Здесь Gi{w)=G[z-{w)\ g\{w) = g[z+{w)\ А и В
—неподвижные точки сдвига a{t).
Решение задачи A8.32) следует искать в классе функций,
ограниченных на концах w = а, w = b vi ^г. бесконечности.
Действительно, ограниченность решения Ф1(ш) = Ф+[г(ш)] в
окрестностях концов W = а, W = b вытекает из ограниченности
Ф+(г) в окрестностях точек г = Л, г = В, а ограниченность на
бесконечности следует из того, что Oi(oo)= Ф+(го) есть
конечное число.
Вычислим индекс xi задачи A8.32). Пусть
Поступая как и в п. 18.2, из условия G{t) G [а(/)] = 1 заключаем,
что [arg G @]l+ =^ [^^& ^ Шь- = ^^- Поэтому
[arg G, (w\^ = [arg G [z- (w)] ]^^ = - [arg G @]^- = - хя. D3.24)
Из того же равенства G{t)G[a(t)] ^ 1 следует, что G{t) может
принимать в точках t = А, t = В лишь значения -fl, —1. Такие
же значения принимает коэффициент Gi{w) на концах о; = а,
W = b контура Li. Рассмотрим отдельно случаи четного и
нечетного к.
1) к — четное. Из равенства
arg Gi F) — arg G^ (a) = — xjt, D3.240
вытекающего из D3.24), следует, что либо G[{a)= G[{b)= 1,
либо Gi(a)= Gi{b)= —1. В первом случае оба конца являются
точками автоматической ограниченности, так что к\ = —к/2. Во
[j^ j_ 1  X 4- 2
5— = к—-
2) УС — нечетное. Тогда в силу D3.24^ либо G\ (а) =
= —GiF)= 1, либо Gi(a)=—Gi{b)=—1. В обоих случаях
[;^-| ^ -±. I
Окончательно индекс задачи вычисляется по формуле
если X четное и G (Л) == G (В) = 1,
к = \ — тг — 1. если к четное и G (Л) = G (S) = — 1,
если X нечетное,
2 ^
х+1
или, что то же.

454 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
где т- обозначает число тех концов w = а, w =^ Ь, для которых
Gi{w)= —1. (Очевидно, т~ может принимать значения О, 1,2.)
Учитывая, что в силу допущения решений, не исчезающих на
бесконечности, число их на единицу больше индекса, приходим
к следующей теореме.
Теорема. Пусть выполнены условия A8.21). Если х +
+ ^~ ^ О, то число I решений однородной задачи Карлемана
равно 1 —^^^ , а неоднородная задача безусловно
разрешима и ее решение линейно зависит от I произвольных
постоянных. Если к + ^~ > О, то / = О, а для разрешимости
неоднородной задачи необходимо и достаточно выполнения ^ 1
условий разрешимости.
Выписав по формулам п. 41.5 общее решение Ф\{хю) задачи
Римана, получим общее решение Ф{г)^=^Ф\[т{г)] задачи
Карлемана A8.20).
Замечание. Можно искать решения задачи A8.32), не
ограниченные в окрестности тех концов, где G\(w)^=^ —1.
Порядок особенности в таких концах равен 1/2. Возвращаясь к
задаче Карлемана A8.20), мы получили бы решение Ф+B:),
имеющее в неподвижных точках сдвига (в одной из них или в
обеих) полярную особенность первого порядка. Допущение
таких решений, не интегрируемых в окрестности неподвижных
точек, увеличивает индекс задачи на тг до величины х^ -f т~ =
= —^^^^^2—• (^Р- ^ рассуждениями в п. 46.4.)
43.5. Заключительные замечания. Используя методы § 16, можно бея
труда дать решение для случая, когда контур состоит из любого числа
замкнутых или разомкнутых непересекающихся кривых, на каждой из которых
имеется любое конечное число точек разрыва 1-го рода. Однако мы не
останавливаемся на этом, так как в следующем параграфе путем небольшого
видоизменения метода будет дано решение задач для еще более общего
случая, когда допускается самопересечение контура.
Сделаем одно простое замечание по поводу возможных обобщений
изложенного в §§ 42, 43 решения.
Как хорошо известно читателю, общее решение неоднородной задачи
складывается из частного решения неоднородной задачи и общего решения
однородной, причем при выборе другого частного решения известным образом
изменяются постоянные, входящие в общее решение. Строя общее решение
неоднородной задачи, мы обе составляющие его части брали из одного
класса. Это выражалось в том, что в частное решение неоднородной задачи
входила та же каноническая функция, что и в решение однородной:
Ф (г) == X (г) J- \ -^ ^^ + X (Z) Р^ (г).
2я/ J Х^ (т) х — г
Пользуясь произволом частного решения, можно при отыскании общего
решения в каком-нибудь классе функций частное решение неоднородной задачи
брать в любом другом более узком класса.

i 44] ЗАДАЧА РИМАНА ДЛЯ СЛОЖНОГО КОНТУРА 455
Например, общее решение задачи п. 42 2, принадлежащее к самому
широкому классу функций, не ограниченных на всех концах, можно взять в виде
ф /^ч ^ ^а (^) 1 С Rb (Т) dx Рт^, (z)
^ ^ Rb (г) 2д/ J /?а (т) т ~ 2 "^ R (г)
L
(частное решение здесь взято в классе функций, ограниченных на концах ал).
Соответственным образом изменится формула обращения особого интеграла
(п. 42,3).
Остановимся в заключение на сравнительной оценке достоинств двух
методов, изложенных в §§ 41—43.
При решении конкретных задач оба способа равносильны и лучше
пользоваться тем из них, которым решающий лучше владеет. При общих
теоретических рассуждениях, относящихся к рассмотренным задачам, второй
метод (§ 43) оказывается выгоднее, так как здесь формулы содержат только
данные величины, и потому проще, чем соответствующие формулы § 42.
Однако первый способ имеет перед вторым то преимущество, что он не
связан с наличием решения в замкнутой форме; поэтому он применим и в тех
случаях, когда такое решение неизвестно, например в обобщенных задачах
(см. задачу 15 в конце главы), а также в случае многих неизвестных
функций.
§ 44. Задача Римана для сложного контура.
Исключительные случаи
44.1. Постановка задачи. Пусть контур L состоит из
конечного числа простых гладких замкнутых или разомкнутых
кривых, расположенных как угодно на плоскости. Кривые могут
иметь любое конечное число точек пересечения или
соприкасания, а также быть расположенными в любом числе друг внутри
друга. При таком широком понимании контура он может пере*
стать разбивать плоскость на области D+ и D~ и для задачи
Римана следует дать новую формулировку. Предварительно
обобщим определение, данное в § 1, и условимся называть кусочно
аналитической функцию, аналитическую в каждой связной
части плоскости, не содержащей точек контура. В точках контура
существуют непрерывные предельные значения слева и
справа*), за исключением некоторого конечного числа точек
«концов», в которых предельные значения или обращаются в
бесконечность интегрируемого порядка, или, оставаясь
ограниченными, зависят от пути приближения к точке. Под концами
контура мы всегда будем понимать концы разомкнутых кривых,
точки разрыва коэффициентов, а также точки самопересечения
или соприкасания контура (см. примечание к п. 43.2).
Краевая задача Римана может быть сформулирована так:
Определить кусочно аналитическую функцию ФB),
удовлетворяющую на контуре L краевому условию
Ф+@ = о(/)Ф-@ + г@, D4Л)
*) Предполагается, что на всех кривых установлено направление.

456 КРАЕВЫЕ ЗАДАЧИ 1ГЛ. Vl
где G{t), g(t)—функции, удовлетворяш^ие условию Гёльдера
всюду, кроме некоторого конечного числа точек, где они могут
иметь разрывы первого рода*). Кроме того, G{t) Ф 0.
Когда речь идет о выполнении граничного условия, концы и
точки пересечения исключаются.
Сформулированная задача, которая кажется с первого
взгляда очень сложной (первые способы ее решения были в самом
деле весьма сложными), может быть решена довольно просто,
если, используя результаты решения задачи с разрывными
коэффициентами, внести небольшое видоизменение в решение
задачи для случая одной замкнутой кривой и непрерывных
коэффициентов. К изложению этого видоизменения мы переходим.
44.2. Новый метод решения задачи Римана для замкнутой
кривой. Пусть контур состоит из одной замкнутой кривой
и G{t)—непрерывная функция. Применим к решению задачи
Римана метод, которым в п. 43.1 была решена эта задача для
разомкнутого контура.
Выделим на контуре некоторую точку ti и будем считать ее
начальной точкой контура. Замкнутый контур будем
рассматривать как специальный случай разомкнутого, когда оба конца
контура совпадают. Рассмотрим функцию е^^^\ где
Если X = Ind G@# о, то функция \nG(t) будет
испытывать в точке ti разрыв, причем в этой точке будет выполняться
равенство
In G (/i — 0) - In G (/i + 0) = 2пЫ. D4.3)
Согласно формуле (8.3) вблизи точки ti будем иметь
Г(г) = к1п(г^/1) + Го(г), D4.4)
где То{г)—ограниченная функция, стремящаяся при
приближении к точке ti к определенному пределу. Отсюда
/<-) = (г-/0'^'^"^'^ D4.5)
Будем понимать под канонической функцией задачи то же,
что и в п. 14.3. Тогда, как легко проверить, канонической
функцией рассматриваемой задачи Римана будет служить функция
X{z)=={z-t,y''e''^'\ D4.6)
Если G{t) имеет точки разрыва, то, выбирая в качестве ti
первую точку разрыва и поступая так же, как в п. 43.2, полу-
*) Класс g{t) может быть расширен (см. конец п. 41.5).

§ 44] ЗАДАЧА РИМАНА ДЛЯ СЛОЖНОГО КОНТУРА 457
чим, ЧТО формула D4.6) даст каноническое решение и в этом
случае.
На основе построенной канонической функции общее решение
однородной и неоднородной задач может быть получено
обычным способом (пп. 14.4, 14.5, 43.1), и нет нужды особо это
излагать.
44.3. Общий случай. Перейдем к сформулированному в п. 44.1
общему случаю, сделав сначала упрощающее предположение,
что каждая точка может служить концом не более чем одной
кривой контура. Начнем с основного вопроса — построения
канонической функции.
Определение. Канонической функцией задачи Римана
будем называть кусочно аналитическую функцию Х(г),
удовлетворяющую однородному краевому условию
X"^@ = GWX-@
и обладающую следующими свойствами:
1. Она имеет нулевой порядок всюду в конечной части
плоскости, за исключением, быть может, концов *).
2. Вблизи концов принадлежит заданному классу
(ограничена или обращается в бесконечность интегрируемого порядка).
3. На бесконечности имеет наивысший возможный порядок
(равный индексу задачи в данном классе).
Построим каноническую функцию для каждой из простых
кривых Lk {k = 1, 2, ..., /n), составляющих контур L. При этом
будем соблюдать такие правила.
Г. Если Lh — разомкнутый контур, то для него будем строить
каноническую функцию по формулам п. 43.1, т. е.
X, {Z) = {z^ Ь,Г^^ /^ ^'\ Г, (г) = У^ 5 i^ dr. D4.7)
2°. Если Lj — замкнутый контур, то выбираем в качестве на-
чальной точки некоторую точку Ьр которая является одной из
точек разрыва, если такие точки есть на контуре Lj, и может
быть любой точкой, если G{t) непрерывна на Lj. Каноническую
функцию для контура Lj строим по правилам п. 43.2 или п.44.2,
что приводит к формулам
Х,(г) = (г-.й;)-///^^ rj{z) = -^\^^dr; D4.8)
Ч
Kh и Hj в формулах D4.7) и D4.8) суть индексы коэффициента
0{t) по кривым Lft, Lj в заданном классе функций.
*) Напомним, что к «концам» мы причисляем и точки разрыва (см.
п. 43.2).

458 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Величину
m
:<-=^Z^k D4.9)
будем называть индексом задачи Римана для сложного контура
в данном классе.
Докажем, что каноническая функция задачи Римана для
всего сложного контура L = Li + L2 + ... + ^т есть
произведение канонических функций для всех составляющих простых
контуров
т
ХB) = ПХаB). D4.10)
Начнем с доказательства того, что последняя функция
удовлетворяет краевому условию. Пусть / есть точка некоторой
кривой Lj, отличная от концов и точек пересечения кривых L^.
Подставляя в краевое условие функцию D4.10) и учитывая, что для
всякого k ф j Xt (t) = Xk (О, после сокращения придем к
равенству
Х/+(о = о(ОХГ@.
которое тождественно удовлетворяется согласно определению
канонической функции Х;(г).
Свойство 1 канонического решения выполняется в силу
формул D4.7), D4.8). Свойство 2 выполняется в силу того, что, по
определению, все канонические функции для простых кривых
принадлежат заданному классу.
Для установления свойства 3 подсчитаем порядок X{z) на
бесконечности.
Вставляя в формулу D4.10) выражения D4.7), D4.8) и
учитывая, что Fjfoo) =0 для любой кривой Lj (замкнутой и
разомкнутой), получим, что разложение в окрестности бесконечно уда-
/ 1 \^
ленной точки начнется с члена (— J . Этим доказательство
заканчивается.
Легко установить рассуждениями, подобными тем, которые
были приведены в конце п. 41.1, что каноническая функция
определяется с точностью до постоянного множителя.
Если нормировать каноническую функцию условием
lim 2^Х(г)=1,
г->оо
ТО формула D4.10) определит ее единственным образом.

S 441 ЗАДАЧА РИМАНА ДЛЯ СЛОЖНОГО КОНТУРА 459
Учитывая формулы D4.7), D4.8), D4.10), каноническую
функцию можно представить в виде
Х(г) = П(^-^/)"''^'*''. ^^^)-ШУ^^^^' D4.11)
/=-1 L
где &j есть конечная точка кривой, если она разомкнута, и точка,
условно принятая за начало (и конец) контура, если она
замкнута. Здесь в качестве исключительной точки, где каноническая
функция имеет нулевой порядок, взята бесконечно удаленная.
Если по каким-либо соображениям такой точкой должна быть
некоторая конечная точка 2о, то в этом случае каноническую
функцию ХB) следует умножить на бином (г — Zq)**.
После того как построена каноническая функция, общее
решение однородной и неоднородной задач в заданном классе
находится уже многократно примененным способом. Представив
коэффициент задачи Римана в виде отношения канонических
функций
G(/)=i^:^
х- (/)
и приведя краевое условие к виду
Ф+ (О Ф- (t) ^ g it)
Х+@ Х-(О Х+@ '
придем к задаче определения кусочно аналитической функции
по заданному скачку при условии, что искомая функция х} )
имеет на бесконечности порядок —к. Отсюда обычными
рассуждениями получим общее решение
Ф(г) = Х(г)[^(г) + Р,(г)], D4.12)
где
^(") = 7^Sx^-b?. "' - <44.13)
2nt J Х^ (т) т — 2
а Py^iz)—многочлен степени х. При х<0 нужно выписать
—к — 1 условий разрешимости
f ^?M_^/-irf^ = 0 (/=1, 2, ..., -K-l) D4.14)
J Х-ь (т)
и при соблюдении их положить Р^ ^ 0.
Результаты представляются в том же виде, что и в
рассмотренных ранее частных случаях (пп. 14.5, 16.2, 43.1),

460 КРАЕВЫЕ ЗАДАЧИ (ГЛ. VI
44.4. Случай совпадения концов. Остановимся коротко на
особенностях исключенного нами случая, когда в одной точке
сходится более одного конца простых кривых. Как следует из
формулы D4.10), порядок канонической функции Х(г) для
сложного контура равен сумме порядков канонических решений
Xk{z) для составляющих простых контуров. Таким образом, если
в данной точке to встречаются несколько концов, то порядок
в /о канонической функции равен сумме порядков канонических
функций для каждой простой кривой, имеющей конец в данной
точке. Отсюда следует, что порядки последних канонических
функций в точке to нельзя брать произвольными, а можно брать
только такими, чтобы суммарный порядок их в точке to
определял каноническую функцию, принадлежащую заданному в этой
точке классу. При этом должно соблюдаться общее требование
о максимальности порядка на бесконечности*). Указанные
условия еще оставляют некоторый произвол в выборе
канонических функций для простых контуров, оканчивающихся в точке ^о,
который, однако, не оказывает влияния на вид канонической
функции для всего контура.
Поясним сказанное примером.
Пусть в данной точке to встречаются три конца,
перенумерованных числами 1, 2, 3, и пусть для этих концов выполняется
/. <^) = (г - tor e''^ ''\ /= (^) _ (^ _ д^/з ^г^ (г)^
где Г1 (z) — ограниченные в окрестности точки to функции.
Допустим для определенности, что искомая каноническая функция
должна быть ограниченной в точке to.
Легко видеть, что для показателей ки >С2, у^г возможны
следующие три комбинации:
(О, О, -2), (О, -1, -1), (-1, О, --I).
Отвлекаясь от всех прочих возможных множителей, получим
для канонических функций Хь Хг, Хз следующие допустимые
выражения:
*) Последнее не позволяет повышать порядок нуля в конечной точке
выше минимально возможного.

§ 441 ЗАДАЧА РИМАНА ДЛЯ СЛОЖНОГО КОНТУРА 461
Для канонической функции Х(г) получим во всех трех случаях
ОДНО и то же выражение:
44.5. Исключительные точки на концах контура. Рассмотрим схематически
случай, когда исключительной точкой, где коэффициент задачи Римана
обращается в нуль или бесконечность, является концевая точка контура. Пусть
ф+ (/) == G (О Ф- (/), G (t) = {t- af Gi (О, D4.15)
где г — любое действительное число. Будем считать для определенности, что
а — начальная точка контура и, для простоты записи, что других
исключительных точек нет.
Решение по формулам D3.2) имеет вид
Ф(г)=е1'Ч rC) = J^(il^rfT.
2Л1 J Т — Z
L
т^/ ч ^ f 1п(т —а) , , 1 f InGi (т) ,
L L
Нашей задачей является исследование поведения решения в
исключительной точке а. Используя формулы (8.25) и (8.10), будем иметь
г (г) = - -^'"' B - «) + [т ~ '" 2ш-''^ ]'" (^ - ") + Г* (г), D4.16)
где Г* (г) ограничена вблизи а и имеет в а определенный предел. Обозначим
1п Gi (а)
е (z) = arg {z — а), а + /р = •
2я/
После простых преобразований будем иметь
1п2 (Z - а) = 1п21 г - а I + 62 + 2/6 In (z - а).
Вставляя последнее выражение в D4.16), получим
rB) = [--~-eB) + i-r + a]lnB-a)~pe-f
+ /^[1п1г-а| + е2(г)] + Г*(г).
Отсюда
фB) = B-а)^<^)ф*(г),
где
а Ф*(г)—ограниченная в окрестности а функция.
При выводе формул (8.25) и (8.1) мы считали контур L разрезом для
ln(z —а) и 9+ = 9, 9- = 9 —2я; поэтому для всех t на контуре, в том числе
и для / = а, будем иметь
а|)+(г)-г|з-(г) = г.
Если 2 обходит точку а в положительном направлении, то при г > О
i|)B) монотонно убывает, а при г < 9 — монотонно возрастает. Следовательно,

462 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
В точке а решение не имеет определенного порядка. Этот порядок будет
зависеть от пути приближения к точке а; на каждом луче, исходящем из а,
порядок будет постоянным. Это характернейшая особенность
рассматриваемого случая.
Относительно неоднородной задачи укажем лишь следующее. Выражение
g (t)
—:^ , входящее в ее решение D3.10), будет иметь в точке а переменный
порядок; поэтому для разрешимости задачи нужно будет потребовать, чтобы
g{t)=i(t — ci)'gi(t), где г—s^O в случае решений, ограниченных в а, и
г — S < 1 — для неограниченных. Результаты взяты из работы И. М.
Мельника 2).
В работе 3) этот автор на основе исследования интеграла типа Коши
Sin In (т — а) -
112 "Т^ дал решение краевой задачи в случае, когда
L
С (О = п (^ - ^/^ 1п'^ (/- ^^) Cj (/).
При этом точки Ch могут быть как концами контура, так и точками разрыва,
где одно из предельных значений обращается в нуль. Характер результатов
остается тот же, что и в изложенном случае.
§ 45. Краевая задача Гильберта
для кусочно аналитической функции*)
Естественным обобщением обеих краевых задач Гильберта
и Римана является такая задача, когда на одной части контура
задается краевое условие типа задачи Гильберта, а на другой —
типа задачи Римана. Сформулируем одну такого рода задачу,
получившую название краевой задачи Гильберта для кусочно
аналитической функции.
45.1. Постановка задачи. Пусть L — простая, гладкая
замкнутая кривая, ограничивающая область D. В последней
расположен контур /, состоящий из конечного числа замкнутых или
разомкнутых кусочно гладких кривых, раздельных или
имеющих любое конечное число точек пересечения. Определить
функцию Ф{г), кусочно аналитическую в D (см. п. 44.1),
удовлетворяющую на контуре краевому условию:
0''(t) = G{tH'{t) + g{t) на /. (R)
Коэффициенты краевых условий берем в тех же классах,
в которых в § 29 решалась задача Гильберта, а в § 44 — задача
*) Материал этого параграфа изложен по рабоге И. С. Рогожиной 1).
Более общие случаи: в классе обобщенных аналитических функций (см.
п. 39.2) и в классе аналитических функций на римановых поверхностях (см.
п. 53.1) рассматривали соответственно Г. С. Б а р х и н, 3. Д. Усманов 1)
и А. И. Сербии 3).

§ 451 КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 463
Римана, т. е. будем считать, что а + ib удовлетворяет условию
Гёльдера и а^ ^ Ь^ ф Q. Функции G, g удовлетворяют условию
Гёльдера всюду, кроме отдельных точек, где они могут иметь
разрывы первого рода. Кроме того, g{t) может в отдельных
точках обращ.аться в бесконечность интегрируемого порядка.
Решение рассматриваемой краевой задачи производится
путем комбинирования методов решения задач Гильберта и
Римана. Отметим особенности постановки задачи.
1. Краевому условию (Н) здесь должна удовлетворять не
аналитическая функция, а функция более широкого класса —
кусочно аналитическая с линией скачков /.
2. Кусочно аналитическая функция, удовлетворяющая
краевому условию (R), определяется не во всей плоскости, а лишь
в области /).
Указанные особенности постановки задачи позволяют
вводить в решение в виде множителей некоторые аналитические
функции. При обычной постановке задач эти множители
вырождаются в тривиальные постоянные; здесь же они остаются
функциями и целесообразный их подбор делает возможным
удовлетворить одновременно обоим краевым условиям.
После предварительных рассуждений перейдем к отысканию
решения.
45.2. Отыскание решения. Начнем рассмотрение с
простейшей задачи, когда оба коэффициента а + fb и G равны
единице:
Re[O@] = ^(s), (НО
Краевому условию (R') задачи о скачке удовлетворяет
интеграл типа Коши
^•(^) = iSf^^^- D5.1)
Если к последнему добавить в качестве слагаемого
произвольную, аналитическую в D функцию ФгС^), то
Ф{г) = ФМ + Ф2{^) D5.2)
будет по-прежнему удовлетворять краевому условию (R').
Подберем теперь Ф2(г) так, чтобы удовлетворялось также и
краевое условие (Н^. Подставляя D5.2) в (Н^, получим для
определения Ф2B:) краевое условие задачи Шварца
Re[Ф,(/)] = ^E)-Re[Фl(/)] D5.3)
с новой известной правой частью c{s)—Re[Фl(/)]. Решая ее
(п. 27.2) и вставляя решение в D5.2), получим решение задачи

464 КРАЕВЫЕ ЗАДАЧИ 1ГЛ. VI
(НО, (R0- 0^0 будет содержать произвольную чисто мнимую
постоянную. Заметим здесь же, что если бы у функции Ф2B)
допускался в некоторой точке полюс, то задача D5.3) была бы
задачей А (п. 27.3) и ее общее решение содержало бы в
качестве слагаемого решение задачи Ао (формула B7.8)).
Перейдем к общей задаче (Н), (R). Теория краевой задачи
Гильберта и задачи Римана позволяет привести краевые
условия (Н), (R) к виду (Н^, (R^. Для первой это делается
делением на регуляризующий множитель (п. 29.1), для второй —
представлением коэффициента G в виде отношения краевых
значений канонической функции G (t) = Х^(t)/Х"(t) (п. 44.3). Но
после этих операций краевые условия будут содержать искомую
функцию с различными аналитическими множителями. Для их
уравнивания будем пользоваться особенностью постановки
задачи, позволяющей вводить в решение аналитические
множители.
Обозначим хн = IndL(a + ^^), ^r—индекс по / задачи (R)
в некотором выбранном классе решений. Выберем в качестве
исключительной точки, где допустим ненулевой порядок,
некоторую точку го, подчиненную единственному ограничению, что
она должна лежать в области, где определена Х+(г)*).
Деля краевое условие (Н) на p{s)—регуляризующий
множитель функции а-\-ib (формула B8.10)), а в (R) полагая
G = Х+/Х~, получим
Ф+@ ф-@ ^ g{t) Р„.
х+@ х-(О х+@ '
При уравнивании искомых функций в (Н'^), (R'') множитель
(/ —2:о)"^н^~'^^^^ можно непосредственно внести в краевое
условие (R^O» но функцию 1/Х+(/) можно будет внести внутрь
краевого условия (Н^0> очевидно, тогда и только тогда, если
Х(-г) будет принимать на контуре L чисто действительные
значения. Таким образом, предварительно нужно решить такую
вспомогательную задачу:
Найти функцию Х(г), обладающую в области D всеми
свойствами канонической функции задачи (R) {см. п. 44.3) и удо-
влетворяюи{ую дополнительному условию:
ImX@ = 0 на L D5.4)
Пусть Z{z)—каноническая функция обычной краевой задачи
Римана с краевым условием (R), определяемая формулой D4.11).
*) Напомним, что такая область лежит слева от контура / при его полд-
"«^ительном обходе.

§ 45] КРАЕВАЯ ЗАДАЧА ГИЛЬБЕРТА 465
Будем искать функцию Х(г) в виде произведения Z{z) на
некоторую произвольную функцию, аналитическую в Z) и не
обращающуюся там в нуль. Последнюю представим в виде е^^^Ч
Итак,
X{2) = Z{z)e^^^'K D5.5)
Теперь подберем \|)(г) так, чтобы выполнялось условие D5.4).
Имеем
Im[Z(Oe^'^^'^] = 0.
Для удовлетворения последнего равенства достаточно (хотя и
не необходимо), чтобы
Последнее означает, что Imln [Z(Oe^^^^^] = 0, т. е.
Rei|)@ = —ImlnZ@ на L.
Для определения г|)(г) получили задачу Шварца. Подбирая
некоторым образом входящую в решение чисто мнимую
произвольную постоянную, найдем определенное решение задачи.
После этого краевые условия (Н), (R) превратятся в
L(/-eof"X+(/)J p(s)X+@
(t - z,f^ Х+ (/) (/ - го)''" Х- (/) (/ - го)""" Х+ (t)
на /. (R^^O
Полученная краевая задача есть решенная в начале этого
пункта задача (Н^), (R') с тем лишь дополнительным условием,
что искомая функция z— — должна в исключительной
точке го иметь порядок не ниже хн + >cr.
45.3. Исследование разрешимости. Задача (Н^'')» (R'^0
связана с исходной задачей (И), (R) цепью однозначных и
однозначно обратимых операций, поэтому исследование
разрешимости исходной задачи равносильно исследованию разрешимости
задачи (Н^"), {ЯП-
1) x==% + >^R^O.
В этом случае задача (Н'''^) есть задача А. Пусть w{z) —
функция, отображающая конформно область D на единичный
круг и переводящая исключительную точку zq в начало коорди-
нат. Тогда Q{z) = i% + Yi {(^k [^i^)]^ — Cklw{z)]""^}, согласно
fe=0
B7.6), будет решением задачи Aq для области D.

466 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Пусть
2^' j (т - го) " Х+ (т) ^ ~ ^
— частное решение задачи о скачке (R'^0» *5 — оператор Шварца
для области D и
^B) = 5(^-ReOi). D5.7)
Используя рассуждения п. 45.2, получим решение
рассматриваемой задачи в виде
ф (Z) = {z^ гоГ X {Z) е'"^''' [Ф, {г) + Ч^ (а) + Q, (з)]. D5.8)
Так как оно содержит в качестве слагаемого общее решение
однородной задачи (Н'^'), то, очевидно, является общим
решением задачи (Н'^'). Задача (R^'O допускает больший произвол
в решении, именно: она содержит произвольный многочлен
степени X относительно 1/(г — го). Однако из требования
одновременного удовлетворения условию (Н'^') вытекает, что
коэффициент при нулевой степени многочлена должен быть чисто
мнимым. Отсюда следует, что решение D5.8) является наиболее
общим также и для краевого условия (R'^O- Таким образом,
решение задачи содержит 2% + 1 произвольных действительных
постоянных.
2) х<0.
В этом случае нужно положить QB)seO и потребовать,
чтобы функция 01 (г) + Ч^(г) в точке Zq имела нуль порядка |х|.
Это даст |х| комплексных условий разрешимости. В случае,
если для области D известно явное выражение оператора
Шварца (в частности, для круга), условия разрешимости
выписываются явно. На подробностях мы не останавливаемся.
Комбинируя методы, изложенные здесь, с методами § 17,
можно дать полное решение аналогичной задачи, когда краевое
условие задачи Римана заменяется условием задачи со сдвигом.
§ 46. Краевая задача Гильберта с разрывными коэффициентами
Рассмотрим краевую задачу Гильберта (п. 27.1), допуская,
что в краевом условии
а E) u{s) + b {s) v{s) = c {s) D6.1)
функции a{s)y b(s)y c{s) могут испытывать разрывы 1-го рода
в конечном числе точек контура.
Для решения этой задачи возможны различные пути. Можно,
например, обобщить данное в гл. IV решение задачи Гильберта

§ 46] ЗАДАЧА ГИЛЬБЕРТА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ 467
на случай разрывных коэффициентов. При этом само это
обобщение может быть произведено двумя способами, аналогично
тому, как это сделано для задачи Римана (§§ 41, 43) (см.
задачи 7, 8 в конце главы). Второй способ заключается в
использовании установленной в § 30 сводимости задачи Гильберта
к задаче Римана.
Желая воспользоваться уже полученным решением задачи
Римана с разрывными коэффициентами, мы изберем второй
путь*). Этим путем можно решить задачу Гильберта для
окружности и полуплоскости. Общий случай можно свести к
рассматриваемым конформным отображением.
46.1. Задача Гильберта для полуплоскости. На основании
рассуждений п. 30.2 в рассматриваемом случае решением задачи
Гильберта D6.1) для верхней полуплоскости является решение
Ф+ задачи Римана
^ ^^^ а (t) - ib (t) ^ ^^^^ а (О - lb it) • ^^^"^^
удовлетворяющее условию
ф- {2) = ф^ B) = Ф+ {г) D6.3)
(по поводу обозначений см. п. 12.1).
Особенно легко получить решение задачи Гильберта из
общего решения задачи Римана, если последнее взять в форме,
вытекающей из рассуждений п. 44.2 **).
Будем рассматривать ось абсцисс как замкнутую кривую
с начальной и конечной точками в начале координат,
замыкающуюся в бесконечности. Для простоты будем считать
коэффициент G{t) непрерывным на бесконечности, т.е. G(—оо) =
= G(+oo). Согласно D4.6) каноническое решение задачи
Римана D6.2) можно дать в виде
ХB)=2->«^Г(г)^ D6.4)
где ***)
— оо
e(/) = argG(/) = arg(-|i|),
D6.5)
*) Рекомендуем читателю восстановить в памяти пп. 30.1 и 30.2.
**) Здесь в исправленном виде воспроизводится решение, помещенное
в первом издании книги.
***) Интегралы с бесконечными пределами, вообще говоря, понимаются
в смысле главного значения.

468 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
а к — индекс функции G(t) в выбранном классе решений.
Общее решение дается обычной формулой
0{z) = X{z)[W{z) + P^{z)]. D6.6)
Однако, если Ч'(г) представлять, как обычно, интегралом
типа Коши, то при х > О интеграл окажется расходящимся. Это
затруднение можно преодолеть, если использовать введенный
в п. 4.6 интеграл D.38) и определить Ч^(г) на основании D6.4)
формулой
оо
W{z) = ^ { '-^ Z ^^. D6.7)
Справедлива (при х ^ 0) следующая
Теорема. Функция Ф'''(г), определяемая формулой D6.6),
при условии, что в ней коэффициенты многочлена Py^{z)
действительны, удовлетворяет условию D6.3) и, следовательно,
является решением задачи Гильберта для верхней полуплоскости
в заданном классе решений.
Доказательство. В силу того, что Ф^{z) и Ф~(г)
задаются одним и тем же аналитическим выражением, можно
в условии D6.3) не обращать внимания на значки +, -, т. е,
требовать выполнения условия
Ф(г) = ФB). D6.8)
Здесь использованы обозначения п. 12.1. Так как функция ХB)
действительна *), то Х(г)= Х(г) для любого г. Следовательно,
каноническая функция удовлетворяет краевому условию
однородной задачи Гильберта. Последнее может быть представлено
в виде _
(а - ib) Х+ (/) + (а + ib) Х"" {t) = О,
откуда на контуре
(а + ib) Х+ (t) = - (а - ib) Х-*" (/).
С помощью последнего соотношения получим
оо
С (т) dt
ni J [а(т) + /^(т)]т^Х+(т) x-z
ni J
-i [a{x)-ib(%)]e
^ ('^) ^1_ — w (y\
,r+(T) x-z — ^^^^
*) Под действительными функциями понимаются функции комплексного
аргумента, принимающие действительные значения при действительных
значениях аргумента.

§ 46] ЗАДАЧА ГИЛЬБЕРТА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ 469
Отсюда вытекает, что если у многочлена Р^ (г) коэффициенты
взять действительными {P^{z)= P^{z)), то формула D6.6)
определяет функцию, удовлетворяющую условию D6.8).
В случае х < О решение дается той же формулой D6.6)
{Ру^ = 0) при выполнении |х| условий разрешимости.
Для решения задачи Гильберта мы воспользовались методом
решения задачи Римана, изложенным в п. 44.2. При решении
практических задач можно использовать также и метод § 42.
Если при этом все интегралы окажутся действительными, то
решение задачи Римана будет также и решением задачи
Гильберта. Это непосредственно вытекает из того факта, что для
действительных функций и только для них выполняется
равенство Ф{2)= Ф(г).
46.2. Пример. Для иллюстрации изложенных методов рассмотрим
конкретный пример *).
Найти функцию F{z)= и + iv, аналитическую в нижней полуплоскости,
по краевому условию на действительной оси:
и = а(х) (-l<jc<l),
Uqu — гоО = о {х < --\, х> I),
где Ко, Vo — определенные постоянные, удовлетворяющие условию ul + г>1==\,
а(х) — заданная функция.
Рассматриваемая задача есть частный случай краевой задачи Гильберта
с разрывными коэффициентами
Re{la{x) + ib(x)]F(x)] = c{x)
при
а(;с) = 1, 6(л:) = 0, с{х) = а{х) (-1<дг<1),
a{x) = Uoy b{x) = Voy с(х) = 0 {х <—\у х > I).
Соответствующая ей задача Римана имеет вид
ф-^(х) = 0{х)Ф'(х) + §{х);
где е^^ = «о + i^Oi причем путем изменения в случае надобности знака в
краевом условии можно добиться того, чтобы удовлетворялось условие
О < ф < я.
Рассматриваемая краевая задача будет равносильна последней задаче
Римана в том смысле, что всякая функция Ф""(г), удовлетворяющая условию
ф- (z) = Ф"^ (г), будет ее решением.
Задачу Римана будем решать по методу § 41. Имеем
G (-1 - 0) _ ,2/Ф G(l-O) _ ,2^ф
Отсюда
П ' JX
ф ф
Yi = ^ — «ь Y2 = — -^ — »<2.
*) Этот пример заимствован из работы В. С. Рогожина 2).

470 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Целые числа Xi, Хг подбираются в зависимости от требуемого класса
решений. Если искать решение, ограниченное на бесконечности и обращающееся
на концах —1, 1 в бесконечность интегрируемого порядка, то нужно взять
xi = 1, Х2 = 0.
Рассматриваемый случай отличен от исследованного в § 42 тем, что здесь
бесконечно удаленная точка принадлежит контуру. Области D+ и D-
равноправны по отношению к бесконечно удаленной точке, поэтому
фундаментальные вспомогательные функции, устраняющие разрыв коэффициента, здесь
для обеих функций Ф+, Ф- нужно брать по образцу функции (ii-(z) (см.
формулу D1.7)). Выбирая в качестве го точки dtt, положим
Тогда придем к задаче Римана
orW = Gi(x)Oi-(A:) + gi(^).
Согласно общей теории коэффициент
должен быть непрерывной функцией. Желая лучше осветить это
обстоятельство, рассмотрим более подробно механизм устранения разрыва.
X /
В интервале (—1, 1) C(jc)=—1, поэтому Gi{x) = лГ^' ^Р^ пере-
X ~t" I
ходе через точки —1 или +1 ^М переходит к значению —е^^^. В произве-
декии ( —q--r I I —ц—г ] , по определению фундаментальной
функции, первый множитель разрывен в точке —1, второй — в точке -fl. При
переходе через точки —1, 1 слева направо эти функции приобретают
множители соответственно
Отсюда легко получаем, что на всей действительной оси
Записав краевое условие задачи Римана в виде
(X + i) Ф+ (х) = - (;с - /) ФГ {x) + g{x){x+\) " (д^ - 1)«,
легко получаем
Bг+ОФ+(г) = Т+(г) + Со + С1г,
-(z-i) Фр (Z) = ^" B) + с^ + c^z,
где
,,(,) =±llii ( aW(/ + l/-"(l-0^ ,,
^ ^ ш J t — z
-1

§46]
ЗАДАЧА ГИЛЬБЕРТА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ
471
а Со, Ci ¦— произвольные постоянные. Отсюда
^ л.
«*м-(ШГ (St)"^^*^^^^
CiZ
:(г+1)" (г-1) " [4r+(z) + Co + c,zh
Л-у
Рис. 17.
=:=-(г+1)" B-1) " [>Г-(г) + Со + ^1г].
Для полной определенности многозначной функции / (г)=B: + 1)^^"""* (г—1)""^^"
укажем еще, каким способом должен быть проведен разрез, соединяющий
ее точки ветвления —1, 1.
Вставляя решение однородной задачи
(Ч^+ = Ч*"- = 0) в однородное
краевое условие (а = 0), получим,
что на участке (—1, 1) оси
выполняется равенство f^{x) =»
= f~'(x), т. е. на этом участке
функция продолжается
аналитически. Следовательно, разрез
нужно провести по отрезкам
действительной оси (—оо, —1), A, оо).
Укажем, наконец, какими
должны быть выбраны величина (—1)^^"
и произвольные постоянные со, Сх
для того, чтобы
удовлетворялось условие Ф'"(г) = Ф~B) = Ф'^B). Для вычисления JXz) положим
2+1 =г,е'«', 2 - 1 = Г2е'«^ Тогда (рис. 17) г -f 1 = n^-'^S г - 1 = гге^(гя-а^)^
Следовательно,
Далее, положив (—1 )'''" = в"Р, будем иметь
Ф- (.) = _4- J <^mt + i)-bi-i)^ ,,^_ ^-.„^, (^^
-1
Вставляя все величины в равенство Ф" (г) = Ф"*" (г), получим
-{co + c,z)e^^'^=^Co + c,z.
Из равенств с^е^^'^ = — с^ (Aj = 0, 1) вытекает, что i'V'^^^Ov"'^) ^^"^^
величина действительная. Поэтому
Со = - //?ое'^, Ci = - iR,e\
где /?Q и /?j — действительные постоянные.

472 КРАЕВЫЕ ЗВДАЧИ [ГЛ. VI
Отсюда получим решение исходной задачи в окончательном виде
JL-1 ^±.
^B:)-ф-(г)«/A+2)" A-г) ^ [Чг, (z) + Ro +Riz],
где
^ я J / — 2
-1
46.3. Смешанная краевая задача аналитических функций.
В качестве применения изложенной теории рассмотрим один
частный случай краевой задачи Гильберта с разрывными
коэффициентами, так называемую смешанную краевую задачу
аналитических функций, встречающуюся во многих приложениях.
Дадим ей общую формулировку.
Пусть замкнутый контур L точками аи fti, ..., а^, Ьщ
разделен на 2т частей. Совокупность дуг (а^, bh) обозначим L\
совокупность дуг {bk, ah^i)—U' (^ = 1, 2, ..., m; a2m+i = «i).
Требуется определить аналитическую в ?)+ функцию
F{z) = u + iv, D6.9)
удовлетворяюи^ую краевому условию
u = f{s) на L\ v = h{s) на U\ D6.10)
где f(s)y h{s)—заданные функции, удовлетворяюи^ие условию
Гёльдера, В точках а^, Ьи функция F(z) должна принадлежать
некоторому заданному классу.
Рассмотрим случай, когда контур L есть действительная ось.
Принципиально задачу всегда можно свести к этому случаю
путем конформного отображения области D+ на верхнюю
полуплоскость. При этом только необходимо считать, что F{z)
ограничена на бесконечности.
Будем предполагать, что бесконечно удаленная точка оси не
совпадает с точками деления а^, Ь^. Следовательно, U будет
состоять из т конечных отрезков (а^, Ь^), а L^' из m— 1
конечных отрезков и двух бесконечных (&т, оо), (— оо, ^i).
Краевые условия D6.10) могут быть записаны в виде одного
краевого условия задачи Гильберта, заданного на всем
контуре L:
a{s)u(s)-\-b{s)v{s)-=c{s) на L, D6.11)
где нужно считать
а=1, 6 = 0, c = f{s) на U\
а^О, 6=1, c = h{s) на U\
Составим соответствующую краевую задачу Римана
ф-*-@-О@Ф"@ + «@. D6.12)

§ 46] ЗАДАЧА ГИЛЬБЕРТА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ 473
Согласно формуле D6.2)
G@ = -f±l = ~l, g{t) = ^ = 2fit) на L^
G@= + 1, g{t) = 2ih{t) на U\
Мы пришли к краевой задаче D2.12^), рассмотренной
в п. 42.2, и можем прямо воспользоваться полученными там
результатами. Приведем решение для трех наиболее важных
классов; получаемые при этом формулы принадлежат М. В.
Келдышу и Л. И. С ед о в у 1).
Г. Решение, не ограниченное вблизи всех
концов а^, 6ft:
-[[{2-a,)(z-h).
При дополнительном условии ф(сх)) = 0 Рт{^) нужно заменить
на Pm-ii^)- Остальные формулы выпишем при этом
дополнительном условии.
2°. Решение, ограниченное вблизи концов ah и
не ограниченное вблизи концов ft^:
^^^^-'Ш^ш]T7i^T^^'^^^ D6.14)
V~m У т
3°. Решение, ограниченное вблизи всех
концов:
Ф(г) = /?(.)у1т$|^^. D6.15)
L
причем здесь должны выполняться условия разрешимости
5Ш"^'"'^^==0 (/=!, 2 т).
D6.16)
Легко доказать, что выписанные формулы, дающие решение
задачи Римана D6.12), если в них коэффициенты многочлена
Рт{^) считать действительными, будут вместе с тем давать ре*
шение исходной задачи Гильберта. Для этого, согласно
замечанию в конце п. 46.2, нужно доказать, что все интегралы, входя*

474 Краевые задачи [гл. VI
щие в эти формулы, действительны. Последнее вытекает из
следующих рассуждений.
Если т е L', то отрицательных биномов т — а^, т — bk
нечетное число, поэтому R{%) и J ;^{ имеют мнимые значения. Но
здесь g{x)=2f{x) — действительная функция, поэтому, в силу
наличия множителя у-т-, весь интеграл будет действительным.
Если т е и\ то отрицательных биномов четное число, R (т)
Rb(T:) " g(r) h{x)
и в ' : действительны, а ^ . = —^—тоже действительная
функция. Поэтому интеграл снова действителен.
Р (z)
Легко видеть, что функция „^Д ^^'^^ общее решение
однородной задачи в наиболее широком классе функций, не
ограниченных на всех концах. Формула D2.24) даст решение в любом
классе, когда требуется конечность на любых р концах и
допускается обращение в интегрируемую бесконечность на остальных
2т — р концах. При р<,т задача имеет т — р линейно
независимых решений, при р > т единственное решение существует
при выполнении р — т условий разрешимости D2.25).
В заключение укажем, что если какой-либо из интегралов
окажется расходящимся, то нужно будеть, аналогично тому, как
это сделано в п. 46.1, перейти к введенному в п. 4.6 интегралу
D.38).
46.4. Задача Дирихле и ее видоизменения для плоскости со
щелями. Исключим из комплексной плоскости отрезки
действительной оси (a/i, bh) (fe = 1, 2, ..., m), и пусть D есть
оставшаяся область. Под границей области будем понимать
выброшенные отрезки (разрезы), проходимые дважды, причем
верхний берег проходится в направлении положительной оси,
нижний — в противоположном. Основная задача будет
заключаться в определении гармонической в области D функции по
значениям ее на берегах разреза.
По своему характеру эта задача есть задача Дирихле для
многосвязной области в том специальном случае, когда все
контуры, ограничивающие область, вырождаются в отрезки оси
абсцисс, проходимые дважды. Рассматриваемый здесь
специальный случай существенно отличается от рассмотренного в § 37
случая многосвязной области тем, что здесь нет точек плоскости,
отличных от точек D -^ L. Напомним, что трудности решения
задачи Дирихле для многосвязной области связаны с
возможностью многозначных решений. В § 37 эти трудности разрешались
путем явного выделения многозначной части (In (г — 2^)), что
возможно только при наличии точек, не принадлежащих D + L.
Поэтому поставленная задача не может быть решена методом

§ 46] ЗАДАЧА ГИЛЬБЕРТА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ 475
§ 37. Решение будет дано на основе других соображений,
опирающихся на рассмотрение краевых задач с разрывными
коэффициентами. Результаты, как увидим далее, также существенно
отличаются от соответственных результатов § 37.
Начнем с рассмотрения задачи, которая имеет
самостоятельный интерес и явится вспомогательной для решения задачи
Дирихле.
Требуется определить аналитическую и однозначную
в D функцию Ф(г) = и -f ^'^ по заданным на разрезах значениям
ее действительной части:
^г+ = /+@, u'^rit) на L, D6.17)
где /+(/)> /"(О—заданные функции, удовлетворяющие условию
Гёльдера. Будем считать краевые значения непрерывными
функциями; тогда должны быть выполненными условия
/'•Ы = ГЫ, f^{bk) = n{bk) {k=\, 2, ..., m). D6.18)
Введем в рассмотрение наряду с искомой функцией Ф(г)
также функцию ФB:) = ФB), уже встречавшуюся в пп. 30.2 и
46.1. Как было установлено ранее, если Ф(г) аналитична в Z), то
и Ф{г) также аналитична в___ней. Когда z приближается к
действительной оси, то Ф(г) и Ф(г) стремятся к своим предельным
значениям на оси из разных полуплоскостей, причем эти
предельные значения комплексно сопряжены.
Сведем предложенную задачу к ранее рассмотренным,
воспользовавшись приемом Н. И. Мусхелишвили *). Выпишем
тождество
ф(^) = 1[фB:) + ФB)]+~[Ф(г)-Ф(г)] = Ч^B) + аB:) D6.19)
и рассмотрим две аналитические в D функции
Ч(г) = \[Ф{г) + Ф{г)], Q{z) = \[Ф(z)-Ф{z)]. D6.20)
Исследуем их поведение на всей действительной оси.
На участках (а^, Ьи) будем иметь
Re Ч (О = ]- [Re Ф (/) + Re Ф Ш = | [/+ (О + f" {t)l
ReQ@ = i[r@-/"@].
D6.21)
*) Н и. Мусхелишвили пользуется этим приемом не для сведения к
смешанной задаче (последнюю он решает позже), а для непосредственного
решения задачи методом п. 30.2.

476 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Обозначим и остальную часть оси за вычетом отрезков (а^, fc/i).
На и обе функции аналитически продолжимы через ось и
обладают свойствами
Ч^@ = 41Ф@ + Ф@] = НеФ@,
а@ = 4[Ф@-Ф@] = ПтФ@,
что равносильно условию
1тЧ^@ = 0, Re Q @ = 0 на Г.
Сопоставляя последние равенства с равенствами D6.21),
получим, что функции Ч^(г), QB) на всей оси абсцисс удовлетворяют
следующим краевым условиям:
ReW@=4[f^@ + r@] на L, 1тЧ^@=-0 на L\ D6.22)
ReQ@ = j[/^@-f"@] на L, ReQ(/) = 0 на L\ D6.23)
Следовательно, отыскание функции ^(г) привелось к
решению смешанной краевой задачи аналитических функций,
рассмотренной в предыдущем пункте. Для функции же й (г) задача
сводится к отысканию аналитической в полуплоскости функции
по заданным на оси абсцисс значениям ее действительной части
при условии аналитической продолжимости функции в
дополнительную полуплоскость. В силу условий непрерывности D6.18)
краевое значение ReQB) на оси есть непрерывная функция.
Функция Ч^(-г) определяется по формулам п. 46.3, где нужно
положить
ff@ = -|-[/''W + /~@] на L, g@ = 0 на V.
Отыскание функции ЙB:) производится применением оператора
Шварца, который для действительной оси, как известно,
совпадает с интегралом типа Коши.
Следова'^ельно, будем иметь
"«-iS^^^^^f^'*'- («.24)
Выпишем решение исходной задачи в классе функций,
конечных на каких-либо концах с\, ^2,..., Ср и имеющих интегрируемую
бесконечность на остальных 2т—р концах с дополнительным

§ 46] ЗАДАЧА ГИЛЬБЕРТА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ 477
условием Ф(о0) = О. По формулам D2.24) и D6.24)
L
где
VP /2m
П(^-Ы /?2(^)=V П (г-С,).
В случае, когда р ^ т, нужно положить Pm-v-\ B) ^ О и
добавить (при р > т) р — т условий разрешимости:
D6.26)
Читатель сам легко выпишет, пользуясь формулами D6.13) —
D6.16), решения для всех наиболее важных классов.
Если отбросить условие непрерывности D6.18), то з силу
свойств интеграла типа Коши (п. 8.1) второй интеграл в
формуле D6.25) будет давать функцию с логарифмической
особенностью. Следовательно, в этом случае ограниченных решений
задачи не существует. Если решение смешанной задачи взято
в классе функций, конечных на данном конце, то все решение
будет иметь логарифмическую бесконечность.
Такое решение Н. И. Мусхелишвили называет почти ограни-
ценным. Особенность этого типа вообще характерна для
решения задачи Дирихле с разрывными краевыми значениями,
имеющими разрыв первого рода.
Сравнение полученных результатов с результатами § 37
показывает следующее существенное различие. Для многосвязной
области в случае контуров, не вырождающихся в щели,
решение рассматриваемой задачи в классе однозначных функций
возможно лишь при специальном подборе заданных краевых
значений (условия однозначности C7.20)). Для той же задачи
6 случае контуров, вырождающихся в щели, решение возможно
при произвольных краевых значениях, если только допускать
решения, имеющие на концах интегрируемую бесконечность.
В этом случае становится возможным Даже нетривиальное
решение однородной задачи.
Причина такого, на первый взгляд парадоксального явления
кроется в негладкости контура на концах щелей. Угол между
левым и правым касательными векторами здесь равен 2я.
Поэтому функция, конформно отображающая плоскость с разрезом

478 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
на область, ограниченную гладким контуром (например, круг),
в окрестности конца Zq разреза имеет вид
Отсюда следует, что решению задачи на плоскости с
разрезом, имеющему на конце разреза некоторый порядок а,
соответствует решение на гладком контуре, имеющее в точке So
порядок 2а. Следовательно, полученному решению, обращающемуся
на концах в бесконечность порядка 1/2, соответствует на
гладком контуре решение, имеющее в ^о простой полюс. Но
допущение у решения задачи полярной особенности первого порядка
увеличивает число линейно независимых решений (или
уменьшает число условий разрешимости) на единицу. Этим и
объясняется кажущееся расхождение между решениями на гладком
контуре и на плоскости с разрезами *).
Замечание. Формулы D6.25) останутся в силе и в том
случае, если на концах, где допускается интегрируемая
бесконечность, функции /+@» /"(О обращаются в бесконечность
интегрируемого порядка (см. п. 43.4).
Перейдем теперь к решению задачи Дирихле, т. е. к
определению гармонической и ограниченной в D функции и{х, у),
удовлетворяющей краевому условию
«+ = /+(/),«" = /"(/) на L, D6.27)
где f+@» /~@—заданные функции, удовлетворяющие условию
непрерывности D6.18). Для применяемого далее метода
решения требуется, чтобы производные их удовлетворяли условию
Гёльдера.
Применим способ решения, указанный М. В. Келдышем
иЛ.И.Седовым 1). Обозначим ф (г) = « + iv аналитическую
функцию, действительная часть которой есть искомая
гармоническая функция. Функция эта будет, вообще говоря,
многозначной. Производная ее
будет, как легко установить, функцией однозначной. В самом
деле, вследствие однозначности и мнимая часть v может лишь
получать постоянные приращения при обходе по любому пути,
охватывающему какой-нибудь отрезок (а^, bk). Отсюда следует,
что производная будет возвращаться к начальному значению
при обходе в области D по любому пути, т. е. будет функцией
однозначной.
*) Разъяснение дано в диссертации Э. И. Зверовича б).

^ 2ni J
§ 46] ЗАДАЧА ГИЛЬБЕРТА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ 479
Применим полученные в настоящем пункте результаты для
отыскания Ф^B:), учитывая, что последняя на бесконечности
обращается в нуль не ниже второго порядка.
В самом широком классе функций, имеющих интегрируемую
бесконечность на всех концах (и имеющих на бесконечности
нуль второго порядка), решение будет иметь вид
L
f'^ (Т) - f'- (Т) . , Co + C,Z+...+Cm^2z'^'^ f.r. от
7=1 ^^ + ЖЩ • D6-2^)
L
Легко видеть, что все члены правой части имеют на
бесконечности нуль второго порядка. Для первого и третьего члена
это очевидно. Относительно второго члена в этом можно
убедиться интегрированием по частям, учитывая, что
проинтегрированная часть в силу непрерывности функций /+(/)> /"(О
обратится в нуль.
Функция Ф(г) определится по формуле
г
ф B) = J ф' (г) dz + С, D6.29)
о
где под С следует понимать действительную постоянную.
Для определения действительных постоянных Со, Сь ..., Ст-2,
С воспользуемся равенствами Re Ф(аА)=/(а^). Полагая в
D6.29) z = «й (^ = 1, 2, ..., т) и беря интеграл по пути, не
пересекающему L (например, по левому берегу оси абсцисс),
получим т уравнений
Ч
Re J Ф'{z)dz+C = f-^ {Uk). D6.30)
о
Для доказательства разрешимости последней системы
рассмотрим соответствующую однородную. Последнюю получим,
положив в краевой задаче /+(/)=/~(/) s 0. Будем иметь
р^^ со + с,г+.^.+ст^,т^'' dT + C^O (/^=1,2, ..., m).
о D6.31)
Путем последовательного вычитания получим систему т — 1
уравнений
Ч+\
Re J =0 (ft=l,2, ..., m-1)*

480 КРАЕВЫЕ ЗАДАЧИ [ГЛ, Vt
Учитывая, что в сумме \ + \ первое слагаемое имеет чисто
мнимое подынтегральное выражение, придем к такой системе:
J co + CIT+.^.+.^-2т^-^ ^^^Q (fe=l,2, ..., m-1).
D6.32)
Так как знаменатель имеет постоянный знак, то для
выполнения равенств числитель должен по крайней мере один раз
менять знак на каждом отрезке (Ь^, аи+\). Следовательно,
многочлен степени т — 2 меняет знак по крайней мере т — 1 раз.
Но такой многочлен тождественно равен нулю. После этого
очевидно, что и С = 0.
Таким образом, однородная система D6.31),
соответствующая системе D6.30), имеет только нулевые решения.
Следовательно, неоднородная система однозначно разрешима при любой
правой части. Отсюда вытекает и разрешимость самой задачи
Дирихле. Одновременно найден и алгоритм для получения
решения.
Заметим, что в книге Н. И. Мусхелишвили [16]
указывается еще другой способ решения задачи Дирихле, не
требующий предположения дифференцируемости краевых значений.
Способ этот опирается на решение еще одной вспомогательной
задачи (см. задачу 11 в конце главы).
§ 47. Характеристическое уравнение для разомкнутых контуров
47.1. Основные понятия и обозначения. Начнем изложение с
простейшего случая, рассмотрев сначала уравнение с
непрерывными коэффициентами и контуром, составленным из
непересекающихся разомкнутых кривых. Перенесение результатов на
общий случай сложного контура, составленного из любого
конечного числа расположенных как угодно замкнутых и
разомкнутых кривых (см. § 44), в предположении, что коэффициенты
уравнения имеют разрывы 1-го рода в конечном числе точек,
будет почти автоматическим.
В дальнейшем мы будем пользоваться обозначениями и
терминами для интегральных уравнений из гл. III, в особенности
п. 20.1, а для задачи Римана — из гл. VI, в первую очередь
§§ 42, 43.
Итак, пусть контур L = Li + L2 + • • • + ^т состоит из т
разомкнутых непересекающихся гладких кривых. Аналогично
п. 20.1 особый оператор и особое интегральное уравнение будем

§ 47] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 481
записывать в виде
Kq,^ait)c(>{i) + -L^mjl^(^)dx==f{t) D7.1)
или
^a{t)^(t) + ^\-^dx+\k{t,x)c^{x)dx = f{t). D7.2)
L L
Функции a{t), b{t)= M{ty t) будем считать
удовлетворяющими условию Гёльдера. От функции
в отличие от п. 20.1, будем требовать соблюдения условия
Гёльдера по обеим переменным. Для этого достаточно потребовать,
чтобы ядро M{t, х) удовлетворяло условию Гёльдера по
переменной t и имело частную производную по т, удовлетворяющую
условию Гёльдера по обеим переменным.
Решение ф(/) уравнений будем отыскивать в тех классах,
к которым принадлежат краевые значения решений задач Ри-
мана, рассмотренных в §§ 41 —45, т. е. в классах функций,
удовлетворяющих условию Гёльдера всюду внутри кривой и
ограниченных или допускающих интегрируемую бесконечность на
концах. (Последнее требование должно каждый раз уточняться.)
В качестве свободного члена f{t) можно допустить функцию
того класса, в каком брался в п. 41.5 свободный член g{t)
задачи Римана. Вначале для простоты формулировок будем
считать функцию f{t) удовлетворяющей условию Гёльдера.
Причина усиления по сравнению с п. 20.1 требования,
накладываемого на регулярное ядро k{t, t), состоит в том, что
нужно обеспечить интегрируемость произведения k{t, т)ф(т) на
тех концах, где будут допускаться неограниченные решения.
Определим обычным образом союзный оператор
КЧ =a(Oi|)@ -i J -~^г|)(т)^т, D7.3)
L
^ait)^{t)-^\ IMlilL dT + \k' {t, t) ^ (t) dx, D7.4)
L L
где
6(T) = M(T,T). k'it,r) = ^.'''''\-_T'''^ ¦

482 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Уравнение K't|? = О будет однородным уравнением, союзным
данному.
47.2. Решение характеристического уравнения. Начнем с
решения характеристического уравнения
К°ф ^a{t)if{t) + ^\-^dx = f (t). D7.5)
L
Вводя аналитическую функцию
L
И рассуждая аналогично п. 21.1, придем к краевой задаче
Римана для контура L:
0''{t) = G{tH'{t) + g{t\ D7.6)
^ ^^^ a(t) + b (/) ' ^^^^ а (t) + b{t) * ^^''''
при дополнительном условии Ф(сх)) = 0.
Будем рассматривать нормальный (неисключительный)
случай, когда G{t) нигде не обращается ни в нуль, ни в
бесконечность, что для исходного уравнения соответствует условию
а(/)± 6@=7^0.
Для упрощения дальнейших формул разделим
предварительно все уравнение D7.5) на ^JcL^{t) — b^ {(), так что будем
считать, что коэффициенты этого уравнения удовлетворяют условию
а2@-б2(/)=1. D7.8)
В связи с необходимостью разбиения на классы решений
особого интегрального уравнения приведем одновременно
классификацию решений задачи Римана.
Будем все концы а^ и Ьи единообразно обозначать буквами
Си С2у . . . , С2т. Пусть Си ^2, ...» Cq НС ЯВЛЯЮТСЯ К О н ц а М И
автоматической ограниченности (неособенные), остальные концы
Cq+u ..., С2т будсм считать особснными, Т. С. концами
автоматической ограниченности. Разобьем все концы на три группы:
Си ^2> •••» ^р\ ^р+Ь •••! ^q\ ^<7+Ь •••> ^2т» D7.9)
Кусочно аналитическую функцию, являющуюся решением
краевой задачи Римана D7.6), удовлетворяющую всюду на L,
кроме концов, условию Гёльдера, имеющую на концах I группы
интегрируемую бесконечность и ограниченную на остальных
концах, назовем принадлежащей классу Н{си с^у ..., Ср). Точки

§ 47] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 483
Си Г2, ..., Ср, В которых допускается обращение решения в
бесконечность, будем называть концами, определяющими класс*).
Класс решений, ограниченных на всех концах (самый узкий
класс), обозначим Hq.
Указанную классификацию будем применять не только к
решениям задачи Римана, но и вообще ко всяким кусочно
аналитическим функциям. Введем еще понятие о союзных классах.
Если в приведенном выше определении класса поменять
местами точки I и II групп, то придем к классу, союзному с
данным. Таким образом, если Н{сиС2у ..., Ср) — данный класс,
то Н'(сиС2у ..., Ср)=^Н{ср^и ..., Cq) будет союзным ему
классом.
Решение характеристического уравнения D7.5) получим по
формуле Сохоцкого:
ф@ = Ф+@-Ф"@. D7.10)
Будем исходить из формул п. 43.1 для решения задачи
Римана с разомкнутым контуром. Рассуждая совершенно так же,
как в п. 21.2, придем к формуле
+ Х+@Г1~-^1Г-^{^^~^^ ^Рн-.1@1. D7.11)
L о (О J [ 2я/ J Х+ (т) т - / 2 '^ ' ^ ^ J ^ ^
Последнее выражение показывает, что класс решений
интегрального уравнения совпадает с классом решений
соответствующей ему задачи Римана. (Напомним, что по условию
свободный член f{t) принадлежит тому же классу, что и искомое
решение.)
т
Вуюся в выражение Х'^@ = П(< —6*)"*** VG@"^^^'^ значе-
ния 0@, g{t) из формул D7.7) и учитывая условие D7.8),
*) Введенная нами классификация несколько отличается от
классификации Н, И. Мусхелишвили [16]. Последний считает основным наиболее
широкий класс функций, имеющих интегрируемую бесконечность на всех
неособенных концах, а остальные классы получает путем сужения. Поэтому
у него точками, определяющими класс, являются все неособенные концы, в
которых требуется ограниченность решения. У нас же основным является
наиболее узкий класс решений, ограниченных на всех концах. Остальные классы
получаются расширением основного путем допущения на некоторых концах
интегрируемой бесконечности. Последние концы как раз и определяют класс.
Произведенное нами изменение классификации необходимо для достижения
единообразия с классификацией в исключительных случаях, когда G{t)
допускает нули и полюсы. Там точки, где решение обращается в бесконечность,
рассматривались не как обычные, а как исключительные.

484 КРАЕВЫЕ ЗАДАЧИ [ГЛ, VI
преобразуем формулу D7.11) к виду
Ф@ = а@/@-^^^^ zixi т^\ +&(OZ(OPk~i@, D7.12)
L
где
Z(/) = [a@ +6@] Х+@ = [а(/)-6@1 Х"@ =
т
= П(^-&*Г *«"'". D7.13)
Если X ^ О, ТО нужно положить Pk-i@ — О- При х < О
решение заданного класса существует тогда и только тогда, когда
удовлетворяются условия разрешимости
S4w'^'"'^^ = 0 (^=1' 2. •••' -«)• D7.14)
Последний член формулы D7.12) представляет собой общее
решение однородного характеристического уравнения К° ф = 0.
Вводя аналогично п. 21.2 оператор R:
Rf^aif)fm-±m^^^, D7.15)
запишем общее решение характеристического уравнения в виде
ф@=-/?/+1: С,фЛО, D7.16)
где ф/1(/)= 6@ Z(/)/'^-^— собственные функции оператора К°,
т. е. линейно независимые решения однородного
характеристического уравнения К°ф = 0.
Исследуем вопрос о классах решений. Введем для
последних классификацию, аналогичную приведенной выше
классификации решений задачи Римана. Различие будет лишь в том,
что здесь будет идти речь не о кусочно аналитических
функциях, определенных во всей плоскости, а о функциях, заданных
лишь на контуре.
Определение. Решение ф(/) особого интегрального
уравнения, удовлетворяющее всюду на L, кроме, может быть,
концов, условию Гёльдера, имеющее в точках I группы D7.9)
интегрируемую бесконечность и ограниченное вблизи всех осталь-

§ 47] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 435
ных КОНЦОВ, будем называть принадлежащим классу A(ci, Сг, ...
Точки Си С2, ..., Ср, в которых решение обращается в
бесконечность, будем считать определяюи^ими класс.
Решение интегрального уравнения, принадлежащее классу
А(Ср+1, ..., Cq), будем называть решением класса, союзного по
отношению к классу h(cu с^у ..., Ср). Легко видеть, что
предельные значения кусочно аналитических функций класса
Н{с\у ..., Ср) являются функциями класса h\cu ^2, ..., Ср).
Класс решений, ограниченных на всех концах (самый узкий
класс), будем обозначать Ло. Эту классификацию будем
применять не только к решению особого интегрального уравнения, но
и вообще к любым функциям, заданным на контуре.
На основании формулы D7.13) и свойств канонической
функции (формулы D3.3) — D3.5)) функция Z(/)*) будет иметь вид
2т
2@ = «)о(ОП(<-<^аГ* (Y* = a, + iM D7.17)
где (Оо@ удовлетворяет условию Гёльдера и нигде не
обращается в нуль, а Re ул определяется условиями
— 1 < ttfe < О для /г = 1, 2, ..., р,
0<а^<1 для ^ = p-f 1, ..., ^, D7.18)
a;fe = 0 для /г = 9 + I, ..., 2/п.
Из выражения для функции Z(/) и формулы D7.11) следует,
что если решение задачи Римана D7.6) взято из класса
Я(с1, ..., Ср), то решение интегрального уравнения D7.5)
будет принадлежать классу Л(^1,..., Ср).
Исследуем поведение решения в окрестности точек
автоматической ограниченности с^ (^ = (/ + 1» • • •» 2т). Для этих
точек Yft = Фл- Если Pft 7^ О, то в силу формулы (8.7) решения
D7.12) хотя и ограничены в точке с^, но не имеют
определенного предела. Если же р^ = О, то G(Cft)= О и тогда &(c/i)= 0.
Особый интеграл в D7.12) имеет на основании формулы (8.1)
логарифмическую особенность. Но решения оказываются
непрерывными в точке Cfe в силу того, что Ь{с\^ = 0.
Индекс X задачи Римана D7.6) в данном классе будем
называть индексом самого интегрального уравнения. Свойства
характеристического особого уравнения можно формулировать так
же, как в п. 21.2, где решение и индекс нужно считать
принадлежащими одному классу. Мы их здесь не будем повторять. Так
же как и для задачи Римана. допущение неограниченности ре-
¦) Н. И. Мусхелишвили [16] называет ее канонической функцией
интегрального уравнения D7.5) данного класса.

486 КРАЕВЫЕ ЗАДАЧИ ГГЛ. VI
шения вблизи какого-нибудь неособенного конца увеличивает
число решений интегрального уравнения на единицу.
Максимальное число решений уравнение имеет в классе h(cu ^2, .. •
..., Cg) и минимальное в классе Ао. Разность числа решений
в этих классах равна числу q неособенных концов. (При этом
число условий разрешимости понимается как число решений,
взятое со знаком минус.)
Легко проверить, учитывая свойство функции Z(t), что R
переводит всякую функцию f{t) класса h{cu ..., Ср) в функцию
ф@ того же класса. Это оправдывает введенное в начале пункта
условие, накладываемое на свободный член /(/).
Замечание 1. Как уже указывалось в п. 43.4, при
отыскании общего решения краевой задачи Римана в каком-нибудь
классе Н{си ..., Ср) можно брать частное решение
неоднородной задачи, входящее в формулу общего решения, в любом
другом более узком классе H{ci, ..., Гг) {г <i р). Обозначим X{z)
каноническую функцию задачи Римана в классе Н{си ..., Ср),
а Xi{z)—в классе Н(си ..., Сг)\ соответствующие им по
формуле D7.13) канонические функции характеристического особого
интегрального уравнения обозначим Z{t) и Z\{t),
Тогда общее решение характеристического уравнения в
классе h{cu ..., Ср) может быть дано в виде
'fit)==a{t)f{t)-±^^l^\-^-:^ + bm{t)P,.i{t). D7.110
Замечание 2. Если в качестве свободного члена /(/)
брать функции более широкого класса, как это делалось для
g{t) в конце п. 41.5, то решение рассматриваемого уравнения
может иметь дополнительные особенности соответственно
особенностям свободного члена. О характере этих особенностей
достаточно подробно говорилось в конце п. 41.5 и здесь на этом
останавливаться не будем.
Замечание 3. Отметим следующее свойство
ограниченных решений характеристического уравнения, которое будет
использовано нами в дальнейшем. Пусть концевая точка Ch не
является точкой автоматической ограниченности (неособенный
конец). Тогда всякое решение ф@ характеристического
уравнения D7.5) с гёльдеровской правой частью, ограниченное в точке
Cft, обращается в этой точке в нуль:
ф(с,)=-0.
Действительно, в силу формул D2.10) и D7.10) решение
уравнения вблизи конца Ck имеет вид ф@ = (^ — Сл)"*^'^*Фо (О,
где фо@—ограниченная в окрестности Сн функция. При этом
определяющая порядок на конце действительная часть показа-

§ 471 ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 487
теля ak из-за ограниченности решения не может быть
отрицательной; в силу неособенности конца а^ ф 0. Следовательно,
ak > О, Отсюда вытекает формулированное выше замечание.
47.3. Решение уравнения, союзного с характеристическим.
Рассмотрим уравнение
К°Ч ^ а (О Ф (О - Д- S ^ ?.!/^^ dx = f (/), D7.19)
L
союзное характеристическому D7.5).
Введя кусочно аналитическую функцию (см. п. 21.3)
придем к краевой задаче
b(t)f(t)
a(t)-b (t) '
D7.21)
где G{t) определяется формулой D7.7). Однородную задачу
Q"*" (/) = -^-TTr-Q""(/) называют союзной по отношению к задаче
Ф+(/) = 0(/)ф-(/). Если Х(г) есть каноническая функция
задачи Римана D7.6), то, очевидно, Х^(г)= 1/Х(г) будет
канонической функцией задачи D7.21). При этом, если X(z)
принадлежит некоторому классу Н(си ..., Ср), то X'(z) принадлежит
союзному классу Н\ Если порядок на бесконечности
канонической функции X(z) (равный индексу задачи в классе
fJ{cu ..., Ср)) есть X, то, очевидно, этот порядок для Х'(г) =
= 1/ХB) будет —к. Следовательно, индекс х^ союзной задачи
в союзном классе Н{Ср^и .••, Cq) решений равен индексу
данной задачи х с обратным знаком.
Общее решение краевой задачи D7.21) в классе Н{Ср+и ...
..», Cq) можно записать в виде
QW=J^S "la-MT ^ + |XW|- >•-,и. D7.22)
L
где P_x-i есть многочлен степени —к — 1 с произвольными
коэффициентами.
Из решения D7.22) задачи Римана по формуле Сохоцкого
b (t) л|) (/) = Q+ (t) - Q- (О D7.23)
обычными выкладками получим решение союзного уравнения
D7.19):
^(t)--a it) fit) + ^ \ ^ ^'^^^] f ^'^ dT + j^ Р-,-, (О, D7.24)

488 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
которое, очевидно, будет функцией союзного класса h{cp+u .¦.
Если —X ^ О, то нужно положить Р-к-1 (О ^ о, причем если
—к <С О, то должны удовлетворяться условия разрешимости
J Z (т) & (т) / (т) т/-1 dr = О (у = 1, 2, ..., к), D7.25)
L
Формула D7.24) показывает, что линейно независимыми
решениями союзного уравнения D7.19) являются функции 'ф/@ =
= YTt) ^^~\i = 1, ..., —х). Следовательно, условия
разрешимости D7.14) данного характеристического уравнения D7.5) могут
быть записаны в виде
S/W^/(T)dT = 0 (/=1,2, ..., ->с). D7.26)
L
Это вторая теорема Нётера (см. п. 23.2), доказанная здесь
для частного случая характеристического уравнения. Эта
теорема, так же как и другие теоремы Нётера, будут доказаны
в п. 48.5 для общего случая полного уравнения.
47.4. Примеры. 1. В качестве первого примера рассмотрим
характеристическое особое интегральное уравнение 1-го рода.
Положим в уравнении D7.5) a(t)^0, В силу условия a(t)±b{t)^ О
b(t) не обращается в нуль нигде на L. Разделив на 6(/), уравнение можно
представить в виде
^ ^т = / (/).
1 [ Ф(т)
я/ J т — i
t
L
Следовательно, решение интегрального уравнения 1-го рода есть обращение
особого интеграла типа Коши. Задача эта была решена нами в п. 42.3. В этом
случае все концы неособенные (д = 2т). В классе h(cu ..., Ср) задача
имеет при р "^ т р — т линейно независимых решений, при р <. т имеет
решение лишь при выполнении т — р условий разрешимости.
Соответствующие формулы мы выписывать еще раз не будем.
2. Рассмотрим интегральное уравнение, встретившееся при решении одной
конкретной механической задачи
/
«Ф@ + ^^$^^т = 6„ + М.
О
Контуром L служит отрезок действительной оси (О, /); а, ао, fli, bo, 6i
—действительные постоянные.
Обычным приемом сводим его к краевой задаче Римана
0^{t) = G{tH-(t) + g(t\
Г а\ = д — ^ (До + ait) ... ^ bo + bit
^^ a + i(ao + a,t)' ^^'^ a + i(ao + ait)'

§ 47] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 489
Мы пришли к краевой задаче, рассмотренной в п. 43.3. Решение исходного
уравнения получим по формуле Сохоцкого
ф(/) = ф-^@-Ф"(/).
Предоставляем читателю самому выписать решение, пользуясь формулами
D3.20) и D7.12).
3. Рассмотрим на отрезке [а, р] однородное уравнение с постоянными
коэффициентами:
3
аф @+^5 -^^ dx = О D7.27)
а
И укажем на его примере один способ вычисления некоторых особых
интегралов. Отыскивая по общим формулам решение однородного уравнения и
подставляя его в само уравнение, придем к тождеству, дающему выражение
для некоторого особого интеграла. Возьмем в D7.27) а = / ctg \кп (О < ц <
< 1). Тогда О (/) = е^""'^ . Индекс в классе функций, не ограниченных на
обоих концах, равен 1. В соответствии с формулой D7.12) найдем, что общее
решение уравнения D7.27) имеет вид
Ф@=-
Подставляя его в уравнение D7.27), приходим к тождеству
^(,_af(p-x)-^r-0°U-«)^p-0'-'> ^"<"<'^' ^''-''^
которое будет использовано нами в дальнейшем в п. 54.2 гл. VH.
Читатель может найти в задаче 21 к этой главе более сложные особые
интегралы, вычисленные указанным способом.
47.5. Уравнение на действительной полуоси. Во всех
предыдущих рассуждениях настоящей главы контур предполагается
конечным и, следовательно, «концы» — конечными числами.
Покажем здесь на простейшем примере, как поступить в случае,
когда «конец» находится в бесконечности. Рассмотрим
характеристическое уравнение
оо
«@<р@ + -1^5 T^dx = f{t). D7.29)
О
Для его решения возможны два пути:
1. С помощью замены независимой переменной свести
уравнение к уже изученному случаю конечного контура.
2. Провести непосредственно для бесконечного контура
рассуждения, аналогичные тем, с помощью которых решалось
уравнение на конечном контуре.
Мы используем первый путь. Он дает наиболее простой
способ определения допустимых на бесконечном конце классов

490 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
решений. Введем новую пару переменных а, s подстановками
-_ g f_ s , do 1 _ (l-5)(l~a)
D7.30)
Действительная положительная полуось переходит при этом
в отрезок [О, 1]. Вводя обозначения
a{t) = A{s\ b{t) = B{s\ •ISlL = F{s\
D7.31)
приведем заданное уравнение к виду
1
л (S) ^К^) + ^ S 1:^ dcr = f is). D7.32)
О
Возьмем в последнем уравнении на верхнем конце два обычных
класса решений: ограниченные
\y\){s)\<M
и неограниченные интегрируемые
1^EI<у^ @<а<1).
На основании равенств D7.31) и вытекающего из D7.30)
соотношения 1—s= 1/A +/) получаем, что соответствующие
им решения исходного уравнения в окрестности бесконечности
должны удовлетворять следующим соотношениям:
1Ф@1<ТТТ' (^7.33)
I Ч^ (^) К ТТД^ (О < а < 1). D7.34)
Таким образом, решениям, ограниченным на верхнем конце,
соответствуют решения, обращающиеся на бесконечности в нуль
порядка не ниже первого. Неограниченным интегрируемым
решениям соответствуют решения, обращающиеся на
бесконечности в нуль любого положительного порядка. В дополнение
отметим, что в условии D7.33) убывание точно первого порядка
будет иметь место лишь в том случае, если бесконечно
удаленная точка является концом автоматической ограниченности
(G(oo)>0). Во всех других случаях вместо D7.33) должно
выполняться условие

§ 47] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 491
Из соотношения /(/) = (!—s)f (s) = y^ следует, что
использованным в этой главе классам свободного члена —
ограниченным или неограниченным — будут соответствовать на
бесконечном конце классы свободных членов, обращающихся в нуль
порядка не ниже первого или любого положительного порядка.
Теоретически использованное нами преобразованное
уравнение D7.32) может служить и для практического решения по
формулам настоящего параграфа первоначально заданного на
бесконечном контуре уравнения D7.29). Можно решать исходное
уравнение также и непосредственно в классах D7.33), D7.34),
используя метод настоящего параграфа (на подробностях не
останавливаемся).
Укажем в заключение, что так как ненулевые на
бесконечности решения здесь отсутствуют, то исчезают и трудности (см.
п. 21.6), связанные с теорией таких решений.
47.6. О методе неполной факторизации *). Существо этого
метода выясним, рассматривая задачу Римана
Ф^ (/) = G (О Ф- (о + g (О, t е L, D7.35)
на простом гладком замкнутом контуре L. Как мы видели, эта
задача решается путем «факторизации» коэффициента 0@» т. е.
представления его в виде отношения
0@ = 1^. t^L. D7.36)
В простейшем случае, когда G{t)^0 и IndG(/)c=0,
функции Q+ и Q"*, называемые факторизующими, являются
аналитическими и не имеющими нулей соответственно внутри и вне
контура L. Но уже при Ind 0(()ф О у этих функций приходится
допускать нули или полюсы. Обычно в качестве факторизующих
используются канонические функции (см. § 14), у которых нули
или полюсы допускаются в единственной точке — бесконечно
удаленной. Следует, однако, подчеркнуть, что вполне пригодны
факторизующие функции, у которых нули или полюсы
сосредоточены в любой другой точке комплексной плоскости (даже
контурной!) или одновременно в нескольких точках. При этом ход
решения задачи остается прежним: аналитическое продолжение
и использование обобщенной теоремы Лиувилля. Отличие будет
заключаться в том, что вместо многочлена с произвольными
коэффициентами, который появлялся при решении в случае
положительного индекса, теперь будет рациональная функция с
постоянными параметрами, число которых на единицу больше
индекса. Таким образом, любая факторизация ведет к цели.
*) Материал настоящего пункта взят из работ Ю. И. Черского 3), 4).

492 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Разумеется, чем существеннее отличается факторизующая
функция от канонической, тем больше будет дополнительных
трудностей при окончательном решении задачи Римана, но
сейчас нам важно отметить принципиальную возможность решения.
У факторизующих функций, кроме полюсов, можно допустить
и другие особенности, в частности, разрыв вдоль некоторых
линий. Такие функции и используются в методе неполной
факторизации.
Пусть, например, функция Q+B:) аналитична и не имеет
нулей внутри L, а Qr{z) аналитична и не имеет нулей вне
контура L, за исключением точек лежащего вне L разомкнутого
контура Г, на котором Й-(г) терпит разрыв 1-го рода.
Как обычно при решении задачи Римана, подставим D7.36)
в D7.35) и запишем известную функцию
В виде разности предельных значений функций, аналитических
внутри и вне L,
Получим
-^li^~.A+(^)=.^lM.~./г-(/)=f (О t^i. D7.37)
Аналитическое продолжение через контур L, возможное
ввиду левого равенства D7.37), показывает, что F{t) есть
значение на контуре L новой неизвестной кусочно аналитической
функции F{z) с единственным скачком вдоль Г. Искомые
функции Ф+(/) и Ф~@ выражаются через F{t) равенствами
ф+ {t) = Q-^ (t) F (t) + Q+ @ Л"^ (О,
' ''' /eL. D7.38)
ф' (t) = Q' {t)F {t) + Q- {t)h-' it),
Найдем краевое условие для определения функции F{t).
С этой целью зададим на Г направление обхода и условимся
обозначать предельные значения аналитических функций
значком + (снизу) при подходе к Г слева и значком — (снизу) при
подходе к Г справа. Из непрерывности функции Ф^{г) вне L
следует равенство
Ф;(т) = Ф:(т), те г,
или, подробнее,
Q; (т) f + (т) + Q; (т) h' (т) = QI (т) F-{x) + QI (т) Л" (т), т е Г.
D7.39)

§ 47] ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 493
Это — краевая задача Римана на контуре Г с неизвестной
кусочно аналитической функцией F{z), Определив последнюю,
найдем по формулам D7.38) решение исходной задачи Римана
D7.35).
Для самой задачи Римана применение такой неполной
факторизации может оказаться целесообразным лишь в редких
случаях, когда, например, коэффициент G{t) на L является
обобщенной функцией (линейным функционалом), у которой
предполагается заданной лишь неполная факторизация. Но
изложенные выше соображения иногда приносят пользу при решении
других задач теории аналитических функций, в краевом условии
которых имеется более двух слагаемых, содержащих искомые
функции. К этим задачам обычный метод факторизации
неприменим.
Рассмотрим одну такую задачу. Требуется найти функцию
ФB), кусочно аналитическую (линией скачков служит
действительная ось) и ограниченную на всей плоскости, по краевому
условию
• Ф+ (х) + ЛФ"'(-х)- Ф~ (х) = g {х\ D7.40)
1
л/х'+\
— оо < л: < оо, ^/х^+ 1 > 0.
Предложенная краевая задача есть задача с сопряжением
и сдвигом (а(.^) = —а:). Как мы видели в пп. 39.3, 39.4, такого
рода задачи в общем случае не решаются в замкнутой форме,
а приводятся к интегральным уравнениям. С помощью метода
неполной факторизации, как далее будет показано, можно
свести поставленную задачу к задачам, разрешаемым в
квадратурах.
Функцию Ф+(—х) можно рассматривать как краевое
значение функции Ф+(—z). Последняя может быть получена из Ф+(г)
с помощью двух операций: преобразованияФГ(г) = Ф'^ (—г),
переводящего Ф+(г) в аналитическую в нижней полуплоскости
функцию Ф~ (г), и преобразования симметрии Ф+ (— 2) = Ф~ (г),
переводящего (см. п. 30.2) ФГ (г) в функцию, аналитическую в
D+. Следовательно, Ф+(—х) есть краевое значение функции,
аналитической в Z)+.
Функция л/х^ + 1 является краевым значением
аналитической функции Уа:^ -+-1, имеющей точки разветвления dzt. Из
условия л/х^ + 1 > О следует, что разрез между точками
разветвления, закрепляющий однозначную ветвь, не может пересекать
действительную ось. Следовательно, он должен проходить через
бесконечно удаленную точку. Проведем его по мнимой оси.

494 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Запишем краевое условие, как обычно, в виде, удобном для
аналитического продолжения
D7.41)
В отличие от обычного решения краевой задачи Римана, F{z)
уже не будет многочленом, а будет иметь в верхней
полуплоскости ту же особенность, что и функция / ^ . т.е. линию
скачков вдоль участка мнимой оси Г = {i, i оо). Задача свелась к
определению функции F{z), аналитической в плоскости,
разрезанной вдоль Г.
В равенстве D7.41) заменяем х на —х и переходим к сопря-
женным значениям. Исключая из полученной системы Ф+(—х),
получим
D7.42)
Аналитическую функцию с линией скачков можно
представить в виде интеграла типа Коши вдоль этой линии с искомой
плотностью:
ioo
^(^) = iSf4^^ + ^- D7.43)
Определим поведение ф(т) на концах i, i^- Из выражения
D7.41), учитывая ограниченность Ф+B) в точках i и too,
получим, что F{z) на бесконечности должна быть ограниченной,
а в точке i допустим рост порядка \z — i\-^^K Отсюда, учитывая
свойства интеграла типа Коши, получим, что ф(т) должна
удовлетворять условиям
Используя непрерывность Ф'^ (z) на Г:
Ф'^(/|/-0) = Ф+(/1/ + 0),
составим интегральное уравнение для ф(т). Беря в выражении
D7.42) по формулам Сохоцкого предельные значения F{z) на
Г слева и справа и подставляя в последнее равенство с учетом

§ 471 ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ 495
соотношения V(^> — 0)^ + 1 = — V(^> + 0)^ + 1, получим
Полагая ((>{iy)= u{y)+iviy), g^{iy)= g\{iy)+ig2{iy). c =
= ci + ^^2 И отделяя в последнем равенстве действительную и
мнимую части, получим для определения и(у) и v{y) два
самостоятельных характеристических уравнения:
оо
L D7.45)
Л VF^=T t» (г/) -1 J i^ ЙЛ = 2g, (^,) + с,.
1
Класс их решений определяется условиями D7.44). Следует
учитывать также необходимые условия разрешимости задачи:
f(VIfIl)+^VIH?), „,.«,
= .(_V!^) + ,.(_VI^). если I.KI.
Эти условия устраняют полюсы у функции D7.42), вызванные
наличием множителя ;^2д.2 4-^2—1 ^ формуле D7.42). Решая
систему уравнений D7.45) (см. п. 47.5) совместно с условиями
D7.46), найдем ф(т), а с ней и решение поставленной задачи.
Методом неполной факторизации решается краевая задача
Римана для системы двух пар функций
Ф!" {х) = V^4^ ФГ {х) + Ф2- (X) + g, {х\
л. 1 (—00<JC<00),
где Я и а — постоянные. К этой задаче приводится основная
смешанная задача для упругого полупространства, а также
некоторые другие задачи математической физики.
Наконец, метод неполной факторизации может
пригодиться при изучении некоторых новых задач. Пусть, например, в

496 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
факторизации D7.36) функция Q-{z) наряду с разрывом Г имеет
еще нули на счетном множестве точек а^ и простые полюсы на
счетном множестве точек Ьд (^ = 1, 2, ...). Тогда задача Ри-
мана D7.35) сведется к другой задаче, в которой у искомой
функции F{z), кроме разрыва Г, допускаются полюсы в точках
uk. При этом наряду с краевым условием D7.39) будет еще
счетное множество условий вида F{bh) = с^ (^ = 1, 2, ...), где Ch —
известные числа. Таким образом, при исследовании краевых
задач для кусочно мероморфных функций со счетным множеством
дополнительных условий можно использовать связь этих задач
с обычной задачей Римана.
47.7. Характеристическое уравнение в банаховых пространствах.
С. Г. Сам ко 8) распространил исследование Ю. И. Черского 1)
относительно задачи Римана в банаховом простарнстве на более общий случай,
соответствующий разомкнутому контуру и разрывным коэффициентам (см.
п. 16.3). Было рассмотрено в банаховом пространстве X общее сингулярное
уравнение вида
(Л,+ Л2Р5)ф = /, D7.47)
соответствующее краевой задаче Римана и являющееся аналогом
характеристического уравнения на разомкнутом контуре и с разрывными
коэффициентами. Оператор S по-прежнему определяется условием S^ = Д S Ф ±/, а
оператор Я, определяемый как проектор: Р^ = Я, соответствовал операции
умножения на характеристическую функцию
P(t)
^Г 1, t^L,
I О, t^L,
контура L. Разрешимость уравнения D7.47) зависит от целого числа х,
определяемого, как и в работе Ю. И. Черского 1), представлением
где аксиоматически определяемые операторы Ч'± являются аналогами
умножения на предельные значения аналитических функций, а U^ — аналог
умножения на степень t^. Существенное отличие от рассмотрений Ю. И. Черского
здесь состоит в том, что операторы W^ не являются ограниченными в
рассматриваемом пространстве X, действуя из X в более широкое
пространство Xi. При некоторых предположениях относительно операторов Ai, Аг
решение уравнения D7.47) получено в явном виде.
§ 48. Полное уравнение для разомкнутых контуров
и разрывных коэффициентов
Теория полного интегрального уравнения D7.1) в рассматри*
ваемом случае, так же как и в случае замкнутого контура,
состоит из двух частей:
1. Регуляризация, включая сюда разработку способов
регуляризации и исследование связи между решениями исходного
особого и полученного регулярного уравнений (вопросы
равносильной регуляризации).

§ 48] УРАВНЕНИЕ ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 497
2. Основные свойства особого уравнения (теоремы Нётера).
Способы исследования будут главным образом те же, что и
в случае замкнутого контура и непрерывных коэффициентов
(гл. III).
Как мы увидим, отличие рассматриваемого случая от случая
замкнутого контура заключается в том, что произведение двух
интегрируемых функций ф(/), \|)@ может оказаться неинтегри-
руемым. Чтобы обеспечить интегрируемость произведения, нужно
позаботиться о том, чтобы оба множителя не обращались
в бесконечность на одном и том же конце. Вспоминая свойства
введенных в § 47 союзных классов, мы легко заключим, что
произведение функций, принадлежащих союзным классам, всегда
окажется интегрируемым.
Оригинальная часть дальнейшей теории будет заключаться
в выяснении в каждом случае вопроса о том, из какого класса
(см. § 47) должны браться соответствующие функции.
48.1. Регуляризация решением характеристического
уравнения. Основные сведения о регуляризации полного особого
интегрального уравнения изложены в §§ 22 и 24, понятиями и
обозначениями которых мы будем здесь постоянно пользоваться.
В рассматриваемом случае применимы те же три способа
регуляризации, что и для замкнутого контура: регуляризация
слева, регуляризация справа, регуляризация решением
характеристического уравнения. Наиболее простым для исследования
поведения возникающих ядер и допустимых классов решений
является последний способ, с него и начнем изложение. Для
простоты рассмотрим сначала случай непрерывных
коэффициентов и разомкнутого контура. Распространение этого
исследования на случай разрывных коэффициентов не представляет
трудностей.
Запишем полное уравнение D7.1) в форме
a{tL>{t) + ^\^dx=f{t)-^\k{t,r)cp{T)dx D8.1)
L L
ИЛИ В символической форме
К>=:/-./^Ф D8.10
и решим его как характеристическое, рассматривая правую часть
как известную функцию. Решение будем искать в некотором
классе h{cu ^2, . • •, ^р)= Л. Будем для простоты предполагать,
что f{t) удовлетворяет условию Гёльдера. Если, как было
предположено в п. 47.1, k{t, т) удовлетворяет условию Гёльдера по
обеим переменным, а ф@ принадлежит классу Л, то, как легко
вывести, йф удовлетворяет условию Гёльдера, следовательно, и
вся правая часть равенства D8.1) удовлетворяет этому условию.

498 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Применив формулу D7.12), получим (см. п. 24.6)
(p{t)+\K{i,x)q>{x)dx = f,{t\ D8.2)
L
где
Kit, x)^RMt, r) = a{t)kit, T)-Am(^5li^-) 'i''
T,) T,-/'
L
„+ '¦ D8.3)
m
= [а@-М0]Х-(/) = П(<-6*Г"*е^'"»
Если x^O, TO нужно положить Ях-1^0> причем при x<0
должны выполняться функциональные соотношения
J [S W-^'"' ^^1 -^ ^'^'^' = ^'-' zf ^^ D8.4)
(/=1,2, .... -х).
Последние условия можно представить еще в форме
5р,(т)ф(т)^т = /,. D8.40
где положено
P/W = J-^^'-'rf^ fl=\i>-'^dt. D8.5)
Если заданное уравнение D8.1) разрешимо, то условия D8.4)
окажутся выполненными.
48.2. Исследование регуляризованного уравнения. Исследуем
ядро /С(/, т) и свободный член /i(/) уравнения D8.2),
полученного в результате регуляризации исходного особого уравнения
D8.1). Эти функции при сделанных в п. 48.1 предположениях
относительно заданных функций k{ty т), f{t), будут, очевидно,
удовлетворять условию Гёльдера во всех точках контура,
отличных от концов. Рассмотрим поведение их на концах.

§ 481 У1>АВНЁНИЕ ДЛЯ РАЗОМКНУТЫХ КОНТУРОб 499
Согласно формуле D7.17)
2/п
^it) = щ{t)Il{t-c,У>^¦, \k = ak + ih, D8.6)
— l<a^fe<0 для /г=1, 2, ..., р,
0<а;^<1 для k = p+l,...,q,
ajfe = 0 для А = ^+1, ..., 2m,
0H(О—функция, удовлетворяющая условию Гёльдера и не
обращающаяся в нуль.
Из формул D8.3) легко вывести, что функции /С(/, т) и /i(/)
на концах си ^2, • • •, ^р будут вести себя как функция Z@, т. е.
обращаться в бесконечность порядка ak- На остальных концах
они будут ограничены. Таким образом, ядро K{ty т) и свободный
член /i(/), имея на концах си ..., Ср неподвижную
бесконечность, не удовлетворяют тем условиям, которые накладываются
на эти функции в теории Фредгольма*). Однако легко путем
замены переменных для функции ф и аргумента интегрирования
X избавиться от неподвижных бесконечностей и привести
уравнение к виду, когда ядро и свободный член подчиняются всем
условиям теории Фредгольма.
Действительно, обозначим
Г@ = П(^-с*Л D8.7)
И произведем подстановку
Ф@ = Г(Офо@. D8.8)
Уравнение D8.2) примет вид
Фо (Ч + j ^1ц) Фо \V ^ = Y^ •
L
Теперь у нас исчезли неподвижные бесконечности по
переменной /, но появились такие же по переменной т. Чтобы избавиться
от последних, сделаем еще замену независимых переменных:
X i
Ti= \T{x)dx, U= ^T{t)dt на Lu (Л=1, 2, ..., m). D8.9)
¦) Только в случае подвижной бесконечности порядка меньше единицы,
т. е. бесконечности вида (т —0~" @<а<1), этот порядок при итерации
уменьшается и существует такой номер т, что т-е итеративное ядро
ограничено.

500 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Обозначая фо[^(^1)] снова через q)o{t\), придем к уравнению
<fo{ti)+\KAtu r,)cfo{x,)dT, = fAti\ D8.10)
в котором новое ядро K\{ty т) и свободный член f2{t) будут
ограничены на новом контуре интегрирования Г.
Заметим, что так как обращение формул D8.9) происходит,
вообще говоря, не однозначно, то новый контур Г может
оказаться самопересекающимся, что не имеет существенного
значения. Найдя все решения уравнения Фредгольма D8.10), с
помощью формулы D8.8) получим решения уравнения D8.2),
принадлежащие классу h{cu ..., Ср).
Так как решения уравнения D8.2) и D8.10) связаны простой
зависимостью D8.8), то, хотя уравнение D8.2) и не является
в строгом смысле фредгольмовым, но для него оказываются
справедливыми все теоремы Фредгольма. Все различие будет
в том, что его решения не будут ограниченными, как это
предусматривается теорией Фредгольма, а будут принадлежать
классу h{cu ..., Ср).
Следовательно, можно утверждать, что в результате
регуляризации мы приводим особое уравнение к уравнению
Фредгольма.
Если взять однородное уравнение
^{t)+\K{x, 0*(т)^т = 0, D8.11)
союзное уравнению D8.2), и произвести в нем замену
переменных, аналогичную D8.8), D8.9), то легко установить, что
придем к уравнению Фредгольма
b{ti)+\KAru /i)to(Ti)rfTi = 0, D8.12)
союзному уравнению D8.10).
48.3. Характеристическое уравнение на сложном контуре и с
разрывными коэффициентами. Прежде чем перейти к
исследованию полного уравнения с разрывными коэффициентами,
рассмотрим соответствующее характеристическое уравнение. Как
мы уже видели в §§ 41—46, теория краевой задачи Римана
в общем случае произвольного сложного контура и разрывных
коэффициентов принципиально мало отличается от случая про-

§ 48] УРАВНЕНИЕ ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 501
стых разомкнутых контуров. Учитывая тесную связь особых
интегральных уравнений с краевой задачей Римана, того же нужно
ожидать и для этих уравнений.
Рассмотрим характеристическое уравнение
K.°^^a{t)q,{t) + ^\^dx = f{t), D8.13)
В предположении, что контур L состоит из любого конечного
числа замкнутых или разомкнутых, как угодно расположенных
кривых. Коэффициенты a{t), b{t) будем считать
удовлетворяющими условию Гёльдера всюду на контуре, кроме конечного
числа точек /ь ..., tu где они испытывают разрывы 1-го рода.
Все концы кривых, а также точки разрыва будем единообразно
называть «концами» (см. п. 43.2) и обозначать Си ^2, ..., Сг-
Для простоты считаем, что концы не совпадают с точками
самопересечения контура. Так же как и во всех аналогичных
случаях, требуем, чтобы уравнение удовлетворялось всюду, кроме
концов и точек самопересечения. Предположим выполненным
условие a^{t)— b^{t) = 1.
Пусть Си С2, ..., Cq — неособенные, а Cq^u ...» Сг —
особенные концы. Совершенно аналогично п. 47.2 введем союзные
классы h{cu ..., Ср)= h, h(cp+u .. •, Cq)= h\ Будем искать
решение уравнения в некотором классе Л. Свободный член
уравнения f{t) в общем случае можно считать принадлежащим этому
же классу Л.
Решение уравнения D8.13) в замкнутой форме можно
получить совершенно тем же способом, что и в рассмотренных ранее
простых случаях (пп. 21.2, 47.2). Введя аналитическую функцию
Ф(-)=2к$^^-. D8-14)
придем к краевой задаче Римана
Ф+@ = О@Ф"@ + ^[@. D8.15)
В предположениях § 44 при условии Ф(оо) = 0.
Взяв по формулам D4.11) —D4.13) решение этой задачи
в некотором классе Я, по формуле Сохоцкого
ф(/) = ф+(/)_ф-(/) D8.17)

502 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Придем к решению исходного уравнения D8.13). Оно
представится формулами
<fit) = a{t)f{t)-^^^^\-l^^ + bii)Z(t)P,^,{t), D8.18)
7.{t) = [a{t) + b{t)]X*{t) = [a{t)-b{t)]X-{t) =
^П^^-'^*)""*^''"' Г(г)=2^г5^^^т. D8.19)
Л-1 L
где числа хл выбираются на каждом конце в соответствии с
выбранным классом решений.
Если X ^ О, то нужно положить Р^_1 {t) ^ 0; при х < О
должны выполняться условия разрешимости
5^^'^'^'^ = 0 (/=>' 2--- -^)- D8.20)
Аналогично решается уравнение
K-''^^a{t)^{t)-±\^^^^dx = fit),
L
союзное характеристическому.
Пример. Пусть L —- единичная окружность, Li и L2 — соответственно ее
прямая и левая полуокружности.
Решим характеристическое особое уравнение
Ш J x-t е"'D<2+1) \tJri)
где
а (t) = ch nty bit)^ — sh nt на Ij»
. -o„»„„.. фушо», D^)"" 3...,. o,p«e«H.o» ^.b», . „„„,.
щем классе функций:
a) A(/, -/); 6) Л@.
Вычислив по формулам D8.16) коэффициенты G{t), g(t), придем к крае^
Bofi задаче Римана
ф-^ (О = а (О Ф- it) + ^<^^+J!<^; + ^> (i^)^.
где
С(/) = е"^ на Lb GU) = e^"^ на la-

§ 48] УРАВНЕНИЕ ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 503
Это есть краевая задача, рассмотренная нами в п. 43.3 (пример 2), при а=1/2.
Можно воспользоваться данным там решением, наложив на него
дополнительное условие ф--(оо)= 0.
а) Для получения нужного нам решения класса h{i, —i) надо в формуле
D3.22) положить а = 1/2, с = 0. Получим
(Ь+ (^\ - (l:ZL\^ 6(/г~1)а^" + 4B^ + 1)Dг + /)
z-i^— 6 (/2-1)
«-<'>-G^)
422+1 •
Учитывая данные при решении краевой задачи указания относительно способа
определения предельных значений, будем иметь
it
Ф W-(,7qrrJ aF+i «а L,
it
^~/ЛТ б(//-1) ^^nt
4/2+1
Отсюда
Ф~«)-G+т)"' ^V;^/^-"' на L,.
ф С) = (,7+7J 4F4n «" ^ь
ff
^"=Dfl)
/ - / \Т 12 {it - 1) sh я/ + 4 (/2 + 1) D/ + /)
4/2+1
6) в классе h{i) индекс уравнения х = —1, поэтому уравнение разрешимо
лишь при выполнении условия
С (T-/)DT+/)g-"^
J 4т2 + 1
• cfT = 0.
Последнее равенство, как легко проверить, удовлетворяется. Аналогично
предыдущему получим
^+ /А _ .nt .. . ..(t- i ^T 6/ + 4в-^^ D/^ - 3// + 1) „^ •
Ф (<) = 4731ГГ (ТТТ) ^ ^^^' sh я< + 4 D/* - Зй + 1I на Ц.

504 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
48.4. Регуляризация полного особого уравнения. Прежде
всего заметим, что при рассмотрении полного уравнения мы
встречаемся с одной особенностью, отличающей случай
разрывных коэффициентов от случая разомкнутых контуров. Способ
выделения характеристической части, заключающийся в
использовании тождества
В случае разрывной функции М становится неприменимым, так
как вблизи точки разрыва подынтегральная функция имеет
особенность вида (т — t)-K В частности, операторы вида
S"^^^:?^%(T)rfT D8.21)
С разрывной функцией a{t) не являются регулярными. Таким
образом, полное особое интегральное уравнение нужно брать
сразу с выделенной характеристической частью:
Кф = К°ф + /гф =
^a{t)cp{t) + ^\-^dx+\ k{t, x)cp{x)dx = f{t), D8.22)
L L
По ЭТОЙ же причине союзное уравнение
K'^^a{t)^{t)^lr\^^^dx+ \k{x,t)y^{x)dx^!(i)
L L
нужно рассматривать как самостоятельный вид, не сводимый
к предыдущему.
Рассмотрим вопрос о регуляризации особого уравнения
D8.22). Применим способ композиции особых операторов. Здесь,
однако, регуляризующие операторы в виде B2.16) непригодны.
Можно показать, что применение регуляризаторов в таком виде
приводит к уравнениям, не являющимся, вообще говоря,
уравнениями Фредгольма. Это вносит серьезные трудности в
исследование полных уравнений с разрывными коэффициентами.
Избегнуть затруднений можно путем подбора специального регу-
ляризатора. Оператором, приспособленным для роли регуляри-
зующего, здесь будет служить оператор
W = a,0/@-iiMMJm_^, D8.23)
который выступал в роли разрешающего при решении
неоднородного характеристического уравнения. Покажем, что этот one-

§ 48] УРАВНЕНИЕ ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 505
ратор является регуляризующим для оператора К как слева,
так и справа. Возникающие здесь трудности связаны с тем, что
при составлении композиций /?К° и K°R нельзя воспользоваться
формулами композиции п. 22.1, поскольку в случае разрывных
коэффициентов операторы вида D8.21) не являются
регулярными. Поэтому мы применим прием, использованный ранее
применительно к задаче Римана: сведем уравнение с разрывными
коэффициентами к уравнению с непрерывными коэффициентами.
Следуя этому приему, получим регуляризатор R как
композицию двух операторов, из которых один регуляризует получаемое
уравнение с непрерывными коэффициентами, а другой —
некоторое простейшее уравнение с разрывными коэффициентами.
Пусть вначале х = 0. Как известно (формула D8.18)),
уравнение К°ф = / тогда безусловно разрешимо и ф =/?/. Отсюда
K°Rf ^ / и /?К°ф ^ ф. Следовательно, в случае х = О оператор
R является для оператора К и левым и правым регуляриза-
тором.
В общем случае, следуя способу сведения задачи Римана
с разрывным коэффициентом к задаче с непрерывным
коэффициентом, проделаем те же операции для характеристического
уравнения. Для простоты ограничимся изложением для случая,
когда L — простой замкнутый контур. Пусть в соответствии с
построениями § 41
.,о-П(/-..)'.=^,
где o)+W = n (^-<*)'*. «>-@ = П {т=^Т' "
^^y^f— со (О •
Коэффициент Gi{t) непрерывен. Задаче Римана с этим
коэффициентом соответствует, согласно B1.8), характеристическое
уравнение
С непрерывными коэффициентами «i (/) = у A + Gi), 6i (t) =
= -г- A — Gi). Процесс сведения задачи Римана с коэффициентом
G{t) к задаче с коэффициентом Gi{t) в операторной форме
можно записать так:
K° = QKi + r, D8.24)

506 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
где Т — оператор с регулярным ядром, а
Оф = ^[A+со@)Ф@ + -Ц|^5^4^] D8.25)
— характеристический оператор с разрывными коэффициентами
специального вида. Читателю предоставляется самостоятельно
проверить равенство D8.24) с учетом того, что теперь
непрерывные коэффициенты ai(t) и b\(t) можно переставлять с особым
оператором с точностью до регулярного слагаемого.
Коэффициент задачи Римана, соответствующей оператору
D8.25), равен (о(/). Так как
то из формул D1.19) — D1.21) непосредственно следует, что
индекс оператора Q равен нулю. Таким образом, мы пришли
к двум более простым характеристическим операторам К? и Q:
коэффициенты первого непрерывны, а у второго коэффициенты
хотя и разрывны, но индекс равен нулю. Согласно D8.24)
регуляризация исходного оператора К сводится к регуляризации
операторов Ki и Q. Для оператора КГ левым и правым регу-
ляризатором служит оператор
/?.Ф = а,(/)ф@—^S^rfT.
Для оператора Q, имеющего индекс, равный нулю, как
показано выше, соответствующий оператор D8.23) будет левым и
правым регуляризатором. Так как для оператора Q
1П(|)'*'(Т)~1Пй)~(Т)
М-
x-t -^
4t) = e i =ш+@©-@,
то его регуляризатор D8.23) имеет вид (с точностью до
множителя, не обращающегося в нуль)
/?аФ = ((»(О + 1) Ф (О + ^^^^^ соМО (О-(О J ^г^^;^-^.
ш J со (т) сэ (т) т — /
Из D8.24), таким образом, следует, что левым и правым
регуляризатором для исходного оператора К будет оператор
/?==/?i/?Q. D8.26)
Можно показать, произведя перемножение операторов в D8.26),
что полученный оператор R отличается от оператора D8.23)
лишь регулярным слагаемым. Не останавливаясь на выкладках,
укажем только, что и здесь, при перемножении операторов

§ 48] УРАВНЕНИЕ ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 507
В D8.26), нужно воспользоваться тем, что коэффициенты
оператора Ri можно представлять с особым оператором с
точностью до регулярного слагаемого.
Имея в виду приложения указанных выше методов к
исследованию вопросов равносильной регуляризации и выводу
основных свойств (теоремы Нётера), рассмотрим вопрос о
собственных функциях оператора R, построенного для решения
уравнения К°ф = / в классе h{cu ..., Ср).
Рассмотрим уравнение
Я^^атЦ)~±Щ^\Щ^^!Ц). D8.27)
Введя новую функцию ф@= ф@/2@> получим
характеристическое уравнение
'¦w*«-^Sl^<'-if
(t)'
Если f{t) принадлежала классу h{cu ..., Ср), то, как легко
видеть, f{t)IZ{t) будет принадлежать классу A(Cp+i,..., с^). Индекс
последнего уравнения в классе A(Cp+i, ..., с^) будет —к. Решив
обычным способом последнее уравнение в классе A(cp+i, ..., г^),
получим решение исходного уравнения D8.27) в классе
Л(сь ..., Ср) по формуле ф(/)== Z@^@- Это решение
представится в виде
Ф(/) = к7 + б@я^н-1@-
Если X > О, то нужно положить P-x-i (О = О, причем в случае
X > О должны выполняться X условий разрешимости
^f{t)t^''Ut = 0 (/=1,2,.../ н). D8.28)
L
Таким образом, мы пришли к следующему результату:
При X ^ О однородное уравнение /?ф = О неразрешимо. Не-
однородное уравнение при х = О разрешимо безусловно и одно-
значно, а при х > О разрешимо (однозначно) лишь при
выполнении X условий D8.28).
При X < О однородное уравнение /?ф = О имеет х линейно
независимых решений. Неоднородное уравнение безусловно
разрешимо, и решение его зависит от х произвольных постоянных.
Используя выведенные свойства оператора /?, можно перейти
к вопросу о равносильной регуляризации в том смысле, как это
было определено в п. 24.1.
Если индекс оператора К в некотором заданном классе
неотрицателен (х^О), то мы применяем регуляризацию слева.

508 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Уравнение
/?Кф = /?/
будет уравнением Фредгольма, равносильным исходному
особому уравнению D8.22).
Если X s^ О, то применяем регуляризацию справа. Введя
новую функцию (o(t)y подстановкой
Ф = /?со D8.29)
приходим к уравнению
K/?(D = /, D8.30)
которое будет равносильно исходному особому уравнению в том
смысле, что в данном классе оба уравнения D8.22) и D8.30)
одновременно разрешимы или неразрешимы и в случае
разрешимости каждому решению уравнения D8.30) по формуле D8.29)
соответствует определенное решение исходного уравнения
D8.22) и, обратно, каждому решению ф@ исходного уравнения
по формуле
со(/) = К°ф + й@^^_х-1@
соответствуют решения уравнения D8.22).
Таким образом, задача равносильной регуляризации в
обобщенном смысле в случае разрывных коэффициентов и
разомкнутых контуров решена совершенно в той же форме, что и для
непрерывных коэффициентов и замкнутых контуров.
48.5. Основные свойства особого уравнения. Все
предшествующие результаты приводят к мысли, что основные свойства
особого уравнения, выражающиеся так называемыми теоремами
Нётера, в основном те же, что и для замкнутого контура.
Вывести эти свойства можно так же, как это сделано в § 23 для
замкнутого контура.
Прежде всего, легко устанавливаем, что если функции ф(/)
и г|)@ таковы, что \|)Кф и фК'-ф интегрируемы, в частности, если
Ф и \|) принадлежит союзным классам, то справедливо
тождество
J г|)Кф dt = J фК'г|) Л. D8.31)
L L
Далее, проводя такие же рассуждения, как в п. 23.2, придем
к основным свойствам рассматриваемого типа уравнений. Эти
свойства по аналогии с теоремами, полученными в простейшем
случае Нётером (см. Исторические сведения к гл. III и VI),
называются иногда теоремами Нётера, Не повторяя вывода этих
теорем, приведем их формулировку.

§ 48] УРАВНЕНИЕ ДЛЯ РАЗОМКНУТЫХ КОНТУРОВ 509
Теорема 1. Число линейно независимых решений {любого
класса) однородного уравнения Кф = О конечно.
Теорема 2. Необходимое и достаточное условие
разрешимости в данном классе h неоднородного уравнения Кф == /
заключается в выполнении равенств
\f(t)^{t)dt = Q, D8.32)
L
где t|)@—любое решение союзного класса Л' союзного
однородного уравнения К'ф = 0.
Теорема 3. Если п — число линейно независимых решений
класса h однородного уравнения Кф = О, х — индекс уравнения
в этом классе, an' — число линейно независимых решений
союзного класса h' союзного однородного уравнения К'г|) = О, то
П'-п' = к. D8.33)
48.6. Теория Нётера особых уравнений со сдвигом Карлемана на
разомкнутом контуре. Особое интегральное уравнение со сдвигом имеет (в обозначениях
п. 23.5) следующий вид:
ЛГф = а (О Ф (/) + ^ (О Яч> + с (t) Scp + d (О С5ф == f (/), D8.34)
где Q — операция карлемановского сдвига- Qtp = ф[а@]. Следуя в основном
схеме, изложенной в п. 23.5, для этого уравнения можно получить теоремы
Нётера при выполнении некоторых предположений относительно
коэффициентов а@. b(t), c(t), d(t).
Пусть контур разомкнут и сдвиг а(/) изменяет направление обхода
Коэффициенты a{t), b{t), с(/), d{i) будем считать непрерывными. Применяя
к оператору N введенный в п. 23.5 оператор
Л?Ф = а [а @1 Ф (/) - 6 (t) дф - с [а (t)] 5ф — е/ (t) QScp,
придем (с учетом, что теперь З^ф I) к уравнению
NNcp = m (О Ф (t) + n(t)S(p + q (t) S^(p + Гф = f, (/), D8.35)
где Т — оператор с регулярным ядром, fi (t) = Nf, m (t) = a (t) a [a (t)] —
-b{t)b [a @1, n {t)=a [a (t)] c(t)-a (t) с [a (/)]+b [a (t)] d (t) - b (t) d [a (/)],
q{t) = d{t)d[a(t)] — c(t)c[a{t)]. Оператор D8.35), оказывается, можно
представить в виде композиции двух особых операторов с ядром Коши. Тем
самым вопрос о справедливости теорем Нётера для уравнения D8 34)
сводится к вопросу об их справедливости для уже изученных особых уравнений
без сдвига Не приводя окончательного результата, отошлем читателя к
работе Н. К. Карапетянца и С. Г. Самко 2), в которой проведено
указанное здесь исследование.
В более общем случае, когда коэффициенты уравнения разрывны, дело
обстоит сложнее. Не останавливаясь на этом, укажем только, что
справедливость теорем Нётера в случае разрывных коэффициентов и сдвига,
сохраняющего направление обхода, показана в работе Н. К. Карапетянца и
С. Г. Самко 3).

510 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
§ 49. Краевая задача Римана с бесконечным индексом
Краевая задача Римана и другие краевые задачи решались
нами при условии, что их индексы — определенные конечные
числа. Отсюда вытекало, что единственно возможной
особенностью канонической функции в ее исключительной точке
является полюс; следствием этого была конечность числа линейно
независимых решений или условий разрешимости*). В случаях,
когда задача допускала замкнутое решение или исчерпывающее
качественное исследование, линейно независимые решения или
условия разрешимости выражались через произвольный
многочлен.
Однако уже давно ставились проблемы, приводящие в общей
постановке к краевым задачам с бесконечным индексом. Еще
в 1945 г. была опубликована работа Н. И. Ахи ез ер а 1) об
обращении интеграла типа Коши на счетном множестве
отрезков действительной оси, а в последующие годы — работы
С. А. Фрейдкина 1), В. А. Пааташвили 2) и др. о задаче
Римана на счетном множестве контуров. Но все эти авторы
выбирали для решения такие частные классы функций, в которых
индекс оставался конечным. Ряд других работ не увидел света
из-за того, что авторы их не смогли преодолеть трудности,
связанные с бесконечным индексом.
В случае бесконечного индекса поведение канонической
функции в окрестности ее исключительной точки аналогично
поведению аналитической функции в окрестности существенно особой
точки. Отсюда следует, что множество линейно независимых
решений или условий разрешимости описывается здесь уже не
многочленом, а целой функцией. Поведение последней в
окрестности ее существенно особой точки весьма многообразно, а это
вызывает при исследовании краевых задач серьезные трудности.
Для их преодоления требуется не только использование
существующего классического аппарата целых функций, но и
решение ряда новых проблем, ранее в этой теории не возникавших.
Мы не в состоянии войти в подробности сложной теории
краевых задач с бесконечным индексом и в последующем
ограничимся лишь схематическим очерком.
49.1. Некоторые сведения из теории функций. Для удобства
дальнейших формулировок приведем некоторые основные
понятия из теории функций, аналитических внутри угла, и, в
частности, из теории целых функций.
Пусть f{z)фO — функция, аналитическая внутри угла 0:^
^ а < arg Z ^ р ^ 2я. Тогда порядком этой функции в
рассматриваемом угле называется точная нижняя граница р тех
*) Исключением является вырожденный случай (п. 25.4).

§ 49] КРАЕВАЯ ЗАДАЧА PVIMAHA С БЕСКОНЕЧНЫМ ИНДЕКСОМ 511
чисел V > о, для которых равномерно по 6 е [а, р]
lim —-^—-^ = 0.
Если р — конечное положительное число, то, упрощенно
говоря, либо max | f (ге^^) \ ^ е^^, либо max | f (ге^^) \ ^ е"^^ при
г->-оо. Таким образом, порядок характеризует рост функции
или ее убывание внутри угла. В обоих случаях при любом е > О
справедлива оценка
\f(z)\<e\-^'^\ 2-^ со.
Для изучения поведения функции f(z) конечного порядка
р > О по отдельным лучам arg г = 9 вводится индикатор, т. е.
действительная функция
hf{U) = Jhn ^"'^У^^' (а<9<р).
Если Л/(Оо)<0, то f{z)->0 при г->оо по лучу arg 2 = 00
В случае Л/(9о) > О функция f{z) неограничена на этом луче.
Наконец, если Л/(9о)= О, то функция может быть как
ограниченной, так и неограниченной.
Для целой функции F{z)^ const более употребительным
является другое определение порядка, равносильное
приведенному *):
In in max \F{z)\
P= hm ^ .
Заметим, что в смысле такого определения порядок любого
многочлена равен нулю.
Для целой функции с корнями на одном луче часто
используется представление через интеграл типа Коши. Например,
пусть
оо
/1-1
и /г (х) — число корней г^ на интервале (О, х). Тогда
оо
\ п {х) JC rfjc < оо и
о
fC) = exp|-ej-^^rf.|. D9.1)
*) Эти определения в общем случае равносильны только для
неограниченных внутри угла функций.

512 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Верно и обратное утверждение. Если некоторая неубывающая
кусочно постоянная с целочисленными значениями функция
п{х)'^0 такова, что \ n{x)x~^dx<оо^ то функция f(z), пост-
0
роенная по формуле D9.1), является целой. Корни ее
расположены на положительном луче и совпадают с точками разрыва
функции п{х).
Приведем еще теорему Фрагмена — Линделёфа для угла.
Пусть функция f{z) является аналитической внутри угла а ^
^ 0 ^ р и при любом 8>0и7 = я/(Р — а) допускает оценку
|/(г)|<е«»^'^ a<arg2:<p, г->оо.
Тогда из ограниченности /(г) на сторонах угла вытекает ее
ограниченность всюду внутри угла.
В частности, для угла О ^ 9 ^ 2я эта оценка должна иметь
вид
49.2. Однородная задача с бесконечным индексом степенного
порядка в случае одностороннего завихрения*). Индекс
непрерывной на замкнутом контуре L функции G{t) был определен
ранее (п. 13.1) как изменение argG(^), выраженное в полных
оборотах, или, что то же, интегралом
-^JrfargGW. D9.2)
L
В случае разомкнутого контура или разрывного коэффициента
(с ограниченным arg G{t)) индекс задачи также выражается
через эту величину (см. формулы D2.8), D2.9)).
Предположим теперь, что на контуре L (замкнутом или
разомкнутом) есть точка /о, в односторонней (двусторонней)
окрестности которой argG(/) неограничен. Тогда будем говорить,
что функция G{t) имеет в to одностороннее (двустороннее)
завихрение. Краевую задачу Римана, у которой коэффициент G(t)
имеет в некоторой точке контура завихрение, назовем задачей
с бесконечным индексом. Кроме того, если в этом случае
интеграл D9.2) равен + оо или — оо, то будем говорить, что задача
имеет соответственно плюс-бесконечный или минус-бесконечный
индекс.
Свойства решений краевых задач с бесконечным индексом
существенно зависят от порядка стремления arg G (t) к беско-
*) Изложение настоящего пункта дано по работам Н. В. Говорова
1),2),3),4).

§ 49] КРАЕВАЯ ЗАДАЧА РИМАНА С БЕСКОНЕЧНЫМ ИНДЕКСОМ 513
нечности. в настоящее время исследованы случаи, когда arg G{t)
растет как степенная функция (бесконечный индекс степенного
порядка) и логарифмическая функция (бесконечный индекс
логарифмического порядка).
Рассмотрим теперь однородную задачу Римана для одного
из случаев бесконечного индекса степенного порядка. Для
простоты в качестве контура L возьмем луч I ^ ^ ^ оо. Будем
считать, что в краевом условии
ф+ (/) = G (t) ф- (/), К / < оо, D9.3)
коэффициент G{t) удовлетворяет следующим требованиям:
1) 1п| G@ I ^ Я^Д1, оо] (условие Гёльдера с показателем jxo
на отрезке 1</<оо: | In | G(/i) |-1п| G(^2) 11< ^иг^-^г'^"^);
2)аг§С@ = 2яф@^^ 1</<оо,0<р<оо, ф(/)еЯ^[1, оо],
В точке t= оо коэффициент G{t) имеет одностороннее
завихрение. Кроме того, при X > О индекс задачи плюс-бесконечен
и при К < О минус-бесконечен.
Решения задачи будем рассматривать в классе ограниченных
во всей плоскости функций Ф{г) Ф 0.
В дальнейшем нам придется иметь дело с интегралами типа
Коши, плотности которых неограничены. Поэтому вместо
использованного ранее интеграла будем рассматривать интеграл вида
(см. конец п. 4.7)
2:^+^ Г ф (т) dx
2я/ ^J т^+^(т-г) *
получаемый из интеграла типа Коши, если в его разложении по
степеням — формально отбросить q + 1 начальных членов.
Введем в рассмотрение функцию
Эта функция является аналитической вне луча I ^ / ^ оо и
отлична там от нуля. Кроме того, она удовлетворяет краевому
условию D9.3). Для рассматриваемого случая бесконечного
индекса ХB:) играет ту же роль, что и каноническая функция
однородной задачи с конечным индексом. Эта аналогия
проявляется еще и в том, что, как оказывается, любое ограниченное
решение задачи представимо в виде
Ф(г) = Х(г)У^B), D9.5)

514 Краевые задачи [гл. vt
где F{z)—некоторая целая функция. Будем поэтому называть
Х(г) канонической функцией рассматриваемой задачи. При
конечном индексе к Х(г)'^-т7 при 2->оо, т.е. Х(г) по всем лу-
Z
чам arg Z = const изменяется одинаково — стремится к нулю
или бесконечности степенного порядка |х|. В случае
бесконечного индекса дело обстоит иначе. Из условия задачи вытекает,
что In G(t) при /-> + оо обращается в бесконечность степенного
порядка.
Поэтому, переходя в D9.4) к конечному контуру и
используя представление для интеграла типа Коши со степенной
особенностью (п. 8.3), можно установить, что каноническая
функция Х(г) имеет в угле О ^ 6 :^ 2я порядок р с индикатором
h^ (G) ^ lim ^"'^У^^' = ^^ cos р (9 - я) D9.6)
^ г>-оо г^ sin яр
(о<е<2я)
при р нецелом и
Ах (в) = lim ^"'^^^^^^^' = - Я cos р9 (О < 9 < 2я) D9.7)
Г->оо Г*^ In Г
для целого р. При этом стремление к пределу в обоих случаях
равномерно по 9 е [О, 2я]. Анализ правых частей в D9.6) и
D9.7) показывает, что только при Л > О и р < 1/2 (т. е. в
случае плюс-бесконечного индекса степенного порядка меньше 1/2)
каноническая функция имеет всюду отрицательный индикатор
и, следовательно, убывает по всем направлениям. Если же р >
> 1/2*), то по одним направлениям (при /гх(9) < О)Х(г) имеет
убывание, а по другим (где их (9) > 0) — рост
экспоненциального порядка р. Поэтому в общем случае X{z) ведет себя при
г -^ оо подобно аналитической функции в окрестности ее
существенно особой точки. В этом и состоит принципиальное отличие
задачи с бесконечным индексом от случая конечного индекса.
Решение задачи Римана с бесконечным индексом в общем
случае сводится к отысканию таких целых функций F (г), которые,
упрощенно говоря, достаточно быстро убывают по тем
направлениям, где Х(г) неограничена, и одновременно не слишком
быстро растут там, где X{z) убывает. Проще всего такие
целые функции можно подобрать в случае Я > О, р < 1/2, когда
I X (г) I < се~^ '^'^, с, а > 0. Действительно, из D9.6) вытекает,
что в этом случае выполняется также оценка | X (г) | > тв"*^'^'^
т, &>0. Поэтому из ограниченности произведения X(z)F{z)
следует, что во всей плоскости | ^(г)! < Cj |Х(г) Г^ < Св^'^'Р.
*) Случай р = 1/2, исследуемый особо, мы не приводим (см. Н. В. Г о-
воров 3)).

§ 49] КРАЕВАЯ ЗАДАЧА РИМАНА С БЕСКОНЕЧНЫМ ИНДЕКСОМ 516
В частности, на контуре In | f (О К — In | Х± (t) \ + const, 1 <
</<оо. Если Р/7--порядок роста F {z), то эти соотношения
можно записать в виде:
1) 9f<9\ D9.8)
оо
2) In I f (О К - / ^ ^ ^f_!^]^^ dx + const, 1<^<оо. D9.9)
Легко показать, что и обратно, если целая функция F{z)
удовлетворяет условиям D9.8), D9.9), то функция ФB) =
= X{z)F{z) является ограниченным решением задачи. В самом
деле, на основании D9.9) эта функция ограничена на луче
1 ^ ^ ^ оо. Далее, в силу D9.8) Ф(г) во всей плоскости при
любом е > О допускает оценку | Ф(г) | < е'^'^'^^ z-^oo. Так как
О < р < 1/2, то по теореме Фрагмена — Линделёфа для угла
О ^ avgz ^ 2я функция Ф(г) ограничена во всей плоскости.
Таким образом, общее решение задача с плюс-бесконечным
индексом (Я > О, р< 1/2) дается формулой D9.5), где F(z) —
произвольная целая функция порядка pi?, для которой
выполняются условия D9.8), D9.9).
Этим условиям удовлетворяет любая целая функция F{z)
порядка pf < р. Действительно, для такой функции при любом
8 > О \F{z)\< ехр {I Z f^^^)y г -> сх>. Но в рассматриваемом
случае I ХB:) |<б~^'^'^, а>0, z-^oo. Поэтому оценка D9.9),
означающая, что ln|f(/)|< — 1п|Х=^(/) 1 +const, вытекает из
требования Pf < р. В частности, условиям D9.8) и D9.9)
удовлетворяет произвольный многочлен, так как порядок его равен
нулю. В более общем случае целой трансцендентной функции
/^W = ^^"n(l-^) @<|2fJ<|32l< ...)
ДЛЯ выполнения этих условий достаточно потребовать, чтобы
-— \пп ^
•im -пгкГГ"~ ^^ ^ ^•
Таким образом, при плюс-бесконечном индексе степенного
порядка меньше 1/2 из бесконечного множества ограниченных
решений задачи можно выделить счетное множество линейно
независимых (например, ф^(г)= z^'Y^(z) (^ = О, 1, 2, ...)).
В случае плюс-бесконечного индекса степенного порядка
р > 1/2 каноническая функция Х(г) является неограниченной.
Отыскание класса целых функций F{z), дающих по формуле
D9.5) ограниченные решения задачи, производится гораздо
сложнее. Оказывается, что порядок каждой из таких целых

516 КРАЕВЫЕ ЗАДАЧИ [ГЛ VI
функций должен быть равен р. Более того, каждое ограниченное
решение необходимо имеет бесконечное множество корней,
являющихся нулями целой функции F{z), Этим множеством
решение определяется однозначно (с точностью до постоянного
множителя). Поэтому исследование задачи в случае Я > О,
р > 1/2 представляет собой, по существу, выяснение тех
условий, которым должно удовлетворять множество корней
ограниченного решения задачи. Отправной точкой такого исследования
являются свойства функций, аналитических и ограниченных
внутри угла О ^ argz :^ 2я. Не имея возможности входить в
подробности этого весьма сложного исследования, приведем лишь
окончательный результат:
Общее решение рассматриваемой однородной краевой задачи
Римана с плюс-бесконечным индексом (К > 0) имеет вид
Ф(.)=«-ехр{^ \ i-«(;>-jyw,,|n_
1-^
\Zn\
где с = const, т — целое положительное число, {Zn}—
последовательность отличных от нуля чисел, удовлетворяюи^их
условиям:
1) сходится ряд } —7=^> ^п^^пб'^'^, 0<9;1<2я;
2) существует конечный предел
г t
lim -j^[^[l^{x)xf-n{x)\^ = y>0:
Г->оо Vr J / J X
1 1
3) сходится интеграл
\ [ф W x^ — n (л:)] a:"^ dx;
1
4) на контуре выполняется при t->-^ oo оценка
rt"l I
где n{x)— число точек Zn в круге |2| ^ л:.
Заметим, что существует бесконечно много различных
последовательностей {Zn}y удовлетворяющих этим условиям.
Однородная задача с минус-бесконечным индексом {к < 0)
не имеет ограниченных решений Ф(г) Ф 0.

§ 49] КРАЕВАЯ ЗАДАЧА РИМАНА С БЕСКОНЕЧНЫМ ИНДЕКСОМ 517
В СВЯЗИ С ЭТИМ интересно отметить следующее. В случае
прямолинейного контура и коэффициента G{t)^H (G(/)=7^0)
однородная задача с отрицательным индексом неразрешима. Если
же контур перестает быть прямолинейным вблизи точки to,
а \G(t)\->0 при t-^toy то однородная задача с отрицательным
индексом (конечным или бесконечным) может оказаться
разрешимой. Соответствующие примеры построены Н. В.
Говоровым 4). Им же получены два условия, выполнение каждого из
которых обеспечивает неразрешимость однородной задачи с
отрицательным индексом.
49.3. Неоднородная задача с бесконечным индексом
степенного порядка для одностороннего завихрения*). Рассмотрим
теперь неоднородную задачу
Ф^@ = О@Ф"@ + г@, 1<^<оо, D9.10)
где
1) агёС@ = 2яф@Л 0<р<оо, Ф(О е ЯЛ 1,00],
причем j^ <М'<1, -1 <ФAХ0, ф(оо) = Я=7^0;
2) ln|G(OI, г@еЯ[1, оо], gr(l) = g(oo) = 0.
Будем считать сначала, что Я. > О, т. е. индекс задачи плюс-
бесконечен. Воспользуемся тем же приемом, что и в случае
конечного индекса (§ 14). Пусть ^o{z)—такое частное решение
соответствующей однородной задачи, для которого выполняются
условия
-4^^Я11, оо], Iim-4^ = 0. D9.11)
^0'"@ ^^оо W+(t) ^ ^
Тогда функция
^»<^>=^S^7^ *«-'^'
будет частным решением рассматриваемой задачи. Общее
решение можно получить как сумму ФоB:) и общего решения
соответствующей однородной задачи.
В случае конечного индекса в качестве Ч^о(<г:) можно было
выбрать каноническую функцию Х(г). Если же индекс
бесконечен, то, вообще говоря, нельзя положить Wo{z)^ ХB:), так как
либо X{z) неограничена, либо могут не выполняться условия
D9.11), т.е. интеграл в D9.12) может оказаться расходящимся.
*) Изложение настоящего пункта проведено по работам Н. В
Говорова 5), 6).

518 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
Поэтому основная трудность в рассматриваемом случае
заключается в построении такого специального решения ^о{^)
соответствующей однородной задачи, которое удовлетворяет
условиям D9.11). Это решение определяется не единственным
образом. Наиболее простую структуру оно имеет в случае, когда его
корни специальным образом расположены на кривой ф = г"Р.
Сформулируем окончательный результат исследования:
Неоднородная краевая задача Римана D9.10) с
плюс-бесконечным индексом {X > 0) допускает бесконечное множество
ограниченных решений, общая формула которых имеет вид
Ф(г) = Фо(г)+^B), D9.13)
где функция Oo{z) определена формулой D9.12), а 'V{z) —
общее решение соответствующей однородной задачи. При этом
функция ^q(z) определена формулой
где По{х) означает число точек последовательности {г^} W =
= Гпе "' ) на отрезке [1; л:] и определяется равенством
По (х) = max |о, [ ^ та^^ {ф (/) f + Щ^
{гп —точки разрыва щ{х)).
В случае минус-бесконечного индекса строится мероморфное
решение Ч^о(^) соответствующей однородной задачи, имеющее
бесконечное множество специально расположенных полюсов.
Тогда рассматриваемая неоднородная задача при Я, < О имеет
единственное решение D9.13) лишь при выполнении счетного
множества условий разрешимости. Эти условия выражаются
в требований, чтобы интеграл типа Коши в D9.12) обращался
в Hy,jfb во всех полюсах Wo{z).
49.4. Задача с бесконечным индексом логарифмического
порядка для одностороннего завихрения*). Рассмотрим теперь тот
случай краевой задачи Римана
ф-*-@ = О(/)Ф"(/) + г@, 1<^<оо,
когда argG(/) растет к^к некоторая степень логарифма.
Именно, будем считать, что функции G{t) и g{t) удовлетворяют
условиям:
1) _ arg О (О = Ф @1п"^
*) Изложение дано по работам П. Г. Юрова 1)—5).

§ 491 КРАЕВАЯ ЗАДАЧА РИМАКА С БЕСКОНЕЧНЫМ ИНДЕКСОМ 619
где о < а < оо, а функция ф(/) принадлежит классу Дини —
Липшица D^[l; оо] с показателем р > а + 2, т.е. для
произвольных t\y /2 ^ [1; оо] должно выполняться
кроме того, ф (оо) Ф 0;
2) ln\Git)l g{t)^D,[U оо] p>max{2;a}, g{oo) = 0.
Решения задачи разыскиваются в классе ограниченных
функций.
Как и в случае бесконечного индекса степенного порядка,
для исследования однородной задачи (при ^(/)^0) вводится
каноническая функция Х(г) по формуле D9.4) (при ^ = 0).
Отыскание класса целых функций f{z), даюш.их в случае плюс-
бесконечного индекса ограниченные решения по той же формуле
D9.5), снова производится с учетом асимптотических свойств
Х(г). Однако, если в рассматриваемом случае перейти в D9.4)
к конечному контуру, то плотность полученного интеграла типа
Коши будет иметь особенность уже не степенного, а, вообще
говоря, нецелого логарифмического порядка. Для исследования
асимптотического поведения таких интегралов П. Г. Юров 1),
2) ввел новый метод, использующий теорию конечных
разностей. В итоге такого исследования можно установить, что для
канонической функции Х(г) справедливо следующее
представление при г ^-> оо:
ixwi=e,p{-^'g',;,°;;;"+o(m-ui)}.
Отсюда видно, что в случае плюс-бесконечного индекса (т. е.
когда ф(оо)>0) каноническая функция ограничена во всей
плоскости и является одним из решений однородной задачи. Все
ограниченные решения даются формулой D9.5), где F(z)
—произвольная целая функция нулевого порядка, удовлетворяющая
на контуре оценке, аналогичной D9.10).
Примером такой функции может служить любой многочлен,
оо
а также трансцендентная целая функция F(z)= Ц Сдз'*, для
которой
г:— Inn ^
lim :: < а.
П->оо
ininVknl"
Поэтому и в случае плюс-бесконечного индекса
логарифмического порядка а > О из множества ограниченных решений
задачи можно выделить счетное множество линейно независимых:
Ф,(г)=2:^Х(г) (Л = О, 1,2,...).

520 КРАЕВЫЕ ЗДДАЧИ [ГЛ VI
Если индекс минус-бесконечен {ф(оо)<0), то |Х(г)|->оо
при z-^oo и однородная задача ограниченных решений ф{г)Ф
^ О не имеет.
При исследовании неоднородной задачи с плюс-бесконечным
индексом логарифмического порядка (ф(оо)>0) возникают те
же трудности, что и в случае степенного порядка. Поэтому снова
приходится строить специальное решение ^o{z)
соответствующей однородной задачи, удовлетворяющее ограничениям:
-ff-^D,[l; со], д>1, Иш^ = 0.
Однако построение такого решения оказывается возможным
лишь в случае а ^ 1. Потребовав, чтобы его корни были
расположены на отрицательном луче —сю -< / ^ 1, можно
построить это решение в виде
'^«<=^) = XW«P|^i Tjj^r^j '-dx
(здесь символ [и] обозначает, как обычно, целую часть числа
и). Тогда частное решение рассматриваемой неоднородной
задачи при ф(оо)> О можно получить по той же формуле D9.12).
Общее решение представляется в виде суммы этого частного и
общего решения соответствующей однородной задачи.
Если О < а < 1, то исследование неоднородной задачи
значительно усложняется. Приходится накладывать на свободный
член g(t) большее по сравнению со случаем а ^ I ограничение:
g(t)^ Н[1\ оо]. Для получения частного решения неоднородной
задачи строится специальное неограниченное (но не слишком
сильно растущее при z-^oo) частное решение ^o(z)
однородной задачи. Это решение таково, что соответствующий ему
интеграл типа Коши в D9.12) стремится к нулю при г-> оо.
Стремление оказывается достаточным для того, чтобы функция Фо(<г),
определенная формулой D9.12), была ограниченной и давала
частное решение неоднородной задачи.
Результаты исследования неоднородной задачи с
минус-бесконечным индексом логарифмического порядка (при ф(оо)< 0)
аналогичны соответствующим результатам для
минус-бесконечного индекса степенного порядка.
49.5. Случай двустороннего завихрения. Впервые краевая задача Римана
с бесконечным индексом степенного порядка меньше единицы для
двустороннего завихрения была рассмотрена Ф. Д. Берковичем и Н. В.
Говоровым 1) при изучении краевой задачи Карлемана:
ф+ (/) = G (О Ф+ (-t) + g (О, - оо</<оо, D9.14)

§ 491 КРАЕВАЯ ЗАДАЧА РИМАНА С БЕСКОНЕЧНЫМ ИНДЕКСОМ 521
где In I G (t) I, g{t)^H [- oo; со], ^ (± со) = 0, arg G (t) = 2яф (t) | t |P,
0 < p < I, Ф (— /) ^ — ф(/), Ф (+ oo) = Л=й=0. Эта задача изучалась сведением
к краевой задаче Римана для полуплоскости
ф+ (t) = G (t) ф- (О + g(tl - оо<^<со. D9.15)
Для исследования последней использовалась теория, развитая Н. В.
Говоровым для одностороннего завихрения.
В дальнейшем Ф. Д. Беркович 1), 2) указал класс интегральных
уравнений типа свертки первого рода, которые приводятся к краевой задаче Кар-
лемана D9.14), Римана D9.15) и задаче Гильберта:
Ф+ (/) == G (О Ф+ (/) -f g (О, - оо</<оо,
с бесконечным индексом. Он же исследовал эти задачи в предположении, что
G (t) = е^^^^ [Х + К Ш афО, Х + Kit) ФО, -oD<t<oo. При этом
функции /С@, ^@ принадлежат кольцу ^о преобразований Фурье функций из
L(—сх), оо). Это исследование опирается на свойства преобразований Фурье
и теоремы Винера и Винера — Леви для функций из кольца ^о.
Ф. Д. Беркович и Е. М. Конышкова 1) дали решение задачи
Римана D9.14) в классе ограниченных функций, в предположении, что G{t) =
=re^^^^Go{t)j а =5^ О, а функции Go(t) и g(t) удовлетворяют условию
Гёльдера на всей действительной оси. Это решение использовано Е. М. Коны ш-
ковой 1) для изучения характеристического сингулярного интегрального
уравнения с бесконечным индексом.
Общий случай однородной задачи с бесконечным индексом степенного
порядка меньше единицы для двустороннего завихрения рассмотрен М. Э. Т о-
лочко 1). В этой работе изучена задача D9.15) (при g(t)^0) с
коэффициентом G{t), удовлетворяющим условиям:
1) 1п10@1еЯ[-оо, 00];
2) argO (О =2яф @U1^. где 0<р<1, а непрерывная при /->±оо
функция ф (t) принадлежит некоторому классу функций, более широкому,
чем класс Гёльдера на каждом из лучей —оо</^0 и 0^/<оо; кроме
того, ф (— оо) =^1, ф(+ оо) = Л2, Л| + Я|>0.
Отметим, что в этой задаче впервые встречается случай «неопределенно
бесконечного» индекса, когда числа ii и Лг имеют одинаковые знаки и
изменение argG@ на контуре вообще не определено.
Основные результаты исследования выражены в виде определенных
соотношений для заданных величин Xi, Яг и р, определяющих поведение
argG(/) при ^->±оо. Так, например, если эти величины удовлетворяют
одному из условий:
1) ^<Р<Т' ^^<^' ^2>0;
2)
1 / X ч^^п ^^
0<Р<у, Я1Я,2>0, ^^j <со5ря;
3) i-<p<l, Я,<0, ^2>0,
то рассматриваемая однородная задача имеет бесконечное множество
ограниченных решений.
Все остальные случаи для Хи Лг и р разделяются на две группы, когда
ограниченных решений нет и когда разрешимость задачи зависит от
дополнительных свойств argG(r).

522 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
49.6. Задача на счетном множестве контуров. По своим свойствам и
характеру исследования такая задача примыкает к задаче для односвязной
области в случае бесконечного индекса.
Впервые краевая задача Римана на счетном множестве разомкнутых
контуров встречается в работах Н. И. Ахиезера 1), И. Н. Карцивадзе и
Б. В. Хведелидзе 1), 2), С. А. Фрейдкина 1), 2), 3), В. Д.
Фролова 3). Однако постановка задач в этих работах предусматривает такие
классы решений, в которых индекс остается конечным.
В случае счетного множества замкнутых контуров задачу Римана
рассматривали В. А. Пааташвили 2), 3), а также Л. И. Чибрикова и
П. X. Мкоян 1). В первой из этих работ выбранный метод — переход к
нулевому на всех кривых индексу — позволил исследовать, в сущности, только
случай конечного индекса, т. е. случай, когда индекс коэффициента G{t)
отличен от нуля лишь на конечном множестве кривых. Во второй работе
исследование ведется в другом направлении, так как решения рассматриваются
в классе кусочно мероморфных функций.
Один из случаев, когда индекс коэффициента G(t) отличен от нуля на
бесконечном множестве замкнутых кривых, рассмотрен М. Э. То л очко 2).
Краевое условие однородной задачи
ф+ (/) = G (/) Ф- (/)
предполагается определенным на некоторой счетной совокупности простых,
гладких, замкнутых кривых Спу сходящихся к бесконечности. Важнейшим из
условий, налагаемых на кривые Спу является требование, чтобы
последовательность некоторых точек [zn] внутри Сп составляла так называемое
^-множество при показателе р (О < р < 1/2), введенное в теорию целых функций
Б. Я. Левиным [13]. Это ограничение представляет собой требование
особой равномерности в расположении кривых Сп. Такое же условие налагается
и на последовательность кривых с положительными индексами G(t),
Коэффициент G(t) на каждой из кривых Сп отличен от нуля и удовлетворяет
условию Гёльдера с показателем и постоянной, не зависящими от п. Решения
задачи рассматриваются в классе ограниченных функций.
Исследование задачи существенно опирается на оценку при z-^oo
канонической функции Х±(г), построенной по методу непосредственного решения
задачи Римана (§ 43) Если t^ и ^^ — некоторые точки тех кривых Са и
Cky для которых lnd(> G (t)=yig>Oy Ind^ G (/) = HJ^<О, то
y±i^ У^ ^'"^ (V 1 С InG(T) .)
TTri-^i '.«-1 с„ )
no-i)
Поведение при г -> со функции X* (г) вполне определяется мероморфной
функцией И и — -7") Ц (^ ) • ^Р*^ оценке последней исполь-
k S
зуется то обстоятельство, что последовательность точек {ts} образует /?-мно-
жество.
Не имея возможности привести полное исследование задачи,
сформулируем лишь окончательные результаты. Они выражаются в Ферминах теории
целых функций.

ИСТОРИЧЕСКИЕ СВЕДЕНИЯ 523
Пусть р^ и р_ — показатели сходимости точек {ts} и {tk)i
In 5 In^
р , = lim ;—-, р = lim —, , , .
^+ s^oo ln\ts\ ^- fe->oo \n\tk\
Пусть, далее, h^ F) и Л_ (9) — индикаторы целых функций 1 ( 1 —г- ) *
S
г
И 11 I 1 7~ ) . Тогда справедливы утверждения:
k
1) При выполнении одного из условий
а) р-<р+;
б) Р- = Р+, min{/i^(e)}>max(/z_(e)},
9 0
рассматриваемая однородная задача на счетном множестве кривых допускает
бесконечное множество ограниченных решений Ф^ (г) = Х^ (г) f (г), где
T(z)—произвольная целая функция порядка Pf ^ р, удовлетворяющая на
кривых Сл (/г = 1, 2, ...) оценке
\F{t)\<Cp\X'^ (О Г^ {Ср = const).
2) Если р+<р_, то ограниченных решений ф-(г)#0 задача не имеет.
§ 50. Исторические сведения
Вопрос о решении задачи Римана с разрывными коэффициентами возник
одновременно с постановкой самой задачи. Риманом [^1] (см. Исторические
сведения к гл. И) задача с самого начала была поставлена как задача
с разрывными коэффициентами. Первые решения задачи в такой постановке
были даны Гильбертом (Hilbert [10]) в 1905 г. и Племелем (Plemelj 2))
в 1907 г. при самом зарождении теории краевых задач. Задача Римана
для разомкнутого контура впервые встречается у Карлемана (Carleman 1))
в 1922 г. (см. Исторические сведения к гл. II и III).
Полное решение задач Римана с разомкнутыми контурами было дано
в 1941 г. независимо двумя авторами: Н. И. Мусхелишвили 1) методом,
который был изложен нами в § 43, и Ф. Д. Гаховым 2) метрдом §§ 41, 42*).
В этой же работе Ф. Д. Гахов дал также решение задачи с разрывными ко-
эффициeJ^taми. Методом И. И. Мусхелишвили она была решена несколько
позже Д. А. Квеселава 5). Прямыми предшественниками этих завершающих
ра0от являются работы Гильберта и Племеля для решения Ф. Д. Гахов а и
работа Карлемана для решения И. И. Мусхелишвили.
Гильберт, Племель и Карлеман, владевшие методом решения задач с
разрывными коэффициентами и разомкнутыми контурами, не дали полного их
решения только потому, что в то время еще не было эффективного решения
этой задачи в простейшем случае замкнутого контура и непрерывных
коэффициентов. Характерным является то, что Н. И. Мусхелишвили, Ф. Д. Гахов,
*) Строгое рбоснование этого метода стало возможным лишь на основе
выведенных И. И. Мусхелишвили формул о поведении интеграла типа Коши
в точках разрыва плотности (см. пп. 8.1 —8.4).

624 КРАЕВЫЕ ЗАДАЧИ 1ГЛ. VI
Д. А Квеселава решали задачи с разрывными коэффициентами и
разомкнутыми контурами сразу, сводя одну к другой, тогда как ранее каждая из
этих задач решалась самостоятельно своими собственными методами, причем
работы, в которых давалось решение этих задач, отделены промежутком в
16 лет.
Ф. Д. Гахов [7] дал дальнейшие применения своего метода в теории
краевой задачи Римана со многими неизвестными функциями. Путем
использования функций от матриц фундаментальные функции, устраняющие разрыв,
здесь удалось записать в том же виде, что и в случае одной неизвестной
функции, с тем лишь различием, что показателем X здесь является матрица.
Тем же методом Л. И. Чибрикова 1) дала решение обобщенной задачи
Римана с разрывными коэффициентами и для разомкнутых контуров (см.
задачи 15, 16 в конце главы).
Метод И. И. Мусхелишвили нашел применение при решении задачи
Римана для сложных контуров. Первое решение этой задачи, данное Тшицин-
ским (Trjizinsky 1)), было очень громоздким. Д. А. Квеселава 3) предложил
брать каноническое решение задачи в виде произведения канонических
решений для простых составляющих контуров, что внесло значительные
упрощения в решение. Однако все еще оставались сложности из-за различия
способов образования канонических решений для замкнутых и разомкнутых
контуров. Ф. Д. Гахов и Л. И. Чибрикова 1) предложили для получения
канонического решения в случае замкнутого контура применить тот же метод, что
и при решении задачи для разомкнутого контура (см. п. 44.2), и дело
свелось к решению задачи с разрывными коэффициентами. (Разрывным здесь
является не сам коэффициент, а его логарифм.) Применение этого приема
окончательно упростило решение задачи в случае сложного контура, и оно
приняло тот же вид, что и решение для многосвязной области. В [16] все
изложение теории краевых задач и особых интегральных уравнений,
относящееся к случаю разрывных коэффициентов и разомкнутых контуров, с самого
начала ведется для общего случая контуров с самопересечением.
Частный случай краевой задачи Гильберта с разрывными
коэффициентами — смешанная краевая задача аналитических (Ьункций — рассмотрен Воль-
терра (Volterra 1)) еще в 1883 г. С тех пор эта задача решалась многими
авторами с помощью различных частных приемов. В основе этих приемов
лежит свойство функции
уП(г-а,)B-^,)
при переходе через точки ад, bk действительной оси переходить от
действительных к чисто мнимым значениям, и наоборот.
Результаты, близкие к законченным, получены в работе Синьорини (Sig-
norini 1)). Полное решение дано М. В. Келдышем и Л. И. Седовым 1). Теми
же приемами ими решены другие аналогичные задачи, как, например, задача
Дирихле для плоскости со щелями.
Общий метод сведения смешанной краевой задачи к задаче Римана
с разрывными коэффициентами был применен впервые Ф. Д. Гаховым в 1941 г.
в работе 2) как иллюстрация к доказанной там сводимости краевой задачи
Гильберта к задаче Римана. Обоснование метода сведения задачи Гильберта
к задаче Римана с разрывными коэффициентами было проведено И. И.
Мусхелишвили [16]. Там же дано приложение этого метода к решению многих
частных случаев указанной задачи (задача Дирихле для плоскости со щелями
и ей подобные).
Теория особых интегральных уравнений с разомкнутыми контурами,
изложенная в § 47 и пп. 48.1, 48.2, была построена в 1942 г. Н. И. Мусхелишвили
и Д. А. Квеселава в работе 1). В дальнейшем развитии теории существенную
роль сыграла работа Д. А. Квеселава 5) A944 г.). Главное ее значение
заключается в том, что в ней было изучено применение оператора R (п. 48.4)

ЗАДАЧИ К ГЛАВЕ VI 625
как регуляризатора слева и справа и на основании этого дано простое
построение теории особого уравнения. Особое уравнение в случае разрывных
коэффициентов было рассмотрено Ф. Д. Гаховым [6], однако метод
исследования, примененный в этой работе, был тот же, что и у Н. И. Мусхелишвили
и Д. А. Квеселава; ввиду известной читателю тесной связи между случаями
разомкнутых контуров и разрывных коэффициентов, эта работа содержит
мало оригинальных результатов.
Из ранних работ по этому вопросу можно упомянуть только работу Кар-
лемана (Carleman 1)), о которой уже была речь в гл. II, III. Им было дано
решение неоднородного характеристического уравнения с постоянными
коэффициентами для отрезка оси [О, 1] в классе функций, ограниченных на одном
конце и обращающихся в бесконечность на другом. Решение в этом классе
производится безусловно и однозначно. Никакого упоминания о возможности
других классов решений в работе нет.
Имеется ряд работ, в которых исследование ведется при более широких
предположениях относительно разрывов коэффициентов. В статьях И. Б, Си-
моненко 2), 3) и др. изучены краевая задача Римана и особые уравнения
с измеримыми коэффициентами, в предположении, что колебание arg G{t)
в точках разрыва остается меньше п. Аналогичного характера результаты
получены И. И. Данилюком 1), 2). Эти исследования продолжены В. А.
Пааташвили 1) и В. Д. Фроловым 1), 2). Ряд работ И. Ц. Гохберга и Н. Я.
Крупника 1), 2) и др. посвящен исследованию особых уравнений с разрывными
коэффициентами в пространствах Lp. К этим работам примыкает статья 3)
указанных авторов, в которой исследованы операторы, представляемые в
виде сумм произведений особых операторов на разомкнутом контуре и с
разрывными коэффициентами. В некоторых работах рассмотрены случаи
разрывов другого типа — почти периодического и др. Изложение исследований
этого рода дано в книге- И. Ц. Гохберг и Н. Я. Крупник, Введение
в теорию одномерных сингулярных интегральных операторов, Кишинев, изд.
АН Молд. ССР, 1973. Мы не имеем здесь возможности останавливаться на
подробностях.
О возникновении и развитии теории краевых задач с бесконечным
индексом достаточно говорилось в тексте (§ 49). Здесь добавим лишь, что главную
трудность в этой теории представляет отыскание ограниченных решений.
Получение решений, имеющих на бесконечности рост любого порядка, не
представляет никаких трудностей.
Задачи к главе VI
1. Доказать, что решение задачи Римана для разомкнутого контура не
зависит от вида той кривой, которой мы дополняем данный разомкнутый
контур до замкнутого. (Ф. Д. Гахов [6].)
2. Пусть L — единичная окружность и Li, Lz — соответственно ее верх*
няя и нижняя полуокружности.
Решить для контура L краевую задачу Римана
2я-5 5-я J.4
Ф+@ = 0(/)ф-(/) + (/~1) " (/+1) « .^ф^ (|а|<1),
где
G (t) = е^^' на Li, G (t) == е^^ на Lj,
/ t — I \5/"
a многозначная функция f . , . J задается некоторой своей определенной
ветвью. Рассмотреть классы функций, имеющих интегрируемую бесконечность

526 КРАЕВЫЕ ЗАДАЧИ [ГЛ Vt
В точках
а) /i==l, /i = -I;
б) /i = l;
в) /i == - 1
и ограниченных во всех остальных точках плоскости г.
г) Решить задачу в классе всюду ограниченных функций.
д) Показать, что в классе функций, всюду ограниченных и
обращающихся на бесконечности в нуль, задача имеет решение лишь при специальном
подборе параметра а; указать эти значения параметра и найти решение в
этом случае.
Ответ.
а\ <h^{-\-^ ^^^ ( ^Л'\\1Г\ (^ ^г\ 2:sin4a+ flC0s4fl ^4^ ,
+ ^J^2 + ^о + с,г],
5-я
, аA — г) cos4a + (а^ + г) sin4a _4; , 1
+ а(г^ + а=) * + ^J'
5--Я
ф-Ы-Г-1±-1'\ =^ ra(l-g)cos4a + (a^ + ?)8in4a ,4/ . Л.
5-2Я
в)Ф+(г) = а'«(|±|) " [i?±i)^lz_?2!i2l,-« +
(g^-г) sin 4а 4г , 1
5-2Я
rt,-,-ч _/'Z+1 Ч я г (Q'-^)s'a-aB+l)cos4a _.м , J
Ф (^) = (,7^rrj L ГEч^Р) " +'J=
5-я
¦¦ч fl)+(-^ -f- 1^Г^+М « ae'*'-BSin4a + acos4o)
г; Ф lz;-B i;^^^_,j аB:2 + а2)
5-я
<л-/,\ /1 ¦,\(Il^lL\ " г sin 4а + а COS 4а ,-4f.
д) a=±i. ф+(.) = (.-1)(?±-'-) "
5-я .
5~я
»-<^)-Ш)
z+lN-irfz-De-"^

ЗАДАЧИ К ГЛАВЕ VI 527
—ЗТ ] понимается функция, аналитическая в плоскости,
разрезанной вдоль Li, предельные значения которой изнутри круга совпадают
с соответственной функцией, входящей в краевое условие.
3. Пусть L, Li, Lz означают то же, что и в предыдущей задаче.
Решить краевую задачу Римана
К е'^^^ на L2
в самом широком классе функций, имеющих бесконечность интегрируемого
порядка в обеих точках разрыва.
Ответ. Индекс задачи в заданном классе х = —2, поэтому задача,
вообще говоря, неразрешима. Решение существует при а =« ± -г- и опреде-
5
ляется в этом случае формулами
е^^^ + 1
ф-Ь(г) = (г^-1)(|±|)«
25^2 - д2 »
42
2+1\-1Г 22-1
«-w-(f^)'
25^2 — я2 '
2-f 1 Ч^^/^
Под ( _ . 1 понимается функция, аналитическая в плоскости,
разрезанной вдоль Lzy предельные значения которой изнутри единичного круга
совпадают с функцией 1.1 , входящей в краевое условие.
4. Пусть L —гладкий замкнутый контур и G(t)—функция, не
обращающаяся в нуль и удовлетворяющая условию. Гёльдера всюду, кроме точек
^ь hy •••» ^i> где она имеет разрывы 1-го рода. Определим индекс G(t) как
причем на участках L между точками разрыва аргумент изменяется
непрерывно, а при переходе через точку разрыва удовлетворяет одному из условий:
О< arg С (tk~ 0) - arg G (tk + 0)<2я,
- 2я< arg G {tk - 0) - arg G (tk + 0)<0.
Показать, что определенный таким образом индекс совпадает с индексом,
определенным в п. 41.4. (Н. И. Мусхелишвили [16], § 78.)
5*. Пусть L есть контур, состоящий из т разомкнутых кривых, и пусть
f@—заданная функция, удовлетворяющая условию Гёльдера, а Pm-\(t) —
многочлен степени т—1, коэффициенты которго не задаются заранее.
Показать, что интеграл типа Коши
j\-^dx=.nt) + Pn-,(t)

628 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
допускает обращение в классе функций, ограниченных на всех концах, и что
многочлен Pm-\(t) при этом однозначно определяется. (Н. И. Мусхелишвили
[16], §87.)
6*. Пусть L и f{t) те же, что и в предыдущей задаче, и Ck — постоянные,
не задаваемые заранее. Показать, что интеграл типа Коши
ni
допускает обращение в классе ограниченных функций и что все постоянные са
при этом однозначно определяются. (И. И. Мусхелишвили [16], § 88.)
7*. Пусть на гладком замкнутом контуре L задана действительная
функция f{s), непрерывная на L, кроме точек /i, ^2. ..., ^и где она имеет разрывы
1-го рода. Обозначим предельные значения f{s) в точках разрыва f{Sk — 0) =
«=s Uky f{Sk + 0) = bk. Показать, что решение задачи Дирихле
u = f(s)
для области D, ограниченной контуром L, может быть представлено в виде
/
Ч-h_, y-h
и (дг, у) ^v(x,y) + Y, -^^ arctg ^—^ (/, = а, -f /р,),
где v(x,y)—решение задачи Дирихле с непрерывными коэффициентами.
Доказать, что в классе функций, имеющих порядок роста ниже логарифмиче-
(«{^> у) л л
—^—-—>0 вместе с расстоянием ri точки разрыва ti до
произвольной точки области), это решение единственно.
8*. Решить задачу Гильберта с разрывными коэффициентами методом
п. 28 2 (путем отыскания регуляризующего множителя). Использовать при
этом результаты предшествующей задачи. (В. К. Столярова 1).)
9*. Пусть область D симметрична относительно оси абсцисс и искомая
функция Ф(г) получена продолжением из верхней полуплоскости в нижнюю
по симметрии. На части контура области D, лежащей в верхней
полуплоскости, задана действительная часть ФB:), а на симметричной части контура —
мнимая. Доказать, что такая смешанная краевая задача безусловно
разрешима в классе ограниченных функций. (А. В. Бицадзе 1).)
Указание. Сначала отобразить область D на единичный круг.
10*. Пусть область D есть плоскость с разрезами (а^, Ь^) оси абсцисс
(п. 46.4). Определить аналитическую и ограниченную в области D функцию
ФB) = и + It)у если на берегах разреза задано
и"^ = f"^ (О + ^fe, и- = Г (О + cj^ на {а^, bf,) (^=1,2,..., m),
где f+, /~ — заданные функции, удовлетворяющие условию Гёльдера, Ck —
постоянные, не задаваемые дарйнее. Показать, что задача безусловно и
однозначно разрешима и что все постоянные Ck при этом однозначно
определяются. (Н. И. Мусхелишвили [16], § 91.)
П*. Исходя из результатов предыдущей задачи, решить задачу Дирихле
для плоскости с разрезами вдоль действительной оси (п. 46.3), не
предполагая дифференцируемобти краевых ^наодйий. (Н. И. Мусхелишвили [16], §91.)
т
Указание. Рассмотреть функцию U {х, у) ~ и (х, у) + ^ ^k^k (^)' ^^^
fe-i
^h (^) = j:zrr; [(^ - ^k) ^" (^ - ^k) - (^ - Ч) J" (^ - «л)]-

ЗАДАЧИ К ГЛАВЕ VI 529
12. Найти функцию w = /(г), отображающую нижнюю полуплоскость
(/ < О на полуплоскость, ограниченную прямой и = kv, с разрезом по
вертикальному отрезку длины С, выходящему из начала координат, при условии,
что интервалу |j^|< 1 соответствуют берега разреза, а интервалам \х\'> 1 —
лучи прямой и = kv.
Ответ.
f(z)=:±iCe^'^{z+\)'' B-1) "".
С — действительная постоянная, ф = arctg k. Знак в формуле берется в
зависимости от того, направлен ли разрез вверх или вниз.
Указание. Воспользоваться тем, что искомая функция должна быть
решением краевой задачи Гильберта из примера п. 46.4 при а = О в классе
функций, ограниченных в точках z = —1, г = 1 и растущих как z при
z-^ со.
Используя геометрические свойства функции Жуковского W ==^-^lz -] J
и ее логарифма, решить две следующие краевые задачи:
13. Найти f(z)= и + iv, аналитическую в нижней полуплоскости,
ограниченную в точках 2 = —1, 2 = 1 и растущую как |2| при z-^oo по
краевому условию:
Im / (д:) = О при л:<—1 и а:>1,
\f(x)\ = \ при ~1<а;<1.
14. Найти f{z)=u + iVy аналитическую в нижней полуплоскости,
ограниченную в точках Z = —1, 2 = 1 и растущую как 1п|г| при z-^oo по
краевому условию:
т Р/ ч f О при д:< -1,
( п при л: > 1,
Re/(A;) = 0 при —1 < ;с < 1.
15*. Дана краевая задача
Ф+[а@] = С(/)ф-@,
где соблюдаются все условия § 17, за исключением того, что у коэффициента
G(i) допускаются разрывы 1-го рода в точках tu /2» ...» ti.
Показать, что подстановкой
ф+B) = П[г-а(У]Нф+B),
данная краевая задача приводится к такого же рода краевой задаче с
непрерывным коэффициентом
(Л. и. Чибрикова 1).)
16*. Показать, что предыдущая краевая задача в случае, когда контур L
разомкнутый и a(t) переводит контур на себя с сохранением направления,
методом п. 42.1 может быть приведена к задаче
Ф"" [«1 (/)] « Qi (t) Ф- (/)

530 КРАЕВЫЕ ЗАДАЧИ [ГЛ. VI
ДЛЯ замкнутого контура с разрывным коэффициентом Gi(i) и непрерывной
функцией ai(/). (Л. И. Чибрикова 1).)
17. Дано обобщенное особое интегральное уравнение
L L
(см. задачу 10 к гл. III и задачу 15), где L — замкнутый контур; a(t), b(t)
имеют разрывы 1-го рода в конечном числе точек. Свести его к краевой
задаче Римана со сдвигом и дать исследование. (Л. И. Чибрикова 1).)
18. Сделать то же для случая, когда L — разомкнутый контур.
19. Показать, что интегро-дифференциальное уравнение крыла самолета
—а
может быть приведено к интегральному уравнению Фредгольма
а
Г (/) + \ а: (и т) г (т) dx==F (/) + ^1 + ^2 arcsin 1,
—а
где
2пВ (т) a^-tx- V(a^ - Р) {а' - т^)
а
F{i)= 5 B{x)K{t,x)f(x)dx,
—а
Си С2 — произвольные постоянные.
Указание. Воспользоваться формулой обращения интеграла типа Коши
в классе функций, не ограниченных на обоих концах, и затем полученное
уравнение проинтегрировать по t.
20. С помощью тождества, получаемого подстановкой в уравнение
Ь
{asgn(x-c) + ^\^(x) + X\-^^dt=^(i, a<c<b,
Till J f X
a
p T^ ±(I ±a), a<x<b,
его решения (см. п. 47.4, 3°), убедиться в справедливости следующих
равенств, где
_ 1 а-Р+1 _ 1 I а+Р-1
^ ~ 2ш а-р~1 ' '^"~ 2п1 ^"^ а+р+1 '
0<ReM,<l, 0<Rev<l:
b
J (t-ar(b-ty-''\c-t\''->4t-x)
_ cos ЦЯ + cos УЯ + (cos ЦЯ — COS уя) sgn (с — л:).
"¦" {x-a)^^(b-x)^-''\c-x\''-^^ '

ЗАДАЧИ К ГЛАВЕ Vt 631
оо
^. f sin цл + sin УЯ + (sin цл — sin уя) sgn (и — Я)
cos \in + COS УЯ + (cos м-я — cos уя) sgn (о — Я) л -^ л ^ л
= - я , я > о, v>0;
b
\ { [(sin цл + sin уя) sgn (g — /) + sin \хл — sin уя] {At + В) ,. __
J (/-a)i-»^F-0^"''k-^l^"^''(^~A:)
[(cos \хл — COS уя) sgn {с — x) + COS ця + COS уя] (Ax + ^)
Re (м- + v) < 1, i4 и В — произвольные числа;
оо
, f du ^ * / \ sgn (Я — и)
г) \ г-ц = ^ ctg (ия) ^—'^
Я>0, 0<Re[i<l/2, t;>0;
оо
f [(sin 11Л + sin Уя) Sgn (ц — Я) + sin [хл — sin уя] (b + дц) du
[(cos М-Я — cos Уя) sgn (у — Я) + COS \хл + COS уя)] (b + flP)
""' |Я-.уГ+^1;1-^
Я>0, у>0, Re(n + y)<l;
f F + an) Sgn (U'-X)du . , . b + av
Я>0, 0<Ren<l/2, о>0.

ГЛАВА VII
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ, РАЗРЕШИМЫЕ
В ЗАМКНУТОЙ ФОРМЕ
Точное решение интегральных уравнений требует, как
правило, применения бесконечных процессов (метод
последовательных приближений, бесконечные системы линейных
алгебраических уравнений и Ttn.). Однако имеются отдельные типы
интегральных уравнений, для которых удается получить решение,
выражающееся через конечное число квадратур от заданных
функций, или, как говорят, в замкнутой форме. Некоторые такие
уравнения были решены в § 21. Они характеризуются тем, что
их ядро является аналитической функцией основной переменной.
Методом решения этих уравнений, как правило, служит
аналитическое продолжение в комплексную плоскость. Путем
введения вспомогательной аналитической функции и использования
решения краевой задачи Римана удается получить их решение
в замкнутой форме.
Примером применения указанного метода является данное
в § 21 решение характеристического особого интегрального
уравнения с ядром Коши. Аналитическое продолжение в
комплексную плоскость там осуществляется интегралом типа Коши, для
которого искомое решение уравнения служило плотностью.
Формулы Сохоцкого для предельных значений интеграла позволили
свести уравнение к краевой задаче Римана. Аналогичный метод
с надлежащими изменениями позволяет получить в замкнутой
форме решения некоторых других типов уравнений. В §§ 51, 52
будут рассмотрены особые интегральные уравнения с ядрами
автоморфного типа, главная часть которых есть ядро типа
Коши. Здесь используются аналоги формул Сохоцкого. В силу
специфики интегрального представления возникающая здесь
краевая задача Римана обладает той особенностью, что искомой
функцией в ней является не произвольная аналитическая
функция, как это было ранее, а аналитическая функция специального
класса, именно автоморфиая функция. Появляется потребность
в изучении краевых задач в этом новом классе функций, в связи

§ 51) УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 533
с чем приходится привлекать теорию самих автоморфных
функций.
Возникшая теория краевых задач в классе автоморфных
функций естественным образом расширялась и обобщалась.
Выяснилась ее тесная связь с краевыми задачами для областей,
расположенных на римановых поверхностях. За последние
полтора десятка лет теория таких краевых задач развилась в
богатую, широко разветвленную, основывающуюся на сложном
математическом аппарате самостоятельную дисциплину.
В этой главе рассматриваются также уравнения со
степенными и логарифмическими ядрами. Последние являются
интегрируемыми функциями, поэтому по внешнему виду эти
уравнения кажутся неособыми. Однако решающим здесь является то
обстоятельство, что они являются уравнениями первого рода.
Это относит их к классу уравнений, подчиняющихся теории Нё-
тера.
Для решения обоих классов уравнений можно было бы
использовать описанный выше способ аналитического продолжения
в комплексную плоскость и сведения их с помощью аналогов
формул Сохоцкого к краевой задаче Римана. Однако изучение
вопроса показало, что для развития их теории, в особенности
для исследования допустимых классов заданных и искомых
функций, целесообразнее использовать их непосредственную
связь с изученными в гл. III и VI уравнениями с ядром Коши.
§ 51. Уравнения с автоморфными ядрами
с конечной группой*)
Для решения полного уравнения, которое будем записывать
в виде
а@ф@+-1^ 5[т^ + ^(^ '^)]фМ^^ = /@, E1.1)
введем, аналогично тому, как это делалось для
характеристического, функцию
^(^) = i S[t^ + ^(^' т)]ф(т)йт. E1.2)
Чтобы Ф{г) была однозначной аналитической функцией,
необходимо, прежде всего, чтобы ядро K{t, т) было однозначным
аналитическим относительно переменной t. Это первое
естественное ограничение для применимости метода. Допустим, что оно
*) Материал этого параграфа написан по работе Ф. Д. Гахова и
Л. И. Чибриковой 1).

534 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ (ГЛ. Vll
выполнено. Существенное отличие функции, определяемой
интегралом E1.2), от функции, определяемой интегралом типа Ко-
ши, заключается в том, что первая, кроме линии Lq, может иметь
еще другие линии особенностей, являющиеся особыми линиями
функции K{z,x), при условии, что переменная т пробегает
контур интегрирования Lq, Чтобы указанный метод мог привести
к цели, необходимо, чтобы для всех возможных линий разрыва
функции E1.2) особое уравнение E1.1) дало возможность
составить краевые условия задачи Римана. Типы особых
интегральных уравнений с ядром Коши, для которых дается в
дальнейшем решение в замкнутой форме, подбираются на основе
высказанных здесь общих соображений. Основная их
характеристика — автоморфность ядра.
Вопросы этого рода заставят нас выйти за пределы
элементов теории функций комплексного переменного и привлечь
теорию автоморфных функций.
51.1. Некоторые сведения о конечных группах
дробно-линейных преобразований и об автоморфных функциях. Пока
приведем простейшие факты из теории автоморфных функций*).
Совокупность всех дробно-линейных подстановок образует
группу. Эта группа, вообще говоря, бесконечная. Здесь будут
рассмотрены лишь конечные группы дробно-линейных
подстановок.
Пусть даны подстановки оI(г), ..., а)т{^)- Если образовать
множество, содержащее данные подстановки, обратные к ним и
построенные из них всеми возможными способами произведения,
то это множество образует группу. Такая группа называется
порожденной подстановками а)\{г), ..., (дт{^), а сами эти
подстановки называются основными подстановками группы. Группы,
порожденные одной подстановкой, называются циклическими.
Знание циклических групп важно потому, что каждая группа
содержит циклические подгруппы.
Выясним, каковы должны быть коэффициенты а, р, у, б
подстановки
чтобы она порождала конечную циклическую группу.
Предположим, что определитель подстановки coi равен единице:
a6-pY=l. F1.4)
Этого всегда можно добиться, разделив коэффициенты
подстановки на V«6"^PY*
*) Подробности можно найти в книге [28] или в книге: В. В. Голубев,
Лекции по аналитической теории, М. — Л., Гостехиздат, 1950.

§ 51] УРАВНЕНИЯ С АВТОМТ)РФТТЬГМИ ЯДРАМИ 635
Так как циклическая группа, порожденная подстановкой coi,
будет содержать все ее последовательные итерации
©2 = (Oi @i), СОз = (Oi @1 @i)), ...,
то, для того чтобы группа была конечной, необходимо и
достаточно, чтобы одна из этих итераций тождественно обращалась
в г, например, чтобы
0„B) = г.
Выведем выражение для п-и итерации ©«(-г). Для этого
воспользуемся следующим представлением для дробно-линейной
функции {[28], стр. 24):
где li, I2 — неподвижные точки подстановки (oiB), а /С — число,
не равное единице:
«=-г^. E1.6)
которое при выполнении условия E1.4) удовлетворяет
соотношению
/С + -^ = (а +6J-2. E1.7)
Из E1.5) получаем
(On{z)-li _ j^n z-l
= r
;i
откуда находим
Из полученного выражения следует, что а)п{^)^г тогда и
только тогда, когда /С^ = 1, т. е. когда
/С = в ^ (Aj=1,2, ..., Ai-l).
Подставляя значение К в E1.7), получим
2nik 2nik
(а + б)*-2 = е « +в « =2cos^,
откуда
(a + 6J = 4cos2^
и, еле довательно,
a + 6=±2cos-^ (А; = 1,2, .... п-1). F1.8)

536 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
Последняя формула используется далее. Равенства E1.4) и
E1.8) являются необходимыми и достаточными условиями для
того, чтобы циклическая группа, порожденная подстановкой
E1.3), была я-членной.
Рассмотрим в качестве примеров случаи, когда п=2 и п=3.
1) дг = 2, й=1; cos-^ = cos-y = 0.
Условие E1.8) дает 6 = —-а, и подстановка
аа^ + Р
@B:) =
yz-
при — а^-—Py=1 является общим видом подстановки, которая
совпадает со своей обратной: со [© (г)] = г.
2) Аг = 3, ^ = 1,2; cos-j' = y, cos-y- = —у.
Условия E1.8) имеют вид а + б=±1, и получаем два двух-
параметрических семейства подстановок:
«>(^)=v/.!|-«. a(l+a) + PY = -l,
удовлетворяющих условию соз (z) ^ г.
Дадим теперь определение автоморфных функций и
установим некоторые их свойства. Функции, инвариантные по
отношению к некоторой группе дробно-линейных подстановок,
называются автоморфными функциями.
Рациональные автоморфные функции образуют единственный
класс однозначных функций, автоморфных по отношению к
конечным группам.
Точки или фигуры, получаемые одна из другой при помощи
подстановок группы, называются эквивалентными. Автоморф-
ная функция принимает в эквивалентных точках одни и те же
значения. Область, которая не содержит двух различных
эквивалентных между собой точек, но которая содержит точки,
эквивалентные любой точке плоскости относительно
рассматриваемой группы, называется фундаментальной областью
группы (соответственно фундаментальной областью автоморфной
функции).
Если некоторая группа не содержит целых линейных
подстановок и
<^Лг)==Щ^ {k = l,2,...,m)

§ 51] УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 537
— основные подстановки группы, то фундаментальной областью
является внешность так называемых изометрических
окружностей основных подстановок, уравнения которых
Автоморфные функции имеют в фундаментальной области
одинаковое число нулей и полюсов и вообще любое свое значение
принимают одинаковое число раз. Из этого свойства следует,
что если автоморфная функция в фундаментальной области не
имеет полюса, то она тождественно равна постоянной.
Особую роль в теории автоморфных функций играет так
называемая основная функция группы. Это автоморфная функция
(где а — любое фиксированное число), принимающая в каждой
фундаментальной области любое свое значение один раз.
Если функция
F{z)=Z^{z) F1.10)
не вырождается тождественно в постоянную, то она является
основной автоморфнои функцией, имеющей полюс в бесконечно
удаленной точке.
В дальнейшем понадобится автоморфная функция, имеющая
полюс некоторого порядка х в бесконечности. Через функцию
E1.10) она выражается простым многочленом Py^iF). Если же
F(z) имеет полюс в конечной точке, то она может быть
представлена в виде
где Zoo — бесконечно удаленная или любая эквивалентная ей
точка.
51.2. Приведение одного полного особого интегрального
уравнения к краевой задаче. Пусть Lq — некоторая гладкая
кривая, которую в дальнейшем для простоты будем считать
замкнутой, и
<^o{t) = ty ®i@, ••., ^n-iit)
— дробно-линейные функции, составляющие группу.
Рассмотрим уравнение
«(Оф@+^ ГЕ [^^-7^Г^)]ф(-)^- = /@. E1.12)
Lq /S"

838 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
где а (О, b{t), /(/)—заданные функции, удовлетворяющие
условию Гёльдера, причем a^{t)—b^(t)= 1.
Введем функцию
Ф(-) = ^ГЕ [тз^~ТЗГ^ E1.13)
удовлетворяющую условию Ф(оо)=0. Она будет аналитична
всюду, кром.е кривой Lq и кривых Lky уравнения которых
т —coftB)= о или 2 = сй~^(т), т е Lq {k= 1, 2, ..., /г— 1).
Рассмотрим поведение Ф(г) на линиях Lu. Когда z
пересекает кривую Lq, со~^(г) пересекает кривую Lft. Подставив
в E1.13) (o^Hz) вместо г, заметим, что все слагаемые в сумме
изменяются непрерывно, кроме (^ + 1)-го, которое обращается
в интеграл типа Коши с линией скачков Lq. Предположим, что
все функции (о~^ (z) переводят кривую Lq в кривые Lk с
сохранением направления и все кривые Lk либо не имеют общих
точек, либо пересекаются в конечном числе их. Тогда легко
видеть, что для всякой точки кривых Lft, не совпадающей с
точками самопересечения, при аг-хл)^^ (/) е L^(/е Lq) будет
справедливо равенство
фЧсоГЧО] = ±{ф@ +
В силу того, что (Ok{z) образуют группу, сумма, стоящая в
правой части последнего равенства, лишь порядком слагаемых от-
личается от суммы ^ L-I^m - >r~i(cxDI' Поэтому на
контурах Lk будут справедливы формулы, аналогичные
формулам Сохоцкого:
Фit) = Ф+ [щ' @]-Ф-[(О,-' @],
if ГЕ [т:г^;@-Т1Г^]фМ^-= E1.14)
Lp fe-0 ^
^O^W{t)\ + 0^[^'{t)\ {k^O, 1, ..., Az-l).
Вставляя последние выражения в интегральное уравнение
E1.12), получим, что функция Ф(г) будет удовлетворять

§ 51] УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ В39
краевым условиям
которые можно еще переписать в виде
Ф^'{t)^G[щ{t)]Ф''{i) + g[щ{t)] (Aj-0, I, ..., Az~l), E1.15)
где введены обычные обозначения
По характеру краевых условий задача напоминает известную
краевую задачу Римана. Но во избежание ошибок нужно
подчеркнуть, что она не является задачей Римана в чистом
виде. Различие заключается в том, что ищется функция,
имеющая определенное аналитическое представление E1.13).
Поэтому при решении задачи необходимо заботиться о том, чтобы
наряду с удовлетворением краевым условиям на линиях Lk
функция имела заданный аналитический характер.
Исследуем подробнее функцию 0{z). Подставляя в
равенство E1.13) (Oj{z) вместо z и учитывая, что (Oj{z) образуют
группу, получим, что 0{z) будет удовлетворять условию
Ф[<^,{г)] = Ф{г), E1.17)
т. е. остается инвариантной при подстановках группы.
Следовательно, искомая функция Ф(г) есть автоморфная
функция с заданной группой 0HB), 0IB), ..., o)n-iB)
подстановок.
Таким образом, заданное особое уравнение E1.12) сводится
к краевой задаче, в которой требуется определить автоморфную
кусочно аналитическую функцию ФB:), имеющую п линий
разрыва Lfe, на которых ее предельные значения удовлетворяют
краевым условиям E1.15) и дополнительному условию ф(оо) =
= 0.
Заметим, что краевые условия E1.15) для кривых Lu ...
..., Ln-i можно было бы получить из краевого условия для
кривой Lo при помощи соотношения E1.17).
Рассуждениями, аналогичными проведенным в п. 21.1, можно
доказать, что решение полученной краевой задачи равносильно
решению исходного уравнения E1.12).
Замечание. Если в преобразованиях группы имеются
такие, которые отображают кривую Lq с изменением направления,
то рассуждения нужно немного изменить.
Пусть преобразования группы ©^^ (z), а>^^ (г), ...
отображают контур Lo с изменением направления. Тогда для кривых

640 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
Lk. (/=1,2, ...) функции Ф'^B:), Ф~(г) меняются местами и
краевое условие E1.15) должно быть заменено на
^^(')-opi;ioi'^-(')-.[„J,[j';:r|l.,(,)] " Ч <5'-'5')
(/=1,2,3,...).
51.3. Решение краевой задачи. Перейдем к решению краевой
задачи E1.15), к которой сведено решение особого уравнения
E1.12). Контур L = Lo + Li + ... + Ln-i, на котором задано
краевое условие, будет, вообще говоря, самопересекающимся.
Для решения краевой задачи воспользуемся методом § 44. Как
было условлено, будем считать, что контур Lo замкнут. Тогда и
все контуры Lft, эквивалентные Lo, будут тоже замкнутыми.
Как установлено в п. 44.3, каноническую функцию ХB:) для
совокупности контуров Lo, Li, ..., Ln-\ можно построить как
произведение канонических функций ХоB:), XiB:), ..., Xn-\{z)
для каждого из этих контуров в отдельности. Однако в данном
случае нет надобности строить каноническую функцию для
каждого контура Lft, так как если Хо(г) есть каноническая функция
для контура Lo:
Xo+@ = G(/)Xo-@,
то, заменяя в этом равенстве t ^ Lq на (Oft(/), t ^ Lk, получим
^t[щ{t)] = G[щ{t)]Xo[щ{t)] {k = 0, 1, ..., n~l). E1.18)
Отсюда следует, что Х^^(<г) = Хо[(о^^(г)].
Таким образом, канонические функции краевой задачи для
контуров Lk, эквивалентных контуру Lo, являются функциями,
эквивалентными канонической функции ХоB:) для основного
контура Lq.
На основании п. 44.2
Хо(г) = (г~^оГ''/»<^
где ^0 — некоторая точка контура Lo, отличная от точек
пересечения, X — индекс функции G{t),
¦¦.«'iSJl^*. E1.19)
Следовательно, каноническая функция для всего контура L
представится в виде
Х(г) = П Хо К(^)] = П [щ{г)-иГ''е^-' . E1.20)
/г-О fe-0

§ 51] УРАВНЕНИЯ С АВТОМОРФКЫМИ ЯДРАМИ 641
Она отлична от нуля всюду, кроме, может быть, бесконечно
удаленной точки и точек, ей эквивалентных, где она имеет порядок
УС и инвариантна относительно всех подстановок группы
Х(г) = Х[(о,B)] (/^=1,2, ..., /г~1). E1.21)
Найдем теперь общее решение однородной задачи
ф+(/) = О[о),(/)]ф-@, t^L, (/j = 0, 1, ..., Аг-1), E1.22)
удовлетворяющее условию Ф(сх)) = 0.
Внося в краевое условие выражение для G[(Ok{t)] из
равенства
получим
Ф"^ (t) Ф-@
X-^@ = G[(D,@]X-@,
t^L, (^ = 0, I, .,., n-1).
^ , Ф (г)
Последние равенства показывают, что функция ^' ' анали-
тична во всей плоскости, кроме бесконечно удаленной точки и
точек, ей эквивалентных, где она может иметь полюсы порядка
•к—1. Кроме того, из E1.17) и E1.21) следует, что эта
функция остается инвариантной относительно всех подстановок oyhiz)
группы. Следовательно, она есть рациональная автоморфная
функция, имеющая в фундаментальной области полюс порядка
к— 1 *), а такая функция имеет вид (см. формулу E1.11))
Ф(г) Pyi-i(F)
X{z) lF(z)--F{z^)r-' '
где F{z)—основная функция группы E1.9), P^-i —
произвольный многочлен степени не выше х — 1, а ^оо означает бесконечно
удаленную или одну из эквивалентных ей точек.
Таким образом, в случае положительного индекса >с > О
однородная задача E1.22) имеет к линейно независимых решений,
определяемых формулой
При X ^ О однородная задача решений не имеет.
*) В этом рассуждении сказывается отличие решаемой задачи от
обыкновенной краевой задачи Римана. Если бы мы решали последнюю задачу,
не учитывая равенства E1.13) и вытекающего из него равенства E1.17), то,
применяя, как обычно, обобщенную теорему Лиувилля, получили бы, что от-
ношение ^ / ч есть многочлен степени п(к— 1).
X(z)

542 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
Если В качестве основной автоморфной функции можно взять
функцию E1.10), то решение принимает более простой вид:
Ф{2) = ХB)Р^-,(П E1.24)
Переходим теперь к решению неоднородной задачи E1.15)
Обычным многократно применявшимся приемом приводим
краевое условие к виду
х"^(/) х-(О х+@ > > » /
Это есть задача определения аналитической (в рассматриваемом
случае, кроме того, автоморфной) функции по ее скачку.
Используя формулы E1.14), непосредственной проверкой легко
убедиться, что кусочно аналитическая функция
4rB) = -LV [^ Ё1 E1.25)
остается инвариантной относительно всех преобразований
группы и удовлетворяет последнему краевому условию.
Следовательно, функция
является частным решением неоднородной задачи E1.15).
Прибавляя сюда общее решение однородной задачи, получим общее
решение неоднородной задачи E1.15):
Ф(г)=хи{т(.)+^^^^;_-;;;у,}. E1.26)
где Х(г)—каноническое решение, определяемое формулой
E1.20), а Т(г) выражается формулой E1.25).
При X < О нужно положить Р^\ s= О и, кроме того,
потребовать, чтобы 4f{z) на бесконечности обращалось в нуль (—х+ 1)-
го порядка. Разложение последней в окрестности бесконечно
удаленной точки будет иметь вид
^(^)=~Щ\^Щ^''^У'-
«»' W
Приравнивая нулю коэффициенты при z"^ (/=1, 2, ..., —х),
получим условия разрешимости задачи
¦^ у «);(T)(o/-'(t)dT = 0 (/=1.2 -к). E1.27)
г.. ^ ^^^ *-о

§ 5\] УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ б43
Таким образом, так же как и в случае обыкновенной задачи
Римана, мы имеем следующие результаты:
Однородная краевая задача E1.22) при х>0 имеет х
линейно независимых решений, исчезаюи^их на бесконечности, при
X ^ О неразрешима.
Неоднородная краевая задача E1.15) при х ^ О безусловно
разрешима. При х < О она разрешима лишь при выполнении
—X условий E1.27).
51.4. Решение интегрального уравнения. Из решения E1.26)
краевой задачи E1.15) по формуле Сохоцкого
ф(/) = ф+@-.ф-@ E1.28)
найдем решение исходного интегрального уравнения E1.12).
Рассуждая совершенно так же, как в пп. 21.2 и 47.2, придем
к равенству
+^^'"['-^]{'^'"-i....,-7.lV'}-
Вставляя сюда значения X{t), W{t) из формул E1.20),
E1.25) и G(t)y g{t) из формул E1.16) и учитывая наложенное
условие a^{t)— b^{t) = 1, получим
(т) dx
V{t) = a{t)f{t)^b{t)Z(t)J^±\l
Z(t) t —соЛО ^
где
Z it) = [a it) + b @1X+ (/) = [a it) - b {t)\ X" {t) =
n-l "s'roi^ftW]
^nKCO-^ol-^e*-» , E1.30)
fe-0
,._ 1 e InQ(T) . /j/A_±wziMl
Если x^O, TO нужно положить Ях-1^0» причем при х<0
для разрешимости уравнения должны выполняться условия
5r^a,;(T)(o/-i(^)J4{^dT = 0 (/=1,2, .... -п). E1.31)
-fe«0

544 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
Таким образом, для интегрального уравнения придем к
результатам, аналогичным тем, которые были получены в
предыдущем пункте для соответствующей краевой задачи.
51.5. Пример. Решим особое интегральное уравнение
1x1=1
= fP f(t) (О < а < 2, р - целое).
Вводим кусочно аналитическую, автоморфную по отношению к группе
соо (г) = 2, (Oi B) = а —• z, функцию
|Т|=1
Она имеет две линии разрыва: единичную окружность Lq и окружность
Lii |т —а| = 1, получающуюся из Lq при помощи преобразования ©i (г) =
= а — Z.
Краевые условия на контуре L = Lq + Li имеют вид
Ф+(/) = ^2Рф~@ + /@ на Lo,
ф+(/) = (а-0^^ф-(/) + /(а-0 на Ij.
Канонические функции для простых составляющих контуров
определяются выражениями
Х+(г) = 1, Хо-(г) = г-2р, Х+(г)=1, Xf (г) = (а--гГ^^
Дальнейшие рассуждения являются иллюстрацией не только для
изложенного в настоящем параграфе метода, но и вообще для решения краевых
задач в случае пересекающихся контуров. Из-за перекрывания областей,
ограниченных простыми составляющими контурами, задачи эти представляют
своеобразные трудности; поэтому мы изложим решение с большими
подробностями, чем это делали обычно.
Каждая из кривых Lk делит плоскость на две дополнительные области
D^, Z)^ (^ = 0, 1). Весь контур L делит плоскость на четыре связные области,
которые удобно обозначать как произведения тех простых областей,
пересечением которых они получены (рис. 18).
В каждой из этих областей на основании формулы XB) = IJ ^ki^)
каноническая функция будет задаваться выражениями
ХB) =
Хо+Х+ = 1 в D^Dt,
X+Xf = (a-2:)-2^ в D^DY.
X^Xf = 2-2^@-г)-2Р в Z)^Df.
ФB) имеет в бесконечно удаленной точке порядок 2, X(z)—порядок 4р.
Отношение ¦ ^ / \' имеет порядок D/? —2). Учитывая, что бесконечно уда-
л {Z)

§511
УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ
545
ленная точка является неподвижной точкой группы и принадлежит,
следовательно, обеим фундаментальным областям (последние суть полуплоскости,
ограниченные прямой, проходящей через точку г = а/2), порядок этот нужно
разделить на два.
Рис. 18.
За основную автоморфную функцию группы возьмем функцию
F{z).
1
1
а — 2 2 (а — 2)'
имеющую простой полюс в начале координат*).
Общее решение однородной задачи при р > О будет иметь вид
-2р-
(/^)
¦ = ^0 +
С\
[FB)-7^@0)p-l " ' FB)
Общее решение краевой задачи запишется так:
Х(г) С /W Г 1 . J
I
... +
С2р-\
ФB) =
2л/
Iti-i ^'^^ LT--2 т —a + 2j
сГт + Со +
+ с,2(а-2)+ ... +С2р-:22/'-^ (а-2J^-1
(здесь постоянные сла* заменены на са).
При вычислении интеграла нужно помнить, что для Х+(т) на различных
участках кривой L берутся различные выражения (l на Lq и (а — т)"^^ на
4') **)•
*) Простейшая функция 2 + о)B) не может быть использована, потому
что она обращается в постоянную.
**) Может показаться, что имеем интеграл с разрывной плотностью. На
самом деле это не так. Если внести ХB) внутрь интеграла и рассматривать
плотность —т / (т^)» то, как легко видеть, она будет вести себя при
переходе через концы участков Lq, L^ как непрерывная функция.

546 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ VH
Если /7^0, решение будет иметь вид
Ф(,)^Х(?1С_Ц1)- ^ 1^— ,,.
2ш J Х^(т) т2-22-а(т-2)
Lo
причем в случае /? < О должны выполняться согласно общей теории —2р
условий разрешимости. Последние можно получить путем разложения Ф(г)
в ряд по степеням F (г) = —т- г-.
2. ^Сь ~"~ Z)
Легко проверить справедливость равенств
2ni J X"*" (т) F (т) F(x)-F(z) f->l
Lo /¦•1
1 С Мт) Г(т) ,,
С, = \ г; 7П "Т.
Для разрешимости задачи необходимо и достаточно, чтобы
Используем решение краевой задачи для решения исходного интегрального
уравнения. Имеем
Z (О = [а (/) + М01 Х+(О =/-^х+(/).
Общее решение интегрального уравнения можно представить в виде
) х+
(г2Р-1)х+{0 с f(T) 2т-а
Й^7~Г 72—^2 ^ г dr +
2ш i^J^j Х^(т) r'-t'-a(x-t)
+ у (/-2" - 1) Х+ {/) к + с,< (а - /) + ... + С2р-,/2р-' (а - О'""'].
При р < О для разрешимости уравнения должны выполняться —2р
условий
Bт - а) [т (а - т)]^-^ ^т = О (/=1,2,...,- 2р).
51.6. Случай, когда вспомогательная аналитическая функция
не обращается на бесконечности в нуль*). В ядрах
рассмотренных интегральных уравнений брались дополнительные члены
вида —^—1—г. Благодаря этому вводимые вспомогательные
функции Ф{г), так же как и интегралы типа Коши, обладали
*) Исследования этого пункта изложены по работе И. А. Парадоксе-
вой 3).

§ 511 УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 547
свойством ф(оо) = 0. Это позволяло на основе обобщенной
теоремы Лиувилля выписать общее решение, в котором все
слагаемые многочлена Py,^\{F) представляют собой линейно
независимые решения однородного уравнения. Если указанные
дополнительные члены исключить из ядра, то появляются осложнения
с выделением действительно линейно независимых решений.
Рассмотрим коротко этот случай.
Итак, пусть интегральное уравнение имеет вид
^(^)Ф^ + -1^3Е хЛ (t) Vb)dr = f{t). F1.120
Соответствующая вспомогательная аналитическая функция
запишется в форме
Здесь приходится различать два существенно различных
случая.
Г. Подстановки группы целые. В этом случае, как
вытекает из свойств автоморфных функций, функция Ф (г) имеет
в бесконечно удаленной точке один простой нуль в каждой
фундаментальной области. Отсюда легко получить*), что формула
E1.23) и в данном случае дает общее решение, содержащее х
линейно независимых решений.
2^ Подстановки группы дробные. В этом случае
2 щ{г)ф const и F{z)^==^Yi ®*(^) можно принять за основ-
ную функцию группы.
При разложении Ф(г) в ряд в окрестности бесконечно
удаленной точки свободный член этого разложения будет
задаваться следующим образом:
fe-OL *
Если последний интеграл при подстановке в него общего
решения интегрального уравнения тождественно обращается
в нуль при произвольных значениях входящих сюда параметров,
то рассматриваемый случай ничем не будет отличаться от
рассмотренного выше и общее решение снова будет даваться
формулой E1.23).
*) Здесь нужно учесть, что бесконечно удаленная точка есть
неподвижная точка группы (см. рассуждения при решении примера 51.6).

548 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ VII
Предположим теперь, что интеграл E1.32) не обращается
тождественно в нуль. Тогда ф(ооO^0 и в решении краевой
задачи и интегрального уравнения многочлен Ях-i нужно
заменить на Р^. Таким образом, в общее решение будет входить
X + 1 параметров. Однако не все они будут независимыми.
Между ними, оказывается, существует линейное соотношение.
Перейдем к его выводу.
Сохраняя прежние обозначения, выпишем для
рассматриваемого случая решение краевой задачи и особого интегрального
уравнения
0{z) = X{z)[W{2) + P^{F)l E1.33)
^^t) = ait)fit)^bmit)f^
+ b{t)Z{t)P^{F). E1.34)
Для получения искомого линейного соотношения подсчитаем
значение Ф(оо) двумя способами. Один раз из решения E1.33)
краевой задачи, другой раз из самого определения ФB)
(формула E1.32)), подставляя в последнее ф@ из решения E1.34)
особого уравнения.
Учитывая, что каноническая функция имеет на бесконечности
нуль порядка >с, а F'*= 2:+ X! щ{^)\ —полюс такого же
порядка, и обозначая с^ коэффициенты многочлена Р^, из E1.33)
найдем
Ф (оо) = lim [Х (г) c^F"" (z)] = ао^, E1.35)
2>оо
где
а= lim [2>«Х(г)].
2->оо
сравнивая E1.32) и E1.35), получим равенство
Ч^'^'ШЬ ] т-со,(оо) ^^ -
L fe-OL '^ J
n—l р г-
=-25-Езт-Глоо)И^)^(^)-
fe-OL * L
b (tVZ (
ni
Если коэффициент при с^^ не обращается в нуль, то
последнее соотнощение позволяет выразить параметр Су^ через осталь-

§ 51] УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 549
ные. Вставляя найденное отсюда значение Су^ в формулу E1.34),
получим общее решение, содержащее х линейно независимых
параметров.
Пусть теперь коэффициент при с^ равен нулю. Докажем, что
соотношение E1.36) не может удовлетворяться тождественно и
что, следовательно, один из параметров ^о, ^ь . •., с^_^ можно
выразить через остальные. В самом деле, при сделанном
предположении равенство E1.36) может быть записано в виде
2ш Z-I J т —©^.(оо)
k-OL '^
Если допустить, что последнее равенство удовлетворяется
тождественно, то это будет означать, что Ф(оо)= О, что
противоречит первоначальному предположению. Таким образом, во
всех случаях общее решение содержит х линейно независимых
параметров.
51.7. Дополнительные замечания. Нами рассмотрен здесь лишь один
простейший тип полного особого интегрального уравнения, разрешаемого в
замкнутой форме. В работе Ф. Д. Гахова и Л. И. Чибриковой 1) дано
решение еще ряда других типов, поддающихся решению аналогичными
методами. Уравнения эти можно разделить на две группы: первая — уравнения,
решаемые, так же как и в п. 51.4 (см. задачу 6 в конце главы), с помощью
автоморфных функций; вторая — уравнения, решение которых производится
с помощью более сложных функций, именно функций, приобретающих при
преобразовании группы некоторые множители. К последней группе
принадлежат известные уравнения, использованные Т р и к о м и [26] и А. В. Б и-
цадзе 1) при решении краевых задач для уравнений смешанного типа (см.
задачи 8 и 9).
Читателю, желающему подробнее ознакомиться с вопросом, можно
обратиться к упомянутой выш# работе Ф. Д. Гахова и Л. И. Чибриковой. Однако
следует предупредить, что в этой работе имеется одна существенная
неточность. Ядра интегральных уравнений берутся там без членов т—г-,
Т @^ @0)
и поэтому соответствующие автоморфные функции, вообще говоря, не
обращаются на бесконечности в нуль. Изложенное в предыдущем пункте
исследование зависимости между к -\- 1 входящими в общее решение параметрами
там не проведено. Поэтому число линейно независимых решений, указанное
в этой статье, на единицу больше действительного их количества.
Сделаем еще два замечания.
1®. Если Lq — разомкнутая кривая, то и все эквивалентные кривые Lh
будут тоже разомкнутыми. Здесь возникают обычные вопросы о классах
решений. Если концы кривых Lk не совпадают между собой, то вопрос о
допустимых классах решается совершенно так же, как и в случае
характеристического уравнения, заданного на сложном контуре (п. 44 3) Если же концы
совпадают, то особенности могут налегать друг на друга и решение,
построенное для каждой простой составляющей кривой в классе интегрируемых
функций, может оказаться неинтегрируемым. Поэтому в этом случае требуется
дополнительное исследование (см. п. 44.4).
2®. Чтобы не усложнять дело, мы считали контур Lo, на котором задано
уравнение, простым. Не предстарит осложнений случай, когда Lp есть

650 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
совокупность замкнутых и разомкнутых кривых, имеющих конечное число
точек пересечения.
Об обобщениях на случай бесконечных групп мы скажем в следующем
параграфе.
§ 52. Уравнения с автоморфными ядрами
с бесконечной группой*)
Естественно сделать попытку обобщить постановку задачи на
случай бесконечной группы. Как показывает исследование, было
бы затруднительным сделать это обобщение, исходя из
предыдущих формул, путем перехода к пределу. Проще для случая
бесконечной группы формулировать задачу заново так, чтобы
случай, рассмотренный ранее, входил как частный. Начнем с
постановки краевой задачи. Для простоты ограничимся случаем
замкнутого контура.
52.1. Краевая задача Римана. Пусть D — одна из областей,
целиком состоящая из обыкновенных точек некоторой
функциональной группы дробно-линейных преобразований:
щ{г)^г, ©1(г), ©2B), ...,
и пусть Lo есть некоторая гладкая замкнутая кривая, целиком
расположенная в области D, Обозначим L/i (fe = 1, 2, ...)
кривые, эквивалентные Lo, т. е. кривые, в которые переходит
кривая Lo при преобразованиях группы. Будем считать, что
кривые Lh не налегают друг на друга, хотя и могут пересекаться.
Назовем функцию ФB), определенную в D, кусочно
аналитической автоморфной функцией, если она обладает
следующими свойствами:
1. Автоморфна относительно подстановок группы:
Ф[ф,(г)] = Ф{г).
2. Аналитична во всех точках области D, кроме точек
контура L = Lo -f Li + • • •
3. Непрерывно продолжима на каждую точку контура L, за
исключением точек самопересечения, вблизи которых она огра-
HH4wa.
Задача Римана состоит теперь в том, чтобы найти кусочно
аналитическую автоморфную функцию Ф(г), удовлетворяющую
на кривой Lo краевому условию
0Ut) = G{tH-'{t) + g{tl E2.1)
где 0{t), g(/)—заданные на Lo функции, удовлетворяющие
условию Гёльдера, причем 0{1)Ф 0.
*) Содержание этого параграфа взято из работы Л. И. Ч и б р и к о-
вой 2).

§ 521 УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 551
Кривые Lh для функции 0(z) будут также линиями разрыва.
Аналогично тому, как это делалось в § 51, легко было бы
составить для них краевые условия. Однако в этом нет
необходимости, так как решение, которое далее получим, учитывая
краевое условие E2.1) и автоморфность искомой функции, будет
автоматически удовлетворять краевым условиям на всем
контуре L
Приступим к решению сформулированной задачи. В его
основе, как и в обыкновенном случае (§ 14), лежит задача о скачке
0^(t)-0-{t) = g{t). E2.2)
Обыкновенный интеграл типа Коши не даст ее решения, так как
не будет соблюдено требование автоморфности. Построим
аналог интеграла типа Коши для автоморфных функций.
Пусть F{z)—основная автоморфная функция группы,
имеющая в фундаментальной области R полюс (простой) го, и g{t) —
заданная на контуре Ц функция, удовлетворяющая условию
Гёльдера. Построим интеграл
^(^)-wSg(^)F(x)-F(.)^^- E2.3)
Он определяет кусочно аналитическую автоморфную функцию,
имеющую линию разрыва Lq и обращающуюся в точке го
(а также и во всех эквивалентных ей точках) в нуль. Ядро
интеграла может быть представлено в виде
где Q — непрерывная на Lq функция. Отсюда легко вытекает,
что для предельных значений Ф(г) на Lq будут справедливы
формулы, аналогичные формулам Сохоцкого D.9), D.10):
Ф^О-Ф-@ = 5@,
и
Следовательно, интеграл E2.3) дает решение задачи о скачке
E2.2) в классе кусочно аналитических автоморфных функций,
обращающихся в точке Zq в нуль. Решение задачи с нулевым
скачком и нулем в точке zq будет в силу теоремы об
аналитическом продолжении и свойств автоморфных функций
тождественным нулем. Отсюда следует, что решение E2.3) в
рассматриваемом классе будет единственным.

552 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
Канонической функцией Х(г) задачи E2.1) назовем авто-
морфную функцию, удовлетворяющую однородному краевому
условию
X-^(/) = G(/)X-@
и имеющую всюду в фундаментальной области R нулевой
порядок, за исключением точки Zo, где она имеет наибольший
возможный порядок X, равный индексу G{t). Легко показать, что
каноническая функция с точностью до постоянного множителя
определяется формулой
Х(г)=[^(г)-/^(/о)]"'^^Ч E2.5)
где F{z)—введенная выше основная автоморфная функция
с простым полюсом в Zo,
r(-) = iJlnG(r)^^^y^dT; E2.6)
to — начальная точка интегрирования в последнем интеграле
(ср. п. 44.2).
Обычными рассуждениями получим общее решение задачи
E2.1) в виде
0{z) = X{z)[W{z) + PJF)l E2.7)
где
Чг (^) = _L С ^ifiL _ILi±_ dr^ E2.8)
^ 2я/ J Х^ (т) F{x)-F(z) ' ^ '
X{z) определяется формулой E2.5), Р^ — произвольный
многочлен степени к.
Если на искомое решение накладывается условие Ф (zq) = О
(что встретится при решении особого уравнения), то Р^ нужно
заменить на Рх-ь
Если в последнем случае х ^ О, то нужно положить P^-i^O,
причем при X < О должны выполняться условия разрешимости
\^^[F{x)]'-'r{x)dx = 0 (/=1,2 -«). E2.9)
J Л (т)
Последнее получается разложением интеграла E2.8) в ряд по
степеням F{z) и приравниванием нулю первых —х
коэффициентов этого разложения.
Формулировка и решение задачи для случая разомкнутых
контуров не представляют никаких трудностей.

§ 52] УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 553
52.2. Особое интегральное уравнение. Рассмотрим особое
интегральное уравнение
а (t) Ф (О + -^ S Ш^ ^ (^) dr = f (t), E2.10)
и
где, как обычно, заданные функции a(t), b{t)y f{t)
удовлетворяют условию Гёльдера, а Lq, F{t) означают то же, что в п. 52.1.
Вводя кусочно аналитическую автоморфную функцию
'^^'^=ш\р^)Упг)^(-)^х E2.11)
ц
и используя формулы E2.4), придем к краевой задаче Римана
Ф*(t) = G{t)ф-{t)+g{t), E2.12)
рассмотренной в предыдущем пункте. При этом в силу свойства
основной автоморфной функции F(z) (простой полюс в Zq)
функция Ф{г) должна удовлетворять дополнительному условию
Ф(го)=0.
Воспользовавшись полученным в п. 52.1 решением краевой
задачи E2.12), по формуле Сохоцкого
Ф@ = ф-'@-Ф"@
получим решение интегрального уравнения E2.10):
(f{t)^a{t)t{t) -.— ] 2(T) F(T)^F(t) ^^ +
+ 6@Z@P^-i(f), E2.14)
где
Z @ = [a (t) + b it)] X+ @ = [a it) - b {t)] X" (/) =
= [F{t)^F{to)r''e^<'\ E2.15)
Если X ^ 0, нужно положить Яи-1 ^ 0. При x < О должны
удовлетворяться условия разрешимости
^2r^[F{'t)]^-'F^{x)dx = 0 (/=1, 2, ..., ~х). E2.16)
С fM
to
Рассуждения, необходимые для получения последних
формул, вполне аналогичны использованным в п. 51.4.
В заключение заметим, что если группа окажется конечной,
то исследуемое здесь уравнение E2.10) обратится в изученное
в предыдущем параграфе уравнение E1.12).

554 УРАВНЕНИЯ РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ VII
52.3. Некоторые приложения. На первый взгляд может
показаться, что автоморфные функции есть весьма специальный
класс, встречающийся лишь в исключительных случаях. Это
совсем не так. Автоморфными функциями являются обыкновенные
периодические функции, а также двоякопериодические.
Следовательно, такие употребительные в анализе и его приложениях
функции, как показательные, тригонометрические и
гиперболические, принадлежат к этому классу; ими же являются
наиболее употребительные из высших трансцендентных —
эллиптические функции. К таким функциям приводят различные
периодические и двоякопериодические процессы, происходящие в
природе. Отсюда проистекает обилие приложений, которые имеет
изложенная теория. Укажем некоторые из них, в первую
очередь математические.
Г. Задача Римана для периодических
функций. Найти кусочно аналитическую периодическую с периодом
2я функцию Ф(г), предельные значения которой на гладком
замкнутом контуре L, целиком находящемся в полосе периода,
удовлетворяют краевому условию:
ф-^(/) = О@ф-@ + г@, E2.17)
где G{t), g{t), как и выше, удовлетворяют условию Гёльдера и
G@?=0.
Группа преобразований здесь порождается подстановкой
0I B) = Z + 2я. Фундаментальной областью является
вертикальная полоса шириной 2я, например полоса О ^ Re 2 ^ 2л.
Основной автоморфной функцией здесь служит е^^ = е-Уе^^. На
верхнем конце полосы она обращается в нуль, а на нижнем
имеет простой полюс*). (Нижний конец полосы играет роль
точки Zq.)
Согласно формуле E2.3) решение задачи о скачке
ot{t)-or{t) = g{t)
дает функция
Ф.(.)=^] S(r)J^ = ^\ ,(x)[ctg:L=:? + /]d., E2.18)
имеющая на нижнем конце полосы периодов нуль первого
порядка. Каноническая функция, согласно E2.5) и E2.6),
*) Бесконечно удаленная точка является для целой функции е^'*
существенно особой и при у-^ оо она имеет полюс бесконечно большого порядка.
Но бесконечно удаленная точка принадлежит всем фундаментальным
областям. Поэтому порядок полюса должен быть распределен между всеми ими.
Из общего свойства основной автоморфной функции принимать каждое свое
значение один раз следует, что в нижнем конце каждой полосы периодов
порядок полюса нужно считать равным единице. То же справедливо и для
порядка нуля в верхнем конце полосы.

^ S2t УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 555
определится выражением
X{z) = {e^'-e"')e^^'\
^ (^) = ^ J '" ^ (^) ctg-b=^ dt. F2.19)
L
Общее решение задачи, согласно E2.7), E2.8), получаем в виде
Ф (г) = X (Z) I J ^^ [ctg ^ + /] dr + Р, (в'-)}. E2.20)
L
Если ищется решение, обращающееся на нижнем конце полосы
в нуль, то Py^ нужно заменить на P^_i. В этом случае при х ^ О
нужно положить Py^^\ ^ О, причем при X < О должны
выполняться условия
$ЗР^«'''*""^'^ = 0 (*=1, 2, .... -X). E2.21)
2°. Задача Гильберта в периодических
функциях для полуплоскости. Найти функцию F{z)=u + ш,
аналитическую в верхней полуплоскости и имеющую период 2я
по граничному условию
а (х) и{х) + Ь {х) v{x) = c {х\ E2.22)
где а(х), Ь{х), с{х)—2я-периодические функции.
Методом п. 30.2 сводим последнее условие к условию задачи
Римана:
^ ^ aix) — lb (х) ^ ^ ' а (д:) — tb (х) ^ '
Относительно кусочно аналитической функции Ф+(г)=^B:),
ф-B)= f (г), удовлетворяющей в силу последних соотношений
условию
ф-B) = ф+(г), E2.24)
краевое условие E2.23) можно считать заданным на отрезке
[О, 2я]. Применяем формулы E2.19). Обозначая
arg(a + /&) = arctg4|j- = e@,
будем иметь
Г(г) =
2п 2я
-IS l"[-SI]='8T^'"-l!r$ [2e(x) + »lctg^^.

556 УРАВНЕНИЯ. РАЗРЕШИМЫЕ 6 ЗАМКНУТОЙ ФОРМЕ ГГЛ. VII
Начальная точка интегрирования здесь to = 0. Вводя в
каноническую функцию E2.19) постоянный множитель С и подбирая
последний согласно условию X(z)=X{z)y будем иметь
с учетом E2.24) решение задачи получим в виде
[2я
JLf ?JT) ^i l^Z±dT +
2ш J X+ (t) [a (T) - ib (t)] ^2 ^
+ Y, Ы cos kz + ^k sin kz) . E2.25)
k-o J
При X < 0 в решении нужно отбросить последнюю сумму.
Кроме того, должны быть удовлетворены условия
2я 2я
С (т) COS kx . Г с (т) sin kx . ^
X"*- (т) [а (т) - ib (т)] '^ """ J Х+ (т) [а (т) - /6 (т)] ^ ""
о о
(* = 0, 1, ..., --Х—1).
3"^. Смешанная краевая задача аналитических
функций в периодических функциях для
полуплоскости. Рассмотрим решенную в п. 46.3 смешанную
задачу. Определить аналитическую в верхней полуплоскости
функцию F(z) = и + iv по краевому условию
u = f{t) на L'=Z «А,
t' E2.26)
v = h{t) на L'' = 2 ^л«й+1
л-1
При условии, ЧТО заданные интервалы а^&й, Ь^а/ц-! (й = I, 2, ...
..., /п) лежат на отрезке [О, я] и что искомая функция
периодически продолжается с периодом я.
Поступая совершенно так же, как в п. 46.3, придем к
краевой задаче Римана
где
Git) = -l, g{t) = 2f{t) на L\
G t)^l, g@ = 2A@ на L'\

§ 52] УРАВНЕНИЯ С АВТОМПРФНЫМИ ЯДРАМИ 557
ДЛЯ кусочно аналитической периодической с периодом я
функции ФB), удовлетворяющей условию Ф{г) = Ф(-г).
Для рассматриваемого случая основная функция в^Ч Будем
иметь
О
1 А г 1 гт sin (г-6.)
= 2SrS 5 nictgir-z)dr = ^ln]l -rF=4-
fe-1 a^j fe-1 ^ '^^
В классе функций, ограниченных в Ь^ и интегрируемых в а^,
каноническая функция запишется так:
Решение задачи в указанном классе дает формула
ФB)=
=1 л/п S^ [z iVn?^''Wc.g(,-.).,+
+ S S Vn ж|^^(^)«=*б(--^)^- + ^ • E2.27)
где ao — произвольная действительная постоянная.
Аналогично можно получить решение в других классах.
4°. Отыскание потока, обтекающего
периодическую решетку. Дадим одно механическое приложение
рассмотренной теории. Пусть в плоскости z дана решетка
профилей, образованная р рядами отрезков, для которых у = тпу
ak<x <bh (^ = 1, 2, ..., р; m = О, ±1, ±2, ...), и ? рядами
отрезков, для которых
У^2п+]_^^ ^/<^<^У (/=1, 2, ..., q; n = 0, ±1, ±2, ...),
обтекаемая потенциальным потоком несжимаемой жидкости.
Определение функций скоростей потока сводится *) к
определению функции Ф{г)=и — iVy удовлетворяющей следующим
условиям:
*) См., например, Л. И. Седов, Плоские задачи гидродинамики и
аэродинамики, Гостехиздат, М., 1950 г.

558 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ VH
а) Ф{г)—кусочно аналитическая периодическая с периодом
7ii функция с линией скачков
б) Ф(+сх)) = 0, Ф(—оо) конечно;
в) в точках Uky Cf + ^F (z) конечна, в точках bk, rf/ + -у-
интегрируема;
г) на L мнимая часть Ф(г) должна принимать при подходе
к L сверху и снизу заданные значения
t;+ = f+(^), ^"^f-^t) на L, E2.28)
причем на конце значения f+@ и /"(О совпадают.
Сформулированная задача есть рассмотренная в п. 46.4
задача Дирихле для плоскости со щелями с дополнительным
условием периодичности и с тем несущественным различием, что
вместо действительной части и задается мнимая часть v.
Вводя аналогично п. 46.4 функции
^{г) = -^[Ф{2) + Ф{гI а(^) = ^[Ф(г)-ФB)],
придем для ^ к рассмотренной выше смешанной задаче, а для
Q к задаче определения аналитической (периодической)
функции по заданной на L мнимой части \т Q(t) = f+(t) — /"(/).
Основной функцией будет в^^ Функция Q определяется
формулой
, B) = J- ( 2/в^МГ(т)-Л(т)]./т _
2я/ ^J
2ш- J е^^'-е^'
Qi
= -^ J [/"" (т) - Г (т)] [cth (т -- 2) + 1] dx. E2.29)
Для функции ^{z)
г (Z) = 2^7" S In (-I) cth (т - 2) rfx =
- 2 '" [И sh (г - а,) 11 ch (г-е,)\'
Отсюда каноническая функция в требуемом классе функций
будет иметь вид

§ 52] УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 559
Решение смешанной задачи определится формулой
ЦТ B) = JZAM С ^^^У/7'^ [cth (т - 2) + 1] dr. E2.30)
271 о А (Т)
Решение поставленной задачи дается суммой полученных функций
0B) = 4^B) + QC). E2.31)
Рассмотрим еще пример на использование эллиптических
функций.
5°. Задача Римана для четной эллиптической
функции. Для двоякопериодической функции с периодами оь
0J одной из фундаментальных областей будет параллелограмм
с вершинами О, (Оь coi + 0J, С02. Основной автоморфной функцией
будет функция Вейерштрасса f{z). В вершинах
параллелограмма периодов она имеет полюсы второго порядка. Одну из
эквивалентных между собою вершин, например г = О, примем
за Zq. Контур L будем считать простым гладким замкнутым,
лежащим внутри параллелограмма периодов. Решение задачи Ри-
мана производится целиком по схеме п. 52.1.
Решение задачи о скачке определится формулой
Каноническая функция задается выражением
а общее решение для % ^ О запишется в виде
^ 2Ш U Х-^Ст) ^(т)-~^(г) ^ ^^^ \ п^ \ J
L
Если X < о, то нужно положить Р^ ^ о, для X < — 1 должны
выполняться следующие условия разрешимости:
t-^S>^-4T)r(t)dT = 0 {/5 = 1,2,..., -х-1).
Случай двоякопериодической функции имеет особенности по
сравнению со случаями автоморфных функций, рассмотренных
ранее; именно здесь отсутствует основная автоморфная функция,
имеющая в фундаментальной области один простой полюс.
В силу этого произвольная двоякопериодическая функция выра

560 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VH
жается рационально не через одну, а через две двоякопериоди-
ческие функции (р и ^0- По этой причине решения задачи
Римана для случаев четной или нечетной и произвольной двоя-
копериодических функций существенно отличаются друг от
друга.
Мы ограничимся здесь рассмотренным случаем четной
функции. Решение для двух остальных случаев, а также решение
ряда других задач с использованием периодических и двоякопе-
риодических функций можно найти в работе Л. И. Чибрико-
вой 2) (см. задачи 10, 11 в конце главы). В следующем
параграфе, где в общем виде будет поставлена равносильная краевой
задаче в классе автоморфных функций краевая задача на рима-
новых поверхностях, станет ясней причина возникающих для
краевых задач в классе эллиптических функций затруднений:
ранее приходилось иметь дело с автоморфными функциями
нулевого рода, здесь впервые встретились функции первого рода.
52.4. Интегральное уравнение с неосновной автоморфной
функцией. Рассмотрим интегральное уравнение
а (/) Ф (О + ^ 5 я(тТ~Я@ Ч^ (^) ^^ = ^ (^)^ E2-33)
и
где, в отличие от уравнения E2.10), входящая в ядро автоморф-
ная функция H(z) принимает в фундаментальной области R
каждое свое значение не один, а v раз.
Введем кусочно автоморфную функцию
Ф(^)=2киы-Я(.)Ф(^)^^- E2.34)
и
Она будет обращаться в нуль в v точках Zi,..., ev (кратный
нуль повторяется столько раз, какова его кратность), где H{z)
имеет полюсы. Знаменатель ядра Я(т)— Н{г) для каждой точки
t е Lo будет обращаться в нуль v раз.
Поэтому Ф(г) будет иметь в фундаментальной области v
линий разрыва, именно Lq и v— 1 кривых Lo\ ..., 1(Г"^\
уравнения которых определяются в неявной форме решением
уравнения
H{z) = H{x) (т^/.о). E2.35)
Если Ч^(г) обозначает функцию, обратную H{z), то
уравнения контуров Lfe^(/ = 0, 1, ..., V —1; fe = 0, 1, 2. ...) будут
задаваться ветвями 4^k многозначной функции Ч^:
z = ^l'[H(x)] (TsLo; /=0, 1, ..., v-1; k=0, 1,2, ...). E2.36)

§ 521 УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ 561
Предположим сначала, что точки ветвления функций Wk\z)
не лежат внутри контура Lq. Тогда все контуры ЬЦ^ будут также
замкнутыми.
Из самого определения 4fk^(H{}?k\t)]^t) вытекает
H{z) = H{wT[H{z)]} = H{zy
Следовательно, функция H{z) будет автоморфной не только
относительно заданной группы m{z) линейных преобразований,
но также и относительно группы *) преобразований
(нелинейных) W^P[H{z)l
На контуре Lq для предельных значений Ф(г) будут
справедливы формулы, аналогичные E2.4),
Ф^@-Ф~(О = Ф@,
Используя их, обычным путем придем на Lq к краевой задаче
Римана
Ф^(/) = С(Оф-@ + г@, E2.38)
G = ^, S=^^ E2.39)
Составлять краевые условия для остальных линий разрыва Lo\
лежащих в R (так же, как и для эквивалентных им, лежащих
в других фундаментальных областях), нет нужды, так как
решение краевой задачи E2.38) с учетом автоморфности его
относительно всех преобразований группы автоматически
удовлетворит краевым условиям на всех линиях разрыва.
Существенное отличие решаемой здесь задачи от
соответствующих задач, решенных ранее, заключается в том, что
искомая функция Ф(г), в силу представления E2.34), должна быть
функцией от Я (г).
Выразив решение задачи о скачке (частное решение
неоднородной задачи) интегралом вида E2.3), мы автоматически удо
влетворим этому условию. Если, кроме того, общее решение
однородной задачи в случае положительного индекса взять в форме
многочлена от функции Я (г), то будут удовлетворены все
условия. С учетом этих обстоятельств, поступая аналогично тому,
как это делалось в предыдущем, получим решение краевой
задачи, а затем по формуле E2.37) и решение исходного уравне-
*) То, что преобразования Wj составляют полную группу, вытекает из
того, что ими исчерпываются все особые линии Lq , лежащие в
фундаментальной области.

562 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ 1ГЛ Vtl
ния E2.33). Выпишем последнее, считая, как обычно, с? — Ь^ =
= I:
+ 6@2@^4-1 (Я). E2.40)
где
Z (О = Х+ (О \а (О + Ь @] = Х- (/) \а Ц) - b (/)],
ХB) = [Я(г)-Я(<оI-'еГ<^\ E2.41)
и
to — начальная точка интегрирования контура Lq.
Если контур Lq разделяет точки ветвления функций Ч^^^ так,
что часть их содержится внутри контура, а часть вне, то кривые
Lq^ будут разомкнутыми. Однако это не вносит в решение
каких-либо осложнений. Особенностью решения краевых задач и
интегральных уравнений для разомкнутого контура, как
известно из гл. VI, является то, что здесь возможны решения
различных классов, именно ограниченные и неограниченные на
концах. Но в данном случае разомкнутые контуры Lo эквивалентны
замкнутому контуру Lo, на котором решение непрерывно и,
следовательно, ограничено. Отсюда в силу эквивалентности на
контурах Lo^ возможен лишь один класс ограниченных решений.
Решение уравнения и в этом случае выражается формулами
E2.40), E2.41). Относительно случая, когда контур Lo есть
разомкнутая линия (или даже совокупность разомкнутых
линий), можно сказать то же, что и в замечании Г п. 51.7.
52.5. пример. Рассмотрим интегральное уравнение
где Lo — окружность | 22 — 1 | = 1, F (z) = ^ .— основная автоморфная
функция группы ©о B) = Z, ©1 (z) = _ I .
фундаментальными областями группы являются внешность и
внутренность окружности |2г — 1|= 1. Внешность, где расположен контур Lo,
назовем /?о, а внутренность Ru Автоморфная функция ядра H{z)=F^(z) имеет
полюсы второго порядка в области Rq в бесконечно удаленной точке, а в
области /?1 — в точке 2 = 1/2.

§ 52] УРАВНЕНИЯ С АВТОМОРФНЫМИ ЯДРАМИ
Вспомогательная кусочно автоморфная функция
563
''^'^-ш\н("'-н(г)<^^'^''
имеет в Ro нуль второго порядка в бесконечно удаленной точке. В каждой
фундаментальной области ФB) имеет по две особые линии; их уравнения
следующие:
ъ Ro\ г = т,
2т— 1
в /?,:
2т-1
(т е Z,o),
(т е Lo),
(io)
D")
(^-i)
, = yU)(^) = Zlli±ig^l+2lZLL
(fs^-o)-
W")
Преобразования ^^q\ ^j^^ являются ветвями многозначной функции
[^Bг — 2) + 2^]^ —^(г^ + 2z — I) = О, точками ветвления которой являются
точки г = —1±л/2. Они лежат вне Lo, поэтому все контуры здесь
замкнутые.
Краевое условие на контуре Lo имеет вид
V 2/-1 ; B/-i)^
На остальных трех контурах краевые условия могут быть получены заменой
переменных.
Так как число линий разрыва Ф(г) конечно, то каноническую функцию
можно найти как произведение канонических функций для каждого из
простых контуров. Для Lo каноническая функция может быть найдена по
способу п. 14.6. Будем иметь
^+,, P^(z) r^~B"-V2")'
Х^ (z) ¦¦
х-(г) =
=[¦
2г— 1
1
¦]¦
P+(z) 2-B + V2^
Для остальных контуров канонические функции могут быть найдены заменой
переменных, исходя из свойства автоморфности. (Еще проще найти их по
тому же способу п. 14.6.) Контуры Lq, L^q\ Lj, LJ^^ разбивают плоскость на
пять областей: D^, dJ)^>+, D+, D^^^^, D"" = D^ .DJ,^^"-Df .D^/^"". Для всей
совокупности областей каноническую функцию получим в виде
Х(г) =
Г 1-22 1^
L 22 -f 42 - 2 J •
г 22-1 ^
122-42 +2 J •
г 22-1 Y
L B2 + 42-2) B2 -. 42 + 2) J '
z^D^.Dt,
VI)+
» ^1
A) +
D'.

564 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ ГГЛ VIl
Каноническая функция при х>0 имеет нули порядка 2х в точках 2 = 1/2, оо.
Ф (z)
В фундаментальной области Rq функция ^ ' . имеет при и>0 полюс порядка
2х — 2 в точке z = оо. Исходя из этого, получим решение краевой задачи
ф (,) = хм С __1A) -^^lliqiL .г + Х (г) Р,_, If ^ (г)].
ц
Решение исходного уравнения будет иметь вид
•Р^^ I ^1,<2_4/ + 2; J 2B<-1)''
+ \P + 4t-2) V ~ \t'-4t-2) J ^
W J_ Г /(т) 2F(T)F(T)dT
2Я/ J Х+ (Т) Bт - 1)" f 2 (^) _ ^J2 (^)
в случае х<0 нужно положить P^-i ^ ^' Решение будет существовать, если
будут выполнены условия
§ 53. Краевые задачи на римановых поверхностях
Рассмотренные в предыдущем параграфе краевые задачи в
классе автоморфных функций тесно связаны с краевыми
задачами для областей, расположенных на римановых поверхностях.
Точнее говоря, в случае римановых поверхностей
алгебраических функций (так называемых компактных поверхностей) оба
класса краевых задач равносильны.
Прежде чем перейти непосредственно к краевым задачам,
приведем схематически важнейшие для наших целей свойства
римановых поверхностей.
53.1. Некоторые сведения о римановых поверхностях, п-знач-
ная алгебраическая функция w = w{z), определяемая
неприводимым уравнением
аоB)ш"+ ... +an^i{z)w + an{z) = 0,
коэффициенты которого многочлены от г, может быть
рассматриваема как однозначная, если аргумент z считать
изменяющимся на некотором геометрическом многообразии, называемом
римановой поверхностью (Р. П.) этой функции. Точное
определение Р. П. и их теория опираются на сложный математический

§ 53] КРАЕВЫЕ ЗАДАЧИ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 565
аппарат: топологию, теорию алгебраических функций и абеле-
вых интегралов, автоморфных функций и др. Мы не
предполагаем у читателя таких знаний и поэтому в последующем будем
опираться только на наглядные представления и аналогии с
теорией однозначных аналитических функций.
Р. П. изображается двумя равносильными способами:
1) п листами обычной плоскости, скрепленными вдоль
разрезов, соединяющих точки ветвления (поверхность наложения).
Об этом уже шла речь в п. 3.3.
2) Пространственной поверхностью. Употребительны два
типа таких поверхностей: а) сфера с прикрепленными к ней
ручками, б) кренделеобразная поверхность с некоторым
числом дыр.
Все указанные способы задания топологически равносильны.
Пространственная форма Р. П. удобна тем, что на ней весьма
наглядно выражается ее важнейший инвариант —pod Р. П. Л.
В случае а) это число ручек у сферы, а в случае б) — число дыр
у кренделя*). В простейшем случае рода нуль Р. П.
топологически равносильна обыкновенной сфере. Характерная
особенность ее та, что любой замкнутый контур разбивает ее на
раздельные части. Пространственным изображением следующих
по сложности Р. П. рода единица будет в случае а) сфера с
одной ручкой (гиря), а в случае б)—тор (бублик). Здесь
можно провести пару замкнутых сечений, не разбивающих
поверхность на раздельные части, а превращающих их в одно-
связные области. Например, тор путем проведения сечений по
меридиональному и параллельному кругам и непрерывной
деформации можно превратить в прямоугольник с
отождествленными противоположными сторонами.
В общем случае поверхность рода h путем проведения h пар
так называемых канонических сечений можно превратить в
4/1-угольник с попарно отождествленными сторонами**).
В теории униформизации доказывается еще более
глубокий факт, именно, что любая компактная Р. П. рода Л,
рассеченная по 2Л каноническим сечениям, может быть с помощью
автоморфных функций отображена конформно на
фундаментальный 4Л-угольник автоморфной функции. В частности, Р. П.
нулевого рода отображаются рациональными функциями на
*) В случае поверхности наложения род Р. П. выражается через число
листов и точек ветвления. Если п — число листов, а v — число точек
ветвления, считаемых столько раз, какова их кратность, то род выражается
формулой Л=-^+1—л.
**) В общем случае можно определить род Р. П. как число пар
канонических сечений, которые нужно провести, чтобы превратить Р. П. в односвяз-
ную область.

566 УРАВНЕНРТЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VI!
обычную комплексную плоскость. Отсюда вытекает упомянутая
в начале параграфа равносильность краевых задач на Р. П. и
в классе автоморфных функций.
Подсчет числа линейно независимых решений краевой задачи
Римана на обыкновенной плоскости (§ 14) опирался на подсчет
числа линейно независимых рациональных функций, имеющих
в плоскости заданное число Ti полюсов, раздельных или
совпадающих. Число таких функций х+ I. (В § 14 фактически имели
дело лишь с частным случаем, когда задавался один полюс
кратности X на бесконечности.) С такой же проблемой
приходится иметь дело и в краевых задачах на Р. П. Однако здесь
она решается сложней. Из-за требования однозначности
искомой функции (обращение в нуль так называемых циклических
постоянных) входящие в нее произвольные постоянные должны
удовлетворять некоторой системе линейных уравнений. Поэто-"
му число линейно независимых рациональных функций
выражается формулой
r = x+l-L E3.1)
где I — ранг указанной системы. Одно из важнейших
предложений теории алгебраических функций — теорема Римана—Роха—
дает выражение для ранга g: 1 = h — t, где i — число так
называемых всюду аналитических абелевых дифференциалов A-го
рода), имеющих нули в тех точках, где искомая рациональная
функция имеет полюсы. Доказывается, что это число лежит в
пределах О ^ i ^ Л. Отсюда
г = >с+1-А + /. E3.10
Несмотря на кажущуюся полную определенность последней
формулы, в действительности точные результаты имеются лишь
для X = О, где I = Л, и X > 2Л — 2, где i = 0. Алгоритм
вычисления числа i настолько сложен, что практически число /
нужно считать неизвестным и, следовательно, г — числом
неопределенным. Этим задается и степень определенности числа линейно
независимых решений краевой задачи Римана (см. следующий
пункт).
Все сказанное относилось к замкнутой Р. П. Пусть задана
Р. П. с отверстиями, ограниченными простыми, взаимно не
пересекающимися кривыми; тогда она называется Р, П, с краем.
Из нее можно образовать новую замкнутую Р. П., так
называемый дубль данной Р. П.^
Для этого нужно к данной Р. П. по контурам отверстий
прикрепить другой экземпляр Р. П., тождественный с первым. Из
наглядных соображений можно подсчитать род дубля Р. П.
рода hem отверстиями. У двух экземпляров Р. П. будет 2h
ручек. Из т скреплений одно используется для образования из

§ 531 КРАЕВЫЕ ЗАДАЧИ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 667
двух раздельных экземпляров Р. П. единой поверхности.
Остальные т — 1 скреплений могут быть деформированы в ручки.
Таким образом, дубль имеет род 2Л + m— 1.
Рассмотренные Р. П. характеризуются тем, что на них можно
задать на любой замкнутой кривой одно единое для нее
положительное направление (например, против часовой стрелки).
Такие поверхности называются ориентируемыми или
двусторонними. Кроме них, существуют еще неориентируемые или
односторонние поверхности. Из них наиболее наглядно
представляемой, а потому наиболее популярной, является так называемый
лист Мёбиуса. Моделью общей неориентируемой поверхности
можно считать сферу с h ручками и с + т отверстиями, из
которых с заклеены листами Мёбиуса.
Полную теорию римановых поверхностей можно найти в
книге [25]. Ее первая глава содержит весьма популярное
наглядное изложение идеи Р. П. Еще более наглядное и
популярное (но в то же время глубокое) можно найти в гл. VI книги
Д.Гильберта и С. Кон-Фоссе н а «Наглядная геометрия»,
М., ОНТИ, 1936.
53.2. Краевая задача Римана. На Р. П. эта задача ставится
совершенно так же, как и на обычной плоскости. Контур в
общем случае может состоять из конечного числа замкнутых или
разомкнутых раздельных или пересекающихся кривых. Случай,
когда среди кривых контура имеются замкнутые, не
разбивающие поверхность на раздельные области, не представляет
исключения. Дело обстоит совершенно так же, как в п. 44.1:
строится функция, аналитическая всюду, кроме точек контура,
для которой Ф-@ — предельные значения на контуре слева и
справа (иногда в области могут в изолированных точках
допускаться полюсы). Путь решения также аналогичен изложенному
ранее для плоской области. Пусть, как и ранее, х = Ind G(t).
1. Решается задача о скачке с помощью специально
построенного аналога ядра Коши. (Способ построения последнего
основан на сложных теориях и не может быть изложен в
популярной форме.)
2. Строится каноническая функция. С помощью ее общая
краевая задача сводится к задаче о скачке в классе функций
с X допустимыми полюсами при х > О и с требуемыми —х ну-
лями при X < 0.
3. С помощью теоремы Римана — Роха подсчитывается
число линейно независимых решений при х > О или условий
разрешимости при X < 0. Выписывается явное решение задачи
через аналоги интеграла типа Коши.
Главная трудность, которую приходится преодолевать,
состоит в том, что для поверхности рода А > О нельзя построить
аналог ядра Коши, имеющий единственную полярную особен-

568 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ VH
ность. Наряду с «полезным» полюсом с главной частью l/(z—т)
он имеет еще h «паразитических» простых полюсов. Их в
дальнейшем приходится устранять. «Паразитические» полюсы
аналога ядра Коши для канонической функции являются
существенно особыми точками. Наличие их являлось главным
препятствием на пути решения краевой задачи. Оно было устранено
путем использования решения так называемой «проблемы обра-
имения Якоби» (см. [25], гл. VII).
Сформулируем результаты о числе I линейно независимых
решений однородной задачи.
Если X < О, то / = 0; если же к> 2h — 2, то / = х + 1 — h.
Случаи индекса О ^к^2к — 2 называются особыми. Здесь
l = K+l-l, E3.2)
где I — ранг некоторой матрицы, выражаемый согласно теореме
Римана — Роха формулой g = Л — L Можно выписать еще
точную оценку для /:
тах{0, х-Л+1}</<[у] + 1. E3.3)
Результаты для неоднородной задачи формулируются
значительно сложнее. Условия разрешимости здесь выражаются через
решение сопряженной краевой задачи, которая формулируется
как задача для аналитических дифференциалов. (Точных
формулировок мы не приводим.)
В заключение отметим, что употребленное выше
выражение— решение записывается в явной форме — нужно понимать
условно. Алгоритм построения аналога ядра Коши настолько
сложен, что уместнее говорить о теоремах существования, чем
об эффективном решении. Имеются лишь частные случаи, когда
явное выражение аналога ядра Коши удается построить.
Прежде всего, это случай Л = 1, когда этот аналог выражается через
эллиптические функции (см. раздел 5"^ п. 52.3). Исследован
также так называемый гиперэллиптический случай. Но в последнем
при возрастании h трудности быстро растут.
С помощью краевой задачи можно решить определенный
класс особых интегральных уравнений, которые можно назвать
характеристическими с ядром — аналогом ядра Коши на данной
Р. П. Но в отличие от уравнений, широко используемых в
приложениях, упомянутый класс имеет пока в основном лишь
теоретический интерес. Мы на нем не останавливаемся.
53.3. Краевая задача Гильберта. Краевая задача Гильберта
ставится на Р. П. с краем. Пусть заданная Р. П. с краем имеет
т+1 отверстий, граница которых — простые гладкие
замкнутые кривые 1-0» ^ь • • • » ^т«
Отыскивается аналитическая на Р. П.

§ 53] КРАЕВЫЕ ЗАДАЧИ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 569
функция ФB) = U + iv, удовлетворяющая на контуре L = Lq +
+ i'l + ... + ^m краевому условию
at/ + &t; = с, E3.4)
Строится дубль р. п. и на нем задача решается путем
доопределения на второй экземпляр поверхности по симметрии. На
дубле возникает краевая задача Римана. Ввиду полной
тождественности обоих экземпляров поверхности метод применим здесь
не только как в п. 30.2 для простейших контуров (прямая,
окружность), но и в самом общем случае контура, составленного
из любого конечного числа произвольных гладких кривых.
Подсчет числа линейно независимых решений или условий
разрешимости производится на основе решения задачи Римана
с учетом требования симметрии. В частности, отсюда при Л = О
(род дубля т— 1) можно получить исследование вопросов
разрешимости краевой задачи Гильберта для многосвязной плоской
области. При подробном всестороннем исследовании можно
получить в несколько иных терминах все результаты, найденные
в § 36 методом регуляризующего множителя и интегральных
уравнений. Л. И. Чибрикова связала вопрос о числе решений
в исключительных случаях индекса О^х^т—1 с
классической в теории алгебраических функций задачей о «пробелах»^
т. е. отрицательных ответов в задаче о построении
алгебраической (рациональной на Р. П.) функции с данными полюсами и
нулями.
53.4. Различные обобщенные задачи. Для областей на Р. П. изучены почти
все краевые задачи, рассмотренные в настоящей книге. О двух основных
задачах говорилось выше. Первая их постановка на Р. П. любого конечного
рода дана Ю. Л. Родиным 1), 2) иКоппельманом [Koppelman W. 1),
2)]. Ими же получены основные результаты по теории разрешимости.
Л. И. Чибрикова, используя теорию униформизации, в ряде работ
рассмотрела те же задачи в классе автоморфных функций на ее
фундаментальной области — плоской модели разрезанной по каноническим сечениям Р. П.
О работах Л. И. Чибриковой по решению краевых задач в классе
автоморфных функций, равносильных краевым задачам на Р. П. нулевого и первого
рода, подробно говорилось в предыдущем параграфе. Главными ее работами
по обш^й теории являются 6), где привлечена «проблема обращения Якоби»,
и 7), связавшая решение краевой задачи Гильберта с классической
проблемой теории алгебраических функций о пробелах. Э. И. 3 в е р о в и ч в
обзорной статье [9] и др. дал наиболее общую постановку краевых задач на
абстрактных Р. П., указал оценку E3.3) и дал в 4) практически
осуществимый алгоритм решения в случае гиперэллиптических Р. П. В [9] приведена
обширная библиография. Р. Н. Абдуллаев 1)—3) указал число решений
в исключительных случаях индекса О ^ х ^ 2/i — 2 через 9-функцию Римана.
Краевые задачи со сдвигом рассмотрел В. И. Показ ее в 1), задачи
с сопряжением — Л. И. Чибрикова и Л. Г. Салехов 1). Задачу
Гильберта для кусочно аналитической функции (см. § 45) исследовала Л. И. Ч и б-
р и ко в а 10). Еще более общую задачу, когда в краевое условие задач
Римана и Гильберта входят производные, изучил А. И. Сербии 1), 2). Краевые
задачи для обобщенных аналитических функций решали Ю. Л. Родин 3),4),

570 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМ1ШУТ0Й ФОРМЕ [ГЛ Vlt
А. И. Сербии 3). В. И. П ок а зеев 2), 3) и др. Л. И. Чибрикова 9)
и Л. И. Чибрикова и Г. В. Марков 1) рассмотрели постановку краевых
задач на неориентируемых Р. П.
Имеется еще много других заслуживающих внимания работ, но из-за
недостатка места мы ограничимся сказанным. Далее мы изложим схематически
некоторые приложения теории краевых задач на Р. П. к теории краевых
задач для плоских областей.
53.5. Принцип локально-конформного склеивания'^). В
конце § 18 указывалось, что в случае многосвязной области крае-»
вая задача Карлемана
ФW{t)] = G{t)Ф{t) + g{t), a[a{t)]^t, E3.5)
может быть решена методом конформного склеивания, если
функция сдвига a{t) переводит каждую кривую контура в себя.
Рассмотрим теперь общий случай. Пусть контур состоит из
т+ 1 кривых, из которых 2Л функцией а (О отображаются по^
парно друг в друга, а остальные т-\-1—2/i переходят в себя.
Преобразуем на последней группе кривых краевые условия,
аналогично тому, как это делалось в п. 18.3 в краевые условия,
заданные на разомкнутом контуре. Первые 2Л кривых отождест-»
вим (склеим) попарно, ставя на них в соответствии точки / и
а (О- Тогда плоскость превратится в Р. П. рода Л (с Л
ручками). Краевое условие E3.5) перейдет в краевое условие
задачи Римана. Следовательно, краевая задача Карлемана
E3.5) переходит в краевую задачу Римана на Р. П. рода А,
заданную на h замкнутых и /п+1—2Л разомкнутых кривых.
Отсюда можно получить число линейно независимых решений
или условий разрешимости задачи.
Приведем один иллюстрирующий пример. Пусть на контуре
кругового кольца 1<|2|</? задано краевое условие задачи
Карлемана
Ф[а(/)] = О@Ф@ + §@, \t\ = R. E3.6)
где функция сдвига а(/) ставит в соответствие точки граничных
окружностей, лежащие на одном радиусе, а G{t) и g(t)
удовлетворяют условиям A8.21). Краевое условие задается на одной
из окружностей; на другой оно определится автоматически в
силу a[a{t)]^ t. Склеим граничные окружности, отождествляя
точки t и a{t). Тогда на возникающей Р. П., равносильной тору,
краевое условие E3,6) перейдет в краевое условие краевой
задачи Римана
0''iti) = G(t,H'{t,) + g{t,). E3.7)
*) Мы ограничимся общими соображениями, не проводя доказательств,
которые довольно сложны. Их можно найти в работах Э. И. 3 в е р о в и-
ча 2), [9] ив работе 9. И. Зверовича и В. А. Чернецкого 1), из
которых взято содержание настоящего пункта.

§ 531 КРАЕВЫЕ ЗАДАЧИ НА РИМАНОВЫХ ПОВЕРХНОСТЯХ 571
Отсюда можно получить полное исследование вопросов
разрешимости поставленной задачи Карлемана.
Заметим в заключение, что, кроме задач со сдвигом,
методом локально-конформного склеивания можно решать также и
краевые задачи с сопряжением.
53.6. Симметрия относительно алгебраической кривой. Пусть
алгебраическая кривая L задана уравнением f{x,y)=Q, где
/ — неприводимый многочлен. Каждой точке z = x4-iy
комплексной плоскости уравнение
' I 2 ' 21 )~^
(см. П. 12.1) ставит в соответствие точки z*, симметричные
относительно L. Если степень этого уравнения относительно г* есть
гг, то каждой точке г, не лежащей на L, будет соответствовать
п симметричных точек
2* = Ф/(ё) (/=1, 2, ..., п). E3.8)
Из них существует лишь одна — обозначим ее г' — обладающая
тем свойством, что когда 2:->L, то и г'->L. Точки z и z^
составляют пару точек, симметричных относительно кривой L Если
с помощью функций OfeB) строить новые симметричные точки,
то получим последовательность (конечную или бесконечную)
пар симметричных точек zuy Zk. (Пара симметрии приводит к
исходной точке только в случае прямой или окружности.)
Л. А. Аксентьев 3), 4), 5), непосредственно продолжая
исследования Д. А. Граве, показал, что
1. Конечное число пар симметрии будет тогда и только
тогда, когда уравнение алгебраической кривой имеет вид
|(г —ai) ... (г —aj| = r|B: —6i) ... (e — ftjl-
2. Взятое по всем парам симметричных точек конечное или
бесконечное произведение
^«, ^) = П Т-? т^ (^« ^ ^> E3.9)
(в последнем случае при условии его равномерной сходимости)
дает функцию, осуществляющую конформное отображение од-
носвязной области, ограниченной контуром L, на единичный
круг. Отсюда непосредственно (см. п. 27.2) получается оператор
Шварца.
3. Получены простые достаточные условия сходимости
бесконечного произведения.
Второй цикл работ по использованию метода симметрии для
решения краевых задач связан с перенесением рассматриваемой

572 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ VII
области на Р. П. Исходное уравнение алгебраической кривой
при X, у комплексных определяет Р. П. R, на которой пары
(а:, у) действительных задают кривую L. Эта Р. П. называется
поверхностью симметрии кривой L, а кривая — линией
симметрии или осью симметрии R, Функции E3.8), определяющие
симметричные точки, рассматриваются как ветви единой
алгебраической функции, однозначной на /?. Тогда краевая задача,
заданная первоначально в плоской области, ограниченной
алгебраической кривой L, переходит в краевую задачу на Р. П.
симметрии. Теория краевых задач на Р. П. позволяет провести
исследование вопросов разрешимости.
Л. И. Чибрикова 11) решила, таким образом, краевую
задачу Гильберта и дала исследование некоторых задач теории
упругости. Л. И. Чибрикова и Л. Г. Салехов 1), 2)
указали решение краевой задачи с сопряжением. На подробностях
мы не останавливаемся.
§ 54. Интегральные уравнения со степенным ядром
Особенность всех ранее рассмотренных нами интегральных
уравнений заключалась в наличии члена, обращающегося при
совпадении аргументов в бесконечность первого порядка. Здесь
будут исследованы уравнения с ядром, обращающимся при
совпадении аргументов в бесконечность степенного порядка
меньше единицы. Па характеру бесконечности это ядро фредголь-
мова типа. Однако уравнения будут первого рода и оказывается,
что это делает их особыми. Применяемый метод решения —
сведение к особому уравнению с ядром Коши — роднит их с
изученными нами ранее уравнениями.
Вначале будут рассмотрены интегральные уравнения со
степенным ядром, играющие ту же роль, что и характеристическое
и союзное с ним уравнения в теории уравнения с ядром Коши,
а затем будет исследован общий случай полного уравнения со
степенным ядром.
54.1. Интегральное уравнение Абеля. Из курса
математического анализа известно, что классическое уравнение Абеля
X
с ^(^1 dt = g{x), 0<ц<1, E4.1)
J (х-if
о.
Ихмеет единственное решение, определяемое формулой

§ 541 ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СО СТЕПЕННЫМ ЯДРОМ 573
Для дифференцируемых функций g(x) решение записывается
равенством
Формулу E4.2) можно представить еще в виде
Действительно,
X—8 х—е
J_ { 8(t)dt _g{x-e) , . [ g(t)dt _
dx ) {x-tV-i^ e'-i* ^ ^M ^x-tf-^^~
a ^ ' a ^ '
x—e
_g(x-E)-g{x) , g{x) . ^^ .Л С S(x)-g(t) ^^ /p-. p-v
^rrs +(,_«)i^. +(»-*^) i (,^,J-. dt E4.5)
Устремляя 8 к нулю, видим, что если g{x) — гёльдеровская
функция с показателем Я > I — \i, то первое слагаемое
исчезает.
Формула E4.4) имеет по сравнению с E4.3) то
преимущество, что требует от g(x) лишь гельдеровости с показателем
Я > 1 — ц.
Мы будем иногда пользоваться обозначениями следующих
интегралов:
связанных с уравнением Абеля и известных в теории
интегральных преобразований под названием интегралов дробного
порядка,
54.2. Связь особого интеграла с ядром Коши с интегралами
со степенным ядром*). Как показано в п. 22.1, композиция
особого оператора с оператором, имеющим регулярное ядро, сама
имеет регулярное ядро. В применении к регулярному ядру
степенного вида это обстоятельство может быть уточнено.
Докажем, что композиция особого оператора с некоторым
оператором со степенным ядром является оперг.^тором со степенным же
*) Изложение пп. 54.2—54.7 следует работам С. Г. Самко 3), 6), 7), 9).

574 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ VIl
ядром. Именно, получим следующие две формулы:
^ i
1 [ /P-^Y~*^ dt f ф(т) dx ^
a d
J- [ ^^ [ f'^ — ^V"^ Ф (t) dx _^
7i^ ix-tf )\t-a) x-t "^
a a
Ввиду полной идентичности доказательств остановимся только
на E4.7). Переставляя в левой части порядок интегрирования
по формуле Дирихле, приведем ее к виду \ К{х, т)ф(т) dx, где
а
Если х>х, то этот интеграл — особый. Он вычислен нами ранее
(см. формулу D7.28)):
К {х, х) = ctg \лп {х — т)"**.
Если же х<х, то, положив f = л: + ^ _ 7— (В — т) /'' "^^^У^им
/C(,,,)=(m:!l( /^» iiziiinL. E4.10)
Таким образом,
^, , 1 ctg ^xя (;^ - т)Л т<д^,
(, cosec |ля (т ¦— д:) "^э т > х,
что и доказывает E4.7).
Тождества E4.7), E4.8) позволят дать простой способ
сведения рассматриваемых ниже уравнений со степенным ядром
к особому уравнению с ядром Коши. Заметим еще, что из

^ 541 интегральный УРАВНЕНИЯ СО СТЕПЕННЫМ ЯДРОМ 575
тождества E4.8) можно получить следующее выражение для
особого интеграла:
1 Г ф (т) t/T , , . ,
а
. (х-а)'-^ d [ dt Г ф(т)^т ,-. .
^ я dx) (x-t)'-^} ^^^a)'-\^(x-tr' ^
для этого следует решить E4.8) как уравнение Абеля
относительно функции
1 f / т —а \i-iA ф(т)с/т . , ч
а
(формула E4.11) применима при любом jx, 0<|i< 1).
54.3. Обобщенное уравнение Абеля с внешними
коэффициентами. Рассмотрим интегральное уравнение
а X ^
Заданные на отрезке [а, р] действительные функции а{х), Ь{х)
будем считать не обращающимися одновременно в нуль и
удовлетворяющими условию Гёльдера с показателем Я > 1 — [л.
Решения будем разыскивать в классе функций ф(л:) вида
где ф* (jc) — гёльдеровская на [а, р] функция. Относительно
правой части предполагается, что она имеет вид
где f*{x) удовлетворяет условию Гёльдера с показателем
Приведем с помощью тождества E4.7) обобщенное
уравнение Абеля E4.12) к особому уравнению с ядром Коши.
Обозначим

/.W=-.» u-
576 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. УП
Из тождества E4.7) находим, что
ft ft
Подставляя в уравнение E4.12), приводим его к виду
а, {X) 0{x)+^\^dt = t, {х\ E4.16)
а
где обозначено
их {х) = а{х) — Ь {х) cos \хщ bi (х) = / sin \inb {х\
fix) E4.17)
Пришли к особому уравнению на разомкнутом контуре,
изученному в § 47. Коэффициент задачи Римана, соответствующей
уравнению E4.16), равен
^^^^_а,(х)-^ЬАх)_ а(х)^Ь{х)е^-^
Уравнения E4.12) и E4.16) равносильны в следующем смысле.
Всякому решению ф(х) уравнения E4.12) соответствует по
формуле E4.15) решение Ф(л:) уравнения E4.16). Обратно, из
всякого решения Ф(д:) уравнения E4.16) по формуле E4.4) можно
получить решение
уравнения E4.12). Укажем схематически, не вдаваясь в
подробности, как связан класс функций Ф{х) с классом функций ф(л:).
Если ф(х) имеет вид E4.13), то Ф{х) внутри интервала (а, р)
удовлетворяет условию Гёльдера с показателем Х> I — [х, а на
концах X = (Ху X = р имеет особенности порядков меньше [i и 1
соответственно. Обратно, если Ф{х) внутри (а, р)
удовлетворяет условию Гёльдера с показателем X > 1 — |л, а при х = а,
jc = р имеет особенности порядков меньше |i и 1 соответственно,
то функция ф(л:) удовлетворяет условию Гёльдера внутри
(а, Р) и имеет на концах особенности порядков меньше 1.
Проверка этого осуществляется непосредственным применением
формул E4.15), E4.19) и требует ряда несложных выкладок,
которые предоставляются читателю (см. задачу 18 в конце
главы).

$ 64] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СО СТЕПЕННЫМ ЯДРОМ 677
Таким образом, чтобы найти все решения ф(л:) уравнения
E4.12) вида E4.13), уравнение E4.16) следует решать в классе
функций, неограниченных на обоих концах л: = а, л: = р, и из
таких решений выбрать те, которые при лс = а имеют
особенность порядка меньше jli. Согласно формулам D7.12), D7.17),
D3.3) решение Ф(-^), отыскиваемое в классе функций,
неограниченных при .^ = а, имеет в этой точке особенность порядка
где \х — 8 — порядок особенности правой части f\{x), а
9==argG(a) выбрано в интервале [О, 2я). Следовательно, при
О < 2п[1 можно взять все неограниченные решения уравнения
E4.16). Если же 0 ^ 2я|и1, то следует отыскивать ограниченные
при х = а решения уравнения E4.16).
54.4. Обобщенное уравнение Абеля с внутренними
коэффициентами. Рассмотрим уравнение
\j^^^+llB^''-S(x), E4.20)
предполагая, что ф(/) и g{t) имеют, как и выше, вид E4.13),
E4.14) соответственно. По-прежнему a{t) и b{t) не обращаются
одновременно в нуль на [а, р]. Здесь можно несколько ослабить
предположения относительно a{t) и b{t) и считать их
произвольными гёльдеровскими (не обязательно с показателем
К> 1 —ц).
Исключая с помощью тождества E4.8) второй из
интегралов в E4.20), получим
\ j;^\a it) (fit)-cos vinbit)(f it) +
+ ^\{T^y~"^^T^dx] = gix). E4.21)
a -^
Отсюда, согласно формуле E4.2) и в соответствии с
обозначениями E4.17), будем иметь
/ \ / \ I 1 С /" т — а \ 1 -^А ^, (т) ф (t) J
а.(х)Ф(^)+--5G3Г5-) T-V ^^ =
sin \хп d
X
С g (t) dx
dx J (x-xy
a

578 УРАВНЕНИЯ, РАЗГ>ЕШИМЫЕ В ЗАМКНУТОЙ ФОРМВ [tJt. VII
Вводя новые функции
получаем особое уравнение
аг(х)Ф1 (х) + ^\ Ы1}^dx = g,{X). E4.22)
а
Решения (pi{x) этого уравнения следует разыскивать в классе
функций, имеющих на концах особенности порядка меньше \i
при л: = а и меньше 1 при а: = р. Порядок особенностей
решений уравнения E4.22) определяется числом 9 = argG(a);
пусть 9 выбрано в интервале [О, 2я), тогда при 9 < 2я^г все
решения ф1(д:) уравнения E4.22) имеют при х = а особенность
порядка меньше [х; если же 9 > 2n\iy то неограниченное при
X = а решение имеет особенность порядка больше [i и поэтому
при 9 ^ 2п\1 следует решать уравнение E4.22) в классе
ограниченных при х = а функций.
54.5. Случай постоянных коэффициентов. Остановимся особо
на важном случае, когда коэффициенты уравнений E4.12),
E4.20) постоянны:
а
Уравнение E4.23) можно записать также в виде
а '
а + b а — b
С\ — -^— , С2 — —2— .
Уравнения такого типа широко используются в приложениях
при решении, например, контактных задач теории упругости,
пластичности, ползучести материалов, некоторых задач теории
игр и др.
Пусть
О = arg G (а) = 2 arg (а — Ье^^) =
= Jin + 2 arg [cg cos ^ — ici sin ^^1

§ 54] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СО СТЕПЕННЫМ ЯДРОМ 679
выбрано в пределах О < 9 < 2я (очевидно, 0 = 0 лишь при Ь^О).
Решая уравнение E4.16), соответствующее E4.23), после простых
преобразований получим
X
г ф (О dt _ а — 6 cos ЦП f / ч ,
^fii=—^l(^-^n;^(^'-)'^fit)^
Anix-a)^"^ (fi-xf 2« «
в случае 9 < 27t\i {с — произвольная постоянная) и
X
f ф (t) dt fl — 6 cos ЦП с / ч
J (др.— t)^ А
а
Q Q ?
f{t)dt
1^(х^аГ^{^^х)^^'\
ej _е
а (/-а) 2« (P-t)^ ^{t-x)
в случае 9>2яИ'. Здесь обозначено
A'^a''-2abcos\m + b' = 4(^c\QOS^^ + clsin'^).
Для определения функции ф(/) остается решить обычное
уравнение Абеля. Уравнение E4.23), таким образом, имеет в
классе гёльдеровских функций с интегрируемыми особенностями
на концах единственное решение тогда и только тогда, когда
Не останавливаясь на выкладках, приведем окончательный
вид решения для случая 9 ^ 2п[1:
X
, V а sin м-я rf с f (t) dt
а
_± /sinjmY f 2{t) д_([ dx \ t(s)ds \ .. ,-, 24^
Z@ = (i-o) ^^ ^>'(р_о^"\

680 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ 1ГЛ. УП
При выводе этой формулы особый интеграл нужно
преобразовать по формуле E4.11), заменив в ней предварительно \i на
(Читателю предоставляется получить аналогичную формулу
для случая 6 < 2я|11.)
Отметим частный случай, привлекавший внимание многих
авторов,
Для этого уравнения 9 = A + ii)n > 2[гя, так что его
единственное решение дается для любой правой части вида E4.14)
формулой E4.24), в которой
а = 6 = 1, A = 4sin2i^, Z@ = (^-a) ' ф-t) ^ .
54.6. Полные уравнения со степенным ядром. Рассмотрим
уравнения общего вида
^Ч^ ^ S Т^ГТг "^ ^^^ "^^ ^ ^ ^^^' ^^^'^^^
а '
предполагая, что функция c{Xyt) может иметь разрыв первого
рода при л: = /, т. е. с (л:, t) = а{х, t) при / < л:, с(х, t) = b{x, t)
при / > л:, так что
а ^ X
Функции a{x,t),b{x,t) будем считать гёльдеровскими по
совокупности переменных л: и ^ с показателем Х> I — |л. Решения
{р{х) и правая часть f{x) будут принадлежать классам функций
вида E4.13) и E4.14) соответственно. Покажем, что уравнение
рассматриваемого вида приводится к полному особому
уравнению с ядром Коши. С помощью обозначения
уравнение E4.26) можно записать в виде
X ^ 3
E4.26')

§54]
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СО СТЕПЕННЫМ ЯДРОМ
681
Рассматривая это уравнение как обобщенное уравнение Абеля
с внутренними коэффициентами (изученное в п. 53.4), запишем
его на основании E4.21) в виде
dt
{x-tf
[а {t, t) — cos \xnb (/, t)] Ф (/) +
3
, siniLin f / T —a \l-ii ^(t, т)ф(т) , '
a
= / W - 5 /C {x, t) Ф (t) dt E4.26'0
Отсюда, решая обычное уравнение Абеля, получим
Кф1^а1(А:)ф1(л:) +
3 3
+ i S ^^1У^ dx+\k {X, т) ф1 (т) dx = f, {х\ E4.27)
а а
где
ai {х) = а (л;, л:) — cos \inb (л:, дс), 6i (л;) = / sin [хкЬ (л:, л:),
X
/ \ I \1-ц / \ Z I \ sin ця / ч1-ц ^ f f (х) dx
(fi(x) = {x-a) **ф(х), /i(;^) = —^(;^-а) —) /^l.Ui-n>
а ^
л:
а ^
Используя формулу E4.4), можно показать, что ядро ^(x,t)-—
регулярное: оно допускает оценку
с
\k{x, т)|<-
JC—т
|1-Я,
где % — показатель гёльдеровости функций a{x,t), b{x,t).
Таким образом, решение рассматриваемого уравнения
E4.25) свелось к решению равносильного особого уравнения с
ядром Коши. Последнее можно известными способами свести
к уравнению Фредгольма. Заметим, что можно сразу получить
уравнение Фредгольма методом, аналогичным методу Карле-
мана — Векуа, если уравнение E4.26') решать как характери-»
стическое способом, указанным в п. 54.4.
Установленная связь уравнения E4.25) с особым
уравнением с ядром Коши дает возможность получить теоремы Нётера

582 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VH
ДЛЯ ЭТОГО уравнения. Однако для справедливости этих теорем
союзные классы для уравнения E4.25) нужно будет вводить
способом, отличным от принятого в § 47 для уравнений с ядром
Коши. Само союзное уравнение здесь вводится обычным
способом:
^'* = S V"^ * (^> ^^ = ^ W- F4.28)
Рассмотренные выше уравнения E4.12), E4.20) с внешними
и внутренними коэффициентами оказываются союзными друг
другу. Обозначим для краткости г=(/ — а)^"^. Сравнивая
оператор М в форме E4.26'), E4.26^') с оператором К из E4.27),
видим, что
Afф = г A - |i) /^^ I Кгф = f, E4.29)
где использовано обозначение E4.6). Для союзного оператора
М' тогда будем иметь
M'^^T{\-\i) гК' у /^Ч = g, E4.30)
где К' —особый оператор с ядром Коши, союзный оператору
К. Сопоставляя E4.29) с E4.30), заключаем, что союзные
классы для функций ф(а:), '^{х) должны быть выбраны так, чтобы
функции
Принадлежали союзным классам в смысле определения в § 47.
Тогда в указанных для ф(л:) и i|)(jk:) классах для исходного
уравнения E4.25) и союзного с ним справедливы все три теоремы
Нётера.
54.7. Уравнения со степенным ядром на бесконечной прямой.
Рассмотрим теперь уравнения вида
предполагая, что а(х), Ь{х) удовлетворяют условию Г?льдера
с показателем А. > 1 — \л на всей прямой, включая бесконечно
удаленную точку. Решения ф(^) будем разыскивать в классе
гёльдвровских функций, обращающихся на бесконечности в
нуль порядка V > I — ц, что обеспечит сходимость интегралов
в левой части уравнения. Правую часть ]{х) будем считать

§ 54) ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ СО СТЕПЕННЫМ ЯДРОМ §83
гёльдеровской с показателем ^ > 1 — |и, обращающейся на
бесконечности в нуль произвольного порядка.
Решение уравнения
S^-'«.
аналогичного уравнению Абеля E4.1), лишь для достаточно
быстро убывающих на бесконечности функций /(''^) : |/(х) | ^
^ с|А:|-|А-в при л:->оо, дается прежней формулой
, ч jinjm ^ f / (О dt
Если же f{x) имеет на бесконечности нуль произвольного
порядка, будем пользоваться формулой, аналогичной E4.4):
X
^/.л_ A-|х)яшця г f(x)'-f(t) ^^_
— 00 ^
оо
^A^>хMшцяГ i(x)^n^-t) ^t^ E4.32)
п J t ^
Имеют место тождества типа E4.7), E4.8):
оо / X оо
if dt f ф (т) rfr , f Ф (т) ^т , ^^ ^ f Ф (т) dx
— \ \ ^ ^ ^ .. = ctg ия \ ¦ „ +С08ес{1я \ ^ ^ ^ ,,,
—оо —оо —оо X
— оо —00 —оо X
С помощью первого из этих тождеств уравнение E4.31) можно
привести (рассуждая, как в п. 54.3) к уравнению с ядром Коши:
оо
а. {X) Ф {х) + Ь, {X) -1. J ^ dt = f {X), E4.33)
— оо
где ai{x), bi{x) те же, что и в E4.17), а
— оо
Решив уравнение E4.33), найдем функцию ф(:'^), выразив ее
через Ф{х) по формуле E4.32).

g84 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. Vti
Точно так же может быть рассмотрено на бесконечной
прямой уравнение вида E4.31) с внутренними коэффициентами.
И, наконец, следуя схеме п. 54.6, можно рассмотреть на
бесконечной прямой и полные уравнения. (Не останавливаясь на
этом, отошлем читателя к работам С. Г. Сам ко 9) —13).)
В заключение для уравнения с постоянными коэффициентами
а — b
приведем формулу, дающую его единственное решение:
оо
, ч _ A — (i) sin ця f ci + С; sign (х — t) ..,. , ,,., ,
'Р^'^^^ Тп i \x-tr^—[fW-fW]^,
где A TO же, что в п. 54.5. Если f{x) убывает на бесконечности
достаточно быстро, |/(^) | ^ ^|л:|""^""®, то эту формулу можно
привести также к виду
00
Ал flfjc J I jc — /1^ **
—оо
54.8. Некоторые другие результаты. Рассмотренное выше
уравнение E4.12) со степенным ядром можно решать и иным
путем — осуществляя аналитическое продолжение в
комплексную плоскость с помощью функции
Ф(г) = [(г-а)(р-гI—(-^.
J {t-zf
а
Для Предельных значений Ф^(л:) выводятся формулы,
аналогичные формулам Сохоцкого D.8). С их помощью уравнение
E4.12) сводится к краевой задаче Римана. Именно так было
впервые решено К. Д. Сакалюком 1) уравнение E4.12), а
также уравнение E4.20) «с внутренними коэффициентами».
Остановимся на других результатах, относящихся к
уравнениям со степенным ядром.
Г. Уравнение, обобщающее уравнение E4.12),
«wSlil^ E4.34)
а X
где Р{х)—многочлен, решено К. Д. Сакалюком 2),
рассмотревшим также некоторые другие классы интегральных
уравнений со степенным ядром (К. Д. С а к а л ю к 3)).

§ 55] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЛОГАРИФМИЧЕСКИМ ЯДРОМ 585
2^ Обобщенное уравнение Абеля E4.12) можно решить в
замкнутой форме и в том случае, когда оно задается на
произвольной гладкой дуге. Такое исследование было проведено
К. Д. Сакалюком 6) и позже Петер с ом [Peters 1)],
который рассмотрел также уравнение вида E4.34) с внутренними
коэффициентами в случае гладкой дуги.
3°. Решение уравнения, аналогичного уравнению E4.12),
в случае нескольких непересекающихся отрезков, дано
Ф. В. Чумаковым 2).
§ 55. Интегральные уравнения с логарифмическим ядром
Здесь будут исследованы интегральные уравнения,
содержащие в ядре логарифмическую особенность. Простейшее
уравнение такого рода
1
^\n\t-x\(p{t)dt = f{x) E5.1)
о
было еще в 1922 г. решено в замкнутой форме Карлеманом
(Carleman 1)). Рассмотрим некоторые общие классы
интегральных уравнений с логарифмическим ядром.
55.1. Характеристическое уравнение с логарифмическим
ядром*). Исследование начнем с решения уравнения
a{x)\^cp{t)dt + ^\\n^^(p{t)dt==f{x\ E5.2)
а а
которое будем называть характеристическим. Как увидим далее,
его теория вполне аналогична теории особого
характеристического уравнения с ядром Коши.
Будем считать, что действительные коэффициенты а{х), Ь{х)
имеют производные, удовлетворяющие на [а, р] условию Гёль-
дера, и не обращаются одновременно в нуль: а^{х)+ Ь^(х)ФО.
Решения ф(;^) будем разыскивать в классе функций вида
ФМ=..- ..-е:_..1-е> E5.3)
где ф*(а:) удовлетворяет условию Гёльдера. Относительно пра^
вой части равенства будем предполагать, что она
дифференцируема и ее производная имеет вид
f-W--„_„,.f.';^_„,-.. ES.4)
где g{x) удовлетворяет условию Гёльдера.
*) Изложение пп. 55.1—55.3 дано по работам С. Г. Сам ко,

586 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VIi
Следуя схеме § 54, установим связь между интегралом с
логарифмическим ядром и интегралом с ядром Коши. Эта связь
аналогична соотношениям E4.7), E4.8) и имеет вид
Р t 3
а а а
l5«(li2te = _l(,nll^,W,,. E5.6)
Доказательство равенств E5.5) —E5.6) получим, переставляя
в их левой части порядок интегрирования и вычисляя
получающиеся внутренние интегралы.
Заменяя в уравнении E5.2) слагаемое с логарифмическим
ядром его выражением через особый интеграл согласно
формуле E5.5), получим особое уравнение с ядром Коши:
э
а{х)Ф{х) -^ 5^Л = /(^), E5.7)
а
где
0{x)^\^{t)dt. E5.8)
а
Здесь необходимо подчеркнуть, что в силу E5.8) следует
искать не любые решения уравнения E5.7), а только
дифференцируемые (и, следовательно, ограниченные на обоих концах)
и удовлетворяющие условию
Ф(а) = 0. E6.9)
Решая уравнение E5.7) в классе функций, ограниченных на
обоих концах, согласно формуле D7.12) получаем (в
предположении, что а?- {х) + Ь2 (jc) == 1)
э
<1>{х)^а{х)!{х) + ^Ъ{х)\ ^У/) Д^^ +Ь{х)Ъ{х)Р,^,{х\
а
E5.10)
где X — индекс уравнения E5.7) в классе функций,
ограниченных на обоих концах, а функция Z {х) = [а (дс) — ib (х) IX+ {х)
имеет (см. D7.17)) следующий вид:
Z {х) = (JC - а)^' (р - хУ' ©о [хУ E5.11)
Здесь функция щ{х) удовлетворяет условию Гёльдера и всюду

§ 55] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЛОГАРИФМИЧЕСКИМ ЯДРОМ 687
отлична от нуля. Показатели уь Y2» определяемые по формуле
D2.7), оказываются действительными, поскольку
при этом 0^Yi<l»0^Y2<l в силу ограниченности решений.
Можно показать, что если правая часть f{x) удовлетворяет
условию E5.4), а коэффициенты а (л:), Ь{х) имеют производные,
удовлетворяющие условию Гёльдера, то все ограниченные
решения Ф{х) уравнения E5.7), определяемые формулой E5.10),
дифференцируемы всюду, кроме, быть может, концов д: = а,
jc = р, и их производные
имеют вид E5.3). Доказательство этого мы не приводим.
Исследуем выполнимость условия E5.9). Если Ь(а) = 0, то
Yi = О и интеграл в E5.10) имеет при ;с = а логарифмическую
особенность. Но Ь{х) дифференцируема, так что |6(а:)| =
^=\b{x)—b{(x)\^c\x — a\ и поэтому из E5.10) Ф(а) =
= а (а)/(а). Так как 6(a) = О, то а (а) ф 0; следовательно, для
разрешимости уравнения E5.2) необходимо, чтобы /(а) = 0.
Если же 6(a) =7^ О, то в силу E5.12) точка л: = а не может быть
точкой автоматической ограниченности. Поэтому условие
ф(а)=0 оказывается выполнимым при любой правой части
рассматриваемого класса в силу замечания 3 из п. 47.2.
Сформулируем окончательный вывод:
1) Пусть х^О. Если 6 (а) =7^ О, то уравнение E5.2)
безусловно разрешимо в классе функций (^(х) вида E5.3) при любой
правой части f{x), удовлетворяющей условию E5.4). Если же
b (а) =5 О, то для разрешимости уравнения необходимо и
достаточно, чтобы
f(a) = 0. E6.13)
Решение уравнения в обоих случаях дается формулой
¦- а
+ b(x)l{x)P^^,{x)\ E5.14)
2) Пусть X < 0. Для разрешимости уравнения в случав
b(oL)ф^'0 необходимо и достаточно выполнения условий
Jm//-id/ = 0 (/-1. 2, .... -х). F5.16)

58Й УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ {ГЛ. VH
В случае Ь{а) = 0 к условиям E5.15) нужно присоединить
требование E5.13). При выполнении условий разрешимости
единственное решение уравнения дается формулой E5.14), в
которой Р^_1 (л:) = 0.
Уравнение
a{x)\q>{t)dt-j^^\\n^^^cf(t)dt = f{x) E5.20
X а
аналогично уравнению E5.2). (Читателю предоставляется
провести его иследование самостоятельно по изложенной выше
схеме. Укажем только, что для этого уравнения нужно
соответствующим образом видоизменить тождество E5.5).)
Уравнение с внутренними коэффициентами
X 3
\a{t)(p{t)dt-\-^\b (t) \пЦ^ ф (О dt = f {х) E5.16)
а а
сводится К особому уравнению непосредственным
дифференцированием с дополнительным условием равносильности /(а) = 0.
55.2. Уравнение с логарифмической особенностью в правой
части. Покажем, что уравнение E5.2) допускает при Ь{^)ФО
решение в классе E5.3) и в более общем случае, когда правая
часть имеет при л: = р логарифмическую особенность
!{х) = Г{х)\пф--х1
где /*(л:) удовлетворяет условию E5.4). Покажем, что решение
ф(а:), найденное для такой правой части по формуле E5.14),
по-прежнему принадлежит рассматриваемому классу. Так как
функция [/*(а:)—/*(р)]1п(р —х) удовлетворяет условию E5.4),
то достаточно рассмотреть случай /(х) = 1п(р — х). Покажем,
что решение E5.14), т. е.
+
[т^+^^ЫШгЩ Р='^
принадлежит классу E5.3)*). Для первого слагаемого это
очевидно, для второго нетрудно получить, используя исследование
интегралов со степенно-логарифмическими особенностями в
п. 8.5. Остается рассмотреть выражение в квадратных скобках
*) Член [Z(jc)Ph-i MY> очевидно, принадлежит этому классу.

§ 65] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЛОГАРИФМИЧЕСКИМ ЯДРОМ 889
в окрестности конца л: = р. Для простоты ограничимся
рассмотрением главной части в Z(x), т. е. будем считать, что 7.(л:) =
s=(p — х)^\ (Нетрудно показать, что это предположение не
ограничивает общности.) Тогда с помощью замены р —1 =
= (Р — х)х получаем
E5.18)
Осуществляя теперь дифференцирование, после ряда
преобразований приведем выражение в квадратных скобках в E5.17) к
виду
X р
где функция А{х) имеет уже интегрируемую особенность. При
этом мы воспользовались тем, что согласно D7.28)
• s= -- я: ctg Y2^- E5.20)
0 ' ^ 0
Так как
то
Следовательно,
X «и ""^^ Д^~-2
G(P)=:62«^Y.^
a(P)-b(p)ctgY2^ = 0,
поэтому первое слагаемое в E5.19) имеет при л: = р
интегрируемую особенность, что и требовалось.
55.3. Обобщенное уравнение Карлемана. Рассмотрим
интегральное уравнение
X 3 е
aAx)\(f{t)dt-\'a2{x)\(p{t)dt-\^^\ln\t-x\(f{t)dt^f{x),
а X а
E5.21)
являющееся непосредственным обобщением уравнения Карле^
мана E5.1). Предполагаем, что [ai{x)—a2(x)Y +Ь^{х)ФО.
Будем решать уравнение E5.21) сведением к E5.2), считая, что

500 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. Vtl
условие E5.4) для правой части выполнено. Перепишем
уравнение в виде
[a,{x)^aAx)]\^{t)dt+^\\n^-f^
= f{x)-cm{x), E5.22)
где обозначено
3
т (х) = -^ 1п (Р - ;с) + «2 {х\ с = J ф (О dt. E5.23)
а
Правая часть уравнения E5.22) принадлежит классу E5.4),
если 6(Р) = 0. Если же &(Р)=7^0, то применимы рассуждения
предыдущего пункта. Следовательно, в обоих случаях для
решения уравнения E5.22) можно воспользоваться формулой
E5.14). Применяя последнюю, получим (при х ^ 0)
<f(x) = -^{b{x)Z{x)P^.,{x)-cF{x) +
+ [a,W-a,W]/W + -^i^^SzW^)}' E5.24)
а
где
3
F {X) = [щ {X) - а, {X)] т {х) + ^^Щ^ J ТЩ^)' ^^^'^^^
а
При ЭТОМ В случае ft(a) = 0 нужно в соответствии с E5.13)
потребовать, чтобы
f{a)-ca2{a) = 0. E5.26)
Для вычисления неопределенной пока постоянной с
подставим выражение E5.24) в интеграл в E5.23). Получим
с [1 + f (Р) - F (а)] = Ф (Р) - Ф (а), E5.27)
где Ф(д^) обозначает ту часть фигурной скобки в E5.24),
которая не содержит постоянной с. Может случиться, что равенство
E5.27) обращается в тождество. Опуская соответствующие
выкладки, укажем, что это действительно будет так, если,
например, Ь{а)ФО, Ь(р)?=0 или г?(а)= 6(р)= ai(p) = a2(a)= 0.
В этих случаях 1 + f(р)—F(a) = О, Ф(Р) = Ф(а) = 0 и
постоянная с остается произвольной. Следовательно, число
решений уравнения (или при х < О число условий разрешимости)

^ 55] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЛОГАРИФМИЧЕСКИМ ЯДРОМ 591
зависит не только от х, но и от обращения или не обращения
в нуль значений ^(а), Ь(р), ai(p), а2(а).
В случае х < О, записывая условия E5.15) для правой части
уравнения E5.22), приходим к системе равенств
kj=c\if (/=1,2,...,— к), E5.28)
где обозначено
а а
В случаях, когда постоянная с определяется из E5.27)
однозначно, равенства E5.28) дают — х условий разрешимости.
В случаях же, когда с остается произвольной, если
одновременно хотя бы одно из чисел jij отлично от нуля, можно за счет
выбора с удовлетворить одному из условий E5.28).
Применим, в частности, полученные результаты к самому
уравнению Карлемана
э
-^^(p{t)ln\t-x\dt = f{x). E5.10
а
Здесь а(л:) = 0, 6(а:) = 1, х = —1, z {х) = д/(^ — «)(? — ^), а
постоянная из E5.29)
(i,= \ln(p-0(^-a) ЧР-0 'dt
а
равна
jtln
P-g
(соответствующее вычисление мы не приводим). На основании
предыдущих рассуждений приходим к следующему выводу:
1. Если р — а ?=4, то уравнение Карлемана E5.1')
безусловно разрешимо в классе E5.3) и имеет единственное
решение, определяемое по формуле
/^л^ 1 Г С ^/(t-a)(fi-t)r{t)dt
I 1 С f{t)dt
"^ In Р~" j V(/-a)(p-0
E5.240

592 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
2. Если !р —а==4, то для разрешимости уравнения необхо-
димо и достаточно, чтобы \ f (О (^ — а)''^^^(Р —/)~^^^d/ = 0 и тогда
а
3
^^^ nV(A:-a)(p-jc) [J t-x J
где С — произвольная постоянная.
Формулы E5.24^, E5.24^') следуют непосредственно из
общей формулы E5.24), если учесть равенство
-^[у(,-а)(р-;,){ ^ffl-^^ 1 =
J t-x
-1) f (t) dt
^/(x-a)(^-x) i t-x
на доказательстве которого мы не останавливаемся.
Аналогичное E5.21) уравнение с внутренними коэффициен»
тами
\aiit)<f{t)dt+\a2{t)<f{t)dt +
а X
+ L^b{t)\n\x-t\(p(t)dt = f{x) E5.30)
а
сводится К особому уравнению
3
[а, {X) - а, {X)] ф (л;) - ± 5 6 (/) ЛШ,^сИ = Г {х) E5.31)
а
непосредственным дифференцированием. Уравнение E5.30)
равносильно уравнению E5.31) с дополнительным условием
5 ^2 (О ^{t)dt + '^^b @1п (^ - а) ф {t) dt = f (а). E5.32)
а а
Подставив решение уравнения E5.31) в E5.32), получим
равенство, связывающее входящие в решение при к > О
произвольные постоянные,

§ 55] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С ЛОГАРИФМИЧЕСКИМ ЯДРОМ 593
55.4. Некоторые другие типы интегральных уравнений с
логарифмическим ядром. Упомянем вкратце, не вдаваясь в
подробности, некоторые другие результаты, относящиеся к
уравнениям с логарифмическим ядром.
Г. Следующее уравнение, содержащее одновременно ядро
Коши и логарифмическое,
+
«W Рф(л:)-^Ф@^Ч
\((>{t)dt=f{x) E5.33)
сводится согласно E5.5) к особому уравнению
Р
а (X) ф (X) + -^ 5 -^^ dt = f{x)- cb {X) In (p - X), E5.34)
где
Ф(а:)=РФ(а:)—\ф(Ой^ и c = — ^(^{f)dt.
а а
Решив особое уравнение, исходное решение ф(а:) определим
из линейного дифференциального уравнения рф' (х) — ф (а:) =
.= Ф'(л:) при дополнительном условии ф(а) = —Ф(а).
Уравнение E5.33) было решено в работе автора (Ф. Д. Г ахов 6))
другим способом — применением метода аналитического
продолжения непосредственно к самому уравнению E5.33).
Можно указать ряд интегральных уравнений с другими
комбинациями ядер (ядра Коши, степенного и
логарифмического), сводимых к краевой задаче Римана (или уравнению
с ядром Коши). Но, как правило, возникают серьезные
затруднения на второй стадии решения, когда приходится определять
искомую функцию по уже найденному решению краевой задачи.
Вопросы этого рода еще мало исследованы.
2°. Рассмотрим интегральное уравнение
X
о
оо
+ •^5 {P{t-x)\n\t-x\^-q(t-x)]i^{t)dt = f{x\ E5.35)

694 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ 1ГЛ. VII
частные случаи которого нередко встречаются в приложениях.
Здесь P{z), Q{z) — заданные целые функции. В общем случае
решение такого уравнения наталкивается на трудности,
связанные с поведением функций P{z)y Q{z) на бесконечности. Если
известно конкретное асимптотическое поведение функций P{z),
Q{z) на бесконечности, то уравнение можно свести методом
аналитического продолжения к краевой задаче Римана. Общая
теория уравнения E5.35) еще ждет своего завершения. Мы
ограничимся здесь указанием одной общей схемы,
руководствуясь которой можно решать уравнения такого вида при
конкретном задании функций P{z)y Q{z),
Введем функцию
оо
ФB) = ф(гM [P{t-z)\n{t-z)-i-Q{t^z)](f{t)dt,
О
где аналитическая вне полуоси (О, со) функция фB) должна
быть подобрана так, чтобы biz) стремилась к нулю при 2:->оо.
Подбор функции i|)(z) в каждом конкретном случае
производится на основе изучения асимптотических свойств ядра при
г->оо.
Для функции Ф(г) нетрудно получить*) аналог формул
Сохоцкого
оо
ф+(;с) = г|)+(хM [P{t-x)ln\x-t\ + Q{t-x)](f{t)dt-
о
X
-ni^^{x)^P{t-x)(f{t)dt,
E5.36)
0-(je) = ,|,-(jc)J [P{t-x)\n\x-t\-\-Q{t-x)]<f{t)dt +
о
X
-f mVW \P{t-x)(f{t)dt
0
Выражая с помощью этих равенств интегральные слагаемые
в E5.35) через предельные значения Ф='=(л:), придем к
краевому условию задачи Римана
ф^ {х)= " <"^ + '^ ^'^ ^^ ^'^ Ф- (х) - 2ш ^^ ^'^' ^'^ , E5.37)
^ ^ а (jc) - ib (х) ф- (л:) ^ ^ а (х) - ib (х) ^ '
*) Вывод формул E5.36) можно найти в статье Ф. Д. Г ахов а 6),
е которой была дана излагаемая схема решения уравнения E5.35).

§ 55] ИНТЕГ15АЛЬНЫЁ УРАВНЕНИЯ С ЛОГАРИФМИЧЕСКИМ ЯДРОМ б95
заданному на действительной положительной полуоси. Пусть
решение краевой задачи найдено; тогда искомое решение ф@
определится из интегрального уравнения
X
2шtя(^-x)ф(oл=-^^--^^ F5.38)
J ф {х) '^^ (х)
Последнее уравнение типа Вольтерра с разностным ядром
принадлежит к классу так называемых уравнений типа свертки.
Путем применения одностороннего преобразования Лапласа
это уравнение легко решается в замкнутой форме.
Проиллюстрируем указанный путь решения уравнений
E5.35) примером.
Пример. Решим интегральное уравнение
оо
J Н^^^ (^ I ;с - /J ) ф (О dt = / (jc), jc> О, F5.39)
о
где k — постоянная, Н^^"^(г) — первая функция Ханкеля нулевого рода.
Используем известное представление
где /о (г) —функция Бесселя нулевого рода, QB)--некоторая целая функция.
Таким образом, здесь Р ^ Joy а = О, b = п. Для функции Ханкеля при
г -> оо известно следующее асимптотическое представление:
«..»«-. ^ + 0A).
Поэтому в рассматриваемом случае t|) (г) = —7=-. Задача E5.37), к которой
yz
сводится уравнение E5.39), имеет вид
Ф+(;с)-ф-(:^) = ^^/(^).
ух
Решая полученную задачу о скачке, приходим к уравнению
]Jolk(t--x)](p{t)dt^^/^^ ±l^——f(t)dt.
о о
Остается для отыскания функции ф@ применить преобразование Лапласа.
3^ Решение уравнения Карлемана E5.1) в случае контура,
состоящего из п отрезков действительной оси дано в работе
J. Thomas 1). Уравнение вида E5.16) на таком контуре
рассмотрел Ф. В. Ч у м а к о в 6).

696 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ {ГЛ. VII
§ 56. Исторические сведения
Материал § 51 написан по работе Ф. Д. Гахова и Л. И. Чибриковой 1);
о содержании этой работы уже говорилось в тексте.
Из ранних работ по этому вопросу следует прежде всего упомянуть
работу Геллерстедта [Gellerstedt 1)] A936 г.), затем работы С. Г. Михлина
[15], Д. И. Шермана 2) A948 г.), А. В. Бицадзе 1) A953 г.). Во всех
перечисленных работах метод решения характеристического уравнения
применяется к решению полных уравнений частного вида.
Материал § 52, как уже указывалось, написан по работе Л. И.
Чибриковой 2).
В дальнейших работах Л. И. Чибрикова дала много новых примеров
использования автоморфных функций для решения различных краевых задач.
Отметим ее работы 3), 4), где решены некоторые краевые задачи для
дифференциальных уравнений смешанного (эллиптико-гиперболического) типа, и
в особенности работу 5), содержащую решение в замкнутой форме через
автоморфные функции краевой задачи Гильберта для некоторых
многоугольников, ограниченных дугами окружностей.
В конце пятидесятых годов начали появляться работы Ю. Л. Родина и
В. Коппельмана (W. Koppelman) по решению краевых задач для областей,
расположенных на римановых поверхностях. В это же время Л. И.
Чибрикова, продолжая исследования по краевым задачам в классе автоморфных
функций, пришла к краевым задачам на фундаментальном многоугольнике
автоморфной функции с любым числом р пар конгруэнтных сторон. В силу
известных теорем об униформизации алгебраических функций автоморфными
последние задачи полностью равносильны краевым задачам на римановых
поверхностях рода /7, рассеченных по р парам канонических сечений. В
дальнейшем обе ветви теории слились воедино, отличаясь разве что
терминологией. Наиболее общая постановка этого рода задач дана Э. И. Зверовичем [9].
К настоящему времени теория краевых задач на римановых поверхностях
сложилась в широко разветвленную дисциплину, носящую, в главных чертах,
законченный характер. О важнейших приложениях, основанных на принципе
локально конформного склеивания и принципе симметрии относительно
алгебраических кривых, достаточно подробно говорилось в тексте. На других
приложениях мы не останавливаемся.
Идея решения уравнений со степенным и логарифмическим ядром
методом аналитического продолжения была выдвинута в 1922 г. Т. Карлеманом
[Carleman 2)]. Это —та же, по существу, идея аналитического продолжения,
которая была использована им же при решении характеристического
уравнения с ядром Коши. В указанной работе было решено уравнение Абеля с
постоянными пределами интегрирования E4.23'), а также простейшее уравнение
с логарифмическим ядром E5.1). Использованные Карлеманом
вспомогательные аналитические функции имели точку ветвления на бесконечности, что
вызвало некоторые трудности в решении.
Обобщенное уравнение Абеля с внутренними или внешними
коэффициентами было впервые решено К. Д. Сакалюком 1), 4), использовавшим метод
Карлемана аналитического продолжения. Ограничительные предположения,
сделанные в упомянутых работах, были ослаблены Л. ф. Вольферсдорфом
[L. V. Wolfersdorf 1)], использовавшим обобщенное уравнение Абеля при
решении краевых задач для дифференциальных уравнений смешанного типа,
и С. Г. Самко 3), 6). Последний автор предложил другой подход к решению
уравнений и рассмотрел их также на бесконечной прямой (см. С. Г. Самко
8)—13)). Полные уравнения со степенным ядром рассматривались в работав
Ф. В. Чумакова 1) и С. Г. Самко 7), 10), 11), 13). Основные соотношени
п. 54.2, связывающие интегралы со степенными ядрами с интегралами с ядром
Коши, были получены в работах С. Г. Самко 3)—6) и Л. ф. Вольферсдорфа
[L. V. Wolfersdorf 2)]. Отметим также работу [L. v. Wolfersdorf 4)], в кото-

ЗАДАЧИ К ГЛАВЕ VII 69/
рой обобщенное уравнение Абеля с постоянными коэффициентами было
применено к некоторым задачам теории игр.
Имеется ряд ранних работ, посвященных решению различных частных
случаев обобщенных уравнений Абеля. Так, Н. И. Ахиезер и В. А. Щербина 1)
получили решение уравнения Абеля E4.23') с постоянными пределами
интегрирования, а также уравнения E5.1) с логарифмическим ядром в качестве
частного случая из формул обращения некоторых интегралов с
гипергеометрическим ядром. К этой работе близка статья У. Уильямса [W. Е. Williams 1)],
рассмотревшего аналогичные уравнения в связи с приложениями в задачах
электростатики. М. Г. Крейн 1) в исследованиях, связанных с обратной
задачей Штурма — Лиувилля, пришел к некоторому методу решения
интегральных уравнений, откуда, в частности, получил решение уравнений E4.23') и E5.1),
В 1958 г. Хейнс и Мак-Ками [А. Е. Heins, R. С. Мае Сашу 1)] указали,
что метод аналитического продолжения позволяет свести решение
интегрального уравнения вида
оо
5 lP(x--t)\n\x-'t\ + Q{x^t)](p{t)dt^f{xh
о
где Р и Q — целые четные функции, к простейшему уравнению типа свертки
X
\ Р (x — t) (p{t) dt ^ f (jc). В качестве иллюстрации метода они дали реше-
0
ние уравнения E5.36). Материал п. 55.4 частично взят из статьи автора 6),
частично публикуется впервые.
Рассмотренные в п. 55.1 интегральные уравнения E5.2), E5.2')
изучались в случаях 6(а)= 6(Р)= О в работах Ф. В. Чумакова 3)—5).
Изложенное в пп. 55.1—55.3 исследование уравнений с логарифмическим ядром в
общем виде выполнено С. Г. Самко и ранее не публиковалось. Некоторые
другие типы интегральных уравнений с логарифмическим ядром рассматривались
К. Д. Сакалюком 3), 5).
Следует указать, что работа по выявлению типов особых интегральных
уравнений, разрешаемых в замкнутой форме, начата сравнительно недавно и
в настоящее время продолжается. Здесь можно ожидать получения новых
результатов.
Задачи к главе VII
1. Показать, что уравнение
|t|-i
принадлежит к типу уравнений E1.12), и дать его решение.
Ответ.
fB)=92-i=^ («>0).

598 УРАВНЕНИЯ, РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VII
2. Тем же методом дать решение следующего уравнения с разомкнутым
контуром:
1
о
8. Дано особое интегральное уравнение
а@<Р@ +
/i-O L ^ ^ ft J
где (Do B)^2, ©1B), ..., ©rt-i B?)— группа дробно-линейных
преобразований, Н (г) — рациональная функция, не имеющая полюсов на Lq, а^ — 6^ = 1.
Показать, что при помощи аналитической автоморфной функции
уравнение сводится к краевой задаче
tsLk (А = 0, 1, .... rt— 1).
Получить отсюда для х> —v+ I решение уравнения A) в виде
ф@-а(<)И<)-
-b(tJ{tJ^ ^^ JZOFT T-«>,W T-a),(oo)J^^ +
b{t)Z{t)P^+y-AF)
+
[^(')-^'(ОГ'П[^(')-^(^/)]
/-1
Z (/) = [a (f) + H (t)b (/)] X"*" (/), X @ — каноническая функция задачи B),
2y —полюсы функции H{z). (Ф. Д. Гахов и Л. И. Чибрикова 1).)
4. Дано особое уравнение
а@Ф@ + И02 ^ Ц:^зг^;(^-Т31^]фМ'^--Д0. A)

ЗАДАЧИ К ГЛАВЕ VII 699
где функции (df^ (г) составляют циклическую группу; р^ (г) — рациональные
функции, удовлетворяющие условиям
/fe-l п-\
Pk (^) = П ^1 К (^)]' П Р\ К W1 = ^-
Показать, что при помощи аналитической функции
^^ Pbiz) ГГ ^ ^1
удовлетворяющей условию
р,B) Ф [со^ (;г)] = Ф (г) (/ = 1, 2 /г- 1),
уравнение сводится к краевой задаче
+ _aK«)]-frKW] д,-,... Pk(()f[4m
^'^ - а [ш^ (/)] + b [<о^ Щ "^ ^^'-^ а [т^ Щ + Ь [<о^ Щ '
t^Lk (ft = 0, 1 rt-1).
Получить отсюда решение уравнения A) в виде
Ф@ = а@/@-
где
В (z) = Go (z) P^f^-^F) ^
[nz)-P{zjf-'Jl[F(z)-F{z,)]
rt-i
во(г)= E PftW:
/5-0
2b 22, ..., гу — нули функции Во (г). (Ф. Д. Гахов и Л. И. Чнбрикова 1).)
5. Показать, что уравнение Трикоми [26]
1
о
принадлежит к типу уравнений A) предыдущей задачи.
6. Свести решение уравнения
«)
2Л-1
A)
ft-о i,
где Wj^W составляют циклическую группу, к краевой задаче
Ф+ ж - ^^ Ь (<)] - ^ К «)] А,- ,,, , (-1)" «>; «) / К «)]

600 УРАВНЕНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФОРМЕ [ГЛ. VU
относительно функции
L-J 2ш J (Ну (т) — Z
/5-0 Lo
Получить отсюда решение уравнения A) в замкнутой форме.
Показать, что уравнение
1
о
использованное А. В. Бицадзе 1) при решении краевых задач для уравнений
смешанного типа, принадлежит к типу уравнений A). (Ф. Д. Гахов и
Л. И. Чибрикова 1).)
7. Показать с помощью разложения на простые дроби, что в случае ко-
Г(т) .
нечных групп ядро г» / \ _ с //\ обращается в
п-1
^ 1'^~®й W T^-0>ife(«>)J*
ft-o
8. Решить интегральное уравнение
у[1 + ('-1)'*C-/)'']ф(/) +
"C-0^ f Н'(х) .,.,.._,,,,
2я«
Z,,
где Lo — окружность | г — 11 = 1/2,
ff-pr,^ 1 _ 16-гЧ4-г')
" -'^^^> F B) - 42 D - 2) '
f (г) — основная автоморфиая функция группы Г:
щ{г)^г. со.(г) = 4-г. Р{г) = ^ + -^, х>0.
Ответ.
(/-D'^O-o'^+l 1-«-1)''(з-<)'<
*^^ 2(<-!)'* C-0" (^-DHO-O"
^r_D^l01_f_l_ Г ..Г Зт^-12т-16-1'' Я-(т)
'^L3/2-12/-16j 2ш )'^'l D-т)т J H(x)-H(t)'^^
2(/-1)«C-0'' L 3/2-12/-16 J **"¦
ал
Г$я(^:^'Р^^т = /(о.
9, Показать, что интеграл
J
д/

Задачи к главе Vit eoi
где И (г) «= — cos г, Lq — окружность
cos 2
г — == ~ , допускает
обращение
,,, If Я' (т) ,, V ,
Указание, f (г) = cos 2 есть основная автоморфная функция,
порожденная группой подстановок (Oi (г) = 2 + 2я, ©2 (z) = — г.
10. Пусть F (г) одно- или двоякопериодическая функция с периодом ©,
имеющая нуль первого порядка при г = 0. Показать, что для интеграла
(О
о
(О
при выполнении условия \f{t)dt = (^ справедлива следующая формула
обращения: о
(О
о
F'
Обобщить на случай, когда отношение ^ заменяется отношением двух
периодических с периодом © функций Fu /^2, удовлетворяющих условию
/?^@)=1, /?2@)=1. (Л. И. Чибрикова 2), стр. 107.)
И. Исходя из результатов задачи 10 вывести следующие формулы
обращения для функций Якоби Oi, sn, СП и dn:
i *.
2л
/(T)rfT;
4j;s
4fe
СП (т •-- t) dn (т — i)
sn (т — /)
о
Ak
3) -^^ '"!^~%(T)rfT = f«),
ш J sn (т ~ /) ^ ^ ^ ' ^ "
о
4J^5
СП (т — /) . , . J
— ^ / (т) ^т;
«fW^iIrS
sn (т — /)
о

602 У^>А6НЁНИЯ. РАЗРЕШИМЫЕ В ЗАМКНУТОЙ ФО^'МЁ [ГЛ, VII
ik Ak
^ ЯГ J sn (т -- /) / \ /» Y V / Я1 J sn (т — о
о о
о о
Ak
О
4J^
i^\ 1 С СП (Т — О ? / \ ^
^ ^ я/ J sn (т — о dn (т — о
о
12* Получить формулы обращения Гильберта (б.б), F.7) при условии
2я 2Я
\ и (а) rfa = \ t; (а) cfa = О, исходя из результатов задачи 10,
о о
13^, Решить уравнение типа Абеля
X
J(A:-/f<pW^ = /W @<ц<1).
а
Ответ.
X
ЦЯ dx^ J {x-tf
14. Решить интегральное уравнение Шлёмильха
Д/2
-|-\ ф (;с Sin 6) fife = / (jc).
Ответ,
я/2
^(x)^f@) + x^ r{xsin^)d^.
о
(Э. Т. Уиттекер и Дж. Н. Ват с он, Курс современного анализа, ч. 1,
Физматгиз, 1962, стр. 323.)
15. Доказать тождество
J т —а: dx J л/x'-t J V(T —а)(т —О
а at
16. Решить уравнение
е 9{t)dt _
.-JL
если а) / (X) = (jc - а)" (п = О, 1, ...); б) / {х) = Цх - а) (р - ;t)]" ^.

Ответ.
а) ф {х) =
cos-^
Г(ц)/г!(р"-
ЗАДАЧИ К ГЛАВЕ VII qq^
п
Т(п + цI(х-а)(р-х)] 2 t=o
б) <Р W = ^f~ ч Их - а) (Р - ;.)]Т-'.
(С. г. Самко 6).)
17. Показать, что общее решение уравнения
fT^^T.%ffl^^°fw
\x-tr
имеет вид
i^^
[(^-а)(р-;^)] 2
8fn2Ji?L JC ц * Р и
2 d г /^ ~ а\Т dt d f д?т Г /Р - s\7 /E)^5
где с — произвольная постоянная.
18. Показать, что если функция ф(д:) удовлетворяет на [а, р] условию
Гёльдера с показателем Л < |х, то функция
X
а
имеет вид f(x)^ . j^-^ (^~а)^~^ +i|?(^g), где ф (дг) удовлетворяет
условию Гёльдера порядка Х+\—ц. (Q. И. Hardy, J. Е. Littlewood I).)
19. Доказать, что для дифференцируемых функций g{x) формулы F4.2),
F4.3), дающие решение уравнения Абеля, можно привести к виду
sinju, f|Xf (/) + (/-а) g-ffl^^
^' ' п(х-а) J (jc-^)l-^
(К. Д. Сакалюк 1).)
Ж Интегральное уравнение
X
$ф(Од/-^-=^Т^Л = /{*). с>0.
а
теории тонкого крыла самолета (Л. И. Седов, Плоские задачи
гидродинамики и аэродинамики, М., «Наука»» 1966) привести к уравнению Вольтерра
второго роДа. (С. Г. Самко 4).)

ПРИЛОЖЕНИЕ Т
ИНДЕКС КАК ГОМОТОПИЧЕСКИЙ ИНВАРИАНТ
1. Гомотопия функций. Пусть L — простой гладкий замкнутый
контур, содержащий внутри себя точку 2 = 0. Обозначим М совокупность
всех непрерывных и не обращающихся в нуль на L функций G(t).
Функции <Jo@ и G\(t), принадлежащие множеству М, назовем
гомотопными (С/о@ ^ ^i(O)» если существует функция 0(/,ЗС), непрерывная по
совокупности переменных ^ е L, А, е [О, 1], такая, что
1) G{U Я):?&0;
2) G(t, 0) = GoW, G(U 1) = G,@.
Другими словами, если Go@ ^ 0\(t), то кривые ш = (?о(/), а> = Oi@
можно непрерывно стянуть друг в друга, не проходя при этом через начало
координат.
Покажем, что если G(t)^M и х «=« Ind 0@, то G{t) ^t\ В самом деле,
на контуре L существует однозначная ветвь функции [t~^G{t)] , и функция
G (/, Я) = t'^ [r'^G (t)]^
осуществляет гомотопию между функциями t^ и G (/). Далее, если G (i)
гомотопна t^f то G (t) не гомотопна никакой другой степени /. Действительно,
если допустить, что G {t) ^ t^^ ^ t^\ то тогда /^i"'*^^!. Но, очевидно,
окружность W =» /**>~'*2 Q центром в начале координат нельзя стянуть в точку
к; = 1, не проходя через начало.
Таким образом, функции Go{t) и Gi{t) из множества М гомотопны тогда
и только тогда, когда индексы этих функций равны.
Простейшим представителем в каждом классе гомотопии (т. е. в классе
эквивалентных друг другу функций) является функция t'^y а индекс
является гомотопическим инвариантом.
Дальнейшие сведения о гомотопии функций (векторных полей)
читатель может найти в книге М. А. Красносельского «Векторные поля на
плоскости», М., Физматгиз, 1963, где даются различные приложения понятия
гомотопии. Нас будет интересовать использование этого понятия лишь в теории
особых интегральных операторов.
2. Гомотопия операторов. Два оператора Нётера *) Л^о и Nu
действующие в банаховом пространстве, назовем гомотопными друг другу,
*) Об операторах Нётера в банаховом пространстве см. п. 23.4.

ПРИЛОЖЕНИЕ I 605
если существует оператор N^y непрерывно зависящий от параметра Я, такой,
что:
1) Л^д, является оператором Нётера при каждом значении X е [О, \]\
Непрерывность оператора Л^^^ по параметру Л понимается, как обычно, в том
смысле, что II Nj^ — Nj^ \\~^^ при ^ ->
используясь теоремой В п. 23.4 об устойчивости индекса по отношению к
малым изменениям оператора, нетрудно доказать, что если два оператора
Нётера гомотопны, то их индексы равны.
3. Гомотопия особых интегральных операторов.
Рассмотрим множество операторов вида
Л^Ф = а(/)ф(/) + 6(/Mф + Гф, A)
где S — особый оператор с ядром Коши на замкнутом контуре, Т —
регулярный оператор, a{t), b(t)—непрерывные коэффициенты, причем выполнены
условия
Л (О = а (/) + Ь(()ФО, В (t) ^a(t)-b (t) Ф 0.
Покажем, что можно добиться гомотопии операторов вида A) с
помощью гомотопии коэффициентов. Справедлива следующая
Лемма. Операторы No и Ni вида A) гомотопны в пространстве Lp
(р > 1), если соответствующие функции Ло@, ^о@ гомотопны функциям
Действительно, пусть Ao(t) г^ Ai(i), Bo{t) ^ Bi(t), и пусть Л(/,X),
B(t,K) —функции, осуществляющие гомотопию. Легко показать, что оператор
,, ^ __ Л it, К) + В (/, К) А (U %)-В (U Я)
Njjp = 2 Ф W Н 2 ^^ "^ ^
непрерывен по Я, в пространстве Lp и удовлетворяет условиям 1), 2) и,
следовательно, осуществляет гомотопию операторов Nn и Л^1.
4. Вычисление индекса одного класса особых
операторов со сдвигом. Метод гомотопии позволяет вычислять индекс
операторов путем замены данного оператора более простым, ему гомотопным.
Этим способом часто пользуются для вычисления индекса различных
операторов. Рассмотрим в качестве иллюстрации особый интегральный оператор со
сдвигом:
М,^а,),,) + Ь,Шат + ^\^1^ + Ш\Л^. B)
L L
где a(t)—сохраняющий направление обхода на L некарлемановский сдвиг,
имеющий неподвижные точки. Предположим для простоты, что a(t) имеет
единственную неподвижную точку ^о-
Пусть
а(/)±с@?«0. C)
Будем еще дополнительно считать, что выполнено условие
I а (to) ± с Но) \>\Ь (to) ± d (to) I max {I, | a' (to) |}. D)
Можно показать, что при выполнении условий C), D) оператор B)
является оператором Нётера. Мы не станем останавливаться на доказательстве
этого, отсылая читателя к статьям В. Г. Кравченко 1), 2), из которых
взят рассматриваемый пример.

606 ПРИЛОЖЕНИЕ II
Введем оператор
L0 L0
Условия C), D) для этого оператора выполняются при любом значении
Xs[0, 1]. Следовательно, оператор А^х нётеров и осуществляет гомотопию
между исследуемым оператором со сдвигом N\t^ N ц особым оператором
с ядром Коши
ЛГоФ-а(Оф@ + ^5^^-
L
Поэтому
Ind N == Ind Л^о = Ind ^ ^^}, 7 ^!!! .
а (О + с (t)
Аналогичный прием использовали Г. С. Литвинчук 1) при вычислении
индекса особых операторов с карлемановским сдвигом, а Н. Л.
Василевский 1) при вычислении индекса некоторых особых уравнений с полярно-
логарифмическим ядром (см. приложение 11).
Для построения оператора Л^х» осуществляющего гомотопию двух
произвольных операторов Нётера Л^о и Л^ь нет какого-либо единого правила;
здесь — простор для искусства исследователя.
ПРИЛОЖЕНИЕ II
ОПЕРАТОР С ПОЛЯРНО-ЛОГАРИФМИЧЕСКИМ ЯДРОМ
Пусть на гладком замкнутом контуре L определен оператор
/Ce-a@/+MOAfe (^Ф ^ lb" j (J ^,)Le ^^}
О)
При е > О ядро оператора Afg имеет особенность интегрируемого порядка
и оператор /Се является фредгольмовым. При е *= О оператор Afg обращается
в сингулярный оператор с ядром Коши S и, следовательно, Кг подчиняется
теории Нётера. Возьмем для измерения порядка бесконечности ядра вместо
степенной шкалы более тонкую. Из элементарных функций такой будет
логарифмическая (с повторными логарифмами и их степенями).
Среди операторов с промежуточным по сравнению с оператором М^ при
е > О и 8 = О порядком особенности простейшим будет оператор
XT ^ f ф(т)бГТ ,^.
^Ф-1НГЗ(т-<Iп(т--<)' <2)
Спрашивается, как влияет ослабление порядка особенности, вызываемое
внесением в ядро оператора 5 множителя-г—7-—-гг-, какой теории (фредгольмо-
вой или нётеровой) будет подчиняться оператор
Q^al+bN? C)
Изложим кратко решение этого вопроса^

Приложение it 60?
Как и в § 22, при исследовании оператора S воспользуемся методом
аналитического продолжения в комплексную плоскость. Пусть ф(т)
удовлетворяет условию Гёльдера. Нетрудно показать, что интеграл Л^ф существует
в смысле главного значения. Введем аналитическую функцию
ф(г) L-{ Ф^^-^ D)
^ ^ 2ni J (т - 2) In (т - z) • ^^'
Обозначим to = Хо + iyo точку контура L с минимальной ординатой.
Соединим ее с бесконечно удаленной точкой лучом Г, не касающимся L в to. Будем
считать функцию 1п(т — z) переменной т главной ветвью логарифма,
определенной условием 1п(т —г)= О при t — 2=1, непрерывной на L всюду, кроме
точки to.
функция ФB) будет иметь особыми линиями контур интегрирования L
и кривую С, определенную уравнением w = i{s)— 1. Для упрощения
дальнейшего исследования будем предполагать, что линии L и С не пересекаются.
Этого можно достигнуть, например, подчинив L условию, что разность любых
двух точек с одинаковыми ординатами остается по абсолютной величине
меньше единицы. Методами, близкими к использованным в § 4 при
исследовании интеграла типа Коши, доказывается
Теорема 1. Интеграл D) является функцией, кусочно аналитической на
плоскости с линиями скачков L, С, Г. Ее предельные значения на контуре L
даются формулами
Ф+@ = со(Оф@ + Л^Ф, (б)
ф-(/) = Л^ф, F)
где
-W=^ln[n-jjr|fb)-l
(аналоги формул Сохоцкого).
Функция (О (О уже не удовлетворяет условию Гёльдера и это приводит
к необходимости рассматривать оператор N не на множестве функций,
удовлетворяющих условию Гёльдера, а в пространстве Lp, Оператор N,
определенный на функциях класса Н равенством B), допускает продолжение до
оператора, ограниченного в пространстве Lp. Всюду в дальнейшем свойства
рассматриваемых операторов выводятся сначала на функциях класса Я, а
затем по непрерывности переносятся на функции из Lp.
Теорема 2. Если ait)-—непрерывная на L функция, то Na — aN-^
вполне непрерывный оператор.
Исследование показывает, что оператор N тесно связан с оператором S,
поэтому целесообразно изучать свойства не оператора Q, а более общего
оператора
A=^aI+bN + cS + T, G)
где а, 6, с — непрерывные функции, а Т — вполне непрерывный оператор.
С помощью аналогов формул Сохоцкого E), F) доказывается
Теорема 3. Справедливы соотношения
N (©/ + Л^) =- О, Л^ (/ -f S) = О, (/ - S) (©/ + iV) « 0.
Отсюда с использованием теоремы 2 непосредственно вытекает
Следствие. Имеют место равенства
N^ =^ - GiN + Т\ Л^5 = - Л^, SN=^(i)I + N-(oS + Г\
еде Т\ Т" — вполне непрерывные операторы.

б08 Приложение it
Последние соотношения позволяют получить формулы композиции
операторов типа Л, а именно, коэффициенты оператора
А = А,А2 = aI+bN-{-cS + T
в очевидных обозначениях выражаются формулами
а = aia2 + С\С2 + ^1^2®»
b = aib2 + Cia2 — b\b2(i^ + ^162 "- ^1^2»
с = 01^2 + C\a2 — Cib2(ii.
Отсюда легко вытекает, что оператор
Л ^ {a-b(i>)I-bN--cS
будет левым и правым регуляризатором для Л, причем
АА^{а+ с)(а-'Ь(д-сI+ Ти
ЛЛ = (а + с) (а -- бсо — с) / + Гг.
(8)
Следовательно, справедлива
Теорема 4. Для того, чтобы оператор А был нётеровым, достаточно
выполнения на контуре L условия
{а + с) (а - 6© - с) =7& 0. (9)
Индекс оператора Л можно получить методом гомотопии (см.
приложение I). Оператор
Л^^(а-Л-^)/+A-ЯNЛ^+(с+Я-у-M + Г, Яе[0, 1],
гомотопно преобразует оператор Л в сингулярный оператор с ядром Коши
A.^{a-^)l+{c + -f-)s + T. A0)
Следовательно, индекс оператора Л совпадает с индексом оператора Ли
Отсюда следует
Теорема 5. Индекс оператора А вычисляется по формуле
Изложенная теория при с = О дает ответ на первоначально
поставленный вопрос.
Теорема 6. При условии а{а~ Ьсо) ф О оператор Q есть нётеров и его
индекс вычисляется по формуле
Ind
I Г а-ЬтЛ
Однако, принадлежность обоих операторов Q ^ а! + bN и К^ ^ а! + bS
к общему для них классу нетеровых операторов еще не означает, что все их
основные свойства совпадают. Можно указать и такие примеры, когда
оператор Л^ оказывается родственным не сингулярному оператору S, а оператору
со слабой полярной особенностью Afg (е > 0). При а ^ О особое
интегральное уравнение 1-го рода (cS + Т)(р = f с^тается по-прежнему нётеровым и
при регуляризации приводится к уравнению Фредгольма 2-го рода; для урав^
нения же 1-го рода (bN + Т)ц) =^ f условие (9) нётеровости нарушается и
соответствующее регуляризованное уравнение оказывается фредгольмовым
уравнением 1-го рода.

ПРИЛОЖЕНИЕ III 609
В исключенном из рассмотрения случае пересечения контуров L и С
теория оказывается значительно сложнее, чем изложенная. Здесь приходится
привлекать к рассмотрению еще некоторые специальные операторы сдвига.
Но в принципиальном отношении окончательные результаты одинаковы со
сформулированными выше. В случае оператора N более общего вида
1^ «,«JLC Ф (т^) ^т^
in)"^ 2ш J (-r-./)in(T-OlnIn(T-0 ... 1П(%('^- О '
где
0< т<1, 1п^(т—0 = In In(^_j)(T —О»
теория еще более усложняется, но в принципиальном отношении и здесь
результаты остаются неизменными.
Рассмотренная в настоящем приложении проблема была поставлена авто-
Йом книги в середине 50-х годов. Первые шаги в ее решении в 1956 г. сделал
[. М. Мельник 1), получивший для интеграла
ф(г)=-1,С- iWrfT ^ @<т<1),
^ ' 2л1 J (т — z) In'" (т — 2) '
L
диалоги формул Сохоцкого. Изложенная здесь теория, а также ее обобщения,
построена недавно молодым одесским математиком Н. Л. Василевским!).
ПРИЛОЖЕНИЕ П1
ИСПОЛЬЗОВАНИЕ КРАЕВЫХ ЗАДАЧ В ТЕОРИИ ПРИБЛИЖЕНИЯ
ФУНКЦИЙ
1. Интерполяция целых функций. Общая задача интерполяции
аналитических функций состоит в определении аналитической функции по счетному
множеству значений ее самой или ее производных на некоторой системе
точек. Здесь речь пойдет только об интерполяции целых функций. Из
конкретных задач отметим следующие.
Задача Ньютона. Найти целую функцию F(z), если известны ее
значения в целых точках
F(n)^an (« = 0, 1,2,...). A)
Задача Линдстона. Найти целую функцию F{z) по значениям ее
четных производных в двух точках
F^^""^ @) = an, F^^^^ A) = bn (« = О, 1,2,...). B)
Задача Абеля — Гончарова. Найти целую функцию F(z) по
значениям ее последовательных производных
F^''H^n)==an {« = 0, 1,2,...). C)
Разрешимость и единственность решения поставленных выше задач
существенно зависят от характера роста целой ф>'нкции. Целую функцию
оо
^W'^S ^f^^ будем называть функцией сравнения, если 1) Лп > О
л-о
(п = О, 1, 2, ...) и 2) An+i/An монотонно стремится к нулю. Говорят, что
целая функция F(z) сравнима с Л (г), если существует т (О < т < оо) такое,
что для всех z
\F(z)\^MA(T\2\l D)

610
ПРИЛОЖЕНИЕ III
где Л1 =: M(f, т)> 0; точную нижнюю грань чисел т, для которых имеет
место соотношение D), называют А-типом функции F(z).
Справедливо утверждение: для того, чтобы целая функция F (г) =
оо
2 anZ^ имела А-тип, равный а, необходимо и достаточно, чтобы
л-О
lim sup L^itL
rt->oo I An
Un
(J.
Для Л-сравнимых функций F {г) ^ ^ UnZ^ имеет место обобщенное
n=»0
представление Бореля
f(^)^-^^A(zt)y-{t)dt,
E)
где Y
-w-Z
On
n-0
An t
irt+i
аналитическая в окрестности бесконечно
удаленной точки функция. При A(t) = е* интегральное представление E)
превращается в обычное преобразование Бореля для целых функций
экспоненциального типа.
С помощью преобразования Бореля E) задачи A), B) и C) сводятся
к решению некоторой проблемы моментов в комплексной области.
В последнее время Ю. А. Казьмин в ряде работ (см. 1)—7))*)
применил к решению проблемы моментов методы теории краевых задач
аналитических функций. Это позволило ему исчерпывающим образом решить ряд
важных задач теории интерполяции в самой общей постановке.
Приведем схематически, следуя в основном работе 3), решение общей
проблемы моментов методом краевых задач.
Пусть w{z) аналитична и однолистна в односвязной конечной области О»,
и пусть заданы аналитические в D^ функции Aa(z) (s = О, 1, ..., р—1),
а также р последовательностей {а»в] и р целых чисел /л, О ^ /, :< р— 1 (не
обязательно различных). Общая проблема моментов состоит в следующем:
I. Существует ли аналитическая в замкнутой области D- функция y~(z),
для которой имеют место равенства
JI
2я/
• \lw(z)f'^^'As{z)y''(z)d2=^ans
F)
(л==0, 1, 2,...; 5 = 0, 1, ..., р-1),
где Tz —простой замкнутый гладкий контур, лежащий в области /)^, и
Y"'B) аналитически продолжима вплоть до контура Гг?
П. Если существует хотя бы одна функция yiz), удовлетворяющая
системе уравнений F), то как по числам ana (моментам), находящимся в
правых частях равенств F), восстановить все множество решений {у(г)) си*
стемы F)?
Пусть функция w^w{z) отображает область D, на область D^, и
2 = г(оу)—обратная функция. Равенства F) могут быть записаны в эквива-
*) Ссылки даются на список литературы в конце данного приложения.

ПРИЛОЖЕНИЕ HI en
лентной форме
-^ ^w"'^'^^'A,[2(w)]2 (w)y-[z(w)]dw==a^^. G)
Условимся обозначать 5^ и В~ соответственно внутреннюю и внешнюю
области, ограниченные контуром Га,. Предположим, что область В^ инвариантна
относительно вращений на угол 2я/р, т. е. 65J = В^, 6 = ехр 2я//р. Из G)
оо
следует, что функции as {w) = V _|^J _^^ (s = О, 1, ..., р — 1) должны
быть аналитическими в замкнутой области В~ (если решение существует)
и G) эквивалентно следующей системе краевых уравнений:
Z ^s[^(^^^I ^' (^^^) ^^^^'^ '^YU (а;6^)] - ра,iw) = 4^+ (ш), т^Т^ (8)
(s = 0, 1. ..., р-1).
В (8) функции ^g (w) аналитичны в замкнутой области Bj. Система (8)
приводит к рассмотрению следующей краевой задачи: найти аналитическую
в области В^ функцию Ф~ (w) и р функций Ф^ (ш), аналитических в
области В^у если на контуре Г^^ выполнены условия
5 Л, [г (w^^)] z' (а;6^) 6^ ^^^^ ^>ф- (а;6^) + ра, (ш) = Ф+ (ш) (9)
ft-O
(s = 0, 1 р~1).
Если определить
Д (ш) = det II Л, [г (ш5*I г' (шй*) «* С*-' •) С"Lo
отличен от нуля, то, как можно показать, краевая задача (9) разрешима и
ее решения CD-(а;) совпадают с некоторым подмножеством решений i|j-(a))
краевой задачи Римана
г|)+ (йу) = Л (w) ф" (ш) + В (ш),
где функция В(ш) выражается через известные функции и является
аналитической в кольцеобразной области, содержащей контур Г». Интеграл типа
Коши
/ ч 1 f ф- [ш @] .,
где ф-(о;)—общее решение системы (9), дает полное решение общей
проблемы моментов. В частности, в рассматриваемом случае Л(а>)# О и, в
предположении, что область Dtc является -инвариантной, необходимым и
достаточным условием разрешимости проблемы моментов является аналитич-

612 ПРИЛОЖЕНИЕ Ml
ность функций «s (w) = 2^ "^ ^^ в области В^. Доказательства мы не
приводим.
Укажем еще некоторые полученные Ю. А. Казьминым результаты
В предположении, что Д(ш)#0, дано полное решение проблемы моментов
2л
для областей Dz, образы которых Dw погружаемы в некоторую
инвариантную область. Однако здесь решение задач I и II, относящихся к F),
значительно усложняется. Тем не менее новый подход к решению общей
проблемы моментов F), использующий результаты теории краевых задач, и в
упомянутом случае позволил дать описание совокупностей {ans}, для которых
задача разрешима, и найти в квадратурах ее пол*1ое решение. Это в свою
очередь позволило получить решение ряда конкретных интерполяционных
задач (см. Ю. А. Казьмин 4)).
В работе Ю. А. Казьмина 5) найдены необходимые и достаточные
условия единственности общей проблемы моментов для важных в
приложениях областей Dz, образы которых О^ не являются погружаемыми в
инвариантные области. В частности, это нашло приложение в
установлении необходимых и достаточных условий полноты фундаментальной системы
решений одного класса разностных уравнений.
Отметим, что постановка проблемы F) допускает различные варианты.
Это, помимо многочисленных приложений в теории интерполирования, может
быть использовано при исследовании некоторых вопросов аналитической
теории чисел. В качестве иллюстрации приведем один результат. Будем
говорить, что целая функция F{z) принадлежит [^, а), <7 > 1, О ^ а < -foo,
если для любого т > а выполняется неравенство
If (г)|<Л1(Лт)ехр-^"''^'^'
2\nq •
Последовательность комплексных чисел Сп = осп + фп назовем финально-
целозначнойу если существует такой номер Л^, что для п'^ N действительные
числа an и Рп являются целыми.
Теорема I. Пусть F(z)e[G,0), ^ > 1. Если последовательность
комплексных чисел
л (rt + l)
]
U ' Fmi (rt = 0, 1, 2, ...)
хотя бы для одного комплексного р, 1 < j р | < <7, является финально-цело-
значной, то F(z) ^ 0.
Теорема II. Каким бы малым ни было е > О, всегда можно указать
такое N = N{e)'> О, что интерполяционная задача
F(p'^) = 0 (n==N, iV-f 1, ...).
где р —комплексное, |Р|> \я\> h в классе целых функций [t/, г) имеет
нетривиальные решения (Ю. А. Казьмин 7)).
Это предложение продолжает исследования А. О. Гельфонда (см.
1)—3)), связанные с изучением значений, принимаемых целыми функциями
в точках, образующих геометрическую прогрессию {Р"}. Доказательство
теоремы существенно использует обобщенное преобразование Бореля E) и
последующее сведение к краевой задаче Римана в ее классической постановке.

ПРИЛОЖЕНИЕ III 613
2. О разложениях в ряды по многочленам Аппеля и их обобщениям.
Введенные в 1880 г. Аппелем 1) многочлены составляют обширный класс,
содержащий многие классические системы многочленов. Последовательность
аппелевых многочленов (А. М.) {Ап{г)} определяется равенством
F(t)e''^Y.^n(z)t^ A0)
rt=0
оо
в котором Р (t) = ^ ctj^t^ — степенной ряд с комплексными коэффициен-
тами а^^, причем а^ =7^ 0. В явном виде А. М. А^ (г) выражаются через
числа uj^ следующим образом:
п
^»(^)=Е-(ЯА)Г^""* (« = 0.1,2,...).
Условие аоФО равносильно тому, что степень многочлена An(z) в
точности равна п. Класс Л^*> А. М. определяется как совокупность
всевозможных систем многочленов {Л«(г)} с производящими функциями вида A0).
Многие хорошо известные последовательности многочленов являются
частными случаями А. М. класса Л(*). Примерами (с точностью до нормировки)
могут служить системы полиномов Бернулли, Эрмита, Лагерра и многие
другие. Многочисленные примеры А. М. собраны в справочной книге Г. Б е й т-
мана, А. Эрдейи 1).
Рассматривались различные обобщения А. М., которые тоже носят
название •систем А. М. класса Л<*). Сюда относятся А. М. с производящими
функциями вида
F (t) е^^ <^> = ? Л« (г) t^ W(t)=f^ Wkt\ ri =^ О, (II)
И далее А. М. с производящими функциями еще более общего характера
F(t)A[zW(t)\=^Y.^n{z)t\ A2)
rt-O
В A2) A(z) является функцией сравнения, а W(t) однолистна в некоторой
окрестности начала.
Майкснером был изучен вопрос об ортогональности с весом на
действительной оси последовательности А. М. с производящими функциями вида A1).
Им было показано, что таких систем всего пять, в том числе среди А. М.
с производящими функциями вида A0) лишь одна система многочленов
Эрмита является ортогональной (с весом е~^'^') на действительной оси.
Вопросы, относящиеся к разложениям в ряды по А. М. с производящими
функциями вида A0) и A1) — A2), а также связи А. М. с различными
функциональными уравнениями, рассмотрены многими авторами. В статьях
Ю. А. Казьмина 8), 9) впервые к решению задачи о разложении в ряды
по А. М. аналитических функций, а также к исследованию ряда
примыкающих проблем были применены результаты теории краевых задач. Это
позволило с новой точки зрения осветить проблематику теории А. М. и дать весьма
простые решения ряда относящихся к ним задач.

614 ПРИЛОЖЕНИЕ ni
С. Н. Бернштейн 1) ввел в рассмотрение системы многочленов {5п (г)}
и [Сп{г)], определяемые разложениями
she/ + ch/(l-
chzt-
cht
- sh / A -
-z)
-2)
rt-0
oo
2] Cn{z)t^.
cht
rt-O
Указанные последовательности многочленов {Sn(z)} и {Cn(z)} и
многочисленные разрозненные системы многочленов, изучением которых занимались
Дж. М. Уиттэкер и его школа, а также Ю. А. Казьмин 10)—13),
приводят к следующему обобщению классов А. М.
Пусть р — целое число, р ^ 1. Класс Л^р) систем функций Аппеля
определяется следующим образом. Последовательность функций {д^ {z)]^^q
принадлежит А^р\ если
р —1 оо
J] Ak it) л (гб% (/)) = J] ^« (Z) t\ б = ехр ^,
где Л (г) — функция сравнения, W{t)—аналитична и однолистна в некоторой
окрестности начала координат, а Ak(t)^ A(\t\<C о), k = О, 1, ..., р—\.
В работах Ю. А. Казьмина 12), 6) рассмотрен вопрос о представлении
Л-сравнимых функций квазистепенными рядами по функциям {qn ('2^)}~-о ^
е Л^^\ С помощью теории краевых задач дано исчерпывающее решение
этого вопроса.
ЛИТЕРАТУРА
Ар pel Р. 1) Ann. Sci. Ecole Norm. Sup. 9 A880), 118—144.
Бейтман Г., Эрдейи А. 1) Высшие трансцендентные функции, т. 2
A966), т. 3 A967), «Наука».
Бернштейн С. И. 1) О некоторых свойствах циклически монотонных
функций, Соч., т. 2, изд-во АН СССР, 1954. 493—516.
ГельфондА. О. 1) Исчисление конечных разностей, Физматгиз, 1967.
2) Sur de development des fonctions entieres d'ordre fini en serie dMnter-
polation de Newton, Rend. Lincei U A930), 377—381.
3) О функциях, целочисленных в точках геометрической прогрессии, Ма-
тем. сб. 40, № 1 A933), 42—47.
Евграфов М. А. 1) Интерполяционная задача Абеля — Гончарова,
Гостехиздат, 1954.
Казьмин Ю. А. 1) Проблема моментов в комплексной области, Вестн.
МГУ, сер. матем., механ., Кя 1 A967), 3—11.
2) Об одной общей задаче из теории интерполяции, ДАН СССР 194, № 6
A970), 1251-1254.
3) Общая проблема моментов в комплексной области, Ргос. of the
Conference on the Constructive Theory of Functions, Budapest A969), 1972,
225—254.
4) К проблеме моментов в комплексной области, ДАН СССР 204, № 6
A972), 1309—1312.
5) Общая проблема моментов. Теоремы единственности, ДАН СССР 205,
Ко 1 A972), 19-22.

ПРИЛОЖЕНИЕ IV 615
6) Методы интерполяции аналитических функций и их приложения, Докт.
диссерт., МГУ, 1972.
7) Об интерполировании целых функций в точках, образующих
геометрическую прогрессию, ДАН БССР XVIII, № 5 A974), 402—405.
8) Сингулярные точки и разложения Аппеля, Mathematica 1, 1970, 75—85.
9) О базисах из последовательных примитивных, Матем. заметки 3, № 3
A968), 237—246.
10) О степенных разложениях целых функций экспоненциального типа,
Вестн. МГУ, № 1 A968), 43—63.
11) О разложениях в ряды по степеням (г — с^")^, Матем. заметки 1,
№6 A967), 683—688.
12) О разложениях в ряды по полиномам Аппеля, Матем. заметки 5, № 5
A969), 509—520.
13) О полиномах Аппеля, Матем. заметки в, № 2 A969), 161—172.
ПРИЛОЖЕНИЕ IV
ПРИМЕНЕНИЕ КРАЕВОЙ ЗАДАЧИ РИМАНА
В ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Уже длительное время некоторые задачи теории массового обслуживания
(теории очередей) решаются сведением к соотношениям типа краевой задачи
Римана. В последнее время задачи, решаемые этими методами, проникли
даже на страницы широко распространенных учебных руководств, таких,
например, как учебники Б. В. Гнеденко [4]*) и А. А. Боровкова [6].
Однако терминология и обозначения, используемые в вероятностных работах,
отличаются от принятых в теории краевых задач, что, несомненно,
препятствует взаимообогащению этих теорий.
Цель настоящего приложения — с одной стороны привлечь внимание
специалистов по теории вероятностей к отрасли математики, из которой они
могут черпать методы решения своих задач, а с другой — указать
специалистам по краевым задачам на новое поле приложения их теорий.
Начнем с изложения вспомогательного вопроса — методов решения
интегральных уравнений типа свертки. Эти уравнения, являясь богатым полем
приложений для краевых задач, имеют сами обширнейшие применения и в
классических областях математической физики, и во многих ее современных
разделах, а также во многих вопросах математической экономики.
1. Интегральные уравнения типа свертки
Преобразование Фурье и некоторые его свойства
1. Преобразование Фурье. Формулы
оо
Vf^ ^f(i)e''"dt = F{x) (-оо<;^<оо),
ОО
K-'f=^ J F(/)e-'''df = /(jc) (-оо<д;<оо)
(I.l)
*) Ссылки даются на список литературы в конце данного приложения.

61 б ГТРИЛОЖЕНИЕ fV
определяют две взаимно обратные операции — прямое и обратное
преобразование Фурье*). Установление условий (необходимых или достаточных),
при выполнении которых функция представима интегралом Фурье, является
сложной задачей. Условий, которые были бы одновременно необходимыми и
достаточными, не существует, т. е., как и в случае разложимости в ряд
Фурье, представимость функции интегралом Фурье является самостоятельным
свойством, не сводимым к другим (непрерывности, дифференцируемости
и т. п.). Наиболее стройная теория возникает в том случае, когда за основу
берется инвариантный для преобразования Фурье класс Аг- Однако тогда
интегрируемость нужно понимать уже в смысле среднего квадратического,
кроме того, теорию краевой задачи Римана также нужно строить в классе L2.
Будем считать, что /(a:)sL2, \xf(x)\^L. Тогда F{x) принадлежит Z.2»
кроме того, будет дифференцируемой и, следовательно, тем более
удовлетворять условию Гёльдера, что обеспечит справедливость всех приводимых далее
формул. Ограничимся этим утверждением и дальше на подобного рода
вопросах не будем останавливаться. Прямое преобразование Фурье будем
обозначать большими буквами, а обратное — соответствующими малыми.
2. Свертка. Интеграл
оо оо
—00 —00
называется сверткой функций k (х), ф (х).
Справедлива пара взаимно обратных формул:
7(/г¦ф) = 7i^Kф=:^:(л:)Ф(Jc),
оо оо
V-'^{KF)=--^ ^K(t)F(t)e-^'^*^dt= J ft (*-/)ф(Ой< = *»Ф. A.2)
—оо —оо
3. Условие аналитической продолжимости. Односторонние функции.
В п. 4.3 было показано, что произвольно заданная на контуре функция,
вообще говоря, не является предельным значением аналитической в Ь+ или D-
функции. Там, исходя из формул Сохоцкого для интеграла типа Коши, мы
вывели формулы D.11), D.12), дающие условие аналитической
продолжимости с контура в области D±. Сейчас дадим те же условия, выраженные
посредством интеграла Фурье.
Теорема. Для того чтобы заданная на действительной оси функция
F(x) класса L2 была краевым значением функции F'^(z), аналитической в
верхней (нижней) полуплоскости, такой, что
5 \F'^(x + iy)?dx<M,
необходимо и достаточно, чтобы обращалась в нуль на отрицательной
(положительной) полуоси функция f(x), являющаяся ее обратным преобразованием
Фурье.
Функции f±(x), определяемые равенствами
, , , f Их). х>0, . . ^ Г О, д:>0,
•f(x), х<0,
*) Мы берем преобразование Фурье с несимметричными коэффициентами
A, 1/2я) потому, что в такой форме оно используется при решении
рассматриваемых далее вероятностных уравнений.

ПРИЛОЖЕНИЕ IV 617
будем называть соответственно правой и левой односторонней от f{x).
Очевидно, справедливо соотношение
/W=/+W-/_(Jc). A.4)
В силу сформулированной теоремы преобразования Фурье от правой и
левой односторонней функции будут краевыми значениями функции,
аналитической в верхней и нижней полуплоскости:
Vf^ = 5 f+ И)е^'^dt^^fit)е^^^dt = F+ (х),
—оо о
оо О
" о (Ь5)
Сведение интегральных уравнений типа свертки
к краевой задаче Римана
1. Уравнение Винера — Хопфа. Заданное на положительной полуоси
уравнение
оо
1ф ^Х(р{х)+[ /г (JC - О ф (О dt = f (л:), д: > О (Я, = const), A.6)
о
называется односторонним или (по историческим мотивам) уравнением
Винера— Хопфа. Решаем его преобразованием по Фурье. Предварительно
прибавляем к правой части некоторую произвольную левую одностороннюю
функцию ф-(^) так, чтобы уравнение выполнялось на всей оси, функции ф(д^),
f(x), определенные лишь для х > О, будем считать правыми односторонними.
Получим
^Ф+ W + ^ ¦ 9+ = /+ М + Ф- Mf
после преобразования Фурье с учетом A.2) и A.5) будем иметь
ЯФ"^ (х) + К (х) Ф"^ (х) = f^ (х) + Ф- (л:) (- оо < а: < оо).
Решая относительно Ф+(л:), придем к краевой задаче Римана на
действительной оси:
Искомая функция находится путем обратного преобразования Фурье
Ф(а:) = Ф+(а:) = 7-^Ф+.
2. Уравнение с двумя ядрами и парные уравнения. Методами, близкими к
описанному выше, решаются два типа интегральных уравнений, обобщающих
уравнения Винера — Хопфа.
Уравнение с двумя ядрами
Л^ф^ — ^зФ- + ^1 * Ф+ — ^2 * ^- ~ ^ (— 00 < jf < 00)

618 ПРИЛОЖЕНИЕ IV
СВОДИТСЯ к краевой задаче Римана
Парные уравнения
Л^ф + Ajj • ф = f_^, д: > 0; Я.2Ф + ^2 * ^ ~ ^-' ^ < ^»
сводятся к краевой задаче Римана
относительно вспомогательной кусочно аналитической функции Q-(z), по
которой исходная функция ф(л:)= Уц> определяется формулой
^^^^^FW + Q-U)
^1 + /Ci (д:) •
Рассмотренные здесь уравнения далее не встретятся, потому ограничиваемся
сказанным.
Нетрудно было бы каждый из трех рассмотренных типов уравнений
свести к особому уравнению с ядром Коши (характеристическому или его
транспонированному); подробнее об уравнениях типа свертки сказано в работах
Ю. И. Черского [1] и Ф. Д. Гахова и Ю. И. Черского [2].
Преобразование Лорана Дискретные уравнения
типа свертки
1. Преобразование Лорана. Пусть
а= ..., а-з, а-ь «о, аи ^2, .- A.10)
— бесконечная последовательность (бесконечномерный вектор), для которой
оо оо
ряд ^ \ап\ сходится. Очевидно, сходятся также оба ряда ^ | «л |,
П = —оо п—о
п—1
Тогда функция
оо
/I» —оо
называется преобразованием Лорана последовательности A.10). Операция
отыскания по формулам
^'*===l!r S Л{г)г'^-Чг A.12)
I2|-l
членов последовательности (составляющих вектора) A.10) называется
обратным преобразованием Лорана. Символически: А (z) = Ma, а = М-М.
Последовательности
4. f an. п>0, _ f О, Az>0,
<-{о, п<0, " ««={-«„. п<0, <''^)

ПРИЛОЖЕНИЕ IV 619
называются соответственно правой и левой односторонней
последовательностью.
Очевидно, справедлива
Теорема. Для того чтобы заданная на единичной окружности функция
оо
л (О = 5^ fl/i^" была краевым значением функции Л±(г), аналитической
в единичном круге {вне единичной окружности), необходимо и достаточно,
чтобы последовательность а» была правой {левой) односторонней,
2. Дискретные уравнения типа свертки (с разностными индексами). Выра-
оо
жение а*;с= ^ ^n-k^k ('^ = О» =Ь Ь =Ь2, ...) называется дискретной
fee—оо
сверткой двух векторов а, х. На основании правила перемножения степенных
рядов легко выводится равенство
М(а*х)= f^ J а„_,д^,2''= I; a^z'» f) x^z" = А(г)Х(г).
П=—оо fee—оо щ = —оо п= —оо
A.1^)
Дискретное преобразование Лорана от дискретной свертки равно
произведению дискретных преобразований Лорана от свертываемых векторов.
Бесконечная система уравнений с бесконечным числом неизвестных
оо
^^n+Z^n-k4^fn (« = 0» 1,2,...) A.15)
fe-0
называется дискретным аналогом уравнения Винера — Хопфа. Доопределим
систему на отрицательные значения индексов путем прибавления к правой
части некоторой левой односторонней последовательности Хп {п =—1,—2, ...)
и возьмем от обеих частей преобразование Лорана: умножим каждое из
уравнений на t^ и сложим. Получим
[Я + Л(/)]Х+@ = ^@ + Х-@.
Решая относительно X (t), придем к краевой задаче Римана
Дискретные аналоги интегральных уравнений типа свертки с двумя ядрами
Кхп +CL * X — b * X = fn {п — Оу ±1, ±2,...) и парных уравнений ^i%+
+ а * X = ffif rt ^ О, Х2Хп + b * X = ^п* « < О, также легко свести к
краевым задачам Римана. Подробности можно найти у В. С. Рогожина [3].
2. Две задачи из теории массового обслуживания
Сведения из теории вероятностей
1. Пусть I — случайная величина их — некоторое ее численное значение.
Вероятность Р того, что | примет значение, меньшее, чем х, называется
функцией распределения вероятностей случайной величины g. Символически:
F{x)=^P[l<x]. B.1)
X
Функция р{х), связанная с F{x) равенством F {х) =^ \ р {t) dt, называется
—оо
плотностью распределения вероятностей случайной величины %. Если F{x)

620 ПРИЛОЖЕНИЕ IV
дифференцируема (что мы в дальнейшем будем предполагать), то
р (X) = F' (л:). B.2)
По определению, вероятность Р может принимать лишь значения
О :^ Р ^ 1. Следовательно, функция распределения F(x) неотрицательна,
огргничена и согласно B.1) неубывающая. Плотность р(х)—неотрицательна.
2. Плотность распределения суммы gi + ^2 двух независимых случайных
величин равна (в случае непрерывного распределения) свертке плотностей
оо
р{х)= [ p^^Hx-t)p<^Ht)dt. B.3)
а в случае дискретного распределения — равна дискретной свертке
Pn=-Z PnlkP^k^ (« = О, ±1, d=2, ...). B.4)
/5-1
В случае, если плотности имеют в отдельных точках разрывы 1-го рода,
в формуле B.3), кроме интегрального члена, появляются еще дискретные
слагаемые, соответствующие разрывам плотности.
3. На практике часто приходится иметь дело со случайными величинами,
способными принимать лишь неотрицательные значения. Тогда F(x)=p(x)^0
при X <. 0. Следовательно, функция распределения и плотность распределения
в этом случае являются правыми односторонними функциями, и их
преобразования Фурье {характеристические функции) являются краевыми значениями
функций, аналитических в верхней полуплоскости. Начало координат здесь,
как правило, является точкой разрыва плотности и (при условии, что нет
других разрывов) формула B.3) принимает вид
оо
Р(х)=^ Р^^^ (X - /)р^2) (t) dt + р<2) @)рA) (X). B.5)
о
Среднее время начала обслуживания
Вероятностные соображения, на основании которых составляются
рассматриваемые ниже уравнения, подробно излагаются в [4], § 62, здесь же мы
ограничимся краткой схемой.
В моменты времени ^г (г == 1, 2, ...) поступают требования на
обслуживание. Введем следующие обозначения: Vr = ^r+i — ^г — промежуток времени
между двумя требованиями, уг — длительность обслуживания г-го клиента,
Wr — длительность ожидания обслуживания.
Из простых соображений вытекает соотношение
( Wr + Ur, Wr+Ur> О,
^^- = 1 О, wr + ur<0. ^'-'^
"r = Y;.-v^. B.7)
Пусть kr, фг — плотности распределения соответственно величин Wr, Wr*
Очевидно, при х < О фг = 0. Считаем, что при г-^оо kr, фг имеют
определенные пределы k(x), (р(х). Из равенств B.6) и B.5) переходом к пределу

ПРИЛОЖЕНИЕ IV 621
при г-^оо получаем для определения ц)(х) интегральное уравнение Винера —
Хопфа:
оо
Ф (Jt) - U (JC - о ф it) dt=^(p @) k (а:), х>0. B.8)
о
Решаем его по методу п. 1 на стр. 617. Заменяем Ц)(х) на ф+(л:),
доопределяем уравнение на отрицательной полуоси внесением в правую часть
произвольной левой односторонней функции Ц)-(х) и берем от обеих частей
равенства преобразование Фурье. Получаем краевую задачу Римана
относительно Ф±(г)
Ф+ (х) [1 - К^ (х)] = ф @) К^ (х) + Ф- (х) B.9)
в классе функций, исчезающих на бесконечности.
Переходя к исследованию полученной краевой задачи, заметим, что так
как Ur согласно B.7) представляет собою алгебраическую сумму двух
случайных величин Yr, —Vr, то ее плотность распределения k(x) будет сверткой
их плотностей h(x), f{—х):
k(x)=^ J f(x + t)h(t)dt
В качестве f(x) можно взять наиболее распространенный показательный
закон распределения f(x) = Хе~^^, х > 0; f{x) = О, Jf < 0. Тогда
оо
О
K''{x)^F(^x)H{x) = —j^H{x)
и краевое условие примет вид
Ф+(а:)[д:-Л/ + Я,/Я+(л:)] =
= (JC - Xi) Ф" (JC) - ф @) Я/Я+ (Х) (- сх) < ;С < 00). B.10)
Так как коэффициент и свободный член краевого условия аналитически
продолжимы в комплексную плоскость, то решать задачу будем способом
аналитического продолжения (см. п. 14.6) без обращения к общим формулам.
Не указывая точного значения Я+(г), используем лишь два ее очевидных
свойства:
оо оо
Я+ (Ki) = \h(t) e-^^dt Ф О, Я+ @) = ^ Л (О dt = 1.
о о
Отсюда следует \х - Я/ + Я/Я+ (jc)L,o
= О (других нулей на оси, как легко
показать, нет), и так как [г — Л/]^„;^^ = О, то коэффициент задачи Римана
B.10) имеет индекс единицу и полюс на контуре интегрирования в начале

622 ПРИЛОЖЕНИЕ IV
координат. Следовательно, имеем дело с исключительным случаем. По
теореме Лиувилля
[х - я/ + Л/Я+ (jc)] Ф+ (х) + Я/ф @) Я+ {х) = (JC - Xi) ф- (х) = С,
^+ С~Я/ф@)Я+(г)
2 - Я/ + Я/Я"*" (г) *
Определяя произвольную постоянную С из условия ограниченности решения
в начале координат, получим С = ф@)Я1 и
ф(,)^Я<р@)[1-Я^г)]
оо
Постоянную ф@) можно определить из равенства Ф @) = \ ф (O^f/ =* 1 — ф @).
о
Формула B.11) позволяет вычислить искомое среднее время ожидания, а
также другие представляющие интерес вероятностные величины (математическое
ожидание, дисперсию и т. д.).
Вероятность наличия в обслуживающей системе
п требований
Пусть Pn{t) (л = О, 1, 2, ...) обозначают в момент времени t искомые
вероятности. Для их определения составляется следующая бесконечная
система линейных дифференциальных уравнений:
р;@--ЯРо@ + цР,@,
Р; (/) = - (Я + ц) Р„ (О + ЯЯ„_, (О + liPn+i it) (л = 1, 2, ...). B.12)
где Я, [г — постоянные коэффициенты.
Эта система возникает не только при решении поставленной задачи, но
и служит математической моделью для обширного класса задач, известных
под названием процессов размножения и гибели. Подробный вывод их
имеется, например, в книге [5] (гл. 4), а также в уже упомянутом
руководстве [4] (§§ 51, 61). Не останавливаясь на выводе, перейдем к решению
системы.
Примем, что в начальный момент в системе ожидают обслуживания /
требований, т. е.
'"<»•={::::;;
последние равенства при решении системы B.12) будут служить начальными
условиями. Представляя правые стороны уравнений в виде дискретной
свертки, запишем систему в виде
К (О = Е «rt-Л (^) + У^^п^о (О (« = о, 1, 2, ...), B.13)
/S-0
где Cq = — (Я 4 fi), Oj = Я, a^j = ц, "i^ = ^» k ^ О, ±1, й„ = 1 при л = О
и 6^ = О при пфО.
Для решения системы используем приемы решения дискретных уравнений
свертки (стр. 619). Доопределяем равенства B.13) на отрицательные
значения индекса п путем прибавления к правой части произвольной
последовательности Q~ (п = — I, —2, ...), затем умножаем все уравнения на
соответствующие степени г и суммируем по всем л = О, ±1, ... (преобразова-

ПРИЛОЖЕНИЕ TV 623
ние Лорана). После некоторых несложных преобразований получим равенство
^^ ^f ^^ - [-^ ~ (^ + »i) + Яг] Р+ (г, t) -- liPo (/) = Q- (г, /), B.14)
оо
тле Р'^ {z, i) = ^ Pfi (i) z'^ — ^ротвоАяихая функция для последовательно-
сти Pn{t). в силу вероятностных соображений ^PnU) ограничена, по-
этому Я(г, t) аналитична в единичном круге. Произвольная последовательность
— оо
On (О берется такой, чтобы Q" (г, О = ^ 0« (О 2?" была аналитичной
вне единичного круга. л--1
Соотношение B.14) представляет собою на единичной окружности
краевую задачу типа задачи Римана. Умножая B.14) на 2, а затем применяя
теорему об аналитическом продолжении и теорему Лиувилля, получим
г Ц^ - [ji - (Я + |i) г + Кг^] Р+ ~ iizPo - С
Подставляя 2 = 0, найдем
С = - fiP+ (О, /) = - [iPo @.
Для отыскания Р+B,0 остается решить линейное дифференциальное
уравнение
Z ^^ ^^' ^^ - [й - (Я + |i) 2 + Хг^\ Р+ (г, О + ,х (I - 2) Ро (/) =^0 B.15)
при начальном условии Р+B,0) = 2^ Искомые вероятности Pn(t) находятся
I д^ I
как коэффициенты ряда Тейлора по формулам Рп (t) == "^fT"^ ^ (^» ^)
Фактическое решение уравнения B.15) в нашу задачу не входит.
г=о
Заключительные замечания
Рассмотренные задачи, характерные наличием одного канала
обслуживания и равными возможностями клиентов, принадлежат к числу простейших.
Более сложный класс задач — хотя и с одним обслуживающим каналом, но
с предпочтением, отдаваемым отдельным видам требований
(«приоритетные», — приводит к краевой задаче Римана для функций также одного
переменного, но зависящих от ряда параметров. Многоканальное обслуживание
при наличии различных требований приводит к краевым задачам для
функций многих переменных.
ЛИТЕРАТУРА
1. Черский Ю. И., О некоторых особых интегральных уравнениях,
Уч. Зап. Казанск. ун-та 113, Яо 10 A953). 43—55.
2. Г а X о в Ф. Д. и Черский Ю. И., Особые интегральные уравнения
типа свертки. Изв. АН СССР, сер, матем. 20, 1956, 33—52.
3. Рогожин В. С, Один класс бесконечных систем линейных
алгебраических уравнений. Докл. АН СССР 114, JVb 3 A957), 486—489.
4. Гнеденко Б. В., Курс теории вероятностей, «Наука», 1969.
5. С а а т и Т., Элементы теории массового обслуживания и ее
приложения, «Сов. Радио», 1971.
6. Боровков А. А., Теория вероятностей, «Наука», 1976

ЛИТЕРАТУРА
А. Руководства, монографии и работы обзорного характера
1. Векуа И. Н., Новые методы решения эллиптических уравнений, Гостех-
издат, 1948.
2. Векуа И. Н., Обобщенные аналитические функции, Физматгиз, 1959.
3. Векуа Н. П., Системы сингулярных интегральных уравнений, «Наука»,
1970.
4. Владимиров В. С, Методы теории функций многих комплексных
переменных, М., Физматгиз, 1964.
5. Гахов Ф. Д., Линейные краевые задачи теории функций комплексной
переменной, Изв. Казанск. физ.-матем. об-ва X, сер. 3, 1938, 39—79.
6. Гахов Ф. Д., Краевые задачи аналитических функций и сингулярные
интегральные уравнения, Изв. Казанск. физ.-матем. об-ва XIV, сер. 3,
1949, 75—160.
7. Гахов Ф. Д., Краевая задача Римана для системы п пар функций, УМН
VII, вып. 4 E0), 1952, 3—54.
8. Годунов С. К., Уравнения математической физики, «Наука», 1971.
9. 3верович Э. И., Литвинчук Г. С, Краевые задачи со сдвигом для
аналитических функций и сингулярные функциональные уравнения, УМН
23, вып. 3, 1968, 67—121.
10. Hilbert D., Grundzuge der Integralgleichungen, Leipzig — Berlin, 2-te
Aufl., 1924, Drittes Abschnitt.
11. Иванов В. В., Теория приближенных методов и ее применение к
численному решению сингулярных интегральных уравнений, «Наукова думка»,
Киев, 1968.
12. Лаврентьев М. А. и Шабат Б. В., Методы теории функций
комплексного переменного, «Наука», 1973.
13. Левин Б. Я., Распределение корней целых функций, Гостехиздат, 1956.
14. Михайлов Л. Г., Новый класс особых интегральных уравнений и его
применения к дифференциальным уравнениям с сингулярными
коэффициентами, Тр. АН Тадж. ССР, т. 1, Душанбе, 1963.
15. Михлин С. Г., Сингулярные интегральные уравнения, УМН III, вып. 3
B5), 1948, 29—112.
16. Мусхелишвили Н. И., Сингулярные интегральные уравнения,
«Наука», 1968.
17. Мусхелишвили Н. И., Некоторые основные задачи математической
теории упругости, «Наука», 1966.
18. Привалов И. И., Граничные свойства аналитических функций,
Гостехиздат, 1950.
19. Picard Е., Lemons sur quelques types simples d'equations aux derivees
partielles, Paris, 1927.
20. Pоinсаre A., Lemons de Mecanique Celeste, t. Ill, Ch. X.
21. Риман Б., Сочинения, Гостехиздат, 1948.

ЛИТЕРАТУРА
625
22. Смирнов В. И., Курс высшей математики, т. III, ч II, «Наука», 1969;
т. IV, Физматгиз, М., 1958.
23. Смирнов М. М , Уравнения смешанного типа. «Наука», 1970.
24. Сохоцкий Ю. В., Об определенных интегралах и функциях,
употребляемых при разложении в ряды, С.-Петербург, 1873.
25. Спрингер Дж., Введение в теорию римановых поверхностей, ИЛ, 1960.
26. Трикоми Ф., О линейных уравнениях смешанного типа, Гостехиздат,
1947.
27. Тумашев Г. Г. и Нужин М. Т., Обратные краевые задачи и их
приложения, Изд-во Казанск. ун-та, 1965.
28. Форд Р., Автоморфные функции, ОНТИ, 1936.
29. Xалилов 3. И., Линейные уравнения в линейных пространствах, изд.
АН Азерб. ССР, Баку, 1949.
30. Xведелидзе Б. В., Линейные разрывные граничные задачи теории
функций, сингулярные интегральные уравнения и некоторые их
приложения, Тр. Тбил. матем. ин-та АН Груз. ССР ХХШ, 1956, 3—158.
Б. Оригинальные работы
Абдуллаев Р. Н. 1) Об условии разрешимости однородной задачи
Римана на замкнутых римановых поверхностях, ДАН СССР 152, № 6, 1963,
1279—1281.
2) К условиям разрешимости однородной задачи Римана на замкнутых
римановых поверхностях, Сообщ. АН Груз. ССР 35, № 3, 1964, 519—522.
3) Однородная задача Римана на замкнутых римановых поверхностях,
ДАН СССР 160, № 5, 1965, 983—985.
Авхадиев Ф. Г., Гайдук В. Н. 1) Применение почти выпуклых
функций к обратным краевым задачам, Изв. вузов, Математика, № 6, 1968,
3-10.
Аксентьев Л. А. 1) Достаточные условия однолистности трех
обратных краевых задач, Уч. зап. Казанск. ун-та 117, № 2, 1957, 32—35.
2) Об условиях разрешимости и условиях однолистности, Тр. семинара
по обратным краевым задачам, Изд-во Казанск. ун-та, вып. 2, 1964, 12—20.
3) Построение оператора Шварца методом симметрии, Тр. семинара по
обратным краевым задачам, Изд-во Казанск. ун-та, вып. 2, 1964, 3—И.
4) Построение оператора Шварца методом симметрии, Тр. семинара по
краевым задачам, Изд-во Казанск. ун-та, вып. 3, 1966, 11—22.
5) Построение оператора Шварца методом симметрии, Тр. семинара по
краевым задачам, Изд-во Казанск. ун-та, вып. 4, 1967, 3—10.
Аксентьев Л. А., Авхадиев Ф. Г. 1) Об одном классе
однолистных функций, Изв. вузов, Математика, № 10, 1970, 12—20.
Алексеев А. Д. 1) Об особом интегральном уравнении на контуре из
класса Я, ДАН СССР 136, № 3, 1961, 525—528.
2) Особое интегральное уравнение на контуре из класса /?, Тр. Тбил.
матем. ин-та АН Груз. ССР 27, 1960, 275—291.
Андрианов С. Н. 1) О существовании и числе решений обратной
краевой задачи теории аналитических функций, Уч. зап. Казанск. ун-та 113,
№ ю, 1953, 21—30.
Антоневич А. Б. 1) Об индексе псевдодифференциального оператора
с конечной группой сдвигов, ДАН СССР 190, № 4, 1970, 751—752.
2) Эллиптические псевдодифференциальные операторы с конечной
группой сдвигов, Изв. АН СССР, сер. матем 37, № 3, 1973, 663—675.
Аржанов Г. В. 1) О нелинейной краевой задаче типа задачи Римана,
ДАН СССР 132, № 6, I960, 1227—1230.
2) О нелинейной краевой задаче типа задачи Римана, Сиб. матем. ж. 2,
№ 4, 1961, 481—504.

626
ЛИТЕРАТУРА
Арутюнян Н. X. 1) Плоская контактная задача теории пластичности
со степенным упрочнением материала, Изв. АН Арм. ССР XII, № 2, 1959,
77-105/
Арутюнян Н. X., Манукян М. М. 1) Контактная задача теории
ползучести с учетом сил трения, ПММ 27, в. 5, 1963, 813—820.
Аткинсон Ф. В. 1) Нормальная разрешимость линейных уравнений
в нормированных пространствах, Матем. сб. 28 G0), № 1, 1951, 3—14.
Ахиезер Н. И. 1) О некоторых формулах обращения сингулярных
интегралов, Изв. АН СССР, сер. матем. 9, 1945, 275—290.
Ахиезер Н. И., Щербина В. А. 1) Об обращении некоторых
сингулярных интегралов, Уч. зап. Харьковск. ун-та XXV, сер. 4, 1957, 191—198.
Бабкин Б. Н. 1) Об одном условии существования решения
интегрального уравнения первого рода, Уч. зап. Пермск. ун-та 131, 1966, 126—129.
Бархин Г. С, Усманов 3. Д. 1) Задача Гильберта для кусочно-
регулярной обобщенной аналитической функции, Сб. «Исслед. по краевым
задачам теории функций и диф. ур-ний», Душанбе, 1964, 113—132.
Батырев А. В. 1) Приближенное решение задачи Римана —
Привалова, УМН 11, вып. 5, 1956, 71—76.
Башкарёв П. Г., Нечаев А. П. 1) К теории краевых задач со
сдвигами, Докл. АН УССР А, № 2, 1973, 99—102.
Беркович Ф. Д. 1) Интегральные уравнения типа свертки с
бесконечным числом решений, Сб. «Матем. анализ и его приложения» изд-во Ростовск.
ун-та, 1969, 27—33.
2) О приложении краевых задач с бесконечным индексом к исследованию
интегральных уравнений, Материалы Всес. конфер. по краевым задачам,
Изд-во Казанск. ун-та, 1970, 49—54.
Беркович Ф. Д., Говоров Н. В. 1) О краевой задаче Карлемана
с бесконечным индексом, Сиб. матем. ж. 12, № 5, 1971, 1001—1014.
Беркович Ф. Д., Конышкова Е. М. 1) Об одном случае краевой
задачи Римана с бесконечным индексом, Сообщ. Рост, научн. матем. об-ва,
Ростов-на-Дону, 1968, 158—164.
Бицадзе А. В. 1) К проблеме уравнений смешанного типа, Тр. матем.
ин-та АН СССР 61, 1953, 1—60.
Бородин М. А. 1) Краевые задачи для голоморфных функций в
пространстве одного и нескольких комплексных переменных, Кандидатская
диссертация, Донецк, 1969.
Боярский Б. В. 1) Об обобщенной граничной задаче Гильберта,
Сообщ. АН Груз. ССР 25, № 4, 1960, 385—390.
Василевский Н. Л. 1) Об условиях нётеровости и формула для
индекса одного класса интегральных операторов типа потенциала, ДАН СССР
202, No. 4, 1972, 747—750.
Векуа И. Н. 1) О сингулярных линейных интегральных уравнениях,
ДАН СССР 26, № 8, 1940, 335—338.
2) Интегральные уравнения с особым ядром типа Коши, Тр. Тбил. матем.
ин-та АН Груз. ССР X, 1941, 45-72.
3) К теории сингулярных интегральных уравнений, Сообщ. АН Груз. ССР
III, № 9, 1942, 869—876.
4) Об одной линейной граничной задаче Римана, Тр. Тбил. матем. ин-та
АН Груз. ССР XI, 1942, 109—139.
5) О некоторых свойствах решений систем уравнений эллиптического типа,
ДАН СССР 98, № 2, 1954, 181—184.
Векуа Н. П. 1) Об одной обобщенной граничной задаче Карлемана
для нескольких неизвестных функций, Изв. АН СССР, сер. матем. 20, № 3,
1956, 377—384.
Владимиров В. С. 1) Задача линейного сопряжения для
голоморфных функций, Изв. АН СССР, сер. матем. 29, № 4, 1965, 807—834.

ЛИТЕРАТУРА
627
2) Теорема об «острие клина» Боголюбова, ее развитие и применение,
Сб. «Проблемы теоретической физики», поев. Н. Н. Боголюбову в связи с его
шестидесятилетием, «Наука», 1969, 61—67.
Гагуа М. Б. 1) О некотором применении кратных интегралов типа
Коши, Сб. «Исследования по совр. пробл. теории функц. компл. переменного»,
Физматгиз, 1960, 345—352.
Гайдук В. Н. 1) Об однолистности решений обратных краевых задач,
Тр. семин. по краев, задачам, Изд-во Казанск. ун-та, вып. 9, 1972, 39—48
Ганин М. П. 1) Краевые задачи теории полигармонических функций,
Уч. зап. Казанск. ун-та 111, № 10, 1951, 9—13.
2) Краевые задачи для полианалитических функций, ДАН СССР 80, № 3,
1951, 313—316.
3) Эквивалентно-регуляризующий оператор для системы сингулярных
интегральных уравнений, ДАН СССР 79, № 3, 1951, 385—387.
4) Об одной общей краевой задаче для аналитических функций ДАН
СССР 79, № 6, 1951, 921—924.
5) Об одной общей краевой задаче для аналитических функций,
Диссертация, Казань, 1952.
Гахов Ф. Д. 1) О краевой задаче Римана, Матем. сб. 2 D4), № 4, 1937,
673-683.
2) Краевые задачи теории аналитических функций и сингулярные
интегральные уравнения, Докторская диссертация, Тбилиси, 1941.
3) Об обратных краевых задачах, ДАН СССР 86, № 4, 1952, 649—
652.
4) Об обратных краевых задачах, Уч. зап. Казанск. ун-та 113, № 10,
1953, 9—20.
5) Об обратной краевой задаче для многосвязной области, Уч. зап. Ро-
стовск. пед. ин-та 3, 1955, 19—27.
6) О новых типах интегральных уравнений, разрешимых в замкнутой
форме, Сб. «Проблемы механ. сплошн. среды», изд-во АН СССР, 1961, 102—
114.
7) О нелинейной краевой задаче, обобщающей краевую задачу Римана,
ДАН СССР 181, № 2, 1968, 271—274.
8) О нелинейной краевой задаче типа задачи Римана в многосвязной
области, Rev. roum. math, pures et appl. XIII, № 9, 1968, 1319—1326.
9) Вырожденные случаи особых интегральных уравнений с ядром Коши,
Дифференц. ур-ния 2, № 4, 1966, 533—543.
10) О нелинейной краевой задаче с допустимыми нулями на контуре,
ДАН СССР 210, № 6, 1973, 21—24.
Гахов Ф. Д., Зверович Э. И., Самко С. Г. 1) Приращение
аргумента, логарифмический вычет и обобщенный принцип аргумента, ДАН СССР
215, № 3, 1974, 432—435.
Гахов Ф. Д., Какичев В. А. 1) Случаи вырождения двумерных
сингулярных интегральных уравнений с ядрами Коши и постоянными
коэффициентами, Сб. «Функцион. анализ и теория функций», вып. 4, изд-во Казанск.
ун-та, 1967, 91—96.
Гахов Ф. Д., Крикунов Ю. М. 1) Топологические методы
комплексного переменного и их приложения к обратным краевым задачам, Изв. АН
СССР, сер. матем. 20, 1956, 206—240.
Гахов Ф. Д., Мельник И. М. 1) Особые точки контура в обратной
краевой задаче теории аналитических функций, Укр. матем. ж. И, № 1, 1959,
25—37.
Гахов Ф. Д., Хасабов Э. Г. 1) О краевой задаче Гильберта для
многосвязной области, Изв. вузов, Математика, т. 2, № 1, 1958, 12—21.
Гахов Ф. Д., Чибрикова Л. И. 1) О некоторых типах сингулярных
интегральных уравнений, разрешаемых в замкнутой форме, Матем. сб. 35,
№ 3, 1954, 395—436.

62а
ЛИТЕРАТУРА
2) О краевой задаче Римана для случая пересекающихся контуров, Уч.
зап. Казанск. ун-та 113, № 10, 1953, 107—110.
Говоров Н. В. 1) О краевой задаче Римана с бесконечным индексом,
ДАН СССР 154, № 6, 1964, 1247—1249.
2) Об ограниченных решениях краевой задачи Римана с бесконечным
индексом степенного порядка, ДАН СССР 182, № 4, 1968, 750—753.
3) Об ограниченных решениях однородной краевой задачи Римана с
бесконечным индексом степенного порядка, Сб. «Теория функц., функц. анализ и
их приложения», Изд-во Харьк. ун-та, вып. 11, 1970, 3—-34.
4) Об условиях неразрешимости однородной краевой задачи Римана с
отрицательным индексом ее коэффициента, Уч. зап. Каб.-Балк. ун-та 19, 1963,
137—141.
5) Неоднородная краевая задача Римана с бесконечным индексом, ДАН
СССР 159, № 5, 1965, 961—964.
6) Краевая задача Римана с бесконечным индексом, Докторская
диссертация, Харьков, 1968.
Гохберг И. Ц. 1) Задача факторизации в нормированных кольцах,
функции от изометрических и симметрических операторов и сингулярные
интегральные уравнения, УМН XIX, вып. 1, 1964, 71—124.
Гохберг И. Ц., Крупник Н. Я. 1) О спектре сингулярных
интегральных операторов в пространстве LP, Studia Mathematica 31, 1968, 347—362.
2) Сингулярные интегральные операторы с кусочно-непрерывными
коэффициентами и их символы, Изв. АН СССР, сер. матем. 35, № 4, 1971, 940—
964.
3) О сложных линейных сингулярных интегральных операторах, Матем.
исследования 4, вып. 4, Кишинев, 1969, 20—32.
Данилюк И. И. 1) О задаче Гильберта с измеримыми коэффициентами,
Сиб. матем. ж. 1, № 2, 1960, 171—197.
2) К теории одномерных сингулярных уравнений, Сб. «Пробл. механ.
сплошн. среды», Изд-во АН СССР, 1961, 135—144.
Джваршейшвили А. Г. 1) О кратных интегралах типа Коши, Rev.
Roum. math, pures et appl. 9, № 5, 1964, 409—424.
2) Об особом интеграле, Тр. Тбил. ун-та 84, 1962, 161—184.
3) Об интегралах типа Коши — Стилтьеса, Тр. Тбил. матем. ин-та АН
Груз. ССР 34, 1968, 22—50.
Зверович Э. И. 1) Краевые задачи со сдвигом на абстрактных рима-
новых поверхностях, ДАН СССР 157, № 1, 1964, 26—29.
2) Краевая задача типа задачи Карлемана для многосвязной области,
Матем. сб. 64 A06), № 4, 1964, 618—627.
3) Краевые задачи со сдвигом на абстрактных римановых поверхностях,
Сиб. матем. ж. VII, № 4, 1966, 804—819.
4) Построение в явном виде аналога ядра Коши на римановых
поверхностях некоторых алгебраических функций, Матем. заметки 8, № 6, 1970,
693—701.
5) Теория двухэлементных краевых задач на римановых поверхностях и
ее приложения, Докторская диссерт., Одесса, 1971.
6) Метод локально-конформного склеивания, ДАН СССР 205, № 4, 1972,
767—770.
Зверович Э. И., Литвинчук Г. С. 1) Односторонние краевые
задачи теории аналитических функций, Изв. АН СССР, сер. матем. 28, № 5,
1964, 1003—1036.
Зверович Э. И., Чернецкий В. А. 1) Краевая задача Карлемана
на римановой поверхности с краем, Укр. матем. ж. 22, № 5, 1970, 591—599.
Зерагия П. К. 1) Об интегрировании полигармонических уравнений,
Тр. Тбил. матем. ин-та АН Груз. ССР VIII, 1940, 135—163.
Иванов В. В. 1) Приближенное решение особых интегральных
уравнений, ДАН СССР ПО, № 1, 1956, 15—18.

ЛИТЕРАТУРА
№
2) О применении метода моментов и смешанного метода к
приближенному решению сингулярных интегральных уравнений, ДАН СССР 114, № 5,
1957, 945—948.
3) Некоторые свойства особых интегралов типа Коши и их приложения,
ДАН СССР 121, № 5, 1958, 793—794.
Исаханов Р. С. 1) Об одном классе сингулярных интегро-дифферен-
циальных уравнений, ДАН СССР 132, № 2, 1960, 264—267.
2) О некоторых граничных задачах линейного сопряжения, Тр. Тбил.
матем. ин-та АН Груз. ССР 28, 1962, 73—84.
Какичев В. А. 1) Граничные свойства интеграла типа Коши многих
переменных, Уч. зап. Шахт. пед. ин-та 2, вып. 6, 1959, 25—90.
2) Преобразование Коши обобщенных функций, ДАН СССР 134, № 6,
1960, 1287—1290.
3) Краевые задачи линейного сопряжения для функций, голоморфных
в бицилиндрических областях. Сб. «Теория функций, функц. анализ и их
приложения», вып. 5, Харьков, 1967, 37—58.
4) Методы решения краевых задач линейного сопряжения для функций,
голоморфных в бицилиндрических областях. Сб. «Теория функций, функц.
анализ и их приложения», вып. 14, Харьков, 1971, 3—15.
5) Мультипликативные краевые задачи для функций, голоморфных в
бицилиндрических областях, Сб. «Теория функций, функц. анализ и их
приложения», вып. 12, Харьков, 1970, 12—20.
6) О регуляризации сингулярных интегральных уравнений с ядрами Коши
для бицилиндрических областей, Изв. вузов, Математика 7 F2), 1967, 54—64.
7) Вырожденные двумерные сингулярные интегральные уравнения с
ядрами Коши для бицилиндрических областей I и И, Сб. «Теория функций,
функцион. анализ и их приложения», вып. 7, Харьков, 1968, 13—19 и вып. 8,
1969, 25—28.
8) Интеграл Шварца и формулы Гильберта для аналитических функций
многих комплексных переменных, Изв. вузов, Математика 2, 1959, 80—93.
9) Задача Гильберта для функций, голоморфных в бикруге, и некоторые
ее приложения. Сб. «Теория функций, функцион. анализ и их приложения»,
вып. 18, Харьков, 1973, 3—18.
Карапетянц Н. К., Самко С. Г. 1) Об одном новом подходе к
исследованию сингулярных интегральных уравнений со сдвигом, ДАН СССР
202, № 2, 1972, 273—276.
2) Сингулярный интегральный оператор со сдвигом на разомкнутом
контуре, ДАН СССР 204, № 3, 536-539.
3) Сингулярные интегральные уравнения со сдвигом Карлемана в случае
разрывных коэффициентов и исследование нётеровости одного класса
линейных операторов с инволюцией, ДАН СССР 211, № 2, 1973, 281—284.
Карцивадзе И. Н., Хведелидзе Б. В. 1) Об одной формуле
обращения, Сообщ. АН Груз. ССР X, № 10, 1949, 587—591.
2) Об интеграле типа Коши, Тр. Тбил. матем. ин-та АН Груз. ССР XX,
1954, 211—244 (на груз, яз., с подробным русским резюме).
Квеселава Д. А. 1) Решение одной граничной задачи теории функций,
ДАН СССР 53, № 8, 1946, 683—686.
2) Некоторые граничные задачи теории функций, Тр. Тбил. матем. ин-та
АН Груз. ССР XVI, 1948, 39—80.
3) Граничная задача Гильберта и сингулярные интегральные уравнения
в случае пересекающихся контуров, Тр. Тбил. матем. ин-та АН Груз. ССР
XVII, 1949, 1—27.
4) Задача Римана — Гильберта для многосвязной области, Сообщ. АН
Груз. ССР VI, № 8, 1945, 581—590 (на груз. яз.).
5) Сингулярные интегральные уравнения с разрывными коэффициентами,
Тр. Тбил. матем. ин-та АН Груз. ССР XIII, 1944, 1—27 (на груз. яз. с
подробным русским резюме).

630
ЛИТЕРАТУРА
Келдыш М. В. 1) Конформные отображения многосвязных областей на
канонические области, УМН VI, 1939, 90—119.
Келдыш М. В., Седов Л. И. 1) Эффективное решение некоторых
краевых задач для гармонических функций, ДАН СССР 16, № 1, 1937,
7—10.
Комяк И. И. 1) Нелинейная краевая задача типа задачи Римана с
положительными показателями, Изв. АН БССР, сер. физ.-матем. наук, № 6,
1970, 83—87.
Конышкова Е. М. 1) О решении характеристического сингулярного
интегрального уравнения с бесконечным индексом, Сообщ. АН Груз. ССР 65,
№ 3, 1972, 535—538.
Кордзадзе Р. А. 1) Об индексе сингулярных интегро-функциональных
операторов, ДАН СССР 185, № 4, 1969, 753—756.
Кравченко В. Г. 1) К теории Нётера функциональных уравнений с
некарлемановским сдвигом, ДАН СССР 201. № 6, 1971, 1275—1278.
2) К теории Нётера интегро-функциональных уравнений со сдвигом, Укр.
матем. ж, 24, № 6, 1972, 752—762.
Красновидова И. С, Рогожин В. С. 1) Достаточные условия
однолистности решения обратной краевой задачи, УМН VIII, вып. 1 E3),
1953, 151—153.
Крейн М. Г. 1) Об одном новом методе решения линейных
интегральных уравнений первого и второго рода, ДАН СССР 100, № 3, 1955, 413—416.
Крикунов Ю. М. 1) О решении обобщенной краевой задачи Римана
и линейного сингулярного интегро-дифференциального уравнения, Уч. зап.
Казанск. ун-та 112, № 10, 1952, 191—199.
2) О решении обобщенной задачи Римана, ДАН СССР 85, № 2, 1952,
269—272.
3) Обобщенная краевая задача Римана и линейное сингулярное интегро-
функциональное уравнение, Уч. зап. Казанск. ун-та 116, № 4, 1956, 3—29.
4) Дифференцирование особых интегралов с ядром Коши и одно
граничное свойство голоморфных функций, Сб. «Краевые задачи теории функц.
компл. перем.», изд-во Казанск. ун-та, 1962, 17—24.
Кудряшов С. Н. 1) К теории однолистности решения внешней
обратной краевой задачи, Тр. семин. по краев, задачам, изд-во Казанск. ун-та,
вып. 7, 1970, 193—197.
Купрадзе В. Д. 1) Теория интегральных уравнений с интегралом
в смысле главного значения по Коши, Сообщ. АН Груз. ССР II, № 7, 1941,
587—596.
2) О проблеме эквивалентности в теории особых интегральных уравнений,
Сообщ. АН Груз. ССР II, № 9, 1941, 793-798.
3) К теории интегральных уравнений с интегралом в смысле главного
значения по Коши, Изв. АН СССР, сер. матем. 5, № 3, 1941, 255—262.
Литвинчук Г. С. 1) Теория Нётера системы сингулярных
интегральных уравнений со сдвигом Карлемана и комплексно сопряженными
неизвестными, Изв. АН СССР, сер. матем. 31, № 3, 1967, 563—586; 32, № 6, 1968,
1414—1417.
2) Об устойчивости одной краевой задачи теории аналитических
функций, ДАН СССР 174, № 6, 1967, 1268—1270.
3) Об одной задаче, обобщающей краевую задачу Карлемана, ДАН
СССР 139, № 2, 1961, 290—293.
4) Об одном типе особых функциональных уравнений и краевых задач
со сдвигом для аналитических функций, Изв. АН СССР, сер. матем. 25, № 6,
1961, 871—886.
5) К теории краевых задач со сдвигом Карлемана ДАН УССР, сер. А,
Ко И, 1967, 1019—1022.
6) Об индексе и нормальной разрешимости одного класса
функциональных уравнений, ДАН СССР 149, № 5, 1963, 1029—1032,

ЛИТЕРАТУРА
631
Литвинчук Г. С, Нечаев А. П. 1) К теории обобщенной краевой
задачи Карлемана, ДАН СССР 189, № 1, 1969, 38—41.
2) Обобщенная краевая задача Карлемана, Матем. сб. 82, № 1, 1970,
30-54.
Литвинчук Г. С, Хасабов Э. Г. 1) О краевой задаче Гильберта
со сдвигом, ДАН СССР 142, № 2, 1962, 274—277.
2) Об индексе обобщенной краевой задачи Гильберта, УМН 20, вып. 6,
1965, 124—130.
3) Об одном типе сингулярных интегральных уравнений, Сиб. матем. ж.
5, № 3, 1964, 608—625.
4) Один класс сингулярных интегральных уравнений и обобщенная
краевая задача типа задачи Карлемана, Сиб. матем. ж. 5, № 4, 1964, 858—880.
Луканкин Г. Л. 1) О некоторых краевых задачах для функций двух
комплексных переменных, Уч. зап. Моск. обл. пед. ин-та, вып. 269, 1969,
23-48.
Магнарадзе Л. Г. 1) Об одном обобщении теоремы Племели —
Привалова, Сообщ. АН Груз. ССР VIII, N° 8, 1947, 509—516.
2) Теория одного класса линейных сингулярных интегро-дифференциаль-
ных уравнений, Сообщ. АН Груз. ССР 4, № 2, 1943, 103—110.
Мылышев В. А. 1) Уравнения Винера — Хопфа в четверть-плоскости,
дискретные группы и автоморфные функции, Матем. сб. 84 A26), № 4, 1971,
499—525.
2) Случайные блуждания, уравнения Винера — Хопфа в
четверть-плоскости, автоморфизмы Галуа, Изд-во МГУ, 1970.
Манджавидзе Г. Ф., Хведелидзе Б. В. 1) О задаче Римана —
Привалова с непрерывными коэффициентами, ДАН СССР 123, № 5, 1958,
791-794.
Манджавидзе Г. Ф. 1) Об одном классе сингулярных интегральных
уравнений с разрывными коэффициентами, Сообщ. АН Груз. ССР 11, № 5,
1950, 269—274.
Маркушевич А. И. 1) Об одной граничной задаче теории
аналитических функций, Уч. зап. МГУ, т. I, вып. 100, 1946, 20—30.
Мельник И. М. 1) Предельные значения аналитической функции,
представленной криволинейным интегралом, Сообщ. АН Груз. ССР XVII, № 8,
1956, 681—688.
2) Исключительный случай краевой задачи Римана, Тр. Тбил. матем.
ин-та АН Груз. ССР 24, 1957, 149—162.
3) Поведение интеграла типа Коши вблизи точек разрыва плотности и
особый случай краевой задачи Римана, Уч. зап. Ростовск. ун-та 43, вып. 6,
1959, 57—71.
Михайлов Л. Г. 1) Предельные значения аналитической функции,
представленной криволинейным интегралом, Уч. зап. Тадж. ун-та I, 1952,
32—55.
2) Краевая задача типа задачи Римана для систем дифференциальных
уравнений первого порядка эллиптического типа, Уч. зап. Тадж. ун-та X,
1957, 32—79.
Михлин С. Г. 1) Проблема эквивалентности в теории сингулярных
интегральных уравнений, Матем. сб. 3 D5), 1938, 121—141.
2) Об одном классе сингулярных интегральных уравнений, ДАН СССР
24, № 4, 1939, 315—317.
Моткин А. С. 1) Сингулярные интегральные уравнения по
бесконечному контуру, Изв. АН БССР, сер. физ.-мат. наук, № 4, 1967, 36—46.
2) О числе решений сингулярного интегрального уравнения на
бесконечном контуре, Изв. АН БССР, сер. физ.-мат наук, № 4, 1969, 72—77.
Мусхелишвили Н. И. 1) Приложение интеграла типа Коши к
одному классу сингулярных интегральных уравнений, Тр. Тбил матем. ин-та
АН Груз. ССР X, 1941, 1—43.

632
ЛИТЕРАТУРА
Мусхелишвили Н. И., Квеселава Д. А. 1) Сингулярные
интегральные уравнения с ядрами типа Коши на разомкнутых контурах, Тр. Тбил.
матем. ин-та АН Груз. ССР XI, 1942, 141—172.
Наталевич В. К. 1) Нелинейные сингулярные интегральные
уравнения и нелинейные краевые задачи теории аналитических функций, Уч. зап.
Казанск. ун-та 112, № 10, 1952, 155—190.
Нужин М. Т. 1) О некоторых обратных краевых задачах и их
применении к определению формы сечений скручиваемых стержней, Уч. зап. Казанск.
ун-та 109, № 1, 1949, 97—120.
2) Об обратных краевых задачах для многосвязных областей, Изв. вузов,
Математика 5, 1964, 69—77.
Пааташвили В. А. 1) Об одной разрывной задаче линейного
сопряжения с суммируемым коэффициентом, Сообщ. АН Груз. ССР 34, № 3, 1964,
519—524.
2) О линейной задаче сопряжения в случае счетного множества
замкнутых контуров, Сообщ. АН Груз. ССР 37, № 1, 1965, 31—36.
3) О линейной задаче сопряжения в случае счетного множества
замкнутых контуров, Тр. Тбил. матем. ин-та АН Груз. ССР 34, 1968, 103—122.
Парадоксова И. А. 1) Об одном интегральном уравнении с авто-
морфным ядром, ДАН СССР 125, № 3, 1959, 496—499.
2) Об одном сингулярном интегральном уравнении, связанном с
циклической группой дробно-линейных преобразований, Изв. вузов, Математика 5,
1960, 136—143.
3) О числе решений одного полного сингулярного интегрального
уравнения, Уч. зап. Ростовск. пед. ин-та, вып. 5, 1960, 51—58.
Пилиди В. С. 1) О многомерных бисингулярных операторах, ДАН
СССР 201, № 4, 1971, 787—789.
2) Локальный метод в теории операторных уравнений типа
бисингулярных интегральных уравнений, Сб. «Матем. анализ и его прилож.», т. III,
изд-во Ростовск. ун-та, 1971, 81—105.
Показеев В. И. 1) Краевая задача Карлемана для фундаментального
многоугольника, Сб. «Краевые задачи теории функц. компл. перем.», изд-во
Казанск. ун-та, 1964, 40—57.
2) Об одном представлении обобщенных аналитических автоморфных
функций, ДАН СССР 155, N° 3, 1964, 528—531.
3) Задачи Римана — Карлемана для одного класса обобщенных
аналитических функций, Изв. АН Казах. ССР, сер. физ.-матем. наук 1, 1965,
72-81.
Попов Г. Я. 1) Некоторые свойства классических многочленов и их
применение к контактным задачам, ПММ 27, вып. 5, 1963, 821—832.
Привалов И. И. 1) Об одной граничной задаче, Матем. сб. 41, № 4,
1934, 519—526.
Рабинович В. С. 1) Многомерное уравнение Винера — Хопфа для
конусов, Сб. «Теория функций, функцион. анализ и их приложения», вып. 5,
Харьков, 1967, 59—67.
Рогожин В. С. 1) Некоторые краевые задачи для полигармонического
уравнения, Уч. зап. Казанск. ун-та ПО, № 3, 1950, 71—94.
2) Нахождение формы тела по заданному импульсивному давлению при
ударе, ПММ 23, вып. 3, 1959, 589—591.
3) Новое интегральное представление кусочно-аналитической функции и
его приложение, ДАН СССР 135, № 4, 1960, 791—793.
4) О числе решений внешней обратной краевой задачи, Уч. зап. Ростовск.
ун-та 46, вып. 7, 1959, 155—158.
5) Достаточные условия однолистности решения обратных краевых
задач, ПММ 22, вып. 6, 1958, 804—807.
6) Краевые задачи Римана и Гильберта в классе обобщенных функций,
Сиб. матем. ж. 2, № 5, 1961, 734—745.

ЛИТЕРАТУРА
633
7) Краевая задача Римана в классе обобщенных функций, Изв. АН
СССР, сер. матем. 28. № 6, 1964, 1325—1344.
8) Общая схема решения краевых задач в пространстве обобщенных
функций, ДАН СССР 164, № 2, 1965, 277—280.
Рогожина И. С. 1) Об одной краевой задаче со смещением для
кусочно аналитических функций, Изв. вузов, Математика, № 2 D5), 1965,
139—151.
Родин Ю. Л. 1) Об условиях разрешимости краевых задач Римана
и Гильберта на римановых поверхностях, ДАН СССР 129, № 6, 1959, 1234—
1237.
2) О задаче Римана на замкнутых римановых поверхностях, ДАН СССР
132, № 5, 1960, 1038—1040.
3) Интегралы типа Коши и краевые задачи для обобщенных
аналитических функций на замкнутых римановых поверхностях, ДАН СССР 142, № 4,
1962, 798—801.
4) Алгебраическая теория обобщенных аналитических функций на
замкнутых римановых поверхностях, ДАН СССР 142, № 5, 1962, 1030—1033.
Рысюк Н. А. 1) Нелинейная краевая задача типа задачи Римана с
действительными показателями в классе автоморфных функций, Изв. АН
БССР, сер. физ.-матем. наук, N° 4, 1973, 51—56.
Сабитов И. X. 1) Об одной граничной задаче линейного сопряжения,
Матем. сб. 64, A06), № 2, 1964, 262—274.
2) Об общей краевой задаче линейного сопряжения на окружности, Сиб.
матем. ж. 5, № 1, 1964, 124—129.
Сакалюк К. Д. 1) Обобщенное уравнение Абеля, ДАН СССР 131,
№ 4, 1960, 748—751.
2) Обобщение интегрального уравнения Абеля, Уч. зап. Кишиневск, ун-та
50, 1962, 95—102.
3) Некоторые особые интегральные уравнения с полярными, степенными
и логарифмическими ядрами, Уч. зап. Кишиневск. ун-та 50, 1962, 103—109.
4) Обобщенное интегральное уравнение Абеля с внутренними
коэффициентами, Уч. зап. Кишиневск. ун-та 82, 1965, 60—68.
5) Интегральные уравнения с логарифмическими и
полярно-логарифмическими ядрами, Уч. зап. Кишиневск. ун-та 70, 1969, 17—23.
6) Интегральные уравнения со степенными, логарифмическими и
полярными ядрами, разрешимые в замкнутой форме, Кандидатская диссертация,
Кишинев, 1963.
Самко С. Г. 1) О разрешимости в замкнутой форме сингулярных
интегральных уравнений, ДАН СССР 189, № 3, 1969, 483—485.
2) Общее сингулярное уравнение в исключительном случае, Дифференц.
ур-ния I, №. 8, 1965, 1108—1116.
3) Обобщенное уравнение Абеля и уравнение с ядром Коши, ДАН СССР
176, № 5, 1967, 1019—1022.
4) О сведении некоторых интегральных уравнений первого рода теории
упругости и гидродинамики к уравнениям второго рода, ПММ 31, вып. 2,
1967, 343—345.
5) К теории обобщенного интегрального уравнения Абеля, Сб.
материалов 7-й и 8-й аспирантск. конф. РГУ за 1964—1965 гг., Изд-во Ростовск.
ун-та, 1968, 56—61.
6) Об обобщенном уравнении Абеля и операторах дробного
интегрирования, Дифференц. ур-ния IV, № 2, 1968, 298—314.
7) О теории Нётера для обобщенного интегрального уравнения Абеля,
Дифференц. ур-ния IV, № 2, 1968, 315—326.
8) Общий сингулярный оператор и интегральный оператор с автоморф-
ным ядром, Изв. вузов, Математика, № 1, 1969, 67—77.
9) Обобщенное уравнение Абеля на прямой, Изв. вузов, Математика, №8
(99), 1970, 83—93.

634
ЛИТЕРАТУРА
10) Об операторах типа потенциала, ДАН СССР 196, № 2, 1971, 299—301.
11) Об интегральных уравнениях с ядром типа потенциала, Изв. вузов,
Математика, № 4, 1971, 78—86.
12) Об одном классе операторов типа потенциала на прямой, Изв. вузов,
Математика, № 5, 1971, 92—100.
13) О пространстве Ia(LP) дробных интегралов и об операторах типа
потенциала, Изв. АН Арм. ССР VII!, 1973, 359—383.
Сербин А. И. 1) Об одной обобщенной краевой задаче Римана на
конечной римановой поверхности, Сб. «Краевые задачи теории функц. компл.
перем.», изд-во Казанск. ун-та, 1964, 86—94.
2) Об общей краевой задаче на конечной римановой поверхности, Сб.
«Краевые задачи теории функц. компл. перем.», изд-во Казанск. ун-та, 1964,
95—105.
3) О краевой задаче Римана для обобщенных аналитических функций на
замкнутой римановой поверхности, Изв. вузов, Математика, № 4, 1964,
131—143.
Симоненко И. Б. 1) Краевая задача Римана с непрерывным
коэффициентом, ДАН СССР 124, № 2, 1959, 278—281.
2) Краевая задача Римана с измеримым коэффициентом, ДАН СССР 135,
№ 3, 1960, 538—541.
3) Краевая задача Римана для п пар функций с измеримыми
коэффициентами и ее применение к исследованию сингулярных интегралов в
пространстве Lp с весами, Изв. АН СССР, сер. матем. 28, № 2, 1964, 277—306.
4) О многомерных дискретных свертках, Матем. исследования 3, № 1 G),
Кишинев, 1968, 108—122.
5) К вопросу о разрешимости бисингулярных и полисингулярных
уравнений, Функцион. анализ и его приложения 5, вып. 1, 1971, 93—94.
6) Новый общий метод исследования линейных операторных
интегральных уравнений I и II, Изв." АН СССР, сер. матем. 29, вып. 3, 1965, 567—586,
и вып. 4, 1965, 775—782.
Соболев С. Л. 1) Об одной предельной задаче теории
логарифмического потенциала и ее применение к отражению плоских упругих волн, Тр.
Сейсм. ин-та, № 11, 1930, 1—18.
Соколов И. А. 1) О краевой задаче типа Римана для бианалитических
функций в случае произвольного контура, Изв. АН БССР, сер. физ.-матем.
наук, № 6, 1969, 29—38.
2) О краевой задаче типа Римана для полианалитических функций на
окружности, Изв. АН БССР, сер. физ.-матем. наук, № 5, 1969, 64—71.
3) О краевой задаче типа задачи Римана со сдвигом для
полианалитических функций на окружности, Изв. АН БССР, сер. физ.-матем. наук, № 1,
1970, 118—121.
4) Первая краевая задача типа Римана для полианалитических функций
в случае произвольного контура, Вестник БГУ, серия I — математика, физика,
механика, № 2, 1970, 20—23.
Сосунов А. С. 1) Об одном сингулярном интегральном уравнении
с двумя ядрами Карлемана, Материалы П-й научн. конфер. молодых ученых
Ростовск. обл., Секция естеств. наук, Ростов-на-Дону, 1968, 111—113.
2) Формула индекса одного класса сингулярных интегральных уравнений
с двумя сдвигами Карлемана, Материалы Всесоюзн. конфер. по краев,
задачам, Казань, 1970, 249—253.
Столярова Э. К. 1) Общая линейная краевая задача для уравнений
эллиптического типа, Уч. зап. Казанск. ун-та 111, № 8, 1951, 149—160.
Толочко М. Э. 1) О разрешимости однородной краевой задачи Римана
с бесконечным индексом для полуплоскости, Изв. АН БССР, сер. физ.-матем.
наук, № 5, 1972, 34—41.
2) О разрешимости однородной краевой задачи Римана для бесконечно
связной области, ДАН БССР 18, № 5, 1974, 398—401.

ЛИТЕРАТУРА
6С5
Тузик А. И. I) Об исключительных случаях особых интегральных
уравнений с ядром Коши, Вестник БГУ, сер. I, № 2, 1969, 3—7.
2) К решению особых интегральных уравнений с ядром Коши в
исключительном случае, Изв. АН БССР, сер. физ.-матем. наук, № 2, 1970, 125—127.
Усманов Н. К. 1) Граничные задачи дифференциальных уравнений
в частных производных первого порядка эллиптического типа, Тр. Ин-та физ.
и матем. Латв. ССР, вып. 1, 1950, 41—100.
2) К граничным задачам функций, удовлетворяющих системе
дифференциальных уравнений, Тр. Ин-та физ. и матем. Латв. ССР, вып. 2, 1950,
59—100.
Фрейдкин С. А. 1) Решение одного класса сингулярных интегральных
уравнений, Учен. зап. Кишиневск. ун-та 11, 1954, 13—17.
2) Краевая задача Римана и сингулярные интегральные уравнения с
кусочно постоянными коэффициентами в случае счетного множества интервалов,
Учен. зап. Кишиневск. ун-та 70, 1964, 27—38.
3) Задача линейного сопряжения и сингулярные интегральные уравнения
в случае счетного множества интервалов, Учен. зап. Кишиневского ун-та 82,
1965, 12—39.
Фролов В. Д. 1) К теории сингулярных интегральных уравнений с
измеримыми коэффициентами, ДАН СССР 189, № 6, 1969, 1185—1188.
2) О сингулярных интегральных уравнениях с измеримыми
коэффициентами в пространствах Lp с весом, Матем. исследования 5, вып. 1, Кишинев,
1970, 141—151.
3) Сингулярные интегральные уравнения на бесконечной системе дуг,
Матем. исследования 6, вып. 1, Кишинев, 1971, 146—157.
Хасабов Э. Г. 1) Обобщенная краевая задача Гильберта, Уч. зап.
Ростовск. ун-та 46, № 7, 1959, 257—278.
2) Краевая задача типа задачи Карлемана, Изв. вузов, Математика, №2,
1963, 124—133.
Хведелидзе Б. В. 1) О краевой задаче Пуанкаре теории
логарифмического потенциала для многосвязной области, Сообщ. АН Груз. ССР 2,
№ 7, 1941, 571—578, № 10, 1941, 865—872.
2) Замечания к моей работе «Линейные граничные задачи», Сообщ. АН
Груз. ССР XXI, № 2, 1958, 129—130.
Хускивадзе Г. А. 1) Об Л-интегралах типа Коши, Сообщ. АН Груз.
ССР 27, № 6, 1961, 633—670.
2) О сопряженных функциях и интегралах типа Коши, Тр. матем. ин-та
АН Груз. ССР 31, 1966, 5—54.
3) Об интегралах типа Коши — Стилтьеса, Тр. Тбил. матем. ин-та АН
Груз. ССР 34, 1968, 160—169.
Чернецкий В. А. 1) О конформной эквивалентности краевой задачи
Карлемана краевой задаче Римана на разомкнутом контуре ДАН СССР 190,
№ 1, 1970, 54—56.
2) О конформной эквивалентности граничной задачи Векуа граничной
задаче Маркушевича на разомкнутом контуре, ДАН УССР А, № 3, 1972,
218—220.
Черский Ю. И. 1) Общее сингулярное уравнение и уравнение типа
свертки, Матем. сб. 41, № 3, 1957, 277—295.
2) К решению краевой задачи Римана в классе обобщенных функций,
ДАН СССР 125, № 3, 1959, 500—503.
3) О методе неполной факторизации, ДАН СССР 189, № I, 1969, 53—56.
4) Метод неполной факторизации, Тр. семин. по краевым задачам, Изд-во
Казанск. ун-та, вып. 7, 1970, 293—296.
5) Задача сопряжения на двулистной поверхности, Матем. исследования
3, № 3, Кишинев, 1968, 139—149.
Чибрикова Л. И. 1) Особые случаи обобщенной задачи Римана, Уч.
зап. Казанск. ун-та 112, № 10, 1952, 129—154.

636
ЛИТЕРАТУРА
2) О краевой задаче Римана для автоморфных функций, Уч. зап.
Казанск. ун-та 116, № 4, 1956, 59—109.
д2и д2и
3) К решению краевой задачи Трикоми для уравнения -г—j + sign у д-2 =
=0, Уч. зап. Казанск. ун-та 117, № 9, 1957, 48—51.
4) Эффективное решение краевой задачи Гильберта для некоторых
многоугольников, ограниченных дугами окружности, Уч. зап. Казанск. ун-та 117,
№ 2, 1957, 22—26.
5) Новый метод решения одной краевой задачи смешанного типа, Уч.
зап. Казанск. ун-та 117, № 9, 1957, 44—47.
6) Краевая задача Римана для автоморфных функций в случае групп
с двумя инвариантами, Изв. вузов, Математика 6, 1961, 121—131; 3, 1962,
195—196.
7) К решению краевой задачи Гильберта, Тр. семин. по обратным
краевым задачам, вып. 2, Казань, 1964, 201—212.
8) О граничных задачах для прямоугольника, Сб. «Краевые задачи
теории функц. компл. перем.», Изд-во Казанск. ун-та, 1964, 15—39.
9) Граничная задача Римана на римановой поверхности с краем, Сб.
«Краевые задачи теории функц. компл. перем.», изд-во Казанск. ун-та, 1964.
3-14.
10) К решению краевых задач методом симметрии, Тр. семинара по
краевым задачам, вып. 3, Казань, 1966, 202—228.
11) О методе симметрии в теории упругости, Изв. вузов, № 10 F5), 1967,
102—112.
Чибрикова Л. И., Марков Г. В. 1) О некоторых краевых задачах
на неориентируемых поверхностях, Тр. семинара по краевым задачам, вып. 3,
изд-во Казанск. ун-та, 1966, 225—229.
Чибрикова Л. И, Мкоян П. X. 1) Задача Римана для счетного
множества контуров с двумя предельными точками, Изв. вузов, Математика,
№ 3, 1972, 90-102.
Чибрикова Л. И., Рогожин В. С. 1) О сведении некоторых
краевых задач к обобщенной задаче Римана, Уч. зап. Казанск. ун-та 112, № 10,
1952, 123—127.
Чибрикова Л. И., Салехов Л. Г. 1) К решению общей задачи
линейного сопряжения аналитических функций в случае алгебраических
контуров, Тр. семин. по краевым задачам, вып. 5, изд-во Казанск. ун-та, 1968,
224-249.
2) Применение метода симметрии при решении одной задачи линейного
сопряжения, Изв. вузов, № 9, 1968, 94—105.
Чикин Л. А. 1) Особые случаи краевой задачи Римана и сингулярных
интегральных уравнений, Уч. зап. Казанск. ун-та 113, № 10, 1952,
57—105.
2) Об устойчивости краевой задачи Римана, ДАН СССР, 111, № 1, 1956,
44—46.
3) Устойчивость краевой задачи Римана, Уч. зап. Ростовск. ун-та 43,
вып. 6, 1959, 119—125.
4) Два алгоритма для вычисления индекса функции с помощью ЦВМ,
Сб. «Вопросы вычисл. матем. и вычисл. техники», Изд-во Ростовск. ун-та.
1965, 60—66.
Чумаков Ф. В. 1) Общая теория интегральных уравнений со
степенным ядром, Дифференц. ур-ния II, № 4, 1966, 544—559.
2) Уравнение типа Абеля на сложном контуре, Изв. АН БССР, сер. физ.-
матем. наук, № 1, 1971, 55—61.
3) Интегральные уравнения с логарифмическим ядром, Дифференц.
ур-ния IV, № 2, 1968, 336—346.
4) Об одном обобщении уравнения Карлемана, Изв. АН БССР, сер. физ.-
матем. наук, № 4, 1972, 113—116.

ЛИТЕРАТУРА
637
5) Обобщенное уравнение Карлемана с внутренними коэффициентами
Изв. АН БССР, сер. физ.-матем. наук, № б, 1972, 104-106.
6) Решение в замкнутой форме некоторых интегральных уравнений с
логарифмическим ядром на сложном ко ;туре, Вестник БГУ, сер. 1, № 2, 1972,
5-9.
Шерман Д. И. 1) К общей задаче теории потенциала, Изв. АН СССР,
сер. матем. 10, 1946, 121—134.
2) О приемах решения некоторых сингулярных интегральных уравнений,
ПММ 12, 1948, 423—452.
3) Об одном случае регуляризации сингулярных уравнений, ПММ 15,
1951, 75—82.
4) О некоторых задачах теории потенциала, ПММ 9, 1945, 479—488.
5) О связи основной задачи теории упругости с одним особым случаем
задачи Пуанкаре, ПММ 17, 1953, 685—692.
Юров П. Г. 1) Интегралы типа Коши и уравнения в конечных
разностях, Изв. АН БССР, сер. физ.-матем. наук, № 3, 1967, 67—74.
2) О представлении интегралов типа Коши, Матем. заметки 6, № I, 1969,
55-63.
3) Однородная краевая задача Римана с бесконечным индексом, Изв.
вузов, Математика, № 2, 1966, 158—163.
4) Неоднородная краевая задача Римана с бесконечным индексом
логарифмического порядка а ^ 1, Материалы Всесоюзн. конфер. по краевым
задачам, Казань, 1970, 279—284.
5) Один из случаев краевой задачи Римана с бесконечным индексом
логарифмического порядка, ДАН БССР, 12, 1968, 489—491.
В. Литература на иностранных языках
Berg L. 1) Losungsverfahren fur singulare Integralgleichungen I, Math.
Nachr. 14, H. 4—6, 1955, 193—212.
2) Uber die Resolvente einer singularen Integralgleichungen, Math. Nachr.
15, H. 5—6, 1956, 339—352.
Bertrand G. 1) Le probleme de Dirichlet et le potentiel de simple
couche, Bull. sci. math. XLVII, 1923, p. 282—288 et 298—307.
Bittner L. 1) Plemelische Randwertformeln fur mehrfache Cauchy-Inte-
gral, J. angew. Math, und Mech. 39, № 9—11, 1959, 347—349.
Carleman T. 1) Sur la resolution de certaines equations integrates,
Arkiv mat., astr. och. phys. 16, № 26, 1922, p. 1—19.
2) Abelsche Integralgleichung mit konstanten Grenzen, Mat. Z. 15, 1922,
111—120.
Demtchenko. 1) Problem mixtes harmoniques, Paris, G. V., 1933.
Gellerstedt S. 1) Quelques problemes mixtes, Arkiv mat., astr. och
phys. 26, № 3, 1936.
Hardy G. H., Littlewood J. E., 1) Some properties of fractional
integrals I, Math. Z. 27, 1928, 565—606.
Harnac A. 1) Beitrage zur Theorie des Cauchy'schen Integrals, Ber.
Sachsisch. Ges. Wiss, Math. phys. K. 37, 1885, 379—398.
Haseman С 1) Anwendung der Theorie der Integralgleichungen auf
einige Randwertaufgaben, Gottingen, 1907.
Heins A. E., Mac Сamy R. C. 1) A function — theoretic solution of
certain integral equation, Quart. J. Math. 9, № 34, 1958, 132—143.
Hilbert D. 1) Ober eine Anwendung der Integralgleichungen, Verhandl.
des III Internat. Mathematiker Kongresses, Heidelberg, 1904.
Jacob С 1) Sur quelques nouvelles extensions du theoreme du cercle,
Annali di matematica pura ed appi. 1970, 84, 263—278.
Koppelman W. 1) The Riemann — Hilbert problem for finite Riemann
surfaces. Comm. Pure and Appl. Math. 12 : 1, 1959, 13—25.

638
ЛИТЕРАТУРА
2) Singular integral equations, boundary value problems and the Riemann-
Roch theorem, Journ. Math, and Mech. 10:2, 1961, 247—277.
Kraut E. A., Lehman G. W. 1) Diffraction of electromagnetic waves
by a right-angle dielectric wedge, Journ. Math. Phys. 10, 1969, 1340—1348.
Leonard A. 1) Two-dimensional Quarter Space problems in one-speed
transport theory, Journ. Math. Phys. 12, 1971, 754—766.
Lundgren Т., Chiang D. 1) Solutions of a class of singular integral
equations, Quart. Appl. Math. 24, № 4, 1967, 303—313.
No ether F. 1) Ober eine Klasse singularer Integralgleichungen, Math.
Ann. 82, 1921, 42—63.
Peters A. S., 1) Some integral equations related to Abel's equation and
the Hilbert transform, Comm. Pure and Appl. Math. XXII, 1969, 539—560.
Plemelj I. 1) Ein Erganzungssatz... Monatsh. Math, und Phys. XIX,
1908, 205—210.
2) Riemannsche Funktionenscharen, Ibid., 211—245.
Prossdorf S. 1) Zur Theorie singularer Integralgleichungen nicht nor-
malen Typs, Wiss. Z. Technol. Hochsch. Karl-Marx-Stadt 11, № 3, 1969, 353—
357.
Przeworska-Rolewiez D. 1) Sur les equations involutives et leurs
applications, Studia math. 20, № 2, 1961, 95—117.
2) Equations avec operations algebraiques, Studia math. 22, № 3, 1963,
337—367.
Riabouchinsky 1) Sur la determination d'une surface, d'apres les
donnees qu'elle ports, С R. Akad. sci., t. 189, 1929.
Signorini 1) Sopra un problema ol contoro nella teoria delle funzioni
di variabile complessa, Ann. mat. C), t 25, 1916.
Susea A. 1) О generalizare a problernei Riemann omogene, St. cercet.
mat. 19, N° 1, Бухарест, 1967, 155—161.
Thomas J. 1) Uber ein Integralgleichungsystem aus der Theorie des
logarithmischen Potentials, Journ. fur d. r. und angew. Math., № 223, 1966,
1—15.
Trjizinsky W. 1) Singular integral equations, Trans. Amer. Math.
Soc. 60, № 2, 1946.
Volterra V. 1) Sopra alkune condizioni caratteristische per functioni
di variabile complessa, Ann. mat. B), t. 11, 1883.
Wiener N. und Hopf E. 1) Uber eine Klasse singularer
Integralgleichungen, Sitzungsber, Berliner Akad. Wiss., 1931, 696—706.
Williams W. E. 1) A class of integral equations, Proc. Cambr. Phil.
Soc. 59, 1963, 589—597.
Wolfersdorf L. v., 1) Abelsche Integralgleichungen und Randwert-
probleme fur die verallgemeinerte Tricomi-Gleichung, Math. Nachr. 27, 1965,
161—178.
2) Ober eine Beziehung zweischen Integralen nichtganzer Ordnung. Math.
Zeit. 90, № 1, 1965, 24—28.
3) Zur Losung der verallgemeinerten Abelschen Integralgleichung mit kon-
stanten koefficienten. Zeit. Angew. Mat. und Mech. 49, № 12, 1969, 759—761.
4) Zur Theorie der Spielle fiber dem Einheitsquadrat mit Auzahlungs funk-
tionen von der Form eines Schmetterlings, Wiss. zeit. Univ. Rostock. 19. Math.
Naturwiss. Reihe, 6/7, 1970,

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоморфные функции 536 , 539
, кусочно аналитические 550
А-задача 269 , 387
Ао-задача 269 , 387
— , обобщенная 271
Аппеля многочлен 613
Аргумента принцип 99
, обобщенный 100
Бигармоническая функция 303
Бисингулярный оператор 221
Бореля преобразование 610
Винера — Хопфа уравнение 617
Гёльдера условие 20 — 22
Гильберта формулы обращения 59
Гомотопия оператора 604 , 605
Грина функция 265 , 382
— — , комплексная 266 , 382
Дирихле задача 265 , 376
— — для полуплоскости со щелями 474
Индекс задачи Гильберта 280 , 385 , 398
Римана 107 , 132 , 140 , 370
для разомкнутого контура 441
« с разрывными коэффициентами 433
— интегрального уравнения 176 , 293
— как гомотопический инвариант 604
— особого оператора 200 , 214
— функции 101
, частичный 105
Интеграл особый (сингулярный) 23 , 24 , 27
, главное значение 23 , 28
— типа Коши (определение) 16
— (аналог) для автоморфных
функций 551
— , кратный 81
— , обобщенный 78
по действительной оси 44
— сложному контуру 76
< , предельные значения 33 , 52 , 78
— Фурье 616
— Шварца 58
Интегральное представление кусочно
аналитических функций 347 , 354 , 363 , 366 , 372 ,
412 , 538
— уравнение Абеля 572
с автоморфными ядрами с конечной
группой 567
__ • — бесконечной группой 585
сингулярное (см. особое)
с логарифмическим ядром 585 — 593
со степенным ядром 572 — 585
¦ типа свертки 617
• Фредгольма 173 — 176
Интегро-дифференциальное уравнение 374 ,
416
Интерполяция целых функций 609
Каноническая функция задачи Римана
107 , 119 , 142 , 448 , 449 , 457 , 540
неоднородной 135
Классы решений задачи Римана 428 , 433 ,
482 — 483
особого интегрального уравнения
484 — 485 , 501 , 507
Композиция особых операторов 198
Концы автоматической ограниченности
(особенные) 441
Краевая задача Гильберта для бикруга 291
внешней области 285
— — кусочно аналитической функции
462
многосвязной области 375 — 408
односвязной области 280
— полианалитических функций 303
полуплоскости 282 , 467
в периодических функциях
555
на римановой поверхности 568
, постановка 264
со сдвигом 158 , 420
союзная 393
Карлемана 163 , 452 , 570
с бесконечным индексом 520
•» — Римана , абстрактная 146
для бицилиндрических областей
123
— ~ многосвязной области 139
односвязной области 106
¦» периодических функций 554
— ¦— полианалитических функций 316
полуплоскости 118
разомкнутого контура 439 , 447
сложного контура 455
, исключительные случаи 130 , 461
, корректная постановка 188
, многомерная 129
на римановой поверхности 567
счетном множестве контуроз 522
, приближенное решение 146
с бесконечным индексом 510
— — — — непрерывным коэффициентом 144
со сдвигом 146
и сопряжением 157 , 419
— с разрывными коэффициентами 428 ,
448
с сопряжением 416
типа задачи Гильберта 344
Римана 365
. для многосвязной области 412
Кривые класса Ляпунова 58
Кусочно аналитическая функция
(определение) 455

640
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Лиувилля теорема , обобщенная 99 , 100
Логарифмический потенциал 85
Локально конформного склеивания
принцип 570
Лорана преобразование 618
Непрерывности модуль 19
— принцип 95
Нётера теоремы 208 , 509
Обратная краевая задача для
многосвязной области 408
односвязной области 320 , 321 ,
324 , 337
Обращение особого интеграла 65
— на разомкнутом контуре 444
Оператор Нётера 214
— нормального типа 177
— особый (сингулярный) 57 , 172 , 198
• , абстрактный 146 , 214 , 496
, норма 57
— , регуляризующий (регуляризатор) 201
— сопряженный 225 , 226
— союзный (транспонированный) 173
— с полярно-логарифмическим ядром 606
— характеристический 173
— Шварца для многосвязной области 381
односвязной области 265
Особое интегральное уравнение с ядром
Гильберта 292
Коши 241 , 249
для сложного контура и
разрывных коэффициентов 496
на действительной оси
188 - 194
полуоси 489
, полное 172
, разрешимое в
замкнутом виде 183
, сингулярное решение 228 ,
230
, сопряженное 225
— со сдвигом Карлемана 215
на разомкнутом
контуре 480 , 496 , 509
— ¦ • — , союзное
(транспонированное) 173
с сопряжением 219
—. , характеристическое 173 , 500
— , приближенное решение 194
Плотность интеграла типа Коши 16
— распределения вероятностей 619
Поверхность Римана 564
, дубль 566
рода h 565
с краем 566
Полианалитическая функция 302
Полигармоническая функция 302
Полицилиндрическая область 81
, остов 81
Порядок аналитической функции 99
Преобразование Фурье 615
Пуанкаре — Бертрана формула
перестановки 63 , 81
Равносильная регуляризация оператора 223
Регуляризация особого интегрального
уравнения 198 , 244 , 504
— решением характеристического
уравнения 232 , 253 , 497
— слева 202 — 204 , 252
— справа 202 , 204 , 205
Регуляризующий множитель 273
действительный 275
для многосвязной области 386 , 390
с постоянным модулем 277
Регулярная часть особого интегрального
уравнения 172
Резольвента интегрального уравнения 174 ,
175
, сингулярная 228 , 229
Римана — Роха теорема 566
Свертки типа уравнения 617 , 619
Симметрии принцип 96 — 98
Симметрия относительно алгебраической
кривой 571
аналитической кривой 97
окружности и прямой 97
Смешанная краевая задача аналитических
функций 472 , 556
Собственные значения и функции 174
Сохоцкого формулы 37 , 38 , 44 , 47 , 78 , 79 ,
82 , 83
Спектр особого уравнения 180 , 181
— уравнения Фредгольма 175
Точки автоматической ограниченности 433
486
Угловой порядок области 398
Факторизации неполной метод 491
Факторизация функций 109
Фредгольма теоремы 174 — 175
Фундаментальная область 536
Функция , аналитическая в угле 510
, индикатор 511
— , интегрируемая со степенью 57 , 144
— распределения вероятностей 619
— сдвига 146
—• с двусторонним завихрением аргумента
512 , 520
• односторонним завихрением
аргумента 512
— фундаментальная 430
Характеристическое уравнение в
банаховом пространстве 496
Шварца задача 265
— — с логарифмической особенностью на
контуре 329
— формула 58
Ядро Гильберта 59
— Коши 16
— Шварца 58