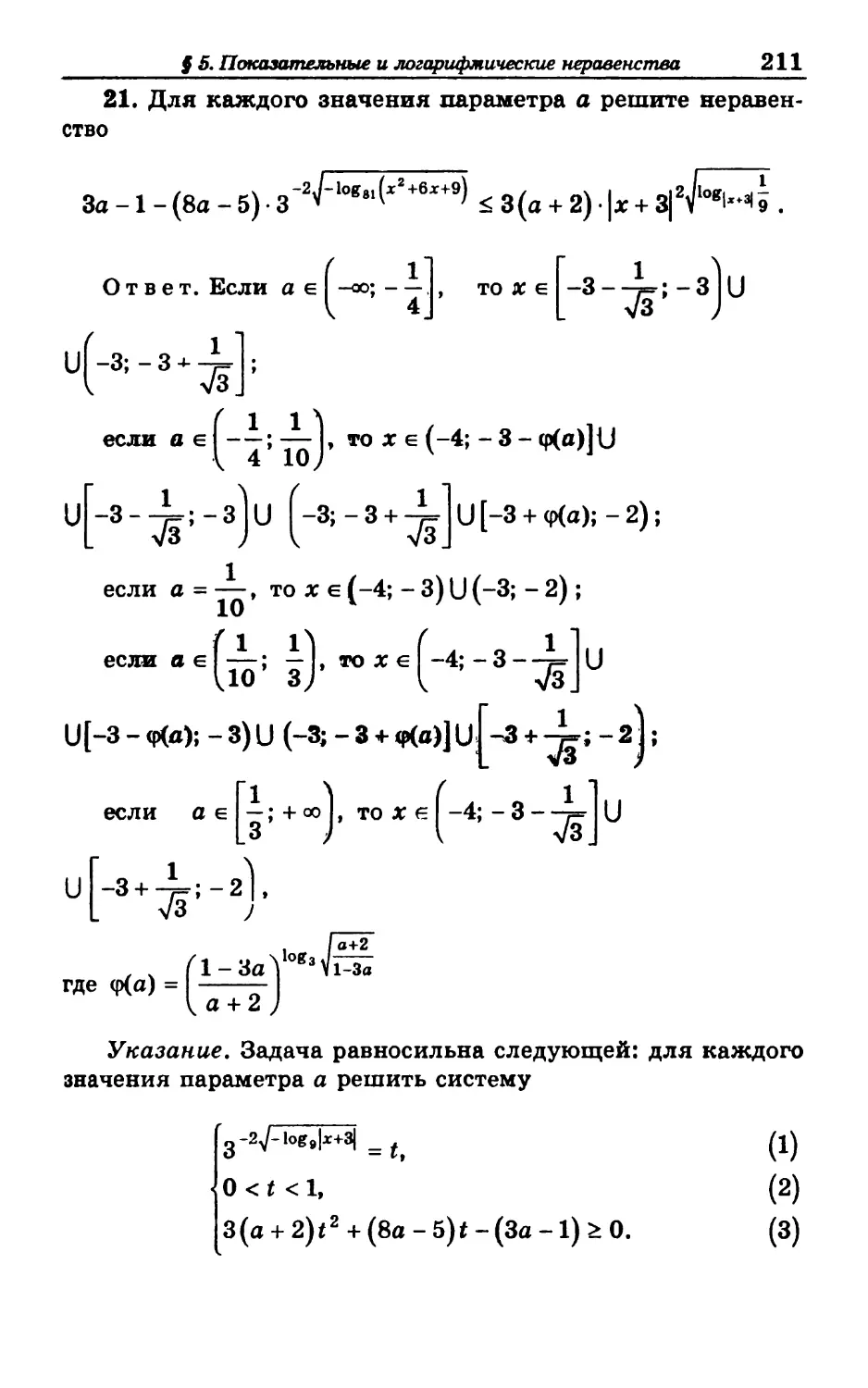Автор: Моденов В.П.
Теги: геометрия топология математика задачи с параметрами
ISBN: 5-472-02628-8
Год: 2007
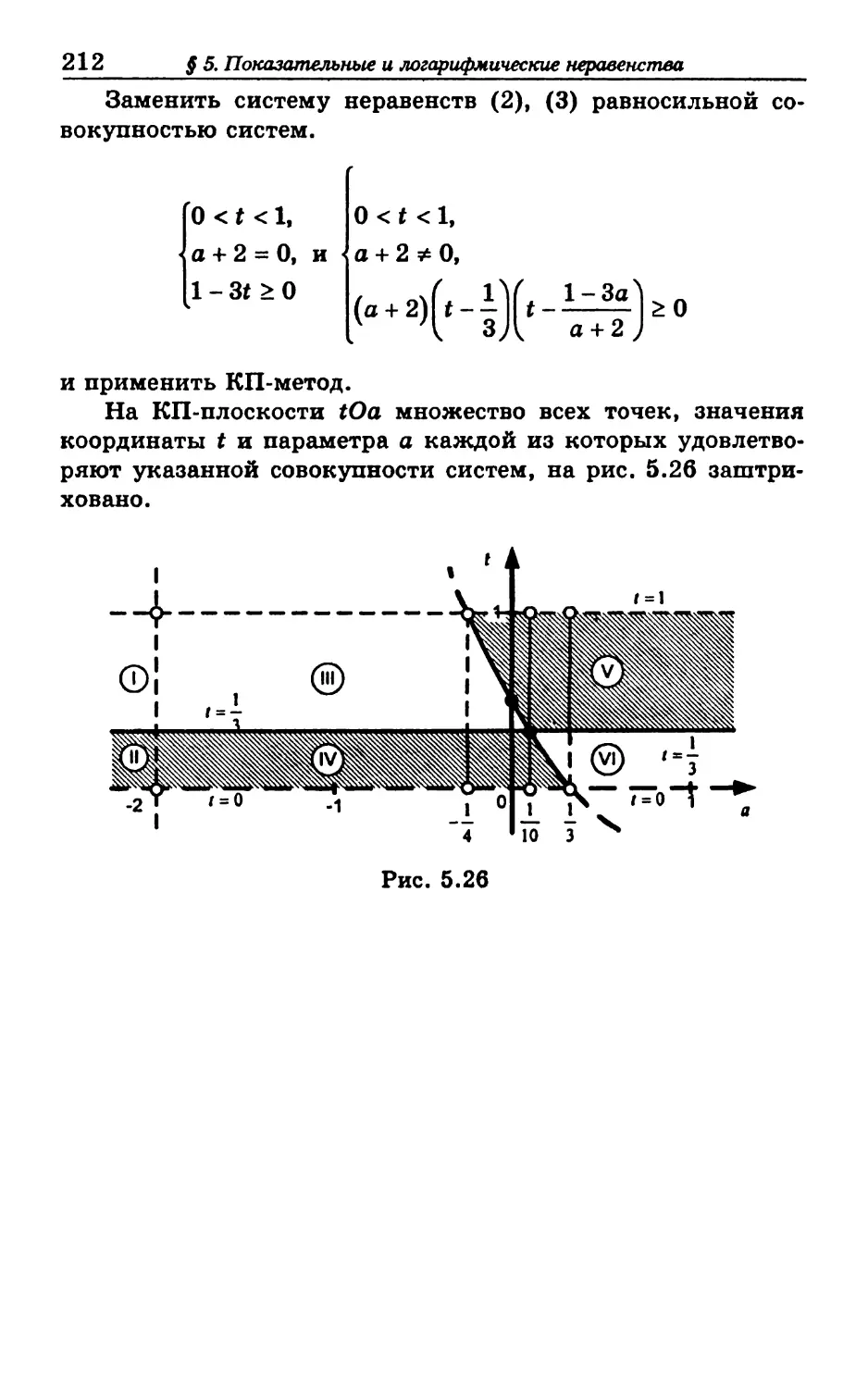
Текст
АБИТУРИЕНТ
В.П. МОДЕНОВ
КООРДИНАТНО-ПАРАМЕТРИЧЕСКИИ
МЕТОД
В.П. Моденов
ЗАДАЧИ
С ПАРАМЕТРАМИ
КООРДИНАТНО-
ПАРАМЕТРИЧЕСКИЙ
МЕТОД
Учебное пособие
Издательство
«ЭКЗАМЕН»
МОСКВА
2007
УДК 514(075.3)
ББК 22.151 5 я72О
М74
Моденов, В. П.
М74 Задачи с параметрами. Координатно-параметрический
метод: учебное пособие / В.П. Моденов. — М.:
Издательство «Экзамен», 2007. — 285, [3] с. (Серия «Абитуриент»)
ISBN 5-472-02628-8
Книга написана профессором Московского государственного
университета им. М.В. Ломоносова и предназначена для учащихся
общеобразовательных учреждений, готовящихся к вступительным
экзаменам по математике в вуз.
Рассматривается метод аналитической геометрии, названный
автором координатно-параметрическим, который позволяет
эффективно решать широкий класс задач с параметрами,
составляющих неотъемлемую и наиболее трудную часть
экзаменационных заданий.
Метод иллюстрируется примерами оригинального решения
задач, предлагавшихся на вступительных экзаменах по
математике в МГУ
УДК 514(075.3)
ББК 22.151.5 я729
Подписано в печать с диапозитивов 22.09.2006 г. Формат 84x108/32
Гарнитура «Школьная». Бумага типографская. Уч.-изд. л. 8,23
Усл. печ. л. 15,12. Тираж 50 000 (2-й завод— 5000) экз. Заказ № 3683(2)
ISBN 5-472-02628-8 €> Моденов, В.П., 2007
© Издательство «ЭКЗАМЕН», 2007
СОДЕРЖАНИЕ
Введение 4
§ 1. Рациональные алгебраические уравнения с
параметрами 16
§ 2. Рациональные алгебраические неравенства с
параметрами 59
§ 3. Иррациональные уравнения и неравенства с
параметрами 107
§ 4. Показательные и логарифмические уравнения с
параметрами 149
§ 5. Показательные и логарифмические
неравенства с параметрами 171
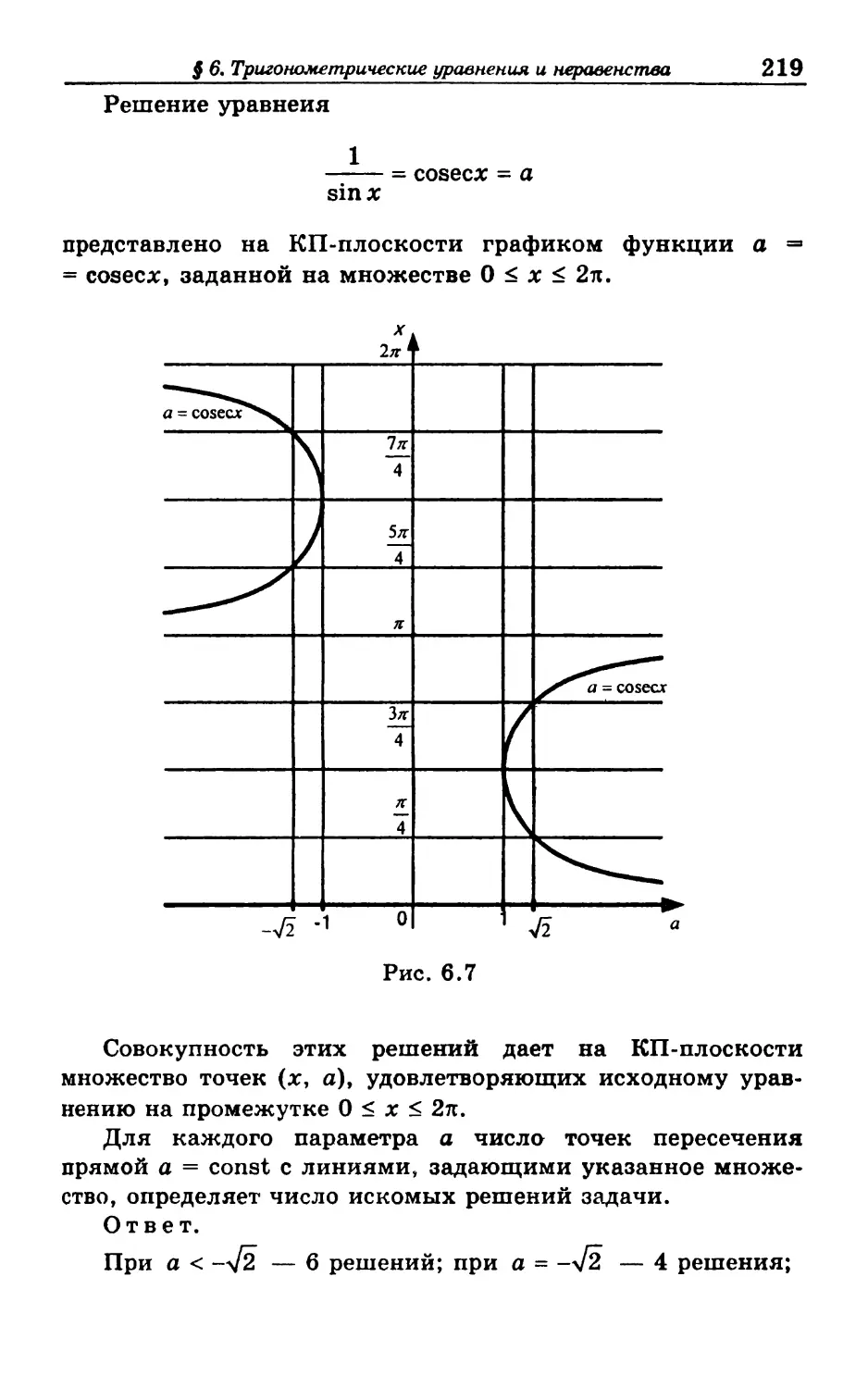
§ 6. Тригонометрические уравнения
и неравенства с параметрами 213
§ 7. Различные трансцендентные уравнения
и неравенства с параметрами 250
§ 8. Задачи на движение 269
Заключение 286
Список литературы 287
«Но когда эти науки (алгебра и геометрия)
объединились, они энергично поддержали друг
друга и быстро зашагали к совершенству*.
Ж Л. Лагранж
Введение
В течение многих лет в вариантах заданий на
вступительных экзаменах по математике в Московском
государственном университете им. М.В. Ломоносова предлагаются
задачи с параметрами [1-6]. Их решение часто вызывает у
абитуриентов определенные трудности, поскольку эти
задачи, как правило, связаны с исследованием искомых
решений в зависимости от значений параметров.
При решении задач с параметрами наряду с
аналитическими методами достаточно эффективно применяется метод
аналитической геометрии — координатный метод Декарта.
Решение данным методом, например, уравнения,
содержащего параметр, приводит к необходимости
рассмотрения на координатной плоскости однопараметрического
семейства линий и связан с построением множеств и
графиков функций.
Поэтому иногда этот метод относят к графо-аналитичес-
ким методам.
Можно, по аналогии, ввести понятие координатнопара-
метрической плоскости хОа или аОх, где х — координата,
а — параметр, и построить координатно-параметрический
метод (КП-метод) решения широкого класса задач с
параметрами.
Тридцать лет назад автор [3, 4] впервые применил
КП-метод в сочетании с концепцией равносильности
математических высказываний, реализованной в виде
логических схем рационализации и алгебризации, то есть замены
иррациональных и трансцендентных уравнений и
неравенств на равносильные им рациональные алгебраические.
Решая уравнения и неравенства с параметрами,
целесообразно выполнять равносильные преобразования, так как
проверка может оказаться весьма затруднительна.
Введение 5
Поэтому потребовалась специальная методика решения
подобных задач.
Предлагаемый подход к решению уравнений, неравенств
и других задач основан на замене одного математического
высказывания (уравнения, неравенства, смешанной системы,
совокупности систем и т.д.) другим равносильным
математическим высказыванием.
Решением высказывания с одной переменной А(х) будем
называть множество X всех значений этой переменной, при
которых высказывание истинно.
Два высказывания А(х) и В(х) будем называть
равносильными и обозначать знаком равносильности
А(х) о В(х),
если множества их решений совпадают.
Те же определения сохраняются и для высказываний с
несколькими переменными и параметрами.
Концепция равносильности высказываний позволила
сформулировать алгоритмы решения уравнений и
неравенств в виде экономичных логических схем. В п. 4
Введения будут приведены логические схемы решения уравнений
и неравенств и даны ссылки на работы, где эти схемы были
впервые опубликованы.
Понятие равносильности позволяет сформулировать
логическое отрицание высказываний.
Обозначим логическое «не» знаком -i, а высказывание,
противоположное А(х), — через А(х).
Тогда правила логического отрицания высказываний,
содержащие кванторы (знаки) всеобщности V и
существования 3, формулируются следующим образом:
е X : А(х)) о Зх е X : А(х)
-,(3х е X : А(х)) oVxeX : А(х)
То есть при логическом отрицании данных высказываний
кванторы всеобщности и существования меняются друг на
друга, а высказывание заменяется на противоположное.
Введение
Используя понятие равносильности, можно
сформулировать метод подстановки для решения уравнений (или
неравенств).
[х е X, [/(О = 0.
Методика равносильных высказываний особенно
эффективна при решении задач с параметрами и в сочетании с
КП-методом поможет абитуриентам успешно справиться с
решением широкого класса задач.
1. Координатно-параметрический метод (КП-метод).
Пусть на плоскости даны две взаимно перпендикулярные с
общим началом (точкой О) числовые оси. Одну из них {Ох)
назовем координатой; другую (Оа) — параметрической, а
плоскость (хОа или аОх) — координатно-параметрической,
или КП плоскостью.
Метод решения задач с параметрами, использующий
КП-плоскость, назовём координатно-параметрическим,
или КП-методом.
Он основан на нахождении множества всех точек
КП-плоскости, значения координаты х и параметра а
каждой из которых удовлетворяют заданному в условиях
задачи условию (соотношению).
Если указанное множество точек найдено, то можно
каждому допустимому значению параметра а = const
поставить в соответствие координаты х точек этого множества,
дающие искомое решение задачи, или указать те значения
параметра, при которых задача не имеет решения.
2. Решение КП-методом уравнений с параметрами.
Рассмотрим уравнение
F(x, а) = 0, (В.1)
где F(x, а) — некоторая функция переменной х и числового
параметра а.
Пусть на КП-плоскости найдено множество всех
точек, значения координаты х и параметра а каждой из
которых удовлетворяют рассматриваемому уравнению.
Введение
Может оказаться, что при любом допустимом значении
параметра уравнение решений не имеет (х е 0), либо для
некоторых значений параметра х е 0 или уравнение имеет
конечное число решений, или бесконечное множество.
Записывая ответ, поставим в соответствие каждому
допустимому фиксированному значению параметра а
значения искомой величины х — координаты
соответствующих точек найденного множества.
Отметим два частных случая.
1°. Координата х есть функция параметра а:
х = /(а), (В.2)
неявно заданная уравнением (В.1). (Вопросы существования
неявно заданной функции рассматриваются в курсе высшей
математики.)
На КП-плоскости хОа с горизонтальной
параметрической осью Оа множество всех точек, значения координаты х
и параметр а каждой из которых удовлетворяют уравнению
(В.1), представляет собой график функции (В.2), где роль
аргумента функции играет параметр.
2°. Параметр а есть функция координаты х:
а = ф(х), (В.З)
неявно заданная уравнением (В.1).
В этом случае можно рассматривать КП-плоскость аОх
с вертикальной параметрической осью Оа и
интерпретировать множество всех точек, значения координаты и
параметры каждой из которых удовлетворяют уравнению (В.1),
как график функции (В.З), где роль аргумента функции
играет координата.
Следует отметить, что в рассматриваемом КП-методе
центральное место занимает нахождение множества всех
точек КП-плоскости, определяемых уравнением (В.1).
Более просто обстоит дело, когда левой частью уравнения
(В.1) являются многочлены первой или второй степеней.
Так в курсе аналитической геометрии доказывается, что
уравнения вида
Р(х, а) = О, (В.4)
где Р(х, а) — многочлен второй степени относительно х и а,
определяет на КП-плоскости линии: эллипс (в частности,
8 Введение
окружность), гиперболу, параболу или пару прямых
(пересекающихся, параллельных или сливающихся в одну).
Например, на КП-плоскости хОа уравнения
х2 -ha2- 1 = 0, ха-1=0, х2-а = 0
определяют соответственно окружность, гиперболу и
параболу, а уравнение
х2-а2
\х + а = 0,
= 0 о
[х - а = 0
определяет пару пересекающихся (взаимно
перпендикулярных) прямых.
3. Метод «частичных областей» (МЧО) при решении
неравенств и систем неравенств, содержащих параметры.
Идея так называемого в прикладной математике метода
«частичных областей» (МЧО) заключается в том, что
решение задачи в исходной области сводится к решению ее или
совокупности более простых задач в каждой из «частичных
областей», из которых составляется (или которыми, как в
альтернирующем методе Шварца, покрывается) исходная
область [5, с. 14].
Так же как метод «промежутков» (в одномерном
случае), МЧО может быть применен при решении КП-методом
уравнений и неравенств с параметрами, содержащих
переменную и параметр под знаком абсолютной величины.
Применение МЧО при решении неравенств с
параметрами во многом аналогично применению метода
«интервалов» для решения неравенств с одной переменной.
Рассмотрим неравенство
Р(х, а) > 0, (В.5)
где Р(х, а) — многочлен, аргументами которого являются
переменная х и параметр а.
Пусть уравнение
Р(х, а) = 0 (В.6)
определяет некоторые линии (как, в частном случае,
уравнение (В.4)) на КП-плоскости.
Введение 9
Разобьем этими линиями КП-плоскость на конечное
число п «частичных областей» Glt G2,...,Gn, ограниченных
линиями Р = 0.
В каждой из «частичных областей» Gjii = 1, 2, ..., п)
многочлен Р(х, а) отличен от нуля, так как точки, в
которых P(xt а) = 0 принадлежат границе этих «частичных
областей».
Справедлива теорема: В каждой из областей Gx (/ = 1,
2, ..., л), на которые линии Р = 0 делят КП-плоскость,
многочлен Р(х, а) либо положителен, либо отрицателен.
Таким образом, решение неравенства (В.5) —
множество всех пар чисел (jc, а), при которых неравенство
выполняется, образует совокупность (объединение) тех областей
G{ (i = 1, 2, .„., л), в которых значение многочлена Р(х, а)
положительно.
Для установления, какое из неравенств Р > 0 или Р < 0
выполняется в данной области достаточно, например,
вычислить значение Р(х, а) в какой-нибудь определенной
точке этой области.
Аналогично рассматривается решение неравенства
P(jc, а) < 0, (В.7)
где Р(х, а) — многочлен, аргументами которого являются
переменная х и параметр а.
Решением системы алгебраических неравенств
Pt(x, а) > 0, Р2(х, а) > 0,... Рт(х, а) > 0 (В.8)
заключается в отыскании для каждого из неравенств
системы областей, в которых оно выполняется, и в
нахождении общей части (пересечения) всех этих областей.
Решение дробного неравенства равносильно решению
либо совокупности систем неравенств
Р>0,
Q>0;
(Р<0,
[Q<0,
(В.9)
10 Введение
либо решению алгебраического неравенства
2°. ^>0«PQ>0 (B.10)
Здесь Р = Р(х, a), Q = Q(xt a) — многочлены аргументов
х и а.
Аналогично,
р
3°. — < 0
Q<0;
fP<0,
Q > 0;
(B.ll)
p
4°., — <0oP-Q<0 (В.12)
Q
Рассмотрим неравенство вида
F(x, a) > О, (В.13)
где F(x, a) — некоторая (неалгебраическая) функция
переменой х и параметра а.
Сформулируем для этого неравенства алгоритм МЧО на
основе КП-метода.
1°. Найдем на КП-плоскости ОДЗ (область допустимых
значений переменной и параметра) — множество всех
точек, при значениях координаты х и параметра а каждой из
которых выражение F(xy а) определено.
2°. Построим на КП-плоскости линии1, состоящие из
всех точек, при значениях координаты х и параметра а
каждой из которых выражение F(jc, а) обращается в нуль
или не. существует, и разобьем этими линиями найденную
ОДЗ на «частичные области».
3°. Исследуем знак выражения F(x, а) в каждой из
полученных «частичных областей». Для этого достаточно, на-
1 Условия, которым должна удовлетворять функция F(x, a),
чтобы уравнение F(x, a) = 0 задавало линии, а функция F(xt а)
сохраняла знак в каждой из «частичных областей», ограниченных
этими линиями, устанавливаются в курсе высшей математики.
Введение 11
пример, установить знак выражения F(x, а) в какой-нибудь
точке каждой из «частичных областей».
Решением рассматриваемого неравенства будут те из
«частичных областей», в которых выражение F(x, а)
положительно. Неравенство F(x, a) < О решается аналогично.
4. Логические схемы решения типовых
иррациональных и трансцендентных уравнений и неравенств.
Простейшие иррациональные уравнения и неравенства
допускают сведение их к рациональным уравнениям и
неравенствам.
Логическая схема решения типового ирационального
уравнения заключается в замене этого уравнения
равносильной ему смешанной системой, состоящей из
рационального уравнения и неравенства:
ф > О,
(в14)
[3, с. 93]
где f = f(x, а), ф = ф(дг, а) — функции переменной и
параметра.
Логические схемы решения двух типовых
иррациональных неравенств имеют вид:
/7 Гф > о,
1°. //<Ф»Г , 2 (В.15)
О < / < ф2;
> ф <=>
Ф<0;
(В.16)
/>Ф2,
Ф>0,
[3, с. 133]
где / = f(x, а), ф = ф(дг, а) — функции переменной и
параметра.
Общий метод решения иррациональных уравнений и
неравенств основан на применении рационализирующих
подстановок (метод рационализации) (см. Моденов В.П.
12
Введение
Решение иррациональных уравнений // Математика в
школе, 1970, № 6. С. 32-35.)
Идея решения трансцендентных (логарифмических и
показательных) уравнений и неравенств заключается в
замене их равносильными уравнениями, неравенствами и
системами, не содержащими трансцендентных функций.
Логические схемы решения типовых логарифмических
и показательных уравнений основаны на замене их
равносильными смешанными системами:
1°.
2°.
\ogu fx = \ogu f2
JO < и * 1,
U = ft > 0,
0.
-<p2) = 0.
(В.17)
[4, с. 126]
(В.18)
Используя свойства функций, получаем логические
схемы решения типовых логарифмических и показательных
неравенств:
1°. \ogufl>\oguf2<^
0<u*l,
A>o,
/2>o,
(»-1)-(Л-/2)>0.
> tf4
2°.
одз
О(у-1)(ф1-ф2)>0.
одз
(B.19)
[4, с 163]
(B.20)
[4, с. 147]
Аналогичные схемы имеют место для неравенств
противоположного знака.
Введение JJJ
Обобщая эти логические схемы на строгие и нестрогие
неравенства, имеем:
1°. F = log ft — log
ОДЗ
где ОДЗ:
О < и * 1,
(i-<P2)v(>> (В,22)
ОДЗ
где ОДЗ: v > 0.
Здесь знак v означает любой из знаков > , >, < , <,
Всюду и, v, fu /2, ф1? ф2 — функции, в общем случае,
переменной х и параметра а.
Широкий класс трансцендентных уравнений и
неравенств допускает решение методом подстановки путем
сведения их к типовым.
5. Метод декомпозиции при решении трансцендентных
уравнений и неравенств1. Простейшее неравенство,
выражающее свойство сохранения знака трансцендентной
функции и допускающее замену его равносильным в ОДЗ (или в
её подмножестве М) неравенством, не содержащим этой
функции, будем называть базовым неравенством, а саму
трансцендентную функция — базовой функцией.
Например, базовыми являются типовые неравенства
(В.21) (В.22), а базовыми функциями — трансцендентные
функции F и Ф .
Рассмотрим неравенство (как строгое, так и нестрогое) в
каноническом виде
FVO, (B.23)
в котором F = F(x,a), трансцендентная (содержащая
логарифмическую, показательную и другие неалгебраические
функции) функция переменной х и параметра а.
1 См. Моденов ВЛ. // Математика в школе. 2001. № 5. С. 64-68.
14 Введение
Предположим, что левая часть (В.23) допускает
представление в виде произведения и (или) частного
(декомпозицию) некоторых базовых функций.
Пусть например,
F = F Ф,
где F и Ф — базовые функции, определяемые
соотношениями (В.21), (В.22).
Тогда согласно рассматриваемому методу
F = F Ф vO<^>P QvO
м
или подробнее:
ЬЛ
о(и -1) • (А - U) • (w -1) • (<Pi - Ф2) v О,
м
где М:
О < и ф 1,
w, у, Л» /2» 9i» Фг — функции, в общем случае, переменной
х и параметра а.
Следует заметить, что Р и Q — многочлены аргументов
jc и а у для решения полученного неравенства Р • Q v 0
особенно эффективен КП-метод.
6. Экзаменационные задачи с параметрами [1-6].
КП-метод иллюстрируется на примерах решения задач из
вариантов вступительных экзаменов по математике в МГУ
им. М.В. Ломоносова. Как правило, это задачи повышенной
сложности. Универсальность предлагаемого метода
позволяет решить достаточно широкий класс таких задач.
Даны некоторые применения КП-метода для решения
текстовых задач на движение (где роль параметра играет
время), различного типа уравнений и неравенств, содержа-
Введение 15
щих параметр, задач с целочисленными значениями
координат и параметров, а также задач на логическое отрицание.
Текстовые задачи на движение решаются с
использованием методики теоретической механики, записывая
уравнение движения для каждого его участника. Эти уравнения
связывают координаты движущегося тела со временем,
зависимость между которыми достаточно наглядно
иллюстрируется на КП-плоскости, что позволяет достаточно просто
проводить математическую постановку соответствующей
текстовой задачи.
Задачи, связанные с решением уравнений и неравенств,
содержащих параметр, заменяются равносильными,
допускающими простое решение на КП-плоскости. Здесь с
угпехом используются предлагаемые алгоритмы,
логические схемы и их реализации.
Задачи с целочисленными значениями координат и
параметров решаются с использованием следующей идеи.
Область КП-плоскости с искомыми целочисленными значе
ниями координат и параметра покрывается координатной
(например, прямоугольной) сеткой конечных размеров, в
узлах которой координата и параметр принимают
целочисленные значения. Затем проверкой устанавливается, какие
из конечного числа целочисленных значений в узлах сетки
принадлежат покрываемой области КП-плоскости, то есть
удовлетворяют условию задачи.
Специально рассматривается общая методика решения
задач на логическое отрицание. В сочетании с КП-методом
она позволяет достаточно эффективно решать многие
задачи, вызывающие у абитуриентов трудности.
х = а\ <=>
I Iй * °'
[x = a,
f a < 0,
[x = -a.
§ 1. Рациональные алгебраические уравнения
с параметрами
Пример 1.1, Для каждого значения параметра а решить
уравнение F (х, а) = х - \а\ = 0•
Решение. Перейдем от неявного к явному заданию
функции и, воспользовавшись определением абсолютной
величины (модуля) числа, заменим уравнение равносильной
ему совокупностью смешанных систем:
(1.1)
На координатнопараметрической плоскости (КП-плос-
кости) хОа с горизонтальной параметрической осью Оа
множество всех точек (х; а), значения координаты и
параметра каждой из которых удовлетворяют полученной
совокупности смешанных систем, представляет собой
изображенный на рис. 1.1а график функции х = \а\, аргументом
которой является параметр а.
Точки КП-плоскости хОа, значения координаты и
параметра каждый из которых удовлетворяют смешанной
системе I, расположены на части прямой х = а,
находящейся в полуплоскости а £ 0 с границей а = 0 (на рис. эта
полуплоскость заштрихована), то есть на луче с началом
х = 0, а = 0 и направлением вдоль биссектрисы первой
четверти КП-плоскости.
Аналогично, точки КП-плоскости хОа, значения
координаты и параметра каждой из которых удовлетворяют
смешанной системе II, расположены на части прямой
х = -а, находящейся в полуплоскости а < 0 (на рис. 1.1а
эта полуплоскость заштрихована), то есть на луче с
началом в точке х = 0, а = 0 и направлением вдоль биссектрисы
второй четверти КП-плоскости.
Следовательно, каждому значению параметра а
соответствует одно-единственное значение координаты дс, а именно, ес-
ли а < 0, то х — -а, если а = 0, то х = 0, если а > 0, то х = а.
§ 1. Рациональные алгебраические уравнения с параметрами 17
На рис. 1.16 то же множество изображено на
КП-плоскости аОх с вертикальной параметрической осью
Оа. Каждая из прямых семейства а = const пересекает
изображенное множество в точке с координатой х,
определяющей решение исходного уравнения, а именно, если
а = const < 0, то х =» -а, если а = const = 0, то х ■* 0, если
18 § 1- Рациональные алгебраические уравнения с параметрами
а = const > 0, то х = а, то есть получаем тот же самый ре*
зультат, что и в первом случае.
Ответ. Если а < О, то х = -а,
если а = 0, то х — 0, если а > О, то х = а.
Пример 1.2. На координатно-параметрической
плоскости хОа изобразить множество решений уравнения
§ 1. Рациональные алгебраические уравнения с параметрами 19
Решение. По определению абсолютной величины
действительного числа х имеем:
И-а
И.
х > О,
х = а;
х <0,
х = -а;
а >0,
х = а;
а >0,
х = -а.
(1.2)
Ответ. На рис. 1.2 рассматриваемое множество
изображено жирной линией.
Пример 1.3. Для каждого значения параметра а решить
уравнение
Решение. Изобразим на КП-плоскости хОа множество
всех точек (х; а), значения координаты и параметра каждой
из которых удовлетворяют заданному уравнению.
х= 1
1-я
В первой четверти КП-плоскости при х £ 0, а > 0
уравнение принимает вид
х + а = 1.
Значит, это множество в первой четверти изображается
отрезком прямой х = 1 - а, а следовательно в силу сим-
20 § 1. Рациональные алгебраические уравнения с параметрами
метрии относительно осей Ох и Оа искомое множество на
всей КП-плоскости представляет собой контур квадрата
(см. рис. 1.3).
Ответ. Если а < -1, то х е 0; если а = -1, то х = 0;
если -1 < а < 0, то х = -1 - а, х = 1 + а;
если 0 < а < 1, то х = -1 + а, х = 1 - а;
если а - 1, то х = 0; если а > 1, то х е 0.
Пример 1.4. Для каждого значения параметра а решить
уравнение
|х + а\ + |х - а\ = 2.
Решение. На КП-плоскости хОа прямые х — -а и
х = а пересекаются в точке О и разбивают КП-плоскость на
четыре «частичные» области I-IV. Рассмотрим исходное
уравнение в каждой из этих областей, заменив его
равносильной совокупностью смешанных систем:
I.
П.
III.
IV.
Следовательно, на КП-плоскости множество всех точек
(х; а), значения координаты х и параметра а каждой из
которых удовлетворяют рассматриваемому уравнению,
представляет собой контур квадрата с центром в точке О и
сторонами, параллельными осям Ох и Оа.
х<а,
х > -а,
х + а + а-х =
х > а,
х£-а,
х + а + х-а =
х£а,
х < -а,
-х - а + х - а
х < а,
х<-а,
-х - а + а - х
2;
2;
= 2;
= 2;
I.
И. «
III.
IV. -
х^
X >
а =
х >
х>
X ^
X <
а =
х <
X £
X =
а,
-а,
1;
а,
-а,
^а,
-а,
-1;
:а,
-а,
§ 1. Рациональные алгебраические уравнения с параметрами 21
ч
-1
\
MIM
/
X i
1
N. П
\
/
УIII
<5
-1
х=\
'/
\
IV \^
х=-1
/
О
X
\
1 в
N
Рис. 1.4
Ответ. Если а < -1, то х е 0;
если а = -1, то -1 < х £1;
если -1 < а < 1, то х = -1, я - 1;
если а = 1, то -1 < х < 1; если а > 1, то х е 0.
Пример 1.5. Для каждого значения параметра а решить
уравнение
Решение. Применяя метод «частичных областей» и
определения абсолютной величины, заменим уравнение
совокупностью трех систем
(П)
(Ш)
х<0,
-2х + 1-х = а;
f 0<;*<:i,
[2дс +1 - х = а;
2х + х -1 = а;
а)
(П)
(Ш)
X
х =
С
X
X =
<о,
1-а
3 '
XZ1,
а + 1
3 '
о
(D
(П)
(Ш)
х =:
а
х =
1-а
3 '
а^2,
а-1;
>2,
а + 1
3
22 § 1* Рациональные алгебраические уравнения с параметрами
На КП-плоскости решением рассматриваемого уравна
ния в первой частичной области (I): х < О (полуплоскости)
1-а
является луч х = , во второй области (II): 0 < х < 1
3
(полосе) — отрезок прямой х = а - 1, в третьей области
(III): х > 1 (полуплоскости) — луч х = .
3
Используя решение на КП-плоскости, нетрудно
записать ответ, поставив в соответствие каждому значению
параметра а значение х на полученной ломаной линии.
Рис. 1.5
Ответ, а < 1: х € 0, 1 < а < 2: \х = -, х = а-1>;
а > 2:
Пример 1.6. Исследовать число решений уравнения
|2|х|-4| = х + а
в зависимости от величины действительного параметра а.
Решение. Используя определение абсолютной
величины, преобразуем уравнение в каждой из «частичных»
областей, на которые делят прямые х = -2, х = 0 и х - 2
j 1. Рациональные алгебраические уравнения с параметрами 23
КП-плоскость, и заменим его равносильной совокзщностью
смешанных систем:
|2|*|-4| =
I.
II.
III.
IV.
х < -2,
Зх + а + 4 = 0;
-2 < х < 0,
-х + а - 4 = 0;
0 < х < 2,
3* + а - 4 = 0;
jc. > 2,
-# + а + 4 = 0.
Изображенное на КП-плоскости хОа множество точек (х, а),
координаты х и параметр а которых удовлетворяют
исходному уравнению, дает возможность ответить на вопрос о
числе решений этого уравнения.
Рис. 1.6
Ответ. Если а < -2, то нет решений;
если а = -2, то одно решение;
24 § 1- Рациональные алгебраические уравнения с параметрами
если -2 < а < 2, то два решения;
если а = 2, то три решения;
если 2 < а < 4, то четыре решения;
если а = 4, то три решения;
если а > 4, то два решения.
Пример 1.7. При каких значениях параметра а все
решения уравнения
удовлетворяют неравенству 4 < х < 6?
Решение.
(х + 2а> О,
F(x, а) = 3 х + 2а - За + х -15 = 0 <=>
Г* + 2а < О,
П. J
[ = 0.
Прямая х + 2а = 0 разбивает КП-плоскость л:Оа на две
«частичные» области I и И. (Пусть эта прямая
принадлежит как I, так и II области.) Часть прямой
4х + За - 15 = 0,
принадлежащая I «частичной» области, дает решения
системы I, а часть прямой
2х + 9а + 15 « 0,
принадлежащая II «частичной» области, дает решение
системы П.
Следовательно, решение системы I, удовлетворяющее
условию 4 < х ^ 6, на КП-плоскости есть отрезок луча с
началом в точке а = -3, х = 6 и концом а = —, х = 4.
3
Аналогично, решение системы II, удовлетворяющее
условию 4 < х ^ 6, есть также отрезок луча с началом а = -3,
23
х = 6 и концом а = , х = 4. (Эти отрезки на КП-плос-
9
кости изображены жирными линиями.)
§ 1. Рациональные алгебраические уравнения с параметрами 25
Рис. 1.7
Оба решения удовлетворяют неравенству при всех
значениях параметра а из отрезка
23
Ответ. -3 < а £ .
Ь ?]•
Пример 1.8. Указать значения параметра а, при
которых уравнение
ах = |*|
имеет единственное решение, и найти это решение.
Решение. Воспользуемся определением абсолютной
величины и заменим данное уравнение равносильной ему
совокупностью смешанных систем
х<0,
26 § 1- Рациональные алгебраические уравнения с параметрами
а- 1
Рис. 1.8
На координатно-параметрической плоскости хОа
изобразим множество точек, значения координат и параметров
которых удовлетворяют этой совокупности.
Ответ. При а е (-оо; -l)u(-l; l)u(l; +<х>) уравнение
имеет единственное решение х = 0.
Пример 1.9. Для каждого действительного значения
параметра а решить уравнение
Решение. Данное уравнение является линейным
относительно х. Логическая схема исследования линейного
уравнения имеет вид:
ах = Ь
- b •
a'
a = 0, b * 0 : x e 0;
a = b = 0 : Vjc <E R.
(1.3)
Следовательно, рассматриваемое уравнение равносильно
(а -1)(а + 1)х = (а -1)(2а + 3),
§ 1. Рациональные алгебраические уравнения с параметрами 27
1° а^1,а^-1:31дс = ;
2° а = -1: *€0;
3° а = 1 : Ух е R.
На координатно-параметрической плоскости д;Оа множество
точек, значения координаты и параметра которых
удовлетворяют исходному линейному уравнению, состоит из
гиперболы и прямой а = 1.
-5 -4 -3 -2 }
X
h
• 2
1.
0
-1
I "2
I "3
1
1
1
ч
2д + 3
2 3 4 5а
Рис. 1.9
Ответ. Если -оо < а < -1, то х =
2а + 3
* + 1 ;
если а = -1, то jc е 0;
если -1 < а < 1, то * =
если а = 1, то Vjc € R;
2а + 3
если 1<а< + оо,то л: =
2а 4-3
a-fl '
28 § 1- Рациональные алгебраические уравнения с параметрами
Пример 1.10. Для каждого значения параметра а,
удовлетворяющего условию |а| < 3, найти решение (х, у)
системы уравнений
х - у = а,
2х + у = 3.
Решение. Исключая последовательно переменные х и
у, получим систему уравнений
Зх = а + 3,
Зу = 3 - 2а,
х =
а
3-
+ 3
3
-2а
где а < 3.
Рис. 1.10
На координатно-параметрических плоскостях хОа и
уОа множества точек, значения координат и параметра
которых удовлетворяют рассматриваемой системе,
представляют собой отрезки, расположенные на прямых х =
а + 3
3-2а
§ 1. Рациональные алгебраические уравнения с параметрами 29
Пример 1.11. Для каждого значения параметра а
решить (относительно х) систему уравнений
1\а - jc| + 2а = 6,
\2а - х\ + За = 6.
Решение. 1-й способ.
Применяя логическую схему
= ф <=>
/ + Ф = 0;
Ф>0,
/ - Ф = 0,
(14)
заменим данную систему уравнений равносильной ей
совокупностью четырех смешанных систем:
а < 2,
(а - х) + (6 - 2а) = 0,
(2а - х) + (6 - За) = 0;
а <2,
(а - дг) + (6 - 2а) = О,
(2а - х) - (6 - За) = 0;
а <2,
(а - х) - (6 - 2а) = О,
а <2,
(а-х)-(б-2а) =
(2а-х)-(6-За) =
Первая смешанная система имеет при любом а £ 2
решение х = 6 - а. Вторая — решений не имеет. Третья и
четвертая при а = 2 и а = 0 имеют соответственно решения
дг = 4 и х = -6.
2-й способ.
Применяя метод «частичных областей» (МЧО) и
определение абсолютной величины действительного числа,
заменим данную в условии задачи систему уравнений
равносильной ей совокупностью следующих четырех смешанных
систем:
30 § 1- Рациональные алгебраические уравнения с параметрами
(I)
(III)
х > 2а,
х>а,
(х-а) + 2а = 6,
(х - 2а) + За = 6;
х < 2а,
х < а,
(а - х) + 2а = 6,
(2а - jc) + За = 6;
(И)
х <2а,
л:>а,
(х - а) + 2а = 6,
(2а - jc) + За = 6;
(IV)
х > 2а,
х < а,
(а - jc) + 2а = 6,
(д:-2а) + 3а = 6.
Решение первой смешанной системы дает в I «частичной
области» КП-плоскости луч с началом в точке х = 4, a = 2,
направленный вдоль прямой х = 6 - а. Вторая и четвертая
смешанные системы решений не имеют. Решение третьей
смешанной системы определяет в III «частичной области»
плоскости точку х = -6, a = 0.
Таким образом, на КП-плоскости хОа множество всех
точек, значения координаты х и параметра а каждой из
которых удовлетворяют исходной системе уравнений, состоит
§ 1. Рациональные алгебраические уравнения с параметрами 31
из точки х = -6, а = О и луча х = 6-а, а < 2, с началом в
точке х = 4, а = 2 (см. рис. 1.11).
Ответ. Если а < 0, то х = 6-а; если а = 0, то х = -6 и
л: = 6; если 0 < а < 2, то х = 6-а.
Пример 1.12. Найти все значения параметра а, при
которых уравнение
(2 - х)(х + 1) = а
имеет два различных неотрицательных корня.
Решение. На КП-плоскости хОа множество всех
точек (jc, а), значения координаты и параметра каждой из
которых удовлетворяют данному уравнению, представляет
собой параболу — график функции
а = (2-х)(х + 1).
Парабола пересекает ось Ох в точках я = -1, а = 0 и
х = 2, а = 0. Вершина параболы jc = 1/2, а = 9/4. В ней
оба корня совпадают. При 2 < а < 9/4 оба корня
неотрицательны.
Ответ. 2<а< 9/4.
32 § !• Рациональные алгебраические уравнения с параметрами
Пример 1.13. Найти все значения параметра а, при
которых уравнение
х2 -х-а = 0
имеет хотя бы одно решение, удовлетворяющее неравенству
Решение. На КП-плоскости хОа множество всех
точек (х; а), координата и параметр каждой из которых
удовлетворяют заданному уравнению, представляет собой
график функции
а = х2-х,
то есть параболу. Эта парабола пересекает ось Ох в точках
х = 0, а = 0 и х = 1, а = 0. Вершиной параболы является
1 1 „ 1
точка х = —, а = —. Неравенству х > — удовлетворяют все
2 4 2
точки полуплоскости (на рис. 1.13 она заштрихована) без
1
границы х = — .
Значения параметра а, при которых все точки параболы
находятся в данной полуплоскости, являются искомыми.
Ответ, а > —.
4
§ 1. Рациональные алгебраические уравнения с параметрами 33
Пример 1.14. Для каждого параметра а решить
уравнение
х2 +\х
\х\ + а = 0.
Решение. По определению абсолютной величины
имеем;
х2 +\х\ + а = 0
а = -х - х,
х>0;
а = -х2 + х
х <0.
На КП-плоскости хОа множество точек (я/а), значения
координаты и параметра каждой из которых удовлетворяют
первой смешанной системе совокупности, представляет собой
часть параболы а = -х2-х, расположенную в полуплоскости
х > 0, а множество точек (х; а), значения координаты и
параметра каждой из которых удовлетворяют второй
смешанной системе совокупности, — часть параболы а = -х2 + х,
расположенную в нижней полуплоскости х < 0 без границы.
2 ' '
Рис. 1.14
2-3683
34 § 1- Рациональные алгебраические уравнения с параметрами
Зная уравнения ветвей парабол, запишем ответ.
~ ~ 11- Vl -4а -1 + Vl-4a
Ответ. Если а < 0, то х е < ;
[22
если а = 0, то х = 0; если а < 0, то х е 0.
Замечание. Можно сделать подстановку |jc| = t > 0.
Пример 1.15. Для каждого значения параметра а найти
все значения х, для которых
min(x2,a) = 1.
Решение Воспользовавшись свойством абсолютной
величины
min(/, ф) =
+ Ф- I f - Ф I
и заменяя уравнение равносильной совокупностью
смешанных систем
min(jc у а) =
- x - a
= i
находим искомое решение.
\хг<а,
\х2=1,
Рис. 1.15
§ 1. Рациональные алгебраические уравнения с параметрами 35
Тот же результат нетрудно получить, используя КП-плос-
кость хОа.
Ответ. Если а < 1, то х е 0; если а = 1, то г > 1 и
х < -1; если а > 1, то х = I и х = -1.
Пример 1.16. Найти наименьший член
последовательности
хп = п2-9п-100. (п = 1, 2, ...).
Решение. На КП-плоскости хОа точки
рассматриваемой последовательности расположены на параболе
х = а2-9а-100
с вершиной а = 4 — ,х = -120— (рис. 1.16).
I hi I I t
I I I I
14 j 16 18 а
i •
i
i
1
-60
\зо]
-120 '
Рис. 1.16
Следовательно, наименьшее значение
последовательность принимает при натуральных значениях параметра
Ответ. х4 = х6 = -120.
36 § 1- Рациональные алгебраические уравнения с параметрами
Пример 1.17. При каждом значении параметра а
решить уравнение
Решение. Раскрывая модули, заменим данное
уравнение равносильной совокупностью смешанных систем:
2х2-5
х<-2;
3 = о,
-2 их
-2х2 +
-\<,х
3 = о,
1 5 X <
= а,
<-1;
5 = а,
<1;
2;
2х2 - 5 = а,
Изображая на КП-плоскости д:Оа множество точек (х, а),
значения координаты и параметра которых удовлетворяют
этой совокупности систем, сформулируем ответ на
поставленную задачу.
Рис. 1.17
§ 1. Рациональные алгебраические уравнения с параметрами 37
Ответ. Если а < 3, то х е 0;
если а = 3, то х е [-2; -1]и[1; 2];
о к [ /5 +а /5-а
если 3 < а < 5, тохе -J ; -J ;
I К « \ £
если а = 5, то л: е |—л/5;О;л/б>;
к ( /5 +а /5 +а)
если а > 5, то л: е ^- ' •-' >
5-а /5 + а
Пример 1.18. При каких значениях а уравнение
)2
3(*-2)2-|х-2|
имеет ровно два различных решения?
Решение. На КП-плоскости множество, задаваемое
уравнением
х > 2,
а=(х-2)(7-Зх),
а=|*-2|-3(х-2)2 о
состоит из симметричных относительно прямой х = 2
частей двух парабол с вершинами, соответствующими
значению параметра a = 1/12, и общей точкой х = 2, a = 0.
Рис. 1.18
Ответ, a < 0, а=—.
12
38 § 1- Рациональные алгебраические уравнения с параметрами
Пример 1.19. Найти значения параметра а, при
которых оба корня уравнения
х2 + х + а = О
действительны и больше а.
Решение. Изобразим на КП-плоскости прямую х = а
и параболу
х2 + х + а - О .
Они пересекаются в двух точках
х = О, а = 0 и х = -2, а = -2.
График зависимости от параметра первого корня jc = хх(а)
представляет собой верхнюю ветвь параболы,
расположенную выше оси х = -1/2 и, следовательно,
хх(а) > а при а < 0.
График зависимости от параметра второго корня х = х2(а)
представляет собой нижнюю ветвь данной параболы и,
следовательно, х2(а) > а при а < -2.
Таким образом, оба корня больше а при а < -2.
Рис. 1.19
§ I. Рациональные алгебраические уравнения с параметрами 39
Другое решение мы получим, если найдем искомые
значения параметра из условия расположения числа а левее
корней квадратного трёхчлена
f(x) = х2 + х + а
то есть из условия:
D = 1 - 4а > О,
f(a) = а2 + 2а > 0 <=> а < -2,
Ответ, а < -2.
Пример 1.20. Найти все значения а, при которых
уравнение
х2 - 4х - 2\х - а\ + 2 + а = О
имеет ровно два решения.
Решение. Воспользовавшись определением
абсолютной величины, заменим данное уравнение равносильной
совокупностью двух смешанных систем:
I.
II.
х - а > 0,
х2 - 6х + За + 2 = 0;
х - а < 0,
х2 - 2х - а + 2 = 0.
На КП-плоскости хОа решением первой смешанной системы
-jc2+6jc-2
являются точки параболы а =
расположенные
в полуплоскости х > а, а решением второй смешанной
системы — точки параболы а = х2 - 2х + 2, расположенные в
полуплоскости х < а, без ее границ.
На рис. эти точки парабол изображены жирными
линиями.
40 § 1- Рациональные алгебраические уравнения с параметрами
Рис. 1.20
Следовательно:
если -оо < а < 2, то исходное уравнение имеет два
решения;
если а = 2, то три решения;
7
если 2 < а < —, то четыре решения;
3
7
если а = —, то три решения;
3
7
наконец, если а > —, то два решения.
3
Ответ, -оо < а < 2, — < а < + со.
Замечание. Тот же результат можно получить,
использовав теорему о расположении числа относительно корней
1Л5адратного трехчлена.
Пример 1.21. Найти все значения параметра а, при
которых уравнение
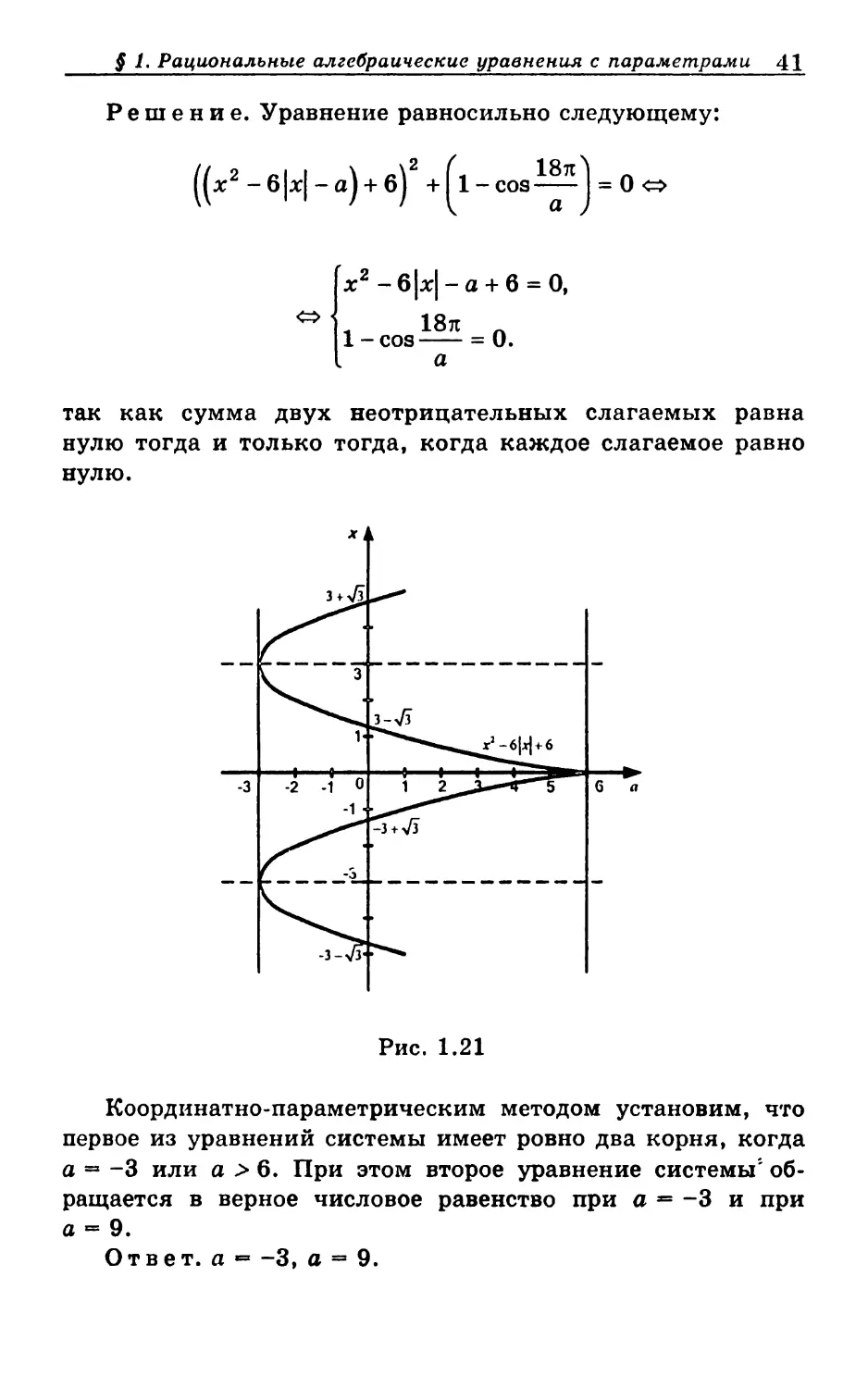
(х2 - б|х| - а) + 12(*2 - в|х| - а) + 37 = cos^
имеет ровно два корня.
§ 1. Рациональные алгебраические уравнения с параметрами 41
Решение. Уравнение равносильно следующему:
= v <=>
х2 — 6|jc| — а н- 6 = 0,
18л п
1-cos = 0.
а
так как сумма двух неотрицательных слагаемых равна
нулю тогда и только тогда, когда каждое слагаемое равно
нулю.
Рис. 1.21
Координатно-параметрическим методом установим, что
первое из уравнений системы имеет ровно два корня, когда
а в -3 или а > 6. При этом второе уравнение системы'
обращается в верное числовое равенство при а = -3 и при
а = 9.
Ответ, а •= -3, а = 9.
42 § I» Рациональные алгебраические уравнения с параметрами
Пример 1.22. Найти все значения параметра а, для
каждого из которых существует только одно значение х,
удовлетворяющее системе уравнений
х2 + 5* + 4| - 9х2 + 5* + 4 - 10x|x| = О,
х2 - 2(а + 1)х + а(а + 2) = 0.
Решение. Раскрывая модули, находим решение
первого уравнения
\х + 1| • \х + 4\ - 9х2 + 5* + 4 - 10х|*| = 0 о
Г-4 < * < -1,
Решаем второе уравнение
х2 - 2(а +1) х + а (а + 2) = 0 о Г = а>
Изобразим полученные решения на КП-плоскости хОа.
Решением исходной системы уравнений являются отрезки
прямых (изображены жирными линиями).
Гх = а + 2 при - 6 < а < -3
[х = а при - 4 < а ^ -1,
а также точки пересечения этих прямых с прямой х = 1.
Следовательно:
если а < -6, то система не имеет решений;
если -6 < а <-4, то имеет одно решение;
если -4 < а < -3, то два решения;
если -3 < а < -1, то одно решение;
если а = -1, то два решения;
если -1 < а < 1, то не имеет решений;
если а = 1, то одно решение;
если а > 1, то система не имеет решений.
§ 1. Рациональные алгебраические уравнения с параметрами 43
Ответ. -6 < а <-4, -3 < а < -1, а = 1.
Пример 1.23. При всех а решить уравнение
и определить, при каких а оно имеет ровно два решения.
Решение. Применяя метод частичных областей и
раскрывая модули в каждой частичной области КП-плос-
кости, получим, что исходное уравнение равносильно
совокупности трех смешанных систем
I.
х < -3,
III.
П.
х > 1,
-3 < х < 1,
(а + 1)х = а + 1;
Первая смешанная система при а ф 1 имеет единственное
7 + а , Л
решение х (гипербола), а при а = 1 не имеет реше-
а-1
ний; вторая смешанная система при а ф -1 имеет
единственное решение х = 1, а при а = -1 множество решений
44 § 1- Рациональные алгебраические уравнения с параметрами
-3 < х < 1; третья смешанная система при а Ф 1 не имеет
решений, а при а = 1 имеет множество решений х > 1.
Рис. 1.23
Жирной линией дано изображение на КП-плоскости
множества всех пар чисел (а,#), удовлетворяющих
рассматриваемому уравнению.
Ответ. Если -со < а < -1, то х = 1;
если а = -1, то -3 < х < 1;
если -1 < а < 1, то ровно два решения: х = 1 и л: =
а-1
если а = 1, то jc > 1; если 1<а< + со,тоя = 1.
Пример 1.24. Найти зависимость корней уравнения
х4 + jc3 - Зах2 - 2ах + 2а2 = О
от значений параметра а.
Решение. Рассматривая данное уравнение как
квадратное относительно параметра а, найдем его корни а в аг(х)
§ 1. Рациональные алгебраические уравнения с параметрами 45
и а = а2(х). Это позволяет разложить левую часть уравнения
на множители
О = X + X
х2
а = —
На КП-плоскости хОа точки (х, а), значения координат х и
параметра а для которых удовлетворяют рассматриваемому
уравнению, расположены на двух параболах
2 х2
а = х + х и а = _
с вершинами соответственно
а = -1,
4
-- и а - О, х = О.
2
Рис. 1.24
Ответ. Если а < —, то уравнение не имеет корней»
4
46 § 1- Рациональные алгебраические уравнения с параметрами
1 1
если а — - — , то х = —;
4 2
1 Л -1 - >/4а +1 -1 + у/4а +1
если — < а < 0, то х = и х =
4 2 2
если а = 0, то х = -1 и х = 0;
Л о -l-ViaTl i—
если 0 < а < 2, то х = , х = -V2a ,
-1 + >/4а +1
х = и х
если а = 2, то х = -2, х = 1 и х — 2;
-1 - V
_ /г 1 V4a +1 -1 + V4a +1
если а > 2, х = - V2a , х = , х =
2 2
и х = «Ла .
Пример 1.25. Для всех значений параметра а решить
уравнение
4 2а -1 2
X + X +■
12
х +
а 1| ^ g-fl
3 6|+ 6 '
Решение. Применяя метод подстановки, сводим
данное уравнение к равносильной системе
х + =
18
£±1.
6
Так как абсолютная величина всегда неотрицательна, то
будем рассматривать решение данной системы на КП-плос-
кости Юа, когда
§ 1. Рациональные алгебраические уравнения с параметрами 47
При а > -1 выражение, стоящее под знаком абсолютной
величины в левой части уравнения, является
неотрицательным.
Следовательно, рассматриваемая система равносильна
х2 +
Н-"•
18
[а >-1.
<=>
2 а 1
х +i"6
а + 1 > О
а_ _ 1\ _ 2а -1
3 б| 6 '
2а-1>0
2 а 1
3 6
[а + 1 > О,
3 б
[2а -1 >0;
2"а
-1,
2 о
д:2=0,
1а = 2-6х2,
[а > -1,
а = -2х\
[а > -1,
Изобразив на КП-плоскости хОа решение полученной
совокупности систем, запишем ответ.
Ответ. Бели а < -1, то решений нет;
если а = -1, то дс = ±-=;
/ а 12-а
если -1 < а < 0, то х = ±Л—, х = ±J ;
Y ^ Y о
если а = О, то х = 0, х = ±-т=;
Зв*
если 0<а<—,tojc = ±J ;
2 V 6
48 § 1- Рациональные алгебраические уравнения с параметрами
если — < а < 2, то х = 0, х = ±J ;
2 V 6
если а > 2, то х = 0.
§ 1. Рациональные алгебраические уравнения с параметрами 49
Пример 1.26. Предприятие производит телевизоры и
является прибыльным. Известно, что при изготовлении п
телевизоров в месяц расходы предприятия на выпуск одного те-
левизора составляют не менее
40 500
п
+ 270
тыс. руб., а цена реализации каждого телевизора при этом
о
не превосходит 540 л тыс. руб. Определить
ежемесячный объем производства, при котором может быть получена
наибольшая из возможных в данных условиях прибыль.
Решение. Пусть х (тыс. руб.) — ежемесячная
прибыль предприятия при изготовлении п телевизоров.
Тогда по условию задачи
о х < 540л - —л2 - 40 500 - 270 + |90ге - 40 500| <=>
10 ' '
х < х{п) =
_3^
ю]
если п < 450,
х, (п) = п2 + 360п - 81 000, если п > 450.
. w 10
27000
У
-4-
\!
1 1 I
^2 (Л)
N
\
-4-
-4-
0 150 300 450 600 750 900 1050 1200 п
Рис. 1.26
50 § 1- Рациональные алгебраические уравнения с параметрами
На КП-шюскости хОп координата х является кусочно-
гладкой функцией натурального аргумента л, график
которой состоит из частей двух парабол
х = xl(n) и х = х2(п).
Так как
х[ (п) = 0 о п = 300,
х*2 (п) = 0 <=> п = 600,
то максимальное значение х = 27 000 функции х = х1(п)
и х = х2 (п) достигают соответственно при п = 300 и
п = 600.
Ответ. 300 или 600 телевизоров.
Упражнения
1. Установить, при каких значениях параметра а
уравнение
jc|jc + l|-a = 0
имеет ровно три корня.
Ответ, а-—, a = 0.
4
2. Для каждого значения а определить число корней
уравнения
- 2х - 3
= а.
Ответ. Если а < 0, то нет корней;
если а = 0, то два корня;
если 0 < а < 4, то четыре корня;
если a = 4, то три корня.
3, На координатно-параметрической плоскости аОх с
вертикальной параметрической осью Оа изобразить
множества всех точек, значения координаты х и параметра а
каждой из которых удовлетворяют уравнениям:
а) а = х + |х| + |х-1|; б) \а\ = ||х2 - 4J - ll;
§ l. Рациональные алгебраические уравнения с параметрами 51
4. На координатно-параметрической плоскости аОх с
горизонтальной параметрической осью Оа изобразить
множества всех точек, значения координаты х и параметра а
каждой из которых удовлетворяют уравнениям:
a) min(a, x) = 1;
6)|x-a| + |x + a|
г) х2 + а2 = х\
д)х2-|а-х| = 2х;
е) х2 + а2 =а2х2 + 1.
5« Применяя КП-метод, исследовать в зависимости от
значений параметра а решения уравнений:
а) {а + \)х = а2 -1;
Ответ. Если а < -1, то х = а-1;
если а = -1, то Vx е Ш;
если а > -1, то х =» а - 1.
Указание. Исследовать как линейное относительно х
уравнение, рассмотрев на КП-плоскости два случая:
а + 1 * О,
х = а -1;
а+1 = 0,
б)
а-1
2ах + с
= 1;
Ответ. Если а = 0, а = 1, то нет решений;
если
0, а * 1, то дг = -
Указание. Применяя логическую схему решения
типового дробно-рационального уравнения
Р п
— = 0
Q
Р = 0,
Q * 0,
(1.5)
52 § 1* Рациональные алгебраические уравнения с параметрами
заменим задачу о решении данного в условии уравнения
равносильным высказыванием 2ах = а — 4 ^ —3.
в) * + 2х = 1;
1-f ах
Ответ. Если а = 2, а = ±-j29 то х е 0;
1-а
если а * 2, а ф ± -J2, то х =
2-а
Указание. Заменим уравнение равносильной системой:
(2 - а) • х = 1 - а,
f ах ф 0.
На КП-плоскости хОа множество всех точек, значения
координаты х и параметра а каждой из которых
удовлетворяют этой системе, состоит из всех точек гиперболы
1-а „ 1
2-а а-2
за исключением двух: а = V2f х = —з-r и а = -J2, х = -т».
V2 V2
Для каждого значения параметра а решить КП-методом
уравнения:
6. |х| - а = 2.
Ответ. Если а < -2, то хе0;
если а ■= -2, то х в 0;
если а > -2, тохв -2-а, х в 2 + а.
7. |x + 2| + |jt-l| + |jc-4| = a.
Ответ. Если а < 6, то х е 0;
если а в 6, то х в 1;
если 6 < а < 9, то х в 7-а, х в а-5;
3-а 3+а
если а £ 9, то х = , х = —-—.
3 3
8. |х|-|х + 2| + а = 0.
Ответ. Если а < -2, то х е 0;
если а = -2, то х £ -2;
§ 1. Рациональные алгебраические уравнения с параметрами 53
а-2
если -2 < а < 2, то х = ——;
если а = 2, то х > 0;
если а > 2, то х е 0.
9. н-Н-».
Ответ. Если а < -1, то х = а-1, х = -а - 1;
если а — -1, то х = 0;
если -1 < а < 1, то х е 0;
если а — 1, то х — 0;
если а > 1, то х = 1 - а, х = а - 1.
10. |а-х| + х + а = 2.
Ответ. Если а < 1, то х = 1;
если а = 1, то х < 1;
если а > 1, то х е 0.
Ответ. Если а < -1, то х е 0;
если а = -1, то Vx e R;
если -1 < а < 1, то х е 0;
если а = 1, то х = 0;
1-а а-1
если а > 1, то х = , х = .
Ответ. Если а < -1, то х = -а + 1, х = -а - 1, х = а + 1,
-а-1;
если а = -1, то х = 0, х = 2, х = -2;
если -1 < а < О, то х = -а + 1, х = а - 1;
если а = 0, то х = -1, х = 1;
если О < а < 1, то х = а + 1, х — -а - 1;
если а = 1, то х - 0, х = -2, х - 2;
если а > 1, то х = -а - 1, х = -а + 1, х = а - 1, х =
1 + 1.
13. |х + а -1| = |х - а +1|.
Ответ. Если а < 1, то х = 0;
если а = 1, то Vx e R;
если а > 1, то х = 0.
54 § 1- Рациональные алгебраические уравнения с параметрами
Указание. Использовать логическую схему:
= ф.
/ = -ф.
(1.6)
а
5:
14. а2 +4ах-Ьх2 = 0.
Ответ. Если а < 0 , х = а, х
если а = 0, то х = 0;
если а > 0, то х = —, х — а.
5
Указание. Разложить левую часть уравнения на
множители и заменить уравнение равносильным:
-| р* I I , II , |-| | 4
Ответ. Если а < О, то х е 0;
если а = 0, то 0 < х < 1;
если 0 < а < 1, тоО<дг<1-а;
если а = 1, то jc = 0;
если а > 1, то jc e 0.
16. |х| + х = \а\ + а.
Ответ. Если а < 0, то х < 0;
если а > 0, то х = а.
17. Для каждого допустимого значения параметра а
КП-методом решить уравнения:
1 - 2
а)
х +
Ответ. Если а < 0, то х = -1, х = 1-—;
а
если 0 < а < 3, то х е 0;
если а
З.то*^;
если а > 3, то х = 1, х = 1 .
а а
§ 1. Рациональные алгебраические уравнения с параметрами 55
1 + - -
б) х - - = 2
а
Ответ. Если а < -1, то х = 1;
а
если -1 < а < 0, то х = -3;
если а = 0, то х е 0;
2
если а > 0, то х = 1.
а
в)
= 4-
■4
Ответ. Если а < 0, то х = — + 1;
а
если 0 < а < 2, то х е 0;
если а = 2, то л: < 3;
если 2 < а < 3, то х = 3;
если а > 3, то л: = — + 1.
а
18. Найти все значения параметра а, при которых имеет
решение систем, уравнений
р + у2 = 1,
[х2 + ху + у2 = а.
1 3
Ответ. — < а < —.
2 2
Указание. Заменить систему равносильной:
х = cos t,
у = sin t,
19. Для всех значений параметра а решить КП-методом
системы уравнений:
f2|jc-a| + a = 2,
jjjc - а\ - 2а = 6.
Ответ. Если а < -2, то х е 0;
56 § 1- Рациональные алгебраические уравнения с параметрами
если а = -2, то х = -4, х = 0;
если а > -2, то х е 0.
1H+W-1-
Ответ. Если а < -1, то х е 0;
если -1 £ а < 0, то х = -1-а;
если а = 0, то х = -1, х = 1;
если 0 < а < 1, то х = 1 - а;
если а > 1, то х е 0.
20. Для всех значений параметра а решить КП-методом
уравнение
Ответ. Если а < 0, то х = ±
2
если а > 0, то х е 0.
21. Найти все значения параметра а, при которых ровно
один корень уравнения
х2 - 4х + а = О,
имеющего различные корни, принадлежит интервалу (1; 4),
Ответ. О < а < 3.
22. Найти все значения параметра а, при которых
корни уравнения
х2 -6х + а = 0
удовлетворяют условию х2 = х.
Ответ, а - -27, а - 8.
23. Найти все значения параметра а, при которых
уравнение
х2 + 4х - 2|х - а\ + 2 - а = О
имеет ровно два различных решения.
7
Ответ, а < -—, а > -2.
3
§ 1. Рациональные алгебраические уравнения с параметрами 57
24. Найти все значения параметра а, при которых
уравнение
имеет единственное решение.
2 1
Ответ.а^-4, а = —, а= —» а £ 4.
3 2
25. Найти все значения параметра а, при каждом из
которых корни квадратного трехчлена х2 + ах + 1 различны и
лежат на отрезке [0; 2].
Ответ. — £ а < -2.
2
26. Найти все значения параметра а, при каждом из
которых уравнение
х|х + 2а| + 1 = 0
имеет единственное решение.
Ответ. а< , а>1.
27. Для каждого целого значения параметра а найти все
целые корни уравнения
4 (а + х) = ах.
Ответ, а =-12, х - 3; a - -4, х - 2; а = 0, х - 0;
а - 8, х = 8; а - 12, х = 6; а « 20, х - 5.
Указание. Заменить уравнение равносильным (а * 4):
. 16
х 4 +
а-4
28. Найти все значения параметра а, при которых
каждое из уравнений:
а) |х2 - 2x1 + |х2 - Зх •*- 2| = х2 - 4х •*• а;
б) |х2 -1| + |х2 - х - 2| = х2 - Зх + а
имеет ровно три различных корня.
От в ет. а) а = 4, а = —; б) а = 2, а = —.
4 3
58 § •?• Рациональные алгебраические уравнения с параметрами
29. При каких значениях а все корни уравнения
Sax2 + (За3 - 12а2 - l)x - а (а - 4) = О
удовлетворяют условию |х| < 1 ?
Ответ, а = 0,2 + 7з <а <2 + >/б.
Указание. Рассмотреть два случая: а = О и а ф 0. Во
втором случае — уравнение квадратное и имеет корни
1 2 А
х = — и х = -а + 4а.
За
30. Для каждого значения параметра а найти все
значения х, удовлетворяющие уравнению
и указать, при каких а оно имеет ровно два решения.
Ответ. Если а = 1, то х > 1;
если а = -1, то -3 £ х < 1;
если |а| > 1, то х = 1;
j i * 7 + а
если |а| < 1, то х = ;
а -1
при |а| < 1 ровно два решения.
31. Найти все значения параметра а, при которых
уравнение
5 • |х - За|
- а2| + 4х = а
1) имеет бесконечное множество решений,
2) не имеет решений.
Ответ. 1) а е 0; 2) а < -8, а > 0.
§ 2. Рациональные алгебраические
неравенства с параметрами
Пример 2.1. Для каждого значения параметра а решить
неравенство
х-|а|>0.
Решение. На КП-плоскости хОа изобразим
множество всех точек (х; а), значения координаты и параметра
каждой из которых удовлетворяют данному неравенству. Это
множество состоит из всех точек, расположенных выше
графика функции х = |а| (см. Пример 1.1 § 1).
Каждому значению параметра а соответствуют точки
изображенного множества с искомыми значениями координат.
Ответ. Если а < О, то х > -а;
если а = О, то х > 0;
если а > 0, то х > а.
Пример 2.2. Для каждого значения параметра а решить
неравенство
Ы - а < 0.
60
§ 2, Рациональные алгебраические неравенства
Решение. Воспользовавшись определением
абсолютной величины числа, заменим данное неравенство
равносильной ему совокупностью систем неравенств:
| - а < 0 о
Г х £
\х -
{х
\-
х £ 0,
х - а < 0,
х<0,
х - а < 0,
II.
х <а,
х <0,
г > -а.
Изобразим на КП-плоскости хОа с горизонтальной
параметрической осью Оа множество всех точек (jc; а), значения
координаты х и параметра а каждой из которых
удовлетворяют совокупности систем неравенств I и П.
Рис. 2,2
Ответ. Если а < 0, то х е 0;
если а > 0, то -а < х < а.
Пример 2.3. Для каждого значения параметра а решить
неравенство
§ 2. Рациональные алгебраические неравенства
61
Решение. Изобразим на КП-плоскости хОа
множество всех точек (х; а), значения координаты х и параметра а
каждой из которых удовлетворяют данному неравенству.
Выражение Ф(х, а) = |*| + |а| -1 обращается в нуль на
контуре квадрата |х| + |<*| = 1 (см. Пример 1.3 § 1) и во всех
точках (например, в точке х = 0, а = 0) внутри этого
квадрата Ф(х, а) < 0 .
Следовательно, искомое множество состоит из точек
данного квадрата, включая границу.
Ответ. Если а < -1, то х е0 ;
если а — -1, то х в 0;
если -1<а^0,то -1-а£х
если 0<а<1,то -1 + а^х£
если а = 1, то х в 0;
если а > 1, то х е 0 .
Пример 2.4. Найти наименьшее и наибольшее значения
параметра t, при которых координата х и параметр а
каждой из точек множества КП-плоскости хОа удовлетворяют
смешанной системе:
х - 2а = t.
(1)
(2)
62
§ 2. Рациональные алгебраические неравенства
Решение. Множество всех точек КП-плоскости хОа%
значения координаты х и параметра а каждой из которых
удовлетворяют соотношению (1), представляет собой
фигуру, заштрихованную на рисунке.
Уравнение (2) задает на КП-плоскости семейство
параллельных прямых
х = 2а + t.
(3)
(На рис. 2.4 изображены пунктиром прямые этого
семейства при значениях параметра t = -4, t * 0 и t = 4.)
X '
Рис. 2.4
Искомыми будут наименьшее и наибольшее из всех тех
значений параметра t, при которых соответствующие этому
параметру прямые семейства (3) пересекут фигуру
множества (1).
Ответ, t — -4, t = 4.
Пример 2.5. Для каждого значения а решить неравенство
(х-а)(х-2)<0.
Решение. См. рис. 2.5.
§ 2. Рациональные алгебраические неравенства
63
Ответ. Если а < 2, то а < х < 2;
если а = 2, то jc = 2;
если а > 2, то 2 < х < а .
Пример 2.6. Для каждого значения параметра а решить
неравенство
х-а
х + 2 ~
Рис. 2.6
64
§ 2. Рациональные алгебраические неравенства
Решение. На координатно-параметрической
плоскости хОа множества точек, значения координаты и
параметра которых удовлетворяют рассматриваемому неравенству,
представляет собой области II и IV (см. рис. 2.6).
Ответ. Если а < -2, то а < х < -2 ;
если а = -2, то х е 0 ;
если а > -2, то -2 < х ^ а .
Пример 2.7. Найти значения параметра а, при которых
неравенство
(х-а)(х-а-2)>0
является следствием неравенства
(1)
(2)
Решение. На координатно-параметрической
плоскости хОа решение неравенства (1) состоит из множества
точек, находящихся в полуплоскости ниже прямой х = а и в
полуплоскости выше прямой х = а + 2, а решение
неравенства (2) состоит из множества точек, находящихся внутри
полосы 1 < х < 3.
Следовательно, все решения неравенства (2) содержатся во
множестве решений неравенства (1) при а < -1 или а > 3 .
Ответ. При а <, 1 или а t 3 .
§ 2. Рациональные алгебраические неравенства
65
Пример 2.8. Найти все значения а, при которых
неравенство
*о
х + 2а - 2
выполняется для всех х из промежутка 2 < х < 3
Решение. Найдем решение неравенства
х - (За +1)
х - (2 - 2а)
0.
(1)
На КП-плоскости числитель обращается в нуль на прямой
х = За + 1, а знаменатель — на прямой х = 2 - 2а. Эти
прямые разбивают КП-плоскость на четыре частичные области
I-IV.
В каждой из частичных областей выражение F(xt а) с
двумя переменными сохраняет знак и меняет его при
переходе через границы этих областей. Чтобы установить знак
F(jc, a) в какой-либо из областей I-IV, достаточно взять
любую точку из этой области.
Например, при х = 2, a = 1 F(2, 1) > 0. Следовате-хьно,
всюду в I области F(x, a) > 0.
3-3683
66
§ 2. Рациональные алгебраические неравенства
Аналогично, определяя знак выражения F(x, а) в
других областях, получим, что неравенство выполняется в I и
III областях, причем граница х = За + 1 является его
решением, а граница х = 2-2а не принадлежит множеству
решений рассматриваемого неравенства (на КП-плоскости
это множество заштриховано).
Пересечение данного множества с множеством точек,
удовлетворяющих неравенству 2 < х < 3, (полосой) дает
решение неравенства (1) на промежутке
S X S о {£),
Следовательно, неравенство (1) выполняется сразу для
всех х из промежутка (2) при а < — и а £ —.
2 3
12
Ответ. а<—, а> —.
2 3
Пример 2.9. Найти все значения параметра а, при
которых неравенство
(х-За)(х-а-3)<0
выполняется при всех х, таких, что
(1)
(2)
Рис. 2.9
§ 2. Рациональные алгебраические неравенства
67
Решение. На КП-плоскости хОа множество точек
{х; а), значения координаты и параметра каждой из
которых удовлетворяют неравенству (1), состоит из областей I и
Ш, ограниченных прямыми х = 3аих = а + 3 (на рисунке
эти области заштрихованы).
Искомыми будут значения параметра 0 < а < —, при ко-
3
торых все точки из этих областей (области III) имеют
координаты, удовлетворяющие условию (2).
1
Ответ. О < а < — .
Пример 2.10. Найти все значения параметра а, при
которых для всех х, удовлетворяющих условию 0 < х < 1,
справедливо неравенство
х - 2а
х - а
Решение. На КП-плоскости хОа множество точек
(х; а), значения координаты и параметра каждой из
которых удовлетворяют дробно-линейному неравенству, состоит
из областей I и III, причем границы этих областей,
совпадающие с прямой х = а, данному множеству не
принадлежат (х * а).
Рис. 2.10
68
§ 2. Рациональные алгебраические неравенства
Искомые значения параметра а, при которых все точки,
расположенные в полосе 0 ^ х < 1 (на КП-плоскости
заштрихована), находятся также в областях I и III,
удовлетворяют условиям а < О или а > 1.
Ответ, а < О, а > 1.
Пример 2.11. Найти все значения параметра а, при
каждом из которых неравенство х2 + 2\х - а\ > а2 справедливо
для всех действительных х.
Решение. По определению абсолютной величины
получим:
х2 + 2\х - а\ Z а2 <=> (х2 - а2) + 2\х - а\ > 0 <^
<=> (х - а)(х + а) + 2\х - а\ > 0 о
х - а = 0;
х - а > 0,
(х-а)(х
х - а < 0,
I. х - а = 0;
х-а >0
х + а + 2 £ 0;
х - а < 0,
П.
III.
На КП-плоскости хОа решение уравнения I есть множество
всех точек (х, а) прямой I: х = а, решение системы II —
множество точек, расположенных одновременно выше
прямой х = а и на прямой дг + а + 2 = 0 и выше ее, решение
системы III — множество точек, расположенных
одновременно ниже прямой х = а и на прямой дг + а-2 = 0и
ниже ее.
§ 2. Рациональные алгебраические неравенства
69
дг + я + 2
Рис. 2.11
Следовательно, сразу для всех х исходное неравенство
справедливо при значениях параметра а е [-1; l].
Ответ. -1 £ а < 1.
Пример 2.12. Найти все значения параметра а, для
каждого из которых выполняется неравенство х2 + 2ах + а2 -1 > О
при всех х из отрезка 1 < х < 3 .
Решение. Разложим левую часть неравенства на
линейные множители, заменив его равносильным
F (jc, а) = (х + а +1) (х + а -1) > 0 .
Рис. 2.12
70
§ 2. Рациональные алгебраические неравенства
На КП-плоскости хОа решение данного неравенства
представляет собой «частичные» области I и III, то есть
полуплоскости, на которых F(x, а) > 0 . Следовательно,
рассматриваемое неравенство выполняется для всех х из
отрезка (полосы) 1 < х < 3 при всех значениях параметра
а < -4 и а > 0 .
Другой способ решения задачи.
Искомые значения параметра а должны удовлетворять
совокупности следующих условий для квадратичной функции
D = 4 > О,
D = 4 > О,
а > О,
а<-4.
/'(4) = 6 + 2а <0;
Ответ, а<-4, а > 0.
Пример 2.13. Для каждого значения параметра а
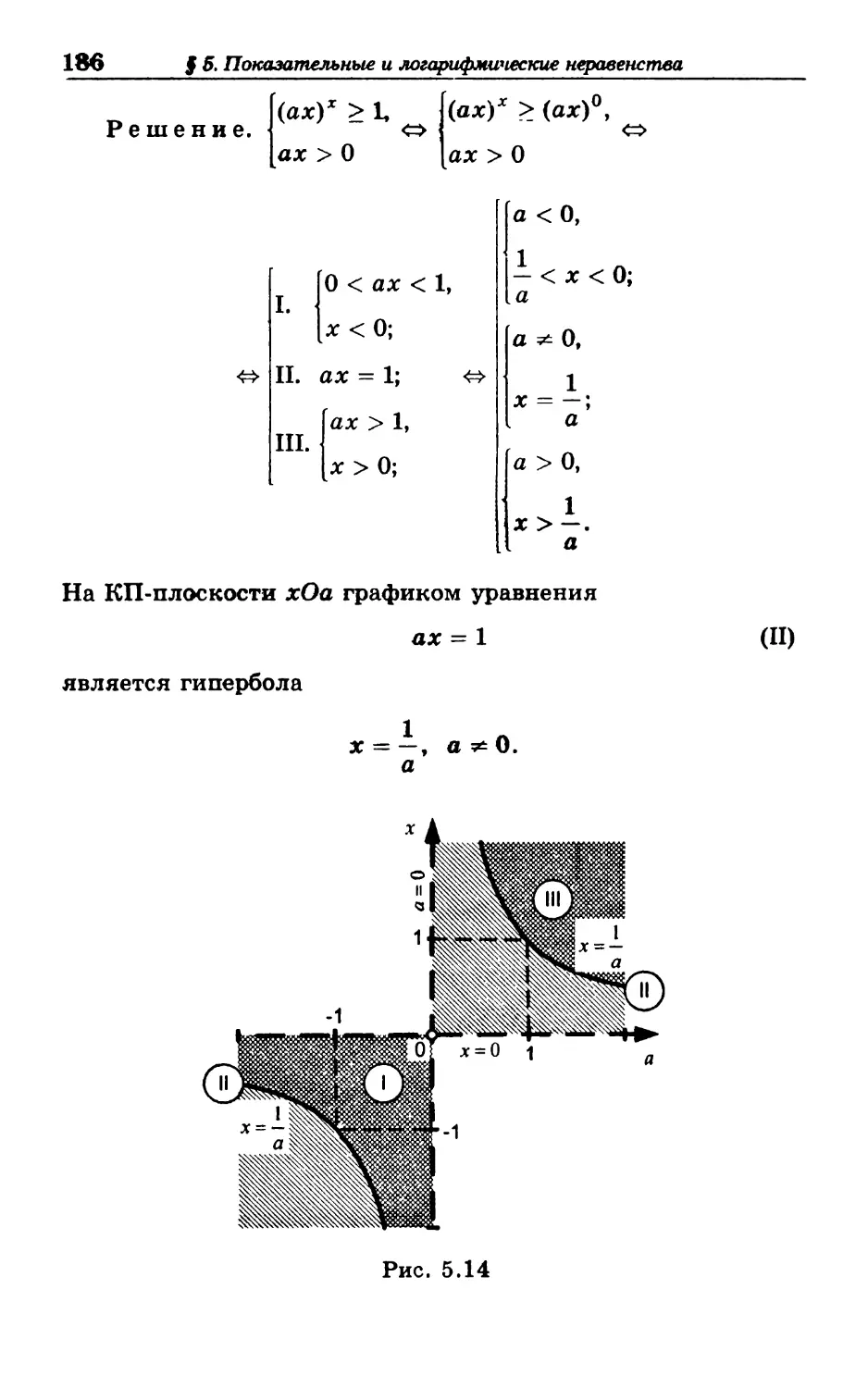
решить неравенство ах~\ > 0.
Решение. Данное неравенство является линейным
относительно х и равносильно следующему: ах > 1.
Логическая схема исследования линейного неравенства
данного типа имеет вид:
ах > b
а>0
= 0
а
[если Ь < 0, то х е R;
[если Ь > 0, то х G 0;
(2.1)
а < 0 : х < —.
а
§ 2. Рациональные алгебраические неравенства
71
Следовательно, рассматриваемое неравенство
равносильно
1° а >0: х>1/а;
2° а = О : х е 0;
3° a < 0 : я < I/a.
На координатно-параметрической плоскости хОа
множество точек, значения координаты и параметра которых
удовлетворяют исходному линейному неравенству,
находится при а < О ниже ветви гиперболы, а при а < 0 —
выше другой ветви гиперболы (на рис. это множество
заштриховано).
Рис. 2.13
Ответ. Если -оо < а < 0 , то х < I/a ;
если a = 0, то х е 0 ;
если 0<а<+оо,то х > 1/а .
Пример 2.14. Для каждого значения параметра а
решить неравенство
х + 1 < a(2 - jc).
Решение. Данное неравенство является линейным
относительно х и равносильно следующему:
(a + 1)jc < 2а - 1.
72
§ 2. Рациональные алгебраические неравенства
В общем случае логическая схема исследования
линейного неравенства данного типа имеет вид:
а > 0: х <-;
а
ах <Ь <=>
а = 0:
[если Ь > 0, то х е R;
[если Ь < 0, то х е 0;
(2.2)
а <0 :х>-.
а
Следовательно, рассматриваемое неравенство равносильно
совокупности
1°
2°
3°
а >-
2о-1
2а-1
Рис. 2.14
На координатно-параметрической плоскости хОа множество
точек, значения координаты и параметра которых удовле-
§ 2. Рациональные алгебраические неравенства
73
творяют исходному линейному неравенству, находится вне
2а-1
ветвей гиперболы х = — и на прямой а = -1
а + 1
Ответ. Если -оо < а < -1, то х >
2а -1
а + 1
если а = -1, то V# G R ;
если -1 < а < +00 , то х <
2а-1
а + 1
Пример 2.15. Для каждого значения параметра а
решить неравенство
Решение. На КП-плоскости хОа множество точек-
значения координаты и параметра которых удовлетворяют
данному неравенству, состоит из точек параболы и точек,
расположенных левее от нее (на рис. это множество
заштриховано).
Рис. 2.15
Уравнения нижней и верхней ветвей параболы имеют
вид:
х = хг(а) = -1 - Vl + а, х = х2(а) = -1 +
Ответ. Если а < -1, то Vx G Е;
если а = -1, то х = -1;
если а >-1, то (-оо; х1(а)^и^х2(а); +оо) .
74
§ 2. Рациональные алгебраические неравенства
Пример 2.16. Найти все значения параметра а, при
которых неравенство
выполняется для всех х е (-оо; +<х>) .
Решение. Воспользовавшись определением
абсолютной величины числа, заменим неравенство равносильной
ему совокупностью систем:
I. х
III.
х > а,
х > 1,
Ъх-2а> 4,
х < а,
х<1,
2а - х > 2,
И.
IV.
л:> а,
JC < 1,
3jc - 2а > 2,
х < а,
x>h
х + 2а > 4.
На КП-плоскости #Оа множество всех точек (х; а),
значения координаты х и параметра а, каждой из которых
удовлетворяют данной совокупности, на рис. заштриховано.
Рис. 2.16
§ 2. Рациональные алгебраические неравенства
75
Следовательно, при каждом значении параметра а > —
исходное неравенство выполняется для всех х е (-оо; +оо).
3
Ответ, а > —.
2
Пример 2.17. Для каких значений а система неравенств
-хг +12х-а
х < 2
выполняется хотя бы при одном значении xl
Решение. На КП-плоскости прямая х = 2 пересекает
параболу а — -х2 +12* в точке а = 20, х = 2.
Рис. 2.17
Множество точек КП-плоскости, соответствующих
значениям х и а, для которых выполняется система
неравенств
а < -х2 +12*,
х<2
заштриховано и представляет собой пересечение
множества точек, расположенных на параболе а = —х2 + 12дг и
левее ее, с множеством точек прямой х = 2 и ниже этой
прямой.
Ответ, а < 20 .
76
§ 2. Рациональные алгебраические неравенства
Пример 2.18. Найти все значения параметра а, при
каждом из которых неравенство ах2 — \х\ < О справедливо для
всех х < О .
Решение. Сведем задачу к исследованию на КП-плос-
кости хОа системы неравенств:
\ах2-х<,0,
[х < 0,
о
<; 0,
(ах + 1) х <> 0,
х < 0.
Последняя система равносильна совокупности следующих
систем неравенств:
j
[х < 0;
а >0,
И.
а <0,
. х=0
Рис. 2.18
Искомыми будут значения параметра а = 0 и а < 0,
которым соответствуют решения первой (луч) и третьей
системы (область II) совокупности.
Ответ. а<0.
§ 2. Рациональные алгебраические неравенства
77
Пример 2.19. Найти все значения а, при которых любое
значение х, удовлетворяющее неравенству
ах2 + (l-a2)x-a > О,
по модулю не превосходит двух.
Решение. При а = О неравенство принимает вид х > О
и, следовательно, не все его решения по модулю не
превосходят двух. Поэтому найдем все значения а * 0, при
которых из неравенства
Ф(дг, а) = ах2+ (l-a2)x-a =
следует неравенство
(1)
(2)
Множество точек КП-плоскости хОа, значения координаты
и параметра каждой из которых удовлетворяют
неравенству (1), состоит из «частичных областей» I, III и V, вдоль
78 § 2. Рациональные алгебраические неравенства
границ которых выражение Ф(#, а) = 0 (это множество
заштриховано).
Множество точек, координата каждой из которых
удовлетворяет условию (2), представляет собой полосу,
включающую границы
х = -2 и х = 2.
Следовательно, искомыми являются значения параметра
— 2 < а < —, при которых любая точка заштрихованного
множества принадлежит полосе (2), то есть если координата
х и параметр а каждой такой точки (х, а) удовлетворяют
неравенству (1), то отсюда следует, что они удовлетворяют
двойному неравенству (2).
Ответ. -2 < а < .
2
Пример 2.20. Найти все значения а, при которых из
неравенства
а*2-х + 1-а<0 (1)
следует неравенство
0 < х < 1. (2)
Решение. Разложим левую часть неравенства (1) на
множители
и заштрихуем на КП-плоскости множество точек (jc, a),
значения координаты и параметра которых удовлетворяют
этому неравенству.
Искомыми значениями параметра а будут те, при
которых все решения неравенства (1) содержатся в полосе
О < х < 1, то есть значения а е —;
2
Ответ. а
1
2*
§ 2. Рациональные алгебраические неравенства
79
Рис. 2.20
Пример 2.21. Найти все значения параметра а, при
каждом из которых существует хотя бы одно решение
неравенства
х2 +(5а + 2)jc + 4a2 + 2a < О,
удовлетворяющее условию х2 4- а2 = 4 .
Решение. Задача равносильна нахождению на КП-плос-
кости хОа множества всех точек (х, а), значения координаты
и параметра каждой из которых удовлетворяют смешанной
системе
: + a)(jc + 4a + 2) < О, (1)
J + a2=4. (2)
Решая системы уравнений
| х + а = О,
х + 4а
2
х +а
+ 2
2
=
= 0,
4;
х = -2,
30
а■ =
а -
х = -V2, а = V2;
х = V2, а = -V2;
16
,
17
80
§ 2. Рациональные алгебраические неравенства
находим точки пересечения прямых х = -а и х = -4а-2 с
окружностью л:2 + а2 = 4 . Искомое множество
представляет собой дуги этой окружности, находящиеся внутри
заштрихованной области-решения (1).
1 л
Ответ. -V2 < а < ; 0 < а < >/2 .
17
Пример 2.22. Найти все значения а, при которых
система неравенств
1х2 + 2х + а < 0,
х2 - 4х - 6а < 0
имеет единственное решение.
Решение. На КП-плоскости хОа решением данной
системы неравенств является пересечение множеств I и П.
Множество I состоит из всех точек плоскости,
расположенных на параболе
= -хг-2х
(1)
§ 2. Рациональные алгебраические неравенства
81
и левее ее, а множество II — из точек, расположенных на
параболе
(2)
и правее ее.
Рис. 2.22
Параболы (1) и (2) пересекаются в точках, для которых
х = 0, а = 0 и х = -- < -1, а = — < 1.
7 49
В вершине А параболы (1)
Точки О к А являются соответственно самой левой и самой
правой точкой полученного множества решений системы
неравенств.
Следовательно, при а < 0 и а > 1 рассматриваемая
система неравенств не имеет решений; при а = 0иае1 —
имеет единственное решение; при 0 < а < 1 — бесконечное
множество решений.
Ответ. а-=0, а = 1.
82
§ 2. Рациональные алгебраические неравенства
Пример 2.23. Найти все действительные значения
параметра а, при которых из неравенства 0 < х < 1 следует
неравенство
Дх,а) = (а2 + а-2)х2-(а + Ъ)х - 2 < 0.
Решение. Требуется найти значения а, при которых
f(xt а) < О при всех х е [0; 1]. Так как
а2 + а -2 = (а + 2)(а - 1),
то исходное неравенство равносильно совокупности
следующих систем:
о,
[а = -2,
а ф-2,
а*1,
[(а-1)*-2]-[(а + 2)* + 1]£0. (*)
где
1
а + 2
— корни квадратного
а-1
трехчлена /(х, а).
Исследуем знак f(x,a) в каждой из «частичных»
областей I и IV. Пусть, например, х = О, а = -1, тогда (*)
выполнено. Пусть х = -3, а = -1, тогда неравенство (*) также
выполнено. Решение (*) есть области II и V.
§ 2. Рациональные алгебраические неравенства
83
Х-ДГ2(Я)
Рис. 2.23
На КП-шюскости хОа решение неравенства f(x, a) <> О
есть множество, состоящее из двух лучей и областей И и
IV, ограниченных ветвями гипербол
х - х^а) и х = х2(а).
Следовательно, это неравенство выполняется для всех
х е [0, 1] при а е [-3, 3].
Ответ. -3 < а < 3.
Пример 2.24. Для каждого значения параметра а
решить неравенство
Решение. Сделаем замену параметра и сведем
неравенство к равносильной ему системе неравенств:
2а = bt
х > О,
84
§ 2. Рациональные алгебраические неравенства
2а = Ь,
На КП-плоскости хОЬ множество всех точек (х, о),
значения координаты и параметра каждой из которых
удовлетворяют полученной системе неравенств, состоит из точек
верхней полуплоскости х > О, расположенных на линии
X
и правее от нее, а также на линии
(1)
(2)
и выше нее, то есть частичная область II, в которой левая
часть последнего неравенства (*) системы принимает
отрицательные значения, с границами этой области (1) и (2),
вдоль которых она обращается в нуль (на рис. область П
заштрихована).
-3
Выражая из (1) и (2) х через параметр &, запишем
уравнения границ области II:
§ 2. Рациональные алгебраические неравенства
85
х > О : х = хх (b) =
О < х <
> 1:
а также аналитические условия, задающие область II при
различных значениях параметра Ь:
b < -2: хг(Ь) <x< x2(b), x > x3(b);
b > -2: х > xt(b).
Возвращаясь к первоначальным значениям параметра а,
получим ответ.
Ответ. Если а £ -1, то а +
х > -а + Va2-1;
"~2
если а > -1, то х > +а + sa + 1.
Пример 2.25. Для каждого натурального значения
параметра а найти все натуральные значения х,
удовлетворяющие системе неравенств
47<22a-2a2,
4a > 7x + 14.
Решение. Система равносильна следующей:
х < -а2 +11а .
х<-а-2.
7
В I четверти КП-плоскости хОа множество всех точек (х, а),
для которых действительные хна удовлетворяют данной
86
§ 2. Рациональные алгебраические неравенства
системе неравенств, представляет собой область ABC,
ограниченную интервалом (АВ) прямой
включая этот интервал, частью (ВС) параболы
и интервал (АС) параметрической оси с концами
.1 11 + 727
а = 3— и а = .
2 2
На рис. это множество заштриховано.
Рис. 2.25
Покроем это множество прямоугольной сеткой с размером
3<а<9, 0 < * < 3,
во внутренних узлах которой а и х натуральные и
принимают следующие значения: ае{4, 5, б, 7, 8}, jcG{1,2}.
§ 2. Рациональные алгебраические неравенства
87
Проверкой убеждаемся, что из десяти внутренних узлов
данной прямоугольной сетки только для трех из них
натуральные значения а и х удовлетворяют исходной системе
неравенств, а следовательно являются искомыми.
Ответ. При а = 6, х = 1; при а = 7, jc = 1hjc = 2.
Пример 2.26. Для каждого целочисленного значения
параметра q найти целочисленные решения неравенства
х2 -
-g| -g<0.
Решение. Рассматриваемое неравенство равносильно
следующей совокупности систем неравенств:
I.
х2 - Ъх + 5 + Зд - Зх - q < О;
х2 - Ъх - 5 + Зх - 3q - q < 0;
\q±x,
На КП-плоскости xOq множество значений (x,g),
удовлетворяющих полученной совокупности систем неравенств,
ограничено двумя параболами и на рис. заштриховано. В
вершинах парабол jc = 1, g = 1 и
11
4, q — —.
Покроем данное множество прямоугольной сеткой с
целочисленными значениями координат хт и параметра qn:
l<jcm<5, l<gn<6, (m= Гб; п= Гб).
Проверяя выполнение условия задачи, находим среди
множества всех точек в узлах сетчатого прямоугольника те
точки, которые принадлежат заштрихованному множеству,
88
§ 2. Рациональные алгебраические неравенства
то есть дают на КП-плоскости целочисленные решения
задачи. (Эти точки в узлах прямоугольника изображены
жирно, а точки, которые не дают решение, — крестиками.)
Рис. 2.26
Ответ. Если q = 1,то х в 1;
если q = 2, то х — 2, х = 3;
если q = 3, то х = 2,х = 3;
если q = 4, то х — 3, х = 4;
если q = 5, то х «= 3, х = 4, х = 5.
Пример 2.27. Найти, при каких значениях а не
существует х, для которого выполнено неравенство
х2 + х-а < 0.
Решение. Искомые значения параметра а находятся
из следующих равносильных высказываний:
К: х2+х-а<0) <=>
<=> (Vx G R : х2 + х - а > О) <^
<=>D(a) - 1 + 4а<0о а <-- .
4
§ 2. Рациональные алгебраические неравенства
89
Тот же результат нетрудно получитт КП-методом (см.
рис. 2.27)
Рис. 2.27
Ответ, а < .
4
Пример 2.28. Найти, при каких значениях параметра а
не существует х < О, для которых справедливо неравенство
ах2-\х\ > 0.
Решение. Искомые значения параметра а находятся
из следующих равносильных высказываний:
н(3*<0: ах2-\х\>
Vx<0: ах2
Va G Е;
х < 0,
: ax2-\x\<0*>
: (ах + 1)х
ах +1 > 0;
< 0 : a < 0.
a < ;
л:
90
§ 2, Рациональные алгебраические неравенства
Рис. 2.28
Ответ. а<0. (См. пример 2.18).
Пример 2.29. Найти все значения р, при каждом из
которых множество решений неравенства
(р-х2)(р + jc-2) < О
не содержит ни одного решения неравенства х2<1.
Решение. Искомые значения параметра р находятся
из следующих равносильных высказываний:
-|(Э*€1-1;Ц: Ф(р,х) = ip-x2)ip + jc-2) < 0} «>
[-l;l]: Ф(р,х) = (р-х2)(р + *-2)>0. (*)
На КП-плоскости хОр выражение Ф(р, jc) с двумя
переменными (р, х) обращается в нуль на параболе р = х2 и
прямой р + jc - 2 = 0, пресекающей параболу и прямую
х = 1 в точке р = 1, я — 1, и прямую х = - 1 в точке
р-8, * = -1.
В каждой из трех «частичных» областей I, II и Ш
полосы -1<х<1 это выражение сохраняет знак (для
установления этого знака достаточно вычислить значение
рассматриваемого выражения в какой-либо точке «частичной»
области).
Так как Ф(р, х) > 0 в I и III областях, то сразу для
VxE[-l; 1] неравенство (*) выполняется, когда либо
р < 0, либо р > 3.
§ 2. Рациональные алгебраические неравенства
91
Рис. 2.29
Ответ, р < 0, либо р > 3.
Пример 2.30. Определить, при каких значениях
параметра а не для всех отрицательных значений х
выполняется неравенство
х2 + \х - а\ - 3 > 0.
Решение. Воспользовавшись правилом логического
отрицания и определением абсолютной величины,
получим для нахождения а следующие равносильные
высказывания:
-л (V х < 0:х2 + \х - а\ - 3 > 0) о
оЗх < 0:х2 + |х-а|-3<0<=>
[ х - а > 0,
<=> Зх < 0 :
I.
П.
х2 + х-а-3<0,
х - а < 0,
Множество точек КП-плоскости, значения координаты
х и параметра а которых удовлетворяют полученной сово-
92
§ 2, Рациональные алгебраические неравенства
купности систем неравенств, представляет собой
объединение двух областей, ограниченных параболами и прямой
х = а. Точки этого множества расположены в нижней
полуплоскости при -3— < а < 3 (рис. 2.30).
4
Рис. 2.30
Ответ. -3— < а <3.
4
Пример 2.31. Найти все значения параметра а, при
которых неравенство
\х2 - 2х + а\ > 5
не имеет решений на отрезке [-1; 2].
Решение. Воспользовавшись логическим отрицанием
высказывания и логической схемой
(2.3)
данную задачу сформулируем следующим образом: найти
все значения параметра а, при которых
§ 2. Рациональные алгебраические неравенства
93
-1 Ых е [-1; 2]: \х2 - 2х + а| > б) <=>
о V* е [-1; 2]: |х2 - 2* + а| < 5 о
<=> V* е [-1; 2]: -х2 + 2х - 5 < а < -д:2 + 2х + 5. (*)
Это значит, что на КП-плоскости jcOa требуется найти все
точки (х;а), значения координаты и параметра каждой из
которых для всех хе[-1; 2] (точек полосы -1 < х <, 2)
удовлетворяют системе неравенств (*) (точки расположены в
заштрихованной области на параболах и между этими
параболами). Этим множеством точек является
прямоугольник (отмечен на рис. двойной штриховкой)
{-1 <; х Z 2; - 4 £ а < 2}.
Рис. 2.31
Ответ. -4
Упражнения
На координатно-параметрической плоскости хОа
изобразить множества точек, значения координаты х и
параметра а каждой из которых удовлетворяют заданным
неравенствам и для каждого значения параметра а решить
относительно х эти неравенства:
94 § 2. Рациональные алгебраические неравенства
Ответ. Если а < О, то х < 2а;
если а > О, то х > 2а.
Указание. Записывая неравенство в виде
дробно-линейного, заменим его равносильной совокупностью двух систем
неравенств:
х-2а
2а
х-2а> О,
а > 0;
х - 2а < О,
а <0.
Можно также применить метод «частичных» областей
(МЧО), рассмотрев четыре частичные области, на которые
КП-плоскость хОа делят прямые х = 2а и а = 0, и
исследовав знак выражения Ф(х, а) в каждой из этих областей.
2. х2 <а2.
Ответ. Если а < О, то а й х <, -а;
если а = 0t то х « О;
если а > О, то -а < х < а .
3. *-|а|<0.
Ответ. Если а < 0, то х < -а;
если а = 0, то х < 0;
если а > 0, то х < а.
4. |х| - а > 0 .
Ответ. Если а < 0, то \/х G Е;
если а = 0, то jc < 0 или л: > 0;
если а > 0, то х < -а или х > а.
5. |а - jc| > 2.
Ответ. Для любых а: л: < а - 2 или х > а + 2 .
6. |а|-Н>1.
Ответ. Если а < 0, то а + 1<я<-а-1;
если а = -1, то х = 0;
§ 2. Рациональные алгебраические неравенства 9J5
если -1 < а < 1, то xG0;
если а = 1, то х = 0;
если а > 1,то 1-а<х<а-1.
Ответ. Если а < -1, то Vx G Е ;
если а =--1, то л: < 0 или х > 0;
если -1<а<0,тох< -1-а или х > 1 + а;
если 0<а< 1, то я < -1 + а или х > 1 - а;
если а = 1, то х < 0 или я > 0;
если а > 1, то Vjc e E .
8. ах + 1 > 0.
Ответ. Если а < 0, то х < —;
а
если а = 0, то Vx G Е;
если а > 0, то х > .
а
9. а(х-1) > х-2.
_ _ Л а-2
Ответ. Если а < 1, то х < ;
а-1
если а = 1, то Vx G Е;
а-2
если а > 1, то х > .
а-1
10. х2 -8ах + 15а2 < 0.
Ответ. Если а < 0, то 5а < х < За;
если а = 0, то х € 0 ;
если а > 0, то За < х < 5а.
Указание. Разложить левую часть неравенства на
линейные множители: (х-3а)(х-5а) < 0.
11. х2 - (а + -)х + 1 > 0, (а * 0).
а
Ответ. Если а < -1, то х < а;
если -1 < а < 0, то х < —;
а
если 0 < а < 1, то х > —;
а
если а > 1, то х > а.
96
§ 2. Рациональные алгебраические неравенства
Указание. Разложить левую часть неравенства на
линейные множители: (х - а)\ х > 0.
V Ч *)
12. ах2 -(а2 +
Ответ. Если а < -1, то а < х < —;
а
если а = -1, тох £ 0;
если -1 < а < 0, то — < х < а ;
а
если а = 0, то х < 0;
если 0 < а < 1, то х > —;
а
если а > 1, то х > а.
Указание. Неравенство равносильно совокупности трех
систем:
а=0,
-оо < л: < 0;
а >0,
X
а <0,
х2 -
-И)
х + 1 > 0;
■ — \х-
13. ах2 < 1.
Ответ. Если а < 0, то Ух G R ;
если а > 0, то —т= < х < —?= .
у/а yja
14. ал: > —.
Ответ. Если а < 0, то х < 0;
если а > 0, то --7=- < х < 0 , jc >
va
§ 2. Рациональные алгебраические неравенства 97
16. пХ <2.
х-а +1
Ответ. Если а<0,тох<а-1, х > — '-;
а-2
2(1-а)
* , jc > а-1;
2
если 0 < а < 1, то х <
а-2
2(1-а)
если 1<а<2;тох< а-1, х > —* '- ;
а-2
если а - 2, то х < 1;
если а > 2, то
^izfls^a-!.
16. а2+х2>4.
а-2
Ответ. Если а < -2, то Ух €R;
если -2 < а < 2, то jc < -V4 - а2 , л: > \l4-a2 ;
если а > 2 , то Vx G 1R .
17. а2 + х2<2(а-|х|).
Ответ. Если а < О, то х G 0;
если а = 0, то х = О;
если 0 < а < 2, то 1 - ^2 - (а -1)2 £ х < -1 + ^2 - (а -1)2 ;
если а = 2, то х = 0;
если а > 2, то х е 0 .
Ответ. Если а < -1, то х G 0; если а = -1, то х > 0 ;
если -1 < а < О, то х > -vl - а2 ; если а > 0, то х > -1.
На КП-плоскости изобразить множества всех точек,
значения координаты х и параметра а каждой из которых
удовлетворяют данным системам, и для каждого параметра
а решить относительно х эти системы:
Ответ. Если а < -3, то х е 0;
44683
98 § 2. Рациональные алгебраические неравенства
если а = -3, то х = — 2;
если -3 <^ а < 0, то -Vl - а 5 # < 1 -t- a ;
если 0 < а < 1, то - Vl - а s*5 Vl - а ;
если а = 1, то jc = 0;
если а > 1, то х е 0 .
|а + jc| + |а - х) < 4,
20.
И * 1.
x> Vo2 -2а + 1.
Ответ. Если а < -1, то х е 0;
если а = -1, то х = 2;
если -1 < а < 1, то 1 - а < х < 2;
если а=1, то 0 < х < 2 ;
если а > 1, то х G 0 .
х2 + а2 > —
21. " 4'
х2 +а2 <4.
Ответ. Если а < -2, то х € 0;
если -2 < а < — , то -л/4 - а < х < V4 - а ;
если —<а<—, то -V4 - а <л: <-J а , J а <
<х < V4-a" ;
< а < 2 , то - V4 - а < х < V4 - а ;
если а > 2 , то х е 0 .
22.
Ответ. Если а < , то х < а;
V2 J2 гг
если < а < — , то х < -VI — а ;
2 2
если а = — , то х =
§ 2. Рационалоныс алгебраические неравенства
99
л
если — < а < 1, то х < -VI - а , VI - а < х < а ;
2
если а > 1, то jc < а.
Ответ. Если а < 1, то х Е 0;
если 1 < а < 2 , то -у]а(2-а) < х < у]а(2-а) ;
если а = 2, то х = 0;
если а > 2, то х е 0 .
24.
jc>0,
а >0.
Ответ. Если а < 0, то х € 0 ;
если а = 0, то х = 2;
если
0 < а < 2, то >А -а2 < jc < 1 + д/2 - (а - I)2 ;
если
если а = 1 + V2 , то jc = 1;
если а > 1 -f v2 , то л: € 0 .
Ответ. Если а < -2, то jc G 0;
если а = -2, то jc = 0;
о
если -2 < а < —, то -2 - а < jc < 2 + а;
~~ 2
о
если — <а<-1, то 1-ьа<дг<-1-а;
Сл
если а = -1, то jc = 0;
если -1 < а < — , то jc e 0 ;
100 § 2. Рациональные алгебраические неравенства
1 3 3
если а = ,то х = , х = —;
2 2 2
если — < а < 0, то -2 - а < х < -1 + а, 1-а<х<2 + а;
если 0 < а < —, то -2 -ь а < jt < -1 - а, 1 + а<х<2-а;
с»
1 3 3
если а = — , то х — —, х = — ;
2 2 2
если — < а < 1, то х е 0 ;
если а = 1, то jc = 0;
если 1 < а < —, то 1-а<^<-1 + а;
2
о
если — < а < 2 , то -2 + а<х<2-а;
если а = 2, то х = 0;
если а > 2, то л: G 0 .
Найти площади фигур, которые изображаются на
КП-плоскости множествами всех точек, значения
координаты х и параметра а каждой из которых удовлетворяют
системам неравенств:
26.
[*2+а2<2.
Ответ. S = 1 + — .
2
2? Г*2 + а2<4*-4а-6,
[х> 1.
Ответ. S = 1 + — .
2
Найти площади фигур, которые изображаются на
КП-плоскости множествами всех точек, значения
координаты х и параметра а каждой из которых удовлетворяют
соотношениям:
§ 2. Рациональные алгебраические неравенства
101
28. х2+а2+б(х-|а|)<0.
Ответ. 5 =
29.
Ответ. S = 15.
30. При каких значениях Р площадь фигуры, заданной
на КП-плоскости хОа условием
\2х + а\ + \х - а + 3| < Р ,
будет равна 24?
Ответ. Р = 6.
Найти наименьшее и наибольшее значения параметра tt
при которых координата х и параметр а каждой из точек
множеств КП-плоскости хОа удовлетворяют смешанным
системам:
х - a = tt
х>0,
а >0,
х + а £ 1,
*тах = 1.
31.
£2.
Ответ. ^ = -
За + х = f,
jc>0,
32. а £ О,
jc + а £ 1,
2х + а < 2.
Ответ. ^ = 1, t
[ж - а = t.
Ответ. <nUn = -l. _
fl^N + |a|s2,
«54. <
[х - 2а = ^.
Ответ. tmln - -4, <mftX = 4.
6.
1.
102 § 2. Рациональные алгебраические неравенства
35. Найти все значения а, при которых неравенство
(х-За)(х-а-3)<0
выполняется при всех значениях ху таких, что 1 < х < 3 .
Ответ. О < а < —.
3
36. Найти все значения параметра а, при каждом из
которых неравенство
х~а <о
х-8а
выполняется для всех х таких, что 2 < х < 4.
Ответ. — < а < 2.
2
37. Для каждого допустимого значения параметра т
6-7т
х
решить неравенство т ~ > 0.
Ответ. Если т<0 или т > 2, то х е -оо; и
I m-2 J
и(-3;+оо);
если 0<т<2,то х е (-со; -3) и ; -н» .
{т-2 )
38. Найти все значения параметра а, при которых
неравенство
о
х + 4х - а
>6
не имеет решений на отрезке [-3; 0].
Ответ. -6 <а <2.
39. Найти все значения параметра а, при каждом из
которых неравенство
х2 + 2|*-а| > а2
справедливо для всех значений х.
Ответ. -1 < а < 1.
§ 2. Рациональные алгебраические неравенства 103
40. Найти все значения параметра а, при каждом из
которых неравенство
2 > \х + а\ + х2
имеет хотя бы одно положительное решение.
Ответ. -2 — < а < 2 .
4
41. Найти все значения параметра а, при каждом из
которых неравенство
3-\х -а\> х2
имеет хотя бы одно отрицательное решение.
13
Ответ. < а < 3 .
4
42. Найти все значения параметра р, при каждом из
которых множество решений неравенства
(Р-х2)(р + х-2)<0
не содержит ни одного решения неравенства х2 < 1 .
Ответ, р < О,р > 3 .
43. Для каждого допустимого значения параметра а
2 о , 1 2
решить неравенство х +2л: + 1> .
а а2
Ответ. Если а < 0 или 0 < а < 2, то Ух eR;
если а = 2, то Vjc е [Щх ^ -l} ;
-а - у/а -2 -а + \la-2
если а > 2, то л: < или л: > .
а а
44. При каких значениях параметра а система
неравенств
[х2 + а2 <4,
ИМ
выполняется для всех х из отрезка V2; V3 ?
Ответ. -1 < а < 1.
104 § 2. Рациональные алгебраические неравенства
45. Найти все а, при каждом из которых существует
хотсЬ бы одно решение х системы
х2 + (5а + 2) х + 4а2 + 2а < 0,
х2 + а2 = 4.
Ответ. -у/2<а< , 0 < а < S .
17
Указание. Записать неравенство смешанной системы в
виде
(л: + 4а + 2)(л: + а) < 0
и применить КП-метод.
46. Найти все значения параметра а, при которых
неравенство
(а-1)х + 2а + 1 >0
выполняется при всех значениях х, удовлетворяющих
условию
2
Ответ. — < a < 4.
5
47. Найти все значения параметра а, при которых
любое значение xt удовлетворяющее неравенству
ax2+(l-a2)x-a >0,
по модулю не превосходит двух.
Ответ. -2 < a < —.
" "~ 2
Указание. Если а ^ 0, то данное неравенство
равносильно следующему:
\(х-а)\ х + —1>0.
V а)
§ 2. Рациональные алгебраические неравенства 1Q5
48. Найти все значения параметра а, при которых для
всех х, по модулю не превосходящих единицу, выполняется
неравенство
^0
а2-ах-1
-1-л/б
Ответ, а < , а > 2.
49. Изобразить на КП-плоскости множество всех точек,
значения координаты х и параметра а каждой из которых
удовлетворяют неравенству
Ы > max х, х2, — .
11 I 2)
50. Для каждого вещественного числа а решить
неравенство
х2-а2
Ответ. Если а ^ 0 , то х < - \а\ или х > \а\;
если а =» 0, то х — любое действительное число, кроме
х = 0 и х = 1.
Указание. Так как при Va ^ 0 : х2 - 2х + 2'а' > 0 , то
рассматриваемое неравенство равносильно совокупности
двух систем:
61. Найти все действительные числа а, при которых
неравенство
7a2+a-2 „
х + < 7 а -1
х + а + 1
не имеет положительных решений х.
Ответ. -1 < а < — .
106
§ 2. Рациональные алгебраические неравенства
Указание. Задача равносильна следующей: ♦ Найти а,
при которых для Vx > 0 выполнено неравенство
х +
> 1а - 1
х + а + 1
52. Найти все значения параметра Ьу при каждом из
которых число целочисленных решений неравенства
х2 +3* + 3|л: + Ы-Ь <0
максимально.
Ответ. b = 4 , -<b <-.
4 2
53. Для каждого значения параметра а решить
неравенство
< х.
Ответ. Если а < -1, то о + v« + 1 < л: < -а - va - 1 ,
если а > — 1, то х > а
§ 3. Иррациональные уравнения
и неравенства с параметрами
Пример 3.1. Найти все значения а, при каждом из
которых корни уравнения
yjx + 3- Wx-1 + V* + 8 - 6V*-1 =
существуют и принадлежат отрезку [2; 17].
Решение. Применяя метод подстановки
выделяя полный квадрат и воспользовавшись формулой
If2(t) =
(3.1)
заменим задачу равносильной задачей о нахождении
параметра а, при каждом из которых корни уравнения
\t-2\ + |t-3| = a (1)
существуют и принадлежат отрезку [1; 4] (если л;е[2; 17],
то у/х-1 = te [1; 4], и наоборот, если >Jx -\ = * е [1; 4], то
; 17]).
Уравнение (1) по определению абсолютной величины
равносильно совокупности систем:
(2)
!<
5-
2<
а =
3<
2t-
t <
2t =
t <
1;
t<
2,1
=«;
3,
4,
«(3)
i/а КП-плоскости aOt с вертикальной параметрической
осью О а множество всех точек (t; а), значение координаты
108
§ 3. Иррациональные уравнения и неравенства
t и параметра а каждой из которых удовлетворяет
уравнению (1) при te[l; 4], представляет собой график функции
а = |* - 2| + \t - 3|, заданной на отрезке [1; 4] (см. рис. 3.1а).
Следовательно, искомые значения параметра 1 < а < 3.
На рис. 3.10 дана интерпретация решения задачи на
КП-плоскости Юа с горизонтальной параметрической
осью Оа.
3 4 5 а
б
Рис. 3.1
Ответ. 1 < а < 3.
Пример 3.2. Для каждого значения параметра а решить
уравнение
= а.
§ 3. Иррациональные уравнения и неравенства
109
Решение. По определению квадратного
арифметического корня имеем
= а<=>
a* 0,
(3.2)
Ча координатно-параметрической плоскости хОа решением
исходного рационального уравнения является множество
точек этой плоскости, расположенных на части параболы
находящиеся в правой полуплоскости
а £ 0.
Ответ. Если a < 0, то х е 0;
если а £ 0, то х = а2.
Пример 3.3. Решить уравнение
-v/jc + х = а.
Решение. Применим рационализирующую
подстановку:
-- х = а
О,
/1 + 4а -1
a > 0.
по
§ 3. Иррациональные уравнения и неравенства
На координатно-параметрической плоскости Юа жирной
линией изображена часть верхней ветви параболы
а = t + t2,
расположенная в верхней полуплоскости
/1
Рис. 3.3
Ответ. Если а > 0, то х =
/1 + 4а - 1
если а < О, то х е 0.
Пример 3.4. При каких а уравнение
имеет решение?
Решение. Применяя рационализирующую
подстановку, получим
i \у]х-1 =t>0,
§ 3. Иррациональные уравнения и неравенства
111
На координатно-параметрической плоскости ЮЬ жирной
линией изображено решение смешанной системы
Рис. 3.4
Исходное уравнение имеет решение при
1 3
6 = 1 + а < - <=> а < —.
4 4
2
Ответ. При а < — .
4
Пример 3.5. Найти все значения параметра а, при
которых уравнение
имеет решение, принадлежащее промежутку [0; 1].
Решение. Применяя логическую схему алгоритма
решения типового иррационального уравнения (В. 14),
заменим данное уравнение равносильной ему смешанной
системой
*>0,
x + a = *2,~ \a = x(x-l).
112
§ 3, Иррациональные уравнения и неравенства
На КП-плоскости хОа множество точек (х; а), значения
координаты и параметры каждой из которых удовлетворяю?
рассматриваемой смешанной системе, состоит из точек,
расположенных в верхней полуплоскости (включая
параметрическую ось х = 0) и на параболе а
хг-х.
2--
Рис. 3.5
Искомые значения параметра а ищутся из условия
нахождения части этой параболы (с вершиной в точке х = —,
2
а = —) в полосе 0 < х £ 1 (на рис. эта полоса заштрихо-
4
вана).
Ответ. — < а < 0.
4
Замечание. На координатной плоскости хОу данная
задача равносильна задаче нахождения значений параметра,
при которых на множестве 0 < х й 1 каждая кривая одно-
параметрического семейства у = л]х + а пересекается с
прямой у = х.
Пример 3.6. При каких а уравнение
>Jx + 2a2 • [х2 - (а - 1)х - а] = О
имеет только два различных корня?
§ 3. Иррациональные уравнения и неравенства
113
Решение. Заменим уравнение равносильным:
х + 2а2 = 0;
/х + 2а2 (х-а)(* + 1) = 0 w , _
]х>-2а2;
х > -2а2.
Решим совокупность КП-методом.
Ответ, а = -1; --т=- £ а < —; 0 < а £ -т=*.
у/2 2 &
Пример 3.7. Для каждого действительного
положительного а найти все действительные корни уравнения
х = х.
Решение. Так как функция
f(x) = >/а + х (а > 0)
строго монотонная, то
/[/(*)] = х <=> f(x) = х,
114
§ 3. Иррациональные уравнения и неравенства
т.е. исходное уравнение равносильно уравнению
yja + х = х.
Рис. 3.7
Воспользовавшись логической схемой решения
иррационального уравнения (см. Введение, В. 14), получим
{* > 0, а > О f х > 0, а > О
а + х = х2 [а = х2 - х.
Решением полученной смешанной системы на КП-плоскос-
ти является верхняя часть параболы
а = х2-х,
расположенная в области х > О, а > 0, то есть jtje
1 + V4a +1
Ответ, х
Пример 3.8. Для каждого значения параметра а * 0
решить уравнение
§ 3. Иррациональные уравнения и неравенства
115
Решение. Заменим данное уравнение равносильными
уравнениями и смешанной системой, применяя схему (В. 14):
(х + у1х2 -а )3(х + yjx2 -а )(х ->1х2 -а ) = а <=>
j ]2
(х + yjx2 - a f-a = а <=> (jc + yjx* - a )3 = 1
> (x + V*2 -a )3-l3 = 0 <=> (л:-1 + 7л:2 -a )x
х[(л: + л/л:2 -a )2 4- (jc + л/л:2 -a ) + 1] = 0,
= л: + 7л:2 -a : / + у + 1 > 0)
f 1 - x > 0,
— а
На КП-плоскости хОа решением полученной смешанной
системы является множество всех точек прямой
расположенных в полуплоскости
X < 1,
I
§ 3, Иррациональные уравнения и неравенства
при всех значениях параметра
О * а < 1,
то есть луч без точки х = —, а = О с началом в точке х = 1,
а- 1.
Ответ. Если 0*а<1, тодг= ,
2
если а > 1, то х е 0.
Замечание. Можно применить рационализирующую
подстановку Эйлера t = х + V*2 -а ([3], с.103; «Математика
в школе», 1970, № 6, с. 32-35).
Пример 3.9. Найти все значения параметра р, при
которых уравнение
_ 9 =
имеет единственное решение.
Решение. Воспользовавшись логической схемой
(В. 14), заменим данное уравнение равносильной смешанной
системой:
)х + 2 = х-2
(х - 2 Z О,
<=>
2
jc + — = -2р = а.
На КП-плоскости хОа решение смешанной системы
представляет собой график функции
X
на множестве х £ 2 (изображен жирной линией).
§ 3. Иррациональные уравнения и неравенства
117
Следовательно, исходное уравнение имеет единственное
о
решение при а > 3, то есть при р < —.
Х i i
5 а
Рис. 3.9
Ответ, р <> —.
Пример 3.10. Найти все значения параметра а, при
которых уравнение
yfax - х + 1
имеет решение.
Решение. Применяя логическую схему (В. 14) замены
типового иррационального уравнения равносильной ему
смешанной системой, получим
(х +1 > 0,
[
х > -1,
а = 2 + * + —.
х
118
§ 3. Иррациональные уравнения и неравенства
Изображая на КП-плоскости хОа множество точек (х; а),
значения координаты и параметра каждой из которйгё
удовлетворяют последней смешанной системе, получаем
ответ на поставленную задачу.
х, i
Рис. ЗЛО
Ответ, а < О, а > 4.
Пример 3.11. Для каждого значения параметра а
решить неравенство
Решение. Заменим данное неравенство равносильной
ему совокупностью систем:
а - 1 < О,
а -1 > О,
и изобразим на координатно-параметрической плоскости
хОа множество точек, значения координат и параметров
которых удовлетворяют этой совокупности.
§ 3. Иррациональные уравнения и неравенства
Ц9
Ответ. Если а < 1, то х > 0;
если а > 1, то х = 0.
Пример 3.12. Для каждого значения параметра а
решить неравенство
(х2 - (а + 2)х - 2а2 + 4а) Vl-* < 0.
Рис. 3.12
120 § 3. Иррациональные уравнения и неравенства
Решение. Разложив квадратный трехчлен на
множители, заменим неравенство равносильным:
(х - (2 - а))(х - 2а) Vl-x <> 0.
На множестве х < 1 КП-плоскости хОа множители,
стоящие в левой части неравенства, обращаются в нуль
соответственно вдоль луча х = 2-а с началом в точке х = 1, а = 1,
вдоль луча х = 2а с началом в точке х = 1, а = — и вдоль
прямой х = 1, а между ними сохраняют знак.
В заштрихованных областях (без границ) левая часть
неравенства принимает отрицательные значения, то есть
выполняется строгое неравенство.
Ответ. Если а < —, то 2а ^ х ^ 1;
если — < а < 1, то х = 1;
если а > 1, то 2 - а < jc < 1.
Пример 3.13. Найти все значения а, при которых
каждое решение неравенства
х2 + а <; 0 (1)
удовлетворяет неравенству
(2х + a)y/3-x <0. (2)
Решение. На КП-плоскости хОа множество I
решений неравенства (1) состоит из точек, расположенных на
параболе а = -х2 и левее от нее.
Заменим неравенство (2) равносильной совокупностью
систем
2х + а < 0, |3 - х = О,
3 - jc > 0 И[аеЕ.
Следовательно, на КП-плоскости множество II решений не-
d
равенства (2) состоит из точек прямой х = 3, луча х = — с
2
началом на этой прямой и области, ограниченной этими
§ 3. Иррациональные уравнения и неравенства
121
прямой и лучом. (На рис. эта область множества II
решений неравенства (2) заштрихована.)
Рис. 3.13
Парабола а = -х2 пересекает прямую х = 3 в точке х = 3,
а = -9, а луч — в точках х — 09 а а 0 и х = 2, а = -4.
Каждая точка (х;а) множества I принадлежит
множеству II при значениях параметра -9 ^ а ^ -4 и а = 0.
О т в е т. -9 £ а < -4, а = 0.
Пример 3.14. Для каждого значения параметра а
решить неравенство
> х.
Решение. Возводя на множестве х>0 обе части
неравенства в квадрат, заменим его соответственно
равносильным иррациональным неравенством и равносильной
совокупностью рациональных неравенств (В. 16):
а + \х\ > 0;
I.
П.
х<а;
а > х2 - х.
122
§ 3. Иррациональные уравнения и неравенства
На КП-плоскости хОа множество точек (х; а), значения
координаты и параметра каждой из которых удовлетворяют
последней совокупности систем неравенств, представляет
собой объединение множества точек I, расположенных в
нижней полуплоскости х < О на прямой х = а и ниже этой
прямой, и множества точек II, расположенных в верхней
полуплоскости х > О (включая параметрическую ось х = 0)
на параболе а = х2-х и правее от нее. (На рис. эти
множества заштрихованы.)
Уравнение нижней ветви параболы
а верхней — х = х2 (а) = ■
Запишем ответ, сопоставляя каждому значению
параметра а координату х соответствующих точек множества
решений исходного неравенства:
а < --: х < а;
4
а = — : х = —,
4 2
§ 3. Иррациональные уравнения и неравенства
123
-- < а < 0: х < а, хг(а) <х< хг(а);
4
а = 0: х < 1;
а > 0: х < х2(а).
Ответ. Если а< , то х < а;
4
1 Л 1 - Vl + 4а 1 + Vl + 4а
если — <а<0, то х < а и < х <
4 2 2
если а > 0, то х <
1 + VI + 4а
Пример 3.15. Пусть f(x) = у]х2 - 2х + 1 - 1,
** >fx - а, а — параметр. Решить относительно х
неравенство f(g{x)) < 0.
Решение. Так как у/х2 - 2х + 1 = |* - 1|, то
f(g(x)) = \>/х~ -а- 1|- 1.
Следовательно, необходимо решить неравенство
\yfx - а - 1|-1 < 0 <=> -1<7х-а-1
<=>а
2.
Решим каждое неравенство полученной системы неравенств
и изобразим на координатно-параметрической плоскости
хОа множества их решений.
I. yfx > a
И. у/х < а + 2
а <0,
а >0,
д:>а2,
Га + 2 > О,
(0 < х < (а + 2)2 .
124
§ 3, Иррациональные уравнения и неравенства
Множество решений первого неравенства состоит из точек
КП-плоскости, расположенных в верхней полуплоскости
х £ О левее ветви параболы х = а2, а множество решений
второго неравенства — правее ветви параболы х = (а + 2)а.
Искомое решение есть пересечение этих множеств.
Ответ. Если а < -2, то х е 0;
если -2 < а < О, то 0 <, х <> (а + 2)2;
если 0 <> а < + оо, то а2 < х <> (а + 2)2.
Пример 3.16. Для каждого значения параметра а
решить неравенство sx2 -а < 1 — дг.
Решение. Применяя логическую схему (В. 15), сведём
решение данного неравенства к решению равносильной
системы рациональных неравенств:
1 - х > О,
х2 - а > О,
х2-а<(1-х)2
а <х2,
1 + а
х <
(1)
(2)
(3)
На КП-плоскости хОа решение полученной системы
неравенств (1)-(3) есть множество точек (х, а), расположенных
одновременно ниже прямой х = 1 и на ней (1), на параболе
а = х2 и левее её (2) и, наконец, ниже прямой х = (3).
§ 3. Иррациональные уравнения и неравенства
125
Рис. 3.16
Прямая х = касается параболы а = х2 в точке с
координатой и значением параметра, определяемого условием
1 + а
х =
1 + 2
*~ 2 '
Уравнения верхней и нижней ветвей параболы а = х2
имеют вид х = Va и х = -у/а .
На рис. множество решений заштриховано.
1 + а
Ответ. Если а < 0, то
если 0 < а < 1, то
хй-у/а , Va ^^< ; если а > 1, то х ^ - у/а .
Пример 3.17. Для каждого значения параметра а
решить неравенство
а - 2
126
§ 3. Иррациональные уравнения и неравенства
Решение. Неравенство равносильно совокупности
систем
fa > 1,
Jx + 1 > = Ь;
1
I 7
\1х + 1
а-1
а~2
а-1
В силу логической схемы (В. 16) неравенство
1х + 1 > Ь <=>
* -1;
х>Ь2-1.
Применяя логическую схему решения типового
иррационального неравенства (В. 15), получим
Jx + 1 < Ь <=>
<Ъ2.
На КП-плоскости множество решений этого неравенства
заштриховано.
Условие
fo<l,
\a-2
{а-1
выполнено, когда а < 1. Условие
= Ь>0
[e>l,
|g-2
= Ь <0
выполнено, когда 1 < а < 2, а условие
§ 3. Иррациональные уравнения и неравенства
127
\а >1,
|а-2
[а-1
= Ь>0
— при а > 2.
хк
Рис. 3.17
Ответ. Если а < 1, то -1 < х <
если 1 < а < 2, то х > -1;
если а > 2, то х >
Пример 3.18. При каждом значении параметра а найти
все решения неравенства
+ 4а > 0.
Решение. Применяя логическую схему (В. 15), сведем
решение данного неравенства к решению системы
рациональных неравенств:
: х + 2а <=>
х + 2а > 0,
Зах + 4а2 > 0,
<=> ,
■('♦тЬ
х(х + а)
128
§ 3. Иррациональные уравнения и неравенства
Рис. 3.18
На КП-плоскости решение полученной системы неравенств
представляет собой множество, состоящее при а = 0 из луча
х > О, а при а > О — из всех точек I четверти без точек па-
4
раметрической оси х = 0, а также точек угла — а £ х £ -а
3
без его стороны х = -а. На рис. 3.18 это множество
заштриховано.
Ответ. Если а < 0, то хе0;
если а «= 0, то х > 0;
4
если а>0,то — а£х<-аих>0.
3
Пример 3.19. Для каждого значения параметра а
решить неравенство
Решение. Применяя логическую схему (В.16)
решения типового иррационального неравенства, получим
§ 3. Иррациональные уравнения и неравенства
129
{а + 1 < О,
П.
а < -1,
(а-х)(а + х)>0;
а > -1,
На КП-плоскости хОа решением системы I есть область I,
ограниченная отрезком прямой с концами, имеющими
координаты jc^-Ihjc^I.h полупрямыми х = -а и х = а.
Решением системы II является прямая И, ограничен-
ыая указанным выше отрезком прямой а= -1 и частью
параболы
проходящей через концы этого отрезка и имеющей
вершину с координатой х = 0 и значением параметра а = —.
2
Уравнение верхней ветви параболы
х = х{(а) = у]-(2а +1) ,
S-3683
130
§ 3. Иррациональные уравнения и неравенства
а нижней —
Решением исходного неравенства является объединение
областей I и II (на рис. 3.19 заштриховано).
Ответ. Если а < -1, то а < х < -а;
если -1 < а <- —, то ~J-(
если а = - —, то х = 0;
х < yj-
если а > —, то решений нет.
Замечание. Данная задача может быть решена также
/а2 - х2 при а ф 0 оп-
методом координат: уравнение у
ределяет на координатной плоскости однопараметрическое
семейство полуокружностей радиуса \а\ с центром в начале
координат, расположенных в верхней полуплоскости, а
уравнение у = а + \ — семейство прямых, параллельных
оси Ох,
Пример 3.20. Решить неравенство
ах > х.
Решение. Заменим иррациональное неравенство
совокупностью иррациональных уравнения и неравенства, а
затем — равносильной совокупностью смешанных
рациональных систем и систем рациональных неравенств (В. 14),
(В.16):
\ах — х
lax2 > х
х>0,
ах2 = х2;
х <0,
ах2 > 0;
л:>0,
ах2 > х2;
(I)
(и)
(III)
(IV)
х = 0,
а€ К;
х>0,
о = 1;
х<0,
а >0;
§ 3. Иррациональные уравнения и неравенства
131
Изобразим полученные множества на КП-плоскости хОа.
Рис. 3.20
Ответ. Если а < 0, то х = 0;
если 0 £ а < 1, то х < 0;
если а > 1, то Vx € К .
Пример 3.21. При каждом значении параметра а
решить неравенство
Решение. Применяя рационализирующую подстанов-
ку, заменим задачу равносильной
л/2а = b > 0,
-/2а =Ь>0,
На КП-плоскости уОЬ множество точек, значение
координаты и параметра которых удовлетворяют неравенствам
системы, заштриховано.
5*
132 § 3. Иррациональные уравнения и неравенства
У
Записывая решение в новых переменных и возвращаясь
к старым, получим ответ.
Ответ. Если b < О, то у е 0, то есть если а < О, то
х е 0;
если 0 < b < —, то b < у < 1-6, то есть если О < а < — ,
2 8
то 0 < х < 1-2л/2а ;
если b = —, то у е 0, то есть если а = — , то х е 0;
2 8
если — <Ь<1,то1-6<1/<6, то есть если — < а < —,
2 8 2
то 1-2л/2а < л: < 0;
если 6 > 1, то 0 < у < 6, то есть если а > —, то
-2а < х < 0.
Пример 3.22. Для каждого значения параметра а
решить неравенство
Jx + х < а - х.
Решение. Применяя логическую схему решения ти-
пового иррационального неравенства, сведем данное
неравенство к равносильной ему системе рациональных
алгебраических неравенств:
§ 3. Иррациональные уравнения и неравенства 133
п - X > О,
х2 + х £ О, о
х2 + х <, (а - х)
х < а,
2а)х<а2
а<~\'
х <а,
х(х + 1)>0,
х > х(а)
|*<-1
а>--,
х < а,
<х(а),
где
2а
Рис. 3.22
Множество точек КП-плоскости хОа, значения
координаты и параметра каждой из которых удовлетворяют
134
§ 3. Иррациональные уравнения и неравенства
данной совокупности систем неравенств, на рис.
заштриховано.
Ответ. Если а < -1, то х е 0;
1 а2
если -1 < а < - —, то < х < -1;
2 1 + 2а
если — < а < 0, то л: < -1;
2
„2
если а > 0, то х < -1, 0 < х <
2а
Пример 3.23. Определить, при каких значениях а
решения неравенства
образует на числовой прямой отрезок длины 2|а|.
Решение. Применяя логическую схему решения
данного типового иррационального неравенства, заменим его
равносильной совокупностью систем рациональных
неравенств:
I.
II.
х + а > 0;
х>0,
х + а> х2;
<=>
2 ^ ' 2
На КП-плоскости хОа заштриховано множество точек
(х; а), значения координаты и параметра каждой из
которых удовлетворяют рассматриваемой совокупности систем
неравенств I и II.
f 3. Иррациональные уравнения и неравенства 135
-3
Рис. 3.23
Искомые значения параметра а должны удовлетворять
совокупности следующих условий:
1
х2(а)-х1(а) = -2а;<^
а >0,
х2 (а) + а = 2а;
,-!,.
|~7<а<0,
4
= -2а;
<=>
|а>0,
[yjl + 4а = 2а -1;
а >0,
2а -1 > О,
1 + 4а = (2а -1)2;
Ответ, а = (1-л/2)/2; а = 2.
а =
а = 2.
136
§ 3. Иррациональные уравнения и неравенства
Пример 3.24. Для каждого значения параметра а
решить систему неравенств
а + \х\ - 4 < 0.
(1)
(2)
(3)
Решение. На КП-плоскости хОа множество точек
(х;а), значения координаты х и параметра а каждой из
которых удовлетворяют системе неравенств, состоит из всех
точек полосы -1 < х < 1 (с границами х = -1 и х = 1),
расположенных правее полуокружности а =» yjl — х2, включая
ее, и левее ломаной линии а — 4 - |jc|, включая ее. (На
рисунке это множество точек заштриховано.)
-1
Уравнение верхней части полуокружности а = \1 — х
имеет вид
О <а <> 1;
О £ а £ 1,
уравнения звеньев ломаной: л: = 4-а, дс = а - 4, 3^а<4.
Ответ. Если а < 0, то х е 0;
если а в 0, то х я -1 и х = 1;
§ 3. Иррациональные уравнения и неравенства
137
если 1 < а < 3,то -1 <> х < 1;
если 3<а<4, то а - 4 < х < 4 - а;
если а = 4, то х = 0;
если а > 4; то jc e 0.
Пример 3.25. Найти все значения параметра а, при
каждом из которых среди решений неравенства
+ а > х
есть ровно два различных целочисленных решения.
Решение. Применяя логическую схему (В. 16)
решения иррационального типового неравенства, получим
• -а <=>
I.
Множество всех точек (х,а) КП-плоскости хОа, для
которых значения х и а удовлетворяют полученной
совокупности систем, на рис. заштриховано.
Системе I удовлетворяют значения х и а для точек,
расположенных при -1 < а < 0 ниже прямой х =» а, но выше
нижней ветви параболы a = -х2 и на ней, а при
О < а < оо — ниже прямой х = а и правее параболы а = х2 и
на ней.
Системе II удовлетворяют значения х и а для точек,
расположенных на прямой х = а и выше ее и при a < 0 ниже
параметрической оси х = 0, левее кубической параболы
a =»
а при 0 < а < 1 — правее этой параболы.
138
§ 3. Иррациональные уравнения и неравенства
Рис. 3.25
Следовательно:
при -5 < а й -1 неравенство имеет одно целочисленное
решение х = -1;
при -15 < а < -5 — два: х = -1 и х = -2;
при а < -15 — три и более решений: х = -1, jc = -2,
х = -3 и т.д.;
при 0 < а < 1 неравенство имеет одно целочисленное
решение х = 0;
при а = 1 — два решения х = 0их = -1;
при а > 1 — три и более решений.
Ответ. -15 й а < -5, а = 1.
Упражнения
1. На координатно-параметрическои плоскости аОх с
вертикальной параметрической осью построить множество
всех точек (jc; а), значения координаты х и параметра а
каждой из которых удовлетворяют следующим
соотношениям:
а) а = \l2x-x2; б) а = V*2 - 2* .
2. Для каждого значения параметра а определить число
решений уравнения
V2R7
а.
Ответ. Если а < 0, то решений нет;
если а = 0, то три решения;
§ 3. Иррациональные уравнения и неравенства
139
если 0 < а < 1, то четыре решения;
если а = 1, то два решения;
если а > 1, то решений нет.
3. Найти все значения параметра а, при каждом из
которых уравнение
х-2 у1х-2-2 = а
имеет единственное решение.
Ответ, а = -1, а > 0.
Указание. Исследовать равносильную смешанную
систему
Ux-2 =t>0,
\t2-2t = a.
4. Для каждого значения параметра а решить уравнение
x-Ja-x2 =1.
Ответ. Если а < 1, то х е 0;
если а > 1, то х = .
Указание. Заменить уравнение равносильной
смешанной системой (В. 14):
I а - х2 = (х -1)2, \2х2 - 2х + 1 = а,
U
\ja- х = х-1 <=>
5. Для каждого значения параметра а решить уравнение
yJ2x + а - >Jx - 1 = 2.
Ответ. Если а < 2, то х = 11 - а + 4>/б- а ;
если 2<а<6, то*=11-а± 4>/б- а ;
если а = 6, то л: = 5;
если а > 6, то л: 6 0.
140 § 3. Иррациональные уравнения и неравенства
Указание. Заменить рассматриваемое уравнение
равносильной ему смешанной системой
IV*-1 = t > 0,
|а = 6-(*-2)2
6. Найти все значения параметра а, при которых
уравнение
Vl + х2 = а-х
имеет решения.
Ответ, а > 0.
Указание. Исследовать равносильную смешанную
систему
[а - х > О [х < а.
7. Для каждого значения параметра а решить уравнение
у]х2 - 1 = а-х.
Ответ. Если а < -1, то х е 0;
если -1 < а < 0, то х = — I а + — ;
2 V а)
если 0<а<1, тох€0;
если а > 1, то * = —I а + — I.
Указание. Заменить уравнение равносильной ему
смешанной системой
Ix2-l = (a-x)\ ^ f2ax = a2 + l.
[a - jc > 0 (л: < a.
8. Найти все значения параметра Ь, при которых
уравнение
= jc-2
имеет единственное решение.
О т в е т. Ь > 3/4 .
§ 3. Иррациональные уравнения и неравенства
141
Указание. Сделав замену параметра, исследовать систему
2(6-1) = а,
[2(6-1) = а,
lax +1 = х - 2
ах
х-2>0
2(6-1) = а,
КП-методом. Тот же результат можно получить, если
воспользоваться тем, что уравнение f(x) я 0 имеет
единственное решение на множестве х £ 2 при условии /(2) < 0 <=>
1 3
о а > — <=>Ь > — .
2 4
9. Найти действительные корни уравнения
ху/х + V*3 -2 = /п,
где m — положительный параметр.
Ответ. Если 0 < т < V2 , то х е 0;
если m
;> V2,
ТО JC
2т
Указание. Исследовать равносильную систему при т > 0:
о/х :
m-t
= m2 ■»- 2,
142 § 3. Иррациональные уравнения и неравенства
На КП-плоскости Ют множество всех точек, значения
координаты t и параметра т > О каждой из которых
удовлетворяют последней смешанной системе, представляет собой
т 1
часть графика функции t = 1 , расположенную в по-
2 т
луплоскости t < т.
Для каждого значения параметра а решить уравнения.
10.
у1х - а = у/2х - 1 + а .
Ответ. Если а < —, то * = 1 - 2а; если а > —, то х е 0.
3 3
Указание. Воспользовавшись логической схемой:
(3.3)
заменить данное уравнение равносильной ему смешанной
системой:
х-а = 2х-\ + а > 0.
На КП-плоскости хОа множество всех точек, значения
координаты и параметра каждой из которых удовлетворяют
этой системе, представляет собой луч, находящийся в по-
11
луплоскости х > а, с началом в точке х = —, а = —, на-
3 3
правленный вдоль прямой
х = 1 - 2а.
\2
ТО X
fl + xY 1 + х
Ответ. Если а < -— ,
4
1 f / I / ^\2
= - Va2 - 1 - a ± V2a2 - 2aVa2 -1-5
4V У
если а = — ,тох=1;
4
если а > — , то х е 0.
4
§ 3. Иррациональные уравнения и неравенства
143
Указание. Заменить уравнение равносильной системой
г = t> 2,
и использовать КП-плоскость tOb.
12.
-х2- a\
Ответ. Если а < 0, то х е 0;
если а = О, то л: = 0;
л/б-1 /-
если 0 < а < , то х = ± Vа ;
л/5-1
если а > , то х е 0.
Указание. Заменить уравнение равносильной
смешанной системой
U2 = х\
\х2 + аг<1.
13. Найти значение параметра а, при каждом из
которых уравнение
- jc +jc + — = 0
имеет решение.
Ответ,-— < а < 0.
20
Указание. Заменить уравнение системой
5а = Ь7
-*-— = *<!,<=>
5а = 6,
-*- — = * < 1, о
4
y/b + t = t
-X - — = f < 1,
4
144 § 3. Иррациональные уравнения и неравенства
Да КП-плоскости ЮЬ множество всех точек, значение ко-
эрдинаты t и параметра Ь каждой из которых
удовлетворяют смешанной системе, представляет собой часть пара-
Золы Ь = t2-t, находящуюся внутри полосы 0 < t <, 1 при
-- < Ъ < 0 о < а < 0.
4 20
14. Изобразить на координатно-параметрической
плоскости хОа фигуру, образованную множеством точек,
значения координаты х и параметра а каждой из которых
удовлетворяют двойному неравенству
vi найти ее площадь.
Ответ. S = ---.
4 2
15. На КП-плоскости хОа найти площадь фигуры,
заданной условиями
Ответ. S = 2/г+ 7.
16. На КП-плоскости хОа изобразить множество точек,
значения координаты х и параметра а каждой из которых
удовлетворяют неравенству
и при каждом значении параметра а решить это
неравенство.
Ответ. Если а < — , то х е 0;
4
1
если а = - — , то
4
§ 3. Иррациональные уравнения и неравенства
145
Указание. Заменить неравенство совокупностью систем
рациональных неравенств:
II:
х + а >х2;
х <0,
х + а > 0;
х <0,
х>-а.
17, Для каждого значения параметра а решить неравен-
Ответ. Если а < О, то х <
если 0<а<1,тох<- Va , va < х < ;
если a £ 1, то х £ -\fa .
Указание. Заменить иррациональное неравенство
системой рациональных неравенств:
1 - х > О,
х2 - а £ 0, <:
18. Найти все значения параметра а, при каждом из
которых неравенство
V2jc + а > х
имеет хотя бы одно неотрицательное решение х.
Ответ, a > 1.
Указание. Заменить иррациональное неравенство
равносильной совокупностью систем рациональных неравенств:
*<о,
[2* + a > 0;
(х>0,
2д:
>х2.
146
§ 3. Иррациональные уравнения и неравенства
19. Определите, при каких значениях параметра а
решения неравенства
образуют на числовой прямой отрезок длины 3|а|.
2
Ответ, а = —; а = -6.
9
20. Для каждого значения параметра а найти решения
неравенства
Ответ. Если а < -1, то х е 0;
если -1 < а < —, то < х < -1;
2 1 -f 2а
если — < а < 0, то л: < -1;
„2
если а > 0, то х < -1, 0 < х <
2а
21. Найти все значения а, при которых каждое решение
неравенства
х2 - а < О
удовлетворяет неравенству
(а - 3*)V* + 5 > 0.
Ответ, а = 0; 9 < а < 25.
Указание. Воспользоваться логической схемой
(1)
(2)
/~>0<=>
Г(/5К
и>
['=
Li/-
0,
0;
0,
существует
(3.4)
и заменить неравенство (2) равносильной ему
совокупностью систем
§ 3. Иррациональные уравнения и неравенства
147
а - Зх > О,
х + 5 > О;
х = 5 = О,
-оо < а < +оо.
22. Для каждого действительного значения параметра а
решить неравенство
(-х2 + (2а - 6)х + За2 4- 18а) v* +4 > 0.
Ответ. Если -оо < а < -2, то -4 < х <, - а - 6;
4
если -2 < а < — ,тодг = -4;
3
4
если -— < а < + оо, то -4 < л: < За.
3
Указание. Заменить неравенство равносильным
(х - За)(х + а + 6)V* + 4 ^ 0.
23. При каждом значении параметра а найти все
решения неравенства
х + 2а - 2у1зах + а2 > 0.
Ответ. Если а < 0, то х е 0;
если а = 0, то х > 0;
если а > 0, то -— < л: < 0, 8а < х < + оо.
3
Указание. Заменить данное иррациональное
неравенство равносильной ему системой рациональных:
/о 2 * + ^а
V3ajc + а <
2
24. Пусть f(x) = ylx2 -4л:+ 4-3, g(x) = Vjc - а, а —
параметр.
Решить относительно х неравенство f(g(x)) ^ 0.
148 § 3. Иррациональные уравнения и неравенства
Ответ. Бели а < —5, то х е 0;
если -5 < а < 1, то 0 £ х <> (а + 5)2;
если а > 1, то (а - I)2 <> х ^ (а + 5)2.
25. Для каждого значения параметра b < 0 решить
неравенство (относительно х)
Ответ. Если Ь < -1, то х < -1, х > 1;
если -1 < b < 0, то --
26. При каждом значении параметра Ь решить
неравенство
у/х + 4Ь2 > х + 2\Ъ\.
Ответ. Если 0 < \b\ < 1/4 , то 0 < х < 1 - 4|Ь|;
если \b\ = 1/4, то х е 0;
если 1/4 < \Ь\ <; 1/2 , то 1 - 4|&| < * < 0;
если |Ь| > 1/2 , то -462 £ х < 0.
27. Найти все значения Ьу при каждом из которых
среди решений неравенства
> х + Ь
есть ровно два различных целочисленных решения.
Ответ. Ь - -1; 5 < Ь <> 15.
§ 4, Показательные и логарифмические
уравнения с параметрами
Пример 4.1. Для каждого действительного значения
параметра а решить уравнение
9"|х"21 - 4 • 3"1*-21 - а = 0.
Решение. Методом подстановки сводим исходную
задачу к равносильной задаче решения смешанной системы
о < t < 1,
(-|* - 2| = Iog3(2 -
1-3<а<0
= 2 ± Iog3(2 -
\ , ч л г-
3-
*. а
Рис. 4.1
На КП-плоскости Юа решение смешанной системы
О < tu 1,
tt a) = О
150
§ 4. Показательные и логарифмические уравнения
представляет собой множество точек, находящихся при
—3 < а < О на нижней ветви параболы t = t^a) в полосе с
нижней границей t = О и верхней -t = 1, включая верхнюю
границу. На рис. 4.1 данная полоса заштрихована.
Ответ. Если а < -3, то решений нет;
если -3 < а < О, то х = 2 ± Iog3(2 - yJ4 + a);
если а > 0, то решений нет.
Пример 4.2. При каких значениях а уравнение
1
х—
4х-(а+ 2)-2 * +2а-2 * =0
имеет ровно два решения?
Решение. Умножая обе части уравнения (при х ± 0)
2
на 2х ^ 0 , получим уравнение, ему равносильное:
г *д и ,д )
2а = 0<=> 2 х-а • 2 *-2 =0о
2 * =а,
хД
2 * =2
— = log2 а = bt
х
* + ! = i.
(1)
(2)
Уравнение (1) равносильно на множестве х * 0 квадратному
уравнению
х2 - 6* +1 = О,
которое имеет ровно два решения, если его дискриминант
положителен:
D = b2-4>0<=>\b\>2<=> |log2 а| > 2
а > 4.
Уравнение (2) действительных решений не имеет.
§ 4. Показательные и логарифмические уравнения
151
На КП-плоскости хОЬ множество всех точек (х\ Ь),
значения координаты и параметра каждой из которых
удовлетворяют уравнению (1), представляет собой график функции
Ь = х + —,
х
(3)
получающийся при суммировании графиков прямой Ь = х и
гиперболы Ь = — .
X
Рис. 4.2
Следовательно, при Ь < -2 (0 < а < 1/4) и при Ь > 2
(а > 4) существует ровно два решения уравнения (1), так
как прямая Ь = const пересекает в этом случае график
функции (3) в двух точках. Уравнение (2), получаемое из
(1) при Ь = 1, решений не имеет.
Ответ. О < а < —, а > 4.
4
Пример 4.3. При всех а решить уравнение
152
§ 4. Показательные и логарифмические уравнения
Решение. Логическая схема алгоритма решения
логарифмического уравнения данного типа имеет вид (В. 17):
\oguf =
fO < и * 1,
(4.1)
Следовательно, рассматриваемое нами уравнение
равносильно следующей смешанной системе
О < х + 1 * 1, Г-1 < х * О,
ах = (х +1)2 ^ [*2 + (2 - а)х +1 = 0 °
а - 2 = 6,
-1 < х * О,
(1)
(2)
(3)
На КП-плоскости хОЬ множество всех точек (х, Ь),
значения координаты и параметра каждой из которых
удовлетворяют уравнению (3), представляет собой график
функции (3). Решением системы (2), (3) является та часть этого
множества, которая принадлежит полуплоскости -1 < х * О
без прямых х = -1 и х = 0 (на рисунке эта полуплоскость
заштрихована).
Рис. 4.3
§ 4. Показательные и логарифмические уравнения
153
При х * 0 уравнение (3) равносильно квадратному
уравнению
х2 -Ьх + 1 = О,
корни которого являются функциями параметра Ь (|б| > 2):
хг(Ъ) =
х2(Ь) =
Ь-ЯЬ*-А
& + Vfc -4
причем при \b\ = 2 они совпадают.
Запишем решение системы (2), (3) для каждого
значения параметра Ь: если Ь < -2, то х — хг(Ь); если -2 < Ь < 2,
то х е 0 ; если Ъ = 2, то х = 1; если Ь > 2, то х = хДЬ) и
х = *2(&)« Возвращаясь к первоначальному значению
параметра, получим ответ.
Ответ. Если а < 0, то х = х2(а) =
если 0 < а < 4, то jc e 0;
если а = 4, то х = 1;
если а > 4, то jc = jcx(a) =
х = *2(а) =
Пример 4.4. При каких значениях Ь уравнение
1
X
25х - (2Ь + 5) • 5 * + 10Ь • 5 х = О
имеет ровно два решения?
Решение. Заменим уравнение ему равносильными:
,4-3.
(2Ь + 5) • 5 * +106 = 0 о
<=>
х+
5 *=5,
<=> х f — = log5 26 = a.
= 26
154
§ 4. Показательные и логарифмические уравнения
Применяя КП-плоскость хОа, получаем, что последнее
уравнение имеет ровно два решения при а < -2 и а > 2,
Следовательно, искомые значения Ь находим из
совокупного 26 <-2,
сти неравенств
Llog52b>2.
1 25
Ответ. 0<Ь<—, Ь>—.
50 2
Пример 4.5. Для каждого значения а решить уравнение
0о\ yJx+a+2 /. .\Vx2+a2-6a-5
og23) =(loge4)
Решение. Уравнивая основания, получим:
= -V-jc2 +a
f x + a + 2 = 0,
^ {*2 + a2 -6a -5 = 0
+ a + 2 = 0,
(1)
§ 4. Показательные и логарифмические уравнения 155
х = -а - 2,
2а2-2а-1 = <
(2)
На КП-плоскости хОа решение системы уравнений (1)
изображается точками пересечения прямой с окружностью
радиуса л/Г? и с центром в точке х = О, а = 3, а решение
совокупности систем (2) — двумя точками пересечения пар
прямых (см. рис.)
Рис. 4.5
1-V3 -5 + V3
Ответ. Если а = , то х = ;
2 2
если а =
V3 -5-л/з
, то х = ; при всех других а
решений нет.
Пример 4.6. Определить, при каких а уравнение
bgV2rj(4x + а) = 4
имеет решения, и найти эти решения.
156
§ 4. Показательные и логарифмические уравнения
Решение. Для применения метода, использующего
равенство одноименных функций, запишем уравнение в
следующем равносильном виде:
а) =
Воспользовавшись логической схемой решения такого
логарифмического уравнения (В. 17), заменим
логарифмическое уравнение равносильной системой:
[о < V2-JC * О,
f 0 < 2 - х * 1,
= (V2 - *)4 > 0 [4* + а = (2 - х)2 > 0.
4jc-
На КП-плоскости решением последней системы является
нижняя ветвь х = х^а) = 4 - «y/fsTba параболы а = (2 - xf -
- 4* = x2-8jc 4- 4, расположенная в полуплоскости д; < 2 (при
а > -8) кроме множества точек прямой х = 1 (при a = -3).
-с-
Рис. 4.6
Ответ, а > -8,а ^ -3 : х - 4-
Пример 4.7. Определить, при каких значениях
параметра а уравнение
имеет ровно два решения.
§ 4. Показательные и логарифмические уравнения
157
Решение. Так как
Iog2(4x - а) = х о Iog2(4x - а) = log2 2х
4х - а = 2
2' = t > О,
L*2 - t - а > О,
то исходная задача равносильна следующей. Требуется
найти, при значениях каких а смешанная система
{t > 0 (полуплоскость),
а = t(t -1) (парабола)
имеет ровно два решения t = t^a) и t =
-2
-1 -
Рис. 4.7
На КП-плоскости Юа решение рассматриваемой
смешанной системы представляет собой часть параболы
а - t(t - 1),
расположенную в верхней полуплоскости, не включая
параметрическую ось. Следовательно, ровно два решения
будет при значениях параметра
1
~-<а<
158
§ 4. Показательные и логарифмические уравнения
Этот же результат можно получить иначе, если
воспользоваться тем, что число X = О расположено левее двух корней
квадратного уравнения f(t, a) = t2 - t - а = 0, когда
О < t, <t9 <=>
D = 1 + 4а > О,
1
ДО) = -а > 0, <=>--< а < 0.
f(0) = -K0
Ответ. — < а < 0.
4
Пример 4.8. Для любых допустимых значений а решить
уравнение
Решение. Применяя логическую схему решения
данного типового логарифмического уравнения (В. 17), заменим
его равносильной смешанной системой:
0 < а ^ 1,
2 -Sa = a2-3x>0
0 < а * 1, (1)
Х<Т' (2)
(х - а)(х + а + 3) = 0. (3)
На КП-плоскости хОа множество точек (х; а), значения
координаты и параметра каждой из которых удовлетворяют
условиям (1) и (2), состоит из точек полуплоскости а > О
без точек координатной оси а = 0 и прямой а = 1, лежащих
2
ниже параболы jc = — (на КП-плоскости это множество
3
точек заштриховано).
Следовательно, решение системы (1)-(3) изображается
точками прямых х - а = 0 и х + а + 3 = 0,
принадлежащими полученному множеству.
Ответ. Если 0 < a < 1, 1 < a < 3, то jc = -a - 3;
если a > 3, то х = -а - 3, х = а.
§ 4, Показательные и логарифмические уравнения
159
Рис. 4.8
Пример 4.9. Для каждого действительного значения
параметра а > О решить уравнение
Решение. Применяя логическую схему (4.1) решения
логарифмического уравнения получим:
Ja>0,
\\oga2_x2[(axf -l] =
а >0,
О <а2 -х2
1,
(ах)2 -1 = а2 -х2
На КП-плоскости хОа множество точек, удовлетворяющих
системе неравенств, расположено в полуплоскости а > О
между биссектрисами х = аих = -а первого и четвертого
координатных углов. Решение уравнения изображается
160
§ 4. Показательные и логарифмические уравнения
прямыми jc = -1h^ = 1, параллельными параметрической
оси. Все точки этих прямых, принадлежащие указанному
множеству и удовлетворяющие условию
аг-хг*\,
то есть а * V2 , дают решение исходной задачи.
Рис. 4.9
Ответ. Если 0 < а < 1, то # е 0 ;
если 1 < а < V2 , то дс ^ -1 и х = 1;
если а = V2 , то х е 0 ;
если а> 72,тох = -1их = 1.
Пример 4.10. Для любых значений а решить уравнение
V2x2~3a-16 = yJ2a2-3x -16 .
Решение. Воспользовавшись логической схемой
= в
(4.2)
заменим данное уравнение равносильной ему смешанной
системой:
§ 4, Показательные и логарифмические уравнения 161
|ох2-3а _ оа2-3ж
и применим КП-метод.
(х - а)(х + а + 3) = О,
а2-4
Рис. 4.10
Ответ. Если -1 < а < 4, то х = - а - 3;
если а < -1, а > 4, то х = - а - 3, # = а.
Пример 4.11. Указать все значения а, при которых
уравнение
loga х
\а + loga
= 0
имеет решение, и найти все соответствующие решения.
Решение. Заменяя данное уравнение равносильной
системой, применим метод подстановки и КП-метод.
6-3683
162 § 4- Показательные и логарифмические уравнения
t i.
Рис. 4.11
О < х * 1,
О < a * 1
loge х = t * О,
О < a / 1,
loga д: = ^ 0,
a + * > 0,
0 < a * 1;
loga x = t* 0,
a + f < 0,
a = -*2-2f,
0 < a * 1;
(1)
(2)
§ 4. Показательные и логарифмические уравнения
163
[О < a < 1,
[ioga x = Vl-a - 1;
[О < а < 1,
II.
[О < а < 1,
\х = а
Wl+3a
На КП-плоскости Юа множество решений системы I
полученной совокупности представляет собой часть верхней
ветви параболы (1), расположенную в полуплоскости t > - а
при 0 < а < 1, а множество решений системы II — часть
нижней ветви параболы (2), расположенную в
полуплоскости t < - а при 0 < а < 1. На рис. 4.11 эти решения
изображены сплошными жирными линиями.
Ответ. 0<a<l:x = aVI^-1, х = а1'7Г7^.
Пример 4.12. Найти все значения а, при каждом из
которых уравнение
(jc2 - (а + 1)х + 3(а - 2)) • log(a_x)(2a - х -1) = О
имеет хотя бы один корень на отрезке [-1; 2], а вне этого
отрезка корней не имеет.
Решение. Воспользовавшись логической схемой вида
(В.17),
logu / = 0 <=>
О < и * 1,
/-1 = 0,
(4.3)
получим:
(*2 - (a + l)x + 3(a - 2)) • log(a_x)(2a - x - 1) = 0 о
О < a - x * 1, (1)
(x - 3) • (* - (a - 2)) • (2a - * - 2) = 0. (2)
На КП-плоскости хОа изображено множество всех точек
(х; а), значения координаты х и параметра а каждой из
которых удовлетворяют системе (1), (2). Условию (1) удов-
6*
164
§ 4. Показательные и логарифмические уравнения
летворяют точки, расположенные в полуплоскости х < а
кроме точек прямой х = а - 1. Условию (2) удовлетворяют
точки прямой х = 3 без точек л: = 3, а = 3 и х = 3, а = 4,
прямой х = а - 2 и прямой х = 2а - 2 без точек х = 2,
а = 2 и х = 0, а = 1. Следовательно, системе (1), (2)
удовлетворяют значения координаты и параметра каждой из
точек прямой х = а - 2 и лучей х = Зих = 2а-2 без
указанных точек (на КП-плоскости эта прямая и лучи
изображены жирными линиями).
Рис. 4.12
Множество всех точек (х; а), значения координаты х
каждой из которых удовлетворяют неравенству -1 <х<2,
расположено в полосе и включает границы х = -1 и jc = 2.
(На рис. 4.12 данная полоса заштрихована.)
Таким образом, искомыми являются значения
параметра 1<а<3иа = 4, при которых существуют точки прямой
х = а - 2 и лучей х = 3, х = 2а - 2, расположенные в
полосе, а точки вне этой полосы не находятся на указанных
прямой и лучах.
Ответ. ae[l; 3]u{4}.
§ 4. Показательные и логарифмические уравнения
165
Упражнения
1. На координатно-параметрической плоскости аОх с
вертикальной параметрической осью Оа изобразить
множество всех точек, значения координаты х и параметра а
каждой из которых удовлетворяют соотношениям:
|log2 x\
log2 x '
в) a=\g\x\-\gx2;
2х-\
б) а = \ogxy[x;
г) a = 2llog2^;
е) а = 3log^(x"2);
з) а = 21*х;
к) а = logy2;
м) |a| = a
n)a = xXgx\
л) a = log x
н)
2. На КП-плоскости аОх с вертикальной
параметрической осью Оа изобразить множество всех точек, значения
координаты х и параметра а каждой из которых
удовлетворяют уравнению:
и для каждого значения параметра а найти решения этого
уравнения.
Ответ. Если а < 0, то х е 0 ;
если а = 0, то х = -1, х = 1;
если а > 0, то х = -2е, х = -2 °; * - 2~а, х = 2а.
3. На КП-плоскости хОа с горизонтальной
параметрической осью Оа построить множество всех точек, значения
координаты х и параметра а каждой из которых
удовлетворяют уравнению:
\oga x = 2t
и для каждого значения параметра решить это уравнение.
166
§ 4. Показательные и логарифмические уравнения
Ответ. Если а < О, то х е 0 ;
если 0 < а < 1, то л: = а2; а = 1, то л: е 0 ;
если а > 1, то х = а2.
Указание. Заменить логарифмическое уравнение
равносильной ему смешанной системой:
О < а ф 1,
х > О,
4. Установить, при каких значениях параметра а система
\ах = 2 - а,
имеет решения, и найти эти решения.
Ответ. Если а = 1, х = 1.
5. Для каждого значения параметра а решить систему:
Ответ. Если а < -1, то х е 0 ;
если -1 < а < 1, то х = 0;
если а > 1, то х е 0 .
Указание. Воспользоваться неравенствами:
О1~\А < О
. о 1 w _
6. Найти все значения параметра а, при каждом из
которых уравнение
= а
имеет ровно два корня.
Ответ, а > 1.
§ 4. Показательные и логарифмические уравнения
167
7. Найти все значения параметра а, при каждом из
которых уравнение
имеет а) ровно два корня; б) четыре корня.
Ответ, а) а = 0; б) а > 0.
8. Найти все значения параметра а, при каждом из
которых уравнение
Iog2(|*| - I)2 = 2а
имеет а) ровно два корня; б) ровно три корня; в) четыре
корня.
Ответ, а) а > 0; б) а = 0; в) а < 0.
9. Найти максимальное значение параметра а, при
котором уравнение
2-*2 = а
имеет решение.
Ответ, а^ = 1.
10. Найти все значения параметра а, при каждом из
которых уравнение
имеет два различных решения.
Ответ. 7 < а < 7,5; а > 7,5.
Указание. Заменить логарифмическое уравнение
равносильной ему смешанной системой
0 < a-6,5 ф 1,
х2 + 1 = (а - Ъ)х > 0
b = a - 5,
3,5
— < b ф —,
2 2
x
11. Найти все значения параметра а, при каждом из
которых уравнение
168
§ 4. Показательные и логарифмические уравнения
Iog3(9x + 9а3) = х
имеет два решения.
Ответ. О < а <
Указание. С помощью замены переменной 3* = t > О и
параметра 9а3 = Ь задачу можно свести к равносильной:
«найти все значения параметра bf при каждом из которых
уравнение
имеет два положительных решения».
Её решение: 0 < Ь < —.
4
12. Определить, при каких значениях параметра а
уравнение
имеет решения, и найти эти решения.
Ответ. Если а > -4, а Ф -1, то х = 3 -
13. Для каждого положительного значения параметра а
решить уравнение
log2 a • logx 4 = 1
Ответ. Если 0<а<1,тох = а2;
если а =» 1, то х е 0 ;
если а > 1, то jc = а2.
Указание. Заменить уравнение равносильной ему
смешанной системой
а > 0,
0 < х * 1,
a > О,
0 < ж * 1,
= log2a2
14. Для каждого значения параметра а решить уравнение
§ 4. Показательные и логарифмические уравнения 169
Ответ. Если а < 1, то х = ±log12fl +Vl -а) ;
если а = 1, то х = 0;
если а > 1, то х е 0 .
Указание. Заменить задачу равносильной о решении
смешанной системой
J12M = t > 1,
15. Указать все значения параметра а, при которых
уравнение
log2 х + \oga х + log4 х = 1
имеет решения, и найти эти решения.
21og2a
Ответ. Если а > 0, а * i, а * 1, то х = 231ogza+2.
16. Для каждого допустимого значения параметра а
решить уравнение
loge(jc2 - 4a) = loga(a2 - 4х).
Ответ. Если 0 < a < 1, 1<а<4, тох = а + 4;
если а > 4, то # = -а; х = а + 4.
17. Для каждого значения параметра а решить уравнение
^2*2-4а _ 32 = V2a2+4* - 32 .
Ответ. Если -1 < а < 5, то х = а + 4;
если а <-1, а > 5, то х = - а; х = а + 4.
18. Для каждого значения параметра а решить уравнение
(Iog62)va+J:+Z =(log425)v
-1-V5 -3 + V5
Ответ. Если a = , то х =
2 2
-1 + ^5 -3 - &
если a = , то х = ;
2 2
при всех остальных а решений нет.
170 § 4. Показательные и логарифмические уравнения
19. Для каждого значения параметра а решить уравнение
у]а(2х -2) + 1 =1-2*
Ответ. Если 0 < а < 1, то х = log2a;
при всех других а решений нет.
Указание. Применить метод подстановки и рассмотреть
систему
2х = t > О,
20. Указать все значения а, при которых уравнение
2\lg(ax)\ ■ log, 10 = (41ga - 3) • logx210 - U
имеет решение, и найти все соответствующие решения.
Ответ. Если a = 10, то х = —;
10
если 10 < a < 1000, то х = —, х = 102-^1+8lga ;
10
если а > 1000, то л: = —, х =
10 1000
Г1 з]
21. Для каждого значения а е\—т=; — найти количест-
Lv2 2J
во корней уравнения
Здесь {#} означает дробную часть числа х.
Ответ. Два.
22. Найти все значения а, при каждом из которых
уравнение
(х2 + (1 - а)х - 3(а + 2)) • log(;c_a)(* - 2а -1) = О
имеет хотя бы один корень на отрезке [-2; 1], а вне этого
отрезка корней не имеет.
Ответ, a e[-3; -l]u{-4}.
§ 5. Показательные и логарифмические
неравенства с параметрами
Пример 5.1. Для каждого допустимого значения
параметра а решить неравенство
loga(7-jc)>21oga(jc-l).
Решение. В области допустимых значений
переменной и параметра заменим данное неравенство
равносильными системами (В. 19):
О < а * 1,
7 - х > О,
х - 1 > О,
loga(7-*)>loga(*-l)2,
0 < а * 1,
1 < х < 7,
0 < а * 1,
1 < х < 7,
(а - IX* + 2)(х - 3) < О
0 < а * 1,
1 < х < 7,
(а_1Кх_3)<0.
Построив на КП-плоскости хОа множество всех точек,
значения координаты х и параметра а каждой из которых
удовлетворяют полученной системе, (на рис. это множество
заштриховано) запишем ответ.
Ответ. Если 0 < а < 1, то 3 < х < 7;
если а > 1, то 1 < х < 3.
172
§ 5. Показательные и логарифмические неравенства
Пример 5.2. Найти и изобразить на координатно-
параметрической плоскости хОа множество всех точек,
значения координаты х и параметра а каждой из которых
удовлетворяет системе неравенств
Iog2_fl(2-x)>0,
Iog4_x(2a-2)>0.
Решение. Воспользовавшись логической схемой
решения типового неравенства (В. 19):
logu/ >0o
О < и * 1,
/>0,
(u-W-1):
(5.1)
раменим исходную систему логарифмических неравенств
равносильной:
0 < 2 - a * 1,
2 - x> 0,
[(2 - a) -1] • [(
0<4-**l,
2a - 2 > 0,
[(4 -x)-l]
0,
- 2) -11 > 0
1 < a < 2,
*<2,
1 - x > 0,
«-!>o.
(i)
(2)
(3)
(4)
Рис. 5.2
§ 5. Показательные и логарифмические неравенства
173
На КП-плоскости искомое множество есть пересечение
полуполосы (1), (2) с полуплоскостями (3), (4).
Ответ. Прямоугольник — < а < 2, 1 < # < 2.
Пример б.З. Для каждого параметра а решить
неравенство
Решение. Алгоритм решения рассматриваемого
типового логарифмического неравенства сформулируем в общем
виде с помощью следующей логической схемы (В. 19):
(5.2)
Для данного в условии задачи логарифмического
неравенства равносильная ему совокупность систем алгебраических
неравенств имеет вид:
logu/>lo
fO < и < 1,
[О < / < u;
fu>l
0 < а < 1,
H<i,
1 - х2 < а;
а > 1,
l-jc2>a.
0)
(2)
(3)
На КП-плоскости хОа решение первой системы неравенств
совокупности есть множество всех точек (х;а), значения
координаты и параметры каждой из которых удовлетворяют
неравенствам (1)-(3). Это множество можно рассматривать
как пересечение полос 0<а<1 и |#|<1 без границ с
множеством точек, расположенных на параболе а = 1 — х2
и правее от неё. На рис. множество, задающее на
КП-плоскости решения системы (1)-(3), заштриховано.
174
§ 5. Показательные и логарифмические неравенстеа
Вторая система неравенств совокупности решений не
имеет.
При а < 1 парабола а = 1 - х2 имеет две ветви — ниж-
яюю
а верхнюю
х = хх{а) = -VI - а
х = х2(а) = у/1-а.
Следовательно, для каждого значения параметра 0 < а < 1
решением исходного неравенства являются множества
-1 < х < хх(а) и х2(а) < х < 1.
При всех других параметрах а неравенство решений не
имеет.
Рис. 5.3
Ответ. Если 0<а<1, то-1<х< -Vl-a,
Vl-a < x < 1;
при остальных а решений нет.
Пример 6.4. Для каждого допустимого значения
параметра а решить неравенство
§ 5. Показательные и логарифмические неравенства
175
Решение. Записывая данное неравенство в
стандартном виде, применим логическую схему решения типового
логарифмического неравенства путем замены его
равносильной системой алгебраических неравенств (5.2):
\og{x_a)(x + а) > \og{x_a)(x - а) о
О < х - а * 1,
х + а > О,
<=>
а)-(х-а)]>0
и применим КП-метод.
а < х * а +1,
х > а,
[* - (а +1)] а > О
Рис. 5.4
Ответ. Если а < -1/2, то х е 0;
если -1/2 < а < 0, то -а < х < а -f 1;
если а = 0, то 0<#<1 и х > 1;
если а>0, то х>а + 1.
Пример б.б. Найти все действительные значения а, при
которых каждое решение неравенства
log0f5*2>log0i5(x + 2)
является решением неравенства
49х2 - 4а4 < О.
176
§ б. Показательные и логарифмические неравенства
Решение. Найдем множество решений
логарифмического неравенства
log05х2 > \og0tb(x + 2)
Г-1 < х < О,
[О <х <2.
(1)
На координатно-параметрической плоскости хОа это
множество представляет собой полосу без прямой х = 0,
ограниченную прямыми х = -1 и jc = 2.
Найдем множество решений неравенства
49х2-4а4 <0<*\х\й-а2 (2)
и изобразим (заштрихуем) это множество на КП-плоскости.
Рис. 5.5
Каждое решение (1) содержится среди множества (2)
при а < -y/l и а > yff.
Ответ, а < -V7, а > >/7.
Пример 5.6. Для каждого значения параметра а решить
неравенство
§ 5. Показательные и логарифмические неравенства
111
Решение. Методом подстановки сведем задачу к
равносильной:
13х = t > О,
\9t2+Sat-a2 <0
3х = t > О,
а
(1)
(2)
На КП-плоскости Юа неравенство t > О задает верхнюю
полуплоскость (без параметрической оси t = 0).
Прямые линии t = -а и t = — разбивают КП-плоскость
у
на четыре частичные области I-IV. Вдоль этих линий левая
часть неравенства обращается в нуль, а между ними
сохраняет знак: положительный в I и III областях,
отрицательный — во II и IV областях (задающих на КП-плоскости
решение неравенства (2)).
Решение системы неравенств (1), (2) на КП-плоскости
есть пересечение полуплоскости f > 0 с областями II и IV
(на рис. это пересечение множеств заштриховано).
t i
Рис. 5.6
Записывая для каждого значения параметра а решение
рассматриваемой системы и воспользовавшись
применяемой подстановкой, получим ответ на поставленную задачу:
Х78
§ 5. Показательные и логарифмические неравенства
а < О : 0 < t < -а, 0 < 3х < -а, х < \og3(-a), ч *
а = 0 : f g 0, <=> л: g 0, <=> jc e 0,
а>0: 0<^<^ 0<Зх<^ x<log3[-|.
Ответ. Если а < О, то jc < log3(-fl)J
если а = О, то jc € 0;
если а > О, то х < log3 — .
Пример 6.7. Для каждого значения параметра а решить
неравенство
Решение. Логарифмируя по основанию 3, получим
неравенство, равносильное данному
<=> Vx + 1 > (а -1) • log8 2 = 6.
8
Используя логическую схему решения типового
иррационального неравенства (см. Введение), получим
/ х + 1 > Ь
х + 1 £ 0;
На КП-плоскости множество решений полученного
неравенства заштриховано и представляет собой часть
полуплоскости х£-1, расположенную левее ветви параболы
Ь = V х + 1
Ъ>0,
х = Ь2 -1.
Так как log3 2 > 0, то Ь < 0 при а < 1 и Ь > 0 при
f 6. Показательные и логарифмические неравенства
179
Рис. 5.7
Ответ. а<1: х > -1;
Пример 5.8. Для каждого значения параметра а решить
неравенство
logx(x-a) > 2.
Решение. Применяя логическую схему решения
типового логарифмического неравенства, заменим данное
неравенство равносильной ему системой неравенств (В. 19):
\ogx(x - a) > \ogx x2 о
О < х * 1,
х > a,
(1)
(2)
На КП-плоскости хОа в области, задаваемой системой
неравенств (1) и (2), решением неравенства будет область I,
состоящая из множества точек верхней полуплоскости,
лежащих выше линии х = а и области III. Обозначим
уравнения нижней и верхней ветвей параболы а = -х2 -Ь х :
, v 1 - Vl - 4a , v 1 + Vl - 4a
x=xl(a)= , x = x2(a) = .
180
§ 5. Показательные и логарифмические неравенства
Рис. 5.8
Ответ. Если а < О, то 1 < х <
если а = 0, то jc G 0;
если 0 < а < —, то а<х<
< х < 1;
если — < а < 1, то а < jc < 1;
4
если а > 1, то jc g 0.
Пример 6.9. Найти все значения а, при которых
неравенство
Ioga(*2 + 4)>1
выполняется для всех значений х.
Решение. Применяя логическую схему решения
типового логарифмического неравенства (см. Введение, В. 19),
получим
[О < а * 1,
24
§ 5. доказательные и логарифмические неравенства
181
2
Прямая а = 1 и парабола а = х + 4 разбивают
КП-плоскость на три «частичные области* I—III.
х
,a) = (a-l)(x2+4-a)>0
во II области (на КП-плоскости она заштрихована).
Следовательно, исходное неравенство сразу для всех х
будет выполняться, когда 1 < а < 4.
Ответ. 1<а<4.
Пример 5.10. Определить, для каких а неравенство
bg_o_(*2+2)>l
а+1
выполняется при любом действительном х.
Решение. Заменим задачу равносильной о решении
системы:
logb(x2 +2)>logbb,
-со < х < -И»,
а + 1
Ь9
(1)
-со < х < +оо.
На КП-плоскости хОЪ найдем пересечение множеств точек,
значения координаты и параметра каждой из которых
удовлетворяют неравенствам (1) и (2). Условие (3) будет
выполняться для полосы
1<6<2, -оо<х< +оо,
182
§ 5. Показательные и логарифмические неравенства
принадлежащей этому пересечению. Искомые значения
раметра находим при решении системы
К
а+1
< 2 <=> а < -2.
Рис. 5.10
Ответ, а < -2.
Пример 5.11. Определить, при каких а неравенство
выполняется при любом действительном х.
Решение.
а(а +1) = Ь,
-оо < х <
-оо < х < -И»
а(а + 1) = Ь,
О < Ь * 1,
(&-1)фс| + 4
-оо < jc < +Q0.
(1)
(2)
На КП-плоскости хОЪ заштриховано множество точек (я, Ь)
(область II), для которых координаты х и значения
параметра Ь удовлетворяют системе (1), (2), а также часть этого
множества 1 < Ь < 4 (полоса без границ), где эта система
выполняется для любого х. Следовательно, исходное лога-
§ 5. Показательные и логарифмические неравенства
183
рифмическое неравенство выполняется при любом
действительном х, когда
а(а +1) < 4 <=>
а* +а-1 >0,
а2 + а-4 <0.
Ответ.
Рис. 5.11
УГ7 ^ 1 + V5 V5-1 ^ ^
<а< ; <а<
Пример 5.12. Найти все действительные значения а,
при которых каждое решение неравенства
log! л:2 >logx(jc +
2 2
является решением неравенства
49х2 -4а4 < О
(1)
(2)
Решение. Применяя логическую схему решения
типового логарифмического неравенства, получим
-1<х<2,
х ^ 0.
49*2 - 4а4 < 0 о х2 < — о Ы < — = Ь.
~ 49 М ~ 7
184
$ 5. Показательные и логарифмические неравенства
На КП-плоскости хОЬ множество точек, для которых х и Ь
удовлетворяют неравенству
\х\<Ь,
представляет собой угол АОВ.
х
Следовательно, каждое решение неравенства (1) (полоса
без точек параметрической оси) является решением
неравенства (2) (то есть принадлежит углу АОВ) при всех
Ь > 2 о \а\ > у/7.
Ответ. |a|>V7.
Пример 6.13. Решить неравенство
log* х - 2b\oga x + 2|loga x - b\ + 2 < О,
где 0 < а ^ 1 и b — действительные параметры.
Решение. Методом подстановки заменяем данное
неравенство равносильной смешанной системой
J |
U2 + 2* + 2 - Ь2 < 0 ° Ш + I)2 < Ь2 - 1 = a
§ 5. Показательные и логарифмические неравенства 185
&2 -1 = а > 1 о
|logo х - Ц < V&2-1 -1
Рис. 6.13
Ответ.
\Ъ\ > л/2, а > 1:
\Ь\ > >/2, 0 < а <
\Ь\ < л/2 : х е 0.
Пример 5.14. Для каждого действительного значения
параметра а решить неравенство (ах)х £ 1 при условии ах > 0.
186 § 6. Показательные и логарифмические неравенства
\(ах)х
Решение, j
[ах >
i 1°
1*
И. а:
о
0
(ах)
ах >
< ах < 1,
<0;
с = 1; <=>
\ах > 1,
III.
[х>0;
На КП-плоскости хОа
является гипербола
с ^
0
а
1
а
а
а
и
<
<
>
IX
0,
0,
1
а
0,
1
а
<=>
<0;
графиком уравнения
ах = 1
_ 1
а'
а ^0.
(И)
Рис. 5.14
§ 5. Показательные и логарифмические неравенства
187
Множество точек, координаты х и значения параметра
а которых удовлетворяют системе I, расположено в третьей
четверти над нижней ветвью этой гиперболы, а множество
точек, координаты х и значения параметра а которых
удовлетворяют системе III, — в первой четверти над
верхней ветвью гиперболы.
Ответ. Если а < О, то — < х < 0;
а
если а = 0, то неравенство решений не имеет;
если а > 0, то х > —.
а
Пример 5.15. Для каждого действительного значения
параметра а решить неравенство
Решение. Переходя к равносильному на множестве
х > 2 неравенству и применяя логическую схему решения
типового неравенства (В. 19), получим:
loge[x(x-2)]>logea,
х> 2
0 < а ф 1,
х> 2.
х2(а)
Рис. 5.15
188
§ 5. Показательные и логарифмические неравенства
На КП-плоскости хОа область а > 0, х > 2 делится прямой
а = 1 и верхней ветвью параболы
х =
на «частичные» области I-IV. В каждой из этих частичных
областей функция
сохраняет знак и является положительной в I и III областях.
Ответ. Если а < 0, то решений нет;
если 0<а<1, то 2<х<1 + >]l + a\
если а = 1, то решений нет;
если а > 1, то х > 1 + ТГТа.
Пример 5.16. Для каждого значения параметра а
решить неравенство
Решение. Заменим неравенство равносильным (В.19)
О < а ф 1,
loga(x - a) + loge(x + a) > 0
jc > a,
2a2)
loge(*2-a2)>0
0 < a * 1,
> a,
(a-lX*2-a2-l)>0
0 < a * 1,
jc > a,
(a - IX* - Va2+1K* + Va2+1) > 0.
Применяя КП-метод, получим ответ.
§ 5. Показательные и логарифмические неравенства
189
Рис. 5.16
Ответ. Если 0<а<1, то а < х < уа +1;
если а > 1, то х > уа2 +1.
Пример 5.17. Для каждого допустимого значения а
решить неравенство
2 - logo х < loge(* -1).
Решение. Заменим неравенство равносильными
о loge а2 - loge х < loge(* -1) о
2
о logo— <loga(*-l).
Применяя логическую схему решения типичного
логарифмического неравенства (В. 19):
(5.3)
заменим логарифмические неравенства равносильной
системой
190
§ 6. Показательные и логарифмические неравенства
0 < а * 1,
(а-1)
— -(х-1)
О < а ф 1,
jc > 1,
<0
О < а * 1,
х> 1,
(а-1)-
О < а * 1,
- л:- а2
>0
где
О < а * 1,
2
0 < а < 1,
1 < л: < JCjj
х > xJa).
Рис. 5.17
На КП-плоскости решение представляет собой две
частичные области I и III и находится аналогично между
интервалов при решении неравенств с одной переменной.
§ 5. Показательные и логарифмические неравенства
191
В каждой из частичных областей I-IV выражение с
двумя переменными
Ф(х,а) = (а-1)[х-хг(а)]
сохраняет знак и меняет его на противоположный при
переходе через границы этих областей х = хг(а) и а = 1.
Для определения знака Ф(х, а) в каждой из
рассматриваемых областей достаточно, например, установить его знак
в любой точке (х,а) из этой области.
Следует заметить, что построение графика функции
х = хх(а), задающей границу частичных областей, здесь не
требуется. Достаточно знать, что график расположен выше
прямой х = 1.
Ответ. 0<а<1: К х <
а > 1: х>
Пример 5.18. Для каждого значения параметра а, при*
надлежащего отрезку [-1;0], решить неравенство
Решение. Воспользуемся логической схемой решения
типового логического неравенства (5.2).
Рассматриваемое в условии задачи логарифмическое
неравенство будет равносильно следующей системе:
-1 < а < О,
О < х + а * 1,
х2 - (а + 1)лг + а > 0, °
-1 <, а < О,
-а < х * 1 - а,
192
§ 5. Показательные и логарифмические неравенства
-1 £ а < О,
х * 1 - а,
На КП-плоскости хОа заштрихуем пересечение множеств
точек, значения координаты и параметра которых
удовлетворяют неравенствам последней системы.
Построенное пересечение множеств дает решение
рассматриваемой задачи.
Рис. 5.18
Ответ. Если а = -1, то 2 < х < -к»;
если -1 < а < —, то 1 < х < а + 2 и 1 - а < х < -Ьоо;
2
1 3 3
если а = —, to1<jc<— и— < х < -нх>;
2 2 2
если — <а<0, то 1<х<1-а и а + 2£х< -и»;
2
если а = 0, то 2< х < -и».
§ 5. Показательные и логарифмические неравенства
193
Пример 5.19. Для любых допустимых значений а
решить неравенство
loga(3ax-5)<* + l.
Решение. В силу логической схемы решения
типового логарифмического неравенства (5.3) имеем:
loge(3a*-5)<logea*+lo
О < а ф 1,
Зах-5>0,
(a-l)[(3a*-5)-ax+1] <0
О < а * 1,
>3'
(а-1)[(3-а)^-5]<0
II.
III.
0 < а < 1,
.-of,
(3 - a)t - 5 > 0;
1 < а < 3,
ax=t>-,
3
(3 - a)t - 5 < 0;
а >3,
(3 - a)t - 5 < 0;
I.
III.
0 < а < 1,
3-а
1 < а < 3,
5 х л
-<а -I
а>3,
а* = ^ > -
5 <^
3-а
0 < а < 1,
7-3683
194
§ 5. Показательные и логарифмические неравенства
На КП-плоскости Юа решение совокупности смешанных
систем заштриховано.
-1 Г
г
г
г
г
Рис. 5.19
Ответ. Если 0 < а < 1, то л: < log
а|3-<
5
если 1 < а < 3, то loga — < л: < logo
3 \3 —•
если 3 < a < оо, то л: > loga —.
3
Пример 5.20. Найти все значения р, для которых
неравенство
log(;c_p)(x2) < 2 (1)
выполняется хотя бы для одного числа х такого, что
И < 0,01. (2)
§ 5. Показательные и логарифмические неравенства
195
Решение. Приведя логарифмическое неравенство (1)
к стандартному виду, применим логическую схему его
решения (5.3)
О < х - р ф 1,
х * 0,
р < х * р +1,
х*0,
(3)
На КП-плоскости *0р изобразим пунктиром линии х = р>
х=р + 1, д: = 0, р = 0, jc = р/2. Эти прямые линии
разбивают КП-плоскость на частичные области.
Рис. 5.20
Объединение частичных областей, состоящих из точек
р), координата и параметр которых при р < — 2,
196
§ 5. Показательные и логарифмические неравенства
-2 < р < 0 и р > О удовлетворяют системе неравенств (3),
на рис. заштриховано.
Решение неравенства (2) представляет собой полосу
-0,01<х<0,01.
Следовательно, построив пересечение множества решений
системы (3) и данной полосы, получим ответ на исходную
задачу.
Ответ. р<0,99; -0,02 < р < 0; 0<р<0,01.
Пример 5.21. Для каждого значения параметра а
решить неравенство
\ogx2(x-a)>l.
Решение. Заменим неравенство равносильным
типовым логарифмическим неравенством и применим к нему
логическую схему (В. 19)
log Ax-a) > log а х2
0 < х2 * 1,
х - a > 0,
§ 5. Показательные и логарифмические неравенства
197
х * О,
X * ±1,
х > а,
- хг(а)][х - х2(а)] < О,
= л:2(а) = - + Л--а —
урав2 \4 л ' 2 \4
нения соответственно нижней и верхней ветвей параболы
-х2 + х - а = 0 . Применяя КП-метод, получим ответ.
Ответ. Если а < 2 ,то ^(а) < * < -1, 1 < х < х2(я);
если а = -2 , то 1 < х < х2(я) = 2 ;
если -2 < а < -1, то -1 < х < хг(а), 1 < х < х2(а);
если -1<а<0,то а < х < хх(а), 1 < х < х2(а);
если а = 0 , то х е 0;
если 0 < а < — , то а < х < хЛа), х9(а) < х < 1;
4
если — < а < 1, то а < * < 1;
4
если а > 1, то х G 0 .
Пример 5.22. Среди множества всех решений неравенства
лайти такое, которое соответствует наибольшему значению
параметра а.
VlT*4a2=(>/2)2 (С,)
Рис. 5.22
198
§ 5. Показательные и логарифмические неравенства
Решение. Воспользовавшись логической схемой
решения типового логарифмического неравенства (5.2), получим:
п ~
а >0,
1
X,
а >0,
О < х2 + а2 * (л/2)2,
[х2 + а2 - (л/2)2][х2 + (а -1)2 -1] < О
На КП-плоскости хОа заштриховано множество всех точек,
соответствующих значениям координаты х и параметра а,
которые удовлетворяют полученной системе.
Эти точки, расположенные на окружности Сх
единичного радиуса с центром в точке х = 0 , а = 1 и внутри её, но
вне окружности С2 радиуса V2 с центром в начале
координат, а также точки полуплоскости а > 0, расположенные
на окружности С\ и вне её, но внутри окружности С2.
Максимальному значению параметра а = 2
соответствует решение д: = 0 (точка А).
О т вет. х = 0.
Пример 5.23. Для каждого значения параметра а
решить неравенство
Решение. log3 (V*2 - 2a* + 1 - l) < log3 3
-2a* + 1-
§ 5. Показательные и логарифмические неравенства
199
2а = b,
x(x-b)>0,
x -Ьх-15<
<=>
0
I <
II <
2a =
x >
X >
b>
2a
x <
X <
b<
= by
o,
ft.
= b,
o,
b,
x -
—;
X
15
На КП-плоскости хОЬ множество точек (х, Ь), значения
координаты и параметра которых удовлетворяют квадратному
уравнению
х2 -Ьх-15 = 0,
является графиком функции
15
x
200 § 5. Показательные и логарифмические неравенства
Корни этого квадратного уравнения
задают на КП-плоскости нижнюю х = х^(Ь) и верхнюю
х = х2(Ь) ветви рассматриваемой функции.
На КП-плоскости хОЬ заштриховано объединение
областей I и II, определяющих решение совокупности систем
неравенств I и П. Запишем полученное решение аналитически
для разных значений параметра Ъ и а:
если Ь < 0, то хг(Ь) < х < bt 0 < х <> х2(Ь) ;
если Ь = 0, то - Vl5 £ х < 0, 0 < х <, yflE ;
если Ь > 0, то JC1(b) <jc<0, b < x <, x2(b).
Возвращаясь к параметру а, находим для каждого
значения а решение исходного логарифмического неравенства.
Ответ. Если а < 0 , то а - yja2 -Ь15 < х < 2а,
если а = 0 , то -Vl5 <x<0, 0<x< Vl5 ;
если а > 0, то а —уа2 +15 < х < О,
2а < х < а + >/я2 +15 .
Пример 5.24. Для любого допустимого значения а
решить неравенство
Iog2a(\ogsx2)>l
и найти, при каком значении а множество точек х, не
являющихся решениями неравенства, представляет собой
промежуток, длина которого равна 6?
Р' шение. Беря в качестве базовой функции разность
леп рифмической функции и применяя декомпозицию
дважды, получим (В.21):
Iog2a(log3*2)-I>0<=>
<=> Iog2a(log3 x2) - log2e 2a
§ 5. Показательные и логарифмические неравенства
201
ода
(2а -
- 2а) > 0 о
ода
2a)
»(2а - l)(log3 x2 - log3 3Za) >0 <*
ОДЭ ОДЭ
где
ОДЗ:
1
21
На КП-плоскости хОа решение заштриховано (достаточно
изобразить множество решений при х>0и
воспользоваться симметрией относительно параметрической оси.)
Рис. 5.24.
202 § 5. Показательные и логарифмические неравенства
Ответ.
1)Еслиае(0; 1/2), то х е (-За; -1)и(1;За);
если а е(1/2; е + оо), то х е (-оо; -За)и(3°; +оо).
2) Множество точек х, не являющихся решениями
(включая промежуток |*| < 1, не входящий в ОДЗ),
образует промежуток Г-За; За1, имеющий конечную длину.
Длина этого промежутка равна 6 при а = 1, что является
ответом на второй вопрос.
Пример 5.25. Для каждого значения параметра р из
интервала 0 < р < — решить неравенство
4
\ogx+p2<\ogx4.
Решение. Применяя метод декомпозиции (см
Введение), запишем исходное неравенство на множестве
М:
0<р<-,
4
0 < х * 1,
0 < х + р ф 1,
принадлежащим области допустимых значений переменно?
х и параметра р, в каноническом виде и, представив левую
часть неравенства как произведение и частное базовых
функций, заменим его равносильным на множестве М
рациональным алгебраическим неравенством (В.21):
log 2-21ogx2<0 » log 22-\ogx2<0 о
м к Р) м
1 1 lognX-\ogo(X+ р)2 л
^<0 <=>
py log2x м
х-(х + р)2 х2 -(1-2р)х+ р2 _
М (^ + р-1).(^-1) м [*-(1-р)].(*-1) м
» [х - ^i(P)] • [х - хя(р)] • [^ - (1 - Р)] • (х -1) > 0, (♦)
At
§ 5. Показательные и логарифмические неравенства
203
где
= --p-yj-- p
причем
p) < х2(р) и лсДр) = х2(р) при р = - .
4
Если 0<р<-,то 0< хх(р) < — , — < л:2(р) < 1 - р < 1
4 4 4
О х = 0
Рис. 5.25
Методом интервалов получим решение неравенства (*) и
дадим интерпретацию его на КП-плоскости хОр.
Ответ. OJt-P-Jt-
^ 4
204 § 5. Показательные и логарифмические неравенства
Упражнения
1. Изобразить на КП-плоскости хОа множество точек,
значения координаты х и параметра а каждой из которых
удовлетворяют следующим неравенствам:
а) ах >1;
б) logax<0;
в) \ogxJha (2х + За) > 1;
1оем-о5)4;
д) 2а2 < log2 х (З|а| - 21og4 x).
2. Указать, где на КП-плоскости jcOa расположены
точки, значения координаты х и параметра а каждой из
которых удовлетворяют неравенству
где р = yjx2 + (a - I)2
Ответ. Вне окружности радиуса 10 с центром в точке
2
а = 1, х = 0 или внутри окружности радиуса — с центром
3
в той же точке.
3. Определить площади фигур, расположенных на
КП-плоскости и состоящих из точек (х;д), значения
координаты х и параметра а каждой из которых удовлетворяют
следующим неравенствам:
а) logx,+e,(* + a)>l;
б) logxi+at(x-a)>l.
2
Ответ, а) 1; б) - + 2>/з .
3
Указание, а) Фигура состоит из всех точек (#; а)
полуплоскости х > —а, лежащих одновременно внутри
окружности радиуса 1 с центром в точке 0 и внутри окружности
1 1
радиуса —р=- с центром в точке х = а = — .
V2 2
§ 5. Показательные и логарифмические неравенства
205
4. Изобразить на КП-плоскости хОа множество точек,
значения координаты х и параметра а каждой из которых
удовлетворяют неравенствам, и для каждого допустимого а
решить эти неравенства:
а) ах>1, (0<а*1);
Ответ. Если 0<а<1, толг^О;
если а > 1, то х > 0 .
Указание. Заменить неравенство равносильной системой:
0 < а * 1,
б) logax>0;
Ответ. Если 0<а<1, toO<jc<1;
если а > 1, то х > 1.
Указание. Заменить логарифмическое неравенство
равносильной системой:
0 < а ф 1,
в) \ogax>l;
Ответ. Если 0 < а < 1, то 0 < х < а ;
если а > 1, то а £ jc < +оо .
Указание. Заменить неравенство равносильной системой:
О < а * 1,
Ответ. Если 0 < а < 1, то а < х < 1;
если а>1, то1<х<а.
206 § 5. Показательные и логарифмические неравенства
Указание. Записать неравенство в виде
loga*
я заменить его в
ода:{о<^1
равносильным дробно-линейным: < 0 .
х-1
д) log* х - \oga x < О;
Ответ. Если 0<а<1, то а < jc < 1;
если а > 1, то 1 < х < а.
Указание. Разложить левую часть неравенства на
множители loge х - (loga x — l) < 0 и заменить его в
равносильным неравенством: (х - 1)(х - а) < 0 .
е) lg(l - *) < а ;
Ответ. 1 - 1Оа < х < 1 при любом а £ R .
5. Для каждого значения параметра а решить неравенство
Ответ, х = 2 у если a = -к + 2fe-rc, feGZ;
О < х < 1, если a G R .
Указание. Применить метод подстановки и рассмотреть
равносильную систему
log2 х = t,
t + - < Ь = -2 cos a,
t
§ 5. Показательные и логарифмические неравенства 207
6. Для каждого допустимого значения параметра а
решить неравенства:
а) loga(logxa)>0;
Ответ. Если 0<а<1, то 0 < я < а ;
если а > 1, то 1 < дс < а .
б) logx(loga*)>0;
Ответ. Если 0<а<1, то а < х < 1;
если а > 1, то х > а .
Для каждого значения параметра а, применяя КП-метод,
решить системы неравенств:
^(a + x-l)>\ogl х,
5 5
7.
л/л: - а -1
Ответ. Если а < 2, то х е 0 ;
если а = -2, то я = 3 ;
если -2 < а < О, то1-а<х<3;
если 0 < а < 1, то1 + а<х<3;
если а > 1, то х G 0 .
8 J*>log2|a|,
Ответ. Если а < —, то х > Iog2(-a);
1
если а = —, то х > -1;
ij
если а > —, то х > 2а .
9. i
" |log2 {2x - а2 + 4) > log2 (х +1).
Ответ. Если а < -2, то х G 0 ;
если -2 < а < -л/2, то а2 - 3 < х < 3 + а ;
если -л/2 < а < 0, то -1<х<3 + а;
если 0<а<л/2, то -1<х<3-а;
208 § 5. Показательные и логарифмические неравенства
если V2<a<2, то a2 - 3 < х < 3 - a ;
если а > 2, то х € 0 .
При каждом допустимом значении параметра а решить
неравенства:
10. loge(x-2)+logex>l.
Ответ. Если 0<а<1, то 2 < Jt < 1 + yjl + а ;
если а > 1, то х > 1 -f yfli-a .
11. xlog°x <а, 0<*;*1.
Ответ. Если 0<а<1, тоО<х<а, л: > —;
а
если а>1, то — < jc < 1, l<jc<a.
а
12. Для всех значений m решить неравенство
Ответ. Если m < 1, то х < 1;
если т > 1, то jc < 1 - [(m - l)log2 3] .
13. Найти все значения р, при которых каждое решение
неравенства
является решением неравенства
2 2р-5 б
хг +-*- л: >0 .
2р 2р
5
Ответ. -— < р < 0.
2
Указание. Заменить логарифмическое неравенство
равносильной системой
3 - рх > О,
О < х +1 * 1,
§ 5. Показательные и логарифмические неравенства 209
Воспользоваться тем, что решением квадратичного
неравенства
2р) \ 2р) v \ 2р
на множестве О < х +1 ^ 1 является х > — .
2р
14. Найти все значения параметра а, при которых
неравенство
16х <30 4*-а
не имеет ни одного целочисленного решения.
Ответ.а < 224 .
Указание. Методом подстановки 4х = t > О задачу
можно свести к равносильной: «Найти все значения параметра а,
при которых неравенство а < -t2 +30t не имеет ни одного
целочисленного решения*. Её решение КП-методом даёт
t > 14, t e N.
15. Для всех значений параметра 0 < а < 1 решить
неравенство
Ответ. i^< х <2.
2-а
16. Для каждого значения параметра а,
принадлежащего отрезку [0; 1], решить неравенство
Ответ. Если а *= 0, то х>2;
если 0<а<-, то1<х<1 + а, х>2-а;
2
1 3 3
если а = — 9 то 1 < х < — f д: > —;
2 2 2
210 § 5. Показательные и логарифмические неравенства
если — < а < 1, то 1 < jc < 2 - а, х > 1 + а ;
если а = 1, то х > 2 .
17. Найти все значения р, при которых неравенство
logx_px2 <2
вьшолняется хотя бы для одного числа х, такого, что|дг| < 0,01.
Ответ. ре(-оо; -0,99)U(-0,02; 0)U(0; 0,01).
18. Найти все значения р, при которых периметр
фигуры, заданной на КП-плоскости аОх условием
будет наименьшим.
Ответ, р = ±>/2 .
19. Множество F состоит из всех точек КП-плоскости
аОху значения координаты х и параметра а каждой из
которых принимают целочисленные значения и
удовлетворяют неравенству
Определить точки множества F, наименее удалённые от
точки х = 2, а = —2 .
Ответ. (Ю;5),(-6;-9),(-5;-10).
20. Множество точек, расположенных внутри фигуры F,
задано на КП-плоскости аОх условием
lOa-24-a2)
850
1147 V
Множество F(t) получается из F поворотом вокруг
точки О против часовой стрелки на угол t. Найти площадь
фигуры, образованной точками, каждая из которых при
некотором t G [0; -л] принадлежит множеству F(t).
Ответ. S =
§ 5. Показательные и логарифмические неравенства 211
21. Для каждого значения параметра а решите неравен-
ство
За -1 -(8а -5)• 3^ 1оМ*2+вН <3(а + 2)-|х + 3|2К^
Ответ. Если а е -оо; . , то х е -3--^; -3 U
если а е
("-Т;ТоГ Т° х G ("4; " 3 "
если «=—, тол:е(-4;-3)и(-3;-2);
если а е
U[-3 - <Ка); - 3) U (-3; - 3 + <р(а)]uf-З + -=; - 2);
—; + оо 1, то х е -4; - 3 —^ U
если а е
где ф(а)
-f—
П-За
2)
Указание. Задача равносильна следующей: для каждого
значения параметра а решить систему
О < t < 1,
3(a + 2)t2 + (8a - 5)^ - (3a -1) > 0.
(1)
(2)
(3)
212
§ 5. Показательные и логарифмические неравенства
Заменить систему неравенств (2), (3) равносильной
совокупностью систем.
О < t < 1,
а + 2 = 0, и
1-3*>0
О < t < 1,
а + 2 ф О,
и применить КП-метод.
На КП-плоскости Юа множество всех точек, значения
координаты t и параметра а каждой из которых
удовлетворяют указанной совокупности систем, на рис. 5.26
заштриховано.
Рис. 5.26
§ 6. Тригонометрические уравнения
и неравенства с параметрами
Пример 6.1. Определить область значений параметра а,
при которых уравнение
2cos2jc - 4acosx + a2 + 2 = О
не имеет действительных решений.
Решение. Так как
cos2jc = 2cos2jc - 1,
тс данное уравнение можно записать следующим образом:
4сов2дг - 4acos:c + а2 = 0 <=>
<=>(2cosx - a)2 = О <=> 2cosx = a.
Полученное тригонометрическое уравнение не имеет
действительных решений при всех значениях параметра \а\ > 2.
На рис. 6.1 дана интерпретация решения на КП-плос-
кости аОх с вертикальной параметрической осью.
Ответ. \а\ > 2.
Пример 6.2. Для каждого допустимого значения
параметра а найти решения уравнения
sin*
принадлежащие промежутку
[-Н
214
§ 6. Тригонометрические уравнения и неравенства
Решение. На рис. 6.2 дана интерпретация решения
на КП-плоскости с вертикальной параметрической осью.
-1
Рис. 6.2
Ответ. Если -1 < а < О, то х = arcsin a;
если 0 < а < 1, то х е {arcsina; я-arcsina};
если а = 1, то х = — .
2
Пример 6.3. При каких значениях параметра а
уравнение
sin2 3* - [ а + - |sin3* + - = О
имеет ровно три корня, расположенных на отрезке
Решение. Обозначая a = Здс, заменяем задачу
равносильной: при каких а уравнение
2 I I I ^
sin a - a + — sin a + — = 0 <=>
sin a = —,
sin a =
имеет ровно три корня на отрезке 2я < а < Зтг ?
Ответ получаем, используя КП-плоскость аОа. На
рассматриваемом отрезке первое уравнение имеет ровно два
корня сх; и а2, а второе — ровно один корень аэ, при а = 1.
Ответ. При а = 1.
§ 6. Тригонометрические уравнения и неравенства
215
1
I
1
ay
ai
In
/
/
\
о
1 a
--
-л
ч
1
<
2
-j
/
\
1
/
f
1
Рис. 6.3.
Пример 6.4. При каких значениях а уравнение
cos2jc + 2cosjc - 2а2 - 2а + 1 = О
имеет ровно три решения на промежутке
О < х < 2л?
Решение. Рассматриваемое уравнение равносильно
совокупности двух следующих уравнений:
[cos х = a, [cos х = а,
<=>
[cos х = -а -1 L"cos # -1 = л-
Применяя КП-метод, получаем ответ.
216
§ 6. Тригонометрические уравнения и неравенства
= 2/г
-cosx-\
-2 -1 О
Рис. 6.4
Ответ, а = -1, а = 0.
Пример 6.5. При каких значениях а уравнение
sin24* + (а2 - 3) sin4jc + а2 - 4 « 0
имеет ровно четыре корня, расположенных на отрезке
Решение. Квадратное относительно sin4:c уравнение
имеет два корня -1 и 4 - а2. Следовательно, задача
равносильна следующей: найти значение а, при которых имеет
ровно четыре решения система
4л: = а,
4-а2 = р,
fsin а = -1,
[since = р,
6кйа<> 8тс.
С помощью решения задачи на КП-плоскости (а, р)
получим р в 0.
Откуда находим а — ±2.
§ 6. Тригонометрические уравнения и неравенства
217
= 8/г
15/г
-1 6л
Рис. 6.5
Ответ, а = ±2.
Пример 6.6. Для каждого значения а найти число
решений уравнения
atgx + cos2jc e 1,
принадлежащих промежутку 0 й х £ 2п.
Решение. Заменим задачу равносильной:
[sin х = О,
[a = sin 2x,
cos jc 4t О,
О й х <> 2%.
Изобразим на КП-плоскости множество точек (х, а),
значения координаты и параметра которых удовлетворяют
полученной системе.
218
§ 6. Тригонометрические уравнения и неравенства
х = 2тг
х-— {
х- к
х- — '
д: = 0
X L
>>
0
—
а
Рис. 6.6.
Ответ. Если а < -1, то три решения; если а = -1, то
пять решений;
если -1 < а < 0, то семь решений; если а « О, то три
решения;
если 0 < а < 1, то семь решений; если а = 1, то пять
решений;
если а > 1, то три решения.
Пример 6.7. Для каждого значения а найти число
решений уравнения
cosjt-ctgjc - sin* = acos2x,
принадлежащих промежутку 0 < х < 2л.
Решение. Рассмотрим равносильную смешанную
систему
сое х - sin х о
= а•cos 2x
sinx
\0<х<>2к
cos 2х
О < х < 2л.
\ а = О,
Vein* )
Уравнение cos2* = 0 имеет при любом а на промежутке
Л я Зя 5л
О <, х < 2п четыре решения х = —, х = —, х = — и
4 4 4
х = —, изображенных на КП-плоскости прямыми, парад-
4
лельными оси Оа.
§ 6, Тригонометрические уравнения и неравенства
219
Решение уравнеия
= cosecjc = a
sin л:
представлено на КП-плоскости графиком функции а
= cos ее х, заданной на множестве О < х < 2тх.
\
In
4
Рис. 6.7
Совокупность этих решений дает на КП-плоскости
множество точек (дс, а), удовлетворяющих исходному
уравнению на промежутке 0 < х < 2л.
Для каждого параметра а число точек пересечения
прямой а = const с линиями, задающими указанное
множество, определяет число искомых решений задачи.
Ответ.
При а < ->/2 — 6 решений; при а = -V2 — 4 решения;
220
§ 6. Тригонометрические уравнения и неравенства
при ->/2 < а < -1 — 6 решений; при а = -1 — 5 решений;
при -1<а<1 — 4 решения; при а = 1 — 5 решений;
при 1 < а < >/2 — 6 решений; при a = y[l — 4 решения;
при а > V2 — 6 решений.
Пример 6.8. При каких значениях параметра а
уравнение
sin* + создг + sinxcosx — a
имеет решения?
Решение. Левая часть уравнения представляет собой
симметрический многочлен относительно функций и = sinjc
и и = cosjc. Так как всякий симметрический многочлен
Р(ц, и) = P(i>, u) можно выразить через основные
симметрические функции
и + у = z
и
tt
то, применяя для рассматриваемого тригонометрического
уравнения подстановку
sinjc + cosjc = z, | z
\< >/2 ,
сведем задачу к равносильной задаче о нахождении
значений параметра а, при которых существует решение
смешанной системы
\z2 + 2z = 2а +1 = b,
Рис. 6.8
§ 6. Тригонометрические уравнения и неравенства
221
Воспользовавшись КП-методом, найдем (см. рис.)
Ответ. -1
-
Пример 6.9. Для каждого значения параметра а решить
уравнение
sin4* + cos4* = a.
Решение. Так как
1 = sin2* + cos2* ol= (sin2* + cos2*)2 •=
= sin4* + 2sin2*cos2* + cos4*,
то
sin4 * + cos4 * = 1 —sin2 2* = а о
2
sin2 2* = t,
{sin22x =
sin2 2* = 2(1-a),
* = — ±-arcsinJ2(l-a), HZ,
2 2 ч \ '
-<a<l.
2 ~ ""
222
§ €. Тригонометрические уравнения и неравенства
Ответ, а < — : х € 0;
— < а < 1: л; = — ± — arcsin J2(l-a);
2 2 2 у v '
а = 1: х = —;
2
а > 1: х е 0, ft eZ.
Пример 6.10. Для каждого значения параметра а найти
решения смешанной системы
[-4 < х < -2.
Решение. Заменим уравнение смешанной системы
равносильной ему совокупностью:
ctg x = ■
VoeR.
1
Уз'
kez,
-2
x =
Va
-4
JC =
x *
-4
3
e I
<
г -
<
x<
a,
tv, Л
x<
-к, n e z,
-2,
-2
л: = -•
Va
2tv
3'
a ^ tv,
2<a<4.
На КП-плоскости хОа множество всех точек, значения
координаты х и параметра а каждой из которых
удовлетворяют рассматриваемой смешанной системе, состоит из
прямой х = , параллельной оси Оа, и отрезка прямой
3
х « -а ф -к без точки х = - -к, а = -к.
Ответ. Если а < 2, то jc = ;
3
§ 6. Тригонометрические уравнения и неравенства
223
Рис. 6.10
если 2 < а < — , то х = и х = -а;
3 3
2я 2л
если а = — , то х = ;
3 3
2л 2л
если — <а<л,то х = и х = -а;
3 3
2л
если а = л, то х = ;
3
если л < а < 4, то х = и х = -а;
3
если а > 4, то х = .
3
Пример 6.11. Найти все значения параметра
а € —; — , для каждого из которых уравнение
sin2x + sinx + sin(:c - а) = sina + sin(:c + a)
имеет ровно 5 различных корней на промежутке ; — .
224
§ 6. Тригонометрические уравнения и неравенства
Решение. Применим метод разложения на
множители и заменим данное уравнение равносильной
совокупностью уравнений:
2sinjccosx + sin* - sin a (1 + 2cosjc) = 0 <=>
<=> (1 + 2cosx)(sinx - sin а) = 0 <=>
1.
sin x = sin а
X i
5/г
Рис. 6.11
§ 6. Тригонометрические уравнения и неравенства
225
х = --
2
х ~~з
х = (-)
4*
2*
д: = —,
3
х = а +
дг = -а
Z.
На КП-плоскости хОа жирными линиями изображено
множество всех точек (дс, а) прямоугольника
<— < а ^ —; < х <, —к
1 2 2 4 4]
которые удовлетворяют уравнениям полученной
совокупности.
Искомые значения а те, при которых прямые,
параллельные оси Ох, пересекают данное множество ровно в
2л
б точках. (Заметим, что прямые х = — и х = п - а, а так-
3
4я к v
же прямые х = и х = -п - а пересекаются при а = —).
3 3
Ответ. -¥<а<~. -^«^ «"f ° = ^
Пример 6.12. Найти все значения параметра а,
удовлетворяющие условию 0 < 25 - а2 Ф 1, из которых для всех
значений х выполняется неравенство
а <
V8 si
sin х + cos х .
Решение. Заменим задачу равносильной о
нахождении на КП-плоскости множества всех точек, значения
координат х и параметра а каждой из которых удовлетворяют
системе неравенств
0<25-а2 ?t 1,
а < V8 sin jc + cos x,
-оо < х < +00
724 *| а | < 5,
а < 3sin(x + <p
-оо < х < -foo,
226
§ 6. Тригонометрические уравнения и неравенства
где
О < ф = arcsm — < — .
3 2
Искомое множество представляет собой пересечение
множества точек, задаваемых неравенством а < 3sin (x + ф), с
множеством
JV24 *| а | < 5,
[-00 < X < +оо.
На рис. 6.12 искомое множество изображено двойной
штриховкой.
Ответ. -5 < а <-V24, - V24 <а <-3.
Пример 6.13. Для каждого значения параметра а
решить уравнение
| а — sin х | = а + sin x.
Решение. Воспользовавшись определением
абсолютной величины действительного числа, заменим данное
уравнение равносильной совокупностью смешанных систем:
§ 6. Тригонометрические уравнения и неравенства
227
X
\
In
л
-п
-2л
(
ч
ч
ч
)
к
)
1
1 х = п
..
х = 0 ^
1
х = -л
х = -2;г
Рис. 6.13
[а > sin л:,
[sin х = 0;
а < sin дс,
а > 0,
sin х = 0;
[а = 0,
sinx > О
а > О,
jc = /rrc, k e
а = О,
2Н-К < х < (
На КП-плоскости хОа решение первой системы
совокупности изображается лучами, параллельными параметрической
оси, второй — отрезками координатной оси.
Ответ, а < 0: х е 0;
а = 0: 2k tv < х < (2k + 1) tv , k e Z ;
>0 a = b,fee Z.
Пример 6.14. Для каждого действительного значения
параметра а найти множество корней уравнения
cos2;c + 2cosx - а + 1 = О
228
§ 6. Тригонометрические уравнения и неравенства
Решение. Применяя метод подстановки, получим
cos2x + 2cosx - а + 1 = 2cos2x + 2cosx - а =» 0 <=>
cos х = t,
-1 < t < 1,
(*)
COS ДС =
-1 ± VI + 2a
2 '<=>
0 < a < 4,
-1 + Vl + 2a
COS JC =
— < а < 0 : х = 2kn ± arccos
2 ~ ~ [ 2
0 < a < 4 : x = 2frrc ± arccos
Рис. 6.14
§ 6. Тригонометрические уравнения и неравенства
229
На КП-плоскости Юа множество точек (t, а), для которых
значения координат t и параметра а удовлетворяют
смешанной системе (*), представляет собой часть параболы
а = 2t(t + 1),
находящейся внутри полосы -1 < / < 1 и на её границах.
п * / ч -1 + Vl + 2а
Верхняя ветвь параболы t = t^a) = нахо-
дится в этой полосе при
~
а нижняя ветвь t = t2(a) =
2а
при
1
~2~а~
Ответ.
Если — < а < 0, то х = 2kn ± arccos — —
2 "" ~ 2
если О < а £ 4, то х = 2fcrc ± arccos \9 k e Z .
Пример 6.15. Для каждого действительного числа а
решить уравнение
|соз 2х\ = lain2 х - а\, 0 << х < 2я.
Рис. 6.15
230
§ 6. Тригонометрические уравнения и неравенства
Решение. Выражая косинус удвоенного аргумента
через квадрат синуса однократного аргумента и применяя
метод подстановки, сведем задачу к решению смешанной
системы:
0 < х < 2х,
sin2 х = t,
0 < * < 1,
Jl - 2*| = \t-a\
(1)
(2)
(3)
(4)
0 < х < 2л,
sin2 x = t,
0 < t < 1,
l + a
t = 1 - a.
(1)
(2)
(3)
(4)
Здесь мы при решении уравнения (4) применим
следующую логическую схему «раскрытия» модуля возведением
в квадрат:
\f(x)\ =
[/(*) +<р(*) = 0.
На КП-плоскости Юа множество точек (t, a), значения
координат и параметра каждой из которых удовлетворяют
смешанной системе (3), (4), состоит из точек линий (4),
принадлежащих полосе (3). (На рис. эта полоса заштрихована.)
Сформулируем результат решения КП-метода
смешанной системы (3), (4) для каждого числа а:
если а < -1, то £20;
если а = -1, то t = 0;
л /ч п + 1
если -1 < а < 0, то t = ;
если a = 0, то t — —, t = 1 ;
3
если 0 < a < — , то t = , t = 1 - a;
2 3
если а = — , то * = — ;
1 1
если — < a < 1, то * = 1 - a, t =
2
§ 6. Тригонометрические уравнения и неравенства 231
2
если а = 1, то t = -1, t = —;
3
а -hi
если 1 < а < 2, то t = ;
3
если а = 2, то t = 1;
если а > 2, то t£0.
Возвращаясь к начальной переменной х,
воспользовавшись подстановкой (2) и условием (1), получим ответ.
Ответ. Если а < -1, то корней нет;
если а = -1, то х = 0, х = к, х = 2я;
если -1 < а < 0, то
/а + 1 . /а + 1
х = arcsin J , jc = я - arcsin J ,
V з V з
\а + 1 _ . /а + 1
х = тс + arcsin J , х = 2тг - arcsin J ;
V з V з
если а = 0, то
п Зтг .1 .1
х = — ,х = — , х = arcsin-p, х = я-arcsin-р ;
2 2 >/3 v3
х = к + arcsin -т=-, х = 2п - arcsin —j= ;
V3 V3
если 0 < а < — , то
х = arcsin Vl-а, л: = я - arcsin Vl-а ,
jc = я + arcsin Vl-а , дс = 2я - arcsin Vl-а ,
. /l + а . /l + а
х = arcsin,./ , л: = я - arcsin J ,
V 3 V 3
/l + а о . /l + а
х = 2я - arcsin J
1 я Зя 5я 7я
если а = —, то х = —, х = —, х = —, х = — ;
2 4 4 4 4
если — < а < 1, то
2
х = arcsin Vl-а, х = я - arcsin Vl-а ,
х = я + arcsin Vl-а, х = 2я - arcsin Vl-а ,
232 §6. Тригонометрические уравнения и неравенства
ll + a . /l + a
х = arcsin J , x = n - arcsin J ,
V 3 V 3
. ll + a o . ll + a
x = n + arcsin J , x = 2n - arcsin i
V 3
если a = 1, то
(2
x = 0, x = 7Г, x = 2tt, x = arcsin./—, jc =
# = 71 + arcsm J—, jc = zrc -
если 1 < a < 2, то
. /a + 1 . /a + 1
jc = arcsm J , x = n - arcsin J ;
V 3 V 3
. /a + 1 _ . /a + 1
x = я + arcsin J , x = 2n- arcsin,,
V 3
n Sn
если a = 2, то л: = —, x = — ;
2 2
если a > 2, то корней нет,
Замечание, При записи окончательного ответа
использована следующая равносильность:
х = arcsm
0<л:
„ х = п - arcsin
sin х = t0,
0<t <1 x = n + arcsin
x = 2n - arcsin
Пример 6.16. Найти все действительные числа р, при
которых существует единственное число х,
удовлетворяющее системе:
[cos 2nx = 1,
1(2* + 4р2 - 11)(б* - р2 - 34) < 0.
Решение. Данная смешанная система равносильна
системе
f 6. Тригонометрические ур нения и неравенства
233
a = p2l
cos 2 л*
(2* + 4а
а = Р2>
x = k€t
(2х + 4а
:0,
= 1,
-11)
0,
5,
-11)
•(6*-
(бх-
а-34)
а-34)
<0;
<0;
Прямые 2х + 4а-11 = 0и6х-а-34 = 0 разбивают
КП-плоскость на хОа на «частичные» области I-IV, в
каждой из которых левая часть неравенства системы сохраняет
знак. Решением этого неравенства на КП-плоскости есть
области I и III.
Рис. 6.16
234 §6. Тригонометрические уравнения и неравенства
Единственное целочисленное решение х = k e Z при а > О
есть х = 5 и принадлежит области I для всех значений
параметра
(1 3
a е —; —
U 4
Следовательно, при всех действительных значениях
параметра р, удовлетворяющих условию
существует единственное число х = 5, удовлетворяющее
исходной смешанной системе.
Ответ. — <Ы <— .
2 ]п 2
Пример 6.17. Найти все целые корни уравнения
cos
Г-(з* - >J9x2 +160* + 800 И = 1 .
Решение. Заменив данное уравнение уравнением с
целочисленным параметром, запишем следующие
равносильные высказывания:
-(Зл: - yJ9x2 +160* + 800) = 2лп, х G Z, п
yJ9x2 + 160* + 800 = 3* - 16л, * G Z, n G Z,
13* - 16n > 0, * G Z, n G Z
9*2 + 160* + 800 = (3* - 16л)2 ^
16
x>-n, neZ,
x = -|24n - 40 - -Ш-
§ 6. Тригонометрические уравнения и неравенства
235
= -(24п-40-х),
х>ул,
25
х =
Зп + 5
х =-(24л-40-х),
х + 24л + 40 < 0,
х =
25
Зл + 5
, л G Z.
(1)
(2)
(3)
На КП-плоскости х Оа найдем точки, имеющие
целочисленные значения координат х и параметра а,
удовлетворяющие условиям (3) и (2). Эти точки принадлежат нижней
ветви гиперболы
25
х =
За + 5
■25
Рис. 6.17
236 §6. Тригонометрические уравнения и неравенства
расположенной в полуплоскости х + 24а + 40 < 0 . При
а < -10 точки, расположенные на этой ветви гиперболы,
имеют дробные значения координат. Проверкой
убеждаемся, что допустимым целочисленным значениям
a G {-10,-9,-8,-7, -6, -5,-4,-3,-2} только а = -10 и
а = -2 соответствуют целочисленные значения х = — 1 и
х = — 25 точек, принадлежащих рассматриваемой ветви
гиперболы.
Следовательно, в силу (1) х = -31 и х = -7.
Ответ, х = -31, х = -7.
Замечание. Можно дать другое решение задачи. Чтобы х
и п были целыми, должны выполняться условия Зд + 5 =
= -1, 5, -25, при п = -2, 0, -10 соответственно. Условию
(2) удовлетворяют только # = -25 и х = -1 при п — -2 и
п = -10.
Пример 6.18. Найти все корни уравнения
tg\ —cosл: = cte[—sin* I
принадлежащие промежутку
-я <, х <, Зя .
Решение. Имеют место следующие равносильные
высказывания:
tgjjcos*) = ctgjjsin*) О tgjjcos*) = ctg[| -|sinx)
—cosx = sin# + kn *■ — + mn
2 2 2 2
cos x -f sin x = 2k 4-1,
(2k 4-1)2 < 2,
cos x ^ 2m + 1,
(Aj, m g Z)
f cos x + sin jc = 1
[cos jc * ± -1;
jcos x + sin x = -1,
[cos* ^ ±1
d, peZ'
§ 6. Тригонометрические уравнения и неравенства
237
Рис. 6.18
На КП-плоскости хОа, где параметры а = р е Z, искомыми
значениями х являются точки полосы -п ^ х £ Зя,
расположенные на прямой jc = — + 2па и имеющие координаты, со-
ответствующие целочисленным значениям параметра а = р е
е {-1, 0, 1, 2}.
Ответ. Ж6|--;-5Т;Т|.
Пример 6.19. Для каждого значения параметра а * О
решить неравенство
sin* + acosx < a.
238
§ 6. Тригонометрические уравнения и неравенства
Решение. Применяя универсальную
рационализирующую подстановку, заменим неравенство равносильной
смешанной системой:
а* О,
2t
1-t2
t2 1 + t2
t(at-l)>0.
*!-••
a >0,
1.
a
a <0,
Решим совокупность систем КП-методом (см. рис.).
Следовательно, если а < 0, то — < tg— < 0; если а > О,
а 2
ш х ^ х 1
то tg — < О и tg — > — .
2 2 а
Записывая решение простейших тригонометрических
неравенств, получим ответ.
Ответ. Если а < 0, то 2/nv + 2 arctg — < * < 2/rrc;
а
если а > 0, то 2Ы + 2 arctg— < jc < tv 4-
а
§ 6. Тригонометрические уравнения и неравенства
239
Пример 6.20. На координатно-параметрической
плоскости хОа указать все точки, значения координаты х и
параметра а каждой из которых таковы, что выражение
+ 2a -
положительно при всяком значении t, и изобразить
область, образуемую этими точками.
Решение. Так как данное выражение можно
преобразовать к виду:
Ф = sin2 [t + a) + 2 sin (t + a) cos (a - x) + — =
= [sin {t + a) + cos (a - x)] + — cos2 (a - x),
то при всяком значении t (такое t существует при любых х к
а, например, t = х) выражение в квадратной скобке
равно нулю.
Следовательно,
[ф > 0, W e R,
[sin (t + a) + cos (a - x) = O,
cos2(a-x)>0,
4 v о
1 ,
__<Cos(a-
We JR;
3
2tt
3
240
§ 6. Тригонометрические уравнения и неравенства
Рис. 6.20
На КП-плоскости хОа множество всех точек (jc, а),
значения координаты х и параметра а каждой из которых
удовлетворяют этому двойному неравенству, состоит из всех
точек, находящихся внутри любой полосы, образованной
парами параллельных прямых:
а -х =
а - х = kn + — ,
3
где ke Z.
Пример 6.21. При каких значениях параметра а не для
всех действительных значений х справедливы неравенства
ИЛИ
2cos
2cos2
!(2"-')
-I
>a
< а +
sin
(22*-*M)
Решение. Применяя правило логического отрицания
и метод подстановки, получим для нахождения а
следующие равносильные высказывания:
§ 6. Тригонометрические уравнения и неравенства
241
-Л/* е R :
Рис. 6.21
R : 2соз2(22'-ж2) = a + Vising2*-*41),
f
0 < t й 4,
cos f - v3 sin t = a -1
= t.
0 < t < 4,
2соэ|( + -|-
Зя к . Зя n
Так как я<4<2я,то <4< — + —.
2 3 2 3
Следовательно,
242 §6. Тригонометрические уравнения и неравенства
На КП-плоскости для 0<£<4и-1<а<2 жирной линие|
(а = 2 cos t + — + 1) изображено решение полученной сме
V %)
шанной системы.
Ответ. -1 < а < 2
Пример 6.22. Пусть х1 — наибольший отрицательный
корень уравнения
>/з sin х - 3 cos x = 2а - 1,
а х2 — наименьший положительный корень уравнения
2cos2jc-2sin2* = а .
Найти все значения а, при каждом из которых \хг\ < х2.
Решение. На КП-плоскости хОа изображены
(жирными линиями и точкой) множества всех точек,
координаты которых задают зависимости от параметра а
наибольшего отрицательного корня х = хх (а) уравнения
( п\ 2а-1
2а-1 <=> sin х— = г*~
\ 3) 2^3
и наименьшего положительного корня х = х2(а) уравнения
2cos2 x-2sin2 х = а о а = 2cos2x .
Анализ этих зависимостей показывает, что
если >/з<а-1,тоО< ^(а)! < —, — < х2(а);
2 6 3
если а — -1, то |^с1(а)| = х2(о) = — ;
3
если -1 < а < 2, то \хх(а)\ > х2(а);
если а = 2, то (^(а)! = х2(а) = п .
§ 6. Тригонометрические уравнения и неравенства
243
Рис. 6.22
Следовательно,
\Xl(a)\ < х2(а)
a = 2.
Ответ. --V3<a<-l,a = 2.
2
244 § 6. Тригонометрические уравнения и неравенства
Упражнения
1. На координатно-параметрическои плоскости аОх с
вертикальной параметрической осью Оа изобразить
множества всех точек, значения координаты х и параметра а
каждой из которых удовлетворяют следующим
соотношениям:
а) в = 1™£]. б) a=|sin*|ctg*;
sin л:
в) а = Vsin2* + l-2sinjc ; г) а = (sin | x | + cos | x |) ;
д) а=|а|создг; е) а2 + СО82х = 1;
ж) | а \= sin | х |; 3) а =| а - sin x \;
и) а =| а - tg* |; к) | а + х |= sin | x \.
л) а > sin | х |;
2. Ha координатно-параметрическои плоскости хОа с
горизонтальной параметрической осью Оа изобразить
множества всех точек, значения координаты х и
параметра а каждой из которых удовлетворяют следующим
соотношениям:
a) sin2:c = sin2a; б) cos(jc + a) = cos(# - a);
в) sin* = cos(* + a); r) sin x =\ sin a |;
Д) cos I x I + sin I a |= 0 ; e) •
ж) tg(sin* + sina) = 0; з) tgxtga = 1;
и) sinjc > sina; к) tgx > tga.
л) | sin x | + | sin a |< 2 ;
3. Для каждого значения параметра а решить
неравенство
I tgx \< a
Ответ. Если а > 0, то -arctga + kn < х < knt kn < х <
< arctga + kn;
если a <i 0, то x e 0; k e Z.
4. Определить все действительные значения а, при
каждом из которых уравнение
§ 6. Тригонометрические уравнения и неравенства 245
cos4 х - (а + 2)cos2 х - (а + 3) = О
имеет решения, и найти все эти решения.
Ответ. -3 < а <, -2: х = ±arccosVa + 3 + knf k e Z.
Указание. Сделать подстановку cos2* = t, 0 < t ^ 1.
5. Найти все целые значения параметра а, при которых
уравнение
2 - 2cos2x = За + 4sin*
ныеет хотя бы одно решение.
Ответ, а е {0; 1;2}.
Указание. Сделать подстановку sin* = t, -I £ t <> 1.
6. Найти наибольшее значение параметра а, при
котором х удовлетворяет уравнению
sin4x - cos4* = a.
Ответ, a^ = 1.
Указание, sin4* - cos4* = -cos2*.
7. Для каждого значения параметра а решить уравнение
sine* + cosex = a.
Ответ. Если a < —, то * е 0;
4
1 Ли , iv
если а = т,то * = — ±т;
4 z 4
1 л kn \
если — < а < 1, то * = — ± — arcsin
4 2 2 V
если а = 1, то л: = —; если а > 1, то х б 0; ft e Z.
2
Указание. Уравнение равносильно
sin2 2* = -(1- а) = 6,
3V у
Для каждого значения параметра а решить уравнения:
246 § 6, Тригонометрические уравнения и неравенства
8. sin х =| а |
Ответ. Если а < -1, то х е 0;
если а = -1, то х = — + 2ftrc ;
если — 1 < а < 0, то х = -arcsina + 2ft/г, х = arcsina
+ (2ft + 1)гс;
если а = 0, то х = 2Ля, jc = (2Л + 1)я;
если 0 < а < 1, то х = arcsina + 2Ля, х = -arcsina-
+ (2Л + 1)я;
если а = 1,то х = — + 2Лтг;
2
если а > 1, то х € 0; ft e Z.
9. | а |= а сое х.
Ответ. Если а < 0, то х = 2ft + 1;
если а = 0, то Уде е Ш ;
если а > 0, то х = 2ft; fte Z.
10. sin7t(|a| + |*|)-Vl-a2-*2 =0.
Ответ. Если а < -1, то х е 0;
если а = -1, то х = 0;
если -1 < а < О, то х е l-yl - а2; -1 - а; 1 + a; vl - a
если а = 0, то х е {-1; 0; 1};
О < а < 1, то х g l-Vl-а2; -1 + а; 1 - а; Vl-а2 ;
если
если а = 1, то х = 0; если а > 1, то jcg0.
11. Для каждого значения параметра а решить смешан
ную систему
sin10 х + cos7 x = 1,
jc > a,
Ответ. Если а < 0, то * = 0; х = —;
§ 6. Тригонометрические уравнения и неравенства 247
71 Л
если 0 < а < — , то х = — ;
2 2
если а > — , то х е 0.
12. Найти все значения параметра а, при которых
система
Ugnx = О,
a2-l)(2*-3)<0
шеет единственное решение.
Ответ. При -1 < а < 1.
Указание. Система равносильна
х = k e Z,
a2<JC<i.
- "2
13. Сколько корней на отрезке хе[-п; я] имеет уравнение
х2 + а =
зли параметр Ь имеет наименьшее возможное значение
рмм квадратов корней квадратного трехчлена
Ответ. Ь = — . Если a < -1-я2, то х е 0;
если -1-п2<а < 1, то два корня;
если а = 1, то один корень;
если а > 1, то х е 0.
14. При каких значениях параметра а уравнение
_ 1+|cosjc1
sin | jc |
меет: ровно два корня; б) ровно четыре корня?
Ответ, а) а = -1, а = 1; б) а < -1, a > 1.
248 §6. Тригонометрические уравнения и неравенства
15. При каких значениях а уравнение
cos2jc + 2cosjc - 2а2 - 2а + 1 = О
имеет ровно одно решение на промежутке 0 < х < 2л?
Ответ, а = -2, а = 1.
16. При каких значениях а уравнение
cos2jc + 2(2а - l)sinx - 2а2 + 2а - 1 = О
имеет ровно три решения на промежутке 0 <, х < 2л?
Ответ, а = 0, а = 1.
17. Для каждого значения а найти число решенив
уравнения
actgx - 1 = cos2jc,
принадлежащих промежутку 0 < х ^ 2л.
Ответ. При а < -1, а = О, а > 1 — два решения;
при а = ±1 — четыре решения;
при -1<а<1,а*0 — шесть решений.
18. На КП-плоскости хОа указать все точки, значения
координаты х и параметра а каждой из которых таковы,
что логарифм выражения
Ф(х,а,О= — (cos л: — 1) +sina-f
2
-f cos 2 (t + a) -f 2 sin (t + a) cos x
при всяком значении t существует, и изобразить область,
образуемую этими точками.
Ответ. Искомое множество состоит из всех внутренних
точек квадратов, образованных пересечением двух
множеств параллельных прямых, уравнения которых
находятся из условия
sina = cos*.
Указание. Преобразовать выражение к виду
Ф(х, a, t) = sin a -cos x + 2 sin(f+ a)—cos*
§ 6. Тригонометрические уравнения и неравенства 249
При любых а п х существует такое t, при котором
sin (t + a) cos x = О»
v ' 2
например, t = -a + arcsin —
Так как по условию задачи должно быть выполнено
неравенство Ф(х, а, О при всех значениях tt то задача
сводится к нахождению множества всех точек (х, а), для которых
sina - cos* > 0.
19. Для каждого значения параметра а решить
уравнение
sin2 х + sin2 2x + sin2 Sx - 2а(sin x + sin2x + sinЗх) +
+ cos* - созЗ* -f 2a2 = 0.
Ответ. Если a = 0, то х = Ля, jc = , Л, л е Z;
3
если а * 0, то jc e 0.
Указание. Уравнение равносильно
/ \2 / ч2 fa = sin x + sin 2x,
(sinjc + sin2*-a) +(sin3*-a) =0o
[a = sin 3*.
§ 7. Различные трансцендентные уравнения
и неравенства с параметрами
Пример 7.1. Для каждого значения параметра а найти
все значения х, при которых смешанная система
logeinxcosx = l,
О < х < 1,
х = а + sin (arcsin (x - а)).
Дать геометрическую интерпретацию решения на коор-
динатно-параметрической плоскости хОа с горизонтальной
параметрической осью.
Решение. Так как
sin(arcsin/) =
(7.1)
то рассматриваемая смешанная система равносильна
х = — + 2/ггс, k е
4
О < х < 1,
-К л:-а <1
Рис. 7.1
§ 7. Различные трансцендентные уравнения и неравенства 251
На КП-плоскости решение системы состоит из точек
отрезка прямой х = — , заключенного внутри параллелограмма
4
со сторонами х = О, х = 1,их = а-1, х = а + 1 (на рис. он
заштрихован).
Ответ. а< 1 : х € 0;
4
а > — + 1:
4
0
Пример 7.2. Для каждого значения параметра а найти
все значения х, при которых справедлива смешанная
система
sin их = О,
х - а = sin (arcsin (x - а)),
х + а = arcsin (sin (x + а)).
252 §7, Различные трансцендентные уравнения и неравенства
Решение. Так как
arcsin(sin t) = t
—
(7.2)
Ответ. Если а < -1, то х e 0;
если -1 < a < 1 —, то х = 0;
2
если 1-— ^ a < 0 , то x = -1, x = 0;
если a = 0, то x = -1, л: = 0, л: = 1;
если 0<ай — 1, то ж — 0, ж я 1;
если 1<а<1,тол:=10;
если а > 1, то х е 0.
Пример 7.3. Для каждого значения параметра 0 < а * 1
решить уравнение
(loga sin jc)2 + \oga sin jc - a = 0 .
Решение. Применяя метод подстановки, заменим
уравнение равносильной совокупностью смешанных систем:
0 < a < 1,
t2 +t-a =
logosinx = t < 0,
t2 +t-a = O;
0 < a < 1,
/1 + 4а -1
-1 - Vl + 4а
Vl+40-1
Ответ. Если 0 < a < 1, то х = ferc + (-1) arcsina 2
если a > 1, то Jt = Ая + (-1)* arcsina 2 , где k e Z.
§ 7. Различные трансцендентные уравнения и неравенства 253
-2
Рис. 7.3
Пример 7.4. Для каждого допустимого значения
параметра а решить уравнение
lg (arctg*) + lg(arcctgjc) = а .
Решение. Воспользуемся тождеством
arctg х + arcctg x = — ,
2
заменим уравнение равносильной смешанной системой:
arctg* > 0,
— arctg* > 0, <^>
2
arctgjcf- - arctg* j = 10°;
arctgx
0<t<
2:
= t,
f.
= 10"
(l)
(2)
= b > 0. (3)
На КП-плоскости ЮЬ множество всех точек (t;b)t значения
координаты и параметра каждой из которых удовлетворяют
смешанной системе (2), (3), представляет собой часть
параболы.
254 § 7. Различные трансцендентные уравнения и неравенства
расположенной в области задаваемой неравенствами
системы (2), (3) (на рис. эта область заштрихована).
Следовательно, если
то
= t12(a)
n±yJn2-1610a
Рис. 7.4
Ответ. Если а <, \g— , то х = хг 2(а) = tgtl2(a)
16
. п±у/п2 -16 10а
-tg ;
при остальных значениях а корней нет.
§ 7. Различные трансцендентные уравнения и неравенства 255
Пример 7.5. Для каждого значения параметра 0 < а * *_
решить неравенство
1 1
—: : >
Решение. Применяя метод подстановки, заменим
данное выражение равносильной системой
ГО < а < 1,
L
<=>
U
1
a*lnx = tt
fO < a < 1,
|а>1,
1<*<
1а
(1)
(2)
(3)
at -1 1 -1
2 1
Если 0 < a < 1, то а < 1 < < —; если a > 1, то
1 + а а
1 2 л
— < < 1 < а .
а 1 + а
На КП-плоскости Юа множество точек (t; а), значения
координат и параметра каждой из которых удовлетворяют
системе (2)-(4), заштриховано. Следовательно, для каждого
значения параметра 0 < а*1 решение системы (2)-(4) имеет
вид:
2
если 0 < а < 1, то 1 <t < ;
1 + а
1 2
если а > 1, то — < t < и 1 < t < a.
а 1 + а
Воспользовавшись подстановкой (1) и переходя к
первоначальной переменной, получим:
если 0 < а < 1, то
,a8in* <_JL.0loge(-A_|<sinx<0;
1 + a
(5)
256 § 7. Различные трансцендентные уравнения и неравенства
ii.ii
i \ -I-
24 \ |
Рис. 7.6
если а > 1, то
а 1 + а
l<asinx £а
logfl
(в)
О <sinx£l.
Решая полученные простейшие двойные
тригонометрические неравенства (5)-(7), находим ответ.
Ответ. Если 0 < а < 1, то
2kn + arcsinlog
< х < 2kn ,
( 2 \
(2k + 1) ж x < (2k + 1) я - arcsin log e ;
если a > 1, то
/ 2 \ Г 2 "\
- l) n - arcsin loga < x < 2kn + arcsin log. ,
{1 + a) U + aJ
x * — + 2kn , 2kn < x < (2k + 1)tt , k
§ 7. Различные трансцендентные уравнения и неравенства 257
Пример 7.6. Для каждого действительного параметра а
найти все значения х из интервала 0 < х < - ,
удовлетворяющие неравенству х
Решение,
Го < х < 1,
[sin дс - а < 0;
inA: - а > 0.
Ответ. Если а < 0, то 1 < д: < — ;
2
если 0 < а < sinl, то 0 < х < arcsina, 1 < х < — ;
2
если sinl <а<1, toO<jc<1, arcsina < x < —
если а>1,тоО<дг<1.
9-3683
258 §7. Различные трансцендентные уравнения и неравенства
Пример 7.7. Для каждого значения параметра а найти
решения неравенства
\ogax + xa \oga-<xa
удовлетворяющие условию
Решение. На множестве М из области допустимых
значений переменной х и параметра а, удовлетворяющих
условиям
М
О < х <-,
2
О < а * 1,
запишем исходное неравенство в каноническом виде и
представим его левую часть как произведение двух базовых
функций:
(loga*-logaa)(*ain*-xfl)<0
~(a-l)(x-a)(x-l)(sinx-a)<0
<=> (а - 1)(х - а)(х - 1)(х - arcsin а) < О,
так как
sin х - a v 0 <=> sin дс - sin (arcsin a) v 0 <=> x - arcsin a v 0.
M V 7 M
На координатно-параметрической плоскости хОа решение
рассматриваемой задачи изображено в виде
заштрихованных областей.
Ответ. Если 0 < а < sin 1, то х е (a; arcsin а) и 1; — ;
V 2 у
если sinl < а < 1, то хе(а; l)u arcsin а; — ;
v 2 У
§ 7. Различные трансцендентные уравнения и неравенства 259
Рис. 7.7
если 1 < а < — , то х е \
2
если а > — , то хе(0; 1).
Пример 7.8. При каких значениях параметра а
неравенство
ч2а>*+1 V16arcsin~4(*
х2+2а2х+1 V
(Х
Не имеет решений на отрезке [-5; 6]?
Решение. Пусть
и = ах2 + 2а2х + 1, / = ^16 arcsin 4 (х + За)
(1)
Тогда при всех значениях переменной х и параметра а из
области допустимых значений (ОДЗ), определяемых
условиями
-За < х Z -За
260 § 7. Различные трансцендентные уравнения и неравенства
имеем f
arcsin2(:c
На КП-плоскости хОа множество (2) есть полоса с
границами х = -За - 1 и х = -За + 1 без точек прямой х = -За.
В силу логических схем
F>0\
guf>0, lu> 1,
/>1 °/>l
получим logu / ^ |logu /| <=> logu / > 0 и, так как f > 1,
Ух е D(f), то
Jlogu / > О, Г
u > 1,
x e D(f).
(3)
Запишем систему (З), воспользовавшись обозначением (1) и
условиями (2), следующим образом:
ах2 + 2а2х + 1 > 1,
-За -1 < х < -За, о
-За < х < -За +1;
ах(х + 2а) > 0,
-За -1 < х < -За,
-За < х £-За + 1.
(4)
Изобразим на КП-плоскости (заштрихуем) можество всех
точек (jc; a), значения координаты и параметра каждой из
которых удовлетворяют системе неравенств (4).
Для изображения на КП-плоскости решения неравенства
Ф(х, а) = ах(х + 2а) > 0 (5)
разобьем ее на шесть «частичных» областей линиями
a = 0; х - 0; х -= -2а,
вдоль которых Ф(дг, а) = 0. При переходе через эти линии
выражение Ф{х, а) меняет знак на противоположный и
сохраняет его в каждой из рассматриваемых областей I—VI.
§ 7. Различные трансцендентные уравнения и неравенства 261
Пусть, например, х = 1, а = 1 — точка I области. Так
как Ф(1, 1) = 3 > 0, то всюду в I области Ф(х, а) > 0.
Следовательно, во II области Ф(я, а) < 0, в III — Ф(х, а) > 0 и
т.д. Решением неравенства (5) является I, III и V частичные
области без границ.
Пересечение эих областей с множеством (2) дает на
КП-плоскости изображение искомого множества (4) (на рис.
оно заштриховано). Зная изображение решения исходного
неравенства на КП-плоскости, нетрудно найти значения
параметра а, при которых точки с соответствующими
координатами хе[-5; 6] не принадлежат полученному
множеству (4), т.е. это неравенство не имеет решений на отрезке
[-5; 6].
-4
Рис. 7.8
Ответ, а < -1, а = 0, а > 2.
262 §7. Различные трансцендентные уравнения и неравенства
Упражнения
1. На координатно-параметрическои плоскости изобра
зить множество всех точек, значения координаты х и пара
метра а каждой из которых удовлетворяют следующим со
отношениям:
а) а = \g tgx + \g ctgx; 6) sin x = log2 a;
в) 3cos^ = log2(a-3); r) a + loghinjc)2 = 0;
3
д) a-logsinxcosx = 0; e) loga sin* > 0;
ж) loga |sinx|>0; з) logCO8X(|a| - 2) > 0;
и) | sinx \a + | cos* |a= 1; к) a = arccos(cosjc);
л) a = arcsin (| sin x |); м) arcsin x = arccos a.
2. При каких значениях параметра а уравнение
2tgx = a
имеет на промежутке
ровно один корень?
Ответ. 0 < а < 1.
3. Найти кони уравнения
при максимальном значении параметра а.
Ответ, х - — + kn , k eZ .
2
4. Для каждого значения параметра а установить число
корней уравнения
arcsin (sin x) = а
m промежутке
0 < х < 2п.
Ответ, а < —, х е 0;
2
§ 7. Различные трансцендентные уравнения и неравенства 263
п
а = — : один корень;
с*
— < а < 0: два корня;
а = 0: три корня;
п
0 < а < —: два корня;
П
а = — : один корень;
а > — : х е 0.
5. Для каждого значения параметра а установить число
корней уравнения
lgsinx = a
на промежутке
0 < х < 3/г,
О т в е т. а < 0: четыре корня;
а = 0: два корня;
а > 0: х е 0.
6. Для каждого значения параметра а установить число
корней уравнения
2i+ein* =1_a
на промежутке
0 < х ^ 2к.
Ответ, а < -3: х е 0;
а = -3: один корень;
-3 < а < -1: два корня;
а = -1: три корня;
-1 < а < 0: два корня;
а = 0: один корень;
а > 0: х g 0.
Указание. Рассмотреть систему
Isin jc = log2 —г— = &•
ч 2 )
0 < jc £ 2л.
264 §7. Различные трансцендентные уравнения и неравенства
7. Для каждого допустимого значения параметра а
решить уравнение
loga (sin x + cosх) = 2 •
Ответ. Если 0 < a * 1, | a |= 3/2 , то
х = — + 2kn ± arccos-7= ;
4 V2
при остальных а решений нет.
8. Для каждого значения параметра а решить уравнение
y]\g sin nx = а
Ответ, а < 0: х е 0;
а > 0: х е 0.
9. Для каждого значения параметра а решить
неравенства:
Ответ, а) а < 0: х е 0;
0 < а < 1: |х jc^— , Л €
а > 1: х е 0;
б) а < 1: х е 0;
а> 1: |хх* *2L,*€
1 2'
10. Для каждого значения параметра а решить
неравенство
а) cos* > а2 +лЬ-х2 -1, б) 2arcsin(x2 + а) > я(2-а).
Ответ а) а = 0: jc — 0;
пря о сальных а решений нет.
б) а = 1: х = 0;
щи остальных а решений нет.
11. Для каждого значения параметра а решить
смешанные системы:
f х = sin (arcsin x),
> а:
§ 7. Различные трансцендентные уравнения и неравенства 265
Ответ, а < -1: -1 <, х < 1;
-1 < а <, 1: а <, х <, 1;
а = 1: х=1;
а > 1: х е 0.
Указание. Рассмотреть равносильную систему
неравенств:
Г-1 < х < 1,
\х> а.
а)
I
л: = sin (arcsin x),
(1)
(2)
Ответ.а<1:х = 1;а> 1:хб 0.
Указание. Решение уравнения (1) подставить в (2) и (3).
J
в) j jc = sin(arcsin x),
[х > а;
Ответ, а < -1: х = -1, х = 0;
-1 < а^О: д: = 0;
а > 0: х е 0.
52х+122х=132х,
г)
х = sin (arcsin jc) ,
х > а;
Ответ, а < 1: х = 1,
а > 1: х е 0.
log8inxcosx =
Д)
jc = sin (arcsin дс),
Ответ, а < — : х е 0;
4
Я ^ ^. Я 71
— < а < — : лг = —;
4 4 4
а > - ; х е 0.
4
266 § 7. Различные трансцендентные уравнения и неравенства
12. Для каждого значения параметра а решить
смешанную систему
tgnx = О,
а = sin (arcsin a),
О < х < а2.
Ответ, a < -1: х е 0;
а = -1: х = О, х = 1;
-1 < а < 1: х = 0;
а = 1: х = 0, х = 1;
а > 1: х € 0.
13. Для каждого допустимого значения параметра а
решить систему уравнений относительно х:
I-V2 = yj\ogx ax • loga х
а = sin (arcsin a).
Ответ, а < 0: х £ 0;
О < а < 1: х = а"2;
а > 1: х е 0.
14. Для каждого допустимого значения параметра а
решить смешанные системы:
|х = arcsin (sin x),
х>а;
Ответ. а< — : — <х<—;
2 2 2
п п т п в
~12<а<~2'а~Х ~~2'
п п
а > — : х е 0.
2
Указание, х - arcsin (sin x)<=> — ^ х < —.
§ 7. Различные трансцендентные уравнения и неравенства 267
Isin6 х + cos5 x = 2 - sin2 jc, (1)
x = arcsin (sin x), (2)
lg|a|. (3)
Ответ. a < -— : x e 0;
2
П . 71
--<a<0:x = -;
a = 0: x e 0;
0<a< — :x=—;
2 2
a > - : x is 0.
2
Указание. Решая уравнение (1), применить неравенства
sin5 x + cos5 x < sin2 x + cos2 x < 1, 2 - sin2 x > 1
и, получив множество его корней х = — + 2&я , k € Ъ, вы-
брать из этого множества при k = 0 корень х = —, который
2
удовлетворяет уравнению (2).
15. Для каждого значения параметра а решить систему
уравнений относительно х:
1х2 + 4* cos (a*)+ 4 = 0,
пх = 4 arcsin (sin а).
Ответ, а = — + 2ттт, /м £ Z : х = 2;
при остальных а решений нет.
16. При каких значениях параметра а неравенство
. | sinх - V3cosx-a-4 I
log_2a_13 > 0
выполняется для любых значений х?
13
Ответ, a <-11; -7 < а < — .
268 §7. Различные трансцендентные уравнения и неравенства
17. Для каждого значения параметра а решить
уравнение
Ответ, а < 0: х ё 0;
а > 0: х = kn± arcsin 2 * 2а , fe £ Z.
18. При каких значениях параметра & в уравнение
tg\b\=\og2(cosx-\x\)
имеет ровно один корень?
Ответ, b = fc/г, k e Z.
Указание. Ввести параметр а = tg | b \ и,
воспользовавшись четностью правой части уравнения относительно х
а = 1о£2(соз*~|дг|),
показать, что уравнение имеет ровно один корень при а = 0.
19. Найти периметр фигуры, заданной на КП-плоскости
хОа условиями
J2 | а + 2 | arcsin((* -1)2 j < л(а + 2),
[2 | х -11 -a > 0.
Ответ. 10 + 2л/5.
20. Найти все значения р, при которых фигура,
заданная на КП-плоскости хОа условием
I * I ^ (Vp-UI) + arcsin(sin{p -1 * I))'
представляет собой 14-угольник.
_ 5л 7я
Ответ. —<Р^ — .
2 F 2
§ 8. Задачи на движение
Решая текстовые задачи на движение, изобразим на
КП-плоскости зависимость координат от времени для
каждого из движущихся тел. Получим простой алгоритм
построения системы уравнений и неравенств для определения
искомых величин.
Пример 8.1. Из города В в город А в 5 ч 30 мин вылетел
самолёт. В 8 ч 30 мин из А в Б вылетел вертолет. Скорости
самолета и вертолёта на всём пути постоянные, и они летят
по одной трассе. После их встречи вертолёт прибыл в Б
через 9 ч, а самолёт прибыл в А через 2 ч. Найти время
прибытия самолёта в город А.
Решение. Направим координатную ось от А к Б с
началом в А. Отсчёт времени t будем проводить от момента
вылета самолёта из города Б.
Изобразим на КП-плоскости xAt зависимости от
времени t координат х самолёта (прямая BD ) и вертолёта
(прямая EN).
Обозначим через т (час) (т > 0) время полёта вертолёта
из города А до встречи с самолётом в С.
Из подобия двух пар прямоугольных треугольников
СЕР и CNM, CDP и СВМ имеем пропорцию
270
§ 8. Задачи на движение
т
9
СР
СМ 3 + т
Отсюда находим положительное т = 3.
Следовательно, самолёт прибудет в город А через 8 ч, то
есть в 13 ч 30 мин.
Ответ. 13 ч 40 мин.
Пример 8.2. Из города А в город Б, расстояние между
которыми 200 км, мотоциклист ехал 6 ч. Сначала он
двигался со скоростью Vl9 превышающей 15 км/ч, а потом со
скоростью V2, причём время движения с каждой скоростью
пропорционально этой скорости. Через 4 ч после выезда
мотоциклист был в 120 км от города А. Определить
скорости Vx и V2.
120
2 3 4 f, 5 6 *
"Л
i, 3 4 5 6'
Рис. 8.2
Решение. Изобразим на КП-плоскости xAt две
возможные зависимости координаты х от времени t, обозначив
через tl (ч) время движения мотоциклиста со скоростью Vt.
По условию задачи имеем уравнения
= ^/1+^(6-/,)
(1)
(2)
Если
4 < t{ < 6,
то 120 = АУХ то есть Vt = 30 (км/ч).
(3)
§ 8. Задачи на движение
271
Исключив из уравнений (1) и (2) К2, получим для
определения t! квадратное уравнение 3/j2 - 28/j + 54 = 0 .
Корни этого уравнения не удовлетворяют условию (3),
Следовательно, первый случай не может иметь место. Если
(4)
(5)
О </, <4f
то по условию задачи имеем уравнение
120 = ^+^(4-/!),
откуда, с учётом уравнений (1) и (2), получим
V2 = 40, t2 = 2 и Vt = 20.
О т в е т. V{ = 20 (км/ч), V2 = 40 (км/ч).
Пример 8.3. Расстояние между городами А и В равно
80 км. Из А в В выехала машина, а через 20 мин —
мотоциклист, скорость которого равна 90 км/ч. Мотоциклист
догнал машину в пункте С и повернул обратно. Когда
машина прибыла в В, мотоциклист проехал половину пути от
С к А. Найти расстояние от А до С.
(т.*.)
Рис. 8.3
272
§ 8. Задачи на движение
Решение. Примем город А за начало координат,
направив ось х от А к В. Обозначим через D середину отрезка
АС, через хв, хс и хр =—— координаты точек В9 С и D
соответственно. Расстояния между А и Б, А и С, С и D равны
$ав=\*в-ха[ sac=\xc~xa[ SrD=\xD-xc\.
Изобразим на КП-плоскости xAt зависимости координат
машины и мотоциклиста от времени г обозначив через tc
время движения машины до пункта С, а через Т — время
её движения до города В.
Пусть V (км/ч) — скорость машины. Запишем
уравнения движения машины и мотоциклиста от А до В9 от А до
С и от С до D.
80 = V-T,
Sac =90-\U "j
т =
80
Sac='
Из двух последних уравнений находим: SAC = 60, V-60.
Ответ. 60 км.
Пример 8.4. Из пункта А в пункт В со скоростью
80 км/ч выехал автомобиль, а через некоторое время с
постоянной скоростью выехал второй. После остановки на
20 мин в пункте В второй автомобиль поехал с той же
скоростью назад, через 48 км встретил первый автомобиль,
шедший навстречу, и был на расстоянии 120 км от Б в
момент прибытия в В первого автомобиля. Найти расстояние
от А до места встречи автомобилей, если АВ = 480 км.
Решение. Пусть V (км/ч) — скорость второго
автомобиля, (V > 80); S (км) — искомое расстояние от пункта А
ло места первой встречи автомобилей в пункте С.
§ 8. Задачи на движение
273
Воспользовавшись изображенными на КП-плоскости
xAt зависимостями от времени координат автомобилей, из
заштрихованных треугольников имеем систему двух
уравнений для нахожденияУ и S:
ч -
48 120-48
80 ~ V '
480 - S - 48
80
480 - S
1
—
3
48
;
V
<=>
120' (\ П 4сЛ7 = 12°' ~lV = 12°*
(480"S) -h^-T^ =o l480-S = 320; \s = 160.
80 120
Ответ. 160 км.
Пример 8=5. Из города А в город Б, находящийся на
расстоянии 105 км от А, с постоянной скоростью V км/ч
выходит автобус. Через 30 мин вслед за ним из А со скоростью
40 км/ч выезжает автомобиль, который, догнав в пути
автобус, поворачивает обратно и движется с прежней скоростью.
Определить все те значения V, при которых автомобиль
возвращается в А позже, чем автобус приходит в В.
Решение. Пусть tl (ч) — время движения
автомобиля до встречи с автобусом; S (км) — расстояние от города А
274
§ 8, Задачи на движение
до места встречи, (S < 105); At (ч) — разность между
временем возвращения в А автомобиля и временем прихода
автобуса в В (по условию At > 0).
Изобразим на КП-плоскости xAt графики зависимостей
от времени координат автобуса и автомобиля. Уравнения
движения автомобиля и автобуса, записанные для момента
встречи автомобиля с автобусом, имеют вид
Откуда находим
U =■
2(40 - V)
Решая систему неравенств
S =
2W
40 -V
д,-
\ 105
) V
>0;
40
1
— н
2
UK
-V
V
40-
105,
V
105
получим множество искомых значений V,
Л/
Рис. 8.5
Ответ. 30 <V< 33,6.
Пример 8.6. Из пункта А в пункт В с постоянными
скоростями выехали два мотоциклиста, а из В в А
одновременно с ними выехал третий мотоциклист с постоянной
§ 8, Задачи на движение
275
скоростью 60 км/ч. Через 45 мин расстояние между
первым и вторым было в два раза больше, чем между первым
и третьим. Через 1 ч после старта расстояние между
первым и вторым было равно расстоянию между первым и
третьим, а расстояние, которое осталось проехать третьему
до А, было равно расстоянию между первым и вторым
через 1ч 30 мин после старта, а также было равно —
расстояния между первым и третьим через 1ч 30 мин после
старта. Найти расстояние между пунктами А и Б.
Решение. Обозначим через SAB (км) искомое
расстояние между А и Б, через Vt (км/ч) и V2 (км/ч) —
скорости первого и второго мотоциклистов соответственно.
Изобразим на КП-плоскости xAt зависимости от
времени координат мотоциклистов.
Рис. 8.6
По условию задачи имеем систему уравнений:
у.-ул--
(1)
(2)
(3)
(4)
276 § 8. Задачи на движение
Рассмотрим случай V2 > Vx.
Раскрывая модуль, из (1) и (2) получим
П-^д-540
К,- - ,V2=
Следовательно, из уравнения (3) находим
Sab - 90 (V, - 50, V2 = 70).
Найденные значения удовлетворяют уравнению (4).
Случай V2 < Vx нереализуем.
Ответ. 90 км.
Замечание. Точное геометрическое построение КП-плос-
кости показывает, что третий мотоциклист прибудет в
пункт А через 1 ч 30 мин, то есть искомое расстояние равно
90 км. Приведенный рисунок соответствует именно этой
ситуации, но решение, естественно, дано в общем виде, не
основываясь на этом рисунке.
Упражнения
1. Из города А в город В выезжает велосипедист, а через
3 ч после его выезда из города В выезжает навстречу ему
мотоциклист, скорость которого в три раза больше скорости
велосипедиста. Велосипедист и мотоциклист встречаются
посредине между А и Б. Если бы мотоциклист выехал не
через 3, а через 2 ч после велосипедиста, то встреча
произошла бы на 15 км ближе к А Найти расстояние между
городами А и В.
Ответ. 180 км.
2. Два тела, первоначальное расстояние между
которыми 100 см, движутся навстречу друг другу. Если первое
тело начнет двигаться на 25 с раньше второго, то они
встретятся через 5 с после начала движения второго тела. Если
же второе тело начнет двигаться на 25 с раньше первого, то
они встретятся через 35 с после начала движения второго
тела. Найти скорости обоих тел, полагая, что они движутся
равномерно.
Ответ. 3 см/сек и 2 см/сек.
3. Из пункта А в пункт В едут грузовой и легковой
автомобили. В первый день пути легковой автомобиль про-
§ 8. Задачи на движение 277
ехал на 200 км больше, чем грузовой. Во второй день
легковой автомобиль проехал на 100 км больше, чем в первый
день, а грузовой — в 1,5 раза больше, чем в первый день.
Какое расстояние проехал каждый автомобиль в первый
день, если за два дня пути легковой автомобиль проехал на
350 км больше, чем грузовой?
Ответ. 500 км и 300 км.
4. Из одного и того же города вышли два поезда,
причем первый из них прошел 240 км, а второй — 300 км.
Скорость первого поезда на 10 км/ч больше скорости второ
го, а на свой путь первый потратил на 4 ч меньше, чем
второй на свой путь. Определить скорости обоих поездов.
Ответ. 40 км/ч, 30 км/ч.
5. Два автомобиля выехали одновременно из одного
пункта и едут в одном направлении. Первый автомобиль
едет со скоростью 40 км/ч, скорость второго составляет
125% скорости первого. Через 30 мин из того же пункта и
в том же направлении выехал третий автомобиль, который
сначала обогнал первый и через 1,5 ч после этого обогнал
второй. Какова скорость третьего автомобиля?
Ответ. 60 км/ч.
6. В соревнованиях по бегу на дистанции 120 м
участвуют три бегуна. Скорость первого из них больше скорости
второго на 1 м/с, а скорость второго равна полусумме
скоростей первого и третьего. Определить скорость третьего
бегуна, если известно, что первый бегун пробежал дистанцию
на 3 с быстрее третьего
Ответ. 8 м/с.
7. Из пункта А в пункт В выехал автомобиль и
одновременно из пункта В в пункт А выехал велосипедист.
После встречи они продолжали свой путь. Автомобиль, доехав
до пункта В, тотчас повернул назад и догнал велосипедиста
через 2 ч после момента первой встречи. Сколько времени
после первой встречи ехал велосипедист до пункта А, если
известно, что к моменту второй встречи он проехал 2/5
всего пути от В до А?
Ответ. 8 ч 45 мин.
8. Автомобиль, идущий со скоростью 100 км/ч, выехал
из пункта А в пункт Бив пункте С встретился с
велосипедистом, выехавшим на полтора часа раньше из В в А со
скоростью 10 км/ч. Если бы скорость автомобиля была на
278 § 8. Задачи на движение
20 км/ч больше, а скорость велосипедиста — на 5 км/ч
больше, то встреча произошла бы на 10 км ближе к А.
Каковы расстояния АС и СВ.
Ответ. 150 км и 30 км.
9. Из пункта А по одному шоссе выезжают
одновременно два автомобиля, а через час вслед за ними выезжает
третий. Еще через час расстояние между третьим и первым
автомобилями уменьшилось в полтора раза, а между третьим
и вторым — в два раза. Во сколько раз скорость первого
автомобиля больше скорости второго? (Известно, что третий
автомобиль не обогнал первых двух.)
Ответ. В 9/8 раза.
10. Расстояние между пунктами А и В равно 60 км,
причем 2/3 дороги приходится на шоссе, а оставшаяся
часть — на грунтовую дорогу. Найти скорость движения
автомобиля по грунтовой дороге и по шоссе, если на шоссе
скорость его движения на 20 км/ч выше его скорости по
грунтовой дороге, а на весь путь он затратил всего 2 ч.
Ответ. 20 км/ч и 40 км/ч
11. Из пункта А в пункт В выехал автомобиль и
одновременно из пункта В в пункт А выехал велосипедист.
После встречи они продолжали свой путь. Автомобиль, доехав
до пункта В, тотчас повернул назад и догнал велосипедиста
через два часа после момента первой встречи. Сколько
времени 'после первой встречи ехал велосипедист до пункта А,
если известно, что к моменту второй встречи он проехал
2/5 всего пути от В до А? (Скорости автомобиля и
велосипедиста постоянны.)
О т в е т. 8 ч 45 мин.
12. В пункт D выехали одновременно два велосипедиста:
первый велосипедист выехал из пункта А, второй — из
пункта В. За время движения скорости их постоянны. По пути
следования оба велосипедиста проезжают пункт С, от
которого вплоть до пункта D они едут по одной и той же дороге.
Расстояние от пункта А до пункта С равно 90 км, от пункта
В до пункта С — 40 км. Первый велосипедист проехал пункт
С на один час позже второго, а в пункт D они прибыли
одновременно. Найти скорость каждого велосипедиста, если
известно, что первый ехал от пункта А до пункта С столько же
времени, сколько второй ехал от пункта С до пункта D.
Ответ. Скорость первого велосипедиста 30 км/ч,
второго — 20 км/ч.
§ 8. Задачи на движение 279
13. Пункт А находится по реке выше пункта В. В одно и
то же время из пункта А отплыли вниз плот и первая
моторная лодка, а из пункта В вверх — вторая моторная
лодка. Через некоторое время лодки встретились в пункте С, а
плот за это время проплыл третью часть АС,
Если бы первая лодка без остановки доплыла до пункта
В, то плот за это время прибыл бы в пункт С. Бели бы из
пункта А в пункт В отплыла вторая лодка, а из пункта В в
пункт А — первая лодка, то они встретились бы в 40 км от
пункта А.
Каковы скорость обеих лодок в стоячей воде, а также
расстояние между пунктами А и Б, если скорость течения
равна 3 км/ч?
Ответ. 6 км/ч, 21 км/ч, 45 км.
14. Из двух пунктов А и Б, расстояние между которыми
равно 78 км, выехали одновременно навстречу друг другу
два велосипедиста (соответственно РА и Рв) и встретились
через 3,9 ч. Через сколько часов встретятся эти же
велосипедисты, если они выедут из тех же пунктов одновременно
навстречу друг другу и если скорость велосипедиста РА
увеличится вдвое, а скорость велосипедиста Рв уменьшится на
2 км/ч? Известно, что скорость велосипедиста РА меньше
9 км/ч, а точка второй встречи велосипедистов отстоит от
точки первой встречи на 16,8 км в сторону пункта В.
Ответ. Через 3 часа.
15. Два велосипедиста и пешеход одновременно
отправились из пункта А в пункт Б. Более чем через час после
выезда у первого велосипедиста сломался велосипед, и он
продолжал путь пешком, двигаясь в 4,5 раза медленнее,
чем на велосипеде. Его обгоняют: второй велосипедист —
через 5/8 ч после поломки, а пешеход — через 10,8 ч после
поломки. К моменту поломки второй велосипедист проехал
в два раза большее расстояние, чем то, которое прошел
пешеход к моменту, на 5/36 ч более позднему, чем момент
поломки.
Через сколько часов после начала движения сломался*
велосипед?
Ответ. Через 4 часа.
16. От А до Б s км. Из А в Б вылетел вертолет, а через t
ч — самолет. Он догнал вертолет в d км от А, долетел до В,
сразу же повернул обратно, в d км от В встретил вертолет и
280 § 8. Задачи на движение
вернулся в А позднее, чем вертолет прибыл в Б. Насколько
раньше вертолет прибыл в Б, чем самолет вернулся в А?
Ответ. На
2d2 У
17. Товарный поезд, шедший из А в Б, прибыл на
станцию С одновременно с пассажирским, шедшим из Б в А со
скоростью в т раз большей, чем товарный. Оба поезда,
простояв на станции С t ч, затем продолжили свой путь, причем
каждый из них увеличил скорость на 25% по сравнению со
своей первоначальной скоростью (скоростью до прибытия в
С). При этом товарный прибыл в Б на tt ч позже, а
пассажирский прибыл в А на t2 ч позже, чем если бы они
двигались без остановки со своими первоначальными скоростями.
Насколько раньше товарный поезд вышел из А, чем
пассажирский из Б?
Ответ. На 5 /и(/-/2) Ч ч-
18. Из пункта А в пункт В выходит в 8 ч утра скорый
поезд. В этот же момент из Б в А выходят пассажирский и
курьерский поезда, причем скорость пассажирского поезда
в два раза меньше скорости курьерского. Скорый поезд в
пункт Б прибывает в 13 ч 50 мин того же дня, а встречает
курьерский поезд не ранее 10 ч 30 мин утра. Найти время
прибытия пассажирского поезда в пункт А, если известно,
что между моментами встреч скорого поезда с курьерским
и скорого поезда с пассажирским проходит не менее часа.
Ответ. В 16 ч 45 мин.
19. Из пункта А в пункт С в 9 ч утра отправился
скорый поезд. В это же время из пункта В, расположенного
между пунктами А и С, выходят два пассажирских поезда,
первый из которых следует в пункт А, а второй — в пункт
С, причем скорости пассажирских поездов равны. Скорый
поезд встречает первый пассажирский поезд не гизж* , чом
через 3 ч после его отправления, потом проходив пу и т В
не ранее 14 ч того же дня и, наконец, прибывает в пуш.т С
одновременно со вторым пассажирским поездом через 12 ч
после встречи с первым пассажирским поездом. Найти
время прибытия в пункт А первого пассажирского поезда.
О т в е т. 16 ч 30 мин.
§ 8, Задачи на движение 281
20. В 7 ч утра из пункта А в пункт В по течению реки
отправляются катер и байдарка. Байдарка прибывает в
пункт В в 17 ч этого же дня. Катер же, дойдя до пункта В,
мгновенно повернул обратно и на своем пути из В в А
встретил байдарку не позднее 15 ч, а прибыл в пункт А не
ранее 23 ч того же дня. Найти время прибытия катера в
пункт В, если известно, что собственная скорость (т. е.
скорость в стоячей воде) катера в два раза больше собственной
скорости байдарки.
Ответ. В 13 ч 00 мин.
21. В 9 ч утра из пункта А выезжает велосипедист,
который едет до пункта В. Через 2 ч после выезда велосипедиста
из А в В выезжает автомобилист, который догоняет
велосипедиста не позже 12 ч дня. Продолжая движение,
автомобилист прибывает в пункт В, мгновенно поворачивает и едет из
В в А На этом пути автомобилист встречает велосипедиста и
потом прибывает в пункт А в 17 ч того же дня (т.е. дня
выезда велосипедиста). Найти время прибытия велосипедиста в
пункт В, если известно, что между двумя встречами
велосипедиста и автомобилиста прошло не более 3 ч.
О т в е т. В 18 ч 00 мин.
22. Утром из пункта А в пункт В отправляется по
течению реки моторная лодка. Одновременно из В в А выходит
катер, собственная скорость (т. е. скорость в стоячей воде)
которого в 1,4 раза больше собственной скорости моторной
лодки. Известно, что лодка и катер встречаются в 12 ч дня,
потом лодка прибывает в пункт В не позже 15 ч дня, а
катер прибывает в пункт А не раньше 15 ч дня. Найти время
отправления лодки из пункта А в пункт В, если известно,
что на путь из В в А лодка затрачивает не более 9 ч, а
катер на путь из А в В затрачивает не менее 4,5 ч.
Ответ. В9ч утра.
23. Расстояние между станциями А и В равно 360 км. В
одно и то же время из А и из В навстречу друг другу
выезжают два поезда. Поезд, выехавший из А, прибывает на
станцию В не ранее чем через 5 ч. Если бы его скорость
была в 1,5 раза больше, чем на самом деле, то он встретил
бы второй поезд раньше, чем через 2 ч после своего выхода
из А Скорость какого поезда больше?
Ответ. Скорость поезда, вышедшего из В, больше.
24. Пункты А и В расположены на одной реке так, что
плот, плывущий из А в В со скоростью течения реки, про-
282 §8. Задачи на движение
ходит пункт от А до Б за 24 ч. Весь путь от А до Б и
обратно моторная лодка проходит не менее чем за 10 ч. Если бы
собственная скорость моторной лодки увеличилась на 40%,
то тот же путь (т.е. путь от А до Б и обратно) занял бы у
лодки не более 7 ч. Найти время, за которое моторная
лодка проходит путь из А в Б в случае, когда ее собственная
скорость не увеличена.
Ответ. За 4 часа.
25. В 9 ч утра из пункта А выезжает велосипедист,
который едет до пункта Б. Через 2 ч после выезда
велосипедиста из А в Б выезжает автомобилист, который догоняет
велосипедиста не позже 12 ч дня. Продолжая движение,
автомобилист прибывает в пункт В, мгновенно
поворачивает и едет из Б в А. На этом пути автомобилист встречает
велосипедиста и потом прибывает в пункт А в 17 ч того же
дня. Найти время прибытия велосипедиста в пункт Б, если
известно, что между двумя встречами велосипедиста и
автомобилиста прошло не более 3 ч.
Ответ. 18 часов.
26. От пристани А к пристани В, находящейся от А на
расстоянии 12 км, вниз по течению отходит моторная
лодка, скорость которой в стоячей воде равна 6 км/ч.
Одновременно с ней из Б в А выходит катер, скорость которого в
стоячей воде равна 10 км/ч. После встречи они
разворачиваются и возвращаются к своим пристаням. Определить все
возможные скорости течения реки и, при которых лодка
приходит в А не раньше чем через 1 час после возвращения
катера в Б.
Ответ. 2<у<6.
Два тела равномерно движутся по окружности в одном
и том же направлении, и одно из них догоняет другое через
каждые 46 с. Если же эти тела с теми же скоростями
движутся в разных направлениях, то они встречаются через
каждые 8 с. Определить скорость движения тел по
окружности, зная, что ее радиус равен 184 см.
Ответ. 27л см/с, 19я см/с.
28. Три гонщика (А, потом Б и затем С) стартуют с
интервалом в 1 мин из одной точки кольцевого шоссе и
двигаются в одном направлении с постоянными скоростями.
Каждый гонщик затрачивает на круг более двух минут.
Сделав три круга, гонщик А в первый раз догоняет В у
§ 8. Задачи на движение 283
точки старта, а еще через 3 мин он вторично обгоняет С.
Гонщик Б впервые догнал С также у точки старта,
закончив 4 круга. Сколько минут тратит на круг гонщик А?
Ответ. 3 мин.
29. Между пунктами А и Б расположен пункт С,
причем АС = 17 км, ВС = 3 км. Из пункта А в пункт В выехала
машина, которая, не проехав и двух километров,
остановилась. Через некоторое время она двинулась дальше в пункт
Б, и в этот же момент из пункта С в пункт В отправились с
постоянными скоростями пешеход и велосипедист, каждый
из которых, достигая Б, сразу же поворачивает назад. С
кем из них раньше поровняется машина, если скорость
машины в 4 раза больше скорости велосипедиста и в 8 раз
больше скорости пешехода?
Ответ. Машина сначала встретит велосипедиста.
30. Если пассажир в городе А сядет в поезд, то он
доберется до города Б через 20 ч. Если же он дождется
отправления самолета (а ждать придется более 5 ч^, то он
доберется до города Б через 10 ч, (в эти 10 ч, естественно,
включено и время ожидания). Во сколько раз скорость
самолета превышает скорость поезда, если известно, что
самолет догоняет поезд через 8/9 ч после своего
отправления? (Предполагается, что самолет летит вдоль железной
дороги и проходит по воздуху то же расстояние, что и
поезд по земле.)
Ответ. Скорость самолета в 10 раз больше скорости
поезда.
31. Города А и Б расположены на берегу реки, причем
город Б расположен ниже по течению. В 9 ч утра из города
А в город Б отправляется плот, плывущий относительно
берегов со скоростью течения реки. В этот же момент из
города В в город А отправляется лодка, которая встречается с
плотом через 5 ч. Доплыв до города А, лодка мгновенно
повернула обратно и приплыла город Б одновременно с
плотом. Успели ли лодка и плот прибыть в город Б к 9 ч
вечера (того же дня)?
Ответ. Не успели.
32. Туристы выехали на лодке из пункта А в пункт В,
расположенный ниже по течению реки. Первую половину
пути АВ они шли на веслах, а потом включили мотор и
прибыли в пункт Б через 4 ч после выхода из А. Если бы
284 §8. Задачи на движение
весь путь из А в Б они шли на веслах, то он занял бы у них
5 ч 20 мин. На обратном пути из Б в Л они четверть пути
В а шли на веслах, а затем включили мотор и прибыли в
пункт А через 7 ч после выхода из В. Сколько времени
занял бы у них обратный путь, если бы весь этот путь они
шли на веслах?
Ответ. 16 часов.
33. Из порта одним и тем же курсом вышли в разное
время два корабля, идущие с одной и той же скоростью. Со
второго корабля, идущего сзади, отправляется
быстроходный катер, который догоняет первый корабль и сразу же
возвращается на свой корабль. Катер находится в пути 13 ч
20 мин. Если бы перед выходом катера оба корабля
одновременно уменьшили свою скорость на 10 км/ч, то катер
находился бы в пути 11 ч 40 мин, а если бы они
одновременно увеличили свою скорость на 10 км/ч, то катер
находился бы в пути 17 ч 30 мин. На сколько раньше вышел из
порта первый корабль, чем второй?
Ответ. На 14 часов.
34. В реку впадает приток. На притоке на некотором
расстоянии от его устья расположен пункт А На реке на том же
расстоянии от устья притока расположен пункт Б. Время,
которое требуется моторной лодке, чтобы доплыть от пункта
А до устья притока и обратно, относится ко времени, которое
требуется ей, чтобы доплыть от пункта В до устья притока и
обратно, как 32:35. Если бы скорость моторной лодки была
на 2 км/ч больше, то это отношение было бы равно 15:16, а
если бы скорость моторной лодки была на 2 км/ч меньше, то
это отношение было бы равно 7:8.
Найти скорость течения реки. (Расстояния измеряются
вдоль притока и реки соответственно.)
Ответ. 4 км/ч.
35. Из пункта А в пункт Б выезжает автомобиль, и
одновременно из Б в А с меньшей скоростью выезжает
мотоцикл. Через некоторое время они встречаются, и в этот
момент из Б в А выезжает второй мотоцикл, который
встречается с автомобилем в точке, отстоящей от точки встречи
автомобиля с первым мотоциклом на расстоянии, равном 2/9
пути от А до В. Если бы скорость автомобиля была на
20 км/ч меньше, то расстояние между точками встречи
равнялось бы 72 км, а первая встреча произошла бы через 3 ч
§ 8. Задачи на движение 285
после выезда автомобиля из пункта А Найти длину пути
между А и В. (Скорости мотоциклов одинаковы.)
Ответ 300 км.
36. Из города А в город В через равные промежутки
времени и с равной скоростью выезжает один за другим 21
автобус, каждый из которых проходит путь АВ за 2 ч 40
мин. При этом первый автобус прибывает в город В в тот
момент, когда из города А выезжает двадцать первый
автобус. Прибыв в город В, каждый автобус мгновенно
поворачивает и движется обратно к городу А. Из города А
одновременно с двадцать первым автобусом выезжает в город В
легковая машина, которая через t мин обгоняет двадцатый
автобус. Найти t и время, за которое легковая машина
преодолевает расстояние АВ, если, встретив первый автобус,
легковая машина после этого встречает второй автобус
через (t - 9) мин. Автобусы занумерованы в том порядке, в
каком они выезжают из города А.
Ответ, t = 12 мин. Расстояние АВ легковая машина
преодолевает за 96 мин.
Заключение
Данное пособие безусловно будет способствовать
изучению учащимися оригинальной и эффективной методики
решения задач с параметрами, которые, как уже
отмечалось во введении, являются для многих абитуриентов
задачами повышенной трудности и требуют глубокого знания
школьного курса математики и высокой логической
культуры.
В этом пособии в рамках существующей школьной
программы и в форме, доступной для эффективного
восприятия учащимися, изложена система математических
методов, способствующая углублению школьного курса
математики и сближению его с вузовским курсом.
Вводя тридцать лет назад логические схемы решения
типовых уравнений и неравенств, основанные на
концепции равносильности математических высказываний, автор
преследовал цель алгоритмизации школьного курса
математики, стремился к логически более строгому его
построению, использующему современный математический язык и
символьное программирование, чтобы развить навыки
алгоритмического мышления учащихся и подготовить их к
восприятию идей и методов прикладной математики. Время
показало эффективность такого подхода.
Список литературы
1. Моденов П.С., Новоселов СИ., Пособие по математике
для поступающих в вузы. М.: Изд-во Моск. ун-та, 1961. —
431 с.
2. Потапов М.К., Розов Я.Х., Дорофеев Г.В. Краткое
пособие по математике для поступающих в Московский
университет. М.: Изд-во Моск. ун-та, 1964. — 208 с.
3. Моденов В.П., Пособие по математике, физике и
химии для поступающих в вузы. М.: Изд-во Моск. ун-та,
1969. — 340 с.
4. Моденов В.П. Пособие по математике. Ч. И. — М.:
Изд-во Моск. ун-та, 1972. — 401 с.
5. Моденов В.П. Пособие по математике. Ч. I. M.: Изд-
во Моск. ун-та, 1977. — 480 с.
6. Справочник для поступающих в Московский
университет. — М.: Изд-во Моск. ун-та, 1969-2002.
Учебное издание
Моденов Владимир Павлович
ЗАДАЧИ С ПАРАМЕТРАМИ
Координатно-параметрический метод
Издательство «ЭКЗАМЕН»
ИД №05518 от 01.08.01
Гигиенический сертификат
№ 77.99.02.953.Д.008330.09.06 от 14.09.2006 г.
Корректор ИД. Баринская, Г.Л/. Мороюва
Дизайн обложки // Р Захаркина
Компьютерная верстка Е Ю. Лысова
105066, Москва, ул. Александра Лукьянова, д. 4, стр. 1.
wvAv.examen.biz
E-mail: по общим вопросам: info@examen.biz;
по вопросам реализации: sale@examen.biz
тел./факс 263-96-60.
Общероссийский классификатор продукции
ОК 005-93, том 2; 953005 — книги, брошюры,
литература учебная
Текст отпечатан с диапозитивов
в ОАО «Владимирская книжная типография»
600000, г Владимир, Октябрьский проспект, д п
Качество печати соответствует
качеству предоставленных диапозитивов
По вопросам реализации обращаться по тел.: 263-96-60.
В.П.МОДЕНОВ
ЗАДАЧИ С ПАРАМЕТРАМИ
КООРДИНАТНО-ПАРАМЕТРИЧЕСКИИ МЕТОД
Книга написана профессором Московского
государственного университета им. М.В. Ломоносова
и предназначена для учащихся общеобразовательных
учреждений, готовящихся к вступительным
экзаменам по математике в вуз.
Рассматривается метод аналитической
геометрии, названный автором координатно-
параметрическим, который позволяет
эффективно решать широкий класс
задач с параметрами, составляющих
неотъемлемую и наиболее трудную
часть экзаменационных заданий.
Метод иллюстрируется
примерами оригинального
решения задач,
предлагавшихся
на вступительных
экзаменах
по математике
в МГУ.
ЭкзАбитур.Задачи с параметр.и
Цена:149р.00к.
>p.l
III
I7854720262S4 07.04.09
г химия
АЛГЕБРА
ГЕОМЕТРИЯ
ФИЗИКА
ГЕОГРАФИЯ
РУССКИЙ
НФОРМАТИКА
ЛИТЕРАТУРА
БИОЛОГИЯ
ИСТОРИЯ
АНГЛИЙСКИЙ
НЕМЕЦКИЙ
РАНЦУЗСКИЙ