Г. А. Тиняков, И. Г. Тиняков
ЗАДАЧИ С ПАРАМЕТРАМИ
издание третье, переработанное и дополненное
Москва — 1996
Г. А. Тиняков, И. Г. Тиняков
ЗАДАЧИ С ПАРАМЕТРАМИ
издание третье, переработанное и дополненное
Москва - 1996
ВВЕДЕНИЕ
Предлагаемое пособие посвящено одному из самых трудных вопросов конкурсных задач вступительных экзаменов по математике. В первой части демонстрируются методы решения задач с параметрами на примерах решений 87 задач с параметрами. Мы сохранили деление задач с параметрами на четыре группы:
1.	Уравнения с параметрами.
2.	Неравенства с параметрами.
3.	Системы уравнений с параметрами.
4.	Системы неравенств и смешанные системы с параметрами.
По сравнению с предыдущим изданием существенно расширены методы решения задач с параметрами. Часто приводятся несколько решений одной и той же задачи с целью показать различные методы решения. В конце этой части даются 38 задач для самостоятельного решения, снабженные ответами.
В Дополнении даются решения задач с параметрами, предлагавшихся на вступительных экзаменах различных факультетов МГУ в 1993-95 годах, и предлагаются еще 35 задач для самостоятельного решения, снабженные ответами.
Желаем успехов!
Геннадий Анатольевич Тиняков, Игорь Геннадьевич Тиняков.
Телефон: 186-18-85.
2
Задаче 1. При каких значениях параметра а все решения уравнения з|х + 2а | - За 4-х -15 = О удовлетворяют неравенству 4£х£б?
Решение. Разобьем эту задачу на две. Сначала найдем решение заданного уравнения как функцию параметра а.
3(х 2а) - За + х - 15 « О х 4- 2а £ О
-3(х 2а) - За + х - 15 - О х 4- 2а £ О
4
4- 2а £ О 4
Г - _9а±15
2
-	♦ 2а £ О
ai-3 х._2й±15’ 2
а£-3
2
Итак, получены два семейства решений, каждое из которых Найдем те значения параметра а, при которых каждое из заключено в пределах от 4 до 6.	-3^
[4.1Ь2^6 4 а 2 -3
зависит этих семейств решений
от параметра о.
Для первой системы:
Для второй системы:
Наконец, решая систему
. 9а 4- 15 4S--—
а £ -3
3
-З.а.-* 9
У 1	1
ai~3 <=>-3SeS-i. а 2-3	3
Ч35 23
U-3	9
получим те значения параметра а, при
1
3
которых все решения заданного уравнения удовлетворяют условию задачи. 23
Ответ: -3 £ а £---.
9
Замечание. Предложенную задачу можно решить, пользуясь наглядными геометрическими соображениями. Введем функцию /(х) «з|х + 2а|-За + х-15. Определяющей точкой этой функции является точка х = -2а. Снимая знак модуля, получим, как задается функция правее точки х = -2а и левее точки х = -2а.
(х + 2а а О	. .
f / ч в .	,	, т.е. правее точки х = -2а функция /цх) монотонно возрастает.
т.е.
левее точки
|/2(х) =-2х - 9а - 15*
х«-2а функция /2(х) монотонно убывает, при этом f(~2a) > fi(-2a) = f2(-2a) = -5а - 15. Рассмотрим сначала случай, когда Д-2а) > 0,
У/(-2а) =-5а-15>0
т.е. -5а - 15 > 0. В этом случае заданное уравнение не имеет решений.
3
Если /(-2а) = 0, т.е. -5а - 15 « О о а « -3 и -2а -6, то заданное уравнение будет иметь при этом единственное решение.
Если /(-2а) < 0, т.е. -5а - 15 < 0 <=> а > -3, то заданное уравнение при этом будет иметь два решения, которые должны удовлетворять
условиям
/1(б) « 9 + За £ О /2(4)«-23-9а 2*0
х
<=> -3 £ а £-------.
9
Задача 2. Найти все целые значения параметра fc при каждом из которых уравнение
х
2
S-4sin2 х -8 сох2
Зк имеет решения. Найти все эти решения.
Решение. 5- 4хй3х - Всад3 у- 3* «5- 4^1 -сад3 х)- 4(1 4-садх)- 3*о kcot2x~4садх4- 1   (2садх-1)а -3*4-4с»садх----^-4 . Так как *gZ, то уравнение будет иметь хотя бы одно решение тогда и только тогда, когда к » -1, либо к « 0, либо к «1.
			х « 2nlt	1 € Z
При	*•-1	имеем	X « ~ 4- ХП,	л € Z * L 2
при	*«0	имеем	х « ± jx 4- 2xm,	m € Z;
при		имеем	x « x ± arccos^^-^ + p € Z .
Задача 3. Определить, при каких значениях параметра а уравнение fog2(4x - а)ж * имеет ровно два решения.
Решение. /^2(4х-а)«хо4х-а«2х о 2^ -2х-а«о. Эго квадратное уравнение относительно 2х > 0 (!!!). Поэтому для того чтобы оно имело два положительных корня, необходимо и достаточно, чтобы одновременно выполнялись следующие два
неравенства:
£
4
2
Ответ: ~1<в<0. 4
4
Задача 4. Найти все значения действительного параметра р, при которых квадратное уравнение (Зх) +13' -15] х + 4 = 0 имеет ровно одно решение.
Решение. Для того чтобы квадратное уравнение имело одно решение (два одинаковых
( V
решения), необходимо и достаточно, чтобы его дискриминант D« 3' -151 -4-9-4
был равен нулю. О = 0 <=>
Ответ: р~--. 2
Задача 5. При каких значениях параметра а уравнение tin23x
а
зтЗх + - = 0 2
имеет ровно три корня, расположенные на отрезке -у £ х £ я ?
Решение.
2я ---£ X £ я
L 3
о
а) (ЛИЗх-1) » 0 уравненнс Зх . 1
2я £ Зх £ Зя	2
на отрезке 2я £ Зх Зя имеет два корня. Поэтому для того чтобы исходное уравнение имело ровно три корня на заданном отрезке, необходимо и достаточно, чтобы уравнение tin Зх « а имело на этом отрезке один корень. Очевидно, что это будет при а «1.
Ответ: а = 1.
а = 2 а а 3
Задача б. При каких значениях параметра а произведение корней квадратного уравнения х2 - 2х + (а2 - 5а + б)» 0 равно нулю?
Решение. Произведение корней квадратного уравнения равно нулю тогда и только тогда, когда по крайней мере один из корней равен нулю. Подставляя х = 0 в заданное уравнение, получим а2 ~5а + 6 в (а - tya - 3) = 0 <=>
Ответ: а = 2, а = 3.
Замечание. Согласно основной теореме алгебры квадратное уравнение с действительными коэффициентами всегда имеет два корня: два различных действительных корня, два одинаковых действительных корня или два комплексно-сопряженных корня. Так как произведение корней приведенного квадратного уравнения равно свободному члену (согласно формулам Виета), то а2 - 5а + б » 0 .
5
Задача 7. Найти все значения параметра а , при которых уравнение г f>x 9-J3 л
х + ~==^ + —— + 36 = 0 имеет единственное решение, ул л а cos а
Решение, йня того чтобы квадратное уравнение имело единственное решение, необходимо и достаточно, чтобы его дискриминант был равен нулю. Поэтому
Таким образом, решение поставленной задачи сводится к решению следующей смешан-
ной системы
sin a cos а sin а > О
4 14-сага - -V-ли a = 2 sin a cos a _ I sin 2a - ллИ-а) « 0 O <2	2	О <	/ О
|яла>0	1лла>0
За - J а + ~
2 sin-----cos —s- «= О o
2	2
। ял a > 0
3a-*
ЛЯ-—4--0«
sin a > 0
a 4-*
COS---SL  0 o ,
2 sin a > 0
3a-J ----
2
sin a > 0
a-^ + 2*/, /cZ a " 18 * ♦ 2nW’m * Z
a + *
—— у + ял, л eZo a « 4* + 2яи, n «Z
Z *	0
sin a > 0
*eZ«
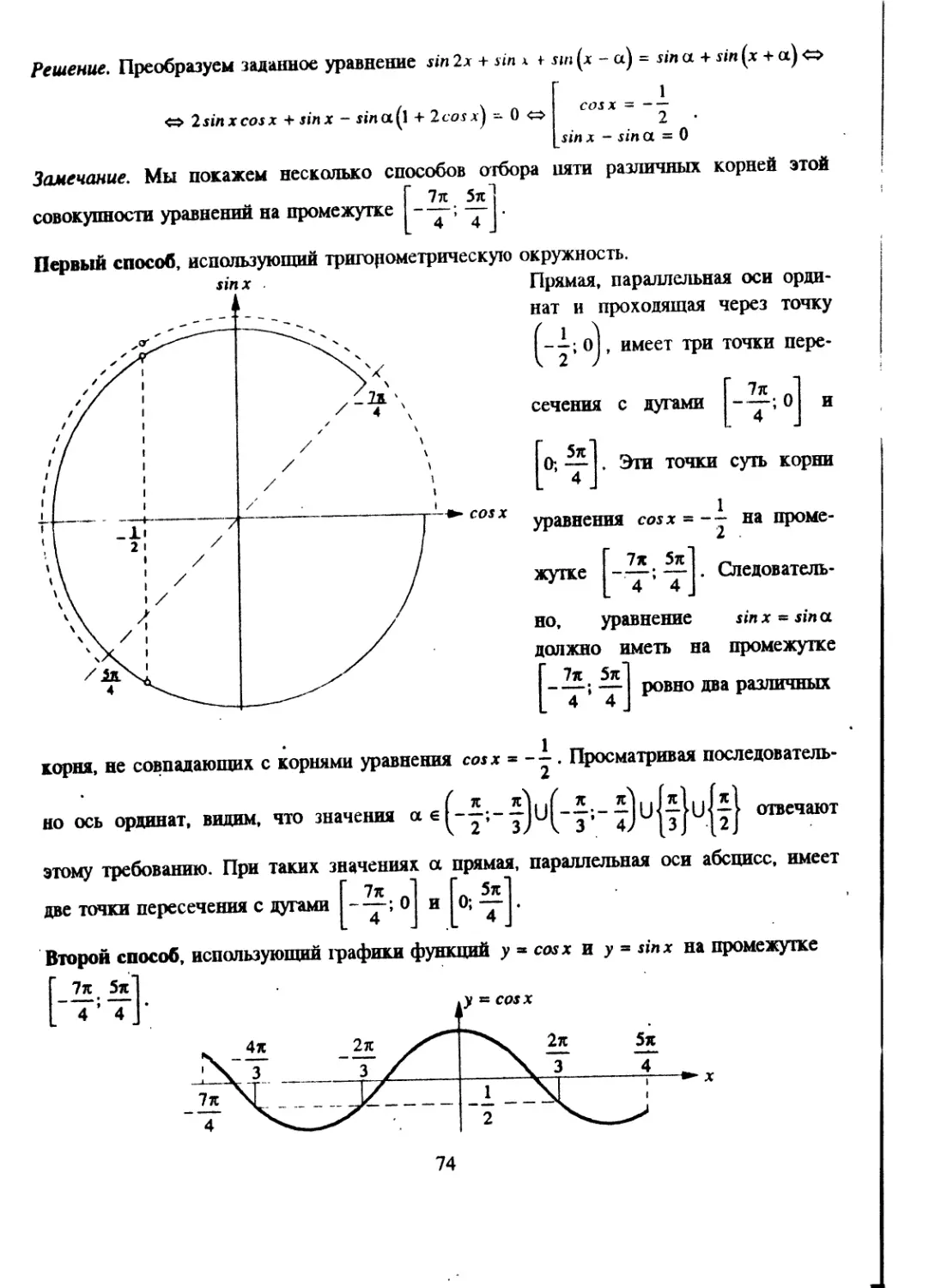
Наиболее тонким вопросом при решении последних систем является удовлетворение неравенству яла>0. В случае второй системы все решения этому неравенству удовлетворяют, так как они лежат во второй четверти, где яла > о. В случае же первой системы из общего решения нужно выделить те, которые лежат в первой и второй четвертях. Это удобно сделать на тригонометрической окружности.
Ответ: а «	+ 2nl; a =	+ 2itm; a «	+ 2яп, l,m,n €Z.
18	18	o
Задача 8. Найти все значения параметра Ь, при которых уравнение b2x2 - b- tg(cosx) 4-1 = 0 имеет единственное решение.
Решение. Заданное уравнение симметрично по х относительно нуля, т.е. если х0 является решением этого уравнения, то и -х0 также будет решением этого уравнения. Поэтому единственным решением заданного уравнения может быть только х = 0. Полагая в заданном уравнении х = 0, получим -Ь tgl 4-1 = 0 <=> b = ctgl.
Условие b-ctgl будучи необходимым, вообще говоря, не является достаточным для единственности, решения, так как может оказаться, что помимо решения х = 0 при b - ctgl имеются и другие решения. Поэтому исследуем исходное уравнение при Ь = ctgl.
б
ctg2\ • x2 - ctg\• tg(cosx) +1 « 0 <=> ctg2\• x2 +1 = ctgl • tg^cosx).
Мы покажем, что других, кроме х = 0, решений у этого уравнения нет. Для этого оценим левую и правую части этого уравнения.
Очевидно, что ctg2lx2 + 1 £ 1, Vx. Причем в этом неравенстве равенство достигается только при х = 0.
-1	для любых х, причем в этом двойном неравенстве равенство
справа достигается для тех х, для которых cosx = 1, а слева - для которых созх » -1.
Это и доказывает, что х = 0 является единственным решением этого уравнения.
Ответ: b^ctg\.
Задача 9. Определить, при каких значениях параметра а уравнение logfi— Jte + a = 2 имеет решения. Найти эти решения.
Решение этой задачи дает следующая цепочка эквивалентных соотношений
	 12х + а - (2-х)2 V2x + а = 2«/о#2_ж(2х + а) = 2<*2-х>0 2-х*1	х2-6х + 4- а«0 2-х>0	<=> 2-х#1
х » 3 ± V5 + а 2-х>0	<=>
2-х#1
х = 3 - 7$ + а
а > -4
а # -1
Ответ: х = 3-j5 + a: а > -4, а # -1
Задача 10. Найти все значения параметра к, для которых уравнение
х2 - 2Лх + fc2 + 21 -1 = 0 имеет два различных действительных корня.
Решение, Для того чтобы квадратное уравнение имело два различных действительных корня, необходимо и достаточно, чтобы его дискриминант был строго больше нуля. Поэтому D -	-4 = 12~^2+21-1)а1-21>0<*1<у.
Ответ: к<-.
1
Замечание, Полезно заметить, что если обозначить /(х) = х2 - 2Лх + Л2 + 2Л-1, и заметить что хс = к - ось симметрии параболы /(х), ветви которой направлены вверх, то заданное уравнение имеет два различных действительных корня тогда и только тогда, когда f(k) < 0 <=> к < у.
7
Задача 11. Найти все значения величины Л, при которых уравнение
х (х +1) (х + h) (х + h +1) = h2 имеет четыре действительных различных корня.
Решение,
Так как х(х + 1)(х + л)(х + л + 1)и^х2 + х(1 + л))(х2 + х(1 + л) + л|, то полагая х2+х(1 + л)-г,
получим /2 +Л/-Л2 -Оо г«-у±у~- + л2 «ь1—. Поэтому
X2 + х(1 + Л) « h - » — х2 + х(1 + Л) » h—
Для того чтобы каждое из этих квадратных уравнений имело два действительных различных корня, необходимо и достаточно, чтобы их дискриминанты были положительны, т. е. должна выполняться следующая система неравенств
^44.н(чмН'М>"~
Ответ: |л|>^5+2; | Л | < 7$ - 2.
Задача 12» При каких значениях параметра р уравнение
4 х - ^р4р х + 4^4Р - 1 j + р = О имеет корни и каковы знаки корней при различных значениях р? Решение, Заданное уравнение эквивалентно уравнению 4х2 - 4^р4рх + 4^4* -1) + р = 0. Из этого уравнения непосредственно заключаем, что р ъ. О. Для существования корней у заданного уравнения необходимо и достаточно, чтобы его дискриминант был неотрицателен, поэтому D = 4р4р -16(4F -1) - 4р s 4^4? - lj (р - 4) £ 0. Так как р £ 0, то 4Р -1 £ 0 и из неравенства D £ 0 заключаем, что уравнение имеет корни при р = О и р £ 4. Для определения знаков корней нужно определить знак свободного члена и знак коэффициента при х Коэффициент при х всегда неположителен, а свободный член всегда неотрицателен. Следовательно, при р = 0 оба корня равны нулю, а при Р 4 оба корня положительны.
Ответ: при р = 0 оба корня равны нулю;
при р £ 4 оба корня положительны.
8
Задача 13. Найти все значения а, которые удовлетворяют условию 5 < а < 16 и при \cosnx-siniuc | относительно х
которых уравнение 1 + cos
имеет хотя бы одно решение, удовлетворяющее условию 1 £ х £ 2.
(ах	/|\|cojxx-j»nxx|
~ + 8 / 1 * a (. з J	£ 1, то отсюда следует, что
ах Зх х --+	-- 2-8---2
хх = — + хт, 4
5а Зх х имеем уравнение — + — = — + л 8	8	2
5<а<1б€>5<у +	< 16 €> 25 < х(1 + 8л) < 80. Откуда л»1;и»2;и»3, а а « у;
СО4
cos юс - sinKx = О
= — + ял, л е Z	$
. Так как 1^х£2, то х»-. И для а meZ	4
л е Z<=> а = у + -у-, л € Z. Удовлетворим условию
17х
““ 5
и а » 5х соответственно.
= О
Ответ:
9»	17»	.
а a —; а » -у; а = 5х.
Задача 14. Найти все значения параметра Ь, при которых уравнение 2(3-д)х2 + 4(1-b)x + |2h-5| = |2£ + 7| имеет два различных корня и сумма этих корней отрицательна.
Решение. Исходное уравнение будет иметь два различных корня тогда и только тогда, когда £>«(2(1-ь))2 — 2(з —	[2Z> — 51 — 12Л>-f7[)>0 и М3. При этом сумма корней от-
рицательна в том и только том случае, когда у-у > о. Снимая знак модуля в интервалах знакопостоянства каждого из выражений, входящих под знак модуля, получим
Ответ: b<-2-V21; -1 < b < 1; b > 3.
Задача 15. Найти все пары действительных чисел шил, при которых уравнение (зх2 - 2т2 +mnj + ^Зт2 -тп + 2п2 - 12х| +4 = 4х~? имеет хотя бы одно решение.
9
Решение. Данное уравнение эквивалентно следующему
(зх2 - 2т2 + тл)2 + (зт2 - тп + 2п2 - 12х)’ + (х - 2)2 = 0. Очевидно, что сумма квадратов
равна нулю тогда и только тогда, когда каждое из слагаемых равно нулю.
(х-2 = 0	[х = 2
Зх2 - 2т2 + тп = 0	<=> 2m2-тл = 12
Зт2 - тп + 2п2 - 12х = О Зт2 - тп + 2п2 = 24
Таким образом, нужно найти решение следующей системы fm-2^ r,	(««V?
[2m2 - тл » 12	о [Зт2 - тп 4 2л2 • 24	2т2 - тл « 12 Зш2 - тл ♦ 2л2 о
	
	2лг - тл
2т2 - тп  12		я л • —т 2		т  -2^2
3-Х. + 2Х.2 „ 		 2 о		2т2 - тл « 12 о		(п.^ .
7 «| S м I		л « *т 2т2 - тл • 12		т « -2 л-2
				т  2
				я • -2
Ответ: Iм
In ж у2
т ® -2^2, [»» “ “2 (т » 2 п « -^2 V* “ |л « -2
Задача 16. Найти все значения параметра а, при которых уравнение
[а2 - 4а 4- 4^4 + 4 sin2 х + 8 sin х) + 2^16а -16 - 4а2)(1 4- sin ж) - 8а 4- 28 « О имеет по крайней мере одно решение.
Решение. Данное уравнение эквивалентно следующему
(в - 2)*(14- sin xf - 2(в - 2)2(1 + sin ж) • 2а - 7 о (а - 2)2 (ria2 х-1)»2а-7о сор х «
7-2а
Очевидно, что при а » 2 заданное уравнение не имеет решений. Для того чтобы это уравнение имело по крайней мере одно решение, необходимо и достаточно, чтобы
7
Ответ: а к Ч; 3«; а £ -.
2'
Задача 17. Найти все значения параметра а, при которых уравнение [а2 - 6а 4- 9^2 + 2sin х - cos2 ж) + (12а -18 - 2а2)(1 + sin ж) 4- а + 3 * О не имеет решений.
Решение. Имеем, как в предыдущей задаче, что исходное уравнение эквивалентно
10
следующему сох2 х «	. Чтобы это уравнение не имело решений, необходимо и
(Л-3)
Ответ:
1 < а < 6 а < -3
Задача 18. При каких значениях параметра b решение уравнения 6 + 4Ьх « 7Ь + 12х меньше 1?
Решение. Выпишем следующую цепочку эквивалентных соотношений
6 + 4Ьх « 7Ь + 12х <» 4(3 - b)x « -1Ь + 6 С=> X =	.
Теперь удовлетворим условию х < 1.	< 1 <=> -2 < Ь < 3.
Ответ: -2 < b < 3.
Замечание. Предложенную задачу можно решить, пользуясь наглядными геометрическими соображениями. Введем функцию f(x) = 4{ь - з)х - 1Ь + б.
„	fb-3>0	fb>3
При <	„ч .. .	Л • система
г « 4(Ь - 3) - 1Ь + б > 0 [ь < -2
несовместна.
Первое условие соответствует тому, что линейная функция f(x) монотонно возрастает, а второе условие соответствует тому, что эта функция обра
щается в нуль в точке, лежащей левее точки х » 1.
„ (b - 3 < 0	fb<3	„
При <	,,	Л<=м. л о -2 < Ь < 3. Первое
г /(1) = ~ЗЬ - б < 0 |Ь >-2	к
условие соответствует тому, что линейная функция f(x) монотонно убывает, а второе условие соответствует тому, что эта функция обращается в нуль в
-15 и в нуль эта функция ншде
точке, лежащей левее точки х « 1. При Ь » 3 /(х)«
не обращается.
Задача 19. При каких значениях параметра а уравнение (а +1) х2 - ах + (а - 3) « О имеет не более одного действительною корня?
Решение. Заметим прежде всего, что при а « -1 уравнение будет первого порядка и его
11
корень х « 4. Если а # -1, то уравнение будет квадратным относительно х и оно имеет не более одного действительного корня ( т.е. имеет либо два одинаковых действительных корня, либо два комплексных корня) тогда и только тогда, когда его дискриминант неположителен. Поэтому D = а2 - 4(а + 1)(а - 3) а -За2 4* 8а +12 £ 0.
Ответ: а = -1;
Задача 20. Найти все значения параметра pt при которых уравнение
J(x + 3p-3x-4V\x + *\ + p-2K+2) + log, —-—2_±£_±±_——_ « о
*	м	'	2(р-я)|х4-2|-х -4х4-2яр
имеет хотя бы одно целочисленное решение.
Решение. Данное уравнение эквивалентно следующему
J(x 4- Зр -Зя-4)(|х4-я| + р- 2я + 2) + log* --
= 0.
Сумма двух неотрицательных слагаемых равна нулю тогда и только тогда, когда каждое из них равно нулю. Поэтому имеем
х 4- Зр - Зя - 4 = 0
|х + я| + р-2л + 2 = 0
3(р - я) = 4 - л
= я - 2
’з(х 4- 2) = 4 - х х 4-2 £ 0
3(р - я) ® 4 - х
х + 2 < 0
3(р - я) = 4 - х
-х £ х £ 2
Так как х должно быть целым числом, то первая система решений не имеет. Из второй системы находим, что х = -5 и соответствующее р=»я 4- 3. Из третьей системы находим, что х = -2 при р = я или х = -3 при р = я +1.
Ответ: р = я; р = я +1; р ж я 4- 3.
Задача 21. При каждом значении параметра b решить уравнение 25х +£2(Ь-1)-5л -В5 «0.
12
Решение. 25' + b2(b -1) • 5' - bs = 0 <=> 51' + b’(/> -1) • 5' - bs = О 5
решений
_’ь2 "[-В3'
Отсюда непосредственно видно, что при b = 0 наше уравнение не имеет решений, при Ь>0 имеет решение 5' = Ь2 в s1^*	= 2log5 b, а при Ь<0 имеет два семейства
5' = Ь2 в 5to,s*’ о х = 2foft|h|, b < О
5’ = -Ь3 в о х = 3 b |, b < О
Ответ:	Если Ь > 0, то х = 2log5 Ь;
если Ь = 0, то решений нет;
если Ь< 0, то х = 3/о$5|ь| или х = 2/о^5|ь|.
Задача 22. Найти все значения параметра к, при которых один корень уравнения х2 - (к + 1)х + к2 + к - 8 = 0 больше 2, а другой корень ме ыпе 2.
Решение. Положим /(х) » х2 - (к + 1)х + к2 + к - 8. Тогда условие задачи выполняется в том и только том случае, когда относительно точки х = 2 квадратный трехчлен /(х) расположен так, как пока
зано на рисунке справа, т.е.
/(2) < 0 « 4 - 2(Ы) +12 + Ь 8 = ^ - Ь б = (Ь 3)(Ь 2) < 0 о -2 < U 3.
Ответ: -2 < к < 3.
Задача 23. При каких значениях параметра b уравнение
((x-b)2 -2b-4)(x-bf ж-2Ь-3 имеет отрицательных корней больше, чем положительных?
Решение. Исходное уравнение эквивалентно следующему
(х-d)4 -(2d + 4)(x-Z>)2 +2h + 3 = 0<=>(х-д)2
1
2д + 3
Если 2Ь + 3 < 0, то у этого уравнения два комплексно сопряженных и два действитель
ных отрицательных корня.
Рассмотрим теперь случай, когда 2Ь + 32*0. При этом исходное уравнение имеет д + 1
четыре действительных корня х =
д-1
Ь + ^2д + 3
д - ^2д + 3
Определим, при каких значениях b эти корни определены и отрицательны.
13
6 + 1<0<=>Ь<-1
b -1 < 0 сэ b < 1
b + <j2b + 3 < 0 <=> - — £b < -1 2
b- V2b + 3 <0 «>--£b <3 2
Заметим, что при Ь = -1 два корня обращаются в нуль, а два других при этом отри-
цательны. Итак, Ь $ -1.
Ответ: b £ -1.
Задача 24. При всех а решить уравнение |х-2| + а|х + з|=5 и определить, при каких а оно имеет ровно два решения.
Решение. Сначала снимем знак модуля, для чего найдем интервалы знакопостоянства каждого из выражений, входящих под знак модуля.
х-2------------------------ 2 + + + +
----------------!----------|------------
х + 3-------- -3 + + + + + + + + + + +
|х - j|+ в|х + 31» 5 с
4x-2)-o(x + 3|«S, xS-3 -(x-2) + 4* + 3)-S,-3SxS2. (х - 2) + я(х + 3)  5, х i 2
Решим каждое из трех полученных уравнений в соответствующей области определения.
Для первого уравнения имеем
а * -1 х£-3 а # -1 х = -3
Для второго уравнения имеем
'-(х - 2) +о(х + 3) = 5 Г(а - 1)х = -3(а -1)
-3 £ х £ 2	[-3 £ X <> 2
а = 1
-3 £ х £ 2 а # 1
х = -3
Для третьего уравнения -
7-За * = а + 1 2^2
-1 < а £ 1
7-За . X =-----
а+1
Чтобы определить, при каких а это уравнение имеет д решения, удобно эти решения изобразить графически.
М
Отсюда непосредственно видно, что при | а | < 1 уравнение имеет ровно два решения.
Ответ: При |а|>1 х»-3;	при о = -1 х£-3;
при а = 1	-3£х£2;	при |а|<1, х = -3 или л = -——.
Замечание. Данную задачу можно решить графически. Для этого разрешим предложен-
ное уравнение относительно параметра а.
	j	с « -3, а е R	3 + х 	с; —1 -г *
а|х + 31« 5-1х - 2 |о		R сч 	 1 tn Н + 1 И- Я к а	-(х + 3) — «1, -3<jS2 3 + х 7-х 	,	л 2 2 х + 3
			
Строим графики полученных функций, т.е. 5-|х-2|
у « а и у в —р--г2.
Из графиков непосредственно видно при	х - -3	а - любое;
при	-«о < х	<	-3	а = -Г,
при	-3 < х	£	2	а « 1;
7 - За ПОИ	х а---	-1 < а <	1.
г л + 1
Задача 25. Найти все значения к, при которых один корень уравнения (Л - 5) л2 - 2Лх + Л - 4 в о меньше 1, а другой корень больше 2.
Решение. Пусть /(л)«(к - 5) х2 - 2кх + к - 4. Возможны следующие два случая
Первый случай характеризуется следующей системой условий к -5 > О	f
-/fl) « fc - 5- 2Л- 4 < О	<^5<Л<24.
Д2)«4(*-5)-4* + *-4<0
Второй случай характеризуется следующей системой условий 15
*-5<0
/() = X- 5- 2* + t- 4>0 Эта система неравенств несовместна.
/(2) = к - 24 > О
Ответ: 5 < к < 24.
Задача 26. Найти все значения т, при которых оба корня уравнения 2х2 + тх - 2 = 0 а) меньше 1; б) больше -1.
Решение. Пусть /(х) = 2х2 + тх - 2.
а)	Оба корня этого квадратного трехчлена будут меньше 1 при одновременном выполнении следующих условий:
1)	D = т2 +16 > 0 ( Условие существования двух различных действительных корней).
2)	- ^ < 1 (Условие того, что ось симметрии параболы Дх) проходит левее точки 1).
3)	/(1) = т > 0 (Условие того, что правее точки 1 нет действительных корней).
Решая эту систему, получим т > 0.
6)	Оба корня квадратного трехчлена /(х) будут больше *1 при одновременном выполнении следующих условий:
1)	D я т2 +16 > 0 (Условие существования двух различных действительных корней).
2)	-— > -1 (Ось симметрии параболы Дх) проходит правее точки -1).
3)	/(-1)  -т > 0 (Условие того, что левее точки -1 нет действительных корней).
Решая эту систему, получим т < 0.
Ответ: а) т > 0; б) m < 0.
Задача 27. Найти все значения параметра а, при которых больший корень уравнения
хг +^^Длл2а-16»0 на больше, чем квадрат разности
»	COS2 О
уравнения х* - хзта +--- -1 = 0.
4
корней
Решение Найдем больший корень уравнения х2 +	sin 2а -16 = 0. Имеем
уз
2 х + 4 . „	/	л sin 2а] Л -	-
х jm2a-16s^x + 4)^x-4 + —| =0. Отсюда следует, что большим корнем
. sin 2а о	,	cos2 а
является х = 4-----. Заметим, что для уравнения	+-------1 = 0
УЗ	4
дискриминант £>
?	sin2 а	cos2 а
1	4	4
cos 2а Л
------> 0, поэтому оно имеет два 4
16
действительных корня для любых значений параметра а. Теперь, пользуясь теоремой
_	„	«	2	cos2 а «
Виета, найдем квадрат разности корней уравнения х - х зт а +----------1=0. Имеем
4
(х, - х2)2 = (х> + х2)2 - *х\х2 = 5™2 а “ cos2 а + 4 s 4 - cos 2а . Наконец, составляем
уравнение, отвечающее условию задачи 4 -	« 4 - cos 2а + J— о cos 2а - —.?* » J—
<3	1 . „	1	/„*11	„ я . я	„
о	cos2а-зт2а « —== о соя 2а + —» —=• а» 2а + - « ±- + 2ял, л eZ »
2	2 V2 V ^2	6	4
я	„
а » — + ял, л е Z 24
5я а --------+ ял», т е Z
24
Ответ: а = — + ял, л € Z; а = - — + пт, т € Z 24	24
Задача 28. Найти все значения параметра Ь, при которых уравнение
(1 +b)x2 - 2Ьх + 2 = |(ь + 1) х -1| имеет ровно одно решение.
Решение. Заметим, что при b = -1 заданное уравнение имеет единственное решение х = 0. Если Ь # -1, то заданное уравнение эквивалентно следующему
2	2	1 |л а „I
(1+Ь)х2-2fer + 2 = |(fc + l)x-2|<=>* b + lX+b + l Ь + 1К* + 1)Х“2|-
Введем в рассмотрение функцию
/W = x2’^Tx+7TF’77tI^ + 1)x’2I-Супюст’
венной точкой этой функции является точка х =-------. Снимая знак модуля, получим
(h + 1)х - 2 <> 0 / \	2	2	1 //,	2 ЗЬ 4-1	4
/1(х)»х--------х +----------|(Ь + 1)х-21 = х-------х +------
7 Ь + 1 b + 1 h + l" 7	7 Ь + 1 Ь + 1
\b + 1)х - 2 0
/2(х) = х2------X + —— +	((ь + 1)х - 2) = х2 -     X *
I К 7 Ь + 1 Ь + 1 b +	7	7 b + l
В точке х = обе функции Л(х) и f2(x) принимают одно zf И >> 3~Ь
ИЛИ
и то же значение
Рассмотрим случай
точке х = 0, то рассмотрим два случая.
17
d2
2
< ——. т.е. точка х = 0 лежит левее точки
—у. Имеем для дискриминанта функции /2(х)
I -—-) = о «> Ь = 1. При Ь = 1 для Д(х) имеем \Ь +1/
= х2 - 2х + 2 = (х -1)2 +1 £ 1, т.е. функция Д(х) ни ни каком множестве не обращается в нуль.
2
2) 0 >	, т.е. точка х = 0 лежит правее точки
х = —. В этом случае /2(х) не обращается в нуль на множестве х£——. Поэтому функция Д(х) Ь 4- 1
2 должна иметь один нуль на множестве х £---. Это
соответствует тому, что
/	\2	,	/—
Z>! = ( 3,fc * \ | —— =	-ЮЬ-15 _ 0 b _ jtjylO pih о о из э значений b
14MJ fc + 1	4(b + l)2	9
2
не удовлетворяет условию 0 >-----<=> ь < -1. Поэтому этот случай не имеет места.
Случай, когда	*0 дает более одного
решения для исходного уравнения, что видно из приведенного справа рисунка.
Ответ: b = -1; b = 1.
Задача 29. При каких значениях параметра к уравнение х2 + 2(Л - 1)х + к + 5 = 0 имеет хотя бы один положительный корень?
Решение, Обозначим /(х) = х2 + 2(к - 1)х + к + 5. Тогда для того чтобы этот квадратный трехчлен имел по крайней мере один действительный корень, необходимо и / \2
достаточно, чтобы D =	- q = (к - 1)2 - (к + 5) £ 0 <=> (к - 4^к + 1) 2 О о .
Ось симметрии параболы /(х) = х2 + 2(Л - 1)х 4- к + 5 определяется так хс = 1 - к и при к £ -1 она будет лежать правее нуля, а при к 4 она будет лежать левее нуля.
В первом случае всегда имеется по крайней мере один положительный корень.
18
Во втором случае для существования положительного корня необходимо и достаточно, чтобы До) = к + 5 < 0 <=> к < -5. Но так как к Z 4, то этот случай невозможен.
Ответ: к £ -1.
Задача 30. Определить все значения параметра а, при которых уравнение log3 х + 3 loga х + log9 х = 5 имеет решения, и найти эти решения.
Решение. Заметим, что а > 0, а * 1. Приводим все логарифмы к основанию а.
log3 х =	; log х = —. Поэтому заданное уравнение эквивалентно следую-
l°ga 3	loga 9
щему
(з/о£9 а + l)loga х = 5 <=>
log9 а + 1 # 0
,	5
log х =	_
3(^9 а + 1)
5
Ответ: х = fl3(to*»e+l) fl>0, а#1, а#-. 9
Задача 31; Определить, при каких значениях параметра а уравнение
а
2
= 4 4 | х | - а2 имеет ровно три корня. Найти эти корни.
Решение. Построим графики функций у = х -
У “4
40х|- а2^ 4|х|-а2£0
-40 х | - в2^ 4| х | - а2 <0
-4^4х + а2)
L 4
-4^4х - в2!
а2 0 S х $ ——
4 4^4х + в2) а2
----£ х S 0
I 4
|4|*|-в2|-
Заданное уравнение должно иметь ровно три корня.
19
2
Это равносильно тому, что прямая у = х - должна иметь с ломаной у ровно три общие точки, которые должны принадлежать четырем звеньям ломаной. Поэтому эта прямая должна проходить через точку, принадлежащую одновременно двум звеньям ломаной, т.е. через вершину ломаной. Таких вершин у нашей ломаной , ОI, |	, 01. Из рисунка непосредственно видно, что последний
) V 4	)
случай невозможен (пунктирная линия на рисунке), ибо в этом случае прямая и ломаная имеют лишь одну общую точку. Рассмотрим случаи (1) и (2).
Случай (1). Общая точка - (о, 4а2). Подставив координаты этой точки в уравнение а = 0
а _	. При а » 0 заданное уравнение превращается в
, “ 8
уравнение х = 1б|х|, которое имеет лишь один корень х»0. При
уравнение будет иметь ровно три корня х « -	; х « 0 и х •	.
Случай (г). Общая точка -	Подставив координаты этой точки в
а2
уравнение прямой, получим 0 « —— - ~ <=>
три:
л 2 а
прямой, получим 4а = - - <=>
заданное 8
а«0 _	Л
Л. Значение а « 0 не годится, как и в а «-2
случае (1).
Ответ:
15	17
При а = -2 заданное уравнение будет иметь ровно три корня х а >1; х = - их- —
при в--1
136 ’* * “ ° И * “ 120 ’
15 - V 1; х « — и х * —.
17	15
при а»-2
Задача 32. Для каждого значения параметра а решить уравнение 4cos xsina. +2sinxcosa-3cosa » 2^7 .
Решение. Перенесем -Зсоуа в правую часть и разделим обе части полученного уравнения на корень квадратный из суммы квадратов коэффициентов при cosx и sinx, т.е. на ^16 sin2 а+ 4 cos2 a s 2^4-3 cos2 а . В результате получим
2лла	соха	2^7 + 3casa /	\	2у7 + 3cosa
-============ caj л + -==s====sr sin х * —====== о cos(x - <р) « —======•, у4-3саг2а y4-3cas2a 2у4-3сох2а	2у4-3сох2а
2sina	соха
ГДе сахф« ’'унгя; '/. , ллф «-====•.
у4*3сси2а	у 4 ~3cos2 а
20
Утверждается, что 2^7 + 3 cos а 2^4-3 cos2 а , Действительно,
28 + 12^7 cos а + 9 cos2 а 2 4^4 - 3 cos2 а) €> 12 +12^7 cos а + 21 cos2 a я 3^2 + ^7 caraj 0 .
2	[з
Равенство достигается тогда и только тогда, когда cosa = - — при этом sin a = ±J- .
V7	17
Таким образом, заданное уравнение имеет решения при тех и только тех
a
для
которых cosa = --=г. При других значениях а уравнение не имеет решений.
при других а решений нет.
Имеем соя х + -| = 1ох«-- + 2кл, п €Z . \	6/	6
имеем соа х + — I = 1« х = ~~ -I- 2*1, i«z. \ б J	б
X «= - — + 2лл, и € Z ;
6
— + 2*7, / eZ б
Задача 33. Определить, при каких значениях параметра b уравнение
(b - 3) х2 - (ъ1 - 5ь)( | х | -1) + 6 » 0 имеет единственное решение.
Решение. Из вида уравнения следует, что если х0 является решением данного уравнения, то и -х0 также есть решение этого уравнения, т.е. исходное уравнение симметрично по х относительно нуля и поэтому оно имеет по крайней мере два решения для всех х, отличных от нуля. Отсюда следует, что если данное уравнение имеет единственное решение, то это может быть только х = 0. Подставляя значение х = 0 в исходное уравнение, получим
b2 - 5Ь + 6 s (b - 2)(b - 3) « 0
Ь*2 Ь = 3'
Однако может оказаться, что помимо х - 0 при этих значениях параметра b имеются и другие решения. Поэтому исследуем заданное уравнение при полученных значениях параметра Ь.
1. При Ь = 2 исходное уравнение обращается в уравнение
21
Таким образом, при b = 2 исходное уравнение имеет три различных решения, т.е. значение параметра Ь = 2 будучи необходимым, не является достаточным для единственности решения заданного уравнения.
2. При Ь = 3 исходное уравнение обращается в уравнение | х | = 0, которое имеет единственное решение х = 0, т.е. значение Ь = 3 является необходимым и достаточным для единственности решения заданного уравнения.
Ответ: Ь-3,
Задача 34. При каких значениях параметра к корни уравнения х2 + 2$к - з) х + 9 = О лежат в промежутке (-6, 1) ?
Решение. Пусть f(x) = х2 + 2(i - 3) х + 9. Тогда > Д-б) I
для выполнения условия задачи необходимо и \	I	Л
достаточно, чтобы одновременно выполнялись . а \	!_____/ а »
следующие четыре условия:	-б	। **	1
1) О-(f) -9-(*-3)2-9> О о к(к - б) > 0	1
( Квадратный трехчлен Дх) имеет два действительных корня). 2) -6 < хс = 3 - fc < 1 <=> -9 < -к < -2 е>2< к <9
( Ось симметрии параболы Дх) принадлежит интервалу (-6,1)).
3) /(-б) = 36 -12(Дг -з) + 9>0€>*<^ ( Нет корней левее точки х « -6).
4) Д1) я 1 + 2(к - з) + 9 > 0 о к > -2 ( Нет корней правее точки х «1).
27 Объединяя все эти результаты, окончательно получим 6 < к < —. 4
27 Ответ: 6<к < —.
'	А
Задача 35. Найти все значения параметра а, при которых уравнение х|х-2а|-1-а = 0 имеет единственное решение.
Решение. Обозначим /(х) = х|х-2а|-1-а. Существенной точкой этой функции
является точка х = 2а. Снимая знак модуля, получим
/(х) = х|х-2д|-1-а<=>
х - 2а £ о
/10 = х(х - 2а) - 1 - а
х - 2а <. О
/г0 = ~*(х - 2а) - 1 - а
/(2а) = Л(2а) = /2(2а) = -1 - а , т.е. значения функций /Дх) и /2(х) в точке х = 2а
22
совпадают и равны -1-а; правее точки х = 2а ветви параболы /1(х) направлены вверх, а левее точки х = 2а ветви параболы /2(х) направлены вниз, причем обе параболы Л(х) и /2(х) имеют одну и ту же ось симметрии хс = а.
Рассмотрим случаи, когда f(2a) = -1 -а > 0 и /(2а) = -1 - а < 0. При этом точка хс = а может лежать левее и правее точки х = 2а.
Заметим, что при а = -1 заданное уравнение обращается в уравнение х I х + 21 = 0 и,
следовательно, имеет два решения х = 0 и х = -2.
Итак, рассмотрим, случай /(2а} = -1 - а > 0.
/(2а) = -1 - а > О
Д(а) = -a2 - а -1 > 0 - нет решений. 2a < a
/(2a) = -1 - а > О
' 7	- нет решении,
a < 2a
Теперь рассмотрим случай /(2a) = -1 - a < 0.
Заметим, что при а = 0 исходное
f/(2a) = -1 - а < О
Г' 7	о -1 < а < 0 .
[ 2a < a
j-
/2(a) = a2 - a- l<0<=>0<a<-—
a <2a
уравнение приобретает вид x | x | -1 = О
и имеет
единственное решение х = 1.
23
Объединяя все результаты, получим, что заданное уравнение имеет единственное 1	1 + V5
решение при -1 < а < —-—.
Ответ: -1 < а <---
2
Решение I. к2х2 + £х-2 = 0<=>*х =
Задача 36. При каких значениях к корни уравнения к2х2 + Ь - 2 = О будут действительными и один корень по абсолютной величине будет больше 1, а другой корень по абсолютной величине будет меньше 1?
На наш взгляд заслуживают внимания несколько решений этой простой задачи.
1
Теперь удовлетворим условиям
1
-2
задачи I- < 1 и
- ~ > 1. Откуда получаем 1 < | к | < 2.
Решение 2. Пусть /(*) = к2х2 + кх-2. Тогда очевидны следующие соотношения: i) D » Ъ2 - 4ас « к2 + 8р = 9к2 > 0 (Условие того, что корни заданного уравнения
2) Один корень меньше -1, а другой принадлежит интервалу (-1.1).
+*-2>0 t „
Л-1) = Р- *- 2<0
Один корень больше 1, а другой принадлежит интервалу (-1,1).
/(1) = *2 +£-2<0	„ L ,
« / \	-2 < к < -1.
/(-1) = *2-*-2>0
Решение 3. Условие задачи соответствует тому, что один нуль функции /(х) принадлежит промежутку (-1,1), а другой нет, т.е.
< О «> (* - 2)(t - 1)(к + 1)(к + 2) < О
к
Ответ: -2 < * < -1, 1<* < 2.
Задача 37. Найти число решений уравнения 71 - х2 = в зависимости от значений параметра а.
24
d	[i T	1 — x2 ® (x +	(2x2 4- 2ax + a2 —1 = 0
Решение. yl-x=x + a<=>	\	/ «=> <
x + a£0	(	x+a£0
Обозначим f(x) = 2x2 +2ax + a2 - 1. Это однопараметрическое семейство парабол,
а
ветви которых направлены вверх и ось симметрии хс = -у • а) Полученная смешанная система не будет иметь ни одного решения
либо при D = 2-а2 < 0 <=> |«| > ^2 (Это означает, что нет действительных корней),
либо при
а
2	<=> а < -1 (Эта система означает, что парабола f(x) не
/(-д) = а2-1>0
имеет нулей, лежащих правее точки х = -а).
б) Полученная смешанная система будет иметь ровно одно решение в одном из трех
случаев
1)
а
2	<=> а = -1 (Точка х = -а является корнем квадратного трехчлена
/(-a) в а2 -1 = 0
/(*) = 2х2 + 2ах + а2 - 1, ось симметрии параболы /(х) лежит левее точки х = -а, и, следовательно, вторая точка пересечения параболы /(х) с осью х лежит левее точки
х = -а),
2) /(-а) в а2 - 1 < 0 <=> -1 < а < 1 (Один нуль функции /(х) лежит левее точки х = -а,
а другой правее этой точки).
3)
"а < " 2	<=> а = V? (Квадратный трехчлен /(х) имеет единственную общую
О в 2 - а2 = 0
точку с осью х и эта точка лежит правее точки х = -а).
Итак, при -1 £ а < 1 и а = 5/2 заданное уравнение имеет ровно одно решение.
в) Наконец, полученная смешанная система будет иметь два решения при
о
~а < а > 0
/(-в) = о2 -12>0<=> |а|^1 <=>1*О <5/2
D в 2-а2 > 0	|а| < ^2
(Это условие того, что две точки пересечения параболы /(х) с осью х лежат правее точки х = -а).
Замечание. Заданную задачу можно решить графически. Построим графики функций у = 71 - х2 и у = х + а . Графиком первой функции является полуокружность радиуса 1 с центром в начале координат, а графиком второй функции является прямая, 25
наклоненная к осн Ох под углом 45° и отсекающая на оси Оу отрезок а. Когда а меняется от -<ю до -юо, тогда это будет семейство параллельных прямых. Считая число общих точек графиков функций у = 71 - х2 и у = х + а, когда а меняется от -<ю до -но, получим приведенные выше ответы.
Ответ: а> J1, а <-1	- нет решений;
а «7?. -1£а<1	- одно решение;
1 £ а < V2	- два решения.
Задача 38. Найти все значения параметра с, при которых уравнение | х2 - 2х | +1 х2 - Зх + 21» х2 - 4х + с
имеет ровно три различных корня.
Решение. В заданном уравнении уединим параметр с справа и построим трафики левой и правой частей, т.е. я » х2 -2х + х2 -Зх + 2 -х2 +4х и у2 = <?.
Заданное уравнение имеет ровно три различных решения в том и только том случае,
когда 1рафики функций и у2 « с пересекаются в трех различных точках. Из приве-
денного рисунка видно, что это выполняется лишь для двух значений с а 4 и с = —. 19
Ответ: с » 4; с » —-.
4
Задача 39. Найти все значения параметра к» при которых уравнение 2х-|х-Р |»11*-Э|л + 4*|
1. Не имеет решений.
2. Имеет конечное непустое множество решений.
26
Решение. Обозначим Дх)» 2х - [ х - к2 | -1И + 31 х + 4к |. Существенными точками этой функции являются точки х = к2 и х = -4* . Рассмотрим два случая.
1.	Точка х =-4* лежит левее точки х = к2,
Снимая жакн модуля, получим
Лх)
-4к£х£к2
, к	Заметим, что на множест-
/2(х) = 6х-Р + к
хЪк2
т.е.
-4Л к
ве x£-4Jt функция Дх) постоянна, а на множествах -4&£х£*2и х^к2 -монотонно возрастает. Поэтому заданное уравнение не имеет решений тогда и только I-Jt2 — 23Л >0
тогда, когда <	<=> -23 < к < -4. Этот факт хорошо виден на приведенном
При
выше рисунке.
-к2 - 23£ = О к = -23 все точки х из множества х £ -4* удовлетворяют
заданному уравнению, т.е. уравнение имеет бесконечно много решении. ЕслиР-Ш,<0
то заданное уравнение имеет единственное решение.
Вывод 1. Заданное уравнение при
* > О имеет единственное решение, при к = -23
имеет бесконечно много решений, при -23 < к < -4 не имеет решений.
2.	Теперь рассмотрим случай p£-4Jt<=>-4£*£0, который соответствует тому, что точка х = -4* лежит не левее точки х = к2. Снимая знаки модуля, получим
х s /Р |л(х) = -*2-23* к2 £ х £ -4Л	_
.	7	. Заметим, что на мно-
Л»)

жестве х£к2 функция Дх) постоянна, на множестве к2 £ х £ -4* - монотонно убывает, а на множестве
27
х z -4к - монотонно возрастает. Поэтому заданное уравнение не имеет решений в том
и только том случае, когда
При
-к2 - Zik = О к2 S -4*
к2 S -4к
к2 — 15* > О к2 i -4к
<=> -4 £ к < 0.
заданное уравнение будет иметь бесконечное множество
к = О
решений. Итак, второй случай, когда -4 £ к £ 0 полностью исследован.
Вывод 2. Заданное уравнение не имеет решений при -4 <. к < 0, при к = 0 имеет бесконечное множество решений.
Объединяя результаты выводов 1*2, окончательно получаем, что заданное уравнение ие имеет решений при -23 < к < 0, имеет бесконечное число решений при к = -23 и при к = 0, имеет конечное число решений при к < -23 и к > 0.
Ответ:	1. -23 < к < 0;
2. *<-23; *>0.
Задача 40. Найти все действительные значения а, при которых корни уравнения х2 + х +а = 0 будут действительными и оба корня будут больше а.
Решение, Обозначим f(x)« х2 +х+а. Тогда условие задачи выполняется тогда и только тогда, когда одновременно выполняются следующие три условия:
1)
2)
D«fe2-4ec = l- 4a^0 (Корни заданного уравнения действительны).
(Ось симметрии параболы f(x) проходит правее точки а).
3) /(а) = а2 +а > 0 (Нет корней, лежащих левее точки а).
Наглядно эти условия видны из приведенного выше рисунка. Решая систему неравенств, получим
Ответ: а < -2.
Задача 41 Определить все значения параметра о, при которых ровно одно решение неравенства ^(а + 3)(а2 + а - б) х3 - Ja4 + в3 - 6а2 х2 4 Ja3 + За2 х - а2 £ 0 удовлетворяет условию 1 £ X £ 4 + а .
28
Решение, Перепишем заданное неравенство в следующей эквивалентной форме + З)1 2(а - 2) х3 - ^а2(а + 3)(а 2) х2 + ^а2(а 4-3) х - а2 £ 0 .
Отсюда видно, что все корни существуют при а £ 2; а = -3.
Если а = -3 до заданное неравенство обращается в неравенство -9 £ 0, справедливое для любого х, а условие 1 £ х £ 4 + а обращается в равенство х = 1. Следовательно, при а = -3 поставленная задача будет иметь единственное решение х = 1.
При а £ 2 неравенство можно записать так
(а + 3)7а - 2 х3 - а^(а + 3)(а - 2) х2 + а^а + 3 х - а2 £ 0 о
<=>	+ з)(а - 2) х2^7л + 3 х - aj + а^а + 3 х - а) £ 0 <=>
<=> (V(a+зх° $ *2 +	+ 3 х - £ 0 <=> Ja + 3 х-а£0<»х£	.
Для того чтобы система
х <; -7-?7.'.-.v
+3 имела при а 2 2 ровно одно решение, 1 £ х £ 4 + а
необходимо и достаточно, чтобы
Z4	а 1 4- <13
Ответ: а = -3; а -------
2
Задача 42 Найти все значения параметра а, при которых неравенство
5 sin 2 х + 2а sin х cos х + cos2 х + а +1 £ 6 выполняется для любых значений X.
Решение. Преобразуем заданное неравенство, выразив sin2 х и cos2 х через cos 2х.
1	2	I
5sin х + 2аsinхcosх + cos х + а + 1£6<^
, 1 - cos 2х . „	1 + соs 2х	, К
5----------+ a sin 2х +----------+ а + 1 £ 6 €>
2	2 I
<=> 13 — 2 cos 2х+аял2х4-а + 1|£б<=>
л / 2 . a 2cos2x Г 2 7 asin2x
4 -	4- 4 -=====• + V«r 4- 4 -===== + а
№ 4-4	уа2 4-4
£ 6 <=>
<=> 4 + у а2 4-4 sin(2x - ^?) 4- а £ б , где cos<р «	— , sin <р » -j===^.
I	ya2 + 4	ya2 4- 4
Так как x - любое, то -1 £ $ш(2х - р) £ 1, т.е. а должно одновременно удовлетворять
£ б
£ б
неравенствам
-10 £ а - Уа2 4-4 2 о
-10 S а + /а2 4- 4 S 2
'	24
---24 а' л
5 о-----s а ь 0 .
а £0	5
Ответ: -—£а^0. 5
29
Задача 43 При каждом значении параметра а найти все решения неравенства х + 2а - д/зах + 4а2 > 0 .
Решение, х + 2а - уЗах + 4а2
х > О, а = О
— I у/зах 4-4а2 1 - уЗах + 4а2 + ~ а > О, а * О
За К	)	3
В таком виде заданное неравенство легко анализируется.
Действительно, если а < о, то неравенство не имеет решении, так как — < 0, а
каждое из выражений		7зах 4- 4а2 - 2а и ^Зах 4- 4а2 - а больше нуля.	
Если а>0, то Ответ: при при при	7зох + 4а2 > 2а о 0 £ ^Зах + 4а2 < а 4 а > 0	—а £ х 3 а ® 0	х > 0 ; а < 0	нет реше]		х > 0 4 —а £ х < -а L з < -а; х > 0; кий.
Задача 44 Найти все действительные значения а, при каждом из которых неравенство а2 + а - sin2 х -2аcos х > 1 выполняется при любом действительном значении х.
Решение. Преобразуем заданное неравенство следующим образом а2 + а - sin2 х - 2а cos х > 1е» cos2 х - 2а cos х 4- а2 4- а - 2 > 0.
Обозначим f(cos х) = cos2 х - 2а cos х а2 + а - 2. Это однопараметрическое семейство квадратных относительно cosx трехчленов. Графиками этого семейства будут часта парабол, соответствующие -1 £ cos х <; 1, так как х - любое действительное число, причем любая парабола этого семейства выпукла вниз, так как коэффициент при cos2 х равен 1, а ось симметрии хс = а может быть расположена левее точки х = -1, т.е. хе < -1, принадлежать отрезку [-1,1], т.е. -1 £ хс £ 1, и быть правее точки х = 1, т.е. хс > 1. Опишем каждый из этих случаев.
f*<•<-1 f °<-i	3 + 713	А1}
|/(-1) > 0 ** |а2 + За - 1 > 0 ** ° < ~ 2 Лсо,х)	/\
Второе неравенство системы соответствует \ j Д'"1)/ ] тому, что f(cosх)> 0 при	1
-----4---------------------4—^.
-1 1
30
[-1 £ хс £ 1	[-1 £ а £ 1 _
2) I ( ) > 0 <=> I о . Эта система неравенств решении не имеет.
[х>1	[ а> 1	1 + 7s
3) < А <=> S о	<=> а >----.
' |/(1) > 0	[а2 - а - 1 > 0	2
л	3 + 713	1 + ^5
2	2
Замечание. Решим предложенную задачу иначе. Преобразуем заданное неравенство следующим образом
а2 + а - sin2 х -2а cosx > 1 « cos2 х -2а cosx + а2 4- д - 2 > 0 <=> (cosx - а)2 4- а - 2 > 0 .
В таком виде неравенство легко анализируется. Действительно, если | а | £ 1, то за счет cosx слагаемое (cosx-я)2 всегда может быть сделано нулем. Отсюда вядао, что данное неравенство не может выполняться для любых действительных х при | а | <. 1.
Рассмотрим случай а>1. Тогда слагаемое (cosx-а)2 не может быть меньше, чем /	\2 т-г	____ 1(1 - в)2 4- в - 2 > в	1«2 -« ~ 1 > О
(1 - а) . Поэтому решим систему р /	{	<=> а > —~—.
[ а > 1	(а>1	2
Рассмотрим случай а < -1. Тогда слагаемое (cos х - в)2 не может быть меньше, чем (-1 - а)2 . Поэтому решим систему
(-1-а)2 4-д-2>0 _ (о2+За-1>0 _	3 + 713
а < -1	I а < -1	2
Задача 45. Найти все значения действительного параметра с, для которых неравенство
справедливо при всех х.
Решение.
1 +	4-1) £ log^cx2 4- 4х 4- с) 5^х2 4-1) £ сх2 4- 4х 4- с> 0
-оо < X < 00	-СО < X < СО
сх2 4- 4х 4- с > О (5- с)х2 -4х + 5- с£0.
-со < X < 00
Замечание. Трехчлен у - ах2 +Ъх + с больше нуля для любых х тогда и только тогда,
когда а > о и его дискриминант отрицателен.
с > о
Воспользовавшись этим замечанием, получим
Ответ: 2 < с £ 3.
31
Задача 46. Для каждого неотрицательного значения параметра а решить неравенство 16а3х4 + 8а2х2 + 16х + а + 4 £ 0 .
Решение. Заметим, что при а = 0 неравенство справедливо для х £ - Преобразуем 4
левую часть неравенства следующим образом
16а3х4 + 8а2х2 + 1бх + а + 4 в а(лах2 +1) + 16х + 4 в а\ (ла2 +1] - 16х2 |+16ах2 + 16х + 4 
а а ^4ох2 - 4х + 1Д4ах2 + 4х +1j + 4\4ах2 + 4х + ij s |4ах2 + 4х + 1д4а2х2 - 4ах + а + 4J .
Таким образом, нужно найти решение неравенства ^4ах2 + 4х + 1^4а2х2 - 4лх + а + 4^£0 при а > 0. Квадратный трехчлен 4а2х2 - 4ах + а + 4 s (2ах -1)2 + а + 3 больше 3 для любых х при а > 0. Следовательно,
^4ах2 + 4х +1) ^4а2х2 - 4ах + а + 4^ 0	(4ах2 + 4х +1 £ О
а > 0	( а > О
Если а £ 1, то неравенство справедлив для любых х.
_	-1 “ 71 - а	-1 + 71 “ «
Если 0 < а < 1, то неравенство справедливо при х £--—-----и при х £------—-----.
Ответ:	Если а = 0, то х £	;
4
если 0 < а < 1, то X <;	и х Ъ	;
2а	2а
если а £ 1, то -со < х < оо.
Задача 47. При каждом значении параметра а указать, для каких х выполняется неравенство 4х*+,а2 - 65 - 4Jt'1a +1 > 0.
Решение. Очевидно, что при а £ 0 неравенство выполняется для любых х. *
Если а > 0, то исходное неравенство эквивалентно следующему
4»
Ответ: При а £ О -со < х < оо; при а > О
х > 1 - log4 а
х < -2- log4 а '
Задача 48. Пусть с > 0, d > 0. Найти решение неравенства
1 1
— 4--
х d
Решение. Умножим обе часта заданного неравенства на x2cd>0. Тогда получим эквивалентное неравенство dix2c2 -х4 >xcd + x2c, которое эквивалентно совокупнос-32
ти следующих двух систем
xd 4- х2 < О
х2(с2-х2Ьо ' ' <=>
xd + х2 £ О
d2(c2x2 - х4 j > x2c2d2 + 2х3с2d + х4с2
х(х + d) < О (с - х)(с + х) £ О
х(х + d)z О
х3 ^с2 + d2 j ч- 2с2 dj < О
либо
-с £ х < 0, при условии d > с;
<£> -d < х < 0 , при условии d £ С.
нет решении» при условии d > с;
2c2d
<=> - ----г < х £ -d , При условии d £ С.
с2 + d2
Окончательно получаем
2c2d
Ответ: - ~------- < х < 0, при условии d £ с;
с2 + d2
-с £ х < 0, при условии d > с.
Задача 49. Найти все значения параметра а, при которых неравенство (х - За) (х - а ~ 3) < О
выполняется для всех х таких, что 1 £ х 3.
Решение. Введем в рассмотрение функцию /(х) = (х - За) (х - а - з). Это однопараметрическое семейство парабол, ветви которых направлены вверх. Тогда заданное неравенство превращается в /(х) < О, которое выполняется для всех х таких, что 1 £ х £ 3, в том и только том случае, когда
Д1) 3 (1 - За)(1 - а - 3) = з(а -	+ 2) < 0	0 < а х
/(з) з (3 - 3о)(3 - я - 3) н 3(а - 1)а < 0	3
33
X2 + к2
Задача 50. Найти все значения параметра к, при которых неравенство -7-г £ 1
Цб + х) выполняется для всех х, удовлетворяющих условию -1 < х < 1.
Решение. Заметим, что при -1 < х < 1 всегда 5 < б + х < 7, и, следовательно к > 0. Поэтому предложенную задачу можно переформулировать так:
найти все положительные значения к, при которых неравенство х2 - кх + к2 - 6к ъ 0 выполняется для всех х, удовлетворяющих условию -1 < х < 1.
Введем функцию /(х) = х2 - кх + к2 - 6к. Это однопараметрическое семейство пара-
бол, имеющих ось симметрии хс = у > 0, и Возможны два случая:
1)	Ось симметрии параболы Дх) принадлежит отрезку [-1, 1]. Этот случай можно описать так: 0<|$1
. Эта систем* решений не имеет.
2)	Ось симметрии параболы Дх) лежит правее точки х«1. Этот случай вписывается так:
->1	~	2	’
2
ветви которых направлены вверх.
Ответ: к^-----
2
Задача 51. Определить, при каких а неравенство х2 + |л-л|-3 < 0 имеет хотя бы одно отрицательное решение.
Решение. Заданное неравенство эквивалентно совокупности двух систем неравенств х - a £ 0
, . t	/. (х) = х2 + (х - а) - 3 < 0
х-л |-3 < 0 <=>	v 7
’	х - а £ 0
|/2(*) = *2 ~(х-а)-3<0
Рассмотрим первую систему совокупности. Функция Д(х) = х2 + х - а - 3 задает однопараметрическое семейство парабол, ветви которых направлены вверх и ось симметрии которых хс^ = -1. Точка х = а может находиться левее и правее точки хс - “у • Поэтому первая система совокупности будет иметь отрицательное решение в одном из 34
следующих двух случаев:
13
4
2
'( П	13
/11 — Iе-----а
[Ч 2/	4
£ а < 0 2
[/1(а) = а2-3<0
Рассмотрим вторую систему совокупности. Функция /2(х) = х2 - х + а - 3 задает однопараметрическое семейство парабол, ветви которых направлены вверх и ось симметрии которых хс = -. Поэтому вторая система совокупности будет иметь отрицательное
решение в одном из следующих двух случаев:
а £ О /2(0) = а-3<0 а < О /2(а) = л2-3<0
Объединяя результаты, получим < а < 3.
4
Л	13
Ответ:-----< а < 3.
4
Задача 52. Найти все значения а, при каждом из которых неравенство fofll хх2 + ах + 5 +1] /о£5|х2 + ах + б] + loga 3 £ О
имеет ровно одно решение.
Решение. Заметим, что а > 0, а * 1. Рассмотрим два случая 1)0<а<1;2)а>1.
1) При 0 < а < 1 исходное неравенство эквивалентно следующему неравенству
2	>
4-1 £ log$ 3 .
Хх2 + ах + 5 +
Это же неравенство справедливо тогда и только тогда, когда ^х2 + ох + 5 £ 2. Достаточность этого условия очевидна. Покажем необходимость. Если ^х2 +ах + 5 < 2, то
2
2
<1 и неравенство не выполняется.
Таким образом, имеем
2
35
Неравенство х2 + ах +1 в (х +	+1 -	£ 0 выполняется для любых х при
О < а < 1, т.е. при 0 < а < 1 исходное неравенство не может иметь единственной) решения.
2) а > 1. При этом исходное неравенство эквивалентно следующему неравенству log^lx2 + ах + 5 +	+ ex + 5J 4-	£ logs 3 .
Последнее неравенство справедливо тогда и только тогда, когда ^х2 + ах +5 £ 2. Дока* зательство этого утверждения аналогично доказательству подобного утверждения для . —.......................................................  Г	2
сдучая 0 < а < 1 и мы его опустим. Итак, имеем ух2 + ах+5£2о]х +ах+1^0.
[х2 + ах -н5 £ О
Положим fi (х) = х2 + ах +1 и /2 (*) = *2 + + 5 • Это два однопараметрических семейства парабол, ветви которых направлены вверх и которые имеют одну и ту же ось симметрии хс=~у. Причем /2(х) =/1(х)+ 4 Для каждого фиксированного значения а, т.е. вершина параболы /2(х) всегда расположена выше вершины параболы /1(х). Пользуясь этим, получим, что неравенство д(х) = х2 + ах +1 £ 0 имеет {О а2 -4 = 0	„ г,
а = 2 . При ЭТОМ а > 1
значении а функция ^(х) = 0, а функция /2(х) = 4 > 0.
Ответ: а = 2.
Задача 53. Найти все значения q, при каждом из которых множество решений неравенства ^g - х2)(д + 2х - 8) < 0 не содержит ни одного решения неравенства х2 £ 4.
Решение, Обозначим /(g) = (д - х2 j(g + 2х - 8). Посмотрим, в каких пределах изменяется величина -(2х - 8), когда х2 £ 4. Имеем	f(q)
х2 ^4« -2 х £ 2 <=> 4 -(2х - 8) £ 12,	\	/
2 \ 4 У П
т.е. точка g = х2 всегда лежит левее точки *	’	УЦ2х-ъ\ q
g = -(2x-8).	*
Отсюда получаем, что множество решений неравенства (д - х2 )(д'+ 2х - 8) < 0 содержит хотя бы одно решение неравенства х2 £ 4 тогда и только тогда, когда
36
0 <q <12. Поэтому для	и для q £ 12 множество решений неравенства
[q - х2 j($ + 2х - 8) < 0 не содержит ни одного решения неравенства х2 4.
Ответ: $£0; $£12.
Замечание. Эту задачу можно решить иначе, пользуясь наглядными геометрическими соображениями. Действительно, нужно найти те значения параметра <?, при которых функция /(х) = ($-х2к$ + 2х--8) на множестве -2£х£2 неотрицательна. Это
возможно в одном из двух случаев:
($-х2)|	£0
V /1х=-2	<»$£12;
(9 + 2х-8)|х=2^0
(?-х2)	*0
'	/1х=о	$ £ 0 .
(« + 2*"<=2 *°
В первом случае функции д(х) = $ - х2
и /2 (х) = q + 2х - 8 одновременно
неотрицательны на отрезке -2 £ х $ 2, а во втором - неположительны на этом отрезке.
Задача 54. Найдите все значения х, удовлетворяющие неравенству (2 - а) х3 + (1 - 2а) х2 - 6х + ^5 + 4а - а2) < 0 хотя бы при одном значении а, принадлежащем отрезку [-1; 2 ].
Решение. Перепишем заданное неравенство в другой форме, а именно как квадратное относительно параметра а, т.е.
-а2 - (х3 4- 2х2 - 4) а + ^2х3 + х2 - 6х + 5) < 0.
Обозначим /(а) = -а2 -(х3 4-2х2 -4^а + ^2х3 -t-х2 - бх + 5). Заметим, что ветви параболы /(а) направлены вниз, Найдем сначала те значения х, при которых заданное неравенство не выполняется ни при каком значении af принадлежащем отрезку [-1; 2]. Это будут те и только те значения х, для которых
- Эх (х ' 2Х* -1) 0	Г-2 i S 0 .	/(-1)___fl2\
|/(2)B-3't+3Xx-l);:0~[ х = 1 ’ Итак, мы нашли те значения х, при которых ________—;---------;—_V—
заданное неравенство не выполняется ни для	/	”1	2	\
одного значения а, из отрезка [-1; 2 ].
Поэтому для х, таких что х е (- <ю; - 2) (0 ; 1) (1; + оо) заданное неравенство будет
37
выполняться хотя бы при одном значении а, принадлежащем отрезку [-1; 2 ].
Ответ: х е ( - оо; - 2) и ( 0 ; 1) (1; + оо).
Задача 55. Определить, при каких а неравенство loga(a+y (| х |+ 4) > 1 выполняется при любом действительном х
Решение, Имеем
/о«а(а+1) ( I * I + 4) > 1 = ,о«.(а+1) а (в + 0
-00 < X < 00
а(а +1) > 1 | х | + 4 > а(а +1)
-00 < х < 00
О < а(а +1) < 1 | х | + 4 < а(а + 1)
-00 < х < оо
Вторая система решений не имеет. Решим первую систему
+1) > 1
| х | + 4 > а(а +1)
-00 < х < 00
1 < а(а +1) < 4 Ф»
а2 + а -1 > О а + а - 4 < О
- i + Jii 1 + 5/5 5/5-1	5Д7-1
Ответ:----------<а<--------; ------< а <------.
2	2	2	2
Задача 56. Найти все действительные значения а, при которых каждое решение неравенства log±x2 log±{x + 2) является решением неравенства 49х2 - 4а4 <; 0.
Решение.
Решим неравенство logrx2 £ log^lx + 2)	0 < х2 <ix + 2o<J^*<0.
2	2	(0 < х £ 2
Положим 49х2 -4а4 £ 0 <=> -уа2 £ х £ ^а2. Всякое решение первого неравенства будет являться решением второго тогда и только тогда, когда
I*2*"1
J Ф» а2 £ 7 |а | £ у7 .
-а2 2*2 7
Ответ: | а | £ 7*7.
Задача 57. Найти все действительные значения т, для которых неравенство тх2 - 4х + 3m +1 > 0 выполняется при всех положительных значениях х
38
Решение. Пусть f(x) ж тх2 - 4х + Зт +1. Заметим, что т > 0 . В противном случае
заданное неравенство не может выполняться для всех положительных значений х. Так
как ось симметрии параболы /(х) проходит правее нуля, ибо
4
х = — > 0, то заданное с 2т
неравенство выполняется для всех положительных х тогда и только тогда, когда D = 4 - т(3т + 1) < О
V ' т > 1.
т > О
Ответ: т > 1.
Задача 58. При каких значениях параметра т неравенство тх2 - 9тх + 5т +1 > о выполняется для любых действительных значений х?
(х 2
х —------т +1 > о. Отсюда непосредственно видно,
2/	4
что заданное неравенство выполняется для любых действительных значений х в том и т 0	4
только том случае, когда _ 61 + 1>0<=>0£т< —.
4
4
Ответ: 0£т < —. 61
Задача 59. Найти все значения параметра т, при которых всякое решение неравенства 1 £ х £ 2 является решением неравенства х2 - тх +1 < 0.
Решение. Обозначим /(х) = х2 - тх +1. Тогда неравенство х2 - тх +1 < 0 выполняется для всех х, принадлежащих отрезку [1; 2], в том и только том /(1) s 2 - т < 0	5
случае, когда е &т>-. f[2) s 5 - 2m < 0	2
л	5
Ответ: т>~.
2
Задача 60. При каких значениях параметра а все числа из отрезка 1 £ х £ 5 удовлетворяют неравенству Зах + 27зх + 1 -6х + а- 5<0?
Решение. Выполним для заданного неравенства ряд элементарных преобразований Зах 4- 2л]3х +1 -6х + а- 5<0о(а- 2)(3х +1) + 2^/Зх +1 - 3 < 0 <=> <=> (а - 2^3х + 1)2 + 2^7+1 - 3 < 0 .
Итак, получено квадратное относительно V3x + 1 неравенство, зависящее от параметра
39
а. Обозначим 7з* +1 =t £ 0. Когда х изменяется в пределах от 1 до 5, t будет изменяться в пределах от 2 до 4. Поэтому первоначальную задачу можно переформулировать так: при каких значениях параметра а все числа из отрезка 2 <; t £ 4 удовлетворяют неравенству (а - l)t2 + 2г - 3 < 0 ?
Для решения этой задачи обозначим /(г) = (а - 2)г2 + 2г - 3 и рассмотрим три случая.
1)	Случай а - 2 > 0. При этом ветви параболы /(г)	у/(г)
2	4 у
направлены вверх, а ось симметрии параболы распо- -------♦-----•—-у~—
ложена левее нуля. Все числа из отрезка 2 £ t £ 4	«
удовлетворяют неравенству (а - 2)г2 + 2г - 3 < 0 тогда и	(4)
только тогда, когда	/(2)
(а - 2 > О
/(4) s 16а 27 < 0 ‘ система неравенств решений не имеет.
2)	Случай а - 2 = 0 . При этом неравенство (а - 2)г2 + 2г - 3 < 0 превращается в нера
венство 2г - 3 < 0, которое не выполняется ни для одного t из отрезка 2 £ г £ 4.
3)	Случай а - 2 < 0. Тогда парабола /(г)=(« - 2)г2 + 2г - 3 выпукла вверх, ось
40
Задача 61. Найти все пары значений а и Ь, для которых система уравнений Ьх (2х - у) + (у - 1)(2х - у) = Ьх + у - 1 4х2 + у2 + аху -1 = 0 имеет не менее пяти решений.
Решение. Разлагая первое уравнение системы на множители, получим эквивалентную f(bx + у - 1)(2х - у - 1) = 0 совокупность следующих систем v	<=>
[ 4х + yz + аху -1 = 0
f Ьх + у - 1 = 0
(4х2 + у2 + аху - 1 = 0
f 2х - у - 1 = 0 [4х2 + у2 + аху -1 = 0
у = 1 - Ьх
^4 + Ь2 - abjx2 - (2Ь - а)х = 0
у = 2х - 1
(8 + 2а)х2 - (4 + а)х = 0
Если 4 + Ь2 - аЬ # 0, то первая система имеет не более двух решений. Аналогично, если 8 + 2а # 0, то вторая система также имеет не более двух решений. Первая система имеет бесчисленное множество решений в том и только том случае, когда
{4 + Ь2 - аЬ = 0	fa = 4	fa = -4
<=> < или < 2b — a = 0	( Ь = 2	[6 = —2
f8 +2a = 0 f a = -4
Для второй системы имеем {	<=> <
( 4 + а = 0 [-оо < Ь < оо
Ответ: а = 4, Ь = 2; а = -4, - оо < Ь < оо .
Задача 62. Найти все действительные значения а, для каждого из которых существуют четыре натуральных числа (х, у, и, v) удовлетворяющие системе уравнений ху(40 + ху) = (150 - a) (а - 90) а (вы2 4- 18v2 - a) = (4м2 - 9v2)
Решение. Разрешим второе уравнение системы относительно а.
а2 - 2^4и2 +9v2ja + ^4и2 - 9v2j
(2м + 3v)2
(2м - 3v)2 *
= 0 <=> а = 4м2 + 9v2 ± 12mv 
Отсюда видно, что а является квадратом целого числа. С другой стороны, из первого уравнения системы заключаем, что так как выражение слева больше 41, ибо х и у - натуральные числа, то 90<а<150. Существуют лишь три числа, удовлетворяющие одновременно этим двум условиям а « 100, а = 121 и а = 144.
Подставляя эти значения а в первое уравнение системы, получим, что только при а » 100 произведение ху является натуральным числом.
Ответ: a = 100.
41
Задача 63. Найти все значения параметра а, при которых система уравнений
имеет хотя бы одно решение.
Решение. В первом уравнении системы освободимся от знака модуля.
6.!cos~~ - 5
V 4
л я? 1
о. cos — - 1
V 4
12^cos^ +5 = 5
OS
ХУ cos— = О
4
. ф - 2х) sin —----- = О
12
х = 1 + 2п - 6т у = 2 + 4п п,т е Z
S •£* 1	4	6
- нет решений.
- нет решений.
Второе уравнение системы разрешим относительно
Icos^ S 1
8. Получим
Теперь решаем систему
Х2+(У-О)2=1 х = 1 + 2п - 6т <=>
у = 2 + 4и, п,т G Z
х = 1, и = 3m у - а = О у = 2 + 12m, т € Z х = -1, п = -1 + Зт у - о = О у = -2 + 12m, m € Z
[cos — + 1 = 5
2
2
2
7 = 5
2
8 - 2 = 0 <=>
Ответ:
о = 2 + 12m, т € Z
а = -2 + 12m, т € Z ’
42
Задача 64. Найти все значения параметра а, для каждого из которых существует только одно значение х, удовлетворяющее системе уравнений
|х2 +5х+4|-9х2 + 5х + 4 - 10х|х | = О
х2 -2(а + 1)х+а(а+2) = 0
Решение. Первое уравнение системы зависит только от неизвестного х. Разрешим его, для чего снимем модуль, найдя интервалы знакопостоянства каждого из выражений, входящих под знак модуля.
J х2 + 5х + 41 - 9х2 + 5х + 4 - 1 Ох | х | = 0 <=> 2(х2+5х + 4) = 0	, х^_4
,-4£х£-1	-4 £ х <, -1
2(х2 +5x4-4j = O >-i^x^O<=>[ х = 1 (х2 + 5х +4) - 10х2 =0’ х * 0
Второе уравнение системы решим, выразив х как функцию параметра а.
х2 - 2(а + 1)х + а (а + 2) = 0 <=>
х = а
х = а + 2
Теперь посмотрим, каково будет количество решений системы, когда а пробегает все значения от -оо до -ню.
нет
решений
।------одно решение-------
а * Э1- т к-  *—за *
-6	-4 I -3	-1 решений 1 решений
два решения
Таким образом, одно решение у системы будет тогда и только тогда, когда -6 £ а < -4;
-3 < а < -Г, а = 1.
Ответ: -6 £ а < -4; -3 < а < -1; а = 1.
Задача 65. Найти все значения а, при каждом из которых существует единственная
тройка чисел (х, у, z), удовлетворяющая системе
х + у + z = х2 + 4у2 х + 2у + 3z = а
Решение. Выразим z через х, у и а из второго уравнения системы и результат подста-
вим в первое уравнение. Получим
X -S у + z = х2 + 4у2 х + 2у + 3z = а
7 =	— -1.x — 2-у
4 3 зЛ зу
х2 - 2-х 4- 4у2 - 2-у =
3 z 3 z 3
43
Преобразуем второе уравнение полученной системы, выделив полные квадраты.
х2 - } X + 4/ - {у = } а е» (х - |)2 + (1у -	| а + $.
Полученное уравнение будет иметь единственное решение тогда и только тогда, когда + -П- = о <=> а = — О-.
3	144 V а 48 *
Замечание. Можно при а = выписать и само решение (|,	•
Ответ: а = - £.
48
Задача 66. Найти все значения параметра а, при которых система
(з -	+ (з + 2^-За«х2 + бх+5
у2 - ^а2 - За + б|х2 « 0 имеет единственное решение.
-6 £ х £ О
Решение. Так как (з - 2^^» -—Ж (3 *	’ ТО данная система симметрична
по у относительно 0, т.е. если (х0, у0) - решение данной системы, то и (х0, - у0) также будет решением данной системы. Поэтому для того чтобы система имела единственное решение необходимо, чтобы у « 0. Подставляя значение у = 0 В заданную систему»
получим следующую систему			
		а « 2	(а = 2
2	у.	- /		(х + З)2 « 0» - б £ х £ 0	«о < |х = -3
х + 6х х -3(в + 1) (а - 2)(и - 3)х2 « 0 <о		1Д	/ в ж 3 х2 4* бх + 12 « 0, - б £ х S 0	- нет решений.
-6 £ х £ 0		а « -1 х « 0	(а == -1 (х Ж 0
Проверим, что при а = -1 у системы нет других решений, кроме
|3 - 2V2 J + |з + 2V2 J + 3 £ 5, причем равенство достигается при у » 0.
х2 + 6л + 5 s 5, когда -6 <; х <; 0, причем равенство достигается либо при х = -6, либо
при х = 0. Но при
у = 0 не удовлетворяется второе уравнение системы. Поэтому а = -1
{X s 0 у-о
44
Проверим теперь значение а = 2.
В силу второго уравнения системы у = 0. Но тогда первое уравнение системы будет х2 + 6х + 9  (х + з)2 = 0 . Поэтому при а = 2 заданная система имеет единственное _______ х = -3
У = 0 *
Ответ: а = -1; а = 2.
решение
Задача 67. Значениями переменных х, у являются действительные числа. Найта все целые значения т, йри которых система уравнений х(х + 2у - 4) + 4т2 = 8 4- 4у - у2 у2 - 2у + 2 = 4х(у - х - 1) + 2^т2 + т)
имеет решения. При найденных целых значениях т найти все решения этой системы.
Решение. Уравнения заданной системы можно записать в следующей эквивалентной форме
(х + у)2 - 4(х + у) + 4т2 -8 = 0 (2х - у)2 + 2(2х - у) + 2 - 2т2 - 2m = 0
Для того чтобы каждое уравнение системы имело решение, необходимо и достаточно, чтобы их дискриминанты были неотрицательны.
£>1=4- 4т2 + 8 £ 0	т2 £ 3
D2 = 1 - 2 + 2m2 + 2т £ 0 <=> ' 2m2 + 2m-l£0<»m = l.
т € Z	т G Z
При т а 1 система будет выглядеть так
(х + у)2 - 4(х + у) - 4 = 0	( X + у = 2 ± 2^2
(2х - у)2 + 2(2х - у) - 2 = 0	[2х - у = -1 ±	*
х =
V -у “ а
Решая полученные четыре системы уравнений относительно х и у, получим четыре решения
г _ 1>2^-Уз	(	1-2^+^	„ _ 1-2^-Тз
Х “	3	..	3	3
v - 5+4 Л г5/З '	= 5-4^2-^ ’	.. = 5-4J2+J3 '
/	3	1/3	1/3
которые и дают ответ.
Задача 68. Найти все значения параметра а, при каждом из которых система 5-г1х1 + з|х|-2 = 5у +3х2-5а
X2 + у2 = 1
имеет единственное решение.
45
Решение. Из вида уравнений системы заключаем, что если (х0, у0) является решением системы, то и (-х0, у0) также является решением системы, т.е. заданная система симметрична по х относительно нуля. Поэтому заданная система будет иметь по крайней мере два решения для всех х * 0. Единственное решение возможно лишь при х = 0.
При этом из второго уравнения системы имеем, что либо у = 1, либо у = -1.
[х = 0	2
Подставляя в первое уравнение системы <	, получим, что а = —.
(у « 1	5
_	[ х = 0	8
Подставляя же <	, имеем а » - -.
(у = -1	5
Замечание. Однако может оказаться, что при этих значениях параметра а помимо этих решений есть и другие.
Поэтому исследуем теперь заданную систему при полученных значениях параметра а.
Заметим, что из второго уравнения системы следует, что | х | £ 1 и | у | £ 1.
2
Подставив а = — в первое уравнение системы, получим
5-г'
.2
Левая часть этого уравнения 5-2^'+з|х|-Зх2 £ 5, причем равенство достигается лишь при х = 0, а правая часть 5у £ 5, причем равенство достигается лишь при у « 1.
*	2	[х = 0
Таким образом, при а = - исходная система имеет единственное решение < 5	[у = 1
/,	2\	[х = 0	[х«1
|1-у2| + 10 и, например,	|^0>
~ 1 удовлетворяют заданной системе. Таким образом, при а = исходная [у = 0 .	5
система имеет белее одного решения. л	2
Ответ: а == —.
5
8	I
При а = -~ имеем 5-2'
Задача 69. Найти все значения а, при каждом из которых система уравнений (а - 2)sinx 4- cosy « 1 loga(2cosy) = log* z logz(l + 7sinx) =1
имеет хотя бы одно решение относительно х, у и z. При каждом таком значении а найти все решения.
Решение. Очевидно, что а > 0, а # 1 и z > 0, z * 1.
46
(о - 2) sin х 4- cos у = 1 /о«„(2 cos у) = loga(l + 7 sin x) 5^a = 1 z > 0, z * 1
cos у = 1 - (a - 2) sin x 2 cos у = 1 +7 sin x
cos у > 0
a > 0, a # 1
z > 0, z # 1
x = (-1)" arcsin + im,n e Z у = ± arccos 2g*^ + 2топ, m € Z 1 = 5^a 2 £ a < 5, a* 1
Задача 70. Найти все значения о, при каждом из которых для любого значения b сис-
х - by 4- az2 = 0	м „	z ч
. л ч	имеет по крайней мере одно решение (х, у, г).
2bx4-(b-6)y-8z = 8	Н
тема
х = by - az2 2b\by - az2 j 4- (b - б) у - 8z = 8
x = by - az2 \2b2 + b - 6j у - 2abz2 - 8z = 8
Рассмотрим случай, когда 2b2 + b - 6 = 0 <=>
3
При Ь « у система выглядит так
При b « -2 система выглядит так
Решение. Выразим из первого уравнения х через у и z, и подставим результат во второе уравнение системы.
х ~ by + az2 =0 2bx + (b - б)у - 8z = 8
Проанализируем второе уравнение полученной системы. Если 2b2 + Ь - 6 # 0, то можно указать тройку чисел, которая будет решением системы. Например, решением за-
у	w ( 3b	8 .Л
данной системы будет тройка —--------, —--------, 0 .
У2Ь2 4-6 - 6 2£2 + Ь - 6 J
2 • b = -2
х - |у + az2 = 0
3	2	8	8 • Умножим первое уравнение на -3 и
сложим со вторым. Тогда получим 3az2 + 8; + 8 « 0. Это уравнение имеет по крайней
2
мере одно решение при D = 16 - 24а £ 0 <=> a £ -.
х + 2у 4- az = 0 Умножим первое уравнение на 4 -4х - 8у - 8г = 8
и сложим со вторым. Тогда получим 4дг2 - 8г - 8 = 0 az22г - 2 = 0. Это уравнение имеет по крайней мере одно решение при D = l + 2a£0<=>a^-i.
Теперь очевидно, что при -у £ a £ ~ заданная система будет иметь по крайней мере одно решение при любом Ь.
л	1	2
Ответ:
2	3
47
Задача 71. Найти все значения а, при каждом из которых система уравнений
’ имеет ровно четыре различных решения. -1
Решение. Заданная система может быть приведена к симметричному виду
Заметим, что если (u0>v0) является решением этой системы, то и (v0.«0) также решение.
Каждое из уравнений системы
следовательно, система будет
у|х-1|»и0
иметь четыре решения, и еще четыре решения будет
имеет ровно два решения, а
1
Таким образом, исходная система будет
иметь система
" vo
иметь восемь решений.
Исходная система имеет четыре решения, когда м0 3 vo = у • ПРИ этом а в “	* а
также тогда, когда
% 8 1 1 0 Л, при этом а » —.
>=°	Р	4
Достаточность этих условий становится очевидной, если второе уравнение исходной системы расписать через элементарные симметрические многочлены и выделить полный квадрат, т.е.
2
= 1-4.
» —4а <=> 2
Ответ: а = - —; 32
£ 4
Задача 72. Найти все пары значений (а, р), при каждой из которых система 8х +(а2 +аВ + р2)у = 4	х
\ г Г имеет бесконечно много решений. (а-р)х + 26у = 2
уравнений
48
Решение. Каждое из уравнений системы определяет на плоскости (X, У) прямую.
Заданная система имеет бесконечно много решений тогда и только тогда, когда две прямые, заданные этими уравнениями, совпадают, т.е. коэффициенты уравнений,
задающих эти прямые, пропорциональны.
8 а2 + оф + р2 4 а-р’ 26	~ 2 °
(	а~р=4
|а2 +сф + р2 = .52
jot = 6 (Р = 2 а = -2
Р = —6
Ответ: а = 6, р = 2; а = -2, р = -6.
2
(1 - а}х 4- 2(а - 3)у 4- а 4-1 = 0
Задача 73. При каких значениях параметра а система уравнений Зу + 2 + ху = О /	. х ✓ ч „ Л имеет единственное решение?
х(у + 1 - а) + у(2а - 3) 4-а 4- 3 = О
Решение. Вычтем из второго уравнения системы первое и получим следующую эквивалентную систему
Зу + 2 + ху = О х(1 - а) + у(2а - б) + о +1 = 0
Если а = 1 илй а = 3, то второе уравнение системы имеет единственное решение, подставляя которое в первое уравнение, получим единственное решение системы.
Если исключить у из этой системы, то получим квадратное уравнение
(1 - а)х2 4- 2(2 - а)х 4-15 -	0, которое имеет один двукратный корень тогда и только
тогда, когда его дискриминант равен нулю.
D = (2-a)2 - (1 - а)(15 - а)  12а - 11 = 0 «а = |у.
При этом заданная система будет иметь единственное решение.
Ответ: а = —; а « Г, а » 3. 12
Задача 74. При каких действительных значениях параметра а существует хотя бы одно действительное значение х, удовлетворяющее системе
х2 4- (2 - За)х 4- 2а2 - 2а < 0 ? ах - 1
Решение. Из уравнения системы заключаем, что а * 0. Умножим обе части неравенства на а2 > 0 и заменим в полученном эквивалентном неравенстве ах = 1. Тогда будем иметь
2о4 - 2а 3 - За2 4- 2а +1 < 0 <=> 2а2 ^а2 - 1) - 2а(а2 - lj - (а2 - 1) < 0
49
Задача 75. Определить4, при каких целых к система уравнений
(arctgx)2 + (arccos у)2 = я2 к
я имеет решения, и найти все эти решения, arctg х 4» arccos у = -
я	я	2 я2
Решение. Так как - — < arctgx < —, то 0 £ (arctgx) < —. 2	2	'	7	4
Так как 0 £ arccosy £ я , ТО 0 £ (arccosy)2 £ я2 .
Поэтому О £ (arctgx)2 4- (arccosy)2 < ~L .
Откуда, принимая во внимание второе уравнение системы, получаем к = 1. Тогда заданную систему можно записать так
(arctgx + arccos у^ - 2(arctgx)(arccosy) = я2 я
arctgx 4- arccosy » —
(arctg x)(arccos у) =
я
arctg х 4- arccos у » —
Используя теорему Виета, по этой системе можно составить соответствующее ей квадратное уравнение, корнями которого будут arctgx и arccosy.
2	8
Л	,	ж	1ж2	Зж2	*1
О	X	«	— ±	<— +-	—
4	Ц16	8
4
Поэтому
XI-
arctg х =---
4
Ж1-* = '«--
Ответ:
arccos х = —1— 4
я 1-<
4 я(1 + у = cos —---
4
у « СО5 —----
:	4
Задача 76. Найти все значения параметра а, при которых равносильны системы
w Г ах + Зу « 6а - 4 уравнении <	и
[ х 4- у » 2а
х2 - 2у4 - 6х 4- 8 « о
х2 + у2 - (2а + 4)х + 1(а2 + а +	= 0 ‘
Решение. При а = 3 первая система несовместна, а вторая система выглядит так 50
х = 2, а = 0	х = 4, а = 1
, либо
х « 2, о = 1	х = 4, о = 2
х2 - 2у4 - 6х + 8 = О х2 + у2 - 1Ох + 28 = О ’
Левую часть второго уравнения этой системы преобразуем следующим образом х2 + у2 - 10х + 28  (х - 5)2 + у2 + 3 £ 3 .
Следовательно, вторая система при а = 3 не имеет решений. Таким образом, обе системы при а = 3 несовместны.
Если а # 3, то первая система имеет единственное решение. Заметим, что если если (х0, у0)  решение второй системы, то и (*О’~Уо) также будет решением этой системы. Поэтому для того чтобы вторая система имела единственное решение необходимо, чтобы у = 0.
(ах = 6а -4	х = 2, а = 1
х - 2а	[х = 4, а = 2
Вторая система при у = 0 выглядит так х2 - 6х + 8 = О
2 /л л/ 2	л <=> либо
х2 - (2а + 4)х + 21а2 + а + 21 = О
Отсюда видно, что только при а = 2 решением и первой, и второй системы будет х « 4 и, следовательно, системы равносильны.
То, что при а « 2 вторая система имеет единственное решение, следует из второго уравнения этой системы, которое после подстановки значения а « 2 превращается в уравнение х2 + у2 - 8х +16 « 0 <z> (х - 4)2 + у2 « 0.
Ответ: а « 2; а « 3.
Задача 77. Найти все значения параметра Ь, при которых система неравенств 2b sin2(x + у)+ b > 4b3 sin(x + у) + Ь3
\ / 4	\ э	выполняется нри любых х и у.
х2 + Ь4 +11у2 + Ь>2ху
Решение, Второе неравенство предложенной системы можно записать так х2 +{bA + 1)у2 + Ь> 2ху <=> (х - у)2 4- b4y2 + b > 0 .
Так как это неравенство должно выполняться при любых х и у, то Ь > 0. В противном случае неравенство не выполняется для х = у = 0.
Первое неравенство системы с учетом Ъ > 0 можно преобразовать так 2sin2(x + у) - 4Ь2 ял(х + у) + 1 - Ь2 > 0 .
Введем функцию /(аш(х + у)) = 2 л’л2(х + у) - 4Ь2 sin(x + у) +1 - Ь2. Это однопараметрическое семейство частей парабол, соответствующих значениям аргумента -1 £ sin(x + у) £ 1. Ось симметрии этого семейства парабол определяется так
51
хс а Ъ2 > 0 и может принадлежать отрезку [-1,1], а может лежать правее точки х = 1.
В первом случае	Во втором случае
Задача 78. При каких значениях параметра р система неравенств х2 + 2рх + 4р2 + 2р + 4 £ 4 sin у + Зсозу
О £ у £ 2х имеет единственное решение?
Решение, В левой части первого неравенства выделим полный квадрат, а в правой части введем вспомогательный угол разделив и умножив ее на 5, и положив
cosy «	sin у = |. В результате получим
дг2 + 2рх + 4р2 + 2р + 4 £ 4 sin у + Зсозу <=> (х + pf + Зр2 + 2р + 4 £ 5sin(y + <р) . 2
р 4-	+ у £ у, т.е. левая часть неравенства не меньше у
И ПОЭТОМУ ~ £ sin(y + <р) $ 1.
Если £ sin(y + ф) < 1, то существует по крайней мере два значения 0 £ у £ 2п, удовлетворяющие этому неравенству.
Если sin(y + ф) = 1, то у определяется однозначно. Неравенство принимает вид (х + р)2 + Зр2 + 2р + 4 £ 5. И заданная система имеет единственное решение тогда и р = -1 1 .
/=3
только тогда, когда Зр2 + 2р
Ответ: р = -1; р = -
*3
52
Задача 79. Найти все действительные числа р, при которых существует единственное число х, удовлетворяющее системе cos2xx = 1 (?x+4p2 -11)(бх-р2 -34)<0‘
Решение. Решим сначала уравнение систем
coslicx = 1 <=> 2юс = 2ял, n е Z о л = л, л 'е Z .
Теперь решим неравенство.
«	11 _ 2	11	.	34 р2 34 е
Так как------2р* £ — < 6, а — + £—'* — >5, то для того чтобы единственное целое
2	2	6	6	6
fll 2 34 1 2I Л число х = п лежало в промежутке----------2р, — + —р I, необходимо и достаточно.
\ 2	6	6 )
чтобы выполнялось одно из двух условий: 7 11 о 2 «
— - 2р2 > 3
34 1
6 £ — + — р2 < 7 6 б
4<-у-2р2 £5
I ^4 1 2 х б
- система несовместна.
1	2	3
— £ р2 < -4	4
1 , . J5T Ответ:	р < —
2	2
Задача 80. Найти все значения а, при которых система неравенств {х2 + 2х + а £ 0 х2 - 4х - ба £ 0
имеет единственное решение.
Решение. Введем в рассмотрение функции /Дх) = х2 +2х + а .и /2(х) = х2 - 4х - ба. Функция /Дх) задает семейство парабол с осью симметрии х^ = -1. Функция /2(х) задает семейство парабол с осью симметрии хг = 2. Отсюда следует, что система неравенств, задаваемая этими функциями, может иметь единственное решение в одном из следующих трех случаев.
53
Во-первых, неравенство /Jx) £ 0 имеет единственное реше-fx = -1
ние 4	, которое является решением неравенства, зада-
ла = 1
ваемого функцией /2(х), т.е. /2(~1)|а=1 = 9- 4- 6 =-1<0.
Во-вторых, неравенство /2(х)$0
имеет единственное решение
2, которое 3
должно удовлетворять неравенству /Дх) £ 0. Но fx (2)
= 9---1 = —>0!
\	3	3
Отсюда видим, что этот случай де имеет места.
Ответ: а = 0; а = 1.
В-третьих, больший нуль функции /Jx) совпадает с меньшим нулем функции /2(х), т.е.
-1 + Vl - = 2 - 74 4- 6а <=> а = 0.
Задача 81. Найти все значения а, при каждом из которых существует единственная пара целых чисел х,у, удовлетворяющая уравнению
Зх2 +11ху 4-Юу2 = 7 и двум неравенствам
х + у > 0 , 4д2х - Зау < 0.
Решение. Решим сначала заданное уравнение в целых числах, для чего разложим ле-
вую часть уравнения на множители					
					X а 9
			х 4- 2у » ±1		у = -4
			Зх 4- 5у = ±7		х - -9
(зх2 + 11ху + 10/ = 7 _	(х+2у)(3х + 5у) = 7		х,у € Z г	с*		у = 4
[	Х,у € Z	Х,у € Z		X 4- 2у а ±7		х » -33
			Зх + 5у = ±1		У а 20
			х,у € Z		' X а 33
					у а -20
Замечание. В каждой из систем одновременно берутся в правой части либо знаки +, либо знаки -.
Затем, подставляя каждое из полученных решений в два заданных неравенства, полу-[х =-9 |х =-33
чим, что решения | и | не УдовлетвоРяют неравенству х + у > 0.
54
I х = 33
Второе неравенство 4а 2 х - Зау < 0 для решения < дает [у = -20
4 • 33а2 + 3 • 20а < 0 <=> а
5
11
(jy Q
из неравенства 4а 2 х - Злу < 0 получаем
Итак,
Отсюда
4'9а2 + 3 • 4а < 0 <=> а(3а + 1)<0€>--<а<0.
нет к одно .г два нет а
решений решение решения 0 решений
5	1
видно, что при - — < а - у существует единственная пара целых чисел, а
именно
х = 33
20 * У®0®7161®0^111^ У^виям задачи.,
л	5	1
Ответ: — < а £ —.
11	3
Задача 82. При каком значении параметра b система неравенств
У * (* - ь)2 xi (у- b)2
имеет единственное решение?
Решение. Заметим, что если точка Мх - (х, у) удовлетворяет заданной системе неравенств, то и точка М2 = (у, х) также удовлетворяет этой системе. Отсюда следует, что для того чтобы данная система неравенств имела единственное решение необходимо, чтобы х = у.
Но тогда систему неравенств можно преобразовать следующим образом /	\2
х £ (х - ь)2 <=> |Jx - ь) -	<; ь + —.
Это неравенство имеет единственное решение тогда и только тогда, когда Ь =
4 ‘
Докажем обратное, т.е. проверим, что система
у * (» +1)2
'	, которая получается из
заданной при Ь = - —, имеет единственное решение. Действительно, сложив эти два
неравенства системы, получим
X + у i (х +	+ (v +о (х - })2 + (у - {) £ о .
55
Отсюда видно, что последнее неравенство имеет единственное решение <
У
1’а
следовательно, и исходная система имеет при Ь = - — единственное решение. •	4
Отет: Ъ = ~ — 4
Задача 83. Найти все положительные х, при которых из системы неравенств abx ^2а +9b + x t а £ 0, Ь £ О следует неравенство ab £ 4.
Решение. Среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Поэтому
abx £ 2а + 9b + х	(ata £ б^^аЬ + х	(^abVx - bjijdb - х £ О
ai*0,Z>2>0, х>0	|a 2> О, Ь 0, х > О	а£0, Ь£0,х>0
Введем функцию f[4abj = x^Tabj “ 65/2 Та£ - х. Это однопараметрическое семейство частей парабол, которые определены на множестве 0 £ 4аЬ <00 и ветви которых
направлены вверх.
Для того чтобы из заданной системы неравенств следовало неравенство аЪ % 4 <=> Jab £ 2 (при a £ 0, Ь £ 0), необходимо и достаточно, чтобы
f /(0)« -х < 0	(х>0 Л л [-
. ч . г- <=><	/- €> 0 < х £ 4у2
/(2) « 4х - 12у2 - х 0 |х £ 4V2
Ответ: 0 < х £ 4^2.
Задача 84. Найти все положительные числа а, для которых не существует действительных чисел х и у, одновременно удовлетворяющихГнстеме 1бх2 + (4 - 5а)(х3 4- х| - ^-а^х2 +	0
4х _ 1 ~ У t ay f а х2 + 1 5у 1 - у 4 0 < у < 1
Решение.
Разделим обе части первого неравенства на
1 / ? ««
-|хх + 1J •. В результате
получим
56
А 4х V * А 4х _ А 4х 4 -------- + (4 - 5а) —--------- - 5а £ 0 <=> 4 ——
U2 J_1 J V Hi < J	L2 .
4х
2~1
Заметим, что в силу уравнения системы - > 0 . График л. 1
функции ....... представлен на рисунке. Поэтому нера-
х2 +1
венство — будет иметь решение при любых а > 0 . х2 +1	4
С другой стороны, должны выполняться следующие условия
- 5аР—I + 5а £ О
> У J v У }
\2	А Л
+5(а-8)	+20а£0‘
У J ' Ч У )
hZ + _2L + £
5y 1 - у 4	4
1 - у ay а л --^ + —2_ + - ^2
5у 1 - у 4 О < у < 1
a > О
Первое неравенство имеет решение тогда и только тогда, когда (d = 25а2. - 20а £ О 4 <	а Ъ —.
( а > 0	5
Второе неравенство имеет решение тогда и только тогда, когда
, D « 25(а - 8)2 - 320а ;> 0	0 < Q 72 - 16714
а £ 8, а > 0	5
Заметим, что требование а £ 8, которое получается из второго неравенства последней системы, существенно. Лишь при таких а последняя система неравенств совместна.
Итак, при у £ а £	и только при таких а, существует пара (х, у),
4
удовлетворяющая исходной системе. А тогда либо при 0 < а < у, либо при а >	не существует (х, у), удовлетворяющих одновременно исходным
условиям.
Л Л 4	72-16-714
Ответ: 0 < а < -; а >-----------.
5	5
Задача 85, При каких значениях параметра b система уравнений
Ьх + 2Ьх + у + ЗЬ-3-0 имеет единственное решение? by2 + х - 6by + 11Ь + 1 = 0
Решение. Преобразуем данную систему следующим образом
57
fbx2 +2Ьг+у + ЗЬ-3 = 0 1*(* + 0 + (у “ 3) + 2Ь = 0 [by2 + х - 6by + 1 lb + 1 = 0 [b(y - З)2 + (х + 1) + 2Ь = 0
Замечание. Из виЛа последней системы заключаем, что если точка М = (х0+1, у0 - з) является решением этой системы, то и точка N = (у0 - 3, х0 +1) также есть решение полученной системы. Это следует из того, что при подстановке координат этих точек в систему первое уравнение переходит во второе, а второе - в первое. Единственность решения будет тогда, когда при перестановке координат точек мы ничего нового не получаем, т.е. переставляемые координаты должны быть одинаковы. Однако нам представляется, что заслуживает внимания и следующий метод решения этой задачи.
Вычитая и первого уравнения системы второе, получим b
0.
Откуда либо х +1 = у - 3, либо х +1 = i ь
Заметим, что при Ъ = 0 данная система имеет единственное решение <
[ у = 3
Подставляя х +1 = у - 3 в первое уравнение заданной системы, получим
Это квадратное уравнение относительно х +1, которое имеет единственное решение тогда и только тогда, когда его дискриминант равен нулю, т.е.
1 - 8Ь2
2у2
Подстановка х +1 = ~(у - 3), Ь * 0 в первое уравнение заданной системы дает
/]	/ i А2 з
b ~-(у- 3)	+ (у-3)ч-2Ь = 0<^Ь (у-3)-----+ — + 2Ь==0.
•	х v х 7	Vх 7 2bJ 4Ь
Если Ь > 0, то все слагаемые в левой части полученного уравнения положительны, и, следовательно, оно не имеет решений. Аналогично, если Ь < 0, то все слагаемые в левой части последнего уравнения отрицательны, и оно также не имеет решений.
Ответ: b = 0; b - ±—“.
2V2
Задача 86. Найти все значения а, при которых решения системы неравенств {х2 +6х + 7 + а£0 х2 + 4х + 7 £ 4а
образуют на числовой оси отрезок длины, равной единице.
Решение. Введем функции /i(x) = х2 + 6х + 7 + а и /2 (*) = *2 + 4х + 7 ~ 4а • Они зада
58
ют однопараметрические семейства парабол, ветви которых направлены вверх и оси симметрии равны xq = -3 и х^ = -2 соответственно.
Могут быть представлены лишь следующие три возможности.
1.	Решения неравенства /i(x) £ 0 образуют на оси х отрезок, длины равной 1, н этот
отрезок целиком принадлежит решениям неравенства /2(х) £ 0 . Этот случай описывается следующей системой
25 30 п ------+ 7 + а = 0
4	2
49 28 „ л Л
------+ 7 - 4а £ 0
4	2
2.	Длина отрезка, заключенного между большим корнем уравнения /1(х) = ° и меныпим корнем уравнения /2(х) = 0, равна 1. Этот случай записывается так
-3 + ^2- а = -2 - -Аа-З +1 а = 1.
3.	Решения неравенства /2(х) 0 образуют на оси х отрезок, длины равной 1, и этот
отрезок целиком принадлежит решениям неравенства /i(x) £ 0. Этот случай описывается следующей системой
9
—-6 + 7-4а = 0
4
9 —-9+7+а£0
. 4
Последняя система несовместна. Значит, на самом деле реализуются только первые два случая.
Ответ: а = 1; а = -.
4
Задача 87. Найти значения параметров и и v, при которых существуют два различных вещественных корня уравнения х^х2 + х - в) = и , являющихся одновременно корнями уравнения х^х2 - б) = v.
Решение, Пусть Xi и х2 общие корни заданных уравнений. Тогда с одной стороны, xJxi2 + *1 -8)= и	,		х
} -	<	=>(*1-*2)1*1 + *1*2 + *2 +*1+*2-8)=0.
*21*2 +*2-8| = и	'	'
Откуда, учитывая, что xj # х2, получаем х2 + х,х2 + х2 + xj + х2 - 8 = 0.
59
С другой стороны,
Г2)(Х1 +*1*2+Х2
о
2
Откуда, учитывая, что q * х2, получаем х/ + хгх2 + х2 -6 = 0.
Итак, получена система двух уравнений с двумя неизвестными, из которой могут быть определены значения этих неизвестных.
х/ +ххх2 + х22 +xi +х2 “ 8 = 0 о f Х{ +2Х2 = 2 о 1*1 + х2 = 2	1*1 = 1 ±
*12+*1*2+*22-6 = 0	|(х1+хг) “*1Х2 = 6 I *1*2 = -2 [х2=1тТз
Подставляя любое из этих значений в каждое из заданных уравнений, получим значения параметров и и v.
и = (1 +	+ Vi)2 + (1 + -/з) - 8^  (1 + ^)(-3 + 3^  з(у1з - 1)(7з +1)  6.
V = (l + л/з)(ji + Лз)2 - б)  (1 + ^з)(-2 +2-/з] . г(7з - 1)(£ +1) . 4.
[и = 6
Ответ: {
IV = 4
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1. При каких значениях параметра а уравнение лп24х4-(а2 -з)ял4х + а2 - 4 = 0
Зп
имеет ровно четыре корня, расположенные на отрезке — £ х £ 2я ?
Ответ: а = -2, а = 2.
Задача 2. Найти все значения параметра а , при которых уравнение
2 2х 1	« IZ л
х 4- -===• +------+ 2у2 = 0 имеет единственное решение.
у since cosa,
Ответ: а = -^ я + 2ят; а = 2. я + 2ял, m,n е Z.
Задача 3. Найти все значения параметра a, i ж которых уравнение х2 - 2а- л‘л(с0$х) + а2 = 0 имеет единственное решение.
Ответ: а = 0; а = 2 лл1.
Задача 4. Найти все действительные значения величины h, при которых уравнение х4 - hx3 - (2й + 1)х2 + hx + 1 = 0 имеет не более двух корней, больших единицы.
Ответ: ^20 - 4 < h < -.
2
60
Задача 5. Найти все значения а, которые удовлетворяют условию 2 < а < 5 и при которых уравнение	хх | j = соу^лх - относительно х имеет хотя бы одно
решение, удовлетворяющее условйю 2 £ х £ 3 . _	9л 15л
Ответ: а = —; а =------.
13	13
Задача 6, Найти все пары действительных чисел а и Ь, при которых уравнение
(зх - а2 + ab - &21 + (lx2 - а2 - abj + х2 + 9 в 6х имеет хотя бы одно решение.
Ответ:
(а = 3
= 3’
а = -3
Ъ = -3’
а - 2^ ь = 7з ’
а =
ь = -4з
Задача 7. Найти все значения параметра а, при которых уравнение
log J------—-— --------------------J(x ~5а + Юл - 34)(1 л-х|-а + х + 2) - О
4х - х1 - 2(в - 2х)| х - 21 + 4ла	Д1 1	’
имеет хотя бы одно целочисленное решение.
Ответ: а = 2к - 8 ; а = 2л - 1; а = 2л.
Задача 8. Определить, при каких значениях параметра а уравнение х~~=2|2|х|-а2| имеет ровно три корня. Найти эти корни.
п	1	1	л	1
Ответ:	при д = — х ----; х = 0 и х = — .
4	20	12
1	1	3	3
при а = -1 х = —; х = — и х = —.
2	10 б
Задача 9. Для каждого значения параметра Р решить уравнение
3cosxsin$ + 2sinxcos$ - 4со$Р = 3-^3 .
Ответ:	при р = — + 2лт, т € Z	х = — 4- 2лл, и е Z ;
6	6
при Р » - — + 2пк, к € Z	X в — + 2л/, I € Z;
6	6
при других р решений нет.
Задача 10. Найти все значения параметра д, при каждом из которых уравнение
4~l x~e I log&\x2 - 2х + з) + 2'** >2х log Д21 х - а | + 2) = 0 имеет ровно три решения, з
л 1 . 3 Ответ: а = —; а = 1; а = —.
2	2
Задача 11. Определить, при каких значениях параметра b уравнение (3 ~ b)x2 - (z>2 - 5hj( J х J - 1) + 6 = 0 имеет единственное решение.
Ответ: b = 2; b = 3 .
61
Задача 12.
Ответ:
Задача 13.
Ответ: с
Задача "4.
Ответ:
Задача 15.
Найти число решений уравнения у 4 - х2 - а в зависимости от значений параметра а, а < 0, а > 2	-	нет решений;
а » 2	-	одно решение;
О £ а < 2	-	два решения.
Найти все значения параметра с, при которых уравнение
| х2 - 1 j +1 х2 - х - 2 J = х2 - Зх + с имеет ровно три различных корня.
= 2; с = —. 3
Найти все значения параметра < при которых уравнение 5|х - За | +|х - а2 14- 4х « а
1. Имеет бесконечное множество решений.
2. Не имеет решений.
1.	0;
2.	(-<о; - 8)(j(0; 4- «>).
Найдите все значения х, удовлетворяющие неравенству (а + 2)х3 - (1 + 2а) х2 - 6х + ^а2 + 4а - б) > 0 хотя бы при одном значении а, принадлежащем отрезку [-2; 1 ].
Ответ: х € (- »; - 1) v(- 1; 0)и(2; + <ю).
Задача 16. При каких значениях параметра а все числа из отрезка -1 £ х £ 3 удовлетворяют неравенству 2ах + 2у2х + 3- 2х+За-5<0?
Ответ: а < —. 2
Задача 17 Определить все значения параметра а, при которых ровно одно решение неравенства Ja3 -2а2 - 4а + 8 х3 ~ Ja3 - 2а2 х2 4- ^а4 -4а2 х - а2 £ 0 удовлетворяет условию 2а £ х £ 713 а .
Л Л 7п Ответ: а = 0; а ------.
2
Задача 18 Найти все значения параметра а, при которых неравенство
3	sin2 х + 2а sin х cosx + cos2 х + а £ 3 выполняется для любых значений х.
12 Ответ:-------£ а £ 0 .
5
Задача 19 Найти все действительные значения Ь, при каждом из которых неравенство cos2 х + 2b sin х - b2 < b - 2 выполняется при любом действительном значении х.
62
Ответ:	o)U 0;
„ К 3 + V17	,	„
Ответ: Ъ <---------— ; b > 2 .
2
Задача 20. Для каждого неотрицательного значения параметра а решить неравенство а3хА + 2а2 х2 -8х+а+4£0.
Ответ:	Если а = 0, то х £ -•;
2 Л ,	„ 1-71-в 1 + Vb^a
если 0 < а < 1, то х £------ и х 2.--------;
а	а
если а £ 1, то -а> < х < оо .
Задача 21. Пусть в > 0, Ъ > 0. Найти решение неравенства JД--—
!х2 в2 •» Ъ
2л2Ъ ------— , при условии а £ b ; а2 + Ъ2)
[-a; 0)U(0; а], при условии а > b.
Задача 22. Найти все действительные значения а, для каждого из которых существуют четыре целых числа (х, у» и, v) удовлетворяющие системе уравнений х2 + у2 = (107 - а)(а - 91) 54^и2 - v2 j = я(15и +3v - а)
Ответ: а « 99.
Задача 23. Найти все значения параметра а, при которых система уравнений
имеет хотя бы одно решение.
Ответ: -1 + 6Аг, 3 + б/; 6m; 2 + бл, к.1,т,п 6 Z .
Задача 24. Найти все пары значений а и Ъ, для которых система уравнений
х2 - у2 + д(х + у) = х- у+ а	.
v '	имеет не менее пяти решений.
х2 + у2 4-Лху- 1 = 0
Ответ: -oo<a<ao,fce:2; а = ±1, b = -2.
Задача 25. Найти все значения о» при каждом из которых для любого значения Ъ система
{Ьх — у - az2 = О
(Ь б) 2Ь 4	4 ПО мсРе W10 решение (х, у, г).
Ответ: - — £ а £ —.
4	3 .
63
Задача 26. Найти все значения параметра а, при которых система
(2 - 4з]* +(2 + Л})’ - 5 = а - 2у +/
• х2 + ^2 - а - a2 ) у2 =0	имеет единственное решение.
0£у<;2
Ответ: а = - 3; а = - 2.
Задача 27. Найти все пары значений ( а, Р ), при каждой из которых система уравнений
8х +(а2 - ар +р2|у = 4
(а + р)х 4- 26у = 2
имеет бесконечно много решений.
Ответ: а = 6, р = -2; а = -2, р = 6.
Задача 28. Определить, при каких целых к система уравнений
(arcsiny^ arccosx = •—-'	7	16
/	. U . Я2
arccos х + \arcsm у) » к —
имеет решения, и найти все эти решения.
я21
Ответ: к = 2; х = cos—; у « ±1.
4
Задача 29. При каких значениях параметра а система уравнений
ах2 + 4ах - у 4- 7а 4-1 = 0 ау2 - х - 2ау 4- 4а - 2 = 0
имеет единственное решение?
Ответ: а = 0; а = ±-Д=г.
Задача 30. При каких значениях параметров а и b можно найти два различных вещественных корня уравнения х3 - 5х2 4- 7х = а , которые будут также корнями уравнения х3 - 8х 4- b = 0 ?
Ответ: а » 2; b = 3.
Задача 31. Найти все значения а, при каждом из которых система уравнений
^|у+з| = 1-.Д7|
16а-9-бу = 25х2 + у2
имеет ровно четыре различных решения.
Ответ: а = —; а =------<
16	128
Задача 32. При каком значении параметра а система неравенств
у £ х2 4-2а [х £ у2 + 2а
имеет единственное решение?
64
Ответ: а = — .
8
Задача 33. Найти все значения параметра Ь, при которых система неравенств (2bcos2(x - у) + 8Ь2 cos(x - у) + 8b2(fc + 1) + 5Ь < О < v	f v /	выполняется П|
[	x2 +y2 + 1 > 2bx + 2y + b b2
Ответ: b < -1------- — < b < 0.
2^2	2
Задача 34. При каких значениях параметра р система неравенств
х2 + 2рх + 3р2 + 3р +3 £ 3siny - 4 cos у	о
r r г	' имеет единственное решение?
О £ у £ 2к
Ответ: р = -2; р = —.
Задача 35. Найти все неотрицательные числа р, при которых существует единственное дсйстви-tgitx = О
(5х + 25р + 19)(2р - 13 - 4х) !> О ’
тельное число х, удовлетворяющее системе
„ 1 6
Ответ: — <, р < —.
2 F 25
Задача 3(*. Найти все значения а, при каждом из которых существует единственная пара целых чисел х,у, удовлетворяющая уравнению -15х2 + 11ху - 2у2 = 7 и двум неравенствам х < у; 2а2 х + Зау < 0 .
Л	13	19
Ответ:-----< а £------.
3	5
Задача 37. Найти все значения а, при которых решение системы неравенств
х2 ~~ 2х Ct “ 1
образует на числовой оси отрезок длины, равной единицы. ж2 - 4х £ 1 - 4а
Ответ: а = —; а= 1.
4
Задача 38. Найти все положительные числа а, для которых существует бесконечно много действительных чисел х и у, одновременно удовлетворяющих системе 18х2 4- ~(1 - а)^х3 + 9х) - ~а(х2 +	0
бх	1 ау а	Л
-------= — + —, у>0 х2+9 Ь 3 6
_	4	26-4-J22
Ответ: — < а <--------.
3	3
65
ДОПОЛНЕНИЕ
Задачи с параметрами, предлагавшиеся на вступительных экзаменах различных факультетов МГУ в 1993*1995 годах
1. (Механико-математический факультет, 1993) При каких значениях параметра а,
1 имеет
принадлежащих интервалу
решения?
Решение. Левая часть заданного уравнения неотрицательна, а правая * неположительна. Поэтому
-1) у + тип, m € Z
cos6x -1 = 0
( Я я А д6-----; —
\ 2 2)
Я (	/	_ А
а = 3V +' ' + 3mJ neZ^meZ о
п GZ
я а = —
3
а = 0 я а = —
3
:оме^ание. Выдожеше
п + (-l)w +3mj « Z, т.е. является целым числом как сумма
трех целых чисел. Очевидно, что при любом фиксированном значении m существуют три последовательных значения и, при которых это выражение принимает значения *1; 0; 1.
Ответ: -у; 0; у.
2. (Механико-математический факультет, 1993) Найти все значения а, при которых уравнение 4х + (а2 3 + 5^ 2х + 9 - а2 = 0 не имеет решений.
Решение. Так как 4х = 22* > 0, (а2 + 5)-2х >0, то при 9-а2£0 левая часть
заданного уравнения будет строго больше нуля, т.е. заданное уравнение не имеет решений. Если 9 - а2 < 0, то существует ровно одно решение.
Замечание. Рассмотрим функцию /(г) = t2 + La2 + 5р + 9 - а2 на множестве t > 0. Это
-	а2 + 5
однопараметрическое семейство парабол с осью симметрии tc =-----— < 0 не имеет
точки пересечения с положительной полуосью t тогда и только тогда, когда /(О) = 9- а2 0 о |а| £ 3 .
Ответ: | а | £ 3.
3. (Механико-математический факультет, 1993) Найти все значения а, для которых неравенство /o#Ja cos2x + 11 + а2 - sin2 х) cosx + 4 + а! < 1 выполняется при всех х.
66
Решение. (а cos2x + 0 + °2 “ ™2 x)cosx + 4 + а) < 1  l°8s5 <=> I	X € R
О < а соз2х ++ а2 - sin2 xj cosx 4- 4 + а < 5 х € R
cosx ух2 4- 2а cosx + cos2 xj + 4 > О cosx (а2 + 2а cosx + cos2 хj - 1 < 0 <=> х е R
cos х (а + cos х)2 + 4 > О
cosx (а + cosx)2 -1 < О . Проанализируем полученную систему.
х е R
Рассмотрим те значения х, для которых cosx £ О. Тогда для всех таких х первое неравенство системы выполняется, а для левой части второго неравенства имеем оценку сверху:
cosx(a 4- cosxf - К (а + cosxf - 1 а а2 4- 2а cosx 4- cos2 х - К
а2 + 2а, а £ О а2 - 1, а < О
Здесь оценка а2 +2а получена заменой cosx единицей, а оценка а2 -1 - заменой
cosx нулем.
Теперь рассмотрим те значения х, для которых cos х <> 0. Тогда для всех таких х второе неравенство системы выполняется, а для левой части первого неравенства имеем
оценку снизу:
cosx(a 4- cosx)2 4- 4 £ -(а 4- cosx)2 4- 4 s -а2
- 2аcosx - cos2 х 4- 4 £
-а2 4- 4, а 2. О
-а2 4- 2а 4- 3, а < О
Здесь оценка -а2 4-4 получена заменой cosx нулем, а оценка -а2 4-2а+3 - заменой cosx минус единицей.
Используя эти оценки, получим, что система выполняется для всех значений х тогда и
	а £ 0 ’ а2 4- 2а £ 0 -а24-4>0
только тогда, когда	<=> -1 < а < 0.	Ответ: -1 < а < 0. а < 0 ’ а2-КО -а2 4- 2а 4- 3 < 0
4.	(Факультет ВМК, 1993) Найти все значения д, при которых область определения функции у ------------------т=~ совпадает с областью определения функции
Зео«-2со?х--^а
у =______!______.
sin3 х 4- cos3 х - а 3cosx -2cos3 х - -Jia
67
Решение.
Прежде всего заметим, что если х0 удовлетворяет уравнению
sin3 х + cos3 х - а » 0, то и
я
---
2	0
удовлетворяет этому же уравнению. Действительно,
. •»[ X | а | К |	Л .а
ял--------хп + cos3---------хп - о = 0 <=> sin хл
\2	® J	\2	°
+ cos3 л0 - а = 0 . Поэтому область опреде-
ления функции у =--------------------будет совпадать с областью определения
3cosx - 2cos3 х - <j2a
.	i	, -ji_______
функции у = —------------------------1-----------j=- в одном из двух случаев:
sin3 х + cos3 х - a 3cos х - 2 cos3 х - \2а
либо уравнения sin3 х + cos3 х - а = 0 и **cosx - 2cos3 х - ^2 а = 0 имеют одинаковые
корни, либо уравнение sin3 х + cos3 х - а = 0 не имеет корней.
Рассмотрим эти случаи. В первом случае, если уравнение sin3 х + cos3 х - а = 0 имеет
корень х0, то как показано выше, оно обязательно будет иметь корень ~~хо-Подставляя эти значения корней в уравнение 3cosx - 2cos3 х - ^2 а = 0, получим
3cosXq
3sinxQ
-2cos3 хп- 42 а = 0	/	\	/ 3	. з \ л
„ 0 г- => 3(cosxA - sinxn) - 2(cos3 xn - sm3 xn) = 0 <=>
-2sin3xo-Jla = O 1	0	°' V °	°>
/	\/	\ cosxn - sinxn = 0 tgxa = 1	я
<=> (cosxn - sinxn) l - sin2x = 0 <=>	" u	u <=> xft = — + xn, n € Z
V 0	°/	sin2x0 = 1 sin2xQ =1	0	4
Подставляя это значение x0 в каждое из уравнений, получим те значения параметра а,
которые обеспечивают выполнение этого условия.
. 3Гя	, 2 л , 1
sm l — 4-ял +cos | — 4- ял I - а = 0 о ±—=• - а = 0 <=> а = ±—=? .
V4 J U J	2V2	<2
Зсоя — 4- ял | - 2cos3[ — + ял] - ^2 л = 0« i-—?	- ^2 а - 0 о а = ±1.
U ) U )	6 £
Т.е. первое уравнение выполняется для одних значении параметра а, а второе - для других. Поэтому первый случай невозможен, т.е. рассматриваемые уравнения не мотуг иметь одинаковых корней.
Рассмотрим второй случай. Уравнение sin3 л 4- cos3 х - а - 0 не будет иметь корней тогда и только тогда, когда [а| > 1.
Действительно, | sin3 х + cos3 х | £ | sin3 х | +1 cos3 х | £ sin2 х 4- cos2 х = 1,
Ответ: |л|>1.
5.	(Физический факультет, 1993) Число х = 5 является одним из корней уравнения Зх2 + рх + q = 0, где q < 0 . Найти действительные корни уравнения Зх4 4- рх2 4-^ = 0.
68
Решение. Уравнение Зх2 + рх + q = 0 имеет два корня хх = 5 и х2 = -^ < 0. Если в уравнении Зх4 + рх2 + q = 0 положить х2 = г £ 0, то получим уравнение
Поэтому
3t2 + pt + q = 0, которое по условию задачи имеет два корня rt = 5 и t2 = А < 0 .
х2 = 5
2 _	< 0 • Откуда действительными корнями являются х = ±^5 .
“ 15 С
Ответ: ±^5 .
6.	(Факультет почвоведения, 1993) Найти все действительные числа о, при которых 7а2 + а - 2	_	,	___м
неравенство х + —-—< 7а -1 не имеет положительных решений х.
Решение. Запишем заданное неравенство в следующей эквивалентной форме, умножив его на (х + а +1)2.
х +12—"L2—?. < 7<з — 1 <=> (х2 - 2(3а - 1)х - 5а - 1](х + а +1} < 0. х+а + 1	\	’
Для трехчлена х2 - 2(3а - 1)х - (5а +1) имеем
D =	-9=(За-1)2 +(5я + 1) = 9а2 -а + 2 = ^За-|} +^^>0-
Поэтому функция Дх) = (х2 - 2 (За - 1) х - 5а - 1) (х + а +1) имеет три точки пересечения с осью х. Полученное неравенство не имеет положительных решений при одновременном выполнении следующих условий: За - 1 < О -а - 1 < О	<=>-1£а£--.
До) = (-5а - 1)(а +1) £ О	5
Эти условия в совокупности означают, что все нули функции Дх) = (х2 -2(За - 1)х - 5а - 1)(х + а +1) лежат левее нуля.
Ответ: -1£а£-~. 5
7.	(Геологический факультет, 1993) Найти все действительные значения параметра К9 при которых в области (2х-7)2+4(у-з)2 £25 лежит ровно одна точка графика функции у = 2х +	к) JcasfyKnx) + 2cos(Kкх) - 3 +1.
Решение. Для существования квадратного корня необходимо, чтобы со$(к лх) = 1; для существования логарифма необходимо, чтобы К > 0. Поэтому
69
соз(К юг) = 1 <=> Ктх = 2ял, л g Z о i = —, л е Z .
А
Имеем у = 2х +1 = — +1. Подставляя эта значения х и у в неравенство, получим I» К
( 4п	J}2	а(4п	(4л V	, f 4л^	_^л	1	л
)	\К	)	\К)	\К)	2	К
Для того чтобы ровно одна точка графика функции у попала в заданную область, необходимо и Достаточно, чтобы одновременно выполнялись следующие условия:
2 К	п£К£2п
1±1 >1 К< п+1 „
к <х>	Из этой системы неравенств можно заключить, что
Л1 1	к>*-2
g < 2 ЛС > 0, л € Z
К > 0, л € Z
| п > °	. Откуда 0 < п < 3.
[2л - 2 < К < п +1
Отсюда заключаем, ввиду л e Z , что л может принимать только два значения п = 1 и л » 2 . Подставляя эти значения л в систему неравенств, получим при л = 1, 1 £ К < 2; при л = 2 , 2 < К < 3.
Ответ: 1 £ К < 2; 2 < К < 3.
8.	(Географический факультет, 1993) При каких значениях параметра а четыре корня уравнения л4 + (а - з)х2 + (а + ю)2 = о являются последовательными членами арифметической прогрессии?
Решение. Заданное уравнение симметрично по х относительно нуля, т.е. если х является решением, то и -х также является решением. Поэтому корни заданного уравнения будут расположены симметрично относительно начала отсчета.
Кроме того, из определения арифметической прогрессии следует, что
[ £
3d =	*1 ® 0	__
2	2 <=>	? . Итак, заданное уравнение имеет следующие корни
-х. + d = х.	з
1	1 х, »—d
Р 2
3 d d 3	'	,
2' 2d* К0Т°Рые явлаются последовательными членами арифметической прогрессии. Имеем
70
х4 + (в -3)х2 +(а + ю)2 « [х + — rflfx + —Ifx - —Ifx - — <f) = x4 - — d2x2 + —J4 . v 7 v 7 I 2 Д 2Л 2A 2 J 2	16
Сравнивая коэффициенты при одинаковых степенях х, получим
		о-З = -	*d2 2		а = -7
ь 1 U) н 1 1<Л		а +10 »			d = ±2
2			4		109
л					а 		
(в + ю)2 = £<**		о-3 = -	-d2 2		7
			з *		d « ±2 J—
		а +10 = -	--d2		17
			4		
Замечание. Мы определили не только требуемые значения параметра а, но и нашли соответствующие значения d, а следовательно, и сами корни. Последнее обстоятельство может быть использовано для контроля правильности решения.
Ответ: а = -7; а = -—.
7
9* (Факультет психологии, 1993) Уравнение (а - 1)х2 - (а + 1)х + 2а -1» 0 имеет действительные корни хр х2.
1) Найти все значения параметра а, при которых оба корня меньше L
2) При а # 1 найти все значения параметра Ь, чтобы выражение (xj - b)(x2 - ь) не зависело от параметра а.
Решение. 1) Заметим, что а # 1. В противном случае заданное уравнение становится линейным и имеет только один корень х = у. Поэтому
1 о + 1 2а ~ 1 Л
2-----х+------= 0.
о-1	о-1
Пусть /(х)» х2-----J-х + —— - однопараметрическое семейство парабол с осью
0—1	0—1
и ветвями, направленными вверх. Тогда для того чтобы
симметрии хс «
парабола из этого семейства имела с осью х две различные общие тогой, лежащие левее точки х»1, необходимо и достаточно, чтобы одновременно выполнялись следующие три условия:
a)	-g * |- J-t* .[ - g ~?fl + 14д ~3 > о (Условие существования
™ U(a-l)J а-1	4(а-1)2
двух различных действительных корней);
Ь)	х ж < 1 (Ось симметрии параболы /(х) лежит левее точки х = 1); р О f Л — 1 1	' '
71
с)	/(1) > о <=> ——р > О (У параболы f(x) нет корней, больших 1).
»	7 - 2^7
Решая эту систему неравенств, получим —-— < а < 1.
2) При а # 1 в силу теоремы Виета имеем
4- Х2 = --
. Поэтому х =------
12	а-1
(х1_^2.а)^л_(Ж1+^+^Ь^1-^О2=Р-, + 2+1^.
Это выражение не зависит от а при Ь = - .
Ответ: 1) -—< а < 1; 2) Ь = -.
7	2
/(х) а х2 + 2| х - а | - а2 <=>
10.	(Институт стран Азии и Африки, 1993) Найти все значения параметра а, при каждом из которых неравенство х2 + 2|х - а | £ <т2 справедливо для всех действительных х.
Решение. Введем в рассмотрение функцию /(х) = х2 + 21 х - а | - а2 . Определяющей точкой этой функции является точка х = а. Посмотрим, как ведет себя эта функция правее точки х = а и левее этой точки.
х - а £ 0 /1(х)“х2 +2(х-а)-а2 х - а £ 0 /2(х) = х2 - 2(х - а) - а2
В точке х = а имеем f(a)*= /До) = /Да) = 0. Заданное неравенство выполняется для всех действительных х тогда и только тогда, когда одновременно выполняются неравенство /Дх)£ 0 для всех х z а и неравенство /Дх)£ 0 для всех х £а. Для того чтобы неравенство /Дх) £ 0 выполнялось для всех х £ а, необходимо и достаточно, чтобы ось симметрии хс = -1 функции /Дх) лежала не правее точки х «а, т.е. -1 £ а. Совершенно аналогично, для тою чтобы неравенство /Дх) £ 0 вьшолншТось для всех х£а, необходимо и достаточно, чтобы ось симметрии = 1 функции /Дх) лежала не левее точки х « а, т.е. а <. 1. Наглядно это видно на рисунке. Откуда получаем -1 £ а £ 1.
Ответ: -1 £ а s 1.
72
11.	(Механико-математический факультет, 1994) При всех значениях параметра а решить уравнение 2х2 + 2аг - а2 = yjlx + 2а + За2 .
Замечание, Если обе части заданного иррационального уравнения возвести в квадрат, то получим алгебраическое уравнение четвертой степени, которое довольно трудно разложить на множители. Поэтому пойдем по другому пути, выделив два раза в левой части уравнения полный квадрат. Все преобразования легко проследить по следующей цепочке эквивалентных соотношений.
Решение. 2х2 + 2ах - а2 = ^4х +2а А-За2 <=> 2| х2 + ах + — | -	= 2 Jx + ~	<=*
I 4 J 2 V 2	4
Ответ: {о}, {1}, а = 0;
1>д4>71Узд2
2
12.	(Механико-математический факультет, 1994) Найти все значения параметра
к я
2* 2
а е
, для каждого из которых уравнение
sin 2х 4- sin х + sin (х - а) = sin а + sin (х + а)
имеет ровно 5 различных корней на промежутке
7к 5п
4 ’ 4
73
Решение, Преобразуем заданное уравнение sin 2х + sin л т sm (х - а) = sin а + sin (х + а) <=>
Isinxcosx 4* sinx - «иа(1 + 2cosх) -0 сэ
1
COSX =-----
2	•
sin х - sin а = О
Замечание. Мы покажем несколько способов отбора пяти различных корней этой _____________________„	Г 7л 5л совокупности уравнении на промежутке------;— .
Первый способ, использующий тригонометрическую окружность.
Прямая, параллельная оси орди-
нат и проходящая через точку
имеет три
точки пере-
сечения с дугами
. Эти точки
суть корни
1 уравнения cosx = на проме-
жугке
1п 5л ~~4~’ Т
Следователь-
но, уравнение sinx = sin а.
должно иметь на промежутке
7л 5л
4 * 4
ровно два различных
2^=0 4
и
4
1 п
корня, не совпадающих с корнями уравнения cosx = —. Просматривая последователь-
но ось ординат, видим, что значения а е
л
2*
отвечают
5л
этому требованию. При таких значениях а прямая, параллельная оси абсцисс, имеет ________	Г 7л Л1 Г 5л
две точки пересечения с дугами-----; 0 и 0; — .
I 4	4
4
Второй способ, использующий графики функций у « COSX и
у = sinx на промежутке
7л 5л 4 ’ 4
у = cos X
74
Из графика функции у = cosx непосредственно видно, что уравнение cosx = ~~ на
промежутке
должно
7л 5л ~Т’ Т
2 л	4 л
имеет три корня: ±—,	. Значит, уравнение sinx = sin а
Г 7л 5л иметь на промежутке ——; —
4л
Т’
ровно два различных корня, не совпадающих
л л
причем, по условию задачи, а е —; — 2 2
{у = sin х
2л л л
л л 2л 3 2 3
. 2л с ±—, 3
_7я _4л 4 ~ 3
Среди всех прямых параллельных оси х, нужно выбрать те, которые с графиком Г 7л 5я1	-
у = «лх, хе ——; — , имеют ровно две общие точки. Из приведенного рисунка L 4	4 J
получаем
Третий способ, использующий решение заданного уравнения. х	Гс	г г
1
COSX в-
2
7	5
—я£ х£ —я k 4	4
sinx-sina = О л	л
—	—
2	2
7	5
----Я £ X<> —л k 4-4
±1*
L з
А . х-а х+а 2 sin--cos---= 0 <=>
2	2
я я — ^а^ —
2	2
7	5
—я £х£ —я
4	4
Л 2л 4л х = ±—;----
3	3
х = а + 2лл, п eZ
я	л	7	5
— £ а £	—л £ х £ —п
Д 2	2	4	4
Теперь изобразим на плоскости (а;х) решения этих
систем. Найдем те значения параметра а €
при
л £
2’ 2 ’
которых прямая, параллельная оси ОХ, имеет пять различных точек пересечения с
75
ломаной ABCDE и прямыми х = ±— и х = - — .
Ответ: а е f-~;-7Ы-7;- тЫтЫт! • к 2‘ 37 к 3 4J (3) |2j
13.	(Физический факультет, 1994) Для каких значений а система неравенств
-х2 + 12х - а к О х <, 2
выполняется хотя бы при одном значении л?
Решение. Введем в рассмотрение функцию /(х) = -х2 t 12* - а . Графиком этой
функции является парабола с осью симметрии хс »6. Ветви этой параболы направлены вниз. Поэтому условиям задачи будет удовлетворять такая картинка. Откуда /(2) = -4 + 24 - а 0 <^> а < 20.
Ответ: а <> 20 .
14.	(Биологический факультет, 1994) Найти все значения величины х, при которых неравенство (2с - б)х2 + (32 - 10с)х - (8 з с) < 0 выполняется для всех с, удовлетворяющих условию 2 < с < 4.
Решение. Перепишем заданное неравенство в следующей эквивалентной форме ^2х2 - 10х - 1) с - 6х2 4 32х - 8 < 0 .
Обозначим /(с) = ^2х2 - lOx ljc - 6х2 + 32х - 8. Это однопараметрическое семейство прямых, причем в качестве параметра выступает переменная х. Для того чтобы неравенство /(с) < 0 выполнялось при всех 2 < с < 4, необходимо и достаточно, чтобы
одновременно выполнялись следующие два условия:
7(2) = -2х2 + 12х - 10 £ 0
/(4) = 2х2 - 8х - 12 £ 0
с
Решая эту систему неравенств, получим
х2 - 6х + 5 в (х ~ 5)(х - 1) £ 0
х2 - 4х - 6 в (х - 2 - V10 j(x - 2 + Tioj £ 0
2 - <10 £ х £ 1
5 £ х £ 2 + 710
Ответ: [2 - 710; 1 ]u[5*» 2 + 710
15.	(Факультет почвоведения, 1994) При каких значениях параметров а и b система f b + cosax £2
неравенств < 2 2ь + 9 £ 0 имеет единствеш1ое решение?
76
Решение. Из первого неравенства системы имеем, что Ь £ 2 - cosax <> 3. Неравенство х2 4- 2Ьх + 9 0 (х + ь)2 + 9 - Ъ2 £ 0 при | Ь | < 3 не имеет решений и имеет единст-
венное решение тогда и только тогда, когда
Ь = 3 „
_ 3 . При этом имеем
b = 3 х = -3
. Подставляя эти значения b и х в первое неравенство системы, получим
при
Ь = 3 х = -3
3 + cos За £ 2 <=> cos За = -1 <=> За = я(2и 4-1)
при
b = -3 х = 3
-3 + cos За £ 2 <=> cos За £5<=>-<ю<а<<ю.
Замечание. При Ь < -3 первое неравенство системы при любом фиксированном а
выполняется для всех х, а второе неравенство системы имеет решения, заключенные на отрезке -b - 4b2 - 9 s х $ -Ь +	- 9 . Поэтому система неравенств при b < -3 не
будет иметь единственного решения.
Ответ:
o = ^(2n + l).«eZ ддн («€(-«,®)
& = 3 I ^ = -з
16.	(Географический факультет, 1994) Найти все значения параметра а, при которых уравнение 2 + ^4х - х2 - 3 = а + J\-a2 + 2ах - х2 имеет ровно одно решение.
Решение. Перепишем заданное уравнение в следующей эквивалентной форме
2 + ^4х - х2 - 3 = а + 71 - а2 + 2ах - х2 <=> 2 +	- (х - 2)2 = а +	- (х - о)2 .
Имеем 2^2 + ^1-(х-2)2 £ 3 и а £ а +	~(х - а)2 £ а +1. Отсюда заключаем, что
заданное уравнение имеет решение только при 1 s а <> 3. Заметим, что при а = 2 правая часть последнего уравнения превращается в левую и уравнение выполняется для любых значений х € [ 1, 3 ]. Итак, исследуем уравнение 2 +	-(х- 2)2 = а +	- (х - а)2 при а е [ 1, 2 )ll(2, 3 ]. Рассмотрим левую часть
уравнения, у = 2 +	- (х - 2)2 - это уравнение полуокружности с центром в точке
(2,2) и радиуса R = 1. Эта полуокружность фиксирована. Аналогично у = а ч- - (х - а)2 - уравнение полуокружности с центром в точке (а, а) и радиуса R = 1. Центр второй полуокружности перемещается по биссектрисе первого координатного угла в зависимости от значений параметра а. Когда а е [ 1,2)и(2,3], то эти две полуокружности имеют только одну общую точку. При а = 2 полуокружности совпадают.
77
Замечание. Возможно и аналитическое решение данной задачи. Возводя обе части заданного уравнения в квадрат, получим следующую цепочку эквивалентных соотношений.
2 + ^4х-х2 - 3 = а + ^1-а2 + 2ах - х2 <=> (2 4- ^4х ~ х2 - з) = (а + х/1 - «2 + 2ах - х21 <=>
Итак, должны одновременно выполняться следующие условия:
-а2+2ах-х2
а2 +2ах-х2 +х
2-а+у4х-х2 -3 +х
’4х-х2
4х-х2
О
2[а~2+^1-а2 +2ах-х2 +х
а2 +2ах~х2 +х
1-а2 +2ах-х2 +х-2
а-2=0 4х-х2-3^0 '	а-2#0
а=2
1£х£3
у4х-х2 -3 =д-х
-а2 +2ах-х2 =2-х
а*2
2х2 -2(а+2)х+а2 +3=0 а -х£0, 2-х£0
Первая система совокупности имеет бесконечно много решении. Вторая система совокупности имеет единственное решение, если функция
Дх) = (а - х)2 - 4х + х2 +3 = (2- х)2 -1 + а2 - 2ах + х2 s 2х2 - 2(а + 2)х + а2 +3
принимает отрицательные значения при х = а и х = 2 , т.е.
/(х)|	= /(х')| 2 за2 - 4а + 3 я (а - 1)(а -3)<0<=>1<а<3.
Легко получить, что вторая система совокупности при а = 1 и а = 3 имеет единственное решение. Учитывая, что а * 2, окончательно получим а е [ 1; 2)11(2; 3 ].
Ответ: а €[ 1; 2 )U(2; 3 ].
17. (Факультет психологии, 1994) Известно, что х = 1, у = -1 одно из решений
системы
/г Г1П1я)
2дх + by = v3 rgl—-—I
Найти все решения данной системы.
ах2 + by2 =2
D	m	f 1111Х )	Я| Я 1
Решение. Так как --------- = tg 1185л + — I = tg— = -=, то заданная система выглядит
\ 6 J \ 6J 6
[ 2ах +Ьу = 1_	[ х = 1
так { 2 + 2	. Поскольку < одно из решении системы, то
78
- Ь = 1 а = 1
<=> < и поэтому исходная система будет иметь такой вид а + Ь = 2 [Ь = 1
2х + у = 1 I у = 1-2х х2 + у2 = 2	[х2 + (1 - 2х)2 = 2
5х2 - 4х - 1 = О у - 1 - 2х
Ответ: (1,-1); I—, -
18. (Институт стран Азии и Африки, 1994) При каких значениях параметра а уравнение а2х2 + 2at^2 - 11 х +	-2 = 2^2 - 3 имеет решение?
Замечание. Так как в заданное уравнение наряду с параметром а входят х, х2, ух-2 то попытка разрешить его относительно х обречена на неудачу.
Решение. Выделим в левой части уравнения полный квадрат относительно ах, оставляя в покое член V* - 2 .
а2х2 +	+ Jx-2 = 2-Ji - 3 » (ах +	- 1)2 + Jx-2 = 0 .
Сумма двух неотрицательных слагаемых равна нулю тогда и только тогда, когда каждое из этих слагаемых равно нулю. Поэтому из последнего уравнения получим
ах + ^2 - 1 = 0 _ х-2 = 0
х = 2
\-^2 .
а
2
л
Ответ: ------
2
19. (Механико-математический факультет, 1995, предварительный экзамен) Пусть Xj - наибольший отрицательный корень уравнения <J5sinx -3cosx = 2а-\, а х2 - наименьший положительный корень уравнения 2 cos2 х - 2 sin2 х = а.. Найти все значения а, при каждом из которых | хх | £ х2.
Решение. Преобразуем заданные уравнения.
/т .	,	,	1 • Л 2« - 1	(	1 - 2а
уЗ sin х - 3cosx = 2а - 1 <=> — sinx-cosx =-=- <=> coj x + — =-?=-.
2	2 2-fi У 6)	2^3
2cos2 x - 2sin2 x = a cos2x = — . 2
Для того чтобы эти два уравнения одновременно имели решения, необходимо и доста
79
1 г	ъ
точно, чтобы — уз $ а £ 2 . Решим первое уравнение и найдем х{.
( я^ 1 - 2а	я	1 - 2а
cos х + — =-------т=- <=> х =--± arccos-----т=- •+ 2 тел, п е Z .
‘ I 6J 2л/з 6	2>/з
Теперь нужно выделить наибольший отрицательный корень.
„	1 - 2а п 1 г '	я	1 - 2а
ЕСЛИ 0 £ arccos--=г- < — <£>-уЗ £ а < -1 , ТО х. =-+ arccos--=-
2^3 б 2	1	6	2<3
Если
я	1 - 2а
— £ arccos-==- £ п	,	_	1 oz.
6	_	я	1 ~ 2а
-1 £ а £ 2, ТО х. =	- arccos-т=- .
'-,6s.S2	6
2
Решим второе уравнение и найдем х2 .
cos 2х = — <=> х = ± — arccos — + пт, т Е Z. 2	2	2
Теперь нужно выделить наименьший положительный корень.
Если
_	1 а Я
О < — arccos — £ —
2	2	2
--^3£а£2 i 2
1 /г	1 а
<=>---уЗ £ а < 2, ТО х~ = — arccos — .
2	2	2	2
= я.
Рассмотрим ~ - VI <; а < -1. При этих значениях параметра а имеем о < |х, | £ ~, а у £ х2 £ -агссо/у - -~Ч . Таким образом, при у - ^3 £ а < -1 неравенство [xj | £ х2
выполняется.
Теперь рассмотрим -1 £ а < 2. При этих значениях параметра а имеем
1.
О £ х2 £ —. Таким образом, неравенство |xj | £ х2 €=> |xj |« х2 = ~ 3	3
При а «2 имеем | 1« х2 «я, т.е. это значение параметра также удовлетворяет условию задачи.
Ответ: | - 7з; -1 U {2}.
20. (Механико-математический факультет, 1995, основной экзамен) Найти все значе-
ния параметра а из отрезка [ 0; 2я ], при которых система уравнений
f х2 +у2 +2z(x + y + z)-sina = 0
а г- г з имеет хотя бы одно решение.
1(х +1) sin2 — + у2 ух 4- а2 + sfa-а = 0
80
Решение. Преобразуем заданную систему уравнений к следующему эквивалентному виду
(х + г)2 + (у + z)2 - sin а = О
(х +1) sin2 — + у2 7* + а2 Jz + sin—а = О
?	'	2	2
Из первого уравнения системы и условия а 0; 2я] заключаем, что sin а £ О Г 0 < а < к
О £ а £ 2я а = 0; я; 2х
Из второго уравнения системы и условия а е[ 0; 2я] заключаем, что
х * 0, z £ О
sin—а £ 0 <=>
2
О £ а £ 2я
х Ъ 0, z Ъ О
3
я < —а < 2я _
2	&
—а = 0; я; 2г,Зя;
.2
х % О, Z £ о
2	4
-я < а < — я
3	3
2 4
а « 0; —я; —я; 2 я.
3	3
Таким образом, решения у заданной системы могут существовать лишь при а * 0; я; 2я или —я < а < я. Так как sin—а « Злп~ - 4sin3 —, то 3	2	2	2
, 2 а .3 л . з а . о а _ . а .а smr — + ли — а  ~4sm9 — + sm — + 3sm — a sm — 2	2	2	2	2	2
✓	x 2
49 fl o . of ------------2 sin — 16 k4-------2/
£ 0
ибо | < | £ J, После этой оценки второе уравнение системы можно записать так
. 2 а 2 Г 2 Г .а 49 xsm* — + у\х + а Vz + sm------
2 7	2 16
fl 0 . а)2 ----2sm — I
U 2J
= 0.
Сумма неотрицательных слагаемых равна нулю тогда и только тогда, когда каждое из
этих слагаемых равно нулю. Пользуясь этим замечанием и тем, что неравенство
. а sm —
2
49
16
1 „ . а ---2 ли — .4-2>
£ 0 обращается в равенство лишь при а = 0; я; 2я получаем,
что при этих значениях а система имеет решение х = у = z - 0. При других значениях а система решений не имеет.
Ответ: 0; я; 2я.
21. (Факультет ВМК, 1995, предварительный экзамен) Для каждого значения параметра а решить неравенство I х + 2а I £ —.
х
Решение. Из вида заданного неравенства следует, что х > 0. Поэтому заданное неравенство эквивалентно следующей системе
81
(х(х + 2а) - 1)(х(* + 2а) + 1) <, О X > О
fx|x+ 2a| S 1	|х2(х+ 2а)2 $1
I *>0 I х>0
S О
Решим первую систему.
О < х £ -а + ^а2 + 1 |ф1
Заметим, что точка х = 0 действительно расположена так, как показано па рисунке, т.е. между корнями квадратного трехчлена, ибо если 0 < -а - Та2 +1
[ -а > О [а2 +1 < а2 ’
то решений нет, а если -а + Ja2 +1 < 0 <=> Ja2 +1 < д 1 < 0, то также нет решений.
Легко видеть, что -а - Ja2 + 1 < -а - 7а2 -1 < -а + Та2 -1 < ~а + Та2 + 1 • Определим теперь, где на числовой оси х может быть расположена точка х » 0, При рассмотрении первой системы мы показали, что точка х « 0 не может быть расположена левее точки -а - Та2 +1 и правей точки	-а + 7а2	+1 * Поэтому
-	а - 7л2	+ 1 < 0	<	-а - 7д2	- 1	(1)
-	а - 7о2	- 1 < 0	<	-а + 7о2	- 1	(2) .
-	а + 7л2	- V < 0	<	-о + Те2	+ 1	(3)
Решим каждое из этих неравенств на множестве | а | £ 1.
(1). (7o2 t l > а & а < -1. При этом [у а2 1 < -а
О < х £ -а - То2 - 1 -а + 7а2 - 1 £ х £ -а + 7а2 +1
— > а - решений нет. Та2-! > а
(3).
Та2 +1 > а
Та2 - 1 < а
<=> а 2 1. При этом 0 < х £ -а + 7а2 +1.
82
Объединяя все результаты, получим ответ.
Ответ: При а < -1, х 6 (0; - а - Та2 - 1|U|-а + ^а2 - 1; ~ а + Ja2 + 1
при а £ -1, х е [О, - а + у а2 + 1
22. (Физический факультет, 1995, предварительный экзамен) Найти минимальное значение произведения ху, где х и у удовлетворяют системе уравнений
х + у = За - 1
х2 + у2 = 4а2 - 2а + 2 ’
решение. Второе уравнение системы можно записать в следующей эквивалентной форме (х + у)2 - 2ху = 4а2 -2а+ 2. Подставляя в это уравнение х + у « За -1, получим
(За - 1)2 - 2ху = 4в2 - 2а 4- 2. Откуда легко определяется ху.
ху
5а2 - 4а -1 2
10	10
а Отсюда получаем, что минимальное значение произведения ху равно и оно достигается при а = -|.
9 Ответ:------.
10
23. (Физический факультет, 1995, основной экзамен) Для всех значений параметра а решить неравенство 3^^ > 20"1.
Решение. Очевидна следующая цепочка эквивалентных соотношений.				
3^ > 2»-’ с* з^Т >			2	V*+ 1 > (a - l)fo£3 2 <=>
	-	а - 1 < 0		xi* -1
		х + 1 £ 0		a < 1
		o-liO	** х +1 > (a - l)2 log^ 2		x > (a - l)2 log2 2-1 a 2 1
Ответ: Если а < 1, х * -1; если а z 1, х > (а -1)2 log2 2 -1.
24. (Биологический факультет, 1995) Найти все значения параметра а, при которых уравнение (х2 - б| х | - а}2 +. 12^х2 - б| х | - aj + 37 =	имеет ровно два корня.
Решение. Заданное уравнение эквивалентно следующему
^х2 - б|х |-aj + e) + 1 — со5 ——— = 0 .
83
Сумма двух неотрицательных слагаемых равна нулю тогда и только тогда, когда каждое из этих слагаемых равно нулю. Поэтому
х2 - б|х|-л+6=0
| f2 - б|х|-а + 6 = 0
, Л
1 - cos-----= О
Обозначим /(х) = |х|2-б|х|-а + 6. Построим график этой функции. Из графика видно, что уравнение (л)2 - б|х|-л+6 = 0 имеЬт ровно два корня в следующих случаях:
1)	/(0) < 0 <=> а > 6 . При этом второе уравнение системы обращается в верное равенство лишь при а = 9.
2)	/(з) = /(-з) = 0 <=> а = -3. При этом значении а второе уравнение системы
обращается в верное равенство. Ответ: -3; 9.
25.	(Факультет почвоведения, 1995, предварительный экзамен) Определить область значений параметра а, при которых уравнение 2cos2x - 4acosx л-а2 +2 = 0 не имеет действительных решений.
Решение. Заметим, что cos2x = cos2 х - sin2 х = 2 cos2 х -1. Поэтому заданное уравнение можно преобразовать так
2cos2x - 4а cosx + а2 + 2 = 0 <=> 212COS2 х - 1) - 4а cosл 4- а2 4- 2 = 0 <=>
4cos2 х - 4а cosx +а2 = 0 <=> (2 cosx - а)2 « 0 <=> cosx =	.
Полученное простейшее тригонометрическое уравнение не имеет действительных ре-
шений тогда и только тогда, когда
Ответ: | а | > 2 .
> 1 <=> |а| > 2.
26.	(Факультет почвоведения, 1995, основной экзамен) При каких значениях параметра b система уравнений + * “ х + 2х имеет два решения?
( х2 + у2 = 2х
Решение. Преобразуем заданную систему, цыделив в каждом из входящих в нее
уравнений полный квадрат. Получим
4у = 4Ъ 4- 3 - х2 ' х2 + у2 = 2х
y =	+ Ь + 1
(* - 1)2 + у2 = i
а
а
2
84
Пер»06 уравнение преобразованной системы задает однопараметоическое семейство парабол с осью симметрии = 1. ветви которых направлены вниз.
Второе уравнение задает окружность с дентром (1; 0) н радиуса 1. Эта окруж-
ность фиксирована, кривые. Покажем,
Построим эти что функция имеет с окруж-
ностью (х -1)2 + у2 = 1 ровно одну
общую точку. Для этого достаточно доказать, что для любого s е (О; 1] выполняется
неравенство
["(» - О2 +	<=> “S2 +1 > V1-S2 <=> ~s4 + |е2 > О.
Таким образом, при Ь = 0 заданная система имеет единственное решение. Из приведенного рисунка получаем, что при -2 < Ъ < 0 заданная система имеет ровно два решения. При Ь = -2 система имеет единственное решение, а при Ь < -2 и при Ь > О система не имеет решений.
Замечание. Возможно и следующее решение предложенной задачи. Из второго уравнения системы заключаем, что у2 = 2х - х2 « 1 - (х - l)2 s 1. Отсюда следует, что | у | $ 1. Если | у | = 1, то х ~ 1 - единственное решение второго уравнения системы, а сама
{х = 1	( х — 1
при b = 0 , либо < при Ъ = -2 .
У = 1	(У = -1
К аждому значению у, заключенному в промежутке -1 < у < 1, соответствуют два значения х Подставляя выражение 2х - х2 = у2 из второго уравнения системы в - рвое, получим у2 - 4у + 4Ь + 3 = 0. Введем функцию /(у) = у2 - 4у + 4Ь + 3. Это однопараметрическое семейство парабол с осью симметрии ус = 2 и ветви этих парабол направлены вверх. Для того чтобы функция /(у) имела один корень, ' финадлежапшй промежутку -1 < у < 1, необходимо и достаточно, чтобы одновременно выполнялись следующие условия:
/(1) < 0 fl-4 + 4fc+3<0	(2><0
? \ л <=> С	<=><	<=> -2 < Ъ < 0.
/(-1) > О [1 + 4 I- 46 4- 3 > 0 |Ь > -2
Ответ: -2 < Ъ < 0 .
85
27.	(Геологический факультет, 1995, предварительный экзамен) Пусть /(*) »	- 4л + 4 - 3, g(x) = Jx - а, а - параметр. Решить относительно х
неравенство /($(*)) £ 0 •
Решение.	« jg2 -4 g ^4 - 3 « | g - 21 - 3 = 1Jx - а - 21 - 3 £ 0.
Итак, нужно решить относительно х неравенство н/х-а-2-3£0<*
cs а - 1 £ Jx £ а + 5 о
а-г 1 £ О а + 5 £ О
О £ х £ (а + 5)2 а - I £ О а + 5 2 О
(а - 1)2 £ х £ (а + if
-5 £а £ 1
О £ х £ (а + 5)2 а £ 1 (а - 1)2 £ л £ (а + if
Ответ: При а < -5 решений нет; при -5 £ а £ 1, 0 £ х £ (а + if;
При а £ 1, (a-\f £ х £ (а + if .
2& (Геологический факультет, 1995, предварительный экзамен) Для каждого
решить систему
tog2(|a|x2 -Зх + 4)	д_ЫЬ„).
/о$2(-3х + 4)
X < 1
Решение.
в I*2
* 1, причем верхнее неравенст-
во в этой системе обращается в равенство когда
|а |х2 = О х < 1
а € R х < 1
х « О, а = О,
Для правой части уравнения заданной системы имеем 5''x^x+l) £ 1, причем равенство достигается когда х = О или х = -1.
х = О
х = -1 ‘
Поэтому при а = О,
при а * О, X = 0 .
Ответ:
при а # 0, х = 0 .
29.	(Геологический факультет, 1995, основной экзамен) Найги все значения параметра а, при которых неравенство I61 < 30 4х - а не имеет ни одного целочисленного решения.
86
Решение. Введем в рассмотрение функцию Д4*|я 42* - 30 • 4* + а. Это одно* параметрическое семейство парабол относительно 4* с осью симметрии 4\ * 15 и ветви этих парабол направлены вверх.	/ v
Ближайшее к 15 число, соответствующее Л4 /\ целому значению х, - это 16 = 42. Поэтому	\	} X х
для того чтобы заданное неравенство не	Xjgj	4
имело ни одного целочисленного решения, необходимо и достаточно, чтобы /(1б) £ 0 <=> 162 - 30 • 16 + а £ 0 о а г 224.
Ответ: а 2 224.
30.	(Географический факультет, 1995, предварительный экзамен) Найти все значе ния параметра а, при каждом из которых функция у(х) «log^^cosx + Jisinx - в) определена при всех значениях переменной х
Решение. Путем введения вспомогательного угла преобразуем заданную функцию к эквивалентному виду.
у(х) = ^25-а2 (C<W х + ^8 s*n х “ = ^25 в213 cos х + лл х j - а | =
« ^25-о2 (^лл(х + ф) “ а)» гае <р = arcsin—.
Так как эта функция должна быть определена при любых значениях х, то
одновременно должны выполняться следующие условия:
25 - а2 > О 25-а2 # 1 <=> -3 - а > О
-5 < а < -2^6
-2# < а < -3 ’
Ответ. (-5; -2Тб|и(-2^6; -з|.
31.	(Географический факультет, 1995, основной экзамен) Сколько корней на отрезке х € [ - я; я ] имеет уравнение х2 + а » 3bcosx, если параметр b есть наименьшее возможное значение суммы квадратов корней квадратного трехчлена х2 - х^5~ Зе2 + — - с2 ?
2
Решение. Если хх и х2 - корни квадратного трехчлена х2 - х
+ *2 = т/з - Зе2 и XjX2 ж у - с2. Находим х2 + х2 «	+ х2)2 - 2х,х2 = 2-с2. Для
того чтобы существовал ^5 - Зс2 , необходимо и достаточно, чтобы
^5 - Зс2 + ~ - с2, то 2
87
5-Зе2 ^0«c2 S Тогда Ь = mm{x2 =	=
Итак, предложенная задача свелась к следующей: сколько корней на отрезке х е [ - я; я ] имеет уравнение х2 + а = cosx 1 Решим эту задачу графически.
Уравнение х2 + а = cosx имеет два решения на отрезке х € [ - п\ я ], когда
-1-я2 £ а < 1.
При а = 1 уравнение имеет одно решение. При а > 1 это уравнение вообще не имеет решений.
При а < -1 - я2 это уравнение не имеет решений на отрезке х € [ - я; я ].
Ответ: При а €	-1 - «2)и(1х + ®) - корней нет;
при а € 1-1 - я2; 11 - два корня;
при а » 1 - один корень.
32.	(Экономический факультет, 1995) Найти все х € | - 7; 2 ], для которых неравенство х|я(х + 2) - Sarctgllm2 + 12m +1711 > 0 выполняется при любых целых т.
Решение. Т.К. 2m2 + 12m + 17 = 2(m + З)2 - 1 £ -1, TO £ arctg^lm2 + 12m + 17^ < у.
Поэтому -4я < -barctgfem2 + 12m + п) £ 2я и должны одновременно выполняться два х(я(х +2)-4я + яе) > 0	|х(х-2 + с)>0 oV У//// ..
такикнеравенсзва	> J ~	+ 4)	~
Отсюда следует, что заданное неравенство не выполняется при х е [-4; 2 - s] при s-> 0, т.е. на полуинтервале [ -4;2),и выполняется при х €[ -7;-4) U {2}.
Ответ: х б[-7;-4)и {2}.
33.	(Экономический факультет, 1995) Найти наименьшее значение выражения а2+(Ь + 1)2 на множестве таких чисел а и Ь, для которых уравнение 11 х + 2|- 21 + ах + 2а + ь = 0 имеет ровно три различных корня. Указать, при каких а и b достигается это наименьшее значение.
88
Решение. Построим график функции у «11 х + 21- 21
-х - 4,
х £ 0 -2^х^0 - 4 £ х 3 -2
J х I , х £ -2 |х + 4|,х£-2
точки, которые должны принадлежать четырем звеньям ломаной. Поэтому эта прямая должна проходить через точку, принадлежащую одновременно двум звеньям ломаной, т.е. через вефшину ломаной. Таких вершин у нашей ломаной три: а(0; о), В(-2; 2) и С (-4; 0). Подставляя координаты точек А, В и С в уравнение прямой, получим
< 2 л 1 <Г	2V 1 1
| = 5а - 4а + 1 =	- -J + - £ -, при
А(0; 0) :	0 = -2а	= -2а и а
ЭТОМ
2	,	„
-х и еще две общие точки находятся из условий:
2
—х = х + 4 5
2
х = -х - 4
В (-2; 2):
Ь — —2 И
этом у
20
7
20 ’
3
И а‘
.2
и еще
две общие
точки находятся из условий:
2V К 1
2
5
8
5
2	8
— х + —
5	5
2	8
. 5Л + 5
£
7 . Отсюда непосредственно видно, что наименьшее значение о
3
выражения а1 + (h +1)2 равно и достигается при а = ±^, Ь - -у.
Л 1	2 L 4
Ответ: - при а = ±~, Ь = —.
5	5	5
89
34.	(Экономический факультет, 1995, отделение менеджмента) Найти все значения
параметра р, при которых уравнение х - 2 = ^-2(р + 2)х + 2 имеет единственное
решение.
Решение. Заданное уравнение эквивалентно следующей смешанной системе
X - 2 = J-2(p + 2)x 4-2 <=>	“ 2) =	* 2)х * 2 .
¥	I х-2^0
Если ввести в рассмотрение функцию /₽(х) »(х - 2)2 +2(р + 2)х - 2 s х2 + 2рх 4- 2, то
предложенную задачу можно переформулировать так: найти, при каких значениях параметра о функция fp(x) имеет единственный нуль, расположенный на промежутке
2 £ х < <ю . Это может быть в следующих ,
В первом случае (рисунок слева) /₽(2) < О
Во втором случае (рисунок справа)
М2)-0 «
з
Ответ: р^-—.
35.	(Факультет психологии, 1995) Найти все значения параметра а, при которых неравенство cos 2х 4- а £ 2^х2 +16 -	имеет единственное решение.
a+cos2x
Решение. Заметим прежде всего, что если х является решением неравенства, то и -х будет решением неравенства, т.к. х2=(-х)2 и cos(-2x) = cos2x. Поэтому единственным решением неравенства может быть лишь х = 0.
16 (а +	"•	4-1) 4-16 (а - З)2 Га « 3
При х = 0 имеем 1 + а £ 8------<=> ------------------£ 0 о- ----— £ 0 <=>
а 4-1	а 4-1	а 4-1	[а < -1
Исследуем заданное неравенство при а = 3 и а < -1.
При а « 3 имеем cos 2х 4- 3 £ 2т/х2 4-16 - ---t— <=> (3 4- соз2х -ух2 4- 1б) £ 0 <=> 3 + еаг2х \
3 4- cos 2х - 7х2 +16 = 0 <=> 4 £ 4х2 4-16 = 3 4- cos 2х £ 4 . Откуда х = 0.
90
4“ cos2x - V*2 + 16j
При a < -1 получаем------------------------£ 0 или а + cos2x < 0. Но последнее
а + cos2x
неравенство при а < -1 справедливо для любых х
Ответ: а = 3.
36.	(Институт стран Азии и Африки, 1995) Найти все значения параметра а, при которых неравенство х2 + 4х + 6а |х + 21 + 9а2 £ 0 имеет не более одного решения.
Решение. Заданное неравенство можно переписать в следующей эквивалентной форме: х2 + 4х + 6а | х + 21 + 9а2 £ 0 <=> | х + 2 |* + 6а | х + 2 (+ 9а2 - 4 £ 0 .
Корни этого квадратного относительно |х + 2| трехчлена будут |х + 2| = -За±2. Для того чтобы неравенство |^-»’2|2 + 6а|х + 2| + 9а2 -4 £ о имело не более одного решения, необходимо н достаточно, чтобы его больший корень х = -За+2 был 2
неположителен, т.е. -За + 2£0<=>а£ —.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.	(Механико-математический факультет, 1993) При каких значениях параметра а, принадлежащих интервалу ; oj , уравнение 2 cos(x + а) - 1 = sin 6х - 1 имеет решения?
Ответ:
12	12
2.	(Механико-математический факультет, 1993) Найти все значения Ь, при которых уравнение 9х + ^2 + б) 3х - Ь2 +16 = 0 не имеет решений.
Ответ: | b | <; 4.
3.	(Механико-математический факультет, 1993) Найти все значения а, для которых неравенство cos2x - (1 + а2 - cos2 xj sin х + 4 - а^ <1 выполняется при всех х.
Ответ: 0 < а < 1.
4.--(Факультет ВМК, 1993) Найти все значения Ь, при которых область определения функции у --	--------------- совпадает с областью определения функции
Зяих - 2х + 2£
VI 1
3sinx - 2 sin3 х +2b sin3 x + cos3 x + ^2b
91
Ответ: b >------.
1 1	2
5.	(Физический факультет, 1993) Уравнение ах2 4- Ьх + 2 = 0, где а < О , имеет одним из своих корней число х = 3. Найти действительные корни уравнения ах4 + Ьх2 4-2 = 0.
Отлет: ±^3 .
6.	(Факультет почвоведения, 1993) Найти все действительные числа а, при которых
Та1 - а - 2	_	„	t
неравенство х 4-----------< -7 а не имеет решений х, больших 1.
х - а
Ответ: ~ < а £ 1.
7,	(Геологический факультет, 1993) Найти все неотрицательные действительные значения параметра а, при которых в области (у 4- 2)2 - 4х £ 0 лежат ровно три точки трафика функции у = 2х ^cos (2а к х)- cos4 (о к х) -4- 2.
Ответ: — < а < 1; 1 < а < — . 4	4
8.	(Географический факультет, 1993) При каких значениях параметра а четыре корня уравнения х4 4- (а - 5)х2 4- (а 4- 2J2 = О являются последовательными членами арифметической прогрессии?
Ответ: а = -	; а - -5.
13
9.	(Факультет психологии, 1993). Уравнение (а - 1)х2 - (2а 4- 1)х 4- 2 4- 5а - 0 имеет действительные корни Xj, х2 .
1)	Найти все значения параметра а, при которых оба корня больше 1.
2)	При а * 1 найти все значения параметра Ь, чтобы выражение (xj - b)(x2 ~ нс зависело от параметра а.
Ответ: 1) 1 < а < - —3^2 ; 2) Ь = — . 4	3
10.	(Институт стран Азии и Африки, 1993) Найти все значен.л параметра о, при каждом из которых неравенство х2 4- 5|х 4- а | £ а2 справедливо для всех действительных х.
Ответ: - — £ а £ - . 2	2
92
11.	(Механико-математический факультет, 1994) Найти все значения параметра <р е [О, ж], для каждого из которых уравнение sin2x + cos х - sin (х + ф) = cos ф + sin (х - ф) имеет ровно «	м	Г 5ж 7ж
5 различных корней на промежутке-; —
[44
Ответ: ф € f0;	{х}.
\ 67 \6 4/ I 6 J ' '
12.	(Механико-математический факультет, 1994) При всех значениях параметра а решил, уравнение ajalx2 + 2ах] а Jx + 1 +а .
Ответ: |-1}, а = 0;
1 - 2а + 71 + 4а2
Л+2а + ^4а2 -3 2а
а£ 1 .
13.	(Физический факультет, 1994) Для каких значений b система неравенств {х2 - 16х + b £ 0	*	о
выполняется хотя бы при одном значении х?
х Ь 10
Ответ: Ь $ 60.
14.	(Биологический факультет, 1994) Найти все значения величины х, при которых неравенство (4 - 2а)х2 + (13а - 27)х 4- (33 - 13а) < 0 выполняется для всех а, удовлетворяющих условию 1 < а < 3.
Ответ: [з -Тб; 2 lufs; 3 + 7б1.
15.	(Факультет почвоведения, 1994) При каких значениях параметров а и b система f а + sin Ъх £ 1
неравенств < 2	+ j q имеет единственное решение?
Ответ:
fl ® 2	Г а « -2
,. Ж л	_ ИЛИ S	\ •
Ъ = — + 2Ю1, п € Z [о € [-<», оо)
16.	(Географический факультет, 1994) Найти все значения параметра а, при которых . уравнение а 4 7бх - х2 - 8 = 3 4- 71 + 2ах - а2 - х2 имеет ровно одно решение.
Ответ: а 6 [ 2; 3)U(3; 4 j.
17.	(Факультет психологии, 1994) Известно, что одним из решений системы уравнений ах + by + sin
является х = 2 , у = -1. Найти все решения данной системы.
а
93
M л ( 13 2) Отмт.- (2, - l):	-j .
18, (Институт стран Азин н Африки, 1994) При каких значениях параметра а уравнение
а2х2 +2a|V3-1)х +Vx-4 = 2^-4 имеет решение?
Ответ: -------.
4
19.	(Механико-математический факультет, 1995, предварительный экзамен) Пусть х( -наибольший отрицательный корень уравнение 4 cos2 х - 4 ял2 х = а , а х2 - наименьший положительный корень уравнения Ji sin х + 3 cos х = 1 - а . Найти все значения а, при каждом ИЗ КОТОрЫХ | Xj | £ х2.
Olfutm: [1 - 2^3; - 2]u{4} .
20.	(Механико-математический факультет, 1995, основной экзамен) Найти все значения параметра а из отрезка [ - к; к j, при которых система уравнений
х2 + у2 + 2z2 - 2z(x + у) + sina « 0
<	\	? а 1 г г г 3 имеет хотя бы одно решение.
(у +1) cos2	+ а ух - сот—а • 0
Ответ: -я; 0; я.
21.	(Факультет ВМК, 1995, предварительный экзамен) Для каждого значения параметра а
решить неравенство — + 2а £ х.
х
Ответ: При а < -1, х €| а + Ja2 + Г, - а - Ja2 - 11 U | - а + yla2 - 1; + <ю];
при a 2 -1, х € а + у а2 +1; + а>
22.	(Физический факультет, 1995, основной экзамен) Для всех значений параметра т
Ответ: Если т < 1, х £ 1; если т £ 1, х < 1 - (т - l)2 log2 3 .
23.	(Биологический факультет, 1995) Найти все значения параметра а, при которых уравнение 1х2 - б| х | + а) + 1о(х2 - б|х| + а) + 26 = cos^- имеет ровно два корня.
94
Ответ: -4; 8.
24.	(Факультет почвоведения, 1995, предварительный экзамен) Определить область значений параметра Ъ, при которых уравнение соз2у + Abcosy + 2b2 +1 = 0 не имеет действительных решений.
Ответ: | b | > 1.
25.	(Факультет почвоведения, 1995, основной экзамен) При каких значениях параметра а {х2 4о = 4v — 2х — 5
7	не имеет действительных решений?
х + 2х + у = О
Ответ: (-»; - 2) U (О; + <»).
26.	(Геологический факультет, 1995, предварительный экзамен) Пусть /(ж) • Jx* - 6х + 9 - 2, #(х) = 4~х - а, а - параметр. Решить относительно х неравенство /(«(«))so.
Ответ: При а < -5 решений нет, при -5 $ а £ -1, 0 £ х <. (а 4- 5)2;
при а 2 -1, (д + 1)2 £ х £ (а + 5)2;
27.	(Геологический факультет, 1995, предварительный экзамен) Для каждого а решить
систему
toft(|a|x2 -4x4-5) = 2-|,|(,+э)> toft(-4x + 5)
х < 1
Ответ: При а » О,
х«0 х«-3
при а в 0, х = 0.
28.	(Геологический факультет, 1995, основной экзамен) Найти все значения параметра о, при которых неравенство 9я < 20 • 3х 4- а не имеет ни одного целочисленного решения.
Ответ: а £ -99.
29.	(Географический факультет, 1995, предварительный экзамен) Найти все значения параметра а, при каждом из которых фумортл у(х) = loga2a2^4sinx^acosx + 5)
определена при всех значениях переменной х
Л (, i-VbI/i-Vu 1 + 71з1/ i + Vi3 J
Ответ: 1-3; --— U --—; -1 U 2; --— U -’—; 3 .
\	2 7 I 2	7 \	2/k2 J
95
30.	(Географический факультет, 1995, основной экзамен) Сколько корней на отрезке
х 6 [ - я; я ] имеет уравнение х2 - а = — b cos х, если параметр b есть наименьшее 11	4
возможное значение суммы квадратов корней уравнения х2 - х^Зс2 - 1 л- с2 - 1 = 0 7
Ответ: При а € (-«о; - 1)и|я2 4-1; + <ю| - корней нет; при а « -1 - один корень, при а е 1-1; к2 +11 - два корня;
31.	(Экономический факультет, 1995) Найти все хб[-3; 1|, для которых неравенство х^х(х +1) - 4агс/#{зт2 + 12m + 1ф> 0 выполняется при любых целых т.
Ответ: х е [ —3;—2 ) U {1 }•
32.	(Экономический факультет, 1995) Найти наименьшее значение выражения a2 + (b -1)2 среди тех а и Ь, для которых уравнение ||х-4|-2|-ах + 4а-£я0 имеет ровно три различных корня. Указать, при каких а и Ъ достигается это наименьшее значение.
Ответ: у при а « ± у, Ъ » у.
33.	(Экономический факультет, 1995, отделение менеджмента) Найти все значения параметра Ь, при которых уравнение х - 2 «	- 1)х +1 имеет единственное решение.
3
Ответ: Ь^—.
4
34.	(Факультет психологии, 1995) Найти все значения параметра а, при которых неравенство г— *2 । у cosx - 2ух2 + 9 --------------а имеет единственное решение.
a + cosx
Ответ: а = 2.
35.	(Институт стран Азии н Африки, 1995) Найти все значения параметра а, при которых неравенство х2 - 6х + 4а|х - 31 + 4а2 £ 0 имеет не более одного решения.
3
Ответ: а £ —.
2
Литература:
1. Справочники для поступающих в МГУ в 1972-96 годах. МГУ, М., 1972-96.
2. Г.А. Тиняков, И.Г. Тиняков. Задачи с параметрами. М., 1994.
96