Пространство и время в микромире - Блохинцев Д.И.

Автор: Блохинцев Д.И.
Теги: ядерная, атомная и молекулярная физика физика издательство наука пространство-время микромир темпоральная теория
Год: 1982
Похожие
Пространство-время. Явные и скрытые размерности.
Пространство и время в макро-, мега- и микромире
Природа пространства и времени
Пространство, время, материя. Лекции по общей теории относительности
Текст
                    О И ВРЕМЯ В МИКРОМИРЕ
Д.И. Блохинцев
ПРОСТРАНСТВО
И ВРЕМЯ
В МИКРОМИРЕ
Д.И. Блохинцев
ПРОСТРАНСТВО
И ВРЕМЯ
В МИКРОМИРЕ
ИЗДАНИЕ 2-Е, ИСПРАВЛЕННОЕ
МОСКВА «НАУКА*
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 8 2
Scan AAW
22.31
Б 70
УДК 539.12
Блохинцев Д. И. Пространство и время в микромире.—2-е изд.,
испр. — М.: Наука. Главная редакция физико-математической лите-
ратуры, 1982.
Монография посвящена критическому анализу пространственно-
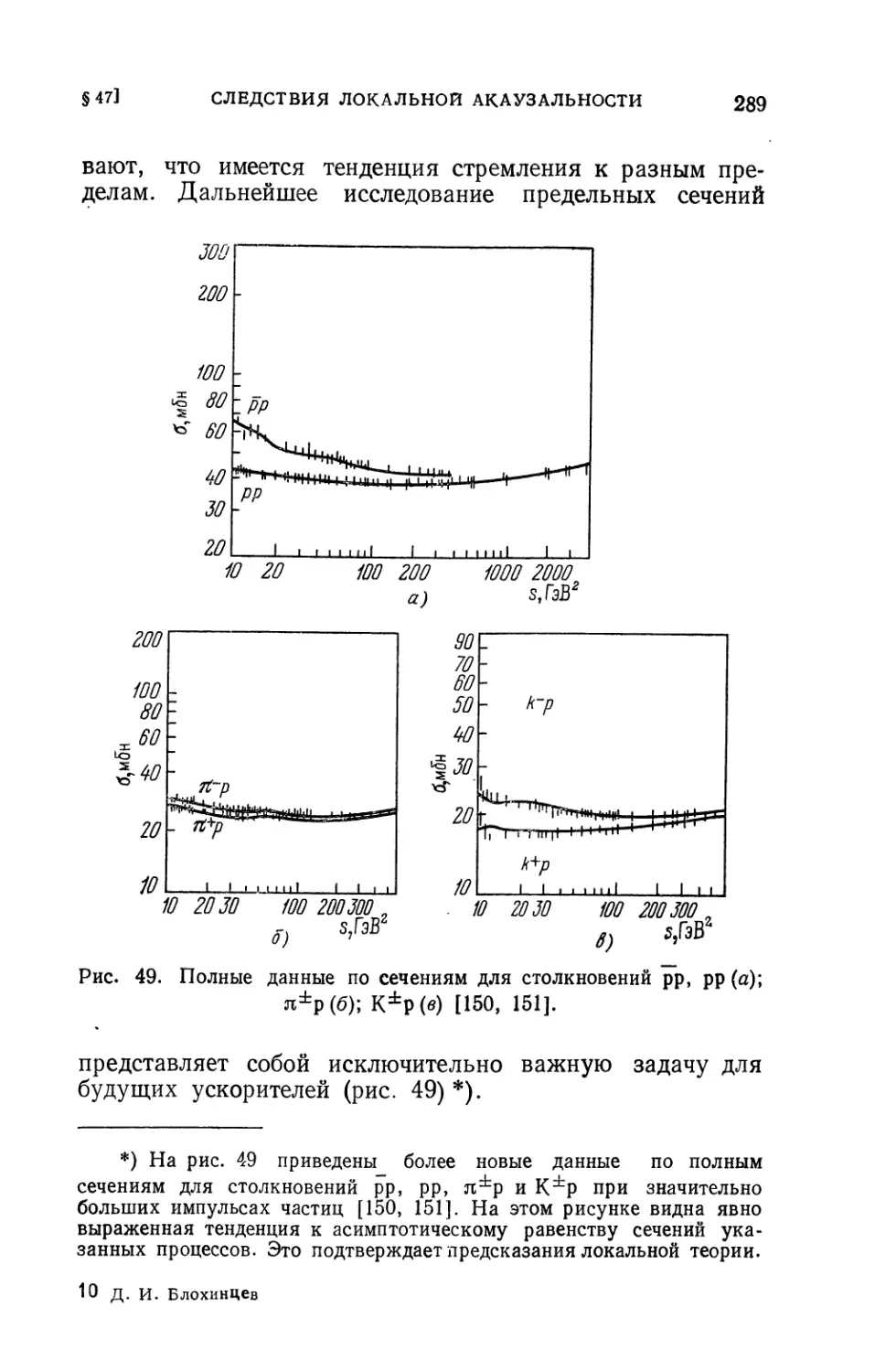
временного описания мира элементарных частиц. В ней высказыва-
ется мысль, что трудности современной теории связаны с неправиль-
ными геометрическими представлениями при описании взаимодействий
элементарных частиц на малых расстояниях, дан подробный анализ
этих трудностей и изложен ряд новых направлений, связанных с раз-
личными модификациями пространственно-временных соотношений.
Наряду с обычными хеометрическими представлениями, вырабо-
таннымиТклассической наукой на основе анализа явлений в макро-
мире, в этой книге с большой оригинальностью изложены вопросы,
касающиеся описания различных геометрических соотношений в мик-
ромире: измерение координат и времени частиц в релятивистском
и нерелятивистском случаях, локализация частиц, распространение
сигналов в нелинейных теориях поля, квантование пространства —
времени и т. д.
В монографии изложены вопросы, связанные с условиями микро-
и макропричинности в квантовой теории поля. Здесь много инте-
ресных результатов, принадлежащих автору, например связь между
нарушением причинности в малых пространственно-временных облас-
тях и наблюдаемыми процессами при рассеянии элементарных частиц.
Большинство результатов, приведенных в книге, ранее почти не было
опубликовано.
Книга рассчитана на студентов, аспирантов и научных работ-
ников, занимающихся теоретической физикой.
Рис. 52, табл. 4, библ. 147 назв.
Б
1704020000—112
053(02)-82 Л
© Издательство «Наука»
Главная редакция
физ и ко- математической
литературы 1982
ОГЛАВЛЕНИЕ
Предисловие................................................ 5
Введение................................................... 7
Глава I. Геометрические измерения в макромире............	9
§ 1.	Арифметизация пространства—времени.................. 9
§ 2.	Физические методы арифметизации пространства —
времени............................................ 11
§ 3.	О делении многообразия событий на пространство и
время.............................................. 19
§ 4.	Аффинное многообразие.............................. 27
§ 5.	Риманово многообразие.............................. 32
§ 6.	Физика арифметизации пространственно-временного
многообразия....................................... 37
§ 7.	Арифметизация событий в случае нелинейной теории
поля .............................................. 41
§ 8.	Общая теория относительности и арифметизация прост-
ранства—времени........................................ 46
§ 9.	Хроно геометрия.................................. 50
Глава II. Геометрические измерения в микромире............ 53
§ 10.	Замечания об измерениях в микромире.............. 53
§ 11.	Измерение координаты микрочастицы................ 55
§ 12.	Механика измерения координаты микрочастицы ...	62
§ 13.	Косвенное измерение координаты микрочастицы в
данный момент времени................................... 73
Глава III. Геометрические измерения в микромире в реля-
тивистском случае...................................... 78
§ 14.	Фермионное поле................................. 78
§ 15.	Соотношение неопределенностей для фермионов ...	83
§ 16.	Бозонное поле................................... 36
§ 17.	Локализация фотонов............................. 91
§ 18.	Расплывание релятивистских пакетов.............. 95
§ 19.	Координата Ньютона — Вигнера.................... 98
§ 20.	Измерение координат микрочастицы в релятивистском
случае................................................ 101
Глава IV. Роль конечных размеров элементарных частиц 105
§ 21.	Поляризация вакуума. Размер электрона..........	105
§ 22.	Электромагнитная структура нуклонов............ 109
§ 23.	Мезонная структура нуклонов....................Л13
§ 24.	Структура частиц в теории квантованных полей ...	123
4
ОГЛАВЛЕНИЕ
Глава V. Причинность в квантовой теории.................... 135
§ 25.	Замечания о причинности в классической теории поля	135
§ 26.	Причинность в квантовой теории поля............... 143
§ 27.	Распространение сигнала «вну?ри» микрочастицы . .	151
§ 28.	Условия микропричинности в квантовой теории поля	157
§ 29.	Микропричинность в теории матрицы рассеяния ...	163
§ 30.	Причинность и аналитические свойства матрицы рас-
сеяния .............................................. 169
Глава VI. Макроскопическая причинность .................... 183
§ 31.	Формальная теория S-матрицы....................... 183
§ 32.	Пространственно-временное описание с помощью S-
матрицы.............................................. 193
§ 33.	Масштаб для асимптотического времени Т.........	198
§ 34.	Нестабильные частицы (резонансы).................. 202
’ § 35. Условия макроскопической причинности для S-мат-
рицы ............................................. 210
§ 36.	Примеры акаузальных функций влияния............... 217
§ 37.	Пример построения акаузальной матрицы рассеяния 222
§ 38.	Дисперсионные соотношения для акаузальной Sa-
м атрицы............................................. 231
Глава VII. Обобщение причинной связи и геометрии . . .	236
§ 39.	Две возможности обобщения......................... 236
§ 40.	Евклидова геометрия в микромире................... 244
§ 41.	Стохастическая геометрия.......................... 250
§ 42.	Дискретное пространство — время........• ...	256
§ 43.	«Квазичастицы» и квантование пространства ....	263
§ 44.	Флуктуации метрики................................ 269
§45.	Нелинейные поля и квантование пространства-времени 275
Глава VIII. Вопросы эксперимента
§ 46.	Заключительные замечания теоретического характера 283
§ 47.	Экспериментальные следствия локальной акаузаль-
ности................................................ 284
§ 48.	Экспериментальные следствия моделей с «внешним»
вектором............................................. 294
Дополнения................................................. 299
Литература................................................  341
Именной указатель.......................................... 346
Предметный указатель....................................... 347
Посвящается
светлой памяти
ШИФРЫ ДРАБКИНОЙ
ПРЕДИСЛОВИЕ
Путь к пониманию закономерностей, господствующих
в мире элементарных частиц, еще не найден. Современ-
ный физик-теоретик принужден довольствоваться компро-
миссными концепциями, которые в лучшем случае обе-
щают частный успех за счет общности и единства.
В этой ситуации критический анализ основных поня-
тий современной квантовой теории может быть и своевре-
менным, и полезным. Можно надеяться, что значение
этого анализа сохранится даже и в том случае, если
в скором времени будут открыты существенно новые пути
к пониманию основ физики элементарных частиц. В на-
стоящей монографии избран определенный аспект этого
анализа — проблемы геометрии в микромире. Обсуждению
этих проблем мы предпослали очерк, посвященный гео-
метрическим измерениям в макромире, которые, по край-
ней мере в ограниченном круге задач, представляются
достаточно ясными и могут служить в качестве исходных
для обсуждения ситуации в микромире. Понятия и мето-
ды, пригодные в макромире, могут быть перенесены в
микромир лишь косвенно и требуют большой степени
абстракции.
Во многих важных случаях для осмысливания физи-
ческого содержания той или иной динамической перемен-
ной, имеющей геометрическое значение, например прост-
ранственно-временных координат частицы х, у, г, t, необ-
ходимо прибегать к мысленным опытам, практическая
осуществимость которых более чем сомнительна, но кото-
рые во всяком случае совместимы с основными принци-
пами геометрии и квантовой механики.
Еще большая дистанция в пустынном море абстракт-
ных построений отделяет макроскопические понятия
пространства-времени от того способа употребления
координат х, у, г, /, который принят в релятивистской
квантовой теории поля.
6
ПРЕДИСЛОВИЙ
В монографии показано, что наличие структуры у эле-
ментарных частиц ставит вообще под сомнение возмож-
ность ^точного определения координат элементарной
частицы х, у, г, t и еще в большей степени координат
элементов, образующих эти частицы (если такие элементы
существуют не только в воображении). Это важное обстоя-
тельство обнаруживается на уровне анализа даже самых
благоприятных мысленных экспериментов.
В этой связи возникает сомнение в логической закон-
ности употребления символов х, у, г, t в качестве прост-
ранственно-временных координат, пригодных для описа-
ния явлений внутри элементарных частиц. Это обстоя-
тельство предоставляет теоретику определенную свободу
в выборе пространственно-временных и причинных связей
внутри элементарных частиц, иными словами, произвол
в выборе геометрии в малом.
Последние главы книги посвящены описанию некото-
рых моделей, позволяющих иллюстрировать обрисованную
выше ситуацию. В заключение обсуждаются эксперимен-
тальные данные и экспериментальные возможности, имею-
щие отношение к геометрическим проблемам и проблемам
причинности в микромире.
Данная монография основана в значительной мере на
работах автора, опубликованных в разное время и в раз-
личных изданиях. Многие из этих работ выполнены со-
вместно с учениками. Автору было отрадно найти возмож-
ность осветить в монографии и некоторые оригинальные
исследования своих учеников: Б. М. Барбашова (совместно
с Н. А. Черниковым), Г. И. Колерова и Г. В. Ефимова.
Автор глубоко признателен им за обсуждения, способст-
вовавшие разъяснению многих неясных и спорных вопро-
сов. Особенно признателен автор за полезные советы и
замечания М. А. Маркову и Б. М. Барбашову, взявшим
на себя труд критически прочесть рукопись книги, и
Г. И. Колерову за существенную помощь в подготовке
рукописи.
Хотелось бы надеяться, что идеи этого труда ока-
жутся полезными для тех, кого волнуют фундаменталь-
ные проблемы современной атомной физики.
Апрель 1969 г.	Д, Блохинцев
Дубна — Москва
ВВЕДЕНИЕ
Защищаемое здесь истолкование Геометрии
нельзя непосредственно применять к субмо-
лекулярным (меньшим, чем молекулы) про-
странствам... может оказаться, что такое
экстраполирование столь же неправильно,
как и распространение понятия температу-
ры на частицы тела молекулярных разме-
ров *).
А. Эйнштейн
Современная философия рассматривает пространство
и время как формы существования любого вида материи.
Поэтому естественно считать, что закономерности геомет-
рии являются самыми общими и простирают свою власть
и значимость на любые события и явления в мире, ко-
торый мы знаем.
□Термин «событие» мы пока не будем уточнять, под-
разумевая под ним некоторое физическое явление, выра-
жающееся в том или ином изменении состояния материи.
Со времени Эйнштейна и Минковского [2, 3] в геомет-
рии' объединяют рассмотрение пространства и времени,
поэтому современная геометрия нераздельно включает в
себя понятие движения. В сущности, это понятие, а вмес-
те с ним и понятие'?времени неявно всегда фигурировали
в геометрии: одна из основных операций евклидовой
геометрии—совмещение геометрических фигур косвенно
вводит в геометрию понятие перемещения в пространстве,
т. е. движения.
В известной «Эрлангенской программе» [4] Ф. Клейн
положил в основу геометрии групповой подход, который
опять-таки можно рассматривать как косвенное введение
в геометрию понятия движения.
Оставляя сейчас в стороне эти вопросы, мы можем
в самом общем виде сказать, что предметом геометрци
является упорядочение событий.
*ЕСм. [1].
8
ВВЕДЕНИЕ
Каждому событию мы намерены выдать паспорт, в
котором было бы отмечено его «местожительство».
Объединенная геометрия пространства—времени позво-
ляет рассматривать соседство событий не только в про-
странстве, но и во времени. Поэтому оказывается возмож-
ным положить в основу упорядочения событий причин-
ность, т. е. форму генетической связи между событиями.
Наш современный опыт учит, что такая возможность
действительно существует и основана на объективных
закономерностях, свойственных нашему миру. Однако,
строго говоря, мы не знаем, как далеко простирается
эта возможность. Область очень больших масштабов —
космология и область очень малых масштабов—мир эле-
ментарных частиц не настолько еще изучены, чтобы
можно было высказать вполне определенные суждения
о значимости причинности.
Мы привыкли считать х пространственной координа-
той, а / — временем и употребляем их в этом смысле
даже внутри элементарных частиц. Однако что соответст-
вует им в действительности?
Не^должны ли пространственно-временные отношения
радикально измениться в области столь малых масшта-
бов, которые характерны для мира элементарных частиц?
Эта книга и будет посвящена анализу проблем прост-
ранства и времени, возникающих в микрокосмосе.
ГЛАВА 1
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ
В МАКРОМИРЕ
§ 1. Арифметизация пространства—времени
Упорядочение событий предполагает возможным при-
писать каждому элементарному событию Р определенные
числа х19 х2, ...» хп — координаты этого события. Число
необходимых координат п определяется числом измере-
ний рассматриваемого пространственно-временного мно-
гообразия (например, физическое пространство четырех-
мерно: три координаты пространственные х±=х, х2 = у,
x3 = z, четвертая координата x^t—временная).
Совокупность этих п чисел (х)=х1? х2, .хп будет
образовывать «паспорт» элементарного события.
При этом под элементарным событием Р мы будем
подразумевать такое событие, которому можно приписать
только одну совокупность чисел (х). Поэтому термины
«элементарное событие Р» и «точка Р» в нашем прост-
ранстве— времени эквивалентны. Приписывание каждому
событию координат мы будем называть арифметизацией
точек пространства—-времени (чтобы не сказать слово,
мало популярное в науке: паспортизация точек прост-
ранства— времени). К процессу арифметизации точек
пространства—времени должны быть предъявлены неко-
торые математические (логические) требования, например
требование однозначного соответствия точек пространства—
времени Р координатам (х); кроме этого, должны быть
указаны те физические методы, с помощью которых, по
крайней мере в принципе, может быть осуществлена
предполагаемая арифметизация. Иными словами, мы
должны указать физические процессы, на которых могут
быть основаны методы арифметизации.
Точки пустого пространства по самому смыслу тер-
мина «пустое» ничем не отличаются друг от друга*).
*) Мы сейчас не касаемся вопроса о том, можно ли считать
реальное физическое пространство пустым.
10
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
Поэтому физически реальный способ различения точек
пространства—времени может быть ^основан только на
реальных событиях в этих точках. Иными словами, воз-
можна арифметизация реальных событий, а не точек
пространства — времени «самих по себе». Принимая экви-
валентность элементарных событий и точек пространства—
времени, мы с самого начала исключаем неопределенные
операции с пустотой.
Таким образом, арифметизация точек пространства —
времени должна основываться на возможности различе-
ния этих точек независимо от самой арифметизации;
точка (= элементарное событие) должна иметь индиви-
дуальные признаки, характерные для осуществляющегося
там события. В такой постановке проблемы арифметиза-
ция еще содержит очень большой произвол. Характер
этого произвола может быть виден из следующего при-
мера. Пусть рассматриваемое пространство заполнено
материей, имеющей непрерывно меняющийся цвет.
Каждая точка Р содержит определенную смесь сине-
го и желтого цветов. Каждой комбинации цветов (по-
скольку цвет всех точек различен) мы могли бы сопо-
ставить любым образом пару чисел х2, лишь бы
множество чисел х± и х2 было равномощно с мно-
жеством цветовых точек. Огромный произвол такого
сопоставления виден из того, что мы могли бы при
переходе к различным цветовым областям допускать
любые скачки в значении пар чисел х2 без того, чтобы
нарушать однозначное соответствие чисел хи х2 и цвета
точки («элементарного события»).
Допустим теперь, что мы располагаем способом из-
мерения цветовых концентраций синего и желтого цвета
в любой точке. Тогда концентрация синего цвета а и
концентрация желтого b могли бы быть взяты в качестве
пар чисел (а, Ь) ддя арифметизации наших событий. Та-
кая арифметизация отражала бы прямым образом струк-
туру нашего многообразия — непрерывный характер из-
менения цвета точек. Выбор любой другой системы
арифметизации такой, что х1 = Х1(а, Ь) и х2 = Х2(а, Ь)
(предполагаем взаимную однозначность пар (хп х2) и (а, &)),
имел бы теперь уже твердое физическое обоснование в
«предпочтительной», или «естественной», системе арифме-
тизации (а, Ь).
§ 2]	ФИЗИЧЕСКИЕ МЕТОДЫ АРИФМЕТИЗАЦИИ	Ц
Эта «предпочтительность», или «естественность», бази-
руется на существовании физического метода определе-
ния цветового состава «событий», не связанного перво-
начально с арифметизацией.
Выбирая другую систему арифметизации (xt, х2), в
частности скачкообразную, мы должны были бы, анали-
зируя события в нашем цветовом пространстве, помнить,
что скачки в системе паспортизации точек введены искусст-
венно. Так, искусственно было бы, например, на одной
и той же улице вводить несколько нумераций домов, из
которых каждая не продолжает соседнюю, а является
новой и произвольной.
Приведенный простой пример показывает, что способ
арифметизации точек пространства — времени должен ос-
новываться на реальных процессах и наиболее прямым
образом отображать объективную структуру пространст-
ва— времени. Арифметизация невозможна без привлече-
ния материальных процессов. Поэтому невозможно и от-
деление физики от геометрии [5, 6].
§ 2. Физические методы арифметизации
пространства — времени
В доэйнштейновский период теоретическая физика
опиралась на геометрию Евклида и на представление о
некотором абсолютном времени. Как абсолютное про-
странство Евклида, так и абсолютное время были сце-
ной, на которой мог бы быть поставлен любой спектакль:
идея о связи материальных явлений с геометрией про-
странства и времени в то время еще была чужда физикам.
Вот как И. Ньютон определял пространство и время
в своих «Математических началах натуральной философии»:
«Абсолютное, истинное и математическое время само по
себе и в силу своей природы протекает равномерно и
безотносительно к какому-нибудь другому объекту, и оно
называется также длительностью... Абсолютное простран-
ство по самой своей природе и безотносительно к какому-
либо другому объекту остается всегда одинаковым и не-
подвижным...» [7].
В этих определениях подчеркивается полная незави-
симость геометрии от физики.
12
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ
[ГЛ. I
Однако, как впервые было показано Г. Гельмгольцем
[8], геометрия Евклида базируется на представлении о
существовании твердых тел. На основании предположе-
ний:
I.	Пространство п измерений есть n-кратно протяжен-
ное многообразие Э?п(х), иными словами, каждый элемент
многообразия (точка) определяется и непрерывно изменяю-
щимися величинами — координатами элемента:	х., ...
..., хп.
II.	Допускается существование подвижных, но неизме-
няемых (твердых) тел или систем точек; между 2п коор-
динатами каждой пары точек, принадлежащих твердому
телу, существует уравнение, не зависящее от движения
твердого тела и одинаковое для всех взаимно совпадаю-
щих пар точек.
III.	Допускается вполне свободная подвижность твер-
дых тел (предполагается, что каждая точка может не-
прерывно перейти в другую, поскольку этому не препят-
ствует связь, налагаемая пунктом II).
IV.	Два совмещающихся тела совмещаются и после
того, как одно из них подвергалось вращению около не-
которой оси (однозначность).
Рассматривая эти положения для случая п = 3 и до-
пуская бесконечность пространства, Г. Гельмгольц пока-
зал, что величина
3
ds2 = ^dx2{ (2.1)
i=l
остается неизменной при всех вращениях твердой систе-
мы около точки dxt = 0. Поэтому эта величина и может
быть принята за меру пространственного удаления—точек
х19 х2, х3 и x1 + dx1, x2 + dx2i x3-Pdx3*).
В заключение своего исследования Г. Гельмгольц
подчеркивает, «...что вся возможность системы наших
пространственных измерений зависит, как показывает
предыдущее изложение, от существования таких тел при-
роды, которые ^достаточно близко подходят под наше
понятие о твердых телах. Независимость совместимости
*) Результат ,Г. Гельмгольца ведет к римановскому мероопре-
делению длины; ср. § 5,
§ 2]	ФИЗИЧЕСКИЕ МЕТОДЫ АРИФМЕТИЗАЦИИ	13
от положения и направления совмещающихся форм и от
пути, которым они приведены к совпадению, есть тот
факт, на котором основывается возможность измерения
пространства».
С современной точки зрения мы так резюмировали бы
исследования Г. Гельмгольца: геометрия Евклида основы-
вается на группе движений твердого тела. Эта группа
является непрерывной шестипараметрической группой,
включающей в себя операции вращения О3 и трансля-
ции Т3.
Вместо движения твердого тела мы можем рассматри-
вать преобразование точек самого евклидова многообразия
х' = Ах,	(2.2)
где Л—некоторая линейная операция над координатами
х(х±, х2, х3), оставляющая неизменными внутренние, гео-
метрические отношения твердого тела и переводящая точ-
ку Р (х) многообразия St (х) в точку Р (х') многообразия
91 (х'). Эта более широкая точка зрения позволяет ввести
в рассмотрение не только непрерывные преобразования,
соответствующие движению, но и дискретные преобразо-
вания координат. Таково, в частности, преобразование
инверсии, меняющее знак координат Р
х9~—х.	(2.3)
Все указанные операции оставляют инвариантной
фундаментальную форму:
L(x, х') = (х1—xj)2+(x2—Х2)2 + (х3—х;)а, (2.4)
где (хх, х2, х3) и (Xi, х2, х3) суть координаты двух точек
Р (х) и Р(х'). Эта форма есть не что иное, как квадрат
расстояния между точками Р (х) и Р (х').
В соответствии с изложенными идеями относительно
существа геометрии Евклида мы видим, что в основу
определения меры в этой геометрии может быть взят
идеально жесткий масштаб, снабженный делениями.
Этот древнейший способ измерения расстояний имеет
немалое практическое значение и в наше время.
Арифметизация точек пространства может быть про-
изведена теперь с помощью операции откладывания же-
сткого масштаба. Появление в том или ином месте кон-
14
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
ца или другого деления масштабного стержня само по
себе есть материальное событие, и в этом случае процесс
арифметизации точек пустого пространства сам собою
сопровождается наполнением пространства материей.
Точка пространства Р с координатой х (мы будем часто
обозначать такую точку символом Р (х)) означает ту
точку, которую занимает конец единичного жесткого
масштаба /, если он отложен х раз.
Жесткость масштаба предполагает и его неизменность
с течением времени. Поэтому, если повторить операцию
откладывания жесткого стержня в более позднее время /,
то, отложив его вновь х раз, мы, по определению, придем
в ту же точку пространства Р(х).
Заметим, что существует изящная возможность про-
верить евклидов характер пространства п измерений,
если обмерить с помощью жесткого масштаба п-мерный
тетраэдр, натянутый на (/г+1) точек, являющихся его
вершинами.
Возьмем одну из этих точек за начало координат, а
координаты остальных точек обозначим через х^, где
1 = 1, 2, ..., п—номера точек, а=1, 2, ..., п — номера
координат. Объем такого тетраэдра Vn выражается фор-
мулой
•^2 • • •
у2 у2
л2 * • • ЛП
Х% ... X"
2 п
(2-5)
Заменяя здесь строки на столбцы и перемножая опреде-
лители, получим
(xxxx) (х’х2) ... (х1хП)
V2 — ——
Vn (nl)2
(х2х’) (х2х2) ... (х2хп)
(2.6)
(хпх]) (х"х2) ... (хпх")
Общий элемент этого детерминанта имеет вид
atk= ^х1ахка = х1хк = ^[(х‘ —хку — (х')2 — (х*)2]. (2.7)
а=1
§ 2]	ФИЗИЧЕСКИЕ МЕТОДЫ АРИФМЕТИЗАЦИИ	15
Иными словами, объем Vn есть функция только попар-
ных расстояний между вершинами тетраэдра. Для п-мер-
ного евклидова пространства Vn+1 — 0; если бы для этого
пространства оказалось Vn+1y=0, то это означало бы,
что геометрия пространства неевклидова.
Для того чтобы произвести исчерпывающую арифме-
тизацию событий, необходимо еще установить способ из-
мерения времени. Наряду со стандартным стержнем-мас-
штабом необходимо иметь и стандартные часы. К таким
часам также предъявляется требование «жесткости», имен-
но, требование постоянства их периода т. Тогда проме-
жуток времени t будет означать число отсчитанных перио-
дов т, которые мы можем считать единичными. Эта
предполагаемая «жесткость» часов математически экви-
валентна однородности времени.
Соответственно этой однородности времени, рассмот-
ренная ранее группа преобразований в евклидовом про-
странстве должна быть дополнена операцией трансляции
во времени Т4, оставляющей инвариантной длительность
промежутка времени t = t2—
Таким образом, общее групповое преобразование,
«характерное» для геометрии Евклида — Ньютона, может
быть представлено в виде произведения операций:
ё=63Т3Т\Р.	(2.8)
Рассмотренные выше преобразования относятся к опре-
деленной системе отсчета. При этом под системой отсчета
мы разумеем совокупность твердых тел и жестких часов,
неподвижных относительно друг друга и служащих для
арифметизации точек пространства и времени.
Можно вообразить себе и другую систему, движущую-
ся равномерно со скоростью v относительно первой. Для
определенности будем считать, что эта скорость направ-
лена по оси Ох. Тогда преобразование координат и вре-
мени гласит:
x'^-x^vt, х2 = х2, х'3 = х3, t' — t. (2.9)
Это — преобразование Галилея. Строго говоря, оно уже
выходит за пределы геометрии, оперирующей раздельно
с пространством Э13(х) и временем $(/). Значение этого
16
геометрические измерения в МАКРОМИРЕ [ГЛ. J
преобразования вскрывается, если мы перейдем к меха-
нике.
Преобразование Галилея оставляет инвариантным уско-
рение, так как
d2x'_d2x'__d2x
di72 ~~~di*~~ dt2 ’
и, следовательно, основной закон механики — второй закон
Ньютона остается неизменным. Эту неизменность выра-
жает принцип относительности Галилея: все механические
явления протекают одинаковым образом во всех инерци-
альных системах отсчета.
Объединим теперь формально пространство 9t3 (х) и
время $ (t) в одно общее многообразие sJt4 (х, /). Обозна-
чая операцию преобразования Галилея (2.9) через g-3, мы
можем записать общую операцию в многообразии про-
странства—времени 91 (х, t) в виде произведения операций:
(2.П)
Это — собственное преобразование Галилея. Оно может
быть расширено до несобственного преобразования, если
операцию g расширить добавлением операции инверсии
Р координат и операции обращения времени Т. Послед-
няя операция означает замену
—	(2.12)
Тогда общая операция несобственного преобразования
Галилея запишется в виде
е.-еРТ.	(2.13)
В заключение этого раздела сделаем несколько заме-
чаний относительно выбора системы координат. Рассмат-
ривая геометрию Евклида, мы пользовались декартовой
системой координат хг, х2, х3, в которой фундаменталь-
ная форма L(x, х') имеет вид (2.4).
Далеко не в каждой системе координат внутренние
свойства пространства — времени выражаются естествен-
ным образом. Немало парадоксов общей теории относи-
тельности связано с тем, что истинные явления недоста-
точно отделяются от «псевдоявлений», обусловленных
§ 21
ФЙЗИЙЕСКЙЕ МЁТОДЫ аёифметйзацйй
17
выбором, иногда неудачным, системы координат или, во-
обще говоря, методом арифметизации событий.
Чтобы пояснить эту мысль, рассмотрим способ ариф-
метизации точек пространства посредством измерения
натяжения упругой нити так, что длина х у нас будет
выражаться в единицах силы f, растягивающей нить.
Поскольку для малых натяжений имеет место закон Гука:
x—af	(2.14)
(здесь а — постоянный коэффициент), то все геометриче-
ские измерения могли бы быть выражены в единицах,
измеряющих f. В силу пропорциональности (2.14) для
чисел f сохранились бы все соотношения геометрии
Евклида. Однако природа вещей такова, что, начиная с
некоторого значения натяжения /, начинаются отступления
от закона Гука и он принимает вид
х = Ф(/)^а/ + рр + ...,	(2.15)
или
/-Ф~ЧЧ>	(2.15')
где ф"1—функция, обратная ф.
Отношение окружности круга к его диаметру теперь
выразилось бы так:
_ ^окр	Ф "1 (2ЯГ)
f /диам ф-1(^)
(2.16)
Число Лу зависело бы теперь от размера круга. Подоб-
ным же образом усложнялась бы и теорема Пифагора:
Гав + Гвс Ф Гас-
(2.17)
Известное неравенство для сторон треугольника АВС:
АВ + ВС > С Л,	(2.18)
также могло бы не выполняться для треугольников с боль-
шой стороной СЛ, так как с ростом растяжениях = С А сила
натяжения fCA становится относительно меньше (длина
нити стремится к оо при конечном значении f).
Посмотрим, как выглядело бы у нас равномерное дви-
жение. Предполагая, что у нас есть хорошие («жесткие»)
часы, получим
(2.19)
18
ГЕОМЕТРИЧЕСКИЕ ИЗМЕНЕНИЯ В МАКРОМИРЕ [ГЛ. I
Иными словами, равномерно движущееся тело представ-
лялось бы нам движущимся замедленно.
Рассматриваемый здесь способ арифметизации прост-
ранства посредством растяжения упругой нити сам по
себе не является бессмысленным и не может быть отверг-
нут. На самом деле, ввиду однозначного соответствия
между растяжением х и силой f он является одним из
допустимых способов упорядочения точек в пространстве.
Более того, для малых масштабов, в области примени-
мости закона Гука, предложенный способ равносилен
обычному—измерению с помощью жестких масштабов.
Почему же мы все же должны предпочесть применение
жестких стержней?
Ответ на этот вопрос может быть дан из сравнения:
а) степени универсальности метода и
б) степени общности закономерностей, которые выяв-
ляет тот или иной предлагаемый метод арифметизации
пространства.
Обратимся сперва к пункту а).
Все реальные стержни по-разному отклоняются от
идеального «абсолютно жесткого» стержня. Однако име-
ется обширная область масштабов и температур, когда
эти отклонения невелики и могут быть учтены в форме
поправок.
Упругие нити также по-разному отличаются от иде-
ально упругой нити, строго следующей закону Гука, но
эти отклонения не являются поправками и существенно
влияют на результаты измерений. Таким образом, уни-
версальность «динамометра» как прибора для определения
длин очень невелика. Каждый динамометр вносил бы
индивидуальные особенности своего характера в прост-
ранственно-временные отношения событий.
Второй пункт (б) также не говорит в пользу измере-
ния расстояний растяжением упругой нити. Применяя
этот метод, мы бы установили, что малые круги имеют
постоянные отношения лу, а большие круги имеют раз-
личные отношения (см. 2.16). Аддитивность отрезков, во-
обще говоря, не имела бы места: АВ 4- ВС Ф АС. Для
некоторых треугольников выполнялось бы неравенство
сторон треугольника, для других оно не имело бы места;
тело, не подверженное действию сил, «двигалось» бы
замедленно и т. п.
§ 3]	О ДЕЛЕНИИ МНОГООБРАЗИЯ СОБЫТИЙ	19
Так бы и выглядел для нас мир, в котором геомет-
рические измерения производятся растяжением нитей и
динамометром.
Если бы мы своевременно перешли к арифметизации
жесткими масштабами, мы обнаружили бы известные
соотношения геометрии Евклида и закон инерции. Ока-
залось бы, что для всех окружностей 2nr/D = ny для
всех треугольников АВ ВС С А, для всех тел, не
подверженных внешним воздействиям, d*x/dt2 = Q и т. п.,
т. е. закономерности, ранее имевшие силу только для
малых масштабов,	—то значение натяжения, при
котором функция ф (/) уже заметно отличается от af (а=
= const)), в новой системе арифметизации сами по себе
распространяются на всю область значений х и стано-
вятся всеобщими.
Таким образом, не всякая система арифметизации
пространства и времени выявляет внутренние закономер-
ности пространственно-временных отношений.
Итак, среди возможных систем и методов арифметизации
существуют методы, обладающие максимальной универ-
сальностью и максимальной способностью выявить наиболее
общие закономерности во взаимоотношении событий.
§ 3. О делении многообразия событий
на пространство и время
Если некоторое событие Р способно оказать влияние
на событие Р', то такое событие можно использовать как
сигнал, распространяющийся из точки Р в точку Р' в
многообразии событий 9?W(P)*).
Совокупность событий Р', на которые способны вли-
ять события, происходящие в Р, образует многообразие
(Р, Р'). Это многообразие мы будем называть абсо-
лютным будущим по отношению к точке Р. Совокупность
событий Р', способных повлиять на события в Р, обра-
зует многообразие (Р, Р'), которое мы будем назы-
вать абсолютным прошедшим по отношению к точке Р.
*)	(^) означает п-мерное многообразие событий; (х) озна-
чает многообразие, но арифметизованное, т. е. каждой точке Р припи-
саны координаты (х). Это иногда будет отмечаться символом Р(х)-
Очевидно, что (Р (х))	(х).
20
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
Если имеет место порядок причины и следствия, то обла-
сти и не имеют общих точек, кроме самой точки Р:
$+п$_=о.	(3.1)
Многообразие, объединяющее области $+ и
£+и$_=2:(Р, Р'),	(3.2)
назовем временной областью (по отношению к точке Р).
Всю остальную часть многообразия событий:
®(Р, Р') = 91(Р)—£(А Р'),	(3.3)
назовем пространственной областью или, попросту, про-
странством (по отношению к точке Р).
Чтобы конкретизировать этот принцип деления много-
образия (Р) на пространственное © (Р) и временное
&(Р), предположим, что физическим событием является
значение некоторого скалярного поля <р = ср(Р), удовле-
творяющего дифференциальному уравнению второго по-
рядка в многообразии 9t„(P):
<3-4>
где коэффициенты Лар и Р в общем случае являются
функциями поля <р и его
, f	первых производных <ра =
= Q—внешний источ-
ник поля, зависящей толь-
\	JP/юнт	ко от точки Р, а, 8=1,
\	nnnULf	_	1
Рассмотрим теперь как
Рис. 1. Слабый разрыв на поверх- распространяется сигнал,
ности фронта волны.	подчиняющийся уравне-
нию (3.4). Под сигналом
мы будем подразумевать волну, фронт которой определяется
функцией
S = S(x1( х2, ..., xn) = const,	(3.5)
причем на границе фронта имеет место разрыв первых
производных (см. рис. 1). Такой разрыв называют сла-
бым. Из теории дифференциальных уравнений известно
[9, 10], что уравнение для поверхности такого разрыва
О ДЕЛЕНИИ МНОГООБРАЗИЯ СОБЫТИЙ
21
§3]
определяется полностью коэффициентами при вторых про-
изводных уравнения (3.4):
(3-6)
Это уравнение, с точностью до членов порядка 1/со, сов-
падает с уравнением для фазы Ф волн высокой частоты со:
Ф —	со —> оо.	(3.7)
Именно, подстановка (3.7) в (3.4) при со —> оо приводит
к уравнению
Лар^^ + оГ-^О.	(3.6')
р дха дхр \ (О J	4	1
Уравнение (3.6) есть уравнение геометрической оптики.
Векторы нормалей к поверхности
ф = ф(Х1, х2, ..., x„) = const	(3.5')
совпадают с направлением лучей и имеют компоненты
АГ 9Ф /	\
— (а—1, 2, ..., и).
дха v	}
Возьмем произвольный действительный вектор
g(gn g2, ..., grt) и образуем квадратичную форму:
FQ, g)-4aPUp.	(3.8)
Если эта форма дефинитна:
F(g, g)>0 или F(g, g)<0	(3.9)
для любых то уравнение для вектора нормали #
F(AT, TV) —О	(3.10)
будет иметь мнимые корни, и, следовательно, нет ника-
кого распространения поля ср в многообразии 91л(х). В
этом случае события образуют застывший в неподвиж-
ности мир. Если же мы будем насильственно варьировать
полетф, например, путем вариации источника поля Q (х)
в окрестности некоторой точки Р так, что
6Q(x)=s64(x—хр),	(3.11)
где 8 — малое число, то состояние поля <р изменится во
всем многообразии 9£л(х).
22
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
Уравнение (3.4) в этом случае является уравнением
эллиптического типа [9], и никаких выделенных много-
образий внутри (х) не возникает.
Рассмотрим второй случай, когда форма (х) не
дефинитна:
(3.9')
в зависимости от области значений переменных В этом
случае, который называют гиперболическим, имеются дей-
ствительные направления N, которые удовлетворяют урав-
нению (3.6). Совокупность этих направлений образует
Рис. 2. Временные многообра-
зия 5£+ и и пространствен,
ное многообразие ©. ABCD —
сечение характеристического
конуса.
Рис. 3. Два характеристических
конуса для полей <р и ip.
характеристический конус. Этот конус (см. рис. 2) раз-
деляет многообразие (х) относительно каждой точки Р
на две области: S ($ =	+$£_) и @. Область может
быть достигнута любыми сигналами, исходящими из Р
и имеющими скорость распространения меньше скорости
сигнала уф, характерной для поля ср. Подобным же обра-
зом область !£_ содержит точки Р', сигнал из оторых
может достигнуть точки Р, если его скорость Об-
§ з]
О ДЕЛЕНИИ МНОГООБРАЗИЯ СОБЫТИЙ
23
Рис. 4. Сплошные пря-
мые линии — распростра-
нение звука: волнистая
линия —распространение
света. Звуковой сигнал
«В"—А"» воспринимается
как нарушающий «аку-
стическую» причинность.
ласть @ содержит точки, которые достигаются сигналами
из Р, имеющими скорость v >tty.
Мы можем сказать иначе: характеристический конус
разбивает многообразие 9£„(х) на многообразия $ и @
по отношению к сигналу типа ср. В области $ (в верх-
нем конусе) лежат события, которые могут быть генети-
чески связаны с событием в точке Р\ в области !£_ (в ниж-
нем конусе) лежат события, мо-
гущие влиять на характер собы-
тия Р.
Рассмотрим теперь случай, ког-
да имеются два типа полей ср и
гр, имеющих различные скорости
распространения tty и tty, и пусть
|^ф|<|^|- На рис. 3 изобра-
жены характеристические конусы
для этих двух полей. Рассмотрим,
какая возникнет ситуация^ в за-
висимости от того, с помощью
какого из сигналов (ср или гр)
произведено разделениеД на про-
странство и время. Предположим
для определенности, что tty есть
скорость звука, a tty— скорость
света (| tty | < | tty |). Предполо-
жим, далее, что среди населения
есть группа слепых, не воспри-
нимающих сигнала гр; их недос-
таток будет основанием для выбо-
ра ими звукового поля в качестве
поля, с помощью которого они
устанавливают связи между яв-
лениями. Итак, эти люди разделяют многообразие (Р)
на $ф и @ф и не будут иметь понятия о делении
на и Как будет выглядеть для них взаимосвязь
событий в многообразии %1п (Р)?
Рассмотрим эту связь, пользуясь графиком на рис. 4.
Пусть А и В—две пространственно удаленные точки.
Расстояние между ними могло бы быть измерено звуко-
вым сигналом tty или твердым масштабом. Пусть событие
в А есть искра, порождающая звук и свет. В точке Д'
наблюдатель А примет звук, отраженный от точки В'
24
Геометрические измерения в макромире [гл. i
(эхо); но свет искры, достигающий точки В", может поро-
дить звук, который достигнет наблюдателя А в точке А",
предшествующей по времени точке А'. Слепой наблюда-
тель А придет к заключению, что звуковое явление А"
нарушает порядок причины и следствия: сигнал А" пришел
раньше, чем его можно было ожидать, если его причи-
ной является отражение звука в точке В.
Однако этот же наблюдатель мог бы обнаружить
постоянство, с которым явление Л" предшествует явлению
Л', и прийти к правильному заключению, что помимо
сигнала звукового поля ср существует еще и другое, скры-
тое от него поле ф, распространяющееся со скоростью сц,
большей скорости звука уф. Иными словами, предполо-
женная им предельная скорость иф на самом деле не
является таковой: есть другая скорость	Итак,
слепой наблюдатель был бы поставлен перед дилеммой:
или допустить события, которые нарушают причинность
(относительно разделения	(Р) = $ф + @ф), или пере-
смотреть способ, которым он разделил 91„(Р) на £ и
Мы видим, что для упорядочения событий с соблюдением
причинности необходимо пользоваться сигналом, имеющим
наибольшую скорость из всех возможных.
Насколько тесно связано деление на пространство и
время с физикой явлений, можно видеть из того обстоя-
тельства, что если бы не обнаружилось постоянства в
предшествовании события А" событию А', то наблюда-
тель пришел бы к прискорбной для его науки мысли о
существовании явлений, не подчиняющихся причинности.
Такую ситуацию нетрудно себе представить, если до-
пустить, что состояние среды («эфира»), в которой рас-
пространяется сигнал ф, было бы не менее капризно,
чем, скажем, состояние земной атмосферы, и это состоя-
ние оказывало бы влияние на скорость сигнала . Время
АА" подвергалось бы тогда случайным колебаниям, что
крайне затруднило бы интерпретацию «непредвиденного»
явления в А".
В заключение этого раздела рассмотрим один любо-
пытный пример, могущий служить дополнительной иллю-
страцией к принципу деления многообразия 91 (Р) на
временное $ и пространственное @ многообразия [11].
Пусть поле <р подчиняется скалярному уравнению
Клейна; рассмотрим сперва случай двух измерений (хх и
§ 3]
О ДЕЛЕНИИ МНОГООБРАЗИЯ СОБЫТИЙ
25
х4). В этом случае
-4?±™-<Р-0.	(3.12)
dxl дх{
Будем считать, что х4—/ есть время *), а хг = х есть
пространственная координата; в уравнении (3.12) мы до-
пустили два знака для tn2 (т пропорционально массе
частиц поля ф). Полагая ф ~ e+z (wf“Ax), получим
со = ± Vk2 ± т2.	(3.13)
Отсюда следует, что для частиц с реальной массой т2>0
групповая скорость волн, а следовательно и скорость сиг-
нала, будет равна
« = ^ = 1^1.	(3.14)
Для случая т2 < 0, напротив,
и=Л>1.	|3.15)
СО '	'
Стало быть, в первом случае сигналы будут распрост-
раняться внутри конуса $ (см. рис. 5), и если события
упорядочены с помощью пре-
дельно быстрого сигнала
w— 1, то в силу того, что
1, для всех сигналов бу-
дет соблюдаться нормальный
порядок причины — следст-
вия. Если же т2 < 0, то сиг-
налы , р аспростр аняющиеся
со скоростью и > 1, будут на-
рушать причинность (они
будут распространяться внут-
ри пространственного кону-
са ®).
Однако легко видеть, что
принятая нами интерпретация
переменных и х4 в много-
образии Э12(х) является в
случае т2 < О неправильной
[11]: действительно, по оп-
ределению временной области
которой распространяются си:
Рис. 5. В случае т2 > 0 х4 = £,
= при т2 < 0 х4 = х, x1 — tt
т. е. пространственные и вре-
менные области меняются ме-
стами.
$ это есть область, внутри
налы. Поэтому правильная
♦) В уравнении (3.12) скорость света с положена равной единице,
26
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ
ГЛ. I
интерпретация требует в случае т? < 0 положить
Xi = x и х4=я/; это видно и непосредственно из уравнения
(3.12), которое переходит само^в себя при замене т9—►
—> — т9, х4 7-“ х<.
В случае четырех измерений, Э14 (х), положение дел
несколько сложнее. Уравнение в этом случае примет вид
-и »,2т
дх% дх* дх\ 3x2] v
'(3-12')
и форма написания этого уравнения предполагает, что мы
намерены рассматри ать х4 как время t, а х4, х2, х3 —
как три пространственные координаты. Найдем выраже-
ние функции Грина для этого уравнения. Для этого об-
ратимся к неоднородному уравнению
5^2"	± tn G 8 (X4) 6 (X8) 6 (x2) 6 (Xf). (3.16)
Полагая
G(x) = $G(^«*d^,	(3.17)
4	3
где qx— S 4txt— S 7Л—<7Л> и подставляя это в (3.16),
tf=l	fe = !
получим
6 ’ (3,18>
откуда
G = У [<Г8 ± т9-<%\ ’	(3> 19)
где q—(qi, q2, q3)', в случае /и* > О мы можем рассмат-
ривать qt как частоту <в = ± V^a+/n2. Групповая ско-
рость всех волн, идущих из точки х —0, будет и =
=d<B/3£s^ 1, и мы можем интерпретировать координату х4
как время t, а х4, х2, х3—как три пространственные ко-
ординаты; при т2<0 (знак минус в уравнении (3.19))
сигналы из точки х = 0, со скоростью u = da/dk^l,
пойдут внутри конуса © (так же как в случае двух из-
§ 4]
А ФФЙННОЕ МНОГООБРАЗИЕ
27
Рис. 6. При т2 > О
сигналы из вершины
характеристического
конуса Р сосредото-
чены внутри области
которую и следует
считать временной; в
случае т2 < 0 они
распространяются в
области ®, в этом
последнем случае
x1 = t1, x2 = h, х4 — х.
мерений), и если мы и в этом случае будем настаивать
на рассмотрении х4 как времени, то придем к противоре-
чию с определением этого понятия: область влияния при
т2 < 0 есть область вне светового конуса (см. рис. 6).
Мы должны признать, что имеем
дело с многообразием, в котором
имеется три времени: — xlf t2 = x2,
t3=^x3 — и одно пространственное
измерение х — х4.
§ 4. Аффинное многообразие
Как было разъяснено выше, в
принципе возможны различные спо-
собы арифметизации многообразия
событий.
Некоторые из них будут естест-
венно выделять самые глубокие чер-
ты пространственно-временных со-
отношений, другие будут подобны
кривому зеркалу, в котором дей-
ствительность изображается в иска-
женном виде. Эта карикатура может
зайти так далеко, что действитель-
ность станет почти неузнаваемой
(или, говоря философским языком,
почти непознаваемой).
Наиболее общие черты геометрического многообразия,
которые должны быть отражены в принятой системе
арифметизации, могут быть отмечены: а) непрерывностью
и б) характером топологической связности *). Пункт а) мы
расшифруем так: будем предполагать, что у каждой точ-
ки Р (х) многообразия Э1„(Р(х)) есть окрестность, обра-
зованная соседними точками.
Если без разрывов деформировать это многообразие,
то соседние точки продолжают оставаться соседними и
структура нашего многообразия будет характеризоваться
исключительно особенностями топологической связности
*) Ограничение а) исключает из нашего рассмотрения многооб-
разия, состоящие из счетного множества точек (например, простран-
ственные решетки).
28
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
(пункт б)), т. е. совокупностью деформаций, не наруша-
ющих непрерывность многообразия. На рис. 7 в качест-
ве примеров многообразий приведены трехмерные поверх-
ности. Поверхности тел а и Ь, с и d попарно топологически
эквивалентны; но поверхности а и b не эквивалентны по-
Рис. 7. Топологически экви-
валентные поверхности.
верхностям с и d, так как
первый род поверхностей нель-
зя непрерывной деформацией
перевести во второй род.
Произведем такую арифме-
тизацию многообразия, что со-
седние точки многообразия бу-
дут отмечаться соседними числа-
ми. Ввиду непрерывности много-
образия эти числа будут также
непрерывны.
В соответствии с раз-
мерностью п многообразия
(Р (х)) =	(х) количество
чисел, характеризующих лю-
бую точку многообразия, рав-
но п. Эти п чисел мы наз-
вали ранее координатами (х) — (хх, х2, ...,х„) точки Р.
Координаты можно выбирать различным образом, и с ма-
тематической точки зрения достаточно, чтобы различные
допустимые системы координат могли быть взаимно од-
нозначно связаны между собою, если не во всем много-
образии sJt„(x), то по крайней мере в отдельных его ча-
стях, покрывающих все многообразие 91п(х). Если такие
части суть 8t'n (х), 91^ (х),	(х) ..., то

Общее преобразование координат в одной из таких
областей (которая может покрывать и все многообразие
fR„(x)) можно записать в виде [12, 14]
х'^ — р1 (х),	(4.1)
где /ц(х) — дифференцируемые функции, ц—1, 2, ..., п.
Обозначим
d/и	ц
dx* dxv	v
(4.2)
§ 4j
А ФФЙЙНОЁ МЙОГООБРАЗЙЁ
Й9
так что
dx^==a»dxv.	(4.3)
Мы будем считать, что уравнение (4.3) разрешимо отно-
сительно dxv, так что детерминант
|а£|=#0.	(4.4)
В многообразии 91„(х) можно рассматривать функции
точки Р: скалярное поле ср(Р), поле векторное (Р)
(pi— 1, 2,..., п), тензорные поля различных рангов
piv-(p) (р,, v, . .. = 1, 2,	п), которые преобразу-
ются следующим образом при преобразовании координат
(4-1):
ф'(Р')=^ф(Р')^ф(Р),	(4.5)
A'»(P’)^a»(P)Av(P),	(4.5')
T'nv- (/>')==ан (/>)av(/>) . .	Tap	-(P),	(4.5")
причем под P' разумеется точка, возникающая из точки
Р при преобразовании (4.1). Векторы	и	тензоры,	преоб-
разующиеся по законам (4.3), (4.5') и (4.5"), называются
контравариантными.
Можно рассмотреть векторы Аи (Р) и тензоры TV,V'„(P'),
преобразующиеся по закону
A^(P')^(P)AV(P),	(4.6)
Т^... (P')=₽°(P)₽V₽(P).. .TaP... (Р), (4.6')
где
=	(4-6")
Такие векторы и тензоры называются ковариантными [14].
Поскольку векторы в различных точках многообразия
преобразуются различным образом (коэффициенты a!J(P)
и Рц(Р) суть функции точки Р), то сравнение двух век-
торов в различных точках многообразий А (Р) и А (Р')
не может быть произведено без дальнейших определений:
для сравнения этих векторов нужно перенести вектор
А (Р) в точку Р' параллельно самому себе. При этом ком-
поненты вектора Л11(Р) претерпят изменение 6Лц(см.
30
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. 1
рис. 8). Рассмотрим это изменение для случая бесконечно
близких точек Р (х) и Р' = Р (x + dx). Величина бД^
должна быть функцией самих компонент перемещаемого
вектора (так как для нулевого вектора 6Д^ = О!) и к то-
му же линейной функцией (сумма векторов должна пре-
образовываться как вектор); далее, величина 6Д^ должна
Рис. 8. Параллельный перенос
вектора по замкнутому контуру
РР'Р", состоящему из отрезков
геодезических линий.
(ещению (при dx11 — 0,
6Дм-=0). Поэтому 6Д»1 мож-
но представить в виде
6Д^ — Г^ДаМ (4.7)
где суть функции точ-
ки Р.
Коэффициенты назы-
ваются коэффициентами аф-
финной связности (или сим-
волами Кристоффеля). Пол-
ное изменение вектора А (Р)
при переходе от точки Р к
Р' будет равно
DA^dA» — бДи, (4.8)
и, следовательно,
по xv будет
производная компоненты
вектора А11
Dxv
дДм-
dxv
-НГ^Да.
(4.9)
Это—так называемая ковариантная производная [13].
Рассмотрим теперь некоторую линию в n-мерном мно-
гообразии
^ = Х^(т),
(4.Ю)
где т—параметр, с помощью которого задается линия.
Среди различных линий, проходящих через точки Р и Р',
есть такая, касательная к которой
dx»
dr

(4.П)
§4]
АФФИННОЕ МНОГООБРАЗИЕ
31
остается параллельной самой себе, т. е. на этой кривой
ковариантная производная от касательного вектора равна
нулю:
Du* du^ + r^uadx^ =* О	(4.12)
или, иначе,
^ + ГйРм«и₽ = 0.	{(4.12')
Такая линия называется геодезической [12—14].
В силу самого определения параллельного переноса
должен сохраняться «угол» между касательной к геоде-
зической линии и любым другим вектором, если его пере-
носить вдоль этой линии; поэтому для любого вектора А
имеем
РЛй = 0.	(4.13)
Рассмотренное изменение компонент вектора при парал-
лельном переносе является постулатом аффинной геомет-
рии и теснейшим образом связано с понятием кривизны
аффинного многообразия.
Рассмотрим бесконечно малый контур С, составленный
из геодезических линий (см. рис. 8). Перенесем вектор А
параллельно самому себе вдоль этого контура. Тогда из-
менение компонент вектора определится выражением
(4.14)
С
применяя теорему Стокса, получим
<4-15)
2 [ дхр	дхР J '
где А/ра—компоненты площадки, натянутой на контур С.
Частные производные, входящие в г(4.15), могут быть
с помощью (4.13) выражены через компоненты вектора Л.
В результате получим
АЛ^-^йраЛ^,	(4.16)
где
dpi*
+	(4.17)
32
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
есть тензор кривизны многообразия (тензор Римана).
Можно доказать, что этот тензор антисимметричен отно-
сительно индексов о, р, т. е.
=	(4.18)
причем
/?Йра + ^ра + ^аа = 0.	(4.19)
§ 5. Риманово многообразие
Рассмотренное выше аффинное многообразие еще слиш-
ком общо. Если аффинную геометрию дополнить поня:
тием расстояния между двумя точками, иными словами,
внести в многообразие метрику, то мы придем к метри-
ческой геометрии, или к римановой геометрии.
Вместо расстояния между точками Р и Р' мы будем
употреблять более общее понятие интервал, имея в виду
включить в многообразие не только пространство, но и
время.
Интервал между двумя бесконечно близким точками
Р (х) и Р (х+dx) будем обозначать через ds. Согласно
основной гипотезе Римана величина ds2 есть квадратич-
ная форма разностей координат точек Р и P'i
ds*—g^^d^dx*,	(5.1)
где gnV = gnV (Р) есть симметричный тензор g^-gw, на-
зываемый метрическим тензором. Поворотом системы
координат в окрестности точки Р и надлежащим выбором
масштабов форма (5.1) может быть приведена к канони-
ческому виду [14]
*’ = 8^)’,	(5.1')
п
где бцц = ± 1 • Величину f — 2 ецн называют сигнатурой
ц = |
метрики. Если сигнатура равна числу измерений, f = n,
то метрическая форма имеет вид
ds2= 2 (dx*)3	(5,1")
Н=1
§5]
РИМАНОВО МНОГООБРАЗИЕ
33
и выражает теорему Пифагора в бесконечно малом для
n-мерного пространства *). Если то интервал ds* 2
можно представить в виде
dsa=2 (dx»)g— 2 (dx*)*,	(5. Г")
ц= |	ц=т+1
так что f=^2m—В этом случае теорема Пифагора
соблюдается в каждом из многообразий (х) и 5R„_OT(x);
такое пространство называют псевдоевклидовым.
Выбор квадратичной формы для ds2 был неоднократно
предметом обсуждения. Фактически эта гипотеза Римана
означает, что в окрестности каждой точки Р имеет место
«обычная» геометрия, основанная на представлении о
твердых телах; для этого типа геометрии обоснование
квадратичной формы, определяющее понятие расстояния,
было дано Г. Гельмгольцем (ср. § 2). Таким образом, об-
щий случай римановой геометрии ведет либо к евклидовой,
либо к псевдоевклидовой геометрии в окрестности каждой
точки n-мерного многообразия Э?„(х).
Напомним несколько важных формул геометрии Ри-
мана.
Метрическая форма (5.1) позволяет определить и ска-
лярное произведение двух векторов (ЛВ), взятых в точке Р:
(ЛВ)-^Л^-Л^,	(5.2)
где
B|I~g,|XVBv	(5.3)
есть ковариантная форма вектора В.
Разрешая (5.3) относительно Bv, получим
В*=^в^	(5.4)
где g^v ~M^v/g9 a есть минор определителя
g=lg>l-	(5-5)
Из определения преобразования тензоров (см. § 4) сле-
дует, что скалярное произведение есть инвариант отно-
сительно преобразования координат (4.3). При параллель-
♦) Заметим, что здесь понятие бесконечно малого имеет чисто
математический смысл. Физически это могут быть кубические кило-
метры в Галактике или кубические ферми внутри атомного ядра.
2 Д. И, Блохинцев
34
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ 1ГЛ. I
ном переносе из Р в соседнюю точку Р' не должны
меняться длина вектора А (точнее, ее квадрат):
L*=(AA)	(5.6)
и угол между любыми векторами А и В:
АВ
COS 0 = - .- >--: ,
‘	/(ЛЯ)Г(вв)’
т. е. ковариантная производная от скалярного [произве-
дения (АВ) должна равняться нулю:
D(AS)=0.	(5.8)
Это соотношение позволяет выразить коэффициенты аф-
финной связности Г£ф через метрический тензор gllv. Ока-
зывается, что
™ = 1 ci,a (dg™ I	dga^\
а3 2	\ дх$ дха дх®) '
(5-9)
На основании (5.9) и (4.17) можно получить и выраже-
ние тензора кривизны через вторые производные метри-
ческого тензора. Если ввести ковариантный тензор кри-
визны
—	,	(5.10)
то оказывается, что
Р О ( d2gl*V , d2ga(3	d2gnp	dzgq(3 \
2 \dxadx3 дх^дх?	дхадх?	дх^дх? J ‘
+ £ра(ВД1?-ВД₽).	(5.11)
В общей теории относительности существенную роль
играют симметричный тензор
— Rpiav	(5.12)
и скалярная кривизна
7? = g^vRiiv	(5.13)
Таким образом, в метрической геометрии Римана все
важные в аффинной геометрии величины выражаются через
метрический тензор и его производные.
Рассмотрим еще групповые свойства в геометрии Ри-
мана. Для этой нелн вместо общего преобразования коор-
РИМАНОВО МНОГООБРАЗИЕ
36
динат (4.1) обратимся к бесконечно малому преобразова-
нию
хц/ =	^(х),	(5.14)
где |(х)—бесконечно малый вектор.
Это преобразование можно также рассматривать как
бесконечно малое смещение точки Р в точку Р' =--Р(х,У).
При таком смещении метрический тензор претерпевает
преобразование
, __дхР дх° .
~ дх/й дх'У ^₽<т
=^v(P)-^p(P) ^yP-gpv(P) д^Р •	(5.15)
С другой стороны, исходная метрика в точке Р' мо-
жет быть выражена через метрику в точке Р посредством
разложения
gpv (Р') = ^v(P) +	(Р) + ...	(5.16)
Отсюда изменение тензора g^v, вызванное смещением
Р —+ Р', будет равно
Дд.   ~	dtp dguv р .	/4 17^
A^v — — gw	gpv^F — -^р"Ьр +•• (5-17)
Метрика не изменится при этом смещении, если Ag^^O,
т. е. если
£HP^ + gpv^ + -j^£p==°-	(5.18)
Это—уравнения группы бесконечно малых смещений. Их
называют уравнениями Шиллинга [12, 14]. Если для мно-
гообразия fftn(P) с метрикой (5.1) можно найти беско-
нечно малый вектор ^(Р), удовлетворяющий уравнениям
Киллинга, то многообразие (Р) допускает группу пре-
образований, характеризуемую вектором (Р). В частно-
сти, в случае евклидова пространства	и урав-
нения Киллинга гласят:
& +	(5.19)
откуда
,
(5.20)
2*
36
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ (ГЛ. I
где о$=! — aJJ и аР суть бесконечно малые постоянные.
Стало быть, группа движений евклидова пространства
состоит из вращений 0(a) и трансляций Т (а). Из приве-
денных выше формул видно, что метрическая формула
(5.1), определяющая геометрию в малом, полностью ха-
рактеризует риманово многообразие. Она как бы явля-
ется той элементарной клеткой, из которых складывается
вся структура геометрии в целом.
Мы уже останавливались на основаниях, которые
диктуют выбор квадратичной формы (5.1) для квадрата
интервала.
В своей знаменитой диссертации [15] Риман впервые
указал на связь постулатов геометрии с физикой, кото-
рая приобрела фундаментальное значение в общей теории
относительности Эйнштейна. Современная физика, как
мы увидим позднее, вновь стоит перед необходимостью
критического пересмотра геометрических представлений
применительно к микромиру. Поэтому в заключение этого
отдела будет весьма уместно привести гениальные слова
Римана относительно геометрии в малом:
«Вопрос о том, справедливы ли допущения геометрии
в бесконечно малом, тесно связан с вопросом о внутрен-
ней причине возникновения метрических отношений в про-
странстве. Этот вопрос, конечно, также относится к об-
ласти учения о пространстве, и при рассмотрении его
следует принять во внимание сделанное выше замечание
о том, что в случае дискретного многообразия принцип
метрических отношений содержится уже в самом понятии
этого многообразия, тогда как в случае непрерывного
многообразия его следует искать где-то в другом месте.
Отсюда видно, что то реальное, что создает идею про-
странства, образует дискретное многообразие, или же
нужно пытаться объяснить возникновение метрических
отношений в чем-то внешнем—силами связи, действую-
щими на это реальное.
Решение этих вопросов можно надеяться найти лишь
в том случае, если, исходя из ныне существующей и про-
веренной опытом концепции, основа которой положена
Ньютоном, станем постепенно ее совершенствовать, руко-
водясь фактами, которые ею объяснены быть не могут;
такие же исследования, как произведенные в настоящей
работе, именно имеющие исходным пунктом общие поня-
§(51
ФИЗИКА АРИФМЕТИЗАЦИИ СОБЫТИЙ
37
тия, служат лишь для того, чтобы движению вперед к
успехам в познании вещей не препятствовали ограничен-
ность понятий и укоренившиеся предрассудки.
Здесь мы стоим на пороге области, принадлежащей
другой науке—физике, и переступать его не дает нам
повода_сегодняшний день» [15]*).
§ 6. Физика арифметизации
пространственно-временного многообразия
Приписывание физическим событиям определенных
координат не является только математической операцией.
Выдача «паспорта» каждому событию сама по себе пред-
полагает определенные манипуляции с материальными
объектами, необходимыми для определения положения
события в пространстве и времени.
Классическим способом арифметизации являлось при-
менение равномерно идущих часов («жестких» часов) и
жесткого масштаба. Однако проблема согласования
часов и масштабов в системах отсчета, движущихся отно-
сительно друг друга, потребовала использования сигна-
лов, законы распространения которых обладали бы наи-
большей общностью и простотой. Эта проблема стала
особенно острой применительно к телам, движущимся
с большими скоростями (исторически такими телами яви-
лись электроны, скорость которых сравнима со скоро-
стью света). Сигналами, наиболее естественно удовлетво-
ряющими поставленным выше условиям, являются свето-
вые сигналы. Скорость этих сигналов оказывается также
предельной для всех материальных тел и полей. В част-
ности, скорость сигнала, распространяющегося по твер-
дому масштабу, значительно меньше скорости света с.
Поэтому мы не имеем права в пределах точности, тре-
буемой теорией относительности, считать твердый стер-
жень абсолютно жестким: необходимо иметь в виду его
упругость и способность к деформациям. Формально мож-
но сказать, что теория относительности исключает воз-
можность существования абсолютно жестких стержней.
*) Г. Вейль в статье, посвященной Ф. Клейну, замечает, что,
может быть, в основе геометрии лежат все же дискретные много-
образия: «...теперь менее, чем когда-либо, можно поклясться, что в
основе геометрии не лежит дискретное многообразие» [16].
38
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
Поэтому, согласно идее, высказанной еще Г. Вейлем [17]
и развитой Р. Марцке [18], мы не будем прибегать к
помощи жестких масштабов, а используем импульсы света
(вспышки) для измерения как расстояний, так и проме-
жутков времени.
Световые часы могут быть построены из двух зеркал,
обращенных друг к другу и не поглощающих света. Если
Рис. 9. Световые
часы: А и В — зер-
кала, L — импульс
света.
между такими зеркалами заключить
импульс света, то он будет попеременно
отражаться то от одного зеркала, то
от другого (см. рис. 9).
Число отражений N может быть
принято для отсчета времени. Такие
«световые» часы, конечно, необязатель-
ны. Мы могли бы взять и любой дру-
гой периодический процесс, например
отражение звука или равномерное вра-
щение волчка. Заметим, что в любом
случае у нас нет априорных оснований
быть убежденными в строгой равномер-
ности хода избранных часов. Неравно-
мерность хода часов могла бы быть
обнаружена лишь в том случае, если
бы наблюдалась неравномерность в хо-
де всех явлений. Тогда было бы естест-
венно заподозрить неравномерность ча-
сов, как причину наблюдаемых изме-
нений в скорости протекания всех
явлений. Выбором других, более совер-
шенных (более независимых от внеш-
них обстоятельств) часов мы бы окончательно убедились
в том, что прежние часы «пошаливали».
Световые часы с зеркалами имеют то преимущество,
что, согласно принципам теории относительности, доста-
точно хорошо обоснованным экспериментально, скорость
света с не зависит ни от движения источника света (в
данном случае от зеркал), ни от движения наблюдателя.
Таким образом, равномерность хода световых часов осно-
вывается на весьма общих принципах, а природа зеркал
и возможное изменение их состояния оказываются несу-
щественными, лишь бы расстояние между ними не меня-
лось и поглощение света оставалось бы незначительным.
§6]
ФИЗИКА АРИФМЕТИЗАЦИИ СОБЫТИЙ
39
Отсутствие дисперсии световых волн в пустоте явля-
ется важным условием возможности использования све-
товых импульсов в световых часах и в качестве сигналов
для установления метрики.
Действительно, пусть световой сигнал задан в прост-
ранстве при t = Q в форме ср (х, 0). Представим его в виде
суперпозиции плоских волн:
Ф (х, 0)= $ C(k)eikxdk.	(6.1)
k>0
Этот сигнал в момент t иметь форму
<р(х, 0 =	=	ct, 0) (6.1')
(где со есть частота, со =с| k |, с—скорость света), т. е
сигнал не меняет своей формы и не расплывается в про-
странстве. Иными словами, черточки и точки азбуки
Морзе не сливаются друг с другом по мере распростра-
нения сигнала *).
Теперь мы обратимся к мысленному опыту по опреде-
лению интервалов между явлениями. На диаграмме
(рис. 10, а) по вертикали отсчитывается время /, а по
горизонтали — пространственная координата х. Линия АА'
есть мировая линия наблюдателя А; в его распоряжении
имеются два зеркала, образующие световые часы: первое
зеркало имеет мировую линию АА', второе зеркало—близ-
кую мировую линию СС'. Зигзагообразная линия между
А А' и СС' есть мировая линия светового импульса, от-
ражающегося последовательно от зеркал А и С. Каждый
излом этой линии может быть использован как отсчет
времени. Пусть мировая линия другого тела В будет ВВ'.
Для того чтобы определить интервал sAB между событиями
А и В, пошлем из А световой импульс в В, где поставим
зеркало, отправляющее сигнал обратно, в А, Будучи
испущен в момент времени tr = t—АВ1с(ъъ световым ча-
сам в Л), этот сигнал вернется в Л в момент времени
t2 = tA-AB/c. Поэтому интервал $лв между событиями А
и В будет определяться формулой
5*лв = /Л = /2-^>0.	(6-2)
*) Эта особенность светового импульса сохраняется и в трехмер-
ном случае (см. § 17).
40
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
Причем Z1 = 2V1t и = где N± и М2—число отраже-
ний, отсчитываемых по световым часам, ат—период часов.
В рассматриваемом случае интервал s2aB больше нуля.
Такой интервал называют временным.
Рис. 10. Измерение интервала sAB между событиями Л и В с помощью
отражения светового импульса, а) Интервал временной; б) интервал
пространственный, А А' — мировая линия наблюдателя А; СС' — линия
второго зеркала его часов, В В' — мировая линия события В.
На рис. 10, б приведен пример, когда световой сигнал
из А не может достигнуть события В. Нетрудно видеть,
что в этом случае следует считать tx < 0 (см. точку (0,
на рис. 10,6), тогда интервал подчиняется прежней фор-
муле:
A R2
=	(6.3)
§ 71 АРИФМЕТИЗАЦИЯ В НЕЛИНЕЙНОЙ ТЕОРИИ ПОЛЯ 41
однако он теперь меньше нуля. Интервал в этом случае
называют пространственным.
Если скорость света является предельной, то рассмот-
ренный способ арифметизации событий производит деление
многообразия событий (я) на пространственное © (я) и
временное % (я) с помощью светового конуса
г 2
s'=t’ —^=0,	(6.4)
где
г2 = х2 +у* + г*.
Вместе с тем вводится вполне определенная форма
причинной связи событий. Событие в мировой точке Р
может влиять лишь на событие, находящееся внутри верх-
него конуса 5£+ (Р) (см. рис. 6), определяемого уравнением
-=0.
с
(6.5)
Все события, находящиеся внутри конуса абсолютного
прошедшего (Р):
/4-—=0,
1 с
(6.6)
могут влиять на событие в Р. События, находящиеся
в пространственной области
г2
^<0,	(6.7)
не могут быть связаны причинным образом (генетически)
с событиями в точке Р.
В связи с тем, что все геометрические соотношения
определяются часами и световыми сигналами, иногда гео-
метрию четырехмерного многообразия с сигнатурой f=—2
называют хроногеометрией (см. [18]).
§ 7. Арифметизация событий
в случае нелинейной теории поля
Этот параграф должен служить иллюстрацией к прин-
ципам деления многообразия событий 9ft (я) на простран-
ственное ь©(я) и временное £(я), изложенным в § 3.
42
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
В случае нелинейной теории поля скорость сигнала зави-
сит от величины поля и его производных. Поэтому само
деление 91 (х) на пространственное и временное многооб-
разия существенно зависит от динамики движения сигнала.
В частности, характеристический конус (см. рис. 2) в этом
случае искривлен, а при некоторых значениях поля и его
производных может стать даже мнимым. Чтобы не услож-
нять изложения, будем считать поле скалярным и огра-
ничимся двумя измерениями: xt = xf x^ = t.
В качестве основы такой теории примем вариационный
принцип с функцией Лагранжа, зависящей от инвариантов,
образованных из поля ф (х, f) и его первых производных
р = дф/д/, q = дф/дх*). Такими инвариантами являются
7=4 Ф2.	(7.1)
(7.Г)
Функция Лагранжа J27 будет равна
=	(7.2)
а вариационный принцип гласит:
6L = j6=g’dxd(=O.	(7.3)
Ясно, что в такой форме теория гарантирует инвариант-
ность относительно преобразования Лоренца. Выполняя
варьирование, замечая, что
№=^(рЪр— <7б?) + ^ФбФ>	(7-4)
допуская, как обычно, исчезновение поверхностных членов
в интеграле (7.3) и приравнивая нулю коэффициент при 6ф,
получим из (7.3)
dt дК Р )^дх \ дК
дХ
д!
(7-5)
Ф —О
*) Эта теория представляет собою скалярный вариант нелиней-
ной электродинамики М. Борна и Л. Инфельда, развитой ими в 30-х
годах [19, 20]. В изложении скалярной теории мы следуем работе [21].
§ 7] АРИФМЕТИЗАЦИЯ В НЕЛИНЕЙНОЙ ТЕОРИИ ПОЛЯ 43
ИЛИ
Д^2- + 2В^- + С-Й-4-/?ф = 0,	(7.6)
dt2 1 dtdx 1 дх2 ’ ч	х '
где
А = —(14-ар2), B = apq, С = (1—aq2), R = y—2|3/( (7.7)
и
d2<£id<£ Q д2^ id^ дХ id^ /7 Q4
а~ дК2/дК ’Р~дКд1 / дК ’ д! I д\ ‘
В случае, когда S? линейно зависит от инвариантов К, /,
когда а = р = 0 и у = const, мы возвращаемся к линейному
уравнению Клейна для скалярного поля ср. Характери-
стические направления уравнения (7.6) определяются из
уравнения (см., например, [22] или [23])
Л^ + 2В^4-С = 0,	(7.7')
где
Е-у	(7.8')
есть скорость распространения фронта волны, который мы,
как и ранее в § 3, считаем слабым, разрывом. Из (7.7)
находим
± У 14-2аК—<хрд
1+ар2
(7.9)
или, при малых а (/(, /),
g=± 1 =р-уа(р±<7)24- ...
(7.Ю)
Если теперь представим себе, что на отрезке а < х < b
при / = 0 задано некоторое начальное состояние <р, p,q =
= dq/дх, то, как видно из (7.9) и (7.10), оно будет рас-
пространяться по характеристикам со скоростью £, отли-
чающейся от скорости света с, которая в обозначениях
этого параграфа равна ±1. На рис. 11, а и 11,6 пред-
ставлены два возможных случая распространения поля:
а) когда скорость распространения |||<1 и б) когда
|£| > 1; в последнем случае нелинейный сигнал нарушает
релятивистскую причинность и арифметизация многообра-
зия событий должна быть пересмотрена.
44
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
Интересно и то обстоятельство, что в нелинейной тео-
рии нельзя исключить и такую ситуацию, когда при оп-
ределенных значениях <р, р и q характеристические на-
правления станут мнимыми, так что уравнение (7.6) будет
принадлежать к эллиптическому типу. В этом случае поня-
тие причинной последовательности событий потеряет свой
смысл, и мы будем иметь дело со связанным «комком»
событий, которые взаимно друг друга7£обусловливают, но
Рис. 11. Характеристики нелинейного поля.
не следуют одно из другого [21]. Если допустить, что
такое положение имеет место где-то внутри частиц, в об-
ласти сильных полей, то вдали от частиц уравнение должно
становиться уравнением гиперболического типа. На поверх-
ности, где совершается этот переход, детерминант
В*—АС= 1+2аЯ	(7.11)
обращается в нуль. Переход от эллиптического типа к ги-
перболическому сопровождается разрывом первых произ-
водных поля ф (р или q или обоих) (см. [10], [23]).
В заключение заметим, что теория нелинейного элек-
тромагнитного поля очень сходна с теорией скалярного
поля. В этом случае инварианты К и / имеют вид
К = Ча(8а—ЛГа), / = (8ЯГ),	(7.12)
§7] АРИФМЕТИЗАЦИЯ В НЕЛИНЕЙНОЙ ТЕОРИИ ПОЛЯ 45
где 8 и Ж имеют смысл напряженностей электромагнит-
ного поля. Варьируя электромагнитные потенциалы А и <р
такие, что
8 =— -^-—gradtp, 3e=TotA, (7.13)
получим из вариационного принципа (7.3) уравнения элек-
тромагнитного поля:
™ = rotB, divD=0,	(7.14)
где D и В суть электромагнитные индукции:
d=m&—N#e, b=mm+n&,	(7.15)
а величины M и N равны
Вторая группа уравнений
^ = — rot 8, div 3¥ = 0	(7.16)
(7.17)
получается непосредственно из (7.13). Для одномерного
случая 8 (<£*, 0, 0), ^f(0, Я? , 0) и <§x = £(t,z), 3%у =
= получаем из (7.14) и (7.16)
(1 +«<£*) +
+ (1-а^)^ = 0,
А
дг "Г dt
d*XtdX ,,
где по-прежнему а = ^5-/-^. Уравнение для характери-
стического направления % = dz/dt будет теперь иметь вид
(1 4-а«?2) ^4-2а<£^-(1— а^») = 0,
откуда
(7.18)
t_± К1+2аК-а^
S“'	1+а<£2
(7-19)
или, при малых а,
|»±1Ч=|а(^±^)’4-...	(7.20)
46
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
Как видно из изложенного, нелинейная теория поля
допускает скорость сигналов, которая может оказаться и
меньше и больше скорости света с или даже стать мнимой.
Поэтому теория относительности, допуская постоянство
скорости света в пустоте, неявно предполагает линейность
теории [24]. Подробно вопросы распространения сигналов
в нелинейной теории М. Борна рассмотрены в работе [25].
В § 43 мы вернемся к теории М. Борна в связи с кван-
тованием пространства—времени.
§ 8. Общая теория относительности
и арифметизация пространства — времени
В общей теории относительности метрика риманова
многообразия событий становится зависящей от движения
материи.
Коэффициенты в метрической форме, определя-
ющей интервал между близкими событиями
ds2 =	(х) dx11 dxv,	(8.1)
в общей теории относительности являются функционалом
от энергии — импульса тензора материи Т^х):
gyw (#) =	{7\v (•£)}•	(8-2)
Эта функциональная связь определяется с помощью зна-
менитого уравнения Эйнштейна [13, 14, 26]:
=	,	(8-3)
где к = 8лу/с2 = 1,86-10~27 см/г—гравитационная постоян-
ная Эйнштейна *), R^—тензор кривизны 2-го ранга, а
R— скалярная кривизна (см. § 5).
К уравнению (8.3) должны быть добавлены: а) урав-
нения движения материи (например, уравнения релятиви-
стской гидродинамики, если материя может быть пред-
ставлена в виде жидкости или газа, или уравнения элек-
тромагнитного поля, если материей является это поле,
и т. д.), б) граничные и начальные условия.
*) Здесь у=6,67-10~8 см3/(г-с2) есть гравитационная постоянная
Ньютона.
§ 8j
связь с общей теорией относительности
47
Общая теория относительности допускает столь же
общее преобразование координат, как и геометрия Ри-
мана (ср. § 5):
х^'=Г(х),	(8.4)
где функция (х) непрерывно и взаимно однозначно
отображает Di4 (х) на 914(х'). Огромный произвол, содер-
жащийся в этом преобразовании, должен использоваться
с большой степенью осторожности. Формальное равнопра-
вие различных систем координат на самом деле может
сводиться почти к нулю особенностями, присущими самой
задаче. Математически произвольный выбор системы коор-
динат должен быть проконтролирован изучением возмож-
ности реализовать выбранную систему координат физиче-
скими методами: иными словами, должны быть указаны
физически осуществимые методы измерения интервалов
в многообразии событий.
Основная особенность геометрии Римана—псевдоевкли-
довостъ в бесконечно малом подсказывает, что ранее рас-
смотренный метод определения интервала между событиями
Л и В (ср. § 6) может быть перенесен и в общую теорию
относительности, если только события А и В бесконечно
близки друг к другу. Пусть в выбранной системе коор-
динат квадрат интервала имеет вид
^=^44 (dx*y + 2gisdx*dxs + grsdxr dxs, (8.5)
где s, r= 1, 2, 3.
Для светового сигнала ds2 = 0, так что
dx*=Г(gisd^_g^ dxr d	(8 6)
У gh gu
где два знака ± отвечают прямому, из Л в В, и обрат-
ному, из В в Л, сигналам.
Обратимся теперь к чертежу на рис. 10 (стр. 40) и
будем считать события А и В бесконечно близкими. Ко-
ординаты события А будут Хд = Хд=Ха=Хд=0, а коор-
динаты события В—dxB, dxB, dxB,dXB- Собственное время
в точке А получим из (8.5), полагая dxs=0:
ds=dx=V~g^ (dxl).	(8.7)
Из рис. 10 имеем
(dxB—dx[), di:2='ygi4(dxt) — dxt), (8.8)
48
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
где dx* есть изменение dx\ соответствующее приходу сиг-
нала из Лх в В, a dx*—то же для сигнала из В в Л2.
Эти величины определяются из формулы (8.6).
Перемножая теперь dxr и dx2, получим
ds^B = dxt dx2—gu (dx^Y 4- grs dxr dxs, (8.9)
т. e. обобщение формулы (8.5). Это—для временного ин-
тервала sAB.
Аналогично для пространственного интервала получим
—dsiAB — — dxldxi = — gii (dx%)s—grsdxrdxs. (8.9')
Полагая здесь dxB=0, найдем выражение для расстояния
между Л и В:
dl*=dx1dx2 = — grsdxrdxs,	(8.10)
или	_____________
dl = V —grsdxrdxs.	(8.10')
Расстояние между двумя точками А и В, удаленными на
конечное расстояние
л
lAB=4V-grsdx'dx°,	(8.11)
В
будет зависеть от пути интегрирования. Можно опреде-
лить «истинное» расстояние как расстояние вдоль геоде-
зической линии:
в _________________________________
/•O=J	(8.12)
А
причем интеграл (8.12) взят при условии, что координаты
кривой Xs (а) удовлетворяют уравнению
d2x? . р dxf dx&______
do2 ' J'kdo do
(8.12')
Согласно основному уравнению Эйнштейна (8.3) при
наличии материи кривизна пространства отлична от нуля
и в общем случае из-за движения материи зависит от
времени. Поэтому проблема арифметизации многообразия
событий в общей теории относительности становится весьма
сложной *).
♦) См. подробности в [14] и [18].
СВЯЗЬ С ОБЩЕЙ ТЕОРИЕЙ ОТНОСИТЕЛЬНОСТИ
49
§ 81
Наиболее естественным способом арифметизации со-
бытий представляется последовательная арифметизация от
одного события к соседнему, бесконечно близкому. Поль-
зуясь световыми сигналами, мы можем определить расстоя-
ние от точки А до соседней точки В и синхронизовать
часы в А и В. При этом, по определению, одновременными
будем считать момент В (х, t) и момент Лв(0, t), соответ-
ствующий среднему между отправлением сигнала из точки
А± и получением отраженного сигнала в точке Л2 (см.
рис. 10):
Vg^ dxi=Y (dx1 + v g44 dxl 4- dr2 4- Vg~ dxf) =
= y(dTi+dTs)—Sisdxs/]/"g^.	(8.13)
Если событие Ав поместить в эту точку, то dxY =— dx2i
разность времени х4 между двумя «одновременными» со-
бытиями А и В будет составлять
dxfc = — gis dxs/gti	(8.13')
и являться той величиной, на которую следует «подвести»
часы в В. Следует заметить, что мы производили измере-
ния, исходя из метрики в точке А.
Мы могли бы также производить измерения, исходя из
метрики в точке В.
Ввиду того, что собственное время в точках А и В
протекает различным образом, результаты измерений рас-
стояний будут также различны. При малости расстояния Л В
эти различия будут иметь место лишь во втором порядке.
Действительно, различия в интервалах, измеренных в А и
В, составляют
Азлв = [guv (В)—guv (Л)] dx* dxv =
= •••]dxlldxV- <8-14)
Подходящим выбором системы координат выражение
в квадратных скобках, содержащее первые степени диф-
ференциалов, может быть обращено в нуль. Таким обра-
зом, существенное различие в измерениях интервала из
точек А и В определяется величинами четвертого порядка
малости. Это последнее различие может быть связано
50
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
с кривизной пространства и поэтому выбором системы
координат, вообще говоря, ликвидировано быть не может.
Вернемся теперь к вопросам арифметизации многообра-
зия событий. Мы видели, что, по крайней мере для ок-
рестности точки, в общей теории относительности сохра-
няется арифметизация, характерная для специальной тео-
рии относительности: все дело сводится к измерению
промежутков времени и к посылке световых сигналов.
Поэтому естественным выражением интервала является
псевдоевклидово:
ds*=c*dt*— (dx* + dxf 4- dxl),	(8.15)
где cdt — dx^ и di есть собственное время, a dx19 dx2, dx3
суть длины по осям 1,2, 3, измеренные с помощью све-
тового сигнала. В системе координат, где интервал имеет
вид (8.15), значения координат совпадают с числовыми
значениями промежутков времени и расстояний.
Таким образом, в принципе мы имеем две возможно-
сти. Мы можем приписать событиям более или менее
произвольные четверки чисел (соблюдая лишь топологи-
ческую непрерывность) и затем с помощью часов и световых
сигналов калибровать эту систему, т. е. связать эти числа
со значением интервалов между бесконечно близкими со-
бытиями.
Другой путь соответствует только что изложенному
выше: производятся измерения промежутков времени и
расстояний между событиями, и на эти измерения «натяги-
вается» подходящая система координат.
§ 9.	Хроногеометрия
Арифметизация событий, a priori произвольная, на са-
мом деле требует применения определенных физических
методов, вторые сами по себе должны совершенствоваться
как в отношении расширения круга применимости, иными
словами, в отношении общности метода, так и в отноше-
нии увеличения точности.
Долгое время физика пользовалась для измерения вре-
мени астрономическими часами —вращением Земли, а
в качестве масштаба длины —платино-иридиевым стерж-
нем— «стандартным метром».
§ 91
ХРОНОГЕОМЕТРИЯ
51
В последние годы стандарты времени и длины заим-
ствуются из атомной физики. Наиболее точными часами
являются часы атомные или молекулярные, а в качестве
стандарта длины принята длина волны К красно-оранже-
вой линии спектра инертного газа криптона (Кг86); длина
стандартного метра оказывается тогда равной 1 650 763,73 X.
Атомные и молекулярные часы обязаны своим происхож-
дением развитию техники атомных или молекулярных
пучков и „практическому применению индуцированного
излучения [18]. Пучок атомов цезия дает очень узкую
линию и обеспечивает стабильность частоты (частота со-
ставляет приблизительно 9000 Мгц) до 10"12 за несколько
месяцев. Столь же высокой стабильностью обладает и
излучение атомов водорода (длина волны около 21 см,
частота 1420 Мгц). Подробности об устройстве атомных
или молекулярных часов можно найти в статье [27]. Вместо
масштаба длины можно пользоваться скоростью света
в пустоте. Наиболее точные современные данные приводят
к величине [27]
с=299 792,5 ± 0,4 км/сек.
Применение часов в качестве стандартов для арифметиза-
ции пространственно-временного многообразия следует
рассматривать как наиболее совершенный и наиболее уни-
версальный метод арифметизации, какой в состоянии
предложить современная физика. Поэтому геометрию,
лежащую в^основе современной физики, часто называют
хроногеометрией, подчеркивая этим названием фундамен-
тальную роль светового сигнала и часов. Нет оснований
думать, что геометрические измерения в макроскопическом
мире перестанут интересовать физиков и геометров. Пробле-
ма арифметизации в нестационарном мире, видимо, еще
ждет своего решения. Еще более глубокие проблемы воз-
никают в том случае, когда нестационарность имеет сто-
хастический характер, так что метрический тензор g^v ста-
новится случайной величиной.
Однако мы не будем вдаваться в эти проблемы боль-
шого мира. Напротив, обращаясь к главному предмету
этой монографии, к геометрии микромира, мы будем
исходить из предположения, что по крайней мере в ста-
ционарном макромире или в ограниченных областях не-
стационарного макромира принципы арифметизации в фи-
52	ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МАКРОМИРЕ [ГЛ. I
зических событиях достаточно ясны и мы понимаем, что
означают символы х, у, г, / для макроскопического события:
в основе осмысливания их физического значения лежит
хроногеометрия.
Принципы хроногеометрии будут на протяжении моно-
графии в явной форме или в форме неявного предположения
использоваться в качестве основы для обсуждения геоме-
трических измерений в микромире.
Переходя в дальнейшем к проблемам микромира, мы
увидим, шаг за шагом, постепенно нарастающую степень
абстракции в применении понятий пространственно-вре-
менных координат х, у, z. t в мире элементарных частиц.
Мы должны подготовить себя к тому, что это возрастание
абстрактности граничит с отрицанием самого физического
смысла этих переменных, которые привыкли считать про-
странственно-временными координатами.
ГЛАВА II
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ
В МИКРОМИРЕ
§ 10.	Замечания об измерениях в микромире
В стандартных курсах квантовой механики любят
подчеркивать влияние прибора на состояние измеряемого
микрообъекта.
Однако более фундаментальным обстоятельством для
понимания истинной ситуации в микромире является при-
знание факта совершенно обязательного влияния микро-
объекта на состояние макроскопического прибора.
Существенно отметить, что измерительный прибор
должен быть нестабильной макроскопической системой:
только такую макроскопическую систему микроявление
способно вывести из состояния неустойчивого равнове-
сия и тем самым породить развитие макроскопического
явления. Это макроскопическое явление и может быть
использовано для измерения состояния микросистемы.
Схематически ситуацию в квантовой механике можно
изобразить с помощью условной формулы
9М=Л1Н-(Л 4-D),	(10.1)
где ЭК означает всю макроскопическую обстановку, в ко-
торой «живет» микросистема р, а М означает ту часть
макрообстановки, которая диктует исходное состояние
микросистемы р. Повторение микросистемы р, погружен-
ных в одну и ту же макроскопическую обстановку М,
образует квантовый ансамбль 91:
91=Л1 + р, Л44-р, 7И + р, ...	(10.2)
Взятая в скобку (Д-f-D) часть 991 образуется макроско-
пическим прибором, который состоит из анализатора А
и детектора D.
Предполагается, что эта часть всей обстановки не
оказывает существенного влияния на формирование со-
стояния микросистемы в обстановке М (иначе прибор
54
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ [ГЛ. II
(Л+/^’нельзя было бы отделить от формирующей части Л4).
Это обстоятельство является также необходимым для воз-
можности замены одного прибора (A-J-jD) другим прибо-
ром (Л+Z))', приспособленным для анализа Состояния
микрообъекта р, по другим измеримым параметрам этой
микросистемы. Анализатору сортирует микросистемы по
Рис. 12. Схемы измерений в квантовой механике. Источник частиц S
и щель С образуют часть М макрообстановки определяющую
исходный ансамбль ¥0 Л4 = £-|-С; дифракционная решетка А А'
является анализатором; она разлагает То на пучки с определенным
импульсом фГа, фГ8, счетчики Гейгера Гъ Г2, Г3, ...
являются детектором D: D = Г1 + Г2 + Г3 + ...; наконец, *Щ = Л1 +
+ M + Z)).
состояниям. Назначение детектора D заключается в реги-
страции наличия микросистемы в том или ином состоянии.
Детектор является неустойчивой макроскопической систе-
мой, способной под воздействием микросистемы менять
свое состояние. Пример, иллюстрирующий эту систему,
приведен на рис. 12, где показаны источник частиц S и
щель С, которые создают направленный поток частиц.
Этот источник и щель образуют часть М обстановки,
определяющей исходный ансамбль. Для простоты мы будем
считать, что он описывается волновой функцией То*).
Дифракционная решетка А А' разлагает этот пучок в спектр
по различным импульсам р частиц первоначального пучка.
*) То есть мы будем считать ансамбль «чистым» (см» [281),
11]
ИЗМЕРЕНИЕ КООРДИНАТЫ МИКРОЧАСТИЦЫ
55
Математически это означает, что исходная волновая функ-
ция ¥0, описывающая состояния исходного ансамбля
частиц, разлагается решеткой в спектр:
(ю.з)
где есть состояние с определенным импульсом, рав-
ным ps, a CPs —- амплитуда этого состояния. Наконец,
детектор D образован ловушками микрочастиц 1\, Га,...
..., Г„; этими ловушками могут служить, например,
счетчики Гейгера: при попадании туда заряженной микро-
частицы возникает лавина электронов, приводящая к газо-
вому разряду в соответствующем счетчике. Счетчик Гей-
гера, находящийся под напряжением, является неустой-
чивой макроскопической системой, которая и регистрирует
факт появления микрочастицы в одном из возможных
состояний фРа, ...
Этот пример иллюстрирует тот факт, что вся инфор-
мация о явлениях в микромире идет через явления в
макромире путем развития нестабильных макроскопи-
ческих явлений*).
§ 11.	Измерение координаты микрочастицы
Нерелятивистская квантовая механика формально до-
пускает как угодно точные измерения координаты микро-
частицы х, у, г в данный момент времени t [28, 30].
Как и все физические величины, координаты х, у, г
изображаются в квантовой механике эрмитовыми опера-
торами х, у, г, Эти операторы вместе с соответствующими
операторами рх, ру, рг проекций импульса на оси Ох,
Оу, Ог подчиняются известным правилам коммутации **):
[х, рх] = lA, [у,~ pj=th, [г, рг]=th,, (11.1)
[Д р] = [у- z] = [z, х]=о,	(11.И
[Рх» Рг,]=[Рг/> рг] = [рг> Рх] = 0.	(11.1")
*) Эта точка зрения на измерения в микромире последовательно
проведена в монографии [29].
**) Здесь, как обычно, [Л, В] = ЛВ—В А.
56
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ [ГЛ. II
В отличие от пространственных координат четвертая ко-
ордината— время / — не описывается в квантовой меха-
нике (нерелятивистской и релятивистской) каким-либо
оператором, а остается классической величиной (парамет-
ром). Поэтому в квантовой механике время t рассматри-
вается существенно неравноправно с пространственными
координатами х, у, z. Такая неравноправность времени
и пространства сохраняется и в релятивистской квантовой
механике. Это обстоятельство не должно удивлять нас,
так как характерное для теории относительности «равно-
правие» времени t и координат х, у, z не превышает того,
которое содержится в форме
s2 = сЧ* - (х* + у2 + z2).	(11.2)
Как только мы обращаемся к рассмотрению реальных
физических явлений, особое значение времени выступает
совершенно отчетливым образом. Действительно, важней-
шие задачи физики формулируются таким образом: по
начальным значениям динамических переменных опреде-
лить их значения в будущем. Иными словами, даются
значения переменных при / = 0, требуется найти их зна-
чения при />0 (или /<0). Такая задача в механике
вытекает из существа динамических законов. В теории
поля соответствующая задача есть задача Коши. По самому
существу динамических законов мы не можем, например,
корректно поставить задачу: «даны /, у и z при х=0,
определить их значения при х#^0». Это важнейшее об-
стоятельство выражается в квантовой механике в том, что
в пространстве переменных х, у, 2, t (пространство Э14 (х))
не наложено никаких связей на эти переменные, в то
время как в пространстве сопряженных импульсов рх,
Руу Pz> Pt = E*) (пространство 9t4 (р)) наложены связи,
вытекающие из динамики.
Именно, в нерелятивистской теории в отсутствие внеш-
них полей
£==^7’ Ру’ Рг)’ U1’3)
где т — масса частицы.
*) Четвертая компонента импульса р/ есть энергия Et
§ 11]
ИЗМЕРЕНИЕ КООРДИНАТЫ МИКРОЧАСТИЦЫ
57
В релятивистской теории соответственно
Е = + Ур2+т2.	(П-3')
В силу соотношений (11.3) или (11.3') пространство (р)
сводится к пространству меньшего числа измерений 9ts (р).
В релятивистском случае (11.3') это пространство есть
пространство Лобачевского (см. § 31).
ТВ [квантовой механике соотношения (11.3) и (11.3')
можно рассматривать также как следствия уравнения
Шредингера:
=	(11.4)
где W — волновая функция, а Н—оператор Гамильтона.
Этот оператор есть функция операторов импульса рх, ру, pz.
Видом гамильтониана Н задается динамика в квантовой
механике. В частности, заметим, что релятивистское урав-
нение Дирака, в которое время входит совершенно сим-
метрично с пространственными координатами (ср. § 14),
может быть также записано в несимметричном, «шредин-
геровском» виде (11.4).
Для стационарных состояний волновая функция Т
зависит от времени только через множитель е . В этом
случае из (11.4) следует
=	(11.5)
т. е. возможные значения энергии Е (или, что то же,
значения четвертой компоненты импульса Pt = E) суть
собственные значения оператора Гамильтона Н. Как из-
вестно, эти значения могут быть даже и дискретными,
в то время как «сопряженная», четвертая координата t
непрерывна. В силу этого обстоятельства не существует
соотношения [31, 32]
[pt, t]=ih (pt=E}f	(11.6)
подобного соотношениям (11.1), (ПЛ'), (ПЛ"). Поэтому
не существует и соотношения неопределенностей
(11.6')
58
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ
[ГЛ. II
подобного соотношению неопределенностей для х и рх:
-----------------------i2
Ьх'Ьр*^,	(11.Г”)
вытекающему, как известно, из операторного соотноше-
ния (11.1). Вместо (11.6') существует соотношение
___	4:2
(11.7)
где, однако, т не есть статистическая дисперсия времени,
а вполне определенный промежуток времени, такой, что
за время т средние значения динамических переменных L
(не являющихся интегралами движения) изменяются на
величину AL, сравнимую с их статистической дисперсией
VjU [29, 33].
” После того как мы поставили на место время t, обра-
тимся к измерению свойств оператора координаты х.
В дальнейшем для наших целей достаточно ограничиться
одним измерением х. Согласно основным принципам кван-
товой механики наблюдаемыми значениями х' перемен-
ной х являются собственные значения оператора х, кото-
рые определяются уравнениями
хфЖ'=х'фх-,	(11.8)
где %, есть собственная функция оператора х, принад-
лежащая собственному значению х’. Явный вид зави-
сит от выбранного представления. В импульсном пред-
ставлении есть функция от рх, а оператор х равен
(П.9)
В координатном представлении есть функция х и опе-
ратор х равен
х = х.	(11.10)
Из уравнения (11.8) следует, что в импульсном пред-
ставлении
фж- (/\) =
1рХХ
ехрт~
V
(11-11)
§ 111
ИЗМЕРЕНИЕ КООРДИНАТЫ МИКРОЧАСТИЦЫ
59
а в координатном представлении
фх-(х) = 6(х—х').
(Н.12)
При выбранной нами нормировке функций они
связаны между собой унитарным преобразованием:
00
Фх'(х)= $ S(x\px)<fc(px)dpx,
— 00
где матричные элементы S(x|px) равны

/ 1рх \
ехрГт)
V 2rck
(ПЛЗ)
(Н.14)
Из вида собственных функций оператора х следует,
что в состоянии с определенным значением х = хг уча-
ствуют состояния с любым импульсом pxf ОТ —оо ДО оо,
1
2nk
причем с одинаковым весом, равным |S (х\рх) |2 =
Поэтому точное измерение координаты микрочастицы х
требует привлечения в пределе бесконечно большой
энергии.
Необходимая энергия может быть заимствована из
энергии самой частицы или из другой физической системы,
участвующей в измерении (например, от какой-либо части
измерительного прибора). Поэтому в случае измерения
координаты вмешательство прибора в состояние микро-
частицы является и неизбежным, и существенным. Учиты-
вая это вмешательство, лучше говорить не об измерении
координаты микрочастицы х, а о локализации [30] микро-
частицы около точки x=xf в результате ее взаимодействия
с измерительным устройством.
Возникшее после локализации- частицы состояние
быстро расплывается, так что средние значения квадра-
тичного отклонения Дх2=(х--х)2 (черта означает усред-
нение по ансамблю) будут быстро возрастать с течением
времени.
Чтобы рассмотреть расплывание локализованного при
/ = 0 в точке х=х' состояния, будем рассматривать (х)
60
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ
[ГЛ. II
как предел последовательности функций (х, а) при
а —► 0:
ехр
Фх' (х, а) = —
(х—х')2\
~ а2 )
Уп а
(11.15)
= Л f exp(-4^+-gX-(A
2л/& J \	4	Ть /
— 00
fвеличина С(px) = -Lexp f—~гРх~есть та же
\	2пИ \	’ л- /
волновая функция, но взятая в /^-представлении'); при
а —> 0 имеем
lim фх- (х, а) = 6(х—х').
а -> О
В силу уравнения Шредингера
dt
(11.16)
(Н-17)
(H = pll2m есть оператор Гамильтона'для свободной ча-
стицы, а т — масса этой частицы) каждая плоская волна
-iPxxfti
фРл. (х) = z_- в суперпозиции волн (11.15) обращается
V 2лй
при t > 0 в
ехрЦРхх^Е()
(11.18)
где Е(р^ = рЦ2т есть кинетическая энергия микроча-
стицы, имеющей импульс рх и массу т. Поэтому к мо-
менту времени t волновая функция (11.15) превратится
в функцию
“• '>=274
(11.19)
Этот интеграл вычисляется подстановкой
г=Ир,+В),	в=^- КИ-20)
§ 11]
ИЗМЕРЕНИЕ КООРДИНАТЫ МИКРОЧАСТИЦЫ
61
В результате интегрирования получается
Из этой формулы нетрудно вывести, что ширина пакета
<и-22)
и возрастает с течением времени; при а—>0, когда
(х, а)-+8(х—х'), скорость возрастания размеров па-
кета становится порядка v ~klma—>оо, что формально
допустимо в нерелятивистской теории.
Рассмотренные выше собственные функции оператора х
квадратично неинтегрируемы. Мы можем рассмотреть
другой класс функций (х, а), которые остаются квадра-
тично интегрируемыми:
ехр(_(^\
Фх- (х, а) =-' •	(П-23)
у/ л V а
Такого рода функция при а—>0 стремится к]/д(х —х').
Для этой функции
|ФИх, a)|adx=l	(11.24)
при любом а. Нетрудно видеть, что в состоянии, описы-
ваемом функцией (11.23), величина Дх2 равна
Дх2 = ^
(11.25)
и при а—>-0 Дх2=0. Что же касается оператора х, то
он будет действовать на функцию (х, а) следующим
образом:
хфх-(х, а)=х'фЛ-(х, а) + Д(х', х, а),	(11.26)
где
Д (х', х, а) = у/л Ya
(11.26')
у л у a J
и при а—>0
Д (х', х, а) —>- р/ л У а (х—х') 6 (х—х')==0. (11.27)
Поэтому при а—>0 функция (11.23) с любой степенью
точности удовлетворяет уравнению (11.3).
62
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ |ГЛ. II
§ 12. Механика измерения координаты микрочастицы
Рассмотренные до сих пор соображения относительно
измерения координаты микрочастицы х являются в зна-
чительной мере формальными.
С этой, формальной, точки зрения измерение коорди-
наты означает, что некоторое исходное состояние, опи-
сываемое волновой функцией ф0(х), «стягивается» к со-
стоянию
ф0(х)-^^(х).	(12.1)
Однако осуществление процесса локализации частицы
около какой-нибудь точки х=х' не является простым
даже в мысленном эксперименте.
В этой связи является важным разделение измерений
на прямые и косвенные, введенное Л. И. Мандельшта-
мом [34]. В случае прямых измерений само измерение
происходит в первом звене, соединяющем микрообъект
с макроскопическим прибором. Во втором типе измерений
имеется одно или несколько опосредствующих звеньев.
Например, если пучок свободных микрочастиц падает
на фотопластинку и попадание частицы вызывает на фо-
топластинке «пятно», то такое явление можно назвать
прямым измерением координаты свободной частицы.
Однако это пятно имеет размеры не меньше размеров
атомов пластинки на самом деле даже много больше, так
как наименьшее пятно имеет размер чувствительного зерна
фотопластинки, в котором падающая частица вызывает
цепную реакцию; поэтому исходная волновая функция,
описывающая падающий пучок ф0(х), стягивается при
таком измерении не к фх/(х) = б(х—х'), а к некоторой
функции (х, а), которая имеет размер а, не меньший
размера атомов фотопластинки. Теория, однако, никак не
ограничивает размера атомов, которые формально могут
быть и очень малыми, поэтому внутреннего противоречия
в теории нет.
Примером косвенного измерения может служить изме-
рение координаты электрона в атоме. В принципе такое
измерение может быть выполнено путем наблюдения рас-
сеяния узкого пучка микрочастиц на связанном в атоме
электроне. Рассеяние этих частиц может непосредственно
регистрироваться на экране и относится уже к прямым
$ 12]	МЕХАНИКА ИЗМЕРЕНИЯ КООРДИНАТЫ	63
измерениям. Узкий пучок микрочастиц, являющийся зон-
дом, которым прощупывают местонахождение электрона
в атоме, представляет собою промежуточное звено в из-
мерении координаты атомного электрона; поэтому такое
измерение есть измерение косвенное.
А. Прямое измерение координаты. Обратимся теперь
к математической стороне дела и рассмотрим взаимо-
действие микрочастицы с атомом фотопластинки [29].
Поскольку нас интересует сейчас принципиальная сто-
рона дела, мы будем допускать те или иные идеализа-
ции, совместимые с принципами теории. Фотопластинку
будем рассматривать как систему бесконечно тяжелых
атомов, расположение которых в пространстве известно
точно. Первоначальное микроявление, которое является
«затравкой» для последующей фотохимической реакции,
пусть состоит в возбуждении атома таким образом, что
его электрон переходит из состояния ф0(х) в состояние
%(х) (здесь х—координата электрона в атоме). Если
а —размер атома, то ф0 и быстро исчезают для |х|^>а.
Координату микрочастицы обозначим через Q и предпо-
ложим, что энергия взаимодействия микрочастицы
с электроном атома имеет S-образный вид:
F=g6(x—Q),	(12.2)
где g—-константа взаимодействия. Энергия возбуждения
атома пусть будет е = 8п — 80, энергия микрочастицы
Е=р*!2т, т — масса частицы, р~ее импульс до взаи-
модействия с атомом, р' — ее импульс после взаимодей-
ствия с атомом. Мы будем считать, что Е^>г. Таким
образом, источником большой энергии, необходимой для
локализации микрочастицы, будет служить энергия самой
микрочастицы. Возбуждение перехода Ео Еп, точно
локализованного в пространстве атома, играет роль ана-
лизатора А, сортирующего микрочастицы по их коорди-
натам Q с точностью до размеров атома а. В дальней-
шем возбужденный атом может инициировать скрытое
изображение в чувствительном зерне фотоэмульсии. Эти
или подобные процессы играют роль макроскопического
детектора О, разрушающего интерференцию различных
состояний микрочастиц. Мы не будем вдаваться в детали
расчета работы детектора и ограничимся расчетом первой
функции измерительного устройства — анализом частиц
64
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ [ГЛ. II
по координатам. Макроскопичность анализатора А в на-
шем случае выражается в предположении, что масса атома
фотопластинки^’предполагается бесконечно большой, так
что его положение в пространстве определено вполне точно.
Волновая функция рассматриваемой системы (микро-
частица р +анализатор Л) в начальный момент времени
/ = 0 будет иметь вид
ф0 (х, Q) = ip0 (х)	(12.3)
Эта функция описывает атом в невозбужденном состоя-
нии и микрочастицу в состоянии плоской волны с им-
пульсом р. Для t > 0 представим волновую функцию
этой системы в виде
Ф(х, Q, /)=Ф0(х, Q)e^ + q)(x, Q, t),	(12.4)
где частота со0 = (£,-|-е0)/А; функцию ср (х, Q, i) будем
считать малой и вычислим ее по теории возмущений. По
известным формулам теории возмущений (см., например,
[28], гл. XI) имеем
ср (x,rQ, 0 =
t
= У d3p' ^2 dxeiQ^ (пр91 W1Ор) (х)	, (12.5)
п О
где (пр* | W | Ор) есть матричный элемент энергии взаи-
модействия, взятый между исходным состоянием Фо (х, Q)
(12.3) и”возбужденным состоянием
Фп«Р) = %(х)^'^Ч	(12.3')
Этот матричный элемент равен
(пр'|1Г|0р)=$Ф;(х, Q)W(x, Q)<DS(x, Q)dxdQ=
=g^n(Q, 0)<Ш Q)dQ=
. =g$p,Io(Q)e':(p~p'’ m1idQ=gpnAq)< q=p—p’- (12.6)
Здесь p„o(Q)=4’n(Q)^(Q)> a P„»(?) есть компонента
Фурье от p„0(Q).
Далее, Q„ есть частота перехода:
о _ 1 ( Р3 ,	р’1	\
2М 8'7 ’
§12] .	МЕХАНИКА ИЗМЕРЕНИЯ КООРДИНАТЫ	65
Если мы рассмотрим малые t:	то
ф (х, Q, t) = у J d3p' р„0 (7)	% (х) t =
п
= У4^(х)Р„0К)^р/Ч.	(12.7)
th
п
Чтобы яснее представить себе результат, допустим, что
в сумме по возбужденным состояниям важен лишь один
член номера и остальные рот0^0, если т^п. Тогда
имеем
ф (х, Q, 0 = f Д % (х) р„о (Q)	(12.8)
Отсюда видно, что при малых /, т. е. вскоре после взаи-
модействия, волновая функция микрочастицы равна
^(Q) = P„o(Q)^₽/ft	(12.9)
и в точности воспроизводит переходную плотность элек-
трона в атоме рп0(х). Эта функция есть волновой пакет
с распределением вероятностей для координаты микро-
частицы
^n(Q)=|p„o(Q)lz	(12.Ю)
и со средним импульсом
p = ^Jo„(Q)^O„(Q)dQ«|p|.	(12.11)
(Здесь знак « означает, что равенство соблюдается с
точностью до импульса электрона в атоме, равного по
порядку величины А/а<?|р|.)
Таким образом, акт возбуждения атома сопровож-
дается локализацией микрочастицы в волновом пакете
(12.9), так что возбуждение атома можно рассматривать
как переход частицы из состояния плоской волны
при / = 0 в локализованное состояние (Q), определяемое
выражением (12.9) при 0<^/<^1/Пп. При t—> оо обра-
зовавшийся пакет расплывается. Однако если возбуждение
атома инициирует химическую или другую реакцию, то
необходимо включить в рассмотрение эту цепь явлений,
ведущую в конечном акте к макроскопическому событию.
Состояние при t—> со не будет тогда сводиться к рас-
плыванию пакета, а будет описывать новое состояние,
3 Д. И. Блохинцец
66
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ [ГЛ. II
возникшее в результате процесса возбуждения атома
с последующей химической реакцией.
Б. Косвенное измерение координаты микрочастицы.
Обратимся теперь к косвенному измерению координаты
микрочастицы. Для этого рас-
Рис. 13. Дифракция узкого
пучка. Э — Э — поглощающий
экран; Д—диафрагма диамет-
ром а; Д-£ — ширина пучка на
расстоянии г от диафрагмы;
А 2	2 I	2
Д±=а +^2Г •
смотрим сперва теорию луча,
который должен служить щу-
пом для измерения коорди-
наты микрочастицы, находя-
щейся в связанном состоянии,
например координаты внутри-
атомного электрона.
На рис. 13 показан эк-
ран Э — Э с диафрагмой Д.
Эта диафрагма формирует
пучок микрочастиц, имеющих
энергию Е = р212т = 1мй, им-
пульс p = hk. Суперпозиция
плоских волн, имеющих за-
данную полную энергию, но
различные направления рас-
пространения, имеет вид
J Л(а)ехр {f£r[cosft cosa-f-
+ sin ft sin ах
X cos (ф — P)] — iat} sinadadp,
(12.12)
где r, ft, ф суть полярные ко-
ординаты радиуса-вектора г; а,р—полярные углы волно-
вого вектора k. Интегрируя по углу dp, находим
ф= A (a) sin а da exp {ikr cos ft cos a — no/} x
X Jo (kr sin ft sin a)
(12.13)
(здесь JQ (x) — функция Бесселя нулевого порядка); при
ft = jt/2 мы получаем значение волнового поля на поверх-
ности экрана. Это поле должно исчезать вне отверстия
диафрагмы. Можно положить f (r) = Be~r^aZ в качестве
простейшей аппроксимации, выражающей непрозрачность
экрана для г > а. В интеграле (12.13) существенную
роль играют только малые углы, поэтому мы можем
§ 12]
МЕХАНИКА ИЗМЕРЕНИЯ КООРДИНАТЫ
67
аппроксимировать его с помощью формулы
00
•^=eikz-i<s>t J yj (a)adaexp (—/0 (&r sin •&•«).
(12.14)
При z=0 имеем
Ве-г*/а*= J j^krdjA (a)ada, .	(12.15)
о
откуда *)
Л(а) = -^ехр(-^).	(12.16)
Подставляя это выражение для Л (а) в формулу (12.14)
и пользуясь опять обращением (12.15), получим, что при
больших г и малых 4 интенсивность волн в пучке |ф|2
равна
|я,)2=/^уехр/|^02\	(1217)
Из этой формулы следует, что пучок частиц, выходящий
из отверстия радиуса а, расширяется благодаря дифрак-
ции, и притом таким образом, что квадрат его попереч-
ных размеров р2=г20з определяется средней величиной:
(12.18)
Если представить себе этот процесс во времени, полагая
r=vt =pt/m, то найдем, что
Дх=7йИ	(12.19)
в соответствии с ранее полученным результатом для рас-
ширения волнового пакета в поперечном направлении.
Для того чтобы пучок являлся хорошим зондом, необ-
ходимо, чтобы его ширина была существенно меньше
размеров системы d, внутри которой изучается положение
микрочастицы, т. е. с учетом начальных размеров имеем
условие
+	(12.20)
*) См., например, [35],
3*
68
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ
(ГЛ. II
или, при a<^d,
Эти условия являются крайне жесткими и, если иметь
в виду реальные объекты, практически неосуществимыми.
Действительно, не видно путей для создания щели или
другого устройства для получения пучка шириной а < d,
если под d разуметь атомные размеры. Однако теория
формально допускает как угодно узкие щели и поэтому
внутренне непротиворечива. Имея это в виду, рассмотрим
взаимодействие микрочастицы, находящейся в связанном
состоянии, с микрочастицами пучка, служащего зондом
для определения положения первой связанной частицы.
Пусть масса первой частицы есть /л, ее координата х,
собственные функции %(х), Еп — соответствующие уровни
энергии. Эти функции удовлетворяют уравнению
(12.21)
где Нт(х) — оператор Гамильтона, описывающий дина-
мику связанной частицы. Пусть масса частицы пучка-
зонда есть р, ее координата Q, оператор импульса Р.
Тогда ее гамильтониан есть попросту
/W)	(12.22)
Положим опять, как в § И, что взаимодействие т-ча-
стицы и ц-частицы—точечное, т. е.
W, Q)=g6(x-Q),	(12.23)
где g — константа взаимодействия. Волновая функция
m-частицы вместе с пучком-зондом ф(х, Q) будет удо-
влетворять уравнению Шредингера
[Нт (x)4-^(Q) + F(x-Q)W. Q)=E^(X, Q). (12.24)
Представим ip (x, Q) в виде
W, ф=ФоИио(<?)+ 2 ^n(x)un(Q), (12.25)
где Фо(лг) описывает состояние m-частицы до взаимодей-
ствия, и0 (Q) описывает пучок ц-частиц вместе с упруго
рассеянной волной. Подставим эту функцию в (12.24) и
§ 12]	МЕХАНИКА ИЗМЕРЕНИЯ КООРДИНАТЫ
69
после скалярного умножения на 'фтС*) найдем систему
уравнений для функций um(Q):
g-4- (Еа-Е)]иа (Q) =-£ф0 (Q) С (Q) и0 (Q), (12.26)
причем мы пренебрегли произведением W 2 ФД*) и«(0)’
П =/= О
как величиной второго порядка малости (при малой g).
Для упругого рассеяния, описываемого u0(Q), имеем
согласно (12.26):
(va + ^) и0 (Q)	1 ф0 (Q)|2 ив (Q) =р (Q), (12.27)
где /г2 = 2ц£/А2. Отсюда известными методами находим*)
«О (Q) = Фо (<?)+5 @ (Q- Q') Р (О')dQ’, (12.28)
где функция ф0 (Q) описывает исходный узкий пучок (см.
формулу (12.12)), а функция u0(Q) описывает этот пучок
вместе с рассеянной волной; ®(Q-Q') есть функция
Грина однородного уравнения (12.27):
__I Q- Q' |
®«?—Q0 = fe-[-q-g-| 	(1229)
а величина р(Q) равна
Р(0) = -^|Фо(0)|2Фо(0)-	(12-30)
Если обратиться к большим расстояниям от области рас-
сеяния |Q| = r—>оо, то формула (12.28) приводит к из-
вестному результату**)
«о(0) = Фо(0)+^-^А(^),	(12.28')
где амплитуда рассеянной волны Л(^) равна
A(q) = ^eWp(Q)dQ-,	(12.31)
здесь вектор q=pr —р есть передаваемый при рассеянии
импульс.
Из формулы (12.28) видно, что источником рассеянных
волн является область, где плотность р (Q) существенно
*) См., например, [28], гл. XIII.
*♦) См., например, [28].
70
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ [Гл. II
отлична от нуля. Эта область есть область пересечения
пучка-зонда ц-частиц <р0 (Q> 0 с областью локализации
m-частицы. Эта область определяется поведением функ-
ции |ф0(О)|2.
Следовательно, область, где р (Q) существенно отлична
от нуля, имеет определенные координаты в плоскости
Рис. 14. Определение координаты в косвенном опыте. Э — Э—погло-
щающий экран, а—диаметр диафрагмы, с помощью которой создается
узкий пучок-зонд.
(х, у) (с точностью до’ширины пучка а) и одну неопреде-
ленную координату z, направленную вдоль пучка (рис. 14).
Если теперь с помощью какого-либо детектора мы фикси-
руем рассеянную атомом ц-частицу, то тем самым будет
доказано, что в момент рассеяния m-частица имела коор-
динаты х, у, равные координатам диафрагмы, ограничи-
вающей пучок р-частиц, с точностью до ширины пучка
Дх, Аужа. Следует заметить, что это утверждение было
бы совсем точным, если бы пучок имел резкую границу.
На самом деле такой границы не существует и имеется
конечная вероятность того, что ц-частица рассеивается на
m-частице, находясь вдали от оси пучка, на расстоянии,
§ 12]	МЕХАНИКА ИЗМЕРЕНИЯ КООРДИНАТЫ	71
большем а. Далее, из-за диффузности границы атома
m-частица может оказаться весьма^далеко от центра атома,
в той области, где пучок-зонд расширился настолько, что
его размеры Д±^>«.
Итак, даже в этом мысленном опыте, допускающем
узкую гщель'ги^точечное взаимодействие, суждение об ис-
тинной координате, связанной в атоме m-частицы, может
быть только вероятностным.
Строгая постановка вопроса была бы такая: найдена
рассеянная р-частица; какова вероятность того, что она
рассеяна m-частицей, находящейся в некоторой резко
ограниченной области Q (х)? Чтобы ответить на этот вопрос,
заметим, что величиной, определяющей полную вероят-
ность какого-либо упругого рассеяния р-частицы связан-
ной m-частицей, является интеграл
/=J|A(^)|2^,	(12.32)
гдеХ(^) — амплитуда рассеянной волны (12.31). Величина/
(12.32) измеряет в условных единицах полный поток
упруго рассеянных р-частиц.
С помощью (12.31) этот интеграл можно переписать
в виде
7 = (4SFjp^')p(x")A^’ x'-x^d^x'd^', (12.33)
где функция Д(#, х) (х = х' — X") определяется формулой
Д (<7, ^sin^sin^sin^z, (12 34)
a Qi, Q%, Qs — максимальные значения проекций вектора q
на оси координат. Из выражения (12.33) видно, что веро-
ятность упругого рассеяния / нельзя представить как
сумму вкладов от отдельных пространственных областей,
а она определяется суммой корреляций.
Однако если длина волны к пучка-зонда мала по срав-
нению с областью вариаций величины р(х), то пределы
интегрирования >по qx, qy, q2 можно заменить на ±°о;
это эквивалентно замене функции Д (q, х) на функцию
S (x). Тогда вместо (12.33) получаем
(12.35)
72
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ
[ГЛ. II
и вероятность того, что рассеяние произошло в области Q,
можно представить в виде
=	(12.36)
Z Q
В этих расчетах мы предполагали, что взаимодействие
ц-частицы и m-частицы является точечным (см. (12.23)).
Если оно не точечное, то определить вероятность I (Q)
в области Q меньшей сферы взаимодействия вообще не-
возможно. Действительно, заменяя в (12.23) 6 (х—Q) на
распределенную функцию взаимодействия V (х—Q), так
что
Г(х — Q)=gV(x — Q),	(12.23')
и повторяя выкладки, ведущие к уравнению (12.27), по-
лучим вместо (12.27)
W + k*)u0(Q) = pv(Q),	(12.27')
где
Ри (Q)=J v (x-Q) 11|>0 (х) I3<р0 (Q) d3x. (12.30')
Отсюда следует, что
7r=^ jP1/(x')Pr(x")A(^, х'—х") d3x’d3x", (12.33')
или при X—s-0, |^| —*-оо получаем, аналогично (12.35),
Л/ = (4^^рНх)Л.	(12.34')
Формально можно ввести, как и прежде, величину
IA®) = (^P*v№d3x.	(12.35')
Однако из (12.30) видно, что величина ру (х) нелокально
связана с функцией |ф0(х)|2, так что в интеграле (12.35)
имеется вклад и от тех областей пространства, где вели-
чина | ф0 (х)|2 равна нулю. Интерпретация интеграла (12.35)
может быть сохранена в том случае, если |ф0(х)|2 весьма
гладко распределена внутри масштабов, определяющих
сферу взаимодействия, т. е. область, вне которой потен-
циал взаимодействия V(x —Q) пренебрежимо мал,
§ iз] косвенное Измерение координаты	73
§ 13. Косвенное измерение координаты
микрочастицы в данный момент времени
До сих пор измерение координаты х микрочастицы
относилось к неопределенному промежутку времени. Для
того чтобы измерить координату х для определенного
малого интервала времени Д/, необходимо усложнить
работу диафрагмы в мысленном опыте формирования пучка-
зонда. Необходимо допустить, что имеется возможность
открыть эту диафрагму в некоторый момент времени, ска-
жем при / = 0, и закрыть ее вновь в момент t = \t. Тогда
вместо луча, показанного на рис. 14, возникнет пакет,
ограниченный не только по осям Ох и Оу, но и в направ-
лении своего движения по оси Oz.
Этот пакет будет расплываться в соответствии с фор-
мулами, приведенными в § 11. Итак, теперь вместо зонда-
пучка ц-частиц мы будем применять зонд-пакет ц-частиц.
Такой волновой зонд-пакет может быть представлен супер-
позицией плоских волн, распространяющихся преиму-
щественно в направлении Oz (см. рис. 14). В соответствии
со сказанным волновую функцию р,-частиц, с помощью
которых мы намерены зондировать положение т-частицы,
связанной внутри микросистемы, представим в виде
фо«2, O=fc(p)exp(-r^y^))-^77, (13.1)
где
с (р) =ехр ,»~г>2 ^д°/7(Рг~р)2^ •	(13 •2)
Здесь р—средний импульс в направлении движения пакета
(по оси Oz), величина 1/й2 есть мера среднего квадратич-
ного отклонения проекций импульса ДР2, ДР2, ДР2.
Пользуясь методом расчета, изложенным в § 11, при до-
статочно большом параметре b функцию ср0 (Q, t) можно
привести к виду
i(co/-&C)
’’	(13'3)
где функция f (Q, t) равна
f(Q, () = ехрГ-е±2£-^1.	(13.4)
Д||
?4
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ [ГЛ. 11
Е	р2
В этих формулах оз = —;	есть средняя энергия
р-частиц; Р—их средний импульс, направленный по оси 0£;
k=2p/ii—волновой вектор; и —р/р —средняя скорость по
оси О£; Д1, Ду —средние ширины волновых пакетов
в поперечном и соответственно в параллельном р-пучку
направлениях. В соответствии с (11.22) имеем
2
Al=Af,=a*+A_^	(13.5)
где a2^ii2!b2. Пусть, как и в § 12, гамильтониан т-ча-
стицы есть Нт(х), а гамильтониан р-частицы есть H^Q)
(см. формулы (12.21) и (12.22)). Тогда уравнение Шре-
дингера для волновой функции ¥ (х, Q, /) системы
«т-частица +волновой пакет р-частицы» запишется в виде
ih = [нт (х) + Н4Q) + W- Q)] Т,	(13.6)
где W есть энергия взаимодействия m-частиц и р-частиц.
Это взаимодействие мы будем считать точечным (см. фор-
мулу (12.23)). Представим теперь функцию T (х, Q, t)
в виде
I А/
Чг=Ф(х, Q, t) exp
(13.7)
где Ео есть энергия m-частицы в состоянии ф0(х). Функ-
ция Ф(х, Q, t) может быть представлена в виде суммы:
Ф(х, Q, 0=Фо(*)фо(а. t) + u(x, Q, i), (13.8)
где и(х, Q, t)—рассеянная волна, а ф0 (х) <р0 (Q, t) —
волна первичная. Представляя, далее, и (х, Q, t) в виде
ряда
и(х, Q, /) = Zh„(Q, /)ф„(х)	(13.9)
п
по собственным функциям (х) оператора Гамильтона
Нт m-частицы, мы найдем обычным путем (ср. § 12) си-
стему уравнений для функций ип\
О, (13.10)
§ 13]
КОСВЕННОЕ ИЗМЕРЕНИЕ КООРДИНАТЫ
75
аналогичную системе (12.26) *). В частности, для упру-
гого рассеяния получим
i4^~Cbo=m(O)|2<p°(Q’ °- (1311)
Чтобы найти решение этого уравнения, заметим, что
уравнение для функции Грина ® однородного уравнения
(13.11) гласит:
(13Л2)
и имеет известное решение [29, 36]:
т. 1	/ i (С— О')®\
® =------ГГ ехр ( —	Д-2 ) Для t>t.
(13.13)
(13.13')
®=0
для t <Zt'.
Поэтому решение неоднородного уравнения (13.11) может
быть представлено в виде
«0(О, O=<po(Q, 0 +
/ i т (Q-Q')2\
е ехр ~Г'2’Т^Т )
+а ----У ,, Л-------— । Ч’о <^') I2 Фо d^' dt'>
и	(t — t )
(13.14)
где в коэффициенте а объединены все постоянные мно-
жители.
Функция rz0(Q, 0 описывает упруго рассеянные р,-ча-
стицы. Рассмотрим теперь случай, когда размеры ji-пакета
продольные Дц и поперечные Д± велики по сравнению
с основной длиной волны k = hlp. В этом случае изме-
нение показателя экспоненты функции f (Q, t) (13.4) за
время периода колебаний tth/E, очень мало, и мы можем
выполнить интегрирование по dt' в (13.4), учитывая за-
висимость функции Фо (О, 0 от /' только через множитель
Вводя обозначение т=/'—t в (13.4),
применим к показателю экспоненты в (13.4) метод пере-
*) При этом мы опять предполагаем малость константы взаимо-
действия g.
76
ГЕОМЕТРИЧЕСКИЕ ИЗМЕРЕНИЯ В МИКРОМИРЕ [ГЛ. II
вала. Интеграл, который необходимо взять, имеет теперь
вид
е-^(т)
о
dx,
(13.15)
где
д 2
F (т) = -тут—сот
4 ’ ±Dx ‘
(13.16)
и 4D = 2^/p,, Д2 = | Q' — Q |2. Приравнивая нулю dF (т)/с(т,
найдем
хт = ± 1/-^- =± |g'~Q|,	(13.17)
т — V 4Z)co — v	4	'
причем знак минус соответствует запаздывающему, а знак
плюс—опережающему действию. Это соотношение ука-
зывает на то, что рассеянная волна приходит из точки Q'
в точку Q за время хт, определяемое скоростью р,-частиц
и =	Замечая, что d2F (x)/dx2 равна
(13J8>
найдем, что
где (3— постоянный коэффициент. Возвращаясь теперь
к формуле (13.14), получим
«»(Q. O = <Po(Q, 0 +
+ a J . । q—q' ।	t v )dQ, (13.20)
где а' —некоторый новый коэффициент, а функция p (Q, t)
равна
P(Q, 0 = ^r^o(Q)l2<Po(Q,	(13.21)
и отличается от прежнего результата (12.28) только за-
висимостью от времени пакета волн ср0 (Q, /). Эта зави-
симость позволяет говорить о том моменте времени, когда
§13]	КОСВЕННОЕ ИЗМЕРЕНИЕ КООРДИНАТЫ
11
в акте рассеяния р,-частицы измеряется координата
т-частицы.
Если, как это было сделано в § 12, рассмотреть боль-
шие расстояния, т. е. |Q| = r—^oo, то из (13.20) полу-
чается
pikr
=	(13.22)
где амплитуда рассеянной волны А(д, Q, t) равна
A(q, Q, 0 =	IQ'rQI)^3Qr <13-23)
и отличается от (12.31) запаздывающей зависимостью от
времени.
Вычисляя теперь полную интенсивность / интегриро-
ванием | Л(<7, Q, /)|2 по d3q в предположении очень ко-
ротких волн (\—>0), мы получим вместо (12.36)
W Q, 0 = (4^$р2(<?'. t—(13.24)
7 й
В этой формуле, в отличие от (12.36), указывается мо-
j. I О'— QI
мент времени t = t—1	 1 •, когда произошло рассея-
ние, причем Q есть радиус-вектор точки наблюдения,
a Q'— радиус-вектор области Q, внутри которой произо-
шло рассеяние.
Величина / (Q, Q, /) есть мера вероятности того, что
наблюдаемая в точке в момент t рассеянная р,-частица
возникла в результате рассеяния в области Q в момент
IQ- Q'l
времени t = t———
ГЛАВА III
ГЕОМЕТРИЧЕСКИЕ
ИЗМЕРЕНИЯ В МИКРОМИРЕ
В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
§ 14. Фермионное поле
Поле свободных фермионов описывается четырехком-
понентным спинорным оператором ф(х). Этот оператор и
сопряженный ему оператор ф (х) подчиняются уравнениям
Дирака
+	=	(14.1)
—т)=0;	(14.Г)
хи (ц=1, 2, 3, 4) суть компоненты четырех мерного ра-
диуса-вектора произвольной точки Р. Они определены
следующим образом: х = (х1У х2, х3), x± = ict. Здесь, как
обычно, t—действительное время, с—скорость света,
а уц— известные матрицы Дирака:
ТцЬ4-ТгТц=2бцу.	(14.2)
Компоненты спиноров гр и гр подчинены правилам ком-
мутации
(Фа(х), Фр (х)} = 0, (фа(х), фр(х')} = 0,	(14.3)
{Фа(х), Фр(х')} = 1'5ар(х—х'),>	(14.3')
. а, 0=1, 2, 3, 4,
где скобки {Я, В} означают антикоммутатор АВ^-ВА.
Далее, функция Sap (%—х') есть матричный элемент
перестановочной функции S (х—х'), равный*)
5ар(х—х') = —	----т\ D(x—x'),	(14.4)
\ дхц, / ар
!) См. дополнение I, формулы (1.3), (1,15).
$ 14j	ФЕРМИОННОЕ ПОЛЁ	?9
где
Dw=^etpx^#p- <i46)
В этой формуле р есть вектор импульса, Е— энергий^
равная Е = -)-]/p2-j-m2.
Если в качестве фундаментальной системы функций
взять плоские волны е‘Рх (рх=рх— Ef), то спиноры ф
и ф могут быть представлены в виде
ф= 2 5 d3 4p {ar (р) ur (р) e‘Px-\-b+ (p')vr(—p)e~I'Px}, (14.6)
Г=1, 2
ф= 2 J d3p{a?ur(p')e~'Px+br(p)vr(—р)е+‘Рх}.	(14.6')
г=1.2
Здесь ur(p), vr (—р) —спинорные амплитуды плоской
волны. Они удовлетворяют уравнениям Дирака
(ip + tri) и (р) = 0,	-(14.7)
(—ip + m)v(—р) = 0	(14.7')
(оператор p = yv,pll, рц==(р, Е/с)) и нормированы в соот-
ветствии с уравнениями
2 «UpM'(p)* = V,	(14.8)
а=1
4
2 ^(-p)<(-p)* = V.	(14.8')
а= 1
Четырехкомпонентный спинор иг(р)е'р* означает волну,
описывающую отрицательно заряженный фермион (элект-
рон) с импульсом р, энергией £ = +Vp24-m2 и ориен-
тацией спина, определяемой индексом г(=1, 2). Волна
vr (—р)е~'Рх описывает положительно заряженный фер-
мион (позитрон) с импульсом р, энергией Е = +К/»2+та
и спином г. Операторные свойства спиноров фиф пере-
несены на амплитуды а, а+, Ь, Ь+, которые являются
операторами, подчиняющимися условиям антикоммутации:
{аг(р), а?. (р')} = 6гг-63 (р—/>'),	(14.9)
(Sr(p), ^(р')} = ^63(р—р');	(14.9')
go	МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАВ (гл. ш
все остальные (антикоммутаторы операторов а, а+, Ь, Ь+)
равны нулю.
Эти правила коммутации обеспечивают выполнение
правил коммутации для операторов ф(х) и 'ф(х) (14.3),
(14.3').
Физический смысл операторов а, а+, Ь, Ь+ таков.
Оператор аг(р), действуя на функционал Y, описы-
вающий состояние фермионного квантованного поля, умень-
шает число электронов пг (р) в состоянии (р, г) на еди-
ницу:
«Д/>)Т(..., пДр), ...) =¥(..nr(p)-l, ...), (14.Ю)
а оператор а+г (р) порождает электрон в состоянии (/». г):
пг(р),	пг(р)+1, ...).(14.10')
Операторы &, Ь+ имеют то же значение для позитрона:
...) = T(...,nr(p)-l, ...), (14.10")
Ь+(р)Ч(...,п+г(р), ...)=W(...,n+(p)+l> ...). (14.10'")
Заметим, что в силу статистики Ферми—Дирака числа
заполнения пг(р) ограничиваются значениями 0 и 1 *).
Из уравнений (14.1) и (14. Г) следует закон сохране-
ния для электрического тока:
^ = °,	(14.11)
ц
причем компоненты этого тока определяются формулой
=	(14.12)
где е — заряд электрона.
Четвертая компонента этого тока:
/4 = ^фу4ф	(14.13)
может иметь различный знак в зависимости от того, элект-
роны или позитроны дают больший вклад в плотность
электрического заряда в данном месте.
*) Подробности о квантовании дираковского поля можно найти
в курсах квантовой теории поля. Мы здесь следуем обозначениям,
принятым в [37, 38].
ФЕРМИОННОЕ ПОЛЕ
81
§ 14]
Однако если обратиться к одночастицному состоянию,
то величина р имеет определенный знак и после деления
на заряд частицы е может рассматриваться как плотнссть
вероятности w (х) найти частицу в данном месте х в мо-
мент времени Л
Чтобы доказать это важное обстоятельство, обратимся
к рассмотрению одночастичного состояния, например
электрона. Это состояние в общем случае будет состоя-
нием с неопределенным импульсом р и неопределенной
ориентацией спина г. Функционал, описывающий такие
состояния, имеет вид
Т(1)= 2	П 6(«;)ds/. (14.14)
г'=1»2	Р=^Р'
Г=^Гг
Матричный элемент оператора фермионного поля ф}.
соответствующий переходу из состояния вакуума ¥ (0):
в состояние Т(1),на основании (14.6), (14.10) — (14.10"7
и (14.11) будет равна
ф (х) = <¥ (0) | ф (х)| Т (1)> = $ cr (р) d3p иг (р) е^х (14.15)
и описывает волновой пакет фермиона с ориентацией
спина г, с импульсами, определенными амплитудой с(р),
и положительной энергией Е = +	т2.
Нормировка функционала поля
<Y(1), W(l)>-1,	(14.16)
ведет к условию нормировки для амплитуды с(р):
с* (р) с (р) d3p = 1.	(14.17)
Рассмотренный матричный элемент оператора ф(х) поля
(14.15) имеет смысл волновой функции электрона ф(х)
в дираковской теории одного электрона.
Вычислим теперь среднее значение четвертой компо-
ненты тока Jt или, что удобнее, величину w = Jjie вод-
ночастичном состоянии Т (1) (14.11). На основании (14.13)
и (14.15) имеем
и>(х) = <Ф(1)|ф?4ф|Чг(1)> =
4
= 'Ф (*) ?4Ф (х) = ф* (х) Ф (х) = 2 Фа W фа (X) > 0. (14.18)
а=1
82
-МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
(гл. Ilf
Положительная дефинитность величины w (х) позволяет
рассматривать ее как плотность вероятности для одно-
частичного состояния. В силу закона сохранения (14.11)
полная вероятность
IF = (ф, Ф) = $ фу4ф^3х = J w (%) d3x (14.19)
остается постоянной во времени:
= ^d3x= — У div Jd3x~ — J	= 0.(14.20)
В заключение заметим, что фундаментальные функции
%,л*.	<14-21)
”) = eXPt'^/7£Z)^(jP)	(Г =1,2), (14.21')
входящие в разложения (14.6) и (14.6'), образуют пол-
ную систему функций, причем условие полноты при t' = t
гласит:
2 5 $ d3p^*p, г (х, a)tyP,r(x', 0) = 63 (х — х') 6аР. (14.22)
Г=1 U, V
Здесь суммирование распространено по обеим ориента-
циям спина r= 1,2 и двум знакам энергии (спиноры ии v).
Если же мы ограничимся одним знаком энергии, например
Е > 0, и соответственно одним спинором и, то вместо
(14.22) получим
2
2 \ г(х, а)%, г(х', а') = — i (у45^(х—%')),(14.23)
г= 1 “
где
Sip (х—х') = — (тй	—/п) Д+ (х—х') (14.24)
И
<14-25)
Отсюда видно, что б3 (х—х') не разлагается по фунда-
ментальной системе функций фр, г(х, ос), если ограни-
читься состояниями только положительно частотными
§ 15] СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ДЛЯ ФЕРМИОНОВ 83
(электроны) или только отрицательно частотными (пози-
троны).
То обстоятельство, что функция SJp(x—х') размазана
в области кх^Ъ/тс, наводит на мысль, что дираковская
частица вообще не может быть локализована точнее, не-
жели в пределах своей комптоновской длины волны.
В следующем параграфе мы рассмотрим этот вопрос под-
робно.
§ 15. Соотношение неопределенностей
для фермионов
Рассмотрим одночастичное состояние T'(l). Для та-
кого состояния мы можем применять обычное, некван-
тованное уравнение Дирака для одного фермиона, с тем
лишь важным ограничением, что мы обязаны использо-
вать состояния только с одним знаком энергии Е —
= +V>+m’>0.
Волновая функция ф(х), описывающая такое состоя-
ние, может быть представлена в виде
2
Ф (х, t) = X СГ (Р) иГ (Р) е‘'рх- (15.1)
Мы будем считать ее квадратично интегрируемой. Вычи-
слим среднее квадратичное отклонение какой-либо коор-
динаты, например г, в этом состоянии в какой-либо мо-
мент времени.
Без всяких ограничений, попросту выбором системы
отсчета, мы можем предположить, что средние значения
z = 0, t = 0 и средний импульс р также равен нулю. Для
простоты достаточно рассмотреть состояние с однойТоп-
ределенной ориентацией спина r= 1 или г = 2. В выбран-
ной системе отсчета среднее значение квадратичного от-
клонения Дг2=(г—z)2 = z2 с помощью (14.18) запишется
в виде
Дг2 = $ ш (х, t) z2 d?x = $ ф* (х, t) г2ф (х, t) d3x. (15.2)
При условии нормировки
t)d3x=\.	(15.3)
84
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
(ГЛ. Ш
Выражение (15.2) может быть преобразовано с помощью
соотношения
гф (х) = Д- f  с (р) и (р)	=
1 J (2л)/г '	И’ dPz
= i Г g [с (р) и (/>)] с{р х
J (2л)’/'	др2
(15.4)
Записывая подобным же образом произведение гф*(х)
и выполняя интегрирование по d3x, найдем
X^ = ^dsp	(Р)1
дрг
дрг
(15.5)
4г’ЧЧ^П“М^1с<',)|!|-®7Г+
о5-5')
Первый интеграл справа, как мы увидим, ведет к обыч-
ному соотношению неопределенностей; вторые два инте-
грала характерны для релятивистской теории и требуют
специального исследования.
В принятой нами системе отсчета мы можем считать
без существенных ограничений, что’амплитуда с(р) имеет
вид
(15.6)
О
где функция f (| р |/| Ро ]) действительна и убывает доста-
точно быстро для \р\/Ро^> 1- Это означает, что величи-
на pQ характеризует разброс импульсов Др| в рассмат-
риваемом состоянии; на самом деле,
М = (рг-рг)2=р1=
J Р» \ Ро /
= р? $ В4 dl cos2 0 d£ip (I)=a,pl	(15.7)
Здесь рг = |р'| cos'l), t/Q = sinft<f&dcp,	а'—ко-
эффициент порядка 1.
Для действительной амплитуды с(р) формула (15.5')
упрощается в силу нормировки спинора и*и = 1 (см. 14.8)).
§15] СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ДЛЯ ФЕРМИОНОВ 85
Учитывая эту нормировку, получим
f d*p + р рс* (р) |Г. (15.8)
Вводя теперь вместо |р| переменную g = |p|/p0, перепи-
шем первый интеграл в (15.8) в виде
<15'9)
о
(коэффициент а"-—порядка 1), а второй интеграл в виде
/2—,	(15.Ю)
Ро 6 J	\ Ро J
где функция М (|, т/р^ определяется интегралом
—")= A. fp-^dQ.	(15.11)
\ р0 j 4п J дрг dpz	v
Эта функция вычислена в дополнении II и равна
, х [да	(1512>
\ Ри / I Зро /72	$•	/72	/ I г* 1 nA
Ввиду этих свойств функции М (£, т!ра) мы имеем
(>₽,дл” <|5-1з>
/,-|#₽"для i>l, (15.13")
[ ро	Ро
где |У и Р"—коэффициенты порядка 1.
Возвращаясь теперь к формуле (15.8) и восстанавли-
вая в явной форме ее размерность, получим
Дг2=а-^=-+ для \pl<^mV, (15.14)
Др® тъс2
___	£2	___
Azz = y^=-	ДЛЯ Дрг^>/ПаСа. (15.14)
ДР*
Из этих формул, в которых а, р, у суть численные
коэффициенты порядка единицы, видно, что добавочные
86
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
[ГЛ. III
релятивистские члены, обусловленные зависимостью спи-
норов от импульса, не являются существенными, так как
в (15.14) добавочный член мал по сравнению с первым,
а при Др2^>т2с2 имеет место формула (15.14'), отличаю-
щаяся от старшего члена в (15.14) лишь численным ко-
эффициентом. Из формулы (15.14) следует, что при Др2 —>оо
величина разброса соответствующей координаты Дг2 мо-
жет быть сделана как угодно малой.
Таким образом, хотя функция б(х—х') не входит
в класс функций, допустимых для одночастичного состоя-
ния, теория все же допускает возможность как угодно
точно локализованных одночастичных состояний с опре-
деленным знаком энергии (в классе квадратично интег-
рируемых функций)*).
§ 16. Бозонное поле
Поле бозонов, не имеющих спина, описывается ска-
лярным (или псевдоскалярным) оператором ф (%), который
может иметь, кром^ того, определенные свойства симметрии
в изотопическом (зарядовом) пространстве.
Мы рассмотрим комплексное скалярное поле, описы-
вающее заряженные частицы. Такое поле подчиняется
уравнению Клейна**):
(□2 —т2)ф-0,	'	(16.1)
(П2_т*)ф+ = 0,	(16.Г)
и правилам коммутации:
[ф(х), ф+ (х')] = Ю (х—х'),	(16.2)
где [Л, В~\ = АВ — ВА есть обычный коммутатор, а функ-
ция D(x — x') определяется формулой (14.5):
здесь k—импульс бозона и со—его энергия (в системе
единиц, где А=1). Остальные коммутаторы
[<р(х). ф(И] = [ф* (*)> ф*(х')] = о.	(16.2')
*) В этом параграфе мы следовали работе [30].
**) См. [37, 38].
ВОЗОННОЕ ПОЛЕ
87
§ 161
Бозонное поле ф (х), аналогично фермионному полю, мо-
жет быть представлено в виде разложения по фундамен-
тальной системе ортогональных функций:
Ф (х) = $ dsk {a (к) и (Jt) etkx+b+ (к) U*(k) e~ikx},
(16-4)
ф+ (x) = J d3k {a+(k) U* (k) e~ikx + b(—k)U(— k) eikx},
(16.4')
где
(0=m —масса бозона. Операторы a, a+,
b и b+ имеют смысл, аналогичный операторам в разложе-
ниях (14.6) и (14.6') для фермионного поля. Именно,
они подчиняются правилам коммутации:
[Н(й), 5+ (Л?)] = 63(Л? —Л?'),	(16.6)
[ь (А), ь+ (&)]=бз (&—£');	(16-6')
остальные коммутаторы: [a, а'], [а+, а+'], [Ь, Ь'], [Ь, &+'],
[а, Ь'] — равны нулю. Физический смысл операторов а, а+,
Ь, Ь+ таков:
оператор a(k), действуя на функционал Т, описывающий
состояние бозонного квантованного поля, уменьшает число
положительно заряженных бозонов п+ (й) в состоянии
с импульсом k и энергией со = +V&+ т2 на единицу:
а(А?)Т(..., п+(й),	/г+(*)-1> •••); (16-7)
оператор а+ (А) порождает положительно заряженную
частицу в состоянии (k, ®):
а+ (Л)Т (..., n+(k),	п+ (Л)Ч-1, ...).(16.7')
Операторы b (k) и Ь+ (к) имеют тот же смысл для отри-
цательно заряженных бозонов:
Ь(Л)Т(..., п~{к),	п~ (к) — 1, ...), (16.8)
8S
Микромир в релятивистском случае
[ГЛ. И1
Ь+(Л)Т(..., п~ (А),	п- (Jfe)4-1, . ,.).(16.8')
Из уравнений (16.1) и (16.И) следует закон сохранения:

= 0,
(16.9)
где
С6.10)
причем четвертая компонента имеет смысл оператора
плотности электрического заряда:
Л=Ф=‘е{ф*>^-—^-ф} •	(16.11)
Однако, в отличие от случая фермионов, как будет
видно из дальнейшего, бозонам нельзя приписать поло-
жительно дефинитной плотности вероятности ui(x) = p/e,
даже для одночастичного состояния с определенным зна-
ком энергии. Обратимся теперь к рассмотрению такого
состояния. Пусть Т(1) есть функционал поля, описываю-
щий одночастичное состояние с неопределенным импуль-
сом бозона k и определенным знаком энергии со > 0. Этот
функционал можно представить в виде, совершенно ана-
логичном случаю фермионного поля (ср. (14.14)):
Т (1) = J A (й) d*k8 (п+ (А) - 1) х
Хб[п-(Л)] п S[n+(£')№"(*')]•	О6-12)
k=^k'
Матричный элемент оператора бозонного поля, соот-
ветствующий переходу из состояния вакуума Т (0) в со-
стояние Y (1), описываемому формулой (16.12), на осно-
вании (16.4), (16.4'), (16.7)—(16.8') будет равен
ф (х) <Т (0) | $ (х) | Т (1)> = $ A (k) U (Л) eikx d3k
(16.13)
и описывает волновой пакет бозона с импульсом, опре-
деленным амплитудой A (k), и положительной энергией
116]
БОЗОННОЕ ПОЛЕ"
89
В силу нормировки функционала
<Т(1), ¥(1)>= 1	(16.14)
получается нормировка для амплитуды A(k):
J Д*(й)Л (Jt)d*k=l.	(16.15)
Рассмотренный матричный элемент ф (%) оператора
поля ф(х) (16.13) имеет смысл волновой функции бозона
в одночастичной теории скалярного поля.
Вычислим теперь средние значения четвертой компо-
ненты тока J4 или, что удобнее, величину w(x) = Jjie
в одночастичном состоянии Y(1) (16.12). На основании
(16.11) и (16.13) имеем
= i (ф* (х)^г~^Ф W) >	(16.16)
причем ф(х) определяется формулой (16.13), где инте-
грирование по d3k распространено только по положитель-
ным энергиям: kx = kx — ®t, со = 4-)/Л2 + т2. Величина W,
выражающаяся формулой
W = (ф, ф) ^^w(x)d3x=i У —jfi-q^d3x9 (16.17)
сохраняется в силу уравнения непрерывности (16.9):
=	d3x — — J div J d3x = \JNda = 0. (16.18)
Обобщенную величину
(Ф, 4>) = i
(16.17')
можно рассматривать как скалярное произведение двух
одночастичных функций: ф и ф. Если в качестве этих
функций взять фундаментальные решения
Фй (х) =
i (kx~ со/)
(2л) /г л
(16.19)
90
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
[ГЛ. III
то они образуют полную систему функций, причем усло-
вие полноты при t=^t' гласит:
$ <Рб (*) <P/e (*') d?k = А+ (х—х'),	(16.20)
где функция А+ (х) равна
• р i (kx—CD/)
д+(*)=7оЦз £----------d3k. (16.21)
' 7	(2л)3 J со	'	7
В силу этого обстоятельства функция 63(х — х'), соот-
ветствующая «точной» локализации бозона, не принад-
лежит к классу функций, представимых разложением
(16.13). Пользуясь тем, что одночастичная волновая
функция ср (х) с определенным знаком энергии удовле-
творяет уравнениям
. dtp •дф* ~ * — 1 -^-=СОф •,	(16.22) (16.22')
где оператор о/ равен
<о =	—	(16.23)
используя формулу (16.11), плотность ш(х) можно пред-
ставить в виде
w (х) (й)ф*ф + ф*аир).	(16.24)
Уже из вида формулы (16.24) видно, что она сама собой
не гарантирует положительной дефинитности. В допол-
нении III приведен пример состояния бозонного поля,
описанного суперпозицией двух волн ф2 и (pj с сильно
различающимися импульсами k2 и kr и имеющих энер-
гию одного и того же знака (й)2^>(0! > 0):
Ф W
С1 । Cq
77= Фх + -Гг= ф2-
у 2©! У 2со2
(16.25)
В этом случае
®(х, 0	^П- |^|соз[(#2 — kt,x)—(®2—®i)/+a]| ,
(16.26)
S 17j
ЛОКАЛИЗАЦИЯ ФОТОНОВ
91
и если |c2/cil> 1, то эта плотность осциллирует в про-
странстве с периодом порядка 1/| Л?2 — Л?х| и осциллирует
во времени с периодом 1/| со2—сох |.
Физически наблюдаемой и положительно дефинитной
величиной в случае бозонного поля является плотность
энергии этого поля е(х); оператор этой величины 8 (х)
может быть выведен из тензора энергии-импульса бозон-
ного поля: х
— дх^ Qxv 2 °“Ц дх^ дх^ 1П р
Отсюда
8(х) = — Г4Дх) = у(^^ + уФ+?ф + т2(₽+ф)-	(16.28)
Стало быть, среднее значение е(х) в состоянии ЧГ(1)есть
е(х) = <Т(1)|е(х)|¥(1)> =
= 4 (^‘ll + V,P*VrP + mVv) >0.	(16.29)
§17. Локализация фотонов
Электромагнитное поле принадлежит к классу бозон-
ных полей, но, в отличие от скалярных мезонных полей,
оно описывается векторным оператором—оператором век-
тор-потенциала Ли(х), где р = 1, 2, 3, 4, с компонентами
л (Л1, Л2, Л3), ф=—д4.
Этот потенциал определен с точностью до градиент-
ного преобразования:
А^х)=А^х) + д-Ш,	(17.1)
где f (х)—произвольная функция, удовлетворяющая урав-
нению Даламбера:
□ VW = °-	<17J')
Ввиду этого произвола собственные значения вектор-по-
тенциала не являются физически измеримыми величинами.
92
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
(ГЛ. Ш
Измеримыми величинами являются компоненты антисим-
метричного тензора электромагнитного поля:
дА р 		и	у ^v~dxv дх^	(17.2)
или, в векторных обозначениях,	
„	1 дА 8=-р>-v<₽»	(17.2')
^?=rot А,	(17.2")
где g есть оператор напряженности электрического поля,
а —оператор напряженности магнитного поля.
Особенностью свободного электромагнитного поля яв-
ляется его поперечность. Поэтому из четырех компонент
вектора Лц только три независимы. Это накладывает
условие на выбор волнового функционала Т:
(¥ Т) = 0.	(17.3)
Если это условие соблюдено в начальный момент времени,
то оно, как можно показать, будет соблюдаться и в даль-
нейшем в силу уравнений движения*). При соблюдении
условия (17.3) уравнение для вектор-потенциала электро-
магнитного поля гласит:
□ 2Ли = 0.	(17.4)
Правила коммутации операторов А записываются в форме:
[ЛДх), 4V (%')] = — iD(x—х')8^,	(17.5)
причем D (х) при т = 0 имеет вид
где со = | Л|. Разложение вектор-потенциала по фундамен-
тальной системе функций имеет вид
4
= 2 d3ke^ [Л (Л) U (Л) е1кх+ At (fe) U* (k) e~ikx], (17.7)
Л= 1
*) Подробности о квантовании электромагнитного поля см. в [371
или [38].
§ 17]
ЛОКАЛИЗАЦИЯ ФОТОНОЁ
93
где U (к) = 1/К2ш, kx=kx—со/, суть компоненты еди-
ничного вектора, определяющего поляризацию, а /U(ft)
и Ah(k)—операторы амплитуд парциальных волн. Заме-
тим, что в этом разложении участвуют все четыре поля-
ризации (две поперечные, одна продольная и одна вре-
менная). При соблюдении условия (17.3) на основании
уравнений (17.2') и (17.2") для наблюдаемых величин ё
в УС получим разложения
2
ё(х)= 2 р3^(ЛН*)^(х)-Л1(й)^(х))е\	(17.8)
Л=1 v
2
^(х) = j 2 d3k [keK\ (А (Л) ик (х) - At (£) и*к (х)),(17.8')
Л=1
где участвуют лишь две поперечные поляризации: %= 1, 2.
Из правил коммутации (17.5) следуют условия коммута-
ции для амплитуд ЛДЛ):
[Л (ft),	(ft')] = S3 (ft-ft') 6U„	(17.9)
[A(ft), 4Uft')] = H\+(*)> A,(ft')] = 0. (17.9')
Единственной физически наблюдаемой величиной, которая
подчиняется закону сохранения, в случае векторного поля
является тензор энергии-импульса поля 7\v(x); оператор,
представляющий этот тензор, имеет вид
отсюда имеем
ты (X) = - | (82+^2),	(х) = - i (8 х - iSk.
(17-11)
Закон сохранения для тензора (х) гласит:
= 0>	(17.12)
в частности, для оператора плотности энергии
е(х) = -Л«(х)	(17-13)
94
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
[ГЛ. Ill
получаем из (17.12)
-^-+div5(x) = 0,	(17.14)
С/*
где S (х) есть оператор вектора потока энергии, имеющего
компоненты S (х) =	Обратимся теперь к однофо-
тонному состоянию с неопределенным импульсом k.
Для этого заметим, что операторы амплитуды Д%(й),
Лх (А?), в силу правил коммутации (17.9) и (17.9'), дей-
ствуют на волновой функционал Т совершенно таким же
образом, как рассмотренные ранее в § 16 операторы ска-
лярного поля (ср. формулы (16.7) и (16.7')). Для одно-
фотонного состояния этот волновой функционал имеет вид
Т(1) = $ЛДЛ)^6(пДЙ)-1) П II ММ*')], (17.15)
где А % (А?) —-произвольная амплитуда волны с волновым
вектором k и поляризацией X (Х= 1, 2).
Пользуясь правилами действия операторов (fe), A£(fc)
на волновой функционал (эти правила выражаются фор-
мулами, в точности совпадающими с формулами (16.7)
и (16.7') для операторов скалярного поля a(k) и а+ (А?)),
найдем, что матричный элемент оператора Ах(х) равен
Ах(х) = <Т(0) | Ак(х) |¥(1)> = $ Лх (Л) U (к) d’k.
(17.16)
Функция /Ц(х) содержит только положительные частоты
и поэтому удовлетворяет уравнению Шредингера:
дА« (%)
1-^ = <>>АК(х),	(17.17)
где w = + K—А2- Подобному же уравнению удовлетво-
ряет и сопряженная функция ЛЦх):
_1-Лф^ = оДх+(х).	(17.17')
Однако ввиду несамосопряженности оператора со величина
Л^Лх не подчиняется какому-либо уравнению сохранения.
Как уже отмечалось, величиной, сохраняющейся и со-
ставленной из реально измеримых (наблюдаемых) величин,
§181 РАСПЛЫВАНИЕ РЕЛЯТИВИСТСКИХ ПАКЕТОВ	95.
является величина плотности энергии s(x) =— Т44(х),
которая выражается через электрическое g (х) и магнитное
(х) поля.
Нетрудно вычислить, что среднее значение плотности
энергии 8 (х) в однофотонном состоянии равно
8 (х) = <Т (1) | е (х) | Т (1)>«
= 1 [8 (х) 8* (х) + (х)	(х)],	(17.18)
где 8 (х) и (х) суть матричные элементы операторов
g (х) и ^?(х) для квантового перехода Т (0) —(1).
Таким образом, в случае свободного электромагнитного
поля нельзя построить величину, которая могла бы играть
роль плотности вероятности нахождения фотона в том или
ином месте пространства в заданный момент времени.
Однако существует плотность энергии, которая может быть
сосредоточена в какой-либо ограниченной области про-
странства.
§ 18. Расплывание релятивистских пакетов
В предыдущих параграфах были рассмотрены состоя-
ния, соответствующие сильной локализации квантовых
полей (локализованные пакеты).
Такие состояния не являются стационарными, а изме-
няются с течением времени, и притом таким образом, что
степень локализации поля уменьшается: первоначально
острый волновой пакет расплывается так, что величины
Дх2, Az/2, Az2 возрастают со временем. Характерные черты
этого расплывания являются общими для всех полей,
поэтому достаточно рассмотреть скалярное поле. Возьмем
волновой пакет в форме *)
ф(х, 0 = ^^-el^x-^d3k	(18.1)
(со = +	+ и положим
c(A.) = JVexp-fc^,	(18.2)
J) См. [30].
!96
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
[ГЛ. III
где W есть нормировочный множитель: N
так как плотность р(х, t) равна
1/)/Ь3 /л3;
р(х, о =
(18.3;
<го локализация при t = 0 будет сильной, если ср (аг, 0),
или дф*(х, 0)/д^, или обе эти величины сильно локали-
зованы.
Подставляя (18.2) в (18.1), найдем
(k —
Xz
= — ieik^x £=-=== ,	(18.4)
V а? Ул3
где а=\/Ь и а—>0 при Ь—^оо, так что состояние (18.1)
принадлежит к классу состояний, сильно локализованных
при = 0.
При t > 0 будем иметь
iNel^x-^I(x, t),	(18.5)
<p(x, /)*= — е{^х~^Цх, f),	(18.5')
где
Цх, t) =
= \d3kexp [——+ i(ft —ftjx—i(to—(Oj)^ , (18.6)
причем в формуле (18.5') предположено, что \кг\^>Ь.
Для определенности направим вектор к± по оси Ох так,
что fti = (^ix, 0, 0). Тогда
и q = k—kt. Простое вычисление ведет к результату
I (х, о==^Х^)ехР га(*> о
___(X—PA.Z)2	у2+г2 ~
2Д2	2Aj_ _
(18.8)
§181 РАСПЛЫВАНИЕ РЕЛЯТИВИСТСКИХ ПАКЕТОВ	97
где A (t) — медленно меняющаяся величина, а—действи-
тельная фаза, а величины Д ц и Д^_ равны соответственно
= +	(18.9)
Д1(0 = 72+-5-^.	(18.9')
Полагая А2 (0) = 1Д>2, эти формулы можно переписать
в виде
Дц (/) = А3(0) +	(18.10)
Д1(/) = А2(0) + ^^?,	(18.10')
где K = iilp есть длина волны, р—импульс частицы,
v = дЕ/др = р/Е—ее скорость.
Из формулы (18.10) видно, что при /п = 0 волновой
пакет не расплывается в продольном направлении, как
это и должно быть для частиц с массой покоя т = 0
(в этом случае волны де Бройля не имеют дисперсии
в пустоте, так что d®/dk = c = const).
Что касается формулы (18.10'), то она совпадает с фор-
мулой (12.19), выведенной из теории дифракции для пучка,
выходящего из узкой щели шириною А(0) = я.
Однако имеются существенные различия в поведении
релятивистского и нерелятивистского пучков. Действи-
тельно, ширина пучка растет пропорционально h2t2v2
(см. 12.19); в нерелятивистском случае h2v2==\v2 ==
= — = const, а в релятивистском —XV=s^z/£z, при
Е>• оо, А.2и2—>0. Для дисперсии в продольном направ-
лении (в нерелятивистском случае она такая же, как и
в поперечном направлении (Дц =Д±)) в релятивистском
случае появляется дополнительный множитель (т/Е)*
стремящийся к нулю при £—>оо, который существенно
уменьшает рост Дц (t) с течением времени. В этом выра-
жается тенденция к поведению, сходному с поведением
частиц без массы покоя, для которых Дц(£) = const.
Переписав формулу (18.10) в виде
Ар
А2 (0)

Д2±(/>Д2 (0)
(18.10")
4 д. и» Блохинцев
98
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
[ГЛ. III
где Ло = h/mc, мы можем трактовать уменьшение скорости
роста (0 как эффект замедления времени t'= а
для движущейся системы-—как эффект «близнецов»: время
жизни быстро движущегося пакета возрастает в Е/т раз.
Таким образом, релятивистские эффекты оказывают
стабилизирующее влияние на волновые пакеты.
Рассмотренные выше особенности релятивистских паке-
тов являются общими для полей различной ковариантно-
сти, что видно из того обстоятельства, что все эти черты
связаны не столько с видом амплитуды пакета с (к),
сколько с законом дисперсии волн де Бройля в пустоте:
о8-11»
который ведет себя совершенно различным образом при
k^>tn и k<^jn.
§ 19.	Координата Ньютона—Вигнера
Как было показано ранее, в релятивистском случае
S (х) не может быть собственной функцией оператора
координаты элементарной частицы, так как не может быть
построена из состояний с положительной энергией.
В этой связи Т. Ньютон и Е. Вигнер [39] ввели новый
оператор положения частицы q, свойства которого опре-
деляются исходя из понятия локализованного состояния ф.
Они постулируют следующие свойства состояний, пред-
ставляющих частицу, локализованную в момент времени t
в точке х == у = z = 0:
а)	эти состояния образуют линейную совокупность,
т. е. суперпозиция двух локализованных состояний есть
также локализованное состояние;
б)	эта совокупность преобразуется сама в себя при
вращениях около начала координат и при отражениях
пространственных и временных;
в)	если ф есть локализованное состояние, то простран-
ственное смещение этого состояния делает его ортогональ-
ным к состояниям, локализованным в начале координат;
г)	должны выполняться некоторые требования регуляр-
ности, позволяющие применять к локализованным состоя-
ниям операторы группы Лоренца.
§ 191
КООРДИНАТА НЬЮТОНА
ВИГНЕРА
99
Найти эти состояния особенно просто в случае бесспи-
новой частицы.
В импульсном представлении волновая функция бес-
спиновой частицы ф есть функция импульса k и k0 = со =
= +
Из требования б) в случае скалярных частиц вытекает,
что ф есть функция от k2 или, что то же, от со, т. е.
гр = (со).
Используем теперь требование в). Оператор простран-
ственного смещения Т3 (а) в импульсном представлении
сводится к умножению на eika:
Ф (Л) = f з (а) ф (со) =з eikaty (со).	(19-1)
Это состояние должно быть ортогонально к состоянию,
локализованному в начале координат, т. е. к ф(со). В ка-
честве ф (Л) и ф (со) мы возьмем ковариантные амплитуды
в разложении
4>(x)=^^(k)elkx
(19.2)
так что ф (fe) = A (k) К® и 1]) (со) = В (со) |Ло. Согласно
(16.17') скалярное произведение ф на ф будет иметь вид
(ф'Ф) = j <р*ф ;	(19.3)
подставляя сюда значения ф и ф, получим
e-ika d3k = 0,
СО
(19.4)
если а#=0. Отсюда следует, что [ ф (со) |2/со = const, т. е.
ф(со) & со1/*; например, можно положить
Ф(®)
___ со1/2
(2л)3/2'
(19.5)
Применяя к (19.5) оператор смещения, получим функ-
цию, представляющую собой состояние, локализованное
около точки х:
(k) = Т (х) ф (со) = eikx.
(19.6)
4*
100
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
[ГЛ. Ш
Нетрудно убедиться, что эта функция есть собственная
функция оператора qx.
который и является оператором координаты элементар-
ной частицы по Ньютону —Вигнеру.
Действительно, применяя оператор qx к функции (19.6),
получим
q>$x (k) =	(*)>	(19.8)
так что х есть собственное значение оператора qx в со-
стоянии фх(Л), локализованном около точки х при / = 0.
Обратимся теперь к координатному представлению со-
стояния, локализованного около точки х = 0 в момент
времени / = 0. Согласно (19.2) и (19.5) имеем
(19'9>
где есть функция Ганкеля первого рода порядка * б/4.
При г —> 0 ф (г)	при г —> оо	ф (г) &е~тг.
Отсюда видно, что область локализации состояния-' по
порядку величины определяется комптоновской длиной
волны частицы iilmc (в формуле (19.9) с=1 и ^=1).
Из поведения в нуле функции ф (г) следует, что лока-
лизованные состояния принадлежат к классу ненорми-
руемых.
Рассмотренное в этом разделе «локализованное» со-
стояние ф (со) и новый оператор координаты qx естественно
вытекают из принятых выше постулативных требований
а), б), в), г) *). Однако физическая интерпретация этих
состояний и операторов qx, qy, qz связана с рядом труд-
ностей, не позволяющих этим операторам конкурировать
с обычными координатами х, г/, г.
Первая из этих трудностей заключается в том, что
состояние, локализованное при t = 0 в точке х = 0 в одной
системе координат, не будет локализованным (в смысле
выполнения условий а), б), в), г)) в движущейся системе
♦) Заметим, что так как мы ограничились случаем бесспиновых
частиц, то нам не было необходимости использовать все пункты а),
б) в), г).
§ 2oj	ИЗМЕРЕНИЕ КООРДЙЙАТ МЙКРОЧАСТЙЦЫ	101
координат, даже если точки х = 0 и х' = 0 совпадают
при l-=t' = 0. В силу этого обстоятельства операторы
дь <7j/> Яг не обладают свойствами релятивистской кова-
риантности.
Вторая трудность заключается в том, что нельзя ука-
зать даже мысленный опыт, который позволил бы изме-
рить операторы qx, qy, qz, иными словами, выделит
локализованное состояние ф(со).
Создается впечатление, что оператор координаты Нью-
тона-Вигнера q является оператором координаты центра
тяжести волнового пакета <р(р), представляющего состоя-
ние, которое по определению называется локализованным.
Ввиду этих затруднений мы предпочитаем работать
«со старыми» координатами х, у, г и /, которые могут
быть измерены, по крайней мере в мысленном опыте.
Такой опыт основан на допущении возможности полу-
чения как угодно узких пучков, как угодно короткой
длины волны X—>0) и, стало быть, на допущении прин-
ципиальной возможности существования сколь угодно
узких диафрагм (а—^0).
Хотя такие допущения и представляются весьма фор-
мальными, тем не менее они имеют преимущество опре-
деленности.
§ 20. Измерение координат микрочастицы
в релятивистском случае
Постановка задачи об измерении координат микро-
частицы в релятивистском случае весьма сходна с тако-
вой в нерелятивистском случае, которая была подробно
рассмотрена в §§ 11, 12.
Так же как и в нерелятивистском случае, мы должны
различать прямое и косвенное измерение.
В случае прямого измерения речь идет об измерении
координаты свободной частицы. В § 14 было показано,
что для частиц со спином 1/2, подчиняющихся уравнению
Дирака, допустимы одночастичные состояния с положи-
тельной энергией, как угодно точно локализованные около
точки х = хг в момент времени t — t'. Из законов расплы-
вания таких состояний следует, что этот крайне локали-
зованный волновой пакет состояния будет расширяться
102
МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ
|ГЛ. III
со скоростью света, если только он сам не движется
с очень большой скоростью, так что средний импульс ча-
стицы в таком пакете р^>тс (т — масса частицы).
В этом случае (см. § 18) продольное расширение пакета
практически прекращается, а скорость поперечного рас-
ширения уменьшается в т/Е раз (Е ]/р2-{-т2).
Локализованные одночастичные состояния в случае
частиц со спином 0 (подчиняющихся уравнению Клейна —
Гордона) и со спином 1 (фотоны, подчиняющиеся урав-
нениям Максвелла) существуют разве в виде специальных
исключений.
Как было показано в § 16 и § 17, в этих случаях
разумнее говорить о локализации мезонного поля, нежели
о локализации мезонов или фотонов. Другая особенность
релятивистского случая заключается в значительном умень-
шении произвола в выборе возможных взаимодействий:
взаимодействие должно подчиняться определенным требо-
ваниям релятивистской инвариантности. Однако эти тре-
бования все же оставляют еще широкие возможности
для обсуждения мысленных опытов, так как теория отно-
сительности не накладывает никаких ограничений на массы
и заряды частиц, кроме ограничения, относящегося к усло-
вию существования частиц в связанном состоянии. Именно,
энергия связи частиц должна быть существенно меньше
ее собственной энергии:
АЕ<тс2.	(20.1)
Обратимся теперь к обсуждению прямого измерения
координаты, рассмотренного для нерелятивистского случая
в § 12. Мы можем, как и в § 12, считать, что атом фото-
пластинки является бесконечно тяжелым (7Ис2^>Е, Е —
энергия частицы) и поглощаемая при возбуждении атома
энергия & = 8п — 80 также мала в сравнении с энергией
частицы (Е^>е), координату которой мы измеряем. Для
того чтобы придать релятивистски инвариантный вид
6-образному взаимодействию (12.2), мы можем считать,
что оно обусловлено обменом очень тяжелыми мезонами.
В этом случае
р~г/а
W = g^-r~,	(20.2)
§ 20]	ИЗМЕРЕНИЕ КООРДИНАТ МИКРОЧАСТИЦЫ	ЮЗ
где а — комптоновская длина гипотетического тяжелого
мезона, g — константа связи, г =	—Q)2. В пределе
бесконечно тяжелого мезона а—>0 функция (20.2) сосре-
доточивается в объеме порядка а3—>0. При указанных
выше условиях атом фотопластинки остается нерелятивист-
ской системой и релятивистское рассмотрение распростра-
няется только на описание движения свободной частицы,
координату которой определяют с помощью наблюдения
последствий возбуждения атомов фотопластинки, и на ее
взаимодействие с этими атомами.
В борновском приближении, в котором мы и проводили
расчет в § 12, релятивизм не внесет никаких изменений
принципиального характера в те выводы, которые были
сделаны в § 12 относительно физических процессов при
таком измерении. В частности, замена 6-образного взаи-
модействия (12.2) на взаимодействие посредством ультра-
тяжелых мезонов (20.2) и замена шредингеровской волно-
вой функции на четырехкомпонентный спинор, удовлетво-
ряющий уравнению Дирака, оставляют в силе вывод о
том, что при малых промежуточных временах (ср. (12.8))
возбуждение атома сопровождается локализацией микро-
частицы вблизи атома. Этот же вывод сохраняет свое
значение и для мезонов, удовлетворяющих волновому
уравнению Клейна.
Обратимся теперь к косвенному измерению. В этом
случае речь идет об измерении координаты частицы, на-
ходящейся в связанном состоянии, с помощью наблюдения
рассеяния узкого пучка-щупа. Прежде всего'следует заме-
тить, что поскольку мы предполагаем, что микрочастица,
находящаяся в связанном состоянии, сохраняет свою инди-
видуальность, то тем самым мы уже предопределяем ма-
лость масс-дефекта АВ по сравнению с собственной
энергией частицы тс2. В силу этого релятивистские эффекты
будут носить характер поправок, не могущих повлиять
на основные выводы, сделанные в § 12 при обсуждении
нерелятивистского косвенного измерения. Более сущест-
венным является то обстоятельство, что узкий пучок,
необходимый для прощупывания местоположения связан-
ной микрочастицы в релятивистском случае, по причинам,
описанным в § 18, может быть сделан значительно более
узким и имеющим значительно меньший угловой раствор,
нежели это допустимо для нерелятивистских пучков,
104	МИКРОМИР В РЕЛЯТИВИСТСКОМ СЛУЧАЕ [ГЛ. III
В заключение этого обсуждения —несколько разъяс-
нений касательно возможности реализации таких узких
пучков-щупов. Речь идет, конечно, не о практической их
реализации, а лишь о мысленной возможности, совмести-
мой с принципами теории. Необходимую узкую щель
шириной а^>к (при ft.—^0) мы можем представить себе
сделанной в диафрагме, которая образована сильно погло-
щающим веществом. Если необходимое поглощение обу-
словлено рождением новых очень тяжелых и, следовательно,
медленных частиц, то их рождение не будет «загрязнять»
наш пучок-щуп. Существование диафрагмы с такими свой-
ствами не противоречит принципам квантовой теории
поля и поэтому может служить формальным основанием
для рассмотрения крайне узких пучков и малых волновых
пакетов (см. дополнение IV).
ГЛАВА IV
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ
ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
§ 21. Поляризация вакуума. Размер электрона
Анализируя возможности измерения пространственно-
временных координат элементарной частицы, мы пред-
полагали сами частицы точечными. Поэтому точность опре-
деления координат микрочастицы ограничивалась возмож-
ностью создания как угодно узких пучков-зондов, обла-
дающих контактным взаимодействием с микрочастицей,
положение которой в пространстве—врёмени измеряете
таким зондом. Последнее требование о контактности взаимо-
действия необходимо, чтобы исключить эффекты, связан-
ные с существованием конечного (или даже бесконечного)
радиуса взаимодействия.
Как было показано, теория в принципе допускает та-
кую возможность в форме мысленного эксперимента.
Однако из этой же теории следует, что физическая кар-
тина точечной частицы является на самом деле прибли-
женной. В высших приближениях по степеням константы
взаимодействия возникают эффекты, которые могут^рас-
сматриваться как проявление структуры частиц. Эта
структура носит динамический характер, и ее не удается
свести к распределению в пространстве какого-либо ве-
щества'
Мы начнем рассмотрение вопросов структуры с про-
стейшего случая бесконечно тяжелой, точечной, электри-
чески заряженной частицы. Такая частица создает во-
круг себя кулоновское поле, потенциал которого равен
V(r)=y,	(21.1)
где е—заряд частицы, а г—расстояние от частицы до
точки наблюдения.
Взаимодействие этой частицы с другой заряженной
частицей, которая рассеивается на первой, может быть
106
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
представлено диаграммой Фейнмана, изображенной на
рис. 15, а, М означает тяжелую точечную частицу,
линия 1—2 показывает вход и выход рассеивающейся
частицы, а пунктирная линия q—линию виртуального
фотона, который передает импульс от одной частицы к
Рис. 15. а) Диаграмма, описывающая рассеяние заряженной частицы
(линия 1—2) на бесконечно тяжелой (неподвижной) заряженной
частице М; q—виртуальный фотон, б) Диаграмма, учитывающая
поляризацию вакуума. Эта диаграмма дает поправки к закону Кулона,
обусловленные поляризацией вакуума, q и qr—виртуальные фотоны,
е+, е~—позитрон и электрон виртуальной пары.
другой. Помимо этой простейшей диаграммы есть и дру-
гие диаграммы, дающие вклад в рассматриваемый про-
цесс. Одна из них изображена на рис. 15, б. Эта диаграм-
ма описывает рождение пары позитрон — электрон (петля
е+, е") виртуальным фотоном q, аннигиляцию этой пары
с последующим испусканием фотона q, который опять
же обусловливает обмен импульсами между частицами.
Эта сложная диаграмма учитывает, в первом неисчезаю-
щем приближении, эффект поляризации электронно-по-
зитронного поля кулоновским полем тяжелой частицы М.
Расчет этого эффекта весьма громоздок, и мы отсылаем
читателя за необходимыми выкладками к курсам кванто-
вой электродинамики*).
Вычисление показывает, что учет поляризационных
поправок приводит к новому выражению для потенциала
точечного заряда, именно вместо (21.1) получается
V (/)=££>,	(21.2)
*) См., например, гл. VIII в [37], гл. VI в [38].
§ 21]*
ПОЛЯРИЗАЦИЯ ВАКУУМА. РАЗМЕР ЭЛЕКТРОНА
107
где величину е(г) называют эффективным зарядом. Как
показывает вычисление, эффективный заряд оказывается
равным:
(eh 4-^-ln M-Y + • • для г Л, (21.3)
I I	ОЭ1 \ '	/	J
е(г) =5 (	г .1	\»/	1
e l	л / И) +  • • }дляг>Л. (21.3')
Здесь a = e*rfic, А.=%!тс, т—масса электрона. Из этих
формул видно, что эффективный заряд при малых г ве-
лик; по мере возрастания расстояния г этот заряд все
сильнее и сильнее экранируется поляризацией вакуума,
так что при г^>Л он становится равен заряду частицы е,
наблюдаемому макроскопически*). Из формулы (21.3')
видно также, что эффективный заряд распределен в обла-
сти, размер которой по порядку величины равен компто-
новской длине электрона (Й//пс = 3,86-10"11 см). Суще-
ствование поляризации вакуума приводит к принципиаль-
ной возможности рассеяния света на бесконечно тяжелой
заряженной частице.
Известно, что в силу линейности уравнений Максвел-
ла статическое поле и поле волны накладываются друг
на друга без искажения. Поляризация вакуума нарушает
эту линейность. В первом неисчезающем приближении
взаимодействие кванта света с полем тяжелой частицы
через поляризацию вакуума описывается диаграммой, при-
веденной на рис. 16. Внешние линии 1 и 2 показывают,
как и ранее, вход и выход рассеивающего фотона. Круг
из линий е± иллюстрирует образование виртуальных пар
позитронов и электронов, порождающихся при поляриза-
ции вакуума; линии q, q' — линии виртуальных фотонов,
передающих импульс тяжелой заряженной частице М.
Следует иметь в виду, что при взаимодействии фотона
с тяжелой заряженной частицей (например, с ядром ато-
ма) при частоте фотона со|>2тс2/^ преобладающим эф-
фектом будет рождение пар позитронов и электронов
(е+, е") и, следовательно, поглощение фотона. Это погло-
щение ведет к упругому дифракционному рассеянию фо-
*) Следует, однако, иметь в виду, что формулы (21.3) и (21.3')
являются приближенными и справедливы лишь до тех пор, пока ПО’
правки | е (г) —е | малы по сравнению с е,
108
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
1ГЛ. IV
тона. Полное сечение
из сечения
ния упругого рассеяния,
упругого рассеяния ауп складывается
упругого^дифракционного рассеяния ОуП и сече-
связанного с поляризацией ваку-
ума* ОуП, которая обусловле-
на процессом, показанным
на диаграмме (рис. 16).
Так как сечение рожде-
ния пар а± велико, отноше-
ние (Ууп к ОуП мало:
Рис. 16. Диаграмма, описыва-
ющая рассеяние света на не-
подвижной заряженной частице
М. Рассеяние фактически проис-
ходит на электронах и позит-
ронах (е^) поляризованного ча-
стицей М вакуума; здесь так
же, как на рис. 15, q и q' —
виртуальные фотоны, е±—вир-
туальные пары.
Оуп   3 / тс2
Оуп л2 \ ha)
(ср. [37], § 55).
Заметим, что при часто-
тах ©<^2тс2, когда реаль-
ные пары позитронов и элек-
тронов урождаться не могут,
эффект поляризации вакуума
jln^- (21.4)
/ тс2
может быть описан с помощью
тензора диэлектрической по-
стоянной вакуума &{к и тен-
зора магнитной проницаемос-
ти
^k = 8lk + -^{2(^ + ^)8lk + 7^k},	(21.5)
© о
pik = 8tk + -L{2 (8a-№)^-7^J, (21.5')
© о
где 8, напряженности электрического и магнитного
полей, St и [(i=l, 2, 3) —проекции этих векторов
на оси координат, <£0—некоторое критическое поле, опре-
деляемое по порядку величины соотношением
^о^=2тс2,	(21.6)
т. е. разность потенциалов в таком поле на протяжении
к/тс равна энергии, необходимой для рождения пар.
Таким образом, в результате поляризации вакуума во-
круг заряженной частицы создается связанная с ней
заряженная «атмосфера», протяженность которой опре-
деляется комптоновской длиной волнь) электронов ft/mc.
§22]
ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА НУКЛОНОВ
109
В силу этого явления частица теряет свою точечную при-
роду.
В частности, если мы представим себе, что частица
локализована в очень узком волновом пакете, размеры
которого меньше Тъ/тс, то ситуация будет соответствовать
рассмотренному выше случаю покоящейся тяжелой части-
цы: вокруг частицы в области порядка it/mc создается
заряженная зона, за счет которой может осуществиться
взаимодействие такой частицы с частицей зонда, и поэтому
будет возникать неустранимая неопределенность в опре-
делении положения частицы, равная по порядку величины
Ах~—=3,86-10"11 см.	(21.7)
В случае электромагнитных взаимодействий эта ат-
мосфера очень «разрежена», что следует из малости кон-
станты электромагнитных взаимодействий a=e2/fic= 1/137.
Поэтому случаи взаимодействия в «атмосфере» частицы
в области поляризации вакуума будут крайне редки по
сравнению со случаями точечного взаимодействия: в пода-
вляющем большинстве случаев неопределенность в опре-
делении координат частицы не будет связана с протяжен-
ностью атмосферы частицы.
В частности, поправки к рассеянию электронов, к ком-
птон-эффекту, к тормозному излучению и другим элек-
тромагнитным эффектам, обусловленным поляризацией
вакуума в окрестности электрона (или позитрона), весьма
малы (см. [37]).
§ 22. Электромагнитная структура нуклонов
Совсем иная ситуация имеет место в тех случаях, ко-
гда протяженность атмосферы частицы возникает за счет
сильных взаимодействий. Из-за значительной величины
константы сильных взаимодействий g (g2/4rific== 16) атмо-
сфера, возникающая вокруг сильно взаимодействующих
частиц, ни в коем случае не является разреженной.
Иллюстрацией к этому утверждению может служить
электромагнитный форм-фактор *) нуклонов, определяю-
*) Этот термин заимствован из теории рассеяния рентгеновских
лучей. «Форм-фактор» учитывает в этой теории неточечный характер
распределения зарядов и токов внутри атрмр^.
по
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
(ГЛ. IV
щий распределение токов и зарядов в нуклоне. Диаграм-
ма Фейнмана на рис. 17, а представляет процесс рассея-
ния на протоне, причем электрон считается точечным.
Линии 3 и 4 суть линии, изображающие рассеивающий-
ся электрон; 1 и 2— линии протона, Г — вершинная часть,
которая изображена заштрихованным треугольником,
чтобы подчеркнуть протяженный характер нуклона, q —
Рис. 17. а) Жирная линия 1—2 — линия протона; q — виртуальный
фотон; линия 3—4—линия рассеивающегося на протоне электрона,
Г — вершина, область около протона, излучающая или поглощающая
виртуальный фотон, б) Эта диаграмма вскрывает структуру вершины Г
(в первом приближении); в вершине А излучается л +-мезон, который
в вершине В излучает виртуальный фотон q в вершине С л+-мезон
поглощается виртуальным нейтроном (линия АС), который превра-
щается в рассеянный протон (2).
линия виртуального фотона, обеспечивающего обмен
импульсом между протоном и электроном. На рис. 17, б
приведена диаграмма, которая поясняет происхождение
протяженности нуклона: в узле А протон посредством
сильного пион-нуклонного взаимодействия испускает л+-
мезон и превращается в нейтрон (линия п); л+-мезон в
точке В испускает (или поглощает) виртуальный квант
q, и, наконец, в точке С этот мезон поглощается нейтро-
ном, который превращается в рассеянный протон (ли-
ния 2). Благодаря описанному процессу вокруг протона
создается пионная атмосфера, которая и порождает эф-
фект протяженности нуклона. Размер этой атмосферы
определяется комптоновской длиной волны мезона
tvlmc=\,A - 10"хз см.
Рассмотренная нами диаграмма, поясняющая проис-
хождение протяженности нуклона, имеет условное зна-
§22]
ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА НУКЛОНОВ
111
чение: благодаря значительной величине константы вза-
имодействия пионного и нуклонного полей вклад других
диаграмм, описывающих процессы с большим числом
виртуальных мезонов, не может быть малым. Кроме того,
оказываются существенными резонансы во взаимодейст-
виях этих мезонов между собою. По этой причине расчет
эффектов, обязанных своим существованием мезонной
атмосфере нуклона, представляет значительные и еще не
преодоленные до конца трудности.
Однако можно построить феноменологическую тео-
рию мезонной атмосферы нуклона в терминах форм-фак-
торов. Для этой цели вычислим матричный элемент от
вершинной частицы Гц(х2, хх, у), не ограничивая себя
простейшими диаграммами, типа изображенной на рис.
17, б, так как такое ограничение в случае сильных взаи-
модействий вообще не обосновано*).
Величина Гр, (х2, хх, у) представляет собою нуклонный
ток с учетом всех эффектов взаимодействия с вакуумом.
Удобнее вычислить матричный элемент от энергии взаи-
модействия этого тока с полем виртуального фотона,
которое мы будем описывать вектор-потенциалом
(22.1)
Эта энергия взаимодействия равна
W (х3—хх) = 5 Гц(х2. х1г y)Ail(y)d*y. (22.2)
Заметим, что в силу однородности вакуума величина Гц
трансляционно инвариантна и, следовательно, зависит
лишь от разности координат х2, xlt у, поэтому мы можем
вместо этих координат ввести более удобные х = х2 — хг
и Х = у —Тогда
Гц (х2, хх, у)	Гц (X, х) =
= (гМ (“> ₽)е£ (“х+м	(22.3)
так что Гц (а, (3) есть фурье-образ от ГИ(Х, х).
В дополнении VA для пояснения приведено вычисление вер-
шины Гц (х2, хх, у) на основе теории возмущений (диаграмма
рис. 17, б); это простое вычисление годилось бы в случае слабей связи
между нуклонами и мезонами.
112	РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ [ГЛ. IV
Условие сохранения тока, эквивалентное калибровоч-
ной инвариантности, требует, чтобы
или
Гц (а, Р)аи=0.	(22.4')
Вычислим теперь матричный элемент от энергии W (х2—лу)
для перехода нуклона из состояния с импульсом pi = Pt
в состояние с импульсом р2 = ру. Эти состояния описы-
ваются спинорами
'^f(x2) = uf{p/)eipfXt, 'ф£(х1) = цг(р1-)е’1'/,гх‘. (22.5)
Имеем
(f I W I 0 = 5 ’Ь' (хг) W	~X1) (xi) d*Xi- <22-6)
Подставляя сюда W (x2—xx) из (22.2) и пользуясь (22.3),
получим
(f | F | i) = (2л)4 64 (pf — pi+q) uf (j}f) Гц (q, P) ut (pt) (q).
(22.7)
Таким образом,
(/|Гц|1) = (2л)464 (/?/—pi — q)iif(p/)ril(q, P)ui{pi'}, (22.8)
где a~iq = pf—p( есть передаваемый при взаимодействии
импульс, а (3 = Р = pf + Pi — сумма конечного и началь-
ного импульсов.
Определим теперь структуру вектора тока:
Л=«/ (р/) Гц {q, Р) Ui (Pl)-	(22.9)
Заметим, что для построения этого вектора в нашем рас-
поряжении имеются матрицы Дирака	и векторы
q = pf — pi, P = pf + pi (матрицы Дирака у5 и приво-
дят к псевдовекторам); таким образом, ток имеет вид
7ц=ыу (pz)	+	(Pz). (22.10)
где коэффициенты a, b, с, d и е—скаляры. Используя
уравнение Дирака для спиноров uf (pf) и u( (р() и допол-
нительное условие (22.4'), которое теперь гласит:
/ц<7ц=0,	(22.4")
§22]
ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА НУКЛОНОВ
113
можно упростить выражение (22.10) и свести его к виду
J*=uf (Pf) {В (<72) ТЦ.4-С (<?2) U; (р{) (22.11)
(см. дополнение VB). Здесь В (<?2) нС(</2) — единственные
форм-факторы, которые остаются после упрощения исход-
ной формулы (22.10). Для точечной частицы с зарядом е
и с аномальным магнитным моментом р. имеем В(0)=е,
С (0) = ip. Поэтому удобно принять следующую нормировку
для форм-факторов:
В(<72)=^(<72)>	(22.12)
C(^)=ipF2(^),	(22.13)
F1(0)=F2(0) = l.	(22.14)
При этой нормировке нуклонный ток принимает вид
Л=«/ (р,) {eFt (?2) Уц + фВ2 (72) щ (р£). (22.15)
Обратимся к случаю, когда обмен импульсом q рас-
сматривается в системе центра масс частиц. В случае
упругого рассеяния электронов на протонах это будет
система центра масс электрона и протона. В этой системе
абсолютная величина импульсов частиц остается неизмен-
ной, изменяется только их направление, так что |	|=| р{ |,
и, следовательно, четвертая компонента вектора q равна
нулю (cj=(g, 0), q=qf—qlt q2 = q*)- В этой системе
координат мы можем определить пространственный образ
нуклона; именно пространственный образ для распреде-
ления плотности электрического заряда р(Х) будет
р (X)=е у Fx (^) exp (iqX)	(22.16)
и для распределения магнитного момента ц(Х)
р (X) = р у F2 (q*) exp (iqX) .	(22.16')
Из этих формул видно, что
Jp(X)d3X=eF1(O) = e,	(22.17)
$ р (X) d3x = p,F2 (0) = р.	(22.17')
На основании (22.16) и (22.16') можно определить сред-
ний квадратичный электрический радиус нуклона <гг>е
114
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
и средний квадратичный магнитный радиус <г2>и посред-
ством формул
=	=	(22.18)
<r% = ±J1i(X)rM>X = ±(^)i).	(22.18')
V
0,9
0,8
0,1
0,5-
04-
0,3-
02
01
f 20 90 60 80 100 > 110 160
рерм
Рис. 18. Кривая изображает
форм-факторы Fi и F2 как
функции квадрата передаваемо-
го импульса q2\ в пределах
ошибок опыта Fx и F2 изобра-
жаются одной и той же кривой.
Последние выражения получаются на основании фурье-
разложений (22.17) и (22.17') дифференцированием их по q2.
Из формул (22.16) и
(22.16') следует, что форм-
фактор F-l (д2) определяет раз-
мазывание в пространстве
электрического заряда ну-
клона, а форм-фактор F2(q2)—
размазывание его магнитного
момента.
Таким образом, форм-
факторы F± и F2 отобража-
ют пространственно-времен-
ную структуру нуклонов. Эта
структур а л был а^впервые об-
н ар ужен адэкспер иментально
при изучении рассеяния элек-
тронов в водороде и в дей-
терии в знаменитых работах
Р. Хофштадтера (см. 40 — 42]). Основной результат его
исследований сводится к тому, что
Г1р (<72)=Г2р (<72),
ЛЖ)«0, F2n(?2) « Лр(<72).
(22.19)
(22.19')
где индексом р отмечены форм-факторы для протона, а
индексом п—те же форм-факторы для нейтрона. На рис. 18
приведены современные данные об электромагнитных форм-
факторах нуклонов [43]. Электрические радиусы оказы-
ваются равными: для протона ге = ]/'<г?>е = 0,8-10“13 ел/,
для нейтрона ге = 0. Магнитные радиусы ги = ]/г<г2>и
у них одинаковы и равны ге.
Определенная формулами (22.16) и (22.16') простран-
ственная структура нуклонов носит несколько условный
характер. Эта условность вытекает из того обстоятельства,
§22] ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА НУКЛОНОВ 115
что с точки зрения квантовой теории поля электромагнит-
ная структура нуклона описывается вершинной функцией
Г^ДХ, х), являющейся функцией двух переменных: Х =
= У—X1	, х=х2 — Xi, а не одной переменной; далее,
эта структура описывается динамически, с учетом движе-
ния нуклона в процессе его взаимодействия с виртуаль-
ным фотоном.
В дополнении VA рассмотрена подробнее связь между
вершиной ГИ(Х, х) и плотностями р(Х), р(Х), определяе-
мыми формулами (22.16) и (22.16'). Именно там показано,
что эти формулы имеют прямой физический смысл для
тяжелого нуклона и для малых передач импульса
(7И—масса нуклона). В этом случае плотность р (X) может
быть представлена формулой
РЦ (X) = $ rg (q, 2М) e‘«xd*q, (22.20)
в которой в явном виде учтено предположение q2<^ZAM2.
Вернемся теперь к нашей теме—к вопросу об изме-
рении положения нуклона. Из-за конечности размеров
пионной атмосферы нуклона, как бы точно ни была ло-
кализована частица в пучке-зонде, по наблюдению рас-
сеяния этой пробной частицы нельзя определить положе-
ние нуклона точнее, чем в пределах его размеров Ах^ ге.
В рассматриваемом случае электромагнитных взаимодей-
ствий радиус взаимодействия, строго говоря, бесконечно
велик; эта особенность электромагнитного (кулоновского
и магнитного) взаимодействия сама по себе будет серьез-
ным препятствием для определения положения нуклона
в мысленном эксперименте, иллюстрированном на рис. 14.
Однако это обстоятельство не имеет принципиального зна-
чения. Вместо электромагнитного взаимодействия можно
рассмотреть слабое взаимодействие, которое является кон-
тактным, точечным взаимодействием. Однако, как мы
сейчас покажем, в это взаимодействие входят те же форм-
факторы Ft(q2) и f2(72), которые характерны и для
электромагнитного взаимодействия.
Для определенности рассмотрим процесс, обратный
Процессу захвата р-мезона протоном р;
n4-v—>р-|*рЛ	(22 21)
116
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
|ГЛ. IV
Здесь п — нейтрон, v — нейтрино. Исходные частицы ней-
тральны, и поэтому эффекты, связанные с электромагнит-
ным взаимодействием, отсутствуют.
Взаимодействие, описывающее этот процесс, является
контактным и имеет вид [44]
W =	(22.22)
где GP есть константа слабого взаимодействия, Gp =
= gFlhc(mcl1iy, т — масса нуклона, gP=2-10“49 эрг-см?
есть константа Ферми; эта константа может быть выра-
жена через длину A.P=.V gpl1ic= 0,6- 10“1в см, характер-
ную для слабого взаимодействия. есть нуклонный
(«сильный») ток:
(Н=1, 2, 3, 4).	(22.23)
Здесь i|)N, ipN суть нуклонные волновые функции (прото-
на или нейтрона): оператор для точечных нуклонов
имеет вид
^n=eYn. + I>CTuWv	(22.24)
Далее, т+ есть оператор изотопического спина, превра-
щающий нейтрон в протон (т. е. он меняет значок N=n
на N = р).
Ток J® есть «слабый» ток и имеет вид
—	(22.25)
где tpv— волновая функция нейтрино, фц—волновая функ-
ция ц.-мезона; —оператор, составленный из матриц уц
и у6 (см. подробности в [44]).
Наличие оператора т+ = у + ir2) (для обратного
перехода фигурировал бы оператор т“=у (tj — ir2)) ука-
зывает, что Jp является линейной комбинацией компо-
нент изотопического векторного тока Jfu, /ц2, J^s:
iWPn»	(22.23 )
где <т=1, 2, 3. Однако компоненты тока в точности
соответствуют электромагнитному току, поэтому опера-
тор (см. (22.24)) должен содержать те же форм-фа^-
§22]
ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА НУКЛОНОВ
117
торы F1(qT) и которые характерны для нуклонов
(см. (22.19) и (22.19')); иными словами, в токе учиты-
вается заряженная пионная атмосфера нуклона. В силу
этого обстоятельства контактный характер взаимодей-
ствия (22.22) нарушается и оно становится нелокальным.
Диаграммы Фейнмана, отображающие контактное
взаимодействие (22.22) и взаимодействие с учетом ко-
нечных размеров нуклона, приведены на рис. 19, а, б.
Рис. 19. Диаграммы, описывающие слабое взаимодействие (процесс
n-j-v—>р + Н”)- а) Диаграмма для контактного взаимодействия;
б) диаграмма, учитывающая «конечные размеры нуклона (его форм-
фактор).
Благодаря возникновению пространственно-временного
распределения нуклонных зарядов и токов в вершине Г,
даже в мысленном эксперименте, допускающем как угодно
узкий пакет нейтрино, служащий зондом для определе-
ния положения нуклона, невозможно определить место
рассеяния нейтрино точнее в пределах размера нуклона,
т. е. в области Ах]~ге (или г^. Таким образом, мы
видим, что существование форм-факторов элементарных
частиц, отображающихЖих пространственно-временную
структуру, приводит к [принципиальной невозможности
локализовать элементарную частицу в пространстве—вре-
мени точнее, нежели в пределах ее размеров, т. е. точнее,
чем с точностью
Ах ~ г0,
Д/
р
(22.26)
где Гд—радиус частицу.
118
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
§ 23. Мезонная структура нуклонов
В этом разделе мы обратимся к теории упругого рас-
сеяния пионов на нуклонах в области высоких энергий
(выше порога рождения мезонов). В этом случае опре-
деляющее значение имеют неупругие процессы, так что
упругое рассеяние оказывается дифракционным. Соот-
ветственно этому амплитуда рассеяния Т q) будет
чисто мнимой (Дп —энергия мезона в системе центра
масс, £’я = 'Кт24-Л2, a q—переданный импульс, |^| =
= 2fesin'&/2, §—угол рассеяния) и может быть прямо
выражена через дифференциальное сечение упругого
рассеяния:
-£-=|Т(Гя,	=	Q)-	(23.1)
Таким образом, имея экспериментальные данные для
, можно найти амплитуду Т (Еп, q). С другой сто-
роны, эта амплитуда, как известно, представляется ря-
дом по полиномам Лежандра Pz(cos$):
00
7(£Я) 0=^L(2/+1)(1-^OP^cos^ (23.2)
где
T]z(^) = Sz(^) + fvz(^), Vz>0,	(23.2')
есть комплексная фаза. В случае достаточно коротких
волн (Х<|а, а—размер рассеивающей волны системы)
сумму по I можно заменить интегралом, полагая
ZAZ —► bdb/^=k2bdb, где b—параметр удара. Далее, при
больших Z и малых $ полином Pt (cos {}) можно заменить
на функцию Бесселя
Уо (Z sin &) JQ(bq).
Тогда (23.2) переписывается в виде
со
Т{Еп, q) = -^^bdbl\-e-Mk>]J.{bqY (23.3)
О
§ 231
МЕЗОННАЯ СТРУКТУРА НУКЛОНОВ
119
В силу ортогональности функций Бесселя Jo (bq) это ин-
тегральное соотношение может быть обращено:
00
1 _ е2й) (b, k> = j Т {Ея, /о (bq) q d(h
О
(23.4)
Таким образом, из опыта можно определить фазу
т] (Ь, k) как функцию энергии мезона k = ]/Е2 — т* и
Рис. 20. а) Сфера очерчивает нуклон, АВ — путь луча внутри нуклона,
b—параметр удара; б) частично поглощающий экран, эквивалентный
нуклону; этот экран дает ту же дифракционную картину (для малых
углов рассеяния), что и реальный нуклон.
параметра удара b. С другой стороны, в пределах гео-
метрической оптики изменения фазы первичной волны
2т] (&, k) могут быть вычислены интегрированием по лучу
показателя преломления п:
в
2т] (&, fe)=^n(fe, x)ds.	(23.5)
А
На рис. 20 указан путь интегрирования внутри нуклона.
В работах [42, 45] был проведен анализ эксперимен-
тальных данных по рассеянию пионов на нуклонах
(л+р). Результат этого анализа приведен на рис. 21, где
по оси ординат отложен коэффициент поглощения К (г) —
мнимая часть коэффициента преломления п (действитель-
ная его часть в рассматриваемом случае крайне мала) —
в функции расстояния от центра нуклона г в системе
центра масс. Как видно, поглощение убывает по мере
удаления от центра нуклона и практически исчезает за
120
РОЛЬ конечных размеров частиц
[ГЛ. IV
пределами г 0,7-10"13 см. Совпадение этой величины
с данными об электромагнитном радиусе нуклона (ге =
= ^ = 0,8-10"13 см} указывает на то, что поглощение
Рис. 21. Сплошная кривая — коэффици-
ент поглощения пионов К (г) как функ-
ция расстояния от центра нуклона г
для энергии пионов Е = 1,3 Гэв; штрихо-
вая кривая—то же для энергии пионов
£’ = 5 Гэв.
мезонов нуклоном и распределение токов и зарядов в нук-
лоне вызвано одной и той же физической причиной —ме-
зонной атмосферой нуклона.
В какой мере может быть обоснована рассмотренная
выше простая оптическая картина взаимодействия мезо-
нов с нуклонами?
Современная теория поля не открывает прямых путей
,цля расчета сильных взаимодействий, к классу которых
относится взаимодействие л-мезонов с нуклонами. По-
этому можно дать лишь условное обоснование, характер-
ное для приемов современной теории: 1) допустить ма-
лость константы взаимодействия g (условие, необходимое
для обеспечения сходимости рядов), 2) допустить возмож-
ность перенормировок в каждом из приближений по сте-
пеням g, 3) в полученных окончательных уравнениях
отказаться от ограничений на величину константы g.
§23]
МЕЗОННАЯ СТРУКТУРА НУКЛОНОВ
121
Следуя по этому пути, мы придем к уравнению, ко-
торое будет иметь вполне определенную структуру, но для
практического применения потребует еще дополнительных
предположений [46] *). Это уравнение, как показано в до-
полнении VI, имеет вид
(Е2п—К2)ф(х) = $ U (х, x'-,E)ty(х')d°x', (23.6)
где К2 —— v2 + /n2 (т — масса мезона), Е = Еп-\-Е^,
En—энергия нуклона в той же системе, U (х, х'; Е) —
нелокальный, вообще говоря, комплексный потенциал,
действующий со стороны нуклона на мезон; ф(х)—вол-
новая функция для относительного движения нуклона и
мезона, взятая при совпадающих временах, так что х —
= х2 — х1( t — t2—/1 = 0.
Эквивалентное другое уравнение гласит:
ф (х) = J V (х, х'; Е) ф (xz) d3x',	(23.7)
где — оператор Дирака,	здесь М —
масса нуклона, а V (х, х'; £)—потенциал, действующий
со стороны мезона на нуклон.
Связь между U (х', х; Е) и V (х, х'; Е) также описа-
на в дополнении VI. Неполнота теории, лежащей в основе
уравнений (23.6) и (23.7), выражается в том, что эти
нелокальные и комплексные потенциалы могут быть вы-
числены в явном виде только в виде ряда по степеням
константы взаимодействия g. Отказываясь от предполо-
жения о малости константы g, мы должны делать спе-
циальные предположения о виде U или V. Подобная
ситуация имеет место в теории атомного ядра, где слож-
ное взаимодействие нуклонов заменяется потенциальной
ямой, описывающей это взаимодействие усредненным
образом.
Если длина волны % относительного движения частиц
существенно больше размера области а, где нелокальные
*) Подобный путь применяется и в теории дисперсионных соот-
ношений. Необходимая для обоснования аналитических свойств
амплитуда рассеяния матрицы рассеяния строится по теории возму-
щений и предполагает малость взаимодействия. Сами же дисперсион-
ные соотношения применяются в области сильных взаимодействий, без
ограничений на величину константы взаимодействия.
122
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
потенциалы U или V существенно отличны от нуля, то
уравнения (23.6) и (23.7) принимают крайне простой вид:
(Е£-/<2) Ф (х) - U (х, Е) ф (х),	(23.6')
(En-^°n)i|)(x)-V(x, Е)ф(х),	(23.7')
где
U(x, E) = $U(x, х'-, E)^d*xr,	(23.8)
V(x, E) = $V(x, x'-, E)^d3x'	(23.8')
и отношение ф (х')Др (x) под знаком интеграла заменено
на единицу. Уравнения (23.6') и (23.7') имеют вид урав-
нений Шредингера (или Дирака) с комплексным, завися-
щим от энергии потенциалом U (х, Е) (или V (х, Е)).
Уравнения (23.6) и (23.7) упрощаются и в другом
крайнем случае, при	Заметим, что это условие
в силу соотношения, справедливого для коротких волн:
or = ггса* (1 — Р),	(23.9)
где о—сечение упругого рассеяния, р (0 < Р < 1) —
прозрачность нуклона, может быть написано в виде
а
Т
Г Л_|1/21>1
(23.9')
При соблюдении этого условия представим волновую
функцию в форме, характерной для геометрической оп-
тики, именно положим
ф (х) — exp {ikS (х)},	(23.10)
где S (х)-—функция действия, & = у . Подставляя (23.10)
в (23.6), соберем члены при степенях k2 (считая, что
k2 —> оо). Члены при k2 дают уравнение эйконала:
(у$)2 = п2,	(23.11)
где п—комплексный показатель преломления, подчиняю-
щийся уравнению
\-n* = ^U (х, х’; E)expik{S(x')-S(x)}d3x'. (23.12)
§24]
СТРУКТУРА ЧАСТИЦ В КВАНТОВАННЫХ полях
123
Разложим разность S (х') —S (х) и показатель экспоненты
под интегралом по степеням (х’ — х):
S(x') — S (х) = VS (х) (х —х') + ... =
= пр cos 04-..., (23.13)
где р = х—х'. Тогда выражение (23.12) примет вид
l-na = pjt7(x, х + р. Е) eiknPcosedap. (23.14)
Подставляя справа вместо показателя преломления п = 1,
получим первое приближение для п2 — 1. Далее результат
можно уточнять итерацией. Полагая n = a-\-i$, нетрудно
убедиться, что необходимым условием сходимости итера-
ции будет &(3—const при k—> оо.
Основываясь на оптической теореме, согласно которой
мнимая часть амплитуды Т (£я, q) упругого рассеяния
вперед (т. е. при 7 = 0) связана с полным сечением огп
соотношением *)
1тТ(Ея, 0) = А-пп	(23.15)
(здесь Ел = ]/~т2+ k2), и пользуясь тем опытным фактом,
что полное сечение jrN-взаимодействия не возрастает
с ростом энергии £я, а стремится к постоянной величине,
можно показать, что величина &|3 при k —> оо убывает и
тем самым необходимое условие сходимости в (23.14)
обеспечено [47].
Изложенный здесь оптический подход к описанию
пространственной структуры мезонной атмосферы нуклона
является лишь одним из возможных аспектов изучения
этой структуры [48].
Количественные и качественные выводы, получаемые
из оптической модели нуклона, таким образом, нахо-
дятся в согласии с основами квантовой теории мезонного
поля.
§ 24. Структура частиц в теории квантованных полей
Структура элементарных частиц изучается посредст-
вом упругого рассеяния частиц, служащих частицами-
зондами.
*) Эта теорема есть следствие свойства унитарности матрицы
рассеяния; см. дополнение ХП(4).
124
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
Современная теория раздельно рассматривает три вида
взаимодействий: сильное, электромагнитное и слабое.
В силу этого мы вынуждены говорить о трех типах
структур элементарных частиц соответственно этим трем
типам взаимодействий.
Понятие структуры элементарной частицы отличается
от классического понятия структуры того или иного
объекта. Основанием для этого служат следующие обстоя-
тельства.
Из экспериментальных данных по упругому рассея-
нию частиц восстанавливается амплитуда рассеяния Tfi,
соответствующая переходу рассеивающихся частиц из не-
которого начального состояния i в конечное f. Восста-
новление этой амплитуды из опытных данных само по
себе представляет серьезную проблему, известную под
названием полного опыта [49].
Амплитуда Tfi есть функция двух инвариантов: s =
(Р— полный импульс рассеивающихся частиц) и t = — q*,
где q есть переданный при рассеянии импульс, равный
разности конечного и начального импульсов одной из ча-
стиц: q=pj — т. е.
Tfl = A(t,s).	(24.1)
Информация, содержащаяся в амплитуде, относится
к обоим состояниям изучаемой частицы, i и отличаю-
щимся импульсами и pf. Поэтому эта информация
преподносится нам в виде интерференции двух структур,
в классическом понимании относящихся к двум различ-
ным состояниям движения изучаемой частицы. Из обще-
известных «оптических» соображений следует, что мы
можем рассчитывать на получение информации о про-
странственно-временной структуре объекта в масштабах b
только в том случае, если изучаются события, акты рас-
сеяния, при которых переданный импульс q^ii/b. Вели-
чину b мы можем рассматривать как параметр удара.
Длительность столкновения будет определяться временем
порядка x = b/v, где v — скорость частицы зонда, близкая
к скорости света.
За время т изучаемая частица сместится на расстоя-
ние порядка Ittb/v- р/М, где р — приобретенный ею
импульс, а М — ее масса. Для того чтобы «структура»
относилась к исходному состоянию частицы-объекта, не-
§24]
СТРУКТУРА ЧАСТИЦ В КВАНТОВАННЫХ ПОЛЯХ
125
обходимо, чтобы нетрудно видеть, что это равно-
сильно требованию h/M-p/qа так как импульсы р
и q одного порядка, то получается, что
(24.2)
т. е. мы можем изучать классическую структуру частицы
только в масштабах Ь, существенно превышающих комп-
тоновскую длину волны изучаемого объекта. Эта качест-
венная оценка согласуется с более основательной оцен-
кой, данной в дополнении V к § 22 в связи с описанием
электромагнитной структуры нуклона.
Другая сторона дела заключается в том, что по мере
увеличения энергии частицы-зонда, а следовательно, и
по мере увеличения верхней границы передаваемого им-
пульса l^fmax —(здесь р—относительный импульс час-
тицы-зонда и частицы-объекта) возрастает относительная
роль неупругих процессов и картина объекта, наблюдае-
мая по рассеянию частиц, приобретает характер дифрак-
ционной картины от сильно поглощающего тела. Как
было замечено в работе [45], если в некоторой области
b < 7? поглощение становится полным, так что эта область
может рассматриваться как абсолютно черное тело, то
вместе с этим всякая информация о структуре этой обла-
сти сводится к нулю*). Величину R можно назвать «эле-
ментарной длиной», обусловленной динамикой неупругих
процессов.
Поэтому поведение отношения сечения упругих про-
цессов сту к полному сечению оп при неограниченном воз-
растании энергии (s —> оо)
lim —= ?	(24.3)
°п
может иметь принципиальное значение для будущей тео-
рии. Важным также является вопрос о поведении сече-
ния неупругих процессов ану. Если бы стну —> 0 при s —> оо,
то это означало бы, что элементарные частицы при пре-
дельно высоких энергиях становятся прозрачными и «абсо-
лютная чернота» исчезает; если же limo'Hy>0, то при
*) Заметим, что для разных взаимодействий это состояние может
наступать (если вообще наступает) при существенно различных энер-
гиях и существенно различных масштабах.
126
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
1ГЛ. IV
столкновении элементарных ^частиц могли бы возникать
за счет их высокой энергии макроскопические количества
материи, вплоть до целых вселенных. В этом случае эле-
ментарные процессы оказались бы способными порождать
процессы макроскопические и обнаружилось бы общее
поле активности микро- и макромира [51]. Однако «reve-
nons a nos moutons»*). Чтобы глубже заглянуть в дина-
мику упругого рассеяния при высокой энергии, предста-
вим себе, что мы в состоянии суммировать все высшие
Рис. 22. Слева — функция s (z/x, у2 | xlt х2), справа — ее разложение по
диаграммам Фейнмана: а) диаграмма первого порядка по g; б) одна
из диаграмм второго порядка (g2): в) одна из диаграмм третьего по-
рядка (g3); г) одна из диаграмм четвертого порядка (g4) и т. д.
диаграммы Фейнмана, дающие вклад в амплитуду упру-
гого рассеяния. В^качестве иллюстрации на рис. 22 при-
ведены эти диаграммы для поля ср, описывающего неза-
ряженные скалярные частицы. Энергия взаимодействия
в таком поле может быть записана в виде
Г =	(24.4)
и
где g — некоторая константа связи.
Суммирование подобных диаграмм, взятых в коорди-
натном представлении и имеющих две входные линии
(%i и х2) и две выходные линии (у± и z/2), приводит
к функции-«четыреххвостке»:
s = s(x4, х3, х2, хх),	(24.5)
описывающей процесс рассеяния частиц (две частицы
в начальном состоянии, две—в конечном).
*) Старая французская поговорка: «Вернемся к нашим баранам».
§24]
СТРУКТУРА ЧАСТИЦ В КВАНТОВАННЫХ ПОЛЯХ
127
В дополнении VII показано, что матрица рассеяния
S, описывающая все возможные процессы со скалярными
незаряженными частицами, может быть сведена к сово-
купности скалярных функций:
s(Xj),
S(%1, х2),
s(xn х2, х8),
(24.6)
s(x1, х2, хп),
каждая из которых является вакуумным средним по все-
возможным процессам взаимодействия частиц, сопровож-
дающимся рождением частиц и их уничтожением.
В силу однородности вакуума эти функции являются
функциями только разностей координат xik — х£—xk,
в частности, s(Xi) = const. Далее, в рассматриваемом
случае скалярного поля эти функции зависят лишь от
скалярных произведений x£kxnm, притом равноправно от
всех х£.
Матричные элементы матрицы рассеяния, описы-
вающие переход из некоторого начального состояния
х2, • ••, хп), в котором имеется п частиц, в конеч-
ное состояние фу(г/1, у2, ..., ут), в котором имеется т
частиц, выражается через функции (24.6) следующим
образом:
$fi ~ fi ~ У Ф/ G/1> Уг» • • • > Ут) X
Xs(yn у2, ..., ут\х» Х2, . .., Х„) фг- (%i, Х2, . ..,х„)Х
X d4yt d*y2 ... d*ym d*xr d*x2 ...	(24.7)
где аргументы функции s(Xj, x2, ..., xN), N = n^m,
относящиеся к конечному состоянию f, обозначены теперь
через у19 у2, ..., ут и отделены чертой от аргументов
xlf х2, ..., хп, относящихся к начальному состоянию i.
Такие разбиения аргументов функций 5(хь х2, ...,xN)
на принадлежащие начальным и конечным состояниям
позволяют записать эти аргументы в виде матрицы,
строки которой (у) относятся к конечному состоянию /,
а столбцы (х)—к начальному состоянию i\
128
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
х у		Х1	Х1, х2	Xi» Х21 х2	
	1				
У1		s (г/i 1 *i)	s (г/i 1 xlt х3)		
У1> У 2		«('Л, У 2 1 *1)	«(У1. У2 1 *1,		
У1, Уъ, Уз					
					
(24.8)
Не все элементы, последовательность которых намечена
в таблице, отличны от нуля и не все описывают реаль-
ные физические процессы с реальными частицами. На-
пример, взаимодействие (24.4) вообще исключает функции
s(x|y) с нечетным числом всех аргументов. Элементы
типа s (у11 %!, х2, х3) отличны от нуля, но не могут
описывать реальный процесс, так как масса покоя части-
цы Q/i) должна бы быть >3т. Это противоречит предполо-
жению о спектре частиц, в котором с самого начала до-
пущены только частицы с массой покоя т. Соответст-
вующий элемент Sfi для реальных частиц автоматически
обратится в нуль. Мы не будем углубляться в эти част-
ности.
Обратимся к той стороне дела, которая является для
нас первостепенной. Допустим, что мы можем сколь угодно
точно локализовать частицы в пространстве и времени.
Иными словами, допустим, что можно взять волновые
функции и Г/фу в виде произведения ^четырехмерных
64-функций:
т	п
^/ = П6Ж~у?)> ^<=П(хч~х'чУ	(24-9)
<7=1	<7=1
Тогда интегрирование в (24.7) сразу выполняется, и мы
получим
= s (у19 у2, ..., ут | х19 x2f • • •, хп). (24.10)
Отсюда следует, что функции s(y|x) из (24.8) дают
наиболее полную информацию о пространственно-времен-
§24] СТРУКТУРА ЧАСТИЦ В КВАНТОВАННЫХ ПОЛЯХ 129
ном течении процесса взаимодействия N = m + n частиц.
Поэтому именно эти функции следует рассматривать как
функции, дающие полное описание структуры скалярных
элементарных частиц, взаимодействующих между собой
путем излучения и поглощения подобных себе частиц.
* Мы могли бы сузить рамки нашего описания, связав
с понятием структуры частицы лишь ту из функций
s (у | х) из (24.8), которая описывает упругое рассеяние,
именно функцию у21 %i, х2). В этом случае одна из
частиц может рассматриваться как зондирующая струк-
туру другой. Такая точка зрения возможна, но, конечно,
не обязательна. Так или иначе, описание структуры час-
тицы на основе S-матрицы носит динамический характер
и неотделимо от процессов, с помощью которых эта
структура проявляется.
На рис. 22 с помощью графиков Фейнмана для спе-
циального случая S = gq* иллюстрировано это динами-
ческое понимание пространственно-временной структуры
частиц. В качестве примера выбрана функция s(y19 y2\xlt х2).
Эта функция представляется суммой вкладов от опера-
тора (24.4), разложенного по степеням g. Каждый такой
вклад может быть представлен суммой графиков Фейн-
мана, имеющих число четверных узлов, равное степени g.
Первый график (я) описывает взаимодействие (упругое
рассеяние) точечных частиц, следующие графики показы-
вают участие виртуальных частиц, создающих облако
вокруг исходных частиц (хх, х2 [ у19 у2). Это облако имеет
динамический смысл: в каждом из узлов частицы порож-
дают другие частицы, которые в результате последующих
превращений, начинающихся с исходных частиц и х2,
заканчиваются конечными частицами уг и у2. Суммиро-
вание всех диаграмм и усреднение их по вакууму озна-
чает учет всех возможных путей, ведущих из (хп х2)
В («/!, t/2).
Если теперь обратиться к реальным частицам, то сле-
дует вспомнить о существовании трех типов взаимодей-
ствий. Одна и та же частица может участвовать в раз-
личных взаимодействиях. Например, протон сильно взаи-
модействует с пионами, электромагнитно — с электроном,
посредством слабого взаимодействия — с нейтрино. Этим
взаимодействиям отвечают различные S-матрицы, и харак-
5 Д. И. Блохинцев
130
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
!гл. iv
тер структуры частицы, отображающейся в каждом из
этих взаимодействий, может быть своим, специфическим
именно для этого взаимодействия. Весьма вероятно, что
в дальнейшем будут установлены внутренние связи этих
взаимодействий, и тогда различные структуры будут
поняты как проявление одной и той же сущности *).
Далее, не следует забывать, что изложенное в этом
разделе представление о пространственно-временной струк-
туре частиц базируется на теории, достаточно обоснован-
ной лишь для случая электромагнитных взаимодействий.
Математически это представление опирается на сово-
купность функций s(y\x) (см. (24.8)), которые могут быть
получены из теории, однако являются ненаблюдаемыми
величинами. Ненаблюдаемость этих величин вытекает из
принципиальной невозможности построить четырехмерные
6-образные волновые пакеты в пространстве и времени
(24.9) и использовать их в качестве функций начальных
и конечных состояний.
В действительности начальное состояние фг и конеч-
ное состояние фу являются суперпозициями плоских волн,
для которых р%= +]/т2 + /72. Поэтому информация отно-
сительно функций s (z/| х), вытекающая из знания матрич-
ных элементов Sfi матрицы рассеяния S, оказывается
крайне ограниченной. Суть дела заключается в том, что
спектральное разложение функции Sfi в пространстве
импульсов 9? (р) составляет лишь малую часть спектраль-
ного разложения функций s(y|x)**).
Для более подробного обсуждения этого вопроса обра-
тимся к реальному случаю упругого рассеяния л-мезона
на нуклоне. Ввиду различия этих частиц нам будет удоб-
нее записать функцию s(y\x) в виде
s (у I х) = s (у2, x2\Xj, yt), '	(24.11)
где xt — координата нуклона в начальном состоянии
% (xx) = (рх) eiP1X1,	(24.12)
*) В атомной физике ядерно-элактронная структура атома яв-
ляется единой основой для понимания образа атома как в свете
рентгеновских лучей, так и в свете пучка электронов.
**) С подобной ситуацией мы уже встречались при изуцециц рер-
щинь! Гр, (Л, х) (см- § 22),
§ 241 СТРУКТУРА ЧАСТИЦ В КВАНТОВАННЫХ ПОЛЯХ 131
а х2 — его координата в конечном состоянии
ф/(х2) = ц/(р2)е-^,
(24.13)
У1 и Уъ—координаты л-мезона в начальном и конечном
состояниях соответственно:
/Mi —	e-ik2y2
г'(й)=Т5Г’
Введем теперь новые координаты
X = Х± Х2,	= ~2~ X 2" (^1 + У г)9
Х = ^(х1-^х2), ^ = ^Х—(уг — у^,
так что
8 (Ра, Х8 | У it %i) = S {х, £х, ^2).
(24.14)
(24.15)
(24.16)
Эта последняя функция имеет спектральное разложение
s (х, gg) = $ ;s (a,	р2) exp [i (ах+р^+р^)] d4a d4Pj d4P2,
(24.17)
где интегрирование по переменным а, рх, Р2 не ограни-
чивается поверхностью масс.
Вычисление матричного элемента Sfi от функции
(24.17) для состояний
Ф/ = Ф/(х2)<р/(у2), Ф1-=Ф1-(Х1)ф1(У1)	(24.18)
ведет к результату
Sfi= б4 (Ра + ^-рх-^йДр^Х
sy — Pi—ki, —q, *х+-4<7 )
. х“--------(24Л9)
Таким образом, функция s(a, рх, р2) оказывается из-
вестной только для значений а = —(Pi + ^i), ₽i = —
P2 = ^i+y?-
Заменим теперь в (24.17) элемент объема d4ad4pxd4p2
так:
d4ad*pid*p2 = d*pxd4<? =	dq9d3q. (24.20)
5*
132
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
Здесь En—энергия первичного нуклона в системе центра
тяжести, Еп — энергия первичного мезона в той же си-
стеме координат. Подставляя теперь s из (24.19) в (24.17),
мы не получим всю функцию s(x, |2), а только ее
«видимую» часть As:
As(x, ?г)=ДЯу s р±— klt —q, ki + ^q^X
xexp [—i (Pi + &i)Xi —+ »	£2]^, (24.21)
где через AQ обозначены все множители в (24.20), кро-
ме d?q.
Рассмотрим частный случай, полагая х=0, £2 = 0;
тогда переменная % получает смысл расстояния между
нуклоном и мезоном; при этом
As(0, g, 0) =
= AQ js (—Pi—klt —q, fci + y </) exp (— iqtydsq. (24.22)
Если теперь ограничиться областью, в которой +
+ -^q&kif т. е. случаем высокой энергии первичного
мезона и малого передаваемого импульса q2, то в (24.20)
можно пренебречь величиной q в выражении = +
Тогда (24.21) можно рассматривать как преобразование
Фурье по переменной q\ обозначим
s(— л —	— q, ^o=0 = s(E, q2),	(24.23)
где E = EN-\- Еп есть полная энергия системы.
Величина
As(0.’J’ о) = f s (Е, q9) е‘9х d3q (24.24)
дает представление о пространственной структуре в нук-
лон-мезонном взаимодействии. Однако на основании (24.19)
удобнее ввести величину
V (Е, 1) = $ V (Е, q) d3q (24.25)
(здесь
V (Е, q)=s^’q^Y	(24.26)
§24]
СТРУКТУРА ЧАСТИЦ В КВАНТОВАННЫХ ПОЛЯХ
133
которая является аналогом потенциала взаимодействия
мезона с нуклоном. Действительно, в крайнем случае
Рис. 23. Сравнение теоретических кривых для дифференциального
сечения do/dQ упругого рассеяния пионов на протоне как функция
косинуса угла рассеяния 0. Сплошная линия получена исходя из
эффективного потенциала (24.28), штриховая — из потенциала (24.28')«
малого потенциала V(E, £) амплитуда рассеяния выра-
жалась бы формулой
Tfi(E, q) = uf(pf)V(E, q)Ul(p{),	(24.27)
что согласуется с (24.19), если принять определение
(24.26).
Величину V (Е, 1) из (24.25) мы будем называть «эф-
фективным» потенциалом мезон-нуклонного взаимодей-
ствия [50].
На рис. 23 приведены экспериментальные данные для
дифференциального сечения упругого (л+р)-рассеяния.
134
РОЛЬ КОНЕЧНЫХ РАЗМЕРОВ ЧАСТИЦ
[ГЛ. IV
Считая амплитуду (лр)-рассеяния чисто мнимой (дейст-
вительная часть этой амплитуды мала), построим две
кривые, аппроксимирующие эти экспериментальные дан-
ные. Эти кривые соответствуют двум потенциалам (24.27):
г ?2"1
V (£, ё) = iV0 (£) exp [- у ,	(24.28)
V (Е, g) = tV0(£)exp(f~g/Q).	(24.28')
Из этих формул первая лучше согласуется с опытными
данными, нежели вторая (см. рис. 23). Длина а в обоих
случаях оказывается равной а = 0,6 4-0,7-10-13. Такая
длина соответствует обмену двумя л-мезонами или век-
торным р-мезоном.
Таким образом, «эффективный потенциал» V (£, |) дает
представление о структуре нуклона, согласующееся с пред-
ставлением о мезонной атмосфере нуклона.
ГЛАВА V
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
§ 25. Замечания о причинности
в классической теории поля
Понятие упорядочения событий включает в себя важ-
нейшую концепцию причинности, основанную на хроно-
геометрическом делении многообразия событий на времени-
подобное и пространственноподобное. Поэтому причинность
можно рассматривать как геометрическую категорию и ис-
следование вопросов причинности есть лишь один из воз-
можных аспектов анализа геометрии.
Мы начнем анализ причинности в микромире с неко-
торых замечаний, относящихся к классической теории
поля.
В классической теории линейного поля причинность
наиболее непосредственно выражается с помощью функ-
ции Грина ®, которая представляет собой поле, возни-
кающее от неограниченно точно локализованного в про-
странстве и во времени импульсного источника поля
Qo (х):
Qo (х) = —64 (х) =—6 (/) 63 (х).	(25.1)
Для скалярного поля функция Грина подчиняется неод-
нородному уравнению Клейна:
(□z—т1 2)®=—6(х).	(25.2)
Согласно дополнению I (см. (1.12) — (1.14)) получим для
запаздывающей функции Грина ®ret
1 D (х) при
@ t (х) — < п
ret' ’	( 0 при
(25.3)
136
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
где функция D (х) совпадает с перестановочной функ-
цией, определенной формулой (1.3), и для опережающей
®adv
Л (О ПРИ > О,
®advW=| _D(X) при /<0.	(253)
Особенно простые формулы получаются при т=0,
что в терминах квантовой теории соответствует частицам,
не имеющим массы покоя. В этом случае, как нетрудно
получить из (1.3),
	®ret(*) =	( 1 6(<-r) 4л г 0	при />0, при t < 0	(25.4)
и	®advW =	0 	1 6(<+') 4л г	при 4 > 0. при t < 0.	(25.4')
Решение ®ret (х) представляет собою бесконечно узкий
импульс, расходящийся из точки г = 0, решение ®ad¥(x)
соответствует такому же импульсу, сходящемуся в точку
г = 0 (см. рис. 24). Первое решение описывает импульс,
передающий 'влияние 'события (импульса) в точке г = 0
на удаленные [от г = 0 точки. Второе решение передает
влияние событий (импульсов)/расположенных вне точки
г = 0, на эту точку.^При массе покоя частиц, отличной
от нуля, вслед за этим сосредоточенным импульсом рас-
пространяется «хвост» более медленных влияний, который
J (__itYl 1/"X2 )
описывается членом с функцией ——-==—- (см. (1.3)).
На языке корпускулярной теории существование этого
хвоста можно интерпретировать как эффект частиц, дви-
жущихся со скоростями, меньшими скорости света с.
Оба решения, ®ret(x) и ®advW> обращаются в нуль
вне светового конуса. Это означает, что взаимодействие
из точки хх = 0 не может распространиться в удаленные
от нее точки со скоростью, большей скорости света с.
Равным образом оно не может прийти в точку хх = 0 из
точек х2, удаленных от нее, со скоростью, превышающей
скорость света с. На рис. 25 изображены три возможных
случая влияния; а) точка х2 лежит внутри светового ко-
§25] ПРИЧИННОСТЬ В КЛАССИЧЕСКОЙ ТЕОРИИ ПОЛЯ 137
нуса будущего по отношению к точке (условно обоз-
начим х2> х^\ влияние на х2 описывается функцией
Рис. 24, а) Бесконечно узкий импульс, расходящийся из точки г = 0;
б) бесконечно узкий импульс, сходящийся к точке г = 0.
Рис. 25. Иллюстрация запаздывающего и опережающего взаимодействий.
а) Запаздывающее взаимодействие между точками хг и х2. Функция
Грина ®ret отлична от нуля внутри заштрихованной области (х2 > *1)',
б) то же для опережающего взаимодействия. Функция Грина ®adv
отлична от нуля в заштрихованной на рисунке области (х2 < *1)!
в) точки х2 и %! не могут быть связаны каким-либо взаимодействием.
®ret (х)> х—х3 —> 0; б) точка х3 лежит в конусе абсо-
лютного прошедшего по отношению к точке хх (условно
xi < xi); влияние х2 на xt в этом случае описывается
функцией ®adv(x)’> в) когда х2 и хх лежат по отношению
138
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
друг к другу в пространственно-подобной области, т. е.
вне обоих световых конусов (условно обозначаем х2~х^
обе функции Грина ®adv(x) и ®retW обращаются в нуль,
так что нет никакой физической связи между точками
х2 и х±.
С помощью функций Грина можно выразить поле ср (х),
обусловленное любым распределенным в пространстве и
времени источником Q (х). Дифференциальное уравнение
для такого поля имеет вид
(□z—mz) ср (х) = — Q (х).	(25.5)
С другой стороны, запаздывающая функция Грина
®ret(*2~*i) удовлетворяет уравнению
(□1—m2)@ret (х2—х0 = —S(x2—хх).	(25.6)
Умножая это уравнение на Q (хх) и интегрируя по d4x1?
получим
(□ 1 — m2) $ ®ret (*2 — *i) Q (*i)	= — Q (*2)• (25.7)
Сопоставление с (25.5) показывает, что поле ср в точке х2
будет равно
Ф (Х2)=фо (х2) + $ ®iet (х2 - хх) Q (хх) d*xlf (25.8)
где (р0 (х2) есть решение однородного уравнения (уравне-
ние (25.5) при Q = 0).
Если поле порождается только источником Q (xj, то
фо(х2) = О и вместо (25.8) получается
ф (х2) = $ ®ret (х2—хх) Q (хх) d^Xj,. (25.9)
В простейшем случае, при т = 0, на основании (25.4)
найдем
ф Wj 6(Z2-Z1~r)- $ W d^ <25-10)
(здесь r = I x2 — xx I) или
ф W =i j	— d*xi-	<25-1
Отсюда видно, что поле <р (х2) в точке х2(/2, х2) склады-
вается из запаздывающих воздействий, отправляющихся
из точек х± в момент времени t^ = t^—r!c (с=1). Это
§25] ПРИЧИННОСТЬ В КЛАССИЧЕСКОЙ ТЕОРИИ ПОЛЯ 139
и есть наиболее прозрачное выражение причинности
в классической теории поля.
При т#=0 согласно (1.3) и (25.3) будем иметь не-
сколько более сложное выражение для поля ф (х2), именно:
т(*.)=^Р(,,7г’Х1) fe,+
x}d‘d’x'- (2512)
При этом область интегрирования Q в последнем ин-
теграле в соответствии с (25.3) ограничена условиями
(^2~^1)* > t2 — t1'>0. Отношение v=r/\ —/г|< 1=с
можно рассматривать как скорость распространения
взаимодействий, происходящих за счет «частиц», имеющих
скорость v, меньшую скорости света.
Допустим теперь, что в области около х2 распределен
заряд Q2(x2). Определим величину
W = Q2 (х2) ф (х2) d*x2	(25.13)
как плотность действия (интеграл по времени от энер-
гии взаимодействия). Обозначая теперь источник поля
в области хг через Qita)» получим, что
w= J Q2 (х2) ® (х2-хх) fe) d‘x2d‘xx, (25.14)
где ® (x2 —xx) = ®ret (x2—xx) —®adv (Xi —Xj.
Такая запись симметричным образом учитывает дей-
ствие одного заряда на другой и, в силу (25.3) и (25.3'),
обеспечивает запаздывающее действие заряда, располо-
женного «раньше», на заряд, расположенный «позднее».
Возьмем теперь вторую функциональную производную
от действия W по функциям источников Q2 и & в точ-
ках х2 и xt соответственно. Получаем
<25'
Отсюда следует, что
&W -О	/95
если х2 ~ хх, т. е. если точки х2 и хх лежат по отноше-
нию друг к другу вне светового конуса, так что интер-
140
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
|ГЛ. V
вал (х2—хх)3 является пространственно-подобным. Условие
(25.16) выражает тот физический факт, что влияние одного
заряда на другой не может распространяться со ско-
ростью, большей скорости света.
В заключение этого раздела заметим, что функции
Грина, удобные для описания причинности, сами по себе
являются лишь математическими абстракциями, так как
импульсный источник
Q(x)=gS(/)S3(x),	(25.17)
порождающий поле, описываемое функцией Грина, несов-
местим с представлением о сохранении заряда. Закон
сохранения заряда требует, чтобы выполнялось уравнение
непрерывности
^- + divy=0,	(25.18)
где /—плотность тока, соответствующего заряду Q. Из
этого уравнения следует, что в случае импульсного ис-
точника (§6 (/) 68 (х)) плотность тока J (х) должна иметь
вид
=	(25.19)
так как
div? (т)==7а(7')=б3^-
Таким образом, ток, соответствующий импульсному ис-
точнику Q (см. (25.17)), оказывается распределенным
в пространстве и имеет высокую сингулярность по вре-
мени (производная 6-функции).
Более реальным представляется случай точечного ис-
точника, движущегося по некоторой траектории
x(t)=X(t).	(25.20)
Плотность заряда и тока имеют в этом случае вид
Q(x) = g63[x-X(0],	(25.21)
У(х)=£^63[х-Х(0].	(25.21')
Эти величины, как легко проверить, удовлетворяют урав-
нению непрерывности (25.18). Подставляя эти выраже-
§25] ПРИЧИННОСТЬ В КЛАССИЧЕСКОЙ ТЕОРИИ ПОЛЯ 141
ния для Q (х) и /(х) в формулу (25.9), мы найдем ска-
лярный и векторный потенциалы:
где точки t, х, достигаемые «сигна-
лом» от движущегося точечного за-
ряда, лежат на поверхности
. (25.23)
Рис. 26. Запаздываю-
щее взаимодействие
между двумя «точеч-
ными» частицами;
х2 = Х2(/) и %i =
= Х± (/) — положения
этих частиц в мо-
мент времени /2 =
= /х = /, —
— “с”) — эффективное
положение частицы 1.
Здесь 7?—расстояние
между точками хг
и х2.
Рис. 26 иллюстрирует передачу
сигнала от одной частицы ta) к дру-
гой'^) посредством запаздывающей
функции Грина ®ret (х2-~ *i).
Рассмотрим теперь потенциалы
<р (х) и А (х) вдали от точки
х(^ t —0. Для определенности можно
принять, что движение заряда проис-
ходит в ограниченной области
|х| < М. Тогда
(25.24)
(25.24')
В этой области пространства fR4(x) потенциал ф(х) не
имеет значения для причинности, так как первый член
g/r (х) статический, и поэтому с ним не связана передача
какого-либо сигнала; второй член имеет порядок О (1/г3).
Таким образом, только векторная часть потенциала А(х)
осуществит передачу сигнала.
142
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
Предположим, далее, что ток J=gX63(x —X) со-
здается осциллятором, которому сообщено движение си-
лой F (/):

(25.25)
где со— собственная частота осциллятора, т— его масса,
у — коэффициент трения. Самое резкое движение осцил-
лятора, какое можно себе представить, возникает под
действием мгновенного удара, т. е. в случае, когда
F (0 = 46(0-	(25.26)
Принимая во внимание, что
t
Х(0 = ^- у ®(^-T)F(r)dT,	(25.27)
где ®(/)—функция Грина уравнения (25.25):
v о,	t < о,
найдем из (25.26) и (25.27)
Х(/) = 4®(0-	(25.29)
Если со у/2 — малое трение, то
X(^) = Ae-?/2/C0SW/;	(25.30)
в случае большого трения
Х(/) = Ае-?/_	(25.31)
В первом случае максимум тока достигается при t ~ 2/у
и ток длится примерно такое же время; во втором слу-
чае максимум тока имеет место при t = 0 и длится также
в течение времени порядка /^2/у. Ширина импульса А/
в обоих случаях определяется величиной у/2.
§263
причинность 6 Квантовой теории Поля
143
Таким образом, предельно короткий импульс будет
передаваться осциллятором, обладающим предельно боль^
шим трением. Этот элементарный расчет иллюстрирует
способ, которым на практике мог бы быть осуществлен
источник, порождающий короткий сигнал,
В классической (макроскопической) физике не ста-
вится никаких принципиальных ограничений относительно
размеров области, в которой локализован источник, отно-
сительно частоты его колебаний и его коэффициента тре-
ния. В частности, заряд может быть сосредоточен в сколь
угодно малой области пространства (что и выражается
в приведенном расчете функцией б3(х — %(/))) и иметь
сколь угодно малую амплитуду колебаний А при любой
частоте со и любом коэффициенте трения у —ситуация,
типичная для последовательной теории, сама по себе она
не ставит каких-либо ограничений.	л
Ограничения приходят извне. Уменьшая размеры ис-
точника, мы в конце концов придем к источникам, имею-
щим молекулярные размеры, и тем самым перейдем
в область микромира, где произвол в выборе источника
в отношении его массы, частоты, трения и амплитуды
колебаний существенно сокращается. При этом принци-
пиальное значение приобретает соотношение неопределен-
ностей Гейзенберга, которое связывает пространственно-
временную локализацию источника с неопределенностью
в его энергии Д£ и импульсе Др.
§ 26. Причинность в квантовой теории поля
В квантовой теории поля распространение взаимо-
действия из одной области 91 (хх) в другую 91 (х2) опи-
сывается с помощью квантованных полей. Операторы,
представляющие эти поля, подчиняются правилам ком-
мутации (см. (14.3) и (16.2)):
для скалярного комплексного поля ср (я)
[ф (х2) > Ф+ (*i)] = ID (х2—хх),	(26.1)
для скалярного действительного поля ср (х) = ф+ (х)
[ф(х2), ф(Х1)] = 1’О(х2— хх),	(26.2)
144
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
для векторного поля Ди(х)
[Лц (х2), Av (х,)] = iD (х2 — Xi) 6gv	(26.3)
И ДЛЯ спинорного ПОЛЯ Чра (х)
Йа(х2), %(Xi)} = iSap(x2—Xi).	(26.4)
Остальные коммутаторы равны нулю.
Функции D(x2—Xi) и Sap(x2— xj описывают корре-
ляцию полей в различных точках пространства —времени.
Важнейшей особенностью этих функций является то, что
они исчезают для пространственноподобных интервалов,
т. е. для (t2 — Qz — (х2—х^СО. Поэтому корреляция
между значениями полей, разделенных пространственно-
подобным интервалом х2~х±, отсутствует*). Это можно
толковать как отсутствие какой-либо причинной связи
между значениями полей, взятых в областях SR (х2) и 9t(Xx),
расположенных пространственноподобно друг другу так;
что для всех точек x2£fR(x2) и	будет х2~хг.
В этой связи условия коммутации**) (26.1)—(26.4),
которые обычно называют условиями локальной комму-
тативности, можно также рассматривать как условия
микропричинности в квантовой теории поля. Заметим,
что другие формулировки микропричинности, которые
будут описаны позднее, так или иначе подразумевают
соблюдение условий локальной коммутативности вида
(26.1)-(26.4).
Операторы квантовых полей могут быть разложены на
две части: одну, содержащую операторы рождения час-
тиц (ее называют положительно-частотной частью), и дру-
гую, содержащую операторы уничтожения (это отрица-
тельно-частотная часть). Чтобы не загромождать дальней-
шие выкладки лишними обозначениями и индексами, мы
обратимся к случаю действительного скалярного поля ср(х).
*) В случае спинорного поля обращается в нуль не коммутатор
[Л, В], а антикоммутатор {Л, В}. Однако, пользуясь (26.4), нетрудно
показать, что для физически наблюдаемых билинейных комбинаций
вида ф(х)Г'ф(х) (где Г — некоторая спинорная матрица), взятых
з двух точках и х2, будет исчезать их коммутатор.
**) Мы не будем касаться здесь аксиоматических исследований,
которые допускают несколько ослабленные условия — коммутативность
в среднем по вакууму.
§26]
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ ПОЛЯ
145
Разложение этого поля на положительно-частотную часть
Ф+ (х) и отрицательно-частотную ф" (х) имеет вид
ф (х) = ф+ (х) + <Р" (х),	(26.5)
причем
Ф+ (х)=J а+	d3k,	(26.6)
= (26.6')
J у 2ш
где (o = ]/£2-|-mz . Из (26.6) и (26.6') видно, что ф+ (х)
содержит только операторы рождения а+ (й), а ф“ (х) —
только операторы уничтожения я(£)*). Поэтому опера-
тор ф+ (хх) есть оператор рождения частицы в точке хь
а оператор ф" (х2) есть оператор поглощения частицы
в точке х2. Оператор ф“(х2)ф+(х1) будет оператором рас-
пространения частицы из точки хх, где она рождается,
до точки х2, где она поглощается. При этом t2 > t±. Опе-
ратор ф" (хх) ф+ (х2) при > t2 описывает рождение
частицы в точке х2 и ее поглощение в точке хР
Матричные элементы этих операторов и являются
функциями влияния в квантовой теории поля. При этом
единственными отличными от нуля элементами являются
вакуумные средние, т. е.
<	Тв|ф- (х2) <р+ (хх) |¥0> при /2>/х,	(26.7)
<	%> | ф_ (хх) ф+ (х2) | Чг0> при t2 < Zx.	(26.7')
Здесь То—функционал поля, описывающий состояние
вакуума. Оба выражения можно объединить в одно,
если воспользоваться понятием хронологически упорядо-
ченного произведения, «Т’-произведения», двух операторов.
По определению Т-произведение поля ф(хх), взятого
в точке хх, на поле ф (х2), взятое в точке х2, равно
Ф (х2) ф (хх), если /2 > /х, (26.8)
Ф (хх) ф (х2), если t2 < /х. (26.8')
Т ф(х2)ф(хх) =
*) Подобные разложения возможны и для любого квантованного
поля ф, Лц и т. п.
146
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
(ГЛ. V
Заметим, что Т-произведение релятивистски инва-
риантно. Действительно, для времениподобного интервала
х2 xi неравенства 2g /2 инвариантны относительно
преобразования Лоренца. Для пространственно-подобного
интервала х2 ~ х± операторы ср (хх) и ср(х2), согласно (26.2),
коммутируют, и поэтому их порядок в (26.8) несуществен.
Замечая, что ф" (х) То (0) = 0 («устойчивость вакуума»),
нетрудно видеть, что оба выражения (26.7) и (26.7')
объединяются формулой
<	Ч'О I Тф (х2) <р (xj I Чг0> = iDc (х2 — xj, (26.9)
где Dc (х) есть причинная функция, определенная в до-
полнении I (см. 1.5). Физический смысл равенства (26.9)
заключается в том, что левая его часть есть среднее по
всем процессам, когда в одной точке частица излучается,
а в другой точке —поглощается.
Функция Dc(x) имеет вид (см. (1.5))
Dc(x)=	_
= i 6	~ 6	(т +
оЛ у X
+ 0 (- х2)	™ К, (т .	(26.10)
4л2 J/ —х2
Эта функция симметричным образом учитывает запазды-
вающее и опережающее взаимодействия подобно класси-
ческой функции Грина ® (х) в (25.14). Ее существенное
отличие от классических функций влияния заключается
в том, что она не равна нулю и вне светового конуса.
Действительно, при x*=(t2 — t^ — (х2—л\)2<0 из (26.10)
следует
De(x)=	.	(26.10')
4л У —х2
Заметим, что при т]/—х2	1 это выражение при-
обретает вид
Dc(x) =----------------Й=У/2 е~тУ~ , (26.10")
cV ' 4л К—х2 \2 т/—х2 /	V
т. е. вне светового конуса функция Dc (х) экспоненциально
затухает на протяжении комптоновской длины волны
частицы Ть/тс (в формулах (26.10), (26.10'), (26.10") при-
нято л= 1, с= 1).
§26]
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ ПОЛЯ
147
При т = 0 имеем вне светового конуса
<26Л1>
т. е. убывание Dc (х) вне светового конуса более мед-
ленно, нежели при т=^=0 (см. дополнение I, формулы
(1.6) и (1.8)).
На первый взгляд может сложиться впечатление, что
это свойство функции Dc (х) противоречит причинности,
поскольку позволяет распространяться взаимодействию
и вне светового конуса. Мы покажем теперь, что из-за
соотношения неопределенностей Гейзенберга такого про-
тиворечия в действительности не возникает. Для доказа-
тельства этого важного положения рассмотрим две микро-
системы (частицы или системы частиц) Л и В, отдаленные
друг от друга в пространстве*).
Пусть в системе А происходит событие а, а в си-
стеме В—-событие В, причем событие а предшествует со-
бытию &, так что ха < хь. Здесь ха — координата события а,
а хь — координата события Ь. Предполагается, что события
а и b могут быть распределенными в пространственно-
временных областях и тогда ха, хь—точки из этих
областей (все или их часть).
Мы будем считать b следствием события а (причины),
если система Л, как результат события а, посылает в си-
стему В «сигнал», инициирующий в В событие Ь. Тем
самым предполагается, что в процессе каузального взаимо-
действия энергия Еа системы А уменьшается (потеря
энергии на отправленный «сигнал»), а энергия Ев си-
стемы В увеличивается (прием «сигнала»); соответственно
должны изменяться и импульсы этих систем. Иными сло-
вами, «сигнал» несет положительную энергию 8 = Йсо
и соответствующий импульс p = hk. Эти утверждения
имеют смысл только в том случае, когда разброс энергии ДЕ
и импульса \ptt\Elv (у —-скорость системы) в рассмат-
риваемых системах А и В мал по сравнению с энергией
кванта и с его импульсом соответственно:
Д£л<А(о, Д£в<Й®,	(26.12)
Дрл«г<4’	<26Л2')
*) В противном случае мы должны рассматривать Л + В как
одну неразложимую на части систему С.
148
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
Здесь L —размеры области, в которой локализованы
микросистемы А и В (мы считаем эти размеры одинако-
выми). В случае невыполнения этих неравенств нельзя
определить, какая из систем, А или В, излучает сигнал
и какая его поглощает.
Мы видим, что координация событий в терминах при-
чины-следствия требует одновременно и пространственно-
временной локализации микросистем, и достаточной опре-
деленности их энергии Е и импульса р. Это обстоятельство
имеет фундаментальное значение для проблемы причин-
ности в микромире: мы можем изучать причинную связь
только между волновыми пакетами, которые по самой
своей сути являются размазанными, нечетко определен-
ными объектами в пространстве—времени. Поэтому при-
чинная связь ги причинная последовательность явлений
в микромире могут быть установлены лишь в пределах
определенного «допуска», величина которого определяется
пространственным размером волнового пакета Ax = L. Этой
неопределенности в пространственных размерах будет
соответствовать временная неопределенность ^t^^xfc.
Эти соображения будут иметь важнейшее значение
для определения понятия макроскопической причинности
в теории элементарных частиц (см. гл. VI).
Теперь же мы обратимся к иллюстрации этих общих
соображений простым примером.
Рассмотрим два волновых пакета (см. рис. 27, а).
Первый из этих пакетов распределен внутри простран-
ственно-временной области (хх) и имеет пространственную
протяженность Ах « L и временную длительность А/ & Т.
Мы будем считать, что этот волновой пакет имеет энер-
гию Е± с точностью А£ ж Ь/Т и импульс^ с точностью
(предполагается, что E^kE^ Pi^>APx).
В пространственно-временной области Э?(х2) сосредоточен
другой пакет/ который можно считать имеющим" ту же
протяженность L (и длительность Т), энергию Е2^> АЕ<> ж
и импульс Р2 ДР2 h/L.
Заряд первого пакета Q (х^, порождающий поле ср (х2),
можно представить в "форме
• Q:Wsg(^)p	.	(26.13)
§26]
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ ПОЛЯ
149
где пространственная часть—функция р (хх) существенно
отлична от нуля в области 913 (хх) А3, около точки xf,
со есть характерная частота квантового перехода, происхо-
дящего в волновом пакете. Функция g (tjT) существенно
отлична от нуля лишь в области (£х) &Tf 91 (xj =
Рис. 27. а) Пакет в области 91 (х2) расположен позднее пакета, нахо-
дящегося в области 91 (*i) [91 (х2) > 9t(*i)]. Взаимодействие пакетов
обусловливается излучением пакетом 91 (хх) кванта энергии Асо (> 0),
который поглощается пакетом, находящимся в области $ (х2). б) Пакет
91 (х2) расположен ранее пакета, находящегося в 9t (хх) [$ (х2) < 91 (хх)].
В этом случае взаимодействие обусловливается испусканием пакетом
91 (хх) отрицательного кванта (to < 0) и поглощением его пакетом
в 91 (х2). Этот процесс эквивалентен излучению кванта to > 0 паке-
том в 91 (х2) и поглощению его пакетом, расположенным в 91 (хх).
= 9i3 (хх) x9tx (Q. Ее можно рассматривать как величину
заряда волнового пакета, который адиабатически, т. е.
в течение времени Т 1/со, включается и выключается
около момента времени /х = 0. Можно, например, поло-
жить, что
1 Т
Л ^ + 72’
1 L
я xl + L2 ’
(26.14)
Этот процесс адиабатического включения и выключе-
ния заряда противоречит закону сохранения заряда и
поэтому имеет чисто формальное значение. Мы прибегаем
к этому искусственному приему лишь для того, чтобы
выделить эффект, порожденный источником поля не только
150
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
1ГЛ. V
от области пространства 9i3 (Xi) ж А3, но и за определен-
ное время « Т.
Более близким к действительности было бы рассмотре-
ние волнового пакета, движущегося по некоторой траек-
тории. Тогда «включение» и «выключение» области Э13 (xj
происходило бы само собой за время Т где v —
скорость пакета. Адиабатичность такого «автоматического
включения» и «выключения» области (хх) будет соблю-
дена, если
<26'15>
или
(26.15')
где к есть длина волны кванта, излучаемого или погло-
щаемого волновым пакетом.
Рассмотрим теперь квантовый аналог действия W
(25.14). Согласно определению причинной функции (26.9)
именно она играет в квантовой теории роль той функции
Грина, которая связывает события в одной области про-
странства— времени с событиями в другой. Поэтому
W = i J Q (х2) Dc (х2— хх) Q (хх) d*xr. (26.16)
Отсюда видно, что
Jq (х2) 6Q (Xi) ~~Dc ~	(26‘ 7)
и что, в отличие от (25.14), эта величина не исчезает вне
светового конуса.
Для выяснения свойств величины W удобнее вычис-
лить поле (р (х2), создаваемое пакетом Q (хх) в области К (х2):
<Р (х2) = $ Dc (х2 — Q (%i)	*).	(26.18)
Наиболее слабое затухание функции Dc (х) вне светового
конуса имеет место при ш = 0, т. е. для поля, не имеющего
частиц с массой покая, отличной от нуля.
*) В силу свойств симметрии функции Dc(x2 — аД можно было
бы так же вычислять поле ср (д^), создаваемое зарядом Q (х2) в 3? (xj;
результат вычисления симметричен относительно областей 91 (хЛ и
91 (х2).
§27] РАСПРОСТРАНЕНИЕ СИГНАЛА «ВНУТРИ» МИКРОЧАСТИЦЫ 151
Функция Dc(x2— хх) описывает процесс взаимодейст-
вия посредством сигнала с положительной энергией, сим-
метричного относительно обеих пространственно-временных
областей 9ft (хх) и 9i(x2). Рис. 27 иллюстрирует сказанное.
Что же касается «аномального» поведения причинной
функции Dc (х2—хх) вне светового конуса, то соотношение
неопределенностей не позволяет «уличить» частицу в на-
рушении каких-либо законов причинности [52, 53].
§ 27. Распространение сигнала «внутри» микрочастицы
В предыдущем параграфе было показано, что, хотя
причинная функция Dc (х), определяющая распространение
взаимодействия в квантовой теории поля, и не исчезает
вне светового конуса, тем не менее невозможно обнару-
жить распространение сигнала со скоростью, большей
скорости света, в частности с бесконечно большой ско-
ростью.
Этот «парадокс» 7)с-функции был рассмотрен для слу-
чая взаимодействия двух точечных частиц.
Сходный парадокс возникает для микрочастицы, име*
ющей конечные размеры. Суть дела заключается в том,
что форм-фактор частицы F (д) (§ 22), где q — импульс,
передаваемый при взаимодействии, не исчезает для про-
странственноподобных значений q и, следовательно, ча-
стице можно приписать жесткое пространственное распре-
деление зарядов и токов
р (х) = F (д) e^xd3qt	(27.1)
способное передать сигнал с бесконечно большой скоростью.
Для разъяснения возникающей ситуации достаточно огра-
ничиться рассмотрением взаимодействия виртуального
фотона со спинорной частицей.
Поле фотона k будем описывать вектор-потенциалом
Лц(х), а спинорное поле частицы, имеющей массу,— опе-
ратором ф(х). Оператор взаимодействия в первом прибли-
жении по заряду е может быть написан в виде
W = j (х3, х2, хх) Лм (х2) d4x3 d4x2 d4xx, (27.2)
152
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
где Jg(x3, х2, хг)—плотность тока, создаваемого спинор-
ной частицей (см. диаграмму на рис. 28). Амплитуда ве-
роятности перехода частицы из состояния i в состояние f,
Рис. 28. Графическое изо-
бражение тока /ц, (х3, х2, X])
для спинорной частицы,
имеющей конечные размеры;
хх— вход частицы, х3 — вы-
ход; в точке х2 происходит
взаимодействие с внешним
полем А (х).
вызванного этим взаимодей-
ствием, будет равна
= х I	2) d*XZ9
(27.3)
где </1	(х2) | есть матрич-
ный элемент плотности тока
(х3, х2, хг), отнесенный к
переходу i-+f:
I Jii (x2) | i> =
= $	(*з) J X2, Xx) t|)(. (xx) X
X^Xad’Xx. (27.4)
Мы будем считать волновые функции фу и произ-
вольными, с тем лишь ограничением, что они являются
суперпозициями состояний только с положительной энер-
гией:
% (Х3) = $ Cf (р3) Uf (р3) exp (— ip3x3) d3p3,	(27.5)
(Xj) = J ct (px) ut (pi) exp (ipxXx) d3Pi;	(27.5')
здесь uf, щ — биспиноры Дирака, , ct — амплитуды со-
стояний с импульсами р3, р/, р3, р? > 0. Обозначая р3 —
— p± = q и пользуясь соотношением
<р31 -7ц (Х2) | Р1> = $ exp (— ip3x3) Jл (х3, х2, Хх) ехр х
X (— ipiXj d*x3 dix1 = Jn(q) exp (iqx2),	(27.6)
получим из (27.4), (27.5) и (27.5')
<f I -7 ц W I i> = J c? (ft) Ct (pt) uf (p3) J * (?) щ (pi) x
X exp (iqx2) d3pt d3p3, (27.7)
§27] РАСПРОСТРАНЕНИЕ СИГНАЛА «ВНУТРИ» МИКРОЧАСТИЦЫ 153
где /цО?)—оператор тока в импульсном представлении.
Этот оператор согласно (22.15) может быть записан в виде
Л (7) = eFi (<72) 7ц + ip,CTM,v^vF2 (q2),	(27.8)
где е—заряд частицы, р—ее магнитный момент, Fi(<72),
F2((?2)—электрический и магнитный форм-факторы части-
цы. Величины F± и F2 при таком определении безразмерны
и должны зависеть лишь от отношения q^lq^ где qm —
некоторое значение q, определяющее скорость убывания
F± и F2 при |^| —>оо. Размер частицы R связан с qm
соотношением R = 1iiqm.
Для того чтобы рассмотреть распространение сигнала
внутри частицы, мы будем считать состояния фу и ф;
локализованными волновыми пакетами. Фотонное поле Ац
будем считать также локализованным *). Для определен-
ности мы положим
,3/2	(	1	Л
9 (Р) = ехР { ~2 bf &ipx'\ • (27-9)
л?/2	(	1	1
Q (Р)=^ехР\— pty—ipXij > (27.9')
Лр.(х) = ац exp {— i \k (x—X)—kt (t—7’)]}x
xexp	• (27.9")
Волновые функции (27.5) и (27.5') представляют собой
волновые пакеты со средними импульсами р, и ph лока-
лизованные при / = 0 около x = xf, Х(, при средних квад-
ратичных отклонениях
F 2	_______ i
^(P~PfY = ^' А(х-х/)2>а^+р-^&/, (27.10)
uf	fnc
где коэффициенты а и 1, т—масса частицы (ср. § 15).
Те же соотношения относятся и к пакету (27.9').
Поле Лц(х) представляет собою волновой пакет вир-
туальных фотонов с характерным волновым вектором
k (k, /г0) и «скоростью» распространения и, локализован-
ный при Т=0 около х = Х, в области шириной порядка
Дх « а, Д/« а/с. Такой выбор формы пакета виртуальных
*) См. дополнение VIII, формула (VIII.4).
154
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
|ГЛ. V
фотонов соответствует предположению, что он мог бы
быть излучен реальной физической частицей.
Заметим, что если бы было возможно использовать
бесконечно узкие пакеты в пространстве и во времени
б-образного типа фу (х3) = б4 (х3 —xz), фг. (хг) = б4 (хх—%.),
А & б4 (х2—X), то, как видно из (27.2)—(27.4), амплитуда
перехода оказалась бы равной непосредственно (xz, X, xz)
и факт распространения сигнала с запрещенной скоростью
был бы установлен.
Однако мы не можем использовать волновые пакеты,
протяженность которых как угодно мала. Действительно,
прием сигнала частицей заключается в устанавливаемом
факте изменения ее импульса pt —> pf. Это изменение
должно быть больше разброса импульсов кр^Ъ/Ь^
Apf ж h/bf1 \k ж hl а в исходных и в конечных пакетах,
т. е. (считая bf жЬ^Ь)
<27л1)
Отсюда вытекает также неравенство

(27.1 Г)
С другой стороны, размеры всех трех пакетов должны
быть меньше размеров частицы:
6Z<7?, b^R, a<^R.	(27.12)
Так как условия (27.11) — (27.12) не противоречат
квантовой механике, то на первый взгляд создается прин-
ципиальная возможность уловить сигнал, идущий внутри
частицы со скоростью, большей скорости света. Однако,
как показывает дальнейший расчет, эта возможность ока-
зывается иллюзорной.
Для доказательства этого утверждения вычислим ам-
плитуду вероятности Тfi для волновых пакетов ф/? ф. и
А, удовлетворяющих условиям (27.11), (27.1 Г) и (27.12).
Эта амплитуда определяет интенсивность сигнала, прини-
маемого в центре частицы и ее периферической области.
§ 27] РАСПРОСТРАНЕНИЕ СИГНАЛА «ВНУТРИ» МИКРОЧАСТИЦЫ 155
Согласно (27.3) имеем
Tfi — У J4/3x2 J ‘FPs&Pi х
хехр{—у &2 [(р3-р/)2 + (/>1—А-)2] +	х
X u*f (рз) F (р) ut (pj) exp [— ikx2] x
хехр [_^{(х2-Х)2 + [(х2-и/)-(Х-иТ)]^}]. (27.13)
При этом, чтобы избежать излишних выкладок, мы
положили xi = xf = Q, bf,bt = b.
Далее, введено обозначение F (q) = a,lly^Jll(q). Если
размеры пакетов b и а во много раз больше величин
hl Pi и h/k, то интегрирование в (27.13) сразу выполняется
и дает обычный в теории рассеяния результат:
Tfi^^[k-q)u*f (p^F^u^).	(27.14)
Однако координаты места посылки сигнала (точка х2) и
места его приема (точки х± и х3) в этом случае полностью
выпадают и поэтому остаются неопределенными.
Обратимся теперь к случаю пакетов малых размеров
а и Ь, но все же удовлетворяющих условиям (27.11),
(26.1 Г), (27.12).
По предположению | qfi \^>h/b^> qm (импульсачастицы),
поэтому множитель F (<?) можно вынести из-под знака ин-
теграла. Мы вынесем также из-под знака интеграла мед-
ленно меняющиеся величины
Далее заметим (см. дополнение VIII), что
<7o = £(A)-£(A)=£/-^+^-V<T]+ .... (27.15)
где
l=ps— Pf, n=Pi—Pi,	Vi^Ei- (27.15')
Интегрируя теперь по £ и q, получим
тfi ~~Т u*f	F Ui ехр I-1 ('kX~ Й°7'^х
X {d3xdte-®^, (27.16)
156
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
где
Ф (х, 0 = i (k—q) x—i (k0 — qt)t + ^ (x— Vtt^ +
+ 2^ (x -X)2 +	[(x - »/) - (X- uT)Y (27.17)
Рис. 29. Иллюстрация к распро-
странению сигнала внутри
микрочастицы. Перекрытие вол-
новых пакетов начального (р,)
и конечного (ру) состояний до
некоторой степени имитирует
64-образный источник. А изоб-
ражает пакет фотонов. Взаимо-
действие возникает, когда все
эти пакеты перекрываются.
(причем здесь для сокра-
щения переобозначено q,i=
=q, Ef—Ei = q0).
Таким образом, амплитуда
Тл определяется перекры-
тием в пространстве и во
времени четырех пакетов. Эта
ситуация изображена на рис.
29. Существенно, что пакеты
в точках х, t 0 и х « X,
t ограничены не только
в пространстве, но и во
времени, так что они до
некоторой степени имитиру-
ют идеальные 6-образные
сигналы типа 64(х).
Вычисление последнего ин-
теграла в (27.16) приводит
к результату
Tfi	F Ui ехр	х
Хехр[-¥(Х,Т)], (27.18)
где Т (X, Т) равно (см. дополнение VIII)
Т (X, Т) =X* + (Х~иту-[2Х-«Т]2-
-^(Х-«Т, »)2-^[(2Х-«Т) (Х—иТ, «)] +
(27Л9)
Коэффициенты Л2, В2, С2, А2 суть функции ширины
пакетов а и b и трех скоростей Vh Vft и. Эта квадратич-
ная форма положительно-дефинитна, и экспоненциальный
§281
УСЛОВИЯ МИКРОПРИЧИННОСТИ
157
множитель ехр[—Т (X, Т)] —► О при больших |Х| как
ехр (—X2/d2), где d2&a2 (или &Ь2). Это означает, что
факт передачи сигнала от периферии к центру частицы
может быть замечен лишь в том случае, если расстояние
от периферии до центра |Х| не превышает ширину па-
кетов а или Ь.
Однако в этом случае волновые пакеты сильно пере-
крываются внутри частицы и передача импульса осущест-
вляется непосредственным контактом.
Воображаемое пространственное распределение токов
/ц(х3, х2, хх), которое могло бы передать сигнал с беско-
нечно большой скоростью, и в этом случае полностью
выпадает из игры. Таким образом, пространственно про-
тяженную частицу, оказывается, также невозможно ули-
чить в передаче сигнала, идущего со скоростью, большей
скорости света [54].
Результаты § 26 и этого параграфа можно рассматри-
вать как указание на то, что в схему квантовой теории
поля можно ввести отклонения от принятой формы при-
чинности, которые из-за соотношения неопределенностей
будут совместимы с классическими представлениями о при-
чинности.
§ 28. Условия микропричинности
в квантовой теории поля
Состояние системы в квантовой теории определяется
волновой функцией Т—вектором в пространстве Гиль-
берта, зависящим от времени t и от динамических пере-
менных Qx, Q2, Q3, ..., Qn, характеризующих рассматри-
ваемую систему. В случае теории поля число таких
динамических переменных бесконечно велико (N —> оо3),
так как посредством их надлежит описать мгновенное со-
стояние полей во всем пространстве 9i3 (х). Поэтому вол-
новая функция в этом случае является функционалом и
зависит от некоторых функций А (х), В(х), ..., характе-
ризующих рассматриваемые поля. Далее, из релятивист-
ских соображений целесообразно рассматривать Т не как
функцию /, а как функционал от некоторой пространст-
венноподобной поверхности о = а(х), которая только
в частном случае вырождается в плоскость t = a(x)=
= const.
158
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[гл. v
Подчеркивая функциональную зависимость волнового
функционала Т от поверхности а(х) и полей А (х),
В (х), ..., мы будем писать аргументы Т в фигурных
скобках:
Лг=Лг{ст(х), А(х), В(х), ..(28.1)
Нормировка этого функционала, определяющая норми-
ровку вероятностей,
(¥,¥)=	(х), В(х),	(28.2)
где интеграл взят в пространстве функций А (х), В (х), ...,
должна сохраняться во времени, иными словами, не дол-
жен зависеть от выбора поверхности ст(х).
Рассмотрим теперь значение полевого функционала Т
на поверхности о', которая отличается от поверхности о
jc+dx
Рис. 30. Пространственноподобная поверхность о (х) и ее вариация
в области (%, x-\-dx).
только в окрестности точки х и лежит позднее ее (см.
рис. 30). Если о'и о отличаются бесконечно мало:
а' (х) = а (х) + 6о (х),	(28.3)
то новый функционал Т =	А(х), В(х), ...} мы
можем выразить через функциональную производную
бТ/бо (х) функционала по поверхности а (х) в точке х (см.
дополнение IX):
Т'	Т{</}=Т {а, А, В, ...} + j	(*)&х.
(28.4)
Заметим, что величина' бо (х) d?x есть бесконечно малый
четырехмерный объем, заключенный между поверхностями
о и а' (см. рис. 30).
Мы обратимся теперь к принципу причинности, кото-
рый сформулируем классическим образом: последующее по
времени состояние Т' однозначно определяется предшест-
§28]
УСЛОВИЯ микропричинности
159
вующим состоянием Т. Отсюда следует, что определенное
в (28.4) приращение функционала должно однозначно оп-
ределяться самим этим функционалом.
Далее, в силу линейности теории связь между прира-
щением функционала Т'—Т и самим функционалом Т
должна быть линейной. На основании этих аргументов,
пользуясь принятым определением функциональной про-
изводной, мы можем написать
<28S>
где т] —линейный эрмитов оператор. Множитель i про-
диктован требованием постоянства нормы функционала
(Т, Т). Действительно, варьируя норму (Чг, ¥), нетрудно
проверить, что вариация 6 (Т, ¥) только в том случае
равна нулю, если оператор rfj антиэрмитов, т. е. если
(fiq)+=—И]+ =—и], так что оператор т] эрмитов. Его
можно представить в виде
П =----(28.6)
где W, по определению, есть эрмитов оператор энергии
взаимодействия полей и является функцией операторов
этих полей А (х), В (х), ...
Уравнение (28.5) теперь приобретает вид
=	(28.7)
6а (х)	v ’
Это—известное уравнение Томонага—Швингера. Функ-
циональная производная б¥/6сг(х) и функционал Т яв-
ляются инвариантами. Отсюда следует, что оператор W
должен быть релятивистским инвариантом.
При W =0 функционал 4е оказывается постоянным.
Это означает, что мы выбрали так называемое представ-
ление взаимодействия, когда свободные невзаимодействую-
щие поля описываются постоянным по времени функциона-
лом Tq.
Возьмем теперь вторую вариацию от функционала Т,
варьируя эту же пространственноподобную поверхность
160
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
сг(х) около некоторой другой точки у. Из (28.7) получим
X / V = (*)	= -V (X) F («) т. (28.8)
6а(х)6о(^) v 76а(//)	&	4 7 w v 7
Выполняя теперь эти же вариации в другом порядке и
вычитая результаты, найдем
[Г(х), F(z/)] =0 при х~у, (28.9)
т. е. операторы энергии взаимодействия полей, взятые
в разных точках х и у, должны коммутировать, поскольку
точки х и у лежат на разных пространственно-подобных
поверхностях так что не могут быть соединены световым
сигналом.
Так как оператор W есть функция операторов кван-
тованных полей Л(х), В(х), то условие (28.9) будет вы-
полнено само собой при соблюдении условия локальной
коммутативности полей, т. е. условия микропричинности,
описанного в § 25. Поэтому условие (28.9) может рас-
сматриваться как важнейший вывод из принципа микро-
причинности. Впервые оно, в несколько иной форме, было
получено Ф. Блохом [55].
В заключение заметим еще одно существенное след-
ствие принципа причинности: изменение волнового функ-
ционала Т за конечное время, при переходе от одной
пространственно-подобной поверхности ах (х) к лежащей
позднее поверхности а2 (х), можно представить как уни-
тарное преобразование с оператором U (сг2, ах), являющее-
ся последовательностью бесконечно малых унитарных
преобразований.
Действительно, из (28.4) и (28.7) следует, что *)
¥' = Т {01 + ба (х)} = ( 1 -4- W7 U) ба (х) d3x\Y {а (х)}.
\ Ъ	/
(28.10)
Применяя этот оператор во всех точках поверхности с\(х),
мы получим значение функционала Т" на поверхности ах (х),
лежащей позднее, но бесконечно близко к поверхности
*) Мы опускаем здесь зависимость Т от динамических перемен-
ных А (х), В (х).
§ 2 81
УСЛОВИЯ МИКРОПРИЧИННОСТИ
161
о\ (х). При этом, в силу (28.8), порядок применения опе-
раторов ( 1 —l-r W (х) бст (х) dsx) несуществен.
\ Ть	/
В результате получим
Т"=Т{ст;'(х)} =
С"1
СТ1
d*x Т{ах(х)}.
(28.10')
Таким же образом перейдем от поверхности ох к по-
верхности о/', лежащей позднее поверхности ох, но
бесконечно близко к ней. Повторяя эту операцию беско-
нечное число раз, найдем
(28.11)
где унитарный оператор U (а2, ах) равен
&(ст2, ст1)=Техр( —С F(x)d4x ).	(28.12)
\ ft J	/
<h
Здесь буква Т указывает на упорядочение по времени.
Унитарность оператора U (а2, ох) непосредственно следует
из эрмитовости оператора W. Формулу (28.12) для опе-
ратора U (о2, ох) совместно с условием (28.9) можно рас-
сматривать как выражение принципа микропричинности
на языке волновых функционалов.
Из (28.7), (28.11) и (28.12) следует, что оператор
(7 (о2, сгх) удовлетворяет уравнению Томонага—Швингера.
Запишем его в специальном виде, полагая ох =—оо,
сг2=сг. Тогда имеем
1А8^’~те) = Г(х)#(п, -оо).	(28.13)
Для специального случая плоской пространственно-
подобной поверхности в=пх, где п—единичный времени-
подобный вектор (n2 = 1, п0>0), вариация So сводится
к малому смещению de всей плоскости о по направлению
вектора п, так что So =dad3x. Умножая уравнение (28.13)
на d3x и интегрируя по трехмерному объему, получим
/А= W (ст) и (стп — ОО), (28.14)
6 д. И. Блохинцев
162
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
где
w (а) = J W (х) d3x = J W (х) б (о—пх) d*x. (28.15)
В этой форме уравнение Томонага—Швингера напоминает
обыкновенное уравнение Шредингера в представлении
взаимодействия *).
Обратимся теперь к связи оператора U с матрицей
рассеяния S. По определению матрица рассеяния S пре-
образует состояние микросистемы, заданное в бесконечно
удаленном прошлом Т (— оо), в состояние микросистемы
в бесконечно удаленном будущем Т(4-оо):
Y(+oo)=ST(—оо).	(28.16)
Из (28.11) следует, что Т (— оо) есть предельное значение
Y{Oi}, когда поверхность сг1 отодвигается в —оо, а
Y (-|—оо)—предельное значениеТ{ст2}, когда поверхность ст2
отодвигается в ф-со**). Следовательно, матрица рассея-
ния S есть унитарный оператор
§S+=7.	(28.17)
являющийся предельным значением оператора U {ст2, crj
при ст2—>-4-оо и ffj —i—оо:
I
h
S=t7{o2, ст1}=7'exp
F(x)d4x), (28.18)
где интегрирование в экспоненте распространено уже на
все пространство—время Э?4 (х).
Вместо матрицы S часто вводят матрицу амплитуды
рассеяния Т, связанную с матрицей S соотношением
§=I + iT.
(28.19)
*) Релятивистский характер представления взаимодействия и урав-
нение в форме (28.14) впервые были указаны в дипломной работе [56],
**) В § 32 мы рассмотрим подробно физический смысл предель-
ного перехода о —> ± оо.
§29] МИКРОПРИЧИННОСТЬ В ТЕОРИИ МАТРИЦЫ РАССЕЯНИЯ 163
Соотношение унитарности для матрицы Т, как это следует
из (28.17), имеет вид*)
i(f+— f)=ft+.	(28.20)
Обозначая частное начальное состояние через
(ЧГ£=ЧГ(—оо)), а частное конечное состояние через
получим амплитуду вероятности перехода i-+f;
SZ/ = <47|S|^.>,	(28.21)
и при —вероятность перехода из состояния i в со-
стояние f;
(28.22)
§ 29. Микропричинность в теории матрицы рассеяния
Впервые Штюкельберг [53] и его коллеги пытались
развить теоретическую схему, в которой S-матрица вво-
дилась в теорию непосредственно, без обращения к урав-
нению Шредингера (28.7), связывающего, в отличие от
S-матрицы, бесконечно близкие по времени и пространству
состояния. При этом было обращено внимание на прин-
ципиальную важность формулировки принципа причинно-
сти непосредственно для самой S-матрицы. Существенный
успех в этом направлении был достигнут позднее в ра-
ботах Н. Н. Боголюбова, который применил несколько
формальный, но оказавшийся весьма эффективным прием
локального адиабатического «включения» хи «выключения»
взаимодействия [38].
Матрица рассеяния S является функционалом от опе-
ратора энергии взаимодействия. Введем другой, вспомо-
гательный, оператор
Wg(x)=g(x)W(x),	(29.1)
где функция g (х) принимает любые значения в интервале
от 0 до 1.
Если построить матрицу рассеяния на основе взаимо-
действия	то она будет функционалом от g(x) —
♦) Из этого соотношения вытекает оптическая теорема, приведен-
ная в § 23 (см. (XII.4)).
6*
164
причинность в квантовой Теории
1гл. v
величины, определяющей степень «включения» взаимодей-
ствия в той или иной области пространства—времени:
S=S{g(x)}.	(29.2)
При g(x)=0 взаимодействие полностью выключено и
S {g (%)} = 1, при g (х) = 1 взаимодействие полностью вклю-
чено и S {g (%)} = S—полной матрице рассеяния (28.18).
Рассмотрим теперь специ-
альный случай, когда функ-
ция включения g(x) отлична
от нуля в двух областях про-
странства— времени: 912(х)и
Э1х(х), причем область &t2(x)
лежит целиком позднее неко-
торой пространственноподоб-
ной поверхности а(х), а об-
ласть Э1х(х)—раньше ее (см.
рис. 31). Очевидно, что
£(*)=& (*)+&(*), (29.3)
Рис. 31. Две области $х (х) и
W, из которых вторая ле-
жит полностью позднее (выше)
пространственноподобной по-
верхности о(х). В области
$ftx (х) взаимодействие вклю-
чено с силой, определяемой
«зарядом» gi(x); в области
Sft2 (х) это же взаимодействие
определяется зарядом g2 (х).
причем gx#=0 в 91х(х), а
g2y=0 в 912(х). Волновой
функционал Т {о} на по-
верхности о может ..быть
получен из начального состо-
яния Y (— оо) с помощью
S-матрицы, зависящей толь-
ко от взаимодействия в об-
ласти 91х(х); взаимодействие
в будущем, в области К2(х), не должно влиять на со-
стояние Yjo}:
(29.4)
Конечное состояние ¥ {g} получится из ¥ {о} применением
оператора S {g2 (х)} *):
¥{g ^}=S{g2 (х)} S (x)} ¥ (- co), (29.5)
*) Заметим, что ввиду выключения взаимодействия на поверхности о
функционал 4е {о} = 4е { 4- оо, g (х)}.
§29] МИКРОПРИЧИННОСТЬ В ТЕОРИИ МАТРИЦЫ РАССЕЯНИЯ 165
откуда следует, что
§kW}=S{g2(x)}S{g1(x)}.	(29.6)
Сравним теперь два случая, которые друг от друга от-
личаются только взаимодействием в области 9J2(x), так
что
g' (x)=g'i(x)+g1(x) и g" (x)=^(x)+gx(x). (29.7)
Составим выражение S (g") S+ (g'). Согласно (29.6) имеем
§ (Я") =5 (g% S (gx), §+ &') = S+ fei) S+ (Й),	(29.8)
следовательно,
S(g")S+(gf)=S^S^g')f	(29.9)
т. e. это выражение не зависит от предшествующей истории
системы в области SRx(x).
Удобно сформулировать этот вывод в дифференциальной
форме. Будем считать, что g'2(y) и gz(y) отличаются друг
от друга бесконечно мало, так что 6g(y) = gl (#)—gaG/),
причем 6g- (у) у=0 в SR2 (у), т. е. в области, лежащей позднее о.
В этом случае
s (g") = s (g') + J-gr 6g' (g) dy.	(29.10)
Опуская теперь штрихи, мы можем записать (29.9)
в форме
S(g + Sg)S+(g) = l+6§(g)S+ (g)-	(29.11)
Это выражение не должно зависеть от поведения g
в области Э^х (х).
Поэтому вариационная производная от выражения
(29.11) по g (х) (причем точка х С 9tx (х)) должна равняться
нулю. Следовательно,
-rr-rf-SmS+tg)') =0,	(29.12)
если точка x предшествует по времени точке у (у > х)
Соотношение (29.12) релятивистски ковариантно. В случа
пространственного интервала между точками х и у (х ~ z/e
выбором системы координат всегда можно сделать у «позд
166
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
нее» х. Поэтому условие (29.12) выполняется и в том
случае, когда точки х и у разделены пространственно-
подобным интервалом. Условие (29.12) является выраже-
нием принципа причинности на языке матрицы рассея-
ния.
Как было показано (см. [38]), на основе требований:
1) релятивистской инвариантности, 2) унитарности,
3) причинности (в форме (29.12)) можно построить S-мат-
рицу, не обращаясь к уравнению Шредингера*).
Отсылая читателя к монографии [38], где изложены
необходимые доказательства, мы ограничимся здесь пост-
роением этой матрицы с точностью до второго прибли-
жения по константе взаимодействия. Таким образом,
дальнейшие выкладки являются только иллюстрацией к
изложенным в этом параграфе идеям.
Запишем митрицу S в виде функционального ряда по
степеням g(x):
s = 1 + Tf J Si (*i) ё (*1)
+ IF j s2 (xlt x2) g (xx) g (x2) d4 xt d4 x2 + • • • (29.13)
Поскольку мы условились считать, что ’ при полном
включении взаимодействия g(x)=l, то мы примем, что
операторы Sx, S2, ..., Sn, пропорциональны степеням
81, е2, ..., е" некоторого малого параметра, имеющего
смысл константы связи («заряда») **).
Подставляя выражение (29.13) для S в условие унитар-
ности (28.17), получим, с точностью до е2,
Sx(x)-|-Sx (х) =0,	(29.14)
S2 (х, у) + St (х, у) + Sx (х) St (у) + Sx (у) S+ (х) = 0 (29.15)
и т. д. ***).
Из первого соотношения следует, что
Sx (х) = it (х),	(29.16)
*) При этом необходимо еще выполнение некоторых математи-
ческих требований к операторам, входящим в структуру S-матрицы
(см. [38]).
**) Например, в электродинамике e — elVtic.
*♦*) Здесь мы ввели новые обозначения х1=х, х2 = г/, что удобно,
поскольку мы ограничиваемся вторым приближением.
§29] МИКРОПРИЧИННОСТЬ В ТЕОРИИ МАТРИЦЫ РАССЕЯНИЯ 167
где £(х)—некоторый эрмитов оператор:
L(x)=L+(x).	(29.17)
Условие (29.15) выполняется автоматически при выпол-
нении (29.16) и условия причинности (29.12). Подставив
в (29.12) разложение (29.13), после несложных выкладок
найдем условие причинности (с точностью до е2):
S2(x, «/) + §1(x)Si’(z/)=0	(29.18)
при у>х.
Учитывая (29.16), находим S2 (х, у)'.
S2(x, у)— — L(x)L(y) при у>х. (29.19)
Ввиду равноправия точек х и у имеем
S2(z/, х)—$г(х, у) —— L\y)t(x) при у<х. (29.19')
Оба выражения перекрываются в области х ~ у и будут
совместны, если
[L (х), L («/)] =0 при х ~ у. (29.20)
Это требование называют требованием локальности.
Оба выражения (29.19) и (29.19') можно объединить
в одно, если воспользоваться знаком Т-произведения:
S2(x, y)=i2T[L(x) L(y)l	(29.21)
Подставляя полученные выражения для S,(x) и S,(x, у)
в ряд (29.13), найдем
S(g) = Z+jj-jL(x)g(x)d‘x+
+ £ Т {j L (х) L (у) g (х) g (у) d*x d*y} + ... (29.22)
Продолжая последовательно изложенную процедуру,
можно получить весь ряд (29.13), который суммируется
в символическую экспоненту:
S (g) = Т { expt7 J L (х) g (х) d4x} .	(29.23)
Эта формула при g (х) = 1 'совпадает с формулой для
матрицы § (28.18), полученной на основе уравнения Щре-
168
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
дингера для волнового функционала, если положить
в (29.23)
L(x)= —1|Г(х).	(29.24)
Ть
Поэтому требование локальности (29.20) совпадает с уста-
новленным ранее условием Блоха (28.9).
Из выражения (29.23) следует, что требование реляти-
вистской инвариантности S-матрицы будет выполнено,
если при неоднородном преобразовании Лоренца
Хц, = L^Xy -р	(29.25)
(символически xr =Lx-[-a) функция включения g(x) будет
скаляром, а оператор энергии взаимодействия W (^ — ре-
лятивистским инвариантом. Это значит, что при преобра-
зовании имеет место соотношение
g(x) ->-g' (х') =g(L~1 (х'—а)),	(29.26)
иными словами, новая функция g' имеет ту же величину
в той же физической точке пространства—времени, что
и непреобразованная функция g.
Далее, оператор энергии взаимодействия W (х) есть
функция операторов полей Л (%), В(х), которые преобра-
зуются при преобразовании Лоренца по формулам
Д' (V) =SL A [L-1 (х' - а)],	(29.27)
причем вид матрицы зависит от ковариантных свойств
поля (для скалярного поля Sl = 1, для векторного поля
она совпадает с матрицей L, так что Sl= L, и т. п.).
Так как оператор Л'(х') дает совершенно ту же физи-
ческую информацию, что и непреобразованный оператор
А (х), то оба оператора, согласно общим принципам кван-
товой теории, должны быть связаны унитарным преобра-
зованием
Л'(х')=/7£Л(х)^Г1,	(29.28)
причем унитарный оператор Ul полностью определяется
лорепцевым преобразованием (29.25).
ПРИЧИННОСТЬ И СВОЙСТВА S-MATPHUbi
169
§ 301
Если оператор энергии W является инвариантом, то
при этом преобразовании будем иметь
F' = W' {А' (х')[ = W {А' (х')} =
= W {UlA (х) UI^UlWIA (х)} Ul1==W{A (х)} = №(х).
(29.29)
Так как матрица S есть функционал (29.23) от опера-
тора W, то тем самым доказывается релятивистская инва-
риантность матрицы S.
В заключение этого раздела заметим, что наличие син-
гулярных функций типа D(x), S(x), входящих в правило
перестановки компонент квантованных полей, и функций
Dc(x), Sc(x), входящих в Т-произведение квантованных
полей, приводит к тому, что элементы матрицы рассеяния
S оказываются расходящимися и для получения физически
осмысленных результатов в функциональном ряде (29.13)
необходимо произвести определенные изменения, которые
исключат вклад предельно малых расстояний.
Эти «определенные изменения» получили название пра-
вил перенормировки. Эти правила подробно освещены в су-
ществующей литературе (см. [37, 38]), и мы не будем
воспроизводить их в этой монографии, цель которой совер-
шенно иная. Мы ограничимся лишь замечанием, что эти
правила, привнесенные извне, таковы, что не нарушают
основных требований релятивистской ковариантности, уни-
тарности и причинности в применении к S-матрице. Однако
нельзя освободиться от впечатления, что эти правила пере-
нормировки поддерживают жизнь современной теории поля
за счет потери изящества и логической стройности этой
теории.
§ 30. Причинность и аналитические свойства
матрицы рассеяния
Важным следствием микропричинности являются опре-
деленные аналитические свойства матричных элементов
матрицы рассеяния Tfi (амплитуд рассеяния), определяю-
щих вероятности квантовых переходов из некоторого на-
чального состояния i в конечное f.
Впервые на эти свойства было обращено внимание еще
в классической электродинамике Р. Кронигом [57] и Г. Кра-
i70
причинность ё квантовой теорий
[ГЛ. V
мерсом [58], которые, исходя из требования, чтобы скорость
распространения сигналов не превосходила скорости света
в пустоте, установили интегральное соотношение между
действительной частью показателя преломления световых
волн Re/г (со) (со—частота колебаний) и его мнимой частью
Im и (со):
Re п (со) = Re п (0) - — ?	”(а/) da'.	(30.1)
л J со (со —со2)
о
Соотношения такого типа получили название дисперсион-
ных соотношений. Основой дисперсионных соотношений
является теорема Коши. Связь их с причинностью может
быть иллюстрирована следующим простым примером.
Пусть в точке х=0 находится микрочастица, рассеи-
вающая падающую на нее волну. Эту падающую волну
мы представим в виде интеграла:
dz, (30.2)
Рис. 32. Контур интегриро-
вания в комплексной пло-
скости со для t > 0 и t < 0.
где 8—>0.
Перенесем интегрирование в (30.2) в комплексную
плоскость z=co-HT и замкнем при t—x/c > 0 контур ин-
тегрирования бесконечно боль-
шим полукругом R = | z | —> оо
в нижней полуплоскости Г < 0
(см. рис. 32). При этом в
интеграле появится «режущий»
множитель ехр [Г (t —х/с)], так
что при R —> оо вклад от инте-
грала по полукругу будет ра-
вен нулю. При t — x/c<0 кон-
тур следует замкнуть в верх-
ней полуплоскости, «режущий»
множитель ехр [— Г (/ —х/с)}
при R —+ оо уничтожит вклад
от интегрирования по беско-
нечному полукругу. Интеграл
(30.2) в первом случае окажется равным вычету в точке
z=coo— fg, а во втором случае, в силу отсутствия сингу-
лярности в верхней полуплоскости,— нулю.
§30]	ПРИЧИННОСТЬ И СВОЙСТВА S’MATPHUbl	171
Таким образом, при е—»-0
I A exp Т— icoo	— у, когда t—-£ > 0,
Фо	= 1	х
'	'	[	когда t—— < 0.
(30.3)
Пусть, далее, Т (<о) есть элемент матрицы рассея-
ния, трансформирующий плоскую падающую волну
ехр[—i®(/—х/с)] в волну рассеянную'(мы сейчас огра-
ничиваемся одним пространственным измерением). Тогда
вся рассеянная волна приобретает вид
+л°	ехрГ— iz'(t——^1
T(Z-)-...(30.4)
— 00
где s —>- 0. Из принципа причинности следует, что рассеян-
ная волна ф(/, х) не может возникнуть раньше, чем па-
дающая волна ф0(/ — х!с) достигнет рассеивающей частицы.
Иными словами,
ф(/, 0) = 0 для t < 0.	(30.5)
Очевидно, что это требование не будет выполняться при
любых Т(со).
Будем рассматривать Т (со) как функцию комплексной
переменной z=co-HT. Пусть Т (г) исчезает на круге бес-
конечно большого радиуса 7?=|z|—^оо и имеет особен-
ности только на действительной оси. При этих ограниче-
ниях на поведение амплитуды Т (г) в комплексной плоско-
сти z —со + гТ мы можем переписать (30.4) для точки х = 0
в виде^
+оо	Г1
АР	o — izt
г*('•°) 4 J т<*>	* F(30.4')
— 00
(здесь е—>0).
По предположению функция Т (z) регулярна на беско-
нечно больших полукругах 7? —оо и не имеет особенностей
внутри них. Г Поэтому мы можем применить к (30.4') тот
же метод интегрирования, что был использован для вычис-
ления интеграла (30.2). Обходя возможные особенности
172
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
Т (z) на действительной оси сверху (z=co + fs, s > 0) и
замыкая контур интегрирования при t > 0 полукругом
в нижней полуплоскости, мы получим некоторое значение
ф(/, 0), вообще говоря отличное от нуля. При t <0
контур замыкается сверху и ввиду отсутствия особенно-
стей ф(/, 0)=0.
Таким образом, если амплитуда Т (со) обладает ука-
занными выше аналитическими свойствами, то рассеянная
волна (30.4') удовлетворяет условию причинности (30.5).
Применим теперь теорему Коши к амплитуде Т (со):
<30 6)
с
В качестве контура интегрирования возьмем линию,
идущую по реальной оси, обходящую сверху точку z=co
и замыкающуюся в нижней полуплоскости бесконечно
большим полукругом R =| z | —> оо. С учетом того, что на
этом полукруге Т =0, интегрируем по бесконечно малому
полукругу около точки z =со и, разделяя Т (со) на дейст-
вительную и мнимую части, получим
’<“>=И 'У"У'	<зо7>
— 00
где знаком обозначено главное значение интеграла около
точки со' =со ± р, р —► 0. Соотношение (30.7) есть простей-
шее дисперсионное соотношение для амплитуды рассеяния
Т(со).
Допустим теперь, что амплитуда Т (z) имеет другие
особенности, кроме тех, которые лежат на действитель-
ной оси.
Рассмотрим сначала случай, когда амплитуда Т (z)
имеет существенно особую точку при | z| —оо. Положим
T(z)=f(z)e-lZT,	(30.8)
где х—а/с, а — некоторая длина, а функция Т (z) обла-
дает свойствами, рассмотренными ранее. Тогда
со
-ф(/, 0)=-А- f Т (2) е~ tz-^-- dz.	(30.9)
1 v ' 2ш J z — (о)0 —4	7
§30]
ПРИЧИННОСТЬ И СВОЙСТВА S-МАТРИЦЫ
173
Применяя к этому интегралу изложенный выше метод
вычисления, мы убедимся, что гр(/, 0) будет не равна
нулю уже при t >-тТ, т. е. рассеянная волна возникает
ранее, чем волна падающая достигает микрочастицы. Такое
поведение нарушает причинность и может интерпретиро-
ваться как наличие у микрочастицы некоторых линейных
размеров а («элементарная длина»), причем сигнал внутри
частицы распространяется бесконечно быстро. Таким обра-
зом, нарушение корректного поведения амплитуды Т (г)
при | 21 —оо ведет к нарушению причинности.
Допустим теперь, что амплитуда Т (г) имеет полюсы
на мнимой оси z = ± *Л. Нетрудно видеть, что и в этом
случае будет нарушаться причинность, так^ как теперь
из-за наличия полюса z =iA (Л > 0) в верхней полуплоско-
сти амплитуда рассеянной волны гр(/, 0) при /< 0 будет
равна
ф (/, 0) = Л	е+А/
т ’ 7 гЛ—(в0	’
(30.10)
что нарушает причинность во времени | /1 ~ 1/Л; при t > 0
возникает дополнительный член с множителем e~At, зату-
хающий при /5>1/Л.
Как видно из (30.7), дисперсионные соотношения свя-
зывают действительную часть амплитуды рассеяния с мни-
мой. В некоторых случаях интеграл в (30.7) можно выра-
зить через наблюдаемые величины, и поэтому экспери-
ментальная проверка дисперсионных соотношений может
служить для проверки основных положений современной
локальной теории поля, в частности важнейшего для всей
теории принципа микропричинности.
Однако установление аналитических свойств элементов
матрицы рассеяния Sfi исходя из общих принципов ло-
кальной теории поля представляется сложнейшей и еще
не решенной задачей.
Только в простейшем случае упругого рассеяния ча-
стиц, благодаря работам М. Гольдбергера [59], К. Симан-
чика [60], Н. Н. Боголюбова J61] и др., был достигнут
существенный прогресс. В частности, для упругого рас-
сеяния вперед (на угол 0° = 0) л-мезонов на нуклонах
удалось получить дисперсионное соотношение, не содер-
жащее ненаблюдаемых величин.
174
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
Наиболее последовательное по математической стро-
гости доказательство этих соотношений принадлежит
Н. Н. Боголюбову, и мы отсылаем читателя к его моно-
графии [61]. В этом разделе мы ограничимся только очер-
ком теории дисперсионных соотношений в той мере, в ка-
кой это будет необходимо нам для дальнейшего.
Основой для построения дисперсионных соотношений
для nN-рассеяния является релятивистское обобщение
теоремы об аналитичности фурье-образа функции, исче-
зающей при t < 0.
Пусть F (х) есть функция от х (х, t), исчезающая вне
светового конуса абсолютного будущего, т. е. при х<ь0.
Рассмотрим ее фурье-образ F (k):
F (k) = J F (x) exp (ikx) d'x.	(30.11)
Напомним, что kx=<nt—kx, так что при комплексных
значениях k, т. е. при k —+ k + iq, ® —> со -Н'Г, экспонента
в (30.11) приобретает вид ехр [—i (&х —<о/)4-(0лг—Г7)].
В области значений Г, где
Г’—> 0, Г > 0,	(30.12)
можно выбрать такую систему координат, что q = 0. Тогда
множитель elkx в (30.11) приобретает фактор обрезания
e~Tt, и благодаря ему интеграл (30.11) и его производные
по k любого порядка будут сходиться. Тем самым дока-
зывается, что фурье-образ F (й) является аналитической
функцией переменной’^ в области (30.12); можно также
показать, что при | k | —оо F (fe) имеет рост не выше
некоторой степени | k |" (см. [61]).
Дисперсионные соотношения устанавливаются для ма-
тричных элементов Тf{ матрицы Т (см. § 24). Для упру-
гого рассеяния л-мезона на нуклоне волновые функции
исходного состояния (i) и конечного (f) могут быть взяты
в форме, описанной в § 24 (см. (24.14), (24.18)):
(30.13)
-ik'yn _
=~^=-uP'e~ip'x‘,	’ (30.14)
У со	7
§ 30]
ПРИЧИННОСТЬ И СВОЙСТВА S-МАТРИЦЫ
175
где р=(р, р0 = J/rM2+p2) (М—масса нуклона), k =
= (Л, ka =со = )//и2 + А2) (т—масса мезона); в конечном
состоянии те же величины отмечены штрихами. Спинорные
индексы нуклона и индексы изотопического спина мезона,
чтобы не загромождать формул, мы не выписываем.
Амплитуда Тл есть матричный элемент четыреххвостки
s (х2, уг | х1( yj, взятый для состояний (30.13) и (30.14).
Вводя координаты У-|(й + (/ф У=^У1 — У1 и Х =
= (Xi+xJ, х=х2—х1( нетрудно убедиться, что интерес
сующий нас матричный элемент Тл может быть записан
в виде
TZi = (p', k'\T\p, k)~
Р'> pY <30-15*
у 4(0(0	\	2	/
Специально в лабораторной системе координат для рас-
сеяния вперед (так что //=р=(0, 0, 0, Л4) и k' =k —
— (k, со)) имеем
тл	Тс (k).	(30.16)
' у 4сосо s
Значком с у функции Te(k) в (30.15) и (30.16) мы под-
черкиваем, что функция Те (k) является фурье-образом
некоторой функции Тс(х), аналогичной по своему про-
странственно-временному поведению причинной функции
Dc (х) *):
Тс (6) = $ Тс (х) eikx d*x.	(30.17)
Однако исследование аналитических свойств удобнее про-
водить на величинах, имеющих свойства запаздывающих
или опережающих величин.
Можно показать, что можно ввести запаздывающую
функцию Ttei (&), аналогичную запаздывающей функции
Dret(&), которая для реальных частиц, т. е. при р2.=М2-
*) Заметим, что во втором порядке теории возмущений Тс (х) =»
•= Df (х).
176
причинность в квантовой теории
[ГЛ. v
и	на поверхности энергии p-\-k=p' A~k' совпа-
дает с функцией Tc(k)\
Tc(k')=TIet(k>-	(30.18)
Наряду с Tiai (k) можно ввести и опережающую функцию
Tadv(4, аналогичную Dadv(4> а также их разность
T(fe)=7’ret(Z;)-TadvW.	(30.19)
Функции Ttet(k) и Tadv(k) при инверсии вектора k под-
чиняются некоторым условиям симметрии, именно:
T;el(fe)=Tret(-A!),	(30.20)
Ttei(k) = Taiv(-k).	(30.20')
В дальнейшем нам пригодится еще разложение ампли-
туды Т (/?) на дисперсионную (эрмитову) часть D и абсорб-
ционную (антиэрмитову) часть iA:
T(k)==D(k) + iA(k).	(30.21)
Для рассеяния вперед без изменения спина нуклона
и изотопического спина мезона (т. е. для когерентного
рассеяния) в силу эрмитовости матриц D и А величины
D (со) и А (со) действительны.
Заметим еще одну тонкость. В силу законов сохране-
ния вектор k в экспоненте (30.17) содержит иррациональ-
ность, которая вносит неудобства. Действительно, в ска-
лярном произведении kx = &)t—kx абсолютная величина
вектора k зависит иррационально от со: [Л| =]/со2—т2 =%.
Поэтому, записывая скалярное произведение kx в виде
со/—kx = со/—ekx,	(30.22)
где e = kl\k\, мы освободимся от иррациональности по со
в (30.17), если вместо (30.17) будем рассматривать функ-
ции, симметризованные и антисимметризованные по сле-
дующей схеме:
ТДе, %)=Т(е, %) + ?(—е, %),	(30.23)
ЛДе. Ч=4г(е. Ч-П-е. Ч].	(30.23')
которые зависят лишь от %2. Из (30.23) и (30.23') следует:
Т{е, Ч = |[Л(е. Ч+^(е, %)]•	(30.24)
30]
ПРИЧИННОСТЬ И СВОЙСТВА S-МАТРИЦЫ
177
Симметризованная по такой схеме абсорбционная часть
амплитуды А имеет определенную симметрию относительно
изменения знака со, именно:
(— со) — +	(со),	(30.25)
ИЛ-^)=-ИаИ-	(30.25')
Эти соотношения будут использованы в дальнейшем.
Окончательное исследование аналитических свойств
Проводится ДЛЯ функций 7\et (со) и 7^ (со), симметризо-
ванных по схеме (30.23) — (30.23').
Весьма сложное и кропотливое исследование приводит
к следующему результату: функции 7ret (со) и 7\ау(<й)
представляют собой одну аналитическую функцию Т (со) в
комплексной плоскости со, которая в области Imco > 0 сов-
падает с Tret (со), а в области
Imco < 0—с T^ady (со). Т (со) име-
ет разрезы на действительной
оси на отрезках — оо < со < —ш
и оо > со >т и полюсы при
0> = ±^=*±<V (30.26)
Она исчезает на круге | со | =
=	> оо.
На рис. 33 изображена ком-
плексная плоскость со и жир-
ной линией обведен контур С,
внутри которого Т является
аналитической функцией со.
Если амплитуда Т (со) все
же растет, как со", то вместо
нее можно ввести величину
7',W=(^)U <30.27)
Рис. 33. Контур интегриро-
вания амплитуды Т (со) на
комплексной плоскости со.
На рисунке показаны разре-
зы^от —7? до —m и?от
до 4-7? (/?|—>оо), а также
простые полюсы в точках
<о=± cog.. Полюс (п-4-1)-го
порядка в точке есо0 вызван
делением амплитуды на вели-
чину (со — со0)" + 1.
(где соо — произвольная точка), которая будет отличаться
от Т (со) наличием дополнительного полюса в точке со=соо
и будет стремиться к нулю на окружности |со|—^оо.
К функции Т' (со) можно применить теорему Коши,
выбрав контур интегрирования, как показано на рис. 33;
178
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЁОРИИ.
1ГЛ. V
перейдя к пределу при R—>оо, получим дисперсионное
соотношение для Т' (со):
- 00 + ie
Т (со)_____ 1 Р Т (со') da)'
(со—®о)" + 1	J (со'— соо)"+1 (со'—ю) "*~
+ 00 4-18
00 -18
+ f	; •	(30.28)
1	J (со — соо)п + 1 (со — со)	v 7
-00-18
Обозначим скачок Т (со) на разрезах (— оо, —т) и
(пг, оо) через ДТ (со) и, умножая (30.28) на (со—соо)п+1,
найдем
— т
т (со) = (Р-во)"*1 С	—Cffz-T--------rdco' +
v 7 2ш J (со—coo)" + 1 (со—со) 1
— со
I (СО—(Oo)n+1 С АТ (со')	, , .
2зи J (со'—соо)" +1 (со'—со)	*”
m
+ (_!)» Дсо-ш,, y+i__g*
> \Wg + (00/ соН-со^. ‘
/ ^_^y + l_g2_ Л
\со^-соо; (О —СО*	г	V )
Здесь g2—вычеты Т (со) в точках со — ±со*, а постоянные
коэффициенты ^определяются вычетами в точке со=соо.
Далее, скачок АТ (со) на разрезах функции Т(со) опре-
деляется из того соображения, что абсорбционная часть Л,
которая отлична от нуля при со < —m и со > -Ь пг, меняет
свой знак при переходе от Im со > 0 к Im со < 0, в то
время как дисперсионная часть амплитуды D (со) изме-
няется непрерывно. Поэтому скачок АТ (со) равен
АТ (со)=2М (со).
(30.30)
Теперь можно воспользоваться симметрией (30.25),
(30.25') и заменить интегрирование по отрицательным со
интегрированием по положительным со.
Выбор показателя п остается произвольным, а его
наименьшее допустимое значение должно быть уставов-
§30]
ПРИЧИННОСТЬ И СВОЙСТВА S-МАТРИЦЫ
179
лено из косвенных соображений. Согласно оптической
теореме (XI 1.4)
Л(<о) = ^ополн(со),	(30.31)
где k — импульс мезона в системе центра масс, а сгполн (со) —
полное сечение процесса л + N —>- N + • • •
Для того чтобы получить теперь из (30.29) конкретные
дисперсионные соотношения для рассеяния нейтральных
л °- и заряженных л^-мезонов, необходимо восстановить
зависимость амплитуды рассеяния от спиновых и изото-
пических индексов.
Эта сторона не представляет уже интереса для темы
нашей монографии, и мы ограничимся приведением окон-
чательного результата. Обозначим дисперсионные и аб-
сорбционные части амплитуды рассеяния через О0, Е>±,
До, Д± для нейтральных (индекс 0) и для заряженных
(индекс ±) мезонов соответственно. Тогда дисперсионные
соотношения запишутся в следующем виде:
(со2—(0р)
+ -(®г-<0£
л
(30.32)
Do (со) — Dq (со0) =	-7~z-------------гг т
'	7 М g (со2—cog) (со?—®g)
Г	со' А 0 (со') dco'
j (со'2—со2) (со'2—со?)
т
(0g (со2 — (Ор).
Z?! (со) Dr (соо) — —7~2 \ / 2 2Т “Г
М ((О2 — (0g ) ((Оо — (0g )
2. (<о2 — со?) £ —	,
‘л	' J ((О'2—(О2) ((О'2—(Оо)
т
DM-^D. Ы - %-	4
(00	М ((О2 — (0g ) ((00 — (0g )
+1 (0 (со2 -со2) £ ——dco',
л v 'j (со'2— со2) (со'2—со?)
т
(30.32')
(30.32")
где
(со) = D+ (со) + D_ (со),	(30.33)
£>а (со) = D+ (со)—(со),	(30.33')
180
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
Ах (со) = А + (со) + А _ (со),	(30.33")
Л2 (со)=Л+ (со)—А- (со),	(30.33"')
а две произвольные константы и с± в многочлене
п
сга? исключены вычитанием из дисперсионных соот-
о
ношений амплитуд О(со0) и ^О(со0), взятых в опреде-
ленной точке со = соо.
Абсорбционные части А± (со), Ло(со) могут быть вы-
ражены с помощью оптической теоремы (30.31) через
наблюдаемые на опыте полные сечения; наконец, кон-
станта g определена из взаимодействия при низких энер-
гиях.
Таким образом, дисперсионные соотношения (30.32)—
(30.32") могут быть проверены на опыте, и тем самым
может быть установлена справедливость локальной тео-
рии поля или, напротив, показана ее несостоятельность.
Другой важный вывод из локальной теории, основан-
ный также на аналитических свойствах амплитуды рас-
сеяния, относится к асимптотическому поведению полного
сечения для частиц и античастиц.
В работе [62] на основании дисперсионных соотноше-
ний для упругого рассеяния вперед л-мезонов на нукло-
нах и с помощью оптической теоремы (см. § 23) было
показано, что полные сечения взаимодействия л+- и лг-
мезонов на нуклонах при предельно больших энергиях
(со —оо) должны быть равны между собой:
Orjt + N = O'jT’N	при	со—>оо.	(30.34)
В последнее время для установления асимптотических
соотношений между сечениями различных процессов при-
влекается ^теорема о поведении аналитической функции
f (z) внутри угла, образованного лучами, в зависимости
от тех пределов и С2, к которым она стремится вдоль
этих лучей [63]. Эта теорема утверждает, Гчто если бы
функция / (г), аналитическая внутри угла имела
различные пределы, С±^С2, вдоль лучей ОС± и ОС2, то
она росла бы внутри угла не медленнее экспоненты.
Обращаясь к нашей задаче, будем рассматривать
плоскость z как комплексную плоскость энергии со ме-
зона: гг=со; если [взять теперь в качестве угла СхОСа
§30]
ПРИЧИННОСТЬ И СВОЙСТВА S-МАТРИЦЫ
181
угол л (верхнюю полуплоскость), а под функцией f (z)
подразумевать амплитуду упругого рассеяния частицы а
на частице Ь, продолженную^ верхнюю полуплоскость,
то при z = co—>оо функция f (z) будет совпадать с ам-
плитудой Т (со) упругого рассеяния вперед для процесса
a + b->a + b;	(30.35)
при со—> оо и г = со —> — оо эта же функция будет совпа-
дать с той же амплитудой Т (<&) для «перекрестного» про-
цесса *):
а4-Ь —> а4-Ь,
(30.35')
где а означает античастицу по отношению к частице а.
В силу доказанной ранее аналитичности амплитуды
упругого рассеяния в верхней полуплоскости и характер-
ного для локальной теории предположения об ограниче-
нии роста амплитуды полиномиальным ростом (~соп),
на основании изложенной выше теоремы предельные зна-
чения Сх и С2 амплитуды f(z), т. е. ее значения при
со = ±оо, должны быть равны. Из-за равенства мнимых
частей амплитуды на основании оптической теоремы дол-
жны быть равны и полные сечения. В частности, считая
частицу а л-мезоном, а частицу Ь —нуклоном, мы при-
дем к равенству (30.34).
На основании этой же теоремы асимптотические со-
отношения были установлены не только для полных се-
чений nN-рассеяния, но и для многих других реакций,
и не только для полных, но и для дифференциальных
сечений [64].
Приведем некоторые из этих соотношений.
а)	Для полных сечений’при со —> оо одинаковы сече-
ния следующих реакций:
л++р—>... и л”-|-р’
К+ + р-+... И К" + р>	(30.36)
р + р—►... и р + р—...,
S++p—►... и S“ + p —...,.
где точками справа обозначены все возможные продукты
реакций, указанных слева.
*) О «перекрестных» реакциях см. подробнее § 31.
182
ПРИЧИННОСТЬ В КВАНТОВОЙ ТЕОРИИ
[ГЛ. V
б)	Для дифференциальных сечений при со —> оо и при
заданной передаче импульса одинаковы сечения:
л+ + р +р и л~+р—>л"+р,
К+4-р —К+4-р	и К- + р->К" + р, I т7
п+_|_р_^К+ + 2+ и К" + р-+л- 4-2+, I { ио/;
л" + р—>К°+Л	и К°+р-^я++А. ,
В заключение этого раздела приведем основные прин-
ципы локальной теории поля, которые использованы при
выводе дисперсионных соотношений для амплитуды рас-
сеяния Т и асимптотических соотношений для сечений а.
I.	Соблюдение микропричинности, которое означает
отсутствие влияния из одной области пространства—вре-
мени 3%i(x) в другую 91Z (х), если точки, принадлежащие
этим областям, разделены пространственно-подобным ин-
тервалом
Х2 Хх, Хх С ^4 (*^)> ^2 С
и если интервал времениподобный, т. е. xz > 0, но х2 < хх
(следствие должно наступать позднее причины!).
II.	Существование спектра стабильных частиц с по-
ложительной энергией:
Ро = /р2+ ml,	(30.38)
где ms — масса частиц (s=l, 2, ...).
III.	Амплитуда Г (со) при со —> оо растет не быстрее,
чем полином:
IТ (со) I < a I со I",
(30.39)
где п—целое положительное число.
ГЛАВА VI
макроскопическая причинность
§ 31. Формальная теория S-матрицы
Прежде чем обратиться к основному предмету этой
главы, мы напомним некоторые важнейшие свойства
S-матрицы.
Как было показано в § 28, S-матрица есть унитарная
матрица, преобразующая начальное состояние свободных
частиц Ч\-, данное при t — —оо, в конечное состояние
свободных частиц Ту, рассматриваемое при /=-|-оо:
T^ST,-.	(31.1)
Эту матрицу обычно представляют в виде (см. (29.4))
S = I + iT.	(31.2)
Условие унитарности
SS+ = 2	(31.3)
может быть превращено в тождество, если положить
S = A	(31.4)
где	т] — эрмитов оператор: П = г|+,	(31.5)
или	путем другой подстановки: & Т-1К /+ IK. '	(31.6)
где	К.—опять-таки эрмитов оператор: к=к+.	(31-7)
Понятие асимптотических состояний и Y/ нуж-
дается в обстоятельном исследовании. В частности, пре-
184
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
дел / —^±оо мы рассматриваем пока чисто формально,
не указывая, в каком смысле следует понимать этот
предел.
К этим вопросам мы вернемся позднее. Асимптоти-
ческие состояния цо самому своему смыслу определяются
полным набором динамических переменных р, характе-
ризующих состояния свободных частиц. В качестве этого
набора переменных мы выберем импульсы этих частиц,
так что
(31.8)
(31.8')
где (р)— совокупность импульсов в начальном состоянии,
а (р') — совокупность импульсов в конечном состоянии:
(p) = (pw, ря_х, рх), если в начальном состоянии
имеется п частиц, и (/?') = (рт+п, рт+п-и •••, р„+1), если
в конечном состоянии имеется т частиц. Для свободных
частиц четвертые компоненты импульсов имеют опреде-
ленное значение:
P<ss = + VplA-ml, s=l, 2, т + п, (31.9)
где ms—масса s-й частицы. Совокупность значений пе-
ременных р=(р0, р) образует трехмерное многообразие
9i3(p), совпадающее с поверхностью однополостного ги-
перболоида
Ро— р2 = т\ р0>0.
(31.10)
Это многообразие является пространством Лобачев-
ского *), скалярная кривизна которого R (ср. (5.13))
определяется массой частиц и равна
л = -^.	(31.11)
Заметим, что вторая полость гиперболоида
Ро = — К/ЙЧ-Р5	, (31.10')
может быть использована для изображения состояния
античастиц.
*) Это обстоятельство было последовательно использовано в
работе [65]; см. также [66].
§31]	ФОРМАЛЬНАЯ ТЕОРИЯ S-МАТРИЦЫ	185
Таким образом, пространство, в котором определены
асимптотические состояния i и f, является композицией
нескольких пространств Лобачевского:
91,- (р)=9t3 (рО ® 9t3 (р2) ®	®	(Р„) • (31.И')
Так же построено и пространство
9?z (р')=gi3 (р;+1) ® э?3 (р;+2) ® . ®913 (Р'п+пгу (31 л 1")
Пространство 9tz (р) мы будем называть пространством
начальных состояний, пространство Э^(р')— простран-
ством конечных состояний. Оба пространства будем на-
зывать пространствами асимптотических состояний.
Заметим, что пространство 91 (р) по самому своему
смыслу совпадает с множеством собственных значений
оператора импульса р свободных частиц и оператора
энергии р0; каждому собственному значению оператора р
и определенному знаку оператора р0 может быть сопо-
ставлена собственная функция фр (х) этих операторов.
Поэтому точкам пространства может быть однозначно
сопоставлена совокупность всех собственных функций
фр(х) операторов р и pQ. Эта совокупность образует
пространство Гильберта SR {ф}. В этом пространстве функ-
ции фр (х) и их произведения являются векторами и
тензорами, образующими "полную систему ортонормиро-
ванных функций.
В избранном нами представлении асимптотических
состояний Tz и Tz строки матрицы S характеризуются
импульсами (//) в^конечном состоянии f, а столбцы —
импульсами (р) в начальном состоянии i. Поэтому мы
можем написать:
S/;. = <p'|S|p>==
==<Pm+ra, Pm+«-l> •••> Рп+1 I I Pit’ Pn-i’ •••> Pl>’
(31.12)
Для дальнейшего удобно выделить, в соответствии
с (31.3), из S-матрицы единицу I. Тогда (31.12) перепи-
шется в виде
Sfi = <p'\i\p> + i<p'\t\p>,	(31.13)
186
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
где
<р'\Т\р> =
= <\Pm+n> Pm+n-if •••> Рп+1 | Т | Pnt Рп-1, •••>	Р1>»
(31.14)
S-матрица должна быть релятивистским инвариантом
(ср. § 29). Пусть при преобразовании Лоренца импульсы
(р) преобразуются с помощью матрицы лоренцева пре-
образования *)
p = Lp,	(31.15)
где под (р) понимается совокупность новых преобразо-
ванных импульсЬв. При этом векторы состояний Т (р)
подвергаются унитарному преобразованию с помощью
некоторой унитарной матрицы
V (р) = UL4 (L"xp) = UlV (р),	(31.16)
где временно через V обозначен вектор состояния в но-
вой системе координат. Применяя это преобразование
к равенству (31.1), получим
UL4r/(L“1p) = t7LS (L-1^)	(L^p), (31.17)
т. e.
4f=S(p)4{,	(31.18)
где
S(p)=(7LS(L-1p)(7i;1.	(31.19)
Релятивистская инвариантность требует, чтобы закон
преобразования был один и тот же во всех системах
отсчета, поэтому должно иметь место соотношение
S (L-1p) = § (р).	(31.20)
Это и есть условие релятивистской инвариантности
теории, выраженное на языке импульсных переменных.
В отсутствие внешних полей физическое явление в
силу однородности пространства —времени не может
♦) Матрица L отлична от матрицы L в (29.25).
§31]
ФОРМАЛЬНАЯ ТЕОРИЯ S-МАТРИЦЫ
187
зависеть от начала отсчета времени и от положения на-
чала координат. Поэтому матрица рассеяния 5 должна
быть трансляционно инвариантна. Из этого требования
вытекает условие
DS—SD = 0,	(31.21)
где D—оператор трансляции. Этот оператор имеет вид
D = ехр (1Рц,ац),	(31.22)
где оператор есть оператор полного импульса рас-
сматриваемой физической системы, а ац — вектор произ-
вольного смещения. Из (31.21) и (31.22) следует, что
Рц5-5Ри=0,	(31.23)
т. е. матрица S коммутирует с оператором полного им-
пульса Р. Поэтому ^-матрица должна быть диагональной
относительно оператора полного импульса Р. В силу
этого матричные элементы Sfi должны быть пропорцио-
нальны 6-функции от полного четырехмерного импульса,
т. е. пропорциональны функции
64(Р'-Р),
где Р' = 2р' = 2 Pn+s и Р = 2р= S ps.
s=l	S=1
Заметим, что матричный элемент от I равен
п
<р' I Ц Р> = 63 (р' — Р) = П 53 (Ps— ps),
s= 1
т. е. произведению трехмерных 6-функций. Для
из этого произведения всегда можно выделить четырех-
мерную 6-функцию от полного импульса, так что
<Р' 111 Р> б3 (/>' —Р) — б4 (2 р' — 2 р) I (р' | р); (з 1.24)
здесь /(р'|р) выражен через относительные импульсы.
Элемент матрицы <р' |Т|р> также должен быть пропор-
ционален б4(2р'—2р)’ т- е-
<р' | т I р> = 64 (£/ -2р)Т (р' IР).	(31.25)
188
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
1ТЛ. VI
Дальнейшая детализация вида матричных элементов
может быть сделана на основе того соображения, что за-
кон перемножения любых двух матриц А и В, взятых
в импульсном представлении, в релятивистски инва-
риантной теории должен быть релятивистски инвариан-
тен. Мы имеем
<р' | АВ | р> = J </ | А | р"> d3p" <р" | В | р>. (31.26)
Однако элемент объема d3p" не является инвариантом.
Мы обеспечим релятивистски инвариантный характер
умножения матриц, если представим матричные элементы
матриц в виде
_А(Р’> Р)______
У 2р'о ... К2р0
<р'|Л|р> =
(31.27)
где р0 есть четвертая компонента импульса, а А (р', р)
есть инвариантная функция импульсов (/?') и (р). Дей-
ствительно, в этом случае вместо (31.26) получим
<р'|ЛВ|р> =
= -	=	(31.26')
V 2р0 •.. V %Ро j V 2ро 2ро у 2р0
о	«	&р"
Возникший здесь элемент объема —есть элемент
2ро
объема в пространстве Лобачевского, который является
релятивистским инвариантом.
Окончательно матричные элементы S-матрицы запи-
шутся в виде
5/(. = <р' |5|р> =
Т(Р’\Р)
(31.28)
У^р’о ... У~^рл
где Т(р'\р) есть инвариантная функция импульсов на-
чального и конечного состояний.
Рассмотрим теперь подробнее структуру матрицы S
в простейшем случае одного сорта скалярных незаря-
женных частиц, имеющих массу покоя т. Мы предпо-
ложим, что взаимодействие между ними таково, что оно
не приводит к образованию ни стабильных комплексов
§311
ФОРМАЛЬНАЯ ТЕОРИЯ S-МАТРИЦЫ
189
с массой Л1, меньшей суммы масс исходных частиц, ни
неустойчивых комплексов с массой Л1*, большей суммы
масс исходных частиц. Возможные процессы в этом про-
стейшем случае ограничиваются рассеянием, рождением
и поглощением частиц. В этом случае имеется лишь один
сорт скалярных частиц, способных рассеиваться, рож-
даться и поглощаться. В табл. 1 для краткости строки
Таблица 1
Матрица рассеяния для простейшего случая скалярных частиц
	1	2	3	4	5	6	7	8
1	1,1							
2		2,2	2,3	2,4	2,5	2,6	2,7	2,8
3		3,2	3,3	3,4	3,5	3,6	3,7	3,8
4			4,3	4,4	4,5	4,6	4,7	4,8
5		5,2	5,3	5,4	5,5	5,6	5,7	5,8
6		6,2	6,3	6,4	6,5	6,6	6,7	6,8
7		7,2	7,3	7,4	7,5	7,6	7,7	7,8
8		8,2	8,3	8,4	8,5	8,6	8,7	8,8
матрицы (/) нумерованы числом частиц т, возникаю-
щих в конечном состоянии, а ее столбцы (t) нумерованы
числом частиц в начальном состоянии п. В каждой
клетке (т, п) записан матричный элемент <m|S|n>,
определенный в асимптотическом пространстве 91 (р, р') =
= 9?z (р)® 91/ (р'), имеющем 3 (m-j-n) измерений. Элемент
(1, 1) есть единица; диагональные элементы (2, 2),
(3, 3), ..., (т, т) описывают упругое 'рассеяние частиц
(мы определим упругое рассеяние как такое рассеяние,
в котором не рождается новых частиц, частицы не погло-
щаются и не меняют своего внутреннего состояния). Эле-
менты с т^п описывают переходы, сопровождающиеся
рождением или поглощением частиц. Пустые клетки
означают матричные элементы, равные нулю. Заметим,
что все элементы, находящиеся на диагонали т + п =
= const, описываются функциями Т(р',р) (31.28) с од-
ним и тем же числом переменных 3(m-|-n). Это обстоя-
190
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
тельство позволяет, по крайней мере в некоторых тео-
ретических схемах, рассматривать все функции
<т\Т\п> = Т(р’1, р2, p'm\ plt р2, рп)
как одну функцию
T(p) = T(plt р2, .... рт- рт+1, рт+п), (31.29)
в которой не различаются начальные и конечные состоя-
ния. Такого рода симметрия начальных и конечных
Рис. 34. Иллюстрация к
перекрестной симметрии. На
рис. а) 1, 2, 3—частицы в
начальном состоянии, а час-
тицы 2', 5', 4' — в конеч-
ном состоянии. На рис. б)
частица 3 причислена к чис-
лу частиц конечного состо-
яния, но уже в роли анти-
частицы 3. Узел $ один и
тот же на обеих диаграммах.
совокупность пространств
странство:
Обратимся
ных» частиц
состояний носит название пере-
крестной симметрии. В общем
случае для реакции, в которой
в начальном состоянии (t) име-
лись частицы a, b, с, d, ... (все-
го п), а в конечном состоянии
(/)—частицы х, у, 2, w, ...
(всего т),
а b с d -f-...
...—>х-f-у-f"2-|-и-|- ... (31.30)
функция Т (р) (31.29) будет той
же, что и для реакции
• • • “F х -J* z -р • • •
...—d-j-e-f-...
(31.30')
где любое число частиц пере-
несено слева направо и, на-
оборот, справа налево, но с
заменой частиц на античасти-
цы (знак
Рис. 34 поясняет на част-
ном примере эту ситуацию.
Наличие перекрестной симмет-
рии позволяет рассматривать
fRz(p) и Э^(р') как одно про-
Э1(р)=^(р)®Э1/(р')-	(31.31)
теперь к случаю, когда помимо «исход-
с массой т имеется еще и стабильная
§31]
ФОРМАЛЬНАЯ ТЕОРИЯ S-МАТРИЦЫ
191
частица с массой т < М < 2т. Такую частицу можно
рассматривать как результат слияния двух частиц с мас-
сой /п, сопровождающегося дефектом масссы Д = 2т —
— М > 0. Существование этой частицы должно быть
учтено в асимптотических состояниях тем, что соответ-
ствующее пространство Лобачевского будет иметь кри-
визну (см. (31.11)) R = — 1/М*.
Таблица 2
Матрица рассеяния для случаев двух сортов скалярных
частиц — частиц с массой т и частиц с массой Л,
причем т < М < 2т. Нумерация строк и столбцов матрицы идет
в порядке возрастания массы покоя
Ч i	1	М	2	М+1	3	2М	4	2М+1
1	1.1						(	
м		М, м						
2			2,2	2, М+1	2,3	2,2М	2.4	2,2М+1
М+1				М + 1, М+1	М + 1,3	М+1,2М	М + 1,4	М+1, 2М + 1
3			3,2	3, М + 1	3,3	3,2М	3,4	3.2М + 1
2М			2М, 2	2М, М+1	2М, 3	2М, 2М	2М, 4	2М, 2М+1
4			4,2	4, М + 1	4,3	4,2М	4,4	4.2М + 1
2М+1			2М +1,2	2М + 1, М+1	2М+1,3	2М+1, 2М	2М+1,4	2М+1, 2М + 1
В табл. 2 изображена структура матрицы рассеяния
в этом случае. Нумерация строк и столбцов по-прежнему
установлена в порядке возрастания суммарной массы
покоя частиц, участвующих в конечном и начальном
состояниях. Во избежание громоздкости обозначений
масса легкой частицы т принята за 1. Существование
взаимных превращений частиц усложняет матрицу.
Кроме единичного матричного элемента (1, 1) имеется
еще один-единственный элемент (/И, 7И), который изобра-
жает движение частицы М по инерции. Элементы (7И, 2)
и (2, М) равны нулю, так как в силу предположения
т < М < 2т частица М не может распадаться на две
192
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
частицы т, равным образом невозможен и процесс
слияния двух частиц т в одну Л+частицу. Однако
такие процессы уже с участием трех частиц возможны,
так как третья частица может унести избыток энергии,
возникающий при слиянии двух m-частиц в одну
Л+частицу. Поэтому матричные элементы (М + 1, 3)
и (3, М+1), вообще говоря, не равны нулю. Среди
матричных элементов есть и такие, которые описывают
процессы исключительно между М-частицами (напри-
мер, элемент (2М, 2М) описывает упругое рассеяние
М-частиц, элемент (ЗМ, 2М) — рождение М-частицы при
столкновении двух М-частиц и т. п.).
Обратимся теперь к случаю, когда М-частица имеет
массу, большую 2m, т. е. М > 2m. Теперь мыслимы две
возможности: а) частица М стабильна, тогда процессы
М 2m запрещены; б) частица М нестабильна, в этом
случае процессы Mz^F2m возможны. ?В табл. ЗЦприве-
дена матрица рассеяния для случая стабильных М- и
Т^а’б|л*иГц а 3
Структура матрицы рассеяния для случая двух скалярных частиц
с массой т и массой ЛТ, причем 2/n’< М < Зт, однако частица М
предполагается стабильной
\ 1 f\	1	2	М	3	М+1	। 4	М + 2	2М
1	М							
2		2,2		2,3	2, М + 1	2,4	2, М + 2	2, 2М
М			ММ					
3		3,2		3,3	3, М+1	3,4	r3, М + 2	3, 2М
М+1		М + 1,2		М+1,3	М+1, М+1	М + 1,4	М+ 1, М + 2	М+1, 2М
4		4,2		4,3	4, М + 1	4,4	4, М + 2'	4, 2М
М + 2		М + 2,2		М + 2,3	М+2, М+ 1	М + 2,4	М + 2, М + 2	М + 2, 2М
2М		2М, 2		2М, 3	2М, М +1	2М, 4	2М, М + 2	2М, 2М
m-частиц, способных, однако, при взаимодействии рож-
даться, поглощаться и рассеиваться. В отличие от мат-
рицы, приведенной в табл. 2, в рассматриваемом слу-
чае столбец и строка, содержащая М-частицу, стоят
после столбца и строки с двумя m-частицами. Для опре-
§ 32]	ОПИСАНИЕ С ПОМОЩЬЮ 3-МАТРИЦЫ	193
деленности предположено, что 2m < М < 3m, поэтому
третий столбец и третья строка следуют за столбцом М.
и строкой М соответственно.
Матричные элементы (7И, 2) и (2, /И) равны нулю в
силу предположенной стабильности 7И-частицы; это не-
который специальный запрет. Процессы М-\-т^2т
не предполагаются запрещенными; в частности, процесс
2m—^М-\-т можно рассматривать как неупругий удар,
сопровождающийся поглощением одной легкой частицы
m и рождением тяжелой /И-частицы. Процессы 3mZ=t7H
запрещены условием М < 3m, поэтому соответствующие
матричные элементы (3, 7И), (7И, 3) равны нулю.
В настоящее время известно очень большое число
нестабильных частиц. Поэтому случай, когда ТИ-частица
является нестабильной, представляется крайне важным.
Однако обсуждение этого случая невозможно без обра-
щения к пространственно-временному описанию явлений.
Поэтому мы отложим на время обсуждение случая б) и
обратимся к некоторым тонкостям, связанным с пробле-
мой пространственно-временного описания явлений с по-
мощью матрицы рассеяния.
§ 32. Пространственно-временное описание
с помощью S-матрицы
По самому своему определению S-матрица трансфор-
мирует исходное состояние заданное при tr=—оо,
в конечное состояние Wy, которое изучается при t2 = + оо.
В § 28 было показано (см. (28.18)), что S-матрица яв-
ляется пределом унитарного оператора U {о2, ai}, транс-
формирующего состояние {с^}, заданное на простран-
ственно-подобной поверхности о^, в состояние Т^{о2} на
поверхности о2. В случае плоских пространственных
поверхностей эти поверхности вырождаются в плоскости
о2 = /2» так что
S- lira t/(/2, Q.	(32.1)
f 1	оо
/f ->+ оо
Мы должны теперь уточнить смысл, в котором сле-
дует понимать пределы ^—> — 00, t2 —+ Рассмотрим
7 Д. И. Влрхинцев
194
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
(ГЛ. VI
простейший случай, когда в начальном состоянии имеются
только две частицы А и В. Будем считать, что начальное
состояние задано при t = и описывается волновыми
пакетами иА и ив соответственно. Тогда
Vz(M = «a(Q«b(^x).	(32.2)
Можно допустить, что эти пакеты образовались в
результате прохождения диафрагм А и В, которые были
открыты на некоторое время вблизи момента времени
t± =— Т. Предположим, что начальные размеры паке-
тов суть	= а (а± есть размер пакета в направ-
лении, перпендикулярном, а а и—в направлении, па-
раллельном направлению движения). Расстояние между
пакетами при t± = — Т пусть будет R^>a. Мы будем
считать, что эти пакеты имеют достаточно определенный
средний импульс рА^> кр жк/а, рв|> Ар жЪ/ст, соответ-
ствующая средняя скорость пакетов будет vA = dEA/dpA
иив = дЕв/дрв, где ЕА=Упг2с^ + с2рА, ЕВ=Уtn2c* * + с2pl —
их средние энергии. В системе центра масс относитель-
ная скорость пакетов будет v = vA—vB, а ЕА = ЕВ} в
дальнейшем мы будем опускать индексы А и В, по-
скольку существенно лишь относительное движение па-
кетов. Если радиус взаимодействия частиц есть b *), то
при Ь^>а пакеты аА и ив придут во взаимодействие
через время Т ~ R/v. В этом случае частицы можно счи-
тать асимптотически свободными в течение времени
(32.3)
начиная с t=tv В случае, когда 6<а, следует иметь
в виду, что величина а определяет точность, с которой
может быть определена локализация частицы; поэтому
при b < а вместо (32.3) будем иметь условие
Т =	(32.3')
V V	v '
Так как	(X— характерная для пакетов длина
волны), то в обоих случаях в асимптотической области
_________
*) Как известно, радиус взаимодействия b не всегда определим.
В частности, в случае кулоновского взаимодействия он бесконечен.
Мы сейчас исключаем из рассмотрения этот случай,
§ 32J	ОПИСАНИЕ С ПОМОЩЬЮ S-МАТРИЦЫ	195
После взаимодействия при /2 = + 7" волновая функ-
ция конечного состояния Ту (t2) запишется в виде
W = «а (Q «в (/,) + «(«,	(32.4)
где функция uA(t2)uB(t2) описывает первоначальные па-
кеты в момент /2, а функция и (t2) —асимптотическую
рассеянную волну. Рассеянная волна и при больших рас-
стояниях г между рассеянными частицами имеет вид *)
pi kr	pikr
M(r) = C^-+D^-+...,	(32.5)
где~^=1/^, a C, D, ...—не зависящие от г коэффици-
енты. Асимптотическое выражение для этой волны при
t2 = Т = R/v есть
'pi kR
u(R)=C^-
(32.6)
и предполагает расстояние r = R настолько большим по
сравнению с X, что в (32.5) можно пренебречь вторым
членом (DeikRiR2) и всеми остальными. Следовательно,
асимптотическая область совпадает с той областью, кото-
рую принято называть волновой зоной (7?^>Х).
В переводе на «язык времени» пренебрежение членами
порядка 1/Z?2 означает, что при переходе к пределу
t2 = T -н^ + оо члены порядка \/Т удерживаются, а члены
порядка 1/Т2 уже считаются исчезающе малыми.
Заметим, что существует и верхний предел для Т,
если мы хотим сохранить пространственно-временное опи-
сание для процесса столкновения. Действительно, описа-
ние с помощью волновых пакетов предполагает, что пер-
воначальный пакет (заданный при — Т) не слишком
расплывается к моменту столкновения частиц, в против-
ном случае момент столкновения становится совершенно
неопределенным.
Согласно теории релятивистского волнового пакета,
пакет, имевший в начальный момент времени ширину Д,
*) В общем случае рассеянная волна описывает также вновь
рожденные при столкновении частицы. Простоты ради мы ограничи-
ваемся сейчас упругим столкновением.
7*
196
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ	[ГЛ. VI
с течением времени расплывается таким образом, что про-
дольная ширина Дц (/) будет равна (см. (18.10) и (18.10'))
Д|1=./(32.7)
и поперечная Дх (/) —
Дх=	(32.7')
Ввиду наличия в (32.7) множителя (т/Еу равенство
(32.7') является более критичным, нежели (32.7). Огра-
ничение расплывания пакета в течение процесса соуда-
рения означает, что Д± пРи t = 2T не сильно отличается
Рис. 35. Здесь изображены волновые пакеты и ц2, выходящие из
диафрагм А и В поглощающего экрана в момент времени /1== —Т.
Около / = 0 происходит столкновение; и и2—те же пакеты (частично
рассеянные) (при /2 = + Т. b — радиус взаимодействия, а—ширина
щели в экране, R = AB = vT— асимптотическое расстояние между
пакетами. На рис. 35, а рассмотрен случай b^>a, R > Ь\ на рис. 35,6 —
b<^.a, R^>a, и наконец, на рис. 35, в показан случай чрезмерно
сильного расплывания пакетов, когда всякая информация о причин-
ности теряется.
от Ajl при / = 0. Следовательно, должно быть a*^№v2T2==
=K2R2. Объединяя теперь это неравенство с неравен-
ствами (32.3) и (32.3'), получаем
или а)^>к.	(32.8)
На рис. 35, а показаны следы, образованные пакетами,
выходящими из диафрагм А и В. Этот рисунок иллюст-
§32]
ОПИСАНИЕ С ПОМОЩЬЮ S-МАТРИЦЫ
197
рирует случай, когда радиус взаимодействия частиц
больше размера пакета а. Рис. 35, б относится к случаю,
когда Ь<^а, так что область возможного взаимодействия
определится размерами пакета а. В обоих случаях пред-
положено, что расплывание пакетов за время Т невелико.
Наконец, рис. 35, в иллюстрирует случай, когда пакеты
расплываются так быстро, что всякая информация о мо-
менте столкновения теряется полностью.
Рассмотренное ограничение на пределы | /21, 11± | —> оо
относится к любым частицам.
Нестабильные частицы приносят новые ограничения,
имеющие принципиальное значение. Действительно, пусть
в первичном пучке (Tz) имеется частица с периодом рас-
пада tz. При | /11 > tz нестабильная частица распадается
и падающий пучок изменит свою природу. При |/i|<^tz
нестабильную частицу можно считать стабильной. Следо-
вательно, для предела tt =— Т возникает ограничение
т>Т>|(или >£).	(32.9)
Подобное же ограничение возникает и в случае наличия
нестабильных частиц в конечном состоянии; нестабиль-
ность частиц можно игнорировать, если
tz>T>4^h >£).	(32.9')
Допустим теперь, что в спектре частиц имеется неста-
бильная частица с массой Л4, причем 2m < М < 3m, так
что частица М может распадаться на две т-частицы:
Al—>2т. Пусть период распада этой частицы есть т.
Тогда возможны два подхода к построению S-матрицы.
Если асимптотические состояния задавать для Т <^т, то
частицу М можно считать стабильной и S-матрица будет
иметь структуру, изображенную в таблице 2. В этом
случае пространство Э? (р) включает два типа пространств
Лобачевского: первый тип — с кривизной, определяемой
массой частиц т, другой тип — с кривизной, определя-
емой массой тяжелых частиц М.
Однако можно рассмотреть также случай, когда асимп-
тотическое время Т^>т. При этом в асимптотических
состояниях вообще не будут появляться нестабильные
198
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
(ГЛ. VI
Л4-частицы, так как за время Т^х они распадаются на
две m-частицы. В этом случае асимптотическое простран-
ство строится полностью из пространств Лобачевского,
имеющих кривизну, характерную для частиц с массой ш.
Матрица рассеяния будет теперь иметь вид, представлен-
ный в таблице 1, характерный для случая, когда т-ча-
стицы вообще не образуют никаких комплексов.
Однако «память» о возможности образования неста-
бильной А4-частицы остается и выражается в том, что
матричный элемент (2.2), описывающий упругое рассея-
ние двух m-частиц т~\-т-+ т-\-т, имеет резонанс при
относительной энергии двух m-частиц, равной массе
7И-частицы. Условно такой резонанс можно было бы
представить как процесс рассеяния, происходящий через
образование промежуточной 7И-частицы:
т + т М —> tn + т.	(32.10)
Ширина Af ~Й/т этого резонанса определяется временем
жизни Л4-частицы *).
Из приведенного выше обсуждения следует, что ха-
рактер асимптотического пространства 9i (р) и характер
асимптотических состояний и Ту существенно зависят
от того, в каком смысле понимается в (32.1) предельный
переход tr—> — оо, /2—>4-00.
§ 33. Масштаб для асимптотического времени Т
Известные сейчас взаимодействия частиц принято де-
лить на сильные, электромагнитные и слабые.
Эти взаимодействия определяют масштаб времени т,
который служит критерием для выбора асимптотического
времени Т. В случае сильных взаимодействий, какими
являются взаимодействия барионов между собой, барио-
нов с мезонами и мезонов между собой, радиус области
взаимодействия b по порядку величины равен комптонов-
ской длине л-мезонов, т. е. Ь = 1г1тпс= 1,4-10“13 см.
Время т5, в течение которого распадается комплекс
сильно взаимодействующих частиц, будет т5 = b/v, где
v—скорость частиц. Для v&c получим т^^б-10”24 с.
*) Более подробное описание нестабильных частиц с помощью
S-матрицы см. в § 34.
§33]
МАСШТАБ ДЛЯ АСИМПТОТИЧЕСКОГО ВРЕМЕНИ
199
При этих взаимодействиях образуются возбужденные
состояния барионов—барионные резонансы и мезоны.
Те и другие являются неустойчивыми частицами. Бари-
онные резонансы образуются по схеме
m + N —> N*	N + т,	(33.1)
соответствующая
36.
N
Рис.
рионного
нистая линия—пион (л),
прямая — барион (W).
Жирная линия — возбуж-
денный нуклон (N*). Обе
вершины Z „ 2 _______
N
Диаграмма ба-
резонанса. Вол-
где m — какой-либо мезон, N — барион, N*—возбужден-
ный барион. На рис. 36 изображена
диаграмма Фейнмана. К числу
подобных реакций относится, на-
пример, реакция
jt + N->N*/2->ji + N, (33.2)
где N — нуклон, a Ni/2-— резонан-
сное состояние, имеющее кванто-
вые числа 7\ = 1/2 (Т3—третья
компонента изотопического спина,
<7 = 1/2, (спин), Р-четность +,
странность S = 0. Энергия этого
резонанса лежит около 1400 Мэв.
В настоящее время известно
большое число барионных резо-
нансов [67]. Ширина этих резо-
нансов Г по порядку величины
равна ~100 Мэв, так что время жизни
равно
А и В «силь-
ные» .
этих частиц
т*=р- = 6-10-« с,
т. е. оказывается того же порядка, что и время сильного
взаимодействия исходных частиц т5. Такой же порядок
величины имеет время жизни мезонов, распадающихся
посредством сильного взаимодействия, например:
р->л4-л, р°—>т] + л, К* К 4-я.	(33.3)
Соответствующие диаграммы показаны на рис. 37.
Поэтому, выбирая	мы должны считать бари-
онные резонансы и мезоны, распадающиеся посредством
сильного взаимодействия, нестабильными частицами; они
не будут входить в асимптотическое пространство 91 (р).
Заметим, что определенное выше время жизни бари-
онных резонансов и мезонов относится к системе покоя.
200
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
(ГЛ. VI
Если распадающаяся частица движется, то время ее
жизни т' возрастает}^ Е/tn раз, где Е—энергия неста-
бильной частицы, а т—ее мас-
са покоя:
. Е
*' = ^.	(33.4)
Phq. 37. «Сильные» верши-
ны для распадов р-, р°- и
К-мезонов.
По этой причине ультрареля-
тивистские частицы могут быть
обнаружены на очень значитель-
ных расстояниях R от места
их рождения:
7?«ст' = ст-^-.	(33.5)
В силу этого нестабильная
частица при Е^>т может
перейти в класс условно ста-
бильных (если	, и
ее существование должно быть
отображено в пространстве 5R (р).
СредиЗнеустойчивых частиц,
возникающих при сильных
взаимодействиях, имеются л°-
мезоны. Такие мезоны распадаются на два у-кванта, так
что в механизме распада
л° —у + у
(33.6)
участвует электромагнитное взаимодействие. На рис. 38
показана диаграмма такого распада. Кроме сильной вер-
шины А имеются две электромагнитные вершины В и В'.
Эти вершины пропорциональны константе электромагнит-
ного взаимодействия e/Vhc = ]/“&, поэтому в выражение
вероятности такого распада входит множитель а2 =
= (e2lhcy « 10"4. Благодаря ему время распада л° —> у+у
много больше времени Ту. Оценка диаграммы с учетом
фазового объема для вершин В и В' дает время жизни
л°-мезона tvV 10“Х6 с.
Для Т, удовлетворяющего неравенству
Тр	(33.6 )
§33]
МАСШТАБ ДЛЯ АСИМПТОТИЧЕСКОГО ВРЕМЕНИ
201
может считаться стабильной частицей. При
в асимптотическое пространство 9i (р) следует
от места взаимодействия
л°-мезон
7>Sv
включить фотоны, так как вдали
вместо мезона л° будут наблю-
даться у-кванты.
Значительное число мезонов
и возбужденные барионы, рас-
падающиеся с изменением стран-
ности (Д5 =/= 0), имеют еще боль-
шее время жизни, так как в
механизме их распада участву-
ет слабое взаимодействие. Рас-
пад л±-мезонов можно описать
диаграммой, изображенной на
рис. 39. Диаграмма состоит из
одной «сильной» вершины А и
вершины «слабого» взаимодей-
ствия W. Ввиду малости кон-
станты этого последнего взаимо-
действия время жизни л^-мезо-
нов, распадающихся по схеме
(33.7)
Рис. 38. Диаграмма для
распада л° —У + у'. Вер-
шина А—сильное взаимо-
действие, здесь л°-мезон дис-
социирует на пару нуклон
(N) — антинуклон (N); в
точке В нуклон испускает
фотон у. В точке В' нуклон
N аннигилирует с антину-
клоном N и испускает фо-
тон у'.
(здесь р —мю-мезон, v—ней-
трино), составляет тя±~10“8 с.
Следовательно, если мы
л±-мезоны каю стабильные частицы, мы должны брать
намерены рассматривать
Рис. 39. Диаграмма распада л*-
мезона на р-мезон и нейтрино v.
А — «сильная» вершина, W—вер-
шина, описывающая слабое взаимо-
действие.
значения времени Т, удов-
летворяющие нер авенству
10"8 с>7п>10’?4 с.
Распады барионов (ги-
перонов), сопровождаю-
щиеся изменением стран-
ности, например распад
S-->n + e’ + v (33.8)
(S "—гиперон,	п—ней-
трон, е“—электрон, v—
антинейтрино), происходят
по диаграмме, изображенной на рис. 40. Здесь имеется
два «сильных» узла А и В и один узел слабого взаимо-
202
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
действия W, описывающий процесс
А° —> р+ 4-e~4-v.	(33.9)
Взаимодействие, характерное для этого процесса, счи-
тается «элементарным» слабым взаимодействием (см. [44]).
Время жизни частиц, распадающихся с участием таких
слабых процессов, составляет 10~10 с.
Из изложенного видно, что переход к пределу /2—->
оо, — оо в S-матрице должен пониматься с серь-
Рис. 40. Диаграмма, описываю-
щая распад 2“-гиперона на
нейтрон п, электрон а- и анти-
нейтрино v.A—вершина силь-
ного взаимодействия, вер-
шина слабого взаимодействия,
В — вторая вершина сильного
взаимодействия.

езными ограничениями, выте-
кающими из анализа возмож-
ных физических процессов. В
зависимости от выбора Т ме-
няется характер асимптоти-
ческого пространства и асим-
птотических состояний
и Ту.
§ 34. Нестабильные
частицы (резонансы)
Возвратимся теперь к
случаю, когда в спектре масс
присутствует нестабильная
частица, имеющая массу
3m > М > 2m.
Как было разъяснено выше, если в асимптотике вре-
мя Т можно выбрать таким, что Т<^т, где т = Й/Г есть
время жизни нестабильной частицы (Г — ширина резо-
нанса), то частицу М можно считать стабильной и вклю-
чить ее в асимптотическое пространство 9т (р). Поэтому
при Т рассмотрение сводится к проведенному ранее
в § 31, когда предполагалось существование двух сортов
стабильных частиц с массами m и М.
Мы сосредоточимся сейчас на противоположном слу-
чае, когда Т^>т.
В этом случае в асимптотическом пространстве 91 (р)
будут фигурировать частицы лишь одного сорта с массой
m < М. Частица с массой М будет обнаруживаться
р виде резонансного состояния, которое при
§34]
НЕСТАБИЛЬНЫЕ ЧАСТИЦЫ (РЕЗОНАНСЫ)
203
практически полностью распадается на исходные стабиль-
ные частицы—т-частицы.
Резонансному состоянию можно приписать определен-
ную массу М (ширина резонанса Г и, следовательно,
полный импульс Р = (Р, Ро), где Ро=+]/Р2 + 7И2.
Этому состоянию можно также приписать оператор
внутреннего момента количества движения который
складывается из спинов m-частиц (если они его
имеют) и из орбитального момента их относительного
движения	= p^xv —	(р, v=l, 2, 3, 4). Внутрен-
ний момент резонансного состояния Д’ц определяется
следующим образом:
(34.1)
где Ецарх —полностью антисимметричный единичный тен-
зор, Мар — полный момент количества движения:
Ма(з = £а|з4-§ар.	(34.2)
В системе центра масс псевдовектор Кц сводится к
оператору трехмерного момента количества движения
М (М23, М31, М12) [68].
Тогда в этой системе координат оператор имеет
собственные значения, характерные для нерелятивист-
ской теории:
K^hjfJ + V), Kz = hmj,	(34.3)
где
—J <.mj < + J, J = 0, 1, 2, ... или J — у. •••
(34.4)
Таким образом, резонансному состоянию, которое при
Л4^>Г представляется нестабильной частицей, приписы-
вается не только масса 7И, полный импульс Р, но и соб-
ственный момент количества движения /С.
| Резонансные состояния мезонов обычно называют об-
щим именем «резононы». За резонансным состоянием ба-
рион + мезон сохраняют название «резонанса*.
204
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ	[ГЛ. VI
Как резононы, так и резонансы кроме названных ха-
рактеристик имеют и другие (изотопический спин, внут-
реннюю четность, странность). Однако мы не будем под-
робнее останавливаться на этих вопросах, относящихся
к систематике и спектроскопии элементарных частиц,
ограничимся сделанными замечаниями и возвратимся
к анализу простейшего случая возможного резонанса
в системе двух скалярных частиц массы т. Мы будем
изучать резонанс в системе центра масс, так что
Р=рх4-/>2 = 0 (А, р2~импульсы частиц), и сосредото-
чимся на относительном движении этих частиц, и притом
с определенным моментом количества движения J.
Асимптотическая волновая функция, описывающая
относительное движение двух m-частиц, может быть пред-
ставлена в виде суммы сходящихся и расходящихся
сферических волн:
фу (г, 0==7" [a(s)e£pr-}-b(s)e_£₽'']e“i££,	(34.5)
где р—импульс относительного движения, Е—энергия
частиц в системе центра масс, г—расстояние между ча-
стицами, Z — их общее время (см. дополнение X).
В дальнейшем удобно импульс р и энергию Е считать
функциями инвариантной энергии:
s = Pl—Р>.	(34.6)
В системе центра масс имеем
5 = Р1 = Еа = (Е1 + Е2у = 4тг + 4р>,	(34.7)
откуда
/>2 = ls—ma,	(34.8)
так что
ip(s)=- ]/(34.9)
—iE = — V~s	(34.10)
И
фу- (г, /) =у [a (s) e~Vm‘~siir-\-b (s) e+^m‘-s/tr] e~v~sl.
(34.11)
$34]
НЕСТАБИЛЬНЫЕ ЧАСТИЦЫ (РЕЗОНАНСЫ)
205
Будем теперь рассматривать s как комплексную пере-
менную и для устранения двузначности радикалов в
(34.11) сделаем в комплексной плоскости (s) разрезы на
действительной оси от з =—оо до $ = 0 и от s = 4m2 до
s=4-oo (см. рис. 41).
Рис. 41. Комплексная плоскость переменной s. Показано два разреза:
от s =—оо до s=0 и от s = 4m2 до s =
Через эти разрезы мы будем продолжать функции
комплексной переменной s на второй лист римановой по-
верхности. Первый лист этой поверхности («физический»)
мы определим таким образом, что на нем
(34.12)
Re 1/ тг—4"= 81/2 sin <р > О,
г	4	Л
где
8, 8‘/2>0 и —/и24-у = еег<₽.	(34.13)
На втором листе («нефизическом») положим
т*—А = 8*/«еТ(ф+я)>
-----L	(34.14)
Re у тг—-j- = — e^’slnyqp.
Импульс p(s) на основании (34.9) и (34.12) определится
теперь следующим образом:
а)	на физическом листе
ip(s) = — У ma—-^-=ieWteWt,	(34.15)
p(s)=Imp(s)>0;	(34.15')
206
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
(ГЛ. VI
б)	на втором, нефизическом листе
fp(s)=r— р^т2—~ = — is1/2ei^2t (34.16)
р (s) = — в1/W2, Im р (s) < 0.	(34.16')
Таким образом, физический лист поверхности (s) отобра-
жается на верхнюю полуплоскость поверхности (р), а не-
физический—на ее нижнюю полуплоскость.
Заметим еще, что в стационарном состоянии компо-
нента* потока частиц J, направленная по радиусу-вектору,
должна равняться нулю. Отсюда следует
b(s) = a*(s*).	(34.17)
Условие, определяющее дискретные уровни нашей си-
стемы, стабильные или резонансные, гласит:
6($) = 0,	(34.18)
причем для стабильных уровней
•s —— iE и 0 < Е < 2m.	(34.19)
Резонансные уровни лежат в области непрерывного
спектра. Для них имеем
—Y~s = — iE—Г,	(34.20)
где Е > 2m, Г > 0. Выбор знаков в (34.20) обеспечивает
экспоненциальный распад резонансного уровня при
t~>оо. Из (34.20) следует, что
s = E2—<2iEV	(34.21)
(для Г<^£), так что Re s > 0, Ims<0.
В случае стабильных уровней из (34.11), (34.12),
(34.18) и (34.19) следует
(г, 0==ya(s)exp(—z^r-iEt).	(34.22)
Заметим, что на втором римановом листе мы имели бы
гр-(г, t) =у a(s)exp (4-e1/2r—iEt), ' (34.22')
так что следовало бы вместо (34.18) требовать a(s) = 0.
В силу (34.17) это условие давало бы те же уровни.
§ 34]
НЕСТАБИЛЬНЫЙ ЧАСТИЦЫ (РЕЗОНАНСЫ)
207
Вернемся теперь к нестабильному уровню. Если бы
мы оставались на первом физическом листе, то попасть
из верхней полуплоскости в нижнюю точку s = E2 —
— 21ЕГ (Г < 0), лежащую под разрезом, мы могли бы
только путем обхода точки s==4m2, как это показано
стрелкой на рис. 41. При этом аргумент функции ip(s)
(см. (34.9)) получил бы дополнительную фазу +2л, т. е.
в этом случае
ip (s) = + eV2 exp	(<p—-n) -j-	= ie1/3 exp ,
(34.23)
где определяется выражением
Ф = — arctg £(1_2fOT3/£2j + 2лп + 0	, (34.24)
в котором n = 0 для первого листа и п = 1 для второго.
Поэтому на физическом листе имеем
p(s) = p'—ix', р' = е1/2 cos —, х' =— e^sin-S-,
(34.25)
так что р' > 0 и х' > 0. Следовательно, на физическом
листе волновая функция (34.22) имела бы вид
фДг, /) = у- a (s) exp [i p'r — iEt] exp [x'r—17]. (34.26)
Нетрудно видеть, что это решение противоречит уравне-
нию непрерывности для потока J, так как оно умень-
шается с ростом г (х' < 0) и с ростом t (Г > 0).
Правильная для нестабильного уровня волновая
функция (г, t) находится на втором, нефизическом ли-
сте. Действительно, в этом случае согласно (34.16') имеем
р (s) = — 81/2 exp	= р"-f- ix",
р" — s1/2 cos f > 0, х" = 81/2 sin f > 0,
так что волновая функция приобретает вид
фу(г, /) = у a (s) exp [i (р"г — £У)]ехр(—к"г—17), (34.28)
имеющий правильное поведение в плоскости (г, t).
(34.27)
208
МАКРОСКОПИИ ЕС КАЯ ПРИЧИН НОСТЬ
[ГЛ. VI
Обратимся теперь к изучению пространственно-вре-
менных свойств общего асимптотического решения (34.5).
Для этой цели будет целесообразно изменить нормировку
решения (34.5) таким образом, чтобы рассеянная волна
и (р, г) имела вид
z ч Sj(P)exp [Z(pr—£/)]
п(р, г) =---------^7---------
(34.29)
где Sj(p)—элемент матрицы рассеяния в состоянии с
полным моментом количества движения J для упругого
рассеяния при энергии Е и относительном импульсе р.
Нормировка (34.29) соответствует первичной асимптоти-
ческой волне в форме
Ро V ’ l> ~ 2ipr	2i^r  V*1 •
Сопоставление формул (34.29) и (34.30) с (34.5) показы-
вает, что
=	(34.31)
(34-32>
где в функцию g(s) мы объединили множители, регуляр-
ные вблизи полюса E = ER —/Г.
Предположим теперь, что начальная волна ф0 задана
в виде волнового пакета
ф(г, 0= $ с(р)ф0(г, t)dp.	(34.33)
— 00
Выбор ф(г, t) в виде пакета позволяет локализовать
момент столкновения частицы около t==0. Считая, что
функция с(р) сосредоточена около p = pR> мы можем
переписать (34.33) в виде
0=2f^?exP Р
—21^7 ехр	Ркг~Еи^ (Г + М> (34.34)
где vR = (dE/dp)R есть относительная скорость частиц
вблизи резонансной энергии Е « ER, Функция f убывает
$34]
НЕСТАБИЛЬНЫЕ ЧАСТИЦЫ (РЕЗОНАНСЫ)
209
вне интервала
|г±^|>|,	(34.35)
где Д—ширина пакета в импульсном пространстве:
с(р)«0	(34.35')
для \р—Ря|>Д.
Отсюда следует, что столкновение произойдет около
момента времени
t — Й/At^
(предполагаем, что ширина пакета Д больше радиуса вза-
имодействия частиц).
Далее, мы будем считать, что
=	(34.36)
где Л—длина распада. Рассеянная волна, возникающая
при столкновении пакетов (34.34), согласно (34.29) и
(34.33) будет иметь вид
00
ui Г) = У с (/?) ехр [ (рГ ~ Е/)] ё (S) dp-
— 00
(34.37)
Положим р—Pr = %, тогда
/.)==ехр[/(^-^)] х
Г	g-i’J-
X \ c(pj>-H)exp[i£(r — Pj?O]g(s)-----т-dl. (34.38)
J	§ + i —
Теперь мы видим, что если g(s) и с(р) таковы, что кон-
тур интегрирования в (34.38) можно замкнуть по боль-
шому полукругу*), то при (г—vRt) < 0 это замыкание
должно быть сделано в* нижней полуплоскости, а при
(г —> 0 —в верхней.
*) Если с (р) достаточно быстро убывает при росте радиуса
круга |р — рр |—>оо, то поведение остальных функций под знаком
интеграла в (34.38) оказывается несущественным.
210
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
В результате мы получим
и (р, г) = — i2nhc eXPtt(p^A	ехР [<r—^0 4]
для r — vRt<.® (34.39)
и
и(р, г) = 0 для г—1^>0.	(34.39')
Так осуществляется причинность в резонансном рас-
паде: распады вообще не происходят в области г > vRt,
которая не достигается резо-
Рис. 42. Распад резонансов,
образующихся около точки
г = 0. В области 0 < г < vRt
резонансы распадаются экспо-
ненциально. В области г > vRt
их волновая функция и (г) рав-
на нулю.
нансами, рождающимися при
г ~0, t = 0 (с точностью до
допуска h/k).
В области г < vRt резо-
нансы распадаются экспонен-
циально с константой распа-
да T = hvR/A (рис. 42).
Приведенный здесь ана-
лиз нестабильных состояний
показывает, что S-матрица
способна правильно описать
пространственно-временное
поведение нестабильных ча-
стиц («резононов» и «резо-
нансов»).
В дополнении XI для удобства читателя приведен де-
тальный расчет нерелятивистского резонона, который
может служить иллюстрацией к изложенной в этом па-
раграфе теории.
§ 35. Условия макроскопической причинности
для S-матрицы
В 1942 г. В. Гейзенберг выдвинул свою знаменитую
программу развития квантовой теории, в основу которой
была положена идея описания явлений в мире элемен-
тарных частиц с помощью S-матрицы вместо волновой
функции.
Значение этой программы не было отвергнуто даль-
нейшим развитием теоретической и экспериментальной
физики. De facto методы, основанные на понятии волно-
вой функции, явно уступили методам, основанным на
§35] УСЛОВИЯ макропричинности для 5-МАТРИЦЫ 211
изучении аналитических свойств S-матрицы. Теперь ги-
бель волновой функции кажется почти очевидной. Однако
нет особых оснований радоваться этому факту: совре-
менный математический аппарат S-матрицы не имеет
продолжения в область малого, в самую «кухню» эле-
ментарных событий.
Нередко теоретические схемы, оперирующие только
S-матрицей, похожи на производство, в котором есть
только два цеха: цех приема полуфабрикатов и цех упа-
ковки готовой продукции, цех же переработки отсут-
ствует.
Аналитическое продолжение S-матрицы с поверхности
масс и поверхности энергии в некоторой мере позволяет
заглянуть в этот «цех переработки», в самое «производ-
ство» элементарных событий. Все же методы аналитиче-
ского продолжения, по всей видимости, не в состоянии
дать полную картину физических явлений в мире эле-
ментарных частиц.
Мы должны признать, что наши современные воз-
можности весьма ограничены. Однако два обстоятельства
говорят в пользу метода S-матрицы:
а) в мире элементарных частиц, по-видимому, нет
явлений, которые не могли бы быть описаны в терминах
S-матрицы; б) S-матрица, по крайней мере в принципе,
принадлежит к числу наблюдаемых величин. Поэтому
мы имеем основания рассматривать S-матрицу как такую
теоретическую конструкцию, которая может сохранить
свою значимость и в будущей теории.
Таким образом, изучение S-матрицы представляется
вполне разумным направлением в теоретической физике,
и, следуя ему, мы будем надеяться, что S-матрица оста-
нется и в будущем тем языком, на котором и в дальней-
шем будет возможно выразить наблюдаемые результаты.
Такая вера в S-матрицу обязывает нас формулировать
принцип причинности непосредственно на языке S-матри-
цы, не прибегая к какой-либо теории поля и к условиям
микропричинности.
На первый взгляд в самой постановке вопроса имеется
неустранимое противоречие, заключающееся в том, что
212
МАКРОСКОПИИ ЕСК АЯ ПРИЧИННОСТЬ
[ГЛ. VI
Рис. 43. Описание столкновения с
помощью волновых пакетов. Паке-
ты Wi и «2 образуются при t± = — Т
в диафрагмах экрана Л и В. В мо-
мент времени 0 происходит
столкновение пакетов (черная об-
ласть S). Далее пакеты вновь уда-
ляются, постепенно расплываясь.
Это увеличение размеров первич-
ных пакетов показано на рисунке
для момента времени /2 = +Т,
Рассеянные волны не показаны.
S-матрица определена в пространстве импульсно-энерге-
тических переменных, в многомерном пространстве Лоба-
чевского 9i3(p); для описания же причинной связи по
самому смыслу этой связи необходимы пространственно-
временные переменные, определенные в пространстве Э?4(х).
В силу этого причинность на языке S-матрицы может
быть сформулирована лишь с той степенью определен-
ности» которая ограничи-
вается возможностью одно-
временного использования
обоих пространств fR3 (р)
и fR4(x). Такая возмож-
ность характерна для клас-
сической макроскопичес-
кой физики.
Поэтому причинность,
которую мы будем изу-
чать в этом разделе, мы
называем макроскопичес-
кой причинностью [69, 70].
Одновременное исполь-
зование обоих пространств
Ot3(p) и Ж4 (х) покоится
на принципиальной воз-
можности построить вол-
новые пакеты, которые в
течение времени от t± = —Т
до /2 = + Т (Т — асимпто-
тическое время) настолько
мало расплываются, что
в течение времени 27,
охватывающего процесс сближения волновых пакетов, их
столкновение и последующий разлет могут представлять
локализованные в пространстве и времени частицы. Воз-
можность существования таких пакетов была показана
в § 18 (см. [30, 74]).
Там же выведены условия для описания процесса
столкновения с помощью волновых пакетов. Эти условия
гласят:
(35.1)
§35] УСЛОВИЯ МАКРОПРИЧИННОСТИ ДЛЯ 3-МАТРИЦЫ 213
где ft— характерная для пакета длина волны, а—размер
пакета, R — расстояние между пакетами, R = Tv, v —
относительная скорость пакетов.
На рис. 43 изображены волновые пакеты (xj и
и2(х2), описывающие частицы в начальном состоянии.
При выполнении условий (35.1) эти пакеты мало изме-
няются за время от tr = — Т до t2 = -\-T.
Обратимся теперь к математическому описанию столк-
новения этих пакетов, пользуясь теорией S-матрицы.
Мы выпишем формулы в явном виде для скалярных ча-
стиц. Согласно (31.28) матричный элемент S-матрицы
в импульсном представлении записывается в форме
S/f = <р' 111 р> + & (Р'-Р)	.	(35.2)
V 2р0...2ро
Более подробно функции <р' 111 р> и Т (рг, р) для
перехода из состояния (р)==(рп, рп„г, ...,рг, pj в со-
стояние (р') = (ри+п, pm+n_i, .... Pn+i, рп+1) запишутся
в виде
<p'|7|p> = f[63(j7„+J— ps) при m=n, (35.3)
1-1
иначе <pf 111 p> = 0, и
T (p > p) __ (Pm + n^ Ргп + п — Ъ • • • > Ръ> Pi) zgg
V2po- • «2ро	V2pm+n V"%Pm+n-i... V2p?
где числитель есть инвариантная функция импульсов,
a pi, р2, ..., Рот+л~их четвертые компоненты.
Для определенности будем считать, что в начальном
состоянии имеется только две частицы, которые опи-
сываются волновыми пакетами иДх^ и и2(х2), принадле-
жащими к классу пакетов, удовлетворяющих условиям
(35.1). Такие пакеты могут быть представлены интегралами
«(*) = ^^ J«(P)exp(ipx)^, (35.4)
где р°=угт2+рг. Волновая функция начального состоя-
ния в импульсном "представлении запишется в виде
(3SS>
214
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
Тогда волновая функция конечного состояния‘$,out(p4, р3)
для т = 4 (упругое столкновение) получится из (35.5)
с помощью преобразования посредством S-матрицы (35.2):
^out (Pv Рз) = ^in (Р4> Рз) +
+ i [ & (р4 + р3 - Рз ~ Pi)	й2 (р3) (pj ,
J	V2p%2p°	2p22pi
(35.6)
и волновая функция для т > 4 (рождение при столкнове-
нии новых частиц) будет иметь вид
^out(pm> Рт-и •• •> Рз) =
= + i J fi4 (pm + Pm—1 + • • • + рз—Рз—Pi) X
T(Pm, Pm — 1....Рз, Pt, Pl) - z„x~ / „ \ ^P2 &P1
U2 \P 2) W1 \P1) —q —q-
Zp2 Zpi
К2pm2pm-i • • • 2рз
(35.7)
Из (35.4) следует, что
= '(2^? I U ехр ipX^d*X- (35,8)
Это соотношение позволяет нам перейти в (35.6) и (35.7)
к координатному представлению. Для этого мы выразим
в (35.6) и (35.7) амплитуды и2(р2) и u^pj с помощью
(35.8) через ^(xj и и2(х2), далее умножим слева (35.6)
и (35.7) на экспоненту
1	exp [t (ртхт +	 ! + ... + р3х3)]	,35 ~
хТ	V2рт2р°т-1 . • • 2рз
и проинтегрируем произведение по d3pmdzpm^i ... d3p3.
В результате мы получим
^OUt (^4»	= ^in (*^4» ^з) Ч~
+ i J ® (х4, х31 х2, %i) и2 (х2) и± (х^ d3x2d3Xi, (35.10)
и в общем случае, когда т > 4,
^OUt (^zn»	* * * > -^з) =
—	®	^т,—1» • * • > I -^2’ *^1) ^2 (*^2)	(^i) d^x2d^Xi,
(35.11)
§35] УСЛОВИЯ МАКРОПРИЧИННОСТИ ДЛЯ S-МАТРИЦЫ 215
где функции ®(хл, хт^, х3|х2, хх) определены сле-
дующим образом:
®(хт, хт.ь х3\х3, Хх) =
_d2®o (,хт> хт — 1) • • • > хз I ^2> *1) /ок 1 л\
~	dt2dtT	’
Здесь t2=x2, ti=Xi суть четвертые компоненты векторов
х2 и хх, а функция ®>0(хт, хт_1У ..., х3|х2, хх) равна
®D С^/zP %т—I» • • •» *з | *2, Хх) =
= $fi4(pm + Pm-1 + ••• +Рз-р2 — Р1)Х
X Т(рт, рт_ь .... р3- р3, Р1)Х
хехр [i (ртхт + р„1_1х,„_1+ ... +рвх3—р2х3—р1х1)]х
X ^afpam~1 •••	. (35.13)
2рщ2рт_1 ... 2pi
Из (35.13) видно, что функция ®0 есть не что иное, как
один из матричных элементов Т (см. также (35.2)), взя-
тый в координатном представлении. Функции ®х и ®0
удовлетворяют уравнению Клейна по любому из своих
аргументов:
(□s2-m2) ®о = О, (Ql-m2) ®х=0;	(35.14)
5=1,2, ..., т. Эти функции описывают процесс столкно-
вения в терминах свободных частиц. Они являются ана-
логами функций s (хт, хт_1, ..., xx), рассмотренных в § 24
(см. (24.5) и (24.6)), но не совпадают с ними, так как
спектральное разложение функций s(xm, хт_1, ..., хх)
выходит за пределы пространства Лобачевского 913(р).
Функции s(xm, хт_л, ..., х29 хх), основанные на пред-
ставлении матрицы рассеяния S через локальные поля
(см. дополнение VII), могут не существовать, в то время
как функции ® (хот, хт_19 ... | х2, хх) основываются на
более общем предположении о существовании матрицы
рассеяния S, взятой для реальных частиц и на поверх-
ности энергии.
Сформулируем теперь принцип макроскопической при-
чинности: волновые пакеты и (хх) и и (х2), представляю-
щие начальное состояние Oin(x2, хх), дают исчезающе
216
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
(ГЛ. VI
малый вклад в рассеянную волну <Dout (хт, хт_^ ..х3)
если в асимптотической области, т. е. для
|Х,—xk\s>R, \t.-tk\^T,	(35.15)
точки Xj, х2, ..., хт лежат вне области, ограниченной
условиями
(х2 - X1y=(t2- ttf- (х2 -Х1у > 0	(35.16)
и
(х,- — Xj)2 > 0,	— /х > Т,
(х{ — х2у>0, ti — t2>T
(35.17)
(35.17')
(i = 3, ..., т— 1, т). Эти условия поясняются рисунком 44
Рис. 44. Макроскопическая причин-
ность. АВС—световой конус у вол-
нового пакета Ui(xi), А'В'С' — све-
товой конус у пакета w2 (*г)- из (хз)
и (х4) — волновые пакеты, описы-
вающие рассеянные волны. Относи-
тельное расположение четырех па-
кетов, показанное на рисунке, со-
ответствует выполнению условий
макроскопической причинности.
на примере упругого
столкновения (т=4).
Обозначим область, оп-
ределенную условиями
(35.15) — (35.17'), симво-
лом SUl(x). Тогда на язы-
ке функций @ (х) =
= ® (хт, ха_1, ... | х2, Хх)
принцип макроскопической
причинности может быть
выражен следующим обра-
зом: функции ® (х) должны
исчезать достаточно
быстро вне области ЭЛ (х):
® (х) —>0 вне ЭЛ (х).
(35.18)
Таким образом, макро-
скопические условия при-
чинности вносят ограниче-
ния на поведение функций
® (х) только в асимптоти-
ческой области. Слова «ис-
чезать достаточно быстро» должны пониматься в смы-
сле: «существенно быстрее, нежели исчезают обычные
каузальные взаимодействия».
Заметим, что эти взаимодействия исчезают в волновой
зоне, как 1/7?. Поэтому акаузальные взаимодействия
должны исчезать существенно быстрее, чем 1//?. Если
§36]
ПРИМЕРЫ АКАУЗАЛЬНЫХ ФУНКЦИЙ ВЛИЯНИЯ
217
они исчезают в области ближе волновой зоны сигнала,
т. е. при	где А.—длина волны, то они вообще не
могут быть обнаружены экспериментально. Поэтому опи-
санное выше условие макропричинности оставляет очень
широкие возможности для различных модификаций микро-
причинности и, стало быть, для изменения геометрии в
малом. Можно сказать, что S-матрица отличается край-
ней веротерпимостью и готова ассимилировать самые
различные теоретические схемы описания взаимодействия
элементарных частиц и их внутренней структуры, по-
скольку изменения относятся к малым пространственным
расстояниям и малым промежуткам времени ^b/v.
Теоретические схемы, в которых нарушается микропри-
чинность, мы будем называть акаузальными (или нело-
кальными, ср. § 26). Если акаузальность не нарушает
макропричинности, то мы будем называть такие схемы
локально-акаузальными.
Таким образом, для построения такой схемы доста-
точно, чтобы: а) S-матраца оставалась локально-акау-
зальной. Далее, следует вспомнить необходимое условие
унитарности S-матрицы (31.3): б) S-матрица должна быть
унитарной *). Совмещение этих обоих условий оказывается
не тривиальным и представляет собою основную проблему
нелокальной теории. В следующем параграфе мы рассмот-
рим примеры функций распространения, удовлетворяющих
условию локальной акаудальности, а в § 37 будет приве-
ден пример построения S-матрицы, удовлетворяющей усло-
виям а) и б).
§ 36. Примеры акаузальных функций влияния
Рассмотрим сперва акаузальный аналог причинной
функции £>с(х), которая симметрична относительно про-
шедшего и будущего: Dc (%)=/= 0 для 8 = + 1и для 8 = —1.
В силу этого она весьма удобна для построения симмет-
ричной относительно запаздывания и опережения акау-
зальной функции влияния.
♦) Можно обсуждать, насколько действительно необходимо усло-
вие унитарности, однако отказ от этого требования ведет к очень
серьезным трудностям (см. дополнение XII).
218
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
|ГЛ. VI
Для простоты мы рассмотрим случай, когда масса
покоя частиц поля, переносящего взаимодействие, равна
нулю. В этом случае, согласно дополнению I (формула
(1.6)), имеем
t = t2—r = \x2—Xi|.	(36.1)
Разлагая здесь 6 (х2) и , получим другое представле-
ние этой формулы:
dc W = i ts+ (^ - И+б- (/+г)] •	(36.1')
Образуем теперь акаузальную функцию Dc(x, а), кото-
рая при достаточно малом значении параметра а аппрок-
симирует причинную функцию Dc(x). Для этого заменим
и
п2 1
6(х2) на 6(х2,а) = ^-^	(36.2)
на г-^6(х2,а).	(36.2')
Тогда Dc(x, а) приобретает вид
РДх,а)=А-[б(х2, а) + »-^6(х2,а)] =
1 р 1	-1 Г 1_________Ml (36.3)
4л|лх2+^2 2ш/72 —ш2 Ti t — ^Jj’
где
т1 = + ]/*г2 — ia2, т2 =— V г2—ia2.	(36.4)
Вычислим теперь полеф(х2), создаваемое в точке x2(x2it2)
источником Q(x), локализованным около точки х^х^ Q
в пределах пространственно-временной области Q (xt)^L3T.
Пусть этот источник описывается выражением
<2 (*i) =Р	g (у-) ela,ti,
(36.5)
S 36]
ПРИМЕРЫ АКАУЗАЛЬНЫХ ФУНКЦИЙ влияния
219
где со > О, ®Т^> 1, LzacT. В частности,
р(т)Чда7'	<ЗМ>
как это было в § 26.
Поле ср(х2), создаваемое источником Q (Xj) (36.5)
посредством акаузальной функции влияния Dc (х, а) (36.3),
вычисляется по формуле
00
Ф (Х2)=j р	у Dc (х, a) g 0*-) dtt. (36.7)
Подставляя сюда Dc(x, а) из (36.3), найдем
ф (х2) =
=8^2 Jр (т-) J ё (т)eiat
(36.8)
где t = t2—tr. В комплексной плоскости tr= и мы
имеем полюсы при tr=t2—тх, t1 = t2—т2 и 1г = ±1Т.
Интеграл в (36.8) при со > 0 можно замкнуть в верхней
полуплоскости бесконечно большим полукругом. Полюс
t± = iT дает вклад, исчезающий при соТ оо как е~®т,
так что остается единственный вычет от полюса 1г=12—тп
Im?! < 0.
Таким образом, получается
ф<**)=- i Jp (1) y|=^exp[to &-иг2-И] X
х g(<2~l^-2~ta2) • (36.9)
Выражение
®ret (Г, t2, ^^expE/coQ^-y^-^)]	(36 10)
у г2—Ш2
можно рассматривать как запаздывающую функцию
Грина для почти периодического источника (частота со).
Как видно, эта функция не имеет сингулярности при г=0,
а при переходит в функцию Грина ®ret (г, /2), вы-
численную в § 26 с помощью функции Dc(x). Правиль-
220
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
(ГЛ. VI
ный характер причинной связи при г ^>а в рассматривае-
мом примере обеспечивается двумя обстоятельствами:
а)	надлежащим выбором сингулярностей функции
Dc (х, а) и
б)	выбором источника: источник Q (хх) локализован
в пространственно-временной области Q UT |>> X3 и
имеет положительную частоту со > 0, что отвечает излу-
чению кванта с положительной энергией Йсо > 0. В случае
со < 0, Асо < 0 вместо выражения (36.10) мы получили бы
выражение для ® (г, t2,a), аппроксимирующее опережаю-
щий потенциал:
a.Jv(r, t„ <,)= “Р['"(',+, (36.Ю-)
V г2—la2
Эта формула есть результат замыкания интеграла (36.8)
в нижней полуплоскости, где имеются полюсы lt =— Т,
1г = 12—т2, 1тт2>0.
Заметим, что если бы мы взяли очень малые L и Т,
то мы пришли бы к существенному нарушению макро-
скопической причинности. Чтобы пояснить эту мысль, до-
статочно рассмотреть малые Т (соТ tv 1). В этом случае
нельзя пренебречь в интеграле (36.8) вкладом от вычета
около полюса Z1 = +i7’. С учетом этого вклада получаем
= ЧлУ J Р (~Г) d3X1 (t2 — iT)2—(r2 — ia2)
ie-®T Р (Xi \ d3xi /Q~ Q,.
~ SF i P U) ' <36-9)
Характер знаменателя в (36.9') указывает на то, что
Ф (х2) содержит симметрично опережающее и запазды-
вающее влияния. Тем самым нарушается макроскопи-
ческая причинность. Отсюда видно, в какой мере важна
достаточная плавность источника Q (хг) в пространстве —
времени для формулировки причинности: необходимо,
чтобы величина со? была много больше единицы. Это
условие совпадает с условием достаточной определенности
энергии источника как по ее знаку, так и по величине.
Как будет показано в § 38, формулировка нарушения
микропричинности, обеспечивающая локальность такого
нарушения, не может быть осуществлена без привлече-
ния времениподобного вектора п (который может счи-
§36]
ПРИМЕРЫ АКАУЗАЛЬНЫХ ФУНКЦИЙ ВЛИЯНИЯ
221
таться единичным, так что п2=1); физический смысл
этого вектора может быть весьма различен. В рассмат-
риваемом примере роль такого вектора играет вектор
(со, Л), где со—характерная частота источника, k—харак-
терный импульс. В частности, мы видели, что изменение
знака со сопровождается заменой запаздывающих потен-
циалов на опережающие.
Обратимся теперь к примеру акаузальной функции
влияния, в которой вектор п вводится в явном виде в
саму функцию влияния.. В этом примере, как и в обычной
каузальной теории, любые функции влияния могут быть
получены суперпозицией запаздывающих и опережаю-
щих функций Грина с функциями D+ и D~.
В частности,
W=^adv (X) + D~ (x)=Dret (x)-D + (x), (36.11)
и согласно (26.18), если имеется источник поля Q (у), то
поле <р(х), возникающее в точке х, определяется фор-
мулой
ф (х) = $ Dc (х—у) Q (у) d*y. (36.12)
Вместо этих каузальных функций влияния Dc(x), £>ret(x)
^adv (х) построим акаузальные, регулярные в вершине
светового конуса. Для этого воспользуемся форм-факто-
ром р(х, п), в который явно вводится некоторый време-
ниподобный единичный вектор п:
р(х,п) = р(4),	(36.13)
где
7?2 = 2(пх)2—х2>0	(36.14)
есть инвариантная положительно-дефинитная квадратич-
ная форма переменной х*). Мы предположим, что форм-
фактор (36.13) быстро исчезает (например, экспонен-
циально) при Ria—>оо, так что величина а имеет смысл
радиуса той области, внутри которой нарушается микро-
причинность. Мы допустим, что этот форм-фактор не
имеет в нуле сингулярности сильнее 1/7?.
*) В системе отсчета, где п= 1,0, 0, 0, инвариант 7?2=/2-}-х2^0,
222
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[гл. vi
Акаузальные функции влияния определим формулами
D+t (х, а) = J D+t (х-%) р (g, п) d*l,	(36.15)
tfa’dv (х, а) = $ Da-dv (X-g) р (£, n) d^. (36.15')
Соответственно этим формулам измененное «акаузальное»
поле <р (х, а) определится вместо (36.12) формулой
<р (х, а} = $ Dc (х—у, a) Q (у) dly, (36.16)
где
Dc (х—у, а) = $ Dc (х—у—В) р (g, n) d*% =
= °ret (х—у, a)—D+ (х—у, а).	(36.17)
Введение такого форм-фактора физически эквивалентно
допущению, что каждая точка источника поля Q (у) раз-
мазывается с помощью форм-фактора (36.13) в области
(х) « а4 и, следовательно, порождает поле так, как его
порождает заряд, распределенный в малой области по-
рядка а4. В силу такой локализации форм-фактора р (?, п)
поведение акаузальной функции Dc(x—у, а) при боль-
ших |х0—/0| и —_у|, т. е. при
1*0—^>|>«> \х—у\^>а,	(36.18)
асимптотически совпадает с поведением акаузальной
функции De(x—у). Тем самым доказывается выполнение
условий макроскопической причинности (35.15) — (35.17').
§ 37. Пример построения акаузальной
матрицы рассеяния
Мы будем исходить из предположения, что существует
унитарная S-матрица, построенная на основании локаль-
ной теории, предполагающей соблюдение условий микро-
причинности. Мы будем также считать, что все беско-
нечности устранены из этой матрицы, скажем, посред-
ством перенормировки. Таким образом, исходная матрица
S будет содержать только матричные элементы, которые
описывают реальные физические процессы. Следовательно,
ее матричные элементы определены на поверхности энер-
§ 37] ПРИМЕР ПОСТРОЕНИЯ АКАУЗАЛЬНОЙ S-МАТРИЦЫ 223
гии (реальные частицы) и выражаются формулами вида
(31.28).
Наша задача будет заключаться в нахождении акау-
зальной матрицы рассеяния Sa, удовлетворяющей усло-
виям макропричинности и условию унитарности (ср. § 35).
Эту матрицу мы будем считать «близкой» к некоторой
локальной матрице S (точное значение слова «близкая»
выяснится позднее). Представим теперь исходную локаль-
ную матрицу рассеяния S в форме
§ = А	(37.1)
где т)—эрмитов оператор фазы такой, что
П = П+-	(37.1')
Мы будем считать, что взаимодействие не сильное и до-
пускает представление операторов S и т| в виде рядов по
степеням константы взаимодействия g;
S = 7+Sg«S„,	(37.2)
/2=1
(37.3)
/г=1
Подставляя эти ряды в (37.1), найдем, что
п ;k
= V- (ПаЪ • • • ^) 6а+&+...+с,	(37.4)
k = 1 ab . . . с
где произведение (т]ат]6 ... т|с) содержит k множителей.
Из (37.4), в частности, следует
гч	~	Z4	/2 л
3, = ^ 52 = И)2+^-П12+...	(37.4')
Эти формулы выражают оператор S через оператор тр
Существенно, что они разрешимы и в обратном направ-
лении, так что можно выразить оператор т, через опера-
тор S. Структура матричных элементов оператора т], ра-
зумеется, совпадает со структурой матричных элементов
224
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
(ГЛ. VI
матрицы рассеяния (см. (31.28)), так что мы можем на-
писать
<р'|л|р> = 6‘(Ур'-Ур),-М^Ь. (37.6)
где г)(р', р)—инвариантная функция импульсов р и р'.
Введение матрицы т) вместо матрицы § существенно вот
в каком отношении: нарушая тем или иным способом
микропричинность, можно нарушать и унитарность матри-
цы 5, что поведет, по всей видимости, к тяжелым по-
следствиям. Между тем, если исходить из оператора rj, то,
переходя от микропричинного оператора rj к акаузаль-
ному т]а, достаточно позаботиться о соблюдении новым
оператором условия эрмитовости (37.Г). Эрмитовость же
оператора является условием симметрии и потому легко
проверяется. Тем самым гарантируется и унитарность
акаузальной матрицы рассеяния Sa. Прямая же проверка
унитарности матрицы Sa является делом весьма сложным,
а может быть, и невыполнимым.
Для того чтобы иметь возможность проверить выпол-
нение матрицей §а условий макропричинности, необхо-
димо обратиться к пространственно-временному описанию,
которое следует теперь сформулировать на языке опера-
тора фазы т]. Для этого напомним, что, согласно § 35,
условия макроскопической причинности формулируются
для функции ® (х) (см. (35.18)), которая определена фор-
мулами (35.12) и (35.13). В последнюю формулу входит
матричный элемент, непосредственно связанный с 5-мат-
рицей формулами (35.2) и (35.3).
С помощью (35.2) и (35.4) можно представить функ-
цию Т (р', р) в виде ряда по степеням константы взаи со-
действия g и по степеням величин т]х, т]2, ..., т)*, ...
(см. (37.4)). Пользуясь законом умножения матриц в прост-
ранстве Лобачевского (см. (31.26)), нетрудно показать,
что это разложение имеет вид
Т(р', p)=gr\1(p', p)^g2'nAp'>p)+^g2nl(P,> р)+...=
=g’ii(p'> р)+£Ч(р'> р)+
+ 4g2fr)1(p', Р")^У\ЛР\ Р)+..., (37.6)
* О	<£Рп
§37] ПРИМЕР ПОСТРОЕНИЯ АКАУЗАЛЬНОЙ 3-МАТРИЦЫ 225
где под р' следует подразумевать совокупность импуль-
сов рт, Рт_\,..Рз в конечном состоянии, аподр—сово-
купность импульсов в начальном состоянии р2, р, (см.
(35.2) и (35.3))*).
Таким образом, формула (37.6), будучи расписана
подробнее, гласит:
Т(рт, Рт-1, .... р3, р2, Pi)=CTi(P»> Pm-i,  ,Р2, Р1) +
4-24(рт, Pm-i, .... р2, Pi)+ ~
+ j-g3 f ’ll (Pm, Pm-1’ • • • > P2> P’l) • • • X
z J	2p2 2pi
XT)i(PJ» Pi.....Pa> Pi)*b--- (37.7)
Вставляя это выражение для функции Т в соотношение
(35.13), мы выразим функцию ®0 через матричные эле-
менты оператора фазы тр
®о(*и, хт_ь .... х3, х2, Хх) =
= (Pm+Pm~i+  • • +Рз—Р2 — Р1)х
x{CTi(p«,.pm-i>  • р2, Р1)4-гЧ(р,л, рт-1>   > Рз. Pi) +
+ yg2fni(Pm. Рт-1, •••. pa'. Pl)	х
v	2р2 2pi
xt)i(pL Pl....Рз, Pi)+---}x
Хехр /[рл+р^.^-хЧ- ... +РЛ—РзХ2 —РЛ]Х
(378)
%Рт %Рт —1 2рх
Функция ® (х^,	..., х2, %х), трансформирующая
падающую волну в рассеянную, получается из ®0(хлр
^/л-1» •••, -^2» *i) путем дифференцирования по х2 и х[
(см. (35.12)).
Таким образом, функция ® (хт, xm^if ..., хг), оказы-
вается функционалом от матричных элементов Tji(p', р),
ЛгСр', Р), оператора фазы т). Зная свойство этих эле-
ментов и пользуясь (37.8), можно проверить выполнение
условий макроскопической причинности (35.15) —(35.17').
•) Как и в § 35, мы в явном виде принимали, что в начальном
состоянии имеется лишь две частицы. Обобщение на большое число
частиц не представляет проблемы.
« ГТ
226
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
Обратимся теперь к простому примеру акаузальной
матрицы Sa. Предположим для определенности, что ис.
ходная каузальная матрица S описывает процессы в ска-
лярном поле ф(х), причем энергия взаимодействия имеет
вид *)
W = g,:<p® (х):,	(37.9)
где ф (х) есть оператор скалярного поля, g — константа
взаимодействия. Пользуясь обычным методом диаграмм
Фейнмана [37, 38], нетрудно показать,“что описывающий
рассеяние матричный элемент оператора т] в первом по-
рядке тождественно равен нулю
ти^О.	(37.10)
Матричный элемент второго порядка т]2, описываю-
щий рассеяние, равен матричному элементу оператора s2
(ср. (37.4)) и описывается суммой следующих ’’диаграмм
Аналитическое выражение этого элемента имеет вид
1Ъ(р4. Рз> Рг, Pi) = {Dc(p3 — p1) + Dc(p2 + p1}, (37.12)
где Dc(q) есть фурье-образ причинной функции Dc(x), а
q—импульс, передаваемый по внутренней линии диаг-
рамм (37.11).
Согласно (37.8) и (37.12) для упругого рассеяния
имеем
®0(х4, х3, х2, x1) = \8i(pi + p3—p.i—p1){bc(ps—p1) +
+Dc(p2 + pJ}expi(pixi + p3x3 — p2x2—p1x1)^ • • • ;йг •
2р4 2pi
(37.13)
*) Ср. дополнение VII. В этом дополнении отмечено, что система
с взаимодействием g(p3 неустойчива. Однако если ограничиваться т§о-
рдей возмущений, то это обстоятельство несущественцр.
§371 ПРИМЕР ПОСТРОЕНИЯ АКАУЗАЛЬНОЙ 3-МАТРИЦЫ 227
Предполагается, что начальное состояние частиц
Ч'ы (*2, хг) задано в виде волновых пакетов и2 (х2) и иг (хх)
типа, рассмотренного в § 35 (ср. (35.4)):
^*in (^'2, ^1) == ^2 (*^2) ^1 (*^1) •	(37. 1 4)
Пользуясь теперь формулой (35.10), после длинных вы-
кладок, приведенных в дополнении XIII, получим для
рассеянных волн в случае упругого столкновения
VOut(X4, Х3) = U2 (х4)	(%3) +
+i$ d*xd*yD+ (х^—у) D+ (xs — x) Dc (x—y) u2 (y) u± (x) +
+ i у dtxd4yD+ (x4 —^±£) D+ (x3—^±£) x
xDe(^-)«2(x)U1(x), (37.15)
где первый интеграл определяется первой диаграммой
(37.11), а второй—второй диаграммой (37.11). Функции
D+ (х) определены в дополнении I формулой (1.10).
Dc — причинная функция.
Выражение, полученное для рассеянной волны, осно-
вано на обычной локальной теории, в которой соблю-
даются условия микропричинности.
Заменим теперь функцию Dc(x—у), входящую в вы-
ражение (37.15), акаузальной функцией Dc(x—у, а):
Dc(x-y, a) = \Dc(x-y-Z)p{^	(37.16)
Здесь p(g, п)—форм-фактор, зависящий от некоторого
единичного временного вектора п и элементарной длины
а. Этот форм-фактор предполагается локализованным
в области 9ft4 (g) tz4. Вектор п будет определен позднее.
Как было показано в § 36, такая замена каузальной
функции Dc(x — у) на акаузальную Dc(x—у, а) обеспе-
чивает выполнение условий макроскопической причинно-
сти (35.15) —(35.17').
Из (37.16) следует соотношение
Dc <х> = 72Н)Г S еХр 1 РХ^С	Р ('Р’ ^Р'
8*
228
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
где Dc (р) есть фурье-образ от функции Dc (х), а р (р, п)
есть фурье-образ от функции р (5, п):
р(р, п) = J Р (n) exp ipld*%.	(37.18)
В качестве примера форм-фактора р (|, /г) можно взять
(см. [69, 72])
Р(£.	(37.19)
где
R? = 2(5, п)2-52.	(37.20)
а—элементарная длина. Из (37.18) — (37.20) имеем
р(р, п) = -~-.—,2 М 2 ,	,	(37.21)
г 7 2 (рп)2—р2+/И2 ’	4	7
где М=1/а есть большая масса, соответствующая малой
элементарной длине а, В системе, где вектор п = (1, 0, 0, 0),
имеем
р (р, п\ =	2Я!----.	(37.21')
Теперь обратимся к выражению (37.16) для акаузаль-
ной функции Dc(x, а). Предположим, что масса частиц
равна нулю. В этом случае (см. [70])
+ <3722>
где
1 г
б± (г) = ЙГ J e±‘V2dv, А -+ 4- ОО.	(37.23)
о
Вычислим сперва ту часть (х, а) акаузальной функ-
ции (37.16), которая происходит от члена с б+ (t—г) в
(37.22). Заменим в интеграле
D+ (х, а) = $ D+(x-5) Р (I, «) d'l . (37.24)
/на t—т(/ = 54) и г(х) на г (х —|) = г (х)4-«54- ...,
где а есть единичный вектор в направлении вектора х.
§371 ПРИМЕР ПОСТРОЕНИЯ АКАУЗАЛЬНОЙ S-МАТРИЦЫ 229
Тогда, пользуясь (37.23), находим
А
D+ (х, а) = J р (g, п) d3l dr Jexp [iv (t—r—r~at,)]dv=
0
A
= 8^7 J exP [lW~r>Jp(V’ v’ a«)^ =
0
« A
1 r	M2	1
8л2г j exPUv r)] 2va4-AP dv — gnar A+ (t A, M)
(37.25)
при A -> oo.
Вычисление функции A+ (t—г, оо, M) проделано в
дополнении XIV и ведет к результатам (XIV. 10) и
(XIV. 11). При |/—г|>а
А+ (t — г, оо,—А =
\	а)
/-1	\ 1 г\! 2а2	\ . л. 1	/	|/—т | \
= 6	+ 0 (-P=7p ) +Т-РТ ехр ('
(37.26)
При |/—г|-*-0 эта функция регулярна и имеет предел
1
а У~2 ’
А+
(37.27)
Функция 6+ (/—г) имеет вид (см. (1.9))
б + (/ - г) = 1 [б (/-г) + 4-	.	(37.28)
Поэтому второй член в (37.26), убывающий, кака2/(/—г)3,
и третий, экспоненциальный, являются поправками к
каузальной функции 6+(/—г). Тем самым подтверждает-
ся выполнение условий макропричинности.
Теперь следует проверить выполнение условия уни-
тарности матрицы рассеяния. Согласно (37.1) достаточно
проверить эрмитовость оператора фазы т)а. На основании
230
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
(37.12) и (37.17) имеем для акаузального оператора
вместо (37.12)
П2(р4. Л- ^2. P1) = ~DC(P3 — Р1)Р(Р3 — Р1, «) +
+^(P2 + Pi)p(pa + Pi, «)• (37.12')
Отсюда следует, что если потребовать выполнения соот-
ношений
р(рз—Pi, п)--=~Р* (Р1—Рз, «),	(37.29)
Р(Р2 + Р1> «) = Р*(Р3 + Р4. «).	(37.30)
то матричный элемент т) (р4, р3, р2, /7Х) будет эрмитовым,
если вектор п не меняется при эрмитовом сопряжении.
Для этого достаточно, чтобы этот вектор был симметри-
чен при перестановке импульсов начального (р2, р±) и ко-
нечного (р4, р3) состояний. В частности, можно положить
Р
У"Р* ’
(37.31)
где Р = Pi + р2 = р3 + есть полный импульс сталки-
вающихся частиц. Другая возможность —
П
(37.32')
где П = р3 + рх. Система отсчета, в которой вектор П = 0,
называется системой Б рейта.
При симметричном выборе вектора п акаузальная матри-
ца Доказывается и унитарной, и макроскопически при-
чинной.
Мы проводили расчет в явной форме с точностью
до g2. Однако этот расчет может быть продолжен и на
более высокие порядки разложения операторов S и г] по
степеням g.
Поэтому результат этого раздела можно резюмиро-
вать следующим образом: если существует макропричин-
ная и унитарная матрица рассеяния S (по крайней мере
с точностью до O(gN), где N— некоторое целое положи-
тельное число), то с той же степенью точности сущест-
вует и акаузальная унитарная матрица рассеяния Д,
удовлетворяющая принципу макроскопической причин-
ности.
§38] ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ ДЛЯ Sa-МАТРИЦЫ 231
§ 38. Дисперсионные соотношения
для акаузальной 5а-матрицы
Нарушение макропричинности тотчас же отражается
на аналитических свойствах матричных элементов
S-матрицы. В частности, дисперсионные соотношения для
упругого рассеяния вперед, рассмотренные в § 30, уже не
будут иметь места. Характер возможных изменений этих
соотношений зависит от конкретной формы нарушения
микропричинности. Мы рассмотрим такую форму нару-
шения микропричинности, которую разумно называть
минимальной.
Пусть Т (k) есть амплитуда упругого рассеяния обыч-
ной, локальной теории, a Ta(k) — акаузальная ампли-
туда того же процесса. Мы будем считать нарушения
микропричинности минимальными, если: а) функция Та (k)
имеет тот же спектр, что и функция Т (&); иными слова-
ми, если амплитуда Т (k) отлична от нуля в некоторой
области 9?3 (£), то спектр Ta(k) не выходит за пределы
этой области; б) условия симметрии, свойственные ампли-
тудам Tret(k) и TadV(k) (30.20), (30.20'), остаются в силе
и для соответствующих акаузальных амплитуд Ta(k):
Tarei(k) = Taaliv(-k),	(38.1)
Kret(k) = TaTet(-k)-,	(38. Г)
в) степень роста | Та (k) | при | k | ->• оо не превышает сте-
пени роста | Т (k) |; г) соблюдаются условия макроско-
пической причинности.
Простейшая форма акаузальности (нарушения мик-
ропричинности), удовлетворяющая этим условиям, рас-
смотрена в работах Д. И. Блохинцева и Г. И. Колерова
[69], [72], которым мы и следуем в дальнейшем.
Пусть Т (х) и Та (х) суть амплитуды Т (k) и Та (k) в
координатном представлении:
Т (х) = J Т (k) e~ikxd'k,	(38.2)
ta (x) = $ Ta (k) e~ikx d*k.	(38.2')
Следуя идеям, изложенным в § £7, положим
т9 (х) = J Т (x-g) Р (g, п) d*t, (38.3)
232
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
1ГЛ. VI
где р (|, п)—форм-фактор, зависящий от некоторого вре-
мениподобного единичного вектора п. В качестве такого
единичного вектора п в цитированной работе [69] принят
вектор, параллельный вектору П = р' -j-p, где р—импульс
нуклона & исходном состоянии, а р'—его же импульс в
конечном состоянии. В системе Брейта, где р'4-р = 0,
вектор п имеет компоненты п=1, 0, 0, 0. Далее, мы
предполагаем, как это было описано в §§ 36, 37, что
форм-фактор р(£, и) есть функция отношения 7?/а, где
а—элементарная длина, a R9—положительно-дефинит-
ный инвариант:
Я’ = 2да-£’>0,	(38.4)
исчезающая достаточно быстро при /?/а-»-оо.
Р(£, п)=р(4)->0.	(38.5)
В силу условия (38.5) из (38.3) следует, что если компо-
ненты вектора х величины | xt | a (i = 1, 2, 3, 4), то ве-
личину t (х—5) можно вынести из-под знака интеграла,
положив в ней £ = 0, а интеграл от р(|, п) в простран-
стве Э14(5) можно нормировать на I. Таким образом,
при |х;|^>а получается
7\(х)«Т(х),	(38.6)
что и следует рассматривать как соблюдение макропри-
чинности.
Переходя в (38.3) к импульсному представлению, по-
лучим
Ta(k) = T {k)p(k, п),	(38.7)
где p(k, п) есть фурье-образ форм-фактора р(£, п). Если
р (5, п) есть функция R/a, то нетрудно показать, что
p(k, п) будет функцией инварианта
7 = 2 (Ы)? — ^>0-	(38.8)
Из (38.7) следует, что условие спектральности а) соблю-
дается автоматически. Условия симметрии б) будут так-
же выполнены, если
р (k, п) = р (—k, и),	(38.9)
p*(k, n)^p(—kt и),	(38.9')
§38] ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ ДЛЯ ?а-МАТРИЦЫ 233
т. е. если р (k, п) есть четная и действительная функция
вектора k. Наконец, условие в) не будет нарушено, если
функция р (k, п) при | k | -+• оо ограничена.
Соблюдения условий а), б), в) и г) достаточно, чтобы
вывести дисперсионные соотношения для акаузальной
амплитуды Ta(k) совершенно таким же путем, которому
следуют при выводе дисперсионных соотношений в обыч-
ной каузальной теории (ср. § 30). Поэтому в случае ми-
нимальной акаузальности мы можем выписать диспер-
сионные соотношения для амплитуды упругого рассеяния
вперед Тв(со), прямо используя формулу (30.30), с той
только разницей, что при обходе по бесконечно удален-
ному кругу мы должны учесть особенности, возникаю-
щие за счет форм-фактора p(k, п) = р(со). Тогда вместо
соотношения (30.29) мы получим более общее:
Тв(«>) = Т(ш) + ф(®),	(38.10)
где Т (со) равно (30.29) с учетом (30.30), а дополнитель-
ный член ф(со) имеет вид
f
ф (<в) = («>-ш0)«»-ы £ Res 2^,	(38.11)
причем сумма взята по особенностям (полюсам) функции
р(со), а Лв(о)—мнимая (абсорбционная) часть амплиту-
ды Тв(со) (см. (30.30)).
Из действительности и четности функции р (со) сле-
дует, что если она имеет полюс в точке <о = ®,, то она
имеет полюс и в точке со = —со,. Эти полюсы не могут
лежать на действительной оси, так как в этом случае
они описывали бы реальные состояния. Поэтому они
должны обязательно иметь мнимую часть 1тсо,#:О, и
притом достаточно большую. Положим | ImcoJ» 1/а, где
а—элементарная длина.
Если величина а мала и в рассматриваемой области
энергия со невелика, так что	то мы можем замк-
нуть контур интегрирования (см. рис. 33) кругом ра-
диуса R таким, что R < 1/а, но все же столь большим,
что можно пренебречь вкладом в лнтеграл от интегриро-
вания по этому кругу. Очевидно, что при этих условиях
мы получим обычные каузальные дисперсионные соотно-
234
МАКРОСКОПИЧЕСКАЯ ПРИЧИННОСТЬ
[ГЛ. VI
шения. При 7? > l/а возникнут дополнительные акаузаль-
ные члены.
Если элементарная длина а достаточно мала, то акау-
зальная матрица Sa отличается от каузальной матрицы
S только в области энергий со^> 1/а = М. Поэтому при
М оо матрица Sa оказывается «близкой» к исходной
каузальной матрицей. Такую матрицу Sa мы называем
почти локальной или почти каузальной.
В заключение этого раздела выпишем дисперсионные
соотношения для лЬТ-рассеяния вперед с учетом акау-
зальности рассматриваемого вида. Для определенности
положим
Р («) = -Tra-i------Т , 7И = — .
(38.12)
Эти соотношения будут отличаться от каузальных соотно-
шений дополнительными членами ip(co), проистекающими
от вычетов функции р (со) в точках со = ±1М.
Именно, в отличие от формул (30.32) —(30.32"), бу-
дем иметь
Do0 (®) ~DaQ (®0) = -Ь	+
+ £(И2_Ю2)^
т
со'Лд0 (со') d(&'
(со'2 —СО2) (to'2 —(Oq)
Wo (®).
(38.13)
(
со'Лд1 (со') dco'
(со'2—со2) (со'2—СОо)
+
+ (“)>
(38.13')

G>g (<02 —Юр)
(co2—<в|)(со§—<в|)
co
+ Afi)((d2_(02)C	WW (38.13")
ЭТ	J (co'2—co2) (co'2 — co0)
tn
где амплитуды £>о0(<»), Dal (co), De2(®), ЛвО(со), Ла1(со),
Aa2 (co) имеют тот же смысл, что и амплитуды каузаль-
§ 38] ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ ДЛЯ Зд-МАТРИЦЫ
235
ной теории в формулах (30.32) — (30.32"), тельные члены равны			а дополни-
	Фо(“)	2	2	(38.14)
	Ф1 И :	о	2 p(”)<ii(iM)'	(38.14')
	Ф2 (ю)	М2 +	(38.14")
где	d0, ^1, d2—некоторые константы, равные		значениям
величин
d — ^al d = ®а1 (ю) d = ^g2
°	Р(®)	1 р(со) 2	р(0>)
в точке со^Ш.
Как видно из этих формул, дополнительные члены
существенны только при частотах со М.
ГЛАВА Vji
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ
И ГЕОМЕТРИИ
§ 39.	Две возможности обобщения
В современной теории предполагается, что геометрия,
известная нам из макроскопической физики, сохраняет
свою значимость и в области микромира. Вместе с этой
геометрией в область микромира переносится и та форма
причинной связи, которая установлена на основе изучения
макроскопических явлений.
Две физические идеи лежат в основе современной кон-
цепции:
а)	идея об однородном и изотропном пространстве —
времени Эйнштейна—Минковского и
б)	идея о переносе взаимодействия физическими полями
(электромагнитным полем, полями мезонным, нейтронным
и т. п.)
Последовательное применение этих идей в физике эле-
ментарных частиц в области особо малых промежутков
времени и особо малых расстояний приводит к физически
нелепым выводам: энергия взаимодействия частиц на ма-
лых расстояниях и их собственная энергия оказываются
бесконечно большими. Этот нежелательный результат воз-
никает как в квантовой, так и в классической физике и,
возможно, указывает на общее для обеих концепций
происхождение трудностей.
Остановимся подробнее на этой стороне дела. В клас-
сической физике распространение слабого (линейного)
сигнала из мировой точки Р (xt) в мировую точку Р (ха)
определяется функцией Грина ® (см. § 25). Постараемся
построить эту функцию, исходя из наиболее общих пред-
положений, относящихся к геометрии и причинности.
Из ^предположения об однородности пространства и
времени следует, что функция Грина может быть?функ-
цией только разности координат точек Q (xt) и Р(ха), т. е.
функцией разностей х = х2~х1 и —
§391	ДВЕ ВОЗМОЖНОСТИ ОБОБЩЕНИЯ	237
Требование изотропности пространства — времени при-
водит к дальнейшему ограничению: функция & должна
зависеть не просто от разностей ха—xlt t2 — t^ но от
четырехмерного интервала х3. = I3—х3 = (t2 — 3 —
— (х2—xtf. Наконец, оказывается еще возможным вве-
сти направление времени в = //| = ±1 для х3 > 0 и на-
правление по пространственному лучу л = х/| х | = ± 1 для
х3 < 0.
Таким образом, функцию Грина можно представить
в виде
® = @(х2, е, т]).	(39.1)
Такая функция является инвариантом собственного преоб-
разования Лоренца, но может не сохраняться при дис-
кретных преобразованиях Т (инверсия времени) и Р
(инверсия в пространстве).
Связь между мировыми точками Р (хх) и Р (х2) выра-
жается с помощью функции Грина в форме*)
Ф (х2) = ® (-Vя, 8» л) Q (xi)	(39.2)
где ф (х2) есть поле в точке Р (х2), a Q (хх) есть источник
этого поля, сосредоточенный около точки Р (хг). Анало-
гичным образом можно написать поле ф (хх), возникающее
в точке PtxJ под действием источника Q(x2), сосредото-
ченного в окрестности точки Р (х2). Связь, выраженная
в (39.2), еще не гарантирует выполнения релятивистского
принципа причинности, который: а) ограничивает скорость
распространения всех взаимодействий верхним пределом
скорости света и б) требует, чтобы причина (источник Q,
помещенный в точке (Р (хг)) вызывала следствие (поле ф
в точке Р (х2)) в более поздний момент времени, т. е.
t2 > t2. Для того-чтобы удовлетворить этим требованиям,
найдем вариацию поля ф (х2) в точке Р (х2) при варьиро-
вании источника Q(xx) в произвольной точке Р (xt) или,
что удобнее, вычислим непосредственно функциональную
производную от поля ф (х2) по источнику Q (хх) (см. до-
полнение IX). Из (39.2) имеем
<39'3>
♦) Gp, § 25.
238
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Отсюда видно, что требования а) и б) будут соблюдены,
если на функцию Грина наложить следующие дополни-
тельные ограничения:
® =	+1), если х2 > О, 8 = 4-1,	(39.4)
( если х2>0, 8 = — 1, (39.4')
® = 0	<
(если х2<0, 8=±1	(39.4")
(параметр т] теперь не входит в функцию ®, так как она
равна нулю при х2<0).
При соблюдении условий (39.4)—(39.4") релятивист-
ские требования причинности уже удовлетворены, но это
еще не значит, что функция ® описывает какое-либо
физическое поле. Для того чтобы функцию ® можно было
рассматривать как некоторое физическое поле*), созда-
ваемое импульсными источниками, необходимо, чтобы оно
подчинялось линейному неоднородному дифференциаль-
ному уравнению
=	(39.5)
где источник Q (xj имеет вид точечного импульса:
Q(x1) = 64 (x1) = 63(x1) 6 (/1).	(39.6)
Линейный характер оператора L вытекает из предполо-
жения о слабости рассматриваемого сигнала, а импульс-
ный характер источника Q соответствует обычному опре-
делению функции Грина как элементарного сигнала,
вызванного возмущением в окрестности только одной
точки Р (xj.
В силу предполагаемой релятивистской инвариантно-
сти оператор L должен быть функцией даламбертиана
□ = — d2/dZ2 + d2/dx24-d2/dz/2 4-d2/dz2, так что
L = £(□).	(39.7)
Функция L может быть или многочленом, или бесконеч-
ным рядом:
N
n = Q
Cnzn .
2n! ’
(39.8)
*) Поэтому возможно обобщенное взаимодействие, не сводящееся
к концепции физического поля; такого рода взаимодействие изуча-
лось в работах автора_[24, 74—77].
§39]
ДВЕ ВОЗМОЖНОСТИ ОБОБЩЕНИЯ
239
здесь N конечно или бесконечно. В последнем случае
оператор £(□) может оказаться нелокальным, т. е., дей-
ствуя на некоторую функцию f (х), он будет воспроизво-
дить функцию в некоторой другой смешанной точке <р (х'),
х'=/=х*). Фурье-образ функции (39.4)—(39.4") есть функ-
ция инварианта &2 = <о2—k2:
® (х2, 4-1) = J @ (k2) eikx dtx,	(39.9)
где kx = (tit—kx. Подставляя (39.9) в (39.5), найдем
£(62)® (/?)-1.	(39.10)
Отсюда следует, что нули функции L(fe2) являются
полюсами функции Грина ®(&2)**). Эти полюсы ведут
к сингулярностям функции ® (х2) на световом конусе
х2 = 0. В дополнении I, где выполнено фурье-преобразо-
вание (39.9) для фурье-образов ®(£2), имеющих полюс
первого порядка, показано, что эти сингулярности имеют
вид 6(х2), Inx2, 1/х2.
Можно было бы допустить, что ситуация в вершине
светового конуса меняется в том смысле, что обычные
геометрические соотношения теряют свою силу из-за изме-
нения самой природы явлений, разыгрывающихся на
малых расстояниях и на малых промежутках времени.
В этом смысле следовало бы ожидать существования не-
которой «элементарной длины» а, которая характеризо-
вала бы масштаб, ограничивающий применение обычных
причинных соотношений со стороны больших |х| и |/|,
по мере приближения |х|, |/| по величине к масштабу а.
На возможное значение такого масштаба для физики
элементарных частиц впервые было указано в работах
Г. В. Ватагина [82] и М. А. Маркова [83].
Позднее идея о существовании масштаба, ограничи-
вающего область применимости современной квантовой
*) На это обстоятельство было указано в работе [74]. В ра-
боте [78] доказано, что это различие зависит от поведения предела
I Cn l1^ при п —> оо. Нелокальный оператор из класса (39,8) был
использован для построения варианта нелокальной теории поля, сво-
бодной от расходимостей [79].
**) Уравнения типа (39.5) были рассмотрены в работах [80, 81]
При этом была обнаружена трудность, заключающаяся в том, что
при N > 1 тензор импульса-энергии частиц становится недефинитным.
240
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
теории и, может быть, и теории относительности, неодно-
кратно воскресала в различных формах, и по сию пору
теоретическая мысль постоянно возвращается к ней.
Важнейшим обстоятельством в связи с представлением
об элементарной длине является факт недефинитности
метрики пространства Эйнштейна—Минковского. В той
области многообразия (х), где применимость псевдоев-
клидовой геометрии не вызывает сомнений, не существует
никакого понятия близости двух событий Р (xj и Р (х2),
кроме выражаемого условием х2 = 0. Это условие означает
лишь то, что точки Р (х^ и Р (х2) могут быть соединены
световым сигналом, разделяющие же их пространственные
r = |x2 —Xi| и временные t = t2—tr промежутки могут
быть как угодно велики. Можно сказать, что равенство
х2 = 0 «не знает», почему оно выполняется: по той ли
причине, что обе величины г и t порознь велики, но г =
или по той причине, что г = 0 и / =	[24].
Допустим теперь, что релятивистский принцип при-
чинности выполняется лишь приближенно, и предположим
сперва, что это относится к пункту а), ограничивающему
скорость распространения сигналов скоростью света. При
таком предположении функция ® (х2, 8, т]) уже не обязана
исчезать вне светового конуса, так что условие (39.4)
теперь не выполняется: ® (ха, 8, т)) при отказе от пред-
положения а) не исчезает в пространственной области.
Вместе с тем появляется возможность взаимодействий,
которые отличают направление по лучу (т) = ±1) и, сле-
довательно, не сохраняют четность.
Отклонение ® (х2, 8, т]) от условий (39.4)—(39.4") не
должно быть слишком значительным: для больших про-
межутков времени	где а —элементарная длина,
условие (39.4') должно выполняться с большой степенью
точности. Введем эту элементарную длину явно в выра-
жение ® (х2, 8, т)):
® = ® (х», 8, Г),	,	(39.9')
I х2 I
и будем считать, что при	оо
@ (х2, 8, Л. ® (*2> 8),	(39.9")
§391
ДВЕ ВОЗМОЖНОСТИ ОБОБЩЕНИЯ
241
где ®(х2, б)—функция Грина каузальной теории (т. е.
исчезающая вне светового конуса). Соответствие требует,
чтобы при |х2М2|^>1 функция влияния ® (39.9) стано-
вилась бы исчезающе малой. При соблюдении этого усло-
вия сигнал, приходящий из точки Р (хх) в Р(х2), будет
распространяться со скоростью ^ = (х2 —	— Q = x/t,
практически равной скорости света с=1.
В самом деле, из условия
|х2|=ф2-х2|<а2	(39.11)
следует, что

(39.12)
так что при 111 а будет я2=1. Это условие является
релятивистски инвариантным. Действительно, в системе
отсчета, движущейся относительно первой вдоль оси Ох
со скоростью и, имеем
х' = у(х — lit), t' — y(t — ux), у = (1 —и2)-1/*.	(39.13)
Следовательно,

а2
t'2
а2(1—д2)
/2(1 — Я02 ’
(39.14)
где v' = х'Ц'. Если | х |, |/| и |я| мало, то \х' | и |/'|
также ~а при и ж 1. Из (39.14) опять следует близость
|<?'| к 1, кроме точки 1—#я = 0. Однако в этой точке
= О, х' = ytv (1 — и2) =	]/1 — и2,
так что |/'| и |х'| малы (порядка а). Если же |/'| и
|х'|^>а, то из (39.14) следует ®'2	1.
Таким образом, нарушив закон распространения сиг-
нала в области | х |, | £| мы можем все же сохранить
ограничение |zf|<^c=1 для|л:| и |/|^>а, т. е. для мак-
роскопических масштабов [85].
Особого рассмотрения требует второе условие причин-
ности (б), согласно которому t2 > t19 так что 8-^ + 1
(см. (39.4)). Трудность заключается в том, что различие
между 8 = +1 и 8 = —1 имеет смысл только внутри све-
тового конуса х2 > 0 и не может быть сформулировано
для функций Грина, отличных от нуля вне светового
242
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ 1ГЛ. VII
конуса, т. е. при ха < 0. Поэтому предельный переход
(39.9") с соблюдением запаздывающего характера взаимо-
действия (8=4-1) не может быть осуществлен последо-
вательно.
Происхождение этой трудности прямым образом свя-
зано с недефинитностью метрики в пространстве Эйн-
штейна-Минковского, с отсутствием там понятия бли-
зости двух пространственно-временных точек.
Эта трудность может быть преодолена только при
учете существования материи, в частности материальных
источников поля.
Суть дела заключается в том, что для определения
понятия близости двух точек Р (хх) и Р (х2) в простран-
стве Эйнштейна—Минковского помимо радиуса-вектора
(х = х2 — х1У t2 — t1=^t), соединяющего мировые точки
Р (хх) и Р(х2), необходимо еще иметь какой-либо второй
времениподобный вектор п (этот вектор без ограничений
мы можем считать единичным, n2 = 1) *). С помощью такого
вектора кроме инвариантов х2, п2 = 1 мы можем еще обра-
зовать инвариант (хп) и с его помощью построить поло-
жительно-дефинитную величину (также инвариант):
7?2 = 2 (хп)2 -х2 > 0.	(39.15)
В системе отсчета, где п = (1, 0, 0, 0), инвариант пре-
вращается в сумму квадратов:
7?2 = г24-/2,	(39.15')
т. е. в положительно-дефинитное евклидово расстояние
между точками Р (хх) и Р(х2). С помощью этого «рас-
стояния» понятие близости между двумя мировыми точ-
ками Р (хх) и Р (х2) может быть определено следующим
образом: точки Р(хх) и Р (х2) считаются близкими, если
R^a,	(39.16)
и удаленными, если
R^>a,
(39.17)
Такова формальная сторона дела. Физический смысл
времениподобного вектора п может быть весьма различ-
ным. Следует различать два принципиально различных
*) Такого рода вектор уже использовался нами при исследовании
причинности (см. (37.24) и (38.4)).
§39]
ДВЕ ВОЗМОЖНОСТИ ОБОБЩЕНИЯ
243
класса векторов п: а) вектор п связывается с движением
материи, расположенной в точках Р (х^ и Р(х2), напри-
мер, этот вектор может быть тождествен четырехмерной
скорости Uq движения источника поля Q, находящегося
в точке P(Xi), или скорости UA приемника поля, нахо-
дящегося в точке Р (х2), или скорости их центра масса Uт.
Во всех этих случаях вектор п связывается с движе-
нием материи, расположенной в точках Р(хх), Р(х^.
В этом случае вектор п мы будем называть внутренним.
Введение в теорию внутреннего вектора п сохраняет все
соотношения теории относительности для свободных частиц,
не приводит к нарушению однородности и изотропности
пространства или к выделению какой-либо преимущест-
венной системы отсчета.
Другая возможность (б) заключается в том, что век-
тор п выделяет какую-то преимущественную систему от-
счета. В этом случае мы будем называть вектор п внеш-
ним. Такой вектор может быть связан с какими-либо
выделенными системами отсчета [105], например с систе-
мой отсчета, сопутствующей движению материи в расши-
ряющейся Вселенной *), или с системой, связанной с
физическим вакуумом (если этот вакуум рассматривать
в духе старого понимания эфира); это может быть система,
связанная с дискретным, квантованным пространством
[94, 104], или система отсчета наблюдателя [91].
В заключение заметим, что эйнштейновское толкова-
ние переменных х и t теряет свою значимость во всех
случаях акаузальности, так как в области |х|,
нет сигнала, который имел бы стандартную скорость
с=1.
Однако это обстоятельство не должно нас смущать,
так как конечные размеры реальных частиц и без того
исключают возможность измерить переменные х и t внутри
частиц и тем самым ставится под сомнение физическая
реальность этих переменных: пространственно-временное
описание структуры частиц может быть не менее иллю-
зорным, чем классические орбиты электронов внутри
атомов.
♦) Эта классификация возможных типов вектора п введена в ра-
ботах [69, 72].
244
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
§ 40. Евклидова геометрия в микромире
В этом разделе мы рассмотрим модель причинной
связи, которая на больших расстояниях сводится к обыч-
ной причинной связи, основанной на принципе постоян-
ства скорости света в пустоте, а на малых расстояниях
настолько меняет свой характер, что скорость распро-
странения светового сигнала может стать мнимой. Пер-
вый тип причинной связи соответствует псевдоевклидовой
геометрии пространства Эйнштейна—Минковского, второй
тип—евклидовой геометрии четырехмерного пространства.
Такая модель не должна казаться ни слишком стран-
ной, ни даже слишком фантастичной, если вспомнить,
например, особенности нелинейной теории поля.
В § 7 было показано, что при определенных условиях,
в области большого поля ф и больших градиентов этого
дф	д(р
поля Р =	’ хаРактеРистики уравнении поля
могут стать мнимыми. Вместе с тем возникает то, что мы
назвали «комком» событий', совокупность реальностей,
связанных между собою, однако не вытекающих друг из
друга. Иными словами, такие реальности не могут быть
упорядочены во времени: понятия «раньше» и «позже» для
них не существуют. Вообще разумно заметить, что если
элементарная частица не разложима на составные части,
которые могли бы быть соединены световыми сигналами,
то нет никаких оснований предполагать, что причинная
связь внутри элементарных частиц или в тесных комплек-
сах этих частиц, возникающих в течение соударения,
будет такой же, какая характерна для событий, отделен-
ных друг от друга расстояниями, существенно превосхо-
дящими размеры элементарных частиц.
В дальнейшем мы и будем рассматривать именно такие
комплексы, которые по установившейся у эксперимента-
торов терминологии будем называть «событиями» или
«звездами». Каждое такое «событие» или «звезда» харак-
теризуется ее лучами, которые на математическом языке
описываются импульсами рк входящих и выходящих
частиц (для N-лучевой звезды &=1, 2, ..., N) *); эти
импульсы (векторы) можно в пределах комплекса пере-
*) Мы здесь несколько расширяем понятие АГ-лучевой звезды,
включая в число ее лучей также и нейтральные частицы.
$40]
ЕВКЛИДОВА ГЕОМЕТРИЯ В МИКРОМИРЕ
245
нести параллельно самим себе так, что все они будут
исходить из одной точки, например из центра масс. Эту
точку назовем «фокусом» события.
Положение фокуса нарушает однородность вакуума,
а векторы рк выделяют определенные направления, кото-
рые нарушают его изотропность; однако мы будем допу-
скать, что «звезда» как целое может быть смещена в про-
странстве и времени tHa любую величину и повернута
любым образом без“того, чтобы внутри нее что-либо
изменилось.
Это означает, что вакуум сам по себе мы считаем
однородным и изотропным, и только существование
«звезды» de facto выделяет в нем избранную точку («фокус
звезды») и избранные направления—направления ее лу-
чей рк.
Обратимся теперь к математической формулировке
этих идей. В современной локальной теории взаимодей-
ствие частиц описывается функциями s(xn х2, ..., xv)
в разложении матриц S по степеням операторов поля <р(х)
(см. § 29). Матричный элемент от такой коэффициентной
функции
<Рм Pn-1’ • • •, PN-m I S (*1> X2, XN) I Ptf-n-!,
pN-m-2' • • • > p2. P1> = $ dlXN. . .dix1s (xlt X2, .... XN) X
xexp i (pNxN+ ... + pN_mxN_m-
-pff-m,1xN_a.1— ... —PiXx) (40.1)
равен амплитуде вероятности перехода частиц из началь-
ного состояния, характеризуемого импульсами plf р2, ...
. . ., Рдг-^-n в конечное состояние, характеризуемое
импульсами pN^m, pN.
Функции s (xlf х2, ..., xN) трансляционно инвариантны.
Выразим это свойство в явной форме. Для этого введем
вместо координат х19 х2, ..xN новые, связанные с ними
линейными преобразованиями:
(а=1, 2, 3, 4),	(40.2)
k
2л*=1	(й=1, 2, .... N),	(40.2')
k
& =	(а=1, 2, 3, 4),	(40.3)
k
Sa'* = 0 (j = 1, 2, ..., АГ—1). (40.3')
k
246
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Операция трансляции t (d):
T(d)x = x + d,	(40.4)
в силу условий (40.2') и (40.3') дает
T(d)X = X + d,	(40.5)
T(d)£ = B.	(40.6)
Таким образом, при трансляции t (d) пространство
(X) смещается на величину d, а пространство 91 (£)
тождественно переходит само в себя.
При однородных преобразованиях Лоренца эти про-
странства также преобразуются независимо друг от друга.
Действительно, выполним в (40.2) и (40.3) преобразова-
ние Лоренца x=Lx, где х — новые координаты. Подроб-
нее это преобразование запишется в виде
xka=LaPxkp,	(40.7)
где АаР суть матричные элементы матрицы L. Из (40.7),
(40.2) и (40.3) получим
Ха =	= Ла3 2 А% = LaPXp (40.8)
И
^‘^ар-^р в ^ар	= Lap£p, '(40.9)
или, в короткой записи,
X=LX,^=L&.	(40.10)
Иными словами, при преобразовании Лоренца простран-
ства 914 (х) и 914 (£) преобразуются порознь, каждое внутри
себя. Если теперь совершить преобразования (40.2) и (40.3)
над переменными х2, ... xN, то функция s окажется
зависящей только от переменных
s(xn х2, .... XaOE?4s’(Bi, • • •. Bv-i), 1(40.11)
т. е. она определена в пространстве относительных пере-
менных 914Лг_4(£).
§40]	ЕВКЛИДОВА ГЕОМЕТРИЯ В МИКРОМИРЕ	247
Далее, эта функция, будучи сама по себе' инвариан-
том лоренцевского преобразования, зависит лишь от ска-
лярных произведений
k=^ 2,	(4012)
Здесь
J	0	при а^=р,
+1, —1, —1, —1 ПРИ а=₽»
так что позволительно написать
s (51, 5г, • • •, 5дг-1) = 5 (• • •, 5/, ...) =
= s(/12, Р3, ..., Iik. . ,.) = s(..., Iik, ...), (40.13)
При этом следует иметь в виду, что из всех Af(Af--l)/2
инвариантов Iik имеется только (47V —10) независимых.
Таким образом, функция s определена в пространстве
914дг_4 (£) и является функцией скалярных произведе-
ний Iik.
Предположим теперь, что характерная для локальной
теории причинная связь меняется в окрестности элемен-
тарных частиц. Как было разъяснено в § 39, для опре-
деления понятия окрестности необходимо нарушение
изотропности пространства—времени, что формально
может быть осуществлено путем введения в функцию
s (51, 52, • • •, 5?v-i) времениподобных векторов п.
Такая возможность возникает в реальной «звезде», так
как самым фактом своего существования «звезда» нару-
шает изотропность пространства и времени. В частности,
любой из векторов пк (пк=1, пк0 > 0), определяющих
направление лучей звезды:
пк=-^=, где k = l, 2, 3, ..., N, (40.14)
V pk
может быть принят в качестве необходимого нам век-
тора п. Могут быть также использованы их линейные
комбинации, например вектор, определяющий направле-
ние движения фокуса звезды *):
w
п = Р-Ул- (40.15)
*) Ср. §§ 37, 39.
248
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Учет анизотропии пространства— времени, обуслов-
ленной анизотропией реальной звезды, позволяет обоб-
щить коэффициентные функции s(^, £2,	таким
образом, чтобы внести в них явную зависимость от на-
правления мировых линий лучей, например:
S(11, U .... 1дг_1; «1, па, tiH-i) (40.16)
или, в более частном случае,
s(li,l2, .... ^-i; п).	(40.17)
Тем самым вводятся новые инварианты типа
£'7=2(п£')2—1/2>°	(40.18)
и
= 2 (ng<) (ntf)-1‘1к	(40.19)
или безразмерные инварианты
=	(40.20)
где а —элементарная длина. Сохраняя релятивистскую
инвариантность «события» в целом, мы можем, используя
векторы /г, помимо инвариантов Iik (40.12) допустить за-
висимость функций $ (51, 5г, • • •, 5дг- х; и) от инвариантов
/?'*(£, я) (40.18) и (40.20). Мы выберем эту зависимость
следующим образом: заменим скалярные произведения
(40.12) более общими, именно положим
I* = а (z) Ilk + b (?) Rik,	(40.21)
где
(£"+£**),	(40.22)
а инварианты Iik и Rik определены формулами (40.13)
и (40.19).
Релятивистская инвариантность коэффициентной функ-
ции s (^, |2, ..., ?дг_х; п) при введении инвариантов
вместо инвариантов Iik полностью сохраняется.
Однако может быть нарушена макроскопическая при-
чинность. Чтобы избежать этой катастрофы, выберем функ-
ции а (г) и b(z) таким образом, что при г —^0
а(г)-+Ъ,	6(z)-+l,	(40.23)
§40]
ЕВКЛИДОВА ГЕОМЕТРИЯ В МИКРОМИРЕ
249
а при г оо
a(z)—+\,	b(z)-+Q.	(40.23')
Далее следует заметить, что мы понимаем «окрест-
ность элементарной частицы» как малость величин | xt — хк |:
(40.24)
Это условие в общем случае вовсе не совпадает с усло-
вием малости инвариантов (40.18)—(40.20), которое озна-
чает малость величин ||'|:
(40.25)
Согласие между этими условиями может быть достиг-
нуто только при специальном выборе переменных gz, если
принять
^51 ~%1 ^2* В2 =^2 %3> • • •>	1 =	1”—-	(40.26)
При соблюдении условий (40.23), (40.23') и (40.26)
возникает ситуация, когда при z —►00 мы будем иметь
дело с обычной причинной связью, так как в этом слу-
чае Iak —► Ilk\ однако при z —► 0 Iik—+Rik, так что обыч-
ная причинная связь будет полностью разрушена: вместо
последовательности событий мы будем иметь дело с их
«комком», не упорядочивающимся во времени. Действи-
тельно, в этом последнем случае в системе отсчета, где
п = (1, 0, 0, 0), инвариант Iik принимает вид
е =	=	(40.27)
а=1
характерный для евклидовой геометрии.
Вместе с тем возникает новая симметрия: при задан-
ном п для малых |£«|, ||jj | имеет место симметрия четы-
рехмерной сферы (или четырехмерного эллипсоида).
Если все скалярные произведения векторов ...
определить посредством инвариантов Iik, то можно будет
сказать, что в пространстве fR(|) введена своеобразная
геометрия, такая, что она, будучи при | |z | а псевдоев-
клидовой, при	переходит в евклидову.
Результат измерения длины между двумя точками А
и В в таком пространстве зависел бы от масштаба, кото-
рым эта длина измеряется: больше оц элементарной длины а
250
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ |ГЛ. VII
или меньше ее. Эта парадоксальная ситуация не должна,
однако, нас удивлять, так как малые значения координат £
ненаблюдаемы.
Поскольку в физически наблюдаемых матричных эле-
ментах матрицы рассеяния (40.1) мы ограничиваемся
соблюдением условий макроскопической причинности, то
эта «парадоксальность» оказывается запрятанной очень
глубоко.
§ 41.	Стохастическая геометрия
В основе стохастической метрической геометрии лежит
предположение, что каждой паре элементов Р, Q стоха-
стического пространства 9? (Р) можно сопоставить функ-
цию распределения FPQ(z), которая интерпретируется как
вероятность того, что расстояние r(P, Q) между точками
Р и Q меньше г. Этой функции приписываются следую-
щие свойства:
1)	FPq (z) = 1 для всех г только тогда, когда
Р = §\
2)	^pq(2) = 0 для всех z^O;
3)	FPq = FqP—симметрия;
4)	если FPQ[(z)=l и Fq₽(m) = 1, то
Fpr(z + u) = 1.
Эти свойства отображают обычные свойства расстоя-
ния в метрическом пространстве
1) r(P, Q)=0 только тогда, когда Р = Q; )
г (Р, Q) > 0;
3) r(P, Q) = r(Q, РУ,
4) r(P, Q) + r(Q, R)>r(P, Р).
Эта метрика возникает из стохастической метрики как
частный случай, если
Рр^^Н[г-г(Р, Q)]	(41.2)
и
Я(?) = 1 для z>;o,	(41.2')
ZZ(z) = O для z<:0	(41.2")
? (41.1)
> (41.Г)
(см. [86, 87]).
§41]
СТОХАСТИЧЕСКАЯ ГЕОМЕТРИЯ
251
С физической точки зрения стохастическая метрика
ведет к стохастической арифметизации пространства.
Действительно, элементы пространства Р арифмети-
зуются таким путем, что каждому элементу Р, отмечен-
ному каким-либо определенным физическим содержанием,
приписывается число х(Р) (координата), которое полу-
чается измерением расстояния г (Р, 0) от некоторого услов-
ного элемента (0) («начала координат»).
Стохастический характер расстояния r(P, Q) приводит
к тому, что если измерено
r(P, 0)=L,	(41.3)
то истинное расстояние I между элементами Р и 0 равно L
с вероятностью
dW(L, l) = w(L, l)dl.	(41.4)
Поэтому арифметизация пространственного многооб-
разия становится стохастической и каждой измеренной
координате х(Р) элемента Р может быть приписана истин-
ная координата X (Р) только с некоторой степенью веро-
ятности.
В дальнейшем мы будем понимать под стохастическим
пространством именно такое пространство 9ist(X), кото-
рое стохастически отображается на пространство измеря-
емых координат 91 (я), и введем вероятность
dW(X, x) = w(X, x)dx.	(41.5)
Эта формула отличается от формулы (41.4) только тем,
что расстояниям L и I приписан знак ±, так что их
теперь следует рассматривать как координаты точки Р,
измеряемую и истинную. Если наше пространство одно-
родно, то вероятность (41.5) есть функция только раз-
ности X—х\ в этом случае вместо (41.5) мы можем
написать
dW(X, =	(41.6)
где а—некоторый масштаб длины, характеризующий раз-
брос частных значений стохастической координаты х около
ее среднего значения я = Х(Р).
Стохастическому пространству был посвящен ряд работ
[88—92]. Мы не намерены входить в подробный крити-
252
обобщение Причинной связи и геометрии [гл. vn
ческий анализ этих работ. Не будет большой ошибкой
сказать, что идейное содержание этих работ может быть
объединено в предположении, что «истинные» координаты
(х, t) физического события Р ввиду некоторой принци-
пиальной неточности, свойственной прибору, измеряю-
щему х, /, или самому событию Р, определяются лишь
с некоторой степенью вероятности. Эти слова следует
понимать в том смысле, что если представить себе ан-
самбль лаборантов, обладающих тождественными и самыми
совершенными (идеальными) приборами для измерения
координаты события Р, то они все же получат различные
результаты для х = х(Р), распределенные статистически
около среднего значения х = Х(Р):
x = X(P) = j^(*=-x}^	(41.7)
с характерной статистической дисперсией, равной
Д72 = (Х—х)2 = j(X—х)2ш(^^)у = а2, (41.8)
при условии нормировки
И*?)*-1	(4L9)
Более детально можно указать по крайней мере три
возможности, которые ведут к стохастическому простран-
ству 9ist (X):
а)	идеальный прибор, измеряющий расстояния, имеет
принципиально неустранимую неточность Дх^а;
б)	объекты, «частицы», с помощью которых фиксиру-
ются точки пространства, имеют конечные размеры а,
что ведет к Дх^а;
в)	среда, в которой распространяется сигнал, служа-
щий для измерения расстояний, турбулентна, так что
скорость сигнала флуктуирует.
Главное отличие физических теорий стохастического
пространства—времени от теорий, разработанных мате-
матиками [86, 87], заключается в том, что физическое
пространство имеет недефинитную метрику, в то время
как метрика, описываемая распределением Fpq(z) (41.1),
предполагается положительно-дефинитной. В силу неде-
финитности метрики физического пространства—времени
§41]	СТОХАСТИЧЕСКАЯ ГЕОМЕТРИЯ	253
формула (41.6) не может быть обобщена на реальное
пространство—время просто путем увеличения числа из-
мерений.
Действительно, инвариантность вероятности dW отно-
сительно преобразования Лоренца требует, чтобы плот-
ность вероятности w была функцией инварианта. Единст-
венным возможным инвариантом является интервал
s?=(X—х)’=(Т— ty—(X—х)2.
Однако вероятность
=	(41.6')
ненормируема и не может представлять распределения
стохастической переменной х(Р), сосредоточенной около
точки Р (а не около светового конуса s2 = 0).
Для того чтобы получить сосредоточенное около точки Р
распределение, следует помимо четырехмерного вектора
(X—х) еще иметь в своем распоряжении времениподоб-
ный вектор п. Имея такой вектор, можно построить ранее
встречавшийся нам инвариант I (п, X—х) (см. (39.15)) и
образовать положительно-дефинитное расстояние Р:
Р = + /2(п, X—х)’—s2	0.	(41.10)
Вероятность dW может теперь рассматриваться как
функция этого расстояния:
dW(X—x, ti)=w^~.	(41.11)
Эта вероятность может быть сосредоточена около точки
X (Р) и может давать ограниченное значение для сред-
него квадратичного отклонения
5T2 = j(X-x)^(4)^«a2.	(41.8')
Вводя в формулу для вероятности dW вектор п, мы
встречаемся с уже рассмотренной нами ран^е проблемой
выбора этого вектора (ср. § 39).
В соответствии с упомянутыми выше возможностями
а) и б) *) рассмотрим сначала первую из них.
*) Возможность в) будет рассмотрена в § 42.
254
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЁТРИИ (ГЛ. VII
а)	Вектор п связан с системой отсчета наблюдателя,
так что вектор п совпадает с направлением мировой линии
этого наблюдателя (ср. [50, 91]). В этом случае усредне-
ние физических величин, зависящих от стохастической
координаты х мировой точки Р, будет приводить к резуль-
татам, зависящим от наблюдателя.
Действительно, пусть F (х) есть физическая величина,
функция стохастической переменной х = Х — %. Ее наблю-
даемое среднее значение будет
= ^Р(0) eiC*~w (Q, и)	(41.12)
где F (Q)—фурье-образ F(x), a w (Q, n) -фурье-образ плот-
ности вероятности и). Вектор п для каждого наблю-
дателя имеет компоненты п=(1, 0, 0, 0). Поэтому вели-
чина w (Q, п) не будет инвариантом при переходе от одной
системы отсчета к другой. В частности, это ясно из сле-
дующего физического соображения. Пусть F (х) есть пло-
ская волна. В одной системе отсчета она может иметь
частоту со такую, что соа<^1 (а —мера дисперсии стоха-
стической координаты х), так что среднее F (X) практи-
чески не будет отличаться от истинного F (х); в системе
же отсчета другого наблюдателя из «за эффекта Допплера
величина юа может быть >1, и тогда \F (X)|<^|F (х)|.
Поэтому в теоретической схеме, рискующей опериро-
вать с вектором п, привязанным к наблюдателю, должно
быть проявлено особое внимание к величинам, инвари-
антность которых не подлежит сомнению. К таким вели-
чинам принадлежит, например, полная вероятность рож-
дения определенного числа и определенного сорта частиц.
Эта величина могла бы зависеть от системы отсчета только
в том случае, если бы существовала выделенная система
отсчета (например, система, связанная с физическим ва-
куумом, если его рассматривать в старом смысле как
некоторую среду, как «эфир» *).
б)	Обратимся теперь ко второй возможности, когда
стохастичность координаты х(Р) обусловлена конечными
*) Заметим, кстати, что А. Эйнштейн не боялся употреблять этот
термин.
§41]
СТОХАСТИЧЕСКАЯ ГЕОМЕТРИЯ
255
размерами частиц. В этом случае физическое событие Р
отождествляется с наличием в этой точке частицы, имею-
щей конечные размеры а. Стохастичность координаты х(Р)
возникает теперь по той причине, что не представляется
возможным определить, какая именно точка внутри ча-
стицы (в пределах Ах^а) рассеяла сигнал, как бы точно
ни был он локализован в пространстве—времени*).
Мы можем представить себе, что пространство—время
заполнено такими частицами, которые мы имеем возмож-
ность отличать друг от друга, как это предполагается
в лагранжевом методе описания течения жидкости.,В этом
случае времениподобный вектор п в формуле (41.12) может
быть отождествлен с четырехмерной скоростью частицы и.
Рел ятив истская	инв ар и антность	вер оятности
dW(X—х, п) при переходе от системы отсчета одного
наблюдателя к системе отсчета другого будет соблюдаться
в силу того, что вектор и подчиняется теперь преобразо-
ванию Лоренца. Допущение зависимости вероятности от
переменных = Х—х и и одновременно означает пред-
положение о коммутативности этих переменных:
[u, g] = 0.	(41.13)
Поэтому естественно рассматривать переменную £ как
переменную, описывающую внутреннюю структуру частиц.
В частности, в цитированной выше работе [89] пред-
полагается, что масса покоя частицы т может быть пред-
ставлена оператором т, зависящим от внутренней коор-
динаты £ и вектора четырехмерной скорости частицы и.
Именно:
т (£, u) = m04-a
(41.14)
Переходя в систему покоя частицы (п=1, 0, 0, 0), не-
трудно видеть, что метрика в пространстве 91(£) есть
метрика положительно-дефинитная, евклидова метрика:
1	=	+	+	**)• Волновая функция
*) Это предположение о точной локализации сигнала эквива-
лентно в данном случае предположению об «идеальности» прибора,
измеряющего координату частицы х(Р).
**) Такая метрика, основанная на условии (41.13), была введена
₽ работе [93], посвященной теории релятивистского волчка.
^л+2
256
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
свободной частицы, движущейся с импульсом Р, имеет вид
. Рх
^р(х, ^)=фр(|)е к	(41.15)
и подстановка ее в уравнение Дирака (14.1) приводит
к уравнению
Р)]ФР(В) = О, (41.16)
где mQ, Р) есть оператор (41.14), в котором скорость и
выражена через полный импульс и = Р1УгР9.
Однако все следствия этой любопытной теоретической
схемы не были изучены.
§ 42.	Дискретное пространство — время
Этот раздел посвящается анализу идей о дискретном
«квантованном» пространстве—времени. Само понятие
«квантования» пространства—времени не является доста-
точно определенным. Здесь мы будем употреблять это
понятие в отношении теоретических схем, предполагаю-
щих ту или иную дискретность пространства—времени,
не вытекающую из какой-либо динамики материи, а имею-
щую чисто геометрический характер. В наиболее простой
форме идея о дискретном квантовании пространства—вре-
мени заключается в предположении, что точки простран-
ственно-временного многообразия не образуют континуума,
а представляют собою некоторое дискретное, счетное или
даже конечное множество. В частности, можно предполо-
жить, что оно образовано точками некоторой решетки
(см. [94—97]).
Предполагая ту или иную дискретность пространст-
венно-временного многообразия, мы сталкиваемся с двумя
проблемами:
а)	с проблемой преобразования этого многообразия от
одной системы отсчета к другой, движущейся (относи-
тельность);
б)	с проблемой предельного перехода от дискретности
к континууму современной теории (соответствие).
Эти проблемы могут быть 'иллюстрированы на при-
мере четырехмерного многообразия ©4(Х), каждая точка
которого X определяется координатами х^п^а, х^=пца.
§ 42]	ДИСКРЕТНОЕ ПРОСТРАНСТВО — ВРЕМЯ	257
х3 — п3а, t = va, где nlt п2, п3 и v суть целые числа и
длина а — постоянная решетки.
Пусть гр (х, f) есть поле, описывающее некоторую фи-
зическую реальность, способную распространяться в
пространстве ©4(х). Слово «распространяется» мы по-
нимаем теперь в том смысле, что: а) существует связь
между значением поля гр в любой точке х (х, t) и его воз-
можными значениями в соседних точках; б) мы допу-
скаем, что существует деление многообразия (х) на
пространство ©3(х) и время S\(Z), (ср. § 3). Предпола-
гая, далее, что поле гр обладает свойством линейности,
и понимая под соседними точками «ближайшие», т. е.
точки с координатами
хг ± а, х2, х3, t\ х1( х2 ± а, х3, t\ xlt х2, х3 ± а, /;
х1( х2, х3, t ±а,
мы можем написать для гр уравнение
агр(хх, х2, х3, /)4*
4-Р1[ф(Х14-а, х2, х3, О + гр(*1~а, х2, х3, /)] +
+ ₽2[гр(Х1, х2 + а, х3, О + гр(Х1, х2—а, х3, /)] +
+ ₽з[гр(Х1, х2, х3 + а, 04-гр(х1, х2, х3—а, <)] +
+ у[гр(Х1, х2, х3, <-|-а)+гр(х1, х2, х3, /—а)] = 0. (42.1)
Если многообразие ©4 (х) однородно, то коэффициенты а,
Pi> Рг, Рз, У не зависят от х и /; если оно к тому же и
изотропно по переменным хп х2, х3, тор1=р2 = р3. Выде-
ляя время, мы допустим, что знаки коэффициентов р и у
противоположны. Тогда уравнение (42.1) удобно пере-
писать в виде
(а 4- 2р + 2у) гр + р [Д4гр+Д2гр-J- Д3гр] + уД4гр = 0, (42.2)
где Дп Д2, Д3, Д*— вторые конечные разности по пере-
менным xlf х2, х3 и t соответственно. По определению
Д;гр = гр(..., Xt + a, . ..)-f-гр(..., Х;—а, ...) —
—2гр (..., xf, ...), (42.3)
где точками обозначены аргументы, не подвергающиеся
смещению + а.
В целях сокращения интересующего нас исследова-
ния уравнения (42.3) ограничимся в дальнейшем спе-
9 Д. И. Блохинцев
258
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
циальным случаем а + 2Р + 2у = О, р = —у, так что вместо
(42.2) получается более простое уравнение:
Ахф-|-Агф4-А3ф—Ati|)=0.	(42.4)
Это уравнение имеет собственные функции в виде пло-
ских волн
ф=const .еМпл-ео,	(42.5)
где импульс П (Пи П2, П3) и энергия е связаны уравне-
нием дисперсии этих волн, получающимся из (42.4) под-
становкой туда выражения (42.5):
sin2 4-sin2 4-sin2 — sin2 (^\ =0. (42.6)
Уравнение (42.4), решение (42.5) и дисперсионное урав-
нение (42.6) обладают в пространстве Э13 (П) симметрией
пространственной кубической решетки и, следовательно,
инвариантны относительно группы симметрии этой решетки.
Что касается преобразований в одной из плоскостей
(Щ, в), то эти преобразования меняют ролями одну из
координат xk и время /; одновременно одна из компонент
импульса Щ меняется с энергией в.
Эти дискретные и конечномерные преобразования на
первый взгляд ничего общего не имеют с преобразова-
нием Лоренца. Однако при | Па |	1 уравнение диспер-
сии (42.6) принимает вид
П2 + П2 + П2—82 - О (Па4),	(42.7)
где через О (Па4) обозначен остаток порядка (Па)4. Одно-
временно	конечные разности	в (42.4) могут быть	заменены
на	вторые	производные, так	что	вместо (42.4)	получаем
О(П	,428
dxVdxl^dxl	dt*	^Шг)ф.	№)
Таким образом, для достаточно малых импульсов | П |
имеет место лоренцевская инвариантность; при больших
импульсах, | П | ~ П/а, ситуация решительно меняется и
остаются в силе лишь дискретные преобразования, харак-
терные для решетки. Несмотря на наличие такого соот-
ветствия с обычной теорией, мы не можем избежать в этой
теоретической схеме существования выделенной системы
отсчета—системы решетки ®4(х); эта система выделяется
§42]
ДИСКРЕТНОЕ ПРОСТРАНСТВО - ВРЕМЯ
259
тем, что для частиц, имеющих в этой системе малые им-
пульсы, пригодны обычные соотношения специальной
теории относительности.
Обратимся теперь к другому подходу — к идее диск-
ретного пространства—времени, основанному на рассмот-
рении координат как операторов смещения в ис-
кривленном пространстве импульсов Э?4 (р) [98]. Наиболее
прямой путь к построению таких операторов исходит из
идеи ограничения, накладываемого на квадрат импульса*):
P2=pl—Pl—Pl—PK^,	(42.9)
где а—некоторая характерная для этой теории длина
(постоянная Планка К и скорость света с приняты здесь
равными 1). Условие (42.9) физически означает ограни-
чение на квадрат массы частиц: т2=^ 1/а2.
Введем теперь однородные координаты г|0, т|х, т]2, т]
и 1% такие, что
^ = 4^ (11=1,2,3,4).	(42.10)
В этих координатах выражение (42.9) для предельных
значений р принимает вид
П1—Пз—По = О.	(42.11)
Наряду с этой квадратичной формой рассмотрим пяти-
мерную гиперсферу
П1—ni—Пз—По = — а2	(42.12)
и определим теперь операторы как операторы беско-
нечно малых вращений, оставляющих инвариантной эту
гиперсферу. Эти операторы таковы:
xa = ia(i]o^—. а = 1, 2, 3, (42.13)
(42-13')
*) Можно также рассмотреть другой тип ограничения, именно
р2^>—1/а2 (см. [100]).
9*
260
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Здесь х4ее=? есть оператор времени. Эти операторы могут
быть дополнены операторами момента количества дви-
жения:
а, Р, у=1,2, 3, (42.14)
УЙа=1’(Т,4^ + Т1“^г)’	«=1,2,3.(42.14')
Нетрудно показать, что нетривиальные правила переста-
новки гласят:
[ха, xp] = ia2Lv,	(42.15)
[х4, ха] = ia2My,	(42.15')
[Ха, P₽] = i(6ap + a2PaP₽),	(42.16)
1а> р4] = «(1—«2Р«),	(42.16')
[Ха, Р^ = 1а2рар4.	(42.16")
Тем же путем из (42.14) и (42.14') получим
La = x^pv— Хурр,	(42.17)
Ма=хар4 + х^ра,	(42.17')
т. е. операторы La и Ма суть компоненты обычного опе-
ратора четырехмерного момента количества движения.
Подобным же образом можно найти и операторы ха,
х4 = / в импульсном представлении:
+	a=l,2, 3,	(42.18)
i = xt = i'	aiPiPv.-g^- (42.18')
Эти операторы действуют в пространстве 3t4(p), в котором
наложено ограничение (42.9). Собственные функции этих
операторов, удовлетворяющие требованиям конечности и
однозначности, находятся из уравнений
Ж(р) = ^(р)>	(42.19)
?Ф/(Р) = ^(Р),	(42.19')
§42]
ДИСКРЕТНОЕ ПРОСТРАНСТВО — ВРЕМЯ
261
где х и t—собственные значения операторов х (индекс а
сейчас опущен) и ?. Нетрудно убедиться, что
(р) = ехР [t/n arctg а (р)], где	(42.20)
а(р) = ар1]/1—azp2,	(42.20')
а т есть целое число.	
Подобным же образом получим	
Ф* (р) « ехр [гтр (р)],	(42.21)
где	
Р(р)=1п-Д^=-. '	К1 —а2р2	(42.21')
Таким образом, спектр собственных значений перемен-
ной х—дискретный: х = та, m = Q, ±1, ±2, а спектр
переменной t = xa—непрерывный. Такое «квантованное»
пространство впервые было получено Г. Снайдером [98].
Геометрия пространства 3t4(p), в котором определены
приведенные выше операторы и их собственные функции,
может быть полностью получена как геометрия многооб-
разия точек, возникающего при проектировании гипер-
сферы (42.12) из ее центра на плоскость т]0=+а [99,
100]. На рис. 45 это показано для случая трех измере-
ний. Осуществляя такую проекцию, нетрудно убедиться,
что мы придем к формуле (42.10), причем*)
= <42'22>
Из (42.10) и (42.12) нетрудно получить и выражение для
квадрата элемента длины в пространстве Э(4(р):
do2=(l—a2p2)-i[dp2 + (l—д^р2)-1 (pdp)2], (42.23)
где
dp*=dpl—dpi—dpi—dpi,	(42.24)
p dp=Pi dpi—pj dpY—p3dp3—p3 dp3.	(42.24')
*) Другие возможные варианты геометрии пространства (р)
могут быть получены путем перемещения центра проекции по оси т]0
(ср. [100]).
262
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ |ГЛ. VII
Элемент объема, соответствующий этой метрике, равен
dQ (р) = К—g dpt dpa dp2 dp1 = (l — агр2)~^2dpt dp3 dp2 dplt
________	(42.25)
где V—g=(l—a2p2)-5/2 есть детерминант, составленный
из метрического тензора g^, определяющего квадратич-
ную форму (42.23).
Рис. 45. а) Проектирование гиперсферы тД—щ—т)о = — я2 на плоскость
НН и Н'Н'—две ветви гиперсферы; рр— плоскость -q0==4-a;
т] и т)'—две точки гиперсферы, проектирующиеся в точку р плоскости
рр (пространство х3(р)). б) То же в проекции для плоскости (щ, т]0).
Введенные ранее операторы для ха, х4, £а, Ма яв-
ляются эрмитовыми операторами в пространстве $i4(p)
с элементом объема dQ(p).
Теперь можно определить операцию трансляции в про-
странстве Э?4(р). Трансляции в пространстве Э14 (р) явля-
ются отображениями вращений гиперсферы (42.12). По-
этому эти трансляции некоммутативны: сдвиг вектора р
на вектор k (обозначение: р (+) k) не тождествен сдвигу
вектора k на вектор р (обозначение: ^(+)р)*). Преобра-
зование волновой функции ср (р) в пространстве sJt4 (р)
при бесконечно малом смещении пространства на век-
тор k может быть записано в виде
<Р (Р (+) = 1 —	(42.26)
Вычисление показывает, что операторы в (42.26) сов-
падают с операторами (42.18) и (42.18'), как этого и
♦) См. подробности в [100].
§ 43] «КВАЗИЧАСТИЦЫ» И КВАНТОВАНИЕ ПРОСТРАНСТВА 263
следовало ожидать из того факта, что сдвиги в простран-
стве 014(р) суть вращения в пространстве 3i5 (ц).
Отсутствие ассоциативности в сложении импульсов при-
водит к тому, что обычные законы сохранения энергии—
импульса в схеме Снайдера становятся приближенными.
При практическом применении этой изящной геомет-
рической теории к квантовой теории поля встретились
серьезные затруднения [101, 102]. Эти затруднения свя-
заны с так называемыми угловыми расходимостями, кото-
рые возникают при вычислении диаграмм Фейнмана в про-
странстве импульсов. Эти угловые расходимости в обычной
теории не являются существенными, так как могут быть
уничтожены поворотом на л/2 пути интегрирования в пло-
скости р4, р = |р|*). При таком повороте недефинитная
метрика в плоскости (р0, р) превращается в дефинитную
евклидову метрику. В случае «снайдеровской» геометрии
в пространстве импульсов единственная модификация, воз-
никающая при вычислении диаграмм Фейнмана, проис-
ходит за счет появления множителя ]/—g в элементе
объема (42.25). Но, как видно из (42.25), этот множитель
имеет разрез в комплексной плоскости (р0, р) при р2 =
=р2—р2=1/а2. Этот разрез не позволяет выполнить ука-
занный поворот на л/2. В этой связи в работах [101,
102] была предпринята несколько искусственная попытка
сперва сделать поворот, а потом ввести снайдеровскую
метрику и путем аналитического продолжения вернуться
в физическую область недефинитной метрики. Такой прием
в некоторых рассмотренных частных случаях оказался
осуществимым **).
§ 43. «Квазичастицы» и квантование пространства
В работе [104] было сформулировано оригинальное
уравнение, эквивалентное уравнению Томонага—Швин-
гера, однако особенно удобное для применения в искрив-
ленном импульсном пространстве.
*) Заметим, что аналитические свойства матричных элементов
обычной, локальной теории допускают такой поворот.
**) Следует также отметить работу [103], в которой применяется
геометрия импульсного пространства с непостоянной кривизной;
в этом варианте геометрии, может быть, будет преодолена обсуждае-
мая трудность.
264
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ	£ГЛ. VII
Пусть <г = /гхесть пространственноподобная плоскость,
причемп—единичный времениподобный вектор (/г2=1),
направленный в будущее (/г0 > 0). Согласно (28.14) имеем
. ^(^-oo)=^(a)6Z(or> _oo)i	(43Л)
где П?(сг) есть энергия взаимодействия (в «представлении
взаимодействия») *).
Согласно (28.18) S-матрица равна
S=l + iT = U(+oof —оо).	(43.2)
Представим оператор U (ст, —оо) в виде интеграла:
+ ОО
и (а, -оо) = 1 + A j R (пт) eiox, (43.3)
— 00
где R (пт)—некоторый новый оператор, а т—инвариант-
ный параметр, сопряженный о; е—>+0. Из (43.2) и (43.3)
при о—> + оо следует
5= 14-1^ (0),
Я(0) = Т.
Положим теперь
+ 00
№(а) = А. J ^(nx)eimdx
— 00
(43.4)
(43.5)
(43.6)
и подставим (43.3) и (43.6) в уравнение (43.1). Нетрудно
видеть, что это уравнение будет удовлетворено, если под-
чинить оператор R (пт) условию**)
+ 00
/?(пт) = >(пт) + ^- f Г(пт-пт')-Д^(пт'). (43.7)
— ОО
*) В (43.1) положено Й = 1.
**) В дополнении XV приведен прямой и бодее подробный рывод
уравнения (43.7).
§43] .квазичАстицы» й Квантование пространства £б§
Рассмотрим специальный случай самовоздействующего
скалярного поля ф (х) с кубическим взаимодействием *):
^(x)=g:$(x)3:.	(43.8)
Полагая
Ф (х) Jе‘кХ^ d*k’ (43-9)
получим на основании (43.6), (43.8) и (43.9)
X У 64 (пт—Лх—k2—ka): ф(6х) ф(&2) q>(fcs): d4fex	d*ka,
(43.10)
где векторы fex, k2, ka имеют смысл импульсов частиц.
Итерируя теперь уравнение (43.7), найдем оператор 7?
в виде ряда по степеням константы взаимодействия g:
Я (пт) = 2 Rs(nx),	(43.11)
S = 1
где
Й. (лт) =-^r j > W —Тт,	х   •
X-f—	(43.12)
и-- С.у-1-1Ь
Если привести это выражение к нормальному виду, то
получается
3$
р,(пт)=2 \ 64(ПТ—ЙХ—Й2—X
т=1 J
Х$т(т, £х, k2,..., km):'^(ki)^(k2)...if(km):d^kidik2...dikm.
(43.13)
Здесь функции являются интегралами от произведе-
ний функций А+ (й) = 0 (&4) 6 (k*—т2) и функций g(xr) =
— -Л-z—-—г • Из-за наличия множителей Д+ (k) в этой
*) Этот специальный случай легко обобщается и приводится
здесь лишь ради простоты.
266
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИЙ [ГЛ. VII
теории все частицы в промежуточных состояниях явля-
ются реальными частицами, для которых &2 = т2 и &4>0.
Виртуальность частиц в промежуточных состояниях, ха-
рактерная для обычной теории возмущений, в этом новом
подходе выражается в .появлении дополнительных инте-
грирований по переменным т2, ..., содержащим-
ся в функциях g(Tr) = ^_—
ные интегрирования должны быть учтены при построении
диаграмм, изображающих функции Rs(n%).
Необходимое обобщение метода диаграмм Фейнмана
может быть сделано следующим образом.
Будем сопоставлять сплошным внешним линиям, как
обычно, операторы поля ср (k) и при т#=0 дополним их
внешними пунктирными линиями так, чтобы соблюдался
закон сохранения
£i + £2+ ... +km—пт = 0.	(43.14)
Сплошные внутренние линии сопоставим функциям Д+ (&),
а функции распространения g(yr) будем изображать пунк-
тирными линиями. Эти линии будут соединять все вер-
шины. На рис. 46 изображены некоторые простейшие диа-
граммы.
Следует напомнить, что для перехода к физической
S-матрице необходимо положить т = 0. Поэтому простей-
шая диаграмма а) не описывает реального физического
процесса, так как она описывала бы распад одной из
частиц на две или обратный процесс синтеза, что проти-
воречило бы закону сохранения энергии — импульса. Две
диаграммы на рис. 46, б суть диаграммы собственной энер-
гии. В них предполагается интегрирование по перемен-
ным q и т. Более сложная диаграмма на рис. 46, в описы-
вает рассеяние частиц.
В целом весь механизм взаимодействия реальных
частиц может быть описан как обмен реальными части-
цами с участием «квазичастиц», имеющих импульсы /гтх,
пт2, . ..,ит5в1 (пунктирные линии), причем переменные
тх, т2, ..., Ty-i пробегают значения от —оо до +°°-
Оказывается, что все расходимости в этой схеме рас-
чета возникают только за счет интегрирования по этим
переменным, т. е. по импульсам квазичастиц в промежу-
точных состояниях. Поэтому можно избежать расходи-
§43] «КВАЗИЧАСТИЦЫ» И КВАНТОВАНИЕ ПРОСТРАНСТВА 267
мостей, если ограничить область интегрирования по пере-
менным т. Это можно сделать, если перейти к искрив-
ленному т-пространству и допустить, что точки компонент
импульса размещены не на прямой от —оо до 4-оо, а на
окружности радиуса Й/а, где а—некоторая «элементарная»
длина, причем ^диаметрально противоположные точки
Рис. 46. Простейшие диаграммы в теории квантованного пространства:
а) вершина для трех реальных частиц kly k2, k3 и «квазичастицы» %т;
б) диаграммы собственной энергии частицы с учетом возможного
испускания или поглощения «квазичастицы» %т; в) диаграмма для
рассеяния реальных частиц klt k2, k3,	—«квазичастица».
круга отождествляются. В этом случае интегрирование
ограничивается пределами
2а	2а
(43.15)
При а —> 0 такая окружность переходит в прямую и пре-
делы интегрирования по т раздвигаются от — оо до + оо.
Группа трансляций на прямой и группа трансляций
на окружности с отождествленными противоположными
точками изоморфны. Различие преобразований в сущест-
венном сводится к изменению операции сложения импуль-
сов тх и т2, которая на указанной окружности будет гла-
сить:
т1( + )т2 = т1 + т2 по модулю^. (43.16)
Иными словами, складывая импульсы, мы должны оста-
ваться в пределах —лЙ/а, 4-л^/я. Уравнение (43.7) те-
перь перепишется в виде
+ л
R (пт) = t (пт) +^~ С > (п | т (-) т') R (пт'). (43.7')
-л
268
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Отсюда можно получить условие унитарности
R (0) -R+ (0) = iR (0)/?+ (0)	(43.17)
и связь между матрицами t и R:
T = R(0),	(43.5')
а также другие соотношения, характерные для теории
при а = 0.
Однако преобразование к координатному пространству
очевидным образом меняется. Действительно, все функ-
ции переменной т в этой новой схеме должны быть пе-
риодическими функциями этой переменной с периодом
2лЙ/а. Поэтому фурье-преобразование по переменной т,
т. е. вдоль вектора п, должно иметь вид
| лк
f(a) = J е'°7(т)йт.	(43.18)
а
Это преобразование имеет смысл только в том случае,
если сопряженная к т пространственная переменная о = пх
дискретна и принимает значения, кратные элементарной
длине:
0, ± а, ±2а, ... , ± та.	(43.19)
Таким образом, допущение новой группы трансляций
ведет к квантованию пространства — времени вдоль нап-
равления вектора п. В силу нового закона сложения (43.16)
внешние пунктирные линии могут соответствовать реаль-
ным квазичастицам с импульсом 2лЛ/а. Поэтому диаграмма
рис. 46, а при nx=^2nh/a будет уже описывать реальный
процесс с участием квазичастицы высокого импульса.
Эти процессы аналогичны известным процессам «пере-
броса» в теории кристаллических решеток, где сохране-
ние импульса для частиц, движущихся в решетке, имеет
место только по модулю 2лЛ/а (а —постоянная решетки);
импульс 2як/а передается в этом случае бесконечно тя-
желой решетке.	|
Обычный закон сохранения энергии —импульса в рас-
сматриваемой схеме не имеет места, что есть прямое след-
ствие неоднородности времени в направлении вектора
§44]
ФЛУКТУАЦИИ МЕТРИКИ
269
которое приобретает структуру дискретной решетки. Физи-
чески это нарушение можно интерпретировать как погло^
щение или излучение «квазичастиц», имеющих импульс
2nh/a.
Описанная схема квантованного пространства—вре-
мени обладает простотой и изяществом.
Деликатным пунктом, требующим особого внимания,
является зависимость физических величин (импульса реаль-
ных квазичастиц и элементов матрицы рассеяния) от еди-
ничного вектора п. Этот вектор указывает то направление,
в котором пространство —время имеет слоистую структуру,
т. е. направление, которое является выделенным направ-
лением, нарушающим характерную для геометрии Эйн-
штейна—Минковского изотропность пространственно-вре-
менного континуума. Возникающая здесь ситуация сходна
с той, которая имеет место в случае временного единич-
ного вектора п, с помощью которого может быть обеспечена
локальность акаузальности (см. §§ 36, 37).
Видимо, возможны следующие три интерпретации:
а) вектор п является «внешним» (см. § 38), например, он
может быть связан с движением гипотетического «эфира»
или галактик [2]; б) вектор п есть собственный вектор
наблюдателя, так что он в каждой системе отсчета имеет
значение п — (1, 0, 0, 0). В этом случае возникает ситуа-
ция, обсужденная в § 39; в) вектор п является произволь-
ным единичным времениподобным вектором. В этом случае
квадраты матричных элементов Tfi (п), величины | Tfi (п) |2,
были бы пропорциональны вероятности того, что в про-
цессе перехода f—приняли участие «квазичастицы»,
реальные и виртуальные, имеющие импульсы, параллель-
ные вектору п.
§ 44. Флуктуации метрики
В тех областях пространства, где имеется турбулентное
движение материи, сопровождающееся значительными слу-
чайными изменениями плотности материи или значитель-
ными случайными иррегулярностями скорости движения
материи, метрический тензор g^v (8.1) становится случай-
цой величиной. Тем самым становятся случайными вели-
чинами промежуток времени tpq и расстояние xPq, раз*
270
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
деляющие два события Р и Q. В этом случае можно
ГОВОрИТЬ ЛИШЬ О ВерОЯТНОСТИ ТОГО, ЧТО tpq = t И XpQ = /*).
Предположим, что тензор энергии —импульса материи
может быть представлен в виде суммы:
Т^ = Т^ + 8Т^,	(44.1)
где описывает глобальное движение материи, харак-
теризуемое большими периодами времени Т и большими
масштабами L, в то время как дополнительный член
является следствием турбулентного движения материи и
характеризуется малыми периодами времени и ма-
лыми масштабами Среднее значение 67^ за про-
межутки времени ~Т и в масштабах ~L принимается
равным нулю:
67^ = 0,	(44.2)
где черта сверху означает усреднение по турбулентному
движению. Разложим соответствующим образом и метри-
ческий тензор ggv:
S|XV”b	(44.3)
/^ = 0.	(44.3')
Ограничиваясь линейным приближением по величинам
и Agv, из уравнения Эйнштейна для метрического
тензора ggv (8.3) можно получить уравнение, справедли-
вое для малых oTnv и (см., например, [13] или [14]).
Это уравнение имеет вид
—у □?A(lv = x^v,	(44.4)
где
□=«?’<445>
=	(44.6)
ST = gf₽6Tap,	(44.7)
♦) Этот параграф может рассматриваться как обсуждение третьей
возможной причины сто хаотичности пространства и времени, отмечен-
ной в пункте в) § 41. В этом параграфе мы следуем работе [106].
§441
ФЛУКТУАЦИИ МЕТРИКИ
271
и = 8лу/га, у = 6,7-10’8 см3/г«с2 есть постоянная гравита-
ции Ньютона. Из уравнения (44.4) находим
ftnv (*) = — 2хП72/Ц¥ (*),	(44.8)
где П*2 есть оператор, обратный оператору П2 (индекс
х указывает, что оператор действует на переменную х).
Пользуясь этим выражением для h^v(x), выпишем ста-
тистическую корреляцию величин h^x), взятых в двух
точках пространства—времени х и х':
Йр/v W (^ ) = 4х2Шх2Пх'2С|Мкх0 (^» % )>	(44.9)
где величина
QwaP (^, % ) — /цу (я)/ар (X )	(44.10)
есть статистическая корреляция компонент тензора /hv,
взятых в двух точках пространства—времени х и х'.
Как было объяснено в § 8, пространственно-временной
промежуток между событиями Р и Q равен
р
SpQ= V^zb^iiydXydxv.	(44.11)
о
Для малых АИу получим
р
С — сО I * 1 С (х) dx^ dxv
s”-s,,» + 2 J
(44.12)
где Spq есть значение интервала sPq при = 0. В силу
(44.2) и (44.8) имеем
Aspq = Spq—SpQ = 0,	(44.13)
Далее, для среднего квадратичного отклонения Aspq =
= ($pq—SpqY получим из (44.12)
Aspq =
р р	,	,
1 С С dx^dxy	dxa dxp
4 (У qJ Vdxv. «4	dx3
W ^a₽	)
(44.14)
272
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
или, подставляя сюда выражения для корреляции из
(44.9), найдем
Aspq = х2
С dXvdxv
dx'
* П;2 Ш Cgv“₽ (Х’ Х>)'
(44.15)
В частном случае, если направление PQ совпадает с
направлением одной из координат, выражение (44.15) су-
щественно упрощается:
^(Р) я
х;«2)Г±^и(х)
х J	а*2	xf). (44.16)
<<«> uv
Как видно из этой формулы, проблема сводится к вы-
числению корреляции СщцаДх, х') и величины
% ) “ х2Пх2 Пх? Сщщц (х, х ).	(44.17)
Обратимся теперь к микромиру. В микромире стати-
стический характер метрики может быть следствием флук
туаций поля физического вакуума. Существование такого
рода флуктуаций, так же как и флуктуаций электрического
заряда вакуума, можно считать доказанным на основании
открытия и измерения сдвига уровня электрона в атоме
водорода *).
Избегая излишних для сути дела усложнений, мы рас-
смотрим флуктуации скалярного поля ср (х) с массой по-
коя частиц т. Функция Лагранжа в этом случае имеет вид
L = 1	(44.18)
2 \ дхадх$	/
*) Впервые на возможность такого сдвига было указано автором
этой монографии (см. [143] и [144]).
§44]
ФЛУКТУАЦИИ МЕТРИКИ
273
и соответствующий тензор энергии—импульса выражается
формулой
(44.19)
где ф(х)—оператор скалярного поля и предполагается,
дц)
дх„ дхл
сс р
что произведения вида
написаны в форме нормаль-
ного произведения (ср. дополнение VII).
Стало быть, среднее по вакууму от f'llv(x) равно’
нулю:
<0|fgv(x)|0>=0,	(44.20)
так что в этом случае 67^, =е Tp,v.
Пользуясь (44.6), нетрудно найти, что
Wx) = ;^(х),^Ф(х) _j.gfivfn2-? (х)..	(44.2i)
ОХц,	и Ху
Следовательно,
—у «W1’';’ (>)] = [^7	— т г"’1’ ’’ (х’>]
(44.22)
Для вычисления этой величины следует иметь в виду, что
среднее по вакууму от произведения нормальных произ-
ведений определяется формулой
<0|:ф (х)ф(^)::ф(х)ф(и): |0> =
= —А_ (х—г) А_ (у—и}—А_ (х—«) А_ (г/—г), (44.23)
где Д_ (х)—сингулярная функция, определенная в допол-
нении XIII*). Из (44.23) следует

dip (х) дф(х) . . дф (у) дц>(у) \ ___д2Д_ (х—у) д2Д_ (х—у)
дха дхр • • дур дуа • /	дха ду& дХр дуа
д2&_ (х—у) д2Д_ (х — у)
~ дха,^Уа дха дУр
(44.24)
*) Для получения этой формулы необходимо переместить в произ-
ведении полей ф (х) ф (у) ф (г) ф (и) все операторы рождения частиц
налево от операторов уничтожения.
274
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Введя вместо функции Д_ (х) ее фурье-образ Д_ (р):
Д_ (х) = §А_ (P)e,J’xdiP==(2^)1 Jр*—т*	(44.25)
с
(контур С показан ниже на рис. 49, и пользуясь (44.23)
и (44.24), получим из (44.22)
м m	С Д-(р)Д (<?) е*<р+|?’ В)
х { Рц<7ц+у	(Рц+tfu) + ^ёю.т* р4р dlq, (44.26)
где £=х'—х, а а—численный коэффициент порядка~1.
Нетрудно видеть, что этот интеграл расходится на верх-
нем пределе |Рц||^ц|^-К—а именно при В=0 полу-
чается
Л1ц1Фц(0)=₽^/<\	(44.27)
а при l = t для 1
=T^^cos/Ct	(44.27')
Здесь р и у—численные коэффициенты. Из-за этой расхо-
димости нет смысла более детально вычислять величину
Afpppj,. Однако формулы (44.27) и (44.27') полезны в
том отношении, что из них видно, что флуктуации метри-
ческого тензора, обусловленные флуктуацией поля ваку-
ума, существенны лишь в области масштабов
1
К

(44.28)
где Ag есть длина, равная
Ag = ]/^ = ]/л^ = 0,82-10-32 см,	(44.28')
гдеЛс =&/тсесть комптоновская длина частиц, a rg =v.m —
гравитационный радиус частицы. Существенно, что флук-
туации не зависят от массы частиц вакуумного поля,
поскольку эта масса т ^^/Лсс«10_5 г*).
*) См. работу [107], где обсуждаются частицы «Максимовы» с пре
дельной массой т^ = 1ъ1Ксс.
$ 45]
НЕЛИНЕЙНЫЕ ПОЛЯ И КВАНТОВАНИЕ
275
Флуктуации поля в масштабах длины Ac^=hlmc дают
ничтожный вклад в флуктуации метрического тензора.
Как видно из (44.28'), критический масштаб Ag есть
среднее геометрическое из гравитационного радиуса части-
цы rg и ее комптоновской длины ti/mc. Длина Ag значи-
тельно превосходит гравитационный радиус частицы, но
все же еще много меньше длины, характерной для сла-
бых взаимодействий AF~10“16 см.
Итак, если слабым взаимодействиям суждена опреде-
ляющая роль в структуре элементарных частиц, то гра-
витационные явления либо вообще несущественны в мире
элементарных частиц, либо сосредоточиваются в таких
глубинах, доступ к которым возможен лишь в мечтах.
§ 45. Нелинейные поля и квантование
пространства— времени
В этом разделе мы рассматриваем задачу о квантова-
нии нелинейного поля ср (%, /), описываемого уравнением
Борна—Инфельда в двумерном пространстве—времени
9t2(*)- Это уравнение выводится из вариационного прин-
ципа:
6S=0, S = — ^Ldxdt,	(45.1)
причем функция Лагранжа определена формулой
Л = -(1+<р*-Ф?)1/а.	(45.1')
где ср* == dq/dx, qt = dq)/dt. Эта функция является частным
случаем функции Лагранжа, рассмотренной ранее в § 7.
Масштаб градиента поля ср0, являющийся мерой нелиней-
ности, принят в (45.1') за единицу.
Из этого вариационного принципа получается урав-
нение
(1 — Ф?) <Рхх + 2<MPt<pxf—(1 — Ф |) Ф< t = о,	(45.2)
где
д2ф	д2ф ______д2ф
^>хх=~дх*’ ^Xt==dxdi’ (Pit = ~d^'
При <р0—>-оо, что соответствует q>x, <pt—*-0, из (45.2)
получается линейное волновое уравнение
Фхх—Ф« = °.	(45.2')
276
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Если положить 2 = ф(х, t), то это уравнение можно
рассматривать как уравнение для экстремальной поверх-
ности в пространстве с метрикой ds2=dt2—dx2—dz2.
Действительно, интеграл S в вариационном принципе ра-
вен площади такой поверхности. Заметим, что уравнение,
вытекающее из лагранжиана
L = - (1+<Й+фП1/2.	(45.3)
приводило бы к уравнению минимальной поверхности в
обычном евклидовом пространстве с метрикой ds2=dx2-\-
+ dy24-dz2. Такой поверхностью является, например, по-
верхность мыльной «пленки», натянутой на заданный
контур.
На первый взгляд задача о квантовании нелинейного
поля не имеет ничего общего с квантованием простран-
ства—времени. Однако, как было показано в работах
[108, 109], существует весьма прямая связь между этими
проблемами *).
Для того чтобы показать эту связь, обратимся к за-
даче Коши для уравнения (45.2). Возьмем начальные
условия при /=0 в форме
Ф(х, 0)=а(х), фДх, 0)=Ь(х)	(45.4)
и предположим, что эти функции удовлетворяют условию
гиперболичности
1+а'2(х)—Ь*(х)>0.	(45.5)
Для решения задачи Коши введем новые переменные а,
Р, которые будут аналогами переменных а =х—t, р = x-\-t>
являющихся характеристиками линейного уравнения
(45.2'), и будем рассматривать переменные %, t и г^ф
как функции новых переменных а и Р:
х = х (а, Р), t == t (а, Р),
ф = ф(/(а, Р)), х(а, р))^г(а, Р).	(45.6)
Вводя вектор г = г(а, Р) с компонентами /, х и z и
определяя скалярное произведение векторов г± и г2 фор-
мулой
(Г1Г2) = Х1Хг—ZiZ„	(45.7)
*) В дальнейшем мы следуем этим работам.
§ 45]
НЕЛИНЕЙНЫЕ ПОЛЯ И КВАНТОВАНИЕ
277
мы можем переписать уравнение (45.2) в виде
— 2 (rarp) DafJ + гlDaa = 0,	(45.8)
где
г — Эг г - — Га~ да ’ Г₽— ар		д2г ’ Гаа~да^’		 д2г Г“Р—даЭ₽	(45.8')
и Dpa есть детерминант			
=	О Q-	8	02. МММ Q.	8	со. Н X Ц ^8 .^ео.		(45.8я)-
(здесь значки р и о пробегают два Гиперболичность уравнения приводит		значения: к условию	а и р).
(rartf	— г2аг$> 0,		(45.9)
и характеристики уравнения (45.8) мулами		определяются фор-	
Га = |	0, ф=0.		(45.10)
Равенства (45.10) вместе с (45.8) образуют систему
уравнений для трех искомых функций: t(a, Р), х(а, Р)
и г (а, р).
Из (45.10) и (45.8) следует, что
£>ар = 0,	(45.11)
и, следовательно,
г«₽=Лга4-Вгр,	(45.12)
где А и В — произвольные функции переменных аир.
Из (45.10) и (45.12) имеем
(Га₽га) = (гагэ)В=1^-^=0,	(45.13)
(гв₽Гр) = (гаГр)Л =1-^-г|=0	(45.13')
и, так как (гаГр)=/:0, Л=В=0.
Таким образом, мы приходим к окончательной си-
стеме уравнений:
Г^О, Гр = 0, гар^О.	(45.14)
278
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ. VII
Из последнего уравнения в (45.14) сразу же следует, что
г (а, Р) = гх(а) + г2(Р),	(45.15)
где гх и г2 —два произвольных вектора. Тогда первые
два уравнения (45.14) теперь запишутся в виде
(^У = 0,	|'ад' = 0.	(45.16)
Пользуясь произволом в выборе переменных аир,
выберем их таким образом, что при / = 0, а=р=х.
Тогда начальные условия (45.4) запишутся в
t (a, a) = t1 (а) 4* t2 (а) = 0,
х(а, а)=х1(а)-|-х2(а) = а,
z(a, a) = z1(a)4-z2(a) = a(a).
„	d©(x, t)
Выразим теперь производную ’
ные от t, х и z по а и р:
виде
(45.17)
(45.17')
(45.17")
— через произвол-
и*
дф ___	ха za		х[ (a) zi (а) х2(Р) г2 (₽)
dt	Ха ^а х3 Z3		(a)	(а) х;(Р) /2(Р)
(45.18)
при а=р получаем
#=На)
	Xi (a.)	(а) х2 (а) г2 (а)
	х( (a) t'i (а) х2 (a) t'2 (а)
(45.18')
Далее, из (45.14) имеем при а=р
(а)2—(а)2—z( (а)*=0
(а)г—х2 (а)а — г; (а)2=0.
Запишем теперь искомое решение в форме
3
Г (а, ₽) =4 Кр + р (Р)н4 Sл dl-
(45.19)
(45.19')
(45.20)
§451
НЕЛИНЕЙНЫЕ ПОЛЯ И КВАНТОВАНИЕ
279
При этом из равенств (45.17) — (45.17") следует, что век-
тор р(а) равен
р (а) = [0, а, а (а)],	(45.21)
а вектор л (а)
л(а) = [л<(а), Яд. (а), лг(а)] (45.22)
определяется из равенств (45.12) и (45.19), (45.19'). Не-
сложное вычисление приводит к результату
(45.23)
где
L (а) = [14- а' (а)г-Ь (а)2]*/*.	(45.23')
Величины nt, пх и ng имеют простой физический
смысл.
Действительно, при / = 0
лг=л(х, 0)=-^	(45.24)
есть импульс, канонически сопряженный полю <р; далее,
nx = G(x, 0) = — л (х, 0) а' (х) = л (х)	(45.25)
есть плотность количества движения поля <р, и, наконец,
nt=H(x, 0)=-|^-q>t—L = nz<pt—L (45.26)
есть-плотность энергии поля при f = 0. Решение (45.20)
можно теперь переписать в виде
₽
/(a,	+	(45.27)
а
3
х (а, ₽) =	+1 f G (X) dk,	(45.28)
<6	"с/
а
0
z (а, Р) =4 [о (а) + а (р)] -Ц J л (к) dk. (45.29)
280
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ (ГЛ. VII
Из этих решений следует, что переменные t, х и и,
рассматриваемые как функции переменных аир, зави-
сят также от динамических переменных Я, G, л, взятых
на пространственной поверхности / = 0. Зависимость t
и х от этих динамических переменных является след-
ствием того факта, что в случае нелинейного уравнения
характеристические линии не являются прямыми линиями
а = х — t, р = х-Н, а искривлены, и это искривление
зависит от величины поля ф и его производных ф*, ф^.
Уравнения (45.27)— (45.29) можно переписать в виде
(45.27')
(45.28')
1
т)=т+4 у [Я(Х)-1]а,
S- т
g + T
Z(g, T) = |[fl(^T)4-a(g-T)] + |y n(X)dX, (45.29')
где
p = g + a=g-T, r=l(0-a), | =	(45.30)
Будем теперь рассматривать поле <р (|, т) = г Q, т) как
Гейзенбергов оператор <р (£, т) в пространстве 9t2(£, т),
причем при т = 0 правило квантования скалярного поля
гласит:
[ф(|, 0),	O)]=-U(g'-g).	(45.31)
Такое квантование поля <р само собой ведет к кван-
тованию величин t и х, которые становятся операторами.
Действительно, хи/ теперь не коммутируют с полем <р.
Чтобы показать это, образуем скобки Пуассона
[<р(£, т),/(£', т)] и [q> Q, т), х(£', т)] и вычислим их, огра-
ничиваясь первыми не исчезающими по величине 1/<р0
членами *).
*) Здесь снова масштаб поля ф0 отличен от единицы и считается,
что <р0>|<р|.
§ 45]
НЕЛИНЕЙНЫЕ ПОЛЯ И КВАНТОВАНИЕ
281
В этом приближении операторы# (а) и G (а) в (45.27'),
(45.28') и (45.29') можно взять в линейном приближении:
G(a)=gn(a),	(45.25')
(45.26')
Тогда получим
[ф(5, т), /(£', т)] =
v+t
= А f [ай+т) + а(5-т)ЛМ]Л,	(45.31')
4фо/т
[ф(|, т), xQ', т)] =
= 4" f [а(В + т) + а(?-т), G(X)]a,	(45.32)
4ф0 J
5'-т
где G (а) и Н (а) взяты из (45.25') и (45.26') и восста-
новлена явно размерность формул введением явно мас-
штаба градиента поля <р0.
Пользуясь теперь правилом перестановки (45.31) и
замечая, что а(|±т) получаются из а(|) просто смеще-
нием координаты | на величину ±т, найдем
[И, т), /(£',т)] =
£'+т
J л (Х){6[%-(В-ЮЖ[X-(g-т)]}а =
V-t
_ 1
~’ 2<ро«
[ф (6. т), Х(Г. т)] =
z<pgl J un
б'-т
1	(да(%+х) , daft— тП (.e
= ^И"^Г~+—(45
(45.33)
причем правые части (45.33) и (45.34) следует заменить
на 0, если переменная £ лежит вне интервала
Г-2т<|<Г + 2т.	(45.34')
282
ОБОБЩЕНИЕ ПРИЧИННОЙ СВЯЗИ И ГЕОМЕТРИИ [ГЛ.УП
Как известно, если две физические величины изобра-
жаются линейными эрмитовыми операторами Л и В, а
их коммутатор есть С = [Л, В], то средние квадратичные
отклонения АЛ2, АВ2 величин Л и В в любом состоянии
подчиняются неравенству
ДТ2 ДВ2^ 1|С*|	(45.35)
(см., например, [ПО]). На основании этого обобщенного
соотношения неопределенностей из (45.33) и (45.34) по-
лучим соотношения для средних квадратичных отклоне-
ний Дф2, Д/2 и Дх2:
Д<р(|,т)2 Д/(В, т)2>^|л(? + т)+л(|-т)|2, (45.36)
4ф0
Дф(|,т)2 Дх(|,т)2> -^|^.<|+т)+аФ(|р)|2. (45.37)
Отсюда следует, что при т > 0 данной точке с коорди-
натами t и х не соответствует никакое определенное зна-
чение поля ср. Поле ср оказывается определенным не
в пространстве Э12 (х, /), а в пространстве 912 (£, т). В силу
этого обстоятельства при т > 0 точке пространства Э?2 (£, т)
не соответствует никакая определенная точка в простран-
стве 9t2 (*, 0 *)•
Из правил коммутации также видно, что «квантова-
ние» пространства—времени 9t2(x, t) возникает только
в той области пространства — времени 9i2(L т), где не-
линейность велика. При — л (?) —>0 и — -Й- —> 0 пере-
F Фо w	Фо	н
менные ф, t и х коммутируют, так как t и х становятся
опять С-числами.
Рассмотренный в этом разделе пример нелинейного
поля интересен с той точки зрения, что квантование про-
странства— времени не привносится извне, а вытекает
из самой динамики нелинейного поля.
*) Однако в рассматриваемом приближении х и t коммутируют.
ГЛАВА VIII
ВОПРОСЫ ЭКСПЕРИМЕНТА
§ 46. Заключительные замечания
теоретического характера
Идея этой монографии покоится на предположении,
что S-матрица, асимптотически описывающая микроявле-
ния, сохранит свое значение и в будущей теории.
Это предположение не противоречит тому, что методы
конструирования этой матрицы могут подвергнуться прин-
ципиальным изменениям и могут существенно отличаться
от современных методов, будь они основаны на традицион-
ном представлении о лагранжиане взаимодействия локаль-
ных полей или на более абстрактных понятиях, характер-
ных для аксиоматического подхода.
Второе предположение, которое мы существенно ис-
пользовали, это предположение о справедливости совре-
менной теории свободных частиц. Иными словами, мы
предполагали, что современная теория асимптотически,
для больших расстояний между частицами, правильно
отображает физическую реальность.
Эти предположения послужили нам основой для об-
суждения возможных отклонений от современной теории,
отклонений, относящихся к области особо малых масшта-
бов пространства и времени. Мы рассмотрели два прин-
ципиально различных класса возможных модификаций
современной теории, которые условно характеризовали
с помощью временного вектора п, «внутреннего» или
«внешнего» (см. § 39).
Мы обратимся сейчас к первому классу. В этом классе
сохраняется современное представление об однородности
и изотропности пространства и времени. Вместе с тем
асимптотические импульсное пространство 9ts(p) (см. § 31)
и пространство—время 9t4(x) сохраняются в том виде,
в котором они знакомы нам из современной теории. Воз-
можные отклонения от современной локальной теории
284
ВОПРОСЫ ЭКСПЕРИМЕНТА
[ГЛ. VIII
поля носят в этом случае сами по себе локальный харак-
тер, т. е. сосредоточиваются в малой пространственно-
временной области (объемом ~я4, если под а разуметь
«элементарную» длину) в окрестности взаимодействующих
частиц. С помощью рассмотренных схем локального нару-
шения микропричинности (ср. §§ 36—40) мы стремились
очертить «магический» круг—ту пространственно-времен-
ную область, ситуация внутри которой, может быть, могла
бы быть описана только посредством принципиально новых
понятий, выходящих за пределы наших современных
представлений. Поэтому рассмотренные нами теоретические
схемы носят характер моделей. Этот модельный характер
выражается в том, что для локализации акаузальности
мы обращались к пространственно-временному описанию
с помощью переменных хи/, которые определены для
свободных и точечных частиц. «Полноправность» этих пере-
менных применительно к малым расстояниям и к малым
промежуткам времени может подвергаться сомнению.
Однако логическая последовательность этих моделей
поддерживалась тем, что обращение к пространственно-
временному описанию было необходимо нам лишь как
прием, позволяющий заручиться гарантией того, что мак-
роскопическая причинность осталась ненарушенной.
После этого мы вновь возвращались в импульсное
пространство, построив таким путем акаузальную ^-ма-
трицу, близкую к некоторой исходной каузальной матри-
це S. Модельный характер рассмотренных акаузальных
схем делает особенно острой проблему эксперименталь-
ного изучения фактов, которые могли бы указывать на
неполноту обычной локальной теории.
§ 47. Экспериментальные следствия
локальной акаузальности
Важнейшими следствиями локальной акаузальности
является изменение аналитических свойств, характерных
для локальной амплитуды рассеяния Г (со). В силу этого
возникают отклонения от обычных дисперсионных соот-
ношений. По этой же причине нарушаются соотношения
между асимптотическими сечениями (см. §§ 30, 38). Эти
следствия акаузальной теории могут быть проверены на
опыте. Для экспериментальной проверки дисперсионных
§47]
СЛЕДСТВИЯ ЛОКАЛЬНОЙ АКАУЗАЛЬНОСТИ
285
соотношений необходимо, чтобы они содержали только
известные из опыта величины и не содержали величин
ненаблюдаемых.
Этим необходимым свойством обладают дисперсион-
ные соотношения для амплитуды упругого рассеяния
вперед л-мезонов на нуклонах. Поэтому только это рас-
сеяние пригодно для проверки такого принципиального
пункта теории, как микропричинность. Соответствующие
дисперсионные соотношения были приведены в § 30.
Сравнивать с опытом можно только дисперсионные соот-
ношения для заряженных мезонов, т. е. для амплитуд
Ох(со) и £>2 (со) (см. § 30, формулы (30.32') и (30.32")).
В качестве точки вычитания соо обычно принимают
энергию покоящегося мезона, так что соо = т, £\(со) =
= Если в формулах (30.32') и (30.32") выразить
абсорбционные части амплитуд А± и А2 при помощи
оптической теоремы (см. (XIII.4)) через полные сечения
о+ и а_, то эти формулы могут быть представлены в виде
Z) (со) = £> (т) +  ---у—т-г-о---т—Г2~ +
14 7 1 м / т2 \ 2	/ /и\2
гч / ч	2fe2
D, (со) =4г----------—т
2' ' М „	( т2
<о2— тт
^^^(ст+(ю') + ст-(47.1)
m
gM 1
2 т2
т
Здесь &2 = со*—т2, где k — импульс мезона, а константа
p = (g2/4) (т2/Л42) = 0,081 и определяется из опытов по
рассеянию л + -мезонов низкой энергии.
Наибольшую трудность при сравнении с эксперимен-
тальными данными представляет экстраполяция полного
сечения о»± (со) для крайне высоких энергий; эта экстра-
поляция необходима для выполнения интегрирования в
(47.1) и (47.Г).
Экстраполяционная формула гласит:
а±=а+-^;
(47.2)
286
ВОПРОСЫ ЭКСПЕРИМЕНТА
[ГЛ. VIII
постоянные а, b и показатель п подбираются на основа-
нии опытных данных (см. [111 —114]). Первые опыты по
определению действительной части амплитуды рассеяния
на крайне малые углы D (со) были сделаны в Дубне [115,
116]. Анализ экспериментальных данных и сравнение их
с результатами вычислений по дисперсионным соотноше-
ниям (47.1) и (47. Г) с помощью экстраполяционной фор-
мулы (47.2) производились в работах [111 —114]*).
В настоящее время наиболее полные данные полу-
чены в работе [148]. На рис. 47 приведены эксперимен-
тальные данные для отношения действительной части
амплитуды к мнимой а = D (со)/А (со) в функции импуль-
са мезонов k. Сплошные кривые—результат вычисле-
ний величины а с помощью дисперсионных соотношений
(47.1) и (47.1') и экстраполяционной формулы для
о± (47.2). Из этих кривых следует, что дисперсион-
ные соотношения, выведенные на основании локаль-
ной (каузальной) теории, находятся в хорошем согла-
сии с опытом вплоть до импульсов эт-мезонов k ж
^20 4-26 ГэВ/с* **).
Обратимся теперь к дополнительным членам, обуслов-
ленным локальной акаузальностью амплитуды (см. §38).
Согласно формулам (38.13) и (38.13') мы можем написать
£»а1(®) = Г»1(®) + ^Н,	(47.3)
Яа2 (®) = О2 (со) + (со),	(47.3')
где слева Dal(o) и Dea(co)—акаузальные амплитуды;
амплитуды D± (со) и D2 (со) вычисляются по формулам
♦) В настоящее время используется несколько иная параметри-
зация полных сечений. А именно, вместо (47.2) можно записать
о± = (а+±а_)/2	(о+—а_—>л~р).
Тогда
о+(Л) = о0 + о1[1п(^1)]2 + ^а-1, )
„ ,	>	10 ГэВ/с.
Постоянные о0, ai> 6, a> ар и с—определяются из сравнения
с экспериментальными данными. (Прим, ред.)
**) Эксперименты, выполненные в ФНАЛ, позволяют сделать
вывод о справедливости дисперсионных соотношений по крайней мере
до значений £=100 ГэВ/с (см. [149]). (Прим, ред.)
§47]
СЛЕДСТВИЯ ЛОКАЛЬНОЙ АКАУЗАЛЬНОСТИ
287
(47.1), (47.Г); и ф2 означают дополнительные, ака-
узальные члены*). В дополнении XVI (формулы
Рис. 47. Отношение а действительной части амплитуды рассеяния
к мнимой. Кривые вычислены по дисперсионным соотношениям (47.1)
и (47.Г) с помощью экстраполяционной формулы (47.2) [148].
(XVI. 1 Г) и (XVI. 12)) чпроизведено необходимое преоб-
разование формул (38. i3) и (38.13'), в результате чего
*) Напомним, что о означает энергию мезона в лабораторной
системе отсчета.
288
ВОПРОСЫ ЭКСПЕРИМЕНТА
[ГЛ. VIII
получено
Н Р (Ю) (°+ (Л1) + (М))’ (47-4)
=	+	(47.4')
где а±(Л4) суть полные сечения при со = Л4, а О±(7И) —
действительные части амплитуды в точке со = 2И.
Как видно, при со^ТИ эти поправки к действитель-
ным частям амплитуды рассеяния D (со) становятся весьма
О £ 4 6 8 10 /2 14 16 18 40
4, ГэВ/с
Рис. 48. Полные сечения для процессов рр, рр, ^р, л^р в функции
импульса (по данным [117, 118]).
существенными, поэтому они были бы замечены в описан-
ных опытах, если бы элементарная длина а=Л/М была
больше 10“16 см.
Обратимся теперь к экспериментальной проверке ра-
венства полных асимптотических сечений (см. § 30).
На рис. 48 приведены кривые полных сечений для
столкновений рр, рр, л±р, К±р по данным [117, 118].
Как видно из этих кривых, асимптотические равенства
сечений, предсказываемые локальной теорией (ср. (30.36),
(30.37)), при импульсе частиц до 20ГэВ/с еще не осу-
ществляются.
Является ли это расхождение эксперимента и теории
следствием недостаточности доступных величин энергии
частиц или уже может рассматриваться как указание на
неполноту локальной теории, пока остается открытым
вопросом. Некоторые кривые (К^р) как будто подчерки-
§47]
СЛЕДСТВИЯ ЛОКАЛЬНОЙ АКАУЗАЛЬНОСТИ
289
вают, что имеется тенденция стремления к разным пре-
делам. Дальнейшее исследование предельных сечений
Рис. 49. Полные данные по сечениям для столкновений рр, рр (а);
л±р (б); К±р(в) [150, 151].
представляет собой исключительно важную задачу для
будущих ускорителей (рис. 49) *).
*) На рис. 49 приведены более новые данные по полным
сечениям для столкновений рр, рр, лт^р и К^р при значительно
больших импульсах частиц [150, 151]. На этом рисунке видна явно
выраженная тенденция к асимптотическому равенству сечений ука-
занных процессов. Это подтверждает предсказания локальной теории.
10 д. И. Блохинцев
290
ВОПРОСЫ ЭКСПЕРИМЕНТА
!гл. УШ
Квантовая электродинамика Гявляется классическим
образцом локальной теории. Поэтому в последние годы
немало усилий было приложено к тому, чтобы обнару-
жить отступления от предсказаний этой теории.
Одним из важнейших критериев справедливости кван-
товой электродинамики является измерение множителя
Ланге g, определяющего отношение магнитного момента
частицы к ее механическому моменту. Для электрона и
рЛ-мезона этот множитель близок к 2.
Экспериментальные данные для ц-мезона могут быть
резюмированыТформулой [121]
|(g-2)9Kcn=4(g-2)Teop ± 0,6 (£)’,	(47.5)
где а = exilic есть постоянная тонкой структуры. Указан-
ное в (47.5) отклонение от предсказания локальной кван-
товой электродинамики формально можно описать с по-
мощью изменения ц-мезонной функции распространения
Dc(q) (здесь q—передаваемый импульс). Для этого за-
меним локальную функцию Dc (q) на нелокальную Ьс (q, а)
посредством формулы
a)=Dc(q)--------!—j-. (47.6)
q u
В этой формуле'нелояльность введена с помощью по-
следнего члена, содержащего малую длину а,
—масса ц-мезона) *). Чтобы получить соответствие
с опытными данными, надо, чтобы длина а была < 10“14см.
Экспериментальные данные показывают, что' множитель
Ланде g — 2 для электронов с высокой степенью точности
совпадает с этим же множителем для ц-мезонов. Разли-
чия относятся к членам порядка (а/л)3. Однако в той
области, где становятся существенными члены столь вы-
сокого порядка, квантовая электродинамика ! перестает
быть замкнутой теорией: возникает необходимость учиты-
вать эффект сильных взаимодействий, а в случае сущест-
вования промежуточного бозона — учитывать также и сла-
бые взаимодействия [121].
*) Эта оценка приведена в работе [122] и является условной,
так как замена (47.6) может служить лишь для оценки возможных
нелокальных эффектов и не претендует^на строгость.
§47]	СЛЕДСТВИЯ ЛОКАЛЬНОЙ АКАУЗАЛЬНОСТИ	291
В связи с проверкой квантовой электродинамики изу-
чалось рождение пар (е+е") и пар (ц+ц“) при большой
передаче импульса [121], а также упругое рассеяние элек-
тронов и мезонов на протонах (при передаче импульса q
до нескольких ГэВ/с) [145]. Основной вывод из этих
экспериментов сводится к тому, что очевидных отступле-
ний от предсказаний локальной квантовой электродина-
мики не обнаруживается вплоть до а< 10~14см.
Многозначительным является тот факт, что в пределах
этих же масштабов не обнаруживается различия в свой-
ствах ц-мезона и электрона, несмотря на большое различие
их масс (mu/me~200) [145]. Этот факт может служить
указанием на то, что различие масс электрона и мезона
должно быть отнесено к пространственно-временным об-
ластям порядка 10~15см (или меньше!). Существенно, что
оценка масштаба нелокальное™ а, основанная на изуче-
нии лр-рассеяния, данная в работе [114], приводит к зна-
чениям а= \/М ж 10“16 см. Поэтому становится вероят-
ным, что масса частиц определяется не столько сильным
и электромагнитным взаимодействиями, сколько слабым,
которое, видимо, играет более фундаментальную роль
[144—146]. Напомним, что длина а, характерная для
слабых взаимодействий (см. § 22), равна a = AF 10’16см.
Современная локальная теория приводит к знаменитой
СРГ-теореме, согласно которой применение операций за-
рядового сопряжения С, пространственной четности Р
и обращения времени t не меняет состояния элементар-
ных частиц. Формально это записывается равенством
СРТ = 1.	(47.7)
Операция СР называется операцией комбинированной
четности.
Существенная связь трех операций видна уже и из
того факта, что в диаграммной технике Фейнмана^анти-
частицы можно рассматривать как частицы, движущиеся
во времени в обратном направлении [127]. Более глубокие
основания равенства (47.7) лежат в правильной связи
статистики частиц с их спином [128]. В аксиоматическом
подходе к квантовой теории поля СРТ-теорема доказы-
вается исходя из локальной причинности, положитель-
ности энергии частиц и лоренцевской инвариантности [129].
Ю*
292
вопросы эксперимента
|ГЛ. VIII
Нарушение СРТ-теоремы означало бы нарушение
основных принципов локальной теории и могло бы быть
связано с возможными изменениями принципа причин-
ности в микромире или, более общо, геометрии микромира.
Однако СРТ-инвариантность, видимо, соблюдается
с большей степенью точности. Одним из следствий этой
инвариантности является утверждение о равенстве масс
частиц т и античастиц т. В настоящее время очень точно
измерялась разность масс Kl- и Ks-мезонов. Из этих
измерений можно вывести заключение, что | —^Ю“14;
этот результат указывает на весьма строгое соблюдение
операторного равенства (47.7).
Из СРТ-теоремы следует также равенство времен
жизни частиц т и античастиц т. Действительно, масса
нестабильных частиц есть комплексная величина т =
= /n0 + ip здесь Л—константа распада. Поэтому ра-
венство тит так же следует из СРТ-теоремы, как и ра-
венство масс т и т. Произведенные до сих пор сравни-
тельные измерения времен распада л+- и л“-мезонов
приводят к результату
——1=0,064 ±0,069,
т. е. с доступной сейчас точностью эти времена оказы-
ваются равными [147].
Другим указанием на соблюдение СРТ-теоремы может
служить совпадение множителей Ланде g, точнее, вели-
чины^—2) для р~- и р+-мезонов, именно [145]: (g—2)+ =
= (11624-5)-10~6, a (g—2)_ = (1165±3).1О"6. Поэтому
пока разумнее считать, что СРТ=1. Сложнее обстоит
дело с комбинированной четностью СР. Несколько лет
тому назад было обнаружено несохранение этой четности
при распаде долгоживущего К^-мезона (Кг-мезон а) на два
л-мезона [123, 124]. Если через К0 обозначить состояния
К°-мезона, а через К°—состояние анти-К0-мезона, то
короткоживущее состояние К-мезона (К?) будет
К5 = _^(К’+К0),	(47.8)
§47]
СЛЕДСТВИЯ ЛОКАЛЬНОЙ АКАУЗАЛЬНОСТИ
293
а состояние долгоживущее (К§) —
Ki=pb(K»-K')).	(47.8')
Первое из этих состояний есть состояние четное относи-
тельно операции СР, второе состояние—нечетное. С дру-
гой стороны, состояние пары мезонов (льл“) относительно
CP-четное. Действительно, операция четности Р меняет знак
состояния л-мезона в силу его псевдоскалярности и меняет
направление радиуса-вектора, соединяющего два мезона.
В силу этого волновая функция, описывающая состояние
пары мезонов, приобретает множитель (—l)z (здесь I —
орбитальный момент). При зарядовом сопряжении С со-
вершается замена л+ л~ благодаря чему появляется
второй множитель (—1/.
Таким образом, четность состояния л+л" доказана.
В силу этого распад
KL->jr++n-	(47.9)
запрещен, если CP-четность сохраняется.
В опыте, описанном в работе [123], которая впервые
была доложена на Международной конференции в Дубне
в 1964 г., было показано, что распады типа (47.9) все же
имеют место, хотя и с малой степенью вероятности: от-
ношение вероятностей распадов
(47.10)
Обнаружено нарушение CP-четности при распаде К-мезона
на л-мезон и лептоны в реакциях [126]
К£-> Ji- + p++v,	(47.11)
и
Кг —> л+ +pl" + V,
(47.11')
К£ —* л- +е+ 4-v,
К£ —* л+ 4-е_ + v.
(47.12)
(47.12')
Асимметрия наблюдалась в том, что реакции (47.11) и
(47.12) оказались предпочтительнее, чем реакции (47.1 Г)
294
ВОПРОСЫ ЭКСПЕРИМЕНТА
(ГЛ. VIII
и (47.12'). Между тем, в силу четности К^-мезона по
отношению к операции СР, реакции (47.11) и (47.1 Г) и
соответственно (47.12) и (47.12') должны бы происходить
с одинаковой скоростью.
Нарушение CP-четности могло бы означать либо на-
рушение ОРТ'-теоремы (47.7), либо неинвариантность фи-
зических явлений относительно операции инверсии вре-
мени t, т. е. несимметрию прошедшего и будущего. Эта
несимметрия хорошо известна в области макроскопических
явлений и вообще в повседневной жизни, но совершенно
непривычна в механике и в теории поля [130].
В какой мере нарушение CP-четности (а следовательно,
и асимметрия времени) может быть связано с проблемами
причинности и геометрии микромира, существенным об-
разом зависит от степени общности нарушения СР-инва-
риантности *).
Пока еще не найдено других явлений, кроме распада
К-мезонов, в которых обнаруживалось бы несохранение
CP-четности. Этот факт препятствует развитию геометри-
ческой точки зрения на явление несохранения СР.
§ 48. Экспериментальные следствия моделей
с «внешним» вектором
Обратимся теперь к другому классу моделей, который
по нашей классификации мы относим к классу моделей
с внешним вектором п.
В этих моделях, в отличие от случая локальной ака-
узальности, лоренцевская инвариантность нарушается и
становится в том или ином смысме приближенной. Это
отступление от лоренцевской инвариантности обусловли-
вается либо выделением той или иной системы отсчета,
как это имеет место в некоторых моделях стохастического
пространства (см. § 41), либо нарушением однородности
и изотропности пространства—времени, как это харак-
терно для моделей с дискретным или квантованным про-
странством— временем (см. § 42).
*) В этой связи см. работы [132, 133].
§48] СЛЕДСТВИЯ МОДЕЛЕЙ С «ВНЕШНИМ» ВЕКТОРОМ 295
В § 44 были рассмотрены нулевые колебания (флук-
туации) скалярного поля ср (х), порождающие флуктуации
метрического тензора g^v.
В обычном понимании^вакуума эти флуктуации, так
же как и флуктуации заряда вакуума, не нарушают од-
нородности и ^изотропности пространства—времени, так
как в любой [точке пространственно-временного конти-
нуума 9?4(х) они протекают одинаковым образом. Однако
возможен и другой взгляд на физический вакуум, более
старомодный, согласно которому вакуум представляет
собой выделенную в нашей Вселенной систему отсчета.
Сколь бы невероятными ни казались эти предположения,
логически они не могут быть исключены из рассмотрения.
В частности, в работе [105] было обращено внимание
на то обстоятельство, что по мере возрастания масшта-
бов число реальных систем отсчета, допустимых в качестве
инерциальных, существенно сокращается. Действительно,
для частиц, движущихся, например, в атомном ядре,
ускорения достигают величины 1032см/с2, для макроско-
пических систем они порядка 108см/с2, для планет они
порядка 1 см/с2, а для звезд или галактик эти ускорения
составляют лишь 10“8см/с2. Поэтому, если для атомных
систем все макроскопические системы являются инерци-
альными, то для больших систем трудно указать систему
более инерциальную, нежели система, связанная со звез-
дами или галактиками. Имея в виду известное расшире-
ние видимой Вселенной, ^было бы более правильно рас-
сматривать системы отсчета, локально покоящиеся и
медленно меняющиеся по мере перехода к более удален-
ным галактикам. Весьма возможно, что такой «наиинер-
циальнейшей» системой отсчета может служить система,
покоящаяся относительно недавно открытого «реликтового»
излучения, наполняющего нашу Вселенную.
После этих общих замечаний вернемся вновь к мик-
ромиру и для определенности рассмотрим -упругое рас-
сеяние частиц.
Это рассеяние в обычной локальной теории полностью
характеризуется амплитудой рассеяния A (s, /), завися-
щей от двух инвариантов s = P* и t = q2 (Р — полный
импульс частиц, q — импульс, переданный при рассеянии).
Если существует некоторый «внешний» времениподобный
единичный вектор /г, то амплитуда рассеяния А может
296
ВОПРОСЫ ЭКСПЕРИМЕНТА
[ГЛ. VIII
еще дополнительно зависеть от двух инвариантов а =
= а(п, Р) и p=tz(n, q), где а—элементарная длина.
Таким образом,
А = А (s, f, а, Р).	(48.1)
Предположим теперь, что лабораторная система почти
покоится относительно некоторой «привилегированной»
системы отсчета (системы, выделенной неоднородностями
пр остр анства—времени, н аибольшей инер ци альностью
и т. д.), так что в лабораторной системе п = (1, 0, 0, 0);
в этой системе отсчета а = аЕ, $ = aq0. Рассмотрим теперь
в той же системе отсчета упругое рассеяние во встречных
пучках. В частности, если центр масс сталкивающихся
частиц покоится, то а = а	, р=0, а т есть
масса покоя частицы.
Таким образом, рассеяние в лабораторной системе и
рассеяние в системе центра масс будут различны. Разу-
меется, что это различие может стать заметным лишь
при достаточно большой энергии сталкивающихся частиц
(или при достаточно большом переданном импульсе).
В противном случае а р 0 и А A (s, /, 0, 0).
Что говорит по поводу такой возможности опыт?
Весьма точные данные имеются по знаменитому теперь
распаду К°—>л++л“, который обстоятельно промерен
при двух энергиях.
Вероятность рассматриваемого распада dW, согласно
локальной теории, есть функция двух инвариантов s = P2
и г = Рр± — Р2 — Рр2, где Р—четырехмерный импульс
Кг-мезона, а р± и р2— импульсы л^-мезонов:
dW = dW(s, г).	(48.2)
Эта вероятность пересчитывается обычным образом из
одной системы отсчета в другую, в частности, будучи
известна для покоящегося мезона, она может быть вы-
числена для мезона движущегося простым пересчетом
инвариантов s и г.
^Критерием справедливости такого преобразования,
основанного на обычной кинематике теории относитель-
ности, может служить инвариантность массы покоя рас-
§48] СЛЕДСТВИЯ МОДЕЛЕЙ С «ВНЕШНИМ» ВЕКТОРОМ 297
издающегося К°-мезона. Опыты, произведенные при энер-
гиях Кг-мезона Ео = 1 ГэВ [134] и EQ = 10,7ГэВ [135],
показывают, что разброс Дтк возможных значений массы
покоя мезона /пк в первом случае составляет ~0,7%,
а во втором ~ 1 % при одном£и том же среднем значе-
нии /пк. Таким образом, эти^опыты показывают, что
релятивистская кинематика в области нескольких .ГэВ
соблюдается с точностью ~ 1 %.
В физике прошлого столетия фундамента пьное значе-
ние имели законы сохранения. Современная теория при-
дает симметриям и групповым свойствам более фунда-
ментальное значение.
Законы сохранения с этой точки зрения являются
следствием определенных симметрий. В частности, законы
сохранения энергии — импульса и момента количества
движения являются следствием однородности и изотроп-
ности пространства—времени. Нарушения такой одно-
родности и изотропности должны были бы приводить
и к нарушениям законов сохранения. В этой связи уместно
напомнить, что в общей теории относительности, опери-
рующей с неоднородным пространством Римана, не су-
ществует локального закона сохранения энергии—им-
пульса.
Поэтому представляется интересным знать, с какой
точностью и обстоятельностью доказаны законы сохранения
энергии и импульса применительно к миру элементарных
частиц, особенно в области высоких энергий. Оказывается,
что ответить на этот вопрос нелегко, так как значимость
этих фундаментальных законов признается самоочевидной
и по этой причине специальные опыты для проверки их
не ставились.
Между тем нужно ясно представлять себе, что воз-
можное нарушение этих законов могло бы быть следствием
нарушения однородности и изотропности пространства—
времени в микромире, и вряд ли есть основания делать
идею об однородности и изотропности пространства —
времени предметом веры физиков.
Какие же сведения о законах сохранения можно по-
черпнуть из современного эксперимента в области высо-
ких энергий? Оказывается, что наиболее точные данные
могут быть получены из изучения упругих столкновений
протонов. Оказывается, что релятивистские законы сохра-
298
ВОПРОСЫ ЭКСПЕРИМЕНТА
(ГЛ. VIII
нения энергии—импульса при упругом столкновении про-
тонов
Pi + Р* = Р'1 + Pi,	(48.3)
Е (л) + Е (р2) = Е (pl) + Е (рО (48.3')
(здесь рх, р2 — импульсы протонов до столкновения,	—
их импульсы после столкновения, Е = ]^р2 + т2—энергия
протона) соблюдаются в интервале £ = 24-10 ГэВ в пре-
делах точности около 3%.
Соответствующая длина волны в лабораторной системе
координат составляет К ~ 10“15см. Далее, можно считать
достаточно убедительно установленным, что резких скач-
кообразных нарушений кинематики (48.3) и (48.3') на уровне
10% нет, но они могли бы быть на уровне 3% [136].
Однако по этому вопросу нет никаких опытных данных.
Между тем, если существует какая-либо неоднородность
пространства—времени, связанная с ультрамалыми мас-
штабами, порядка а, то ожидаемые нарушения законов
сохранения должны быть значительными, \E~1icla,
хотя, быть может, и редкими. Такая ситуация
возникает в теории «квазичастиц», рассмотренной в § 43.
Очевидно, что подобные нарушения трудно отличить от
процессов с участием нейтральных частиц: в тех случаях,
когда имелась бы утечка энергии и импульса, возникала
бы естественная возможность интерпретировать событие
как результат рождения нейтральных частиц. Поэтому
более интересным было бы наблюдение случаев спонтан-
ного увеличения энергии — импульса в условиях доста-
точной защиты от внешних нейтральных излучений.
ДОПОЛНЕНИЯ
Дополнение I (к §§ 14 и 16)
Сингулярные функции в теории поля. Функция D (х)
в (14.4) (и такая же функция в (16.3)) возникает из четы-
рехмерного интеграла
1 р pikx
I (%) =	— \ —--------- d*k,
v 7	(2л)4 J k2—т2
(1.1)
где, как обычно, d*k = dkQd3k, kx^k^t—kx, k2=k%—k2
в «бозонном» обозначении; для фермионов мы будем упот-
реблять вместо вектора k вектор р.
Подынтегральное выражение в (1.1) имеет полюсы
в точках
Ао = ~4~	Л2 -}“ /722 — zb
(1.2)
(или, для фермионов, в точках kQ= ±Vp2 + m2=± Е)-
Поэтому результат интегрирования в (1.1) по dk0 зависит
от выбора в комплексной плоскости переменной#0 контура,
по которому обходят эти полюсы.
Различные возможности изображены на рис. 50.
В частности, функции D (х) соответствует контур Со.
Ниже мы приводим список сингулярных функций и
явные выражения, возникающие из интеграла (1.1) в за-
висимости от выбора контура интегрирования.
1.	Функция D (х) — «перестановочная»; контур инте-
грирования Со. Эта функция имеет вид

-i'W (б w
/и2 /г (тУ х2)
? тУ х*
0(х2) ,	(1.3)
300
ДОПОЛНЕНИЯ
где х2 = /2—x2=t2—г2 (считая с=1), Jj(z) есть функ-
ция Бесселя. При этом
0(Ю = 1. £>0, 8® = +1, |>0,
0® = О, g<0, e(g) = —1, g<0. ц ’
2.	Функция Dc(x)—«причинная»; контур интегриро-
вания С. Явное выражение для этой функции имеет вид
6 <**) — 811у-у 0 (*’) 111 ('пКх')—<ЛГ, (тУх!)]+
+	(1.5)
Здесь	/С1(г)—функции Бесселя в обычных
обозначениях.
Рис. 50. Различные контуры интегрирования в комплексной плоскости
k0 = u + iv для получения сингулярных функций/), Dc, £>±, Z)ret, Dadv
Функция Dc при т=0 принимает вид
Рс(х) = ±6+(х2),	(1.6)
ДОПОЛНЕНИЯ
301
где
00
6+ (Z) = JL f e«o(z+re) da — ^.—1	(i j)
' 1 2 л J	2л z +18	v 1
0
при 8—^0. Подобным же образом
00
6‘<z)=iHe’'““’'a‘to=;sri	(I8)
о
при 8 —> 0. Эти формулы эквивалентны такой форме
записи:
б£(г) = |[в(г)±Л|].	(1.9)
пригодной при интегрировании по действительной оси,
если при интегрировании члена 1/z брать главное значе-
ние интеграла около z = 0.
3.	При интегрировании по контурам С+ и возни-
кают функции О±(х):
D±(x)=|{D(x)±iDx(x)},	(1.10)
где функция (х) получается при интегрировании по
контуру причем в явной форме:
ад) =
от8 Ki (т Ух2)
т/х8
от8 (т Ух2)
2л8 т
при X8 > О,
при х8 < 0.
(1.11)
(1.И')
4.	Наконец, при интегрировании по контурам Cret и
Cadv возникают функции Diet (х) и Daiv(x), совпадающие
с функцией Грина для неоднородного уравнения:
(□-m8)Dret(x) = -6(x),	(1.12)
(□-m8)Dadv(x) = -6(x),	(1.12')
	D(x)	при	с	>0,	(1.13)
^ret (^) —	0	при	t<	со,	(1.13')
	0	при	t-	>0,	(1.14)
^adv С^) ~ |	D(x)	при	t<	СО;	(1-14')
Dret (х) есть запаздывающая функция Грина, a О^(х) —
опережающая,
302
ДОПОЛНЕНИЯ
Соответствующие функции для фермионного поля
получаются действием на^ функцию D (х) оператора
--------т ) • А именно, перестановочная функция для
фермионного поля S (х) равна
S(x) = -(V11^--m)D(x).	(1.15)
Выражение причинной функции для фермионного^ поля
таково:
«с(х)=-(Тц^--/и)рс(х).	(1.16)
Наконец, запаздывающая функция Sret (х) и опережающая
Sadv (х) для этого же поля определяются формулами
Sret (*) = —	fn) £>ret (x),	(1.17)
Sadv(*) = -(b^-m)£>adv(x)	(1.17')
и удовлетворяют неоднородным уравнениям
(b^T-m)Sret(x) = -6(x),	(1.18)
m) 5adv(x)= —6(Х).	(1.18')
Доказательство формул, приведенных в этом допол-
нении, можно найти в курсах квантовой теории поля
[37, 38].
Дополнение II (к § 15)
Компоненты спинора ига(р) для £>0 могут быть
N,
г = 2
«1 = 0,
u2 — N,
п*
«з = —г~ъ N,
о т _1_ h ’
(П.1)
записаны в виде
г — 1
u1 = N,
и2 = 0,
и — рг
Ua~ т+Е
П »,
«4 = —гг Д',
4	т-\-Е ’
кт 1 Л । т \ i/2
где —(J + t)
«4 =-------пЦ? N,
4	т -4- F. 1
, Ц^р^ру.
ДОПОЛНЕНИЯ
303
Отсюда находим, что
ди* ди	диа _ 1 / < . tn \ -1 т2р% .
dpz dpz~~ 2^ dpz dpz ~~ 8 V 1 "Г E J E* "Г
a=l
Замечая, что»
находим
ИЛИ
__ 1 P ди* ди
~ 4л J dpz ~др~
Jp*dQ = -|np4,
4? ПРИ Р<тс>
при р>тс
1	4 т2 1
4^"3 TfP ПРИ
т
Ро9
т
А?
Интеграл от М (£) имеет вид

(П.З)
(П.4)
(П.4')
(П.5)
(П.5')
(П.6)
Этот интеграл при т/р0—>оо равен
(IL7)
При т/ро —>- 0 имеем
т/р0	~
J	над. (П.8)
0	т/р0
304
ДОПОЛНЕНИЯ
Первый интеграл в (II.8) стремится к нулю, как (т/р0)3;
второй интеграл в (II.8) стремится к единице и дает вклад
в /2 порядка 1/р§. Этот вклад объединяется с вкладом
интеграла Д в (15.9).
Дополнение III (к § 16)
Пример, на который мы ссылаемся в § 16, таков.
Пусть поле ф(х) (16.13) имеет амплитуду A(k), рав-
ную
4W=iexp(-<t^)+iexp(-fc;b!i). (III.1)
Вычислим w(x, 0). На основании (16.16) имеем
сехр	+*&*)
Ф (х, 0)=С1 j —--------->- d3k +
Ci	(	b2x2 t \ . c2 / b2x2 .	\ /тут
=£ exP (-----2“ + tk^x) + 57 exP (—r + lk*x) ’ 11 -2)
причем предположено, что |ftx—k2\^>b. Отсюда
/ b2x2	\	f b2x2 \
акр = ct exp (--g- + ifcjX j4- c2 exp (-+ i fe2x j.
(III.3)
Пользуясь (16.24), имеем
w (x, 0)=y (а><р*ф -|- <р*акр) —
= е-ъ^ lg-114-1^1 cos {\kx 4-a)4-
+ 1^1соз(Дйх4-а)4-^}, (Ш.4)
где AAf=Af2—й1( a = arg(c2/c!). Полагая	получим
w(x, Q)=e-b‘xl^~ [ 14-1 1 cos (Ab: 4-а)]- (Ш.5)
При | c2/cx ( > 1 величина w (x, 0) осциллирует. Заметим,
что в силу предположения |й2—плотность не
ДОПОЛНЕНИЯ
305
сильно локализована (Ь мало!). Осцилляции имеют период
порядка 1/| k2 — в пространстве и порядка 1/|со2—ссц |
во времени.
Дополнение IV (к § 20)
Поглощающая диафрагма. Рассмотрим решения урав-
нения Дирака для частицы массы т и энергии Е, дви-
жущейся в поле сильно поглощающей диафрагмы. Мы
обязаны предположить определенную ковариантность
взаимодействия частиц диафрагмы с рассматриваемой
нами частицей. Предположим ради (определенности, что
взаимодействие имеет векторный характер. Пусть четвер-
тая компонента этого взаимодействия есть V.
Тогда уравнение Дирака гласит:
(ар+Рт)ф= (Е—V) ф.	(IV. 1)
{ФI
?, получим ДЛЯ ф
% '
{&Р {E-v+m)	Ф = (Я-V-m) <Р,
где о—матрицы Паули, а
(IV.2)
(IV.3)
В области, где У=0 (вне экрана и внутри щели), имеем
р*Ф = (Е\—mz) ф.	(IV.4)
Ограничимся для простоты двумя измерениями и на-
правим пучок по оси Оу. Замечая, что р2 =— V2 =
=— (д2/дх2-}-д2/ду*), находим ф в виде
<р ~ ехр (i (kxx 4- kyy)),	(IV.5)
E*=k3+k*+m3=ks+m3,	(IV.6)
E=..+yk3 + m3.	(IV.6')
В области внутри толщи экрана, где 1/#=0, уравнение
(II.2) записывается в форме
раФ + [(£—У)2—™2] ф = 0	(IV.7)
или
7?ф + [(£—V)*—т2]ф==0.	(IV.7')
306
ДОПОЛНЕНИЯ
Если бы энергия V была действительной, мы бы имели
два случая:
а)	V < 0 (притяжение); в этом случае величина
[(£—У)2—m2] = q2 = q2 4- q2 > k2 и решение имеет вид
волны
Ф - exp (i (qxz + qvy)Y	(IV.5')
При Е<т могут появиться и связанные состояния.
Если V < —2т, то возникают и такие связанные состоя-
ния, в которых электронные и позитронные состояния
перепутываются.
б)	V > 0 (отталкивание); в этом случае величина
[(£—V)2—т2] при достаточно больших Е положительна,
так что решение опять можно представить в виде (IV.5'),
но только с иным значениехМ волнового вектора q'x, q'y.
При (Е—У)2—т2 > 0 частица проходит над барьером.
При (Е—У)2—т2 =— Z2 < 0, A,24-A| = V волна будет
иметь вид
Ф « exp (± \хх ± lyy),	(IV.5")
причем внутри бесконечного барьера мы должны взять
одно из этих решений, соответствующее затуханию вол-
ны ф.
Наконец, при больших значениях У (V > 2т) барьер
становится опять прозрачным; это соответствует перекры-
тию [внутри барьера уровней т и —т, т. е. случаю
большой поляризации вакуума, когда поле способно по-
рождать^пары позитронов и электронов.
Обратимся к интересующему нас случаю поглощаю-
щего чисто мнимого потенциала. Полагая V = iW, получим
?2ф + [(E2-m2)—2iEW — W2] ф = 0.	(IV.8)
Из этого уравнения видно, что при IF —> оо оно превра-
щается в уравнение вида
72ф — №2ф = 0	(IV.8')
и, следовательно, имеет экспоненциальные решения с дей-
ствительными показателями Кх, Ку, %24-А,£ = IF2 > 0:
Ф ~ ехр (± 1хх ± \г/),
(IV.9)
ДОПОЛНЕНИЯ
307
и при больших W (больших Кх, Х9) эти волны будут
крайне быстро затухать внутрь экрана. Существенно, что
в этом случае не возникает «парадокс Клейна» и реше-
ния с +т не перепутываются между собой.
Дополнение V (к § 22)
А. Формально пространственно-временная структура
нуклона определяется вершиной Гц (см. (22.3)), завися-
щей от двух переменных Х=у—(xt + x^l2 и х=х2—хх:
Ги=Гц(Х, х).	(V.1)
Происхождение функции двух аргументов Гц (X, х) может
быть пояснено с помощью теории возмущений. Вычислим
вершину Гм для взаимодействия, описываемого лагран-
жианом
F=g {фу5тхф<рх 4- фу5т2ф<р2} +
+ ie	+т«) WMh- (V.2)
Здесь операторы гр и гр описывают нуклонное поле («го-
лые» протоны и нейтроны), операторы <рх и ср2—заря-
женное мезонное псевдоскалярное поле, Тр т3 и т2—обыч-
ные матрицы изотопического спина. Первый член описы-
вает «сильное» взаимодействие нуклонного и мезонного
полей, g есть константа этого взаимодействия; ее мы
будем считать формально также достаточно малой, чтобы
можно было применять теорию возмущений. Второй член
описывает взаимодействия мезонного поля с электромаг-
нитным полем; это поле характеризуется вектор-потен-
циалом А^. Наконец, третий член описывает электромаг-
нитное взаимодействие «голого» нуклона. Для нейтрона
этот член равен нулю, так как в этом случае (1 + т3) = 0.
Вычислим теперь элемент матрицы рассеяния фотона
на нуклоне в первом порядке по е и во втором порядке
по константе g. Таким образом, нам надо вычислить
среднее по мезонному вакууму от энергии взаимодейст-
вия W, учитывая члены порядка е, eg, eg2. Следуя обыч*
308
ДОПОЛНЕНИЯ
ному методу диаграмм Фейнмана, мы получим для сред-
него по мезонному вакууму
<0|Г|0>=$ 7ц(х)Ди(х)^х4-
+ $ Ai (хх, х2, у) Au (х) d4xx d*x2 dty, (V.3)
где
Jv. (х) = - ф (х) (1 + rs) уЗ (х) ,	(V.4)
Ш- х2, #) = 1е£2ф(х2){у63с(х2—хх)у8т3х
X [Д (х2—z/) dDc^~^-Dc (Х1-у) ^c-(g~y)l I (Х1).
L	иУц	У J J
(V.5)
Ток (V.4) обусловлен зарядом «голого» протона, а ток
(V.5)—зарядом мезонной атмосферы, сосредоточенной
около нуклона. Этот последний ток соответствует диа-
грамме Фейнмана, приведенной на рис. 22, б. В этой
формуле Sc(x2—хх) есть причинная функция для нук-
лона (см. ее определение в (14.3) и (1.16)); Dc(x2—у),
Dc(xx—у) — причинные функции для мезона. Выражение
стоящее в фигурных скобках формулы (V.5), является,
с точностью до множителя leg2, вершинной функцией,
Гц (хх, х2, у) второго порядка по g. Как видно, она зави-
сит лишь от разностей координат хХ) х2, у и поэтому
может быть представлена в виде функции переменных
X—у и х, причем Х = у—(хх-]-х2)/2. Таким образом,
с полевой точки зрения пространственно-временная струк-
тура нуклона описывается функцией двух переменных.
Различие точек входа хх и выхода х2 учитывает эффект
отдачи нуклона (изменение его положения) при пере-
ходе из начального состояния ф(хх) = фДхх) в конечное
Ф (х2) = Ф/(х2). В этом отражается динамический харак-
тер структуры нуклона, описываемый вершиной ГИ(Х, х).
Фурье-образ этой величины Г (а, 0) есть функция матриц
Ун и векторов а, 0. Для дальнейшего будет достаточно
ограничиться членами Г, диагональными относительно
спиновых индексов. Нетрудно показать, что эти члены
имеют структуру
Гц (а, 0)=ацФ (а2, ар, р2) Фи (а2, ар, р2),	(V,6)
ДОПОЛНЕНИЯ
309
где Ф—функция, зависящая от инвариантов а2, ар, Р2.
Заметим, что точно такой вид имела бы величина Ги(а, Р),
если бы нуклон был бесспиновой, скалярной частицей.
Из рассеяния частиц, как следует из формулы (22.7),
можно найти значение функции f„(a, Р) только при a = q
и р = Р:
Гц(«у, Р)=Фи(<72, 0, Р2)=Ф[1((?2, 0, 4ЛР—g2). (V.7)
Определяемый^отсюда пространственный образ
рц(Х)=$ Ги(<7, P)e^d*q	(V.8)
имеет физический смысл лишь при q2<^4M2 (Р2&4М2).
Действительно, переменная 0(=Р) сопряжена координате
х = х2—xlf но не координате Х = у между тем
согласно (V.7) переменная 0 в (V.8) оказывается функ-
цией переменной a = q. Поэтому мы должны положить
рм(Х)=$Гц(<7,22И)^^	(V.9)
и ограничиться значениями q2<^AM2.
Отсюда следует/ что 'пространственное распределение
р (Х) имеет физический смысл лишь для тяжелого, почти
покоящегося нуклона и'для малых переданных импуль-
сов q.
Б. Для упрощения формулы (22.10):
(V.10)
заметим, что из векторов q, Р и уи можно построить только
следующие скаляры: q2. Р2, у^ц, уцРц (скаляр qP==O)\
далее, скаляр Р2 выражается через скаляр q2 (Р2 =
= 4М2—q2), скаляры Уу/Уу, и у^Рц могут быть исключены
с помощью уравнений; Дирака
(ул—М) и(р)=0,	(V.11)
й(р)(тиДц4-Л1) = 0,	(V.11')
где М—масса нуклона. В силу этих соотношений коэф-
фициенты а, Ь, с, d, е являются функциями только q3,
310
ДОПОЛНЕНИЯ
На основании уравнений (V.11) и (V. 11') имеем также
(«/1 iffgVJPv !«,-) = (йу |—| uz),	(V. 12)
(i/у |	|«;)= (w/12Л4уц Pц | uz).	(V.12 )
Эти соотношения позволяют исключить из (V.10) члены,
пропорциональные р^ и о^Р?. После исключения этих
членов ток Уц приобретает вид
=	+	+	(Р/)>	(V. 13)
где Л, В, С суть форм-факторы функции, зависящие
только от q2.
Пользуясь теперь соотношением (22.4"), получаем
о =	^Uf{pf){Aq2 + Ву^ + Ca^q^} u^pi). (V. 14)
Множитель равен нулю в силу уравнений (V. 11) и
(V. 11'), а сумма огИУ^¥ = 0 в силу антисимметрии матриц
Оцд,. Отсюда следует, что форм-фактор Л(<?2)^0.
Окончательно ток приобретает вид
=йу (Ру) {В (р2) Уц4- С (р2) OuvPv} ut (Pi).	(V. 15)
Дополнение VI (к § 23)
Уравнение (23.6) для упругого jcN-рассеяния было
получено таким путем. Пусть Ф5 = Ф5 (k19 k2, k3, ..., ks) —
волновая функция системы из s мезонов и нуклонов
(здесь kly Л2, • ••, ks— их импульсы). При взаимодейст-
вии мезоны и нуклоны могут рождаться и уничтожаться.
Поэтому волновые функции Ф5 с различным числом частиц
связаны между собой цепочкой уравнений
(Vi. 1)
s'=£s
Здесь Нй—гамильтониан невзаимодействующих частиц,
полная энергия системы, U7SS-—матричный элемент
оператора энергии взаимодействия. Из всех функций Ф^
нас интересует одна Ф2(^х, й2)=ф(й, р), где = Л есть
импульс мезона, а Л?2 — р есть импульс нуклона. Для
ДОПОЛНЕНИЯ
311
выделения этой компоненты перепишем систему уравне-
ний (VI. 1) в виде
(Vi.2)
s'#=2
(£-tf0)Os,= 2	(VI.2')
s"#=s'
Введем «элементарную матрицу» рассеяния г (см. [41]):
г = 8+(Е —Я0)Г,	(VI.3)
где 6+(z)—функция, определенная в дополнении I фор-
мулой]^!. 7).
С помощью этой матрицы уравнения (VI.2) и (VI.2')
могут быть записаны в символическом виде:
(Е~Я0)ф=^Ф,	(VI.4)
Ф = гФ-|~гф;	(VI.4')
отсюда итерацией получим уравнение для интересующей
нас функции ф:
(£—	(и^Ф)дг_>оо. (VI.5)
1 —г
Если предположить, что: а) все расходящиеся члены
исключены из этого уравнения и б) остаточный член при
N —+ оо стремится к нулю, то это уравнение может быть
записано в виде
{E—E(k, p)}^(k, р) =
= $ ® (Л, РI р') Ф (£', р') dak' d3p', (VI.6)
где ® (A, p\k', р') есть матричный элемент оператора
® =	(VI.7)
E(k, p) = EAk) + EN(p)	(VI.8)
есть сумма энергий л-мезона En(k) и нуклона EN(p).
Для реальных процессов E = HQ и матрица г из-за мни-
мости функции
6+ (Е-Я0) = тА_ + ш6 (£ — //„) (VI.9)
312
ДОПОЛНЕНИЯ
будет давать вклад в мнимую часть оператора ®. Таким
образом, этот оператор ® является комплексным и эта
комплексность обусловлена реальными неупругими про-
цессами.
Перейдем теперь к системе центра масс, в которой
k + p = Уравнение (VI.6) тогда запишется в виде
{Е~ EN(q) — En(q)}q>(q) = J® (£, q\q')ty(q')d3q' (VI.10)
или, в координатном представлении,
{Е—H°N(x) —Z7“[(x)}i|>(x) = $F(£,
(VI.H)
Здесь Н^(х) и Н°л(х) суть гамильтонианы свободного
движения нуклона и л-мезона соответственно. Применяя
к обеим частям этого уравнения один раз оператор
[£— Л^(х)] + Ял(х), а другой раз оператор [£ + Ял(х)]—
— Нм(х), получим уравнения
U(x, х'-, E)ty(x') d3x', (VI.12)
[£N-tf0N(x)]ip(*) = $ V(x, х'-, E)^(x')d3x'. (VI.13)
Эти уравнения приведены в тексте под номерами (23.6)
и (23.7).
Эти уравнения можно получить также из цепочки
уравнений для релятивистских многовременных волновых
функций для системы частиц ф (х19 х2, ..., хк, ..., xN)
(здесь xk=tk, xk есть время и координата ^-частицы,
см. [47]). Наиболее последовательно этот путь получения
уравнения для одновременной функции ф (/, х1У t, х2) =
= xlt х2) осуществлен в работе [48] на основе
теории функций Грина. Авторы получили уравнение, ко-
торое они называют квазипотенциалъным. Преимущество
этого нового вывода одновременного уравнения заклю-
чается в том, что следуя ему: а) автоматически выполнены
необходимые перенормировки, б) потенциал оказывается
локальным и приближенно может быть выражен через
амплитуду рассеяния.
ДОПОЛНЕНИЯ
313
Дополнение VII (к §§ 24 и 29)
Взаимодействие полей в современной теории описы-
вается оператором функции Лагранжа £(х), которая
обычно представляет собою произведение операторов рас-
сматриваемых полей. Это произведение должно удовлет-
ворять требованиям релятивистской инвариантности, не-
которым условиям симметрии и требованию соответствия
с классической теорией, если таковая существует. В част-
ности, для взаимодействия электромагнитного поля
с электронно-позитронным полем ф лагранжиан L имеет
вид
£ = ---рДхМДх),	(VII.1)
где ток Ju(x) равен
2ц(х)=еф(х)уц,ф(х).	(VI 1.2)
Константой связи в данном случае является элементар-
ный электрический заряд е. В случае скалярного элек-
трически нейтрального поля ф = ф+ лагранжиан отобра-
жает взаимодействие этого поля с самим собой. Простей-
шей формой такого лагранжиана является
<VIL3>
где %—некоторая константа связи*).
При достаточно малой константе взаимодействия и
при полностью включенном взаимодействии матрица рас-
сеяния S
S = TexpijL(x)d4x	(VI 1.4)
может быть представлена в виде функционального ряда
(см.’(28.11), (29.22))
5=Е 4т Ут 1 dix> • • • dix«-
п = 0
(VII.5)
*) Заметим, что L — ф3 ведет к динамически неустойчивым си-
стемам; L — ф2 ведет к тривиальным линейнымтуравнениям.
314
ДОПОЛНЕНИЯ
Ввиду того, что лагранжиан L (х) является произве-
дением операторов поля ф, или гр, или Л, каждый член
ряда (VI 1.5) представляет собою сумму произведений
операторов рождения частиц at и операторов их уничто-
жения ak. Последовательность этих операторов, перево-
дящая начальное состояние поля ¥; в конечное Ту,
описывает историю частиц (в смысле графиков Фейнмана),
в результате которой состояние Tz превращается в состоя-
ние Ту. Вычисление матричного элемента SyZ = <Ty|S|Tz>,
описывающего этот переход, может быть существенно
упрощенно, если расположить множители в (VI 1.2) таким
образом, чтобы все операторы уничтожения стояли справа
от операторов рождения.
ТогдаТчасть операторов уничтожения, действуя на Tz,
переводит "его в функционал вакуума То, часть операторов
рождения, действуя слева на функционал Ту, также
переводит его в функционал вакуума То. Вычисление
действия остальных «лишних» операторов сведется к на-
хождению их среднего по вакууму.
Такое^изменение расположения операторов называется
операцией представления Т-произведений через нормаль-
ные V-произведения. Она выполняется на основе легко
проверяемого^соотношения (см. [37, 38]).
т {ф (X) ф (у)} = N {ф (х) ф ш + Dc (х—у), (VII .5')
справедливого для операторов бозонного поля ф(х), и со-
отношения
т {ipa (х) 4>р («/)}=N {гра (х) грэ (у)} + [S, (х—г/)]ар, (VII .6)
справедливого для операторов фермионного поля фф. Заме-
тим, что для комбинаций операторов вида (ф, ф) или
(ф, ф) I- и V-произведения равны между собою. Причин-
ные функции Dc (х) и Sc (х) определены в дополнении I
и называются также свертками. Средние по вакууму от
нормального произведения, очевидно, равны нулю. Поэтому
неисчезающий вклад в матричные элементы S{f создается
из произведений сингулярных функций типа Dc(x—у)
и Se (х — у) и из крайних, «обрамляющих» операторов
уничтожения и рождения частиц, действующих на функ-
ДОПОЛНЕНИЯ
315
ционалы Туг и Tz *). В соответствии со сказанным в прос-
тейшем случае действительного скалярного поля <р (х)
ф (х) = J d3k {a (k) ик (х) 4- а+ (k) Uk (х)}, (VI1.7)
где Uk (х) = е‘кх/У 2<в , (о = '|/йг4"/и2 > матричный эле-
мент Зд. имеет вид
sfi =(^/|а+ (^i) «+ (^) • • -а+ (km) $ Ф,(уи y2t .... ут) х
X $тпф1 (*i> х2,	х„) d^ dly2... diym х
Xdix1diy2... dixna (&() a (k'2).. .n(&m)| ^1), (VII.8)
где через Smn обозначены суммы произведений всех опе-
раторов a+(k)Uk(x) и a(k)Uk(x), за исключением «об-
рамляющих» операторов, которые явно выписаны в (VII.8).
Функция Фу равна
У2. •••> '/J = S^1(z/i)t/ft2(</2). • -Vkm{ym),
(VII.9)
где 2 означает сумму по всем перестановкам /п-частиц,
р
имеющихся в конечном состоянии; подобным же образом
ФДХЬ ха, .... xn) = ^UAx^UAx^.-.U^ (VII.9')
р 1	2	П
есть симметризованная функция n-частиц в начально i
состоянии. Из самого определения «обрамляющих» опе-
раторов следует, что
Sfi =* $ Ф/О1> У* • • •. Ут) S (yt, у2, . . . , Ут\хи Х2.Х„) х
ХФ,- (хп х2, .... х„) d4y± diy2.. .d*ym d*X!d*x2.. .d*xn,
(VII. 10)
где
s(yi, У2....Ут\хи x2, ..., x„)==<Y0/S„OT|¥0> (VII. 11)
— средние по вакууму от всех комбинаций операторов
рождения и уничтожения частиц, описывающих проме-
*) Некоторые матричные элементы могут расходиться. Мы здесь
не будем описывать способы регуляризации («перенормировки») таких
элементов. Эти методы изложены в специальных курсах квантовой
теории поля.
316
ДОПОЛНЕНИЯ
жуточную историю поля от = —оо до t2 ~ °о, ведущие
из состояния i в состояние f.
Из этого краткого очерка следует, что матрица рас-
сеяния S может быть представлена в виде последова-
тельности функций
s„=s(x1, х2, .... х„),	(VII.12)
каждая из которых представляет собой вакуумные сред
ние по истории n-частиц. При этом разбиение на час-
тицы в начальном состоянии (%) и на частицы в конеч-
ном состоянии (у) не является существенным,! как это
видно уже из формулы (VI 1.9). Каждая функция*из числа
функций (VII. 11) может представлять различные физиче-
ские процессы в зависимости от ее возможного разбиения
на начальные (i) и конечные (/) частицы. Именно, функ-
ция s(xx, х21 ..., хп) может представлять процессы
$(У11^2> •••>
S (^1» У2 | Х19 X2t •••> Х»-!’	* мттт 1 Q\
S(Z/1, У29 •••> Уп-1\ХП)-	7
Не все из этих разбиений на i- и /-состояния будут опи-
сывать реальные процессы, происходящие с физическими
частицами. Например, первое разбиение в (VII. 13) озна-
чало бы, что частица уг есть резонансное состояние
(п—1) частицы (х1? х2, ..., xn_i), что противоречит
спектральному разложению (VII.7), предполагающему
лишь один сорт частиц с массой т, и притом стабильных.
Дополнение VIII (к § 27)
А. Виртуальные фотоны нельзя рассматривать отдельно
от их источника. Допустим, что таким источником яв-
ляется частица, локализованная около точки х — 0 и со-
вершающая там квантовый переход вблизи момента вре-
мени t = 0. Ток, создаваемый частицей при этом пере-
ходе, будет равен
JW = jd3p3d3pxexp [—уа2[(Рз—Р/)2 + (Л—л)2)]] X
X ехр[— i(kx—V)] м/(Рз) (Pi)- (VIII.1)
ДОПОЛНЕНИЯ
317
Поле пакета виртуальных фотонов, возникающих при
этом переходе, описывается уравнением
Л g (X, t) = (□2_|_m2) J» W = j ^Р1 ^2_^2_|_m2) X
хехР [— ^-\kp3—pfY+{pi—Pi)2A—^kx—kot) .
(VI11.2)
Для вычисления интегралов в (VIII.2) положим
Р1=£4-А,	А=п+Р/»	(VI1I.3)
так что
Р-— Р1 = (Я—1) + (Р/—Pt), k^(Pf-Pi),
Роз—Рп = Е (р3)—Е (/>,) =Ef—Ei 4-	v£,l+ • •
k^wEj—Ei, ^Ef=uf, ^Ei^Ui-
(VIII.3')
Будем считать, что пакет мал, но =
Далее, для простоты примем, что излучающая частица
является точечной (т. е. будем считать, что ее масса
Тогда для потенциала, пакета получаем из
(VIII.2)
Лр.(х, /) »ехр.р(Лх—kot)—^-((х—Ufty-\- (х—И/02)]
(VIII.4)
— выражение, которое и было принято в основном тексте
(при этом было положено #z = 0, uf=u).
Б. Заметим, что интеграл
/=$ $е-ф(* t^dxdt,	(VIII.5)
— со
где
Ф(х, t) = A2x2 + Bxt + C42 + Dx + Et + G, (VIII.6)
при Д2=4Л2С2—В* > О равен
I = ^.ev,	(VIII.7)
318
ДОПОЛНЕНИЯ
где
4=£e*+-£d*—^ED-G. _ (VIII.8)
В нашем случае
да _ о Г' ЮМ	ГР/+<Р/ ' и г
а2 62 J L 62 a2 J	L 62 "Г a2 J ’
(VIII.9)
где
Л2=^- + ^-’	(VIII.10)
1 / V? 4- Яг	w2 \
С2=Н~ЛГ-+^)’	(VIII.10')
в=—(-^4^+4-L	(viii.ю")
D — i(k—0)4-JL(2X— uT),	(VIII.10'")
E = -i(k0-q0)+±[(X-aT, «)]. (VIII.1O1V)
(Здесь q0—разность четвертых компонент векторов р3
и рг) При специальных значениях А, А, С, В:
А2=^г[2 (®f + ®.2 + «2)+ (»/+».•-«)2]> (VIII.И)'
		л2=4«	(VIII.1Г)
	С2 = —	(р2 ©г2 4- и2),	(VIII. 11")
	в=-		(VIII.11'")
получаем			
ПГ		 X2 2а2	(х—иту 2а2	Т^(2Х-»Т)24-	
^-^(Х-кТ, иГ+-^(2Х-иТ)(Х-иТ, и)-
~^-(k-чУ—^-(^e-^) + ImY,	(VIII.12)
где ImT означает мнимую часть Т. Так как при k=q,
k0 = qt) Im4f=0, то в (VIII.12) ImT вообще можно опус-
тить.
ДОПОЛНЕНИЯ
319
Действительная часть от Y есть положительно-дефи-
нитная квадратичная форма переменных X и Т. Приведем
ее частные значения при a = b, X± = 0,	Т = 0
(здесь Х„=Д(Х«)} :
d*=2a* [1 +4	(VIH.13)
для Хв = 0, Т = 0
Y=-^,	(VIII.13')
для Х = 0, Т #=0
¥ = —(VIII.13")
р
где
_	2	+ + «2) ++«)2
Р2=2а2 - -V-f /.	. (VI11.14)
2 (г>2	г»2 + и2) и2
Дополнение IX (к § 28)
Пусть V есть функционал от некоторой функции,
определенной в пространстве 97 (х):
Т=¥{«(х)}.	(IX.I)
Варьируем функцию и(х) около точки х:
и' (х) = и (х) 4- бы (х),
где вариация би (х) отлична от нуля в окрестности
точки х0.
Если новый функционал можно представить в виде
T, = T{и,(x)} = Чf{н(x)}4-$/7{и(x')}6и(x,)dx,, (IX.2)
то предел
W = Ига	F)„W) (IX.3)
QU W	6u dx-^ 0	°“ W ax
называют функциональной производной функционала V
по функции и (х) в точке х. Другое, более формальное
320
ДОПОЛНЕНИЯ
определение таково:
Тl“'WI7<r|“WI ,	(IX.3')
где 8и (х') = еб (х—х'). В этом определении явно под-
черкнута локализация вариации около точки х. Очевидно,
что определения (IX.3) и (IX.3') эквивалентны.
Если и(х) = в (х) есть пространственноподобная по-
верхность, то
_ iirn W (х)}-Т{о(х)}	ТХ4
ба(х)“^™0	бсо	’
где бео = бег (х) d3x есть четырехмерный объем, заключен-
ный между поверхностями ст'(х) и ст (х) (ср. рис. 30).
Если функционал ¥{и(х)} задан рядом
Т{«} = Т0(х) +
+ ТГ У 'Ф (*1) и (*1) dx± + Ц- у ф (хп х2) и (Хх) и (х2) dx±dx3 +
+ УГ У 'Ф (xlt х2, х3) и (хх) и (х2) и (х3) dxx dx2 dx3, (I X .5)
то его функциональная производная в точке х будет
-а~ц (х) = (*) + 2Т J Х^ U dx2 +
+ тгУ'Ф(х1- x)u(x1)dx1 +
+ Ц- ф (х, х2, х3) и (х2) и (х3) dx2 dx3 +
+ -у- У Ф (Хх, х, х8) и (Xj) и (х3) dxx dx3 +
+	х2, х) и (хг) и (х2) dxTdx2+ ... (IX.6)
Дополнение X (к § 31)
Релятивистская волновая функция для двух частиц.
Рассмотрим волновую функцию для двух свободных час-
тиц, описываемых плоскими волнами
T|)(Xi,	х2, ^2) = ехр (p^i—EiQ]exp [Z (/?2х2—Е2/2)].
(Х.1)
ДОПОЛНЕНИЯ
321
Эта функция имеет физический смысл только в том слу-
чае, когда точки хп t± и/х2, t2 лежат на пространственно-
подобной поверхности.
Введем новые координаты:
Х=ах1+рх2> Т=а/1+р/а, 1
х=х1-х2)	/ = fx-f2,	J	(	’
где а, ₽ > 0, a-J-P=l.
Отсюда
=	/1==Т+Р/, 1
х2 = Х—ах, t2 = T—at. J	(	'
Полный импульс будет
Р=Р1+р2,	E = E± + E2.	(Х.4)
В этих переменных волновая функция (Х.1) имеет вид
ф(Х, Т, х, Z) = exp[f (РХ—ЕТ) + Црх—s/)], (Х.5)
где
P = PPi—8=рЕ1—а£*2	(Х.6)
суть относительные импульс и энергия.
Поскольку точки (xn Q и (х2, /2) лежат на простран-
ственной поверхности, то можно положить /1 = ^2; тогда
/=0, а Т есть общее для обеих частиц время.
В системе центра масс Р=0, так что в этой системе
при t± = t2 имеем
ф(Х, Т, х, 0) = exp[f(px—ЕТ)].	(Х.7)
Здесь величина
E=E(p) = Vml+/fi +Vml+f (Х.8)
есть полная энергия двух частиц в системе центра масс.
В дальнейшем мы изменим обозначение, заменяя Т на
при этом х есть относительная координата частиц, a t —
их общее время. В этих обозначениях разложение функ-
ции ф по сферическим волнам имеет вид
00
г|)(х, 0= 2(2/+l)PJcosft)fy(pr)e-‘£<P>' (Х.9)
/ = 0
11 Л. И. Блохинпетч
322
ДОПОЛНЕНИЯ
и для бесспиновых частиц не отличаются от нерелятиви-
стского. В этой формуле г есть расстояние между части-
цами в системе центра масс,
Rdpr) = J‘+^-r),	(Х.10)
у рг
Ji+i/2(z)—функция Бесселя, —полином Лежандра.
Асимптотический вид функции (Х.9) будет
ф(х, (2/+l)Pz(cosft)[az(£)exp(i(pr —£/)) +
I =0
+ &z(£)exp(— i(pr — Ef)y\, (X.ll)
. /л
где az(£) = / 2, ^(£)==a*z(5).
Дополнение XI (к § 34)
Резонансные состояния. Нерелятивистская теория.
Рассмотрим рассеяние двух частиц, способных к резо-
нансному взаимодействию.
Для определенности предположим, что резонанс имеет
место в s-состоянии *).
Представим волновую функцию s-состояния в виде
	1	/ Et\ <р (g 0=7 (kr) ехР (—]•	(XI.1)
Функция	ф подчиняется уравнению	(XI.2)
где	te	4 ' fa	(XI.3)
Е есть полная энергия, k — волновой вектор, т — приве-
денная масса взаимодействующих частиц: l//n=l/m1+
+ l/m2, У (г) —потенциальная энергия их взаимодействия
в s-состоянии.
) Вычисления для других состояний аналогичны.
Дополнения
323
Специализируем вид У(г) следующим образом (7? —ра-
диус сферы действия):
k2 (г) = 0
k2(r)=kl =
2mV0
А2
для R < r,
для a < r < R,
(XI-4)
(XI.4')
k2 (r) = 0
дляО<г<й (XI.4")
(см. рис. 51). Выбранный вид V (г) допускает существо-
вание резонансных уровней в непрерывном спектре.
Рис. 51. Вид потенциала V (г), приводящего к резонансу при энергии
Е = Е%. На графике пунктиром изображена также волновая функция
ф для Е = Ец.
Решение уравнения (XI.2) записывается в виде
ф,=аег*-(''-Л) + Ье“Н;‘<г_я) для R < г,
ф11=ае+Х(г-Я)-|-ре-М'--Я) дляа<г<7?,
ipni = ysin£r	для 0 < г < а.
(XI.5)
(XI.5')
(XI. 5")
Сшивка этих решений на границах r = R и г=а при-
водит к уравнениям
а + Ь=а4-Р,л
ik t	„> для г = а,
у(а-&)=а-р J
ае~л +PeA=ysin ka, -j
ае~л — реА = у-’yc.Qska / ДЛЯ Г~R’
(XI.6)
(XI.6')
11*
324
ДОПОЛНЕНИЯ
где А=Х(7?— а) > 0. При Л—>оо (R —>оо) из (XI.6) и
(XI.6') имеем условие
D+(£)=l-|-ActgA!a=O,	(XI.7)
определяющее дискретные стационарные уровни для слу-
чая бесконечно широкого барьера.
При конечной величине возникают квазистационарные
резонансные уровни [28]. Для вычисления положения
этих уровней перепишем систему уравнений (XI.6) и
(XI.6') в виде
2a = Aa-t-A*b, Ma-\-M*b=^-ys\nka, (XI.8)
2₽=4*а + Л&, Na + N*b=±-у %-cos ka, (XI.8')
А A
где
Д = 1+^., Л1 = Ле-Л4-4*еЛ, N=Ae~A -Л*ел. (XI.9)
Из (XI.8) и (XI.8') имеем
где
D_(k) — 1 — 4-ctgJfea.	(XI.10')
Пусть kR—один из корней уравнения (XI.7). Тогда
О.(4) = [^]1.1я(4-*я) + ...,	(XI.11)
[т]4..я = -^А<ад-	(XI.11-)
где
Д(М=1+4+^(1+^-)>0.	(XI.12)
лц ля \ rrJ
Поэтому вблизи резонанса отношение (XI. 10) принимает
вид
а _ А [&—(&£ 4-6) —/Г]
Ь~ л* [fe_(^4-6)4-tT] ’
(XI.13)
ДОПОЛНЕНИЯ
325
где
Г = 1ш Г4i е~2Л kR	,
LA* Я Д J
6 = Re ГАе-*л^£^Ж1 .
I /1	ZA j
(XI.14)
(XI.15)
Заметим, что около резонанса амплитуда волновой функ-
ции во внутренней области у стремится к оо.
Действительно, около резонанса
=	4(Я*2-^)	= 4(Л^-Л2) 2 - Л
a sin kga [Л1* + N*] sin kga
(XI.16)
так что при Л—> оо и при Е ж Ед, у/а—>оо: частицы
накапливаются внутри потенциального барьера, в облас-
ти 0 < г < а.
Решение г]^ (kr) при r>R перепишем теперь в виде
суперпозиции первичной s-волны ^ = (sinkr)/kr и волны
е е&г
рассеянной и = [—:
(XI.17)
Простое вычисление на основании формул (XI.5), (XI.9)
и (XI. 13) приводит к результату
_ e-nkR. k—ikR k—kR—irR	(xi jgx
1 2ik k + i'kRk^kR + iVR'	V ’
где
k-R— kR-\-&R.
Матрица рассеяния S преобразующая падающую волну
e~ikr в волну рассеянную eikr, на основании (XI.17) и
(XI. 18) будет иметь вид
=	(XI. 19)
’	k + tlRk—kR + iVR
Первый множитель объединяет факторы, нарушающие
причинность. Это нарушение обусловлено конечным радиу-
сом действия потенциала V (г). Второй множитель опи-
сывает резонанс около точки k = kR.
326
ДОПОЛНЕНИЯ
а)	Аналитические свойства решения в комплексной
плоскости Е. Учитывая, что k2 = <2tnEfa и полагая для
упрощения записи 2т/А2=1, мы можем записать реше-
ние % (см. (XI.5)) в виде
tpj (&г)=аехр [-У—Е (г— /?)] + & ехр [У— E(r—R)]
(XI.20)
и положим
£' = ее‘ф, е=|£|, ei/2 = | fV21.	(XI.21)
Определим: на «физическом», первом листе римановой
Рис. 52. Комплексная плос-
кость (Е). На рисунке показан
переход из точки первого лис-
та (крестик) в точку второго
листа (жирная точка).
поверхности
У—Е = 81/2 ехр [yi (<р—л)] ,
Re/=£r=
=8VaSin ±ср0. (XI.22)
На «нефизическом», втором
листе этой же поверхности
определим Е формулами
]/"—£ — 8 i/2t (<р + л),
ReK^B =
=—е^зшуф^О (XI.22')
и проведем разрез от £ = 0 до £ = + <эо, который будет
отделять эти листы друг от друга (см. рис. 52).
Волновой вектор k в соответствии с (XI.5), (XI.20)—
(XI.22) определится следующим образом:
на физическом листе
ik= —	+181/2ехр (i	(XI.23)
^ = 8!/2ехр (i у) , Im&>0; (XI.23')
на нефизическом листе
ik = — У=Ё=- i8i/2exp(i-j),	(XI.24)
k = — s1/2ехр (i, ImA<0. (XI.24')
ДОПОЛНЕНИЯ
327
Таким образом, физический лист поверхности (В) ото-
бражается на верхнюю полуплоскость переменной k, а не-
физический—на нижнюю полуплоскость переменной k.
Заметим, что в стационарном состоянии компонента
потока, направленная по радиусу-вектору, должна рав-
няться нулю. Поэтому
6(Е)=а(Е*).	(XI.25)
Далее, из симметрии верхней и нижней полуплоскостей
(Е) имеем
а(Е*)=а*(Е).	(XI.26)
Рассмотрим сперва стабильные уровни, которые в опи-
санном выше примере могут быть при А = 0 (R —>оо).
На первом листе имеем
ф (г, t) = [а (Е) ехр (— 8W) +
4-Ь (Е) ехр (е^г)] ехр (— iEt). (XI.27)
Второе решение неограничено растет при г—>оо; поэтому
мы должны потребовать (собственное решение уравнения
(XI.2)), чтобы
6(Е) = 0.	(XI.28)
Это уравнение определяет стабильные уровни, которые
определяются нулями функции на поверхности (Е), ле-
жащими на вещественной полуоси Е < 0.
Заметим, что на втором, нефизическом листе мы имели
бы при Е < 0
ф (г, t) = [а (Е) ехр (s^r) + j
+ &(Е)ехр (—8‘/2r)]exp (— iEt), (XI.29)
так что уровни определялись бы из условия
a(E) = 0.	(XI.28')
В силу условия (XI.25) уравнения (XI.28') и (XI.28) ве-
дут к одному и тому же результату.
б)	Нестабильные уровни. Рассмотрим возможные уров-
ни при комплексных значениях Е, когда ReE>0. По-
требуем опять
6(Е) = 0,
(XI.30)
328
ДОПОЛНЕНИЯ
Пусть
E — ER—tr,	(XI.31)
так что
exp (—iE/) = exp (— iERt—Г/).	(XI.32)
На физическом листе имеем
ik=— V—Е = — е1/2ехр ^yi(y4*2n—л)] =
= — е1/2ехр [-у1'(у + л)] =—ie1/2exp у), (XI.33)
где
у=—arctg Jr-2л/г, /г = 0, 1, (XI.34)
откуда
k = — k'— ix',	(XI.35)
k' =е*/2cos-y, х' =— e1/2siny,	(XI.35')
так что k' >0, х' < 0.
Таким образом, функция на физическом листе имела
бы вид
ф (г, f)=a (Е) ехр [— ik' (г—7?)+н'(г—Е)] ехр (—iERt—Г/).
(XI.36)
Это решение противоречит уравнению непрерывности, так
как ф(г, t) уменьшается с ростом г(х'<0) и с ростом t
одновременно.
Обратимся теперь к решению на втором, нефизичес-
ком листе. В этом случае
ik = — V—Е —— ie1/2 ехр (i у), k — — е1/2 ехр (i у)
и <р=у-}-2л, где у < 0, так что k—k" + ix",
F = e1/2cos-J, H’=eV2sin-|-,	(XI.37)
k’>0, x"<0,	(XI.37')
и волновая функция при г > Е имеет вид
ф(г, f) = а(Е)ехр (ik"r—х"г)ехр(—iERt—Г/). (XI.38)
ДОГЮЛНЁНЙ&
329
Это решение растет с ростом г(х"<0) и убывает с рос-
том^/. Полагая —х' = + |х"|, получим
ф(г, f) = a(E) ехр [f (k"Rr— ERt)]zwp(n"r— Г/). (XI.38')
Полученное решение совместимо с уравнением непрерыв-
ности и потому является правильным [138].
Этот переход с первого листа плоскости (£) на второй
лист легко уясняется, если вернуться к рис. 52. Нуль
E~ER—iT лежит снизу разреза 0 < ER <-|-оо; на рис. 52
он отмечен крестиком. Оставаясь на первом листе, мы
можем попасть из точки E = ER-\-iV в точку E = ER—/Г
только путем обхода разреза слева. При этом фаза вол-
нового вектора k меняется на eiJi и сходящаяся и расхо-
дящаяся волны меняются местами. Чтобы сохранить
условие (XI.30) и прежнее определение расходящихся и
сходящихся волн, мы должны перейти на второй, нефи-
зический лист прямо через разрез ОЕ.
в)	Пространственно-временные свойства резонансных
уровней. Зададим начальное состояние ф? в виде локали-
зованного волнового пакета
i|)« = jc(Z!)^exp[— iE(k)t]dk, (XI.39)
сосредоточенного около значения k = kR*). Для опреде-
ленности положим
c{k) = c для kR—А < k < kR-\- А,
c(k) = 0 вне этого интервала.
Волновой пакет (XI.39) будет иметь вид
^1 (г, t) =	ехр [i (kRr—ERf)\f(r—vt)—
exP Ь1	+ ERt>)-\f(r + vt),	(XI .41)
где функции f(r± vt) существенно отличны от нуля вблизи
r±vt = ^.	(XI.42)
Мы возьмем А >/?. Поэтому столкновение произойдет
около момента времени
(XI.43)
(XI.40)
*) Мы предполагаем, что kR не слишком близко к нулю.
330
ДОПОЛНЕНИЯ
Обратимся теперь к рассеянной волне us(kr, t). Согласно
(XI. 17), (XI. 18) и (XI.39) она будет иметь вид
us{kr, t) —
*й+д
kR~^
Заменяя здесь гладкие функции, обозначенные через g(x),
их значениями в точке k = kR, получим
„,(4г ,0 = сехР1^эд-И] ц ад х
X У ехр [г (г —(XI.44')
-д
Замкнем, считая А—>оо, контур интегрирования полу-
кругом внизу, что можно сделать при г—и/^0. Получим
«,	о =	ехР I? (V-ВД] (-2/Г) х
Хехр [— i (г—vt) iT] =
= ^TSkRR)	Г (f- (Х 1 -45>
Если г — vt > 0, то мы замыкаем в верхнем полукруге и
получим
us(kr, /) = 0 для г—vt > 0,	(XI.45')
что совпадает с результатами § 34.
Дополнение XII (к § 35)
Соотношение унитарности для матрицы рассеяния
S = I-\-it гласит:
SS+ = I + if— if+ + ff+ = 1	(XII.1)
или
Im7, = lf7,+.	(XII.2)
ДОПОЛНЕНИЯ
331
Это операторное равенство можно записать в матричной
форме:
Im Та|з = "2"^^ ТауТ^.
v
В частности, для диагонального члена а = (3, замечая, что
Тау = Туа> имеем
ImTaa=l£|Tav|2.	(ХП.З)
V
Применим это равенство к рассеянию частиц. Тогда
Таа означает амплитуду рассеяния «вперед» (т. е. рассея-
ние без изменения состояния частиц), а сумма членов
|Tav|2 означает полную вероятность перехода из началь-
ного состояния а во все другие состояния у. Следова-
тельно, 21 I2 пропорциональна полному сечению оп.
Более подробное вычисление приводит к результату
Im7(0) = Aan,	(XII.4)
где Т (0) = Таа, а k есть импульс частиц в системе цент-
ра масс. Равенство (XII.4) носит название оптической
теоремы. Оно кажется логически необходимым следствием
теории S-матрицы, так как выражает сохранение вероят-
ностей: уход частиц из начального состояния а компен-
сируется их возникновением в других возможных состоя-
ниях у. Условие унитарности (XI 1.2) не является столь
обязательным, как условие (XII.3), ведущее к оптичес-
кой теореме. Однако, отказываясь от унитарности, мы
теряем математические обоснования формулы (ХП.З). По-
этому отказ от требования унитарности матрицы S или
противоречие с этим требованием ведут к трудно преодо-
лимой ситуации.
Дополнение XIII (к § 37)
Для вычисления упруго рассеянных волн исходим
из формулы (35.10), где функция ® определена посредст-
. вом функции ®0, данной формулой (37.13). Мы начнем с
' рассмотрения первого случая; второй вычисляется проще,
332
ДОПОЛНЕНИЯ
Запишем четырехмерную 6-функцию в виде
б4(Р4 + Рз — р2 — pi) = \diaexpia(pt+p3—р3—рг) (XIII.1)
и функцию Dc (7) в виде
Д(7) = р‘рД(₽)^₽9>	(ХШ.2)
где q=p3— р± или p24~Pi- Подставляя эти выражения в
(37.13), дифференцируя (37.13) по д/дх2 и д/дх° и поль-
зуясь формулой (35.10), получим
^Out (^4 > ^s) = ^2 (^4)	(*з) 4“ J d^Otd^f) X
X ехр i [а (р4 4- р3 — р2 — р±) 4- р4х4 4- р3х3—р2х2 — /^ху] х
X {Dc (₽) ехр [i₽ (р3—рО]4-Д. (₽) ехр [ip (р2 + а)]} X
X dsP1d3p2u3 (х2) U1 (Х1) d*x2d4i, (XIII.3)
где предположено, что первичная волна Tin(x2, х±) пред-
ставляет собою два волновых пакета и2(х2) и и1(х1). Вы-
полним сперва интегрирование по х1} получим
J Ui (Xi) ехр (— ipiXi) d3Xi =	. (X111.4)
Пользуясь теперь (35.4), выполняем интегрирование по рг
и получаем
J	ехр I - ipl (а + ₽>] d3pi = (— а~₽) (х 111.5)
для первого слагаемого в фигурных скобках и
У ехр ipi d3pi = “1 (₽—а) (X111.6)
для второго слагаемого в тех же скобках. Подобным же
образом поступаем с интегрированием по х2 и р2.
Наконец, интегрирование по р3 ведет к функциям
Jexp[ip3(a4-p4-x3)]^|=Z)+(a + P + ^)	(ХШ.7)
И
J ехр [ip3 (а 4- х8)] ^ = D+(a + x3).	(X111.7')
ДОПОЛНЕНИЯ
333
Так же выполняется интегрирование и по р4. Полагая
теперь после интегрирования первого члена в фигурных
скобках а = — %, а-|-(3 = — у, а после интегрирования
второго члена а—f} = — х, (а-|~Р) = — у, получим окон-
чательно
^out (^4» *з)-^2 (^4) ^1 (^з) 4"
+ i $ dixdiyD+(xi—y)D+ (x3—x)Dc(x—y) иъ(х) и2 (у) +
+ ip‘xd^D+(x4+^)D+(x,-^)x
xDe	(XIII.8)
Дополнение XIV (к § 37)
Вычисление функции Д+ (t — r, А, 7И) при А —>- оо сво-
дится к табличным интегралам. Действительно, положим
2m2=/И2, t—г = х=т&, тогда интеграл
со
р piVR
Д+(8, ОО, 7M) = 7H2 0 2
\	/ J 2v2 + Af2
о
(XIV.l)
легко приводится к виду
А+(8, оо, A4) = 6+(8)4-m^7(x),	(XIV.2)
где
7(х) —^2—
О
eizxdz—^^^elzxdz
О
= 1 [- е~хЕ+1 (х) + exEi (- х)].
Здесь
Ei (—х) = — ^^-dt,
E+i (x)=Ei—in
(XIV.3)
(XIV.4)
(XIV.4')
334
ДОПОЛНЕНИЯ
(эти формулы можно найти в известных таблицах •)).
Асимптотические разложения этих функций имеют вид
£Ц_х) = _£_ф_1 + ?!_.. 1	(XIV.5)
A* I	Л Л	J
£+*(x) = -i«+y [l+l+g+...].	(XIV.5')
Поэтому интеграл I (х) при х—>оо равен
=	+	(XIV.6)
и, следовательно,
=	+	(XIV.7)
W'A'	\ Л J
Отсюда на основании (XIV.2) имеем
Д+(е, ОО, М) = 6+(8) + 0	(XIV.8)
Напомним, что 6+ (е) определяется формулой
6+ (е) = 6 (8) + 1	(XIV.9)
(см. (1.9)). Поэтому два последних члена в (Х.9) при
т = М/У2 —>оо является поправочными. Вспоминая зна-
чение т = М/У^^ 1/я]/2 и полагая & = t — г^>а, полу-
чим окончательно
Д+(/-г, оо, 1) =
t-r
=&4t-r) + O [^] + ^1=	. (XIV. 10)
При t—г<^—а получается та же формула с заменой
t — г на —(t—г). Из (XIV.1) следует, что при t — г—*0
функция Д+(/—г, оо, 1/а) регулярна и стремится к по-
стоянному значению
(» “ I)-т- W
*) Таблицу функций Е, Янке и Ф. Эмде, стр, 99, 100, ГостеХ’
издат, 194§,
дополнений
335
Дополнение XV (к § 43)
Уравнение (43.7) может быть выведено следующим
образом *). Пусть S-матрица в координатном представле-
нии дана( как обычно, в виде упорядоченной по времени
экспоненты:
3 = Т ехр (i $ L (х) dx) >	(XV. 1)
где £(х) —лагранжиан, а Т — знак упорядочения по вре*
мени (ср. дополнение VII).
Полагая
$ = /-НЛ	(XV.2)
из (XV. 1) получаем, что
Т — У, “jj У (-^i) • • • L (xs)) dx±... dxt —
S=1
= 2 i«-1 S 9 (/x-Q...0 (G-i-Q L (xx).. 1 (x,) X
S = 1
Xdxx...dx,= 2f,. (XV.3)
s = l
Придадим выражению (XV.3) полностью четырех-
мерный вид, заменяя 0(/) инвариантными функциями
0(пх), где
nx — nj—^nx, а пг=1, п4 > 0.	(XV.4)
В результате получим
2 Ts = 2 15-1 6 («,	—х2) ... 0 (п, х,_х—х,) х
s= 1
XL (хх) ... L (x,) dxx ... dxs. (XV.5)
Как известно, зависимость величин Ts от п в (XV.5)
является чисто фиктивной, так как при (xz—xz+1)2 > 0
всегда 0 (^ —//+х) = 0 (п, х,-—х,-+1), а при (х,—х,+1)2<0
*) В этом дополнении мы следуем работам [139, 140].
336
Дополнения
функция 0(п, х{—xz+1) не дает вклада й СиЛу условия
«локальности»
[£(х,.),	(XV.6)
Ёьшолняюгцегося в этой области.
Положим для определенности
L(x)=g:^:,	(XV.7)
где ф—скалярное поле, и произведем теперь в (XV.5)
преобразование Фурье, полагая
оо
0(»> f	<xv-8)
4JVL	I-to
— oo
L (p) = J e~!PxL (x) dx =
= -p^=- J 6 (p—k2—k2—k3): ф (kJ ф (fe2) ф (fe3) :d£x dk2 dk3,
(XV.9)
где
Ф (fe) = f e~ikx4 <*)dx-	(XV. 10)
В результате будем иметь
Л=£(0),	(xv.ii)
j £(-/гт)^£(пт),	(XV.ll')
Г =	* _х С L (— пт) rfT1. L {пт1—%т2)  rfT2;- ...
J (2лр-1 J '	' тх —ie ' 1	2/ т2—te
— оо
...-^^£(пт5_х).	(XV.11")
Выражения (XV. 11) можно рассматривать как после-
довательные итерации некоторого линейного интеграль-
ного уравнения
оо
Л(лт) = £(пт)=^- j L^-nT')^^R{tiTl) (XV.12)
ДОПОЛНЕНИЯ
337
при условии, что
f=2f,4(0).	(XV. 13)
S =1
Уравнение (XV. 12) является инвариантным уравне-
нием движения для матрицы рассеяния в р-представ-
лении.
Покажем, например, пользуясь уравнением (XV. 12),.
унитарность матрицы S. Для этого перепишем (XV. 12)
в виде
R (пт) = L (пт) -f- J L (пт') F (т—т') dt', (XV. 14)
где
= <XVJ5>
Учитывая, что при эрмитовом сопряжении
L+ (пт) = L (— пт),
(XV. 16)
уравнение, сопряженное (XV. 14), можно записать так
R + (— пт) = L (пт) 4- $ F+ (т'—т) L (пт') dt', (XV. 17)
причем
^(т,-т) = ^У-(т+^ •	(XV-18)
Из (XV. 14) и (XV. 17) следует равенство
R (пт) — R+ (— пт) =
= J L (пт')Р (т—т') dr’ — J F+ (т'—t)L (nTr)dTr.
(XV. 19)
С другой стороны, с помощью тех же уравнений после
простых преобразований можно показать, что
R+ (— пт') F (т—т') dT' — J F+ (т'—т) R (пт') dr' =
= J L (пт’) F (т—т') dT—
— $ F+ (т'—т)L (пт)dr' +	(т)—Фа(т),	(XV.20)
ДОЙОЛЙЁЙЙД
333
где
Фх (Т) = $ F+ L (пт') F (т—т") dr' di", (XV.21)
ф2 (т) = J F+ (т" — т) L (пт') F (т"—т') dr' dT"; (XV.21')
Произведем теперь в (XV.21) последовательные замены
переменных интегрирования:
т' —т"-^?, т' —т"-^т] в Фх(т), (XV.22)
т"_т"—т-^? в ф2(т). (XV.22')
В результате получим
Фх (т) = Ф2(т) = J F+ (?) L (п, Т + S-Т)) F (я) dl drj. (XV.23)
Теперь из (XV. 19) и (XV.20) с учетом (XV.23), вы-
текает, что
Д (пт) — R+ (—пт) —
= J [7? + (—пт) F (т—т')—F* (т'—т) R (пт')] с/т',
или
R (пт) — R + (— пт) =
=i J7^=7?	+(— от') R (пт—пт')+ R+(пт'—пт) R (пт')].
(XV.24)
Полагая в (XV.24) т = 0 и используя формулу
Tl^ = pl + l-Jl6(T),	(XV.25)
будем иметь
R (Q)-R+ (0) = iR+ (0) R (0),	(XV.26)
т. е. условие унитарности матрицы §= 1-H-R (0). Соот-
ношение (XV.24) можно рассматривать как условие
унитарности S-матрицы при т=/=0.
ДОПОЛНЕНИЯ
339
Дополнение XVI (к § 47)
Согласно формулам (38.14') и (38.14") добавочные
члены Yi и Y2 имеют вид
2	2
<XVL1)
A42 + to0
2	2
(XVI.l')
Формулы в этом виде непригодны для сранения с
опытом, так как действительная d и мнимая а части
функции N взяты в формулах в точке со = Ш.
Для оценки функций и Т2 можно воспользоваться
аналитичностью амплитуды в угле от 0° до 90° и боль-
шой величиной М. Для этого рассмотрим функцию
f(z)=I£>=PO2,	(XVI.2)
где
P(Z) = Z^W*	(XVI.3)
Функция f (z) на действительной оси при z = co—>4-00
стремится к постоянному пределу, который мы обозна-
чим через ia. Это предположение эквивалентно пред-
положению о постоянстве полных асимптотических се-
чений о±. В частности, согласно оптической теореме
(см. (XI 1.4))
Rea± = ^.	(XVI.4)
Из (XVI.2) и (XVI.3) при |z| = V, V-^ + оо на осно-
вании теоремы Линделёфа [63] имеем
=	(XVI.3)
и для z = + iV
(xvi.6)
Отсюда
N (jV) = ({)зN (V) = — iN (V).	(XVI.7)
340
ДОПОЛНЕНИЯ
Поэтому
d (iV) = Re N (iV) = + a (V), (XVI.8)
a (iV) = Im N (iV) = — d (V)	(XVI .8')
при большом V. Если характерная частота М настолько
велика, что при V = М уже достигается асимптотическое
значение функции /(z), то можно положить
d(iM) = a(M),	(XVI .9)
a(iM) = d(M),	(XVI.9')
или, имея в виду, что р (М) = 1/2, получим
±d(iM) = A(M),	(XVI. 10)
±a(iM) = — D(M).	(XVI.10')
Поэтому формулы (38.13) и (38.13') можно переписать
в виде
ед=р (®) И°+ (М)+л» (/И)], (XVI.11)
ед—(xvi.ii')
или, выражая амплитуды Л± через полное сечение
А± (/И) =	о± (/И), получим
(со) = —Р («>) [а+ (М) + а- (М)]. (XVI .12)
4л у М. -j-m2
ЛИТЕРАТУРА
1.	Эйнштейн А. Геометрия и опыт.— Л., 1923.
2.	Эйнштейн А.— В кн.: Принцип относительности: К электроди-
динамике движущихся тел, М.: ОНТИ, 1935.
3.	Минковский Г.— В кн.: Принцип относительности: Пространство
й время, М.: ОНТИ, 1935.
4.	Клейн Ф.— В кн.: Об основаниях геометрии: Эрлангенская про-
грамма, М.: Гостехиздат, 1956.
5.	Гравитация и относительность.— М.: Мир, 1965.
6.	Синг Дж. Общая теория относительности.— М.: ИЛ, 1963.
7.	Ньютон И. В кн.: Крылов А. Н.— М.: Изд. АН СССР, 1936,
т. VII/Математические начала натуральной философии.
8.	Гельмгольц Г.— В кн.: Об основаниях геометрии: О фактах,
лежащих в основании геометрии, М.: Гостехиздат, 1956-
9.	Смирнов В. И. Курс высшей математики.— М.: Физматгиз, 1958,
т. IV, т. 91.
10.	Курант Р., Фридрихе К- Сверхзвуковое течение и ударные
волны.—М.: ИЛ, 1950.
11.	Блохинцев Д. И. Метрика пространства времени.— Дубна: Пре-
принт ОИЯИ, Р-2152, 1965.
12.	Петров А. 3. Пространства Эйнштейна.— М.: Физматгиз, 1961.
13.	Фок В. А. Теория пространства, времени и тяготения.— М. Гос-
техиздат, 1955.
14.	Ландау Л. Д., Лифшиц Е. М. Теория поля.— М.: Наука, 1967.
15.	Риман Б.— В кн.: Об основаниях геометрии: О гипотезах, ле-
жащих в основе геометрии.— М.: Гостехиздат, 1956.
16.	Вейль Г.— В кн.: Об основаниях геометрии: Комментарий к ст.
Б. Римана—М.: Гостехиздат, 1956.
17.	Weyl Н. Raum, Zeit und Materie.— Berlin, 1918.
18.	Марцке P., Диллер Д.— В кн.: Гравитация и относительность,
М.: Мир, 1965.
19.	Born М.— Proc. Roy. Soc., 1934, v. A143, p. 410.
20.	Born M., Infeld L.— Proc. Roy. Soc., 1934, v. A144, p. 425.
21.	Блохинцев Д. И.— ДАН СССР, 1952, т. 82, с. 553.
22.	Смирнов В. И. Курс высшей математики.— М.: Физматгиз, 1958,
т. IV, с. 311.
23.	Карман Т. Сверхзвуковая аэродинамика.— М.: ИЛ, 1968.
24.	Блохинцев Д. И.— Атомная энергия, 1963, т. 14. с. 105.
25.	Блохинцев Д. И., Орлов В. И.—ЖЭТФ, 1953, т. 25, с. 513.
26.	Паули В. Теория относительности.— М.: Гостехиздат, 1947.
27.	Дю Моид.— УФН, 1961, т. 73, вып. 4, с. 333.
342
ЛИТЕРАТУРА
28.	Блохинцев Д. И. Основы квантовой механики.— М.: Высшая
школа, 1963.
29.	Блохинцев Д. И. Принципиальные вопросы квантовой меха-
ники.— М.: Наука, 1966.
30.	Блохинцев Д. И.— В кн.: Физика высоких энергий и теория
элементарных частиц: О локализации частиц.— Киев: Наукова
Думка, 1967.
31.	Паули В. Общие принципы волновой механики.— М.: Гостехиз-
дат, 1947.
32.	Широков М. И. Препринт ОИЯИ Е-2478—Дубна, 1965.
33.	Мандельштам Л. М. Собрание сочинений.— М.: Изд. АН СССР,
1950, т. III, с. 397.
34.	Мандельштам Л. И. Собрание сочинений.—М.: Изд. АН СССР,
1950, т. V, с. 347.
35.	Мотт И., Мэсси Г. Теория атомных столкновений.— М.: ИЛ,
1951.
36.	Фейнман Р. Вопросы причинности в квантовой механике.— М.:
ИЛ, 1955.
37.	Ахиезер А. И., Берестецкий Б. В. Квантовая электродина-
мика.— М.: Физматгиз, 1959.
38.	Боголюбов Н. Н., Ширков Д. В. Введение в теорию квантовых
полей.— М.: Гостехиздат, 1957.
39.	Newton Т., Wigner Е. Rev. Mod. Phys., 1949, v. 21, p. 400.
40.	Хофштадтер P. Электромагнитная структура нуклонов.— М.:
ИЛ, 1962.
41.	Дрелл С.Г., Закариадзен Ф. Электромагнитная структура нукло-
нов.—М.: ИЛ, 1962.
42.	Блохинцев Д. И., Барашенков В. С., Барбашев Б. М.— УФН,
1959, т. 68, с. 417.
43.	Chew К. W. et al. XII Международная конференция по физике
высоких энергий в Дубне.— М.: Атомиздат, 1964, т. I, с. 861.
44.	Окунь Л. Б. Слабые взаимодействия элементарных частиц.—
М.: Физматгиз, 1963.
45.	Blokhintsev D., Barachenkov V., Grishin V.— Nuovo Cimento,
1958, v. 9, p. 249.
46.	Блохинцев Д. И.— ДАН СССР, 1946, т. 53, с. 205.
47.	Blokhintsev D.— Nuovo Cimento, ser. X, 1964, v. 33, p. 1094.
48.	Логунов А. А. и др. Препринт ОИЯИ, Д-1191.— Дубна, 1962,
Nuovo Cimento, 1963, v. 30.
49.	Пузиков Л. Д., Рындин Р. М., Смородинский Д. А.— ЖЭТФ,
1957 т 32 с. 592
50.	Blokhintsev D.— Nuclear Physics, 1962, v. 31, p. 628.
51.	Блохинцев Д. И.— УФН, 1959, т. 69, вып. 3.
52.	Fierz М.— Helv. Phys. Acta, 1950, v. 23, p. 731.
53.	Stuekelberg E., Rivier D.— Helv. Phys. Acta, 1949, v. 22, p. 215.
54.	Блохинцев Д. И.— В кн.: Пространство, время, причинность.
Препринт ОИЯИ, Д-1735.— Дубна, 1964.
55.	Bloch F.—Sov. Phys., 1943, v. 5, p. 301.
56.	Мейер А. А. Дипломная работа.— Физ. фак. МГУ, 1945.
57.	Kronig R.— J. Amer. Opt. Soc., 1926, v. 12, p. 547.
58.	Kramers H. A.— Atti Congr. Inst. Fisici Como, 1927, v. 2, p. 545,
59.	Goldberger M. L.— Phys, Rev., 1955, v. 97, p. 508.
ЛЙТЁРАТУРА
343
60.	Symanztk К., Jost D. Reports of the Conference in Siatle, 1956.
61.	Боголюбов H. H., Медведев Б. В., Поливанов M. /<. Вопросы
теории дисперсионных соотношений.— М.: Физматгиз, 1958.
62.	Померанчук И. Я-— ЖЭТФ, 1958, т. 34, с. 725.
63.	Нейман Н. Н. В кн.: Вопросы физики элементарных частиц.—
Ереван, 1962.
64.	Логунов А. А., Тодоров И., Нгуен Ван Хьеу—УФН, 1966, т. 88,
вып. I.
65.	Черников Н. А. Препринт ОИЯИ, Р-723.— Дубна, 1961.
66.	С мор одинокий Я. А.— Препринт ОИЯИ, Р-11Р9.— Дубна, 1962;
Fortschr. d. Phys. 1965, Bd. 113, Hf. 4.
67.	Rosenfeld A. H. et al. Preprint JINR, R1-3129, 1967.
68.	Широков Ю. М,— ЖЭТФ, 1957, т. 33, с. 861.
69.	Blokhintsev D. /., Kolerov G. I.— Nuovo Cimento, Ser. X, 1966,
v. 44, p, 974.
70.	Blokhintsev D. /., Kolerov G. I.— Nuovo Cimento Macroscopic
Causality.— Centre Theor. Phys. Trieste, IC/67/36, 1967.
71.	Blokhintsev D.— Acta Phys. Acad. Sci. Hung., 1967, v. 22. p. 307.
72.	Blokhintsev D. I., Kolerov G. I.— Nuovo Cimento, Ser. X, 1964,
v. 34, p. 163.
73.	Блохинцев Д. И., Виноградов В. М. Препринт ОИЯИ, Р2-3506.—
Дубна, 1967.
74.	Блохинцев Д. И.— Ученые записки МГУ, сер. Физика, 1945,
книга III, вып. 77, с. 101.
75.	Блохинцев Д. И.— ЖЭТФ, 1946, т. 16, с. 480.
76.	Blokhintsev D.— J. Phys. USSR, 1946, v. 10, p. 167.
77.	Блохинцев Д. Я.—ЖЭТФ, 1947, т. 17, с. 266.
78.	Нейман Н. Н.— ЖЭТФ, 1964, т. 47, с. 1966.
79.	Ефимов Г. В. Препринт ОИФИ, Р2-3390.— Дубна, 1967.
80.	Блохинцев Д. Я.—ЖЭТФ, 1947, т. 17, с. 116.
81.	Blokhintsev D.— J. Phys. USSR, 1940, v. 2, p. 453.
82.	Wat agin G — Zs. Phys., 1934, v. 88, p. 92.
83.	Markov M. A.— J. Phys. USSR, 1940, v. 2, p. 433.
84.	Блохинцев Д. И.— ЖЭТФ, 1948, т. 18, с. 566.
85.	Блохинцев Д. И— ЖЭТФ, 1951, т. 22, с. 254.
86.	Menger К-—Proc. Nat. Acad. Soc. USA, 1951, v. 37, p. 226.
87.	Schweiser B., Selar A.— Pacific J. Math., 1960, v. 10, p. 313.
88.	March A.—Zs. Phys., 1934, v. 104, p. 93; 1937, v. 105, p. 620.
89.	Марков M. А. Гипероны и К-мезоны.— M.: Физматгиз, 1964.
90. Ingraham R. I.— Nuovo Cimento, Ser. X. 1964, v. 34, p. 182.
91.	Ingraham R. I. Renormalization Theory of Quantum Field with
a Cut-off.— N. Y.: Gordon et Beach, 1967.
92.	Tikawa H. Research Inst. Fund. Phvs. Kyoto Univers., RiFP-55,
1966.
93.	Широков Ю. М,— ЖЭТФ, 1951, т. 21, с. 748.
94.	Ambarzumian V., Ivanenko D.— Zs. Phys., 1930, v. 64, p. 563.
95.	Darling B.—Phys. Rev., 1950, v. 80, p. 460; 1953, v. 91, p. 1252.
96.	Das. A.— Nuovo Cimento, 1960, v. 18, p. 482.
97.	Вяльцев A. H.— Дискретное пространство — время.— M.: Наука,
1965.
98.	Snyder Н.— Phys. Rev., 1947, v. 71, p. 38.
99.	Гольфанд H. А.—ЖЭТФ, 1959, т. 37, с. 504.
344
ЛИТЕРАТУРА
100.	Кадышевский В. Г.—ЖЭТФ, 1961, т. 41, с. 1885; ДАЙ СССР,
1962, т. 147, с. 588.
101.	Голъфанд Н. А.—ЖЭТФ, 1962, т. 43, с. 256; 1963, т. 44, с. 1248.
102.	Кадышевский В. Г.— ДАН СССР, 1962, т. 147, с. 1336.
103.	Тамм И. Е. XII Международная Конференция по физике высо-
ких энергий в Дубне.— М.: Атомиздат, 1964, т. II, с. 229; Proc,
of Int. Conf, on Element. Part.—Kyoto, 1965, p, 314.
104.	Кадышевский В. Г.— В кн.: Пространство, время, причинность.
Препринт ОИЯИ Д-1735.— Дубна, 1964.
105.	Blokhintsev D.— Phys. Letts., 1964, v. 12, p. 272.
106.	Blokhintsev D.— Nuovo Cimento, 1960, v. 16, p. 382.
107.	Марков M. А. Препринт ОИЯИ, E2-2973.— Дубна, 1966.
108.	Барбашев Б, М., Черников Н. А. Препринт ОИЯИ, Р-2151.—
Дубна. 1965.
109.	Барбашев Б. М., Черников Н. А.— ЖЭТФ, 1966, т. 50, вып. 5.
НО. фон Нейман И. Математические основы квантовой механики.—
М.: Наука, 1967.
111.	Barashenkov	V.	S.—	Fortschr. Phys., 1962, v. 10, p.	205.
112.	Barashenkov	V.	S., Dedya	V. I.— Nucl.	Phys., 1966,	v.	64,	p.636.
113.	Hohler G., Ebel G., Giesiche I.— Zs. Phys., 1964, v. 108, p. 430.
114.	Foley К- J-	st	al.—	Phys.	Rev. Letts.,	1963, v. 11,	p.	425.
115.	Kirillova L.	et	al.—	Phys.	Letts., 1964,	v. 13, p. 93.
116.	Никитин В. А. и др. Школа физиков в Ереване, 1965.
117.	Gabraith W. et al. XII Международная конференция по физике
высоких энергий в Дубне.— М.: Атомиздат, 1964, т. I, с. 109.
118.	Lindenbaum S. I. XII Международная конференция по физике
высоких энергий в Дубне.— М.: Атомиздат, 1964, т. I, с. 188.
119.	de Pagter I. et al.— Phys. Rev. Letts, 1964, v. 12, p. 739.
120.	de Pagter I. et al.— Proc. Int. Sump, on Electron and Photon
Interactions, 1965, v. 11, p. 360.
121.	Drell S. D. Раппортерский доклад, Proc. XIII Int. Conf, on
High Energy Physics.— Berkeley, 1967, p. 85.
122.	Drell S. D.— Ann. Phys.. 1958, v. 4, p. 75.
123.	Christensen I. H., Cronin I. W., Fitch V. L., Tarlay R.
XII Международная конференция по физике высоких энергий
в Дубне.— М.: Атомиздат, 1964, т. II, с. 105.
124.	Терентьев М. В.— УФН, 1965, т. 86, вып. 2, с. 231.
125.	Dorfman D. et al.— Phys. Rev. Letts, 1967, v. 19, p. 987.
126.	Bennet S. et al.— Phys. Rev. Letts, 1967, v. 19, p. 993.
127.	Feynman R.— Phys. Rev., 1949, v. 76, p. 749 (см. пер. в кн.:
Новейшее развитие квантовой электродинамики, М.: ИЛ, 1954).
128.	Паули В.— В кн., Нильс Бор и развитие физики, М.: ИЛ, 1958.
129.	Tost R.— Helv. Phys. Acta, 1957, v. 30, p. 409.
130.	Блохинцев Д. Я.—ЖЭТФ, 1947, т. 17, с. 924.
131.	Шапиро И. С.—УФН, 1957, т. 61, с. 313.
132.	Арбузов Б. А., Филиппов А. Т. Препринт ОИЯИ, Р2-2578.—
Дубна, 1966.
133.	Арбузов Б. А., Филиппов А. Т. Препринт ОИЯИ, Р2-3067.—
Дубна, 1966.
134.	Christensen /. Н. et al.— Phys. Rev. Letts, 1964, v. 13, p. 138.
135.	Bonard X. D. et al.—Phys. Rev. Letts, 1965, v. 15, p. 58.
136.	Никитин В. А. и др.— ПТЭ, 1963, № 6, с. 18.
ЛИТЕРАТУРА
345
137.	Blokhintsev D. I.— Comp. Rendus USSR (Dokladay), 1946,
t. 53, № 3.
138.	Ландау Л. Д., Лифшиц E. M., Квантовая механика.— M.:
Физматгиз, 1963.
139.	Кадышевский В. Г. Препринт ОИЯИ, Р-1327,—Дубна, 1963.
140.	Кадышевский В. Г. Препринт ОИЯИ, Р-1328,— Дубна, 1967.
141.	Смородинский А. Д.— УФН. т. 39, с. 325.
142.	Иваненко Д. Д.— В кн.: Сдвиг уровней атомных электронов.—
М.: ИЛ, 1950.
143.	Panovsky W. Electromagnetic Interactions Proc. XIV Conf, on
High Energy Physics.— CERN, 1968, p. 23.
144.	Blokhintsev D.— Nuovo Cimento, Ser. X, 1958, v. 9, p. 925.
145.	Blokhintsev D. Proc. Berkeley Conf, on Instrumentation.— Ber-
keley, 1960, p. 198.
146.	Blokhintsev D.— Fortschr. Phys., 1969.
147.	Cronin I. W. Proc. XIV Int. Conf, on High Energy Physics.—
CERN, 1968. p. 300.
148.	Hohler G., Kaiser F. Reviev and Tables of Pion-Nucleon For-
ward Amplitudes. Preprint KfK 3027.— Karlsruhe, 1980.
149.	Ankenbrandt C. et al. Preprint Fermilab. Pub. 80/27—exp.,
1980.
150.	Brach E. et al. Preprints CERN/HERA, 72—1,2. 1972; 73—1,
1973.
151.	Carol A. S. et. al. Preprint Fermilab., Pub. 75. Exp.—7100—
104, 1975.
ИМЕННОЙ УКАЗАТЕЛЬ
Блох 160, 168 Блохинцев 231, 238, 272 Боголюбов 163, 173, 174 Борн 42, 46, 275 Брейт 230, 232 Ватагин 239 Вейль 37, 38 Вигнер 92, 100, 101 Гейзенберг 143, 147, 210 Гельмгольц 33 Гильберт 157, 185 Гольдбергер 173 Гордон 102 Грин 26, 75, 134, 137, 138, 140— 142, 146, 150, 219, 221, 236— 239, 241, 301, 312 Дирак 78—80, 83, 101, 103, 112, 121, 122, 256, 305, 308 Инфельд 42, 275 Киллинг 35 Клейн 24, 37, 43, 86, 102, 103, 134, 215 Колеров 231 Коши 56, 170, 172, 177, 276 Крамере 169 Кристоффель 30 Крониг 169	Ланде 290, 299 Лобачевский 57, 184, 185, 188, 197, 198, 215, 224 Мандельштам 62 Марков 239 Марцке 38 Минковский 236, 240, 242, 244, 269 Ньютон Т. 98, 100, 101 Риман 32—34, 36, 47 Симанчик 173 Снайдер 261 Томонага 159, 161, 162, 263 Фейнман 106, ПО, 126, 129, 199, 226, 263, 266, 291, 308 Ферми 80, 146 Хофштадтер 114 Швингер 159, 161, 162, 263 Шредингер 57, 60, 94, 122, 162, 163, 168 Штюкельберг 163 Эйнштейн 36, 46, 48, 236, 240, 242, 244, 254, 269, 270
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютное будущее 19
— прошедшее 19
Асимптотические состояния 183,
184, 197
Борновское приближение 103
Вектор внешний 243, 269, 282, 294
— внутренний 243, 282
Волновая зона 195, 217
Волновой функционал 158, 159,
164
-----, нормировка 158, 159
Временная область 20, 48
Временной интервал 48
Геодезическая линия 31
Гипотеза Римана 32, 33
Диаграммы Фейнмана 106, ПО,
117, 126, 199, 202, 226, 267
Дисперсионные соотношения 170,
172, 174, 180
Дифференциальное сечение упру-
гого рассеяния 118
Задача Коши 56, 256
Закон Гука 17
— сохранения заряда 140
Запаздывающая функция; ферми-
онное поле 302
Инвариант 32, 44, 124, 159, 188
Интервал 32, 39, 40, 144
—	временной 40
—	пространственный 41
Калибровка системы 40, 50
Квазипотенциальное уравнение
312
Ковариантная производная 30
Ковариантный вектор 29
— тензор 29
Комбинированная четность 291
«Комок» событий 44
Контравариантный вектор 29
— тензор 29, 34
Косвенное измерение 62, 73, 103
Коэффициенты аффинной связно-
сти, см. Символы Кристоффеля
Локализация частиц, полей 59, 65,
70, 83, 86, 95, 101, 117, 128, 148,
153
Локальная акаузальность 217, 284
Локальности требования 167, 220
Матрица амплитуды рассеяния 162
--------, унитарность 163
— рассеяния 102, 127, 162 ид.
----, локальность 167
----, почти локальность 234
----, релятивистская инвариант-
ность 168, 186
----, трансляционная инвари-
антность 187
----, унитарность 162, 183, 217,
229, 330, 337
348
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Матрицы Дирака 78, 112
Мезонная атмосфера нуклона 120
Метрическая геометрия 32
Метрический тензор 32, 34
Мировая линия 39
Обобщенное взаимодействие 238
Общее преобразование координат
28, 47
Оператор Дирака 121
— координаты Ньютона — Вигне-
ра 98
Опережающая функция, фермион-
ное поле 302
Оптическая теорема 123, 163, 179,
331
Параметр удара 124
Перекрестная симметрия 190
Плотность действия 139
Полный опыт 124
Поляризация вакуума 107
Правила коммутации, бозонное
поле 87
-----, векторное поле 144
----- операторов 55
-----, скалярное действительное
поле 143
-----, — комплексное поле 143
-----, спинорное поле 144
-----, фермионное поле 78
-----, электромагнитное поле 92
Представление взаимодействия
159, 162
Преобразование Лоренца 42, 146,
168, 186
Причинная функция 146, 150, 226
-----, фермионное поле 302
Причинность макроскопическая
215, 216, 224, 227, 229
— микроскопическая 144, 212, 222
-----, минимальное нарушение
231
—, принцип 158, 160, 171
Пространственная область 20
Пространственные решетки 27
Пространство асимптотических со-
стояний 185, 199, 283
— Гильберта 185
— конечных состояний 185
Пространство Лобачевского 57,
184, 212, 224
— начальных состояний 185
— псевдоевклидово 33, 47, 50
— Снайдера 261, 263
— стохастическое 251
— Эйнштейна — Минковского
236, 242, 269
Прямое измерение 61, 101, 102
Резонансы 203, 210
«Резононы» 203, 210
Риманова геометрия 32
Свертка 314
Сигнал 20, 23, 25, 37, 49, 147
Сигнатура метрики 32, 41
Символы Кристоффеля 30
Система Брэйта 230
Слабый разрыв производной 20, 43
Событие 14, 244, 252
Соотношение неопределенностей
143, 147
Средний	квадратичный радиус
нуклона, магнитный 114
—---------, электрический 113
Тензор кривизны многообразия,
см. Тензор Римана
—	Римана 32
—	энергии-импульса поля 93
Теорема Коши 170, 172, 177
—	Линделёфа 339
—	Стокса 31
Точечность частицы 105
Требование локальности 168
Т-произведение 145, 161, 167
Уравнение Борна — Инфельда 275
—	геометрической оптики 21
— Даламбера 91
— Дирака 83, 103, 112, 256, 305
---релятивистское 57, 78
— Клейна 24, 43, 86, 103, 215
— Томонага — Швингера 159, 162
— Шредингера 57, 60, 68, 94, 122
— Эйнштейна 46, 48, 170
Уравнения Киллинга 35
Условие Блоха 160, 168
— локальной акаузальности 217
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
349
Условия локальной коммутации
144, 212, 222
— симметрии амплитуды 231
— спектральности амплитуды 231
Физическое поле 238
Фокус события 245, 247
Формфактор 109, 111, 114, 151
Функция Грина 26, 69, 75, 135, 236
-----запаздывающая 135, 138,
219» 301
Функция Грйна опережающая
136, 221, 301
— Лагранжа 42
Характеристический конус 22
Хроногеометрия 41, 50
Эффективный заряд 107
— потенциал мезон-нуклонного
взаимодействия 133
Дмитрий Иванович Блохинцев
Пространство и время в микромире
Редакторы М. К. Волков, Т, Г. Корышева
Техн, редактор И. Ш. Аксельрод
Корректор Л. И. Назарова
ИБ № 11975
Сдано в набор 12.02.82. Подписано к печати
28.07.82. Т-11167. Формат 84Х1081/зг. Бумага
тип. № 1. Литературная гарнитура. Высокая печать.
Условн. печ. л. 18,48. Уч.-изд. л. 17,83. Тираж
10 000 экз. Заказ № 31. Цена 1 р. 40 к.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Октябрьской Революции и ордена Трудового
Красного Знамени Первая Образцовая типография
имени А. А. Жданова Союзполиграфпрома при
Государственном комитете СССР по делам изда-
тельств, полиграфии и книжной торговли. Москва,
М-54, Валовая, 28.
Отпечатано в типографии № 2 изд-ва «Наука»,
Заказ 1921	Москва, Шубинский пер., 10.
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
117071, Москва, В-71, Ленинский проспект, 15
ГОТОВИТСЯ К ИЗДАНИЮ
В 1982 ГОДУ :
Каталог книг Главной редакции физико-математической лите-
ратуры издательства «Наука», вышедших в 1965—1980 гг.— М.: Нау-
ка, Главная редакция физико-математической литературы.
Каталог содержит полный перечень библиографических описаний
книг, выпущенных Главной редакцией физико-математической лите-
ратуры издательства «Наука» за 16 лет (1965—1980). Материал систе-
матизирован по тематическому принципу (литература по математике,
физике, механике и процессам управления и астрономии). В отдель-
ный раздел выделена «Библиотечка «Квант». В большинстве случаев
раскрывается содержание описываемых книг, приводятся учебные
грифы или перечисляются параграфы и главы. Для удобства пользо-
вания каталогом он снабжен именным указателем авторов, титуль-
ных редакторов и переводчиков.
Для научных работников, инженеров и преподавателей, пользую-
щихся физико-математической литературой, а также специалистов,
работающих в органах научно-технической информации, билиотеч-
ных и книготорговых работников.
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУР Ы
117071, Москва, В-71, Ленинский проспект, 15
ГОТОВИТСЯ К ПЕЧАТИ:
Паули В. Теория относительности: Пер. с англ.— 2-е изд.
испр. / Под ред. В. Л. Гинзбурга и В. П. Фролова.
Книга написана известным физиком-теоретиком и является клас-
сической книгой по теории относительности. Она включает основы и
Систематическое построение специальной теории относительности.
Кроме того, она содержит общую теорию относительности, а также
рассмотрение теорий о природе заряженных элементарных частиц.
Предыдущее издание выходило в 1947 г.
Для научных работников, аспирантов и студентов старших кур-
сов, интересующихся вопросами теоретической физики.