В. А. Лукас
ТЕОРИЯ УПРАВЛЕНИЯ
ТЕХНИЧЕСКИМИ СИСТЕМАМИ
3-е издание, переработанное и дополненное
Компактный учебный курс
для студентов, обучающихся в вузах по направлению
высшего профессионального образования
«Автоматизация и управление»
Екатеринбург 2002
ББК 33 1 32
Л 84
УДК 681 5 011 (075 8)
Л у кас В. А.
Л 84 Теория управления техническими системами Компактный учеб курс
для ву юв - 3-е издание, перераб и дополн - Екатеринбург Изд-во
УГГГА 2002 - 675 с ил 214
И сложены основные принципы и аетоды теории управления техниче-
скими объектами фундаментальные принципы построения автоматических
систем \ правления, методы их математического описания и структурного
анализа критерии оценки устойчивости и качества таких систем при детер-
минированных и случайных воздействиях, способы оптимизации структуры
и параметров систем, основы анализа дискретных и нелинейных систем
управления
Наряду с традиционным структурным представлением систем управ-
ления (метод «вход-выход») использован современный векторно-
матричныи метод пространства состояний (МПС) Изложены основанные на
МПС критерии оценки наблюдаемости и управляемости объектов управле-
ния основы оптимальной фильтрации сигналов и оптимального оценивания
состояния объектов управления, методы синтеза оптимальных систем
управления при полной и неполной информации об объекте
Третье издание дополнено изложением базовых принципов синтеза ал-
горитмической структуры замкнутых систем управления, элементов теории
многосвязных систем, сведений из новейшей области теории управления -
fuzzy-управления, основанного на теории нечетких множеств
Излагаемые принципы и методы иллюстрированы конкретными при-
мера ми Особое внимание уделено физическим трактовкам математических
положений теории у правления
Первое издание (1977 г) вышло под заглавием «Основы теории авто-
матического управления», второе издание, переработанное и дополненное
(1990 г) - под заглавием «Теория автоматического управления»
Для студентов, обучающихся в ву зах по направлению «Автоматизация
и у правление»
© Издательство «Недра», 1977
© Издательство «Недра», 1990
© Уральская государственная
горно-геологическая академия 2002
© Лу кас В А, 2002 с изменениями и
дополнениями
Оглавление
Предисловие	7
Сокращения и условные обозначения, принятые в книге	14
Введение	16
Глава 1. ВВОДНЫЕ СВЕДЕНИЯ О СИСТЕМАХ
УПРАВЛЕНИЯ	26
1 1 Основные понятия теории управления	26
1 2 Функциональная и алгоритмическая структуры системы
управления	34
1 3 Принципы построения и классификация систем
управления	39
1 4 Примеры систем управления	48
Контрольные задания и вопросы	35
Глава 2. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ
ЛИНЕЙНЫХ ЭЛЕМЕНТОВ И СИСТЕМ УПРАВЛЕНИЯ	56
2 1 Общие понятия о передаточных свойствах элементов и систем 56
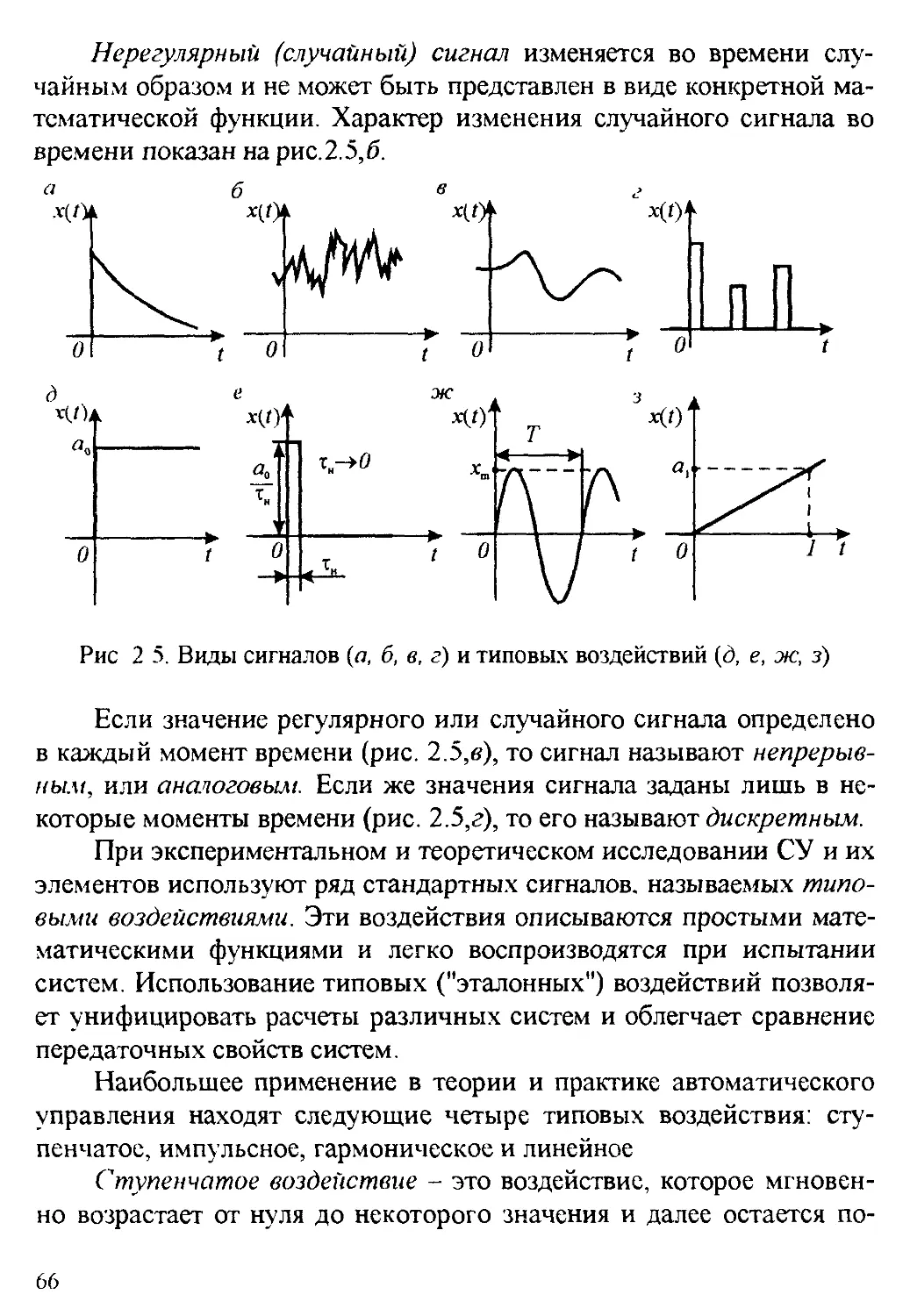
2 2 Временные и спектральные характеристики типовых во ^действий
и сигналов	65
2 3 Статические характеристики элементов	78
2 4 Линейные дифференциальные уравнения как динамические
характеристики	86
2 5 Временные характеристики	94
2 6 Операторный метод и передаточная функция	99
2 7 Частотные характеристики	107
2 8 Статические и динамические характеристики типовых соединений
элементов	115
2 9 Векторно-матричная форма описания многомерных элементов и
систем управления	123
2 10 Комплексный пример математического описания объекта
управления	143
2 11 Элементарные операции машинного математического
моделирования	151
Контрольные задания и вопросы	157
Глава 3. ХАРАКТЕРИСТИКИ ТИПОВЫХ ДИНАМИЧЕСКИХ
ЗВЕНЬЕВ ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ	159
3 1 Классификация звеньев	159
3 2 Безынерционное звено	161
3 3 Инерционное звено первого порядка	165
3 4 Инерционные звенья второго порядка	172
3 5 Интегрирующие звенья	183
3 6 Дифференцирующие звенья	190
3 7 Звено запаздывания	195
3 8 Приближенные модели динамики инерционных статических
объектов управления (ОУ)	201
Контрольные задания и вопросы	208
Глава 4. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ХАРАКТЕРИСТИКИ
ТОЧНОСТИ СИСТЕМ УПРАВЛЕНИЯ (СУ)	210
4 1 Правила преобразования алгоритмических структур	210
4 2 Примеры составления передаточных функции и уравнений
динамики СУ	220
4 3 Передаточные функции типовой одноконтурной СУ	226
4 4 Точность статических и астатических СУ при типовых
воздействиях	233
Контрольные задания и вопросы	250
Глава 5. АНАЛИЗ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ
УПРАВЛЕНИЯ	252
5 1 Понятие, виды и общее условие устойчивости	252
5 2 Алгебраические критерии устойчивости	259
5 3 Критерий Михайлова	266
5 4 Критерий Найквиста	272
5 5 Построение областей устойчивости	282
5 6 Влияние структуры и передаточного коэффициента СУ
на устойчивость	295
Контрольные задания и вопросы	301
Глава 6. ОЦЕНКА КАЧЕСТВА УПРАВЛЕНИЯ	304
6 1 Понятие и показатели качества	304
6 2 Приближенная оценка качества по частотным характеристикам 317
6 3 Интегральные показатели качества	328
6 4 Оценка чувствительности СУ	337
6 5 Оценка > правляемости и наблюдаемости многомерного ОУ 343
6 6 Общие сведения о методах расчета переходных процессов
на ЭВМ	349
Контрольные задания и вопросы	357
Глава 7. МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ СИСТЕМ
УПРАВЛЕНИЯ	359
7 1 Общие сведения о синтезе СУ	359
4
7 2 Основные принципы синтеза алгоритмической структуры
одноконтурной СУ	362
7 3 Синтез СУ с желаемыми динамическими свойствами	374
7 4 Стабилизация и коррекция частотных свойств СУ	381
7 5 Улучшение качества систем при помощи дополнительных
каналов управления	396
7 6 Оптимизация и выбор настроечных параметров СУ	412
Контрольные задания и вопросы	433
Глава 8. АНАЛИЗ И СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
УПРАВЛЕНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ	435
8 1 Общие сведения о статистическом подходе к расчету СУ 435
8 2 Характеристики случайных сигналов	439
8 3 Типичные случайные сигналы	451
8 4 Преобразование случайного сигнала линейным динамическим
звеном	455
8 5 Вычисление и минимизация дисперсии сигнала ошибки
управления	462
8 6 Определение оптимальной передаточной функции СУ
(задача Винера)	471
8 7 Оптимальная фильтрация векторных случайных сигналов
(фильтр Калмана)	477
8 8	Оптимальное оценивание состояния многомерного ОУ	484
Контрольные задания и вопросы	487
Глава 9. ОСНОВЫ АНАЛИЗА ДИСКРЕТНЫХ СИСТЕМ
УПРАВЛЕНИЯ	489
9 1	Общие сведения о дискретных СУ	489
9 2 Функциональная и алгоритмическая структуры
амплитудно-импульсной СУ	494
9 3	Математическое описание амплитудно-импульсной СУ	501
9 4 Основное условие и критерии устойчивости импульсных СУ 512
9 5	Оценка качества импульсных СУ	517
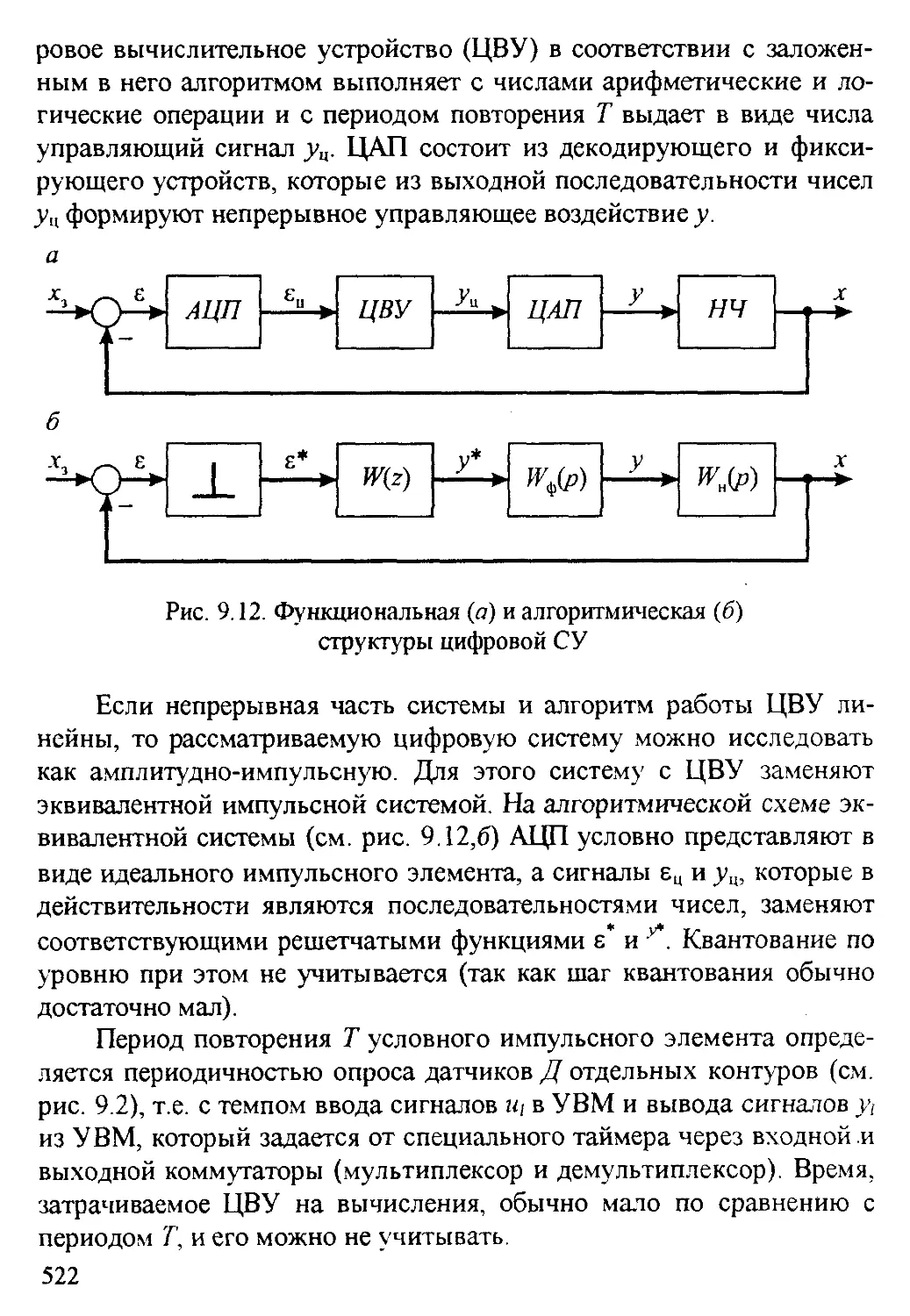
9 6 Структура и характеристики цифровой СУ	521
Контрольные задания и вопросы	526
Глава 10. ХАРАКТЕРИСТИКИ И ОСНОВНЫЕ МЕТОДЫ АНАЛИЗА
НЕЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ	528
10 1 Особенности нелинейных СУ	528
10 2 Типовые нелинейные элементы СУ	532
10 3 Метод фазовых траекторий	537
10 4 Метод гармонической линеаризации	547
5
10 5 Оценка абсолютной устойчивости с помощью критерия Попова 559
10 6 Основные сведения о вибрационной и статистической
линеаризации	563
Контрольные задания и вопросы	576
Глава 11. ПРИНЦИПЫ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ И
АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ	578
11 1 Общая характеристика и классификация задач оптимального
управления	578
11 2 Принцип максимума и метод динамического
программирования	593
11 3 Системы, оптимальные по быстродействию	607
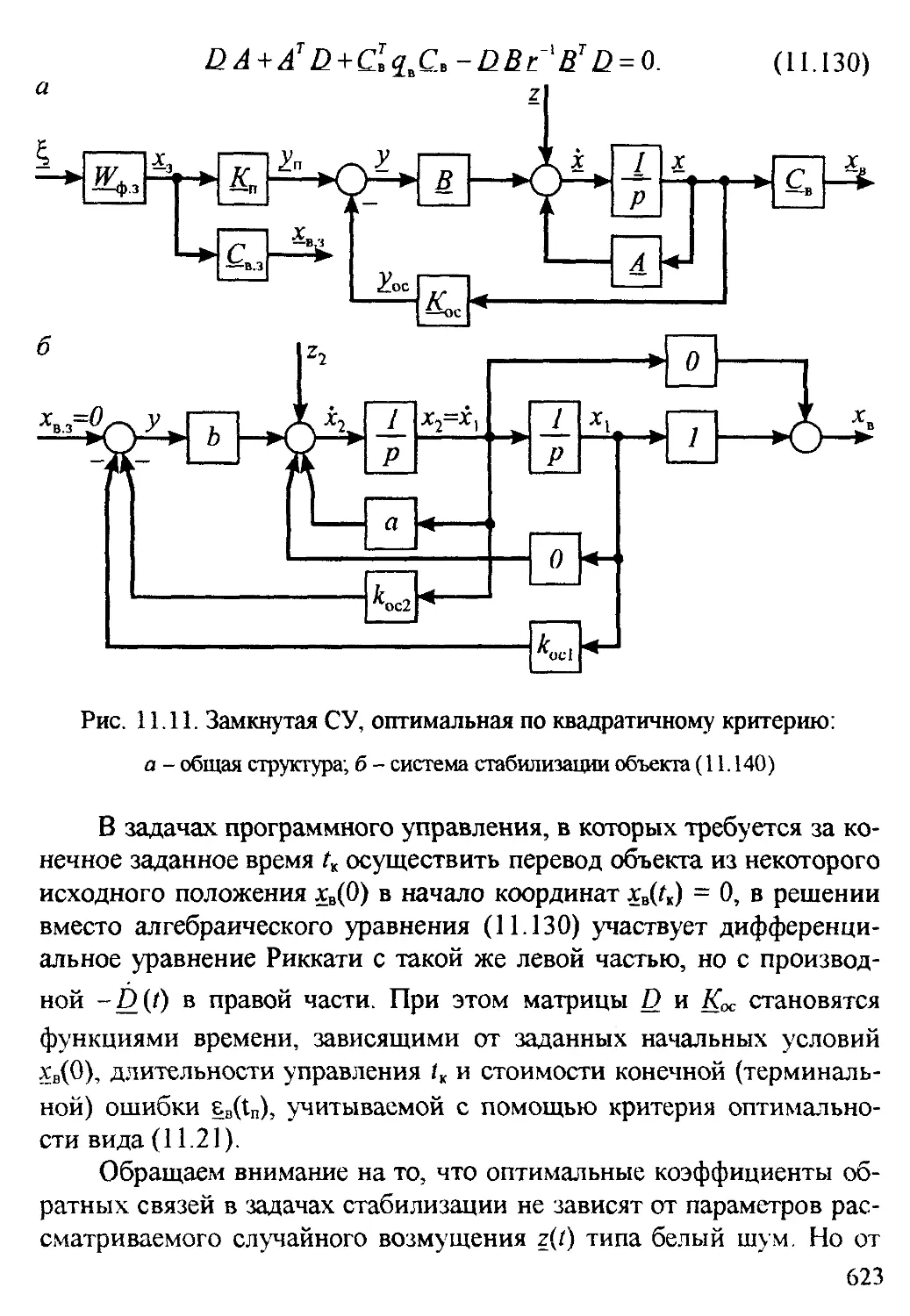
11 4 Системы, оптимальные по квадратичным критериям	620
11 5 Адаптивные системы управления	637
Контрольные задания и вопросы	642
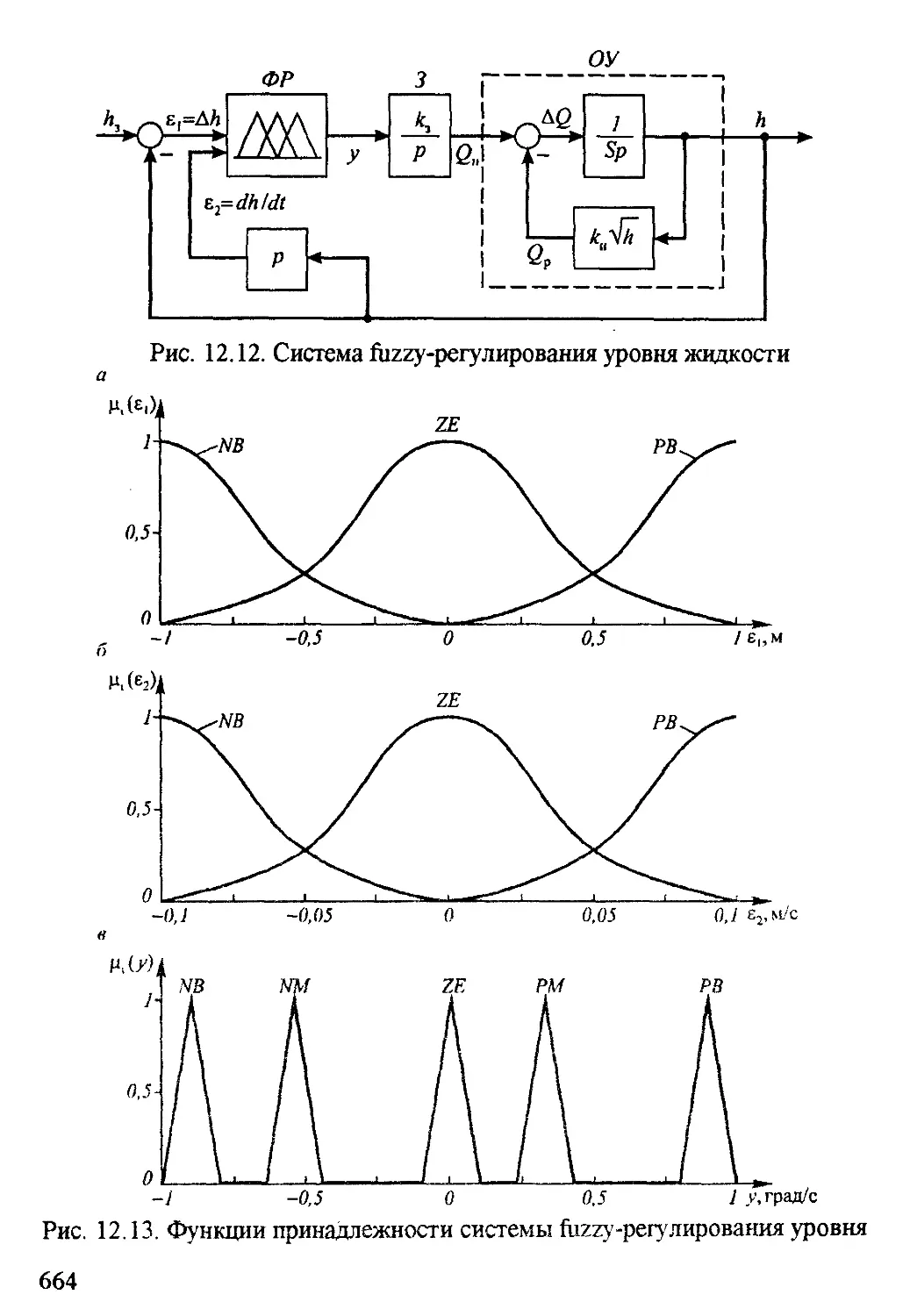
Глава 12. ОСНОВЫ FUZZY-УПРАВЛЕНИЯ	644
12 1 Общие сведения о fuzzy-управлении	644
12 2 Основные понятия и операции fuzzy-логики	646
12 3 Структура и принцип действия систем fuzzy-управления	656
12 4 Пример системы fuzzy-управления	662
Контрольные задания и вопросы	666
Заключение	668
Список литературы, рекоменду емой для самостоятельного
углубленного изучения теории управления	670
Ру сско-английский указатель основных терминов	671
6
ПРЕДИСЛОВИЕ
Предлагаемая читателю (студенту и преподавателю) книга, хотя
и названа автором нетрадиционно (но достаточно точно), по своему
содержанию и структуре близка большинству изданных в России и
за рубежом монографий и учебников по теории автоматического
управления и регулирования При этом автор исходил из того, что
термин «управление» (в англоязычной литературе - control) отражает
более широкое понятие, охватывающее и процесс регулирования, а
слово «автоматическое» относится почти исключительно к техниче-
ским объектам и системам и, следовательно, является в данном на-
звании излишним Попытки же некоторых специалистов ввести но-
вое название - «Теория управления» - и тем самым расширить тра-
диционную научную и учебную дисциплину «Теория автоматическо-
го управления», сформировавшуюся как дисциплина об управлении
именно техническими объектами, на биологические и социоэконо-
мические системы ограничиваются пока лишь несколькими просты-
ми примерами и вряд ли вообще целесообразны
Таким образом, в книге по существу изложены основы класси-
ческой и современной теории автоматического управления (ТАУ),
широко вошедшей в инженерную практику и вузовские учебные
планы Причем содержание книги охватывает основные разделы
теории управления, установленные соответствующим Государствен-
ным образовательным стандартом
Указанный на титульном листе жанр книги («учебный курс»),
по убеждению автора, вполне отражает ее предназначение, позволяет
отойти от процедур присвоения министерских грифов «учебник» или
«учебное пособие», дает автору необходимую свободу на выражение
своих дидактических взглядов и подходов
В характеристике жанра книги напрашивалось еще определение
«авторский» (курс), но это было бы излишне претенциозно, так как
авторство, как в большинстве учебных курсов, заключается прежде
всего и в основном лишь в рациональном и доходчивом изложении
научных сведений из монографических и журнальных публикаций
7
Естественно, что при подборе сведений и структурировании мате-
риала книги любому автору не удается избежать определенного
субъективизма и пристрастия к «любимым» разделам и методам.
Определение «компактный курс» подчеркивает попытку автора
охватить кратко и достаточно сбалансированно основные разделы
ТАУ и соразмерить объем книги с реальным объемом учебного вре-
мени (300-400 часов, в том числе 150-200 часов аудиторных заня-
тий). предусматриваемым учебными планами по направлению «Ав-
томатизация и управление». Определение «компактный» оправдано
еще и потому, что рассматриваемый в курсе круг разделов (включая
статистическую динамику и оптимальное управление) до сих пор
излагался в двух и более томах.
Теория управления техническими системами (или традиционная
ТАУ) - одна из базовых учебных дисциплин, преподаваемых студен-
там указанного направления. Целью преподавания ТАУ являются
формирование у студентов прочных знаний об общих принципах
построения и законах функционирования автоматических систем
управления, основных методах анализа и синтеза непрерывных и
дискретных систем управления при детерминированных и случайных
внешних воздействиях, привитие студентам твердых практических
навыков по составлению функциональной и алгоритмической схем
конкретной автоматической системы управления техническим объ-
ектом. определению передаточных функций и параметров отдельных
конструктивных элементов системы, записи передаточных функций
и уравнений динамики линейной системы, расчету статической и
динамической точности управления, анализу устойчивости линейной
системы, оценке показателей качества процесса управления с ис-
пользованием программных компьютерных систем типа «MATLAB»
и «SIMULINK».
Для достижения этой цели преподавания и формирования у сту-
дентов навыков по математическому анализу и расчету автоматиче-
ских систем управления необходимо в процессе преподавания доби-
ваться понимания студентами излагаемых положений ТАУ, способ-
ствовать возбуждению интереса студентов к изучаемой дисциплине,
с помощью простых и наглядных примеров из механики и электро-
техники убеждать студентов в «физичности» математических мето-
дов ТАУ и в их доступности для каждого студента.
8
В процессе изучения ТАУ студент должен приобрести следую-
щие знания и умения, необходимые инженеру в практической работе
по созданию и эксплуатации автоматических систем управления.
Студент, изучивший ТАУ, должен знать:
-	фундаментальные принципы построения систем управления,
классификацию систем по основным алгоритмическим признакам и
соответствующие алгоритмические схемы, достоинства и недостатки
замкнутых и разомкнутых систем, роль обратной связи в системах
управления;
-	методику линеаризации статической характеристики отдель-
ного элемента, запись уравнений статики и динамики элемента в
отклонениях;
-	формы описания динамических свойств линейных одномер-
ных элементов и систем управления: дифференциальное уравнение,
временные характеристики (переходную и импульсную), передаточ-
ную функцию, частотные характеристики, их взаимосвязь; векторно-
матричную форму описания многомерных элементов и систем;
-	классификацию динамических звеньев по виду их передаточ-
ных функций, характерные особенности инерционных статических
звеньев первого и второго порядков, интегрирующих и дифференци-
рующих звеньев;
-	правила преобразования алгоритмических схем и получения
эквивалентных передаточных функций систем управления, принцип
суперпозиции, методику записи уравнения динамики системы с не-
сколькими входными воздействиями, закономерность влияния обще-
го передаточного коэффициента системы на точность управления;
-	понятие и условие устойчивости линейной системы управле-
ния, основные критерии устойчивости и приемы их практического
применения для анализа устойчивости, закономерность влияния об-
щего передаточного коэффициента на устойчивость системы;
-	прямые и косвенные показатели качества процесса управле-
ния, методику их приближенной оценки, закономерности влияния
общего передаточного коэффициента на показатели;
-	основные принципы, методы и приемы синтеза систем с за-
данными показателями качества, методику выбора настроечных па-
раметров типовых управляющих устройств, условия обеспечения
инвариантности систем к внешним возмущениям;
9
-	математическое описание импульсной системы управления в
z-форме, условие и критерии устойчивости импульсной системы;
-	характеристики случайных сигналов, законы их преобразова-
ния линейным звеном, методику вычисления дисперсии сигнала
ошибки управления при случайных воздействиях;
-	особенности и характеристики нелинейных систем, основные
понятия и порядок применения метода фазовых траекторий, сущ-
ность и использование метода гармонической линеаризации, понятие
и критерий абсолютной устойчивости нелинейной системы;
-	общую характеристику и классификацию задач оптимального
управления, структуру систем, оптимальных по быстродействию, по
квадратичным критериям, принципы построения адаптивных систем
управления;
-	основы применения fuzzy-логики в системах управления.
Изучив ТАУ, студент должен уметь:
-	составить по принципиальной схеме конкретной автоматиче-
ской системы управления ее математическую модель в виде алго-
ритмической структурной схемы, определить передаточные функции
отдельных конструктивных элементов и числовые значения парамет-
ров, входящих в эти передаточные функции, записать для линейной
системы уравнение динамики и передаточные функции по задающе-
му и возмущающим воздействиям;
-	вычислить установившиеся значения ошибок управления при
ступенчатом и линейном воздействиях в статической и астатической
системах с известными передаточными функциями и параметрами;
-	проанализировать с помощью алгебраического или частотного
критерия устойчивость линейной системы;
-	оценить по приближенным формулам или определить экспе-
риментально (с помощью вычислительной машины) основные пока-
затели качества процесса управления;
-	выбрать передаточную функцию и настроечные параметры
типового управляющего устройства, обеспечивающие получение
требуемых показателей качества системы;
-	проанализировать устойчивость импульсной системы управ-
ления, заданной в виде передаточной функции в z-форме;
-	вычислить дисперсию сигнала ошибки управления в линейной
системе при случайном воздействии;
10
-	определить методом гармонической линеаризации амплитуду
и частоту автоколебаний в одноконтурной нелинейной системе
управления;
-	решать сформулированные выше задачи с помощью про-
граммных компьютерных систем типа <<MATLAB>>/«SIMULINK»;
-	освоить самостоятельно по специальной литературе новый
раздел или метод ТАУ, не излагавшийся в курсе.
Для успешного изучения ТАУ студентам необходимо знать сле-
дующие разделы предшествующих дисциплин учебного плана:
-	из математики: элементы линейной и векторной алгебры, ис-
следование функций с помощью производных, неопределенный и
несобственный интегралы, функции нескольких переменных, обык-
новенные дифференциальные уравнения, ряд и интеграл Фурье, эле-
менты теории функций комплексного переменного, операционное
исчисление, элементы математической статистики и вариационного
исчисления;
-	из электротехники: характеристики электрических цепей при
синусоидальном токе, основы комплексного метода, классический,
операторный и частотный методы расчета переходных процессов в
линейных электрических цепях с сосредоточенными параметрами,
основы синтеза электрических цепей;
-	из теоретической механики: уравнения Лагранжа, принцип
Д’Аламбера, общее уравнение динамики, гармонические колебания
материальной точки.
На рис. П. 1 изображена структура предлагаемой книги и лекци-
онного курса «Теория управления техническими системами (ТУ
ТС)» с сокращенными условными названиями частей и глав. В скоб-
ках указаны ориентировочные объемы лекционного времени в часах.
Объем излагаемого в книге материала превышает на 20-30 % реко-
мендуемые часы, что позволяет преподавателю варьировать содер-
жание своего лекционного курса, расширяя или сокращая те или
иные разделы в соответствии с интересами и традициями кафедры,
преподающей курс и/или выпускающей студентов.
Материал книги и двух ее предыдущих изданий сформировался
в процессе длительного (в течение 40 лет) преподавания автором
курса ТАУ студентам, специализировавшимся по автоматизации
технологических процессов. Улучшению и актуализации содержания
11
материала способствовали замечания и пожелания преподавателей
родственных кафедр, членов общероссийской учебно-методической
комиссии по автоматизации производства в разных отраслях
промышленности (председатель комиссии проф. В С. Балакирев), а
также научно-педагогические стажировки автора в вузах Германии.
Гл. 4 - Точность
СУ (6)
Гл. 1 - Введение
в ТУ (4)
Гл. 2 - Модели
СУ (6)
Гл. 5 - Качество
СУ (6)
Гл. 7 - Синтез
СУ (12)
Гл. 3 - Звенья
СУ (6)
Гл. 6 - Устойчи-
вость СУ (8)
Гл. 8 - Статистичес-
кая динамика СУ (10)
Гл. 10 - Нелинейные
СУ (10)
Гл. 9 -Дискретные
СУ (10)
Гл. 11 - Оптимальные
СУ (10)
Гл. 12 - Fuzzy-
управление (8)
Рис. П. 1. Структура книги и лекционного курса
по теории управления техническими системами
Одобрительные отзывы и пожелания коллег по специальности
подвигли автора на переработку книги и подготовку ее третьего из-
дания, которое, возможно, восполнит в какой-то мере огромный де-
фицит учебной литературы по ТАУ (последние учебники и учебные
пособия в России были изданы 15-20 лет назад).
12
Выражаю благодарность многолетнему коллеге В.П. Баранов-
скому и Л.Н. Авдеевой за помощь при переработке и оформлению
рукописей настоящего и предыдущих изданий книги. Особая призна-
тельность - профессору Л.Д. Певзнеру за ценные замечания и сове-
ты.
Екатеринбург - Берлин
Май 2002 г
В. Лукас
13
СОКРАЩЕНИЯ И УСЛОВНЫЕ ОБОЗНАЧЕНИЯ,
ПРИНЯТЫЕ В КНИГЕ
7. Сокращения основных терминов
ТС - техническая система
ОУ - объект управления
УУ - управляющее устройство
СУ - система управления
ИО - исполнительный орган
ИУ - исполнительное устройство
Д - датчик
ОС - обратная связь
ПК - передаточный коэффициент
ПФ - передаточная функция
ДПФ - дискретная передаточная функция
АФ(Ч)Х - амплитудно-фазовая (частотная) характеристика
АЧХ - амплитудная частотная характеристика
ФЧХ - фазовая частотная характеристика
2. Условные обозначения основных переменных и функций
x(t) - входной сигнал элемента СУ, выходной сигнал ОУ и СУ
(управляемая величина)
y{t) - выходной сигнал элемента СУ, входной сигнал ОУ (управ-
ляющее воздействие)
Хз(0 - задающее воздействие СУ
z(0 - возмущающее воздействие на СУ
е(/) - сигнал ошибки (рассогласования) в СУ
о(0 - единичное ступенчатое воздействие
5(/) - единичное импульсное воздействие
х„„ ут ~ амплитудные значения сигналов x(f) и Х0
х(0, Х0 _ векторы сигналов
р - оператор Лапласа, оператор дифференцирования
со - круговая частота, оператор преобразования Фурье
Х(р) - изображение непрерывного сигнала x(t) по Лапласу
X(z) - z-изображение дискретного сигнала x(i Г)
14
Х(](я} - изображение непрерывного сигнала х(/) по Фурье
к - ПК элемента (или соединения элементов)
W(p) - ПФ элемента (или соединения элементов)
W(ja) - АФХ элемента
W(z) - ДПФ элемента
Л(сй) - АЧХ элемента
^(со) - ФЧХ элемента
Ф(р), Ф(и) - соответственно ПФ и ДПФ замкнутой СУ
h(t) - переходная характеристика (функция) элемента или СУ
w(t) - импульсная (весовая) характеристика (функция) элемента
или СУ
А
= - равно по определению
= - требуется равенство (должно быть равно)
15
ВВЕДЕНИЕ
Теория управления техническими системами (ТУ ТО), или тра-
диционная теория автоматического управления (ТАУ), - научная
дисциплина, предметом изучения которой являются информацион-
ные процессы, протекающие в системах управления техническими и
технологическими объектами. ТУ ТС выявляет общие закономерно-
сти функционирования, присущие автоматическим системам различ-
ной физической природы, и на основе этих закономерностей разра-
батывает принципы построения высококачественных систем управ-
ления.
ТУ ТС при изучении процессов управления абстрагируется от
физических и конструктивных особенностей систем и вместо реаль-
ных систем рассматривает их адекватные математические модели.
Основными методами исследования в ТУ ТС являются математиче-
ское моделирование, теория обыкновенных дифференциальных
уравнений, операционное исчисление и гармонический анализ. Оха-
рактеризуем кратко каждый из них.
а	б
„V) 1Ж-
------► И(/>) ---------►
Рис. В.1. Схематичное представление
математических методов,
используемых в ТУ ТС
Метод матема-
тического моделиро-
вания, объединяющий
самые разнообразные
способы и приемы
описания и представ-
ления физических
объектов и явлений,
при данном первом,
общем знакомстве
можно условно, схе-
матично определить с
помощью наиболее часто используемого приема - графическим изо-
бражением простого объекта, имеющего один входной сигнал x(t) и
один выходной сигнал^Л в виде прямоугольника (рис. В.1,<з). Сим-
вол А внутри прямоугольника означает некоторый математический
16
оператор (функцию, интеграл и т.п ), который связывает входной и
выходной сигналы, меняющиеся во времени.
Этот прием лежит в основе структурного математического мо-
делирования, которое можно проиллюстрировать на следующем
примере. Пусть имеется система из двух алгебраических уравнений,
связывающих независимые (входные) переменные Xi и х2 с зависи-
мыми (выходными) переменными у\ и у2.
ОпЛ=йл;’
>
«21Л +«22 У 2 = Ь2Х2^
(В.1)
причем переменные хь х2, У1, Уг, как правило, изменяются во време-
ни.
В алгебре систему (В.1) и подобные системы решают, выражая
каждую из зависимых переменных через другую и через «свою» не-
зависимую:
(В.2)
а затем перекрестными подстановками выражений (В.2) в уравнения
(В.1) находят переменные .У] и у2 в явном виде, т.е. как функции от
Х1, Х2.
Такой процесс решения системы (В.1) можно представить в ви-
де блок-схемы на рис. В.2,а. Если теперь раскрыть функции f\ и f2 ,
то получится структурная модель системы, изображенная на рис.
В.2,б. Эту модель можно использовать не только для однократного
решения системы (В 1) при фиксированных значениях независимых
переменных Xi и х2, но и для многоразового (в т.ч. непрерывного)
ее решения при меняющихся во времени входных переменных Xi и
х2. При этом структурная математическая модель реализуется в виде
соответствующего вычислительного устройства, имеющего такую же
!	** •'	17
Рис. В.2. Структурная модель системы
двух линейных уравнений (ВЛ):
а - обобщенная; б - подробная
блок-схему, а перемен-
ные X), Хг, уь уг имити-
руются в виде электри-
ческих сигналов соот-
ветствующей величины.
Теория обыкновен-
ных дифференциаль-
ных уравнений, акцен-
тирующая свое внима-
ние на физические ас-
пекты и приложения
получаемых решений,
служит главной мето-
дологической основой
ТУ ТС, а сами обыкно-
венные дифференци-
альные уравнения -
наиболее общей и пол-
ной формой математи-
ческого описания сис-
тем управления. Дифференциальные уравнения связывают меняю-
щиеся во времени входные и выходные переменные и их производ-
ные. В простейшем случае дифференциальное уравнение имеет вид
ф(/)М=/[х(0,Я0]-
(В.З)
Из дифференциального уравнения получают его общее решение
и так называемую импульсную переходную функцию w(t) (подроб-
нее см. главу 2), с помощью которой можно связать выходную пере-
менную y(t) и входную x(t) (см. рис.В.2,(5) в форме интеграла свертки
(интеграла Дюамеля)
y(t) = [x(t- &)w(&)d&.
о
(В.4)
18
Метод операционного исчисления, в основе которого лежит пре-
образование Лапласа
00
Х(р) = fx(t)e ~p‘dt,
О
(В.5)
позволяет алгебраизировать дифференциальные уравнения - перейти
к так называемым операторным уравнениям, связывающим изобра-
жения Х(р) и Y{p) входного и выходного сигналов через передаточ-
ную функцию W(p) (рис.В.2,в)
W(p) = Г(Р)/Х(Р).
(В. 6)
Сама передаточная функция связана с импульсной переходной
также преобразованием Лапласа:
оо
W(p) = [ Mt)e-p,dt.
О
(В.7)
Метод гармонического анализа основан на известном из курса
математики преобразовании Фурье, имеющем вид
«о
X(ja>) = f
-00
(В.8)
С помощью преобразования Фурье (В.8) находят изображения
Х(/со) и У(/со) входного и выходного сигналов и y(t), характери-
зующие частотные спектры этих сигналов. Изображения сигналов по
Фурье связаны (рис. В.2,г) частотной передаточной функцией

(В.9)
которая также является изображением функции времени w(t) по Фу-
рье:
19
W(j(o) = f w(t)e~J<a,dt.
-QO
(B.10)
Частотные характеристики элементов и систем управления, по-
лучаемые с помощью преобразования Фурье, имеют ясный физиче-
ский смысл и широко используются в ТУ ТС.
Все четыре метода, кратко представленные выше, образуют ма-
тематический аппарат ТУ ТС. На его базе разработан комплекс «соб-
ственных» методов ТУ ТС, излагаемых в настоящем курсе.
ТУ ТС (или традиционная ТАУ) вместе с теорией построения и
функционирования элементов систем управления (датчиков, регуля-
торов, исполнительных устройств) образует более широкую отрасль
науки - автоматику (от греческого слова «аутоматос» - самодвижу-
щийся). Автоматика в свою очередь является одним из разделов тех-
нической кибернетики. Техническая кибернетика изучает сложные
автоматизированные системы управления технологическими процес-
сами (АСУТП) и предприятиями (АСУП), построенные с использо-
ванием управляющих вычислительных машин (УВМ).
Техническая кибернетика наряду с биологической и социоэко-
номической кибернетикой - составная часть кибернетики, которую
ее родоначальник, американский математик Н. Винер, в 1948 году
определил как науку об управлении и связи в технических системах
и живых организмах.
Рис. В.З. Связь ТУ ТС с другими науками
20
Связь ТУ ТС с кибернетикой и другими науками показана на
рис.В.З.
Первые теоретические работы в области автоматического
управления появились в конце XIX века, когда в промышленности
получили широкое распространение регуляторы паровых машин и
когда инженеры-практики стали сталкиваться с трудностями при
проектировании и наладке этих регуляторов. Именно в этот период
российский ученый и инженер И.А. Вышнеградский выполнил ряд
научных исследований, в которых паровая машина и ее регулятор
впервые были проанализированы математическими методами как
единая динамическая система. В дальнейшем российские ученые
А.М Ляпунов и Н.Е. Жуковский создали основы математической
теории процессов, происходящих в автоматически управляемых ма-
шинах и механизмах.
Приблизительно до середины XX столетия теория регуляторов
паровых машин и котлов развивалась как раздел прикладной меха-
ники. Параллельно разрабатывались методы анализа и расчета авто-
матических устройств, применяемых в электротехнике. Формирова-
ние теории управления в самостоятельную научную и учебную дис-
циплину произошло в период с 1940 по 1960 годы. В это время в
России и за рубежом были изданы первые монографии и учебники, в
которых автоматические устройства различной физической природы
рассматривались едиными методами.
В становлении российской школы теории управления большую
роль сыграли математические работы академиков А.А. Андронова и
В.С. Кулебакина, профессоров И.Н. Вознесенского, Б.В. Булгакова,
А. А. Фельдбаума. Крупный вклад в развитие ТУ ТС во второй поло-
вине XX века внесли академики Н.Н. Красовский, Б.Н. Петров,
ВС. Пугачев, А.А. Воронов, С.В. Емельянов, Г.С. Поспелов,
А А. Красовский, Я.З. Цыпкин, профессора М.А. Айзерман, В.В. Со-
лодовников, Е.П. Петров, А.А. Первозванский.
Основные этапы и даты истории развития теории управления
приведены в табл.В. 1.
Развитие современной теории управления из так называемой
«классической» теории регулирования, основанной на четырех вы-
шеупомянутых математических «китах», и формирование ее новей-
ших методов схематично проиллюстрированы на рис. В.4.
21
Рис. В.4. Развитие содержания и методологии теории управления
В настоящее время ТУ ТС наряду с новейшими разделами об-
щей теории управления (исследование операций, системотехника,
теория игр, теория массового обслуживания) играет важнейшую роль
в совершенствовании и автоматизации управления производством,
строительством и транспортом.
Автоматизация является одним из главных направлений научно-
технического прогресса и важным средством повышения эффектив-
ности производственных процессов Современное промышленное
производство характеризуется ростом масштабов и усложнением
технологических процессов, увеличением единичной мощности от-
дельных агрегатов и установок, применением интенсивных, высоко-
скоростных режимов, близким к критическим, повышением требова-
ний к качеству продукции, безопасности персонала, сохранности
оборудования и окружающей среды. Экономичное, надежное и безо-
22
пасное функционирование сложных промышленных объектов может
быть обеспечено с помощью лишь самых совершенных принципов и
технических средств управления.
Современными тенденциями в автоматизации производства яв-
ляются широкое применение ЭВМ для управления, создание машин
и оборудования со встроенными микропроцессорными средствами
измерения, контроля и регулирования, переход на децентрализован-
ные (распределенные) структуры управления с микроЭВМ, внедре-
ние человеко-машинных систем, использование высоконадежных
технических средств, автоматизированное проектирование систем
управления
Таблица В.1
Основные этапы и даты истории развития теории управления
Этапы	Сущность этапа	Основные события и имена
0 (1765-1804)	Первые промышленные регуляторы	1765, И.Ползунов - поплавковый регулятор уровня воды в паровом котле 1788, Дж Уатт (J Watt) - центробежный регулятор частоты вращения паровой машины 1804, Ж Жаккар (J Jacquard) - программное управление ткацким станком
I (1868-1893)	Первые теоретические исследования регуляторов	1868, Дж.Максвелл (J.Maxwell) - работа «О регуляторах» 1876, И.Вышнеградский - статьи о регулято- рах прямого и непрямого действия 1893, А Стодола (A Stodola) - «О регулиро- вании турбин»
II (1877-1938)	Создание математических основ теории управления	1877, Э Раус (Е Routh); 1892, А Ляпунов, 1895, А.Гурвиц (A Hurwitz) - математические условия устойчивости систем регулирования 1905, М. Толле (М Tolle) - «Регулирование двигателей» 1909, НЖуковский - «Регулирование хода машина 1928, К.Кюпфмюллер (К Kupfmuller) - «О динамике автоматических регуляторов с усилением» 1932, XНайквист (Н Nyquist), 1938, А Ми- хайлов - частотные критерии устойчивости
23
Окончание табл ВИ
Этапы	Сущность этапа	Основные события и имена
III (1940-1956)	Формирование теории управле- ния в инженер- ную дисциплину	Первые монографии и учебники. 1940, А.Леонард (A.Leonhard),В.Оппелът (W. Oppelt) 1944, Р. Ольденбург (R. Oldenburg),X. Сарто- риус (И. Sartorius) 1947, X.Джеймс (Н. James), Н.Никольс N. Nichols), Р. Филлипс (R. Phillips) 1954, А.Фельдбаум 1955, Дж. Траксел (J. Truxal) 1956, М.Айзерман.
IV (1948-2002)	Становление и развитие современной теории управления	1948, Н.Винер (N. Wiener) - «Кибернетика или управление и связь в живом организме и машине» 1956 - организация Международной феде- рации по автоматическому управлению (International Federation of Automatic Control - IFAC) 1956, Л. Понтрягин; 1957, P Веллман (R. Bellman) - математические принципы оптимального управления 1959-1963, Р.Калман (R.Kalman), А.Летов - теория синтеза оптимальных регуляторов в пространстве состояний 1965, Л.Заде (LZadeh) - основы теории нечетких множеств, fuzzy-логика 1950-1990, А.Воронов, В.Солодовников, А.Фельдбаум, Я.Цыпкин - развитие российской школы теории управления 1950-2000, Х.Боде (H.Bode), X Честнат (Н.Chestnut), Х.Квакернаак (H.Kwakernaak), В. Уткин (V Utkin), Р.Изерманн (R.Isermann), К.Острем (K.Astrdm), В.Кучера (V.Kucera) - развитие теории управления за рубежом I960 - 2002 - 1-15-й международные кон- грессы IF АС, тематические симпозиумы IFAC
24
В последнее десятилетие XX века в теории управления и прак-
тике автоматизации возникли и стали применяться новые технологии
проектирования СУ, получившие объединяющее название - «Com-
putational Intelligence» (англ. - компьютерный интеллект), или «Soft
Computing» (мягкие вычисления)1 fuzzy-логика, искусственные ней-
ронные сети и эволюционные (генетические) алгоритмы оптимиза-
ции. Общим для трех названных технологий является то, что в них
используются принципы биологических систем и субсимвольная
обработка информации.
25
Глава 1. ВВОДНЫЕ СВЕДЕНИЯ
О СИСТЕМАХ УПРАВЛЕНИЯ
1.1. Основные понятия теории управления
Введем основные понятия теории управления, ориентируясь на
терминологию, принятую большинством авторов книг по автомати-
ческому управлению и регулированию, а также на рекомендации
Российской Академии наук и Министерства образования России [1]
и на многоязычный словарь, изданный Международной федерацией
по автоматическому управлению [2].
Одним из исходных, базовых понятий теории управления явля-
ется понятие «система». Система - это множество связанных друг с
другом элементов, образующее определенную целостность При этом
целостность определяется тем, что связи элементов системы между
собой проявляются сильнее, чем их связи с другими элементами, с
окружающей средой. Системы можно классифицировать по различ-
ным признакам (основаниям). При наиболее общем подходе все сис-
темы можно разделить на абстрактные и материальные
Абстрактные системы являются продуктом человеческого мыш-
ления К ним относятся, например, различные научные теории, гипо-
тезы, методы, системы математических уравнений.
Материальные системы, представляющие собой целостные со-
вокупности материальных объектов, в свою очередь, делятся на не-
живые и живые системы.
К живым системам относятся живые организмы и растения и их
сообщества, к неживым - различные объекты неорганической при-
роды (физические, химические, геологические и т п).
Особый класс живых материальных систем образуют социаль-
ные системы - объединения людей различных уровней и масштабов
(семьи, населенные пункты, армии, государства)
По характеру взаимодействия с внешней окружающей средой
материальные системы делятся на закрытые (замкнутые) и открытые
(незамкнутые) В открытой системе постоянно происходят ввод и
26
вывод энергии и/или вещества В закрытой системе такого обмена с
ее внешней средой не происходит Согласно второму закону термо-
динамики, в каждой закрытой системе после определенного проме-
жутка времени (с момента ее закрытия) прекращаются все макроско-
пические процессы и система приходит в состояние равновесия, при
котором все физические величины, характеризующие ее макроско-
пическое состояние (температуру, давление и т п), остаются неиз-
менными во времени Такое состояние равновесия закрытой системы
и сама система могут быть названы статическими
В открытой системе из-за непрекращающегося обмена с внеш-
ней средой устанавливается стационарное состояние, которое можно
с разной степенью строгости и удачности назвать динамическим,
подвижным, проточным или пульсирующим равновесием В состоя-
нии такого динамического равно-
весия открытая система совершает
локальные, малые колебания отно-
сительно макроскопического со-
стояния термодинамического рав-
новесия.
Открытую систему, находя-
щуюся в динамическом равнове-
сии, в теории управления называ-
ют динамической системой, или
процессом Второй термин исполь-
зуется потому, что он подчеркива-
ет последовательную смену со-
стояний (стадий) развития какого-
либо явления
Рис 1.1 Виды
технических систем (ТС)
Открытые системы могут быть как естественными, так и искус-
ственными, специально созданными человеком Искусственная от-
крытая система сконструирована, как правило, так, что у нее обмен
энергией или веществом с внешней средой происходит целенаправ-
ленно и достаточно длительно Причем, процессы обмена и преобра-
зования энергии (вещества) в открытой системе происходят в одном
определенном направлении, т.е. являются необратимыми
В инженерной теории управления наибольший интерес пред-
ставляют неживые материальные объекты в виде различных техни-
27
ческих систем Техническая система (ТС) - совокупность машин и
аппаратов, осуществляющих преобразование, транспортирование и
накопление энергии, вещества или информации Примерами ТС яв-
ляются генератор электрической энергии, химический реактор, ком-
пьютер (рис 1 1)
Рис 1 2 Взаимодействие ТС
с внешней средой
Всякая ТС, как и любая другая
открытая система, взаимодействует с
внешней средой (рис 1 2) Причем,
внешняя среда всегда оказывает на
ТС мешающее влияние, т е воздей-
ствие, нарушающее нормальное
функционирование ТС Поэтому
факторы влияния внешней среды на
ТС называются возмущающими воз-
действиями, или возмущениями Для
названных выше примеров ТС воз-
мущающими воздействиями могут
быть соответственно мощность (кВт), расходуемая потребителями
электроэнергии, содержание (%) полезного компонента в исходном
сырье, поступающем в реактор, и температура (°C), при которой экс-
плуатируется компьютер
Из-за постоянного воздействия на ТС различных возмущений
приходится предпринимать специальные воздействия, направленные
на компенсацию нежелательного влияния среды или на желательное
изменение ее работы Процесс осуществления целенаправленных
воздействий на ТС, обеспечивающих ее нормальное функционирова-
ние, называют управлением А саму ТС, нуждающуюся в этих специ-
ально организованных воздействиях, называют объектом управления
(ОУ) Целенаправленные воздействия на ОУ являются управляющи-
ми Их обычно обозначают символом у, а возмущение - z
Для рассматриваемых трех примеров ТС управляющими воз-
действиями соответственно могут служить, например, частота вра-
щения (об/с) ротора электрогенератора, расход катализатора (кг/с),
подаваемого в реактор, и команды ввода данных («enter», «input» и
т п)
В приведенных выше определениях и примерах использовался
термин «воздействие», заимствованный из повседневной практики и
28
естественного языка Строгое определение понятия «воздействие» в
научной литературе отсутствует Его можно определить, лишь указав
его существенные признаки
1) воздействие всегда проявляется в передаче энергии, вещества
или информации от одного элемента к другому элементу системы,
2) интенсивность процесса этой передачи характеризуется од-
ной или несколькими физическими переменными (величинами)
Поскольку в теории управления при математическом анализе
любой системы, наряду с количественными характеристиками энер-
гетических и материальных потоков, рассматривается информацион-
ный аспект обмена, то каждое воздействие при этом выступает одно-
временно как материальный носитель информации, те как сигнал
Сигналом называют изменение во времени физической величины,
которое отображает в соответствии с принятой условностью инфор-
мацию, содержащуюся в воздействии Поясним понятие сигнала на
примере воздействия в виде потока горячей воды, который передает
одновременно и вещество (воду), и энергию (тепло) Этот поток ко-
личественно характеризуется такими физическими величинами, как
подача воды (кг/с) и подача тепла (Дж/с) Если любая из этих вели-
чин изменяется во времени, то она может рассматриваться как сиг-
нал. передающий информацию о данном тепловом воздействии
Рис 1 3 Возмущающие и управляющие воздействия на ТС
Пользуясь теперь понятием «сигнал», вернемся к понятию «тех-
ническая система» Существенной особенностью ТС или ОУ являет-
ся их возможность, способность влиять на потоки вещества или
энергии большой мощности с помощью управляющего воздействия
29
y(f) значительно меньшей мощности. Поэтому ОУ с позиций теории
сигналов можно рассматривать как модулятор, изменяющий по за-
данному, желаемому закону y(t) расходную характеристику (кг/с или
Дж/с) или какой-либо другой информативный признак x{t) выходно-
го потока объекта (рис. 1.3,6?). Процесс модуляции характеристик
основного потока объекта по закону изменения управляющего воз-
действия y{t) можно проиллюстрировать на простом примере венти-
ля, устанавливаемого обычно на трубопроводе для регулирования
потока жидкости или газа (рис. 1.3,6). Изменяя целенаправленно
управляющее воздействие y{t) - в данном случае угол поворота
(р (град) вентиля, можно при нестабильном давлении р (Н/м2) в маги-
страли трубопровода, являющемся возмущением z(f), менять или
поддерживать на постоянном уровне выходной сигнал объекта x(f) -
расход q (м/с). На рис. 1.3,6 показаны графики изменения во времени
сигналов (p(f) = y{t) и q{f) = x{f) до и после увеличения в момент вре-
мени /0 управляющего воздействия y{f) - угла поворота вентиля.
Выходной сигнал x{t) объекта управления, который с помощью
управляющего воздействия y{t) поддерживается на заданном уровне
или изменяется по желаемому закону,
динатой, или управляемой величиной.
называется управляемой коор-
Рис. 1 4. Обобщенная структура
системы управления (СУ)
У геройство, осуществ-
ляющее целенаправленные
управляющие воздействия
на ОУ, называют управляю-
щим устройством (УУ)
Совокупность ОУ и УУ.
взаимодействующих между
собой, называют системой
управления {СУ).
В самом общем, обоб-
щенном виде структура СУ
показана на рис. 1.4.
Управляемой величиной x{t) может служить физическая вели-
чина, которая либо измеряется (непосредственно на выходе объекта),
либо вычисляется по нескольким измеряемым величинам. Управляе-
мыми величинами первого типа являются, например, температура,
давление, напряжение, скорость, содержание полезного компонента
30
в готовом продукте и т.п. Примером величин второго типа служат
коэффициент полезного действия энергетической установки, соот-
ношение количества двух продуктов разделительной установки
Часто выход и состояние объекта управления характеризуются
несколькими величинами x}(t), х2(0, ..,х„(7) Тогда принято говорить
об ц-мерном выходном векторе объекта x(t), компонентами которого
являются величины x}(t), x2(t),..., xn(t) Объект в этом случае называ-
ют многомерным.
Управляемая величина является выходной величиной объекта и
зависит от двух входных воздействий: возмущающего z(t) и управ-
ляющего y(t). В общем случае эти воздействия также могут быть
векторными величинами
Возмущающие воздействия могут быть координатными и пара-
метрическими Координатные воздействия - это физические величи-
ны, которые обычно сами являются характеристиками состояния
внешней среды или выходными сигналами других технических уст-
ройств, не входящих в состав рассматриваемой СУ Параметрические
возмущения также являются следствием влияния внешней среды, но
проявляются в изменениях параметров объекта (Параметрами объ-
екта являются его передаточные коэффициенты, постоянные времени
и т п).
Кроме основного возмущения zo(t), действующего на объект, на
функционирование системы может влиять дополнительное возмуще-
ние 2д(0, приложенное к У У (см. рис. 1.4). Обычно такие возмущения
проявляются в нестабильности напряжения источников энергии,
питающих УУ, в изменениях температурного режима, влияющих на
работу УУ, и т.п.
Зависимость управляемой величины от входных воздействий
для одномерного объекта можно выразить при помощи некоторого
алгебраического алгоритма или математического оператора Ао, ха-
рактеризующего объект как преобразователь сигналов:
x(t) = Ay>{t),z(t)\	(II)
Символом Ао в выражении (1 1) обозначена некоторая совокуп-
ность математических операций, которые необходимо выполнить,
чтобы по функциям времени y(t) и z(t) найти функцию x(t)
31
Для «-мерного объекта будет п зависимостей вида (1.1), связы-
вающих п управляемых величин x2(t),..., xn(f) с несколькими
управляющими и возмущающими воздействиями.
Зависимость (1.1) вместе с требованиями, предъявляемыми к
управляемой величине (и в некоторых случаях - к управляющему
воздействию), составляют алгоритм функционирования объекта.
Управляющее воздействие вырабатывается в УУ в соответствии
с алгоритмом (законом) управления и в зависимости от истинного и
предписанного значений управляемой величины. Информация об
истинном значении управляемой величины поступает в управляющее
устройство в виде контрольного воздействия xK(t), или сигнала
обратной связи, а информация о предписанном значении - в виде
задающего воздействия x3(t). Иногда управляющее воздействие вы-
рабатывается с учетом изменений возмущающих воздействий zo(t) и
Za(t) (см. рис. 1.4).
Алгоритм управления (алгоритм функционирования управляю-
щего устройства) в самом общем случае выражает зависимость
управляющего воздействия от задающего воздействия, управляемой
величины и возмущающих воздействий. Для одномерной СУ он за-
пишется так:
y(t) = Лу[х,(/),	z0(t), хд(/)].	(1.2)
Алгоритм функционирования ОУ (1.1) и алгоритм управления
(1.2) в совокупности образуют алгоритмы функционирования СУ.
Воздействия z(t) и x3(f) являются внешними для рассматриваемой
системы, а воздействия^/) и хк(/) - внутренними. Передача внешних
и внутренних воздействий происходит через элементы СУ, которые в
совокупности образуют несколько цепей воздействий. На рис. 1.4
можно указать, например, цепи воздействий от величины х3(/) к ве-
личине y(t) и далее к х(/), от z(t) к x(t).
Различают три аспекта любого воздействия: энергетический,
метаболический и информационный. Энергетический аспект прояв-
ляется в процессах преобразования и передаче энергии, метаболи-
ческий - в процессах преобразования формы и состава вещества.
Информационный аспект заключается в том, что и при энергетиче-
ском, и при метаболическом проявлениях каждое воздействие явля-
32
ется одновременно носителем информации. Информационный аспект
наиболее важен для изучения процессов, происходящих в СУ. Эти
процессы заключаются в преобразовании сигналов, т.е. мате-
матических переменных.
Рис. 1.5. Система управления горнодобычной машиной
Проиллюстрируем введенные понятия на примере конкретной
системы управления. На рис. 1.5 изображена структура СУ режимом
работы горнодобычной машины (например, роторного экскаватора).
Заметим, что такую же структуру имеет и система управления режи-
мом работы материалообрабатывающего станка Назначение СУ -
поддержание постоянной нагрузки основного привода рабочего ор-
гана (роторного колеса или фрезы) путем изменения скорости пере-
мещения органа. Управляемой величиной х в системе является элек-
трическая мощность Рн, потребляемая преобразователем П и переда-
ваемая через основной двигатель До рабочему органу. Сигнал их,
пропорциональный мощности Рн, вырабатывается датчиком нагруз-
ки ДН и передается в элемент сравнения ЭС, где он сравнивается с
заданием =РН3. В зависимости от знака и величины сигнала рассо-
гласования wp, регулятор нагрузки РН формирует сигнал на увеличе-
ние или уменьшение частоты вращения привода подачи. Этот сигнал
через управляемый преобразователь УП, двигатель Дп и механизм
подачи преобразуется в управляющее воздействие - линейную ско-
рость подачи vn = У- (Полагаем, что мощность привода подачи дос-
таточно большая и поэтому сопротивление перемещению рабочего
33
органа может не учитываться). Основным возмущающим воздейст-
вием z0 является момент сопротивления или нагрузки Ма на основной
привод, зависящий от крепости разрушаемого горного массива (или
твердости обрабатываемого материала).
В качестве объекта управления в данной системе можно рас-
сматривать весь основной привод (рабочий орган, двигатель До, пре-
образователь Z7). К управляющему устройству относятся привод по-
дачи и регулятор нагрузки PH.
1.2. Функциональная и алгоритмическая
структуры системы управления
Изучение и математический анализ системы управления суще-
ственно облегчаются, если ее предварительно расчленить (мысленно,
разумеется) на типовые элементы, выявить физические взаимосвязи
между элементами и отобразить их в какой-либо условной форме на
схеме.
Следует заметить, что процесс формализации физических явле-
ний, происходящих в системе управления, весьма трудоемок и ответ-
ственен. Он требует хорошего знания конструкции и принципа дей-
ствия системы и ее элементов. Лишь тщательное и правильное вы-
полнение этого процесса обеспечивает полезность и эффективность
последующих расчетов.
Система управления может быть разделена на части по различ-
ным признакам: по назначению частей, алгоритмам преобразования
информации и конструктивной обособленности. Соответственно
различают функциональные, алгоритмические и конструктивные
структуры. При этом под структурой понимают совокупность свя-
занных между собой частей чего-либо целого.
Функциональная структура отображает функции (целевые на-
значения), выполняемые отдельными частями системы. Такими
функциями могут быть: получение информации о состоянии объекта,
преобразование сигналов, сравнение сигналов и т.п. Части функцио-
нальной структуры называются элементами и блоками. Названия
элементов и блоков указывают на выполняемые функции, например:
воспринимающий элемент, управляющий блок, исполнительный
блок.
34
Алгоритмическая структура характеризует алгоритмы преоб-
разования информации в системе и представляет собой совокупность
элементарных алгоритмических звеньев и связей между ними. Алго-
ритмы всех звеньев, входящих в систему, в совокупности соответст-
вуют алгоритму функционирования системы.
Элементарное алгоритмическое звено - часть алгоритмической
структуры СУ, соответствующая элементарному алгоритму преобра-
зования сигнала. Каждое элементарное звено выполняет одну про-
стейшую математическую или логическую операцию. На схемах
элементарные звенья изображают прямоугольниками, внутри кото-
рых записывают соответствующие операторы преобразования сигна-
лов. Иногда вместо операторов в формульном виде приводят графи-
ки зависимости выходной величины от входной или графики пере-
ходных функций.
Различают следующие виды элементарных звеньев, статиче-
ские, динамические, арифметические и логические
У статического звена мгновенное значение выходного сигнала
зависит только от значения входного сигнала в данный момент и не
зависит от характера изменения входного сигнала во времени Связь
между входным и выходным сигналами статического звена описыва-
ется обычно алгебраической функцией. К статическим звеньям отно-
сятся различные безынерционные (нелинейные и линейные) преоб-
разователи. Статическим звеном является, например, двухпозицион-
ное реле (рис.1.6,п). На рисунке показаны также условное изображе-
ние реле на схемах и графики изменения входного и выходного сиг-
налов.
Динамическое звено преобразует входной сигнал в соответствии
с операциями интегрирования и дифференцирования во времени.
Значение выходного сигнала динамического звена зависит не только
от текущего значения входного сигнала, но и от его предыдущих
значений, т.е. от характера изменения входного сигнала. Большинст-
во динамических звеньев описывается обыкновенными дифференци-
альными уравнениями. К классу динамических звеньев относятся
конструктивные элементы, обладающие способностью накапливать
35
a
б	в
Рис 1 6 Элементарные алгоритмические звенья
а ~ статическое, б - динамическое, в - арифметическое, г - логическое
какой-либо вид энергии или вещества На рис 1 6,6 в качестве при-
мера динамического звена приведена дифференцирующая гС-цепь
Арифметическое звено осуществляет одну из арифметических
операций сложение, вычитание, умножение или деление сигналов
На рис 1 6,в показано условное обозначение наиболее часто встре-
чающегося в автоматике арифметического звена - звена, выполняю-
щего алгебраическое суммирование сигналов Его называют сумма-
тором На рисунке приведены также два примера суммирования сиг-
налов - электрического (гальванического) и магнитного
Логическое звено выполняет какую-либо логическую операцию
логическое умножение ("И"), сложение ("ИЛИ”), логическое отрица-
ние ("НЕ”) и гд Входной и выходной сигналы логического звена
являются обычно дискретными и рассматриваются как логические
переменные
На рис 1 6,г приведен пример логического звена "НЕ" в виде так
называемого транзисторного ключа
Графическое изображение любой структуры системы, содержа-
щее условное изображение ее частей, называют структурной схемой
В соответствии с классификацией структур различают три типа
структурных схем функциональные, алгоритмические и конструк-
тивные
К конструктивным схемам относятся кинематические схемы
различных устройств, принципиальные и монтажные схемы электри-
ческих соединений и т п
Функциональные и алгоритмические схемы состоят из у словных
изображений элементов и звеньев (обычно в виде прямоугольников)
и различных связей, изображаемых в виде линий со стрелками
Стрелки показывают направление передачи воздействия Каждая
линия соответствует обычно одному сигналу или одному воздейст-
вию Иногда применяют жирные или сдвоенные линии на функцио-
нальных схемах - для обозначения материальных и энергетических
потоков, на алгоритмических схемах - для обозначения векторных
величин Около каждой линии указывают физическую величину,
характеризующу ю данное воздействие
Обычно вначале составляют функциональную схему системы,
затем - алгоритмическую
37
Структурные схемы могут быть составлены с большей или
меньшей степенью детализации. Схемы, на которых показаны лишь
главные или укрупненные части системы управления, мы будем на-
зывать обобщенными Такой схемой является, например, функцио-
нальная схема, приведенная на рис 1.4
а
о
Рис 1 7 Функциональная (я) и алгоритмическая (б)
структуры системы управления
На рис 1.7,6? в качестве примера изображена функциональная
структура СУ, в состав которой входят наиболее распространенные
функциональные элементы: задающий элемент (ЗЭ), сравнивающий
элемент (СЭ). датчики управляемой величины х (Дх) и управляющего
воздействия у (Ду), регулирующее устройство (РУ), усилитель мощ-
ности (УМ), исполнительный механизм (ИМ), исполнительный (ре-
гулирующий) орган (ИО).
В качестве исполнительных механизмов используют электри-
ческие, гидравлические и пневматические двигатели, электромаг-
ниты Регулирующими органами обычно служат заслонки, вентили,
различные дозирующие устройства (питатели) Они передают управ-
ляющее воздействие непосредственно на объект, изменяя количество
38
поступающих в объект вещества или энергии (сырья, воды, воздуха,
топлива, катализаторов и т.д.).
На функциональных схемах конкретных систем управления ука-
зывают не общее назначение блоков, а их конкретное наименование
- например, двигатель (Д), тиристорный преобразователь (ТП), тахо-
генератор (ТГ), электронный усилитель (ЭУ) и т п.
На рис. 1.1,6 приведена алгоритмическая схема системы, функ-
циональная структура которой была рассмотрена выше. Легко заме-
тить, что в данном примере каждому элементу функциональной
структуры (см.рис. 1.7,а) соответствует определенное алгоритмиче-
ское звено. В общем случае такое совпадение необязательно. Часто
элементарное алгоритмическое звено соответствует искусственно
выделяемой части функционального или конструктивного блока
Например, нелинейный инерционный объект может быть представ-
лен на алгоритмической схеме в виде последовательного соединения
соответствующих статического и динамического звеньев
1.3. Принципы построения и классификация систем управления
Классификация систем управления может быть осуществлена по
самым различным принципам и признакам, характеризующим назна-
чение и конструкцию систем, вид применяемой энергии, используе-
мые алгоритмы управления и функционирования и т д Классифика-
ция систем по различным основаниям показана на рис 1.8
Рассмотрим вначале классификацию систем по наиболее важ-
ным для теории управления признакам - признакам, которые харак-
теризуют алгоритм функционирования и алгоритм управления сис-
темы. Этими признаками являются: 1) цель управления и связанный
с ней характер изменения задающего воздействия (и соответственно
управляемой величины), 2) конфигурация цепи воздействий и 3) спо-
соб выработки управляющих воздействий.
В зависимости от характера изменения
задающего воздействия во времени системы
управления делят на три класса- стабилизирующие, программные и
следящие системы
39
Системы управления
По виду диффе-
ренциального
уравнения
По виду
сигналов
По виду уста-
новившегося
режима
По принадлеж-
ности источ-
ника энергии
По виду
применяемой
энергии
По
назначению
«с
£
jt
3
3
£
£
*
а:
£
сз
S
з:
о
5
ч>
I
Ч)
Ч)
g
Рис. 1.8. Классификация систем управления:
о







5
§
с
£
а - по алгоритмическим признакам; б - по неалгоритмическим признакам
Стабилизирующая система управления (система стабилизации)
- это система, алгоритм функционирования которой содержит пред-
писание поддерживать значение управляемой величины постоянным.
х(Г) ® х3 = const.	(13)
Знак ~ означает, что управляемая величина поддерживается на
заданном уровне с некоторой ошибкой.
Стабилизирующие системы - самые распространенные в про-
мышленной автоматике. Их применяют для стабилизации различных
физических величин, характеризующих состояние технологических
объектов. Примером стабилизирующей системы является СУ темпе-
ратурным режимом в отапливаемом помещении (см. рис. 1.10 в сле-
дующем разделе).
Алгоритм функционирования программной СУ содержит пред-
писание изменять управляемую величину в соответствии с заранее
заданной функцией времени fn(t)
=	(1.4)
Программной системой является, например, СУ шахтной подъ-
емной установкой (см. рис. 1.11). Управляемой величиной в системе
служит скорость движения подъемного сосуда в шахтном стволе.
Закон изменения скорости может быть задан как функция времени
или как функция пути, пройденного подъемным сосудом с начала
движения (см.рис.1.10,б). В первом случае программа называется
временной, во втором - параметрической.
Следящая система управления предназначена для изменения
управляемой величины в соответствии с изменениями другой вели-
чины, которая действует на входе системы и закон изменения кото-
рой заранее неизвестен:
х(0 « х,(0 = /С(Г),	(1.5)
где fc(t) - произвольная функция времени.
41
Следящие системы, называемые также системами позициониро-
вания, используются обычно для дистанционного управления пере-
мещением механических объектов в пространстве. Управляемой ве-
личиной в этом случае является либо расстояние (перемещаемого
объекта) от какой-либо начальной точки, либо угол поворота (вра-
щаемого объекта), отсчитываемый от начального положения. Сле-
дящие системы применяют также для дистанционной передачи пока-
заний. Примером следящей системы является система управления
положением шибера (см. рис. 1.14 в 1.4).
В стабилизирующих, программных и следящих системах цель
управления заключается в обеспечении равенства или близости
управляемой величины x(t) к ее заданному значению x3(f). Такое
управление, осуществляемое с целью поддержания равенства
(1.6)
называется регулированием.
Управляющее устройство, осуществляющее регулирование,
называют регулятором, а саму систему - системой регулирования.
В зависимости от конфигурации цепи
воздействий, различают три вида систем управления: с
разомкнутой цепью воздействий, с замкнутой цепью и комбиниро-
ванные.
В системе управления с разомкнутой цепью воздействий (крат-
ко - разомкнутая система) входными воздействиями управляющего
устройства являются только внешние (задающие и возмущающие)
воздействия, т.е. в них не осуществляется контроль управляемой
величины.
Разомкнутые системы можно разделить, в свою очередь, на два
класса; системы, осуществляющие управление в соответствии с из-
менением только задающего воздействия (рис. 1.9,я), и системы,
управляющие при изменении возмущения (рис. 1.9,6).
Алгоритм управления разомкнутой системы первого типа имеет
вид
(1.7)
42
Рис. 1.9. Функциональные структуры систем управления
с разомкнутой (а, б), замкнутой (в) и комбинированной (г)
цепью воздействий
Чаще всего оператор Ау устанавливает пропорциональную связь
между задающим воздействием х3(г) и управляющим воздействием
y{t), а сама система в этом случае осуществляет программное
управление.
Системы первого типа работают с достаточной эффективностью
лишь при условии, если влияние возмущений на управляемую вели-
чину невелико и если все элементы разомкнутой цепи обладают дос-
таточно стабильными характеристиками. Так, например, автоматиче-
ская система стабилизации расхода (дозирования) сыпучего мате-
риала, показанная на рис. 1.12, может работать с разомкнутой цепью
воздействия лишь в том случае, если удельный вес, крупность и сы-
пучие свойства материала постоянны или меняются в небольших
пределах.
Разомкнутые системы, действующие по заданию, называют
также циклическими системами. Характерными представителями
циклических систем являются различные автоматы, выполняющие
по жесткой программе, без свободы выбора действий, одноразовые
или многоразовые операции. К этой группе относятся, например,
различные системы управления пуском электродвигателей, включе-
нием в работу конвейерных линий и т д.
Циклические системы могут иметь довольно сложную конст-
рукцию и выполнять сложные управляющие функции. Принципы
функционирования сложных циклических систем специфичны, и
43
изучает их специальная теория - теория конечных автоматов. В дан-
ной книге эти принципы не рассматриваются
В системах управления по возмущению (см.рис. 1.9,6) управ-
ляющее воздействие зависит от возмущающего воздействия и от
задающего воздействия:
XO = 4k('),z(r)],	(1.8)
причем в большинстве случаев оператор Ау может быть разделен на
две, не зависящие друг от друга составляющие:
У(') = Л (0 + У, (0 = 4 к (0 ]+Л [*(')]	(1.9)
Оператор А3 соответствует, как правило, простому пропорцио-
нальному преобразованию сигнала x3ft). а оператор Ав может быть и
более сложным, например, устанавливать нелинейное соотношение
между сигналами уъ(!) и z(t).
В большинстве случаев разомкнутые системы управления по
возмущению выполняют функции стабилизации управляемой вели-
чины.
Преимущество разомкнутых систем управления по возмущению
- их быстродействие: они компенсируют влияние возмущения еще
до того, как оно проявится на выходе объекта. Но применимы эти
системы лишь в том случае, если на управляемую величину действу-
ет одно или два возмущения и если есть возможность измерять эти
возмущения. Сравнительно легко можно измерять, например, темпе-
ратуру, расход вещества, газа, ток нагрузки на генератор. Поэтому
если эти величины действуют на объект как возмущения, то обычно
стремятся стабилизировать их при помощи дополнительной системы
или ввести в основную систему управления данным объектом сиг-
нал, пропорциональный такому воздействию.
В системе управления с замкнутой цепью воздействий (кратко -
замкнутая система, или система с обратной связью) на вход управ-
ляющего устройства поступают как внутреннее (контрольное) воз-
действие, так и внешнее (задающее). Обобщенная функциональная
структура замкнутой системы изображена на рис 1.9,в.
44
Управляющее воздействие в замкнутой системе формируется в
большинстве случаев в зависимости от величины и знака отклонения
истинного значения управляемой величины от ее заданного значе-
ния:
y(Z) = ^[£(O],	(1.10)
где б(0 = x3(f) - x(t) - сигнал ошибки (называемый также сигналом
рассогласования). Замкнутые системы называют часто системами
управления по отклонению.
В замкнутой системе контролируется непосредственно управ-
ляемая величина и тем самым при выработке управляющих воздей-
ствий учитывается действие всех возмущений, влияющих на управ-
ляемую величину. В этом заключается преимущество замкнутых
систем. Но из-за наличия замкнутой цепи воздействий в этих систе-
мах могут возникать колебания, которые в некоторых случаях дела-
ют систему неработоспособной. Кроме того, сам принцип действия
замкнутых систем (принцип управления по отклонению) допускает
нежелательные изменения управляемой величины: вначале возму-
щение должно проявиться на выходе, система "почувствует" откло-
нение и лишь потом выработает управляющие воздействия, направ-
ленные на устранение отклонения. Такая "медлительность" снижает
эффективность управления. Несмотря на наличие определенных не-
достатков, этот принцип широко применяют при создании систем
управления.
Примеры замкнутых систем приведены в 1.4.
Основное внимание в настоящей книге будет уделено именно
замкнутым системам управления.
В комбинированных системах (рис. 1.9,г) создают две цепи воз-
действий - по заданию и по возмущению, и управляющее воздейст-
вие формируется согласно оператору
y(t) = 4[£(r)] + 4,[z(0]	(111)
Эффективность работы комбинированной системы управления
всегда больше, чем у порознь функционирующих замкнутой или
разомкнутой систем.
45
В зависимости от способа выработки
управляющих воздействий, замкнутые системы делят-
ся на беспоисковые и поисковые.
В беспоисковых системах управляющие воздействия вырабаты-
ваются в результате сравнения истинного значения управляемой ве-
личины с ее заданным значением. Такие системы применяют для
управления сравнительно несложными объектами, характеристики
которых достаточно хорошо изучены и для которых заранее извест-
но, с каким знаком и насколько нужно изменить управляющее воз-
действие при определенном отклонении управляемой величины от
заданного значения. Упомянутые выше системы регулирования,
поддерживающие равенство x{t)=x2(t) путем постоянного сравнива-
ния этих двух сигналов, относятся по рассматриваемому признаку
классификации к беспоисковым.
В поисковой системе основные управляющие воздействия фор-
мируются с помощью пробных управляющих воздействий и путем
анализа результатов пробных воздействий. Такую процедуру поиска
правильных управляющих воздействий приходится применять в тех
случаях, когда характеристики объекта меняются или известны не
полностью; например, известен тип зависимости управляемой вели-
чины от управляющего воздействия, но неизвестны числовые значе-
ния параметров этой зависимости. Поэтому поисковые системы на-
зывают также системами с неполной информацией.
Наиболее часто принцип автоматического поиска применяют
для управления объектами, характеристики которых имеют экстре-
мальный характер. Целью управления является отыскание и поддер-
жание управляющих воздействий, соответствующих экстремальному
значению управляемой величины. Такие системы поиска называют
экстремальными системами.
Особый класс систем управления образуют системы, которые
способны автоматически приспосабливаться к изменению внешних
условий и свойств объекта, обеспечивая при этом необходимое каче-
ство управления путем изменения структуры и параметров управ-
ляющего устройства. Они называются адаптивными, или самопри-
способляющимися, системами. В составе адаптивной системы
управления имеется дополнительное устройство, которое меняет ал-
горитм управления основного управляющего устройства таким обра-
46
зом, чтобы система в целом осуществляла заданный алгоритм функ-
ционирования. Алгоритм функционирования адаптивной системы
предписывает обычно максимизацию показателя качества, который
характеризует либо свойства процесса управления в системе в целом
(быстродействие, точность и т.п ), либо свойства процессов, проте-
кающих в управляемом объекте (производительность, извлечение
полезного компонента и т.п.).
Более подробно адаптивные системы будут рассмотрены в гл. 11.
Рассмотрим теперь кратко классификацию систем управления
по некоторым дополнительным признакам.
В зависимости от принадлежности ис-
точника энергии, при помощи которого создается управ-
ляющее воздействие, системы могут быть прямого и непрямого дей-
ствия. В системах прямого действия используется энергия управ-
ляемого объекта. К ним относятся простейшие системы стабилиза-
ции (уровня, расхода, давления и т.п.), в которых воспринимающий
элемент через рычажную систему непосредственно действует на
исполнительный орган (заслонку, клапан и т.п ). В системах непря-
мого действия управляющее воздействие создается за счет энергии
дополнительного источника.
По виду сигналов, действующих в системах, системы
управления делят на непрерывные и дискретные. Дискретные систе-
мы, в свою очередь, делят на импульсные, релейные и цифровые
(подробнее см. в 10.1).
Системы управления, у которых управляемая величина в у с -
тановившемся режиме зависит от величины возмущаю-
щего воздействия, называются статическими, а системы, у которых
не зависит, - астатическими. Примеры систем и математические
условия астатизма систем будут даны в гл.4.
По виду дифференциальных уравнений,
описывающих элементы систем, последние делят на линейные и не-
линейные. В линейной системе все элементы описываются линей-
ными алгебраическими и дифференциальными уравнениями. Если
хотя бы один элемент системы имеет нелинейную зависимость вы-
ходной величины от входной, то вся система является нелинейной.
47
1.4. Примеры систем управления
Проиллюстрируем изложенные в 1.1-1.3 общие понятия и
принципы управления на конкретных примерах. Ниже описаны сис-
темы управления некоторыми техническими объектами. Описание
систем дано применительно к упрощенным принципиальным схе-
мам, на которых показаны лишь главные цепи управляющих воздей-
ствий.
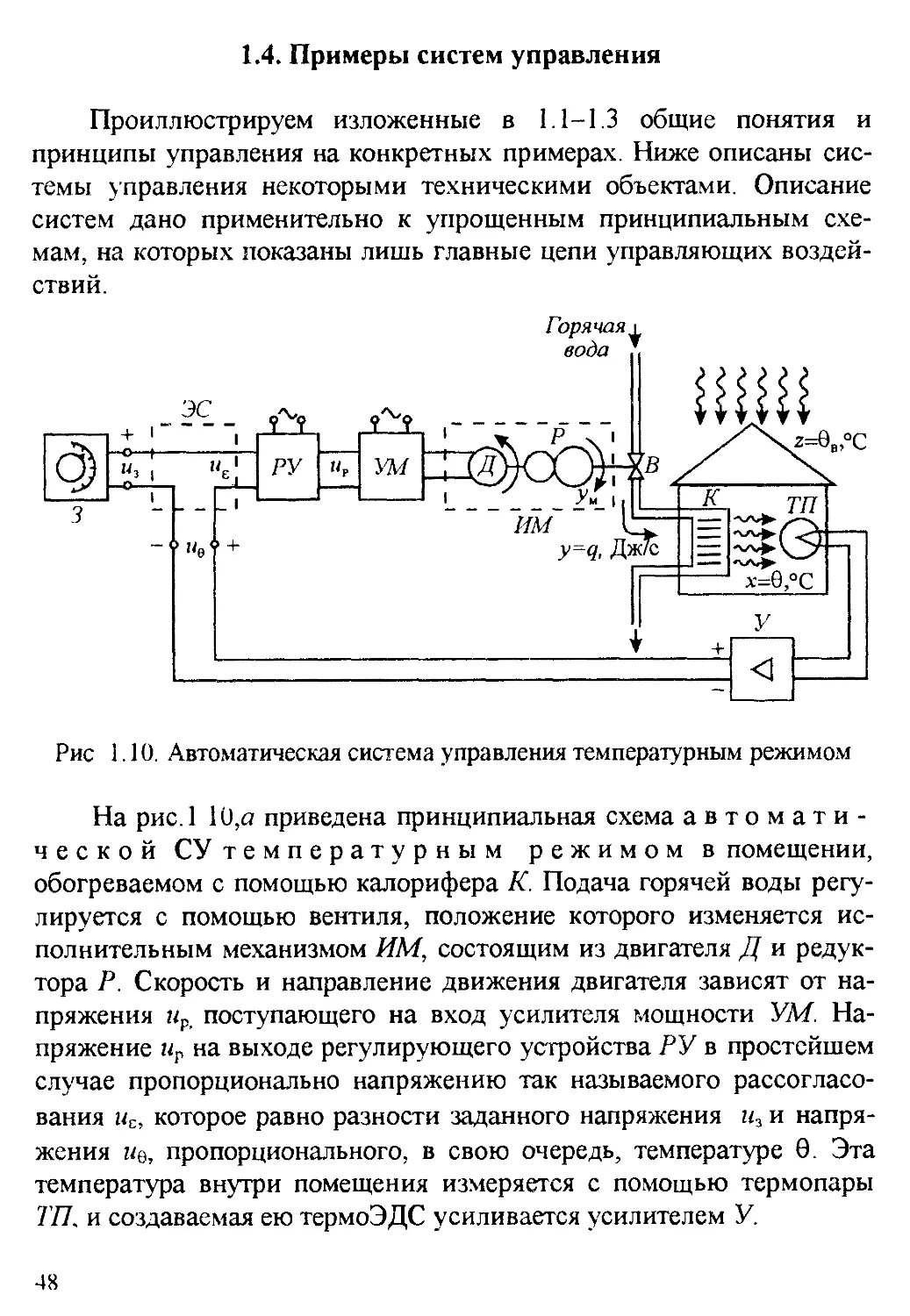
Рис 1.10. Автоматическая система управления темпера1урным режимом
На рис. 1 10,я приведена принципиальная схема автомати-
ческой СУ температурным режимом в помещении,
обогреваемом с помощью калорифера К. Подача горячей воды регу-
лируется с помощью вентиля, положение которого изменяется ис-
полнительным механизмом ИМ, состоящим из двигателя Д и редук-
тора Р. Скорость и направление движения двигателя зависят от на-
пряжения пр поступающего на вход усилителя мощности УМ. На-
пряжение Пр на выходе регулирующего устройства РУ в простейшем
случае пропорционально напряжению так называемого рассогласо-
вания ис, которое равно разности заданного напряжения п3 и напря-
жения uq, пропорционального, в свою очередь, температуре 0. Эта
температура внутри помещения измеряется с помощью термопары
7’77. и создаваемая ею термоЭДС усиливается усилителем У.
48
При отклонении измеряемой температуры 0 внутри помещения
от заданной 03 в элементе сравнения ЭС появляется сигнал рассогла-
сования wE соответствующей величины и знака, который, усиленный
по мощности в УМ, приведет в движение двигатель Д, редуктор Р и
вентиль В, Это движение и процесс открытия или закрытия вентиля
будут происходить до тех пор, пока температура 0 на станет равной
03. Регулирующее устройство РУ вырабатывает сигнал ир, который в
простейшем случае пропорционален сигналу иЕ (т.е. разности 03 - 0),
а при более сложном алгоритме управления может быть пропорцио-
нален интегралу и/или производной сигнала иЕ.
Заметим, что данная система стабилизации температуры с по-
мощью обратной связи может быть построена и как комбинирован-
ная система Для этого необходимо измерять основное возмущение -
внешнюю температуру 0В - и подавать соответствующий электриче-
ский сигнал в элемент сравнения ЭС.
На рис. 1.11,а приведена упрощенная принципиальная схема
автоматической системы управления шахт-
ной подъемной установкой. Назначение системы -
изменение скорости v подъемных сосудов в зависимости от их по-
ложения h в шахтном стволе. Другими словами, задача системы -
управление подъемной установкой по определенной программе
(рис. 1.11,6), заданной в параметрической форме.
Подъемная машина приводится в движение двигателем посто-
янного тока Д, который питается от генератора Г. Энергия, необхо-
димая для подъема сосудов, подводится к генератору от сетевого
двигателя СД. Скорость подъемного двигателя Д пропорциональна
напряжению на его якорных зажимах, которое, в свою очередь, про-
порционально напряжению на обмотке возбуждения генератора ОВГ.
Напряжение возбуждения иъ создается тиристорным преобразовате-
лем ТП, который играет в данной системе роль возбудителя. Напря-
жение ив пропорционально напряжению ир, которое равно разно-
сти между напряжением и3 и игг. Напряжение игг на зажимах
тахогенератора ТГ, выполняющего в системе роль датчика частоты
вращения, пропорционально в каждый момент времени линейной
скорости V. Напряжение и3 является задающим воздействием Оно
снимается с потенциометра П, движок которого перемещается спе-
49
циальным профилированным кулачком К. Этот кулачок выполняет
функцию задающего элемента. Профиль кулачка соответствует тре-
буемой программе изменения скорости (см.рис. 1.11,6).
Рис. 1.11. Автоматическая система управления
шахтной подъемной установкой
При перемещении подъемных сосудов по стволу кулачок К, свя-
занный с подъемной машиной и с главным редуктором Р\ через
вспомогательный редуктор А, поворачивается и изменяет заданное
значение скорости.
Согласно изложенным в 1.3 принципам классификации, система
управления подъемной установкой является замкнутой программной
системой регулирования непрямого действия.
50
На рис. 1.12 приведена принципиальная схема автомати-
ческой системы стабилизации расхода сы-
пучего материала, поступающего на переработку в техно-
логическую установку. Объектом управления в данной системе явля-
ется шнековый питатель 77. Питатель приводится в движение двига-
телем постоянного тока Д, который питается от силового магнитного
усилителя СМУ.
Рис. 1.12. Автоматическая система стабилизации
подачи сыпучего материала
Количество материала q, проходящее через питатель в единицу
времени, измеряется при помощи весоизмерителя В, который состоит
из короткого ленточного конвейера и магнитоупругого датчика МД.
Количество материала, находящееся на конвейере, пропорционально
массовому расходу материала q. Следовательно, сила тяжести F
будет также пропорциональна расходу q. Электрическое напряжение
пв на выходе магнитоупругого датчика, в свою очередь, пропорцио-
нально силе F. Напряжение мв, являющееся сигналом текущего рас-
хода q. сравнивается с задающим напряжением и3. Сигнал разности
этих двух напряжений усиливается в усилителе ЭУ и поступает на
обмотку управления магнитного усилителя.
При изменении удельного веса и сыпучести материала массовый
расход q будет отклоняться от заданного значения q3 При этом будет
51
возникать сигнал рассогласования ир и, в зависимости от знака сиг-
нала ир, будет увеличиваться или уменьшаться частота вращения
шнека. Положительное или отрицательное приращение скорости
компенсирует возникшее ранее отклонение расхода q от значения q3.
На рис. 1.13 показана принципиальная схема автоматиче-
ской системы стабилизации уровня жидко-
сти в резервуаре. Уровень измеряется с помощью поплав-
Рис. 1.13. Автоматическая система
стабилизации уровня жидкости
кового датчика уровня
ДУ, который замыкает
цепи контактов К\ или
К2.
Когда уровень h
(управляемая величина)
равен заданному значе-
нию, подвижный кон-
такт находится в ней-
тральном (среднем) по-
ложении. При этом
якорная цепь исполни-
тельного двигателя ИД
обесточена и он не вра-
щает регулирующий
клапан РКл. Если уро-
вень h снизится или по-
высится, с потенциометра П через контакты К2 или К] на двигатель
будет подано напряжение иа необходимой полярности, и он будет
открывать или закрывать клапан. Процесс увеличения или уменьше-
ния подачи qn будет происходить до тех пор, пока уровень не при-
мет заданное значение.
Для дистанционного управления перемещением различных объ-
ектов в пространстве применяются следящие автоматические систе-
мы. На рис. 1.14 показана принципиальная схема следящей
системы управления положением шибера.
Перемещение шибера осуществляется при помощи исполнительного
двигателя ИД, который связан с шибером через редукторы Р\ и Р2 и
винтовую передачу ВП. Элементом сравнения заданного и действи-
52
тельного положений шибера является электрический мост Л/, движки
которого механически связаны с рукояткой оператора и с шибером.
Пульт	В цехе
оператора
Рис. 1.14. Следящая система управления положением шибера
Для перемещения шибера оператор, находящийся на удалении
от шибера, небольшим усилием ставит движок Д в новое положение.
При этом мост разбалансируется, возникнет напряжение пр, пропор-
циональное разности перемещений х3 - х. Это напряжение усилится
в усилителе У, и на якорных зажимах двигателя ИД возникнет на-
пряжение = иу. Двигатель начнет перемещать шибер со скоростью,
пропорциональной рассогласованию х3 - х. Это перемещение будет
происходить до тех пор, пока шибер не займет новое положение х,
соответствующее положению рукоятки оператора х3.
Рассмотрим теперь систему, относящуюся к классу поисковых
систем На рис.1 15,п схематично изображена структура экстре-
мальной системы управления режимом горения га-
зообразного топлива в камере сжигания КС. Принцип действия сис-
темы основал на экстремальном характере зависимости количества
выделяющегося при горении тепла (или в конечном итоге - темпера-
туры 0 (°C) в камере) от подачи воздуха qB (м/с) при постоянной
подаче топлива (рис. 1.15,6). Для каждого значения qT (Дж/кг) ме-
няющейся теплотворной способности топлива, являющейся возму-
щением, существует наилучшее соотношение между подачами газа и
воздуха, и максимальная температура пламени 0 достигается при
53
определенном расходе воздуха. Поэтому задача СУ - отыскивать при
разных, заранее неизвестных значениях qT наилучшие значения д3.
Рис. 1.15. Экстремальная система управления режимом сжигания топлива
Температура измеряется в СУ при помощи термопары 777. Сиг-
нал uq, пропорциональный температуре 0, усиливается электронным
усилителем ЭУ. В элементе сравнения ЭС в каждый дискретный мо-
мент времени вычисляется разность Дне между предыдущими и
последующими значениями сигнала uQ. Задержка сигнала на проме-
жуток времени создается элементом запаздывания ЭЗ.
Сигнал Дие с периодичностью Д/, обеспечиваемой генерато-
ром тактовых импульсов ГТИ, переключает двухпозиционное реле
ПР, которое реверсирует исполнительный двигатель ИД. Исполни-
тельный двигатель через редуктор Р открывает или закрывает вен-
тиль В и тем самым увеличивает или уменьшает подачу воздуха в
камеру сжигания.
Если текущее значение м©(0 больше предыдущего uQ(t - ДО, то
ИД очередной раз изменит положение вентиля в прежнем направле-
нии. Если же текущее значение станет меньше предыдущего, т.е.
разность Дме станет отрицательной, то реле среверсирует двигатель,
и подача воздуха начнет изменяться в противоположном направле-
нии.
54
Этот процесс реверсирования ИД многократно повторяется,
благодаря чему температура сжигания приближается к своему "пла-
вающему" экстремуму то по левой, то по правой ветви характеристик
6 =Л?.)
Контрольные задания и вопросы
1	Проиллюстрируйте основные понятия теории управления на приме-
ре системы управления температурным режимом (см.рис.1.10).
2.	Какие признаки элементов системы управления отражаются на ее
функциональной схеме?
3.	Назовите наиболее распространенные, типичные функциональные
элементы систем управления.
4.	Составьте функциональную схему системы управления шахтной
подъемной установкой (см. рис. 1.11).
5.	Что отражает алгоритмическая схема системы управления?
6.	Приведите примеры элементарных алгоритмических звеньев.
7.	На какие три класса делятся системы управления в зависимости от
характера изменения задающего воздействия и управляемой величины?
8.	Назовите три класса систем, отличающихся конфигурацией цепи
воздействий.
9.	Какие достоинства и недостатки имеют разомкнутые системы
управления?
10.	Какие достоинства и недостатки имеют замкнутые системы управ-
ления?
11.	Предложите разомкнутую структуру и составьте соответствующую
функциональную схему системы управления температурным режимом (см.
рис. 1.10), в которой изменяются основные возмущения - температура 9
окружающего воздуха и давление воды в магистрали.
12.	При каких условиях система стабилизации сыпучего материала
(см. рис. 1.12) могла бы функционировать как разомкнутая?
55
Глава 2. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ
ЭЛЕМЕНТОВ И СИСТЕМ УПРАВЛЕНИЯ
2.1. Общие понятия о передаточных свойствах
элементов и систем
Любая СУ представляет собой совокупность нескольких уст-
ройств, в которых происходят явления различной физической поро-
ды Одна и та же система может включать в себя, например, механи-
ческие, электрические и гидравлические элементы Эти части СУ
взаимодействуют между собой по сложным законам механики, элек-
тротехники, гидравлики Взаимодействие частей системы между со-
бой так же, как и функционирование самого объекта управления, за-
ключается в преобразовании, хранении и передаче энергии, вещества
или информации Но эти процессы в системе управления, в отличие
от многих других физических систем, строго ориентированы, те
воздействия передаются только в определенном направлении
Направленность передачи воздействий в СУ обеспечивается
благодаря наличию у одного или нескольких конструктивных эле-
ментов системы так называемого детектирующего свойства Это
свойство заключается в том, что рассматриваемый элемент не оказы-
вает обратного действия на предыдущий элемент, а его выходная ве-
личина не влияет на свою входную Например, электрический четы-
рехполюсник обладает однонаправленностью передачи воздействий,
если он не нагружает предшествующий четырехполюсник, т е если
выходное сопротивление предшествующего элемента существенно
меньше входного сопротивления рассматриваемого четырехполюс-
ника
Обычно свойством однонаправленности обладают те элементы
системы, которые передают информационные воздействия К таким
элементам относятся в первую очередь измерители и преобразовате-
ли сигналов Конструктивные части системы, через которые переда-
ются энергетические и материальные воздействия, этим свойством,
как правило, не обладают
56
Заметим, что только благодаря наличию элементов направлен-
ного действия в СУ создается замкнутый контур передачи воздейст-
вий, при помощи которого и осуществляется целенаправленный про-
цесс управления Без таких элементов системы управления были бы
неработоспособны или малоэффективны
Рис 2 1 Функциональная структура автоматической системы
стабилизации подачи сыпучего материала
Рассмотрим, как происходит передача воздействий в конкретной
системе управления На рис 2 1 показана функциональная структура
автоматической системы стабилизации подачи сыпучего материала,
описанной в 1 4 В этой системе электрическая энергия, поступаю-
щая из сети, преобразуется при помощи двигателя в механическую,
которая через редуктор Р передается на вал шнекового питателя П
Питатель перемещает материал из бункера на весоизмеритель В и
далее в технологический аппарат, перерабатывающий данный мате-
риал Количество энергии, передаваемой двигателем питателю, из-
меняется в зависимости от величины управляющего сигнала щ и от
величины момента сопротивления, действующего на вал шнека Мо-
мент сопротивления зависит от физических свойств материала
(удельный вес. крупность, вязкость) и от частоты вращения шнека
Это означает, что в электромеханической части системы, состоящей
из силового магнитного усилителя СМУ, приводного двигателя Д,
реду ктора Р и питателя П. действует внутренняя обратная связь (см
57
пунктирную линию), т.е. что рассматриваемая часть системы не об-
ладает свойством однонаправленности.
Свойством однонаправленности передачи воздействия в данной
автоматической системе обладают ленточный весоизмеритель, маг-
нитоупругий датчик МД и электронный усилитель ЭУ. Действитель-
но, никакие искусственные изменения выходных величин этих эле-
ментов не могут привести к изменению их входных величин. Напри-
мер, сила F не может изменить количество руды, проходящей через
весоизмеритель, а напряжение на выходе датчика не может повлиять
на силу F
Анализ процессов, происходящих в системах управления, и эф-
фективное решение задач расчета и проектирования систем возмож-
ны лишь с применением языка и методов математики. Причем, пер-
вым этапом при исследовании или конструировании СУ является
составление математического описания (математической модели) ее
элементов и системы в целом
Составление математического описания конструктивного эле-
мента СУ состоит из следующих последовательных процедур: при-
нятие исходных допущений, выбор входных и выходных перемен-
ных, выбор систем отсчета для каждой переменной, применение фи-
зического принципа, отражающего в математической форме законо-
мерности преобразования энергии или вещества.
Наиболее распространенной и самой общей формой описания
передаточных свойств систем управления и их элементов являются
обыкновенные дифференциальные уравнения. Для элемента, имею-
щего один входной сигнал x(t) и один выходной сигнал y(t), обыкно-
венное дифференциальное уравнение записывается в общем случае
следующим образом:
фо, т.	х'-м Л-°	»
Уравнение (2.1) связывает неизвестную функцию y(t) и ее про-
изводные у'(О,- У” v) с независимой переменной t и известной (за-
данной) функцией времени x(t). Уравнение (2.1) называют уравнени-
ем динамики или движения элемента.
Уравнение (2.1) может быть линейным и нелинейным Линей-
ным оно является, если функция Ф линейна по отношению ко всем се
58
аргументам. Если же переменные y(t), x(t) и их производные входят в
выражение функции Ф в виде произведений, частных или степеней,
то уравнение является нелинейным.
В выражение для функции Ф, кроме основных переменных,
входят постоянные величины, называемые параметрами. Числовые
значения параметров зависят от конструктивных данных описывае-
мого элемента - от масс, индуктивностей, емкостей и т.п
Если переменная у, характеризующая состояние элемента, кро-
ме времени зависит еще от другой независимой переменной, которая
является пространственной координатой, то элемент описывается
дифференциальным уравнением с частными производными. Сам
описываемый элемент называют в этом случае элементом с распре-
деленными (в пространстве) параметрами. Элементами с распреде-
ленными параметрами являются, например, сушильные барабаны,
дистилляционные химические колонны и другие аналогичные уста-
новки, в которых процессы преобразования энергии и вещества про-
исходят по всей длине аппарата.
Отметим, что почти все реальные объекты управления являются
элементами с распределенными параметрами. Однако при практиче-
ских расчетах с большей или меньшей степенью приближения их
рассматривают как элементы с сосредоточенными параметрами.
б
Рис. 2.2. Механическая (а) и электрическая (б) колебательные
диссипативные системы с сосредоточенными параметрами
Для наиболее часто используемых в СУ механических и элек-
трических конструктивных элементов составление математической
модели существенно облегчается с помощью метода механоэлек-
трических аналогий. На рис.2.2 показаны две типичные конструк-
тивные части СУ - механическое колебательное устройство (а) и
59
электрический колебательный контур (б) В обеих частях, содержа-
щих по два накопителя энергии и рассматриваемых как физические
системы, протекают аналогичные процессы под действием внешнего
фактора (силы FBH или напряжения пвн) происходят движение, пони-
маемое в обобщенном физическом смысле (механическое перемеще-
ние массы т на расстояние s или накопление электрического заряда
q в емкости С ), и преобразование одного вида энергии в другой (ки-
нетической Ек в потенциальную Еп или магнитной Ем в электриче-
скую Еэ, и наоборот) При этих процессах передачи и преобразования
энергии неизбежно происходят ее потери на преодоление силы тре-
ния Fyp или на нагрев активного сопротивления г Такие физические
системы называют диссипативными
Рис 2 3 Структурная математическая модеть
динамических систем (см рис 2 2)
Математические связи между физическими переменными обеих
колебательных систем представлены обобщенной структурной моде-
лью на рис 2 3, где реальные физические связи и воздействия указа-
ны сплошными стрелками а вычисляемые переменные (энергии Ап,
FK и Ffl) - пунктирными
60
Для составления этой и подобной модели удобно использовать
метод механоэлектрических аналогий, сущность которого отражена в
табл 2 1
Таблица 21
Переменные состояния и параметры диссипативных
динамических систем (см. рис. 2.2)
Обобщенные перемен-	Переменные и параметры	
ные и параметры	механическая система	электрическая система
Показатель интенсивно- r dQi сти L = 1 di	Сила F, Н	Напряжение и В
Количественный показа- тель <2i ~V\dt	Импульс р = mv, Н с	Магнитный поток Ф = П Вс
Показатель интенсивно- Г dQz СТИ /э - di	Скорость v, м/с	Сила тока i Кл/с=А
Ко птчественный показа- ть = $I2dt	Путь S, м	Заряд q Кл=А с
Мера инерционности к лин	Масса т> кг	Индуктивность L Гн
Мера емкости (упругости) куп	Коэффициент упругости к^, Н/м	Обратная емкость 1 ±_ в С’ Ф " Кл
Мера диссипативности (сопротивления) ктр	Коэффициент трения Н тр’ м/с	Активное сопротивление г Ом=В/А
Энергия в 1-м накопите- ле Ех Дж	Кинетическая энергия mv2 ЕК= — ,Дж	Магнитная энергия Li £м=-5-.Д«
Энергия во 2-м накопи- теле Е2 Дж	Потенциальная энергия fcvns2 Еп = 2 , Дж	Электрическая энергия Си2 Еэ=-у-,Дж
Энергия диссипации Ед, Дж	Энергия потерь на трение Етр =iETpvdt > Дж	Энергия тепловых потерь Er =\uridt Дж
61
Составим теперь математическую модель (дифференциальное
уравнение и алгоритмическую схему), отражающую физические свя-
зи между входной и выходной величинами электромагнита и харак-
теризующие его передаточные свойства Электромагнит, схематично
изображенный на рис.2.4,а, состоит из электрической обмотки, не-
подвижного сердечника и подвижного якоря. В автоматике такие
электромагниты широко используют в качестве исполнительного
устройства СУ, перемещающего различные исполнительные органы
(задвижки, вентили, шиберы и т.п.).
Рис. 2.4. Конструктивная (а) и алгоритмическая (б) схема электромагнита
Входной величиной является напряжение u(t), приложенное к
обмотке электромагнита. Напряжение u(t) в процессе работы элек-
тромагнита изменяется в соответствии с алгоритмом управления сис-
темы (в общем случае - по произвольному закону) Будем считать,
что источник напряжения 1 обладает достаточно большой мощно-
стью и что напряжение и(1) не зависит от электромагнитных про-
цессов, происходящих в обмотке.
В качестве выходной величины целесообразно принять элек-
тромагнитную силу F3(t), которую создает магнитное поле и которая
действует через подвижный якорь на последующий элемент 2 систе-
мы управления
62
Согласно второму правилу Кирхгофа, алгебраическая сумма
ЭДС и напряжений в цепи обмотки в каждый момент времени равна
нулю.
u(t)-i(t)r+e(t) = O,	(2.2)
ЭДС самоиндукции e(f) равна скорости изменения потокосцеп-
ления:
e(t) = -c№(t)!dt,	(2.3)
а потокосцепление самоиндукции Т(0 равно произведению тока 1(f)
и индуктивности L:
4(t) = Li(t).	(2 4)
Индуктивность цепи, в свою очередь, зависит от величины зазо-
ра между сердечником и якорем, т е. от перемещения якоря s(t) и от
тока в цепи. Эта зависимость в общем случае имеет довольно слож-
ный характер Однако при наличии воздушного зазора насыщение в
магнитопроводе не наступает, ток практически не влияет на индук-
тивность, и индуктивность может рассматриваться как функция
только одной переменной - перемещения s(f), т.е. L[s(f)].
Отметим, что индуктивность зависит также от размеров, формы
и магнитных свойств сердечника. Но эти факторы в процессе работы
электромагнита не меняются и поэтому при описании передаточных
свойств электромагнита учитываются в коэффициентах уравнений.
Подставляя выражения (2.3) и (2.4) в равенство (2 2), получаем
нелинейное дифференциальное уравнение цепи обмотки
u(0 - i(t)r - l[s(0]^^ - z(0	= 0.
(2.5)
Электромагнитная сила как известно из электротехники,
пропорциональна в каждый момент времени квадрату тока и обратно
пропорциональна величине зазора (перемещения)
(0 = сэ>2 (/)/?(<),
(2.6)
63
где с3 - коэффициент, учитывающий число витков обмотки и пло-
щадь сечения сердечника.
Алгебраическое соотношение (2.6) и дифференциальное урав-
нение (2.5) совместно описывают электромагнит как преобразователь
сигнального (информационного) воздействия в силовое (энергетиче-
ское) воздействие. Выражая из (2.6) ток через силу и перемещение и
подставляя ток в уравнение (2.5), можно получить одно общее урав-
нение электромагнита в форме (2.1)
ад, ад, ад, ад, г,с,]=о. (2.7)
Нетрудно убедиться, что в левую часть уравнения (2.7) войдут
произведения и степени переменных F3(t), s(f) и их производные.
Следовательно, полученное дифференциальное уравнение является
нелинейным. Причем один из параметров уравнения является пере-
менным’ индуктивность L зависит от меняющейся величины s(t)
Наглядное представление о внутренних процессах электромагнита и
о его передаточных свойствах дает алгоритмическая схема (рис.
2.4,6), которая соответствует уравнениям (2.5) и (2.6).
Особенностью электромагнита, рассматриваемого как структур-
ное звено системы управления, является наличие у него внутренней
обратной связи: электромагнитная сила F3(t) создает перемещение
s(t), а перемещение s(t), в свою очередь, влияет на силу F3(t) и
индуктивность L. Поэтому при математическом описании электро-
магнит рассматривают обычно совместно с конструктивным элемен-
том 2, на который действует сила F3(t) и от противодействия которо-
го зависят результирующая сила и перемещение s(f). В практических
расчетах обычно учитывают лишь влияние перемещения на силу
F3(t), а индуктивность L считают неизменной и равной некоторой
средней величине Lq.
В заключение сформулируем ряд положений, определяющих
методологию формализованного представ-
ления и математического описания элементов и
систем управления.
1.	Система рассматривается как цепь взаимодействующих (фи-
зически и информационно) элементов, которая обладает способно-
64
стью передавать физические воздействия и информационные сигна-
лы в одном, строго определенном направлении
2.	Каждый конструктивный элемент системы рассматривается
как преобразователь входного воздействия в выходную реакцию.
3	На основе априорных сведений о физической природе каждо-
го элемента и закономерностях его функционирования составляется
математическая модель, которая на языке соответствующей научной
дисциплины отражает существенные для данной цели взаимосвязи
между входными и выходными переменными элемента.
4.	При составлении математического описания отдельных эле-
ментов и системы в целом всегда приходится прибегать к некоторой
идеализации реальных физических процессов, происходящих в эле-
ментах, к определенным упрощениям физических закономерностей,
отбрасыванию второстепенных факторов Удачность и допустимость
всех этих упрощений зависят от глубины знаний исследователя сис-
темы в данной области физики и технологии, от его инженерной ин-
туиции и всегда подлежат экспериментальной проверке
2.2. Временные и спектральные характеристики
типовых воздействий и сигналов
Виды воздействий и режимов в системах управления. Боль-
шое разнообразие конструкций и условий работы систем управления
определяет многообразие воздействий и сигналов, наблюдаемых в
системах Изучение и математический анализ конкретных систем
существенно упрощаются, если пользоваться принятой в теории
управления типизацией воздействий и сигналов
Рассмотрим основные разновидности сигна-
лов и воздействий. В зависимости от характера изменения
сигнала во времени и от формы его математического представления,
различают регулярные и нерегулярные сигналы
Регулярный (детерминированный) сигнал изменяется по опреде-
ленному закону и может быть описан конкретной математической
функцией времени К классу регулярных сигналов относятся различ-
ные периодические сигналы и непериодические импульсы конечной
длительности На рис 2.5/7 в качестве примера регулярного сигнала
показан импульс, описываемый экспонентой
65
Нерегулярный (случайный) сигнал изменяется во времени слу-
чайным образом и не может быть представлен в виде конкретной ма-
тематической функции. Характер изменения случайного сигнала во
времени показан на рис.2.5,б.
Рис 2 5. Виды сигналов (а, б, в, г) и типовых воздействий (д, е, ж, з)
Если значение регулярного или случайного сигнала определено
в каждый момент времени (рис. 2.5,в), то сигнал называют непрерыв-
ным, или аналоговым. Если же значения сигнала заданы лишь в не-
которые моменты времени (рис. 2.5,г), то его называют дискретным.
При экспериментальном и теоретическом исследовании СУ и их
элементов используют ряд стандартных сигналов, называемых типо-
выми воздействиями. Эти воздействия описываются простыми мате-
матическими функциями и легко воспроизводятся при испытании
систем. Использование типовых ("эталонных") воздействий позволя-
ет унифицировать расчеты различных систем и облегчает сравнение
передаточных свойств систем.
Наибольшее применение в теории и практике автоматического
управления находят следующие четыре типовых воздействия: сту-
пенчатое, импульсное, гармоническое и линейное
Ступенчатое воздействие - это воздействие, которое мгновен-
но возрастает от нуля до некоторого значения и далее остается по-
66
стоянным
функция
(рис.2.5,д). Ступенчатому воздействию соответствует
д
Хс(() =
О при t < 0;
aQ при t > 0.
(2.8)
При анализе и расчете систем удобно использовать ступенчатое
воздействие, у которого величина а0 = 1. Его называют единичным
ступенчатым воздействием (единичным скачком) и обозначают а(0
или 1(/). Математическое выражение, описывающее единичный ска-
чок, имеет вид
<т(0 = 1(0
д (ОприГсО;
[1 при t > 0.
(2.9)
Функцию времени (2.9) называют также функцией Хевисайда
Любое неединичное ступенчатое воздействие можно обозначить
atfs(t). Единичное ступенчатое воздействие, возникающее в момент
времени t = t\, обозначают o(f -1\).
Ступенчатые воздействия чаще всего используют при испыта-
ниях и расчетах систем стабилизации, так как эти воздействия наи-
более близки к реальным входным (задающим и возмущающим) воз-
действиям систем стабилизации.
Импульсное воздействие представляет собой одиночный им-
пульс прямоугольной формы (рис.2.5,е), имеющий достаточно боль-
шую высоту осо / ти и весьма малую (по сравнению с инерционностью
испытываемой системы) продолжительность ти —> 0. Очевидно, что
площадь такого импульса всегда равна а0.
При математическом анализе систем управления используют
единичное импульсное воздействие, которое описывается так назы-
ваемой дельта-функцией, или функцией Дирака
г. . А
ад =
0 при t Ф 0;
оо при t = 0,
(2.10)
причем
67
JO
I 8(t)dt = 1.
-OQ
(2.11)
Согласно выражениям (2.10) и (2.11), дельта-функцию можно
рассматривать как импульс, имеющий бесконечно большую высоту,
бесконечно малую длительность и единичную площадь. Дельта-
функцию можно определить так же, как предел разности двух еди-
ничных ступенчатых функций:
£(0 = lim [cr(O - cr(t - АГ)]
(2.12)
или как производную единичного скачка:
8(t) = dcr(t)/dt,
(2.13)
соответственно единичная ступенчатая функция равна интегралу
дельта-функции:
/
- j 8(&)d&.	(2.14)
О
Нсединичное импульсное воздействие с площадью <70 обознача-
ется ао<^0-
Если единичный импульс действует в момент времени t = то
ему соответствует так называемая смещенная дельта-функция
- G), которая тоже удовлетворяет условию (2.11)
Основное свойство дельта-функции выражается соотношением
со
Jx(5)<?(5-r)tf5 = x(/),
-СЮ
(2.15)
которое обозначает, что неединичная импульсная функция
полученная как произведение произвольной функции х(&)
на дельта-функцию, существует только в момент & ~ t, и что пло-
68
щадь ее равна значению функции х(19) в точке & - t. Это свойство
дельта-функции называют фильтрующим или "выхватывающим".
Выражение (2.15) можно также рассматривать как разложение
некоторой функции x(t) на сумму бесконечно большого числа эле-
ментарных импульсов вида х(«9)$3 - f)d&. Каждый элементарный
импульс действует лишь в момент времени & = t и имеет площадь
х(
В качестве стандартного гармонического воздействия исполь-
зуют обычно сигнал синусоидальной формы, описываемый функци-
ей
х(/) = хт sin со t, (— оо < t < qo),	(2 16)
где х„, - амплитуда сигнала; со = 2 л /Т - круговая частота, рад/с; Т -
период сигнала, с.
Гармонический сигнал, начинающий действовать в момент вре-
мени t = 0 (рис. 2.5,ж), описывают при помощи единичной ступен-
чатой функции
х(Г) = o(f)xm sin со t, (О < t < оо).	(2.17)
Гармонические воздействия (2.16) и (2.17) широко используют-
ся при исследовании точности и устойчивости как стабилизирую-
щих, так и следящих и программных СУ. Это объясняется двумя об-
стоятельствами: во-первых, тем, что реальные возмущения часто
имеют периодический характер и поэтому могут быть представлены
в виде суммы гармонических составляющих и, во-вторых, тем, что
математический аппарат анализа автоматических систем хорошо
разработан именно для случая гармонических воздействий
Для следящих и программных систем типовым является линей-
ное воздействие, начинающееся в момент t - 0 (рис 2.5. з).
х(/) = сг(/)<7]/,	(0<f<co).	(2.18)
где коэффициент характеризует скорость нарастания воздействия
х(г).
69
Рассмотрим теперь возможные состояния и возможные
режимы перехода СУ от одного состояния к другому. Со-
стояние системы будем характеризовать изменением управляемой
величины во времени. Очевидно, что состояние системы и режимы
перехода зависят как от формы задающего или возмущающего воз-
действия, так и от свойств самой системы.
Различают два режима работы СУ и их элементов: статический
и динамический. Статическим режимом называют состояние сис-
темы (элемента), при котором управляемая (выходная) величина у
не изменяется во времени, т.е y(f) = const.
Очевидно, что статический режим (или состояние равновесия)
может иметь место лишь тогда, когда входные воздействия постоян-
ны во времени Связь между входными и выходными величинами в
статическом режиме описывают алгебраическими выражениями.
В динамическом режиме работы системы (элемента) управляе-
мая (выходная) величина непрерывно изменяется во времени -
у(0 = var
Динамические режимы имеют место, когда в системе после на-
несения внешних воздействий происходят процессы установления
заданного изменения выходной величины. Эти процессы называют
процессами управления. Они описываются в общем случае диффе-
ренциальными уравнениями.
Рис. 2.6. Переходные и установившиеся режимы при типовых воздействиях
Динамические режимы делят: на неустановившиеся и устано-
вившиеся Неустановившиеся, или переходные, режимы имеют ме-
сто сразу после изменения внешних воздействий. Конкретный вид
70
функции y(t) в переходном режиме зависит от типа воздействия и от
собственных динамических свойств системы. Установившийся ре-
жим работы наступает после окончания переходного процесса, когда
выходная величина элемента или системы изменяется во времени по
такому же закону, что и входное воздействие. При этом говорят, что
элемент (система) совершает вынужденное движение.
Нетрудно заметить, что статический режим является частным
случаем установившегося (вынужденного) режима при x(r) = const.
Понятия "переходный режим" и "установившийся режим" ил-
люстрируются графиками изменения выходной величины y(f) при
трех типовых воздействиях (рис.2.6). Граница между переходным и
установившимся режимами показана вертикальной пунктирной ли-
нией.
Основные сведения из гармонического анализа воздействий
и сигналов. В инженерной практике при описании и исследовании
систем управления широко применяется разложение реальных сиг-
налов сложной формы на элементарные сигналы синусоидальной
формы. Математический метод представления сложных сигналов
(периодических и непериодических) в виде совокупности элементар-
ных гармонических составляющих (гармоник) называется гармони-
ческим анализом.
Рассмотрим основные положения этого метода. Как известно из
курса математики, любая периодическая функция с периодом Т
x(t) = ^t+iT), (/ = 0;1;2....),	(2.19)
удовлетворяющая условиям Дирихле (конечное число разрывов на
интервале периода 7), может быть разложена в бесконечный сходя-
щийся тригонометрический ряд - ряд Фурье
V (ak cos a\kt + bk sin co{ki),
k=\
(2 20)
где <O] - 2 л/7' - частота основной гармоники, рад/с; со;- = <&\к - частота
к-тл гармоники, рад/с; <з0, ак, Ьк - независимые от t коэффициенты
(коэффициенты Фурье), которые определяются по формулам
7)
т
ак=— \ x(&)cosco}k9d9, (£ = 0,1,2, ),	(2 21)
Т т
2
Т
ьк =-]x(5)smfi),£ftZ5, (£ = 1,2, )	(2 22)
* т
2
Переменная интегрирования 3 в (2 21) и (2 22) рассматривается
на интервале от -772 до +772 Постоянная составляющая а0 / 2 ряда,
соответствующая £ = 0, равна среднему за период Т значению сигна-
ла
Если функция х(3) на интервале (-772, 772) четная, то в разло-
жении (2 20) будут присутствовать только косинусоиды, а если эта
функция нечетная, то ряд будет содержать только синусоиды
Таким образом,
при помощи ряда Фурье удается сложный периодический сигнал
выразить аналитически в виде суммы простых гармонических
сигналов, называемых гармониками
Ряд Фурье обладает замечательным свойством при заданном
конечном числе членов он дает лучшее приближение (по критерию
суммы квадратов отклонений), чем любое другое разложение функ-
ции x(f)
Ряд Фурье удобно использовать, если он записан не в тригоно-
метрической форме (2 20), а в виде суммы экспоненциальных функ-
ций eja>i, соответствующих, как известно, единичным вращаю-
щимся векторам С помощью известной формулы Эйлера
е±,а = cosaiysina	(2 23)
и ее модификаций
cos а = (е?а + е Ja)/2, sm а = (eja -eja)/2j,	(2 24)
ряд (2 20) можно преобразовать к комплексной форме ряда Фурье
72
Z Jt--ao
(£ = 0,+1,+ 2, ),
(2 25)
T
где	|-v('9)r '"“‘'5 = «1+.A,	(2 26)
? T
/2
(знак минус для к > 0, а плюс для к < О)
Отметим, что в формуле (2 25) суммирование производится как
по положительным, так и по отрицательным значениям к Это озна-
чает, что комплексная форма ряда Фурье допускает существование и
положительных, и отрицательных частот со* = cojfc Так как каждому
комплексному слагаемому с положительным к соответствует
сопряженное слагаемое с отрицательным к, то при суммировании в
(2 25) останутся только действительные величины
Слагаемые в (2 25) называются комплексными гармониками, а
сомножители X(ja\k) в этих слагаемых - комплексными амплитуда-
ми
Зависимость модуля Хк комплексной амплитуды Xfycpk) от час-
тоты (Dk = С0]£ называют амплитудным спектром сигнала х(/)
Для периодического сигнала спектр амплитуд, равных на каж-
дой частоте
к ~ Хкт — V ак +^к >
(2 27)
удобно изображать в виде так называемой решетчатой функции -
последовательности отрезков (спектральных линий) длиной хкт,
перпендикулярных к оси На рис 2 7,6 показан в качестве при-
мера амплитудный спектр конкретного сигнала - периодической по-
следовательности прямоугольных импульсов (рис 2 7,а) с амплиту-
дой хи и скважностью 77ти = 4
Амплитудный спектр любой последовательности прямоуголь-
ных импульсов описывается следующей функцией аргумента к
(2 28)
73
Рис. 2.7. Примеры периодического (а) и непериодического (в) сигналов
и их амплитудные спектры (б, г)
Анализируя общее выражение (2.28) и конкретный график ам-
плитудного спектра (см.рис. 2.7,6), можно установить ряд харак-
терных свойств спектра любых периодиче-
ских сигналов:
1.	Спектры всегда дискретны - они содержат только такие гар-
моники, частоты которых кратны основной частоте он. Некоторые
гармоники могут отсутствовать.
2.	Чем больше период Т сигнала, тем меньше интервал он = 2т6Т
между соседними частотами и, следовательно, ’’гуще” спектр. При
Т —> оо, т е. для единственного импульса, описываемого непериоди-
ческой функцией времени, спектр становится сплошным. Но ампли-
туды хкт при возрастании периода будут уменьшаться.
3.	С уменьшением длительности импульсов ти (при неизменном
7) амплитуды гармоник также уменьшаются, а спектр становится
"гуще”.
4.	Если одновременно с уменьшением длительности ти импуль-
сов увеличивать амплитуду х„, например, по закону хи = 1/ти, то их
74
последовательность (см.рис. 2.7,я) будет стремиться к последова-
тельности дельта-функций, а амплитудный спектр - к постоянному
для всех частот значению хкт = 1 Т
Перейдем теперь кхарактеристикам непериоди-
ческих сигналов. Любой непериодический сигнал в виде
импульса конечной длительности (см.рис. 2.7,в) можно рассматри-
вать как предельный частный случай соответствующего периодиче-
ского сигнала (см.рис. 2.1,а), если устремить период Т к бесконечно-
сти, не изменяя при этом длительность импульса. Очевидно, что при
Т —> оо расстояние между соседними спектральными линиями
(см.рис. 2.7,6), равное Дю = <»i = litIT, будет уменьшаться и стре-
миться к а дискретная переменная - к непрерывной (о Дис-
кретный спектр становится непрерывным Так как при этом модули
xkm стремятся к нулю, то для непериодических сигналов вместо ам-
плитуд Хк используют относительные амплитуды
X(ja>}k) = XJ&(0.	(2.29)
Учитывая, что До = 2it/T и 1/Т -= Д(о /2л, сумму (2.25) при пре-
дельном переходе Т —> оо можно заменить интегралом Фурье
х(1) = ^-]х(}а>)е^Ю,
— <Ю
(2.30)
а выражение (2.26) для комплексной амплитуды - так называемым
преобразованием Фурье
оо
X(ja>) = fx(t)e“‘dt
-00
(2.31)
Непериодический сигнал х(/), представленный в виде интеграла
(2.30), можно по аналогии с периодическим сигналом, разложенным
в ряд (2.25), рассматривать как сумму бесконечно большого числа
комплексных гармоник с бесконечно малыми комплексными ампли-
тудами
75
dX = X(ja>)da>/27r.
(2.32)
Так как амплитуда dX характеризует спектр, приходящийся на
интервал от со до со + с/со, то величину
X(jCo) = 2ndX/d(O
(2.33)
называют комплексной спектральной плотностью, а зависимость ее
модуля рТ(/со)| от частоты - спектральной плотностью амплитуд.
На рис 2.7,г показана спектральная плотность амплитуд для
одиночного прямоугольного импульса (см.рис. 2.1,в). Она описыва-
ется функцией
Х(;щ)! = 2х г
' J	ИИ
sin (су ги/2)
и
(2.34)
Обратим внимание на особенности спектральных
свойств непериодического сигнала:
1.	Спектр всегда непрерывен и характеризуется не абсолютны-
ми значениями амплитуд гармоник (они бесконечно малы), а плотно-
стью амплитуд гармоник, приходящихся на интервал с/со.
2.	При уменьшении длительности импульса его спектр расши-
ряется вдоль оси со, а значения плотности амплитуд уменьшаются.
3.	Если одновременно с уменьшением длительности ти прямо-
угольного импульса (см.рис. 2.1,в) увеличивать его амплитуду хи по
закону хи = 1/ти, то импульс стремится к дельта-функции, а его спек-
тральная плотность - к постоянной величине, равной единице на
всем диапазоне частоты от -оо до -н» .
Формулы (2.30) и (2.31), называемые соответственно обратным
и прямым преобразованием Фурье, являются основными в гармони-
ческом анализе непериодических сигналов и широко используются в
теории управления. С помощью прямого преобразования (2.31) для
любого сигнала x(t), удовлетворяющего условиям Дирихле и являю-
щегося интегрируемым, можно найти его изображение по Фурье,
которое символически обозначается так:
76
X (у®) =	{х(/)}
(2.35)
Процедура обратного преобразования Фурье соответственно
обозначается с помощью символа :
х(0 = ^--'{¥(;«)}.
(2.36)
Если прямое преобразование (2.31) записать для относительного
времени t = t/TM и относительной частоты оо = &Т№, где Тм - некото-
рый масштабный множитель, то можно получить одно из важнейших
свойств преобразования Фурье:

(2.37)
которое означает, что
при растяжении (сжатии) графика функции x(t) в 7М раз
вдоль оси времени график спектральной плотности |Х(/со)|,
во-первых, сжимается (растягивается) вдоль оси частот в Тм
раз и, во-вторых, увеличиваются (уменьшаются) в Тм раз ее
значения, т.е. чем короче импульс x(t), тем шире и ниже гра-
фик I X(jo) .
Другое важнейшее свойство преобразования Фурье выражается
равенством Парсеваля
2,.	1
at = —
2тг
f \X(ja)\2 da.
(2 38)
Соотношение (2.38) имеет следующий физический смысл. Во
многих практических задачах автоматики сигнал x(t) характеризует
электрический ток или скорость перемещения, соответственно квад-
рат такого сигнала пропорционален мощности, а его интеграл - энер-
гии Согласно такому смыслу левой части равенства (2 38) рассмат-
ривают и правую часть как сумму энергий отдельных гармоник, час-
тоты которых расположены в полосе dco около со. Поэтому функ-
цию |А"(/со)|2, характеризующую распределение энергии среди
гармоник сигнала x(t), называют энергетической спектральной
плотностью (спектральной плотностью мощности).
Пример. Найдем спектральные характеристики Д/со), ) Д/со) | и
IД/®) г экспоненциального импульса , возникающего в момент t = О
x(l) = c(l)xKe
О при
/<0,
при t £ О,
(а > О)
(2.39)

Отметим, что функция (2.39) удовлетворяет условиям применимости
преобразования Фурье. Изображение функции (2.39), по Фурье, согласно
(2.31)
т е

а + ju>
а+ущ’
*и
a+jo)
(»>«)
(2.40)
(2.41)
Спектральная плотность амплитуд
(2.42)
Энергетическая спектральная плотность
а2 +со
(2.43)
2.3.	Статические характеристики элементов
Передаточные свойства элементов и систем в статическом ре-
жиме описывают при помощи статических характеристик. Статиче-
ской характеристикой элемента называют зависимость его выход-
ной величины у от входной величины х
У = /(*) = у{х}
(2.44)
в установившемся статическом режиме
78
Статическая характеристика конкретного элемента может быть
задана в формульном виде (например, в виде алгебраической функ-
ции у - сх2) или в виде графика (рис. 2.8,а).
Рис. 2.8 .Статические характеристики элементов с одной (п) и
двумя (б, в) входными величинами
В общем случае, когда состояние элемента или системы зависит
от нескольких входных воздействий xitx2, . ., х„„ то статическая ха-
рактеристика представляет собой функцию нескольких независимых
переменных
у = /(х,,х2,...,хш)	(2 45)
Функция двух переменных Х] и х2 может быть, как известно,
изображена в виде поверхности в трехмерном пространстве с декар-
товыми координатами у, х(, х2 (рис.2.8,6) или в виде семейства линий
сечений этой поверхности, соответствующих нескольким фиксиро-
ванным значениям одного из аргументов (рис 2 8,в)
Так как статический режим является частной формой дина-
мического режима, то соответствующая статическая характеристика
может быть получена как частный вид дифференциального уравне-
ния (2.1) Для этого необходимо в дифференциальном уравнении
элемента приравнять все производные по времени нулю (что соот-
ветствует определению понятия статический режим), и тогда полу-
чим уравнение статики элемента
79
х =0.
(2.46)
Из уравнения (2.46) можно получить аналитическое выражение
статической характеристики в явном виде (2.44).
Рис. 2.9. Виды статических характеристик
Большинство конструктивных элементов систем в статическом
режиме характеризуется строгими однозначными соотношениями
между значениями входной и выходной величин (рис.2 9,а,б,в). Эти
элементы называют статическими, или позиционными. Но некото-
рые элементы систем не обладают определенными передаточными
свойствами в статическом режиме: при различных значениях вход-
ной величины х выходная величинау может принимать одно и то же
значение (рис.2.9,г), или, наоборот, при одном и том же значении х
величина у может принимать любые значения (рис.2.9,6) Такие эле-
менты называют астатическими. К ним относятся, например, интег-
рирующие звенья, которые будут описаны в главе 3.
По виду статических характеристик элементы делят на линей-
ные и нелинейные. Статическая характеристика линейного элемента
(см рис 2 9,6) описывается линейной функцией у = b + ах У нели-
нейных элементов связь между входной и выходной величинами вы-
80
ражается обычно в виде степенных функций, степенных полиномов,
дробных рациональных и более сложных функций.
На рис.2.10 показаны примеры линейного элемента - двигателя
постоянного тока с независимым постоянным возбуждением (п) и
нелинейного - генератора постоянного тока с неменяющейся часто-
той вращения якоря (в) и их статические характеристики - соответ-
ственно по каналу "мя - л” (б) и по каналу ”/в - ег" (г).
Рис. 2.10. Примеры линейного (а, б) и нелинейного (в, г) элементов
Нелинейные элементы, в свою очередь, подразделяют на эле-
менты с существенно нелинейной статической характеристикой и
элементы с несущественно нелинейной (линеаризуемой) характери-
стикой.
Статическая характеристика является несущественно нелиней-
ной, если она описывается непрерывной дифференцируемой функци-
ей. Практически это математическое условие означает, что график
функции^ = Дх) должен иметь гладкую форму (см.рис. 2.9,п). В ог-
раниченном диапазоне изменения входной величины х такая харак-
теристика может быть приближенно заменена (аппроксимирована)
линейной функцией. Приближенная замена нелинейной функции ли-
нейной называется линеаризацией. Линеаризация нелинейной харак-
81
теристики правомерна, если в процессе работы элемента его входная
величина меняется в небольшом диапазоне вокруг некоторого значе-
ния X = Х0.
Статическая характеристика считается существенно нелинейной,
если она имеет изломы или разрывы. На рис. 2.9,в в качестве приме-
ра приведена характеристика реле, которое при достижении входно-
го сигнала х (ток в обмотке реле) некоторого значения Х] изменит
выходной сигнал у (напряжение в коммутируемой цепи) с уровня у^
до уровня у’2. Замена такой характеристики прямой линией с посто-
янным углом наклона привела бы к существенному несоответствию
между математическим описанием элемента и реальным физическим
процессом, происходящим в элементе.
Линеаризацию гладких статических характеристик можно осу-
ществлять либо по методу касательной, либо по методу секущей.
Линеаризация по методу касательной за-
ключается в разложении функции у(х) в интервале вокруг некоторой
точки х0 в ряд Тейлора и в последующем учете первых двух членов
этого ряда:
у(х)«у(х0) + У(х0)(х- х0),	(2 47)
где у'(хо) = /(хо) - значение производной функции /(х) в заданной
рабочей точке А с координатами Хо и у0. Геометрический смысл такой
линеаризации заключается в замене кривой fix) касательной ВС, про-
веденной к кривой в точке (рис. 2.11,я).
При расчете систем управления удобно линейные статические
характеристики вида (2.47) рассматривать в отклонениях перемен-
ных у и х от значений yQ и Xq:
У~Уо = У,(хо)(х~хо)	(2.48)
или
Ьу-кЬх,	(2.49)
где Дх = х - Хо, Ду = у - Хо, к = у'(х0). Следовательно, переход от за-
писи (2.48) к записи (2.49) уравнения статики соответствует перехо-
ду от исходной системы координат хОу к системе ДхЛДу.
82
Рис. 2.11. Линеаризация статических характеристик
проведением касательной (а) и секущей (6)
Коэффициент пропорциональности к между отклонениями
входной и выходной величин в статическом режиме называют пере-
даточным коэффициентом.
Передаточный коэффициент является основным параметром
линейных и линеаризованных элементов статического типа:
его числовое значение полностью характеризует передаточные
свойства элемента в статике.
Размерность передаточного коэффициента равна отношению
размерности выходной величины к размерности входной величины.
|	(2.50)
Например, у электрического двигателя передаточный коэффи-
циент по каналу "напряжение - частота вращения" имеет размер-
ность (об/с)/В
Если исходная статическая характеристика задана в формуль-
ном виде, то передаточный коэффициент находят как значение про-
изводной в рабочей точке.
I	W(x0) =	,	(2.51)
83
а если характеристика задана графически, то передаточный коэффи-
циент может быть определен как тангенс угла а наклона касатель-
ной (см. рис.2.10,а).
k = (rny/mx)tga,	(2 52)
где ту и тх - масштабные коэффициенты величин у и х
Линеаризация может быть выполнена и в том случае, если вы-
ходная величина является гладкой функцией нескольких перемен-
ных. Линеаризованная статическая характеристика в отклонениях
будет иметь вид
Ду = £.Дх. + £,Дх, + . + £ Дх.	(2 53)
где к}, к2, ..., кт - передаточные коэффициенты, равные значениям
частных производных вида (2.51) функции (2 45) в рабочей точке (у0,
ХЮ, х20, ,хто).
Линеаризацию по методу секущей осуществ-
ляют непосредственно на графике - проведением прямой линии (на
рис 2 10,6 линия ВС) таким образом, чтобы в некотором заданном
диапазоне изменения аргумента х спрямленная характеристика бы-
ла в среднем как можно ближе к исходной линеаризуемой характе-
ристике /(х)- При этом передаточный коэффициент линеаризован-
ной характеристики определяют как отношение соответствующих
друг другу приращений:
|	к = Ду/Дх	(2 54)
Формулой (2 54) для определения коэффициента к можно поль-
зоваться и при применении метода касательной.
Метод секущей можно использовать и при аналитическом ре-
шении задачи линеаризации. При этом указанное выше нестрогое
условие близости линеаризованной характеристики к исходной фор-
мализуется в виде критерия минимума суммы квадратов отклонений
В заключение отметим, что линеаризация по методу касатель-
ной дает хорошее совпадение вблизи рабочей точки и худшее у гра-
84
ниц рабочей зоны, а аппроксимирующая прямая, полученная по ме-
тоду секущей (наименьших квадратов), имеет меньшее среднее рас-
хождение с исходной характеристикой, хотя ее наклон может и не
совпадать с наклоном кривой в рабочей точке.
Пример 1. Линеаризуем нелинейную статическую характеристику
Р (рис. 2.12,6) расходомера газа (рис. 2.12,а), состоящего из шайбы Ш
в трубопроводе и дифференциального манометра ДМ. Из аэромеханики из-
вестно, что перепад давлений р= р\ -рг (Н/м2) на шайбе, сужающей пло-
щадь сечения трубопровода, связан с расходом q (м3/с) квадратичной зави-
симостью
p = cq\	(2.55)
2
где с - постоянный коэффициент; в дальнейшем принято с = 100 (Н/м ) /
Рис. 2.12. Пример линеаризации нелинейного элемента
Линеаризацию осуществим в заданной точке qo = 7 м3/с и
Ро = 4,9-103 Н/м2. Передаточный коэффициент определим по формуле (2.51)
как производную функции (2.55) в заданной точке:
* = (pP/^)q=q^7
= 2cqQ =1400
Н/м2
м3/с
(2 56)
Теперь можно записать линеаризованные уравнения статики расходо-
мера в абсолютных значениях
Р = Ро+л(<7-<7о) = 4-9 103 +1400(<7-7)
(2 57)
или в отклонениях
85
iXp = k&q = 1400Дд,
(2 58)
справедливые в заданной точке.
Передаточный коэффициент к можно определить и по графику на рис
2.12 - проведением касательной в точке Л.
Пример 2. Линеаризуем нелинейное уравнение электромагнита, рас-
смотренного в 2.1. Уравнение статики электромагнита можно получить,
приравнивая в уравнении (2.5) производные по времени нулю и подставляя
в него значения тока из (2.6). Уравнение статики связывает две входные
величины - напряжение и и перемещение 5 - с одной выходной величиной
F3=c3u2/г212 ,	(2 59)
где сэ = ур2цо872 - конструктивный параметр электромагнита, зависящий от
числа витков w, площади сечения сердечника S и магнитной проницаемо-
сти воздуха цо; г - активное сопротивление обмотки.
Передаточные коэффициенты электромагнита для рассматриваемых
двух входных воздействий определим как значения частных производных
функции (2 59) в точке (и0, /о), соответствующей некоторому заданному ус-
тановившемуся режиму:
А, =	=lc,UJr2ll (Н/В);
/-/о
к, =	= - leer'll (Н/м).
/=/о
(2.60)
(2.61)
Линеаризованное уравнение статики электромагнита в отклонениях от
заданного режима
ДЕЭ = ^иДы+^1Д7
(2.62)
2.4.	Линейные дифференциальные уравнения
как динамические характеристики
, В 2 1 было указано, что наиболее общей и наиболее полной
формой математического описания систем управления и их элемен-
тов является дифференциальное уравнение вида (2 1). Для большин-
86
ства реальных элементов исходное уравнение (2.1), составленное
строго в соответствии с законами физики, оказывается нелинейным
Это обстоятельство сильно усложняет все последующие процедуры
анализа Поэтому всегда стремятся перейти от трудно разрешимого
нелинейного уравнения (2.1) к обыкновенному линейному диффе-
ренциальному уравнению вида
(2.63а)
или в свернутом виде
' dt‘ J dtJ
(2 636)
где x(t) и y(t) - входная и выходная величины элемента или систе-
мы, а, Ь} - коэффициенты уравнения
Уравнения (2 63а) и (2.636) устанавливают связь между входной
и выходной величинами как в переходных, так и в установившихся
режимах
Приравнивая все производные в уравнениях динамики (2.63а) и
(2 636) нулю, можно получить уравнение статики элемента (системы)
в следующем общем виде
аоу(О - box(t) или y(t) = — x(t) = kx(t)
«о
(2.64)
Заметим, что аргумент t в уравнениях статики обычно не пишут,
так как в установившемся статическом режиме переменные x(t) и y(t)
не изменяются во времени
Коэффициенты дифференциального уравнения называют пара-
метрами Они зависят от различных физических констант, характе-
ризующих скорость протекания процессов в элементах Такими кон-
87
стантами являются, например, массы движущихся частей, индуктив-
ности и емкости электрических цепей, теплоемкости нагреваемых
элементов.
Иногда параметры некоторых элементов систем изменяются во
времени, причем скорость их изменения соизмерима со скоростью
процессов управления в системе. Тогда систему называют нестацио-
нарной, или системой с переменными параметрами Системой с пе-
ременными параметрами является, например, система управления
приводом поворота мощного экскаватора, если в процессе его пово-
рота одновременно происходит выдвижение рукояти с ковшом. По
мере удаления ковша от центра вращения платформы экскаватора
существенно увеличивается маховый момент вращающихся вокруг
вертикальной оси масс, и, следовательно, существенно будет менять-
ся один из коэффициентов дифференциального уравнения.
В большинстве же практических случаев коэффициенты урав-
нения существенно не изменяются и системы являются системами с
постоянными параметрами. В дальнейшем будут рассматриваться
только такие системы.
Если при составлении линейного дифференциального уравнения
(2 63) использованы линеаризованные статические характеристики
или приняты допущения о линейности тех или иных взаимосвязей, то
уравнение справедливо лишь для малых отклонений входной и вы-
ходной величин от их значений в статическом режиме Дх(/) = x{t) -
Хо, Ду (О - ХО - Уо- Однако с целью упрощения записей часто в ли-
нейном уравнении отклонения обозначают теми же символами (без
знака Л), что и сами величины.
Для систем управления, описываемых линейным уравнением
(2 63), справедлив принцип наложения, или супер-
позиции, согласно которому
изменение выходной величины y(t), возникающее при действии
на систему нескольких входных сигналов x}{t), равно сумме из-
менений yi(t) величины y(t), вызываемых каждым сигналом в от-
дельности
Это свойство линейных систем имеет большое практическое
значение, так как благодаря ему значительно облегчаются все расче-
ты
88
Рассмотрим теперь типовые формы записи линейного диффе-
ренциального уравнения (2.63), используемые в различных задачах
теории управления.
Как и в других областях науки и техники, все физические пере-
менные, входящие в уравнение, могут быть выражены в относи-
тельных единицах. Для этого каждое слагаемое делят на постоянную
величину, имеющую размерность той переменной, которая входит в
это слагаемое. Постоянные величины называют базовыми. В качест-
ве базовых величин принимают обычно номинальные или устано-
вившиеся значения переменных у и х.
Удобной формой записи линейных дифференциальных уравне-
ний является символическая, или операторная. Переход к этой фор-
ме осуществляют введением сокращенного условного обозначения
операции дифференцирования: d ...!dt= р. Соответственно z-ю про-
изводную переменной у обозначают
d'yifildt' = p'y(t)
тогда уравнение (2.63) в символической форме будет иметь вид
^пРп + 4,-1 р"' + • • • + 44+4 W) =
= (\РИ +\-1Р””1 + .- + bxp+b^x(t).
(2 65)
(2.66)
Многочлены от р степени л и ти, находящиеся в левой и пра-
вой частях уравнения (2.66), называют дифференциальными опера-
торами. Каждый такой оператор устанавливает соответствие между
функцией времени и определенной совокупностью производных
этой функции. Многочлен
а„Р"+ ar,-.P"~‘ +-+a!p + a, = D(p)
называют собственным оператором, а многочлен
b^” +Ьт_хрт~' + .. + Ьхр+Ьй=К(р)
- входным оператором, или оператором воздействия.
(2.67)
(2.68)
89
Название собственный обусловлено тем, что многочлен D(p)
характеризует собственное движение элемента, т.е. движение при
отсутствии внешних воздействий. Оператор D(p) называют также
характеристическим.
Дифференциальное уравнение, записанное в символической
форме (2 62), называют операторным уравнением динамики элемента
(системы).
У всех реальных элементов и систем порядок наивысшей произ-
водной во входном операторе не может быть больше порядка наи-
высшей производной в собственном операторе, т.е. обычно т < п.
Если в процессе каких-либо формальных выкладок образуется урав-
нение, у которого т > п , то говорят, что это уравнение соответствует
физически нереализуемой системе.
Уравнения элементов невысокого порядка (и < 3) в теории
управления принято записывать в так называемой стандартной фор-
ме. При стандартной форме записи уравнение преобразовывают
таким образом, чтобы коэффициент при выходной величине был ра-
вен единице. При этом коэффициент перед входной величиной в
правой части уравнения становится равным передаточному коэффи-
циенту, а коэффициенты при производных выходной величины бу-
дут иметь размерность времени в степени, равной порядку соответ-
ствующей производной. Например, уравнение второго порядка
(а2р2 +axp + a^)y{t) =(b{p + bQ}x(t)	(2.69)
путем деления всех членов на коэффициент п0 может быть приведено
к стандартной форме
fcp2 +TtP+\)y(t) = k(Tp+fytf),	(2.70)
где к = Ьо/а0. Т = bt/bw 7] = а, /а0; Т2 = а2 /а0.
Коэффициенты Т, Т\, Т2 принято называть постоянными вре-
мени. Они характеризуют динамические свойства элемента или сис-
темы.
Часто при исследовании автоматических систем оказывается
удобным переход от естественного времени t, измеряемого в секун-
90
дах, минутах и т.д., к так называемому безразмерному (относитель-
ному) времени t. Этот переход осуществляется с помощью некото-
рого постоянного (в общем случае произвольно выбранного) множи-
теля Ты, имеющего размерность времени
t = t/T. .
(2.71)
В качестве множителя Тм часто принимают постоянную времени
одного из элементов, входящих в систему. Величину, обратную
множителю Гм, называют масштабом времени и обозначают
т =1/Т .
t	м
Оператор /-кратного дифференцирования по безразмерному
времени р1 =d'/dt связан с обычным оператором дифференциро-
вания р1 =d‘ / dt’ соотношением
Р = рТм.
(2 72)
Используя соотношение (2.68), можно любое дифференциаль-
ное уравнение записать в безразмерном времени, измеряемом в ус-
ловных единицах Тм. Например, уравнение (2.69) будет иметь вид
“ГР2+^-Р + «о >(0 = ~~р + h МО-
Um 'м ) Um J
(2.73)
Если коэффициент преобразования времени выбирать по опре-
деленному правилу, а именно
=Va»/°o>	<2-74)
то можно максимально упростить дифференциальное уравнение
Так, уравнение (2.73) примет вид
(рг +А{р + 1)у(0 = (Вхр + В0)х(О,
(2 75)
где 4 =aJ^aQa2 ,ВХ = bx/^aQa2 ;BQ =Ь0/а0.
91
В левой части уравнения вместо трех числовых коэффициентов
п0, 0ъ 02 остался лишь один коэффициент Ль Такая компактная фор-
ма записи была впервые применена И.А Вышнеградским (для урав-
нения 3-го порядка) и называется формой Вышнеградского.
Важным преимуществом этой формы является то, что введение
безразмерного времени t в дифференциальное уравнение не влияет
на характер искомой функции y(t) (меняется только масштаб незави-
симой переменной f). Поэтому изменение масштаба времени широко
применяют при исследовании и моделировании систем управления
При этом прибегают как к ускорению времени (Тм> 1с и mt < 1), так
и к замедлению времени (Тм < 1с и mt > 1).
Изменение масштаба времени облегчает во многих случаях ана-
лиз динамики СУ, позволяет получить результаты в наиболее общем,
универсальном виде.
Очевидно, что уравнение статики можно получить из оператор-
ных уравнений динамики (2.66), (2.69), (2.70), (2.73) и (2.75), прирав-
нивая в них оператор р нулю.
Пример 1. Составим дифференциальное уравнение химического реак-
тора непрерывного действия с идеальным перемешиванием жидкой среды
(рис 2.13,а). В реактор с рабочим объемом V (м3) поступает жидкость, со-
держащая частицы некоторого компонента с концентрацией свх = х (кг/м3)
В реакторе происходит частичное превращение этого компонента в газ по
закону реакции первого порядка - его выход q (кг/с) пропорционален кон-
центрации с компонента в реакторе и объему V\
q = kpcV,	(2 76)
где kp - константа скорости реакции.
Будем считать, что расход жидкости через реактор постоянен.
Qi = Qz= Q = const. Тогда уравнение материального баланса рассматривае-
мого компонента
d[^ty]/A = c„(-(;e1 -cBla(t)Q2 -kpc(t)V .	(2 77)
Концентрация ctblx в выходном потоке жидкости благодаря интенсив-
ному перемешиванию равна в каждый момент времени концентрации с
внутри реактора, т.е. свых = с = у. Учитывая это, уравнение (2.77) можно
привести к стандартной форме
92
Рис 2 13 Схемы химического реактора (а) и
механического колебательного устройства (б)
Tl^-+y(t) = kx(t),
at
(2.78)
где к = Q/\Q+kpv] - передаточный коэффициент реактора по рассматривае-
мому каналу "с^ - свых”; 7] = V/\Q + kpV) - постоянная времени реактора.
Пример 2. Составим дифференциальное уравнение механического ко-
лебательного устройства (рис. 2.13,6), состоящего из подвижной части с
массой т (кг) и упругого элемента с коэффициентом упругости к^. В каче-
стве входной переменной х будем рассматривать силу F (Н), а выходной у
- перемещение л (м) центра массы.
Согласно известному закону механики - принципу Д Аламбера - ак-
тивная (внешняя) сила F уравновешивается суммой сил инерции Fm, тре-
ния и упругой реакции Fy^
Fm(t)+F^(t) +F^(t) = F(t).	(2.79)
Сила инерции пропорциональна ускорению и массе:
Fm(l) = m d24(t)/dt2	(2.80)
Силу трения будем считать пропорциональной скорости движения.
F^ (t) = k^ds( t)/dt.	(281)
Сила упругой реакции пропорциональна перемещению
93
•^*уп(О “ kyn5(t).
(2.82)
Подставляя выражения (2.80), (2.81) и (2.82) в уравнение сил (2.79),
получим линейное дифференциальное уравнение общего вида
d2sft) , ds(t) ,	, .	Л_.
w—^-+krp—^- + kyns(t)=F(t)	(2.83)
и после деления на к^ - в стандартной форме:
Г22	^- + s(t) = kF(t),	(2 84)
dt dt
где к = \/куп - ПК устройства, м/Н; 1\ = ктр]куп, Т2 = Jm/kyn - постоянные
времени, с.
2.5.	Временные характеристики
Дифференциальное уравнение является самой общей формой
описания элемента и не дает наглядного представления о передаточ-
ных свойствах элемента. Наглядное представление об этих свойствах
дает функция y(t), являющаяся решением дифференциального урав-
нения. Но одно и то же дифференциальное уравнение может иметь,
как известно, много решений, конкретный вид которых зависит от
начальных условий и от характера функции x(t), т.е. от начального
состояния элемента и от вида внешнего воздействия. Поэтому при-
нято динамические свойства элементов и систем характеризовать
решением, соответствующим нулевым начальным условиям и одно-
му из типовых воздействий. В качестве типовых воздействий прини-
мают единичное ступенчатое, дельта-функцию или гармоническое.
Наиболее наглядное представление о динамических свойствах
элемента дают его переходные функции или переходные характери-
стики. Переходной функцией (характеристикой) h(t) называют изме-
нение выходной величины y(t) во времени, возникающее после по-
дачи на вход единичного ступенчатого воздействия, при нулевых
начальных условиях. Переходная функция может быть задана в виде
94
графика (рис.2.14,а) или в формульном виде. Формульное выражение
функции h(f) для конкретного элемента можно найти, решая его диф-
ференциальное уравнение при x(t) = o(t) и при у(~0) = Ул~0) ~
= ,.= у(и' (-0) = 0. Второе условие означает, что выходная величина
у и ее производные до (п- 1)-го порядка непосредственно перед
подачей ступенчатого воздействия равны нулю.
Переходная функция h(t), как и любое решение неоднородного
дифференциального уравнения вида (2.63), имеет две составляющие:
вынужденную hB(t) и свободную hc(fy.
(2.85)
Вынужденная
составляющая hB(f)
переходного про-
цесса представляет
собой, как известно,
частное решение
исходного уравне-
ния. При единич-
ном ступенчатом
воздействии о(/)
вынужденная со-
ставляющая равна
установившемуся
значению выходной
величины, которое
для статических
элементов может
h(t) = hB(t) + hc(t).
Рис 2.14. Переходная (а) и импульсная
переходная (б) характеристики
быть определено непосредственно из дифференциального уравнения
(при нулевых производных)

(2.86)
95
Свободная составляющая hc(t) может быть найдена как общее
решение соответствующего однородного дифференциального урав-
нения в следующем виде (при отсутствии одинаковых корней):
mo=£cZ',
*=1
(2.87)
где \к ~ корни характеристического уравнения; Ск - постоянные ин-
тегрирования, зависящие от начальных условий
Если же среди п корней характеристического уравнения (п - Z)
корней одинаковы и равны между собой, т.е. Xj = Х2 = ... = Х„.|, то
свободная составляющая принимает более сложный вид:
п-1
п
к~п-1+\
(2.88)
ы
Характеристическое уравнение, соответствующее определен-
ному дифференциальному уравнению, представляет собой, как из-
вестно, алгебраическое уравнение, степень и коэффициенты которо-
го совпадают с порядком и коэффициентами левой части этого диф-
ференциального уравнения. Для дифференциального уравнения, за-
писанного в форме (2.63), характеристическое уравнение имеет вид
«Л +Ч,-Л'”1 + ...+М + *о =° •	(2.89)
Структура характеристического уравнения (2.85) совпадает со
структурой левой части дифференциального уравнения, записанного
в символической форме (2.66), и со структурой собственного (харак-
теристического) оператора D{p) [см. (2.67)]. Поэтому при записи ха-
рактеристического уравнения часто вместо символа X, обозначающе-
го неизвестную переменную алгебраического уравнения, используют
тот же символ р. Но при этом р означает уже не операцию диффе-
ренцирования, а некоторое комплексное число, которое является ре-
шением (корнем) характеристического уравнения.
96
Для линейных элементов и систем, кроме принципа суперпози-
ции, справедливо еще одно общее правило: реакция у(0 на нееди-
ничное ступенчатое воздействие t7o^(O равна произведению переход-
ной функции h(t) на величину множителя ао, те. y(t) = aoh(t). Это
свойство широко используется при исследовании и расчете линей-
ных систем.
Импульсной переходной функцией w(t) называют изменение вы-
ходной величины y(t), возникающее после подачи на вход дельта-
функции, при нулевых начальных условиях (рис. 2.14,6).
Если входное воздействие представляет собой неединичный
импульс бто8(О, ординаты функции выходной величины y(t) будут в
ао раз больше ординат функции w(t), т.е. y(t) = aow(t).
Импульсная переходная функция w(t) равна производной от
переходной функции h(t):
|	w(t) = dh(t)/dt	(2.90)
и, наоборот, переходная функция равна интегралу от импульсной
переходной:
/
о
(2.91)
При помощи импульсной переходной функции элемента можно
определить его реакцию на входное воздействие произвольного вида.
Связь между изменениями входной и выходной величин во времени
устанавливается интегралом свертки (интегралом Дюамеля)
QO	О0
ХО = ( x(&)w(t - &)d9 = f x(t - &)w(&)d9.
о	0
(2.92)
Интегральное соотношение (2.92) вытекает из следующих рас-
суждений. Любое входное воздействие х(/) можно рассматривать
(рис. 2 15.(1) как непрерывную последовательность коротких импуль-
сов х(3)б/35(/ - 3), имеющих площадь x(Q)d§ и действующих в мо-
97
менты t = 3, где 0 < 3 < оо. Так как смещенная дельта-функция
5(/ - 3), действующая на входе элемента, создает на его выходе сме-
щенную импульсную переходную функцию w(l - 3), то каждому не-
Рис. 2.15. К пояснению
интеграла свертки
единичному входному импульсу
x(3)c/36(r - 3) на выходе будет соот-
ветствовать реакция, пропорцио-
нальная импульсной функции, т.е.
реакция dy = x(3)w(r - 3)^3 (рис.
2.15,6). Полный переходный процесс
y(t) на выходе согласно принципу су-
перпозиции получается как результат
суммирования реакций на все вход-
ные импульсы (рис. 2.15,в), т.е. как
результат их интегрирования по ар-
гументу 3 от 0 до оо, что и требова-
лось доказать [см. первую запись ин-
теграла (2.92)].
Изложенное обоснование инте-
грала свертки (2.92) объясняет второе
распространенное название функции
w(t) - весовая. Действительно, эта
функция определяет вес (долю), с ко-
торым каждый входной импульс, по-
лученный при разложении сигнала
х(Г), участвует в формировании ре-
зультирующего выходного сигнала y(f).
Так как следствие не может опережать причину, действует усло-
вие физической осуществимости: при t < 0 весовая функция w(t) = О
или при 3 > t - 3) = 0. С учетом этого верхний предел интегри-
рования в (2.92) может быть уменьшен до t.
Переходные характеристики h(t) и w(t) называются также вре-
менными.
Пример 1. Найдем переходную функцию h(t) элемента, описывае-
мого уравнением
(aiP + ao)XO = 6оХО
(2 93)
98
Переходная функция имеет две составляющие:
Л(/) = ^(0 + ^(0	(2.94)
Вынужденная составляющая согласно (2.86) в данном случае
Лв(0 = (Ь0/а0)о(0.	(2.95)
Свободную составляющую будем искать в виде
hc(t) = С^10'.	(2.96)
Учитывая начальное условие у(0) = 0, получим С] = (- Ьо /а0 )□(/). Тогда
Л(0 = —(1-е~°°'/о’)о(0
«о
(2 97)
Пример 2. Определим при помощи интеграла свертки реакцию эле-
мента (2.93) на воздействие вида х(0 =
Импульсная переходная функция элемента согласно (2.90)
w(0 = ^-е-О0//О1.
ai
(2.98)
Функцию y(t), описывающую изменение выходной величины после
подачи линейного воздействия, получим, подставляя выражение (2.98) в
интеграл (2.92):
о 1
•G(/)
(2 99)
2.6.	Операторный метод и передаточная функция
Наиболее распространенным методом описания и анализа эле-
ментов и систем управления является операторный метод (метод
99
операционного исчисления). В основе метода лежит преобразование
Лапласа
Х(р) = У’{л(/)} = pldt.
о
(2.100)
которое устанавливает соответствие между функциями действитель-
ной переменной t и функциями комплексной переменной р. Функ-
цию времени x(t), входящую в интеграл Лапласа (2.100), называют
оригиналом, а результат интегрирования - функцию Х{р) - изобра-
жением функции х(0 по Лапласу.
Таблица 2.1
Изображение простейших функций времени по Лапласу
Наименование функций	ХО	х(р) =
Дельта-функция	8(0	1
Ступенчатая	w(0	ао/р
Степенная	Л/о (0 (« = 0,1.2. )	_	..	(О'=1) 	
Экспонента	е ^<3(1)	1/(р + а)
Синусоида	(sin со0о(0	<о/(р2 + С02)
Косинусоида	(cos соГ)о(Г)	р/(р2 +С02)
Периодическая _ 			 	.	..		-J	х(1) = x(t +Т)	
Преобразование Лапласа выполнимо, как известно, лишь для
таких функций времени, которые равны нулю при t < 0. Это условие
обеспечивается обычно умножением функции x(t) на единичную
ступенчатую функцию cr(0. С математической и физической точек
зрения такой искусственный прием вполне корректен, так как функ-
ции x(t) описывают процессы в СУ, начинающиеся с некоторого мо-
мента времени, а этот момент времени всегда может быть принят за
начало отсчета.
100
В табл. 2.1 приведены изображения простейших
функций времени, наиболее часто используемых в расчетах СУ.
Основные свойства преобразования Ла-
пласа, используемые при анализе автоматических систем, указа-
ны в табл.2.2.
Таблица 2.2
Основные свойства преобразования Лапласа
Наименование	Оригинал	Изображение
Линейность	ах(0	aX(p)
	Х1 (0 ± х2 (0	У1 (p) + A 2 (p)
Правило дифференциро- вания (при нулевых на- чальных условиях)	d	’	X(p)p' . ...
Правило интегрирования (при нулевых начальных условиях)	t t J...[x(tf)tZi5’ 0 0	X(p)lp'
Изменение масштаба времени (теорема подо- бия)		XipTJT.
Смещение аргумента оригинала (теорема за- паздывания)	x(r-T)	X(p)epx
Смещение аргумента изображения (теорема затухания)	Х(Г)е'а'	X(p+a)
Теорема о начальном значении оригинала	lim x(0 t—>0	lim pX(p) p—►
Теорема о конечном значении оригинала	hm x(/) t—>00	hm pX(p) p—>0
Правило свертки ориги- налов	t |х1(г-й)-х2(«Х/гх= 0 = x1(r)*x2(/)	A'i (p)X2(p)
Наиболее важными свойствами преобразования Лапласа явля-
ются свойства, формулируемые обычно в виде правил:
при нулевых начальных условиях дифференцированию оригинала
x(f) по переменной t соответствует умножение изображения
101
Х(р) на комплексную переменную р, а интегрированию оригина-
ла соответствует деление Х(р) на р.
Именно на этих двух свойствах основан операторный метод ре-
шения дифференциальных уравнений. Метод заключается в сле-
дующем. Исходное дифференциальное (или интегродифференциаль-
ное) уравнение, записанное относительно искомой выходной функ-
ции v(f), заменяют на алгебраическое уравнение относительно изо-
бражения У(р) (эту процедуру называют алгебраизацией дифферен-
циального уравнения), затем, решая алгебраическое уравнение при
заданном Х(р). находят изображение У(р) и, наконец, по изображе-
нию Y(p) определяют функцию y(t). Этот обратный переход от изо-
бражений к оригиналам в большинстве практических задач может
быть осуществлен при помощи таблиц, имеющихся в специальных
справочниках по операционному исчислению.
Широкое распространение операторного метода в теории
у правления обусловлено тем, что с его помощью определяют так на-
зываемую передаточную функцию, которая является компактной
формой описания динамических свойств элементов и систем
Применим преобразование Лапласа к линейному дифференци-
альному уравнению (2.63), полагая, что до приложения внешнего
воздействия система находилась в покое и что все начальные усло-
вия равны нулю. Используя свойство линейности и правило диффе-
ренцирования (см. табл.2.2), можно получить алгебраическое урав-
нение в изображениях
D(p)Y(p) = K(p)X(p),	(2.101)
где 1)(р) = апр" + апА рпЛ + . +ахр + а^
К{р) = Ьтрт + ЬтА ртЛ +...+ bxp + bt>.
Сравнивая уравнение (2.101) с уравнением в символической
форме (2 66), можно заметить полную аналогию их структур. Разли-
чие уравнений лишь в значении символа р: в первом уравнении он
обозначает операцию дифференцирования, во втором - комплексную
переменную.
Введем теперь понятие передаточной функции (сокращенно -
ПФ). Передаточной функцией W{p) называют отношение изображе-
102
ния выходной величины к изображению входной величины при ну-
левых начальных условиях:
А
W(p)=Y(p)/X(p) = ^{у(/)}/^{х(О}	(2.102)
Для системы, описываемой уравнением (2.63), ПФ равна отно-
шению входного оператора К(р) к собственному оператору D(p):
.... К(р) Ьтрт +Ьт ,рт 1 +... + b{p + bQ
/Л/ I П 1 •	' - т	Ц
Е>(Р)	апР” +ап^рп' +... + a{p + aQ ’
(2 103)
Как следует из определений (2.102) и (2.103), ПФ представляет
собой некоторый динамический оператор, характеризующий прохо-
ждение сигналов через линейный элемент (рис. 2.16,а).
в
Х(р)
Z(p)-l/pC
Рис. 2.16. Схемы для определения передаточной функции
электрического четырехполюсника
Передаточную функцию формально можно получить из диффе-
ренциального уравнения заменой в нем символа кратного дифферен-
цирования на соответствующую степень р и делением образованного
таким образом многочлена правой части уравнения на многочлен
левой части.
Передаточную функцию электрических
четырехполюсников удобно получить, пользуясь поняти-
ем операторного сопротивления. Для этого четырехполюсник необ-
ходимо представить в виде схемы делителя напряжения (рис. 2.16,6),
состоящей из двух операторных сопротивлений Zi(p) и Z2(p). Тогда
ПФ между напряжениями щ и и2 может быть определена как отно-
103
шение выходного сопротивления ZBblx(p) = Z2(p) к входному ZBX(p) =
Zx(p) + Z2(py.
W( м =	= Ze-x(P) = Zz(P)
«№ Up) z^py+z^pY
(2.104)
где Z](p) и Z2(p) найдены как эквивалентные операторные сопротив-
ления входного и выходного участков, состоящих из типовых эле-
ментов электрических цепей (рис. 2.16,в).
Рассмотрим теперь основные свойства и осо-
бенности передаточных функций систем управле-
ния и их элементов.
Передаточная функция элемента связана с его импульсной пе-
реходной функцией преобразованием Лапласа:
00
W(p) = _^{и’(Г)}= J w(t)e~ptdt,
о
(2.105)
соответственно и наоборот
но=
(2.106)
Поскольку переходная характеристика h(t) и импульсная пере-
ходная функция w(r) связаны друг с другом интегральным соотноше-
нием (2.91), то, учитывая третье свойство преобразования Лапласа
(см.табл. 2.2), можно записать следующее равенство.

(2.107)
А теперь в соответствии с теоремами о начальном и конечном
значениях оригинала (см.табл 2.2) можно с учетом равенства (2.107)
получить следующие соотношения:
A(oo) = FK(0) и /?(0) = ^(ос).
(2.108)
104
У реальных элементов систем, описываемых обыкновенными
дифференциальными уравнениями вида (2.63), ПФ представляет со-
бой правильную рациональную дробь, у которой степень многочлена
числителя меньше или равна степени многочлена знаменателя, т.е.
т < п. Все коэффициенты ПФ - действительные числа, характери-
зующие параметры элемента (системы).
ПФ является функцией комплексной переменной р = а ± ур, ко-
торая может быть при некоторых значениях переменной р обращать-
ся в нуль или бесконечность. Значение переменной р, при котором
функция W(p) обращается в нуль, называют нулем, а значение, при
котором обращается в бесконечность, - полюсом передаточной
функции. Очевидно, что нулями передаточной функции являются
корни полинома К(р), а полюсами - корни полинома D(/?) Корни по-
линомов числителя и знаменателя могут быть комплексными, мни-
мыми и вещественными числами (в том числе и нулевыми) Если эти
корни известны, то ПФ может быть представлена в следующем виде:
(2.109)
ап\р-^КР-^)Лр-^)
где у, - корни многочлена К(р) (нули ПФ); X, - корни многочлена D(p)
(полюсы ПФ).
Таким образом, каждой конкретной ПФ с заданными коэффици-
ентами соответствует вполне определенное сочетание нулей и полю-
сов. По распределению нулей и полюсов ПФ на комплексной плос-
кости с координатами а иур можно судить о свойствах элемента или
системы.
Если полиномы D(p) и К(р) имеют один или несколько нулевых
корней, то ПФ удобно записывать в такой форме, чтобы полюсы и
нули были выделены в явном виде. Так. если ПФ имеет в точке р = 0
полюс кратности v, то её удобно записать в виде
W(p) = kW‘(p)/pv.	(2.110)
где W*(р) прир 0 стремится к единице.
105
ПФ (2.106) имеет полюсы в точке р == 0, когда один или несколь-
ко младших коэффициентов многочлена Z)(p) равны нулю.
о0 = Oi = ... = ov.| =0, (v = 0; 1, 2; ...). Такую ПФ можно представить
в виде

ьтрт + ьт_}рт~х + ..лЪ}р + Ьо
~pv(cinpn-v+aH_}pn-l-v+... + av+}pv+x +ov)
(2 111)
или после преобразований
где В, = b,/ Ьо при i = 0; 1, 2; ... w, Я, = а, / av при i = v + 1; v + 2; n,
к-bo I av
Величину v называют порядком астатизма Коэффициент к
имеет размерность
И=[.у]/М['Г
(2 113)
и с некоторой условностью может быть назван передаточным коэф-
фициентом. Условность заключается в том, что понятие "передаточ-
ный коэффициент" было введено в качестве характеристики статиче-
ского режима, а у элементов с v Ф 0 статический режим работы не
существует.
Если v = 0, то элемент называется статическим, а его переда-
точная функция при р = 0 равна передаточному коэффициенту
W(0) = kW'(0) = bJaQ = к
(2 114)
Пример 1. Определим ПФ механического устройства, рассмотренного
в 2 4 Для этого запишем его дифференциальное уравнение (2 84) в изобра-
жениях:
Г22р2з( p) + T}ps( p) + s(p)=kF(p)
(2 115)
106
и найдем отношение изображения выходной величины s(p) к изображению
входной величины F(pY
W(p) = s(p)]F(p) = k/frfp2 +TlP + l)
(2 116)
Пример 2. Найдем ПФ электрического колебательного контура, кото-
рый представлен в виде четырехполюсника (рис 2 16,6), причем входной
участок образован последовательным соединением резистора г и индуктив-
ности L, а выходной - из емкости С.
Операторные сопротивления участков Z\(p) = г + pL, Z2(p) = \[pC
Согласно (2.104) ПФ равна

Щ(р) r + pL + \/pC T2p2+Txp + l’
(2.117)
где Т2 - у/ьС; Т} -гС .
2.7.	Частотные характеристики
Частотные характеристики описывают передаточные свойства
элементов и систем в режиме установившихся гармонических коле-
баний, вызванных внешним гармоническим воздействием Зная час-
тотную характеристику элемента, можно определить реакцию эле-
мента на гармоническое воздействие любой частоты, а также на
сумму гармонических воздействий различной частоты Частотные
характеристики широко используются в теории и практике автома-
тического управления, так как реальные возмущения, действующие
на системы, могут быть представлены как сумма гармонических сиг-
налов.
Рассмотрим физическую сущность и разно-
видности частотных характеристик Пусть на
вход линейного элемента (рис. 2.17,я) в момент времени t = 0 подано
гармоническое воздействие определенной частоты о
x(t) - xm sinrztf
(2 118)
107
0«о<х>
x(t) -vmsin®C	W(/co)	yW=y„sm((£>t+(p)
		
-00<0) <4-00
Рис 2 17 Схема для определения понятий частотного метода
Через некоторое время, необходимое для протекания переход-
ного процесса (т е для исчезновения свободной составляющей), эле-
мент войдет в режим установившихся вынужденных колебаний, а
выходная величина y(t) будет изменяться по гармоническому закону
с той же частотой со, но с отличающейся амплитудой ут и со сдвигом
Дгф по оси времени (рис 2 17,6)
У(0 = Ут sin(cwf + <p),
(2 119)
где ср — (Д/ф / Г)-360° - фазовый сдвиг между входным и выходным
сигналами, 0
Повторяя такой эксперимент при фиксированном хт для различ-
ных значений частоты (от 0 до со), можно установить, что амплитуда
у„, и фазовый сдвиг ср выходного сигнала конкретного элемента зави-
сят от частоты воздействия Подавая гармоническое воздействие на
вход различных элементов, можно убедиться, что величины ут и ср
зависят также от типа и параметров элемента Следовательно, зави-
симости амплитуды ут и сдвига ср от значений частоты со могут
служить характеристиками динамических свойств элементов
Так как амплитуда выходного сигнала ут зависит еще и от ам-
плитуды входного сигнала хт, то целесообразно при описании пере-
даточных свойств элементов рассматривать отношение амплитуд
v_,/x„.
Зависимость отношения амплитуд выходного и входного сигна-
лов от частоты называют амплитудной частотной характеристикой
108
(сокращенно - АЧХ). Она обозначается Л (со) Зависимость фазового
сдвига между входным и выходным сигналами от частоты называют
фазовой частотной характеристикой (ФЧХ) ср(со) Возможный вид
этих характеристик показан на рис. 2 18,а и б Аналитические выра-
жения Л (со) и ср(со) называют соответственно амплитудной и фазо-
вой частотными функциями
Рис. 2.18. Частотные характеристики:
а - амплитудная, б - фазовая, в - амплитудно-фазовая, г - логарифмическая
АЧХ показывает, как элемент пропускает сигналы различной
частоты Оценка пропускания производится по отношению амплитуд
ут1хт АЧХ имеет размерность, равную отношению размерности вы-
ходной величины к размерности входной. ФЧХ показывает, какое
отставание или опережение выходного сигнала по фазе создаст эле-
мент при различных частотах
Графики АЧХ и ФЧХ (см.рис. 2 18,с? и б), расположенные со-
вместно, друг под другом, в западной литературе называют диаграм-
мой Боде
109
Амплитудную и фазовую частотные характеристики можно
объединить в одну общую - амплитудно-фазовую частотную харак-
теристику (АФЧХ или АФХ). Амплитудно-фазовая частотная ха-
рактеристика W(jo) представляет собой функцию комплексного
переменного jo, модуль которой равен Л (со), а аргумент равен ср(со).
Каждому фиксированному значению частоты со1 соответствует ком-
плексное число FKQcO;), которое на комплексной плоскости можно
изобразить вектором, имеющим длину А(со;) и угол поворота
(рис. 2.18,в). Отрицательные значения ср(со), соответствующие отста-
ванию выходного сигнала от входного, принято отсчитывать по ча-
совой стрелке от положительного направления действительной оси.
При изменении частоты от нуля до бесконечности вектор W(jo)
будет поворачиваться вокруг начала координат, одновременно будет
увеличиваться или уменьшаться длина вектора Кривая, которую при
этом опишет конец вектора, и есть АФХ. Каждой точке характери-
стики соответствует определенное значение частоты.
Проекции вектора W\jo) на действительную и мнимую оси на-
зывают соответственно действительной частотной характеристикой
и мнимой частотной характеристикой Обозначают их так:
Р(о) = Re IP(jo), Q(o) - Im W(jo). Отметим, что действительная час-
тотная характеристика Р(о) - всегда четная функция частоты, а мни-
мая характеристика Q(o) - всегда нечетная функция.
Аналитическое выражение для АФХ конкретного элемента
можно получить из его передаточной функции - путем под-
становки р - jo:
W(jo)^W(p)
(2.120)
поэтому АФЧХ иногда называют частотной передаточной функцией.
АФХ W(jo), как и любая комплексная величина, может быть
представлена в показательной форме
W(j- А(аз)е}<р(ш},
(2.121)
алгебраической
НО
W(ja>) = P(a)) + jQ(a>)
(2.122)
или тригонометрической
W(jco) = A(a))cos (p{(o) + jA(a)}s\n (p((o).
(2.123)
Связь между различными частотными функциями следующая:
Л(щ) = |^(»| = ^P\a>) + Q\a)Y
(2.124)
<р(й)) = argFF(jTy) = arctg(2 (щ)/Р(щ)).	(2.125)
Поскольку АФХ так же, как и ПФ, представляет собой
обычно дробь, то ее модуль может быть найден по известному пра-
вилу - как отношение модуля числителя к модулю знаменателя:
А(а>) =	= |^( 7^)|/|^(7^)|,
(2.126)
а аргумент функции Wfjo) - как разность аргументов числителя и
знаменателя:
(р(а>) = argPT(/(D) = arg А (у а») - arg/7 (.7^) 	(2.127)
При практических расчетах СУ удобно использовать частотные
характеристики, построенные в логарифмической системе коорди-
нат. Такие характеристики называют логарифмическими. Они имеют
меньшую кривизну и поэтому могут быть приближенно заменены
ломаными линиями, составленными из нескольких прямолинейных
отрезков. Причем эти отрезки в большинстве случаев удается по-
строить без громоздких вычислений, при помощи некоторых про-
стых правил. Кроме того, в логарифмической системе координат лег-
ко находить характеристики различных соединений элементов, так
как умножению и делению обычных характеристик соответствует
сложение и вычитание ординат логарифмических характеристик.
111
За единицу длины по оси частот логарифмических характери-
стик принимают декаду Декада - интервал частот, заключенный
между произвольным значением со, и его десятикратным значением
Юсо, Отрезок логарифмической оси частот, соответствующий одной
декаде, равен 1
Обычно в расчетах используют логарифмическую амплитудную
частотную характеристику (ЛАЧХ)
Цсо) = 201g А(а>),	(2 128)
ординаты которой измеряют в логарифмических единицах - белах
или децибелах (сокращенно дБ)
Бел - единица измерения отношения мощностей двух сигналов
Если мощность одного сигнала больше (меньше) мощности другого
сигнала в 10 раз, то эти мощности отличаются на 1 бел (1g 10 = 1) Так
как мощность гармонического сигнала пропорциональна квадрату
его амплитуды, то при применении этой единицы для измерения от-
ношения амплитуд перед логарифмом появляется множитель 2 На-
пример, если на некоторой частоте Л (со) = 100, то это означает, что
мощности входного и выходного сигналов отличаются в 1002 раз, т.е
на 21g 100 = 4 бела или на 40 децибел, соответственно и
£(со) = 201^Л (со) = 40 дБ
При построении фазовой частотной характеристики логарифми-
ческий масштаб применяют только для оси абсцисс
На рис 2 18,2 показаны ЛАЧХ L(co) (жирная линия) и соответ-
ствующая ей приближенная (асимптотическая) характеристика La(©)
в виде прямолинейных отрезков (тонкая линия). Частоты, соответст-
вующие точкам стыковки отрезков, называются сопрягающими и
обозначаются сос
Правила и примеры построения приближенных логарифмиче-
ских характеристик конкретных элементов будут даны в главе 3
АФХ устанавливает связь между входным и выходным сигна-
лами не только для случая, когда они являются гармоническими
функциями, но и тогда, когда они имеют произвольный вид Поэтому
АФХ можно определить как отношение изображения по Фурье вы-
ходной величины К(/со) к изображению входной величины Х(усо)
112
W(ja>) = Y(ja>)/X(ja>).
(2.129)
В этом случае комплексная переменная ja изменяется от -со до
+оо, так как любой реальный сигнал может быть разложен на сумму
только попарно сопряженных вращающихся векторов.
АФХ элемента связана с его импульсной переходной функцией
преобразованием Фурье (2.31):
W (уш) =	= j w(f)e
о
(2 130)
При применении двустороннего преобразования (231) к функ-
ции w(f) учтено, что при t < 0 w(t) = 0, и поэтому нижний предел ин-
тегрирования принят равным нулю
Если формулу (2.130) применить для импульсной переходной
функции, записанной в безразмерном времени t = t/T то АФХ ста-
нет функцией безразмерной частоты со = со7м
(2.131)
J 1
О м
где Гм - масштабный множитель, принятый за единицу времени.
Соотношение (2.131) означает, что если растягивать (сжимать)
график функции w(f) вдоль оси времени в Гм раз, то графики ампли-
тудной и фазовой характеристик будут сжиматься (растягиваться)
вдоль оси частот о в Ти раз. Это свойство используется при построе-
нии безразмерных частотных характеристик и при анализе связи пе-
реходных процессов с частотными свойствами системы управления.
По виду частотных характеристик все элементы и системы де-
лятся на две группы: минимально-фазовые и неминимально-фазовые.
Минимально-фазовыми являются элементы (системы), у которых все
полюсы и нули передаточной функции W(p) имеют отрицательные
действительные части. Такие элементы дают минимальный фазовый
сдвиг ф(со) по сравнению с любыми другими элементами, имеющими
такую же амплитудную характеристику Л(со), но у которых действи-
113
тельная часть хотя бы одного полюса или нуля положительна. Эта
особенность частотных характеристик будет проиллюстрирована в
3.3.
Минимально-фазовые элементы обладают ценным для практи-
ческих расчетов свойством: их частотная передаточная функция пол-
ностью определяется одной из трех составляющих - Л (со), Р(о) или
2(®). Это существенно упрощает задачи анализа и синтеза мини-
мально-фазовых систем.
Пример. Найдем аналитические выражения для частотных характери-
стик элемента, ПФ которого имеет вид
ff'(P) = (Ь\Р +^Махр + а0).
Амплитудно-фазовая функция элемента
= (Vю + bo)/(a}jG3 + а0).
(2.132)
(2.133)
Выражение для амплитудной частотной характеристики найдем как
отношение модулей числителя и знаменателя:
Л(го) =
+Ьр
al jro + а0
=	+ bfa21+ а2со2 ,
(2.134)
а для фазовой - как разность аргументов числителя и знаменателя
(со) = arg(Z>0 + jd2co)-arg(a0 +Jax(j)) = arctgfo co/dj-arctgfo co/a0). (2.135)
Анализируя выражение (2.135), нетрудно убедиться, что элемент
(2.132) с положительными коэффициентами at и Ь, является минимально-
фазовым. Если хотя бы один из них отрицательный, то фазовый сдвиг
(2.135) уже не будет минимальным.
Рассмотренные в 2.5-2.7 временные, передаточные и частотные
характеристики однозначно связаны между собой прямым и обрат-
ным преобразованиями Лапласа и Фурье. Эти взаимные связи и со-
ответствия сведены в табл.2.3.
114
Таблица 2.3
Взаимные соответствия динамических характеристик
Характеристики	Л(г)	КО	W(p)	W(ja>)
Переходная /?(/) =	1	t J w( в )• d3 0		
Импульсная w(Z) =	dh(t) dt	1		X-1
Передаточная W(p) =	p-zfyf!)}		1	
Частотная ИЛ(/©) =		#-{»(/)}	if	1
2.8.	Статические и динамические характеристики типовых
соединений элементов
Алгоритмическая структура любой СУ представляет собой ком-
бинацию трех типовых соединений элементов: последовательного,
параллельного и встречно-параллельного (охват обратной связью).
Если эти соединения состоят из элементов направленного действия
(см.2.1), то каждое соединение может быть по простым правилам
заменено одним элементом, статические и динамические свойства
которого эквивалентны свойствам всего соединения.
При последовательном соединении (рис. 2.19,а) выходная вели-
чина каждого предыдущего элемента является входным воздействи-
ем для последующего элемента. Если элементы линейны и в статике
характеризуются передаточными коэффициентами к\,к2, ...,kt, ..., кп,
то, согласно определению передаточного коэффициента, можно за-
писать систему равенств
у.=к.х.=к.х;
* 1 1 7
У2=к3х2=к3у>;
у^к^ = klyi_l;
(2.136)
у„ =к„х„ = kv..
* п	п П	П иг П 1 J
115
a
Рис. 2.19. Типовые соединения линейных элементов:
а - последовательное; б - параллельное;
в - встречно-параллельное (с обратной связью)
Исключая из (2.136) промежуточные переменные У\, у2, •• •, Ki.
у„ у,,, получим равенство
y = kik1..k, ,.к„х,	(2.137)
из которого следует, что ПК эквивалентного элемента
^,=^/х = ^2..Л-Л? = П*' •	(2.138)
i=i
Таким образом,
общий ПК последовательно соединенных элементов равен про-
изведению передаточных коэффициентов этих элементов.
Размерность общего передаточного коэффициента равна про-
изведению размерностей коэффициентов.
Так как при последовательном соединении выход каждого пре-
дыдущего элемента является входом последующего, то передаточ-
ные коэффициенты всех элементов должны определяться путем ли-
116
неаризации статических характеристик в точках, соответствующих
одному и тому же режиму.
Параллельным соединением называют такое соединение, при ко-
тором на вход всех элементов поступает одно и то же воздействие, а
их выходные величины (с соответствующими знаками) суммируются
(рис. 2.19,6). Согласно этому определению,
= X = X —	“ X =
Л2
(2.139)
y = yl+y2+... + y,+... + y„.
(2.140)
Подставляя в (2.140) уравнения статики отдельных элементов
У, = к,х,<
(2.141)
получим
У = (к1+к2^
... + ki+...+ kn)x.
(2.142)
Отсюда следует, что
эквивалентный ПК параллельно соединенных линейных элемен-
тов равен сумме передаточных коэффициентов элементов:
(2.143)
Отметим, что суммирование сигналов в одной точке возмож-
но лишь в том случае, если они имеют одинаковую размерность. По-
этому коэффициенты всех параллельно соединенных элементов и их
общий коэффициент кэ всегда имеют одну и ту же размерность.
Встречно-параллельным соединением двух элементов (соедине-
нием с обратной связью) называют такое соединение, при котором
выходной сигнал первого элемента поступает на вход второго, а вы-
ходной сигнал второго элемента с соответствующим знаком сумми-
руется с общим входным сигналом (рис. 2.19,в). Первый элемент, в
котором направление передачи сигнала совпадает с направлением
передачи общего сигнала, называют элементом прямой цепи. Второй
117
элемент, у которого направление передачи сигнала противоположно
направлению передачи общего сигнала, называют элементом об-
ратной связи.
В зависимости от знака сигнала обратной связи различают по-
ложительные и отрицательные обратные связи. Если сигнал обрат-
ной связи уос суммируется (на схеме знак "+") с общим входным сиг-
налом х, то обратная связь является положительной. Если сигнал
обратной связи вычитается из общего сигнала (на схеме знак "-"), то
обратная связь является отрицательной.
Рассмотрим статические свойства соединения с обратной свя-
зью. Пусть элементы прямой и обратной связи линейны и характери-
зуются коэффициентами кП и кж. Тогда, согласно определению поня-
тия «обратная связь», можно записать уравнения:
прямой цепи
У = к^\	(2.144)
обратной связи
Уос= kxy,	(2.145)
и узла суммирования
Хп=* + Лс-	(2146)
Подставляя выражение (2.145) в (2.146), а затем выражение
(2.146) в (2.144), получим уравнение статики всего соединения с об-
ратной связью
y = xfcn/(l±VoJ	(2.147)
Отсюда эквивалентный ПК
к,=кЛ±Ш,
(2.148)
где знак соответствует отрицательной обратной связи, а знак
положительной. Формула (2.148) выражает одно из фундаменталь-
ных правил теории управления:
эквивалентный ПК элемента, охваченного отрицательной об-
ратной связью, равен коэффициенту прямой цепи, разделенному
на единицу плюс произведение коэффициентов прямой и обрат-
ной связи.
118
Размерность эквивалентного ПК равна размерности коэффици-
ента кп Произведение коэффициентов какос всегда безразмерно.
Из выражения (2.148) следует, что отрицательная обратная связь
уменьшает эквивалентный коэффициент, а положительная - увели-
чивает Если при положительной обратной связи произведение ко-
эффициентов кпкж равно единице, то коэффициент кэ возрастает до
бесконечности. А если кпкж > 1, то положительная обратная связь
превращает соединение в инвертор (элемент, изменяющий знак
входного сигнала) с эквивалентным коэффициентом кэ
Анализируя формулу (2.148), можно показать, что отрицатель-
ная обратная связь уменьшает отклонения выходной величины, воз-
никающие в исходной прямой цепи из-за нестабильности коэффици-
ента кп, в (1 4- кпкж) раз. Нестабильность самого коэффициента кж
обратной связью не компенсируется.
Соединение с отрицательной обратной связью обладает еще од-
ним замечательным свойством:
при достаточно большом значении произведения кПкж эквива-
лентный ПК практически не зависит от коэффициента кп.
Действительно при кпкж » 1
= W	(2149)
Это свойство широко используется при конструировании высо-
ко стабильных устройств из элементов с меняющимися коэффициен-
тами.
Таким образом,
отрицательная обратная связь всегда уменьшает проявление
нестабильности параметров охватываемого элемента и ока-
зывает стабилизирующее действие на передаточные свойства
прямой цепи.
Заметим, что в случаях, когда статические характеристики от-
дельных элементов нелинейны, то нельзя применять формулы
(2 138), (2.143), (2.148) и эквивалентные характеристики соединений
можно определить только графическими построениями Эти по-
строения эквивалентных характеристик проиллюстрированы на рис
2.20, 2.21 и 2.22 для всех трех типовых соединений при конкретных
видах нелинейных характеристик исходных элементов
119
a
Рис. 2.20. Построение эквивалентной статической характеристики
последовательного соединения трех нелинейных элементов
Рис. 2.21. Построение эквивалентной статической характеристики
параллельного соединения трех нелинейных элементов
120
б
Рис 2.22. Построение эквивалентной статической характеристики
встречно-параллельного соединения двух нелинейных элементов
Рассмотрим теперь правила нахождения экви-
валентных динамических характеристик ти-
повых соединений.
Выражения для эквивалентных ПФ типовых соединений можно
получить так же, как и выражения (2.138), (2.143) и (2.148) для ПК.
Эквивалентная ПФ последовательного соединения из п элемен-
тов равна произведению п ПФ элементов
ч'Ар) =
1=1
(2.150)
Соответственно эквивалентная АФЧХ последовательного со-
единения также равна произведению:
п
п
(2.151)
1=1	1=1
Эквивалентная АЧХ этого соединения может быть получена как
модуль произведения (2.151) и равна произведению отдельных АЧХ:
A(®) = F.O®)|=rp>)>
/=1
(2 152)
12]
а эквивалентная ФЧХ - как аргумент произведения и равна сумме
ФЧХ.
п
<РЭ (<у) = arg W3 (;7у) = £ (pt (со).
1=1
(2.153)
В соответствии с (2.152) эквивалентная ЛАЧХ может быть по-
лучена как сумма ЛАЧХ отдельных элементов, соединенных после-
довательно:
я
Л(<а) = ХД(®)-
1=1
(2 154)
Эта возможность широко используется в практических расче-
тах.
При параллельном соединении п элементов эквивалентная ПФ
равна сумме п ПФ элементов:
п
1=1
(2.155)
Как сумма могут быть найдены и такие эквивалентные характе-
ристики параллельного соединения, как Жэ(7со), h3(t) и w3(r).
Наконец, для соединения с обратной связью эквивалентная ПФ,
аналогично (2.148),
^(р)=ВД/(1±^(Ж« (/>)),
(2.156)
где знак "+" соответствует отрицательной обратной связи, а знак
положительной.
Нетрудно убедиться, что при больших значениях ПК прямой
цепи эквивалентная ПФ встречно-параллельного соединения с отри-
цательной обратной связью, аналогично (2.149), принимает вид

(2.157)
122
Соотношение (2.157) выражает свойство так называемой пре-
дельной системы, динамические свойства которой определяются
только свойствами звена обратной связи.
2.9. Векторно-матричная форма описания многомерных
элементов и систем управления
Современные СУ сложными технологическими объектами со-
держат часто элементы с несколькими входными и несколькими вы-
ходными переменными. Такие элементы называют многомерными.
Многомерными элементами являются прежде всего сами объек-
ты управления. Например, электрический генератор переменного
тока имеет две выходные переменные - напряжение и частоту - и
две входные - напряжение возбуждения и частоту вращения ротора.
Примером более сложного многомерного элемента является такой
объект управления, как химико-технологический процесс в раздели-
тельной колонне, который характеризуется десятками входных и вы-
ходных переменных. К входным переменным процесса разделения
относятся выходы получаемых продуктов (например, метанола, эта-
нола и пропанола) и большое количество контролируемых режимных
параметров (концентрации выделяемых компонентов и температура
среды в различных точках колонны). К входным управляемым пере-
менным в данном случае относятся, например, подача исходной сме-
си и подача пара в колонну. Основными возмущающими воздейст-
виями являются концентрации полезных компонентов в разделяемой
смеси.
Многомерными элементами могут быть и другие части систем
управления - например, сложные управляющие устройства в виде
микроЭВМ, выполняющие роль многоканальных регуляторов.
В приведенных примерах выходными переменными многомер-
ного элемента являются реальные физические величины, которые,
как правило, поддаются измерению. Однако, как будет показано ни-
же, в качестве выходных переменных могут фигурировать и некото-
рые абстрактные переменные - например, производные от реальных
выходных переменных, не имеющие конкретного физического смыс-
ла, и тогда даже элемент с одним входом и одним выходом (но опи-
123
сываемый дифференциальным уравнением выше первого порядка'),
может рассматриваться как многомерный.
Математическое описание передаточных свойств любых линей-
ных многомерных элементов может быть осуществлено в двух раз-
личных видах. 1) при помощи рассмотренных в 2.4-2.7 динамических
характеристик (дифференциальных уравнений, временных, переда-
точных и частотных функций), записанных для реальных входных и
выходных переменных; 2) при помощи дифференциальных уравне-
ний в форме Коши, записанных для абстрактных выходных перемен-
ных (переменных состояния). Будем для краткости обозначать пер-
вый способ описания - ВВ (вход-выход), а второй - ПС (переменные
состояния).
Рассмотрим сущность обоих способов.
Способ описания ’’вход - выход’’. Пусть имеется многомер-
ный элемент (рис. 2.23,я) с т входными переменными хь х2, ..., X;-,
..., хт и п измеряемыми (наблюдаемыми) выходными переменными
у 1,у2, ...,уI, ...уп. В общем случае каждая входная переменная связа-
на с каждой выходной переменной. (На рисунке показаны лишь
связи переменных х^ и yi с остальными). Если взаимосвязи по всем
каналам Хк - у/ линейны или линеаризованы, то в общем случае эле-
мент можно описать следующей системой п неоднородных диффе-
ренциальных уравнений:
п	т
(/ = 1;2,...;и),	(2.158)
1=1
где D,i(p) и - выходные и входные дифференциальные опера-
торы вида (2.67) и (2.68).
Систему (2.158) можно записать более компактно - в виде одно-
го векторного дифференциального уравнения
D(p)y(t) = K(p)x(t),
(2.159)
где y(t) и x(f) - векторы выходных и входных переменных, пред-
ставленные в виде матриц-столбцов У = [УьУ2--У/ Уп К и
124
х - [x1,x2,...,x£,...,xmT[, a D(p) и K_(p) - матрицы операторов Dt^p) и
Kii&p), имеющие размеры соответственно (п х п) и (и х т).
Рис. 2.23. Модели «вход-выход» многомерного элемента
Отмстим, что у большинства реальных конструктивных элемен-
тов каждая выходная переменная зависит только от входных пере-
менных хк и не связана уравнениями с другими выходными перемен-
ными, и в этом случае матрица D диагональная. Если же хотя бы ме-
жду двумя выходными переменными существует внутренняя связь
(на рис. 2.23,а показана связь между у/ иу„), матрица D уже недиаго-
нальная.
Запишем векторное дифференциальное уравнение (2.159) в изо-
бражениях по Лапласу, полагая при этом начальные условия нуле-
выми-
D(p)y(p) = K(p)x(p).	(2.160)
Теперь можно определить матрицу передаточных функций (пе-
редаточную матрицу) элемента
125
w^pY-WM
f?(p) = .......... =	D'\p)K(p) =
D(p)K(p)
\D(P)
(2.161)

Р(р) = Dtl{p)
где D~x(p) - матрица, обратная по отношению к D(p\,
- присоединенная матрица для D(pY - алгеб-
раические дополнения элементов D,i(p).
Элементы матрицы W(p) представляют собой ПФ WuAp) по от-
дельным каналам Xk-yi. В частном случае, когда матрица D(p) диаго-
нальная, т.е. когда в левой части каждого уравнения системы (2.158)
содержатся только одно слагаемое с переменной yh передаточные
функции по отдельным каналам можно найти более просто - пользу-
ясь определением понятия ПФ:
У(Р) = W(p)x(p).
(2.162)
Согласно принципу суперпозиции, каждая выходная переменная
элемента может рассматриваться как сумма (см.рис. 2.23,6).
ffi
yi(p) = YwMxk(py	=
(2.163)
Пользуясь введенной передаточной матрицей многомерного
элемента, его схему на рис. 2.23,6 можно заменить схемой на рис.
2.23,в, которой соответствует операторное уравнение
у(р) = W(p)x(p).
(2.164)
Матрицы, элементами которых служат весовые функции
или переходные функции h^t), называются соответственно весовой
wik(t) и переходной hu^t) матрицами. Весовая и передаточная
матрицы связаны соотношением, аналогичным формуле (2.105)
126
W(p} = J?{w(/)}= \^(t)e~ptdt.	(2.165)
о
Если все воздействия приложены к элементу одновременно в
момент t = 0, то аналогично интегралу свертки (2.92) можно записать
QO
y(t) - J *(#)!*& ~ 9)d9
о
(2.166)
или в скалярной форме
у, w=Ё (х* ~ $
i=l о
(2.167)
(Z = 1;2;...;л).
Способ описания в переменных состояния. Рассмотрим сущ-
ность способа применительно к задаче описания многомерного объ-
екта управления. Учтем при этом, что при описании объектов управ-
ления выходные (управляемые) переменные принято обозначать
символом х, а входные (управляющие) - у (рис. 2.23,г). Математиче-
скую модель объекта представляют в виде двух уравнений - уравне-
ния состояния и уравнения выхода.
Уравнение состояния линейного объекта отражает его динами-
ческие свойства и записывается в виде векторного дифференциаль-
ного уравнения в форме Коши
+ By(t) + z(/)>	(2.168)
где х(0 - вектор состояния, представляющий собой вектор-столбец
размерностью п х 1 с компонентами X\(f), Xi(t),..., xn(t), называемыми
переменными состояния объекта; y(t) - вектор управляющих
воздействий - то же вектор-столбец с размерностью т х 1, вклю-
чающий компоненты yi(0, ^(О, -- , Ут(Х)', z(t) - вектор-столбец возму-
щений Z](r), z2(0>-действующих на входе объекта; 4=[«у]Ихт,
В=[6у]Мхт - матрицы постоянных коэффициентов, зависящих от кон-
127
структивных параметров объекта; первый индекс в размерности мат-
риц А и В соответствует количеству строк, второй - количеству
столбцов.
Векторное уравнение (2.168) эквивалентно системе п скалярных
дифференциальных уравнений первого порядка
п	т
*,(0 = LaZ/f)+SV/'> + z,(0, (i = l;2;...;n).	(2.169)
7=1	7=1
При описании электрических и механических объектов, обла-
дающих способностью накапливать энергию, в качестве переменных
состояния часто принимают токи через индуктивности, напряжения
на емкостях, перемещения и скорости движения масс. Как известно,
эти величины определяют накопленную энергию (магнитную, элек-
трическую, потенциальную, кинетическую) и характеризуют, следо-
вательно, инерционные свойства объекта. Для одномерного объекта
и-го порядка переменными состояния могут служить выходной сиг-
нал и его производные до (и - 1)-й включительно.
Однако в общем случае переменные состояния могут и не иметь
конкретного физического смысла - они будут формальными, абст-
рактными переменными, лишь удовлетворяющими уравнениям со-
стояния.
В некоторых частных случаях переменные состояния оказыва-
ются связанными между собой соотношением
*,(') = *,.,('), (> = 1;2;(2.170)
и тогда они называются фазовыми переменными.
«-мерное пространство, координатами которого служат пере-
менные состояния X), называют пространством состояния, а рас-
сматриваемый способ описания соответственно - методом про-
странства состояний (МПС).
Полная математическая модель линейного многомерного
объекта, кроме уравнений состояния, содержит еще так называемое
уравнение выхода, или уравнение наблюдения, связывающее пере-
менные состояния (промежуточные переменные) и управляющие
128
воздействия с выходными измеряемыми (наблюдаемыми) перемен-
ными хв:
xB(t) = Cx(t) + Dy(t) + g(t)	(2.171)
или в скалярной форме
п	т
х„Ю = £с„х/') + £^Л(') + 8,(0, ('= 1;2;...;/),	(2.172)
7=1	J=\
где хв (0 = [хв1 (0, хв2 (0, - Лв1(0]Т ” /-мерный вектор-столбец выход-
ных переменных объекта; g(O = [gi(O, g2(0>- ,gz(O]T ~ /-мерный
вектор-столбец возмущений, действующих на выходе объекта;
C=[cJ/xm, D=[dtJ]ixm - матрицы постоянных коэффициентов, характе-
ризующие безынерционное влияние переменных состояния и управ-
ляющих воздействий на выход объекта.
Матрица выхода С отражает статические передаточные свойства
как самого объекта, так и измерительного устройства, с помощью
которого получаются выходные сигналы хв. Поэтому матрицу С на-
зывают еще матрицей наблюдения, а в вектор возмущений g вклю-
чают и помехи, возникающие в измерительном устройстве.
Модели объекта, записанной при помощи переменных состоя-
ния в виде уравнений (2.168) и (2.171), соответствует алгоритмиче-
ская структура на рис. 2.24. В звене, стоящем между х и х, выполня-
ется операция
(2.173)
где 1/р - оператор интегрирования; 1 - единичная матрица вида
Г1	0	0	...	01
0	1	о	...	о
0	О	1	...	о
О О 0 ... 1
129
Рис. 2.24. Модель многомерного объекта управления
в переменных состояния
Из уравнений состояния (2.168) и выхода (2.171) может быть
получено следующее матричное уравнение статики многомерного
линейного объекта.
хв = КуУ~К^ + ё,
(2.174)
где К\= В - G4и Кв ~ СА 1 - матрицы передаточных коэффици-
ентов объекта соответственно по каналам управления и возмущения.
С помощью переменных состояния можно представить в виде
модели (2 168), (2.171) динамический объект управления, имеющий
один вход и один выход и описываемый передаточной функцией ви-
да (2.103) с т = п\
w(n} =	= ьпРп+ь^Рп'х +-+^р+ь0
™о\Р/	/ X	п	л-1
Яр) а»р +ап^р +...+^р+«0
(2.175)
Этой ПФ соответствует алгоритмическая структура, показанная
на рис. 2.25. Такая форма представления динамического объекта
(2 175) в переменных состояния называется стандартной, или нор-
мальной, а также формой Фробениуса. При ней переменные состоя-
ния связаны соотношением (2.170), т.е. являются фазовыми.
во
Рис. 2.25. Модель динамического объекта управления (2.175)
в переменных состояния для случая т = п
Существуют и другие формы представления, при которых пере-
менные состояния не связаны соотношением (2.170).
В частном, но распространенном случае, когда в ПФ общего ви-
да (2.103) т < п - 1, матрицы, входящие в уравнения (2 168) и
(2.171), имеют вид
131
(2.176)
где Т - знак транспонирования, а матрицы В и С вырождаются соот-
ветственно в матрицу-столбец b и матрицу-строку с.
Если в передаточной функции (2.175) полиномы числителя и
знаменателя имеют одинаковый порядок, т.е. т = п, то матрица
D - b а О, а матрица С имеет более сложный вид, соответствую-
щий структуре на рис. 2.25.
Покажем, что объекту, описываемому передаточной функцией
(2 175) с т = п - 1, в пространстве состояний действительно соответ-
ствуют матрицы (2.176). Преобразуем дифференциальное уравнение
\апрп +а„_}рп~} + .. +а}р + aQ)xB(t) =
= (bn,pm +bm_ipm~' +. .. + bxp + b0)y(t),
(2.177)
к нормальной форме Коши (2.168) или (2.169). Для этого введем
вспомогательную переменную X\(f) и запишем уравнение (2.177) в
виде пропорции
*At)/(bmpm +bm }pm~l + ... + bip + bu) =
= У(О/{апрп +ап-\Рп~{ +	+ «о)=х1(О.
(2.178)
Очевидно, что соотношению (2.177) соответствуют два уравне-
ния
рт-' + ... + b,p + htl)x,(r)=x,(t)-	(2.179)
[а„р" +а„^р" '+...+ atp + а,,)х,(1) = y(t).	(2.180)
132
Введем обозначения
*1(0 = х2(Г), Х2(О = Х3(О, -X-1(0 = х„(0,	(2.181)
тогда вместо уравнения (2.180) получим
1г	11
ХЛ(О =----К-1ХЯ(Г) +	+... + а>х2(/) + ад(0] + — y<J). (2 182)
ап	ап
Объединяя последнее уравнение с выражениями (2.170), полу-
чим систему уравнений в форме Коши
х,(0 = х,+1(0, / = 1;2;...;л-1;
хЛ(0 = —-[ая-!*я(0 + an-2xn-i(0 + ••• + а\х2 (О + яоХ(')] + — y(t)\ (2'183)
ап	J
Применяя соотношения (2.181) к уравнению (2.179), находим
выражение для выходной переменной
х. (0 - Ьтхт^ (0 + Ьт лхт (0 + .. + ь,хг (г) + bQx{ (0.	(2.184)
Теперь нетрудно видеть, что именно при матрицах вида (2.176)
полученные уравнения (2.183) и (2.184) эквивалентны уравнениям
состояния (2.168) и выхода (2.171).
Уравнениям (2.183), (2.184) и матрицам (2.176) соответствует
структурная модель, показанная на рис. 2.26.
От модели объекта, записанной по способу ПС, можно перейти
к описанию по способу ВВ.
Для этого необходимо векторные уравнения (2.168) и (2.171) за-
писать, как и обычные скалярные дифференциальные уравнения, в
изображениях по Лапласу (с учетом ненулевых начальных условий).
Тогда вместо уравнения состояния (2.168) получим (при z = 0):
рХ(р) - Хо = А Х(р) + В Y(p)	(2.185)
или
133
Х(р) = (Pl - dV -I« + (Pl - A)'BY(p)
(2 186)
и вместо уравнения выхода (2.171) (при g = 0):
*\(P) = QX(P) + DY(P),
(2.187)
где (pl_- А) 1 - резольвента матрицы А, ей (резольвенте) соответст-
вует экспоненциальная матричная функция-оригинал
А1
е-.
.188)
Рис. 2.26 Модель динамического объекта управления (2 175)
в переменных состояния для случая т < п - 1
134
Объединенное операторное уравнение, связывающее вход y(t)
и выход хв(0, имеет вид
2С,(Р) = С(р1-^)1^0+С(р1-Л)-'ВВД + ОХ(р) (2 189)
Теперь из операторных уравнений (2.186) и (2.189) при нулевых
начальных условиях можно получить матричные ПФ рассматривае-
мого ОУ:
по каналу ” у - х"
ГГ'(р) = Х(р)1т(р)={р\-АУ'В	(2.190)
и по каналу " у - хв"
К(р) =^B(/’)/W = C(pl-4)-1B + P. (2.191)
Матричный передаточный коэффициент по каналу "у- хв"
£ = lim W'o(p) = D-СА~'В,
(2.192)
где к* - [£„ jZxm - матрица передаточных коэффициентов кр, а кр -пе-
редаточный коэффициент по каналу "у, - хв;".
По матричным передаточным функциям (2.190) и (2.191) можно
найти соответствующие им матричные импульсные переходные (ве-
совые) функции:
по каналу "у-х"
w:(0 = ^'te(p)}=eJ,B	(2 193)
и по каналу " у - хв"
^(О = S’-'	(/>)}= СеА,В + Д5(Г).
(2 194)
135
Изображению (2.186) вектора состояния x(f) соответствует сле-
дующее полное решение векторного дифференциального уравнения
состояния (2.168):
х(0 = е~х0 +	By(&)d&,	(2.195)
О
где второе слагаемое получено по правилу свертки (см. табл.2.2) как
оригинал произведения двух изображений, входящих во второе сла-
гаемое уравнения (2.186).
Аналогично по изображению (2.189) вектора выхода хв(0 можно
найти полное решение для объединенных уравнений (2.168) и (2.171)
(при I) = О)-
хв(Г) = Се-х0 +	(2.196)
о
Первые слагаемые в выражениях (2.195) и (2.196) соответствуют
свободным составляющим вектора состояния x(f) и вектора выхода
xB(Z) и зависят только от начальных условий х0 и от собственных
свойств ОУ, т е. от матриц А и С, а вторые описывают вынужденные
составляющие векторов x(t) и хв(0, зависящие как от собственных
свойств (матриц А, В и С), так и от входных воздействий - компо-
нентов вектора v(t).
Для частного случая, когда все управляющие воздействия пред-
ставляют собой единичные ступенчатые функции, т е. когда v(t) -
g(0, из выражения (2.196) получается матричная переходная харак-
теристика ОУ по каналу "у - хв" (при 2 = 0)
Л;(0 = j>L(«W =f Ce^BdB	(2.197)
о	о
Экспоненциальная матричная функция (или матрица экспонен-
циальных функций) Ф(0 = e~f, входящая в решения в (2.195) и
(2 196). называется системной, или фундаментальной, матрицей.
Она определяет фундаментальную систему линейно независимых
136
решений xt(t) однородного векторного дифференциального уравне-
ния x{t) -- Ax(t):
X,(r>
Ф„(0;..ФДО
(2.198)
...ф,Л')
Каждый элемент Ф,у(0 фундаментальной матрицы описывает
изменение ?-й переменной состояния, когдау-я переменная состояния
имеет начальное значение ху0 = 1.
Через переходную матрицу Ф(0 можно выразить матричную ве-
совую функцию (2.194) при D = 0:
^(г) = СФ(г)В.
(2.199)
Каждый элемент матричной весовой функции (2.199) опре-
деляет реакцию выхода xBJ(t) на импульсное воздействие 5(f), прило-
женное ко входу yt(t) в момент t =0, тогда как другие составляющие
вектора управления y(t) и начальное значение хву(0) равны нулю.
При численном решении матричных дифференциальных урав-
нений используются следующие свойства фундаментальной матри-
цы:
1) Ф(0) =	= Z; 2) Ф(оо) = е-* = 0; 3)Ф’‘(Г) = Ф(-0;
4)Ф‘(0 = Ф(/7); 5)Ф(0Ф(Г2) = Фа, +Г2);
б)Фа-гу)=Ф(0Фчау).
>	(2.200)
Для удобства математических операций (в частности, для диф-
ференцирования) и численного решения матричных уравнений сис-
темную функцию Ф(/) представляют в виде бесконечного степенного
ряда.
137
(2.201)
ф(о = ^ =
1=0 п
= 1 4- At +
Динамические свойства объекта можно оценить и без решения
его уравнения - по собственным значениям матрицы Л, которые яв-
ляются корнями характеристического уравнения матрицы А
^11	^12’ ••а\п
t?2i, а22 -к, ...п2„
det (Л - kl) =
(2.202)
а • а ' ...а -к
ш ’ п2 ’ пп
Эти корни совпадают с полюсами р, передаточных функций
объекта (2.190) и (2.191). Это утверждение следует из известного
свойства определителя квадратной матрицы

(2.203)
где п - размерность матрицы А.
При определении передаточных функций по формулам (2.190) и
(2.191) приходится оперировать с обратными матрицами вида
G' = [/G, которые вычисляются по следующему правилу Лейбница-
Крамера:
G'=G^/dctG,	(2.204)
п
где
Sn\Sn2"S
- исходная матрица,
(2.205)
пп _
138
- адъюнкта матрицы G.
(2.206)
Объекты управления, представленные в пространстве состояний
уравнениями (2.168) и (2.171), могут быть соединены между собой,
как и простые звенья, - последовательно, параллельно и встречно-
параллельно. Причем соединения этих объектов могут быть полными
- когда векторы входов и выходов соединяемых объектов совпадают
по всем компонентам, и неполными - когда указанные векторы сов-
падают частично. На рис. 2.27 показан простейший случай последо-
вательного соединения двух ОУ, при котором выходной вектор хв1
первого объекта полностью совпадает с входным вектором у вто-
рого объекта, т.е.хВ] = у . Уравнение состояния такого объединенно-
го (эквивалентного) ОУ будет иметь вид
*(')
_i(0
(2.207)
а уравнение общего выхода
(2.208)
Рис. 2.27. Последовательное соединение двух ОУ,
представленных в пространстве состояний уравнениями (2.168) и (2.171)
139
Для более сложных случаев последовательного соединения, ко-
гда хв1 И для других соединений существуют соответствующие
формулы для вычисления эквивалентных матриц Аэ, В3, Сэ и D3. Эти
громоздкие вычисления сложных, составных матриц удобно выпол-
нять с помощью прикладной программной системы MATLAB (от
слов "матричная" и "лаборатория»).
Пример. Составим уравнение состояния (2.168) и уравнение выхода
(2 171) для смесительного резервуара (рис 2.28) емкостью V (м3), в который
одновременно подаются два регулируемых потока жидкости Q\ и Q2 (м3/с),
содержащие один и тот же компонент с постоянными концентрациями сю и
с2П (кг/м3) В качестве выходных переменных этого объекта управления бу-
дем рассматривать расход Q, концентрацию с компонента в выходном пото-
ке О и уровень h (м) жидкости в баке, а в качестве входных - расходы Q\ и
бС
Рис 2.28 Смесительный резервуар как объект управления
Уравнения материального баланса имеют вид:
по массе жидкости
dV(t)ldt = Q}(l)+Q2(j)-Q(jY,
(2.209)
и по массе компонента
+	(2 210)
Расход жидкости из бака, согласно законам гидравлики,
140
(2.211)

где Кн - коэффициент истечения; 5 - площадь поверхности жидкости, м2.
С учетом (2 211) последнее слагаемое в (2.210), соответствующее рас-
ходу q(t) компонента из резервуара, равно
9(О = Ф)0(О = Ф)*И7Г(ОЛ
(2 212)
Для некоторого фиксированного установившегося режима, характери-
зуемого значениями Vo, Qo, Q}0, Q2{), c0, h0, q0 и соотношениями
01O+02O~0O’ 9o -CO0O’ 00 - V^o/S, Cq - (c]Q0io + c2O02o)/cO0O •
(2.213)
можно нелинейную функцию (2.212) двух переменных c(t) и Г(0 линеари-
зовать:
q = f{c,V)»qQ + cq	+А-и Дс
(2.214)
Аналогично линеаризуются и остальные слагаемые уравнений (2.209)
(2.210), представляющие собой произведение двух переменных или нели-
нейную зависимость от V.
Введем следующие обозначения для отклонения всех переменных от
их значений в рассматриваемом режиме
Д01 0) = 01 (0 - 010 = У\О)- Л02 0) = 02 0) - 020 = v2 ('),'
ДУ(t) = У(1) - Уо =x1(Z), Дс(/) = c(t) - С(1 = х2{1) = хъ2(1\ >
ДА(/) = h(t) -h0= xb3(z), A0(z) = 2(Z) - Q = ЛВ1 (z)
(2.215)
Тогда, учитывая соотношения (2.213), можно исходные уравнения
(2.209) и (2.210) записать в отклонениях от установившегося режима
-*1 (О » У\(0+у 2 (0 ~	*i 0),
^0 *2 (0 + ад 0)ssqo>zl(O + C2O.v20)--^5-^10)-0O^20)
о
(2 216)
141
Обозначая VqIQq = Т к исключая из второго уравнения ^(0, можно
получить искомые уравнения состояния
1
*1 (0 =	(0+л (')+п(0,
•	1	- с0 /<ч.с10-с0
*2<0 =	*2(0+—  л (0+— ----------J2<0-
1	•'О	к0
(2.217)
Выходные переменные Q(t), c(t) и h(t) однозначно выражаются через
переменные состояния (в отклонениях):
(2.218)
*.i«)=лес»)=<?(') - а«-ч«),
X* л
хв2 (t) = &c(t) = c(t) - с о = х2 (ty,
Очевидно, что для рассматриваемого объекта матрицы Л, ВиС
О
-1/Т
О’
1
о
(2.219)
где 621-(с10-с0)/Г0 ; ^22 ~ (с2о со)/го-
Системная матрица в данном случае имеет вид
Ф(О = е-
'е ~t/1T;
0;
1
О
„-ЧТ '
С*
(2.220)
а резольвента матрицы Л
(pw)-'
’1/Ср + 1/2Г).
о.
(2.221)
о
l/(p + l/7jj
Импульсная переходная матрица рассматриваемого объекта по каналу
" У (0 - £в(0" согласно (2.199),
142

(2.222)
_L--t/2T.	1	-t/2T
C*	•	c*
IT	IT
_b2\e~t/T^	b22e~‘/T .
Соответствующая согласно (2.197) матричная переходная характери-
стика ОУ
Й(0 =


(2.223)
Передаточная функция по каналу "у-хв" (при D = 0),согласно (2.191) и
с учетом правила (2.204),
’(1/2Т)/(р + 1/2Т), (1/27-)/ (р + 1/27’)'
Ь21/(р + 1/г);	i>22/(p+l/7-) .
(2 224)
2.10. Комплексный пример математического описания ОУ
Проиллюстрируем
изложенные методы и
приемы математическо-
го описания на конкрет-
ном примере двух дос-
таточно распространен-
ных (особенно в учеб-
ных целях) механиче-
ских объектов - так на-
зываемого "переверну-
того маятника" (рис.
2.29,6?) и мостового кра-
на (рис. 2.29,6), которые
описываются идентич-
ными дифференциаль-
ными уравнениями. "Пе-
ревернутый маятник"
представляет собой
пример неустойчивого
Рис. 2.29. Колебательные механические
объекты управления:
а - перевернутый маятник, б - мостовой кран
объекта, по своим динамическим свойствам он эквивалентен некото-
143
объекта, по своим динамическим свойствам он эквивалентен некото-
рым реальным объектам управления, в частности ракете на стартовой
площадке
Используем известные из курса теоретической механики урав-
нения Лагранжа второго рода. В качестве обобщенных координат
примем перемещение тележки sT(Y) и угол отклонения маятника (гру-
за) а(/) от вертикального положения. Горизонтальная составляющая
перемещения маятника (груза) относительно начала координат О,
очевидно, равна (см.рис. 2.29)
МО = Л <0 + (О = Л (О +1 sm МО,
(2.225)
а вертикальная
zT (г) = I -1 cos a(t),
(2 226)
где верхний знак соответствует маятнику, а нижний - мостовому
крану. Соответствующие составляющие скоростей перемещения
5rt(r) = sT(0+/a(0cosa(r),
(2.227)
zr(0 = la(t) sin a(t)
(2 228)
Кинетическая энергия механической системы "тележка - маят-
ник (груз)"
Ек =	(0 +	+ /q(0cos a(z))2+ (/a(/)sin а(г))2 =
(О + 2 mrls(t )d(0 cos а(0 + тг12а2 (t).
(2.229)
Потенциальная энергия системы
Еп = ±т r gl cos a(t),
(2.230)
144
Функция Лагранжа равна разности кинетической и потенциаль-
ной энергии:
т	?ит + тт .2, ч
£ — Ек—Еп— - s (/) +
—1+ 25(/)a(/)cos
(2.231)
Уравнения Лагранжа 2-го рода для принятых обобщенных ко-
ординат 5Т(О и а(0 (без учета диссипативных потерь энергии на тре-
ние) имеют вид
dfdL'
ds j
(2.232)
(2.233)
где ys{t) и ya(t) - обобщенные непотенциальные силы, которые в дан-
ном случае равны ys{t) = F(t) и ya(t) - 0.
После дифференцирования функции (2.231) по переменным
иа(О и подстановки производных в (2.232) и (2.233)
получим два нелинейных дифференциальных уравнения для обоб-
щенных координат:
la(t) + s(t) cos a(t) + g sin a(t) = 0;	(2.234)
(mT + mr)s(0 + wrZa(Ocos a(f) ± wr/d2(/)sin a(/) = F(t). (2.235)
Учтем, что для малых углов a(t)«n/2, как известно,
sin a(Z) « a(0 и cosa(r) ~ 1, и пренебрежем в уравнении (2.235)
слагаемым с a2(Z) как величиной второго порядка малости. Тогда
получим линеаризованные дифференциальные уравнения механиче-
ской системы "тележка - маятник (груз)"
145
+ 5(0 + ga(0 = 0 i
(wT + wr)y(0 + >Hr/d(0 = F(0-
(2.236)
(2.237)
Для того, чтобы перейти к уравнениям в пространстве состоя-
ний, необходимо вначале уравнения (2.236) и (2.237) путем перекре-
стных подстановок преобразовать к виду, при котором старшие про-
изводные выражены явно:
d(t) = ^F(t)±^^^a(t)=bFiF^ + aa.a(t)- (2.238)
тт1	тт1
S(t) = -F(t) + ^-a(t) = brlF(t)+b„a(t),	(2.239)
тт	тТ
т	т
где bFX = aa = ±(m1+mr)g/m1F,	ba= + mrg/m1.
Каждое из уравнений второго порядка (2.238) и (2.239) можно
заменить на два уравнения первого порядка:
a(t) = ш(0,
(b(t) = a(t) = bFXF(t)+aaa(t)\
fs(O = v(0,
\y’(t) = s(t) = bF2F(t)+baa(t).
(2.240)
(2.241)
Как видно из систем (2.240) и (2.241), выходная (зависимая) пе-
ременная а(0 в первой системе является входной (независимой) во
второй. Это обстоятельство вынуждает в дальнейшем рассматривать
порознь две подсистемы с условными названиями - "Маятник" и
"Тележка".
Введем для обеих подсистем обозначения, принятые в методе
пространства состояний, и учтем, что выходные переменные подсис-
146
темы "Маятник" являются одновременно входными (управляющими)
переменными подсистемы "Тележка":
^(0=Ki(0; а(0=хм1(0; а(0=ш(0=* 2(0;
^(0 = *вм1(0; а(0 = хвм2(0;
(2.242)
F(t) = ут1; а(Г) = ут2(0; s(t) = хт1 (г); s(t) = v(0 = *т2(0;
а(0 = *bti(O;*(O =*вт2(0; *(0 = хвтз-	(2.243)
Заметим, что выходные переменные подсистемы "Тележка" яв-
ляются выходными переменными всей системы "Тележка - маятник
(груз)" и что скорость перемещения тележки v(t) = s(t) в некоторых
случаях также может представлять интерес как выходная переменная
системы.
Теперь уравнения (2.240) и (2.241) можно записать в стандарт-
ной для МПС форме - как уравнения состояния указанных подсис-
тем:
*М1 (0 = 0- ХМ1 (0 +	(0 + о • ум1 (0;
*м2 (0 = «м21 *М1 (0 + 0 • Хм2 (0 + &м21 ?М1 (0i
xTi(0 = 0 • хт1 (0 + лТ12хт2(0 + 0 • ут1(Г) + 0 • ут2(0;
Хт2 (0 = 0- Хт1 (0 + 0 • Хт2 (0 + &т21 Ут 1 (0 + &Т22Л2 (0,
(2.244)
(2.245)
где яМ12 = 1; Ям21 = Ла = ±{m,+mr)glmJ-, b^\ = bn = - 1/mJ; атП = 1;
^т21 = Ьр2 = 1//«т; Ьт22 = ba = + mrglnii.
Согласно введенным обозначениям (2.242) и (2.243), скалярные
уравнения для выходов обеих подсистем имеют вид
^в м1 (0 0 " ^м1 (0	' ^м2 (0 ^м11.Ум1 (0>
<
Л М2 (0 = См21 ХМ2 (0 + 0 • *м2 (0 + 0 • л.1 (0;
(2.246)
147
хв Т1 (о = о • хт1 (г) + о • хт2 (/) + о • ^Т1 (/)+JT12 ут2 (О;
5 хвт2(Г) = ст21хт1 (О + О • хт2 (/) + О • Л1 (О + О • Л1(О;
л тз (0 = О • ХТ1 (0 + ст32хт2 (г) + О • >>т1 (Г) + О • ут2,
(2.247)
ГДе CM21 1,^М11	1, ^т32	1» <^т11	!•
Скалярные уравнения состояния (2.244), (2.245) и выхода
(2.246), (2.247) можно представить в виде структурной модели на
рис. 2.30/7.
б
Маятник
Тележка
Рис. 2.30. Линейная модель перевернутого маятника
(мостового крана) в пространстве состояний
148
В более компактной векторно-матричной форме уравнения со-
стояния подсистемы "Маятник"
i.(') = 4ихи(') + Вм? (О,	(2.248)
подсистемы "Тележка"
i,(')=4I5,(')+sI?,(0,
(2.249)
а уравнения выхода, соответственно,
где
Хм(0
1»и(О=свх„(о+рм/ (о;
'Хм1(0‘
_Хм2 (0_
а(Г)
со(г) ’
•*

= ’F(01
_X»m2(OJ La(')j
’МО’
_M0_
a(Oj’
Г Wl
*BT1(O
Хвт2 (О
_ХвтЗ (0_
а(0
s(r)
_v(0_
(2.250)
(2.251)
Векторно-матричные уравнения (2.248)-(2.251) представлены в
виде структурной модели на рис. 2.30,6. Две подсистемы соединены
между собой последовательно, причем выход первой подсистемы
149
полностью, по обеим компонентам F(t) и а(0, совпадает с входом
второй. В этом случае общие уравнения всего соединения могут
быть определены с помощью формул (2.207), (2.208) или программ-
ной системы "MATLAB".
По структурной модели на рис. 2.30,я можно определить пере-
даточные функции рассматриваемого ОУ по отдельным каналам, в
частности ПФ по каналу "F - а"

W (р)*=^
Г(Р)
~ ^м21
(2.252)
а через нее ПФ по каналу "F- s"
OS
(2.253)
При wT» тг ПФ (2.253) существенно упрощается:
И\ЛР) = ^(P)/F(p)^l/mTp2,
(2.254)
она соответствует 2-му закону Ньютона для движущейся массы
При рассмотрении объекта в замкнутой СУ приходится учиты-
вать ПФ электропривода тележки. При достаточно большой мощно-
сти привода можно полагать, что частота вращения двигателя и, сле-
довательно, скорость тележки s(t) = v(t) пропорциональны питаю-
щему напряжению ад(/), т.е.
(р) = v(p )/ил (р)=кп /(Т„р + 1Х
(2.255)
где кп - ПК привода
учитывающий коэффициенты двигателя,
редуктора и приводных шкивов (шестеренок); Тп - постоянная вре-
мени привода (с).
150
Тогда, учитывая соотношения (2.252), (2.254) и L\s(f)}= р$(р),
можно записать общую передаточную электромеханического объек-
та управления по каналу "ид - а"
-a^\TnP + i) =
+ knm,p/(m,+mr)g
f +mTl
k(mt+mr)g
(2.256)
или при mr» mr
W0(p)~
-Kp/S _ ~k0P
(2.257)
где k0 = kn/g, T = Jl/g - соответственно передаточный коэффици-
ент и постоянная времени ОУ.
2.11. Элементарные операции машинного
математического моделирования
Для экспериментального исследования динамических свойств
СУ широко применяется машинное моделирование, осуществляемое
на различных видах ЭВМ. Используются два основных метода ма-
шинного моделирования, метод аналогового моделирования, реали-
зуемый на АВМ, и метод цифрового моделирования, реализуемый на
ЦВМ.
При аналоговом моделировании решение динамической задачи
воспроизводится в виде электрического переходного процесса, адек-
ватного свойствам исследуемой СУ. Результат решения наблюдают
на экране осциллографа или регистрируют с помощью записываю-
щих приборов.
151
Цифровое моделирование заключается в выполнении опреде-
ленной последовательности вычислительных процедур, соответст-
вующих решению дифференциальных уравнений системы. Результат
решения получается на экране дисплея или выводится на печатаю-
щее устройство.
При аналоговом и цифровом моделировании систем управления
наиболее широко применяется методика структурного моделирова-
ния, согласно которой в машинной модели воспроизводится физиче-
ская структура исследуемой системы, расчлененная на элементарные
математические операции (интегрирование, умножение на постоян-
ный коэффициент, суммирование и др.). Эти элементарные операции
реализуются при аналоговом моделировании на операционных уси-
лителях. а при цифровом - соответствующими программами вычис-
лений.
Как было показано в 2.9, любая сложная динамическая система
и-го порядка, описываемая матричными уравнениями (2.168) и
(2.171), может быть представлена в виде структурной модели, со-
стоящей только из интеграторов, сумматоров и блоков умножения
сигналов на постоянный коэффициент (см. рис. 2.25 и 2.26).
Ниже описаны основные операционные элементы, используе-
мые при аналоговом и цифровом моделировании линейных систем.
Рис. 2.31. Операционные элементы аналоговых моделей.
а - потенциометр; в - операционный усилитель; г - операционный
усилитель интегрирующий, б, г, е - соответствующие условные
обозначения элементов
152
Простейшим элементом аналоговой модели является потенцио-
метр (рис. 2.31,а), умножающий входное напряжение их на постоян-
ный коэффициент а:
(2.258)
где а = г,/г - коэффициент, который можно изменять от 0 до 1. На
схемах модели потенциометр изображается в виде кружочка (рис.
2.31,0.
Основным элементом при аналоговом моделировании служит
операционный (решающий) усилитель - электронный усилитель по-
стоянного тока с большим коэффициентом усиления (к = 104... 106),
охваченный отрицательной обратной связью. Характер математиче-
ских операций, выполняемых таким усилителем, зависит от опера-
торных сопротивлений ZBX(p) и Zoc(p), включенных на входе и в об-
ратную связь усилителя. Передаточная функция операционного уси-
лителя, связывающая входное и выходное напряжения,
| W(p) = uy(p)/u^p) = --ZJp)/ZJ,p),	(2.259)
где знак минус указывает, что одновременно с математическим пре-
образованием входного сигнала усилитель меняет его полярность на
противоположную.
Так, если на входе и в обратную связь включены активные со-
противления Г) и г2 (рис. 2.31,в), то операционный усилитель выпол-
няет функции масштабного блока - умножает входной сигнал их на
постоянный коэффициент
= ~г/г„	(2.260)
который можно изменять в широких пределах. Условное обозначе-
ние масштабного усилителя показано на рис. 2.31,г.
В частном случае, когда Г\ = г2 и квх= -1, масштабный усилитель
используется как инвертор - только для изменения полярности
входного сигнала.
153
Если на входе стоит резистор г}, а обратная связь образована
емкостью С с операторным сопротивлением	(р) = 1/рС (рис
2.31 ,д), то операционный усилитель является интегратором с пере-
даточной функцией
»,(p) = Zoc(p)/ZBX(p) = -(l/pC)/r1 =-l/r,q>.	(2.261)
Условное обозначение интегратора на рис. 2.31,е. Коэффициент
£вх = !/>*/? характеризует скорость интегрирования входного сигна-
ла.
Масштабный и интегрирующий усилители могут одновременно
выполнять суммирование нескольких входных сигналов. При таком
совмещении основной функции усилителя и функции суммирования
операторное сопротивление обратной связи для всех суммируемых
сигналов всегда одинаково, а входные сопротивления для отдельных
сигналов могут быть различными. Поэтому коэффициенты кт для
отдельных масштабируемых или интегрируемых слагаемых также
могут быть разными.
Рис. 2.32. Операционные элементы цифровых моделей
Рассмотрим теперь основные операционные элементы цифро-
вых моделей. Цифровое моделирование непрерывных систем осно-
вано на дискретизации обыкновенных дифференциальных уравнений
вида (2.177) - на приближенной замене их разностными уравнения-
ми, которые связывают между собой дискретные значения
х(/,) = х(/Д/) и y(tt) - входного и выходного сигналов x(t) и y(t).
154
При этом непрерывная независимая переменная 0 < t < оо заменяется
дискретной переменной t, - 0; 1Д/; 2Д/;...; zzV; оо. Переход к
дискретным значениям сигнала x(f) и дискретному времени может
быть осуществлен с помощью идеального ключа (рис. 2.32,а), кото-
рый через равные интервалы времени Дг на короткое мгновение за-
мыкается и выдает дискретные значения xt- = x(iAt) и у,- =	= kxt
(рис. 2.32,6).
В разностных уравнениях вместо обычных дифференциалов dy
и dx, используемых в обыкновенных дифференциальных уравнениях,
применяют разности (отсюда название уравнений!):
dy{t)« Ду(О = y(ti) - y(tf_x) = у,- у,-!;	(2.262)
dx(t)« Дг(^) = x(t.) - хО^ ) = х{-	,
(2.263)
а вместо производных по времени - отношение конечных прираще-
ний (2.262) и (2.263) к шагу дискретизации по времени ДЛ Поэтому
элементарным операциям непрерывного дифференцирования
y(t) = dx(t)/dt
и интегрирования входного сигнала
dy(t) = x(t)dt
(2.264)
(2.265)
в дискретной форме будут соответствовать разностные уравнения
yi={x;~X{_[)/M-
У{ = У;-\ + ХА1 •
(2.266)
(2.267)
На схемах цифрового моделирования уравнения дискретного
дифференцирования (2.266) и интегрирования (2.267) изображают в
виде полных схем вычислений (рис. 2.32,в и г) или в условном виде
(рис. 2.32,г и е).
155
Как видим, для цифрового моделирования операции дифферен-
цирования или интегрирования требуется выполнение лишь арифме-
тических операций суммирования, умножения на постоянный коэф-
фициент и запоминания предыдущего значения сигнала на один шаг
Д/, которые легко программируются. Процедура запоминания или
задержки дискретных значений реализуется при программировании
вычислений с помощью оператора присваивания
Л:=У,-|.	(2.268)
согласно которому в ячейке памяти происходит пошаговая замена
предыдущего значения на последующее.
Формула (2.267) и схема на рис. 2 32,д соответствуют алгоритму
приближенного численного интегрирования непрерывного сигнала
x(f), представленного своими дискретными значениями x(tt) = xt, по
наиболее простому методу - методу Эйлера (вариант обратной раз-
ности или прямоугольников с упреждением). Поскольку в этом алго-
ритме каждое последующее значение выражается через предыдущее,
он называется рекурретным.
Приближенное решение исходных дифференциальных уравнений
с помощью их цифровых моделей дает удовлетворительные ре-
зультаты только в тех случаях, когда шаг интегрирования kt
достаточно мал по сравнению с постоянными времени иссле-
дуемой системы и с темпом изменения сигналов x(t) и y(f) во
времени.
Например, для дифференциального уравнения первого порядка
с постоянной времени Т = aja\ шаг интегрирования рекомендуется
принимать
ДГ<(0,1...0,2)Г.	(2.269)
В главе 3 приведены аналоговые и цифровые модели типовых
динамических звеньев систем управления, построенные на описан-
ных выше простейших операционных элементах.
156
Контрольные задания и вопросы
1	В чем заключается свойство однонаправленности передачи воздей-
ствий отдельным элементом (например, электрическим четырехполюсни-
ком)?
2.	Назовите внешние и внутренние переменные, а также параметры
математической модели электромагнита (рис. 2.4,6).
3.	Какие типовые воздействия используются при изучении динамики
элементов и систем?
4.	Поясните понятие переходного и установившегося режима на гра-
фике процесса y(f), возникшего на выходе статического элемента после сту-
пенчатого воздействия на его вход.
5.	Как будет выглядеть график амплитудного спектра отдельного гар-
монического сигнала с xim = 10 В и частотой = 2 рад/с?
6.	Как изменяется график спектральной плотности |2Г(усо)| любого ко-
нечного импульса при увеличении его длительности?
7.	Проинтегрируйте квадрат экспоненциального импульса (2.39) по
времени и его спектральную плотность мощности (2.43) по частоте и убеди-
тесь в этом частном случае в справедливости равенства Парсеваля (2.38).
8.	Постройте линеаризованную статическую характеристику двигателя
л = Дмя), соответствующую к = 0,05 (об/с)/В. Укажите на ней точку номи-
нального режима - «о = 200 В, и0 = 10 об/с.
9.	Как классифицируются элементы систем управления по виду стати-
ческих характеристик?
10.	Линеаризуйте уравнение множительного элемента
у = /(x],x2) = 5xjx2 в точке xi0 = 1 В, *20 = 2 В. Запишите линеаризованное
уравнение для абсолютных значений (см. формулу (2.48)) и для отклонений
[формула (2.49)].
11.	Как из дифференциального уравнения элемента получить его урав-
нение статики? Найдите из дифференциального уравнения общего вида
(2.63,а) выражение для ПК.
12	Запишите уравнения химического реактора и механического уст-
ройства в примерах к 2.4 в символической (операторной) форме.
13.	Как получить в общем случае ПФ h(f) из дифференциального урав-
нения?
14.	Как связаны друг с другом переходная и весовая функции?
15.	Дайте определение ПФ и запишите соответствующее выражение.
16.	Как из дифференциального уравнения элемента получить его ПФ?
157
17.	Продемонстрируйте на простейшем электрическом четырехполюс-
нике типа r-С или r-L методику получения ПФ, основанную на понятии
операторного сопротивления.
18.	Как от передаточной функции элемента перейти к его уравнению
динамики в изображениях, а затем - в оригиналах?
19.	Как из ПФ получить выражение для АФХ?
20.	Постройте график ИХ/со) произвольного вида и укажите на нем ве-
личины А (а) и <р(со).
21.	Приведите основные формулы, связывающие АФХ, АЧХ и ФЧХ
между собой.
22.	Какой физический смысл имеют ординаты ЯЧХ элемента? Как по
ним оценить условия пропускания элементом гармонического сигнала?
23.	По каким правилам определяются эквивалентные ПК для последо-
вательного, параллельного и встречно-параллельного соединений линейных
элементов? Запишите соответствующие формулы эквивалентных ПК для
случая двух соединенных элементов.
24.	Запишите в векторной форме модель многомерного ОУ в перемен-
ных состояния. Какой смысл имеют компоненты векторов x(t),
25.	Составьте уравнения состояния и выхода для электрического r-L-C
четырехполюсника, изображенного на рис. 2.2,6, рассматривая в качестве
входной переменной 7 = ивн, а выходной - хв = ис.
26.	Составьте структурную модель в пространстве состояний (см.рис.
2.26) для механического устройства (см.рис. 2.13,а), используя его диффе-
ренциальное уравнение (2.83).
27.	Составьте аналоговую и цифровую модель непрерывного элемента,
описываемого дифференциальным уравнением
«0^+а1ХО = МО-	(2-270)
at
158
Глава 3. ХАРАКТЕРИСТИКИ ТИПОВЫХ
ДИНАМИЧЕСКИХ ЗВЕНЬЕВ ЛИНЕЙНЫХ СУ
3.1.	Классификация звеньев
Функциональные элементы, используемые в СУ, могут иметь
самое различное конструктивное выполнение и самые различные
принципы действия Однако общность математических выражений,
связывающих входные и выходные величины различных функцио-
нальных элементов, позволяет выделить ограниченное число так на-
зываемых типовых алгоритмических звеньев. Каждому типовому
алгоритмическому звену соответствует определенное математиче-
ское соотношение между входной и выходной величинами. Если это
соотношение является элементарным (например, дифференцирова-
ние, умножение на постоянный коэффициент), то и звено называется
элементарн ым.
Алгоритмические звенья, которые описываются обыкновенны-
ми дифференциальными уравнениями первого и второго порядков,
получили название типовых динамических звеньев. Это понятие и
связанные с ним приемы анализа автоматических систем были пред-
ложены в 1938 г. российским ученым А.В. Михайловым. В дальней-
шем методика анализа, основанная на расчленении СУ на типовые
звенья, широко вошла в практику инженерных расчетов и в настоя-
щее время является доминирующей
Типовые динамические звенья являются основными составными
частями алгоритмических структур непрерывных систем управления,
и поэтому знание их характеристик существенно облегчает анализ
таких систем
Классификацию типовых звеньев удобно осуществить, рассмат-
ривая различные частные формы дифференциального уравнения вто-
рого порядка
+C7j	+ aoy{t) p + box(t).	(3.1)
at at	at
159
В табл. 3.1 приведены значения коэффициентов уравнения (3.1)
и названия для наиболее часто встречающихся звеньев.
Таблица 3.1
Значения коэффициентов уравнения (3.1) типовых звеньев
Номер звена	Наименование звена	аг	а\	ао	bi		Примечание
1	Безынерционное (пропорциональное)	0	0	1	0	к	
2	Инерционное 1-го порядка (апериоди- ческое)	0	Т	1	0	к	
3	Инерционное 2-го порядка (апериоди- ческое)	т?	т\	1	0	к	Тх > 2Т2
4	Инерционное 2-го порядка (колеба- тельное)	г22	Т}	1	0	к	< 2Т2
5	Идеальное интегри- рующее	0		0	0	к	
6	Реальное интегри- рующее	т	1	0	0	к	
7	Идеальное диффе- ренцирующее	0	0	1	к	0	
8	Реальное дифферен- цирующее	0	т		к	0	
9	Изодромное (про- порционально- интегрирующее)	0	1	0	к\	к	
10	Форсирующее (про- порционально- дифференцирующее)	0	0	1	к\	к	
11	Интегро-дифферен- цирующее с преоб- ладанием интегри- рующих свойств	0	т	1	ki	к	(Ь/к^Т
12	Интегро-дифферен- цирующее с преоб- ладанием дифферен- цирующих свойств	0	т	1	ki	к	(к,/к)>Т
160
Отметим ряд общих закономерностей. Звенья, у которых коэф-
фициенты и 6о^О, обладают статизмом, те. однозначной связью
между входом и выходом в статическом режиме. К их названиям по-
этому часто добавляют слова статическое или позиционное. К этим
звеньям относятся № 1, 2, 3, 4, 10, 11, 12.
Звенья, у которых а<уё0, а^О и а^ёО, обладают инерционностью
(замедлением). К ним относятся звенья № 2, 3, 4, 6, 8, 11, 12.
У звеньев № 1, 5 и 7 только два коэффициента не равны нулю.
Они являются простейшими, или элементарными. Все остальные ти-
повые звенья могут быть образованы из элементарных путем после-
довательного, параллельного и встречно-параллельного соединений.
Если один из коэффициентов левой части уравнения (3 1) отри-
цателен, то звено будет неустойчивым и, как будет показано на при-
мере в 3.3, неминимально-фазовым.
Ниже в 3.2-3.6 рассмотрены характеристики модели и примеры
звеньев № 1-8. Характеристики звеньев № 8-12 могут быть получе-
ны как характеристики соединений звеньев при помощи формул
(2.150)-(2.156).
3.2.	Безынерционное звено
Безынерционное звено является простейшим среди всех типо-
вых звеньев. Оно передает сигнал со входа на выход мгновенно, без
искажений его формы. В звене может происходить только усиление
или ослабление мгновенных значений входной величины.
Связь между мгновенными значениями входной величины x(t) и
выходной величины y(t) описывается алгебраическим уравнением
=	(3.2)
Передаточные свойства звена определяются лишь одним пара-
метром - передаточным коэффициентом к.
При единичном ступенчатом воздействии х(/)=о(/), приложен-
ном в момент 1=0, выходная величина мгновенно изменяется и при-
нимает значение к (рис. 3.1,а). Переходная функция звена имеет вид
161
h(t) = kcr(t),
(3.3)
а импульсная переходная (рис. 3.1,6)
w(t) = kd(t).
в
Aft»)*'
к 
~о'
г
cp(w)M
jQ(®)“
к
	* ~д........*
ср(®)=0	®...........г со=0?.ооЛ Р(<в)
Рис. 3.1. Характеристики безынерционного звена
Уравнение звена в операторной форме
Y(p) = kX(p),
(3.5)
отсюда ПФ
W(p} = Y(p)!X(p) = к.
(3.6)
Амплитудно-фазовая характеристика (АФХ) звена описывается
функцией
W(jco) = k,	(3.7)
которой на комплексной плоскости соответствует одна точка на дей-
ствительной оси (рис. 3.1,е) Амплитудная частотная характеристика
(АЧХ)
Л(ш) =	= к
(3.8)
162
представляет собой прямую, параллельную оси частот (рис. 3 1,е).
Это означает, что
сигналы любой частоты (от нуля до бесконечности) проходят
через безынерционное звено с одинаковым отношением ампли-
туд входной и выходной величин, равным к.
Выражение для фазовой частотной характеристики (ФЧХ) (рис.
3.1,г)
ф(со) = afgW(jco) = arctg(O/ к) = 0	(3.9)
показывает, что безынерционное звено не создает фазовых сдвигов
между входной и выходной величинами. Это и оправдывает название
звена
Логарифмическая амплитудная частотная характеристика
(ЛАЧХ) безынерционного звена
£(ш) = 201g А(ш) = 201g к
(3.10)
так же, как и его АЧХ, является прямой линией, параллельной оси
абсцисс (рис. 3.1,д).
На алгоритмических схемах безынерционное звено изображают
в виде прямоугольника, внутри которого указывают буквенное обо-
значение или числовое значение передаточного коэффициента к (рис.
3.2/7)
Рис. 3.2. Модели и примеры безынерционного звена
Аналоговой моделью безынерционного звена служит операци-
онный усилитель (рис 3 2,6), используемый в режиме масштабного
163
усиления (см. 2.10), с коэффициентом При цифровом моде-
лировании безынерционному звену соответствует блок умножения
дискретных значений входного сигнала х, на постоянный коэффици-
ент к (рис. 3.2,в).
Распространенными примерами безынерционного звена являют-
ся редуктор (рис. 3.2,г), потенциометрический датчик углового пере-
мещения ^>(рис. 3.2,д), тахогенератор, используемый в качестве дат-
чика частоты вращения п (рис. 3.2,е).
Передаточный коэффициент редуктора зависит от соотношения
диаметров или чисел зубьев ведомой и ведущей шестерён:
*р=^1М =zi/z2.	(3.11)
Передаточный коэффициент потенциометрического датчика за-
висит от величины напряжения uq, подводимого от внешнего источ-
ника к зажимам потенциометра, и от величины полного хода движка
0b:
Ч=«аМ, В/’.	(3.12)
Передаточный коэффициент тахогенератора зависит от числа
пар полюсов р, числа проводников в пазах якоря N, числа пар парал-
лельных ветвей обмотки якоря а и магнитного потока возбуждения Ф
(в веберах):
~ ct® = pN®/a, В/(об/с).
(3.13)
У серийных тахогенераторов коэффициент £тг находится в пре-
делах от 1 до 10.
Следует заметить, что понятие безынерционного звена является
продуктом математической идеализации. На самом деле все реаль-
ные конструктивные элементы СУ обладают некоторой инерционно-
стью, так как передача энергии со входа на выход элемента не может
осуществляться мгновенно. Однако, если инерционность того или
иного элемента на 2-3 порядка меньше, чем у остальных элементов
рассматриваемой системы, то его считают безынерционным звеном.
Так, например, при описании и анализе системы управления тепло-
164
вым объектом, инерционность которого характеризуется, как прави-
ло, постоянной времени от нескольких десятков до тысяч секунд,
датчик температуры (термопару, термосопротивление) можно рас-
сматривать как безынерционное звено
3.3.	Инерционное звено первого порядка
Дифференциальное уравнение звена имеет вид
dt
(3 14)
где к - передаточный коэффициент, характеризующий свойства зве-
на в статическом режиме, Т - постоянная времени, характеризующая
инерционность звена.
Переходную функцию звена можно найти как сумму общего и
частного решений уравнения (3.14). Применяя методику, изложен-
ную в 2.5, получим следующее выражение для переходной функции
Л(Г) = £(1-е-'/г)о(0.	(3.15)
График переходной функции изображен на рис. 3.3,а Методами
аналитической геометрии нетрудно убедиться в том, что касательная
к кривой h(t) в точке /=0 отсекает на горизонтальной прямой h=k от-
резок, равный постоянной времени Т. Переходная функция при t=T
равна 0,632£, а при /=37 функция h(t) достигает значения 0,95£. В
приближенных расчетах обычно считают, что при t=3T переходный
процесс практически закончился
Импульсная переходная функция звена может быть получена,
как известно, путем дифференцирования функции h(t) Для
инерционного звена первого порядка импульсная функция имеет вид
(рис. 3.3,6)
НО = у^"го-(Г).	(3.16)
165
Рис 3 3 Характеристики инерционного звена первого порядка
Применяя к левой и правой частям уравнения (3 14) преобразо-
вание Лапласа, получим уравнение динамики звена в операторной
форме
[Tp + l]Y(p) = kX(P)
(3 17)
Из уравнения (3 17) находим передаточную функцию звена
W(p) = Y(p)/X(p) = к! (Гр +1)
Подставляя в передаточную функцию p=J(&, получим АФХ
IT(yffl) = к/ (Т/а +1)
(3 18)
(3 19)
Умножая числитель и знаменатель функции (3 19) на выражение
(l-jTw), сопряженное со знаменателем, можно избавиться от вели-
чины j в знаменателе и представить АФХ в виде суммы действитель-
ной и мнимой частей
166
= P(a>) + jQ(a>),
(3 20)
где P(<o) = Re fP(ju) = */ (1 + T2u>2),
2(0)) = Im W(ую) = - кТа/ (1 + T2a2)
(3 21)
Выражения (3 21) можно рассматривать как уравнение АФХ
1Г(/со), заданное в параметрической форме в системе координат Р(со)
и jQ(&) Роль третьей переменной (параметра) играет частота со
Если выразить мнимую составляющую Q(co) через действитель-
ную Р(со), то можно убедиться, что АФХ представляет собой полу-
окружность с центром в точке (к/2, /0) и с диаметром, равным к
(рис 3 3,е)
Распределение точек, соответствующих различным значениям со
вдоль кривой зависит от величины постоянной времени Т На
графике показаны характерные точки со=О, со=оо и сос = 1/Г
Выражение для АЧХ можно получить либо по формуле (2 124),
либо по формуле (2 126) Для рассматриваемого звена проще исполь-
зовать формулу (2 126)
А(а>) = |1Г(у®)| = |it|/|7y® +1| = к/^\ + Т2а>2
(3 22)
График функции Л(со) изображен на рис 3 3,в По графику вид-
но, что
гармонические сигналы малой частоты (со<сос) пропускаются
звеном хорошо - с отношением амплитуд выходной и входной
величин, близким к передаточному коэффициенту к Сигналы
большой частоты (ю>юс) плохо пропускаются звеном отноше-
ние амплитуд существенно меньше коэффициента к Чем
больше постоянная времени Т, т е чем больше инерционность
звена, тем меньше АЧХ вытянута вдоль оси частот или, как
принято говорить в автоматике, тем уже полоса пропускания
частот
Таким образом, инерционное звено первого порядка по своим
частотным свойствам является фильтром низкой частоты
167
В практических расчетах ширину полосы пропускания соп звень-
ев и систем определяют по ординате Л(соп), равной (0,05...0,10)fc. Для
инерционного звена первого порядка соп=(2О... 1О)сос.
ФЧХ инерционного звена первого порядка согласно формуле
(2.125)
ф(со) = arctg [^(co)/7>(cd)] = arctg оз/’.	(3.23)
График функции (3.23) показан на рис. 3.3,г. Чем больше часто-
та входного сигнала, тем больше отставание по фазе выходной вели-
чины от входной. Максимально возможное отставание равно 90°.
При частоте сос = 1/7’ сдвиг фаз равен -45°.
Рассматриваемое звено является минимально-фазовым. Фазовый
сдвиг, создаваемый этим звеном, меньше, чем у любого другого зве-
на с такой же амплитудной характеристикой. Например, у неустой-
чивого инерционного звена первого порядка
W(ia>) = к/ (Tja> -1)	(3.24)
АЧХ не отличается от характеристики (3.22), а фазовая, согласно
формуле (2.125), составляет
Ф(<о) =-180° + arctg (оГ	(3.25)
При изменении частоты со от 0 до оо фазовый сдвиг (3.25) изме-
няется от -180° до -90°.
Рассмотрим теперь ЛАЧХ звена Точная ЛАЧХ описывается
выражением
£(<й) = 201gA(ro) = 201g*-20Ig>/l + r2oo2.	(3.26)
В практических расчетах используют приближенную или асим-
птотическую характеристику Г(со), представляющую собой ломаную
в виде двух асимптот (рис. 3.3,д). Первая асимптота (низкочастотная)
получается при малых частотах, когда величиной Г2®2 в выражении
(3 .26) можно пренебречь и принять:
168
L(co) ~ £нЧ((о) - 201gк
(3.27)
Низкочастотная асимптота от частоты не зависит и представляет
собой прямую, параллельную оси частот и отстоящую от нее на рас-
стоянии 20 1g к.
Вторая асимптота (высокочастотная) заменяет точную характе-
ристику при больших частотах, когда ТЛо2» 1, и единицу под корнем
в формуле (3.26) можно не учитывать Выражение для этой асимпто-
ты
£((О)«ДЧ =201g£-201g7co.	(3 28)
Эта асимптота зависит от частоты. В логарифмической системе
координат она представляет собой прямую, имеющую отрицатель-
ный наклон и проходящую через точку с координатами
со = 1/Т, L((o) = 201g £. Подставляя в формулу (3.28) два значения час-
тоты со 1 и со2= 1 Осо 1, можно убедиться, что приращение высокочастот-
ной асимптоты, приходящееся на одну декаду, равно -20 дБ
Значение сопрягающей частоты сос, при которой пересекаются
обе асимптоты, найдем из условия £нч(а>с)=£вч(сос):
201g к = 201g к - 201g Та)с,	(3.29)
отсюда
®С=1/Г.
(3.30)
Можно показать, что наибольшая ошибка, получающаяся от
приближенной замены точной характеристик (3 27) двумя асимпто-
тами, равна 3 дБ (при частоте сос).
На алгоритмических схемах инерционное звено первого порядка
представляют либо в виде модели "вход-выход" (рис 3 4,а), либо в
виде модели в переменных состояния (рис. 3.4,6).
При аналоговом моделировании рассматриваемое звено реали-
зуют при помощи схемы набора, приведенной на рис 3 4,в Коэффи-
циенты аналоговой модели (при единичном масштабе времени)'
а{=к/Т, а2=\/Т	(3 31)
169
a
e x(t)
Рис. 3.4. Модели инерционного звена первого порядка
Цифровая модель звена может быть реализована в виде блок-
схемы (рис. 3 4,г), соответствующей модели в переменных состояния
(см.рис. 3.4,6) и содержащей цифровой интегратор (см. 2.10) с шагом
интегрирования АЛ Для обеспечения удовлетворительной точности
моделирования отдельного инерционного звена шаг интегрирования
должен быть
Дг<(0,1 ..0,2)7’.
(3.32)
Инерционными звеньями первого порядка являются конструк-
тивные элементы, которые могут накапливать и передавать энергию
или вещество. В электрических элементах накопителем энергии
электрического поля служит конденсатор, а магнитного - индуктив-
ность. В механических элементах потенциальная энергия накаплива-
ется в пружинах и других упругих элементах, а кинетическая - в
движущихся массах. Простейшим примером такого элемента служит
электрический пассивный четырехполюсник (рис. 3.5,я), состоящий
из резистора с сопротивлением г, Ом, и конденсатора с емкостью С,
Ф Выходная величина четырехполюсника - напряжение и2 - после
подачи на его вход постоянного напряжения щ изменяется пропор-
ционально величине накапливаемого в емкости заряда. В первые мо-
менты времени заряд растет быстро (см рис 3 3,п), а затем, по мере
170
приближения напряжения и2 на обкладках конденсатора к входному
напряжению щ, ток заряда становится все меньше, и скорость
возрастания напряжения и2 постепенно падает до нуля.
Рис. 3.5. Инерционные звенья первого порядка
Параметры передаточной функции (3.18) применительно к рас-
сматриваемому четырехполюснику: к = 1; Т = гС (с).
Свойствами инерционного звена первого порядка обладают
также электрические элементы с индуктивностью L, Гн, у которых
выходной сигнал пропорционален току через индуктивность. Про-
стейшим примером такого элемента является цепь, изображенная на
рис. 3.5,6. Передаточный коэффициент цепи к=1, а постоянная вре-
мени Т = L/r , с.
Более сложным примером звена такого рода является широко
применяемый в СУ электрический генератор постоянного тока (рис.
3.5,в), у которого в качестве входной переменной рассматривается
напряжение возбуждения ив, а выходной - ЭДС ег, наводимая в об-
мотке якоря генератора. Передаточный коэффициент генератора по
указанному каналу
кг =сепкн wB/rB, В/В,
1 V П D / D 7 I >
(3.33)
где се - константа, зависящая от конструктивных параметров генера-
тора, В/Вб (об/с); п - частота вращения якоря, 1/с; кп - коэффициент
наклона линеаризованной характеристики намагничивания генерато-
ра, Вб/А; wB - число витков обмотки возбуждения, приходящееся на
один полюс; гв - сопротивление обмотки возбуждения, Ом. Постоян-
ная времени генератора
171
Tr=Ljr*,c,	(3 34)
где Лв - индуктивность обмотки возбуждения, Гн
3.4.	Инерционные звенья второго порядка
Дифференциальное уравнение звена
т? + Т} + y(t) = kx(t),	(3 35)
dt dt
ему соответствуют уравнение динамики в изображениях по Лапласу
(или в операторной форме)
[т]р2 + Ttp + 1]г(р) = кХ(р)	(3 36)
и передаточная функция
I И'(р) = У(.Р)/Х(р) = к/(т2 р2 +Т,р +1)	(3 37)
Характеристическое уравнение звена
Г2У+7> + 1 = 0	(3 38)
имеет два корня
р11ЦсТ1±л1г2-4Т2)/:>Т2	(3 39)
Общее решение дифференциального уравнения, определяющее
свободное движение звена, согласно выражению (2 87), имеет вид
у(0 = С^'+С2^'
(3 40)
Характер переходного процесса звена зависит от вида корней
(3 39). которые могут быть действительными или комплексными
Если 7’1 >271, то оба корня действительные Обозначим их
172
р, = -1/Г3. А = -1/Л.
(3 41)
где Тз и Тд - некоторые условные постоянные времени, причем Тз>14
Ниже будет показано, что при T\>2Ti переходная функция звена
имеет монотонный, апериодический характер Поэтом} звено в этом
случае называют апериодическим второго порядка
При Т\>2Тз знаменатель передаточной функции (3 37) можно
разложить на два множителя и представить ее в следующих двух эк-
вивалентных формах
(3 42)
W(p) = kl(7\p + !)(/> + !),
(3 43)
согласно которым инерционное звено второго порядка (рис 3 б.я)
можно представить либо как последовательное (рис 3 6,6), либо как
параллельное (рис 3 6,в) соединение двух инерционных звеньев пер-
вого порядка
Рис 3 6 Алгоритмические схемы инерционных звеньев второго порядка
173
Если Z’i<27'2, то корни уравнения (3 38) комплексные
Рм =-а±;Р,
(3 44)
где а = 71 /27<, р =
Решение (3 40) в этом случае содержит гармонические состав-
ляющие, и звено называют колебательным
Наконец, возможен случай, когда Г]=0 При этом оба корня бу-
дут мнимыми, а переходная функция будет представлять собой неза-
тухающую синусоиду Инерционное звено второго порядка с 7\=0
называется идеальным колебательным, или консервативным
Наряду' с общими признаками (статизм, инерционность) аперио-
дическое и колебательное звенья имеют и существенные различия
Рассмотрим в отдельности характеристики этих звеньев
Переходная функция апериодического звена
второго порядка может быть получена сложением общего
решения (3 40) с частным решением, соответствующим вынужден-
ной составляющей при х(/)=а(/) Переходная функция имеет вид
/?(/) = Q +С2е //Л + Ь(/)
Подставляя начальные у словия
А(О) -0 и /?'(0) = 0
в выражение (3 45). находим
(= -И,а(/)/(7, -1\). С, = -И>(/)/(7’ - Г4)
Тогда переходная ф} нкция
h(t) = k 1 ----- —е t7' + -—4; е ///д о(/)
<	~ *4	I з ~ 4	)
(3 45)
(3 46)
(3 47)
(3 48)
174
Временные характеристики h(t) и w(t) апериодического звена
показаны на рис 3 7,а и б В соответствии с представлением аперио-
дического звена второго порядка в виде последовательного соедине-
ния двух инерционных звеньев первого порядка (см рис 3 6,6) все
его частотные характеристики (рис 3 7,в, г, д. е) могут быть полече-
ны по аналогичным характеристикам звеньев первого порядка, при-
веденным в 3 3, - правилам умножения комплексных (векторных)
величин
Рис 3 7 Характеристики апериодического звена второго порядка
Апериодическое звено второго порядка так же. как и звено пер-
вого порядка, хорошо пропускает сигналы низкой частоты и
плохо - сигналы высокой частоты
Дифференциальное уравнение колебательного з в с -
н а записывают обычно в следующем виде
Г1^1+2?Г^И+У(1) = кх(11
at	at
(3 49)
где 7-Г? - постоянная времени, характеризующая инерционность
звена, =	- относительный коэффициент демпфирования,
характеризующий колебательность звена (0 < ^ < 1)
175
Передаточная функция колебательного звена
№(р) = Цр)/Х(р) = к/(тгр! + 2£Гр + 1)
Корни соответствующего характеристического уравнения
Pl2=-a.±fi = -(i,/T)±j4iTe/T,
(3 50)
(3 51)
где а = £,/7’ - коэффициент затухания, $ = ^1-1^ /Т - круговая час-
тота затухающих колебаний, рад/с
Подставляя в общее решение (3 40) значения комплексных кор-
ней (3 51) и складывая его с частным решением kv{f), получим пере-
ходную фу нкцию колебательного звена
h(l) = (>'“•1Vl' + С,е< “	+ ka(t)
(3 52)
С помощью формулы Эйлера (2 23) можно функцию (3 52) пре-
образовать к виду
h(t) - Се at sm(|3f + ф) + &o(f)	(3 53)
Используя начальные условия /?(0) и Л'(0)=0, найдем
С = -fo(r)7а2 + р3 /р = -Ь(')А/1 - V 	(3 54)
Ф = arctg(j3/a) = aresm рТ1 = arccos £	(3 55)
Окончательно переходная функция может быть записана в сле-
дующей форме
(3 56)
176
Свободная составляющая переходной функции (рис 3 8,а) пред-
ставляет собой синусоиду, амплитуда которой убывает по экспонен-
циальной огибающей (пунктирная линия) Период затухающих коле-
баний
Чем больше коэффициент £ и чем меньше постоянная Т, тем бы-
стрее затухают колебания
Если коэффициент демпфирования ^=0 (что соответствует
Т\=0), то на выходе звена после подачи единичного ступенчатого
воздействия возникают незатухающие колебания с частотой
о>0 = 1/Г
Скорость затухания колебательных переходных процессов при-
нято оценивать степенью затухания
v=(4 -А)/4	,
(3 58)
177
представляющей собой отношение разности двух соседних амплитуд
(рис. 3 8,а) к первой из них. Чем ближе величина \|/ к единице, тем
быстрее затухают колебания.
Степень затухания \|/ зависит от соотношения действительной и
мнимой частей комплексного корня. Действительно, если в выраже-
ние для огибающей в формуле (3 56) подставить два значения Л от-
личающиеся на период затухающих колебаний Т3 - 2л/Р, то можно
получить
= 1 - е2’га/₽ = 1-е2л/и
(3.59)
Отношение р. = 0/а называют степенью колебательности. Ис-
пользуя выражение (3.51), можно установить связь между степенью
колебательности р, и коэффициентом демпфирования

(3.60)
Определим теперь зависимость максимального значения hM пе-
реходной функции от коэффициента демпфирования Дифферен-
цируя выражение (3.56) по t и приравнивая производную нулю, по-
лучим
(3 61)
Л = h(t ) = k( 1+е	.
(3.62)
АФХ колебательного звена (рис. 3.8,е) описывается функцией
IT(ja>) = ЛгДт’Ч/ю)2 + 2^7/ш +1],
ей соответствуют АЧХ (рис. 3.8,в)
Л(ш) = к/ 7(1-Г2©2)2 +4^272со2
(3 63)
(3 64)
178
и ФЧХ (рис 3 8,г)
(р(сэ) = -arctg 22,7 со/(1 - Т2($2)]
(3.65)
АЧХ при частоте
(3.66)
имеет максимум (резонансный пик), равный
A„=A(<S>M) = k/^l-2p .
(3.67)
Максимум существует, если 1-2^2 > 0, т.е. если £,< 0,707.
Из выражений (3 66) и (3.67) следует- чем меньше коэффициент
тем ближе резонансная частота сор=сом к собственной частоте неза-
тухающих колебаний о)о = \/Т и тем больше резонансный пик.
Таким образом, по графику АЧХ (см.рис. 3.8,в) видно, что
колебательное звено, как и все инерционные звенья, хорошо про-
пускает сигналы низкой частоты и плохо - сигналы высокой
частоты, если частота гармонического входного сигнала близ-
ка к частоте собственных колебаний звена, то отношение ам-
плитуды выходного сигнала к амплитуде входного больше пере-
даточного коэффициента к.
Аналоговую (рис. 3 9,6) и цифровую (рис. 3.9,в) модели инерци-
онного звена второго порядка удобно составлять в соответствии с его
моделью в переменных состояния (рис. 3.9,а). Коэффициенты анало-
говой модели
а,=к/р =k/T2 - аг=Т2/Т{ =2ЦТ- а3 = 1/Z,2 = 1/?'2. (3 68)
Инерционными звеньями второго порядка являются обычно та-
кие конструктивные элементы СУ, которые содержат два накопителя
энергии или вещества Если в одном из них накапливается потенци-
альная энергия, а в другом - кинетическая, то элемент системы мо-
179
жет обладать колебательными свойствами Колебательность элемен-
та зависит от условий обмена энергии между указанными накопите-
лями если канал передачи энергии обладает существенным сопро-
тивлением (электрическим или механическим), то в нем происходит
заметное поглощение или рассеивание энергии, и элемент близок по
своим свойствам к апериодическому звену второго порядка, если же
потери энергии при обмене незначительны, то процесс обмена будет
иметь колебательный характер
Рис 3 9 Модели инерционного звена второго порядка
Мерой потерь энергии в канале передачи служит коэффициент
демпфирования £ чем меньше потери, тем меньше в пределе, ко-
гда сопротивление канала равно нулю и потерь нет, коэффициент
180
£,=0 При этом элемент сохраняет в себе неизменным первоначаль-
ный запас энергии, и колебательный процесс обмена энергией между
накопителями не затухает
Классическим примером инерционного звена второго порядка
служит четырехполюсник, состоящий из резистора г, индуктивности
I и конденсатора С (рис 3 10,а) Коэффициенты дифференциальных
уравнений (3 35) и (3 49) для этого четырехполюсника
* = ], T2=T = 4lC, T^TgT^rC, =	(3 69)
При г=0 параметры Ti=0 и £=0 и четырехполюсник становится
идеальным колебательным контуром
Рис 3 10 Инерционные звенья второго порядка
Другим распространенным примером инерционного звена вто-
рого порядка является электрический двигатель постоянного тока с
независимым возбуждением (рис 3 10,6) Если в качестве входной
переменной рассматривать ЭДС еи, подводимую от источника регу-
лируемого напряжения, а в качестве выходной - частоту вращения
вала п, об/с, то двигатель по этому основному каналу описывается
передаточной функцией
д
и(Р)
М?)
VJ3p2+t„p + \)
(3 70)
где кд = 1/се Ф - ПК двигателя по управляющему воздействию,
(об/с)/В, Т3 -LJгя - электромагнитная постоянная времени якорной
цепи, с, 7М = 2л*7гя/сесмФ2 - электромеханическая постоянная вре-
181
мени, с; J - момент инерции вращающихся масс (якоря, редуктора,
рабочей машины), приведенных к валу двигателя, кг-м, гя и Ья -
соответственно активное сопротивление и индуктивность всей якор-
ной цепи (включающей в себя и выходную цепь источника напряже-
ния), Ом и Гн; се и см =се/2тг - конструктивные постоянные
двигателя, В-Вб' (об/с)*1 и Н-м/А-Вб; Ф - магнитный поток возбуж-
дения, Вб.
Инерционность двигателя обусловлена процессами накопления
электромагнитной энергии в индуктивности якорной цепи и кинети-
ческой - во вращающихся массах. Потери энергии происходят в ак-
тивном сопротивлении якорной цепи.
Параметры передаточной функции (3.70) для серийных двигате-
лей постоянного тока находятся в пределах: £д=0,01... 0,03 (об/с)/В,
Тэ = 0,01...0,1 с; Ти=0,01...0,1 с. Причем у двигателей средней и
большой мощности всегда Тм > 4ТЯ и коэффициент демпфирования
£ =	1, т.е. двигатель эквивалентен апериодическому зве-
ну второго порядка.
В СУ часто встречаются механические устройства, которым со-
ответствует схема замещения, приведенная на рис. 3.10,в. Составляя
уравнение равновесия моментов, можно показать, что такое устрой-
ство описывается уравнением инерционного звена второго порядка с
параметрами
* = 1/*уп,7н-М; Т2=Г = 72ж//360^,с; Т, = 2^ = к^/куп,с,
(3 71)
где J - момент инерции вращающихся масс, кг м2;	- коэффициент
упругости вала, Нм/°; к^ - коэффициент трения, Н м/(°/с).
Коэффициент трения учитывает потери механической энергии,
подводимой к валу, на преодоление силы трения в подшипниках и
силы внутреннего (вязкого) сопротивления, возникающего в самом
валу при его деформации. От этих потерь, называемых диссипатив-
ными, зависит колебательность рассматриваемого устройства.
182
В заключение отметим общие свойства статиче-
ских (позиционных) звеньев, рассмотренных в 3.2,
3.3 и 3 4.
1	. В установившемся режиме выходная переменная у звена од-
нозначно связана с входной х уравнением статики
у = кх
2	ПК звена связан с ПФ соотношением
к = W(p)
(3 72)
(3.73)
3	Звенья являются фильтрами низкой частоты (кроме безынер-
ционного), т.е. хорошо пропускают низкочастотные сигналы и плохо
- высокочастотные; в режиме гармонических колебаний они создают
отрицательные фазовые сдвиги.
3.5.	Интегрирующие звенья
Различают два вида интегрирующих звеньев- идеальные и ре-
альные Общей особенностью интегрирующих звеньев является про-
порциональность производной выходной величины мгновенному
значению входной величины Причем у идеального интегрирующего
звена пропорциональность существует в любой момент времени по-
сле подачи ступенчатого воздействия, а у реального - только после
завершения переходного процесса в звене.
Дифференциальное уравнение идеального интегри-
рующего звена
-^- = кх{1)
dt
(3 74)
Коэффициент пропорциональности к зависит от конструктив-
ных параметров звена и имеет размерность
183
(i] = W/M(']
(3 75)
Уравнению (3 74) равносильно интегральное соотношение
ЯО = к J x(9)d& + >(0),
О
(3 76)
которое в явной форме выражает зависимость выходной величины от
входной и объясняет название звена звено интегрирует входной сиг-
нал
Подставляя в соотношение (3 76) х(Э)=ст(0, можно получить пе-
реходную функцию
h(t) = ktcr(t)
(3 77)
График функции h(t) показан на рис 3 11,а (линия 7)
Рис 3 11 Характеристики идеального (7) и
реального (2) интегрирующих звеньев
184
Импульсная переходная функция звена (рис 3 11,6)
w(t) = МО	(3 78)
ПФ идеального интегрирующего звена
I	= к/р	(3 79)
АФХ звена
W (jm) = к/	- jk / (&	(3 80)
на комплексной плоскости изображается в виде прямой, совпадаю-
щей с мнимой осью (рис 3 11,е - линия 7)
АЧХ
Л (со) = |FK(/co)| = к/о)
(3 81)
представляет собой гиперболу (рис 3 11,в - линия 7), которая при
со=0 стремится к бесконечности Эту особенность можно условно (по
аналогии со статическими звеньями) объяснить наличием ПК, равно-
го бесконечности
При увеличении частоты значения Л (со) стремятся к нулю Это
свойство сближает интегрирующие звенья с инерционными
ФЧХ идеального интегрирующего звена
/	\	+	~к/(£> АЛ"
<р(со) = arctg—-— = -90
(3 82)
показывает, что сдвиг фаз, создаваемый звеном, на всех частотах
одинаков и равен -90° (рис 3 11,г - линия 7)
ЛАЧХ
£(со) = 201g Л(со) = 201g к - 201g со	(3 83)
185
представляет собой прямую с наклоном -20 дБ/декаду, проходящую
через точку с координатами ш=1, £(<o)=201g к (рис. 3.11,д).
Рассмотрим теперь характеристики реального интег-
рирующего звена. Его дифференциальное уравнение
г d2y(t) t dy(t)
dt2 dt
= *x(0,
а передаточная функция
W(p) = к/р(Гр +1).
(3.84)
(3.85)
Нетрудно заметить, что звено с передаточной функцией (3.85)
может рассматриваться как последовательное соединение двух эле-
ментарных звеньев (рис. 3.12,а): идеального интегрирующего с пере-
даточной функцией 1/р и статического инерционного звена первого
порядка с постоянной времени Т и передаточным коэффициентом к.
Поэтому все частотные характеристики реального интегрирующего
звена могут быть получены по характеристикам этих простых звень-
ев, по соответствующим правилам перемножения комплексных (век-
торных) величин.
Рис. 3.12. Модели реального интегрирующего звена
186
Модели "вход - выход" реального интегрирующего звена, изо-
браженной на рис. 3.12,а, соответствуют модели: в переменных со-
стояния (рис. 3.12,в), аналоговая (рис. 3.12,6) и цифровая (рис.
3.12,г). Коэффициенты аналоговой модели
ах=к/Т\ а2=\1Т.
Рис. 3.13. Интегрирующие звенья
Интегрирующие свойства присущи всем объектам управления, в
которых происходит накопление вещества или энергии без ее одно-
временной отдачи в окружающую среду. Классическим примером
объекта с интегрирующими свойствами служит резервуар с жидко-
стью (рис. 3.13,а), если в качестве входной переменной рассматри-
вать подачу жидкости Q, м3/с, а выходной - уровень жидкости А, м.
Действительно, уравнение баланса жидкости
= Q(t)dt,
(3.87)
где S - площадь поверхности жидкости, м2, легко приводится к урав-
нению вида (3.74) или (3.76). При этом коэффициент
k = \/S, м’2.
(3.88)
Интегрирующими звеньями являются также различные испол-
нительные двигатели и механизмы - устройства, которые перемеща-
ют регулирующие органы (шиберы, заслонки, вентили и т.п ). Вход-
ной величиной этих устройств служит обычно количество энергии
или вещества, поступающих в устройство, а выходной - линейное
или угловое перемещение какого-либо элемента. Степень идеально-
187
сти (безынерционное™) таких интегрирующих звеньев зависит от
величины масс перемещающихся (вращающихся) частей исполни-
тельного устройства и приводимого им в движение регулирующего
органа.
Идеальным интегрирующим звеном можно считать (с некото-
рыми допущениями) гидравлический исполнительный механизм
(рис. 3.13,6), у которого входной величиной является количество
жидкости Q, м/с, поступающей в единицу времени в полость цилин-
дра, а выходной - перемещение /, м, поршня со штоком. Действи-
тельно, если масса перемещающихся частей пренебрежимо мала и
если усилие, создаваемое давлением гидронасоса, существенно
больше сил сопротивления, то перемещение поршня определяется
уравнением баланса жидкости вида (3.87), а коэффициент к - выра-
жением (3.88).
Свойствами идеального интегрирующего звена обладает при
некоторых условиях инерционное звено первого порядка. Например,
апериодическая rC-цепь (см.рис. 3.5,а) при частотах входного воз-
действия со »сос = 1/Т может приближенно рассматриваться как
интегрирующее звено. Действительно, если в частотной функции
(3.19) пренебречь единицей в знаменателе, то она совпадает с функ-
цией (3.80).
Реальными интегрирующими звеньями являются электрические
исполнительные двигатели постоянного и переменного токов. На
рис. 3.13,в изображен двухфазный асинхронный двигатель. Его
входная величина - напряжение переменного тока иу, В, приложен-
ное к обмотке управления, выходная - угол поворота вала ср,°. Дей-
ствующее значение напряжения ис на обмотке возбуждения считает-
ся неизменным. При некоторых допущениях (инерционность обмот-
ки управления пренебрежимо мала, статические механические ха-
рактеристики двигателя предварительно линеаризованы, диапазон
изменения напряжений иу ограничен) двигатель может быть описан
передаточной функцией (3.85). Передаточный коэффициент двигате-
ля (°/В.с) приближенно может быть рассчитан через номинальные
значения частоты вращения пК, об/с, и управляющего напряжения
wy н:
188
£«360ли/луи,7(В-с).
(3.89)
Постоянная времени Т (с) зависит от приведенного на вал дви-
гателя момента инерции вращающихся частей J, кг м2
Т = 2лЛин/Мп,с,
(3.90)
где Мп - номинальное значение пускового момента, Н м.
В случаях, когда исполнительный двигатель используется для
управления объектом с большой инерционностью, можно постоян-
ную времени Т не учитывать и считать двигатель идеальным интег-
рирующим звеном.
Общие свойства и особенности интегри-
рующих звеньев:
1.	После подачи ступенчатого входного воздействия х(0=хост(0
выходная переменная y(t) неограниченно возрастает и по окончании
переходного процесса изменяется по линейному закону
|	y(t) = kx^ t>Q.	(3.91)
При снятии входного воздействия выходная переменная сохра-
няет достигнутое значение, поэтому интегрирующие звенья можно
использовать в качестве запоминающих элементов (элементов с па-
мятью).
2.	В передаточную функцию обязательно входит сомножитель
1/р; поэтому
=^к, а РК(0) = оо.	(3.92)
3.	Интегрирующие звенья, как и инерционные статические, яв-
ляются фильтрами низкой частоты; в режиме гармонического коле-
бания они вносят отрицательные фазовые сдвиги.
W(p)
189
3.6.	Дифференцирующие звенья
Дифференцирующие звенья могут быть идеальными (безынер-
ционными) и реальными (инерционными). Мгновенное значение вы-
ходной величины идеального дифференцирующего
звена пропорционально в каждый момент времени мгновенному
значению входной величины
dx(t)
уМ=к~^г-
at
(3.93)
Коэффициент пропорциональности к зависит от конструктив-
ных параметров звена и имеет размерность
Рис. 3.14. Характеристики идеального (7) и
реального (2) дифференцирующих звеньев
Переходная функция звена получается непосредственно из
уравнения (3.93) - подстановкой и дифференцированием единичной
ступенчатой функции:
190
h(t) =
(3.95)
График переходной функции идеального дифференцирующего
звена показан на рис. 3.14,а (линия 7).
Импульсная переходная функция (рис. 3.14,6 - линия 7)
w(t)=kdd(t)/dt.
Передаточная функция звена
W(p) = kp.
(3.96)
(3.97)
Амплитудно-фазовая функция

(3.98)
совпадает с положительной частью мнимой оси (рис. 3.14,е - линия
7).
АЧХ звена
Л(со) = £со	(3.99)
показывает (рис. 3.14,в - линия 7), что чем больше частота входного
сигнала, тем больше амплитуда выходного сигнала. Эта особенность
дифференцирующих звеньев вытекает непосредственно из основного
уравнения (3.93): чем быстрее изменяется во времени сигнал x(t), тем
больше его производная в правой части и тем больше выходной сиг-
нал y(t).
Сдвиг фаз, создаваемый идеальным дифференцирующим зве-
ном, на всех частотах одинаков (рис. 3.14,г - линия 7)
ЛАЧХ звена
<р(со) = arctg— = +90°.
£(со) = 201g кт
(3.100)
(3.101)
191
- прямая линия с наклоном +20 дБ/декаду, проходящая через точку с
координатами со = \/к, £(со) = 0 (рис. 3.14,д - линия 1).
Реальное дифференцирующее звено пред-
ставляет собой последовательное соединение идеального дифферен-
цирующего звена и инерционного звена первого порядка (рис.
3.15,а). Его уравнение
w (0=t^(n
dt z dt
(3.102)
а передаточная функция
W(p) = kpftTp +1).	(3.103)
Рис. 3.15. Модели реального дифференцирующего звена
Нетрудно убедиться, что звено с передаточной функцией (3.103)
можно представить и в виде параллельного соединения безынерци-
онного и инерционного звеньев (рис. 3.15,6).
192
Временные характеристики h(t) и w(f) реального дифференци-
рующего звена показаны на рис. 3.14,6? и б линиями 2.
Аналитические выражения для частотных характеристик реаль-
ного дифференцирующего звена можно получить по соответствую-
щим функциям идеального дифференцирующего и инерционного
звеньев первого порядка. Графики этих характеристик показаны ли-
ниями 2 на рис 3.14,6, в, г, д.
На рис. 3.15 приведены модели реального дифференцирующего
звена в переменных состояния (в), аналоговая (г) и цифровая (д). Ко-
эффициенты аналоговой модели
о.х=к1тг-, <х2=1/Т; а3=к/Т.	(3.104)
Большинство конструктивных элементов автоматики, обладаю-
щих способностью дифференцировать входной сигнал по времени,
описывается уравнениями реального дифференцирующего звена
Исключением являются лишь так называемые кинематические диф-
ференцирующие звенья, у которых дифференцирующая связь между
входом и выходом образуется чисто формально Например, если в
качестве входной величины безынерционного редуктора (см.рис.
3.2,г) рассматривать угол поворота ведущего вала (pi, а в качестве
выходной величины - частоту вращения ведомого вала гь, то свойст-
ва редуктора как алгоритмического звена будут очевидно описывать-
ся уравнением (3.93).
Рис. 3.16. Дифференцирующие звенья
Реальными дифференцирующими звеньями являются электри-
ческие цепи, изображенные на рис. 3.16,6? и б. Читатель может убе-
диться, что они описываются ПФ вида (3.103). Причем, для цепи с
емкостью к=Т=гС, а для цепи с индуктивностью к = Т = L/r Оче-
193
видно, что чем меньше постоянная времени Т, тем ближе свойства
этих цепей к свойствам идеального дифференцирующего звена. Но
при этом абсолютные значения выходного сигнала и2 становятся ма-
лыми и их приходится дополнительно усиливать.
Примером идеального дифференцирующего звена служит элек-
трический тахогенератор (рис. 3.16,в), если в качестве входной пере-
менной рассматривать не частоту вращения (как в 3.2), а угол пово-
рота <р его вала. В этом случае коэффициент к (В.с/°), входящий в ПФ
(3.79), определяется также по формуле (3.13), но с учетом размерно-
сти угла поворота:
Л: = р#Ф/360а,В-с/0.	(3.105)
Особенности дифференцирующих звень-
е в :
1.	При подаче на вход звена ступенчатого воздействия на его
выходе возникает большой кратковременный импульс, а затем по
окончании переходного процесса выходная переменная становится
равной нулю. Если входной сигнал не изменяется во времени, то вы-
ходной равен нулю. Если же входной сигнал x(t) растет по линейно-
му закону x(t)=a\t, то выходной
y(t) = ах= const.
(3.106)
2.	В передаточную функцию всегда входит сомножитель р, по-
этому
I	W(P)^=0	(3.107)
и дифференцирующие звенья в статике не передают входные сигна-
лы.
3.	Дифференцирующие звенья являются фильтрами высокой
частоты, т.е. хорошо пропускают высокочастотные сигналы и плохо
- низкочастотные. Они вносят положительные фазовые сдвиги.
194
3.7. Звено запаздывания
Звено запаздывания так же, как безынерционное статическое
звено, передает сигнал со входа на выход без искажения его формы.
Однако все мгновенные значения входной величины выходная вели-
чина принимает с некоторым отставанием (запаздыванием). Способ-
ностью задерживать сигнал во времени, не изменяя его формы, обла-
дают многие элементы промышленных автоматических систем. В
первую очередь к таким элементам относятся транспортирующие
устройства (конвейеры, ленточные питатели, трубопроводы), при
помощи которых подают различные материалы (сырье, топливо, реа-
генты) в технологические аппараты. Запаздыванием часто обладают
и сами технологические аппараты. Особенно заметно запаздывание
проявляется в аппаратах, которые имеют большие размеры и в кото-
рых происходят распределенные в пространстве процессы массооб-
мена (шаровые мельницы, флотомашины, сушильные барабаны).
Уравнение звена запаздывания
ЯО = х(г - х) ,	(3.108)
где т - длительность запаздывания.
Уравнение (3.108) не является дифференциальным и относится к
классу особых уравнений со смещенным (запаздывающим) аргумен-
том. Оно указывает, что выходной сигнал y(t) повторяет все измене-
ния входного сигнала x(i), но с отставанием на время т
Подставляя	можно сразу получить его переходную
функцию
ад=о(г-т),	(3.109)
а подставляя х(0=б(0,_ импульсную
M'(f) = 5(t - т).	(3.110)
Обе эти временные характеристики показаны на рис. 3 VI,а и б.
Применяя теорему запаздывания (см. табл. 2.2), можно записать
уравнение (3.108) в изображениях по Лапласу
195
Y(p) = X(p)ep\
отсюда ПФ звена
W{p) = Y(p)/X(p) = e~p\
(3.1И)
(3.112)
АФХ звена
IV(ja) = е Jcn = cos сот - j sin сот
(3.113)
представляет собой окружность с центром в начале координат и с
радиусом, равным единице (рис. 3.17,е).
Рис. 3.17. Характеристики звена запаздывания
Сравнивая выражение (3.113) с показательной формой записи
АФХ общего вида (2.121), легко установить, что у рассматриваемого
звена АЧХ (рис. 3.17,в)
Л (со) = 1 = const
(З.Н4)
196
и ФЧХ (рис. 3.17,г)
(р(со) = -сот.
(3.115)
Характеристики (3.114) и (3.115) могут быть получены и с по-
мощью формул (2.124) и (2.125):
Л(со) = \cos2 сот + sin2 сот = 1;
(3.116)
ср(со) = arctg(- sin cot/cos сот) = -сот.
(3.117)
Звенья запаздывания в большинстве случаев ухудшают устой-
чивость систем и делают их трудно управляемыми.
Если звено запаздывания входит в контур системы управления,
то характеристическое уравнение системы будет уже не простым ал-
гебраическим, а трансцендентным. Решение и анализ трансцендент-
ных уравнений связаны с большими трудностями Поэтому часто в
практических расчетах трансцендентную ПФ (3.112) раскладывают в
ряд Пада и, учитывая только два или три члена ряда, приближенно
заменяют ее дробной рациональной функцией
W(p) -е «(1 - 0,5т/?)/(1 + 0,5т/?)
или более точно
1 - 0,5т/? + 0,083т2/?2
1 + 0,5т/? + 0,083т2/?2
(3.118)
(3.119)
Другим возможным способом приближенной аппроксимации
звена запаздывания (рис. 3.18,6?) является представление его в виде
последовательного соединения п инерционных звеньев первого по-
рядка с одинаковыми постоянными времени Т, - i/n (рис. 3.18,6):
W(p) = e~pT
(3 120)
причем чем больше п, тем точнее такая аппроксимация.

197
Приближенным представлениям (3 118) и (3 119) соответствуют
аналоговые модели на рис 3 18,в,
где	^=4/1, а2=2/т,	(3 121)
и на рис 3 18,г,
где	а, =а2 = 2/т	(3 122)
а	б	в
Рис 3 18 Модели звена запаздывания
Модель (3 118) дает удовлетворительное приближение, если
частота входного сигнала со< 1,5/т . рад/с
Цифровая модель звена запаздывания (рис 3 18,д) реализуется
обычно в виде программы циклического смещения (переадресации),
которая задерживает на шагов или тактов дискретные значения
входного сигнала х,
У,=х,,_	(3 123)
где /э = т/Д/ - число тактов, соответствующее длительности запаз-
дывания т при интервале дискретности Д/
Наиболее характерным примером звена запаздывания является
ленточный питатель (рис 3 19,я), который транспортирует какой-
либо сыпучий материал Запаздывание между количеством материа-
ла О], кг/с, высыпающимся в единицу времени на питатель, и коли-
чеством материала О?, кг/с, на сходе питателя зависит от длины L, м,
и скорости движения v, м/с
198
t^L/v, с
(3 124)
Другим распространенным примером звена запаздывания явля-
ется трубопровод (рис 3 19,6), по которому в технологический объ-
ект управления подается какая-либо жидкая среда в количестве (м3/с)
^2=^1 и с концентрацией полезного компонента (кг/м3) x2(0~Yi(^-T)
Рис 3 19 Звенья с запаздыванием
Отметим, что необходимость рассматривать питатель, трубо-
провод и другие транспортирующие устройства как звенья запазды-
вания возникает лишь в тех случаях, когда они являются элементами
замкнутых систем управления
Таким образом, звено запаздывания отличает-
ся следующими характерными особенностя-
м и
1 Оно передает любые входные сигналы без искажения их фор-
мы, но задерживает их на интервал т, в установившемся режиме (при
t > т) выходной сигнал
(3 125)
2 Как и у других статических (позиционных) звеньев, переда-
точная функция
W(p)p0=k = l
(3 126)
3 По свойствам АЧХ звено запаздывания эквивалентно безы-
нерционному пропускает и высокочастотные, и низкочастотные
199
сигналы с одинаковым отношением амплитуд, равным единице; по
свойствам ФЧХ оно эквивалентно инерционным звеньям: создает
отрицательный фазовый сдвиг, пропорциональный запаздыванию т и
частоте со
Приведем пример технического устройства, в котором наряду с
запаздыванием проявляются интегрирующие свойства, - конвейер-
ный весоизмеритель (рис. 3.20,с?). Количество материала т, кг, нака-
пливаемого на ленте, в каждый момент времени
t
t-T
(3.127)
где 0i(3) - массовая подача материала на конвейер, кг/с; t = L/v -
длительность нахождения элементарной порции материала на дви-
жущейся ленте конвейера, с.
Рис. 3.20. Ленточный весоизмеритель
Найдем ПФ весоизмерителя, связывающую массу т и подачу О\
при нулевых начальных условиях. Для этого представим интеграл
(3 127) как разность двух интегралов
/	/-г
о	о
(3.128)
200
и найдем соответствующее изображение Лапласа-
т{р)=омме-
(3 129)
Р Р
При получении изображения второго интеграла в (3.128) учтено,
что J)=Z-t>0 и что при /<()	и /и (/)=().
Искомая ПФ
W(p) = m(p)/Ql(p) = [\-e~pz)/p.
(3.130)
Переходная характеристика весоизмерителя показана на рис
3.20,6. После ступенчатого изменения величины x=Qi материал на
ленте накапливается по интегральному закону до тех пор, пока через
интервал т расходы Q\ и СР не сравняются.
Заметим, что передаточной функцией (3.130) описываются так-
же так называемые фиксаторы, которые используются в импульсных
системах управления (см. главу 10).
Если в качестве выходного сигнала рассматривать среднее зна-
чение Q - т/т расхода материала, проходящего через весоизмери-
тель, то ПФ

(3.131)
Она соответствует оператору скользящего усреднения, исполь-
зуемому часто при первичной обработке измеряемых сигналов.
3.8. Приближенные модели динамики
инерционных статических объектов управления
При автоматизации технологических процессов наиболее часто
приходится встречаться с инерционными статическими объектами,
переходные характеристики которых имеют специфическую
^-образную форму (линия 1 на рис 3 21). Наклон, кривизна характе-
201
ристики и ее расстояние от оси ординат зависят от динамических
свойств конкретного объекта
Рис. 3 21. Переходные характеристики реального ОУ (7) и его приближен-
ных моделей второго порядка (2) и первого порядка с запаздыванием (3)
Для практических расчетов систем управления такими объекта-
ми каждую 5-образную кривую переходного процесса, снятую при
единичном ступенчатом воздействии, достаточно охарактеризовать
следующими параметрами, определяемыми непосредственно по гра-
фику (см рис Зг21): передаточным коэффициентом к0, постоянной
времени То и полным запаздыванием то, которое складывается из так
называемого чистого или транспортного запаздывания тч и переход-
ного запаздывания тп, т е То=*ч+*п
Параметры То и то определяются достаточно легко - проведени-
ем касательной АВ к наиболее крутому участку переходной характе-
ристики Выделение горизонтального участка OD, соответствующего
запаздыванию тч, связано обычно с некоторыми трудностями (из-за
202
помех, влиявших при снятии переходной характеристики), и поэтому
параметр тч можно установить лишь с определенной погрешностью
При расчете настроечных параметров систем управления объек-
тами с 5-образными переходными характеристиками ориентируются
либо на параметры ко, То, то, тч и тп, которые обобщенно (но не
полно!) характеризуют статику и динамику реального объекта, либо
используют упрощенные модели объекта, коэффициенты которых
однозначно выражаются через указанные экспериментальные пара-
метры.
Модели п - г о порядка Если заведомо известно, что
описываемый сложный объект состоит из нескольких одинаковых
объектов первого порядка, соединенных последовательно, то наибо-
лее точное приближение к 5-образной характеристике обеспечивает
ПФ
(3 132)
т е. наилучшей моделью динамики объекта является последователь-
ное соединение и инерционных звеньев первого порядка с одинако-
выми постоянными времени Тп! и звена запаздывания с тч
Модель (3.132) целесообразно использовать при исследовании
СУ на аналоговых или цифровых вычислительных машинах Посто-
янную времени ТО1 и порядок п этой модели можно вычислить по
экспериментально найденным параметрам То и тп (или то) с помощью
соотношений, приведенных в табл. 3.2
Модель (3.132) может служить удовлетворительной аппрокси-
мацией и в тех случаях, когда объект состоит из неодинаковых
звеньев. Важно только, чтобы у такого объекта число неодинаковых
звеньев было не менее трех, а их постоянные времени не сильно от-
личались друг от друга. Тогда кривая переходного процесса сохраня-
ет 5-образную форму и динамика объекта может быть охарактеризо-
вана теми же параметрами То, то, тч и тп-
Достоинством модели (3 132) является возможность воспроиз-
водить с ее помощью относительно большое полное запаздывание то,
состоящее только из переходного запаздывания тп В практических
задачах анализа и синтеза систем управления замена чистого запаз-
дывания тч переходным тп обычно допустима При этом исключается
203
необходимость применения специальных блоков АВМ или программ
ЦВМ, моделирующих чистое запаздывание.
Таблица 3.2
Связь между параметрами 5-образной переходной характеристики
(рис. 3.21) и параметрами аппроксимирующей модели (3.132)
— п	тп ^0	Т ‘ о т 1 01	Тп	1 т 01	1	И	Тп т * О	Т ‘ о т 1 01	т 2 OZ
1	0,000	1,00	0,00	13	1,005	8,74	8,77
2	0,107	2,72	0,29	14	1,053	9,12	9,62
3	0,222	3,69	0,82	15	1,115	9,41	10,50
4	0,323	4,46	1,44	16	1,180	9,69	11,42
5	0,420	5,12	2,15	17	1,220	10,09	12,27
6	0,518	5,69	2,95	18	1,265	10,40	13,16
7	0,595	6,22	3,70	19	1,295	10,70	13,90
8	0.673	6,71	4,52	20	1,320	11,10	14,90
9	0,745	7,16	5,34	25	1,500	12,00	19,50
10	0.816	7.59	6,20 |	30	1,660	12.60	24,30
11	0.871	7,99	7,04	35	1,800	13,30	29,20
12	0,942	8,38	7,90	1 40	1,950	13,60	34,20
Типичная кривая переходного процесса ODCE (см рис. 3.21),
имеющая участок чистого запаздывания OD и участок инерционного
перехода DCE, может быть смоделирована двумя способами
При первом способе переходный участок DCE, характеризуе-
мый отношением тп/Г0 (на рис 3.21 оно равно 0,75), воспроизводят
на АВМ или ЦВМ дробно-рациональной частью передаточной функ-
ции (3.132) с порядком п и постоянными времени Т01 (для рассматри-
ваемого на рисунке частного случая, согласно табл. 3 2, я=9 и
Го, = 7’0/7,16, а участок OD, соответствующий сомножителю в рХц,
- при помощи блока чистого запаздывания или программы цикличе-
ского смещения
Если в табл 3.2 не удается подобрать параметр п (целое число')-
который обеспечивает значение тп/Г0 , близкое к эксперименталь-
ному, то изменяют положение точки D, т.е искусственно перерас-
пределяют значения тч и тп (при неизменно суммарном т0). Перерас-
пределение осуществляют таким образом, чтобы получить ближай-
204
шее целое значение п. Затем для принятого п по соотношениям
Го/Го, или Тп/Л» > приведенным в табл. 3.2, и по эксперименталь-
ным значениям То или тп вычисляют второй параметр модели (3 132)
- постоянную времени Tot.
При втором способе моделирования полагают, что полное за-
паздывание т0 состоит только из переходного тп, т.е. что То-^п и всю
переходную кривую ODCE, характеризуемую отношением т0/Г0 ,
моделируют лишь дробно-рациональной частью с параметрами п и
То1, а чистое запаздывание в (3.132) считается равным нулю (Для
кривой на рис. 3.21 т0/Т0 «1,25, ц=18 и Т01 = Го/10,4) Необходи-
мость в блоке запаздывания или программе смещения при этом от-
падает. Но переходная характеристика с большим п приближается к
трапециевидной форме - ломаной ОАВЕ - и может, следовательно,
существенно расходиться с исходной аппроксимируемой кривой.
В классе моделей второго порядка достаточно хо-
рошее приближение к s-образным переходным кривым дает переда-
точная функция с одинаковыми постоянными времени и запаздыва-
нием’
»№> = k„e-r': 1(Т„р +1)\	(3.133)
где То, = 7^ /2,72; т' = т0 - т'п = т0 - 0,107Го; т'п - переходное запаз-
дывание модели (3.132) для ц=2. Как видим, параметры данной мо-
дели однозначно выражаются через параметры То и т0 эксперимен-
тальной переходной характеристики.
Передаточной функции (3.133) на рис 3.21 соответствует линия
2, которая начинается в точке D' Очевидно, что при данном способе
аппроксимации почти весь интервал т0 должен быть смоделирован
как чистое запаздывание, т.е. тч=т'о-
Модель (3.133) является наиболее рациональной для рассматри-
ваемых объектов, так как, с одной стороны, она обеспечивает доста-
точно хорошую аппроксимацию, а с другой - ее параметры легко
определяются по переходной характеристике.
Если на графике переходной функции объекта h0(t) не просмат-
ривается характерный для s-образных кривых прямолинейный уча-
сток, а сама переходная кривая приближается к установившемуся
205
значению h0(co)=k0 сравнительно медленно, пересекая вертикаль из
точки В ниже значения Ло=0,80Хго, то более точную, чем модель
(3 133), аппроксимацию может обеспечить ПФ с запаздыванием тч и
разными постоянными времени
»№>)=м "7(Х1/>+1)(тяр+О
(3 134)
Постоянные времени Toi и То2 определяют не через параметры То
и тп, а по некоторым характерным точкам графика переходного про-
цесса
В большинстве случаев модель (3 134) обеспечивает достаточ-
ную для практических расчетов точность, если принять
То1 /То2 = 0,5 При этом постоянные времени То\ и То2 определяют
следующим образом По ординате /?(Л)=0,63^о экспериментальной
переходной характеристики находят момент времени t2, отсчитывае-
мый от точки D (т е без учета чистого запаздывания тч), а затем вы-
числяют 7’)2=0,64/2 и ТО1=0,5Го2 Такая аппроксимация целесообразна,
когда /?(0,5/2)>0,3&о
В классе моделей первого порядка 5-образную
характеристику можно приближенно заменить экспонентой с запаз-
дыванием (линия 3 на рис 3 21) Параметры Т'о и т'о передаточной
функции
<3 135)
выбирают так, чтобы экспонента пересекала аппроксимируемую
кривую в двух точках и проходила в среднем наиболее близко к ней
Очевидно, что такое математически нестрогое требование мо-
жет быть выполнено при разных сочетаниях параметров Т'о и Т'о
Один из возможных способов определения параметров модели
(3 135) заключается в следующем Полагают, что экспонента начина-
ется в той же точке, что и характеристика модели с двумя одинако-
выми постоянными времени (точка D 'на рис 3 21), т е
т0 «то-0,11То,
(3 136)
206
а постоянную времени принимают
То = 0,64Го
(3 137)
Заметим, что применяемая часто модель первого порядка с па-
раметрами Г0=Т0 и т'0=т0 дает слишком грубое приближение к ре-
альному объекту
Пример. Аппроксимируем рассмотренными моделями динамику теп-
лового объекта, экспериментальная переходная кривая которого характери-
зуется параметрами к0=2,5 °С/(Дж/с), То= 100 с, тп=то=30 с (тч=0)
Отношению тп/Го=0.3 в табл 3 2 соответствует ближайшее значение
порядка модели (3 132) /7=4 Далее находим постоянную времени
7’0,^774,5-22 с и переходное запаздывание тп=7’о-0.32-32 с. которое будем
полагать приблизительно равным исходному т0 Тогда модель (3 132) в дан-
ном случае примет вид
1Г0(р) = 2,5/(22р + 1)4	(3 138)
Рассматриваемую характеристику можно аппроксимировать и моде-
лью (3 132) с чистым запаздыванием Действительно, принимая п=3, полу-
чим согласно табл 3 2 тп=0,227’о=22 с, 7’о,=7’0/3,7«27 с, тч=т0-тп= 30-22=8 с
Соответствующая модель третьего порядка
W'o(p) = 2,5es'’/(27p + l)3	(3 139)
Аналогично с помощью табл 3 2 можно определить для и=2
71О1=То/2,7»37 с, Tq=To-0,l 1Г0«19 с и конкретный вид модели (3 133)
И/0(р) = 2,5е-19р/(37р + 1)2	(3 140)
Самой простой и в то же время достаточно точной (в большинстве
практических случаев) аппроксимацией является модель первого порядка с
запаздыванием (3 135)
^О(р) = 2,5? 19^/(б4р + 1),	(3 141)
где То=0.647о=64 с. а чистое запаздывание т'0= 19 с принято таким же, как
у предыдущей модели
207
Контрольные задания и вопросы
1	Запишите частные формы уравнения (3 1), соответствующие про-
стейшим (элементарным) типовым звеньям
2	Получите из уравнения (3 1) уравнение статики позиционных звень-
ев и выразите их передаточный коэффициент к через коэффициенты а0 и Ьо
3	Как будет изменяться выходной сигнал y(t) безынерционного звена,
если на его вход подать линейное воздействие? Нарисуйте график у(1)
4	Как влияет безынерционное звено на амплитуду и фазу синусои-
дального входного сигнала?
5	Определите передаточные коэффициенты к следующих безынерци-
онных звеньев рычага с плечами 6=25 см, /2=50 см, делителя напряжения с
Г1=г2=10 кОм
6	Напишите передаточную функцию инерционного звена первого по-
рядка
7	Как проходят через инерционное звено первого порядка гармониче-
ские сигналы низкой и высокой частоты?
8	Выведите передаточные функции четырехполюсников, изображен-
ных на рис 3 5,а и б, пользуясь понятием операторного сопротивления Z(p)
(см 2 104) и формулой
^(?) = ^ВЫЧ (?)/Zbx (?)
9	При каком соотношении между постоянными времени Т} и Т2
инерционное звено второго порядка имеет апериодический переходный
процесс и при каком - колебательный?
10	Выведите передаточную функцию четырехполюсника, изображен-
ного на рис 3 10,а
11	Назовите характерные свойства, присущие всем инерционным ста-
тическим звеньям в установившемся режиме и при гармонических воздей-
ствиях
12	Напишите передаточную функцию идеального интегратора
13	Выведите передаточную функцию редуктора (рис 3 2,г),с Ар=0,01,
который используется как интегратор, т е у которого х=п}, об/с, а у=(р2,°
14	В чем сходство и в чем отличие частотных свойств у интегрирую-
щих и инерционных статических звеньев?
15	Напишите передаточную функцию идеального дифференциатора
16	Объясните, почему тахогенератор в одном случае (рис 3 2,е) явля-
ется безынерционным (пропорциональным) звеном, а в другом (рис 3 16,в)
- идеальным дифференцирующим
17	Почему дифференцирующие звенья плохо пропускают медленно
меняющиеся входные сигналы ?
208
18	Нарисуйте график выходного сигнала ХО звена запаздывания при
подаче на его вход линейного воздействия
19	Напишите передаточную функцию звена запаздывания
20	Определите для звена запаздывания с т=10 с фазовый сдвиг (в ра-
дианах и градусах) и амплитуду выходного сигнала ХО ПРИ действии на его
входе синусоидального воздействия х(0 с ©=2 рад/с и хт=50 кг/с
21	Какая из рассмотренных в 3 8 моделей является наиболее точной
для объекта с s-образной переходной характеристикой (см рис 3 20), а какая
- наиболее простой4?
22	Подберите по табл 3 2 порядок п моделей (3 132) для объекта с па-
раметрами То= 100 с и то=60 в двух вариантах а) без выделения чистого за-
паздывания, б) с выделением чистого запаздывания тч=30 с Определите для
обоих вариантов постоянные времени Tot
209
Глава 4. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ХАРАКТЕРИСТИКИ
ТОЧНОСТИ СИСТЕМ УПРАВЛЕНИЯ
4.1.	Правила преобразования алгоритмических структур
Для оценки точности, устойчивости и качества управления
замкнутых СУ необходимо знать их уравнения статики и динамики.
Уравнение динамики замкнутой СУ можно получить на основе сово-
купности уравнений отдельных элементов, образующих систему, -
путем последовательного исключения промежуточных переменных.
Наиболее удобным для решения этой задачи объединения математи-
ческих моделей элементов является метод структурных преобразо-
ваний, согласно которому по структуре системы с помощью несколь-
ких простых правил находят ее общую (эквивалентную) ПФ, а затем
- соответствующее уравнение динамики.
Информация о структуре СУ и передаточных свойствах ее эле-
ментов может быть задана в виде обычной алгоритмической схемы
(см. 1.2) или в виде сигнального графа.
Сигнальный граф системы управления представляет собой ори-
ентированный граф - совокупность дуг, изображающих отдельные
звенья и указывающих направление передачи сигнала, и вершин, со-
ответствующих входным и выходным сигналам звеньев. Отдельному
звену алгоритмической схемы, изображаемому прямоугольником, на
сигнальном графе системы соответствует стрелка, соединяющая
вершины х и у (рис. 4.1,я). Около стрелки указывается передаточная
функция звена.
Рис. 4.1,6, в и г иллюстрирует соответствие между изображе-
ниями типовых соединений двух элементов на алгоритмических
схемах и на сигнальных графах. Если к вершине подходят несколько
дуг, то соответствующий ей сигнал равен сумме всех выходных сиг-
налов этих дуг. Если из вершины исходят несколько дуг, то входные
сигналы всех дуг одинаковы и равны сигналу данной вершины. При
необходимости изобразить отдельно сигнал одной из суммируемых
210
дуг вводят дополнительную дугу с Ж(р) =1 (см. графы на рис. 4.1,в и
Алгоритмические схемы
Сигнальные графы
Рис. 4.1. Алгоритмические схемы и
сигнальные графы соединений элементов
Знак, с которым сигнал вводится на алгоритмической схеме в
сумматор, на сигнальном графе учитывается вместе с ПФ дуги. Бла-
годаря этому сигналы всех дуг, подходящих к вершине, складывают-
ся со знаком плюс.
Граф СУ строят по ее алгоритмической схеме, заменяя каждое
звено (прямоугольник) дугой, а каждый сумматор (кружок) - верши-
ной (кружком меньшего диаметра). При этом узлы разветвления сиг-
налов, используемые на алгоритмических схемах, на графах оказы-
ваются совмещенными с вершинами.
Для упрощения (свертывания) сложных алгоритмических схем и
сигнальных графов применяют следующие три главных пра-
вила преобразования^ помощью которых определяют
эквивалентные ПФ типовых соединений звеньев (см. также 2.8).
211
Эквивалентная ПФ последовательно соединенных звеньев равна
произведению передаточных функций всех звеньев, входящих в
соединение.
Например, для соединения двух звеньев (см.рис. 4.1,6)
W3{p) = WSp)W2(p).
(4.1)
Эквивалентная ПФ параллельно соединенных звеньев равна ал-
гебраической сумме передаточных функций всех звеньев, входя-
щих в соединение.
Например, для соединения двух звеньев (см.рис. 4 1,в)
WSp} = +WSp)±W2(p).
(4.2)
Эквивалентная ПФ соединения с отрицательной (положитель-
ной) обратной связью равна ПФ прямой цепи, деленной на еди-
ницу плюс (минус) произведение передаточных функций прямой
цепи и цепи обратной связи.
Так, для соединения из двух звеньев (см.рис. 4.1,г)

(4.3)
С помощью изложенных трех главных правил удается преобра-
зовать любую исходную алгоритмическую схему, не содержащую
перекрестных связей, к одноконтурной схеме (рис 4.2,а).
Алгоритмическую схему замкнутой СУ (и саму систему) назы-
вают одноконтурной, если при ее размыкании в какой-либо точке
образуется цепь, не содержащая параллельных соединений и внут-
ренних обратных связей. На рис. 4.2,6 показана цепь, полученная при
размыкании замкнутой СУ (см.рис. 4.2,а) между точками А и В. Она
не содержит параллельных соединений и обратных связей.
Получаемая при размыкании одноконтурной СУ цепь последо-
вательно соединенных элементов, стоявших внутри замкнутого кон-
тура, называется разомкнутым контуром СУ. В соответствии с этим
определением
212
ПФ разомкнутого контура WvJp) одноконтурной системы рав-
на произведению ПФ всех элементов, стоящих внутри контура
системы. ПФ элементов, стоящих вне замкнутого контура, ни-
когда не входят в произведение WpK(p).
Например, для системы на рис. 4.2,а

(4 4)
при этом учтен сумматор (перед звеном FF3), в котором знак сигнала
в контуре меняется на противоположный, т.е. главная ОС в данном
случае является отрицательной. ПФ W5(p) и fF6(p) не входят в произ-
ведение (4.4), так как эти элементы стоят вне замкнутого контура.
Рис. 4.2. Алгоритмические схемы одноконтурной СУ (а) и
ее разомкнутого контура (б)
ПФ разомкнутого контура является одной из важнейших харак-
теристик замкнутой СУ. От нее зависят устойчивость и показатели
качества процесса управления (см. главы 5 и 6) Она обязательно
входит в выражение ПФ замкнутой системы.
213
В общем случае на замкнутую СУ могут влиять несколько
внешних воздействий (задающих и возмущающих), а при анализе и
оценке ее свойств часто возникает необходимость рассматривать не-
сколько выходных переменных. Например, в СУ на рис. 4.2,я четыре
внешних воздействия (х5, х2, х6, х4) и четыре выходных переменных
(У1, у2, Уз, У4)- Для каждой пары "вход-выход" замкнутой системы мо-
жет быть записана своя ПФ по следующему правилу:
Передаточная функция Фу^р) одноконтурной СУ между к-м
входом Хк и 1-м выходом yi равна ПФ прямой цепи Wik(p), делен-
ной на единицу плюс ПФ разомкнутого контура, т.е.
<W> = УАр)Ыр) = ^(р)Д1 + И;к(р)),	(4.5)
при этом предполагается, что обратная связь в системе отрицатель-
ная. Знак обратной связи в одноконтурной СУ устанавливают с уче-
том всех перемен знака, происходящих в сумматорах при прохожде-
нии сигнала по замкнутому контуру.
Например, для системы на рис. 4.2,о ПФ по каналу "х5-у3"
ф35(р)
уАр) _ ~ ^Ap^ApWApWAp)
М/>)	i + ^(p)
(4.6)
где ^(p^fp^fp^fp^fp).
При записи (4.6) учтено, что в схеме на рис. 4.2,а знак внутри
контура изменяется только один раз (в сумматоре после звена JV3),
т е что обратная связь отрицательная. Эта перемена знака происхо-
дит и с сигналом в прямой цепи и учтена в числителе (4.6) в виде
минуса.
ПФ по любому из каналов xk-yi записывается по правилу (4.5)
независимо от остальных каналов - в предположении, что остальные
входные воздействия равны нулю.
Если исходная алгоритмическая схема многоконтурная и со-
держит перекрестные связи, как, например, на рис. 4 3,я,
то для ее свертывания к одноконтурной приходится применять, кро-
214
ме трех главных правил (4.1), (4.2), (4.3), вспомогательные
правила структурных преобразований, приведенных в табл. 4 1.
а
Рис. 4.3. Пример структурных преобразований алгоритмической схемы
Действительно, ни для одного из трех типовых соединений по
три элемента (^-^2-^4, W2-W3-W5, ^-И^-Иб), образующих схему на
рис 4.3,я, нельзя сразу применить главные правила, так как начало
или конец одного эквивалентного соединения оказались бы при этом
внутри другого соединения. Поэтому приходится эти перекрещи-
вающиеся контуры предварительно "развязывать" - устранять пере-
крестность. Она всегда может быть устранена несколькими различ-
ными путями. Так, пользуясь вспомогательным правилом 3 из табл.
4.1, можно перенести узел разветвления со входа на выход звена W3,
добавив одновременно перед звеном обратную функцию W3~}. С
помощью правила 5 можно сумматор перенести на выход звена W2
включив последовательно с Ж5 звено W2, а затем по правилу 2
поменять местами сумматоры А и В. В итоге получится схема без
перекрестных связей (рис. 4.3,6), которую легко свернуть по главным
правилам.
215
Таблица 4.1
Вспомогательные правила структурных преобразований
	Операция	Исходная схема					Преобразованная схема					
1	Перестановка узлов разветвления	Axt=x х |	х					X	’ t X					
		х2=х|					|х2=х					
2	Перестановка сумматоров	х2 1 *зТ					X, I > П Х1+Чп х X| Sr	у 1хз					
3	Перенос узла разветвления через звено вперед	X		W 		у	А	- w		У г		
		I/								w' ‘ lx		
4	Перенос узла разветвления через звено назад		• W				V		w 		У	
					J i;		W					
5	Перенос сумматора через звено вперед									|X2		
		1*2			w					W		
							х1^	w -		у		
6	Перенос сумматора через звено назад	xt>	W		Г*2 дГ у		w' xii			W		
216
Для двух внутренних соединений схемы (см рис 4 3,6) эквива-
лентные ПФ
=	(4 7)
^3.2,5 (р) = w2 00/(1 - WWWi)	(4 8)
Теперь схему можно рассматривать как одноконтурную с ПФ
разомкнутого контура
W„(p) = ^.Лр^СрШр)/^,(Р) 	(4 9)
ПФ замкнутой СУ (см.рис. 4 3,6) по каналу х-у согласно прави-
лу (4 5)
v(n) №12Ар)№щ(р)
Фст(р) = —=	(4.10)
" х(р) \ + WvSp)
или с учетом выражений (4.7), (4.8), (4.9)
Ф , ) =_________Wx{p)W2(p)W^p)-W^p)W^p)__________
у 1+^(р)^(р)^(р)-^(р)^(р)^(р)-^4(р)^6(р) 
(4.П)
Для многоконтурных схем, более сложных, чем рассмотренная,
процедуры предварительных переносов и последовательного свер-
тывания оказываются достаточно трудоемкими. Поэтому для таких
схем целесообразно использовать формулу Мейсона
1 т
ФЛр'> =—2^ы(р)^.(р'>,
(4 12)
где №цф)(р) ~ ПФ /-го прямого канала, связывающего вход Хк с выхо-
дом у}; т - число таких каналов, Д(р) - специальный полином, кото-
рый определенным образом характеризует совокупность всех замк-
нутых цепей системы, содержащих обратные связи, и вычисляется
217
как сумма из передаточных функций разомкнутых контуров этих це-
пей и из произведений передаточных функций разомкнутых конту-
ров пар и троек не соприкасающихся друг с другом цепей с обрат-
ными связями:
Д(Р) = 1 -	+2X(/Wp) ~Х^(р)^(рК(р) + ... . (4.13)
i	ij	i,JJ
Полином Д;(р) составляется по правилу, аналогичному (4.13), но
только для цепей с обратными связями, не соприкасающихся с z-м
прямым каналом. Знаки всех сигналов прямых каналов и обратных
связей учитываются в формулах (4.12) и (4.13) перед соответствую-
щими ПФ.
Формула Мейсона особенно удобна для применения, когда
структура системы представлена в виде сигнального графа.
Рис. 4.4. Сигнальный граф системы (а) и
бразующие его прямые каналы (б) и замкнутые контуры (в)
Проиллюстрируем использование формулы на примере систе-
мы, алгоритмическая схема которой приведена на рис. 4.3,я. Соот-
ветствующий ей сигнальный граф показан на рис. 4.4,а, причем зна-
ки сигналов перед сумматорами С и В учтены на графе вместе с ПФ
W6 и Ид. Для наглядности на рис. 4.4,6 и в отдельно изображены гра-
фы двух прямых каналов и трех замкнутых цепей. Поэтому можно,
218
пользуясь формулой Мейсона, получить сразу в окончательном виде
ПФ по каналу х-у, которая полностью совпадает с ПФ (4.11), полу-
ченной с помощью предварительных переносов и последовательным
свертыванием. Так как все контуры в данном примере соприкасаются
(имеют общие ветви или вершины), то парные произведения и триа-
ды в формуле отсутствуют. Нет также в сигнальном графе (рис. 4.4,а)
контуров, не соприкасающихся с прямыми каналами, поэтому
Ai(p)=l и Д2(р)=1.
После определения ПФ между всеми т входами хк и одним из
выходов yi можно на основании принципа суперпозиции записать
уравнение динамики замкнутой системы для рассматриваемого вы-
хода^:
т
у№ =	(414)
Л=1
Так как у одноконтурной СУ знаменатели всех ПФ Ф^(р) одина-
ковы, то уравнение (4.14) для нее можно записать в таком виде:
л (И1+^(р)]=
(4 15)
где FFpK(p) - ПФ разомкнутого контура.
Выражение в квадратных скобках в левой части уравнения
(4.15) представляет собой не что иное, как собственный оператор
системы. Если приравнять его к нулю, то получим характеристиче-
ское уравнение одноконтурной системы в обобщенном виде
I	l + ^(p) = 0.	(4.16)
Выражению (4.16) соответствует следующее правило:
характеристическое уравнение замкнутой одноконтурной сис-
темы представляет собой приравненную нулю сумму единицы и
ПФ разомкнутого контура.
Если ПФ разомкнутого контура предварительно записана в виде
отношения полиномов К(р) и D(p), то характеристическое уравнение
одноконтурной системы будет иметь вид
219
D(p) + K(p) = O.
(4.17)
Для многоконтурных систем характеристическое уравнение по-
лучается приравниванием нулю полинома (4 13) Например, для сис-
темы на рис. 4.13,4? характеристическое уравнение
А(Р) = 1 +	(p)W2 (p)W6 (р) - W2(p)W3 (p)W5 (р) - W4 (p)W6 (p) = 0.
(4 18)
В разделе 4.2 на примерах одноконтурных СУ проиллюстриро-
ваны изложенные приемы определения ПФ и уравнения динамики
замкнутой СУ.
4.2.	Примеры составления передаточных функций
и уравнений динамики СУ
Система управления частотой вращения двигателя. Автома-
тическая система, упрощенная принципиальная схема которой при-
ведена на рис. 4.5,я, широко применяется для регулирования частоты
вращения различных машин и механизмов. Систему используют как
в режиме программного управления, так и в режиме стабилизации
скорости. В качестве исполнительного устройства в системе приме-
нен генератор постоянного тока Г. Возбуждение генератора осуще-
ствляется от тиристорного преобразователя 777. Управляющий сиг-
нал иу, действующий на входе преобразователя, формируется в опе-
рационном усилителе У в зависимости от величины и знака сигнала
рассогласования ир - разности напряжений и3 и мтг. Формирование
сигнала иу может происходить по простейшему, пропорциональному
закону или по более сложному алгоритму (см. 4.3).
Кроме главной обратной связи (по частоте вращения двигателя),
в системах такого рода применяют обычно обратные связи по на-
пряжению или току якорной цепи (см. пунктирную линию на рис.
4 5,а). Ниже будет рассматриваться только главная обратная связь.
Алгоритмическая схема СУ частотой вращения двигателя пока-
зана на рис. 4.5,6. На этой схеме двигатель представлен в виде двух
звеньев. Жд и Wa't выходные величины которых суммируются.
220
a
Рис. 4.5. Система управления частотой вращения двигателя:
а - принципиальная схема, б - алгоритмическая схема
ПФ двигателя по управляющему воздействию - ЭДС генератора
(см. 3.4)
= "(р)/<Цр) =	+ Гир +1),
(4.19)
по возмущающему воздействию - моменту нагрузки
< (р) = п(р)/Мс (р) = -к,(Т,р + 1)/(гиТ,р’ + тир +1).	(4.20)
ПФ генератора (см.3.3)
(р) = <?, (р)К (р) = кг/(Тгр +1).	(4.21)
221
Тиристорный преобразователь по сравнению с двигателем и ге-
нератором может рассматриваться как практически безынерционное
звено:
^тп(Р) = «в(Р)Лу(/?)«^Тп-
(4.22)
Будем считать, что операционный усилитель выполняет про-
стейший алгоритм - пропорциональное усиление:
^y(P) = Wy(P)/Wp(/>)=^y.
(4.23)
Тахогенератор является безынерционным звеном'
^г(Р) = “тг(Р)/"(/?)=^тг-
(424)
Согласно правилу (4.5) ПФ замкнутой СУ по задающему воз-
действию
»(р)
’ “Ар) i + ^(p)
а по возмущающему воздействию
ФВ(Р)
п(р) = ^д (Р)
мс(р)~1 + &рЛр)’
(4.26)
где fFpK(p) - ПФ разомкнутого контура
= ^(Р^М^Ар^АрШр).	(4.27)
После подстановки в выражения (4.25), (4.26) и (4.27) ПФ от-
дельных элементов получим
Ф ( и) = МлЛА.
(4.28)
222
ФАр) =
\(T,P+f)(Trp+f)	.
^p + i^p1 +Tup + l}+k’
(4.29)
^(р) = к/(т,р + 1XW + ТнР +1),	(4.30)
где k=kykTnkvkJ5kxr - ПК разомкнутого контура.
ПФ (4.28) - (4.30) можно записать в форме (2.103) - в виде от-
ношения двух полиномов.
Согласно принципу суперпозиции уравнение динамики в опера-
торной форме
»(р) = и3(р)Ф3(р) +МС(Р)ФЪ(Р)	(431)
или в развернутом виде
kp+ikry + тиР+1)+t]»(p>=
= кукткткдиАр) - к^Т,р + 1ХГгр +	(р).	(4.32)
Характеристическое уравнение системы
(?;p+iXv,p2+^p+i)+t=o.
(4.33)
Подставляя в уравнение динамики (4.32) значение р=0, получим
уравнение статики
(434)
Система стабилизации подачи сыпучего материала. Соста-
вим ПФ и уравнение системы стабилизации подачи сыпучего мате-
риала, описанной в 1.4 и 2 1. При этом воспользуемся приведенными
в главе 3 ПФ конструктивных элементов системы.
223
На рис. 4.6 приведена алгоритмическая схема, составленная со-
гласно принципиальной (см.рис. 1.12) и функциональной (см рис
2 1) схемам системы.
Рис. 4.6 Алгоритмическая схема системы
стабилизации подачи сыпучего материала
Питатель по каналу "частота вращения - расход материала"
представляет собой статическое инерционное звено с ПФ

(4.35)
где кп - ПК питателя, (кг/с) / (об/с); Тп - постоянная времени питате-
ля, с
Весоизмеритель (3.131) будем описывать приближенно - инер-
ционным звеном первого порядка с 7’в-0,5т:
’К(р)=е„(р)/е(^=1/(7’.р+1).
(4 36)
Двигатель постоянного тока, вращающий шнековый питатель, в
рассматриваемой инерционной системе достаточно учитывать как
звено первого порядка:
w,(p) = n„(p)/u.(p) ~ kJ^',p+1),
(4 37)
где kR - ПК двигателя, (об/с)/В; 7Д~7’М - электромеханическая посто-
янная времени, с
224
Электромагнитная постоянная времени двигателя Тэ значитель-
но меньше постоянных времени Тп и Тъ Поэтому в данной системе
величину Тэ можно не учитывать.
Магнитный усилитель по этим же причинам можно считать бе-
зынерционным звеном

(4 38)
Электронный усилитель, редуктор и магнитоупругий датчик в
данной системе являются практически безынерционными звеньями
(4 38) с ПК кзу, к? и к^ (В/Н)
Кроме указанных конструктивных элементов в алгоритмичес-
кую схему системы входят еще два условных звена с эквивалентной
ПФ
W3{p) = *g, (Н/(кг/с)),	(4 39)
где т - время нахождения элементарной порции материала на ленте
весоизмерителя, с; g « 9,8 - ускорение силы тяжести, м/с“
Эти два условных звена включены в схему для перехода от
среднего массового расхода (?ср к количеству тп материала,
находящегося на ленте, и от количества тп к силе тяжести F, которая
непосредственно действует на магнитоупругий датчик. Если ПК дат-
чика задан сразу с размерностью В/(кг/с), то звено (4 39) в алгорит-
мической схеме отсутствует.
Возможные при работе системы изменения удельного веса и
сыпучих свойств материала учтены на алгоритмической схеме (см
рис 4.6) в виде эквивалентных изменений расхода материала АОВ
Характеристики эквивалентного возмущения АОВ определяют обыч-
но экспериментальным путем - измерением расхода Q при разомк-
нутом контуре системы, т е при постоянной частоте вращения шне-
ка. Таким способом можно определить, например, максимальное
значение отклонений расхода Q (от некоторого среднего значения),
возникающих из-за изменений сыпучих свойств материала
Согласно правилу (4 5) ПФ системы по задающему воздействию
225
®,<p') = Q(p'>/uAp) =
______^(р)^(р)ГЛрЩ(рШр)_______
1+^,,(р)^(р)^д(р)^г(рШр)^р)^,(р)^(р)'
(4.40)
После подстановки ПФ отдельных звеньев функция (4.40) при-
мет вид
Ф3(/>) =
МмЛя^п^в/’ + О
(гпР + 1ХгвР+1Хгдр+1)+г
(4.41)
где k^k^k^k^kpknTgk^ - ПК разомкнутого контура.
ПФ системы по возмущающему воздействию АОВ
ф.(р)=2(р)/дс.(р)
(4.42)
или в развернутом виде
(Л./’ + 1Х7’.Р + 0(7> + 1)
(7’„р+1ХЛр + 1Хт'аР + 1)+*'
(4.43)
У равнение динамики системы в операторной форме
Q{p) = и3(р)Ф3(р) ± Дй(^)Фв(Р)-	(4-44)
Уравнение статики системы
к к к к к
эумудрп
±да—
1 + £
(4.45)
1
4.3.	Передаточные функции типовой одноконтурной СУ
Под типовой одноконтурной системой управления (регулирова-
ния) будем понимать систему, которая была описана в 1.2. Ее функ-
циональной схеме (см.рис. 1.7,а) соответствует обобщенная алго-
226
ритмическая схема на рис. 4.7,я. Объект управления характеризуется
одной выходной переменной х, которую требуется стабилизировать
на заданном уровне х3. На стабилизируемую переменную х через со-
ответствующие ПФ влияют возмущения z$ и Zz, действующие непо-
средственно на выход объекта и на его вход (через регулирующий
орган РО). Отклонения хв и ув, вызываемые этими возмущениями,
компенсируются в системе целенаправленными изменениями
Рис. 4.7. Алгоритмические схемы типовой одноконтурной СУ
На входе регулятора с ПФ Wp' действует сигнал рассогласования
ие. Этот сигнал формируется в результате сравнения (алгебраическо-
го суммирования) сигналов и3 и их, пропорциональных соответствен-
но задающему воздействию х3 и управляемой величине х. Сигнал их
вырабатывается датчиком WR, а сигнал и3 формируется в задающем
элементе W3.
Для анализа и расчета типовой системы (см.рис. 4.7,я) удобно
пользоваться преобразованной алгоритмической схемой на рис. 4.7,6.
В этой схеме датчик отнесен к регулятору, и условно принято, что во
входном сумматоре сравниваются непосредственно физические ве-
личины х3 и х. Сигнал ошибки 8 имеет, следовательно, ту же размер-
227
ность, что и величины х, и х, и поэтому по значению е можно прямо
судить о точности системы. Помеха z\ при этом также оказывается
выраженной в единицах измерения х-в виде эквивалентного
сигнала хп.
Обратная связь в схеме, приведенной на рис. 4.7,6, называется
единичной.
При переходе от исходной схемы (см.рис. 4 Т,а) к эквивалент-
ной с единичной обратной связью (см.рис. 4.7,6) использовано пра-
вило 6 из табл. 4.1 (о переносе сумматора назад) и учтено, что за-
дающий элемент и датчик - обычно безынерционные звенья с пере-
даточными коэффициентами к3 и кД, причем всегда к3 =1]кл.
Очевидно, что при этом задатчик оказывается присоединенным к
регулятору с передаточной функцией
W = W/>).	(4 46)
Регулирующий орган с ПФ отнесен на преобразованной
схеме к объекту:
^о(Р) = ^ро(Р)^(Р).	(4.47)
Возмущениям и гз соответствуют эквивалентные внешние
воздействия у& и хв на вход и выход объекта, выраженные в единицах
измерения управляющего воздействия у и управляемой величины х
Запишем передаточные функции и уравне-
ния динамики типовой одноконтурной сис-
темы, схема которой изображена на рис. 4.7,6.
ПФ системы по задающему воздействию имеет вид
ф х^ = х^ = wpo(pWp)
”	*,(/>) хп(р) 1 + ^р(Ж0(р)’
(4.48)
а по возмущающему воздействию
228
(4 49)
х(р) = WAP>
у Ар) ^wv(P)wo(p)
Согласно принципу суперпозиции общее изменение выходной
величины х, возникающее при совместном действии входов х3 и ув,
равно сумме изменений, создаваемых каждым воздействием в от-
дельности Отсюда уравнение динамики системы в краткой записи
х(р) = х3(р)Фч,(р) + ув(^)ФЛ(р)	(4 50)
или в развернутом виде
х(р) = хАр)
wapWAp)
i+wapWAp)
+ у (р)--------.
y^A+WAp)wo{p)
(4 51)
Часто при расчете систем передаточные функции и уравнение
динамики записывают не для управляемой величины х, а для сигнала
ошибки е. Сигнал ошибки
е = хз-х	(4 52)
также может рассматриваться как сумма двух составляющих.
s =	+ £в >
(4 53)
где е3 - составляющая сигнала ошибки, обусловленная изменениями
задающего воздействия; ев - составляющая сигнала ошибки, обу-
словленная изменениями возмущающего воздействия у&
Для каждой составляющей сигнала ошибки можно
записать ПФ, связывающие эти составляющие с соответст-
вующими внешними воздействиями. ПФ системы (см рис 4 7,6) по
задающему воздействию согласно правилу (4 5)
\	8з(Р)	1
ф (п) = —-----=-----------------
Х3(р)	1 + ^р (рШрУ
(4 54)
229
а ПФ no возмущающему воздействию
ф (р)=Ж JQ?) .
уЛр) ^^(pW0(p)
(4.55)
Уравнение динамики системы, записанное для сигнала ошибки,
будет иметь вид
е(р) = £3 (р) + ев (р) = х3 (р)Фа (р) + ув (р)Фев (р)	(4.56)
или
1	-W (р)
£(р) = х3 (р)------------+ v (р)------.	(4.57)
Д^1 + ^р(Ж0(р)	l^^(p)W0(p)
Если в системе (см.рис. 4.7,я) заданы характеристики возмуще-
ния z3 (вместо ув), то в числители ПФ (4.49) и (4.55), входящих в
уравнения (4.51) и (4.57), следует подставлять функцию Жов (вместо
>о).
Обратим внимание на две характерные связи между ПФ для
управляемой величины и для сигнала ошибки. Во-первых, сравнивая
выражения (4.48) и (4.54), можно установить, что
Фез(р) = 1-Ф„(РХ	(4.58)
и, во-вторых, легко заметить, что
Ф£В(Р) = ~ФВ(Р).
(4.59)
Аналогично можно записать ПФ и для других входных воздей-
ствий (например, по каналам хп-х, хп-£, хв-х, хв-е). При их учете в
уравнениях динамики замкнутой системы (4.56) и (4.60) появятся
дополнительные слагаемые, соответствующие воздействиям хп и хв
Таким образом, в общем случае сигнал ошибки в системе на
рис.4.7,б может складываться из четырех составляющих:
230

(4 60)
где e3 - составляющая, обусловленная неточным воспроизведением
системой задания х3 на выходе объекта; ев, еп, ех - составляющие,
обусловленные неполной компенсацией регулятором влияния воз-
мущений у*, хп и помехи хв на управляемую величину х Причем, ка-
ждая составляющая в (4.60) пропорциональна величине воздействия,
создавшего ее.
Рассмотрим теперь типовые алгоритмы управ-
ления (законы регулирования), применяемые в ли-
нейных СУ.
Простейший закон регулирования реализуется при помощи бе-
зынерционного звена с ПФ
^р(Р) = ХР)/е(р) = ^п = *₽•	(4.61)
Согласно выражению (4.61) управляющее воздействие и в ста-
тике, и в динамике пропорционально сигналу ошибки е. Поэтому та-
кой закон регулирования называется пропорциональным (П).
Достоинства П-регулятора - простота и быстродействие, недос-
татки - ограниченная точность (особенно при управлении объектами
с большой инерционностью и запаздыванием)
Закон регулирования, которому соответствует ПФ
Wf(p> = kJp = kflTnp,	(4 62)
называется интегральным (И). При интегральном законе регулиро-
вания управляющее воздействие у в каждый момент времени про-
порционально интегралу от сигнала ошибки е. Поэтому И-регулятор
реагирует главным образом на длительные отклонения управляемой
величины от заданного значения. Кратковременные отклонения
сглаживаются таким регулятором.
Достоинства интегрального закона - лучшая (по сравнению с
пропорциональным законом) точность в установившихся режимах
(см. 4.4). Недостатками интегрального закона регулирования являют-
231
ся худшие свойства в переходных режимах: меньшее быстродейст-
вие и большая колебательность.
Наибольшее распространение в промышленной автоматике по-
лучил пропорционально-интегральный (ПИ) закон регулирования
= +kjp = k„ + k,/T„p = kp(T„p + l)/T„p.	(4.63)
Благодаря наличию интегральной составляющей ПИ-закон ре-
гулирования обеспечивает высокую точность в установившихся ре-
жимах, а при определенном соотношении коэффициентов кп и кИ за-
кон обеспечивает хорошие показатели и в переходных режимах.
Наилучшее быстродействие достигается при пропорционально-
дифференциальном (ПД) законе регулирования
W4 +кДР = кр(ТДР + 1)-
(4.64)
ПД-регулятор реагирует не только на величину сигнала ошибки,
но и на скорость его изменения. Благодаря этому при управлении
достигается эффект упреждения. Недостатком пропорционально-
дифференциального закона регулирования является ограниченная
точность.
Наиболее гибким законом регулирования (в классе линейных
законов) является пропорционально-интегрально-дифференциальный
(ПИД) закон
к	Lp + 1 + TLp2
^P(p) = *n +~^ + кДр = кр^ и^-,	(4.65)
Р	ТпР
или
(4.66)
который сочетает в себе преимущества более простых законов
(4.61)-(4 64).
232
Коэффициенты и постоянные времени, входящие в ПФ типовых
регуляторов, называются настроечными параметрами и имеют сле-
дующие наименования: кп, ки, кд - коэффициенты пропорциональной,
интегральной и дифференциальной частей; кр, кр - передаточные
коэффициенты регулятора; ТИ,ТИ’ - постоянные времени дифферен-
цирования.
Параметры, входящие в различные записи (4.65) и (4.66) ПИД-
закона, связаны между собой соотношениями
к«=к,=кг[т.р+т.р}1т.; к,=к,!т.=кг/т.- к^к,г,=к,'1\, 
(467)
из которых следует, что кр^кр, ТН^Т^ Тд= Тд.
4.4.	Точность статических и астатических СУ
при типовых воздействиях
Общие понятия о точности управления. Назначение любой
СУ - изменение выходной величины x(t) в соответствии с измене-
ниями задающего воздействия x3(t). В большинстве случаев эта
задача СУ заключается в поддержании равенства
х(Г)-х3(Г)
(4.68)
при любых изменениях задающего и возмущающих воздействий.
При анализе точности различают две функции системы: воспро-
изведение задающего воздействия и подавление (компенсация) воз-
мущений.
Из-за инерционности объекта и регулятора обе эти функции вы-
полняются любой реальной системой с погрешностью в каждый мо-
мент времени после внешнего воздействия существует разность
е(0 = х3 (f) — х(/),
(4.69)
характеризующая точность системы. Чем меньше мгновенные значе-
ния сигнала ошибки e(f), тем больше (лучше) точность системы
233
Как было показано в 4.3, сигнал ошибки е(/) в типовой СУ
(см.рис. 4.7,6) содержит составляющую е3(Г), которая характеризует
точность выполнения системой функции воспроизведения задающе-
го воздействия, и несколько составляющих, которые в сумме харак-
теризуют точность выполнения функции подавления возмущений.
Из формул (4.54)-(4.57) следует одно из важнейших правил тео-
рии управления:
в типовой одноконтурной системе, состоящей из объекта
Wo(p) и регулятора W?(p), полная ошибка регулирования s(t) и ее
составляющие и в статике, и в динамике обратно-
пропорциональны выражению (l + Wp(p)W0(p)), т.е. точность
регулирования тем лучше, чем больше усилительные свойства
регулятора.
Вычисление мгновенных значений сигнала ошибки и его со-
ставляющих при произвольном законе изменения внешних воздейст-
вий представляет собой сложную задачу. Поэтому точность систем
принято оценивать по значениям е3 и ев в статическом режиме рабо-
ты системы. Соответственно различают статическую точность и ди-
намическую точность.
Статическая точность. Ниже показано, что в статическом ре-
жиме ошибки возникают только в статической системе и что в аста-
тической системе они равны нулю Поэтому статическую точность
оценивают только при анализе статических систем.
Статической системой управления называется система, объект
и регулятор которой являются статическими элементами, т е.
Wo(0) = ko и FFp(O) = fcp.	(4.70)
Подставляя в уравнения динамики (4.51) и (4.57) одноконтурной
системы (см.рис. 4.7,£) р=0 и учитывая выражения (4.70), получим
уравнения статики статической системы:
для управляемой величины
х —г + у  —
1+Ып	1 + *Л
р о	р о
(4.71)
234
и для сигнала ошибки
(4.72)
Если вместо возмущения ув задано z3 (см. рис 4 7,а), то в числи-
тели вторых слагаемых в (4.71) и (4.72) следует подставлять ПК ков,
характеризующий канал z3-x.
Первое слагаемое в правой части уравнения (4.72) характеризует
так называемую статическую ошибку по задающему воздействию, а
второе - статическую ошибку по возмущению. Обе эти ошибки тем
больше, чем больше внешние воздействия, и тем меньше, чем боль-
ше знаменатель (1+&р&0). Следовательно,
точность статической системы тем лучше, чем больше ПК
разомкнутого контура.
Точность статической системы принято оценивать коэффици-
ентом статизма
5 = Дх3/Дхр,
(4 73)
где Дхр - отклонение управляемой величины х от заданного значения,
создаваемое возмущением ув=у’во при разомкнутом контуре регули-
рования; Дх3 - отклонение управляемой величины, создаваемое тем
же возмущением уво в замкнутой системе. Коэффициент статизма
показывает, во сколько раз отклонение выходной величины управ-
ляемого объекта меньше отклонения этой величины у неуправляемо-
го объекта (при одном и том же значении возмущающего воздейст-
вия).
Очевидно, что
ч = ДуА	(4 74)
И
Ч=АЛЛ/0 + Мо)	(4 75)
Отсюда коэффициент статизма
235
5 = l/(l + V») = l/(M,
(4.76)
где k-k^k^ - ПК разомкнутого контура.
Точность статической системы считается удовлетворительной;
если коэффициент j находится в пределах 0,1 ... 0,01. Следователь-
но, общий ПК разомкнутого контура статической системы должен
находиться в диапазоне 10 ... 100.
Приведем примеры расчета статической точности конкретных
систем.
Пример 1. Оценим статическую точность системы стабилизации час-
тоты вращения двигателя (см. в 4.2 рис. 4.5), если известно, что А\=4; 4^=2;
А'г=4.5; Ад=0,1; ^=2,5; £л'=0,01.
Пусть требуется при расчетном моменте нагрузки Л/с(!=ККЮ Н м под-
держивать неизменной частоту ло=1О об/с.
Предполагаем, что все элементы системы линейны. По уравнению
(4.34), описывающему статику системы, можно рассчитать необходимое
значение задающего воздействия и3. Оно равно w30«30 В.
Если в процессе работы момент нагрузки будет изменяться от 900 до
1100 Нм, т.е. М/с=200 Н м, то в системе будут возникать статические
ошибки, максимальное значение которых
Д//3 = ев = ДА/сАгд70 + к) = 200 • 0,01/(1 +9) = 0,2об/с,	(4.77)
где k~kykulkv кл к^=9 - ПК разомкнутого контура.
В неуправляемом двигателе (т.е. при разомкнутом контуре системы)
такие же изменения момента создавали бы отклонения частоты вращения,
равные
Длр =ШсАд' =200-0,01 = 2 об/с.	(4.78)
Следовательно, коэффициент статизма системы
S =	= 0,2/2 = 0,1	(4.79)
Это значение коэффициента s получается и при вычислении его непо-
средственно по формуле (4.76).
Пример 2. Определим необходимое по условию статической точности
значение ПК электронного усилителя в системе стабилизации расхода ма-
236
териала (см. в 4.2 рис.4.6). Пусть ПК элементов системы равны, питателя
Ап=40 (кг/с)/(об/с), редуктора А'р=0,1. двигателя А’д=0,2 (об/с)/В. магнитного
усилителя кыу=5‘, датчика Агмд=0.5 В/(кг/с).
Предположим, что из-за изменения свойств материала его расход при
и=const отклоняется от некоторого среднего значения на величину
А<2В=5 кг/с, а допустимое отклонение расхода ДО;1=0.5 кг/с. Тогда необхо-
димое значение коэффициента статизма
5 = ДСд/Д0в= 0,5/5 = 0,1	(4 80)
Соответствующее этой точности значение общего ПК системы
к = (1/5)-1 = (1/0.1)-1 = 9,	(4.81)
отсюда необходимое значение ПК электронного усилителя
кзу =к/кпкгкак^к^ = 9/40-0,1-0,2-5-0,5 =4,5	(4 82)
Динамическая точность. Динамическую точность систем оце-
нивают по величине сигнала ошибки в установившемся динамиче-
ском режиме. Установившийся динамический режим наступает, как
известно, после окончания переходного процесса. В этом режиме
управляемая величина и сигнал ошибки имеют только вынужденную
составляющую.
В зависимости от свойств системы и от точки приложения
внешнего воздействия вынужденная составляющая сигнала ошибки
либо равна постоянной величине, либо неограниченно возрастает.
Постоянную вынужденную составляющую можно определить при
помощи теоремы о конечном значении оригинала. Возрастающую
вынужденную составляющую находят при помощи метода коэффи-
циентов ошибок.
Рассмотрим вначале методику определения по-
стоянных составляющих сигнала ошибки. Оп-
ределим установившееся значение сигнала ошибки типовой одно-
контурной СУ (рис. 4.7,6) при изменении внешних воздействий x3(f)
или ув(/) по закону ступенчатой функции
237
хз(О = «о°(О
(4.83)
и по закону степенной функции
x.(t)=aqtqc(t), (g = 1;2;3;...).
Пусть ПФ регулятора имеет вид
а объекта
(4.84)
(4.85)
(4.86)
где множители W$(p) и W*(p) прир—>0 стремятся к единице.
Показатели vp и v0 характеризуют порядок астатизма регулятора
и объекта.
Согласно выражениям (4.85) и (4.86) ПФ разомкнутого контура
будет иметь вид
1Г(р) = kW(p)lp-,
(4.87)
где к=к^0 - ПК разомкнутого контура; v=vp+v0 - порядок астатизма
контура; ^Т*(/>)=^Кр*(р)И/0*(р) - множитель, который при /?—>0 стре-
мится к единице.
Типовая СУ называется астатической v-го порядка, если ее ре-
гулятор обладает астатизмом v-ro порядка, т.е. содержит v интегри-
рующих звеньев. В промышленной автоматике обычно используются
системы с v=l и 2. Астатическими являются системы с И-, ПИ- и
ПИД-регуляторами.
Подставляя ПФ (4.85) и (4.86) в выражение (4.57), получим изо-
бражение сигнала ошибки типовой системы
е(Р) = х3(р)
pv +kW*(p)
+ У3(Р)
pVtk0W0\p)
р*+kW\p)
(4.88)
238
Из выражения (4.88) следует, что составляющая с, обусловлен-
ная изменением задающего воздействия х3, зависит от общего поряд-
ка астатизма v, а составляющая ев, обусловленная изменением воз-
мущающего воздействия ув, зависит только от порядка астатизма ре-
гулятора.
Установившееся значение сигнала ошибки определим, исполь-
зуя теорему о конечном значении оригинала (см табл 2 2).
lime(r) = lim ре(р).
^—>00	р-*0
(4.89)
Знаменатели обоих слагаемых в выражении (4.88) при р->0
стремятся к значению 1+& (при v=0) или к значению к (при v>0).
Предельное значение числителей зависит от вида функций х3(/) и ув(0
и от показателей астатизма v и vp.
Если подставить вместо х3(р) и ув(р) в формуле (4 88) изображе-
ния ступенчатой функции
х3(р) = уАр)=^/р
или степенной функции
х3(р) = Л(Р) = М!/Pq+' >	=-
(4.90)
(4.91)
то можно найти установившиеся значения сигнала ошибки.
В табл. 4.2 приведены установившиеся значения составляющих
е3 и ев для ряда распространенных случаев (g=0; 1; 2 и v=0; 1; 2).
На основании результатов, приведенных в табл. 4.2, можно
сформулировать следующие общие правила.
I.	Если суммарный порядок астатизма v типовой системы равен
показателю q степенного задающего воздействия, то система в уста-
новившемся режиме имеет ошибку воспроизведения
е3(р) = ^’/£ = const,
(4.92)
которая тем меньше, чем больше ПК разомкнутого контура системы
239
2	Постоянная ошибка подавления ев(оо), возникающая в устано-
вившемся режиме при <?=vp, обратно пропорциональна ПК регулято-
ра.
3.	Если порядок астатизма vp регулятора больше показателя q
воздействия, то установившиеся значения ошибок е3(оо)=0 и ев(оо)=0.
4.	Если порядок астатизма v меньше показателя q, то е3(оо)=оо и
8В(СО)=00
Таблица 4.2
Установившиеся значения ошибки типовой системы (см. рис. 4.7,6)
			  Порядок астатизма	Вид воздействия		
		a0o(0	ai/a(0	£12^(0
	\=0	a J (1+Л)	CO	CO
	V=1	0	a} / к	00
	v=2	0	0	2а2/ к
	vp=0; vo=0	aokQ/(l+k)	CO	CO
	 vp=0; vo=l	ao/kv	00	00
	vp= 1; vo=0	0	01 /kp	00
	vp=l; vo=l	0	(7i / kp	co
	vp=2; vo=0	0	0	2^2 /
На рис. 4.8 показана серия переходных функций, установившие-
ся участки которых иллюстрируют сформулированные правила. На
рис. 4.8,(7 показаны переходные функции статической (v=0) и астати-
ческих (v=l и v=2) систем при ступенчатом изменении задающего
воздействия, а на рис. 4.8,6 - переходные функции тех же систем при
линейно нарастающем задающем воздействии
Рассмотрим теперь более общий метод расчета установившихся
значений сигнала ошибки - метод коэффициентов
о ш и б о к . С помощью этого метода можно определить возрастаю-
щие во времени вынужденные составляющие сигнала ошибки. Ме-
тод применим, если внешние воздействия на систему изменяются
достаточно медленно (по сравнению с инерционностью самой систе-
мы) и благодаря этому могут быть описаны функцией времени,
имеющей конечное число I производных Обычно 7=2; 3.
240
Рис 4.8. Переходные процессы в статической и астатической СУ при
ступенчатом (а) и линейном (б) изменении задающего воздействия
Рассмотрим сущность этого метода применительно к одному
входному воздействию x3(t).
Разложим ПФ системы в ряд по возрастающим степеням
ФЛ/>) = С<, +С.Р + С-У + (?,/ + ... = £с,/,',	(4.93)
1=0
где
члены ряда, называемые коэффициентами ошибок.
241
Тогда изображение ошибки, обусловленной изменением задаю-
щего воздействия, можно представить в следующем виде:
е3(р) = Мр)<Мр) = [Со + С\Р + • •• + ciPl R(P)-	(4.94)
Каждому слагаемому вида С, ргх3(р) во временной области соот-
ветствует составляющая ошибки	dt* . Поэтому сигнал
ошибки можно записать в виде суммы
Е3 (0 — С0Х3 (Z) + С}
dlx3(t)
Г . . . Т С |	
(4.95)
В выражении (4.95) учтены только Z первых членов, так как ос-
тальные производные входного сигнала по условию равны нулю.
С помощью формулы (4.95) можно определить закон изменения
вынужденной составляющей сигнала ошибки, обусловленной как
изменением задающего воздействия, так и изменением возмущающе-
го воздействия. Во втором случае коэффициенты С, находят разло-
жением ПФ Фев(р) В ряд
В обоих случаях коэффициенты ошибок в виде ряда (4.93) нахо-
дят делением числителя ПФ на ее знаменатель (по правилу деления
многочленов). (Результат деления при этом получается непосредст-
венно в виде ряда (6.93)).
Если ПФ системы записана в форме (2.103), то коэффициенты
ошибок можно найти при помощи рекуррентной формулы
(4.96)
Пример 3. Определим установившуюся составляющую сигнала ошиб-
ки типовой системы (см.рис. 4.7,6) при изменении задающего воздействия
по закону
x3(/) = 20z2o(z)	(4.97)
Пусть ПФ разомкнутого контура имеет вид
242
»'(р) = */р2(Лр+0(Г2Р + 1).
(4.98)
где НО; Ti=O,l с; Т2-0,2 с.
В данном случае показатель воздействия q=2 и порядок астатизма сис-
темы v=2. поэтому, согласно табл. 4.2, установившаяся ошибка воспроизве-
дения
Е3(оо) = 2а2Д = 2-20/10 = 4 .
Пример 4. Определим теперь установившуюся составляющую сигнала
ошибки при изменении задающего воздействия по закону
лг3 (г) = (s +1 Of + 20f2)o(0	(4.99)
Пусть ПФ разомкнутого контура имеет вид
f?(p) = k/P(TlP + lXr2j9 +1),	(4 100)
где W0, 7]=0,1 с; 72=0,2 с.
Так как в данном случае порядок воздействия q=2 больше порядка ас-
татизма системы v=l, то вынужденная составляющая сигнала ошибки пред-
ставляет собой неограниченно возрастающую функцию. Для отыскания
этой функции воспользуемся методом коэффициентов ошибок.
ПФ системы для сигнала ошибки
к
ф“(р) = TTtL >=	=	+b2p2 +Ь'рУ(ър3 +а^р2 +aiP+ao)>
1 + ^(р) р^р + Ц^р+Ц + к
(4.101)
где />з=а3=7) 72=0,02 с2; />2=^2=7i+72=0,3 с; />1=а]=1; />о=О; a0=^=10 с’1.
Порядок знаменателя л=3, числителя т=3. По формуле (4.96) можно
определить три первых коэффициента ряда (4.93):
Со = Мао = 0; G = bJao = № =°Дс;
С2 =	- ЬЛ)/а1 = ((Г, + Т2 X - 1)/к2 = 0,02 с.)
(4.102)
Производные задающего воздействия (4.99) равны
<&3(0/Л = 10+40Г, d2x3(t)/dt2 =40, d3x3(t)/dt3 =0	(4.103)
243
Отсюда выражение для вынужденной составляющей сигнала ошибки
, .	_ dxAt\ „ d2x3(t) , „ .
б3(0 = С1-^2 + С2-y-^ = l,8 + 4t	(4.104)
dt dr
Если в воздействии (4.99) последнее слагаемое отсутствует, то
вторая производная воздействия равна нулю, а первая - 10. Вынуж-
денная составляющая сигнала ошибки в этом случае равна постоян-
ной величине s3=Ci 10=1. Это же значение ошибки можно получить,
пользуясь табл. 4.2: при v=l и линейном воздействии с коэффициен-
том «1=10 установившееся значение сигнала ошибки
£3 =а}/к = 10/10 = 1.
Точность при гармонических воздействиях. При изменении
внешнего воздействия (задающего или возмущающего) по гармони-
ческому закону управляемая величина и сигнал ошибки системы
также изменяются по гармоническому закону. Поэтому точность
системы при гармоническом воздействии оценивают отношением
амплитуды сигнала ошибки к амплитуде внешнего воздействия. Чем
меньше это отношение, тем лучше качество системы.
Рассмотрим основные соотношения и закономерности, характе-
ризующие точность выполнения системой функции воспроизведения
полезных и подавления вредных внешних воздействий.
Пусть на типовую систему (см.рис. 4.7,6) влияют задающее воз-
действие x3(t), основное возмущающее воздействие хв, приложенное
к выходу объекта, а также дополнительное возмущение (помеха) хп.
Помеха хп учитывает случайные флуктуации, возникающие в задаю-
щем и измерительном элементах, а также в канале обратной связи.
Помеха хп, приложенная ко входу системы, воспринимается сис-
темой как задающее воздействие и поэтому создает дополнительную
ошибку воспроизведения.
Переходя от ПФ (4.48), (4.49), (4.54) и (4.55) к соответствующим
частотным функциям и их модулям, можно найти отношение ампли-
туд входных и выходных сигналов в режиме установившихся гармо-
нических колебаний:
244
|фи(»
Р	Р	Г
° m _	_ гп
%зт	^вт	^вт
Ф^(Уй»= —= —= —
XXX
зт пт пт
1
1 + ^(70)
W{j^)
1 + W(jeb)
(4.105)
(4.106)
где Ж(/со)= fFp(/(o)IFo(/(o) - АФХ разомкнутого контура, а индекс т
обозначает амплитудные значения входных и выходных сигналов.
При известных частоте и амплитуде внешнего воздействия по
формулам (4.105) и (4.106) можно вычислить амплитуды рассматри-
ваемых выходных сигналов: ошибки ет и управляемой величины хт.
Из выражения (4.105) следует, что
на каждой фиксированной частоте сов амплитуда сигнала
ошибки обратно пропорциональна величине 11+ИХ/сов) |.
Эта закономерность аналогична зависимости статической
ошибки от ПК разомкнутого контура (см. формулу (4.72)).
Из выражения (4.105) следует также, что в разомкнутой системе,
т.е. когда Ж(/(о)=0, амплитуды выходной величины и сигнала ошибки
равны амплитуде внешнего воздействия:
Y = Р — X
т т впп
Г = X
° т 'Л'зт *
(4.107)
Проанализируем в общем виде свойства АЧХ ФеХД0) и
Фхз(Л°) 1> рассматривая их как отношение модулей числителя и зна-
менателя.
Учтем, как изменяется в общем случае АФХ Ж(/(й) разомкнуто-
го контура, входящая в выражения (4.105) и (4.106). Так как в контур
большинства реальных систем входит обычно несколько инерцион-
ных звеньев, то АФХ РК(/со) проходит через (п-т) квадрантов (рис.
4.9). При этом модуль вектора с ростом частоты уменьшается
от к (для статической системы) или от оо (для астатической системы)
до нуля, а угол поворота вектора изменяется соответственно от нуля
или от -я/2 до (n-m)Ti/2, где п - порядок знаменателя, а т - порядок
числителя передаточной функции
245
Анализируя изменения векторов (см.рис. 4.9), нетрудно устано-
вить, что входящий в выражения (4.105) и (4.106) знаменатель
I 1+РГ(7(й) | по мере роста частоты вначале уменьшается до некоторо-
го значения, меньшего единицы, а затем увеличивается и стремится к
Рис. 4.9. АФХ разомкнутого контура СУ:
1 - статической; 2 - астатической
единице. Следовательно,
амплитудные характери-
стики | ФезО’СО) | И
Фхз(Л&) имеют при не-
которой частоте сор мак-
симум - резонансный
пик (рис. 4.10). Резо-
нансная частота сор при-
близительно равна часто-
те со л, при которой вектор
РГ(/сй) повернут на угол
-180 °(см.рис. 4.9).
Наличие у ампли-
тудных характеристик
Фез(/со) | и | ФхзО'со) I резонансного пика свидетельствует о колеба-
тельности системы.
Рис. 4.10. АЧХ типовой СУ:
1 - статической; 2 - астатической
246
Анализируя форму характеристики Фез(/'со) , изображенной на
рис. 4.10,67, можно сделать следующие выводы:
1.	Если частота (йв внешнего воздействия х3 или хв мала
(сов«(йр), то амплитуда сигнала ошибки намного меньше амплитуды
воздействия, т.е. система хорошо выполняет функции воспроизведе-
ния и подавления.
2.	Если частота воздействия х3 или хв велика (сов»сор), то ампли-
туда сигнала ошибки равна амплитуде воздействия, т.е. система бес-
полезна. Объясняется это тем, что при быстрых изменениях внешних
воздействий система из-за инерционности объекта и регулятора не
успевает реагировать на эти воздействия.
3.	Если частота воздействий близка или равна резонансной час-
тоте (wB«wp), то амплитуда сигнала ошибки больше амплитуды воз-
действий, т.е. система управления даже вредна.
График функции Ф^Х/со) , приведенный на рис. 4.10,6, показы-
вает, что низкочастотные помехи, возникающие в задающем или из-
мерительном элементе, создают большую ошибку воспроизведения.
Амплитуда этой ошибки приблизительно равна амплитуде помехи.
Если частота помехи близка к резонансной частоте, то амплитуда
сигнала ошибки даже превышает амплитуду помехи. Наконец, если
частота помехи велика, то амплитуда ошибки мала, так как помеха
гасится при прохождении через совокупность инерционных звеньев с
эквивалентной АФХ Ж(/со).
На основе выявленных закономерностей можно сформулиро-
вать требования к виду амплитудной характеристики разомкнутого
контура.
Учтем, что при малых частотах функция | JVQa) | »1, и поэтому
можно пренебречь единицей в знаменателе выражения (4.105):
ф„ М»1/И» .
(4.108)
При больших частотах функция | PKQco) | «1 и можно полагать
|флз(7“)| «|^(» .
(4.109)
247
Рис 4.11. АЧХ разомкнутого
контура СУ:
1 - статической, 2 - астатической
действия хзт, то характеристика
Приближенные соотно-
шения (4.108) и (4.109) можно
использовать для выбора фор-
мы и конкретного расположе-
ния характеристики | РУ(/со) |
по известной частоте и
амплитуде внешнего воздейст-
вия и по максимально допус-
тимой амплитуде сигнала
ошибки. Например, если на
некоторой низкой частоте (он
максимальная амплитуда сиг-
нала ошибки ет должна быть в
Si раз меньше амплитуды воз-
разомкнутого контура (рис. 4.11)
должна проходить не ниже точки с координатами сйн, 5ь Если, кроме
этого, необходимо, чтобы амплитуда составляющей ошибки, созда-
ваемой высокочастотной помехой хп, была в 62 раз меньше амплиту-
ды помехи, то функция I | должна проходить не выше точки с
координатами <х>в, 1/52.
Рассмотрим теперь влияние закона регулирования на форму
АЧХ системы. На рис. 4.12,67,б,в толстой линией изображены графи-
ки функции I Фез(7Сй) I при пропорциональном законе регулирования
Тонкими линиями показаны эти же характеристики при различных
сочетаниях коэффициентов пропорциональной, интегральной и диф-
ференциальной составляющих закона регулирования (4.65).
Рис. 4.12,67 иллюстрирует влияние пропорциональной состав-
ляющей на точность системы. Увеличение коэффициента кп улучша-
ет точность системы на низких частотах, но повышает колебатель-
ность системы.
Добавление интегральной составляющей к пропорциональной
приводит к уменьшению ошибки на очень низких частотах, но сме-
щает резонансный пик в область низких частот и увеличивает коле-
бательность системы (см.рис. 4.12,6).
Рис 4 12,в показывает, что введение в пропорциональный закон
регулирования дифференциальной составляющей улучшает точность
248
системы на низких частотах, однако смещает резонансный пик в
область высоких частот и увеличивает колебательность системы.
Рис. 4.12. Влияние пропорциональной (а), интегральной (б) и
дифференциальной (в) составляющих на форму АЧХ замкнутой СУ
В заключение обобщим изложенные зависимости сигнала
ошибки от свойств системы в виде следующей фундаментальной за-
кономерности:
точность воспроизведения системой управления задающего
воздействия и точность подавления ею внешних возмущений
тем лучше, чем больше передаточный коэффициент регулято-
ра.
Пример 5. Оценим точность типовой системы стабилизации (рис.
4.7,6) при изменении возмущающего воздействия по гармоническому зако-
ну. ПФ разомкнутого контура
К(Р) = к/Р(ГР + \\
где £=0,05 с'1; Т=20 с.
Пусть на выходе объекта действует возмущение
Лв(0 = лвт sinwB/.
(4.110)
(4.111)
где Хвт=5 - амплитуда колебаний; сов=0,02 с1 - частота колебаний
Очевидно, что при отсутствии регулирования амплитуда колебаний
выходного сигнала будет равна амплитуде колебаний возмущения хв, при-
ложенного непосредственно к выходу объекта, т.е. хт~Хып~5-
Найдем ПФ замкнутой системы по каналу хв-х:
249
фхв (J®) = Ф£3 О) =	=
1 +iv(p)
Тр2 +р
Тр2 + р +к
(4.112)
Согласно формуле (4.105) амплитуда хт колебаний выходного сигнала
около стабилизируемого значения
хт ~ хвт Фез Ов ) ~ хвт
[^2 4.-2
уТ ®в + 7®в
«5-0,4 = 2.
(4.113)
Система стабилизации уменьшает амплитуду колебаний выходного
сигнала приблизительно в 2 раза. Этот же результат можно получить и по
приближенной формуле (4.108).
Контрольные задания и вопросы
1.	Как изображаются отдельное звено W и его сигналы х и у на алго-
ритмической схеме и на сигнальном графе системы?
2.	Запишите выражения для эквивалентных ПФ типовых соединений
из двух элементов.
3.	Что такое разомкнутый контур системы и чему равна его ПФ?
4.	По какому общему правилу вычисляется ПФ замкнутой СУ для
произвольного канала хк-ур
5.	Определите передаточную функцию одноконтурной системы
(см.рис. 4.2) по каналу х$-у\.
6.	Найдите с помощью формулы Мейсона передаточную функцию
многоконтурной системы (см.рис. 4.3,д и рис. 4.4,а) между вершинами А и
В.
7.	Как перейти от известной ПФ замкнутой СУ по одному каналу х-у к
операторному уравнению динамики этого канала?
8.	Как записывается в общем случае характеристическое уравнение
замкнутой системы через ПФ разомкнутого контура?
9.	Составьте характеристическое уравнение системы стабилизации по-
дачи сыпучего материала (см. рис. 4.6 в 4.2).
10.	Нарисуйте обобщенную алгоритмическую схему типовой однокон-
турной СУ, состоящей из объекта Wo регулятора W?.
11.	Какие внешние воздействия обычно рассматриваются при анализе
типовой системы? Чему равен сигнал ошибки в системе с единичной обрат-
ной связью?
250
12.	Запишите ПФ типовой замкнутой СУ (см.рис. 4.7,6) по основным
каналам.
13.	Запишите передаточную функцию ПИ-регулятора.
14	Из каких составляющих складывается сигнал ошибки в типовой
системе? От каких внешних воздействий они зависят?
15.	Как связаны сигнал ошибки и его составляющие с ПФ разомкнуто-
го контура?
16.	Как влияет ПК разомкнутого контура на статическую и динамиче-
скую точность систем?
17.	Укажите характерные признаки ПФ Wp(p) и №о(р) в статической
системе регулирования.
18.	Какая система называется астатической? От наличия каких типо-
вых звеньев в контуре системы зависит ее астатизм?
19.	При каком соотношении между степенным показателем q внешне-
го воздействия и порядком астатизма v установившаяся ошибка равна ну-
лю?
20.	Как зависит установившаяся ошибка от ПК разомкнутого контура
при v=q?
21.	Как при гармоническом внешнем воздействии с частотой ©в
амплитуда сигнала ошибки &т связана со значением FF(/®B)?
22.	Как в типовой системе (см.рис. 4.7,6) влияет частота внешнего воз-
действия х3 (или хв) на точность его воспроизведения (или подавления)?
Объясните закономерность этого влияния, учитывая инерционность объекта
и регулятора.
251
Глава 5. АНАЛИЗ УСТОЙЧИВОСТИ
ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ
5.1.	Понятие, виды и общее условие устойчивости
Одной из важнейших характеристик СУ наряду с точностью яв-
ляется ее устойчивость. Причем если показатели точности определя-
ют степень полезности и эффективности системы, то от устойчивости
зависит работоспособность системы. Система, не обладающая устой-
чивостью, вообще не способна выполнять функции управления и
имеет нулевую или даже отрицательную эффективность (т. е. систе-
ма вредна). Неустойчивая СУ может привести объект в аварийное
состояние. Поэтому проблема устойчивости систем является одной из
центральных в теории управления.
Раскроем вначале физический смысл понятия «устойчивость».
Устойчивость СУ - это свойство системы возвращаться в исходное
состояние равновесия после прекращения воздействия, выведшего ее
из этого состояния. Неустойчивая система не возвращается в исход-
ное состояние, а непрерывно удаляется от него.
Наглядное представление о понятии «устойчивость» дает рис
5.1, на котором показаны три вида равновесия механической систе-
мы. а - устойчивое; б - нейтральное; в - неустойчивое.
С)_
777777777^77777777
Рис. 5.1. Виды равновесия механической системы
Неустойчивость замкнутой СУ возникает, как правило, из-за
неправильного или очень сильного действия главной обратной связи.
Неправильное действие главной обратной связи имеет место, напри-
мер, в тех случаях, когда из-за ошибки, допущенной при монтаже
системы, связь оказывается положительной (вместо отрицательной),
252
которая практически при любых параметрах делает систему неустой-
чивой. Возникающую при этом неустойчивость называют статиче-
ской.
Более сложным и более распространенным видом неустойчиво-
сти является динамическая неустойчивость. Она проявляется в сис-
темах с отрицательной обратной связью, при достаточно большом
значении передаточного коэффициента разомкнутого контура (к > 8)
и при количестве инерционных звеньев, не меньшем трех. Причиной
динамической неустойчивости обычно является значительная инер-
ционность элементов замкнутого контура, из-за которой в режиме
колебаний системы сигнал главной обратной связи сильно отстает от
входного сигнала и оказывается с ним в фазе. А это означает, что
связь, выполненная конструктивно как отрицательная (в статическом
режиме!), в динамике — в режиме гармонических колебаний — про-
является как положительная.
Рассмотрим теперь математическую сущность устойчивости и
неустойчивости. Согласно данному выше физическому определению,
устойчивость зависит только от характера свободного движения сис-
темы. Свободное движение линейной или линеаризованной системы
описывается однородным дифференциальным уравнением
а
п
dnx(t)
сГ \(t)
--------+ЯП-2
Л“1
сГ 2x(t)
4-...+аох(О = О,
(5.1)
где x(t) = xc(t) - свободная составляющая выходной величины сис-
темы.
Вынужденная составляющая выходной величины, зависящая от
вида внешнего воздействия и правой части дифференциального
уравнения (2.63), на устойчивость системы не влияет.
Дадим математическое определение понятия «устойчивость».
Система является устойчивой, если свободная составляющая xc(t)
переходного процесса с течением времени стремится к нулю, т. е.
если
limrc(0 = 0.	(5.2)
/->00
253
Очевидно, что при этом выходная величина системы будет
стремиться к вынужденной составляющей, определяемой внешним
воздействием и правой частью уравнения (2.63). Устойчивость в
смысле условия (5.2) принято называть асимптотической.
Если свободная составляющая неограниченно возрастает, т. е.
если
lim хс (г) = оо,
/—>00
(5.3)
то система неустойчива.
Наконец, если свободная составляющая не стремится ни к нулю,
ни к бесконечности, то система находится на границе устойчивости.
Найдем общее условие, при котором система, описываемая
уравнением (5.1), устойчива. Решение уравнения (5.1) при отсутст-
вии у него одинаковых корней равно сумме
п р t
х (0= Z С е *
С	к
k = 1
(5.4)
где Ск - постоянные, зависящие от начальных условий; рк - корни
характеристического уравнения
а рп +а рп 1 +а рп 2+... + а =0.
п	n-Г	п-2	о
(5.5)
Корни характеристического уравнения могут быть действитель-
ными {рк - Ct*), мнимыми (рк =J$k) и комплексными
Рк = ак ±jfik,
(5.6)
причем комплексные корни всегда попарно сопряжены между собой:
если есть корень с положительной мнимой частью, то обязательно
существует корень с такой же по модулю, но отрицательной мнимой
частью.
254
Переходная составляющая (5.4) при t —> оо стремится к нулю
лишь в том случае, если каждое слагаемое вида
к
стремится к
нулю. Характер этой функции времени зависит от вида корня рк.
Рассмотрим все возможные случаи расположения корней рк на ком-
плексной плоскости (рис. 5.2) и соответствующие им функции х (t),
которые на рис. 5.2 показаны внутри кружочков (как на экране ос-
циллографа)
Рис 5 2 Влияние корней характеристического уравнения СУ
на составляющие ее свободного движения
1 Каждому действительному корню рк = а.к в решении (5.4) со-
ответствует слагаемое вида
а г
х(0 =С^е к .
(5.7)
Если ак < 0 (на рис. 5.1 корень р}), то функция (5.7) при t -+ <ю
стремится к нулю. Если ак > 0 (корень р3), то функция (5.7) неогра-
255
ниченно возрастает. Если = 0 (корень то эта функция остается
постоянной.
2. Каждой паре сопряженных комплексных корней /^ = о* +
и рк+\ = ак- в решении (5.4) соответствуют два слагаемых, кото-
рые могут быть объединены (см. 3.4) в одно слагаемое:
a t
х(0 = 2Се
* sin (В t + ш
к к
(5 8)
Функция (5.8) представляет собой синусоиду с частотой pfe и с
амплитудой, изменяющейся во времени по экспоненте. Если дейст-
вительная часть ак двух комплексных корней (на рис. 5.2 корни р4 и
Ps), то колебательная составляющая (5.8) будет затухать. Если ак > О
(корни р% и рд), то амплитуда колебаний будет неограниченно возрас-
тать. Наконец, если ак = 0 (корни /?ви /27), т. е. если оба сопряженных
корня - мнимые (рк = + j$k, рк+\ = - jpfe), то xk{t) представляет собой
незатухающую синусоиду с частотой pfe.
Если среди корней характеристического уравнения (5.5) имеют-
ся / равных между собой корней pi, то в решении (5.4) вместо I сла-
гаемых вида
появится одна составляющая
(Co+Q+C/+..+См('-1) = е«'.
(5.9)
Учитывая, что функция вида е~ы при любом b убывает быст-
рее, чем возрастают слагаемые вида tг, можно доказать, что и в слу-
чае кратности корней решение (5.4) будет стремиться к нулю лишь
при отрицательности действительной части кратных корней pi.
На основании приведенного анализа можно сформулировать
общее условие устойчивости:
для устойчивости линейной СУ необходимо и достаточно,
чтобы действительные части всех корней характеристическо-
го уравнения системы были отрицательными.
256
Если хотя бы один корень имеет положительную действитель-
ную часть, то система будет неустойчивой
Обратим внимание на то, что устойчивость системы зависит
только от вида корней характеристического уравнения и не зависит
от характера внешних воздействий на систему Устойчивость есть
внутреннее свойство системы, присущее ей вне зависимости от
внешних условий
Используя геометрическое представление корней (5 6) на ком-
плексной плоскости (см.рис 5 2) в виде векторов или точек, можно
дать вторую формулировку общего условия
устойчивости (эквивалентную основной)
для устойчивости линейной системы необходимо и достаточ-
но. чтобы все корни характеристического уравнения находи-
лись в левой полуплоскости
Если хотя бы один корень находится в правой полуплоскости,
система будет неустойчивой.
Мнимая ось jP является границей устойчивости в плоскости
корней Если характеристическое уравнение имеет одну пару чисто
мнимых корней (рк = + 7 Ра- Pk+i = - уР*), а все остальные корни нахо-
дятся в левой полуплоскости, то в системе устанавливаются незату-
хающие гармонические колебания с круговой частотой со - |pt | В
этом случае говорят, что система находится на колебательной грани-
це устойчивости, а частоту колебаний на границе устойчивости на-
зывают критической.
Если уравнение имеет более одной пары мнимых корней, то
система неустойчива
Точка р - 0 на мнимой оси соответствует так называемому ну-
левому корню. Если уравнение имеет один нулевой корень, то систе-
ма находится на апериодической границе устойчивости Если таких
корней два, то система неустойчива
Применяя сформулированное выше условие для оценки устой-
чивости реальных систем, не следует забывать, что линейные урав-
нения типа (5 1), как правило, получаются в результате у прощений и
линеаризации исходных нелинейных уравнений Возникает вопрос, в
какой мере оценка устойчивости по линеаризованному уравнению
257
будет справедлива для реальной системы Не окажут ли существен-
ное влияние на результат анализа отброшенные при линеаризации
члены разложения'? Ответ на этот вопрос был дан русским математи-
ком А М Ляпуновым в 1882 г в докторской диссертации «Общая
задача об устойчивости движения» Он сформулировал и доказал
следующую теорему если характеристическое уравнение линеаризо-
ванной системы имеет хотя бы один нулевой корень или одну пару
мнимых корней, то судить об устойчивости реальной системы по
линеаризованному уравнению нельзя Отброшенные при линеариза-
ции малые члены могут сделать систему устойчивой или неустойчи-
вой, и поэтому устойчивость реальной системы необходимо оцени-
вать по исходному нелинейному уравнению
Таким образом, для суждения об устойчивости линейной систе-
мы достаточно определить лишь знаки действительных частей кор-
ней характеристического уравнения
В математике и теории управления разработан ряд правил, с
помощью которых можно судить о знаках корней, не решая характе-
ристическое уравнение и не находя числовые значения самих корней
Эти правила называются критериями устойчивости
Простейшим критерием устойчивости является условие поло-
жительности коэффициентов характеристического уравнения
Положительность коэффициентов уравнения (5 4) является необхо-
димым (но недостаточным') условием устойчивости системы Это
означает, что если все коэффициенты положительны, то система мо-
жет быть устойчивой, но может быть и неустойчивой Но если хотя
бы один коэффициент уравнения отрицателен или равен нулю, то
система наверняка неустойчива
Критерии устойчивости могут быть алгебраическими и частот-
ными Алгебраические критерии устанавливают необходимые и дос-
таточные условия отрицательности корней в форме ограничений,
накладываемых на определенные комбинации коэффициентов харак-
теристического уравнения Частотные критерии определяют связь
между устойчивостью системы и формой частотных характеристик
системы
При анализе устойчивости систем управления обычно решают
одну или несколько из следующих задач 1) оценивают, устойчива
258 ’
или нет система при заданных параметрах, 2) определяют допусти-
мый по условию устойчивости диапазон изменения некоторых неза-
данных параметров системы, 3) выясняют, может ли система при
заданной структуре быть в принципе устойчивой
Первая задача может быть решена с помощью критериев, изло-
женных в 5 2—5 4, вторая — построением областей устойчивости
(5 5), третья — с использованием условий структурной устойчивости
(5 6)
5.2.	Алгебраические критерии устойчивости
Наибольшее распространение в инженерной практике получили
критерии Гурвица и Рауса Ниже приводятся формулировки и мето-
дика применения этих критериев без доказательства их справедливо-
сти
Критерий Гурвица был сформулирован и доказан в 1895 г не-
мецким математиком А Гурвицем (A Hurwitz) Гурвиц разработал
свой критерий, решая чисто математическую задачу — задачу иссле-
дования устойчивости решений линейного дифференциального
уравнения Однако следует отметить, что обратился он к этой задаче
по просьбе словацкого ученого А Стодолы (A Stodola), занимавше-
гося вопросами регулирования турбин
Применительно к задачам теории управления критерий Гурвица
можно сформулировать так
линейная СУ, описываемая характеристическгсм уравнением
°„р" +	+ а.-гР"-2 + + а» = 0,	(5 10)
устойчива, если положительны все п+1 коэффициентов а, и все
п определителей Д вида
259
ai а3 a5...a2l_j
а0 а2 a4 - a2i-2
О (Ц а3 ..^21-3
i = 1;2;...п.
А. =
(5.Н)
Если хотя бы один из определителей (5.11), называемых опреде-
лителями Гурвица, отрицателен, то система неустойчива.
Матрицы (5.11), по которым вычисляют определители Гурвица
А», составляют следующим образом: на главной диагонали записы-
вают все коэффициенты характеристического уравнения от сц до at (в
порядке возрастания индекса), затем в каждом столбце выше диаго-
нальных коэффициентов записывают коэффициенты с последова-
тельно возрастающими индексами, а ниже - с последовательно убы-
вающими индексами; на место коэффициентов с индексами больше п
или меньше нуля проставляют нули. При этом каждая 7-я матрица
получается квадратной размером 7x7.
Всегда главный определитель А„
А» б/фАи-].
(5.12)
Если главный определитель А» = 0, а все остальные определите-
ли положительны, то система находится на границе устойчивости. С
учетом выражения (5.12) это условие распадается на два
ао= 0 или An.i = 0.
(5.13)
Условию До = 0 соответствует один нулевой корень, т. е. аперио-
дическая граница устойчивости, а условию An.i = 0 - пара мнимых
корней, т е колебательная граница устойчивости
260
Рассмотрим частные случаи критерия Гур-
вица для п = 1; 2; 3; 4. Раскрывая определители, фигурирующие в
общей формулировке критерия, можно получить следующие условия
1	Для уравнения первого порядка (п = 1)
(5.14)
условие устойчивости
ао> 0 и а} > 0.
(5.15)
т е положительность коэффициентов уравнения является в данном
случае необходимым и достаточным условием. Действительно, при
<70> 0 и <71 > 0 единственный корень уравнения будет отрицательным'
Р\ =- (<70/<71) < 0.
2	. Для уравнения второго порядка (п = 2)
«2^+0^ +00 = 0
(5 16)
условие устойчивости
а0 >0, Л] = с?] > 0, а7 > 0.
(5.17)
Таким образом, и для системы второго порядка необходимое ус-
ловие устойчивости (положительность коэффициентов) является од-
новременно и достаточным.
Частота колебаний на границе устойчивости
«кр
(5.18)
Для уравнения третьего порядка (п = 3)
ар3 + ар2 + ар + а0 = 0
(5.19)
<71/7+ <70 = О
условие устойчивости
261
aQ >0; A! = «1 > 0; a2 > 0; a3 > 0;
«1
ao
a3
a->
— <7it?2 “ °0°3 '> 0> Л3 — °0^2 > 0.
(5.20)
Последнее неравенство при aQ > 0 эквивалентно неравенству
Д2 > 0. Следовательно, для системы третьего порядка, кроме положи-
тельности всех коэффициентов, требуется, чтобы Д2 > 0. Учитывая
выражение для Д2, можно сформулировать следующее мнемониче-
ское правило оценки устойчивости систем третьего порядка:
произведение средних коэффициентов уравнения должно быть
больше произведения крайних.
Частота колебаний на границе устойчивости
“кр = Vя! /Я3 = 7Я0 /°2 
4. Для уравнения четвертого порядка (п = 4)
а.р4 + а3р3 + а;>р2+ ар+ а0 = 0,
(5 21)
(5.22)
кроме положительности всех коэффициентов, требуется выполнение
условия
Д3 =а}а2а3 - aoaj - а2а4 > 0 .	(5.23)
Нетрудно доказать, что при положительности всех коэффициен-
тов условие (5.23) обеспечивает выполнение и условия Д2 > 0.
Таким образом,
для устойчивости систем не выше четвертого порядка необхо-
димо и достаточно, чтобы все коэффициенты характеристи-
ческого уравнения и определитель были положительны.
Критерий Гурвица целесообразно применять для анализа устой-
чивости систем не выше пятого порядка. При п > 5 вычисление опре-
делителей становится громоздким.
262
Пример 1. Определим с помощью критерия Гурвица, устойчива ли
система управления частотой вращения двигателя (см 4.2) при следующих
значениях параметров:
Гм = 1 с; Тэ = 0,1 с; Тг= 0,5 с; к = кук^кгкЛ^ = 14.
Характеристическое уравнение системы
(Тгр + 1)(ГМ Т3р2 + Т„р+Х) + к = О.
(5.24)
(5.25)
Приводя это уравнение к форме (5.19), получим значения коэффициен-
тов:
а2 = T„TJr = 1 • 0,1 • 0,5 = 0,05 с3;
= Ц, + TJ\ = 1  0,1 + 1  0.5 = 0.6 с!;
а, =	+ т, “1+O.5-1.5 с.
а0 - 1 + к = 15.
Все коэффициенты характеристического уравнения положительны, т. е.
необходимое условие устойчивости выполняется. Проверим, выполняется ли
достаточное условие: вычислим определитель
Д2 = 0^2	= 0,6 1,5 -0,05-15 - +0,15,
(5.27)
он больше нуля, следовательно, система устойчива.
Решим теперь обратную задачу: определим, какое максимальное зна-
чение общего ПК к допустимо по условию устойчивости.
Максимально допустимое значение коэффициента к найдем из условия
нахождения системы на колебательной границе устойчивости
Максимально допустимое значение коэффициента к найдем из условия
нахождения системы на колебательной границе устойчивости
Д«-1 = Д2 = я1а2 “ а0аЗ г 0
Отсюда
а0 < «1«2/аз =0-6-1,5/0,05 - 18,
(5.28)
(5.29)
263
а максимально допустимое значение общего ПК
к = а0 — 1 < 18— 1 = 17.
(5.30)
Условию нахождения системы на апериодической границе устойчиво-
сти (д0 = 0) соответствует второе предельное значение передаточного коэф-
фициента
к>-\.	(5.31)
Поясним физический смысл этого результата. Знак «минус» соответст-
вует положительной обратной связи в главном контуре системы. Следова-
тельно, рассматриваемая статическая система устойчива и при положитель-
ной обратной связи, но если общий передаточный коэффициент по модулю
меньше единицы
Отметим, что точность системы в режиме положительной обратной
связи совершенно неудовлетворительна.
Критерий Рауса, предложенный в 1877 г. английским матема-
тиком Э Дж. Раусом (E.J. Routh), целесообразно использовать при
анализе устойчивости систем выше четвертого порядка. Для этого из
коэффициентов характеристического уравнения (5.10) составляют
следующую табл 5.1.
Таблица 5.1
Коэффициенты Рауса
Столбец	1	2	3		к	• •
Строка						
1	Гц = ап	Г12 = ап-2	Г13 “ °л-4	• « •	Г] к	• . .
2	^21 —	1	Г22 = йп-3	^23 ~ fln-S	• « •	Г2к	•
3	/* 31	/* 32	Гзз	* « •	ГЗк	‘ • •
/	Г/1	t * • Г/2	ГгЗ	. . .	rtk	. . •
и + 1	дл+1,1	• • • °л+1,2	^л+1,3	• • •	ап+\,к	
В первой строке 0=1) таблицы записаны коэффициенты урав-
нения с четными индексами, во второй 0 = 2) - с нечетными В по-
следующие строки (/ > 3) помещены коэффициенты Рауса, которые
264
получены как комбинации коэффициентов двух вышестоящих строк
по формуле
rtk= rt-2, к+1 - (г-2,1 П-1Л+1/ г-1,1),	(5,32)
где i - номер строки, к - номер столбца.
Сам критерий формулируется так:
линейная СУ устойчива, если положительны все коэффициен-
ты первого столбца таблицы Рауса (включая ап и anJ.
Если не все коэффициенты столбца положительны, то система
неустойчива. При этом число перемен знака среди этих коэффициен-
тов соответствует числу правых корней характеристического уравне-
ния.
Алгоритм вычисления коэффициентов (5.32) легко запрограм-
мировать, и поэтому критерий Рауса используют для анализа систем
высокого порядка (п > 5) с помощью ЭВМ.
Достоинством критериев Гурвица и Рауса является то, что с их
помощью можно оценивать устойчивость как замкнутых, так и ра-
зомкнутых систем. Вывод об устойчивости при применении этих
критериев делается непосредственно о той системе (замкнутой или
разомкнутой), уравнение которой анализируется.
Пример 2. Определим с помощью критерия Рауса, устойчива ли сис-
тема, описываемая характеристическим уравнением
2/+ Зр5 + 4/+ 5р3+ 6р2+ 7р+ 8 = 0.	(5.33)
Коэффициенты Рауса:
Гц = ап = а6= 2; rn = ап.2 = аА = 4; гв= ап.А = а2= 6; ru= ап.6 = а0= 8;
Г21 = «л-1 = «5 = 3; г2? = ап.з = «з = 5; г2з = а„.5 = а} = 7\ г2А = 0;
Гз1 = Г\2 - О'] 1 г21! Г21) = аА- (а6 а3/ я5) = 4 - (2 • 5/3) « 0.67;
Г32 =''1з-(гп Г2з/^21) = «2 - («в «1/«5) = 6 - (2 • 7/2) = -1;
Гзз= Г14- (Гц г2А! Г21) = «0 - «б • 0= 8; гЗА = 0; г35 = 0;
265
'’и = Г22 ~ (г2\ Г32/ Г31) = 5 - 3(-1 )/0,67 » 9,48;
г42 = Г22 - (/*21 Гц/ Г31) = 7 - (3 • 8/0,67) = -28,8; г4з= 0; гАА = 0;
Г51 = Гн-(г31 гА21 г41) = -1 - 0.67(-28,8)/9,48 = 1,25;
Г52 = Гзз - (Г31 Г43/ ^41) = 8; Г53 = 0;
''ei = ^*42 - (^*41 'Зг/ ''si) = -28,8 - 9,48 • 8/1,25 = —89,5; Гб2 = 0;
Г1\ =г52 - (''SI Гбг/ ''бО = 8.
Один из коэффициентов г,] первого столбца отрицателен (гб] = -89,5).
Следовательно, система (5.33) неустойчива. Так как знак коэффициентов
этого столбца меняется дважды (до и после гб1), то уравнение (5.33) имеет
два правых корня.
5.3.	Критерий Михайлова
Критерий Михайлова относится к группе частотных критериев
устойчивости. Он был сформулирован и обоснован в 1936 г. россий-
ским ученым А. В. Михайловым в работе «Гармонический метод в
теории регулирования», которая получила высокую оценку на кон-
курсе работ молодых ученых и послужила началом широкого приме-
нения частотных методов в теории автоматического управления.
Позднее германские специалисты А.Леонард (A.Leonhard) и
Л Кремер (L.Cremer) независимо от Михайлова, сформулировали
аналогичный критерий, и поэтому в западной литературе он получил
название критерия Михайлова-Леонарда-Кремера.
Критерий Михайлова так же, как и критерий Гурвица и Рауса,
основан на анализе характеристического уравнения системы, и по-
этому с его помощью можно судить об устойчивости и замкнутых, и
разомкнутых систем.
Пусть левая часть характеристического уравнения, называемая
характеристическим полиномом, имеет вид
F(p) = anpn + an_xprt~i +...+ а0.	(5.34)
266
Подставим в этот полином вместо переменного р чисто мнимый
корень, который в дальнейшем будем обозначать усо Тогда получим
функцию комплексного переменного
F(Z<b) = <7n(7CD)"+ ^(/со)"1 +...+ а0.
(5.35)
которую можно так же, как амплитудно-фазовую характеристику,
представить в виде суммы действительной и мнимой частей:
F(7(d) = F(0)+72(«).
(5 36)
Действительная часть Р(со) содержит только четные степени пе-
ременного со:
Р(со) =п0 - ао2 + аса4- ...,	(5.37)
а мнимая часть Q(o>) - только нечетные:
<2(со) =аа- аа3 + ...
(5.38)
Каждому фиксированному значению переменного со соответст-
вует комплексное число, которое можно изобразить в виде вектора на
комплексной плоскости. Если теперь изменять параметр со от 0 до оо,
то конец вектора F(/co) опишет некоторую линию (рис. 5.3,я), которая
называется характеристической кривой, или годографом Михайло-
ва. По виду этой кривой можно судить об устойчивости системы.
Формулировка критерия Михайлова та-
кова:
линейная СУ, описываемая уравнением п-го порядка, устойчива,
если при изменении со от 0 до оо характеристический вектор
системы F(jco) повернется против часовой стрелки на угол
пл/2, не обращаясь при этом в нуль.
Это означает, что характеристическая кривая устойчивой систе-
мы должна при изменении со от 0 до оо пройти последовательно через
п квадрантов. Из выражений (5.37) и (5.38) следует, что кривая F(/co)
267
всегда начинается в точке на действительной оси, удаленной от на-
чала координат на величину ао
На рис 5 3,6 приведены характеристические кривые, соответст-
вующие устойчивым системам Кривые имеют плавную спиралеоб-
разную форму и уходят в бесконечность в том квадранте, номер ко-
торого равен порядку уравнения Если характеристическая кривая
проходит п квадрантов не последовательно или проходит меньшее
число квадрантов, то система неустойчива (рис 5 3,в)
Рис 5 3 Характеристические кривые (годографы) Михайлова
268
Если кривая F(/co) проходит через начало координат, то система
находится на границе устойчивости Действительно, если характери-
стическое уравнение имеет один нулевой корень = 0 (апериодиче-
ская граница устойчивости) или одну пару чисто мнимых корней
Pi = ± ypjt (колебательная граница устойчивости), то функция F(j($)
при со = 0 или со = обратится в нуль
В практических расчетах удобно применять следствие из
критерия Михайлова
система устойчива, если действительная и мнимая части ха-
рактеристической функции F(]<£>) обращаются в нуль поочеред-
но (рис 5 3,г), т е если корни уравнений
Р(со) = 0 и О(со) = О
(5 39)
перемежаются Это утверждение вытекает непосредственно из фор-
мулировки критерия Михайлова - из условия последовательного
прохождения кривой F(/co) через п квадрантов
Докажем справедливость критерия Ми-
хайлова Характеристический полином (5 34), согласно извест-
ной теореме алгебры, можно разделить на множители
F(p) = an(p-p}) + (p-p2)	(р-рп),
где р], рг. , рп - корни характеристического уравнения
Подставим в выражение (5 40) p=j®, тогда получим
F(/co) = п„(/со - /20 (/со - р2)	(ja - рп)
(5 40)
(5 41)
Каждый сомножитель (/со - д) можно рассматривать как вектор,
начало которого находится в точке рк, а конец - на мнимой оси, в
точке /со (рис 5 4,а) При изменении параметра со от 0 до оо вектор
(/со - рк) будет поворачиваться на определенный угол, т е будет из-
меняться аргумент этого вектора
Результирующий угол вектора F(ju) при изменении со от 0 до оо
будет равен сумме углов поворота отдельных сомножителей
269
A argF(7w) = f A arg(7W-p, )
0 a) <r	।	0«в«г	ft
(5 42)
Направление вращения отдельных векторов зависит от того, в
какой (правой или левой) полуплоскости лежит корень Условимся
считать вращение против часовой стрелки положительным Тогда
каждый вектор (/со - д), соответствующий отрицательному действи-
тельному корню, при изменении со от 0 до оо повернется на угол +я/2,
а вектор, соответствующий положительному действительному кор-
ню, - на угол -я/2 (рис 5 4,6) Каждая пара векторов, соответствую-
щая двум сопряженным корням в левой полуплоскости, повернется
на общий угол +7Г, а пара векторов, соответствующая двум сопря-
женным корням в правой полуплоскости, повернется на угол — тс
(рис 5 4,в)
Рис 5 4 Влияние расположения корней на
аргумент характеристической функции
Результирующий угол поворота вектора F(/co) при изменении со
от 0 до оо будет равен
AargFQco) = (п - 1)л/2 - М2,
(5 43)
где / - число корней в правой полуплоскости
Из приведенных рассуждений и выражения (5 43) следует, что
если все корни характеристического уравнения лежат в левой полу-
270
плоскости (/ = 0), то вектор F{jas) повернется на угол mtH, если же
хотя бы один корень находится в правой полуплоскости (/ #= 0), то
угол поворота вектора будет меньше ил/2 Это и требовалось дока-
зать
Критерий Михайлова удобно применять для анализа устойчиво-
сти систем высокого порядка (и > 5)
Пример. Определим с помощью критерия Михайлова, устойчива ли
система, характеристический полином которой имеет вид
F(p) = а$р5 + аАр4 + а3р3 + а2р2 + а}р + а0,	(5 44)
где а5 = 0,16, аА = 1,7, а3 = 6,0, а2 = 9,6, at = 6,7, а0 = 8
Подставляя в выражение (5 44) р - найдем мнимую и действитель-
ную составляющие характеристической функции
= а5а>5 - а3а3 + а\(£>,	(5 45)
Р(со) = аАо>4 - а2($2 + п0	(5 46)
Подставляя в выражения (5 45) и (5 46) конкретные значения парамет-
ра со, можно вычислить координаты ряда точек прямой F(ja>) и по ее виду
оценить устойчивость системы Однако этот путь требует сравнительно мно-
го вычислений (обычно 10-15 точек в интервале со = 0 оо) Поэтому вос-
пользуемся следствием из критерия Михайлова
Найдем положительные корни уравнений
п5®5-п3®3 + П)® = 0,	(5 47)
аА($4 - а2(&2 + п0 = 0	(5 48)
Первое уравнение всегда имеет один нулевой корень сом)= 0 Вычислим
корни уравнения
п5со4-п3со2 + П] = 0,	(5 49)
для этого введем промежуточную переменную z = со2
а$22-a3z + П] = 0	(5 50)
271
Корни вспомогательного уравнения (5.50)
Z1.2
(5.51)
После подстановки числовых значений получим:
z\ - 1,15; z2 = 35.
Положительные корни исходного уравнения (5.49)
®М2=1.1;	сом3 = 5,9.
Аналогично найдем положительные корни уравнения (5.48):
С0д1 ~ 1,0,	С0д2 2,2.
Нетрудно заметить, что корни мнимой и действительной составляю-
щих чередуются. Следовательно, система устойчива.
Если хотя бы один из корней вспомогательного уравнения получится
отрицательным или комплексным, то это будет означать, что не существует
соответствующего положительного корня со, при котором кривая F(/co) пере-
секает оси Р(со) или /Q(co). Кривая F(ja) в этом случае не пройдет через п
квадрантов, и система будет неустойчивой.
5.4.	Критерий Найквиста
Критерий был сформулирован в 1932 г. американским физиком
X.Найквистом (Н.Nyquist), занимавшимся исследованием свойств
электронных усилителей с обратной связью. Позднее А.В. Михайлов
обосновал этот критерий и показал возможность применения его для
анализа систем управления.
В отличие от критериев Гурвица, Рауса и Михайлова, которые
основаны на анализе характеристического уравнения системы, кри-
терий Найквиста позволяет судить об устойчивости замкнутой сис-
темы по АФХ ее разомкнутого контура. В этом заключается сущест-
венное преимущество критерия, т.к. построение АФХ разомкнутого
контура для большинства реальных систем оказывается проще, чем
272
построение годографа Михайлова. Особенно упрощается это по-
строение для одноконтурных систем, состоящих из типовых звеньев.
А в тех случаях, когда неизвестно математическое описание одного
или нескольких конструктивных элементов системы и оценить их
свойства можно только экспериментальным определением частотных
характеристик, критерий Найквиста является единственно пригод-
ным.
Основная формулировка критерия
Найквиста:
система управления устойчива, если АФХ W(ja>) разомкнутого
контура не охватывает точку с координатами (-1; jO).
Эта формулировка справедлива для систем, которые в разомк-
нутом состоянии устойчивы. Таковыми являются большинство ре-
альных систем, состоящих из устойчивых элементов.
На рис. 5.5,а изображены АФХ разомкнутого контура, соответ-
ствующие трем различным случаям: 1 - система устойчива; 2 - сис-
тема находится на колебательной границе устойчивости; 3 - система
неустойчива.
Рис. 5.5. АФХ разомкнутого контура (а) и
физическая трактовка критерия Найквиста (б)
273
Употребленное в формулировке критерия Найквиста понятие
охвата точки имеет некоторую неопределенность, из-за чего в случа-
ях сложной формы кривой FF(/co) могут возникнуть затруднения в
суждении об устойчивости системы. Поэтому для большей ясности
рекомендуется такой прием. Надо проследить мысленно за движени-
ем вектора fP](/co) = 1 + FF(/co), вращающегося вокруг точки (-1; уО) и
скользящего по кривой Угол поворота вектора ^(/со), равный
л, означает охват точки (-1; уО), а угол, меньший л, - неохват.
Для использования изложенного приема к астатическим систе-
мам, которые содержат интегрирующее звено и АФХ которых начи-
нается в минус бесконечности на мнимой оси, характеристику FF(/g))
предварительно дополняют в четвертом квадранте дугой окружности
бесконечно большого радиуса.
Для суждения об устойчивости систем, имеющих АФХ сложной
конфигурации (кривая АФХ пересекает действительную ось левее
точки (-1; у'О) несколько раз), можно также использовать «прави-
ло переходов», сформулированное российским ученым Я 3
Цыпкиным: АФХ не охватывает точку (-1; уО), т. е. система устойчи-
ва, если при возрастании © разность между числом положительных
(сверху вниз) и отрицательных (снизу вверх) переходов АФХ через
ось абсцисс слева от точки (-1; j 0) равна нулю.
Если АФХ начинается или заканчивается на отрезке (-оо;-1), то
считают, что характеристика совершает полперехода.
Частота, при которой АЧХ А(®) (модуль функции FF(/<o)) при-
нимает значение 1, называется частотой среза. Обозначение этой
частоты ©ср. Частоту, при которой фазовый сдвиг (р(со) равен -л, обо-
значают (0л.
Пользуясь введенными обозначениями, можно записать сле-
дующее условие нахождения системы на границе устойчивости:
Л(шя) = 1;
ф(соя) = -л.
(5.52)
274
Очевидно, что при нахождении системы на границе устойчиво-
сти (Оср =
Дадим физическую трактовку основной формули-
ровки критерия Найквиста. Предположим, что на входе
системы (см.рис. 5.5,6) действует гармонический сигнал g(0=<gmSin
с малой амплитудой gm. Пусть частота со окажется равной частоте сол,
при которой фазовый сдвиг ср(<о), создаваемый звеном РК(/со), равен
-к. При этом сигнал отрицательной обратной связи окажется в фазе с
сигналом g(t) и мгновенные значения сигналов поэтому будут скла-
дываться
Если на частоте со = модуль j^(/®)| окажется равным единице,
т. е. если выполняется условие (5.52), то в контуре системы будут
поддерживаться незатухающие колебания даже после исчезновения
внешнего воздействия g(f), т.е. система будет находиться на границе
устойчивости. Характеристика W(j(o) при этом проходит через точку
(-1;;0).
Если на частоте <о = сол модуль )РК(/а>эт)) < 1, то после исчезнове-
ния внешнего воздействия колебания в контуре затухнут, т.е. система
устойчива. Характеристика не охватывает точку (— 1; jO).
Если же модуль |^(/<ол)| > 1, то амплитуда сигналов в контуре
будет неограниченно возрастать, т.е. система будет неустойчивой.
Характеристика W(j(o) в этом случае охватит точку (-1; j'O).
Таким образом, особая роль точки (-1; jO) заключается в том,
что она, во-первых, соответствует превращению отрицательной об-
ратной связи в положительную и, во-вторых, является граничной
между режимами усиления и ослабления сигналов звеном РК(/<о).
Иногда на практике встречаются системы, в контуре которых
имеется одно или несколько неустойчивых элементов. Такие сис-
темы в разомкнутом состоянии неустойчи-
в ы Для суждения об их устойчивости необходимо использовать
следующую формулировку критерия Найк-
виста:
система управления устойчива, если АФХ W(jco) разомкнутого
контура охватывает 1/2 раз точку с координатами (-1; jO), где
275
I - число правых корней характеристического уравнения ра-
зомкнутого контура.
Количество охватов при этом можно определять по правилу
Цыпкина - как разность между числом положительных и отрица-
тельных переходов характеристикой W(j&) отрезка (-оо; -1).
Данная формулировка критерия Найквиста является более об-
щей, чем предыдущая. Действительно, если разомкнутая система
устойчива (т. е. если Z = 0), то для устойчивости замкнутой системы
АФХ должна точку (-1; уО) охватывать нуль раз, т.е. не охва-
тывать.
Из обеих формулировок следует, что для суждения об устойчи-
вости системы необходимо предварительно установить, устойчива ли
она в разомкнутом состоянии. Обычно эта вспомогательная задача
решается сравнительно легко, при помощи критерия Гурвица. Для
этого приравнивают к нулю знаменатель ПФ W(p) разомкнутого кон-
тура и анализируют это характеристическое уравнение.
Во многих практических случаях устойчивость разомкнутого
контура может быть оценена без каких-либо вычислений, непосред-
ственно по виду входящих в контур звеньев.
Докажем теперь м ат е м а т и ч е с к и справедли-
вость критерия Найквиста. Рассмотрим вспомога-
тельную функцию
W\(p) = 1 + JV(p).	(5.53)
Представим ПФ разомкнутого контура, входящую в выражение
(5.53), в виде отношения двух полиномов К(р) и D(p)\
^)=1+адДДД.	(5.54)
D(p) D(p) D(p)
Числитель функции W\(p) представляет собой характеристиче-
ский полином системы, а знаменатель - характеристический поли-
ном разомкнутого контура. Так как у реальных систем степень поли-
276
нома К(р) не превышает степень полинома D(p), то степени обоих
характеристических полиномов F(p) и D(p) всегда равны.
Проследим, как изменяется угол поворота вектора ^(/со) ПРИ
изменении со от 0 до оо. Согласно правилу деления комплексных чи-
сел, этот угол равен разности аргументов числителя и знаменателя
функции IT] (/со):
Acpj (со) = AargF(jco) - AargD(jco).
(5.55)
Выше, в 5.3, было показано, что характеристический вектор ус-
тойчивой системы «-го порядка при изменении со от 0 до оо повора-
чивается против часовой стрелки на угол п тс/2. Это правило спра-
ведливо как для замкнутой системы, так и для ее разомкнутого кон-
тура, т.е. и для вектора F(/co), и для вектора £)(/<о). Отсюда можно
сделать вывод: если разомкнутый контур устойчив, то для устойчи-
вости замкнутой системы необходимо и достаточно, чтобы разность
аргументов (5.5) была равна нулю. Результирующий угол (pi (со) будет
равен нулю лишь в том случае, если годограф вектора ^i(/co) при
изменении со от 0 до со не охватит начало координат (рис. 5.5,в).
Годограф РГ1(/со) представляет собой АФХ РГ(/со), сдвинутую на
единицу вправо Поэтому в осях координат характеристики W(jo)
начало координат вектора ^(/со) соответствует точке (-1; уО). Оче-
видно теперь, что изменение угла <pi(co) будет равно нулю, если ха-
рактеристика W(j(o) не охватит точку (-1; уО). Таким образом, спра-
ведливость основной формулировки критерия Найквиста доказана.
Аналогичными рассуждениями можно доказать справедливость
и второй формулировки критерия
Пример 1. Определим с помощью критерия Найквиста максимально
допустимое значение общего ПК системы, состоящей из трех инерционных
звеньев первого порядка с одинаковыми постоянными времени Т\=Т2-Тз=Т
ПФ разомкнутого контура системы
W(p) = kl(Tp + I)3.
(5.56)
277
Амплитудная частотная функция контура
А(аз) - I I = к / (Vr2co2 +1 )3,
(5 57)
фазовая частотная функция
ф(со) = argPTfjro) = -3arctg®r
Система будет находиться на границе устойчивости, если АФХ ра-
зомкнутого контура пройдет через точку (-1, уО), те если при некоторой
частоте со - соя = одновременно выполняется условие
Л(®1ф) = 1, ф(СО|ф) =
Для рассматриваемой системы условия (5 59) имеют вид
=1.
-Загс12со„Т = -я
Из условия (5 61) имеем
юкрг= 7з
(5 59)
(5 60)
(5 61)
(5 62)
Подставляя выражение (5 62) в условие (5 60), получим искомое зна-
чение передаточного коэффициента к = 8
Из приведенного решения следует также, что предельное значение ПК
не зависит от абсолютного значения постоянных времени Т
Критерий Найквиста удобно использовать для анализа
устойчивости систем, содержащих звено
запаздывания Если звено запаздывания включено последо-
вательно с остальными звеньями (рис 5 6, а), то АФХ разомкнутого
контура может быть представлена как произведение
И\до) = W'Qo) е ,
(5 63)
278
где W '(j(n) - эквивалентная амплитудно-фазовая функция остальных
звеньев
а
Рис 5 6 Оценка устойчивости СУ с запаздыванием
а - структура СУ, б - АФХ разомкнутого контура
Характеристику	строят следующим образом Вначале
строят кривую W (/со), а затем каждый вектор, соответствующий час-
тоте поворачивают на угол со,т (рис 5 6,6)
Отметим, что звенья запаздывания, как правило, ухудшают ус-
тойчивость систем
Пример 2. Определим, будет ли устойчива статическая система, со-
стоящая из пропорционального управляющего устройства и статического
впм
инерционного объекта первого порядка с запаздыванием (3 135), при сле-
дующих значениях параметров
к = кук0 = 7, То - 100 с, то = 20 с
АФХ разомкнутого контура
W (/со) = (F, (/со) И", Qm) = ке	+1),	(5 64)
амплитудная функция контура
Л (со) = к/ 7г02®2 +1,	(5 65)
фазовая функция
279
ф(со) = -arctgtoT0 — сот о
(5.66)
Найдем вначале частоту соя, при которой ф(соя) - -л. Решая методом
последовательных приближений трансцендентное уравнение
-arctgcon100-on20 =-я,	(5.67)
получим соя « 0,085 с .
Теперь вычислим значение Л (со) при частоте соя = 0,085:
Ди)1<0=о,о85 = 1/1002(0,085)2 +1 * 0,82 < 1.
(5.68)
Следовательно, АФХ не охватит точку (-1; /0). Система устойчива.
Найдем теперь так называемое критическое запаздывание iOKp - зна-
чение то, при котором рассматриваемая система станет неустойчивой. Для
этого из условия Л (соср) = 1 определим ®ср = 0,069 с-1. При этой частоте
инерционная часть разомкнутого контура создает фазовый сдвиг
Фи(®ср) = - arctgC0cp^o = -82°. Соответственно, на запаздывающую часть оста-
ется угол ф3(соср) = -180° -(-82°) = -98°. Отсюда критическое запаздывание
кр — ФзС^ср )/57,3cOqj « 25 С.
Если разомкнутый контур системы образован последовательным
соединением типовых динамических звеньев, то целесообразно час-
тотную характеристику контура строить в логарифмиче-
ской системе координат и об устойчивости системы
судить по виду этой характеристики. При этом используют следую-
щуюразно в идность основной формулировки
критерия Найквиста:
система устойчива, если при достижении фазовой частотной
характеристикой значения - 180° логарифмическая амплитуд-
ная характеристика будет отрицательной (рис. 5.7,а, линия 1).
Действительно, если £(о>) < 0, то Я(а>) < 1. Поэтому отрицатель-
ность £(<в) при 9(0)*)= -180° свидетельствует о том, что АФХ ра-
зомкнутого контура не охватывает точку (-1,/0).
280
Логарифмические частот-
ные характеристики L(o) и q>(o)
разомкнутого контура находят
суммированием ординат соот-
ветствующих характеристик
отдельных звеньев. Фазовые
характеристики отдельных
звеньев строят либо по несколь-
ким вычисленным точкам, либо
при помощи специальных шаб-
лонов Амплитудные характе-
ристики отдельных звеньев
строят приближенно - в виде
совокупности прямолинейных
Ц(й), дБ А
Рис. 5.7. Логарифмические частотные
отрезков по простым правилам,
изложенным в главе 3.
Критерий Найквиста, при-
меняемый в логарифмической
характеристики статических систем:
I - устойчивой; 2 - находящейся на
границе устойчивости, 3 - неустойчивой
системе координат, называют часто логарифмическим критерием.
Рис. 5.8. Пример оценки
устойчивости по логарифмическим
частотным характеристикам
Пример 3. Определим по
логарифмическим частотным
характеристикам устойчивость
статической системы, состоя-
щей из трех инерционных
звеньев первого порядка с по-
стоянными времени =0,2 с;
Т2 = 0,1 с. Тз = 0,05 с. Переда-
точный коэффициент разомк-
нутого контура к = 20.
Сопрягающие частоты
звеньев ®с] = 1/Д = 5 с-1;
<ой = 1/7’2 = 10 с, ШсЭ = 1/7, =
20 с’1.
В соответствии с этими
значениями построены при-
ближенная ЛАЧХ L(w) (рис.
5.8,а) и фазовая характеристи-
281
ка ф(ю) (рис 5 8.6) разомкнутого контура, которая получена согласно выра-
жению
ф(со) = -arctgcoT7! - arctgcoT^ - arctgcoT^	(5 69)
По графику видим, что при <р(со) = -180° функция Л(со) > 0 Следова-
тельно, система неустойчива
5.5.	Построение областей устойчивости
Понятия и метод построения областей При помощи критери-
ев устойчивости, сформулированных в (5 2)-(5 4), можно установить
факт устойчивости или неустойчивости системы, все параметры ко-
торой заданы Однако часто при проектировании и наладке систем
возникает более общая задача анализа устойчивости — определение
допустимых (по условию устойчивости) пределов изменения некото-
рых параметров системы В качестве таких варьируемых параметров
обычно рассматривают коэффициенты и постоянные времени управ-
ляющего устройства, которые можно целенаправленно изменять при
настройке системы Иногда допустимые пределы изменения опреде-
ляют и для параметров объекта (если последние изменяются при
работе системы) Варьируемыми параметрами могут служить также
коэффициенты характеристического уравнения, которые, как извест-
но, однозначно связаны с передаточными коэффициентами и посто-
янными времени элементов системы
Допустимые пределы варьирования параметров системы можно
определить путем построения областей устойчивости Областью
устойчивости называют область в пространстве варьируемых пара-
метров, каждой точке которой соответствуют только левые корни
характеристического уравнения Область устойчивости выделяет из
всех возможных значений варьируемых параметров лишь те значе-
ния, при которых система устойчива Поверхность, ограничивающая
область устойчивости, называется границей области устойчивости
На рис 5 9,а показана область устойчивости, построенная в
пространстве двух коэффициентов характеристического уравнения -
а, и ак Каждой точке, находящейся ниже заштрихованной кривой
(например, точке Л'), соответствуют только левые корни (например,
282
точки р'} и р'2 на рис 5 9,6) Любой точке, находящейся выше кри-
вой (например, точке А"'), обязательно соответствуют хотя бы один
действительный корень или пара комплексных корней, расположен-
ных справа на плоскости корней (точки р"’ и р'^'У Границей об-
ласти устойчивости в данном примере является заштрихованная кри-
вая Каждой точке этой кривой (например, точке А") соответствует
пара чисто мнимых корней (точки Р'х и р2 )
Рис 5 9 Области устойчивости в плоскостях коэффициентов (а) и
корней (б) характеристического уравнения
Граница области устойчивости в принципе может быть найдена
путем многократного применения одного из критериев устойчивости,
при различных значениях варьируемых параметров Но такой путь
связан с большим объемом вычислений Эффективным способом
отыскания границ областей устойчивости является метод P-разбие-
ния, разработанный российскими учеными А А Соколовым и
Ю И Неймар ком
С\ щность метода D-разбиения заключается в следующем Пусть
анализируемая система описывается характеристическим уравнени-
ем п-го порядка
283
апРП +аплРПЛ +ап-гРП'2 + ••• + *() = 0-	<5-70)
Расположение всех п корней характеристического уравнения на
комплексной плоскости а - ДЗ зависит от значений коэффициентов
а0, а}, ..., а„. В общем случае в пространстве варьируемых коэффи-
циентов, например at и 64 (см.рис. 5.8,6/), существуют такие значения
коэффициентов, при которых / корней расположены справа, а (л - /)
корней - слева от мнимой оси /р Совокупность всех таких значений
образует в пространстве коэффициентов область, которую можно
обозначить D(n - /; /)• Очевидно, что могут существовать области и с
другим распределением корней: D(n - / - 1; 1+1), D(n -1-2, 1+2) и
т.д Область D(n; 0) является областью устойчивости.
Процесс построения в пространстве параметров (или коэффици-
ентов) областей с различным распределением корней называется
D-разбиением. Линии, разграничивающие эти области, называются
кривыми D-разбиения.
Переход из одной области в другую область пространства коэф-
фициентов соответствует переходу одного действительного или пары
комплексных корней через мнимую ось /0. Следовательно, каждой
точке, лежащей на границе между двумя областями, соответствует
либо нулевой корень р = 0, либо пара чисто мнимых корней р = ± J0.
Поэтому кривую D-разбиения можно рассматривать как отображение
мнимой оси плоскости корней. Указанная особенность кривых
D-разбиения используется при отыскании их уравнений. Для этого в
уравнение (5.70) подставляют p-jft или p=j® и решают уравнение
относительно варьируемых параметров. Совокупность значений
варьируемых параметров, соответствующих всем возможным значе-
ниям о (от -оо до +оо), дает все точки кривой D-разбиения Выделе-
ние области D(w; 0) среди остальных областей производят при помо-
щи специальной процедуры — штриховки кривых D-разбиения.
Построение области устойчивости по одному параметру.
Применим метод D-разбиения для построения области устойчивости
в плоскости одного параметра. Предположим, что варьируемый па-
раметр к входит в характеристическое уравнение линейно.
284
F(p) = к A(p) + B(p) = О,
(5.71)
где А(р) и В(р) - степенные полиномы отр.
Подставляя в уравнение (5.71) р=](а и разрешая его относитель-
но параметра к, получим
к = - В(/со) / А (/о) = P(g)) +
(5 72)
Придавая теперь переменной о значения от 0 до оо, можно в
системе координат Р(о) - jQi®) построить кривую D-разбиения (рис.
5 10,6)
Imk^
в
Рис. 5.10. Область устойчивости в плоскости одного параметра:
а - граница устойчивости в плоскости корней,
б - общий случай D-разбиения, в - пример построения
Так как составляющая всегда четная, a Q(ca) - нечетная
функция переменной о, то кривая D-разбиения всегда симметрична
285
относительно действительной оси Р(о). Поэтому при построении
области устойчивости достаточно найти лишь одну ветвь кривой D-
разбиения, соответствующую, например, положительным значениям
со, а вторую ветвь можно нанести как зеркальное отражение первой
Кривая D-разбиения (см.рис. 5.10,6) делит плоскость параметра
к на несколько областей, соответствующих различным вариантам
расположения корней. Выделить из этих областей область устойчи-
вости D(n, 0) можно при помощи штриховки. Правило штриховки
основано на том, что кривая D-разбиения является отображением
мнимой оси плоскости корней (рис. 5.10,я). В системе координат а—
усо область устойчивости находится слева от мнимой оси усо, и ось
принято штриховать слева (при движении вдоль оси от -оо до +оо) В
теории функций комплексного переменного доказано, что в плоско-
сти варьируемого параметра область устойчивости также находится
слева от кривой D-разбиения Соответственно кривую D-разбиения
также штрихуют слева (при движении вдоль кривой от -оо до +оо)
После нанесения штриховки выявляют область с наибольшим
числом левых корней. При этом учитывают, что каждому переходу с
заштрихованной стороны кривой D-разбиения на незаштрихованную
сторону (стрелка 1 на рис. 5.10,6) соответствует переход одного кор-
ня из левой полуплоскости в правую, а пересечению кривой D-
разбиения в обратном направлении (стрелка 2 на рис. 5 10,6) соот-
ветствует переход одного корня из правой полуплоскости в левую
Переходя последовательно из одной области в другую, можно вы-
явить область с наибольшим числом левых корней (см рис 5 10,6,
область D(n; 0)). После этого при помощи одного из критериев необ-
ходимо проверить, является ли выявленная область областью устой-
чивости, т е. проверить, все ли корни левые.
В практических задачах параметр к является действительной ве-
личиной (передаточный коэффициент, постоянная времени) и его
допустимые пределы изменения определяются не всей областью D(n,
0), а только отрезком действительной оси Р(о), заключенным внутри
области D(w; 0).
Пример 1. Построим при помощи метода D-разбиения область устой-
чивости системы, состоящей из трех инерционных звеньев первого порядка
286
с постоянными времени 7} =0,1 с, Т2 = 0,2 с и Т3 = 0,4 с. Область устойчи-
вости будем строить в плоскости общего ПК к.
Характеристическое уравнение системы
а\р +1\т2р + 1ХГ3р +1) + к=0	(5.73)
Подставим в уравнение р =у(3 и решим его относительно коэффициен-
та к
к = -(T,ja> + 1)ГТ2joj + l)(T3jo> +1) = [(7-,7-2 + TtT, + Т2Т3 )ш2 -1] +
+ ЖЛГгЛш3 - (Г, + Т2 + 73)<о] = (0,14ш2 -1) + /(0.00&? - О,7ш) (5 74)
Подставляя в выражение (5.74) различные значения переменной оо,
можно построить кривую D-разбиения (рис. 5.10,в). При помощи штриховки
и соответствующих рассуждений о переходах корней нетрудно установить,
что областью с наибольшим числом левых корней является область £>(3; 0)
В этой области все корни левые, т.е. она является областью устойчивости
Действительно, при к=0 все три корня характеристического уравнения (5 73)
отрицательные р\ = -1/Д, р2 = -МТ2, р3 = -1/Т3.
Допустимый диапазон изменения передаточного коэффициента рас-
сматриваемой системы от -1 до +1 ] ,2.
Построение области устойчивости по двум параметрам Рас-
смотрим теперь случай, когда требуется исследовать влияние двух
параметров на устойчивость системы. При этом все остальные пара-
метры системы должны быть заданы. В качестве варьируемых пара-
метров обычно принимают постоянную времени Т одного из конст-
руктивных элементов системы и передаточный коэффициент к ра-
зомкнутого контура или одного из элементов. Предположим, что
варьируемые параметры к и Т входят в характеристическое уравне-
ние системы линейно, т.е. уравнение не содержит ни произведений к
и Т, ни их степеней выше первой. Тогда уравнение может быть пред-
ставлено в следующем виде.
F(p) = кА(р) + ТВ(р) + С(р) = 0,	(5 75)
287
где А(р), В(р\ С(р) - полиномы от р, коэффициенты которых не за-
висят от к и Т.
Если варьируемые параметры входят в уравнение нелинейно, то
следует попытаться ввести такие две новые переменные, которые
были бы функционально связаны с к и Т и входили бы в уравнение
линейно. Во многих практических случаях это удается сделать.
Согласно общей методике £)-разбиения, подставим в характери-
стическое уравнение (5.75) вместо переменной р мнимый корень /р,
тогда получим тождество
kA(jo>) + ТВ(/&) + C(jd)) = О,
(5.76)
которое при каждом фиксированном значении о можно рассматри-
вать как уравнение с неизвестными кнТ.
Отметим, что с позиции критерия Михайлова уравнение (5.76)
можно рассматривать как условие прохождения характеристического
вектора F(j(a) через начало координат, т.е. как условие колебательной
границы устойчивости.
Каждый из трех полиномов, входящих в уравнение (5.76), после
возведения у® в четные и нечетные степени можно представить в
виде суммы действительной и мнимой частей:
Л(» = Л1(ш) + ;Л2((о);'
В(усо) = В, (со) + jB2 (со); >
С(у(о) = С1(со) + уС2(со).
(5.77)
Подставляя (5.77) в (5.76) и группируя действительные и мни-
мые слагаемые, получим
[кА,(®) + ТВ}(а>) + CH®)] + j [Ы2(ю) + TB2(g>) + С2(®)] = 0. (5.78)
Известно, что комплексная величина равна нулю только в том
случае, если одновременно равны нулю ее действительная и мнимая
части. Поэтому условие (5.78) эквивалентно двум уравнениям
288
Ы] (cd) + ТВ} (cd) + Q (cd) = 0; I
kA2 (cd) + TB2 (co) + C2 (cd) - 0.^
(5.79)
Эта система двух уравнений дает возможность определить для
каждого фиксированного значения со два неизвестных киТ
Решим систему (5.79) методом определителей:

(5.80)
где
Т = А2/А =/2(со),
(5.81)
4 (<d); Вх (cd)
4(cd);B2 (cd)
= А} (cd)B2 (cd) - A2 ((o)Bx (cd);
-C) (cd);B](cd)
-C2 (cd);B2(cd)
4 (cd);-C1 (cd)
A2 (cd);-C2(cd)
= -С, (cd)B2 (cd) + B2 (cd)Bj (cd);
^2
= -Ax (cd)C2 (cd) + A2 (cd)Cj (cd).
Выражения (5.80) и (5.81) представляют собой уравнение кри-
вой D-разбиения, заданное в параметрической форме. Подставляя в
эти выражения различные значения параметра со (в диапазоне от -со
до +со), можно построить основную границу области устойчивости
(кривая АВС на рис. 5.11).
Так как полиномы Ai(co), В](со) и Cj(co) - четные функции, а по-
линомы Л2(со), В2(со) и С2(со) - нечетные функции, то определители А,
А] и А2 являются нечетными функциями переменной со Из этого сле-
дует, что кривая D-разбиения при изменении со от -со до +со прохо-
дит дважды через одни и те же точки: первый раз при изменении со
от -оо до 0 и второй раз - при изменении со от 0 до +оо.
289
Рис 5 11. Область устойчивости в плоскости двух параметров
Кривая £)-разбиения, построенная в плоскости двух параметров,
штрихуется по следующему правилу:
если определитель Д > 0, то штриховка наносится слева (при
движении вдоль кривой в сторону увеличения со); если опреде-
литель Д< 0, то штриховка наносится справа.
Обращаем внимание на то, что это правило сформулировано к
вполне определенному порядку построения кривой D-разбиения, а
именно уравнение, получающееся от приравнивания к нулю дейст-
вительной части, должно быть написано в первой строке системы
(5 79); параметр, стоящий в обоих уравнениях на первом месте, не-
обходимо откладывать по оси абсцисс.
Так как при прохождении переменной о через нуль знак главно-
го определителя А меняется на противоположный, то штриховка
кривой D-разбиения всегда двойная
Уравнения (5.79) определяют в плоскости k-Т одну-единствен-
ную точку (при фиксированном значении w) лишь в тех случаях,
когда эти уравнения совместны и линейно независимы, т е когда
290
определители Д, Д; и Д2 не равны нулю Если же при некотором зна-
чении со все три определителя одновременно обращаются в нуль или
бесконечность, то решения (5 80) и (5 81) становятся неопределен-
ными. Это означает, что при данном значении со уравнения (5 79)
эквивалентны, т е что одно отличается от другого на постоянный
множитель В системе координат к-Т таким «исключительным» зна-
чениям сои соответствуют так называемые особые прямые (на рис
5.11 линии BF, АЕ и СЕ). Уравнением особой прямой может служить
любое из уравнений (5.79):
Т = [-С](2)(а>и) _^41(2)(сои)]/В](2)(®и)	(5 82)
Во многих практических задачах параметры к и Т входят соот-
ветственно в коэффициенты и ап характеристического уравнения
(5.70). В этом случае уравнения двух особых прямых получают при-
равниванием указанных коэффициентов к нулю:
aQ = 0; ап = 0.	(5.83)
Первое уравнение соответствует сон = 0, второе - сои = со
Штриховку особых прямых выполняют по сле-
дующим правилам. Особые прямые, соответствующие <п„ = 0 и сои =
= <х>, штрихуют один раз (на рис. 5.11 линии АЕ и СЕ, а прямые, со-
ответствующие 0 < со < оо, штрихуют дважды (линия BF) В точках
пересечения (или сопряжения) особой прямой с основной кривой
О-разбиения, соответствующих со = сон, заштрихованные стороны
прямой и кривой должны быть обращены друг к другу (точки А, В и
С) Причем, если в точке пересечения определитель Д меняет знак, то
штриховка особой прямой переходит на противоположную сторону
прямой. Если же знак определителя не меняется, то направление
штриховки остается прежним.
После нанесения штриховки выявляют области с наибольшим
числом левых корней. На рис. 5 11 три области имеют предположи-
тельно распределение корней £>(и; 0) Они и являются «претендента-
ми» на области устойчивости
291
Пример 2. Построим при помощи метода D-разбиения область устой-
чивости системы, состоящей из статического объекта третьего порядка
И'о(Р) = М(7> + 1)3
(5 84)
и пропорционально-интегрального управляющего устройства
^у(р) ~ кп + кц/Р’
Параметры объекта известны. ко = 0,1; То = 1 с.
Область устойчивости будем строить в плоскости двух настроечных
параметров управляющего устройства кп и кц
Характеристическое уравнение системы имеет вид
кп . ки
1 +--^-Т(*п+—) = 0
(7>+1)3 Р
(5 86)
или после преобразований
Г3/ +ЗТ0У +ЗТор2 +(1+*„*„)р + Мк = О-	(5 87)
После подстановки р = усо характеристическое уравнение превращается
в тождество, которое распадается на два уравнения
Т03со4 -ЗТ0со2 +кокК = 0,
-З7"2со3 +(1+кока)ы = 0
(5 88)
Приведем систему (5 88) к виду (5 79)
ЛпО+Мо-7>2(3-Г02ог) = 0,
к^со(я+кп0+ш(1-УГ2(й2') = 0
(5 89)
Определители этой системы
Д = -А2<о, Д] =А0оХ1-ЗГ2со2), Д2 =-АоТ^оуХЗ-/“со2)	(5 90)
292
Уравнение границы устойчивости в параметрической форме

(5 91)
= Д2/Д = 7'0<о2(3-7'2ш2уЛ0 = /2(о>)
(5.92)
Подставляя в выражения (5.91) и (5 92) значения со от 0 до оо, получим
основную границу устойчивости (кривая А С на рис 5.12,4?) Основную гра-
ницу дополним особой прямой, соответствующей значению сон = О
а0= коки= 0 иликК = 0.
(5 93)
Рис. 5.12. Примеры построения областей устойчивости
Особая прямая, соответствующая значению ®и = оо, находится в беско-
нечности.
Вдоль основной границы нанесем двойную штриховку Так как при
положительных значениях со главный определитель А < 0, то штриховать
необходимо справа (при движении от со = 0 до со = оо). Особую прямую
штрихуем так, чтобы в точках пересечения прямой с основной границей
штриховка была направлена в одну сторону. В точке со = 0 штриховка осо-
бой прямой переходит на противоположную сторону.
Таким образом, плоскость параметров кп и к„ оказалась разбитой на
четыре области: D(4; 0), D(3, 1), D(2; 2), D(l; 3).
Областью устойчивости является область D(4, 0) В этом можно убе-
диться при помощи критерия Гурвица
Обратим внимание на то, что ПК объекта к0 входит в выражения (5 91)
и (5.92) в первой степени, причем входит одинаково в выражение для кп и
длякн.
293
Если коэффициент интегральной составляющей кн = 0, то данная сис-
тема превращается в систему, рассмотренную в (5.4) (пример 1). Функция
(5 92) обращается в нуль при со2 = 3/Г2. Подставляя это значение в функ-
цию (5.91), получим, как и в указанном примере, предельное значение об-
щего ПК системы кп ко = 8, не зависящее от постоянной времени То.
Пример 3. Построим область устойчивости системы, состоящей из не-
устойчивого объекта
H'M^k^T^p + iyCT^p2-!)3
(5.94)
и пропорционально-дифференциального регулятора с отрицательной диф-
ференциальной составляющей
№р(р) = кп-кдр.
(5.95)
Пусть ко = I, Т’о] = I с, То2 = 2 с. Область устойчивости будем строить
по параметрам регулятора кп и кд.
Характеристическое уравнение системы
(7'о2 ~кдкоТо\)р2 +(кпкоТо\ ~кдко)Р + кпко “1 = 0
(5.96)
при заданных параметрах объекта оно принимает вид
кп(Р + ^) + кд(~р2 ~р) + 4р2 -1 = 0
(5.97)
После подстановки р= ja> получим систему двух уравнений
/сп1 + /сдсо2 -4со2 -1 = 0;
к со+А'л(-со)+0 = О
Определители системы
Д = -со-со3,Д1 = Д2 =-со(1+со2)
Уравнение границы устойчивости в параметрической форме
(5.98)
(5-99)
294
А'п = (1+4со2)/(1+со2), кд =(1+4со2)/(1 + со2)	(5.100)
Основная граница устойчивости, соответствующая этим двум одинако-
вым функциям, представляет собой отрезок прямой А С (рис. 5.12,6). Основ-
ную границу А С дополняют две особые прямые, соответствующие частотам
соИ1 = 0 и со„з = оо:
ао=^п - 1 = 0 илиАгп = 1;	(5.101)
«2 =	+ 4 = 0 или ка = 4.	(5.102)
Штриховка основной границы и особых прямых, выполненная по из-
ложенным выше правилам, указывает, что в плоскости настроечных пара-
метров кп и кл существуют две области устойчивости D(2; 0).
5.6.	Влияние структуры и передаточного коэффициента
СУ на устойчивость
В предыдущих параграфах было показано, что устойчивость
системы зависит как от вида характеристического уравнения систе-
мы, так и от конкретных числовых значений коэффициентов уравне-
ния. Существуют системы, которые устойчивы при любых значениях
параметров. Такие системы называют структурно неустойчивыми.
Структурно неустойчивую систему можно сделать устойчивой, толь-
ко изменив ее структуру. У структурно неустойчивой системы в про-
странстве любых ее параметров области устойчивости не существует.
Рассмотрим в качестве примера одноконтурную систему, содер-
жащую одно инерционное звено и два идеальных интегрирующих.
Характеристическое уравнение такой системы имеет вид
(1\р + l)p2+fc = 0,	(5.103)
оно не содержит слагаемое с р в первой степени. Очевидно, что в
данном случае не выполняется необходимое условие устойчивости -
условие положительности коэффициентов, и никакие вариации па-
295
раметров ki и Т\ не могут привести к появлению слагаемого с р в
первой степени. Следовательно, эта система структурно неустойчива.
Все системы, приведенные в (5.2)-(5.5), являются структурно
устойчивыми.
У рассматриваемых ниже одноконтурных систем алгоритмиче-
ская структура однозначно характеризуется типом и числом элемен-
тарных динамических звеньев, образующих контур системы.
Существуют звенья, которые, как правило, ухудшают устойчи-
вость системы, и звенья, которые почти всегда улучшают устойчи-
вость. К первой группе звеньев относятся следующие:
идеальное интегрирующее
W(p) = к!р,
неустойчивое статическое звено первого порядка
W(p) = кЦТр - V)
консервативное (идеальное колебательное)
W(p) = k/(fp2 + 1).
(5.104)
(5.105)
(5.106)
Звеньями, улучшающими устойчивость системы, являются фор-
сирующие звенья. Обычно применяют форсирующие звенья первого
порядка
W(p)=l+k}p.
(5.107)
Отметим, что широко применяемый в промышленной автомати-
ке пропорционально-интегральный закон регулирования соответст-
вует последовательному соединению идеального интегрирующего
звена и форсирующего звена первого порядка:
W(p) = (к}р + к»)/р
(5.108)
296
Поэтому влияние этого закона на устойчивость двоякое: при
больших значениях коэффициента интегральной составляющей ки
устойчивость хуже, при больших значениях коэффициента кп устой-
чивость лучше.
Рассмотрим общие условия структурной ус-
тойчивости одноконтурной системы. Характе-
ристическое уравнение системы в общем случае имеет вид
D(p) + К(р) = О,
(5.109)
где D(p) = ndt(p) - произведение знаменателей ПФ отдельных
звеньев, входящих в контур системы; К(р) - произведение числите-
лей этих же функций.
Условия структурной устойчивости зависят от общего порядка и
характеристического уравнения (5.109) и от вида полиномов D(p) и
К(р}. В полином D(p) входят знаменатели «плохих» звеньев
(5.104)-(5.106), а в полином К(р)~ числители «хороших» - форси-
рующих звеньев (5.107). Обозначим: q - количество идеальных ин-
тегрирующих (5.102), t - количество неустойчивых (5.105), г - коли-
чество консервативных звеньев (5.106), входящих в систему.
Если форсирующих звеньев в контуре нет, т.е. если К(р) = к
(где к - общий ПК разомкнутого контура), то условие структурной
устойчивости системы выражается в виде двух неравенств:
<7 +Г <2;
4г <п.
(5.110)
Для более сложных видов полинома К(р) условия структурной
устойчивости одноконтурных систем приводятся в специальной ли-
тературе.
Общие свойства многоконтурных систем (систем, содержащих
внутренние обратные связи) изучены еще слабо. Для всех этих сис-
тем пока не найдены условия структурной устойчивости. Лишь для
одного класса многоконтурных систем - класса систем со статиче-
297
скими неперекрестными обратными связями - установлено правило:
если все контуры системы структурно устойчивы, то сама система
структурно устойчива. Обращаем внимание на то, что обратное ут-
верждение несправедливо. Один или несколько контуров могут быть
структурно неустойчивы, а вся система - структурно устойчива.
Рассмотрим теперь влияние одного из основных парамет-
ров системы - ПК разомкнутого контура на ее устойчивость. Учтем,
что у одноконтурных систем коэффициент к входит в выражение
АФХ W\j&) как множитель:
= £A?(/cd)/D(/cd),
(5.1Н)
где Х*(/со) | «-о = I •
Это означает, что длины вектора W(j®) при всех значениях со
пропорциональны коэффициенту к. При увеличении коэффициента к
АФХ расширяется (рис. 5.13,я) и приближается к критической точке
(—1,70). Следовательно, увеличение ПК разомкнутого контура приво-
дит к нарушению устойчивости системы.
298
Это правило справедливо для большинства реальных систем, у
которых АФХ имеет форму плавной спирали (см.рис. 5.13,л). Однако
существуют системы, у которых АФХ имеет клювообразную форму
(рис. 5.13,6). В таких системах к нарушению устойчивости может
привести не только увеличение, но и уменьшение ПК.
Значение ПК, при котором АФХ проходит через точку (-1; уО),
называют предельным, или критическим.
В существовании предельного коэффициента можно убедиться и
при помощи критерия Михайлова. Действительно, у простых одно-
контурных систем коэффициент к входит только в коэффициент я0
характеристического уравнения, причем у статических систем
а0 = 1 + к, а у астатических -ао = к. Если увеличивать коэффициент к,
то будет увеличиваться только коэффициент ао и характеристическая
кривая F(/co) без деформации будет перемещаться вправо (рис.
5.13,в). Очевидно, что при некотором предельном значении коэффи-
циента ап, а следовательно, и коэффициента к, кривая Т^со) пройдет
через начало координат, т. е. система будет на границе устойчивости.
Таким образом, установлена одна из важнейших в ТАУ законо-
мерностей:
чем больше общий ПК разомкнутого контура системы регули-
рования, тем ближе замкнутая система к границе устойчиво-
сти.
Предельное значение ПК зависит от соотношения постоянных
времени звеньев, образующих контур системы. Рассмотрим, напри-
мер, статическую систему, состоящую из трех инерционных звеньев
первого порядка с передаточными коэффициентами к\, к2, к3 и посто-
янными времени Т\, Т2, Т3. Характеристическое уравнение такой сис-
темы
а3р3 + а2р2 + а\р + а0 = О,
где а3=Г1Г2Г3;а2=Г1Г2 + Г1Г3 + Г2Г3;
а} = Г] + Т2 + Т3; ао= 1 + к2 к3 = 1 + к.
(5.112)
(5.113)
Согласно критерию Гурвица, система третьего порядка будет
находиться на границе устойчивости, когда
299
Д2 = #1 <72 — <7о <73 = О
(5 114)
Подставив в условие (5 114) коэффициенты (5 113), получим
(7, Т2 + Г1Г3+ Т2 Г3)( Л + Т2 + Г3) - Г, Т2 Т2 (1 + £пр) = О (5 115)
Разрешив это равенство относительно кар и выполнив некоторые
дополнительные преобразования (деление на ап), получим выражение
для предельного коэффициента
Анализируя зависимость (э 116), можно доказать, что предель-
ный коэффициент тем больше, чем больше разность между двумя
наиболее различающимися постоянными времени (например, и Т2)
и чем ближе третья постоянная
времени Г3 к среднеарифмез и-
ческому значению двух пер-
вых
На рис 5 14 показаны об-
ласти устойчивости рассматри-
ваемой статической системы
третьего порядка Области по-
строены в плоскости относи-
тельных постоянных времени
Т2/Т\ и Т2/Т\ для нескольких
фиксированных значений об-
щего передаточного коэффи-
Рис 5 14 Предельные ПК системы циента системы
из трех инерционных звеньев	На основании выражения
(5 116) можно сформулировать
важное практическое правило предельное значение ПК системы
зависит от соотношения постоянных времени и не зависит от их
абсолютных значений
300
Приведенное правило справедливо для систем любого порядка,
и поэтому всегда при конструировании систем стремятся как можно
больше «раздвинуть» постоянные времени Однако изменение посто-
янных времени с целью увеличения ПК и улучшения точности сис-
темы во многих случаях оказывается невозможным или нецелесооб-
разным Действительно, при конструировании элементов системы
обычно принимают меры, направленные на максимальное уменьше-
ние постоянных времени, а поэтому дальнейшее их уменьшение, как
правило, невозможно Увеличение же постоянных времени нецелесо-
образно, т к ведет к ухудшению быстродействия всей системы
Эффективным средством достижения требуемой точности сис-
темы при сохранении ее устойчивости является изменение структуры
системы - путем добавления специальных стабилизирующих и кор-
ректирующих устройств (см главу 7)
Контрольные задания и вопросы
1	Дайте физическую трактовку понятия «устойчивая СУ»
2	Запишите соответствующее этому физическому определению мате-
матическое условие асимптотической устойчивости системы
3	Сформулируйте общее условие устойчивости линейной системы
Объясните, почему действительные корни характеристического уравнения
системы должны быть обязательно отрицательными
4	Покажите (используя необходимое условие устойчивости), что одно-
контурная статическая система с положительной обратной связью и ПК
|£ | > 1 всегда неустойчива
5	Убедитесь (используя критерий Гурвица), что замкнутая система,
образованная из двух инерционных статических звеньев первого порядка,
устойчива при любых значениях общего ПК
6	Покажите с помощью критерия Гурвица, что предельное по условию
устойчивости значение ПК к системы, состоящей из идеального интегри-
рующего звена и двух одинаковых инерционных звеньев с постоянной вре-
мени Т\ = Т2 = Т, равно к^, = 2/Г Найдите предельное значение передаточ-
ного коэффициента для случая, когда Т} ф Т2
7	Сформулируйте критерий Михайлова Объясните, почему' характе-
ристическая кривая обязательно начинается на действительной оси Для
анализа каких систем (замкнутых или разомкнутых) можно использовать
критерий Михайлова?
301
8.	Докажите с помощью критерия Михайлова, что система второго по-
рядка, описываемая характеристическим уравнением
а2рг + а}р + ао =
(5.117)
устойчива при любых положительных значениях коэффициентов уравнения.
9.	Получите результат задания 6 с помощью критерия Михайлова. Ис-
пользуйте условие прохождения характеристической кривой через начало
координат: F(ja>) = 0.
10.	Сформулируйте критерий Найквиста для случая, когда разомкну-
тый контур системы устойчив. Дайте физическое объяснение особой роли
точки (-1; уО). В чем достоинства и недостатки критерия Найквиста?
11.	Определите с помощью критерия Найквиста, при каких значениях
коэффициента к устойчива замкнутая система, разомкнутый контур которой
представляет собой неустойчивое звено первого порядка
№(р) = к/(Тр - 1) = 0.
(5.118)
Используйте для этого понятие «полуохват».
12.	Покажите с помощью критерия Найквиста, что в замкнутой систе-
ме, состоящей из идеального интегрирующего звена
№(р) = к/р
и звена запаздывания
Щр) = е~р',
(5.119)
(5.120)
предельные (критические) значения запаздывания и передаточного коэффи-
циента связаны соотношением
т = 2п/к.
(5.121)
Используйте для этого условие (5.52).
13.	Объясните, почему при построении областей устойчивости методом
D-разбиения в характеристическом уравнении делается подстановка р = jcn.
14.	Найдите методом D-разбиения допустимый диапазон изменения
передаточного коэффициента системы, рассмотренной в задании 6.
15.	Для системы, состоящей из ПИ-регулятора и инерционного объекта
второго порядка с двумя одинаковыми постоянными времени Di = То2, по-
стройте область устойчивости в плоскости настроечных параметров кп и кК.
302
16.	Какие типовые динамические звенья ухудшают структурную устой-
чивость одноконтурных систем и какие улучшают ее?
17.	Как влияет общий ПК разомкнутого контура системы на ее устой-
чивость в замкнутом состоянии?
18.	Покажите, что в замкнутой системе, состоящей из п одинаковых
инерционных звеньев первого порядка с Tt = Т, предельное по условию ус-
тойчивости значение общего ПК разомкнутого контура не зависит от посто-
янной времени Т и
А’пР =fvtg2(7r/«) + 1 I
Используйте условия прохождения АФХ разомкнутого контура через
точку (-Г.;0), т. е. условия (5.52).
303
Глава 6. ОЦЕНКА КАЧЕСТВА УПРАВЛЕНИЯ
6.1. Понятие и показатели качества управления
Понятие качества управления Качество СУ определяется со-
вокупностью свойств, обеспечивающих эффективное функциониро-
вание как самого ОУ, так и управляющего устройства, т е всей СУ в
целом Свойства, составляющие эту совокупность и имеющие коли-
чественные измерители, называют показателями качества системы
управления
Качество СУ, как и любого технического устройства, может
быть оценено такими общепринятыми показателями, как вес систе-
мы, ее габариты, стоимость, надежность, долговечность и т п Сово-
купность этих общетехнических показателей характеризует качество
СУ в широком смысле
В теории управления и в практике автоматизации термины «ка-
чество системы», «качество управления» используют, как правило, в
более узком смысле рассматривают только статические и динамиче-
ские свойства системы Эти свойства предопределяют точность под-
держания управляемой величины (выходной величины объекта) на
заданном уровне в установившихся и переходных режимах, т е
обеспечивают эффективность процесса управления Для
такого, более узкого, понятия качества СУ, охватывающего только ее
статические и динамические свойства, применяют термин «качество
управления», а сами свойства системы, выраженные в количествен-
ной форме, называют показателями качества управления
Точность системы в установившихся режимах как одна из важ-
нейших характеристик качества управления была рассмотрена от-
дельно, в главе 4 В настоящей главе будут рассмотрены показатели
качества, характеризующие точность системы в переходных режи-
мах
Точность системы в переходных режимах оценивают при по-
мощи прямых и косвенных показателей Прямые показатели опреде-
ли
ляют по графику переходного процесса, возникающего в системе при
ступенчатом внешнем воздействии Косвенные показатели качества
определяют по распределению корней характеристического уравне-
ния или по частотным характеристикам системы
К особой категории качества относятся так называемые инте-
гральные оценки, которые вычисляют либо непосредственно по пере-
ходной функции системы, либо по коэффициентам ПФ системы
Подробно эти оценки будут рассмотрены в 6 3
Точность системы в переходных режимах определяется величи-
ной отклонений управляемой переменной x(t) от заданного значения
x3(f) и длительностью существования этих отклонений Величина и
длительность отклонений зависят от характера переходного процесса
в системе Характер переходного процесса, в свою очередь, зависит
как от свойств системы, так и от места приложения внешнего воздей-
ствия
При самой общей оценке качества обращают внимание прежде
всего на форму переходного процесса Различают следующие ти-
повые переходные процессы (рис 6 1,а,б) колеба-
тельный (линия У), монотонный (линия 2) и апериодический (линия
3)
Рис 6 1 Типовые переходные процессы
а - по заданию, б - по возмущению
Каждый из трех типовых процессов имеет свои преимущества и
недостатки, и предпочтение той или иной форме процесса делают с
учетом особенностей ОУ Так, например, в электромеханических
объектах со сложными кинематическими передачами (прокатные
305
станы, экскаваторы, подъемные установки) нежелательны резкие
знакопеременные усилия, и поэтому при выборе настроек СУ такими
объектами стремятся к апериодическим и монотонным процессам. В
СУ технологическими процессами и аппаратами большой емкости
допустимы колебательные переходные процессы, т. к. кратковремен-
ные отклонения управляемых величин не нарушают, как правило,
нормальный режим работы аппарата и не ухудшают существенно
показатели процесса.
Рассмотрим основные показатели качества управления приме-
нительно к типовой одноконтурной системе регулирования, описан-
ной в 4.3 (см. рис. 4.7,0.
Прямые показатели. На рис. 6 2 приведены графики переход-
ных процессов, вызванных ступенчатым изменением задающего воз-
действия х3 (0 (а) и возмущения ув, действующего на входе объекта
(0 За начало отсчета для выходной величины x(t) принято значение
х(-0), которое было до подачи ступенчатого воздействия
Одним из главных прямых показателей качества является ко-
эффициент перерегулирования о, который равен отношению первого
максимального отклонения хм управляемой переменной х(/) от ее ус-
тановившегося значения х(со) к этому установившемуся значению
(см рис. 6.2,0:
а =	^°^100 = -4-100, %.	(6 1)
х(оо)	х(оо)
Качество процесса управления считается удовлетворительным,
если коэффициент перерегулирования не превышает 30-40 %
Для переходных процессов, вызванных возмущающим воздей-
ствием ув на входе объекта (см.рис. 6.2,0, коэффициент перерегули-
рования можно определять как отношение второго (отрицательного)
максимального отклонения Л2 к первому максимальному отклонению
di
а = —------100 =	100, % .	(6 2)
хм - х(оо) 4
306
a
Рис 6 2. Прямые показатели качества процесса управления
а - по каналу задания, б - по каналу возмущения
Показатель, вычисляемый по данной формуле для переходных
процессов по каналу возмущения, называют также колебательно-
стью
Другой важной характеристикой таких процессов служит дина-
мический коэффициент регулирования Ra, который равен отношению
первого максимального отклонения хм к отклонению выходной пере-
307
менной x(t) нерегулируемого объекта, вызванному тем же возмуще-
нием, т. е.
R =^-100,%.
Д к0
(6.3)
Коэффициент показывает, насколько эффективно компенси-
рующее действие регулятора на объект.
Отметим, что и само первое максимальное отклонение хм, воз-
никающее от возмущения на входе объекта, является показателем
качества. При формировании требований к системе указывают до-
пустимое значение максимального отклонения (непосредственно в
единицах измерения управляемой величины).
Длительность существования динамических отклонений управ-
ляемой величины x(t) от ее нового установившегося значения х(оо)
принято оценивать с помощью нескольких характерных моментов
времени Самым важным из этой группы показателей является дли-
тельность переходного процесса tn - интервал времени от момента
приложения ступенчатого воздействия до момента, после которого
отклонения управляемой величины x(t) от ее нового установившегося
значения х(оо) становятся меньше некоторого заданного числа 5П, т. е.
до момента, после которого выполняется условие )х(/) - х(оо)| < 5П.
В промышленной автоматике величину 5П принимают обычно
равной 5 % от установившегося значения х(оо), т. е. 5П = 0,05 х(оо).
При оценке длительности переходных процессов, вызванных еди-
ничным возмущающим воздействием ув на входе объекта (см.рис.
6 2,6), величину 5П можно принимать равной 5 % от значения ПК
объекта к0, т. е. 6П = 0,05 к0, а для процессов, вызванных воздействи-
ем хв на выходе объекта,— 5 % от начального отклонения х(+0), т. е.
Sn = 0,05 х(+0).
Дополнительными временными показателями качества являют-
ся (см.рис. 6.2,ц): время нарастания ta, время достижения первого
максимума /м и период затухающих колебаний Т3. Эти показатели
вместе с ta характеризуют быстродействие системы регулирования
308
Прямым показателем качества служит также степень затухания
V — (А ~ ^з)/Д -1 “ /Д >
(6.4)
где Л] и Аз - соседние максимальные отклонения (амплитуды) одного
знака (см.рис. 6.2,6). Интенсивность затухания колебаний в системе
считается удовлетворительной, если ц/ = 0,75-0,95.
Колебательность системы можно оценивать, наряду с показате-
лями сиу, числом переходов N величины x(t) через установившееся
значение х(оо) на интервале tn.
Три главных
показателя качества
- коэффициент пе-
ререгулирования а,
первое максималь-
ное отклонение хм и
длительность tn -
тесно связаны меж-
ду собой. Они зави-
сят от всех пара-
метров системы, но
наиболее сильно -
от ПК разомкнутого
контура Причем с
увеличением этого
коэффициента мак-
Рис 6.3. Влияние ПК разомкнутого контура
на показатели переходного процесса
симальное отклонение по каналу возмущения всегда уменьшается, а
перерегулирование и длительность переходного процесса, как прави-
ло, увеличиваются (рис. 6.3). Отыскание наилучшего компромисса
между этими двумя противоречивыми тенденциями является одной
из основных задач синтеза систем управления.
Рассмотренные прямые показатели качества удобно использо-
вать в тех случаях, когда график переходного процесса x(t) можно
получить экспериментально - в реальной системе регулирования или
путем моделирования системы на ЭВМ. Если же такой возможности
309
нет или она связана с определенными трудностями решения или мо-
делирования дифференциальных уравнений высокого порядка, то
пользуются косвенными показателями качества, которые вычисляют-
ся без построения графика переходного процесса, по коэффициентам
уравнения или по частотным характеристикам системы.
Частотные показатели. Наиболее важными и одновременно
удобными косвенными показателями являются частотные показате-
ли, которые определяются по частотным характеристикам замкнуто-
го и разомкнутого контура СУ.
По амплитудной частотной характеристике А (о) замкнутой сис-
темы по основному каналу х3 - х (рис. 6.4) оценивают частотный
показатель колебательности М, равный отношению максимума Ам
характеристики к ее начальному значению Л(0):
|	M=AJA(0).	(6.5)
Чем больше это отношение, тем сильнее колебательность систе-
мы (тем больше перерегулирование о) и, как следствие, больше дли-
тельность переходного процесса tn. Качество системы считается
обычно удовлетворительным, если показатель М находится в преде-
лах 1,1-1,5.
Для оценки качества многомерной СУ, характеризуемой мат-
ричной ПФ Ф(усо), используют так называемую //«-норму или норму
310
АФХ в пространстве Харди (Hardy), которая применительно к одно-
мерной СУ соответствует максимуму АФХ:
ЦФО^Ь = тах|Ф(»|,
(6.6)
а применительно к многомерной СУ - наибольшему значению среди
всех одиночных значений максимумов матрицы {Ф^(уа>)}:
||Ф( J<»)L = supmax^ Ф«(»
kJ m I со
(6.7)
Естественно, что при пользовании этим показателем качества
стремятся выбором РКУ (/со) обеспечить минимум нормы (6.7).
Косвенными частотными показателями быстродействия систе-
мы служат характерные частоты (см.рис. 6.4): резонансная частота
Юр, частота незатухающих колебаний соо ~ ®Р и частота пропуска-
ния со„ х Зюо-
Рис. 6.5. Запасы устойчивости системы
По АФХ РК(/со) разомкнутого контура (рис. 6.5,а) определяют
запас устойчивости по амплитуде
311
дл = |1-ЖО1,
(6 8)
и запас устойчивости по фазе
Аф = к - |ф((Оср)|,	(6 9)
которые вместе характеризуют удаленность кривой от крити-
ческой точки (-1, jO) При проектировании систем обычно задаются
запасом по амплитуде АЛ > 0,5-0,6 и по фазе Аф > 30-60° При этом
обеспечивается, как правило, и удовлетворительное качество процес-
са управления
Запасы устойчивости необходимо принимать в связи с тем, что
некоторые параметры ОУ могут произвольно изменяться в процессе
работы системы Например, постоянные времени электрических ма-
шин экскаваторного привода из-за изменения температуры окру-
жающего воздуха могут существенно отклоняться от своих номи-
нальных (расчетных) значений Расхождения между фактическими
значениями параметров объекта и значениями, при которых выпол-
няется анализ устойчивости системы, могут иметь место и по другим
причинам Так, при математическом описании объекта применяется
определенная идеализация — отбрасываются второстепенные факто-
ры Погрешности возникают также при экспериментальном опреде-
лении и при линеаризации характеристик объекта
При решении задач синтеза систем (см главу 7) запасы устой-
чивости удобней задавать в логарифмических координатах (рис
6 5,6) В этом случае запас устойчивости по амплитуде определяют
по выражению
AL = 2O|lg^(con)|	(6 10)
Указанным выше значениям АЛ соответствует Л/, > 6-8 дБ
Корневые показатели Для косвенной оценки качества управ-
ления используют также корневые показатели, определяемые по
расположению корней р2,	, рп характеристического уравнения
замкнутой системы
312
a^pn + an{pn] + +аа = 0	(6 11)
на комплексной плоскости (рис 6 6,а)
Рис 6 6 Корневые показатели качества
Наиболее общим корневым показателем качества является сред-
нее геометрическое значение модулей корней
“о = +V|p1;,2 Р„|.
(6 12)
которое легко вычисляется через крайние коэффициенты характери-
стического уравнения
“о = +V°o ia«
(6 13)
Среднегеометрический корень «о определяет на действительной
оси комплексной плоскости а - /J3 (рис 6 6,а) точку, являющуюся
геометрическим центром всех корней характеристического уравне-
ния Величина осо имеет размерность с-1 и служит обобщенной мерой
быстродействия системы чем меньше показатель Оо, тем ближе «со-
звездие» корней к мнимой оси и тем больше длительность переход-
ного процесса
Для колебательной системы второго порядка, рассматриваемой
в 6 2, показатель Оо равен частоте незатухающих колебаний
313
Обратим внимание, что в числитель подкоренного выражения в
формуле (6.13) входит коэффициент а0, который зависит от ПК к
разомкнутого контура: у статических систем а0= 1 + к, у астатиче-
ских - а0 - к. Отсюда можно сделать вывод: чем больше коэффици-
ент к, тем лучше быстродействие системы (при прочих равных усло-
виях — одинаковой конфигурации «созвездия» корней).
Основное влияние на характер переходного процесса оказывают
корни, расположенные ближе к мнимой оси. Эти корни дают наибо-
лее длительные составляющие переходного процесса и называются
доминирующими.
Расстояние от мнимой оси до ближайшего к ней корня называ-
ется степенью устойчивости Т|. Если ближайший корень действи-
тельный (на рис. 6.6,а корень р\), то доминирующей составляющей
переходного процесса будет экспонента с показателем степени
А=-ц:
= С^,
(6.14)
если же ближайшими к мнимой оси являются два сопряженных ком-
плексных корня, то доминирующей будет одна колебательная со-
ставляющая, которая затухает также по экспоненциальной состав-
ляющей (6.14). В обоих случаях длительность переходного процесса
(для 5П = 0,05 Ск) определяется приближенной формулой
Гп^З/ц,
(6.15)
где знак равенства относится к случаю действительного домини-
рующего корня, а знак неравенства — к случаю комплексных доми-
нирующих корней.
При выборе настроечных параметров регулятора всегда стре-
мятся скомпенсировать (исключить из уравнения) доминирующие
(наименьшие корни), которым соответствуют наибольшие постоян-
ные времени объекта, и тем самым улучшить быстродействие систе-
мы.
Колебательные свойства СУ предопределяет та к-я пара ком-
плексных корней рк = (Хк ± jPk, у которой наибольшее отношение
314
|p*r |/ |at |
(6.16)
или наибольший угол & между двумя симметричными лучами
(см.рис. 6.6,а). На рис. 6.6,а такой парой, предопределяющей доми-
нирующую колебательную составляющую переходного процесса,
являются комплексные корни р\ и рз.
Отношение цд мнимой части 0 к действительной части а доми-
нирующей пары комплексных сопряженных корней называют сте-
пенью колебательности.
В практических расчетах чаще используют так называемый
корневой показатель колебательности
тд = ак/$к = 1/рь	(6.17)
также определяемый через доминирующую пару комплексных кор-
ней. При выборе настроек регуляторов стремятся получить значения
т = 0,2-0,5.
Специальными математическими исследованиями установлено,
что в системе любого порядка наиболее быстрый апериодический
переходный процесс имеет место, когда все п корней равны между
собой. Максимальное быстродействие системы достигается при не-
большой колебательности (ст < 10 %). Для этого все комплексные
корни (и один действительный при п нечетном) должны распола-
гаться на одинаковом расстоянии г| от мнимой оси, а мнимые части
должны образовать арифметическую прогрессию с разностью
Д0 = р). Причем для каждого порядка уравнения существует опти-
мальное отношение Др/q: для второго порядка оно равно 1,00, для
третьего - 1,45, четвертого - 0,79, пятого - 1,50.
Рекомендации по выбору коэффициентов характеристического
уравнения, соответствующих различным требованиям к переходному
процессу, приводятся в 7.3.
Определение показателей ц и ц по уравнению с известными ко-
эффициентами является в общем случае такой же трудоемкой зада-
чей, как и отыскание самих корней. Легче решается обратная задача
- определение коэффициентов уравнения и параметров системы, при
315
которых все корни лежат в области с заданной степенью устойчиво-
сти (рис. 6.6,6) или колебательности (рис. 6.6,в). Для этого может
быть использован изложенный в главе 5 метод Р-разбиения. Только
вместо обычной замены р = у© в характеристическом уравнении не-
обходимо сделать подстановку р = -г] + J© или р- - (|©|/ц) + у©, где
т] и ц - заданные числа.
Выполняя далее все обычные процедуры метода £)-разбиения,
можно получить области заданной степени устойчивости и колеба-
тельности в пространстве варьируемых коэффициентов и параметров
системы.
Корневые показатели Оо, г], цд и тид важны для понимания про-
блемы качества и ее связи с проблемой устойчивости, но использу-
ются реже других, т.к. их непосредственное определение для кон-
кретной системы высокого порядка (« > 3) представляет собой слож-
ную вычислительную задачу.
Влияние распределения корней на ха-
рактер переходного процесса и на устойчивость
хорошо иллюстрирует диаграмма, построенная И. А. Вышнеград-
ским для нормированного характеристического уравнения третьего
порядка
р3 + Я2р2 + 4р + 1 = 0.	(6.18)
Область устойчивости в плоскости параметров А] и А2 (рис. 6.7)
состоит из трех областей, соответствующих различному распределе-
нию корней. Область I, ограниченная линией abc, соответствует трем
действительным (и не равным друг другу) корням и апериодическо-
му переходному процессу. Область II, ограниченная линией abd,
соответствует паре комплексных корней и одному действительному
корню, причем действительный корень ближе к мнимой оси, чем
комплексные. Переходный процесс в этом случае монотонный. В
области III, заключенной между границей устойчивости и линией
abc, тоже пара комплексных корней и один действительный, но к
мнимой оси ближе расположены комплексные корни. Переходный
процесс колебательный.
316
На диаграмме показано также распределение корней для разгра-
ничительных линий. В точке Ь, где Ai =А2 = 3, все три корня дейст-
вительные и равные друг другу.
В заключение отметим, что при наличии нулей ПФ замкнутой
системы оценка качества только по ее полюсам (корням характери-
стического уравнения) мо-
жет привести к существен-
ным ошибкам. Наличие
нулей способствует увели-
чению перерегулирования
и уменьшению длительно-
сти переходного процесса
Существуют и другие
показатели процесса
управления - например,
такие, как чувствитель-
ность, наблюдаемость и
управляемость, которые
будут изложены в 6.4 и 6.5.
В 6.6 будут изложены
основные приемы аналого- рис 57 Диаграмма Вышнеградского
вого и цифрового модели-
рования непрерывных линейных систем, которые используются для
получения переходных характеристик h(t) и прямой оценки качества.
6.2. Приближенная оценка качества
по частотным характеристикам
Исходные соотношения. Возможности оценки качества по час-
тотным характеристикам основаны на существовании однозначной
связи между временными и спектральными характеристиками сиг-
налов, которая выражается обратным и прямым преобразованиями
Фурье (2.30) и (3.31).
Воспользуемся преобразованием (2 30) и найдем связь переход-
ной функции h(t) замкнутой СУ с ее АФХ Ф(/<а). Изображение по
317
Фурье Х(/(о) входного сигнала x(t) согласно (2 129) равно произведе-
нию
Ф(7®),
(6.19)
где Х(/ю) - изображение задающего воздействия х3(Г) произвольного
вида Изображение единичного ступенчатого воздействия x3(f) = c(t)
можно получить как частный случай изображения (2.40) экспонен-
циального импульса (2.39) при хи = 1 и а= 0: Х3{/а) = 1/ja Тогда
x(t) = h(t) =
2л 1 jo)
ОО
(6 20)

Вычисление ПХ h(t) по формуле (6 20) достаточно громоздко и
трудоемко, поэтому ее стремятся получить путем аналогового или
цифрового моделирования системы (см 6 6).
Приближенную оценку прямых показателей качества ст и tn (без
вычисления и построения переходной характеристики) удобно осу-
ществлять на основе гипотезы об эквивалентности динамических
свойств замкнутой СУ свойствам колебательного звена второго по-
рядка (см 3 4). Рассмотрим подробнее сущность этой гипотезы и
методику оценки показателей качества реальной системы через па-
раметры ее упрощенной колебательной модели.
Связь показателей качества с параметрами приближенной
модели. Простейшей моделью, пригодной для приближенного опи-
сания динамики одноконтурной системы и приближенной оценки
показателей качества процесса управления по основному каналу
Хз - х, может служить инерционное звено второго порядка
>Мр) = kl(T2p- + 2к,Тр + 1),
(6.21)
обладающее колебательными свойствами (коэффициент демпфиро-
вания < 0,7) и передаточным коэффициентом к, равным (для аста-
тической системы) или близким (для статической) единице Прибли-
женная замена реальной СУ, у которой АЧХ |Фс(/со)| имеет, как пра-
вило, характерный резонансный пик при частоте о)р (см рис 6 4,(7),
318
заключается в подборе параметров Т и 4 модели (6.19) таким обра-
зом, чтобы обеспечить в существенном диапазоне частот 0 < о < 2а>р
наиболее близкое совпадение АЧХ системы и ее модели, т. е. чтобы
|Фс(Ло)Ы^м(7(о)|.
(6 22)
При этом обычно достаточно обеспечить совпадение трех пара-
метров АЧХ' начальных значений [Фс(/0)[ » [1Тм(/0)[, резонансных
частот о)рС ~ о)рм и максимальных значений |Фс(/сор)| « |И/м(/сор)|, опре-
деляющих, как известно, частотный показатель колебательности М
(см. формулу (6.5)).
Очевидно, что при адекватности (6.22) частотных характеристик
будут близки друг другу и переходные характеристики реальной сис-
темы и ее приближенной модели:
ад «
(6 23)
С помощью модели (6 21) удается реальный контур регулирова-
ния, представляющий собой в общем случае сложную динамическую
систему высокого порядка, описать достаточно простыми формула-
ми Так, АЧХ замкнутого контура
Л(<о) = |Фс(/<о)[ «Л„(й) = l/Vd-rW)2 + 44TW,	(624)
а переходная функция (см формулу (3.56))
h(t) * hu(t) = [1-—-e-atsm(pf + ф)]о(Х)
(6.25)
частота затухающих
колебаний;
со0 =---частота незатухающих колебаний; a = НД’ - коэффициент
затухания, (р = arctg (р/а).
319
В выражения (6.24) и (6.25) входят лишь два числовых парамет-
ра Т и которые связаны с частотами незатухающих (о0), затухаю-
щих (о3) и резонансных (сор) колебаний и с частотным показателем
колебательностиМизвестными соотношениями (см. 3.4):
со0 = 1/7-; <о,=7Г¥/Л	= ф - 2^/т;	(6.26)
M = A(af)/A(0) = l/2^>l^.	(6.27)
По модельной переходной характеристике (6.25) можно полу-
чить аналитическое выражение для двух главных показателей каче-
ства:
коэффициента перерегулирования
о = е^^100,%
(6.28)
и длительности переходного процесса (при 5 %-ной зоне)
tn < Лп 20Д « 3T/Z, .
(6.29)
Зависимости важнейших частотных и временных показателей
качества от коэффициента демпфирования показаны на рис. 6.8. В
диапазоне реальных (часто используемых на практике) значений
0,25 <£>< 0,55, которым соответствуют показатели колебательности
2,1 > М > 1,1, эти зависимости могут быть с точностью, достаточной
для практических задач, аппроксимированы следующими простыми
выражениями:
а «Ю/fc Гп«ЗГ/§;
М«0,545Д; ар/ш, «1,2 - £./
(6.30)
320
С помощью приближенных формул (6.30) можно динамические
показатели качества замкнутой системы выразить через параметры ее
разомкнутого контура.
Зависимости пока-
зателей качества от па-
раметров разомкнутого
контура. Так как при
синтезе систем регулиро-
вания всегда стремятся
показатели замкнутой
системы оценивать по
характеристикам ее ра-
зомкнутого контура, ко-
торые более просты и
непосредственно выби-
раются разработчиком, то
для модели (6.21) замкну-
той системы желательно
Рис 6.8. Зависимости показателей каче-
ства от коэффициента демпфирования
найти соответствующую модель разомкнутого контура Нетрудно
убедиться, что простейшим разомкнутым контуром, который при
замыкании образует колебательное звено (6.21), является реальное
интегрирующее звено
^pK(^) = Woi^+l)
(6 31)
Действительно, ПФ замкнутой системы, изображенной на рис
6.9,о, по основному каналу
jMfL = а- =	1
1 + ^рк(Р) Т0}р2+р + к Т*\ р2+ Х р+\
к к
(6 32)
где к ~ ПК разомкнутого контура; Toi - постоянная времени инерци-
онного звена контура (обычно объекта).
321
Очевидно, что модель (6.32) замкнутой системы по каналу зада-
ния будет эквивалентна колебательному звену (6.21), если параметры
разомкнутого контура связаны с параметрами этого звена следую-
щими соотношениями:
или
Тофк = Т\ \/к = 2^Т
кТ0^\№- То1=Т/2^.
(6.33)
(6.34)
Параметры Т и колебательной модели (6.21) замкнутой СУ
можно выразить в явном виде через параметры к и То\ разомкнутого
контура системы.
г=1/Шо=^7ёл=1/2#лГ-
(6.35)
Из формул (6.35) вытекают следующие общие законо-
мерности:
1. Частота а)0 собственных незатухающих колебаний замкну-
той системы, равная 1/Т и характеризующая инерционность
системы, тем больше, чем больше общий передаточный коэф-
фициент к разомкнутого контура и чем больше его постоянная
времени.
2. Колебательность замкнутой системы, характеризуемая ве-
личиной //£ тем сильней, чем больше произведение передаточ-
ного коэффициента к и постоянной времени То1 разомкнутого
контура.
При выполнении соотношений (6.33), (6.34) и (6.35) ПФ замкну-
той системы (рис 6.9,а) по каналу хв - х имеет вид
1	=	= _тЩщуГр_
1 + И$к(Р) Т^р'+р + к Тг р1 +2фр + Г
(6.36)
соответствующая ей АЧХ
322
Д,,(ш) =	+ 4^7’W/^(l-PW)1 +4^Гг<02 .	(6 37)
Типичная форма амплитудных характеристик (6.24) и (6.37) по
каналам задания и возмущения показана на рис. 6.9,б,в. Обратим
внимание на то, что резонансный пик у характеристики Лмв(со) все-
гда больше, чем у Лм(со), и частота сорв > сор.
Рис. 6.9. Алгоритмическая структура (а) и частотные характеристики (б, в)
приближенной модели колебательной СУ
Проанализируем связь между частотными характеристиками
замкнутой системы и ее разомкнутого контура. Передаточной функ-
ции (6.31) соответствует амплитудная характеристика
и фазовая
Ч>р K(<o) = -y-arctg7’ol<o.
Лн*
(6.38)
(6 39)
323
Выразим с помощью соотношений (6 33) и (6 34) параметры Т&
и к через Т и Тогда передаточная функция (6.31) и частотные
функции (6 38) и (6 39) примут вид
И/рк(р)~ l/(T2p2 + 2^7р);	(640)
Лр,(®) = 1/г®^Г2ш2 + 4?2 ,	(641)
<ррк(ш) = -^ -arctg(7m/2^)	(6 42)
Рис 6 10 Амплитудная (д) и фазовая (б) частотные характеристики
разомкнутого контура модели (631)
На рис 6 10 показаны характеристики (6 41) и (6 42) как функ-
ции относительной (безразмерной) частоты □ = со Г = со/со0, где
324
coo = ИТ - частота собственных незатухающих колебаний замкнутой
системы (при % - 0).
Используя известное условие ЯрК(со ) = 1 (см. 5.4), можно из
(6.41) получить следующее выражение для относительной частоты
среза:
Пср=О)ср7- = А/71 + 4^4 -2V .	(6.43)
Для реальных значений 0,25 < < 0,55
« 7l - 2V /г = шр,
(6.44)
т. е. частота среза разомкнутого контура приблизительно равна
резонансной частоте замкнутой системы.
Подставляя приближенное значение частоты среза (6 44) в фор-
мулу фазовой характеристики (6.42), можно установить связь между
запасом устойчивости по фазе Дер (рад) и коэффициентом демпфиро-
вания %:
5 « O^tgAtp/^l + 0,5(tgA<p)2 .	(6.45)
Относительную частоту среза со 7’ = со /со0 также можно вы-
разить через запас устойчивости по фазе
T<av = 1Д/1+ 0,5(tgA<p)2 .
(6.46)
В рассматриваемом диапазоне значений эти зависимости
можно линеаризовать и представить в удобной для практических
расчетов форме:
£ « 0,5 Дер; Т ~ (1,2 - 0,5Дф)/соср.
(6.47)
325
Таким образом, с помощью формул (6.47) удается параметры 2,
и Т колебательной модели (6.21) замкнутой системы определить че-
рез обобщенные параметры ®ср и Л(р частотной характеристики ра-
зомкнутого контура, форма и положение которой выбираются при
решении задачи синтеза (см. главу 7).
Формулы для приближенной оценки показателей качества
системы Объединяя теперь зависимости (6.30), (6.35) и (6.47), полу-
чим следующие простые формулы для приближенной оценки показа-
телей качества системы регулирования по известным (заданным или
выбираемым) параметрам ее разомкнутого контура:
а «0,27^7
Л “67;,;
а « 0,2/Дф;
(7"2	/
7~-3 /шсрЛ
Дф	) /
М ъ 1,1/Дф.
(6 48)
Аналогично можно получить формулы для частоты среза и пе-
риода затухающих колебаний:
«ср « «р ;
Л =	« 2дГ01 /^Го1 -0,25 .
(6.49)
Формулы (6.48) и (6.49) обеспечивают достаточную для инже-
нерных расчетов точность в диапазоне 30° < Дер < 60°, который соот-
ветствует значениям 0,25 < £ < 0,55.
Грубую оценку длительности переходного процесса можно дать
только по частоте среза'
/п«(7 Ю)/щср .
(6 50)
В заключение укажем, как следует определять базовые парамет-
ры к и Z'oi приближенной модели (6.31) в тех случаях, когда разомк-
326
нутый контур реальной системы имеет более сложную ПФ, чем
(6 31) Например, если реальная система астатическая с ПФ
Ws,,(p) = ktk2..kJp(T}p + \)(T2p + i) .(Г„р + 1),	(651)
где Т] >Т2>.. > Тп, то базовые параметры
п
к = кхк2..кп и Т01=ЕТ,.
1-1
(6.52)
то
Если же реальная система статическая с ПФ
И/р«(Р) = ^^..Л„/(ЛР + 1)(Лр + 1)...(Г„р + 1),
,	и
к = k\k2..kjl\ и Tai = YT,.
1=2
(6 53)
(6 54)
В более сложных случаях, когда числитель WpK(p) представляет
собой полином от р, то пользоваться моделями (6 31), (6.21) и соот-
ветствующими им формулами (6 48), (6 49) можно лишь с опреде-
ленной осторожностью.
Пример. Оценим приближенно показатели качества статической сис-
темы регулирования с передаточной функцией разомкнутого контура
^«(^ = ^«/(^ + 1X^+1) (Лр+В,
где крк = 8; 1\ = 10 с; Т2= 1,5 с; Т3 = 0,5 с.
Определим параметры упрощенной модели (6.31).
к = к9К / Тх = 0,8, Го1 = Т2 + Т2 = 2 с.
(6 56)
В соответствии с (6.35) параметр £ модели (6 21)
£ =	= 1/2^0,8-2 = 0.4.
(6.57)
327
он находится в пределах 0,25 < £ < 0,55, для которых справедливы приме-
няемые ниже приближенные формулы
Согласно (6 48), коэффициент перерегулирования
о « 0,2^кТ^ = 0,2д/0.8 2 = 0,25 = 25 %,	(6 58)
длительность переходного процесса
Zn«67;,|=6-2= 12с,	(6 59)
показатель колебательности
М « 1,17^7 = 1Д V°>8 2 = t375	(6 60)
6.3.	Интегральные показатели качества
Каждый из рассмотренных выше прямых и косвенных показате-
лей качества характеризует лишь одно какое-либо свойство системы,
лишь один признак переходного процесса или частотной характери-
стики Причем все показатели связаны с настроечными параметрами
регулятора сложными зависимостями, имеющими, как правило, про-
тиворечивый характер изменение параметра приводит к улучшению
одних показателей качества и к ухудшению других Это обстоятель-
ство существенно затрудняет выбор параметров регулятора Поэтому
в инженерной практике широко используются интегральные показа-
тели или оценки качества
Интегральные оценки представляют собой определенные ин-
тегралы по времени (в пределах от 0 до оо) от некоторой функции
управляемой переменной x(t) (или сигнала ошибки е(7))
Q = IfaWMdt
о
(6 61)
Подынтегральная функция f0 выбирается таким образом, чтобы
интеграл (6 61) лучше характеризовал качество системы и проще
328
выражался через коэффициенты передаточной функции замкнутой
системы Чтобы интеграл был сходящимся, в функцию вводят не
абсолютные значения x(t) или е(/), а их отклонения от конечных,
установившихся значений
Простейшей интегральной оценкой является линейная инте-
гральная оценка
00
2Л =
о
(6 62)
которая равна площади, заключенной между прямой х(оо) и кривой
переходного процесса x(t) (рис 6 11,о) Интегральная оценка (6 62)
учитывает как величину динамических отклонений, так и длитель-
ность их существования Поэтому чем меньше оценка, тем лучше
качество процесса управления
Рис 6 11 Интегральные оценки качества
Разность под знаком (6 60) равна динамической или переходной
составляющей сигнала ошибки
329
х(со) - x(t) = х3 - Е(со) - х(/) = е(Г) - £(со) = 8П(Г),
(6 63)
поэтому интегральную оценку (6 62) чаще определяют в таком виде
Сл = J £п = /1£(0 “ e(oo)]43fr	(6 64)
о	о
Интеграл (6 64) соответствует площади под кривой переходной
составляющей сигнала ошибки, вызванной изменением задающего
воздействия (рис 6 11,а) или возмущающего воздействия (рис
6 11,6) Площадь под кривой еп(0 будет тем меньше, чем быстрее
заканчивается переходный процесс и чем меньше отклонения сигна-
ла от х3 Поэтому настроечные параметры регулятора необходимо
выбирать таким образом, чтобы интегральная оценка была мини-
мальна
Недостатком линейной интегральной оценки Qn является то, что
ее можно применять лишь для заведомо неколебательных, апериоди-
ческих переходных процессов Действительно, из рис 6 11,в ясно,
что интеграл (6 64), вычисленный для знакопеременной кривой /,
будет существенно меньше интеграла, вычисленного для апериоди-
ческой кривой 2 (хотя качество переходного процесса 2 явно лучше)
В связи с этим для колебательных переходных процессов при-
меняют такие интегральные оценки, у которых знакопеременность
подынтегральной функции тем или иным способом устранена Таки-
ми оценками являются, например, модульная интегральная оценка
a = j|e„(o^	(6 65)
О
и ее модификация
QL =	(6 66)
О
Оценка (6 66) придает больший вес тем значениям сигнала
ошибки, которые имеют место в конце переходного процесса
330
Оценки (6 65) и (6 66) можно использовать только при исследо-
вании систем на моделях, т к их вычисление через коэффициенты
ПФ (без нахождения £п(/)) невозможно
При анализе и синтезе систем регулирования с колебательными
свойствами наиболее широко используется квадратичная инте-
гральная оценка
(6 67)
о
которая равна площади под кривой (/) (рис 6 11,г)
Квадратичная оценка (6 67) так же, как и линейная, учитывает и
величину и длительность отклонений Однако из-за возведения сиг-
нала £п(/‘) в квадрат первые (большие) отклонения приобретают в
конечном значении интеграла существенно больший вес, чем после-
дующие (малые) отклонения Поэтому минимальные значения оцен-
ки (6 67) всегда получаются у колебательных процессов с малым
затуханием
С целью устранения этого недостатка применяют так называе-
мую улучшенную квадратичную оценку
е;=1К(о+7^(ок
о
(6 68)
которая, кроме самих отклонений, учитывает с весовым коэффици-
ентом Т* производную отклонений Обычно весовой коэффициент
Т& выбирают равным желаемому времени нарастания /н или прини-
мают в пределах
г„/6<7\ </„/3,
(6 69)
где tn - желаемая длительность переходного процесса
Достоинством квадратичных оценок (6 67) и (6 68) является
возможность их вычисления без предварительного отыскания пере-
331
ходного процесса - непосредственно по коэффициентам передаточ-
ной функции замкнутой системы, записанной для сигнала ошибки в
следующей стандартной форме:
£(Р) = е(Р) =	±1	= ±bmpm + Ьт_1рт~х + ,., + Ь0
*3 (р) хв (р) 1 + Wp (p)W0 (р)	апрп + ап_{рп~х +... + а0 ’
(6.70)
где знак «плюс» перед дробью соответствует каналу х3 - е, а знак
«минус» - каналу хв - е.
Дня вычисления квадратичной ошибки (6.67) необходимо пред-
варительно найти изображение Еп(р) переходной составляющей ев(0
сигнала ошибки, которое при единичном ступенчатом воздействии
х3(0 или хв(0 равно
р
(6.71)
Далее изображение (6.71) записывают как отношение следую-
щих полиномов.
_ cQpn-1 +с{рп-2 + ... + сп_{ _ С(р)
d^p”+dlPn~l + ... + dn D(p)
(6.72)
Для вычисления квадратичной оценки (6.67) по изображению
(6.72) используют равенство Парсеваля (2.38), которое в данном слу-
чае имеет вид
2» =Ьп('И = — 1J
о	2ту -«о	2ту -«о
сем
D(jco)
2
(6.73)
332
Значения интеграла (6.73) для стандартных подынтегральных
выражений в виде отношения полиномов (6.72), степени которых
равны иип-1, удобно находить по следующей общей формуле:
=_L j teL(y(0)=JL j	=
2nj^\D(ja)\2	2лЛ|/)(ущ)|2	2<Д„
(6.74)
где
£>(» =	+ J.or1 +... +^(ущ)1 +dn-	I
Г(усо) = |С(усо)|2 = v0(yco)2('’"n +V1(yco)2('”2) +... + v„_2(yco)2 4-v^;.
(6.75)
dx d3 d5.......0
6?0 ^2 ^4......Q
................0
............d.-fi
..........d„ ,d„
П — L П
V0 Vi V2...........-v„-l
dj..........0
0 d, d,.................0
(676)
............^-.0
..........^n-2^n
Обращаем внимание на то, что для получения коэффициентов
полинома Г(усо) следует вначале найти квадрат модуля полинома
С(усо), а затем все слагаемые с четными степенями со привести к
виду с четными степенями (усо), поменяв при необходимости знаки
слагаемых.
Определитель Ли представляет собой старший определитель
Гурвица, и поэтому при приближении системы к границе устойчиво-
сти определитель Д п —> 0, а оценка (?кв —> оо.
333
Формулу (6.74) можно использовать и для вычисления улуч-
шенной оценки (6.68). Необходимо лишь интеграл (6.68) разбить на
два слагаемых, а изображение производной привести к виду (6.72).
Следует отметить, что абсолютные значения любой интеграль-
ной оценки сами по себе не представляют интереса. Они служат
лишь для сопоставления различных вариантов настройки одной и
той же системы.
Все рассмотренные интегральные показатели используют не
только для оценки качества, но и для определения опти-
мальных значений настроечных парамет-
ров системы. Оптимальными считают такие значения, кото-
рые соответствуют минимуму интегрального показателя
mm
(6 77)
Рис 6 12 Зависимость
интегральной оценки от
одного параметра СУ
Предположим, что необходимо
найти оптимальные значения ка-
ких-либо двух параметров (напри-
мер, kt и Ti), входящих в ПФ систе-
мы (6 70). Для этого надо с помо-
щью формулы (6.74) выразить по-
казатель Q как функцию парамет-
ров kiVtTr.
Q =Лк,, Tt),	(6.78)
а затем взять частные производные
и приравнять их к нулю:
8Q(k,, Tt )/дк, = 0;
8Q(k,, Т, )/5Т, = О?
(6 79)
Решая систему (6.79), можно найти искомые оптимальные зна-
чения к10пт и Thm. На рис. 6.12 показана зависимость интегральной
оценки О от одного параметра к,.
334
При сложном характере функции (6.78) задачу минимизации
решают численными методами.
Отметим, что в некоторых случаях функция Q(kt, Ti) может не
иметь минимума. Тогда варьируемые параметры выбирают по наи-
меньшему значению интегрального показателя Q внутри или на гра-
нице области, задаваемой из условий запаса устойчивости, точности
в установившемся режиме и др
Пример 1. Определим квадратичную интегральную оценку (6 67) для
системы регулирования, представленной в виде колебательной модели
(6.21), и найдем оптимальное соотношение между параметрами к и То} ра-
зомкнутого контура (6.31).
ПФ системы по каналу х3-х (см.рис. 6.8,а)
Фхз(р) = \/(Т2р2+2^Тр+^
(6 80)
где Т2 = ТоХ/к, 2ф - 1Д, $ = 1/27^
ПФ по каналу х3 - е
Фа(.р) = \-Фа(р) = (Т2р2 +1^Тр)/(Т2р2 + 2$Тр + Г)
(6 81)
Изображение переходной составляющей сигнала ошибки при единич-
ном ступенчатом воздействии
Еп (р) = - [Аз (Р) - Фа (0)] =
Р	Т2р2+2Е,Тр + 1 D(p)
(6 82)
где п = 2,с0 =d0 =Т2,сх = dx - 2^T,d2 =1
Для применения основной расчетной формулы (6.74) запишем изобра-
жение (6.82) в частотной форме и преобразуем полиномы числителя и зна-
менателя изображения к виду, соответствующему (6.75).
|Я„(;о>)|2 =
С(/а»|2 = |<М2 =
|«7<о)|2 Т^Ою)2+2УО<»)+12
335
(Г2(о)2+(2%Г)2
*	-	2
Г2(»2+2Щ»+1
-Г4(у(о)2 4-4^2Г2
Г2(»2 +2Щ/(о) + 12
(6.83)
Сравнивая последнюю запись полиномов £>(/со) и И(/со) с их общей
формой (6.75), видим, что в данном случае
и = 2, v0 =-Г4; v1=4^2r2,
d0=T2-, dx=2isT\ d2=l.
(6.84)
Определители (6.76), входящие в (6.74):
Д2 = dxd2 = 2$Т; Av2 =
VOV1
dod2
= vod2 - dov,- -T4 -
(6.85)
Согласно основной формуле (6.74), искомая интегральная оценка
е„ • (-о"4'
Д\ з-Г4-4£27’4 Т
----L_ = (-1)3--------ь-----=	+ —.
2d0 A 2	2Т “ 2tT	4^
(6.86)
Найдем оптимальное значение коэффициента демпфирования
32кв/^ = т-ж2 = о,
(6.87)
отсюда ^оГГГ = 0,5. Следовательно, оптимальное соотношение между пара-
метрами к и ТоХ имеет вид кТоХ = 2.
Пример 2. Определим теперь для системы, рассмотренной в примере
1, значение коэффициента соответствующее минимуму улучшенной инте-
гральной оценки (6.68).
Представим интеграл (6.68) как сумму двух интегралов:
а, =а +а=^юл+т’,2м2юл.
о	о
(6.88)
Значение интеграла Q\ получено в примере 1. Для вычисления второго
интеграла запишем изображение производной ё2(г):
336
^„(0} = pen(p)-s„(O) = pJ\P+^ -1 = -l/P'72 + ВД«1) (6.89)
Tlpl + 2£7> + l
или в частотной форме
кКа>Г
Г1(»2+2^7'(»+1
+1
Г2(»2 + 2§Т(» + 12
(6.90)
В данном примере
и = 2; dQ=T2', d[=2^T‘ d2=\; v0=O, v1=l;
А2 = dxd2 = 2^Т- Av2 = -rfovj = -Г2.
(6.91)
Применяя формулу (6.74), с учетом сомножителя Т2 получим
а=г,2/4<г.
(6.92)
Приравняем производную суммы интегралов к нулю:
отсюда
bm=G,5^+T2/T2.
(6.93)
(6.94)
При предварительно выбранном значении 7’в = Т, которое соответст-
вует желаемой длительности переходного процесса t„ я 37’, оптимальное
демпфирование ® 0,707, а оптимальное соотношение кТо\ » 0,5.
6.4.	Оценка чувствительности СУ
В предыдущих разделах при анализе точности устойчивости и
качества СУ предполагалось, что ПФ и значения параметров ОУ
остаются в процессе эксплуатации системы постоянными. Однако в
337
реальных промышленных условиях из-за ряда причин вариация на-
грузок на объект (изменение температуры, износ оборудования, ста-
рение изоляции и тп.), параметры системы скачкообразно или по-
степенно изменяются и их действительные значения почти всегда
отличаются от расчетных. Влияние вариаций параметров ОУ на ста-
тические и динамические свойства СУ называют параметрическими
возмущениями, а влияние изменчивости ее операторов - оператор-
ными возмущениями.
Изменения параметров и операторов СУ могут происходить с
разными скоростями по сравнению со скоростью протекания пере-
ходных процессов в СУ. Для задач анализа и синтеза СУ целесооб-
разно выделять изменения параметров, происходящие в течение од-
ного переходного процесса, и изменения, происходящие существенно
медленнее, в периоды между отдельными переходными процессами
Например, в СУ мостовым краном (см. 2.11) длина подвески груза I
может меняться в течение процесса управляемого перемещения те-
лежки крана, а величина груза тг может быть различной в каждом
последующем цикле «подъем - перемещение».
Изменения оператора (т.е. ПФ) ОУ происходят, как правило,
при его переключении с одного режима на другой или при сущест-
венном изменении условий его эксплуатации.
Вариации параметров и оператора ОУ можно учитывать как не-
стабильность его модели JV0M - как погрешности или отклонения Л№о
фактической ПФ объекта №о от расчетной модели. При этом приме-
няют две формы учета погрешности: аддитивную, при которой
^0(p)=^0M(p) + AaW0(p),	(6.95)
и мультипликативную
И;(р) = Woм (р) + AMW0(p)W0 м (р).	(6 96)
В теории чувствительности рассматривают изменения парамет-
ров и операторов, происходящие сравнительно медленно - в течение
не одного переходного процесса Более быстрые изменения и их
338
влияние на свойства СУ изучаются в специальной теории нестацио-
нарных систем
Чувствительность - это свойство системы изменять свои вы-
ходные координаты и показатели качества при отклонении того или
иного ее параметра от расчетного (номинального) значения. Для обо-
значения противоположного свойства пользуются термином гру-
бость Системы, сохраняющие свои свойства при значительных па-
раметрических или операторных возмущениях, называют грубыми,
или робастными.
Следует заметить, что общепризнанного четкого разграничения
между понятиями «нечувствительность» и «робастность» в настоя-
щее время не существует. Но в большинстве публикаций по пробле-
мам чувствительности и робастности под робастностью понимают
нечувствительность СУ к изменениям параметров ОУ, происходя-
щим в определенной ограниченной области. При этом робастная СУ
должна обладать показателями качества, входящими в заданную
область Например, корни характеристического уравнения робастной
СУ должны располагаться в области с заданной степенью колеба-
тельности (см.рис. 6.6,в) при изменениях некоторого параметра ОУ в
ограниченной области.
Далее будут рассматриваться лишь сравнительно простые прие-
мы оценки чувствительности СУ.
Количественными оценками чувствительности служат функции
и коэффициенты чувствительности Функция чувствительности
представляет собой частную производную какой-либо передаточной
характеристики (например, h(t), Ф(р)) или какого-либо показателя
качества (например, с, Л/) по изменяющемуся параметру к,. Напри-
мер, для передаточной функции Ф(р, kt), зависящей от параметра к,
функция чувствительности
.	(6.97)
*	1 ю
где к,0 - расчетное (исходное) значение параметра к.
339
Часто вместо функций чувствительности в виде отношения
дифференциалов (6.97) используют относительную функцию чувст-
вительности

дФ(р,кг) к,
dk, k_k Ф(р,к1)
to
(6.98)
Аналогично можно определить функции чувствительности и для
частотных характеристик. Для числовых показателей качества (о, М)
чувствительность оценивается при помощи коэффициентов чувстви-
тельности.
Функция чувствительности (6.97) приближенно определяет так
называемую дополнительную ПФ
Д4Ф(рЛ,)«5*(р)М,.
(6.99)
При ступенчатом координатном воздействии на систему допол-
нительная ПФ будет порождать дополнительное изменение (движе-
ние) выходной координаты
Л х(0 = S* (ОМ,,
(6.100)
(6.101)
где
х‘(о=[эй(гл,)Ж]л
i io
- функция чувствительности переходной характеристики по отноше-
нию к параметру к,.
Из выражения (6.100) следует:
чем меньше значения функции чувствительности (т.е. чем гру-
бее система), тем меньше дополнительное отклонение выход-
ной координаты и, следовательно, лучше качество системы.
340
Так как функция Sk в общем случае может быть комплексной
величиной, то, говоря об уменьшении или увеличении функции чув-
ствительности, имеют в виду уменьшение или увеличение ее модуля.
Одной из важных характеристик типовой системы, состоящей
из регулятора W? (р) и объекта Wo (р) - к0 W*(p) (см. 4.3), является
относительная функция чувствительности
S
ф
кО
(р) = [8Ф(р,к0)/Зк,]
к0
(6.102)
5
которая отражает влияние нестабильности ПК объекта к0 на ПФ
замкнутой системы Ф(р).
Если в (6.102) подставить функцию (4.48) типовой системы, то
получим выражение
1 + W (p)WQ (р) ’
г
(6.103)
которое означает.
-	относительная чувствительность типовой замкнутой СУ к
изменениям свойств объекта полностью определяется только
передаточной функцией разомкнутого контура;
-	обратная связь при достаточно большом усилении разомкну-
того контура обеспечивает не только инвариантность выход-
ного сигнала к координатным (сигнальным) возмущениям, но
одновременно ослабляет и влияние параметрических возмуще-
ний.
Заметим, что и в случае операторного возмущения (например,
изменения ПФ Wo(p)) относительная функция чувствительности
5* (/?) также имеет вид (6.103).
Относительная функция чувствительности является функцией
комплексной переменной р ~ у®, и к ней предъявляется обычно тре-
341
бование, чтобы ее модуль в существенном диапазоне частот оставал-
ся ограниченным:
S(>) <	(»'
5
или
1 + »;(;<О)И'1,(;(Я)>|и'1(7(о)|,
(6.104)
(6.105)
Рис. 6.13. Ограничения на относи-
тельную функцию чувствительности
где №](/&) - заданная функция.
Требование (6.105) означает, что АФХ разомкнутого контура
должна быть удалена от критической точки (- 1; уО) хотя бы на рас-
стояние (усо)|. Ограниче-
ния на модуль функции
У (у©) проиллюстрированы
на рис. 6.13. На нем выделе-
ны важные для оценки чув-
ствительности частоты (йн, йр
и сов.
Для дополнительных
приращений, обусловленных
чувствительностью линейной
СУ к параметрическим воз-
мущениям, справедлив прин-
цип суперпозиции. Так, если
передаточная функция зависит от нескольких изменяющихся пара-
метров, то дополнительная ПФ
Ш X
1=1
соответственно дополнительное движение
/Я Л
Дх(Г)« SS*(r)A*,.
1=1	'
(6.106)
(6.107)
342
Пример. Найдем для колебательной модели (6.21) и (6.31) соотноше-
ние между ее параметрами к и То\, при котором чувствительность показате-
ля колебательности М к изменениям коэффициента к отсутствует.
Показатель колебательности данной системы согласно формулам (6 27)
и (6.35)
М = 2кТоХ /^kTQX -1, (при АТо1 £ 0,5).
Коэффициент чувствительности этого показателя
= fajH = 2roi(2*oroi "О
I дк )k=tg (4к0Т01 -1)3/2
(6.108)
(6.109)
равен нулю при условии коТо1 = 0,5, что соответствует £ = 0,7.
Этот результат означает, что система является нечувствительной (гру-
бой) к вариациям параметра к только тогда, когда сам показатель М = 1, т е
когда система неколебательна.
6.5. Оценка управляемости и наблюдаемости многомерного ОУ
При проектировании СУ сложными многомерными объектами
необходимо предварительно оценить такие структурные свойства
объектов, как управляемость и наблюдаемость. Изложим кратко по-
нятия и условия управляемости и наблюдаемости, разработанные
американским математиком Р. Калманом.
Пусть имеется многомерный линейный стационарный объект
управления, представленный в виде модели в переменных состояния
(см. 2.9):
х(0 = Ax(t) + By(t);	(6.110)
хв(0 = Сх(Г),	(6 111)
где А, В, С - матрицы постоянных коэффициентов с размерами соот-
ветственно п х п, п х m, I х т.
Объект (6.10) является полностью управляемым, если его можно
с помощью некоторого ограниченного управляющего воздействия
343
ХО перевести в течение конечного интервала времени tK из любого
начального состояния х(0) = х0 в заданное конечное состояние
х(гк) = 0.
Интуитивно ясно, что для осуществления такого перевода объ-
екта необходимо (но недостаточно!), чтобы каждая из переменных
состояния Xj{j = 1; 2;...; п) зависела хотя бы от одной из составляю-
щих yt(i = 1; 2;...; т) вектора управления у (t). Очевидно также, что
об управляемости объекта с п переменными состояния и т управ-
ляющими воздействиями нельзя судить только по соотношению этих
размерностей, т. к. она зависит еще и от структуры матриц А и В.
Математически условие полной управляемости формулируется
так: стационарный объект (6.110) полностью управляем, если и толь-
ко если блочная матрица размером п х т, определяемая выражением
О =\в,АВ,АгВ..
(6.112)
и называемая матрицей управляемости, имеет ранг, равный размер-
ности п пространства состояний объекта, т. е. если
rang Qy = п.
(6.113)
Запись в правой части (6.112) означает матрицу, у которой пер-
вые т столбцов со столбцами матрицы В, следующие т столбцов -
со столбцами произведения матриц АВ и т.д., а последние т столб-
цов образованы столбцами произведения матриц Ап~ХВ. Запятые в
блочной матрице (6.12) отделяют друг от друга простые (неблочные)
матрицы. Напомним также, что ранг матрицы находят как наиболь-
ший порядок отличных от нуля квадратных миноров матрицы.
Необходимое и достаточное условие (6.113) означает, что мат-
рица управляемости (6.112) должна содержать п линейно независи-
мых столбцов.
В частном случае, когда ранг г матрицы В больше единицы, ус-
ловие управляемости имеет вид
344
тзп%[В,А-В,...,Ап~гB] = n.	(6.114)
Если управление у (t) - скалярная функция времени и матрица
В превращается в матрицу-столбец, то для полной управляемости
необходимо и достаточно, чтобы квадратная матрица управляемости
Qy не была вырожденной, т. е. чтобы ее определитель
det Qy * 0.	(6.115)
В другом частном случае, когда А - диагональная матрица и все
ее элементы различны, для управляемости необходимо и достаточно,
чтобы матрица В не содержала нулевых строк.
Если ранг матрицы Оу меньше п, то система будет не полностью
управляемой.
Наряду с управляемостью состояния x(t) можно рассматривать
управляемость выхода xB(t) объекта. Условие управляемости выхода
объекта
ranggy, = rang[C-B,C-X.B,C-4! В,...,С-А’''В] = /.	(6.116)
где / - размерность вектора хв(0-
Перейдем теперь к понятию и условию наблюдаемости. Линей-
ный стационарный объект, описываемый уравнениями состояния
(6 НО) и выхода (6.111), является полностью наблюдаемым, если
при известном векторе y{t) по результатам наблюдения (измерения
или измерения и вычисления) выхода хв(/) можно определить (вос-
становить) предыдущие значения переменных состояния x(t). Если
матрица С - квадратная и невырожденная, то решение задачи на-
блюдения становится тривиальным, т к в этом случае возможно
преобразование
J(O = C'£.W	(6 117)
Для полной наблюдаемости или восстанавливаемости объекта
необходимо (но недостаточно!), чтобы каждая переменная состояния
345
xj(f) {] ~ 1; 2;...; л) была связана по меньшей мере с одним из выход-
ных сигналов xw(0 (/ = 1; 2;...; Z), т.е. чтобы хотя бы один из коэффи-
циентов Су,	не был равен нулю. Другими словами, для на-
блюдаемости необходимо, чтобы матрица выхода С не содержала
столбцов, все элементы которых отличны от нуля.
Необходимым и достаточным условием полной наблюдаемости
является следующее требование к матрице наблюдаемости QH.
tangQ„=tang[C\A' -С\(А'У С\...,(А')"-} -С'} = п, (6.118)
где т - символ транспонирования матрицы. Если же ранг этой мат-
рицы меньше п, то система будет не полностью наблюдаемой.
В частном случае, когда выход хв(г) - скалярная величина и
матрица С состоит соответственно лишь из одной строки, необходи-
мое и достаточное условие наблюдаемости сводится к невырожден-
ности квадратной матрицы наблюдаемости QH.
Если А - диагональная матрица с различными элементами, то
для наблюдаемости необходимо и достаточно, чтобы матрица не
содержала нулевых столбцов.
Для объектов, заданных скалярной ПФ W0(p) =K(p)/D(p), усло-
вием одновременного наличия и управляемости и наблюдаемости
является отсутствие общих корней у полиномов К(р) и Dip).
Пример 1. Оценим управляемость и наблюдаемость ОУ, алгоритмиче-
ская структура которого изображена на рис. 6.14,а. Матрицы управнений
состояния и выхода имеют вид
’1 -Г
О -2 ’
с = р о
(6.119)
Непосредственно по схеме на рис. 6.14,а можно записать ПФ ОУ:
^О(Р) =
(6.120)
346
В соответствии с замечанием, сформулированным непосредственно
перед примером, ОУ не может быть одновременно и управляемым, и на-
блюдаемым, Но одно из этих качеств может иметь место. Их наличие мож-
но определить с помощью условий (6.113) и (6.114).
а
Рис. 6.14. Пример оценки управляемости и наблюдаемости ОУ
Матрица управляемости состояния имеет вид
(6.121)
ее определитель второго порядка равен нулю, т.е.
rang Qy = 0 < п = 2.
(6.122)
Следовательно, состояние ОУ неуправляемо.
Матрица наблюдаемости
ее определитель
rang 2н = 2.
(6.123)
(6.124)
Следовательно, ОУ наблюдаем.
Пример 2. Оценим управляемость и наблюдаемость ОУ, алгоритмиче-
ская структура которого изображена на рис 6.12,6. Матрицы уравнений ОУ
(6.125)
347
Характеристическое уравнение ОУ
[р1-л]=
р + 2 О
1 />+1_
= (р + 2)(р + 1) = 0
(6.126)
имеет корни р\ = -2 ир2 = -1.
В соответствии с формулой (2.191) ПФ ОУ по каналу y-xt

р+2	1 (р + 2)(р+1)
р+1
(р+1\р + 2) р + 2
(6.127)
У полиномов числителя и знаменателя ПФ есть общие корни р = -1,
поэтому ОУ не может быть одновременно и управляемым, и наблюдаемым
Ранг матрицы управляемости
rang 2У = rang Ь 4®] = rang
= 1 < п = 2,
(6.128)
т. е. ОУ неуправляем.
Ранг матрицы наблюдаемости
rang =rang |С, >4TC)=rang
О -1
1 -1
(6.129)
т. e ОУ наблюдаем.
Пример 3. Оценим управляемость и наблюдаемость смесительного
бака, рассмотренного в примере к 2.9 как объект управления. Его матрицы
имеют вид (см. (2.197))
где Ь2\ = (сю - с0)/Г0; Ь2\ = (сю - со)/Ро Очевидно, что п = 2; т = 2, Z = 3.
348
Так как матрица А - диагональная с неодинаковыми элементами, то
для управляемости необходимо и достаточно, чтобы матрица В не имела
нулевых строк Очевидно, что это условие в данном примере выполняется.
Однако, если концентрации компонента сю и с2о во входных потоках
одинаковы, то и концентрация в выходном потоке будет с = с0 = сю = с20 и
элементы Ь\2 = Ь22 = 0. т. е состояние объекта управляемо лишь частично
Управляема только одна переменная состояния - xy(f) = ДИ(0, а вторая -
х2(/) - &c(t) - неуправляема, что легко объяснить с физической точки зре-
ния
Применяя условие (6 116), можно убедиться, что при Сю * с20 объект
(6 130) управляем и по выходу rang Qy в = / =3
Оценим теперь наблюдаемость объекта. Применим условие (6 118)
= rang
= rang
rang QH = rang
1/27, 0, 1/5 (-1/27,	0 Yl/27, °’
_ o, 1,	0 \ О, -1/7Д 0, I,
"1/27, 0, 1/5, -1/472, 0, -1/2751
0.	1, 0,	0,	-1/7,	0
1/5T _
0 J ~
(6 131)
т e объект полностью наблюдаем
6.6. Общие сведения о методах расчета
переходных процессов на ЭВМ
Переходная характеристика h(t), по которой непосредственно
оценивается качество системы управления, может быть получена с
помощью расчетов, выполняемых на АВМ и ЦВМ Используемые
при этом различные математические методы и технические приемы
можно объединить в две группы методы структурного моделирова-
ния и методы численного интегрирования. При структурном модели-
ровании исходной основой для расчетов является алгоритмическая
схема системы, состоящая их типовых динамических звеньев или из
элементарных операционных элементов (см рис. 2 11), а сама рас-
четная модель имеет такую же структуру, как и имитируемая систе-
ма Для применения методов численного интегрирования рассчиты-
349
ваемая система управления должна быть представлена в виде сово-
купности дифференциальных уравнений.
Структурное моделирование на АВМ и ЦВМ. Изложим мето-
дику структурного моделирования применительно к конкретной сис-
теме регулирования, которая описывается по каналу х3-х передаточ-
ной функцией
ф( ) = Х(Р) = b2p2 +b}p + bQ
Хз(Р) ^зР3 +а2р2 +а\Р + а0
(6.132)
или неоднородным дифференциальным уравнением в операторной
форме
(а3р3+а2р2 + axp + aa)x(t) = (b1p2 +b,p + 6о)*з(О-	(6.133)
Рис. 6.15. Диаграмма состояния СУ (6.132), (6.133)
Передаточной функции (6.132) и дифференциальному уравне-
нию (6.133) эквивалентна, как известно (см. 2.9), система уравнений
первого порядка, записанная в нормальной форме Коши. Переход к
нормальной форме удобно осуществлять с помощью так называемой
диаграммы состояния - сигнального графа системы, составленного
аналогично алгоритмической схеме на рис. 2.26. Диаграмма состоя-
ния, соответствующая (6.132) и (6.133), показана на рис. 6.15. Пря-
мые стрелки-дуги между вершинами х4, хз, хг и Xi означают операции
либо непрерывного, либо дискретного интегрирования с единичными
350
коэффициентами. Если диаграмма в дальнейшем используется для
аналогового моделирования, то каждой указанной дуге соответствует
непрерывный интегратор (см.рис. 2.31Де), а если для цифрового -
дискретный (рекуррентный) интегратор (см.рис. 2.32Де).
Диаграмма состояния может использоваться и для анализа соот-
ветствующей импульсной системы, но в этом случае передаточные
свойства интегрирующих дуг описываются с помощью оператора
задержки (см. главу 9).
Согласно диаграмме на рис. 6.15, можно записать в форме Ко-
ши систему из трех дифференциальных уравнений состояния
рх,(0 = х2(0;
рх2(О = х3(г);
(6.134)
Р*з(О = 1-ад (0 - «1^(0 -«2^(0 + х3(01
и алгебраическое уравнение вида
х(0 = bQxx(t) + ^х2(/) +b2x3(t\	(6.135)
где х, (t), х2 (t) = х, (Z), хз (t) = х2 (Z) = х, О - вспомогательная перемен-
ная и ее производные (см. 2.9).
При аналоговом моделировании из операцион-
ных элементов, описанных в 2.11, составляется структурная схема
модели, соответствующая диаграмме состояния (рис. 6.15) и уравне-
ниям (6.134), (6.135). При этом может применяться масштабирование
как основных переменных х3, х, так и времени.
Масштаб тх основных переменных выбирается таким, чтобы
машинные переменные и = тх х3 и их = тх х не выходили за рабо-
чий диапазон напряжений Масштабирование по времени (см 2.4)
осуществляется как с целью замедления переходного процесса
(mt > 1), так и с целью его ускорения (mt < 1). При mt = 1 процесс
получается на АВМ в реальном масштабе времени. Масштаб време-
ни целесообразно выбирать, исходя из предполагаемой длительности
351
tn переходного процесса и желательной длительности tn решения по-
дачи на ABM mt = tM /tn
Структурная схема моделирования может составляться также из
аналоговых моделей типовых звеньев, описанных в главе 3 В этом
случае структура модели воспроизводит не диаграмму состояния
(см рис 6 15), а совпадает с алгоритмической схемой моделируемой
системы регулирования
При обоих вариантах составления схемы моделирования на
АВМ (из простейших операционных элементов и из типовых моде-
лей) необходимо обращать внимание на знаки промежуточных сиг-
налов и их соответствие исходной схеме
Для цифрового моделирования (6 134) и (6 135)
можно записать соответствующие разностные уравнения
X' (l + l) = Xl (l) + X2 (l)&,
x2(z + l) = x2 (z) + x3(z)Ar,
x3 (z +1) = x3 (z) + —- [- aoxt (z) - a, x2 (z) -a2x3(i) + x3 (z)]zV
} (6 136)
x, (z) = 6OX1 (z) + 5, x2 (z) + b2x3 (z)
Уравнения (6 136) записаны применительно к самому простому
варианту численного интегрирования - методу Эйлера или прямой
разности, согласно которому дискретное (приближенное) значение
y(z) интеграла
y(t) = jx(S)d&
(6 137)
равно
^(z)=jz(z-l) + x(z-l)A/
(6 138)
ИЛИ
y(z +1) = y(z) 4- x(z)Az
(6 139)
где А/ - по шаг интегрирования
352
Получаемые по этому методу достаточно простые разностные
уравнения легко программируются для ЦВМ
Идея и принципы структурного моделирования СУ на ЦВМ
реализованы в виде различных специальных пакетов прикладных
программ Эти программы предназначены для решения широкого
круга задач имитационного моделирования и машинного проектиро-
вания СУ Пакеты составлены, как правило, на специализированном
для задач ТУ проблемно-ориентированном языке, основой которого
являются типовые функциональные блоки динамические звенья,
сумматоры, нелинейные и логические функции Из всех таких паке-
тов доминирующее распространение получили программные систе-
мы «MATLAB»/«SIMULINK» и «MATKAD»
Поскольку при вычислении в ЦВМ выходного сигнала х(1) неза-
висимой переменной фактически является не время, а текущий номер
1 шага интегрирования, то получаемый в виде таблицы переходный
процесс будет соответствовать реальному масштабу времени
Численное интегрирование на ЦВМ Расчет переходных про-
цессов в системах регулирования высокого порядка удобно выпол-
нять методом матричных рядов Для этого векторные уравнения
состояния и выхода (см (2 168) и (2 171)), описывающие замкнутую
систему (например, по каналу уъ-г)
= Аэх(1) + В3у (Г),
в
е(0 = С3х(0,
преобразуют в разностную форму
х(/ + 1) = Л3*х(/) + ^ув(0,
§0) = C3x(z)
(6 140)
(6 141)
(6 142)
(6 143)
Матрицы А*, В*3 зависят от исходных матриц Л3, Вг и от спосо-
ба приближенного интегрирования векторного уравнения первого
порядка (6 140) и в общем виде представляют собой матричные сте-
пенные ряды типа (2 201) (отсюда название метода) При прибли-
353
женном интегрировании по формуле Эйлера (или прямоугольников)
с шагом А/ эти матричные ряды содержат только первые слагаемые:
+ В*=1Аг + В3.	(6.144)
Разностное уравнение (6.142) можно представить как прибли-
женную модель исходной непрерывной системы (6.140), записанную
с приближением нулевого порядка для дискретных моментов време-
ни t - t, = i&t, (i = 0; l;...oo). Модель выражает состояние системы на
(/ + 1)-м шаге через ее состояние на предыдущем i-м шаге, т.е., по
существу, является рекуррентным алгоритмом решения исходного
уравнения. Согласно этому алгоритму, вычисление дискретных зна-
чений переменных состояния x(i) и сигнала ошибки e(z) сводится к
последовательному выполнению в ЦВМ однотипных преобразований
матриц - умножению постоянных матриц А *, В* и С3 на векторы-
столбцы х(0 и у (/). Значения вектора-столбца внешнего возденет-
—в
вия у (/) вводятся в ЦВМ в табличной форме.
—в
Кроме описанного метода матричных рядов, для расчета пере-
ходных процессов систем высокого порядка могут использоваться
различные стандартные методы численного интегрирования диф-
ференциальных уравнений (например, Рунге-Кутта, Адамса-Баш-
форта, Хемминга и др.). Эти методы реализованы обычно в виде
библиотечных подпрограмм, которые входят в стандартное матема-
тическое обеспечение ЦВМ.
Для обращения к таким подпрограммам модель системы, для
которой рассчитывается переходный процесс, должна быть пред-
ставлена в нормальной форме Коши (6.134). Если исходное уравне-
ние системы является неоднородным - с правой частью, как (6.133),
то приходится, кроме обычных (предначальных) условий х(-0), учи-
тывать так называемые эквивалентные начальные условия х(+0),
имеющие место непосредственно после приложения ступенчатого
воздействия.
Для обеспечения необходимой точности расчета шаг дискрети-
зации At при любом способе цифрового моделирования или числен-
354
ного интегрирования должен быть выбран достаточно малым по
сравнению с каким-либо базовым показателем инерционности иссле-
дуемой системы. В качестве такого показателя обычно принимают
резонансную частоту сор или близкую к ней частоту среза соср (см. 6.2).
По частоте среза разомкнутого контура можно оценить верхний до-
пустимый предел шага интегрирования
М < (0,5... 1,0)/ ©ср,
(6.145)
а также ожидаемую длительность переходного процесса, которая при
удовлетворительной настройке системы регулирования
/п «(7... 10)/ ©ср.
(6.146)
Обычно рекомендуются следующие параметры режима вычис-
лений:
конечное время счета
/к — /п ® Ю/
(6.147)
шаг интегрирования
А/< (0,005... 1,010)/к;
(6.148)
шаг вывода на печать
/в = (5...10)Д/к.
(6.149)
Кроме того, для шага интегрирования должно быть выполнено
условие
& < TmJ2
(6.150)
где Тт1п - наименьшая постоянная времени системы.
355
Пример. Составим программу цифрового моделирования типовой сис-
темы (см.рис. 4.7,6), состоящей из инерционного объекта с запаздыванием,
д
Ио(р) = х0(р) / у(р) = к0 1(Тор +1)	(6.151)
и ПИ-регулятора
И^(р) = У (р) / е<Р) = кп + кК 1р.	(6.152)
Дифференциальное уравнение объекта, связывающее управляющее
воздействие ХО с выходом x(t) инерционной части объекта, имеет вид
То+ х(Г) = М(Г)	(6.153)
at
или
x{t)^koy{t)(To-x(t)lTo.	(6.154)
Применяя метод Эйлера (формулу прямой разности), можно записать
соответствующее (6.154) разностное уравнение объекта
х(/) = x(i -1) + [М(( -1) - *0 - 1)]д//го •	(6.155)
Для ПИ-регулятора запишем порознь разностные уравнения,
пропорциональной части
Уп(0 = кп е(/)
и интегральной части
Уи (0 = У и V -1) + k^i ~ 1) At
(6.156)
(6.157)
При моделировании переходного процесса х(/), вызванного единичным
ступенчатым изменением задания x3(f) = о(0, сигнал ошибки
(6.158)
Для получения переходного процесса по каналу - хо при возмущении
y3(t) = a(f) к суммарному управляющему воздействию добавим единицу.
356
y(i) = Уп (J)+У и (i) +1 = Лгпе(/ )Лгие(/ - 1)Д/ +1,
а задание при этом будет считать нулевым, т.е. е(/) = -хо(/).
Запаздывающую связь
х0 (О = х0 (t - то) или х0 (i) = x(i - i3 У
(6.159)
(6.160)
где /3 = То/А/, можно реализовать специальной процедурой циклического
смещения значений х(/) на /3 шагов.
Контрольные задания и вопросы
1.	Какие свойства СУ принято рассматривать при оценке ее качества?
2.	По какой динамической характеристике системы регулирования
оценивают прямые показатели качества? Какие из них характеризуют коле-
бательность системы, а какие - ее быстродействие?
3.	Нарисуйте графики переходных процессов по каналам задания и
возмущения, соответствующие перерегулированию ст = 50 %.
4.	Какие из частотных показателей характеризуют колебательность
системы, а какие - ее быстродействие?
5.	Как связано расположение корней характеристического уравнения
на комплексной плоскости с устойчивостью и колебательностью системы?
6.	Как связан ближайший действительный корень характеристического
уравнения с длительностью переходного процесса?
7.	На каком характерном свойстве замкнутой системы регулирования
основана ее приближенная замена эквивалентным колебательным звеном? В
чем заключается условие эквивалентности колебательного звена и аппрок-
симируемой замкнутой системы?
8.	Назовите два параметра колебательного звена, характеризующих его
динамические свойства.
9.	Как влияет коэффициент демпфирования % колебательной модели на
показатели качества ст и Гп?
10.	Каким типовым динамическим звеном является разомкнутый кон-
тур колебательной модели? Назовите два параметра разомкнутого контура,
характеризующих его динамические свойства.
11.	Как влияют параметры к и То\ разомкнутого контура на динамиче-
ские свойства замкнутой системы?
357
12.	Прокомментируйте опорные формулы (6.48), связывающие показа-
тели качества системы с параметрами к, Toi, ®ср и Д<р разомкнутого контура:
как влияет каждый из этих параметров на показатели ст, tn и Л/?
13.	Определите параметры £ и Т колебательной модели и показатели
качества ст и замкнутой системы, если ПФ разомкнутого контура
И/рк(^) = ^рк/(7’|^+1)(7’2^+1),
(6.161)
где кр1с = 0.33; 7\ = 2 с; Т2= 1 с.
14.	Какие параметры графика переходного процесса учитываются ин-
тегральными оценками?
15.	Какой из двух переходных процессов лучше - с большой инте-
гральной оценкой или малой? Почему?
16.	Для каких переходных процессов можно применять линейную ин-
тегральную оценку?
17.	Почему для колебательных переходных процессов приходится
применять модульные или квадратичные оценки?
18.	Определите квадратичную интегральную оценку для системы, со-
стоящей из ПИ-регулятора и объекта в виде реального интегрирующего
звена (см. пример 1 в 6.3).
19.	Что представляет собой функция чувствительности системы к па-
раметрическому возмущению?
20.	Какие системы называют робастными?
21.	Дайте физическое определение понятия управляемого объекта.
22.	При каком физическом условии объект называют наблюдаемым?
23.	Составьте для системы на рис. 6.9,о диаграмму состояния по кана-
лу х5 - х.
24.	С помощью каких операционных элементов реализуются интегри-
рующие ветви диаграммы состояния при аналоговом и цифровом моделиро-
вании?
25.	Как выбираются параметры режима вычислений tK, &t и ta при рас-
чете переходного процесса?
358
Глава 7. МЕТОДЫ СИНТЕЗА
ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ
7.1.	Общие сведения о синтезе систем управления
Все математические задачи, решаемые в теории управления,
можно объединить в два больших класса - задачи анализа и задачи
синтеза систем управления.
В задачах анализа полностью известна структура системы, зада-
ны все (как правило) параметры системы, и требуется оценить какое-
либо ее статическое или динамическое свойство. К задачам анализа
относятся расчет точности в установившихся режимах (глава 4), оп-
ределение устойчивости (глава 5), оценка качества системы (глава 6).
Задачи синтеза можно рассматривать как обратные по отноше-
нию к задачам анализа: в них требуется определить структуру и па-
раметры системы по заданным показателям. Простейшими задачами
синтеза являются, например, задачи определения передаточного ко-
эффициента разомкнутого контура по заданной ошибке или по усло-
вию минимума интегральной оценки. Более сложные задачи синтеза
рассматриваются в данной главе, а также в разделах 8.5, 10.6, главе
11.
Синтезом системы управления называют процедуру определе-
ния ее структуры и параметров по заданным показателям качества.
Синтез является важнейшим этапом проектирования и конструиро-
вания системы. В общем случае при проектировании системы необ-
ходимо определить как алгоритмическую, так и ее функциональную
структуру, т.е. решить задачу так называемого полного синтеза.
Алгоритмическую структуру системы (или ее части) находят
при помощи математических методов и на основе требований, запи-
санных в строгой математической форме. Поэтому процедуру оты-
скания алгоритмической структуры часто называют теоретическим
синтезом или аналитическим конструированием системы управле-
ния.
359
Синтез функциональной структуры, или технический синтез,
системы заключается в выборе конкретных элементов (с учетом их
физической природы) и в согласовании статических и энергетиче-
ских характеристик смежных элементов. Эта процедура проектиро-
вания не имеет пока математической основы и относится к области
инженерного искусства. Выполняя синтез функциональной структу-
ры, прежде всего согласовывают входные и выходные сигналы
смежных элементов. Сигналы должны иметь одинаковую физиче-
скую природу и одинаковые несущие величины. При выборе вида
энергии и конструкции отдельных элементов руководствуются прак-
тическими соображениями об их простоте, надежности, минималь-
ных габаритах и стоимости. Кроме этого учитывают условия экс-
плуатации элементов: температуру окружающей среды, агрессив-
ность среды, вибрацию, взрывоопасность и т.п. На выбор функцио-
нальной структуры часто влияют традиции и опыт проектирования
аналогичных систем.
Последовательность решения задачи полного синтеза может
быть различной. В некоторых простых случаях задачу удается ре-
шить в идеальной (с методологической точки зрения) последова-
тельности: сначала определить при помощи математических методов
алгоритмическую структуру системы, а затем подобрать соответст-
вующие конструктивные элементы. Однако применение этой иде-
альной последовательности при проектировании сколько-нибудь
сложных промышленных систем управления, как правило, оказыва-
ется по ряду причин невозможным. В первую очередь возникают
трудности в подборе конструктивных элементов: в ограниченной
номенклатуре серийно изготавливаемых средств управления может
не оказаться устройств с необходимыми алгоритмическими свойст-
вами. Поэтому задачу синтеза в большинстве случаев решают сле-
дующим образом.
Сначала, исходя из требований к назначению системы, учитывая
условия ее работы, по каталогам серийного оборудования выбирают
функционально необходимые элементы системы: регулирующий ор-
ган (РО), исполнительное устройство (ИУ), датчики (Д). Эти элемен-
ты вместе с объектом управления (ОУ) образуют неизменяемую
часть системы (рис. 7.1). Затем на основании требований к статиче-
ским и динамическим свойствам системы определяют ее изменяе-
360
мую часть, в которую входят усилительно-преобразующий блок
(УПБ) и различные корректирующие устройства (КУ). Алгоритмиче-
скую структуру изменяемой части находят с учетом свойств уже вы-
бранных функционально необходимых элементов, а техническая
реализация этой части осуществляется с использованием стандарт-
ных унифицированных регуляторов и различных корректирующих и
компенсирующих устройств. Корректирующие устройства (КУ\ и
КУ2 на рис. 7.1), включаемые в контур последовательно или в виде
внутренней обратной связи, служат для улучшения динамических
свойств системы. Компенсирующие устройства (КУ^) включаются
между датчиком Д, воспринимающим возмущающее воздействие, и
усилительно-преобразующим блоком, и служат для улучшения
точности системы (см. 7.5).
Рис. 7.1. Функциональная структура синтезируемой системы управления
Таким образом, процедуры определения алгоритмической и
функциональной структур всей системы тесно переплетаются друг с
другом. Нередко эти процедуры приходится выполнять по нескольку
раз, чередуя их. А окончательное решение о структуре системы при-
нимается, как правило, на основе компромисса между точностью и
качеством, с одной стороны, и простотой и надежностью - с другой.
Заключительным этапом проектирования системы управления
является параметрическая оптимизация - расчет настроечных пара-
метров выбранного регулятора.
После решения задачи синтеза обычно выполняют анализ син-
тезированной системы: методами, изложенными в главах 4, 5 и 6,
361
проверяют, обладает ли система необходимыми показателями точно-
сти, устойчивости и качества.
На всех этапах синтеза и анализа систем целесообразно приме-
нение цифровых вычислительных машин. Моделирование систем на
вычислительных машинах позволяет исследовать большое количест-
во вариантов структур и параметров и тем самым существенно уско-
рить решение задачи синтеза.
7.2.	Основные принципы синтеза алгоритмической структуры
одноконтурной системы управления
При синтезе (проектировании) алгоритмической структуры СУ
стремятся выполнить следующие главные требования:
1)	система должна как можно лучше, точнее воспроизводить
любые изменения задающего воздействия x3(f) на выходе x(f) объекта
управления;
2)	система должна максимально лучше устранять влияние воз-
мущений (как внешних, так и внутренних) на управляемую коорди-
нату' х(/);
3)	система должна быть устойчивой.
Первым двум главным целям синтеза соответствуют следующие
математические условия:
передаточная функция СУ по каналу задания должна быть равна
единице:
А >	'
Ф3(р) = х(р)/х3(р) = 1,	(7.1)
а передаточная функция по каналам возмущений, например, по воз-
мущению х8(0, приложенному на выходе объекта, равна нулю:
Ф. <Р) = 4Р)/х. (Р) = 1 - фз (Р) = 0.
(7.2)
Для полного и точного решения задачи синтеза алгоритмиче-
ской структуры линейной СУ должна быть известна ПФ Wo(p) объек-
та управления, характеристики задания x3(f), возмущений yB(f) и хв(/),
действующих соответственно на входе и выходе объекта, а также
362
свойства помех хп.з.(0 и хп.и.(0, возникающих соответственно в кана-
лах задания и измерения (рис. 7.2). Такое решение задачи в общем
случае - при одновремен-
ном влиянии нескольких
внешних воздействий -
затруднительно из-за ее
математической сложнос-
ти, отсутствия, как пра-
вило, информации о
внешних воздействиях
Синтезируемая Неизменяем 1ая
часть	часть
Рис. 7.2. Исходная структура для
задачи теоретического синтеза
xn(f), *в(0 и yB(t), а также из-за физических ограничений на величину
управляющего воздействия y(f). Однако для лучшего понимания
сущности задачи синтеза и всей проблематики теории систем управ-
ления полезно знать ряд фундаментальных идей и принципов по-
строения СУ, справедливых для отдельных частных случаев рас-
сматриваемой задачи синтеза.
1.	Компенсация инерционности объекта. В простейшем слу-
чае, когда возмущающие воздействия отсутствуют, управление мож-
но осуществлять, как известно из гл.1, по разомкнутой схеме (рис.
7.3,л). Если при этом ПФ Wy(p) управляющего устройства принять

(7.3)
то обеспечится полная (структурная) компенсация
инерционности объекта, и система управления будет
мгновенно и точно воспроизводить на выходе объекта задающее воз-
д
действие х3(г), так как ПФ всей системы при этом Ф3(р) = х(р)/х3(р) =
= Wy(p\Wo(p) = \.
Полная компенсация инерционности объекта может быть дос-
тигнута и с помогцью отрицательной обратной связи, если управ-
ляющее устройство будет иметь бесконечно большой передаточ-
ный коэффициент.
Действительно, схема полной компенсации инерционности,
приведенная на рис. 7.3,47, согласно правилам преобразования схем
(см. 4.1), эквивалентна схеме на рис. 7.3,6, а се можно преобразовать,
в свою очередь, к схеме на рис. 7.3,в, перенеся узел разветвления со
входа на выход объекта. Нетрудно убедиться, что ПФ системы
управления (см.рис. 7.3,в) (теперь уже замкнутой, с единичной отри-
цательной обратной связью) и в этом случае будет равна
д
Ф3(р) = х(р) / х3(р) = 1, т.е. в каждый момент времени x(t) = x3(f). Если
ПК ку меньше бесконечности, но значительно больше единицы, то
д	д
Ф3(р) ~ 1, а ФЖр) = £ (р)/ х3(р) = 1 - Ф(р) « 0, что соответствует вы-
водам о влиянии ПК разомкнутого контура на точность замкнутой
СУ (см. гл. 4).
отрицательной ОС
Так как выполнить теоретические условия (7.1) и ку = оо физиче-
ски невозможно, на практике применяют частичную (парамет-
рическую) компенсацию инерционности: устраняют
влияние одной-двух (обычно самых больших) постоянных времени
объекта. Для этого последовательно с инерционным объектом
W =	+ IX?;,/’ +1)-(К..Р +1).	(7.4)
где Т0] > Го2 > ... > Топ, включают компенсирующее устройство в
виде форсирующего звена первого-второго порядка с ПФ
^(^ = ^(7'х,р + 1ХГйр + 1),
(7.5)
у которого постоянные времени должны быть равны компенсируе-
мым постоянным времени объекта, т.е.
364
|	Тл=Т„,Та^Та,	(7.6)
а передаточный коэффициент
|	< = 1/*о 	(7.7)
Нетрудно убедиться, что при такой частичной компенсации ПФ
системы по каналу «х3 -х»
д
Ф(Т’) = х(р)/хД/>) = и;(р)и;(р) = 1/...(г„„^+1Х7;,/>+1), (7.8)
т.е. система при малых частотах близка по своим свойствам к фильт-
ру низкой частоты с ПК k = 1, а в диапазоне высоких частот, где про-
являются малые постоянные времени ... То.п.\, Топ, отношение ампли-
туд xm/x3m < 1.
Следует заметить, что практическое применение идей полной и
частичной компенсации инерционности объекта связано всегда со
значительными трудностями. В частности, невозможно, как правило,
точно реализовать обратную ПФ объекта (7.3); большой ПК ку вызы-
вает большие, нереализуемые управляющие воздействия у и приво-
дит к неустойчивости замкнутой СУ; форсирующие звенья вида
(7.5), используемые для частичной компенсации инерционности объ-
екта, реально имеют свою, дополнительную инерционность.
Тем не менее, несмотря на трудности практической реализации
систем с идеальной, предельной структурой (см.рис. 1.3,а и в) на ос-
новании изложенного в п.1 можно сформулировать следующий,
весьма важный для задач синтеза фундаментальный принцип струк-
турно-параметрической оптимизации систем управления.
для компенсации инерционности объекта управляющее устрой-
ство должно представлять собой динамическое звено с пере-
даточной функцией, равной или близкой обратной ПФ объекта,
а в системе с отрицательной ОС ПК разомкнутого контура
должен быть как можно больше.
2.	Компенсация возмущения на выходе объекта. Если на объ-
ект управления действует возмущение хв (рис. 7.4,а) и оно поддается
измерению, то теоретически можно синтезировать систему управле-
365
Рис. 7.4. Компенсация возмущения на выходе объекта:
а - прямая, г - с помощью отрицательной ОС
ния с полной компенсацией возмущения. Для этого ПФ управляюще-
го устройства должна быть так же, как и в задаче компенсации инер-
ционности объекта,

(7-9)
366
и тогда, согласно схеме на рис. 7.4,а, выходной сигнал х(р) = хв(р) +
+ Ху(р) = Хв(р) + [*з(р) - xB(p)]FKv(p)^o(p) = хз(р), т.е. система будет
точно воспроизводить задание х3 на выходе х, несмотря на наличие
возмущения хв.
Разомкнутую схему прямой и полной компенсации (см. рис.
7.4,а) можно преобразовать (аналогично схеме на рис. 7.3) к схеме в
отрицательной ОС (рис. 7.4,г). При переносе узла разветвления J со
входа объекта (рис. 7.4,6) на выходе х, через сумматор 3 (рис. 7.4,в),
согласно правилам преобразования (см. главу 4), на схеме появится
дополнительное воздействие хв, приложенное к сумматору 4 со зна-
ком минус. Это воздействие, перенесенное далее через сумматор 2 к
сумматору 7, скомпенсирует воздействие хв, которое желательно бы-
ло получить согласно идее прямой компенсации (см. рис. 7.4,а). В
результате преобразований вместо схемы с прямой компенсацией
возмущения (см. рис. 7.4,п) получена схема с отрицательной ОС и с
бесконечно большим ПК ку. Но она не учитывает наличие и свойства
задающего воздействия х3(Г) и помехи хп(/), действующей на входе.
Отсюда второй фундаментальный принцип синтеза систем
управления, аналогичный первому:
для компенсации измеряемого возмущения, действующего на
выходе объекта, управляющее устройство должно представ-
лять собой динамическое звено с передаточной функцией, рав-
ной обратной ПФ объекта, а для компенсации любых некон-
тролируемых возмущений с помощью отрицательной ОС ПК
разомкнутого контура должен быть как можно больше.
3.	Управление с помощью модели объекта. Полную компен-
сацию возмущения хв, действующего на выходе объекта (см.п.2),
можно осуществить и без непосредственного измерения хв, вычисляя
его с помощью модели объекта (рис. 7.5,п). Действительно, при точ-
ном совпадении передаточных функций модели и объекта, т.е. при
^ом(р) - Wo(p) и ху м = ху, образующийся на выходе сумматора 2
сигнал хв м(/7) = х(р) - ху м(р) = \ху(р) + хв(р)] - ху м(р) = хв м(р) является
косвенно измеряемым возмущением хв. Очевидно, что это вычислен-
ное с помощью модели объекта возмущение хвм можно, как и при
прямой компенсации (по схеме на рис. 7.4,а), подать со знаком минус
на вход УУ, ПФ которого, согласно принципу 2, должна быть по-
прежнему равна №у(р) = 1/№о(р). Если теперь перенести сигнал ху.м с
367
a
Компенсация возмущения
Рис. 7.5. Управление с помощью модели объекта:
а - косвенная компенсация возмущения, б - по отклонению
сумматора 2 на сумматор 2'(рис. 7.5,6) с соответствующей перемен-
ной знака, то разомкнутая структура компенсации возмущения (см.
рис.7.5,а) превращается в замкнутую с отрицательной обратной свя-
зью и с регулятором
и;и(р)=
Wy(p)
1-^у(Жм(р)
(7.10)
имеющим внутреннюю положительную обратную связь в виде моде-
ли объекта. Очевидно, что при Wy(p) = l/JF0(p) регулятор (7.10) экви-
валентен пропорциональному звену с ПК кр = оо, обеспечивающему,
как известно, абсолютную точность (еуст = 0) и максимальное быст-
родействие (tn = 0), и поэтому его называют идеальным. Звено
1Ком(р), входящее в состав идеального регулятора, после очередного
изменения управляющего воздействия у прогнозирует его влияние на
выход объекта, т.е. вычисляет составляющую ху м, которая поступает
368
на вход УУ со знаком плюс. Туда же со знаком минус поступает со-
ставляющая ху, которая, при условии эквивалентности объекта и его
модели, равна ху м. В результате основной контур системы оказывает-
ся как бы разомкнутым, что исключает возникновение колебаний и
неустойчивости.
Заметим, что идея регулятора с внутренней моделью объекта (в
англоязычной литературе - Internal Model Control) может использо-
ваться и в случае, когда Wy(p) * 1/1¥о(р).
Таким образом, с учетом выводов в п.1 и 2 можно сформулиро-
вать еще один важный принцип синтеза алгоритмической структуры
замкнутой СУ:
идеальный регулятор должен включать в себя модель объекта
управления - №ом(р) и представлять собой встречно-
параллельное соединение в виде прямой цепи с ПФ \/W0(p), охва-
ченной положительной обратной связью с ПФ W0(p).
4.	Структурно-параметрическая оптимизация систем управ-
ления объектами с запаздыванием. Часто встречающиеся в про-
мышленной автоматике инерционные объекты с чистым, или транс-
портным, запаздыванием можно представить в виде следующей ПФ:
ад = ШЛ	(7.11)
где 1Р0'(р) - дробно-рациональная функция, характеризующая инер-
ционную часть ОУ; то - чистое запаздывание объекта.
Для объектов такого типа выполнить условия компенсации не
удается, так как, согласно формулам (7.3), (7.9), в ПФ У У появится
сомножитель е+рх°, который соответствует идеальному упредителю,
и точная реализация которого технически невозможна. Поэтому с
целью упрощения искомой структуры У У и облегчения ее техниче-
ской реализации целесообразно допустить, чтобы для объектов, со-
держащих чистое запаздывание т0, синтезируемая система воспроиз-
водила задающее воздействие х3 с запаздыванием то, т.е. чтобы ее ПФ
по каналу «х3 - х» была равна не единице, а
Ф3(р) = 1-е’рх°.	(7.12)
369
Соответственно ПФ замкнутой системы по каналу «хв - х» будет
Фв(р) = 1-Ф3(р)=1-е-^.
(7.13)
Для выполнения условия (7.12) достаточно, чтобы ПФ У У была
равна
Wy(Py = \lw\P).	(7.14)
Соответственно ПФ регулятора (7.10) для объектов с запаздыва-
нием примет вид
WVAP) =
V w0 (р)
1----
W0{P)
_ i/4'(p)
(7.15)
Регулятор (7.15), называемый по имени автора идеи (7.12) регу-
лятором Ресвика, компенсирует лишь инерционную часть объекта
W°(p), но не устраняет из контура системы запаздывание е-р1°, ко-
торое всегда отрицательно влияет на устойчивость и качество замк-
нутой СУ. Кроме того, недостатком системы с регулятором Ресвика
является ее критичность или сильная чувствительность к малым ва-
риациям запаздывания объекта: система устойчива только при точ-
ном равенстве запаздывания объекта то и запаздывания то м, модели-
руемого в регуляторе, т.е. при т0 = т0 м.
Устранить эти два недостатка и исключить полностью запазды-
вание из главного контура системы можно с помощью регулятора-
упредителя, предложенного американским специалистом Смитом.
Идея упредителя Смита заключается в том, чтобы выбором его ПФ
ИупР(р) исходную структуру на рис. 1.6,а сделать эквивалентной
структуре на рис. 1.6,6, содержащей УУ с произвольной ПФ №у(р).
Действительно, приравняв ПФ обеих замкнутых систем по каналу
«х3 - х», можно получить следующую ПФ упредителя Смита:
370
w„(p)=
fp,(p)
1 + и; (p)»Up)(1 -еР'-)’
(7.16)
которой соответствует структура на рис. 7.6,в.
а
Рис. 7.6. Структурная компенсация запаздывания
с помощью упредителя Смита
Если теперь на схеме рис. 7.6,в перенести согласно правилам эк-
вивалентных преобразований узел 7 на выход х', а узел 2 на выход х,
то кроме отрицательной обратной связи по сигналу х', как на рис.
7.6,6, образуются два единичных канала с выхода х на выход х3, ко-
торые имеют противоположные знаки и, следовательно, взаимно
компенсируют друг друга. Таким образом, можно убедиться, что за-
паздывание действительно устраняется из замкнутого контура. Это
позволяет выбирать ПФ Wy(p) без учета запаздывания, в частности,
по ключевой формуле (7.1), или принимать в качестве У У любой из
371
типовых регуляторов (см. главу 4). Если при этом ПК ку -> со , то уп-
редитель Смита (7.16) эквивалентен регулятору Ресвика (7.15).
Хотя регулятор Ресвика (7.15) практически осуществить нико-
гда не удается, анализ его свойств позволяет оценить предельные
возможности управления объектами с запаздыванием, а также вы-
явить наилучшие законы управления такими объектами.
Передаточным функциям (7.12) и (7.13) соответствуют идеаль-
ные переходные процессы прямоугольной формы, заканчивающиеся
за минимально возможное время tn = т0- По каналу «ув - х» переход-
ный процесс имеет ступенчато-апериодический характер и длитель-
ность tn»(З...4)то-
Применим регулятор Ресвика для широко используемых при-
ближенных моделей промышленных объектов с запаздыванием:
без инерционной составляющей
^(р)=^-'--,
с инерционной частью первого порядка
^(Р) = ^-/(ГаР + 1)
и с инерционной частью второго порядка
w^p}=
(7 17)
(7.18)
(7.19)
Для объекта с чистым запаздыванием (7.17) ПФ регулятора
(7.15) принимает вид
^p«(p)=iA0(i-^’)-
(7.20)
При низкочастотных внешних воздействиях, а именно при
(йв« (йс= 1/т0, допустима приближенная замена
е рт° а 1- рт0
(7.21)
372
и идеальный регулятор (7.20) эквивалентен И-регулятору (4.63):
*<Л/Р = *Р/ГиА
(7.22)
гдеЯи = Кр/ 7 и = 1 / кото.
При высокочастотных воздействиях регулятор (7.20) действует
как дискретный: после каждого очередного изменения управляюще-
го воздействия у он выжидает в течение интервала т0, благодаря это-
му контур системы оказывается как бы разомкнутым, а устойчивость
ее улучшается.
Для инерционного объекта 1-го порядка с запаздыванием (7.18)
идеальный регулятор (7.15) с учетом условия (7.21) становится экви-
валентным ПИ-регулятору (4.64).
(7.23)
где кп = кр = То / кото, кК = кр I ТК = 1 / ^ото, что дает еще дополнитель-
ные соотношения: крк0 = То / т0 и Ти = То.
Наконец, для инерционного объекта 2-го порядка с запаздыва-
нием (7.19) регулятор Ресвика при низких частотах эквивалентен
ПИД-регулятору (4.65), (4.66):
ЙК (р)«	= к К +клр = к f 1+-L + /;Z
₽	VoP	Р ₽1 ТКр
(7.24)
где кп кр (7о1	Т02) / кохо, кК кр / Тц 1 / к0хо, кд крТд
=ТоХТо2) / кото.
На основании изложенного в п.5 можно сформулировать сле-
дующие важные правила структурно-параметрической оптимизации
систем управления объектами, обладающими запаздыванием:
чистое запаздывание объекта, отрицательно влияющее на ус-
тойчивость системы управления, можно устранить из замк-
нутого контура системы с помощью регулятора, моделирую-
373
щего это запаздывание; для безынерционного, инерционного
первого порядка и инерционного второго порядка статических
объектов, обладающих чистым запаздыванием, наилучшими из
типовых линейных являются соответственно И-, ПИ- и ПИД-
регуляторы, при этом передаточный коэффициент регулятора
должен быть прямо пропорционален постоянным времени объ-
екта и обратно пропорционален передаточному коэффициенту
объекта и времени запаздывания.
7.3. Синтез системы управления с желаемыми
динамическими свойствами
Изложенные выше принципы синтеза направлены на достиже-
ние идеальных целей - обеспечение равенств (7.1) и (7.2). Однако их
выполнение в реальных технических СУ оказывается невозможным.
Поэтому на практике для замкнутой системы (рис. 7.7,я) вместо пре-
дельных условий (7.1) и (7.2) задаются требованиями
д
ф, (р) =
Х(Р) .. ^PVW
х,(р) 1+^у(рШр)
(7.25)
или / и
д
ФАР> =
*Ар) 1 + ^у(Ж0(р)
(7.26)
где Ф3 ж(р), Фъ.-Ар) ~ ПФ замкнутой СУ, обладающей желательными
статическими и динамическими свойствами, соответственно по ка-
налу задания и возмущения. (Для краткости будем называть эти ПФ
желаемыми).
Желаемую ПФ Фж(р) обычно выбирают, исходя из условия по-
лучения переходной характеристики Лж(0 определенного типа. Раз-
личные типовые, или стандартные, характеристики Лж(0 будут рас-
смотрены ниже.
Из выражения (7.25) можно для задачи воспроизведения задания
хД) получить следующую ПФ УУ:
374
^у.з(р) =
Фз.ж(Р) 1
1-Ф3.ж(Р)^о(Р)
(7.27)
5
которой соответствует схема на рис. 7.7,6. Если на схеме перенести
узел 1 на выход звена l/PF0(/>) и принять Фж(р) = 1, то будет очевидна
ее идентичность схеме с идеальным регулятором на рис. 7.5,6.
Для задачи компенсации возмущения хв(0 ПФ УУ, согласно вы-
ражению (7.26), должна быть
(7.28)
^.(р)=
1-ф„(р) 1
ф„(р) 1ГЛр)'
Рис. 7.7. Синтез системы с желаемыми свойствами
Желаемые виды переходной характеристики hx(f) и соответст-
вующей ПФ Фж(р) могут быть выбраны не только для основных ка-
налов «г3 - х» и «хв - х», но и для любого другого, например <<ув - у»,
если для проектировщика представляет интерес характер изменения
управляющего воздействия y(t) при действии возмущения ув(0 на
входе объекта.
375
Так как выбором ПФ №у(р) можно выполнить лишь одно из ус-
ловий типа (7.25) и (7.26), то при желании одновременного удовле-
творения основного условия (7.25) и второго условия типа (7.26) в
схему синтеризуемой системы приходится включать дополнительное
устройство - предварительный, или входной, фильтр с ПФ РКф(р) (см.
рис. 7.7,а). Тогда, выбрав сначала ПФ УУ по второму условию, на-
пример по формуле (7.28), ПФ фильтра определяют по условию
Ф'3(р)
*(р)
*э'(Р)
=	(Р)
^у(рШр)
i + wy(p)w0(p)
=ф3ж(р)>
(7.29)
д
с учетом уже выбранной Wy(p) = №ул(р):
ф 1-ф„(/>)
(7.30)
Обратим внимание, что при выборе ПФ Wy(p) по формуле (7.27)
ПФ разомкнутого контура
д
wrAp) = ^г(р)^(р) =
ф„(р)
1-ф,,(р)’
(7.31)
т е. не зависит от свойств ОУ.
Рассмотрим теперь процедуру определения ПФ УУ для объекта
и желаемой системы, описанных в виде следующих дробно-
рациональных ПФ:
. b_pm +Ьт_1рт4 +... + b.p + bQ В(р) . ч
W0{p} = ^~n------------------L =	(w<«)
anP +an-xP + ...+a,p + a0 л(р)
(7.32)
ФЖ(Р) =
avpv +av^pv~' +...+а}р + а0 a(p)’
(p<v). (7.33)
Передаточная функция УУ, полученная в соответствии с фор-
мулами (7.27) или (7.28), в общем случае будет иметь вид
376
W(p)=-^----=	(r<5)
y dsp'+ds^+...+dip + d, D(p)
(7.34)
Для конкретных каналов, по которым заданы желаемые ПФ
(7.25) или (7.26), ПФ УУ будут иметь вид
^.3(Р) =
Мр)А(р)
\а(Р) - Р(р)}В(р) ’
Wy_Ap) =
[«(/?)-Д(р)]Л(/?)
№)В(р)
(7.35)
(7.36)
Для физической реализуемости ПФ (7.34) необходимо желае-
мую ПФ Ф^р) выбирать так, чтобы порядок полинома С{р) оказался
не больше порядка полинома D(p), т.е. для ПФ (7.35) должно быть
r-n+p<s~m+v или п - т < у - р,
(7.37)
а для ПФ (7.36)
г = n + v <s = т+ р или п-т< p-v.
(7-38)
При решении практических задач синтеза выбор желаемых ПФ
Фж(р) ограничивают определенными формами, которые называются
стандартными и которые имеют более простой вид, чем ПФ (7.33):
Фж(Р) =
____________А____________
av pv + ccv^p'{ + ...+atp + a0
(7.39)
377
00
Стандартные полиномы р(/?) желаемой ПФ для v = 1; 2;...; 6
Таблица 7.1
Биноминальная форма	Форма Баттерворта
5 + со0 S2 + 2сОо5 + С0„ s3 + 3co0s2 + Зсо25 + со* 5 4 + 4сО053 + 6(Bq52 +4со^5 + со£ s5 + 5co0s4 +10cOqS3 + lOcoJs2 + 5cojs + co„ s6 + 6co0s3 +15а>о$4 + 20cOg.s3 +1 5cOq52 + 6co35 + co®	5 + C0o s1 +l,4coos + ci)* s’ + 2,Oco0s2 + 2,0<o25 + co3 s* + 2,6co053 + 3,4<o2/ + 2,6co35 + coj 5s + 3,24<й05< + 5,24<o2№ + 5,24<d252 + 3,24с0д5 + co’ № + 3,86coo№ + 7,64<Bo-s4 + 9,14coJ№ + 7,46<oj52 + 3,860’5 + coj
min J 0	min tn
S + COo s2 + 1,4см + cOg 53 + l,75co0s2 + 2,1 5co25 + co3 s4 + 2,lco0s3 + 3,4co2s2 + 2,7co3s + coj s3 + 2,8co0s4 + 5,0co2s3 + 5,5cOq52 + 3,4co„s + co3 s6 + 3,25co0№ + 6,60cOq54 + 8,60co3s3 + 7,45cOq52 + 3,95co3s + co*	s + co0 s2 + l,4a>0s + co2 s3 +l,55co0s2 + 2,10co2s + co3 s4 + l,60coos3 +3,15co„s2 + 2,45cols + col s5 +1,575co0j4 +4,05cOq53 +4,IOco^s2 +3,025сОд5 + сОо s6 + 1,45co053 + 5,10co„54 + 5,30cOq53 + 6,25cOq52 + 3,425со^ + со£
a
б
Рис. 7.8. Стандартные переходные характеристики желаемой СУ
Коэффициент р0 числителя, исходя из условия статики Фзж(0) =
= 1, принимают равным ро = а0, а коэффициенты знаменателя а0,
аь..., av выбирают по одной из стандартных форм, приведенных в
табл. 7.1 и соответствующих разным видам ПХ Аж(/) (рис. 7.8).
Простейшая стандартная форма называется биноминальной, так
как ей соответствует желаемая ПФ со знаменателем в виде бинома:
(7.40)
где (о0 - относительная частота. ПФ (7.40) соответствует, в свою оче-
редь, последовательному соединению из v инерционных звеньев пер-
вого порядка с одинаковыми постоянными времени Т, = 1/со0, и сле-
довательно, с одинаковыми полюсами pt = - <в0- На апериодический
переходный процесс такого соединения ориентируются лишь в
тех редких случаях, когда перерегулирование в синтезируемой сис-
379
теме нежелательно. При этом, как видно по графикам Лж(г) на рис.
7.8, переходные процессы имеют наибольшие длительности tH и tn по
сравнению с другими стандартными формами.
Более часто используется стандартная форма Баттерворта (англ.
- Butterworth), полиномы Р(р) которой имеют v корней ph располо-
женных в левой полуплоскости равномерно на дуге с радиусом о0,
отстоящих друг от друга на одинаковые углы тс/л и подчиняющихся
следующей общей формуле:
Pt = соо ехр + 2/ - 1)/2и.
(7.41)
Наиболее распространенной является форма полинома 0(р), ко-
торой соответствуют переходные процессы с минимальным значени-
ем улучшенной модульной интегральной оценки следующего вида
(см. 6.3):
й =	(7.42)
О
Наконец, четвертая из рассматриваемых стандартных форм
применяется, когда необходимо обеспечить минимальную длитель-
ность /п (время вхождения ПХ Лж(0 в 5-процентную зону).
Пример. Определим для ОУ
»№)=—=
Л(р)
_________1________
5р3 + Пр2 + 7р + 1
(7.43)
ПФ УУ, обеспечивающую по каналу «х3 - х» переходный процесс с мини-
мальным значением интегрального показателя (7.42) и с длительностью на-
растания tH = 8 с.
Для объекта (7.43) с п - т = 3 условие реализуемости (7.37) будет
v - ц > 3 или для упрощенной желаемой ПФ (7.39) - v > 3. В соответствии
с табл. 7.1 для v = 3
«(Р) = Р3 +1,75со0р2 +2,15со2р + со0,
(7.44)
где учетом заданной длительности нарастания со0 = 4/8 = 0,5 с1.
Тогда для реального времени
380
(7.45)
а(р) = р3 + 0,875р2 +0,5375/7+0,125,
а ПФ УУ в соответствии с формулой (7.35) будет
0,125(5р3+11рг+7р+1)	5р3+11р2+7р+1 _ С(р)
у3 Р ”	+0,875р2 + 0,5375р+0,125-0,125)1 " р(8р2 +7р+4,з) " D(p)'
(1А6)
Заметим, что от выбираемой длительности нарастания /н выходной ве-
личины x(t) сильно зависят дифференцирующие свойства УУ и первый
«выброс» управляющего воздействия y(t): чем меньше tn, тем больше пре-
обладают дифференцирующие свойства над интегрирующими и тем больше
«выброс» y(t).
7.4. Стабилизация и коррекция частотных свойств
системы управления
Сущность стабилизации и коррекции. Стабилизация и кор-
рекция представляют собой процедуры улучшения динамических
свойств СУ путем включения в ее контур дополнительных конструк-
тивных элементов, имеющих заранее выбранные характеристики.
Под стабилизацией понимают процедуру, осуществляемую с целью
придания устойчивости структурно-неустойчивой системе или с це-
лью повышения запаса устойчивости структурно-устойчивой СУ, а
под коррекцией - процедуру, осуществляемую для улучшения каче-
ства переходного процесса (уменьшения его длительности и колеба-
тельности).
Стабилизация и коррекция тесно связаны между собой: измене-
ние запаса устойчивости всегда приводит к изменению колебатель-
ности и длительности переходного процесса в СУ, и наоборот, - при
изменении колебательности меняется запас устойчивости. Как пра-
вило, увеличение запаса устойчивости приводит к уменьшению ко-
лебательности и к увеличению длительности переходного процесса.
Стабилизацию и коррекцию осуществляют включением в ос-
новной (функционально необходимый) контур СУ последовательно-
го или параллельного корректирующего устройства (КУ). Последо-
вательное КУ с ПФ WK пс(р) включают в прямую цепь основного кон-
тура между элементами и W2(p), образующими исходную, не-
381
скорректированную систему с ПФ РГнс(р) (рис. 7.9,а), а параллельное
(точнее - встречно-параллельное) КУ включают в виде отрицатель-
ной (иногда положительной) обратной связи с ПФ fKK0C(p), охваты-
вающей одно или несколько элементов прямой цепи (рис. 7.9,6).
*
а
Рис. 7.9. Схема включения последовательного (а) и параллельного (6) КУ
В качестве КУ обычно используются электрические гС-
четырехполюсники. В табл. 7.2 приведены схема и частотные харак-
теристики трех наиболее простых и в то же время наиболее часто
применяемых четырехполюсников.
На рис. 7.10 в качестве примера приведена принципиальная
схема следящей СУ. Управляемой величиной в системе является
угол поворота а. Угловое перемещение объекта ОУ осуществляется
исполнительным двигателем ИД который питается от усилителя
мощности У. Сравнение угла поворота а выходного вала с заданным
углом а3 осуществляется при помощи сельсин-пары, работающей в
трансформаторном режиме. Сигналом рассогласования в системе
служит напряжение переменного тока на выходе сельсин-
трансформатора СТ. Действующее значение этого напряжения про-
порционально разности углов а и о,. Фазочувствительным элемен-
том ФЧВ сигнал рассогласования преобразуется в напряжение по-
стоянного тока, которое воздействует на усилитель У. Качество этой
следящей системы, состоящей из описанных функционально
382
Типовые корректирующие устройства
Таблица 7.2
необходимых элементов, можно улучшить при помощи двух КУ,
включаемых в контур последовательно (КУ1) или в виде обратной
связи (КУ2). Во втором случае кроме самого КУ2 используется еще
тахогенератор ТГ, преобразующий частоту вращения ИД в электри-
ческое напряжение постоянного тока.
Рис. 7.10. Следящая СУ с последовательным и параллельным КУ
Каждый из указанных выше способов включения КУ имеет оп-
ределенные достоинства и недостатки. Последовательное КУ проще
включать в контур (для этого не нужны дополнительные входы у
суммирующих элементов). Но оно ослабляет основной сигнал и по-
этому требует применения дополнительного усиления. Кроме этого,
качество СУ сильно зависит от стабильности характеристик самого
КУ, а при выходе его из строя вся СУ становится неработоспособ-
ной.
Параллельное КУ уменьшает влияние координатных и парамет-
рических возмущений, действующих в охватываемых элементах.
При включении такого КУ в контур не возникают трудности согла-
сования мощности сигналов, так как оно всегда подключается к вы-
ходу более мощного элемента. Но параллельное КУ уменьшает ПК
охватываемого участка, а следовательно и всего разомкнутого кон-
тура.
ПФ разомкнутого контура СУ, скорректированной при помощи
последовательного КУ (см. рис. 7.9,а),
384
(7.47)

где f^HC(p) - W\(p)' W2(p) - ПФ разомкнутого контура нескорректиро-
ванной системы,
ПФ разомкнутого контура СУ, скорректированной при помощи
параллельного КУ (см. рис. 7.9,6),
WIK(P)
Ж
Ж (/?) = Щ(р)---------------W3(p) =-----,	(7.48)
Л/'1±Ж2(/,)ЖК0С(р)	\±W0(p)^(p)
где Жнс(р) = Ж](р)Ж2(р)Ж3(р) - ПФ разомкнутого контура нескоррек-
тированной системы; Ж0(р) = Ж2(р) - ПФ части прямой цепи контура,
охваченной обратной связью.
Одни и те же свойства скорректированной системы можно по-
лучить включением в нескорректированную СУ как последователь-
ного, так и параллельного КУ. Приравнивая правые части выражений
(7.47) и (7.48), легко найти условие эквивалентного влияния этих
устройств на свойства нескорректированной системы:
или
и;Пс(р)=
1
l±W0(p)WK0C(p)
ЖК0С(Р)=±
1 -	<Р)
WO(P)WKM
(7.49)
(7.50)
Выбор того или иного способа включения КУ определяется
удобством технической реализации.
Последовательная коррекция. АФХ разомкнутого контура
СУ, скорректированной с помощью последовательно включенного
КУ
О) = Л„	(»)FK„ (со) = Ат	,к (ш)е^'“
(751)
отсюда
385
Лк('у) = 4Л®И„(®);
(7.52)

(7.53)
т.е. коррекция АФХ может быть достигнута как изменением АЧХ,
так и ФЧХ нескорректированной системы.
На рис. 7.11 показано, как деформируется АФХ нескорректиро-
ванной СУ, проходящая близко к границе устойчивости (см. штрихо-
вые линии), при изменении ее амплитудной (см. рис.7.11,а) и фазо-
вой (см. рис.7.11,б) составляющей. В первом случае достигается
уменьшением модулей Л (со,) в некотором диапазоне частот от сон до
сов (амплитудная коррекция). Для этого АЧХ КУ должна в указанном
диапазоне иметь значения, меньшие единицы (см. рис.7.11,в). Во
втором случае достигается уменьшение фазовых сдвигов (р(со;) (фа-
зовая коррекция), для чего КУ должно создавать положительные
(опережающие) сдвиги (см. рис. 7.11,в).
Рис. 7.11. Амплитудная (а) и фазовая (б) коррекции АФХ исходной СУ
Следует заметить, что при использовании в качестве КУ мини-
мально-фазовых звеньев одновременно происходят и амплитудная, и
фазовая коррекции. Причем часто их влияния противоположны, и
приходится искать компромиссные решения.
Рассмотрим теперь, как влияют КУ трех основных типов
(см.табл. 7.2) при их последовательном включении.
Интегро-дифференцирующее звено
386
(7.54)
1\р +1
IF (р) =	—
к 7> + 1
с преобладанием интегрирующих свойств (т.е. с Т2 > Т\ используют
для коррекции высокочастотной части АЧХ - для подавления высо-
ких частот. При его включении в контур АЧХ в области высоких
частот опускается (рис.7.12,а). Это позволяет уменьшить частоту
среза, не изменяя общий ПК контура, или, наоборот, увеличить ПК,
не изменяя частоту среза.
Достоинством данного способа коррекции является уменьшение
ошибок, вызываемых высокочастотными помехами. Недостаток спо-
соба - снижение полосы пропускания СУ и, как следствие, ухудше-
ние быстродействия. Поэтому способ может использоваться лишь в
тех случаях, когда допустимо снижение быстродействия СУ.
КУ (7.54) создает в определенной области частот отставание по
фазе. Чтобы это отставание не ухудшило запас устойчивости СУ,
сопрягающие частоты = 1/7\ и оъ = 1/Т2 должны находиться левее
частоты среза со^, скорректированной СУ. Соответственно постоян-
ные времени КУ целесообразно выбирать из условий.
7’,«(10...20)/®ср;	(7.55)
Ц10...20>р,Х,	(7.56)
где А'р к - требуемый по условию точности ПК разомкнутого контура.
Пассивное интегро-дифференцирующее звено
=	а<1)	(7.57)
Tip + l
с преобладанием дифференцирующих свойств (т.е. с Т\ > Т2) подав-
ляет низкие частоты и уменьшает общий ПК контура. Так как
обычно по условию точности нельзя допускать уменьшения общего
ПК, то приходится одновременно с включением в контур пассивного
четырехполюсника (7.57) обеспечить сохранение ПК на требуемом
387
уровне при помощи дополнительного усилителя или путем увеличе-
ния исходного ПК. Тогда звено может быть использовано для подня-
тия высококачественного участка ЛАЧХ (см. рис.7.12,6). Кроме того,
рассматриваемое КУ создает в определенной области частот опере-
жение по фазе.
Рис. 7.12. Коррекция ЛАЧХ при помощи последовательных КУ
Достоинство коррекции с помощью звена (7.57) состоит в том,
что наряду с дополнительным увеличением общего ПК удается уве-
личить и частоту среза, т е. одновременно улучшить и точность, и
быстродействие СУ. Недостатки данного способа: необходимость
дополнительного усиления, ухудшение помехозащищенности в об-
ласти высоких частот.
Фазоопережающие свойства звена (7.57) тем сильнее, чем боль-
ше отношение его постоянных времени T-JT^. Но отношение ТУТ?
нельзя выбирать очень большим, так как это ведет к существенному
ослаблению сигнала при его прохождении через КУ. Ведь ПК кк у
388
рассматриваемой rC-цепи обратно пропорционален указанному от-
ношению: кк - Т\!Тг . Поэтому на практике принимают
TJT2 = 10...50 или кК = 0,10.. .0,02,	(7.58)
соответственно приходится обеспечивать дополнительное усиление с
коэффициентом кд = 10... 50.
Постоянную времени выбирают приблизительно равной наи-
большей постоянной времени неизменяемой части. В тех случаях,
когда наибольшая постоянная времени превышает остальные посто-
янные времени на порядок и более, а также когда на входе действуют
высокочастотные помехи, постоянная 7\ может быть принята мень-
ше, чем наибольшая.
Наиболее часто для последовательной коррекции используют
интегро-дифференцирующее звено
^(P) = /7‘P+v " +	(7-59)
(T,p+iXrtP+iy
обладающее свойствами полосового фильтра. В области низких час-
тот у этого звена преобладают интегрирующие свойства, а в области
высоких - дифференцирующие свойства.
При включении звена (7.59) в контур происходит подавление
средних частот (см. рис. 7.12,в). Это позволяет увеличить общий ПК
и частоту среза СУ (т.е. улучшить ее точность и быстродействие) без
ухудшения помехозащищенности при высоких частотах.
При выборе параметров КУ (7.59) руководствуются следующи-
ми соображениями. Сопрягающие частоты 1/7з и \/Т\ должны быть
меньше частоты среза скорректированной системы. Тогда область
частот, в которой КУ вносит отставание, будет находиться левее час-
тоты среза. Постоянную времени 75 целесообразно принимать рав-
ной наибольшей постоянной времени неизменяемой части СУ. Же-
лательно также, чтобы частота среза находилась между сопрягаю-
щими частотами 1/75 и 1/Т4, т.е. в области максимального опереже-
ния фаз, создаваемого КУ. Благодаря этому достигается наибольший
запас устойчивости по фазе.
389
Параллельная коррекция. Параллельная коррекция осуществ-
ляется с помощью КУ, включаемых встречно-параллельно с частью
прямой цепи основного контура, т.е. охватывающих одно или не-
сколько элементов прямой цепи обратной связью (см. рис. 7.9,6). Об-
ратной связью (ОС) охватывают, как правило, инерционные статиче-
ские элементы корректируемой СУ.
В отличие от главной ОС, корректирующие ОС называют внут-
ренними, или местными.
Корректирующие ОС могут быть отрицательными или положи-
тельными, жесткими или гибкими. Жесткую ОС осуществляют через
безынерционное или инерционное статические звенья, у которого,
как известно, ПФ WK ос(О) Ф 0. Это означает, что такая связь действует
как в статическом, так и в динамическом режиме. Гибкую (упругую)
ОС выполняют при помощи дифференцирующего звена, у которого
^кос(О) = 0. Следовательно, сигнал гибкой ОС действует только в
динамическом режиме, т.е. когда выходной сигнал охватываемого
участка изменяется во времени.
АФХ разомкнутого контура СУ, скорректированной при помо-
щи внутренней ОС (см. рис. 7.9,6),
^ск (JCO) =	(7со)
1±^(7щ)^кос(7СО)
^3 О) -
1±^(»^кос(7СО)'
(7.60)
Произведение ^(/coj^oc^'to), входящее в знаменатель выраже-
ния (7.60), характеризует свойства внутреннего контура. Очевидно,
что коррекция будет эффективной лишь тогда, когда внутренний
контур устойчив.
В диапазоне частот, для которого справедливо неравенство

(7.61)
АФХ (7.60) скорректированной СУ приблизительно равна АФХ не-
скорректированной СУ:

(7.62)
390
т.е. ОС практически не влияет на свойства СУ. Соответствующий
диапазон частот является несущественным для задачи коррекции.
Для жестких ОС условие (7.61) выполняется при высоких часто-
тах, а для гибких - при низких частотах.
В диапазоне частот, где справедливо неравенство
WAjn)W^j(o) »1,
(7.63)
АФХ скорректированной СУ составляет

(7.64)
где FFho(/co) =	- АФХ элементов, не охваченных коррек-
тирующей ОС.
Соотношение (7.64) означает, что свойства скорректированной
СУ в определенном диапазоне частот зависят только от свойств ОС и
от свойств элементов, не охваченных ОС, и что характеристики эле-
ментов, охваченных ОС, не влияют на поведение скорректированной
системы.
Диапазон частот, для которого выполняется условие (7.63), яв-
ляется существенным для задачи коррекции. Для жестких ОС усло-
вие (7.63) выполняется при низких частотах, а для гибких - при вы-
соких частотах.
Увеличение ПК звена ОС приводит, как правило, к возрастанию
частоты среза, а увеличение ПК неохваченных элементов - к умень-
шению частоты среза.
При помощи параллельных КУ, как и при помощи последова-
тельных, можно осуществлять амплитудную коррекцию трех видов:
подавление высоких, низких и средних частот. Но влияние одних и
тех же звеньев при их параллельном и последовательном включении
прямо противоположно. Например, дифференцирующее звено в ОС
подавляет высокие частоты в основном контуре, т.е. действует как
интегрирующее звено, включенное последовательно. И наоборот,
интегрирующее звено в ОС подавляет низкие частоты, т.е. действует
как последовательное дифференцирующее.
391
Определение структуры и параметров КУ7 по заданным по-
казателям качества. Для минимально-фазовых СУ, у которых, как
известно, существует однозначная связь между амплитудной и фазо-
вой характеристиками, выбор ПФ и параметров КУ можно осущест-
влять только по АЧХ, причем удобнее делать это по ЛАЧХ. Напри-
мер, для последовательного КУ в соответствии с формулой (7.52)
ЛАЧХ представляет собой разность
4пс(й?) = Ак(^)-/'нс(^)
(7.65)
что позволяет определять ЛАЧХ последовательного КУ графическим
вычитанием ординат.
Для параллельного КУ можно использовать приближенное со-
отношение (7.63), справедливое для существенного диапазона час-
тот:

(7.66)
Решение задачи состоит из следующих пяти последовательных
этапов:
1)	построение ЛАЧХ Ьнс(<а) нескорректированной системы, со-
стоящей из функционально необходимых элементов;
2)	построение желаемой ЛАЧХ £ск(со), соответствующей тре-
буемым показателям качества;
3)	определение ЛАЧХ LK пс(о>) или £к.ос(®);
4)	подбор принципиальной схемы и параметров КУ, соответст-
вующих полученным в п.З ЛАЧХ;
5)	проверочный расчет качества скорректированной СУ.
Выполнение первого этапа обычно не вызывает затруднений.
ЛАЧХ отдельных элементов, образующих неизменяемую часть (при
последовательной коррекции) или неохваченных ОС (при парал-
лельной коррекции), строят по простым правилам, изложенным в
гл.З, а общую характеристику Z,HC(co) или LH0(tB) находят суммирова-
нием ЛАЧХ этих элементов.
392
Наиболее важным и трудоемким этапом является построе-
ние желаемой характеристики Лск(о). При построе-
нии выделяют три ее участка (рис. 7.13): низкочастотный, среднечас-
тотный и высокочастотный.
Рис. 7.13. Типичная форма желаемой ЛАЧХ
Низкочастотный участок предопределяет точность системы в
установившихся режимах. Исходными данными для его построения
служат требуемый порядок астатизма v и величина ошибки s, допус-
тимая при заданном законе изменения входного воздействия. В об-
ласти низких частот ЛАЧХ ZCK(co) представляет собой прямую, про-
ходящую через точку с координатами L(q) = 20 1g к и о = 1 (точка Е
на рис. 7.13) и имеющую наклон - 20 v дБ/декаду, где к - ПК ра-
зомкнутого контура, рассчитанный по условиям точности.
Среднечастотный участок определяет быстродействие и колеба-
тельность СУ. Параметры этого участка (наклон, частота среза, ши-
рина) выбирают согласно заданным значениям коэффициента пере-
регулирования с и длительности переходного процесса /п- Участок,
как было показано в гл. 6, должен иметь наклон - 20 дБ/декаду и пе-
ресекать ось частот при частоте среза соср. Частоту среза можно опре-
делять по приближенной эмпирической формуле
393
С0ср « 0,3 8а//п, 1/с,
(7.67)
где а - коэффициент перерегулирования в %.
Границу среднечастотного участка оъ и со3 выбирают из сле-
дующих соображений. Чем шире участок с наклоном - 20 дБ/декаду,
тем больше запас устойчивости и меньше колебательность системы.
Левую границу принимают
а правую
<(0,50...0,25)<уср,
щ3>(2...4)щср.
(7.68)
(7.69)
Высокочастотный участок слабо влияет на характер переходно-
го процесса. На его положение обращают внимание, если на СУ дей-
ствуют высокочастотные помехи (см. 4.6). Высокочастотную часть
ЛАЧХ Ack((d) строят так, чтобы разность наклонов ее асимптот и
асимптот ЛАЧХ £нс(со) или £Но(<£>) не превышала 20 дБ/декаду. Жела-
тельно, чтобы, начиная с некоторой частоты, характеристики Ьск((я) и
Анс(со) совпадали, тогда КУ получается более простым.
Заключительным этапом задачи коррекции является подбор
конкретной схемы КУ. Для этого используют справочные таблицы,
подобные табл. 7.2.
После выбора КУ строят ФЧХ фск(<») и оценивают запас устой-
чивости по модулю и по фазе.
Пример. Выберем КУ для астатической СУ подъемной установкой
(v = 1). неизменяемая часть которой описывается ПФ
И' (р) = k/pfc р + 0(7> + 1Х?3? +1),
(7.70)
где 71 = 0,5 с; Т2 = 0,25 с; Т3 = 0,125 с.
Структуру и параметры КУ определим исходя из заданных показате-
лей точности и качества. Пусть при заданной скорости изменения входного
воздействия = 1,4 м/с допустимая динамическая ошибка в установившем-
ся режиме ускорения еуст = 0,25 м/с, допустимый коэффициент перерегули-
рования ст = 20 % и длительность переходного процесса tn = 5 с. По формуле
(4.92) для <7=1 находим требуемый ПК:
394
к = ах/&уст =1,4/0,25 = 5,6с’1.
(7.71)
Сопрягающие частоты исходной системы (рис. 7.14,а):
®С1 =1/^ =2с-,;£Ос2 =1/Т2 =4с-,;®с3 =1Д3 = 8с’*.	(7.72)
Рис. 7.14. Пример расчета последовательного КУ
Согласно формуле (7.67), частота среза
®ср ®0,38оДп =0,38-20/5 = 1,5с’1.
(7.73)
Левую граничную частоту среднечастотного участка LCK(o'>) примем со-
гласно рекомендации (7.68)
395
<n2 = 0,5о)ср = 0,75с 1,
(7.74)
из соответствующей точки С (см. рис.7.14,а) проводим асимптот}' со стан-
дартным наклоном - 40 дБ/декаду до пересечения с ЛАЧХ Z,HC(co) в точке F.
Правую граничную частоту и3 этого участка целесообразно выбирать рав-
ной сопрягающей частоте ис2, если это не противоречит рекомендации
(7.69). В данном случае со3 = сос2 = 4 ~ 2,7 соср, что вполне допустимо.
Высокочастотную часть желаемой характеристики £ск(а>) строим так,
чтобы ее изломы происходили при тех же частотах, при которых имеет из-
ломы ЛАЧХ ZHC(o>).
После вычитания характеристики Lllc(w) из Аск(®) находим, что КУ
должно представлять собой полосовой фильтр (см.табл. 7.2). Сопрягающие
частоты фильтра определим непосредственно по графику LK пс(®):
сок1 = 0,75с 1; сок2 =2с *;	=0,2с *; ®к4 =7,1с 1
(7.75)
По ФЧХ фск(со) (см. рис. 7.14,6) можно установить, что у скорректиро-
ванной системы запас устойчивости по модулю ДА=6 дБ, а по фазе -
Д(р=35°.
7.5. Улучшение качества систем при помощи
дополнительных каналов управления
Понятие инвариантности в задачах управления. Одной из
главных целей, преследуемых при синтезе СУ, является обеспечение
требуемой точности в установившихся и переходных режимах. В
главе 4 было показано, что точность СУ в установившихся режимах
можно улучшить, увеличивая порядок астатизма v и ПК к разомкну-
того контура. Но при этом, как правило, уменьшается запас устойчи-
вости, увеличивается колебательность и, как следствие, ухудшается
точность СУ в переходных режимах. Эффективным средством уст-
ранения этого противоречия между условиями точности в устано-
вившихся и переходных режимах служит компенсация внешних воз-
действий путем осуществления инвариантности.
Термин «инвариантность» в общем случае означает независи-
мость одной физической величины от другой. В ТУ рассматривают
независимость выходных координат (управляемой величины и / или
396
сигнала ошибки) от входных воздействий или независимость одних
выходных координат от других.
Математическая теория инвариантности СУ, разработанная рос-
сийскими учеными Г.В. Щипановым, Н.Н. Лузиным, В С. Кулебаки-
ным и Б.Н. Петровым, различает полную и частичную инвариант-
ность. При полной инвариантности выходные координаты не зависят
от характера входных воздействий, а при частичной независимость
выходных координат обеспечивается только по отношению к вход-
ным воздействиям определенного вида (например, к низкочастотным
воздействиям).
Условия полной инвариантности в стабилизирующих и сле-
дящих СУ. В стабилизирующих СУ стремятся получить независи-
мость управляемой величины от возмущающего воздействия, а в
следящих - независимость сигнала ошибок от задающего воздейст-
вия. Для этого в СУ осуществляют дополнительные цепи управле-
ния, называемые компенсирующими связями. Обычно компенсирую-
щие связи применяются в сочетании с основным контуром управле-
ния по отклонению. Как известно из главы 1, СУ, в которой исполь-
зуются совместно принципы управления по отклонению и по возму-
щению, называется комбинированной. Ниже рассматриваются усло-
вия достижения инвариантности именно в комбинированных систе-
мах управления.
На рис. 7.15,я приведена алгоритмическая схема комбинирован-
ной системы стабилизации с компенсирующей связью по возмуще-
нию z. Компенсирующая связь действует на выходную величину со
знаком, который всегда противоположен знаку непосредственного
влияния возмущения на выход. Передаточная функция системы по
возмущению
. * Х(р) Wo:(p)-WSp)Wv(p)WQ(p)
ф (р) = —— =---------------:--------
" Г z(p) l + Wy(p)W0(p)
(7.76)
где W0(p) и Woz(p) - передаточные функции объекта соответственно
по управляющему и возмущающему воздействиям; FKv(p) - переда-
точная функция управляющего устройства; №к(р) - передаточная
функция компенсирующего устройства.
397
Рис. 7.15. Алгоритмические структуры инвариантных
комбинированных СУ с компенсирующими связями:
а - по возмущению; б - по задающему' воздействию
Управляемая величина х(/) не будет зависеть от возмущения z(t),
если передаточная функция (7.76) будет равна нулю:
ф„(/’) = о,
(7.77)
а это возможно, если равен нулю ее числитель. Отсюда условие
полной инвариантности стабилизируемой
величины по отношению к возмущению

(7.78)
Условие (7.78) означает, что
для достижения независимости величины x(t) от возмущения
z(t) необходимо, чтобы динамические свойства двух параллель-
ных каналов, по которым возмущение z(t) действует на величи-
ну x(t), были одинаковыми.
398
Именно благодаря идентичности каналов сигнал, поступающий
на выход через звенья FFK(p), Wy(p) и W0(p), компенсирует сигнал,
идущий на выход через звено Wo:(p).
Согласно условию полной инвариантности (7.78), передаточная
функция компенсирующего устройства должна быть
^(р) = ^(р)/^(р)^(р)-
(7.79)
Компенсирующее устройство представляет собой динамическое
звено, свойства которого зависят от соотношения инерционностей
канала возмущения (РКог) и канала управления (Wy Wo), Если инерци-
онность канала управления больше, чем инерционность канала воз-
мущения, то компенсирующее устройство должно обладать свойст-
вами дифференцирующего звена. Причем, чем больше различие этих
инерционностей, тем выше должен быть порядок дифференцирую-
щего звена. Как известно, дифференцирующие звенья высокого по-
рядка трудно технически реализовать.
Если оба канала объекта обладают запаздываниями т0 и т0- и при
этом т0 > т0-, то компенсирующее устройство не может быть реализо-
вано физически. Действительно, в этом случае компенсирующее воз-
действие должно опережать возмущение на время Дт =	- г,.,-, что
невозможно.
Для обеспечения частичной инвариантности - инвариантности
только в статике - компенсирующее устройство может быть реали-
зовано в виде безынерционного звена с передаточным коэффициен-
том
(7.80)
В следящих системах необходимо добиваться независимости
сигнала ошибки от задающего воздействия. Для схемы, приведенной
на рис. 7.15,6, передаточная функция между задающим воздействием
Хз(0 и сигналом ошибки e(f)
i-^(pWy(pK(p)
l+wy(p)wo(p)
(7.81)
399
Приравнивая функцию (7.81) нулю, находим условие
полной инвариантности ошибки слежания по
отношению к задающему воздействию
1-^(Жу(р)1Го(р) = 0,	(7.82)
отсюда требуемая передаточная функция компенсирующего устрой-
ства
I	WSp) = \IW^p)W°(p).	(7.83)
Компенсирующее устройство в следящих системах так же, как и
в стабилизирующих, должно обладать дифференцирующими свойст-
вами.
По виду передаточных функций (7.76) и (7.81) можно устано-
вить, что введение компенсирующих связей не изменяет характери-
стический полином системы и, следовательно, не влияет на ее устой-
чивость. Нетрудно также заметить, что и в стабилизирующей, и в
следящей системах инвариантность осуществима благодаря наличию
двух параллельных каналов передачи сигналов от точки приложения
воздействия до выходной величины (х или е). Этот структурный при-
знак достижения инвариантности был впервые сформулирован акад.
Б.Н. Петровым в виде принципа двухканалъности. Но наличие двух
каналов является лишь необходимым условием получения инвари-
антности. Достаточным условием служит условие физической реали-
зуемости передаточной функции WK(p) в виде конкретного техниче-
ского устройства: максимальная степень полинома числителя должна
быть меньше или равна максимальной степени полинома знаменате-
ля.
Если передаточная функция WK(p) удовлетворяет условию фи-
зической реализуемости, то в системе возможно достижение полной
инвариантности. Если же передаточная функция WK(p) не удовлетво-
ряет этому условию и может быть реализована только приближенно,
то в системе осуществима лишь частичная инвариантность. В систе-
400
ме с частичной инвариантностью независимость достигается только
при медленных изменениях входных воздействий.
Пример. На рис. 7.16,а приведена принципиальная схема комбиниро-
ванной системы стабилизации частоты вращения двигателя постоянного
тока. Основной контур СУ - контур по отклонению - содержит тахогенера-
тор Т1\ усилитель У и силовой тиристорный преобразователь 777. служащий
регулируемым источником питания двигателя. Возмущающие воздействие
- момент сопротивления Мс - измеряется при помощи упругой муфты М и
встроенного в нее индуктивного датчика. Электрический сигнал пропор-
циональный моменту Л/с. через компенсирующее устройство КУ поступает
на вход усилителя.
Определим ПФ и схемную реализацию КУ, обеспечивающего незави-
симость частоты вращения п от момента Мс.
Алгоритмическая структура СУ изображена на рис. 7.16,6. ПФ двига-
теля по напряжению и по моменту сопротивления имеют вид
(7.84)
Управляющее устройство, состоящее из усилителя и тиристорного
преобразователя, можно приближенно описать ПФ инерционного звена
первого порядка

Тахогенератор и муфту можно рассматривать как безынерционные
звенья:
^Tr(p) = *Tr; Им(р) = 1-м.
Условие инвариантности СУ

(7.87)
Из условия (7.87) находим ПФ компенсирующего устройства
w.(pFy(p)H',(p) МЛ
(7.88)
401
Рис. 7.16. Инвариантная система стабилизации частоты вращения двигателя
Как видно из выражения (7.88), для достижения полной инвариантно-
сти КУ должно быть форсирующим звеном второго порядка. Но практиче-
ски реализовать ПФ (7.88) можно только приближенно - в виде двух диф-
ференцирующих четырехполюсников (7.57), соединенных последовательно
через разделительный усилитель ЭУ (рис.7.17). ПФ такой цепи

(7.89)
где = г1с1;/с1 = г2Дг, + г2),12 = МйЛ	=г4/У*з+МЛ = к213.
(7.90)
Выбирая коэффициенты к\ и к2 достаточно малыми (например, 0,1),
можно добиться приближенного совпадения ПФ (7.88) и (7.89). Инвариант-
402
ность при этом оудет лишь частич-
ной, справедливой при низких час-
тотах Для ее обеспечения пара-
метры КУ должны удовлетворять
следующим равенствам:
'I ~ Л —	~ кд /кцкук
(7.91)
Рис. 7.17. Принципиальная схема
компенсирующего устройства
Использование дополнительных контролируемых величин.
В промышленной автоматике для обеспечения лучшего качества СУ
широко используются схемы с дополнительными (вспомогательны-
ми) контролируемыми величинами хд (рис. 7.18).
Схема на рис. 7.18,а служит для более быстрого реагирования
на изменения основного возмущения z, так как дополнительный сиг-
нал хд измеряется не на выходе всего объекта (после №02), а в его се-
редине (после IFoi). Схема обеспечивает частичную инвариантность
на низких частотах, при которых ПФ по каналу «z-х»
ф(	=___________Мх(р)Ул(р)___________~ 0
н z(p) I +	+
за счет больших значений АФХ H^i(/co) и И^2(/о>). Такие схемы с до-
полнительными сигналами хД, измеряемыми в промежуточных точ-
ках ОУ, широко распространены, например, в теплоэнергетике.
Схема на рис. 7.18.6 используется в системах так называемого
каскадного, или подчиненного, регулирования. Она по существу явля-
ется частным случаем схемы на рис. 7.18,а. Особенность ее заключа-
ется в том, что внутренний контур служит для устранения влияния
возмущения на промежуточную управляемую величину хД, а
внешний - для устранения влияния возмущения z2 на основную
управляемую величину х. Причем, УУ внешнего контура вырабаты-
вает задание хдз для внутреннего.
403
Рис. 7.18. Алгоритмические структуры СУ с
дополнительными контролируемыми величинами
Как правило, внутренний контур, подчиненный, так сказать,
внешнему, менее инерционен, чем внешний, и поэтому полагают, что
при низких частотах ПФ по каналу «хд - хд,3»
д
ф(р) =
ХД(Р) ^у1(Жо)(Р)
Хд.з(р) 1 + (Жо1 (р) " ’
(7.93)
и что промежуточная управляемая величина хд так же, как и в схеме
на рис. 7.18,я, не зависит от «своего» возмущения zj. Приближенное
равенство (7.93) позволяет при анализе динамики внешнего контура
учитывать внутренний как безынерционное звено с ПК к ~ 1.
404
В общем случае внутренних контуров может быть несколько,
причем каждый из них будет являться одновременно и внешним по
отношению к последующему внутреннему (подробнее см. в 7.6).
Системы каскадного регулирования получили наибольшее рас-
пространение в управлении электроприводами.
Обеспечение автономности в многосвязных СУ. В промыш-
ленной автоматике чаще всего приходится иметь дело с многомер-
ными ОУ, у которых по две и более выходных управляемых коорди-
нат. Рассмотрение и описание таких ОУ обычно начинают с мнемо-
нической схемы, подобной схеме на рис. 2.23,п, где выходные пере-
менные зависят только от входных и не зависят друг от друга. Одна-
ко, как будет показано ниже на простом примере, не всегда много-
мерный ОУ может быть сразу, без промежуточных преобразований,
представлен такой схемой и описан системой уравнений вида (2.158).
Рассмотрим вначале ОУ, который непосредственно может быть
представлен схемой на рис. 2.23,а и уравнениями (2.158). Пусть име-
ется резервуар (рис. 7.19,я), в котором смешиваются два потока жид-
костей Qi и Q: (м/с), содержащих один и тот же компонент с посто-
янными концентрациями соответственно Сю и Сго (кг/м3). Управляе-
мыми переменными являются суммарный выходной поток и концен-
трация компонента в выходном потоке, т.е. хв! = Q и хв2 = с, а управ-
ляющими воздействиями - углы поворота вентилей j>i - cxi и у2 ~ &2,
пропорциональные потокам: Qi = и Q2 = къ2о.2.
Пользуясь моделью, полученной для рассматриваемого объекта
в разделе 2.9 (см. уравнения (2.217)), можно для новых входных и
выходных переменных записать следующие линеаризованные урав-
нения в операторной форме:
^в1(р)(2Гр +1) = ^цУ1(р) + кх2у2(рУ\
z ч	>	(7.94)
хв2(р)(Т> + U= W1(P) + к22у2(р), J
где Т --= Vq/Qq, ки = Хгв!, кп = £В2, £21 = Агв1(сю - c^/Q^ к22 = къ2(с2() -
- co)/Qo, а индексом «О» отмечены значения, соответствующие точке
линеаризации исходных уравнений.
405
Рис. 7.19. Примеры двумерных СУ
Системе уравнений (7.94) соответствует алгоритмическая струк-
тура, изображенная на рис. 7.20,а, где
ff',, (р) = /(2Тр +1); Wa (/>) = кп /(2Тр +1);1
^,(Р)=*г,/(7>+1); >М/>) =	+О- J
(7-95)
Такая структура в теории многосвязного регулирования, разра-
ботанной американским ученым М.Месаровичем, названа канониче-
ской P-структурой. Она отличается прямыми перекрестными связя-
ми через звенья PKi2(p) и PK2i(p).
Рассмотрим теперь другой пример (см. рис. 7.19,0 - резервуар с
входным и выходным потоками Q3X и Q, регулируемыми с помощью
вентилей. В качестве управляющих воздействий служат углы пово-
рота вентилей: yi = о,) и у2 = а2, а в качестве управляемых перемен-
ных - расход на выходе x8i - Q (м/с) и уровень жидкости в резервуа-
ре хв2 = h (м). С помощью аналогичных выкладок можно получить
для данного случая следующие линеаризованные уравнения.
(7.96)
406
где ^bi и кв2 - ПК соответственно выходного и входного вентилей;
к ~ кц/2.у[Ио - ПК по каналу «Л-0»; Ли - коэффициент истечения;
S - площадь горизонтального сечения резервуара, м2.
Рис. 7.20. Канонические структуры двумерного объекта:
а - Р-структура; б - Р-структура
Системе уравнений (7.96) соответствует структура на рис.
7.20,6, где Wu(p) = £в1; W«(p) = к / кв}; №ж(р) = - 1/ кв2; W22(p) =
= кв2 / Sp. Эта структура имеет обратные перекрестные связи через
звенья кКж (р) и Woc (р) и называется канонической V-структурой.
Канонические Р- и P-структуры применимы и для многомерных
объектов с п входами у, и п выходами хв,. В этом случае удобно опи-
. сывать объект матричным уравнением. Например, для объекта с
/^-структурой справедливо матричное уравнение
XB(P) = ^(PW)>	(7-97)
где хв(р) = [хв1(р),... Лш(р), • • • Лвл(р)Г и у(р) = [у 1 (р),... ^(р),... ,х„(р)]т -
«-мерные векторы-столбцы входных и выходных переменных;
^(р) = [W ? (р)]Пхл - квадратная матрица из ПФ W? (р).
407
К-структура описывается уравнением
Хв (р) = wv (р){у(р) + W* (р)хъ (р)]
или
хв (р) = [1 - Wv (р)	(р)]-1 Wv (р)у(р),
(7.98)
(7.99)
где И^(р) =
(Р)
- матричная ПФ прямых связей с /=/, (те.
отличающаяся от И^(р)!); W^fp) =
№ж(р)
Ц
- матричная ПФ об-
X л
ратных связей. В матрице И? (р) все элементы, кроме элементов,
стоящих в главной диагонали, равны нулю, а в матрице W^lp), на-
оборот, все элементы, кроме главной диагонали, не равны нулю.
Сравнивая выражения (7.97) и (7.99), нетрудно установить связь
между ПФ для P-модели и ПФ для К-модели:
f?p(p)=[1 - ’Lr(p)?L°c (p)j^(p)-
(7.100)
Заметим, что выражение (7.99) справедливо лишь в случае, если
обратная матрица [1-И'г(р)И/0С(р)у1 существует, т.е. если определи-
тель det Ц-Д^СР^СР)] * 0.
Проблема управления многосвязным объектом заключается в
том, что контуры регулирования каналов x31-xBi и хз2-хв2 (рис. 7.21,а),
рассчитанные порознь - без учета перекрестных связей, при их со-
вместном функционировании на реальном объекте влияют друг на
друга и, как правило, становятся более колебательными и даже неус-
тойчивыми. Поэтому задача синтеза СУ многосвязным ОУ заключа-
ется в обеспечении автономности или развязки отдельных контуров с
помощью дополнительных компенсирующих связей Wy (р) и Wy (р),
которые должны сделать главные контуры с регуляторами Wy (р) и
Wy (р), независимыми друг от друга.
408
Рис. 7.21. Система управления двухмерным ОУ с Р-структурой
В общем случае для СУ «-мерным ОУ с P-структурой можно,
кроме уравнения ОУ (7.97), записать следующее матричное уравне-
ние УУ:
y(p) = Wy(p)E(p),
(7.101)
где Е(р) - [Е\(р),... ,Еп(р)]т - вектор-столбец сигналов ошибок регули-
рования в основных контурах; - [Жу(р)]лхл ~ матричная ПФ
УУ, состоящая из ПФ главных регуляторов Wy (р) (с i=j) и ПФ
развязывающих регуляторов (компенсаторов) W у (р) (с tej).
У
Уравнения (7.97) и (7.101) можно объединить в одно матричное
уравнение всей СУ
x(p) = Wp (р)}^ (р)Е(р).
(7.102)
409
Сложная многосвязная СУ, описанная уравнением (7.102),
должна функционировать так, чтобы каждый /-й контур был незави-
сим от остальных и-1 контуров, т.е. чтобы каждый /-й сигнал ошиб-
ки Б/ действовал только на «свою» выходную величину хв/. Это воз-
можно, если только для всех I от 1 до п выполняется условие
xi(p) = WiK(p)Wu (p)Ei(p), l =
(7.103)
где W* (р) - ПФ корректирующего устройства, которое должно
обеспечить автономность /-го контура.
Сформулированную математически цель обеспечения автоном-
ности (7.103) можно пояснить на примере двухмерного ОУ: ПФ кор-
ректирующих устройств W]K (р) и W* (р) (см. рис.7.21,6) должны
быть выбраны так, чтобы две автономные (развязанные) структуры
на рис. 7.21,6 были эквивалентны исходной структуре на рис. 7.21,я.
Условие (7.103) можно записать в матричной форме
£(р)=»:д(р)»:к(р)е(л
(7.104)
где	(р) = [ Wy (р) ]пхп и УКж (р) = [ УК/ (р) ] - диагональные матри-
цы, состоящие только из элементов Wy (р) и W* (р).
Поскольку выражения (7.102) и (7.104) должны соответствовать
одной и той же СУ, можно записать равенство
wp(pyrv(p)=wp(p)WK(P)
(7.105)
из которого следует общее условие автономности для определения
ПФ главных регуляторов (i=j) и компенсаторов (/ту):
wy(p)=a^(.p)fLK(p)/wp(p)
(7.106)
где УУ^(р) и УК^ (р) - известные матрицы, предопределяемые
свойствами ОУ, а матрица W *(р) выбирается свободно.
410
(7.107)
Проиллюстрируем методику обеспечения автономности в СУ
двумерным ОУ. В этом частном случае матричному равенству
(7.105) соответствуют следующие скалярные уравнения:
для 7=1
Ц'и (Р)^ (Р> + ^12 (р)^ (р)=(р);
И'я <Р)^ (Р) + ^22 <P)^2y! (Р) = 0
и для 7=2
(Р)^у2 (Р) + ^2 (PW& (Р) = 0;	|	7 108)
(p)^12 (Р) + ^22^2 (Р) = ^22 (Ж (Р) J
Из уравнений (7.107) и (7.108) получаются искомые ПФ двух
главных регуляторов и двух компенсаторов:
(Р) = W, (р)И? (р),
и?2 (Р)=- и'и (р)»^ (Р)М (р); >
(р) = -	(р)^ (р)/»22 (р); ’
(7.109)
^22 (р) =	(р)»? (р).
где »г,(р) = 1/[1-^(р)^(Р)М(Р)»,22(Р)].	(7.Н0)
Таким образом, проблема синтеза многосвязной СУ сведена к
задаче синтеза п автономных одноконтурных СУ, которую можно
решить с помощью методов, изложенных в разделах 7.3 и 7.6. При
этом подлежат определению ПФ И^к (р).
В заключение покажем, как обеспечивается автономность в СУ
объектом с И-структурой. Очевидно, что если в уравнение (7.98) ис-
кусственно ввести отрицательное слагаемое	то получим
выражение
х в (р) =	(р)[у(/>) +	(Р)х , (р) - W™ (р)хъ (/>)] =	(р)у(р),
(7111)
411
Рис. 7.22. Система управления двумерным ОУ с ^-структурой
которое означает ничто иное, как независимость отдельных конту-
ров. На рис. 7.22 показано, как с помощью искусственных каналов -
и -W2™ (р) компенсируются соответствующие естественные
каналы ОУ и тем самым реализуется условие (7.111).
7.6. Оптимизация и выбор настроечных параметров СУ
На основе изложенных выше теоретических принципов и мето-
дов синтеза в практике автоматизации разработан ряд методик рас-
чета настроечных параметров СУ, получивших название «инженер-
ные методики». Рассмотрим методики, наиболее часто применяемые
в инженерной практике.
Критерий и метод оптимизации амплитудной характеристи-
ки СУ. При проектировании и наладке СУ объектами, не содержа-
щими чистого запаздывания, наибольшее применение получили два
критерия - модульный оптимум (МО) и симметричный оптимум
(СО).
Критерий модульного оптимума, называемый также критерием
амплитудного, или технического, оптимума, заключается в выполне-
нии следующих требований к форме амплитудной характеристики
I Ф(/со) I замкнутой системы по каналу х3-х (см. рис. 6.4 и рис. 6.9,я):
412
характеристика в как можно более широком диапазоне частот долж-
на быть горизонтальной и равна единице; наклонный участок харак-
теристики должен быть как можно более крутопадающим. Другими
словами, критерий модульного оптимума требует, чтобы настраи-
ваемая система приближалась по своим частотным передаточным
свойствам к идеальному фильтру низкой частоты, имеющему, как
известно, прямоугольную частотную характеристику. Тогда, при от-
сутствии помехи на входе, система будет наилучшим образом вос-
производить задающее воздействие х3 и подавлять возмущение ха.
При наличии на входе высокочастотной помехи частоту пропускания
со0 системы выбирают тоже достаточно большой, но по компромисс-
ному условию совместной фильтрации всех действующих сигналов
(см. главу 8).
Настройка системы по критерию МО обеспечивает малое пере-
регулирование и достаточно быстрое протекание переходного про-
цесса:
о<9%; Гн<5/<о0; Гм<2яДоо; Гп<3я/(йо-
(7.112)
Эти верхние пределы показателей качества соответствуют иде-
альному фильтру низкой частоты, который практически нереализу-
ем.
Амплитудную характеристику, близкую по форме к прямо-
угольной характеристике идеального фильтра, имеет фильтр Баттер-
ворта (см. 7.3), у которого АЧХ
ли=Рм>) = 1/76
(7.113)
На практике обычно используют фильтры с порядком п = 2 . 8.
Нетрудно убедиться, что колебательная модель (6.21) замкнутой сис-
темы при коэффициенте демпфирования £, = 0,7 имеет амплитудную
характеристику (см. формулу (6.24))
4(<o)«i/7i+7v
(7.114)
соответствующую частному случаю фильтра (7.113) с п = 2.
413
Таким образом, в рамках приближенной модели (6.21) критерию
МО соответствует значение коэффициента демпфирования
£ = 0,7,
при этом главные показатели качества
а «5%; Гп «3,2Т = 3,2/®О «4,5ТО1,
(7.П5)
(7.116)
где со о = МТ - частота собственных незатухающих колебаний замк-
нутой системы (при £ = 0), характеризующая полосу пропускания
фильтра; Toi - постоянная времени разомкнутого контура системы.
Для колебательной модели (6.21) нестрогий критерий МО обес-
печивает одновременно минимумы интегральной оценки (6.67) и
улучшенной интегральной оценки (6.68) с весовым коэффициентом
Т = 1
Л в 1 •
При настройке систем более высокого порядка (п > 2) по крите-
рию МО можно обходиться и без приближенной модели (6.21). Для
этого ПФ замкнутой системы по каналу х3-х
Ф(р) = ^о/кр" +л„-1Р'”’ +...+а,р + а0)	(7.117)
приводят к нормированному виду
Ф(р) =	(₽" + А-.Р"’1 + • + Др +1),
(7.118)
где р = рТм - р1т^- оператор Лапласа, соответствующий безраз-
мерному (относительному) времени i = t /Ти ; Тм- масштабный мно-
житель
Тм — 1/cOq ~	/«о •>
(7.119)
безразмерные коэффициенты
414
О1 м
<*2	.
2	<г» 2 ?
а0Тм
^0*м
_ bo
О “	•
«о
(7.120)
Чтобы обеспечить желаемую форму амплитудной характери-
стики, близкую к прямоугольной, коэффициенты нормированной
функции (7.118) выбирают в соответствии со стандартными полино-
мами Баттерворта (табл. 7.3). Именно при таких сочетаниях коэффи-
циентов Ai амплитудная характеристика фильтра принимает вид
(7.113), причем Т-Ти, а относительная частота Оо = ®0Т = 1 соответ-
ствует значению амплитудной функции, равному 0,7 (при Во = 1).
Таблица 7.3
Коэффициенты фильтров Баттерворта
п	Ai		Аз	Л	Аз	Лб	А
2	1,4	1		 11		—	
3	2,0	2,0	1			—	
4	2,61	3,41	2,61	1		—	1  " 
5	3,24	5,24	5,24	3,24	1	—	
6	3,86	7,46	9,13	7,46	3,86	1	——
7	4,5	10,1	14,6	14,6	10,1	4,5	1
8	5,12	13,1	21,8	25,7	21,8	13,1	5,12
Масштабный множитель Ти не влияет на форму переходного
процесса и служит обобщенной мерой быстродействия системы. Его
значение можно выбрать, исходя из требуемых показателей быстро-
действия Ги и tn, по следующим приближенным формулам:
I	rH«„7L, rn«2„7L,	(7.121)
где п - порядок полинома Баттерворта.
Найденное по этим формулам значение Тм обеспечивают за счет
выбора по формуле (7.119) соответствующего общего передаточного
коэффициента разомкнутого контура к, который, как известно, вхо-
дит в свободный член а0: а0 = 1 + к- для статических систем, а0 = к -
для астатических систем.
415
Применительно к колебательной модели (6.21) параметры
фильтра Баттерворта
4 =2^ = 1/^; Tu = T = ^rjk.	(7.122)
В системах, параметры которых выбраны в соответствии со
стандартными полиномами Баттерворта, перерегулирование
|	о«10...15%.	(7.123)
Заметим, что указанные выше значения длительности переход-
ного процесса ?п и перерегулирования о строго выдерживаются толь-
ко в тех случаях, когда числитель ПФ (7.117) не содержит слагаемых
с оператором р. Тем не менее и для систем с более сложным полино-
мом числителя можно пользоваться рекомендуемыми значениями
коэффициентов Баттерворта. При этом также обеспечивается доста-
точно хорошее качество переходного процесса. Кроме того, настрой-
ки, соответствующие полиномам Баттерворта, могут использоваться
как исходные, отправные для отыскания оптимальных настроек сис-
тем, передаточные функции которых имеют числитель в виде поли-
нома от р.
Пример 1. Пусть исходная часть системы, состоящая из функциональ-
но необходимых элементов, описывается ПФ
H'(p) = k/p(Tlp + l)(T2p + i),	(7.124)
где Г] = 1 с, Г2 = 2 с.
Требуется определить настроечные параметры Т3 и ТА последовательно
включаемого корректирующего устройства
И,«<Р) = (7’зР+>Х7’4?+0	(7.125)
и общий ПК к, обеспечивающие критерий МО и желаемую длительность
переходного процесса /п = 6 с.
ПФ замкнутой системы по каналу х3-х
416
<Ир) =
*(Лр + 1ХЛр+1)
T^p’+iT, +Т2 + kT,Tt)p1 + (|+АТ3 + кТ,)р + к
(7.126)
Не обращая внимания на наличие полинома в числителе этой переда-
точной функции, будем подбирать настроечные параметры так, чтобы без-
размерные коэффициенты А\ и А2 полинома знаменателя соответствовали
фильтру Баттерворта.
Определим вначале масштабный множитель Ты, ориентируясь на при-
ближенное соотношение (7.121):
Гм =Гп/2н =6/23 = 1 с.
(7.127)
Теперь в соответствии с формулой (7.119) можно найти необходимое
(для заданного быстродействия) значение общего ПК:
*=«» = а,/Тиэ = 7, 7,/т’ =1-2/1’ =2,с'1.
(7.128)
Для п=3 оба безразмерных коэффициента Баттерворта, согласно табл.
7.2, должны быть равны 2:
. _ а2 -р _Т] +Т2 +кТ2Тд _ 3 + 2ТуГ4 _
^3	/]/2	2
2 = 1-ь^з-ь^ 2 = 1 + 2Т3+2Т4 =
м	гр <р	W	—
а3	Т(Т2	2
(7.129)
(7.130)
Решая совместно эти два уравнения, получим 73 = 0,5 с и Т4 = 1 с.
Оптимизация типовых контуров регулирования. Применим
изложенный метод оптимизации амплитудной характеристики для
расчета настроечных параметров типовых регуляторов (4.61) - (4.65),
используемых для управления следующими инерционными объекта-
ми второго-третьего порядков без запаздывания:
»ГЛР) = к„ /р(То1 р +1);
>г.(р)=*»/(г<,1р+1Хг»гр+1);
WAp} = kJp(T^p + \\^j> + \\
^(Р) = kj^p + fcp + fcp + 1),
(7.131)
(7.132)
(7.133)
(7.134)
417
где 7’oi < ТО2 < То3, причем в общем случае сомножитель с наимень-
шей постоянной времени 7О] приближенно заменяет собой несколько
инерционных звеньев с еще более малыми постоянными времени Toi,
т.е.
п(т;,,р+1)«7;.ир+1
I
i
(7.135)
Моделями (7.131) - (7.134) обычно пользуются для приближен-
ного описания объектов, входящих в типовые контуры регулирова-
ния систем управления электроприводами (контуры регулирования
напряжения, тока и частоты вращения).
Таблица 7.4
Гарантирующие настроечные параметры
типовых регуляторов для объектов без запаздывания
Передаточная функция объекта W0{p)	Условия примене- ния	Крите- рий	Параметры регулятора		
			к' р	г и	д
ко	То2 < 4ГО1	МО	то2	То2	—
амР+пт^р+1) (Л1 <Л>2)			2к„Т„		
	ТО2 > 4ТО}	СО	Г,2 2коТо1	47о1	- 
ко	то2« ТоХ	СО	1 2^0^01	4Го1	 “
p(Tolp + V)(To2p + l) -  	 		Го1 < то2	СО	I МЛ	47’о1	То2
	ко		То2 4Т01	МО	Тоз 2коТо1	ТрЗ	То2
(r^p+ixr^p+ix^p+l) (То[<То2<То.)	Тоз 47’0]	СО	Тоз	4То1	То2
	То2 > 4Го1	со	То2То3 wl,	То2	Юоз
В зависимости от типа и порядка объектов (7.131) - (7,134), а
также соотношений между их постоянными времени, настройка кон-
тура регулирования осуществляется либо по критерию МО, либо по
418
критерию СО (табл. 7.4). Настроечные параметры регуляторов к'
Г' и Г' (см. раздел 4.3), обеспечивающие получение определенных
показателей качества, в дальнейшем будем называть гарантирую-
щими. Такой термин в рассматриваемой задаче точнее, чем исполь-
зуемые часто понятия «оптимальные» (в отечественной литературе)
и «наиболее благоприятные» (в немецкой литературе) настройки.
Если у объекта второго порядка (7.132) То2 < То\, то предпочти-
телен критерий МО. Для выполнения требований критерия приме-
няют ПИ-регулятор (4.63)
(7.136)
с постоянной времени интегрирования Т'п, равной наибольшей
постоянной времени объекта, т.е.
(7.137)
Тем самым достигается полная компенсация (устранение из
уравнения динамики) этой наибольшей постоянной времени, а пере-
даточная функция разомкнутого контура принимает вид
h'(p)=ir,(p)w=Мо +О.
(7.138)
Она совпадает с ПФ (6.31) разомкнутого контура колебательной
модели (6.21), для которой, как показано выше, критерий МО сво-
дится к условию - 0,1. Отсюда в соответствии с формулой (6.34)
при £, ~ 0,7 ПК разомкнутого контура должен быть
к = 1/4^2Го, = 1/27;,.
(7.139)
Учитывая, что для рассматриваемого контура с ПИ-регулятором

(7.140)
419
получим, кроме (7.137), второе условие настройки на МО:

(7.141)
Рис. 7.23. Частотные и переходные характеристики одноконтурной СУ,
настроенной по критериям модульного (а) и симметричного (б) оптимумов
На рис. 7.23,а показаны ЛАЧХ Цоу) разомкнутого контура и
переходная характеристика h(t) замкнутой системы с объектом
(7.132) и ПИ-регулятором, настроенным на МО. ПФ замкнутого кон-
тура, настроенного на МО, имеет вид
Ф(Р) = 1/(2т;У+2г<,1р+1).
(7.142)
ей соответствуют показатели качества
о «4,3 %; /Н«4,7ГО1; /П«4,5ГО1.	(7.143)
420
Если большая постоянная времени То2 превышает меньшую Toi в
20 раз, то объект (7.132) по своим свойствам приближается к реаль-
ному интегрирующему звену (7.123) и описывается функцией

(7.144)
Таким объектом можно управлять с помощью П-регулятора
(4.61)
Wp(p) = kp,	(7.145)
настроенного на МО. Для этого ПК регулятора кр должен быть таким
же, как и при 7'о2 < 4Т’о]. Но в системе с П-регулятором по каналу
ув - е (см.рис. 4.8,6) возникает статическая ошибка ев, равная при
единичном возмущении (ув = 1)
e. = 2kaTjT^.
(7.146)
При То2 > 20То) ошибка ев <0,1 к0, что вполне допустимо.
Для астатических объектов второго порядка (7.131) и (7.144) по
условиям структурной устойчивости замкнутой системы (см. раздел
5.6) нельзя использовать ПИ-регулятор с настройкой Т'н = Г0), пол-
ностью компенсирующей единственную постоянную времени. По-
этому для таких объектов применяют настройку Т'п Ф То|, обеспечи-
вающую лишь частичную компенсацию постоянной времени То\.
Найдем наилучшие соотношения настроечных параметров для час-
тичной компенсации. ПФ разомкнутого контура, состоящего из аста-
тического объекта (7.131) и ПИ-регулятора с Т'и Ф То}, имеет вид
W(p) = к'р
Кр +1 ко
Кр p(Kp + W
(7.147)
ей соответствует ПФ замкнутой системы
421
ф(р) =
к',кЛТиР + 1)
ТпТ<лР' + ТпР2 + k/JHP + kVk°
(7.148)
Применяя к знаменателю функции (7.148) соотношения Баттер-
ворта (см. табл. 7.3), можно получить следующие настройки ПИ-
регулятора:
к'р=кр=1/2коТоХ; 7>7>4То1,
(7.149)
причем Тм = 2Тоь
При полученных настройках ПФ (7.147) и (7.148) принимают
вид
&(р) =
4Го1/> + 1
470|р + 1
8Т>Ч8Т>2+4То!р + 1
Ф(р) =
(7.150)
(7.151)
Передаточной функции (7.150) соответствует симметричная
ЛАЧХ £(<л), показанная на рис. 7.23,6. Поэтому изложенный подход
к выбору настроек получил название симметричного оптимума.
Передаточной функции (7.151) соответствует ПХ замкнутой
системы, показанная на рис. 7.23,6. Переходный процесс в контуре,
настроенном на СО, характеризуется следующими показателями.
о-43%; ZH«3,lTol; /П«14,7ТО1.
(7.152)
Для статического объекта третьего порядка (7.134) с постоян-
ными времени, не сильно отличающимися друг от друга, можно
применять ПИД-регулятор (4.65)

(7.153)
настроенный по критерию МО, с полной компенсацией двух наи-
больших постоянных времени. Причем большую То3 из этих двух
422
постоянных времени необходимо компенсировать постоянной/^', а
меньшую Т02 - постоянной Т'д . Если же хотя бы одна из больших
постоянных времени объекта (7.134) превышает наименьшую в 4
раза, то ПИД-регулятор необходимо настраивать по критерию СО, с
полной компенсацией лишь одной постоянной времени То2.
Для сравнения передаточных свойств контуров, настроенных по
разным критериям, найдем передаточные функции замкнутой систе-
мы по каналу ув-х:
по критерию МО
ф {р) =	= г_____2к^р ______
Wp(p) {2Ог+2Г„,р + 1)(7;г/> + 1)'
по критерию СО
/ х Ф(Р)
ф ( п) =-----------о_оЕ_----
Wp(p) 8/;У+8/;Ут47>тГ
(7.154)
(7.155)
где Ф(у) - передаточные функции (7.142) и (7.151) замкнутой систе-
мы по основному каналу х3-х.
Сравнивая теперь попарно функции (7.142) с (7.151) и (7.154) с
(7.155), обращаем внимание на следующие их особенности и разли-
чия. Все они имеют знаменатели, соответствующие полиномам Бат-
терворта. А это означает, что собственные динамические свойства
систем, настроенных по МО и СО, можно приближенно описать
инерционным звеном первого порядка
Ф(р)«(Г(р) = 1/(Г|р + 1),	(7.156)
где Т3 = 2Т0[ для системы, настроенной на МО, и 7’э = 47’0) для систе-
мы, настроенной на СО. В числителе ПФ (7.151) присутствует фор-
сирующий сомножитель 4Т0\р+1, из-за которого в системе, настро-
енной на СО, переходный процесс по каналу х3-х обладает значи-
тельным перерегулированием (см. рис. 7.23,6). В передаточную
функцию (7.154) в качестве сомножителя входит реальное диффе-
423
ренцирующее звено с постоянной времени То2, из-за чего переходный
процесс по каналу ув-х в системе, настроенной на МО, имеет
большую длительность, чем в системе, настроенной на СО.
Моделирование на ЭВМ и анализ переходных процессов, про-
исходящих в замкнутой системе по каналам х3-х и ув-х при различ-
ных настройках, позволяют сделать следующие выводы о
влиянии критериев настройки и параметров
регулятора на показатели переходного
процесса ио достоинствах и недостатках самих критериев:
1.	Увеличение ПК приводит к уменьшению времени нараста-
ния tH и повышению перерегулирования о.
2.	Увеличение постоянной интегрирования Т'к дает повышение
длительности tn и снижение перерегулирования ст.
3.	Критерий МО предпочтителен при оптимизации систем, от-
рабатывающих в основном изменения задающего воздействия х3, т.е.
следящих и программных систем.
4.	Критерий СО целесообразно применять при настройке сис-
тем, которым чаще приходится реагировать на возмущающие воз-
действия ув, т е. стабилизирующих систем.
5.	Оба критерия обеспечивают по каналу ув-х приблизительно
одинаковые значения первого максимального отклонения хм:
х„/л ® (0,85...1,45)£о/(Го2/Го1),	(7.157)
где коэффициент 0,85 соответствует отношению То21То\ = 2, а 1,45 -
отношению То2/То\ = 8.
6.	При настройке по критерию МО относительная длительность
переходного процесса по каналу ув-х увеличивается с ростом отно-
шения То2ГГо\.
(„/?;, «5 + 1,5(Го2/То1),	(7.158)
а по критерию СО - уменьшается:
г„/Го1=(35...65)/(Го2/То1),	(7.159)
424
где ta соответствует моменту достижения регулируемой величины
значения х = 0,05£о (приув = 1).
7.	При Го2/Го1 = 4 длительности переходного процесса по каналу
ув-х для обоих критериев одинаковы. При То2/То\ < 4 лучшее
быстродействие дает МО, а при Го2/ То] > 4 - критерий СО.
Для снижения и устранения больших перерегулирований, кото-
рые возникают в системе, настроенной по критерию СО, применяют
сглаживание ступенчатого задающего воздействия путем включения
на входе системы специального фильтра - инерционного звена пер-
вого порядка
1Гф(р) = 1/(Гфр +1),	(7.160)
где Гф = 4Toi для астатических объектов (7.131) и (7.133) и для стати-
ческих объектов (7.132) и (7.134) с То2/ Гы > 20. При меньших от-
ношениях постоянную времени можно уменьшить. Естественно,
что быстродействие системы при включении сглаживающего фильт-
ра снижается.
Переходный процесс, соответствующий последовательному со-
единению звеньев (7.151) и (7.160), характеризуется такими показа-
телями:
0*8,1 %; /„«7,67;,; /„«11,77;,.	(7.161)
Пример 2. Пусть объект описывается передаточной функцией
(р) = ко /(Г., р + \\Тлр + fc р +1).	(7.162)
где к0 = 5; То\ = 0,1 с; То2 = 0,2 с; То2 = 0,5 с. Определим тип и параметры
регулятора, обеспечивающие длительность переходного процесса /п < 2 с и
перерегулирование о < 10 %.
В соответствии с условиями табл. 7.4 применяем ПИД-регулятор с на-
стройками по критерию СО:
= Го3/2А'07^1 = 0,5/2 • 5 • 0,1 = 0.5;
К = 4Toi = 4 • 0,1 = 0,4 с; Тл = То2 = 0,2 с.]
(7.163)
425
Для снижения перерегулирования, равного при СО 43 %, необходимо
сигнал задающего воздействия х3 подавать через сглаживающее звено
»W = 1/(7,P + 1)	(7.164)
с постоянной времени 7ф = 47’о1 = 0,4 с. Тогда при выбранных настройках
эквивалентная ПФ замкнутой системы по каналу х3-х
•'/ Кр +8Г«0 +7'../nJ)p’ + 4Гв1(| + 2Го1/Г03)р + 1 -
1+^р(рЯ0(Р)
= l/(o,oo 1 р3 + 0,096р2 + 0,56 р +1).	(7.165)
Постоянная времени звена первого порядка, эквивалентного данной
системе, равна Т3 = 0,56 с. Ей соответствует длительность переходного про-
цесса /п ~	= 3-0,56 » 1,7 с.
Последовательная оптимизация контуров подчиненного ре-
гулирования. Для управления сложными технологическими ком-
плексами и электроприводами промышленных установок применяют
многоконтурные системы с несколькими внутренними обратными
связями по промежуточным переменным Х\, Хг,..., хп.\ (рис. 7.24).
Каждая /-я обратная связь (для простоты все связи на рисунке приня-
ты единичными) образует контур регулирования переменной х,. При-
чем, (1+1 )-й контур охватывает /-й контур, а регулятор (/+1)-го кон-
тура вырабатывает задание х3 для /-го контура. Принцип построения
многоконтурной системы с таким каскадным включением регулято-
ров называют принципом подчиненного регулирования (см. 7.5).
На рис. 7.25 в качестве примера приведена принципиальная
схема системы управления электроприводом, построенной по прин-
ципу подчиненного регулирования. В этой часто применяемой типо-
вой системе осуществлены три обратные связи, главная - по частоте
вращения рабочей машины РМ и две внутренние - по току и по на-
пряжению в яркой цепи двигателя М. Главный контур образован с
помощью тахогенератора ТГ и регулятора частоты вращения РЧВ.
Он вырабатывает задание [7ТЗ регулятору тока РТ, который, в свою
очередь, формирует задание £7НЗ регулятору напряжения PH. По-
следний через тиристорный преобразователь ТП воздействует на
якорную цепь двигателя М.
426
Рис. 7.24. Многоконтурная система подчиненного регулирования
Рис. 7.25. Трехконтурная СУ электроприводом рабочей машины
Расчет настроечных параметров системы, построенной по прин-
ципу подчиненного регулирования, осуществляют путем последова-
тельной оптимизации контуров, начиная с внутреннего (/-1), с объ-
ектом PFoi(p) (см.рис. 7.24). В каждом последующем оптимизируемом
контуре (/ == 2; 3; ...; и) в качестве объекта регулирования рассматри-
вают соединение собственного объекта данного контура W0l(p) и зве-
на, эквивалентного замкнутому (/-1)-му контуру, т.е.
Ж,. „(Лп(р)
=—^L^L^w^p).	(7.166)
1+wr(-
Замкнутый (/—1)-й контур, оптимизированный на предыдущем
этапе расчета по критерию МО или СО и описываемый передаточной
427
функцией (7.142) или (7.151), может быть приближенно представлен
(с учетом сглаживающего фильтра (7.160) для случая СО) инерцион-
ным звеном первого порядка (7.156) с постоянной времени Тэ = 2Toi
или Тэ ~ 4ГО1, где Г01 - наименьшая (некомпенсированная) постоян-
ная времени объекта (z-l)-ro контура. Поэтому условный объект
(7.166) описывается также одной из передаточных функций (7.131) -
(7.134) и выбор настроек очередного /-го контура можно осуществ-
лять в соответствии с рекомендациями табл. 7.4.
Пример 3. Определим ПФ и настроечные параметры регуляторов тока
(Р7) и частоты вращения (РЧВ) двухконтурной системы управления элек-
троприводом, алгоритмическая схема которой показана на рис. 7.26.
Рис. 7.26. Алгоритмическая структура двухконтурной
системы подчиненного регулирования
Пусть известны ПФ двигателя (без учета внутренней обратной связи
по ЭДС). тиристорного преобразователя и датчиков.
W =	1); >г,(р) = 1/г,(7>+1); 1
*
(7.167)
где А’п = 50 В/В: Тп = 0,01 с; гя = 0,1 Ом; Тя = 0.05 с; ки = 0,02 (об/с)/(А-с);
А'дг = 0.01 В/A; АдЧ = 0,5 В/(об/с).
Для внутреннего контура - контура тока, в котором объектом является
инерционное звено второго порядка

дт^и / ^я
(O + iX^p + i)’
(7.168)
428
целесообразно применить ПИ-регулятор с настройкой по критерию МО, т е.
с полной компенсацией наибольшей постоянной времени 7НТ = То2 = Тя =
= 0,05 с и с передаточным коэффициентом (согласно табл. 7.4)
Т02 Тягя 0,05-0,1	^05В
2koToi	2кпкдтТп	2-50-0,01-0,01	’ В'
(7.169)
Эквивалентная ПФ замкнутого контура тока при выбранных настрой-
ках
Ф|(^) = ФГ(^) = —г т—----*	(7.170)
2Т„Рг+2ТпР+} 2ТпР + \
С учетом последнего упрощения объект регулирования в контуре час-
тоты можно представить так:
^оъ(Р) = Ф1(Л(Лч(Р) =т—(7.171)
кдтМ27>+1)
Таким объектом можно управлять с помощью настроенного на МО
П-регулягора с коэффициентом
=	1	= кдг =	0,01	= 25 В
2к0Т0{ 4кдчкыТп 4-0,5-0,02-0,01 В’
(7.172)
но при этом будет возникать существенная статическая ошибка по скорости
А// ^дт
^-рч^дч
= 4к„Тп =4-0,02-0,01 = 8-10'4,
А
(7.173)
зависящая только от динамических параметров двигателя и преобразователя
и, следовательно, принципиально неустранимая. Поэтому в контуре частоты
целесообразно применять ПИ-регулятор, настроенный на СО, т.е. с частич-
ной компенсацией инерционности:
Т = 47’, = 8Г = 0.08 с; кт = —— =	— 25 -.
₽	2^0Г01 4кдчкмТп В
(7.174)
429
Для снижения больших перерегулирований, возникающих при ступен-
чатых изменениях сигнала изч, необходимо его пропускать через сглажи-
вающий фильтр (7.160) с постоянной времени - Ги ч = 0,08 с. При этом
длительность переходного процесса согласно (7.161) будет tn = 11,1Т0\ =
= 11,7-2Тп « 0,23 с, а перерегулирование по частоте вращения о » 8 %.
Определение настроечных параметров типовых регуляторов
технологических объектов с запаздыванием. Используем общие
принципы, изложенные в разделе 7.2, для выбора гарантирующих
настроечных параметров типовых ПИ- и ПИД-регуляторов, которые
обычно используются для регулирования следующих инерционных
объектов первого и второго порядков с запаздыванием:
и;(^) = М'х/(т:> + 1);
tv0(p)=к„е-р'- /(т„1Р + \\Т„2р+1),
И'0(^)=М'</(Лр+1)г,
(7.175)
(7.176)
(7.177)
где То =т0 - 0,11Т0, Г' =О,647'о, Го. =0,377'о, а параметры То и т0
определяются экспериментально - проведением касательной к пере-
ходной характеристике объекта (см. раздел 3.8).
Как было показано в 7.2, наилучшим регулятором для объекта
первого порядка (7.175) является ПИ-регулятор
(7.178)
настроечные параметры кр и 7’и которого составляют
к.=т;/кх, Т„=т'°.
(7.179)
Для объекта (7.176), имеющего инерционную часть второго по-
рядка, наилучшим будет ПИД-регулятор
ИС(р) = *о|1 + — + Тяр
Р	р Т п	лГ
\	1 НГ	J
(7.180)
430
с настроечными параметрами
| кг = (г01 + rj/кл, =тл^тл. у; = ?;,7^/(7;, + /;,). (7.i8i)
Для наиболее рациональной аппроксимации объектов с л-
образной переходной характеристикой - модели (7.177) с двумя оди-
наковыми постоянными времени Го1 = 7’о2 = То, = 0,377’о - параметры
ПИД-регулятора должны быть
|	кр=0,74Т„/кХ; т; =0,747;; Т, =0,187;.	(7 182)
Рекомендации (7.180) - (7.182) по выбору настроечных пара-
метров являются базовыми, отправными, которые подлежат уточне-
нию в зависимости от точки приложения возмущения и от требова-
ний, предъявляемых к переходному процессу в системе регулирова-
ния.
Заметим, что введение дифференциальной составляющей в ПИ-
закон регулирования, как правило, улучшает переходный процесс -
уменьшает первый выброс и длительность. Но при больших отноше-
ниях io/To или при действии в контуре системы случайных помех
ПИД-регулятор следует применять с определенной осторожностью,
после дополнительных исследований системы.
В табл. 7.5 приведены эмпирические формулы, в которых обоб-
щены результаты экспериментальных исследований по определению
настроечных параметров типовых регуляторов для объектов с запаз-
дыванием. Параметры определены путем моделирования систем при
ступенчатых изменениях задающего х3 и управляющего ув воздейст-
вий. Обеспечиваемым показателем качества системы является перс-
регулирование о (0 или 20 %) на выходе объекта.
Формулы для канала х3-х получены без учета ограничения на
величину управляющего воздействия, необходимого для обеспече-
ния заданного показателя о. Если такое ограничение наложено, то
приходится уменьшать коэффициент регулятора (без изменения па-
раметра Ги), например, при максимально допустимом значении
управляющего воздействия умакс = 1,5у(оо). Передаточный коэффици-
ент ПИ-регулятора следует выбирать по формуле
431
(7.183)
Vo
’ o/o
Таблица 7.5
Формулы для расчета настроечных параметров типовых регуляторов
статических инерционных объектов с 5-образной переходной
характеристикой (при xJT0 = 0...1)
Закон	Обобщенный параметр конту- ра	По каналу ху-х		По каналу уъ-х	
		ст = 0	ст = 20 %	ст = 0	ст = 20 %
П	КрАоТо/Го =	0,30	0,70	0,30	0,85
ПИ	KpkoxJTo =	0,35	0,60	0,60	0,75
	TJTO =	1,20	1,00	4,00	2,65
ПИД	ФЛ =	0,60	0,95	0,95	1,20
	=	1,00	1,35	2,40	2,00
	Тд/т0 =	0,50	0,47	0.42 ✓	0,42 	
Пример 4. Определим настроечные параметры ПИ-регулятора, стаби-
лизирующего температуру в сушильной установке изменением подачи топ-
ливного газа. Переходная характеристика установки по указанному каналу
имеет 5-образную форму (см. рис. 3.20) и следующие параметры:
к0 = 0,5 °C/ % хода ИМ; То = 100 с; то = 30 с.
Пусть требуется обеспечить в системе перерегулирование ст < 20 %
при ступенчатом возмущении на входе объекта. Согласно табл. 7.5f форму-
лы для расчета гарантирующих настроек в данном случае имеют вид
АрАото/Го=0,75; TjT0 = 2,65,
(7.184)
отсюда Ар = 0.75-100 / 0,5-30 = 5 % хода / °C;	= 2.65-100 = 265 с.
Полученное произведение АрА'о=2,5 не удовлетворяет условию (7.183).
Это означает, что при ступенчатом воздействии х3(г) = ст(0 управляющее
воздействие у(0 превысит во время переходного процесса свое установив-
шееся значение у(оо) более чем в 1.5 раза. Если такое превышение недопус-
тимо. найденное значение Ар следует уменьшить.
432
Контрольные задания и вопросы
1.	Какие функциональные элементы входят в неизменяемую и изме-
няемую части синтезируемой системы управления?
2.	Исходя из каких условий выбирают элементы неизменяемой и изме-
няемой частей функциональной структуры?
3.	Назовите главные требования, которые необходимо выполнить при
решении задачи синтеза СУ.
4.	Чему должны быть равны ПФ идеальной СУ по каналам задания и
возмущения?
5.	Чему должна быть равна ПФ УУ для компенсации возмущения и
инерционности ОУ?
6.	Как достигается частичная компенсация инерционности ОУ?
7.	При помощи каких типовых динамических звеньев, включаемых по-
следовательно в контур системы, осуществляется полная и частичная ком-
пенсация инерционности объекта?
8.	Что должен представлять собой идеальный регулятор?
9.	Чем затрудняется техническая реализация идеального регулятора?
10.	Какие типовые регуляторы лучше всего подходят для регулирова-
ния инерционных ОУ с запаздыванием?
11.	Как зависит передаточный коэффициент регулятора от передаточ-
ного коэффициента и времени запаздывания ОУ?
12.	Назовите требования к ПХ, которыми руководствуются при выборе
желаемой ПФ.
13.	Запишите выражения, по которым определяют ПФ УУ, исходя из
желаемой ПФ замкнутой СУ.
14.	Нарисуйте алгоритмические схемы последовательной и параллель-
ной коррекции.
15.	Поясните принципы амплитудной и фазовой коррекции на графике
АФХ разомкнутого контура.
16.	Как влияют типовые КУ на ЛАЧХ при их последовательном вклю-
чении? Поясните это влияние на графиках ЛАЧХ.
17.	Какими выражениями связаны АФХ скорректированной и нескор-
ректированной СУ при параллельной коррекции?
18.	Из каких этапов состоит решение задачи выбора КУ? Какие пока-
затели качества являются исходными для построения желаемой ЛАЧХ?
19	. По каким каналам передачи воздействий необходимо добиваться
инвариантности в стабилизирующих и следящих системах? Поясните это на
соответствующих алгоритмических схемах.
20.	Сформулируйте принцип двухканальности как условие, необходи-
мое для достижения инвариантности.
433
21.	Какие типовые динамические звенья используются обычно для
осуществления компенсирующих связей? Почему?
22.	Почему в реальных системах не удается, как правило, обеспечить
полную инвариантность?
23.	Нарисуйте алгоритмическую схему СУ с дополнительной контро-
лируемой величиной.
24.	Нарисуйте алгоритмические схемы двухмерного ОУ с Р- и /^струк-
турой.
25.	В чем заключается задача обеспечения автономности в многосвяз-
ной СУ?
26.	Нарисуйте алгоритмическую схему СУ двухмерным объектом с
/-структурой, обеспечивающую автономность обоих главных контуров.
27.	Какую форму, согласно критерию МО, должна иметь АЧХ идеаль-
ной СУ?
28.	Как связана частота пропускания и0 идеальной СУ с длительно-
стью переходного процесса /п?
29.	Поясните на графике ЛАЧХ название критерия «симметричный
оптимум».
30.	Какие значения показателей качества о и tn обеспечивают критерии
МО и СО?
31.	Для каких систем регулирования лучше применять настройку по
критерию МО, а каких - по критерию СО?
32.	Поясните принцип последовательной оптимизации контуров в сис-
теме подчиненного регулирования.
33.	В каких пределах изменяются рекомендуемые при различных ус-
ловиях значения безразмерного обобщенного параметра kpkoTc/7’o контура
регулирования с запаздыванием?
34.	В каких пределах изменяются рекомендуемые значения безразмер-
ного настроечного параметра TJTO1
35.	Как изменяются гарантирующие настроечные параметры kv и 7’и
при увеличении допустимого перерегулирования а?
434
Глава 8. АНАЛИЗ И СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ
УПРАВЛЕНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
8.1.	Общие сведения о статистическом подходе
к расчету систем управления
В предыдущих главах функционирование СУ рассматривалось
при влиянии на них внешних воздействий регулярного типа. Качест-
во систем оценивалось при типовых воздействиях, описываемых, как
известно, определенными функциями времени (ступенчатая функ-
ция, дельта-функция и т.п.). Соответственно и параметры систем вы-
бирались, исходя из условия достижения того или иного показателя
качества при конкретном внешнем воздействии.
В ряде случаев, когда реальные внешние воздействия достаточ-
но близки к типовым, такой детерминистический подход к анализу и
синтезу систем вполне оправдан и эффективен.
Однако для многих реальных СУ внешние воздействия (задаю-
щие и возмущающие) являются случайными сигналами. Случайными
сигналами являются, например, такие внешние воздействия, как на-
грузочный момент сопротивления в электрических приводах различ-
ных машин и механизмов (металлообрабатывающих и буровых стан-
ков, добычных механизмов), концентрации полезного компонента и
вредных примесей в перерабатываемом химическом сырье, нагрузка
электрического генератора, питающего большое количество потре-
бителей. Часто случайным образом изменяются параметры объектов
управления (параметрические случайные возмущения). Случайную
природу имеют и помехи, возникающие в измерительных устройст-
вах СУ.
Случайным сигналом называется сигнал, значения которого в
каждый момент времени представляют собой случайную величину.
В теории вероятностей случайную величину, изменяющуюся во вре-
мени, называют случайным процессом. Применяют также равносиль-
ные термины - «стохастический процесс» и «вероятностный про-
цесс».
435
Случайный сигнал (процесс), в отличие от детерминированного,
нельзя описать какой-либо одной конкретной функцией времени.
Случайный сигнал представляет собой множество функций времени,
обладающих некоторыми общими вероятностными свойствами. Кон-
кретная функция x(t), которая получается при экспериментальном
наблюдении случайного сигнала на конечном интервале времени,
называется реализацией случайного сигнала.
Свойства случайных сигналов можно описать только при помо-
щи понятий и методов теории вероятностей и математической стати-
стики. Эти понятия должны быть знакомы читателю из соответст-
вующего раздела курса «Математика». В теории управления исполь-
зуются, например, такие статистические характеристики, как матема-
тическое ожидание (среднее значение), дисперсия (средне-
квадратичное отклонение) и т.п.
Различают стационарные и нестационарные случайные сигналы.
У стационарного сигнала статистические характеристики не изме-
няются во времени. Статистические свойства нестационарного сиг-
нала с течением времени меняются.
Сущность статистического подхода к анализу и синтезу систем
управления состоит в том, что при проектировании системы и при
оценке ее качества ориентируются не на самые «тяжелые» (но мало-
вероятные) условия функционирования системы, а на некоторые
средние, наиболее часто встречающиеся условия.
Поясним целесообразность такого подхода на конкретном при-
мере. Для такого показателя качества, как коэффициент перерегули-
рования, наиболее «тяжелым» является ступенчатое воздействие.
Снизить перерегулирование можно уменьшением общего ПК систе-
мы. Но при этом, как правило, ухудшаются ее точность и быстродей-
ствие. Таким образом, если при проектировании системы ориентиро-
ваться на сравнительно редко встречающееся ступенчатое воздейст-
вие, то приходится занижать ПК и тем самым ухудшать точность и
быстродействие во всех других режимах. Очевидно, что правильней
поступить наоборот - ПК выбрать наилучшим для наиболее вероят-
ного режима (преднамеренно допуская большое перерегулирование
при редком, ступенчатом воздействии).
При действии на систему случайных возмущений в ней никогда
не наступает установившийся режим. Она непрерывно переходит из
одного состояния в другое. Управляемая величина x(t) и сигнал
ошибки s(Z) также непрерывно изменяются и представляют собой
случайные сигналы. Поэтому оценку точности системы можно про-
изводить только при помощи статистических характеристик - мате-
матического ожидания и дисперсии указанных двух сигналов.
В данной главе будут рассматриваться только такие случаи, ко-
гда входные и выходные сигналы являются стационарными случай-
ными сигналами, которые можно представлять в виде суммы посто-
янного математического ожидания и переменной центрированной
составляющей. Поэтому сигнал ошибки согласно принципу суперпо-
зиции также можно рассматривать как сумму постоянной и перемен-
ной составляющих, т.е.
е(Г) = тг + £ (Г).
(8.1)
Постоянную составляющую mz сигнала ошибки вычисляют при
помощи методов, изложенных в главе 4, а переменную составляю-
щую £(/) оценивают в среднем - по величине дисперсии D,, кото-
рая равна дисперсии самого сигнала ошибки
D. =D£.
(8.2)
В качестве критерия оптимальности системы при случайных
воздействиях принимают условие
—> min.
(8.3)
Выбор критерия (8.3) целесообразен во всех случаях, когда по-
тери, возникающие из-за неточного поддержания управляемой вели-
чины на заданном уровне, пропорциональны квадрату сигнала ошиб-
ки. Критерий (8.3) получил наибольшее распространение в инженер-
ной практике и обладает рядом преимуществ. Он связан сравнитель-
но простыми соотношениями с характеристиками системы и внеш-
них воздействий. При часто встречающемся нормальном законе рас-
пределения случайного сигнала критерий (8.3) приводит к тем же
результатам, что и другие, более сложные критерии.
437
Преимуществом критерия (8.3) является также то обстоятельст-
во, что при нормальном законе распределения сигнала дисперсию
сигнала можно связать с некоторыми другими статистическими по-
казателями точности - с вероятностью превышения сигналом 8 опре-
деленного уровня 8Д, со средним числом таких выбросов, со средней
длительностью выбросов. Например, при заданной вероятности пре-
вышения 0,003 и допустимом значении 8Д дисперсия сигнала ошибки
должна быть
Dt<e2J^ или сг£<8д/3.	(8.4)
Неравенство (8.4) выражает известное в теории вероятностей
правило «трех сигм».
Среднее за единицу времени число выбросов, превосходящих
значение ед,
п(Ед) = пое~Е‘/щ,	(8.5)
где «о ~ параметр, характеризующий среднюю скорость изменения
сигнала и равный среднему за единицу времени числу пересечений
сигналом линии среднего значения.
Методы расчета систем, подверженных случайным воздействи-
ям, составляют в теории управления отдельную ветвь, называемую
статистической динамикой.
Теоретическим фундаментом для статистической динамики по-
служили работы российских математиков академиков А.Н. Колмого-
рова и А.Я. Хинчина, известного американского ученого Н.Винера.
Большой вклад в применение этого фундамента к задачам управле-
ния внесли российские ученые - акад. В.С. Пугачев и проф. В.В. Со-
лодовников.
В статистической динамике различают следующие три задачи
расчета систем управления:
-	определение статистических характеристик выходных сиг-
налов (управляемой величины и сигнала ошибки) при полностью за-
данной структуре системы, заданных параметрах объекта и управ-
ляющего устройства и известных характеристиках внешних воздей-
ствий;
438
-	определение оптимальных параметров управляющего устрой-
ства при заданной структуре системы, заданных параметрах объекта
и известных характеристиках воздействий;
-	определение оптимальной структуры управляющего устрой-
ства при заданном ОУ и известных характеристиках внешних воз-
действий.
8.2.	Характеристики случайных сигналов
Математический аппарат анализа стационарных случайных сиг-
налов основан на гипотезе эргодичности. Согласно гипотезе эрго-
дичности, статистические характеристики большого числа произ-
вольно выбранных реализацией стационарного случайного сигнала
совпадают со статистическими характеристиками одной реализации
достаточно большой длины. Это означает, что усреднение по множе-
ству реализаций стационарного случайного сигнала можно заменить
усреднением во времени одной, достаточно длинной реализации.
Тем самым существенно облегчается экспериментальное определе-
ние статистических характеристик стационарных сигналов и упро-
щается расчет систем при случайных воздействиях.
Рис. 8.1. Реализации стационарных случайных сигналов
439
Определим основные статистические характеристики стацио-
нарного случайного сигнала, заданного в виде одной реализации на
интервале 0 < t < Т (рис. 8.1,а).
Числовые характеристики. Числовыми характеристиками
случайного сигнала являются среднее значение (математическое
ожидание) и дисперсия.
Среднее значение сигнала на конечном интервале времени Т
можно вычислить по формуле
(8.6)
Если интервал усреднения - длину реализации Т устремить к
бесконечности, то среднее по времени значение хт, согласно гипо-
тезе эргодичности, будет равно математическому ожиданию тх
сигнала:
тх =Л/{х(Г)} = Пт||х(Г)Л.
(8.7)
В дальнейшем для краткости знак предела перед интегралом бу-
дет опускаться. При этом либо вместо знака - будет использоваться
знак «, либо под вычисляемыми статистическими характеристиками
будут подразумеваться их приближенные оценки.
В практических расчетах, когда конечная реализация задана в
виде N дискретных значений, отделенных друг от друга равными
промежутками времени Д/ = Т/ N (см.рис. 8.1), среднее значение вы-
числяют по приближенной формуле
(8.8)
Стационарный случайный сигнал можно рассматривать как
сумму постоянной составляющей, равной среднему значению тх, и
440
переменной составляющей x(t), соответствующей отклонениям слу-
чайного сигнала от среднего:
x(t) = x(t)-mx.
(8.9)
Переменную составляющую х(1) называют центрированным
случайным сигналом.
Очевидно, что среднее значение центрированного сигнала все-
гда равно нулю.
Так как спектр сигнала x(t) совпадает со спектром соответст-
вующего центрированного сигнала x(Z), то во многих (но не всех!)
задачах расчета системы управления можно вместо сигнала x(t) рас-
сматривать х(1).
Дисперсия Dx стационарного случайного сигнала равна средне-
му значению квадрата отклонений сигнала от математического ожи-
дания тх, т.е.

dt.
(8.10)
Дисперсия Dx является мерой разброса мгновенных значений
сигнала около математического ожидания. Чем больше пульсации
переменной составляющей сигнала относительно его постоянной
составляющей, тем больше дисперсия сигнала. Дисперсия имеет
размерность величины х в квадрате.
Применительно к электрическим сигналам дисперсию можно
рассматривать как среднее значение мощности переменной состав-
ляющей сигнала.
Часто в качестве меры разброса случайного сигнала используют
среднеквадратичное отклонение
Для расчета СУ имеет важное значение следующее свойство.
441
дисперсия суммы или разности независимых случайных сигналов
x(t) = Xi(r) ±x2(f)равна сумме (/) дисперсий этих сигналов, т.е.
D=D +DX.	(8.11)
Математическое ожидание и дисперсия являются важными чи-
словыми параметрами случайного сигнала, но они характеризуют его
не полностью: по ним нельзя судить о скорости изменения сигнала
во времени. Так, например, у случайных сигналов x;(f) и х2(0, изо-
браженных на рис. 8.1,6,в, одинаковые математические ожидания и
дисперсия, но, несмотря на это, сигналы явно отличаются друг от
друга: сигнал Xi(f) изменяется медленнее, чем сигнал x2(f).
Скорость изменения случайного сигнала во времени можно
описать при помощи одной из функциональных характеристик -
корреляционной функции и функции спектральной плотности.
Корреляционная функция. Корреляционной функцией Rx(x)
случайного сигнала x(f) называется математическое ожидание произ-
ведений мгновенных значений центрированного х(/), разделенных
промежутком времени т, т.е.
1 Т
Rx(t)^—jx(t)x(t + x)df, (Q<x<T),	(8.12)
* о
где т - варьируемый сдвиг между мгновенными значениями сигнала
(см. рис. 8.1,а). Сдвиг т варьируют от нуля до некоторого значения
тм. Каждому фиксированному значению т соответствует определен-
ное числовое значение функции Rx(x).
Корреляционная функция (называемая также автокорреляцион-
ной) характеризует степень корреляции (тесноту связи) между пре-
дыдущими и последующими значениями сигнала.
При увеличении сдвига х связь между значениями x(t) и x(f + x)
ослабевает, и ординаты корреляционной функции (рис. 8.2,а)
уменьшаются.
Это основное свойство корреляционной функции можно объяс-
нить следующим образом. При малых сдвигах под знак интеграла
442
(8.12) попадают произведения сомножителей, имеющих, как прави-
ло, одинаковые знаки, и поэтому большинство произведений будут
положительными, а значение интеграла большим. По мере увели-
чения сдвига под знак
интеграла будет попа-
дать все больше со-
множителей, имею-
щих противоположные
знаки, и значения ин-
теграла будут умень-
шаться. При очень
больших сдвигах (т —>
оо) сомножители x(f)
Рис. 8.2. Корреляционная функция (а) и
спектральная плотность (б) случайного сигнала
и х(/ + т) практически независимы, и число положительных произ-
ведений равно числу отрицательных произведений, а значение инте-
грала стремится к нулю.
Из приведенных рассуждений следует также, что
корреляционная функция убывает тем быстрее, чем быстрее
изменяется случайный сигнал во времени.
Из определения корреляционной функции следует, что она яв-
ляется четной функцией аргумента т, т.е.
Rx(r) = Rx{~T),
(8.13)
поэтому обычно рассматривают только положительные значения т
Начальное значение корреляционной функции центрированного
сигнала равно дисперсии сигнала, т.е.
*Д0) = ^.
(8.14)
Равенство (8.14) получается из выражения (8.12) при подстанов-
ке т = 0.
Корреляционную функцию конкретного сигнала определяют по
экспериментально полученной реализации этого сигнала. Если реа-
лизация сигнала получена в виде непрерывной диаграммной записи
длиной 7', то корреляционную функцию определяют при помощи
специального вычислительного устройства - коррелятора (рис.
8.3,а), реализующего формулу (8.12). Коррелятор состоит из блока
задержки БЗ, блока умножения БУ и интегратора И. Для определения
нескольких ординат jRx(tk) блок запаздывания поочередно настраи-
вают на различные сдвиги тк.
ПФ
КВ
Рис. 8.3. Алгоритмические схемы вычисления ординат корреляционной
функции (а) и спектральной плотности (б)
Если же реализация представляет собой совокупность дискрет-
ных значений сигнала, полученных через равные промежутки А/ (см.
рис. 8.1,а), то интеграл (8.12) приближенно заменяют суммой
Rx(z) = Rx(k&)*
N-k
£ x(iAt)x(iAt + к At),
i=0
(8.15)
которую вычисляют при помощи ЦВМ.
Для получения достаточно достоверной информации о свойст-
вах случайного сигнала длину реализации Т и интервал дискретности
At необходимо выбирать из условий
Г>(10...20Кч; Д^0,5Гвч,
(«16)
где ТцЧ и Гвч - периоды соответственно самой низкочастотной и са-
мой высокочастотной составляющих сигнала.
444
Заметим, что корреляционная функция может быть определена
и для нецентрированного сигнала x(f) по формулам, аналогичным
(8.12) и (8.15). В этом случае
Rx(i)= R, (т) +тх.
X
(8.17)
Спектральная плотность. Определим теперь спектральную
характеристику стационарного случайного сигнала x(t). Так как
функция x(f) не является периодической, она не может быть разло-
жена в ряд Фурье (2.20). С другой стороны, функция х(/) из-за неог-
раниченной длительности не интегрируема и поэтому не может быть
представлена интегралом Фурье (2.30). Однако, если рассматривать
случайный сигнал на конечном интервале Г, то функция хт(/) стано-
вится интегрируемой и для нее существует прямое преобразование
Фурье:
ОО
%,(»=	(8.18)
-иО
Как известно (см. 2.2), изображение по Фурье Х(/со) непериоди-
ческого сигнала x(t) характеризует распределение относительных
амплитуд сигнала вдоль оси частот и называется спектральной плот-
ностью амплитуд. Там же было показано, что функция lAX/co) I2 ха-
рактеризует распределение энергии сигнала среди его гармоник.
Очевидно, что если разделить функцию (/со) г на длительность Т
случайного сигнала, то она будет определять распределение мощ-
ности конечного сигнала х(t) среди его гармоник. Если теперь
устремить Т к бесконечности, то функция lA' (/со) I2 будет стремить-
ся к пределу
Д	I	17 1
S,(®) = lim Хт(/«>) /Г,	(8.19)
7" —>со
445
который называется спектральной плотностью мощности случай-
ного сигнала. (В дальнейшем мы будем функцию 5Ж(®) именовать
сокращенно - спектральная плотность).
Наряду с математическим определением (8.19), спектральной
плотности можно дать более простое, физическое толкование. Спек-
тральная плотность случайного сигнала х(/) характеризует распре-
деление квадратов относительных амплитуд гармоник сигнала вдоль
оси (0.
Согласно определению (8.19), спектральная плотность - четная
функция частоты. При со —> со функция Sr(co) обычно стремится к ну-
лю (см. рис. 8.2,6). Причем
чем быстрее изменяется сигнал во времени, тем шире график
Sx(g)}.
Отдельные пики на графике спектральной плотности свидетель-
ствуют о наличии у случайного сигнала периодических составляю-
щих.
Найдем связь спектральной плотности с дисперсией сигнала.
Запишем равенство Парсеваля (2.38) для конечной реализации х (t)
и разделим его левую и правую части на Т. Получим
(8.20)
При Т —> со левая часть равенства (8.20) стремится к дисперсии
сигнала Dx (см. формулу (8.10)), а подынтегральное выражение в
правой части - к спектральной плотности £(ю), т.е. вместо (8.20) по-
лучим одну из главных формул статистической динамики:
(8.21)
Поскольку левая часть равенства (8.21) представляет собой пол-
ную дисперсию сигнала, то каждую элементарную составляющую
5x(coz)Jco под знаком интеграла можно рассматривать как величину,
446
пропорциональную дисперсии или квадрату амплитуды гармоники с
частотой
Формула (8.21) имеет большое практическое значение, так как
она позволяет по известной спектральной плотности сигнала вычис-
лять его дисперсию. А дисперсия сигнала во многих задачах расчета
СУ служит важной количественной характеристикой точности.
Спектральную плотность Ух((») можно найти по эксперимен-
тальной реализации сигнала при помощи спектрального анализатора
(см. рис. 8.3,6), который состоит из полосового фильтра ПФ с узкой
полосой пропускания Лео, квадратора Кв и интегратора И. Для опре-
деления нескольких ординат 5Х(®Э полосовой фильтр поочередно
настраивают на различные частоты пропускания (ак.
Взаимосвязь между функциональными характеристиками
случайного сигнала. Н.Винером и А.Я. Хинчиным было впервые
показано, что функциональные характеристики Rx(r) и Ух(со) стацио-
нарного случайного сигнала связаны друг с другом преобразованием
Фурье: спектральная плотность является изображением корреляци-
онной функции, т.е.
У(<у) =	,	(8.22)
— ОО
а корреляционная функция соответственно является оригиналом это-
го изображения, т.е
Л	] оО
Я,(г) = & (со)}=3- /SJcoK'-Wco. (8.23)
Z7T -л
Если разложить множители е±7“г с помощью формулы Эйлера
(2.23) и учесть, что Ях(т), Ух(<о) и cos <от - четные функции, a sintai -
нечетная функция, то выражения (8.22) и (8.23) можно преобразовать
к следующему виду, более удобному для практических расчетов:
\(со) = 2|/?г(т)со5<йт6т,	(8.24)
447
Rx(r) = — f 5(до) cos
it •*
л 0
(8.25)
Отметим, что при подстановке в выражение (8.25) значения т=0
получается формула (8.21) для вычисления дисперсии.
Соотношения, связывающие корреляционную функцию и спек-
тральную плотность, обладают всеми присущими преобразованию
Фурье свойствами. В
частности: чем шире
график функции /?х(т),
тем рке график функ-
ции Sx(co), и наоборот -
чем быстрее убывает
функция Ях(т), тем
медленнее уменьшает-
ся функция Sx((o). Эту7
Рис. 8.4. Взаимосвязь между корреляционной взаимосвязь иллюст-
функцией (а) и спектральной плотностью (б) рируют графики на
рис. 8.4,67,6. Линии 1 на
обоих рисунках соответствуют медленно меняющемуся случайному
сигналу X](f) (см. рис. 8.1,6), в спектре которого преобладают низко-
частотные гармоники. Линии 2 соответствуют быстро меняющемуся
сигналу x2(f) (см. рис. 8.1,в), в спектре которого преобладают высо-
кочастотные гармоники.
Если случайный сигнал изменяется во времени очень резко и
между его предыдущими и последующими значениями корреляция
полностью отсутствует, то функция Rx(r) имеет вид дельта-функции
(линия 3 на рис. 8.4,а). График спектральной плотности в этом слу-
чае представляет собой горизонтальную прямую *S’x(co)=6^ в
диапазоне частот от 0 до со (линия 3 на рис. 8.4,6). Это указывает на
то, что амплитуды гармоник во всем диапазоне частот одинаковы.
Такой сигнал называется идеальным белым шумом (по аналогии с
белым светом, у которого, как известно, интенсивность всех компо-
нентов одинакова).
Отметим, что понятие «белый шум» является математической
абстракцией. Физические сигналы в виде белого шума неосуществи-
448
мы, так как бесконечно широкому спектру согласно формуле (8.21)
соответствует бесконечно большая дисперсия, а следовательно, и
бесконечно большая мощность, что невозможно. Тем не менее часто
реальные сигналы с конечным спектром можно приближенно рас-
сматривать как белый шум. Это упрощение правомерно в тех случа-
ях, когда спектр сигнала значительно шире полосы пропускания сис-
темы, на которую действует сигнал.
У всех случайных сигналов, действующих в реальных физиче-
ских системах, существует корреляция между предыдущими и по-
следующими значениями. Это означает, что корреляционные функ-
ции реальных сигналов отличаются от дельта-функции и имеют ко-
нечную, не равную нулю длительность спада. Соответственно и
спектральные плотности реальных сигналов всегда имеют конечную
ширину.
Характеристики связи двух случайных сигналов. Для описа-
ния вероятностной связи, проявляющейся между двумя случайными
сигналами, используют взаимную корреляционную функцию и вза-
имную спектральную плотность.
Взаимная корреляционная функция стационарных случайных
сигналов X\{t) и определяется выражением
(8.26)
Функция R (т) характеризует степень связи (корреляции)
г1 х2
между мгновенными значениями сигналов X\{t) и x^t), отстоящими
друг от друга на величину т. Если сигналы статистически не связаны
(не коррелированы) между собой, то при всех значениях т функция
R (т) -0.
Для взаимной корреляционной функции справедливо следую-
щее соотношение, вытекающее из определения (8.26):
Rxx (г) = R (-г).
(8.27)
449
Корреляционная функция суммы (разности) двух коррелиро-
ванных между собой сигналов х(Г) = X\(t) ± х2(/)
Ю + R" (Г) ± RV; (г) ±	(Г).	(8.28)
Взаимная спектральная плотность случайных сигналов X\(t) и
х2(/) определяется как изображение по Фурье взаимной корреляцион-
ной функции:
S,„,	(r)}= j RV1 Me-^dT.	(8.29)
-ao
Из определения (8.29) и свойства (8.27) следует:

(8.30)
Спектральная плотность суммы (разности) случайных сигналов
Х)(/) и х2(/):
SXW = \ (*>) +	± 5хЛг (» ± (Jco).
(8.31)
Если сигналы Х](/) и х2(/) не коррелированы между собой, то вы-
ражения (8.28) и (8.230) упрощаются:
/?д(г) = ^(г)4-^(г);1
(8.32)
Соотношения (8.32), а также (8.11) означают, что
статистические характеристики 7?х(т), -Жсо) и Dx совокупно-
сти нескольких некоррелированных друг с другом случайных
сигналов всегда равны сумме соответствующих характеристик
этих сигналов (независимо от того, с каким знаком сигналы
складываются в эту совокупность).
450
8.3. Типичные случайные сигналы
Реальные случайные воздействия, влияющие на промышленные
объекты управления, весьма разнообразны по своим свойствам. Но,
прибегая при математическом описании этих воздействий к некото-
рой идеализации, можно выделить ограниченное число типичных
или типовых случайных сигналов. Корреляционные функции и спек-
тральные плотности типичных случайных сигналов представляют
собой достаточно простые функции аргументов т и со. Параметры
этих функций, как правило, можно определить по эксперименталь-
ным реализациям сигналов.
Простейшим типичным случайным сигналом является белый
шум с ограниченной шириной спектра. Спектральная плотность это-
го воздействия (рис. 8.5,а) описывается функцией
Sx0 ПРИ Н ч
О при со > со
(8.33)
где - интенсивность белого шума; соп - ширина спектра.
Согласно (8.21), дисперсия сигнала

(8.34)
Согласно (8.25), корреляционная функция в данном случае име-
ет вид
Rx (г) = — Sx0 cos о rd о = —^sin con r.
К '	KT
(8.35)
Учитывая (8.34), можно функцию (8.35) записать в следующем
виде:
^(r) = ^(sin4r/4r)
(8.36)
График функции (8.36) показан на рис. 8.5,6. При соп оо белый
шум с ограниченным спектром (реальный белый шум) становится
451
идеальным, а его корреляционная функция (см. рис. 8.5,6) стремится
к дельта-функции 2?х(т) = D&ix), что будет свидетельствовать об
отсутствии взаимосвязи (корреляции) между предыдущими и после-
дующими значениями сигнала x(t).
452
В некоторых задачах теории управления используется случай-
ный сигнал типа цветной шум, у которого спектральная плотность
имеет вид (см. рис. 8.5,в)
при (0H S(OS(OB
При (0<(0н И (0>(0в.
(8.37)
Согласно формуле (8.25), корреляционная функция такого сиг-
нала (см. рис. 8.5,г)
5
R (r) = -^-(sinfi? г-sin (У г).
X '	'	X	В	л /
ПТ
(8.38)
Видно, что реальный белый шум, у которого сон = 0, а сов = со„,
является частным случаем цветного шума.
Наиболее часто в практических расчетах встречается сигнал с
экспоненциальной корреляционной функцией (см. рис. 8.5,е)
Я,(г) = О,е
(8.39)
Такой сигнал называется также марковским.
Применяя к корреляционной функции (8.39) преобразование
(8.24), находим спектральную плотность (см. рис. 8.5/)):
£(д))= Г D e ~a^T' cos andт = —Л
J0
(8.40)
Чем больше параметр ах, тем быстрее уменьшается корреляци-
онная функция и тем шире график спектральной плотности. Ордина-
ты функции &((») при увеличении ах уменьшаются. При ах оо рас-
сматриваемый сигнал приближается к идеальному белому шуму.
При ориентировочных расчетах параметр ад можно определить
непосредственно по реализации сигнала - по среднему числу п0 пе-
ресечений центрированным сигналом оси времени: ах - ппо.
453
В практических задачах возникает необходимость аппроксими-
ровать ступенчатую функцию (8.33) более удобной, аналитической
функцией (8.40). Условиями аппроксимации являются равенство
дисперсий и равенство одного из параметров графиков Sx(co) обоих
сигналов. Обычно приравнивают параметры ах и соп. Если же при-
равнять начальные значения Ух(0), то параметр ах должен быть при-
близительно равен 2соп/л.
Часто случайный сигнал содержит скрытую периодическую со-
ставляющую. Такой сигнал имеет экспоненциально-косинусную кор-
реляционную функцию (см. рис. 8.5,з)
Rx(r) = Z)/"“l|r|cos Дг.
(8.41)
Параметр рх этой функции соответствует среднему значению
«периода» скрытой составляющей, а параметр ах характеризует от-
носительную интенсивность остальных случайных составляющих,
которые наложены на периодическую составляющую. Если показа-
тель ах мал и близок к значению рх/2л, то относительный уровень
этих составляющих невелик, и смешанный сигнал близок к гармони-
ческому. Если же показатель ах велик и равен (5... 10) рд/л, то уро-
вень случайных составляющих соизмерим с «амплитудой» периоди-
ческой составляющей. При ах > 20рх/л корреляционная функция
(8.41) практически (с точностью 5 %) совпадает с экспонентой (8.39).
Корреляционной функции (8.41) соответствует спектральная
плотность
2 ’
(8.42)
— СО
у которой при частоте со = рх имеется явно выраженный пик (см. рис.
8.5 ,ж).
В частном случае, когда «случайный» сигнал имеет чисто регу-
лярный характер и представляет собой косинусоиду или синусоиду,
т.е. когда ах - 0, х(/) = rmsinpx< корреляционная функция также бу-
дет гармонической.
454
Rx(r) = собДг,
(8.43)
л
где Dx= х 12, а спектральная плотность - дельта-функцией:
т
Sx(fl>) = nDt3(a>-0,).
(8.44)
8.4. Преобразование случайного сигнала
линейным динамическим звеном
Исходные соотношения. При воздействии стационарного слу-
чайного сигнала на линейное устойчивое звено (или систему) на вы-
ходе звена возникает также стационарный случайный сигнал, кото-
рый можно рассматривать как преобразованный входной сигнал.
Преобразование входного сигнала проявляется в изменении его ста-
тистических характеристик - математического ожидания, дисперсии,
корреляционной функции и спектральной плотности.
Если входное воздействие x(t) состоит из постоянной или доста-
точно медленно меняющейся составляющей тх и центрированной
случайной составляющей x(f), т.е.
о
х(Г) = тх + х(Г),
(8.45)
то и выходная реакция y(t) звена может быть представлена в виде
суммы
y{t) = ту + y(t).
(8.46)
Согласно принципу суперпозиции, каждая из составляющих y(f)
может быть определена отдельно: ту - как результат преобразования
тх, a y(t) - как результат преобразования x(t). Так, математические
ожидания входа и выхода статического звена с передаточной функ-
цией W(p) связаны между собой уравнением статики
m = тШ) - тк.
ул	л
(8.47)
455
Статистические характеристики переменной составляющей y(f)
определяются более сложными соотношениями. Так как в дальней-
шем рассматриваются законы преобразования только центрирован-
ных составляющих, то значок ° будем опускать.
Базовыми формулами для вывода законов преобразования слу-
чайных сигналов являются интеграл свертки (2.92)
QO
ХО = j - 9)w(&)d9
О
(8.48)
и Фурье-изображение (2.118) весовой функции w(0
О
(8.49)
Законы преобразования во временнбй области. Пусть вход-
ной сигнал x(f) задан своей корреляционной функцией Rx(r) (рис.
8.6,а). Найдем корреляционные функции R^t) и Ry(r).
а
Лду(т)	^(/со)
Рис. 8.6. Преобразование характеристик
случайного сигнала линейным звеном
Взаимная корреляционная функция сигналов x{t) ny{t)
1	1
RJt) ~ т J
1 о
(8.50)
456
Если вместо Х^+т) в выражении (8.50) подставить интеграл
(8.48), записанный для времени = t+т, и выполнить вначале интег-
рирование произведения x(t)x(t+T) по переменной t в диапазоне от 0
до Т, то под интегралом в правой части (8.50) образуется корреляци-
онная функция (8.12) входного сигнала с аргументом, равным разно-
сти т - 3, и формула (8.50) примет вид
QO
ЯДг) = |я,(г-(8.51)
о
Интегральное соотношение (8.51), называемое уравнением Ви-
нера-Хопфа, имеет такой же вид, как интеграл свертки (8.48), и по-
этому функцию Rxy(r) можно рассматривать как реакцию звена на
воздействие, имеющее форму функции Rx(t).
Если в корреляционную функцию выходного сигнала y(f), рав-
ную
1 т
RV(T) ~ ^]У(Оу(/ + r)dt,	(8.52)
о
дважды подставить вместо y(t) и y(t+i) интеграл свертки (8.48) с пе-
ременными интегрирования соответственно $ и «9? и вначале вы-
полнить интегрирование произведения x(t - &\)x(t + т - &т) по t в пре-
деле от 0 до Г, то в правой части (8.52) образуется корреляционная
функция входного сигнала с аргументом, равным т - «9г + <91, и выра-
жение (8.52) примет вид
QO ОС
Ry(t) = J J Rx(r + (9, - 32)w(^)w(^2)d^d32.	(8.53)
о о
В частном случае, когда на входе звена действует единичный
белый шум (5^; = 1) с корреляционной функцией Rx(t) - 5(т), выра-
жение (8.53) с учетом «выхватывающего» свойства дельта-функции
(2.13) может быть упрощено:
457
(8.54)
00
Я,(г) =	+
О
Подставляя теперь в (8.54) т = 0, легко получить формулу для
дисперсии выходного сигнала
со	00
D, = Я,(0) = |[м.9,)Г<Л9, =
О	о
(8.55)
которая показывает, что для вычисления дисперсии выходного сиг-
нала при действии на входе звена белого шума достаточно проинтег-
рировать по времени квадрат весовой функции звена.
Формулу (8.55) можно использовать для вычисления дисперсии
и в тех случаях, когда входной сигнал отличен от белого шума. Для
этого необходимо лишь в (8.55) подставлять весовую функцию не
самого рассматриваемого звена w(t), а функцию w3(t) эквивалентного
звена, которое представляет собой последовательное соединение (см.
рис.8.6,в) исследуемого звена ИЗ и так называемого формирующего
фильтра ФФ. (Подробнее метод формирующего фильтра изложен
ниже).
Законы преобразования в частотной области. В практических
расчетах удобней пользоваться соотношениями между спектральны-
ми характеристиками входа и выхода (см. рис. 8.6,6). Пусть известна
спектральная плотность Выразим через нее спектральные
ПЛОТНОСТИ Sxy{j(ii) и 5Х((1)).
Согласно определению (8.29), взаимная спектральная плотность
сигналов х(0 и y(f)
Д	i	Xе0
М» =	}= К(Ф J“A.	(8.56)
-00
Если вместо Rxy(r) в формулу (8.56) подставить интеграл Вине-
ра-Хопфа (8.51), являющийся сверткой двух функций-оригиналов, и
использовать правило, аналогичное правилу свертки для преобразо-
вания Лапласа (см. табл. 2.2), то с учетом определений (8.22) и (8.49)
получится важное соотношение статистической динамики:
458
S,y(jv>) = ^{RM }=
(8.57)
Равенство (8.57), разрешенное относительно АФХ PF(/co),
используют для определения характеристик объектов управления по
экспериментальным реализациям сигналов x(t) и y(t). Для этого сна-
чала вычисляют корреляционные функции Rx(t) и Яху(т), а затем пе-
реходят к спектральным плотностям 5’Л-(со) и Sxy(/co), которые и под-
ставляют в (8.57).
Согласно (8.22), спектральная плотность выходного сигнала
с©
s (а) = f я,(r)e '"dr.
— 00
(8.58)
Если вместо Ку(т) подставить в (8.58) двойной интеграл (8.53) и
представить образованное выражение с тремя интегралами как про-
изведение интеграла вида (8.22) и двух интегралов вида (8.49) с пе-
ременными интегрирования соответственно т, и Фч, то получим
одну из важнейших формул статистической динамики
ИЛИ

2
5>)^Д<у)|^(;ш)| .
(8.59)
(8.60)
Соотношение (8.60) показывает, что
спектральная плотность выходного сигнала равна спектраль-
ной плотности входного сигнала, умноженной на квадрат ам-
плитудной частотной характеристики звена (системы).
Заметим, что к формуле (8.60) можно прийти и из чисто физиче-
ских представлений. Ведь АЧХ I W(j&) | при каждом значении аргу-
мента со, равна отношению амплитуд гармоник входного и выходно-
го сигналов, т е. ИХ/со,) = ymi/xmi, а спектральные плотности 5х(со) и
5\.(со) при фиксированном значении со, пропорциональны квадратам
амплитуд этих гармоник.
459
Если равенство (8.60) объединить с формулой (8.21), записанной
для сигнала y(t), то получим еще одну важную для практических рас-
четов формулу
-L f s (®)Л« =
2л- Л
2?Г j
-со
(8-61)
по которой вычисляют дисперсию сигналов на выходе СУ.
На соотношении (8.60) основаны понятие и метод
формирующего фильтра. Формирующим фильтром
(ФФ) называют динамическое звено, которое преобразует входной
сигнал в виде белого шума в выходной сигнал с заданными стати-
стическими характеристиками.
Пусть на входе формирующего фильтра ФФ (см. рис. 8.6,в) дей-
ствует белый шум с единичной интенсивностью Уо=1 при всех значе-
ниях со. Тогда спектральная плотность сигнала x(t) на выходе ФФ
согласно (8.60)
W) = l-«'*(»’	(862)
Следовательно, для получения на выходе ФФ случайного сигна-
ла с желаемой функцией Sx(co) необходимо частотную функцию
фильтра выбрать в соответствии с равенством (8.62), т.е.
квадрат АЧХ ФФ должен быть равен спектральной плотности
сигнала, формируемого из белого шума.
Для нахождения функции Жф(/со) заданную спектральную плот-
ность представляют в виде произведения двух комплексно сопря-
женных сомножителей и И'ф(-усо) и из них выбирают тот, ко-
торый имеет нули и полюса в верхней полуплоскости со, т.е. тот, ко-
торый соответствует устойчивому, физически реализуемому звену.
Например, для получения на выходе ФФ случайного сигнала со
спектральной плотностью (8.40)
!О,«,	j2D,g,
2 + су2 а + jco ах - jco ’
(8.63)
460
реализуемым является первый сомножитель, т.е.
= 41D*a*Ka> + >)•
(8.64)
Формирующий фильтр (8.64) представляет собой инерционное
звено первого порядка (см. 3.3) с параметрами
кф = ^2Dxax  Тф = 1/ах.	(8.65)
Последовательное соединение ФФ и исследуемого звена ИЗ на-
зывают эквивалентным звеном. Его АФХ

(8.66)
Метод формирующего фильтра заключается в том, что при ста-
тистическом анализе систем управления перед исследуемым звеном
(или системой) включают ФФ с АФХ, соответствующей спектраль-
ным свойствам реального входного сигнала x(t), и характеристики
выходного сигнала y(t) определяют при подаче на вход эквивалент-
ного звена (или системы) белого шума с единичной интенсивностью
Sxo = 1  Такой переход от исследования реального звена к исследова-
нию эквивалентного в ряде случаев упрощает математические вы-
кладки и задачу анализа. Например, для определения дисперсии вы-
ходного сигнала исследуемого звена достаточно получить (аналити-
чески или экспериментально) весовую функцию w3(r) эквивалентного
звена и согласно (8.55) проинтегрировать по времени ее квадрат.
00
Ч =fk(')T<*
О
(8.67)
Эту же дисперсию можно получить интегрированием в частот
ной области, подставляя в (8.61) Sx(co) = 1:
1
2я
00
-00
(8.68)
461
Заметим, что, приравнивая правые части формул (8.67) и (8.68),
можно получить частный случай равенства Парсеваля (2.38).
Пример. Вычислим дисперсию на выходе инерционного звена первого
порядка с передаточной функцией W(p) = к!(Гр + 1) при действии на его
входе белого шума с интенсивностью и шириной спектра соп »сос = 1/Т.
Решим задачу интегрированием в частотной области - при помощи
формулы (8.61). Дисперсия выходного сигнала
arctg со Т
°>п
1 00
D = — J 5х(со)
у 2п_оо
(8.69)
Дисперсия Dy тем меньше, чем меньше интенсивность SM входного
сигнала и чем больше постоянная времени Т.
8.5. Вычисление и минимизация дисперсии
сигнала ошибки управления
Общие соотношения. Применим формулы, приведенные в 8.4,
для расчета точности замкнутой СУ, обобщенная алгоритмическая
структура которой показана на рис. 8.7,я.
Рис. 8.7. Алгоритмические схемы замкнутой СУ:
а - исходная; б - расчетная
Будем считать, что ПФ №(р), равная произведению передаточ-
ных функций объекта и управляющего устройства, известна. Не за-
462
даны могут быть лишь некоторые параметры управляющего устрой-
ства.
На систему действуют случайные возмущения хп и хв с извест-
ными спектральными плотностями 5п(са) и 5в((о). Задающее воздей-
ствие х3 также является случайным сигналом со спектральной плот-
ностью S3(co). Пусть все три воздействия - центрированные сигналы.
Тогда и сигнал ошибки е будет центрированным.
Если указанные внешние воздействия не коррелированы между
собой, то сигнал ошибки е, возникающий в системе, может рассмат-
риваться как сумма трех независимых составляющих (см. рис. 8.7,6):
£ = £3+£п+£ъ.	(8.70)
Составляющая £3 обусловлена неточным воспроизведением за-
дающего воздействия, а составляющие еп и ев - неполным подавле-
нием возмущений хп и хв.
Соответственно и дисперсия сигнала ошибки может быть пред-
ставлена в виде суммы трех дисперсий:
(8.71)
Каждая из этих трех дисперсий может быть вычислена по фор-
муле (8.61) независимо друг от друга:
(8.72)
(8.73)
(8.74)
Если внешние воздействия коррелированы между собой, то и
составляющие (8.70) сигнала ошибки будут коррелированы, и поэто-
му полную дисперсию Dz можно вычислять только путем интегриро-
463
вания общей спектральной плотности ^(со), найденной с учетом
свойства (8.31).
Методика вычисления и минимизация дисперсии. При под-
становке в формулы (8.72) - (8.74) конкретных функций Ж(/со) и 5'(со)
получаются довольно сложные выражения, интегрирование которых
обычными методами затруднительно. Поэтому используют методи-
ку, изложенную в 6.3 для вычисления квадратичных интегральных
оценок. В соответствии с этой методикой каждую из трех дисперсий
определяют по формуле, аналогичной (6.74):
2л- Л|О(7Й>)|2	2d А
(8.75)
где полиномы Г(/со), D(jgs) и определители и Дп составляются по
формулам (6.75) и (6.76).
В простейших случаях, когда наибольшая степень полинома
£)(/со) п = 1 ;2;3, формула (8.75) дает:
Я, = vo/Wi; Ч = fe -	;
A, = (^*0 + ^1V2 -^3V1)/W3(^2
(8.76)
В полином D{ja) в виде сомножителя входит характеристиче-
ская функция F(/co) = 1 + W(Jd)) замкнутой системы. Поэтому при
приближении системы к границе устойчивости (т.е. при F(/co) —> 0)
интеграл (8.75) резко возрастает.
Для систем с запаздыванием подынтегральное выражение нель-
зя привести к виду (8.75) и дисперсию можно вычислить только при-
ближенно - заменяя запаздывание е1* дробно-рациональной функци-
ей (3.118) или (3.119).
С помощью формул (8.71) - (8.76) можно получить аналитиче-
ское выражение, связывающее полную дисперсию сигнала ошибки
£)е с параметрами внешних воздействий и с параметрами системы
(например, к„ Ti):
D, = f(k„T,\	(8.77)
464
Минимизируя функцию (8.77) по параметрам к, и Ti, можно оп-
ределить их оптимальные значения.
Пример. Определим оптимальное значение ПК для системы с ПФ:
(р)=Vp •
(8.78)
На входе системы (см. рис. 8.7,а) действует задающее воздействие х3
со спектральной плотностью
5'э(со) = 2Г>3а3/(а3+со2)	(8.79)
и помеха хп в виде белого шума со спектральной плотностью
Sn(co) = Sn0 = const при |со|<соп,	(8.80)
причем соп»соср = к.
Дисперсия, обусловленная неточным воспроизведением задающего
воздействия,
п - — 7 2Р3а3
4 2л_ооа3+со2
I \	1 -	2£>3а3|/€о|2
----—— а® =-------- J --------г1--!—«-«со =
1 + k/jcn 2л -оо [а3 + /со) | /со + /с|
- 2£3а3(/со)2
(1(А
(/со)2 +(03+ /с)/со + а3к
(8.81)
Сравнивая выражение (8.81) с типовой формой записи полиномов
(6.75), (6.76), нетрудно установить, что в данном случае
и=2; с70=1; c/i=a3+£; с72=аз£; v0=-2£)3a3; Vi=0.
Окончательно дисперсия
О., =(d«vi-d2vQ)l2d,d,d2 = Dsa,/(a3 +t)	(8.82)
Чем больше коэффициент к, тем меньше дисперсия Dn, т.е. тем точнее
система воспроизводит на выходе задающее воздействие.
Дисперсия, обусловленная влиянием помехи,
465
1 °?
d.
*n J nV ^l+jt/yco
2л
—QO
J CO	£
~ _L 7 5 —2-----------
П — j nv .	I?
Z7C -co ;>л Ц_ Zr
(8.83)
У этого интеграла п = 1; dQ =1; d\ = v0 - S^J?.
Дисперсия
D^vJld^S^kll.	(8.84)
Чем больше коэффициент к, тем больше ошибка из-за прохождения
помехи хп на выход системы.
Суммарная дисперсия сигнала ошибки
De
a3+&
(8.85)
Оптимальное значение коэффициента к найдем из условия
_ ^ЗаЗ ^пО _ q
дк (а3 +к?	2
откуда
fcOnr - ^2D3a3 /S^ а 3.
(8.86)
(8.87)
Оптимальное значение коэффициента зависит только от параметров
воздействий. Чем больше а3 (уже спектр задающего воздействия), тем мень-
ше должен быть к (меньше полоса пропускания системы). Чем больше D3,
тем шире полоса пропускания. Чем больше интенсивность помехи S^, тем
меньше должен быть к и, следовательно, уже полоса пропускания (соср = к).
Влияние ПК разомкнутого контура и спектра воздействий
на точность СУ. Покажем, что минимум функции (8.77) существует,
как правило, и в общем случае. Пусть на систему действуют задаю-
щее воздействие х3 и помеха хп. Как правило, спектр задающего воз-
действия находится в области низки?< частот (рис. 8.8,4/), а спектр
помехи равномерен в широкой полосе частот (см. рис. 8 8,в). С уве-
личением ПК к разомкнутого контура АЧХ | Фа(/4°) | и | Фег((/о>) I по
каналам х3-е и хп-е смещаются в область более высоких частот, а ре-
зонансный пик становится выше (см. пунктирные линии на рис. 8.8,а
и рис. 8.8,в).
466
Рис. 8.8. Влияние ПК разомкнутого контура
на спектральную плотность сигнала ошибки
Так как спектральные плотности ^(со) и <Sen(co) равны произве-
дениям 5'Х®) и ^n(w) на соответствующие АЧХ замкнутой системы,
то при увеличении к ординаты функции ^(со) уменьшаются (см. рис.
8.8,6), а ординаты функции Уеп(со) увеличиваются (см. рис. 8.8,г). Со-
ответственно меняются и составляющие полной дисперсии: £>а
уменьшается при увеличении к, a Dai - увеличивается (рис. 8.9). Оче-
видно, что суммарная дисперсия De при некотором значении к=кот
будет иметь минимум.
На основе анализа графиков на рис.8.8 можно также сделать
выводы о влиянии спектра случайных входных воздействий на
точность их воспроизведения или подавления:
-	низкочастотные (с оо«сор) задающие воздействия х3 хорошо
(почти без ошибки, с коэффициентом к ~ 1) воспроизводятся на вы-
ходе СУ, при этом дисперсия выходного сигнала х приблизительно
равна дисперсии задающего воздействия х3, т.е. Dx « Dx.^ a De« 0;
-	низкочастотные возмущения хв, действующие на выходе ОУ,
хорошо компенсируются системой, при этом дисперсия сигнала
ошибки близка к нулю;
467
Е
Рис. 8.9. Зависимость дисперсии
сигнала ошибки от ПК
разомкнутого контура
- низкочастотные помехи
хп, действующие на входе СУ,
воспринимаются системой как
задающие и почти полностью
воспроизводятся на выходе, в
результате чего составляющая
полной дисперсии £)еп « Dm,
высокочастотные (с
со»(»р) задающие воздействия
х3 практически не воспроизво-
дятся системой (из-за ее инер-
ционности), при этом De ~ Djai
- высокочастотные возмущения хв плохо компенсируются сис-
темой (из-за ее инерционности), при этом составляющая дисперсии
^ЕВ ® DB,
-	любые внешние воздействия с частотой со, близкой к собст-
венной резонансной частоте СУ, проявляются на выходах х и е с со-
отношением амплитуд, большим единицы.
Оценка эффективности и предельных возможностей систем
стабилизации при случайных возмущениях. Эффективность
функционирования стабилизирующей системы при стационарном
случайном возмущении хв, действующем на выходе объекта, можно
оценить отношением дисперсии Dx выходного (стабилизируемого)
сигнала х к дисперсии DB возмущения хв:
k^DjD*.	(8.88)
Очевидно, что чем меньше это отношение дисперсий, тем лучше
система выполняет задачу компенсации влияния возмущения хв на
стабилизируемую переменную х.
Показатель к3 зависит от инерционности элементов, входящих в
контур системы, и от спектра возмущающего воздействия. При
большой инерционности контура и высокочастотном спектре отно-
шение ДД)В« 1, а это означает, что система практически бесполезна.
Если частоты некоторых спектральных составляющих возмущения
окажутся близкими к собственной резонансной частоте системы, от-
468
ношение /Л-/Вй может стать больше единицы, т.е. система будет даже
вредна.
Наилучший эффект стабилизации достигается, когда структура
и параметры регулятора выбраны оптимальными для данного объек-
та и действующего возмущения. Отношение дисперсий £MDB при
этом будет характеризовать наилучшую достижимую точность ста-
билизации и, следовательно, предельные возможности системы в
данных условиях работы.
Оценим предельные возможности системы стабилизации, со-
стоящей из инерционного объекта с запаздыванием
WO(P) =
и идеального для него регулятора Ресвика (см. 7.15)
=	(8.90)
Для этого определим дисперсию выходного сигнала идеальной
системы
ч СО	ч 00
D, = —	(®) Ф, т (Jco)2 da) = — f SB (а) 1 - e'J--
Л	J D v ' D.OJll	'	J-'/Jr * й '
da). (8.91)
После несложных преобразований можно получить следующую
важную формулу для оценки минимально достижимой дисперсии в
системе с запаздыванием:
£>Ж=2[£>,-Л,(го)],
(8.92)
где Яв(т0) - значение корреляционной функции возмущения при ар-
гументе т=т0.
Формулу (8.92) можно вывести и на основе физических рассуж-
дений. Оптимальная система, стабилизирующая выход объекта с за-
паздыванием, вырабатывает через интервал т0 после каждого изме-
нения возмущения xB(f) компенсирующую составляющую ху(/), рав-
ную хв(т-т0). Поэтому выходной сигнал в каждый момент времени (с
учетом знака отрицательной обратной связи)	469
x(t) = Хв (0 + ху (0 = хв (О - хв (t - т0).	(8 93)
Дисперсия выходного сигнала, который так же, как и возмуще-
ние, считается стационарным с нулевым математическим ожидани-
ем,
{к (0 - 0 - г0 )Г }=м к (О - 2х. (Ох. (/ - То) + Х2Л (t - т0)) = 2[DB - Д, (т0)].
(8.94)
Полученный результат совпадает с формулой (8.92).
Как известно, корреляционная функция любого случайного сиг-
нала при изменении ее аргумента т от нуля до значения, называемого
временем спада тсп (или максимальным интервалом корреляции),
уменьшается от значения DB практически до нуля. Поэтому при ва-
риации запаздывания объекта от 0 до тсп эффективность стабилиза-
ции в соответствии с формулой (8.92) находится всегда в диапазоне
0<D,/D,<2.	(8.95)
Причем нижний предел относится к случаям, когда либо запаз-
дывание объекта практически отсутствует, либо возмущение меняет-
ся очень медленно, а верхний - к случаям, когда запаздывание вели-
ко или возмущение имеет более высокочастотный спектр, чем сама
система.
Соотношение Dx = 2DB можно объяснить следующим образом.
При большом запаздывании т0 = тсп компенсирующие воздействия
ху(0 в каждый момент времени не будут уже соответствовать тем из-
менениям возмущения хв(Г-т0), которые вызвали отклонения выход-
ной переменной, и, следовательно, не будут коррелированы с возму-
щающими воздействиями. При этом сигнал x(f) оказывается суммой
двух равных, но независимых друг от друга слагаемых xs(t) и xy(t) -
= хв(/-т0), и поэтому Dx = 2DB.
Для распространенного случая, когда свойства случайного воз-
мущения хв описываются экспоненциальной корреляционной функ-
цией (8.39), формула минимально достижимой дисперсии (8.92) при-
нимает вид
470

(8.96)
Из нее можно определить условие, при котором система стаби-
лизации (даже оптимальная!) становится бесполезной. Очевидно, что
Dx/D3 > 1, когда
ато>0,7.	(8.97)
Учитывая известное соотношение тсп ~ 3/а-, можно условие
(8 .97) записать и в таком виде:
то>0,23тсп,	(8.98)
т е. система стабилизации становится бесполезной, если время спада
корреляционной функции возмущения будет меньше, чем « 4т0.
8.6. Определение оптимальной передаточной функции СУ
(задача Винера)
Назначение любой СУ - изменять выходную величину x(t) по
определенному закону и устранять влияние возмущений на эту вели-
чину. В общем случае СУ должна воспроизводить на своем выходе
не само воздействие х3(Г), а некоторый требуемый сигнал xK(t), свя-
занный с сигналом x3(f) заданным соотношением
хн(0 = х3(Г)Фн(р),	(8.99)
где Фи(^) - заданный оператор идеального преобразования входного
сигнала х3(/).
Вид оператора Фи(р) зависит от назначения системы. В системах
воспроизведения, к которым относятся следящие и стабилизирую-
щие системы, этот оператор равен Фи(р)=1. Если обратная связь в
системе воспроизведения неединичная - с коэффициентом кос 1, то
оператор Фи(/>) равен постоянному числу \/к0,с.
Из-за того, что на входе системы кроме полезного сигнала х3(Г)
действует помеха хп, идеальное преобразование согласно заданному
оператору Фи(р), как правило, невозможно. Сигнал х(/) на выходе
471
реальной системы Ф(р) (рис. 8.10,а) почти всегда отличается от иде-
ального выходного сигнала на величину сигнала ошибки е(г) = хи(/)
- х(г). В связи с этим возникает задача синтеза такой структуры сис-
темы, которая обеспечивала бы наилучшее, в том или ином смысле,
приближение к идеальному преобразованию Фи(р).
б 5_____

Рис. 8.10. Алгоритмические схемы к задаче Винера
Критерием точности приближения реальной структуры к иде-
альной может служить условие минимума дисперсии сигнала ошиб-
ки е.
Задача синтеза структуры линейной системы, оптимальной по
критерию (8.3) при стационарных случайных воздействиях, была
впервые сформулирована и решена Н.Винером и носит его имя.
Ниже излагается упрощенное решение задачи Винера примени-
тельно к расчетной схеме (см. рис. 8.10,6), которая эквивалентна ис-
ходной схеме (см. рис. 8.10,а). Будем полагать, что входные воздей-
ствия х3(г) и хп(Г) не корродированы между собой. Следовательно, и
составляющие с3 и еп сигнала ошибки будут независимы друг от дру-
га. Поэтому можно спектральную плотность сигнала е определять
как простую сумму (8.32) (а не (8.31)!):
5. (со) = St, (со) +	(со) = 5, (со)|Ф„ ()о>) - Ф(»|2 + 5„ (<о)|Ф(»|2.
(8.100)
Дисперсия сигнала ошибки равна интегралу спектральной плот-
ности (8.100):
D. =2- 1к(<о)|Фн(усо)-Ф(7со)|2 +5„(<0)|Ф(»|2}с/<0.	(8.101)
2 л -л
472
Задача Винера заключается в определении такой частотной пе-
редаточной функции Ф(7<в) замкнутой системы, которая обеспечива-
ет минимум дисперсии Ре. Для решения этой задачи формулу (8.101)
необходимо преобразовать к следующей форме, при которой иско-
мая функция Ф(7<в) входит только в одно слагаемое подынтегрально-
го выражения (выкладки здесь не приводятся):
_	1 г 5,(®5n(®)., . . .2 „ . ... . . Ф,(»$,(й>) 1 ,
\<(®)	s„(®)
(8.102)
где ^((о)^^)^^^) - спектральная плотность суммарного входно-
го сигнала.
В первое слагаемое интеграла (8.102) не входит функция Ф(до),
и на него нельзя повлиять при выборе вида этой функции. Второе
слагаемое можно изменять при выборе функции Ф(/со). Так как оба
слагаемых неотрицательны, то условием минимума дисперсии Ре
является равенство
ф(;®)-ф„и®)5,(®)Лвх(®).	(8.ЮЗ)
Отсюда оптимальная ПФ замкнутой системы
Фот(^) = Фи(^)^(^вх(^)-
(8.104)
Оптимальная ПФ зависит от вида заданного оператора идеаль-
ного преобразования Фи(/(о) и от соотношения спектральных плотно-
стей задающего воздействия и помехи.
При отсутствии помехи (5п((о)=0) оптимальная функция равна
заданному оператору идеального преобразования:
ФОГО(7^) = ФИ(7М
(8.105)
Если помеха представляет собой белый шум и ее интенсивность
Sno намного больше уровня полезного сигнала, т.е. ^о»^©), то
473
оптимальная частотная характеристика системы воспроизведения
(Фи(/го)=1)
(8.106)
т.е. повторяет форму кривой спектральной плотности задания.
Частотные функции, определяемые выражением (8.104), оказы-
ваются, как правило, физически не реализуемыми: им соответствуют
весовые функции отличные от нуля при !<().
Оптимальную частотную функцию, удовлетворяющую условию
физической реализуемости (w(f)=0 при t<0), можно определить по
формуле Колмогорова-Винера, которая вытекает из (8.104):
Фопг.р(» =
WJja)
ФЙ(Я)ЭД
(8.107)

5
где ^вх(/<») - частотная функция формирующего фильтра, соответст-
вующего спектральной плотности 5вх(го), т.е.
S„(a>) = Ко)2 =
(8.108)
Квадратные скобки со знаком «+» означают, что второй сомно-
житель - функция, имеющая нули и полюсы только в верхней полу-
плоскости го (или в левой полуплоскости р). Для того, чтобы найти
этот сомножитель, разлагают выражение в скобках на сумму про-
стых дробей и отбрасывают все дроби, имеющие нули и полюсы в
нижней полуплоскости го.
Если синтезируемая система должна включать в себя какую-
либо неизменяемую часть, например объект W0(J(q), то оптимальную
функцию изменяемой части, например регулятора, можно найти по
общей функции ФОптр(/<»)- Так, оптимальная частотная функция регу-
лятора типовой системы (см. рис, 4.7)
^ропт(^) =
(8.109)
474
Следует отметить, что степень числителя у функции РКр.опт(/а))
часто оказывается больше степени знаменателя. Как известно, это
создает трудности технической реализации получаемых функций.
Трудности технической реализации особенно проявляются в тех слу-
чаях, когда объект содержит запаздывание е ° . Как видно из фор-
мулы (8.109), регулятор при этом должен содержать идеальный уп-
редитель с передаточной функцией е+ pt° . Такую функцию можно
реализовать только приближенно.
Минимальная дисперсия Ре, которая теоретически достижима
при оптимальной передаточной функции, равна интегралу от первого
слагаемого в выражении (8.102):
f.MHH
оО
Цф.(»Г
-оО
(8.110)

Из (8.110) следует:
предельно достижимая точность системы тем лучше, чем
меньше перекрываются спектры задающего воздействия и по-
мехи.
В физически реализуемой системе из-за различия функций
ФОпт(/®) и Фопт.рСД0) дисперсия (8.110) возрастает на некоторую вели-
чину ДД; и становится равной
<I>„(/o)).S'.(m)
ФИ(У“)2
S,(<o)Sn(<o) (
>dw, (8.111)
J
где знак «-» вверху у квадратной скобки означает, что это слагаемое
должно иметь только нижние нули и полюсы в плоскости со.
Выражение (8.111) определяет предельную точность синтези-
руемой системы. Дисперсия Ремин принципиально неустранима ни-
какими техническими средствами.
Если на стадии технической реализации передаточная функция
Фоптр(/а>) будет изменена, то точность дополнительно ухудшится.
475
На предельную точность, кроме запаздывания (см. формулу
(8.97)), сильно влияет помеха в канале измерения. Чем выше уровень
помехи тем хуже предельная точность. Например, в системе ста-
билизации (см. рис. 8.7,6?) минимально достижимая дисперсия DCMm
становится равной дисперсии DB возмущения хв (т.е. система стано-
вится бесполезной), когда
S. «0,77)!а.,
ГК/ ?	8/ В ’
(8.112)
где 1)в и ав - параметры возмущения хв типа (8.39).
При совместном действии обоих факторов (запаздывания и по-
мехи) система становится бесполезной при меньшем запаздывании т0
и меньшем уровне Sno-
Пример. Определим оптимальную передаточную функцию и предель-
ную точность следящей системы (Фи(/<о)=1), если
S3(w) = 2L>a/(a2+со2); Sn(co) = 5n0 ,	(8.113)
и корреляция между сигналами х3 и хп отсутствует.
Найдем спектральную плотность суммарного сигнала и разложим ее
на комплексно сопряженные множители:
о / ч с , ч с / ч	ZDa + S-Ja2 + <й2)	. (1 + ycoaYl - усол) .
5 (о?) = 53(со) +5п(<о) =----------------L = А\-----т-З----= ^BX(y®)^BX(-yto),
a +со	(a + усоДа-усо)
(8.114)
где А = 2Da + $по<х2; а2 - STlfj(2Da + З^а2)= ЗпоМ.
Согласно формуле (8.107), оптимальная передаточная функция
Фонт р С/®) ~
a + jay 2Da(a-j(o)__________
7л(1 + y'oa) |_(сг + co2 p/1 (1 - jaya)
Разложим выражение в квадратных скобках на сумму дробей.
53(со) _ 2Da < 1/(1 + aa) a/(l + «а)
^вх(->) ЛЧ а + Л> а-у®
(8.115)
(8.116)
476
Отбросим второе слагаемое, так как оно имеет полюс ® = aJj - -ja, ле-
жащий в нижней полуплоскости. Тогда реализуемая оптимальная функция
примет вид
ФопгрО) = 2£>а/л(1 + ааХ1 + jaa).	(8.117)
Как видим, оптимальная система должна обладать свойствами инер-
ционного звена первого порядка с параметрами
к3 = 2£>а/Л(1 +аа); Г3 = а.	(8.118)
В большинстве реальных случаев 5'поос « 1, при этом коэффициент
к3~ 1. Согласно (8.109), частотная функция разомкнутого контура
^ропт О) = l/T^co = k/jv,	(8.119)
т.е. разомкнутый контур оптимальной системы в рассматриваемом частном
случае является интегратором.
8.7. Оптимальная фильтрация векторных случайных сигналов
(фильтр Калмана)
В предыдущем параграфе задача определения оптимальной ПФ
была решена для одномерных (скалярных) случайных воздействий.
При этом можно было заметить, что процесс решения задачи не за-
висел от того, подразумевается ли под искомой передаточной функ-
цией отдельное звено (например, фильтр в распространенном радио-
техническом понимании) или же замкнутая система управления, ко-
торая в эквивалентном представлении также может рассматриваться
как фильтр, пропускающий полезный сигнал и подавляющий поме-
ху.
Перейдем теперь к задаче синтеза оптимального фильтра, пони-
маемого в обобщенном смысле, для многомерных (векторных) слу-
чайных сигналов. Для описания фильтра и сигналов применим метод
пространства состояний, изложенный в 2.9.
Пусть имеется совокупность стационарных независимых друг от
друга сигналов Х](Г), х2(0, ... , xn(t) с нулевыми математическими
ожиданиями и известными корреляционными функциями 7?Х1(т),
Ах,(т), ... , 7?Хп(т). Эту совокупность случайных сигналов можно
рассматривать как случайный «-мерный вектор x(t) с известной мат-
рицей-столбцом корреляционных функций Rx(i). Положим, что век-
торный случайный сигнал x(t) недоступен для непосредственного
измерения, а вместо него при помощи безынерционного преобразо-
вателя наблюдается (измеряется и вычисляется) /-мерный случайный
вектор хн(/), у которого каждая составляющая xH1(f), хн2(0,	, хнг(г)
представляет собой сумму линейной комбинации составляющих век-
тора х(/) и независимой помехи (ошибки измерения) в виде идеаль-
ного белого шума с известной интенсивностью, т.е. наблюдаемый
вектор
ХН (Г) = хп (Г) + g{t) = С х(0 + g(0,	(8.120)
где С - известная постоянная матрица размера /х« (/>«); g(t) -
/-мерный вектор белого шума, состоящий из / независимых центри-
рованных компонентов gi(0, gi(f), • , gi(0 и характеризуемый из-
вестной матрицей-столбцом интенсивностей помех SgQ =	Sgn,...,
s&f.
Задача оптимальной фильтрации заключается в том, чтобы из
наблюдаемого сигнала хн(0 выделить «-мерный векторный сигнал
x(f), который наиболее близок в определенном смысле к исходному
(полезному) сигналу x(t). Используя терминологию математической
статистики, можно сигнал x(t) назвать оценкой сигнала х(г), а сам
процесс фильтрации - оцениванием.
В качестве меры близости оценки х (/) к истинному сигналу x(t)
примем сумму средних значений квадратов отклонений 8, = хг - х,,
т.е. скалярную величину
6„ = Z	1 = S м {[е,(/)]1 }= £ D,,	(8.121)
1=1	i=l	i=l
или в векторно-матричной форме
a =fr(w^T(0s(')})=HI2[),	(8.122)
478
где £(r) - «-мерный вектор ошибок оценивания, образованный со-
ставляющими 8](Г), б2(0,	М {•} - знак математического ожи-
дания (усреднения по времени); т - знак транспонирования матрицы;
tr(-) - обозначает так называемый след матрицы, который по опреде-
лению равен сумме диагональных элементов матрицы, записанной
внутри скобок.
Матрица Д, равная среднему значению скалярного произведе-
ния, называется ковариационной (или дисперсионной). Диагональ-
ные элементы Д матрицы Д, имеющей размер п х п, равны диспер-
сиям Д, сигналов ошибки, а недиагональные равны взаимным кор-
реляциям (ковариациям)
Оценку х (/), обеспечивающую минимум
Д —>пип
*(/)
(8.123)
называют оптимальной по квадратичному критерию и обозначают
х*(0.
Для решения задачи синтеза оптимального фильтра в простран-
стве состояний представим оцениваемый случайный вектор x(t) как
вектор состояния некоторой динамической системы н-го порядка (см.
2.9), описываемой матричным дифференциальным уравнением
x(t) = А х (0 + В z(f),
(8.124)
где А - постоянная матрица размером п х т. определяющая однород-
ную часть уравнения; z(t} - w-мерный вектор белого шума с нулевым
математическим ожиданием и известной матрицей-столбцом интен-
сивностей В - постоянная матрица размером п х т, определяю-
щая неоднородную часть уравнения и тем самым влияние входного
сигнала на систему.
Очевидно, что динамическую систему, описываемую уравнени-
ем (8.124), можно рассматривать как многомерный формирующий
фильтр для полезного сигнала х(0. Уравнениям формирующего
фильтра ФФ (8.124) и измерителя И (8.120) соответствует алгорит-
мическая схема на рис. 8.11.
F	479
Рис. 8.11. Оптимальный фильтр Калмана
Американским математиком Р.Калманом было показано, что
при такой постановке задачи фильтрации (оценивания) оптимальный
фильтр ОФ представляет собой (см. рис. 8.11) следящую систему с
отрицательной обратной связью, которая состоит из модели одно-
родной части формирующего фильтра, модели идеального измерите-
ля (без помех) и матричного коэффициента фильтра К$. Этот коэф-
фициент в установившемся режиме фильтрации стационарных сиг-
налов представляет собой постоянную (их/)- матрицу
=D,C'S'\
-ф --€- -gO ’
(8.125)
где D? - ковариационная матрица, полученная как решение нелиней-
ного матричного алгебраического уравнения
AD. + 2.4’ + BS,'?-D'CS^CD, =0.	(8.126)
В частном случае, когда сигнал х(/) одномерный (п = 1), в коэф-
фициент фильтра Калмана (8.125) в качестве сомножителя входит
480
дисперсия ошибки оценивания D*, соответствующая минимуму
(8.123).
Выражения (8.125) и (8.126) имеют смысл лишь в том случае,
если все элементы матрицы-столбца S#o отличны от нуля, т.е. если
все I составляющих сигнала хн(Г) содержат помеху. Уравнение (8.126)
имеет единственное положительно определенное решение, если сис-
тема (8.120), (8.124) управляема и наблюдаема (см. 6.5).
Параметры фильтра Калмана, как и в задаче Винера (см. 8.6),
предопределяются характеристиками полезного сигнала (через мат-
рицы Szo, В, А), измерительного устройства (матрица С) и помехи
(матрица З^о). Так, чем больше интенсивность полезного сигнала
и чем меньше интенсивность S^o помехи, тем больше будут коэффи-
циенты и быстродействие следящей системы фильтра и тем луч-
ше она будет воспроизводить все изменения полезного сигнала x(t).
В пределе, когда 5^ >:> ^о, фильтр будет эквивалентен безынерцион-
ному преобразователю с единичными передаточными коэффициен-
тами. В противоположном случае, когда « S^, фильтр эквива-
лентен модели полезного сигнала.
Фильтр Калмана одновременно с оптимальной оценкой х (/) ис-
ходного сигнала х(0 выдает оценку х п(0 для линейной комбинации
х п(0 ~ С x(t), образуемой из исходного сигнала в измерительном
устройстве.
Если какое-либо из входных воздействий z(t) или g (t) не явля-
ется центрированным сигналом, то для получения несмещенных
оценок в схему фильтра необходимо, согласно принципу суперпози-
ции, ввести со знаком минус соответствующее ненулевое математи-
ческое ожидание. На рис. 8.11 пунктирной линией показано, как сле-
дует учесть математическое ожидание Ф 0. Аналогично можно
учесть ожидание т., только оно должно быть предварительно про-
пущено, как и сам сигнал z(t), через блок В и приложено ко входу
интегратора.
Согласно рис. 8.11 матричную ПФ фильтра между наблюдае-
мым (измеряемым) вектором xH(/j и вектором-оценкой x(t) можно
вычислить по формуле
481
Е*(Р) = х(р)/хи(р) = (р1-4 + ^фС)_1^ф
(8.127)
Отметим, что приведенная на рис. 8.11 схема будет служить
фильтром и в том случае, если коэффициент выбран не в соответ-
ствии с выражениями (8.125) и (8.126). Необходимо лишь, чтобы эта
следящая система была асимптотически устойчива. Очевидно, что
при этом ошибка оценивания е(0 в установившемся режиме так же,
как и в оптимальном фильтре, будет стремиться к нулю. Но диспер-
сия ошибки будет больше, чем в оптимальном фильтре.
Пример. Пусть имеется стационарный случайный сигнал х(/) с корре-
ляционной функцией Ях(т) = Охе ’ад , который, как известно, можно полу-
чить. пропуская белый шум с единичной интенсивностью 5'^ = 1 через фор-
мирующий фильтр с передаточной функцией
+р)	<8128>
Если Sjo ф 1, то для получения сигнала x(z) с требуемыми параметрами
Dx и ах в числителе функции (8.128) должно быть выражение j2Dxax/SgQ .
Предположим, что сигнал x(z) измеряется с помехой g(z):
XH(Z) = x(/) + g(/).
(8.129)
где g(t) - стационарный белый шум с корреляционной функцией Rg(z) =
= Sgo8(T) и спектральной функцией Sg(a) - 5^.
Определим структуру и параметры фильтра Калмана, наилучшим об-
разом (в смысле критерия (8.123)) выделяющего из измеренного сигнала
Л
хн(0 оценку x(t) полезного сигнала. Для этого представим формирующий
фильтр (8.128) в виде скалярного дифференциального уравнения в про-
странстве состояний
хн(0 = ax(t) + bz(f).
(8.130)
где а = А = - ах, b = В = j2Dxax при = 1 или же Z> = В = 1 при = 2Dxax.
Очевидно, что в данном случае матрица наблюдения С и матрицы ин-
тенсивностей и Sgo также вырождаются в скаляры и имеют вид
482
С = 1, 520=5г0, Sg0 = 5g0.
Согласно формуле (8.125) коэффициент фильтра
—Ф =^Ф =^e/^g0 •
(8.131)
(8.132)
Сомножитель De находим как решение следующего уравнения, яв-
ляющегося частной формой матричного уравнения (8.126):
aDe + Dea + bSzOb - Dt • 1 • Sg'o • 1 • Dt = 0	(8.133)
или
D,:-2aSs0D<-l>I5;05s(1=0	(8.134)
Положительный корень уравнения (8.134)
O,	(8.135)
а соответствующий ему коэффициент фильтра с учетом принятых обозна-
чений
*ф =	= а ++b2sio/sgo = -а, + & +^Dxax/SgQ. (8.136)
При этом дисперсия ошибки фильтрации
D. = й„ = -a,S,o + ^S82o+2DA5so-	(8.137)
. Передаточная функция фильтра
д х( nA	к л.	кл. / ar + Ад)
И* (р) =	= 7-------г = ~ЛП1Г—(8.138)
*н(р) (p + ax + fy>) 1 + р/(ах+*ф)
соответствует инерционному звену первого порядка с постоянной времени
^зв = 1/(ах +^'ф)- yj^go /Т^х +2DxaT
(8.139)
и передаточным коэффициентом
483
= *Ф Дах +кф) =-- 1	..	(8.140)
^С1Л + 2D дад IS gQ
Нетрудно убедиться, что структура и параметры фильтра Калмана и
фильтра, полученного для этих же условий решением задачи Винера (см.
пример в 8.6), совпадают.
8.8. Оптимальное оценивание состояния многомерного ОУ
Для построения замкнутой системы управления многомерным
динамическим объектом необходимо располагать достаточно полной
информацией о его переменных состояния x(f). Однако в реальных
условиях промышленного объекта часто оказывается, что не все
компоненты вектора состояния x(t) доступны для измерения: либо
отсутствуют соответствующие измерительные устройства (датчики),
либо некоторые переменные в принципе нельзя измерить. При этом
размерность I наблюдаемого вектора хн(0 меньше размерности п век-
тора состояния х(/), и нельзя определить все переменные состояния
х(/) согласно уравнению x(t) = C ’jChCO- В таких условиях задача син-
теза системы называется задачей с неполной информацией о состоя-
нии объекта. Кроме того, результаты даже тех измерений, которые
можно осуществить, содержат обычно случайные ошибки, и задача
синтеза становится задачей с неполной и неточной информацией.
Таким образом, при синтезе управления возникает задача оце-
нивания всех переменных x(t) по имеющейся неполной и неточной
информации о состоянии многомерного объекта. Для решения этой
вспомогательной задачи - определения наиболее вероятных значе-
ний переменных x(t) - в контур системы управления включают спе-
циальное устройство оценивания, называемое также наблюдателем,
или идентификатором состояния.
Структуру устройства, оптимально оценивающего состояние
объекта, удобно выбирать, опираясь на изложенную в предыдущем
параграфе методику синтеза фильтра Калмана. При этом объект, на
входе которого, кроме управляющего сигнала y(t), действует обычно
случайное возмущение z(f), рассматривают как формирующий
фильтр, а наблюдаемый на выходе объекта сигнал хн(0 подают на
вход устройства оценивания (рис. 8.12), которое представляет собой
484
модель объекта, охваченную отрицательной обратной связью по сиг-
налу б'н(0 = хн(0 - х „(/). Для получения оптимальной по критерию
(8.123) оценки состояния стационарного объекта, описываемого
уравнением (8.124) и контролируемого при помощи измерителя
(8.120), матричный коэффициент определяют также согласно вы-
ражениям (8.125) и (8.126). Необходимо только, чтобы объект был
полностью управляем и наблюдаем (см. 6.5).
Управляющее воздействие y(t) рассматривают как дополни-
тельное внешнее воздействие и так же, как детерминированные со-
ставляющие т. и mg, подают на соответствующие входы устройства
оценивания.
Оптимальное оценивающее устройство обеспечивает компро-
мисс между скоростью воспроизведения переменных состояния и
темпом сглаживания помехи наблюдения. Баланс между этими двумя
свойствами определяется соотношением интенсивностей возмуще-
ния z и помехи g .
485
Если помеха g отсутствует, то точное оценивание состояния
возможно лишь в том случае, когда число компонент наблюдаемой
переменной по крайней мере не больше, чем число компонент воз-
мущения z.
Отметим, что оценивающее устройство в виде модели объекта,
охваченной обратной связью, может удовлетворительно работать и
при достаточно произвольно выбранном коэффициенте Кф. Единст-
венным ограничением при выборе этого коэффициента является ус-
ловие устойчивости замкнутого контура оценивания. Обычно мат-
ричный коэффициент Кф выбирают таким, чтобы переходные про-
цессы в контуре оценивания протекали в 2-3 раза быстрее, чем в кон-
туре управления. Необходимо, однако, помнить, что с увеличением
быстродействия контур оценивания приобретает нежелательные
свойства дифференциатора.
Оценивающее устройство, построенное в виде фильтра Калма-
на, обладает определенной степенью избыточности, так как оно оце-
нивает весь вектор состояния x(f), хотя / его компонент можно вы-
числить и по результатам непосредственного измерения. Поэтому
применяют и упрощенные устройства оценивания, имеющие порядок
(Z7-/).
Пример. Определим коэффициент кф оценивающего устройства для
одномерного объекта
fF0(p) = хн{р')/у(р) = ко/^ор+\),	(8.141)
на входе которого, кроме управляющего воздействия y(t), действует случай-
ное возмущение z(f) в виде белого шума с интенсивностью S.o, а наблюдае-
мая переменная хн(0 представляет собой сумму единственной переменной
состояния x(f) и независимой помехи g(f) типа белый шум с интенсивностью
Sgi).
Уравнение состояния объекта
i(/) = ax(f) + by(t) + bz(J),	(8.142)
где а = -1/Г0, b = kJTo, а уравнение наблюдения
*„(/) = *(/) + £(')•	(8.143)
486
Очевидно, что в данном случае
п = 1; / = 1; т = 1; А = B = b, С = 1.
(8.144)
Матричное уравнение (8.126) вырождается в одно скалярное
aD, + D,a +bS!Ob - D,  1  S;J • I  Dt =0	(8.145)
ИЛИ
D2 -2aSg0D, ~b2SgQS20 =0.	(8.146)
Положительное решение этого уравнения
о. - aS + ^2S^,+i2Sj0S,0.	(8.147>
Искомый коэффициент оценивающего устройства, согласно формуле
(8.125)
Ч =Dt/S,e =a+^a2+b2Slt/S!t = -(1/7о)+^(1/Г„)! +*oS,0/ro2S,0.	(8.148)
Полученный результат совпадает с коэффициентом фильтра из приме-
ра в 8.7. Это объясняется тем, что при ах = \/Т0 и b = J2Dx/To рассматри-
ваемый объект (8.141) совпадает с формирующим фильтром (8.128).
Контрольные задания и вопросы
1.	Поясните, в чем заключается сущность статистического подхода к
расчету систем управления.
2.	Какие основные три задачи решаются в статистической динамике
систем управления?
3.	Какие числовые характеристики используются для описания стати-
стических свойств случайных сигналов?
4.	Напишите формулу корреляционной функции. Чему равно ее на-
чальное значение?
5.	Как связана крутизна графика Rx(x) со средней скоростью изменения
сигнала x(f) во времени?
6.	Какой физический смысл имеют ординаты спектральной плотности?
487
7.	Нарисуйте графики Sx((o) для медленно и быстро меняющегося слу-
чайного сигнала.	;
8.	Напишите формулу, связывающую дисперсию Dx со спектральной
плотностью Sx(co) сигнала.
9.	Чем отличаются графики S^co) идеального и реального белого шу-
ма?
10.	Вычислите дисперсию реального белого шума, характеризуемого
параметрами: - 0,1 В2-с, соп = 30 рад/с.
11.	Как связан параметр осх сигнала, характеризуемого экспоненциаль-
ной Rx(i), со средней скоростью изменения сигнала во времени?
12.	Нарисуйте график Sx(co) цветного шума.
13.	Каким соотношением связаны спектральные плотности сигналов на
входе и выходе звена с АФХ 1К(/со)?
14.	Определите спектральную плотность сигнала на выходе интегри-
рующего звена с коэффициентом ки при действии на входе идеального бело-
го шума с интенсивностью S^.
15.	Что такое формирующий фильтр? Как выбирается его АФХ?
16.	Напишите формулу для вычисления дисперсии сигнала на выходе
звена.
17.	Вычислите дисперсию сигнала на выходе дифференцирующего
звена с кл = 1 при действии на его входе белого шума с параметрами 5^ =
0,1; соп= 2 рад/с.
18.	По каким формулам вычисляются составляющие дисперсии сигна-
ла ошибки замкнутой системы?
19.	Как влияет передаточный коэффициент разомкнутого контура на
суммарную дисперсию сигнала ошибки?
20.	Как влияет ширина спектра задающего воздействия (см.рис.8.8) на
точность его воспроизведения?
21.	Какой формулой связана минимально достижимая дисперсия £)х
выходного сигнала идеальной стабилизирующей СУ с дисперсией DB воз-
мущения и с его корреляционной функцией?
22.	Как связана оптимальная АФХ со спектральными плотностями за-
дающего воздействия и помехи?
23.	Поясните идею и принцип построения фильтра Кал мана.
24.	Что представляет собой устройство оценивания состояния объекта
управления?
488
Глава 9. ОСНОВЫ АНАЛИЗА ДИСКРЕТНЫХ
СИСТЕМ УПРАВЛЕНИЯ
9.1.	Общие сведения о дискретных СУ
В современной автоматике широкое применение получили дис-
кретные СУ, или системы дискретного действия. Основным элемен-
том дискретной СУ является управляющая вычислительная машина
(УВМ), которая может использоваться либо в супервизорном режи-
ме, либо в режиме прямого цифрового управления (ПЦУ). В супер-
визорном режиме УВМ вырабатывает задания локальным контурам
регулирования, реализованным с помощью традиционных техниче-
ских средств автоматики. При режиме ПЦУ контуры регулирования
образуются самой УВМ.
На рис. 9.1 изображена функциональная структура системы
ПЦУ, в которой объектом управления является некоторый техноло-
гический процесс (ТП), характеризуемый управляемыми перемен-
ными Xi, х2, ... , хб. Эти выходные переменные объекта зависят от
управляющих воздействий у\, у2, уз, У4 (например, расходов сырья,
катализатора, энергии, рабочей среды) и возмущений z1? z2 (качест-
венные признаки сырья). Электрические сигналы uh пропорциональ-
ные указанным выходным и входным переменным объекта, посту-
пают в УВМ. УВМ в соответствии с заданной целью управления и
требованиями х,3 к качеству продукции и режиму ТП вырабатывает
управляющие сигналы, которые с помощью исполнительных меха-
низмов (ИМ) и регулирующих органов (РО) преобразуются в управ-
ляющие воздействия - расходы у}.
В рассматриваемой системе УВМ работает в так называемом
режиме разделения времени - поочередно подключается к отдельным
контурам регулирования (рис. 9.2). Для этого используются специ-
альные коммутирующие устройства - мультиплексор (МП) и де-
мультиплексор (ДМП), которые одновременно подключают цифро-
вое вычислительное устройство (ЦВУ) к датчику (Д) и исполнитель-
ному устройству (ИУ) l-го контура. Периодичность подключения
контуров к ЦВУ задается специальным устройством - таймером.
489
Преобразование сигналов из аналоговой формы в цифровую и на-
оборот осуществляется аналого-цифровым преобразователем (АЦП)
и цифро-аналоговым преобразователем (ЦАП).
Рис. 9.1. Функциональная структура системы
прямого цифрового управления
Таким образом, в системе с УВМ наряду с непрерывными сиг-
налами уц X], iii действуют и дискретные сигналы щ и у*, представ-
ляющие собой последовательности электрических импульсов, а сама
система управления поэтому относится к классу дискретных.
В дискретной СУ один или несколько сигналов являются дис-
кретными - представляют собой последовательность кратковремен-
ных импульсов.
Различают две категории дискретных СУ. В одной из них СУ
дискретны по своей физической природе - в них информация об
управляемых величинах объективно существует только в дискретные
490
моменты времени, как например, в СУ технологическим процессом,
состояние которого можно оценить только по периодически отби-
раемым пробам выходных продуктов. В СУ другой категории ин-
формация о состоянии ОУ существует непрерывно, но намеренно
преобразуется в дискретную форму для получения некоторых
свойств, улучшающих качество дискретной СУ по сравнению с
непрерывной.
Рис. 9.2. Функциональная структура отдельного контура СУ с УВМ
В состав дискретной СУ наряду со звеньями непрерывного дей-
ствия входят элементы, преобразующие непрерывные сигналы в дис-
кретные, и элементы, выполняющие обратное преобразование. Пре-
образование непрерывного сигнала в дискретный называется кван-
тованием. Различают три вида квантования сигналов: по уровню, по
времени, по уровню и по времени (совместно).
Квантование по уровню заключается в фиксации вполне опре-
деленных дискретных значений непрерывного сигнала (рис. 9.3,а).
При этом непрерывный сигнал (тонкая линия) заменяется ступенчато
изменяющимся сигналом (жирная линия). Смежные дискретные зна-
чения отличаются друг от друга на постоянную величину Аг, назы-
ваемую интервалом квантования по уровню. Переход с одного уров-
ня на другой происходит в моменты времени, когда непрерывный
сигнал достигает очередного фиксированного значения.
Квантование по времени заключается в фиксации мгновенных
значений непрерывного сигнала в равноотстоящие друг от друга
дискретные моменты времени (см. рис. 9.3,6). При этом квантован-
ный по времени сигнал представляет собой так называемую решет-
чатую функцию - последовательность идеальных импульсов. Смеж-
ные моменты времени отличаются друг от друга на постоянную
величину Д/ = Т, называемую интервалом дискретности (интерва-
лом квантования по времени, периодом повторения).
Рис. 9.3. Виды квантования и модуляции непрерывного сигнала
При совместном квантовании по уровню и по времени фикси-
руются дискретные по уровню значения, ближайшие к значениям
непрерывного сигнала в дискретные моменты времени (см. рис.
9.3,«), причем приоритетным является квантование по времени.
В зависимости от применяемого вида квантования все дискрет-
ные системы принято делить на три класса: релейные, импульсные и
цифровые (релейно-импульсные). В релейных системах квантование
осуществляется только по уровню, в импульсных - по времени, а в
цифровых - и по уровню, и по времени.
Квантование по уровню осуществляется при помощи специаль-
ных элементов - квантователей. Простейшими квантователями яв-
ляются двух- и трехпозиционные реле. Они квантуют непрерывный
сигнал соответственно по двум и трем уровням. При достаточно
большом числе уровней и малом интервале квантования, обеспечи-
492
ваемых в УВМ, релейную систему можно приближенно рассматри-
вать как непрерывную.
Квантование по времени осуществляется с помощью импульс-
ного элемента. Импульсный элемент преобразует непрерывный
входной сигнал в последовательность импульсов, амплитуда, дли-
тельность или период повторения которых зависят от значений вход-
ного сигнала в дискретные моменты времени. При эти преобразую-
щее действие квантователя можно рассматривать как процесс моду-
ляции последовательности одинаковых импульсов по закону измене-
ния входного непрерывного сигнала, а сам квантователь по времени
- как импульсный модулятор.
В зависимости от того, какой из параметров моделируемой по-
следовательности импульсов изменяется по закону изменения моду-
лирующего сигнала x(t), различают модуляцию: амплитудно-
импульсную (АИМ), широтно-импульсную (ШИМ) и частотно-
импульсную (ЧИМ). При АИМ значениям моделирующего сигнала
x(t) пропорциональны амплитуды (высоты) импульсов хи (см. рис.
9.3,г):
хизх(О; Г = const: ти= const;	(9.1)
при ШИМ - длительности ти импульсов (см. рис. 9.3,д):
ти=х(/); хи= const; Т = const;	(9.2)
и при ЧИМ - частота <од импульсов (см. рис. 9.3,е):
сод = х(0; *и = const; ти = const,	(9.3)
где Од = 2п/Т - частота дискретизации, или частота повторения.
Совместное квантование сигналов по уровню и по времени в
цифровых СУ осуществляется при помощи АЦП. В АЦП, кроме
квантования по уровню и по времени, происходит кодирование дис-
кретных значений сигнала - представление их в виде последователь-
ности чисел и запись в каком-либо цифровом коде.
Отметим, что при сравнительно большом шаге квантования по
уровню цифровая СУ существенно нелинейна, а при достаточно ма-
493
лом шаге дискретностью по уровню можно пренебречь и рассматри-
вать систему как линейную амплитудно-импульсную.
Дискретные СУ с УВМ находят широкое применение в совре-
менной автоматике благодаря наличию у них следующих пре-
имуществ перед непрерывными системами.
Дискретное управляющее устройство можно использовать для
одновременного управления несколькими однотипными объектами
или каналами ОУ. Для этого оно поочередно с периодом повторения
Т подключается к каждому объекту. Импульсные и цифровые эле-
менты, входящие в дискретные системы управления, обеспечивают
более высокую точность передачи и преобразования сигналов. Сис-
темы управления, скомплектованные из дискретных элементов,
имеют, как правило, меньшие габаритные размеры, вес и стоимость.
Они более надежны и лучше защищены от помех. Дискретные эле-
менты более удобны для агрегатно-блочного построения систем. На-
конец, цифровые вычислительные устройства могут реализовать бо-
лее сложные и, следовательно, более гибкие законы управления.
В последующих разделах главы рассматривается наиболее рас-
пространенный вид дискретных систем - импульсные системы с
ЛИМ. Будет показано, что цифровые системы с УВМ (см.рис. 9.2)
при определенных условиях могут анализироваться как импульсные
с ЛИМ.
9.2.	Функциональная и алгоритмическая структуры
амплитудно-импульсной СУ
В общем случае импульсный элемент может входить в состав
любого функционального блока СУ. Дискретный характер работы
системы может быть обусловлен, например, использованием датчика
периодического действия (различные анализаторы состава вещества).
Но в большинстве случаев дискретность системы связана с наличием
в ее контуре коммутирующих устройств МП и ДМП (см. рис. 9.2),
которые периодически замыкают и разрывают цепь регулирования.
Наиболее типичная функциональная структура импульсной сис-
темы изображена на рис. 9.4,а. К такой структуре могут быть сведе-
ны почти все случаи включения импульсного элемента. Импульсные
элементы ИЭ{ и ИЭ2, которые реально находятся в задатчике и в об-
ратной связи, могут быть учтены одним импульсным элементом ИЭ.
494
Рис. 9.4. Функциональная (а) и алгоритмическая (б)
структуры амплитудно-импульсной СУ
Импульсный элемент ИЭ, осуществляющий в системе квантова-
ние по времени, можно рассматривать как амплитудно-импульсный
модулятор (рис. 9.5,а). Модулятор умножает несущий сигнал - по-
следовательность одинаковых импульсов, поступающих с генератора
импульсов (ГИ), на модулирующий сигнал - входной непрерывный
сигнал x(t). Образующийся при этом на выходе дискретный сигнал
x№(t) представляет собой последовательность импульсов, амплитуды
которых равны или пропорциональны мгновенным значениям непре-
рывного сигнала.
Для облегчения анализа системы с АИМ целесообразно реаль-
ный импульсный элемент ИЭ заменить эквивалентным последова-
тельным соединением идеального импульсного элемента ИИЭ и
формирующего элемента ФЭ (см. рис. 9.5,6). Идеальный импульсный
элемент преобразует непрерывный сигнал х(/) в последовательность
мгновенных равноотстоящих друг от друга импульсов, площади ко-
торых равны значениям входного сигнала в дискретные моменты
времени. Формирующий элемент, или демодулятор, образует из
мгновенных импульсов такие импульсы, которые по форме совпада-
ют с импульсами на выходе реального импульсного элемента.
Реакция формирующего элемента на единичный импульс, т.е. на
дельта-функцию, есть не что иное, как весовая функция Иф(/) этого
элемента. Поэтому, согласно известному соотношению (2.105), ПФ
формирующего элемента должна быть
495
QO
О
(9.4)
где и'ф(/) = wK(t) - функция, описывающая импульс на выходе реаль-
ного импульсного элемента при действии на входе дельта-функции.
Рис. 9.5. Алгоритмическая структура импульсного элемента
Формирующий элемент является звеном непрерывного дейст-
вия, и его удобно при анализе объединять с непрерывной частью
системы (см. рис. 9.4,6). Образующееся при этом соединение назы-
вают приведенной непрерывной частью системы. ПФ приведенной
непрерывной части
=	(9.5)
В наиболее часто встречающемся случае, когда несущие им-
пульсы имеют прямоугольную форму, формирующий элемент дол-
жен преобразовать единичную дельта-функцию в прямоугольный
импульс с единичной высотой и длительностью ти = уТ, где у -
скважность или относительная длительность. Такой импульс можно
496
представить в виде разности двух ступенчатых функций, сдвинутых
на время ти, т.е.
НО = ст(Г)-ст(/-ги).	(9.6)
Отсюда, согласно (9.4), ПФ формирующего элемента
(9.7)
Если длительность импульсов ти существенно меньше основных
постоянных времени остальных звеньев непрерывной части системы,
то формирующий элемент (9.7) может быть приближенно заменен
безынерционным звеном И^ф(р) « ти.
При ти = Т формирующий элемент (9.7) выдает в течение всего
периода повторения Т постоянный сигнал, равный значению входно-
го сигнала в начале периода Т. Поэтому в данном частном (но рас-
пространенном) случае формирующий элемент (9.7) называют фик-
сирующим или запоминающим. Передаточная функция фиксирующе-
го элемента
^P) = (i-e-pT)/p.	(9.8)
Нетрудно убедиться, что ПК фильтра Иф(О) = Т.
Рис. 9.6. Простейший квантователь и фиксатор
Так как фиксацию мгновенного значения сигнала на постоянном
уровне можно рассматривать как простейшую экстраполяцию - экс-
497
трансляцию полиномом нулевого порядка, то формирующий элемент
в указанном частном случае (ти ~ Т) называют также экстраполято-
ром нулевого порядка.
На рис. 9.6 в качестве простейшего примера показаны последо-
вательно соединенные квантователь по времени (К) и запоминающий
элемент (ЗЭ), а также сигналы в этой цепи.
Так как квантователь по времени и запоминающий элемент яв-
ляются важными частями дискретной СУ, существенно влияющими
на ее динамику, проанализируем их частотные свойства. Квантова-
тель по времени, или идеальный импульсный элемент, можно рас-
сматривать как генератор дополнительных гармоник, частота кото-
рых равна частоте дискретизации а>л = 2п/Т. Спектр Х*(ря) сигнала
квантованного по времени по принципу АИМ, равен следую-
щей сумме смещенных спектров непрерывного входного сигнала
=	СЮ
где АХ/cd) - спектр входного (квантуемого) сигнала (рис. 9.7,а). Ви-
дим, что при квантовании по времени амплитуды всех гармоник
уменьшаются в Г раз. Это означает, что импульсный элемент эквива-
лентен по своим свойствам безынерционному звену с передаточным
коэффициентом 1/Г.
В общем случае спектр существенно отличается от спек-
тра X(j&): он содержит как основную составляющую (к=0), совпа-
дающую с X(ja), так и дополнительные составляющие (к = ±1; ±2;
...), возникающие при квантовании.
Если у квантуемого сигнала ширина спектра сох < сод/2, то до-
полнительные составляющие в основном диапазоне частот (-сод/2,
+сод/2) не искажают форму спектра АГ(/(о) (см. рис. 9.7,6), т.е.

(9.10)
но их наличие тем не менее приходится учитывать при восстановле-
нии непрерывного сигнала по его дискретным значениям.
498
а	б
W“)l|	ml
1
Рис. 9.7. Амплитудные спектры входного и выходного сигналов идеального
квантователя и АЧХ фиксатора
Если же частота квантования недостаточно велика и <ох > озя/2,
то в основном диапазоне спектр Х(/(а) искажается прилегающими
составляющими с к+Л (см. рис. 9.7,в).
Таким образом, на основе проведенных физических рассужде-
ний приходим к так называемой теореме о квантовании.
если непрерывный сигнал обладает спектром, ограниченным
частотой сох, то его квантование по времени с частотой
0}Д > 2ах
(9.П)
не приводит к потере информации, т.е. сигнал однозначно и
полностью представляется своими дискретными значениями,
взятыми через интервал квантования
(9.12)
499
Строгое доказательство этой теоремы было дано российским
ученым-радиотехником В.А. Котельниковым (в 1933 г.) и американ-
ским математиком К.Шенноном (в 1949 г.).
Если сигнал х(Г) квантован в соответствии с условиями (9.11),
(9.12) и его спектр X(j&) в основной полосе (-сод/2, <од/2) не искажен
боковыми составляющими, то он может быть снова восстановлен в
непрерывной форме при помощи формирующего элемента в виде
идеального фильтра низкой частоты с ПК k = Т и с АЧХ (см.рис. 9.7,
г - штриховая линия)
^ф(М
при
при
{бу <буд;
<у|><уд,
(9.13)
где (Од = 2сох.
Но, к сожалению, такой фильтр физически нереализуем, и на
практике пользуются фиксатором (9.8), у которого АЧХ
=т
sin ((У772)
щТ/2
(914)
существенно отличается от прямоугольной АЧХ (9.13) (см. рис. 9.7,г
- сплошная линия). Очевидно, что такой реальный фиксатор не-
сколько искажает исходный спектр X(j&) в основной полосе, и кроме
того, пропускает частично гармоники боковых составляющих с
Сй > й)д/2.
При достаточно большой частоте повторения (<од » сод) фикса-
тор (9.8) близок по своим свойствам к звену запаздывания

(9.15)
и импульсную СУ (см. рис. 9.4/7, £) можно рассматривать как чисто
непрерывную, описываемую только передаточными функциями (9.5)
и (9.15). Но при этом эквивалентное звено запаздывания (9.15) ухуд-
шает запас устойчивости системы.
500
Для упрощенного анализа динамики импульсной системы фик-
сатор (9.8) можно описывать приближенно ПФ апериодического зве-
на
(9.16)
которая тем точнее, чем больше частота квантования.
Заметим, что при определении минимально допустимой частоты
квантования для замкнутой СУ по формулам (9.11) и (9.12) следует
учитывать частоту затухающих колебаний в системе со3 и резонанс-
ную частоту (Dp, которые приблизительно равны друг другу (см.
формулы (6.47)) и зависят от наибольших постоянных времени и от
ПК разомкнутого контура. Так как спектр АЧХ замкнутой СУ суще-
ственно шире, чем <о3 и сор (см. рис. 6.4), то с целью обеспечения дос-
таточной точности принимают
. io>„
(9.17)
(9.18)
или
Д1 = 7’<(0,10.0,20)т;.
Для распространенных ОУ с запаздыванием (3.135) период ре-
зонансных колебаний Тр зависит от соотношения параметров То и т0,
и его можно определить по приближенной формуле
т - 2?r ~
Р яЧ-г<,/Т/
(9.19)
9.3.	Математическое описание амплитудно-импульсной СУ
^-преобразование. Математическое описание и анализ им-
пульсной СУ с амплитудной модуляцией существенно упрощается,
если все сигналы в системе (как в импульсной, так и в непрерывной
ее части) рассматривать только в дискретные моменты времени
t = ОТ1; IT1; 2Т; ... ; /Т; ... , оо. При этом каждый непрерывный сигнал
x(t) удобно представлять в виде решетчатой функции времени х(/7)
501
(см. рис. 9.3,6), значения которой определены только для дискретных
моментов времени:
x(t) = x(iT) = x(t),__iT.	(9.20)
Между дискретными значениями аргумента t функция х(/7) рав-
на нулю.
Непрерывная функция x(t) является огибающей для решетчатой
функции x(iT), и каждому конкретному сигналу x(t) соответствует
вполне определенный сигнал x(iT).
При замене реальных непрерывных сигналов решетчатыми
функциями часто оказывается удобным переходить к относительно-
му времени t = t/T, т.е. измерять время числом периодов квантова-
ния Т. В этом случае относительный период Т =1, а решетчатая
функция обозначается x(i).
Последовательность неединичных импульсов, образующих ре-
шетчатую функцию на интервале д<П <оо, можно представить в
виде бесконечного ряда
х(Г) = ^х0Т)<5(<-/Г),
1=0
(9.21)
где 5(Г-/Т) - смещенная дельта-функция, существующая только в
моменты времени t=iT и равная нулю при всех других значениях t.
Применим к сумме (9.21) преобразование Лапласа (2.100). Уч-
тем при этом, что изображение суммы оригиналов равно сумме их
изображений, а также, что, согласно теореме запаздывания (см.табл.
2.2), изображение смещенной дельта-функции равно с. Тогда изо-
бражение решетчатой функции (9.21) по Лапласу
Л-(р) = ^{х-(Г)}=£хО7)е-₽,г.	(9.22)
i=0
Выражение (9.22) называется дискретным преобразованием Ла-
пласа. Оно содержит трансцендентный сомножитель е~р!\ из-за кото-
рого изображения л (/;) и соответствующие передаточные функции
становятся иррациональными функциями аргумента р, чтс создает
502
определенные трудности при их использовании. Поэтому с целью
получения передаточных функций импульсных систем в дробно-
рациональной форме, свойственной непрерывным системам, прибе-
гают к следующей замене аргументов:
(9.23)
и тогда вместо (9.22) получают более удобное для практического ис-
пользования преобразование
Х(г) = ж{х((Т)}= Sx(iT)z',
(=0
(9.24)
называемое z-преобразованием решетчатой функции (или дискрет-
ной последовательности) x(iT).
Для большинства встречающихся в расчетах решетчатых функ-
ций z-преобразование может быть выполнено при помощи таблиц
соответствия, которые приводятся в специальной литературе по им-
пульсным системам. В табл. 9.1 приведены z-изображения лишь для
тех функций времени, которые используются ниже в примерах.
Таблица 9.1
z-изображения простейших функций времени
хо (г>0)	W)	X(p)	*(z)
6(0		1	1
о(/)	<3(iT)=£b(t-iT) i=0	P	z z — 1
t	iT	1 P1	Tz (z-1)2
jQ,	m2	2! P3	T2z(z + 1) (z-1)3
	eaiT=ci (с=е-аТ)	1 p + a	z z — c
503
Главное достоинство и удобство z-преобразования заключается
в том, что сама запись z-изображения (9.21) указывает простой спо-
соб выполнения прямого и обратного преобразования:
1)	чтобы по известной функции времени x(t) найти ее z-
изображение, необходимо лишь каждое дискретное значение
x(iT) умножить на z'', а затем свернуть получившийся степен-
ной ряд в конечную сумму;
2)	чтобы по известному изображению X(z) найти соответст-
вующий сигнал x(t), необходимо представить изображение X(z)
в виде степенного ряда по убывающим степеням z'1; получаю-
щиеся при этом числовые коэффициенты ряда и есть дискрет-
ные значения x{iT) сигнала x(t).
Проиллюстрируем эти правила на простых функциях.
Пример 1. Найдем z-изображение единичной ступенчатой функции
x(f)=cr(f). Соответствующая ей последовательность идеальных импульсов
х(17) = ЮП; » = 0; I;(9.25)
В соответствии с правилом 1 изображение
X(z) = lz° +L?'1 + lz~2 +....	(9.26)
Сумму бесконечного ряда (9.26) можно записать в компактной форме
X(z) = l/(l-z-1)=^-l), •	(9.27)
что и приведено в табл. 9.1.
Пример 2. Найдем функцию времени x(f), изображение которой
X(z)^T z/tz-tf.	(9.28)
Делением числителя на знаменатель выражение (9.28) можно предста-
вить в виде ряда
2T(z) = 17z"1 + 27z~2+37z“3+....	(9.29)
В соответствии с правилом 2 значения решетчатой функции
х(1Г) = \Т\ х(2Т) = 27"; х(ЗТ) = ЗТ;...	(9.30)
504
или
x(iT) = iT.	(9.31)
Откуда нетрудно установить, что
х(0 = /.	(9.32)
Полученное соответствие также приведено в табл. 9.1.
Свойства z-преобразования аналогичны свойствам обычного
преобразования Лапласа. Приведем важнейшие из них.
1.	Линейность
^'{л1х!(0 ± a2x2(t)}=	+ a2X(z).	(9.33)
2.	Теорема о начальном значении оригинала
limx(ZT) = lim X(z).	(9.34)
/->0	Z-><*>
3.	Теорема о конечном значении оригинала
lim x(iT) = lim-—-%(z).
/—>00	J—>1
(9.35)
4.	Теорема о смещении аргумента оригинала (теорема запазды-
вания)
sr{x{iT-lT)}=X(z)z‘.	(9.36)
Соотношение (9.36) означает, что умножение на z-/ соответству-
ст задержке дискретного сигнала на / интервалов.
Перейдем теперь к описанию передаточных свойств разомкну-
тых и замкнутых импульсных систем. Как и для обычных систем не-
прерывного действия, для импульсных систем наиболее удобно ис-
пользовать структурный метод и передаточные функции.
Характеристики типовой импульсной цепи. Введем понятие
типовой импульсной цепи, в которую входит (рис. 9.8) идеальный
импульсный элемент («ключ») и непрерывная часть с передаточной
функцией Будем рассматривать динамику этой цепи, ее вход-
505
ной и выходной сигналы только в дискретные моменты времени iT
(для чего на выходе цепи показан фиктивный квантователь, рабо-
тающий синхронно с входным квантователем). Тогда передаточные
свойства импульсной цепи можно характеризовать с помощью дис-
кретной передаточной функции (ДПФ)
W(z)=Y(z)/X(z),
(9.37)
где X(z) и T(z) - z-изображения входного и выходного сигналов цепи.
Рис. 9.8. Типовой участок импульсной СУ
ДПФ JF(z) импульсной цепи связана с весовой функцией n(f)
непрерывной части ^-преобразованием:
ДО
W(z) = Z{w(zT)}= ^w(/T)z"'.
i=0
(9.38)
Непрерывная часть цепи задана обычно в виде передаточной
функции ЙК(р), поэтому для отыскания функции W(z) необходимо
предварительно находить весовую функцию
Так как в таблицах соответствия обычно рядом указываются
изображения по Лапласу и z-изображения, то функцию W(z) можно
определить сразу по виду функции JY(p). Этому непосредственному
переходу от IY(p) к W(z) соответствует условная запись
W(z) = ЯГ{№(р)}
(9.39)
506
Если в типовой цепи после «ключа» стоит фиксатор (9.8), то
ДПФ всей цепи может быть определена по формуле
И'(г) =	= (1 - г-')лг.	=
= £^М^1 = £^1<Г{йн(,));	(9.40)
z [ р J z
где Wn(p) - ПФ непрерывной части (не включающей фиксатор).
Пример 3. Найдем ДПФ цепи, состоящей из «ключа» и инерционного
звена первого порядка (без фиксатора на его входе)
^(р) = ^о/(7оР + 1)-
(9.41)
Весовая функция звена
или
Нг) = (*<,/Т0>"г»
»<,/-) = (А-с/7„
Согласно табл. 9.1,ДПФ цепи
W{z) = х{(к e/Tt)e~iT/T° }=
Го z - е 10
(9.42)
(9.43)
(9.44)
Для сравнения приведем ДПФ, полученную по формуле (9.37)
для случая, когда на входе звена (9.41) включен фиксатор:
W(z) = к0 (1 - e~TITo )/(z - е~т/То).
(9.45)
Способы получения ДПФ по формулам (9.38) - (9.40) являются
точными, но их применение для реальных систем высокого порядка
оказывается затруднительным. Поэтому в практических расчетах
импульсных систем используют приближенные способы
перехода от ПФ W(p) к ДПФ W(z). Эти способы основаны на замене
507
производной по времени, фигурирующей в уравнении непрерывной
части, так называемой первой разностью:
Ф(0 Ау(Л)	- ЯЛ-i)	/О ,ю
dt Ar	Ar
Подставляя разность (9.46) в дифференциальное уравнение не-
прерывного (аналогового) интегратора
dy(t)!dt = x(f),	(9.47)
можно получить разностное уравнение интегратора
y(iT~) = y(iT-\T)+Tx(iT'),	(9.48)
которое легко записать в z-форме:
r(z) = r(z)z-‘ + 7X(z).	(9.49)
Отсюда ДПФ интегратора
W(z) = Y(z )/X(z) = Г/(1 -z-')=r z/(z -1).	(9.50)
Учитывая, что обычная ПФ интегратора
W(p) = l/p,	(9.51)
нетрудно получить одну из часто используемых формул приближен-
ного перехода от передаточных функций непрерывной части (без
учета фиксатора!) к ДПФ:
(9.52)
Более точный переход от непрерывной системы к дискретной
обеспечивает подстановка Тастина
508
p = Z{z-
(9.53)
Замена (9.52) соответствует приближенному (численному) ин-
тегрированию по методу прямоугольников, а подстановка (9.53) -
интегрированию по методу трапеций.
При достаточной большой частоте дискретности, когда <вд»б)п,
где соп - полоса пропускания непрерывной части системы, прибли-
женные способы перехода, основанные на заменах (9.52) и (9.53),
дают результаты, близкие к точным ДПФ, а частотные свойства им-
пульсной цепи эквивалентны свойствам непрерывной части с АФХ
Wn(jG))/T. Это условие эквивалентности обычно выполняется, если
наибольшая постоянная времени непрерывной части больше периода
квантования Т.
Изложенные приемы математического описания импульсных
систем с помощью z-изображений и соответствующих им разност-
ных уравнений удобно использовать и для цифрового мо-
делирования чисто н е п р е р ы в н ы х систем на ЭВМ.
Переход от обычных передаточных функций W(p) к ДПФ W(z)
осуществляется аналогично - подстановками (9.52) и (9.53). Но если
для цифрового моделирования используются точные ДПФ, получен-
ные по формуле (9.38) или по таблицам соответствия, то необходимо
предварительно, перед переходом к разностному уравнению, найти
ДПФ W' (z), устанавливающую связь между огибающими
входной и выходной дискретных последовательностей:
|	W'(z)=TW(z).	(9.54)
Множителем Т компенсируется ослабление сигналов, которое
вносится реально квантователем в импульсной системе (и которое
отсутствует в моделируемой непрерывной системе!).
Любую ДПФ FF(z) или W'(z) в общем случае можно представить
в виде отношения полиномов переменной z:
W(z) =
Y(z) _bmzm+bm\Zm~{ + ,.. + b^ _K(z)
X{z) anzn +an4zn-' + ... + a0 D{z)
(9.55)
или
509
(9.56)
Передаточной функции (9.56) соответствует следующее опера-
торное уравнение динамики импульсной цепи в z-форме:
anY (z) + a„_,Y (z)z~' +... + a0Y (z)z~n =
bmX(z)zm~n + bm^X(z)zm-l-n + ... + bQX(z)z~n,
(9.57)
по которому легко получить разностное уравнение импульсной цепи
(см. рис. 9.8) или моделируемой непрерывной системы
WiiT)+а„	* 1Г)+•• +- пТ) =
= hrx(iT+(m-n)r)+b,_lx(iT + (m-l-n)r)+ ...+btx(iT-пТ). (9.58)
Разностные уравнения вида (9.58) обладают важным преимуще-
ством перед обыкновенными дифференциальными уравнениями,
разрешенные относительно y{iT), они уже в самой своей записи со-
держат алгоритм решения, который легко программируется на ЦВМ.
Кроме того, разностные уравнения можно также представлять в виде
сигнальных диаграмм состояния, удобных для моделирования. Ос-
новным операционным элементом дискретной диаграммы состояния
вместо аналогового интегратора (см. рис. 6.12) является элемент за-
держки z" .
Пример 4. Определим точную и приближенные ДПФ импульсной це-
пи, состоящей из «ключа», фиксатора (9.8) и идеального интегратора

(9.59)
Согласно (9.40) и табл. 9.1, точная ДПФ
JP(z) =
z-1 kTz кТ
(9.60)
Подстановка (9.52) в (9.59) дает рассматриваемой цепи с фиксатором
следующую приближенную ДПФ:
510 '
W(Z^WH(P)
kTz
(9.61)
а подстановка Тастина (9.53) - более сложную, но более точную ДПФ
W(z)xWK(p)
(9.62)
Характеристики замкнутой импульсной системы. Для опре-
деления ДПФ замкнутой импульсной системы можно использовать
правила структурных преобразований типовых соединений, сформу-
лированные в гл. 4 для непрерывных систем (см. формулы (4.1),
(4.2), (4.3)). Но при этом следует помнить, что:
-	обычные правила структурных преобразований справедливы
для импульсных систем, лишь если каждая ветвь типового со-
единения представляет собой типовую импульсную цепь (см.
рис.9.8), состоящую из идеального квантователя (на входе це-
пи) и непрерывной части;
-	при иной структуре цепи и всего типового соединения эквива-
лентная ДПФ определяется более сложными правилами.
Дря основной схемы одноконтурной импульсной системы (см.
рис. 9.4,6) ДПФ по каналу хз-х
Ф„(г) = X(z)/X,(z) = r(z)/(l + r(z))	(9 63)
и по каналу Хз-£
Д	/	X
Фв(г) = £(z)/Xs(z) = 1/(1+ FF(z)),
(9.64)
где W(z) = K(z)ID(z) - ДПФ разомкнутого контура, представляющего
собой (в данной схеме!) типовую импульсную цепь.
Характеристическое уравнение импульсной системы
1 + W(z) = О
(9.65)
511
или в развернутых формах
D(z)+^(z) = F(z) = Q,
a zn + a tzn 1 +. + ап = О
л-1	.............. 9	*
(9.66)
(9.67)
Пример 5. Определим характеристики замкнутой импульсной систе-
мы (см. рис. 9.4,6), разомкнутый контур которой соответствует цепи, рас-
смотренной в примере 4.
Подставляя точную ДПФ (9.60) в формулы (9.63) и (9.64), получим со-
ответствующие ДПФ замкнутой системы
ФЛ(г) = X(z )/Х3(г) = kT/(z +кТ -1);
(9.68)
Фо(г) = E{z )/X3(z) = (z- l)/(z + kT -1).	(9.69)
Характеристическое уравнение системы
z+W-l=0.
(9.70)
Найдем операторное уравнение динамики системы по каналу х3-£.
Разделив предварительно числитель и знаменатель ДПФ (9.69) на z, полу-
чим
+	(9.71)
Уравнению (9.71) соответствует разностное уравнение в рекуррентной
форме (при 7=1)
е(;) = (1 - кТ)е(х -1)+дгэ (х) - х3 (х -1).
(9.72)
9.4.	Основное условие и критерии устойчивости
импульсных СУ
Динамические свойства импульсных систем с амплитудной
модуляцией во многом аналогичны динамическим свойствам непре-
рывных систем. Поэтому и методы анализа таких импульсных сис-
тем являются аналогами соответствующих методов исследования
непрерывных систем.
512
Устойчивость импульсной системы управления, как и устойчи-
вость непрерывной системы, определяется характером ее свободного
движения. Импульсная система устойчива, если свободная состав-
ляющая переходного процесса xc(iT) с течением времени затухает,
т.е. если
limxc(zT) = 0.
(9.73)
Свободная составляющая xc(iT) является решением однородно-
го разностного уравнения
(anzn +an_}zn'1 + ... + aQ)X(z) = 0.
(9.74)
Решение уравнения (9.74) при отсутствии одинаковых корней
представляет собой сумму

(9.75)
где Ск - постоянные интегрирования, зависящие от начальных усло-
вий; Zk - корни характеристического уравнения
anzn +an_}zn 1 +... + п0 =0.
(9.76)
Из выражения (9.75) видно, что при z-хю решение xc(iT) стре-
мится к нулю лишь в том случае, если все корни Zk по модулю мень-
ше единицы, т.е. если
(к = 1; 2;
(9.77)
Запись (9.77) выражает общее условие устойчи-
вости:
для устойчивости импульсной системы необходимо и доста-
точно, чтобы все корни характеристического уравнения сис-
темы находились внутри круга единичного радиуса с центром в
начале координат (рис. 9.9,а).
513
Если хотя бы один корень zk располагается на окружности еди-
ничного радиуса, то система находится на границе устойчивости.
При I Zk I > 1 система неустойчива.
Таким образом, единичная окружность в плоскости корней z^
является границей устойчивости и, следовательно, играет такую же
роль, как мнимая ось в плоскости корней рк (рис. 9.9,6). Этот вывод
вытекает также из основной подстановки (9.28) метода z-преоб-
разования. Действительно, пусть рк= ак i/Pt. Тогда
zk
= ePtT
atT,t±jPtT
(9.78)
и требование | zk | < 1 сводится к неравенству

(9.79)
откуда следует известное в теории непрерывных систем условие ус-
тойчивости
ак <^-
Рис. 9.9. Области устойчивости в плоскости корней
Для суждения об устойчивости импульсных систем можно ис-
пользовать обычные критерии устойчивости линейных систем (см.
гл.5), но при этом приходится учитывать лишь некоторые особенно-
сти импульсных систем. Так, для того, чтобы применить крите-
рий Гурвица, необходимо предварительно в уравнении (9.76)
514
произвести замену переменной z на переменную w путем
подстановки
z = (w + l)/(w-l)	(9.81)
и получить преобразованное характеристическое уравнение
a'w" + a'_1w"’1 + ... + а[ =0.
(9.82)
Корням уравнения (9.76), расположенным в плоскости корней
внутри единичного круга (см. рис. 9.9,а), теперь будут соответст-
вовать корни преобразованного уравнения (9.82), находящиеся в
плоскости корней слева от мнимой оси (рис. 9.9,в). Действитель-
1, то модуль числителя в выражении (9.81) должен
быть меньше модуля знаменателя, т.е.
но, если
Zk
. А это воз-
можно лишь в том случае, если вектор wk расположен в левой полу-
плоскости (см. рис. 9.9,в).
При использовании критерия Михайлова в характе-
ристический полином F(z) подставляют z = е , изменяют со от 0
до л/Г ив комплексной плоскости строят годограф вектора F(e).
Импульсная система устойчива, если при возрастании со от 0 до тс /Г
характеристический вектор F(e^T} повернется против часовой стрел-
ки на угол пп. Если годограф характеристического вектора проходит
через начало координат, то система находится на границе устойчиво-
сти.
На рис. 9.10,а показаны годографы вектора Fie1®1) для устойчи-
вой (линия 7) и неустойчивой (линия 2) системы второго порядка.
Отметим, что импульсные системы второго и даже первого по-
рядка, в отличие от непрерывных систем такого порядка, могут быть
неустойчивыми даже при положительных коэффициентах характери-
стического уравнения. Это объясняется тем, что фиксатор, содержа-
щийся обычно в контуре импульсной системы, вносит дополнитель-
ное отставание по фазе.
Критерий Найквиста для импульсных систем форму-
лируется так же, как и для непрерывных систем: система устойчива,
если АФХ W(el<i>l) устойчивого разомкнутого контура не охватывает
точку (-1; у0).
515
a jQ(u)L
О
JQWk
Рис. 9.10. Критерий Михайлова (а) и Найквиста (б) для импульсной СУ
На рис. 9.10,6 приведены характеристики устойчивой импульс-
ной системы (линия 7), неустойчивой (линия 2) и системы, находя-
щейся на границе устойчивости (штриховая линия).
Устойчивость разомкнутого контура импульсной системы опре-
деляется устойчивостью ее непрерывной части: если последняя ус-
тойчива, то и весь контур (включая импульсный элемент) устойчив.
Следует иметь в виду, что хотя на устойчивость разомкнутого
контура импульсный элемент и не влияет, на эти свойства замкнутой
системы он оказывает существенное влияние. При малых периодах
повторения частотная характеристика разомкнутого контура совпа-
дает с частотной характеристикой непрерывной части, и устойчи-
вость импульсной системы полностью определяется свойствами не-
прерывной части. По мере увеличения периода повторения у боль-
шинства систем уменьшается предельный ПК и ухудшаются дина-
мические свойства. Однако на некоторые структурно-неустойчивые
непрерывные системы и на системы с запаздыванием, у которых
АФХ заходит в правую полуплоскость, импульсный элемент оказы-
вает стабилизирующее действие. Для таких систем рекомендуется
период повторения Т выбирать из условия
Т>я1со^	(9.83)
где со0 - частота, при которой АФХ непрерывной части пересекает
положительную мнимую ось □(©).
516
Пример. Определим с помощью критерия Гурвица предельное значе-
ние передаточного коэффициента импульсной системы, рассмотренной в
примере 5 раздела 9.3.
Характеристическое уравнение системы
z + AT-l = O.
После подстановки (9.79) уравнение принимает вид
kTw + 2 - кТ = 0.
(9.84)
(9.85)
для него условие устойчивости Гурвица заключается, как известно, в поло-
жительности коэффициентов, т.е.
^=^>0 и а'^2-кТ>0,
(9.86)
отсюда допустимые пределы изменения передаточного коэффициента
О < к < 2/Т.
(9.87)
9.5.	Оценка качества импульсных СУ
Качество импульсных СУ характеризуется такими же показате-
лями, как и качество непрерывных систем: точностью в установив-
шихся режимах, коэффициентом перерегулирования и длительно-
стью переходного процесса.
Коэффициент перерегулирования и дли-
тельность оценивают непосредственно по переходной характе-
ристике. Переходная характеристика импульсной системы строится
гораздо проще, чем у непрерывной системы. Для этого записывают z-
изображение выходной величины при единичном ступенчатом воз-
действии
¥(z) = -—ф(а)
z-1
(9.88)
а затем по изображению находят оригинал - решетчатую функцию
х(/7).
517
В простых случаях функцию x(iT) можно найти при помощи
таблиц обратного ^-преобразования, разлагая предварительно изо-
бражение X(z) на простые дроби.
В тех случаях, когда разделение на дроби связано с трудностя-
ми, целесообразно делением числителя на знаменатель разложить
функцию X(z) в степенной ряд по отрицательным степеням z (ряд
Лорана)
ср
yV(z) = Vc(z”' = с0 +c\z"' + c2z'2 +...+ctz-‘ +... .
i=0
(9.89)
Из самого определения ^-преобразования (9.24) видно, что
коэффициенты степенного ряда (9.89) по степеням z~
представляют собой значения переходной характеристики h(t)
в дискретные моменты времени t = IT (i = 0; 1; 2; ...), т.е.
с0 =x(0);Cj =х(1Т);с2 =х(2Т);...;с/ =x(ZT);....	(9.90)
Импульсные системы обладают особенностью: пере-
ходные процессы в них могут заканчиваться за конечное число пе-
риодов 7, равное порядку системы п. Условием получения конечной
длительности переходного процесса является равенство всех (кроме
первого) коэффициентов характеристического уравнения (9.67) ну-
лю, т.е.
ап . =ап . = ... = а0 =0.
п—J	л—2	U
(9.91)
При этом характеристический полином системы имеет вид
F(z) = n z”,
(9.92)
а изображение выходной величины оказывается конечным рядом от-
рицательных степеней z:
X(z) =-^-Ф(г) = - ---	= Со +	(9.93)
z-1 г -1 anz
п
518
что и соответствует переходному процессу с конечной длительно-
стью, равной /п = пТ.
При любом другом соотношении коэффициентов длительность
переходного процесса будет больше, чем пТ. Поэтому процесс с ко-
нечной длительностью будет оптимальным по быстродействию.
Выполнение условия (9.91) достигается, как правило, введением
в контур системы непрерывных и импульсных корректирующих уст-
ройств.
Точность импульсной системы оценивается по
установившемуся значению сигнала ошибки, которое, согласно тео-
реме (9.35),
f(oo) = lim s(iT) = lim -—^-E(z) = lim-—-Ф£ (z)X3(z).	(9.94)
При ступенчатом воздействии x3(t) = a0o(f) установившаяся
ошибка
f(oo) = lim —
z—+1
___L___£oL = go
l + W(z)z-l 1 + ИД1)
(9.95)
Отсюда видно, что при ступенчатом воздействии ошибка будет
равна нулю, если передаточная функция W(z) разомкнутого контура
имеет хотя бы один полюс, равный единице.
Аналогично можно показать, что при линейном воздействии
x3(f) ~ a\t установившаяся ошибка
/тп
е(со) = lim 7---------------г.
_ 1^1 + W(z))
(9.96)
Как и в непрерывных системах, импульсная СУ имеет нулевую
установившуюся ошибку, если порядок ее астатизма v больше степе-
ни входного воздействия q. При этом порядок астатизма системы оп-
ределяется количеством сомножителей вида (z-1) в знаменателе ДПФ
разомкнутого контура.
Пример 1. Построим переходную характеристику системы, состоящей
из «ключам, фиксатора (9.8) и идеального интегрирующего звена.
ДПФ разомкнутого контура такой системы
519
W(z) = kT/(z-\).
(9.97)
ДПФ системы по задающему воздействию
<Da(z) = kT/(z+kT -i).
(9.98)
При единичном ступенчатом воздействии изображение выходного
сигнала

z кТ
2-1 z+kT
(9.99)
можно легко разложить на две дроби
Z	Z
А(г) =--------7----Г
2-1 г-(]-кТ)
(9.100)
и. пользуясь таблицами обратного z-преобразования, записать переходную
функцию
х(»Т) = 1(17)-(1-ЛТУ.	(9.101)
На рис. 9.11 по выражению (9.101) построены переходные процессы
при кТ = 0,5 (линия 7), кТ = 1 (линия 2), кТ = 1,5 (линия 3). Очевидно, что
при кТ = 1 процесс оптимален: перерегулирование равно нулю, а длитель-
ность процесса минимальна.
520
При каждом конкретном значении параметра кТ переходную функцию
можно найти и путем разложения изображения X(z) в степенной ряд (9.89).
Например, при кТ= 1,5 в результате деления числителя выражения (9.99) на
знаменатель получим
X(z) = l,5z"‘ +0,75z‘2 +l,125z’3 +0,937z~4 +....
(9.102)
Коэффициенты этого ряда соответствуют ординатам колебательного
переходного процесса на рис. 9.11 (линия 3).
Пример 2. Определим для системы, рассмотренной в примере 1, уста-
новившееся значение ошибки при ступенчатом и линейном воздействии.
ДПФ системы для сигнала ошибки

(9.103)
Так как ДПФ разомкнутого контура И’(г) имеет полюс z = 1, то при
ступенчатом воздействии установившаяся ошибка равна нулю.
При линейном воздействии x(t) - установившаяся ошибка
(9.104)
9.6.	Структура и характеристики цифровой СУ
Одним из современных направлений в технике автоматического
управления является использование цифровых вычислительных ма-
шин в режиме ПЦУ. При осуществлении этого режима УВМ вклю-
чают непосредственно в контур СУ. УВМ работает в реальном мас-
штабе времени - в темпе хода технологического процесса вырабаты-
вает управляющие воздействия, которые через исполнительные уст-
ройства передаются на управляемый объект. Одновременно УВМ
выполняет функции задающего и сравнивающего устройств.
На рис. 9.12,t7 показана типичная функциональная структура од-
ноконтурной цифровой системы управления. АЦП квантует непре-
рывный сигнал s по уровню и по времени и представляет его в циф-
ровом коде. При этом образуется последовательность чисел ец, запи-
санных в определенной (обычно двоичной) системе счисления. Циф-
521
ровое вычислительное устройство (ЦВУ) в соответствии с заложен-
ным в него алгоритмом выполняет с числами арифметические и ло-
гические операции и с периодом повторения Т выдает в виде числа
управляющий сигнал уц. ЦАП состоит из декодирующего и фикси-
рующего устройств, которые из выходной последовательности чисел
уц формируют непрерывное управляющее воздействие у.
Рис. 9.12. Функциональная (а) и алгоритмическая (6)
структуры цифровой СУ
Если непрерывная часть системы и алгоритм работы ЦВУ ли-
нейны, то рассматриваемую цифровую систему можно исследовать
как амплитудно-импульсную. Для этого систему с ЦВУ заменяют
эквивалентной импульсной системой. На алгоритмической схеме эк-
вивалентной системы (см. рис. 9.12,6) АЦП условно представляют в
виде идеального импульсного элемента, а сигналы ец и уц, которые в
действительности являются последовательностями чисел, заменяют
соответствующими решетчатыми функциями 6 и у . Квантование по
уровню при этом не учитывается (так как шаг квантования обычно
достаточно мал).
Период повторения Т условного импульсного элемента опреде-
ляется периодичностью опроса датчиков Д отдельных контуров (см.
рис. 9.2), т.е. с темпом ввода сигналов щ в УВМ и вывода сигналов
из УВМ, который задается от специального таймера через входной и
выходной коммутаторы (мультиплексор и демультиплексор). Время,
затрачиваемое ЦВУ на вычисления, обычно мало по сравнению с
периодом Т, и его можно не учитывать.
522
Реализуемый в ЦВУ алгоритм преобразования входной после-
довательности чисел £ц в выходную уц на эквивалентной схеме пред-
ставляют в виде соответствующей ДПФ lFu(z), которая связывает
между собой дискретные значения сигналов е и у . Звено с переда-
точной функцией W^z) называют дискретным фильтром, или циф-
ровым регулятором.
Преобразователю ЦАП в эквивалентной системе соответствует
фиксирующий элемент W$(p), который в течение одного такта сохра-
няет мгновенное значение у .
Для цифровой системы (см.рис. 9.12,а), представленной в виде
эквивалентной импульсной системы (см.рис. 9Л2,б), ДПФ
д X(z) ^(z)JFn(z)
Ф( Z) = --=-------------=
X3(z) l + ^(z)^n(z)
Ka(z)Kn(z) _K(z)
D^D^zy + K^K^z) F(z)’
(9.105)
где Wn(z)=Kn(z)/Dn(z) - ДПФ приведенной непрерывной части, вклю-
чающей объект, исполнительное устройство и фиксирующий эле-
мент; lFu(z)=Fu(z)/Du(z) - ДПФ цифрового регулятора.
Благодаря большим вычислительным возможностям УВМ в
цифровых системах можно реализовать сложные алгоритмы управ-
ления и обеспечить такие переходные процессы, которые недости-
жимы в непрерывных системах.
Рассмотрим один из возможных подходов к решению задачи
синтеза оптимальной цифровой системы. Пусть необходимо полу-
чить переходный процесс конечной длительности ta-lT. При этом
правомерно потребовать, чтобы длительность соответствовала по-
рядку уравнения неизменяемой части системы, который определяет-
ся главным образом объектом. Данное требование можно записать
так:
/ = н,	(9.106)
где п - порядок полинома Dn(z) приведенной части. С учетом усло-
вия конечной длительности (9.91) будем искать ДПФ в таком виде.
523
Q(z) = K(z)/F(z) = K,(z)K„(z)/z' •
(9.107)
Полином числителя K^z) ДПФ цифрового регулятора в данной
задаче можно произвольно принять
Kn(z) = kn = l/kn,
(9.108)
где ки = Кц( 1),кп = A*n( 1) - передаточные коэффициенты регулятора и
приведенной части.
Так как ДПФ JFn(z) приведенной части считается известной, то
можно определить ДПФ ЦВУ.
Ф(и) 1 = Dn(z)/kn
1-Ф(г)И;(г) z‘-Kn(z)/kn
(9.109)
В общем случае ДПФ (9.109) представляет собой отношение по-
линомов
wu(z) =	+--tAz.
E(z} а0+atz +...+asz '
(9.110)
соответственно уравнение ЦВУ в операторной форме
Y(z)[a0 +a{z 1 + ... + asz s) = E(z)[b0 +b}z 1 + ... + brz r).	(9.111)
Выполняя теперь почленно обратное z-преобразование и учиты-
вая теорему запаздывания (9.36), можно получить рекуррентную
формулу
y(i) = —Ybkc(j-k)—~^aky(i -к),	(9.112)
По *=о	По
которая связывает текущее значение y(i) дискретного управляющего
воздействия с текущим и предыдущими значениями сигнала ошибки,
а также с предыдущими значениями управляющего воздействия.
524
Рекуррентная формула (9.112) легко может быть запрограмми-
рована на ЦВМ. Для реализации программы требуется выполнение
операций умножения, сложения и переадресации.
Изложенный метод позволяет синтезировать импульсную сис-
тему, оптимальную по быстродействию. Оптимальный переходный
процесс достигается за счет выбора амплитуд управляющего воздей-
ствия на интервалах заданной продолжительности. В релейных сис-
темах, оптимальных по быстродействию (см. 11.3), наименьшая дли-
тельность процесса достигается выбором моментов изменения знака
постоянного по амплитуде управляющего воздействия.
Пример. Непрерывная часть цифровой системы (см. рис. 9.12,6) со-
стоит из фиксатора (9.8) и двух последовательно соединенных идеальных
интегрирующих звеньев:
»'„(?) =	(9.ПЗ)
Требуется определить алгоритм управления, обеспечивающий мини-
мальную длительность переходного процесса при заданных Т = 10 с и к =
= 0,01 с2.
Согласно табл. 9.1, ДПФ приведенной непрерывной части системы
(9.114)
Очевидно, что в данном случае 1=п=2, А'п=А'п(1)=2А'7г.
Оптимальная ДПФ цифрового регулятора согласно формуле (9.109)
,у ,г, =	2(z-iy/2kT2	=	1 - 2Z-1 + Z-1	= Г(г)
ц z2 - кТ2 (z + 1)/2кТ2	1 - 0,5г”1 - O.5z’2 E(z) ’
Отсюда рекуррентный алгоритм управления
y(i) = е(,) - 2е(/ -1) + е(/ - 2) + 0,5у(/ -1) + 0,5у(/ - 2).	(9.116)
Он обеспечивает окончание переходного процесса за два периода по-
вторения.
525
Контрольные задания и вопросы
1.	Нарисуйте графики синусоиды x(t) = xmsincot, проквантованной по
уровню, времени и совместно, при Ах = х^/4 и At = 0,125 (2л/(в).
2.	Назовите основные функциональные элементы дискретной системы
с УВМ. Каково их назначение?
3.	Поясните на графике принцип амплитудно-импульсной модуляции.
4.	В чем преимущества дискретных (цифровых) систем управления?
5.	В виде какой алгоритмической схемы удобно представлять реаль-
ный импульсный элемент?
6.	Что понимается под приведенной непрерывной частью?
7.	Запишите передаточную функцию фиксатора.
8.	Каково условие квантования непрерывного сигнала с ограниченным
спектром сох?
9.	Запишите выражение (9.21) для последовательности импульсов, об-
разующейся при идеальном квантовании сигнала x(t) = 0,1 Г с интервалом
Т = 0,2 с.
10.	С помощью какой замены переменных получается основная фор-
мула z-преобразования?
11.	Запишите основную формулу 2-преобразования, получающуюся
как преобразование последовательности импульсов по Лапласу.
12.	Как получить изображение X(z) дискретного сигнала х(/Т)?
13.	Как получить значения x(iT) дискретного сигнала, если известно
его изображение X(z)?
14.	Найдите с помощью теоремы запаздывания (9.36) изображение
дельта-функции, смещенной по времени на / интервалов назад.
15.	Определите по формуле (9.38) точную ДПФ импульсной цепи с
двойным интегратором Wn(p}=kjp\ Учтите, что весовая функция такого
интегратора - линейная функция времени, и используйте ряд (9.29) из при-
мера 2.
16.	Используя подстановку (9.52), получите приближенную ДПФ им-
пульсной цепи, состоящей из «ключа», фиксатора и непрерывной части
^/н(р)=А'о/(Д/’+1). Сравните эту приближенную ДПФ с точной (9.45).
17.	Запишите для этой цепи разностные уравнения, соответствующие
приближенной ДПФ (см. задание 16) и точной ДПФ (9.45).
18.	Вычислите и сравните числовые значения коэффициентов а и b
разностного уравнения у(1+1)=ау(0+^0), соответствующие точной и при-
ближенной модели (см. задание 17) при следующих параметрах. ко = 1;
То = 10с; Т=5с.
19.	Убедитесь, что при Т/То>0,\ точная и приближенная модели им-
пульсной цепи с инерционным звеном практически совпадают.
526
20.	Определите точную ДПФ Ф„(г) замкнутой системы, которая обра-
зована импульсной цепью, рассмотренной в задании 16, и единичной обрат-
ной связью.
21.	Какими должны быть корни zk характеристического уравнения,
чтобы импульсная система была устойчива? Объясните это условие устой-
чивости с помощью формулы (9.75).
22.	Как найти ординаты переходного процесса импульсной системы
при ступенчатом воздействии?
23.	Какой вид должно иметь характеристическое уравнение импульс-
ной системы, чтобы длительность переходного процесса была конечной?
24.	Определите ДПФ и рекуррентный алгоритм цифрового регулято-
ра, обеспечивающего конечную длительность переходного процесса в циф-
ровой системе управления (см. рис. 9.12,6) с WH(p)=ko/p(T0p+\) при следую-
щих параметрах: к0 = 0,1; То = 10 с; Т= 1 с.
527
Глава 10. ХАРАКТЕРИСТИКИ И ОСНОВНЫЕ МЕТОДЫ
АНАЛИЗА НЕЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ
10.1.	Особенности нелинейных систем
Система управления (СУ) является нелинейной, если хотя бы
один ее конструктивный элемент (или одно ее алгоритмическое зве-
но) описывается нелинейным уравнением (см. 2.1).
Практически все реальные СУ содержат один или несколько не-
линейных элементов (или так называемых нелинейностей). Нели-
нейными могут быть как элементы неизменяемой части системы, так
и элементы изменяемой (синтезируемой) части.
В первом случае говорят о сопутствующих нелинейностях. К
ним относятся, например, исполнительные органы с ограниченной
пропускной способностью (вентили, клапаны), исполнительные уст-
ройства с ограниченным диапазоном воздействия (электрические и
гидравлические исполнительные механизмы с ограниченным ходом,
регулируемые источники напряжения с насыщением), кинематиче-
ские передачи с зазором или трением. Нелинейной характеристикой
часто обладает и объект управления.
Нелинейная форма характеристик указанных элементов, как
правило, нежелательна, но они функционально необходимы для ра-
боты системы.
Некоторые нелинейные элементы вводятся конструктором в сис-
тему преднамеренно — для улучшения качества управления. Такими
нелинейностями являются, например, релейные управляющие уст-
ройства. Они обеспечивают высокое быстродействие процесса
управления, выгодно отличаются от других управляющих устройств
простотой, надежностью и экономичностью. Применяются также и
нелинейные корректирующие устройства.
Различают два вида нелинейных элементов: существенно нели-
нейные и несущественно нелинейные. Нелинейность считается несу-
щественной, если ее замена линейным элементом не изменяет прин-
528
ципиальных особенностей системы и процессы в линеаризованной
системе существенно не отличаются от процессов в реальной систе-
ме. Если же такая замена невозможна и процессы в линеаризованной
и реальной системах сильно отличаются, то нелинейность является
существенной.
СУ с существенными нелинейностями обладают рядом принци-
пиальных особенностей, которые не присущи линейным системам и
не могут быть выявлены при исследовании линеаризованного урав-
нения СУ.
Главная особенность существенно нелинейных СУ заключается
в том, что они не подчиняются принципу наложения (суперпозиции),
а характер и показатели переходного процесса зависят от величины
внешнего воздействия или начального отклонения. Например, при
малом начальном отклонении Х](0), меньшем некоторого критическо-
го значения х^, переходный процесс может быть апериодическим
(рис. 10.1,а - линия 7), а при большом начальном отклонении
х2(0) > Хжр - колебательным (см.рис. 10.1,а - линия 2).
Рис. 10.1. Особенности нелинейных СУ
Другой важной особенностью динамики существенно нелиней-
ных СУ является зависимость условий устойчивости от величины
внешнего воздействия: СУ, устойчивая при одних значениях началь-
ного отклонения, оказывается неустойчивой при других его значени-
ях. На рис. 10.1,6 показаны переходные процессы X] и х2, один из
которых вызван большим начальным отклонением и сходится к ус-
тойчивому колебательному процессу, а второй, вызванный малым
529
начальным отклонением, расходится и тоже стремится к этому коле-
бательному процессу.
В связи с этим для нелинейных СУ применяют понятия «устой-
чивость (неустойчивость) в малом», «устойчивость (неустойчивость)
в большом», «устойчивость в целом». Система устойчива в малом,
если она устойчива только при малых начальных отклонениях. Сис-
тема устойчива в большом, если она устойчива при больших началь-
ных отклонениях. Система устойчива в целом, если она устойчива
при любых отклонениях.
Специфической особенностью нелинейных СУ является также
режим автоколебаний. Автоколебания - это устойчивые собственные
колебания, возникающие из-за нелинейных свойств системы. На рис.
10.1,6 процессы X] и х2 переходят в автоколебания с момента ta. Ре-
жим автоколебаний нелинейной системы принципиально отличается
от колебания линейной системы на границе устойчивости. В линей-
ной системе при малейшем изменении ее параметров колебательный
процесс становится либо затухающим, либо расходящимся. Автоко-
лебания же являются устойчивым режимом: малые изменения пара-
метров системы не выводят ее из этого режима. Амплитуда автоко-
лебаний хт не зависит от начальных условий и уровня внешних воз-
действий.
Автоколебания в нелинейных СУ в общем случае нежелательны,
а иногда и недопустимы (как незатухающие колебания в линейных
системах). Однако в некоторых нелинейных СУ автоколебания яв-
ляются основным рабочим режимом.
Рассмотрим в качестве примера нелинейной СУ систему стаби-
лизации температуры с нелинейным управляющим устройством
(рис. 10.2). В качестве управляющего устройства применено грехпо-
зиционное реле Р, на обмотку которого подано напряжение разба-
ланса мр моста М. Одним из плеч моста является термосопротивление
ТС, помещенное в рабочее пространство объекта.
При отклонении температуры О от заданной 03 нарушается рав-
новесие моста и реле подает напряжение лд определенной полярности
на исполнительный двигатель ИД, который при помощи задвижки 3
увеличивает или уменьшает подачу топлива в объект.
530
Рис. 10.2. Система стабилизации температуры
с нелинейным управляющим устройством
В этой системе имеется существенно нелинейный элемент -
трехпозиционное реле (см. 10.2), и ей присущи все указанные выше
особенности. Например, при определенных значениях параметров в
системе могут возникнуть автоколебания: температура будет непре-
рывно колебаться вокруг некоторого среднего значения, равного ве-
личине 0з. Автоколебания будут возникать, если открывание и за-
крывание задвижки после включения двигателя будут происходить
очень быстро. При этом температура будет быстро возвращаться к
заданному значению и «проскакивать» зону нечувствительности ре-
ле, а двигатель будет снова и снова то увеличивать, то уменьшать
подачу топлива.
Для устранения этих автоколебаний и улучшения динамических
свойств системы в ней с помощью потенциометра Пж осуществлена
внугренняя отрицательная обратная связь по положению регули-
рующего органа - углу а поворота задвижки 3.
Примером нелинейной СУ является также система стабилиза-
ции уровня жидкости в баке (см.рис. 1.13), описанная в 1.4. Сущест-
531
венно нелинейным элементом этой системы является управляющее
устройство, состоящее из контактов К\ и и потенциометра П.
Нелинейные СУ описываются нелинейными дифференциаль-
ными уравнениями, теория которых разработана не столь полно, как
теория линейных дифференциальных уравнений. Существует ряд
точных и приближенных методов, позволяющих решать лишь неко-
торые частные задачи анализа нелинейных систем. Наибольшее рас-
пространение в инженерной практике получили методы фазового
пространства, гармонической линеаризации, критерий абсолютной
устойчивости и метод моделирования на аналоговых и цифровых
вычислительных машинах.
При анализе нелинейных систем обычно решают следующие за-
дачи:
1)	отыскание возможных состояний равновесия системы и оцен-
ка их устойчивости;
2)	определение возможности существования автоколебаний и
оценка их устойчивости;
3)	выявление соотношений между параметрами системы, при
которых возникают автоколебания;
4)	определение параметров автоколебаний и их связи с парамет-
рами системы.
Математические основы теории нелинейных систем любой фи-
зической природы и любого назначения были созданы в период с
1892 по 1940 год выдающимися российскими учеными А.М. Ляпу-
новым, Н.М. Крыловым, Н.Н. Боголюбовым и А.А. Андроновым. В
последующий период крупные российские специалисты в области
автоматического управления Б.В. Булгаков, Л.С. Гольдфарб и
Е.П. Попов разработали методы исследования нелинейных СУ.
г
10.2.	Типовые нелинейные элементы СУ
Структура и уравнение нелинейной СУ в общем случае могут
быть очень сложными. Степень сложности зависит от количества,
вида и места включения нелинейных элементов. Однако большинст-
во систем, встречающихся в промышленной автоматике, содержат
один существенно нелинейный элемент. Обобщенная алгоритмиче-
532
ская схема таких систем показана на рис. 10.3. На схеме выделены
линейная и нелинейная части системы. Линейная часть включает в
себя все линейные звенья системы и может иметь структуру любой
сложности, в. частности, содержать внутренние обратные связи.
Рис. 10.3. Обобщенная алгоритмическая структура нелинейной СУ
Нелинейная часть образована одним нелинейным элементом,
выходная величина уи которого может быть выражена как функция
входной величины хн и ее производной хн:
(Ю.1)
Структура, изображенная на рис. 10.3, соответствует случаю,
когда нелинейный элемент выполняет функции управляющего уст-
ройства, как например, в системе стабилизации температуры (см.рис.
10.2).
Иногда нелинейный элемент выполняет одновременно и функ-
ции блока сравнения. Так, например, в системе стабилизации уровня
(см.рис. 1.13) выходная величина управляющего устройства (рис.
10.4,а) - напряжение ид - связана с входной величиной - уровнем h
зависимостью, изображенной на рис. 10.4,6. Среднее значение й0
между положениями верхних и нижних контактов может рассматри-
ваться как задающее воздействие.
Простейшими нелинейными элементами являются статические
(безынерционные) нелинейности. У них выходная величина уи зави-
сит только от входной величины хн, причем эта зависимость строго
однозначна.
Примерами статических нелинейностей служат трехпозицион-
ное управляющее устройство (рис. 10.4,а,б) и регулирующая задвиж-
533
ка с «мертвым» ходом (0-фо) и ограниченной пропускной
способностью QM (рис. 10.4,в,г).
Рис. 10.4. Примеры нелинейных элементов
У динамических нелинейностей выходная величина зависит
как от входной величины хн, так и от ее производной хн . Характери-
стика динамической нелинейности всегда неоднозначна. Динамиче-
ской нелинейностью является, например, кинематическая передача с
зазором (рис. 10.4Де).
На рис. 10.5 приведены статические характеристики наиболее
часто встречающихся нелинейных элементов и показано, как эти
элементы преобразуют входной гармонический сигнал xH(0:=xHff)sin со t
в периодический (не гармонический!) выходной сигнал ун(0 при ус-
ловии превышения амплитудой х.нт зоны Ь.
Элемент с характеристикой на рис. 10.5,6/ называется идеаль-
ным или двухпозиционным реле. Аналитически он описывается вы-
ражением
534
C.(+l)
с • О

при хн > 0;
при хя = 0;
при хн < О,
(10.2)
где sign - символ сигнатуры, который выделяет знак (плюс или ми-
нус) переменной, стоящей после символа.
Рис. 10.5. Характеристики типовых нелинейных элементов
Характеристика на рис. 10.5,6 соответствует трехпозиционному
реле с зоной нечувствительности b и описывается выражением
н
+6)].
(10.3)
535
Элемент на рис. 10.5,в называется идеальным двухпозиционным
реле с гистерезисами. Его характеристике соответствует выражение
~ ftyw) ^н)
Лн
+ с при: а) хн > Ь или б) |хн| < Ь и Хн < 0;
г
- с при: а) хн < -Ь или б) хн <Ь и хн > 0
= (с sign(xH - b sign хн),
(Ю.4)
где b - зона неоднозначности.
Характеристику на рис. 10.5,г имеют различные элементы с ог-
раничением выходного сигнала. Величина b в данном случае назы-
вается зоной пропорциональности.
Характеристика на рис. 10.5,д присуща различным конструк-
тивным элементам, имеющим «мертвую» зону Ь.
Наконец, характеристика на рис. 10.5,е описывает, как было уже
отмечено, кинематическую передачу с зазором («люфтом») 2Ь.
Рассмотренные статические и динамические нелинейности от-
носятся к классу нелинейностей с кусочно-линейными характеристи-
ками.
В управляющих устройствах СУ наряду с релейными элемента-
ми часто используются так называемые особые нелинейности, мно-
жительное и делительное звенья, элементы с переменной структурой,
элементы логического типа.
Рис. 10.6. Нелинейные управляющие устройства с переменной структурой
Для улучшения качества систем применяются управляющие
устройства с переменной структурой. В таких устройствах специаль-
ный блок изменения структуры (БИС) может включать в основной
контур системы звенья с различными динамическими свойствами.
536
Например, в устройстве на рис. 10.6,а БИС, в зависимости от значе-
ний сигнала ошибки и его производной, переключает закон регули-
рования с пропорционального на интегральный. Изменение структу-
ры может происходить в зависимости и от других сигналов основно-
го контура. Схема на рис. 10.6,5 при больших сигналах ошибки ра-
ботает как трехпозиционный регулятор, а при малых — как ПИ-
регулятор. В ней изменение структуры происходит за счет зон не-
чувствительности.
Управляющим устройствам с переменной структурой эквива-
лентны и различные логические УУ. На рис. 10.7,(7 изображена
структура логического УУ, изменение которой происходит по сле-
дующему алгоритму, называемому переключающей функцией:
- с при £ > 0 и е > 0;
уп(£,£) = <0 при: п)е>0 и £<0 или 5)е<0 и е>0;	(10.5)
+ с при е<0 и £<0.
а
Рис. 10.7. Алгоритмическая структура (а) и переключающая функция (б)
логического управляющего устройства
б
Логическую функцию (10.5) удобно изображать на графике в
системе координат входных переменных вис (рис. 10.7,5).
10.3.	Метод фазовых траекторий
Метод фазовых траекторий представляет собой графо-
аналитический способ исследования нелинейных СУ. Сущность ме-
537
тода заключается в описании поведения систем при помощи нагляд-
ных геометрических представлений - фазовых портретов.
Свободное движение нелинейной динамической системы управ-
ления с одной управляемой величиной x(t) в общем случае можно
описать с помощью п дифференциальных уравнений первого поряд-
ка (см. 2.9):
dXj(t)(dt = /Дх^О, х2(/), ...,хД0,	0 = 1; 2;п\ (10.6)
где xi(0 = х(0, х2(0 = х, (0, .., хЛ1(0 = Xj (0, хя(0 = х„_} (0 - фазовые
переменные состояния.
Мгновенное состояние системы и ее дальнейшее поведение од-
нозначно определены, если в данный момент времени t=tj известны
значения всех п переменных ху. Эти значения можно рассматривать
как координаты точки (хц х2;..., х„) в «-мерном пространстве, которое
называется фазовым пространством (здесь термин «фаза» имеет тот
же смысл, что и слово «стадия»).
Точку с координатами хц х2;..., хп называют изображающей
точкой, а линию, по которой она перемещается при изменении со-
стояния системы, - фазовой траекторией.
Как известно, конкретной группе начальных условий xi(0) = xi0,
х2(0) = х20;...; х„(0) = х„о соответствует единственное решение системы
(10.6) - определенная совокупность искомых функций времени Xi(^);
x2(f); ... ; xn(f). Поэтому каждой группе начальных условий соответст-
вует только одна начальная точка и единственная фазовая траекто-
рия, а множеству групп начальных условий соответствует целое се-
мейство траекторий, которое называется фазовым портретом систе-
мы. Этот образный термин, предложенный акад. А.А. Андроновым,
оправдан тем, что семейство фазовых траекторий действительно дает
наглядное представление о поведении системы во времени.
Метод фазового пространства наиболее удобен для анализа сис-
тем второго порядка, т. к. их фазовые траектории располагаются в
одной плоскости - в фазовой плоскости переменных xi и х2. Фазовый
портрет этих систем можно построить непосредственно по диффе-
ренциальному уравнению, не решая его.
538
Пусть описание системы представлено в виде системы двух
уравнений первого порядка
бЙС] I(11	(Xj 5 ^"2 )5
~ Уг (^i ’ Xj
(10.7)
где Xi = x - отклонение выходной величины или сигнала ошибки от
установившегося значения.
Если в качестве второй переменной состояния х2 принята произ-
водная переменной Х] = х, т. е. если х2 =х, то всегда функция
/1(хь х2) = х2.
Разделив второе уравнение системы (10.7) на первое, можно по-
лучить уравнение фазовых траекторий в дифференциальной форме
4&2/4&, =/2(х1,х2)/х2,	(10.8)
в котором независимой переменной является величина X] (не время
/!), а зависимой - х2.
Разделяя далее переменные Xi и х2 и интегрируя уравнение (10.8),
можно получить уравнение фазовых траекторий в явном виде
х2 =F(Xj) + C0,	(10.9)
где Со - постоянная интегрирования, зависящая от начальных усло-
вий.
На рис. 10.8,6, г, е показаны характерные фазовые траектории
линейной системы второго порядка, соответствующие затухающему
(рис. 10.8,47), расходящемуся (см.рис. 10.5,в) и незатухающему (рис.
10.8,6) колебательным процессам. Моменты времени /3, t$, когда
кривые x(Z) достигают своих максимумов и минимумов, соответст-
вуют пересечению фазовыми траекториями оси Xi = х, а моменты
прохождения кривых х(7) через нуль (/2, /4) - пересечению оси х2 = х.
Построение фазовых траекторий значительно облегчается, если
учитывать их следующие общие свойства, вытекающие из
анализа выражений (10.7) и (10.8).
Рис. 10.8 Переходные процессы и фазовые траектории
линейной системы второго порядка:
а, б- устойчивой; в, г- неустойчивой; д. е - на границе устойчивости
В верхних квадрантах фазовой плоскости изображающая точка
движется всегда слева направо, а в нижних - справа налево. Это
объясняется тем, что при Xi = х >0 переменная X] = х возрастает, а
при Х2 = х < 0 переменная xj = х убывает.
540
В любой точке фазовой плоскости, где переменная х2 и функция
fi не равны нулю, фазовая траектория имеет только одно определен-
ное направление, соответствующее значению производной dx2/dx\ в
данной точке. Из этого следует, что фазовые траектории в таких точ-
ках не пересекаются.
Согласно выражению (10.8), при х2= 0 производная dx2ldx} = оо,
т.е. фазовые траектории пересекают ось х\ под прямым углом, а пе-
ременная Xi = х достигает своего максимума. Если при х2 = 0 одно-
временно равна нулю функция f, то фазовая траектория в таких осо-
бых точках плоскости не имеет определенного направления, а обе
производные Xj и х2, согласно уравнениям (10.7), равны нулю. По-
следнее означает, что изображающая точка неподвижна, а исследуе-
мая система управления находится в состоянии равновесия.
Особые точки могут быть обособленными или образовывать це-
лые особые отрезки на оси хь Такие отрезки называются отрезками
покоя. У систем с релейными характеристиками длина отрезка покоя
равна зоне нечувствительности 2Ь.
Самые важные для анализа нелинейных систем свойства фазо-
вых траекторий заключается в следующем:
1.	Затухающему (устойчивому) переходному процессу (рис.
10.8	, а) соответствует фазовая траектория, сходящаяся к на-
чалу координат (рис. 10.8,6) или к отрезку покоя.
2.	Неустойчивому процессу (рис. 10.8, в) соответствует фазо-
вая траектория, удаляющаяся от начала координат (рис.
10.8, г).
3.	Периодическому процессу (рис. 10.8,д) соответствует замк-
нутая фазовая траектория (рис. 10.8,е), называемая предель-
ным циклом.
Предельный цикл может быть устойчивым или неустойчивым.
Если все соседние фазовые траектории стягиваются к предельному
циклу, то он является устойчивым и соответствует автоколебаниям.
Если же соседние траектории отходят от цикла, то он является неус-
тойчивым.
По графику устойчивого предельного цикла можно определить
два основных параметра автоколебательного режима - частоту и
амплитуду. Частота соа равна отношению отрезка, отсекаемого траек-
ториеи на оси хз, к отрезку, отсекаемому на оси х\, а амплитуда хт
равна отрезку на оси х\.
Фазовый портрет нелинейной системы, обладающей кусочно-
линейной или разрывной характеристикой, состоит из нескольких
областей с различными фазовыми траекториями. Линии, отделяю-
щие на плоскости одну область от другой, называются линиями пере-
ключения.
В точках пересечения фазовыми траекториями линий переклю-
чения происходит излом траекторий. Это происходит из-за скачкооб-
разного изменения правой части уравнения (10.8).
Пример 1. Построим фазовый портрет и оценим динамику системы
стабилизации температуры (см. рис. 10.2).
Алгоритмическая схема системы приведена на рис. 10.9,а. Объект
управления представлен инерционным звеном первого порядка, исполни-
тельный двигатель — идеальным интегрирующим звеном (без учета меха-
нической и электрической инерции двигателя), измерительная мостовая
схема и задвижка - безынерционными статическими звеньями. Нелинейным
элементом системы является трехпозиционное реле. Входная величина реле
- результирующая магнитодвижущая сила (ампер-витки) основной обмотки
и обмотки обратной связи, выходная - напряжение пд. подаваемое на якор-
ные зажимы двигателя.
Для анализа целесообразно исходную схему преобразовать к расчетной
схеме (рис. 10.9,6), на которой входная величина реле имеет ту же размер-
ность, что и управляемая величина 0. При этом зона нечувствительности
реле b (рис. 10.9,в) должна быть также выражена в градусах. Она равна b ~
Ь}/кл, где Ь\ - зона нечувствительности, выраженная в ампер-витках; кк - ПК
измерительной схемы.
Линейная часть системы (без учета внутренней обратной связи по по-
ложению задвижки) описывается дифференциальным уравнением второго
порядка
=	(1010)
dt dt
где кл = кок3кл - ПК линейной части, °С/(В-с).
Реле описывается нелинейной функцией ид = Дхн), которая может при-
нимать три значения (см. рис. 10.9,в).
+ с
«д = /(*н ) = < 0
542
при хн > Ь;
при |хн| < Ь',	(10.11)
при лн < -Ь.
Рис. 10.9. Исходная (а) и расчетная (б) алгоритмические схемы
системы стабилизации температуры и характеристика реле (в)
При отсутствии внутренней обратной связи сигнал хн = е.
Будем рассматривать только отклонения температуры 0 от ее заданно-
го значения 03, обозначая их символом х. Тогда сигнал ошибки е = -х, а
уравнение замкнутой системы в отклонениях будет иметь вид
_ d х dx , л, .
dr dt
(10.12)
где
/(х) = ^0
при х < -b,
при |х| < Ь\
при х > Ь.
(10.13)
Уравнение (10.12) эквивалентно системе двух уравнений первого по-
рядка, записанной в форме Коши:
dxx/dt = x2-,
dx2 !dt = [~ х2 + к л /(х 1 )]/Го >,
(10.14)
где х\ = х = ДО = 9 - 03, х2 = •
543
Разделив второе уравнение на первое, получим нелинейное уравнение
фазовых траекторий
Л2 /dxx = [-1 + k„ f(xi )/х2 ]/Т0.
(10.15)
В соответствии с видом функции (10.13) разделим фазовую плоскость
(рис. 10.10) на три области. В области I, соответствующей значениям |х| < Ь,
уравнение (10.15) принимает вид
Л* 2 = ~Todx\.
оно легко интегрируется. Его решение
х2 --rjxj +С01,
(10.16)
(10.17)
где Coi - постоянная интегрирования, зависящая от начальных условий.
Таким образом, в средней области I фазовые траектории представляют
собой прямые линии с отрицательным наклоном 1/Г0.
В областях II и III, где соответственно х > b и х < -Ь, аДх]) = -с и
fa}) = +с, уравнение (10.15) принимает такой вид:
Лг/Л1 =(-1ТМ/х2)/то-
(10.18)
Разделяя переменные xi и х2, получим
~ ~Тох2 dx2/(x2±knc\
(10.19)
После интегрирования выражения (10.19) находим уравнение фазовых
траекторий
*1 =-(Го*2 ±Г0 *лсЦ*2 ±Ллс|)+СП(111),	(10.20)
где верхние знаки относятся к области II, а нижние - к области III.
На рис. 10.10 приведены фазовые траектории, построенные при раз-
личных значениях постоянных Со и следующих параметрах системы:
То = 10 с, к„ = 0,04 °С/(В-с), с = 50 В, b = 2 °C.
Жирной линией выделена фазовая траектория, соответствующая на-
чальному отклонению температуры ДО = х0= +10 °C.
544
Рис. 10.10. Фазовый портрет системы стабилизации температуры
По фазовому портрету видим, что после любых начальных отклонений
температуры и ее производной в системе происходит затухающий колеба-
тельный процесс, который продолжается до тех пор, пока отклонения тем-
пературы не станут меньше зоны нечувствительности b = 2 °C.
Пример 2. Построим фазовый портрет и оценим динамику СУ, со-
стоящей из той же линейной части (10.10) и двухпозиционного реле с гисте-
резисом (см. рис. 10.5,в и выражение (10.4)).
Уравнение фазовых траекторий имеет тот же вид (10.15), а характери-
стику реле (10.4) можно представить следующей зависимостью от фазовой
переменной х = ~ -хх,:
если: а)х<-Ь или < b и х > 0;
если : а) х >
(10.21)
В соответствии с этими условиями фазовая плоскость данной СУ раз-
бивается на две области (рис. 10.11). В области I вместо функции yfo) в
уравнение (10.15) необходимо подставить значение -с. а в области II - зна-
545
чение +с. Очевидно, что решения уравнения (10.15) для этих двух областей
будут такими же, как в предыдущем примере, т. е. подчиняться выражению
(10.20), а средняя область отсутствует.
На рис. 10.11 построены разовые траектории, вычисленные по форму-
ле (10.20) при следующих параметрах СУ: Tq = 2 с; кл = 2; с = 1; b = 0,4. По
фазовому портрету7 видно, что система неустойчива в малом и устойчива в
большом и что все траектории стягиваются к предельному циклу (жирная
линия). Следовательно, в системе всегда, при любых ее параметрах будут
возникать устойчивые автоколебания.
Рис. 10.11. Фазовый портрет СУ, содержащей
двухпозиционное реле с гистерезисом
По величине отрезков, отсекаемых предельным циклом на осях коор-
динат, определяем, что амплитуда автоколебаний xma = 1, а частота
соа = 1,1 с"1. Соответственно период колебаний Та - 2л/©а* 5,7 с.
546
10.4. Метод гармонической линеаризации
Метод гармонической линеаризации является приближенным
методом исследования режима автоколебаний нелинейных СУ. Этим
методом можно определить условия возникновения и параметры
автоколебаний как в системах второго порядка, так и в более слож-
ных системах с п > 2.
Метод заключается в замене существенно нелинейного элемента
с характеристикой /(хн) эквивалентным линейным звеном с коэффи-
циентом ки. В замкнутой автоматической системе, работающей в
режиме автоколебаний, условием эквивалентности служит равенство
амплитуд и фаз выходного сигнала эквивалентного звена и первой
гармоники выходного сигнала реального нелинейного элемента. При
этом предполагается, что сигнал на входе нелинейного элемента яв-
ляется синусоидальным. Такое предположение справедливо во всех
случаях, когда линейная часть системы достаточно инерционна и не
пропускает высокочастотные гармоники.
а	б
t	нелинейным элементом
547
Рассмотрим сущность метода гармонической
линеаризации подробнее. Пусть, как и прежде, СУ состоит из
отделимых друг от друга линейной и нелинейной частей (см.рис.
10.3) и нелинейная часть описывается функцией (10.1). Предполо-
жим, что контур системы разомкнут (на выходе линейной части) и
что на входе нелинейного элемента действует синусоидальный сиг-
нал
xH(0 = ^HmsinfiX.	(10.22)
При этом на выходе нелинейного элемента будет возникать пе-
риодический сигнал форма которого зависит от характера не-
линейности и в общем случае существенно отличается от синусои-
дальной. Так, например, на выходе двухпозиционного реле без зоны
нечувствительности (рис. 10.12,а) образуется периодический сигнал
прямоугольной формы (рис. 10.12,6).
Уравнение нелинейной части (10.1) при синусоидальном воз-
действии (10.22) можно записать в таком общем виде:
К(0 = /[х(0, х(0]= sin (of, xHm03coso3f], (10.23)
Периодический сигнал ун(0 может быть разложен в ряд Фурье
(2.20) и тем самым представлен в виде суммы к-х гармонических
составляющих
Л* (0 = акcos + sin cokt = Уь* sin(a*r + у/J,	(10.24)
где коэффициенты пк и 5К определяются по формулам (2.21) и (2.22),
а параметры -
Укт=^к+Ьк', 4k=a™tg(ak/bk)', (& = 1; 2; ...;оо).	(10.25)
У большинства встречающихся в автоматике нелинейных эле-
ментов статическая характеристика кососимметрична относительно
начала координат, т. е. J[xH) - -fl-x^), и для них всегда постоянная
548
составляющая ajl = 0, а коэффициенты всех четных гармоник
Cl2k~ ^2к ~ О И У2кт ~ 0.
Возможность и правомерность замены реального нелинейного
элемента, функционирующего в замкнутой системе в режиме гармо-
нических колебаний, эквивалентным линейным звеном основаны на
следующих общих закономерностях:
1. Амплитуды Укт всех гармоник выше первой почти всегда зна-
чительно меньше амплитуды первой гармоники сигнала уH(t), т.е.
(10.26)
2. Линейная часть большинства нелинейных систем обладает
свойством фильтра низкой частоты:
WSJo>)\»\Wn(jkm), (k = 3-5,..\
(10.27)
т. е. все гармоники, кроме основной, существенно ослабляются ли-
нейной частью и благодаря этому сигнал ул(1) на ее выходе окажет-
ся близким к синусоиде.
На основании этих двух предпосылок можно при анализе замк-
нутой системы учитывать только первую гармонику и сигнал vH(r) на
выходе элемента с кососимметричной характеристикой представлять
приближенно так:
Л(0	= Л1 cos cot+b{ sin^r = ylmsin(cX + ^1).	(10.28)
Учитывая, что
sin <а = х„ (t)/xm; cos at = х„ (<)/х„ а>
и вводя обозначения
q(x} = bjxwn: qXxHm) = aJxHm,
(10.29)
(10.30)
можно вместо выражения (10.28) записать
549
Ун(О«<?(хнт )*M + q}(x
нт )хн(0/со
(10.31)
или в операторной форме
Ун (0 * Ч(Хнт К (0 + ?! (*нт )РХН (')/» 	(10.32)
Таким образом, при выполнении указанных выше предпосылок
нелинейное уравнение (10.23) может быть заменено линейным урав-
нением (10.31). Эта операция называется гармонической линеариза-
цией, а коэффициенты q(xKn} и <7i(xlim) - коэффициентами гармони-
ческой линеаризации.
Коэффициенты гармонической линеаризации зависят от вида
нелинейности f и могут быть определены по формулам (2.21), (2.22)
и (10.29). В табл. 10.1 приведены коэффициенты q и q\ для наиболее
часто встречающихся нелинейностей.
Гармоническая линеаризация принципиально отличается от
обычной линеаризации (см. 2.3), т. к. коэффициенты гармонически
линеаризованного элемента непостоянны, а зависят от амплитуды хнт
входного сигнала. Эта особенность проиллюстрирована на примере
рис. 10.12. Эквивалентная прямолинейная характеристика (тонкая
линия на рис. 10.12,47), устанавливающая связь между входным сиг-
налом хн и первой гармоникой yHi выходного сигнала, имеет различ-
ный наклон при разных амплитудах входного сигнала. Однако при
определенном режиме периодических колебаний, когда значения со и
хнт фиксированы, коэффициенты гармонической линеаризации име-
ют также постоянные значения. Благодаря этому для решения неко-
торых задач анализа нелинейных систем могут быть использованы
понятия и методы теории линейных систем.
Так, из уравнения (10.32) можно получить эквивалентную ПФ
нелинейного элемента
УЛрУхЛР> = Ч^т') + Ч^т,'>Р1о>,	(10.33)
а подстановкой в неер =jo) - эквивалентную АФХ
= <?(*„) +Л, (О	(10.34)
550
Таблица 10.1
Коэффициенты гармонической линеаризации типовых нелинейностей
551
Модуль функции (10.34)
X
Л'т
(10.35)
определяет отношение амплитуды первой гармоники выходного сиг-
нала к амплитуде входного сигнала, а аргумент функции
Фн(ХН/П ) = arctg [^] (х
Н/П	н/п )]
(10.36)
- фазовый сдвиг между первой гармоникой и входным сигналом.
Отметим, что у всех нелинейностей с однозначными статиче-
скими характеристиками коэффициент ^1(хнш) равен нулю, и они не
создают отставания по фазе.
о
в
b
Я-
Рис. 10.13. Зависимости коэффициентов гармонической
линеаризации от амплитуды входного сигнала
На рис. 10.13 приведены графики коэффициентов q и q\, по-
строенные по формулам табл. 10.1. Графики построены в безразмер-
ной форме. В качестве единицы измерения амплитуды хнт принят
параметр Ь, а для самих коэффициентов введен нормирующий мно-
житель Ыс или 1/к.
Линия 1 на рис. 10.13,t7 соответствует нелинейности 1 в табл.
10.1, линия 2 - нелинейности 2. Линия 1 на рис. 10.13,6 соответству-
ет нелинейности 4, линия 2 - нелинейности 5. На рис. 10.13,в, г
представлены графики соответственно для нелинейностей 3 и 6.
У нелинейностей 1-4, имеющих ограничение с, коэффициенты
гармонической линеаризации по мере увеличения амплитуды хпт
стремятся к нулю, т. к. амплитуда первой гармоники выходного сиг-
нала остается постоянной. У нелинейностей 5 и 6 с ростом амплиту-
ды хпт ослабевает влияние нечувствительности Ь, и коэффициент q
стремится к коэффициенту к линейного участка. Нелинейности 3 и 6,
имеющие неоднозначные характеристики, создают отставание по
фазе. С ростом амплитуды хНП) коэффициент q\ этих звеньев умень-
шается и соответственно уменьшается отставание по фазе.
Перейдем теперь непосредственно к использованию
метода гармонической линеаризации для ис-
следования режима автоколебаний.
Если известны ПФ линейной части
W,(P) = K,(P)ID,(P)	(10.37)
и эквивалентная ПФ (10.32) нелинейной части, то можно записать
эквивалентную ПФ разомкнутого контура нелинейной СУ
W(p,xm,co) = (p)WK(р, хт, <у) =	[?(хи) + (хи)р/(о\ (10.38)
и характеристическое уравнение гармонически линеаризованной
системы
f(a хт>®) = Dn (Р) + Кп (Р)Ь(Х.) + (хт =0. (10.39)
553
В режиме автоколебаний амплитуда хт и частота со, как извест-
но, остаются постоянными. Следовательно, и функция ^(/7, хт, со) в
этом режиме постоянна, а выражения (10.38) и (10.39) линейны, и их
можно анализировать обычными методами теории линейных СУ.
Существованию в нелинейной СУ автоколебаний соответствует
нахождение линеаризованной системы (10.39) на колебательной гра-
нице устойчивости. Для определения колебательной границы можно
использовать любой из обычных критериев устойчивости, изложен-
ных в главе 5.
Наиболее удобно исследовать автоколебания при помощи
критерия Михайлова. Для того чтобы установить, воз-
можны ли в системе автоколебания вида x(t) = хта sin соа/ с постоян-
ной амплитудой хт& и частотой ®а, необходимо в характеристическое
уравнение (10.39) подставить чисто мнимый корень р =j&a:
Dn О.) + Кп (X )[^(хта) + qx (хм	/ща ] = 0	(10.40)
и решить его относительно неизвестных хта и <йа.
Решение уравнения (10.40) упрощается благодаря тому, что в
левой части всегда могут быть выделены действительная и мнимая
составляющие, которые порознь также равны нулю.
(10.41)
Одновременное выполнение равенств (10.41) соответствует про-
хождению характеристической кривой F(ju>, хт) через начало коорди-
нат.
Если уравнения (10.41) не имеют положительных действитель-
ных корней соа и хта, то автоколебания в системе невозможны.
После отыскания параметров соа и хта необходимо проверить, со-
ответствуют ли они устойчивым автоколебаниям. Для этого исполь-
зуют следующее условие устойчивости автоколебаний:
554
(ap/&J (ae/5®)' - (ap/ao)' (ee/&J > o,
(10.42)
где звездочка означает, что в частные производные, полученные из
выражений (10.41), необходимо подставить найденные численные
Рис. 10.14. Определение амплитуды и частоты
автоколебаний графическим способом
Если линейная часть описывается уравнением высокого порядка
или содержит запаздывание, то аналитическое решение системы
(10.40) затруднительно или невозможно. В этих случаях автоколеба-
ния можно отыскать при помощи критерия Найквиста.
Согласно критерию Найквиста, система находится
на колебательной границе устойчивости, если АФХ разомкнутого
контура проходит через точку (-1, /0). Следовательно, условием су-
ществования автоколебаний является равенство
=	(10.43)
ИЛИ

(10.44)
555
Левая часть уравнения (10.44) представляет собой АФХ всех
линейных звеньев системы, а правая - обратную характеристику
нелинейного элемента, взятую с противоположным знаком.
Уравнение (10.44) удобно решать графически. Для этого необ-
ходимо построить указанные характеристики в одной системе коор-
динат (рис. 10.14,я). В точках пересечения кривых выполняется ра-
венство (10.44). Эти точки определяют параметры автоколебаний.
Отметка текущей частоты на кривой HSi(/co) определяет частоту авто-
колебаний ша, а отметка текущей амплитуды на кривой \/WK(xm) -
амплитуду автоколебаний xwa.
Если характеристики не пересекаются, то автоколебания отсут-
ствуют.
Факт устойчивости или неустойчивости найденного режима ав-
токолебаний устанавливают при помощи следующего правила,
если точка на кривой l/FFH(x„,), близкая к точке пересечения, но сдви-
нутая в направлении возрастания параметра хт, не охватывается ха-
рактеристикой Wn(jo>), то автоколебания устойчивы, если же охваты-
вается, - то неустойчивы. На рис. 10.13,я точка М2 соответствует
устойчивым автоколебаниям, а точкаМ - неустойчивым.
Пример 1. Определим амплитуду и частоту автоколебаний в системе
стабилизации температуры, работающей без внутренней обратной связи (см.
пример 1 в 10.3) при следующих параметрах системы: кп = 0,04 °С/(В-с);
с = 50 В; b = 2 °C; То = 10 с; Тд = 0,5 с.
ПФ линейной части (с учетом инерционности исполнительного двига-
теля)
»'л(Р) = ‘лЖр + 1)(?’дР + 1)	(10.45)
а эквивалентная ПФ нелинейного элемента - трехпозиционного реле (см.
табл. 10.1)
=	-*2 /’“rn •	(10.46)
Характеристический полином системы
+(г„ +Гд)р2 +р+М(^,)-	(10.47)
556
Подставим в полином (10.47) р = jco и приравняем его действительную
и мнимую составляющие к нулю
, хта ) — knq(xma) (го + Гд)соа О,
б(®а , хтъ )= «а (1 ~ Т0Тд(й1 )= °.
(10.48)
Из второго уравнения системы (10.48) можно определить частоту авто-
колебаний
(10.49)
которая в данном случае зависит только от постоянных времени.
Подставляя значение юа в первое уравнение системы (10.48), получим
уравнение с одним неизвестным - амплитудой хта
/пх2^-(то +ТД)/ТОТД =0,	(10.50)
которое можно привести к виду
-л2 +Ь" = О,
та та	’
(10.51)
где А = п2 (Г, + 7-,)2/16 к2 с2 Т2 Г; .
Прежде чем решать это биквадратное уравнение при конкретных зна-
чениях коэффициентов, исследуем его дискриминант
/) = 1-4Я/>2.
(10.52)
Уравнение (10.51) имеет действительные корни х2а (а в системе соот-
ветственно возможны автоколебания с амплитудой хта) только в том случае,
если дискриминант D > 0, т. е. если
24„сГоГд-я(го+Гл)1,>0.
(10.53)
При заданных в условии примера параметрах неравенство (10.53) не
выполняется, следовательно, автоколебания в системе не могут возникнуть.
557
Из условия (10.53) можно определить предельное значение ПК линей-
ной части:
*я „„ = я* (го + )/2сГ07-д.	(10.54)
При большем значении коэффициента линейной части автоколебания
возможны. Например, при к„ = 0,4 уравнение (10.51) имеет два действи-
тельных решения: хта = 2,1 °C и хта = 12 °C.
Для того чтобы установить, которое из этих двух решений соответству-
ет устойчивым колебаниям, применим общее условие устойчивости автоко-
лебаний (10.42). В данном случае имеем
^k'/dXfn Хт =хЛЯ1 ~ 4кпС (26*” Хта)/7СХтау Хта Ь >
дР/дсо|ш=(О1 = -2(Г0 +Тд)(оа;
%)/дхт = 0; 5Q/<Эсо| Ф=Ш1 = 1-3 T^iOa.
(10.55)
Подставляя значения частных производных (10.55) в условие (10.42) и
учитывая одновременно выражение (10.49) для частоты, получим
4клс(2Ь~ х^а )(1 3)/itxma ух^а Ь >0
(10.56)
или
Хта >	.
(10.57)
Этому условию удовлетворяет только второе решение. Следовательно,
в системе будут возникать устойчивые автоколебания с амплитудой
хта = 12 °C и частотой юа = 1/^Г0Гд* 0,45 с-1. Период колебаний
Та = 2л/0,45 ~ 14 с.
Покажем, что при отсутствии зоны нечувствительности реле в системе
всегда будут возникать устойчивые автоколебания. Действительно, при b = 0
уравнение (10.51) всегда имеет одно действительное решение
•*та
(10.58)
Нетрудно видеть, что при Тд -> 0 амплитуда автоколебаний будет
стремиться к нулю, а их частота, согласно выражению (10.49), - к бесконеч-
ности.
558
Пример 2. Определим амплитуду и частоту автоколебаний системы,
состоящей из трехпозиционного реле (см. позицию № 2 в табл. 10.1)) и ли-
нейной части с запаздыванием:
W = k„e->"/(Tp + l).
(10.59)
Параметры системы: кл = 1, Т= 10 с, т = 5 с, с - 25, b = 1.
Поскольку система обладает запаздыванием, применим графический
способ решения.
На рис. 10.14,6 построены АФХ линейной части и обратная характери-
стика реле
=(10.60)
Характеристика (10.60) дважды проходит вдоль действительной оси
Р(®). При xm = b = 1 характеристика начинается от -оо, при xm = bjl * 1,4
достигает максимального значения пЫ2с, а затем при хт —> оо опять стре-
мится к -оо.
Характеристики линейной и нелинейной частей пересекаются в двух
точках. Согласно приведенному выше правилу, точка М\ (на верхней ветви
обратной характеристики) соответствует неустойчивым колебаниям, а точка
Л/2 (на нижней ветви) - устойчивым. Амплитуда автоколебаний хта 8. а
частота соа ® 0,375 1/с.
10.5. Оценка абсолютной устойчивости
с помощью критерия Попова
При решении практических задач анализа и синтеза нелиней-
ных СУ часто возникает необходимость оценки устойчивости со-
стояния равновесия и определения допустимых вариаций формы и
параметров статической характеристики нелинейного элемента. Эти
две задачи связаны с понятием и критерием абсолютной устойчиво-
сти нелинейной системы.
Пусть в контуре нелинейной СУ (см.рис. 10.3) содержится не-
линейный элемент с характеристикой Дхн), имеющей любую форму,
но не выходящей за пределы определенного сектора [О, £н] (рис.
10.15,а). Состояние равновесия нелинейной системы называется аб-
солютно у стойчивъш, если оно асимптотически устойчиво (см. главу
559
5) при любой нелинейности, относящейся к определенному классу.
Нелинейности считаются относящимися к одному классу, если их
характеристики /(хи) располагаются в секторе между осью абсцисс и
прямой с угловым коэффициентом £н(см. рис. 10.15,я).
Рис. 10.15. Критерии оценки абсолютной устойчивости Попова
На первый взгляд, может показаться, что для оценки абсолют-
ной устойчивости нелинейной системы, состоящей из линейной час-
ти с Wn (р) и нелинейности с Дхн), достаточно оценить устойчивость
линейной системы с передаточной функцией кн Wn (р). Однако это
предположение выполняется только для некоторых частных видов Wn
(р), а в общем случае оно несправедливо и требуются специальные
критерии.
Удобный критерий для суждения об абсолютной устойчивости
нелинейных СУ предложил в 1959 г. румынский ученый В.Попов.
Его критерий основан, как и критерий Найквиста, на использовании
АФХ и имеет простую геометрическую трактовку.
560
В формулировке критерия используется понятие модифициро-
ванной АФХ. Пусть линейная часть устойчива и имеет следующую
АФХ;
WJja>) = P((o) + jQ((o).
(10.61)
Образуем из этой обычной АФХ следующую видоизмененную
АФХ.

(10.62)
у которой мнимая часть получена умножением Q(g)) на оРы, где
Тм = 1 с - нормирующий множитель. Характеристика (10.62) и назы-
вается модифицированной.
Теперь можно следующим образом сформулировать крите-
рий абсолютной устойчивости равновесия нели-
нейной СУ, которая состоит из линейной части с АФХ Wn (/со) и не-
линейного элемента с характеристикой Дхн), расположенной в секто-
ре [0, fcH];
для абсолютной устойчивости равновесия достаточно, чтобы
модифицированная характеристика W* (/со) не охватывала
точку (-l/kK,ty и через эту точку можно было провести пря-
мую, не пересекающую характеристику (/со) (последняя ле-
жит справа от прямой).
На рис. 10.15,6 показан случай, когда критерий Попова выпол-
няется, а на рис. 10.15,в, г — случаи, когда не выполняется.
С помощью критерия Попова решают и обратную задачу, строят
заданную характеристику (/со), затем проводят как можно ближе к
этой характеристике прямую так, чтобы получить наименьший отре-
зок [0 - 1/Агн], и таким образом находят допустимое значение углового
коэффициента кп.
По наклону прямой Попова, «прижатой» к кривой (/со), мож-
но судить о допустимом классе нелинейности: если прямая верти-
кальна, то нелинейность может быть только однозначной, а если она
наклонена, то нелинейность может быть и однозначной, и неодно-
значной (например, с гистерезисом).
561
Линейная часть реальных нелинейных СУ часто представляет
собой последовательное соединение инерционных звеньев с АФХ
и; (jco)=
____________
О, (» (TJo, + ifaja, +1).. (TJa> +1) ’
(10.63)
модуль которой с ростом со монотонно убывает. Исследование абсо-
лютной устойчивости таких систем можно свести к анализу устойчи-
вости соответствующей линейной системы: допустимое значение
углового коэффициента кн находить через предельное значение обще-
го ПК (см. 5.6).
Пример. Оценим с помощью критерия Попова абсолютную устойчи-
вость равновесия нелинейной СУ, состоящей из трехпозиционного релейно-
го элемента (рис. 10.16,а) с параметрами 6=1ис = 8и линейной части
(10 64)
Wa(j^ = k„e-lm/(Tja>+i)
Рис. 10.16. Пример оценки абсолютной устойчивости
Представим АФХ (10.64) в виде суммы действительной и мнимой час-
тей:
562
(10.65)
, ч 7cn (cos сот —Тео sin сот)	к „ (sin сот + Тео cos сот)
(J®) = —------5-5------------ ~ 1 —--------------------
Соответствующая (10.65) модифицированная характеристика
ч &п (cos сот-Тео sin сот) /с„ (sin сот + Тео cos сот)
fF (7со)=- j(o-^--------------------------—----------
, i	т^.ч^ i 1
(10.66)
она показана на рис. 10.16,6. Через точку с абсциссой, равной 1/кл = -0,125,
проведена прямая 7, которая не пересекается с кривой 1Кл*(/со). Следова-
тельно, при заданных параметрах равновесие системы абсолютно устойчи-
во.
Решим теперь обратную задачу: определим допустимое по условию ус-
тойчивости равновесия значение зоны нечувствительности Ь. Для этого,
проведем прямую 2, «прижатую» к характеристике И7* (/ю). Она пересекает
действительную ось в точке с абсциссой примерно 0,11. Отсюда допустимое
значение для углового коэффициента кн < 1/0,11 » 9, а для зоны нечувстви-
тельности 6>с/^н=8/9«0,9. При b < 0,9 состояние равновесия системы будет
неустойчивым.
10.6. Основные сведения о вибрационной и
статистической линеаризации
Как следует из предыдущих разделов данной главы, наличие
нелинейности в контуре системы может существенно ухудшать каче-
ство управления, а в некоторых случаях сделать ее вообще неработо-
способной. Поэтому при проектировании нелинейных СУ обычно
стремятся либо уменьшить влияние нелинейности на динамику сис-
темы, либо обеспечить получение автоколебаний с заданной часто-
той и амплитудой. Коррекция и улучшение свойств нелинейной сис-
темы могут быть осуществлены изменением характеристик как ли-
нейной части, так и нелинейного элемента системы.
Изменение характеристики линейной части достигается спосо-
бами, изложенными в главе 7.
Изменение характеристики нелинейного элемента может быть
получено несколькими способами. Некоторые статические нелиней-
ности можно компенсировать при помощи соответствующих обрат-
563
ных нелинейностей. Для этого параллельно или последовательно с
основной нелинейностью Дхн) включают компенсирующую нелиней-
ность, имеющую обратную характеристику /'(хн). Эквивалентное
соединение при этом будет линейным.
Эффективным средством уменьшения влияния нелинейностей
на свойства систем является наложение на основной, как правило,
низкочастотный сигнал, дополнительного высокочастотного сигна-
ла. Такие принудительные высокочастотные колебания, называемые
вибрационными, существенно снижают отрицательное влияние
люфтов, зазоров, сухого трения в механических передачах на дина-
мику нелинейной системы.
Рассмотрим этот способ подробнее.
Вибрационная линеаризация. Вибрационная линеаризация
заключается в сглаживании нелинейностей при помощи специально-
го высокочастотного сигнала, который подается на вход нелинейного
элемента одновременно с основным сигналом. В качестве этого до-
полнительного сигнала могут быть использованы как собственные
автоколебания системы, так и внешнее воздействие от специального
генератора. Для того чтобы собственные автоколебания происходили
с достаточно большой частотой, применяют внутренние обратные
связи, охватывающие нелинейные элементы.
Изложим математическую сущность вибрационной линеариза-
ции и проиллюстрируем получение линеаризующего эффекта на
примере вибрационной линеаризации идеального реле.
Пусть на входе нелинейного элемента с однозначной характери-
стикой Дхн), включенного в контур системы (см.рис. 10.9,6), дейст-
вуют медленно меняющийся основной сигнал х0(/) и дополнительный
высокочастотный сигнал хд(/) с амплитудой хат и частотой сод (рис.
10.17,я), т. е.
хн(0 = (0 + х0(Г) = х0(Г) + хат sin со/.	(10.67)
При этом частота сод должна быть достаточно большой, чтобы
основной сигнал x0(t) в течение нескольких периодов дополнительно-
го сигналах//)оставался практически постоянным (см. рис 10.17,#).
Амплитуда хдж должна быть достаточной для срабатывания релейно-
564
го элемента (рис. 10.17,6), т. е. хдт > | х0 (г) |. Кроме того, необходи-
мым условием работоспособности такой системы является подавле-
ние линейной частью составляющей с частотой сод и более высоких
гармоник:
^пОд) <
(10.68)
где соп - частота пропускания линейной части.
Рис. 10.17. Вибрационная линеаризация идеального реле
Сигнал yn(t) на выходе нелинейного элемента также будет пред-
ставлять собой сумму медленно меняющейся составляющей уо(0
(рис. 10.17,в), равной среднему значению сигнала и быстро
меняющейся yA(t):
УМ = уМ + УаЮ,	(10-69)
где Л (0 =Уо [xc(0L Л (0 =Л 1хд (01, причем функции/о т.к.
для нелинейного элемента не выполняется принцип суперпозиции.
565
Функции То и 7д можно приближенно определить, если разло-
жить суммарный выходной сигнал yH(t) в ряд Фурье (2.20). При этом
полагают, что на интервале разложения, равном периоду Т сигнала
хд (0, составляющая у0 (/) практически не меняется, т. е. уо(0 к const.
Тогда по аналогии с основной процедурой гармонической линеари-
зации (см. формулу (10.31)) можно вместо нелинейной зависимости
Л (0 = /К, *д(0]
(10.70)
записать гармонически линеаризованное уравнение

(10.71)
Коэффициент q = /д определяется аналогично - по формуле
(10.30). Составляющая /, соответствует нулевому члену разложения
периодического сигнала yK(t) в ряд Фурье, т.е.
(10.72)
Очевидно, что этот член будет зависеть только от вида функции
/ медленной составляющей х0 и от амплитуды хДЛ/ высокочастотного
сигнала, т. е.
y0=F(x0,xflm) или yQ=FQ(x0).	(10.73)
Так, например, для рассматриваемого двухпозиционного реле
без зоны нечувствительности (см.рис. 10.17, б) зависимость (10.73)
принимает вид
у0 =~arcsin-^~.	(10.74)
7L	ппл
Таким образом, видим, что условия прохождения основного
сигнала х0 через нелинейный элемент зависят от амплитуды допол-
нительного сигнала хд.
566
Для большинства однозначных нелинейностей график функции
f0 (х0) имеет достаточно плавную форму (даже для релейных элемен-
тов). На рис. 10.17,г показана характеристика fo(xQ) идеального реле
при различных амплитудах Эффект сглаживания нелинейностей
для медленной составляющей, достигаемый наложением высокочас-
тотных колебаний, называется вибрационной линеаризацией.
Плавность функции f0 (х0) позволяет осуществить еще и обыч-
ную линеаризацию
(10.75)
где ки ={^PJ^xo)x =0 - ПК нелинейного элемента для медленной
о
составляющей. Например, для двухпозиционного реле ПК
k^lc/xx^.	(10.76)
Эффект сглаживания тем сильнее, чем больше амплитуда высо-
кочастотного сигнала. Однако следует учитывать, что с увеличением
амплитуды хдда уменьшается передаточный коэффициент к*.
Кроме описанного линеаризующего эффекта, с помощью перио-
дического внешнего воздействия на нелинейную систему можно до-
биться подавления или устранения ее собственных автоколебаний.
При соблюдении определенных условий выбора частоты сод и ампли-
туды хдт система под воздействием сигнала хд(?) может перейти из
режима автоколебаний с частотой ©а в режим вынужденных колеба-
ний с частотой (од. Это явление называется захватыванием часто-
ты. Так как вынужденные колебания имеют обычно меньшую ам-
плитуду и большую частоту, чем автоколебания, то такое устранение
автоколебаний также улучшает качество нелинейных систем.
Вынужденные высокочастотные вибрации нелинейного элемен-
та могут вызываться как внешним генератором периодических коле-
баний, так и за счет собственных автоколебательных свойств нели-
нейной системы. Для реализации второго способа в системе органи-
зуется внутренний автоколебательный контур, охватывающий нели-
нейный элемент. Параметры контура выбираются так, чтобы частота
567
автоколебаний была достаточно большой, а их амплитуда превыша-
ла медленную составляющую x0(t).
Одним из вариантов осуществления вибрационной линеариза-
ции за счет внутренних свойств системы является создание так назы-
ваемого скользящего режима.
Вибрационная линеаризация в скользящем режиме. Проил-
люстрируем сущность вибрационной линеаризации в скользящем
режиме на примере релейной системы стабилизации температуры
(см.рис. 10.2).
Для простоты будем полагать, что зона нечувствительности реле
b = 0 и постоянная времени двигателя Тд - 0. Согласно схеме на
рис. 10.9Д входной сигнал нелинейного элемента (с учетом внут-
ренней обратной связи)
Хн =	+ *ОС (ТоР + О/Мо]*
(10.77)
или после преобразований
xH=~kfi + ^p)x,
(10.78)
где = 1 + k<JkJcQ-, Т\ = кж То1(кж + kJcQ\
С учетом выражения (10.78) можно записать дифференциальное
уравнение замкнутой системы СУ
d2x dx t	, <r, dx\
—_-i----= -k„f к.х + к.Т.—
dt2 dt ЛЧ dt)
(10.79)
В системе без внутренней обратной связи линия переключения
на фазовой плоскости описывается выражением хн = 0 и совпадает с
осью ординат (рис. 10.18,а). Если же на входе реле кроме основного
сигнала х подается дополнительный сигнал, пропорциональный про-
изводной от х, то уравнение линии переключения для рассматривае-
мого идеального реле без зоны нечувствительности имеет вид
Т^+х = 0.	(10.80)
568
Рис. 10.18. Фазовый портрет скользящего режима
В системе координат «х-х» уравнению (10.79) соответствует
прямаяMN(рис. 10.18,6), имеющая наклон \П\.
Фазовые траектории по обе стороны линии переключения опре-
деляются такими же уравнениями (10.20), как и в системе без внут-
ренней обратной связи. Но на наклоненной линии переключения
всегда образуется особый отрезок АВ, который в своих крайних точ-
ках касается двух фазовых траекторий (показаны штриховыми ли-
ниями). Вне этого отрезка фазовые траектории подходят к линии
переключения с одной стороны, а отходят - с другой. На самом же
отрезке АВ фазовые траектории подходят к линии переключения с
обеих сторон. Это означает, что изображающая точка, попав на отре-
зок АВ, не может уйти с него. А так как производная х не равна ну-
лю, то изображающая точка продолжит свое движение к началу ко-
ординат, скользя по линии переключения. Такой режим работы сис-
темы называется скользящим.
При скользящем режиме происходят бесконечно быстрые пере-
ключения реле из одного положения в другое. При этом величина х
колеблется с бесконечно малой амплитудой около некоторого средне-
го значения, которое уменьшается до нуля. Средняя составляющая
569
сигнала х подчиняется линейному дифференциальному уравнению
(10.80) и может быть найдена как его решение
х(Г) = хое"г
(10.81)
Убывание сигнала х по экспоненте означает, что в скользящем
режиме нелинейная система подчиняется линейным законам и ее
можно приближенно рассматривать как линейную систему первого
порядка. К этому выводу можно прийти и путем следующих рассуж-
дений. Средняя составляющая сигнала хн в скользящем режиме при-
близительно равна нулю, а среднее значение сигнала х конечно. По-
этому передаточный коэффициент прямой цепи на рис. 10.9,6 можно
считать равным бесконечности. Соответственно ПФ замкнутой сис-
темы в скользящем режиме согласно основному свойству предельной
системы (см. формулу (2.157)) будет равна обратной ПФ звена об-
ратной связи:
Ф(/>) = x(p)/x3(p)«(l/^)/(7;p + l).
(10.82)
Так как все реле обычно имеют зону нечувствительности или
зону неоднозначности и поэтому срабатывают с некоторым запазды-
ванием, то скользящий режим в реальных системах осуществляется
не в виде плавного скольжения, а в виде высокочастотных колебаний
около линии переключения. При этом частота и амплитуда сигнала х
имеют конечное значение, а реле вибрирует с большой частотой.
Статистическая линеаризация. Линеаризующий эффект в не-
линейных системах получается и при воздействии на них высокочас-
тотных случайных сигналов.
Пусть на вход безынерционного нелинейного элемента с косо-
симметричной статической характеристикой
У = /(*)
(10.83)
поступает стационарный случайный сигнал
570
о
x(t) = тх + x(t),	(10.84)
где тх - математическое ожидание входного сигнала x(f); x(f) - цен-
трированная случайная составляющая входного сигнала, у которой
математическое ожидание равно нулю.
Будем искать статистически эквивалентное звено в виде парал-
лельного соединения двух линейных звеньев с коэффициентами ко и
ki (рис. 10.19), одно из которых преобразует только составляющую
тх, а другое - только составляющую х (/). Соответственно выходной
сигнал эквивалентного звена можно представить в виде суммы
©	о
л (0 =	+ y3(t) =	х(0-
(10.85)
Рис. 10.19. Статистически эквивалентное линейное звено
Коэффициенты ко и к\ называют коэффициентами статисти-
ческой линеаризации соответственно для математического ожидания
и для центрированной случайной составляющей.
Параметры ко и к{ линейного звена выбирают, исходя из условия
эквивалентности его выходного сигнала y3(t) сигналу на выходе
реальной нелинейности. В качестве условия статистической эквива-
лентности (т.е. эквивалентности в среднем) используют один из сле-
дующих двух критериев.
Первый критерий заключается в требовании равенства матема-
тических ожиданий и дисперсий обоих сигналов, т.е.
571
ту тУз, Dy Dy3.
(10.86)
Второй критерий требует обеспечения минимума среднего квад-
ратического отклонения сигналауэ(0 от сигнала ХО-
Коэффициент ко согласно обоим критериям получается всегда
одинаковым и равным
kQ=my/mx.	(10.87)
Коэффициент к\ согласно первому критерию
к, =JDJD, =аг/а,	(10.88)
и согласно второму
к, =R„(0)/D'.	(10.89)
Формулы (10.87) и (10.88) вытекают непосредственно из выра-
жений (10.85) и (10.86). Вывод формулы (10.89) приводится в специ-
альных монографиях по теории нелинейных систем.
Знак коэффициента к\ в формуле (10.88) определяется характе-
ром функции Дх) в точке х = тх: если она возрастает, то к\ > 0, а если
убывает, то к\ < 0.
Коэффициент к\ по первому критерию получается обычно не-
сколько заниженным, а по второму - несколько завышенным, поэто-
му в практических расчетах рекомендуется принимать среднее ариф-
метическое значение коэффициентов к\, найденных по обоим крите-
риям.
В качестве примера на рис. 10.20 показаны зависимости коэф-
фициентов статистической линеаризации идеального реле (см.табл.
10.1) от параметров тх и ох входного сигнала. Зависимость, получен-
ная по второму критерию эквивалентности, показана штриховой
линией. Случайная составляющая сглаживает нелинейную зависи-
мость между средними значениями входного и выходного сигналов.
Этот эффект линеаризации под действием случайной составляющей
так же, как и вибрационная линеаризация, улучшает во многих слу-
чаях работу нелинейной системы. Однако при большой интенсивно-
сти случайной составляющей (т. е. при сх » л?х) передаточный ко-
572
эффициент ко для постоянной составляющей становится практически
равным нулю. Кривые на рис. 10.20,6 показывают, что имеет место и
обратное влияние: при возрастании составляющей тх уменьшается
коэффициент к\ ддя случайной составляющей.
Рис. 10.20. Коэффициенты статистической линеаризации идеального реле
Основной задачей, решаемой при помощи метода статистиче-
ской линеаризации, является расчет точности нели-
нейной системы при случайных воздейст-
виях. Изложим методику расчета точности применительно к сис-
теме стабилизации, изображенной на рис. 10.3.
Пусть на входе линейной части системы приложено стационар-
ное случайное возмущение
о
g(0 = mg + g(t),
(10.90)
которое содержит постоянную (или медленно изменяющуюся) со-
ставляющую ms и быстро меняющуюся случайную составляющую
g (0 с известной спектральной плотностью ^(со). Из-за этого возму-
щения в системе в каждый момент времени будет возникать сигнал
ошибки е(Г) = хн(Г), который также будет случайным сигналом. При-
чем сигнал ошибки также может быть представлен в виду суммы
двух составляющих
573
о
е(0 = тЕ + е(г).
(10.91)
Полагая, что нелинейный элемент Дхн) заменен статистически
эквивалентным звеном с двумя каналами ко и (см.рис. 10.19),
можно порознь записать выражения для двух составляющих сигнала
ошибки:
™АР) = rng (р) W* (р)/(1 + Wp)),	(10.92)
Ар) = £(РЖ<Р)/С + М^л(Р))-
(10.93)
Постоянную составляющую сигнала ошибки можно определить
при помощи теоремы о конечном значении оригинала (см. табл. 2.2):
V	< X V	/ X W(p)
т, = hm рт,(р) = hm ртг(р), Д
р-»0	р->о 8	(1 + k0JVn (р))
(10.94)
Случайную составляющую сигнала ошибки можно оценить по
ее дисперсии
D. =
Е	Е
Ца>)
(1ЦВД
dox
(10.95)
2
Выражения (10.94) и (10.95) недостаточны для вычисления по-
казателей и D., т.к. в их правые части входят коэффициенты к0 и
£
к}, зависящие от искомых величин ms и D». Поэтому приходится
е
использовать еще два уравнения статистической линеаризации нели-
нейного элемента
(ю 96)
(10.97)
Решая совместно уравнения (10.94) - (10.97). можно найти по-
казатели точности системы и D..
€
574
В заключение отметим, что изложенный метод применим только
в тех случаях, когда в нелинейной системе отсутствуют автоколеба-
ния. Если же автоколебания в системе возможны, то необходимо
применять метод совместной гармонической и статистической ли-
неаризации, который излагается в специальных монографиях по
теории нелинейных систем.
Пример. Определим дисперсию сигнала ошибки в системе стабилиза-
ции, состоящей из идеального реле и линейной части
^л(Р) = *л/р>
(10.98)
если на входе линейной части действует случайное возмущение с нулевым
математическим ожиданием и спектральной плотностью
Sg (со) = IDa/y^1 + со2).
(10.99)
Найдем вначале коэффициенты статистической линеаризации реле.
Так как т& = 0, то и ms = 0. При те - 0, согласно рис. 10.19,5, по первому
критерию к} - с/<зе, а по второму - кг ~ 0,8 с/ое Примем для дальнейших
расчетов среднее значение этих коэффициентов к\ - 0,9 с/ое.
Согласно выражению (9.95), дисперсия сигнала ошибки
De =	= J 2Па 2л-------------
2л _от а2 + со2 ;со + ^л
dto. (10.100)
Применяя формулу (8.76) для п - 2, получим
= о2 = Da кл /к] (а + к} кл).
(10.101)
Подставляя в выражение (10.101) коэффициент к} - 0,9 с/ое, оконча-
тельно найдем среднее квадратическое значение сигнала ошибки
=^л[(1,1Т>/с)-0,9с/а].
(10.102)
575
Оно увеличивается при возрастании коэффициента кл и дисперсии воз-
мущения D. С ростом управляющего воздействия с среднее квадратическое
значение сигнала о
ПЕЙ
ки уменьшается.
Контрольные задания и вопросы
1.	Назовите основные особенности нелинейных СУ.
2.	Как изменяется выходной сигнал х(/) нелинейной системы в режиме
автоколебаний? Какими параметрами он характеризуется?
3.	Назовите основные виды нелинейных элементов.
4.	Приведите пример существенно нелинейного элемента с однознач-
ной статической характеристикой.
5.	В какой системе координат строится фазовая траектория системы
второго порядка?
6.	Как вид фазовой траектории связан с характером переходного про-
цесса устойчивой и неустойчивой системы?
7.	Как определить по графику фазовой траектории амплитуду и частоту
автоколебаний?
8.	Постройте график выходного сигнала yn(t) трехпозиционного релей-
ного элемента, на входе которого действует синусоидальный сигнал.
9.	Выделите на графике ун(0, построенном в задании 8, его первую
гармонику7 и определите приближенное значение коэффициента q - кК
(см.рис. 10.12), если хт = 5, b = 2, с = 10.
10.	Вычислите точное значение коэффициента q (см.габл. 10.1) для ус-
ловий задания 9 и сравните его с приближенным, полученным графически.
11.	Объясните, почему для нелинейностей, имеющих ограничение вы-
хода, коэффициенты q -д 0 при хт оо, а для нелинейностей с зоной нечув-
ствительности коэффштиенты q возрастают до определенного значения.
12.	Какими свойствами должна обладать линейная часть нелинейной
системы, чтобы можно было полагать, что в контуре циркулирует почти
гармонический сигнал?
13.	Как аналитически (с помощью критерия Михайлова) определить
амплитуду и частоту автоколебаний?
14.	Как графически (с помощью критерия Найквиста) определить ам-
плитуду и частоту'' автоколебаний?
15.	Устойчиьэсть какого состояния нелинейной системы можно оце-
нить с помощью критерия Попова?
16.	Как обобщенно характеризуется нелинейность при оценке абсо-
лютной устойчивости? Какое обстоятельство подчеркивается словом «абсо-
лютная»?
17.	Дайте геометрическую трактовку критерия Попова.
18.	Как влияет угловой коэффициент кн на устойчивость равновесия
системы (при неизменной линейной части)?
19.	Определите максимально допустимое значение кк для системы, ли-
нейная часть которой состоит из трех инерционных звеньев с Т\ = Т2-
(см. пример 1 в 5.4), если кп = 4. (Используйте критерий Попова для систем
с монотонно убывающей АФХ).
20.	Поясните, как и за счет чего достигается вибрационная линеариза-
ция.
21.	Как создается скользящий режим в нелинейной системе?
22.	В чем сущность статистической линеаризации нелинейного элемен-
та?
577
Глава 11. ПРИНЦИПЫ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ И
АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
11.1. Общая характеристика и классификация задач
оптимального управления
Общая задача управления сложным технологическим объектом
управления, описанным в главе 9 (см. рис.9.1), включает в себя
обычно несколько взаимосвязанных подзадач. В структуре СУ таким
объектом (рис. 11.1) в общем случае можно выделить следующие
основные контуры: стабилизации, идентификации и оптимизации
объекта управления, оптимизации стабилизирующего управляющего
устройства.
-1 Критерий
стабилизации
Рис. 11.1. Функциональная структура управления сложным объектом
578
Контур оптимизации объекта управления (ОУ) с помощью спе-
циального устройства оптимизаций УО (или алгоритма оптимизации,
реализуемого в УВМ) определяет наилучший по выбранному техно-
логическому критерию режим функционирования объекта и выдает
соответствующие этому режиму задания (уставки) х3 контуру стаби-
лизации. Контур оптимизации объекта работает обычно в сравни-
тельно медленном темпе и периодически решает задачу статической
оптимизации объекта.
Контур стабилизации, содержащий основное управляющее уст-
ройство (УУ0), работает в одинаковом с объектом темпе и поддержи-
вает с помощью управляющих воздействий у объект в состоянии,
оптимальном для текущих условий. При изменении возмущения z
устройство УУО возвращает объект в заданное состояние, а при изме-
нении задания х% переводит объект в новое требуемое состояние. В
обоих случаях контур стабилизации должен осуществлять наилуч-
ший в определенном смысле перевод объекта из одного состояния в
другое.
Наилучшие переходные процессы в контуре стабилизации обес-
печивает контур оптимизации УУ0, в котором дополнительное
управляющее устройство (УУД) определяет оптимальные для различ-
ных условий параметры основного управляющего устройства (на-
пример, коэффициенты обратных связей кос. При этом контур опти-
мизации УУ0 работает в масштабе времени, одинаковом с контуром
стабилизации, и решает обычно задачу непрерывной, динамической
оптимизации последнего.
Для постоянной или периодической корректировки параметров
А, В объекта служит контур идентификации, в котором устройство
оценки параметров (УОГТ) по наблюдаемым входным и выходным
сигналам объекта определяет текущие значения этих параметров и
вводит их в основное и дополнительное управляющие устройства.
Кроме рассмотренных контуров, в системе управления имеется,
как правило, устройство оценивания состояния (УОС) объекта. Это
устройство определяет наилучшие оценки х переменных состояния
х объекта, измеряемых измерительным устройством (ИУ) неточно
(искаженных помехой g).
579
В каждом указанном контуре и устройстве, как правило, реша-
ется определенная задача оптимизации или оптимального управле-
ния.
Управление называется оптимальным, если оно среди всех
управлений рассматриваемого ограниченного класса обеспечивает
наилучший в определенном смысле результат.
Постановка задачи оптимального управления включает в себя
два основных этапа:
1) выбор желаемого режима функционирования объекта управ-
ления и задание в математической форме цели управления - крите-
рия оптимальности, соответствующего этому режиму;
2) определение математической модели объекта и установление
ограничений на его входные и выходные переменные.
Рассмотрим понятия, связанные с этими этапами, и дадим клас-
сификацию задач оптимального управления в зависимости от видов
критериев и типов ограничений.
Критерии оптимальности. Как известно, всякое управление
заключается в целенаправленном воздействии на объект с целью
улучшения его функционирования. В простейших случаях улучше-
ние достигается за счет устранения и компенсации внешних и внут-
ренних возмущений и поддержания тем самым объекта в некотором
расчетном, номинальном режиме. В более сложных случаях для су-
щественного улучшения функционирования объекта одной стабили-
зации недостаточно, и приходится изменять сам режим работы объ-
екта, его выходные переменные. В обеих указанных задачах управ-
ления при формировании управляющих воздействий, направленных
на улучшение функционирования объекта, используют некоторую
количественную меру, характеризующую качество, эффективность
управления. Эта количественная мера, по которой производятся вна-
чале сравнительная оценка различных режимов функционирования
объекта, а затем выбор наилучшего режима и соответствующего ему
варианта управляющих воздействий, называется критерием опти-
мальности (или критерием качества управления).
Критерий оптимальности обычно принимают в виде некоторой
скалярной величины Q, которую стремятся выбрать таким образом,
чтобы каждому варианту управления у соответствовало вполне оп-
ределенное значение Q( у), а при наилучшем варианте управления
580
у критерии достигал своего экстремального значения
(максимума или минимума). Тогда цель управления может быть вы-
ражена в виде следующей математической записи:
Q -2> extr,
(11.1)
*
а искомое наилучшее управление у может рассматриваться как ар-
гумент экстремизации критерия:
у - argextrC?.
(11.2)
Физический смысл величины Q зависит от характера ОУ и от
назначения оптимизируемой СУ. В качестве величины Q могут быть
приняты различные технические и экономические показатели функ-
ционирования как самого объекта, так и системы в целом. Критерием
оптимальности могут служить величины, которые по своей сути,
смысловому содержанию необходимо максимизировать, - например,
производительность технологического агрегата или коэффициент
полезного действия энергетической установки. Такие величины
можно назвать показателями выгоды Ов, и цель управления для них
записать так:
>тах.	(11.3)
Но критерием оптимальности могут служить и такие величины,
которые требуется минимизировать, например расходы сырья или
энергии на единицу продукции, отклонения качественных признаков
продукции от заданных значений. Они являются показателями по-
терь и цель управления соответственно будет
ft, Amin.
(11.4)
Выбор критерия оптимальности в каждом отдельном случае для
конкретного объекта представляет собой сложную инженерную за-
581
дачу, которая не имеет строгого, однозначного решения. Объясняет-
ся это тем, что многообразие требований к любому реальному техно-
логическому объекту управления принципиально не может быть све-
дено к единой количественной оценке, т.е. нельзя принять единый
показатель, объективно оценивающий сочетания различных качест-
венных признаков объекта. Поэтому указанную задачу выбора кри-
терия оптимальности решают, как правило, эвристически, на основе
глубокого и всестороннего изучения ОУ. При этом вынужденно ог-
раничиваются упрощенным решением - выбором одного показателя,
субъективно принимаемого в качестве основного, важнейшего для
данной задачи управления. Естественно, что удачность выбора еди-
ного критерия зависит от опыта и интуиции постановщика задачи
оптимизации.
Но если все-таки необходимо (по соображениям более высокого
порядка) оценить объект или СУ достаточно полно, учитывая одно-
временно несколько показателей эффективности, то приходится ре-
шать задачу так называемой векторной, или многокритериальной,
оптимизации с векторным критерием
g=fe,a,.,a]T,	(Ц.5)
состоящим из скалярных критериев. А для задач векторной опти-
мизации не существует таких же строгих и мощных методов анали-
тического решения, как для задач со скалярным критерием. Вектор-
ная оптимизация осуществляется, как правило, путем сложных мно-
гоэтапных оценок, имеющих всегда субъективный и эвристический
характер. Поэтому при синтезе оптимальных систем управления
обычно стремятся сразу при постановке задачи заменить исходный
векторный критерий О одним скалярным критерием Q, который был
бы более или менее эквивалентен векторному. Один из простейших
способов такой замены заключается в линейном свертывании (агре-
гировании) компонентов 0 исходного критерия в виде суммы
(uq
где q, - весовые коэффициенты, выбираемые постановщиком с со-
блюдением условия
582
e = S«. = 1-
(11.7)
Заметим, что указанное агрегирование нескольких скалярных
критериев возможно лишь в том случае, если все они однородны -
относятся либо к группе показателей выгоды (11.3), либо - потерь
(11.4).
Рассмотрим основные виды критериев оптимальности, которые
применяются в задачах управления объектом, описываемым в общем
случае нелинейным дифференциальным уравнением состояния
s(O = Z,[s(O, v(r), z(r)]
(11.8)
и нелинейным алгебраическим уравнением выхода
I.(r) = jVl, g(7)],
(11.9)
где x(Z), j/(f), z(t\ g (t) - векторы соответственно состояния, выхода,
управления, возмущения и помехи измерения; fc и /в - матрицы-
столбцы, состоящие из скалярных функций fCi и fBi (i ~ 1; 2;
j' - 1; 2; ...;/). При этом будем полагать в дальнейшем, что вид самих
функций /ci и /В1 во времени не изменяется, т.е. что объект стациона-
рен.
Критерий оптимальности согласно своему смысловому содер-
жанию выражается обычно через компоненты векторов выхода хв(0,
управления и задания хвз(/):
2 = хвл(0, v(r)]
(II .10)
где хвз(г) - вектор-функция времени, определяющая желаемое изме-
нение выходах^/1).
С учетом уравнений (11.8) и (11.9) можно для скалярной вели-
чины Q вместо выражения (11.10) записать зависимость от входных
переменных:
583
q=&(&,(o, xo, g(oi
(hid
Конкретный вид выражений (11.10) и (11.11) зависит от харак-
тера вектор-функций хвз(г) и z(z). Если компоненты этих функций
постоянны или изменяются во времени достаточно медленно по
сравнению с длительностью переходного процесса в объекте, то объ-
ект работает в установившемся или статическом режиме, а критерий
оптимальности (11.10) представляет собой алгебраическую нелиней-
ную зависимость
(Ц.12)
где хв, хв_з, у - векторы с не изменяющимися во времени компонента-
ми. Если же внешние воздействия хвз(г) или z{t) непрерывно изменя-
ются или изменяются ступенчато, но достаточно часто (по сравне-
нию с длительностью переходного процесса), то эффективность
функционирования объекта и системы управления оценивают по
функционалу - определенному интегралу, вычисляемому на заданном
интервале управления /к:
q=ebob J /оксо,	(His)
о
где jo - некоторая скалярная неотрицательная функция, вид которой
выбирают согласно цели управления.
Если целью управления является достижение минимальной дли-
тельности переходного процесса (максимального быстродействия),
то полагают fQ = 1, и функционал (11.13) принимает тривиальный вид
а = {1<Л = г,->т1Г1,	(11.14)
0	-
который по смыслу относится к показателям потерь.
Распространенным критерием оптимальности типа (11.13) явля-
ется квадратичный интегральный показатель качества переходного
584
процесса (см.6.3), который для объекта с одним скалярным выходом
хв имеет вид
Qn = ]s2(t)dt = j [xb3(t)-xb{t)]2dtЛmin,	(И.15)
J	J	v(t)
0	0
а для объекта с /-выходами -
&=£?/&	Ьтз(0-Х/в(0]2^	(Ш6)
1=1	1 = 1 О	~ '
где - х,вз(/) -	= е,(0 - сигналы ошибки.
Учитывая, что операции суммирования и интегрирования пере-
становочны, и записывая сумму квадратов отклонений е, в матрич-
ной форме, можно вместо (11.16) получить
Qn =]£T(t)qE(t)dt^min,
J	—	y(t)
0
(11.17)
где 8(0 - /-мерный вектор-столбец, образованный из ошибок €](0,
е2(0,  , £;(0; Я ~ диагональная неотрицательно определенная (/ х /) -
матрица весовых коэффициентов q\t q->, ..., qi, оценивающих степень
нежелательности отклонений выходных переменных х,в(/) от своих
заданий х,вз(/).
Во многих задачах управления квадрат управляющего воздейст-
вия у(0 пропорционален мощности, потребляемой управляющим
устройством или самим объектом, а интеграл этого квадрата по вре-
мени пропорционален, следовательно, энергии, расходуемой на
управление. Поэтому часто используют критерий минимума расхода
энергии
т
0
у1 (Огу (t)dt —> min,
J —	—	v(/)
0
(11.18)
585
где г - диагональная положительно определенная (т х т) - матрица
весовых коэффициентов	гт, соответствующих стоимостям
энергии отдельных управляющих воздействий.
В некоторых задачах управляющее воздействие y(f) есть не что
иное, как расход топлива, сырья или катализатора. В таких случаях
для многомерного объекта применяют критерий минимума расхода
материального ресурса
(11.19)
Наибольшее распространение в современной теории управления
получил обобщенный квадратичный критерий качества функциони-
рования
Qn = J [sT(O<?s(O + /(OrXo]^^niin,
о “	~	-	Уй)
(11.20)
соединяющий в себе требование минимума отклонений выходных
переменных (критерий максимальной точности (11,17)) и критерий
минимума расхода энергии (11.18).
Встречаются задачи управления, в которых, наряду с качеством
функционирования системы во время переходного процесса, требу-
ется оценивать точность в конечном состоянии объекта. Тогда к
обобщенному критерию (11.20) добавляется составляющая

(11.21)
где q - матрица весовых коэффициентов, оценивающих степень
нежелательности отклонений конечного состояния объекта от задан-
ного.
При случайном характере внешних воздействий х3(г) и z(t) ком-
поненты вектора отклонений е(/) и управлений y(t) также будут слу-
чайными сигналами и критерий оптимальности определяют как
586
среднее значение функционала (11.13) на достаточно большом ин-
тервале времени:
1
(? = lim — ]Q(t)dt.	(11.22)
Иногда в таких случаях среднее значение первичного критерия
находят усреднением не по времени, а по множеству. Например, если
известна функция w(z) плотности вероятности совместного распре-
деления компонентов вектора z, то среднее значение Q может быть
получено интегрированием по всей области Z изменения случайных
величин z\, z2,
Q=M.{0}= J(?(z,y)w(z)6/Z(z).
Z(I)
(11.23)
где M2{.} - знак математического ожидания случайной величины;
c/Z(z) = dz\dz2 ... dzn- бесконечно малый элемент указанной области
и-мерного пространства Z.
Если величина Q в выражениях (11.22) и (11.23) является пока-
зателем потерь, то ее математическое ожидание Q называют средним
риском.
В случаях, когда закон распределения w(z) возмущения z заранее
не известен, а известны лишь диапазоны изменения компонентов
вектора z, можно применять критерий минимакса
Qn (у, l) A min (max)	(11.24)
или критерий максимина
2в(у. zp>max(min).
(Н.25)
Оптимизация по критерию (11.24) или (11.25) позволяет вы-
брать такое управление у_ , которое обеспечивает наилучший резуль-
тат О* или (7* при наиболее неблагоприятном сочетании компонсн-
587
тов вектора возмущений z из всех возможных зол - наименьшее!).
Наглядное представление об этих критериях дает рис. 11.2, на кото-
ром изображена зависимость Qn(y.z) в виде гиперболического пара-
болоида, имеющего так называемую седловую точку.
Рис. 11.2. Минимаксный критерий оптимальности
Очевидно, что в этом примере для показателя потерь Оп наибо-
лее неблагоприятное значение z возмущения всегда соответствует
гребню параболоида, а наилучшее значение у управления - низшей
точке этого гребня.
Недостаток минимаксного и максиминного критериев в том, что
в более легких условиях они дают худшие результаты, чем, напри-
мер, критерий среднего риска. Поэтому их целесообразно применять
лишь тогда, когда неизвестны статистические характеристики внеш-
них воздействий.
Ограничения на процесс управления. Различают два вида ог-
раничений: естественные и условные. Естественными ограничения-
ми являются физические законы, в соответствии с которыми функ-
ционируют объект управления и управляющее устройство. При ма-
тематической постановке задачи управления эти ограничения пред-
ставляются в виде дифференциальных и алгебраических уравнений
объекта типа (11.8) и (11.9). К естественным относятся также огра-
588
ничения значений переменных х(0, xB(f) и y(t), обусловленные осо-
бенностями конструкции объекта и управляющего устройства. На-
пример. частота вращения асинхронного двигателя не может
быть больше синхронной, выходной сигнал усилителя не может
принять значения, большие, чем уровень насыщения. Такие ограни-
чения действуют сами по себе, независимо от желания конструктора
системы.
Условные ограничения на эти же переменные устанавливает
конструктор системы, стремясь не допустить аварийных или каких-
либо иных нежелательных режимов работы объекта. Например, ско-
рость и ускорение движения груза подъемной установки н е
должны превысить значения, допустимые по условиям безопас-
ности. Ясно, что выполнение условных ограничений должна обеспе-
чивать система управления.
При постановке и решении задачи управления необходимо учи-
тывать и естественные, и условные ограничения на переменные х(0,
хв(г) и г(0- В этом случае эти ограничения задаются в виде условий
принадлежности векторов х(/), хв(/) и y(t) к некоторым замкнутым
множествам:
х(Г)е А'; хв(7)е ^B;_v(7)e Г,	(11.26)
где X, Хв, Y - замкнутые множества, заданные соответственно в п, I и
w-мерных пространствах.
Обычно ограничения (11.26) задаются в виде алгебраических
уравнений или неравенств
Х,(х], х2,...,х„)>0; р,(х1в, х2в,...,х/в)>0; vk(y},y2,...,ут)> О,
(11.27)
где 0 < / < п\ 0 <j < 1\ 0 < к < т.
В наиболее простых задачах управления ограничения на компо-
ненты векторов х(0, хв(0 и у(г) накладываются независимо друг от
друга - в виде ограничений по модулю отдельных компонентов:
|х1В[<х)вм; |У<|<у)М,	(11.28)
где х,м, х1В.м, у1М - максимально возможные или допустимые значения
компонентов.
589
Основными ограничениями в задачах оптимального управления
являются уравнение состояния (11.8) и уравнение выхода (11.9), свя-
зывающие между собой все переменные объекта. С целью упроще-
ния задачи эти нелинейные уравнения стремятся заменить линейны-
ми в следующей типовой форме (см.2.9).
Х(0 = А х(0 + (О + z(0;	(11.29)
xB(O = Cx(0 + ^(O+g(0.	(11.30)
Виды задач оптимизации. Тип задачи управления зависит от
характера внешних воздействий и режима работы объекта. Если воз-
действия постоянны или меняются медленно, то объект работает в
установившемся режиме, вектор x(t) = 0, а объект описывается ал-
гебраическим уравнением статики
xb = fA&z,g),	(11.31)
которое для линеаризованного объекта (11.29), (11.30) принимает
вид
xt=Kyy-Kbz + g,	(11.32)
Г№КУ = О-СК'В,К, = СК'.
Задача управления объектом (11.31) или (11.32) по критерию
(11.12) при ограничениях (11.27) называется задачей статической
оптимизации.
В зависимости от вида целевой функции (11.12) и уравнения
статики (11.31) задача статической оптимизации может относиться к
классу задач нелинейного или линейного программирования. Зада-
чей линейного программирования она является, если линейны целе-
вая функция, уравнение статики и ограничивающие уравнения
(11.27). В частном, но распространенном случае, когда целевая
функция (11.12) или статическая зависимость (11.31) имеют экстре-
мальный характер, задача статической оптимизации становится за-
дачей экстремального регулирования.
Задача управления объектом (11.8), (11.9) или (11.29), (11.30) по
критерию типа (11.13) при ограничениях (11.27) называется задачей
590
динамической оптимизации. Разновидности задач динамической
оптимизации и методы их решения будут рассмотрены ниже.
Сформулированным постановкам задач статической и динами-
ческой оптимизации соответствует обобщенная функциональная
схема системы оптимального управления, приведенная на рис. 11.3.
Кроме обычных частей, в системе имеется блок вычисления крите-
рия (БВК).
Рис. 11.3. Обобщенная функциональная структура
системы оптимального управления
Если внешние воздействия на объект и систему управления от-
сутствуют или заданы в виде конкретных функций, то задача управ-
ления называется детерминированной. Если же воздействия имеют
случайный характер, то задача называется стохастической.
В зависимости от полноты априорной и текущей информации о
состоянии объекта, о возмущении z(t) и задании х3(г), имеющейся и
поступающей в управляющее устройство, все системы оптимально-
го управления делятся на системы: 1) с полной (максимально воз-
можной) информацией; 2) с неполной информацией и пассивным ее
накоплением в процессе управления; 3) с неполной информацией и
активным ее накоплением.
Системы с полной информацией работают по «жестким» зако-
нам управления с постоянными настроечными параметрами. Систе-
мы с пассивным и активным накоплением информации изучают ус-
ловия работы объекта и изменяют законы управления согласно этим
условиям, и поэтому они называются адаптивными.
В системах с активным накоплением информации управляющее
воздействие, одновременно с выполнением основной своей функции.
591
осуществляет такое изменение состояния объекта, при котором нака-
пливается максимум информации об объекте и внешних воздействи-
ях. В связи с двойственным характером управления управление в
таких адаптивных системах называется дуальным.
Таблица 11.1
Примеры задач оптимального управления
Огггимизируемый технологический процесс	Критерий оптимальности	Управляющие воздействия	Ограничиваемые переменные
Сжигание газа в топке парового котла	Максимум температуры	Подача возду- ха в топку	Расход топливного газа
Генерирование электрической энергии турбо- генератором	Максимум коэффициен- та полезного действия	Подача пара в турбину	Частота генерируемо- го электрического то- ка
Выемка горной массы роторным экскаватором	Максимум производи- тельности	Скорость бо- кового пере- мещения	Ток и энергия нагрева двигателя, вращаю- щего роторное колесо
Подъем груза шахтной подъ- емной установ- кой	Минимум длительности одного цикла подъема	Движущий мо- мент привод- ного двигателя	Скорость и ускорение подъемного сосуда
Разделение хи- мической смеси в дистилляци- онной колонне	Максимум коэффициен- та извлечения полезного компонента	Подача ката- лизаторов в колонну	Содержание полезно- го компонента в вы- ходном продукте
Сушка влажного вещества (изде- лия) в сушиль- ной установке	Максимум количества удаляемой влаги	Подача горя- чего воздуха в сушильную установку	Температура в су- шильной камере
Стабилизация выходных и про- межуточных переменных технологическо- го процесса	Минимум дисперсии отклонения от задания	Материальные и энергетиче- ские потоки	Расходы материалов и энергии
592
Решение любой задачи оптимального управления и последую-
щая реализация найденного алгоритма в конкретной системе связа-
ны, как правило, с большими трудностями математического и техни-
ческого характера. Поэтому при создании оптимальных систем стре-
мятся либо предварительно упростить математическое описание
объекта, либо реализовать алгоритм приближенно. Такие системы,
синтезированные с упрощениями модели объекта или алгоритма
управления, называются близкими к оптимальным или квазиопти-
малъными.
В заключение приведем несколько примеров задач оптимально-
го управления технологическими объектами (табл. 11.1).
11.2. Принцип максимума и
метод динамического программирования
В теории управления для оптимизации функционалов вида
(11.20), (11.21) при наличии ограничений на векторы управления и
состояния применяют принцип максимума и метод динамического
программирования, разработанные в 1956-1957 годах российским и
американским математиками Л.С.Понтрягиным и Р.Веллманом на
основе классических методов вариационного исчисления Эйлера,
Лагранжа.
Принцип максимума Понтрягина. Пусть объект описывается
следующей системой нелинейных уравнений состояния:
*,(') =	yi(t),...,у„(0]; 1 = 1; 2;3; ..л	(11.33)
или в векторной форме
Х(0 = [/>('),
(11.34)
Заметим, что уравнения (11.33) не содержат в явном виде время
t и описывают так называемые стационарные или автономные объек-
ты. Уравнения нестационарных объектов, у которых время t явно
входит в функции f, можно привести к виду (11.33), если вместо пе-
ременной t рассматривать условную координату x„-i, заданную диф-
ференциальным уравнением
593
=	(11.35)
и удовлетворяющую начальному условию x«+i(0) = 0. При этом к
системе (11.33) добавится еще уравнение (11.35), а размерность про-
странства состояний станет равной п + 1.
Положим, что нелинейные функции f непрерывны по всем ар-
гументам и непрерывно дифференцируемы по компонентам вектора
состояния х. Исходя из физических соображений, принимаем также,
что составляющие вектора управления у являются кусочно-непре-
рывными функциями времени, которые по модулю не превышают
заданные максимально допустимые значения у7М.
У/0 О7М; J = l;2;...,w.
(11.36)
Ограничения (11.36) можно записать и в векторной форме
или y(t) е X,
(11.37)
где y(t) и ум - векторы-столбцы соответственно модулей и макси-
мальных значений управляющих воздействий у70); Y - ограниченное
множество в виде w-мерного параллелепипеда со сторонами 2уум
Заметим, что в общем случае допустимые значения положи-
тельных и отрицательных управляющих воздействий могут быть
различными, и тогда вместо ограничений (11.36) используют нера-
венства
у;м<у7<Уум; j = l;2;...;w,	(11.38)
где у+/м > 0 и у JM < 0 - допустимые по техническим условиям значе-
ния соответственно положительных и отрицательных управляющих
воздействий.
Задача оптимального управления заключается в следующем:
Среди всех допустимых управлений (11.36) или (11.38) найти такой
вектор у(0, который переводит объект (11.34) из заданного начально-
го состояния х(0) = хн в требуемое конечное состояние х(/к) = хк и
обеспечивает при этом минимум функционала
594
(11.39)
О
где функция fo также удовлетворяет условиям гладкости, принятым
для функций fi, а момент времени tK может быть заранее задан или
быть свободным.
Искомый вектор управления и соответствующий ему вектор со-
стояния называют оптимальными и обозначают у (t) и х (/).
Введем в рассмотрение еще одну переменную состояния, опре-
деляемую с помощью интеграла
М') =
о
где fo - функция из критерия (11.40) и 0 < v < t < tK.
Очевидно, что
хо(О) = О и x0(tK) = Q.
(11.40)
(11.41)
Дифференцируя выражение (11.40) по аргументу 3, получим
уравнение
*»=/»[*('),2«)],	(11.42)
которое можно присоединить к исходной системе (11.33). Тогда вме-
сто (11.33) образуется расширенная система уравнений состояния
х,	1 = 0;1;...;п.	(11.43)
Вводя теперь в рассмотрение (п + 1) - мерный вектор состояния
х (/) = [хо(0, Xi(t), ..., х„(/)]т; можно систему (11.43) записать в виде
следующего векторного уравнения состояния:
£ = £[*('), 2<')],	(11.44)
где / = [/о, f ]т - вектор правых частей системы (11.43).
595
Обратим внимание на то, что вектор-функция f не зависит от
дополнительной переменной х0.
Теперь исходную задачу управления можно сформулировать
так: среди всех допустимых управлений можно найти такое, которое
дает решение х (/) уравнения (11.44), удовлетворяющее граничным
условиям х(0) = х (0) = хн, x(G) = хк и имеющее минимальную ордина-
ту7 x*(tK) точки x*(zK) в расширенном (и+1)-мерном пространстве
состояния.
Для решения этой преобразованной задачи с использованием
принципа максимума вводят вспомогательную вектор-функцию
V(0 ~ ['Ио(О,	> Ч'пО)]7, компоненты которой удовлетво-
ряют системе дифференциальных уравнений
=	<=0,(11.45)
в которой частные производные определены вдоль оптимальной тра-
ектории х (/)•
Так как ни одна из функций / не зависит от переменной х0, то
уравнение (11.45) для вспомогательной переменной имеет вид
у0 = 0, а сама переменная ~ const.
Формулировка принципа максимума: управ-
ляющее воздействие Я 0 является оптимальным по критерию (11.39),
если в любой момент времени скалярное произведение Н вектор-
функций у(0 и/[х(0, y(OL вычисляемое вдоль оптимальной траек-
тории х*(/), достигает максимума, т.е. если
я = я [ф(о, /[*(0, яо] = Ф т7[яо, Я0.

max;
0<t <L.
№
(11.46)
596
При этом вспомогательная функция \|/о(О всегда будет представ-
лять собой неположительную константу, которую можно принимать
произвольной, например, x|r0 = -1.
В рассматриваемой задаче с функциями f и fo, не зависящими
явно от времени t, максимальное значение п , соответствующее оп-
тимальному управлению у_ (t), является константой на всем интерва-
ле 0 < t < tK, т.е.
Н' =я{£(0.х’(0,/(')}= const,	(11.47)
а в частном случае, когда конечный момент времени tK не задан, Я*
тождественно равно нулю.
Заметим, что в общем случае - для нелинейного объекта (11.33),
(11.34) условие (11.46) принципа максимума является лишь необхо-
димым, а для объекта с линейными функциями f оно является одно-
временно и достаточным.
Применительно к механическим объектам управления функции
ft означают обобщенные скорости движения, функции ц/, - обоб-
щенные импульсы (количества движения), а гамильтониан Н выра-
жает полную механическую энергию, равную сумме кинетической и
потенциальной энергии. Как известно, полная энергия консерватив-
ной механической системы остается в процессе движения неизмен-
ной и равной нулю. Всякое уменьшение полной энергии будет сви-
детельствовать о диссипативных потерях (на трение и т.п.), и следо-
вательно, - о неоптимальности движения. Именно поэтому гамиль-
тониан Н, согласно принципу Понтрягина, и должен быть макси-
мальным.
Принцип максимума позволяет во многих практических случаях
выбрать оптимальный вектор управления у (/) непосредственно по
виду зависимости скалярной величины Н от вектор-функции yft) и
обойтись тем самым без решения сложной вариационной задачи на
условный экстремум. При этом оптимальный закон управления у (/)
удается выразить через вспомогательные функции ц/, (f).
Вспомогательные функции удобно находить из следующей
симметричной системы уравнений.
597
( dxjdt = дН! дуг\
dyjdt -~дН/дк{,
(11.48)
объединяющей уравнения объекта (11.44) и вспомогательные урав-
нения (11.45) и называемой системой Гамильтона. (Именно поэтому
величину Н называют иногда гамильтонианом).
В том, что система Гамильтона (11.48) действительно объединя-
ет указанные уравнения, нетрудно убедиться, если учесть, что
(11.49)
Пример 1. Проиллюстрируем методику решения задач оптимального
управления с использованием принципа максимума на сравнительно про-
стом примере. Пусть имеется линейный объект
И'о(р) =	Р2 ,
(11.50)
который требуется за конечное время /к перевести из начального состояния
х(0)=х1н, х (0)=х2н в конечное состояние х(/к)=х1к, х (4)=*2к таким образом,
чтобы энергия, затрачиваемая управляющим устройством, была минималь-
ной, т.е. чтобы обеспечивался минимум функционала
Q=]y\t}dt.
о
(11.51)
Уравнения состояния объекта, соответствующие передаточной функ-
ции (11.49), имеют вид
xi(0 = x2(0, х2(0 = ^оХ0,
(11.52)
гдех](0 = хв(0.
Для отыскания вспомогательных функций ц/,(0 запишем выражение
для гамильтониана (11.46)
Н =^ofo+^fl + V2/2 =Vo(Oy2(f) + V](f>2(O+V2(r)/cO.V(O
(11.53)
598
Применяя второе из соотношений (11.48), получаем
tfyo/t7/ = O; =	(й|/2М = -У1,	(11.54)
откуда
VoO) = Co; v1(/) = C1; y2(j) = -C\t+С2.	(11.55)
Теперь гамильтониан (11.53) принимает вид
н = С „у2 (>)+С| х2 т+(С2 - С,	(11 56)
Условие максимума гамильтониана Н по управлению у(0 дает
у у
дН/ду = 2C0y(t)+ С2 - C}t = 0,	(11.57)
откуда закон управления
y(t) =
(11.58)
Умножая управляющее воздействие (11.58) на ПК ко и интегрируя его
по времени, получаем
(11.59)
(11.60)
Подставляя заданные граничные условия в выражения (11.59) и
(11.60), можно найти постоянные интегрирования Сь С2, С3 и С4.
Метод динамического программирования. Метод основан на
сформулированном Р.Веллманом принципе оптимальности: опти-
мальная траектория любой управляемой динамической системы в
каждой промежуточной точке x(t) обладает тем свойством, что, како-
вы бы ни были первоначальное состояние и первоначальное управ-
ление, последующее управление должно быть оптимальным относи-
тельно этого состояния х(/), полученного в результате первоначаль-
ного управления. Принцип оптимальности утверждает, что каждый
участок оптимальной траектории от любой ее промежуточной точки
599
x(t) до конечной точки х(Гк) также оптимален по рассматриваемому
критерию. Так, если имеется единственная оптимальная траектория
1-2 (сплошная линия на рис. 11.4) и на ней рассматривается промежу-
точная точка x(f), то, согласно принципу оптимальности, оптималь-
ной для «начального» состояния x(t) будет траектория 2 (независимо
от того, по какой траектории система пришла в указанную точку). В
справедливости этого утверждения нетрудно убедиться, рассуждая
от противного. Действительно, если бы между точками х(0 и x(tK)
существовала какая-либо другая оптимальная траектория 2', то для
начального состояния х(0) оптимальной была бы не траектория 1-2, а
траектория 1-2'. А это противоречит исходной посылке, что
траектория 1-2 - единственная оптимальная траектория.
Заметим, что начальный участок 1 оптимальной траектории сам
по себе может и не быть оптимальным.
Вследствие отмеченного принципиального различия конечных и
начальных участков оптимальной траектории при применении мето-
да динамического программирования часто используют процедуру
поэтапной оптимизации траектории с попятным движением от ко-
600
нечного состояния к начальному: вначале оптимизируют самый по-
следний отрезок траектории, затем прилегающий к нему предпо-
следний и так далее все предшествующие отрезки до заданного ис-
ходного состояния х(0). При этом на каждом шаге такой поэтапной
оптимизации приходится делать серию предположений о возможных
исходах управления на предыдущем шаге (еще не найденного!), для
каждого из предположений находить оптимальное управление и зна-
чение функционала на рассматриваемом текущем шаге и выбирать из
серии найденных управлений то, которое совместно с уже выбран-
ными для последующих отрезков управлениями обеспечивает общий
минимум функционала.
Несмотря на то, что принцип оптимальности был сформулиро-
ван Р.Веллманом с помощью чисто эвристических, интуитивных
рассуждений и что сама формулировка принципа имела чисто каче-
ственный, нематематический, характер, в дальнейшем на его основе
был разработан строгий математический метод оптимизации, полу-
чивший название динамического программирования и широко ис-
пользуемый как для дискретных, так и для непрерывных систем
управления.
Рассмотрим сущность метода динамического программирова-
ния применительно к непрерывным системам. Пусть имеется неста-
ционарный объект управления, описываемый нелинейным вектор-
ным дифференциальным уравнением
i(0 = Z[x(O, ж 4	(11.61)
и пусть требуется найти управление y(t), минимизирующее функ-
ционал
et(O, t J = JЛ[г(ло, y(t), t]dt	(11.62)
0
при заданных начальном состоянии х(0) = хн, конечном времени G,
ограничении ХО е У и произвольном конечном состоянии х(4)
Согласно принципу оптимальности каждое текущее значение
времени t на заданном интервале 0 < t < может быть выбрано в
601
качестве начала отсчета, и оптимальное управление у* (/), миними-
— 1-2
зирующее функционал (11.62) на этом интервале, будет совпадать на
интервале t < 3 < tK с оптимальным управлением у* (3), минимизи-
—2
руюгцим функционал

]= ]f^(y,9),y(9},9]d9,
I
(11.63)
причем минимальное значение Q - S функционала (11.63) будет
(при найденном оптимальном управлении!) зависеть только от на-
чального для участка 2 состояния х(0 и длительности tK - t процесса
управления:
К Г	1
min	=	0<Г</к.	(11.64)
£ *
отсюда с учетом уравнений объекта (11.61)
-~~ = fo[x(y,t),y(t),r]+	£(0,4	(11.66)
dt	,=i их.
Уравнение (11.66) справедливо для любого допустимого управ-
ления y(t) 6 У, не выводящего объект на границу области F. При
оптимальном управлении y(f) это уравнение с учетом выражения
(11.64) приобретает вид
602
~~dt=	+4 <11 -67)
o<js/k
Уравнение (11.67), называемое уравнением Беллмана, можно за-
писать в более компактных формах:
= min
,у(«)еГ
0<г<?к
x(y,t), y(O,q+
(11.68)
/|*(о, мо, Ф
или
— = min {f0 |х(>>, Г), y(t), J+(gradS, /[х(0, y(t), ф }, (11.69)
Qi y(t)zY '	—	—	\	—*•	— J / '
0<t<tK
где (dSIdxf = dS!dx}, dSldx2, ... , dS/dx^ =dS/dx'1 - вектор-стол-
бец, соответствующий градиенту grad S скалярной функции S век-
торного аргумента х; (...) - обозначение скалярного произведения
векторов.
Уравнение Беллмана представляет собой специфическое диффе-
ренциальное уравнение первого порядка в частных производных
относительно одной переменной У Специфичность уравнения за-
ключается в том, что оно содержит операцию минимизации по аргу-
менту v(0 и поэтому справедливо только для оптимального управле-
ния у (г).
Уравнения (11.67)-( 11.69) выражают необходимое условие оп-
тимальности управления и определяют порядок решения задачи оп-
тимального управления методом динамического программирования.
На первом этапе минимизируют выражение в правой части, для чего
дифференцируют ее по управлению y(t) и приравнивают производ-
ную нулю. В результате минимизации оптимальное управление y(t)
выражается через функции f0, f и не известные пока составляющие
градиента S:
У (0 = /|/о» L gradS] = /[х(0, gradS1].	(11.70)
603
При подстановке выражения (11.70) в уравнение (11.69) послед-
нее уже не будет содержать операцию минимизации и управление
у*(0 и поэтому может быть разрешено относительно неизвестной 5
при граничном условии
st(',vj=o.
(11.71)
Получив, наконец, функцию 5 [х(г), /] и ее градиент gradS’ по ар-
гументу х и подставив его в формулу (11.70), выражают оптимальное
управление через переменные состояния x(t).
В заключение отметим, что в случаях, когда функции f и fQ не
зависят явно от времени t, функция S также не зависит от времени, и,
следовательно, dS/dt = 0.
Пример 2. Определим для стационарного линейного объекта
wokp) =	= к о!р(гор +1)
(11.72)
оптимальное управляющее воздействие у (/), стабилизирующее объект в
положении xi(0) = х2(0) = 0 и обеспечивающее минимум функционала
С[ИО]= 1 |?*в (О+rv2 (f
о
где q,r- положительные константы.
Уравнения состояния объекта
^(0 = х2(0; *2(0 = ax2{t) + by{t),
(11.73)
(11.74)
где Xi(0 = хв(/)„ а = -UT0, b = kJTo.
Для стационарного объекта и функционала, не зависящего явно от
времени, уравнение Веллмана имеет вид
7	> СЛ?
+гу“ +------х2
и о	дх\
(11.75)
Найдем производную выражения в скобках по управлению и прирав-
няем ее нулю:
604
откуда
/(0 =
b dS
2r dx2
(11.76)
(11.77)
После подстановки выражения (11.77) в уравнение Беллмана прихо-
дим к нелинейному дифференциальному уравнению в частных производных
первого порядка
4х?
(11.78)
которое необходимо решить при граничном условии S' [г (оо)] = 0.
Решение уравнения (11.78) будем искать в виде квадратичной формы
5(х1>х2) = с11*12 +2сиХ1Х2 +С22х2
(11.79)
с неопределенными коэффициентами Си, С12, С22, удовлетворяющей ука-
занному граничному условию.
Подставив функцию S’ и ее производные в уравнение (11.78) и при-
равняв нулю коэффициенты, получающиеся при слагаемых х?. х\х2, х2,
получим
(И 80)

Коэффициент Сн нет необходимости определять, так как управление
у зависит только от производной dS/dx2, в которую этот коэффициент не
входит.
Теперь при найденных значениях коэффициентов (11.80) можно вы-
числить производную dS/dx2 и записать окончательное выражение для оп-
тимального управляющего воздействия
являющегося, очевидно, линейной функцией переменных состояния.
605
Связь метода динамического программирования с принци-
пом максимума. Применим уравнение Беллмана (11.67) для случая,
когда функции/ и fQ не зависят явно от времени, т.е. когда dS/dt = 0.
Напомним, что к такому случаю можно свести и задачу с нестацио-
нарными объектом (11.61) и функционалом (11.62). Для этого необ-
ходимо лишь ввести дополнительную переменную состояния х„+],
удовлетворяющую уравнению (11.35).
Расширим вектор-столбец градиента функции S в формуле
(11.69) на один элемент, равный единице, и обозначим его
(11.82)
Учтем, что минимум положительной функции равен взятому с
противоположным знаком максимуму совпадающей с ней по модулю
отрицательной функции. Тогда вместо уравнения (11.67) можно за-
писать
0 = max
,У(/)€У
... У т >
> = тах)ю i
(11.83)
Сопоставляя полученное выражение с условием (11.46) принци-
па максимума, легко убедиться, что они идентичны, если вектор ср
отождествить с вектором у, т.е. если
(11.84)
или
= -1;^ = -dS/дх^ у/г = -cS/dx2, ...,уп = ~dSjdxit.
(11.85)
Поясним смысл выбора оптимального управления в соответст-
вии с выражением (11.83). Для этого введем вспомогательную функ-
цию
Л — >5 (Xg , Xj ,. . ,,Хя ) ^(Хд , Х| , . . .,Хп )+ Хд ,	(11.86)
606
где 5' определяется формулой (11.64), а составляющая х0 - формулой
(11.40). Переменная S' является непрерывной функцией точки в рас-
ширенном пространстве состояния х , и в этом пространстве сущест-
вуют изоповерхности S = const равных значений функционала
(11.63). Согласно выражениям (11.84), (11.85), вектор у является
взятым со знаком минус градиентом скаляра S в пространстве х, и,
следовательно, как любой градиент, ортогонален в любой точке х к
изоповерхностям S = const и к вектору касательной х = f, который
имеет смысл вектора скорости движения изображающей точки х.
Таким образом, условие максимизации скалярного произведе-
ния векторов у и f означает следующее: необходимо в каждый
момент времени выбирать такое управление & чтобы проекция век-
тора скорости х, изображающей точки на вектор отрицательной
нормали к изоповерхностям критерия оптимальности была макси-
мальной, т е. чтобы составляющая вектора х в направлении наиско-
рейшего убывания функционала О была максимально большой. При
этом проекция оказывается отрицательной, а ее максимальное значе-
ние равно нулю.
11.3. Системы, оптимальные по быстродействию
Синтез алгоритмов разомкнутого управления. Применим
принцип максимума для синтеза оптимального по быстродействию
закона управления у (t) линейным стационарным объектом вида
(2.169), который при отсутствии возмущения z(t} описывается систе-
мой уравнений
п	т
МО =
j=i	/=1
(11.87)
607
или одним векторным уравнением
Х(0 = 4 х(0 + £?(0-
(11.88)
Пусть требуется перевести объект из начального состояния
х(0) = хн в конечное состояние х(гк) = хк за минимально возможное
время при ограничениях на управление

(11.89)
Заметим, что при решении задач синтеза замкнутых СУ удобно
в качестве переменных состояния рассматривать не абсолютные зна-
чения координат объекта, а отклонения координат от некоторой из-
вестной вектор-функции xjt), которая задана заранее или формиру-
ется задающим устройством системы в процессе управления.
Оптимизируемый функционал в задаче максимального быстро-
действия имеет, как известно, вид
SWO = I .У('). t\dt = (,= min
(11.90)
т е. подынтегральная функция^ = 1.
С учетом последнего тождества и введенного в предыдущем
разделе условия vg0 = -1 гамильтониан (11.46) для объекта (11.87),
(И.88) примет вид
т Г	1	и	п	т
Я = -1 + уг (0Ц X(t) + Ду(Г)] = -1 + Z Vi (0 Z atj х} (0 + S bt] у J (t)
n	n	n	m
= -1 + S v,(<)	+Sv, (0 SM/0,
1~1	I—I
(11.91)
где функции определяются вспомогательной системой уравне-
ний (11.45)
608
у, (0 = йЯ/йг,	/ = 1;2;...;и
j=i
или в векторной форме
(11.92)
И0 = -4гИ0-
(11.93)
От управляющего воздействия v(f) зависит только третье сла-
гаемое в выражении (11.91), поэтому условие достижения максимума
гамильтониана Н сводится к условию
п	т
max
или
т	п
У тахуДОУ^УЛО-
Яyj(t)	%
(11.94)
(1195)
Так как каждая составляющая у,(/) изменяется независимо от ос-
тальных составляющих вектора у(t), то выражения (11.94) и (11.95)
достигают максимума, если все у7(0 принимают свои максимально
допустимые значения, т.е. если
Л
Т*(0 =	J' = 1; 2;...;т,
i=i
(11.96)
или в векторной форме
y\t) = y sign[BT v(0] = У sign [я r],
—	—м	—	—м
(11.97)
где у м - диагональная матрица т х т, состоящая из максимально
допустимых значений у,м; sign [/Zv] = {sign НУ1}т , i - матрица -
столбец; Ну — дН/ду; = дН/ду}
609
Записи (11.96) и (11.97) означают, что оптимальные управляю-
щие воздействия у (/) представляют собой кусочно-постоянные
функции времени, принимающие в зависимости от знака суммы
V, (0 значения +у/м или - yJU (рис. 11.5), т.е.
i=i
Рис. 11.5. Управляющее воздействие в системе
с максимальным быстродействием
Моменты переключения управляющих воздействий и, следова-
тельно, длительности интервалов постоянства зависят от заданных
начальных и конечных состояний хн и хк, вида ограничений y(t)eY и
от собственных чисел X, матрицы А.
Закон управления (11.96), (11.97) справедлив, если функция,
стоящая после символа sign, принимает нулевые значения только в
изолированных точках. Если же эта функция обращается тождест-
венно в нуль на каком-либо конечном интервале времени, то задача
управления относится к классу особых задач оптимального управле-
ния, для решения которых применяются специальные методы.
Как видно из выражения (11.96), для получения оптимальных
управляющих воздействий в виде известных функций времени у* (/)
610
необходимо найти вспомогательные функции (/), которые являют-
ся решениями системы уравнений (11,92). Вид этих решений зависит
от начальных условий \j/(0) и от собственных значений ц, матрицы
Лт, которые, как известно из теории матриц, связаны с собственными
значениями X, матрицы А соотношением
/ = 1;2;...;л.	(11.99)
Равенство (11.99) означает, что если объект (11.88) устойчив, то
решения (Г) неустойчивы. Это обстоятельство уже само по себе
существенно затрудняет отыскание функций \|/,(/). Кроме того, слож-
ность решения вспомогательной системы уравнений (11.92) опреде-
ляется еще и тем, что начальные условия \|л(0) заранее неизвестны, и
в общем случае их нельзя выразить в аналитической форме через
граничные условия хн и хк основной системы уравнений (11.87). По-
этому условия (0) приходится подбирать методом последователь-
ных приближений до тех пор, пока управления уу(/), получающиеся
при выбираемых значениях ц/, (0), не обеспечат выход вектора х(Г) в
заданное конечное состояние хк.
Однако во многих практических случаях задачу синтеза разом к-
нутой системы с максимальным быстродействием удается решить
без отыскания функций у,-(/). При этом дополнительно к принцип}
максимума используют теорему об п интервалах.
Теорема об п интервалах, сформулированная и
доказанная в 1953 г. российским ученым А.А. Фельдбаумом, утвер-
ждает следующее. Если все корни характеристического уравнения
линейного объекта (11.88) (т.е. собственные значения X, матрицы А)
- действительные числа, то каждая из составляющих у* (t) опти-
мального вектора управления у (/) в задаче (11.88) - (11.90) имеет нс
более п интервалов постоянства своих предельных значений у,м (т.е.
не более (и - 1) переключений с одного предельного значения на
другое), где п - порядок системы уравнений объекта
Алгоритмы оптимального управления, найденные как вектор-
функции времени у (t), могут быть реализованы при помощи разомк-
нутой системы (рис. 11.6,а), состоящей из задающего, вычислитель-
ного и исполнительного устройств. Задающее устройство ЗУ форм и-
611
руст программу управления х3(/) как функцию сигнала времени л
вырабатываемого специальным датчиком (таймером). Вычислитель-
ное устройство ВУ, в зависимости от известных начальных условий
х(0) и задания х3(/), эквивалентного желаемому конечному состоянию
хк, определяет моменты переключения tjs каждого управляющего
воздействия уг Далее вычислительное устройство выдает в рассчи-
танные моменты времени ts команды уп на переключение исполни-
тельного устройства ИУ из одного крайнего положения в другое.
Моменты переключения зависят также от возмущения z, и по-
этому при его наличии управление в разомкнутой системе может
быть осуществлено лишь в том случае, если возмущение известно
как функция времени z(t).
Рис. 11.6. Разомкнутая (а) и замкнутая (б) системы
с максимальным быстродействием
В заключение надо отметить, что определение моментов пере-
ключения в общем случае является весьма сложной задачей, и по-
этому системы с максимальным быстродействием предпочтительней
конструировать как замкнутые.
612
Синтез алгоритмов замкнутого управления. При синтезе
замкнутой системы управления (рис. 11.6,6) дополнительно к прин-
ципу максимума используют метод фазовых траекторий, с помощью
которого определяют уравнения поверхностей переключения
£б..у<=0; / = l;2;...;/w
(11.100)
и так называемые переключающие функции
п
(11.101)
принимающие нулевые значения на поверхности переключения.
Поверхность (линия) переключения в силу непрерывной зави-
симости оптимальной траектории х (г) от начальных условий х(0)
представляет собой непрерывную кусочно-гладкую поверхность
(линию), которая разделяет пространство состояния х на две области,
соответствующие разным знакам управляющего воздействия. Форма
и положение поверхности переключения зависят как от вида и пара-
метров уравнений объекта, так и от вида и параметров внешних воз-
действий x3(f) и z(Z). Если в качестве переменных состояния приняты
отклонения б,(0= x3i(t) - х,(Г), то поверхность переключения обяза-
тельно проходит через начало координат, в котором заканчивается
переходный процесс, начавшийся из любого начального состояния
е(0). Если порядок внешнего воздействия в виде степенной функции
(см.4.4) меньше порядка астатизма объекта, то поверхность пере-
ключения кососимметрична относительно указанного начала коор-
динат.
На рис. 11.7 показана не кососимметричная линия переключения
АОВ для объекта второго порядка, которая делит фазовую плоскость
X! - х2 на две области (заштрихованы под разным наклоном), соот-
ветствующие различным знакам управляющего воздействия, ниже
линии + vM и выше -ум. Причем, ветвь АО соответствует -vM, а ветвь
ОВ - значению +ум. Очевидно, что в зависимости от начального со-
стояния объекта могут иметь место следующие варианты управляю-
613
Рис. 11.7. Линии переключения для ОУ
второго порядка
щих последовательностей, переводящих объект в начало координат.
Если точка начального состояния расположена выше линии пере-
ключения (например, точка Л/i), то вначале управляющее воздейст-
вие должно быть отрицательным, а затем в точке Л/2, расположенной
на линии переключения, управляющее воздействие должно стать
положительным. Если же начальная точка расположена ниже линии
переключения (например, точка М), то управление вначале положи-
тельное, а затем в точке N2 на линии переключения должно стать
отрицательным. В частных случаях, когда начальная точка сразу
оказывается на одной из
ветвей линии переключе-
ния (точки А и В), изме-
нять знак управления в
течение переходного
процесса вообще не тре-
буется.
Знак управляющего
воздействия на первом
интервале определяется
знаком переключающей
функции уп в начальной
точке. Переключающую
функцию стремятся
обычно записать так, чтобы ее знак по обе стороны линии переклю-
чения совпадал со знаком управляющего воздействия, т.е. чтобы
при
при
(11.102)
Таким образом, задача синтеза оптимальной по быстродействию
замкнутой системы сводится к отысканию в пространстве состояния
переключающей функции уп(х) и к ее реализации в вычислительном
устройстве. Оптимальные управляющие воздействия, равные соглас-
но выражениям (11.96) и (11.101)

(11.103)
614
окончательно формируются двухпозиционным исполнительным уст-
ройством, выходные переменные которого принимают только мак-
симальные значения + yJM и - у;м.
Отыскание уравнений поверхностей переключения и переклю-
чающих функций является в общем случае довольно сложной зада-
чей. Особенно задача усложняется при наличии внешних (задающих
или возмущающих) воздействий. В таких случаях приходится либо
заранее учитывать эти воздействия в уравнении объекта, либо изме-
рять их и вводить соответствующие сигналы в вычислительное уст-
ройство, реализующее переключающую функцию. При этом поверх-
ность переключения и переключающая функция оказываются неста-
ционарными, «плавающими» в пространстве состояния.
Сравнительно просто переключающие функции можно найти
лишь для некоторых частных случаев - когда объект описывается
уравнением не выше второго порядка, а внешние воздействия пред-
ставляют собой степенные функции с порядком, не превышающим
порядок объекта.
Пример 1. Пусть дан объект, описываемый линейным дифференци-
альным уравнением второго порядка
*в(0 =
(11.104)
или системой двух уравнений первого порядка
-П (/) = *2 (/); т2 (/) = kQy(t).
(11.105)
где X] = хв. Уравнения (11.104), (11.105) соответствуют широкому классу
механических объектов, в которых происходят процессы перемещения
больших масс без трения. Применительно к таким объектам переменная хв
означает линейное или угловое перемещение, а переменные iB и .гв - соот-
ветственно линейные (угловые) скорости и ускорения. Управляющим воз-
действием у является сила или момент, создаваемые приводом. Коэффици-
ент к0 в таком случае равен единице, деленной на массу или момент инер-
ции.
Требуется найти алгоритм разомкнутого управления y(t), обеспечи-
вающий перевод объекта из заданного начального состояния х(0) = хн = [ xiH,
х2н ]т в заданное конечное состояние х(О = хк = [х1к. х2к]т за минимальное
время и при ограниченном управляющем воздействии I у | < ум. Заметим,
615
что применительно к рассматриваемому объекту ограничение управления
эквивалентно ограничению ускорения:
или
(11.106)
(11.107)
где лм и ум - заданные максимально допустимые по технологическим усло-
виям значения ускорения и момента.
Для удобства решения задачи целесообразно начало координат про-
странства состояний выбрать в точке л>, т.е. полагать, что xiK = 0 и х^ = 0, а
Рис. 11.8. Оптимальные переходные
процессы для ОУ (11.104)
под начальными значениями х]н и х2н
понимать уже начальные координаты
в этой новой системе отсчета.
Согласно теореме об п интерва-
лах, оптимальное управление у (С) для
данного объекта второго порядка
должно иметь два интервала постоян-
ства и одно переключение. Таким
образом, задача сводится к отыска-
нию моментов реверса /п и отключе-
ния 4 управляющего воздействия.
Для этого запишем решения
системы уравнений (11.105) для двух
интервалов времени:
при 0 < t < /п
*2(0 =-*оУм+СИ •	|
х)(0 - \“^оУм Z“/2/+Ci]Z + С\2,J
(11.108)
при
= роУм /“Aj+Cji?+C22J
(11.109)
Используя граничные условия Х)(0) = xjH, х2(0) = х2н; Xj(ZK) = 0, х2(/к) = 0,
находим следующие значения постоянных интегрирования:
616
С] 1 ~ х2ц ’ С2| ~ ^Ih ’ ^-"12 ~ ^оТм^к ’ С22 ~ ^оУм^ к /^ •	(11.110)
Моменты времени гп и tK будем искать методом «сшивания решений.
Условия «сшивания» решений уравнений (11.108) и (11.109) в момент t = /п
имеют вид
(11.111)
Решая совместно систему (11.111) с учетом значений постоянных
(11.110), окончательно получаем
Ai ~ (•* 2h/^oJ’m)'*"'V \ 2н/2£о.Ум )** 1и/^оУм >	(11.112)
ZK = 2/п — X 2к/^оУм ~ % 2н /^оУм 2н/^оУм }^~х 1н/^оУм (11.113)
На рис. 11.8 приведены оптимальные для данного объекта переходные
процессы при произвольных начальных условиях х1н > 0 и х2н > 0.
Пример 2. Определим для объекта (11.104), рассмотренного в преды-
дущем примере, оптимальный алгоритм замкнутого управления v*(x) или
у’(е), обеспечивающий за минимальное время перевод объекта в режим
слежения выходной величины хв(0 за некоторым задающим воздействием
х3(0-
Структура управляющего устройства, реализующего алгоритм у*(е),
зависит от вида воздействия x3(z).
Рассмотрим вначале наиболее простой случай, когда воздействие х3
является ступенчатым, т е. x3(f) = х1з(0 = Х]Ко(г), а начальные условия нуле-
выми: xi(0), х2(0) = 0. Тогда в качестве переменных его состояния объекта
можно принять сигнал ошибки е = ej = х3 - хв = х3 - Х; = х)к - xj и его произ-
водную Ё = с2 = х3 - х2 = - х2, для которых уравнения объекта (11.105) так-
же справедливы:
£1=£2; &2 = -коу-	(11.114)
Для определения переключающей функции и синтеза управляющего
устройства применим метод фазовых траекторий. Исключая из уравнений
(11.114) величину dt, находим дифференциальное уравнение фазовых траек-
торий
£2J£ = -А'оу'г/£[.
(11.115)
617
Интегрируя выражение (11.115), получаем уравнения фазовых траек-
торий в плоскости Е] - е2:
при у = + ум
е|=4гМ.)'м)+С,;	(11.116)
при у = - уи
(11.117)
На фазовой плоскости (рис. 11.9) уравнению (11.116) соответствует се-
мейство парабол с ветвями, направленными влево, а уравнению (11.117) -
семейство парабол с ветвями, направленными вправо. Смещение вершин
парабол по оси Е] определяется постоянными интегрирования С] и С2, зави-
сящими от начальных условий Е] (0) и в2(0).
Рис. 11.9. Фазовые траектории и линии переключения СУ объектом (11.104)
Так как по условию примера процесс должен закончиться в начале ко-
ординат е = 0. то на последнем этапе процесса изображающая точка будет
двигаться обязательно по одной из двух парабол, проходящих через начало
координат. Причем, согласно общему свойству фазовых траекторий
(см. 10.3), движение к началу координат может происходить лишь по одной
ветви каждой параболы, при е2 > 0 - по ветви АО, при е2 < 0 - по ветви ВО
Эти две ветви, принадлежащие параболам из разных семейств, можно
описать одним общим уравнением
618
ej = -E ^sign£2/2fcoyM = -8 5|е2|/2*оум .
(11.118)
Если в начальном состоянии изображающая точка с(0) расположена
выше линии ЛОВ (как. например, точка 0. то под воздействием управления
v = + ум система будет двигаться к завершающему участку' ВО по траекто-
рии CD, подчиняющейся уравнению (11.116). Если же точка расположена
ниже линии АОВ, то у = - ум. и движение происходит по одной из траекто-
рий (11.117) до ее пересечения с ветвью АО.
В обоих случаях при попадании изображающей точки на линию АОВ
происходит переключение управляющего воздействия с одного предельного
значения на другое. Таким образом, линия АОВ является линией переклю-
чения.
Теперь, зная уравнение линии переключения, можно синтезировать
вычислительное устройство (рис. 11.10), которое реализует переключаю-
щую функцию
Уп(е1 >е2)= е) +е	>	С1 И 19)
равную нулю на линии переключения (11.118).
Рис. 11.10. Фазовый портрет системы стабилизации температуры
Статическая характеристика нелинейного элемента НЭ. входящего в
ВУ. соответствует второму слагаемому переключающей функции.
Исполнительное устройство ИУ описывается функцией
У = yMsignyn
(11.120)
619
Очевидно, что в точках, расположенных правее линии переключения,
функция уп > 0 и управляющее воздействие согласно выражению (11.120)
равно +ум. а в точках, расположенных левее, функция уп > 0 и у = - ум.
Для случая, когда задающее воздействие х3 является функцией време-
ни. переключающая функция становится сложнее. Причем, воздействие х3
должно удовлетворять определенному условию: максимальное значение его
второй производной г, м в установившемся режиме не должно превышать
допустимое ускорение объекта, т.е. I хзм I < ко у*.
Уравнения состояния объекта при наличии меняющегося воздействия
принимают вид
ei=e2; ё2=х3-/гоум.	(11.121)
Исключая из них время, можно аналогично получить переключающую
функцию
Уп(е1»е2)=е1 +е зЫ/^оА'мгЛ IellAo^M 	(11.122)
Вычислительное устройство в данном случае будет содержать еще до-
полнительные элементы, которые формируют сигнал, соответствующий
третьему слагаемому в выражении (11.122).
Полная структура ВУ будет оптимальной и для частного случая, когда
задающее воздействие меняется ступенчато.
11.4. Системы, оптимальные по квадратичным критериям
Методика синтеза замкнутых линейных СУ, оптимальных по
квадратичным критериям типа (11.20), была разработана российским
и американским математиками А.М. Летовым и Р.Калманом и полу-
чила название методики аналитического конструирования опти-
мальных регуляторов (АКОР).
Рассмотрим сущность методики АКОР вначале применительно
к таким объектам, у которых переменные состояния поддаются
полному и точному наблюдению. Пусть объект
управления стационарен и задан матричным дифференциальным
уравнением состояния
х(Г) = Ax(t) + By(t) + z(r)	(11.123)
и алгебраическим уравнением выхода
620
хв(О = Свх(/),	(11.124)
где х(0 - n-мерный вектор состояния с компонентами x}(t), x2(t),	,
x„(t); y(f) - m-мерный вектор управляющих воздействий у i (t), y2(t),
?.(*) ~ «-мерный вектор возмущающих воздействий zz(t),
z„(t) типа белый шум с известными интенсивностями 570; хв(0 -
/-мерный вектор выходных (управляемых) переменных хв1(/), хв2(/),
xbZ(0, к значениям которых предъявляются определенные требо-
вания при формулировке цели и задачи управления; А = {ау}п >. п,
В = {^у}п х т, Съ= {Cy}i х п - постоянные матрицы, элементы которых
являются параметрами объекта.
Полагаем, что управляющие воздействия y(t) не ограничены и
что между размерностями векторов выполняются следующие соот-
ношения:
п>т>1.	(11.125)
Стабилизирующие системы при полном и точном наблюде-
нии объекта. Простейшей задачей управления является задача ста-
билизации переменных хв(0 на заданных уровнях хвз0 = const. Для
удобства решения эти уровни принимают за начала отсчета перемен-
ных хв(0, и тогда задача стабилизации будет заключаться в удержа-
нии вектора хв(0 в смещенном начале координат хвз0 = 0 с наимень-
шим среднеквадратичным значением отклонения ев(0 = xB(f) - хвз0 =
= хв(0 Причем, по технико-экономическим соображениям всегда
желательно, чтобы при этом среднеквадратичные значения управ-
ляющих воздействий y(t) были также минимальны. Такой формули-
ровке цели управления соответствует минимизация квадратичного
функционала
2о =
t • 2
к О
хв +/(ОгЯоК
(11.126)
где q - {q,i}„ *п иг = {г = {гц}т х т - диагональные матрицы весовых
коэффициентов qti > 0 и > 0, учитывающих «штрафы» за отклоне-
ния компонент векторов хв(0 ид>(0 от нуля.
621
Весовые коэффициенты q„ и г„ подбирают обычно эксперимен-
тально путем последовательных итераций и сравнений процессов
управления, вычисляемых на цифровой модели системы. Успеш-
ность такого подбора зависит от интуитивно-эвристического пони-
мания разработчиком системы сложного механизма влияния весовых
коэффициентов на показатели качества процесса управления. Глав-
ные закономерности влияния таковы. Чем больше значения коэффи-
циентов qih тем шире полоса пропускания замкнутой системы управ-
ления и, следовательно, лучше ее быстродействие. Чем больше зна-
чения коэффициентов rih тем инерционнее система.
Задача стабилизации выходных координат xB(f) по критерию
(11.126) эквивалентна задаче стабилизации переменных состояния
х(Г) по критерию
Q„ = lim -1 [/ (t)qx + yT (Ory(r)]tfr,
'к 0
(11.127)
где q = Cj q*C„.
Согласно теоретическим положениям, разработанным А.М. Ле-
товым и Р.Калманом,
в СУ (рис. 11.11,а), работающей в режиме стабилизации (т.е.
при Xj(t) ~ 0), оптимальные управляющие воздействия у (t), со-
ответствующие минимуму функционала (11.126) или (11.127),
являются линейными функциями переменных состояния:

(11.128)
где - (т х и)-матрица коэффициентов обратных связей между п
переменными состояния и т управляющими воздействиями:
^=CXBTD.
(11.129)
Матрица/) в формуле (11.129) является симметричной положи-
тельно определенной размера п х п и находится как решение нели-
нейного матричного алгебраического уравнения Риккати
622
DA+A'D + Clqj:^D = 0.	(11.130)
Рис. 11.11. Замкнутая СУ, оптимальная по квадратичному критерию:
а - общая структура; б - система стабилизации объекта (11.140)
В задачах программного управления, в которых требуется за ко-
нечное заданное время t* осуществить перевод объекта из некоторого
исходного положения хв(0) в начало координат хв(4) = 0, в решении
вместо алгебраического уравнения (11.130) участвует дифференци-
альное уравнение Риккати с такой же левой частью, но с производ-
ной -D(t) в правой части. При этом матрицы D и Кк становятся
функциями времени, зависящими от заданных начальных условий
хв(0), длительности управления tK и стоимости конечной (терминаль-
ной) ошибки £B(tn), учитываемой с помощью критерия оптимально-
сти вида (11.21).
Обращаем внимание на то, что оптимальные коэффициенты об-
ратных связей в задачах стабилизации не зависят от параметров рас-
сматриваемого случайного возмущения z(f) типа белый шум. Но от
623
этих параметров зависит минимально достижимое при оптимальном
управлении значение критерия (11.127). Так, если z(t) - векторный
белый шум, то минимальное значение О* критерия (11.127) опреде-
ляется выражением

(11.131)
где tr( ) обозначают так называемый след матрицы, который по опре-
делению равен сумме диагональных элементов матрицы, записанной
внутри скобок; S& - матрица интенсивностей компонент вектора z(t),
имеющая размер п х п.
Оптимальная ПФ замкнутой системы стабилизации (см.рис.
11.11), связывающая медленные изменения задания хв 3 с выходом хв,
а при £ = 0 и Кп = 1 равна
ф(р) =s»(^)/s„(^)=C.(pI-4+fi£«l'&	(11.132)
ей соответствует характеристическое уравнение
pl-A + BKJ, = 0.
I
(11.133)
Как и в задачах фильтрации и оценивания (см.8.6 и 8.7), коэф-
фициенты обратных связей можно определять и не по выражениям
(11.129), (11.130). При этом используют различные методы модаль-
ного синтеза, с помощью которых коэффициенты обратных связей
выбирают таким образом, чтобы придать характеристическому по-
линому (11.133) замкнутой системы определенные требуемые свой-
ства, например, заранее предписанное расположение ее собственных
значений на комплексной плоскости.
Пример 1. Определим для стационарного объекта
Д	/ ч
^0(Р> - *В(РУМр) = к о /(Т0Р +0
(11.134)
оптимальное управление, стабилизирующее скалярный выход объекта
хв(0 = х(/) в начале координат хв 3 = 0 при помощи отрицательной обратной
624
связи по единственной переменной состояния х;(0 = x(t) и обеспечивающее
минимум функционалу

Qn ~
tK о 2
(11.135)
где q. и г - заданные весовые коэффициенты.
Уравнение состояния объекта (11.134) имеет вид
x(t) = ax(t} + by(t) + z(0,
(11.136)
где a = - 1/To, b = kJTo.
Очевидна, что в данном примере А = а, В = b, С, = 1, и матричное
уравнение Риккати принимает вид
da+ad+qB -db—bd = Q.
(11.137)
Положительное решение этого уравнения
d = ar + Ja2r^ +b^qnr
IV	• и
(11.138)
а соответствующий оптимальный коэффициент обратной связи
С =r-1M = L + 5/a2+ijB/r]/i = [-l+1/l+^9B/r I/<•	(11.139)
Пример 2. Определим для стационарного объекта
д	.	.
№о(р) = хв(р)/у(р) = к о/р(Т0р+1)
(11.140)
оптимальное управление, стабилизирующее выход объекта хв(0 = хвз = 0
при помощи обратных связей по переменным состояния х>(0 = хв(/) и х2(0 =
- х( (/) (см. рис. 11.11,6) и обеспечивающее минимум функционалу (11.135).
Запишем уравнения состояния и выхода объекта и минимизируемый
функционал в матричной форме. Очевидно, что (см.рис. 11.11,6)
625
о
о
r = rn =r,
(11.141)
где а = а-п = - l/Т’о, b = b22 = kJTo.
Матричное уравнение (11.130) в данном случае принимает вид
L“21
</121Го i
rf22jL0 a
IF.
11	^12
о о1Г^
1 a d-
11	^12
[_“21 ^22 _
^12
(11.142)
и
О
<?в	0
О О
О 1 r i
. -M
b r
О
О
L“21 “22 J
L“2I “22 J
О
О
Перемножив матрицы в уравнении (11.142) и учитывая, что всегда d\2
= d2\, получим равносильную ему систему трех алгебраических уравнений
^Br-62i/j2 =^,-b2d^d22 +rd]\ +ardn =0,
-b^d22 +2rd\2 +2ard22 = 0.
(11.143)
С учетом условий положительной определенности матрицы D
dxj >0 и d^^d22 d\2 >0,
(11.144)
решения системы (11.143) равны
(11.145)
Согласно выражению (11.129), матрица коэффициентов обратных свя-
зей имеет вид
(11.146)
Соответственно, коэффициент обратной связи для сигнала xj (О
"ocl
(11.147)
626
и для сигнала х2(0
*ос1
= bd 12/г =
(-1Ao)+v(1Ao)+27»i/TAAo  (11.148)
Результатом (11.147) и (11.148) соответствуют алгоритмическая схема,
приведенная на рис. 11.12, и следующая ПФ замкнутой системы стабилиза-
ции
ф/рЛхв(Р) =	+ Q =
Х>(р) 1 + (р&ос2 + ^ocl Yo/pfcp+l)
= р-------Г, -	(11.149)
Т~ р2 + Р\ 7^ + 27° ^Чъ1г1ко + ^в/г
ко У к0
Рис. 11.12. Пример системы стабилизации
Отметим, что если измерение или вычисление координаты состояния
Л
x2(t) затруднено, то ОС кж2 можно осуществить по оценке х (0, полученной
при помощи оценивающего устройства (см. 8.7).
Следящие системы при полном и точном наблюдении объ-
екта. Примечательно, что отрицательные ОС, определяемые выра-
жениями (11.129) и (11.130), остаются оптимальными и для случая,
когда синтезируется следящая СУ объектом (11.123), (11.124) по
критерию
627
й, = 7	к (0& £в (0 + /
* v Л **
(11.150)
где eff) = xB(0 - xB3(0 - /-мерный вектор отклонений компонент век-
тора выхода хв(0 от соответствующих компонент вектора хвз(Г); £в.з(0
= Св.зХз(0 - /-мерный вектор требуемых значений выходных (управ-
ляемых) переменных хв(Г).
Но при этом оптимальное управляющее воздействие y\f) со-
держит, кроме составляющих, пропорциональных переменным со-
стояния х(0, еще слагаемые, пропорциональные компонентам векто-
ра задающего воздействия х3(0-
y\t) = К’х3(0-К’ос*(0 = /п (0+yjt)-
(11.151)
Матричный коэффициент /Г* определяют по выражениям, ана-
логичным (11.129) и (11.130), но вместо матриц Л, В, С„ используют
так называемые расширенные матрицы, получаемые при объедине-
нии уравнений объекта и задающего воздействия. Для этого задаю-
щее воздействие х3(/), которое в общем случае является стационар-
ным случайным вектором, рассматривают как вектор состояния мно-
гомерного формирующего фильтра (на рис. 11.11,а обозначен мат-
ричной ПФ /Рфз), на входе которого действует стационарный белый
шум £ с нулевым математическим ожиданием и известной матрицей-
столбцом интенсивностей т.е.
*3(о=а3х3(о+m
(11.152)
а вектор требуемых значений выходных переменных xB3(t) представ-
ляют в форме (11.124)
х//) = С х (t).
—В.З ' '	-В.З—3 V z
(11.153)
Теперь можно записать объединенную (расширенную) систему
уравнений состояния объекта (с z(t) = 0) и задающего фильтра
628
или
Х(0
Хз (О
А 0 х(О
о 4_ _Хз(О_
О
х(О = Axjf) + By(t) +
(11.154)
(11.155)
где х (Г) = [х(О; Хз(О]т - расширенный вектор состояния.
Соответственно, и критерий (11.126) принимает для расширен-
ной системы (11.155) следующий вид:
2П = lim — J|[х^(t)q хй(t)+yr(ОгХОЙ =
'к-*00^ о 2	~в	-	-
= lim — f^[xT(t)C*4 Свх(Г) + ут(0гИ01^
'к-*00 L о 2 L	-в	~	~ J
(11.156)
где х в(0 С в (О FCbi\ Свз] х(Г).
Очевидно, что задача минимизации критерия (11.156) для рас-
ширенной системы (11.155) эквивалентна задаче синтеза оптималь-
ной по критерию (11.127) системы стабилизации объекта (11.123),
т.е. задача синтеза следящей системы оказалась сведенной к задаче
стабилизации. Решение задачи (11.155), (11.156), в соответствии со
структурой вектора х(0, ищется в виде
/(0 = -к‘х(0 = -к
*(0
Хз(0_
(11.157)
гдеК* = [£ж;-1?п].
Уравнение Риккати (11.130) для расширенных матриц А, В_
С в распадается на четыре уравнения, и его общее решение также
рассматривать как расширенную (блочную) матрицу
629
—12
(11.158)
Входящие в (11.158) простые матрицы находят как решение
следующих трех матричных алгебраических уравнений Риккати:
DUA + ATD„ +Са C-D„Br~xByDu =0;	(11.159)
C„=0;	(11.160)
D„A,+A'D^ +C’ a C. -D' Br~'BrD„ =0.	(11.161)
-ZZ —3	—3 —ZZ — B.3 _£B —B.3	—IZ — —	— —IZ	—	v	7
Оптимальный коэффициент ОС в расширенной задаче равен
Гос = L Вт Dn
(11.162)
и определяется уравнением (11.159), в которое входят только пара-
метры объекта управления и критерия оптимальности. В то же время
оптимальный коэффициент К*, равный
Kn=-LlBDl2,
(11.163)
зависит как от параметров объекта и критерия, так и от параметров
задающего воздействия.
Пример 3. Синтезируем оптимальную следящую СУ объектом
д
(Р) = хМ1у(р) = k о/^оГ + О,
(11.164)
если случайное задающее воздействие x3(t) можно рассматривать как выход
формирующего фильтра
^ф.з(Р)= Xj(P )Д(Р) = V2£>3«3 /(р + аз)>
(11.165)
и требуется, чтобы хв(/) =хв.3(0 = x3(t), т.е. Св з = 1.
630
Уравнения состояния объекта
j(t) = ах(0 + Ьу(О
и фильтра
Х»(0 — а3Х3 (О + ^3^(0»
(11.166)
(11.167)
где а = - 1/Т0; b = kJTQ\ а3 = ~Оз,Ь3 = ^2D,a3 при S^o = 1 или b3 = 1 при S$o =
= 2D3a3.
Для расширенного вектора х (t) = [х(0; х3(0]т уравнение состояния
а критерии
1(0 =
О а3
L(0 +	£(0,
(11.168)
1 *
Qn = lim — f ^(^(О-^эСО)2 +о,2(0]ж =
U ->со t
Лв(О + ГИ2(О dt,
(11.169)
где хв(0 = [1;-1] х(Г).
Таким образом, задача синтеза следящей СУ оказалась сведенной к за-
даче синтеза стабилизирующей СУ этим же ОУ, решенной в примере 1.
Оптимальное управляющее воздействие в следящей системе состоит
из двух слагаемых:
У (О-^'пЛз(0 ^ос^(0-
(11.170)
Оптимальный коэффициент обратной связи в выражении (11.170) бу-
дет таким же, как в стабилизирующей системе, т.е. (см. пример 1)
(11.171)
Согласно выражению (11.160)7 уравнение для коэффициента «п имеет
вид
d}2a3 +[a-br bdu]dn ~qB = 0,
(11.172)
, ♦
ОС ~
631
из него получаем
(11.173)
и соответствующий коэффициент прямой цепи
(11.174)
ПФ замкнутой системы между входом х3(0 и выходом хв(/)
Ф(р) = кпк
(11.175)
Стабилизирующие и следящие системы при неполном и не-
точном наблюдении объекта. Перейдем теперь к задачам АКОР для
объектов с неполной и (или) неточной инфор-
мацией о текущем состоянии, т.е. для таких объектов, у которых
переменные состояния x(t) не поддаются полному и точному наблю-
дению. В этих случаях для построения замкнутых систем управления
Л
приходится вместо сигналов х(0 использовать их оценки х (t), полу-
ченные из наблюдаемых переменных xH(f) при помощи специальных
устройств оценивания состояния (УОС) объекта (см.8.7). Методика
АКОР для объектов с неполным и неточным наблюдением состояния
основана на так называемом принципе разделения, согласно которому
задача синтеза оптимальной системы управления при неполных и
неточных измерениях может быть разделена на две независимые
друг от друга задачи: задачу оптимального оценивания состояния
объекта управления и задачу оптимального управления объектом по
Л
оценкам х(0, которые рассматриваются как истинные значения пе-
ременных состояния x(t). Соответственно оптимальное управляющее
устройство в целом должно состоять из последовательно соединен-
ных оптимального устройства оценивания и регулятора, оптимально-
го при полных и точных измерениях. Причем, параметры этих двух
частей управляющего устройства могут быть определены раздельно
и независимо друг от друга.
632
Стабилизирующая системы управления объектом с неполными
и неточными измерениями содержит устройство У0Со (рис. 11.13,а),
которое оценивает состояние объекта. В следящей системе, в кото-
Л
рой х3(0 * const, кроме основного устройства У0Со, требуется еще
устройство оценивания состояния задающего устройства (УОС3).
Устройство УОС3 выдает оценку х3(г), из которой блок Кп формирует
составляющую у* (/) оптимального воздействия.
Рис. 11.13. Замкнутая система оптимального управления объектом с
неполным и неточным наблюдением состояния и задающего воздействия:
а - полная структура; б - упрощенная структура
633
По алгоритмической схеме на рис. 11.13,(7 можно определить
матричную ПФ УУ, состоящего из УОСо и регулятора Калмана-
Летова (11.128) с матричным ПК Кж. Она равна
Wy (Р) = У(р}/М К^Сп л-ВК^' Кх. (11.176)
Для одномерного ОУ со скалярными параметрами а, b и сн = 1
У У (11.176) вырождается в инерционное звено первого порядка с ПК
k,=^k„/(ra+k^-bkx)	(11.177)
и с постоянной времени
=1/(-о + 4ф-М„).	(11.178)
При анализе динамических свойств систем управления с У ОС
л
полагают для простоты, что х (?) = x(t), и тогда схема рис. 11.13,(7
может быть заменена схемой на рис. 11.13,6, где раскрыта внутрен-
няя структура УОС3. Для последней схемы основная матричная ПФ
между входом хзн(г) и выходом хв(г)
ф(р) = С (pI-A + BK YBKn(pI-A +К. J?„УК. =<ЬЛр}К№. (р),
-—В V — — ос/ nv — —3  фЗ—З.Н/  фЗ —С 7 П фзчг/
(11.179)
где Фс(р) - матричная ПФ контура стабилизации; W$3(p) - матрич-
ная ПФ оптимального фильтра, выделяющего полезный сигнал х3;
Кп - матричный ПК, формирующий компоненты вектора у п(0
Весовые коэффициенты, образующие матрицы q и г, подбира-
ют обычно экспериментально - путем моделирования синтезируемой
системы на ЭВМ. При этом руководствуются следующими сообра-
жениями. Процессы оценивания и управления в системе стабилиза-
ции должны протекать приблизительно в одинаковом темпе. Если
интенсивность помехи измерения g(t) больше интенсивности воз-
мущения z(r), то процесс оценивания медленный, и чрезмерное быст-
634
родействие управляющего устройства будет приводить только к уве-
личению среднеквадратичного значения воздействия у (t) без
уменьшения среднеквадратичного значения ошибки стабилизации
ев(г). С другой стороны, и при малой интенсивности помехи измере-
ния, когда устройство оценивания может быть достаточно быстро-
действующим, нецелесообразно большое быстродействие управле-
ния, так как в этом случае критерий будет возрастать из-за состав-
ляющих y(t).
Пример 4. Определим для объекта
^о(Р) = хАр)/у(р) = К/р(Т0Р + 1)’	(11.180)
рассмотренного в примере 2, параметры следящей системы, осуществляю-
щей по схеме рис. 11.13 оптимальное управление в следующих условиях:
1) скалярное воздействие х3(/) описывается, как и в примере 3, уравне-
нием состояния
x3(t) = a3X3(t)+£(t)	(11.181)
где а3 = ос3; = 2D3oc3 (b3 = 1), но измеряется с помехой g3(/), имеющей ин-
тенсивность т.е.
*зЛ(0 = *3 (')+&(');	(11.182)
2) единственная наблюдаемая переменная хн(/) также представляет со-
бой сумму переменной состояния x}(t) и помехиg(/):
хн(0 = x,(0 + g(0-
(11.183)
Требуется, чтобы управляемая переменная хв(0 = Xi(0 с минимальны-
ми по критерию (11.150) потерями следовала за задающим воздействием
х3(0, т.е.
*в(0 = хв.3(0 = *3(0.
(11.184)
Из выражений (11.181) - (11.184) видно, что в данном примере
Св=[1;0]; Сн=[1;0]; Свз=[1;0]; Сзн=[1;0].	(11.185)
635
Оптимальное устройство оценивания для задающего воздействия вида
(11.181) было определено в примере 8.6. В обозначениях решаемой задачи
уравнение устройства УОС3
где
(0 = ~а3х3 (г) + кфз [х3 н (г) - хз н (г)],
(11.186)
(11.187)
Оптимальные коэффициенты обратных связей по оценкам (Z) и
х2 (0, выдаваемым устройством У0Со, полностью определяются матрицей
Dn, элементы которой получены в примере 2 для стабилизации объекта
(11.140) (см. формулы (11.145)).
Оптимальный коэффициент пропорциональности между сигналами
х3 (1) и yn(f) согласно формуле (11.163) равен
(11.188)
Обозначения к элементов матрицы D\z = Л*12 введены для того, чтобы
отличать их от элементов матрицы Ьн, полученных в примере 2.
Для определения коэффициента кп запишем матричное уравнение вида
(11.160)
К1243	-СЛвСвз = 0.	(11.189)
После перемножения матриц в уравнении (11.189) и решения эквива-
лентной системы скалярных уравнений получаем
£22 - 0; £2i - <?в
з2 + аз
Отсюда искомый коэффициент
(11.191)
(11.190)
636
Согласно (11.179),ПФ системы между входом хзн(/) и выходом хв(/)
к
ф(р)=—:
1/£
___________ / ОС
п1 7"»2
7 о -2
к к
КоКос1
k
о^ос? „ . 1
о ос!
она включает в себя передаточную функцию устройства У0С3, которое
определяет оптимальную оценку х3 (/) задающего воздействия х3 н(г), иска-
женного помехой g3(0, и эквивалентно в данном примере инерционному
звену первого порядка. Кроме того, общая передаточная функция опти-
мальной следящей системы содержит масштабирующий коэффициент £пь
зависящий от параметров задающего воздействия, объекта и от весовых
коэффициентов критерия. Основная часть синтезируемой системы эквива-
лентна в данном случае инерционному звену второго порядка.
11.5. Адаптивные системы управления
Адаптивными (или самоприспособляющимися) называют такие
СУ, которые в условиях непредвиденного изменения свойств управ-
ляемого объекта, внешних воздействий или цели управления автома-
тически изменяют структуру или параметры своего управляющего
устройства, обеспечивая при этом необходимое качество управления.
Для осуществления адаптации (автоматического изменения алгорит-
ма управления) эти системы содержат дополнительное управляющее
устройство - устройство адаптации. Устройство адаптации по ре-
зультатам измерений сигналов в главном контуре управления выяв-
ляет изменения свойств внешних воздействий и объекта и произво-
дит необходимые изменения в управляющем устройстве.
Показатель качества, по которому осуществляется адаптация,
может характеризовать либо работу управляемого объекта, либо
функционирование системы в целом.
Необходимость применения адаптивных систем управления
возникает в случаях, когда условия функционирования и свойства
управляемого объекта изменяются в широких пределах и по заранее
неизвестным законам.
637
Объекты, у которых изменяются собственные параметры и па-
раметры внешних воздействий, называются объектами с неполной
информацией.
Неполнота информации об объекте создает неопределенность в
постановке задачи управления, и обычные принципы построения
системы управления оказываются непригодными или малоэффек-
тивными. Систему приходится строить таким образом, чтобы она в
процессе управления сама (автоматически) получала и использовала
для выработки управляющих воздействий недостающую информа-
цию.
Управление, во время которого происходит изучение характери-
стик объекта, называется дуальным.
Дуальность управления является специфической особенностью
адаптивных систем. От обычных систем они отличаются также более
сложной структурой, возможностью переключений в контуре управ-
ления, наличием логического и запоминающего устройств, использо-
ванием поисковых воздействий.
На рис. 11.14 приведена обобщенная функциональная схема
адаптивной системы управления. Главный контур системы образован
объектом ОУ и основным управляющим устройством УУ0. Дополни-
тельное управляющее устройство УУД вместе с ОУ и УУ0 образует
контур адаптации.
Рис. 11.14. Обобщенная функциональная структура адаптивной СУ
638
Устройство адаптации УУД состоит из анализатора объекта АО,
анализатора внешних воздействий АВ, логического устройства ЛУ и
исполнительного устройства ИУ. Логическое устройство вычисляет
текущее значение показателя качества и вырабатывает необходимые
корректирующие воздействия уд.
Для изучения характеристик объекта и установления его теку-
щего состояния устройство адаптации создает специальные поиско-
вые воздействия хп. Иногда для этой цели используются естествен-
ные флуктуации внешних воздействий.
Устройство адаптации действует, как правило, в более медлен-
ном темпе, чем основной контур управления.
Анализаторы АО и АВ и логическое устройство ЛУ представля-
ют собой вычислительные блоки.
В некоторых случаях устройство адаптации содержит эталон-
ную модель объекта или всей системы, реализованную также в виде
некоторого вычислительного блока. Модель используется для обна-
ружения отклонений характеристик системы. При этом упрощается
структура логического устройства.
Строгая классификация адаптивных систем еще не разработана,
и ниже указываются лишь наиболее важные признаки классифика-
ции.
По характеру изменений, производимых в основном управляю-
щем устройстве устройствами адаптации, адаптивные системы под-
разделяются на самонастраивающиеся и самоорганизующиеся. В
самонастраивающихся системах адаптация осуществляется измене-
нием параметров управляющего устройства или управляющего воз-
действия, а в самоорганизующихся системах адаптация достигается
изменением структуры управляющего устройства.
В соответствии с такой классификацией адаптивных систем
можно дополнительные управляющие воздействия разделить на па-
раметрические и структурные.
По характеру функций, выполняемых устройством адаптации,
адаптивные системы подразделяются на системы со стабилизацией
качества управления и системы с оптимизацией качества управле-
ния. Назначение первых - поддержание показателя качества на за-
данном уровне, а вторых - поиск и поддержание экстремального
значения показателя качества.
639
Адаптивные системы, обеспечивающие в процессе функциони-
рования экстремизацию показателя качества, называются системами
оптимизации. В них задача синтеза оптимального управляющего
устройства решается автоматически и непрерывно, в то время как в
обычных (неадаптивных) системах оптимального управления эта
задача решается однократно - при конструировании или при на-
стройке системы.
Стабилизируемые и оптимизируемые показатели качества могут
характеризовать либо динамический, либо статический режим объ-
екта или главного контура. Стабилизируют, например, такие харак-
теристики динамического режима системы, как колебательность,
частотная характеристика, импульсная переходная функция. Необхо-
димость в их стабилизации возникает при существенных изменениях
параметров объекта (передаточного коэффициента, постоянных вре-
мени, времени запаздывания).
Оптимизировать целесообразно такие показатели, как длитель-
ность переходного процесса в системе, дисперсия сигнала ошибки.
Длительность переходного процесса сильно отклоняется от опти-
мально возможного значения при изменениях указанных параметров
объекта. Минимально достижимое значение дисперсии зависит от
спектральных характеристик внешних воздействий. Если эти воздей-
ствия нестационарны, и их характеристики существенно изменяются,
то необходимо непрерывно или периодически изменять соответст-
вующим образом параметры управляющего устройства.
В зависимости от используемого способа получения информа-
ции о параметрах объекта различают поисковые и беспоисковые
адаптивные системы. В поисковой системе условия экстремума по-
казателя качества находятся с помощью пробных поисковых воздей-
ствий на объект и оценки результатов этих воздействий. В беспоис-
ковой (или аналитической) системе параметры управляющего уст-
ройства, обеспечивающие наилучшие показатели качества, опреде-
ляются для конкретных условий функционирования системы анали-
тически - расчетным путем.
Адаптивные системы, способные в процессе работы совершен-
ствовать свой алгоритм функционирования и тем самым улучшать
качество управления, называются самообучающимися. Такие систе-
мы имеют второй контур адаптации, который анализирует и коррек-
640
тирует работу первого контура адаптации. Причем, второй контур,
накапливая информацию о функционировании первого контура, дей-
ствует значительно медленнее.
Самообучающиеся системы обладают наиболее высокими спо-
собностями адаптации и по своим возможностям приближаются к
живым организмам.
Наибольшее распространение в промышленной автоматике по-
лучили самонастраивающиеся системы с оптимизацией какого-либо
показателя статического режима объекта. Такие системы называются
экстремальными системами управления.
Рис. 11.15. Типичные функциональные структуры адаптивных СУ:
а - с идентификатором ОУ; б - с моделью желаемой СУ
641
В промышленной автоматике наибольшее распространение по-
лучили два сравнительно простых вида адаптивных СУ (рис. 11.15): с
идентификатором ОУ и с моделью желаемой СУ. В СУ первого типа
дополнительное УУД меняет параметры основного УУ0 в зависимости
от изменений параметров ОУ, выявляемых с помощью идентифика-
тора, а в СУ второго типа УУД меняет параметры УУ0 в зависимости
от отклонений свойств реальной СУ от свойств ее желаемой модели.
Более подробно принципы построения математического описа-
ния и анализа адаптивных систем управления изложены в специаль-
ной литературе.
Контрольные задания и вопросы
1.	Приведите примеры критериев оптимальности типа функций выго-
ды и потерь.
2.	Приведите пример технологического объекта оптимального управ-
ления и назовите для него критерий оптимальности, управляющее воздейст-
вие и ограничения.
3.	Приведите пример критерия оптимальности в виде функционала.
4.	Как записывается критерий оптимальности системы по быстродей-
ствию?
5.	Запишите выражение обобщенного квадратичного критерия для
случая скалярного выхода и скалярного управления.
6.	При каких условиях задача оптимального управления может рас-
сматриваться как задача статической оптимизации и при каких условиях она
должна рассматриваться как задача динамической оптимизации?
7.	Нарисуйте обобщенную функциональную схему системы оптималь-
ного управления.
8.	Сформулируйте идею и сущность принципа максимума Понтрягина.
9.	Что утверждает принцип оптимальности Беллмана?
10.	Что представляет собой закон управления в разомкнутой системе с
максимальным быстродействием и ограниченным управлением?
11.	Что утверждает система об п интервалах?
12.	От чего зависят моменты переключения управляющего воздейст-
вия в разомкнутой системе с максимальным быстродействием?
13.	Как формируется закон управления в замкнутой СУ с максималь-
ным быстродействием?
14.	Какой закон регулирования в системе стабилизации состояния и
выхода обеспечивает минимум обобщенного квадратичного критерия?
642
15.	От чего зависят коэффициенты обратных связей в оптимальной
системе стабилизации?
16.	В чем заключается принцип разделения?
17.	Из каких частей состоит управляющее устройство оптимальной
системы, стабилизирующей выход объекта в условиях неполного и неточ-
ного наблюдения?
18.	Какие основные блоки и устройства входят в обобщенную струк-
туру адаптивной СУ?
19.	Охарактеризуйте две типичные структуры адаптивных СУ.
643
Глава 12. ОСНОВЫ FUZZY-УПРАВЛЕНИЯ
12.1.	Общие сведения о fuzzy-у правлении
Английский термин «fuzzy» (произносится «фасзи») примени-
тельно к техническим понятиям означает то же, что слова «нечет-
кий» или «нестрогий». Он был введен в научную литературу в 1965
году американским ученым Л.Заде (L.Zadeh), который определил по-
нятие «нечеткое множество» (англ. - fuzzy set) и распространил ме-
тоды классической теории множеств (т.е. теорию четких множеств)
на нечеткие множества.
Исходная идея теории нечетких множеств (ТНМ) заключается в
том, чтобы принадлежность элементов к тому или иному множеству
определять не в форме однозначных ответов «да» или «нет», как в
традиционной теории множеств, а с помощью ответов типа «может
быть», «вероятнее всего». Для этого используются так называемые
функции принадлежности, которые могут принимать любые проме-
жуточные значения между единицей, соответствующей, как и в ал-
гебре, логике, однозначному «да», и нулем, соответствующим «нет».
Например, житейскую проблему отнесения 30-летнего человека к
альтернативным категориям (множествам) «молодые люди» или
«немолодые люди» можно решить интуитивно, как часто мы и дела-
ем, полагая, что 30-летний с коэффициентом истинности 0,65 являет-
ся молодым, ас коэффициентом 0,35 - немолодым человеком.
Такой подход Заде к описанию множества элементов позволил
использовать строгие процедуры теории множеств и математической
логики для алгоритмизированного получения логических выводов из
нечетко заданных исходных условий, а применительно к задачам
управления - формулировать точные, однозначные управляющие
воздействия на основе приближенных, эмпирических, словесно опи-
санных знаний о свойствах ОУ и обычных действиях человека-
оператора. Подход предоставил возможности математически опери-
ровать с такими нечеткими, но часто встречающимися обыденными
характеристиками, как, например: «много», «мало», «очень много»,
«очень мало».
644
Совокупность методов математического описания нечетких
множеств и формализованного получения логических выводов из
нечетких предпосылок получила название нечеткой, или fuzzy-логи-
ки.
Упрощенная схема выработки управляющих воздействий с по-
мощью процедур fuzzy-логики приведена на рис. 12.1. Главным эле-
ментом схемы является блок реализации логических правил типа
«Если..., то...», которые формулируются на основе знаний экспертов
о данном ОУ и хранятся в специальной базе правил. Здесь же хра-
нятся так называемые функции принадлежности (ФП), с помощью
которых измеренные (т.е. четкие) значения х* входных сигналов х,
преобразуются в соответствующие коэффициенты истинности, т.е. в
нечеткую форму информации. Далее частные логические выводы о
целесообразных значениях отдельных составляющих управляюще-
го воздействия у (нечеткая форма) агрегируются в единое (четкое!)
значение у , соответствующее исходным условиям xz .
Рис. 12.1. Схема выработки управляющих воздействий
с помощью fuzzy-логики
Более подробно и на математическом языке fuzzy-логики меха-
низм выработки управляющих воздействий излагается в последую-
щих разделах 12.2 и 12.3.
Методы fuzzy-логики целесообразно использовать при решении
таких задач управления, как:
-	регулирование ОУ, свойства которых описаны лишь в качест-
венной, нематематической форме;
645
-	управление ОУ с выходными переменными, характеризую-
щими качество продукции или условия комфортности и не поддаю-
щимися измерению (текстура, шероховатость, эластичность мате-
риалов, восприятие человеком температуры, влажности, вибрации и
т.п.);
-	дополнение обычных одноконтурных систем регулирования
вспомогательными контурами для компенсации возмущений, изме-
нения структуры, самонастройки и адаптации основного контура;
-	перенастройка СУ в нестационарных, в том числе аварийных
производственных ситуациях;
-	воспроизведение действий человека-оператора в системах ор-
ганизационного управления верхнего уровня - для контроля, диагно-
стики и оптимизации сложного технологического ОУ.
12.2.	Основные понятия и операции fuzzy-логики
Функция принадлежности и лингвистическая переменная.
Первичным, исходным понятием fuzzy-логики является понятие «не-
четкое множество». Обычное, или четкое, множество в математике
определяют как совокупность каких-либо объектов (элементов мно-
жества), обладающих общими для всех них характеристическими
свойствами. Четкое множество задают либо перечислением всех его
элементов (если оно конечное), либо формулируя строгое правило
отнесения того или иного объекта к рассматриваемому множеству.
Например, обычное множество Л/ц целых отрицательных чисел х, из
исходного базисного множества R рациональных чисел можно пред-
ставить перечислением всех элементов:
Ми = {х1=-1,х2 =-2,х3=-3,...},	(12.1)
а множество М всех отрицательных чисел х из того же множества -
так:
М = {x;x&R,x<0}.	(12.2)
Для описания четких множеств типа (12.1) и (12.2) можно ис-
пользовать характеристическую функцию которая принимает
лишь два значения - 0 или 1:
646
На/(х) =
Л
[о,
если
если
хеМ'
х £ М.
(12.3)
Нечеткое множество характеризуется непрерывной функцией
принадлежности Цл/х) (англ. - membership function), которая может
принимать любые промежуточные значения между 0 и 1 и устанав-
ливает для каждого значения х степень его принадлежности к нечет-
кому множеству М. Нечеткое множество М является подмножеством
базисного множества X и в общем виде может быть записано как со-
вокупность пар различных значений х и соответствующих значений
ФП щ/х):
Рис. 12 2. ФП, характеризующие три зна-
чения лингвистической переменной
"температура в помещении"
ФП могут быть заданы аналитически или графически, чаще все-
го используются кусочно-линейные ФП. На рис. 12.2 в качестве при-
мера приведен график с
тремя ФП Ц;(х), харак-
теризующими множе-
ства температур «про-
хладно», «нормально» и
«тепло». Базисной пе-
ременной х в данном
случае является темпе-
ратура в помещении.
Если нечеткое
множество М содержит
лишь одну пару (х*,
ц(х*)), где ц(х*), то оно
становится четким, а
саму пару называют
синглтоном (англ. - singletori).
Лингвистической переменной (англ. - linguistic vaviable) назы-
вают переменную, которая задана на количественной шкале базис-
ной переменной х и принимает значения в виде слов и словосочета-
ний естественного языка. Отдельное значение лингвистической пе-
ременной, задаваемое с помощью одной ФП, называется лингвисти-
647
ческим термом. Каждому терму соответствует одно нечеткое мно-
жество. В примере на рис. 12.2 совокупность Ml трех термов («про-
хладно», «нормально», «тепло») рассматривается как лингвистиче-
ская переменная, принимающая эти лингвистические значения.
Лингвистическая переменная полностью определена, если зада-
ны множество ее термов и множество соответствующих ФП Ц/(х).
На практике вместо абсолютных значений базисной переменной
х используют обычно ее нормированные значения хн (см.рис. 12.2)
Наилучшим расположением ФП отдельных термов вдоль оси х
является такое, при котором соседние ФП перекрываются, а сумма
значений Ц/(хн) двух соседних термов при каждом значении хн равна
единице.
В теории fuzzy-управления для лингвистического описания вы-
ходной переменной ОУ и сигнала ошибки наиболее часто применяют
универсальный набор из 7 термов с треугольными и трапецеидаль-
ными ФП (рис. 12.3), образованных с помощью комбинаций слов
«отрицательный» (англ. - negative), «положительный» (англ. - posi-
tive), «большой» (англ. - big), «средний» (англ. - medium), «малень-
кий» (англ. - small) и «приблизительно ноль» (англ.- approximately
zero), а именно: negativ big (NB), negativ medium (NM), negativ small
(NS), approximately zero (ZE), positive small (PS), positive medium (PM),
positive big (PB).
Рис. 12.3. Унифицированная система ФП
Процедуру определения значения ФП цм(х*), соответствующего
конкретному значению х* переменной х, называют фазификацией
(англ. - fuzzyficatiori).
Операции с нечеткими множествами. Известные в алгебре ло-
гики операции «И», «ИЛИ», производимые с логическими перемен-
648
ними 1 и 0, могут быть применены и к нечетким множествам. Для
этого вместо переменных 1 и 0, соответствующих истинному и лож-
ному высказыванию, используют ФП ц(х), текущие значения кото-
рых можно рассматривать как степени истинности, принимающие
значения от 0 («ложно») до 1 («истинно»), включая все промежуточ-
ные значения («может быть с вероятностью ц(х)»).
Правила алгебры логики позволяют получать из двух простых
исходных высказываний А и В, соединенных союзами «И», «ИЛИ»,
одно, более сложное высказывание С. Логические операции конъ-
юнкции (операция «И») и дизъюнкции (операция «ИЛИ»), выпол-
няемые над высказываниями А и В или с логическими переменными
1 и 0, аналогичны соответственно операциям пересечения и объеди-
нения, выполняемым над множествами (причем, как четкими, так и
нечеткими).
Правила, по которым определяются результирующие значения
истинности или принадлежности, можно записать в виде алгебраиче-
ских формул и с помощью операторов минимизации и максимиза-
ции.
Так, для операции пересечения (конъюнкции) двух нечетких
множеств А и В, заданных на общем базисном множестве X, ФП ре-
зультирующего множества С, соответствующего союзу «И», равна
Х6А
(12.5)
Для операции объединения (дизъюнкции) двух нечетких мно-
жеств А и В, заданных на общем базисном множестве X, ФП резуль-
тирующего множества, соответствующего союзу «ИЛИ», равна
ВсМ = /^(х) = тах{/<ЛхШ(х)}.
хе А
(12.6)
Графики на рис. 12.4 иллюстрируют, как в соответствии с фор-
мулами (12.5) и (12.6) из ФП, характеризующих исходные нечеткие
терм-множества N, ZE, Р, образуются ФП производных множеств
[NHZE] и[7ЕИЛИР].
649
Рис. 12.4. Примеры пересечения (а) и объединения (б)
двух нечетких множеств
Операции пересечения и объединения, проиллюстрированные
для случая двух исходных множеств А и В, могут быть распростра-
нены и на случай нескольких исходных множеств.
В задачах fuzzy-управления операторы минимизации (12.5) и
максимизации (12.6) используются для агрегирования нескольких
исходных посылок «Если», соединенных соответственно союзами
«И» и «ИЛИ».
Алгоритмы логических выводов. Главной операцией fuzzy-
логики является процедура нечеткого вывода (англ. - fuzzy-
reasoning), заключающаяся в строго алгоритмизированном получе-
нии приближенных решений из нечетких условий. Эта процедура
основана на операции импликации и обобщенном правиле логиче-
ского вывода, используемых в традиционной математической логике.
Импликация - логическая операция соединения двух высказы-
ваний А и В в новое высказывание «Если А, то В», обозначаемое
Ra-+b- Применительно к ТНМ операция импликации описывается
следующей формулой, предложенной последователем Заде - амери-
канским ученым Мамдани:
= (12 7)
Av Н
где цл(х) и цв(у) - ФП, которые заданы на разных базисных множест-
вах X и У, а ц - ФП, которая задана на декартовом произведении
АхВ, представляющем собой множество упорядоченных пар или
650
кортежей (х, у). ФП (12.7) характеризует одновременную принад-
лежность (как при операции «И»!) пар (х, у) из декартова произведе-
ния АхВ к подмножеству, образованному по правилу Ra->b- Процеду-
ру (12.7) можно иллюстрировать числовым примером, приведенным
в табл. 12.1
Таблица 12.1
Пример определения ФП импликации (12.7)
	нХу)	2	4	6	X	
		0,75	1,00	0,50	цДх)
	0,25	0,25	0,25	0,25	1
2	1,00	0,75	1,00	0,50	Гня
3	0,50	0,50	0,50	0,50	.	А -> В г
Заметим, что вместо оператора минимизации в формуле (12.7),
как и в формуле (12.5), можно применять операцию умножения двух
ФП.

(12.8)
что не искажает решения задачи, но существенно упрощает его.
Обобщенное правило логического вывода основано на извест-
ном из математической логики правиле замены (правиле «modus ро-
nens»), позволяющем перейти от истинной посылки А' и истинного
высказывания «Если А, то В» к истинному заключению В'. Правило
замены устанавливает истинность заключения В' лишь в случае ис-
тинности посылки А1 и (!) истинности импликации А-+В. Примени-
тельно к ТНМ обобщенное правило логического вывода можно
сформулировать так:
ФП заключения В' равна максимальному значению ФП пересе-
чения (операции «И») посылки А' и импликации А—>В.
Или в математической форме:
= maxminfцЯх),^(х,у)].	(12.9)
Правило (12.9), называемое инференц-процедурой, с учетом
формулы (12.7) может быть последовательно преобразовано к виду,
удобному для практического применения:	^51
Ш'(У) = max тт{рл(х), riling (х),рв (у)] } = тахтш{тт||1Дх),ц/х)],цв(у)} =
хеА'	xeY
= min max {min [цл< (Д Ня (*)], Нв (?)} = min {у, ps (у)},	(12.10)
хе А
где у = тах тт[цл<(х), цл(х)] - так называемая степень активи-
хеХ
рования правила.
Действие правила (12.10) иллюстрирует пример на рис. 12.5,а.
Операции min, входящей в выражение для у, соответствует пересече-
ние двух ФП - Цл(х) и Цл'(х) (см. заштрихованный треугольник). Да-
лее, согласно выражению для у, берется максимальное значение ФП
p.jrvi', и оно сравнивается с ФП р.5<(у) (см. правый график на рис.
12.5,а). Операция минимизации в основном выражении (12.10) сво-
дится в данном случае к ограничению трапеции Цв'(у) сверху. Поэто-
му инференц-процедуру (12.10) называют максимин-процедурой.
Рис. 12.5. Пример определения ФП управляющего воздействия
по методу максимина (а, б) и максимума произведения (в)
652
В часто встречающемся на практике случае, когда высказывание
А' представляет собой синглтон
Ра(х) = Ра(х) =
при
при
х = х ;
х Ф х ,
(12.11)
т.е. когда, например, в задаче управления х является точно извест-
ным, измеренным сигналом х . Тогда степень активирования у соот-
ветствует просто точке пересечения синглтона с ФП ц,;(х) (см.рис.
12.5,6), а итоговая ФП
//B.(y) = mm{r,//B(y)}
(12.12)
где у = Цл(х*).
Если процедуру минимизации двух ФП в формуле (12.10) заме-
нить операцией их умножения (12.8), то искомая ФП управляющего
воздействия при фиксированном значении х входного сигнала х оп-
ределяется просто как произведение (см.рис. 12.5,в):
Ц-в'(У) = №в(у)-
(12.13)
Поэтому инференц-процедуру (12.13), в отличие от (12.10), на-
зывают процедурой максимума произведения.
Аккумуляция локальных выводов. Если база правил состоит
из N правил П7 в форме
П.:	ЕСЛИ	4,	ТО	Д.1
ИЛИ	П,.	ЕСЛИ	А,	ТО	в2
ИЛИ	П :	ЕСЛИ	А,..	ТО	В ’
ИЛИ	Пл.:	ЕСЛИ	4,	ТО	BN
(12.14)
то локальные выводы В',, соответствующие локальным условиям
А', могут быть объединены в один общий вывод В' с ФП
653
Нв'(у) = тах[цВ' (у),цв- (у),... ,цв^ (у)].	(12.15)
Если внутри отдельных правил П7 имеется по нескольку посы-
лок Ар, соединенных союзами «И», «ИЛИ», то общая ФП правила Ц
определяется соответственно по формулам (12.5), (12.6).
Правило, посылка которого содержат союз «ИЛИ», может быть
преобразовано в несколько правил с посылками, содержащими толь-
ко союз «И». И наоборот - правила с одинаковым заключением мо-
гут быть объединены в одно правило с помощью союза «ИЛИ». На-
пример, правило
П, :ЕСЛИ(хп = ЖИЛИх12 = М/)И х/3 = Ж,ТО у, =NM (12.16)
можно представить в виде двух правил:
Пп : ЕСЛИ xn = NB И хв = NS, ТО yz = NM; 1
П/2: ЕСЛИ xl2 = NM И xZ3 = NS, ТО yz = NM.j
Соответственно два правила, например:
Пл : ЕСЛИ xn = NB, ТО у, = NM;)
П/2: ЕСЛИ хп = NB, ТО у, = NM\
(12.17)
(12.18)
можно с помощью союза «ИЛИ» объединить в одно
П, :ЕСЛИхп = ДЖИЛИх,2 = NB,Wу, = NM. (12.19)
Базу правил (англ. - rule-base) удобно представить в табличной
форме. Покажем, как формируется база правил для пропорциональ-
но-дифференциального (ПД) fuzzy-регулятора. Очевидна следующая
стратегия управления: 1) если сигнал ошибки с = х3-х положителен
(отрицателен), то управляющее воздействие у должно быть положи-
тельным (отрицательным), чтобы сигнал ошибки привести быстрее в
нулю, а выходной сигнал х сделать равным задающему х3; 2) если
производная с сигнала ошибки по времени положительна (отрица-
654
тельна), то сигнал ошибки увеличивается (уменьшается), и соответ-
ственно управляющее воздействие у также должно увеличиваться
(уменьшаться); 3) если же сигнал ошибки и его производная имеют
противоположные знаки и близкие лингвистические значения, то при
выработке управляющего воздействия приоритет должен отдаваться
сигналу ошибки.
Примем для сигнала ошибки и управляющего воздействия по 5
лингвистических значений: NB, NM, ZE, PM, РВ, а для производной
сигнала ошибки - 3 значения: NM, ZE, РМ. Тогда стратегию управ-
ления можно представить в виде следующей базы правил (табл.
12.2):
Таблица 12.2
Лингвистические значения управляющего воздействия
ПД-йигу-регулятора при различных значениях сигнала
ошибки и его производной
Ё	Е	i = l	i = 2	i = 3	i = 4	i = 5
		NB	NM	ZE	PM	PB
j = 1	NM	NB	NB	NM	ZE	PM
j = 2	ZE	NB	NM	ZE	PM	PB
/ = з	PM	NM	ZE	PM	PB	PB
Все 15 правил П;( для выработки управляющего воздействия у,
приведенных в табл. 12.2, можно объединить с помощью союза
«ИЛИ» в 5 правил с одинаковыми значениями yt.
Трем правилам Пп, П]2, П21 с одинаковым значением» = NB со-
ответствует одно правило
Плв :ЕСЛИе = ЖИё = Ж/ИЛИе = А7?Иё = 2Е
ИЛИе = NMHi = NM,W У1 =NB;
(12.20)
аналогично правилам П13, П22, П31 с» = NMсоответствует правило
П : Е С ЛИ £ = NB И Ё = РМ И ЛИ е = NM И Ё = ZE
ИЛИе = 2ЕИё = NM, ТО У! = NM;	(12.21)
правилам П23, П32, TUi су( - ZE эквивалентно правило
655
Пж :ЕСЛИе = УМИё = РМИЛИе = 7ЕИё = 7Е
ИЛИе = РМИё = NM,TOy1 =ZE-	(12.22)
правилам П33, П^, П51 су( = РМ - правило
Пт :ЕСЛИе = 2ЕИё = РМИЛИ£ = РМИё = 7Е
ИЛИе = РВИё = УМ, ТО у, =РМ-	(12.23)
и, наконец, правилам П43, П52, П53 су{ = РВ
Прв :ЕСЛИе = РМИё = РМИЛИе = РВИё = 7Е
ИЛИЕ = РВИЁ = РМ,ТОу/ =РВ.	(12.24)
12.3.	Структура и принцип действия систем fuzzy-управления
Поясним принцип действия систем fuzzy-управления на приме-
ре построения УУ, имеющего два входных сигнал X] и х2 (это могут
быть и сигналы ошибки £i и е2) и реализующего следующую базу из
трех правил:
П]. ЕС ЛИ X] = j ИЛИ х2 = 4 2, ТО у = В}; '
ИЛИП2: ЕСЛИх, = Л21 ИЛИх2 = А22,ТО у = В2Л
(12.25)
ИЛИП3: ЕСЛИX] = Л31 И х2 = Л32,ТОу = В3.
При этом предполагается, что термы Ар, Ар и Ву (J = 1; 2; 3) за-
даны своими ФП.
Пользуясь описанными в предыдущем разделе операциями и ал-
горитмами, можно составить соответствующую базе правил (12.25)
схему инференц-механизма (рис. 12.6), называемого также fuzzy-
процессором. Общую схему fuzzy-управления, приведенную ранее на
рис. 12.1, теперь можно конкретизировать в виде функциональной
схемы на рис. 12.7. В блоке Н происходит нормирование входных
сигналов х, - преобразование их абсолютных значений в нормиро-
ванные х*н . В блоке ФФ осуществляется процедура фазификации -
656
выработка конкретных значений ФП pL, соответствующих значе-
ниям сигналов х*н . В блоке ДН происходит денормирование полу-
ченного управляющего воздействия у*. Действие инференц-
механизма и процедура дефазификации (ДФ) дополнительно к схеме
на рис. 12.6 иллюстрирует графики на рис. 12.8, соответствующие
этому же примеру с двумя входными сигналами и тремя правилами
(12.25). Но теперь абстрактные предпосылки представлены в виде
ФП ц для трех конкретных термов из унифицированной системы
Ал
на рис. 12.3: РВ, NS, ZE. Коэффициенты ау( являются составляющими
степеней активирования у7.
Рис. 12.6. Пример построения инференц-механизма
Процедура дефазификации заключается в выработке конкретно-
го значения у* управляющего воздействия у на основе объединенной
ФП цв (у), полученной из частных ФП цв. (у) с помощью операции
максимизации. Наибольшее распространение из известных способов
дефазификации получил метод центра тяжести, согласно которому
657
значение у находят как абсциссу «центра тяжести» площади, распо-
ложенной под графиком цд,(у) (см. заштрихованную фигуру на рис.
12.8), по следующей формуле средневзвешенного значения:
+i
$Мг(у)у4у
-1_________
+1
j^B'(y)dy
-1
(12.26)
Рис. 12.7. Функциональная схема fuzzy-управления
Из изложенного принципа построения и функционирования
системы fuzzy-управления нетрудно установить, что fuzzy-регулятор
представляет собой безынерционный нелинейный преобразователь с
одним или несколькими входными и выходными сигналами. На ал-
горитмических схемах его принято обозначать прямоугольником, а
внутри прямоугольника изображают три треугольные ФП (рис. 12.9).
Для придания безынерционнному fuzzy-регулятору необходи-
мых свойств к нему часто присоединяют последовательно один из
трех каналов распространенного в промышленной автоматике ПИД-
регулятора. Естественно, что при этом в базе правил самого fuzzy-
регулятора в качестве входных переменных; кроме сигнала ошибки
8, могут фигурировать интеграл и производная этого сигнала по вре-
мени.
Передаточные свойства fuzzy-регулятора без динамических со-
ставляющих можно в простейших случаях описывать с помощью
нелинейных статических характеристик. Покажем это на следующем
658
простом примере. Линейный статический алгоритм пропорциональ-
ного регулятора с передаточным коэффициентом кп
y(t) = V(0
(12.27)
Рис. 12.8. Графическое представление
инференц-механизма для правил (12.25)
659
можно приближенно заменить совокупностью следующих пяти пра-
вил:
П]: ЕСЛИ £ = ЛЯ, ТО у = ЛЯ;]
П,: ЕСЛИ е = NS, ТО у = NS;
П3: ЕСЛИ £ = ZE, ТО у = ZE; >
П4: ЕСЛИ е = Р5, ТО у = PS;
П5: ЕСЛИ £ = РЯ, ТО у =/Я.
(12.28)
Рис. 12.9. Варианты структур СУ с динамическим fuzzy-регулятором
Если теперь допустить, что входная переменная е принимает
только четкие значения, т.е. представляет собой синглтоны, то алго-
ритму (12.28) будет соответствовать нелинейная статическая харак-
теристика у = Де) пятипозиционного реле (рис. 12.10,я).
Рис. 12.10. Статические характеристики релейного (а) и fuzzy-регулятора (б)
Если же правила (12.27) реализуются не в обычном релейном
регуляторе, а в fuzzy-регуляторе - с выполнением процедур фазифи-
660
кации, то статическая характеристика у = Де) может принять совсем
иной вид (см.рис. 12.10,6). Причем форма характеристики зависит
как от формы и взаимного расположения ФП входной переменной,
так и от используемых методов инференции и дефазификации.
В случае двух входных переменных (например, е и е) статиче-
ская характеристика у = Де, ё) представляет собой поверхность, ко-
торую удобнее изображать на плоскости в виде семейства изолиний
y=v*=const. На рис. 12.11 показаны нормированные статические ха-
рактеристики обычного непрерывного ПИ-регулятора (а), описывае-
мого уравнениями
у = 0,5(£- + £) или 8 = -£ + 2у,	(12.29)
и ПИ-fuzzy-регулятора (6) с такой же динамической частью (12.28).
Рис. 12.11. Статические характеристики линейного (а)
и fuzzy-ПИ-регулятора (6)
Рассмотрим теперь кратко порядок синтеза систем
fuzzy-управления. Несмотря на большое разнообразие под-
ходов к построению систем fuzzy-управления и на преобладание эв-
ристических приемов алгоритмизации задач fuzzy-управления, мож-
но выделить следующие обычно выполняемые процедуры синтеза:
1.	Предварительно изучают ОУ, его традиционную модель и
опыт технологов по его эксплуатации.
661
2.	Выбирают измеряемые (наблюдаемые) выходные переменные
Xi и управляющие воздействия устанавливают пределы их измене-
ния и подбирают масштабные коэффициенты, обеспечивающие нор-
мирование всех переменных в безразмерном диапазоне [-1, 1].
3.	Вводят лингвистические переменные xt и yt и представляют
их с помощью нескольких ФП, соответствующих 3-7 термам. При
этом весьма важным для обеспечения качества и эффективности
управления является выбор количества, формы и взаимного распо-
ложения ФП на нормированном интервале.
4.	На основе интервью и анкетирования экспертов (операторов-
технологов, инженеров-конструкторов ОУ) формируют логические
правила (алгоритмы) управления. При этом полезно консультирова-
ние экспертов по объекту экспертом по fuzzy-управлению. В случае
необходимости корректируют выбранные в п. 3 ФП.
Правила с одинаковым заключением (выводом) с помощью
союза «ИЛИ» объединяют в одно правило.
5.	Сформулированные правила проверяют на их полноту, не-
противоречивость и избыточность.
6.	В случае двух входных переменных Xi и х2 составляют табли-
цы лингвистических правил, устанавливающие соответствие между
лингвистическими значениями входных и выходных переменных.
7.	Выбирают операторы импликации и инференц-процедуры и
метод дефазификации.
8.	С использованием специализированного пакета программ
(например, из системы «MATLAB» / «SIMULINK») программируют
все ФП, правила, процедуры агрегирования посылок отдельных пра-
вил и всех правил между собой.
9.	Проводят имитационное моделирование и испытание синте-
зированной стратегии управления в разомкнутом виде и в соедине-
нии с моделью ОУ (четкой или нечеткой) и оценивают работоспо-
собность, устойчивость и качество СУ.
12.4. Пример системы fuzzy-управления
В качестве иллюстративного учебного примера рассмотрим
простую систему регулирования уровня жидкости в резервуаре (рис.
12.12). ОУ в системе представляет собой интегрирующее звено, ох-
ваченное нелинейной отрицательной обратной связью. Эта ОС соот-
662
ветствует закону истечения жидкости из резервуара: расход жидко-
сти Qp (м/с) нелинейно зависит от уровня h (м). Подача жидкости в
резервуар Qn (м3/с) регулируется с помощью задвижки 3, степень от-
крытия которой у (град) пропорциональна подаче Qn. Инерционность
ОУ зависит от площади поверхности жидкости в резервуаре 5 (м2) и
от коэффициента истечения кп.
В качестве управляющего воздействия у рассматривается ско-
рость перемещения задвижки, т.е. y(f) = d(y(t)!dt.
Если имеется возможность измерения скорости изменения
уровня, то один из простейших алгоритмов управления может быть
представлен в виде следующих пяти нечетких правил:
Hj: ЕСЛИ уровень нормальный (gj = ZE), ТО поло -
жение задвижки не изменять (у = ZEy,
ИЛИ П2: ЕСЛИ уровень низкий (gj = РВ), ТО задвижку
открывать быстро (у = РВу
ИЛИ П3: ЕСЛИ уровень высокий (gj = NB), ТО задвижку
закрывать быстро (у = NBy,
(12.30)
ИЛИ П4 : ЕСЛИ уровень нормальный (gj = ZE), И он уве -
личивается (е2 = РВ), ТО задвижку закрывать
медленно (у - NM);
ИЛИ П5: ЕСЛИ уровень нормальный (gj = ZE), И он
уменьшается (g2 = NB), ТО задвижку закрывать
медленно (у=РМ\
Функции принадлежности выходной (в) и входных (а, б) пере-
менных, фигурирующие в правилах (12.30), показаны на рис. 12.13.
663
ОУ
Рис. 12.13. Функции принадлежности системы fuzzy-регулирования уровня
664
£*=Z\h=-0,25 м £^=(dh/dt)=0,05 м/с у =—0,15 град/с
Рис. 12.14. Инференц-процедура в системе fuzzy-регулирования уровня
Соответствующие этим правилам процедуры фазификации и
инференции проиллюстрированы на рис. 12.14 для конкретных зна-
чений Е* и е* . ФП управляющего воздействия определены по мето-
ду максимума произведения (см. заштрихованные треугольники).
Результирующее значение управляющего воздействия у вычислено
по формуле (12.26) как средневзвешенное значение для двух заштри-
хованных треугольников.
На рис. 12.15 показано пространство управления, соответст-
вующее правилам (12.30). Форма поверхности у(£ь ег) зависит от ви-
665
Рис. 12.15. Пространство управления в системе fuzzy-регулирования уровня
да и взаимного расположения принятых ФП и применяемого метода
дефазификации.
Контрольные задания и вопросы
1.	Представьте с помощью трех термов лингвистическую переменную
«температура человеческого тела». Нарисуйте графики соответствующих
ФП.
2.	С помощью каких операторов можно найти ФП пересечения и объе-
динения нечетких множеств, если известна ФП исходных множеств? Пояс-
ните эти процедуры на графиках ФП двух исходных множеств (термов).
3.	Каким логическим операциям соответствуют процедуры минимиза-
ции и максимизации?
4.	Постройте графики ФП нечетких множеств, образованных с помо-
щью союзов «И», «ИЛИ» из трех исходных термов NB, ZE, РВ.
5.	Сформулируйте обобщенное правило логического вывода. Запиши-
те соответствующее математическое выражение для ФП вывода В'. исполь-
зуя ФП посылки Л' и импликации А-»В.
6.	Проиллюстрируйте на двух произвольных графиках ц 4 (х) и ( у)
алгоритм определения ФП управляющего воздействия у при фиксирован-
ном значении х* входного сигнала х.
666
7.	Как по графику |1В-(И можно найти значение у управляющего
воздействия?
8.	Какие основные операции и процедуры осуществляются в системе
fuzzy-управления?
9.	С помощью каких процедур определяют ФП для сложных посылок,
которые состоят из нескольких простых, соединенных союзами «И»,
«ИЛИ»?
10.	С помощью какой процедуры находят результирующую ФП, соот-
ветствующую совокупностиу-х правил, соединенных союзом «ИЛИ»?
11.	Поясните на произвольных графиках ФП ц(х) и р.(у), как происхо-
дят процедуры инференции и дефазификации.
12.	Назовите основные этапы синтезирования системы fuzzy-
управления.
667
Заключение
Изложенный в книге учебный курс призван создать у студентов
целостное представление об одной из важных инженерных наук -
теории управления техническими системами, помочь им овладеть
математическим аппаратом этой теории, сформировать у них знания
основных принципов построения автоматических систем управле-
ния, привить навыки анализа и расчета таких систем, выработать у
будущих специалистов по автоматизации и управлению определен-
ную "философию", систему мышления инженера-автоматизатора.
Один из аспектов этого профессионального мышления заключа-
ется в понимании и осознании следующего. В практической инже-
нерной деятельности часто встречаются проблемы и задачи, которые
с трудом поддаются математической формализации на основе изло-
женных в книге строгих методов. И тогда разработчик системы
управления вынужден опираться еще и на интуицию, сформировав-
шуюся при изучении данного курса, проявлять определенную изо-
бретательность. При этом окончательную оценку принятых решений
можно дать только на основании результатов моделирования и/или
достаточно длительной эксплуатации спроектированной системы в
реальных условиях.
Идеология и методология теории управления, ориентированные
главным образом на технические системы с обратной связью, играют
не только большую прикладную, внутридисциплинарную роль в ав-
томатике, но имеют и важное общепознавательное, междисципли-
нарное значение, так как обратная связь является фундаментальным
668
принципом, используемым и действующим не только в технических,
но и в биологических и социоэкономических системах.
Назначение курса заключается не только в обучении и привитии
знаний теории управления, но и в закладке фундамента для даль-
нейшего углубленного самостоятельного ее изучения по специаль-
ной научной и справочной литературе. Тем более, что за последнее
десятилетие в технологии автоматизации интенсивно развиваются
направления, ставящие новые задачи перед теорией управления: ана-
лиз, синтез и моделирование иерархических и распределенных сис-
тем, обеспечение их надежности и живучести с применением прин-
ципов и средств искусственного интеллекта, создание математиче-
ских моделей взаимодействия человека и автоматизированной сис-
темы управления.
Автор надеется, что решению указанных актуальных, принци-
пиально сложных задач автоматизации и управления также будут
способствовать изложенные в настоящей книге сведения о сравни-
тельно простых, традиционных системах управления, ставших клас-
сическими для учебных целей.
669
СПИСОК ЛИТЕРАТУРЫ, РЕКОМЕНДУЕМОЙ ДЛЯ
САМОСТОЯТЕЛЬНОГО УГЛУБЛЕННОГО ИЗУЧЕНИЯ
ТЕОРИИ УПРАВЛЕНИЯ
1.	Теория управления. Терминология. -М.: Наука, 1988 (Выл. 107).
2.	Multilingual Dictionary of Automatic Control Terminology7. IFAC,
Pittsburg / Dusseldorf, 1967.
3.	Математические основы теории автоматического регулирования:
Учеб, пособ. для втузов: В 2 т. / Под ред. Б.К. Чемоданова. - 2-е изд., доп. -
М.: Высшая школа, 1977.
4.	Теория автоматического управления: Учеб, для вузов: В 2 ч. / Под
ред. А. А. Воронова. - 2-е изд, перераб. и доп. - М.: Высшая школа, 1986.
5.	Первозванский А А. Курс теории автоматического управления: Учеб,
пособ. для вузов. -М.л 1986.
6.	Теория управления: Учеб, для вузов / Авторы: А. А. Алексеев,
Д.Х. Имаев, Н.Н. Кузьмин, В.Б. Яковлев. - СПб: Изд-во СПбГЭТУ «ЛЭТИ».
- 1999.
7.	Изерман Р. Цифровые системы управления / Пер. с англ. И.М. Мака-
рова. - М.: Мир, 1984.
8.	Куо Б. Теория и проектирование цифровых систем управления / Пер.
с англ. П.И. Попова. - М.: Машиностроение, 1986.
9.	The control handbook / edited bu William S.Levine. 1996 bu Press.
670
Русско-английский указатель основных терминов
Автоматика, 20
Алгоритм управления (регулиро-
вания), 32
-	функционирования ОУ, 32
Величина управляемая (регулиру-
емая), 30
Воздействие (как процесс), 28
Воздействие (как сигнал), 29
-	возмущающее, 28
-	задающее, 32
-	импульсное, 67
—	единичное, 67
-	ступенчатое, 66
— единичное, 67
-	управляющее, 28
Возмущение, 28
Годограф Михайлова, 267
Граница устойчивости, 257, 260
Диаграмма состояния, 350
Длительность переходного про-
цесса, 308
Динамическая ошибка, 240
Динамическая точность, 237
Законы регулирования, 231
Запас устойчивости по амплиту-
де, 311
- по фазе, 312
Звено алгоритмическое, 35
- апериодическое, 165,173
-динамическое, 35,159
-дифференцирующее, 190
-запаздывания, 195
- интегрирующее, 183
-статическое, 35, 161
Интеграл свертки, 97
Интервал дискретности (повторе-
ния), 494
Квантование (сигналов) по време-
ни, 491
automatica, automation
control law
funktion law
controled variable
action
action variable
disturbance variable, disturbance signal
reference signal
stepping action
unit impulse (Dirac funktion)
step funktion, ramp funktion
unit-step funktion
control signal, actuating signal
disturbance
Michaylov lokus
stability limit
state graph, state diagramm
duration transient response
transient deviation
dynamic accuracy
control law
gain margin
phase margin
element, component
lag element
dynamic element
derivative element
delay element
integrating element
static element
convolution integral
recurrence interval
sampling
671
Компенсация возмущений, 365,368	disturbance-variable compensation
Коэффициент передаточный, 83	transfer gain
- перерегулирования, 306	peak overshoot
Критерий Гурвица, 259, 516	Hurwitz criterion
- устойчивости, 258	stability criterion
-Михайлова, 266, 517	Michaylov criterion
- Найквиста, 272, 517	Nyquist criterion
- Рауса, 264	Routh criterion
Линеаризация, 81, 547, 563	linearization
Модуляция, 493	modulation.
Область устойчивости, 282	stability domain
Обратная связь, 44	feedback
Объект управления, 28	controlled plant
Ошибка регулирования, 45,231,234	control error, deviation
Переменная состояния, 127	state variable
Перерегулирование, 306	overlap
Постоянная времени, 90	time constant
Предельный цикл, 541	limit cycle
Преобразование Лапласа, 19,100	Laplase transform
-Фурье, 19, 75	Fourier transform
- Принцип наложения (суперпози-	principe of superposition
ции), 88	
Пространство состояний, 128	state space
Регулирование, 42	regulation, closed loop control
Регулятор, 42	controller
Режим динамический, 70	dynamic duty
- переходный (неустановивший-	transient duty •
ся), 70	
- статический, 70	static duty
-установившийся, 71	steady duty
Сигнал, 29	signal
- аналоговый (непрерывный), 66	analogue signal
- гармонический, 69	harmonic signal
- дискретный, 66	digital signal
- ошибки (рассогласования), 45	converted deviation, error signal
- случайный, 66, 435, 451	random signal
Синтез, 359, 362, 375	design
Система управления (регулирова-	control system
ния), 30	
- астатическая, 238	floating control system
672
— дискретная, 492
— импульсная, 494
—	комбинированная, 45
—	нелинейная, 528
—	программная, 41
—	с замкнутой цепью воздейст-
вии, 44
—	следящая, 41
—	с разомкнутой цепью воздейст-
вий, 42
—	стабилизирующая, 41
—	статическая, 234
—	цифровая, 492, 521
Спектральная плотность, 78, 445
Стабилизация, 381
Статическая точность, 234
-	ошибка, 235
-	характеристика, 78
Степень затухания, 177, 309
Суперпозиция, 88
Схема структурная, 37
Точность управления, 233
-	динамическая, 237
-	статическая, 234
Уравнение выхода, 128
-	динамики, 58, 219
-разностное, 155
-	состояния, 127
-	статики, 79, 130
-	характеристическое, 96, 219
Управление (регулирование), 28
-	в замкнутой цепи, 44
-	в разомкнутой цепи, 42
Управляемость, 343
Устойчивость, 253
Устройство управляющее, 30
Фазовое пространство, 538
-	траектория, 538
Функция взаимная корреляцион-
ная, 449
sampling control system
sampled-data control system
compound control system
non-linear control system
programmed control system
closed-loop control system
servocontrol system
open-loop control system
stabilizing control system
static control system
digital control system
spectral density
stabilization, fixed command control
static accuracy
static error
static characteristic
damping factor
superposition
block diagram
accuracy precision
dynamic accuracy
static accuracy
output equation
dynamic equation
difference equation
state equation
static equation
characteristic equation
control
feedback control
feedforward control
controllability
stability
control equiment
phase plane
phase trajectory
cross-correlation funktion
673
-	импульсная (весовая), 97
-	корреляционная (автокорреля-
ционная), 442
-	передаточная, 102
-	переходная, 94
-	чувствительности, 339
Fuzzy-управление, 644
Характеристика импульсная (весо-
вая), 97
-	переходная, 94
-	статическая, 78
-	амплитудная частотная, 108
-частотная, 107
Характеристическая кривая, 267
Характеристический оператор (по-
лином), 90
Характеристическое уравнение, 96
Частота критическая, 257
-	резонансная, 179
-	среза, 274
Чувствительность, 339
Элемент импульсный, 495
-	запоминающий, 497
-	линейный, 80
-	нелинейный, 80
-	сравнения, 38
-	статический, 80
-	формирующий, 495
impulse response, weigting funktion
auto-correlation funktion
transfer funktion
step response
sensitivity funktion
fuzzy-control
impulse response
step response, transient response
stead-state characteristic curve
magnitude plot, amplitude response
frequency response, Bode diagram
(plot)
response curve
characteristic polynomial
characteristic equation
cut-off frequency
resonant frequency
cut-off frequency
sensitivity
sampling element
holding element
linear element
nonlinear element
comparator
static element
shaper
674
Заявки на книгу направлять по адресу:
620144, г. Екатеринбург, ул. Куйбышева, 30
Уральская государственная горно-геологическая академия,
кафедра автоматики и компьютерных технологий
Учебное издание
Вильмар Адольфович Лукас
ТЕОРИЯ УПРАВЛЕНИЯ
ТЕХНИЧЕСКИМИ СИСТЕМАМИ
3-е издание, переработанное и дополненное
Редактор Л.В. Устьянцева
Компьютерная верстка Н.Л. Кузиной
Подписано в печать 14.05.02 г. Печать офсетная. Бумага писчая Формат
бумаги 60 х 84 1/16. Печ.л. 42,125. Уч.-изд.л. 42,0. Тираж 1500 экз. Заказ 502
Информационно-издательский центр
620144, г.Екатеринбург, ул. Куйбышева, 30.
Уральская государственная горно-геологическая академия
АООТ «Полиграфист»
620151, г.Екатеринбург, ул. Тургенева, 20