Автор: Кочетков Е.С. Кочеткова Е.С.
Теги: линейная алгебра алгебра издательство просвещение учебник для школы
Год: 1969
Текст
!
Ялгевра
и элементарные
сруннции
Е, С. КОЧЕТКОВ
Е. С. КОЧЕТКОВА
Алгебра
и элементарные
рункции
Учебное пособие
для учащихся 9 класса
средней школы
Под редакцией доктора
физико-математических наук
О. И. ГОЛОВИНА
Утверждено Министерством
просвещение РСФСР
ИЗДАНИЕ 4-е
ИЗДАТЕЛЬСТВО
«ПРОСВЕЩЕНИЕ»
МОСКВА 1969
ЛИНЕЙНЫЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
Изучение алгебры и элементарных функций мы начинаем
с рассмотрения линейных уравнений и неравенств. Эта тема
знакома нам еще по курсу VIII класса. Прежде чем изучить ее
более глубоко, вспомним некоторые уже известные нам понятия.
Тождества
§ 1
В математике часто приходится иметь деле с равенствами,
то есть с такими записями, в которых два выражения соединены
знаком = (знаком равенства).
Прежде всего обратимся к числам. Если а и b — числа, то
равенство
а = b
означает, что а и b — это просто одно и то же число. Наоборот,
если а и b — разные числа, тс пишут
о # Ь.
Например, 2 = 2, 2 + 3 = 5, 2 — 3 = — 1,
но
7#= 6, 7 + 3 # О, 3 — 7 # 4.
Труднее обстоит дело, когда равенство содержит какие-ни-
будь буквы, которыми обычно мы обозначаем неизвестные ве-
личины. Рассмотрим, например, такие равенства:
о + 4 = 5, аг+ J = —3, (О (2) 1 1 1 о®—1 а + 1 а — 1 (5)
1 + К а — а, (3) ая — Ь- . , а + Ь. (6)
о2—1=(а+ 1)(с —1), (4) а — b
Каждая часть равенства (1)
ниях а. Это означает, что
имеет смысл при любых значе-
какое бы числовое значение мы
3
ни придали букве а, левая и правая части равенства (1) тоже
прнмут некоторые числовые значения.
Аналогичным свойством обладают также равенства (2) и (4).
А вот с равенствами (3), (5) и (6) дело обстоит иначе.
Правая часть равенства (3) определена при любых значениях а,
а левая — лишь при неотрицательных значениях а. (Вспомните:
извлекать квадратные корни можно лишь из положи гельных
чисел и нуля.) Поэтому если равенство (3) рассматривать в целом,
ю следует сказать, что оно определено для всех неотри-
цательных значений а. Левая и правая части равенства (5) оп-
ределены лишь при а =# 1 и а =£ — 1. Если же а = 1 или а = — 1.
то в знаменателях дробей получаются нули, а делить на нуль
нельзя. Поэтому равенство (5) определено при всех значениях а,
отличных от 1 и —1. Правая часть равенства (6) определена
при любых значениях а и Ь, а левая лишь при а =И= Ь. Поэтому
в целом равенство (6) имеет смысл для любых не равных друг
другу чисел а и Ь.
Значения букв, входящих в равенство, при которых имеют
смысл и левая и правая части этого равенства, называются
допустимыми значениями этих букв.
Так, допустимыми значениями а в равенствах (1), (2) и (4)
будут все числа, в равенстве (3) — все неотрицательные числа,
в равенстве (5) — все числа, кроме 1 и — 1. В равенстве (6) до-
пустимые значения а и b складываются из всевозможных пар не
равных друг другу чисел.
Если равенство содержит более одной буквы, то, говоря о допустимых
значениях этих букв, мы должны иметь в виду одновременно к а ж д у ю из
этих букв. Например, можно сказать, что пары чисел (1, 2) и (—5, 6) яв-
ляются допустимыми, а пара (3, 3) — не допустимой для букв а и Ь в равен-
стве (6).
Однако не следует говорить, что значение I является допустимым для
буквы а, так же как не следует говорить и то, что это значение не является
допустимым для а. Ведь все зависит еще и от того, какое значение прини-
мает при этом буква Ь. Если не только а, но и Ъ равно 1, то равенство (6)
теряет смысл; если же b + 1, то при а = 1 это равенство определено.
Хотя в равенстве (1) допустимым является любое число, ле-
вая и правая части этого равенства принимают одинаковые
числовые значения лишь при а = 1. При всех же остальных
значениях а левая часть этого равенства принимает числовые
значения, отличные от 5. Обе части равенства (2) не могут при-
нять одинаковые числовые значения ни при каком значении а.
Ведь выражение а2 4- 1 принимает только положительные значе-
ния, а число — 3 является отрицательным. Прямо противополож-
ным свойством обладает равенство (4). Какое бы значение мы пи
придали букве а, левая и правая части этого равенства примут
одинаковые числовые значения. О равенстве (5) этого сказать
нельзя. При а — 1 и а = — 1 это равенство вообще теряет смысл,
4
а в таком случае нельзя шпорить о том, одинаковые пли неоди-
наковые числовые значения принимают его отдельные части. Но
числа 1 и 1 не входят в область допустимых значении а. По-
этому можно сказать, чю обе части равенства (5) принимают оди-
наковые числовые значения при любом допустимом значе-
нии а. Аналогично можно сказать и про равенство (6). Обе его
части прииимаюг одинаковые числовые значения при любых
допустимых, значениях а и Ь.
Равенство, обе части которого принимают рдинаковые число-
вые значения при любых, допустимых значениях входящих в него
букв, называется тождеством.
К тождествам относятся, например, равенства (4), (5) и (6).
Что же касается равенств (1), (2) и (3), тс их отнести к тожде-
ствам, очевидно, нельзя.
Представляемся вполне естественным потребовать, чтобы понятие тож-
дества удовлетворяло следующему важному свойству, называемому свойством
транзите вност и,
если равенства А = В и В = С являются тождествами,
то и равенство А С являете я тождеством.
Можно, однако, показать, что введенное нами определение тождества
этому требованию удовлетворяет не всегда. Действительно, равенства
|а =(/~а)5, (7)
(К а^ = а (8)
в смысле нашего определения являются тождествами. Каждое нз них имеет
допустимыми значениями все неотрицательные значения а. Однако равенство
I с 1 = а (9)
имеет допустимыми значениями уже все значения а (положительные, отри-
цательные н пуль), а справедливо оно лишь для неотрицательных значений а.
Следовательно, в смысле введенного нами определения равенство (9] не
является тождеством.
Выяснение того, когда такие неприятности могут возникнуть и когда
они не возникают, выходит за пределы нашей программы н потому не мо-
жет быть здесь проведено.-Для избежания же этих неприятностей поступают
таким образом. Вместо того чтобы говорить о тождествах как равенствах,
справедливых для всех допустимых значений входящей в них буквы а,
говорят о тождествах, имеющих место для какого-то заданного множе-
ства значений а. Тогда если равенства А = В я В = С являются тождества-
ми на одном и том же множестве значений а, то для тех же значений а будет
тождеством и рагеиство А = С.
Упражнения
Для каждого из данных равенств (№ 1—10) выяснить, при
каких значениях входящих в них букв определены:
а) левая часть равенства;
б) правая часть равенства;
в) равенство в целом.
1. |/ а = 4^ а.
2. | -U.
И а
3. — — - —. 5. ' 4- —— = t±^?.
/,24-2 Ь-— 9 а _ а 4- 1 а2 3 — а
3. С- 5—.
с!— с Ь — 1 3
5
7 = s. J_ + _=
a»+ 1 a + 1 a2 -a -f- 1 a3 + 1
_ 5 1 !n 1 . I_________ + b+6
M ~ a*-\b* ’2-b^^+2b+4
11. Покажите, что равенство 2 — a — 3a — 4 не является тож-
деством
12. Можно ли сказать, 4io равенства:
„ 1 1 ч 1 г— , 1 х р 1
а) =------------------; в) и х \—=-=-—=
' a3 — й3 (J — b) (а2 + ab + b2) V х V х
б) а3 + b3 = (a -f- b) (а2 — ab А Ь-у,
— выполняются при любых значениях входящих в них букв?
Являются ли эти равенства тождествами?
Уравнения § 2
В предыдущем параграфе все равенства, содержащие букву,
мы разбили на два класса. К одному классу были отнесены
тождества, то есть такие равенства, обе части которых прини
мают одинаковые числовые значения при любых допустимых
значениях буквы. Примером таких равенств могут служить ра-
веис1ва.
a2 _ J = (а + i)(u_ 1), _J_ =
а2— 1 а + 1 ° — *
К другому классу мы отнесли все те равенства, обе части
которых принимают разные числовые значения хотя бы при одном
допустимом значении буквы. К ним относятся, например, равен-
ства:
a + 4 = 5, a2 + 1 = — 3.
Однако к изучению равенств можно подойти н по-другому.
Практика часто ставит перед нами задачу выяснить, при ка-
ких допустимых значениях буквы (или нескольких букв) обе
части того или иного равенства принимают одинаковые число-
вые значения. На равенство в этом случае мы смотрим как на
уравнение относительно указанной неизвестной величины.
Так, если равенство
a + 4 = 5 (1)
рассматривать как уравнение относительно величины а, тс легко
сообразить, что обе его части принимают одинаковые числовые
значения только при a = 1. Действительно, если a = 1, то
а + 4 — 5; если же а ф 1, то а 4- 4 =£ 5. Число 1 называется кор-
нем уравнения (1).
Вообще, корнем уравнения относительно одной неизвестной
величины называется каждое числовое значение этой величины,
6
при котором обе части уравнения принимают одинаковые число-
вьА значения.
То же самиС определение иначе формулируют следующим ой
разим: корнем уравнения относительно одной неизвестной вели-
чины называется такое значение этой величины, при котором
уравнение обращается в числовое равенстве (или которое убив-
летвиряет данному уравнению).
Выше мы привели уравнение (а + 4 = 5), которое имеет лишь
один корень. Существуют уравнения, которые имеют более од-
ного корня. Например, уравнение а2 = 1 имее, два корня. 1 и
— I; уравнение а -f- 2 — 2 + а имеет бесконечно много корней:
каждое число является его корнем. (В этом случае уравнение
является тождеством.) Наконец, можно- указать и такие урав
нения, которые совсем не имеют корней. Примером може1 слу-
жить хотя бы уравнение а- 4* 1 = — 3
Решить уравнение — этс значит:
1) выяснить, имеет ли оно корни, и
2) если имеет, то найти каждый из них.
Отметим (хотя это и несущественно), что в равенствах, рас-
сматриваемых как уравнения, неизвестные величины обычно обо
значаются не начальными буквами латинского алфавита (а, о,
с, . . .), а конечными буквами (к, у, z). Например, вместе а 4- 4 = £
пишут х 4-4=5; вместо а2 4- 1 = — 3 пишут х2 1 = — Зит. д.
Два уравнения относительно одной и той же неизвестной
называются эквивалентными (или равносильными), если каждый
корень первого уравнения является вместе с тем и корнем второго
уравнения, а каждый корень второго уравнения является вместе
с шеи и корнем первого уравнения.
Эквивалентными будут, например, уравнения х 4* 4 = 5 и
х — 1=0, каждое из которых имеет единственный корень 1. Эк
Бивалентными являются и уравнения х~ = 4 и 2х2 = 8. Каждое
из них имеет два корня: 2 и —2.
Уравнения, не имеющие корней, считаются также эквивалент-
ными (например, х2 = — 1 и х2 4* 1 = — 3).
Для решения уравнений оказываются важными следующие
свойства эквивалентных уравнений, которые мы напоминаем
учащимся без доказательства.
1. Если обе части уравнения умножить или разде-
лить на одно и то же число, отличное от нуля, то
получится уравнение, эквивалентное данному.
2. Если какое-нибудь слагаемое перенести из одной
части уравнения в другую, поменяв при этом его знак
на противоположный, то получится уравнение, экви-
валентное данному.
Например, в уравнении
2х — 1 = 5 — х
— I можно перенес m из левой части в правую, а - х, наобо-
рот, из правил части в левую. В результате получим
2х + х = 5 + I,
н.п!
Зл = 6.
Очевидно, что единственным корнем этого (а следовательно,
и исходного) уравнения служит число 2.
Упражнения
13. Эквивалентны ли уравнении.
а) 25х2 = 0 и 5х = 0; г) х2 = — 3 и х — 1 = 3;
б) 9х2 = 25 и 3* = 5, д) хг + I = 0 и х2 4* 2 = 0?
в) (2* — I)2 -- I и 2х — 1 = I;
14*. Сколько Кинней имеет следующее уравнение относительно
неизвестной величины х:
(х — I)2 + (х — а)2 = 0,
где а — некоторое заданное число?
Линейные функции и их графики § 3
Рассмотрим равенство
у = 2х 4- 1 (1)
Каждому значению буквы х это равенство ставит в соответ-
ствие вполне определенное значение буквы у. Если, например,
х = 0, то у = 2 • 0 4- 1 = 1; если х — 10, то у = 2 • 10 4-1=21;
при х = — -1 имеем у = 2 • (—4- 1 - 0 и т. д. Обратимся
еще к одному равенству:
у = х2. (2)
Каждому значению х это равенство, как и равенство (1), ста-
вит в соответствие вполне определенное значение у. Если, напри-
мер, х = 2, то у = 4; при х = — 3 получаем у = 9 и т. д. Равен-
ства (1) и (2) связызают между собой две величины х и у так,
что каждому значению одной из них (х) ставится в соответствие
вполне определенное значение другой величины (у).
Если каждому значению величины х соответствует вполне
определенное значение величины у, то эта величина у называется
функцией от х. Величина х при этом называется аргументом
функции у.
Таким образом, формулы (1) и (2) определяют две различ-
ные функции аргумента х.
• Функция аргумента х, имеющая вид
у = ах 4- Ь, (3)
8
где aw b — некоторые заданные числа,
называйся линейной. Примером ли-
нейной функции может служить любая
из функций:
V = х | 2 (а — 1, b = 2);
у = - 10 (а = 0, Ь = - 10),
у = — Зл (а — — 3, b = 0);
у = 0 (а = b = 0).
Как известно из курса VIII клас-
са, графиком функции у~ах-\-Ь
является прямая линия. Поэтому-
то данная функция и называется ли-
нейной
Напомним, как строится график ли-
нейной функции у — ах + Ь.
1. График функции у=Ь. При
а = 0 линейная функция у = ах J,- b име-
ет вид у = Ь. Ее графиком служит пря-
мая, параллельная оси х и пересекающая
ось у в точке с ординатой Ь. На ри-
сунке 1 вы видите график функции
у = 2 (Ь > 0), а на рисунке 2 — график
функции у — — 1 (£> С 0у
Если не только а, но и £ равно
нулю, тс функция у = ах + b имеет вид
у — 0, В этом случае ее график совпа-
дает с осью х (рис, 3.)
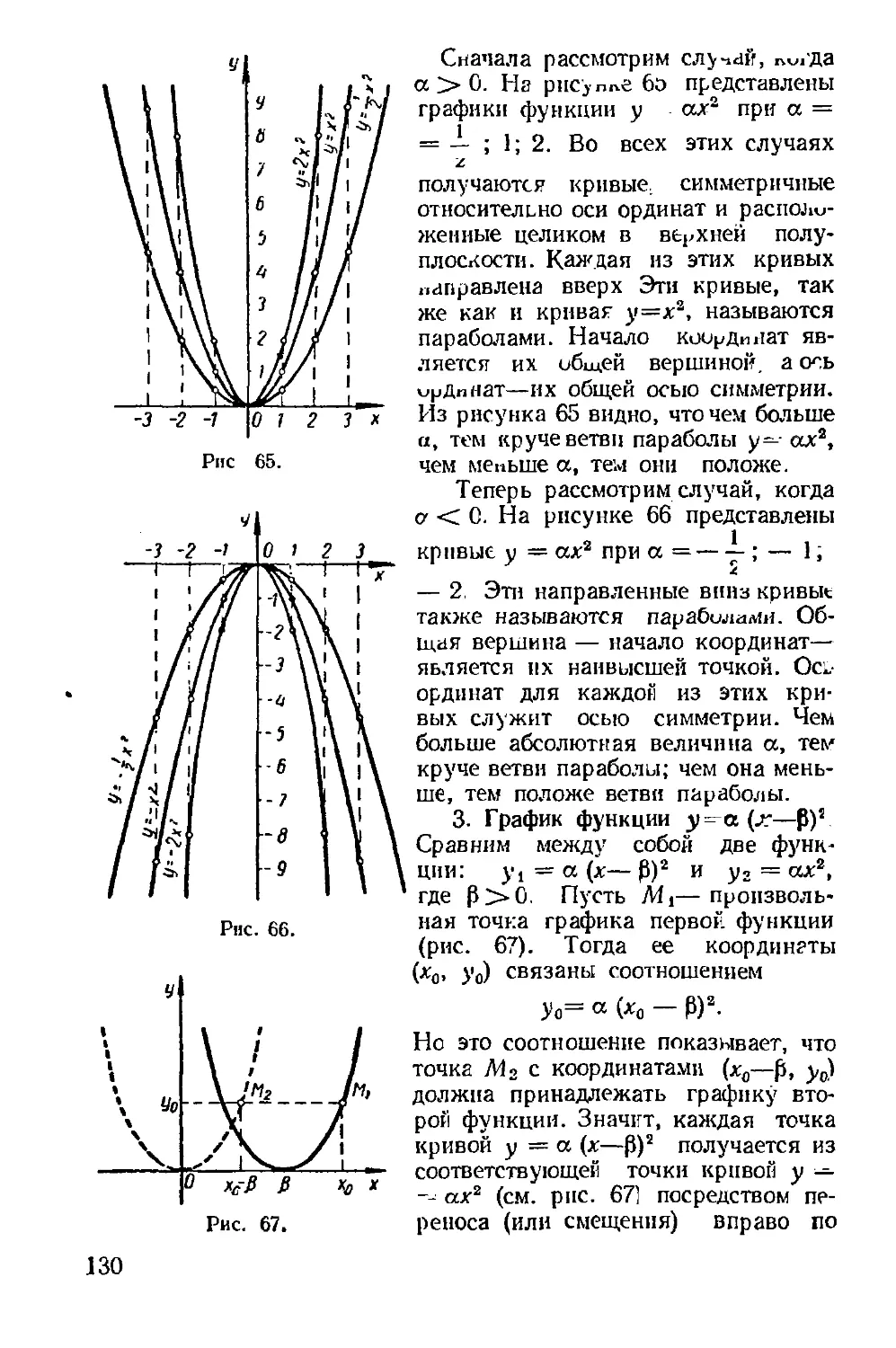
2. График функции уя=ах. При
b = 0 линейная функция у = ах + b
имеет вид у = ах
Если а =# 0, то графиком ее явля-
ется прямая, проходящая через начало
координат и наклоненная к оси х под
углом ср, тангенс которого равен а
(рис. 4). Для построения прямой у = ах
достаточно найти какую-нибудь одну
ее точку, отличную от начала коорди-
нат. Полагая, например, в равенстве
у ~ ах х ~ получим у = а. Следова-
тельно, точка М с координатами (1; а)
лежит на нашей прямой (рис. 4). Про-
водя теперь прямую через начало ко-
ординат и точку М, получаем иско-
мую прямую у = ах.
На рисунке 5 для примера на-
черчена прямая у = 2х (а > 0), а
У
У-0
7) *
Рис. 3.
9
Рис. 8.
на рисунке 6 прямая у =— х
(а < 0).
3. График функции у = ах + Ь.
ПуС1Ь b > 0. Тогда прямая у — ах , b
получается посредством параллель-
ного сдвига прямой у = ох nd b еди-
ниц вверл. В качестве примера на
рисунке 7 показано построение пря-
мой у = — + 3.
2
Если b < 0, то прямая у — ах+ b
получается посредством параллель-
ного сдьша прямой у = ах па — b
единиц вниз. В качестве примера на
рисунке 8 показано построение пря-
„ X п
мои у -------3.
г 2
Прямую у = ах + b можно постро-
ит ь и другим способом. Любая пря-
мая полностью определяется двумя
своими точками. Поэтому для по-
строения графика функции у = ах + b
достаточно найти какие-нибудь две
его точки, а затем провести через
них прямую линию. Поясним это
на примере функции у = — 2х + 3.
При х — 0 у = 3, а при х = 1 у = I.
Поэтому две точки: М с координата-
ми (0; 3) и N с координатами (1;1) —
лежат на нашей прямой. Отметив
эти точки на плоскости коорди-
нат и соединив их прямой линией
(рпс. 9), получим график функции
у — — 2х 4 3. Вместо точек М и N
можно было бы взять, конечно, и
другие две точки. Например, в ка-
честве значений х мы могли бы вы-
брать не 0 и 1, как выше, а — 1 и
2,5. Тогда для у мы получили бы со-
ответственно значения 5 и — 2. Вмес-
то точек Л4 и N мы имели бы точки Р
с координатами (—1; 5) и Q с ко-
ординатами (2,5; —2). Эти две
точки, так же как и точки М и
N, полностью определяют искомую
прямую у — — 2х + 3.
10
Упражнения
15 На одном и том же рисунке
достроить графики функций:
а) у = — 4;
6} у = 2;
в) у == 0;
г) у = 2;
Д) У = 4.
Пересе как, гея ли эти графики
с осями координат? E<_^ih Пересе
каются, то укажите координаты
1ичек Пересечения.
16. На одном и 1GM же рисунке
построить графики функций;
а) у = б) у = у; в) у = х;
г) у = 2х; д) у — 4х.
17. На одном и том же рисун-
ке построить графики функций:
а)у = -р б)у = -|;
в) у = — х; г) у=— 2х; д) у = — 4х.
Построить графики данных
функций (№ -18 -21) и определить
координаты точек пересечения
этих графиков с осями координат.
18. у=3+х. 20. у=—4—х.
19. у=2х—2. 21. у=0,5 (1 —
- Зх).
22. Построить график функ-
ции
у — 2х — 4;
используя этот график, выяснить:
а; при каких значениях х
У = 0;
б) при каких значениях х зна-
чения у отрицательны и при ка-
ких — положительны;
в) при каких значениях х
величины х и у имеют одинако-
вые знаки;
г) при каких значениях х вели-
чины х и у имеют разные знаки.
23. Написать уравнения пря-
мых, представленных на рисун-
ках 10 и 11.
Рие П,
и
24. Какие из известных вам физических законов описываются
с помощью линейных функций?
25. Как построить график функции у — — (ах + Ь), если за-
дан график функции у = ах + Ь?
Линейные уравнения
Уравнение называется линейным, если левая и правая части
его представляют собой линейные функции относительно неиз-
вестной величины.
К таким уравнения™ относится, например, любое из уравне-
ний:
2х — 1 — Зх — 5; 4х — 6 — 7х; 8х — 9 = 0.
Общий вид линейного уравнения таков:
ах ]- b = сх + d, (1)
где а, Ь, с и d — заданные числа, ах — неизвестная величина.
Если в уравнении (1) коэффициенты а и с отличны друг от
друга, то уравнение называется также уравнением 1-й степени.
Так, каждое из приведенных выше линейных уравнений яв-
ляется вместе с тем и уравнением 1-й степени. Уравнение
0 х - 1 (это тоже уравнение!) является'линейным, но не явля-
ется уравнением 1-й степени. Очевидно, что каждое уравнение 1-й
степени можно назвать и линейным уравнением. Однако не каж-
дое линейное уравнение будет уравнением 1-й степени.
Как же решаются линейные уравнения?
Перенося сх из правой части уравнения (1) в левую, а Ь из
левой части в правую, получим эквивалентное уравнение
(а —с) х =d — Ь. Таким образом, всякое линейное уравнение экви-
валентно уравнению вида
тх = п, (2)
где тип — некоторые заданные числа, ах — неизвестная величина.
Если т 0, то уравнение (2) имеет, очевидно, один корень
х = —.
т
Если т = 0, а п 0, то уравнение (2) обращается в
0 • х = п.
Такое равенство не может выполняться ни при каких значениях х.
Следовательно, в этом случае уравнение (2) не имеет корней.
Наконец, прит — п ;= 0уравнение (2) принимаетвид 0-х 0.
12
Эти равенстве верно при любых значениях х Поэтому в дан-
ном случае уравнение (2) имеет бесконечное множесшо корней:
любое число является е^о корнем.
Примеры.
1) Решить относительно х уравнение
ах — 1 = л + 2
Перенося х в левую, а — 1 в правую час"ъ и приводя подоб-
ные члены, получаем
(а — 1) х = 3.
Если а =£ 1, тс уравнение имеет единственный корень х —--.
а — 1
Если же о = 1, то уравнение принимает вид С • х = 3. Такое
уравнение не имеет корней.
Ответ При а #= ’ данное уравнение имеет единственный
з
корень х = ----, а при а = I — корней не имеет,
с — I
2) Решить относительно х уравнение
а — х = 1 — а2х.
Перенося а2х в левую, а о в правую часть и приводя подобные
члены, получаем
(а* — 1)х = 1 — а.
Если о2 — 1 =# 0, то есть а =£ 1 i о =f= — 1, то
J — а. 1
х =---- =--------.
с2— 1 а + 1
Если а = 1, тс рассматриваемое уравнение сводится к такому:
О х = 0.
В этом случае любое число является егс корнем.
Наконец, при с — — 1 получаем
0 • х = 2.
Такое равенство не выполняется ни при каких значениях х.
Ответ. Если а =f= 1 и. а #= — 1, то данное уравнение имеет
единственный корень х =-----—; при а= 1 его корнем является лю-
с + 1
бое число, а при а = — 1 уравнение вовсе не имеет корней
Упражнения
Данные уравнения (№ 26—35) решить относительно х:
26. Зх + 1 = а. 31. а 4- х = а2х — 1.
27. 5 + х = ах. 32. ах — b = ! 4- х.
28. 4 = ах. 33. х = Ь — а2х.
29. х = а2х. 34. ах — Ь2 =- 7.
30. ах — с2 = 4 - 2х. 35. 3 - а2х = л — Ь.
13
36. Может ли уравнение тх ~ п иметь:
а) ровно один корень;
б) рооно два различных л^ни;
в) ровно 1 иОО Оии различных корней;
г) бесконечно много различных корней?
37. Может ли уравнение ал — 1 + Ь2 Имею бесконечно много
различных корней?
38. Может ли уравнение (а — 1)х = а2 — За Г 2 не иметь корней?
39. Отцу 45 лет, а его сыну 15. Через сколоко лет оген
будет с1арше CoiHci.
а) в два раза;
б) в четыре раза?
Кал можно истолловать мцяшательный корень уравнения,
полученный при решении задачи 39 б?
40. Из пунктов А и В отправляются навстречу друг другу
одновременно два пешехода. Первый идет со скирмстью сц км/ч,
а второй — со скоростью v2 км ч (vt =/= n2j Спустя некоторое время
они одновременно изменяют свои скорости: первый пешеход идет
со скоростью v2 км/ч, а второй — со скоростью Ut км’ч. Встреча
пешеходов происходит через час после того, как они изменили
свои скорости, в пункте, равноудаленном от А и В. Какое время
находились пешеходы в пути?
41. Имеется лом стали двух сортов с содержанием никеля
в р% и q% (р =/= q). Сколько нужно взять лома того и другого
сорта, чтобы получить 100 тонн стали с содержанием никеля в г%?
Графический способ решения уравнения тх—п * 1
§ 5
Уравнение вида тх = п, к которому сводится любое линей-
ное уравнение, может быть легко решено графически. На одном
и том же рисунке построим графики двух функций: у = тх и
у = л. Если эти графики пересекутся, то абсцисса точки пересе-
чения и даст нам корень уравнения тх — п.
Если же эти графики не пересекутся, то это будет означать,
что уравнение не имеет корней.
Рассмотрим отдельно три случая.
1. т =/- 0. В этом случае графикам
функции у = тх будет прямая, накло-
ненная к оси х под некоторым углом
<р (рис. 12). Графиком функции у = л
является прямая, параллельная оси х.
Такие две прямые пересекаются и при-
том лишь в одной точке (на рис. 12 —
точка Л1). Абсцисса точки пересечения,
", и есть корень уравнения тх = л.
т
14
2. т = 0, п ф О. В этом случае .,ря-
ма« у = тх сливается с осью х г прямая
у п параллельна оси х (рис. 13).
Прямые у = тх и у = п OnajuiuuiOj СЯ
Параллельными точки пересечения та-
ких прямых не существует. Поэтому
НС CytuCv 1 oyCi И КОриСЙ у раопсНИЯ
)ПХ — п.
3. т = п = G. В этом случае прямые
у == tTlX И у == ft К-^ВПЗДаЮТ, vjIbwaflCb С
осью х (рис. 14) О таких прямых мож-
но сказать, что они пересекаются в
каждой точке оси х. Поэтому е данном
случае любое число является корнем
уравнения тх = п.
Рис. 13.
Упражнения
Решить графически данные
ния-
42. 2х = 4.
43. Зх == О
44. 4х = — 4.
45. 0,5х — 1,5.
уравне-
У = Л (п-01
д=тх (т=о)
46. — 0,8х = О
47. — 2х = — 7
48. 3 — х = 2х — 3.
49. х = 2х 4- 2.
Рис. 14.
с
х
Уравнения, сводящиеся к линейным
§ 6
К решению линейных уравнений сводится решение и некото-
рых других уравнений.
Поясним этс на примере уравнения
т + х _fn
п 4-х п’ ' '
где тип — заданные числа, ах — неизвестная величина. Это
уравнение нельзя назвать линейным, поскольку его левая часть
не является линейной функцией относителпно х. По тако« урав-
нение легко сводится л линейному. Прежде всего заметим, 1,то
л =# О, иначе правая часть данного уравнения не нмелг бы смысла.
Теперь воспользуемся свойством пропорций: если а — то
о d
ad = fee. Применяя это свойство поопорций к равенству (1) полу-
чаем
(лг -f- х) п = {п 4- х) т,
откуда
лги -f- лд = ллг - тх,
.Ь
или
(n — tn.) x — и. (2)
Итак, исходя пЗ нс..|Ипейногс уравнепия (1), мы пришли к ли-
нейному уравнению (zj. Из него получаем: если m #= п, то х — и;
если же т = п, то х — любое число.
Не будет торопиться С ОТВсЗмМ. ПЬрслмд от уравнения (i)
к уравнению (2) фактически свелся к тому, что обе части урав-
нения (1) мы умножили на выражение п (п -|- х). Но в таком слу-
чае уравнение (2) может оказаться и неэквивалентным уравне-
нию (1). Очевидно, чти Потери!о корней при переходе от (1) к (2)
мы не могли (докажите это!) Но как знать, может быть, мы
получили посторонние корни? Вот почему теперь необходимо
сделать проверку полученных корней.
Сначала проверим корень х = 0, который получен из урав-
нения (2) в предположении, что т п. Если в уравнении (1)
положить х = 0, то получим — = Следовательно, при т #= п
п п
и п#=0 х = О — действительно корень уравнения (1). Теперь
проверим, будет ли любое число при т = п =И= 0 корнем уравне-
ния (1). При т — п это уравнение принимает вид
Любое число, кроме — п, удовлетворяет уравнению (3) и,
следовательно, является его корнем. Но х = — п нельзя считать
корнем этого уравнения, поскольку при х = — п левая часть
равенства (3) не определена. Таким образом, при tn = /г =# 0 кор-
нем уравнения (1) является не любое число, как это было для
уравнения (2), а лишь любое число, отличное от — п.
Теперь можно дать ответ; если ti #= 0 и т п, то уравнение (1)
имеет единственный корень х = 0; если же m = п #= 0, то корнем
ею является любое число, кроме — п.
Упражнения
Данные уравнения (№ 50—58)» решить относительно х, счи-
тая а, Ь, т и п заданными;
50. X х — 3 = 3 . 53. а- х — 3 х —2 *+1. х2—4
51. 2 54* а Ь
х — 3 хг— 9 1 -Ьх 1—ах
52. х — 5 а — х — . 55*. а = I — Ьх
х + 7 х-1-7 1 -р Ьх
56. . . = 2х 2х
2Ьх — b — 2х+ 1 Ь — 1 2х — 1
1G
57 Зс a ______________ a 2a
x — a x 2a x — a x — 2a
m n ______________ m- — ti-
x — tn x — n x-—(m-|-n)x-|-//in
59. Уравнение
ax — b j
ax + b
решить.
а) относительно а; б) относительно b\ в) относительно x.
Уравнения, содержащие неизвестное под знаком
абсолютной величины § 7
Абсолютная величина числа а (обозначается * 1а |) определяется
следующим образом:
| а, если а>»0;
| а | = ' —а, если а < 0;
| 0, если а — 0.
Например, 1101 = 10; | — у | = | — 1001 — 100 и т. д.
Каждому значению х соответствует вполне-} определенное зна-
чение |х|. Поэтому равенство у = |х| определяет у как некоторую
функцию аргумента х. График этой функции приведен на рисун-
ке 15 (стр. 18). При х > 0 |х| = х, а при х <. 0 |х| = — х\
поэтому линия у-— |х) при х>0 совпадает с прямой у — х
(биссектриса 1-го координатного угла), а при х < 0 — с прямой
у = — х (биссектриса 2-го координатного угла).
Некоторые уравнения содержат неизвестное под знаком абсо-
лютной величины. К таким относятся, например, уравнения
I х — 11 — 2, |6 — 2х| = Зх -|- 1 ит. д. Решение их основано на
том, что если абсолютная величина некиспириси числа х
равна положительному числу а, то само это число х
равно либо а, либо — а. Так, если |х| = 10, то либо х — 10,
либо х — — 10.
Рассмотрим несколько примеров.
1. Решить уравнение |х — 1 | — 2.
Разность х — 1 должна быть равна либо -J- 2, либо — 2. Если
х 1 = 2, то х = 3; если же х—1 — — 2, то х— — 1. Проверка
показывает, что оба эти значения удовлетгоряют данному урав-
нению.
Ответ. Данное уравнение имеет два корня: xt = 3, х2 = — 1.
2. Решить уравнение |6 — 2х[ = Зх + 1.
Имеем: либо 6 — 2х = Зх + 1, либо 6 — 2х — — (Зх -f- 1). В
первом случае х = 1, а во втором х — — 7.
17
Проверка. При х = 1 6 2x1 =
|4| —4, Зх + 1 =4, с-.едовательно,
.. = 1 — корень данного уравнения.
При х = — 7 |6 — 2х; = |20| — 20,
Зх 4- I = — 20; так как 20 =/= — 20, то
х------/ не есть корень данного урав
нения.
Ответ. Данное уравнение имеет
один корень, х = i.
Подобные уравнения можно ре-
шать и графически. Решим, например
графически уравнение х— 1| = 2.
Для этого нужно прежде всего по-
строить график функции у — |х — 1'.
Это можно сделать следующим об-
разом. Сначала построим график
функции у = х — 1 (рис. 16). Ту часть
этого графика, которая лежит выше
оси х, оставим без изменения. Дли
нее х — 1 > 0 и потому л — 1| = х—1.
Ту же часть графика, которая ле-
жит ниже оси х, отобразим симметрич-
но относительно этой оси. Ведь для
этой части х — 1 < 0 и потому । х — 11=
= — (х — 1). Полученная в резуль-
тате линия (рис. 17 — сплошная ли-
ния) и будет графиком функции у =
= |х— 1|. Эта линия пересекается с
прямой у — 2 (рис. 18) в двух точках;
М । с абсциссой — 1 и М2 с абсцис-
сой 3.
Поэтому уравнение |х— 1| = 2
имеет два корня: Xj = — 1, Xj = 3.
Упражнения
Решить уравнения;
60. 1 — |х| — 0,5.
61. 1 + |х| = а.
62. |1 — х| = 0,5.
63. |1 — х| = а.
64. |х + 3 | = 3 + 2х.
65. |7х — 1| = 21 — 9х.
66. ]5 — х’ = |х 4- 4'.
67. Т — Зх: = 13 — 2х|.
18
68. Гк'паглпте, что график функции у — [х — а| (а"> 0) попу-
чается посредством параллельного ^двига графика функции
у = ]х| на а единиц длины вправо.
кап строится график функции у = |х + а| (а ~> 0)?
69. Используя реоуЛптат задачи 68, построить графики сле-
дующих функций:
а) у = |х — 2j; О) у - |х + 3|.
70. К<:к построить график функции у = \ах + Ь\, если задан
график функции у — ал -j- b?
71. Может ли график функции у = ах + b совпасть <, i рафи-
ком функции у — ]ах £>|?
72. Решить графически уравнения:
а) |2 + х| = 3, б) х = |2 — х|; в) |2х — 3| = 3 — х.
73. Исходя из геометрических соображений, выяснить, всегда
ли имеют корни следующие уравнения:
а) х = [ах + bj; в) |ах ф- = с‘,
б) |2х + Ь\ = 3; г) |пх + Ь| = |сх + d|.
74. Как построить график функции у = a ,х| + Ъ, если задай
график функции у = ах + 0?
Метод интервалов § 8
При решении некоторых уравнений, содержащих неизвестное под знаком
абсолютной величины, часто используют так называемый метод интервалов.
Продемонстрируем этот метод на примере уравнения
1*+ П + I* — 2| =3. (1)
Это уравнение содержит две абсолютные величины: |х + li н |х —21.
Первая из них обращается в нуль при х — — 1, а вторая — при х = 2. На
числовой прямой отметим две точки: А с абсциссой — 1 и б с абсциссой 2
(рис. 19). Тем самым числовая прямая разобьется на три интервала. Первый
А В
-> 2
Рис. 19.
(бесконечный) интервал включает в себя все точки, лежащие левее А. Второй
(конечный) интервал содержит в себе точки А и В, а также все точки, лежащие
между ними. Третий (бесконечный) интервал состоит из всех точек, лежащих
19
правее В. В любам из этих трех интервалов каждое из выражений' ]х + 1|
и \х — 2| легко записывается без знака абсолютной величины. Так,
. . .. _ I — х — 1 в пергом интервале;
Iх-*" 11 — | х + 1 во втором и в третьем интервалах.
Аналогично,
„ ( —х + 2 в первом и во втором интервалах:
Iх___________________| х —2 в третьем интервале.
Поэтому левая часть уравнения (1) представляется следующим образом:
в первом интервале (—х — 1) + (—х + 2) = — 2х + I:
во втором интервале (х + 1) + (—х + 2) = 3;
в третьем интервале (х + 1) + (х — 2) = 2х — I.
Теперь нетрудно найти все корни уравнения (1). Сразу же замечаем, что
любое число из второго интервала
— 1 < х < 2
является корнем: ведь при любом значении х из этого интервала левая
и правая части уравнений (1) принимают одно и то же числовое значение 3.
Обратимся к первому интервалу. Если в нем имеются корни, то они
должны, очевидно, совпадать с корнями уравнения
—2х +1=3.
Это уравнение имеет единственный корень х = —1, который мы уже получили
раньше и который, кстати, ие попадает в первый интервал. (Значение х = — 1
принадлежит второму интервалу.) Таким образом, в первом интервале
уравнение (I) ие имеет корней.
Аналогично можно установить, что уравнение (I) не имеет корней
и в третьем интервале. Предлагаем учащимся убедиться в этом самосто-
ятельно.
Итак, уравнение (I) имеет бесконечное множество корней. Каждое
число, заключенное в интервале
~-1 < х < 2,
является его корнем. Никаких других корней это уравнение ие имеет.
Упражнения
Решить уравнения:
75. х — 1| + 1х + 11=2.
76. )5 — 2х| + ,х + 31 = 2 — Зх.
77. |х] + 1х + 21 + 12 — х| = х + 1.
78. Ц — х I—|х + 3] = |х + 2].
Неравенства
§ 9
Если числа а и b равны между собой, то а — Ь — С. Если же^чис-
ла а и Ь ие равны между собой, то разность а — b либо положи-
тельна, либо отрицательна.
20
Если разность а — b положительна, то говорят, что число а
больше числа Ь\ записывается этс таким образом:
а > b. (1)
Если разность а — b отрицательна, то говорят, что число а
меньше числа Ь\ записывается это таким образом:
а < Ь. (2)
Например, 5 > 3, поскольку разность 5 — 3 = 2 положитель-
на; — 7 < — 6, так как разность (—7) — (—6) = — 1 отрица-
тельна.
Записи (1) и (2) называются числовыми непавенствами, а
знаки > п <, участвующие в них, — знаками неравенства.
Числовые неравенства допускают простую геометрическую
интерпретацию. Будем изображать числа точками числовой пря-
мой. Пусть числу а соответствует точка А, а числу I — точка В.
Тогда, если а > Ь, то точка А будет лежать правее точкг В
(рис. 20, а). Если же а < Ь, то точка А будет лежать левее
точки В (рис. 20, б).
До сих пор мы говорили лишь о таких неравенствах, обе части
которых представляют собой вполне определенные числа. (Прав-
да, для общности рассуждений мы обозначали эти числа буквами.
Однако в математике часто приходится иметь дело и с такими не-
равенствами, отдельные члены которых, выраженные с помощью
букв, могут принимать различные числовые значения например,
> а,
-> 3,
с — 1 < а,
Уа + ^6<С,5.
(3)
(4)
(5)
(6)
0) — в в А 0
Al A f
и) 0 6
Рис. 20.
Допустимыми значениями букв, входящих, в неоавенство, назы-
ваются такие значения этих букв, при которых обе части нера-
венства имеют смысл.
Очевидно, что допустимыми значениями с в неравенстве (3)
служат все положительные числа и нуль, в неравенстве (4) — все
числа, кроме нуля, в неравенстве
(5) — все числа. Для неравенства (6)
допустимые значения а и Ь складыва-
ются из всевозможных пар неотри-
цательных чисел.
Рассмотрим подробнее неравенст-
во (3). Оно, как мы уже говорили,
определено для всех неотрицательных
21
значений а. Однако не каждое из указанных чисел удовлетворяет
этому неравенству. Действительно, при а — 0,25 = 0,5. По-
скольку 0,5 > 0,25, то число а = 0,25 удовлетворяет неравенству
(3). А.вот число 4 ему уже не удовлетворяет, поскольку |/4 < 4.
Таким образом, неравенству, содержащему букву, могут удов-
летворять одни допустимые значения этой буквы и не удовле-
творять другие допустимые значения этой буквы.
Неравенство, которому удовлетворяют все допустимые значе-
ния входящих в него букв, называется тождественным неравен-
ством.
Примером такого неравенства может служить хотя бы нера-
венство (5). При любом значении а а — 1 < а. Неравенство (4)
нельзя отнести к тождественным неравенствам; ему не удовлет-
Упр аж не ни я
79. Найти допустимые значения букв, входящих в неравен-
ства:
_ a) Lf. >5; в) д) |х|>х;
б) 1 ~Ь< ——; г) Г |&| < е) —!—>-----?—.
1— b ” 1 ' *»+Г . ' аг + Ьг а2+*Ч-1
80. Можно ли сказать, что неравенствам
Г а + 5 > 1 и ----- < а
удовлетворяют любые значения входящих в них букв? Являются
ли эти неравенства тождественными?
Основные свойства числовых неравенств
$ 10
1. Если а>Ь, то Ь<.а, и, наоборот, если а<Ь, то
t > а.
Доказательство. Пусть а >» Ь. По определению это оз-
начает, что число (а — Ь) положительно. Если мы перед ним
поставим знак минус, то полученное число — (а —Ь) будет, оче-
видно, отрицательным. Поэтому — (а — Ь) < 0, или b — a<Z0.
А это (опять же по определению) и означает, что Ь<а.
Обратное утверждение предлагаем учащимся доказать само-
стоятельно.
Доказанное свойство неравенств допускает простую геометри-
ческую интерпретацию: если точка А лежит на числовой прямой
22
' Е* правее точки В, то точка В лежит левее точки А, и наоборот
• f (см. рис. 20).
2. Если a>b,ab>c, то а> с.
Геометрически это свойство состоит в следующем. Пусть
Т точка А (соответствующая числу а) лежит правее точки В (соот-
ветствующей числу Ь), а точка В, в свою очередь, лежцт правее
точки С (соответствующей числу с). Тогда точка А и подавно
будет лежать правее точки С (рис. 21).
Приведем алгебраическое доказательство этого свойства не-
равенств.
Пусть а >» b, а b >» с. Это означает, что числа (а — Ь) и (Ь — с)
положительны. Сумма двух положительных чисел, очевидно,
С в а
О ' '—о —' —
с 6 о
Рис. 21.
положительна. Поэтому (а — Ь) + (Ь — с) >» 0, или а — с "> 0. Но
это и означает, что а >» с.
3. Если а > 6, то для любого числа с с> b с,
а — с^> Ь — с. Иными словами, если к обеим частям чис-
лового неравенства прибавить или от обеих частей
отнять одно и то же число» то неравенство не нару-
шится-
Доказательство. Пусть а >» Ь. Это означает, что а — Ь>0.
Но а — b — (а 4- с) — (6 4-е). Поэтому (а 4- с) — (Ь 4- с) > 0. А по
определению это и означает, что a -f- с > b 4- с. Аналогично пока-
зывается, что а — с > b — с.
Например, если к обеим частям неравенства 5 >» 4 прибавить
1 то получим 6 > 5 Отнимая от обеих частей данного
неравенства число 5, получим 0 >»— 1.
Следствие. Любое слагаемое одной части числового
неравенства можно перенести в другую часть нера-
венства» поменяв знак этого слагаемого на противо-
положный.
Пусть, например, а 4- 6 >» с. Требуется доказать, что а > с — Ь.
Для доказательства от обеих частей данного неравенства доста-
точно отнять число Ь.
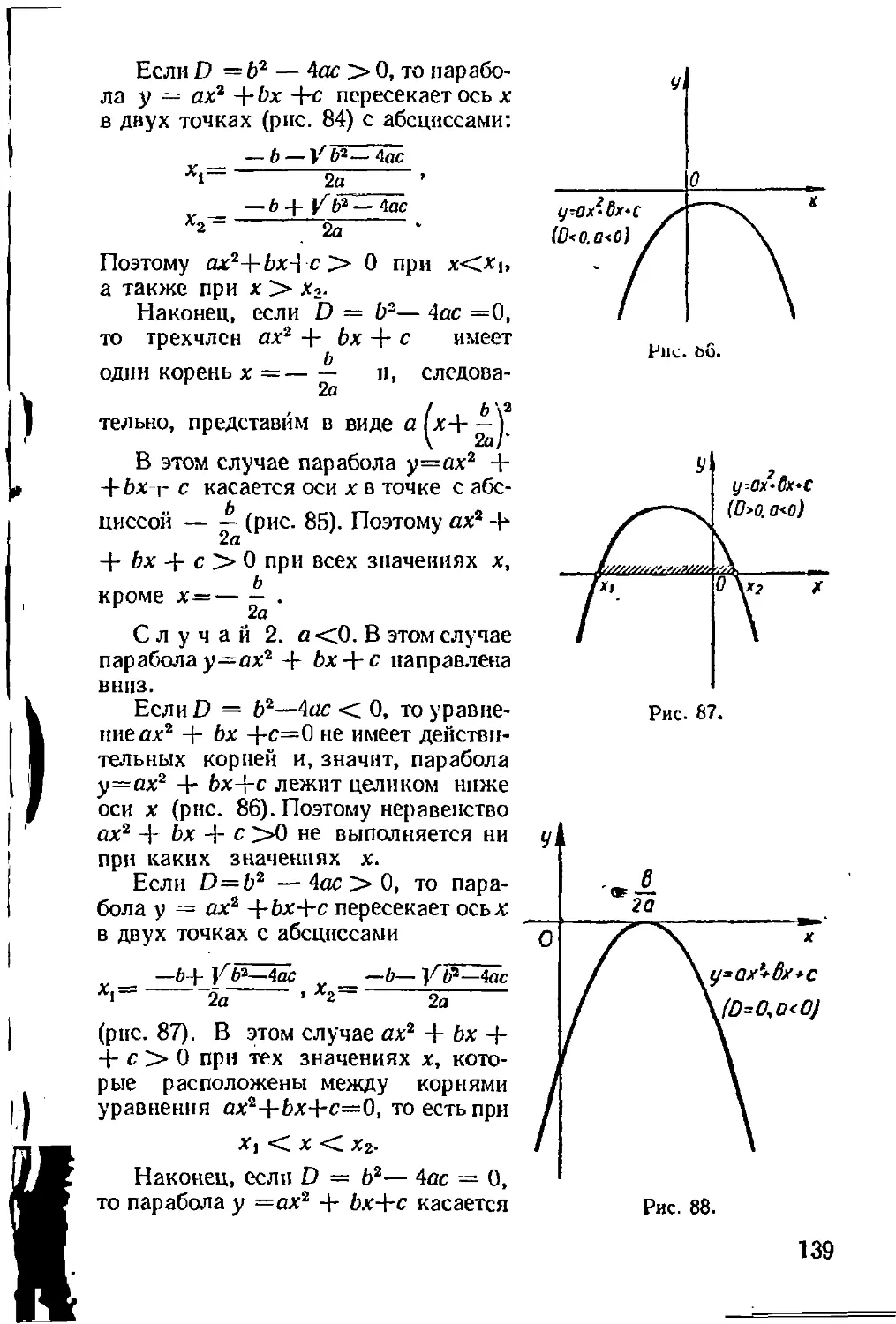
4. Пусть а^>Ь. Если с>0, то ас>Ьс. Если же с<0,
то ас <^Ьс.
Иными словами, если обе части числового неравенства
умножить на положительное число» то неравенство
не нарушится; если обе части неравенства умножить
на отрицательное число» то знак неравенства изме-
нится на противоположный.
23
•Короче это свойство формулируется таким образом:
Неравенство сохраняется при почленном умноже-
нии на положительное число и изменяет знак на про-
тивоположный при почленном умножении на отри-
цательное число.
Например, умножив неравенство 5 > 1 почленно на 7, полу-
чим 35 > 7. Почленное умножение того же неравенства на —7
дает —35 < —7.
Доказательство 4-г о свойства.
Пусть а > Ь. Это означает, что число а — Ь положительно.
Произведение двух положительных чисел а — Ь и с, очевидно,
также положительно, т. е. (а — Ь)с > 0, или ас — Ьс > 0. Поэтому
ас > Ьс.
Аналогично рассматривается случай, когда число с отри-
цательно. Произведение положительного числа а — Ь на отрица-
тельное число с, очевидно, отрицательно, т. е. (а—Ь)с<0; по
этому ас — Ьс < 0, откуда ас < Ьс.
Следствие. Знак неравенства сохраняется при по-
членном делении на положительное число и изменяется
на противоположный при почленном делении на отри-
цательное число.
Это вытекает из того, что деление на число с =#= 0 равносильно
J
умножению на число —.
С
Упражнения
81. Можно ли неравенство 2 > 1 умножить почленно на
а) а2 + 1; б) в) а; г) 1 — 2а + а2,
так чтобы знак неравенства сохранился?
82. Всегда ли 5х больше 4х, а — у меньше у?
83. Каким может быть число х, если известно, что — х > 7?
84. Расположить в порядке возрастания числа:
а) а2, 5а2, 2а2; б) а, 5а, 2а; в) а, а2, а3.
85. Расположить в порядке убывания числа
а — Ь, а — 2Ь, а — ЗЬ.
86. Дать геометрическую интерпретацию третьему свойству
числовых неравенств.
Почленное сложение и вычитание неравенств § 11
Про два неравенства, имеющие одинаковые знаки неравенства
(оба знак > или оба знак <), говорят, что они одинакового
смысла. Например, неравенства а> Ь и 3 > 2 — одинакового
смысла, так как оба они имеют один и тот же знак >; нера-
24
венства а < b и а<с также одинакового смысла, поскольку
имеют один и тот же знак <.
Если одно из неравенств имеет знак >, а другое знак <,
то такие неравенства называются неравенствами противополож-
ного смысла. Например, 16 > 0 и 5 < а — неравенства противо-
положного смысла.
Теорема 1. Неравенства одинакового смысла можно
почленно складывать.
Доказательство. Пусть а > b и с > d. Докажем, что
а + с > b + d.
Так как а > b н с > d, то числа (а — Ь) и (с — d) положительны.
Сумма двух положительных чисел также положительна: (а — Ь) +
+ (с — d) > 0. Но (а — Ь) + (с — d) — {а + с) — (6 -|- d).
Поэтому число (а + с) — (Ь + d) положительно. А это и озна-
чает, что а + с > b + d.
Случай, когда складываются неравенства а < b и с < d, пред-
самостоятел ь но.
лагаем учащимся рассмотреть
Примеры:
, ( 0 > — 100
+ (65 > 64
65 > — 36
( 14 < 15
t — 20 < — 15
— 6<0.
Теорема 2. Два неравенства противоположного
смысла можно почленно вычитать, оставляя знак того
неравенства, из которого мы вычитаем.
Например:
( 2>0 (10 <15
1—3 <6 — I 3> 2
5>—6 7 <13.
Доказательство. Пусть а > Ь и с < d. Покажем, что
а — с > b — d.
Почленное умножение неравенства c<Zd на—1 дает — с>—d.
Сложив это неравенство с данным неравенством а > Ь, получим
а — О b — d.
Случай, когда а < b и с ~> d, предлагаем учащимся рассмот-
реть самостоятельно.
Замечание. Неравенства одинакового смысла почленно вычи-
тать, вообще говоря, нельзя. Например, если бы мы из нера-
венства 2 > 0 вычли почленно неравенство 0 > — 5, то пришли
бы к противоречию: 2 больше 5.
Упражнения
Доказать неравенства:
87. /5 + /10 > 5.
88. /7 + /15 <7.
89. /21 — /5> /20 — J/6.
90« /37 —/14> 6 —/15.
91. /101—/35>4_
92. — 16 </17 —р 390.
25
Почленное умножение неравенств
§ 12
Теорема. Неравенства одинакового смысла с поло-
жительными частями можно почленно умножать.
Доказательство. Пусть а > Ь и с >• d, причем числа а,
Ь, с и d положительны. Докажем, что ас > bd.
Умножив неравенство а > b почленно на положительное
число с, получим ас > Ьс. Умножив затем неравенство с > d
почленно на положительное число Ь, получим be > bd. Теперь
имеем: ас > be, a be > bd. Но тогда по второму основному свой-
ству неравенств (§ 10) должно быть ас > bd.
Аналогично может быть рассмотрен случай, когда a <Z b и
с < d.
Примеры:
f 2> 1
1 6 > 4
12 > 4
( 5> 3
’ I 100 > 10
500 > 30
( 1 < 7
’ I 9< 10
9 <70
Следствие 1. Если а>Ь, причем числа а и b поло-
жительны, то для любого натурального п
ап > Ьп.
Действительно, умножая почленно неравенство а > b само
на себя, получим а2 > Ь2. Умножая затем почленно полученное
неравенство на исходное неравенство а > Ь, получим а3 > Ь3
и т. д.
Следствие 2. Если числа а и Ь положительны и
ап~>Ьп
(1)
(п — натуральное число), то а^>Ь.
Действительно, возможен один из трех случаев: а = b, а< b
\\ а > Ь. Если а = Ь, то ап = Ьп. При а < b мы имели бы: b >а,
и потому по следствию 1 Ьп > ап. И то и другое противоречит
неравенству (1). Остается признать, что а >• Ь.
Пример. Определить, какое число больше: /5 4-/6 или
/з + /8:
Возвысим оба числа в квадрат:
(/5 + /б У = 54-2 /30 + 6 - 11 4-2 /30;
(/3 4- /8 )2 = 3 4-2/24 4-8= 11 4- 21 24.
Квадрат первого числа больше квадрата второго числа. Так
как эти числа положительны, то по следствию 2
/5 4- | 'б > /3 4- /&
26
Упражнения
93. Любые ли два неравенства одинакового смысла можно
почленно умножить? (Рассмотрите пример: 3 > — 10 и —2 > — 7.)
94. а) Всегда ли из а > ft вытекает, что а” > ft"? Ответ по-
яснить примерами.
б) Следует ли из а" <1 ft", что а -< ft? Ответ пояснить при-
мерами.
В задачах № 95—102 сравнить данные числа, то есть выяс-
нить, какое из них больше и какое меньше:
95. /2+|/3 и V7. 99*. ^2 + ^4 и {/26-
96. У5 + УЗ и + 100. (1 +/5 )100 и 3,0°-
£7. /ТТ — ]/Г0 и Кб —101. (1/7Ч-1/2")9 и 4s.
eg. j/8 —JA15 и |(/30— /2). 102. (/5— КЗ )51 и
(/б — /2 )51.
Двойные неравенства § 13 В * * * * * * * * * * * * * * * * * * * *
В дальнейшем нам иногда придется иметь дело с двойными
неравенствами. Так называются неравенства вида:
а < а < а" .
По существу, эта формула объединяет в себе два неравенства:
а' < а и а < а" . Этим и объясняется название «двойное нера-
венством.
Двойные неравенства обладают всеми теми свойствами, о ко-
торых мы говорили в § 10—12, когда рассматривали обычные
неравенства. Например, к каждой части двойного неравенства
можно прибавить любое число k:
а' + k < а + k < а" + k. (1)
Каждую часть двойного неравенства можно умножить на любое
положительное число А:
ka < ka<. ka". (2)
Каждую часть двойного неравенства можно умножить и на лю-
бое отрицательное число /, поменяв при этом знаки неравенства
на противоположные:
Id > la > Id1. (3)
Упражнения
103. В каких пределах заключено число а, если:
а) —1,2 < За < 6; б) — 1,2 < —За < 6?
27
104. В каких пределах заключена сумма а 4- 6, если
1,1 < а < 1,2, a 5,5 < b < 5,6?
105. В каких пределах заключена сумма 2а 4- 36, если
1,98 < а < 1,99, а 0,55 < b < 0,56?
106. В каких пределах заключена разность а — Ь, если
0,1 < а < 0,2, а —0,2 < b < — 0,1?
107. В каких пределах заключено произведение ab, если
а) 0,6 < а < 0,7, 2,3 < b < 2,4;
.6)
— 3- <6< — 3 - ?
7 8
Строгие и нестрогие неравенства
§ 14
Когда хотят записать, что число а не меньше числа b (дру-
гими словами, а больше или равно 6), то используют знак >
и пишут а > Ь. Например, а2 1 > 1. И > 0 и т. д. Если нужно
записать, что число а не больше числа b (другими словами,
а меньше или равно Ь), то используют знак < и пишут а < Ь.
Например, 1 < 1 4- а2, —' |х| < 0 и т. д.
Соотношения а > b и а < Ь, так же как и соотношения а > b
и а < Ь, называются неравенствами. Неравенства, содержащие
знак > или знак <2, называются строгими, а неравенства, со-
держащие знак > или знак с, •—нестрогими. Например, нера-
венства л < 4 и 2л > 6 — строгие, а неравенства 17 > 17 и
3 и 4 — нестрогие.
Все выведенные выше свойства строгих числовых неравенств
R 10—13) легко распространяются и на нестрогие неравенства.
Например, если а > Ь, то b < а; если а > Ь, w Ь-\-с
И т. д.
Упражнения
108. Можно ли писать так: 3 > 3; 5 > 4; а2 4- 62 > а2;
а* 4- Ьй > а2?
109. а) Могут ли одновременно выполняться неравенства
а < b и а 6?
б) Могут ли одновременно выполняться неравенства а < b
и а > Ь?
ПО. Доказать, что если а > b и с < d, то а — с > Ь — d.
28
f
Некоторые способы доказательства неравенств
S 15
Доказать неравенство, содержащее некоторые буквы, — это
значит показать, что ему удовлетворяют любые допустимые или
специально указанные значения этих букв.
Существуют различные способы доказательства неравенств.
Проиллюстрируем некоторые из них па конкретных примерах.
Пример 1. Доказать, что любые положительные числа а
и Ь удовлетворяют неравенству
(1)
причем знак равенства имеет место тогда и только тогда, когда
а — Ь.
l-й способ. Рассмотрим разность
Ее можно привести к виду:
_____-|/777,_ a±b — 2VаЬ __ (V~a —y/~b)z
2 Г 2 2
Но а — Уб )2 > 0. Поэтому > 0. А это и озна-
чает, что > Уа^- Знак равенства в формуле (1) имеет место
тогда и только тогда, когда ]/а— Уб =0, т. е. при а-= Ь.
2-й способ. Предположим, что данное неравенство верно.
Тогда, умножив обе его части на 2, получим:
а 4- Ь > 2\ГаЬ.
Перенесем 2}/Га6 в левую часть:
а + Ь — 2)ЛаБ > 0.
Наконец, перепишем полученное неравенство в виде
(У а- УЬ)г > 0. (2)
Последнее неравенство, очевидно, верно для любых положи-
тельных чисел а и Ь, причем равенство в нем достигается тогда
и только тогда, когда а — Ь. Таким образом, данное неравенство
мы свели к очевидному неравенству. Теперь, производя все
рассуждения в обратном порядке, мы докажем данное неравен-
ство.
Для любых положительных чисел а и b имеем;
0,
29
или
а — 2j'rab 4- b > и.
Знак равенства при этом имеет место тогда и только тогда,
когда а = Ь. Перенося - 2)/ab в правую часть, получаем а +
4- b > 2]Sab, откуда - > К
Сразу трудно было догадаться, что при доказательстве не-
равенства (1) нужно исходить из очевидного неравенства (2).
Вот почему предварительно нам пришлось сделать допущение,
что неравенство (1) верно, и получить при этом допущении
неравенство (2).
Пример?. Доказать, что если произведение положительных
чисел хну равно 1, то (1 + х) (1 4- у) > 4.
Доказательство. Полагая в только что доказанном
неравенстве
а — 1, b = х, получим > Ух, или 1 4" х> 2|/х. Аналогично
показывается, что 1 4- у > 2)/у. Почленное умножение получен
ных неравенств дает:
(1 + X) (1 4- у) > 2уТ • 2К£
или
(1 4-Х) (1 4-У) > 4|/ху.
Но по условию ху — 1. Поэтому
(1 4- X) (1 4- У) > 4.
Упражнения
Доказать неравенства (№ 111—117):
111. (х4-у)г>4ху.
112. х3 4- у3> хгу 4- хуг (х > 0, у > 0).
113. (а 4- b 4- с)г > а (Ь 4~ с — а) + Ь(а + с — b) + с(а + b — с).
‘«4. 4- Д > 1 4-1 (а>0, Ь> 0).
/>* а2 а о
115. — < 1.
I 4- с2
116. as 4- 1 > 2.
а*
П7. +_L_ (а>0, Ь>0).
1 4-аЧ- 6 1 4-а I 4-&
118. Самолет летит из Москвы в Киев и возвращается обратно.
В какую погоду этот рейс будет совершен быстрее: в безветреп-
30
ную или при ветре, дующем с постоянной силой в направлении
Москва — Киев.-'
119. Доказать, что полупернметр треугольника больше каж-
дой из его сторон.
120*. Доказать неравенство
J 3 1 Z 99 L
2 ’ 4 ’ 6 8 ......100 10
Теорема о среднем арифметическом
и среднем геометрическом § 16
Средним арифметическим любых п чисел аь а2, ... , ап на-
зывается число
°i 4~ од Ц~ • • • ~4~ °я
п
Средним геометрическим п положительных чисел at,a2,... , ап
называется число
Г’ • ^2 ‘ • • • 'агГ
Например, для чисел 2 и 8 средним арифметическим будет
число —1—= 5, а средним геометрическим — число ] 2 • 8 4.
Среднее арифметическое чисел 10, 10 и 80 равно
10 + 10 4-80 _ 1
~ ““ — — 0J —
3 з
а среднее геометрическое
3/ 10 • 10 • 80 = |/8000 = 20.
Для чисел 5, 5 и 5 средним арифметическим будет число
+ ~ 5, а средним геометрическим yz5 • 5 • 5 = 5.
Заметим, что во всех трех случаях среднее арифметическое
оказалось не меньше их среднего геометрического, причем рав-
ными они получились лишь в третьем примере, где все рас-
сматриваемые числа равны друг другу. И это не случайно.
Имеет место следующая общая теорема.
Теорема. Среднее арифметическое п положитель-
ных чисел не меньше их среднего геометрического:
> V~^a2 -Т7т«;.
п
Знак равенства в этой формуле имеет место тогда а
только тогда, когда все п чисел alt а2, ... , «„ равны
между собой.
31
В предыдущем параграфе было показано, что для любых
двух положительных чисел а н b справедливо неравенство
2
причем знак равенства имеет место тогда и только тогда, когда
а = Ь. Тем самым была доказана теорема о среднем арифмети-
ческом и среднем Геометрическом двух- положительных чисел.
В общем случае доказательство этой теоремы довольно громоздко
и поэтому здесь не приводится.
Неравенство
-у- > Vab,
верное для любых положительных чисел а и Ь, было известно еще в древ-
ние времена. Рисунок 22 приведен нами для геометрической интерпретации
этого неравенства. На рИеунке
©CD = V AD -DB. СО = АО = °- •
» Обобщение данного неравенства на случай про-
° извольного числа положительных чисел (теорема о
среднем арифметическом н среднем геометрическом)
- было получено французским математиком Коши
(1789—1857). С именем этого выдающегося ученого
_ __ связаны и некоторые другие замечательные нера-
I ис. 22. венства, изучение которых, однако, выходит
за пределы нашей программы.
Пример 1. Доказать, что для любых чисел a, t и с, имею-
щих одинаковые знаки,
a + i + ^>3.
b с а
Действительно, по теореме
о среднем арифметическом и сред-
нем геометрическом
Ь с
— • — >
с а
откуда и вытекает требуемое соотношение.
Пример 2. Доказать, что для произвольного положитель-
ного числа а справедливо неравенство
99а + 1 > ЮО ,0/а™
причем знак равенства имеет место только при а = 1.
Применяя теорему о среднем арифметическом и среднем гео-
метрическом к 100 числам а, а, .... а, 1, получаем
шо-
_99а<1
100 V *
32
откуда Во./екает .ребуемос соотношение. Знак равенства имеет
место лишь в том случае когда все 100 чисел равны между
собой, то есть при а = 1.
Из теоремы о среднем арифметическом и среднем геометри-
ческом вытекает следующее важное следствие.
Следствие. Если произведение п положительных
чисел равно 1, то их сумма не меньше п. Другими словами,
если положительные числа а,, аг, ... , ап удовлетворяют условию
а, а. • ... -ап — 1,
то
“1 аг + • • • + ап > Л* С1)
Действительно,
откуда и получается неравенство (1).
На практике соотношение (1) особенно часто используется
при п = 2. Сумма двух взаимно обратных положитель-
ных чисел не меньше 2:
а - г - > 2 {а > 0).
а
Упр аж нения
Доказать неравенства (№ 121 — 129):
121. (а + Ь) 4 (а>0, Ь > 0).
\ а Ь/
122. j (а + Ь) 4- ~ (а + ₽) (а > 0, b > 0.
а > С, ₽>0).
123. п+^<а-^-
п + 1
124. 2а2 + Ь2 4- с2 > 2с (Ь + с).
125. 1а + Ь] (Ь + с) (с + а) > 8abc (а > 0, b > С, с > 0).
126. y ab>-^~ (а > 0. 6>0)
с1
127. а + Ь + с > У ab + У be -f-] ас (а > 0, b > 0. с > 0).
128. а2 + Ь2 + с2 > at -i- Ьс + ас.
129. (а -|- 1) (t + 1) (с + с) (&+с) >16 abc (а>С I > С, с>0).
130. Доказать, что если сумма положительных чисел о и Ь
равна 1, то:
а) а2 + b2 > 1; 6 а4 + Ь4 > -.
131. Какое наименьшее значение может принять сумме а2 + h2,
если а b = 2, причем числа а и Ь положительные?
2 Заказ 261
33
132*. Доказать, что при любом натуральном значении п
Теоремы о постоянной сумме
и постоянном произведении
§ 17.
Из теоремы о среднем арифметическом и среднем геометрическом выте-
кают две важные теоремы, которые очень часто используются при решении
практических задач.
Теорема о постоянной сумме. Если суммадвух положитель-
ных величин постоянна, то их произведение Судет наибольшим
тогда и только тогда, когда эти величины примут равные
значения.
Напрн.мер, если сумма двух положительных величии а и Ь равна 10,
то возможны случаи: а = 1, 6 = 9; а = 2, Ь - 8; а = 3,5, b = 6,5; а = 4,1,
6 — 5,9; а = 5, b = 5 н т. д. Этим случаям соответствуют следующие значе-
ния произведения ab: 9; 16; 22,75; 24,19; 25. Наибольшее произведение
(25) будет при а = b = 5.
Доказательство теоремы. Пусть сумма двух положитель-
ных величин а и Ь равна с. Тогда по теореме о среднем арифметическом и
среднем геометрическом получаем:
, - а Ь .— с •
) ab < —-—, пли у ab < -.
При этом, если а~Ь, то ]/ab= — ; если же
с
2
а Ь,
Следовательно, ]' ab будет наибольшим при а = Ь. Но тогда, очевидно, н
подкоренное выражение ab будет наибольшим при а = Ь.
Задача. Какой наибольший по площади прямоугольный участок можно
огородить забором длины /2
Решение. Пусть длина участка равна х, а ширина у. Тогда площадь
егобудетравна ху. По условию задачи 2х + 2у = 1. или х + у =2.. Так как
сумма х + у постоянна, то произведение ху будет наибольшим при х = у.
Следовательно, если мы хотим забором длины / огородить наибольший по
площади прямоугольный участок, то должны огораживать участок, имеющий
I Р
форму квадрата. Сторона такого квадрата равна — , г площадь -
4 16
Теорема о постоянном произведении Если произведе-
ние двух положительных величин постоянно, то их сумма бу-
дет наименьшей тогда и только тогда, когда эти величины
примут равные значения.
Например, если произведение двух положительных величин он Ь
равно 16, то возможны случаи: а=1, 6=16; а=2, 6=8, с=4, 6=4, а=5,
16 1
6 — — и т. д. Этим случаям соответствуют- суммы а + 6: 17; 10. 8; 8 — и т. д.
5 5
Наименьшая сумма (8) будет при а = 6 =
Доказательство теоремы аналогично доказательству теоремы о постоян-
ной сумме. Предлагаем учащимся провести его самостоятельно
Задача. Какую наименьшую длину должен иметь забор, чтобы им
можно было огородить прямоугольный участок, площадь которого равна S?
Решение Пусть длина прямоугольного участка равна х, а ширина у.
Тогда длина забора будет равна 2 (х + у). Площадь участка равна ху = S.
34
Так как произведение ху постоянно тс суммг х.4 у будет наименьшей
при * == у = fS. Следовательно, наимеч-шая длина забора равна
2(Г$ 4 Г$1 = 4/S:
Упражнения ,
133- При каких положительных значениях а данные выражения при-
нимают наибольшие числовые значения:
а) а (8 — и); б) (t 4- 2u} (3 — 2af; в)* aV 10 — а2?
134 При каких положительных значениях а данные выражения при-
нимаю! наименьшие числовые значения:
1 8 * 4 2 ,
а) д -г б) в)*
а а У а2-т I
135. В круг радиуса R вписать прямоугольник наибольшей площади
136. Из круглой балки данного диаметра d требуется вырезать балку
прямоугольное поперечного сечения так чтобы количество отходог было
наименьшим. Найти площадь этого сечения.
137. Окно имеет форму прямоугольника. Какова должна быть длина
и ширина этого окна, чтобы онс при данное периметре р пропускало наи-
большее количество света?
Указание Количество пропускаемого света тем больше, чем больше
площадь окна.
138. Решить уравнения:
I 1
а) х -L — = 2: б) х 4- — =1,5; в) х -j-— — 2.
ххх
139*. Одна бригада увеличивало производительность труда ежемесячно
на 2%. Другая бригада в течение первого полугодия увеличивала произ-
водительность труда ежемесячно на 1%, о г течение второго полугодия —
ежемесячно на 3%. Какая и- этих бригад добилась большего увеличения
производительности труда за год:
Приближенные значения числа.
Свойство абсолютной величины суммы § 18
На практике мы почт! нико-да не знаем точных значений
величин. Никакие весы, как бы точны они ни были, не пока-
зывают вес абсолютно точно; любой термометр показывает тем-
пературу с той или инок ошибкой; никакой амперметр не может
дать точных показаний тока i т. д. К тому же наш глаз не
в состоянии абсолютно правильно прочитать показания измери-
тельных приборов. Поэтому, вместо того чтобы иметь дело
с истинными значениями величин, мы вынуждень опепировато
с их приближенными значениями
Тот факт, что а есть приближенное значение числа а, записы-
вается следующим образом:
а ^-а’.
Если а есть приближенное значение величины а. тс. разность
Л = а — а называется погрешностью приближение*.. Например,
* Л — греческаг буква; читается: дельта.
На следующей странице встречается еще одна греческая буква е (чита-
ется: эпсилон).
есчи число 3,7о6 заменить его приближенным значением 3,7, то
погрешность будет равна: Д = 3,756 — 3,7 = 0,056. Если в
качестве приближенного значения взять 3,8, то погрешность будет
равна: Л= 3,756 — 3,8 = — 0,044.
На практике чаще всего пользуются не погрешностью при-
ближения Д, а абсолютной величиной этой погрешности ]Д|.
В дальнейшем Эгу абсолютную величину погрешности мы будем
называть просто абсолютной погрешностью. Считают, что одно
приближение лучше другого, если абсолютная погрешность первого
приближения меньше абсолютной погрешности второго прнбли
жения. Например, приближение 3,8 дли числа 3,756
лучше, чем приближение 3,7, поскольку" для первого
приближения ]Д| = I — 0,0441 = 0,044, а для второго
|Д| = ;0,05б| = 0,056.
Число а' называется приближенным значением числа а с точ-
ностью до е, если абсолютная погрешность этого приближения
меньше, чем е.-.
\а — а'| <е.
Например, 3,6 есть приближенное значение числа 3,671
с точностью до 0,1, поскольку |3,671 — 3,6| = |0,071| — 0,071 <0,1.
Аналогично,
3
— — можно рассматривать как приближенное зна-
8 1
чение числа — с точностью до —, поскольку
5 5
Если а' < а, то а' называется приближенным значением
числа а с недостатком. Если же а, то а' называется при-
ближенным значением числа а с избытком. Например, 3,6 есть
приближенное значение числа 3,671 с недостатком, поскольку
3,6 <3,671, а —есть приближенное значение числа — —
3 8
с избытком, так как---->-----.
2 5
Если мы вместо чисел а и b сложим их приближенные зна-
чения а' и Ь', то результат а 4- Ь’ будет приближенным значе-
нием суммы а Ь. Возникает вопрос: как оценить точность этого
результата, если известна точность приближения каждого сла-
гаемого? Решение этой и подобных ей задач основано на следую-
щем свойстве абсолютной величины:
]а + &|<|а|+1Н
Абсолютная величина суммы любых двух чисел не
превышает суммы их абсолютных величин.
36
Доказательство Если числа а и b положительны,
то и сумма их положительна. В этом случае ja| = а, |6| - Ь,
|а + Ь| = а 4- b и, следива 1вльно, |rz -J- £>| = |а! 4- |&|. Если числа
ah b отрицательны, то и сумма их отрицательна. В этом случае
!а| = — а, |/>; = — b, ja -| Ь' = - (а 4- Ь); поэтому [а 4- также
равняется (а1 4- М
Пусть, наконец, одно из чисел а и Ь положительно, а дру-
гое — отрицательно. Тогда если |а| > , то |а 4- = |oj — |6j,
если же |а| < |6|, то |а 4- 6| — |/>| — |а[. В любом из этих слу-
чаев разность двух положительных чисел |а| и |/>| будет меньше
их суммы Таким образом, если одно из чисел а и b положи-
тельно, а другое отрицательно, то
|а 4- Ч <И 4 |^|.
Осталось рассмотреть лишь случай, когда одно из чисел
а и Ь, а может быть, и оба равны нулю. Учащиеся без особого
труда могут сделать это самостоятельно.
Пример. 1 — 20| С |1J 4-1— 20|.
Действительно,
|1 — 20| = |— 19| = 19,
111 4- I— 20| - 1 4- 20 - 21,
19 < 21.
Упражнения
140. С какой точностью можно измерять длины с помощью
обыкновенной линейки?
141. С какой точностью показывают время часы?
142. Знаете ли вы, с какой точностью можно измерять вес
тела на современных электрических весах?
143. а) В каких пределах заключено число а, если его при-
ближенное значение с точностью до 0,01 равно 0,99?
б) В каких пределах заключено число а, если его прибли-
женное значение с недостатком с точностью до 0,01 равно 0,99?
в) В каких пределах заключено число а, если его прибли-
женное значение с избытком с точностью до 0,01 равно 0,99?
144. Какое, приближение числа л 3,14 лучше: 3,1 или 3,2?
145. Можно ли приближенное значение некоторого числа
с точностью до 0,01 считать приближенным значением того же
числа с точностью до 0,1? А наоборот?
146. На числовой прямой задано положение точки, соответ-
ствующей числу а. Указать на этой прямой:
а) положение всех точек, которые соответствуют приближен-
ным значениям числа а с недостатком с точностью до 0,1;
б) положение всех точек, которые соответствуют приближен-
ным значениям числа а с избытком с точностью до 0,1;
37
в) положение всех точек, которые соответствуют приближен-
ным значениям числа а с ючностью до 0,1.
147. В каком случае абсолютная величина суммы двух чисел:
а) меньше суммы абсолютных величин этих чисел;
б) равна сумме абсолютных величин этих чисел?
148. Доказать неравенства:
а) |а — Ь\ ' |а| + |6|; б)* |а — Ь\ > ||а| — |0]|.
Ко1да в этих формулах имеет место знак равенства?
Приближенное сложение и умножение на число § 16
Пусть а есть приближенное значение числа а с точностью
до et, а Ь' — приближенное значение числа b с точностью до е2.
Тогда сумма а Ь' будет приближенным значением числа а + Ь.
Какова же точность такого приближения? Чтобы выяснить этот
вопрос, воспользуемся свойством абсолютной величины суммы.
Имеем:
|(а + 6) — (а’ + 6')| = |(а — а) + (Ь — й')1 < — «'I + \Ь—й'|.
По условию |а — а'|<е1, a ]t> fe'|<e2. Следовательно,
|(д _|_ Ь) _ (д' _|_ b')|<ei+fc2.
Но в таком случае можно сказать, что а + Ь^а Ь' с точностью
до е t 4- е,. Итак, мы доказали теорему.
Теорема 1. Если а~а' с точностью до ер а b^b'
с точностью до ez, mu а + b як а' + Ь' с точностью до
«1 + е2‘
Примеры. 1) С какой точностью можно найти сумму двух
чисел, если одно из них известно с точностью до 0,1, а дру-
гое — с точностью до 0,2?
Теорема 1 в данном случае гарантирует точность 0,1 + 0,2 =
= 0,3. _
2) Сумму )/1б + V 12 нужно найти с точностью до 0,1. Будем
извлекать корни из 10 и 12 по известному алгоритму:
]/Т0’= 3,16 ... У 12 = 3,46 ...
9 9
611100 64:300
1 I 61 4 256
6261 3900 686! 4400
61, 3756 6 4116
~ 144 284
Двух десятичных знаков вполне достаточно. В этом случае
каждое из слагаемых мы находим с точностью до 0,01. Поэтому
по теореме 1 сумма ]/ТЬ -|- |/ 12 =кЗ,16 + 3,46 - 6,62 будет най-
38
депа с точностью до 0.01 + 0,01 = 0,02 <0,1. Согласно трсбо-
ьанию задачи окончательно запишем: ]/Т0 + j/12^6,6. Огра-
ничиться при извлечении корней лишь одним десятичным зна-
ком было бы нехорошо. В этом случае мы нашли бы прибли-
женные значения слагаемых с точностью до 0,1. Но тогда
у нас пе было бы уверенности в том, что сумма
^3,1 + 3,4 = 6,5 будет найдена с точностью до 0,1 Ведь тео-
рема 1 гарантировала бы лишь точность 0,1 4-0,1 = 0,2, которая
нас не устраивает.
Теорема 2. Если а'— приближенное значение числа а
с точное то ги до е., то ka' есть приближенное значение
числа ka с точностью до k | е. __ _
Например, с точностью до 0,1 ^3,1. Поэтому 51^10^
^5 -3,1 = 15,5 с точностью до 5 • 0,1 =0,5. Аналогично — 7^10
~— 7-3,1 = — 21,7 с точностью до |—7| -0,1 =7-0,1 = 0,7.
Доказательство теоремы 2. Если а' есть прибли-
женное значение а с точностью до е, то |а — а'\ < е. Поэтому
|6а — ka’\ — \k(a — а')| = |й| • |а - а’\ < |й| • е, что и требовалось
доказать.
В заключение рассмотрим следующий пример. Пусть с точ-
ностью до 0,1 а^а — 2,7; b Ь' — 3,6. Требуется найти при-
ближенное значение выражения 5а — ЗЬ и определить точность
этого приближения.
Имеем:
5а — 36 5а' — 36' = 5 • 2,7 — 3 • 3,6 - 13,5 — 10,8 = 2,7.
Точность этого результата можно оценить, используя свойство
абсолютной величины суммы:
|(5а _ 36) _ (5й' _ зб')| = |(5а — 5а') — (36 — З6')| <
< |5а — 5а'| 4- |36 — З6'| =- |5 (а — а')| 4- 13 (6 — 6')| =
= 5 |а — а'| 4- 3| 6 — 6'| < 5 • 0,1 4- 3 • 0,1 = 0,8.
Итак, 5а — 36 2,7 с точностью до 0,8.
Упражнения
149. Вычислить с точностью до 0,1:
а) ]/2 +1/Т7; б)|Л24-|; в)5]/^ г) - 1.
7 "546 75
150. Известно, что с точностью до 0,01 а^ — 3,05; 6~3,01.
Найти приближенные значения выражений:
а) 2а + 76; б) За — 56; в) — а — 46.
Определить точность полученных приближений.
151. Числа а и 6 заданы с одинаковой точностью е. Каким
должно быть е, чтобы с точностью до 0.001 можно было бы найти:
а) а 4- 6; б) а — 6; в) а — 106 ?
39
Эквивалентные неравенства и их свойства
§ 20
До сих пор мы рассматривали тождественные неравенства,
то есть такие неравенства, которые выполняются (обращаются
в числовые неравенства) при всех допустимых или специально
указанных значениях входящих в них букв. К таким отно-
сятся, например, неравенства:
а + 1 > а, й2 > 0, > V а&-
Теперь мы переходим к изучению неравенств, которые выпол-
няются не при всех, а лишь при некоторых (а может быть, и
ни при каких!) допустимых значениях букв. Примером такого
неравенства может служить неравенство
2х > 0.
Оно выполняется при любых положительных значениях х, хотя
допустимыми значениями х являются все числа, в том числе и
отрицательные.
Решить неравенство, содержащее неизвестную величину, — это
значит найти все те значения этой неизвестной величины, при
которых данное неравенство выполняется.
Подобно решению уравнений, решение неравенств обычно
проводится путем сведения их к более простым, эквивалентным
(или равносильным) неравенствам.
Два неравенства, содержащие одну и ту же неизвестную ве-
личину, называются эквивалентными (или равносильными), если
они выполняются при одних и тех же значениях этой величины.
Примером эквивалентных неравенств могут служить нера-
венства 2х > 0 и — Зх < 0, справедливые при всех положитель-
ных значениях х. Неравенства х>0 и х’>0 не эквивалентны,
поскольку первое из них верно только при положительных
значениях х, а второе — как при положительных, так и при
отрицательных значениях х.
Неравенства, каждое из которых не выполняется ни при
каких значениях неизвестной величины, также считаются экви-
валентными. Примером таких неравенств могут служить нера-
венства
х2 < — 1 и — (5х' + 3) > 0.
Эквивалентные неравенства обладают рядом важных свойств,
которые мы приводим без доказательства.
Свойство. 1. Если к обеим частям неравенства при-
бавить или из обеих частей вычесть число или выра-
жение, определенное для всех значений неизвестной
величины, то получится неравенство, эквивалентное
данному.
40
Примеры. 1) Если к обеим частям неравенства х > 2 — х
прибавить число — 2, то в результате получится неравенство
х — 2 > — х. Это неравенство, как утверждает свойство 1, должно
быть эквивалентно данному неравенству х > 2 — х.
2) Прибавим к каждой части неравенства 1 < 1 выражение
X
—!—. В результате получим — 4-----!— < 14----!—. Выражение
*’ 4- 1 х х2 4 1 х2 |- 1
—-— определено при всех значениях х. Следовательно, полу-
х2 4- 1
ченное неравенство эквивалентно данному неравенству < 1.
Существенным условием в 1-м свойстве эквивалентных нера-
венств является то, что выражение, которое мы прибавляем
к каждой части исходного неравенства, должно быть опреде-
лено для всех значений неизвестной величины. Если это усло-
вие не выполнено, то данное и полученное из него неравенства
могут оказаться неэквивалентными. Поясним это на следующем
примере. Прибавив к обеим частям неравенства х > 0 выраже-
ние —1 , мы получим неравенство х 4----— > —-—- Исходное
х — 1 х— 1 х— 1
неравенство верно при всех положительных значениях х и,
в частности, при х = 1. Полученное же неравенство при х = 1
не имеет смысла. Поэтому при х = 1 оно выполняться не может.
Таким образом, рассматриваемые два неравенства не эквивалентны.
Из первого свойства эквивалентных неравенств вытекает
важное для дальнейшего следствие. Любое слагаемое, опре-
деленное для всех значений неизвестной величины,
можно перенести из одной части неравенства в другую,
поменяв знак этого слагаемого на противоположный,
Действительно, пусть дано неравенство
Р (х) + Q (х) > R (х), (1)
где Р (х), Q (х) и R (х) представляют собой некоторые выраже-
ния, зависящие от х, причем Q (х) определено для любых зна-
чений х. Нам нужно доказать, что такое неравенство эквива-
лентно неравенству
Р (х) > R (х) - Q (х). (2)
Доказательство этого факта очень простое: неравенство (2)
получается, если из обеих частей неравенства (1) отнять Q (х).
Пример. Пусть дано неравенство Зх + 1 < 2 — х. Перенеся
— х из правой части в левую, а 1, наоборот, из левой части
в правую, получим:
Зх + х < 2 — 1,
или
4х< 1.
41
Последнее неравенство выполняется, очевидно, при всех значе-
ниях х, меньших у. При этих же значениях х должно, следо
пепельно, выполняться и данное неравенство Зх -Ь J < 2 — х.
Вообще можно доказать, что
другую можно любое слагаемое.
1
Например, слагаемое
х—1
переносить из одной части неравенства в
в неравенстве
можно перенести из л<вэй части в правую. В резу^ю.аз^ .аки,о преобра-
зования получится неравенство
1 1
х >-------- —-------,
X — 1 X — 1
эквивалентное данному (оба неравенства выполняются при всех положи-
тельных значениях х, кроме 1). А вот такое простое преобразование, как
приведение подобных членов, требует большей осторожности Так, если бы
мы в правой части последнего неравенства привели подобные члены, то
получили бы неравенство
х > О,
которое не эквивалентно исходному неравенству.
Свойство 2. Если обе части неравенства умножить
на riujiujtvurriejioHoe число или выражение, принимающее
только положительные значения и определенное для
всех значений неизвестной величины, то получится не-
равенство, эквивалентное данному.
Пример ы. 1) Если обе части неравенства х > 2 — х умно-
жить на положительное число 3, то получится неравенство
Зх > 6 — Зх, эквивалентное данному.
2) Выражение х2 + 1 принимает только положительные зна-
чения и определено для всех значений х. Поэтому неравенство
х < 1 эквивалентно неравенству
х (х2 Н I) < х2 4- 1,
или
х3 hx<x2H 1.
Следует особо подчеркнуть, что то выражение, на которое
мы умножаем обе части исходного неравенства, должно удов-
летворять двум требованиям1.
а) оно обязано принимать только положительные значения и
б) быть определенным для всех значений неизвестной вели-
чины.
42
Если хотя бы одно из этих требований н< удовлетворяете! ,
ИСХОДНОЕ И Г1М*»1¥ 4V11I1WV ПЭ IlK-fU HUpCluCllV 1 ОСД МиГу Г ОКЗэС! Д OV71
неэквивалентными Поясним это на следующих примерах.
') Неравенство х > 0 выполняется только для положительных
опа4еНИИ X. УмНмлхиВ tiu пи'.дсппи гк At Moi им^уЧИМ nvpadcn*
ctbg x‘ >0. Оно верно кат для положительных. Tai и для от-
рицательных значений х. Несоответствие этого результата со
свойством 2 легко объяснить. Ведь выражение х. н: ко трое
мы умножили оое части исходного неравенства х 0,
мает как положительные, таи и отрицательные значения
этот случай свойство 2 не дает никаких гарантий
Умножив неравенство х>0 н; выражение —--,
(х— )2
прини-
А на
мь пс
лучим неравенство —--------> 0.
(х — 1)2
Предлагаем
учащимся самостоя-
тельнс показать, что это неравенство н< эквивалентно данному,
и объяснить, почему 2-е свойство эквивалентных неравенств
здесь не применимо.
Сеойство 3. Если обе части неравенства умножить
на отрицательное число или выражение, которое опре-
делено для всех значений неизвестной величины и при-
нимает только отрицательные значения а знак нера-
венства изменить на противоположный ('^>на<^;<^на'»,
то получится неравенство, эквивалентное данному.
Это свойстве вполне аналогично 2-му свойству. Поэтому
подробно останавливаться н< нем мы не будем.
Упражнения
152. Эквивалентны ли неравенства:
а) х2 > х — 1 и х2 -+- 1 > х,
б) 2х < 0 и 2х 4- ;
X X
в, х — 1 > 0 и бг — 1) -J----> —1—
4 —х 4- х
г) Зх + 1 > 0 и (Зх + Г + pv — 4) > х — 4’
153. Эквивалентны ли неравенства:
а) 2х > 3 и 6 2х > 6 • 3;
б) 2х> с и — 6 • 2х < — С 3; е)2х>3г 2х > 3- ;
4 —х2 4—.-'
в) 2х > 3 и 2х (х3 + -) > 3 (х3 4-1); ж) 2х > 3 п —- 3—;
х — х —4
: ) 2х > 3 и 2х3 > 3;4; з 2г > 3 и — > -Д. ?
1 - /Т
д) 2х > 3 г 2х2 > Зх;
43
Линейные неравенства § 21
Так называются неравенства, левая и праоал части которых
[Расставляют собой линейные функции относительно неизвест-
ной величины. К ним OinGvnivn, например, неравенства
2х — 1 > — х + 3; 7х < 0;
5 > 4 6х; 9 — х х + 5
и т. д. Для определенности мы рассмотрим лишь ^равенства,
содержащие знак > . Линейное неравенство, содержащее знак
имеет вид:
ах + b > сх 4 d. (1)
Если в неравенстве (1) а=/=с, то такое неравенство назы-
вается также неравенством 1-й степени. Очевидно, что всякое
неравенство 1-й степени является вместе с тем и линейным не-
равенством. Обратное утверждение неверно. Например, нера-
венство 0 • х > — 2 является линейным, но не является неравен-
ством 1-й степени.
Перенося сх из правой части неравенства (1) в левую, а Ь
из левой части в правую, получим:
, (а — с) х> d — b.
Таким образом, любое линейное неравенство сводится к экви-
валентному неравенству вида
тх > п, (2)
где т и п — некоторые заданные числа, а х — неизвестная вели-
чина.
Если т > 0, то, деля обе части неравенства (2) на т, полу-
чтм х > — . Это соотношение и определяет множество всех тех
т
значений величины х, при которых выполняется неравенство (2).
Геометрически это множество изображается в виде той части
Л п
т т
Рис. 23. Рис. 24.
числовой прямой, которая лежит справа от точки с абсциссой
— (рис. 23). Сама точка — в это множество не включается.
т т
На рисунке это отмечено стрелочкой, обращенной к точке
с абсциссой ,
т
4-1
Если nt <, 0, то, деля обе части неравенства (2) на т и меняя
при этом знак неравенства На противоположной, получаем
, п
х< —.
т
Это соотношение ипрсл^лпСТ МНОЖССТВО BCtX ТОХ ЗНачСНИН овЛН-
чнаы х, при которых в данном случае выполняется неравенст-
во (2) Геометрически это множество изображается в виде той
части числовой прямой, которая расположена слевг от точки
с абсциссой — (рис. 24). Сама точка х = — в это множество не
т т
включается. На рисунке это отмечено стрелочкой, обращенной
к точке с абсциссой —,
т
Теперь предположим, что т = 0. Тогда неравенство (2) при- •
ннмает вид:
0 • х > п
Если число п отрицательное, то это неравенство выполня-
ется при всех значениях х В противном же случае оно не
имеет решений.
-j\.z ..-.л Wf~''
~ 3
Рис. 25. Рис. 26.
Мы рассмотрели линейные неравенства, содержащие знак
Неравенства, содержащие знаки >, < и <, решаются анало-
гично. Рассмотрим несколько примеров.
1. Решить неравенство
х + 4 > — 2х + 3.
Перенося — 2х в левую, а 4 в правую часть, получаем
Зх > — 1, откуда х > — .
На числовой прямой (рис. 25) отмечены все те значения
которые удовлетворяют данному неравенству.
2. Решить неравенство
3 — 7х > х — 5.
Перенося х в левую, а 3 в правую часть, получим — 8х >
> — 8. Разделим обе части этого неравенства на —8. Поскольку
это число отрицательно, то знак неравенства при этом нужне
изменить на противоположный. Е результате получим х< 1.
Множество всех таких значений х отмечено на рисунке 26 (точ-
ка х — I включается в это множество).
.45
Упражнения
Решить данные неравенства (№ 154-165) и отметить получен-
ные результаты на числовой Примой:
154. 7х — 6 < х 4~ 12.
155. 1 — 2х > 4 — 5х.
156. 1 — х 2х 4- 3.
157. — >0. 3 —х
158. 9 — 7х > — 1 — 17х.
159. + (а>0; b>Q} а — b а ] Ь 4 Л
160. — — С 0.
161. 2 + х -^-<0. Зх -}- 5
162. 163. ах 4- 1 > 2 — 5х. ах 4- b > 3 — 2х.
164. х х-Н. х— 3 х — 2 2 4 3
165. I X — 1 X 4* 1 х 4 > —! их.
При а |- 1 о h 1 каких значениях х определены данные выражения
(№ 166—169):
166. 1/7 4-3x7 168« )/~2х+4.
167. ]/5 - х. 16?я V1 — 2х 4- /х?
170. Может ли неравенство
а2х <. а 4- 1
не иметь решений?
Решить уравнения:
171. |4х — 3 = 4х — 3. 173. [6х — а\ — а — 6х.
172. [7 — 2х| = 2х 7. 174. [ах — 1 = ах — I.
Графический способ решения неравенства тх > п
§ 22
На одном и том же чертеже построим графики двух функций:
у = тх и у = п.
Если т =# 0, то прямая у = тх обязательно пересечет прямую
у — п (рис. 27 для т>0 и рис. 28 для т < 0). Обозначим точку
пересечения этих прямых через Л4. Абсцисса этой точки пред-
ставляет собой корень уравнения тх = п и потому равна —.
46
Если tn > 0, то, как видно из рисун-
ка 27, тх будет больше п для всех х,
больших, чемЕсли т < 0 (рис. 28),
т
то тх будет больше п для всех х, меиь
п
ших, чем - .
гП
При т = 0 прямая у — тх совпадает
с осью абсцисс. Если при этом
число п отрицательно, то тх всегда
будет больше п (рис. 29). В этом случае
любое число х удовлетворяет неравенству
тх п. Если лее число п . неотрица-
тельно (рис. 30), то ни прг каком
значении х тх не будет больше п.
Упражнения
Решить графически данные нера-
венства.
175. 2х — 1 > 3. 177. 1 — 2х > 7.
176. х + 1 > 2х — 1. 178. 3 > 1 — х.
Рис. 27.
Рис. 28.
Системы линейных
неравенств
§23
У. Угтх(т=о1
0 х у.п (п<0)
п
Рис. 2£.
Системой линейных неравенств на-
зывается любая совокупность двух или
более линейных неравенств, содержащих
одну и ту же неизвестную величину.
Примерами таких систем могут слу-
жить системы:
х — 1 > 0, 11 — х < 2х — 5,
2х — 8 > 0; ( 3 — х > — 5;
I 14х — 3 < 7 4- 9х,
1 1 < х — 3.
Решить систему неравенств — это
значит найти все значения неизвестной
величины, при которых выполняется
каждое неравенство системы.
Решим приведенные выше системы.
Пример 1.
| х — 1 > 0,
( 2х— 8>0.
У> у-п (п>о)
п у=тх (т=о)
0 »
Рис. 30.
47
I и
I h
Рис. 31.
2 в
*"' - УК ж/-,
2 в
Рис 32.
Расположим одну под другой две
числовые прямые (рис. 31); на верхней
отметим те значения х, при которых
выполняется первое неравенство (х > 1),
а на нижней — те значения х, при кото-
рых выполняется второе неравенство
(х > 4). Сравнивая результаты на число
вых прямых, замечаем, что оба нера-
венства одновременно будут удовлетво-
ряться при х> 4. О тв ет. х >- 4.
Пример 2.
Г 1 — х < 2х — 5,
( 3 —х>- 5.
Первое неравенство дает — Зх < — 6,
или х > 2, а второе — х > — 8, или
х < 8. Далее поступаем так же, как и
в первом примере. На одной числовой
прямой отмечаем все те значения х, при
которых выполняется первое неравен-
ство системы, а на второй числовой
прямой, расположенной под первой,—все
)ых выполняется второе неравенство си-
2 Ь
2 4
Рис. 33.
те значения х, при коте
стемы (рис. 32). Сравнение этих двух результатов показывает,
что оба неравенства одновременно будут выполняться при всех
значениях х, заключенных от 2 до 8. Множество таких зна-
чений х записывается в виде двойного неравенства 2 < х < 8.
Пример 3. Решить систему неравенств
1 14х — 3 < 7 4- 9х,
[ 1 < х — 3.
Первое неравенство системы дает 5х < 10, или х < 2, вто-
рое х > 4. Таким образом, любое число, удовлетворяющее обоим
неравенствам одновременно, должно быть не больше 2 и боль-
ше 4 (рис. 33). Но таких чисел не существует. Поэтому данная
система неравенств не выполняется ни при каких значениях х.
Подобные системы неравенств называются несовместными.
Упражнения
Решить данные системы неравенств (№ 179—184):
17?. ( 2х— 1 > 1, . 181 / 5* + 3>8, 1 3 — х>0. ’ ( 0,7 — Зх<—2.6.
180. 1 —2х<—9, lg2 ( 2х —3>х —3, [ 3x4-1 <13. ’ [ 4х 4- 3>8 — х.
48
J 3x 4' 7 >9 •{‘2X1 1C4 Iх + 4 <2x-
I 5 + x ;> 2x 4- 2. 1 —x > — 2.
Решить неравенства (№ 185, 186):
185 (2x 4- 3) (2 — 2x, > L. 136. (2 — л) (2x — 15' (x 4- 4, > 0
Найти допустимые значения букв входящих в данные равен-
ства (№ 187, 188):
187. Va— 1 + /5 —За = У~£
уд —2а 4-/За —6 =^~6-
Решить неравенства (К° 189, 190):
189. 1 < 2х — 5 <т. 2. 190. — 2 < 1 — ах < 5.
191. Какой должна был температура 10 л воды, чтобы при
смешении ее с 6 л воды при температуре 15° получи гь виду
с температурой не менее 30° и не более 40°?
192. Одна сторона треугольника равна 4 см, а сумма двух
других 10 см. Найт! эт1 стороны, если они выражаются целым!
числами.
193. Известно, что система двух линейных неравенств не
удовлетворяется ни прг каких значениях неизвестной величины
Можно ли сказать, чти отдельные неравенства этой системь не
выполняются ни при каких значениях неизвестно! величины?
Дробно-линейные функции § 24
В этом параграфе мы рассмотрим некоторые вопросы поведе-
ния функций вида
у = , (1)
сх 4- d
где с, Ь, с и d — заданные числа, причем с отлично от нуля.
Такие функции называются дробно-линейными*.
Прежде всего отменим, что дробно-линейная функция Ч)
d
определена при всех значениях аргумента х кроме х = — — .
1е значения аргумента при которых Функция определена,
в математике принято называл областью определения этой функ-
ции. Поэтому можно сказать, что областью определения дробно-
линейной функции (1) служит множество всех чисел, кроме--------.
Так, областью определения функции у— ^Гх будет множе-
ство всех чисел, кроме у; области определения функции \ --------
состоит из всех чисел кроме 1.
Теперь на частном примере покажем, как можно выяснить,
при каких значениях аргумента х дробно-линейная функция
* Обычно, говоря о функциях вида (1), предполагают, что ad—bc^O.
Это условие мы заменяем здесь более простым условием с =/= б.
49
/
1
7
Рнс. 34.
принимает положительные значения,
при каких — отрицательные значения и
при каких она обращается в нуль.
Пусть
Рассмотрим отдельно числитель и знаменатель данной дроби.
При х > 1 числитель х — 1 положителен, а при х< 1 — отрица-
телен. Этот факт отмечен на верхней прямой рисунка 34: заштри-
хованная область этой числовой прямой соответствует тем зна-
чениям аргументах, при которых числитель х—I положителен,
а незаштрихованная — тем значениям аргумента х, при которых
числитель х — 1 отрицателен. Решая неравенство
о
получаем: х < — . Поэтому знаменатель 3 — 7х данной дроби
будет положительным при х < — ; этот факт отмечен с помощью
7 7
штрихов на нижней числовой прямой рисунка 34. При х>
О
знаменатель будет, очевидно, отрицательным.
Сравнение двух числовых прямых на рисунке дает: при
— < х < 1 знаки числителя и знаменателя данной дроби сов-
з
падают (оба «—»); при х< — и при х > 1 они разные. Поэтому
з
при - <х< 1 данная функция
тельные значения, а при х<С -
значения. В точке х 1 она
вообще не определена (рис. 35).
Описанным способом можно решать*и некоторые неравенства,
содержащие дробно-линейные выражения. Покажем, например,
как решается неравенство
— <4.
х — 1
у=-----— принимает положи-
3 — 7*
и при х > 1 — отрицательные
обращается в нуль, а при х = ~
Перенося 4 в левую часть, получаем эквивалентное неравенство
—-----4 < О,
х- 1
или
Рис. 35.
50
Числитель 6 — 4х полученной
дроби положителен при х < --
3
и отрицателен при х > •
Знаменатель х — I положителен
при х > 1 п отрицателен при
х< 1 (рис. 36). Поэтому дробь
6 — 4х
— -- принимает отрицательные значения
X — 1
2 А
Таким образом, неравенству ------- < 4
х — 1
-3
ченпя х < I и х > .
ZzyzZZZZZZZZZZZZZZZZZZZZ/ZZzZZ
1
Рис. 36.
при Х<1 II при Х>
удовлетворяют все зна-
Подчсркнем, что данное неравенство нельзя решать
почленного умножения на х— 1. Ведь тогда могло бы
читься неравенство, не эквивалентное данному. В самом
мы имели бы
путем
полу-
деле,
2 < 4 {х -
6 < 4х,
1),
3_
2 '
х
Оказались потерянными решения х <_ 1.
Правильным является ответ: х < 1; х >
3
2
Упражнения
Найти области определения данных дробно-линейных функ-
ций (№ 194, 195) и установить, прн каких значениях аргумента
они принимают положительные значения, при каких — отрица-
тельные значения и при каких обращаются в нуль:
164, у=-----. 1 £5. у =------.
Решить неравенства (№ 196—198):
196. -<1. 197. х~-1>2. из. i±J>7.
х х -|- 5 х 4- 3
199. При каких х значения выражения —-— заключены
х— 1
между 0 и 2?
200. Решить неравенство
1 < < 2.
1 — X
Найти допустимые значения букв, входящих в данные выра-
жения (№ 201, 202):
»' /S' + 202. .
51
Решить уравнения:
203. |2A=Jp^.
205. 1*^2° =10-5-.,
! Зх2 Зх2
□ — к
Ь — х
205.
х — а
х -Ь
Неравенства, содержащие неизвестное
под знаком абсолютной величины
§ 25
в этом параграфе мы »<з частных примерах покажем, каг. решаются
неравенства вида
lax + Ь\ < с и \ах + Ь\ > с.
Пример 1. Решить неравенство
|2х - 5| < 1.
Если абсолютная величина некоторого числа меньше 1, то само это
число должно оыть больше — 1, но меньше 1 (рис 37). Поэтому данное
неравенство можно записать в виде двойного неравенства:
— 1 < 2х — 5 < 1.
!__ . ___________________________________।
о /
Рис. 37.
Прибавляя к каждой части такого неравенства число 5 и деля затем полу-
ченное неравенство почленно на 2, мы приходим к следующему результату;
4 < 2х < 6,
2 < х < 3.
Множество таких значений х показано на рисунке 38.
0
1
2 3
Рис. 38.
а
П р и м е р 2. Решить неравенство
13 - х| > 2.
Если абсолютная величина некоторого числа больше 2, то само это
число должно быть либо меньше — 2, либо больше 2 (рнс. 39). Поэтому из
данного неравенства вытекает, что либо
либо
3 — х < — 2,
3 — х > 2.
-3-2-10123
Рис. 39.
52
Первое из этих двух неравенств дает
— х — 5. или х > 5,
а второе
X >-------------1, Г14Г1Г1 Л. I ,
О т d с х < 1, х > 5. Множество '.акнх значений х показано на ри-
сунке 40 в виде двух лучей числовой прямой.
0 12 3 0 5 6
Рис. 40.
Упражнения
Решить следующие неравенства (№ 207—216):
207. |х — 2| < 3.
2U8. |1 — х| > 10.
2U9. |0,5х — 3| < 0,5.
210. |2 х — 4| > 6.
211.
212.
213.
|1 + х| < 2.
|2 — х| > 1.
I— 2х + 1| >
214. |х+ 4| < 3.
215». |3 + Xi >1х|.
5. 216. \ах + 6| < а.
Данные неравенства решить графически:
217. |х ~ 3| < 2. 218. |1 — 2х| > 3. 219. |х | > [1 — х|.
Сиотема двух линейных уравнений с двумя
неизвестными. Совместные и несовместные системы§ 26
Системой двух линейных уравнений с двумя неизвестными
называется совокупность уравнений вида
1а1х + &1у=с1, /к
| ajc + b2y — с,,
где х и у — неизвестные величины, a at, bt, с( и а2, b2, с2 — неко-
торые заданные числа.
Примером системы двух линейных уравнений с двумя неиз-
вестными может служить любая из систем:
2х — Зу = 0, 7х — 5у.= 0; (2) о о II II 54 1 I (5)
100х — 2у — 96, — Зх+ 57у= 111; (3) ( X 4- у - 0, 1 х4-у = 1; (6)
х— 2у — 12, Зу = 3; (1) ( —х + 1,5у = 3, 1 2х — Зу =— 6. (7)
Кстати, любую из этих систем можно назвать системой урав-
нений 1 й степени. Так называются системы вида (1), в которых
53
хотя бы одно из уравнений содержит ненулевой коэффициент
при х или при у.
Если в системе (1) оба свободных члена ct и с2 равны нулю,
то система называется однородной. Если хотя бы один из сво-
бодных членов сх и с2 отличен от нуля, то система называется
неоднородной.
Так, из приведенных выше систем (2) — (7) однородными
будут системы (2) и (5); все же остальные системы неоднородны.
Решением системы уравнений (1) называется такая пара
чисел (xQ, у0), которая каждое уравнение этой системы обра-
щает в числовое равенство*'.
Ср
, ^гУо — ^2’
Например, пара чисел (0, 0) является решением системы урав-
нении (2), поскольку
2 • 0 — 3.0 = 0,
7-0 — 50 = 0.
Пара чисел (1, 2) будет решением системы (3), так как
100- 1 -2-2 = 96,
— 3 - 1 4-57- 2= 111.
Пара чисел (2, 1) не будет решением системы (3), поскольку
100-2 —2. J =£96,
. —3-2 + 57-2^ 111.
Решением системы уравнений (3) не будет и пара чисел (2, 52).
Действительно,
100 • 2 — 2 52 = 96,
но
— 3 • 2 4- 57 - 52=^ 111.
Системы могут иметь различное число решений. Например,
система уравнений (4) имеет, очевидно, единственное решение:
х = 14, у = 1. В самом деле, из второго уравнения этой системы
следует, что у = 1- Подставляя затем это значение у в первое
уравнение, получаем: х — 2 • 1 = 12, откуда х = 14.
Система уравнений (5) имеет, очевидно, бесконечное множе-
ство решений. Действительно, при любом а пара чисел (а, а)
обращает оба уравнения системы в числовые равенства. Поэтому
любая такая пара чисел (а их бесконечное множество) является
решением данной системы.
* Это определение годится и для произвольных систем уравнений с
двумя неизвестными.
51
Наконец, существуют системы, которые вообще не имеют
решений. Примером таких систем может служить система (6).
Если бы она имела решение (х0, //0), то сумма двух чисел х0 и
у0 должна была бы равняться одновременно и 0 и 1. Но этого
быть не может.
Таким образом, существуют системы линейных уравнений,
имеющие ровно одно решение, бесконечное множество решений
и, наконец, совсем не имеющие решений.
Система уравнений, имеющая хотя бы одно решение, назы-
вается совместной, а не имеющая ни одного решения — несов-
местной. Например, системы уравнений (2) и (3) совместны, а
система (6) несовместна.
Для каждой однородной системы уравнений
ape + by — О,
а2х + b2y — О
пара чисел (0, 0) является решением. Поэтому любая однород-
ная система уравнений совместна. В частности, совмест-
ными являются приведенные выше системы (2) и (5).
Решить систему уравнений
I арс 4- b ру =
I ^2-^ ^2
— это значит: 1) выяснить, является ли она совместной, и
2) если она совместна, то найти все ее решения.
Упражнения
220. Можно ли системы:
( х + у = 0, I 2х — Зу = 3, Зх — 7,
I х 4- у = 0; 2х — Зу = 30; 2у = 0
— назвать системами двух линейных уравнений с двумя неиз-
вестными?
221. Показать, что ни при каких значениях а системы урав-
нений
2х 4- 7у = а,
— 5х + бу = а 4- 1
— 11х 4“ бу = Еа— 1,
4х — 5у = а2
не являются однородными.
222. Доказать, что если система двух уравнений 1-й степени
с двумя неизвестными имеет нулевое решение (то есть решение
х = 0, у = 0), то она является однородной.
Верно ли обратное утверждение?
55
Определители второго порядка
§ 27
Когда нам нужно записать сумму двух чисел а и Ь, мы
используем знак + и пишем а 4- 6; для записи разности двух
чисел используется знак — и т. д. Большую роль в математике
играет еще одна форма записи алгебраических действий, которая
нам понадобится для изучения систем двух линейных уравне-
ний с двумя неизвестными. Выглядит эта форма записи так:
а‘| (1)
с d I
Четыре числа а, Ь, с и d записаны в виде таблицы, имеющей
две строки (a, t) и (с, d) и два столбца и . Слева и
справа стоят вертикальные черточки. Все это выражение упо-
требляется для записи разности ad — be и называется определи-
телем второго порядка. Итак,
Например,
2-3
— 5 — 6
а b . .
— ad be.
с d\
(2)
= 2 • (- 6) - (- 3) • (- 5) =- 12 - 15 =- 27:
’ 2 I — 1.6-с—2) - (—3) = 6—6 = 0;
— 3 6 I
а 1
1 а
----- а • а — 1 • 1 = а3— 1.
Числа a, b, с, d называются элементами определителя (1).
Строки (а, Ь) и (с, d) определителя
а b
с d
называются пропорциональными, если хотя бы одна из них по-
лучается в результате поэлементного умножения другой строки
на некоторое число k.
Поясним это определение на двух частных примерах.
Пример!. В определителе
2 6
1 3
первая строка получается посредством умножения каждого эле-
мента второй строки на 2:
2 = 2-1; 6 = 2-3.
66
Значит, строки этого определителя пропорциональны. В роли
k здесь выступает число 2
В данном случае возможно и другое объяснение: вторая
строка определителя получается посредством умножения каждого
1
элемента первой строки на —:
1=1-2; 3=1-6.
2 2
Следовательно, строки этого определителя пропорциональны.
Здесь уже в роли к выступает число —
Пример 2. Строки определителя
О О
О 1
также пропорциональны, поскольку первая из них получается
поэлементным умножением второй строки на нуль:
0 = 0-0; 0 = 0-1.
В этом случае роль k играет число 0.
В отличие от первого примера, здесь вторая строка уже не
может быть получена путем поэлементного умножения первой
строки. Вот почему в определении пропорциональных строк
говорится, что из двух таких строк хотя бы одна должна по-
лучаться в результате поэлементного умножения другой строки
на некоторое число k.
Таким образом, определение пропорциональности строк
(а, Ь) и (с, d) определителя
а Ь
с d
можно записать следующим образом:
либо а = kc,
либо с = k'a,
b = kd, (3)
d = k'b, (4)
где k и k' — некоторые числа. Для одних определителей
выполняются оба эти условия (см. пример 1, в котором k = 2,
k' = lj j для других же определителей имеет место только одно
из них (см. пример 2).
Заметим, что если оба элемента первой строки в определи-
теле
а b
с d
57
отличны от нуля, то пропорциональность строк можно записать
в виде:
с J
а b
Аналогично, если каждый элемент ширей строки данного
определителя отличен от нуля, то
пропорциональность строк
можно записать в виде:
я — А
с d
Упражнения
223. Вычислить определители:
О 0 .
1 —6 ’
1 °1*
—3 о|'
а —а
1 4 а
а
224. Как изменится определитель 2-го порядка, если:
а) поменять местами его строки;
б) поменять местами его столбцы;
в) поменять местами элементы, стоящие на одной диагонали;
г) все элементы первой строки умножить на число а;
д) все элементы второго столбца разделить на число d -/= О?
225. При каких значениях а строки данных определителей
пропорциональны:
а) И 3
|2 а
б)
226. Докажите,
а —4
1 2 ’
что если
в)
7 5
а За
в определителе второго порядка
какая нибудь строка или какой-нибудь столбец состоит из од-
них нулей, то строки такого определителя пропорциональны.
(Это утверждение полезно запомнить. Оно потребуется нам
в следующем параграфе.)
О
О О
6 а
Условие, при котором определитель
2-го порядка равен нулю § 28
Во всех приложениях теории определителей важную роль
играют условия, прщ которых определитель обращается в нуль.
Эти условия мы и рассмотрим в данном параграфе.
Теорема 1. Если строки определителя
а b
с d
пропорциональны, то этот определитель равен нулю.
58
= ak'b — bk'a = 0.
k'a k'b
Доказательство. Пронипнионяльность строк (а. Ь) и
(с, d) означает, что:
либо а = kc, Ь = kd,
либо с = k'a, d = k'b.
(При этом, конечно, не исключается возможность и того и дру-
гого.)
Если и = kc, Ь = kd, ти
a b kc kd . , ' п
~~ = kcd kdc = 0.
cd cd
Аналогично ибсюиг дело и в случае, когда с = к'a. d — k'b'.
а Ь _
с d
Теорема доказана.
Верна и обратная теорема.
Теорема 2. Если определитель
'а Ь'
k d
равен нулю, то строки его пропорциональны.
Доказательство. По условию
ad — be = 0,
или
ad = be (П
Еслп ни один из элементов второй строки (с, d) не равен
нулю, то из (1) вытекает, что
а ___________________________ ь
с d
Но это уже означает, что строки (а, Ь) и (с, d) пропорцио-
нальны.
Если оба числа end равны нулю, то строки определителей
опять же будут пропорциональны (см. задачу 226 из предыду-
щего параграфа).
Остается рассмотреть лишь случай, когда одно из чисел с
и d равно нулю, а другое отлично от нуля. Пусть, например,
с = 0, a d Ф 0. Тогда из (1) вытекает, что а = 0. Но в таком
случае в определителе
а Ь
с d
59
первый столбец будет состоять из одних нулей. Поэтому строки
определителя будут пропорциональны (см. задачу 226).
Доказанные две теоремы приводят к следующему результату.
Определитель
а b
с d
равен нулю тогда и только тогда, когда его строка
пропорциональны.
Упражнения
227. При каких значениях а строки данных определителей
пропор циональны:
а) а 2 б) а — 1 3 в) а а — 1
2а' а- За । ’ a -f- 1 а
228. Столбцы определителя 2-го порядка называются пропор-
циональными, если хотя бы один из них получается в резуль-
тате поэлементного умножения другого на некоторое число k.
Докажите, что’если в определителе 2-ю порядка пропорцио-
нальны строки, то пропорциональными будут и столбцы. Верно
ли обратное утверждение?
Главный и вспомогательные определители системы
двух линейных уравнений с двумя неизвестными § 29
Главным определителем системы уравнений
I atx + fyy = q,
I a2x + b2y = c2
называется определитель
(О
«2 Ь2 '
составленный из коэффициентов при неизвестных х и у. Этот
определитель мы будем обозначать греческой буквой Д (дельта).
Очевидно, что
Д = aib2 — a2bi.
Первым вспомогательным определителем системы уравнений (1)
называется определитель
q
c z i
60
Он получается из главного определителя этой системы уравне-
ний путем замены первого столбца на столбец свободных чле-
нов. Этот определитель мы будем обозначать Дх. Индекс (то
есть значок) х при А указывает, что в главном определителе А
первый столбец (с,|, составленный из коэффициентов при х
\а2)
в системе уравнений (1), заменен на столбец свободных членов
( С1). Очевидно, что
\С2/
Дх= Cib2— c2bi.
Вторым вспомогательным определителем системы уравнений (1)
называется определитель
ai Cjl
аг Сг1
который получается из главного определителя этой системы пу-
тем замены второго столбца на столбец свободных членоз.
Этот определитель мы будем обозначать Ду. Очевидно, что
Ду= ахс2— a2ct.
Пример. Для системы уравнений
Д =
| — х + 2у =— 5,
I — 7х + Зу =— 13
= (— 1) • 3 — (— 7) • 2 =— 3 + 14 = 11;
Дх=
— 5 2
— 13 3
= (— 5) 3 —(— 13) • 2 = — 15 + 26 = И;
* — 1 —5
Д„=
у — 7 — 13
= (—!)• (— 13) - (— 7) • (— 5) = 13—35= — 22.
Вопрос о том, какую пользу приносят введенные нами оп-
ределители Д, Дх и Ду при решении системы уравнений (1),
мы выясним в следующих параграфах.
Упражнения
Найти главный и вспомогательные определители для следу-
ющих систем уравнений:
229. |5-'-ЗУ = 5-
I 2х + Зу = 8.
230. !“ + >“ ’
( х + ау = а.
( 1 1 с
231. / Тх~
I V d
I х — у = 0.
{у
х —=— а,
Зах у = 5а.
61
Правило Крамера
§ 30
Теорема. Если главный определитель системы урав»
нений
I а.х + - q, (1)
I «2^4- М = с2
не равен нулю, то эта система уравнений совместна и
имеет единственное решение:
Например, для системы
| - х |- 2у =— 5,
| — Чх + Зу =— 13,
рассмотренной в конце предыдущего параграфа, Д = 11, Дх = 11,
Ду = — 22. Поскольку Д =# 0, то система совместна и имеет един
ственнсе решение:
Ду - 22 о
у = -1 =---- =— 2.
Л Д Н
Доказательство теоремы мы разобьем на два этапа.
1) Сначала покажем, что при Д =# 0 система (1) не может
иметь более одного решения.
Пусть (х0, у0) — решение системы (1). Тогда
<2i*o + &1Уо = (2)
а2*о 4' ^гУо = ^2- (3)
Умнолтим первое из этих равенств на Ь2, а второе на — и
полученные соотношения сложим. Тогда получится:
(«1&2 — а2Ьдх0 + (Ь1Ьг — МОуо = b2Ci ~ Ь{с2,
или
Д • Хд = ДЛ.
Затем к равенству (2), умноженному на — а,, прибавим равен-
ство (3), умноженное на а,. В результате получим:
(— a2ai + ai<22) хв + (—a2bi + у0 -- —
или
Д ‘ Уо = ду-
Таким образом, если система уравнений (1) имеет решение
(*о. Уо). то
д - *о = Дх<
Д Уо = Дг
62
Вследствие того что Л Ф 9, х0 должен быть равен ^-г, а уг =
Д
= . Никакими другими числами л0 и у0 быть не могут. Нс
эю и означает, что данная система имеет не более одного ре-
шения.
2) Доказывая единственность решения системы уравнений
(1), мы предположи.; I., что решение существует. Но верно
ли такое предположение? Теперь этот вопрос выяснить нетруд-
но. Мы уже показали, «то решением системь уравнений мо-
гут бьгь лишь числа х0 — — и у0 — . Поэтому сейчас нам
А а
нужно будет просто подставить эти значение х i у i уравнения
системы <!' и посмотреть, обратятся л» прг этом уравнения в
числовые равенства. Если обратится, тс тем самым мь дока-
л\ем, “То система уравнение (1 имеет решение х0 = —, у0 =
и, следовательно, является совместной. Б этом и состоит вто-
рой этап доказательства нашей теоремы.
Имеем:
ЧАС 4- Ь$о = дЛ + Й4Ь= 1С?’ -4- * (0,t ~
д
- - = с,
А 1
д
—— огЬLc2 —*— b^a^c2 ~~ Cj - — Ogiy
A _ _
Аналогично показывается, что
4*0 4~ ^г1/о = 4е
Таким образом, если для системы уравнений
эта система имеет и притом единственное решение. Бгс
получить по следующему правилу: находим Дх, ау,
вычисляем искомые величины z и у
(1)_ Д =# б то
~ можно
а затем
, Дг
по формулаь г =
у = ~ . Это правило названо именем швейцарскою математика
К г а м е р а (17С4—1752),
к понятию определителя г
Условие
пришел
теорему.
который одним и: первых
доказал приведенную здесь
= \а 1 =^0
Iе с'\
г (с, d) этого определители
Д
означает что строки (.с. Ь>
порниональнв! (см. § 28). В таком случае говорят что
циенты при неизвестны? х и у в системе уоавненш (1)
порциональны. Поэтому полученный результат можно
лировать следующим образом.
не про- .
коэффи-
не про-
сформу
63
Если коэффициенты при неизвестных хи у в систе-
ме уравнений
| a,x 4- = с„
I а^х 4- Ь2у = с2
не пропорциональны, то эта система совместна и
имеет единственное решение.
Вопрос о пропорциональности коэффициентов при неизвест-
ных часто решается устно. Поэтому устно может быть установ-
лена совместность таких, например, систем, как
j х 4- 2у = 1, | Зх — у = 5, j х + у = а,
I 2х + 5у = 0; I Зх — 2у = 6; | х — у = Ь,
и т. д. Вместе с тем устно выясняется, что каждая из данных
систем имеет лишь одно решение.
Упражнения
233. Данные системы решить по правилу Крамера:
a) f х + 2у = 2, в) [ 2х — Зу — — 3,
| — 2х — Зу = — 8; ( 4х + у = 1?
б) f О.Зх — -у= 1,
{ 5
I — 6х + 5у —- — 19;
234. Можно ли решать по правилу Крамера следующие си-
стемы:
а) 1 ах + 4у ==» 9, б)(х_У=_а> ( - х 4- ау = 0,
I 9х 4- ay = 1; | « ( ау 4- х = at
I Зах + У = 5а; z
235. Решить систему уравнений:
-* 1- + ’ — = 1.
1 — ах 1 ау
__2_____3 _ _ £
1 — ах 1 4- ау 3 ’
Случай, когда главный определитель системы уравнений
равен нулю, а хотя бы один из вспомогательных
определителей отличен от нуля § 31
(1)
Теорема. Если главный определитель системы урав-
нений . , .
f акх-\-Ь^у Гр
I и^х 4~ Ь^у = Cj
равен нулю, а хотя бы один из вспомогательных опре-
делителей отличен от нуля, то система несовместна.
64
Формально доказательство этой теоремы нетрудно получить
методом от противного. Предположим, что система уравнений (1)
имеет решение (х0, у0). Тогда, как показано в предыдущем па-
раграфе,
Д-х0 = Дх, Д-у0 = Ду. (2)
Но по условию Д = 0, а хотя бы один из определителей Дх и Ду
отличен от нуля. Таким образом, равенства (2) одновременно
выполняться не могут. Теорема доказана.
Однако представляется интересным более детально выяснить,
почему система уравнений (I) в рассматриваемом случае несов-
местна.
Условие
ai
^2 ^2
Д =
= 0
означает, что коэффициенты при неизвестных в системе урав-
нений (1) пропорциональны. Пусть, например,
Условие
дх
— ka2, bi — kb2<
с, bt
С2 ^2
=£0
означает, что коэффициенты при у и свободные члены уравне-
ний системы (1) не пропорциональны. Поскольку bt = kb2 , то
Cj kc2.
Следовательно, система уравнений (1) может быть записана
в следующем виде:
I kajc + kb$ = с„
I а2х + Ьгу = с2.
В этой системе коэффициенты при неизвестных соответственно
пропорциональны, но коэффициенты при у (или при х) и сво-
бодные члены ие пропорциональны. Такая система, конечно,
несовместна. Действительно, если бы она имела решение (х0, у0),
то выполнялись бы числовые равенства
k (а2х0 + = сь
®2^о -J” ^гУо ^2'
Но одно из этих равенств противоречит другому: ведь #= kc2.
Мы рассмотрели лишь случай, когда Дх 0. Аналогично
может быть рассмотрен случай, когда Ду 0.
Доказанную теорему можно сформулировать и таким образом.
Если коэффициенты при неизвестных хи у в системе
уравнении (1) пропорциональны, а коэффициенты при
какой-нибудь из этих неизвестных и свободные члены
не пропорциональны, то эта система уравнений несов-
местна.
3 Заказ 261
6S
Легко, например, убедиться в том, что каждая из данных
систем будет несовместной:
| х 4- у = 0, f 2х— 0,5у — 3, f х— у = О,
} 2х Н 2у = 1; I 4х— у=1; I—2х4*2у = 7.
Упражнения
236. (У с т н о.) Показать, что каждая из данных систем
уравнений несовместна:
х — 2у = О,
а) < л
I 4х — 8у = 5;
2х — у = 3,
х — 0,5у = 1;
в)( -* + 3.V=-2,
I 2х — 6у=—1.
Решить системы уравнений:
237. ( 5»«-У = 8.
I — ах + у —0.
239.
238. J 8х + 2аУ ~ 240.
{ 5х 4- 4ау = 2.
х ау
ах 4--— =1 — X,
а— 1
х 4- у — 1 = а?х —а.
Случай, когда и главный и оба вспомогательных
определителя системы уравнений равны нулю § 32
В предыдущих параграфах, изучая систему уравнений
( а,х 4- 6,у = с„ (J)
I ^2^ ^гУ =
мы рассмотрели два случая:
1) случай, когда коэффициенты при неизвестных х и у не
являются соответственно пропорциональными (Д =# 0);
2) случай, когда коэффициенты при неизвестных хи у соот-
ветственно пропорциональны, а коэффициенты при каком-нибудь
неизвестном и свободные члены, не являются соответственно
пропорциональными (Д —- 0, а хотя бы один из определителей
Дх и Ду отличен от нуля).
Осталось рассмотреть еще один случай, когда и коэффи-
циенты при неизвестных х и у и свободные члены соответст-
венно пропорциональны, то есть
at = ka2, b, = kb2, Ci = kc2
или
a2 — k'at, b2= k'bi, c2 = k'ct.
Для определенности мы рассмотрим первый из этих двух вариан-
тов. Система уравнений (1) в этом случае имеет вид:
66
ka2x + kb2y = kc2, ^2)
a2x 4- b2y = c,.
Очевидно, что каждая пара чисел (х0, у0), удовлетворяющая
второму уравнению системы (2), должна удовлетворять и пер-
вому уравнению этой системы. Поэтому, для того чтобы решить
систему уравнений (2), достаточно решить одно лишь второе
уравнение этой системы. Другими словами, достаточно найти
все такие пары чисел (х0, у0), котопые обращают уравнение
а2х + b2y = с2
в числовое равенство.
Предположим, что в этом уравнении хотя бы одни нз коэф-
фициентов а2 и Ь2 отличен от нуля. Пусть, например, Ь2 =/= 0.
Тогда в качестве х0 можно выбрать любое число /; у0 в этом
v jit. ^2 — Q»i
случае найдется из условия а/ + о2Уо == с2» откуда у0 — —-----.
Итак, в рассматриваемом случае система уравнений (2) имеет
бесконечное множество решений. Все они задаются формулами
Сд — Ад/
хо -= Уо =
где t — любое число.
Этот результат мы получили в предположении, что хотя бы
один из коэффициентов а2 и Ь2 отличен от нуля. А если оба
они равны нулю? Тогда система уравнений (2) имеет вид.
J Ox -l Оу = q,
< (<</
I Ох -г- Оу = с,.
Такая система не представляет особого интереса. Если с, = с2 = 0,
то решением ее является любая пара чисел (х0, у0) Если же хотя бы
©дно из чисел ct и с2 отлично от нуля, то система (3) несовместна.
Очевидно, что случай, когда а2 = Ь2 = 0, будет автоматически
исключен, если дополнительно потребовать, чтобь среди коэф-
фициентов при неизвестных х и у в системе уравнений (1) был
хотя бы один отличный от нуля коэффициент.
Мы доказали следующую теорему.
Если коэффициенты при неизвестных и свободны^
члены в системе уравнений (1) соответственно пропор-
циональны и среди коэффициентов при неизвестных
есть хотя бы один коэффициент, отличный от нуля,
то система уравнений (1) имеет бесконечное множество
решений, Все они получаются как решения одного того
уравнения, которое содержит отличный от нуля коэф-
фициент при неизвестном.
з*
67
Пример. Решить систему уравнений
| х-2у = 3,
I 2л — 4у — 6.
Коэффициенты при неизвестных и свободные члены этой системы
уравнений соответственно пропорциональны. Поэтому все реше-
ния этой системы уравнений можно получить как решения одного
лишь первого уравнения
х — 2у = 3.
Полагая х — I, находим, что у = * (I — 3).
Итак, данная система уравнений имеет бесконечное множе-
ство решений:
x = t, у=
где t — любое число. В частности, при t = 0 получается решение
х = 0, у — — — , при t = 5 — решение х = 5, у — 1 и т. д.
Доказанную выше теорему полезно сформулировать и е тер-
минах определителей.
Если коэффициенты при неизвестных и свободные члены
системы уравнений (1) соответственно пропорциональны, то, как
легко получить непосредственно, используя (2),
А= Дх = Ду = 0.
Можно доказать и обратное утверждение. Если А — = Ау = О
и хотя бы один из коэффициентов при неизвестных системы
уравнений (1) отличен от нуля, то коэффициенты при неизвест-
ных и свободные члены такой системы уравнений будут соот-
ветственно пропорциональными. На доказательстве этого факта
мы останавливаться не будем, хотя в принципе это и можно
было бы сделать Но, приняв его на веру, мы можем теперь
доказанную выше теорему сформулировать следующим образом.
Если и главный и оба вспомогательных определителя
системы уравнений (1) равны нулю и среди коэффи-
циентов при неизвестных есть хотя бы один отличный
от нуля коэффициент, то система уравнений (1) имеет
бесконечное множество решений. Все они получаются
как решения одного того уравнения, которое содержит
отличный от нуля коэффициент при неизвестном.
Упражнения
241. (Усти о.) Показать, что каждая из данных систем урав-
нений имеет бесконечное множество решений:
. ( 1х — у = 3, | 2л + Зу = 0, . ( 2х — 1,5у = 3,
а) { б) { - в) { z
( 14х — 2у — 6; ( 4х Н бу = 0; I Зу — 4х =—6.
68
f Решить системы уравнений (№ 242—244):
242.1 ‘-У- 1- 243.1 3'-5У“°
) Зу — Зх =—3 | —15хЦ-25у б.
плл | 7х — 2у = 16,
244. у
I 3,5х— у = 8.
245. Дана система уравнений
( 2х - Зу = — I,
( 4х - бу = 1.
а) Сколько решений имеет каждое уравнение этой системы?
б) Сколько решений имеет система?
246. Сколько различных решений имеет однородная система
уравнений
atx + bty — О,
агх -+ Ь^у = О,
если а)
ai
а2 Ьг
¥=0;
6j
= О?
^2
Таблица основных результатов рассмотрения систем дьух
линейных уравнений с двумя неизвестнымн § 33
Все результаты о системе уравнений
( а1х 4- fe(y = cit
I &%Х 4“ ^2У —’
которые получены в § 30—32, приводятся в следующей таблице:
А Л =0
хотя бы один из опре- делителей £-х у Aj не равен нулк Ад — Ду — 0 и хотя бы один коэффи- циент при неизвестных отличен 01 нуля
L-ii случай 2-й случай 3-й случай
Система совместна и имеет единственное ре- шение: * ’ 4* х ь ’Л’ Система несовместна *- Система совместна и имеет бесконечное мно- жество решений. Все этт решения по- лучаются как решения одного того уравнения, которое содержит отлич- ный от нуля коэффи- циент при неизвестном
69
Пример Решить систему уравнений
ах — у — 3,
— х ау = — 3
Для этой системы
а
— 1
I
а
Д =
= а2—1, ДЛ. -
3 — I
3 а
= 3а -3,
Ду
я 3 I „ , .
I — — Зя "Р 3.
I —3 I
Пусть я’ — 1 ¥= 0, то есть я #= — 1 и я#= 1. То1Да Д #= О
(случай I), и потому система имеет единственное решение:
X &х За —3 _ 3 _ _ — За 4-3 _ _ 3
Д аг — 1 а + 1 ’ Д а* — 1 а + 1’
Если а = — 1, то Д - О, Дх = — 6, Ду — 6. В этом случае
система будет несовместной (случай 2). Если же а — 1, то
Д = Дх = Ду =0 (случай 3). В этом случае система будет иметь
бесконечное множество решений, причем все ини получаются в
результате решения одного лишь первого (второго) уравнения.
При а — 1 первое уравнение обращается в х — у = 3. Все реше-
ния этого уравнения можно записать в виде х — t, у = t — 3, где
t — любое числи.
Итак, к задаче можно дать следующий ответ: если а #= 1 и
а #= — I, то данная система уравнений имеет единственное
решение:
„ з 3
u+1 ? а+Г
если а = — 1, то система несовместна; при а = 1 система имеет
бесконечное множество решений, которые можно записать в виде
х = t, у = t — 3,
где t — любое число.
Метод решения системы двух линейных уравнений с двумя неизвест-
ными, с которым мы познакомились в этой главе, основан на использова-
нии определителей 2-го порядка. В курсе высшей алгебры вводится понятие
определителя порядка п для любого натурального п и излагается
метод решения системы п линейных уравнений с п неизвестными с помощью
таких определителей. Этот метод очень важен как при решении теорети-
ческих вопросов, так и при исследовании систем уравнений с буквенными
коэффициентами. Он широко применяется (как и само понятие определи-
теля) не только в высшей алгебре, но и в других разделах высшей ь<Йте-
матнки, в механике, в теоретической физике.
Однако для практического решения систем линейных уравнений с чи-
сло в ы м и коэффициентами самым экономным (в смысле объема произво-
димых вычислений) оказывается известный вам по курсу VIII класса
метод последовательного исключения неизвестных. Именно нм пользуются
всегда на практике.
70
Упражнения
Решить системы уравнений (№ 247—249):
247. f 2х + = — 6, I ах (а — 1} у = 0,5,
I их + 8у = 12. ( (а — 1) х — ау — а.
24fe I Зх-ау=6 — а,
|—ах 4- Зу = 3 —2а.
250. Доказать, что каждая из данных систем уравнений не
может иметь бесконечно много различных решений:
(а+ 1)х + у = 0,
х 4* (с2 — а -{- 1) у = 1;
251. Доказать, что каждая из данных систем уравнений либо
несовместна, либо имеет бесконечное множество решений:
(4х —6y=u, f (4 — а)х + у — — а,
I 2х — Зу = 1; I (2а — 8) х — 2у = а.
252. (У с т н о.) Выяснить, сколько решений имеет каждая
из данных систем уравнений:
а) х + 2у = о. г) ' 2х 4-у = 9,
х — Зу = 0; 8х — 4у — — 36;
6) 4х - бу = 5, П1 ( х4-17у=0,
я — 8х + 12у = 10; 2х 4 34у ~ 1;
в) < Зх — у = 6, е) ! х— у = 100,
°) * 1 * * * У 6х— 2у = 12; } 1 2x4- Зу = 17.
Графический способ решения систем линейных
уравнений§ 34
(1)
Предположим, что в каждом уравнении системы
1 а,х + Ь^у = с(,
I а2х Ц- Ь2у = с2
хотя бы один из коэффициентов при неизвестных х и у отличен от
нуля. Тогда любое из этих двух уравнений можно рассматри-
вать как уравнение прямой в прямоугольной системе координат.
Действительно, возьмем, например, первое уравнение
ape + bty = ct.
Если bi ф 0, то уравнение можно переписать в виде:
У
р, Р1
71
Рии. 41.
Это уже знакомое нам уравнение
прямой (см. § 3).
При bt = 0 уравнение а^х +
4- Ъ2у — ct принимает вид atx = ct,
или
Это соотношение можно рас-
сматривать как уравнение пря-
мой, параллельной оси у и пересе-
кающей ось х в точке с абсцис-
сой Ь (смотри, например, рису-
нок 41, на котором представлены
прямые х = — 1 и х = 2).
полученные в предыдущих параграфах,
Поэтому результаты,
допускают простую геометрическую интерпретацию. С системой
уравнений (1) свяжем две прямые: прямую atx + bty — ct и пря-
мую а2х + Ь2у = с2 (рис. 42). Если эти прямые имеют общую
точку Л4, то координаты ее (х0, у0) определяют некоторое решение
системы уравнений (1). Обратно: каждое решение системы урав-
нений (1) можно рассматривать как координаты точки, принадле-
жащей одновременно и прямой atx 4- 6ty = ct и прямой а2х 4-
4- Ь2у = с2. Таким образом, система уравнений (1) имеет столько
решений, сколько общих точек содержат прямые atx 4- hy = ct
и а2х 4- b2y = с2.
Любые две прямые либо имеют одну общую точку (пересе-
кающиеся прямые), либо не имеют ни одной общей точки (па-
раллельные прямые)г либо имеют бесконечно много общих то-
чек (сливающиеся друг с другом прямые). Соответственно это-
му система уравнений (1) либо имеет единственное решение (слу-
чай 1), либо
есть не имеет ни одного решения
(случай 2), либо имеет бесконечно
много решений (случай 3). По-
ясним это на трех частных приме-
рах.
Примеры. 1. Системе урав-
нений
несовместна, то
' * — У = 1
соответствуют прямые, представ-
ленные на рисунке 43. Они пере-
секаются в одной точке с коор-
динатами (2; 1). Следовательно,
72
данная система имеет единственное
решение х — 2, у = 1.
2. Системе уравнений
| х — у = 2,
I 2х — 2у — 6
соответствуют параллельные пря-
мые, представленные на рисун-
ке 44. Они не пересекаются ни
в одной точке. Данная система
уравнений несовместна.
3. Для системы уравнений
I 2х 4- у = 1,
| 6г -р Зу = 3
соответствующие прямые сливаются в одну прямую линию
(рис. 45). О таких прямых можно сказать, что они пересекаются
в бесконечном множестве точек, а именно в каждой своей точке.
Поэтому данная система уравнений имеет бесконечное множество
решений. Все эти решения можно представить как координаты
точек, лежащих на этой прямой. Если х принять за t, то для у
получим у = 1 — 2/.
Упражнения
Решить графически следующие системы уравнений (№ 253— 258):
253.
2х — у = 5,
Зх — у = 7.
2S4. х+ У-4’
2х + 2у = 8.
( 2х — Зу = О,
255. 1 Л
1 х— 1,Ьу — 1,5.
256. ( Х у
| у — 2х= 1.
257. р-У = 3’
I 2х = 4.
258. I ~ Х 2у = °’
( Зу = 6.
73
259. Как геометрически можно интерпретировать тот факт,
что любая иднородная сястста дь^Л д..нсйных уравнений с До,ип
неизвестными совместна?
Задачи на повторение
260. При каких значениях а уравнение ах = 2х |- а
а) не имеет п.оннсй;
б) имеет и притом только положительные корни;
в) имеет и притом только отрицательные корни;
г) имеет корни?
261. Отцу 40 лет, а сыну 1и. Через сколько лет отец будет
в k раз старше сына?
262. Решить относительно х уравнение
____Зх1 — 8а_ _ Зх________х
2ах — 2а — 3x4-3 ~ 2а — 3 х— 1 *
263. Сколько точек пересечения имеет прямая у — ах 4- b
а) с осью абсцисс;
б) с осью ординат ?
Доказать неравенства (№ 264—268):
264. -?= + > У а + Vb.
\ b V а
265. (ас bd)2 < (а2 4- Ь2) (с2 4- d2).
266. (п-н4-1 4--^>9 (а>0, б > 0, с> 0).
\ а b с)
267. (а 4- b 4- с)2 < 3 (а2 |- Ь2 4- са).
268*. а1 4- Ь1 4- с4 > abc (а 4- Ь 4- с).
269. Где моторная лодка быстрее пройдет расстояние в 30 км
и возвратится назад: по озеру или по реке?
270. Доказать, что если а 4- b 4- О 3, го и а2 4- Ь2 4- с2 > 3.
271*. Как выгоднее (с точки зрения экономии металла) штам-
повать металлические шайбы: как показано на рисунке 46, а
или как показано на рисунке 46, б? Каждая пластина, из кото-
рой штампуются шайбы, имеет форму прямоугольника со сто-
ронами а и Ь, а диаметр шайбы равен d.
272. Громоотвод защищает от молнии все предметы, расстоя-
ния которых от его основания не превышают его удвоенной
высоты. Какой должна быть высота h громоотвода, чтобы нм
можно было защитить от молнии прямоугольный участок шири-
ной а м и длиной b В каком месте этого участка лучше всего
поставить громоотвод?
Решить неравенства (№ 273, 274):
273. 3<~—-< 5. 274. 3 < 1л —21 <4.
2х — 3 1
74
Рис. 46.
275. Решить систему неравенств:
2х — 1 < 1
х4-1С
Решить системы уравнений (№ 276—279):
£____1=3
276. Iх + ау = Ь> 278. х у
I ах + у = Ь. 2 1 = _ з
* У
277*. / 0Х + 1У1 = 1 +°’ 279. |2Х + ^:Л
[ х + ау = I — а. I х + у —
280. При каких значениях тип прямые Зх — ту -= п я
2х 4- Зу = 5 параллельны?
281. При каких значениях а прямые 4х — Зу = а и — 5х -|-
4- о у = 8 пересекаются в точке, координаты которой отрицатель-
ны?"
282. При каких значениях a u b прямые ах — у = b и
4х + Зу — 10 сливаются в одну прямую?
283. В каком случае однородная система уравнений
( а,х + Ь^у — 0,
I а2х 4- Ь2у = 0
а) имеет только нулевое решение, то есть решение
х — 0, у = 0,
| б) имеет ненулевое решение, то есть такое решение (х0 у#)>
, что хотя бы одно из чисел х0 и у0 отлично от нуля?
I
I 75
284 При каких значениях а решение системы уравнений
х — 7У = 1,
5х + Зу — а
удовлетворяет условию х < 0, у > О?
285. С какой точностью можно найти х и у из системы
уравнений
| 2х — у = а,
I х Ч- Зу = Ь,
если вместо чисел а и b известны ил приближенные значения
с точностью до 0,01? Что можно определить точнее: х или у?
286. (У ст н о.) Сколько различных решений имеет каждая
из систем уравнений:
. ( 2х — у = 0, . L 7х 4- Зу — 2, [ х — 3,5у = 0,
а) у в) | J д) ’ z
I Зх 4- 4у = 1; I 7х — Зу — а; ( 2х — 7у = 0;
_ [ х 4- у — 5, . 6х — 12у =5, , [ 2х — Зу — 1,
б) { г) 5 е) I
12х4-2у = 1; — х4-2у=-; (ох 4-бу =2?
6
287. а) Известно, что уравнение ах = b имеет бесконечное
множество корней. Следует ли отсюда, что любое число xQ
является корнем этого уравнения?
б) Известно, что система уравнений
ахх 4- &1У = q,
4" ^гУ = ^2
имеет бесконечное множество решений. Следует ли отсюда, что
любая пара чисел (х0, у0) является решением этой системы?
288. В каких пределах заключены числа т и п, удовлетво-
ряющие системе уравнений
т — 5п — а,
2т 4- Зп = Ь,
если 0,1 < а < 0,2, а 1,3 < b < 1,4?
ДЕЙСТВИТЕЛЬНЫЕ
ЧИСЛА
Рациональные числа
§ 35
Первой математической операцией, с которой столкнулся
человек, бил счет предметов. В результате счета предметов по-
лучаются целые положительные числа, иначе называемые на
туральными. Расположенные в ниридке возрастании, они об-
разуют натуральный ряд чисел
1, 2, 3, 4...
После натуральных чисел в математику были введены поло-
жительные дроби, то есть числа вида , где т и п — произ-
п
вольные натуральные числа. Введение этих чисел в математику
было вызвано потребностью производить измерения.
Известно, например, что при разливах реки Нила затоплялись огромные
земельные участки древних египтян. После того как вода спадала, каждый
должен был ианти свой участок. Но без умения точно измерять ширину
и длину участка сделать это было невозможно.
Для того чтобы показать, каким образом появляются поло-
жительные дроби при решении задач измерения, мы напомним,
как измеряются прямолинейные отрезки. Из всех отрезков
выбирают какой-нибудь один, например Л В (см. рис. 47 на стр. 78),
и объявляют его «единицей длины». Если в измеряемом отрезке CD
выбранная единица длины укладывается ровно п раз (на рис. 47
п — 3), то длина отрезка CD выражается числом п.
Но не всегда отрезок АВ, представляющий собой единицу
длины, укладывается в измеряемом отрезке целое число раз.
Так, например, на рисунке 48 отрезок АВ вдвое длиннее
измеряемого отрезка CD. Следовательно, половина отрезка АВ
укладывается в CD ровно один раз. Поэтому длина отрезка CD
выражается дробным числом —. Вообще, если отрезок, выбран-
ный в качестве единицы длины, в п раз длиннее измеряемого
отрезка, то длина последнего выражается числом —. Возможен
п
и такой случай, когда n-я часть единицы длины АВ уклады-
77
С р
Рис. 47.
А В
С Р
Рис. 48.
А в
С D
Рис. 49.
вается в измеряемом отрез-
ке CD ровно т раз (см.
рис. 49, па котором п — 3,
т ~ 4). В этом случае длина
отрезка CD выражается дроб-
ным числом — .
п
Таким образом, введение
в математику натуральных
чисел и положительных дро-
бей было вызвано практиче-
скими потребностями людей.
Позднее наряду с этими по-
требностями стали появлять-
ся и потребности теоретиче-
ского характера. Как изве-
стно, натуральные числа и
положительные дроби можно
складывать и умножать друг
на друга. А вот вычесть та-
кие числа одно из другого
удается далеко не всегда.
Например, разности 5—5 и
— 2 никакими натуральными числами и никакими положитель-
Л 8
ными дробями выразить нельзя. Следовательно, действие вычи-
тания в множестве всех натуральных чисел и положительных
дробей, вообще говоря, невыполнимо. Потребности арифметики
еще в древние времена поставили перед математикой необходи-
мость ввести в рассмотрение отрицательные целые числа, нуль и
отрицательные дроби.
Отрицательные числа мы впервые встречаем в работах китайских ма-
тематиков 1 I века до и. э. Нс исключена возможность, что результаты,
содержащиеся в этих работах, были получены еще раньше. В VI—XI веках
отрицательными числами свободно пользовались индийские математики.
В Европе отрицательные числа стали широко использоваться лишь после
работ французского математика Декарта (1596—1650).
После введения отрицательных чисел и нуля математика
стала располагать всеми рациональными числами, то есть чис-
лам», которые можно представить в виде отношения ” , где т
мп — целые числа, причем п #= 0. Сюда входят все целые числа
(положительные, отрицательные и нуль):
3 6
“ 1 2! ~
— 5 _ 10 _ 0=- = °
1 ~ —2 ~ ’ 1 2
78
и все дроби (правильные и неправильные, положительные и от-
рицательные):
1 1_ ь
2’ з’ 5
и т. д.
Упражнения
289. Существует ли средн всех натуральных чисел:
а) наименьшее число, б) наибольшее число3
290. Есть ли среди всех положительных рациональных чисел:
а) наименьшее число;
б) наибольшее число?
291. Есть ли среди всех неположительных рациональных
чисел:
а) наименьшее число;
б) наибольшее число?
292. Среди всех отрицательных чисел, не превышающих по
5 •
абсолютной величине —, указать:
с,
0,
А
I
а) наименьшее рациональное число;
б) наибольшее рациональное число;
в) наименьшее целое число.
293. Если за единицу длины при-
нять отрезок Л В, то длина отрезка CD
Рис. 50.
ГП А
выразится числом — . А каким числом выразится длина того
п
же самого отрезка CD, если в качестве единицы длины вы-
брать отрезок:
а) в k раз меньший отрезка АЬ\
б) в k раз больший отрезка АВ?
294. Какими числами выразятся длины отрезков CtDu C D2
и СдС>3. представленных на рисунке 50, если за единиц]' длины
принять:
а) отрезок CjO б) отрезок CDZ, в) отрезок C-Jjj?
Действия над рациональными числами § 36
Как известно, две дроби т и — равны, то есть изображают одно
п I
и то же рациональное число, в том и только в том случае, когда
ml = nk. Например, — = —, так как 1 • 6 = 3 • 2; = —10 , по-
3 6 7 —14
скольку (— 5) - (— 14) = 7-10; — = —, так как 0 • 5 = 1 • 0 и т д.
1 5
79
Очевидно, что для любого целого числа г, не равного О,
т т • г
п п • г '
Это вытекает из очевидного равенства т (и • г) = п • (т г). По-
этому любое рациональное число можно представить в виде
игношеьпя двуЛ Чисел бесконечным числом способов. Н аирИМСр,
5 _ 2 ~ 1 = ~ 10 ~ -2 . = 15 - и T. Д. и
— 1 7 . — 2 — 14 = ~~3 — 21 — 100 и т. д. 700
0 = £ _ 1 ~ 0 _ — 2 ~ 0 3 0 = — и т. д. 100
В множестве всех рациональных чисел выполнимы действия
сложения, умножения, вычитания и деления (кроме деления на
нуль). Напомним, как определяются эти действия.
Сумма двух рациональных 'чисел ™ и к- определяется
п 1
формулой:
т , k ml + nk
7 7 пГ
Произведение двух рациональных чисел ” и k
п I
формулой:
т k mk
nl nl '
(1)
определяете^
(2)
Поскольку одно и то
/ I 2
писей I например, — = —
же рациональное число допускает несколько за-
3 \
= — = ... I, следовало бы показать, что сумма и
произведение рациональных чисел не
гаемые или сомножители. Например,
зависят от того, как записаны сла-
112 3
— + '-= — + —;
2Т3 4 9
1 1 _ 1 1
2 ' 3 “ 6 ’ 6
и т. д. Однако рассмотрение этих вопросов выходит за пределы нашей
программы.
При сложении и умножении рациональных чисел соблюда-
ются следующие основные закопы:
1) коммутативный (или переместительный) закон сложения:
<7» । г» rt
n I I n'
80
2) ассоциативный (или сочетательный) закон сложения:
3) штмутативный (или переместительным) закон умножения
т k km.
п I In
4) ассоциативный (или сочетательный) закон умножения:
. !l\ . Е. т IР
,п I I q п \ I q
5) дистрибутивный (или
ния относительно сложения:
распределительный) закон умноже-
Сложение и умножение являются основными алгебраическими
действиями. Что же касается вычитания и деления, то эти
действия определяются как обратные по отношению к сложе-
нию и умножению.
Разностью двух рациональных
такое число х,
вами, разность
k
которое в сумме с —
т k
------ определяется
чисел — и — называется
п I
дает Другими сло-
п
как корень уравнения
к
7
Можно доказать, что такое уравнение всегда имеет корень и
притом только один:
ml —nk
Х ~ ~пГ~'
Таким образом, разность двух чисел — и — находится по фор-
п I
муле:
т k ml — nk
п I nl
81
г' т k »
Если числа — и — равны между <д?бои, то разность их
п I
обращается в нуль; если же эти числа ье равны между собой,
то разность их либо положительна, либо отрицательна. При
т k „ т к
------->0 говорят, что число — больше числа —: если же
п i----г п I
т k - n т k
------<0, то говорят, что число — меньше числа —.
п I п <
Частным от деления рационального числа — на рациональ-
п
k
ное число — называется такое число х, которое в произведении
с - диет —. Другими словами, частное — : — определяется
I п п I
как корень уравнения
k
т
п
Еслп у =/= 0, то данное уравнение имеет единственный корень
mZ
nk
Если же - = 0, то это уравнение либо совсем не имеет кор-
ней ^прн — =/= о), либо имеет бесконечно много корней (при
— = 01. Желая сделать операцию деления выполнимой одно-
fl /
зпачно, условимся не рассматривать вовсе деление на нуль. Та-
ким образом, деление рационального числа — на рациональное
п
k к
число - определено всегда, еслп только -- =/= 0. При этом
m к ml
п < nk
Упражнения
295. Вычислить наиболее рациональным способом и ука-
зать, какими законами действий приходится при этом пользо-
ваться ;
82
а>(5,'2 3—)*24;
в) ,333- • 4) - I—
' V 3 / \125
£
16?
о 1\ , 9.
-3^ + Го’
Геометрическое изображение рациональных чисел § 37
Пусть Д есть отрезок, принятый за единицу длины, а
I — произвольная прямая (рис. 51). Возьмем на ней какую-нибудь
точку и обозначим ее буквой О. Каждому положи 1ельному
ill
рациональному числу — поставим в соответствие точку прямой
I, лежащую справа от О на расстоянии в — единиц длины.
Например, числу 2 будет соответствовать точка А, лежащая
справа от О на расстоянии в 2 единицы длины, а числу -у —
5
точка В, лежащая справа от О на расстоянии в — единиц
4
.. *
длины. Каждому отрицательному рациональному числу -
поставим в соответствие точку прямой, лежащую слева от О
|Л I
на расстоянии в -Ч
соответствовать точка
в 3 единицы длины,
единиц длины. Так, числу — 3 будет
С, лежащая слева от О на расстоянии
3 п
а числу------точка D, лежащая слева
3
от О на расстоянии в _ единиц длины. Наконец, рациональ-
ному числу «нуль» поставим в соответствие точку О.
Очевидно, что при выбранном соответствии равным рацио-
i 2
нальным числам (например, — и — 1 будет отвечать одна и та
же точка, а не равным между собой числам различные точки
прямой. Предположим, что числу — соответствует точка Р,
а числу у — точка Q. Тогда, если т > у , то точка Р будет
лежать правее точки Q в
(рис. 52, а); если же - ,
п Г п I с D 0 6 Л I
то точка Р будет пахо- s---------------.—о—। о '° »
диться левее точки Q (рис. -з - '
52, б). Рис. 51.
83
о£
7 о
Рис. 52.
В С О . * В
° 1
Рис. 53.
297. Известно, что точка
Итак, любое рациональное
число можно геометрически
изобразить в виде некоторой,
вполне определенной точки пря-
мой. А верно ли обратное утверж-
дение? Всякую ли точку прямой
можно рассматривать как геомет-
рический образ некоторого рацио-
нального числа? Решение этого во-
проса мы отложим до § 44.
Упражнения
296. Изобразить точками прямой
следующие рациональные числа:
7
— 3; — — ; 0; 2,6.
2
А (рис. 53) служит геометрическим
изображением рационального числа у. Какие числа изобра-
жают точки В, С и D?
298. На прямой заданы две точки, которые служат геомет-
рическим изображением рациональных чисел а и Ь. Найти на
этой прямой точки, изображающие числа а + Ь и а — Ь.
299. На прямой заданы две точки, которые служат геометри-
ческим изображением рациональных чисел а + b и а — Ь.
Найти на этой прямой точки, изображающие числа а и Ь.
Десятичная форма записи рациональных
чисел § 38
На практике обычно пользуются десятичной формой записи
рациональных чисел. Так, вместо пишут 0,5; вместо — — пи-
шут — 0,375; вместо — пишут 1,25 и т. д. Для простоты в
4
дальнейшем мы будем говорить лишь о положительных и пра-
вильных дробях, то есть дробях, заключенных в интервале от
0 до 1.
Чтобы получить десятичную форму записи числа —, нужно
п
т «уголком» разделить на п. Как известно из арифметики, в
результате такого деления получается либо конечная, либо
бесконечная периодическая десятичная дробь. Проиллюстрируем
5 1 29
это на числах —, — и —.
16 3 ИО
84
5| 16 11 3 29 | 110
500,3125 10 0,3333... 290 0.26363...
48 9 220
20 10 700
16 9 660
40 10 400
32 9 330
80 1 700
80 660
0 400
330
70
Поэтому
(конечная десятичная дробь)!
- = 0,3125
16
1 = 0,3333...
3
— = 0,26363...
НО
Период начинается либо
0,333. .), либо после нескольких десятичных знаков, не вхо-
(бесконечная периодическая де-
сятичная дробь с периодом 3);
(бесконечная периодическая де-
сятичная дробь с периодом 63).
сразу же после запятой (например,
дящих в период (например, 0,26363...). Соответственно этому
все периодические десятичные дроби разделяются на простые
(такие, как 0,333...) и смешанные (такие, как 0,26363...).
Период бесконечной десятичной дроби, которая получается
в результате деления целых чисел <уголком», может быть любым
натуральным числом; исключается лишь случай, когда он со-
ставлен из одних девяток. (На строгом доказательстве этого
факта мы останавливаться не будем.) Отметим еще, что любую
конечную десятичную дробь можно рассматривать как бесконеч-
ную периодическую дробь с периодом 0. Например,
0,37 = 0,370000 ...
6,14 = 6,140000 ...
и т. д. Таким образом, любое рациональное число можно
представить в виде бесконечной периодической десятич-
ной дроби, период которой отличен от 9.
Верно и обратное утверждение: любая бесконечная пери-
одическая дробь с периодом, отличным от 9, является
рациональным числом.
Доказательство этого утверждения мы отложим до § 148. А пока напом-
ним лишь известные нз арифметики правила обращения периодических деся-
тичных дробей в обыкновенные. Для простоты мы предположим, что все рас-
сматриваемые нами десятичные дроби положительны и меньше единицы.
85
Правило 1. Для обращения простой периодической дроби
в обыкновенную нужно поступить следующим образом: в
числителе поставить период десятичной дроби, а в знаме-
на теле—число, состоящее из девяток, взятых столько раз,
сколько знаков в периоде десятичной дроби.
Например. 0,333333
9 3
0,454545 — = —;
99 11
243 9
0, 243243243. . . = — = -.
999 37
Правило 2. Для об ращения смешанной периодической деся-
тичной дроби в обыкновенную нужно поступить следующим
об разом: в числителе взять число, стоящее в десятичной
дроби до второго периода, минус число, стоящее в десятич-
ной дроби до первого периода,- в знаменателе нужно напи-
сать столько девяток, сколько цифр в периоде, и приписать
к ним столько нулей, сколько цифр в исходной десятичной
дроби от запятой до первого периода.
Например,
453 - 45 408 34
0,4оЗЗЗЗ ... =-------= — — —;
900 900 75
2745 — 27 2718 151
99000 “ 99000 5500-
0,027454545 .
Заметим, что бесконечным периодическим дробям с периодом 9 также
можно придать определенный смысл, если формально, используя правила
1 и 2. представить их в виде отношения двух целых чисел. Например, пра-
вило 1 дает
9
0,999999 ...= - = 1.
9
45
Согласно правилу 2
49 — 4 45 1
0,499999 . . . = —— = - = - = 0.5.
90 90 2
679 — 67 612 68
0,679999 ... ~---—— = -— = — = 0,68.
900 900 100
5219—521 4698 522
0,521999 . .. =---------=-----=-------= 0,522
9000 9000 1000
и т. д. Все приведенные здесь бесконечные периодические десятичные дроби
с периодом 9 оказались равными конечным десятичным дробям, которые
получаются из данных десятичных дробей, если десятичный знак, стоящий
перед первым периодом, увеличить иа 1, а все последующие десятичные
знаки отбросить. Можно доказать, что это относится не только к рассмот-
ренным, ио и к любым другим периодическим десятичным дробям с перио-
дом 9. Отсюда вытекает, что любая конечная десятичная дробь может быть
представлена в виде бесконечной периодической дроби двумя различными
способами: с периодом 0 и с периодом 9. Например,
0,37 = 0,370000... = 0,369999. . . ;
0.6 = 0.600000... = 0,599999. . . .
Это обстоятельство затрудняет изложение теории бесконечных периоди-
ческих десятичных дробей. Вот почему в дальнейшем мы условимся совсем
не говорить о периодических десятичных дробях с периодом 9. каждый раз
заменяя их соответствующими периодическими дробями с периодом О.
86
. Итак, рациональные числа (и~только они) представимы в ви-
де бесконечных периодических десятичных дробей. А существуют
ли бесконечные непериодические десятичные дроби? Вопрос этот
решается положительно. Чтобы убедиться в этом, достаточно
привести хотя бы один пример бесконечной непериодической
десятичной дроби. Такой пример дает, в частности, дробь
0,101001000100001...
(после запятой выписываются подряд числа 10, 100, 1000, 10000
и т. д.). Попробуйте доказать, что указанная десятичная дробь
действительно является непериодической!
В следующих параграфах будут рассмотрены конкретные
задачи, которые приводят нас к бесконечным непериодическим
десятичным дробям.
Упражнения
300. Записать в биде бесконечных десятичных дробей:
. 15 „ 3 . п .46 , 9
а) б) —7; в) 0; г) д)
301*. Данные периодические десятичные дроби обратить в
обыкновенные:
а) 0,444444...; в) 4,636363...; д) — 2,001777...;
б) 10,521521...; г) 0,573636...; е) 7,090909... .
302. Известно, что несократимая дробь — представима в
п
виде конечной десятичной дроби. На какие числа может де-
литься без остатка число п?
303*. Почему при делении целых чисел «уголком» получаются
всегда периодические дроби?
304*. Доказать, что дробь
0,12345678910111213...,
которая получается, если после нуля выписать подряд все нату-
ральные числа, ие является периодической.
Извлечение квадратных корней
из рациональных чисел
§ 39
Как мы знаем, в множестве рациональных чисел всегда вы-
полнимо действие умножения. В частности, определено произ-
ведение — —. Это произведение, как известно, называется
п п
т (tn
квадратом числа и обозначается —
п \п
т \2 т т
п I п п'
87
Таким образом, если некоторое число является рациональ-
ным, то квадрат его есть также рациональное число. Это число,
очевидно, положительно. А теперь поставим обратную задачу:
всякое ли положительное рациональное число является квадра-
том некоторого рационального числа? На языке алгебраических
уравнений эта задача может быть сформулирована следующим
образом. Дано уравнение хз _ 0
где а — некоторое положительное рациональное число, а
х — неизвестная величина. Спрашивается: всегда ли это уравне-
ние имеет рациональные корни? Ответ на этот вопрос
оказывается отрицательным. Рациональное число а можно вы-
брать так, что уравнение х2 = а не будет иметь ни одного ра-
ционального корня. В этом нас убеждает, в частности, следующая
теорема.
Теорема. Не существует рационального числа,
квадрат которого равен 2.
Доказательство будем проводить методом от противного.
Предположим, что существует рациональное число —, квадрат
п
которого равен 2: /—\2 == 2
\п /
Если целые числа т и п имеют одинаковые множители, то дробь
— можно сократить. Поэтому с самого начала мы вправе пред-
п а т
положить, что дробь несократима.
п
ч т\3 п
Из условия I — =2 вытекает, что
п }
т2 = 2п2.
Поскольку число 2п2 четно, то число т2 должно быть четным.
Но тогда будет четным и число т. (Докажите это!) Таким обра-
зом, т — 2k, где k — некоторое целое число. Подставляя это
выражение для т в формулу т2 — 2п2, получаем: 4/га = 2п2,
откуда д2 =
В таком случае число п2 будет четным; но тогда должно быть
четным и число п. Выходит, что числа тип четные. А это
противоречит тому, что дробь — несократима. Следовательно,
л
наше исходное предположение о существовании дроби — , удов-
п
летворяющей условию ( — j = 2, неверно. Остается признать,
что среди всех рациональных чисел нет такого, квадрат кото-
рого был бы равен 2. Поэтому уравнение
а2 = 2
88
в множестве р а ци опальных чисел неразрешимо. Анало-
гичное заключение можно было. бы сделать и о многих других
уравнениях вида
х2 = а,
где а — положительное целое число. Тем не менее в VI 1 классе
мы неоднократно говорили о корнях таких уравнений. А поло-
жительному корню уравнения х2 — а мы даже дали специальное
название «корень квадратный из числа а» и введя для него
специальное обозначение: а
Итак, к рациональным числам V 2 не принадлежит. А как
же в таком случае можно охарактеризовать ]/2 ? Чтобы ответить
на этот вопрос, вспомним правило для извлечения квадратных
корней. Применительно к числу 2 это правило дает
24' ЮС
4j 96
28 400
1 281
2824 1190О
4 11296
28282.60400
2156564
282841 383600
1 282841
100759
Процесс извлечения корня в данном случае не может закончиться
ни на каком шаге. В противном случае ]/ 2 был бы равен не-
которой конечной десятичной дроби и потому был бы рацио-
нальным числом. А этс противоречит доказанной выше теореме.
Таким образом, при извлечении корня квадратного из 2 по-
лучается бесконечная десятичная дробь Эта дробь не мо-
жет быть периодической, иначе ее, как и всяюйо другую бес-
конечную периодическую дробь, можно было бы представить в
виде отношения двух целых чисел. А это также находится в
противоречии с доказанной выше теоремой. Таким образом, У 2
можно рассматривать как бесконечную непериодическую де-
сятичную дробь.
Итак, к бесконечным непериодическим десятичным дробям
нас приводит, например, действие извлечения корней из целых
чисел.
89
В последующих параграфах мы рассмсприм еще одну задачу,
которая, вообще говоря, никак не связана с извлечением корней,
но которая также приводит нас к бесконечным непериодическим
десятичным дробям.
Упражнения
305. Укажите несколько натуральных чисел, квадратные
корни из которых были бы рациональными числами.
306. Докажите, что если корень квадратный из натурального
чиста представляет собой рациональное число, ю это рациональ-
ное число является непременно целым.
307. Докажите, что уравнение х3 — 5 в множестве рациональ-
ных чисел не имеет корней.
Соизмеримые и несоизмеримые отрезки
§ 40
Отрезок Д называется общей мерой отрезков Af и Д2, если
он укладывается целое число раз в каждом из этих отрезков.
Например, отрезок, EF, изображенный
д> ......... на рисунке 54, укладывается в Л В два
раза, а в CD — 3 раза. Поэтому он
** , , . - Р является общей мерой отрезков АВ
и CD. Аналогично этому, отрезок Д2,
{ { изображенный на рисунке 55, является
общей мерой отрезков At и Д2, по-
Рис. 54. скольку в Д, он укладывается 4 раза,
а в Д2 (в самом себе) — одни раз.
Любые ли два отрезка имеют об-
. . ф щую меру? Ответ на этот вопрос будет
дан несколькими строками ниже. А по-
?ис. 55.
ка мы введем еще одно определение.
Два отрезка, имеющие общую меру,
называются соизмеримыми, а не имею-
щие общей меры — несоизмеримыми.
Теперь вопрос о том, любые ли два
отрезка имеют общую меру, можно
перефразировать таким образом: любые
ли два отрезка являются соизмеримы-
ми? Следующая теорема дает отрица-
тельный ответ на этот вопрос.
Теорема. Диагональ любого
квадрата несоизмерима с его
стороной.
Доказательство будем про-
водить методом от противного. Предполо-
жим, что диагональ АС квадрата ABCD
90
(рис. 56j соизмерима с его стороной АВ Тогда существует об-
щая мера этих отрезков, то есть от резон, который в АВ укла-
дывается ровно п раз, а в АС ровно т раз. Еслг принять этот
отрезок за единицу длины, то длина АВ вырастет числом к,
а длина АС — числом гг.
На диагонали АС построим новый квадрат ACEF, Каи по-
казано на рисунке 56. Очевидно, что площадт этого квадрата
вдвое больше глощадн квадрата A BCD:
$АСЬг ~ ^abcd •
но
$ABCD ~ n*’ а ACEF ~ П'2‘
Поэтому
т2 = 2п2,
откуда
Но это равенстве противоречи'г теореме, доказанной в предыду
щем параграфе «Не существует рационально”© числа, квадрат
которого равен 2».
Следовательно, наше исходное предположение неверно.
Остается признать, что диагональ любого квадрата несоизмерима
с егс стороной.
"'еперь мы можем сделать два важных вывода.
1. Если отрезок CD соизмерим с единицей дли-
ны АВ, то его длина выражается рациональным числом.
Действительно, в силу того что отрезки АВ и CD соизме-
римы, найдется третий отрезок EF, который в АВ укладываемся
ровно г. раз, а в CD ровно т раз. Но г таком случае n-s, часть
отрезка АВ должна укладываться в CD ровно т раз. Поэтому
т
длина CD выражается рациональиыи числом —.
2. Если отрезок CD несоизмерим с единицей длины
АВ, то длина его не выражается никаким рациональ-
ным числом.
Действительно, если бы длина отрезке CD выражалась не
которым рациональным числом, например - , то q-я доля от-
а
резка АВ укладывалась бь в АВ q раз, а в CD р раз. Но в
таком случае 4-10 долю отрезка АВ можно было бы считать
общей мерог отрезков АВ и CD. А этс противоречит условию:
отрезки АВ и CD несоизмеримы.
Упражнения
308. Докажите, что если отрезки АВ n CD соизмеримы, то
п-я доля отрезка АВ соизмерим; с т-й долей отрезка CD
(тип— произвольные натуральные числа).
91
309. Докажите, что если отрезки АВ и CD несоизмеримы,
то n-я доля отрезка АВ несоизмерима с m-й долей отрезка CD
(тип — произвольные натуральные числа).
310. Пусть Aj и Д2 — два соизмеримых отрезка, причем от
резок А,длиннее отрезка Д2. Докажите, что в таком случае
отрезки Д1+ Д2и At — Д2 будут также соизмеримыми.
Верно ли обратное утверждение?
311. Докажите, что в прямоугольном треугольнике катет,
лежащий против угла в 60°, несоизмерим с гипотенузой.
312. Докажите, что если отрезок АВ соизмерим с отрезком CD,
а отрезок CD соизмерим с отрезком EF, то отрезок АВ соизме-
рим с отрезком EF.
313. Докажите, что если отрезок Л В соизмерим с отрезком СО,
но несоизмерим с отрезком EF, то отрезки CD и EF несоизме-
римы.
Глина отрезка, несоизмеримого с единицей
длины § 41
Вернемся к задаче измерения прямолинейных отрезков, ча-
стично уже рассмотренной нами в предыдущих параграфах.
Пусть АВ есть отрезок, принятый за единицу длины, a CD —
измеряемый отрезок. Может представиться два случая:
1) отрезки АВ и CD соизмеримы;
2) отрезки АВ и СО несоизмеримы.
В первом случае длина отрезка СО выразится некоторым ра-
циональным числом — . Во втором случае длина СО не может
п
быть выражена никаким рациональным числом. Этот случай
сейчас будет представлять для нас наибольший интерес. Его-то
мы и рассмотрим. Один из важнейших выводов, к которому
приводит рассмотрение этого случая, состоит в следующем: для
измерения отрезков рациональных чисел не хватает.
Для того чтобы длина каждого отрезка выражалась некоторым
числом, мы должны к уже известным нам рациональным числам
добавить какие-то новые числа.
Как же представить себе эти новые числа?
Пусть отрезок CD несоизмерим с единицей длины — отрез-
ком АВ. Будем откладывать отрезок АВ на отрезке CD, начи-
ная от точки С (рис. 57). Предположим, что в результате двух
последовательных откладываний получается некоторый «остаток»—
отрезок CD, который меньше отрезка АВ. Тогда естественно
считать, что длина CD приближенно выражается числом 2.
Разделим единицу длины АВ на 10 равных частей и одну такую
часть будем откладывать на CD, начиная от точки С Допустим,
что после пяти таких откладываний получается «остаток» — отре-
92
С С СР
Рис. 57.
зок C"D, меньший, чем десятая доля АВ. Тогда естественно
считать, что длина CD приближенно выражается числсм 2,5.
После этого десятую долю АВ разделим, в свою очередь, на
1С равных частей. В результате мы получим — долю АВ.
Будем откладывать* ее н< отрезке C"D, начиная о~ точки С".
Предположим, что после восьми таких последовательных отклады
ваний получаете? «остаток», — отрезок C"'D, меньший, чем
— дол?. АВ Тогда естественно считать что длина отрезка CD
100
приближенно выражается числом 2,58. Описанный процесс можно
было бы продолжать неограниченно. При этом каждый шар
давал бы нам все более и более точные, хотя и всегда прибли-
женные, значения длины отрезка CD, например:
2; 2,583;
2,5; 2,5833
2,58; 2.58337
и т. д.
Почему мы уверены что этот процесс будет продолжаться
бесконечно? Если бы он оборвалс?. на каком-нибудь шаге, на-
пример на третьем, то длине CD выразилась бы точно (а не
приближенно) числом 2,58. Но в таком случае доля АВ
укладывалась бы в АВ 100 раз, а в CD 258 паз. А это проти-
воречит условию, согласно которому отрезки АВ i; CD несоиз-
меримы.
Теперь естественно считать что длина отрезка CD выражается
бесконечной десятичной дробьк
2,58337... .
Эта дробь не может быть периодической, иначе ее можно было
бы представить в виде —, где т и п — натуральные числа. Но
тогда n-я дол? АВ укладывалась бы в АВ п раз, а в CD т раз,
чтс также противоречит несоизмеримости отрезков А. В и CD.
Таким образом, длина отрезка CD выражается бесконечной
непериодической десятичной дробью (2,58337..). К аналогичному
выводу мы пришли бы если вместо отрезка CD рассмотрели
какой-нибудь другой отрезок, несоизмеримый с единицей дли-
ны АВ.
* На рисунке 57 этс уже не отмечено.
93
И1ак, если некоторый отрезок CD несоизмерим с еди-
ницей длины, то его длина записывается в виде беско-
нечной непериодической десятичной дроби.
Упражнения
314 Может ли длина оц?езка Д при одной единице длины
выражаться бесконечной периодической дробью, а при другой
единице длины — бесконечной непериодической дробью? Приве-
дите примеры.
315. Соизмерим ли отрезок CD с единицей длины АВ, если
длина CD выражается:
а) конечной десятичной дробью;
б) бесконечной периодической десятичной дробью;
в) бесконечной непериодической десятичной дробью?
Действительные числа § 42
В предыдущем параграфе мы убедились, что для измерения
отрезков рациональных чисел не хватает. Напомним еще раз,
что рациональные числа — это числа, представимые в виде бес-
конечных периодических десятичных дробей. А длины не-
которых отрезков выражаются бесконечными непериоди-
ческими десятичными дробями. Таким образом, задача изме-
рения отрезков приводит нас к необходимости расширить
множество рациональных чисел путем присоединения к нему
положительных бесконечных непериодических десятичных дробей.
С такой же необходимостью мы столкнулись, по существу,
и в § 39 при рассмотрении квадратных уравнений вида ха = а,
где а — некоторое рациональное (даже натуральное) число. По-
требности алгебры (например, выполнимость действия вычи-
тания) указывают на то, что наряду с положительными целе-
сообразно сразу же ввести в рассмотрение и отрицательные беско-
нечные непериодические десятичные дроби. Поэтому в дальней-
шем, говоря о бесконечных непериодических дробях, мы будем
иметь в виду как положительные, так и отрицательные дроби.
Числа, которые можно представить в виде бесконечных не-
периодических десятичных дробей, называются иррациональными
(то есть «нерациональными»).
Примером иррациональных чисел может служить любое из
чисел )/2, )/з, У5 и т. д. Иррациональность У 2 мы факти-
чески доказали в § 39, а иррациональность чисел j/З и ]/ 5 мо-
жет быть установлена аналогично. Не следует, однако, думать,
что иррациональные числа получаются только при извлечении
корней. Как было показано в предыдущем параграфе, к ир-
рациональным числам приводит и задача измерения отрезков.
94
А измерение отрезков, вообще говоря, не обязательно связана
с извлечением корней.
В § 38, где об извлечении корней не говорилось ни сло-
ва, мы указали иррациональное число 0,101001000100001 ... .
Классический пример иррационального числа, происхождение
которого также не имеет никакого отношения к извлечению
корней, дает число л — 3,1415926535... (отношение длины ок-
ружности к ее Диаметру). К сожалению, мы не можем приве-
сти здесь других убедительных примеров. Но примеры такие
существуют. Поэтому извлечение корней из целых чисел — да
леКо не единственный источник образования иррациональных
чисел. Более того, среди всех иррациональных чисел в изве-
стном смысле больше как раз таких чисел, которые своим про-
исхождением никак не связаны с извлечением корней. Однако
вопрос этот довольно сложен; подробно останавливаться на нем
мы здесь не можем.
Все рациональные и все иррациональные числа, взятые
вместе, образуют множество действительных, или вещественных,
чисел. К изучению этого множества мы приступим в следую-
щем параграфе.
Некоторыми иррациональными числами математики пользовались еще
в древние времена. К ним приводили многие задачи геометрии, которые ие
могли быть решены на базе существовавшей тогда арифметики. Однако в
те времена иррациональные числа рассматривались не как равноправные
с рациональными, а как какие-то исключительные числа, нарушающие гар-
монию арифметики и геометрии. По этой причине некоторые предлагалз
даже изгнать иррациональные числа из математики.
Строгая теория иррациональных чисел была построена лишь во второй
половине XIX века. Основная заслуга в этом принадлежит немецким
ученым Дедекинду (1831 —1916), Кантору (1815—1918) и
Вейерштрассу (1815—1897)
Упражнения
316. а) Любое ли рациональное число является действитель-
ным? А наоборот?
б) Любое ли иррациональное число является действительным?
А наоборот?
317. Длина любого ли отрезка выражается:
а) рациональным числом;
б) иррациональным числом;
в) действительным числом?
Сравнение действительных чисел § 43
В этом параграфе, говоря о действительных числах, мы бу-
дем предполагать, что все они заданы нам в виде бесконечных
десятичных дробей. Сначала рассмотрим лишь положительные
числа.
95
Два положительных действительных числа называются рав-
ными, если все соответственные десятичные знаки их одинаковы*.
Если же одно из чисел содержит знак, не совпадающий с со-
ответственным знаком другого числа, то числа называются
неравными. Например, число 5,6389... не равно числу 3,6389...;
число 0,146... не равно числу 0,148... и т. д.
Пусть аир — не равные между собой положительные действи-
тельные числа **. Если целые части этих чисел различны, то
большим считается то из них, которое имеет большую целую
часть. Например,
5,6348... > 3,9901...;
1,0000... > 0,5777... .
Предположим теперь, что целые части неравных чисел аир
равны между собой. Тогда сравним их первые после запятой
десятичные знаки. Если эти знаки различны, то большим буде!
то из чисел аир, которое содержит больший первый десятич-
ный знак. Если же и эти знаки одинаковы, то сравним вторые
после запятой знаки. Большим из чисел а и Р будет то, у ко-
торого второй после запятой десятичный знак больше. Если же
и эти знаки одинаковы, то сравниваем третьи после запятой
знаки и т. д. Рано или поздно мы придем к разным знакам:
в противном случае числа а и Р были бы равны друг
ДРУГУ-
Примеры. 37,1269... > 37,0394...;
110,0057... > 110,0049...;
0,3333... > 0,3332... .
Теперь покажем, как сравниваются между собой отрица-
тельные действительные числа. Два отрицательных действи-
тельных числа a u р называются равными, если равны их абсо-
лютные значения'.
1а1 = 1Р|.
Если же ‘а> #= ipi, то отрицательные числа а и Р называются
неравными. Например:
— 5,6389... #= — 3,6389...;
— 0,146... #= — 0,147... .
Из двух отрицательных чисел большим считается то, аб-
солютная величина которого меньше. Например:
— 37,1269... < — 37,0394..., так как 37,1269... > 37,0394...;
— 0,3333... < — 0,3332..., поскольку 0,3333... > 0,3332... .
• Бесконечные периодические десятичные дроби С периодом 9 мы исклю-
чаем из рассмотрения.
а НР греческие буквы; читаются соответственно: альфа и бета.
96
Нам осталось установить, как сравниваются между собой
действительные числа разных знаков. Будем считать, что любое
положительное число больше любого отрицательного числа и
числа О, а число 0, в свою очередь, больше любого отрицатель-
ного числа.
Упражнения
318. Между данными числами поставить одие из следующих
трех знаков: >, <, = .
a) 5,6347S... и 5,634s7...’ г) 15,25 ... и ;
б) — 3,4833... и — 3,5829 .. . • д] 0 и — 0,0003 ..
в) — 16,0010. .. и — 16.0001 ..;
319. Выяснить, какое из двух данных чисел больше и ка-
кое меньше (или же показать, чтс эти числа равны друг другу):
а) —71,7171 . .. и 7,1717...; б) - | и - 0,375... ;
О
в) — и 0,5555... (одни пятерки); г) 0,3333... и —.
9 3
Геометрическое изображение действительных чисел § 44
Геометрически действительные числа, так же как и рацио-
нальные числа, изображаются точками прямой.
Пусть I — произвольная прямая, г О — некоторая ее точка
(см. рис. 58 на стр. 98,. Каждому положительному действитель-
ному числу а поставим в соответствие точку А лежащую справа
от О на расстоянии в а единиц длины.
Если, например, а = 2,1356..., то
2 <а < с
2 1 < а < 2,2
2,13<а<2,14
и т. д. Очевидно, что точка А в этом случае должна находиться
на прямой / правее точек, соответствующих числам
2; 2,1; 2,13; ....
но левее точек, соответствующих числам
3; 2,2; 2.14; ... .
Можно показать, что эти условия определяют на прямо? i
единственную точку А, которую мы и рассматриваем как
геометрический образ действительного числа а = 2,1356... .
Аналогично, каждому отрицательному действгтельному чис-
лу р поставим в соответствие точку В, лежащую слева от О на
расстоянии в |0| единиц длины. Наконец, числу «нуль» поставим
в соответствие точки О.
4 Заказ 261
S7
а о___________л I
Во а
Рис. 58.
В______0 л I
~V2 'J 1
Рис. 59.
Так, число 1 изобразится на
прямой I точкой А, находящейся
справа от О на расстоянии в одну
единицу длины (рис 59), число
—У2 -точкой В, лежащей слева
от О на расстоянии в еди-
ниц длины, и т. д.
Покажем, как на прямой I с помощью
циркуля и линейки можно, отыскать лочкн.
соответствующие действительным числам
У 2, р З, р'4, р5 и 1. Д. Для этого
прежде всего покажем, как можно постро-
ить отрезки, длины которых выражаются
этими числами. Пусть ZB есть отрезок,
принятый за единицу длины (рис. 60).
В точке А восставим к этому отрезку
перпендикуляр и отложил на нем отре-
зок АС, равный отрезку АВ. Тогда, при-
меняя теорему Пифагора к прямоуголь-
ному треугольнику АВС, получим
ВС = р АВ- + АС1 = - /~2.
Следовательно, отрезок ВС имеет длину
У 2. Теперь восставим перпендикуляр
к отрезку ВС в точке С и выберем на
нем точку D так, чтобы отрезок CD был
равег единице длины АВ. Тогда из прямо-
угольного треугольника BCD найдем:
BD « Р ВС1 4- CD- = У2 + \ =У~3.
Следовательно, отрезок BD имеет длину ИЗ. Продолжая описанный про-
цесс дальше, мы могли бы получить отрезки BE, BF, ... , длины которых
выражаются числами У 4, У5 и т. д.
Теперь на прямой I легко найти те точки, которые служат геометри-
ческим изображением чисел У 2, УЗ, У4, У5 и т. д. Откладывая, на-
пример, справа от точки О отрезок ВС (рис. 61), мы получим точку С’, ко-
торая служит геометрическим изображением числа У 2. Точно так же,
откладывая справа от точки О отрезок BD, мы получим точку D’, которая
является геометрическим образом числа У 3, и т. д.
0 С В' Г(
» Уг \Гз \1й
Рис. 61.
Не следует, однако, думать, что с помощью циркуля и линейки на
числовой прямой I можно найти точку, соответствующую любому заданному
действительному числу. Доказано, например, что, имея в своем распоря-
жении только циркуль и линейку, нельзя построить отрезок, длина
которого выражается числом л - 3,14 .. Поэтому на числовой прямой Z с
помощью, таких построений нельзя указать точку, соответствующую этому
числу. Тем не менее такая точка существует.
98
б)-----*_______________________
а /з
Рис. 62.
Г__________L Д___________
L г
Рис. G3.
Итак, каждому действительному
числу <х можно iiociaBiTb ь соот-
ветствие некоторую вполне опреде-
ленную точку прямой /. Эта точка
будет отстоять иг начальной точки О
на расстоянии в |си> единиц длины
и находиться справа от О, если
ст > 0, и слева от О, если a <Z 0.
Очевидце что при этом двум нерав-
ным действительным числам будут
соответствовать две различные точки
прямой /. В самом деле, пусть числу
о. соответствует точка /., а числу 0—
точка В. Тогда есл1 a Z> 0, то А будет находитьо правее В
(рис. 62, а), если же a <Z р, то А будет лежато левее В (рис. 62, б).
Говоря в § 37 о геометрическом изображении рациональ-
ных чисел, мы поставили вопрос: любую ли точку прямой мож-
но рассматривать как геометрический образ некоторого I а-
ц и о и а л ь н о г о числа? Тогда мы не могли дать ответ на этот
вопрос; теперь же мы можем ответил на неге вполне опре-
деленно Н< прямой есть точки, которые служат геометрическим
изображением иррациональны:: чисел (например ]'2). Поэтому
не всякая точка прямой изображает рациональное число. Но
в таком случае напрашивается другой вопрос: любую ли точку
числовой прямой можно рассматривать как геоме рическиг об-
паз некоторогс де i.(, 1 в п те л ьп о " о числа? Этот вопрос ре-
шается уже положительно.
В самом деле, пус’ь А — произвольна} точь< прямой I, ле-
жащая справа от С (рис. 63). Длина отрезка ОА выражается
некоторым положительным действительным числом а (ом § 41k
Поэтому точка А является геометрическим образом числа а.
Аналогично устанавливается, что каждая точка В, лежащая слева
о С, может рассматривать^ каг геометрпческии образ отрица-
тельного действительного числа — 0, где 0 — длина отрезка ВО.
Наконец, точка О служит геометрически:. изображение:, числа
нули. Понятно, что две различные точки, прямой I не мо-ут быть
геометрическим образом одного ь того же дейсгвительно'о
числа
В силу указанных выше причин пряма} . на которой указана
в качестве «начальной)- некоторая точк< О (при заданной еди-
нице длины), называется числовой прямой.
Вывод. Множество всех действительных чисел и
множество всех точек числовой прямой находятся
во взаимно однозначном соответствии
Это означает, чтс каждому действительному числу соответствует
одна, вполне определенная, точка числовой прямой и наоборот.
каждой точке числовой прямой при таком соответствии отве-
чает одно, вполне определенное действительное число.
Упражнения
320. Выяснить, какая из двух точек находится на числовой пря-
мой левее и какая правее, если эти точки соответствуют числам:
а) 1,454545... и 1,455454...; в) Он — 1,56673...;
б) — 12,0003... и —12,0002...; г) 13,24... и 13,00....
321. Выяснить, какая из двух точек находится на числовой
прямой дальше от начальной точки О , если эти точки соответ-
ствуют числам:
а) 5,2397... и 4,4996...; в) — 0,3567... и 0,3557... .
б) — 15,0001 и — 15,1000...,'
322. В этом параграфе было показано, что для построения отрезка
длиной в ]/~п с помощью циркуля и линейки можно поступить
следующим образом: сначала построить отрезок длиной в ]/2,
затем отрезок длиной в р^З и т. д., пока не дойдем до отрезка
длиной в п. Но при каждом фиксированном п > 3 этот про-
цесс можно ускорить. Как бы, например, вы стали строить отрезок
длиной в 10?
323*. Как с помощью циркуля и линейки найти на число-
вой прямой точку, соответствующую числу — , если положение
точки, соответствующей числу а , известно?
Десятичные приближения действительных чисел I 49
Пусть а есть некоторое положительное действительное число,
представленное в вйде бесконечной дроби. Вначале мы предпо-
ложим, что эта дробь не является периодической с периодом 0.
(Например, в качестве а не может выступать число 0,5 =
— 0,5000... .) Тогда десятичные приближения числа а с недостат-
ком определяются как числа, которые получаются в результате
последовательного отбрасывания всех его цифр, стоящих после
запятой, начиная с первой цифры, потом со второй, затем с третьей
и т. д. Например, для числа ]/г2 = 1,41421... такими приближе-
ниями будут:
1; 1,4; 1,41; 1,414; 1,4142; 1,41421; ...
Если последнюю цифру каждого из десятичных приближений
числа а увеличить на 1, то мы получим последовательные деся-
тичные приближения числа а с избытком. Например, для числа
]/2 такими приближениями будут:
2; 1,5; 1,42; 1,415; 1,4143; 1,41422; ... .
100
Очевидно, что число а больше любого своего десятичного
приближения с недостатком, но меньше любого своего десятич-
ного приближения с избытком. Например, для числа 2
1 <У2<2
1,4<]/2< 1>5
1,41 <У 2< 1,42
1,414 <]/2< 1,415
1,4142 <У 2 < 1,4143
1,41421 < У 2 < 1,41422
и т. д.
Теперь предположим, что а есть периодическая десятичная
дробь с периодом 0. Примером такого числа может служить число
1,47 = 1,4700... . Десятичные приближения этого числе с не-
достатком естественно определить как числа
1; 1,4; 1,47; 1,470; 1,4700; ...»
а десятичные приближения с избытком — как числа
2; 1,5; 1,47; 1,470; 1,4700, ...
Вообще, пусть нулевой период числа а начинается с k-ro
десятичного знака после запятой (например, для числа 1,47 =
= 1,470000... k = 3). Тогда его первые k — 1 десятичных прибли-
жений с недостатком и первые k — 1 десятичных приближений
с избытком определяются так же, как и в случае, когда рас-
сматриваемая дробь не является периодической с периодом 0.
Все же остальные десятичные приближения считаются равными
числу а. Так, для числа 0,373 = 0,37300... десятичными при-
ближениями будут:
с недостатком 0; 0,3; 0,37; 0,373; 0,3730; 0,37300, ...,
с избытком 1; 0,4; 0,38; 0,373; 0,3730; 0,37300; ... .
Очевидно, что в этом случае число а не меньше любого своего
десятичного приближения с недостатком и не больше любого
своего десятичного приближения с избытком.
Мы показали, как составляются десятичные приближения
(с недостатком и с избытком) для любых положительных действи-
тельных чисел. Аналогично можно определить десятичные при-
ближения и для произвольных отрицательных чисел. Мы не
будем приводить здесь общих определений; покажем лишь, как
следует находить десятичные приближения отрицательных чисел
на примере числа —]/2 = — 1,41421... .
101
Кап мн знаем (см. § 43), из двух отрицательных чисел боль-
ше то. абсолютная величина которого меньше. Поэтому из по-
лученных выше соотношений
1 <У2<2
1,4 < V 2< 1,5
1.41 <У 2 < 1,42
вытекает, что
1,414 < 'У2< 1,415
1,4142 <К2< : 1,4143
1,41421 <У~2< 1,41422
— 2 < - V ~2 < — J
— 1,5 < -Г2< С — 14
— 1,42 < -)<2« С— 1,41
— 1.415 < -У С —1,414
- 1,4143 < ~У~2< С— 1,4142
— 1,41422< — У 2<— 1,41421
Числа, стоящие в левых частях этих неравенств, естественно
назвать десятичными приближениями числа — У 2 с недостат-
ком, а числа, стоящие в правых частях, — десятичными прибли-
жениями числа — 2 с избытком. Очевидно, что число — ] 2
больше любого своего десятичного приближения с недостатком,
но меньше любого своего десятичного приближения с избытком.
Добавим, наконец, что для действительного числа 0 также мож-
но построить десятичные приближения с недостатком и десятич-
ные приближения с избытком. Каждое из таких приближении
считается равным нулю.
Итак, с каждым действительным числом а можно связать
две бесконечные последовательности чисел:
«!, а?', а3', а/...;
„ " ГУ " П " ГУ "
Первая последовательность состоит из десятичных приближений
числа а с недостатком, а вторая — из десятичных приближений
числа а с избытком. При этом
102
czj < a < CZ|
a2‘ < a < a2"
a3' < a < a/r
a4' < a < a4"
и т. д.
важно отметить, что каждое из десятичных приближений
числа а является рациональным числом, хотя само число a
может быть и иррациональным.
Упражнения
324. Найти несколько первых десятичных приближений
(с недостатком и с избытком) для следующих действительных
чисел:
а) / 3; в) 11, д) 4; ж)
/ с
б> — F 3; Г)-1’; е) — 4; 3)
325. Все десятичные приближения действительного числа а
с недостатком, начиная с некоторого, совпадают. Какое
число а: рациональное или иррациональное?
326. Все десятичные приближения действительного числа и.
с недостатком различны. Можно ли утверждать, что число a
иррационально? Ответ пояснить примерами.
Сложение действительных чисел § 46 *
Пока что мы умеем складывать друг с другом лишь р а-
циональные числа. Как мы знаем,
п l nl
А вот какой смысл вкладывается в сумму двух чисел, из кото-
рых хотя бы одно иррационально, этого мы еще не знаем.
Нам предстоит сейчас дать определение того, что понимается
под суммой a 4- Р двух произвольных действительных
чисел а и Р .
Для примера рассмотрим числа -i- и ]/2. Представим их
в виде бесконечных десятичных дробей
= 0,33333...;
V 2 = 1,41421 ... .
103
Сначала сложим соответственные десятичные приближения дан-
ных чисел с недостатком. Эти приближения, как отмечалось
в конце предыдущего параграфа, представляют собой рацио-
нальные числа. А складывать такие числа мы уже умеем:
0+1 = 1
0,3+ 1,4 = 1,7
0,33 + 1,41 = 1,74
0,333 + 1,414 = 1,747
0,3333+ 1,4142= 1,7475
0,33333+ 1,41421 = 1,74754
Затем сложим соответственные десятичные приближения данных
чисел с избытком:
1+2 = 3
0,4 + 1,5= 1,9
0,34 + 1,42 = 1,76
0,334 + 1,415 = 1,749
0,3334+ 1,4143 = 1,7477
0,33334 + 1,41422 = 1,74756
Можно доказать*, что существует и притом единственное
действительное число у**, которое больше всех сумм десятичных
приближений чисел и ]/2 с недостатком, но меньше всех сумм
десятичных приближений этих чисел с избытком:
1 < у <3
1,7<у< 1,9
1,74 < у < 1,76
1,747 <у< 1,749
1.7475 <у< 17477
1,74754 < у <1,74756
По определению это число у и принимается за сумму чисел
Очевидно, что у = 1,7475... .
* Строгое доказательство этого факта выходит за пределы нашей про-
граммы и потому здесь не приводится.
** у — греческая буква; читается: гамма.
104
Аналогично может быть определена и сумма любых других
положительных действительных чисел, из которых хотя бы одно
иррационально. Суть дела не изменится и в том случае, если
одно из слагаемых, а может быть, и оба, будут отрицательными.
Итак, если числа а и р рациональны, то сумма их находится по
правилу сложения рациональных чисел (см. § 36).
Если же хотя бы одно из них иррационально, то суммой
а + р называется такое действительное число, которое больше
всех сумм соответственных десятичных приближений этих чисел
с недостатком, но меньше всех сумм соответственных десятич-
ных приближений этих чисел с избытком.
Определенное таким образом действие сложения подчи-
няется следующим двум законам:
1) коммутативному закону:
а р = Р + а;
2) ассоциативному закону:
(а + Р) + У = « + (Р + ?)-
Доказывать этого мы не будем. Учащиеся могут сделать
это самостоятельно. Отметим лишь, что при доказательстве при*
дется использовать уже известный нам факт: сложение рацио-
нальных чисел подчинено коммутативному и ассоциативному
законам (см. § 36).
Упражнения
327. Данные суммы представить в виде десятичных дробей,
указав не менее трех верных знаков после запятой:
а) V 2 -Ь К 3; г) Г 2 + (-Г 3); ж) | + (- V 5);
4
б) К 2 + |; д) (- Д + у 5; з) 2 +Г з.
В) (-Г2) +ГЗ; е) ^+(-^5);
3218. Найти несколько первых десятичных приближений
(с недостатком и с избытком) для действительных чисел:
а) |+/7; б) J/3 + K7; в) ГЗ +(-/7).
329. Исходя из определения суммы действительных чисел,
доказать, что для любого числа а
а + (—а) = 0.
330. Всегда ли сумма двух бесконечных непериодических
дробей есть дробь непериодическая? Ответ -пояснить примерами.
105
Умножение действительных чисел
§ 47
В этом параграфе мы покажем, как можно прийти к естест-
венному определению произведения двух действительных чисел
п. и р, из которых хотя бы одно является иррациональным.
При этом мы будем исходить из того, что умножение рацио-
нальных чисел нами уже изучено (см. § 36).
Сначала предположим, что числа а и р положительные.
Пусть, например, а = i , а Р = ]/2. Представим эти числа в
виде бесконечных десятичных дробей:
— = 0,33333...; 1,41421 ... .
3
Перемножим соответственные десятичные приближения данных
чисел с недостатком. Эти приближения представляют собой
рациональные числа. А перемножать такие числа мы уже
умеем:
0-1 = 0
0,3 - 1,4 = 0,42
0,33 -1,41 =0,4653
0,333-0,414 = 0.470862
0.3333 - 1,4142 = 0.47135286
0,33333- 1,41421 =0.4713986193
Затем перемножим соответственные десятичные приближения
данных чисел с избытком:
1-2 = 2
0,4 • 1,5 = 0,6
0,34 1,42 = 0,4828
0.334 1,415 = 0,47261
0.3334 • 1,4143 = 0,47152762
0.33334 - 1,41422 = 0,4714160948
Можно доказать, что существует и притом единственное
число у, которое больше всех произведений десятичных при-
ближений чисел -- и К2 с недостатком, но меньше всех про-
3
изведений десятичных приближений этих чисел с избытком:
106
О < y < 2
0,42 < у < 0,6
0,4653 < y < 0,4828
0,470862 < y < 0,47261
0,47135286 < y < 0,47152762
0,4713986193 < Y < 0,4714160318
По определению это число у и принимается
чисел -i- и |/2:
за
произведение
Y = ’- • /2-
Очевидно, что у — 0,471... . Аналогично может быть опреде-
лено и произведение любых других положительных действи-
тельных чисел, из которых хотя бы одно иррационально.
Теперь нужно рассмотреть случай, когда хотя бы один из
сомножителей а и р отрицателен. Если отрицательными яв-
ляются оба сомножителя а и р, то
а • Р = !а| • |pi.
Если же один из сомножителей аир положителен, а дру-
гой отрицателен, то
о- - р = — а; . |pj.
Например.
(-|)-(-/2) = ~-Г2 = 0,471... ;
3 )' =~ (I ’ 2) 0,471 " ‘
Наконец, если хотя бы один из сомножителей равен пулю,
то и произведение считается равным нулю. Например,
)' 2 -0 = 0,
0 (- Г'2)= 0
и т. д.
Теперь мы можем дать общее определение произведения
двух действительных чисел.
Если числа аир рациональны, то произведение их находится
по правилу умножения рациональных чисел (см. § 36).
Если хотя бы одно из чисел а и р иррационально и оба
они положительны, то произведением их называется такое дей-
ствительное число, которое больше всех произведений соответ-
ственных десятичных приближений этих чисел с недостатком,
но меньше всех произведений соответственных десятичных
приближений этих чисел с избытка».
107
Если оби числи tt d Р ишриЦиШелопт, ГПО
а • р = |а| • |р[.
Если одно из чисел а и Р является положительным, а дру-
гое отрицательным, то
а • Р = — (|а| . |р|),
Наконец, если хотя бы одно из чисел а и р равно нулю, тс
а • р = 0.
Нетрудно показать, что определенное таким образом дейст-
вие умножения подчиняется следующим законам:
1) коммутативному Залину.
а • Р = Р а;
2) ассоциативному закону:
(а • р) • у = а • (р • у).
Кроме того, для любых действительных чисел а, Р и у
выполняется соотношение
(а + Р) у = ау 4 Ру,
которое выражает дистрибутивный закон умножения относи-
тельно сложения.
Упражнения
331. Данные произведения представить в виде десятичных
дробей, указав не менее двух верных знаков после запятой:
а)У2-УЗ; г) /2-(-У 5); ж) - ( -/6);
4
б)Г2~4; д)/_1).у2; з)1-У2-КЗ.
в)(-Г2).]/3; е> ^ (—Г5);
332. Найти несколько первых десятичных приближений
(с недостатком и с избытком) для действительных чисел:
а) у • У7; б) /3 • V1-, в) /3 • (- У7).
333. Исходя из определения произведения действительных
чисел, доказать, что для любого числа а
а • 1 = а.
334. Всегда ли произведение двух бесконечных непериоди-
ческих дробей представляет собой непериодическую дробь?
108
Вычитание и деление действительных чисел $ 48
Основными алгебраическим! действиями в множестве всех
действительных чисел, таи же как и в множестве всех рацио
нальных чисел, являются сложение и умножение. Что же
касается вычитания и деления, то эти действия определяются
как обратные по отношению к действиям сложения и умножения
1. Вычитание действительных чисел
Разностью а — Р двух действительных чисе; а и р назы-
вается такое число у, которое, с сумме с Р диет а.
Другими словами, разноси а — р определяется кая корень
уравнения
Р + х = а. (1)
Как и в случае рациональных 4ncej (cn § 36) уравнение '1)
всегда имеет и притом единственное решение. Таким образом
для любых действительных чисел й « ₽ разность а— р
существует и определена однозначно.
Покажем, например, как мо^ут бы-ъ найдены приближен
ные значения разностк
У2 — - .
3
i
Заменив в этом выражении число У 2
ным приближением с недостатком (1; 1,4;
егс любым десятич-
1,41 1,414 ...), а
число— его любым десятичным приближением с избытког.
О
1.1; 0,4 0,34; С,334; ...), мы получим очевидно приближенно!
значение разности У2-----с недостатком. Наоборот, есл>
г выражении У 2—у число У2 заменит! егс любым десятич-
ным приближением с избытком (2; 1,5; 1,42; 1,415; ...), и
число ~ —его любым десятичным приближением с недостатком
(0 С,3; 0,33; 0,333; ...), то полученная разность будет, оче
видно, предстаьлять собор приближенное значение У2 —
с избытком. В частлост!.,
или
1 — 1< У2----—0,
3
0 < VT----<2.
3
109
Это слитком грубое неравенство. Для получения более
точных данных о разности )/2 —- возьмем другие приблкже-
ння /2 и - :
3
1,4 —0,4 — 1,5 —С,3,
или
1,0 </2 — --< 1 2.
з
Это неравенство дает уже гораздо больше информации с раз-
ности У2— . Из него, в частности, вытекает, что с точно-
стью до 0,1
1/2 — 1^ 1 1.
3
Если и такая точность нас не устраивает, мы можем продол-
жить наши рассуждения:
1,41-0,34</2— у< 1,42 — 0,33,
или
1,07 < V 2 — - < 1,09.
з
Отсюда, в частности, получаем, что с точностью до 0,01
/2 — 1^ 1,08.
Описанный способ нахождения приближенных значений раз-
ности ]^2 — -i- можно было бы продолжать и дальше. При
этом будут получаться все более и более точные значения этой
разности. (Заметим, однако, что ни на каком шаге мы не можем
получить точного значения этой разности. Почему?)
2. Деление действительных чисел
Частным а : Р от деления действительного числа а на дей-
ствительное число Р называется такое число у, которое при
умножении на Р дает а.
Другими словами, частное а : р определяется как корень
уравнения
р - х = а. (2]
Можно доказать, что если Р =#= С, то уравнение (2) имеет
и притом единственный корень. Если же р — 0, то это уравне-
ние либо вообще не имеет корней (при а -=?= 0), либо имеет
бесконечно много корней (при а = 0); в последнем случае любое
число является корнем уравнения (2). Поэтому, если р =/= 0, то
НО
частное а:Р существует и определено однозначно; при.
Р = О частное а:? не определено.
Покажем, например, как могут быи найдены поиближен-
ные значения частного а : Р, если а= . ,532 ... a Р = 2.037 ....
Если в выражении с. : Р, число с. заменить его любым десятш-
ным приближением с недостатком (1; 1.5 1,53; 1,532; . .
а число Р — его любым десятичным приближением с избытком
(3; 2,1; 2,04; 2,038 . ..) то полученное частное будет очевидно
представлять собой приближенное значение с- : р с недостатком.
Наоборот, если в выпажениг а : Р числе а заменит! любым со
десятичным приближением с избытком (2. 1,6; 1,54; ’,533. ..._,
а число Р — любым его десятичным приближением с недостатком
(2; 2 0 2,03 2,ОЗ7; ...), то полученное частное будет служить,
очевидно, приближенным значением а : р с избытком.
В частности,
1,532 2,038 < а : р < ,53? : 2,03/,
или
0 75.6 < а : р < 0,7526.
Это дает по меньшей меое два верных десятичных знака
(после запятой; частного:
а : р = 0,75 ....
Упражнения
I к 335. Вычислить с точностью до 0,01
1 а ,/7-/3; в' /6 -1
1 б)/5-| ; г) 0.25 -/£
336. НаРти приближенное значение разности
1,7534 . . — С,6325 . . .
с точностью до 0,001.
337. Вычислить с точностью до 0,0 :
К? . «ч 1 1 . 1"3-
а, —5; б) — : Е 5 в) ----------------- .
1,3657... 3 _^2
338. Найти приближенные значения частного
0,023...
0,041...
I с точностью до:
< а) 0,1; б' 0,01
i 339. Доказать, что для любого действительного числа а,
* отличного от нуля,
а : е — 1.
I 1-.
340. Разность между действительным чишОм а и одним из
его десятичных приближений есть число рациональное. Каким
является само число а: рациональным или иррациональным?
341. Может ли частное от деления иррационального числа
на какое-нибудь его десятичное приближение быть числом
рациональным?
Задачи на повторение
342. Разрешимо ли уравнение
а 4- х = b
(а и Ь -— заданные натуральные числа)
а) В МнОжеСгВе всех натуральных чисел;
б) в множестве всех положительных рациональных чисел;
в) в множестве всех целых чисел?
343. Разрешимо ли уравнение
ах — b
(а и Ь — заданные целые числа)
а) в множестве всех целых чисел;
б) в множестве всех рациональных чисел?
344. Может ли уравнение
]/т + х = ]/п
(тип — заданные натуральные числа)
а) иметь иррациональный корень;
б) иметь рациональный корень;
в) не иметь действительных корней?
345. Числа а + 0 и а — 0 рациональны. Будут ли рациональ-
ными числа а и 0?
346. Если за единицу длины принять отезок Л ь то длина
отрезка АВ выразится рациональным числом; если же в качестве
единицы длины выбрать отрезок Д2, то длина отрезка АВ вы-
разится иррациональным числом. Докажите, что отрезки Д£н Д2
несоизмеримы.
347. Может ли произведение двух периодических десятичных
дробей быть дробью непериодической?
348. Методом от противного доказать, что сумма рациональ-
ного числа с иррациональным числом есть число иррациональное.
Доказанное утверждение сформулировать в терминах бесконеч-
ных десятичных дробей (периодических и непериодических).
112
349. Может ли сумма двух иррациональных чисел быть
числом рациональным? Ответ пояснить примерами.
350. Может ли произведение двух иррациональных чисел быть
числим рациональным? Ответ пояснить примерами.
351. Может ли случиться так, что первые 10 степеней числа а
а, а2, с$, ... , а10
будут иррациональными, а следующие 10 степеней
а11, а'2, а13, ... , а20
— рациональными?
352. Пусть а и b — некоторые рациональные числа. Докажите,
что если а + & |Л2 =/= 0, то и а — b ^2 =/= 0. Привести не менее
двух различных способов доказательства.
353. Доказать, что числа j/З + ]/2 и J/3— ]/2 являются
иррациональными.
КВАДРАТНЫЙ ТРЕХЧЛЕН
III
Выделение из квадратного трехчлена
полного квадрата § 49
Квадратным трехчленом относительна переменной величины
х называется выражение вида ах2 4- Ьх 4- с, где а, b и с — задан-
ные числа, причем и =/= 0.
Преобразуем квадратный трехчлен ах2 4- Ьх 4- с следующим
образом. Прежде всего вынесем за скобки коэффициент при х2:
ах2 4- Ьх Ц- с — а (х24- — х 4- — V
\ а а)
Затем выражение — х представим в виде 2- — • х (удвоенное
а 2а
Ь
произведение числа — на число х):
а (х2 |- b х 4- — = aitfl-f- 2- — • х 4- —V
\ а а) \ 2а а /
К выражению, стоящему в скобках, прибавим и вычтем из него
/>» b „
число —, являющееся квадратом числа—. В результате получим:
ох2 4- Ьх ф с = с 17х2 4- 2 • — х 4- — 'l - — 4- — ].
[\ 2а 4а2/ 4а» а]
о о , о * , & I , ЬХ*
Замечая теперь, что х2 4- 2 • — • х4- — = I х 4- — I, получаем:
ах2 4- Ьх 4- с — а (х 4- — V— - —с. (1)
\ 2а) 4а 7
114
Преобразование квадратного трехчлена к виду (1) называется
выделением полного квадрата. Проиллюстрируем эю преобразо-
вание на некоторЫл частных примерах:
1) — 2№ — 4х + 5 - - 2 (х2 + 2х — =
— 2^(х2 + 2х- 1 (- 1)— 1- = —2^(л + I)2- *
= -2(х+ 1)2 + 7.
Упражнения
Выделить полные квадраты
(№ 354—361):
354 . 2л2 + 4л — 3.
355. 1 х2 — 4х । 16.
3
356. — 5х2 + 20л — 13.
в следующих выражениях
358. (х — 2)(х — 4).
359. ах2 — 4а2х + 4а3 ) 3.
360. 6trx — 9а1 — ах2 + а— 1.
361. (х -|~ о)(х -|~ 6).
357. — 0,5х — 0.25х3 — 2,25.
362. Доказать, что квадратный трехчлен х2 + х + 1 при всех
значениях х принимает положительные значения.
363. Доказать, что квадратный трехчлен — Зх2 + 12х — 13
при всех значениях х принимает отрицательные значения
Квадратные уравнения
§ 50
Уравнения вида
ах2 + Ьх + с — 0, (1)
где х — неизвестная величина, а, Ь, с — данные числа (а =/= 0),
называются квадратными.
Выделяя в левой части квадратного уравнения полный квад-
рат (см. формулу (1) § 49), получаем:
Очевидно, что уравнение (2) эквивалентно уравнению (1)
(см. § 2). Уравнение (2) может иметь действительные корни
только тогда, когда — > 0, или Ь2—4ас > 0 (поскольку 4fl3> 0).
4а*
115
Ввиду той особой роли, которую играет выражение
D = Ь2 — 4ас при решении уравнения (1), этому выражению дано
специальное название — дискриминант квадратного уравнения
ах2 4- Ьх + с = 0 (или дискриминант квадратного трехчлена
ах2-\Ьх+с). Итак, если дискриминант квадратного урав-
нения отрицателен, то уравнение не имеет действи-
тельных корней.
Если же D — Ь2 — 4ас 0, то из (2) получаем:
। > 1 [t2 — 4дс , У Ь3 — 4ас
*+^=± у-^- =±—а
или
х —b± У Ь2 — 4ас — Ь±УР
~~ 2а ~ 2а
Если дискриминант квадратного уравнения неотрицателен,
то это уравнение имеет действительные корни. Они запи-
сываются в виде дроби, в числителе которой стоит коэффициент
уравнения при х, взятый с противоположным знаком, плюс-минус
корень квадратный из дискриминанта, а в знаменателе— удвоен-
ный коэффициент при хг.
Если дискриминант квадратного уравнения положи-
телен, то уравнение имеет два различных действи-
тельных корня:
v -ь+УЪ „ ~ -b-VD
2а 2 2а
Если дискриминант квадратного уравнения равен
нулю, то уравнение имеет один действительный ко-
рень:
х=-±.
2а
(В этом случае иногда говорят, что уравнение имеет два
равных корня: х2=—
Примеры.
1) Для уравнения 2х2 — х — 3 = 0 дискриминант D = (— 1)’—
— 4 2 - (—3) = 25 >• 0. Уравнение имеет два различных корня:
v _ 1 F К25 _ 3
— 4 _ - 2 »
6 4
2) Для уравнения Зх2 — 6х + 3 = О D =(— 6)3 —4 • 3 3=0.
Ото уравнение имеет один действительный корень:
х = -^ = 1.
2-3
116
3) Для уравнения 5х2 4- 4х 4 7 == О D = & — 4 5 • 7 =
= — 124 < 0. Это уравнение не имеет действительных корней.
4) Выяснить, при каких значениях а квадратное уравнение
х2 + ах -г 1 = 0:
а) имее” од и г корень;
б) имеет два разных корня;
в) вообще не имеет корней.
Дискриминант данного квадратного уравнения равен
D = а2 — ‘1.
Если |о| = 2, toD = 0; в этом случае уравнение имее”один кооень.
Если |а' > 2 то D >• 0; в этол; случае уравнение имеет два разных
корня. Наконец, если |а| < 2, то данное уравнение не имеет
корней.
Упражнения
367. — х2 8х — 16 = 0.
368. 2х2 — 12х 4-12 — 0.
369 . 2х — х- — 6 = 0.
виде суммы двух
Решите уравнения (Кр 364—369):
364 . 6х2 — х — 1 = 0.
365. Зх2 — 5х 4- 1 — 0.
366. ;:2 — х 4- 1 = 0.
370. Можно л г. число 15 представит г в
чисел так чтобы их произведение было равно 7С’
371. При каких значениях а уравнение
X2 — 2ах + а ( 4 а) = 0
а) имеет два различных корня;
б) имеет только один корень;
в) не имеет корней’
372. При каких значениях с уравнение
(1 — а) х2 — 4ах 4 4 (1 — а) = (
а) не имеет корней;
б) имеет не более одного корня;
в) имеет не менее одного корня?
373. При какол значении а уравнение х2 4- ах 4- 1 =0 имеет
единственный корень? Чему ог равен':
374. В каких пределах заключено число а, если известно,
что уравнения х2 4- х 4- а = 0 и х2 4- * — е== 0 имеют оди-
наковое число корней:
375. Что вы можете сказать с величине а еелг уравнения
4а (х2 4- X) = с — 2,5 ь х (х — Г) — 1.25 — а имеют одинаково(
число корней?
376. Поезд был задержан на станции не t мин. Чтобь на-
верстать потерянное время, машинис” увеличил скорост: но с км/ч
и на следующем перегоне в b км ликвидировал опоздание. С какой
скоростью поезд шел до задержки на станции?
117
377. Два подъемных крана, работая вместе, разгрузили баржу
за t ч. За какое время может разгрузить баржу каждый кран
в отдельности, если один из них тратит на это на а ч меньше
другого?
378. Один из заводов выполняет некоторый запаз на 4 дня
быстрее, чем Другой. За какое время может выполнить заказ
каждый завод, работая отдельно, если известно, что при сов-
местной работе за 24 дня они выполнили заказ в 5 раз больший?
Решить уравнения (№ 379, 380).
(Обратите внимание на то, что в этих уравнениях неизвестное
содержится в знаменателях дробен. Полученные корни не-
обходимо будет проверить!)
37!'. —+ Л_ = JL + 1.
х- — 1 х + I х — 1
380. —--------L - z 24- .
х т а а — х а-— *3
381*. При каких значениях а уравнения
х2 4- ах 4- 1 = 0 и х2 4- х + а = 0
имеют хотя бы один общин корень?
Частные виды квадратных уравнений * 1
§ 51
В этом параграфе мы изучим некоторые наиболее важные
частные виды квадратных уравнений. При этом каждый раз,
не оговаривая это специально, мы будем предполагать, что
дискриминант рассматриваемого квадратного уравнения неотри-
цателен.
1. Уравнение с «четным коэффициентом при х». Если в
уравнении ах2 4- Ьх 4- с = 0 коэффициент при х имеет вид b = 2k
(например, b — 4, b = 2J/2 и т. д.), то формула для корней этого
уравнения несколько упрощается. Подставив в соотношение
~__ — Ь ± У Ь‘ — 4ос
Х~ ~2а '
вместо b число 2k, получим:
—2k ± |/ 4кг — 4ас — k ± У А2 — ас
X - - -а = — и .
Таким образом, корни квадратного уравнения ах2 4- 2kx + с=0
можно записать в виде дроби, в числителе которой - половина
коэффициента при х, взятого с противоположным знаком, плгос-
118
минус корень квадратный из квадрата этой половины без произ-
ведения коэффициента при х2 и свободное члена., а ь знамена-
теле — коэффициент при хг.
Например, Ч1обы решить уравнение
5х2 — 16х 4- 3 = О,
нет необходимости применять общую формулу
____ — b ± VЬ- — 4ас
х - 2й— — .
В данном случае следует отдать предпочтение доказанной выше
формуле
__ — А ± Уй3 — ас
а
Используя се, получаем:
8+ У64—15 _ 8 + У'49 _ 8 ± 7
А“б ~ f - 5
х( = 1 ; хг =- 3.
ь
2. Приведенное квадратное уравнение. Квадратное уравнение
называется приведенным, если коэффициент при х2 равен 1.
Общий вид приведенного квадратного уравнения таков:
х2 4- рх 4- < = 0, (1)
где р и q — некоторые .числа.
Полагая в общей формуле для корней квадратного уравнения
— I ± У А2 — 4ас
Х ~ 2с
а = I, b = рис = q, получим формулу для корней приведенного
квадратного уравнения:
— Г ± У? — 44 _ Р т/ _ Р J. 1/ I р
х---------5-----------2 ± V —--------2 - Ц2; *
Таким образом,
Корни приведенного квадратногс уравнения равны половине
коэффициента при х, взятого с про~ивоположным знаком, плюс-
минус корень квадратный из квадоата этой половины без сво-
бодного члена.
119
Пример. Пусть х2 4- 4х — 12 — 0.
Тогда
х = — 2±]/4 4- 12 = — 2 ± 4,
или
*1 = 2- х2 = — 6.
Замечание. Любое квадратное уравнение ок2 4- Ьх 4- с =0
можно свести к приведенному квадратному уравнению посред-
ством деления на а:
дх2 4- Ьх 4- с = 0, х2 4- - х 4- - = 0.
а а
Упражнение
382. Решить уравнения, используя в каждом случае наиболее
удобную формулу:
а) Зх2 — 5х 4- 2 = 0; г) х2 4- 7х — 30 = 0;
б) Зх2 — 20х — 52 = 0; д) 5ха 4- 9х — 14 = 0;
в) х2 — 10х ф- 24 = 0; е) 4х2 — х 4- 10 = 0.
Теорема Виета
§ 52
В § 51 мы получили следующие формулы для корней при-
веденного квадратного уравнения с неотрицательным дискрими-
нантом:
Из них вытекает, что
Xi 4- х2 = — р,
Произведение суммы двух чисел на их разность равно разности
квадратов этих чисел. Поэтому
Итак,
*i+*2=—А
^1 ’ "^2 ~ Я'
Если приведенное квадратное уравнение имеет дей-
ствительные корни, то сумма их равна коэффициенту
при х, взятому с противоположным знаком, а произ-
ведение — свободному члену этого уравнения.
120
Это свойство корней приведенного квадратного уравнения
носит название теоремы Виета*.
Пример. Для уравнения х2—7х— 8 — О D=81 > 0. Поэтому
уравнение имеет два различных действительных корня хх и х2.
По теореме Виета
Xi 4- х2 = 7, х, • х2 = — 8.
Предлагаем учащимся решить данное уравнение и убедиться в
справедливости полученных нами соотношений.
Квадратное уравнение общего вида ах2 + Ьх 4- с — 0 делением
на а сводится к приведенному квадратному уравнению
х5 + - х+ - = 0.
а а
Если исходное уравнение ах* + Ьх + с = 0 имеет действительные
Ь с
корни Xj и х2, то и уравнение х2 4— х 4* — = 0 должно иметь
а а
те же самые корни xt и х2. При этом по теореме Виета должно
быть
. Ь о
X14” ^2 « Xj • Xg = — •
а а
Пример. Уравнение 2х1 — 2х — 3 = 0 имеет дискриминант
D — 28 > 0. Поэтому оно имеет два действительных корня xt и х2,
причем
. —2 , —33
*1+ Х2 —---—- = 1, X, • X, = --=— — .
J Z 2 1 2 2
Предлагаем учащимся решить данное уравнение и убедиться
в справедливости полученных соотношений.
В дальнейшем нам потребуется теорема, обратная теореме
Виета. Формулируется она следующим образом
Если существуют действительные числа х1 и х2 та-
кие, что xt-{-x2=—p, xt- x2=q, то эти числа (xt и х2) яв-
ляются корнями квадратного уравнения л2+ = °-
Доказательство. Если х( 4- х2 = — р, то х2 = — р —х,.
Подставляя это выражение для х2 в соотношение xt • х2 — q,
получаем:
хг(— Р — *1) = — PXi — xt2 = q, х? 4> pxi 4- q = 0.
Но это означает, что число х( является корнем уравнения
х2 4- рх 4- <7 = 0. Аналогично доказывается, что корнем этого
уравнения является и число х2. Впрочем, это и так ясно: ведь
числа Xi и х2 входят в формулировку нашей теоремы совершен-
но симметрично.
‘Виет (1540—1603) — французский математик.
121
Упражнения
383. (Усти о.) Решить уравнения:
1) №-3x4'2 = 0;
2) х2 4- 99л- — 100 = 0;
3) х2 4- 54Ьл - 549 =• 0;
4) — х2 4- 6* — 5 = О,
384. Обозначим через х, и х2 корни уравнения
5) - № - 7х + 8 = 0;
6) № — 7х + 12 - = О;
7) Зх2 4- х - 2 - 0;
8) х« — 5х 4-6 = 0.
ха — 7х 4- Ю = 0.
Не находя этих корней, определить:
а) х24- х2- в) 1 4- 1; д) *i 4- хл .
Xj *2 Xj Xj
б) л-з (- л-2; г) А + Л ’
*'Г 4
385. Го же, что и в задаче 384, сделать для уравнения
— Зх2 [- х 4- 24 = 0.
386. При каких значениях х выражение (х — 1) (х 4- 5) равно
(а — I) (а 4- 5)?
387. Доказать, что корни уравнения ах2 4- Ьх 4- а = 0 (если
только они существуют) представляют собой взаимно обратные
числа.
388. Определить число т так, чтобы уравнение
х2 — 12х 4- т = 0
имело два действительных корня, один из которых больше дру-
гого на 2|№5.
389. Определить число а так, чтобы один из корней урав-
нения
4х2 — 15х 4- 4а3 = 0
был квадратом другого
390. При каких значениях а уравнение
х* — 4х 4- а = 0
имеет:
а) действительные корни;
6) действительные корни одного знака;
в) действительные корни разных знаков;
|) один корень нулевой, а другой — положительный;
д) один корень нулевой, а другой — отрицательный?
122
Исследование знаков корней квадратного
уравнения по его коэффициентам § 53
Используя теорему Виета, можно, не решая уравнения
№ -f- рх ь q = 0, определить, какими буду г с>о корни положи-
тельными или отрицательными. Но при этом, конечно, нужно
быть уверенным в том, что рассматриваемое уравнение имеет
корни. Если же корней нет, то говорить о знаках корней не
нмсег смысла. Поэтому на протяжении всего этого параграфа
мы будем предполагать, что рассматриваемое приведенное квад-
ратное уравнение х2 4- рх + q = 0 имеет корпи, то есть дискрими-
нант его неотрицателен.
1) Пусть q > 0, тогда оба корня имеют одинаковые знаки,
поскольку Xf Xi - q~> 0. Еслп к тому же р<_ 0, го Xj х? =
= — р > 0, значит, оба корня положительны. Если р > 0,
то х( + х2 — — р < 0, и тогда оба корня отрицательны. В случае,
когда р = 0, уравнение не будет’ иметь действительных корней,
потому что сумма двух положительных или двух отрицательных
чисел не может быть равна нулю.
2) Предположим теперь, что q < 0. Тогда одни из корней дол
жен быть положительным, а другой — отрицательным, поскольку
х, • х2 = q < 0. Если при этом р > 0, то Xj -г х2 = — р < 0- и,
значит, абсолютная величина отрицательного корня больше поло-
жительного корня. Еслп же р < 0, то х( + х2 = — р > 0. Это
возможно только тогда, когда положительный корень больше
абсолютной величины отрицательного корня. При р = 0
X] + х2 — 0, откуда х, — — х2; в этом случае корни равны по аб-
солютной величине и противоположны по знаку.
3) Осталось рассмотреть случай, когда q = 0. Тогда xt • х2 = 0,
поэтому хотя бы один из корней равен нулю. Пусть для опре-
Я > 0 я < о р = 0
р 0 Р <с р-0 р > 0 Р < о р= 0
х, <0 *1>0 Этот случаи не- возможен ввиду исходного пред- Корпи разных знаков: Корни разных знаков: Корни вза- имно про- тивополож- х, = 0
хг<0 х2>0 »положения, что D>0 Х1 <0, х2 > 0, xt|> х2 X. <0, Xi >0, ! х, |< х2 пые: Xi =— х2 х2 •-=— Р
деленности xt = 0, тогда другой корень найдется из условия
X] х2 = — р, откуда х2 — — р. Значит. в этом случае один ко-
рень равен нулю, а другой представляет собой число, противопо-
123
ложное коэффициенту р. Если же и р = 0, то уравнение имеет
два равных корня: xt — хг — 0.
Полученные результаты исследования знаков корней пред-
ставлены в таблице на предыдущей странице.
Еще раз отметим, что приведенные здесь рассуждения верны
лишь в предположении, что исследуемое уравнение имеет дей-
ствительные корни, то есть его дискриминант неотрицателен.
Рассмотрим несколько примеров на исследование знаков кор-
ней квадратных уравнений.
1) х2 — 8х — 9 = 0. Дискриминант этого уравнения равен
D = 64 4- 36 = 100 > 0. Поэтому уравнение имеет два различ-
ных действительных корня. Вследствие того что х( • х2 — 9,
корни должны иметь разные знаки, а так как xt 4- хг = 8, то
абсолютная величина отрицательного корня меньше положитель-
ного корня.
2) х2 4- 7х 4- 10 — 0. Дискриминант этого уравнения равен
D = 49 — 40 = 9 > 0. Поэтому уравнение имеет два различных
действительных корня. Так как xt-x2 = 10 > 0, то корни имеют
одинаковые знаки. Кроме того, xt 4- хг = — 7, значит, оба корня
отрицательны.
3) х2 — х 4- 1 =0. Для данного уравнения
D = (— I)2 —4 = — 3<0.
Следовательно, это уравнение не имеет действительных корней.
Полученные выше результаты относятся лишь к приведенным,
квадратным уравнениям. Но подобные исследования можно про-
вести и для любых квадратных уравнений ах2 4- Ьх 4- с = 0. Для
этого сначала нужно посредством деления на а привести данное
уравнение к приведенному квадратному уравнению х2 4* — х 4-
а
4- — = 0, а затем для этого уравнения провести описанные выше
а
рассуждения.
Пусть, например, нужно исследовать знаки корней уравне-
ния — Зх2 4- 5х — 2 = 0. Дискриминант этого уравнения равен
D — 25 — 24 — 1 > 0. Поэтому оно имеет два различных действи-
тельных корня.
Разделив обе части уравнения на — 3, получим; х2 — — х 4-
3
2 *
4— =0. Отсюда видно, что корни данного уравнения имеют
3
2
одинаковые знаки, так как х£ • х2= — > 0. Кроме того, xt 4- х2=
5
= - > 0. Следовательно, оба корня положительны.
О
324
396. 6х2 — х — 1 =0.
397. — 20х2 — Зх + 2 = 0.
398. х2 — 6х + 10 - 0.
399. — Зх2 + 17 = 0.
400. — 5х2 + х — 7 =0.
х2 — 4х + 3 = 0
х2 — 6х + 5 = 0.
х2 — х — 42 — 0.
х2 — х — 6 = 0.
Упражнения
Не решая данных уравнений (№ 391—400), определить знаки
их корней:
391.
392.
393.
394.
395. х* 1 2 + х + 1 = 0.
401. При каких значениях а корни уравнения
х2 + (1 — о) х — а = 0
имеют одинаковые знаки и при каких — разные?
402. При каких, значениях а корни уравнения
х2 + (а + 6) х + (2а — 1) (7 — а) = 0
имеют одинаковые знаки и при каких — разные?
Разложение квадратного трехчлена
на линейные множители
$ 54
В этом параграфе мы рассмотрим следующий вопрос: ь ка-
ком случае квадратный трехчлен ах2 + Ьх + с можно представить
в виде произведения
(atx + bt) (а2х + Ь2)
двух линейных относительно х множителей о действительными
коэффициентами ait Ьъ а2, b2 (ai =/= 0, а2 =# 0)?
1. Предположим, что данный квадратный трехчлен ах2 + Ьх + с
представим в виде
Правая часть
и х=—- (а,
«2
ах2 bx с = (OjX + bi) (а2х -+• b2). (1)
„ bi
формулы (1) обращается в нуль при х=-------------
а1
и а2 по условию не равны нулю). Но в таком
случае числа ——и —— являются корнями уравнения
at а,
ах2 -1- Ьх + с = 0.
Следовательно, дискриминант квадратного трехчлена ах2 + Ьх 4- с
должен быть неотрицательным.
2. Обратно, предположим, что дискриминант D = Ьг — 4ас
квадратного трехчлена ах2 + bx J с неотрицателен. Тогда этот
125
трехчлен имеет действительные корни х1 и х2. Используя .е^-
рему Виета, получаем:
ах1 4- Ьл + с = а (л2 + - х j —\= а(хг — (л1 4- л?) ~ 4- х,^) =
v» CL /
— а((х2 — xtx) — (xzx — xtxJJ = а[х (x — x,) —x2 (x — xj] —
= a (x — xj (x • xj.
Итак,
ux2 4- bx 4- c = a (x — xj (x — x2), (2)
где x, и x£ — корни трехчлена ax2 -f- bx F с. Коэффициент а можно
отнести к любому двух линейных множителей, например,
и (х — х,) (х - х2) = (ах — ахд (х — х2).
Но это означает, что в рассматриваемом случае квадратный
трехчлен ах2 4- Ьх 4- <- представим в виде произведения двух-
линейных множителей с действительными коэффициентами.
Объединяя результаты, полученные в пунктах 1 и 2, мы
приходим к следующей теореме.
Теорема. Квадратный трехчлен ах- -}- Ьх -}- с тогда
и только тогда можно представить в виде произведения
двух линейных множителей с действительными коэф-
фициентами,
ахг -ф Ьх + с — (atx 4- Ь) (а?х 4~ Ь
когда дискриминант этого квадратного трехчлена
неотрицателен (то есть когда этот трехчлен имеет
действительные корни).
Пример!. Разложить на линейные множители 6х2 — х — 1.
Корни этого квадратного трехчлена равны х,= * и х2=— .
Поэтому по формуле (2)
6х2 — к— 1 --б(х— -)(х4- — (2х— 1)(3х4- 1).
П р и м е р 2. Разложить на линейные множители х24-х+ 1.
Дискриминант этого квадратного трехчлена отрицателен:
D = I2 — 4 1 • 1 - — 3<0.
Поэтому данный квадратный трехчлен на линейные множители
с действительными коэффициентами не раскладывается.
Упражнения
Разложить на линейные множители следующие выражения
(№ 403—406):
403 . 6х2 — 7х 4- 2. 405. х2 — х 4- 1.
404. 2х2 — 7ах 4- 6a2. 406. х2 — Зах 4- 2a2 — ab — Ь9.
126
Сократить дроби (№ 407, 408).
407 iA" 408 '
12x2 -Ьл —/>2 ’ ' Зо2 |-5а— 2 *
Решить уравнения:
409. -* * * * * * * * * х - -®- =-4л-.
х—10 х—о х2 16х f 60
410*. --------------?_____________1 — .
54 (х—lj . (а 4~ 1 )(а+х) х2+0*—Ох—а
Составление квадратного уравнения
по заданным корням $ 55
Предположим, что нам нужно составить квадратнее уравне-
ние, корнями которого были бы числа xt и ха. Очевидно, что
в качестве искомого уравнения можно выбрать уравнение
а (х - - xj (х — Ха) = 0, (1)
где а — любое отличное от нуля действительное число. С другой
стороны, как было показано в § Ь4, каждое квадратное уравне-
ние с корнями х, и х2 можно записать в виде (1).
Таким образом., формула (1) полностью решает поставленную
выше задачу. Из всех квадратных уравнений корни лу и х2
имеют уравнения вида (1) и только они.
Пример. Составить квадратное уравнение, корни которого
равны 1 и — 2.
О т в е т. Корни 1 и — 2 имеют все квадратные уравнения вида
а (х — 1) (х + 2) = 0,
или
ах2 4- ах — 2а = 0,
где а — любое отличное от нуля действительное число. Напри-
мер, при а = 1 получается уравнение
х2 + х — 2 = 0.
Упражнения
411. Составить квадратное уравнение, корнями которого были
бы числа:
а) 2 и — 3; б) — 1 и — 5; в) А- и ; г) — А и .
412. Составить квадратное уравнение с целыми коэффициен-
тами так, чтобы его корпи были равны:
127
413. Составить квадратное уравнение с целыми коэффициен-
тами, корни которого равны ° и —, а сумма всех коэффици-
ентов равна 36.
414. Могут ли лорпями квадратного уравнения с натураль-
ными коэффициентами быть числа -g- и---?
415. Составить квадратное уравнение с целыми коэффициен-
тами, если известно, что один из его корней равен:
а) 2 + ]/3; б) 3 — /2.
Биквадратные уравнения § 56
Биквадратными называется уравнения вида
ах* + Ьх2 + с = 0, (!)
где а, Ьп с — заданные числа, причем й 0.
Решение таких уравнений сводится к решению квадратных
уравнений. Действительно, полагая в (1) у = х2, получаем:
ay2 + by + с = 0.
Найдя из этого уравнения у и учитывая, что у = хг, легко по-
лучить и х.
Пример. Решить уравнение
х*— 5х2 — 36 = О-
Полагая у = х2, получаем:
у2 — 5у — 36 - 0,
откуда yi = — 4, у г — 9. Поскольку у может принимать только
неотрицательные значения (ведь у = х2), первый из этих корней
является «посторонним». Следовательно, х2 = 9, откуда х( = — 3,
х2 = 3.
Подобным способом можно решать и более широкий круг уравнений,
а именно уравнения вида
а*1'1 + ЬхР + с = 0,
где п — любое натуральное число. Полагая здесь
у = хП,
мы приходим к квадратному уравнению
ay ’ + by + с — 0.
Пример. Решить уравнение
— 7х3 — 8 = 0.
Полагая у = х3, получаем:
у 1 — Ту — 8 = 0,
J28
откуда
У1 = — 1 У» ; 8
В^аачипая, что у = х3, получаем следующих два корпя данного уравнения:
х, = — 1, ха = 2.
График квадратной функции
§ 57
В этом параграфе мы покажем, как строится график квад-
painun функции у = ах2 + Ьл + Наше рассмотрение придет
ся разбить па ряд отдельных этапов.
1. График функции у=лг!. Этот график строится «по точ-
кам». Составим следующую таблицу значений функции:
X — 3 — 2 — 1 1 0 -|О, 1 2 3 ...
у = ха 9 • 4 1 _1 4 G £ 4 L 9 ...
Отметим соответствующие точки на плоскости координат и сое-
диним их плавной кривой (рис. 64). Эта кривая называется па-
раболой. Fla рисунке 64 парабола у = х'“ начерчена лишь при
— 3 < х < 3 При jx, > 3 она уходит (и притом весьма круто)
все выше и выше.
Парабола у = х2 обладает следующими основными свойствами.
1) Она лежит целиком в верхней полуплоскости, Это
соответствует тому, что функция у — х2 принимает только
неотрицательные значения. В начале координат парабола ка-
сается оси абсцисс. Это самая низ-
кая точка графика; она называется
вершиной параболы.
2) Парабола симметрична относи-
тельно оси ординат. Если перегнуть
рисунок 64 по оси у, то левая и пра-
вая части параболы совместятся. Этс
служит графической иллюстрацией того,
что функция у=х2 не меняет своих зна-
чений при изменении знака у аргумента;
(— х)2 = х2.
Такие функции называются четными.
2. График функции у = ах2, Гра-
фик функции у = ах2, так же как и
график функции у — х2, легко строится
Рис. 64.
«по точкам».
5 Заказ 261
129
Рис 65.
-3 -2 -1 0 12 3
Рис. 66.
Сначала рассмотрим случай, ™гда
а > 0. На рисуПЛе бэ представлены
графики функции у ах2 при а =
= — ; 1; 2. Во всех этих случаях
получаются кривые, симметричные
относительно оси ординат и располо-
женные целиком в верхней полу-
плоскости. Каждая из этих кривых
направлена вверх Эти кривые, так
же как и кривая у=х2, называются
параболами. Начало коирДпнат яв-
ляется их ибщ.ей вершиной, а ось
ирДпнат—их общей осью симметрии.
Из рисунка 65 видно, что чем больше
а, тем круче ветви параболы у— ах2,
чем меньше а, тем они положе.
Теперь рассмотрим случай, когда
а < 0. На рисунке 66 представлены
2 1 1
кривые у = ах2 при а =— —; — 1;
— 2. Эти направленные вниз кривые
также называются параболами. Об-
щая вершина — начало координат—
является их наивысшей точкой. Ось-
ординат для каждой из этих кри-
вых служит осью симметрии. Чем
больше абсолютная величина а, тем
круче ветви параболы; чем она мень-
ше, тем положе ветви параболы.
3. График функции у а (?’—Р)!
Сравним менаду собой две функ-
ции: j’j = а (х— Р)2 и у о = ах2,
где р>0. Пусть Mt—произволь-
ная точка графика первой функции
(рис. 67). Тогда ее координаты
(-*4)» Уо) связаны соотношением
Уо= а (х0 — Р)2.
Нс это соотношение показывает, что
точка М2 с координатами (х0—р, у0)
должна принадлежать графику вто-
рой функции. Значит, каждая точка
кривой у = а (х—Р)2 получается из
соответствующей точки кривой у —
-- ах2 (см. рис. 67] посредством пе-
реноса (или смещения) вправо по
130
напраии-пню оси х на расстоя-
ние р Поэтому и вся кривая
у а (х — р)2 получается по-
средством переноса кривой
у=-ах- вправо на Р.
Чапример, кривая у =2 (х— 1)“
получается из кривой у- 2х2, еслп
последнюю сместить па \ вправо
(рис. 68)- кривая у ——0,5 (л — о)2
получается смещением кривой
у — — С,5х2 ппраВм на 3 единицы
(рис 69}
Вершиной параболы у ах2
является точка с координата-
ми (О, U), а осыс симметрии —
прямая х — 0. При смещении
вправо по направлению оси х па
раси1О»ние р точка с координа-
тами (U, 0) переходи” в точку
с координатами ф, 0/ а прямая
х = 0 — в.прямую х-р (рис. 70)
Поэтому вершиной п раСолы
у=а ‘х — Р)2 будет точке с коор-
динатам!.' ф, 0) a ocuio симмет-
рии — прямая л = р.
Парабола у = ах2 направлена
вверх при 0 и вниз при а< 0.
Поэтому такое же направление
будет иметь и парабола у =
— а (х — Р)2.
Итак, графикок функции
у = а {х — Р)1 является парабола,
напреваенная вверх, если а > 0,
I, вниз, если а < С Вершиной
этой параболы является точка с
координатами (р, 0), а осью сим-
метрии — прямая л = р.
Точно так же может быть по-
строен к график функции у =
— а (х P)s где Р > 0 Он пред-
ставляет собой параболу, которая
получается поспедством смещения
параболы у= ах2 влев( на р. Эта
парабола направлена вверх если
а > 0 (рис. 71а), и вниз, если
a<L 0 (рис. 716). Веошина ее на-
ходится в точке с координатами
Рис. 70.
131
Рис. 716.
У
(— Р, 0); осью симметрии служит
прямая х — — ₽.
На рисунке 72 вы видите гра-
фик функции у = 2 (х + I)2. Он
получен посредством параллельно-
го переноса параболы у=2х2 влево
на 1. График функции у =
— — 0,5 (х + З)2 (рис. 73) получен
посредством параллельного пере-
носа параболы у = — 0,5х2 влево
на 3.
4. График функции у =
— а (л — р)2+ у. Этот график по-
лучается посредством смещения
параболы у = а (х—Р)2 по направ-
лению оси у вверх на расстоя-
ние у, если у>0, и вниз на рас-
стояние — у, если у < 0. В ре-
зультате смещения получается
парабола с вершиной в точке, ко-
ординаты которой равны (Р, у).
Осью симметрии такой параболы
служит прямая х = р.
При смещении вверх или вниз
парабола у=а (х — Р)2 не меняет
своего направления. Поэтому па-
раболы у — а (х—р)2 + у н у —
= а (х—Р)2 имеют одно и то же на-
правление: при а > 0 — вверх, а
при а < 0 — вниз.
В качестве примера на рисун-
ке 74 представлен график функ-
ции у = —0,5 (х+3)2 + 1, который
получается смещением графика
у = — 0,5 (х Г З)2 вверх на 1. На
рисунке 75 вы видите график
функции у—2 (х — I)2 — 3, полу-
ченный из графика у — 2 (х — I)2
смещением вниз на 3 по оси сим-
метрии.
5. График функции у — ах2 +
+ Ьх+с. Как отмечалось в § 49
квадратный трехчлен ах3 + Ьх-Ьс
представим в виде
(Л \2 м______4.,с
х + -)— ~
2а/ 4а
132
Последнее выражение имеет вид
а (х — Р)- + у, где
Ь- — 4ас
----
Поэтому графиком функции
у- ax2-j- Ьх с является па-
рабола с вершиной в точке
/ Ь Ь* 1 — 4аг\ Л
(----,---------I. Осью сим-
\ 2а 4а }
метрик этой параболы яв-
ь п
ляется прямая х = — При
а~>0 парабола направлена
вверх, а при а<0 — вниз.
Рис. 74.
Примеры построения
графика квадратной
функции § 58
Пример!. Построить график
функции
у= 2х2 + 12х -|- 17.
Преобразуем квадратный трех-
член 2х2 + 12х 4-17, выделив пол-
ный квадрат:
2х2 + 12х 4- 17 = 2 (х2 4- 6х 4- = 2 f(x2 4-2-3-х 4- 9)— 9 4- =►
= 2^(х 4- З)2— 1] = 2(х 4- З)2— 1.
Теперь построение графика можно выполнить в следующей по-
следовательности .
1) «По точкам» строим график функции у = 2х2 (I, рис. 76).
2) Смещаем этот график на 3 единицы влево. В результате
получаем кривую у = 2 (х 4* З)2 (II, рис. 76).
3) Эту кривую опускаем вниз на 1 (III, рис. 76). Получен-
ная парабола и есть график функции у = 2х2 4- 12х 4- 17. Ее вер-
шина имеет координаты (— 3, — 1), а осью симметрии является
прямая х — — 3.
Пример 2. Построить график функции у =| — 2х2 4- 3|.
Сначала построим график функции у — — 2ха 4- 3 (рис. 77а).
Затем ту часть этого графика, которая лежит выше оси х (для
нее — 2х2 4- 3 >• 0), оставим без изменения, а ту часть графика,
133
Рис. 76.
которая лежит ниже оси х (для нее
—2х24-3<0), отобразим симметрично
относительно оси х. Полученная в ре-
зультате этого кривая (рис. 776,
сплошная линия) и есть график функ-
ции у = |—2х2 + 3|.
Упражнения
Построить графики данных функций:
Рис 77 а.
416. у = — 2х2 + 1.
417. у = 0,5х2 — 2.
418. у = (х — 2)2 4- 3.
419. у = (х + I)2 — 2.
420. у = —2(х ф 1,5)2 4- 1.
421. у = 2х2 — Зх — 2.
422. у = —Зх2 4- 8х 4- 3.
423. у = (х - 3) (х — 5) 4- 1.
424. у —х2 4- 2|.
425. у = Зх2 — 11.
426. у = х2 4- х — 2|.
427. у = —х2 4- Зх — 2|.
Характеристические точки
параболы § 59
Характеристическими точками па-
раболы у =ах24- bx+с мы называем ее
вершину и точки пересечения с осями
координат.
Вершину имеет любая парабола
у=дх24-6х4-с. Координаты этой вер-
шины легко найти, выделив в квад-
ратном трехчлене пх24-6х4-с полный
квадрат (см. § 49). Например, для па-
раболы у = х24-4x4-3 имеем:
х24-4х4-3 = (х 4- 2)2 - 1.
Поэтому абсцисса вершины равна—2,
а ордината —1 (рис. 78).
Точку пересечения с осью у имеет
также любая парабола у — ах24-Ьх4-с.
Абсцисса точки пересечения равна, оче-
видно, пулю, а ордината с. Она полу-
134
чается, если в выражении ах2 4-
4- Ьх-^-с положить х = 0. Например,
точка пересечения параболы у=х2 +
4- 4х 4- 3 с осью ординат (рис. 78)
имеет координаты (0,3).
Точки пересечения с осью х
имеет не всякая парабола у — ах2 4-
4- Ьх 4- с. Если дискриминант D —
— Ь2 — 4ас положителен, то уравне-
ние ах2 4- Ьх 4- с — 0 имеет два раз-
личных действительных корня:
V - -ь+/Р. г _ -ь-уГр
1 2а ’ 2~~ 2а
Рис. 78.
<
I
В этом случае парабола у = ах2 4-
4- Ьх 4- с пересекает ось х в двух
точках с абсциссами Xi и х2 соответ-
ственно. Так, для квадратного трех-
члена х24-4х 4-3 £)=16—12=4>0.
Этот квадратный трехчлен имеет два
корня: Xi— — 1, х2 ——3. Поэтому
парабола у = х24-4х -|- 3 пересекает
ось х в двух точках (рис. 78), абсцис-
сы которых равны — 1 и — 3.
Если D = Ь2 — 4ас = 0, то уравне-
ние ах2 4- Ьх 4- с — 0 имеет один
.. ь
действительный корень х =—- .
В этом случае уравнение параболы
/ . Ь \2
можно записать в виде у = al*4- —
\ 2а/’
Такая парабола касается оси х в
точке с абсциссой ——. Например,
2а
для квадратного трехчлена х2—2x4-1
D= 0. Уравнение х2 — 2х 4~ 1 =0
имеет один корень х = 1.
Поэтому парабола у=х2 — 2x4-1 ка-
сается оси х в точке с абсциссой 1
(рис. 79).
Если D = Ь2—4ас <0, то уравне-
ние ах2 4- Ьх 4- с = 0 не имеет дей-
ствительных корней. В этом случае
парабола не пересекает оси х. Напри-
мер, для квадратного трехчлена
ха 4- 2х 4- 3 D =— 8< 0. Уравнение
х2 4- 2х 4“ 3=0 не имеет действитель-
Рис. 79.
135
Рис. 81.
пых корней. Парабола у = х2+ 2x4 3
не пересекает оси х (рис. 80).
Характеристические точки параиолы
всегда полезно налодить при построе-
нии графика функции у =пх2+ Ьх + с.
Это позволяет более точно построить
график.
Упражнения
Начертить данные параболы, указав
координаты ларактеристических точек
и уравнения осей симметрии:
428. у = 3 (х — 2)2 — 2.
429. 'у - - Си О2 I- 3.
430. у = 3 — 2х — х2.
431. у = 2х2 — 2х — 4.
432. у = л2 + 12т + 22.
433. у — х (1 — х).
Экстремальное значение функции у = ох2 + bx + с § 60
Наименьшее, или минимальное, из всех значений, которые
принимает квадратная функция у — ах2 + Ьх ) с, геометрически
можно истолковать как ординату самой низкой точки параболы
у = ах2 + Ьх + с (рис. 81), а наибольшее, или максимальное, зна-
чение — как ординату самой высокой точки параболы у — ах2 +
+ Ьх + с (рис. 82).
Если а > 0, то парабола у — ах2 + Ьх + с уходит неограни-
ченно вверх (рис. 81). В этом случае самой высокой точки па-
раболы не существует. Поэтому не существует и максимального
значения функции у = ах2 4- Ьх + с. Но в этом случае существует
самая низкая точка параболы — ее вершина. Следовательно,
существует минимальное значение функции. Это минималь-
ное значение (мы будем его обозиачть y(nin) равно ординате вер-
шины параболы. Абсцисса этой верши-
ны (обозначим ее xmin) дает то значение
аргумента х, при котором достигается
минимум функции у — ах2 + Ьх + с.
Если а < 0, то парабола у = ахг+
+ Ьх + с уходит неограниченно вниз
7" (рис. 82). В этом случае самой низкой
точки параболы на существует. Поэтому
не существует и минимального значе-
ния функции у = ах2 + Ьх +с. Зато су-
ществует самая высокая точка пара-
болы — ее вершина. Следовательно,
Рис. 82. существует максимальное значение дан-
136
нои функции. Эю максимальное значение (moi будем обозначав
его у.„ак) равно ординате вершины параболы Абсцисса этой вер-
шины (обозначим ее хП1Э>) дает то значение аргумента х, при кото-
ром достигается максимум функции у — ах2 -г Ьх -Ь с.
В § 57 было установлено, что вершина параболы у = ах8 +6х+ с
независимо от того, положительно а или отрицательно, имеет kg-
°РДИ1,аТЬ1: b b‘— 4ас n
X =-----; у =—------------. 11)
2а 4а
Поэтому можносказать, что если а > 0, тофункция у = ах8 +бх+ с
b* - 4ас „ b
принимает наименьшее значение ymin =----------при xmin =------;
4а 2а
наибольшею значения згой функции не существует. Если а < О,
то функция у = ах8 + Ьх + с принимает наибольшее значение
““ 4ас Ь
ymsx=----------при хтах=------; наименьшего значения функции
4а 2а
в данном случае не существует.
Минимальные и максимальные значения функции иначе на-
зываются экстремальными.
Пример!. Найти экстремальное значение функции у =2х8—
— 4х — 17 и указать, при каком значении х функция принимает
это экстремальное значение.
Поскольку коэффициент при х8 положителен, то данная функ-
ция имеет минимальное значение. Максимального значения она
не имеет. Чтобы определить минимальное значение, найдем коорди-
наты вершины параболы у = 2х8 — 4х — 17. Для этого выделим
полный квадрат:
2х2 — 4х — 17 = 2 х8 — 2х — =
1 2/
= 2 (х8— 2х 4- 1)— 1 — 1? | = 2(Х — I)2—19.
Отсюда заключаем, что координаты вершины параболы таковы;
х = 1, у = — 19. (Эти координаты, конечно, можно было бы по-
лучить и по формулам (1), если в них положить а — 2, b — — 4,
с = — 17.) Следовательно, минимальное значение функции
у — 2х8 — 4х — 17 равно — 19. Оно достигается при х = 1.
Пример 2. Найти экстремальное значение функции
у ----х8 — 4х + 6 и выяснить, при каком значении аргумента х
оно достигается.
Поскольку коэффициент при х8 отрицателен, то данная функ-
ция имеет максимальное значение. Минимального значения она
не имеет. Чтобы найти максимальное значение, выделим полный
квадрат:
— х8 — 4х -+- 6 = — (х8 + 4х — 6) =
= - Цх« + 4х + 4) — 101 = — О-’ + 2)8 - 10.
Отсюда заключаем, что максимальное значение данной функции
равно 10. Оно достигается при х = — 2.
137
Упражнения
Найти экстремальные значения дан-
ных функций и указать, при каких
значениях аргумента они достигаются
(№ 434—437).
434. у = 2х2 + 12х + 13.
435. у = — 2х2 — 4х — 5.
436. у = |6х2 — х — 1|.
437. у = |4х2 — 4х — 3|.
438. Доказать, что если сумма двух
величин постоянна, то их произведе-
ние максимально тогда н только тогда,
когда эти величины принимают рав-
ные значения. (Это утверждение явля-
ется естественным обобщением теоремы
о постоянной сумме на случай любых,
а не только положительных величин;
см. гл. I, § 17.)
4/
(D>o,a>o)
Рис. 84.
Квадратные неравенства
§ 61
х
ах2 4* Ьх 4- с < О,
Неравенства вида
'«агакяха ах2 .4* Ьх 4* с > О,
ах2 4- Ьх 4- с > О,
где а, Ь и с — заданные числа и а =/= О,
называются квадратными (или неравен-
ствами второй степени).
В этом параграфе мы ограничимся
лишь рассмотрением неравенств вида
ах2 4- Ьх 4- с > 0.
Такие неравенства лучше всего решать,
используя геометрическую иллюстра-
цию. Рассмотрим отдельно два случая:
а > 0 и а <. 0.
Случай 1. а > 0. В этом случае
парабола у = ах2 4* Ьх 4- с направлена
вверх. Если D = Ь2 — 4ас <0, то квад-
ратный трехчлен ах2 4- Ьх 4-с не имеет
действительных корней. Значит, пара-
бола у = ах2 4- Ьх+с не пересекает оси х
и расположена целиком выше оси х
(рис. 83). Это означает, что в данном
случае неравенство ах2 -}-Ьх 4- О 0 вы-
полняется при любых значениях х.
138
Если D —b2 — 4ac > 0, то парабо-
ла у — ах2 +bx +с пересекает ось х
в двух точках (рис. 84) с абсциссами:
— Ь — V Ь-— 4ас
X,— ---------о------ >
1 2а ____ ’
_ — Ь + УЬ2 — 4ас
Х2-------~2а *
Поэтому ax2-hbx-j с > 0 при x<*i,
а также при х > х2-
Наконец, если D = Ь2— 4ас =0,
то трехчлен ах2 + Ьх + с имеет
ь
одни корень х ------и, следова-
2а
' { । b \а
тельно, представим в виде а 1х+ — 1
В этом случае парабола у=ах2 +
+Ьх-г с касается оси х в точке с абс-
циссой — (рис. 85). Поэтому ах2 -И
4- Ьх 4- с > 0 при всех значениях х,
ь
кроме х = — — .
Случай 2. а <0. В этом случае
парабола у—ах2 -|- bx + с направлена
вниз.
ЕслиП = Ь2—4ас < 0, то уравне-
ние ах2 + Ьх 4-с=0 не имеет действи-
тельных корней и,значит, парабола
у=йх2 4- Ьх-\-с лежит целиком ниже
оси х (рис. 86). Поэтому неравенство
ах2 4* Ьх 4- с >0 не выполняется ни
при каких значениях х.
Если D = b2 —4ас> 0, то пара-
бола у = ах2 4-to+c пересекает осьх
в двух точках с абсциссами
_ —6+ —4а£ —Ь— —4ас
2а ’ 2~____________________25
(рис. 87). В этом случае ах2 4- Ьх 4*
+ с > 0 при тех значениях х, кото-
рые расположены между корнями
уравнения ах2+Ьх+с—0, то есть при
X) < X < х2-
Наконец, если D = Ь2— 4ас — 0,
то парабола у =ах2 4* bx+с касается
Рис. 88.
139
оси х в точке с абсциссой х = — — (рис 88). В этрм случае не-
га
равенство их- 4- Ьх 4- О 0 не выполняется ни при каких зна-
чениях х.
Замечание!. Из paccMOipennuiu вьискает, что если дис-
криминант квадратного трехчлена ах2 4- Ьх + с положителен, то
это» трехчлен принимает как положительные, так и oiyn-
цательные значения. Если же дискриминант отрицателен, то все
значения квадратного трехчлена имеют один и тот же знак,
а именно знак коэффициента при х2
Замечание 2. При решении неравенства ах24- Ьх + О О
нет необходимости точно строить параболу у = ах2 4~ Ьх 4- с (на-
пример, совсем не нужно искать вершину параболы, точку пе-
ресечения с осью у и т д.). Достаточно лишь грубо представить
себе эту кривую. Единственное, что нужно сделать абсолютно
точно, — это найти корни уравнения ах2 4- Ьх+с— 0 (при D >0).
Примеры решения квадратных неравенств
§ 62
Пример 1. Решить неравенство
2х2 4- 4х - - 6 > 0.
Квадратный трехчлен 2х2 4- 4х — 6 имеет два действительных
корня Xt = — 3, х2 — 1- Поэтому парабола у = 2х2 + 4х — 6 пере-
секает ось х в двух точках, абсциссы которых равны —3 и 1.
Поскольку коэффициент при х2 больше нуля, парабола у = 2х2 4-
4- 4х — 6 направлена вверх (рис. 89). Из рисунка видно, что
трехчлен 2№ 4 4х — 6 положителен при х < — 3 и при х > 1.
П р и м е р 2. Решить неравенство
—х2 + х — I 2> 0.
м Дискриминант квадратного трехчле-
I 11 на — х2 4~ х — 1 отрицателен; Ё>=—3.
-2 -1 .0 Поэтому при всех х значения функции
V А х у — — х2 + х—1 имеют один и тот же
I б / знак, а именно знак коэффициента при
I / х2, то есть минус. Следовательно, нера-
1 / венство — х2 4- х—1 2> 0 не выполняет-
\ / ся ни при каких значениях х.
\ / ПримерЗ. Выяснить, при каких
I / значениях х дробь
\ / х2 ч 2* — 3
\ /I 2х — >?
Рис. 89.
положительна и при
отрицательна.
каких
140
Сначала указанным выше способом
определим знаки числителя и знамена-
теля данной дроби, а затем сравним их.
Числитель х24- '2х — 3 положителен
при х < — 3 и при х>-1 а отрицателен
при — 3 < х< 1 (рис. 90, верхняя чис-
ловая ось). Знаменатель 2% — х2 поло-
-4 3 -2 -1 0 I 2 3
~
I -и
0 2
Рис. 90.
жителей при 0 < х <Z 2 и отрицателен при х < 0 и при х > 2
(рис. 90, нижняя числовая ось). Из рисунка 90 видно, ч<о данная
дробь будет положительна при — 3 < х <Z 0 (в этом случае числи-
тель и знаменатель отрицательны) и при 1 <. х < 2 (в этом
случае числитель и знаменатель положи ел ьны): отрицательной
она будет при х < — 3 (числитель положителен, знаменатель от-
рицателен), при 0 •< х •< I (числитель отрицателен, знаменатель
положителен) и при х 2 (числитель положителен; знаменатель
огрипателен).
Упражнения
Решить данные неравенства (№ 439—446):
439. х2 — 4х + 3 > 0.
440. х2 — 6х + 5 < 0.
441. — 5х2 + Зх + 2 > 0.
442. х (1 — х) > 0.
443. х2 + х + 1 < 0.
444. х2 — х + 1 > 6.
445. х2 — 6х 4- 10 -< 0.
446. — Зх2 + 2х ; ! > 0
447. Найти целые значения х, удовлетворяющие неравенству
4х2 + 4х — 3 < 0.
Решить неравенства (№ 448, 449):
х2 4- 2х — 15
х + 1
<0.
449.^zJ*-J6>0,
х24-&»—
450. Найти целые значения х, удовлетворяющие системе не-
равенств
' х2 — 6> -р 5 Q
. —Зх2+2х—7 ’
X2 < 16.
При каких значениях а данные неравенства (№ 451, 452)
удовлетворяются для всех значений х?
451. (а — 1)х2 — (а + 1) х + (а + 1) > 0.
452. (а — 2) х2 4- 2 (2а — 3) х + 5а — 6 < 0.
453. При каких значениях а уравнение
(а — 3) х2 — 2 (За — 4) х 4- 7а — 6 = 0
имеет действительные корни?
141
454. При каких значениях а уравнение
5(а 4- 4)х2 — 10х а = О
имеет:
а) действительные корни;
б) действительные корни одного знака;
в) действительные корни разных знаков?
455. Не решая уравнения
х2 — (а 4- 1) х 4- (За — 5) = О,
определить знаки его корней.
Решение некоторых систем уравнений
§ 63
В этом параграфе мы рассмотрим некоторые типичные си-
стемы уравнений, решение которых сводится к решению квад-
ратных уравнений.
Пример 1. Решить систему уравнений
х2 4- Зу2 — ху — 2х 4-1 =0,
х — у — 1.
Поскольку второе уравнение этой системы линейно относи-
тельно каждой из переменных х и у, то одна из этих перемен-
ных, например у, легко выражается через другую:
у = х — 1.
Подставляя это выражение для у в первое уравнение системы,
получаем:
х2 4- 3 (х — I)2 — х (х — 1) — 2х 4- 1 - 0,
откуда
Зх2 — 7х + 4 = 0; х1== |; х2 = 1.
следующие значения у: yi = -i- ; у2 = 0.
образом, данная система уравнений имеет два ре-
Этим значениям х согласно второму уравнению системы соот-
ветствуют
Таким
шения:
У1=Т " *2=1- Уг = 0-
О о
Пример 2. Решить систему уравнений
f 14х2 — 5ху 4-Зу2 = 16,
I 6х2 — ху 4- у2 = 8.
Характерная особенность этой системы уравнений состоит в
том, что она содержит лишь выражения х2, у2 и ху, суммар-
ная степень х и у в которых постоянна и равна 2.
142
Для решения данной системы выполним следующие преобра-
зования. Из первого уравнения системы (1) вычтем второе,
умноженное на 2. В результате получим уравнение
2х2 — Зху + у2 = 0, (2)
правая часть которого равна 0.
Заметим, что. х =/= 0. В противном случае из (2) вытекало бы,
что у == 0, а это явно противоречит уравнениям системы (1).
Но если х =/= 0, то уравнение (2) можно почленно разделить
на х2, что дает
Мы получили квадратное уравнение относительно — . Из него
следует, что либо — = 1, либо У- — 2.
X X
Рассмотрим эти два случая отдельно.
1) Если -V- = 1, то у = х. Замена у в первом уравнении дан-
ной системы на х приводит к следующему результату:
14х2 — 5х2 -F Зх2 = 16, или 12х2 = 16.
Следовательно, х=+ 1Z— =+ Л/~ = + —•
“ F 12 31 к з ~~ /з
Отсюда получаем следующие два решения данной системы:
2) Если = 2, то у = 2х. Заменяя у в первом уравнении дан-
ной системы на 2х, получаем:
14х2 — 10х2 + 12х2 = 16,
или
16х2 = 16.
Следовательно, х — + 1. Отсюда, учитывая, что у — 2х, полу-
чаем еще два решения данной системы:
Xg 1, Уз 2, Л-4 = 1, у4 — 2.
Проверка показывает, что ни одно из полученных четырех ре-
шений системы (1) не является «посторонним».
143
Ответ. Данная система уравнений имеет 4 решения:
1)х = — ,у=—; 3) х — 1, у =2;
Уз у ) з у
2 2
2)х =-----у =---------— 4)х=—1,у=—2.
ГЗ J'T
Пример 3. Решить систему уравнений
( х + у = 6,
I ху =— 7.
Если только данная система уравнений имеет решение, то
по теореме, обратной теореме Виета, это решение должно со-
стоять из корней квадратного уравнения (см. § 52):
z8 — 6з — 7 = 0.
Это уравнение имеет корни — — 1, z2 = + 7. Следователь-
но, в роли решений данной системы уравнений могут высту-
пать только следующие две пары чисел:
х, = — 1, у, = 7 и х2 — 7, у2 = — 1.
Элементарная проверка показывает, что каждая из этих пар
чисел является решением нашей системы.
Ответ. Данная система уравнений имеет два решения:
Xt = — 1, yt = 7 и х2 = 7, у2 — — 1,
П р и м е р 4. Решить систему уравнений
( х— у =~ 8,
| ху = — 7.
Из второго уравнения следует, что х (— у) 7. Поэтому
I * + (—у) = 8,
I х-(—у)-7.
Мы получили систему уравнений, вполне аналогичную си-
стеме, рассмотренной в примере 3. Только роль неизвестных
играют не х и у, как в ^примере 3, ахи — у. Поэтому даль-
нейший ход решения этой системы такой же, как в примере 3.
Учащимся предлагается провести его самостоятельно.
П р и м е р 5. Решить систему уравнений
( *’ + у* = 5,
I ху —— 2.
144
Из второго уравнения получаем №у2 = 4. Но в таком случае
по теореме, обратной теореме Виета, х2 и у2 можно рассматри-
вать как корни квадратного уравнения
z2 — 5z 4- 4 = О,
откуда г, = 4, гг = 1. Поэтому возможны два случая: I) х2 4«
и тогда у2 — 1; 2) х2 — 1, и тогда у2 = 4.
Случай 1. Если х = + 2, то у = — 1 (согласно второму
уравнению исходной системы ху = — 2). Если х = — 2, то
у = 1.
С л у ч а й 2. Если х— 1, то у = — 2, если же х = — 1, то
у -2.
Мы получили 4 решения данной системы уравнений:
2, yt 1, Xj= 1, Уз ~ 2,
*2 — 2, у2 = I; х4 = — 1, у4 = 2.
Упражнения
Решить данные системы уравнений:
. | х2 4- Зху — у3 Н 2х — 5у =— 64,
I х —у = —7.
457, 2х3 — Зху — 19у2 х3 —бу2 =-250. = 25, 462. |2>'2-Зх3 = -19, ху =— 6.
458. । 7х3 — бху 4- 12у3 = 108, = 18. [ х 4- ху 4- у = 11, 463. У 1 х— ху 4- у — I.
459. । х4-2у=13, ху = 15. 464 |хУ+>' + х=:|1’ I х?-у 4- у3х = 30.
460. | 2х — Зу =— 18, ху =— 12. 465. И3 + У3=1’ 1 х 4- у — 1.
461, £ Ъ II । . 1 КЭ Л 1- Чс II *1“ ( __ . |2 — О | 466. * У 21’ 1 к 4- у = 3.
Графический способ решения некоторых
систем уравнений
§ 64
Некоторые системы уравнений могут быть решены графнче»
ски. Проиллюстрируем это на примере следующей системы:
I х2 4- у ~ 4,
( х 4- у = 2.
145
На одном и том же рисунке начер-
тил! две кривые, первая из которых
имеет уравнение № + у = 4, или у =
=4 х2, а вторая—уравнение х 4-у=2,
пли у = 2—х. Очевидно, что искомыми
решениями данной системы уравнений
будут координаты точек пересечения
этих двух кривых.
Как видно из рисунка 91. рассмат-
риваемые кривые пересекаются в двух
точках: А с координатами (— 1,3) и В
с координатами (2,0). Поэтому данная
система уравнений имеет два решения:
х-----1, у = 3 и z = 2, у = 0.
Упражнения
Решить графически следующие системы уравнений:
467.Н2 + 2у=Ю,
I х — у =--1.
468. | 2х2 — У=—2>
| Зх Ч у 1.
4С9. 1>'+2х2=3’
I хН-у - 2.
470. । У = Х" ’’
I у =—№ 4- 2х— 1.
Иррациональные уравнения
§ 65
Иррациональными уравнениями называются уравнения, со-
держащие неизвестное под знаком радикала. К таким относятся,
например, уравнения
= 34- Ух; Ух = 5 — 4х;
у4 2 — х = У х 4-6 4-
и т. д.
Мы ограничимся рассмотрением иррациональных уравнений,
которые содержат только квадратные радикалы. В связи с этим
следует напомнить, что квадратные корни можно извлекать
только из неотрицательных чисел. Такие, например, выражения,
как У— 3, У— 25, У — 10, не имеют смысла. Далее, под квад-
ратным корнем из положительного числа мы всегда подразуме-
ваем его арифметическое, то есть положительное, значение. Так,
]/4 — 2, а не — 2; ]Л25 = 5, а не — 5; У 2 = 1,4142 ..., а не
— 1,4142... и т. д.
Этих замечаний уже достаточно для того, чтобы мы могли
рассмотреть несколько типичных примеров иррациональных урав-
нений.
146
Пример 1 Решить уравнение
К* + 2 + = г.
Квадратные корни можно извлекать лишь из неотрицатель-
ных чисел. Поэтому допустимые значения неизвестной величи-
ны х должны удовлетворять системе неравенств
х — 2 0.
1 — х 0
Первое неравенстве этой системы дае'г х 2 второе х < 1.
Очевидно, что одновременно эти условия выполняться нс могут.
Поэтому множестве допустимых значений неизвестной величи-
ны х в данном случае пусто, то есть не содержит ни одно-о
числа. Но в таком случае данное уравнение не может иметь
действительных корней.
Рассмотренный пример учит нас постоянно помнить о следу-
ющей важном обстоятельстве. Прежде чем решать тс иль иное
иррациональное уравнение, нужно быть уверенным, чтс множе-
ство допустимых значений неизвестной величины не пустс. Если
ни одно из чисел не является допустимым для неизвестной ве-
личины. то можне сразу же сказать, что уравнение не имеет
корней.
Пример 2. Решить уравнение
Ух + 2.
Нь один из корней ]/х и У*— х Ht может быть отрицатель-
ным. Поэтому ни при каких действительных значениях величи-
ны х сумма этих корней не может равняться — 2. Следователь-
но, данное уравнение также не имеет корней.
Заметим, что здесь не было необходимости исследовать, какие
значения может принимать неизвестная величина х. Отсутствие
корней данного уравнения мы установили и бе? этого исследования.
Мы рассмотрели два простейших примера иррациональных
уравнений. В следующем параграфе будут рассмотрены более
‘сложные примеры.
Упражнения
Показать, что данные уравнения не имеют корней:
471. J'x — 3 + Ух^З ^— 1. 473« ]/Зх — 5 Ч- ]/6 — х= -7.
472. J '2х —7 + Ух = 0. 474. /4 — 4х f Ух —2 =6.
147
Примеры решения иррациональных уравнений
§66
Обычней способ решения нррацпснапьнгнл уравнений состоит
в освобождении их от радикалов и сведении к уже изученным
нами типам алгебраических уравнений (например, к линейным
или квалратным). Добился 3luiu иногда удается путем почлен-
ного возведения иррационального, уравнения в степень. По-
ясним это на ряде частных примеров.
Пример 1. Решить уравнение ।
х = у 2— х. I
Множество допустимых значений величины х определяется |
неравенством х < 2 Чтобы среди всех этих значении наити
корни нашего уравнения, возведем обе его части в квадрат. В Ш
результате получим: I
х2 = 2 — х, I
х2 + х — 2 = 0, I
откуда
X,- - - 2,
х2 = 1- 6
Каждое из двух полученных чисел попадает в множество до- Г
пустпмых значении величины х. Но это еще не означает, что §
— 2 и 1 — корни данного уравнения. Ведь к уравнению х2 =
= 2 — х мы пришли путем почленного возведения в квадрат ис-
ходного уравнения к
х = ]/2^х? 1
Но к такому же результату мы пришли бы, если бы почленно I
возвели в квадрат не это, а другое уравнение I
х=— У^х,
отличное от данного. Следовательно, в результате выполненных
преобразований мы можем получить новые, посторонние корни —
корни уравнения х = — 2— х, которые нас в данном случае не
интересуют. Вот почему, прежде чем дать ответ к данной за-
даче, необходимо сделать проверку полученных корней.
При х = — 2 левая часть данного уравнения принимает зна-
чение — 2, а правая ]/~4 = 2. Поскольку — 2 #= 2, число — 2 не
есть корень данного уравнения. При х -= 1 обе части нашего
уравнения принимают значения, равные 1. Поэтому 1 — корень I
этого уравнения. • I
Итак, данное уравнение имеет один корень х= 1. Что же '
касается числа — 2, полученного нами выше, то оно, как и )
следовало ожидать, является корнем уравнения х = — )Л2— х .
Пример 2. Решить уравнение
х = 1 ] ’х4 5.
Множество допустимых значении неизвестной величины в
данном случае определяется неравенством х > 5.
Перенося 1 из правой части о ^свую и возводя обе части
полученного уравнения в квадрат мы приходим к уравнению
(х—1)а — (|/х 4-5)2,
х2 - 2х + 1 = х + 5, х2 - Зх - 4 = О,
откуда
х, = 4, X- — — 1.
Проверка показывает, что из этих двух чисел корнем данного
уравнения является лишь число 4. Число — 1 является посто-
ронним корнем.
Ответ. Данное уравнение имеет единственный корень х = 4.
ПримерЗ. Решить уравнение
У х 5 + У 10 — х = 3.
Множество допустимых значений х определяется, очевидно, нера-
венством
5 < х < 10.
Возведя обе части данного уравнения в квадрат, мы получим:
х — 5 + 2 ] (х —5)(10 —х) + 10 — х = 9,
2 /(х —5)(Ю—х) = 4, 5)( Ю—х) = 2.
С последним уравнением мы поступим так же, как и с исход-
ным: возведем его почленно в квадрат. В результате получим:
(х — 5) (10 — х) = 4, —х 2 4- 15х — 50 = 4,
х2 — 15х4~ 51 = 0.
Итак, в результате двукратного почленного возведения данного
уравнения в квадрат в сочетании с другими элементарными пре-
образованиями мы пришли к простому квадратному уравнению,
корни которого равны:
X! = 6, х2 = 9.
Проверка показывает, что оба эти числа являются корнями
данного уравнения.
Ответ. Xj = 6, х2 = 9.
Пример 4. Решить уравнение
]/ х 4- 7 4- ]Лх — 1 — 4-
Множество допустимых значений неизвестной величины х оп-
ределяется в данном случае неравенством х > 1. Это уравнение
149
можно были бы решит 1^14 же способе.», п^горым мы решали
предыдущее уравнение Для этого нам пришлось бы дважды
применять метод почленного возведения в квадрат.
В данном СлучслС niOhwiG предложить г. другой прием.
Умножим почленно данное уравнение на выражение
1/х + 7 —Ух — 1, сопряженное* выражению + 7 + Ух — 1.
В результате, используя формулу для произведения суммы двух
чисел на их разность, получим:
[Ух Ч 7 + Ух — l’XV'^+7 — У Г— I) - 4 (Ух + 7 — Ух - 1),
или
(х +7) — (X- 1) = 4\уТ^7-Ух I).
Отсюда
4(КГ+7 —8,
1 'Т+7 1 '~1 = 2.
Теперь мы имеем:
У’х~+1 + = 4,
У’ х + 7 — Ух — 1 =2.
Складывая почленно эти уравнения, получаем:
2 УГ+7 = 6,
откуда ____
Ух + 7 = 3, х + 7 = 9, х - 2.
В процессе решения данного уравнения нам пришлось обе его
части умножить на Ух + 7 — Ух — 1. Но в результате такого
преобразования могли получиться посторонние корни. Вот по-
чему теперь необходимо проверить, является ли полученное
число 2 корнем исходного уравнения.
При х — 2 левая часть данного уравнения принимает значение
У9 + У Т = 3+1=4.
Следовательно, х = 2 — корень данного уравнения.
Ответ. Данное уравнение имеет единственный корень х = 2.
Рассмотренные методы решения иррациональных уравнений
таковы, что, используя их, мы не можем потерять никаких
* Одно выражение, содержащее знак радикала, называется сопряжен-
ным другому выражению, содержащему знак радикала, если произведение
этих выражений можно записать уже без знака радикала. Так, выражение
Ух + 7 — Ух — 1 является сопряженным выражению Ух + 7 -|-х— 1, по-
скольку (Ух + 7 + Ух — 1) (Ух + 7 — | х— 1) = (х-г_7) — (Л —1)=8; выра-
жение будет сопряженным выражению У а — I, так как
(У а — 1 ) (Уа + 1 )= а — 1, и т. д.
150
KGpneft. Зато, как показывают примеры 1 н 2, мы можем полу-
чить посторонние корни. Поэтому €.дс раз подчеркнем, что про-
верка полученных корней путем их подстановкг в исходные
уравнения является важной составной частью решения ирраци
ОНаЛЬНЫХ jраВНСпиЙ.
Упражнения
Решить уравнения:
475. /?--/х=3 = 2. 479. = 2^х--Ух^З.
476. /1—Зх — 3 ] х 480. I + х/х'?+ 24 —х 4-1.
477. 21 4- У 2г — 7 — х. 481. /а + х + /с — х = ]/Г2а.
478. }'4—х 4- /5+7 = 3. 482. /х^З — /Г+7 =-2— /К)
Из истории развития алгебры
§ 67
Методы решение квадратных уравнений были известны еще в древние
времена. Они излагаются, например, в вавилонских рукописях времен
царя Хаммурапи (XX в. до н. з.), в трудах древнегреческогс математика
Евк/ и дь (III в. до н. э.), в древних китайских и японских трактатах.
Многие математики древности решали квадратные уравнения геомет-
рическим способом. Например, для решения уравнения Г + 10х = 39 по-
ступали следующим образом. Пусть АВ = х, ВС = 5 (= 10 : 2). На стороне
АС = АВ + ВС строилск квадрат, который разбивало на четыре части,
как показано на рисунке 92. Очевидно, что сумма площадей I, II и
III частей равна х3 + Юх, или 39.
Если к этой площади прибавить площадь IV часть, то в результате
получится 64 — площадь всего квадрата. Нс эта же площадь равна (х 4 5'*,
так как ДС = х + 5. Следовательно,
(х + 5; » = 64,
х -+- 5 = 8,
х = Z.
В некоторых древних рукописях содержатся примеры решения приведен-
ных квадратных уравнении; которые, по существу, следуют формуле
Правда, задачи эти решаются не в общем виде, г
лишь при определенных числовых значениях коэф-
фициентов. Однако методы решение не оставляют
сомнения в том, что авторам их были знакомы общие
правила. Здесь следует указать, что в древние вре-
мена буквенные обозначения еще не использова-
лись. Систематически их ввел в математику лиши
французский математик Вьет, чье имя носит
известная нам теорема о корнях приведенного
151
квадратного уравнения. Отрицательные числа также не были шнрокс
известны ученым древности. Поэтому о формуле (1), как таковой, конеч-
но, не могло быть и речи.
Достаточно подробно методы решения квадратных уравнений изложены
в трудах знаменитого узбекского математика а л-Х орезми (IX в.). Одна
из его работ называется «Хисаб ал-джебр вал-мукабала», что в переводе на
русский язык означает «Учение о приведении н о двустороннем отнятии».
В этой книге рассматривались и линейные уравнения. Одним из методов
их решения был метод, названный «ал-джебр». От этого слова и произошлс
название «алгебра».
Задачи на повторение
483. Какие известные вам физические законы описываются
с помощью квадратных функций’
484. Чему равно число с, если при любых значениях а и b
уравнение ах2 4- Ьх + с = 0 всегда имеет хотя бы один корень?
485. При каких значениях а корни уравнения
(а — 1)хг — 2(о + 1) х + (о + 4) = О
равны между собой?
486. Разложить выражение
2х (2х + Ь) — a (4 v — о) — ab
на линейные относительно х множители.
487. Известно, что при любых значениях х функция у =
— ах2 4- Ьх 4- с принимает положительные значения. Докажите,
что а > О, с > 0. Можно ли утверждать, что в рассматриваемом
случае b > 0? Ответ поясните примерами.
488. Известно, что при любых значениях х
а,х2 4- btx 4- > Qzx2 4- b2x 4- с».
Докажите, что ot > а2, с, > с2. Можно ли утверждать, что в рас-
сматриваемом случае bt > b2?
489* - Решить уравнение
X X— 1
X 1
490. При каких значениях х выражение -----------— принимает
значение, равное
_£--L ’
(о4-2)*
491. Решить уравнение
, Ьх 2аЪ
v 4------=-------.
х — 2а х — 2а
492. При каких значениях а корни уравнения
х1 4- х — а (1 + а) = О
152
имеют
а) одинаковые знаки;
б) разные знаки?
493. Могут ли выражения х' — ах 4- 1 и 2г 4- ах 4- 3 быть
равиь при трех различных значения? х?
494. При каких значениях а непавенство ах* 4- (а — 1 х 4*
4- (а — 1) < 0 выполняете? для всех значений х?
Решить неравенства (№ 495, 496):
495. *—+ <0. 496. —А + 2 > 0.
л2 — Ях + 15 х2 - 7х 4- 6
497. При каких значениях а уравнение
(2а — Г,х2 4- (3 - о) х 4- 1 = 0
имеет действительные копии’
498. Прг каких значениях с квадратное уравнение
5 (10 - а) х2 — 1Сх - 6 — а = (
а) имеет корни;
б’ имеет не более одного копня
в) не имеет корней,
г) имеет одинаковые корни;
д) имеет корни одинакового знака;
е' имеет корни разных знаков’
Решить системь уравнений (№ 499—502;:
499. ( »Z*— УГУ = 2’
I ху = 27.
500. । х у К
I ху — 50.
501
х2 — у' = а,
х — у = Ь.
502. у х
х -4- у — 2
Решить уравнения (№ 563—565):
503*. ]/1 4- ал = х 4-1' 1—ах.
504. /1 -‘ X 4-/1 —х = 1
505. ]/22—х —/ТсГ^х = 2.
506. Не решая упавнениг
х2 4- 2ах -- (а2 + 2а — П = 0,
определить знаки его корней
153
Рис. 93 б.
Указание. Освещенность
507. Доказать, что
корни уравнения 4-
+ Ьх с=0 (если толь-
ко они существуют!)
обратны корням урав-
нения
с№ -|- Ьх + а = 0.
508. Могут ли кор-
нями уравнения х2 4-
4- рх + q =0 быть чис-
ла р и 9?
509. При каких зна-
чениях а сумма квад-
ратов корней уравне-
ния х2 4- о%4-(а—2) = 0
будет минимальной?
510*. При каких зна-
чениях а сумма кубов
корней уравнения
~ Зх2 4- З(а-М) х + аг =0
_ будет максимальной?
511. Квадратное
_ уравнение Зха4-Ьх 4- с=
=0 имеет единственный
' ~ корень, равный 1. Че-'
х му равны Ь и с?
_ 512. На неограни-
ченной прямой, со-
_ единяющей два источни-
ка света разной силы Д
_ и У2. определить точ-
ку, равно освещенную
обоими источниками.
Расстояние между ис-
точниками света равно а.
обратно пропорциональна
квадрату расстояния от источника света.
513. Потребность колхоза в ячмене 4000 ц. Если увеличить
урожай ячменя на 8 ц с 1 га, то можно будет уменьшить площадь
посева ячменя на 25 га. Сколько гектаров засеяно ячменем и ка-
кой урожай в центнерах с I га?
514. Написать уравнения парабол, приведенных на рисунках
93 а и 93 б.
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ
ПОКАЗАТЕЛЕМ. СТЕПЕННАЯ ФУНКЦИЯ
IV
Степень с натуральным показателем
Возведение в степень произведения и частного £ 68
Пусть с — произвольное действительное число, ап — натураль-
ное число, большее или равное 2. 1огд< п-я степень числа a
(обозначается а") есть произведение п чисел, каждо1 из котооых
равно а:
an = а а а ... а.
Например,
23 = 2 • 2 2 = 8,
I 3/ ’ 3, \ с/ \ 3/ \ 3, 81
Число а в выражении г" называете основанием, a t — пока-
зателем степени. 1ерв£>н степеныс действительной: числа а назы-
вается самс это число а. По аналогии с л-й степенью (п > 2)
числа а первую степень этого числа следовало бы записывать как
а’, но поскольку это выпажение равно и тс единицу в запиш а1
обычно опускают и пишут просто а.
Степени с натуральными показателями обладают рядом важ-
ных свойств которые мы рассмотрим ниже.
1 е с р е м а 1. Степень положительного числа с любым
натуральным показателем положительна.
Степень отрицательного числа с четным показате-
лем положительна, а с нечетным показателем отри-
цательна.
Действительно -если а~> 0, то сп как произведение п поло-
жительных чисел положительно. Если а <. О, то о2* как произ-
ведение четного числа отрицательных чисел положительно,
a как произведение нечетногс числа отрицательных чисел
отрицательно.
Ч р 1 меры:
'—3)с =• 81 (четное число отрицательных сомножителей)}
(— 2)5 — — 32 (нечетное число отрицательных сомножителей).
155
Теорема 2. Чтобы возвести в степень произведение,
достаточно возвести в эту степень каждый сомножи-
тель и результаты перемножить, то есть
(а Ь)а =апЬп.
Доказательство. По определению степени
(а • Ь)" — (ab) (ab) ... (ab).
п
Используя коммутативный и ассоциативный законы умноже-
ния, получаем:
(ab) (ab) ... (ab) = (а а ... а) {Ь b ... Ь} = апЬП,
Г1 п
что и требовалось доказать.
Мы получили правило возведения в степень для случая двух
сомножителей. На самом же деле оно верно для любого числа
сомножителей, например:
(а • b • с - d)n — a!’br,cr,drl.
Формулу (ab)n — апЬп иногда полезнее читать справа налево
апЬЛ = (ab)'1.
Чтобы перемножить степени с одинаковыми показа-
телями, достаточно перемножить основания этих
степеней, а показатель оставить прежним.
Например,
23 • З3 — (2 • З)3 = 63 = 216;
12* ( *JS= (12 • З3 = 243;
164 • M-V . 44 = (16 • 1 . 4 24 = 16.
\32/ \ 32 /
Теорема 3. Чтобы возвести в степень дробь, доста-
точно возвести в эту степень отдельно числитель и
знаменатель и первыйрезультат разделить на второй,
то есть
умножения дробей
(а \п_ а а
Т) ~ ~b'~b
Примеры:
( 2 \4 2* 16
\ 3 / 3« — 81’
Доказательство. По определению степени и правилу
а _ а- а ... а _ аП
7 — ь-ь ...ь ~ ~ь^'
\ 4J ~ 43 ~ 64'
156
Упражнения
515. (У с т н о ) Какие из данных чисел являются положитель-
ными и какие — отрицательными:
4)-(- Г5)6; 7, (°/3)5; 10) (2-|/5)6;
3) (- З)5;
5)-(-|j3: 8) (-сг/2)88; 1ь(г/7--|р
6) (~ 9) ^2 “ )1?- 12) U - о)*3?
516. Упростить выражения:
а) 2=4=83 В) (49)..(_±у,21<;
б) 53153253(~)3; г) (— -Г.
\125/ \ Г7/ \ 2/\ 15/
517. Степени каких чисел не изменяются при произвольном
изменении показателя?
Умножение н деление степеней с одинаковыми
основаниями § 63
Теорема 1. Чтобы перемножить степени с одинако-
выми основаниями, достаточно показатели степеней
сложить, а основание оставить прежним, то есть
ат • ап = атхп.
Доказательство. По определению степени
ат • а” = аа .. а • а-а ... а = и-а ... а =ат+п.
т п т-^-г
Например,
22 . 2з = 25 = 32; (— 3) • (— З)3 = (- 3? - 81.
Мы рассмотрели произведение двух степеней. На самом же
деле доказанное свойство верно для любого Числа степеней
с одинаковыми основаниями.
Например,
а” ап • а* а' — am+tt+lt+l.
Теорема 2. Чтобы разделить степени с одинаковыми
основаниями, когда показатель делимого больше пока-
зателя делителя, достаточно из показателя делимого
157
вычесть показатель делителя, а основание оставить
прежним, то есть при т^>п
• = а—" (а 0).
Доказательство. Напомним, что частным от деления
одного числа на другое называется число, которое при ум ноже-
ат
нии на делитель дает делимое. Поэтому доказать формулу — =
а”
= ат~", где а Ф 0, это все равно, что доказать формулу
ат~п • ап — ат. i
Если т > п, то число т — п будет натуральным; следовательно,
по теореме 1
, qti __ л)4-л __
Теорема 2 доказана.
Например, 3 - = З10-8 = 3:
9;
— = 46-3 = 4з = б4
43
Следует обратить
доказана нами лишь
доказанного пока
внимание на то, что формула
ат
— - ат~" (а 0)
cP
в предположении, что т 2> п. Поэтому из
нельзя делать, например, таких выводов:
-- -- 38-,° - 3~2
З10 '
К тому же степени с отрицательными показателями нами
еще не рассматривались и мы пока что не знаем, какой смысл
можно придать выражению З-2.
Теорема 3. Чтобы возвести степень в степень, дос-
таточно перемножить показатели, оставив основание
степени прежним, то есть
(лп)'я = апт.
Доказательство. Используя определение степени и тео-
рему 1 этого параграфа, получаем:
т
(ап)т — ап-ап ... ап — an+n+ " +" = апт,
т
что и требовалось доказать.
Например, (2J)2 — 2е -= 64;
1__
1024'
Формулу (ап)т — апт иногда полезнее
апт = (а',')гп.
читать справа налево:
158
Упражнения
518. (У с т н о.) Определить х и
I) 2 • 22 - 2:| • 2' • 25 • 2е = 2 х;
2) 3 • З3 • 3Б • З7 • 3® = 3х;
519. (У ст н о.) Упростить:
з уравнений:
3) 42 4* - 4е - 4* • 4’° = 2х;
4) 1 _ 1_____1_ = I
5 25 125 ' 625 5<‘
8) (9е)7;
9) |^]*;
,0)
4) ;
(-1 2)11
520. (Устно.) Упростить:
п ОС2)15 . 2)
(F 2)17 ’ (-б)*03 '
(21<3)1П
125 ‘
степеней с
3) : 4)
(_3)ico
представить в виде
521. Данные выражения
одинаковыми основаниями:
1) 32 и 64; 3) 8е и 16'; 5) 41№ и 3250;
2) — Ю00 и 100; 4) — 27 и — 243; 6) 817ь • 82М г. 3е00 • 4,а0.
Упростить выражения:
522. (— 2а)в — (— 8а')2 — [— (2а)2]3 — [2 (- а)3)2.
523. (— 2а)10 — (— 13а5)2 — [— (2а)2]Е - [2 • (— а6)]2.
Сравнение степенен
§70
Теорема 1. Из двух степеней с одинаковыми показа-
телями и положительными основаниями больше та,
основание которой больше. Другими словами, если а > &>0,
то при любом натуральном п
ап > Ьп.
Это свойство было доказано нами в главе 1 (§ 12).
Пример. Какое число больше: 2300 или З200?
159
Для решения этой задачи представим данные числа в виде
степеней с одинаковыми показателями, используя тождество
атп = (а,л)л.
Имеем:
2го = 23-100 = (23)100 = 8101, З200 = З2’100 = (Зг)1ос =91М.
Так как 9> 8, то 9IM > 8100. Следовательно,
3200 > 2300
Теорема 2. Если 0 •< а •< 1, то из двух степеней ат и
ап больше та, показатель которой меньше.
Если 1, то из двух степеней ат и ап больше та,
показатель которой больше.
Доказательство. Пусть т>п. Тогда т = n -|- k, где
k — некоторое натуральное число. Поэтому
ат = аг' +* = anak.
Если 0 < а < 1, то 0 < а* <. 1. Следовательно, ст = сп - ак < а'-.
Если же а > 1, то а* > 1. Следовательно, ат— ап • ah > аг.
Например, Y°° <)5°; 3100>350.
\ 3 / \ 3 /
Упражнения
526. Данные выражения представить в виде степеней с
одинаковыми показателями и сравнить их по величине:
1) 4= и 28; 4) 4300 и З40®; 6) и
2) 27я и 9е; 5) - i и (- -Ц3; 7) (-М™ и f 1Г
8 \ 32/ \16/ \2/ ‘
3) 1252 и 2Б3;
527. Данные вырйкения представить в виде степеней с
одинаковыми основаниями и сравнить иЯ по величине:
1) 8® и 163; 3) (— З)7® и (— 27)1®;
2) 4100 и 32®°; 4) 8Р®° 8”°° и 3ю0 • 167®.
528. Ито больше: (ап)т или (ат)"?
Степени с нулевыми и отрицательными
показателями § 71
В § 69 мы доказали (см. теорему 2), что при т > п
^--а"-” (п^О).
ап
Вполне естественно желание распространить эту формулу
и па случай, когда т < п. Но тогда число гп — п будет либо
160
отрицательным, либо равным нулю. А мь. до сих пор говорили
лишь о степенях с натуральными показателями. таким образом,
мы сталкиваемся с необходимостью ввести в рассмотрение сте-
пени действительных чисел с нулевыми и отрицателоными
показателями
Определение!. Любое число а, не равное нулю, в нулевой
степени равно единице, то есть при а =/= О
а0 = 1. (1)
Например, 13,7)» =1 л° =-!; = I
Число С нулевой степени не имеет, то есть выражение 0п не
определено.
Определение 2. Если а =^= 0 н п — натуральное число, то
= 4, (2)
ап
то есть степень любого числа- неравного нулю с целым отои-
цательным показателем равна дроби, числитель котоооь есть
единица, а знаменатель — степень того же числа а, нс с показа-
телем, противоположным показателю данной степени
TJ о_р 1 1 / ’ \-3 1 О
Например, 3 • = — = - ; I---) =----------=----- = — 8.
’ °'2 (-?)’ -5
Приняв ап определения, можно доказать, что при а 0 Фор-
мула
— = ст~п (3)
ап
верна для любых натуральных чисес т и п, а не только для т > п.
Для доказательства достаточно ограничиться рассмотрением
двух случаев: т = п и т < п, поскольку случай т > г уже
рассмо^рег ь § 69.
ant ап
Пусть т = п; тогдг — = -- = 1. Значит, левая часы равен-
а" ап
ства (3) равна 1. Правая же часть npi п = п обращаете! -в
ат~п = ап~п = с°
Но по определению а0 = 1. Таким образом, правая част! равен-
ства (3) также равна 1- Следовательно при т — п формуле (3)
верна
Теперь предположим, что т < и. Разделив числитель и
знаменатель дроби — на ат, получим:
ат _ 1
а1 а" '
6 Заказ 26!
16
an am J
Так как л > m, то — = an~m. Поэтому — =--------. Используя
ат 1 аа ап~'п 1
определение степени с отрицательным показателем, можно
1 ат
записать------= = ат~п. Итак, при т<п — — ат~п, что
ап~т г пп
и требовалось доказать. Формула (3) доказана теперь для любых
натуральных чисел т и п.
Замечание. Отрицательные показатели позволяют записы-
вать дроби без знаменателей. Например,
— = З-1; — = 2 5-1; вообще, а — а • 6-1.
3 5 Ь-
Однако не следует думать, что при такой записи дроби
превращаются в целые числа. Например, З-1 есть такая же
1 2
дробь, как н —, 2 5-1 такая же дробь, как и , и т. д.
3 5
Упражнения
529. Вычислить:
10-2
<- 2)\’
3) 6-4^)] ;
530» Записать без знаменателей дроби:
531. Данные десятичные дроби записать в виде целых выраже-
ний, используя отрицательные показатели:
1) 0,01; 3) — 0,00033; 5) — 7,125;
2) 0,65; 4) — 0,5; 6) 75,75.
Свойства степенен с целыми показателями
§ 72
В § 68 и 69 мы доказали следующие свойства степеней с
натуральными показателями:
1) (а Ь)'п = ат • Ьт;
( а\т — а"1
\Ь J Ьт’
3) ат - аП = ат+п;
4) ат . а” — ат п;
5) (о'")" = атп.
162
Все эти свойства оказываются справедливыми и для степеней
с любыми целыми (положительными, отрицательными и нулевыми)
показателями, если только числа а и Ь не равны нулю.
Докажем, например, что при а Ф О
ат • ап = ат+п, (1)
где тип — любые целые числа.
Поскольку для натуральных чисел т и п формула (1) уже
доказана, то нам остается рассмотреть лишь следующие три
случая: 1) числа т и п отрицательны: 2) одно из чисел т и п
положительно, а другое — отрицательно; 3) хотя бы одно из
чисел т и п равно нулю.
Случай 1. Пусть т и п — отрицательные числа. Тогда по
определению степени с отрицательным показателем
ат-а” = ------------------------- =----!—-
а~"‘ а~п а~т‘С~п
Так как т и п отрицательны, то — т и — п положительны.
Поэтому
а~т • а~" = а~т~н = а~{т+п').
Значит, — = _(Д-пу . Используя определение степени с отри-
цательным показателем, запишем:
----L— = ат+п. •
а~ <«’+п»
Следовательно,
ат. ап = ат+п.
Слу-чай 2. Один из показателей тип положителен,
а другой — отрицателен. Пусть, например, т > 0, а п -< 0. По
определению степени с отрицательным показателем
1 а”-
ат • а” - - ат • — = —,
а~г а~п
Число — п положительно; значит, по доказанному в § 71
. а"‘
— дда—<—п) _ ат+п.
а~г‘
Поэтому
ат -ап — °-— — <zm+".
а-”
С л у ч а й 3. Хотя бы один из показателей тип равен нулю.
Пусть, например, т — 0. Тогда пс определению нулевоЁ степени
ат . ап - - . ап = J . ап — а’,
Ь-
163
но ал‘+п— а°+ '•= ап. Значит, формула
ат . ап — ат+п
верна н в этом случае.
ТакИМ ОбраЗОМ, ilpll Я #= О формула
ат. ап — ат+л
верна для любых целых чисел т и п.
Аналогично могут быть доказаны и остальные четыре свой-
ства степеней с целыми показателями, упомянутые в начале
этого параграфа
Пример ы. 1) 4 6 • 4* = 43 = 64;
2) (З2)-4 -- 3~ь = —.
6561
3) ИтГТ = Кб-1)-2]3 = [52]3 = 5е = 15 625-
В заключение отметим еще два свойства степеней с целыми
показателями (заучивать эти свойства не нужно).
6) Если а > Ь > 0 н и отрицательно, то ап <; L'-, то есть
из овух степеней с положительными основаниями и
одинаковыми отрицательными показателями больше
та, основание которой меньше.
Например,
е-З^и-зИ
5 3<4 3—<-|; — > - (9>4)
\125 64/ \2) 4 '
я Т. д.
7) Если 0 < а <_ 1, то из двух степеней ат и ап больше
та, показатель которой меньше.
Если а> 1, то из двух степеней ат и аП больше та,
показатель которой больше. Под т и п здесь подразумева-
ются любые целые числа, а не только натуральные.
Например,
и т. д.
Предлагаем
/1 \-8^ I 1 \-4 оо - 1 с
I — I > — I , или 32 > 16
\ 2 / \ 2 ) ’
2-5 <_ 2-4, или — < —
32 16
учащимся доказать эти свойства самостоятельно.
Упражнения
532. Вычислить:
а) аъ а~3; а4 • я~г; а* : я-1;
б) За'* • 4а1; 5ап : — а-";
2
а 3 : а
ч
— а~т: а”",
2
2-1 а3 (а +b)
~3-2а~2 (а + Ь)~3-'
164
г) (а — (1 — a)-* 1] •
a-=~a+'
д, (x~2 -r- a-3) • 'лт-2 — a-").
e' — p--'-a—-----; a3 * * * * (a- — 2abb2)'.
‘ a-» —«г»
533. Какое число больше:
aj 5-63 или 5-84; в' 5-вз или [Л—' 3j
б) 5-03 ил: 6‘°8; г) 1 у3 или 5-вз?
\ 5 /
534, Упростить выражение
[? (а-*)]-’- а-1- ]
и найти его чистовое значение при
а — — 4 b — — ’.
2
535. При каком показателе п степень ап не зависит от
основания а?
Функции у =хп при п = 1, 2, 3 § 73
Каждому значении величинь х формула
У = х“,
rjif. п — натуральное число, ставит ь соответствие вполне опре-
деленное значение величины у. Следовательно, эта формула
определяет у как функцию аргумента х. Рассмотрим такие функции
при п = 1, 2, 3.
1. Функция у =х. Эта функция определена дл» всех значе-
нии х. Поэтому можно сказать, что областью определения функ-
ции у = х является совокупность всех чисел.
Данная функция принимает любые числовые значения. Множе-
стве всех значений которые принимает та или иная функция,
называете», областью изменения этой функции. Поэтому можно
сказать, что областью изменения Функции у = л также является
совокупность всех чисел.
График функции у = х (рис. 94) есть пряма»., проходящая
через начале координат и разделяющая первый i тре~ий коор-
динатные углы пополам. Этот график хорошо иллюстрирует
свойстве функции у = х.
165
Так большему значению ар.,мента
х соответствует и большее значение
функции у. Например, при хг :> Xf
Уг> У< (рис 64)- 1 акне функц.л. при-
нято называть монотонно возрастаю-
щими.
ФУНКЦИЯ V = л ncttiil nu.fl. Э'.и озна-
чает, что при изменении знака аргу-
мент на противоположный она, не
изменяясь i iv/ абсолютной величине,
изменяет свои знак па противополож-
ный. График функции у — х симметри-
чен относительно начала координат.
2. Функция у = х2. Eha функция
была подробно изучена нами в главе ID.
Областью ее определения является
множество всех действительных чисел,
а областью изменения — множество
всех неотрицательных чисел. Графиком
этой функции является направленная
вверх парабола с вершиной в начале
координат (рис. 95). Как видно из ри-
сунка, при отрицательных значениях
аргумента х функция у = х2 монотонно
убывает. Это означает, что из двух
отрицательных значении аргумента
большему соответс1вуст меньшее значе-
ние функции. При положительных зна-
чениях аргумента функция у х2 монотонно возрастает. Это
означает, что из двух положительных значении аргумента боль-
шему соответствует большее значение функции. При х = О
функция принимает наименьшее значение, равное нулю. Наиболь-
шего значения функция не имеет.
Функция у = х2 четна. Это означает, что изменение знака
аргумента х на противоположный не изменяет значения функции у.
График такой функции симметричен относительно осн у.
3. Функция у = х3. Областью определения этой функции
является множество всех действительных чисел. Функция является
нечетной, поскольку (—х)3 = —х3. Поэтому для построения ее
графика достаточно составить таблицу значений только для
положительных значений аргумента х:
* 101 т 111112 I 3
0 UU1118127
166
Значения функции для отрицатель-
ных х отличаклся от значений функции
Д чЯ Сии । ЗС1 1 оуЮ1Дг1 X i CJlbuoIX
к только знаками. Например, при х=
i 1 I
= У = --> поэтому при х =-----------
4 61 4
ж * 1 * г с
у будет равен — при х — 2 у = 8;
поэтому при х = - 2 убудет равен 8
11 г. д. Теперь, испильзуя составленную
таблицу и свойство нечетности функции Р,,с- 96.
у = х3, построим график этой функции
(рис. 96). Кривая, изображенная на рисунке 96, называется куби-
ческой параболой.
Кубическая парабола наглядно демонстрирует, что функция
у = х3 всюду монотонно возрастает, принимая любые значения.
Областью изменения этой функции явлиеюм совокупность всех
дейывительных чисел. Следует особо отметить поведение этой
кривой вблизи начала координат. Здесь кубическая парабола под
ходит к осн абсцисс, как бы одновременно и касаясь этой оси
и пересекая ее.
Упражнения
536. Какими общими свойствами обладают функции у = х,
у = г и у = х3?
537. Построить графики функций
а) у — х3— 1; б) у — (х - I)3; в) у = (х + 2)3; г) у = jx3!-
Функции у — х" при п = — 1 и п = — 2
§ 74
1. Функция у = х 1. Областью определения функции у = х *,
1
или у = —, является множество всех действительных чисел,
X
кроме нуля. Эта функция нечетна, так как------------. Поэтому
для построения ее графика достаточно составить таблицу значе-
ний только для положительных значений аргумента х:
Используя эту таблицу и свойство нечетности функции у = х~*,
построим ее график (рис. 97). Этот график, как видно нз рисунка,
состоит из двух кривых, одна из которых целиком находится
167,
в первом, а другая—в третьем коорди-
натном углу. Они симметричны друг
другу относительно начала координат.
Вместе эти кривые называются гипер-
болой, а каждая из кривых в отдель-
ности — бс/нвью гиперболы.
Заметим, что при всех положитель-
ных значениях х функция у —х 1 моно-
тонно убывает. То же верно и для всех
отрицательных значений х. Однако было
бы ошибочно утверждать, что эта функ-
ция является монотонно убывающей
всюду. Например, значению аргумента xt = — 1, соответствует зна-
чение функции yi ~ — 1, а значению аргумента х2 = + 1 — зна-
чение функции у2 -- 1. Имеем: х2 > xt и у2 > У1- Дтя монотонно
убывающей функции из х2 > Xj должно вытекать у2 < yt. Но здесь
это условие не выполняется. Следовательно, говорить, что функция
у = х-1 всюду монотонно убывает, нельзя. Однако можно сказать,
что эта функция убывает на любом отрезке, на котором она
определена (то есть на любом отрезке оси л, не содержащем
нуля).
Функция у = х-1 принимает любые числовые значения, кроме
нуля. Значит, областью ее изменения, так же как и областью
определения, является множество всех действительных чисел,
кроме нуля.
Следует обратить внимание на поведение функции у = х-1
вблизи точки х = 0. Если значения аргумента х неограниченно
приближаются к нулю, оставаясь положительными, то соответ-
ствующие значения функции у неограниченно растут. Если же
значения аргумента х неограниченно приближаются к пулю,
оставаясь отрицательными, то соответствующие значения функ-
ции у неограниченно убывают.
2. Функция у = х~2. Областью определения функции у = х-2,
1
или у =—, является множество всех действительных чисел,
кроме нуля. Так как
то функция у = х-2 четна. Поэтому для построения графика
этой функции достаточно составить таблицу ее значений толькс
для положительных значений х:
168
Значения этой функции при отрица-
тельных х равны ее значениям при
соответствующих ПОЛОЖИТСльнь.Х X.
Например, [—= 2~
пользуя составленнук таблицу и сьой-
ствс четности функции у = х~2, пост-
роим ее график (рис. 98). Он состоит
ИЗ ДВул ВеТВей, одна ИЗ китОрЫл цели-
ком расположена в первом, а другая —
во втором координатном углу. Эти кри-
вые симметричны друг другу относи-
тельно оси ординат. Необходимо подчеркнуть, что ни
них е отдельности нелвзя считать графикоь функции
Только взятые вместе, они образуют этот график.
Функция у — х 2,
1
или у ,
X2
принимаем только
одну из
у = х~2.
положи-
телоные значения. Поэтому график ее расположеЕ целикок выше
осе х. #
Когда значения аргумента х неограниченно растут (или
неограниченно убывают), соответствующие значения функции у
неограниченно приближаются к нулю, оставаясь все время по-
ложительными. При неограниченном приближении значений аргу-
мента х к нулю (как слева, так и справа' соответствующие значе-
ния функцш' у неограниченно расту"'. Эбпастыо изменения функ-
ции у = х~2 является совокупность всех положительных чисел.
Упражнение
538. Построить графики функций:
а' У = (х — О-1; в) у = |; Д' У = х-2 — 2;
б? у = (х 4- 2Г; г) у; = | х Г»; е- у = Щ
х+ 1
Корень п-й степени из действительного числа а § 75
Пусть п — натуральное число, большее пли равное 2, а с —
произвольное действительное число Тогдг корнем л-й степени
из числа а (обозначается а) называется число п-я степень
которого равна а.
Например, У — 8 = — 2, так как (— 2'3 — — 8; V»1 - 3, так
как З4 — 81. Число — 3 также является корнем 4-й степенЕ из
числа 8), поскольку (— З)4 = З4 = 81
Вошло в обычай корпи второй степени называть квадратными,
а корни третьей степени — кубическими. В выражениях тип? а
число 2 обычно опускают и пишут поосто у' а .
169
Фактически корень n-й степени из действительного числа
мы определяем как корень уравнения
х" —- а.
Уравнения, как мы знаем, могут иметь, а могут и не иметь
корней, ючно так же корень n-й степени из числа и миже»
существовать, а может и не существовать Когда же он суще-
ствует и сколько различных значений может он принимать? Этот
вопрос будет рассмотрен в следующих параграфах.
Упражнения
539. В какую сумму обратится денежный вклад в а рублей
через п лет, если ежегодный прирост составляет р%?
540. Определиib ежегодный прирост, если известно, чтс через
каждые 20 лет вклад увеличивается вдвое.
541. Производительность труда увеличивается каждый год
на одно и то же число процентов по сравнению с предыду-
щим годом. В результате за три года она возросла на 27%. На
сколько процентов она увеличивалась ежегодно?
542. На сколько процентов нужно увеличивать производитель-
ность труда ежегодно, чтобы за 7 лет она возросла вдвое?
Корень л-й степени из положительного числа а § 76
Теорема 1. Для любого положительного числа а
существует положительный корень пй степени.
Другими словами, для любого натурального числа п и любогс
положительного числа а уравнение
хП = и
имеет положительный корень.
Мы не будем доказывать эту теорему, а укажем лишь, как
можно находить приближенное значение положительного корня
степени п из положительного числа а. Найдем, например, при-
ближенное значение ^2.
Приближенными значениями корня с точностью до 1 будут,
очевидно, 1 (с недостатком) и 2 (с избытком). сгобы найти пер-
вый десятичный знак приближенного значения 2, найдем
в ряде
1,0; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2,0
два таких последовательных числа, чтобы куб первого из них
был меньше 2, а куб второго — больше 2. Для этого возьмем из
чисел нашего ряда среднее 1,5 и возвысим его в куб. Мы най-
дем: 1,53 — 3,375, что больше 2. Так как числа, стоящие справа
170
ui 1,5, при возвышении е куб дают результат еще больши!, то
м л можем отбросить всю правую половину ряд. и дальше ис-
пытывать лишь числа:
1.1 ',2. 1,3; 1/.
Возвысив Е куб Среднее ИЗ ЭТИХ ЧИСеЛ — 1,2. Пилучпм
1,728, что меньше 2. Куб числа 1,1 будет еще меньше. Значит,
дальнейшему испытанию подлежат только числа 1,3 и 1.4.
Возвысив в куб 1,3, получим 2,197 что больше 2 как, мы
нашли Два числа 1,2 и 1,3, таких, что куб перього из них
меньше 2, а куб второго больше 2. Эп числа и будут прибль-
женнымг* значениями /2 с тичписияо до 0,1 . 1,2 — с недостат-
ком а 1,3 — с избытком
Дл; нахождения солях долей нужно испытать следующие
числа:
1,2 ; 1,22; 1,23; 1,24 ... 1,29.
Взяв в эюм ряде среднее число 1,25 и возвысит его ь куб,
найдем 1,253 = 1,953125, что меньше 2 Значит тсперо надо
испытать только числа
1,26 1,27; 1,28; 1,29.
Имеем: ,263 = 2,000376, что больше 2. Значит, приближен-
ными значениям! fz2 с точностыо до 0, 01 буду": 1,25 (с недо-
статком) и 1.26 (с избытком).
Если указанный процесс нахождения последовательны? де-
сятичных знаков корня продолжать дальше, то мы будем получать
значения j'/2 все с большей и большей точностью
Мы показали на примере, как приближенно, но с любой
степенью точности можно отыскать корень третьей степени из
положительного числа 2 '"акнм же образом можно отыскивать
приближенные значения корня любой степени иг любого поло-
жительного числа.
Оьметик, чтс еслЕ: о представим в виде конечной деся-
тичной дроби, то в принципе с помощью описанного метода
значение корня можно получито абсолютно точно (< ’ н< при-
ближенно».
Теорема 2. Всякое положительное число а имеет
ровно один положительный корень степени п.
Доказательство будем вести методол от противного. Пред-
положим, что существует несколько различных положительных
корней п-г степени из положительного числа и. Пусть b и < —
два таки?: корпя. Тогда
1?-‘ =• сч - а (1)
Так как числа b и с различные, то одно из них больше другого.
Пусть, например, Ь>с. Тогда должно быть Ь" >- г но эт<
противоречит соотношении (1). Знач! т, наше предположение о
171
существовании нескольких различных положительных корней
неверно. Таким образом, существует только один положитель-
ный корень /i-й степени из положительного числа а.
А существуют ли отрицательные корни м-й степени из поло-
жительного числа «? Ответ на этот вопрос дают последующие
теоремы.
Теорема 3. Отрицательных корней нечетной сте-
пени из положительного числа не существует.
Другими словами, при положительном а уравнение
№*+! = а
не имеет отрицательных корней.
Доказательство этой теоремы очень простое, и потому мы
опускаем его. Учащиеся без особого труда могут провести его
самостоятельно.
Теорема 4. Существует и притом только один от-
рицательный корень четной степени из положитель-
ного числа. Он отличается от положительного корня
из этого числа лишь знаком.
Доказательство. Пусть b есть положительный, корень
уравнения
x~k = а(а> 0).
Такой корень существует в силу теоремы 1. Но тогда
= а
и, следовательно,
(_ b)~k = а.
А это означает, что отрицательное число — Ь является корнем
n-ii степени из числа а. Тем самым доказано существование
отрицательного корня.
Предположим теперь, что отрицательных корней степени 2k
нз положительного числа а несколько. Пусть — b и — с — два
таких корня. Тогда
(— Ь)2к - (— с)2* = а.
Отсюда вытекает, что
fc2* = c-k = а.
Следовательно, существует два различных положительных корня
степени 2k из положительного числа а: b н с. Но этс противо-
речит теореме 2. Таким образом, наше предположение о суще-
ствовании двух различных отрицательных корней степени 2k
из числа а неверно. Тем самым доказана единственность отри-
цательного корня.
Теорема 4 доказана.
Объединяя теперь теоремы 1, 2, 3 и 4, мы приходим к сле-
дующему выводу.
172
Существует ровно один корень нечетной степени из
положительного числа. Этот корень положительный.
Существует ровно два корня четной степени из по-
ложительного числа. Эти корни равны по абсолютной
величине и противоположны по знаку.
Примеры. т'32 = 2; |/ 125 = 5; 1*^16 — ±2; ± 3.
Упражнения
543. Найти все значения корней: a) |z 125 б) v .29С.
544. Что можно сказать о числе а, если известно, чтс существуй’”
два различных значения корня
545. Что можно сказать о числе о если известно, « то никакое по-
ложительное число не может быть значением у о?
Арифметическое значение корня
§ 77
Б предыдущем параграфе было показано, что любое поло-
жительное число имеет два корня четной степени: положгтель
ный i отрицательный. Например, J/J = ±3;ri6= + 2 и т. д.
Положительный корень четной степени из положительного
числа называется его арифметическим значением пли арифме
тическим корнем. Так, арифметическим значением 1^9 буде”
число 3, а арисЪметическил значением |^64 — число 2.
2k __
Всюду в дальнейшем под у а (а > С) мы будем подразуме-
вать арифметические корень степени 2/г из числа а. Например
]/16 = 4, 1/25 = 5 и т. д В связи с этим полезно отметит! сле-
дующую важную формулу:
1 х. если х> О
у ^2 __ — х, если х < О,
0 если х — 0.
Другими словами,
/х- = |х|.
Ошибочно было бы написать \Гх2 = л так как при о~рица-
тельных значениях х мы имели бь дело с отрицательным (не-
арифметическим) копнем.
П р и n е р ы:
1) И4-а)?= |4 - а
4 — с если а < 4,
а — 4, если 0 4,
О, еслп о = 4.
2) V (*2 4 х + I)2 = х! 4- г - 1.
173
В данном случае знак модуля можно не писать, так как при
любых значениях х х2 + х (- 1 2> 0.
Упражнения
546« Найти арифметические значения корней:
а) 1<(Т- Г)2~ в) |Г(2^3х + I)2;
о) К(х + 2)2; г) 1<(-Зх’2Трх~_ 1)3.
547* Построить графики функций:
а) У - V(x— l)2; в) у - J/?;
б) у - О У =-
548. Вычислить сумму
|уч-1/(3 - х)2.
549. Построить график функции
у-= Н^’РФ-ГО-х)2.
550« Решить уравнение
] (^“3?" + К(5-х)2 = 2.
551« Решить уравнения.
а) V(х 4- 6)г = х Н 6; в) V(х- + 2х — 3)’- =- х2 Н 2х - 3.
б) у (1 -2х)4 - (1—2х)2; Г) ]<(8 - 4х -=“х2)2 = х2 + 4х — 8.
Корень л-й степени из отрицательного числа — а § 78
Теорема 1. Корней четной степени из отрицатель-
ного числа не существует.
Другими словами, уравнение
xst = — а (а > 0)
не имеет действительных корней.
Мы предлагаем учащимся доказать эту теорему самостоятельно.
Теорема 2.. Существует и притом только один
корень нечетной степени из отрицательного числа.
Этот корень отрицателен.
Другими словами, уравнение
х24+* — — о (а > 0)
имеет единственный корень. Этот корень является отрицательным.
Доказательство. Прежде всего покажем, что корень
нечетной степени 2k Н 1 из отрицательного числа — а не может
быть положительным. Если бы этот корень (обозначим его че-
рез Ь) был положительным, то в равенстве Ь*'1'1'1 — а левая
часть была бы положительной, а правая — отрицательной.
174
Теперь покажем, что отрицательный корень нечетной сте-
пени 2k + 1 из отрицательного числа —а существуем
Число и, положительно, „ потому оно имеет положительный
корень степени 2/г + 1 (теорема 1 § 76/. Обозначим его через Ь.
Тогда
= й>
Отсюда вытекает, чтс
(— 1 _ _ _ а.
Но это н означает, что офыЦательное чнию — b является кор-
нем степени 2/г + 1 из отрицательного числа —а.
Осталось лишь показать, чтс существует не более одного
отрица 1ежьного порня нечетной степени 2k + 1 из числа — а.
для доказательства предположим притивние, т. е. чи. суще-
ствует несколько таких корней. Пусть — Ь и — с — два таких
корня. Тогда
(— 6)2*+’ = — а, (— с)2*+1 = — а. (Г)
Нс так как число 2/? + 1 нечетно, то (— t)2fc_|1 = — 62/k+l;
(—c)2{+i = _ Поэтому из (1) следует, что
№ 1 — с, 1 = а.
к это, в свою очередь, означает, ито положительное число а
имеет два различных положительных корня степени 2k -! 1:
Ь и с; но это противоречит теореме 2, § 76.
Теорема полностью доказана. Объединяя теоремы 1 и 2, мы
приходим к следующему выводу.
Корней четной степени из отрицательного числа
не существует.
Существует ровно один корень нечетной степени
из отрицательного числа. Этот корень является
отрицательным.
Пример ы.
Корней f/—81: I0yz—25 не существует; 32=—2;
125 = — 5.
Упражнения
552. (Устно.) Какие из данных выражений не имеют смысла:
V— 9: / — 8 ; Г - 0,25 ; i-z — 2?
553. Найти области определения следующих функций;
а) .V = Кх — 1; г) у = , '(д ф 2)(х — 7);
б) у = jza — 1; Д) У ? V2 + х + L;
в) у = Зх24 5л—2, е) у = р' 3 — > т у 5’-- 5 .
Извлечение корней из произведения и частного
§ 79
Теорема 1. Корень п-й степени из произведения по-
ложительных чисел равен произведению корней п-й
степени из сомножителей, то есть при п>0, 6>0п
натуральном п
nVab=V~a-Vb. (1)
Доказательство. Напомним, что корень п-й степени из
положительного числа ab есть такое положительное число, п-я
степень которого равна ab. Поэтому доказать равенство (1) —
это все равно, что доказать равенство
(j/ а • у4 Ь)П — ab.
По свойству степени произведения
("/ а • 1Z Ь)п — (у/ а)п • (у^ Ь)п.
Но по определению корпя п-й степени (Уа)п — а, {у^Ь)п = Ь.
Поэтому (у/а • у^Ь)" — ab. Теорема доказана.
Требование а > О, b > 0 существенно лишь для четного п,
. "/------------------
поскольку при отрицательных а и & и четном п корни у а и
yfb не определены. Если же п нечетно, то формула (1) спра-
ведлива для любых а и b (как положительных, так и отрица-
тельных).
Примеры: У16- 121 =1/16 • Г12Т - 4- 11 =44.
У~ 125- 27 = У— Г?5 • ^27 = — 5-3 = — 15.
Формулу (1) полезно использовать при вычислении корней,
когда подкоренное выражение представляется в виде произве-
дения точных квадратов. Например,
У1532 — 722 = ]/ (153 -f- 72) (153 — 72) = У225-81 = 15-9=135-
Теорему 1 мы доказали для случая, когда под знаком ра-
дикала в левой части формулы (1) стоит произведение двух
положительных чисел. На самом же деле эта теорема верна
для любого числа положительных сомножителей, то есть при лю-
бом натуральном Л > 2:
п --------- п П - Пг—
У а, • а2... о*= fa, / аг.. . f ak.
Следствие. Читая это тождество справа налево, мы по-
лучаем следующее правило умножения корней с одинаковыми
показателями:
ft <-— П — ’ П t ft г 1 г'
у Oj • I . у ah = f • • • Gft-
176
Чтобы перемножить корни с одинаковыми пока-
зателями, достаточно перемножить подкоренные
выражения, оставив показатель корня прежним.
Например, V 3 • V 8 • V 6=/ЗДГб = /144 = 12.
Теорема 2. Корень п-й степени из дроби, числитель
и знаменатель которой—положительные числа, равен
частному от деления корня той же степени из числи-
теля на корень той же степени из знаменателя, то
есть при а > 0 и b > О
Доказать равенство (2) — это значит показать, что
(л,— \ л
V «) = а
У~Ы Ь'
По правилу возведения дроби в степень и определению корня
й-й степени имеем:
(rt/-—\л (nf \п
£_?] а
aS~J ty-by V
Тем самым теорема доказана.
Требование а 2> 0 и b > 0 существенно лишь при четном п.
Если же п нечетно, то формула (2) верна и для отрицатель-
ных значений а и Ь.
Примеры: /’зб _ К36 _ 6.
у 49 — V 49 7 ’
3 f 64 _ /—64 _ —4 4
У 27 — /27 “ 3 “ 3'
г.—
справа налево,
мы получаем следующее правило деления корней с одинаковыми
показателями:
Чтобы разделить корни с одинаковыми показате-
лями, достаточно разделить подкоренные выражения,
оставив показатель корня прежним.
Например, 1 *36 — 1/ — = 1/9 — 3
У 14 Г 14 г
177
Упражнения
554. В каком месте доказательства теоремы 1 мы использо-
вали то, что а и о положительны?
Почему при нечетном п формула (1) верна и для отрица-
тельных чисел а и Ь?
При каких значениях х верпы данные равенства (№ 555—5GUJ:
555. |/х2 —9 = ]/ х — 3 • /х + 3.
556. У(х - 2) (8 - х) = Ух — 2 • /8 — х.
557 У(х 4- 1)(г — 5) = рбГП • Ух — 5.
558. у х(х + 1) (л + 2) =-- V х ух + 1 [ х -Ь 2.
559. ]/(» —а)3 =- (У* — а)3.
560. У(х — 5)2= (Ул — 5)2.
561. Вычислить;
а) /1732 — 522; в) У200'2 — 562;
б) /З732 — 2522; г) ]/ 242,52 — 46,52.
562. В прямоугольном треугольнике гипотенуза равна 205 см,
а один из катетов 84 см. Найти другой катет.
563. Во сколько раз:
__ __ з /
а) у 45 больше У 5; е) }/ 256 меньше у й'
Извлечение корня из степени. Возведение корня
в степень. Извлечение корня из корня § 80
Пусть а — произвольное положительное число, а т и п —
натуральные числа, причем т делится без остатка на п. Тогда
У^ = аУ. (1)
Например, У5е = 52 = 25; /З*2 = З3 = 27.
Другими словами, верна следующая теорема.
Теорема 1. Чтобы извлечь корень из степени поло-
жительного числа, показатель которой делится на-
цело на показатель корня, достаточно показатель
подкоренного выражения разделить на показатель
корня, оставив основание степени прежним.
Доказательство. На основании правила возведения сте-
пени в степень имеем:
fm \п тп
а п 1=а П = ат.
т
¥ т Г ~ fl
Но это и означает, что у а"1 — а .
178
Теорема 2. Чтобы корень из положительного чис-
ла возвести в степень, достаточно возсести в эту
степень подкоренное число, оставив показатель кор-
ня без изменения, то есть при а>0
(Го)га = ^. (2)
Действительно,
(у а)т и • у а... у и—у и • а.. .а — у ат.
т т
Если п — нечетное число, то формула (2) верна и для а <; 0.
Пример ьг. (у 2)3 ={/ 23 ~ у 8;
(у Тб)3 = 7Яб3 = = 2= = 4;
(/-2)М'(-2)5 = Г-32.
Теорема з. Величина корня из положительного чис-
ла не изменится, если показатели корня и подкорен-
ного выражения умножить на одно и то же натураль-
ное число или разделить на их общий множитель.
Другими словами: а) если а > 0 и т, п, k — натуральные
числа, то
л у- 1 пЛ у
(3)
2) если а>0 п k общий делитель чисел т и п, то
п
п,— (4)
уа"‘=у а*.
Доказать формулу (3) — это значит показать, что
= ат
По правилу возведения корня в степень
( у а,пкУ — i
Показатель mnk степени делится нацело на показатель nk корня.
Следовательно, по теореме 1 yf amkn — а"1. Поэтому (yz a",k)n=am‘
_ nr— nk i—Т
Это и означает, что у ат— у а"1'1.
Формула (4) легко вытекает из (3). Предлагаем учащимся
самостоятельно убедиться в этом.
Примеры. jZ3 = F32; y^2a = Y^^a*.
Теорема 4. Чтобы извлечь корень из корня, доста-
точно перемножить показатели этих корней, не из-
меняя подкоренного числа, то есть
У у а = а (а > 0).
(5)
179
Доказательстве. По теореме 2
(пт. — пт.—
(. )/ а)- = у а -.
Величина корня не изменится, если показатель корня и
показатель подкоренного числа разделить на иЛ обедни множи-
тель (теорема 3); поэтому / ап = у а. Итак, ( у а) = у а
и -.% тГ~ птг —
Но по определению корня это и означает, что У \' а= у а.
Например, у 4 = / 4,
5 /—
Г Г 2 = V 2.
Упражнения
564« Упростить выражения:
I) 3) 7(=зР; 5) j/?;
2) */3\ 4) 6)
565. Упростить выражения:
1) V (Г 7-2Л 3) Z(K d-Г 5)3;
2) V(1 - /2)2; 4) (/3 —4)2;
566. Упростить выражения:
1) /|(х-1)(х+ 1)14; 2)
567« (Устно). Упростить выражения:
1). 1'4 3) V /8; 5) V/16;
2) 3/ V 5; 4) V /^243; 6) S/ 7;
5) 1Л/5-2)1;
6) Ku - /’гр.
7) //(-3);
8) 9//’9;
Вынесение множителя из-под знака корня
и введение его под знак корня § 81
Иногда подкоренное выражение разлагается на такие мно-
жители, корни из которых извлекаются довольно легко. В таких
случаях выражение можно упростить посредством вынесения
множителя из-под знака корня. Например,
/Т2 = /4^3 = У4 • V 3 = 21/3;
/1250 - гг625-2 = /5У"2 = /5« • / 2 =5/£
Вынесение множителя за знак корня позволяет упростить и
более сложные выражения. Так,
180
/18 +V5G — /98 = /9 24-V25- 2 — /49-2 =
= 3]/ 2-.- 5/2— 7/2 /2;
/8 /24 4 /875 / 27^3 — /ГИГ4»
4- / 125-3 =3/3—2/34- 5/ 3= б/£
Иногда оказывается полезным, наоборот, ввести калой-ни-
буд1 множитель под знак корня.
Пусть, например нужно вычислить приближенное значение
7 / 8 с недостатком с точностью до О, I. Введем 7 под знак
корня. Для_ этого заметим,_что 7 = /49. Поэтому 7/8 =
= /49- / 8 = /49-8 = /392. Извлекая корень из 3^2! обычным
способом, получил «.Лсдующее приближенное значение этого
корня с недостатком с точностью до 0,1: /39219.7 Если бы
мы не ввели 7 под знак корня, а вычислили бь приближенное
значение/8 < точностью до 0.1 ф 8~2,8) и полученный ре-
зультат умножили на 7 то получили.бы 7]/ 8 ~ 19,6, то еств
ошиблись на 0,1. Этот пример показывает, какую пользу может
оказать введение множителя под знак корня.
Кроме того, введение множителя под знак корня приводит
иногда к значительному упрощению выражения. Например,
V 1б/~2 = Т^/Гб^-? = V/2^2 = V/‘29 =
= /2“ = /23= 2/2.
Упражнения
568. Не извлекая копнен, определит,., какое из данных
чисел больше;
а) 2 / 3 или 3 /2; в) 5/ 7 или 8 /3;
б) 2 / 3 или 3 /2- г) ? у' 4 или 4 /2.
569. Вычислить:
а) 2 У 3 — /27 4- 3/12— 2] ''243,
б; /50- 5/ 8 4-V "5 -.-/128;
в; /’г 4- {^250 — >/'686 — /Те.
570. Упростись:
181
571. Вычислить с точностью до 0,01:
а) 2 /7; в) 1/6;
б) 5 /3; г) 2 /7 + 5/3 + ~/б7
572. Вычислить:
а) (2/3—ЗУ 24-/6) • (/6- /T-2/3h_
б) (/8- 3/2 4- /10) • (/2 + /1^ + 3/04);
в) (/ 9 + /_6 + / 4) • (/ 3 - /2);
г) (i^a2 -f- /ab 4 • /б2) • (/ а — / Ь).
573. Что больше:
а) / 2 или /3; в) /8 или /19;
б) /12 или /5; г) ’/2 или ’/з?
Умножение и деление корней
§ 82
1. Умножение корней. В § 79 было получено правило
умножения корней с одинаковыми показателями:
/а, • /а,... /аЛ= /at • a,...ah.
Чтобы умножить корни с разными показателями, пред-
варительно их нужно привести к общему показателю, а затем
умножить как корни с одинаковыми показателями.
Пусть, например, надо умножить /а на /6. Исполь-
зуя теорему 3 § 80, можно написать:
/ д— У ат\ / & = / Ьп.
Отсюда
у а-у b — у а"‘- \'ЬЯ = у а"‘Ьп.
Например, ]/ 3 - /9 = /з’ - /9® = /з37^2 = /З^- З4 =
= /3’=з/£
В качестве общего показателя для корней / д и удоб-
нее всего выбирать наименьшее общее кратное чисел п и т.
Например, если нужно умножить /~2 на /32, то в каче-
стве общего показателя для данных корней удобно выбрать
число 12, являющееся наименьшим. общим кратным чисел 4 и 6.
Теорема 3 § 80 дает: /2=‘/23; /32 = ,/322 ='/2Го.
Поэтому
/2 • у 32 = '/23 • у 2го = '/г*^ 2'/2;
182
2. Деление корней. В § 79 было получено правило де-
ления корней содинаковыми показателями;
П/~
Л/
у ь
Чтобы разделить корни с разными показателями,
предварительно их следует привести к общему показателю, а
затем разделить как корни с одинаковыми показателями.
Например.
— — —* = — У2
У ~2 ~ V 2* 2 3 * 5 * V 23 ~ г
Упражнения
574. Выполнить указанные действия:
а) / а2 • 'Уд) 1 у^й5 : Уа-.
б) у а- • у а; е) у а : у а ’;
г) а У 4а y^4a • аг у/Г4а3;
575. Что больше:
' , З10 ”/3» У 2Б У 2*
а) тт;— или ; б) vzz или 77=?
’ V33 ,Л32 ’ У 2 2‘
Освобождение от радикалов в знаменателе дроби § 83
Некоторые дроби, содержащие в знаменателях радикалы, с
помощью преобразований могут быть сведены к дробям, которые
уже не содержат радикалов в знаменателях. Поясним это па
ряде частных примеров.
Пример 1. Освободиться от радикала в знаменателе
2
дроби ——
У 3 •
Умножив числитель и знаменатель данной дроби на ]/3, по-
лучим:
4r-=X^=2l/3
У з (К з)2 з ’
Пример 2. Освободиться от радикала в знаменателе дроби
5
У 12 ’
183
Число 12, стоящее под знаком радикала, разложим на Мно-
жители 12 2а 3. JXo injJinvjiO Куба пв Хаадает, очевидно, мно-
жителя 2 • З2 - 18. Умножив числитель и знаменатель данной
дроби на /18, получим:
5 _ 5/18 _ 5/18 _ б/18 = 1 Джг^-
/12* “ /12 /18 ~ /^З/^З5 2-3 6
ПримерЗ. Освободиться от радикалов в знаменателе дроби
/~з + /~2
/"з — /’г ’
Умножив числитель и знаменатель данной дроби на /3 +
(это выражение является сопряженным к выражению /3 ~^2),
получим: _
/'3 + /~2 (/~3 + /~2)2_____ 3 + 2 /~6+2
У~3 — /~2 ~ (/З — /~2) (/*3 +/~2) ~ 3-2 ~
= 5 + 2/6.
Пример 4. Вычислить
/~3 + /~2
/"з—/'г
с точностью до 0,1.
В примере 3 мы получили:
1"3 4 V~2
т- =5+2/6.
/ 3 — / 2 г
Но 2/6 = /4-6 = /24 « 4,8 (с точностью до 0,1). Поэтому
5 + 2/б« 9,8 (с точностью до 0,1).
Если бы мы вместо этого в исходную дробь подставили при-
ближенные значения /3 и /2 с точностью до 0,1:
/ 3^1,7; /2^1,4,
то получили бы
/ 3+ /2 3,1
/~3 — /”2 0.3
10,3,
что дает значительную ошибку.
Пример 5. Освободиться от радикалов в знаменателе
дроби
______4
1+/ 3-/V
Освободиться от радикалов в знаменателе данной дроби
можно в два приема. Сначала умножим числитель и знаменатель
184
дъппой дроби на 1 -г Ус 4-/2. В результате мы освободимся
от радикала /2;
4 _ 4[(1+/~з) + /~2] *
’+/"з-/“2 [(1 У'з)-/'2’[(1-1-/-3)+/2Г="
4(1 + /~3 + /~2, 4(1 + /~3+/~2)
— (1 -г V~З)2— (/2)2 “ у + г/'З; —2 ”
4( /~Ь + /~2) = 2(1+/~3+/~2)
“ z + 2 /"3 “ 1 + У~3
Затемчислитель и знаменатель полученной дроби умножил' на
—УЗ. В результате получим'
2(1+ /3 +У~2) _ 2G-t/~?-f-/~2)(l -/1)
1 + /~3 ~ (1 + /~3)( -<~3) =
= 2(1-/-3 + /-3 3 + /-2-Г6) = 2 _ у-£ + у ё;
Пример 6. Освободиться от радикалов в знаменателе
дроби
/~5 4-/~3
/I —/“3"
Умножим числитель и знаменател! данной дроби на непол
ный квадрат суммы чисел У 5 и У 3, то есть н.‘ (У 5)г
+ У 5 • У 3 4-(/З)2. Тогда ь знаменателе получится разноси
кубов чисел У 5 и у' 3 ; (У 5)3—(/ 3): = 5 — 3 = 2, а в чис
лителе (/1 4- У 3' (/^ + /б^З + /З2) = /5= -г- У&~3 4
4-1' 5jЗ2 + 171^3 - УЁГЗ2 -г У3! =
4г ^45 + 3 -= 8 4- 2^75 -т- 2/45.
Поэтому
= C + 2/7F + 2V45
— У~3 ~ 2
5 4 ^75 4 /45 4-f 75 +
= 4--/75-1 1М5.
Упражнения
576. Освободиться от радикалов в знаменателях дробей:
— ч 1 74 1 —/~2 *
/!• 4' ^18’ 1+/1’ 10) 1^25- /Й ’
„ 3 У 7—/1 /"3—1 . 12
) /1’ 5) /-7д.}'-6’ 8\'з-У5 1 3+yi-yV
l 1 15 _____31____
3) |<75 6) 9) y-Q 3/-Ъ ’ 12) 2+/ 2 — / 5-
185
577. Найти приближенные значения данных выражений с
точностью до 0,01:
\ /'ё + /‘5. ,. 13- /У. . 36 — 5/17
——----— ( о) —------, В) ------- —.
/6 — /5 /3—1 2 — /17
578. Освободиться и г радикалов в знаменателях «робей:
ь)7 6) 1 _------;
/5+/2 2-/2+/3-/6 K/fl + |/b
Степень положительного числа с положительным
дробным показателем
§ 84
В § 80 мы доказали следующее утверждение: если а — произ-
вольное положительное число, а т и п — натуральные числа
(п 2), причем т делится без остатка на п, то
т
п/ат - а".
Вполне естественно желание обобщить эту формулу на слу-
чай произвольных натуральных чисел. Но деление в области
натуральных чисел, вообще говоря, невыполнимо. Поэтому част-
ное — может оказаться дробным числом. Таким образом, мы
п
сталкиваемся с необходимостью ввести в рассмотрение степени
с дробными показателями.
Определение. Пусть а — произвольное положительное
число, а т и и — произвольные натуральные числа. Тогда
a" ='f'ra'”. (1)
Например,
9? = /95 = i 9*^9 = 9 5л9 = 9 /3;
8- = = /2° =4.
Степень положительного числа с положительным дробным
показателем есть корень, показатель которого равен знамена-
телю данного дробного показателя, а подкоренное выражение —
степень исходного положительного числа с показателем, равным
числителю данного дробного показателя.
Как мы знаем, величина дроби — не изменится, если чпс-
п
литель и знаменатель этой дроби умножить на какое-нибудь
186
натуральное число k или разделить на какой-нибудь их общий
делитель р*:
т
т mk т р
п nk ’ п п
Р
Вполне понятие что введенное нами определение степени
т
ип будет корректным лишь в том случае, если
/ = а*, <2)
т
Р
т п
ап =а~р. (3)
И эти соотношения действительно выполняются. Докажем,
папример, формулу (2). Имеем:
ГН
ап -- "/а”,
mk
nft-------г
а — ]• amk.
Но
/ ат I а,пк.
Отсюда и получается соотношение (2).
Формула (3), если ее читать справа налево,
« т
р
п т
ар — ап,
выражает по существу то же самое, что и формула (2). Только
т п
роль т здесь играет целое число — , роль п — целое число ,
р р
а роль k — число р. Поэтому в специальном доказательстве
формула (3) не нуждается.
Формулы (2) и (3) выражают следующий факт: величина
степени положительного числа с положительным
дробным показателем не изменится, если числитель
и знаменатель показателя умножить на какое-ни-
будь натуральное число или разделить на их общий
множитель.
т п
* Поскольку р есть общий делитель чисел т и п, числа и —
Р P
являются целыми.
187
- — - я
Например, п3=аь=а9 = .... Ц
Л 1 _?
а1Г’ = а8 = а« «... .
Замечание. Введенное определение степени с дробным по- ]
казателем не распространяется на степени с отрицатель-
ными основаниями. Для отрицательных а формула (1) может •
L 4_ И
вообще потерять смысл. Например, писать (— 2)4 — у — 2 нельзя, ।
поскольку выражение -\f — 2 не определено.
Упражнение
579. Вычислить:
2 э _5
а) 643; в) (-V; д) 1256 : 5;
\ 4 /
1 з_ _
б) 273; г) (-V; е) 1444 : 9.
Основные свойства степени положительного числа
с положительным дробным показателем § 85 I
В этом параграфе мы рассмотрим основные свойства степени
положительного числа с положительным дробным показателем.
Поскольку степень отрицательного числа с положительным дроб-
ным показателем, вообще говоря, не определена, то всегда, не
оговаривая это специально, мы будем предполагать, что осно-
вание степени есть число положительное.
Перечислим основные свойства степени, которые мы хотим
рассмотреть:
т р т^Р / т\р т 1) ап • а“ = а" "• 4) (а"Г = °" т т т т — т р 2) (а bf а" Ьп \ 5) = ап~\ cfl т т — 3) = ~; ' \Ь 1 ™ Ьп Прежде чем приступить к рассмотрению помним следующий важный факт, о котором дыдушем параграфе. 188 р ч . * „ w р если — > —, « Я этих свойств, на- мы говорили в пре-
Величина степени с дробным показателем не .изменится, если
числитель и знаменатель показателя умножить на любое нату-
ральное число или разделить на нх общий множитель;
т
Р-
т тп гп п
_,Л Л к - - - П D
а = а ; а = а р .
Теперь перейдём к доказательству 1-го свойства степени:
т Р тЛ-Р
о" а4 = а" ’
Чтобы перемножить две степени с одинаковыми
основаниями, достаточно показатели степеней сло-
жить, а основание оставить прежним.
Действительно,
т mq р рп
й" = й"-’, й’~ = а9".
Следовательно,
т р mq рп
а aq = aQn - aqn =n^am7i • п^а^.
По правилу умножения корней с одинаковыми показателями
Пу/ ат^ • "уЛй/"' = "^/ а'п<1 аРп = "^атч+Рп.
Но
mq+pn т р
7/й^^м =й = а" 9.
П оэтому
т р т р
по по
а • а4 = а 4 ,
что и требовалось доказать.
Примеры:
J. 3
3 3 . з3 = 33 3 - З1 = 3;
_2 _4 _2 22
3 „5 Л3+5
а • й — а ~а \а б).
1-е свойство степени, доказанное нами для случая двух сомно-
жителей, на самом деле верно и для любого числа сомножителей.
m _Р г т г
Например, сГ • а4 • а- — ап 4
Остальные свойства степени с дробным показателем предла-
гаем учащимся сформулировать и доказать самостоятельно.
Упражнения
580. Доказать тождества:
/ _1 I V / j 1\
a) (fl2+6j\fl2 — /?2) = а—6;
189
fl l\f Я 11 2\
6) (a 3 J- b3/ \a3 — a 3b? 4- b3) = a 4- b\
/ j 1\ / 1 - 1 J\
в) (д3 __ 63Дл3 4- a 3b3 4- b 3) = a — b.
581. Что больше:
j з з
a) 82 или 12 4; в) 12 2 или 183;
11 1 1
6) 643 или 362; г) (-V или (—V?
\18/ \12/ ’
582. Упростить:
£83. Упростить выражения:
584. Какое значение принимает выражение
/ »\ 5
/ 1\1 1 I ю 1 з
7 — 4 2 • — х ' 4- 6 Ух при условии, что х3 — Зх0?
(з 2?°)
Степень положительного числа с отрицательным
дробным показателем § 88
Подобно тому как в § 71 мы определили степень а~п числа
а с отрицательным целым показателем — /г, можно определить
т
и степень а а положительного числа а с отрицательным дробным
т
показателем — —.
п
Пусть а — произвольное положительное число, а т и п — на-
туральные числа. Тогда по определению
т
п
а
190
Степень положительного числа с отрицательным дробным
показателем равна единице, деленной на степень того же числа
с показателем, противоположным показателю данной степени.
_ 2
Например, 8 3 = Ц- = = 1;
83
5
27~т= 1 =—1 = 1 - 1 - 1
J У27& ; 3^ /3* 9/з”
276
Теперь мы знаем, что представляет собой степень положи-
тельного числа с любым рациональным показателем.
Степени с рациональными показателями обладают следующими
основными свойствами:
\)an-aq = an q;
т т т
2) (abf = a”'b”;
т
3) ;
\ b / ™
! т\ р т р
4) (а^)1 = a”'q-9
т
— т р
п —----
5) — = а" ".
р
Частично эти свойства были доказаны нами в предыдущих
параграфах, но лишь для положительных показателей. Теперь же
мы можем доказать их для произвольных рациональных по-
казателей.
Докажем, например, свойство 1.
Для положительных показателей — и — доказательство было
n q
дано в предыдущем параграфе. Поэтому нам нужно рассмотреть
следующие случаи:
1) оба показателя отрицательны;
2) один из показателей отрицательный, а другой — положи-
тельный;
3) хотя бы один из показателей равен нулю.
Пусть т, п, р и q — натуральные числа. Покажем, что
т р т р
a . a~~q = a~"~~q.
Действительно, по определению степени с отрицательным
показателем
т р
п 1 1
а — —, а = —.
m ’ ** jp
п q
а а
191
Поэтому
т р
».e"« = -I-._L = _!—
т т р *
п q п + q
а а а
но
откуда и вытекает требуемое соотношение.
Мы рассмотрели случай, когда показатели
степеней отрицательны. Теперь рассмотрим случай,
из них положителен, а другой отрицателен,
мер, что
т
а"
a Q=an q
11меем:
т
ап
р
я__
т
п
а
_р*
Q
а
а
каждом из двух
когда один
Докажем, напри-
т? т Р
Если — > —, то
л q
ра графе,
по
свойству
5,
упомянутому
в предыдущем па-
т
п
а
р
Q
а
т р
= а
Л?
Если -
п
р
—, то
9
т
п
а
р
Q
а
р гп
а1 ~п
но
Наконец,
если —
п
р
о
а
_ Р
— “>
Я
1
— = а
т
п
то
т
— а"
р
я
т
7 т_ р
— =\ = ап Q
£
Q
а
192
Здесь мы используем определение а0 = 1. Таким образом,
т р т р
ri ~ q _п q
а • а = а
Нам осталось рассмотреть случай, когда из двух степеней
с одинаковыми основаниями хотя бы одна имеет нулевой пока-
затель. Докажем, например, что
— ™ 4-0 ап • а° = ап .
Действительно, а0 = 1 и — 0 = —. Поэтому
п п
т т т т . % 71 — — - 4- 0 1 п п ~ п а" = а • 1 = а, а = а .
а"-
Свойство 1 доказано.
Аналогично можно доказать и все остальные свойства. Заме-
тим, что если в предыдущем параграфе мы могли говорить
о свойстве 5 лишь при — >> — , то теперь, используя опреде-
n q
ления степени положительного числа с нулевым и отрицательным
дробным показателем, мы можем доказать его и для случая, когда
т р
п д'
Например, 3 4 3_4 _ I _ — = 164 5= 16 20 = (2‘) 4 165 Упражнения 585. Вычислить: _ 3 _ _4 а) 9 2; в) fl) \64 _ _4 б) Ц) 3; Г) (25) 2; • Вычислить (№ 586 -592): 3 Г/ 3 \01-0.5 „ —« 586. i| -7,5-4 2 —(—2 \4/ - 587. 0,027 3 — f — 1 V+ 2560'7’ \ 6/ /д\ L /ос- 3 Г/ 4 \ - "1— 588. / ю . 2 I _) 2 I ‘ \1С/ * \36/ |Дз) J _ 2 3_ 5 1 589. (9 ~3У—/25 2>) 10 + [(-Г1 \ / \ 1 L\ 4 / 1 _ j 20 _ 2 5 _ 1 _ 1 ~ А ’ i 2 ‘ 2° д) (27) " 6 • З2,5'• г) (6,25)” 4 - f If. \ О / )-4 .1. 810-25. - 3-* + (5,5)°. 4.16 f \5/ ’ • (36)”7+^U. \ 9 / J 7 V 5
7 Заказ 261
193
4
590.
4 4
4-°‘5—(2|/2) 3
591.
а3 —х
3\z ж д 4- х
I з.з
• 2 (ах) 3.
. °2) 2 > аа0—аа)
1 1 — а*
выражение
-2
592. (1 — я2) 2-------------------
1 + а2 (I—а2)-’
593. Какое значение принимает
2
2 2
(x2+D +U2-!)
П
2 2
-U2- 1)
> tn > 0; 2)
ni
если: I) п
594. Вычислить
’ 2 1
-2 1 3 3 I 2
х а + а х j
595. Упростить выражение
/2 2\/ 2 1\
L4— !> 4 Да 4 +о4) —
-------г ------^~Vab
0; 3) т = п = 1?
I _ J\_ J / _ _2\_ з
13)2 ( < 3) ~2
х ] при х = — а ]
2 )' 2,5 (а - Ь)~1
4
3
2 , 2
а — Ь
(10)
2
. г 1 I
Функции у = х при г = - и г — -
§ 87
2
Функция у — х . Функция
у = х2, или у = ]^х , определена
для всех неотрица-
тельных значений аргу-
мента х; поэтому областью
ее определения является со-
вокупность всех неотрица-
тельных чисел. График этой
функции (построенный «по
точкам») представлен на ри-
супке 99. Функция у —к 2
принимает любые неотрица-
194
тельные значения: поэтому ооластыо
ее изменения является совокупность
всех неотрицать^иНЫл wbu
Данная функция является монотон-
но возрастающей. Это хорошо впднс
на графике, но можсг быть стриги
доказано и без обращения к графику.
(Из двух положительных чисел боль-
шему соответствует больший квадрат-
ный корень.)
j 1
Функция у — х3 . Функция у=х3,
3 ,---------
или у= у х, определена для ьсех дей-
ствительных значений аргумента х.
Однако мы ограничимся рассмотрением
ес поведения лишь для положительных
значений л.
_i
График функции у=х3 для х>0
представлен на рисунке 100. Как видно
из этого рисунка, поведение функции
1
у —х 3 при х > 0 вполне аналогично по-
д-
ведению функции у =х ~: она прини-
мает только положительные значения
и является монотонно возрастающей.
Упражнения
596. Используя график функции у = х2, найдите приближев
ные значения корней:
а) /2; б) /3; в) /5.
597. Построить графики функций"
1) у = Vx^l- 5) у = —2] 'х; 8) у = у/Т+Т;
2) у = ]/х- 1; 6) у = ^х_- 2; 9) у = /х + h
3) у — ]Лх + 2, 7) у — j/x — 2; 10) у = — 2 х.
4) у = + 2;
598. Как располагаются друг относительно друга графики
функций: '___
а) у = \Гх и у = /х + а; б) у = j/x и у = д/х? _
599. На рисунке 101 вы видите график функции у — ]/ х.
По ошибке чертежник забыл отметить на чертеже единицу длины
(масштаб). Как с помощью циркуля и линейки определить по
этому чертежу единицу длины?
7»
195
Общие свойства степенных функций
§ 88
Степенными функциями называются функции вида у = ах',
где а и г заданные действительные числа. Согласно этому опре-
делению показатель степени г может быть как рациональным,
так и иррациональным. Но поскольку мы еще не знаем, что
такое степень с иррациональным показателем, то пока ограни-
чимся лишь случаем, когда число г рационально. Кроме того,
мы будем считать, что а = 1. После того как функция у = х'
будет изучена, исследование функции у = ах' не представит
особых затруднении.
Некоторые частные примеры степенных функций у = х' (при
г = 1, 2, 3, — 1, — 2, 1, —) уже рассматривались нами в § 73
74, 87. Сейчас мы рассмотрим свойства функции при любом
рациональном г.
Поскольку степень х' с рациональным показателем г опре-
делена, вообще говоря, лишь для положительных значений х,
то и функцию у = х' мы будем рассматривать только для поло-
жительных значений аргумента х.
Степенные функции обладают следующими основными свой-
ствами.
Свойство 1. При положительных значениях аргу-
мента х степенная функция у = х' принимает только
положительные значения.
Действительно, если г = 0, то xr = 1 > 0. Если г = —, где tn
п
т
и п — натуральные числа, то х' = х п ~ хт. Но х>0; значит,
хт также больше нуля, потому и хт > 0. Если г = — —, где
п
т т
т и п — натуральные числа, то х " =— .‘Но хп>0; следова-
т
п
X
1 л
тельно, и — >0.
т
п
X
На рисунках 102—104 вы видите графики степенных функций
у = х' при различных значениях г.
Каждая из приведенных кривых расположена выше осн х.
Это и служит графическим подтверждением 1-го свойства сте-
пенной функции.
Свойство 2. Если число г положительно, то при
положительных значениях аргумента х степенная
функция у — х' является монотонно возрастающей.
196
Доказательство. Пустьr=
= — > О, х,> х, > 0. Докажем, что
л
х'2 > х'. Эго и будет означать, чтс
при положительных значениях аргу-
мента х функция у = хг монотонно
возрастает.
Имеем:
0
Рис. 102
т гп
п п /-----------
х'2 = х2 = / х".
Так как х2 > х, > 0, то х3т>х1т,
причем оба эти числа положительны.
Поэтому и
т т
то есть х2 > х", или х2~> хц
Каи видно из рисунка 103, кри-
вые у = хг с ростом л поднимаются
все выше и выше. Это является гра-
фическим подтверждением 2-го свой-
ства степенной функции.
Свойство 3. Если число г
отрицательно, то при поло-
жительных значениях аргу-
мента х функция у = х’ явля-
ется монотонно убывающей.
Доказательство. Пусть
х~ > х.> 0 и г =— - , где т и
z 1 п
п —натуральные числа. Покажем, что
Х2 < Х|.
Это п будет означать, что при по-
ложительных значениях аргумента х
функция у — хГ монотонно убывает.
Имеем:
т т
r “г 1 Т 1
х2= х, хг. = х. =
* Л т ’ 1 1 т
г. п
Х2 XI
197
Так как хг > xt > 0, то по 2-му свойству пененной функции
Следовательно,
или хг2 < xrlt что и требовалось доказать.
В заключение отмстим еще одно свойство степенных функций.
Свойство 4. Если число г положительно, то при
неограниченном приближении х к 0 соответствующие
значения функции у -хТ неограниченно приближаются
к 0; при неограниченном возрастании х соответствую-
щие значения функции у—хг неограниченно возрастают.
Если число г отрицательно, то при неограниченном
приближении х к нулю соответствующие значения
функции у=хг неограниченно возрастают; при неогра-
ниченном росте х соответствующие значения функ-
ции у=хг неограниченно приближаются к нулю.
Это свойство степенных функций легко понять, рассматривая
графики, представленные на рисунках 103 и 104. Строгого до-
казательства этого свойства мы не приводим.
Упражнения
600. Что больше:
/3\6 /3\6 --1 --1
а) /у)11 или^у1; в) 0,357 3 или 0,358 3;
2 \ 2 ____2 ___2
б) (21<3)3 или(3/2/3; г) (/21) 7 или (2/5) 7?
601. Известно, что т, п, р и q— натуральные числа, причем
т . р ..
— > —. Чго можно сказать о положительном числе а, если:
n q
т р гп р
а) ап>а9; б) а п > а ’?
602. Какие из данных чисел больше 1 и какие меньше 1:
ч (3\‘? /2\-Л . /13А
а>(т); «>/)'; в>(Гг)?
Задачи на повторение
603. Какие известные вам физические законы описываются
с помощью степенных функций у — ахг? Какой физический смысл
имеют в них параметры а и г?
198
604. Какие из приводимых ниже формул выражают теоремы
и какие — определения (tn и п — произвольные натуральные числа):
а) а° — 1; б)ат — ~. в)ап = Уагп; г)ат ;ая=ат~'‘?
605. Построить графики следующих функций:
а) у = ]Л(х — 2)2 и у = х — 2;
б) у = -fr(x+ I)3 и у = х + 1;
в) у= У[(х — 3) (х + 2)]2 и у = (х — 3)(х + 2).
( _!\_2 ( J\ _1
606*. Вычислить \а + */ 2 + \а — х21 2 прих = 4(а— 1).
Освободиться от радикалов в знаменателях дробей (№ 607, 608):
607. з + . 608. 2 + /3+Г5 .
к + /2 —/6 ’ 1 + /5 — уз
Расположить в порядке возрастания числа (№ 609—611):
611. (if8-
\5/ ’ \ 27) ’ \25/
612. Доказать тождества (формулы сложных радикалов):
У'а + УЬ^ + + У а~^У=Г[-
Используя формулы сложных радикалов, упростить выра-
жения (№ 613—615):
613. Кб + 2Уб. 614. Кб — V 20. 615. К10—2У2Г.
616. Доказать, что при 1 < х < 2
Кх + 2)Л— 1 + Кх — 2~Ух^1 =2.
Решить уравнения (№ 617—619):
/9 1/ V Г» г — >
617. =[(х/хГГ-2.
__1 J 4 6
Г 2н 5 г, 1 « 3 1 5
618. |(/х) ] =[(уг) ] •
199
/ \ 4
619. 5
W *3 /
G
7
Данные выражения (№ 620—623) упростить путем вынесения
множителей за знак радикала:
620, У'а^Ь. 621. ¥&Ь2. 622. 623. а°Ь7.'
624. Расположить в-порядке возрастания числа:
1. V2, ^з,
625. Вычислить
при
х = 5; у = 20.
626. Вычислить
G 2+ У 2) ' + У"’) + . , 2- ~7^'(х 2 4 У 2).
fl I \
*2 21 -
+у )
если известно, что
1
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
V
Понятия вектора и оси § 89
Все величины, которые изучаются в математике и физике,
можно разбить на две группьк К одной группе относятся ве-
личины, которые полностью характеризуются их числовыми зна-
чениями. Гаковы длина, площадь, объем, время, масса и другие
величины. Если мы скажем, что карандаш имеет длину 10 см
или что температура воздуха равна - - 5°, то длина карандаша
и температура воздуха гем самым буду г определены полностью.
Но наряду с такими величинами существуют и величины, кото-
рые нельзя полностью охарактеризовать числовыми значениями.
Из физики, например, известно, что сила, скорость, ускорение и
некоторые другие величины характеризуются не только своимл
числовыми значениями, но и направлениями. Если на материаль-
ную точку действует сила 5 кГ, то для того чтобы сказать,
к чему это приведет, нужно знать еще направление этой силы.
Для полного описания подобных величин наряду с числовыми
значениями необходимо задавать и их направления.
Величины, которые полностью определяются своими числовыми
значениями, называются скалярными. Величины, которые харак-
теризуются не только своими числовыми значениями, но и на-
правлениями, называются векторными величинами.
В______О А
3-2-1 0 I 2 3 “ 5
Рис. 105.
Любую скалярную величину можно характеризовать отрезком
числовой прямой. Например, длину карандаша 10 см можно харак-
теризовать отрезком ОА (рис. 105), длина которого равна длине
карандаша. Температуру — 5° можно характеризовать на число-
вой прямой отрезком ОВ (рис. 105), где точка В удалена от
точки О на расстояние в 5 единиц длины и лежит слева от О,
указывая, что на улице 5° мороза, а не тепла.
201
£ ,^6 f Такая интерпретация векторных всли-
/ чин была бы неполной. Но подобно тому
4 / как скалярные величины можно харак-
х. / тернзовать отрезками числовой прямой,
f векторные величины можно характеризо-
Рнс. 106. вать направленными отрезками, или век-
торами.
Вектор есть направленный отрезок, то есть отрезок с фиксиро-
ванным положением своего начала и своего конца.
Направлением вектора считается направление от его начала
к его концу. Обычно вектор обозначается двумя буквами, над
которыми ставится стрелочка, обращенная острием вправо. При
этом первая буква обозначает начало вектора, а вторая — конец.
Так, векторы, представленные на рисунке 106, обозначаются
АВ, CD, ~EF.
Единственно существенной характеристикой отрезка является
его длина. Вектор же имеет несколько характеристик: начало,
направление, длину. Каждая из этих характеристик является по-
своему важной. Незнание хотя бы одной из них делает вектор
неопределенным.
Flapяду с понятием вектора, или направленного отрезка,
большую роль в математике играет также понятие направленной
прямой, или оси.
Упражнение
627. Какие из данных величин являются скалярными и ка-
кие векторными: объем, скорость, масса, ускорение, сила тока?
Проекция вектора на ось § 90
Как известно, проекцией точки А на ось / называется
основание В перпендикуляра, опущенного из точки А на эту
ось (рис. 107).
Проекцией вектора АВ на ось I называется величина отрезка
AtBi, соединяющего проекцию начала данного вектора с проек-
цией его конца на ось I (рис. 108—111). Эта величина считается по-
ложительной, если направление вектора А,В{ совпадает с на-
• правлением оси /, и отрицательной в противном случае.
Рассмотрим несколько примеров.
1. Вектор АВ длины г параллелен оси I. Если направление
этого вектора совпадает с направлением оси I (рис. 109, а), то
—
проекция его на ось / равна г. Если же направление вектора АВ
202
противоположно направлению оси I
(рис. 109, б), то его проекция рав-
на — г.
—>
2. Вектор АВ перпендикулярен
оси I (рис. НО). В этом случае
точки А н В проектируются в одну
и ту же точку. Поэтому проекция
вектора АВ на ось I равна нулю.
3. Вектор АВ длины г распо-
ложен по отношению к оси I так.
как показано на рисунке 111. Тогда
его проекция на ось I равна длине
отрезка A tBt или ДС. Из прямо-
угольного треугольника АВС нахо-
дим А С — (катет, лежащий против
угла в 30е, равен половине гипоте-
нузы).
Упражнения
628. Как изменится проекция ве-
ктора на ось, если:
а) длину вектора увеличить вдвое;
б) направление вектора изменить
на противоположное, направление
оси оставить прежним;
в) направление осп изменить на
противоположное, а направленно век-
тора оставить прежним;
г) направление оси и направле-
ние вектора изменить на противопо-
ложные?
629. Что можно сказать о взаим-
ном расположении вектора и оси.
если при изменении направления век-
тора на противоположное проекция
этого вектора на ось не изменяется?
Свободные и связанные
векторы § 91
Как уже отмечалось в § 89, каж-
дый вектор определяется своим на-
чалом (или точкой приложения), на-
ТЛ
I
Рис. 107.
4, в,
Рис. Ill.
203
правлением и длиной. Точку приложения вектора особенно важно
учитывать при решении физических задач. Пусть, например, на
диск, закрепленный на оси (рис. 112), действует сила F — 1 kF,
направленная вертикально вниз. Если эта сила приложена в
точке А, то диск под действием ее будет вращаться по часовой
стрелке. Если эта сила приложена в точке В, то диск будет вра-
щаться против часовой стрелки. Если же сила F приложена
в точке С, то диск будет находиться в состоянии покоя.
В математике в основном рассматриваются лишь такие за-
дачи, в которых точка приложения вектора не играет сущест-
венной роли. Примером может служить хотя бы следующая за-
дача: какой угол образуют между собой векторы АВ и CD
Рис. 112. Рис. 113.
(рис. 113)? В дальнейшем мы будем иметь дело только с такими
векторами. Они называются свободными, в отличие от связанных
векторов, для изучения которых важно знать, где располагаются
их начальные точки. Свободные векторы, где бы они ни начи-
нались, всегда можно перенести так, чтобы их начальные
точки совпали; направления векторов и их длины при этом
останутся прежними. Удобно считать, что точкой приложения
свободного вектора является начало координат. Поэтому в даль-
нейшем мы будем в основном рассматривать лишь векторы, вы-
ходящие из начала координат.
Координаты вектора на плоскости § 92
Пусть хОу — прямоугольная система координат. Проекции х
— ►
и у вектора ОА (рис. 114) на оси абсцисс и ординат называются
координатами этого вектора. Координаты вектора обычно запи-
— ►
сываются в виде (х, у), а сам вектор так: ОА — (х, у).
Рассмотрим несколько примеров.
— ►
1. Пусть вектор ОА длины г лежит на оси х и направлен
в ту же сторону, что и ось х (рис. 115, а). Тогда OAt — (г, 0).
Если бы направление вектора ОА было противоположно на-
204
правлению оси x (рис. 115, б), то мы
имели бы 0А2 = (—г, 0). Аналогич-
но, вектор 0А3, представленный на
рисунке 115,6, имеет координаты
(0, г), а вектор 0А4, представленный
на рисунке 115, г, — координаты
(0, — г).
2. Вектор ОВ^ длины г, образую-
щий с осями координат равные углы
(рис. 116, о), имеет координаты ^^=-,
: У Это легко доказать, рассмотрев
прямоугольный треугольник ОВ^.
► —
Аналогично, векторы 0В2, 0В3 и
ОВ4, изображенные на рисунках
116, б, в и г, соответственно имеют
координаты:
0В2 =
OB.
Y2 / ’
___r_\
Г2 J ’
Координаты являются исчерпы-
вающей характеристикой любого
вектора, гак как по координатам
можно построить п сам вектор. Зная
координаты, легко найти и длину
вектора.
Теорема. Квадрат длины
любого вектора равен сумме
квадратов его координат.
Доказательство. Пусть ко-
— ►
ординаты вектора ОА равны х и у,
а длина г. Покажем, что
г2 = х2 -г- у2. (1)
Если вектор ОА лежит на какой-
нибудь координатной осп, то, как
было показано выше, одна из его
координат равна нулю, а другая
либо +г, либо — г. Б эгом случае
205
равенство (1) верно. Если вектор ОА
лежит в первой четверти (рис. 117),
то (1) следует из теоремы Пифагора,
примененной к Л АВО. Аналогично
обстоит дело и в случае, когда век-
тор ОА лежит в какой-нибудь дру-
гой четверти (докажите это!).
Из доказанной теоремы вытекает
следующее важное для дальнейшего
следствие: любая координата
вектора по абсолютной величи-
не не превышает длины этого
вектора. Другими словами, если век-
тор длины г имеет координаты х и у, то
< г, |у| < г.
Действительно,
г2 = х2 + у2.
Поэтому г2 > х2, откуда
W < г.
Аналогично показывается, что [у|< г.
Упражнения
630. Построить векторы с коорди-
натами: (2; 5); (0; 3); (4; 0); (—1; 2);
(0; - 3); (- 7; - 6).
631. Как изменятся координаты
вектора, если:
а) направление вектора изменить
на противоположное;
б) уменьшить длину вектора вдвое,
не меняя направления?
632. Найти длины векторов с коор-
динатами:
(3; 4); (- 5; 12); (0;—75); (2; ]<5).
633*. Что представляет собой мно-
жество концов векторов, если коорди-
наты (х, у) этих векторов удовлетворя-
ют уравнению (х — а)а +(у—6)2= г2?
206
Обобщение понятий угла и дуги § 93
В геометрии мы рассматривал! в
основном углы, меньшие «полного» уг-
ла, то есть угла в 360°. Чаще всего
(например, в треугольниках) это были
даже углы, меньшие «развернутого»
(180е). Но иногда нам приходилось
иметь дело и с углами, большими
360е. Вспомните хотя бы теорем} об
углах выпуклого многоугольника: сум-
ма всех внутренних углов выпуклого
n-угольника равна
2d (л. - 2',.
Согласно этой теореме сумма внутрен-
них углов выпуклого пятиугольника
равна
2d * 3 = 6d = 540е.
Как же представить себе такой угол?
Любой угол можно рассматривать
как фигуру, образующуюся при враще-
нии луча вокруг своей начальной точки.
Например, угол в 90° получится, еелг
—
луч СА (рис. 118, а) соверши" четверть
полного оборота вокруг точки О. Ана-
логично развернутый угол получится,
если этот луч совершит пол-оборота
вокруг точки О (рис. 118, 6V, полный
угол описывается ь результате одного
полного оборота (рис 118, в) и т. д.
Угол, больший полного, получится,
если луч совершит более одного обо-
рота вокруг точки О. Например, в ре-
, 1 . .
зультаге ) - оборота образуется угол, в
1 - раза больший полного (рис. 119, аУ,
8
е результате двух оборотов получа-
ется угол, в два раза больший пол-
ного (рис. 119, б). Подобные углы
описывают, например, стрелки часов,
лопасти пропеллера самолета и т д.
В то время как саь лу»: при пово-
роте вокруг своей начальной точки
описывает угол, любая его точка, отлич-
207
ная от. начальной точки, описывает дугу
окружности. Если, например, луч совер-
шит четверть полного оборота, то точка Л
(рис. 120, а) опишет четверть полной
дуги (то есть четверть окружности ради-
уса ОА); при двух полных оборотах луча
°) (рис. 120, б) точка А опишет дугу, кото-
рая вдвое больше полной дуги, и т. д.
Представление о таких дугах дает, на-
4 пример, намотанная на катушку нить.
Луч можно вращать вокруг начальной
Рис. 121. б) точки в двух направлениях: по часовой
стрелке и против часовой стрелки. На-
правление против часовой стрелки при-
нято называть положительным, а по часо-
вой стрелке — отрицательным. Соответ-
ственно этому ‘углы и дуги, полученные
вращением оси против часовой стрелки,
принято считать положительными; углы
и дуги, полученные вращением оси по
часовой стрелке, принято считать от-
а’ рицательными.
За единицу измерения углов и дуг,
как и в геометрии, мы примем соответст-
венно угол в 1 градус и дугу в 1 градус.
Угол в 1 градус — это угол, кото-
рый опишет луч, совершив 1/зв0 часть
полного оборота вокруг своей начальной
Рис. 122. б) точки против часовой стрелки. При такой
единице измерения угол, описываемый в
результате одного полного оборота против
часовой стрелки, равен 360°, а по часовой
стрелке — 360°. Угол, изображенный на
7 рисунке 121, а, равен 360° • 1 — = 450°, а
угол, изображенный на рисунке 121, б,
равен — 360° I— — — 540°.
Дуга в 1 градус — это дуга, кото-
рую описывает точка луча при по-
вороте этого луча на угол в 1 градус.
Например, дуга, изображенная на рисун-
Рис. 124.
i''05 _ ке 122, а, равна 1— - 360° = 450°, а дуга,
I а 4
изображенная на рисунке 122, б, равна
.360° = — 270°.
208
Дугу в 1 градус и угол в 1 градус не следует отождествлять
друг с друюм. Это разные, хотя и очень близкие понятия. Чтобы
не путать их, иногда угол в 1 градус называют угловым граду-
сом, а дугу в 1 градус — дуговым градусом. Дуга всегда содержит
столько дуговых градусов, сколько угловых градусов содержит
соответствующий ей угол.
В заключение примем следующее соглашение. Пусть угол <р*
образован вращением луча ОА вокруг точки О (рис. 123). Ис-
ходное положение ОА этого луча будем называть начальной сто-
роной угла <р, а положение ОА', которое он займет в результате
вращения, — конечной стороной угла <р. Если начальные стороны
двух равных углов совпадают, то совпадут, очевидно, и их ко-
нечные стороны. Обратное утверждение, вообще говоря, неверно.
Так, углы в 45° и 45’ + 36(Г = 405г (рис. 124) не равны друг
другу, хотя начальные и конечные стороны их совпадают.
Упражнения
634. Какие углы описывают минутная и часовая стрелки за:
а) 5 мин-, б) 5 ч?
635. В каких координатных четвертях оканчиваются углы:
а) 75° и — 75°; в) 140° и — 140°;
б) 1000° и — 1000°; г) 191° и — 191’?
636. Могут ли углы и — <р оканчиваться в одной и той же
четверти? Могут ли они иметь одну и ту же конечную сторону?
637. Написать общин вид углов, оканчивающихся:
а) на положительной части оси абсцисс;
б) на отрицательной части оси абсцисс;
в) на положительной части оси ординат;
г) на отрицательной части оси ординат;
д) на биссектрисе первого координатного угла;
е) на биссектрисе первого или на биссектрисе третьего коор-
динатного угла;
ж) на биссектрисе четвертого координатного угла.
Теорема об отношениях координат вектора к его длине § 54
Пусть два вектора ОА, = (хь у,) и ОАг = (х2, у2), длины ко-
торых равны соответственно г, и г2, лежат на одной прямой
и направлены в одну и ту же сторону, как показано на рисун-
ке 125. Тогда х, — ОВ,. у, = А,В,; х2 = 6В2, у2= А2В2. Из по-
добия треугольников ОЛ(В, и ОА2В2 следует, что
/IjC, АгВг ОВ, ________ОВг
ОА, ~ ОА3 ОА, ' ОА, ’
* <р греческая буква читается: фв.
209
Рис. 128.
О
Рис. 129.
ИЛИ Уi _ Уз б _ f? Ц)
б г2 Ci г2
-
Если бы векторы ОА, и 0А2 лежа-
ли во второй it,верти (рис. 126), то
аналогично предыдущему мы имели бы
Xi — — OB j, у j — A tB f;
х2 -= — 0В2, у2 - А 2В2;
A,J\ а2в2 0Bt = ов2_
ОА, ~ 0А2 ' 0Д1 0А2
или
У1 _ Уз . — *1 _ — Х2
Г1 Г2 Г1 Г2
откуда снова получаются соотноше-
нпя (I). Таким же образом можно бы-
ло бы рассмотреть и случаи, когда
векторы OAt и ОА2 лежат в Зйили4й
четвертях. Мы и илда пришли бы к со-
отношениям (1).
Формулы (1) справедливы также
в случае, когда векторы OAt и ОА2
лежат на какой нибудь оси коор
дннат. Например, в случае, представ-
ленном на рисунке 127,
xt = 0; yi = rt; х2 = 0; у2 = г2.
11оэтому
У1 — 1 _ Уз. , q _ б
г2 Г2 ’ q г2
Учащиеся могут самостоятельно рас-
смотреть и другие возможные случаи
расположения векторов ОА, и 0А2 на
осях координат и убедиться, что фор-
мулы (1) верны в этих случаях.
Равенства
У1 _ Уз п б = х2
б б б г2
л
указывают на то, что отношения — и —
Г Г
координат х и у вектора к его дли-
не г не зависят от длины вектора. При
изменении длины вектора эти отиоше-
210
ния остаются неизменными, хотя сами координаты х и у при
этом, конечно, изменяю ни.
От чего же в таком случае зависят эти отношения? Чтобы
ответить на этот вопрос, рассмотрим два примера. Если век-
тор ОА длины г лежит па положительной полуоси абсцисс
(рис. 128), то его координаты равны х = г, у = 0. Поэтому дли
такого вектора
* =1, 2=0.
г г
— —
Если же вектор ОА длины г лежит на положительной полуоси
ординат (рис. 129), то, как мы видели выше,
2=0, 2 = 1.
г г
Уже из этих частных примеров видно, что отношения координат
вектора к его длине изменяются при изменении направления
вектора.
Таким образом, мы доказали следующую теорему.
Теорема Отношения
х У
- и -
г г
координат вектора к его длине не зависят от длины
вектора, но зависят от его направления^
Упражнения
638. Зависят ли от длины г вектора ОА:
а) его координаты х и у;
б) отношения — и - ?
Г г
639. Зависит ли отношение — координат вектора от его дли-
У
ны г?
Определение тригонометрических функций угла § 95
Пусть <р — произвольный угол (рис. 130). На конечной сто-
роне этого угла возьмем вектор О А произвольной длины г. Абс-
циссу этого вектора обозначим х, а
ординату — у. Как было показано в пре-
дыдущем параграфе, отношения 2 и 2
г г
зависят лишь от направления векто-
ра ОА, определяемого углом <р, и не
зависят от длины вектора г. Поэтому
эти величины являются своеобразными
Рис. 130.
характеристиками угла <р.
211
Отношение ординаты вектора, образующего с осью Ох
угол <р, к длине этого вектора называется синусом угла <р (обо-
значается sin ф):
sin <р = — . (1)
Отношение абсциссы вектора, образующего с осью Ох
угол ср, к длине этого вектора называется косинусом угла <р (обо-
значается costp):
cos <р = — , (2)
г
Отношение синуса угла ф к его косинусу называется танген-
сом угла <р (обозначается tg ср):
, sin ф
tg ф = —г. (3)
COS ф
Отношение косинуса угла ф к его синусу называется котан-
генсом угла ф (обозначается ctg ф):
ctgcp=S2^P. (4)
Sin ф
Величина, обратная косинусу угла ф, называется секансом
угла ф (обозначается sec tpj.
sec ф = —!— . (5)
COS ф
Величина, обратная синусу угла ф, называется косекансом
угла ф (обозначается cosec ф): -
cosec ф = —— . (6)
sin ф
Легко понять, что для острых углов введенные таким образом
определения полностью совпадают с теми, которые уже известны
нам по курсу геометрии.
Синус и косинус определены для любого угла ф, поскольку
выражения— и имеют смысл при любом положительном г.
Что же касается tg ф, ctg ф, sec ф и cosec ф, то они определены
не для всякого угла ф. Тангенс и секанс в силу (3) и (5) опре-
делены лишь для тех углов, косинусы которых отличны от нуля,
а котангенс и косеканс в силу (4) и (6) — для тех углов, синусы
которых отличны от пуля.
Если cos ф = — — 0, то х — 0. Это может быть лишь тогда,
_
когда вектор О А перпендикулярен оси абсииес (рис. 131, а
и 131, б).
212
В этом случае угол g может принимать
значения
±90°; ±270°; ±450°; ±630°; ... .
Все эти значения можно записать одной
формулой:
g = 90° (2и + 1),
где п — любое целое число (положительное,
отрицательное или нуль).
Таким образом, тангенс и секанс опре-
делены для всех углов д. кроме углов
g = 90° (2я--1).
Если sir g = — = 0, то у = 0. Этс возмож-
г
—
но лишь тогда, когда вектор ОА лежит на оси
абсцисс (рис. 132, а и 132, б). В этом случае
угол g может принимать значения:
±0°; ±180°; ±360°; х540°; ... .
Все эти значения можно записать одной
формулой:
g = 180°п,
где п — любое целое число (положительное,
отрицательное или нуль.) Поэтому котан-
генс и косеканс определены для всех
углов <р, кроме g = 180°//.
Если д =# 90°т (т—целое число), то опре-
делены и tg д и cig д, причем:
Z
. sin С£ г у
tg д = - = — = z;
COS С[ X X
г
X
cos а г х
ctg д = — - - = - .
Sin Ф > у
г
*
И гак,
tg д = - ; ctg д = - . (?)
* у
Каждому у!лу д соответствуют вполне
определенные значения sin д и cos д. Кроме
того, каждому углу д =^= 90е (2п -|-1) соответ-
ствуют вполне определенные значения tg д и
0)
Рис. 131.
О ЛК
0}
Рис 132
213
sec <p, а каждому углу <p =J= 180° n — вполне определенные значения
ctg и cosec <р.
Поэтому sin <р, cos <р, tg <р, ctg <р, sec <р, cosec q являются функ-
циями угла <р. Эти функции называются тригонометрическими
функциями угла.
Ввиду простои связи между углами и дугами (см. § 93)
можно говорить о тригонометрических функциях не только
угла, но н дуги. Под синусом (косинусом, тангенсом и т. д.)
дуги в а дуговых градусов понимают число, равное синусу (коси-
нусу, тангенсу и т. д.) угла в а угловых градусов.
Упражнения
640. Для каких из данных углов 65°, 90°, 180°, 270', 720°,
810°, 900° не определены:
а) тангенс; б) котангенс?
641. (У с т н о.) Найти tga , если известно, что:
a) sin а ==0,6, cos а = 0,8;
б) sin а = 0, cos а = 1;
в) sin а = — 1, cos а -= 0.
642. Существует ли угол а, для которого и tg а и ctg а не
определены?
643. Найти значения тригонометрических функций угла <р,
►
который образует с осью х вектор ОА с координатами (— 2, 2).
644. Найти значения тригонометрических функций угла <р,
который образует с осью х векгор ОА с координатами (1, — р 3).
Тригонометрический круг. Оси тангенсов
н котангенсов § 06
Синус и косинус угла q мы определили отношениями:
sin <п = — , cos ср = - , (1)
Г 9
где х и у — координаты вектора, образующего с осью абсцисс
угол <р, а г — его длина. Поскольку отношения 2- г. — не зависят
от длины вектора, то в качестве г можно выбрать любое
положительное число. Удобнее всего положить г = 1. Тогда
формулы (1) принимают наиболее простой вид:
sin <f = у cos гр — х. (2)
Синус угла <р равен ординате, а косинус — абсциссе
вектора единичной длины, исходящего из качала коор-
динат и образующего с осью Ох угол q (рис. 133).
В § 92 мы доказали, что координаты вектора не превышают
по абсолютной величине длины этого вектора. Поэтому из (2)
214
следует, что синус и ко-
синус любого угла не
могут принимать зна-
чений, больших по
абсолютной величине,
чем 7.
Все векторы единичной
длины целиком лежат в
круге радиуса I с цент-
ром в начале координат
(рис. 134). Этим кругом
удобно пользоваться прг
изучении трпгонометриче
ских функций (особенно
синуса и косинуса ) По-
этому он получил специ-
альное название — триго
неметрический круг
Прямая х= 1 (рис. 135)
называется осью танген-
сов. Каждому углу <р #=
#= 90°(2л- .) можно по-
ставить в соответствие
точку В на оси тангенсов
являющуюся точкой пе-
ресечения конечной сторо-
ны угла ср (еле ее продол-
жения) с осью тангенсов
(рис. 136, а и 136, б).
Тангенс угла ра-
вен ординате соот-
ветствующей точки В
на оси тангенсов.
Действительно, если
угол <р оканчивается в 1-й
четверти (рис.
то согласно
§ 95,
. ВС
tgq.= —
ОС
До ВО как
ордината точки В.
же угол <с
2-й четверти
Рис. 135.
136, а),
формуле (7),
= ™ = ВС.
1
раз и есть
Если
оканчивается
во 2-й четверти (рис.
136, б), то, выбирая на егс
215
Риг. 137.
6)
vl
С
Рис. 138.
конечной стороне произвольную >
точку А и рассматривай вектор
—
ОА, получаем:
1ёф=2=_л£ =-^.
* х _оо ог>
Из подобия треугольников OAD
и ОВС следует, что
AD _ ВС
OD ОС, ’
„ , ВС ВС
Поэтому tgcp =— — =— у =
= — ВС. Но —ВС как раз и есть
ордината точки В.
Аналогично можно доказать
справедливость нашего утвержде-
ния и для углов ф, оканчиваю-
щихся в 3-й н 4-й четвертях.
В отличие от sin ф и cos ф,
принимающих только значения от
—1 до 1 (включая эти два значения),
tg <р может быть равен любо-
му действительному числу.
В самом деле, каким бы ни было
число а, всегда, выбирая на. оси
тангенсов точку В с ординатой а
и соединяя ее с точкой 0, мы по-
лучаем вектор ОВ, образующий с
осью х некоторый угол ф. Тан-
генс этого угла равен а (см.
рис. 137, а для а>0 и рис. 137, б
для а < 0). Поэтому для любого
числа а можно указать такой
угол ф. что tg ф = а.
Прямая у = 1 (рис. 138) назы-
вается осью котангенсов. Каждо-
му углу ф =/= 180°л можно поста-
вить в соответствие точку В на
оси котангенсов, являющуюся точ-
кой пересечения конечной стороны
угла ф (или ее продолжения) с осью
котангенсов (рис. 139, а и 139, б).
Котангенс угла ф равен
абсциссе соответствующей
точки В на оси котангенсов.
216
Это утверждение мы предлагаем учащимся доказать самостоя-
тельно.
Как и tg ф, котангенс угла может быть равен любо-
му действительному числу.
Упражнения
I
645. Используя тригонометрический круг, показать, что для
любого острого угла а
sin а -J- cos а >• 1
646. Показать, чтс углам 35° и 215° соответствует одна и та
же точка на оси тангенсов.
То л\е для углов 215° и — 145°.
647. Используя ось тангенсов и ось котангенсов, показать,
что tg 45° = I g 225° = 1
648. Верны ли утверждения:
а) каждому углу ф соответствует одна вполне определенная
точка оси тангенсов;
б) каждой точке оси тангенсов соответствует один вполне
определенный угол ф?
649. Может ли синус некоторого угла равняться — ?
3
650. Может ли секанс некоторого угла равняться у?
651. Докажите геометрически, используя ось тангенсов и ось
котангенсов, что для любого осгрогс угла ф
1"ф- ctg ф = 1.
Построение угла по заданным значениям
его тригонометрических функций § 97
В этом параграфе мы на конкретных задачах покажем, как
строятся углы по известным значениям их тригонометрических
функций.
Задача 1. Построить угол ф, синус которого равен а.
Если |п| >• 1, то построить такой угол нельзя, потому что
он вообще не существует (синус любого угла пс абсолютной
величине не превышает единицы). Если же [а| < 1, то поступаем
таким образом. Проводим окружность радиуса 1 с центром
в начале координат. На оси Оу отмечаем точку В с ординатой а
(рис. 140) и проводим через нее прямую, параллельную оси
абсцисс. Точки пересечения этой прямой с окружностью обозна-
чим через At и А2. Векторы OAt и С.42 имеют единичную длину,
а их ординаты равны а. Поэтому все углы, для которых OAt
217
Рис. НО
Рис. 141.
и ОА2 являются конечными сто-
ронами, имеют синус, равный а.
Замечали. Если а = I,
то описанным выше спосоОом
мы получаем не два, а только
один вектор ОВ, образующий
искомые углы с положительным
направлением оси абсцисс (рп«,.
141, а) В этом случае <р=&0°+
4- 360°п. Аналогично обстоит
дело и при а = —1 (рис. 141, б).
В этом случае<р= —90J + 360°п.
Задача 2. Построить
угол <р, косинус которого ра-
вен а.
Как и в задаче 1, требуе-
мое построение можно выпол-
нить лишь при |п] < 1.
На оси Ох отмечаем точку В
с абсциссой а и через нее про-
водим прямую, параллельную
оси Ординат (рис. 142; на этом
рисунке число а отрицательно).
Точки пересечения этой прямой
с единичной окружностью обо-
значим через Ai и А2. Искомыми
углами будут углы, для кото-
рых конечными сторонами яв-
ляются OAiViOAz.
Задача 3. Построить
угол <р, тангенс- которого ра-
вен а.
На оси тангенсов отмечаем
точку В с ординатой а (рис. 143).
Все углы, конечные стороны
которых лежат на прямой ОВ,
имеют тангенс, равный а.
Задача 4. Построить
угол ф, котангенс которого ра-
вен а.
На осп котангенсов отмечаем
точку В с абсциссой а (рис. 144).
Все углы, конечные стороны
которых лежат на прямой ОВ,
имеют котангенс, равный а.
218
Упражнение
652. Построить угол ф после’
дующим данным:
I) sin ф = --; 7) tg ф = 3;
2) sin ф = - - С,5,’ 8) tg ф = — 2;
3) sin ф = — 1, 9) ctg ф == 5;
4) cos ф= — у; 10) ctg Ф = — 4;
5) cos ф = 0,4; 11) осе ф = 1,5;
6) соьф = 1; 12) cosec ф— —2.
Значения тригонометрических
функций некоторых
углов § 98
1. Пусть вектор единичной дли-
—
ны О А образует с осью абсцисс
угол <f = 0' (рис. 145). Тогда eio
координаты х и у равны соответ-
ственно 1 и С. Следовательно,
sin 0° — у — 0, cos 0° = х = 1.
Отсюда
tgGJ = —--0,
cos О'
sec 0е = —— — 1.
cos 0е
Котангенс и косеканс этогс угла
не определены.
2. Если ф=90° (рис. 146), то
—->
координаты вектора ОА единич-
ной длины равны л = 0, у = 1.
Следовательно,
sin 90с= у ~ 1, cos 90°= х — 0.
Поэтому
ctg =
sin 90°
cosec 90е = —— = 1.
sin 90'
Тангенс и секанс этого угла не
определены.
Рио Н8.
219
У 3. При ц> = 130м (рис. 147) х =
~ 1, у=0. Поэтому sin 180° — 0,
cos 180° = — 1, tg 180° = 0,
sec 180” = —1. Котангенс и косе-
*---------пя--------*7 канс этого угла не определены.
и 4. При <р = 270° (рис. 148) х = 0,
Рис 149. У — — 1. Поэтому sin 270° =—1,
cos 270° - 0, ctg 270° = 0,
v. cosec 270° = — 1. Тапгенс и се-
Л канс этого угла не определены.
5. Пусть <р — 30° (рис. 149).
--------в—о---------Г Тогда х = ОВ, у—АВ. Р1з Д АОВ
находим- АВ= (катет, лежащий
против угла в 30°, равен поло-
Рис 150. вине гипотенузы). Используя тео-
рему Пифагора, получаем:
ОЯ= /ОЛ’-ЛВ* = У1- ~± = . Поэтому , у= А •
Следовательно,
sin 30°= l; cos30° = ; tg30°= . ctg30’=
6. Пусть <р = 135° (рис. 150). Тогда если ОЛ = 1, то
х — — ОВ —— ~==, у = АВ= (в Д О АВ ОВ — АВ, так как
Z АОВ = 45°).
Следовательно, sin 135° = -А=; cos 135°=-tg 135°==—1;
/2 /2
ctg 135"=— 1; sec 135°=—ф 2 ; cosec 135°= ]/2Г
а 0° 30° 45° 60° 90°
sin а 0 1 2 гг 2' /гг 2 1
cos а I уТ 2 /Г 2 2 2 0
tg а 0 1з_ 3 1 /Г Не суще- ствует
ctg а Не суще- ствует /Г 1 рт 3 0
220
Аналогично можно было бы найти значения тригонометри-
ческих функций и некоторых других углов. Значения тригоно-
метрических функций у слое 0°. 30е. 45°, 60°, 90° следует знать
на память.
Таблица этих значений приведена на странице 220.
Упражнения
Вычислить (№ 653—659):
653. 2 sin 30°+3 cos 30э —2tg30°—4 ctg30°-rsec 30е—cosec30e.
654. 5 sin 45° 4- 2 cos 45е Ь 3 tg 45° — 10 ctg 45° — 4 sec 45э—
7 cosec 45’.
655. sin 60’ + cos 60 J — tg 60° — ctg 60° + sec 60° —cosec 60°.
656. 3 sin 0е — 5 cos 0° + 7 tg O’ + sec 0°.
657. sin 90° — 6 cos 90° + 3 ctg 0° + 5 cosec 0°.
658. sin 270° 4- cos 270° — ctg 270°
659. - sin 180° — Г 3 cos 180’4- — -g 18- 4- sec 180°.
2 i— tg 180°
660. Найти тригонометрические функции углов:
а) — 30°; б) — 45°; в) — 60°; г) — 90°.
Вычислить:
„„, sin 45° cos 60° — cos (— 45°) sin 60°'
uO I * - --- •
tg2 30° — sin2 90° - cos2 270“
662 $eC — 30°) 4- cosec (— 30°)
sin2 (— 30°) 4- cosec2 (— 30°)
Четность тригонометрических функций
§ 99
Углы ч>и —<р образуются при повороте луча в двух взаимно
противоположных направлениях (по часовой стрелке и против
часовой стрелки). Поэтому конечные стороны OAt и ОАа этих
углов симметричны относительно оси абсцисс (рис. 151). Коор-
динаты векторов единичной длины OAt = (xlt у 0 н ОА2 = (x2l yj
удовлетворяют соотношениям:
х2 = % и у2 = У1-
Поэтому
cos (— <р) = cos <р,
sin ( — ср) = — sin <р.
Следовательно, синус является
нечетной, а косинус—четной
функцией угле.
221
Далее имеем:
. sin (— <p) — sin ф
tg (— ф) = — -—— = -------- =— tg <p,
COS (— Ф) COS ф
, cos (— Ф) COS ф
Ctg ( — ф) = ! — =-------2- = — Ctg ф.
sin (—ф) — б!пф
Поэтому тангенс и котангенс являются нечетными
функциями угла.
Упражнение
663. Выяснить, какие из данных функций являются четными
и какие нечетными:
1) у = sin (— х);
2) у = cos (— х);
3) у = tg (2х);
4) у = sin х cos х;
5) у = sec х;
6) у = cosec xj
7) у — sin2 х;
8) у — cos2 х;
9) у = sin х + tg х.
Периодичность функций sin ср и со$ф
§ 100
Предположим, что вектор ОА = (х, у) единичной длины обра-
зует с осью абсцисс угол ф (рис. 152). Если сделать полный
оборот вектора ОА вокруг точки О против часовой стрелки, то
получится угол ф + 360°. Но вектор ОА при этом займет перво-
начальное положение, а потому координаты его х и у не
изменятся. Следовательно,
у = sin ф = sin (ф + 360’),
х = cos ф = cos (ф 4- 360°).
Эти соотношения показывают, что значения функций sin ф и cos ф
не изменяются, если их аргумент увеличить на 360е.
Пусть f (х) есть некоторое выражение, зависящее от перемен-
ной величины х. (Например, f (х) = х2, /(х) = sin хи т. д.) Тогда
равенство
У = f W
определяет у как функцию аргумента к.
Рис. 152.
Если при любых: допустимых
значениях аргумента х
f(x 4- Т) = f (х),
где Т — некоторое отличное от
нуля число, то функция f (х)
называется периодической, а чис-
ло Т—ее периодом Согласно этому
222
определению функции sin х и cos х являются периодическими
с периодом Т=360°.
— >
При п полных оборотах вектора ОА против часовой стрелки
образуется угсл ср +360° и, а по часовой стрелке—угол
ср — 360° п. В каждом из этих случаев координаты х и у вектора
не изменяются, а потому не изменяются sir ср и cos ср. Таким
образом,
cos ср = cos (ср + 360°/i),
sin ср = sir (ср + 360эл), (I)
где п — любое целое число (положительное, отрицательное или
нуль).
Формулы (1) показывают, что каждый из углов
360°; 720°; 1080°; ... (п = 1, 2, 3, . ..),
— 360°; — 720°; — Ю8СЭ; ... (п = — 1, — 2, - 3, . , .)
является периодом функции sin ср и cos ср. Таким образом, эти
периодические функции имеют бесконечное множестве периодов.
Можно доказать, что любая периодическая функция (а не
только sin ср и cos ср) имеет бесконечное множество периодов.
Говоря о периоде функции, удобно из бесконечного множе-
ства всех ее периодов иметь в виду какой-нибудь один вполне
определенный период. Обычно псд ним понимают наименьший
положительный период функции*.
Из всех рассмотренных выше периодов функции sin <р наи-
меньшим положительным периодом является угол в 360°. По,
может быть, существует еще меньший угол, который мы просто
упустили из виду, но который также является периодом функ-
ции sin ср? Ч гобы решить этот вопрос, предположим, что наи-
меньший положительный период функции sin ср равен Г. Тогда
при любом ср
sin (ср + Т) = sin ср.
В частности, при ср = 0 получаем:
sin Т = sin 0е = 0.
Но нулю равны синусы лишь тех положительных углов, кото-
рые кратны углу в 180° (см. § 95)’, то есть углов в 180°, 360°,
540е и т. д. Поэтому единственным «конкурентом» для угла в
360° является угол в 180°. Составляет ли он период функции
sin ср? Если бы это было так, то равенство sin (<~ 4 180°) = sin ср
должно было бы выполняться при всех значениях ср. В част-
ности, при ср = 90° мы получили бы
sin 270° = sin 90°.
* Следует, однако, иметь в виду, что наименьшегс положительного
пе риода у периодической функции может и не быть. Подробнее об этом см.
в гл. IX, часть II.
223
Ho sin 270° = — 1, a sin 90° = 1 (см, § 98 j. Поэтому угол в 1в0°
НС яе>ся периодом функции sin ф. Остается признать, что
периодом [то есть наименьшим положительным периодом)
функции sin <р является угол в 360 .
Аналогично можно доказать, что периодом функции costp
также является угол в 360а.
Предлагаем учащимся убедиться в этом самостоятельно.
Упражнения
664. Доказать следующнс соотношения:
a) sin 740° = sin 20°; в) cos 54° = cos (— 1026°);
б) sin (— 1000°) = sin 80°; г) cos (— 1750°) = cos 50°,
665. Данные вырал\епия Преобразовать так, чтобы входящие
в них углы были положительными и не превышали 360°:
a) sin 820°; б) cos (— 7363°); в) sin (— 600°).
666. Данные выражения преобразовать так, чтобы входящие
в них углы по абсолют ной величине не превышали 180°:
a) cos 729°; б) sin 1268°; в) sin (— 535°); г) cos (— 1001°).
667. Доказать, что угол в 540° является одним из периодов
функции у = cos 2х.
668. Доказать, что угол в 360° является одним из периодов
функции у — tg х.
669. Докажите, что любой период Т функции у = cos х явля-
ется корнем уравнения
cos х — 1.
Верно лп обратное утверждение?
Периодичность функций tg<p и ctg qp
§ 101
Мы знаем, что тангенс угла ф равен ординате соответствую-
щей точки В на оси тангенсов (рис. 153). При повороте вектора
ОЛ, образующего с осью абсцисс угол <р, на 180° против часовой
стрелки вектор изменит свое на-
правление на противоположное,
но соответствующая точка В на оси
тангенсов останется прежней. По-
этому не изменится и тангенс
угла. Следовательно, при любом <р
tg (<р 4- 180°) = tg ф.
Это означает, что функция tg ф
является периодической с пе-
224
рнидом 1шЛ. Нс будет ли угол в 180° наименьшим поло-
жительным периодом этой функции?
Предположим, ч.м »и»мсньи1»й положительный период функ-
ции tg <р раьен 1 Тогда длг всех допустимых значений <р должна
быть
tg (ф + Л = tg <р.
В частности, при <р = 0° получаем:
tg Т = tg 0° = 0.
Hg тангенс положительного угла равен нулю лишь тогда, когда
синус этого угла равен пулю, то есть при Т = 180°, 360°, мО1,
и т. д. Следова>едино, никакой положительный угол, меньший
1г50“= не может быть периодом функции tg <р. Остается признать,
что периодом (то' есть наименьшим положительным периодом)
функции tg <р является угол в 180°.
Аналогично можно доказать, что периодом функции ctg <р
также является угол в 180°. Предлагаем учащимся убе-
диться в этом самостоятельно.
Упражнения
670. Данные выражения преобразовать так, чтобы входящие
в них углы были положительными и не превышали 180°:
a) tg 205°; б) tg (— 185°); в) ctg 300°; г) ctg (— 210°).
671. Данные выражения преобразовать так, чтобы входящие
в них углы по абсолютной величине не превышали 90е
a) tg 375°; б) ctg (—93°); в) ctg 530°.
672. Доказать, что угол ь 120° является одним из периодов
функции у = ctg Зх
673. Доказать, что любой период Т функции у = ctg х явля-
ется корнем уравнения
ctg (х + 90°) = 0.
Верно ли обратное утверждение?
0 периодических функциях § 102
Если функция f(x} периодична с периодом Т, то по значе-
ниям этой функции на любом отрезке длины Т можно восста-
новить ее значения на всей числовой прямой.
Действительно, пусть периодическая функция f (х) задана
в интервале (а, а+ Т), где Т — период этой функции (рис. 154)
Покажем, как можно определить значения этой функции в ин-
тервале (а + Т, а ф- 2Т). Для любой точки b из этого интервала
8 Заказ 261 225
можно указать точку Ь' из интервала (а, а 4- Т), отстоящую от
b на расстоянии Т. В силу периодичности функции f (х)
f (6) = f (£')•
Таким образом, по заданным значениям функции f (х) в интер-
вале (а, а 7) можно восстановить значения этой функции
в интервале (a -j- Т, а 4- 2Т). Затем, исходя из значений функции
f (х) в интервале (а 4- Т, а-]-27), можно восстановить ее значе-
ния в интервале (а 27, а 4- 37). После этого точно так же
можно найти значения функции / (х) в интервале (а 4- 37, а -+ 47)
и т. д. Аналогично можно определить значения функции f (х)
и во всех точках числовой прямой, лежащих левее отрезка
(а, а+Т).
Итак, задание периодической с периодом 7 функции f (х) на
любом интервале длины 7 дает возможность полностью охарак-
теризовать ее на всей числовой прямой. Поэтому для исследо-
вания функции f (х), периодической с периодом 7, достаточно
изучить ее поведение лишь на каком-нибудь интервале длины 7.
Например, для исследования функций у — sin ф и у = сое <р доста-
точно рассмотреть их лишь при 0° < <р < 360°. Для исследования
функции у = tg ф можно было бы ограничиться интервалом
0° < <р < 180°. Но при ф = 90° tg ф не определен. Поэтому в дан-
ном случае целесообразнее выбрать какой-нибудь другой интер-
вал, в каждой точке которого функция у = tg ф была бы опре-
делена. Мы отдадим предпочтение интервалу — 90° < ф < 90°.
Однако в принципе можно было бы выбрать, конечно, и интер-
вал 0° < ф < 180°. Для изучения функции ctg ф целесообразно
выбрать интервал 0° < ф < 180°.
Упражнения
674. Как достроить график функции, периодической с перио-
дом 7, если он задан лишь в интервале 0 < х < 7?
675. Может ли периодическая с периодом 7 функция f (х)
удовлетворить условию
f (2Т) = 2/ (7)?
Если может, то в каком случае? Ответ пояснить примерами.
22G
Изменение функций sin гр и cos ср
§ 103
Используг тригонометрический круг, выясним, каг с изме-
нением аргумента ср изменяются функции sir <р и cos ф.
Пусть угол q. непрерывно возрастает о” 0° до 90°. Тогда
ордината соответствующего вектора (рис. 155, а) будет непре-
рывно возрастать от 0 до 1. Следовательно, при увеличении
угла от 0° до 90° синус его возрастает ст 0 до 1.
Если угол ф непрерывно возрастает от 90° до 18Э°, то орди-
ната соответствующего вектора будет непрерывно уменьшаться
or 1 до 0 (рис. 155, б}. Следовательно, при увеличении угла ф
от 90° до 180е синус его уменьшается от 1 до 0
Точнс так же можно установить, что при возрастании угла
Ф от 180е дс 270° синус его уменьшается от 0 до — 1 (рис 155 в)
а при возрастании угла ф от 270° до 360° синус его увеличи-
вается от — 1 до 0 (рис. 155, г).
Схематично поведение функции sin ф прт изменении угла го
в интервала от 0° до 360° представлено сплошной линиег на ри-
сунке 156. Пунктирная линия схематично показывает изменение
функции sir ф в других интервалах. Он? получен? посредством
периодического продолжения сплошной линии влево г вправо.
Если угол ф оканчивается в 1-г или во 2-й четверти (рис.
155, а и 155 б), тс ордината соответствующего вектор? поло-
жительна. Поэтому синусы углов оканчивающихся в 1-й и во
2-й четвертях, положительны. Еслг же угол ф оканчивается
в 3-й или в 4-й четверти (рис. 155, в и 155, г), тс ордината
соответствующего вектора отрицательна. Поэтом} и синусы
этих углов отрицательны. К такнь же выводам, конечно, можно
было бы прийти и из рассмотрения схемы поведения функции
sir. ф ( рис. 156).
Из отмеченных выше свойстг следует особо подчеркнуть еле
дующее свойство острых углов: чем больше острый угол,
тем больше его синус. Так. sin 55° > sin 54°; sin 13: 56' >
> sin 13°54' и т. д. Это утвервденне, верное для острых углов,
не распространяется на произвольные углы. Например, угол
в 180° больше угла в 0‘. Однако sin 180° - sir 0° = С.
227
8
Аналогично тому, как мы изучили функцию sin <р, может
быть рассмотрена и функция cos <р. Мы предлагаем учащимся
провести это рассмотрение самостоятельно. При этом могут быть
использовацы те же самые рисунки 155, а, 155, б, 155, ей 155, г.
Приведем лишь окончательный результат.
При увеличении угла от 0° до 90° косинус его уменьшается
от 1 до 0; при увеличении угла от 90° до 180° косинус его умень-
шается от 0 до — 1; при увеличении угла от 180° до 270° коси-
нус его увеличивается от — 1 до 0; при увеличении угла от
270° до 360° косинус его увеличивается от 0 до 1.
Схематично поведение функции у — cos х при изменении аргу-
мента <р в интервале от 0° до 360° представлено сплошной
линией на рисунке 157. Пунктирная линия схематично показы-
вает изменение функции cos <р в других интервалах. Такая кар-
тина обусловлена периодичностью косинуса. Как показывают
рисунки 155 и . 157, косинусы углов, оканчивающихся в 1-й
или в 4-й четвертях, положительны; косинусы углов, оканчиваю-
щихся во 2-й или в 3-й четвертях, отрицательны.
Следует особо подчеркнуть следующее свойство косинусов
острых углов: чем больше острый угол, тем меньше его
косинус. Так, cos 55° < cos 54°; cos 13°56'< cos 13°54' и т. д.
Это утверждение, верное для острых углов, не распространяется
на произвольные углы. Например, угол в 270° больше угла
в 180°. Вместе с тем cos 270° > cos 180° (0 > — 1).
Упражнения
676. Определить знаки следующих выражений:
1) sin 153°; 4) sin (— 402е); 7) cos (— 1230°);
2) sin 273°; 5) cos 73°; 8) cos 140°;
3) sin 301°; 6) sin 910°; 9) sin 1000° - cos 1000°.
228
677. Доказать неравенства:
1) sin 6Г > sin 60°;
2) sin 92° < sin 91°;
3) sin 196° > sin 20Г;
4) sin 353° < sin 359°;
5) cos 79* < cos 78°;
6) cos 102° > cos 150°;
7) cos 190“ < cos 200°;
8) cos 290° < cos 310“.
678. Какое число больше:
a) sin 735° или sin (— 1066°);
6) sin (— 313°) или sin 790°;
в) cos 860° или cos 510°;
r) cos (— 20°) или cos (— 10е)?
679. В каких четвертях может оканчиваться угол <р, если:
a) sin ср cos ср > 0; б) sin ср cos <р <Z 0?
680. В каких четвертях может оканчиваться угол ср, если:
a) cos 2ср > 0, sin 2ср < 0; б) cos 2ср < 0, sin 2ср > 0?
681. В каких четвертях может оканчиваться угол а, если:
a) |sin а| = — sin а;
б) |cos а| = cos а;
в) |sin (— а)| = — sin а?
682. Расположить в порядке возрастания величины:
a) sin (— 55°); sin 600°; sin 1295°;
б) cos 654°; cos (- 67°); cos 295°.
683. Как изменяется sin 2cp при изменении угла ср:
а) от 0° до 45°; в) от 135° до 180°;
б) от 90° до 135°; г) от 5760° до 5805е?
684. Как изменяется cos Зср при изменении угла ср от 3660®
до 3690°?
Изменение функций tg ср и ctg ср § 104
Как было отмечено в § 102, для полного исследования функ-
ции tg ср достаточно изучить ее лишь в интервале от — 90° до 90°.
При ср = + 90° tg ср не определен. Но если угол ср, оставаясь
в пределах от — 90° до 90°, хоть немного отличается от + 90',
то выражение tg ср уже определено. Посмотрим, как же ведет
себя функция tg?, когда ее аргумент ср близок к + 90°.
По мере того как угол ср приближается к 90°, оставаясь
меньше 90°, ордината соответствующей точки на оси тангенсов
(рис. 158) неограниченно возрастает. Какое бы большое число
N мы ни взяли, всегда можно указать такой угол ?0 (рис. 159),
что для всех острых углов ср, больших ср0, будет: tg ср > N. Это
229
Риг. 158.
Рис. 159.
свойство тангенсов условно запи-
сывается так:
Н../ tg ф = + ос
Ф -* 90’
(Ф < 90°)
(читается: предел тангенса ф,
когда ф стремится к 90°, остг
ваясь при этом меньше 90е, paofcn
njnuc бесконечности).
По мере того как угол ф при-
ближается к — 90°, оставаясь при
этом больше —90°, ордината соот-
ветствующей точки на оси тан-
генсов, будучи отрицательной, не
ограниченно возрастает по абсо-
лютной величине (рис. 160}. Какое
бы большое число N мы ни взялн,
всегда можно указать такой угол
Фс (рис. 161), чти Для всех углов
ф. меньших ф0, но больших —90°,
будет: [tg ф| > N, причем tg ф <.0.
Это свойство тангенса условно за-
писывается так:
lim tg ф = — со
Ф -> — 90е
(Ф>—90’)
(читается: предел тангенса ф,
когда ф стремится к — 90е, оста-
ваясь при этом больше — 90°,
равен минус бесконечности).
Мы исследовали поведение
функции tg ф вблизи конечных
точек интервала (— 90е, 90°). Ис-
следовать tg ф внутри этого ин-
тервала весьма просто. Как уже
указывалось в § 96, tg ф может
принимать любые числовые зна-
чения. Из рисунка 162 легко по-
нять, что, чем больше значение
аргумента ф в интервале (— 90°,
90е), тем больше будет ордината
соответствующей точки на оси
тангенсов. Следовательно, из двух
произвольных углов этого интер-
вала большему соответствует
больший тангенс.
230
nT^ при
увеличении угла от—90° до
4 90° тангенс его возрастает
От — оо^О + оо.
Схематично поведение функ-
ции tg <р в интервале—90° <’. ф <:
< 90° изображена сплошной ли-
нией на рисунке 1оЗ. Пунктир
ные линии на том же рисунке
дают представление об изменении
функции tg у в других интерва-
лах изменения аргумента ф. Такая картинг объясняется перио-
дичностью тангенса (см. § 102).
Необходимо особо отметить следующее. Еслк угол ф прибли-
жается к 90', Очаоаясь при этом меньше 90°, то tg ф neui-
раниченно возрастает. Если же угол ф приближается г 90°,
оставаясь при этом больше 90° (см. рис. 163), то tg ф неог-
раниченно убывает. Аналогично можно сформулировать и закон
изменения функции tg ф, когда ф -> — 90\
Углам, оканчивающимся в 1-й и 3-й четвертях, соответст-
вуют точки на оси тангенсов с положительными ординатами
(рис. 162). Поэтому тангенсы этих углов полож! тельны. ^лам,
оканчивающимся вс 2-й и 4-й четвертях, соответствуют точки
на оси тангенсов с отрицательными ординатами ^рис. 162). По-
этому тангенсы этих углов отрицательны.
Итак, мы рассмотрели функцию у = tg <р. Аналогично мсжио
было бы исследовать и функцию ctg ф. Нетрудно видеть’
(рис. 164), что
lim ctg ф = + оо , lim ctg ф = —оо
<р — 0° ф-И0’
(ф>0)°, (Ф<180’)
Из двух углов, заключенных в ин-
тервале^0, 180°), большему соответству-
ет меньший котангенс.
Принято говорить, что при увели-
чении угла от 0° до 180е котангенс
его уменьшается от- оодо—оо.
231
Рис. 165
Схематично поведение функции ctg ф представлено на ри-
сунке 165.
Котангенсы углов, оканчивающихся в 1-й и 3-й четвертях,
положительны; котангенсы углив, иканчнвающнлся во 2-й и 4-й
четвертях, отрицательны.
Упражнения
685. Определить знаки следующих выражений:
1) tg 153°; 4) ctg (— 402°) - tg 1°; 7) tg (— 1230”);
2) ctg 270°; 5) tg 73°; 8) tg 140° • ctg 240;
3) tg 301°; 6) ctg (— 910°); 9) tg 546° — 1.
686. Какое число больше:
1) tg 92° или tg 91°; 5) ctg 102°
2) tg 61° или tg 60°; 6) ctg (— 313°)
3) tg 353° или tg 359°; 7) ctg (— 20“)
4) ctg 290° или ctg 310°; 8) tg 407°
иди ctg 150°;
или ctg 790c;
или ctg (— 10°);
или ctg 497°?
687. В каких четвертях может оканчиваться угол ф, если:
a) jtg ф| = tg ф; в) tg 2ф > 0;
б) |ctg (— ф)| = — ctg ф; г) ctg 2ф < 0?
688. В каких четвертях имеют одинаковые знаки:
a) sin ф и tg ф; в) cos ф и tg ф;
б) cos ф и ctg ф; г) tg ф и ctg ф?
689. Какие пары тригонометрических функций имеют одина-
ковые знаки во всех четвертях?
690. Данные выражения расположить в порядке возрастания:
a) tg (- 55е); tg 600°; tg 1295е;
б) ctg 295“; ctg (— 67°); ctg 654°.
691. Какие тригонометрические функции внутреннего угла
треугольника могут принимать отрицательные значения п когда
именно?
692. Могут ли быть отрицательными значения тригонометри-
ческих функций:
а) половины внутреннего угла треугольника;
б) полусуммы двух внутренних углов треугольника;
в) полуразности двух внутренних углов треугольника?
232
Таблицы значений тригонометрических функций
§ 105
В § 98, используя известные из геометрии свойства прямо-
угольных треугольников, мы показали, как можно найги значе-
ния триюпомегрическнл функций некоторых углов, например
30°, 45е, ЬО° и т. д. Кроме того, мь показали как находятся
значения тригонометрических функций углов, конечные стороны
которых лежат на какой-нибудь оси коирдинат (9(У, 180°, 279°
и т. д.). Но до снх пор остается неясным, как отыскиваются зна-
чения тригонометрических функций произвольных углов, таких,
например, как 12°, 91°, 1239° и т. д.
Л1атематика уже давно располагает весьма эффективными
методами определения значений тригонометрических функций
любого углг Однако рассмотрение этих методов выходит далеко
за пределы школьной программы. Поэтому мь: можем лишь от-
метить, что в настоящее время существуют таблицы приближен-
ных значений тригонометрических функций углов с очент высо-
кой степенью точности. В некоторых из эгих таблиц ошибки не
превышают 10-7 = 6,0000001. Мь будем пользоваться «Четырех-
значными математическими таблицами» В. М. Брадпса. В них
на страницах 52—54 приведена таблица, по которой с точностью
до 0,0001 можно определять синусы и косинусь острых углов
с интервалом в одну минуту.
Входными данными в таблицу являются величины углов-
в строках отмечены градусы, а в столбцах — минуты Каж-
дая строка таблицы имеет две помегкп — левую и правую.
Например, первая строка на странице 53 помечена слева
как 35е. а справа как 54°; последняя строка нг тог же странице
j помечена слева как 69°, а справа как 20°. Аналогично, каждый
/ столбец имеет две пометит — верхнюю и нижнюю. Например,
второй столбец на странице 53 сверху помечен как 6', а снизу
как 54'; следующий столбец сверху помечен как 12', г снизу как
48' и т. д.
Нахождение синуса угла. Пусть, например, нужно найти
синус угла 37‘. Отыскиваем число, стоящее нг пересечении
строки с левой пометкой 37° и столбца с верхней пометкой О'.
Это число 0,60;8 (для краткости ь таблице указаны лишь дроб-
ные части чисел, поскольку целые части всех этих чисел равны
нулю). Следовательно, с. точностью до 0.00С1 sin 37°« 0.6018.
Если бы нам нужно было найти sin 37°24', тс мы должны были бы
взять число в строке с левой пометкой 37° и в столбце с верхней
пометкой 24'. Это число 0,6074. Следовательно, с точностью до
0,0001 sin 37°24'« С,6074.
Предположим теперь, что нам нужно найти sin 37°26'. Столбца
с верхней пометкой 26' в таблице нет. В таком случае нужно
воспользоваться поправками, приведенными в правой части
233
страницы. Представим 37°26' как 37°24' + 2'. Теперь к sin 37°24‘ та
та 0,6074 нужно прибавить поправку на 2'. Эту поправку оты-
скиваем в строке с левой пометкой 37° и столбце с пометкой 2'.
Она равна 5.
Поэтому
sin 37°26' = sin (37 24' + 2 ) л- 0,6074
22 5
0,6079.
Итак, с точностью до 0,0001 sin 37’26'?» 0,6079.
Если бы нам нужно было найти sin 37°29', то мы поступили
бы следующим образом: 37°29' — 37°30' — Г. В таблице находим
sin 37°30'а? 0,6088; поправка на Г равна 2. Поэтому
sin 37’29' = sin (37' 30' — L')» 0,6088
--2
0,6086.
Итак, с точностью до 0,0001 sin 37°29' та 0,6086.
Из этих примеров нетрудно понять общее правило учета по-
правки при нахождении синуса: если данный угол больше
того, который отмечен в таблице, то поправка при на-
хождении синуса прибавляется; если же данный угол
меньше того, который отмечен в таблице, то поправка
отнимается.
Это правило легко понять: ведь чем больше острый угол,
тем больше его синус, и, наоборот, чем меньше острый угол, тем
меньше его синус.
Нахождение косинуса угла. Пусть, например, нужно най-
ти косинус угла 37°. Отыскиваем число, стоящее на пересече-
нии строки с правой пометкой 37° и столбца с нижней по-
меткой О'. Это число 0,7986. Следовательно, с точностью дс
0,0001 cos 37°та 0,7986. Если бы нам нужно было найти cos 37°24',
то мы должны были бы взять число в строке с правой помет-
кой 37 и столбце с нижней пометкой 24'. Это число 0,7944. Сле-
довательно, cos 37’24' та 0,7944.
Предположим теперь, что нам нужно найти cos 37’26'. Тогда
мы находим по таблице cos 37’24' та 0,7944, а затем отнимаем
от этого числа поправку на 2'. Эту поправку отыскиваем в строке
с правой пометкой 37° и в столбце с отметкой 2 . Она равна 4.
Поэтому
cos 37*26' = cos (37*24' + 2') та- 0.7944 — 0,0004 = 0,7940.
Итак, с точностью до 0,0001 cos 37*26' ~ 0,7940. Если бы нам
нужно было найти cos 37*29', то мы поступили бы следующим
образом: 37*29' = 37'30'— Г. В таблице находим cos 37*30'
0,7934; поправка на Г равна 2. Поэтому
cos 37’29' ~ cos (37°30' — Г)» 0,7934 + 0,0002 = 0,7936.
Итак, с точностью до 0,0001 cos 37’29' та 0,7936.
234
Из этих примеров нетрудно понять общее правило уче~а по
поавки при нахождении косинуса. Если данный угол больше
того, который отмечен в таблице, то поправка при
нахождении косинуса отнимается; если же данный
угол меньше того, который отмечен в таблице, то
поправка прибавляется.
Е> основе этого правилг лежит следующее свойство kochhvcc
чем больше острый угол, тек меньше его косинус; чек меньше
острый угол, тем больше его косинус.
Нахождение тангенса и котангенса угла, '’’аблицы танген-
сов и котан~енсов приведены у В. М. Брадиса на страницах
55—58 Этг таблицы составлены аналогично таблицам сину-
сов и косинусов, ь поэтому мы не будем подробно их описывать.
Отметим лишь правила учета поправок. Если данный угол
больше того, который отмечен в таблице, то при на-
хождении тангенса поправка прибавляется, а пои на-
хождении котангенса—отнимается* Наоборот, если
данный угол меньше того, который отмечен в таблице,
то при нахождении тангенса поправка отнимается,
а при нахождении котангенса—прибавляется.
Учащимся предлагается самостоятельно обоспэват! этс правило.
Примеры. Найти tg 37°29’.
По таблице находим tg 37°30'«^ 0,7673 Поправк; н< 1 гавна о.
Поэтому tg 37с29' = tg (37°30' —1')» 6,7673 —0,0005 - 0,7668.
Найти ctg 37с29'. По таблице находим ctg 37°30' т 1,3032.
В таблице мы прочитаем простс 3032. Это дробная част.. котан-
генса Целая часть указана ниже. Она оавпа 1 и постоянна для
котангенсов всех углов от 30° и до 35'. Поправка нт ' равна 8.
Поэтому ctg 37°2£' = ctg (37сЗС—:')« 1.3032 + 0,0008 = 1,3040.
В заключение отметим, что тангепсь углов близких к 90°
(от 76° до 90°). и котангенсы углов близких к С" (от 0‘ до 14е},
находятся по таблице (стр. 57, 58' без использования поправок.
Мы показали, как с помощью математических таблиц нахо-
дятся значения тригонометоических функций острых углов. А как
быть еслт интересующий нас у го/ не являетсг острым (напри-
мер, 9Г, 127° и т. д.)1 Этот вопрос мы решим позднее. Пока
лишь отметим что для нахождения синуса, косинуса, тангенса
и котангенса любого угла (в том числе i нт острого!) вполне
достаточне тех таблиц, которые мь только что рассмотрели.
Упражнения
693. Длт каждого из данных углов найти синус, косинус,
тангенс и котангенс:
1) 20°48'; 4) 88°54', 7) 6’°13; 10) 45°07-:
2) 35°06‘; 5) 20°50'; 8) 88°5’'; Н . 8741'
3) 6 °,2'; 6) 35°05'; 9} 44°03'; 12) 65с05’
235
С 94. Самолет, видимый с базы поисковой группы под уг-
лом 12', радирует на базу, что он находится на высоте 800 м
над разыскиваемым объектом. Найти расстояние от базы до ра-
зыскиваемого объекта.
695. При фотографировании обратной стороны Лупы автома-
тическая межпланетная станция находилась ог Луны на расстоя-
нии, примерно равном 65 000 км. Под каким углом была видна
в это время Луна? Радиус Луны принять равным 1740 км.
Использование тригонометрических таблиц
для нахождения острого угла по значениям
его тригонометрических функций § 106
Тригонометрические таблицы можно использовать не только
для нахождения значений тригонометрических функций острых
углов, но и для нахождения острых углов по заданным значе-
ниям их тригонометрических функций.
Пусть, например, нужно найти острый угол <р, синус кото-
рого равен 0,5135. Отыскиваем это число в таблице на страни-
цах 52—54. Замечаем, что оно стоит на пересечении строки с
левой пометкой 30° и столбца с верхней пометкой 54'. Следова-
тельно, 30с54'. Попробуем теперь найти острый угол <р,
синус которого равен 0,9526. Такого числа в таблице нет. Бли-
жайшее же к нему число в таблице равно 0,9527. Представим
0,9526 в виде 0,9527 — 0,0001. Число 0,9527 соответствует углу
72°18', а 0,0001 — поправке на Г. Поэтому 72°18' — 1'= 72с17'.
Таким же образом можно находить углы и по значениям их
косинуса, тангенса и котангенса. Ответы, как правило, будут
приближенными с точностью до Г.
Особое внимание при решении подобных задач нужно обра-
тить на правило учета поправок. Пусть, например, нужно найти
острый угол <р, котангенс которого равен 2,710. В таблице на
страницах 55—58 отыскиваем число, ближайшее к 2,710. Таким
числом является 2,703. Представим 2.710 в виде 2,703 4- 0,007. Чис-
ло 2,703 соответствует котангенсу угла 20°18', а 0,007 — поправке
на 3'. Поэтому искомый угол <р равен 20° 18' —3' — 20° 15’.
Поправку в данном случае нужно отнимать, а не прибавлять.
Ведь из двух острых углов меньшему соответствует больший
котангенс.
Упражнения
696. Найти острый угол по данному значению его синуса
(косинуса):
а) 0,1874; г) 0,9903; ж) 0,9412; к) 0,9441;
б) 0,5577; д) 0,2682; з) 0,4381; л) 0,9944;
в) 0,9078; е) 0,8264; и) 0,8760; м) 0,0020.
236
697. Найти острый угол ф по данному значению его тангенса
(котангенса):
а) 0,2698; г) 19,1900; ж) 3,9910, к) 0,3832;
6) 2,2250; д) 0,0090; з) 1,7400; л) 0,1844;
в) 3,9230; е) 0,5782; и) 2,7440} м) 0,0008.
Радианное измерение углов и дуг 9 107
Подобно тому как расстояния не всегда удобно измерять
в сантиметрах, время в секундах, массу в граммах и т. д. — углы
и дуги не всегда удобно измерять в градусах. Поэтому наряду
с градусом очень часто употребляется и другая единица измере-
ния углов и дуг — радиан.
1 угловой радиан есть центральный угол, опирающийся на
такую дугу окружности, длина которой равна радиусу этой ок-
ружности (рис. 166).
В этом определении фигурирует окружность, и поэтому есте-
ственно поставить вопрос: а не зависит ли угол в 1 радиан от
радиуса этой окружности? Было бы нехорошо, если бы такая
зависимость имела место Ведь тогда один и тот же угол, на-
пример угол в ЗС°, содержал бы разное число радианов в зави-
симости от того, с какой окружностью егс связывать. Однако
в этом отношении все обстоит благополучно. Действительно,
окружность радиуса R имеет длину 2п7?. Поэтому ее дуга длиной
в 7? составляет — часть окружности; нс в таком случае соответ-
1
ствующеи ей центральный угол должен составлять часть
полного угла, то есть угла в 360°:
1 радиан — 57° 17'45".
Такой угол не зависит от R. Очевидно, что
2л радианов — 360°.
Поэтому
1° = радиана ~ 0,017 радиана.
1 дуговой радиан есть такая дуга окружности, которой со-
ответствует центральный угол в 1 угловой радиан.
Вошло в обычаи слово «радиан» в выражениях:
«Ф = 1 радиану», «<р= 10 радианам», «ф =—3 радпа-
нам» и т. д. опускать и писать просто: [
Ф = 1, Ф = 10, ф = — 3 и т. д. ( ° j
Эти выражения не следует путать с выражениями
ф = 1°, ф = Ю°, ф------3° и т. д. Рнс. 166
237
Такие углы, как углы в 30°, 45°, 60° 90°. 135° и др., очень
часто будут встречаться в упражнениях. Радианную меру этих
УГ1ИМО 1 i V1П ton О llGjVinHloI
Л ₽ с. TI Л л Л «г\ 3
<3U'= —; -т5 — —; 01)' = —; 9сг = —; !3b“ = —л и т. д.
6 4 3 2 4
В четырехзначных математических таблицах В. М. Бра«пеа
на страницах 59—61 приведены таблицы для перевода градусной
меры угла (дуги) в радианную. Этими же таблицами можно
пользоваться и для решения обратной задачи, то есть для об-
ращения радианнмй меры угла в градусную. На границах 62,—
— 64 в таблицах В М. Брадиса приведены значения функций
sin q>, cos ф, tg ф для углов ф, выраженных в радианах.
Если под ф понимать угол, выраженный в радианах, то пе-
риодом функций sin ф и cos ф будет угол 2л, а периодом функ-
ций tg ф и ctg ф — угол л.
Упражнения
698. Данные углы выразить в радианах:
а) 40°; б) 150°; в) 315°; г) 1000°.
699. Данные углы выразить в градусах:
а) б) -|л; в) 7л; г) Зл.
700. В какой четверти оканчиваются углы:
1) 2; 3) 5) 3; 7) 100.
2) —2"; 4)0,80; 6) —3,25; 8) — |?
701. Вычислить:
а) о2 sin + Ь3 cos 0 = 2аЬ cos л;
С) 3 cos — — 4 sin3 Зл + 8 tg л;
’ 2 2
з
в) 2 cos л + 6 ctg — л — 5 sin 2л;
з
г) 2 tg 0 -f- sin л — cos — л — ctg л.
702. Для каких значений х. выражение tg ^х—не опре-
делено?
703. Какие из данных величин являются положительными и
какие отрицательными:
a) Sin у1; б) cos 2; в) tg^n; г) ctg 100?
Используя тригонометрические таблицы, вычислить:
704. sin 0,5 + cos 2,7 + tg 0,6 • ctg 2,8.
705. tg 2,5 + ctg 1,5 + sin 0,3 • cos 0,3.
238
706. При каком условии
радианной мере?
707 что больше:
a) sin 0.63 или sin 0 87;
б) cos 1,8 пли cos 1,83;
длина дуги окружности равна
в) sin 4° или sin 4,
г) tg (у) или tg |?
Тригонометрические функции числового аргумента
§ 108
До СИХ пор, говоря о ТршмпмморИчсСКНЛ фуНКЦИЯХ, МЫ СЧИ-
тали, чтс аргументами этих функций являются утлы или дуги
Теперь мы хотим ввести в рассмотрение тригонометрические функ-
ции числового аргумента. Такое желание вполне естественно.
Когда мы говорим, например, о квадратной функции у - ахг,
то под х понимаем просто число. Это число может хараме-
ризовать время в свободном падении тел (S = ^-), сопротивле-
ние электрической цепи в законе Джоуля — Ленца (Q = /У?2) и т. д
Почему же в таком случае, говоря о функции у = tg х, мы под
х Должны понимать обязательно угол?
Определение. Синусом числа х называется число, равное
синусу угла в х радианов. Косинусом числи х называется число,
равное косинусу угла в х радианов.
Аналогично определяются и другие тригонометрические функ-
л у 2 я 1 •
ции числового аргумента х. Например, sin ~ — -g-; cos - — —’
tg л = и т. д. Здесь уже я" и — не углы, выраженные
6 р 3 4 3 6
в радианах, а просто числа.
Упражнения
Какие из данных чисел являются положительными и какие
отрицательными (№ 708, 709):
708. a) sin 3; б) cos 6; в) tg 9; г) ctg 12.
709. a) cos (— 5), б) tg (— 10): в) sin (— 15); г) ctg (— 20)?
Алгебраические соотношения
между тригонометрическими функциями одного
и того же аргумента $ 109
Прежде всего отметим уже известные нам тождества
и Sir ф Z1V tg ф = - ~ (1) COS ф Ctg<p - (2) Sin ф
239
О *
Рис. 167.
Квадрат длины
координат. Из этого
Из этих двух тождеств следует, чтс
tgq> • ctg ф — 1. (3)
Теперь покажем, что для любого угла <р
sin2 ср Н- cos2 ф = 1*. (1)
Предположим, что О А = (х, у) ес~ь век-
тор единичной длины, образующий с осьюх
угол ф (рис. 167). Тогда
cos ф х,
sin ф = у.
любого вектора равен сумме квадратов его
утверждения и вытекает формула (4).
Нам известны также следующие соотношения:
1 /Г-Ч
sec ф =------ (5)
ccs а
И 1
cosec ф =----, (6)
sin ф
К полученным шести тождествам добавим еще два;
I + tg2 ф = sec2 ф, (7)
1 + ctg2 ф — cosec2 Ф- (8)
Докажем, например, тождество (7):
, . .» , . sin29 cos2фsin3® 1 ,
1 + tg2 ф = 1 Н---=--------З-С----й- = —— == 5ес2ф.
COS3 ф COS3 ф COS2(f
Аналогично доказывается и тождество (8).
Упражнения
710. Могут ли sin ф и cos ф одновременно равняться нулю?
711. Могут ли tg ф и ctg ф по абсолютной величине быть:
а) оба больше 1; б) оба меньше 1?
712. Может ли одно из чисел tg ф и ctg ф быть положитель-
ным, а другое отрицательным?
713. Какова область допустимых значений ф в тождестве
tg ф • ctg ф = 1?
714. Доказать неравенство |sec ф| > 1 не менее чем двумя
различными способами.
г> 3 sin a--cos а .
715. Выразить------------- через tg а.
sin а -|- 2 cos а
716. Найти sin а • cos а, если since + cos а — а.
* Выражения sin2 ф. cos2 ф н т. д. употребляются для записи квадратов
(sin<p)2, (cos ф)2 и т. д.
240
Нахождение значений тригонометрических функций угла
по значению какой-нибудь одной из них § 110
Используя основные тригонометрические тождества, получен-
ные в § 109, легкс найти значения всех тригонометрических
функций sin х, cos х, tg х, ctp х, sec x, cosec x, если известно
значение какой-нибудь одной из них. Поясним это на конкретных
примерах.
Пример 1. Найти значения тригонометрических функций
3
ула ср, если известно, что sm ср = —.
5
Из тождества sin2 ср + cos2 ср = 1 находим: cos2 ср — 1—sm2cp=
16 п , 4
= — . Поэтому cos ср - + — .
25 5
Знак + или — следует выбирать в зависимости от того, в ка-
кой четверти оканчивается угол ср. По условию sin ср = > 0.
Значил угол ср оканчивается либс в 1-й, либо во 2-й четверти
Если он оканчивается в 1-й четверти, тс со: ср = + у . Если же
он оканчивается во 2-й четвеоти, то cos ср = —
В первом случае
3
, > sin w 5 3
сог <р 4 4
У
* 1 4
Ctg ф = -— =
<ёф з
втором случае
3 4
tgq>= — ctgcp = — -, s
4 о
1 >г
sec ср = — = 7;
COS ф 4
1 5
cosec ср = ------= —.
sin <p 3
5 5
о — — —; cosec ср = —.
4 4 4 3
Во
Пример 2. Най^и значения тригонометрических функций
угла ср если известно, чтс он оканчивается в 4-й четверто и
х 3
tgcp = —
Используя тождество 1 + tg2 ср = sec2 ср, найдем sec <р:
/ 3~? 5
1 4 ^—7) “7-
Знак + перед радикалом мы взяли потому, чтс угол ср по условию
. 1
оканчивается в 4-и четверти, sec ср = -- , а косинус угла, окан-
cos ф
чивающегося в 4-г четверти, положителен; поэтому положителен
i; sec ср. Далее получаем:
. 1 4
cos ср =-- = —.
seccp 5
241
Теперь, используя тождество sin2 ф 4- соз2ф = 1, найдем sintf;
sin <р ~ — |/ 1 — cos2<p = — —.
5
Здесь перед радикалом нужно брать знак — , поскольку синус
угла, оканчивающегося в 4-й четверти, отрицателен.
Заметим, что в данном случае рациональнее было бы найти
sin <р из тождества tg ф = Однако мы сознательно получили
cos ф
sin ф другим путем, чтобы еще раз показать, как нужно выби-
рать знак (4- или ’—) перед радикалом.
Итак, мы получили cos ф, sin ф, tg ф, sec ф. После этого легко
найти значения и других тригонометрических функций угла ф:
.14 15
ctg ф = -—— =-----; cosec ф = ---=-----.
tg ф 3 sin ф 3
Упражнения
717. Найти значения тригонометрических функций угла а
по следующим данным:
1) sin а = 0,6,0° < а < 90°; 4) cos а = — 0,8, 180° < а < 270°;
2) sin а = — л<а<|я; 5) *8а = ~2, ~ л<а<2л;
3) cos о — 270° < а < 360°; 6) tga=p 180°<а<270°.
718. Найти значения тригонометрических функций угла ф,
если известно, что sin ф = У (а > b > 0) и угол ф окапчп-
а -|- b
вается не в 1-й четверти.
719. Найти значения тригонометрических функций угла ф,
если известно, что tg ф = а2 — 1 (|а| < 1), и угол ф оканчивается
не во 2-й четверти.
Формулы приведения § 111
Теорема. Для любого угла ф
sin (90° 4- ф) = cos ф. (1)
Доказательство. Если угол ф оканчивается в 1-й чет-
верти (рис. 168, а), то угол 90° 4- ф должен оканчиваться во 2-й
четверти. Используя единичный круг, получаем:
sin (90° 4- ф) = BD, cos ф — ОС.
Но треугольники ОАС и B0D равны; поэтому BD — ОС. Отсюда
и вытекает равенство (1).
242
Рис.
168.
случаи, когда угол ф окаи-
Если угол ф оканчивается во
2-й четверти (рис. 168, б), то
угол 90° + <р должен оканчи-
ваться в 3-й четверти. Исполь-
зуя единичный круг, получаем:
sin (90° + ф) = —BD, cos ф =
= —ОС.
Треугольники ОАС и B0D
равны; поэтому BD = ОС. Сле-
довательно, —BD = —ОС, или
sin (90° + <р) = cos ф.
Аналогично можно рассмотр<
чивается в 3-й или в 4-й четверти. Тождество (1) легко прове-
рить и в случае, когда конечная сторона угла ф лежит на
какой-нибудь оси координат. Предлагаем учащимся самосто-
ятельно убедиться в этом.
Из доказанного тождества (1) вытекает ряд других важных
тождеств. Заменив в (1) ф на —ф, получаем:'
sin (90° — ф) = cos (—ф) = cos ф. (2)
Чтобы получить аналогичную формулу для cos (90° — ф), заменим
в (2) ф на 90° — ф. В результате получаем:
sin [90°—(90° — ф)] = cos (90° — ф),
или
зшф = cos (90° — ф).
Итак,
cos (90° — ф) = sin ф. (3)
Из (2) и (3) вытекает:
tg(90° - ф)= 5|'п(99-~ф). = = ctg ф.
Б cos (90° — ф) Sinqp Т
tg(90° — ф) = ctg ф. (4)
Аналогично, ctg (90° — ф) = -os — tg ф,
sin (90 — ф) cos ф
ctg (90° — ф) == tgф. (5)
, Формулы
sin (90° — ф) = cos ф,
cos (90° — ф) = sin ф,
tg (90° — ф) = ctg ф,
ctg (90° — ф) -= tg ф
иногда называют формулами дополнительного угла. Это связано
с тем, что углы 90° — ф и ф дополняют друг друга до прямого
угла. Эти формулы очень просто запомнить: одна функция
заменяется на другую, сходную с ней (синус на косинус,
косинус на синус, тангенс на котангенс, котангенс на тангенс).
Например, sin 40° = cos 50°; tg 70° = ctg 20° и т. д.
213
Теперь получим формулы для угла 90° 4- <р. Одну из таких
формул мы уже доказали выше:
sin (90° + ф) = cos q>.
Остальные формулы легко получаются из формул дополни-
тельного угла и свойства четности (нечетности) тригонометри-
ческих функций. Имеем:
cos (90° -J- ф) = cos [90° — (— ф)1 = sin (— ф) = — sir ф;
tg (90° 4- Ф) = tg[90c — (— ф)] = ctg (— ф) = — ctg ф;
ctg (90° + ф) = ctg [90° — (— ф)] = tg (— ф) = — tg ф.
Исходя из этих формул, можно получить формулы для углов
180° + ф. Например,
sin (180° 4- ф) = sin [90° 4- (90° 4- ф)1 = cos (90° 4- ф)= — sinф;
sin (180° — ф) = sin (90° -Ь (90° — ф)] = cos (90э — ф) = sin ф-
Аналогично доказываются формулы
cos (180° 4- ф) = — cos ф; cos (180° — ф) = — cos ф
Чтобы получить соответствующие формулы для тангенса и
котангенса, можно воспользоваться выведенными соотношениями
_ , sir <р > _ cos ф
для синуса и косинуса, учитывая, что 1£ф=-----с!бф=> -------—.
cos ф sin ф
Однако в данном случае лучше всего исходить из того, что
угол 180° является периодом функций tg ф и ctg ф. Отсюда сразу
же получаем: tg (180° 4- ф) = tg ф,
tg (180° — ф) = tg (— ф) = — tg ф,
ctg (180° 4- ф) = ctg ф,
ctg (180° — ф) = ctg (— ф) = — ctg ф.
Из формул для углов 180° + ф можно получить аналогичные
формулы для углов 270° + ф.
Формулы для углов 360° +ф легко получаются, если учесть,
что угол 360° является общим периодом тригонометрических
функций. Подробно останавливаться на этом мы не будем.
На странице 245 приведена полная таблица нужных нам фор-
мул. Заучивать эти формулы нет нужды. Достаточно помнить
следующее:
1) Если в формуле содержатся углы 180г и 360е (п и
2п), то наименование функции не изменяется; если же
в формуле содержатся углы 90° и 270° ( л и — л), то
наименование функции меняется на сходное (синус на
косинус, тангенс на котангенс и т, д.);
2) чтобы определить знак в правой части форму-
лы (±или—), достаточно, считая угол ф острым, опреде-
лить знак выражения, стоящего в левой части фор-
мулы.
244
— Функция Угол sin х COS J In X Cig J
<Г | sin q> COS Ф tg Ф Ctg 0^
90’—у <Р' COS Ф sin ф Clgq tg<P
ЭО'+ф -г ф) COS ф — sin ф — Ctgq - tg q.
180’ — <р (л — q1 sin ф — cos q* — tgq — с*ЙФ
180’ 4- ср 1л 4 <р) — sin ф — COS Ф tg Ф С1£ф
270°— ф ^-|л —ф) — COS ф — sin ф elf a tgq
270° 4- ф ^-эс4-Ч’) — COS ф sin q? — ctg ф — tg Ф
360’ — ф (2г — ф) — sin ф cos ф — tg q — ctgq
360< 4- ф (2т 4- о) sin q COS <] tg<P ctg ф
Пусть, например нужно определить (90° 4- q>). Гшежце
всего мы замечаем, что в Формуле содержатся утол 90°. Поэтому
в правое части искомой формулы дол же i стоять ctg <р. Чтобь
определит! знак перед c.g <р, предположим, чтс уол q> острый.
Тогда угол 90° -у ср должег оканчиваться во 2-г четверти. I- с
тангенс угла, оканчивающегося во 2-1 четверти, отрицателен.
Поэтому перед ctg q нужно взять знаь — . Итак,
tg (90° со) = — ctg со
Аналогично устанавливается формула
cos (180° — ф — — cos о>.
Поскольку г формуле содержится угол в 189°, наименование
функции не изменяется. Если угол q> острый, то угол. 180" — <р
должен оканчиваться вс 2-й четвегтн. 14с косинус угла,
оканчивающегося вс 2-й четверти, отпццателен. Поэтому в пра-
вок части формулы должен стоять знак — .
245
Полученные выше формулы носят название формул приведе-
нии. Причины такого названия будут выяснены в следующем
параграфе.
Упражнения
Упростить выражения (№ 720—727):
720. sin f ——оА 4- cosf л —а].
\2 ) \2 /
721. . tg^ + ^-ctg^ + a).
722. sin (л + a) — tg (л —a).
723. cos (л — a) + ctg (л 4- a).
724. sin (270° — a) + cos (270° + a).
725. tg (270°+a)—ctg (270 —a).
726. tg (a — 360°) 4- sin (a + 360°).
727. cos (a — 360°) — ctg (a — 360°).
728. Доказать, что если прямые у = ktx и у — k2x взаимно
перпендикулярны, то kik2 = — 1.
729. tg х — 3. Чему равен тангенс дополнительного угла?
730k sin <р = 0,6. Чему равен синус дополнительного угла?
731. Что больше:
sin | — — а] или sin |—|-сс)?
\2 I \ч I
Упростить выражения (.Ne 732—734):
732. sin (л 4- 1) -г cos — 1).
733. sin2 2 (л4- 1) 4" cos3 2 (л— 1).
[sin2 (9л + 0,5) + sin2 (0,5—7,5.4)]-sin — л\
734. -----------------------------1?----/.
/3 \
cos I — л — 0,51 tg (0,5 — 0,5л)
Доказать тождества (№ 735—739):
735. cos (45° ]- a) = sin (45° — a).
736. cos (20° — a) 4- sin (250° 4- a) = 0.
737. sin (112° — a) 4- cos (a 4- 158°) = 0.
738. tg x • tg (90° — x) = 1.
739*. tg 1° • tg2° - tg 3° . . . tg 87° • tg 88° tg 89° = 1.
740. Доказать, что синус суммы двух углов треугольника
равен синусу третьего угла.
741. 1) Доказать, что площадь любого четырехугольника
равна половине произведения его диагоналей на синус угла
между ними.
2) Доказать, что из всех прямоугольников с данной диаго-
налью наибольшую площадь имеет квадрат.
3) Какой четырехугольник с диагоналями di и имеет мак-
симальную площадь?
246
742. Что больше:
a) sin 26° или cos 40°; в) sin 0,63 или cos 0,87;
б) tg 57° или ctg 20°; г) tg - л или ctg -- л?
8 1 &
Определение по таблицам значений
тригонометрических функций любого угла
§ 112
В § 105 мы показали, как, используя «Четырехзначные ма-
тематические таблицы» В. М. Браднса, можно определить, чему
равно значение той или иной тригонометрической функции
острого угла. Теперь ту же самую задачу мы решим для
любого (а не только для острого) угла а.
Прежде всего заметим, что угол а. можно считать положи-
тельным. В противном случае мы воспользовались бы формулами
sin (— а) — — sin а,
cos (— а) = cos а,
tg (—а) = —tga,
ctg (— а) = — ctg а
и свели бы тем самым нашу задачу к нахождению значений
тригонометрических функций положительного угла.
Далее, можно считать, что угол а заключен в пределах
0° < а < 360°, или 0 < а < 2п.
Действительно, во всех иных случаях угол а можно предста-
вить в таком виде:
а — 360° - п сц, или а — 2лл 4- аь
где п — некоторое натуральное число, a cq находится в пределах
0е < а, < 360°, или 0< а < 2л.
Поскольку угол в 360° (или в 2л радианов) есть общий период
синуса, косинуса, тангенса и котангенса, то:
sin а = sin (360° п. + а() = sin а(.
cos а = cos (360° • п aj = cos cxi,
tg а = tg (360° • n 4- а,) = tg at,
ctgа = ctg (360° • n 4- a,) = ctga,.
Таким образом, наша задача сводится к нахождению значе-
ний тригонометрических функций угла аь заключенного в ин-
тервале
0" < «1 < 360°, или 0 < «! < 2л.
Если теперь угол острый, то значения его тригонометри-
ческих функций можно определить по таблицам В. М. Браднса.
Если же Oj > 90°, то
либо ocj — 90° 4-
либо а, = 180° 4- а,,
либо а! — 270° 4- аг,
ГДС Ct, — j/znC Uv рый угол. Используя формулы приведения мы
можем теперь свести нашу задачу к определению значений три-
гонометрических функций острого угла с.2.
Примеры. 1) Найти sin 757°24'.
Имеем-
757°24' - Зои0 • 2 + 37°24'.
Поэ.и.му
sin 757J24' = sin (360° • 2 |- 37°24') = sin 37°24'.
Синус угла в 37°24' находим по таблице В. М. Брадиса.
Приближенно он оказывается равным 0,6074. Поэтому
sin 757°24' « 0,6074.
2) Найти tg (— 1927°30').
Прежде всего заметим, что
tg ( 1927°30') = — tg 1927°30'.
Теперь представим угол в 1927°30' в виде
1927°30' = 360° • 5 + [27°30\
Отсюда tg 1927°30'/ = tg (360° • 5 + 127°30') = tg 127°30'; но
127с30'= 90° + 37°30'. Поэтому, используя фефмулы приведения,
получаем:
tg 127J30' = tg (90° + 37°30') = — ctg 37°30'.
Окончательно получаем, используя таблицы В. М. Брадиса,
tg (— 1927°30') = ctg 37 30' «1,3032.
Итак, для того чтобы находить значения тригонометрических
функций sin х, cos х, tg х и ctg х для любых значений х, вполне
достаточно уметь находить значения этих функций лишь для
6° < х < 90° (или 0 < х < для всех же остальных х значе-
ния функций можно найти, используя уже известные нам три-
гонометрические тождества. Отсюда можно сделать следующий
вывод:
Поведение функций sin л:, cosjc, tg лс и ctg ж при всех
значениях х вполне определяется их поведением при
0<х<^.
Упражнение
743. Используя «Четырехзначные математические таблицы»,
найти синусы, косинусы, тангенсы и котангенсы следующих углов:
1) 112°14'; 5) 283° 13'; 9) 824°22'; 13)5;
2) 217° 47'; 6) 351°05'; 10) 1307°21'; 14)6,3;
3) 233°2Г; 7) 100°17'; 11) 1715°39'; 15)1000;
4) 165’58'; 8) 275°57'; 12) 3928° 15'; 16) 3,14.
248
График функции у = sin лг
§ 113
Как б^ю отмечено в пре
дыдущем параграфе, поведение
функции у = sin х на всей чис-
ловой прямой (или при всех
значениях аргумента х) полно-
стью определяется ее поведени-
г . -к
ем в интервале 0 < х .
Поэтому прежде всего мы по-
строим график функции у =
—siii х именно ь этом интервале.
Составим следующую таблицу значений нашей функции.
п
2
1
Отмечая соответствующие точке на плоскости координат в сое-
диняя их плавной линией, мы получаем кривую, представленную
на рисунке 169. Для построения ее можно было бы выбрать
и большее число точек При этом нам пришлось^бы использо-
вать тригонометрические таблицы.
Полученную кривую можно было бы построить и геометри-
чески, не составляв таблицы значений функции у — sin х. Первую
четверть окружности радиуса 1 (рис. 170) разделим на 8 равных
частей и через точки деления проведем прямые, параллельные
осп х. Ординаты точек деления окружности представляют собой
синусы соответствующих углов. Первая четверть окружности
249
соответствует углам от 0 до - . Поэтому на оси х возьмсь отре-
зок [0, -^j и разделим его па 8 равны* частей. Из точек деления
восставим перпендикуляры до пересечения с ранее проведенными
горизонтальными прямыми. Точки пересечения соединим плав-
ной линией.
Теперь обратимся к интервалу у < х < л. Каждое значение
аргумента х из этого интервала можно представить в виде
+ф.
1Де 0 < ф < . По формулам приведения
sin (^ + Чр) = cos Ф sin (f ~ Ф) •
Точки оси х с абсциссами ф и - —ф симметричны друг
другу относительно точки оси х с абсциссой ,
точках одинаковы. Это позволяет
у = sin х в интервале , nj путем
раження графика этой функции в интервале |о, у
тельно прямой х = ~ (рис. 171).
и синусы в этих
получить график функции
простого симметричного отоб-
, — относи-
2]
Теперь, используя свойство нечетности функции у — sin х,
sin х) = — sin х,
легко построить график этой функции в интервале [—л, 0].
Эго построение выполнено на рисунке 172.
Функция у = sin х периодична с периодом 2л. Поэтому для
построения всего графика этой функции достаточно кривую,
изображенную ня рисунке 172, продолжить влево и вправо
периодически с периодом 2л. Полученная в результате этого
250
Рис. 172.
кривая (рис. 173) называется синусоидой. Она и ппедставляе-”
собой график функции у — sir. л.
Рисунок 173 хорошо иллюстригует все те свойства функции
у = sin х, которые раиоше были доказаны нами. Напомнил э"и
свойства.
1) Функция у = sin х определен; для всех значений х, так
что областью ее определения является совокупность всех дейст-
вительных чисел.
2) Функция у = sin х ограничена Все значения, которые она
принимает, заключены в интервале от —1 до 1, включая эти
два числа. Следовательно, область изменения этой функции
определяется неравенством — ’ < у < 1.
Пт х =— + 21гг. (bvHK-
2
ция принимает наибольшие значения, равные 1, а при :: =
= — ~ + 2/гл — наименьшие значения, равные — ?.
3) Функция у = sin х является нечетной (синусоида симмет-
рична относительнс начала координат).
4J Функциг у = sin х периодична с периодом 2л.
5) В интервалах 2пл < х < л + 2ггл (л — любсх целое число)
она положительна, а в интервалах л + 2fei С х < 2л + 2/гл
(k — любое целое число; она отрицательна. Прг х — /гл функция
обращается в нуль. Поэтом) эти значени? аргумента г (0; ч_л;
1г 2л; ...) называются нулями функции у = sin х.
-Л/С——6) В интервалах —- + 2лл < х <Z
у-яп» 2
___________< <Z -^ + 2лл функция у = sin х монс-
~jA О Ji *
томно возрастает, а в интервалах
— + 2/гл < х < — л + 2/гл она мо-
2 2
Рис. 174. нотонно убывает.
Следует особо обратить внима-
ние на поведение функции у = sin х
вблизи точки х = 0. Как видно из рисунка 174, в окрест-
ности точки х = 0 синусоида почти сливается с биссектрисой
1-го и 3-го координатных углов. Поэтому при малых углах х,
выраженных в радианах, или при малых по абсолютной вели-
чине числовых значениях х (как положительных, так и отри-
цательных)
sin х» х.
Например, sin 0,012» 0,012- sin (— 0,05)» — 0,05;
sin 2’= sin—— = sin — =» -»;0,03.
180 90 9C
Вместе с тем следует отметать, что при любых значениях х
|sin х| < |r|. (1)
Действительно, пусть радиус окружности, представленной на
рисунке . 175, равен 1, a Z АОВ = х. Тогда sin х = АС. Но
АС < АВ, а АВ, в свою очередь, меньше длины дуги АВ, на
которую опирается угол х. Длина этой дуги равна, очевидно, х,
так как радиус окружности равен 1. Итак, при 0<х<
sin х < х.
Отсюда в силу нечетности функции у — sin х легко показать,
Что при —- < х < О
|sin х] < |х|.
0 Наконец, при х = О
|sin х| = |х|.
Таким образом, для |х| < — нера-
2
В венство (1) доказано. На самом же де-
ле это неравенство верно и при >
>, в силу того, что |sm х| < 1, а
- > 1.
Рис. 175. 2
252 .
Упражнения
744. По графику функции у — sir. х определить:
a) sin 2; б) sin 4; в) sm (— 3).
745 Пс графику функции у = sin х определить, какое число
из интервала^—?, ”] имеет синус, равный:
а) 0,6; б) — 0,8. ‘
746. По графику функции у = sin х определить, какие числа
имеют синус, равный -Ь.
747. Найти приближенно (без использования таблиц):
a) sin 1°; б) sin 0,03; в! sir. (— 0,015); г) sin (— 2°30').
График функции y = cosx § 114
Как мы знаем, cosx = sir ^х т
Поэтому еслг cos х принимает некоторое значение с при х = х0,
то при х = х0 + — это же значение а примет г sir х. Если аргу-
мент х толковать как воемя, то можно сказать, что значения
функции у — sin х как бь «запаздывают», иль «отстают: от
соответствующих значений функции у = cos х на . Отсюда
можно заключить, что график функции у — cos х получается
поспедством сдвига графика функции у — sin х вдол0 оси абсцисс
влевс на расстояние ~ (рис. 76).
Итак, график функции у = cos х есть синусоида, сдвинутая
влевс на . Иногда такую кривую называют косинусоидой.
Косинусоида хорошо иллюстрирует все основные свойства
функпиг у = cos х которые раньше были нами доказаны. Пред-
лагаем учащимся еще раз сформулировать эти свойства и дать
им "рафическук интерпретацию.
25Э
Упражнения
748. По графику функции У = сиъ X Определи!в!
а) cos 3; б) cos 4; в) cos (— 2)
749. По графику функции у — cos х определить, какое число
из интервала [0, л] имеет косинус, равный.
а) 0,6; б) — 0,8.
750. По графику функции у = cos х определить, какие числа
имеют косинус, равный у,
751. При малых (по абсолютной величине) значениях х ко-
синусоида у = cos х имеет примерно такой же вид, как и парабола
у = 1 - ~ . (Сделайте чертеж!) Поэтому для малых значений х
cos х ~ 1----.
2
Используя эту формулу, вычислите приближенно:
a) cos Г; б) cos 0,03; в) cos (— 0,015); г) cos (— 2°30')-
Полученные результаты сравните с табличными.
Графики функций у — tg* и y = ctg*
§ И5
Схематично поведение функции у = tg х было представлено
на рисунке 163 (см. стр. 231). Теперь мы начертим точный гра-
фик этой функции. Для этого используем геометрическое по-
строение, аналогичное тому, которое было описано в § 113
для построения синусоиды (см. рис. 170). Мы не будем подробно
останавливаться на этом построении, а ограничимся лишь тем,
что приведем соответствующий рисунок (рис. 177). Учащиеся
без особого труда смогут разобраться в нем самостоятельно.
Теперь, используя график функции у — tg х в интервале
О < X < у, можно построить график этой функции и в интер-
Рис. 177.
254
вале-----С х < 0. Для это-
1 о воспользуемся тождест-
вом
tg (— <г) _ — tg <р.
Оно указывает на то, что
график функции y=tg х сим-
ме«рпчеп относительно нача-
ла координат. Отсюда сразу
же получается та часть гра-
фика, которая соответству-
ет значениям----* < х < С
2
(рис. 178).
Функции у= tg х перио-
дична с периодом л. Поэтому
теперь для построения ее гра
фика нам остается лишь про-
должить периодически кри-
вую, представленную на ри-
сунке 178, влевс и вправо
с периодом л. В результате
получается кривая, которая i
Тангенсоида хорошс иллюстрирует все те основные свойства
функции у = tg х, которые раньше были доказаны нами. На-
помним эти свойства.
1) Функция у — tg х определена для всех значений х, кроме
х = - + пл, где п — любое целое число. Таким образом, областью
ее определения служит совокупность всех действительных чисел,
кроме х = у 4- пл.
2) Функция у — tgx не ограничена. Он? может принимать
как любые положительные, так и любые отрицательные зна-
Рнс. 17».
тангенсоидой
255
чения. Следовательно, областью ее изменения является совокуп-
ность всех действительных чисел. Среди этих чисел нельзя
указать ни наибольшего, ни наименьшего.
3) Функция у = tg х нечетна (тангенсоида симметрична отно-
сительно начала координат).
4) Функция у = tgx периодична с периодом л.
5) В интервалах
- л ,
пл < X <-----Ь пл
2
функция у = tg х положительна, а в интервалах
л . -
— — + пл < х < пл
отрицательна. При х = пл функция у = tg х обращается в нуль.
Поэтому эти значения аргумента (0; +л; +2л; + Зл; ...) слу-
жат нулями функции у = tgx.
6) В интервалах
JT л
------F пл < х < —|- пл
2-----2
функция монотонно возрастает. Можно «сказать, что в любом
интервале, в котором функция у = tg х определена, она является
монотонно возрастающей. Однако ошибочно было бы считать
что функция у = tg х монотонно возрастает всюду. Так, напри-
мер (рис. 179), £. Однако tg (£ Д < tg £.
Это объясняется тем, что в интервал, соединяющий точки
л л . л л
х = — и х = - + — , попадает значение х — — , при котором
функция у = tg х не определена.
Для построения графика функции у = ctgx следует восполь-
зоваться тождеством
ctgx =— tg(х + .
Оно указывает на следующий порядок построения графика:
1) тангенсоиду у = tg х нужно сдвинуть влево по оси абсцисс
л
на расстояние —;
2) полученную кривую отобразить симметрично относительно
оси абсцисс.
В результате такого построения получается кривая, предста-
вленная на рисунке 180. Эту кривую иногда называют ко-
тангенсоидой.
Котангенсоида хорошо иллюстрирует все основные свойства
функции у = ctg х. Предлагаем учащимся сформулировать эти
свойства и дать пм графическую интерпретацию.
256
Упражнения
752. Используя графики функций у = tg х и у — ctg х. найти
наименьшие положительные корни уравнений:
a) tg х = — 3; б) tg х - 2; в) ctg х = — 3; г) ctg х = 2.
753. Используя графики функций у = tg х и у = ctg х, найги
все корни уравнений:
Доказательство тригонометрических тождеств § 116
При доказательстве любых тождеств и, в частности, триго-
нометрических, обычно используют следующие способы:
1) выражение, стоящее в одной части равенства, с помощью
тождественных преобразований приводят к выражению, стоящему
в другой части равенства;
2) выражения, стоящие в левой и правой частях тождества,
с помощью тождественных преобразований приводят к одному
и тому же виду;
3) доказывают, что разность между левой и правой частями
данного тождества равна нулю.
Поясним это на некоторых частных примерах.
Пример 1. Доказать тождество
sin4 а — cos’a = sina а — cos2 а.
Используя формулу для разности квадратов двух чисел, получаем:
sin4a +- cos'a = (sin2 а 4- cos2 а) (sin2 а — cos2 а)
Но sin2 а + cos2 а — 1. Поэтому
sin4a — cos'a = sin2 а — cos2 а,
что и требовалось доказать.
9
Заказ 261
257
Пример 2 Показать тождество
,sin а,-- I '____________________’*_____
г tga 4 ctya
Это тождество мы будем доказывать путем преобразования
выражения, стоящего в правой части.
Способ 1.
sin « sin и sin a
tg a cos a co? <x cos a
-------------------------------------— . sin*a.
tea 4-ctga sin a -os a ’in'a-] cos-a-------------1
co' a sin a a - ,na sina-cosu
Поэтому
1Л_____Jz sin2 a — ! sin a l,
V tg a + ctg a
Способ 2. Прежде всего заметим, что ctg a^G; е про-
тивном случае не имело бы смысла выражение tg а = ——. Но
ctg а
если ctg a^O, то числитель и знаменатель подкоренного выра-
жения можно умножить на ctg а, не изменяя значения дробь.
Следовательно,
tg a _________________________ tg a ctg a
tg a 4- ctg a tg a ctg a 4- ctg2 a
11спользуя
получаем:
П оэтому
тождества tgactga = 1 -и 1 ctg® a = cosec® a,
tga 1 1 . ,
-----------=--------------------=sin® a.
tg a + ctg a 14- ctg2 a cosec2 a
tga
tga 4- ctg a
= |sin aj,
что и требовалось доказать.
Замечание. Следует обратить внимание на то, что левая
часть доказанного тождества (Isin а,) определена при всех зна-
чениях а, а правая — лишь при
, л
а =/= — п.
2
Поэтому при всех допустимых значениях a 1/ =
V tga+ctga
= jsin a j. Вообще же эти выражения не эквнвалентиь друг
другу.
П р и м е р 3. Доказать тождество
sin л -{- aj + cos (я — a) = cos (2п + a) — 3 sin J1 — cj .
Преобразуем левую и правую части этого тождества, используя
формулы приведения:
258
sin I - n 4 a) + cos (л — a) — — cos a — cos a - — 2 cos a;
cos (2n a — 3 sin J — aj = cos a — 3 cos a = — 2 cos a.
Итак, выражения, стоящие в обеих частях данного тождества,
приведены к одному и тому же виду. тем самым тождество - до-
квзано.
fl р и м ер 4. Дилазать тождество
si п о. 4- cos4ce — = — 2 shr a cos2 a.
Покажем, что разност., между левой и право!' частями данного
тождества равна нулю. Имеем:
(sin’ce 4- cos4a — ) — (— 2 sin2 a cos2 a) =
= (sin’a 4* " sin2 a cos2 o. 4- cos4a) — 1 =
= (sin2 a 4 cos2 a)" — 1 — — 1=0.
Tcvi самым тождество доказано.
Пример 5. Доказать тождество
— sin с __ cos а
сог а ’ -} sin с
Это тождество можнс рассматривать как пропорцию. Но
чтобы доказать справедливость пропорции — = —, достаточно
b а
показать, что произведение ее крайних членов ad равно произ-
ведению ее средних членов Ьс. Так мы поступим и в данном
случае. Покажем. чтс (1 — since) (1 4- sin a) = cos a • cos a,
Действительно (1 — since) '1 4- sin ce) = 1 — sin2 c. = cos2 ce.
По поводу этого пример? можно было бы сделать замечание,
аналогичное замечанию к примеру 2.
Упражнения
Доказать тождества (№ 754—763):
sin а , 1 -+ cos a 2
754.----------1--------- -----.
1 -г- cos a sin a sin a
_rr. sin® a + 2 cos2 a — '
755.-------—------------— sin* a.
ctg2 a
756. slna~ tgt~- = tgce.
1 4 cos a
757. 2 (sin6 ce 4- cos6 ce) -r- 1 = 3 (sin4 a -y cos4 a).
758» 1 4- 2 sin o’ • cos ce = ' sin a 4- cos a|.
759ctg2 a — cos® a, = c tg2 a cos2 a
760. |since'| = ]/(sec2ce—1)(1 — sir2ce).
761 2 cos2 a—J cos a— sina 4tgc
1—2 sin о cos c. cose. 4-sine. 1 — tg2a
9*
259
— sin a ______ 1 cos a 1
4- si., u I 4- sin a
7G3. 1/ 1 4 cos a _ 1 4~ ~
V 1 —cos a | sina|
Упростить выражения (№ 764—769):
7C4. 1/ r । r
V 14 cos a г 1 — cos a ' •
765. J/(I + tgaj2 + (1 — tga)3.
766. .1 +1?-?L.
1 4-ctg a
770. Напти значение выражения
/1? I,----------4-----------.
1 -t tg3a 1 I-ctg3a
768. ^“ + ‘10 .
ctga4-ctg ₽
— л 14~ CvS a 4~ cos3 a
7l)9.-----------------.
1 + sec a 4* see2 a
ho, что tga=
2
з‘
5 cos a 4 6 sin a
3 sin a — 7 cos a
CcjIH ИЗиеСГ-
. .1 v 4 sin a — cos a
//1. Напти значение выражения------------- ,
cos a — sisin a
если известно,
что котангенс угла а не определен.
_ .т " 5sin а 4- 6 cosп
7/2, Наити значение выражения-----------------, если извест-
cos a — sin a
по, что ctg a = — .
2
Доказать тождества (№ 773—779):
773.
774.
775.
776.
___etga____
cosec a — 1
sin a _
1 4- cos a
tga4-ctgP
__ cosec a 4- 1
ctg a
1 — cos a
sin a
= tgactgp.
ctga4-tgp
tg (a + n) —2 ctg (a -
2 — 3 cos5 a
sin a cos a
777. sin (a 4- 4- sin (a 4- n) 4- sin fa 4- 4- sin (0 4- 2л) =
= cos [a + 77 j 4- cos (a 4- л) 4- cos (a 4- & л) 4- cos (a 4 2л).
77« 1 2 sin a cos a _ tga 4- 1
sin2 a — cos2 a tga—1
___ i — 2 cos2 a ... .
779. --------------= tga — ctga.
sin a cos a
Арксинус числа a § 117
Пусть про угол <р известно лишь то, чго синус его равен —;
sin <р == 1 .
2
(1)
260
Можем ли мы найти этот угол?
Как известно, sin — = - . По-
6 2
этому ВОЗМОЖНО, чТО <р = - .
Вме^ме с тем в силу исрииднч-
пости синуса
sir (п f 2л I = sin - = 1 .
\6 ) 6 2
Поэтому не исключена также воз-
можность, что ф — — 4- 2л.
ло л, 6
Вообще, каким бы ни было целое чис-
sin I — 4- 2мл )= sin - = - .
.6 ) 6 2
Следиеа1елыю, искомым углом <р может быть любой нл углов
- , - ± 2л; - ± 4л; " ± 6л
6 6 6 6
и т. д. Таким образом, по значению своего синус? угол опре-
деляется неоднозначно.
Такой неоднозначности, однако, можно избежать, если по-
требовать, чтобы искомый угол <р находился в определенных
пределах. Например, при дополнительном условии, что
0<<Р<"
равенство (1) определяет единственный угол: <р •=
Если бы мы в качестве дополнительного ограничения, накла-
дываемого на угол <р, выбрали условие 0<;ф<л, то задача
опять была бы неопределенной. В интервале (0, л) синусоида
у = sin л (см. рис. 181) пересекается с прямой У ~ ~ в Двух
- , а абсцисса
6
точках М, и /Л г. Абсцисса точки М, равна
точки Мг равна — л. Поэтому в интервале (0, л) существует два
6'
ь
на угол ф,
угла ф, синусы которых равны i:
Какие же ограничения нужно
равенство
л
Ф1 = “ ,
6
наложить
чтобы
sin ф =
(2)
а
определяло этот угол однозначно? Одни из возможных путей
решения этой задачи состоит в следующем. Прежде всего за-
метим, что если |о| > I, то равенство (2) вообще не определяет
никакого угла- ведь при любых значениях <р
|sin <р| < 1.
261
Далее, будем считать, что угол
л
изменяется в интервале от —
до Тогда синус его непре-
рывно возрастает от — 1 до +1
(рис. 182). Каким бы ни было
число а, не превосходящее ио
абсолютной величине единицы,
л л
в интервале—— < х < - сину-
соида у = sin х обязательно пересечется с прямой у — а и при-
том лишь в одной точке. Поэтому при любом |а| < 1 равенство
(2) в интервале —определяет и притом единственный
угол <[. Этот угол принято называть арксинусом числа а н обо-
значать arcsin а.
Арксинус а есть угол, заключенный в интервале от----до
+ " (или от —90° до +90°), синус которого равен а.
Приме ры.
1) arcsin - = —
2 6
или arcsin = 30°. Действительно, угол в
— радианов попадает в интервал f-----— и синус его равен —.
6 [ 2 2 J 2
я /
2) arcsin I---у I =— 3-, или arcsin I — -^у I = —60°. Дей-
ствительно, угол в — 60° попадает в интервал (— 90°, 90°) и
/з"
синус его равен-----у .
3) arcsin 1= " , пли arcsin 1 = £0°. Действительно, угол
в радианов попадает в интервал и синус его
равен 1.
Аналогично,
arcsin (— 1) ---------; arcsin 0 = 0
2
и т. д.
Заметим, чго из равенства
sin л = 0
нельзя сделать вывод, что arcsin 0 — л Ведь угол в л радианов
не попадает в интервал и потому не можег рав-
няться арксинусу числа 0.
262
У прояснения
780. Какие значения могут принимать величины а и Ь, если
Ь = arcsin а?
781. Вычислить:
1 Vй з
a) arcsin 0 4- arcsin —+ arcsin ------1- arcsin 1;
7 /2 2
(I \ / р з \
----— —arcsin — -— + arcsin f— 1);
К2 .1 \ 2 /
в) 6arcsin(— 1)— 12 arcsin^- + 5arcsin [-----— | •
2 \ /
782. а) Можно ли из равенства sin я = заключить, что
4 *
• F*2*
arcsin
2 4
б) Можно ли из равенства sin 270° = — 1 заключить, что
arcsin (— 1) — 270°?
783. (У с т н о.) В каких четвертях оканчиваются углы:
a) arcsin 0,6; в) arcsin (— 0,8);
б) arcsin 0,9; г) arcsin (—0,1)?
784. Вычислить: _ _
a) sin (arcsin 0,6); в) cos (arcsin (У 3 — ]/2)J;
б) sin [arcsin (—0,8)1; г) cos ^arcsin .
785. Найти синусы, косинусы, тангенсы и котангенсы углов:
a) arcsin 0,4; б) arcsin (— 0,8).
786. Доказать тождества:
, . I . л\ п
a) arcsin sin — = — ;
\ 12/ 12
б) arcsin (sin 6) — 6 — 2я;
в) arcsin (— х) = — arcsin х.
Уравнение sin х = а
. Каждый корень уравнения
sin х = а
§ 118
(1)
можно рассматривать как абсциссу некоторой точки пересече-
ния синусоиды у — sin х с прямой у = а, и, наоборот, абсцисса
каждой такой точки пересечения является одним из корней
уравнения (1).
При 1а| > 1 синусоида у = sinx ие пересекается с прямой
у = а (рис. 183). В этом случае уравнение (1) корней не имеет.
263
Если «с |о] < 1, то синусоида у = sin х и прямая у = а
имеют бесконечно много общих точек. В случае уравне-
ние (1) имеет бесконечное множество корней
Пусть 0 < а < 1. Тогда в интервале 0 «. х < л имеем две
точки пересечения: А и В (р«с. 184). Точке А попадает е интер-
вал — < х < . Поэтому ее абсцисса равна arcsin а. Что
же касается точки В, то ее абсцисса, как легко понять из
рисунка 184. равна л — arcsin а Все остальные точки пере-
сечения синусоиды у — sin х с прямой у = а мы разобьем на две
1руппы;
• •• » А_г, А_„ А |, А г, ... ,
... , В_ 2, В J, В 2,..
Точки первой группы удалены от А на расстояния, кратные 2л,
и потому имеют абсциссы arcsin а + 2пл, где п пробегает все
целые числа (п = 0, +1, +2, +3, ...). Точки второй группы
удалены от В на расстояния, кратные 2л, и потому имеют
абсциссы л — arcsin а + 2/гл = — arcsin а + (2k +1) л, где k про-
бегает все целые числа (k = 0, +1, +2, ±3, Таким обра-
зом, уравнение (1) имеет две группы корней:
х = arcsin а -Т 2лл (2)
и
х = — arcsin а + (2k + 1) л (3)
Легко понять, что обе эти группы корней можно представить
одной формулой
х — (— l)m arcsin а + гпя, (4)
264
где т пробегает все целик числа (т — 0, +1, -_г2, ±3, .. .).
Действительно, при т черном (ги = 2п) (4/ обращается в (2),
а прг т нечетном (т = 2k 1) — в (3).
Итак, при С < а < 1 ьсе корни уравнения (Г, задаются фор-
мулой (4).
К такому же результату можно прийти и в случае
— 1<а< С
Мы не будел; подробно разбирать это'1' случай, предлагая уча-
щимся сделать это самостоятельно с помощью рисунка 18b
Нам осталось рассмотреть случай, когда и = 0 и а — + 1.
При и = 0 уравнение
sin х = а
имеет корни
х = тл, (5)
где т пробегает все целые числа (т — 0, ±1. +2. —3, ..)
Такой же результат дает и формула (4) при а — 0. Действи-
телоно, arcsin 0 = 0 и потому
(— l)"-’arcsir 0 + тл = тл.
Следовательно, формула (4) формально дает все корни уравне-
ниг (*) и е случае, когда а = 0.
Если а = 1, то корнями уравнения sinx = a будут числа
(рис. 186)
х = " + 2Лл, (6)
4
265
.де k пробегает все пелые числа (k = 0, J.1, ±2, +3, ...}.
Формула (4) oxbjtl.uc.vT .. сличай. Действительно, полагая
в ней а = 1 и учьтиовя, чго arcsin 1 — , получаем:
(— l)m arcsin 1 + тл — (— 1)т - + тл.
2
Если т четно (т = 2k), то
I — 1 )т ai csin 1 + тл — + 2/гл.
Если же т нечетно (т = 2k + I), то
(— l)m arcsin i + /Пл =— + 2А,л+ л = + 2/гл.
И тот и другой случай учитываются формулой (6).
Наконец, если а — — 1, то корнями уравнения sin х = а будут
числа (см. рис. 187):
х =— ~ + 2£л, (7)
где k пробегает .все целые числа (k = 0, ±1, ±2, ±3, . . .) .
Предлагаем учащимся доказать, что при а = — 1 формула (7)
дает тот же результат, что и общая формула (4). Таким обра-
зом, формула (4) задает все корни уравнения (1) при любых
значениях а, если только |о] < 1. Однако при а = 0, а = + 1 и
а = — 1 целесообразнее сразу же использовать формулы (5), (6)
и (7), не обращаясь к общей формуле (4).
В заключение отметим, что формулы (4), (5), (6) и (7) можно
использовать лишь тогда, когда искомый угол х выражен
в радианах. Если же х выражен в градусах, то эти формулы
нужно естественным образом изменить. Например, вместо фор-
мулы (4) нужно использовать формулу
х = (— l)m arcsin а + 180° т,
вместо формулы (5) — формулу
х = 180° т
и т. д.
266
Примеры.
1) Решить уравнение
/ 3
SinX = - .j—
Приведем два возможных оарианта записи решения.
1-й вариант 2-й вариант
1-й вариант
х={— l)"‘ai«ii. у__.18О°77т= * = ( J)'" arcsiii 1^-4-/ил =
=-(— 1)«‘60° -Г 180°т.
Ответ. х—(—1)ть0° + 180эш,
где tn—любое целое люло.
= (— 1)'" " + п,л.
3
Ответ, х (— 1)"' л Н- /лл,
3
где п\ -любое целое число.
Недопустимо в одном п том же решении частично использо-
вать 1-й н частично 2-й варианты. Например, оюет к данному
упражнению нельзя записать в виде
х = (— l)ffl 60° + /нл
или
X =(— 1)т + 180° т.
3
2) Решить уравнение
sin (1 — 2х)= —
В отлнчйе от примера J, здесь искомые значения х нельзя
выражать в градусах. В условии задачи под знаком синуса
стоит выражение 1 — 2х. Наличие единицы указывает, что х —
либо угол, выраженный в радианах, либо просто число. Поэтому
решение данного уравнения нужно записать следующим образом:
1 —2х = (— 1)ш arcsin (— -1-1 + тл =ч— 1)"' (— " ) + /,гл =
.in (— - j + /пл =v
=(— 1)ш+‘ ~ + тл.
Отсюда
х — ~ -И- 1)"‘
*>
3) Решить уравнение sin (30° — х) = 0.
267.
Здесь, как легко понять, под х подразумеваете,! угол, выра-
женный в градусах. Поэтому решение данного уравнения нужно
Записать следующим образом:
30° — х = 180° т, х — 30° — 180° т.
Поскольку под т мы подразумеваем любое целое число (в том
hiivjic и отрицательное), то полученный результат можно,
конечно, представить и в другой фирме, а именно:
х = 30° + 180° и,
1дс п — любое целое число.
Упражнения
Решить уравнения (№ 787 -796):
787. Sin X = 1 792. sinf-—x'j — /3
’ /Г' \3 ) 2
788. sin х = 1 3 , 2 * 793. sin (60° —x) — л 3 ‘
789. sin 2х = 0. 794. sin(2x + 1) = n 4
790. X sin — - 3 = 1. 795. sin nr = 0.
791. sin (2x 4-зо°)=-1. 796.* sin x -f- sin 2x = 2.
Арккосинус числа а § 119
В§ 117 мы отмечали, что равенство
sin ф = а
при $ < 1 однозначно определяет угол ф, если дополнительно
по! ребовать, чтобы он находился в пределах
< Ф < , пли — 90° < ф < 90°.
Аналогичным свойством обладает равенство
соз Ф = а,
(1)
только в качестве дополнительного ог-
раничения, накладываемого на угол ф,
нужно выбрать следующее условие:
0 < ф < л, или 0° < ф < 180*.
Действительно, в интервале 0 < х < л
функция у = cos х непрерывно убывает
от I до — I (рис. 188). Следовательно,
268
в этом интервале при ]а| с 1 косинусоида у = cos х обязательпс
пересечется с прямой у — а и притом только в одной точке. Поэтому
равенство (1) при дополните^Ьпи.п О < < л определяет
угол ф однозначно. Этот угол принято называть арккосинусом
числа а и обозначать arccos а.
Арккосипус и tcmi> уеОл, заключенный в интервале от 0 до л
(или от 0° до 180°), косинус которого равен а.
Пример ы.
1) arccos — — —, или arccos — — 60°. Действительно, угол в
2 3 2
— радианов попадает в интервал [0, ?»] и косинус его равен — .
3 2
2) arccos (_L13 = — л, или arccos = 150°.
Действительно, угол е 150° попадает в интервал |0°, 180°]
/Г
и косинус сги равен — Ц?- .
3) arccos (— 1) = л, или arccos (— 1) — 180°. Действительно,
угол в 180° попадает в интервал [0, 180°| и косинус его
равен — 1.
Аналогично
arccos 1 =0, arccos 0= —
2
и т. д. Заметим, что из равенства
cos (--") = 0
нельзя сделать вывод, что arccos С = — — . Ведь угол в — — ра-
дианов не попадает в интервал 10, л] и потому не может рав-
няться арккосинусу числа 0.
Упражнения
797. Какие значения могут принимать величины а и Ь, если
b = arccos а?
Вычислить (№ 798—801):
798. arccos 0 + arccos (— 1) + arccos 1. _
7S9. arccos 0 4- arccos —U? 4- arccos I-+ arccos .
V 2 \ V'2 2
800. arccos (— 1) —arccos 1 —arccos
801. 5arccos(— 1)— 12arccos-2-6 arccos^—pyj
802. Можно ли из равенства cos Зл = — 1 заключить, что
arccos (— 1) = Зл?
269
803 вычислить:
a) cos (arccos 0,5); в) sin [arccos (]/ 2—2)];
6) cos (arccos 0,2); rj sin [arccos (3 —
804. Найти синусы, косинусы, тангенсы и котангенсы углов:
a) arcsin 0,5; б) arccos 1.
805. (Устно.) В каких четвертях оканчиваются углы.
a) arccos (0,7); в) arccos (— 0,3);
б) aiccus (0,9), г) arccos (1,3)?
Доказать тождества (№ 806—808):
806. arccos (cos у) = у .
807. arccos (— cos = — л.
\ 7/7
808. arccos (— х) = л. — arccos х.
Вычислить (№ 809, 810):
809. arccos (cos 6)
810. arccos (cos 1).
8Н.Мигутли выражения arcsin о и arccos а при положитель-
ном значении а принимать значения:
а) одного знака; б) разных знаков?
Уравнение cos х = а
§ 120
Каждый корень уравнения
cosx — а (1]
можно рассматривать как абсциссу некоторой точки пересечения
косинусоиды у = cos х с прямой у= а, и, наоборот, абсциссу каж-
дой точки пересечения можно толковать как один из корней
уравнения (1). Таким образом, множестве всех корней уравне-
ния (1) совпадает с множеством абсцисс всех точен пересечения
косинусоиды у = cos х с прямой у — а.
Если > 1, то косинусоида у — cos х не пересекается с пря-
мой у — а (рис. 189). В этом случае уравнение (1] не имеет
270
корней. При 1а| < 1 получается бесконечно много точек перс
сечения (см. рис. 190 для а > 0 и рис. 19 для а < 0/.
Все эти точкг пересечения мы разоб.-ем нг две iруПпы:
••• > _2> _1 li 2> ••
• •• , B_z, E_it Е, В\, Ezt ••• -
Точка / имеет абсциссу arccos а, а все остальные гички первой
группы отстоят о, нее на расстояния, кратные 2л. Поэтому нх
абсциссы выражаются ка1 '
arccos г + 2/гл. (2)
Точка Е, как легкс понять из рпсунксв 190 и 91. имеет
абсциссу — arccos а а вес остальные точки второй группы уда
лены от нее на расстояния кратные 2л. Поэтому их абсциссы
выражаются как
arccos а 4- 2лл. (3)
Таким образом, уравнение (1) имеет две группы корней, опреде-
ляемых формулами (2) и (3). Но эп две формулы можно,
очевидно, записать г виде одной формулы
х — + arccos с + 2/лл, (4)
где т пробегает всецелые числа (л = С +1- -ь2, ±2-
Те рассуждения, которые мы проводили при выводе этой
формулы, верно! лишь при |а| =/= 1. Однакс формально соотно-
шение (4) определяет все корни уравнения соз к = с к npi ia| = .
(Докажите это!; Поэтому можно сказать, что формула (4) дает
Рис 191.
271
все корни уравнения (I) при любых значениях а. если только
И < I.
Но все же и трех частных случаях (а = 0, а = — 1, а = + 1)
мы рекомендуем не обращаться к формуле (4), а пользоваться
другими соотношениями. Полезно запомнить, что корни урав-
нения cos х = 0 задаются формулой
х = + пп\ (5)
корни уравнения cos х = — 1 задаются формулой
х = л + 2тл, (6)
и, наконец, корни уравнения cos х = 1 задаются формулой
х = 2тл. (7)
В заключение отметим, что формулы (4), (5), (6) и (7) верны
лишь в предположении, что искомый угол х выражен в радианах.
Если же он выражен в градусах, то эти формулы нужно есте-
ственным образом изменить. Так, формулу (4) следует замени гь
формулой!
х = ±arccos а + 360° п,
формулу (5) формулой
х = 90° 4- 180° п
И 1. д.
Пример ы.
1) Решить уравнение
cos Зх =
По формуле (4) находим:
Зх = + arccos — + 2тл = + ” 4- 2тл.
— 2 1 — 3
Отсюда
х = + - + — тл.
- 9 3
Ответ к задаче можно было бы выразить и в градусах:
х = ±20° + 120° т.
Однако не следует записывать ответ в форме, в которой гра-
9
дусы перемешиваются с радианами (например, х = + 20° + рш
• 3
или х — + - + 120°m 1
~ 9 )
2) Решить уравнение
cosf" — 2х^ = — 1.
'.4 /
272
Очевидно, что здесь искомый угол к выражен в радианах.
Поэтому, используя формулу (6), решение можно записать таким
образом:
- — 2х = л 4- 2тл,
4
откуда
2х = — — л — 2тл,
4
или
3
к =----л — тл.
8
Поскольку под т здесь подразумевается любое целое число
(в том числе и отрицательное), то ответ можно записать в виде
х =
Упражнения
Решить уравнения:
812. cos .V = —
2
813. cos3x = ~^--
814. cos4x = — 1.
815. cos (30° — х) = 1.
816. cos5x= —.
2
Арктангенс и арккотангенс
з
---л 4- тл.
8
817. cosnx = 1.
818. cos (2z — 1) =
(x\ 1Л T"
2°°—-§•)=—
820. sin x + cos x = — 2.
821. cos x + cos 2x = — 2.
822. sin x • cosx = 1.
числа a § 121
Равенство
tg ф = a (1)
определяет угол <p неоднозначно. В самом деле, если <р0 есть
угол, удовлетворяющий равенству (1), то в силу периодичности
тангенса этому равенству будут удовлетворять и углы
фс + «л,
где п пробегает все целые числа (п = 0, + 1, +2, ±3, ...).
Такой неоднозначности можно избежать, если дополнительно
потребовать, чтобы угол ф находился в предела к — •< ф <
Действительно, в интервале
функция у= tgx монотонно возрастает от —оо до 4-оо (рис 192).
Следовательно, в этом интервале тангенсоида обязательно пересе-
273
чстся с прямой у=а и притом лишь в
одной точке. Абсциссу этой точки при-
нято называть арктангенсом числа а и
обозначать arctg а.
Арктангенс а есть угол, заключен-
ный в интервале от — ” до Н ~ (или
от — 90" до + 90°), тангенс которого
равен а.
Примеры.
1) arctg 1 = -я ’ или arctg 1 *= 45°.
4
Действительно, угол в я радианов
попадает в интервал (-,
2)агс,Ц-й)=-1
л\ .
- 1 и тангенс его равен 1.
или arctg /----j = — 30
’ J 3 I
Действительно, угол в — 30° попадает в интервал (— 90", 90"),
1
тангенс его равен—.
Заметим, что из равенства
tg л - 0
нельзя заключить, что aictg 0 = л. Ведь угол в л радианов не
попадает в интервал {—”, и потому он не может быть
арктангенсом нуля. Читатель, по-видимиму, уже догадался, что
arctg 0 = 0.
Равенство
Рис. 193.
ctg <р = а, (2)
так же как и равенство (1), опреде-
ляет угол неоднозначно. Чтобы избавить-
ся от этой неоднозначности, нужно на
искомый угол наложить дополнительные
ограничения. В качестве таких ограниче-
ний мы выберем условие
0 < <р < л.
Если аргумент х непрерывно возрастает
в интервале (0, л), то функция у = ctg х
будет монотонно убывать от +оо до —оо.
Поэтому в рассматриваемом интервале
котангенсоида (рис. 193) обязательно пе-
ресечет прямую у = а и притом лишь в
274
одной точке. Абсциссу этой точки принято пазывяп. арккотан-
генсом числа а и обозначать arcctg о
Арккотангенс а есть угол, заключенный. и интервале от 0 дол
(или от 0° до 180°}, котангенс которого равен а.
Пр н м е р ы
1) arccig 0 = , или arcctg С = 90°.
Депстьшельно, угол в радианов попадает в интервал
(0, л) и котангенс его равен 0.
2) arcctg (—= -|п, или arcctg (—= !20°.
Действительно, угол в 120е попадает в интервал (0°, 180°)
1
и котангенс его равен — р== .
Заметим, что из равенства
ctg (— 45°) = — 1
нельзя заключить, что arcctg I— 1) = — 45°. Ведь у юл в — 45е
не попадает в интервал (0е, 180*) и потому он не может быть
арккотангенсом числа — 1. Очевидно, что
arcctg(— 1) = 135%
Упражнения
Вычислить (№ 823—826):
823. arctgO + arctg 4- arctg]/ 3 4-arctg 1.
824. arcctgO 4- arcctg 4- arcctg]/ 3 4- arcctg 1.
825. arcctgO 4-arcctg(— 1) — arcctg^-4-arcctg (—J 3 ).
\ УЗ/
826. arctg(— 1) + arctg (— J7 3) — arctg(--Д=) — arctg0.
1 V з /
827. Какие значения могут принимать величины а и Ь, если
Ь — arctg а?
828. Какие значения могут принимать величины а и Ь, если
b = arcctg а?
829. В каких четвертях оканчиваются углы:
a) arctg 5; в) arcctg 3; д) —arcctg (—4);
3 I
б) arctg(—7); г) arcctg(—2), е) — л 4-arctg—?
830. Могут ли выражения arctg а и arcctg а принимать зна-
чения: а) одного знака; б) разных знаков?
275
831. Найти синусы, косинусы, тангенсы и котангенсы сле-
дующих углов:
a) arctg в) arcctg
б) arctg (— 0,75); г) arcctg (0,75).
Доказать тождества (№ 832, 833):
832. arctg (— х) = — arctg х.
833. arcctg (— х) = л — arcctg х.
Вычислить:
834. arcctg (ctg 2).
835. arctg (tg 2).
Уравнения tgx = а и ctgx = a § 122
Все корни уравнения
tgx = a
задаются формулой
x — aretga 4- tnn, (1)
или
x = aretga + 180° tn, (2)
где m пробегает все целые числа (т = 0, +1, + 2, ±3, ...).
Предлагаем учащимся доказать это самостоятельно. При этом
следует использовать рисунок 194.
Аналогично, все корни уравнения
ctg х = а
определяются соотношением
х = arcctg а + тл, (3)
или
х = arcctg а + 180° т. (4)
Это хорошо иллюстрируется рисунком 195.
276
Рассмотрим два примера
1) Решить уравнение tg (30° — х) = ]/3.
Используя формулу (2), получаем:
30° — х = arctg J/3+ 180° т = 60° + 180° т.
Отсюда
х = _ 30° — 180’ т.
что можно представить, конечно, и в таком виде:
х = — 30° + 180° k.
2) Решить уравнение ctg (2х— — )= — 1.
\ 4 /
Используя формулу (3), получаем:
2х — я = arcctg (— 1) + тл = — л + тл.
4 4
Отсюда
2х = л + тл = (1 + т) л,
х = J (т + 0-
Поскольку т может быть любым целым числом, то получен-
ный результат можно представить и в более простой форме:
П L.
X = - • к.
Упражнения
Решить уравнения:
836. tg3x = 0.
837. tg(2x +60°)= — 1.
838. tg(i-5x) = r3.
839. tgnx = 1.
840. ctg (30° + 2x) =
2
841. ctg(3x —45°) = —
842. ctg л x = 0.
843. ctg^-x) = — 1.
844. tgx 4-ctgx = 0,5.
845. tgx + ctgx = 2.
277
Более сложные тригонометрические уравнения § 123
Уравнения
sin х = а,
vOo X — tl,
tg X — а,
ctg х — а
являются простейшими тригонометрическими уравнениями.
В этом napai рафе на конкретных примерах мы рассмотрим бо-
лее сложные тригонометрические уравнения. Их решение, как
правило, сведшая к решен ши простейших тригонометрических
уравнений.
Пример 1. Решить уравнение
sin 2х — cos х sin 2х.
тогда равно нулю,
нулю, а другой
он был определен.
п. Если же 1 — cos х = 0, то
Перенося все члены этого уравнения в левую часть и разла
гая полученное выражение на множители, получаем:
sin 2х (1 — cos х) = 0.
Произведение двух выражений тогда и только
когда хотя бы один из сомножителей равен
принимает любое числовое значение, лишь бы
Если sin 2х = 0, то 2х = лл; х = -
2
cos х = 1; х = 2/г л.
Итак, мы получили две группы корней: х = ” л; х = 2kn.
Вторая группа корней, очевидно, содержится в первой, поскольку
при п = 4/г выражение х — - п обращается в х = 2kn. Поэтому
ответ можно записать одной формулой: х ~ ' л(> где п — любое
целое число.
Заметим, что данное уравнение нельзя было решать путем
сокращения на. sin 2х. Действительно, после сокращения мы
получили бы 1 — cosx — 0, откуда х = 2&л. Таким образом, мы по-
, л
теряли бы некоторые корни, например — , л,
Пример 2. Решить уравнение
sin 2х ________________________Q
sin х
Дробь равна нулю лишь в том случае,
равен нулю. Поэтому sin 2х = 0, откуда 2х — пл; х = — п. Из
3
- л.
2
когда ее числитель
278
этих значений х нужно выбросить как посторонние те значения,
при которых sin х обращается в нуль (дроби с Нулевыми зна-
менателями не имеют смысла: деление на нуль не определено)
Такими значениями являются числа, кратные л. В формуле
х = п они получаются при четных п. Следовательно, корнями
данного уравнения будут числа
х i (2k + 1),
где k — любое целое число.
ПримерЗ, Решить уравнение
2 sin2 х + 7 cos х — 5 = 0.
Выразим sin2 х через cos х~. sin2 х = 1 — cos2 х. Тогда данное
уравнение можно переписать е виде
2(1— cos2 х) + 7 cos х — 5 = 0,
или
2 cos2 х — 7 cos х + 3 = С.
Обозначая cos х через у, мы приходим к квадратному уравнению
2у2 — 7у + 3 = 0,
корнями которого являются числа ~ и 3 Значит, либо cos х = ,
либо cos х = 3. Однако последнее невозможно, поскольку коси-
нус любого угла по абсолютной величине не превышает 1.
Остается признать, что cos х = , откуда
х =. ±60° + 360° п.
П р и м е р 4. Решить уравнение
• 2 sin х + 3 cos х — 6.
Поскольку sin х и cos х ио абсолютной величине не превы-
шают 1, то выражение 2 sin х + 3 cos х не может принимать значе-
ний, больших, чем 5. Поэтому данное уравнение не имеет корней.
Пример 5. Решить уравнение
sin х cos х = 1.
Возвысив обе части данного уравнения в квадрат, мы полу-
чим:
sin2 х + 2 sin х cos х + cos2 х — 1, но sin£ х + cos’ х = 1.
Поэтому 2 sin х cos х = 0, Если sin х — 0, то х = пл; если же
cos х = 0, то х = + kn. Эти две группы решений можно запи-
сать одной формулой: х =
л
2
П.
279
Поскольку обе части данного урав-
нения мы возводили в квадрат, то не
исключена возможность, что среди по-
лученных нами корней имеются посто-
ронние. Вот почему в этом примере,
в отличие от всех предыдущих, необ-
ходимо сделать проверку. Все значения
х = • п можно разбить на 4 группы
(см. рис. 196):
1) х — 2/гл; (и = 4/г);
2) х = -2 + 2/гп; (п = 4k + 1);
3) х = л + 2/гл; (п = 4/г 4- 2);
4) х = л 4- 2/гл; (п = 4/г 4- 3).
При.г = 2/глsinх + cosx = 0 4- 1 = 1 • Следовательно, х = 2/гл —
корпи данного уравнения. При х— — 4- 2/гл sin х + cos х — 1 +
2
4-0=1. Значит, х — '^-4- 2/гл — также корни данного уравнения.
При х=л4-2/гл sinx4-cosx=0— 1= —1. Поэтому значения х = л4-
4-2/гл не являются корнями данного уравнения. Аналогично показы-
Q
вается, что х = — л 4- 2/гл не являются корнями.
Таким образом, данное уравнение имеет следующие корни:
х = 2/гл и х = — 4- 2/ил, где k и т — любые целые числа.
2
Упражнения
Решить уравнения:
846. cos х = sin 2х cos х.
847. tg х 4- sin х tg x = 0.
848. cos.r cosec2 x — 0.
849. _ $in.x = o.
1 — COS X
850. COS X Q
1 4- sin x
851. ^==0.
IgA
852. cos x 4- tg x = 0.
855. 2 cos2 x = 3 sin x.
856. cos2 x — 1 = cos (90е — x)
857. 2 sin 2 x = 2 4- 5 cos x.
858. ]/3 tg2 (x 4-40°) =
= ctg(50° —x).
859. sinx 4- cosx = 3.
860. 2sinx—3cosx = 6.
861. sinx 4-cos2x = 2.
862. sin x cos 2x = — 1.
853. tg2 x 4- 2tg x — 3 = 0. 863. cos 2x — 2 sin2 x = — 3.
854. 2 cos2 x 4- 5 cos x — 3 = 0. 864 .sinx — cos x = 1.
865. sin x — cos x.
280
Однородные уравнения
$ 124
Примерами однородных тригонометрических уравнений могут
служить уравнения:
sin х — cos х — О,
sin2x — 5 sinx cosx 4- 6 cos2x = О,
cos2 x — sin x cos x = 0.
Это такие уравнения, все члены которых имеют одну и ту же
общую степень относительно sinx и cosx. Например, все члены
первого уравнения имеют общую степень 1, а все члены других
двух уравнений — общую степень 2.
Решим уравнение sinx — cosx = 0. Для этого заметим, .что
в данном случае cosx не может быть равен нулю. Если бы было
cos х = 0, то должно было бы быть и sin х = 0. Но тогда не
выполнялось бы тождество sin2x + cos2x -= 1. Итак, в данном
случае cosx 5^0. Поэтому обе части данного уравнения можно
разделить на cosx. В результате получим tgx— 1—0, откуда
tg X -- 1, X “ + лл.
4
Аналогично решается и уравнение sin2 х—5 sin х cosx 4-6 cos2 х=0.
Разделив обе части этого уравнения на cos2 х, получим:
tg2x — 5 tgx + 6 = 0; (tgx)i = 2; (tgx)2 = 3.
Поэтому
x = arctg 2 + пл; x = arctg 3 4~ kn.
Теперь решим уравнение
• cos2 x — sin x cos x — 0.
Здесь уже равенство cosx — 0 возможно, поэтому делить
обе части уравнения на cos2 х нельзя. Зато можно утверждать,
что sin х 5^ 0. В противном случае из уравнения вытекало бы,
что cos х = 0. Но тогда не выполнялось бы тождество sin2 х 4-
4- cos2x = 1. Итак, sin х #= 0. Поэтому обе части данного урав-
нения можно разделить на sin2 х. В результате получим:
ctg2x — ctg х = 0,
откуда (ctgx)t — 0; (ctgx)2 = 1. Соответственно этому получается
две группы корней:
х = — 4- пл и х = — 4- kn.
2 1 4
Некоторые тригонометрические уравнения, не являясь одно-
родными, легко сводятся к однородным.
2Ы
Например, если в уравнении
sin х cos х — 0,5
представить 0,о в виде U,b (sin2x 4 cos2x), то получится одно-
родное уравнение sin х cos х = 0,5 sin2x 4- 0,5 cos2 х. Это уравне-
ние предлагаем учащимся решить самостоятельно.
Упражнения
Решшь уравнения:
866. 3 sin х — Jz3 cos х = 0.
867 . 2 cos х — j/2 sin х — 0.
868 . 3 sin х 4- 5 cos х = 0.
869. sin2 х — (1 4- ]/ 3) sin к cos x 4* 4^3 cos2 x = 0.
870. sin2 x — 4 sin x cos x 4 3 cos2 x = 0.
871. J/3 sin2 x — 4 sin x cos x 4- 43 cos2 x — 0.
872. 2 sin x — cos x sin x = 0.
873. Y3 cos x 4- cos x sin x = 0.
874. sin x cos x = —Lt cos2 x.
Гз
875. cos2 x — 3 sin x cos *41=0.
87f. sin2 x 4- 3 cos2 x — 2 sin x cos x — —
2
877. sin x cos x = — 0,25.’
878. sin x 4 cos x = j/2.
Графический способ решения
тригонометрических уравнений § 125
Уравнения, с которыми приходится сталкиваться при реше-
нии практических задач, как правило, значительно отличаются
от тех, которые мы рассматривали в этой главе. Для таких
уравнений иногда вообще нельзя указать никакого способа,
который позволял бы. найти корни абсолютно точно. В таком
случае приходится ограничиваться нахождением лишь прибли-
женных значений корней. Современная математика располагает
эффективными методами приближенного решения уравнений.
Эти методы излагаются в учебниках по вычислительной мате-
матике и требуют определенных знаний, которых у нас пока еще
нет. Поэтому мы остановимся лишь на одном из доступных нам
способов — графическом способе.
282
Пусть, например,
нужно решить уравнение
sin х = 1 — х.
IL одном и том же ри-
сунке начертим два гра-
фика: график функции
y=sinx и график функ
пин у=1 — х (рис. 197).
Эги графики пересекают-
ся в одной точке М. Абс-
цисса этой точки и дает нам единственный корень нашего уравнения:
хяг 0,5.
Для уточнения полученного результата полезно использовать
тригонометрические таблицы. При х — 0.5
sin х» 0.4794,
1 — х = 0,5;
следовательно, sinxCl —х. Но тогда, как легко понять из
рисунка 197, корень уравнения sin х = 1 — х будет больше, чем 0,5.
Проверим значение х = 0,6. Имеем (при х — 0,6);
sinxя? 0,5446,
1 — х = 0,4;
следовательно, sinx Z> 1 — х. Но тогда, как легко понять из
того же рисунка 197, искомый корень хь должен быть меньше,
чем 0,6. Теперь уже мы знаем, что х0 находится в интервале
(0,5; 0,6]. Поэтому с точностью до 0,1
х0» 0,5 (с недостатком),
х0» 0,6 (с избытком).
С помощью таблиц можно найти приближенное значение х0
и с точностью до 0,01. Разделим интервал (0,5; 0,6] пополам.
В средней точке (х = 0,55) этого интервала
sinx» 0,5227,
1 — х — 0,45.
Опять получаем, что sinx > 1 — х. Следовательно, х0 <; 0,55.
Проверим точку х = 0,52 (она близка к средней точке х = 0,525
интервала (0,50; 0,55], в котором заключен корень х0). При
х = 0,52
sin х» 0,4969,
1 — х = 0,48.
283
Снова sin v 1 — х’ поэтому t0 < 0,52 Итак,
0,b0 << х0 << 0,52.
Пиэю.му с точностью до 0,01
х0~ 0,51.
Упражнения
879. Выше мы показали, чго с точностью до 0,01 корень
уравнения sinx = I —х равен 0,51. Определите, какое это зна-
чение корня: с недостатком или с избытком.
880. Найти корни данных уравнений с точностью до 0,01:
a) cosx = х — 1; б) sinx + 0,5 = х.
881. Сколько корней имеет уравнение 10sinx = х?
882. Найти наименьший положительный корень уравнения
tg х = 1 — хс точное!ыо до 0,01.
Тригонометрические неравенства
§ 126
При решении тригонометрических неравенств полезно обра-
щаться к графикам. Пусть, например, нужно решить неравенство
1
COS X > —.
2
На одном и том же чертеже построим графики функ-
ций у = cos х и у =• (рис. 198). Как видно из рисунка,
один из интервалов, в котором выполняется данное неравенство,
заключен между наименьшими по абсолютной величине корнями
уравнения cosx — -i, то есть между точками х = — и х = ?.
Все остальные интервалы, в которых выполняется данное нера-
284
или вправо на расстояния, кратные 2л Поэтому неравенство
cos х выполняется при условии, что
— — + 2/. л < х < — + 2нл,
3 £
где п — любое целое число.
Рассмотрим еще один пример. Решить неравенство
2 cos2 х 4- 3 cos х — 2 0.
Обозначив cos х через у. придем к следующему квадратному
неравенству:
2у2 4- Зу — 2 > 0.
Это неравенство выполняется при у < — 2 и у> - . Поэтому
все решения данного неравенства должны удовлетворять либс
неравенству cos х < — 2, либо неравенству cos х > . Первое из
эти> неравенств не выполняется нн при каких значениях х; вто-
рое же неравенство, как мы показали выше, выполняется при
— — 4- 2пл с х < — 4- 2пл.
3 г
.Упражнения
Решить неравенства:
883. tgx> 1.
884. sinx <—
886. sin’x > cos x.
885. 2 sin2 х — 5 sin х 4~ 3 >• 0.
887. |sinx|>>-^.
Задачи на повторение
Доказать тождества (№ 888—891):
888. (г cos а)2 4* (г sin а sin р)2 4- (г sin а cos р)2
г2
889.
2 |sec а|.
мп । । со?ate*а
8S0. 1 4--------= sec а.
1 4- cos а
891. 1 4- (ctg2 а — tg2a) cos2 а = ctg2 а
Решить данные неравенства (№ 892—894)
острого угла а.
892*. cos (а — 120") > sin (64п |- а)
относительно
285
893* tg (85° — 2a) > ctg (40° — a).
894*. sia (a 4- 3u°) > cos (72" — 2a).
895. Найти косинус, тангенс и котангенс угла ср, если изве-
стно, что sin <р 0,28.
896. Найти синус, тангенс и котангенс угла ф, если известно,
что
cos ф = — 0,96
и угол ф оканчивается не в 3-й четверти.
897. Найти синус, косинус и котангенс угла ф, если известно,
что этот угол оканчивается в 3-й четверти и
= р
0
Найти синусы, косинусы, тангенсы и котангенсы
углов (№ 898—901):
898. arcsin 0,28 и arcsin (— 0,28).
899. arccos 0,96 и arccos (— 0,96).
следующих
900. arctg- и arctg (—— 1
901. arcctg 1 н arcctg (— 1 — ).
3 \ 3 /
Упростить данные выражения (№ 902—905): ’
902.
sin i - — arccos 0,6 |.
\2 /
903.
cos
904.
905.
tg — л — arcsin I — —
12 \ 13/
sin (arctg 0,75 — nJ.
906. a) sin a = sin p. Можно ли сказать, что a = 0?
б) sina = sin p, причем углы аир оканчиваются в одной и
той же четверти. Можно ли сказать, чго a = р?
в) sina = sinр, причем 0<а<л и 0<р<.л, Можно ли
сказать, что a — р?
г) sin a = sin ₽, причем — < a < и — . Мож-
но ли сказать, что a = р?
286
907. Чел Oijiii4aioi<_fi друг от друга функции
у — х и у — sii> (arcsin x>i
Сравните графики этих функций.
908*. Построить график фунпши у — arccos (cos х).
909*. Па плоскости хОу найти множество ьсех точек коорди-
наты (х, у) которых удовлетворяют условию
sin (х 4- у) = О
910. При каких значениях а определены выражения:
д
sin а 4 cos u
е) tg 2а?
В) | ZCO: г) — I
3
a) ------------:
sm с 4-1
б', —-?----------;
cor а — 0,5
Г)
Sin а — cor а
911. При каких значениях а данные уравнения имеют корни
a) tg2 х 4- tg х 4- а = 0; б) sin2 г 4- sin х + а - Ui
Проверить данные равенства (№ 912—915):
912. arcsin (sin 1) — 1.
913. arcsin (sin 2) — л — 2.
914. arccos (cos 1,5) — 1,5.
915. arccos (cos 2,5' — 2,5.
916. Доказать тождества:
a) arcsir r. 4- a'ccos r, =
6) arctg x -f arcctg x =
Вычислить (№ 917—919)
917. aretg^etg |ri.j.
918. arcctg (tg 0,6л).
919. arccos (sin 2).
920. Что больше:
2 3
a; arccos — или arcsin -,
3 4
I 4 . ' 5'
6) arccos)—— j или arccos --);
в) arctg 3 или arctg 4?
Решить данные уравнения (№ 921—930):
921. tg2 x 4- tg2 x — 3tg x - 3.
922. 3 sin2 x 4 2 sin x cos x = 2.
923. sin x — cos 2x 4" sin 4? = 3.
287
924. cos x = |/2 sin® x.
925. sin x H- cosx = 1 + 2sinxcosx.
926. sin (n cos x) = 0.
927. cos 2xsin x = cos 2x.
£28. -----------= 0.
tgx + ctg x
£29. У1 — sin2 x = cos x
930. У1 — cos2x = — sin x.
931. Доказать, что уравнение
sinx + sin 2x + sin3x + ... + sin lOOx = 100
не имеет корней.
ЧИСЛОВЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ
VI
ммп
Числовые последовательности
и способы их задания.
Конечные и бесконечные последовательности § 127
Рассмотрим следующие три совокупности чисел;
1, 2, 3......................... п..... (1)
1-1 2 _1 I- Ц"'* 1 (9)
* 2' о’ 4............. п ’
sin 1, sin 2, sin 3, ... sin n, ... . (3)
Естественно считать, что каждое число в любой из эи:х
совокупностей снабжено номером в соответствии ' тем местом,
которое оно занимает в этой совокупности Например, вс £ го-
рой совокупности число 1 имеет номер :, числе — 2 — номер 2,
1 о
число - — номер 3 и т. д
Наоборот, какой бы номер мы ни указали, е каждой. из
этих совокупностей найдется число, снабженное этим номером.
Например, номер 2 в первой последовательности имев” числе 2,
во второй — число — -
, в третьей — число sir 2. Аналогично, но-
мер 10 имеют: в первое последовательности — число 1С, во вто-
рой — число — — , в третьей — число sin 10 и т д. Таким обра-
зом, в приведенных выше совокупностях каждое число нмее’. вполне
определенный номер и полностью определяется этим номером
Совокупность чисел, каждое из которых снабжено своим номе-
ром п (п — 1,2,3,...), называется числовой последовательностью.
Отдельные числа последовательности называются ее членами
и обозначаются обычно так: первый член at, второй. а? .... п-it
член ап и т. д. Вся числовая последовательности обозначается
at а2, air ..., аП ... или {ап}.
Задать числовую последовательность — это значит указать,
как отыскивается тот или иной ее член, еелг известен номер
занимаемого им места. Существует много различных способов
10 Заказ 261
289
задания числовых последовательностей. Ниже мы остановимся
на некоторых из них.
1. Обычно числовая последовательность задается с помощью
формулы, позволяющей по номеру члена последовательности
определить этот член. Например, если известно, что при любом п
ап = п2,
то
— 1, а2 = 4, а3 = 9 и т. д.
— sin — =1, а2 — sin л — О,
2
При ап—sin ~ п мы получим: at
з
а3 = sin — л = — 1, д4 = sin 2л = 0 и т. д.
2
Формула, позволяющая найти любой член числовой последова-
тельности по его номеру, называется формулой общего члена
числовой последовательности.
2. Бывают случаи, когда последовательность задается посред-
ством описания ее членов. Например, говорят, что последова-
тельность
1,4; 1,41; 1,414; 1,4142; ...
составлена из приближенных значений /2 с недостатком с точ-
ностью до 0,1; 0,01; 0,001; 0,0001 и т. д. В подобных случаях
иногда вообще нельзя установить формулу общего члена; тем
не менее последовательность оказывается полностью определенной.
3. Иногда указывается несколько первых членов последова-
тельности, а все остальные члены определяются этими задан-
ными членами по тому или иному правилу. Пусть, например,
= 1, а2 = 1,
а каждый последующий член определяется как сумма двух преды-
дущих. Другими словами, при любом п > 3
~ &П-1 “Ь @п—2'
Так определяется числовая последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34, ...,
члены которой носят название «чисел Фибоначчи» [по имени италь-
янского математика Леонарда Пизанского (около 1170—1250),
которого называли также Фибоначчи, что означает «сын Боначчо»].
Они обладают многими интересными свойствами, рассмотрение
которых, однако, выходит за пределы нашей программы.
Последовательность может содержать как конечное, так и
бесконечное число членов.
Последовательность, состоящая из конечного числа членов,
называется конечной, а последовательность, состоящая из бес-
конечного числа членов, — бесконечной последовательностью.
290
Например, последовательность всех четных положительных
чисел 2, 4, 6, 8, 10, 12, ... бесконечна, а последовательность
однозначных четных положительных чисел 2, 4, 6, 8 конечна.
Упражнения
932. Написать 4 первых числа последовательности с общим
членом:
\ о „ \ 2п — 1 а) ап = 2 в) а„ = ; з 4-п д) = (— 1)";
б) ап=24-3л; г) ап = sin[2 п); е) °" -lg п + 2 •
933. Найти формулу общего члена последов ател ьностей: для каждой из данных
а) 1, 3, 5, 7, 9, ... ;
б) 2, 4, 6, 8, 10, ... ;
в) 3,-3, 3,-3, 3, ...
г) 1 1 1 2 •
' З’ 9* 27* 81*
д) tg45°, tg22°30', tgll°15', ... ;
. i __2 1 —1 1
6 ' 2’ 4’ 8’ 16* ’“ *
ж) 1, 9, 25, 49, 81, ... .
934. Является ли конечной последовательность всех поло-
жительных корней уравнения:
a) sin х = х — 1; б) tg х = х\ в) sin х = ах 4- 6?
Монотонные последовательности
§ 128
Если каждый член последовательности, начиная со второго,
больше предыдущего, то последовательность называется моно-
тонно возрастающей.
Другими словами, числовая последовательность ait а2, а3, ...
называется монотонно возрастающей, если для любого п
Примером монотонно возрастающей* числовой последователь-
ности является натуральный ряд чисел 1, 2, 3, 4, ... . Другим
примером монотонно возрастающей числовой последовательности
может служить последовательность
Pi» Ps* Р16» Р32» •••
периметров правильных 4-, 8-, 16-угольников и т. д., вписан-
ных в одну и ту же окружность. Действительно, пусть АВ —
* Если при любом п яп-н > ап, то последовательность {оп} называется
монотонно неубывающей. Например, последовательность 1, 1, 2, 2, 3, 3, ... не
является монотонно возрастающей» но является монотонно неубывающей.
10*
291
Рис. 109.
с i ирона квадрата, вписанного е окружность О
(рис. 199). Опустим на АВ перпендикуляр из
центра окружности О и продолжим его до
пересечения с окружностью в точке С, АС и
ВС буду!, очевидно, сторонами правильного
восьмиугольника В треугольнике АВС
АС + ВС> АВ.
Поскольку р4 = 4АВ, р8= 4 (АС 4 ВС), то
р8 > р4. Аналогично Покалывается, ЧТО р1в '_>
Psi Р32 Рт И T. Д.
Если каждый член числовой последователь-
ности, начиная со второго, меньше предыду-
щего, то последовательность называется Монотонно убывающей.
Другими словами, числовая последовательность аь а2, аЛ, ...
называется монотонно убывающей, если для любого п
^п+1 ®п-
Примером монотонно убывающей* числовой последователь-
ности может служить последовательность
1111 1
’ 2* з’ 4’ ’ п’
Другим примером монотонно убывающей последовательности
является последовательность
р р р р
*4’ ' 6’ Г 16’ Г 32’ —
периметров правильных 4-, 8-, 16-угольнпков и т. д., описан-
ных около одной и той же окружности. Доказательство этого
факта мы предлагаем учащимся провести самостоятельно.
Монотонно возрастающие и монотонно убывающие последова-
тельности иногда называются просто монотонными последова-
тельностями.
Не следует думать, что всякая числовая последовательность
является монотонной. Так, например, последовательность
— 1; 1; — 1; 1; ...
с общим членом ап — (— 1)п не принадлежит ни к монотонно
возрастающим, ни к монотонно убывающим последовательностям.
То же самое можно сказать и о последовательности
1 _1 1 __1 1
--------- ’ 2* з* 4’ 5'
* Если при любой п Пп+1 < пп, то последовательность ап называется
монотонно нееозрастакнцей. Например, последовательность 1, 1, - , -,
1 1
— не является монотонно убывающей, но является монотонно
невозрастающей.
292
(__nn-j i
с общим членом a, =----------. Надобные последовательности по
г
лучили название колеблющихся последовательностей.
Упражнения
935. Какие из данных последовательностей являются возраста
юшпмн, какие убывающими какие КОлеблЮЩпмиии
а) 1 3, 5, , 2/i — 1, ;
б) 1. ‘ , 1, ... , 2, ... ;
2 3 г
в) sin 1, sin 2, sin3, ... sin n, ... ; ,
. . Л . Л . Л . Л
Г) tg -, tg-, tg-...... tg- ...;
о О У o/l
д) 1,4, 9, ... , n2, ...;
e) 1; - 0,1; 0,01; - 0,001; ... ; (— О,!)"'1; ... .
936. Доказать, что последовательность с общим членом
а„ = является возрастающей
2п + 1
937. Доказать, что последовательность с общий членом
2п + 3 ,
ат = ——- является 'бывающей.
т 6п — 5
938. Какому условию должны удовлетворять положительные
числа а, Ь, с и d, чтобы последовательность с общим членом
ап = --.2.ь была монотонно возрастающей?
сп + d
939. Доказать, что последовательность с общим членом
1а-+ Гл
ап = I—-—I, где а— некоторое положительное число, отличное
от 1, является монотонно возрастающей.
Ограниченные и неограниченные числовые
последовательности § 129
Числовая последовательность {а,} называется ограниченной
сверху, если все ее члены меньше некоторого числе А
ап< А (п — 1, 2, 3, ...).
Примером такой последовательности может служить после-
дова1ельность
12 3 и
2’ 3* 4’ *** ’ п-b 1......
все члены которой меньше 1:
fln 1.
Здесь в роли А выступает числе 1. Вместе него можно былс
бы выбрать 2, 3, у и т. д., поскольку любое число рассматри-
293
ваемои последовательности меньше катк-
ую дого из этих чисел. Важно не то, ка-
/ \ кое число выбрано в качестве А, а
I О 1 то, что хотя бы одно такое число суще-
I /\ 1 ствуегп.,
\ / X. / Важным примером последовательно-
А>^--------7<Р сти. ограниченной сверху, служит после-
а'2>g' довательность
Р1,С- 20°- А. Р10» Рз2. ••• (1)
периметров правильных 4-, 8-, 16-угольников и т. д., в п и с а н-
п ы х в одну и ту же окружность. Для доказательства ограничен-
ности этой последовательности мы поступим следующим образом.
Наряду с данной последовательностью рассмотрим последо-
вательность
^4. Лр РК> - (2)
периметров правильных 4- 8-, 16-угольников и т. д., о п и с а н-
н ы х около той же самой окружности. Очевидно, что сторона АВ
правильного 2я-уголышка, вписанного в окружность, меньше
стороны А'В' правильного 2п-угольиика, описанного около этой
окружности (рис. 200). Поэтому
Pin<p-S- (3)
Как было отмечено в предыдущем параграфе, последователь-
ность (2) является монотонно убывающей. Поэтому каждый член
этой последовательности, начиная со второго, меньше первого
члена Р4. Следовательно, для любого п > 2
Р2ч < (4)
Из (3) и (4) вытекает, что
< ^4-
Но-Р4= 8т , где г — радиус окружности. Итак, для всех п > 2
Р,„ < 8г-
Это неравенство и говорит о том, что последовательность (1)
ограничена сверху. Роль А в данном случае играет число 8г.
Если члены ограниченной сверху числовой последователь-
ности изобразить точками числовой прямой, то все точки распо-
ложатся левее точки с абсциссой А (рис. 201).
-+
А
Рис. 201.
294
Числовая последовательность {аг} называется ограниченной
снизу, если все ее члены больше некоторого числа В'.
ап> В (п = 1,2, 3, ...).
Примером такой последовательности можег служить нату-
ральный ряд чисел
1, 2, 3, 4, 5...
Он ограничен снизу, так как все его члены больше нуля
(В — 0). В качестве В можне было бы указать и любое отрица-
тельное число или — , — и т д. Как и ь случае последователь-
2 3
пости, ограниченной сверху, здесь важно не то, какое число
выбрать в качестве В, г то, чтс хотя бы одно такое число
существует.
Важным примером последовательности, ограниченной снизу,
является последовательность
Рд. Р$, Р{Г. •••
периметров правильных 4-, 8-, 16-угольников и т. д., описан-
ных около окружности. В этом легко убедиться с помощью
рассуждений, аналогичных тем, которые мы проводили выше
при исследовании последовательности
Р-г Ps> Pie ••• •
Если члены ограниченной снизу числовой последовательности
изобразить точками числовой прямой, тс все точки расположатся
правее точки с абсциссой В (рис. 202).
Числовая последовательность, ограниченная одновременно
и снизу и сверху, называется ограниченной.
Другими словами, числовая последовательность at, а2, .... а„, ...
называется ограниченной, если существуют числа А и В такие,
что^гри любом п
Л < ап <5 (/г = 1, 2, 3, ...).
Очевидно, что все точки числовой оси, соответствующие членам
такой числовой последовательности, заключены в отрезке,
концы которого имеют абсциссы A v. В (рис. 2СЗ).
Пример ы.
1} sin 1, sin 2, sin 3, ... sin n, ...
Для этой последовательности ап — sin п. При любом п
— 2 < sin п < 2.
Поэтому данная числовая последовательность ограничена.
2) 1,4; 1,41; 1,414; 1,4142, ... .
В А в
Рис. 202.
Рис. 203.
295
Члены этой последовательности представляют собой деся-
тичные приближения числа ]/2. Очевидно, что 1 < ап <2, так
что эта последовательность также ограничена.
3) Ограниченными будут, очевидно, и рассмотренные выше
последовательности:
Р«> Ре» Р1в» Р.32»
Р р р р
*4» *8» г 1в» г 32
составленные из периметров правильных 2п-угольников, вписан-
ных и описанных около некоторой окружности.
Упражнения
940. Выяснить, какие из данных
ничспы и какие не ограничены:
последовательностей огра-
-..1 3 5 2п—1
б) —, —, —, ... , --------------, ... :
2 4 6 2/i
в) 2, —3, 4, —5, ... , (— 1У+1 (n+ 1), ... j
. sin I sin 2 sin 3 (—I)"—1 sin/г
г) -,-----, ---, ... , ..................
' 1 2 3 n
941. Приведите пример последовательности, которая была бы:
а) ограниченной сверху, но не ограниченной снизу;
б) ограниченной снизу, но не ограниченной сверху;
в) не ограниченной ни сверху, ни снизу.
942*. Доказать, что последовательность с общим членом
Пп = 1 + — + — + — + —
At О fl
является неограниченной.
Предел бесконечной числовой
последовательности
§ 130
Рассмотрим бесконечную числовую последовательность
с общим членом
(—-1)я~*
п
оп 1 -+
Будем изображать члены этой последовательности точками
на числовой прямой (рис. 204). Понятно, что все последователь-
ные точки с ростом п то слева, то справа все ближе и ближе
296
подходят к точке с абсциссой 1. Алгебраически это означает,
что абсолютная величина разности ап — 1с ростом п становится
все меньше и меньше, неограниченно приближаясь к пулю.
Действительно,
(- »)п~г
Поэтому для всех членов, начиная со 101-го, эта абсолютная
величина меньше 0,01; для всех членов, начиная с 1001-го, она
47^ @6 ^7 ^5
Рис. 204.
меньше 0,001 и т. д. Вообще, какое бы малое положительное
число е мы ни выбрали (например, е = 0,01; 0,001), всегда
можно указать номер N такой, что для всех п > N будет вы-
полняться неравенство
k-М <г-
Это неравенство эквивалентно двойному неравенству
— е < ап — 1 < е ,
из которого вытекает, что
Итак, при любом е > 0 существует такой номер N, начиная
с которого все члены нашей последовательности лежат в интер-
7£
7+ £
Рис. 205.
вале от 1 —в до 1 -(-в (рис. 205). В таких случаях говорят, что
число 1 является пределом последовательности.
Число а называется пределом бесконечной числовой последователь-
ности а ь а 2, ... ,ап,... , если для любого положительного числа
е существует номер N такой, что все члены последовательности,
начиная с o,v+1I попадают в интервал (а — е, с + е).
Другими словами, число а называется пределом бесконечной
числовой последовательности alt а2, ... , ....... если для любого
297
положительного числа е существует номер N такой, что для
всех n > N
\ап—а <Е.
Тот факт, что а есть предел числовой последовательности
at, и.... ап, , записываете»! следующим образом:
lini ап = а
п > W
(читается: предел* ап при п, стремящемся к бесконечности,
равен а).
Результат, полученный в начале этого параграфа, мы можем
записать теперь в виде:
Q -► со £ П J
Примеры § 131
Рассмотрим несколько примеров на вычисление пределов бес-
конечных числовых последовательностей.
Пример!. Доказать, чю предел числовой последователь-
ности
] 1 8 2/t
’3’4’5’ ’ п1 ’
равен 2:
1- 2”
lira ----= 2.
п -» м п 4- 1
Имеем.
। ш 1 2п л| 2п — 2п — 2 1 ~ 2 2
Л 4- 1 | «4 1 ~М- I’
Отсюда видно, что с ростом п абсолютная величина ап — 2
становится и остается сколь угодно малой.
Например, при п > 20 эта абсолютная величина меньше 0,1,
при п > 200 она меньше 0,01 и т. д. Вообще, как бы мало ни
было положительное число е, всегда можно найти номер W
такой, что для всех п > N будет выполняться неравенство
|а,— 2, <е.
2
В самом деле, |о„ — 2| ----. Поэтому написанное выше нера-
п +1
венство можно переписать в виде
2
«4-1
<^Е,
* Нт — первые три буквы латинского слова limes, что по-русски озна-
чает: предел, граница.
298
откуда
9 9
n + 1 > п > — ! -|—.
е е
Если, например, мы хотим, чтобы |тгп — 2| было меньше, чем
е = 0,1, то п нужно выбирать из условия
. 1 1 2
п > — 1 ~ । —,
о.Г
то есть начиная с п = 20. При е = 0,001 мы получили бы
1 + — -
0,00)
Следовательно, условие |йп — 2| < 0,001 выполняется для
всех п, начиная с п — 2000 и т. д.
Если бы мы стали изображать члены рассматриваемой число-
вой последовательности точками числовой прямой (рис. 206),
то заметили бы, что с ростом п они все ближе и ближе слева
О,
4-
1
Ог
и,
_Д_
)
2П
Рис. 206.
подходят к точке с абсциссой 2. Для любого е > 0 можно ука-
зать такой номер Л', начиная с которого все точки будут нахо-
диться в интерва ле (2 —е, 2). Но в таком случае можно сказать,
что все они будут находиться и в интервале (2 —в, 2 -|- е). Это
служит геометрической иллюстрацией того, чтс предел данной
числовой последовательности равен 2.
Пример 2. Доказать, что
sin и' «
lim —- — 0.
П -* «с П
Доказательство.
'sin г qI — 's'n п 1
I п I п п.
Выражение —, а вместе с ним и 1^-2-----01, с ростом п прн-
п п
ннмает все меньшие и меньшие значения. Поэтому, как бы мало
ни было положительное число е , можно указать такой номер
что для всех п > Л7 будет выполняться неравенство
Isin п Л 1 ~
1-------0 < в.
I п I
299
В частности, можно добиться, чтобы было
:s±Lt_0!<0u| (е = 0,01),
I п |
— О' <0,001 (е=0,001)
I п ।
и т. д. Но в таком случае
sin я „
lim-----= 0.
’ П -* еч rl
Упражнения
Исходя из определения
ношения (№ 943 -946):
£43. lim — =
П -* СО п + 1
£44. lim ----------I.
,i - о. 14 яа
предела, доказать следующие соот
645. Гт — = 0.
п "♦ со Г1
£46. lim sinn + coSn = 0
п -* СО П
В упражнениях 9-17—950 указаны общие члены числовых
последовательностей. Для каждой из этих последовательностей
найти предел а и определить номер N так, чтобы для всех п J> N
выполнялось неравенство 'пп — а| <Z. 0,01.
£47. а„
£48. ап
1 —п
1 Г'>
п
2п ] Г
£49. ап
£50« а„
CCS п
п *
sin п — с<л п
п
Сходящиеся и расходящиеся числовые
последовательности
§ 132
Теорема. Числовая последовательность не может
иметь более одного предела.
Для доказательства предположим противное. Пусть некоторая
числовая последовательность Oj, а2, ап, ... имеет несколько
а-е. а а+е
b-е b Ь+с
Рис. 207.
пределов. Допустим, что а и b — два таких предела. Для опреде-
ленности будем считать, что а < Ь. Выберем положительное число
е так, чтобы отрезки (а—е, а + е) и (&—е, Ь + е) не пере-
300
крывалпсь друг другом* (рис. 207). Тогда все числа нашей
.последовательности, начиная с некоторого, должны находиться,
с одной птерины, ь отрезке (а-е,й + е), ас другой — в отрезе
(Ь — е, О + £) Но это невозможно, так как эти отрезки но пере-
крываются. Получено противоречие; значит, предположение
о существовании двух различных пределов неверно.
Итак, любая числовая последовательность может iimoib но
более одного предела. А каждая лг числовая последовательность
-?,/ -0,3
-----ИСА----------1-----------о-----
-1 (. 1
Рис. 208.
имеет предел? Чтобы выяснить этот вопрос, рассмотрим после-
довательность
— 1, 1. — 1, 1г — 1, 1, ...
с общим членом
= (— 1)п.
Каждый ее член, стоящий на нечетном месте, изобразится
на числовой прямой точкой с абсциссой — 1, а каждый член,
стоящий на четном месте, —точкой с абсциссой 1. Уже отсюда
ясне, что если только гиа последовательность имеет предел,
тс он равен либо — 1, либо 1. Пусть, например, предел суще-
ствует и равен— I Тогда все члень последовательности, начи-
ная с некоторого, должны укладываться, например, в интервале
(— I —С, I; — 1 0,1), пли (— 1,1; —С,9), что соответствует
числу е — 0,1 (рпс. 208). Ио это не так, поскольку члены, равные 1,
-----1 О О о .... О - -О О С 0'0 О
6*234567
Рис. 209.
не попадают в этот интервал. Аналогичнс доказывается, что
и 1 не является пределов рассматриваемой последовательности.
Таким образом, последовательность —1 1: — ; ); .. не,
имеет предела.
Рассмотрим еще один пример — натуральный ряд чисел
1, 2, 3, ..., п.
Точки числовой прямой, соответствующие членам этой по-
следовательности (рис. 209), не скапливаются ни у какой точки.
Какую бы точку на числовой прямой мы ни взяли, точки,
* В качестве такого £ можно, например, взять
Ь — с
£ — ----.
4
301
соответствующие натуральному ряду Чг.сел, рано или поздно
«перешагнут» через нее и уйдут как угодно далеко вправо.
Следооа.^лыю, натуральный ряд чисел также не имеет предела.
Числовая nocAedooatntuoiwbinb, имеющая предел, называется
сходящейся, а не имеющая предела — расходящейся.
Например, последовательности
j 1 6 8 2п
’ 3 ’ 4 ’ 5 + 1 ’
и
sin 1 sin 2 sin 3 sin n
1 ’ 2 ’ 3 ....... n ’
(см. примеры 1 и 2, § 131) являются сходящимися, а Последо-
вательности
—1, 1, -1, 1, 1, 1...
1, 2, 3, 4, ...
— расходящимися
Упражнение
951. Какие из данных последовательностей являются сходя-
щимися и какие расходящимися:
а) 2, 4, 6, ... , 2п, ...;
б) I, 3, 5, ... , 2п — 1, ... ;
в)—-, 1, _1, 1.............<=212, ... ;
2 4 6 й 2п
г) 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, . . . ;
Д)1 _1 1 _ 1 ?
6 ’ 7’8* 9 ’ ’ 54 1’
Монотонные н ограниченные последовательности § 133
В предыдущем параграфе мы убедились, что не всякая чис-
ловая последовательность имеет предел. Теперь возникает
вопрос: как же решить, является ли та или иная последова-
тельность сходящейся? Полное решение этой задачи выходит
далеки за пределы школьной программы. Однако с одним до-
вольно широким классом сходящихся числовых последователь-
ностей мы познакомимся в этом параграфе. Справедливы следую-
щие теоремы, которые мы приводим без доказательства.
Теорема 1. Всякая монотонно возрастающая (не-
убывающая) и ограниченная сверху числовая последова-
тельность сходится»
Теорема 2. Всякая монотонно убывающая (не-
возрастающая) и ограниченная снизу числовая после-
довательность сходится»
302
Поясним эти теоремы на двух частных примерах.
Пример I. Последовательность
J- 1,4; 1,41; 1/14; 1,4142;
составлена из десятичны? приближений числа с недостатком.
Эта последовательность является монотонно возрастающей (точ-
nfct, монотонно неубывающей), поскольку каждый ее член, начи-
ная со второго, получается из предыдущего путел приписывания
соответствующего десятичного знака. Вместе с тем эта последо-
вательность ограничена сверху, так как любой ес член меньше
До}л. Следовательно пе теореме 1 данная последовательность имеет
предел. (Этим пределом являете? иррациональное число }/ 2.)
П р к м е р 2. Последовательность
P1G
периметров правильных 4-, 8-, 16-угольников и т. д.. вписан-
ных в некоторук окружность, является монотонно возрастающей
(см. § 128) и ограниченной сверху (см. § 129). Следовательно,
по теореме 1 существует предел этой последовательности. ( К этому
пределу мы еще вернемся в последующих параграфах.)
К аналогичному результату можно прийти, рассма^рива?
последовател ьность
Р F Р
г ' 1С, ..
периметров правильных 4- 8-, 16-уголы1иков и т. д., опиранных
около некоторой окружности. Для этого придется использовать
теорему 2.
В заключение отметим, что иногда указанные две теоремы
объединяют в одну:
Любая монотонная и ограниченная числовая по-
следовательность имеет предел..
Упражнения
952. Докажите, что последовательность
о £ А
’ 2 ’ 3 ’ ’ п
монотонно убывает и ог'раничеиа снизу. Покажите, что пределом
этой последовательности является число 1
953. Доказать, что последовательность
Sk, $32»
площадей правильных 4-, 8-, 16-, 32-угольников и т. д., вписан-
ных в одну и ту же окружность, является монотонно еоз; ..ста-
ющей и ограниченной.
303
Число е
§ 134
Рассмотрим бесконечную числовую последовательность
Покажем, что эта последипателыюсть является монотонно возрастающей
и ограниченной.
1) Применим теорему о среднем арифметическом н среднем геометри-
ческом (см. гл. I, § 16) к л + 1 числу.
получим:
или
Возводя обе части последнего неравенства в (л-|-1)-ю степень, получаем
или
fln+i > ап-
Тем самым доказано,- что рассматриваемая последовательность является
монотонно возрастающей.
2) Теперь докажем, что наша последовательность является ограниченной.
Для этого рассмотрим еще одну последовательность:
С общим членом
Аналогично тому, как мы доказали монотонность последовательности (1),
может быть доказана н монотонность последовательности (2):
^Л+1
Далее,
ап • ьп
л
304
Поэтому для всех п > 1
Так как последовательность (2) монотонно возрастает, все ее члены, начиная
с третьего, больше второго члена. Поэтому для всех п > 3
/ 1 \* 2 I
Ьп> ь, - -2J - ~ •
Следовательно, для всех л > 3
1
Это неравенство верно и при п — 1 н п = 2, так что для всех натуральных п
Тем самым доказана ограниченность последовательности (1).
Теперь на основании теоремы о пределе монотонной ограниченной
11оследователннос1и можно заключить, что предел последовательности (1)
существует Этот предел принято обозначать буквой е:
7 1 \л
lim I 1+ — = е. (3)
л ОО \ Л /
Подсчитано, что е — 2,7182818284... ,
Иногда для запоминания того или иного числа цифры этого числа свя-
зывают с какой-нибудь знаменательной датой. Легко, например, запомнить
первые девять знаков числа е после запятой, если обратить внимание на
то. что 1828 — это год рождения Льва Толстого.
Число е является иррациональным. Более того, как показал французский
математик Эрмит (1822—1901), это число не может быть корнем никакого
алгебраического уравнения с целыми коэффициентами. Такие иррациональные
числа называются трансцендентными (см. гл. 11).
Предел (3) является одним из тех замечательных пределов, которые
лежат в основе многих математических исследований. Число е играет особую
роль в математике. Однако, если бы мы захотели убедиться в этом, нам
пришлось бы заняться уже высшей математикой.
Переменные величины и их пределы
§ 135
Общий член любой числовой последовательности можно рас-
сматривать как переменную величину. Например, последователь-
ность
1, -
2
£ 2
3 ’ 4 ’
имеет общий член ап = — . При разных значениях п величина ап
п
принимает разные числовые значения и потому является пере-
менной величиной.
305
Итак, с каждой числовой последовательностью можно связать
некоторую переменную величину. Обратное утверждение, вообще
говоря, неверно. Наирлмц,, с племенной величиной t, представ-
ляющей собой время, нельзя связать никакую числовую после-
довательность. Члены числовой последовательности изменяются
скачками. Если мы будем изображать члены последовательности
точками ЧИСЛОВОЙ прямой, ТО BCtv числовую ирлМуЮ При 31 иМ
мы не заполним (рис. 210).
0-0 о ... о
P..V, 210.
А вот со временем дело обстоит иначе. Время течет непре-
рывно. Потому все моменты времени нельзя занумеровать
как члены некоторой числовой последовательности.
В этой главе мы будем изучать лишь такие переменные
величины, которые можно рассматривать как общие члены не-
которых числовых последовательностей. Такие переменные ве-
личины мы будем обозначать символами ап, Ьп, сп и т. д.
Пределом переменной величины ап называется предел числовой
последовательности, для которой ап есть общий член.
Например, предел переменной величины
есть по определению предел последовательности
.111 1
’ 2 ’ 3 ’ 4 ’ ’ п ’ " '
Очевидно, что предел переменной величины можно определить
и таким образом.
Число а называется пределом переменной величины ап, если для
любого положительного числа е можно указать номер П такой,
что для всех п> N
К — а|<8.
Так же как и числовые последовательности, переменные ве-
личины могут иметь, а могут и не иметь предела. Например,
переменная величина ап = sin п (см. § 131, пример 2) имеет предел,
п
а переменная величина ап = (— 1)л (см. § 132) не имеет предела.
Над переменными величинами можно производить те же самые
действия, что и над постоянными величинами (то есть числами).
306
Например, уМНОЖИВ hxiptmvnn^nj обЛИЧnnj Ыд — — чЭ 3, 1ЮЛ_у чим
п
1 з
переменную величину оп = — .
п
При сложении переменных величин ап ----------!— и Ьп= — по-
. п -|-1 п
ЛуЧаск-я переменная величина cn=un4-tn=-------j—j + — = - .
Основные теоремы о пределах
§ 13S
Как было отмечено в предыдущем параграфе, не всякая пе-
ременная величина ап имеет предел при п » оо. в этом параг-
рафе мы будем рассматривать только такие переменные величины,
пределы которых существуют. Для таких величин мы без дока-
зательства укажем несколько важных теорем.
Теорема 1. Предел константы равен самой этой
константе:
I im с = с.
п — оо
Говоря о пределе константы с, мы имеем в виду предел числовой
последовательности
с, с, с........с, .. ,
все члены которой равны одному и тому же числу с.
Теорема 2. Постоянный множитель можно выно-
сить за знак предела:
lim (Ла„) = й-Нтая.
П -» «О П -* ее
Пример. В § 130 было доказано, что
lim [1 + <=1^1= 1.
Л -* ео L п J
Поэтому
lim [5[1 + (~ 1)Л~* 11) = 5lim [1 + ~ °-] = 5• 1 =5.
ft 09 I П J П -» 09 |_ П J
Теорема 3. Предел суммы двух переменных величин
равен сумме пределов этих величин:
lim (ап + Ьп) - + lim&„.
307
Пример. В § 130 и 132 было доказано, что
। Г< । (— О'1-1] 1 sinn п
lim 1 +—-— = I, lim---------= 0.
п — w. L л _ л •* о© n
Поэтому
i- I • । (— O'1*1 । sin n 1 Г, . (— l)n-1l sinn , . n i
Inn 1 + —-— 4------------ lim 1 +-—-— + lim----------= 1 +0=1.
Л | И Л J fl — co |_ fl J fl -* Э* fl
Данная теорема верна не только для двух, но и для произ-
вольного фиксированного числа слагаемых. Например,
lim (an + bn + сп + dn) = lim ап + lim bn + lim cn + lim dn.
fl-*cc П — co fl -» О» n -* CO fl-*»
Теорема 4. Предел произведения двух переменных
величин равен произведению пределов этих величин:
lim(a„ • bn) = Hma„ • Iim&n.
fl co n “* oo n -» oo
Пример.
.. (sinn Г, . (—l)n-1T| ...sinn .. Г, . (—I)"'1] л . n
lim | 1 4-------— 1 = lim-----lim 1 + 5—-— =0- 1 = 0.
/I Ч N [ Л fl JJfl-»OO /1 fl -*i» |_ fl J
И эта теорема верпа не только для двух, но и для произволь-
ного фиксированного числа сомножителей. Например,
lim (ап Ьп сп • dn) = lim ап lim bn • lim c„ • lim d„.
fl-*-» П -• CO fl — CO fl -o OO fl -* OO
Теорема 5. Предел дроби равен частному от деле-
ния предела числителя на предел знаменателя, если
только предел знаменателя отличен от нуля:
lim а*
lim
fl -» CO
Пример. Пусть
sin п
Тогда
lim ап
lim ал = = £ = 0
П- « bn limftn 1
fl -» OO
Заметим, что писать
lim Ь„
lim
П ее Iimnn
в данном случае нельзя, поскольку lim ап = 0.
п ее
308
Следует отметить, что, хотя доказательстве приведенных теорем выхо-
дит за пределы школьно? программы, некоторые ученики в состоянии до-
казать их. Поэтому тек учащимся, которые проявляют к математике осо-
бый интерес, мы предлагаем попытаться доказать эти теоремы. А теорему I
должны доказать все,
Замечание. Необходимо напомнить соглашение, которое
мы приняли в начале данного параграфа Мы условились счи-
тать, что все рассматриваемые нами переменные величпиь имеют
пределы. Если же это не так. то приведенные выше теорекы
теряют смысл. Например, нельзя писать (см. теорему 2)
lim5n3 = 5 lim и2.
поскольку предел Гии гг, очевидно, ие существует.
П <зо
В заключение мы рассмотрим пример на вычисление предела
переменной величины с использованием приведенньи выше теорем.
Пусть требуется найти
lim .
п - «. Зл2 — п -|- 5
Разделим числитель и знаменатель данной дроби на гг. В
зультате получим:
1- - — -
л2 +2/1—1 __ п я2
Ея2 — л + 5 1 5
• Г> __ I
ре-
Теперь, используя приведенные
lim +-?п-~1. =
п - «. Зл2 — л + 5 '
выше теоремы, получаем:
lim (1+---7)
lim (з_ 1 _
л - «> \ л л2
Здесь мы воспользовались очевидными равенствами:
lim — = С, lim — = 0.
• П -i СО П Л
Упражнения
Найти пределы:
пел г —л2 + 3 Зла—л
£54. lim ------— . 9<э5» lim. ----.
л - о. 2и£ + 6л — 5 я-»«ола — 5
309
956. lim
n -* О.
2n — 7
пг 4- 7n — 9
958. lim
n -* •
n»+ 1000000
n»+ 1
957. lim
Г •* °-
П (1 — Л)
(П + 1) (n - 2)
959. lim +
n •* » ujrt“ Z/j/i -J-
lim qn при |<?| <4
§ 137
В этом параграфе мы докажем, что если [g] < 1, то предел
lim qn
п -* <*
существует и равен нулю. Нам придется рассмотреть отдельно
два случая: q > 0 и q < 0.
Случаи!. 0 < q < 1. Прежде всего заметим, что lim qn явля-
ется пределом числовой последовательности п-“
q, q\ q\ q", ... . (1)
Эта последовательность при 0 < q <. 1 будет монотонно убыва-
ющей (<т"+1 < <7П) и ограниченной (0 < qn<. 1). Поэтому опа имеет
предел. Обозначим этот предел буквой с и докажем, что с = 0.
Если из последовательности (1) выбросить первый член, то
получится последовательность
g2, q\ q'.... <7Л+1, ..., (2)
которая, очевидно, имеет тот же самый предел с, что и после-
довательность (1). Общий член последовательности (1J естьал = qn,
а последовательности (2) bn = qn+i.
Имеем:
lim qn = с,
п »
lim <7Л+’ — с.
л •* 00
Но <7л+,= q • qn. Поэтому
с — lim qn+' = lim (q • qn) = q lim qn -= qc.
л-*» Л-*« n •• Л
Итак, c = qc, откуда c = 0, поскольку q Ф 1. Таким образом,
при 0 < <7 < 1 предел lim qn существует и равен пулю.
Случай 2. — 1 < q < 0. Докажем, что и в этом случае
lim qn
л -♦ «*
существует и равен 0. Имеем:
]?"~0| = И = |<7|п-
310
Поскольку |<7 < 1, то ]г7"*| при возрасташп- п стремится к
нулю (случай 1).
Следовательно, с ростом п выражение становится и
остается меньше любого наперед заданного положительного числа.
Поэтому, каково бы ни было положительное числе к, можно
указать такой номер п, начиная с которогс будет выполняться
неравенство
— 0 < t.
Но это и означает, что
lim qn = 0.
f. -♦ со
Упражнения
960. Что вы можете сказать о пределе lim о1. если:
а) ру] = 1; п~ -
6) м > I?
961. Существует ли lim д' при
п ** 00
а) <7= 7; б) q=— в) <?=—2;
3 4 а —
Что такое длина окружности § 138
Б главе II мы говорили о том, что такое длина прямоли-
нейного отрезка Чтобы измерить прямолинейны! отрезок /В
(рис. 211), нужно выбрать единицу изменения (например, отре-
зок CD] и сравнить АВ с это! единицей измерения. Длина
отрезка АВ есть число, показывающее, сколько раз единица изме-
рения укладывается в этом отрезке. А что понимать под длиной
окружности? Ведь окружность — кривая линия и откладывать
на ней отрезок CD нельзя. Таким образом ' мы сталкиваемся
с необходимостью определить, чтс такое длина окружности.
Пусть
Ра- Pet Рю • • Р2П+
— последовательность периметров правильных 4-, 8-, 16-у.оль-
нпкоь и т. д., вписанных в окружность радиусг г. Как мы уже
говорили раньше (§ 133), эта последовательность монотонно
возрастает и 01 раничена. Поэтсмг су-
ществует предел А &
Р = 1 in"А 2П-г 1- ----------------------
Л оо
С D
Этот предел мы и назовем длиной ок- (— ----'
ружности радиуса г. Рис. 211.
311
Впишем теперь в окружность радиуса г не 4-, 8-, 16-уголь-
ники и т. д., а, например, правильные 3-, 6-, 12-угольники
и т, д., периметры которых образуют последовательность
Рз> Р12> ••• » Ps.2n-1’ ••• • (2)
Эта последовательность также монотонно возрастает, огра-
ничена и, следовательно, имеет предел
р' = lim р п_ь
п -♦ ос 8*2
Этот предел р’. как и предел р, также естественно назвать длиной
окружности. Но возникает вопрос: равны ли между собой чис-
ла р и р'? Ведь если бы эти числа оказались различными, тс
принятое нами определение длины окружности было бы не-
удачным.
Можно доказать, что числа р и р' равны между собой. Вообще,
как бы мы ни вписывали в окружность правильные много-
угольники, получая каждый последующий путем удвоения числа
сторон предыдущего, последовательность периметров этих много-
угольников всегда будет сходиться к одному и тому же числу,
принимаемому за длину окружности. Более того, если каждый
последующий многоугольник мы будем получать не обязательно
путем удвоения числа сторон предыдущего, а каким-нибудь дру-
гим способом (например, вписывать правильные 3-, 4-, 5-, 6-уголь-
нпки и т. д.), то все равно последовательность периметров этих
многоугольников будет сходиться и притом к тому же самому
числу р, что и последовательность (1).
Доказательство этих утверждений выходит за пределы школь-
ной программы и потому здесь не приводится.
Итак, мы принимаем следующее определение длины окруж-
ности:
длина р окружности радиуса г есть предел последовательности
Рз’ Р1> Ра’ •” » Рп
периметров правильных 3-, 4-, 5-угольников и т. д., вписанных
в ату окружность'.
р = limpn.
п -* «в
Рис. 212.
Упражнение
962. Теперь мы знаем, как определяются
длины прямолинейных отрезков п окруж-
ностей. А как бы вы определили длину про-
извольной кривой (см., например, рис. 212)?
312
Формула для нахождения длины окружности
§ 133
Лемма. Отношение длины окружности к ее диа-
метру постоянно для всех окружностей.
Предположим, что / iB t и А 2В« — стороны правильных п-у 'ель-
ников, вписанных е окружности 0( и С2 соответствеппс (рис. 213).
Тогда треугольники г 02В2.42, как треугольники с соот-
ветственно равными углами, будут подобны; поэтому
/цВ __Л2Вг
OlAl О2А2 ‘
Умножая обе части этого равенства на ~ , получим:
п • А1В1__ г. А2В2
2 • 0^! 5 • 62Л2
Но п • А ,В, =р„, п А?Вй=рп", где рп' и Рп —периметры пра-
вильных n-угольников, вписанных в окружностг 01 и 0; соот-
ветственно. Следовательно,
Рп' _ Рп'' / \
2г2 ’ 2г, ’ W
где Г1 и г2 — радиусы окружностей СА и 02 соответственно.
Поскольку существуют пределы р' = liir. рп и р" — lim р'п, то
должны существовать и пределы r - “
lim Р" = — • lim р'п = —; lim — = — • lim р" = —. (2)
n-*«o 2tj 2гг п — «> 2-г п — «> 2Г а 2г2 п* 2г2
В силу (1) эти пределы должны быть равны. Поэтому
Это равенстве как раз и означает, чтс отношение длины окруж-
ности к ее диаметру постоян-
но для всех окружностей.
Отношение длины окруж-
ности к ее диаметру принято
обозначать греческой бук-
вой л («пи»). Подсчитано чтс
л = 3,141592... . Длг прак-
тических потребностей доста-
точно запомнить лишь три-
четыре цифры после запятой.
Рис. 213.
3.3
Итак, для окружности радиуса г
₽ =л,
Чг
откуда
р = 2лг.
Длина окружности равна произведению ее диамет-
ра на число л.
В разные времена использовались различные приближения числа л.
Один из величайших математиков древней Греции Архимед (III век до
и. э.) нашел довольно точное приближение для л: 3~, что дает два верных
десятичных знака. В XVI веке было получено приближенное значение л
с 35 верными десятичными знаками, в XIX —с 527 верными десятичными
знаками и т. д. Наибольшее число правильных десятичных знаков числа л
(1J ООО) было получено с помощью счетной машины в 1958 году.
Швейцарский математик Ламберт (1728—1777) доказал, что число л
является иррациональным. Немецкий ученый Линдеманн (1852—1939)
усилил этот результат, доказав, чточислол не может быть корнем никакого
алгебраического уравнения с целыми коэффициентами. Такне иррациональ-
ные числа, как известно, называются трансцендентными.
Нахождение приближенных значений числа л
§ 140
Для нахождения приближенных значений числа л представим это число
Р
в виде отношения длины окружности радиуса
к диаметру, то есть как
половину длины окружности радиуса I. Если вместо половины длины такой
окружности взять половину периметра правильного п-угольннка, вписан-
ного в нее, то вместо точного значения л получится его приближенное
значение. С ростом п это приближенное значение должно стремиться к точ-
ному значению. Следовательно,
Рп
2 ’
где р„ — периметр правильного n-угольцика, вписанного в окружность
радиуса 1. Но рп — а ап, где аП — сторона правильного n-угольника. По-
этому
Л
я ап
2
(1)
Теперь воспользуемся известной из геометрии формулой удвое-
ния. Согласно этой формуле стороны ап и а-п правильных п- и 2п-уголь-
ииков, вписанных в окружность радиуса г, связаны соотношением
4,=2г»-2г
314
£
4
При г = к это соотношение принимает вид:
4. = 2-2
1-^
4
(2)
Вспомним еще. что сторона ав правильного шестиугольника, вписанного
г. окружность, равна радиусу этой окружности. Поэтому по формуле (2)
найдем:
°12 = 2 - 2 |/" 1-1 = 2- /Г,
откуда
я,2 = ]/2- V3 к 0,51764.
Затем по формуле (2) найдем я:1:
^=2-2^/ 1_^? = 2-2 j/ 1-2~р- = 2-У2+ГЗ.
Отсюда а: 0,26104. Затем по формуле (2) можно найти a,s. а9в и т. д.
После этого составим таблицу приближенных значении ап и л:
Г, аг. » ап 1 2
6 1,00000 3,000
12 0,51764 3,106
24 0,26104 3,132
48 0,13080 3,139
96 0.06542 3,140
Из этой таблицы видно, что уже при л = 96 получается две верных
десятичных знака чиелг л.
Площадь круга
§ 141
Пусть s4, s8, sie, ..., s4n+i, ... — последовательность площа-
дей правильных 4-, 8-, 16-угольников и т. д., вписанных в окруж-
ность радиуса г.
Легко показать, что последовательность этг монотонно воз-
растает, ограничена и, следовательно, имеет предел
s = 11ГГ S2n+i.
П-* «
315
Можно допазгиь, Mio idKoii Же предел
имеет последовательность s3, s„, s.,...,
\ sn, ... площадей правильных 3-, 4-, 5-уголь-
1 никив и т. д., вписанных в ту же самую
I окружность Этот предел по определению и
/ принимается за площадь круга радиуса г
В Теперь выведем формулу для нахож-
дения площади круга по ею радиусу г.
11усть АВ — сторона правильного п-уголь-
ника (рпс. 214), вписанного в окружность
радиуса г, рп — периметр этого многоугольника, a sn — его пло-
щадь. Имеем:
sn — п - s^oab — П- ± АВ • ОС,
по п АВ = рп. Поэтому
s,.= -’pn-OC. (!)
Покажем, что при п -> оо ОС неограниченно приближается к г.
Действительно ( рис. 214),
г _ ОС = ОА — ОС.
Из треугольника АОС получаем:
о<ол —ос<лс= 1 ав
2
(разность двух сторон треугольника меньше третьей стороны).
Поэтому г — ОС < АВ. Но AB=-'-', р <2лг. Следовательно,
2 п
О <г — 0С<- • 2л — = - . При возрастании п дробь ™ стано-
2 п п п
вится сколь угодно малой. Поэтому | ОС — г| при п — со стано-
вится и остается меньше любого наперед заданного положитель-
ного числа е:
|0С - г| <8
А это и означает, что предел ОС при п -► со равен г. Теперь
из равенства (1) получаем:
s = lim s„ - limM рп ОС 'J = 1 lim (p„ • ОС} =
= - lim p„ • lim ОС = — • 2лг г = лг2.
2 « - ~ л « » « 2
Итак,
S — лг2.
316
Площадь круга радиуса г равна произ-
ведению числа л на квадрит радиуса
этого круга. ।
Упражнение
963. Какое определение вы предложили
бы для площади, ограниченной произвольной
замкну iuii линией (см., например, рис. 215)?
Арифметическая прогрессия
Рис. 21b.
§ 142
Числовая последовательность, каждый член которой, начиная
со второго, равен предыдущему, сложенному с одним и тем же
для данной последовательности числом, называется арифметиче-
ctwu прогрессией.
Примером арифметической прогрессии является натуральный
ряд чисел
1, 2, 3....
Каждое его число, начиная со второго, равнс предыдущему
сложенному с единицей. Другим примером арифметической про-
грессии может служить последовательность
3; 1,5; 0; — 1,5; — 3...
Каждый член этой последовательности, начиная со второго,
равен предыдущему, сложенному с числом — 1,5.
Данное выше определение арифметической прогрессии экви-
валентно, очевидно, такому определению: числовая последователь-
ность at, а2, ... , ап, ... называется арифметической прогрес-
сией, если для любого п
^П+1 4"
где d — некоторое постоянное для данной последовательности
число.
Это число d называется разностью прогрессии.
Например, для натурального ряда чисел d равно 1; для ариф-
метической прогрессии 3; 1,5; 0; — 1,5; - 3; ... разность d
равна — 1,5.
Пусть at — первый член арифметической прогрессии, ad —
ее разность.
Тогда по определению арифметической прогрессии
Сг 4- d,
а^ — й2 d — (й| -|- d) -1- d --- ai 4* 2d,
о, = °з + d = («! 4- 2d) 4- d — at 4- 3d к т, д.
Очевидно, что при любом п > 1
ап а^(п— 1)а. (1)
317
К формуле (1) можно прийти другим путем, который, кстати,
является и более строгим. Пи определению арифметической про-
грессии
а2 = Qj f- d,
а, = а2 + d,
a* =-
йп-1 ~ йц-2 4"
ап = a«-i -I d-
Складывая почленно эти п — 1 равенств, получаем:
(«2 4* аз 4 ai 4 ••• + Д,1-1) + =
= «1 + (а2 + о3 + ••• + пп-2 + an-t) 4' (я — 1) d’
откуда и вытекает формула (1).
Формула (1) позволяет найти любой член арифметической
прогрессии, если известны ее первый член и разность. Поэтому
она называется формулой общего члена арифметической прогрес-
сии. Например, для арифметической пршрессии
— 10; —9,5; —9; ...
at — — 10; d — 0,5.
Поэтому
Gai = сц 4" 20d = — 10 + 10 = 0,
о100= ai 4* 99d = — 10 + 49,5 = 39,5
и т. д.
Упражнения
964. Найти формулу общего члена арифметической прогрес-
сии, для которой:
a) = 5, а2 =—- 5;
б) = - 3, а2 — 0;
в) = 6, а10 = 33;
г) а, = — 4, а17 = — 17;
д) а10 = 0, а40 = — 30.
965. Если к членам одной арифметической прогрессии при-
бавить соответствующие (по номеру занимаемого места) члены
другой арифметической прогрессии, то будет ли полученная по-
следовательность арифметической прогрессией?
966. Доказать, что если числа —!—, ——, —— составляют
Ь + с с + а b -|-а
арифметическую прогрессию, то числа а2, Ь2, с2 также состав-
ляют арифметическую прогрессию.
318
! 967. Образуют ли арифметическую прогрессию положитель-
ные корни уравнения, расположенные в порядке возраствиия:
a) sin х = 0; б) sin х — ; в) tg х— ~ ?
968. При каких значениях а корни данного уравнения
cos х — а.
расположенные в порядке возрастания, образуют арифметическую
прогрессию?
Составить арифметические прогрессии по следующим данным:
969. (а2 + й4 = 16> 970. ( а1 * = 44’
I и, • а, = 28. 1 -г aib = 24.
Характеристическое свойство арифметической
прогрессии
§ 143
Теорема. Каждый член арифметической прогрессии
ai> а2, , an-t, ап, а,,^, ... ,
начиная со второго, равен среднему арифметическому
соседних с ним членов.
Другими словами, при любом п > 2
а^-~Г~\апЛ1 • (П
Действительно, при любом п > 2
ап = ar>_, + d,
ап = "пн —
Почленное сложение этих равенств дает:
= ап~1 4- "пЫ»
откуда и вытекает соотношение (1).
Верна и теорема, обратная к только что доказанной.
Если каждый член числовой последовательности, на-
чиная со второго, равен среднему арифметическому
соседних с ним членов, то такая числовая последова-
тельность является арифметической прогрессией.
Попробуйте доказать это самостоятельно.
Отмеченное в этом параграфе свойство определяет, в част-
ности, причину названия «арифметическая прогрессия».
319
Сумма членов арифметической прогрессии
в 144
Рассказывают, что однажды учитель начальной школы, желая
занять класс на продолжительное время самостоятельной работой,
дал детям «труднее» задание — вычислить сумму всех ньтуралп-
ных чисел от 1 до 100:
14-2 4-34- 4 4-... 4- 10и.
Один из учеников моментально предложил решение. Вот оно:
1 + 2 + 3 + ... + У8 + УУ + 1VU =
= (1 + 100) + (2 4- 99) + (3 + 98) + .. . + (49 + 52) + (50 + 51) =
= 101 + 101 + 4 101 -|- 101 = 101 • 50 = 5050.
50 раз
Вто был Карл Гаусс, ставший потом одним из самых знаме-
нитых математиков мира*.
Идею такого решения можно использовать для нахождения
суммы членов любой арифметической прогрессии.
Лемма. Сумма двух членов конечной арифметичес-
кой прогрессии, равноудаленных от концов, равна сумме
крайних членов.
Например, в конечной арифметической прогрессии
1, 2, 3, ... , 98, §9, 100
члены 2 и 99, 3 и 98, 4 и 97 и т. д. являются равноудаленными
ст копнов этой прогрессии. Поэтому их суммы 2 4- 99, 3 4- 98,
4 4- 97 равны сумме крайних членов 14- 100.
Доказательство леммы. Пусть в конечной арифме-
тической прогрессии
«!, а2 ... , 0,,-р ап
два каких-нибудь члена одинаково удалены от концов. Предпо-
ложим, что один из них есть k-й член слева, то есть ak, а дру-
гой — k-й член справа, то есть ап_А41. Тогда
<’»+°мн = l«i 4- (* — 1) ^1 4- la, 4- (л — k) d]=2a( 4- (n — 1) d.
Сумма крайних членов данной прогрессии равна
at -1- ап = а, 4- 4- (п — 1) d] = 2а1 4- (п — 1) d.
Таким образом,
+ ап = а, 4- ап,
что и требовалось доказать.
* Подобный случай с Гауссом действительно имел место. Однако здесь
он значительно упрощен. Предложенные учителем числа были пятизначными
и составляли арифметическую прогрессию с трехзначной разностью.
320
Используя доказанную лемму, легко полу чпго общую фор-
мулу для суммы п членов любмй арифметической прогрессии.
1 llVI Wiv, .
Sn — °i + Ог 4 ••• Ь °n-i + ап<
Sn = ап+ an-j + + «2 + °1-
Складывая эти два равенства почленно, получаем.
zSn = (at + a J + {а2 + ап_,) + ... + (ап_, а2) + (пп 4- а,),
но
01+ ип~а2~^ °п-1 — °3 + ап-2 — • •• •
Поэтому
2Sn = п (а( + ап),
откуда
$ ,1-С1 + С"-/7.
п 2
Сумма членов конечной арифметической прогрессии
равна произведению полусуммы крайних членов на чис-
ло всех членов.
В частности,
1 + 2 + 3 + ... -I- 100 = п+-‘^0)!°- = 5050.
Упражнения
971. Найти сумму всех нечетных трехзначных чисел.
972. Сколько ударов сделают часы в течение суток, если
они отбивают только число целых часов?
973. Чему раина сумма первых п чисел натурального ряда?
974. Вывести формулу длины пути, пройденною телом при
равномерно ускоренном движении:
м м .
где v0 — начальная скорость в —, а — ускорение в , t— время
сек сек-
движения в сек.
975. Найти сумму всех несократимых дробей со знаменате-
лем 3, заключенных между целыми положительными числами
т и п (т < п).
976. Рабочий обслуживает 16 ткацких станков, работающих
автоматически. Производительность каждого стайка ам . Рабо-
ч
чий включил первый с ганок в 7 ч, а каждый следующий на
5 мин позже предыдущего. Узнать выработку в метрах за пер-
вые 2 ч работы.
977. Решить уравнения:
а) 1 -I- 7 + 13 + ... + х = 280;
б) (х + 1) + (х + 4) + (х 4- 7) + ... + (х + 28) - 155.
11 Заказ 261 321
978. С 1 по 12 июля включительно температура воздуха
ежедневно поднималась в среднем на градуса. Зная, чтс средняя
температура за это время оказалась равной 18— градуса, опре-
делить, какой была температура воздуха 1 июля
979. Найти арифметическую прогрессию, у которой среднее
арифметическое п первых членов при любом п равно их числу.
980. Найти сумму первых двадцати членов арифметической
прогрессии, в которой
аь + °е + <212 + “is — 20.
Геометрическая прогрессия. Формула
общего члена геометрической прогрессии
8 145
Геометрической прогрессией называется такая числовая после-
довательность, каждый член которой, начиная со второго, равен
предыдущему, умноженному на некоторое постоянное для данной
последовательности число, отличное от нуля.
Примеры геометрической прогрессии:
1, 1, 2, 2, ... ,
3 9 27
2, 8, 32, 128, ... ,
12—6, 3, — -.....
2
2 _ 2 _ А
5’ 5’ 5’ 5’ "
В каждой из этих последовательностей любой член, начиная
со второго, получается из предыдущего путем умножения в пер-
в чет-
вом случае на —, во втором — на 4, в третьем — на
3
вертом — на (— 2).
Геометрическую прогрессию, очевидно, можно определить и
таким образом:
числовая последовательность а^, а %, а3, ..., ап, ... называется
геометрической прогрессией, если для любого п
где q — некоторое постоянное для данной последовательности и
отличное от нуля число.
Это число q называется знаменателем геометрической про-
грессии.
Для приведенных выше примеров q равно в первом случае
—, во втором 4, в третьем—в четвертом — 2.
322
Геометрическая прогрессия называется возрастающей, если
|<?| > 1, и убывающей, если |?1 < 1. Так, из приведенных выше
геометрических прогрессии первая |<? = - | и третья |о=—— —
убывающие, а вторая (д — 4) и четвертая (д = — 2) — возра-
стающие.
Пусть знаменатель геометрической прогрессии а1г а2, с3, ...
равен q. Тогда по определению
а2 = а_ • q,
а.л = а2 • q = (at • q} • q - af • о2,
щ = а:- q= (a. - <?2) - q a^ q3
и т. д. Очевидно, что при любом п > 1
a, = a, qn •», (1)
то есть п-й член геометрической прогрессии равен
произведению ее первого члена на знаменатель про-
грессии в степени п—1.
Формула (!) называете? формулой общего члена геометриче-
.ской прогрессии.
Например, для геометрической прогрессии
12, —6, 3, - -, ...
2
а, = 12, q — — Поэтому
(I \© Q Q
“г) = (=2? = -128:
°101 а1 ?100 = 12 • (--V°° = “
\ 2 / 2е*
И Т. Д.
Упражнения
про-
981. Написать формулу общего члена геометрической
грессии, в которой:
a) а, = 2, 1 2 2 д) а, = sin ф, а2 = 2 sin ф;
б) а, = 3, е) = 1£ф, аг = -л 1?ф;
в) а3 = а6 = — 1: ж) at — tg ф, а2 — 1;
г) = — 54, аь = 162; з) — 1, а4 = 8.
11*
323
982. Получить формулу общего члена геометрической про-
грессии путем почленного умножения равенств:
a2 = • q,
аз ~ ’ Ч’
' «д ^n-i ' *?•
(Сравните с арифметической прогрессией, § 142.)
Составить геометрические прогрессии по следующим данным
(№ 983, 984):
[a, — a = — 4,
883. “ *
!«з — «1 - 8.
|“4 Т “1 — —»
«И- к 7
!о3—a2+af = -.
О
985. Найти формулу, выражающую произведение п первых
членов геометрической прогрессии через ее первый член и зна-
менатель.
986. Если все члены геометрической прогрессии умножить
на соответствующие (по номеру занимаемого места) члены другой
геометрической прогрессии, то будет ли полученная последова-
тельность геометрической прогрессией?
987. Две геометрические прогрессии почленно сложили.
В каком случае полученная последовательность будет геометри-
ческой прогрессией?
988. Доказать, что в конечной геометрической прогрессии
произведение членов, равноудаленных от концов, равно произ-
ведению крайних членов.
Характеристическое свойство геометрической
прогрессии с положительными членами § 146
Для любой геометрической прогрессии с положительны-
м и членами верна следующая теорема, которая, в частности,
объясняет название «геометрическая прогрессия».
Теорема. Любой член геометрической прогрессии
с положительными членами
а2, ая,... , an_t, ап, ап+1,...,
начиная со второго, равен среднему геометрическому
соседних с ним членов.
Другими словами, при п > 2
«п = • an+r (1)
324
Действительно, при п > 2
ап = «п-1 <7.
Поэтому
«п = «п-1 °п+1>
откуда н вытекает равенство (1).
На геометрические прогрессии, содержащие отрицательные
члены, эта теорема не распространяется: ведь среднее геометри-
ческое определенс только для положительных чисел.
Верна и теорема, обратная к только что доказанно!'.
Если каждый член числовой последовательности с
положительными членами, начиная со второго, равен
среднему геометрическому соседних с ним членос, то
такая последовательность является геометрической
прогрессией.
Попробуйте доказать это самостоятельно!
Сумма членов геометрической прогрессии § 147
Пусть S„ есть сумма п членов геометрической прогрессии
Sn = at + atq -f- atq2 -- ... + Oi?"'1. (1)
Если знаменатель прогрессии q равек 1, тс Sn = г • at. Если же
он отличен от 1, то поступим следующим образом. Умножим
равенство (1) почленнс на о; в результате получим
qSn = aiq 4* arf + a,q9 + ... +«!<?'. (2)
Затем вычтем почленно из равенства (1) равенстве (2):
Sn — qSn = а + (ctq + ctq2 -т- ... -т- — («iC + ан?2 4”
+ Gitf 4- ... 4- OfC'1'1) — cta“ = a( — aiq4 = at (1 — q
11так,
(1 — q)Sn = ( — q‘},
откуда
5n= (3)
Таким образом, если знаменатель геометрической про-
грессии не равен единице, то сумма п первых членос
этой прогрессии равна дроби, в числителе которой сто-
ит произведение первого члена на единицу минус п-я сте-
пень знаменателя прогрессии, а в знаменателе дроби—
единица минус знам'енатель прогрессии.
325
Примеры.
2 / 2.1
И I4.I4.I+ +-=2' 210' - —~1 = —•
/ 2 ‘ 22 23 — ” 2‘о 2 210 ,024’
1 — т
2) 1 —з + з2—з3 + - +з8 = - 'В-(--ВЛ = 1+2! = 4921>
' 1 —(—3) 4
Существует предание, по которому индийский принц Сирам (VI век)
предложил изобретателю шахмат любую награду, которую только тот захо-
чет. Изобретатель попросил, чтобы за первую клетку шахматной доски ему
Дали одно пшеничное зерно, за вторую — два, за третью — четыре и т. д. —
за каждую следующую клетку вдвое больше, чем за предыдущую. Такое«скром-
ное» желание удивило принца, но он согласился. Когда же подсчитали ко-
личество зерен пшеницы, которое следовало выдать за все 64 клетки шах-
матной доски, то оказалось, что награда в этом размере не может быть
выдана. Действительно, требуемое количество зерен равно:
1 . (j — 2е1)
1 + 2 4- 22 + 24- ... +203 =-*-—- = 2«J — 1 = 18446744073709551615.
Р.сли бы такое число зерен равномерно рассыпать по всей земной суше,
то образовался бы слой пшеницы толщиной около 9 мм.
Упражнения
989. Найти суммы:
а) 1 + 2 -2 22 + ... + 210; г) 1 — 2 + 22 — 23 + ... + 2'2;
б) - —-iд) 1 +х + хй+ ... + х100; ' 2 23 1 23 210 ' 1
в) — + ~ 2 “ + — + — 1 е) X — х®4-х5—... +х13. ' 3 З2 З3 З10
990. За одно качание воздушный насос откачивает часть
воздуха. Сколько процентов воздуха останется после 10 кача-
ний?
991. Бактерия, попав в живой организм, к концу 20-й ми-
нуты делится на две; каждая из них к концу следующих 20 минут
делится опять на две и т. д. Найти число бактерий, образовав-
шихся из одной бактерии к концу суток.
992. Доказать, что в геометрической прогрессии, имеющей
четное число членов, отношение суммы членов, стоящих на чет-
ных местах, к сумме членов, стояших на нечетных местах, равно
знаменателю прогрессии.
993. Решить уравнения;
а) 1 + х Ь ха + х3 + ... + х’9 = 0;
б) 1 +- х + х2 + х3 + ... + х™ = 0.
994. Сумма трех чисел, составляющих арифметическую про-
грессию, равна 30. Если от первого числа отнять 5, от второго
4, а третье число оставить без изменения', то полученные числа
составят геометрическую прогрессию. Найти заданные числа.
326
Сумма бесконечно убывающей
геометрической прогрессии * § 143
До сих пор, говоря о суммах, мы всегда предполагали, что
число слагаемых в этих суммах конечно (например, 2, 15, 1000
и т. д.). Но при решении некоторых задач (особенно высшей
математики) приходится сталкиваться и с суммами бесконечного
числа слагаемых
S = Oi + о2 + ... + ап + ... . (1)
Что же представляют из себя такие суммы? По определению
суммой бесконечного числа слагаемых at, а2, ... , ап, ... называ-
ется предел суммы Sn первых п чисел, когда п -> со:
S = lim Sn = lim (aj + а2 4- ... Н ап). (2)
п -* ев П -* во
Предел (2), конечно, может существовать, а может и не су-
ществовать. Соответственно этому говорят, что сумма (1) суще-
ствует или не существует.
Как же выяснить, существует ли сумма (1) в каждом кон-
кретном случае? Общее решение этого вопроса выходит далеко за
пределы нашей программы. Однако существует один важный част-
ный случай, который нам предстоит сейчас рассмотреть. Речь
будет идти о суммировании членов бесконечно убывающей гео-
метрической прогрессии.
Пусть alt aiq, atq2, ...—бесконечно убывающая геометриче-
ская прогрессия. Это означает, что | q | < 1. Сумма первых п
членов этой прогрессии равна
с _ 0 — ?р)
п 1-ч ‘
Из основных теорем о пределах переменных величин (см. § 136)
получаем:
limSn = lim °-(1 ~ q~ = -°- • lim (I — q") =
n -* n — 1 — 1 — Q r -r «
= ———Him 1 — lim <7”].
1 — n -* ee ft во
Ho lim 1 = 1, a lim qn — 0. Поэтому
n -* •» n -* »
5 limSn = _?!_.
n •© 1 q
Итак, сумма бесконечно убывающей геометрической
прогрессии равна первому члену этой прогрессии, де-
ленному на единицу минус знаменатель этой прогрес-
сии.
327
Примеры.
1) Сумма геометрический прогрессии 1, —, —, —, ... равна
3 0 27
. 5= 1 • =
1-1 2
3
з
а сумма геометрической прогрессии 12; — 6; 3; — —, ... равна
2) Простую периодическую дробь
0,454545 ...
обратить в обыкновенную.
Для решения этой задачи представим данную дробь в виде
бесконечной суммы:
п л-лсле 45 45 . . 45 .
0,4о4545 ... — — ------}•------И- ... •
100 10000 1000000
Правая часть этого равенства представляет собой сумму бесконеч-
но убывающей геометрической прогрессии, первый член которой
45 1
равен —, а знаменатель —. Поэтому
100 100
45
п 100 45 5
0,454545 ... =----------= — = —.
1 99 11
1 — —
100
Описанным способом может быть получено и общее правило
обращения простых периодических дробей в обыкновенные (см. гл.
И, § 38):
Для обращения простой периодической дроби в
обыкновенную нужно поступить следующим образом:
в числителе поставить период десятичной дроби, а
в знаменателе—число, состоящее из девяток, взя-
тых столько раз, сколько знаков в периоде десятич-
ной дроби*
3) Смешанную периодическую дробь
0,58333 ...
обратить в обыкновенную.
328
Представим донную дробс в виде бесконечной суммы:
.. . 58 , 3 3 3 .
0,583дб — — Ч-------+--------Ь------— ~Ь ••• •
100 1000 10000 100000
з
В правой части этого равенства все слагаемые, начиная с —-, об-
разуют бесконечно убывающую геометрическую прогрессию, пер-
3 1
вый член которой равен -----, а знаменатель —. Поэтому
н н 1000 10
3
3______3 1 _ 1000 = _1_
luuo luOun 1UUUUV | _ J Зии’
10
Следовательно,
0,58333 ... = — + — = — =
1U0 300 300 12
Описанным способом может быть получено и общее правили
обращения смешанных периодических дробен в обыкновенные (см.
гл. II. § 38). Мы сознательно не приводим его здесь. Запоминать
это громоздкое правило нет необходимости. Гораздо полезнее знать,
что любую смешанную периодическую дробь можно представить в
виде суммы бесконечно убывающей геометрической прогрессии и
некоторого числа.
А формулу
S = -^—
1 — ?
для суммы бесконечно убывающей геометрической прогрессии
нужно, конечно, помнить.
В качестве упражнения предлагаем вам, помимо приведенных
ниже задач № 995 — 1000, еще раз обратиться к задаче № 301
(стр. 87).
Упражнения
995. Что называется суммой бесконечно убывающей геометри-
ческой прогрессии?
996. Найти суммы бесконечно убывающих геометрических
прогрессий:
б) 3, - 1, -, - ... ;
’ 3 9
в, r»tl. I, ....
/3—1 /3+1
г) 1, х, №, х3, ... (|х|< 1).
329
997. При каких значениях х лри1рсссия
а 4~ х а — л 1а — х\3
а — х а + х’ \а 4 х/ ’
является бесконечно убывающей? Найти сумму такой прогрессии.
998. В равносторонний треугольник со стороной а вписан
посредством соединения середин его сторон новый греугольник;
в этот треугольник тем же способом вписан новый треугольник
и так далее до бесконечности.
Найти.
а) сумму периметров всех этих треугольников;
б) сумму их площадей.
999. В квадрат со стороной а вписан путем соединения се-
редин его С1Орон новый квадрат; в этот квадрат таким же об-
разом вписан квадрат и так далее до бесконечности. Найти сумму
периметров всех этих квадратов и сумму их площадей.
1000. Составить бесконечно убывающую геометрическую про-
25
грессию, такую, чтобы сумма ее равнялась —, а сумма квадра-
4
625
тов ее членов равнялась —.
Задачи на повторение
1001. Будет ли последовательность
1; — 1; 2; — 2; 3; —3; 4; —4; ... :
а) ограниченной снизу;
б) ограниченной сверху?
1002. Доказать, что всякая последовательность, имеющая
предел, ограничена. Верно ли обратное утверждение? Ответ по-
яснить примерами.
1003. Является ли последовательность всех положительных
корней уравнения sin — = 0:
X
а) конечной;
б) ограниченной?
1004. а) Последовательность alt а^, ая ... образует арифме-
тическую прогрессию. Будет ли арифметической прогрессией
последовательность loj, |о2|, | а3], ••• ?
б) Последовательность at, az, ая, ... образует геометрическую
прогрессию. Будет ли геометрической прогрессией последова-
тельность 'at j, |а2|, |а31, ... ?
1005. Докажите, что всякая арифметическая прогрессия пред-
ставляет собой монотонную последовательность. Верно ли это
для геометрической прогрессии?
330
1006. При каком значении л числа
Vк, у/ х, Ух:
а) образуют арифметическую прогрессию;
б) образуют геометрическую прогрессию;
в) образуют одновременно и арифметическую » геометриче-
скую прогрессии?
1007. Найти сумму
|о + —\ + (а2 + —) + — + |О'‘ +
\ а / \ а2/ \ с'1].
1008. В неметрической прогрессы ат+п = А, ат_п — в.
Найти аш и ап.
1009. Существуют ли такие трг члена, который одновременно
являются первыми членами некоторой арифметической и неко-
торой геометрической прогрессии?
1010. В какой арифметической прогрессии сумма двух любых
ее членов является членом той же прогрессии-
1011. Могут ли стороны пр я моу-ильного треугольника обра-
зовывать:
aj арифметическую прогрессию;
б' геометрическую прогрессию?
1012. В арифметической прогрессии сст+71 = А ат_п = В.
Найти с„ и
1013. Могут ли сумма и разность двух членов арифметиче-
ской прогрессии быть последовательными членами той же про-
грессии? Если могут то ь каком случае?
1014. Най^и арифметическую прогрессию, если сумма 7-го
и 9-го ее членов равнг 30, а произведение 6-го и IG-’o членов
равно 209
1015. Доказать, чтс если в арифметической прогрессии для
некоторых р г q {р =* q) Sp = Sq, то Sp^c — 0.
1016. Найти 3-й ь 10-й члены геометрической прогрессии,
если их сумма равнг — 2, а произведение 2-го и Н-гс членов
этой прогрессии равне — 3.
1017*. Могут ли числа 16, 11 12 быть членами (не обязательно
соседними) одноц и той же геометрической прогрессии5
1018. В круг, радиус которого равен /?, вписа! квадрат;
в квадра" вписан круг, а в этот круг вписаг новый квадрат
и так далее дс бесконечности. Определить сумму площадей всех
этих кругов и сумму площадей всех квадратов. "
1019. Построить график функции
1020. Три числа, составляющие арифметическую прогрессию,
дают в сумме 3. Найти эти числа, если при прибавлении к ним
соответственнс 1, 7 и 17 получается геометрическая прогрессия.
33L
1021. Сумма трех чисел, составляющих возрастающую гео-
метрическую прогрессию, рав^а 65. Если от ме.ШЦЛ1и из 3inx
чисел отнять 1, а от большего 19, то полученных три числа
составят арифметическую прогрессию. Найти эти числа.
1022. Нанта четыре 1D1A НО IXV/lV/pniA 1рИ
составляют арифметическую, а последние три — геометрическую
прогрессию, если известно, что сумма крайних чисел равна 37,
а сумма средних 36.
1023*. Можно ли из чисел —, —, —,
2 4 8
1 -
, ... выбрать
бесконечную геометрическую прогрессию, сумма которой равна:
а) Ь 6)
ОТВЕТЫ К УПРАЖНЕНИЯМ
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
1. Левая часть определена для любых неотрицательных чисел а, пра-
вая часть— для любых чисел а, раеенство в целом—для всех неотри-
цательных чисел а. 4. Левая часть определена для всех чисел с, кроме
0 и 1, правая чаью— для всех чисел с, равенство в целом — для ьсех
чисел с, кроме 0 н 1. 5. Левая часть определена для всех а, кроме 0
н —1, правая часть — для всех чисел а, кроме 0 н 1, равенство в целом—.для
всех чисел а, кроме 0, — 1 и 1. 6. Левая часть определена для всех
рпцательных чисел Ь, кроме 1, правая часть — для всех чисел Ь,
стро в целом — для всех неотрицательных чисел Ь, кроме 1. 8. Левая
определена для всех пар (а, Ь), правая — для всех пар, кроме пары
равенство в целом — для всех пар, кроме пары (0, 0). 13.
г) нет; д) да. 14. Еслп а= 1. то один: х— 1 если а
а— 1 5
26. -----. 27. Прпа=-1 нет корней; при а=£1
3
а) Да; б) нет;
1, то ни
иеот-
равеи-
часть
(0. 0).
в) нет;
одного.
то х = 0. 30.
Если а + — 2, то х =
±
а — 1
28. 1 Ipu
и = О
а + ± 1,
то
32. Еслп
а =
1
= ——; если
а — 1
н b — 1. то
а = 1
1, то х—любое; если
а+ 1
при а = — 2 корней нет. 31. Если
4
корней нет; при а + 0 х = .29. Если а =
а
4+
а 2
то корней нет; при а = — 1 х — любое,
нет; еслп а = 1 п b = — 1, то х—любое;
при а +
корней
Да, если т -f= 0: б) нет; в) нет; г) да, если т=
. 36. а)
а — 1
37. Нет. 38. Нет. 39. б) 5 лет назад отец был в 4 раза старше сы-
ч. 41.
1 х =
= п = 0.
па. 40. 2
чае, еслп число
сорта нужно
а + — 19 х
Требуемое количество стали можно получить лишь в
г заключено между числами р и
100 (г —q}
взять----------тони. 50. Нет
P — Q
а -| • 5
—-—, при а = — 19 нет корней.
1 — 2а 3 .
х—--------: при а — 1 п а= — нет корней. 54.
а — 1 4
число является корне»! уравнения; еслп одно из чисел а и Ь равно пулю, а
q. При этом
корней. 51.
53. Если а +
том слу-
первого
5’. При
3
1 и а+ —, то
4
лома
— 1.
Если а = b •— 0. то каждое
333
другое отлично от нуля, то Мирней пет; сил» а 0 и 6 0, го upn а2 =/= 61
х — при 6= а х — любое, кроме —, при 6 = — а корней нет. 55 Ес-
а
любое; если Ь — 0 и а 1,
; при 6 0 и а = — 1 корней
г при
Если а = 0, то х — любое число, кроме
хотя бы одно из чисел т и л равно нулю, то корней нет;
и л отличны от пуля и т = л, то х— любое число, кроме
т + п. 59. Относительно *: если bj- 0, то
то корней нет; при 6 =/= О
56. При 6 дь 0 и
нет.
Ь == 1 урЗопспис не
О, если а =£ 0, то
ли 6 = 0 и а=1,то х
1 а
н а 4 — 1 х— —----
b(а 4-1)
Ь 4= 1 х = 2; нри Ь = О X — любое Ч1КЛ0, прОМе
имеет смысла. 57.
5
х — — а. 58. Если
3
если оба числа т
п; при я^б, л^Оит^лх
корней пет; если Ь — и и a 4= 0, то х — люоое число, кроме 0; при а — о = 0
уравнение не имеет смысла. Относительно о: если хотя бы одно из чисел а и
х равно пулю, то корней нет; если л ^0 и х -/ 0, то 6 = 0. 61. Если а 1,
то X— ±(а—1); при а<1 корней нет. 62. 0,5; 1,5. 63. Если аз>0, то х=1±а;
11 * „ 4
если а < 0, то корней нет. 64. 0. 65. —. 66. —. 67. —2; . 71. Может,
8 2 5
если а = 0, a b — положительное число. 73. а) Нет; например, при а= b = 1;
б) да; в) нет; например, при отрицательном с; г) нет. 75. лг — любое число, за-
ключенное в интервале от — 1 до 1 (включая эти два числа). 76. х — любое
4
число, не превосходящее — 3. 77. Нет корней. 78. — — и — 6. 79. а) а > 0;
б) Ь > О, b 4= 1; в) а Ф 0; г) b — любое; д) х — любое; е) а и b — любые чис-
ла, не равные нулю одновременно. 84. а) Если а = 0, то а2 = 5а2 = 2а2; если
а #= 0, то а* < 2а2 < 5а2; с) если а > 1, то а < а2 < а3; если 0 < а < 1, то
а > а2 > а3; при а = 0 и а — 1 а = а" = а3; если — 1 < а < 0, то а < а3<а2;
если а <—1, то а3 <а<а2; при а——1 а = а3 < а2. 98. Данные числа равны
между_ собой, 99. уГ26_> У 2 4-/4. 100. (1 |- /'5)10° > З100. 102. (/5—
— V 3)51<(/ 6 — / 2)61. 103. а) — 0,4 < а < 2; б) — 2<а<0,4. 104. 6,6<
22 25
<а 4-6 <6,8. 105. 5,61; 5,66. 106. 0,2; 0,4. 107. а) 1,38; 1.68; б)-
т 35 48
118. Быстрее в безветренную погоду. 125. Указание. а 4-6 >2/ab: Ь+О
>2/сЬ; а 4-с> 2/ас. 131. 2. 133. а) а = 4; б)а = -; в)а=-/57134. а) а=1;
d2
б) а = 2; в) 0. 135. Квадрат с площадью 2/?2. 136. Квадрат с площадью —.
р
137. Квадрат со стороной 138. а) 1; б) нет корней; в) — I. 139. Первая
бригада. 142. Ошибка при взвешивании на некоторых электрических весах со-
ставляет не более 0,001 % от истинного веса тела. 149. а) 5,5; б) 3,7; в) 8,6;
г) 0,6. 150. а) 14,97 с точностью до 0,09; б) — 24,20 с точностью до 0,08;
в) —8,99 с точностью до 0,05. 151. а) 0,0005; б) 0,0005; в) 0,00009 (точнее.
—— I. 152. а) Да; б) нет; в) нет; г) да. 153. а) Да; б) да; в) да; г) да; д) нет;
I 1иии/
е) нет; ж) нет; з) да. 155. х > 1. 159. Если а > Ь, то х> — 1; если а< Ь, то
3 — & 3—6
х < — 1. 163. Если а > — 2, то х >---; если а < — 2, то х <---------; если
а 4- 2 а+2
5
а = —2 и 6>3, то х—любое; при а=—2 и 6 < 3 нет решений. 164. х>у.
334
2 2-3
165. Если а > — 1, то х>--------; если а < 1, то х < -—. 171. .
(а-1-1)» (« + 1)2 4
171. Если а > и, то х > —; если а < 0, то х < —; при а = 0 нет корней.
а а
о
181. 1,1 186. — 4 < х< 7 5 187. 1 <и < b > 0. 188. 2 < « < 3,
о
4 3
3 < а < 4,5; Ь —любое. 189. 3 < х < 3,5. 190. Если а > 0, то — — < х < —;
а а
3 ч /
если а < 0, то - < х<——; при а = 0 х — любое. 191. 39“ < t < 55°.
а а
194. Положительна при 2,5 < х < 3; отрицательна при х < 2,5 и при х > 3.
19
196. х < 0; х > 1. 197. 11 < х < — 5. 198. — — < х < — 3. 199. х < 0;
6
х > 2. 200. 0 < х < 201. х > 2. 20з. х < и; х > 2. 205. х < 0, 0 < х < 2.
О
з
207. — 1 < х < 5. 208. х< — 9, к > 11. 212. х < 1, х> 3. 215. х > — —.
2
„ . а + i> а — b
216. При а < 0 решении нет; если а > 0, то-----< х < -----; еслп-а = О,
а. а
b и, то решений нет; при а — b = 0 х — любое. 223. а) —15; б) 3; в) 121;
ж) 1. 224. а) Изменит знак на противоположный; в) не изменится. 225. а) 6;
б) — 2, в) 0; г) при любом а. 227. а) ± 2, б) 0; и) ни при каком значении а
строки данного определителя не пропорциональны. 231. —; —6; —6. 232.4;
5 — а; 5а + За2 (а У- 0). 234. а) Да, если я ± 6; в) да, если ay= 0. 235. Ес-
„ .. „ 2 1
лн а = 0, то решении нет; если а 0, то х = — —, у = —. 237. Если ау= 0,
а 2а
2
то х = —, у = 2; при а = 0 система несовместна. 238. Если а + 0, то х=0,
а
у = при
а = 0 система несовместна. 239. Система несовместна. 210. Если
1
х =------, у = 0; при а=—1 система несовместна; прн а=1 она
а ± 1, то
не имеет смысла. 242. x = t, y = t—1, где 1 - любое число. 243. х = t,
3
у = — t, где t — любое число. 245. а) Бесконечное множество решений; б) си-
5
12 6
стема несовместна. 247. Если а У= ± 4, то х — —-----, у =-------; если а =
4 —а 4 —а
14-3
= — 4, то х = I, у = —-—, где t — любое; при а = 4 система несовместна.
а — 6 + 31
248. Если а =£ ± 3, то х = 2, у = 1; если а — ± 3, то х = 1, у=-----------,
где t — любое число. 249. Если а 4- то
х —
при а~—~ система несовместна. 260. а) 2;
а
а (2а — 3) _ 2а3 — g 4- 1
2(1 —2а)’ У “ 2(1—2а) 1
б) а < 0; а > 2; в) 0 < а < 2;
х — любое
270. Ука-
273. —2,о<
3
г) а г 2. 262. Если а ф 0 и а =г= —, то лс = 4; если а = G, то
z
й
число, кроме 1; при а = — уравнение ие определено. 269. По озеру
зание. Использовать результат упр. №267. 272. h >3 g ,
4
< х < 8. 274. — 2 <ж< — 1; 5 < х < 6. 275. — 1 < х < 2. 27». Если а=£ +1
b
то х = у =-------; если а = 1, то х = i, у = b — /; если
У 14-и
система несовместна; если л = — 1, Ь = 0, то х = у = t
1; кроме того, при | а | < 1 получается
. 27'8. Еслп а = — 1 то
а = — 1, b У- 0, то
где /—„.обое число,
еще одно решение.
/
, у = - „ . 2/8. Ьслп а = — I то л = /, у -------------
а2 — 1 1 — а2 7 14-3/
1
где / — любое число, отличное от 0 н — - ; при а =/= — 1 система несовместна.
О
'ill. X — 1, у
а2 + 2а — 1
х= —1 - -
а
279. Если л 4= 2, то х— — у = а + 1; при а—2 х— /, у = 2 — /, где
9 15
/ — любое число. 280. При т=— —, п Ф — 281. —6,40 <а<3,75. 282. а=
4 10
= — у, b — — —. 284. Указанные условия не выполняются
значениях а. 285. х находится с точностью до 0,006 ^точнее,
/ 3 \ 34 38 9
точностью до 0,005 точнее, — . 288. — < т < —; — <
\ 700/ 65 65 130
п
ни при
4 \
— > а
700/
12
< 130'
каких
у—с
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
II
5 „ km т 2 3
292. а) — б) нет; в) — 2. 293. а) —; б) —. 294. а) 1; -; 2; б) 3;
1 1 +(а—Ь)
в) -; —; 1. 299. Указание. Воспользоваться тождествами а=1---------------
(а + Ь) — (а — Ь)
о =
2
2
. 302. Все делители числа п имеют вид 2т51'. 308. Пусть
А
мера отрезков АВ и CD. Тогда отрезок — будет общей мерой от-
пт
CD
и —. 309. Если бы п-я доля АВ и т-я доля CD
т
имели общую
Пусть Д — об-
получим, что
| употребляется
| Д, — Д2 । т —п.
и Aj — Д2. Обрат-
Д—общая
АВ
резкое —
п
меру Д. то Д была бы и общей мерой отрезков АВ и CD. 310.
щая мера отрезков Aj и Д2. Приняв Д за единицу длины,
| Д, = т, | Д2 | и, где т и п—натуральные числа (значок |
для обозначения длины). Но тогда | А] | + | Д2 | ~ т + п.
Следовательно, Д является общей мерой отрезков Д_
ное утверждение также верно. 313. Доказывается методом от противного с
молью результата задачи 312. 315, а) Да; б) да; в) нет. 318. г) 15,25...>
3 5
319.6) — — >—0,375...; в) =0,5555... (одни пятерки); г) какое
8 9
ПО”
4’
ИЗ
336
чисел бол! ше: 0,3333 ... или — —сказать нельзя; вс»^ии...... ,о.с,
вы десятичные знаки числа 0,3333 ... , стоящие после четвертой тройки’ на-
пример, 0,33331 ... < , но 0,оо335 ... >—.324. а) С недостатком: 1; 1,7, 1,73!
1,732; ... ; с избытком: 2; 1,8; 1,74; 1,7оо; ... ; б/ с недостатком: 2;
— 1,8; — 1,74; — 1,733; ... ; с пзоытком: — 1; — 1,7; 1,73; - 1,732; ...
326. Нет; например -а = = 0,333 ... . 327. а) 3,1'ю ... ; bj 0,317 ,. ;
г) —0,317 ... , д) 1,902 ... ; е) —1,013 ... ; ж) — i,4oo ... ; з) 3,479... ;
328. а) С Недостатков». 3, 3,1; 3 14; 3,145; ... ; б) с недостатком: 4; ч,3; 4,37^
4,377 . ; н} с педмотатком: —1; —1,0; —0,92; —0,914; ... . 330. Нет'
не всегда, например, )' 2=1,4142 ... ; 2—И 2 = 0,5857 ... , но у’2-[(2-
— У 2) = 2,000 ... =2. 331. б) 0,88 ... ; г)—3.16... ; е) — 2,73....
334. Не всегда. 335. а) 0,91 ... . 337. а) 1,03; б)'0,1 4; в) — 1,22 344. а) Мо-
жет, например, при т = 1, п = 2; б) может, например, при т = л; в) нет,
ие может. 345. Да. 351. Нет. 352. 1-й способ Если хотя бы одно из
чисел с. + b К 2 ьа — ЬУ 2 равно нулю то (а + b У" 2 )(о — b\r 2) =0 ст-
(а \= а
— 1 = 2. Число — рационально, но еред» рациональных чисел нет та-
b / о
кого, квадрат которого равен 2. 2-й способ. Число а рационально, а число
b рг 2 иррациопалоно. Следовательно, их сумма не может быть равна рацио-
нальному числу 0.
КВАДРАТНЫЙ ТРЕХЧЛЕН
ill
л «о-I Ь\- (о — о)’
358. (х — З)2 — 1. 359. о(л—2о)2 + 3. 361. “ ) —------362. х24-
/ 1 \2 3
4- х 4. I = I х + — I + — 363. — Зх3 + 12х-13=— 3(х — 2)« — 1. 370. Н ет.
371. а) а < 0; б) а = 0; в) о > 0. 372. а) а < ; б) а< — ; в) а >
373. Либо 1 (при а = —2), либо — 1 (при а = 2) 374. | а | < — 375. а < 0.
376 V = ~с/ + ™ 377 ± ° + 2/ + /4F+T2 ц 379 2
2/ ч 2 .
3 з *
380. При а =— — корней нет, при а — — х = 3 + а. 381. а =— 2.
384. Указание. Воспользоваться тождествами: а2 -|- Ь2 = (а + Ь)2— 2аЬ',
а3 +b3 = (а +b)3~3ab(a+Ь). 38n.au—а— 4. 388.31. 389. о =1,5 и
а = — 2,5. 390. а) а < 4; б) 0 < а < 4; в) а < 0; г) а — 0; д) этот
случай не может иметь места ни при каком значении а. 401. Одинако-
вые при а <0, разные при о > 0. 402. Одинаковые при — <о < 7, раз-
ные при а < и при а > 7. 404. (2х—За)(х— 2а) 406. (ч—2а—Ь)(.ч—а-|-£)
54
409. 8. 410. Если а ± — 1 и а + 53, то х= ——, при а = 53 корней нет.
337
412. a) a (lox-1—/х— zj = О, где a — любое целое число, отличное от нуля.
413. 8чх» 18х 30 = 0. 414. Нет. 415. а) а(х2—4x4- 1) = 0, где а — любое
целое число, с. нуля. 434. х1П1|, = —3, у,шп=—5- 435. xmax = — 1,
Уп.„х = — 3. 436. ymi„ =0; д^.„гагъ.я при х = — и х = — —. 437. ,min=0;
Z о
1 3
достигается при х = — и х = — 439. Либо х<1, либо л > 3. 440. 1<л<5.
2 2
443. Неравенство ие выполняется ни
448. Либо х < —5, либо — I
450 —3; - 2; — 1; 0. 451
— 4, либо 0 < о < 1; в) — 4
_ 8 „ 5
442. 0 < х < 1.
447. — 1; 0
< 8.
5^
3
411.
5
при каких значении*. х
449. Либо | х| <2, либо 6 < х
452. о < 1. 454. б) Либо —5
455. При а = — одни корень равен 0, а другой —При — <а< 3, а также
*5 и U
з 3
5
при а > 7 г.0рни положительны. При о<-— корни разных знаков. Если 3<а< 7,
*5
ю уравнение не имеет корней. 458. х = - У 3, у=— — у 3; х=—— V 3,
5 5 5
6 г— 6КТ зКТ 6КТ зКТ
У = -к 3; х = —— , у = —— ; X ------—, у = — -' -. 459, х=
5 у 7 К7 К 7 К 7
3 1
с=10, у= —; х = 3, у = 5. 460. х=— 3, у =4; х = — 6, у = 2. 461. х=у= —;
х = у = — —. 463. х = 1, у = 5; х=5, у-=1. «64. х=1, у=5; х=5, у=1; х—2,
у=3; х=3, у=2 465. х=0, у=1; х=1. у=0. 466. х = 2, у = — 5. 470. См.
рис. 1». 475. 12. 476. —1. 477. 28. 478. 4; —5. 479. 4. 480. 0; 5. 481. —а; а.
482. 7. 484. с = 0. 485.5. 486. (2х - а) (2х — а 4- 6). 489. Сели а = b = 0,
то х — любое число, кроме 0 и 1: если хотя бы одно из чисел а и b от-
лично от нуля, то корней нет. 490. При х = а и х = —°, если а отлич-
а — 1
но от 1 и — 2; при х = 1, если а = 1;
при а = — 2 задача теряет смысл.
491. Если 6=£—2а, то х=—Ь. При Ь=—2а
уравнение не имеет корней. 493. Нет.
494. а < — у. 495. 3 < х<5. 496. Либо
о
— 2 < х < 1, либо х > 6. 497. При
а < 1 и при а > 13. 498. а) 5 < а < 11;
б) а < 5 и а > 11; в) а < 5 и а > 11;
г) fl=5,fl=ll; д) 5 < а < 6 и .10 < а<11;
е) 6 < а < 10- 499. х=27, у=1; х=-1.
у = — 27. 501. Если Ъ 4- 0, то
1 I а \ 1 / а А
Т— И если
Z \ С? J Z \ D /
338
b = 0, a a =£ О, то система не
имеет решении; при а = 6=О
x=t,
число.
2
у = t, где t — ...обсе
4 2
502. х = —, у = “ >
3 * 3
4
у = - , 504. Нет корней.
505. 6. 506. Кории одинаковых
знаков при а < — i —К2 и при
— 14- V~2 < а <0,5; корни раз-
ных знаков при — 1 — И 2 <
< х < — 1 + К 2~ 508. Могут,
но только при р=<7—0 и р =1,
q = - 2 509. 1. 510. — —.
4
511. 5 = —6, с = 3
Рис. 2*
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ.
СТЕПЕННАЯ ФУНКЦИЯ
IV
517. 0 и 1. 521. 21 (— Юр и (— 10)»; 5) 22М и 2»3°. 522. Ь0а». 523. 1875а10.
/ 1 V / 1 \3
524. <? 525. ар. 526 . 4) (43)100 и (3«)‘°°, (43)lw < (З4)100; 5) [ — ~ и — - ,
Ь (Ь* — ЗаЬ -}- За»)
531. 3) - 33- 10-®. 532. г) 1; д) хг* — а"«; е) — -------——53S. С
(t—а)4 _
537. б) и в) см. рис. 2*. 538. в’,, д) и е) см. рис. 3*. 540. 100 ( 2— 1) %.
541. 100 (3/L27 — 1) %. 542. ЮС (j/ 2 — I) %. 544. а > 0. 515. а < 0.
546. a) |х — 1 |; г) Зх» —х+ 1. 548. 4 —2х при х < I; 2 при 1 < х < 3;
339
б) 8; в) 1;г)<т — b. 574 г)
2х — 4 при х > 3. 649. См. рис. 4*.
650. 3 < х < 5. 551. а; х > — 6; б) х—
любое число; в) л<—3; х > 1 553. а)
х> i; О) множество всех действнтель-
1
ных чисел; в) х < — 2 и х > —;
г) х < — 2 и х > 7; д) множество всех
действительных чисел; е) х>1.
555. х > 3. аоб. 2 < х < 8.
557. х — любое число. 558. х > 0.
659. х > а. 560. х — любое число.
563. а) В три раза 566. 1) /| х2—1 |;
а) 3/Т>2/3;
4/б' — 8 Г 3;
(а > 0). 575.
2) ух2 —х-|-1. 568.
е) 1/^- 572. а)
I а — 1
2а4 V 64cz; д) / и
576. 8) 1(/3 4-/ 5-У 15 — 3); 9)-|(/V-/21+/49);
'/з3 /з= 2 _ 2 __
а)
И) '2(2/Т+/1б—/Т— 1); J2) 6 + 7/2’-у т/10 —/Г577. а) 21, 95;
б) 15.39;
в) —7.24 581
а) 8^ > 12*; в) 12^ > 18’. 582
583. а) —, если а > 0 и b > 0; 0, если а > 0 u b = 0; б) ——
b / х + У у.
г г- 19
(х > 0, у > 0, х* у). 584. — 3 у 9 . 586. 3. 587. 32. 589. —.
7 /ЗХ^ /зД
590. — 591. 4 (| а | =/= | х |). 592. 0. 600. a) (у)11 > l~
? 2 2 _ _2
б) (2/Л 3 < (3/2 ) 3; г) (/21) 7<(2/~5) 7. 601. а) а> 1; б) а < 1.
2
606. ------, если 1 < а <
2 — а
2;
-------, если а > 2; при а
а — 2
< 1 и а = 2 за-
дача теряет смысл. 607. 5—V 2. 608. /3 [- / 5 . 616. У к аз а н н е-
Представить х-|-2/х—1 в виде (х—1Ц-2/х—1 + 1- 617. /16.
618. 1. 619. 1. 620. |а|/а6. 621. а /53. 622. а уГа-Ь‘~. 623. ab /‘оЛГ
624. 1; /-2 = /Т; /"3. 625. 0,1. 626. —.
F 243
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
V
629. Вектор перпендикулярен оси. 633. Окружность радиуса г с центром в точ-
ке с координатами (а, Ь). 634. а)—30° (минутная) и —2°,5 (часовая). 635. а) 1-й
и 4-й; 6) 4-й и 1-й. 636. В одной и той же четверти углы <р и —<р окан-
340
чиваться не wfyi, одпали vnii Iviuijt иметь одну и ту же нвнёчную сторону,
лежащую на осн абсцисс (например, 360’ и —360°, 180° и —180°). 637 а) ЗбО’-п;
б) 180°-f-360’ • п; в) 90’4-360° п; г) 270°4-360” п; д) 45°4-зб0-п; е) чз° 4- *80 п;
ж) — 45° 4-360° н 639. Не.. 642. Нет. 643. sin cos<p= — Ц2,
2-; cosip =Д, tBT = ->'3;
648. а) Да; 6) нет. 619. Нет. 650. Нет. 653. - 2 + 5> 3
tgq^ — 1,
cig*? — —1- 644. sin<p = —
2
9.
2, 5, 7, 8; нечетные: 1, 3, 4, 6,
biii 120° 666. а) cos 9°; б) sin (— 172 );
tg25’; 6) tg 175°; в) ctg 120°; г) ctg 150’.
10’). 675. Может, если / (0) = 0; если
может. 676. Положитель-
II 5); остальные выражения отрнцатель-
в) cos 860’; г) cos (- 10’). 679. а) В пер-
680. а) Во 2-й или в 4-й четверти, 6) в 1-й
681. а) В 3-п и 4-й четвертях; б) в 1-й и 4-п чет-
б) cos(— 67°) < cos 654’ <
Положител ьным и
выражение 2) равно нулю; остальные
686.
пли в 4 л четверти; в) в любой четверти; однако
может быть произвольным. 689. sin х н cosec х,
и ctg х. 690. а) tg (—55°), tg 1295°, tg600°, б) ctg 295’, cig 651°;
ctg«p= — -
>
654. — 14 + ^JC2* 655. 656. — 4. 657. Выражение не on-
__ 3 __
ределено: ctg 0’u cosec 0’не существуют. 658. 1.659. pA3 . 661. —(Jz2 4 > 6)-
4
8 , r._
662. — 3—3) 663. Четные:
665. a) sin 100°; 6) cos 163’; в)
в) sin (— 175°); г) cos 79°. 670. а)
671. a) tg 15’; 6) ctg 87°; в) ctg(
У(0) =/= 0, то указанное условие выполняться не
нымп являются выражения 1)
ны. 678. а) sin 735°; б) sin 790°;
вон пли третьей четверти,
или 3-й четверти.
вертях. 682. а) sin 600’ < sin (— 55’) < sin 1295°;
< cos 295°. 684. Возрастает от — i до 0. 685.
ляются выражения 5) н 7);
ражения отрицательны.
> ctg (— 10°). 687. б) Во 2-н
это не означает, что угол <р
cos х и sec х, tg х
“ ' ' “ ~ 24
ctg (— 67 ). 692. а) Нет; б) пет; в) да. 694. ж 3764 м. 695. а 3°. 698. а)—л;
5 7 50
б) — л; в) — л; г) — л. 699. а)
6 4 '9
3) в 3-н. 701. а) (а — Ь)-\
делено: ctg л не существует. 702. х = пл.
равен 1. 707. а) sin 0,87; б) cos 1,8;
708. Положительными являются выражения а) и б),
яь-
i u-
3) tg 353’< tg 359°; 7) ctg(— 2O’;>
25°43'; 6) 108°. 700. 1) В 1-й; 2) в 3-й
6) 4; в) — 2; г) данное выражение не опре-
706. Когда радиус окружности
в) sin 4°. Указали е. sin 4'’ > О,
sin 4 < 0; r) tg
отрицательными — гыражения в) и г). 709. Положительным являются выраже-
3 tg a — 1 аг — 1
нне а), отрицательными — выражения б), в) и г). 715. —---——. 716.
tg a -J- 2
1 — , tga = -----; 4) sin a =—0,6. tga= 0,75; 5)sina=>
3 17
1 b — a . a2 — 1
cos a , --. 718. cos <p = ———. 719. sin <p = , ==y
/5 b 4- а у a*—2a2 4- 2
717. 2) cos a =
. tga =
2
2
/5
341
cos ® = , =- 729. —. 730. 0,8, если угол ® оканчивается в пер-
* Va“—2а2+ 2 3 т
вой четверти; —0,8, если угол <р оканчивается во второй четверти.
732. 0. 733. 1. 734. — tg 0,5 г: — 0,5463. 742. a) cos 40°; в) cos 0,87. 743. При-
водятся соответственно' синусы, косинусы, тангенсы и котангенсы данных
углов:
1) 0,9257; —0,3783; —2,446; —0,4088; 2) —0,6127; —0,7900; 0,7752;
1,2900; 3) —0,8023; —0,5969; 1,3440; 0,7441; 5) —0,9735; 0,2287; —4,258;
— 0,2348. 747. а) 0,017; в) —0,015. 751. а) 0,9999; в) 0,9999. 764. .
’ |sin а|
765. 2|seca|. 766. tga. 767. 1 768. tga tg 0 (aj=rm, Р^/гл).
( л \ 7
769. cos2 a a — -J-лл . 770. — — . 771. — 1. 772. —16. 780. — l<a< 1,
\ 2 ) 6
Л Л
— 781.
2 2
0,2 ,____
5 /0,21;
/0.21
788. (— I)""11 + лл.
О
a) 195°; 6) — 75°; в) — 1485°. 785. a) 0,4; /0,84;
x 4 3 4 3 л
6) — 7- T: — T: ~T 787- (~ О т + лл.
5 5 3 4 4
n 3
789. — л. 790. — л+блл. 791. —60°+I80°n. 792. 2лл;
---^4- 21гл. 793. Нет корней. 794. -% [— 1 + (— 1)" arcsin -|- лл]. 795, п.
796. Нет корней. 797. — I < о < 1; 0 < 6 < л. 798. 270°. 799. 300°. 800. 30°.
801- —270°. 809. 2л —6. 810. 1. 811. а) Да; б) нет. 812. ± 120° 7 360° л.
л 2 л л „
813. ± — + —пл. 814. — + — л. 815. 30°+360°п. 816. Нет корней. 817. 2п.
1о о Ч
л 1
818. ± — + — + пл. 819. — 390’ + 108071; 510° + 1080°л. 820. Нет корней,
о 2
821. Нет корней. 822. Нет корней. 823.
л . л
827. —оо<а<оо, — — < b < —.
135°. 824. 225°.. 825. 255°. 826. — 75°.
828. — оо<а<оо; 0 < Z> < л.
Рис. 5*
342
12
13’
5
12’
_4
3 ’
838.
1
839. — + л.
4
843.
847.
3
5 ’
4
5 ’
3
12
—; б) — —
5 ' 5
з
834. 2. 835. 2 —я. 836.
4
840. 15° 4 904г. 841.
831. а) — ,
’ 13
5 4
— —; г)— •
12 5
л
"б31"’
7
— —л 4-лл. 844.
12
пл; — — + 2/гл. 848. — + пп.
2 2
я
Нет корней. 845. — 4-
я
корней. 852. ля. 853.
2 '
л
— 4- ля;
4
12
5’
855. (- 1)" ”
о
—10° 4- 18О’/г.
862.
856. /1я; —
866.
я
— 4- 2ля.
2
я
— 4 ля
6
4- ля.
859. Нет корней.
863.
867.
л
2+„я.
arctg /2 4-
л
3
л
873. — 4- пл.
2
— 4- /гл. 877.
6
k я.
870.
я
4
4 12 5
----, в) —--------
3 13 1S
л
—я. 837. —52°30'4-90°п.
<5
842. —4 л.
2
л
55° -j- 60'л.
ля.
849. я -|- 2ля. 850.
— arctg 3 + kn
я
я
846. — -г ля; — 4-йя.
4 2
4- 2ля- 851. Нет
2
854. ± 60° -l 360’л;
-4 2/гл. 857. у4'ш. 858.—40’4180° л:
860. Нет корней- 861. Нет корней,
я
865. 4- пл.
4
ля 869. — 4 ля;
4
864.
ля.
4- ля; arctg 3 4- kn.
Л
875. — + пл; arctg 2
4
„ , л пл
,-1) 12+2‘ 878’
885. х + у 4- 2ля. 892
73° < а < 90°.
2 ’
Нет корней-
я
— 4 2ля; л 4 2/гл.
5
868. — arctg — 4-
л
— 4- ля;
«5
— arctg (2 4- /3 '* 4- пл.
871.
876.
я
— 4-Ля. 872. ля-
я
4
881. 7 корней- 882. 0,47.
24 7 24
895.—, —, если ф оканчивается
25 24 ’
2ля.
24 7 24
ь первой четверти;——, —если ф оканчивается вс втопон четверти.
7 7 24 1 3 „__ 7 24 7 24 7 24
•* й'-й--»-"’—7 — 25 25'
7 24 7 2.4 7 24 7 24 7 2* 5 12 5 12
_ _ _ R99 ... _ 1. — _ _ — _9QQ — — —
24’ 7‘ ‘ 25'25' 24 ’ 7 25’ 25' 24’ 7 13’ 13' 12 5
343
5 12 5 12 3 4 3 4
п----,----------, — ~ . 901. —, —, —, —
. 13 13 12 5 5 5 4 £
3 4 £ <
" 5 ’ “5 “ 4’ ~ 3’
12
902.0 6. 903. —С.6. 901 905. 0,8. 907 См.
5
1
рис. 5*. 908. См. рис. 6*. 911. а) а < —;
С) — 2<а<—. 917. — -. 918.0,9л
4 6
Л Л л
919.2—-. 921. — 4 пл; ±-+1.Я.
2 4 д
922. arctg(— 1 ± / 3) + лл. 923." Нет корней.
л л л
924. ± + 2/1Л. 925, — — 4-пх, 2fcx; — 4-21Л.
X 4 4 2
п л л k
926. — л. 927. + 2пл; — 4- — л. 928, Нет
л * л
корней. 929. — + 2лл < х < — -т 2лл.
Рне 7* 930. л -j 2лл < х < 2л -(-.2/1 л.
ЧИСЛОВЫЕ последовательности
VI
934. а) Да; б) нет; в) да, если а 4 0, при а — 0, |й| < ) данная последова-
тельность бесконечна; при а = 0, (t|> 1 уравнение sin х = ах Ь совсем
2
не имеет корней. 936. Указание. а,,+, — ап = - ---------т---------> 6.
1 " (2л + 3) (2л +1)
938. ad — be > 0. 947. N = 199. 948. N - 24. 949. N -= 100. 950. N = 200.
1 a.
954 ----. 955. 3. 956. 0. 957. — ]. 958. 1. 959. - , если а2 =£ 0; если
2 a2
a2 = 0, a 3j =£ 0, то предел не существует; если а, = а2 = 0, а Ь2 4 0. то пре-
5,
дел равен — и т. д. 961. а) Нет; б) да; г) да при а < 0; нет при а > 0
964. а) ап — 5 — 10 (л — 1); в) ап = 6 + 3 (п — 1). 967. а) Да, б) нет; в) да.
968. — I; 0; 1. 969. Либо а, = 2, d = 3, либо ах = 14, d =—3. 970. Либо
Oj = 2, d = 2, либо а, = 22, d = — 2. 971.247 500. 97В. 156. 975. л- —/л* 2 * 4.
976. 22 м. 977. а) 55; б) 1. 978. 16°. 979. 1, 3, 5......... 980. 100.
981. в) Либо а„ -(— 1)", либо а„ = — 1. 983. 1,-3, 9...... 984. -,
1 1 х101 — 1
— — , -..... 989. г) 2731; д) ---------, если х 4= 1; 101. если
4 8 х— 1
/ 1 \м
х= 1. 990. 100 11 — — ) % 991. 27>. 993. а) —1; б) нет корней. 991. 17,
344
10, 3 или б, 10, 12. 99t> б) —; bj . 997. Если я>0, то при х>0.
4 2
если а < 0, тс пр» х < 0; есл! жеп = С, то данная геометрическая про-рессия
л 3
не будс. vOoinirvuj.eii ни npi каком значении х. 991. а) ба; б; _Е_— а1.
1000. 5 1,
... . 1004. а/ Вообще говори, нет; б) да. 1006. а) 0; I;
(V 5 4- 1 X1* 11/ g i\l‘*
———T.‘.l ; | г г_____I • 6‘ 1; в) 1. Примечание. Последовательност! 0. 0, 0, ...
(1 {а2Я«)(1-а!Л)
мы не относим к геометрическим прогрессиям. 1007. --------——------------ --2п
С“ ( 1 — О*'
1009. какими числами могу г быть лишь равны! числа; и, а, а
А 4- В tr
1012. ап = 2~' ап = А + -(* —А) >014. 1- 3, 5,... н.ш 29, 27.
25, . . 1016. 1 1—3 ил> —3 и 1. 1017; Нет. 1019. См. рис. 7*.
1026. 3, 1,- 1 или 15, — 13. 1021. 5, 15 45. 1022. 12, 16 20, 2Ь.
ОГЛАВЛЕНИЕ I
ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
§ 1. Тождества ............................................................................... 3
§ 2. Уравнения ............................................................................. 6
§ 3. Линейные функции и их графики . - . . 8
§ 4. Линейные уравнении ..................................................................... 12
§ 5. Графический способ решения уравнения тх = п ............................................ 14
§ 6. Уравнения, сводящиеся к линейным ....................................................... 15
§ 7. Уравнения, содержащие неизвестное под знаком абсолютной
величины .............................................................................. 17
§ 8. Метод интервалов ....................................................................... 19
§ 9. Неравенства .......................................................................... 20
§ 10. Основные свойства числовых неравенств . 22
§ 11. Почленное сложение и вычитание неравенств ............................................. 24
§ 12. Почленное умножение неравенств . 26
§ 13. Двойные неравенства . 27
$ 14. Строгие и нестрогие неравенства .... 28
§ 15. Некоторые способы доказательства неравенств . 29
§ 16. Теорема о среднем арифметическом и среднем геометрическом 31
§ 17. Теоремы о постоянной сумме и постоянном произведении . . 31
§ 18. Приближенные значения числа. Свойство абсолютной величи-
ны суммы ......................................................... 35
§ 19. Приближенное сложение и умиожениена число .............................................. 38
§ 20. Эквивалентные неравенства и их свойства ................................................ /О
§ 21. Линейные неравенства ................................................................... 44
§ 22. Графический способ решения неравенства тх > п ..... 46
§ 23. Системы линейных неравенств ............................................................ 47
§ 24. Дробно-линейные функции ................................................................ 49
§ 25. Неравенства, содержащие неизвестное под знаком абсолютной
величины ......................................................... 52
§ 26. Система двух линейных уравнений с двумя неизвестными.
Совместные и несовместные системы ................................ 53
346
§ 27. Определители второго порядка ............................. 56
§ 28. Усл^и..^, ..ри ..„.„ром определитель z-ro порядка равен нулю Ьо
§ 26. Главный и вспомогательный опрело-...>^..и снс.^...^ -;i.цен-
ных уравнений с двумя неизвестными си
§ 30. Правило Крамера ............................................62
§ 31. Случай, когда главный определитель системы уравнений равен
нулю, а хотя бы один ие ь...<.™огательных определителей от-
личен от пуля ................................................. • 6-1
§ 32 Случай, когда .. .лавный и оба вспомогательных определите-
ля системы уравнений равны нулю .................................. 66
§ 33. Таблица основных результатов о системе двух линейных урав-
нений с двумя неизвестными ....................................... 69
§ 34. Графический способ решения систем лннейных уравнений . . 7k
Задачи на повторение ......................................74
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА II
§ 35. Рациональные числа ................................. 77
§ 36. Действия над рациональными числами....................79
§ 37. Геометрическое изображение рацпональныл чисел ........83
§ 38. Десятичная форма запнен рациональных чисел ....... 84
§ 39. Извлечение квадратных корней из рациональных чисел ... 87
§ 40. Соизмеримые и несоизмеримые отрезки ..................90
§ 41. Длина отрезка, несоизмеримого с единицей длины........92
§ 42. Действительные числа .................................94
§ 43. Сравнение действительных чисел ..................... 95
§ 44. Геометрическое изображение действительных чисел ......97
§ 45. Десятичные приближения действительных чисел .........100
§ 46. ’ Сложение действительных чисел .....................103
§ 47. Умножение действительных чисел ......................106
§ 48. Вычитание и деление действительных чисел ............109
Задачи на повторение ................. 112
КВАДРАТНЫЙ ТРЕХЧЛЕН III
§ 49. Выделение из квадратного трехчлена полного квадрата . . .114
§ 50. Квадратные уравнения ..................................115
§ 51. Частные виды квадратных уравнений ... ...........118
347
§ 52. Теорема Виета..................................................120
§ 53. Исследование знаков корней квадратного уравнения по его
коэффициентам ..................................................123
§ 54. Разложение квадратного трехчлена на линейные множители 125
§ 55. Составление квадратного уравнения по заданным корням . . .127
§ 56. Биквадратные уравнения _.............................128
§ 57. График квадратной функции ................*.........................129
§ 58. Примеры построения графика квадратной функции .... 133
§ 59. Характеристические точки параболы ..................................134
§ 60. Экстремальное значение функции у = ах2 -f- Ьх 4- с .... 136
§ 61. Квадратные неравенства..............................................138
§ 62. Примеры решения квадратных неравенств ..............................140
§ 63. Решение некоторых систем уравнений .................................142
§ 64. Графический способ решения некоторых систем уравнений. . 145
§ 6о. Иррациональные уравнения ...........................................146
§ 66. Примеры решения иррациональных уравнений ...........................148
§ 67. Из истории развития алгебры ........................................151
Задачи на повторение ............................................ 152
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ, СТЕПЕННАЯ ФУНКЦИЯ IV
§ 68. Степень с натуральным показателем. Возведение в степень
произведения и частного ........................................155
§ 69. Умножение и деление степеней с одинаковыми основаниями 157
§ 70. Сравнение степеней .......................................159
§ 71. Степени с нулевыми и отрицательными показателями .... 160
§ 72. Свойства степеней с целыми показателями ..................162
§ 73. Функции у = хп при п — 1, 2, 3.......................165
§ 74. Функции у = хп при п = — 1 и п = — 2 ................167
§ 75. Корень л-й степени из действительного числа а .....169
§ 76. Корень п-й степени из положительного числа а ........170
§ 77. Арифметическое значение корня ............................173
§ 78. Корень п-й степени из отрицательного числа—а..............174
§ 79. Извлечение корней из произведения и частного .............176
§ 80. Извлечение корня из степени. Возведение корня в степень.
Извлечение корня из корня ......................................178
§ 81. Вынесение множителя из-под знака корня и введение его под
знак корня .....................................180
§ 82. Умножение и деление корней ...............................182
348
§ 83. Освобождение от радикалов в знаменателе дроби............ . 183
§ 84. Степень положительного числа с положительным дробным по-
казателем .......................................................186
§ 85. Основные свойства степени положительного числа с положи-
тельным дробным показателем .....................................188
§ 86. Степень положительного числа с отрицательным дробным по-
казателем .......................................................190
1
1
§ 87. Функции у = хТ при г — — и г —
• “
88. Общие свойства степенных функций
-............194
3
.............196
Задачи на повторение .................. 198
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ V
§ 89. Понятия вектора и оси .......................................201
§ 90. Проекция вектора на ось .....................................202
§ 91. Свободные и связанные векторы ...............................203
§ 92. Координаты вектора на плоскости..........................204
§ 93. Обобщение понятий угла и дуги............................207
§ 94. Теорема об отношениях координат вектора к его длине .... 209
§ 95. Определение тригонометрических функции угла .........211
§ 96. Тригонометрический круг. Оси тангенсов и котангенсов . . .214
§ 97. Построение угла по заданным значениям его тригонометричес-
ких функций .....................................................217
§ 98. Значения тригонометрических функций некоторых углов . . 219
§ 99. Четность тригонометрических функций .........................221
§ 100- Периодичность функций sin <р и cos ср .......................222
§ 101. Периодичность функций tg ср и ctg ср ........................224
§ 102. О периодических функциях ....................................225
§ 103. Изменение функций sin (р и cos ср............................227
§ 104. Изменение функций tg (р и ctg (р ............................229
§ 105. Таблицы значений тригонометрических функций .................233
§ 106. Использование тригонометрических таблиц для нахождения
острого угла по значениям его тригонометрических функ-
ций ................................................................236
§ 107. Радианное измерение углов и дуг .............................237
§ 108. Тригонометрические функции числового аргумента ..............239
§ 109. Алгебраические соотношения между тригонометрическими
функциями одного и того же аргумента ............................. —
349
§ 110. Нахождение значений тригонометрических функций угла по зна-
чению какой-нибудь одной из них .............241
§111. Формулы приведения ..........................242
$ 112. Определение по таблицам значений тригонометрических функ-
ций любого угла ...................................247
$ 113. График функции у = sin с ...................249
§ 114. График функции у = cosx ....................253
§ 115. Графики функций у = tgx и у = ctgx .........254
§ 116. Доказательство тригонометрических тождеств .257
§ 117. Арксинус числа а ...........................260
§ 118. Уравнение sinx = а .... 263
§ 119. Арккосинус числа а ................... 268
§ 120. Уравнение cosx = а .................. 270
§ 121. Арктангенс и арккотангенс числа а ..........273
§ 122. Уравнения tgx = а и ctgx = а .............. 276
§ 123. Более сложные тригонометрические уравнения .278
$ 124. Однородные уравнения .......................281
$ 125. Графический способ решения тригонометрических уравнений 282
$ 126. Тригонометрические неравенства .............284
Задачи на повторение .................. 285
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ VI
$ 127. Числовые последовательности и способы их задания. Конечные
. и бесконечные последовательности ....................... 289
§ 128. Монотонные последовательности .......................291
§ 129. Ограниченные и неограниченные числовые последовательности 293
§ 130. Предел бесконечной числовой последовательности ......296
$ 131. Примеры .............................................298
§ 132. Сходящиеся и расходящиеся числовые последовательности . 300
§ 133. Монотонные и ограниченные последовательности ........302
' § 134. Число е ........................ 304
§ 135. Переменные величины и их пределы ................305
§ 136. Основные теоремы о пределах .........................307
§ 137. lim при । q | < 1....................................310
п >• о»
§ 138. Что такое длина окружности . ........................311
§ 139. Формула для нахождения длины окружности .............313
§ 140. Нахождение приближенных значений числа л .......... 314
350
§ 141. Площадь круга .....................................315
§ 142. Арифметическая прогрессия.......................317
§ 143. Характеристическое свойство арифметической прогрессии . . 319
§ 144. Сумма членов арифметической прогрессии ............320
§ 145. Геометрическая прогрессия. Формула общего члена геометри-
ческой прогрессии .................................. 322
§ 146. Характеристическое свойство геометрической прогрессии с по-
ложительными членами ......................324
§ 147. Сумма членов геометрической прогрессии .325
§ 148. Сумма бесконечно убывающей геометрической прогрессии . . 327
Задачи на повторение .................. 330
Ответы к упражнениям ................. 333
Евгений Семенович Кочетков
Екатерина Семеновна Кочеткова
АЛГЕБРА
И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
9 класс
Ридом ор Г. С. Уманский
Переплет художника А. С. Котлярова
Художественный редактор В. С Эрденко
Технический редактор В. //. Корнеева
Корректор А. А. Рукосуева
Сдано в набор 23/V 1968 г.
Подписано к печати 29/VIII 1968 г.
60х90*/1б- Бумага тип. № 2. Печ. л. 22.
Уч.-изд. л. 17,11. Тираж 1000 тыс. экз.
Заказ 261.
Издательство «.Просвещение» Комитета
по печати при Совете Министров РСФСР.
Москва, 3-й проезд Марышой рощи. 41.
Саратовский полиграфический комбинат
Росглавполиграфпрома Комитета по пе-
чати при Совете Министров РСФСР.
Саратов, ул. Чернышевского, 59.
Цена без переплета 23 коп. Переплет
бум. 7 коп., бум. ледерин. 12 коп, колен-
кор 15 коп.
<ПРОСВЕЩЕНИЕ>
1969