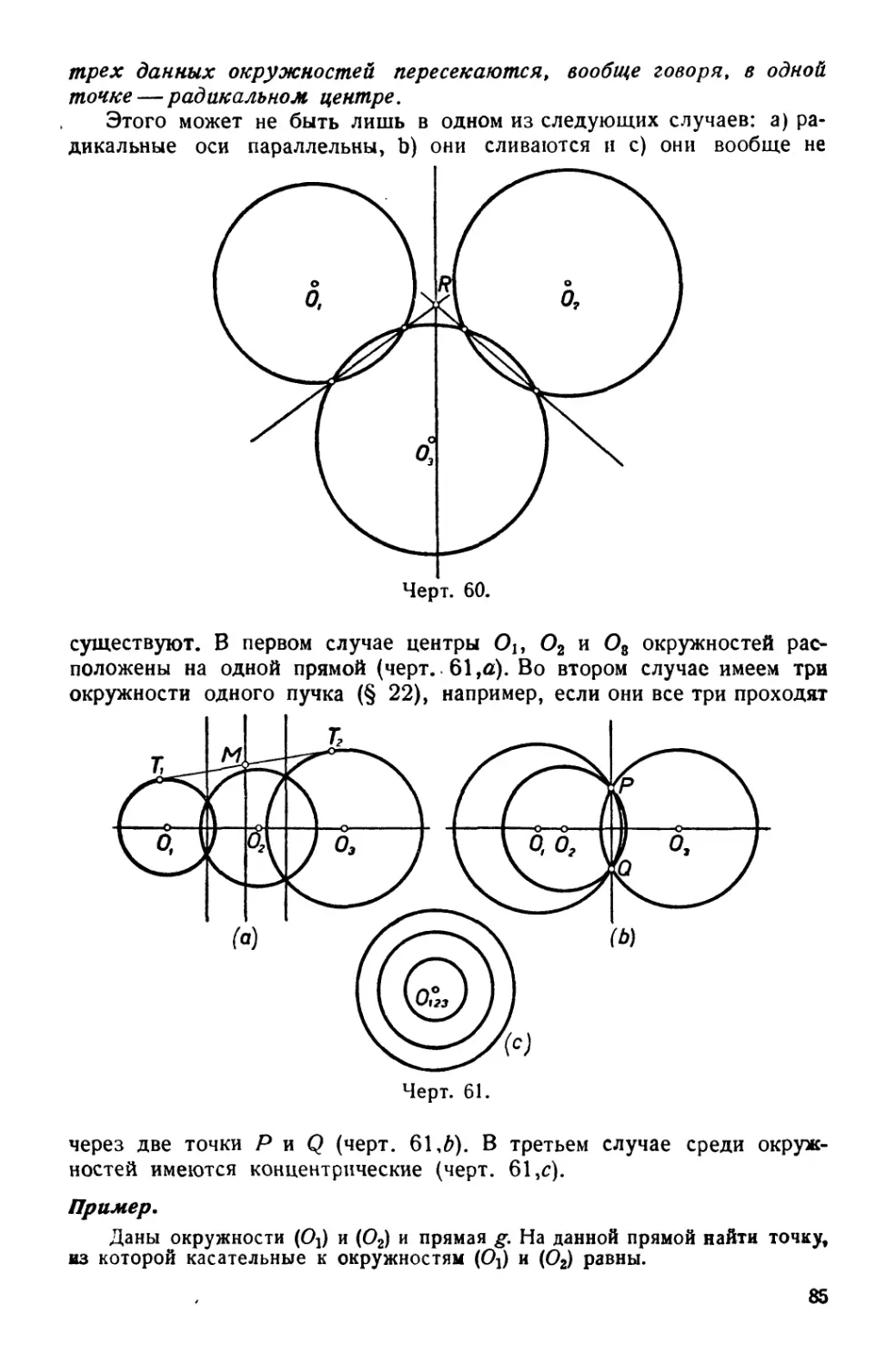
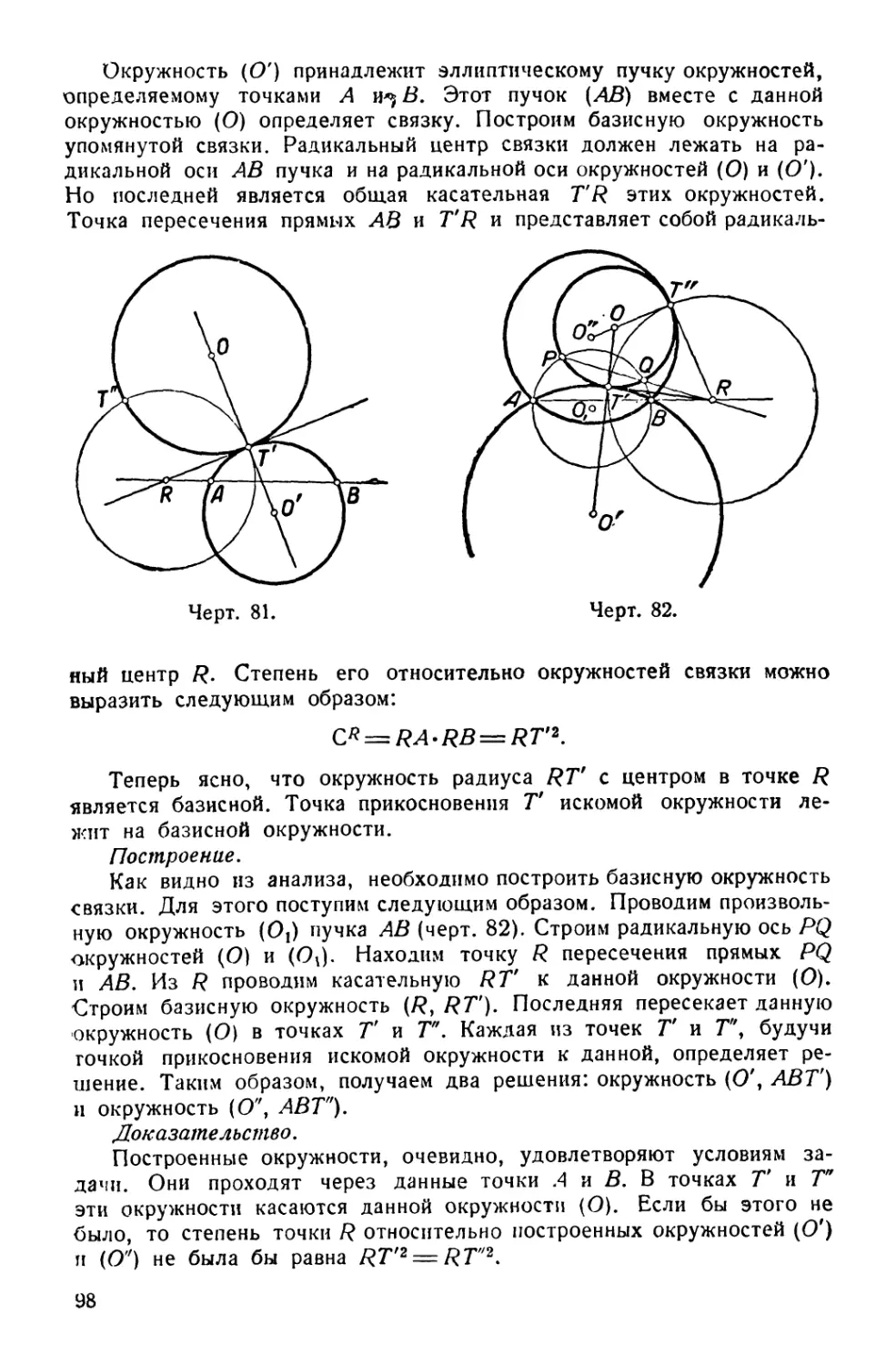
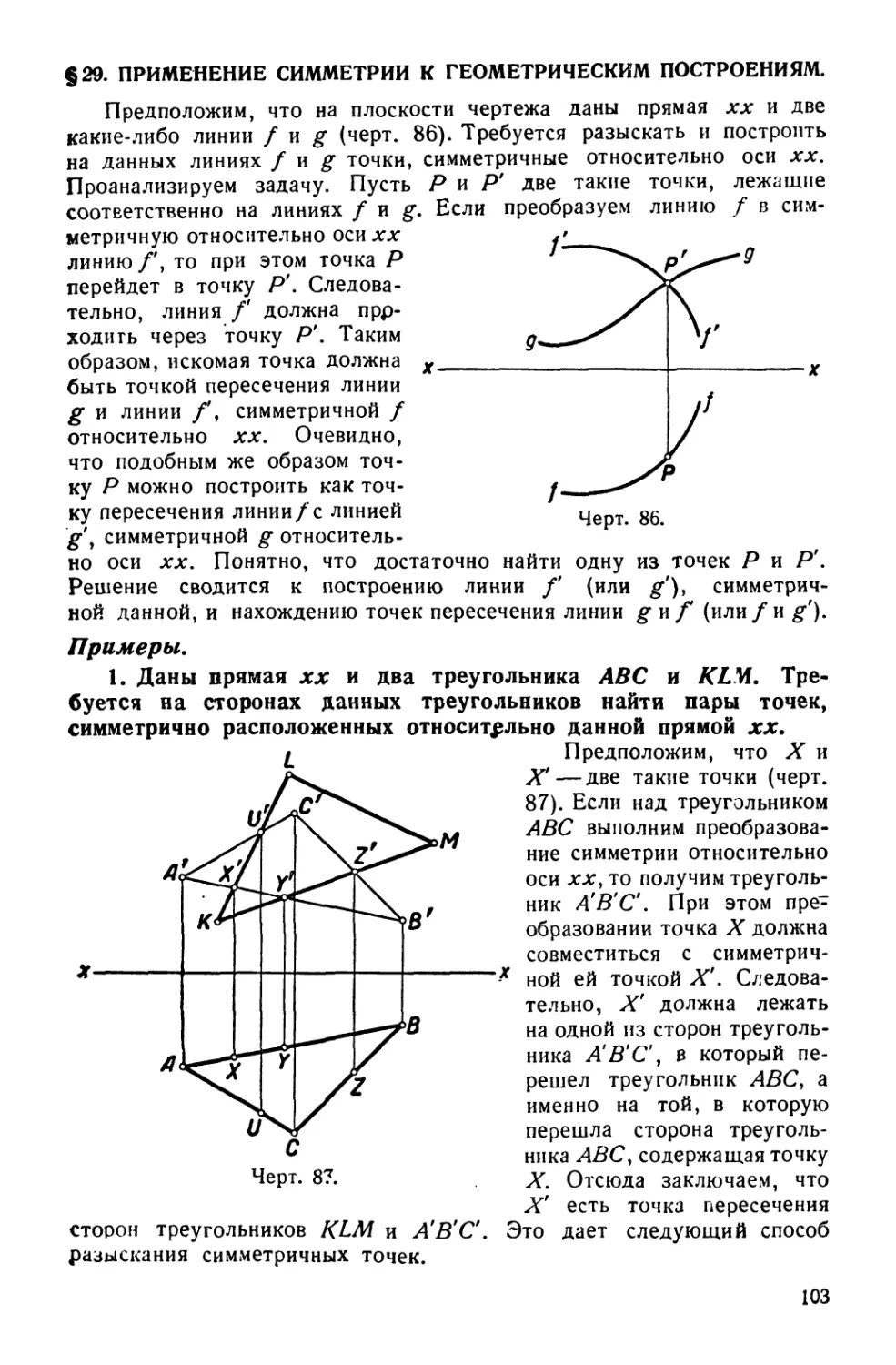
Текст
Ό Ι**
4-52
·· " НИМИ I Ч 9 «
ЕОМЕТ , К
?·*
V ·
чпеВ
t>
г з~ 95
Η. Φ. ЧЕТВЕРУХИН
МЕТОДЫ
ГЕОМЕТРИЧЕСКИХ
ПОСТРОЕНИЙ
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ ПЕДАГОГИЧЕСКИХ ИНСТИТУТОВ.
Утверждено
Министерством просвещения РСФСР
ИЗДАНИЕ 2-е
у4ебно-№:ЙЙго?1Йе&5Ь? Издательство
лшннстврствл просвещении nefcep
Москва 1952
ВВЕДЕНИЕ.
Геометрические задачи на построение являются настолько
существенным фактором математического образования, что на преподавание
этого раздела в средней школе должно быть обращено серьезное
внимание.
Задачи на построение развивают изобретательность, инициативу,
конструктивные способности, столь необходимые будущим строителям
нашей великой Родины.
Значение отдельных моментов решения задачи на построение должно
быть отмечено. Так, в „анализе" учащиеся приучаются к тщательному
изучению задачи, которое должно установить связи и с ко м ы χ
элементов с данными и указать пути решения. Это первый и важнейший
момент решения задачи на построение. Затем выполняется самое
„построение". Учащийся, имея в своем распоряжении заданные элементы
и руководствуясь выводами анализа, должен произвести синтез,
приводящий его к построению искомой фигуры. Следующий этап
решения— „доказательство". Он может показаться излишним, обеспеченным
соответствием построения с данными анализа. Но это не всегда так.
Надо убедиться в том, что найденные необходимые условия являются
достаточными и что построенная фигура удовлетворяет всем
требованиям задачи. Поэтому учащийся приучается давать себе отчет в
логической строгости конструкции, ее соответствии поставленной
задаче.
Наконец, в последней части, завершающей процесс решения,
производится „исследование", т. е. выясняется вопрос об условиях
существования решения, о числе решений и т. п. В задачах более сложных
„исследование" затрагивает иногда настолько тонкие вопросы и требует
такой математической строгости рассуждений, что становится для
учащихся как бы первым опытом, первым подходом к научному изучению
математических проблем.
Уже из этого перечисления основных моментов в процессе решения
конструктивной задачи видно, что мы имеем здесь весьма ценное
орудие математического образования, математического развития учащихся.
Последние находят в задачах на построение разностороннее применение
своих способностей. Кажущаяся простота проблемы только усиливает
интерес к ней и желание найти решение, которое, однако, может
потребовать большого умственного напряжения и изобретательности.
а
Ознакомление учащихся с методами геометрических построений
вооружает их теоретический практически, вносит ясность, ориентирует
в разнообразных вопросах конструктивной геометрии. Однако при этом
необходимо остерегаться механического применения методов
геометрических построений как универсальных рецептов к решению задач. Это
нанесло бы вред, убивая инициативу ученика и приучая его к
пользованию шаблонами. Изучение методов геометрических построений
должно, напротив, усилить творческие возможности учащихся, увеличить
выбор приемов решения, правильно организовать процесс решения
задачи. С этой точки зрения мы и подходим к задачам учителя.
Последний должен владеть теоретической стороной дела, хорошо понимая
вместе с тем практическое значение методов построения.
Первая глава этой небольшой книги, написанной в соответствии
с программой педагогических институтов, посвящена вопросам
обоснования конструктивной геометрии. Преподавателю необходимо
разобраться в этой стороне дела, которая усложняется участием в
геометрических построениях материальных инструментов (линейки, циркуля,
угольника и т. п.). Возникает вопрос: что же такое геометрические
построения — графическое искусство или абстрактная геометрическая
дисциплина? Или, быть может, здесь неизбежно слияние того и другого?
В главе, посвященной этим вопросам, мы постарались показать,
что конструктивная геометрия является частью геометрии как
абстрактной математической дисциплины. В то же время конструктивная
геометрия отражает чертежно-графическую практику. Все чертежные
операции могут быть представлены в абстрактно-геометрической форме.
Таково происхождение этой теоретической дисциплины, обязанной,
в. свою очередь, содействовать разрешению практических проблем.
Вместе с тем мы должны здесь отметить отставание школьных программ
от быстро растущих потребностей жизни (гл. 1. § 7).
Следует иметь в виду, что книга предназначена для учителей и
студентов, уже знакомых с основами высшей математики. Это
позволяет воспользоваться некоторыми обобщающими идеями и попытаться
связать в одно целое разрозненные, многочисленные приемы решения
геометрических задач на построение. В основу нашего изложения
положена идея геометрических преобразований как точечных
преобразований плоскости в себя. Под этим углом зрения рассматривается решение
типичных задач методами симметрии, вращения, параллельного
перенесения, гомотетии и инверсии (гл. V, § 29, 31, 33, 35 и др.). Нам
кажется, что такой подход к задачам на построение вносит некоторую
ясность в пеструю картину методов и приемов решения, предлагаемых
в распространенных задачниках и учебниках. Не следует забывать,
что выбор метода решения задачи на практике нередко оказывается
весьма затруднительным. Установление общих принципов здесь
особенно желательно.
Изложение методов геометрических построений мы заканчиваем
рассмотрением проблемы Аполлония о касающихся окружностях. Для
полного решения этой задачи приходится рассматривать инверсии
с отрицательной степенью и мнимой базисной окружностью, ортого-
4
нальные окружности которой образуют гиперболическую связку.
Считаясь с трудностью такой концепции, трудностью распространения на
нее обычных рассуждений и доказательств, мы предпочли заменить
мнимую окружность действительной, а гиперболическую связку
ортогональных окружностей эллиптической связкой диаметральных
окружностей. Это позволяет провести все построения, основываясь лишь на
действительных элементах плоскости. Заметим кстати, что во всем
изложении мы предполагали, что имеем дело с обыкновенной
эвклидовой плоскостью, чтобы не создавать для учителя затруднений в
применении материала на уроках геометрии в школе. В тех случаях, когда
являлась необходимость рассматривать несобственные элементы
плоскости (например, § 41), сделаны соответствующие оговорки. Самое
выполнение геометрических построений с ними не связано. Таким
образом эти пункты предназначены лишь для учителя.
Несколько слов относительно выбора примеров и задач для
преподавания в школе. Делались попытки дать рекомендуемый список
(см., например, список упражнений, приведенный в статье Брауна
„Математика и физика в школе", № 4, 1936 г.), однако более жела-
телмю, чтобы учитель владел основными методами геометрических
построений настолько, что мог бы производить подбор и даже
самостоятельную композицию несложных примеров и задач. В этом
направлении построен § 17 главы III, в котором показано развитие
задачи с помощью вариации данных, приводящее к различным
геометрическим местам. В заключение отметим необходимость решения в школе
стереометрических задач на построение, столь полезных для развития
пространственного воображения учащихся. В школьных программах
этот момент не получил сколько-нибудь серьезного отражения. В
порядке постановки вопроса мы посвятили ему § 18 главы о
геометрических местах, считая, однако, что приведенный в этом параграфе
материал представляет собой лишь краткое введение в раздел
геометрических построений в пространстве. Включение такого раздела
в школьные программы представляется весьма желательным *).
1) Более подробно этот вопрос рассматривается в статье автора „Вопросы
методологии и методики геометрических построений в школьном курсе
геометрии" („Известия Акад. педаг. наук РСФСР", 1946, вып. VI).
См. также: Н. Ч е τ в е ρ у χ и н, Стереометрические з-адачи на
проекционном чертеже, Учпедгиз, 1952.
Л. М. Л о π о в о к, Сборник стереометрических задач на построение,
Учпедгиз, 1950.
Глава первая.
ОБОСНОВАНИЕ КОНСТРУКТИВНОЙ ГЕОМЕТРИИ
§ 1. ПРАКТИЧЕСКАЯ ГРАФИКА И ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ.
Инженеры и техники в своей практической работе прибегают к
помощи чертежа. При выполнении чертежа они пользуются теми или
другими чертежными инструментами. Наиболее употребительными
инструментами являются линейка, циркуль и угольник. Понятно, что
задачи, которые приходится решать чертежнику, связаны с его
инструментарием. Ему недостаточно убедиться в существовании решения или
даже определить искомые элементы через численные данные. Он
стремится с помощью своих инструментов фактически осуществить на
чертеже построение искомой фигуры. В этом именно и состоит
графическое решение задачи.
Так, пытаясь построить на чертеже отрезок, равный по длине
заданной окружности, чертежник не сможет этого сделать с помощью
своего инструментария. Точно так же он не будет в состоянии
выполнить квадратуру какого-нибудь начерченного круга, т. е. построить
равновеликий ему квадрат. Формулы С—2тгг и £ = тсг2 в этом случае
не помогут ему. Он должен будет признать обе задачи для себя
„неразрешимыми". Ограничивая свой инструментарий линейкой и
циркулем, чертежник вообще не будет в состоянии решить какую-либо
задачу степени выше второй]).
Так, задача об удвоении куба, приводящаяся к кубическому
уравнению χ3 — 2απ = 0, будет ему недоступна. Это означает, что с
помощью своих инструментов (линейки и циркуля) он не сможет построить
на чертеже отрезок, длина которого выражалась бы формулой:
x=za У^
где через а обозначена длина ребра данного куба. Еще меньше
возможностей окажется у чертежника, если в качестве чертежного
инструмента он будет применять лишь одну линейку. Он должен будет
отказаться от проведения параллелей или перпендикуляров, не будет
в состоянии разделить данный отрезок пополам. Лишь те задачи
первой степени, решение которых сводится к проектированиям и
пересечениям (так называемые „визуальные" задачи), будут ему доступны.
!) .Степенью' задачи на построение называют степень уравнения, к
которому приводится решение задачи в аналитической форме.
6
Все это с достаточной ясностью показывает, что самая постановка
задач, возможность их решения, существенно зависит от состава
инструментария, который может быть использован чертежником для
выполнения построений. Так обстоит дело в чертежной практике. Но
абстрактная математика является отображением материальной
действительности. Поэтому вполне естественно, что математическая теория
геометрических построений (конструктивная геометрия) должна
отражать свойства и особенности графической практики.
Наша задача заключается в том, чтобы выразить сущность
конструктивной геометрии в терминах абстрактной математики.
Тогда геометрические построения становятся одной из глав геометрии.
То своеобразное, что отличает конструктивную геометрию,
заключается в том, что не всякая задача, решенная математически, является
задачей, решенной „конструктивно"; что не всякая точка, прямая или
какая-нибудь геометрическая фигура, математически вполне
определенная, может быть „построена". Поэтому, рассматривая точки, прямые,
окружности и другие фигуры обыкновенной эвклидовой геометрии на
плоскости мы должны указать, какие из них являются „построенными44
или какие из них „могут быть построены". Условимся теперь же
называть все такие элементы конструктивными 1). Мы уже видели, что
вопрос о „конструктивности" геометрических элементов зависит от
средств построения (инструментария). Будем считать, что речь идет о
построениях, выполняемых линейкой и циркулем. В тех случаях, когда
для геометрических построений привлекаются другие инструменты
(двухсторонняя линейка, прямой или острый угол, угольник), будут сделаны
необходимые дополнительные исследования.
Итак, постараемся обосновать конструктивную геометрию, при
условии, что построения выполняются линейкой и циркулем.
§ 2. ОПРЕДЕЛЕНИЕ „КОНСТРУКТИВНЫХ" ЭЛЕМЕНТОВ.
Элементами геометрических построений на плоскости служат точки,
прямые, окружности и другие фигуры обыкновенной эвклидовой
геометрии. Некоторые из этих элементов являются „построенными* на
чертеже. Таковы, например, данные элементы во всякой задаче на
построение. Другие элементы могут быть „построены" из данных
с помощью конечного числа операций линейкой и циркулем. Наконец,
третьи элементы не поддаются построению, сколько бы операций
линейкой и циркулем ни было произведено. Они, следовательно, не обладают
свойством „конструктивности". Все остальные элементы являются
„конструктивными". Таким образом, каждая задача на построение
разбивает точки плоскости на два класса: класс К, состоящий из
„конструктивных" точек, и класс Λ/, содержащий все остальные точки плоскости.
Аналогичным образом разобьются на два класса все прямые и все
окружности плоскости. Наша задача теперь заключается в том, чтобы
1) В следующем параграфе содержание этого термина будет точно опре-
7
точно установить, какие элементы должны быть отнесены к классу
„конструктивных". Это достигается с помощью следующих
определений:
Считаются (или называются) „конструктивными*-.
1. Все данные в условии задачи на построение геометрические
образы (точки, прямые, окружности...).
2. Прямая, если она определена двумя „конструктивными*
точками,
3. Окружность, если она определена „конструктивным*
центром и „конструктивным* радиусом (пара „конструктивных" точек).
4. Точка, если она является точкой пересечения двух
„конструктивных"' линии.
Приведенные здесь четыре определения отображают в абстрактной
форме практические построения линейкой и циркулем. Проанализируем
каждое из них в отдельности.
Первое определение устанавливает существование
„конструктивных" элементов, без которых не могут быть применены линейка и
циркуль. Это определение относит к классу „конструктивных" все
элементы, „заданные" в условии задачи на построение. Таким образом,
„данные" конструктивной задачи должны быть выражены в такой
форме, чтобы к ним могли быть применены операции линейкой и
циркулем. Так как каждая геометрическая фигура может быть задана
некоторой совокупностью точек, то мы будем предполагать, что
„данные* каждой задачи на построение выражаются в форме
некоторой совокупности построенных на чертеже точек. Ниже будет
рассмотрен вопрос относительно возможности иного выражения условий
задачи на построение. Пока же нам важно отметить, что как только
задача на построение формулирована, все „данные", согласно
определению 1, входят в класс „конструктивных" точек, который не является,
таким образом, пустым, и геометрические построения могу г быть
произведены.
Второе определение устанавливает „конструктивность* прямой,
определенной с помощью двух „конструктивных" точек (например,
„данных"). На практике „построение" прямой, когда „построены" две
ее точки, выполняется линейкой. Поэтому можно сказать, что
определение второе выражает в абстрактной форме свойство лшнейки.
Это — абстрактное определение „линейки".
Третье определение, подобно предыдущему, выражает свойство
циркуля в абстрактной форме. Можно поэтому назвать его
абстрактным определением „циркуля".
Четвертое (и последнее) определение устанавливает образование
новых „конструктивных" элементов из имеющихся с помощью
применения линейки и циркуля, т. е. через определения 2 и 3.
Это определение устанавливает, что новые „конструктивные" точки
можно получить как точки пересечения „конструктивных" линий.
Перечисленные определения дают нам все, что нужно для
выполнения геометрических построений. В самом деле, согласно первому
определению, в каждой задаче на построение мы имеем некоторую совокуп-
8
ность „конструктивных" точек („данные"). Второе и третье определения
дают возможность образования „конструктивных" прямых и
окружностей (применение линейки и циркуля). Наконец, четвертое определение
открывает возможность получить новые „конструктивные* точки. Таким
образом, геометрические построения в этой абстрактной форме
развиваются аналогично практическим построениям чертежника.
Следовательно, мы можем построить абстрактную математическую теорию,
отображающую практику и опыт материальной действительности.
§ 3. ОБРАЗОВАНИЕ КЛАССА К „КОНСТРУКТИВНЫХ" ТОЧЕК.
В этом параграфе мы рассмотрим на простейшем примере
фактическое образование класса К на основе определений „конструктивных"
элементов, данных в § 2.
Задана на построение.
Дан отрезок АВ (даны концы А и В отрезка). Требуется
построить середину отрезка — точку М.
На чертеже имеем две данные точки А и В (черт. 1), которые
принадлежат к классу К (определение 1). Будем называть их точками
нулевой категории. Совокупность точек нулевой категории обозначим
буквой К0. Она состоит из двух данных точек А и В. Вообще
совокупность точек нулевой категории образует „данные" точки (около
них на чертеже 1 стоит цифра 0).
Прямая АВ „конструктивна" (определение 2), „конструктивны"
также две окружности с центрами в точках А и В и радиусом АВ
(определение 3). Все эти
линии мы будем называть
линиями нулевой
категории. Следовательно, мы
имеем 1 прямую и 2
окружности нулевой
категории.
Точки пересечения
этих линий являются
„конструктивными"
(определение 4). Мы будем их
называть точками первой
категории. Совокупность
точек первой категории
обозначим буквой Кх. Таких точек 4 (около них на чертеже 1
поставлена цифра /). Далее мы имеем: 9 прямых и 22 окружности первой
категории. Это все те линии, которые определяются точками нулевой
и первой категорий, за исключением тех из линий, которые вошли в
нулевую категорию. Все эти линии „конструктивны44 (определения 2 и 3).
Точки пересечения линий первой категории между собой, а также
с линиями нулевой категории „конструктивны" (определение 4),
Совокупность таких точек, за исключением вошедших в нулевую и первую
категории, обозначим буквой К2. Это точки второй категории. Среди
9
них находится и искомая точка Μ (середина отрезка АВ), которая
является точкой пересечения прямой CD первой категории с прямой АВ
нулевой категории. Если бы мы продолжали рассуждения, аналогичные
приведенным выше, то получили бы „конструктивные" элементы (точки,
прямые и окружности) третьей, четвертой, .. . , вообще, п-й
категории. Очевидно, что категории образуют бесконечную
последовательность. Но в каждой из них имеется лишь конечное число элементов.
Будем говорить, в частности, о „конструктивных" точках. Каждая
такая точка должна принадлежать к одной из совокупностей /Q так
как, если бы она не была точкой какой-либо определенной категории
/, то ее нельзя было бы построить с помощью конечного числа
операций линейкой и циркулем. Таким образом
а:=а:0+к1+*2+. ··+*„ + ··· >
т. е. класс „конструктивных* точек образуется „суммированием"
точек всех категорий.
Мы определили состав класса К и теперь можем сказать, что
если точка является „конструктивной", то она принадлежит к классу
К. Точка, не принадлежащая классу /С, „неконструктивна".
Уже из того, что было сказано во введении, ясно, что не всякая
точка плоскости „конструктивна". Так, например, имея на чертеже
прямую с координатными пометками 0 и 1, мы относим точки 0 и 1
к классу К (как „данные"), но на той же прямой имеется точка
с пометкой |/ 2, которая не входит в класс /С, так как ее
невозможно построить линейкой и циркулем при конечном числе операций !).
Отсюда приходим к следующему выводу относительно
разрешимости задачи на построение:
Если искомая точка (точки) принадлежит к классу К, то задача
разрешима линейкой и циркулем при конечном числе операций.
В противном случае задача неразрешима.
Так, например, рассмотренная нами задача о построении середины
отрезка разрешима линейкой и циркулем. Искомая точка Му как мы
видели, является „конструктивной" точкой второй категории;
следовательно, она входит в К2 и в класс /С.
Решить задачу на построение — значит указать порядок
последовательного применения определений 1 —4, приводящий к включению
искомых элементов в класс К („конструктивных").
§ 4. О „ДАННЫХ" И „ПРОИЗВОЛЬНЫХ" ЭЛЕМЕНТАХ.
Как видно из определений 2 и 3 (§ 2), для образования новых
„конструктивных" прямых или окружностей необходимо иметь не
менее двух „конструктивных" точек. С другой стороны, как это
видно из рассмотренного в § 3 примера (построение середины
данного отрезка АВ), имея две „конструктивные" („данные") точки,
!) См. об этом Адлер, Теория геометрических построений, 1940, § 36,
стр. 141.
10
можем построить сколько угодно новых „конструктивных" элементов.
При том предположении, которое было сделано в § 2 относительно
„данных" элементов задачи („данные" выражены совокупностью
точек), мы всегда будем иметь несколько (не менее двух)
„конструктивных" точек и, следовательно, можем построить сколько угодно
точек. Благодаря этому обеспечены все условия для выполнения
построения.
В этом параграфе мы рассмотрим иные условия и иные формы
выражения данных, также соответствующие практике чертежного дела.
Если мы не будем придерживаться требования, чтобы все
„данные" были выражены с помощью точек, то среди „данных"
элементов может оказаться не более одной точки. Но тогда мы не имеем
возможности получить новые „конструктивные" элементы, как это
видно из определений 2, 3 и 4 § 2. Следовательно, в этих
условиях построение невозможно, пока система определений § 2 не будет
дополнена новыми определениями. Вот примеры таких задач на
построение (черт. 2):
1) Дана прямая и точка на ней. Требуется в данной точке
построить перпендикуляр к данной прямой.
2) Дана прямая и точка вне ее. Требуется из данной точки
опустить перпендикуляр на данную прямую.
|) : С l) "~~Xf
А
2) а А)
Черт. 2.
3) Даны две пересекающиеся прямые. Разделить пополам угол,
образованный ими.
4) Дана окружность. Построить ее центр.
В самом деле, в первых двух из этих задач на чертеже имеется
лишь одна „конструктивная44 точка. Применение определений 1—4
§ 2 не дает возможностей получить еще хотя бы одну
„конструктивную" точку или линию. Следовательно, при этих условиях
построение невозможно. В задаче 3) в числе данных нет ни одной
„конструктивной" точки. Применение определений 1 и 4 дает одну
„конструктивную" точку (точка пересечения двух данных прямых).
Но дальнейшее развитие построения невозможно по той же причине,
что и в предшествующих случаях. Наконец, в последней задаче
„конструктивных" точек нет в числе „данных" и применение
определений 1—4 не вносит ничего нового, так что решение задачи
О
11
при этих условиях невозможно. Однако, как мы хорошо знаем из
чертежной практики, такие задачи рассматриваются и легко
выполняются линейкой и циркулем, если воспользоваться для построения
произвольными точками на чертеже. Так, в задаче 1) из центра А
описывается окружность „произвольного" радиуса, пересекающая
прямую а в точках Ρ и Q, после чего решение задачи становится
аналогичным построению, рассмотренному в § 3.
Таким образом, для решения задачи была построена окружность
„произвольного" радиуса, что сводится к пользованию произ*воль-
ными точками нашего чертежа как „конструктивными". Для
определения радиуса нужно иметь две такие точки. Вообще для применения
определений 2 — 4 необходимо, как уже было сказано, не менее
двух конструктивных точек; следовательно, понадобится использовать
две „произвольные" точки, как „конструктивные", если среди
„данных" нет ни одной „конструктивной" точки и они не могут быть
получены через определение 4. Именно так обстоит дело в задаче
4), в то время как в задачах 1), 2) и 3) достаточно применить по
одной „произвольной" точке как „конструктивной".
Все это показывает, что система определений 1—4 является
недостаточной и должна быть дополнена, если на „данные" не
наложены ограничительные условия, как это было сделано в § 2 и 3.
Новое определение, очевидно, должно вводить „произвольные"
точки плоскости как „конструктивные".
Оно может быть формулировано следующим образом:
5. „Данные* в задаче на построение могут быть пополнены
„произвольными" точками плоскости, которые поэтому
считаются „конструктивными".
В случае геометрических построений линейкой и циркулем можно
ограничиться применением „произвольных" точек „конструктивной"
линии. В самом деле, две такие точки позволяют в этом случае
построить сколько угодно новых „конструктивных" точек, как это
видно из построения, рассмотренного в § 3.
Напомним еще раз, что при условии § 2, т. е. когда „данными"
являются исключительно точки, необходимость в определении 5
отпадает.
§ 5. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ С ПОМОЩЬЮ ДВУХСТОРОННЕЙ
ЛИНЕЙКИ.
В предшествующих параграфах мы развивали
абстрактно-геометрическое учение о построениях с помощью линейки и циркуля, причем
чертежные свойства этих инструментов были фиксированы
определениями 2 и 3. Естественно, что система наших определений должна
быть перестроена, если будет условлено, что построения
выполняются с помощью других инструментов. При этом соответствующие
определения должны точно отображать чертежные свойства этих
инструментов, т. е. должны выполняться абстрактные операции,
аналогичные построениям практической графики.
12
Предположим, что единственным инструментом, с помощью
которого выполняются построения, является двухсторонняя линейка.
В чертежной практике и не бывает, как известно, других линеек.
Однако свойство „двусторонности" линейки не отражено в
определении 2 (§ 2), которое соответствует применению лишь одного края
линейки. Для большей ясности мы рассмотрим здесь решение двух
задач: деление пополам угла и отрезка с помощью двухсторонней
линейки.
1) Угол, образованный двумя данными прямыми а и /?,
требуется разделить пополам.
Построение с помощью двухсторонней линейки особенно просто.
Прикладываем линейку к прямой а (черт. 3) и проводим по другому
краю линейки прямую
а'1). Затем
прикладываем линейку к прямой
Ь и также строим
прямую Ь''. Точка
пересечения Μ прямых а' и Ь'
принадлежит искомой
биссектрисе, которую
строим по точкам Sn M.
2) Отрезок АВ
(даны точки А и В)
требуется разделить
пополам (черт. 4).
Прикладываем линейку так, чтобы один ее край проходил через
точку А, а другой через точку В. По первому краю проводим
прямую ау а по второму Ь. Затем
перекладываем линейку в положение,
Черт. 3.
Черт. 4.
симметричное относительно прямой, и чертим прямые а' и Ь'. Точки
пересечения С (прямых а и Ь') и D (прямых b и а') определяют
прямую CD. Последняя делит отрезок АВ пополам в точке М.
1) Буквой „δβ обозначена ширина линейки.
13
Примечание.
Построение возможно при условии: /Ш> 5, где через Ь обозначено
расстояние между краями линейки (ширина линейки).
В случае АВ^с, строим прямую, параллельную прямой АВУ и делим
пополам расположенный па ней произвольный отрезок А'В'. Пусть М'—
середина этого отрезка, а С — точка пересечения прямых А'В и В'А. Тогда
прямая М'С пересекает прямую АВ в искомой середине Μ (черт. 5).
В двух рассмотренных пострбениях были применены операции,
характерные для построений с помощью двухсторонней линейки. Эти
операции заключаются в следующем.
а) Проведение прямой по одному краю линейки.
б) Прикладывание одного края линейки к начерченной прямой
и проведение новой прямой по второму краю.
в) Прикладывание линейки своими двумя краями к двум
начерченным точкам так, чтобы каждый край линейки проходил
через одну точку.
Последняя операция была применена в рассмотренной выше
задаче о делении отрезка пополам.
Из чертежа 4 видно, что такое прикладывание возможно лишь
двумя способами. Линейка в этих двух способах расположена
симметрично относительно прямой АВ. Угол наклона ψ линейки определяется
длиной отрезка АВ:
sincp = -^.
Все перечисленные операции должны найти свое абстрактное
выражение в системе определений „конструктивных" элементов.
Новая система определений (взамен 1 —4, § 2) будет иметь
следующий вид.
Определения 1 и 2 должны быть, очевидно, сохранены, равно
как и определение 4. Эти определения сохраняют свое значение для
построений с помощью двухсторонней линейки. В частности,
определение 2 сохраняет за последней свойство односторонней линейки
[операция а)].
Определение 3 выражает свойство циркуля, поэтому оно
необходимо лишь в том случае, если, кроме двухсторонней линейки,
применяется и циркуль, чего мы, как уже было сказано, не предполагаем.
Взамен него система должна быть дополнена двумя следующими
определениями, соответствующими операциям б) и в).
б*) Прямая, параллельная „конструктивной* прямой а
отстоящая от нее на расстоянии δ (δ = constj, считается
„конструктивной". Константа δ соотЕегствует ширине двухсторонней линейки.
в*) Если имеются две „конструктивные" точки А и В, причем
АВ^>$, то две пары параллельных прямых, отстоящих одна от
другой на расстоянии δ и проходящих соответственно через А и В,
считаются „конструктивными".
Таким образом, три операции а), б) и в), которые могут быть
осуществлены с помощью двухсторонней линейки, фиксированы
соответствующими определениями 2, б*) и в*). Благодаря этому иост-
14
роения с помощью двухсторонней линейки могут быть проведены
в абстрактно-геометрической форме, т. е. они составляют часть
содержания конструктивной геометрии.
Упражнения.
С помощью двухсторонней линейки выполнить следующие построения:
1. Удвоить данный угол.
2. Восставить перпендикуляр к данной прямой в данной на ней точке.
§ 6. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ С ПОМОЩЬЮ „ПРЯМОГО*
ИЛИ „ОСТРОГО УГЛА" И „УГОЛЬНИКА".
В этом параграфе мы ставим своей целью охарактеризовать
построения, производимые с помощью „прямого" или „острого угла",
а также с помощью „угольника".
Предположим, что чертежным инструментом является „прямой
угол" 1).
Рассмотрим прежде всего несколько примеров чертежных
операций, выполняемых с помощью „прямого угла".
1. Отрезок АВ разделить пополам.
Прикладывая одну сторону „прямого угла" к линии АВ и
заставляя вторую сторону проходить один раз через А, а второй
через Ву вычерчиваем
перпендикуляры к прямой в точках А и В
(черт. 6). Затем проводим
произвольный перпендикуляр CD к прямой АС
(параллель к АВ). Получаем
прямоугольник ABCD. Строим его диаго- /f^
нали. Через точку Ε пересечения диагоналей строим перпендикуляр
к АВ, который пересекает эту прямую в искомой точке
Μ—середине отрезка.
2. Удвоение отрезка.
Предположим, что данный отрезок АВ (черт. 7) требуется
удвоить, т. е. на прямой АВ построить отрезок ВС = АВ. Через точку А
1) Последний надо представлять себе как две односторонние линейки,
закрепленные под прямым углом. Таким образом, этот инструмент не имеет
треугольной формы, как чертежный „угольник".
15
проводим произвольную прямую а и строим перпендикуляр AD к ней.
В точке В строим перпендикуляр к АВ, пересекающий прямую а
в точке Е, а прямую AD в точке D. В точках Ε и D строим
перпендикуляры соответственно к прямым а и AD. Обозначим точку их
пересечения буквой F. Строим перпендикуляр FC b прямой АВ.
Нетрудно убедиться, что отрезок ВС = АВ. В самом деле, эти отрезки
являются проекциями двух равных и параллельных отрезков АЕ и DF:
AE#DF.
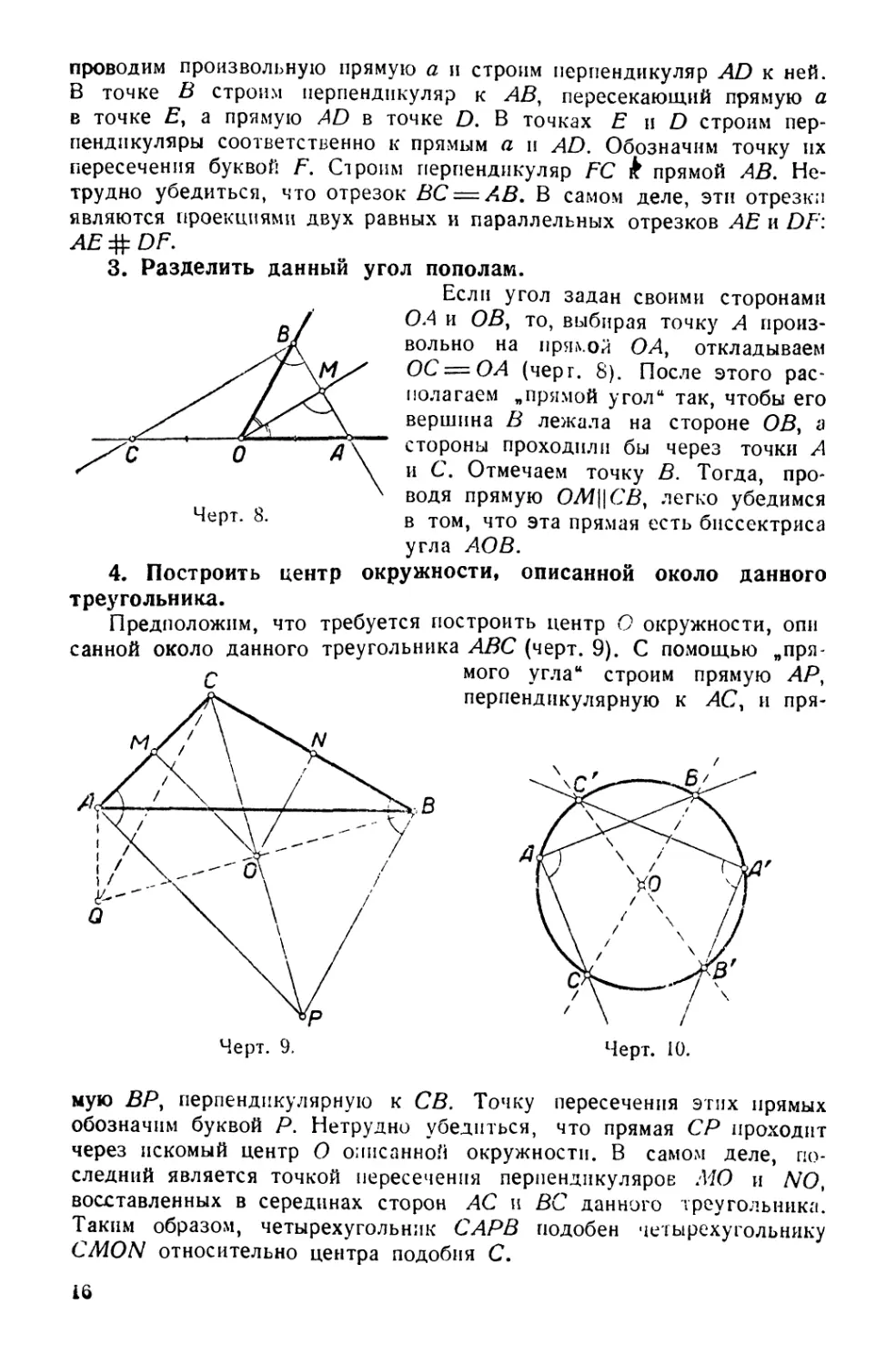
3. Разделить данный угол пополам.
Если угол задан своими сторонами
ОЛ и ОВ, то, выбирая точку А
произвольно на прямой ОАу откладываем
ОС = ОА (черг. 8). После этого
располагаем „прямой угол" так, чтобы его
вершина В лежала на стороне ОД а
стороны проходили бы через точки А
и С. Отмечаем точку В. Тогда,
проводя прямую ОМ\\СВ, легко убедимся
в том, что эта прямая есть биссектриса
угла АОВ.
4. Построить центр окружности, описанной около данного
треугольника.
Предположим, что требуется построить центр О окружности, опи
санной около данного треугольника ABC (черт. 9). С помощью
„прямого угла" строим прямую АР,
перпендикулярную к АС, и пря-
Черт. 8.
Черт. 9.
Черт. 10.
мую ВР, перпендикулярную к СВ. Точку пересечения этих прямых
обозначим буквой Р. Нетрудно убедиться, что прямая СР проходит
через искомый центр О описанной окружности. В самом деле,
последний является точкой пересечения перпендикуляров МО и Л/О,
восставленных в серединах сторон АС и ВС данного треугольника.
Таким образом, четырехугольник САРВ подобен четырехугольнику
CMON относительно центра подобия С.
16
Но это и означает, что точка Р, подобно-соответственная точке О,
лежит на прямой СО (см. о гомотетии, § 34). При этом
СР_СА __СВ _
CO~CM~CN~ '
Таков коэффициент подобия рассматриваемых
четырехугольников.
Ясно, что если будет выполнено построение, аналогичное
построению точки Я, для другой стороны треугольника, например, для
стороны АС, то получим точку Q, причем прямая BQ должна проходить
через центр О. Следовательно, искомый центр О найдется как точка
пересечения прямых СР и BQ.
б. Построить центр данной окружности (черт. 10). На чертеже
„данные" состоят только из окружности. Поэтому применение
произвольных элементов здесь необходимо (§ 4). Помещая вершину
„прямого угла" в произвольную точку А данной окружности,
отмечаем точки В и С пересечения сторон „прямого угла" с
окружностью. Прямая ВС является диаметром окружности. Повторяя
построение для точки А'у получим новый диаметр В'С окружности.
Центр О является точкой пересечения прямых ВС и В'С
Мы ограничимся приведенными примерами, так как
характеристические свойства „прямого угла" как чертежного инструмента уже
достаточно выяснены. Эти свойства могут быть фиксированы
следующими тремя определениями:
а) Определением 2 системы 1—4 (§ 2), сохраняющим за
„прямым углом" свойство односторонней линейки.
б) Прямая, проходящая через „конструктивную* точку и
перпендикулярная к „конструктивной* прямой, считается
„конструктивной*.
в) Точка „конструктивной" линии, из которой две другие
„конструктивные" точки видны под прямым углом, считается
„ конструктивнойu.
Определение б) выражает операцию построения перпендикуляра
при помощи „прямого угла", которой мы преимущественно
пользовались во всех разобранных примерах. Определение в) соответствует
другой более редкой операции „прямого угла". Эта операция
составляет существенную часть примера 3) — п разделить данный угол
пополам*.
Таким образом, построения с помощью „прямого угла"
изображаются системой определений а), б) и в), к которым должны быть
присоединены определение 1 § 2, а также определение 5 § 4 о
произвольных элементах.
Уже те примеры, которые были рассмотрены в настоящем
параграфе, показывают, что применение „прямого угла" как чертежного
инструмента вполне целесообразно. Этот вывод может быть
подкреплен многими построениями, в которых с большим успехом прибе-
ха^т к помощи „прямого угла".
17
Если вместо „прямого угла" в качестве чертежного инструмента
будет применен „острый угол", т. е. система двух односторонних
линеек, образующих постоянный угол φ (0 <^φ <^90°)*), то операции
с помощью этого инструмента вполне аналогичны операциям
„прямого угла".
Мы ограничимся двумя примерами.
1. Удвоение угла.
Пусть данный угол с вершиной О (черт, 11) образован прямыми
а н Ъ. В произвольной точке В стороны Ъ угла прикладываем наш
инструмент—„острый угол" (φ), как
показано на чертеже. Сторона ВА угла φ
определит на прямой а точку А. Теперь
прикладываем угол φ так, чтобы одна
из его сторон проходила через точку Л,
а другая совпадала бы с прямой Ь2).
Тогда вершина угла φ определит на
прямой b точку В'. Теперь снова
прикладываем угол φ к стороне Ьу помещая
его вершину один раз в точке В и
другой раз в точке В'. При этом вторая
сторона определяет нам прямые ВС и
В'СУ пересекающиеся в точке С. Как легко видеть из чертежа 11,
фигура АВСВ' есть ромб. Следовательно, прямая ОС является
искомой, так как имеем: ^тВОС = /^ВОА.
2. От данной точки А' данной прямой а отложить на ней
данный отрезок АВ (черт. 12).
В построении неоднократно применяется проведение прямой,
параллельной данной и проходящей через данную точку, что легко
выполняется параллельным передвижением „острого угла", причем
одна из его сторон скользит сама по себе. Пользуясь этим приемом,
строим прямую A'B'V параллельную данной прямой АВ. Далее
соединяем А и А' и проводим через В прямую BB'V параллельную АА'.
Получаем параллелограм АВВ\А!'. Следовательно, А'В'1 = АВ.
Теперь с помощью „острого угла" строим ромб со стороной
А'В'1 = А'С и углом 2φ при вершине А' совершенно так же, как
это было сделано в предыдущем примере. Наконец, применяем наш
„острый угол" так, чтобы стороны его проходили через точки С и
Β'ν а вершина лежала на прямой а. Положение вершины В'
определит нам второй конец искомого отрезка А'В' (второе положение Я',
очевидно, соответствует откладыванию отрезка в противоположном
направлении). В самом деле, если опишем из А' окружность радиуса
A,C = A'B,l=zABy то последняя должна пройти через точки В' и В".
!) Достаточно ограничиться рассмотрением „острого угла", так как тот
•же инструмент дает и тупой угол, смежный с острым.
2) Читатель заметит, что эта операция вполне аналогична проведению
через данную точку перпендикуляра к данной прямой с помощью „прямого
угла".
18
Это видно из того, что вписанные углы, опирающиеся на дугу СВ'Х
упомянутой окружности, должны равняться острому углу φ, так как
дуге СВ[ соответствует центральный угол СА'В[ = 2ъ.
Заметим, что операция „острым углом", произведенная для
нахождения точек В' и В", вполне аналогична операции и
определению я), рассмотренному ранее для „прямого углаи. Мы можем
теперь установить, какие определения соответствуют операциям при
построениях с помощью „острого угла". Эти определения следующие:
А
Черт. 12.
а!) Определение 2 системы 1 —4 (§ 2), сохраняющее за
„острым углом" свойство односторонней линейки.
б') Прямая, проходящая через „конструктивную" точку и
пересекающая „конструктивную" прямую под углом φ, считается
„ конструктивной".
в') Точка „конструктивной" линии, из которой две другие
„конструктивные" точки видны под углом φ, считается
„конструктивной".
Таким образом, система определений для „острого угла" как
чертежного инструмента аналогична системе определений,
характеризующих „прямой угол". Поэтому можно было бы рассматривать
систему определений а'), б') и в') как общий случай инструмента,
который является „произвольным углом φ". Если φ = 90°, то
наш инструмент — „прямой угол". Если <р<^90°, то это „острый
угол".
Практическим инструментом чертежника является обыкновенно не
„угол", образованный двумя линейками, а „угольник", имеющий
форму треугольника. Этот инструмент образован тремя
(односторонними) линейками и имеет, следовательно, три угла. Употребляются
„угольники" преимущественно двух видов: 1) с одним углом в 90°
и двумя равными острыми углами (по 45°), 2) с тремя различными
углами в 90°, ϋϋ° π 30°.
Если мы будем рассматривать „угольник" как абстрактный
математический инструмент, то его нетрудно заменить соответствующими
19
определениями. В самом деле, „угольник" объединяет в себе
свойства „прямого угла*1 и двух „острых углов". Поэтому операциям
с помощью „угольника" соответствуют определения а'), б') и в'), в
которых угол φ имеет значения 90° и 45° (для угольников первого
вида), или 90°, 60° и 30° (для угольников второго вида).
§ 7. О ТЕОРЕТИЧЕСКОМ И ПРАКТИЧЕСКОМ ЗНАЧЕНИЯХ
ИНСТРУМЕНТОВ ПОСТРОЕНИЯ.
Необходимо внести ясность в этот вопрос, так как опыт
показывает, что и среди преподавателей математики и среди
преподавателей черчения имеется много ошибочных представлений, происходящих
от смешения теоретических и практических требований. Благодаря
этому в школах в области геометрических построений продолжает
сохраняться рутина, противоречащая развитию техники и
практической графики.
Прежде всего часто думают, что геометрические построения
линейкой и циркулем являются „строгими" в теоретическом отношение
и могут поэтому войти в школьный курс геометрии, но что этого
нельзя сказать о других чертежных инструментах, которые „пригодны
лишь для практических целей чертежников".
Из того обоснования геометрических построений, которое было
развито в предыдущих параграфах, с достаточной ясностью видно,
что каждый инструмент (линейка, циркуль, прямой или острый угол,
угольник) может быть охарактеризован рядом свойственных этому
инструменту операций. Последние в свою очередь могут быть
выражены в абстрактно-геометрической форме системой определений,
которые позволяют абстрактно осуществлять геометрические построения
обыкновенной эвклидовой геометрии. Таким образом, геометрические
построения, выполняющиеся с помощью любого из этих
инструментов, становятся частью абстрактной математической науки. Поэтому
не только построения линейкой и циркулем, но и построения с
помощью других инструментов могут быть с одинаковым правом
включены в учебный курс геометрии. С этой точки зрения ни один из
инструментов не имеет преимуществ перед другим. Независимо от
того, какие именно операции будут узаконены соответствующими
определениями, наши построения будут вполне строгими.
Говоря о построении с помощью прямого угла, Адлер!)
подчеркивает, что это построение будет отнюдь не приближенным, „ибо
при идеальном совершенстве2) употребленного инструмента точка X
получалась бы вполне точно".
„Правда,— говорит он,— прямой угол необходимо некоторое время
передвигать, пока он не придет в надлежащее положение; но это
обстоятельство отнюдь не делает нашего построения приближенным,
ибо и при соединений двух точек прямою приходится некоторое
!) Адлер, Теория геометрических построений, Л., 1940, § 22, стр. 94.
2) Это „идеальное совершенство" достигается заменой практических
инструментов соответствующими им абстрактными определениями.
20
время передвигать линейку, пока она не примет надлежащего
положения" .
Различие в геометрических построениях, выполняемых с помощью
тех или иных „инструментов" (в абстрактной форме „определений"),
заключается, следовательно, не в „строгости" их теоретического
обоснования, а в самих построениях, доступных одним „инструментам44
и недоступных другим.
За основу сравнения инструментов в этом отношении лучше всего
избрать „циркуль". С помощью этого инструмента может быть
решена всякая задача на построение второй степени1) и не может
быть решена задача более высокой степени, не сводимая к
квадратным уравнениям. Ту же область построений получаем, применяя
в качестве инструментов линейку и циркуль. Следовательно,
включение линейки в „инструментарий" построений, присоединение ее
к циркулю не дает никакого расширения „области построений".
Короче говоря, все построения, выполнимые циркулем и линейкой,
могут быть произведены и одним циркулем. Это положение было
известно еще итальянскому геометру Маскерони (Mascheroni),
который обосновал его в своей классической работе „La geometria del
Compasso" (1797 г.).
Область построений, выполняемых применением одной линейки
(односторонней), оказывается значительно более узкой, чем
упомянутая выше. Поэтому возникает вопрос о том минимуме применений
циркуля в геометрических построениях с односторонней линейкой,
который обеспечивал бы решение всякой задачи на построение
второй степени. Полное решение этого вопроса было дано в
классическом труде немецкого геометра Якоба Штейнера (Jakob Steiner),
опубликованном в 1833 г.2).
Штейнер показал, что всякая задача на построение второй
степени может быть решена одной линейкой, если в плоскости
чертежа построен один произвольный круг и его центр.
Таким образом, построения с помощью линейки будут обладать
конструктивной силой, необходимой для решения любой задачи второй
степени, при однократном употреблении циркуля.
Так был полностью выяснен теоретический вопрос о
сравнительной конструктивной силе двух классических инструментов: линейки и
у циркуля.
Что же касается других инструментов, то аналогичный вопрос
был решен Адлером. В сочинении, напечатанном в 1890 г. в
„Ученых записках Венской академии", Адлер показал, что каждая задача
на построение второй степени может быть решена с помощью
двусторонней линейки или с помощью прямого или острого угла, а
следовательно, и угольника.
1) А д л е р, Теория геометрических построений. Л, 1940, § 20, стр. 88. См.
сноску на стр. 6.
2) Имеется в переводе на русский язык: Якоб Штейнер,
Геометрические построения, выполняемые с помощью прямой линии и неподвижного
круга, Учпедгиз, М., 1939.
21
Отсюда ясно, что для решения всякой задача на построение
второй степени достаточно одного аз следующих инструментов:
циркуль, двухсторонняя линейка, прямой или острый угол, угольник.
Комбинируя те или другие из этих инструментов, можно составить
инструментарий, достаточный для решения задач более высоких
степеней. Так, Адлером в упомянутой выше работе было доказано, что
каждая задача на построение третьей и четвертой степени
может быть решена с помощью двух
прямых углов.
В последнее время Н. А. Никулин
(Симферополь) доказал, что каждая
задача на построение третьей и
четвертой степени может быть решена с
помощью циркуля и произвольного угла
(в частности прямого угла). При этом
достаточно иметь циркуль постоянного
раствора („диск", как его называет
автор).
Н. А. Никулин показал также, что
задачи на построение третьей и
четвертой степени могут быть решены при
помощи произвольного угла и
двухсторонней линейки *).
Черт. 13. Интересно отметить, что для
выполнения построений при этом была
„узаконена" следующая операция с помощью прямого или
произвольного угла. Предположим, что на чертеже имеются точка Л,
прямая а и окружность К (черт. 13). Прямой угол располагают таким
образом, чтобы его вершина находилась на данной прямой а, одна
из его сторон проходила через точку Л, а вторая касалась бы
окружности К. Обозначим такую операцию буквой (W). Эту операцию
можно рассматривать как обобщение операции Ь) предыдущего
параграфа. В самом деле, если данная окружность вырождается в точку В,
то упомянутая операция (V7) обращается в операцию Ь) прямого угла.
Мы покажем здесь, как выполняется, например, трисекция угла
(задача третьей степени) с помощью операции (W).
Трисекция угла с помощью циркуля и прямого угла (черт. 14).
Пусть угол |5, образованный прямыми ВС и ВХ, требуется
разделить на три равные части. Тогда из произвольной точки С стороны
угла описываем окружность радиусом СВ. Далее на продолжении
стороны ВС откладываем ВА = ВС. Теперь применяем операцию (У7),
*) Н. А. Никулин, Геометрические построения с помощью
простейших инструментов, Симферополь, 1947. См. также: „Известия Крымск. педаг.
ин-та", т. XVI, 1950.
В своих работах о геометрических построениях Н. А. Никулин
доказал, что каждая задача на построение пятой и шестой степени может быть
решена с помощью циркуля, двух прямых углов и постоянного конического
сечения.
22
располагая прямой угол так, чтобы его вершина X лежала на данной
стороне угла ВХ, одна из сторон проходила через точку Л, а вторая
сторона касалась бы построенной окружности. Соединяя точку каса-
3
ния Τ с вершиной В, получаем /'СВТ=а = -тг .
о
Доказательство весьма просто. Пусть прямая BD _]_ АУ, тогда
имеем:
СТ\\ВО\\АХ,
так как все эти прямые перпендикулярны к касательной XT. Следо-
вательно, TD = DX, так как —— = —-= 1.
DX ВА
Таким образом, прямая BD является биссектрисой равнобедренного
треугольника ТВХ. Отсюда имеем:
/_XBD = /_TBD.
С другой стороны, при параллельных BD и СТ имеем накрестлежащие
углы:
^/TBD = Z.BTCy
а последний равен ^/ ТВС, так как треугольник ВСТ равнобедренный.
Следовательно, имеем:
^/XBD = Z.TBD = Z.TBC = a=:
β
(что и требовалось доказать).
Интересно отметить, что, принимая операцию (W), мы вместе
с тем признаем законность построения касательной к окружности
простым прикладывани- χ
ем линейки. В самом деле, X/
такое „прикладывание"
является одним из
элементов операции (1*?).
Между тем, более всего
приходится слышать
возражений против такого
„упрощенного"
построения касательной, которое
называют „нестрогим" и
„неточным". Ясно, что
здесь происходит
смешение теоретической и
практической строгости или
точности построений. С
теоретической стороны
все приведенные выше построения и составляющие их операции могут
быть обоснованы в одинаковой степени строго. Показать это и было
основной целью настоящей главы.
Черт. 14.
23
Таким образом, предпочтение одного „инструмента" другому с
теоретической точки зрения может быть оправдано лишь большей
„конструктивной" силой этого инструмента. Если же речь идет о задаче,
которая разрешается как одним, так и другим инструментом, то
теоретически безразлично, каким инструментом произвести построение.
Мы хотим подчеркнуть поэтому, что именно с теоретической стороны,
с точки зрения абстрактной науки, нет никаких оснований
отказываться от применения таких инструментов, как угольник или
двухсторонняя линейка, вместе с присущими им операциями.
Что же касается практической стороны вопроса, то здесь имеется
очень много моментов, способных склонить чертежника к
предпочтению того или другого инструмента, или той или иной операции.
Здесь могут быть приняты во внимание и сравнительная простота
операции, и ее более легкая (практически) выполнимость, и точность
получаемых построений, и время, затрачиваемое на операцию,
и т. д.
В конце концов эти вопросы решаются опытом, и опыт
показывает, что линейка, циркуль а угольник являются наиболее
необходимыми и полезными инструментами чертежников. В частности,
задачу на построение общей касательной к двум кривым практики
почти всегда решают простым прикладыванием линейки. Получаемая
при этом точность построения оказывается для них вполне
достаточной. Во всяком случае вопрос о выборе тех или иных конструктивных
операций находится в зависимости от практических требований,
предъявляемых к построению. Все это показывает, что традиционный
взгляд на геометрические построения как на построения с помощью
линейки и циркуля (и только этих инструментов!) является
необоснованным ни с теоретической, ни с практической стороны. В
особенности неправильно держаться этой явно устаревшей и отставшей от
жизни „ложноклассической" традиции в школе. Между тем она
продолжает сохраняться во многих учебниках; так, например, в своем
курсе элементарной геометрии известный французский математик
Адамар *) пишет: „Под геометрическими построениями понимают
построения, производимые при помощи линейки и циркуля" (гл. V, § 83).
Несомненно, что классическое направление древних греков, оказавшее
такое огромное влияние на школу (классические гимназии!), сказалось
и в этом вопросе. Но в наше время оно идет вразрез со всей
практикой, и не имеет никаких оправданий. Просто здесь имеет место
некоторая инерция, против которой не ведется борьбы. Между тем
не только в инженерно-технических кругах сознается несоответствие
традиционных построений с практической графикой, но и такой
„теоретик" геометрических построений, как Адлер, пишет следующее:
„циркуль, линейка, прямой и острый угол являются обычными
чертежными инструментами каждого чертежника" 2). Таким образом,
!) Ж. Адамар, Элементарная геометрия, ч. 1, Учпедгиз, М., 1948.
2) Адлер, Теория геометрических построений, Л., 1940, §25,
стр. 103.
24
вопрос о школьном курсе геометрических построений требует
пересмотра. Необходимо, „чтобы теоретическая работа не только поспевала
за практической, но и опережала ее, вооружая наших практиков в их
борьбе за победу социализма44 (Сталин).
§ 8. СХЕМА РЕШЕНИЯ ЗАДАЧИ НА ПОСТРОЕНИЕ.
Первый вопрос, который возникает по отношению к каждой
задаче на построение еще до ее решения, заключается в следующем:
определяют ли те данные, которые имеются в условиях задачи,
искомые элементы, представляющие собой предмет нашего
построения?
Не может ли случиться, что для определения искомых элементов
данных недостаточно, или, наоборот, что требований, выставленных
в условиях задачи, слишком много, так что им невозможно
удовлетворить. Легко видеть, что все три случая возможны. Рассмотрим
хотя бы следующий пример. Построить треугольник по данной
стороне а и противолежащэму углу Л.
Мы имеем только два данных, что недостаточно для построения
определенного треугольника. Для этого необходимо, как известно,
иметь три данных. Поэтому задача имеет бесчисленное множество
решений, которыми являются все треугольники с данным основанием а
и вершиной Л, лежащей в любой точке дуги сегмента, построенного
на основании а и вмещающего угол А (ср. гл. III, § 12, стр. 45).
Таким образом в этом случае задача является неопределенной.
Если в число данных формулированной выше задачи включим еще
одну из сторон искомого треугольника, например, сторону Ь, то
задача станет определенной и искомый треугольник легко может быть
построен. Для этого достаточно из вершины С данного основания
описать окружность радиусом, равным стороне Ь. Точка пересечения
этой окружности с дугой сегмента, вмещающего угол Л, определит
положение третьей вершины искомого треугольника.
Предположим, наконец, что к данным присоединена еще одна
сторона (с) искомого треугольника. В таком случае, как иногда
говорят, задача станет переопределенной, так как три стороны сами по
себе уже определяют треугольник и угол А не может быть задан
произвольно. Поэтому, вообще говоря, невозможно удовлетворить
требованию, чтобы три стороны и угол треугольника имели заданные
величины.
Задачи на построение, как правило, принадлежат ко второму типу,
т. е. к задачам определенным. Лишь те задачи, в которых искомым
является некоторое геометрическое место, принадлежат к первому
типу, т. е. к задачам неопределенным.
В задаче на построение обыкновенно требуется построить какую-
нибудь фигуру, например, многоугольник. Предположим, что искомую
фигуру определяют η точек (например, η вершин многоугольника).
Выясним, сколькими условиями определяется такая фигура, независимо
от ее положения на плоскости.
25
Выделим две какие-либо из η точек и проведем через них ось
координат. Тогда одну из выделенных точек можно принять за начало
координат, а положение второй точки определится одним условием—
координатой этой точки. Проведя вторую ось координат, например,
перпендикулярно к первой, отнесем к построенной системе координат
все остальные (п — 2) точки фигуры. Каждая из них определяется
двумя условиями—своими координатами в установленной системе.
Таким образом, для определения фигуры имеем следующее число
условий:
(п — 2)2+1=2л — 3.
Так, для определения треугольника (п = 3) необходимо задать: 2·3—
— 3 = 3 условия. Для четырехугольника (/г = 4): 2 · 4 — 3 = 5 условий.
Аналогичным образом для определения фигуры (системы η точек)
в пространстве проведем через какие-либо три точки этой фигуры
плоскость координат. На этой плоскости мы выберем две координатные
оси таким образом, чтобы одна из выделенных трех точек стала
началом координат, а вторая оказалась на одной из осей. Проведя третью
ось под произвольным углом к плоскости, установим систему
координатных осей в пространстве. К этой системе отнесем все остальные
точки, которые определяются тремя условиями (своими координатами)
каждая. Для определения же первоначально выделенных трех точек
требуется, как мы знаем, три условия. Таким образом, для
определения нашей фигуры (независимо от ее положения в пространстве)
требуется
(п — 3)3-f 3 = 3/г — 6 условий.
Так, для определения тетраэдра (/г = 4) требуется
3-4 — 6 = 6 условий, например, 6 его ребер.
Перейдем теперь к схеме решения задачи на построение. Схема
эта состоит из четырех основных моментов:
1) анализ задачи,
2) построение,
3) доказательство,
4) исследование.
Анализ задачи на построение является важнейшим моментом
приведенной схемы, так как именно он дает ключ к решению задачи.
Исходным пунктом анализа является искомая фигура (неизвестное).
Цель анализа состоит в установлении связей искомых элементов
фигуры с данными. При этом иногда искомая фигура должна быть
дополнена таким образом, чтобы дополненная фигура или ее части
могли быть построены по данным задачи, после чего может быть
построена и сама искомая фигура.
Несомненно, что главная трудность задачи на построение
заключается именно в анализе задачи; поэтому основное внимание педагога
должно быть направлено к тому, чтобы научить учащихся
производить анализ задачи. В конце настоящего параграфа будут даны
примеры, содержащие некоторые характерные случаи анализа.
26
После того как с помощью анализа установлены связи искомых
элементов с данными, производится построение.
Далее следует доказательство, что построенные элементы
удовлетворяют условиям задачи. Наконец, нужно произвести еще
исследование найденного решения. В этом пункте схемы предполагается
выяснить, каким условиям должны удовлетворять данные, чтобы
решение действительно существовало, и будет ли задача иметь одно
или несколько решений.
Мы поясним процесс решения задачи на построение следующими
примерами.
Примеры.
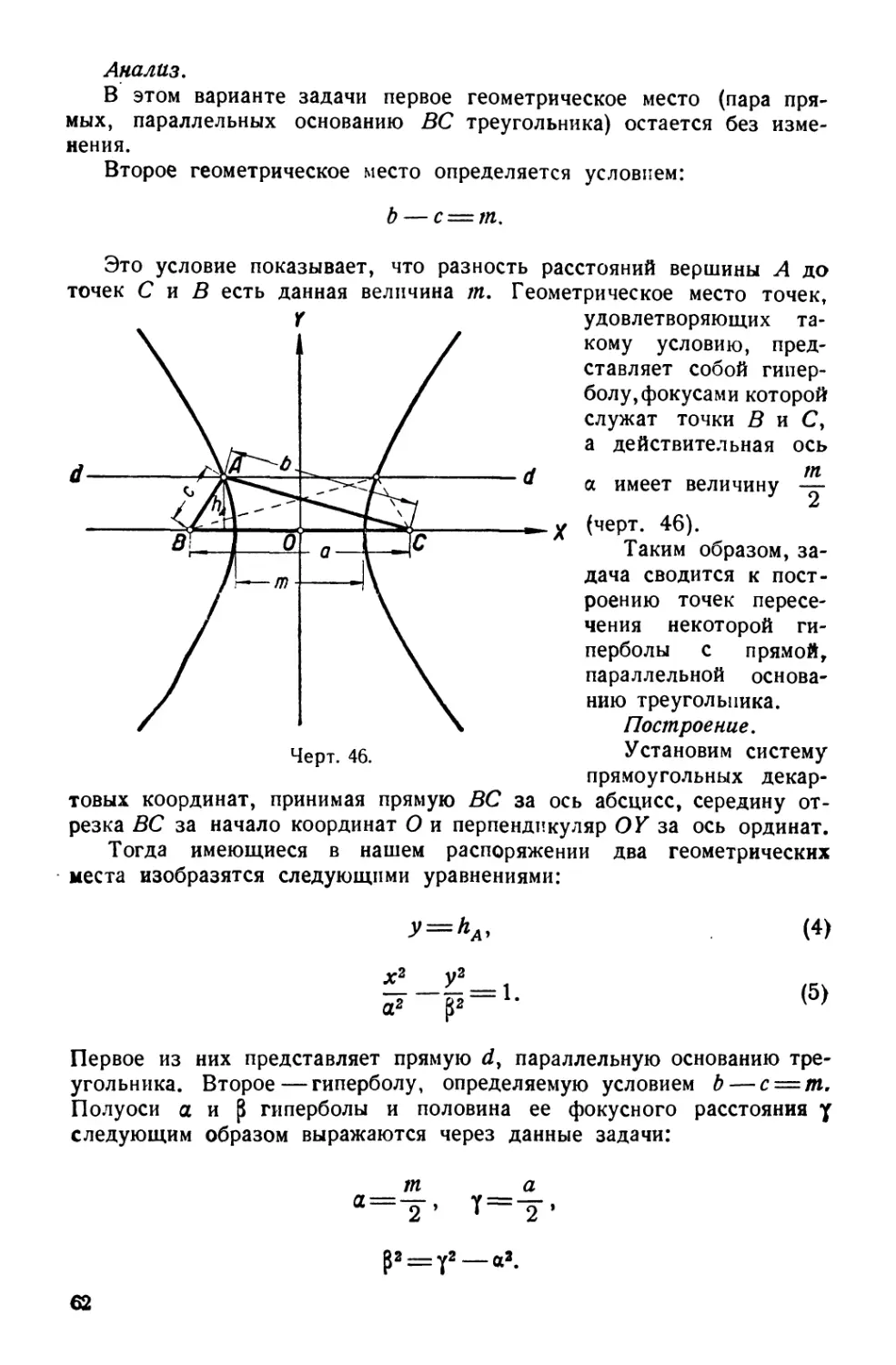
1. По данным сумме и разности двух отрезков построить эти
отрезки.
Данными в этом примере служат отрезки ρ и q (черт. 15),
изображающие сумму и разность искомых отрезков χ и у.
г
Г'1
Г
«в
-~ГПв-у Ί
Υ м м V ^
р -
ч ——*
Черт. 15.
Черт. 16.
Таким образом, имеем: ~*~ >
• 1)
Анализ задачи в этом случае сводится к следующим
рассуждениям. Из формул (1) путем сложения и вычитания получаем:
Р + Я
2 '
2
<2)
Предположим, что искомые отрезки χ и у изображены на чертеже 16
отрезками АВ и ВС. Следовательно,
АВ-\- ВС= АС = χ -χ-у =р.
Откладывая отрезок ВС=у влево от точки В, получим D, причем
. AD = AB — DB = x — y — q,
DC = AC — AD = p — q.
Написанные выше формулы показывают, что
27
Аналогично можно было бы отложить от точки В отрезок АВ = х
вправо и получить точку Е. Тогда будем иметь:
CE=BE — BC = x—y = qy
AE=AC-{-CE = p-{-q.
Первая из формул (2) дает:
_ p + q AE
= АВ.
Эти формулы и устанавливают связь искомых элементов с данными.
Для построения искомых отрезков достаточно проделать
следующие операции (черт. 16).
(1-й способ). Строим: DC = AC—AD = p — q.
Делим отрезок DC пополам. Получаем точку В.
Тогда ВС=у> АВ = х.
(2-й способ). Строим: АЕ = AC -\-CE = p-\-q.
Делим отрезок АЕ пополам. Получаем точку В.
Тогда АВ = х, ВС=у.
Доказательство заключается в показе того, что построенные
отрезки удовлетворяют условиям задачи.
В самом деле:
х-\-у = АВ-\-ВС = АС = ру
x—y = AB — BC=AB — DB=AD = q.
Исследование показывает, что решение возможно в том, и только
в том случае, если
так как сумма любых двух отрезков всегда больше их разности. При
этом задача имеет одно решение, так как по данным ρ и q отрезки
χ и у определяются однозначно.
Если рассмотрим граничный случай, т. е. p = q> то получим:
х 2 — 2 —р'
у = Р^- = Р-=1р = 0.
У 2 2
Следовательно, в этом случае один отрезок равен заданному (р),
а второй обращается в точку.
2. Даны окружность и точка вне ее. Из данной точки
требуется провести такую секущую к окружности, чтобы ее внешняя
часть равнялась внутренней.
28
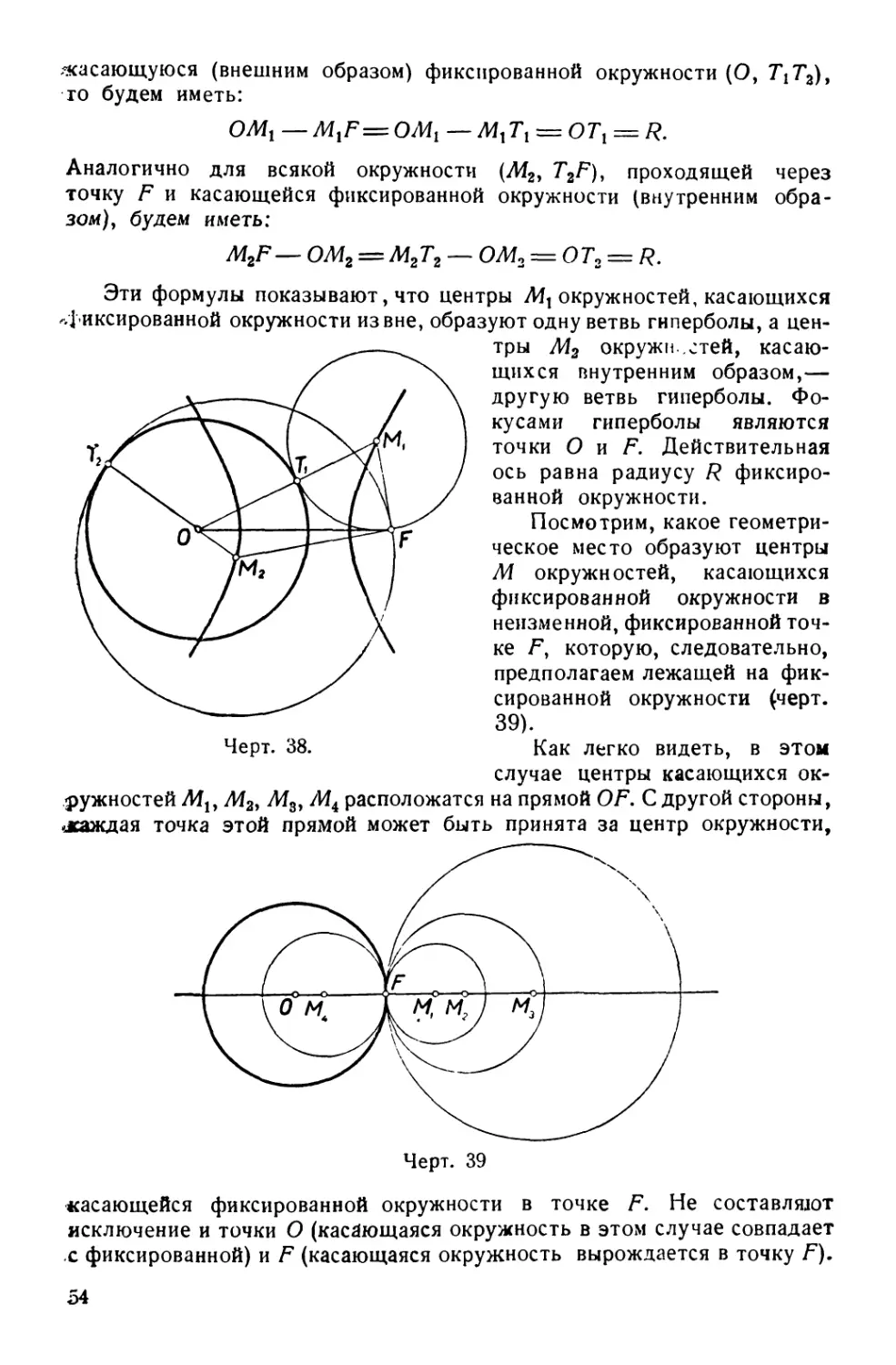
Анализ.
Пусть (черт. 17) имеем окружность (О, АВ) и точку 5 вне ее.
Предположим далее, что прямая SMN и есть искомая секущая. Это
значит, что SM=MN.
Обозначим точки пересечения с окружностью той секущей,
которая проходит через центр ее, буквами А и В. Далее обозначим
отрезки:
SM = xt SA = a.
Радиус окружности ОВ = г.
Тогда будем иметь (по свойству секущей):
SM-SN = SA-SB%
или
2х2 = а(а-\-2г),
откуда получаем:
* = Т/у(* + 2г). (3)
Такова связь искомого с данными.
Она приводит к следующему построению.
Как видно из формулы /V
(3), отрезок SM=x можно
построить как среднее гео-
а
метрическое отрезков — и
а-\-2г. Так как последние
легко получить изданных, то
построение отрезка SM=x
не представляет
затруднений. После чего, описывая
из точки S окружность
радиуса SM, определяем на Черт. 17.
данной окружности точку Λί,
а вместе с тем и направление секущей SMN.
Доказательство.
Предположим, что построение выполнено. Тогда имеем:
SM=x=]fj(a + 2r).
Докажем, что MN=SM.
Обозначим пока хорду MN буквой у.
По теореме о секущей будем иметь:
SM-SN=SA-SB,
или
x(x+y) = a(a-{-2r)t
29
откуда
* ία
= j/|-(a + 2r> = .r.
Таким образом, требуемое доказано.
Исследование.
Так как 5уИ^5Л, то х^я.
Следовательно,
или
Таково необходимое и достаточное условие существования
решения.
Из чертежа непосредственно видно, что при а<^2г> SA<^AB.
Вращая секущую около точки Sy мы увеличиваем внешнюю часть ее,
SM, и уменьшаем внутреннюю, MN. Это изменение происходит
непрерывно, пока секущая не обратится в касательную, причем хорда
MN обращается в нуль. Поэтому при некотором положении секущей
будем иметь равенство: ^ι
SM = SN. ~ Д/М
Решений будет два, так как возможны две симметрично
расположенные секущие.
Если я = 2г, то центральная секущая SAB и дает решение.
В этом случае оно единственное.
Наконец, при а^>2г решение, очевидно, невозможно, так как при
вращении секущей часть SM растет, а часть MN убывает, и
равенство их не может иметь места.
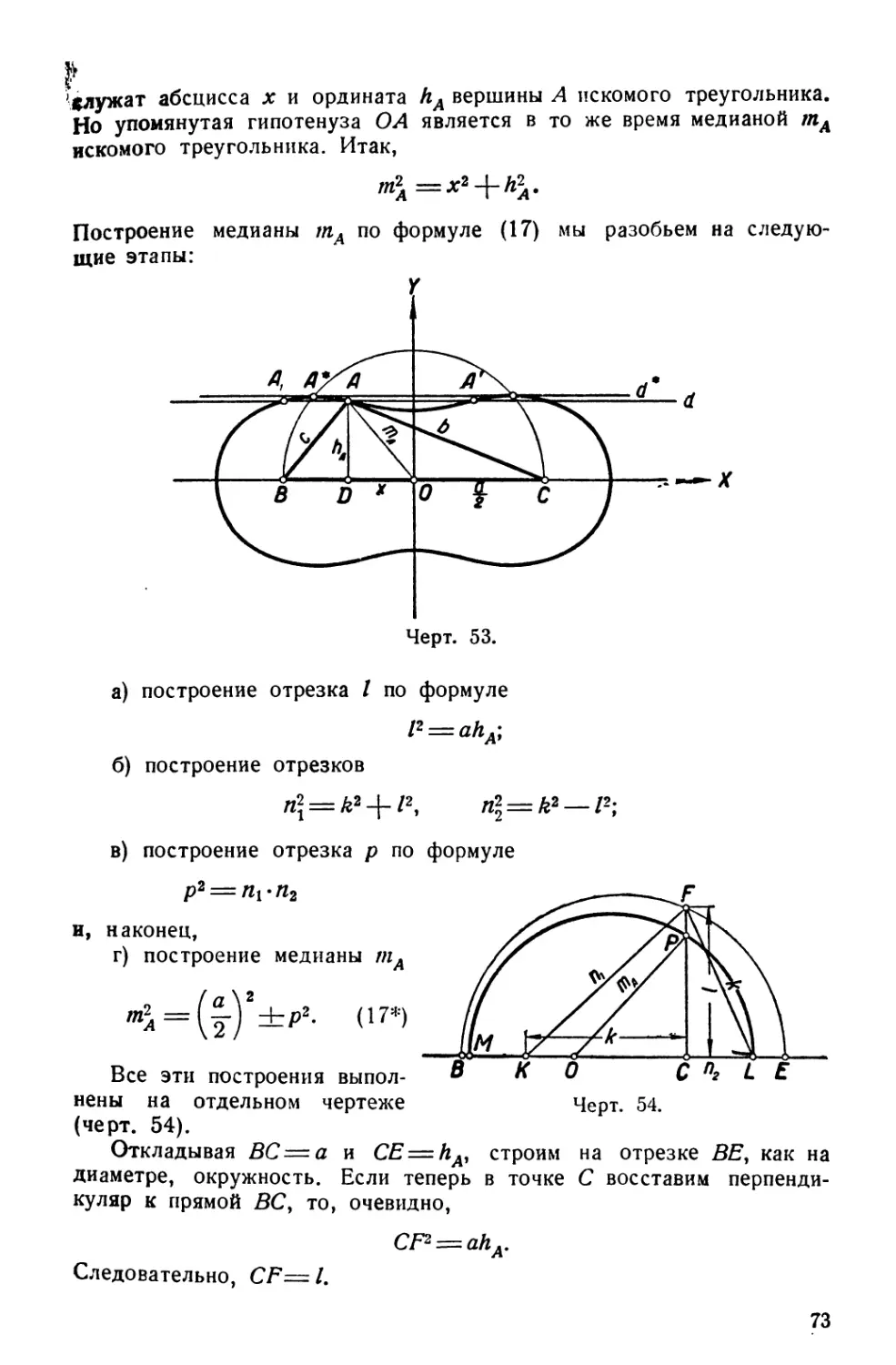
3. Построить прямоугольный треугольник по катету и разности
между гипотенузой и другим катетом.
Анализ.
На этом примере1), по существу чрезвычайно простом, можно
видеть те затруднения, которые встретит учащийся, анализируя
задачу на построение.
Предположим, что искомый прямоугольный треугольник построен.
Пусть это треугольник ABC (черт. 18), в котором катет АС является
данным. Тогда, откладывая на гипотенузе АВ от точки В второй
!) Пример взят из статьи Броуна („Математика и физика в школе,,
1936 г., № 4).
30
ι α
катет (ВС), получим точку D (черт. 18а), так что BD = BC. При
этом отрезок AD> представляя собой разность гипотенузы и катета,
является вторым данным нашей задачи. Таким образом, казалось бы,
связь искомой фигуры с данными в условии ее элементами
установлена. Однако в этой форме она не дает нам способа решения задачи,
так как треугольник ACD, две стороны которого являются данными,
мы все же не можем построить. Мы, следовательно, свели искомую
фигуру к новой фигуре,
два элемента которой
непосредственно даны, но
для построения этой
новой фигуры данных все
же недостаточно.
Попробуем сделать
иначе. Отложим
гипотенузу ВЛ на катете ВС
(черт. 18<5). Получим
точку D, причем BA = BD.
Тогда отрезок CD
представляет собой данную
разность гипотенузы и ка- Черт. 18.
тета. Мы опять перешли
от искомой фигуры к другой (/\ACD), два элемента которой
являются заданными (АС и CD). На этот раз мы достигли цели,
так как треугольник ACD прямоугольный, и, зная два катета, можем
его построить. Перейти от Д ACD к искомому Д ABC уже не
представляет никаких затруднений.
Построение.
Строим прямоугольный треугольник ACD по катетам АС и CD
(черт. 19). Делим гипотенузу AD пополам и восставляем в ее середине
Μ перпендикуляр к AD. Точка В, в которой этот перпендикуляр
пересечет прямую DC, и есть третья искомая вершина треугольнику.
Доказательство.
Треугольник ABC, очевидно, удовлетворяет условиям задачи, так-
как имеем
AB=BD
и, следовательно,
BD — BC = AB — BC = CD.
Исследование.
Так как треугольник возможен лишь при условии
CD<AC
(разность двух сторон треугольника всегда меньше третьей стороны,
черт. 186), то будем исследовать задачу только при этом
предположении. Как видно из чертежа 19, в этом случае перпендикуляр MB
пересекает прямую CD в точке В, которая является искомой
вершиной треугольника. Из построения видно, что решение единственное.
31
В самом деле, если предположим, что, кроме треугольника АВСУ
решением служит также треугольник АВ'С (черт. 20), то придем к
противоречию. Будем иметь:
АВ' — В'С = АВ — ВС= CD.
С другой стороны:
АВ'—В'В<^АВ.
Вычитая из обеих частей неравенства ВС, получим:
АВ' — В'В — ВС<АВ — ВС,
или
АВ' — Б'С<АВ — ВС,
что противоречит сделанному предположению.
Черт. 19. Черт. 20. Черт. 21.
4. Дана окружность и три точки на ней: В, Μ и И. Построить
треугольник, вписанный в данную окружность, для которого три
данные точки служили бы точками пересечения с окружностью
биссектрисы, медианы и высоты, проведенных из одной вершины
треугольника.
(Задача предложена на Московской олимпиаде для оканчивающих
среднюю школу в 1935 г.)
Анализ.
Предположим, что имеем искомый треугольник PQR, вписанный
в данную окружность (черт. 21). Биссектриса, высота и медиана
треугольника, проведенные из вершины Я, пересекают окружность
соответственно в точках В, И и М. Так как прямая РВ является
биссектрисой, то /_RPB= /^QPB и BR = BQ. Опустим из В
перпендикуляр ВС на RQ. Этот перпендикуляр пройдет, очевидно, через
середину С хорды RQ и через центр окружности О. Медиана Ρ Μ
должна пересекать основание RQ треугольника в точке С. С другой
стороны, высота РН, как прямая, перпендикулярная RQ,
параллельна ВО.
32
Построение.
Строим прямую ВО и параллельную ей прямую HP. Точка
пересечения Ρ последней с данной окружностью является вершиной
искомого треугольника. Далее проводим медиану РЖ, которая пересекает
диаметр ВО окружности в точке С. Наконец, через С проводим
прямую, перпендикулярную к ВО. Эта прямая пересекает окружность
в точках Q и /?, которые служат двумя другими вершинами
искомого треугольника.
Доказательство.
Покажем, что построенный треугольник PQR удовлетворяет
условиям задачи. Так как RQJ^BO, то BQ = BR. Следовательно,
прямая РВ является биссектрисой угла Ρ треугольника. Далее прямая
РИ || ВО и, следовательно, РН _[_RQ. Отсюда заключаем, что РН—
высота треугольника PQR. Наконец, прямая РМ делит сторону RQ
в точке С пополам и, следовательно, служит медианой треугольника.
Таким образом, построенный треугольник удовлетворяет
требованиям задачи.
Исследование.
Так как Q/?J_£0, то сторона QR треугольника PQR при
задании точки В может иметь различные (параллельные между собой)
положения, пересекая прямую ВВ'
(черт. 22) в точке, лежащей на отрезке
от точки В до диаметрально
противоположной точки В'. Однако решением
задачи могут служить лишь такие
положения хорды /?Q, которые разделяют
точки Ρ к В, так как в противном
случае точкой пересечения биссектрисы
треугольника из вершины Ρ с
окружностью была бы точка В\ а не В.
Следовательно, PS есть граничное
положение хорды RQ. С другой стороны,
граничным положением хорды RQ
служит точка В, в которой хорда RQ
вырождается в точку В. Такова область
возможных положений хорды RQ. При
этом положение точки И остается всегда неизменным, а положение
точки Μ меняется от точки В до точки S. Отсюда заключаем, что
дуга ИВМ1) должна быть меньше полуокружности,
НВМ<ш,
где г — радиус окружности. Это условие является необходимым и
достаточным, при его выполнении имеем одно решение задачи.
*) Обратить внимание на порядок букв!
33
Глава вторая.
АЛГЕБРАИЧЕСКИЙ МЕТОД.
§ 9. ПРИМЕНЕНИЕ АЛГЕБРЫ К ГЕОМЕТРИИ.
Многие задачи на построение содержат условия или требования
относительно тех или других геометрических величин: отрезков,
углов, площадей, объемов. Эти условия могут быть выражены с
помощью уравнений. Таким образом задача на построение получает
аналитическое изображение. Часто случается, что решение уравнения,
выражающего задачу на построение, позволяет найти и
геометрическое решение, т. е. самое построение. С другой стороны,
чрезвычайно облегчается исследование задачи. Такова идея, на которой
основано применение алгебраического метода к геометрическим
построениям. Идея эта нашла свое дальнейшее распространение и
обобщение в методе координат основоположника аналитической
геометрии— Декарта. Метод координат позволяет сводить различные задачи
геометрического характера к решению и исследованию алгебраических
уравнений. Здесь нет необходимости доказывать преимущества метода
Декарта. Читатель знает это из курса аналитической геометрии.
Нашей задачей является непосредственное применение
алгебраического метода к геометрическим построениям !). Простейшие примеры
такого применения мы находим еще в школьном курсе геометрии.
Так, каждый ученик знает, что построение четвертого
пропорционального к трем данным отрезкам выражается формулой:
be
х = —.
а
Он знает также построение, дающее отрезок:
т. е. среднее пропорциональное двух данных отрезков. Умеет строить
гипотенузу с прямоугольного треугольника по данном его катетам,
т. е. выполнять „построение" для формулы: ^
*) В школьных учебниках приведенные здесь построения выполняются
линейкой и циркулем. Читатель уже знает, что могут быть применены и
другие инструменты (гл. I).
34
Умеет построить катет прямоугольного треугольника b по данным
гипотенузе и другому катету, что соответствует формуле Ь = У с2 — а2,
и т. п. Все эти простейшие построения должны быть хорошо известны
учащимся, так как в конечном счете именно к ним сводится всякое
более сложное применение алгебраического метода.
Так, например, пользуясь построением среднего пропорционального
несколько раз подряд, можем построить любую степень длины
данного отрезка. На чертеже 23 показано, как это сделать. Если длину
отрезка ОА примем за единицу (0.4=1), а длину отрезка ОВ
обозначим буквой л:, то, проведя прямую ВС^АВ, получим:
§ξ=^, или 0С=0В* = х*.
Проведя затем CD_\_BC, будем иметь:
откуда получаем:
ш-т·»"" °°-°в=ос
оо-^-?=Л
Подобным же образом найдем:
ОЕ = х\ OF=x\ OG = x*
На чертеже получается спиралевидная ломаная линия ABCDEFG. ..,
отсекающая на осях координат отрезки, длины которых являются
последовательными
степенями длины χ данного
отрезка.
Продолжая ее за
точку А (по часовой стрелке),
получим последовательно
целые отрицательные
степени х. Особенно просто
выполняется это
построение с помощью „прямого
угла". Применяя к
геометрическим задачам
алгебраический метод, мы
получаем формулы,
выражающие ту или иную
геометрическую величину —
отрезок, площадь, объем
и т. д.
Формулы эти, как нетрудно видеть, должны быть однородными
относительно входящих в них букв. Так, формулы, выражающие
длину отрезка, будут однородными первого измерения. Формулы,
35
выражающие величину площади, — второго измерения. Объемы
выразятся формулами третьего измерения.
Это можно пояснить следующим образом. Представим себе, что
наш чертеж подвергнут преобразованию подобия (§ 34). Тогда
изображенная на нем фигура не изменит своего вида, но все линейные
размеры ее изменятся одинаковым образом, т. е. получат множитель
к — коэффициент подобия. Следовательно, любой отрезок,
выраженный с помощью формулы через другие отрезки фигуры, также должен
получить множитель k. Площади, как известно, получат при этом
множитель k2; объемы — множитель /г3. Таким образом, формулы,
выражающие эти величины, являются однородными соответственно
первою, второго и третьего измерений.
§ 10. ПОСТРОЕНИЕ КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ.
1) По формулам.
Предположим, что условия задачи на построение могут быть
выражены квадратным уравнением. Это уравнение мы напишем в
однородной форме, как это обыкновенно и имеет место при решении
геометрических задач:
х2-\-тх-^-п2 = 0. (1)
Решая написанное уравнение, получим:
Из этих формул ясно, что дело сводится к построению радикала
Г ( т\2
Ί/ I —] —/г2. Но это знакомое построение катета прямоугольного
(т\
треугольника по гипотенузе ( — I и другому катету п.
т
действительные значения для хх и х2 получим при условии — ^ п.
Заметам, что коэффициенты т и η в уравнении (1), выражающие
длины отрезков, предполагаются положительными.
Если бы данное квадратное уравнение имело вид:
х*-\-тх — л2 = 0, (2)
то мы имели бы дело с построением гипотенузы 1/ ( — j -\-пг
прямоугольного треугольника по двум его катетам
(г)"п-
36
В этом случае корни уравнения (2) всегда действительны.
Как ;:егко видеть, керемена знака у коэффициента т не меняет
существа построения.
2) По теореме Виета.
Предположим, что рассматриваемое уравнение имеет еид:
х2-\- тх-{-п2 = 0.
Если обозначгм его корни буквами χγ и лг2, то будем иметь (но
чеореме Виета):
х1-1гх2 = — /д,
Х\Х\
1Л2"
: А/-.
(3)
Вторая из этих формул показывает, что корни имеют оаннткокые
знаки; поэтому первая формула
может быть написана так:
Ι *ι 1 + 1*21=»*·
(4)
Таким образом, достаточно построить
два отрезка, сумма которых равна
данному отрезку /я, а
произведение п2.
С этой целью на отрезке АВ = ш
<черт. 24), как на диаметре, строим
окружность АВМ. Затем строим
прямую M/V, параллельную прямой АВ
и отстоящую от нее на расстоянии п.
Тогда перпендикуляр MP определит
«а прямой АВ точку Р. Отрезки АР
и РВ и представляют корни хх и лг2, взятые по абсолютному
значению. В самом деле, будем иметь:
Черт. 24.
АР-{-РВ=АВ:
-ms
ΑΡ·ΡΒ = ΡΜ2 = η2.
Как уже было сказано ранее, уравнение (1) имеет действительные
корни при условии -^-^п. На чертеже 24 этот факт выступает осо-
ш
<5енно наглядно. В самом деле, при я^> — прямая, параллельная АВ
и отстоящая от нее на расстоянии /г, не пересекала бы окружности
{АВМ).
Если уравнение задачи имеет вид
•тх-
-/г3 = 0,
(2)
то корни его имеют разные знаки, как это видно по их
произведению (—п2). Следовательно, алгебраическая сумма их получается
вычитанием соответствующих отрезков.
Построение корней в этом случае может быть произведено
следующим образом (черт. 25). Из произвольной точки О радиусом
37
0М = — описываем окружность. В произвольной точке Μ этой
окружности проводим касательную к ней и откладываем на ней
отрезок ΜΝ = η. Через точки N и О проводим прямую, которая
пересекает окружность в точках А и В. Тогда отрезки AN и BN
изображают абсолютные величины корней квадратього уравнения. В
самом деле,
AN — BN = AB = m.
ΑΝ·ΒΝ=ΜΝ2=η2.
Очевидно, что корни уравнения (2) всегда действительны и построй
ние (черт. 25) всегда возможно.
Черт. 25.
Продемонстрируем построение корней квадратного уравнения на
задаче о делении отрезка в среднем и крайнем отношениях
(„золотое деление").
Как известно, в этой задаче требуется данный отрезок разделить
на два таких, чтобы больший из них был средним
пропорциональным между всем отрезком и меньшим.
Если обозначим длину данного отрезка через я, а длину искомого
большего отрезка через л:, то условия задачи можно выразить
следующим образом:
а:х = х:(а —х),
что дает квадратное уравнение
х2 ~\-ах — а2 = 0.
Таким образом решение задачи о золотом делении сводится к
построению корней квадратного уравнения, что может быть сделано
как по формуле квадратного уравнения, так и по теореме Виета.
Так, например, если на чертеже 25 положить /я = /г = а, то
отрезок ΒΝ = χ дает решение задачи. Второй корень AN (AN^> a),
очевидно, не удовлетворяет условиям задачи и должен быть отброшен.
38
§ 11. ПРИМЕРЫ.
1. Дана сторона а квадрата. Построить сторону χ другого
квадрата, площадь которого в два раза более площади данного
(задача об удвоении квадрата).
Имеем:
χ2=2β2,
или __
\x\=aV2.
Выражение, которое мы получили для х, показывает, что сторона
искомого квадрата является диагональю данного (черт. 26). На
чертеже ясно видно, что второй квадрат,
построенный на диагонали первого,
удовлетворяет условию задачи.
Черт. 26.
Черт. 27.
2. Дан треугольник ЛВС. Провести прямую, параллельную его
основанию и делящую пополам его площадь.
Пусть ЛВС (черт. 27) — данный треугольник. Предположим, что
PQ—искомая прямая. В таком случае должны иметь
пл. Д ЛВС_ АВ. АС_ 2
пл. /\APQ~~AP-AQ~ 1 '
С другой стороны, имеем:
АВ_АС
AP~AQ'
„ АС
Подставляя найденное выражение —- в формулу отношения площа-
AQ
дей, получим:
АВ-АС АВ*
откуда имеем:
AP-AQ
АР=
АР2
АВ
V2
39
Это решение дает нам очень простое построение: делим отрезок АВ
в точке ΛΊ пополам и строим прямоугольный равнобедренный
треугольник AMN. Тогда гипотенуза AN последнего и даст искомый
отрезок
AN = VMN2 + Μ Α2 = -4^- .
Откладываем от точки А отрезок ΑΡ=ΑΝ и проводим PQ\\BC.
Решение, очевидно, всегда имеется, и притом единственное.
3. Даны треугольники ЛХВХСХ и А2В2С2. Требуется построить
треугольник, подобный первому из данных и равновеликий второму.
Алгебраическое решение этой задачи чрезвычайно элементарно.
Обозначим через SXi alt hx и S2y аъ h2 соответственно площади,
основания и высоты данных треугольников. Тогда можем написать
Sx hxax
Ь2 п2й2
Пусть 5—площадь и а — основание искомого треугольника.
Так как этот треугольник подобен треугольнику AxBxCXi то
можем написать
^λ — ^L·
S а2
С другой стороны, по условиям задачи, S = S2. Поэтому
или
откуда
Таким образом, дело сводится к построению отрезка а по написанной
формуле, что не представляет никаких затруднений. Построение можно
разбить на два, как это видно из следующих формул:
h2a2
ζ — -ϊ-ϊ и a- = axz.
hx
Первое из них — знакомое построение четвертого пропорционального,
второе — среднего геометрического. После того как основание а
найдено, искомый треугольник ABC строим по подобию с треугольников
АХВХСХ. Ясно, что решение всегда имеется и притом единственное.
S,
S,
ас
а2 '
а2 —
5 '
hxax
h2a2 '
h2a2ax
Л, '
40
4. Даны угол и точка на его биссектрисе. Требуется через
данную точку провести прямую так, чтобы точки ее пересечения
со сторонами данного угла определили отрезок данной длины
(задана Паппа).
Анализ.
Предположим, что данный угол образован прямыми АВ и АС
^черт. 28). Пусть Μ — данная точка на его биссектрисе AD.
Предположим далее, что через точку Μ проведена прямая, образующая
в пересечении со сторонами угла отрезок ВС заданной длины а.
Опишем окружность около треугольника ABC и центр ее обозначим
буквой О. Проведем диаметр DE и хорды АЕ и ВО.
Из чертежа видно, что
прямоугольные треугольники ADE и
FDAi подобны (дуги BD и DC
равны; следовательно, точка F
делит хорду ВС пополам).
Следовательно,
DM-DA = DF-DE.
С другой стороны, применяя
свойство перпендикуляра к диаметру,
можем написать
DF-DE = DB\
Таким образом, получаем:
DM-DA = DB\
Если мы для краткости введем
следующие обозначения: AM = m,
MD = x, BD = by то найденная
образом:
λγ(λγ +
Мы получили для отрезка χ квадратное уравнение, которое и
поможет найти решение задачи. Постоянная Ь> входящая в правую часть
уравнения, как это легко видеть из чертежа, определяется из
треугольника BFD, через данный отрезок а и данный угол α (α — / ВАС),
следующем образом:
2cos|-
Построение.
Анализ задачи подготовил Есе необходимое для ее решения. Самое
построение мы проведем обратным порядком, сохраняя, однако,
прежний чертеж (черт. 28). Предположим, что ВС = а — данный отрезок.
Построим на нем дугу окружности (ABC), вмещающую данный угол а.
Пусть D—середина дуги BDC этой окружное ι и. Строим диаметр DE
Черт. 28.
формула нерепшцртся следующим
-т) = Ь\ (5)
окружности и соединяем точку Ε с точкой С. Далее откладываем
CG = —. Тогда
(так как DC = DB = b и треугольник DCG прямоугольный).
Из точки G описываем окружность радиусом GC> которая
пересекает прямую DG в точках И и /(. Поэтому
DH=DQ-GH=-^ + ^^ + b*=x*)9
DK=DH-\-HK=x-\-m = DM + MA = DA.
Если из точки D, как центра, опишем окружность радиусом DK, то
последняя пересечет построенную ранее окружность ЛВС в точке А—
вершине данного угла (вторая точка пересечения дает симметричный
чертеж относительно диаметра DE).
Доказательство,
После того как точка А—вершина угла ВАС—построена,
проводим АВ и АС — стороны угла. Так как вершина А угла ВАС лежит
на дуге, вмещающей данный угол а, то / ВАС = си. Прямая AD,
очевидно, является биссектрисой этого угла, так как BD = DC по
построению. Отрезок ВС> отсекаемый прямой, проходящей через
точку М, имеет данную длину α также.по построению. Остается
убедиться в том, что АМ=т. Это можно сделать следующим образом»
По построению имеем:
AD = KD = x-\-m.
Из чертежа убеждаемся, что
DM-DA = DB*.
(Совершенно так же, как это было получено при анализе задачи.) Но
это означает, что отрезок DM является положительным корнем
уравнения (5), т. е. DM=x. Следовательно,
AM=AD — DM=(x-\-m)— x = m.
Итак, все условия задачи удовлетворены.
Исследование.
Как показывает чертеж, построение точки А связано с
пересечением двух окружностей. Точки пересечения· существуют, если радиус
DK второй окружности не больше диаметра DE первой:
DK^DE,
!) В этой формуле радикал должен быть взят со знаком -f-> так как
отрезок DH—DM не может иметь отрицательной величины. Вообще в этой
задаче все отрезки рассматриваются независимо от направления.
42
или
AD ^ ED,
АЛИ
AM+MD^EF-\-FD.
Но FD^MD; следовательно,
AM<EF.
Замечая, что
EF=JСЦ (из Δ^Ο,
лолучим необходимое условие существования решения в форме:
rn^jctgj. (6)
Дальнейшее исследование показывает, что найденное условие также
и достаточно.
В самом деле, при AM = EF точка Ε (черт. 28) является
вершиной угла, т. е. А совпадает с Е. При этом Μ совпадает с Ρ и
отрезок ВС \_АМ (EF). В этом
случае и будем иметь:
a L α
Разрешим это равенство
относительно а:
a = 2mtgj. (7)
Предположим, что на чертеже 29
изображены данный угол ВАС,
биссектриса AM и данная точка Μ (на
биссектрисе AM). Будем проводить Черт. 29.
различные секущие через точку М.
Эти секущие образуют со сторонами данного угла отрезки ВС
различной длины. Как мы уже видели, при ВС _]_ AM длина отрезка ВС
выражается по формуле (7). От этой величины (которая является
минимумом, см. ниже примечание) длина отрезка при вращении секущей,
непрерывно изменяясь, возрастает до бесконечности. Таким образом,
при выполнении условия (6), т. е. когда
a^2//*tg-,
решение всегда существует.
43
Как мы видели, вообще говоря, имеем два симметричных
(относительно биссектрисы) решения. Они совпадают в случае минимума,
т. е. при ВС±_АМ.
Примечание.
Несложные соображения геометрического характера показывают, что
отрезок ВС имеет минимальную длину, когда он занимает положение,
перпендикулярное к AM (на чертеже 29 это положение обозначено буквами
В0С0). Пусть ВС — любое, произвольное положение отрезка. Докажем, что-
ВС > В0С&
Из точки Му как центра, опишем окружность радиуса MCq. Последняя»
пересечет прямую ЕС по диаметру βγ. Следовательно, $* = В0С0. Поэтому
мы можем сравнить отрезок ВС с отрезком βγ. Как видно из чертежа, точка }
должна лежать внутри отрезка ВС (так как окружность пересекает
отрезок MB). Что же касается второй точки пересечения γ, то она может лежать
внутри или вне (как на черт. 29) отрезка ВС. В первом случае 5C>(fy \t
требуемое доказано. Во втором случае от отрезка βγ можно перейти к
отрезку ВС, прибавляя отрезок, β£ и отнимая отрезок γ£. Если будет доказано,
что $В > γ(7, то отсюда будет следовать, что ВС > βγ.
Построим В0С'\\АС0. Тогда МО = МС и βΟ = γ£. Пусть BqM' —
касательная к окружности в точке Bq. Следовательно, BqM'\\AM. Из подобна
фигур ВВ0С'М' и БАСМ имеем:
ВМ' __ ВМ
М'О " МС #
Но, как видно из чертежа, ВМ > МС, а значит
ВМ' > М'О.
Но тогда и подавно
Щ > }С.
Так как рС — С^, то требуемое доказано.
Глава третья.
ГЕОМЕТРИЧЕСКИЕ МЕСТА.
§ 12. ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИЕ МЕСТА.
Понятие геометрического места является фундаментальным в
геометрии. Мы много раз встречались с ним в элементарной и
аналитической геометрии. Прямая линия, окружность и другие кривые могут
служить примерами геометрических мест точек, удовлетворяющих тому
или другому условию.
Простейшими геометрическими местами, рассматриваемыми в курсе
элементарной геометрии» являются следующие.
1. Геометрическое место точек, имеющих постоянное
расстояние от одной и той же фиксированной точки.
Это место представляет собой окружность, центром которой
служит фиксированная точка, а радиус равен постоянному расстоянию.
2. Геометрическое место точек, равноотстоящих от двух
фиксированных точек.
Известно, что таким местом служит перпендикуляр, восставленный
в середине отрезка, определяемого двумя фиксированными точками.
3. Геометрическое место точек, имеющих постоянное
расстояние от одной и той же фиксированной прямой.
Такое место образует пара прямых, параллельных фиксированной
прямой и находящихся от нее на заданном расстоянии.
4. Геометрическое место точек, равноотстоящих от двух
фиксированных прямых.
Как известно из элементарного курса, таким местом точек служат
биссектрисы угла, образованного фиксированными прямыми, причем
предполагается, что последние пересекаются.
Если же фиксированные прямые параллельны, то искомым
геометрическим местом является их средняя линия (т. е. прямая, им
параллельная и делящая пополам отрезок, определяемый какими-нибудь
двумя точками той и другой прямой).
5. Геометрическое место точек плоскости, из которых
некоторый фиксированный отрезок виден под постоянным углом.
В элементарном курсе доказывается, что это место состоит из
двух одинаковых, симметрично расположенных относительно данного
отрезка, дуг окружностей, проходящих через концы фиксированного
отрезка АВ (черт. 30). Полезно напомнить, как строится центр
какой-нибудь из них.
45
Пусть φ — постоянный угол, под которым виден из точек
геометрического места фиксированный отрезок АВ. Проводим через А прямую
АС, образующую с АВ угол φ. Далее строим АО J_ АС и DO _|_ АВ,
где D есть середина отрезка АВ. Точка О пересечения прямых АО
и DO является искомым центром окружности (АВМ). В самом деле,
из любой точки Μ дуги АМВ отрезок АВ виден под углом <р.
//AMB=^ = ^/BAC = (fy
так как угол ВАС образован хордой и касательной (прямая АС,
перпендикулярная к АО, касательна к окружности).
В частном случае, геометрическим местом точек, из которых
фиксированный отрезок виден под прямым углом, служит
окружность, построенная на этом отрезке, как на диаметре.
Черт. 30. Черт. 31.
§ 13. ГЕОМЕТРИЧЕСКИЕ МЕСТА В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.
Читатель этой книги уже знаком с аналитической геометрией и
мог заметить, что там понятие геометрического места является
основным. Действительно, самый принцип координации точек плоскости
основан на понятии геометрического места. Так, когда мы говорим,
что точка Μ имеет абсциссу х = а> то этим мы выделяем на
плоскости геометрическое место — прямую, параллельную оси Оу и
отстоящую от нее на расстояние а (черт. 31). Следовательно, точка Μ
является одной из точек этой прямой. Но одного геометрического
места мало для определения положения точки М, поэтому
необходимо дать еще второе геометрическое место. Последнее
определяется заданием ординаты точки М. Если эта ордината у = Ь, то мы
получаем второе геометрическое место — прямую, параллельную оси Ох
и отстоящую от нее на расстояние Ъ. Точка Μ теперь определена.
Она должна принадлежать как первому (лг = я), так и второму (у = Ь)
геометрическому месту; следовательно, Μ есть точка пересечения
обоих геометрических мест. Так как в данном случае оба геометри-
46
ческнх места суть прямые линии, то точка их пересечения Μ
определяется однозначно.
Мы рассмотрели координацию точек плоскости в декартовой
прямоугольной системе координат. Аналогичные выводы можно сделать
и в других системах. Так, в полярной системе мы имеем координаты φ
(полярный угол) и ρ (радиус-вектор). Если дан полярный угол φ = α,
то этим определяется первое геометрическое место: луч (полупрямая),
выходящий из полюса О и
образующий с полярной осью ОХ угол α
(черт. 32). Точка Μ должна лежать
на этом луче. Вторая координата
о = а определяет еще одно
геометрическое место: окружность с
центром в полюсе О и радиуса а.
Точка Μ принадлежит также и этому
месту, поэтому она является точкой
пересечения луча с окружностью.
Таким образом, и здесь мы имеем Черт. 32.
однозначное определение точки Μ
с помощью двух геометрических мест. Координатные линии той или
иной системы координат выражаются простейшими уравнениями в этой
системе. Так, уравнения координатных линий в декартовой системе
имеют вид:
лг = я, у = Ь.
Аналогично координатные линии полярной системы изображаются
уравнениями:
φ = α, р = а.
Вообще линия рассматривается в аналитической геометрии именно
как геометрическое место точек. Это геометрическое место
выражается в аналитической форме уравнением
/(х,У) = 0.
Каждое отдельное решение (л:, у) этого уравнения дает точку Μ
нашего геометрического места.
Метод аналитической геометрии и состоит в изучении свойств
кривых (геометрических мест) по их уравнениям. Кривая
(геометрическое место) может быть определена либо геометрическим свойством,
либо уравнением, т. е. аналитическим условием. Иногда, зная
геометрическое свойство точек кривой, составляют ее уравнение, т. е.
выражают это свойство или условие аналитически. Так, например,
зная, что прямую линию можяо рассматривать как геометрическое
место точек, равноотстоящих от двух данных фиксированных точек,
можно вывести уравнение прямой. Обозначая координаты
фиксированных точек через (хи ух) и (лг2, у2)у а координаты точки,
принадлежащей искомому геометрическому месту, через (лг, у)у будем иметь:
V(x — xx)* + (y —у,)* = V(x — x2Y + (у —уг)\ (1)
47
Это уравнение выражает в декартовых прямоугольных координатах
равенство расстояний точки (х, у) от фиксированных точек.
Освобождаясь от радикалов, раскрывая скобки и группируя члены с χ и у,
получим то же уравнение (1) в форме:
2(х2 — х1)х + 2{у2—у1)у + х]-\-уЪ—х1—у1 = 0. (2)
Мы видим, что найденное уравнение перзой степени относительно
Л" и у и представляет прямую, перпендикулярную к прямой,
соединяющей обе фиксированные точки. Как это обстоятельство, так и то,
что найденная прямая проходит через середину отрезка,
определяемого двумя фиксированными точками, легко проверить аналитически.
Аналогичным образом, рассматривая прямую как место точек,
одинаково удаленных от сторон данного угла, придем к уравнениям
биссектрис этого угла. В самом деле, если уравнения сторон угла
заданы в нормальной форме:
а = 0 и [} = 0,
где через а и β сокращенно обозначены левые части нормальных
уравнений сторон, то расстояния некоторой точки (л:, у) до этих
сторон равны левым частям нормальных уравнений, взятых со знаком ( -\- )
или (— )1). Следовательно, они выражаются через dza и zbp-
Приравнивая эти расстояния, по свойству рассматриваемого
геометрического места, получим два уравнения биссектрис данного угла:
α=+β, α=— β. (3)
Приведенные примеры показывают, как находится уравнение линии,
определенной своим геометрическим свойством. Мы воспользуемся
методом аналитической геометрии, чтобы найти геометрическое место
точек, для которых разность квадратов их расстояний от двух
фиксированных точек есть величина постоянная, равная а2.
Пусть Мх (jc,, уг) и М2 (х2, Уъ) — Две фиксированные точки, а
Μ (χ, у) — точка искомого геометрического места.
Тогда, по условию, разность квадратов расстояний от точки Μ
до точек Μχ и М2 есть постоянная величина а2. Следовательно,
(* — *ι)2 + (V — У ι)2 = (х — х2)2 + (У —У 2? + °>2· (4) .
Раскрывая скобки и приводя подобные члены, получим:
2(л2 — Х\)х-\- 2(у2— У\)У = х\-±-у1 — х\ — Уг+а2. (5)
Это уравнение прямой, так как оно первой степени относительно
текущих координат. Как и в случае уравнения (2), прямая (5)
перпендикулярна к прямой Мх М2. Ири я = 0 уравнение (5) переходит, как
это и должно быть, в уравнение (2).
!) В зависимости от положения начала координат О и рассматриваемой
точки относительно прямой.
48
К тому же выводу можно было бы прийти из геометрических
соображений (черт. 33). Опуская из точки Μ перпендикуляр ММ0 на
прямую Мх М2, будем иметь:
МХМ2 = МгМд + М0М2;
м2.\р=м2м1-\-м0м2.
Производя почленное вычитание, найдем:
МгМ* — М2М2 = МгМо — M2Ml (6)
Так как для любой точки Μ перпендикуляра ММ0 правая часть
равенства (6) не изменяется, она постоянна, то можем обозначить ее
через а2:
МхМ2 — М2М2 = а2. (7)
Равенства (6) и (7) показывают, что нашему условию удовлетворяют
все точки перпендикуляра ММ0. Для всякой точки, не лежащей на
прямой ММ0У правая часть будет иметь
другое значение; следовательно, такая точка \M(xj)
не принадлежит к данному
геометрическому месту.
Таким образом, искомое геометрическое
место представляет собой прямую,
перпендикулярную к прямой ΜχΜ2 и
пересекающую последнюю в точке, для которой М,(х„у,) М0| M2(x2tyj
MxMl—J0#tfQ = a2. (8)
Мы рассмотрели несколько примеров, Черт. 33.
в которых роль геометрического места
выполняет прямая линия. В следующем параграфе мы проведем
аналогичное исследование для кривых второго порядка.
§ 14. КРИВЫЕ ВТОРОГО ПОРЯДКА КАК ГЕОМЕТРИЧЕСКИЕ МЕСТА.
L Окружность.
Если говорить о геометрических построениях линейкой и циркулем,
то наряду с прямой линией основное место должно быть отведено
изучению окружности. С нее мы и начнем рассмотрение кривых
второго порядка. Определение окружности как геометрического места
точек, равноудаленных от данной точки (центра окружности),
приводит, как известно из аналитической геометрии, к следующему
уравнению:
(х — х0)2 + (у— у0)2 = г2,
где через χύ и у0 обозначены координаты центра окружности, а через
г — ее радиу^.
Но окружность может быть определена как геометрическое место
точек и другими геометрическими условиями. Рассмотрим, например,
следующую задачу.
49
Найти геометрическое место середин всех хорд данной окруж*
ноет и, выходящих из одной какой-нибудь точки последней.
Отметим на данной окружности (О, АВ) постоянную точку А и
будем проводить через нее хорды (черт. 34). Обозначим через Μ
середину хорды АВ. Требуется найти
геометрическое место точек Αί, образующееся при
перемещении точки В (конца хорды) по
окружности.
Соединяя точку Μ с центром О, получим
прямую ОМ, перпендикулярную к хорде АВ.
Следовательно, угол АМО прямой и опирается
на отрезок АО, как на диаметр окружности,
проходящей через точки О, А и М. Таким
образом, точка Μ всегда лежит на окружности,
построенной на отрезке ОА, как на диаметре.
Эта окружность и является искомым геометрическим местом, так как
нетрудно видеть, что всякая точка ее, будучи серединой проходящей
через эту точку хорды, принадлежит нашему геометрическому месту.
Аналогичным образом можем получить решение второй, более
общей задачи:
Найти геометрическое место середин хорд данной окружности,
проходящих через заданную точку Р.
Соединяем центр окружности О с серединой Μ хорды АВ и с
фиксированной точкой Ρ (черт. 35). Так как ОМ \_АВ, то угол РМО
л:
Черт. 35.
Черт. 36.
прямой. Поэтому точка Μ лежит на окружности, описанной на
отрезке ОР, как на диаметре. Эта окружность и является, очевидно*
искомым геометрическим местом !).
!) В том случае, когда точка Ρ расположена вне данной окружности,
геометрическим местом точек Μ является не вся окружность, построенная
на отрезке ОР, как на диаметре, а только та ее дуга, которая расположена
внутри данной окружности.
SO
Большое значение для геометрических построений имеет
рассматриваемое ниже место точек.
Геометрическое место точек, расстояния которых от двух
фиксированных точек плоскости находятся в постоянном отношении (λ).
Обозначим фиксированные точки буквами А и В, а произвольную
точку искомого геометрического места через Μ (черт. 36). Положим
AM
_ = λ. Далее, проведем биссектрисы MP и MQ углов,
образованных при точке Μ прямыми AM и ВМ. Пусть эти биссектрисы
пересекают прямую АВ в точках Ρ и Q. Следовательно,
Ζ.ΑΜΡ=£ΒΜΡ и ^/BMQ = /_A'MQ.
Точки Ρ и Q, по свойству биссектрис треугольника, должны делить
отрезок АВ в отношении, равном отношению АМ:ВМУ т. е.
AP_AQ_AM
РВ~ BQ~~ BM~ '
Отсюда заключаем, что точки Ρ и Q ултот вполне определенное
положение на прямой АВ.
В самом деле, точка Ρ делит отрезок АВ внутренним образом, а
точка Q—внешним образом в данном отношении λ. Такие две точки
называются „гармонически сопряженными" относительно точек А и В.
Итак, положение точек Ρ и Q вполне определено заданием λ и
не зависит от М,
С другой стороны, прямые MP и MQ как биссектрисы смежных
углов взаимно перпендикулярны. Поэтому, если на отрезке PQ, как
на диаметре, построить окружность PMQ, то построенная окружность
пройдет через каждую точку Ж, удовлетворяющую условию
геометрического места. Только что построенная окружность называется
аполлониевой. Таким образом, всякая точка Μ искомого
геометрического места лежит на соответствующей окружности. Аполлония.
Докажем теперь обратное предложение, т. е. что всякая точка Μ
окружности Аполлония удовлетворяет условию: ^—= λ. С этой целью
через точку В проводим прямую UV, параллельную AM:
UV || AM.
Точки пересечения этой прямой с прямыми MP и MQ обозначим
буквами U и V.
Тогда получим подобные треугольники:
Δ АМРся Д BUP
и
/\AMQcoZ\BVQ.
Из этих треугольников имеем следующие пропорции:
АМ__АР_. AM _AQ
BU ~BP~k' BV ~~BQ
51
Сравнивая левые части этих отношений, находим, что
Таким образом, точка В является серединой гипотенузы
прямоугольного треугольника UMV с прямым углом при вершине М.
Следовательно,
B(J = BV = BM,
и написанные выше пропорции при замене знаменателей первых
отношений дают
АЛ1 _.
вм~А
(что и требовалось доказать).
II. Эллипс, гипербола, парабола.
В курсах аналитической геометрии эллипс рассматривается как
геометрическое место точек, сумма расстояний которых от двух
фиксированных точек плоскости (фокусов) постоянна.
На этом основан известный вывод уравнения эллипса
а2 ' Ь2
Аналогичным образом гипербола определяется как геометрическое
место точек, разность расстояний которых от двух
фиксированных точек (фокусов) постоянна.
То же самое выражается, как известно, уравнением гиперболы
х2 у2
~а~2~ ¥~
Наконец, парабола рассматривается в аналитической геометрии как
ι еометрическое место точек, равноотстоящих от некоторой
фиксированной точки (фокуса) и фиксированной прямой (директрисы).
Выражая расстояния „текущей" точки параболы от фиксированной
точки и фиксированной прямой в координатах и приравнивая их,
получаем известное уравнение параболы (если ось д:-в проходит через
фокус):
у2 = 2рх.
Таким образом, мы определяем параболу через свойство ее точек по
отношению к фокусу и соответствующей директрисе. Аналогичными
свойствами обладают также эллипс и гипербола. Поэтому кривая
второго порядка (эллипс, парабола, гипербола) может
рассматриваться как геометрическое место точек, отношение расстояний
которых до фиксированной точки (фокус) и до фиксированной
прямой (директриса) постоянно. (Постоянное отношение расстояний
52
равно эксцентриситету кривой.) Это позволяет вывести уравнения всех,
трех кривых в одной и той же общей форме. В полярных
координатах это уравнение, как известно, имеет вид
р-^^-г-^ , О)
г 1 -J- e cos ъ
где φ и ρ — текущие полярные координаты кривой второго порядка,
ρ—ее параметр, а е — эксцентриситет. В зависимости от того, будет
ли ^<0' е=\ "л» e^>U уравнение (9) представляет эллипс,
параболу или гиперболу.
Псе это показывает, что кривые второго порядка могут быть
определены различными геометрическими свойствами. С точки зрения
решения конструктивных задач методом геометрических мест,
желательно изучить кривые второго порядка как геометрические места,,
определяемые различными их геометрическими свойствами.
Так, например, и эллипс и гиперболу можно рассматривать как
геометрическое место центров окружностей, проходящих через
фиксированную точку плоскости и касающихся фиксированной
окружности.
Пусть фиксированная точка F (черт. 37), через которую
проходят все окружности, лежит внутри фиксированной окружности. Как
увидим дальше, в этом, и только в этом, случае получим эллипс-
Пусть окружность (МХу TXF)
касается фиксированной
окружности (О, ТХТ2) в точке Т\ и
проходит через фиксированную точку
F. Тогда
ОМх + Ж1/7= ОМх +ΛΤι7Ί =/?,
где через R обозначен радиус
фиксированной окружности. Таким
образом, точки Мх
рассматриваемого геометрического места
(центров окружностей) обладают
свойством точек эллипса
ОМх + M{F= R = const
и поэтому можно утверждать, что
искомое геометрическое место
представляет собой эллипс,
фокусами которого служат центр О фиксированной окружности и
фиксированная точка F, а большой осью — радиус R фиксированной
окружности.
Гипербола может быть получена аналогичным образом, причем
фиксированная точка F должна лежать вне фиксированной
окружности.
Чертеж примет в этом случае следующий вид (черт. 38). Если
рассмотрим окружность (МХу 7\F)y проходящую через точку F и
Черт. 37.
53-
касающуюся (внешним образом) фиксированной окружности (О, Т{Т2),
то будем иметь:
ОМг — MXF= ОМ, —MxTl = OTl = R.
Аналогично для всякой окружности (М2у T2F), проходящей через
точку F и касающейся фиксированной окружности (внутренним
образом), будем иметь:
M2F — ОМ2 = М2Т2 — ОМ2 = ОТ2 = R.
Эти формулы показывают, что центры Мх окружностей, касающихся
фиксированной окружности извне, образуют одну ветвь гиперболы, а
центры М2 окружностей,
касающихся внутренним образом,—
другую ветвь гиперболы.
Фокусами гиперболы являются
точки О и F. Действительная
ось равна радиусу R
фиксированной окружности.
Посмотрим, какое
геометрическое место образуют центры
Μ окружностей, касающихся
фиксированной окружности в
неизменной, фиксированной
точке F, которую, следовательно,
предполагаем лежащей на
фиксированной окружности (черт.
39).
Черт. 38. Как легко видеть, в этом
случае центры касающихся
окружностей Ми М2у Λί3, Μ4 расположатся на прямой OF. С другой стороны,
осаждая точка этой прямой может быть принята за центр окружности,
Черт. 39
касающейся фиксированной окружности в точке F. Не составляют
исключение и точки О (касающаяся окружность в этом случае совпадает
χ фиксированной) и F (касающаяся окружность вырождается в точку F).
54
Черт. 40.
Тактш образом, в этом случае геометрическое место центров Μ
касающихся окружностей представляет прямую OF.
Для образования параболы мы заменим фиксированную
окружность фиксированной прямой ТХТ2 (черт. 40). Тогда для всех
окружностей, проходящих через точку F и
касающихся прямой ТХТЪ будем иметь:
M1F=MlTu
M2F=M2T2,
M,F=MJV
Следовательно, центры Ми М2> MBi...
окружностей лежат на параболе, для
которой точка F служит фокусом, а прямая
ТхТг— директрисой (направляющей).
В рассмотренных ранее построениях
эллипса и гиперболы фиксированная
точка F также служит одним из фокусов
кривой, в то время как роль направляющей
выполняла фиксированная окружность,
имеющая центр в другом фокусе О
кривой и радиус R которой равен оси кривой
(R = 2a). Такая окружность называется
направляющей. Мы видели, что с точки зрения нашего построения
кривых второго порядка роль направляющих окружностей для эллипса
и гиперболы аналогична роли направляющей прямой (директрисы) для
параболы.
§ 15. ОВАЛЫ КАССИНИ.
Рассмотрим две фиксированные точки Ρ и Q и произвольную
(„текущую") точку Μ (черт. 41).
Длины отрезков MP и MQ выражают расстояния точки Μ до
фиксированных точек. Если потребовать, чтобы произведение этих
расстояний имело постоянное значение, то текущая точка Μ не может
у изменять свое положение на
плоскости произвольно, она опи-
рМ (xj) шет некоторую кривую.
Последняя является геометрическим
местом точек, произведение
расстояний которых от двух
фиксированных точек
постоянно.
Выведем уравнение этого
геометрического места. Оси
координат расположим
следующим образом. Ось абсцисс проведем через фиксированные точки Ρ я Q*
Начало координат поместим в середине отрезка PQ, ось ординат —
перпендикулярно оси абсцисс.
55
Если обозначить длину отрезка PQ через 2с, то точки Р, Q η
Μ будут иметь координаты: Ρ (—с, о), Q (с, о) и Μ (л:, у). Условие
^которому должна удовлетворять точка Ж, можно выразить следующим
образом:
MP.MQ = a\
где а означает некоторое постоянное.
Заменяя MP и MQ по формулам расстояния между двумя
точками, получим:
[(х + с)2 Л-у2} Цх - с)2 +у2} = а*.
Раскрывая скобки и производя упрощение, можем переписать это
уравнение в следующей форме:
(х*—с*)2 + 2(х*-\-с*)у*-{-у* = а*. (1)
Полученное уравнение показывает, что искомое геометрическое место
представляет собой кривую четвертого порядка. Она называется овалом
Кассини. Форма овала Кассини зависит от значения параметра а.
При а = с уравнение овала принимает более простой вид:
(χ2 -|-^2)2 _ 2^2*2 _|_ 2<*у2 _ Q. (2)
В этом частном случае кривая называется лемнискатой Бернулли.
Лемниската, как видно из ее уравнения (2), проходит через начало
координат О. Полагая у = О, найдем точки пересечения ее с осью
ОХ. Имеем:
л;4-- 2с2х2 = 0у
х2(х2 — 2с2) = 0.
Таким образом, получаем двойную точку в начале координат
хг = х2 = 0.
Жроме того, кривая пересекает ось абсцисс в точках
хг = с \% x± = — cVt2.
Ось OY лемниската пересекает только в начале координат, так как
при х = 0 получаем у2 (у3-{-2с2) = 0 и точками пересечения служат:
Ух=У2 = 0 и yz^ = ±ci Ϋ2,
причем действительными являются только первые две точки.
Исследуем теперь общее уравнение овала Кассини (1).
1) Предположим, что а<^с.
Полагая в уравнении (1) у = 0, найдем точку пересечения овала
с осью абсцисс. Имеем:
(Х2 — С*)* = а*,
И. Ill
χ* — с'1 = а2, х2 — с'2 = — а2.
.56
Следовательно,
Получаем четыре действительные точки, так как в нашем
предположении (а<^с) подкоренное выражение в обоих случаях положительно^-
Ищем точки пересечения с осью ординат.
Полагая 8 (1) л: = 0, получим:
у*-\-2с2у2-{-с* = а\
или
(у2 + с2)2 = а\
откуда имеем:
у2-^-с2 = а2, у2-\-с2 = — а2
и
3Ί,2 = ± Vo2 - с2, y,A=±i'Va^c2.
Вторая из этих формул дает явно мнимые значения для ординат
точек пересечения кривой с осью OY. Но и первая формула в нашем
предположении (а<^с) дает мнимые значения для у. Следовательно»
кривая не пересекает оси OY. Она состоит, очевидно, из двух
симметрично расположенных относительно оси OY частей. Таким образом^
при а<^с кривая
распадается на пару
симметричных овалов.
2) При а = су как мы
уже видели, получается
лемниската Бернулли.
3) Исследуем случай
а^>с.
Из двух формул (3)
первая всегда дает два
действительных значения
для абсциссы точек
пересечения кривой с осью
ОХ. Вторая из формул (3),
наоборот, в нашем пред- Черт. 42.
положении дает два
мнимых значения. Следовательно, овал пересекает ось абсцисс в двух-
(симметрично расположенных) действительных точках. Чтобы найти
точки пересечения кривой с осью ординат, обращаемся к формулам (4).
Первая из них дает в нашем предположении (а^>с) два
действительных значения. Кривая пересекает ось в двух действительных точках.
Вторая из формул (4) всегда дает, как уже было сказано, мнимые
значения. Вид кривой, соответственно различным значениям параметра
д, изображен гна чертеже 42.
57
§ 16. „МЕТОД ГЕОМЕТРИЧЕСКИХ МЕСТ".
,eq^
Геометрические места широко применяются к решению задач на
построение. Поясним этот метод на примерах.
Рассмотрим задачу на построение:
На плоскости даны (фиксированы) точка А и прямая d
Требуется построить точку Л!, находящуюся на расстоянии а (дано
отрезком) от точки А и на расстоянии Ь (дано отрезком) от
прямой d.
В этой задаче искомая точка Μ должна удовлетворять двум
условиям. Первое условие заключается в том, что точка должна находиться
от фиксированной точки А на
данном расстоянии а. Точки,
удовлетворяющие такому условию, образуют
геометрическое место — окружность
с центром в точке А и радиусом,
равным а (черт. 43). Эту
окружность можно построить.
Следовательно, искомая точка должна лежать
на указанной окружности.
Переходим ко второму условию. Оно
говорит, что искомая точка Μ должна
находиться на данном расстоянии
5 от фиксированной прямой d„
Точки, удовлетворяющие этому
требованию, образуют геометрическое
место — пару прямых, параллельных
прямой d и отстоящих от нее на
расстояние Ь (§ 12, п. 3). Эти прямые также можно построить.
Согласно второму условию искомая точка Μ должна лежать на какой-
либо из построенных параллелей.
Таким образом, искомая точка Λί, удовлетворяя обоим требованиям
задачи, должна принадлежать тому и другому геометрическому месту,
т. е. она является их точкой пересечения. Анализ задачи показывает,
что для ее решения следует построить первое и второе
геометрические места. Нетрудно убедиться, что точки пересечения обоих
геометрических мест действительно являются решениями задачи. В самом
деле, если Μ есть одна из таких точек, то она находится на
расстоянии а от точки Л и на расстоянии Ь от прямой d.
Исследование решения задачи также чрезвычайно облегчается
благодаря применению метода геометрических мест. Надо
исследовать, при каких условиях первое геометрическое место (окружность)
пересекается со вторым (пара прямых). Так как окружность не может
пересекать две прямые более чем в четырех точках, то, в
зависимости от данных (Л, a, d и δ), мы можем иметь от нуля до четырех
решений. На чертеже 43 задача имеет два решения (точки Μ и М).
Разобранный пример показывает, что метод геометрических мест
применяется в тех случаях, когда условия задачи могут быть расчле-
Черт
£8
нены на два независимых требования, каждое из которые/ в
отдельности определяет геометрическое место точек. Тогда точки
пересечения обоих геометрических мест удовлетворяют уже полному условию·
задачи, т. е. дают ее решение.
Метод геометрических мест дает ясную картину возможности
решения задачи и вместе с тем и самый способ построения. В этом
заключаются его преимущества. С другой стороны, оставляя одно
условие неизменным и варьируя второе условие, мы можем объединить
несколько задач на построение в одну группу и рассматривать их как
различные варианты некоторой общей конструктивной проблемы. Опыт
такого исследования задачи мы даем в следующем параграфе.
§ 17. ИССЛЕДОВАНИЕ СТРУКТУРЫ ЗАДАЧИ НА ПОСТРОЕНИЕ.
Задача, которую мы будем исследовать, заключается в следующем..
Требуется построить треугольник, если даны его основание а,,
высота h а и некоторая зависимость между двумя другими
сторонами Ь и су выражаемая равенством /(й, с) = 0.
Решение задачи сводится в сущности к построению вершины А
треугольника, так как две другие его вершины В и С можно считать
данными вместе с основанием а. Для определения вершины А мы
имеем два условия: первое из них заключается в том, что дана
расстояние вершины А от основания а (это расстояние равно вы-
соте h л); второе условие выражается соотношением ДЬ> с)=0
Предположим, что основание а (сторона ВС) треугольника
построено на чертеже. Тогда первое условие говорит, что точка А
лежит на одной из двух
параллельных прямых, лежащих по обе
стороны от а на расстоянии h A (на
чертеже 44 изображена одна из них — d).
Эта пара параллельных прямых
представляет первое геометрическое
место, которому принадлежит искомая
вершина А.
Второе Геометрическое место опре- Черт. 44.
деляется соотношением f(b, c) = 0.
В следующих примерах мы разберем различные случаи,
соответствующие тому или иному заданию соотношения f(b> c) = 0.
1. Даны основание а и высота hA треугольника, а также сумма
двух других его сторон Ь-{-с = т. Требуется построить
треугольник.
Анализ.
Как мы уже видели, задача сводится к построению точки А—
вершины треугольника. Для определения этой точки мы имеем одно
геометрическое место—точка А должна лежать на прямой,
параллельной основанию а и проходящей на расстоянии hA от него (черт. 45).
Таких прямых две (выше и ниже основания); на чертеже показана
59
одна из них — верхняя, так как вторая прямая симметрична первой
относительно оснозания а треугольника так же, как и весь чертеж.
Второе геометрическое место выражается условием: Ь-\-с = т.
Так как b и с представляют собой расстояния точки А до
фиксированных точек С и В—вершин треугольника, то указанное условие
говорит, что сумма этих расстояний для искомой точки должна быть
постоянна. Это означает, что вершина А должна лежать на эллипсе,
.фокусами которого служат точки В и С> а большей осью — отрезок т.
Таким образом, для
определения вершины А
треугольника имеем два
геометрических места — параиарал-
лельных прямых и эллипс.
Наша задача сводится к
построению точек пересечения
этих геометрических мест.
Построение.
Воспользуемся для этого
методом координат.
Расположим ось абсцисс по
основанию а треугольника;
начало координат О в середине
отрезка ВС, а ось ординат
перпендикулярно к прямой ВС. Тогда уравнение первого
геометрического места (прямой d) будет иметь вид:
Черт. 45.
у = /г
л-
(1)
Уравнение второго геометрического места (эллипса) напишется так:
(-)
х2 , у2
а2 ' ψ''
1.
Полуоси α и β эллипса и половина его фокусного расстояния
γ-следующим образом выражаются через данные задачи:
т
а=у г-
■— й2 = а2-
2 ' Р
Решая совместно уравнения (1) и (2), получим:
x = ±jVP-h*A.
(3)
Формула (3) дает абсциссу ОАх искомой точки А, в то время как ее
ордината y = hA.
Построение χ по формуле (3) можно разбить на следующие этапы:
1) строим β по формуле β2 = 22—Y2(α~9, ΐ = .9 '» τ· естР0НМ
катет $ по данным гипотенузе α и другому катету γ;
60
2) строим выражение
т. е. строим катет δ по данным гипотенузе β и второму катету /?4;
3) строим лг = —^—, т. е. строим отрезок л: по трем данным отрез-
Р
кам а, р и о, с которыми он образует пропорцию
Все эти построения легко выполняются циркулем и линейкой, и мы
получили, следовательно, решение поставленной задачи при тех же
средствах построения.
Исследование,
При каких условиях задача имеет решение? Одно из условий
совершенно очевидно. В самом деле, для всякого треугольника
должно выполняться требование
Ь-\-с^>ау
или
Таково необходимое условие существования решения. Это условие,
конечно, недостаточно. Из чертежа 45 видно, что решение
существует в том, и только в том, случае, если прямая d пересекает
эллипс или, в предельном случае, касается его. Это будет иметь
место при условии, что расстояние hA прямой d от большой оси ВС
эллипса не превышает малой оси β эллипса. Другими словами, должно
выполняться условие
или, иначе,
V т2 — а2
Что же касается числа решений, то, как видно из чертежа 45,
прямая d пересекает эллипс, вообще говоря, в двух точках, если
достаточные, условия выполнены. Но два треугольника, которые
получаются из этих решений, являются симметрично-конгруэнтными
(относительно малой оси эллипса). Точно так же вторая параллельная
прямая (нижняя, на чертеже 45 не показана), пересекая эллипс, дает
два треугольника, симметричных двум ранее полученным относительно
большой оси эллипса. Таким обрезом, можно считать, что при
выполнении указанных выше условий задача имеет одно решение.
2. Даны основание а и высота hA треугольника, а также
разность двух других его сторон Ь — с = т. Требуется построить
треугольник.
61
Анализ.
В этом варианте задачи первое геометрическое место (пара
прямых, параллельных основанию ВС треугольника) остается без
изменения.
Второе геометрическое место определяется условием:
Ъ — с = т.
Это условие показывает, что разность расстояний вершины Л до
точек С и В есть данная величина т. Геометрическое место точек,
удовлетворяющих
такому условию,
представляет собой
гиперболу, фокусами которой
служат точки В и С,
а действительная ось
т
α имеет величину —
^χ (черт. 46).
Таким образом,
задача сводится к
построению точек
пересечения некоторой
гиперболы с прямой,
параллельной
основанию треугольника.
Построение.
Черт. 46. Установим систему
прямоугольных
декартовых координат, принимая прямую ВС за ось абсцисс, середину
отрезка ВС за начало координат О и перпендикуляр О К за ось ординат.
Тогда имеющиеся в нашем распоряжении два геометрических
места изобразятся следующими уравнениями:
y = hAy
а2 82 1'
(4)
(5)
Первое из них представляет прямую rf, параллельную основанию
треугольника. Второе — гиперболу, определяемую условием b — с = т.
Полуоси α и β гиперболы и половина ее фокусного расстояния γ
следующим образом выражаются через данные задачи:
~2У
а
β2 = Υ2
-α*.
62
Решая совместно уравнения (4) и (5), получим абсциссу χ точки А
в следующей форме:
*=±ууТ+лГ· (6)
Построение абсциссы χ по формуле (6) распадается на три этапа:
1) построение β как катета прямоугольного треугольника по
гипотенузе γ и второму катету α
причем
а т
2) построение выражения
входящего в формулу (6), т. е. построение гипотенузы Ь по двум
катетам β и hA прямоугольного треугольника;
3) построение абсциссы χ по формуле
Все эти построения выполняются циркулем и линейкой. Таким
образом, мы получаем абсциссу χ и ординату y=hA вершины А
треугольника.
Исследование.
Совершенно очевидно, что в рассматриваемом варианте задачи
необходимым условием существования решения является требование
Ъ — с<^а,
или
так как такое условие обязательно для всякого треугольника. Вместе
с тем, как видно из чертежа 46, это условие является и
достаточным. В самом деле, при любом значении высоты hA прямая d
пересекает гиперболу (в двух точках); следовательно, при соблюдении
этого условия решение всегда существует. Обе параллели,
составляющие первое геометрическое место, пересекают гиперболу в четырех
точках, одной из которых является упомянутая точка Л, а три
остальные точки определяют треугольники, симметричные
треугольнику ABC. Поэтому можно считать, что задача имеет одно решение,
если выполнено условие b — с<^а.
3. Даны основание а и высота hA треугольника, а также
сумма квадратов двух других сторон Ь2-{-с2=р2. Требуется
построить треугольник.
63
Анализ.
Если в числе других данных задан отрезок KL, имеющий длину рг
то последнее условие задачи (Ь2 -\- с2 = р2) утверждает, что стороны
Ь и с треугольника являются катетами прямоугольного треугольника,
гипотенузой которого служит данный отрезок KL=p. Этому
требованию можно придать наглядно-геометрическую форму. На отрезке/?,
как на диаметре, строим окружность (черт. 47); тогда для любой
Υ
— X
Черт. 47.
Черт. 48.
точки Μ этой окружности сумма квадратов ее расстояний до концов
отрезка KL равна р2. Следовательно, отрезки МК и ML
удовлетворяют требованию задачи относительно сторон b и с.
Рассмотрим теперь условия задачи в их совокупности. Расположим
оси координат так же, как и в предыдущих случаях (черт. 48).
Тогда условие, наложенное на стороны b и с, может быть выражена
следующим образом:
АВ2 + АС2=р2,
или
*+fI+У+
(-1)'+*
Производя упрощения в этом уравнении, получим:
2*2 + 2у + |-2 = р*.
Делим обе части уравнения на 2 и вводим обозначение
2 4
64
Тогда написанное выше уравнение примет вид:
х*+у* = г*. (7)
Уравнение (7) показывает, что в данном случае геометрическим местом
Еершины А искомого треугольника служит окружность с центром
в начале координат О и радиусом г
1/2 4
Таким образом, решение задачи сводится к отысканию точек^
пересечения обоих геометрических мест: прямой d, параллельной
оси ОХ, и окружности (7).
Построение.
На чертеже 48 имеются все данные: основание искомого
треугольника ВС = а, высота hA и отрезок ОР=р. Для построения
' |/ 2 4
радиуса г=\/ ^ — окружности проделаем следующие операции.
Строим на отрезке ОР, как на диаметре, окружность и в ней
сторону квадрата OQ. Тогда
OQ=OMV2 = ^V2 = -^r.
у Ζ
Далее на отрезке OQ, как на диаметре, строим окружность и
откладываем OR=OC= —. Получается прямоугольный треугольник OQRy
в котором OQ служит гипотенузой. Катот с^ этого треугольника
выразится следующим образом:
Таким образом, проводя из О окружность радиуса QRy находим
искомое геометрическое место. Точка пересечения его А с прямой d
определяет третью вершину треугольника.
Доказательство.
Предлагаем читателю произнести проверку построения. Для этого
следует найти координаты точки А пересечения обоих геометрических
мест (окружности х2Л-у2 = г2 и прямой v — hA) и доказать, что
ЛЯ2 + АС~ = р*.
Исследование.
Очевидно, что для существования решения задачи необходимо ir
достаточно, чтобы прямая d пересекала окружность (О, г) (или
касалась последней). Это будет иметь место, если
или
65
Так как радиус г должен иметь действительное значение, то должно
быть
2^4'
ЛЛИ
Р>
V2
При выполнении этих условий для р, а и hA задача имеет решение.
Ввиду симметричности чертежа можно сказать, что задача имеет
единственное решение, так как все остальные точки пересечения дают
треугольники, конгруэнтные или симметрично-конгруэнтные первому.
4. Даны основание а и высота hA треугольника, а также
разность квадратов двух других сторон Ь2— с2 = р2. Требуется
построить треугольник.
Анализ.
Первое геометрическое место остается неизменным во всех
вариантах задачи — это пара прямых, параллельных основанию ВС
треугольника. На чертеже 49
изображена одна из этих прямых—d.
Переходим ко второму
условию. Оно выражает требование,
чтобы разность квадратов
расстояний точки А до фиксированных
точек В и С имела данное
значение (Ь2—£2 = р2). Согласно § 13,
совокупность точек,
удовлетворяющих этому требованию, образует
прямую, перпендикулярную к
прямой ВС. Чтобы построить эту
прямую» представляющую второе геометрическое место, достаточно
определить точку Ρ ее пересечения с прямой ВС. Точка Ρ как
принадлежащая геометрическому месту должна удовлетворять условию
Черт,
или
РС1 — РВ'1 = р2,
(PC + РВ) (PC — РВ) =р2.
(8)
Предположим, что среди остальных данных задачи имеется отрезок
MN=p.
Если точка Ρ лежит внутри отрезка ВС, то имеем, очевидно,
РС + РВ = а,
и равенство (8) примет вид:
РС — РВ = £~.
а
(9)
(9*)
66
Если же точка Ρ лежит вне отрезка ВС, то
РС — РВ = ау (10)
и равенство (8) перепишется так:
Р2
РС-\-РВ=£~. (Ю*)
Таким образом, в первом случае для определения Ρ мы имеем
равенства (9) и (9*), причем в этом случае должны иметь1)
^Р2
а р> — , или а ^> р.
Во втором случае будем иметь два равенства (10) и (10*), причем
необходимо выполняется условие
— >я, или pj>a.
Наконец, в случае, когда точка Ρ совпадает с вершиной В2), будем
иметь:
ЯВ=0, РС + РВ = РС — РВ,
или
Р2
- = *, р = а.
Построение.
1) Предположим, что из двух данных отрезков ВС = а и ΜΝ—ρ
первый меньше второго:
£C</WV,
или
Тогда точка Ρ должна лежать вне отрезка ВС и, конечно, левее
точки В, так как
PC2 — РВ2=р*>0.
Для построения точки Ρ воспользуемся формулами (10) и (10*).
РС — РВ = а,
РС+РВ=·^ .
1 а
Р2
Отрезок х = — легко строится, а затем по сумме (х) и разности
1) Так как сумма двух отрезков должна быть больше их разности.
2) Предлагаем читателю на основании сказанного установить область
возможных положений точки Ρ на прямой ВС.
6*
(α) двух отрезков находятся самые отрезки. Мы знаем, что решение
существует, если
как это и имеет место в нашем случае. По отрезку РВ (или PC)
строим точку Р. После того как точка Ρ построена, проводим через
нее перпендикуляр к прямой ВС — получим искомое геометрическое
место. Точка А пересечения этого перпендикуляра с прямой d и есть
искомая вершина тре-
mrf угольника.
На чертеже 50
выполнено построение:
SC=TC = py
TC-SC
ВС
= Г-=в'С.
Тогда
Черт, 50.
В самом деле, будем иметь:
BP=2£=pir.
РС-\-РВ = РС + РВ' = —,
РС — РВ = ВС = а.
2) Если отрезок ВС больше MN, т. е.
то точка Ρ должна лежать внутри отрезка ВС и построение
упрощается.
В самом деле, в этом случае
а
2~
РВ-\-РС = а и РВг
(так как РВ^РС).
Следовательно, если Р' какая-нибудь точка нашего
геометрического места (перпендикуляра к ВС в точке Р), то будем иметь:
р'вурв.
Поэтому мы можем утверждать, что окружность с центром В
радиуса Р'В всегда пересечет наше геометрическое место
(перпендикуляр к ВС в точке Р).
Выберем Р'В произвольно, но больше -^-. Тогда имеем:
р'С* = р* + Р'В\
4В
Таким образом, Ρ'С строится как гипотенуза прямоугольного
треугольника (по катетам ρ и Р'В). Имея отрезки Р'В и PC, делаем
засечки из точек β и С и находим точку Я' искомого
геометрического места. Последнее представляет перпендикуляр, опущенный из
р' на прямую ВС. На чертеже 51 для простоты отрезок Р'В выбран
равным основанию а. Так что
ВР' = ВС = а.
Тогда Р'С находится как гипотенуза прямоугольного
треугольника DBCy в котором катеты
Следовательно,
BD = p и ВС = а = ВР'.
Р'С = DC.
Проводя из центров В и С окружности радиуса ВР' = ВС и
CP' = CD, находим точку их пересечения Я', которая является,
очевидно, точкой искомо- р'
го геометрического места.
Последнее получаем,
опуская из Я'
перпендикуляр Р'Р на прямую ВС.
3) Если MN=BC или
р = а, то будем иметь:
' РС+РВ=РС—РВ=а.
Иными словами, РВ=0.
Таким образом,
геометрическое место
проходит через вершину Ву и
треугольник ЛВС
является прямоугольным. Для его построения восставляем перпендикуляр
к ВС в точке В и находим точку А пересечения его с прямой d.
Очевидно, будем иметь:
/f
Ά
Ρ
k
в
l<*f
[_ Ε
жх
\\\ h
1
1
-а Л?
Черт. 51.
АС2 — АВ2 = ВС\
или
Ь2 — С2 =
с2 = а2=р2.
Исследование.
При всяких а и р, а именно:
или
я</>,
как было показано только что, может быть построена точка Я
пересечения искомого геометрического места с прямой ВС. Следовательно,
геометрическое место, определяемое условием Ь2— с2=р29
существует всегда. Так как оно представляет собой прямую,
перпендикулярную к ВС, а второе геометрическое место прямую d, параллельную
ВС, то точка пересечения А обоих мест существует всегда. Таким
образом, задача всегда имеет решение и притом единственное1).
5. Даны основание а и высота hA треугольника, а также от-
& ^ ^ -
ношение двух других сторон — = λ. Требуется построить
треугольник.
Анализ.
В этом варианте задачи легко определяются оба геометрических
места. Условие постоянства отношения сторон Ь и с (— = Х]яв-
ляется требованием, чтобы расстояния вершины А искомого
треугольника до двух других его вершин находились в постоянном
отношении (λ). Согласно §14, геометрическое место точек А,
удовлетворяющих этому условию, есть окружность Аполлония. Точка
пересечения этой окружности с прямой d дает вершину А искомого
треугольника.
Построение.
Как видно из анализа, дело сводится к построению окружности
Аполлония. Если λ задано геометрически отношением отрезков BP:PQ,
которые для простоты мы предполагаем отложенными на какой-нибудь
прямой ВРУ проходящей через точку В, то, соединяя Q с С и
проводя PM\\QC, найдем точку Μ (черт. 52), для которой
ВМ_ВР_
МС~ PQ~ *
Затем откладываем PQ'z=PQ и соединяем Q' с С. Если теперь
проведем PN\\Q'C, то определим на прямой ВС точку N. При этом
будем иметь:
BN_ BP _
CN~Q'P~
Точки Μ и N делят отрезок ВС в отношении λ внутренним и внеп>
ним образом. Они гармонически сопряжены относительно β и С
1) Второе решение: точка пересечения перпендикуляра к ВС со второй
параллелью дает треугольник, симметричный первому относительно ВС.
70
(§ 14). Как известно (§ 14), отрезок MN является диаметром искомой
аполлониевой окружности. Строя последнюю и находя точки ее
пересечения с прямой dy получим два решения: треугольник ВАС и
треугольник ВАС.
Доказательство предоставляем провести читателю.
Исследование.
При любом λ (заданном геометрически отношением отрезков
BP'.PQ) можем построить точки Μ и N и затем окружность Лпол-
лония. Следовательно, вопрос о возможности решения сводится к
существованию общих точек у окружности Аполлония и прямой d. Это
будет иметь место, если радиус окружности не меньше высоты hA
искомого треугольника.
Найдем выражение радиуса г аполлониевой окружности через
данные задачи:
MN MC + CN
г=_ = —ψ—. (11)
Следовательно, нужно выразить МС и CN через α и λ:
ВМ-\-МС = а,
ВМ а
МС* ~ МС\
или
Отсюда
λ 4-1— —
мс=, а
λ+ι·
Аналогичным образом имеем:
ΒΝ — СМ = а,
ВМ_ _а_
CN CN'
или
λ-1-—
откуда
а
CN = -
λ —Г
Подставив найденные выражения МС и CN в формулу (11), получим:
1
ша_ /__!_ ι __1_\ а\
"2 U-t-Mi^Tj-i^T
71
Таким образом, для существования решения задачи необходимо
и достаточно, чтобы
ак
й=1^Н+ (12)
Как видно из чертежа, при выполнении условия (12) будем иметь
два решения, если г^>/гд, и одно решение, если r = hA. Решения,
связанные со второй параллелью, дают треугольники, симметричные
с найденными.
6. Даны основание а и высота hA треугольника, а также
произведение двух других сторон b-c = k2. Требуется построить
треугольник.
Анализ.
Условие, наложенное на стороны Ъ и с треугольника, показывает,
что вершина А должна лежать на кривой, называющейся „овалом
Кассини" (§ 15). Уравнение этой кривой, если оси координат имеют
расположение, показанное на чертеже 53, примет вид:
(*,-т)+2(х>+т)у,+:у4=*4' (13)
где через а обозначено данное основание искомого треугольника,
а через k2 — постоянная величина произведения двух других сторон.
Будем предполагать, что эта константа в геометрической форме
задана отрезком, равным k. Таким образом, задача сводится к
построению точек пересечения овала Кассини (13) и прямой d>
параллельной оси Ох (черт. 53). Уравнение этой прямой имеет вид:
у = НА. (14)
Подставляя значение у из формулы (14) в уравнение овала (13),
после несложных упрощений получим:
* + 3(^—)*+(**+£),-* = 0. (15)
Решая уравнение (15) относительно л:2, находим:
х2 =j — h\±^V — a*hA. (16)
Таким образом, дело сводится к построению абсциссы χ по
формуле (16).
Построение.
Перепишем формулу (16) в следующем виде:
Х2 + hA =J± V(k2 + a>tA) (*' - ahA)· (17>
Как видно из чертежа, левая часть этой формулы представляет собой
квадрат гипотенузы прямоугольного треугольника, катетами которого
72
•«лужат абсцисса χ и ордината hA вершины А искомого треугольника.
Но упомянутая гипотенуза ОА является в то же время медианой тА
искомого треугольника. Итак,
Построение медианы тА по формуле (17) мы разобьем на
следующие этапы:
Υ
Черт. 53.
а) построение отрезка / по формуле
l2 = ahA;
б) построение отрезков
n\ = k*-\-l\ п\ = № — Г-\
в) построение отрезка ρ по формуле
Р2 = пгп2 —^Р
и, наконец,
г) построение медианы тА
W1
= (|)2±Р2. (17*)
Все эти построения
выполнены на отдельном чертеже
(черт. 54).
Откладывая ВС=а и CE = hA, строим на отрезке BE, как на
диаметре, окружность. Если теперь в точке С восставим
перпендикуляр к прямой ВСУ то, очевидно,
Следовательно, CF=l.
CF2 = ahA.
73
Далее откладываем CK=FL = k. Тогда гипотенуза KF
прямоугольного треугольника KFC и катет CL прямоугольного
треугольника CFL могут быть выражены формулами:
KF2 = k2-\- /2, CL2 = k2 — /2,
т. е.
KF = nu CL = n2.
Откладывая после этого отрезок CM=KF = ni> строим на отрезке
ML, как на диаметре, окружность. Тогда отрезок СР определится
по формуле
СР2 = пгп2,
т. е.
СР=р.
Наконец, соединяя О (середина отрезка ВС) с точкой Я, находим,
что
ор*=оа + ср*,
или
ор2=(1)2+*г·
Из этой формулы видно, что ОР дает одно из двух возможных
значений медианы тА1).
Соответствующую этой медиане вершину А легко построить,
описывая из центра О окружность радиуса тА = ОР. Каждая из
точек пересечения этой окружности с прямой d является вершиной
искомого треугольника. Однако оба треугольника ЛВС и А'ВС
симметрично-конгруэнтны (черт. 53).
Доказательство того, что найденный треугольник удовлетворяет
условиям задачи, вытекает из самого метода решения.
Исследование.
Посмотрим, при каких условиях задача имеет решение.
Формула (17) показывает, что действительное значение для тА может
быть получено лишь при условии, если
k2
k2^ahAl или hA < —. (18)
Л Л а
Это необходимое условие.
k2 a
Если Лл = ~, то mA = j.
При этом я2 = 0, р = 0 и, как показывает формула (17*), оба
значения тА совпадают. Это значит, что точка Ах совпадает с
точкой А (черт. 53), т. е. прямая d* касается овала Кассини в точке Л*.
(ау
^Второе решение дает формула /и^=(—] — р'<
74
rflpn данных а и k высота hAi(i имеет в этом случае максимальное
значение: при больших значениях, т. е. когда hA^> — , задача не
имеет решения.
а
Легко построить точку Л*, принимая во внимание, что тА# = — .
k2
hA*~ — . Следовательно, Л* является точкой пересечения прямой d*
А а
i^ = —J и окружности с центром О и радиуса — . Условие,
полученное нами для высоты /гд, является необходимым. Если
присоединим к нему требование, чтобы /Ид^Лд, то получим достаточные
π k* а
. условия. Для максимального значения пА = — и /ид = — это дает:
a k2 , а /1Лч
— ^5 — , или k^—~. (19
2 α Ϋ2
если 6^^у=. При этом прямая у=1пА пересекает овал Кассини
Следовательно, условие (18) является необходимым и достаточным,
а
'FT
в четырех точках [уравнение (15) имеет четыре действительных корня].
Так как точки пересечения попарно симметричны (относительно оси
ординат), то имеется только два решения, например, треугольники ЛВС
k2
и А,ВС (черт. 53). При Лд = — прямая d(y = hA) касается овала
Кассини. Абсциссу точки прикосновения получаем из уравнения
т
2
±\f<
л-*л-
Граничный случай дает овал при /г = —=, для которого mA = hA.
Тогда для точки прикосновения л: = 0. Прямая d касается овала в его
вершине на оси OY. Соответствующее значение hA = —-. При этих
а а
значениях k = —T=_, /гд = — все четыре корня уравнения (15) равны
нулю, т. е. четыре точки пересечения прямой d с овалом совпадают
а
в вершине (на оси ΟΥ). Таким образом при k= —τ= задача имеет
V %
а
одно решение, если hA^ ~ (прямая d пересекает .овал Кассини в двух
а\
симметричных точках, которые сливаются при hA = —- 1 . При значениях
75
L4 a
k^> r~r= максимум ординаты (а следовательно, и высоты hA) всегда
V 2* *
имеем при лг = 0. В самом деле, при х = 0 получаем из
уравнения (15):
(Лл+тТ-&4=0·
или
Очевидно, возможен только знак -|-; следовательно,
h2A = b'-J- (20)
Это значение hA обращает в нуль свободный член уравнения (15) и дает
л;1 = л:2 = 0.
Сокращая уравнение (15) на л:2, получим:
!+з(
^-т.)=0· (21>
При k^>-j=.y как видно из формулы (20), h2A^> — и корни уравне-
у 2 4
ния (21) мнимы. Это значит, что касательная в вершине овала не имеет
более общих точек с овалом, т. е. формула (20) дает максимальное
CL
значение высоты /г.. Таким образом, для к^—?= необходимо и до-
А Ϋ2
статочно
/а2
k2—γ.
χ предполо
ресекает ов
При этих предположениях имеем одно решение задачи, так как
прямая d пересекает овал в двух симметричных точках, которые сли-
~а2
ваются при hA = 1/ к2 — — .
§ 18. ГЕОМЕТРИЧЕСКИЕ МЕСТА В ПРОСТРАНСТВЕ.
Переход от геометрических мест на плоскости к геометрическим
местам в пространстве позволяет педагогу развивать пространственное
воображение учащихся, сообщая им вместе с тем совершенно
необходимые элементарные сведения о простейших геометрических местах
в пространстве. Плохо, что в школьной программе этот вопрос не
нашел никакого отражения, и окончившие среднюю школу часто
показывают при поступлении в вуз слабое развитие пространственных
представлений.
76
Между тем переход от геометрических мест на плоскости к
геометрическим местам в пространстве вполне естественен и несомненна
может принести пользу в этом направлении.
Мы ограничимся здесь минимальными указаниями о тех „экскурсиях
в пространство*, которые были бы желательны при прохождении
геометрических мест.
В соответствии с геометрическими местами, рассмотренными в § 12,
возникает вопрос о геометрических местах в пространстве, как,
например:
1) Геометрическое место точек в пространстве, имеющих
постоянное расстояние δ от некоторой фиксированной точки О.
Это место есть сфера радиуса δ с центром в точке О.
Пример.
Найти геометрическое место точек, лежащих в данной
плоскости α и удаленных от данной точки О (не лежащей в плоскости а)
на постоянное расстояние δ.
Искомое геометрическое место представляет окружность, по
которой плоскость α пересекает сферу с центром О и радиусом δ.
Пусть учащийся сформулирует, при каких условиях существует
решение.
2) Геометрическое место точек в пространстве, имеющих
постоянное расстояние δ от фиксированной прямой а.
Искомое место представляет цилиндрическую поверхность, осью
которой служит данная прямая а, а ортогональным сечением —
окружность радиуса δ.
3) Геометрическое место точек, имеющих постоянное
расстояние δ от фиксированной плоскости а.
Это место состоит из двух плоскостей, параллельных плоскости а
и отстоящих от нее на расстояние δ.
Полезно комбинировать геометрические места, подобно тому, как
это сделано в нижеследующих примерах:
Примеры.
1. Найти геометрическое место точек в пространстве, имеющих
данное расстояние δ от двух данных точек А и θ.
Искомым местом является окружность — пересечение двух
сферических поверхностей, описанных из центров А и В радиусом δ.
Плоскость окружности перпендикулярна к прямой АВ.
Предложите учащимся сформулировать, при каких условиях
существует решение и когда оно обращается в точку.
2. Найти геометрическое место точек, удаленных на
расстояние δ от двух данных (пересекающихся) плоскостей α и β.
Искомое место состоит из четырех прямых пересечения двух пар
плоскостей, параллельных плоскостям аир.
Выяснить, как расположены эти четыре прямые по отношению
к плоскостям α и β и их линии пересечения.
77
3. Найти геометрическое место точек, расположенных на
расстоянии d от данной точки А и расстоянии Ь от данной плоскости а.
Место состоит, вообще говоря, из двух окружностей пересечения
пары плоскостей, параллельных плоскости а, и сферы с центром
в точке А.
Что можно сказать об условиях существования решения (две
окружности, одна окружность, окружность и точка и т. д.)? Как
расположены искомые места по отношению к данным в задаче?
Более сложные места получаются в следующих примерах:
4. Найти место точек, имеющих заданные расстояния от
данной прямой и данной плоскости (два эллипса).
5. Найти место точек в пространстве, имеющих заданные
расстояния от данной прямой и данной точки (пространственная
кривая четвертого порядка — линия пересечения сферической и
цилиндрической поверхностей).
6. Найти место точек в пространстве, имеющих заданные
расстояния от двух данных прямых (пространственная кривая
четвертого порядка — линия пересечения двух цилиндрических поверхностей).
4) Геометрическое место точек в пространстве, одинаково
удаленных от двух данных точек А и В.
Искомое место представляет плоскость, перпендикулярную к
прямой АВ и проходящую через середину отрезка АВ.
4 5) Геометрическое место точек в пространстве, одинаково
удаленных от трех данных точек А, В и С, не лежащих на одной
прямой.
Искомое место определяется как линия пересечения h плоскостей,
перпендикулярных к отрезкам АВ и ВС в их серединах. Третья
плоскость, перпендикулярная к отрезку АС в его середине, должна
проходить через прямую к. Прямая h может быть также построена как
перпендикуляр к плоскости ABC, проходящий через центр О
окружности, описанной около треугольника ABC.
Пример.
Найти геометрическое место точек, одинаково удаленных от
четырех данных точек А, В, С и Z), не лежащих в одной
плоскости, из которых никакие три не лежат на одной прямой.
Геометрическое место точек, одинаково удаленных от трех данных
точек Л, В и С, есть прямая /ζ, перпендикулярная к плоскости ABC
в центре окружности, описанной около треугольника ABC.
Геометрическое место точек, одинаково удаленных от точек С и D, есть
плоскость γ, перпендикулярная к отрезку CD в его середине.
Обозначим точку пересечения плоскости γ с прямой // буквой О. Тогда
точка О обладает тем свойством, что она одинаково удалена от
всех четырех данных точек Л, В, С и D. Других точек,
обладающих этим свойством, очевидно, не может быть. Отсюда можем
сделать следующие выводы.
Четыре точки пространства А, В, С и D, не лежащие в одной
плоскости и из которых никакие три не лежат на одной прямой,
^
определяют единственную, проходящую через них сферу. Иначе:
около тетраэдра ABCD можно описать шар, центр которого О
есть точка пересечения перпендикуляров к граням тетраэдра,
проходящих через центры описанных около этих граней окружностей.
6) Геометрическое место точек, одинаково удаленных от двух
данных плоскостей α и β.
Искомое место представляет две биссекториальные плоскости
двугранных углов, образованных данными плоскостями α и ji.
7) Геометрическое место точек, одинаково удаленных от
граней a, ji и γ данного трехгранного угла.
Искомое место представляет прямую g пересечения биссекториаль-
ных плоскостей двугранных углов данного трехгранного угла.
Задача. Определить центр S шара, вписанного в данный
тетраэдр ABCD.
Искомый центр 5 есть точка, одинаково удаленная от граней а„
β, γ и δ данного тетраэдра. Эту точку можно получить как точку
пересечения трех биссекториальных плоскостей двугранных углов
тетраэдра, не принадлежащих одному трехгранному углу. Очевидно,
что через точку 5 проходят б биссекториальных плоскостей,
соответствующих б ребрам (двугранным углам) тетраэдра х).
Ограничиваясь этими замечаниями относительно геометрических
мест в пространстве, отсылаем интересующихся геометрическими
построениями в пространстве к следующим источникам:
Η. Φ. Четверухин, Стереометрические задачи на
проекционном чертеже, Учпедгиз, 1951.
Л. М. Лоповок, Сборник стереометрических задач на
построение, Учпедгиз, 1950.
Η. Φ. Четверухин, Вопросы методологии и методики
геометрических построений в школьном курсе геометрии („Известия Акад.
педаг. наук РСФСР", 1946, вып. б).
!) Если учитывать также вневписанные шары, то можем иметь до 8
шаров, вписанных в тетраэдр.
Глава четвертая.
ГЕОМЕТРИЯ КРУГОВ
§ 19. СТЕПЕНЬ ТОЧКИ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ.
Понятие о степени точки, нашедшее широкое применение в
геометрии окружностей, было введено немецким геометром Якобом
Штейнером (Jakob Steiner,
1769—1863).
Предположим, что из
д / \а Z^r^-^У данной точки Μ
проведены прямые, пересекающие
данную окружность (О)
(черт. 55). Одна из них,
ч@ а именно прямая МО,
/t\*^ χ ^s^ J ' проходит через центр
окружности и пересекает
ее в точках Лий Точки
пересечения других
прямых с данной окружностью
Черт. 55. обозначим буквами Аи
&и А2> &2ι · · · Кроме
того, на чертеже 55 имеется касательная МТ.
По известной теореме элементарной геометрии будем иметь:
МА. MB = МА! · МВХ = МА2 · МВ2 = МТ* = const.
Рассматриваемое произведение отрезков секущей постоянно для
данной точки Μ и данной окружности (О). Эту константу и
называют степенью точки Μ относительно окружности (О). Мы будем
обозначать ее буквой С с двумя индексами, из которых верхний
указывает данную точку, а нижний данную окружность. Согласно этому,
будем иметь:
Со = МА · MB = /ИГ2 = const.
Обозначив радиус окружности буквой г, а расстояние точки Μ от
центра О буквой dy получим:
Co=MA-MB = (d + r)(d— r)=:d2 — г2. (1)
Формула (1) дает выражение степени точки через радиус
соответствующей окружности и расстояние до ее центра. Формула (1) будет
SO
справедливой во всех случаях, если введем понятие о знаке степени
точки.
В самом деле, для точки Λί, лежащей вне круга (О),
расстояние d^>r. Поэтому Со^>0. Для точки, лежащей внутри круга, d<V,
степень такой точки отрицательна: Со<^0. Наконец, для точки,
лежащей на окружности, d = r, и степень Со=0. Обратно: по
степени точки можем судить о ее положении относительно окружности.
Так, например, при отрицательной степени точка лежкт внутри круга
и т. д.
Отметим частный случай, когда точка Μ совпадает с центром О.
При этом d = 0 и, как показывает формула (1), Со = — г2.
§ 20. РАДИКАЛЬНАЯ ОСЬ.
Поставим следующую задачу: найти геометрическое место точек*
имеющих одинаковую степень относительно двух данных
окружностей.
Черт. 56.
На чертеже 56 изображены две данные окружности (Οχ) и (02).
Пусть Μ — какая-нибудь точка плоскости. Ее степень относительно
первой окружности выражается по формуле (1):
Со, = d\ — r\
и относительно второй окружности:
ГМ ,2 2
причем через du r{ и d2, гг обозначены расстояния точки Μ до
центров первой и второй окружностей и радиусы последних.
ах
Так как, по предположению, точка Μ должна иметь одинаковую
степень относительно обеих окружностей, то будем иметь:
или
di — r2=d2 г2
1 1 2 2*
Отсюда находим, что
d\ — d\ = r\ — r\ = const.
Таким образом, оказывается, что разность квадратов расстояний точки Μ
до данных точек Ох и 02 есть величина постоянная. В § 13 мы
видели, что геометрическое место точек М, обладающих этим
свойством, есть прямая, перпендикулярная к прямой 0\02. Эта прямая и
называется радикальной осью двух окружностей.
Пусть Μ какая-нибудь точка радикальной оси. Проведем из Μ
касательные МТ\ и МТ2 к той и другой окружностям (черт. 56).
Тогда степени точки Μ относительно этих окружностей выразятся
следующим образом:
с^=мт1 с%=мт\.
Но для точек радикальной оси обе степени равны; поэтому имеем:
или
МТХ=МТ2.
Мы получили характеристическое свойство радикальной оси:
касательные из любой точки
радикальной оси к обеим
окружностям равны.
Таким образом,
радикальную ось можно
рассматривать как геометрическое
место точек, имеющих равные
касательные к обеим
окружностям.
Построение радикальной
оси. Описанные выше .свойства
радикальной оси дают простые
способы ее построения.
Возможны три случая.
1) Окружности (Οι) и (02)
пересекаются (черт. 57). Тогда
точки пересечения Ρ и Q имеют нулевую степень относительно обеих
окружностей, а следовательно, они лежат на радикальной оси.
Поэтому прямая PQ и является радикальной осью данных окружностей.
2) Окружности (Οι) и (02) касаются (черт. 58). Пусть Τ — точка
прикосновения окружностей. Построим их общую касательную в точке 7\
Черт,
82
Рассмотрим произвольную точку /И этой касательной. Степень этой
^очки относительно первой окружности выразится так:
|а относительно второй:
Μ
Черт. 58.
Следовательно, для любой точки Μ прямой МТ будем иметь:
Отсюда заключим, что общая касательная МТ данных
окружностей в точке их прикосновения и является радикальной осью.
3) Окружности не
имеют общих точек (черт. 56).
Пусть прямая SXS2 —
общая касательная данных
окружностей. Точку ее
пересечения с
радикальной осью обозначим бук
вой Р. Тогда по свойств)
радикальной оси буде^
иметь:
C£=CS„
или
Р^ = РЩ;
значит:
PSX = PS2.
Отсюда получаем простой Черт. 59.
способ построения ради
кальной оси. Строим общую касательную SXS2 данных окружностей и
через середину Ρ отрезка ^52 проводим прямую РМ, перпендикуляр-
83
ную к линии центров Οχ02 (РМ _]_ 0χ02). Тогда прямая РМ и является
радикальной осью рассматриваемых окружностей.
Только что приведенный способ неприменим, если одна окружность
находится внутри другой и общей касательной не существует.
Поэтому мы дадим способ, применимый во всех случаях. Пусть (Οι) и
(02) — данные окружности, причем вторая находится внутри или вне
первой (черт. 59). Проведем произвольную новую окружность (О),
пересекающую обе данные. Тогда прямая PXQX есть радикальная ось
окружностей (О) и (Οι), а прямая P2Q2 является радикальной осью
окружностей (О) и (02). Пусть R есть точка пересечения прямых PxQt
и P2Q2. Тогда по свойству радикальной оси для точки R должно быть
одновременно
<$ = <$ С*о=С*о-
Следовательно, С$ =С$, и точка R лежит на радикальной оси
данных окружностей (Οχ) и (02). Поэтому для построения радикальной
оси достаточно из точки R опустить перпендикуляр RS на линию
•центров Ог02.
Примечание.
Если две данные окружности (Οχ) и (ОД концентричны, но не
тождественны, то для любой точки Μ имеем:
άλ = d2, причем ΤχφΓ*
Поэтому
Следовательно, не существует точек, имеющих одинаковую степень
относительно концентрических окружностей.
§ 21. РАДИКАЛЬНЫЙ ЦЕНТР.
В предшествующем параграфе мы уже встретились с построением
точки R (черт. 59), которая имеет одинаковую степень
относительно трех данных окружностей. Такая точка называется рада-
/сальным центром трех окружностей. Нетрудно видеть, что задача
о построении радикального центра имеет, вообще говоря, одно
решение. В самом деле, если имеем три окружности (Οχ), (02) и (03), то
радикальный центр R этих окружностей должен лежать на
радикальной оси каждой пары окружностей. Предположим, например, что
радикальные оси пар (Οχ), (02) и (02), (03) пересекаются в точке R.
Тогда для точки R будем иметь:
С*о=С1 ■ <& = <$·
Отсюда следует, что
а значит радикальная ось третьей пары окружностей (Οι), (08) также
проходит через точку R (черт. 60). Таким образом, радикальные оси
трех данных окружностей пересекаются, вообще говоря, в одной
точке — радикальном центре.
Этого может не быть лишь в одном из следующих случаев: а)
радикальные оси параллельны, Ь) они сливаются и с) они вообще не
Черт. 60.
существуют. В первом случае центры Оь 02 и 08 окружностей
расположены на одной прямой (черт. 61,а). Во втором случае имеем три
окружности одного пучка (§ 22), например, если они все три проходят
Черт. 61.
через две точки Ρ и Q (черт. 61,£). В третьем случае среди
окружностей имеются концентрические (черт. 61,с).
Пример.
Даны окружности (0{) и (02) и прямая g. На данной прямой найти точку,
из которой касательные к окружностям (Oj) и (02) равны.
85
Указание.
Искомая точка должна лежать на радикальной оси данных окружностей.
Произведите исследование задачи.
§ 22. ПУЧКИ ОКРУЖНОСТЕЙ.
Совокупность окружностей, имеющих попарно общую радикальную
ось, называется пучком окружностей.
В зависимости от того, пересекает ли радикальная ось окружности
пучка, касается их, или не пересекает и не касается, имеем три вида
пучков: эллиптический, параболический и гиперболический.
1. Эллиптический пучок окружностей.
Предположим, что (черт. 62) имеются две пересекающиеся
окружности. Точки пересечения окружностей обозначим буквами Ρ и Q.
Черт. 62.
Тогда, как мы видели (§ 20), радикальная ось данных окружностей
проводит через точки Ρ и Q. Следовательно, каждая новая окружность,
имеющая с одной из данных радикальной осью прямую PQ, должна
проходить через точки Ρ и Q, ибо степень этих точек относительно
данных окружностей равна нулю. Таким образом, эллиптический пучок
состоит из всех окружностей, проходящих через точки Ρ и Q. Эти
точки называются центрами пучка.
Из предыдущего видно, что две любые окружности эллиптического
пучка определяют его, так как определяют общую радикальную ось
и центры Ρ π Q.
Задание одной точки, через которую должна проходить окружность
пучка, вполне определяет эту окружность. В самом деле, пусть Μ
такая точка (черт. 62). Тогда окружность пучка должна проходить
через точки Р, Q и /W. Центр ее должен находиться на линии
центров, которой, очевидно, служит прямая Ολ02, перпендикулярная
к хорде PQ в ее середине. Поэтому, восставляя перпендикуляр
к хорде РМ (черт. 62) в ее середине, мы построим точку пересечения
его с линией центров. Эта точка О и является центром
окружности (Л4, Я, Q). В эллиптическом пучке имеется наименьшая
окружность, пли окружность наименьшего диаметра. Нетрудно видеть, что
86
такой окружностью является та, для которой общая хорда PQ служит
диаметром, т. е. центр которой находится в точке пересечения
радикальной оси PQ с линией центров Ох02. Всякая другая окружность
пучка больше минимальной,
так как для нее PQ служит
хордой и, следовательно, ее
диаметр больше PQ.
2. Параболический пучок
определяется двумя
касающимися окружностями.
Радикальной осью таких окружностей
служит общая касательная в
точке их прикосновения 7 (§21)
(черт. 63). Все окружности Черт. 63.
пучка касаются радикальной оси
в точке Т; в той же точке они касаются друг друга. Линия центров
Ολ02 также проходит через Г и перпендикулярна к радикальной оси.
Произвольная точка Μ (не лежащая на прямой 0{02 и радикальной
оси) определяет окружность параболического пучка. Центр ее находим,
восставляя перпендикуляр к хорде МТ в ее середине.
3. Гиперболический пучок.
Рассмотрим теперь случай двух окружностей, не имеющих общих
точек (черт. 64). В § 20 были даны способы построения радикальной
осп в этом случае.
Последняя не имеет общих
точек с окружностями
гиперболического пучка.
Покажем, как
построить окружность пучка,
проходящую через
данную точку М.
Через точку Μ
проводим произвольную
окружность (О), лишь бы она
Черт. 64. пересекала обе данные
окружности. Тогда точка
R есть радикальный центр окружностей (О), (Οχ) и (02). Проведем
прямую RM и обозначим вторую точку пересечения ее с окружностью
(О) через N. Нетрудно убедиться в том, что искомая окружность
пучка, определяемая точкой /И, должна проходить и через точку N.
В самом деле, точка /?, как радикальный центр, должна лежать на
общей радикальной оси пучка. С другой стороны, имеем:
Предположим, что искомая окружность (О') пересекает луч RM в
точках Μ и Ν'. Тогда должны иметь:
87
Сравнивая эти выражения степеней Cg и С#, видим, что они равны;
следовательно,
RN-RM=RN'.RM.
Отсюда и находим, что
RN = RN'.
Таким образом, вторая точка N' совпадает с Л/, и мы имеем хорду MN
искомой окружности. С другой стороны, как мы знаем, центр искомой
окружности О' должен лежать на прямой Οχ02- Отсюда цецтр О'
легко может быть построен с помощью перпендикуляра к хорде ΜΝ
в ее середине (черт. 64).
§ 2а НУЛЕВЫЕ ОКРУЖНОСТИ И ОРТОГОНАЛЬНЫЕ ТРАЕКТОРИИ
Точку можно рассматривать как окружность нулевого радиуса^ или,
коротко, „нулевую окружность". Если точка О —нулевая окружность
(г=0), то степень произвольной точки Μ относительно О выразится
по формуле (1) § 18, а именно:
C% = d* — r2 = d2 = OM2.
Следовательно, степень точки относительно нулевой окружности
выражается через квадрат расстояния от точки Μ до окружности, (или ее
центра О). Это замечание будет нам полезно в дальнейшем.
Посмотрим, какие пучки могут иметь в своем составе нулевые
окружности. Как мы видели в предыдущем параграфе, эллиптические
пучки не имеют нулевых окружностей, так как наименьшей
окружностью эллиптического пучка является окружность, диаметром которой
служит общая хорда PQ (черт. 62).
Для параболического пучка нулевой окружностью является точка
прикосновения Τ (черт. 63). В самом деле, степень произвольной точки
S радикальной оси параболического пучка относительно нулевой
окружности (Т) равна по предыдущему ST2. Но той же величиной выражается
степень точки S относительно любой окружности пучка, так как ST
касательна ко всякой окружности пучка. Следовательно, нулевая
окружность (Т) принадлежит к пучку, так как имеет общую с ним
радикальную ось TS.
Переходя теперь к гиперболическому пучку, мы должны учесть то
обстоятельство, что нулевыми окружностями могут быть лишь точки
линии центров. Это следует из того, что нулевая окружность
совпадает со своим центром, а последний для всякой окружности пучка
лежит на линии центров. Предположим, что Μ—какая-нибудь точка
радикальной оси гиперболического пучка (черт. 65). Степень этой
точки относительно окружности (Ог) равна квадрату касательной МТХ2.
Построим окружность радиуса МТ\ из центра М. Обозначим точки
пересечения этой окружности с линией центров буквами аир.
Нетрудно видеть, что точки а и β будут нулевыми окружностями
гиперболического пучка. В самом деле, степень точки Μ относительно
88
нулевой окружности (α) выражается величиной <хМ2 и равна степени
точки Μ относительно окружности (Oj), которая выражается
величиной МТ\. Следовательно, радикальная ось окружностей (а) и (Ох)
проходит через точку Μ и перпендикулярна к линии центров, т. е.
она совпадает с общей радикальной осью гиперболического пучка.
Аналогичное можно сказать и относительно точки β. Таким образом,
эти точки аир являются нулевыми окружностями гиперболического
пучка.
Чертеж 65 позволяет сделать ряд интересных выводов о так
называемых ортогональных траекториях. Построенная на этом чертеже
окружность радиуса МТХ с
центром в точке Μ является
такой ортогональной
окружностью. Действительно, радиус
МТХ упомянутой окружности
равен касательной, проведенной
из точки Μ к любой из
окружностей гиперболического пучка,
так как точка Μ имеет
одинаковую степень по отношению
ко всем этим окружностям. Но
это значит, что окружность (М)
пересекает все окружности
пучка ортогонально, так как
радиус окружности, проведенной
в точку пересечения, касается
каждой пересекаемой
окружности. Ортогональная окружность Черт. 65.
(М) проходит через нулевые
окружности (а) и (β), что, естественно, должно иметь место, так как
пересечение нулевой окружности сводится к прохождению через нее
окружности (М). Замечая, что точка Μ была выбрана на
радикальной оси произвольно, мы приходим к выводу, что точки радикальной
оси пучка являются центрами ортогональных окружностей, а
касательные из этих точек к любой окружности пучка — радиусами
ортогональных окружностей. Все ортогональные окружности проходят через
точки (а) и (jj) — нулевые окружности гиперболического пучка.
Следовательно, ортогональные окружности образуют в свою очередь
пучок, но уже эллиптический. Центрами его служат нулевые
окружности (а) и (β) гиперболического пучка.
Задача, очевидно, может быть обращена. Действительно, если бы
мы рассмотрели эллиптический пучок окружностей, пересекающихся
в точках α и β, то его ортогональными траекториями, очевидно,
явились бы окружности гиперболического пучка, для которого точки а и β
были бы нулевыми окружностями, радикальная ось aji — линией
центров Ох02у а линия центров МХМ—радикальной осью.
Таким образом, ортогональные траекторий эллиптического пучка
образуют гиперболический пучок, и обратно.
89
Рассмотрим вопрос об ортогональных траекториях для
параболического пучка.
Нетрудно убедиться, что и для параболического пучка его
радикальная ось является
геометрическим местом центров
ортогональных окружностей (черт. 66).
Так как касательная МТг равна
отрезку Ма> то все окружности
ортогонального пучка проходят
через точку а. В этой точке они
касаются друг друга и прямой
0\02. Последняя является их
общей радикальной осью. Таким
образом, пучок, ортогональный
параболическому, также
является параболическим.
§ 24. ПРИМЕРЫ.
1. Построить окружность, проходящую через данную точку А
и касающуюся данной прямой t в данной точке В.
Анализ.
Совокупность всех окружностей, касающихся прямой t в данной
точке В> образует параболический пучок. В задаче требуется выбрать
из пучка ту окружность, которая проходит через точку А.
Предположим, что окружность построена и удовлетворяет условиям задачи
(черт. 67). Тогда OB}_t и OL \_АВ, причем AL = LB.
А
Построение.
Строим прямые ВО и LO. Точка О их пересечения есть искомый
центр.
Дока зательство.
Очевидно, что найденная окружность удовлетворяет условиям задачи.
Исследование.
Прямые ВО и LO не пересекаются лишь в случае, если точка А
лежит на прямой t. Тогда решение невозможно. В остальных случаях
всегда имеем одно решение.
В частности, если точка А лежит на прямой ВО J_ t, то отрезок В А
является диаметром искомой окружности (черт. 68).
90
2. Даны точки Л и В и прямая t. Требуется построить
окружность, проходящую через точки А и В и касающуюся
прямой t.
Анализ,
Окружности, проходящие через точки А и В, образуют
эллиптический пучок. В задаче требуется выбрать из пучка ту окружность,
которая касается прямой t.
Предположим, что задача
решена и искомая окружность
построена (черт. 69). Точку
ее касания с прямой
^обозначим буквой Т. Проведем
секущую АВ. Точку пересечения
прямых t и АВ обозначим бук- f
вой С. Тогда будем иметь: С Τ
СС = СА.СВ=СТ*. ЧеРт· 69·
Таким образом, отрезок СТ может быть построен.
Построение.
Для построения отрезка СТ воспользуемся свойством радикальной
оси. Строим произвольную окружность (О'), проходящую через точки А
и В (черт. 69). Тогда
прямая АВ являетск
радикальной осью
окружностей (О) и (О').
Поэтому степень точки
С относительно обеих
окружностей одинакова
и отрезок касательной
СТ к окружности (О)
равен отрезку СТ ка-
/ сательной к
окружности (О'). Проводим
касательную СТ' и из
точки С описываем
окружность радиусом СТ. Точки пересечения ее с прямой t обозначим
буквами Тх и Тг. Искомая окружность определяется точками А, В и
Тх или Л, В и Т2. Ее нетрудно построить (черт. 70).
Доказательство.
Обе построенные окружности (Л, В, Τ χ) и (Л, В, Т2) принадлежат
к эллиптическому пучку с центрами А и В. Окружность (С, СТ)
(черт. 70) является их ортогональной окружностью, поэтому прямые
СТХ и СТ2 должны быть касательными к соответствующим окружностям.
Следовательно, построенные окружности удовлетворяют условиям
задачи.
Исследование.
Вопрос о существовании решений и о числе их зависит от
расположения данных точек А и В и прямой t на плоскости чертежа.
91
Если точки А и В расположены по одну сторону от прямой t,
причем АВ^^ то имеем два решения задачи, как на чертеже 70.
Если AS || f, то имеем только одно решение (черт. 71), которое
в этом случае находится следующим образом !). Прямая ОТ,
перпендикулярная к АВ и проходящая через середину этого отрезка, определяет
точку касания Т. Затем строим центр окружности О.
Если одна из точек А и В лежит на прямой t, то задача
принимает формулировку предшествующей задачи (пример 1° настоящего
параграфа).
Если обе точки А и В лежат на прямой t, то задача, очевидно,
невозможна.
Наконец, если точки А и В лежат по разные стороны от прямой t,
то, как нетрудно видеть, задача также невозможна. В самом деле,
в этом случае всякая окружность, проходящая через А и В,
пересекает прямую t (черт. 72), которая, следовательно, не может быть
касательной, как это требуется в условии задачи.
§ 25. СВЯЗКИ ОКРУЖНОСТЕЙ.
Рассмотрим совокупность окружностей, относительно которых
данная точка имеет одинаковую степень. Такая совокупность называется
связкой окружностей.
Данная точка является, очевидно, радикальным центром любых трех
окружностей связки. Мы будем ее называть поэтому радикальным
центром связки.
В зависимости от степени радикального центра относительно
окружностей, составляющих связку, различаются три вида связок. Если
степень радикального центра положительна, то связка называется
гиперболической, при отрицательной степени эллиптической;
наконец, если степень равна нулю,— параболической.
1. Гиперболические связки.
Предположим, что даны окружность (Οχ) и точка /?вне ее (черт. 73).
Точка R имеет положительную степень относительно окружности (Οχ),
выражающуюся квадратом отрезка касательной:
с2,=л7£
1) Общий способ в этом случае неприменим, так как прямые АВ и t не
пересекаются.
92
Пусть (02) — окружность, относительно которой точка R имеет ту же
степень
Но так как
где RT2— отрезок касательной из точки R к окружности (02), то
RT2 = RTt.
Следовательно, касательные из точки R ко всем окружностям
связки должны быть равны. Опишем из точки R окружность
радиуса RT2. Она пройдет через все
точки прикосновения касательных
из R к окружностям ^связки, а
значит, пересечет все эти окружности
ортогонально. Будем называть
построенную ортогональную
окружность с центром в точке R
базисной окружностью связки. Тогда
гиперболическую связку можно
рассматривать как состоящую из
окружностей, ортогональных к
базисной.
Ясно, что каждая окружность,
ортогональная к базисной,
принадлежит данной гиперболической связ- Черт. 73.
ке, так как точка R имеет
относительно нее степень, равную квадрату радиуса базисной окружности.
Таким образом, гиперболическую связку можно задать ее
базисной окружностью.
Проанализируем состав
гиперболической связки.
Пусть окружность (R, RT)
является базисной (черт. 74).
Проведем к ней касательную
в точке Г. Тогда, принимая
эту касательную за линию
центров, можем построить
параболический пучок окружностей,
соприкасающихся в точке Г.
Прямая RT будет общей
касательной и радикальной осью
пучка.
Все окружности (Ог), (02),
Черт. 74. (Од), . .., входящие в состав
параболического пучка,
пересекают базисную окружность ортогонально. Следовательно, пучок
полностью принадлежит гиперболической связке. Можно сказать,
93
что две окружности (О,) и (02) связки, соприкасающиеся в точке Т,
определяют параболический пучок, принадлежащий связке.
Подобным же образом две окружности (Ot) и (02) связки, не
имеющие общих точек, определяют гиперболический пучок,
входящий в состав связки (черт. 75). Радикальной осью этого пучка
служит диаметр базисной
окружности,
перпендикулярный к линии центров 0\02.
Точки пересечения аир
базисной окружности с
линией 0\02 являются
нулевыми окружностями
гиперболического пучка. В
самом деле, базисная
окружность служит ортогональной
окружностью
гиперболического пучка (§ 23).
Лее окружности (02) и
Черт. 75. (Од) связки, пересекающиеся
в точках PuQ, определяют
эллиптический пучок окружностей, принадлежащий связке. Ясно,
что каждая окружность, проходящая через точки Ρ и Q, пересекает
базисную окружность ортогонально.
Таким образом, в состав связки входят пучки всех трех типов.
Посмотрим, сколько точек определяют окружность,
принадлежащую к гиперболической связке.
Предположим, что связка
задана своей базисной окруж
ностью (R, RT) (черт. 76).
Докажем, что две произвольные
(не лежащие на одном диаметре
базисной окружности) точки
А и В определяют
окружность связка. Проведем через
точку А какую-нибудь
окружность связки. Такую
окружность легко построить.
Например, можно воспользоваться
окружностью (0\ О'Т)
параболического пучка, принадлежа- Черт. 76.
щего связке. Тогда точка
пересечения А' этой окружности с прямой RA должна принадлежать
искомой окружности, как и вообще всякой окружности связки,
проходящей через точку А. В самом деле, имеем:
RA'.RA = RT* = C%.
Окружность (О), проходящая через три точки Д 5и А\
является искомой.
94
2. Эллиптические связки.
Предположим, что окружность (Οι) принадлежит связке,
радикальный центр которой R лежит внутри окружности (черт. 77).
В этом случае точка R имеет отрицательную степень относительно
окружности (Ох) (§ 19).
Проведем в окружности (Ох) хорду ΜΝ, перпендикулярную к
отрезку 0{R. Степень точки R относительно (Οι) равна
c8t = RM.RN=— r\
где через г обозначена половина длины хорды MN. Построим на
отрезке MN, как на диаметре, окружность. Можно сказать, что
окружность (Οι) пересекает окружность (R) по диаметру последнего и
делит ее пополам. Для краткости мы
будем говорить в таких случаях, что
окружность (Ох) пересекает
окружность (R) диаметрально. Нетрудно
убедиться в том, что все окружно
сти, пересекающие диаметрально ок
ружность (/?), принадлежат к одной
связке. Окружность (R) является
базисной окружностью связки.
Пусть, например, окружность (02)
пересекает базисную окружность (R)
по диаметру PQ. Тогда имеем:
C%% = RP.RQ = — r*.
Следовательно, окружность (02)
принадлежит к той же, что и окружность
(Ot), эллиптической связке с радикальным центром R и степенью —г2.
С другой стороны, если окружность (03) принадлежит к той же
связке, то легко убедиться, что она пересекает базисную окружность
диаметрально. В самом деле, обозначим точки пересечения обеих
окружностей буквами U и V. Проведем прямую UR и обозначим
вторую точку пересечения ее с окружностью (08) через W (на чертеже
последнее построение не проводится). Тогда должны иметь:
Co9 = RU.RW=—r2.
Но так как \RU\ = r, то и \RW\=r. Отсюда и заключаем, что
точка W должна лежать также на базисной окружности, т. е.
совпадать с V. Следовательно, точки U, V и R лежат на одной прямой
и хорда UV является диаметром базисной окружности.
Таким образом, установлено, что эллиптическую связку можно
рассматривать как совокупность окружностей, пересекающих
базисную окружность диаметрально.
Посмотрим, какие пучки окружностей могут входить в состав
эллиптической связки. Так как радикальный центр связки R должен
лежать на радикальной оси такого пучка и притом внутри
окружностей, составляющих связку, то такому условию удовлетворяют только
93
эллиптические пучки. В самом деле, только в эллиптическом пучке
радикальная ось пересекает окружности пучка. Итак, в состав связки
входят лишь эллиптические пучки окружностей.
Убедимся теперь в том, что две точки, не лежащие на диаметре
базисной окружности, определяют окружность эллиптической связки.
Решение задачи аналогично приведенному ранее в случае
гиперболической связки.
Пусть (/?, RM)—базисная окружность связки (черт. 78), А, В—
данные точки.
Строим произвольную окружность (О'), принадлежащую связке и
проходящую через точку А (черт. 78). Для этого проводим
произвольный диаметр MN' базисной окружности и находим центр О'
окружности, проходящей через точки М\ N' и А. Построенная
окружность (О'), очевидно, принадлежит данной связке, так как
пересекает ее базисную окружность (R) диаметрально. Проводим, далее,
прямую AR и отмечаем вторую точку пересечения ее с
окружностью (О'). Обозначим последнюю буквой А'. Тогда будем иметь:
RA · RA = С& = RAT · ЛАГ = — г2.
Отсюда следует, что каждая окружность данной связки, проходящая
через точку А, должна пройти и через сопряженную с ней точку А'.
Поэтому искомая окружность (О) определяется тремя точками: А,
А' и В.
Примечание.
Сама базисная окружность также принадлежит эллиптической связке,
так как степень центра R относительно нее равна—г2.
3. Параболическая связка.
Предположим, что радикальный центр R связки лежит на
окружности (Ох) (черт. 79). Тогда имеем параболическую связку
окружностей, проходящих через точку /?. Степень точки относительно всех
окружностей связки равна нулю. Так как каждые две окружности
связки пересекаются в точке /?, то в состав параболической связки
не могут входить гиперболические пучки. Связка содержит лишь эл-
96
липтические [окружности (02) и (03)] и параболические
[окружности (04) и (05)] пучки. Две точки А и В, не лежащие на одной прямой
с радикальным центром /?, определяют окружность параболической
связки. Это очевидно, так как искомая окружность должна проходить
через точку R [на чертеже 79 окружность (Οδ)].
Заметим, что базисная окружность вырождается в случае
параболической связки в точку — радикальный центр R. Поэтому задание
последнего вполне определяет связку как совокупность окружностей,
проходящих через точку R *).
Из всего сказанного о связках (гиперболическая, эллиптическая
и параболическая) видно, что базисная окружность (в случае
параболической связки—точка) вполне определяет связку.
Поэтому связка определяется также тремя своими окружностями.
В самом деле, данные три окружности определяют радикальный центр
и степень связки, т. е. центр и радиус базисной окружности.
§ 26. ПРИМЕРЫ.
1. Через данную точку А провести окружность, касающуюся
данной окружности (О, ОБ) в данной точке В.
Решение задачи не представляет никаких затруднений. Центр
искомой окружности должен лежать на нормали ОВ. Его легко
построить, имея хорду АВ (черт. 80).
Способ построения показывает, что задача имеет одно решение.
Точка А может лежать вне или внутри данной окружности. Если же
она лежит на окружности, то
искомая окружность совпадает с
данной2). Задача не имеет решения,
если точка А лежит на
касательной t к окружности в точке В.
Если точка А лежит на нормали
ОВ, решением служит окружность
с центром в середине отрезка АВ.
2. Построить окружность,
касающуюся данной окружности
(О) и проходящую через данные
точки А и В.
Анализ.
Предположим, что на чертеже Черт. 80.
81 имеются данные в задаче точки
А и В, окружность (О), а также искомая окружность (О'),
удовлетворяющая услоьиям задачи.
1) Относительно трех геометрических систем — эвклидовой, римановой и
Лобачевского, — интерпретируемых с помощью параболической,
эллиптической и гиперболической связок окружностей, см. Ч е τ в е ρ у χ и н, Введение
в высшую геометрию, стр. 189.
2) Если же точка А совпадает с точкой Ву то решением будет служить
любая окружность, центр которой расположен на прямой ОВ.
97
Окружность (О') принадлежит эллиптическому пучку окружностей,
определяемому точками А и^#. Этот пучок (АВ) вместе с данной
окружностью (О) определяет связку. Построим базисную окружность
упомянутой связки. Радикальный центр связки должен лежать на
радикальной оси АВ пучка и на радикальной оси окружностей (О) и (О').
Но последней является общая касательная YR этих окружностей.
Точка пересечения прямых АВ и YR и представляет собой радикаль-
Черт. 81. Черт. 82.
ный центр R. Степень его относительно окружностей связки можно
выразить следующим образом:
C* = RA.RB = RT'2.
Теперь ясно, что окружность радиуса RT' с центром в точке R
является базисной. Точка прикосновения Υ искомой окружности
лежит на базисной окружности.
Построение.
Как видно из анализа, необходимо построить базисную окружность
связки. Для этого поступим следующим образом. Проводим
произвольную окружность (Ог) пучка АВ (черт. 82). Строим радикальную ось PQ
окружностей (О) и (Ох). Находим точку R пересечения прямых PQ
и АВ. Из R проводим касательную RT к данной окружности (О).
Строим базисную окружность (/?, RT). Последняя пересекает данную
окружность (О) в точках Υ и Г". Каждая из точек Υ и Г", будучи
точкой прикосновения искомой окружности к данной, определяет
решение. Таким образом, получаем два решения: окружность (0\ АВТ)
и окружность (О", АВТ").
Доказательство.
Построенные окружности, очевидно, удовлетворяют условиям
задами. Они проходят через данные точки А и В. В точках Υ и Υ
эти окружности касаются данной окружности (О). Если бы этого не
было, то степень точки R относительно построенных окружностей (О')
и (О") не была бы равна RY2 = RY2.
98
Исследование.
Как показывает чертеж (черт. 82), в общем случае имеем два
решения задачи. При этом необходимо предполагать, что точки А и В
обе лежат либо внутри, либо вне данной окружности. В самом деле,
если одна из них лежит внутри, а другая вне данной4 окружности,
то решение, очевидно, невозможно, так как в этом случае всякая
окружность, проходящая через данные точки А и В, непременно
пересечет данную окружность (О), т. е. не может служить решением
задачи х).
Примечание,
Совершенно аналогичны рассмотренной задаче следующие две:
1) Построить окружность, касающуюся данной окружности (О), а
также данной прямой а в точке А последней.
2) Построить окружность, касающуюся двух данных окружностей,
притом одной из них в данной точке А.
Все различие с разобранным выше примером сводится к тому, что
искомая окружность будет теперь принадлежать к параболическому пучку,
радикальной осью которого служит прямая а или касательная к данной
окружности в точке А. Метод решения тот же. В общем случае имеем два
решения.
3. Найти геометрическое место точек прикосновения всех
окружностей, касающихся данной плоскости и проходящих через две
данные точки, не лежащие в этой плоскости.
Пусть α — данная плоскость, А и В—данные точки (черт. 83).
Продолжим прямую АВ до пересечения с плоскостью а. Точку пере-
Черт. 83.
сечения обозначим буквой 5. Предположим, что {АВТХ)—одна из
касающихся окружностей. Тогда прямая STU соединяющая точку S
с точкой прикосновения окружности Г|, есть, очевидно, касательная
к этой окружности, так как она является линией пересечения пло-
1) Если одна из данных точек лежит на окружности, то задача сводится
к предшествующей (1).
99
скости окружности с касательной к ней данной плоскостью а. При
этом будем иметь:
ST\ = SA-SB = const.
Будем проводить через точки А и В различные окружности,
касательные к плоскости а. Точки прикосновения их с плоскостью обозначим
буквами 7Ί, Г2, 7^, ...
Тогда, по доказанному, должны иметь:
STi = ST2 = STz = const.
Отсюда следует, что искомое геометрическое место точек
прикосновения Τ ι есть окружность с центром в точке 5 и радиусом r—VSA'SB.
Построение такой окружности не представляет никаких затруднений.
§ 27. ПУЧОК ОКРУЖНОСТЕЙ, ДИАМЕТРАЛЬНО ПЕРЕСЕКАЮЩИХ
ДВЕ ДАННЫЕ ОКРУЖНОСТИ.
Пусть имеем две окружности (Ог) и (02) (черт. 84). Рассмотрим
совокупность всех окружностей, пересекающих данные окружности
диаметрально. Мы знаем, что совокупность окружностей,
пересекающих данную окружность диаметрально, образует эллиптическую связку,
для которой данная
окружность является
базисной (§ 25). Поэтому
множество
окружностей, диаметрально
пересекающих две
данные окружности (Οι) и
(02), является
„пересечением" или общей
частью двух
эллиптических связок с
базисными окружностями (Οι)
и (02). Нетрудно
видеть, что эта общая
часть представляет
собой пучок
окружностей, общей радикаль-
Черт. 84. ной осью которых
служит прямая Ох02- В
самом деле, если мы обозначим радиусы данных окружностей буквами
тх и г2, а центры двух каких-либо окружностей, диаметрально
пересекающих обе данные, буквами О' и О", то будем иметь:
/
ffL·
А
ТЗ
=^5<7
/ 1 ,
M^L
в
Q'
о
ι
ι
\
i—^
\α^
*/В* >:
•г~и
L.O' <-0" = ^2·
Первая из этих формул показывает, что точка 01 лежит на
радикальной оси окружностей (О') и (О"), так как имеет относительно
100
них одинаковую степень. По той же причине точка 02 также лежит^
на радикальной оси окружностей (О') и (О"). Отсюда и заключаем,
что радикальной осью окружностей (О') и (О") служит прямая ОхОг.
Итак, окружности, пересекающие (Οι) и (02) диаметрально,
образуют пучок.
Центры окружностей, образующих пучок, лежат на одной прямой.
Зта прямая перпендикулярна к радикальной оси пучка Οι02. В самом
деле, пусть (О')— одна из окружностей этого пучка (черт. 84).
Предположим, что она пересекает окружность (Ог) по диаметру PiQXi a
окружность (02)—по диаметру P2Q2. Тогда имеем:
OOi_LAQi и 0'0tJLP2Q2.
Из прямоугольных треугольников 0'ΡχΟχ и 0'Р202 находим, что
0'0] = г'* — г\ 0'0l = r'z — rl,
или, после вычитания,
0'0\ — 0'0\ = rl—r\ = const.
Отсюда видно, что геометрическое место центров О' есть
перпендикуляр к прямой Ох02. В § 20 было показано, что разность квадратов
расстояний от центров О, и 02 точек радикальной оси данных
окружностей выражается константой (г\—г\). Поэтому найденное нами
геометрическое место центров О' представляет собой прямую,
параллельную радикальной оси данных окружностей и отстоящую от центра Ох
на таком же расстоянии, на каком радикальная ось отстоит от центра 02.
Для построения геометрического места центров диаметрально
пересекающего пучка достаточно найти центр О окружности, лежащий
на прямой Οχ02. С этой целью проводим диаметры АХВХ и AzB2l
перпендикулярные к 0{02, и строим окружность (А\ВХА2В2). Центром ее
и будет служить точка О.
Упражнения,
1. Построить окружность, диаметрально пересекающую три данные
окружности (см. § 27).
2. Построить окружность, ортогональную к трем данным окружностям
(см. § 23).
Глава пятая.
МЕТОД ГЕОМЕТРИЧЕСКИХ
ПРЕОБРАЗОВАНИЙ.
§ 28. СИММЕТРИЯ.
Предположим, что на плоскости дана какая-нибудь прямая хх
(черт. 85). Рассмотрим такое преобразование точек плоскости, при
котором каждая точка Μ плоскости переходит в точку М\
симметрично расположенную с ней относительно прямой хх. Все точки
самой прямой хх при этом преобразуются сами в себя. Такое
преобразование называется осевой симметрией (или отражением).
Прямая хх называется осью симметрии. Достаточно задать ось
симметрии, чтобы определить преобразование. Если на плоскости дана
какая-нибудь кривая, то, рассматривая ее как геометрическое место
точек, мы можем подвергнуть ее преобразованию симметрии. Тогда
данной кривой будет соответствовать новая кривая (ей
симметричная), представляющая собой геометрическое место точек,
симметричных точкам данной кривой.
Таким образом, всякую
геометрическую фигуру на плоскости можно
подвергнуть преобразованиям
симметрии.
Предположим, что мы имеем фигуру
F и симметричную ей фигуру F.
Представим себе, что плоскость чертежа
вращается в пространстве около оси
симметрии хх. Если сделаем поворот на
Черт. 85. 180°, то плоскость совместится со
своим первоначальным положением. При
этом фигура F после поворота совместится с фигурой F
первоначальной плоскости. Отсюда видно, что симметричные фигуры
конгруэнтны, но их нельзя совместить передвижением в плоскости
чертежа, необходима пространственная операция, как, например, поворот
плоскости на 180° вокруг оси хх.
Преобразование симметрии дает тот же самый результат.
Выполненное два раза подряд, оно возвращает фигуру в ее
первоначальное положение. Так, при одном отражении фигура F переходит в F.
При повторении отражения F переходит в F. Следовательно,
двукратное отражение (осевая симметрия) дает тождественное
преобразование, при котором точки плоскости не меняют своего положения.
102
Черт. 86.
§29. ПРИМЕНЕНИЕ СИММЕТРИИ К ГЕОМЕТРИЧЕСКИМ ПОСТРОЕНИЯМ.
Предположим, что на плоскости чертежа даны прямая хх и две
какие-либо линии fug (черт. 86). Требуется разыскать и построить
на данных линиях / и g точки, симметричные относительно оси хх.
Проанализируем задачу. Пусть Ρ и Я' две такие точки, лежащие
соответственно на линиях / и g. Если преобразуем линию / в
симметричную относительно осилгл: ^
линию/', то при этом точка Ρ
перейдет в точку Р'.
Следовательно, линия /' должна прр-
ходигь через точку Р'. Таким
образом, искомая точка должна
быть точкой пересечения линии
g и линии /', симметричной /
относительно хх. Очевидно,
что подобным же образом
точку Ρ можно построить как
точку пересечения линии/с линией
g\ симметричной g
относительно оси хх. Понятно, что достаточно найти одну из точек Ρ и Р'.
Решение сводится к построению линии /' (или g')y
симметричной данной, и нахождению точек пересечения линии g uf (или/и g').
Примеры.
1. Даны прямая хх и два треугольника ABC и KLM.
Требуется на сторонах данных треугольников найти пары точек,
симметрично расположенных относительно данной прямой хх.
Предположим, что X и
X'—две такие точки (черт.
87). Если над треугольником
ABC выполним
преобразование симметрии относительно
оси хх, то получим
треугольник АВ'С. При этом пре^
образовании точка X должна
совместиться с
симметричной ей точкой X'.
Следовательно, X' должна лежать
на одной из сторон
треугольника А'В'С, в который
перешел треугольник ABC, a
именно на той, в которую
перешла сторона
треугольника ABC, содержащая точку
X. Отсюда заключаем, что
X' есть точка пересечения
сторон треугольников KLM и А'В'С. Это дает следующий способ
разыскания симметричных точек.
103
Преобразуем один из данных треугольников в симметричный
относительно данной прямой хх. Найдем точки пересечения последнего
со вторым из данных треугольников. Пусть это будут точки Х\ К\
Z' и LJ'. Тогда эти точки вместе с соответственно симметричными
им X, У, Ζ и U дают, очевидно, все решения предлагаемой
задачи.
2. Даны прямая хх и две точки А и В, лежащие по одну
сторону от данной прямой. Требуется на прямой хх найти такую
точку X, чтобы ломаная АХВ имела наименьшую длину
(черт. 88).
Если точка В' симметрична точке В относительно оси лгдг, то
при любом положении точки X на прямой хх будем иметь:'
ХВ = ХВ\
длина ломаной АХВ равна длине ломаной АХВ'.
Поэтому точка В может быть заменена точкой В\ и достаточно найти
такое положение точки Ху при котором ломаная АХВ' имеет
минимум. Очевидно, что это
будет иметь место в том
случае, когда ломаная АХВ'
является прямой. Отсюда
получаем следующее по- ш
строение точкиЛ': строим
точку В\ симметричную В
Черт. 88. относительно прямой хх>
и проводим прямую АВ'.
Точка X ее пересечения с прямой хх и дает решение задачи.
Доказательство основывается на том, что при найденном
положении точки X ломаная АХВ' имеет минимум, а следовательно, тоже
самое можно сказать про линию АХВ.
Исследование показывает, что решение всегда существует, так
как точки А и В' лежат по разные стороны от прямой хх. Поэтому
прямая АВ' пересекается с прямой хх. Отсюда же ясно, что
решение единственное.
Интересно отметить прием решения, примененный в только что
рассмотренной задаче. Он заключается в том, что данные задачи
частично могут быть изменены (точка В заменяется точкой В') таким
образом, чтобы решение задачи стало вполне очевидным.
Преобразование симметрии применяется здесь с целью частичного изменения
данных, при котором, однако, не изменяется длина исследуемой
ломаной. Этот прием может быть успешно применен и в следующем
примере.
3. Дан угол, образованный прямыми χ и у, к точка Μ внутри
него. Требуется найти на сторонах данного угла такие- точки
X и Υ, чтобы треугольник MXY имел наименьший периметр
(черт. 89).
Произведя отражение точки Μ относительно сторон угла χ и у,
найдем симметричные с Μ точки Μ и М". При любом положении
101
точек X к Υ на сторонах угла будем иметь:
М'Х=МХ и ΜΎ=ΜΥ.
Следовательно, ломаная М*
переходит в новфф^)чку|^Л1' с соблкЬ^ени|Ьм двух следующих
условий (черт. 90)}
1) ОМ' = ОМ,
Ь) ,/ΛίΟΛί' = φ.
Свойства этоАэ преобразования хорошо известны каждому. Каждая
.^фигура F переходит в конгруэнтную фигуру F\ все точки которой
удовлетворяют двум указанным выше услолиям.
103
К понятию о вращении как точечном преобразовании плоскости
можно подойти от преобразования симметрии.
Предположим, что точки плоскости подвергнуты преобразованию
симметрии относительно оси Ох (черт. 91). Пусть например, при этом
преобразовании точка Μ перешла в точку Μ'. Затем преобразованные
точки подвергаются новому преобразованию симметрии, но уже
относительно оси Оу. Обозначим точку, в которую перейдет точка AV при
этом втором преобразовании, через М". Нетрудно убедиться в том,
что эти два последовательно выполненные преобразования симметрии
можно заменить одним—вращением около точки О пересечения осей
Ох и Оу двух рассмотренных симметрии. При этом угол вращения
равен удвоенному углу хОу.
В самом деле, по свойству преобразования симметрии будем иметь:
1) ОМ=ОМ' = ОМ"\
2) ^/MOM" = Z. MOM -f /_ MOM" = 2 Ζ. xOM -f
+ 2 Z.M'Oy = 2(Z.xOM' + ^/M'Oy) = 2 Z.xOy.
Таким образом, преобразование вращения можно
рассматривать как „произведение* двух осевых симметрии (отражений).
§ 31. ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ВРАЩЕНИЯ
К ГЕОМЕТРИЧЕСКИМ ПОСТРОЕНИЯМ.
Предположим, что на чертеже даны две какие-либо линии fug
и точка О (черт. 92). Найдем на линии/такие точки, которые после
*ι вращения линии / около цент-
'\Р_ ра О на угол φ0 оказались бы
9 лежащими на линии g. Пусть
/' есть та кривая, в которую
переходит линия / при
указанном вращении. Тогда, как
легко видеть, искомые точки
будут точками пересечения линии
/' с линией g (на чертеже
92—точки Ρ и Q).
Применение преобразования
вращения к задачам на
построение основано на
рассмотренном выше принципе. При
этом разыскание среди данных
таких точек, которые обладали
бы свойствами точек Ρ и Q,
достигается с помощью
анализа и по большей части не является очевидным из самого чертежа.
Черт. 92.
Примеры.
1. В данный квадрат вписать равносторонний треугольник, одна
из вершин которого дана (на стороне квадрата).
106
Анализ.
Предполагаем задачу решенной; в данный квадрат ABCD вписан
равносторонний треугольник PQR (черт. 93), причем вершина R—
данная точка.
Так как каждый угол равностороннего треугольника содержит 60°,
то вращение вокруг точки R на угол в 60° переводит сторону RP
в сторону RQ и вершину Ρ в
вершину Q. С другой стороны, §-
то же вращение переводит
данный квадрат ABCD в квадрат ρ
A'B'C'D', сторона А 'В'
которого должна проходить через
точку Q, так как с ней
совпадает точка Р'. Это и дает
необходимое указание к решению
задачи.
Построение.
Выполним преобразование
вращении с центром R и углом
в 60°. В частности, нам
достаточно проделать это со
стороной квадрата АВ (на которой
лежит одна из вершин искомого треугольника PQR). Для этого
переводим точки А и В в положение А' и В'. Точка пересечения Q
отрезков АВ' и CD дает решение задачи.
Зная Еершины R и Q искомого равностороннего треугольника
легко построить и третью вершину Р, проводя прямую RP под
углом в 60° к прямой RQ.
Доказательство.
Точка Ρ при вращении вокруг R на угол в 60° переходит в точку
Q; следовательно,
RP=RQ.
Отсюда заключаем, что треугольник PRQ равнобедренный, угол при
вершине R равен 60°, а значит и углы при вершинах Ρ и Q
содержат каждый по 60°. Таким образом треугольник PRQ
равносторонний.
Исследование.
В заьисимости от положения точки R на стороне квадрата будет
изменяться положение вершин Ρ и Q треугольника. Достаточно
исследовать возрос для промежутка MD (от середины Μ стороны AD до
вершины D квадрата ABCD), так как для точек /?, лежащих на
другой половине AM стороны, будем, очевидно, иметь совершенно
симметричную картину. Предположим поэтому, что точкам R
перемещается по стороне AD квадрата от точки Μ до точки D.
Прежде всего можем установить, что при любом положении
точки R в этом промежутке отрезок АВ' пересекает квадрат и,
конечно, в одной точке. Это следует из того, что точка А должна
107
находиться внутри квадрата, в то время как точка В вне его. На
чертеже 94 отрезок АХ'ВХГ получен вращением стороны АВ вокруг
точки j:M на угол в 60°. Ясно, что полуокружность AAX'D лежит
внутри квадрата, так же как и лежащая на ней точка Л/. С другой
стороны, точка Вх должна лежать на окружности, описанной из
точки Μ радиусом MB. Но эта окружность, исключая точки β и С,
лежит вне квадрата. Таким образом, заключаем, что точка Ах —
внутренняя, а Вх —внешняя по отношению к квадрату; поэтому
отрезок ΑχΒι пересекает квадрат в одной точке (Qx).
Аналогичным образом можно убедиться, что точка Л3' находится внутри
квадрата, а точка Bz' — вне него. Это положение Ав'Вг' отрезка
соответствует вращению на 60° вокруг точки D. Вообще при любом
положении центра вращения R на отрезке MD точка А оказывается
внутри, а точка В' — вне квадрата. Следовательно, мы всегда будем
иметь решение задачи и притом единственное.
Далее нетрудно построить интервалы изменения точек Ρ и Q при
перемещении точки R от точки Μ до точки D. Предполагая, что
точка Rt (первое положение для точки R) совпадает с Му мы
получим решение задачи в Биде треугольника P\Q\R\ (черт. 94), причем
M(RJ R2 D(RJ S
^ Черт. 94. Черт. 95.
Другому крайнему положению точки Ry когда она совпадает с D,
соответствует треугольник PzQzR^y причем точка Q3 лежит на стороне ВС.
Таким образом, при движении точки R по отрезку MD точка Ρ
перемещается по прямой АВУ описывая отрезок РгРг. В то же время
точка Q перемещается сперва по стороне DC, проходя отрезок QXC,
и далее по стороне СВ, проходя отрезок CQB.
Отсюда ясно, что для различных положений точки R на стороне
AD всегда имеем решение (треугольник PQR) и притом единственное.
2. Даны две окружности и точка. Из данной точки, как центра,
описать окружность так, чтобы дуга ее, образованная точками
пересечения с данными окружностями, имела данную градусную
меру.
103
Анализ.
Предположим, что (Ог) и (02)— данные окружности, a S—данная
точка (черт. 95). Пусть, например, РР есть искомая дуга и
соответствующий ей центральный угол PSP имеет данную градусную меру φ.
Подвергнем окружность (Ог) вращению вокруг точки S на угол φ.
Она займет новое положение (О/).
При этом вращении точка Ρ окружности (О,) перейдет, очевидно,
в точку Р' окружности (02). С другой стороны, точка Р' должна
принадлежать преобразованной окружности (О/). Таким образом,
искомая точка Ρ является точкой пересечения окружностей (02) и (О/).
Построение.
Окружность (Ох) вращаем на данный угол φ вокруг точки S, что
дает окружность (О/). Тогда точки пересечения окружностей (02) и
(О/) дают решения. На нашем чертеже имеем два решения: точки Р'
и Q'. Проводя из 5 окружности радяусами SP' и SQ', построим
искомые дуги: РР' и QQ\
Доказательство.
Так как точки Ρ и Q переходят в точки Р' и Q' при вращении
с центром S и углом φ, то дуги РР' и QQ' должны содержать, по φ
градусов.
Исследование.
Из чертежа 95 видно, что, в зависимости от того, пересекаются,
касаются или не имеют общих точек окружности (02) и (О/), мы
будем иметь два, одно или ни одного решения задачи.
§ 32. ПАРАЛЛЕЛЬНОЕ ПЕРЕНЕСЕНИЕ.
Под названием „параллельное перенесение" известно такое
преобразование плоскости, при котором все ее точки смещаются на
одинаковые расстояния по параллельным направлениям. Поэтому для
определения параллельного перенесения, как преобразования
плоскости, необходимо знать д дг
направление и интервал
перенесения. Так, на
чертеже 96
произведено параллельное
перенесение^ плоскости,- в
котором точки А, В и
С (треугольника ABC)
переходят в точки А\
В' и С' (треугольника
А'В'С'). Направление
перенесения
определяется каждой из направленных прямых АА' \\ ВВ' || СС. Интервал
перенесения — каждым из отрезков АА' = ВВ' = СС'. Вместо этого
достаточно задать вектор d (черт. 96), определяющий одновременно
направление и интервал данного перенесения.
Черт. 96.
10Э
Как видно из чертежа 96, при параллельном перенесении каждая
фигура переходит в фигуру, конгруэнтную и одинаково
расположенную с первоначальной.^Параллельное перенесение можно осуществить
с помощью двух осевых симметрии, оси которых параллельны между
собой. Так, на чертеже 97 над треугольником ABC выполнено
преобразование симметрии с осью χ χ (первое отражение). Получаем
треугольник А'В'С. Над последним выполнено новое преобразование
симметрии с осью х"х" (второе отражение). Это дает треугольник
Черт. 97.
А"В?С". Ясно, что два произведенных преобразования можно заменить
одним: параллельным перенесением треугольника ABC на расстояние
АХ' = ВВ" = СС = 28 по направлению АА" Ц ВВ" |] СС".
В самом деле, направление этого перенесения перпендикулярно
направлению осей χ χ и х"х\ а интервал его равен удвоенному
расстоянию (25) между осями.
§ 33. ПРИМЕНЕНИЕ ПАРАЛЛЕЛЬНОГО ПЕРЕНЕСЕНИЯ К ЗАДАЧАМ
НА ПОСТРОЕНИЕ.
Начнем с рассмотрения той задачи, которая была ранее
исследована в преобразовании симметрии и вращения.
Пусть / и g— две данные линии. Требуется на линии / найти
такие точки, которые при данном
параллельном перенесении
переходили бы в соответственные точки
линии g.
Предположим, что даны обе
линии / и g", а также вектор d,
определяющий параллельное перенесение
(черт. 98). Пусть Ρ— одна из то
чек, удовлетворяющих поставлен-
о = ~- ному условию. Тогда параллельное
Черт. 98. перенесение d переводит эту точку
в точку Р\ лежащую, согласно
условию, на линии g; с другой стороны, точка Р' должна находиться
на линии /', в которую переходит линия /.
110
Таким образом, искомая точка Р' является точкой пересечения
линий/' и g. Следовательно, все искомые точки (Р', Q',...) могут
быть определены как точки пересечения линий g и /'.
Примеры.
1. Даны две окружности (Ох) и (02), прямая g и отрезок т.
Требуется параллельно данной прямой g провести секущую так,
чтобы она образовала в пересечении с окружностями (Ох) и (02)
хорды, сумма длин которых была бы равна длине отрезка т.
Анализ.
На чертеже 99 имеем
следующие данные:
окружности (Oj) и (02),
прямую g и на ней отрезок
т. Предположим, что
секущая AD дает решение
задачи. Это значит, что
AD\\g и AB-\-CD = m.
Произведем параллельное
перенесение окружности
(02) но направлению g на Черт. 99.
интервал СВ. Пусть при
этом точка D переходит в D', а центр 02 в 0% Тогда хорда CD
перейдет в хорду BD' окружности (02). Следовательно,
AB-\-BD' = AD' = m.
Если из точек Ог и 02 опустим перпендикуляры OxF и O2G
на секущую AD, то, как видно из чертежа, получим:
FG=FB + BG=^ = ?L=EOl
Это позволяет определить интервал переноса. В самом деле, прямая
Сорч\[g и, следовательно, может быть построена. Точка Ε—
основание перпендикуляра ОхЕ— также может быть построена. Откладывая
от Ε на прямой 0202 отрезок Я02 = —, получаем точку 02. Таким
образом интервал переноса найден. Точки пересечения В и В*
окружностей (Ог) и (02) определяют решения задачи.
Построение.
Оно вытекает из сказанного в анализе. Проведя через точку 02
прямую 0202||g-, строим ОхЕ J_ 0202 и откладываем Е02 = —. По-
лучаем точку 02— центр перенесенной окружности. Описывая из 00
окружность радиуса г2 окружности (02), находим точки пересечения В
и В* окружностей (Ot) и (0'2). Секущие, проходящие через точки
ill
В и £* параллельно g, при некоторых условиях (см. исследование),
дают решение задачи.
Доказательство.
Будем предполагать, что АВ -\- BD' = AD', как на чертеже 99.
Тогда легко доказать, что построенные секущие удовлетворяют всем
требованиям задачи. Действительно, как видно из чертежа, имеем:
Следовательно,
АВ -{- BD' = т = АВ + CD,
что и требовалось доказать.
Исследование.
Как мы видели из предыдущего, точки пересечения окружностей
(Οχ) и (0«), если они имеются, дают решение задачи. Таким
образом, мы должны исследовать, при каких условиях окружности (0{)
и (0'2) пересекаются. Эти условия можно выразить, как известно,
следующим образом:
Г\-\-г2^ОхО'2 и г у—г2^ОхО'ъ
где через гг и г2 обозначены радиусы данных окружностей г).
Обозначая через ρ длину перпендикуляра ОхЕ, мы можем выразить
расстояние центров Οχθ'2 из треугольника Ох02Е в виде:
Тогда условия пересечения окружностей примут вид:
Ъ + г,*]/' ffi+fe)* " '.-'з<-|/р2+('!)2.
Причем, как легко видеть, знак равенства соответствует случаю
прикосновения окружностей (при этом возможно только одно решение).
Помимо условий пересечения окружностей должно еще, как мы
видели, выполняться условие расположения точек на прямой AD
в порядке ABD\ т. е. чтобы AD' = АВ-\- BD'. При этих условиях точки
пересечения окружностей (Οχ) и (02) определяют решения задачи.
Проще всего проверить выполнение условий непосредственным
построением окружности (Оо). #
2. Построить треугольник ABC, если даны три его медианы
тА, т^ч тс.
х) Напомним, что радиус окружности 0\ равен г2.
,112
Анализ.
Начнем, как обычно, с искомого треугольника ЛВС (черт. 100).
Пусть Μ— точка пересечения его медиан:
ААт = тА> ВВт = ШВ> ССт = тС-
Рассмотрим параллельное перенесение, определяемое вектором MB.
В этом перенесении отрезок МС медианы ССт переходит в
отрезок ВС\ причем точка С переходит в С. Стороны треугольника
МВС выражаются через медианы искомого треугольника ABC
следующим образом:
МВ=^-тв, МС=-^тАУ ВС = — тс.
Этого достаточно для решения задачи.
Построение.
Строим треугольник МВС' по трем сторонам, которые известны,
так как медианы тл, тв и тс даны. По точке С находим С, для
чего проводим С'С ψ ΒΜ. Затем от- β
кладываем на прямых ВМ и СМ
соответствующие медианы. Получим
точки Вт и Ст. Прямые ВСт и СВт
пересекаются в третьей вершине
треугольника А.
Доказательство.
В треугольнике ABC, который
мы построили, исходя из
треугольника МВС у линия ААт является ме- ^
дианой, так как ВАт = АтС. Линии ' ^ ' '
ВВт и ССт также медианы, так как · 2—^ ·
они пересекаются в точке Му которая ' - ·
делит их в отношении 2:1 (соглас- Черт. 100.
но построению). Длины медиан ВВт
;и ССт равны соответственно тв и тс. Что же касается медианы ААт,
™'--ZAAm = MAm = -z"lA·
Следовательно, ААт = тА.
Исследование. 9
Задача возможна только в том случае, если из отрезков -^- т»,
2 2
~Ттв и ~Ттс можно построить треугольник, или, иначе, если дан-
о о
ные отрезки (медианы) тд, тв, тс образуют треугольник. Как было
показано, в этом случае решение существует. Докажем, что оно
единственное. Для этого достаточно убедиться в том, что перенос
любой вершины искомого треугольника МВС дает то же решение,
что и перенос вершины С (в точку С). Так, если бы была
перенесена вершина В в точку В' (ВВ' 4J= CM), то отрезок В'С
определил бы одну из сторон искомого треугольника. Именно: В'С =АС.
Таким образом, исходный треугольник МВС является разрешающим
ИЗ
треугольником для вполне определенного и единственного искомого
треугольника ABC.
3. Даны три стороны четырехугольника и углы, прилежащие
к четвертой его стороне. Требуется построить четырехугольник.
Анализ.
Предположим, что искомый четырехугольник ABCD, в котором
стороны АВ, ВС и CD являются данными, так же, как и углы А
и D, построен (черт. 101). Предположим далее, что сторона CD
подвергнута параллельному переносу, определяемому вектором CZ?.
В таком случае она займет положение
BD'. При этом прямая BD' наклонена
к прямой AD под данным углом D.
Ломаная ABD' может быть построена, а за
ней и искомый четырехугольник ABCD.
Построение.
Начинаем построение с угла Л, на
одной из сторон которого откладываем
отрезок АВ. Из точки В проводим пря-
Черт. 101. мую BD\ образующую угол D с прямой
AD. На прямой BD' откладываем от
точки В отрезок BD' = CD. Получаем точку D'. Так как D'D = BCy то
для определения точки D опишем из D', как центра, окружность
радиуса ВС. Получаем вершину D. Для построения последней
вершины С проводим BC\\D'D и DC\\D'B. Иначе: переносим отрезок D'B
обратно в положение DC. Теперь все вершины искомого
четырехугольника построены.
Доказательство.
Как видно из построения, в полученном четырехугольнике ABCD
стороны АВ, ВС и CD имеют данную величину. В то же время
углы А и В равны данным.
Исследование.
Решение возможно, если расстояние точки D' от прямой AD
меньше данной стороны ВС, так как только в этом случае
окружность, описанная из точки D', радиуса ВС пересекает прямую AD.
Получаем, вообще говоря, две точки пересечения D и D\. Они
дают решения, если в соответствующих четырехугольниках углы А
и D равны данным углам, а не смежным с ними.
Точка D (черт. 101) дает решение — четырехугольник ABCD, в то
время как точка D] решения не дает, ибо в соответствующем ей
четырехугольнике ABC*DX углы Л и Dj не равны данным углам,
а дополняют их до 180°.
§34. ГОМОТЕТИЯ.
Рассмотрим следующее преобразование точек плоскости. Некото*
рую точку S выберем в качестве центра гомотетии (черт. 102).
Тогда какой-нибудь точке Μ плоскости соответствует точка М\
удовлетворяющая следующим двум условиям:
114
Μ
Черт. 102.
Μ'
1) Μ' лежит на прямой SMy
2) отношение -ргтт = k = const.
' ч SM
Таким образом, гомотетия определяется точкой 5 (центр
гомотетии) и числом k {коэффициент гомотетии). Преобразование это
взаимнооднозначное, так как каждой
точке Μ соответствует вполне определенная ~^
точка М' и наоборот. Точка 5 является
двойной точкой преобразования, так как
она сама себе соответствует.
В самом деле, из написанного выше условия имеем:
SM' = k.SM.
Если Μ совпадает с S, то SM=Oy но тогда и SM' = &·0 = 0.
Отсюда видим, что точка 5 — двойная.
Других двойных точек в преобразовании гомотетии плоскость иметь
не может, так как, если предположить, что точка X — двойная, то
так как с ν
— — k— 1
sx~ *— lf
в этом случае вообще имеем SM' = SM, т. е. все точки двойные
и гомотетия обращается в тождественное преобразование.
Далее нетрудно видеть, что
гомотетия преобразует прямую линию
в прямую же. Так, если все точки
прямой t (черт. 103) преобразованы
посредством гомотетии с центром 5
и коэффициентом /г, то получим
геометрическое место соответственных
точек, удовлетворяющих условию
SM
= k.
L. Пусть точке А данной прямой t co-
« ответствует точка А'. Проведем че-
р ' ' рез А' прямую t\ параллельную t.
Тогда для любой прямой, проходящей через S и пересекающей
прямые / и f соответственно в точках В и В\ будем иметь:
SBT _SA' _
~SB~SA "
Отсюда видно, что прямая f представляет собою геометрическое
место точек, соответственных точкам прямой / в гомотетии.
Следовательно, произвольная прямая переходит в параллельную ей прямую.
Исключение составляют прямые, проходящие через центр S. Так как
в силу условия 1) точки каждой прямой, проходящей через центр S,
переходят при гомотетии в точки той же прямой, то такая прямая
переходит в себя.
115
Следствия.
1. Гомотетия не изменяет величины углов.
В самом деле, гомотетия преобразует каждый угол в угол с
соответственно параллельными сторонами.
2. Гомотетия сохраняет параллельность прямых.
Действительно, две параллельные прямые переходят в две
прямые, параллельные данным.
3. Отношение двух соответственных отрезков равно
постоянному коэффициенту гомотетии (k).
Предположим, что отрезок АВ преобразуется в отрезок А 'В'
(черт. 103). Тогда имеем:
ASAB<Lr;f\SA'B'y
откуда
А'В' SA'
АВ SA
Замечания.
1) Из предыдущего видно, что гомотетия может быть задана центром S
и парой соответственных точек А, А', или же центром S и коэффициентом k.
Так, если на чертеже 103 имеем пару соответственных точек А и А', то для
произвольной точки В легко построить соответственную ей точку В'. Для
этого проводим прямую А'В'\\АВ. Точка встречи этой прямой с прямой SB
и есть искомая.
2) В преобразовании гомотетии коэффициент k может иметь
отрицательное значение. Тогда отрезки SM и SM' должны иметь
противоположные направления и соответственные
точки Μ и М' расположены но
разные стороны от центра S. Таковы,
например, точки А и А\ В и' В' на
чертеже 104. Отрезок АВ переходит
в противоположно направленный от-
А'В'
резок А'В''. Отношение -т^· =k
имеет в этом случае отрицательное
значение.
3) Каждая фигура F в гомотетии
переходит в новую фигуру F',
подобную данной, так как расстояния
всех точек фигуры F изменяются
Черт. 104. при этом в одном и том же
отношении, а углы не изменяются. Поэтому
гомотетия является преобразованием подобия, сохраняющим также
расположение фигур. В элементарной геометрии такие фигуры называются
„подобными и подобно-расположенными*.
§ 35. ПРИМЕНЕНИЕ ГОМОТЕТИИ К ГЕОМЕТРИЧЕСКИМ ПОСТРОЕНИЯМ.
Применение гомотетии к геометрическим построениям основано на
том принципе, который мы неоднократно подчеркивали в главе о
геометрических преобразованиях. Оно заключается в том, что
соответственные элементы после преобразования должны приходить в
совпадение. Поясним эту мысль на примерах.
116
1. Даны точка и две пересекающиеся прямые. Через данную
точку требуется провести секущую так, чтобы отрезки,
образованные на ней точками пересечения с данными прямыми, имели
данное отношение т.п.
Обозначим буквой S данную точку, а буквами fug данные прямые
(черт. 105). Проанализируем задачу. Предположим, что секущая SFG
дает решение задачи. Это означает, что
SF m SG η
SG=T> ИЛИ SF=m=k'
Произведем преобразование гомотетии с центром 5 и коэффициентом k.
Тогда точка G будет соответствовать точке F в этом преобразовании.
Прямая / перейдет в этом преобразовании в
прямую /'. Точка F, как уже было сказано,
переходит в точку G. Так как последняя
принадлежит одновременно прямым /' и £\ то
она является их точкой пересечения. Отсюда
получаем следующее построение (черт. 105).
Из центра 5 проводим окружность радиуса
SM=m. Находим точку пересечения ее с
прямой /. Пусть это будет точка М. Про- Δ
водим секущую SM и откладываем на ней
второй отрезок SN = n. Если произведем
теперь преобразование гомотетии с центром
S и коэффициентом k= — , то точка Μ пе-
т
рейдет в точку N. Прямая / переходит в
прямую /'. Последняя должна быть параллель- Черт. 105.
ной прямой / и должна проходить через
точку N. Строим прямую /' и находим точку G ее пересечении с пря-
мой g. Тогда секущая SG является решением, так как — =— = k*
Из построения видно, что задача имеет одно решение.
2. Даны точка S, прямая / и окружность (О). Требуется
провести через S секущую так, чтобы отрезки, образованные на
ней точками пересечения с прямой и окружностью, имели данное
отношение т.п.
Метод. Преобразуем данную прямую / в прямую /' с помощью
гомотетии (центр 5 и коэффициент & = — ]. Решение определяется
точками пересечения прямой /" с окружностью (О).
Очевидно, что в этом примере вместо окружности может быть
взята любая кривая, лишь бы она была задана графически.
Примечание.
Приведенные примеры показывают, что для построения точек,
определяющих искомые секущие, достаточно выполнить преобразование гомотетии
над одной из двух данных линий. Если эта линия прямая, то гомотетия
117
легко выполняется, и решение задачи может быть получено независимо
от большей или меньшей сложности второй данной линии. Так, в качестве
данных линий можно взять прямую и логарифмическую спираль (черт. 106).
В этом случае задача имеет бесконечное множество решений, которые
ι / определяются точками пе-
I' ресечения логарифмической
спирали с прямой /'.
4. В данный
треугольник ABC требуется
вписать прямоугольник,
стороны которого имеют
заданное отношение,
таким образом, чтобы две
вершины
прямоугольника лежали на стороне
АВ данного
треугольника, а две другие
вершины— одна на стороне
АС и другая на
стороне ВС.
Предположим, что
искомый прямоугольник
PQSR построен (черт.
107). Тогда отношение
QS т
его сторон —п =— » г*е
КО Π
буквами т и η обозначены
заданные отрезки.
Произведем над
прямоугольником PQSR
преобразование гомотетии, имеющей
т
центр в точке А и коэффициент &=—. Получим новый прнмоуголь-
QS
Q'S' m
ник P'Q'S'R', причем —— = & = —. Отсюда Q'S' = m = P R .
Так как при гомотетии
отношение двух отрезков
не меняется, то
Черт. 106.
Q'S' _ QS
RS'~~RS~~
т
η
А
S R'B
Черт. 107.
и, следовательно,
R'S = n.
Построение.
Проводим прямую, параллельную стороне АВ данного
треугольника и отстоящую на расстоянии т от последней. Обозначим точку
пересечения этой параллели со стороной АС треугольника через Ρ.
118
После этого строим прямоугольник P'Q'S'R' со сторонами P'R' = m
и R'S' = n. Вершина Q искомого прямоугольника должна лежать на
прямой AQ\ так как она соответствует точке Q' в гомотетии с
центром А. Следовательно, Q есть точка пересечения прямой AQ' со
стороной ВС треугольника. После того как вершина Q искомого
прямоугольника найдена, построение остальных вершин не представляет
затруднений.
Из построения видно, что задача имеет одно решение.
§36. ПОДОБИЕ ОКРУЖНОСТЕЙ.
Предположим, что точки плоскости преобразованы с помощью
некоторой гомотетии. Выясним, во что переходит при этом
преобразовании произвольная окружность (О) (черт. 108). Пусть гомотетия
задана центром 5 и парой соответственных точек О и О'. Отметим
произвольную точку Μ данной окружности и построим ей
соответственную М'. Для этого достаточно ,
провести 0'М'\\ОМ. Тогда s^ ^\M
О'М'
ОМ
= k = const,
или
0'M' = k-OM.
Черт. 108.
Если точка Μ описывает
окружность (О), то отрезок ОМ=г не
изменяет своей величины, но из написанной выше формулы видно,
что и отрезок О'М'= к-ОМ также не изменяет своей величины;
следовательно, точка Μ также описывает окружность радиуса г' = кг.
Таким образом, преобразование гомотетии переводит данную
окружность (О) снова в окружность (О').
Предположим, что центр гомотетии 5 находится на самой
окружности (О). Преобразование последней дает новую окружность (О').
При этом точка 5 переходит в себя. Других общих точек
окружности (О) и (О) не имеют. Следовательно,
окружность (О') касается окружности (О)
в точке 5 (черт. 109).
Если центр гомотетии совпадает с
центром О данной окружности, то
SM _ОМ'
SM~ ОМ
k= const.
Но OM=r постоянно для данной окруж-
Черт. 109. ности. Следовательно, ОМ' также
постоянно.
Итак, в этом случае окружность (О) преобразуется в
концентрическую окружность (О') (черт. ПО).
119
Возникает вопрос, можно ли две произвольные окружности
рассматривать как соответственные в некоторой гомотетии. Иначе говоря,
существует ли такая гомотетия, которая преобразовала бы одну из
данных окружностей в другую.
Предположим, что даны две окружности (О) и (О') (черт. 111).
Попытаемся определить гомотетию так, чтобы данные окружности
соответствовали одна другой в этой гомотетии.
Так как центры О и О' окружностей являются парой
соответственных точек, то и дело сводится к построению точки 5—центра
гомотетии.
С этой целью проводим параллельные радиусы обеих окружностей
О'М || ОМ.
Прямые ОМ и О'М' должны быть соответственными, так как они
параллельны и проходят через соответственные точки О и О'.
Следовательно, точки Μ и М' также являются соответственными, как точки
пересечения соответственных линий. Поэтому центр гомотетии 5
найдем как точку пересечения прямых 00' и ММ!. Это одно решение
задачи, но может быть и второе. Оно получается, если из точки О'
проведем радиус 0'M'V параллельный радиусу ОМ, но противоположно
направленный. Точку пересечения прямых 00' и ММ[ обозначим
буквой Sj. Таким образом, мы имеем два решения задачи, т. е. два
центра гомотетии—S (внешний центр) и S{ (внутренний центр). Этот
вывод можно формулировать следующим образом.
Две произвольные окружности можно рассматривать как
соответственные в преобразовании гомотетии. Существуют две
гомотетии, переводящие одну окружность в другую. Коэффициенты k
\\ k\ этих гомотетий имеют следующее значение:
к~ ОМ~ г '
0'М\ г
kl = ~0M=~7'
Если из центра гомотетии 5 проведем касательную ST к
окружности (О), то эта прямая окажется также касательной к окружности (О'),
так как точке прикосновения Τ должна соответствовать точка при-
120
косновения Τ (черт. 111)1). Следовательно, центр гомотетии можно
построить как точку пересечения прямой 00' и общей касательной ТТ
к данным окружностям. На чертеже 111 касательные ТТ и ΤχΤχ
пересекают прямую 00' в центрах подобия S и Si.
Разумеется, этот способ построения центров подобия не может
быть применен в случае, когда одна из окружностей лежит внутри
второй (черт. 112), но способ
параллельных радиусов сохраняет свою силу и в
этом случае.
Как на чертеже 111, так и на
чертеже 112 построены оба центра
гомотетии— 5 и Sx. Один из них, £ь делит
отрезок 00' внутренним, а другой, S,
внешним образом в отношении, равном
коэффициенту гомотетии k. Такие две
точки называются
гармонически-сопряженными (§ 14). Чертеж 111 (или
черт. 112) дает нам способ построения
гармонических точек. Пусть, например,
три точки О, О' и Si даны. Требуется
построить четвертую гармоническую 5
(черт. 113). С этой целью через точки О и О' проводим две
произвольные, но параллельные между собой, прямые ОМ\\0'М'. Через точку St
проводим произвольную секущую, которая пересекает параллельные
Μ
Черт. 112.
Черт. 113.
прямые в точках Μ \\ М\. Затем на прямой О'М\ откладываем от
точки О' отрезок О'М = 0'М\. Получаем точку М. Прямая ММ
пересекает прямую 00' в искомой точке S.
§ 37. ТЕОРЕМА МОНЖА (О ПОДОБИИ ОКРУЖНОСТЕЙ). ·>
Для дальнейшего изучения вопроса о подобии окружностей полезно
познакомиться с методом представления окружностей плоскости с
помощью точек пространства -).
L) В самом деле, в точке прикосновения Τ совпали две точки
пересечения прямой с окружностью (О), которым соответствуют две совпавшие
точки окружности (О'), а именно — точка прикосновения Р.
2) У нас этими вопросами занимался проф. Федоров Е. С. («Точное изо-
0 жжение точек пространства на плоскости". .Записки Горного института",
т". 1, СПБ, 1907;.
121
Черт. 114.
Предположим, что на плоскости Ρ имеется окружность с центром О
и радиусом ОМ (черт. 114). Предположим далее, чго на окружности
установлено положительное направление обхода (указано стрелкой).
Восставим в точке О перпендикуляр к плоскости Ρ и отложим на нем
отрезок 00\ равный радиусу окружности (00' = О/И), в сторону,
соответствующую положительному направлению обхода на окружности
по принципу правого винта1)· Тогда точку О' перпендикуляра будем
называть соответственной данной
окружности на плоскости Ρ или
изображающей эту окружность.
Мы видим, таким образом, что
каждой (направленной)
окружности (О) плоскости Ρ
соответствует некоторая точка О'
пространства. Обратно: каждой точке
пространства соответствует
некоторая направленная окружность
«а плоскости Р. В самом деле, пусть О' (черт. 114) — какая-нибудь точка
пространства. Опуская из О' перпендикуляр на плоскость Р, получим
точку О— проекцию точки О'. Опишем из точки О, как центра,
окружность радиуса ОМ =00' и установим на ней направление обхода так,
чтобы из точки О' оно было видно как противоположное
движению стрелки часов. Эта окружность и является соответственной
данной точке О'. Следовательно, каждой точке пространства О'
соответствует на плоскости Ρ
направленная окружность,
центром которой служит
проекция О точки О' на
плоскость Р, а радиусом—
расстояние точки О' от
плоскости Р. Точки на
самой плоскости Ρ надо
рассматривать как
окружности нулевого радиуса,
поэтому они сами и являются своими изображениями. Таким образом,
все точки пространства изображаются окружностями на плоскости Ρ
и обратно.
Предположим, что окружностям (Ог) и (02) плоскости Ρ
соответствуют изображающие их точки 0\ и 00 пространства.
Проектирующая плоскость 0\Ох0202 пересекает плоскость Ρ по линии
центров Ох02 (черт. 115). Если данные окружности (Ох) и (02) одинаково
направленные, то перпендикуляры 0Х0\ и 0202 отложены в одну и
ту же сторону. Прямая Οι02 пересекает линию центров в точке Sl2i
которая, как легко видеть, является центром подобия данных окруж-
!) Следовательно, из точки О' мы увидим направление обхода
противоположным движению стрелки часов.
122
ностей. В самом деле,
^12^2 _ 0*0*2 Огмг
Sl202~Όχθ\~ОхМхУ
где через 02М2 и ОхМх обозначены два одинаково направленных
радиуса данных окружностей.
Для построения второго „внутреннего центра подобия изменяем
направление обхода одной из данных окружностей на противоположное.
Так, если изменить направление обхода окружности (02), то
перпендикуляр в центре 02 должен быть проведен в сторону, противоположную
первому перпендикуляру, и окружности (02) в этом случае
соответствует точка 02. Прямая θ\θ'2 пересечет линию центров в точке SX2l
которая и является вторым „внутренним14 центром подобия
окружностей.
В самом деле, имеем:
Sl202 = 0202 = 02~M2
Sx2Ox Οχθ\ ОхМх'
где 02уИ2 и ОхМх обозначают два противоположно направленных
радиуса окружностей (02) и (Ох).
Таким образом, прямая, соединяющая точки 0\ и 02 (или 02),
изображающие данные окружности, пересекает плоскость этих окруж-
ностой в их центре подобия.
Рассмотрим теперь три окружности на плоскости Я, центры
которых обозначим через Оь 02 и 08 (черт. 116). Предположим, что на
Черт. 116.
всех окружностях установлено одинаковое направление обхода. Тогда
они изобразятся точками Оъ 02 и Оз, лежащими по одну сторону
от плоскости Я, причем перпендикуляры Οχθ[, 0202 и 080з равны
радиусам данных окружностей. Прямые θ[θ2, 020з, ОзО'ь
соединяющие эти точки попарно, пересекают плоскость Я в точках 512, 523 и
S81, которые являются явнешнимиα центрами подобия соответствующих
пар окружностей. Так как, с другой стороны прямые θ\02, 02θ'ζ и
123
О3О1 лежат в плоскости 010-20'з» то точки пересечения их с
плоскостью Ρ должны лежать на прямой пересечения плоскостей 0^0'20'з
и Р. Эта прямая проходит через внешние центры подобия S12, 523, S3i
и называется осью подобая трех окружностей.
Чтобы построить все остальные центры и оси подобия
окружностей, заметим, что как мы видели, изменение направления обхода
какой-либо из окружностей заменяет изображающую точку 0{ на
точку Οι·(/=1, 2, 3), симметричную ей относительно плоскости Р.
Поэтому мы должны рассмотреть шесть изображающих точек θ\ ,
02» 0з» Оь 0'2> 0з· Каждые три из них определяют плоскость,
пересекающую плоскость Ρ по прямой—оси подобия. При этом, однако,
две плоскости, проходящие через тройки точек, расположенные
симметрично относительно плоскости Р, например, плоскости 0'iO'203 и
010*203, пересекают плоскость Ρ по одной и той же прямой и,
следовательно, определяют только одну ось подобия.
Таким образом, есе восемь возможных троек точек должны быть
соединены в пары следующим образом:
Плоскости Оси и центры подобия
1) О'аОООз и Οι α: 0з
2) 0Ί0003 и 0|020з
3) 0^0003 и 0i0003
4) 0'i0203 и 0'i0203
°12 ^23 _^3l
^12 *->23 ^31
Sl2
^31
*->12 ^23 ^31
Приведенная таблица показывает, что всего будем иметь четыре
оси подобия, на каждой из которых лежит по три центра подобия.
Черт. 117.
При этом одна из осей подобая содержат три внешних центра
подобия, а каждая из остальных осей—по одному внешнему и по
124
два внутренних. Это предложение и называется теоремой Монжа.
Четыре оса подобия образуют, таким образом, полный
четырехсторонник, вершины которого являются центрами подобия данных
окружностей. Эта конфигурация изображена отдельно на чертеже 117.
§ 38. СИСТЕМЫ ОКРУЖНОСТЕЙ, ИМЕЮЩИХ ОБЩУЮ ОСЬ ПОДОБИЯ.
Та пространственная интерпретация окружностей, которая была
развита в предшествующем параграфе, позволяет сделать
дальнейшие выводы относительно подобия окружностей на плоскости.
Предположим, что на плоскости Я даны три окружности (0{), (02)
и (03), представленные точками Оь 02 и Оз пространства (черт. 116).
Плоскость 0\0'20з пересекает плоскость Ρ по оси подобия трех данных
окружностей. Пусть О'— какая-нибудь точка плоскости 0\0'2Оъ. Ей
соответствует на плоскости Я окружность, имеющая своим центром
точку О — проекцию точки О' на плоскость Ρ—и своим радиусом
отрезок 00'. Направление обхода на этой окружности устанав/ивается
соответственно указаниям § 37. Как мы знаем, прямая, соединяющая
точку О' с каждой из точек 0\у О у и 03, пересекает плоскость Ρ в
центре подобия соответствующей пары окружностей. Это справедливо
для любых двух точек О' и О' пространства: прямая О'О' пересекает
плоскость Ρ в центре подобия 5 соответствующих окружностей (О)
и (О). Если мы выберем обе точки О' и О' на плоскости 0\0'20ъ ,
то прямая О'О' пересечет плоскость Ρ в точке 5, лежащей на линии
пересечения плоскости 0\020^ с плоскостью Я, т. е. на оси
подобия окружностей (Oj), (02) и (03). Следовательно, любая пара
окружностей, соответствующих двум точкам О' и О' плоскости θ\θ'20^ ,
имеет центр подобия на одной и той же прямой—линии пересечения
плоскости Ρ с плоскостью О^ОгОз. Эту прямую естественно назвать
осью подобия системы окружностей (О), соответствующих точкам О'
плоскости Οχ θ'2 03. Все окружности рассматриваемой системы обладают,
как мы видели, тем свойством, что центр подобия любых двух
окружностей лежит на оси подобия системы.
С другой стороны, в нашем стереометрическом представлении
система окружностей изображается совокупностью точек О' плоскости
0\θ'ιΟ$. Таким образом, каждой плоскости соответствует система
окружностей, и обратно. Плоскость ΟχΟ^Ο'ζ будем называть
плоскостью изображения системы окружностей (О). Осью подобия системы
окружностей является линия пересечения плоскости изображения
с плоскостью Я, в которой лежат окружности системы. Очевидно,
что для определения системы окружностей достаточно иметь три
принадлежащие к ней окружности, так как три точки определяют
плоскость изображения. Можно также определить систему
окружностей одной окружностью и осью подобия, так как прямая и точка
определяют плоскость изображения. Рассмотрим несколько примеров.
125
Черт. 118.
1. Система окружностей задана окружностью (Ог) и осью
подобия х. Требуется построить окружность (02), имеющую центр
в данной точке 02 и принадлежащую данной системе (черт. 118).
Центр подобия 5 окружностей (Oj) и (02) должен лежать на оси
подобия л: и на линии центров Ох02. Следовательно, он является
точкой пересечения этих прямых. Проведем какой-нибудь радиус ОхМх
данной окружности и соединим
Мх с «S. Прямая, проходящая
через 02 параллельно ОгМи
пересекает прямую SMi в точке
М2. Тогда 02М2 — радиус
искомой окружности.
2. Система окружностей
задана осью подобия χ и
окружностью (Ох). Найти
геометрическое место центров О
окружностей системы,
имеющих данный радиус г (черт.
119).
Изображающую плоскость
данной системы обозначим
буквой ω, а точку, изображающую искомую окружность (О),—буквой О'.
Тогда отрезок 00' = гу и, следовательно, искомому геометрическому
месту центров (О) соответствует на плоскости ω геометрическое место
точек (О'), отстоящих от плоскости Ρ на расстояние г. Таким
геометрическим местом точек (О')
является, очевидно, прямая,
параллельная следу х, лежащая в
плоскости ω и имеющая высоту
г над плоскостью Р. Эту
параллель можно получить как линию
пересечения плоскости ω с
плоскостью, параллельной
плоскости Ρ и отстоящей от нее на
расстояние г. Проекция
параллели (с отметкой г)1) на
плоскость Ρ представляет прямую,
параллельную оси х. Эта
прямая ζ и является, очевидно,
искомым геометрическим местом
центров О. Для ее
построения достаточно найти одну ее
точку. Выбрав произвольно точку 5 на оси х, проведем прямую О^,
произвольный радиус ΟχΜλ и прямую MXS. Откладывая на прямой ΜλΟλ
от точки Мх отрезок МхО* = г и проводя 0*0\\MxS% получим точку О
Черт
*) То-есть отстоящей от плоскости Ρ на расстояние г (см. пример 3,
стр. 127).
126
пересечения прямых 0*0 и Оц£, которая и является точкой искомого
геометрического места.
3. На плоскости Ρ даны три прямые хи л:2 и jc3 и три
окружности (Ох), (02) и (08). Требуется построить такую окружность (О),
центры подобия которой с данными окружностями лежали бы
соответственно на прямых х{, х2 и хв.
С помощью пространственного изображения задача может быть
представлена в следующей форме.
Так как окружность и прямая определяют на плоскости систему
окружностей, то данные условия задачи сводятся к системам
окружностей [(ОО,*!], [(02), х2\ и [(03), х3]. В задаче требуется построить
окружность (О), принадлежащую одновременно всем трем системам.
Изображающие плоскости этих систем обозначим буквами ω,, щ и ω3.
Линии пересечения каких-либо двух изображающих плоскостей
представляют собой геометрические места точек, изображающих окружности,
общие двум соответствующим системам. Так, например, линия
пересечения плоскостей o)t и ω2 представляет геометрическое место точек,
изображающих окружности, общие системам [(Oj), хх\ и [(02), х2\.
Подобным же образом точка пересечения плоскостей a>t, ω2 и ω3 изображает
окружность, принадлежащую всем трем системам окружностей. Такая
окружность удовлетворяет всем требованиям задачи и является,
очевидно, искомой окружностью (О). Таким образом решение задачи
сводится к построению точки О' пересечения плоскостей ти щ и ω8
и ее проекции О на плоскость Р. Мы применим здесь методы,
употребляемые в начертательной геометрии. С этой целью введем понятие
о параллелях плоскости изображения ω. Плоскость ω пересекает
плоскость Ρ по оси подобия χ соответствующей системы окружностей.
„Параллелями" будем называть прямые, лежащие в плоскости ω и
параллельные ее следу х. Проведем плоскость //, параллельную
плоскости Ρ и отстоящую от нее на расстоянии /г. Эту величину h будем
называть „отметкой" плоскости И. Последняя пересекает плоскости а)ь
<о2 и ω3 соответственно по трем параллелям £^, ζ!2 и Sg, имеющим
отметку /г. Теперь легко построить линии пересечения плоскостей
изображения; они определяются каждая двумя точками: 1) точкой пересечения
следов (осей подобия) и 2) точкой пересечения параллелей. Так,
например, линия пересечения плоскостей ω{ и ω2 определяется точкой Nl2
пересечения следов хх и х2 и точкой М'п пересечения параллелей £j
и Ц. Аналогично получим точки пересечения N28 и ^з плоскостей
ω2 и со3. Точка О' пересечения прямых M'nNl2 и ΜηΝ2Ζ является
искомой. Как построить ее проекцию О на плоскости Р? Заметим, что
проекция какой-либо параллели £' с отметкой h параллельна
соответствующему следу χ (оси подобия) и представляет собой
геометрическое место окружностей данной системы, имеющих радиус h.
Следовательно, для построения проекции ξ параллели достаточно иметь
одну окружность системы, имеющую данный радиус h.
Самое построение может быть выполнено следующим образом.
Через центр 02 данной окружности (Οι) (черт. 120) проводим гря-
127
мую 41, параллельную оси подобия хх. Прямая ζ, есть, очевидно,
проекция параллели с^ плоскости ω^ Отметка этой параллели равна
радиусу г χ данной окружности (Ох). Чтобы построить параллель Ц'у
плоскости (л>2 с той же отметкой ги или, лучше, ее проекцию ξ2>
необходимо иметь одну ее точку — центр окружности системы [(02),лг2],
радиус которой был бы равен г\. Для этого произвольную точку S>
на прямой х2 соединяем с данным центром 02. Проводим
произвольный радиус 02А2 окружности (02). От точки А2 на прямой А202 от-
Черт. 120.
кладываем отрезок A2C<i = rt и проводим прямую СоС21|-4252. Эта
прямая пересекает прямую 02S2 в точке С2. Далее проводим С2В2\\02А2.
Определяем точку В2, причем отрезок С2В2 = С*А2 = г1.
Следовательно, получили окружность системы [(02), х2\ с центром С2 и
радиусом С2В2 = гх.
Проводя через С2 прямую, параллельную х2, получим проекцию
параллели ζ2· Прямые £г и ξ2 пересекаются в точке МХг. Совершенно
аналогичным построением получается и точка Mzt. Прямые М12Л^2 и
128
^si^si являются проекциями линий пересечения ΜγιΝχι и Μ^χΝζχ
изображающих плоскостей. Точка пересечения О прямых Μί2Νι2 и
Мг\Мь\ является проекцией точки О' пересечения трех изображающих
плоскостей. Таким образом, точка О является центром искомой
окружности. Радиус ее может быть найден по способу, указанному в
примере 1, причем окружность (О) можно рассматривать как окружность^
принадлежащую к любой из трех данных систем.
§ 39. ИНВЕРСИЯ.
В этом параграфе мы познакомимся с преобразованием, которое
называется инверсией или преобразованием обратных радиусов.
Предположим, что имеем окружность с центром в точке О и
радиусом г (черт. 121).
Пусть Μ—какая-нибудь точка плоскости. Точка М\
соответствующая точке Μ по инверсии относительно окружности (О),
определяется следующими условиями:
1) Μ лежит на прямой ОМ,
2) произведение ОМ · ОМ' = г2 =
= const.
Окружность (О) называется основной
окружностью инверсии, а константа г2,
равная квадрату радиуса окружности
инверсии, — степенью инверсий.
Таким образом, инверсия
преобразует каждую точку плоскости в точку
той же плоскости. Исключительной точ- Черт,
кой является центр О основной
окружности инверсии, так как не существует точки О', соответствующей
в инверсии точке О, ибо при любом радиусе г основной окружности
будем иметь: ОМ-ОМ'= 00-00'= 0-00'= 0=£г2, т. е. ни для
какой точки О' не выполняется второе условие инверсии *).
Предположим, что А есть точка основной окружности инверсии. Тогда имеем:
ОА-ОА — гК
Это равенство показывает, что каждая точка основной окружности
инверсии переходит сама в себя. Следовательно, и вся основная
окружность инверсии переходит в себя, причем каждая ее точка сама
себе соответствует. Таким образом, все точки основной окружности
инверсии двойные. Других двойных точек, очевидно, не имеется.
В самом деле, если точка Μ лежит вне основной окружности
инверсии, то будем иметь ОМ^> г; но тогда ОМ' <V, ибо ОМ·ОМ' = г2.
Аналогично и для точки, лежащей внутри основной окружности
инверсии. Вообще можно сказать, что из двух соответственных
(в инверсии) точек Μ и Μ одна лежит вне, а другая внутри основ-
1) В этом рассуждении предполагается, что мы имеем дело с
эвклидовой плоскостью. См. далее § 41 и сноску к нему.
129
ной окружности инверсии. Только точки самой окружности инверсии
преобразуются в себя.
Построение инверсно-соответственных точек. Пусть Μ — какая-
нибудь точка плоскости (черт. 121). В инверсии относительно
окружности (О) ей соответствует некоторая точка Μ'. Построение точки Μ
можно выполнить следующим образом. Из точки Μ проводим
касательную МТ к основной окружности инверсии. Обозначим буквой Τ
точку касания и опустим из нее перпендикуляр ТМ! на прямую ОМ.
Основание Μ этого перпендикуляра и является искомой инверсно-
соответственной точкой. В самом деле, в прямоугольном
треугольнике ОТМ отрезок ОМ служит гипотенузой, а точка Τ — вершиной
•прямого угла. Из вершины Τ опущен перпендикуляр ТМ' на
гипотенузу. По известной теореме элементарной геометрии
ОТ2=ОМ-ОМ' = г2,
что и доказывает наше утверждение о соответствии точек Μ и М'.
Из определения преобразования инверсии еидно, что оно обладает
свойством инволюционноапи, т. е. если М' — точка, соответственная Ж,
то Μ есть точка, соответственная Μ.
Построение инверсно-соответственной точки было нами выполнено
в предположении, что точка Μ—внешняя по отношению к основной
окружности инверсии. Если же точка лежит внутри основной окружности
инверсии, как, например, точка М\ то построение должно быть
произведено в обратном порядке. В этом случае из М' восставляем
перпендикуляр М'Т к прямой ОМ'. Найдя точку Τ его пересечения
с основной окружностью инверсии, строим касательную в этой точке
и определяем соответственную точку М1).
Заметим кстати, что, полагая радиус основной окружности инверсии
равным единице, получим:
ОМ-ОМ'=\, или ОМ' = ^щ, или р' = -,
где через рг и ρ обозначены расстояния от центра инверсии до
инверсно-соответственных точек.
Отсюда и название „преобразование обратных радиусов*.
§ 40. ТЕОРЕМА ОБ АНТИПАРАЛЛЕЛЬНЫХ ПРЯМЫХ.
Предположим, что стороны данного угла АОВ пересечены
прямыми АВ и А'В' (черт. 122) таким образом, что
^/ ОАВ = £ ΟΒΆ' {£ ОВА = /_ ОА'В').
Такие две прямые АВ и А'В' называются антипараллельными
относительно данного угла. Докажем следующую теорему:
1) Из чертежа видно, что прямая ТМ' является полярой точки Μ
относительно окружности инверсии. Точки Μ и М' гармонически сопряжены
относительно точек пересечения прямой ММ' с окружностью инверсии.
130
Если точкам А и В соответствуют в инверсии с
окружностью (О) точки А' и В\ то прямые АВ и А'В' антипараллельны
относительно угла АОВ.
Доказател ъство.
По свойству инверсии
имеем:
ОА.ОА' = ОВ-ОВ' = г2.
Отсюда получаем:
ОВ' _ О А т
О А' ~ OB;
следовательно, Д ОАВ -^
£\ОВ'А\ так как угол
при вершине О у них
общий. Черт. 122.
Из подобия треугольников имеем:
£OAB = Z.OB'A\
/_ΟΒΑ = £ΟΑ'Β'.
Следовательно, прямые АВ и А'В' антипараллельны.
§ 41. ИНВЕРСИЯ ПРЯМОЙ И ОКРУЖНОСТИ.
Рассмотрим сначала прямую АВ, проходящую через центр
инверсии О (черт. 123). Как мы знаем, каждая точка Μ такой прямой
переходит в некоторую точку Μ той же прямой. Точки А и В
пересечения прямой с окружностью переходят сами в себя, точке О нет
соответственной в инверсии (см. § 39)J).
Перейдем к общему случаю. Пусть прямая АВ произвольно
расположена относительно базисной окружности (черт. 124). Опустим из
центра О перпендикуляр О А на данную прямую. Точкам А и В
данной прямой соответствуют в инверсии точки А' и В'. Тогда по
теореме § 40 прямые АВ и А'В' антипараллельны относительно угла АОВ.
Следовательно, имеем:
/_OAB = Z.OB'A'.
Но, согласно построению, ОА [_АВ. Поэтому / ОВ'А' = 90°.
Отсюда заключаем, что точка В' лежит на окружности, построенной
1) Это исключение может быть устранено, если дополнить эвклидову
плоскость «бесконечно-удаленными", или „несобственными", элементами·
Тогда точке О—центру инверсии — будет соответствовать «несобственная
точка" прямой АВ. В самом деле, из формулы
ом'=т
сшдим, что при ОМ—*0, ОМ'—*■ оо.
Следует отметить, что центру инверсии О соответствует несобственная
точка прямой произвольного направления. Но, сохраняя условие
взаимнооднозначного соответствия точек в инверсии, мы должны считать, что
центру инверсии соответствует единственная несобственная точка плоскости.
Следовательно, всякая прямая, проходящая через центр инверсии, должна
также проходить и через несобственную точку плоскости.
131
на отрезке ОЛ'у как на диаметре. Если точка В движется по данной
прямой, то соответственная точка В' описывает окружность !).
О
Черт. 123. Черт. 124.
Таким образом, прямая, не проходящая через центр инверсии,
преобразуется в окружность, проходящую через центр инверсии.
Так как инверсия есть преобразование инволюционное, то, обратно,
окружность, проходящая через центр инверсии, переходит в прямуюt
не проходящую через центр инверсии.
Рассмотрим теперь окружность в общем случае, т. е. произвольна
расположенную относительно базисной окружности. Обозначим ее
центр буквой С (черт. 125). Пусть прямая ОС, соединяющая центр ин-
Черт. 125.
версии с центром данной окружности, пересекает последнюю в точках
А и В. Отметим, кроме того, произвольную точку Μ данной
окружности. Предположим, что точкам Л, В и Μ соответствуют в инверсии
точки А\ В' и М'. Тогда имеем две пары прямых, антипараллельных
относительно угла АОМ, а именно: прямая AM антипараллельна А'М\
прямая ВМ антипараллельна В'М'.
1) Так как эта окружность проходит через центр инверсии, то
соответствующая ей прямая проходит через несобственную точку плоскости. Таким
образом, всякая прямая проходит через несобственную точку плоскости,
соответствующую центру инверсии.
132
Далее имеем:
^/ АМВ = £ ОМВ — £ ОМА,
/_ А'М'В' = £ ОВ'ЛГ — ^/ О А'М'.
Но правые части этих равенств равны в силу указанной Еыше
антипараллельности-прямых AM и А'М\ ВМ и В'М'. Следовательно, равны
и левые части, т. е.
^/АМВ = ^ А'М'В'.
Но угол АМВУ опирающийся на диаметр АВ> — прямой. Это
означает, что угол А'М'В' также прямой. Точка М! лежит на окружности,
построенной на отрезке А'В\ как на диаметре. При движении точки Μ
по окружности (С) точка Μ движется по инверсно-соответственной
окружности.
Далее имеем:
£ М'В'А' = £ ΒΜΝ = / В А N.
Следовательно, прямые AN и В'М' параллельны. Но это означает,
что прямые CN и DM' также параллельны J). Таким образом, прямая NM'
соединяет концы параллельных радиусов двух данных окружностей.
Поэтому она должна проходить через их центр подобия. Последний
лежит на линии центров CD в точке ее пересечения с прямой NM'. Но
такой точкой является центр инверсии О. Отсюда заключаем:
Произвольная окружность (С), не проходящая через центр
инверсии, преобразуется в окружность. Центр инверсии является при
этом центром подобия обеих окружностей.
Упражнения.
1. Провести доказательство этой теоремы для случая, когда окружность
инверсии находится внутри данной окружности (С).
2. В окружность вписан треугольник. Построить фигуру,
инверсно-соответственную вписанному треугольнику относительно окружности.
§ 42. НЕИЗМЕННОСТЬ УГЛОВ В ИНВЕРСИИ.
В настоящем параграфе мы рассмотрим вопрос о сохранении угла
пересечения двух кривых при выполнении преобразования инверсии.
Предположим, что две кривые / и g преобразованы с помощью
инверсии в кривые f и gf (черт. 126). Точка пересечения Μ кривых / и g
переходит в точку пересечения М! кривых f и gf. При этом точки О, Μ
и М! лежат на одной прямой. Проведем из центра инверсии О какой-
либо луч, пересекающий данные кривые в точках А и В, а
соответственные им кривые — в точках А' и В'. Тогда прямые AM и А'М'
антипараллельны относительно угла АОМ. Точно так же антипарал-
лельны прямые ВМ и В'М''. Подобно тому, как это было сделано
в предшествующем параграфе, докажем, что
Z.AMB = ^ А'М'В'.
!) Заметим, что центры С и D обеих окружностей не являются точками
инверсно-соответственными.
133
Будем теперь вращать луч ОА, приближая его к прямой ОМ. При этом
точки А и В будут стремиться к точке Ж, а точки А' и В' — к точке М'.
Секущие AM и ВМ, вращаясь около точки М, будут стремиться к
положению касательных Tf и Τ _ в этой точке. Соответственно с этим
секущие А'М' и В'М', вращаясь около точки ЛГ, стремятся к положению
касательных Tf и Т^ в
точке М'. Следовательно, будем
иметь:
hm^/AMB = j/TfMT
Urn Ζ. Α Μ'Β* = /_ ТГМ'Т^.
Но во все время этого
процесса сохраняется равенство
£АМВ = /_АМ'В'.
По известной теореме о пределах отсюда заключаем, что
\\т/тАМВ=\\т/^А'М,В\ или /_ТfМТ„ =/_Тf M'T^ .
Известно, что углом двух кривых в точке их пересечения называется
угол, образованный касательными к этим кривым в этой точке. Поэтому
полученное нами равенство можно сформулировать следующим образом:
Угол двух пересекающихся кривых не изменяет своей величины
в инверсии.
При этом обратим внимание на следующее обстоятельство. Если
будем рассматривать угол АМВ как угол, образованный вращением
луча МА (против часовой стрелки), то соответственный угол А'М'В1
приходится считать образованным вращением луча М'А" в
противоположном направлении (по часовой стрелке).
Следствие.
Если две кривые соприкасаются в точке М, то
инверсно-соответственные кривые также соприкасаются в инверсно-соответственной
точке М\
Касательные в точке Μ к таким кривым совпадают; следовательно,
угол этих кривых равен нулю.
После инверсии величина угла не изменится. Касательные к
соответственным кривым в точке М' должны совпадать. Но это означает, что
кривые соприкасаются в точке М!.
§ 43. ИНВЕРСИЯ С ОТРИЦАТЕЛЬНОЙ СТЕПЕНЬЮ.
Предположим, что с помощью окружности (О) радиуса г
установлена инверсия, центром которой служит точка О, а степень равна г2
(черт. 127). Произвольная точка Μ плоскости преобразуется в точку М\
которую легко построить (§ 39). При этом будем иметь:
ОМ-ОМ'= г2.
134
Черт. 127.
Пусть Μ"—точка, симметричная с точкой Μ относительно центра
инверсии О. Иначе говоря, точку М" получим, поворачивая отрезок ОМ'
вокруг точки О на 180° против часовой стрелки. Тогда
ΟΜ·ΟΜη = — г2.
Следовательно, точку М" можно рассматривать как
инверсно-соответственную точке Μ в инверсии с центром О и степенью — г2. Таким
образом, приходим к понятию инверсии с отрицательной степенью.
Радиус базисной окружности
такой инверсии является мнимым.
Он равен ги Это
обстоятельство лишает, нас возможности
пользоваться базисной
окружностью для выполнения
построений, подобно тому как мы
это делали в инверсии с
положительной степенью. Но вместо
этого мы можем
воспользоваться действительной окружностью
с тем же центром О и
радиусом г. В самом деле, как видно из чертежа 127, построение точки
М' может быть выполнено в два приема: 1) построение точки М\
соответствующей точке Μ в инверсии относительно окружности (О)
радиуса г, и 2) поворот вектора ОМ' вокруг точки О на 180°.
Предположим, что некоторая фигура F подвергается инверсии с
отрицательной степенью — г2. Выполним это преобразование в два приема:
1) преобразуем данную фигуру F в фигуру F' с помощью окружности
инверсии (О, г) и 2) поворачиваем фигуру F' вокруг точки Она 180°
(против часовой стрелки). Тогда и получим искомую фигуру Р',
соответствующую F в инверсии (О, —г2). Изложенные соображения
показывают, что инверсию с
отрицательной степенью — г2 можно
рассматривать как инверсию с
положительной степенью г2,
сопровождаемую ПОВОРОТОМ ΗΟΚμΝΤ ТОЧКИ О
на 180°.
• Поэтому теоремы о
преобразовании прямых и окружностей в
инверсии, а также относительно
неизменности углов сохраняют свою
силу и для инверсии с
отрицательной степенью, лишь расположение элементов при этом будет иное.
Так, например, если произведем преобразование окружности (С, СП
в инверсии с центром О и степенью — г2, то первый этап построения
относительно окружности инверсии даст нам окружность (СХ\СХТ),
причем точка О является внешним центром подобия обеих окружностей.
Последующий поворот на 180° дает искомую окружность (С2, С2Т"),
соответствующую данной окружности в инверсии с отрицательной сте-
Черт. 128.
135
пенью — г2. Как видно из чертежа 128, точка О является теперь
внутренним центром подобия окружностей (С, СТ) и (С2, С2Г").
Таким образом, теорема, данная в конце § 41, остается справедливой
и для инверсии с отрицательной степенью.
Примечание.
Если центр данной окружности С совпадает с центром инверсии О, то,
обозначая через Μ произвольную точку данной окружности, а через Μ — ей
инверсно-соответственную, будем иметь:
ОМОМ' = const.
Но для данной окружности ОМ= const; следовательно,
ОМ' = const.
То-есть данная окружность преобразуется в концентрическую окружность.
Центром подобия в этом случае служит центр обеих окружностей О,
совпадающий с центром инверсии. Это имеет место как при инверсии с
положительной, так при инверсии с отрицательной степенью. Оба центра подобия
(внешний и внутренний) в данном случае совпадают с центром инверсии.
§ 44. ИНВАРИАНТНЫЕ ОКРУЖНОСТИ В ИНВЕРСИИ.
Предположим, что инверсия задана центром О и степенью г2. Тогда,
как известно, базисной окружностью инверсии служит окружность,
описанная из точки О радиусом г. Эта окружность, как мы видели (§ 39),
является инвариантной относительно инверсии, и все ее точки
переходят сами в себя.
Рассмотрим теперь какую-либо окружность (С), пересекающую
ортогонально окружность инверсии (черт. 129). Точки пересечения обо-
Черт. 129. Черт. 130.
значим буквами А и В. Тогда радиусы О А и ОВ являются
касательными к окружности (С). Это значит, что степень точки О относительно
окружности (С)
С°с = О А2 = ОВ2 = ОМ- ОМ' = г2.
Из этого равенства видно, что точки Μ и Μ соответствуют одна
другой и данной инверсии. Таким образом, каждая точка Μ окружности
(С) кереходит в точку Μ той же окружности, т. е. окружность (С)
инвариантна относительно данной инверсии. При этом, как это видно
из чертежа 129, точки окружности (С), вообще говоря, меняют свое
136
положение на окружности, и только точки А и В являются двойными
fi переходят каждая в себя. Отметим еще, что все внутренние точки
круга (С) остаются внутри круга после инверсии, а внешние точки —
вне круга.
Если степень инверсии отрицательна, например равна — г2, то
окружность с центром в точке О и радиуса г не является базисной.
Мы будем ее называть действительной окружностью инверсий.
Рассмотрим какую-нибудь точку А этой окружности. Инверсия с
центром. О и степенью —г2 состоит, как известно, из двух этапов:
инверсии со степенью г2, преобразующей, точку А в себя, и поворота
Еектора О А на 180°, переводящего точку А в диаметрально
противоположную точку А' (черт. 130). Так преобразуются все точки
окружности (О). Следовательно, эта окружность инвариантна относительно
инверсии со степенью — г2, но все ее точки переходят в диаметрально
противоположные. Окружности, ортогональные к окружности (О), уже
«е будут инвариантными относительно инверсии с отрицательной
степенью — г2. Легко видеть, что каждая из них переходит в
ортогональную окружность, симметричную с данной относительно О.
Рассмотрим окружность (С), диаметрально пересекающую
действительную окружность инверсии (О). Точки пересечения обозначим
буквами А и А'. Нетрудно убедиться в том, что точки внутренней области
круга (С) переходят в точки внешней и наоборот. Пусть ММ' —
какая-нибудь хорда окружности (С), проходящая через точку О. Тогда
•будем иметь:
С£ = ΟΑΌΑ' = ΟΜ- ОМ' = — г2.
Отсюда заключаем, что точки М' и Ж соответствуют друг другу
относительно ингерсил с центром в точке О и степенью—г2.
Следовательно, каждая точка Μ окружности (С), диаметрально
пересекающей действительную окруэ/сность инверсии (О), переходит в точку М'
той же окружности. Окружность (С) инвариантна относительно
инверсии со степенью — г2, но все ее точки меняют свое место на
самой окружности.
Полезно также отметить обратную теорему, соответствующую
только что доказанной.
Ее можно формулировать так:
Если точки Μ и М' инверсно-соответственные, то всякая
окружность, проходящая через эти две точки, является инвариантной
окружностью в инверсии.
В самом деле, степень центра ннЕерсии О относительно любой
окружности, проходящей через точки Мм М\ выражается
произведением ОМ· ОМ', следовательно, равна степени инверсии (черт. 129 и 130).
Если из О проведем какую-либо другую секущую, встречающую
окружность (С) в точках N и ΛΓ, то последние являются
инверсно-соответственными,, так как произведение ΟΝΌΝ' равно степени инверсии.
Таким образом, все точки окружности (С) переходят в точки той же
окружности. Отсюда видим, что всякая окружность (С), проходящая
через точки Μ и М'у инвариантна относительно инверсии.
137
§ 45. ИЗОГОНАЛЬНЫЕ И КАСАТЕЛЬНЫЕ ОКРУЖНОСТИ.
На основании теоремы § 41 каждые две окружности можно
рассматривать как инверсно-соответственные. Пусть, например, имеем»
окружность (Οχ) и (02) (черт. 131). Обозначим буквами S и S их
внешний и внутренний центры подобия.
Если окружности (Ох) и (02) соответственны в инверсии с
центром S, то степень инверсии г3 определяется из условия
r2 = SAl-SA2 = SBl-SB2 = STi-ST2.
Определив таким образом центр 5 и степень г2 инверсии, мы
убеждаемся в том, что в этой инверсии окружности (0|) и (02)
преобразуются друг в друга. В самом деле, преобразуя окружность (Οχ), мы
по теореме § 41 должны получить окружность (02) и обратно.
Аналогичным образом можно рассматривать данные окружности (Oj)
и (02), как соответственные в инверсии с центром S. В этом случае
инЕерсия имеет отрицательную степень —г2, которая определяется по
формуле:
— 72 = SAl -SB2=SBrSA2.
Мы уже знаем, что инверсия с отрицательной степенью —г2
может быть заменена инверсией с положительной степенью относительно
окружности (S, г) с последующим поворотом вокруг точки S на 180°.
Предположим, что окружность (С) ортогональна к базисной
окружности (S, г). В инверсии относительно окружности (Sy г)
окружность (С) переходит в
себя (§ 44).
В той же инверсии
окружности (0{) и (02)
переходят друг в друга.
Предположим, что
окружность (С) пересекает
окружность (Οι) под углом
φ. Окружности (С) и (Ot)
переходят в окружности
(С) и (02). Последние на
основании теоремы § 42
должны пересекаться под
тем же углом φ. Иными
Черт. 131. словами, окружность (С)
пересекает окружности-
(Oj) и (02) под одним и тем же углом φ. Так как окружность (С)
ортогональна к базисной окружности (S, г), то она принадлежит к
гиперболической связке, определяемой этой окружностью (S, г). Но каждая
окружность, принадлежащая этой связке, является изогональной
окружностью для данных окружностей (Οι) и (02).
Аналогичным образом для второй связки, определяемой радикальным
центром 5 и степенью — г2, все принадлежащие ей окружности дна-
138
метрально пересекают окружность (5, г) и являются инвариантным»
относительно инверсии с центром S и степенью — г2. Так как в этой*
инверсии окружности (Ох) и (02) переходят одна в другую, то
каждая окружность (С), принадлежащая эллиптической связке («S, .г)г
изогональна окружностям (О,) и (02).
Легко доказать и обратное предположение:
Каждая окружность, изогональная к двум данным
окружностям iOx) и (02), является инвариантной окружностью в инверсии,-
преобразующей данные окружности одну в другую.
В самом деле, если окружность (С) пересекает данные окружности*
(О,) и (02) изогонально (черт. 132), то это означает, что углы,
образованные радиусами пересекающихся окружностей, равны, т. е.
/_ОхМхС = /^02М2С.
Но треугольник МХСМ2 равнобедренный, поэтому
Ζ.ΟχΜχΜ2 = ^02Μ2Μχ.
Следовательно,
^ ΟχΜχΝχ = Ζ 02Μ2Ν2 = £ 02Ν2Μ2,
и прямые (радиусы) ОхМх и 02Ν2 параллельны. Отсюда заключаем,,
что прямая /W,/V2 пересекает линию центров Ох02 в центре подобия &.
Точки /И, и М2 — соответственные в инверсии (с центром S),
преобразующей окружности (Ох) и (02) друг в друга. Изогональная
окружность (С), проходящая через эти точки, является инвариантной?
окружностью инверсии (§ 44) и принадлежит связке, определяемой»
базисной окружностью инверсии.
В частном случае изогональная окружность может оказаться
касающейся двух данных окружностей. Из доказанной теоремы следует, что*
каждая окружность, касающаяся двух данных окружностей,
является инвариантной относительно инверсии, переводящей данные-
окружности друг в друга. Точки прикосновения Тх и Т2
окружностей являются соответственными в той же инверсии (черт. 132).
Ш
Примечание.
При выводе теоремы об изогональной окружности мы принимали в
качестве угла пересечения двух окружностей угол, образованный радиусами
этих окружностей, направленными в точку их пересечения. Так, на чертеже
132 окружность (С) пересекает окружность (Οι) в точке Μλ под углом 0\М\С
.и окружность (02) в точке М2 под углом 02М2С. В рассмотренном случае
эти углы были равны, почему и самая окружность (С) называлась
изогональной. Центром инверсии, преобразующей окружности (Οι) и (02) друг
β друга, служил внешний центр подобия S.
Черт. 133.
На чертеже 133 изображена изогональная окружность (С) другого типа.
Юна пересекает окружности (Ολ) и (02) соответственно в точках Μλ и М2.
При этом имеем:
т. е. для одной из окружности берётся дополнительный угол (/_ CM^Q). Как
нетрудно убедиться, в этом_случае прямая ΜλΜ2 (или ΝλΜ2) проходит через
внутренний центр подобия 5, который является центром инверсии,
преобразующей данные окружности одну в другую. Изогональная окружность
инвариантна относительно этой инверсии, так как проходит через инверсно-
соответственные точки Μλ и М2.
Соответствующая этому случаю касающаяся окружность (С) касаетсп
окружности (0\) в точке Тг внешним образом, а окружности (02) в точке 7\
внутренним образом, или наоборот. Следовательно, прикосновению разного
рода соответствует внутренний центр подобия. Окружность (С) инвариантна
относительно инверсии с центром 6\
В случае прикосновения одного рода (черт. 132) центром инверсии
является, как мы видим, внешний центр подобия S.
Сказанное может быть резюмировано следующим образом.
Окружность, касающаяся двух данных окружностей, инвариантна
относительно инверсии, преобразующей данные окружности друг в друга.
Центром такой инверсии является центр подобия данных окружностей,
и притом внешний, если прикосновение инвариантной окружности к двум
данным одного рода, и внутренний, если оно разного рода. Точки
прикосновения окружностей являются инвгрсно-соотзетственными. Прямая,
соединяющая эти точки, проходит через соответствующий центр подобия
данных окружностей.
1-Ш
§ 46. ПРОБЛЕМА АПОЛЛОНИЯ О КАСАНИИ ОКРУЖНОСТЕЙ.
Даны три окружности (СМ, (02) и (О.,). Требуется построить окруж-
«ость (О), касающуюся трех данных окружностей.
Эта задача, известная под названием проблемы Аполлония, была
предметом многочисленных и разнообразных исследований. Мы
изложим здесь решение проблемы Аполлония, основываясь на выводах
предшествующих параграфов.
$12 Ъ $23 $3
Черт. 134.
Проанализируем задачу. Предположим, что имеем окружность (О),
касающуюся данных окружностей (Oj), (02) и (03) (черт. 134). На
чертеже окружность (О) имеет с окружностями (Ог), (02) и (03)
соприкосновение одного рода. Тогда, согласно § 45, окружность (О),
как касающаяся окружностей (Οχ) и (02), принадлежит к (гилерболн-
ческой)*) связке с радикальным центром Si2> По той же причине
окружность (О) как касающаяся окружностей (02) и (03)
принадлежит к (гиперболической) связке с радикальным центром S2r
Следовательно, окружность (О) ортогональна к базисным окружностям этих
связок. Отсюда заключаем, что окружность (О) 1фииадлежит пучку
окружностей, ортогональных базисным окружностям (512) и (S23). Ради-
'Кальной осью такого пучка (§ 23) служит линия центров базисных
окружностей, т. е. ось подобия 6'12523. Предположим, что мы умеем
построить какую-либо окружность (ΤιΤ2Τ2) того же пучка. Тогда,
как нетрудно убедиться, мы могли бы построить искомую
окружность (О).
Ц При ином расположении окружностей связка могла бы оказат:.ся
эллиптической, что, однако, не меняет характера рассуждений.
141
В самом деле, построим радикальную ось окружностей (Ох) и»
(ТуТ2Т3). Пусть это будет прямая ΤχΗλ. Точку пересечения ее с осью
подобия SX2S2B обозначим буквой /?,. Точка /?, является радикальным
центром окружностей (О,), (О) и (ТХТ2ТЬ), так как она есть точка
пересечения радикальной оси TXRX окружностей (Ох) и (TXT2TZ) с
радикальной осью SX2S2Z окружностей (О) и (ТХТ2ТЪ)1). Но окружности
(О) и (Ох) должны
касаться по условию,
поэтому их радикальна»
ось проходит через
точку их прикосновения
А. Кроме того, она
должна проходить
через точку /?j.
Следовательно, проводя из
Rx касательную R\At
к окружности (Οι),
определим эту точку
прикосновения А.
Для построения
точки прикосновения В
искомой окружности к
окружности (02)
проводим прямую SX2A и
находим точки ее
пересечения с окружностью
(02). Одна из них со-
Черт. 135. ответствует точке А в
инверсии {SX2). Это и
есть, как мы знаем, точка прикосновения В (§45). Подобным же образом,
применяя центр инверсии 528, построим третью точку прикосновения С.
Таким образом, для решения задачи надо уметь построить
окружность (TxT2Tz)y принадлежащую к пучку окружностей, ортогональных
базисным окружностям (SX2) и (£23).
Воспользуемся для этого точками Т2 и Г8, которые сопряжены
относительно базисной окружности (528). Проводя прямую SX2T2,
находим соответствующую точку пересечения Тх с окружностью (Ох).
Окружность, проходящая через точки Ть Т2 и Г3, ортогональна
к базисным окружностям (SX2) и (£23), так как она проходит через
точки, попарно сопряженные относительно этих окружностей. Мы
знаем, что она пересекает три данные окружности (Ох), (02) и (08)
изогонально (§ 45)2).
1) Обе эти окружности принадлежат пучку, радикальной осью которого
служит прямая S12o23.
*ι Отсюда, между прочим, следует, что построенная изогональная
окружность (Ί\12ϊ:ύ принадлежит также третьей связке — с центром 5Ώ. Это
значит, что три точки 6'12, $23 и 5.Ц лежат на одной прямой (доказательство
теоремы Монжа).
142
Когда окружность (ΤχΤ2Τ3) построена, дальнейшее построение
точек прикосновения Л, В и С уже не представляет, как мы видели,
затруднений.
Так как из точки Rx можно провести две касательные к
окружности (Οχ), то, кроме точки прикосновения А и соответствующей ей
окружности [О (ЛВС)], мы имеем точку прикосновения А' и второе
решение задачи Аполлония — окружность \0' (А'В'С)] *)·
Таким образом, оси подобия Sl2S2dSsl соответствуют два решения
задачи Аполлония. Оба эти решения мы получили в предположении,
что искомая окружность имеет со всеми
данными окружностями прикосновение одного рода.
Таковы окружности \0 (ABC)] и \О'(А'В'С')].
Если мы предположим, что искомая
окружность имеет с окружностями (Οχ) и (02)
прикосновение разного рода, то для двух других
комбинаций (Οχ) (03) и (02) (03) она имеет
прикосновение одного рода в одной из них и
разного рода в другой. Поэтому искомая окружность
должна принадлежать одновременно к трем связ- Черт. 136.
кам. Радикальными центрами этих связок
являются два внутренних и один внешний центры подобия данных
окружностей, которые лежат на оси подобия. Кроме оси о^^з^зь мы име~
£м, как известно, еще три оси подобия, на каждой из которых лежит
один внешний и два внутренних центра подобия. Каждой из этих осей
соответствуют два решения аполлониевой задачи.
Таким образом, проблема Аполлония имеет, вообще говоря, 8
решений. При этом некоторые из этих решений (или даже все) могут
оказаться мнимыми 2).
На чертеже 135 даны все 8 решений аполлониевой задачи3).
Чертеж 136 представляет случай, когда задача не имеет ни одного
действительного решения. В самом деле, если предположим, что
такая окружность существует и касается окружности (Oj) в какой-
нибудь точке Гь а окружности (03) в точке Г3, то отсюда будет
следовать, что упомянутая окружность необходимо пересекает
окружность (02) и не является поэтому решением задачи Аполлония.
*) Решение невозможно, если точка RA окажется внутри окружности (Οι).
В этом случае касательные из Яг мнимы так же, как и соответствующие им
окружности Аполлония.
2) Подробное исследование можно найти в книге А д а м а р а,
Элементарная геометрия, М., 1938.
3) Центры касающихся окружностей обозначены буквами: αΐ5 α2; р1э р^
Τι» Ч* δι> S2.
ЛИТЕРАТУРА.
I. Учебно-методическая литература.
Александров И., Сборник геометрических задач на построение с
решениями, изд. 18, М., 1950.
Глаголев А. Н., Сборник геометрических задач на построение, М.г
1911.
Рашевский, Систематический курс геометрии и методы решения
задач на построение, М.—Л., 1928.
Рябков Г., Сборник геометрических задач на построение для
средних учебных заведений, Одесса, 1894.
Пржевальский Е., Собрание геометрических теорем и задач, М., 1932.
Романовский Б. В., Задачи на построение в стереометрии, М., 1936.
Делоне Б. и Житомирский О., Задачник по геометрии, М., 1936»
Делоне Б.э Житомирский О. и Фетисов А.э Сборник
геометрических задач, М., 1951.
А д а м а ρ Ж., Элементарная геометрия, под ред. Д. И. Перепелкина,
М., 1938.
Воронец А. М.э Геометрия циркуля, М., 1935.
Цюл ьке П., Построения на ограниченном куске плоскости, Огиз, 1936,
Берг М. Ф.э Приемы решения геометрических задач на построение,
М., 1928.
Зет ель С. И.э Новая геометрия треугольника, М., 1940.
Зет ель С. И.э Геометрия линейки и геометрия циркуля, М., 1950.
Перепелкин Д. И., Геометрические построения в средней школе,
М.— Л., 1947.
Четверухин Η. Φ., Методы геометрических построений, М.э 1938.
Четверухин Η. Φ., Вопросы методологии и методики геометрических
построений в школьном курсе геометрии. „Известия Акад. педаг. наук
РСФСР", 1946, вып. 6.
Четверухин Η. Φ., Стереометрические задачи на проекционном
чертеже, М.э 1951.
Л о π о в о к Л. М., Сборник стереометрических задач на построение,
М., 1950.
Μ и с ю ρ к е е в И. В., Геометрические построения, М., 1950.
Гуль И. М., Сборник геометрических задач. М., 1940.
II. Научные работы в области геометрических построений.
Mascheroni, La Geometria del Compasso, 1797.
Pons el et, Traite des proprietes projectives des figures, 1822.
Ш τ e й η e ρ Я., Геометрические построения, выполняемые с помощью
прямой линии и неподвижного круга, М., 1939.
Клейн Ф., Лекции по избранным вопросам элементарной геометрии,
Казань, 1898.
141
Гильберт Д., Основания геометрии, М. — Л., 1948.
Адлер Α., Теория геометрических построений, Л., 1940.
Петерсен, Методы и теория решения геометрических задач на
построение, Харьков, 1883.
Шатуновский С, Об измерении прямолинейных отрезков и
построении их с помощью циркуля и линейки, Одесса, 1925.
Орлов Α., Руководство к геометрическому линейному черчению,-
Казань, 1877.
Некрасов П. Α., Приложение алгебры к геометрии (алгебраический·
метод решения геометрических задач на построение), М., 1897.
Мордухай-Болтовский Д. Д., О штейнеровских построениях на
сфере. „Математический сборник", т. 42, 1935, стр. 535.
Четверухин Н. Ф., Геометрические построения и приближения, М.г.
1935.
Enrique s F., Question! Riguardanti La Geometria Elementare, II,
Bologna, 1910. .
Vahlen Th., Konstruktionen und Approximationen, Leipzig, 1910.
Никулин Η. Α., Геометрические построения с помощью простейших
инструментов, Крымиздат, Симферополь, 1947.
Lebesque Η., Legons sur les constructions geometriques, Paris, Gautier-
Villars, 1950.
Мордухай-Болтовский Д. Д., О геометрических построениях,
в пространстве Лобачевского. Ученые записки научно-исследовательского
института математики и физики Ростовского государственного университетаг
1, 1Уо/.
Нестерович Н. М.. Геометрические построения в плоскости
Лобачевского, Гостехиздат, М. — Л., 1951.
Смогоржевский А. С., Геометрические построения в плоскости»
Лобачевского, М. — Л., 1951.
СОДЕРЖАНИЕ.
Стр.
введение 3
Глава первая.
Обоснование конструктивной геометрии.
.§ 1. Практическая графика и геометрические построения 6
.§ 2. Определение „конструктивных" элементов 7
§ 3. Образование класса К конструктивных точек 9
*§ 4. О «данных* и „произвольных" элементах 10
4 5. Геометрические построения с помощью двусторонней линейки . . 12
<§ 6. Геометрические построения с помощью „прямого" или „острого
угла" и «угольника" 15
§ 7. О теоретическом и практическом значениях инструментов
построения 20
$ 8. Схема решения задачи на построение 25
Глава вторая.
Алгебраический метэд.
§ 9. Применение алгебры к геометрии 34
§ 10. Построение корней квадратного уравнения 36
§ 11. Примеры 39
Глава третья.
Геометрические места.
*§ 12. Простейшие геометрические места 45
4 13. Геометрические места в аналитической геометрии 46
-§ 14. Кривые второго порядка как геометрические места 49
§ 15. Овалы Кассини 55
§ 16. „Метод геометрических мест" 58
§ 17. Исследование структуры задачи на построение 59
-§ 18. Геометрические места в пространстве 76
Глава четвертая..
Геометрия кругов.
^ 19. Степень точки относительно окружности 80
§ 20. Радикальная ось " 81
·§ 21. Радикальный центр 84
§ 22. Пучки окружностей 86
§ 23. Нулевые окружности и ортогональные траектории 88
§ 24. Примеры 90
4 25. Связки окружностей 92
-§ 26. Примеры 97
<§ 27. Пучок окружностей, диаметрально пересекающих две данные
окружности 100
146
Глава пятая.
Метод геометрических преобразований.
Стр.
§ 28. Симметрия 102
§ 29. Применение симметрии к геометрическим построениям .... 103
§ 30. Вращение 105
§ 31. Применение преобразования вращения к геометрическим
построениям 106
§ 32. Параллельное перенесение 109
§ 33. Применение параллельного перенесения к задачам на построение ПО
§ 34. Гомотетия 114
I 35. Применение гомотетии к геометрическим построениям 116
§ 36. Подобие окружностей . 119
* § 37. Теорема Монжа (о подобии окружностей) 121
§ 38. Системы окружностей, имеющих общую ось подобия 125
§ 39. Инверсия 129
§ 40. Теорема об антипараллельных прямых 130
§ 41. Инверсия прямой и окружности 131
§ 42. Неизменность углов в инверсии 133
§ 43. Инверсия с отрицательной степенью 134
§ 44. Инвариантные окружности в инверсии 136
§ 45. Изогональные и касательные окружности 138
§ 46. Проблема Аполлония о касании окружностей 141
Литература 144
Редактор А В. Игнатьева,
Техн. редактор С Τ Шикин.
Корректор 3. Л1. Шабхи.
Обложка художника С Г. Богачева.
Чертежи И. Л. Меделяновского.
Художественный редактор К, П. Васькова.
Подписано в печать 30/V 1952 г А02982.
Тираж 25 тыс. экз. Бумага 60Х921 /,б=4,б25
бум л.=9,25 печ. л. Уч.-изд л. 9,58. Заказ ЛЪ 3272.
Цена без переплёта 2 р. 85 к Переплёт 50 к.
Набрано и отматрицировано β Первой
Образцовой типографии имени А. А. Жданова Глав-
полиграфиздага при Совете Министров СССР
Москва, Валовая, 28.
Отпечатано с матриц в Калужской типографии
Росполиграфпрома Зак 246.