Ч П Е Д Г И 3 • I
Г. А. ВЛАДИМИРСКИМ
СТЕРЕОСКОПИЧЕСКИЕ ЧЕРТЕЖИ
по
ГЕОМЕТРИИ
ГОСУДАРСТВЕННОЕ
УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
Москва* 19 62
Подготовлено к печати и отпечатано по методу
и под руководством С. С. Гуревича
Два экземпляра стереоочков вложены
в кармашек переплета в конце книги.
ОТ ИЗДАТЕЛЬСТВА
Настоящее издание книги «Стереоскопические чертежи по геомет-
рии» предназначено в качестве учебного пособия для учащихся старших
классов очных и заочных средних школ и для лиц, занимающихся
самообразованием.
Явление стереоскопического эффекта, вызывая живой интерес со
стороны учащихся, способствует яркости восприятия и прочности запо-
минания изучаемого учебного материала.
Из разных способов стереоскопического показа наиболее простым
и экономически целесообразным является анаглифический метод, разра-
ботанный в последнее время для издательских процессов достаточно
надежно.
Книга «Стереоскопические чертежи по геометрии» состоит из двух
частей. Первая часть содержит 80 чертежей к Онкольному курсу стерео-
метрии. Каждый чертеж сопровождается кратким текстом, в котором
приводятся название и определение изображенной 'фигуры или сформу-
лирована зависимость между элементами данной фигуры в соответ-
ствии с теоремой. В скобках приведена ссылка на учебник А. П. Кисе-
лева по стереометрии издания 1951 г. и более поздних лет.
1
Во второй части даны изображения 80 фигур к стереометрическим
задачам из «Сборника задач по геометрии». Н. Рыбкина. Сопроводи-
тельный текст к изображенной на чертеже фигуре содержит условие за-
дачи. Ссылка в скобках под текстом указывает параграф и номер за-
дачи из «Сборника задач по геометрии» Н. Рыбкина издания 1955 г.
и более поздних лет.
Прежде чем приступить к использованию этого пособия, рекомен-
дуется внимательно ознакомиться с условиями рассматривания стерео-
чертежей и методическими указаниями.
Учпедгиз просит прислать свои отзывы и замечания как по содер-
жанию, а также и по художественному исполнению по адресу:
Москва, И-18, 3-й проезд Марьиной рощи, дом № 41, Учпедгиз.
ВВЕДЕНИЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Одной из задач преподавания геометрии в средней школе является
задача развития и формирования пространственных представлений и
понятий. В основе развития пространственных представлений учащихся
на уроках стереометрии лежит зрительное восприятие объемного на-
глядного материала, обычно моделей геометрических тел, различных
технических форм, предметов обихода, графических наглядных пособий
и т. п. Систематическое ознакомление учащихся с геометрическими свой-
ствами пространственных фигур и взаимосвязью между их элементами
приводит к обобщению первоначальных пространственных представле-
ний и формированию геометрических понятий. Процесс накопления и
расширения запаса пространственных представлений протекает наиболее
успешно в условиях широкого использования разнообразного нагляд-
ного материала. В этом отношении существенная роль может принад-
лежать стереоскопическим чертежам, которые дают возможность при
изучении курса стереометрии значительно увеличить количество фигур,
дающих в зрительном восприятии объемное изображение.
Следует иметь в виду, что стереоскопический чертеж не может пол-
ностью заменить объемную модель, преимущество которой состоит в том,
что учащиеся имеют возможность рассматривать ее с любой стороны,
в любом ракурсе, в неподвижном положении и движении. Использо-
вать эти качества модели особенно важно при первоначальном ознаком-
лении с какой-либо пространственной фигурой. Поэтому если в рас-
поряжении педагога имеется модель изучаемой фигуры, то первое озна-
комление учащихся с этой фигурой нужно начинать с модели. Однако
не все условия задачи или теоремы могут быть представлены в
объемной модели. Вообще, при дальнейшем формировании пространст-
венных представлений на первое место следует выдвинуть стереоскопи-
ческий чертеж, который в силу целого ряда преимуществ позволит каж-
дому учащемуся в течение произвольного, необходимого ему времени
детально рассмотреть изучаемую фигуру, уточняя общую ее конструк-
цию и выделяя существенные признаки, определяющие форму фигуры.
Такая методика широкого использования стереочертежей после пред-
варительного ознакомления с основными фигурами на объемных моде-
лях обеспечивает для каждого учащегося формирование наиболее точ-
ного и яркого представления изучаемых в стереометрии пространствен-
ных фигур.
При ознакомлении с основными геометрическими телами и при изу-
чении их свойств, излагаемых в учебнике, учащиеся не всегда легко и
правильно понимают структуру пространственных фигур по чертежам,
приведенным в учебнике ’. В этом случае стереоскопический чертеж,
изображающий ту же фигуру, окажет учащемуся значительную помощь.
Сопоставляя стереоскопическую фигуру с соответствующим чертежом
б
1 Подробные сведения о построении стереочертежей можно найти в статье
Г. А. Владимирского «Построение стереоскопических проекций геометрических
фигур», «Математика в школе», Учпедгиз, 1937,	№ 3.
учебника, учащиеся яснее и отчетливее представят себе строение фигу-
ры, изображенной в учебнике, и вместе с тем постепенно освоят те ус-
ловности графического чертежа, которые обычно затрудняют правильное
его восприятие. Необходимо отметить, что в начальном периоде изучения
стереометрии полезным является одновременный показ стереоскопиче-
ской фигуры и чертежа учебника; в дальнейшем необходимо на первое
место., ста вить чертеж учебника и использовать соответствующий стерео-
чертеж только после того, как изучение свойств изображенной на обыч-
ном чертеже фигуры или доказательство теоремы, иллюстрируемой чер-
тежом, будет закончено. Такой заключительный показ стереочертежа
необходим с целью уточнения тех подробностей, которые могли ускольз-
нуть при рассмотрении обычного чертежа, а также с целью устранения
возможных ошибок в понимании формы изучаемой фигуры, допущен-
ных учащимися при неправильном истолковании чертежа учебника.
При решении стереометрических задач (на вычисление и на построе-
ние) учащиеся должны, во-первых, мысленно представить пространст-
венную фигуру, описанную в условии задачи, и, во-вторых, начертить ее
наглядное изображение. Выполнение этих двух требований нередко ока-
зывается весьма трудным для учащихся. Однако сопровождение усло-
вия задачи обычным наглядным рисунком фигуры, описанной в тексте,
нецелесообразно, так как вследствие этого задача в значительной сте-
пени теряет свое образовательное и воспитательное значение. В этом
случае стереочертеж может оказать методическую помощь, так как
только частично снимает трудности решения, заключающиеся в мыслен-
ном представлении пространственной фигуры, описанной в условии за-
дачи. Вместе с тем стереочертеж ни в коей мере не дает ответа на вто-
рое требование — построить в параллельной проекции наглядное изо-
бражение фигуры, которую учащийся видит через стереоочки. Нежела	§
тельный подсказ ответа на это требование устраняется благодаря тому,
что плоские фигуры на стереочертеже построены в центральной (а не
в параллельной) проекции и притом в таком ракурсе, который не при-
нят при параллельном проектировании.
Методика использования стереочертежей при решении задач анало-
гична той, которая указана для стереочертежей первой части альбома.
Стереочертеж необходим, если учащийся не может правильно предста-
вить и изобразить фигуру, заданную в условии задачи; вместе с тем
стереочертеж весьма полезен и в том случае, если его рассмотрит уча-
щийся, сумевший решить задачу, не используя этого наглядного посо-
бия. Такое последующее после решения обращение к стереочертежу по-
зволит учащемуся проверить и, если нужно, уточнить и пополнить свое
мысленное первоначальное представление заданной в условии фигуры.
КАК РАССМАТРИВАТЬ СТЕРЕОЧЕРТЕЖИ
Стереочертежи рассматривают через светофильтры (стереоочки)
таким образом, чтобы синий светофильтр пришелся на правый глаз, а
красный — на левый *.
Рассматривать чертежи, помещенные в этой книге, следует сидя
за столом (или за школьной партой) и положив книгу на стол таким
образом, чтобы плоскость страницы, на которой отпечатан чертеж, была
расположена горизонтально, а нижний край страницы был параллелен
переднему краю крышки стола.
Если крышка школьной парты имеет наклонное положение, то не-
обходимое горизонтальное положение страницы с рассматриваемым
чертежом можно получить, опирая верхний край обложки альбома на
крышку парты и поддерживая надлежащим образом альбом за нижний
край обложки левой рукой, опирающейся на крышку парты.
Форма и размеры фигуры, воспринимаемой через стереоочки, не
остаются неизменными, если изменять положение глаз относительно
1 Подробные описания методов получения и рассматривания объемных печатных
иллюстраций приведены в следующих книгах:
Научно-исследовательский институт полиграф, и издат. пр-ти. С. С. Гуревич,
«Стереоскопическая печать», изд. Гизлегпром, 72 стр., 1933 г.
С. С. Гуревич, «Объемная печатная иллюстрация», изд. «Искусство», 328 стр.,
1959 г.
10
чертежа. Поэтому для получения зрительного образа фигуры, наиболее
соответствующего по форме и размерам условию иллюстрируемой тео-
ремы или задачи, необходимо, рассматривая чертеж через стереоочки,
подыскать наиболее правильное положение глаз перед страницей с чер-
тежом; это можно сделать, слегка перемещая голову вверх и вниз,
вправо и влево, вперед и назад. Лица, пользующиеся при чтении обыч-
ными очками, должны рассматривать стереочертежи через обычные
очки, прикладывая к ним очки-светофильтры. Для освещения чертежей
должен служить рассеянный белый (дневной или искусственный) свет,
равномерно (без бликов) освещающий поверхность чертежа.
Стереоочки (светофильтры) нужно оберегать от царапин, пыли,
загрязнения. Сохранять их нужно в бумажном чистом конверте. Если
светофильтр запылится, его можно осторожно протереть чистой сухой
ваткой. Протирать влажной ваткой светофильтр можно только после
освобождения его от бумажной оправы.
Часть первая
СТЕРЕОСКОПИЧЕСКИЕ ЧЕРТЕЖИ
К УЧЕБНИКУ А. П. КИСЕЛЕВА «ГЕОМЕТРИЯ», ч. II
При рассматривании стереочертежей
внимательно проверьте, чтобы синий
светофильтр пришелся на правый глаз,
а красный—на левый (см. стр. 8 и 10).
/?
1. ПРЯМЫЕ И плоскости
(черт. I—29)
- Ч«рт. 1
Через каждую прямую а в прост-
ранстве можно провести бесчислен-
ное множество плоскостей М,
N, Р,...
(Стр. 4, § 5, черт. 2.)

14
Черт. 2.
Две прямые АВ и DE, не имеющие
общих точек и лежащие в разных
плоскостях, называются скрещива-
ющимися.
(Стр. 5, § 8, черт. 4.)
15
Черт. 3.
Если прямая АВ параллельна ка
кой-нибудь прямой CD, располо-
женной в плоскости г то она пз-
раллельна сами;, п юскос'п
(Стр. 6, § 10, черт. 5.)
Черт. 4.
Если прямая АВ параллельна каж-
дой из двух пересекающихся пло-
скостей Р и Q, то она параллель-
на линии их пересечения CD.
(Стр. 7, § 12, черт. 6.)
17
Черт. 5.
Если две прямые АВ и CD парал-
лельны третьей прямой EF, то онч
параллельны между собой.
(Стр. 7, § 13, черт. 7.)
2. Стереочертежи по геометрии
I

18
Черт. 6.
Если две пересекающиеся прямые
АВ и АС одной плоскости Р со-
ответственно параллельны двум
прямым А\В\ и Л1С1 другой пло-
скости Q, то эти плоскости парал-
лельны.
(Стр. 7, § 15, черт. 8.)
19
Черт. 7.
Задача. Даны две скрещиваю-
щиеся прямые а и b и точка А, не
лежащая ни на одной из данных
прямых. Провести через точку А
прямую, пересекающую обе данные
прямые а и Ь.
(Стр. 9, § 22, черт. 14.)
2*


20
Черт. 8.
Если прямая AAlt пересекающаяся
с плоскостью Mt перпендикулярна
к двум прямым ОВ и ОС, прове-
денным на этой плоскости через
точку пересечения О данной прямой
и плоскости, то она перпендикуляр-
на и ко всякой прямой OD, прове-
денной на плоскости через ту же
точку О.
(Стр. 10, § 23, черт. 15.)
Черт. 9.
Если из одной и той же точки А,
взятой вне плоскости Р, проведены
к этой плоскости перпендикуляр
АВ и какие-нибудь наклонные АС,
AD, АЕ,..., то: 1) две наклонные,
имеющие равные проекции, равны;
2) из двух наклонных та больше,
проекция которой больше.
(Стр. 11, § 26, черт. 16.)


Черт. 10.
Прямая DE, проведенная на плоско-
сти F через основание наклонной
АС перпендикулярно к ее проекции
ВС, перпендикулярна и к самой на-
клонной.
(Стр. 12, § 28, черт. 17.)
Черт. 11,
Если плоскость Р перпендикулярна
к одной из параллельных прямых
АВ, то она перпендикулярна и к
другой CD.
(Стр. 13, § 31, черт. 18.)
Черт. 12.
Если две прямые АВ и CD перпен-
дикулярны к одной и той же пло-
скости Р, то они параллельны.
(Стр. 13, § 32, черт. 19.)
Черт. 13.
Если прямая ВВХ перпендикулярна
к одной из параллельных плоско-
стей Р, то она перпендикулярна и
к другой Q.
(Стр. 14, § 33, черт. 20.)

 26
Черт. 14.
Если две плоскости Р и Q перпенди-
кулярны к одной и той же прямой
АВ, то они параллельны.
(Стр. 14, § 34, черт. 21.)

27
Черт. 15.
Задача. Через данную точку О
пространства провести прямую, пер-
пендикулярную к данной плоско-
сти Р.
(Стр. 15, § 36, черт. 23.)

I
- 28
Черт. 16.
Задача. Даны две скрещиваю-
щиеся прямые а и Ь. Построить
прямую, пересекающую обе данные
прямые и перпендикулярную к ним
обеим.
(Стр. 16, § 37, черт. 25.)
29
Черт. 17.
Двугранным углом называет-
ся фигура, образованная двумя полу-
плоскостями Р и Q, исходящими из
одной прямой АВ. Прямая АВ —
ребро, а полуплоскости Р и Q — гра-
ни двугранного угла.
(Стр. 17, § 38, черт. 26 и 27.)
I

30
Черт. 18.
Если из произвольной точки D реб-
ра АВ провести на каждой грани
по перпендикуляру к ребру, то об-
разованный ими угол CDE назы-
вается линейным углом дву-
гранного угла.
(Стр. 17, § 38, черт. 28.)
31
Черт. 19.
Теоремы: I) Равным двугранным
углам соответствуют равные линей-
ные углы Z.CBD = ^.CiBiDi.
2) Большему двугранному углу
соответствует больший линейный
угол Z.CBD> Z.C\BiDi.
(Стр. 18, § 39, черт. 29.)

Черт. 20.
Прямому двугранному углу соответ-
ствует прямой линейный угол и об-
ратно.
(Стр. 18, § 41, черт. 30.)
L‘f:
Черт. 21.
Если плоскость Р проходит через
перпендикуляр АВ к другой пло-
скости Q, то она перпендикуляр-
на к этой плоскости.
(Стр. 19, § 43, черт. 31.)
3. Стереочертежи по геометрии


Черт. 22.
Если две плоскости Р и Q взаимно
перпендикулярны и к одной из них,
к Q, проведен перпендикуляр, имею-
щий общую точку А с другой пло-
скостью Р, то этот перпендикуляр
весь лежит в этой плоскости Р.
(Стр. 19, § 44, черт. 32.)
Черт. 23.
Линия пересечения АВ двух пло-
скостей Р и Q, перпендикулярных
к третьей плоскости R, есть перпен-
дикуляр к этой плоскости.
(Стр. 20, § 45, черт. 33.)
з

36
Черт. 24.
Углом двух скрещивающихся пря-
мых АВ и CD, для которых дано
положение и направление, назы-
вается угол MON, образуемый по-
лупрямыми ОМ и ON, соответствен-
но параллельными прямым АВ и
CD и одинаково с ними направ-
ленными. Точка О произвольная.
(Стр. 20, § 46, черт. 34.)
37
Черт. 25.
Если проектируемая линия есть
прямая АВ, не перпендикулярная к
плоскости Р, то проекция ее на эту
плоскость есть также прямая ab.
(Стр, 21, § 47, черт. 35.)


Черт. 26.
Углом прямой АВ с плоскостью Р в
том случае, когда прямая наклонна
к плоскости, называется острый
угол АВС, составленный этой пря-
мой с ее проекцией ВС на плоскость.
(Стр. 21, § 48, черт. 36.)
Черт. 27.
Многогранный угол SABCDE нельзя
назвать выпуклым, так как он рас-
положен не по одну, а по обе сторо-
ны от плоскости некоторых граней
(от грани ASB и от грани BSC).
(Стр. 22, § 49, черт. 39.)

— 40
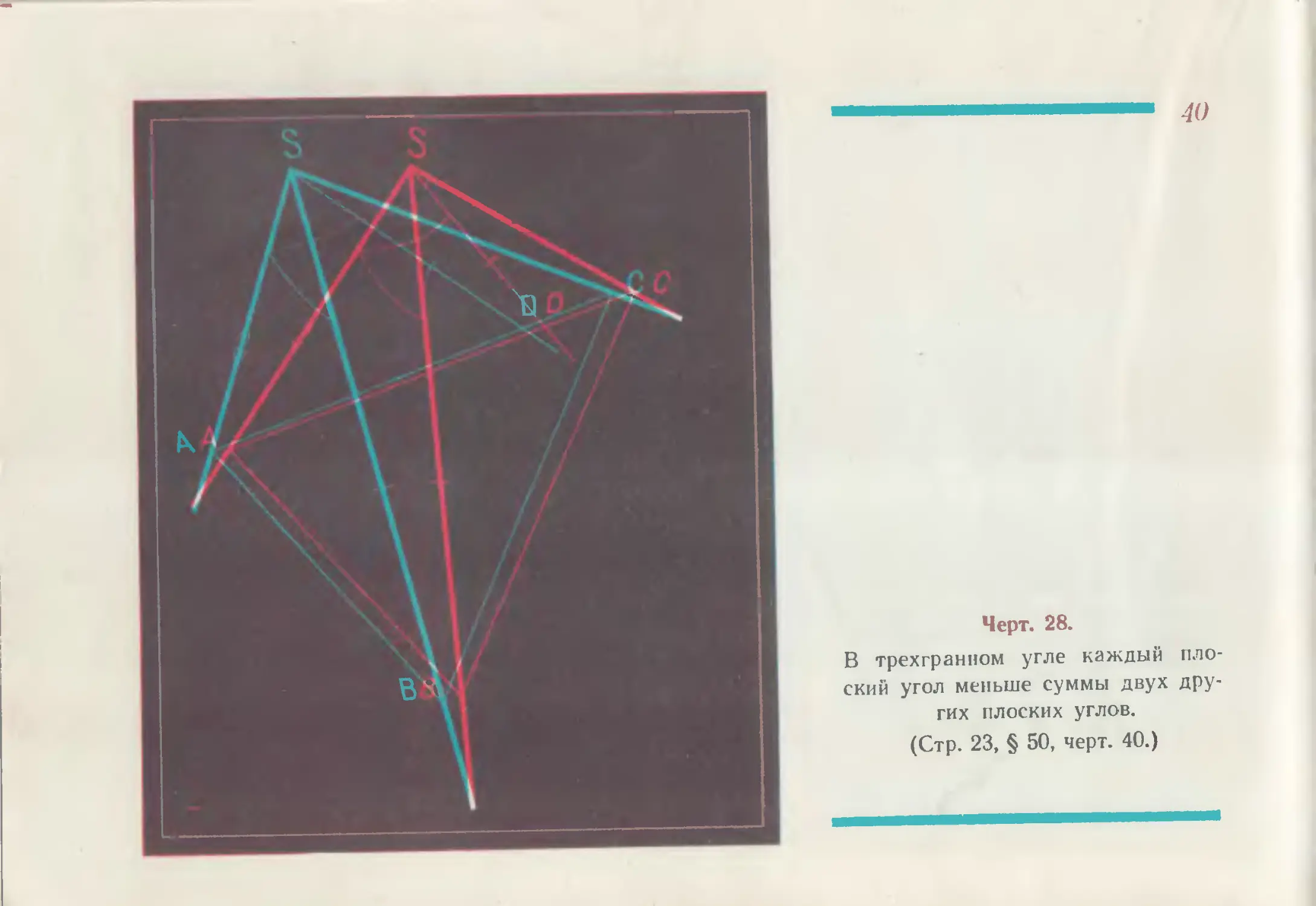
Черт. 28.
В трехгранном угле каждый пло-
ский угол меньше суммы двух дру-
гих плоских углов.
(Стр. 23, § 50, черт. 40.)
41
Черт. 29.
Многогранные углы SABCDE и
ХЛ iBiCiDiEi называются вертикаль-
ными, если ребра одного из них слу-
жат продолжением соответственных
ребер другого.
(Стр. 25, § 53, черт. 43.)


2. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
ТОЧКИ, ОТРЕЗКА И ФИГУРЫ
(черт. 30—39)
Черт. 30.
Плоскости проекций Н и V образу-
ют прямой двугранный угол НхуУ и
служат для построения на них про-
екций фигур, расположенных внутри
этого угла, например а и а' — про-
екции точки А на плоскости Н и V.
(Стр. 26, § 54, черт. 44.)
Черт. 31.
I) Точка А лежит на плоскости Н;
2) Точка В расположена на плоско-
сти V; 3) Точка С лежит на оси ху.
Проекции точек А, В и С лежат на
прямой ху.
(Стр. 27, § 55, черт. 46.)

г
44
Черт. 32.
Проекции отрезков: 1) один конец
В отрезка ЛВ лежит на плоскости
//; 2) один конец D отрезка CD
лежит на плоскости V; 3) отрезок
EF упирается своими концами в
плоскости V и Н.
(Стр. 28, § 57, черт. 50.)
45
Черт. 33.
I) Отрезок АВ перепендикулярен к
плоскости V и упирается в нее.
2) отрезок CD перпендикулярен к
плоскости И и упирается в нее.
(Стр. 29, § 57, черт. 52 и 53J

Черт 34.
Отрезок АВ лежит в плоскости Р,
перпендикулярной к оси ху.
(Стр. 29, § 57, п. 6, черт. 54 и 55.)
Черт. 35.
Отрезок АВ параллелен плоскости
V; его горизонтальная проекция аЬ
параллельна оси ху, а фронталь-
ная проекция а'Ь' равна отрезку А В.
(Стр. 30, § 57, черт. 56.)

I
48
Черт. 36.
Отрезок АВ параллелен плоскости
Н; его фронтальная проекция а'Ь'
параллельная оси ху, а горизонталь-
ная проекция ab равна отрезку АВ.
(Стр. 30, § 57, черт. 58.)
49
Черт. 37.
Отрезок АВ вращением вокруг пря-
мой А а приведен в положение АВ0,
параллельное плоскости V. Фрон-
тальная проекция а'Ь'о равна нату-
ральной величине отрезка АВ.
(Стр. 32, § 60, черт. 64.)
4. Стереочертежи ло геометрии


50
Черт. 38.
По заданным проекциям abc и а'Ь'с'
треугольника АВС и заданной го-
ризонтальной проекции (pq) прямой
PQ, лежащей в плоскости этого тре-
угольника, построена фронтальная
проекция р'д' поямой PQ.
(Стр. 33, § 63, черт. 68.)
51
Черт. 39.
По заданным произвольно горизон-
тальным проекциям a, b, с, d, е, f
вершин шестиугольника ABCDEF
построены горизонтальна(я и фрон-
тальная проекции (abcdef-,
a'b'c'd'e'f') этого шестиугольника.
(Стр. 35, § 65, черт. 72.)

Т
52
3. МНОГОГРАННИКИ
(черт. 40—63)
Черт. 40.
Призмой называется многогран-
ник, у которого две грани — равные
многоугольники с соответственно па-
раллельными сторонами, а все ос-
тальные грани — параллелограммы.
(Стр. 37, § 68, черт. 73.)
53
Черт. 41.
Пирамидой называется много-
гранник, у которого одна грань, на-
зываемая основанием, есть какой-ни-
будь многоугольник, а все осталь-
ные грани, называемые боковыми,—
треугольники, имеющие общую вер-
шину.
(Стр. 38, § 70, черт. 76.)

I
54
Черт. 42.
В параллелепипеде: 1) противопо-
ложные грани равны и параллель-
ны; 2) все четыре диагонали пере-
секаются в одной точке и делятся в
ней пополам.
(Стр. 40, § 72, черт. 81.)
55
Черт. 43.
Если две пирамиды с равными вы-
сотами рассечены на одинаковом
расстоянии от вершины плоскостя-
ми, параллельными основаниям, то
площади сечений пропорциональны
площадям оснований.
(Стр. 42, § 76, черт. 84.)


56
Черт. 44.
Перпендикулярное сечение
призмы — многоугольник abcde,
получаемый от пересечения призмы
плоскостью, перпендикулярной к бо-
ковым ребрам. Стороны этого мно-
гоугольника перпендикулярны к бо-
ковым ребрам призмы.
(Стр. 43, § 78, черт. 85.)
57
Черт. 45.
Любая наклонная приз.ма
ABCDEAiBtCiDiEi равновелика та-
кой прямой призме abcdeajbiCidiet,
основание которой равно перпенди-
кулярному сечению данной наклон-
ной призмы, а высота ой] — ее боко-
вому ребру AAi.
(Стр. 48, § 86, черт. 92.)

• 58
Черт. 46.
Объем прямого параллелепипеда ра-
вен произведению площади основа-
ния (пл. ABCD) на высоту BB}.
(Стр. 48, § 87, черт. 93.)
59
Черт. 47.
Объем наклонного параллелепипеда
равен произведению площади осно-
вания (пл. ABCD) на высоту RS.
(Стр. 49, § 87, черт. 94.)
60
Черт. 48.
Объем треугольной призмы равен
произведению площади основания
(пл. АВС) на высоту призмы Н.
(Стр. 50, § 88, черт. 95.)
61
Черт. 49.
Объем многоугольной призмы равен
произведению площади основания
(пл. ЛБС...) на высоту призмы Н.
(Стр. 50, § 88, черт. 96.)

62
Черт. 50.
Принцип Кавальер и. Если
два тела могут быть помещены в та-
кое положение, при котором всякая
плоскость, параллельная какой-ни-
будь данной плоскости и пересекаю-
щая оба тела, дает в сечении с ними
равновеликие фигуры, то объемы
таких тел одинаковы.
(Стр. 51, § 89, черт. 97.)
63 —
Черт. 51.
Треугольные пирамиды с равнове-
ликими основаниями и равными вы-
сотами равновелики.
(Стр. 52, § 90, черт. 99.)
Черт. 52.
Объем пирамиды равен произведе-
нию плошади ее основания на треть
высоты.
(Стр. 55, § 91, черт. 102.)
65
Черт. 53.
Объем усеченной пирамиды вычис-
ляется по формуле:
v= 1 н^в + ь + увь^,
где Н — высота усеченной пирами-
ды, В — площадь нижнего основания
п b — площадь верхнего основания
усеченной пирамиды.
(Стр. 56, § 92, черт. 104.)
5. Стереочерт-чжи пл геометрии

Черт. 54.
г ПО
Объемы подобных многогранников
относятся, как кубы сходственных
ребер.
(Стр. 59, § 96, черт. 106.)
Черт. 55.
Тетраэдр — правильный четырех-
гранник, поверхность которого со-
ставлена из четырех правильных
треугольников.
(Стр. 60, § 97, черт. 107.)


68
Черт. 56.
Куб, или гексаэдр — правиль-
ный шестигранник, поверхность ко-
торого состоит из шести правильных
четырехугольников (квадратов).
(Стр. 60, § 97, черт. ПО.)
69
Черт. 57.
Октаэдр — правильный восьми-
гранник, поверхность которого со-
ставлена из восьми правильных тре-
угольников.
(Стр. 60, §-98, черт. 108.)

Черт. 58
Додекаэдр — правильный две-
надцатигранник, поверхность кото-
рого составлена из двенадцати пра-
вильных пятиугольников.
(Стр. 60, § 97, черт. Ill.)
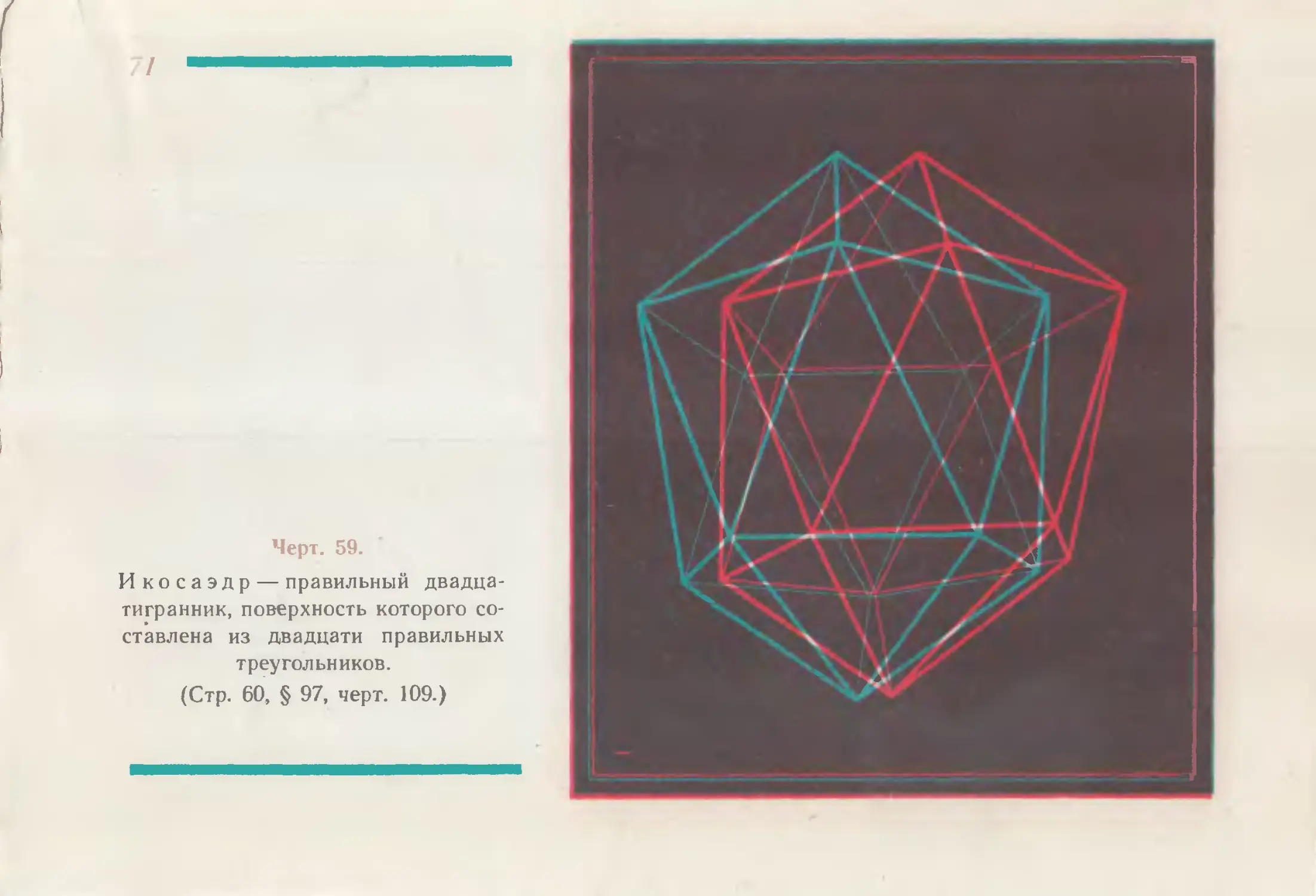
Черт. 59.
Икосаэдр — правильный двадца-
тигранник, поверхность которого со-
ставлена из двадцати правильных
треугольников.
(Стр. 60, § 97, черт. 109.)

7'2
Черт. 60;
Построение тетраэдра.
(Стр. 61, § 98, черт. 112.)
Черт. 61.
Построение октаэдра.
(Стр. 61, § 98, черт. 113.)

71
Черт 62.
Высота правильной треугольной
пирамиды служит для нее осью
симметрии третьего порядка.
(Стр. 66, § ЮЗ, черт. 119.)
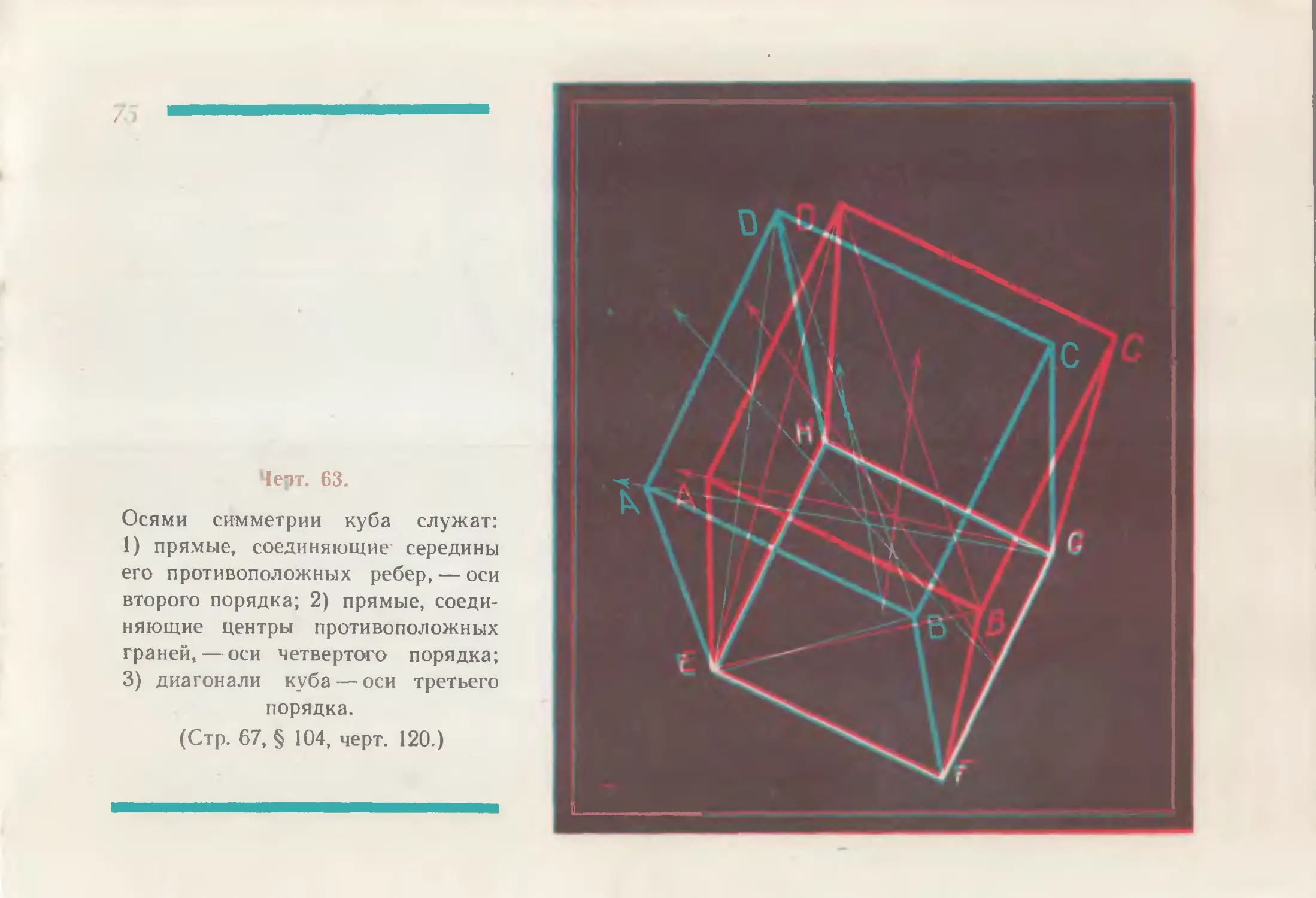
Черт. 63.
Осями симметрии куба служат:
1) прямые, соединяющие- середины
его противоположных ребер, — оси
второго порядка; 2) прямые, соеди-
няющие центры противоположных
граней, — оси четвертого порядка;
3) диагонали куба — оси третьего
порядка.
(Стр. 67, § 104, черт. 120.)


76
4. КРУГЛЫЕ ТЕЛА
(черт. 64—74)
Черт. 64.
Цилиндрическая поверх-
ность, направляющей линией кото-
рой служит парабола MAN и обра-
зующей— прямая АВ.
(Стр. 69, § 106. черт. 122.)
77 '
Черт. 65.
Цилиндр, основаниями которого
являются эллипсы.
(Стр. 69, § 107, черт. 123.)
' 78
Черт. 66.
Прямой круговой цилиндр-
его основаниями служат круги.
(Стр. 69, § 107, черт. 124.)
79
Черт. 67.
Конической поверхностью
называется поверхность, производи-
мая движением прямой АВ, переме-
щающейся в пространстве так, чго
она при этом постоянно проходит че-
рез неподвижную точку S и пересе-
кает данную кривую линию MN.
Прямая АВ — образующая, а линия
MN — направляющая; S — вершина
конической поверхности.
(Стр. 70, § 108, черт. 125.)


80
Черт. 68.
Конусом называется тело, огра-
ниченное частью конической поверх-
ности, расположенной по одну сто-
рону от вершины, и плоскостью, пе-
ресекающей все образующие по ту
же сторону от вершины.
(Стр. 70, § 109, черт. 126.)
81
Черт. 69.
Конус называется прямым
круговым, если его основание
есть круг, а высота проходит через
центр основания.
(Стр. 70, § 108, черт. 127.)
в. Стереочертежи по геометрии


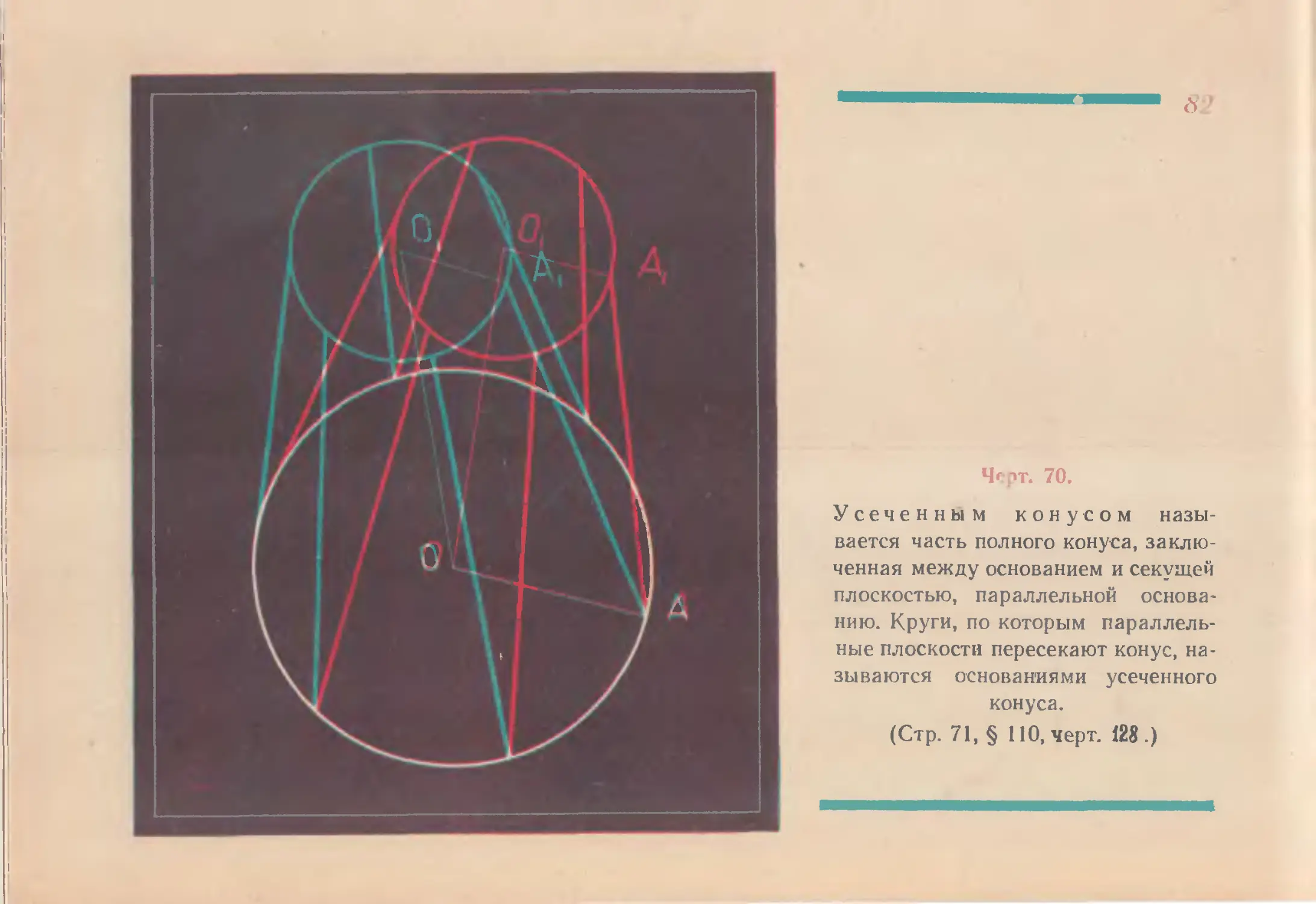
Черт. 70.
Усеченным конусом назы-
вается часть полного конуса, заклю-
ченная между основанием и секущей
плоскостью, параллельной основа-
нию. Круги, по которым параллель-
ные плоскости пересекают конус, на-
зываются основаниями усеченного
конуса.
(Стр. 71, § НО, черт. 128.)
S3
Черт. 71.
Боковая поверхность ц и-
л и н д р а. За величину боковой по-
верхности цилиндра принимают пре-
дел, к которому стремится боковая
поверхность вписанной в этот ци-
линдр правильной призмы при не-
ограниченном увеличении числа бо-
ковых граней этой призмы.
(Стр. 71, § 112, черт. 129.)
I
I

84
Черт. 72.
Боковая поверхность ко-
нуса. За величину боковой поверх-
ности конуса принимают предел, к
которому стремится боковая поверх-
ность вписанной в этот конус пра-
вильной пирамиды при неограничен-
ном увеличении числа боковых гра-
ней пирамиды.
(Стр. 72, § 111, черт. 130.)
Черт. 73.
Всякое сечение шара плоскостью
есть круг.
(Стр. 78, § 126, черт. 137.)

Л6
Черт. 74.
Через две точки, например С и N,
шаровой поверхности, не лежащие
на концах одного диаметра, можно
провести окружность большого кру-
га и только одну.
(Стр. 79, § 129, черт. 139.)
5. ПРИЛОЖЕНИЕ
( -ерт. 75—80)
Черт. 75.
Тело, образованное вращением по-
лукруга вокруг диаметра, назы-
вается шаром, а поверхность, описы-
ваемая при этом полуокружностью,
называется шаровой или сфериче-
ской поверхностью.
(Стр. 77, §.125.)


88
Черт. 76.
Тор, или кольцо. Поверхность
кольца образуется вращением ок-
ружности вокруг оси, расположен-
ной в плоскости этой окружности и
не пересекающей ее.
89
Черт. 77.
Эллипсоид вращения сжа-
т ы й. Поверхность сжатого эллип-
соида вращения образуется враще-
нием эллипса вокруг его малой оси.
Черт. 78.
Параболоид в р а щен и я.
Поверхность параболоида вращения
образуется вращением дуги парабо-
лы вокруг оси симметрии этой пара-
болы.
91
Черт. 79.
Гиперболоид вращения од-
нополостям й. Поверхность од-
нополостного гиперболоида враще-
ния может быть получена движени-
ем прямой, скользящей вдоль двух
равных окружностей; плоскости этих
окружностей перпендикулярны к
оси, проходящей через их центры, и
находятся на расстоянии d друг от
друга; скользящая прямая, не пере-
секаясь с осью, сохраняет неизме-
ненным угол наклона к ней.


92
Черт, 80.
Винтовая поверхность об-
разуется движением прямой, сколь-
зящей одновременно вдоль другой
прямой и вдоль винтовой линии и
сохраняющей при этом параллель-
ность по отношению к некоторой
плоскости.
Часть вторая
СТЕРЕОСКОПИЧЕСКИЕ ЧЕРТЕЖИ
К СБОРНИКУ ЗАДАЧ ПО СТЕРЕОМЕТРИИ Н. РЫБКИНА
При рассматривании стереочертежей
внимательно проверьте, чтобы синий
светофильтр пришелся на правый глаз,
а красный- на левый (см. стр. 9 и 10).
I ПЕРПЕНДИКУЛЯР И НАКЛОННЫ!
К ПЛОСКОЕГИ
(черт. I —17|
Черт I
Ребра прямоугольного параллелепи-
педа равны 3 см, 4 см и 7 см. Опре-
делить площадь сечения, проведен-
ного через концы трех ребер, выхо-
дящих из одной .вершины.
(§ 1, № 3.)

I
96
Черт. 2.
Основанием правильной призмы
служит треугольник со стороной а.
Высота призмы равна Ь. Провести
плоскость через одну из сторон ниж-
него основания и через противопо-
ложную вершину верхнего основа-
ния. Вычислить площадь получен-
ного сечения
(§ 1, № 4.)
97
Черт. 3.
В прямоугольном параллелепипеде
ABCDAjBjC^Dt боковое ребро AiA —
= 56 см, а стороны основания: АВ =
= 33 см и Л£) = 40 см. Определить
площадь сечения, проведенного че-
рез ребра AD и В1СЬ
(§ 1, N? 12.)
7. Стереочертежи по геометрии

• 98
Черт. 4.
Точка О — центр квадрата со сторо-
ной а; ОА — прямая, перпендику-
лярная к плоскости квадрата и рав-
ная Ь. Найти расстояние от точки/
до вершин квадрата.
(§ 1, № 13.)
99
Черт. 5.
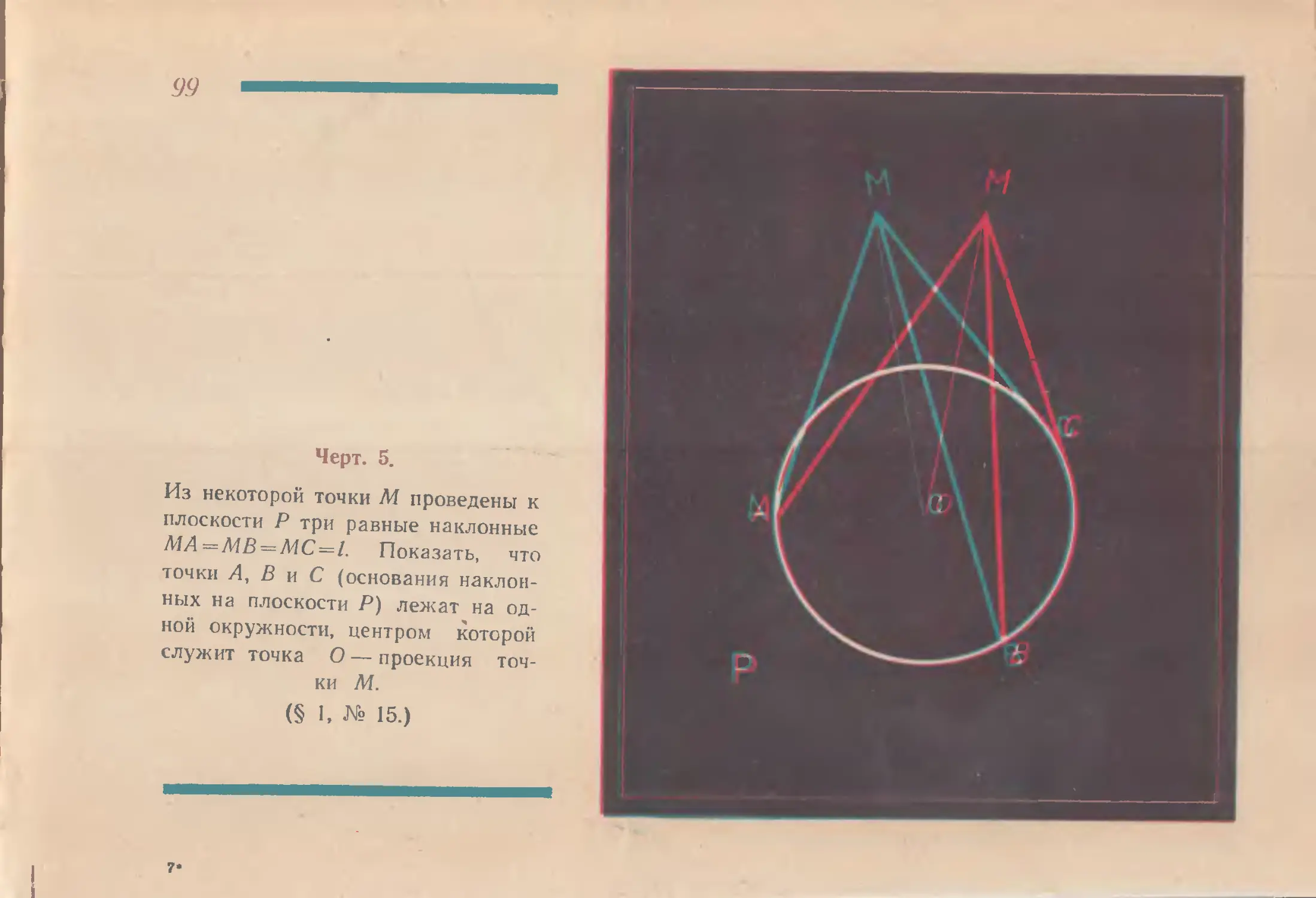
Из некоторой точки М проведены к
плоскости Р три равные наклонные
ЛМ = МВ=МС=1. Показать, что
точки А, В и С (основания наклон-
ных на плоскости Р) лежат на од-
ной окружности, центром которой
служит точка О — проекция точ-
ки М.
(§ I. № 15.)
7*


100
Черт. 6.
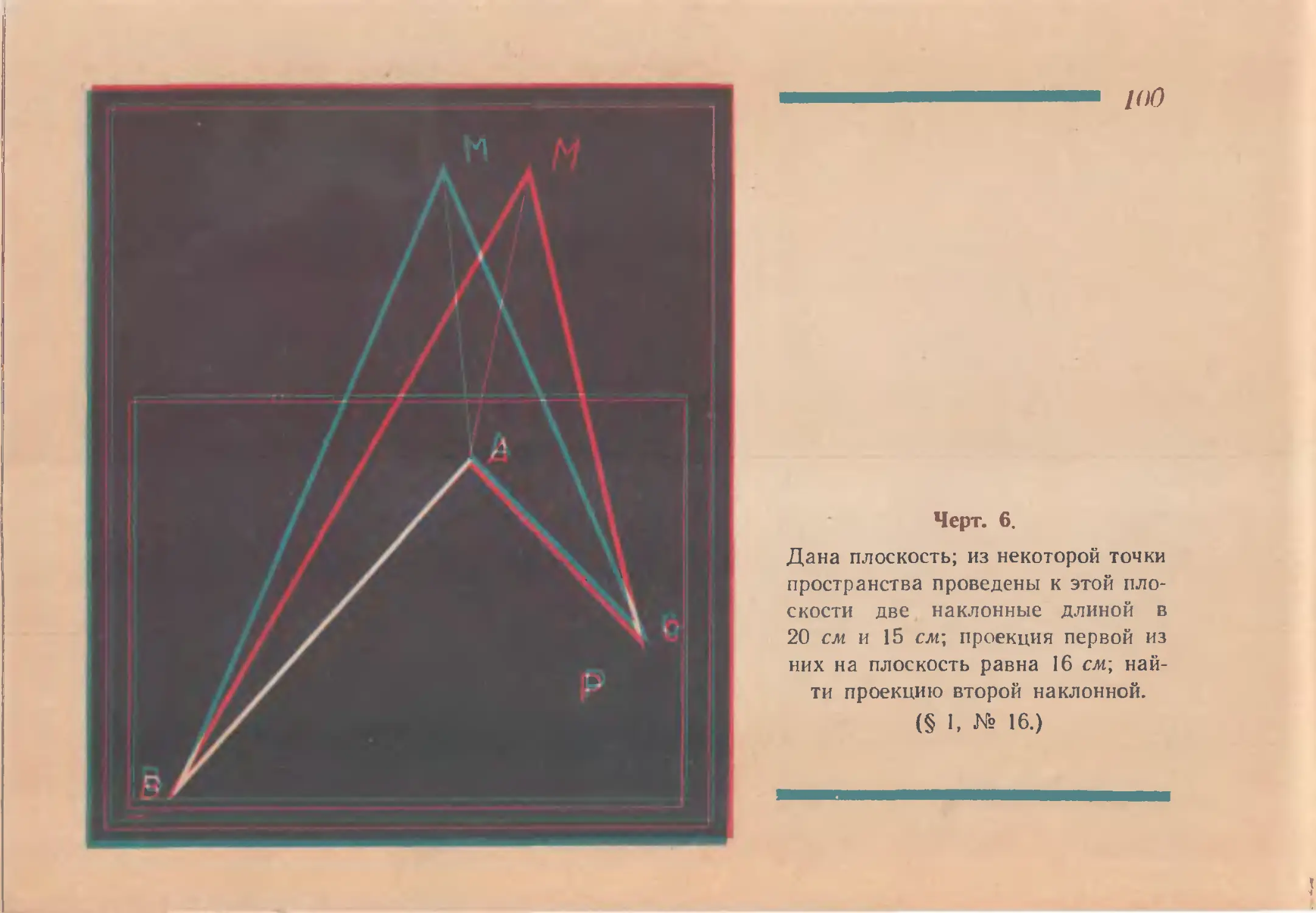
Дана плоскость; из некоторой точки
пространства проведены к этой пло-
скости две наклонные длиной в
20 см и 15 см; проекция первой из
них на плоскость равна 16 см; най-
ти проекцию второй наклонной.
(§ 1, № 16.)
101
Черт. 7.
Из некоторой точки пространства
проведены к данной плоскости пер-
пендикуляр, равный 6 см, и наклон-
ная длиной 9 см. Найти проекцию
перпендикуляра на наклонную.
(§ 1, № 17.)
102
Черт. 8.
Сторона равностороннего треуголь-
ника равна 3 см. Определить рас-
стояние от его плоскости до точки,
которая отстоит от каждой из его
вершин на 2 см.
(§ 1, № 18.)
103
Черт. 9.
Из данной точки проведены к дан-
ной плоскости две наклонные, рав-
ные каждая 2 см; угол между ними
равен 60°, а угол между их проек-
циями— прямой. Найти расстояние
данной точки от плоскости.
(§ 1, № 192.)

104
Черт 10.
В равнобедренном треугольнике ос-
нование и высота содержат по 4 см.
Данная точка находится на расстоя-
нии 6 см от плоскости треугольника
и на равном расстоянии от его вер-
шин. Найти это расстояние.
(§ 1, № 20.)
10.5
Черт. 11.
Дан равнобедренный треугольник
А ВС с основанием 6 = 6 см и боко-
вой стороной а=5 см. К плоскости
треугольника в центре О вписанного
в него круга проведен перпендику-
ляр ОК=2 см. Найти расстояние
точки /( от сторон треугольника и
от вершины В.
(§ 1. № 21.)


106
Черт. 12.
В треугольнике АВС угол .В пря-
мой и катет ВС=а. Из вершины .4
проведен к плоскости треугольника
перпендикуляр AD так, что расстоя-
ние между точками D и С равно /.
Определить расстояние от точки D
до катета ВС.
(§ 1, № 22,.)
107
Черт. 13.
Катеты прямоугольного треуголь-
ника АВС равны 15 м и 20 м. Из
вершины прямого угла С проведен
к плоскости этого треугольника пер-
пендикуляр С£> = 35 м. Найти рас-
стояние от точки D до гипотену-
зы АВ
(§ 1, № 222.)

“ 108
Черт. 14.
В треугольнике АВС угол С пря-
мой; CD — перпендикуляр к плоско-
сти этого треугольника. Точка D
соединена с Л и В. Определить пло-
щадь треугольника ADB, если дано:
С А = 3 дм, ВС = 2 дм и CD = 1 дм.
(-§ 1, № 23.)
109
Черт. 15.
В вершине Л прямоугольника- A BCD
проведен к его плоскости перпенди-
куляр АК, конец К которого отстоит
от других вершин на расстоянии
6 см, 7 см и 9 см. Найти длину
перпендикуляра АК.
(§ 1, № 24)


ЦО
Черт. 16.
На плоскости М даны две парал-
лельные прямые АВ и CD, расстоя-
ние между которыми равно а. Вне
плоскости М дана точка S, удален-
ная от АВ на 6 и от CD на с. Опре-
делить расстояние от точки S до
плоскости М, если известно, что:
1) а = 66, fe=c = 65; 2) о = 6, fe = 25,
с=29.
(§ 1. № 27.)
Ill
Черт. 17.
Если из вершины угла, лежащего
на плоскости, провести наклонную к
плоскости так, чтобы она составля-
ла со сторонами угла равные углы,
то проекция этой наклонной будет
служить биссектрисой данного угла.
Доказать.
(§ 1, № 28ь)


1Г2
2. УГОЛ ПРЯМОЙ линии
с плоскостью
(черт. 18—27)
Черт. 18.
Ребра основания прямоугольного
параллелепипеда имеют длину 4 см
и 3 см\ высота параллелепипеда
равна 5 см. Найти его диагональ и
угол диагонали с плоскостью осно-
вания.
(§ 2, № 1.)
Черт. 19.
Высота правильной четырехуголь-
ной пирамиды равна А; апофема на-
клонена к плоскости основания под
углом в 60°. Найти боковые ребра.
(§ 2, № 3.)
8. Стереочертежи по геометрии

' 114
Черт. 20.
В правильной треугольной пирами-
де боковое ребро равно Ъ и обра-
зует с основанием пирамиды угол в
30°. Найти сторону основания.
(§ 2, № 4.)
Черт. 21.
Отрезок длиной 10 см пересекает
плоскость; концы его находятся на
расстоянии 3 см и 2 см от плоско-
сти. Найти угол между данным от-
резком и плоскостью.
(§ 2, № 7.)

116
Черт. 22.
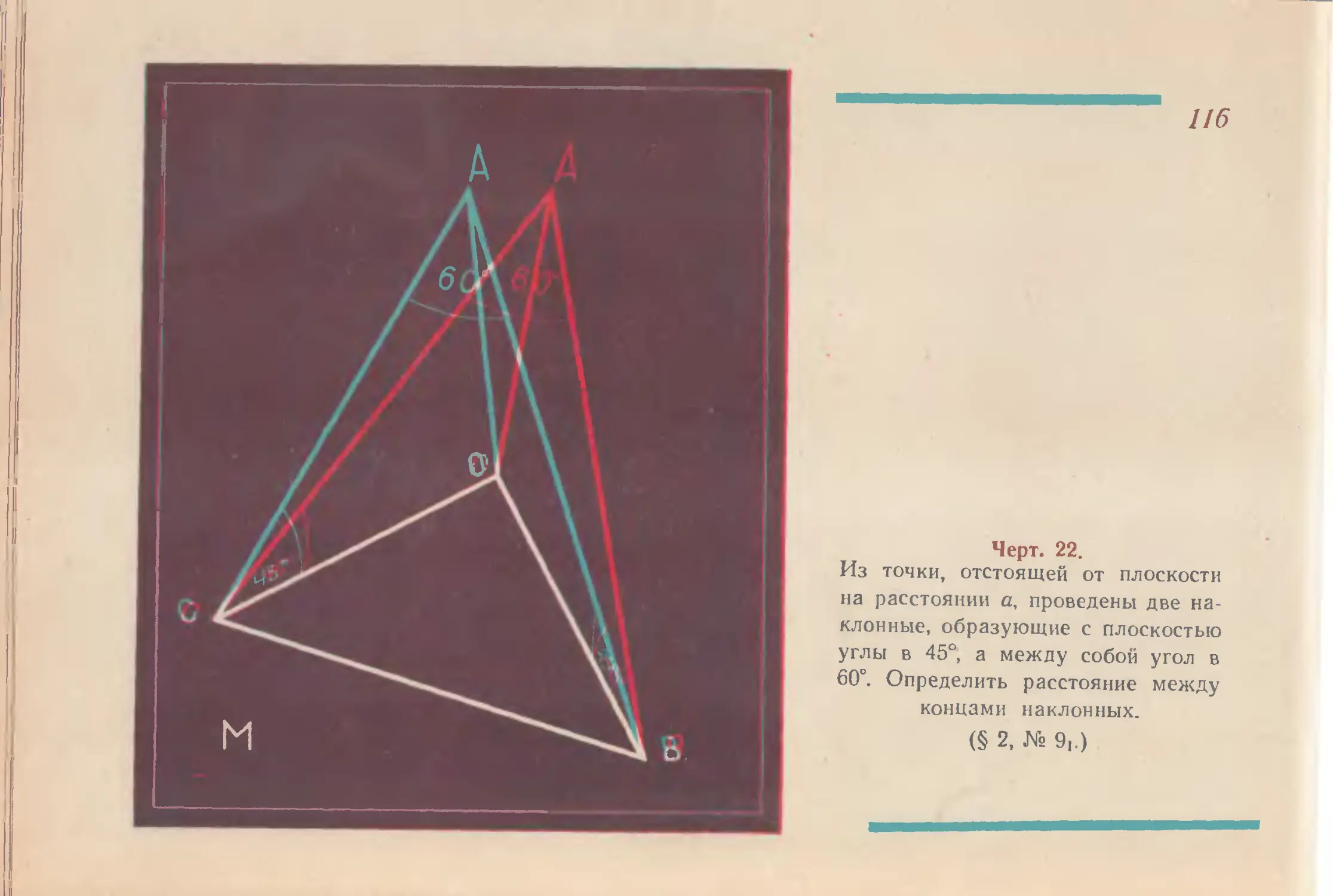
Из точки, отстоящей от плоскости
на расстоянии а, проведены две на-
клонные, образующие с плоскостью
углы в 45°, а между собой угол в
60°. Определить расстояние между
концами наклонных.
(§ 2, № 9,.)
117
Черт. 23.
Из точки, отстоящей от- плоскости
на а, проведены две наклонные под
углом в 30° к плоскости, причем их
проекции составляют между собой
угол в 120°. Определить расстояние
между концами наклонных.
(§ 2, № 10.)


118
Черт. 24.
В плоскости М находится прямая
АВ. Из точки В проведены по одну
сторону плоскости перпендикуляр
ные к АВ прямые ВС и BD, откло-
ненные от плоскости М на 50° и 15°.
Определить угол CBD.
(§ 2,№ И.)
119
Черт. 25.
Если в равнобедренном прямоуголь-
ном треугольнике один катет нахо-
дится на плоскости М, а другой ка-
тет образует с ней угол в 45°. то ги-
потенуза образует с плоскостью М
угол в 30°. Доказать это.
(§ 2, № 12.)


120
Черт. 26.
Если наклонная АВ составляет с
плоскостью М угол в 45°, а прямая
АС, лежащая в плоскости М, со-
ставляет угол в 45° с проекцией на-
клонной АВ, то Z. ВАС = 60°. Дока-
зать это.
(§ 2, № 13.)
Черт. 27.'
Если в правильной треугольной пи-
рамиде высота равна стороне осно-
вания, то боковые ребра составляют
с плоскостью основания угол в 60°.
Доказать.
(§ 2, № 14.)
г
122
3. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
И ПЛОСКОСТИ
(черт. 28—60)
Черт. 28.
А и В — точки вне плоскости М\ АС
и BD — перпендикуляры на эту
плоскость; ЛС=3 м, BD = 2 м и
СВ = 24 дм. Определить расстояние
между точками А и В Два случая.
(§ 3, № 1ь)
Г23
Черт. 29.
Концы данного
125 см отстоят
100 см и 56 см.
проекции.
отрезка длиной в
от плоскости на
Найти длину его
Два случая.
(§ 3, № 2,.)

124
Черт. 30.
Из точки А плоскости М проведена
на'клонная прямая линия, и на ней
взяты точки В и С, причем АВ =
= 8 см и АС = 14 см. Точка В удале-
на от плоскости М на 6 см. Найти
расстояние точки С от плоскости М.
(§ 3, № 3.)
125
Черт. 31.
Отрезок пересекает плоскость; кон-
цы его отстоят от плоскости на рас-
стоянии 8 см и 2 см. Найти расстоя-
ние середины этого отрезка от плос-
кости.
(§ 3, № 5.)
Черт. 32.
Г26
Конны данного отрезка, ле Пересе
кающего плоскость, удалены от нее
на 30 см и 50 см. Как удалена от
плоскости точка, делящая данный
отрезок в отношении 3 : 7? (Два
случая).
(§ 3, № 6.)
127
Черт. 33.
Правильный треугольник спроекти-
рован на плоскость; вершины его
отстоят от плоскости на расстоянии
10 г).и, 1.5 дм и 17 дм. Найти рас-
стояние его центра от плоскости
проекций. (Задача имеет четыре ре
шення. См. черт. 34. 35. 36.)
(§ 3, № 7.)


128
Черт. 34.
Правильный треугольник спроекти-
рован на плоскость; вершины его от-
стоят от плоскости на расстоянии
10 дм, 15 дм и 17 дм. Найти рас-
стояние его центра от плоскости
проекции. (Задача имеет четыре ре-
шения. См. фигуры № 33, 35, 36)
(§ 3, № 7.)
129
Черт. 35.
Правильный треугольник спроекти
рован на плоскость; вершины е;<.
отстоят от плоскости на расстоянии
10 дм, 15 дм и 17 дм. Найти рас
стояние его центра от плоскости
проекций. (Задача имеет четыре ре
шения. См. фигуры № 33, 34, ЗЬ
3. № 7.)
9.	Стереочерчежн по геометрии^
I

130
Черт. 36.
Правильный треугольник спроекти-
рован на плоскость; вершины его
отстоят от плоскости на расстоянии
10 дм, 15 дм и 17 дм. Найти рас-
стояние его центра от плоскости
проекций. (Задача имеет четыре ре-
шения. См. фигуры № 33, 34, 35.)
(§ 3. № 7.)
Черт. 37.
Данный отрезок АВ параллелен
плоскости и равен а. Отрезок BAt,
соединяющий конец В с проекцией
Л| другого конца, составляет с
плоскостью угол в 60°. Определить
длину отрезка ВА\.
(§ 3, № 8.)


132
Черт. 38.
Из точек А и В плоскости М прове-
дены вне ее параллельные между
собой отрезки: АС — 8 см и BD =
= 6 см. Прямая, проведенная через
С и D, пересекает плоскость М (по-
чему?) в точке Е. Отрезок' АВ =
= 4 см. Определить расстояние BE.
(§ 3, № 9.)
333
Черт. 39.
АВ — отрезок на плоскости М, рав-
ный а, АС и BD — отрезки вне плос-
кости Л1, равные Ь, причем отрезок
АС перпендикулярен к плоскости М,
a BD, будучи перпендикулярным к
АВ, составляет с плоскостью М угон
в 30°. Определить расстояние CD.
(§ 3, № 10.)


134
Черт. 40.
По стороне основания а и боковому
ребру Ь правильной треугольной
призмы определить площадь сече-
ния, проведенного через боковое
ребро и ось призмы.
(§ 3, № 13.)
135
Черт. 41.
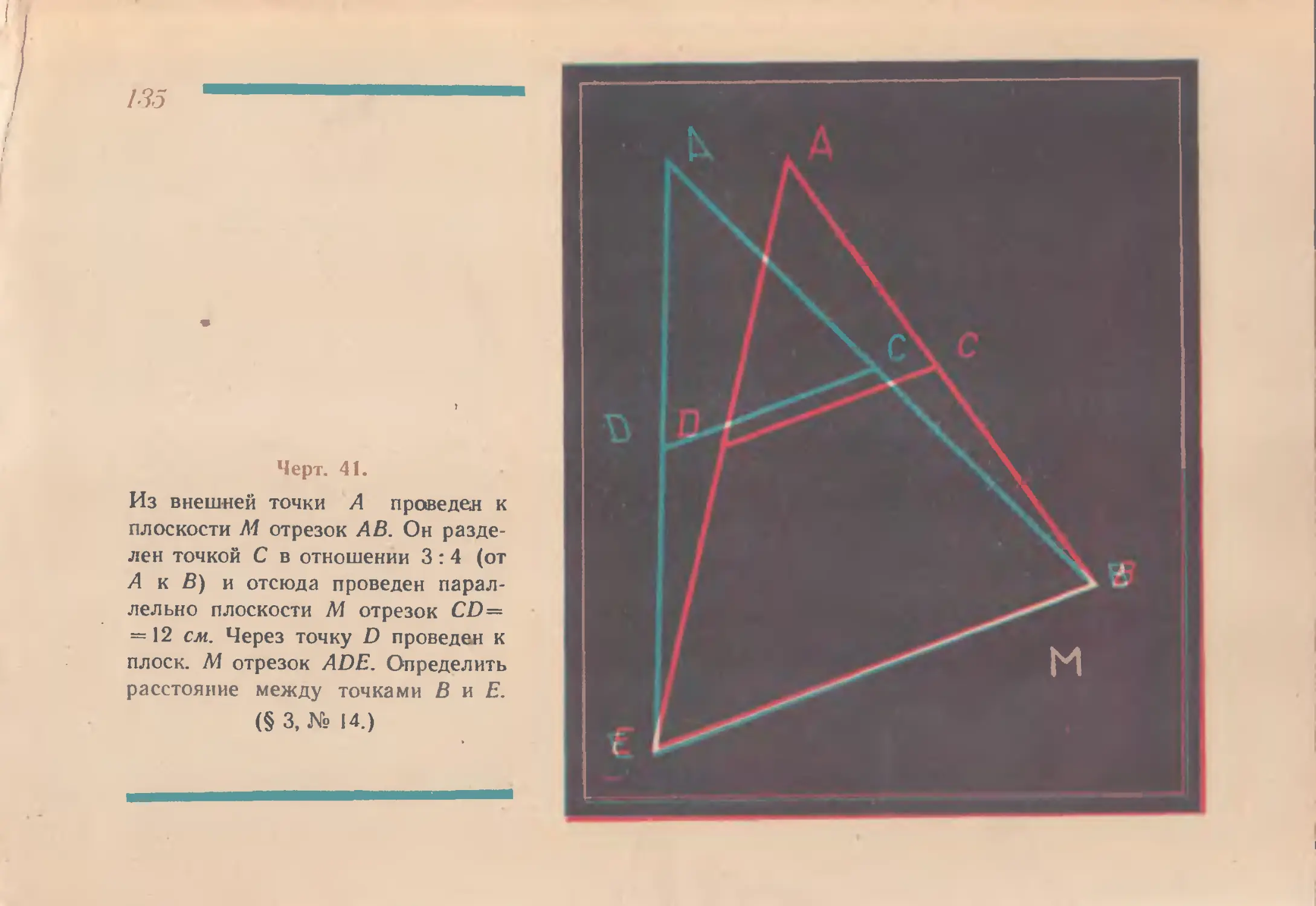
Из внешней точки А проведем к
плоскости М отрезок АВ. Он разде-
лен точкой С в отношении 3:4 (от
Л к В) и отсюда проведен парал-
лельно плоскости М отрезок CD—
= 12 см. Через точку D проведен к
плоек. М отрезок ADE. Определить
расстояние между точками В и Е.
(§ 3, № 14.)


136
Черт. 42.
BDC — отрезок, параллельный плос-
кости М\ ABE, ADF и ACG— пря-
мые, проведенные из внешней точки
А к плоскости М и пересекающие ее
в точках Е, F, G. Определить рас-
стояние между точками Е и G, если
ВС=а, AD = b, DF = c.
(§ 3, № 15.)
137
Черт. 43.
АВ и CD — параллельные отрезки,
лежащие в двух пересекающихся
плоскостях; АЕ и DF— перпендику-
ляры на линию пересечения плоско-
стей. Расстояние AD = 5 см и отре-
зок EF=4 см. Найти расстояние
между прямыми АВ и CD.
(§ 3, № 16.)


13S
Черт. 44.
Основание DA трапеции ABCD на-
ходится на плоскости Р, а основа-
ние СВ отстоит от нее на 5 см. Най-
ти расстояние от плоскости Р точ-
ки М пересечения диагоналей этой
трапеции, если DA : С В = 7 :3.
(§ 3, № 17.)
139
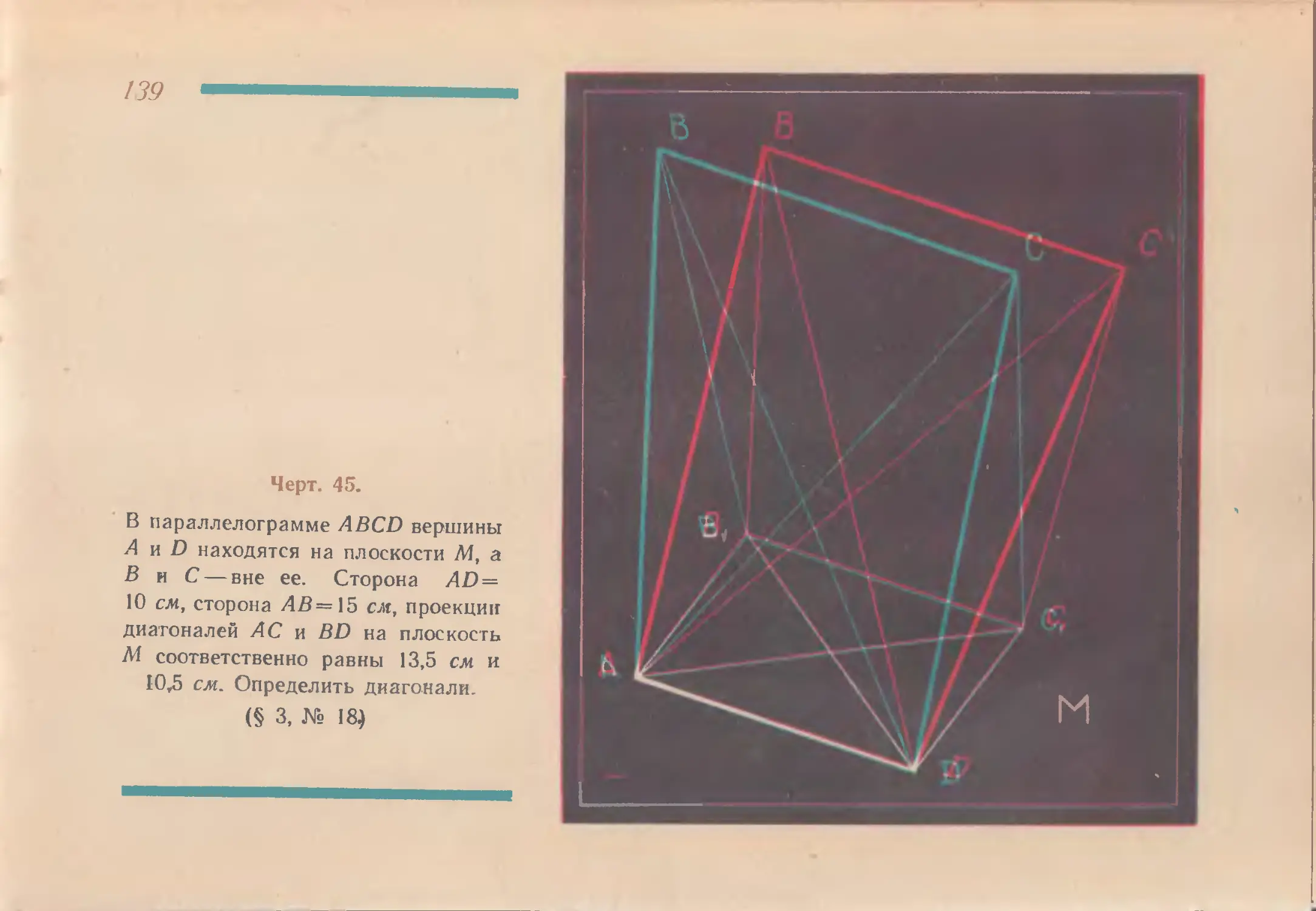
Черт. 45.
В параллелограмме ABCD вершины
А и D находятся на плоскости М, а
В и С — вне ее. Сторона AD =
10 см, сторона ЛВ=15 см, проекции
диагоналей АС и BD на плоскость
М соответственно равны 13,5 см и
10,5 см. Определить диагонали.
(§ 3, № 18}


140
Черт. 46
АВ и CD — две параллельные пря-
мые, лежащие в плоскости М на
расстоянии 28 см одна от другой;
EF— внешняя прямая, параллель-
ная АВ и удаленная от АВ на 17 см,
а от плоскости М — на 15 см. Най-
ти расстояние между EF и CD (два
случая).
(§ 3, № 21.)
141
Черт. 47.
Из концов отрезка АВ, параллель-
ного плоскости М, проведены к ней
перпендикуляр АС и наклонная
BDJ-AB. Определить расстояние
CD, если АВ = а, АС=Ь и BD = c.
(§ 3, № £2.)

142
Черт. 48.
АВ — отрезок, параллельный плос-
кости М\ АС и BD—две равные на-
клонные к плоскости М, проведен-
ные перпендикулярно к отрезку АВ
и в разных направлениях от него.
Отрезок АВ = 2 см и отстоит от плос-
кости М на 7 см, а отрезки АС и
BD содержат по 8 см. Определить
расстояние CD.
(§ 3, № 23.)
/7?
Черт. 49.
В правильной четырехугольной пи-
рамиде провести плоскость через
диагональ основания параллельно
боковому ребру. Сторона основания
равна а, а боковое ребро равно Ь.
Определить площадь полученного
сечения.
(§ 3, № 24.)


141
Черт. 50.
В правильной треугольной пирами-
де SABC сторона основания — а и
боковое ребро — Ь. Провести в
этой пирамиде плоскость через се-
редины ребер АВ и ВС параллельно
ребру SB. Определить площадь по-
лученного сечения.
(§ 3, № 25.)
145
Черт. 51.
Каждое ребро правильной четырех-
угольной пирамиды равно а. Про-
вести сечение через середины двух
смежных сторон основания и сере-
дину высоты и найти его площадь.
(§ 3, № 26.)
10.	Стереочертежи по геометрии


146
Черт. 52.
В кубе с ребром а провести плос-
кость, которая проходила бы через
середины двух смежных сторон верх-
него основания и через центр ниж-
него. Вычислить периметр сечения.
(§ 3, № 28.)
147
Черт. 53.
Расстояние между двумя парал-
лельными плоскостями равно 8 дм.
Отрезок длиной 10 дм своими кон-
цами упирается в эти плоскости.
Определить проекции отрезка на
каждую плоскость.
(§ 3, № 29.)
то*


148
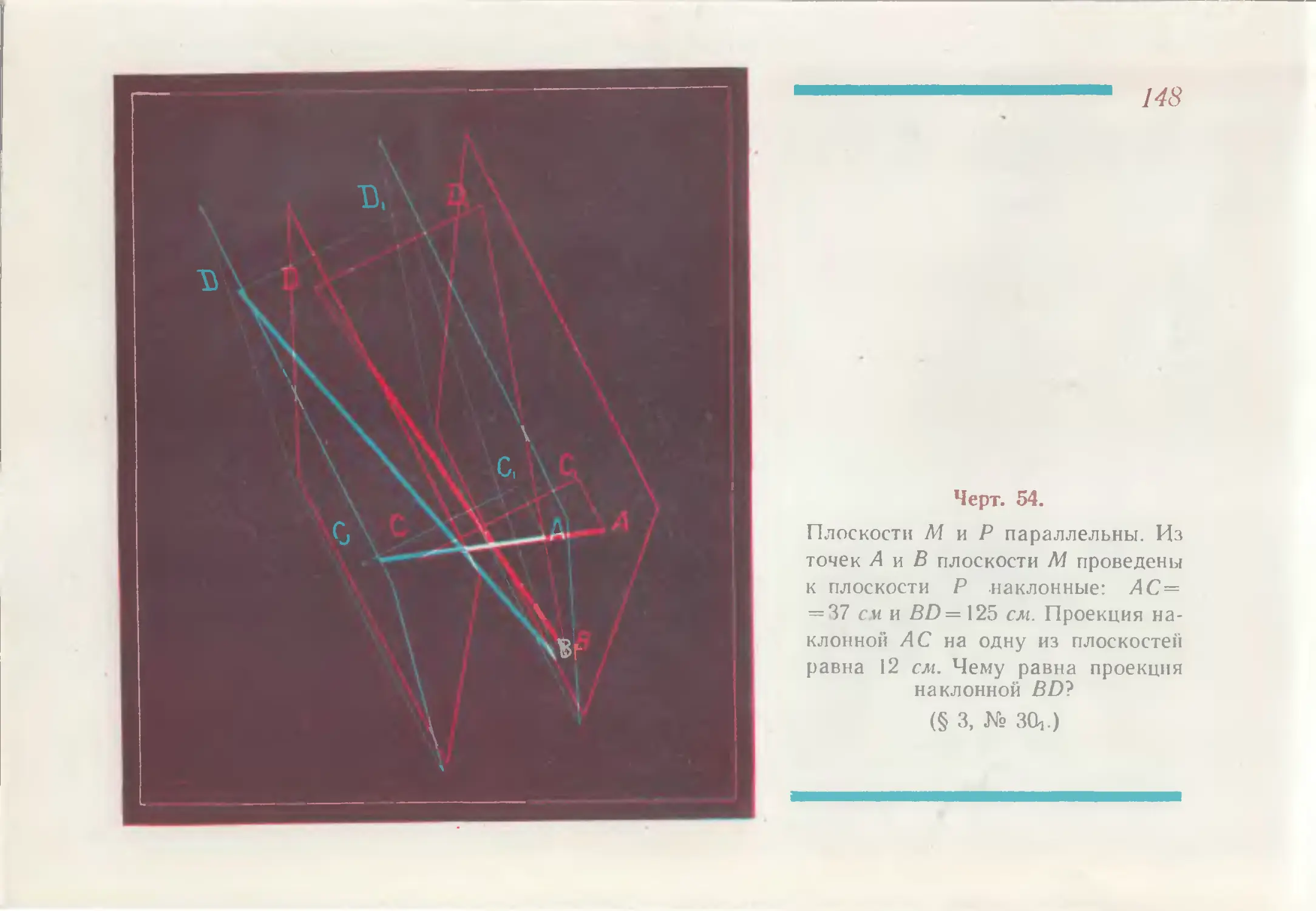
Черт. 54.
Плоскости М и Р параллельны. Из
точек Л и В плоскости М проведены
к плоскости Р наклонные: АС =
= 37 см и В£>=125 см. Проекция на-
клонной АС на одну из плоскостей
равна 12 см. Чему равна проекция
наклонной В£>?
(§ 3, № 30,.)
149
Черт. 55.
Между двумя параллельными плос-
костями заключены перпендикуляр
длиной 4 л и наклонная, равная
6 м. Расстояния между их концами
в каждой плоскости равны по 3 м.
Найти расстояние между середина-
ми перпендикуляра и наклонной.
(§ 3, № 31.)


150
Черт. 56.
Два прямых угла в пространстве
расположены так, что стороны их
соответственно параллельны, одина-
ково направлены и перпендикуляр-
ны к отрезку, соединяющему их вер
шины. Длина этого отрезка равна
а. На стороне одного угла отложен
от его вершины отрезок Ь, а на не-
параллельной ей стороне другого
угла отложен отрезок с. Определить
расстояние между концами этих от-
резков.
(§ 3, № 341.)
151
Черт. 57.
Вершины равностороннего треуголь-
ника со стороной а находятся вне
плоскости М на одинаковом от нее
расстоянии d. Из центра треуголь-
ника проведен перпендикуляр к его
плоскости, равный h и направлен-
ный в сторону, противоположную
плоскости М. Из конца этого пер-
пендикуляра проведены прямые че-
рез вершины треугольника до пере-
сечения с плоскостью М. Опреде-
лить отрезки этих прямых между
вершинами треугольника и плоско
стью М и расстояния между их кон-
цами.
(§ 3, № 35.)


152
Черт. 58.
В кубе ABCDA\BxCtDt середины К
и L противолежащих ребер AAi и
С С] соединены прямыми с вершина-
ми куба В и D{. Найти стороны и
диагонали получившегося четырех-
угольника KBLDi и определить вид
его. Ребро куба равно а.
(§ 3, № 36.)
153
Черт. 59.
В кубе ABCDAiBiCxDt соединить по
порядку середины следующих ре-
бер: AAi, AtBi, BiCi, CtC, CD, DA
и AAt. Доказать, что полученная
фигура есть правильный шести-
угольник, и определить ее площадь
по ребру куба а.
(§ 3, № 37.)


154
Черт. 60.
Основанием правильной призмы
служит шестиугольник со стороной
в 3 дм; высота призмы равна 13 дм.
Определить площадь сечения, про-
веденного через две противолежа-
щие стороны верхнего и нижнего ос-
нований призмы.
(§ 3, № 38,.)
155
4. ДВУГРАННЫЕ УГЛЫ
И ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
(черт. 61—75)
Черт. 61.
На одной грани двугранного угла
даны две точки А и В; из них опу-
щены перпендикуляры на другую
грань: АС=1 дм и BD = 2 дм — и на
ребро: Л£=3 дм и BF.. Найти BF.
(§ 4. № 1ь)


156
Черт 62
Если равнобедренный прямоуголь-
ный треугольник АВС перегнуть по
высоте BD так, чтобы плоскости
ABD и CBD образовали прямой
двугранный угол, то линии DA и DC
сделаются взаимно перпендикуляр-
ными, аВ4 и ВС составят угол в 60°.
Доказать это.
(§ 4, № 3.)
157
Черт. 63.
Определить величину двугранного
угла, если точка, взятая на одной
из граней, отстоит от ребра вдвое
далее, чем от другой грани.
(§ 4, № 4.)

158
Черт. 64.
Из точки, взятой внутри двугранно-
го угла, опущен перпендикуляр на
ребро; он образует с гранями углы
38°24' и УНЗб'. Вычислить величину
двугранного угла.
(§ 4, № 5,.)
159
Черт. 65.
А и В - точки на ребре прямого
двугранного угла; АС и BD — пер-
пендикуляры к ребру, проведенные
в разных гранях. Определить рас-
стояние CD, если А В = 6 см, АС=
= 3 см и BD = 2 см.
(§ 4, № 6,.)

f
160
Черт. 66.
Треугольник АВС, прямоугольны!
при С, опирается катетом АС на
плоскость М, образуя с ней дву
гранный угол в 45°. Катет АС=2 м
а гипотенуза АВ относится к катету
вс, как 3 : 1. Определить расстоя-
ние от вершин В до плоскости М
(§ 4, № 7.)
161
Черт. 67.
Основанием прямой призмы служит
равнобедренный треугольник АВС,
у которого две стороны АВ и ВС
содержат по 7 см, а третья АС =
=2 см. Через сторону АС проведена
плоскость под углом в 30° к плоско-
сти основания, пересекающая проти-
волежащее боковое ребро в точке
D. Определить площадь полученно-
го сечения и отрезок BD бокового
ребра.
(§ 4, № 8.)


162
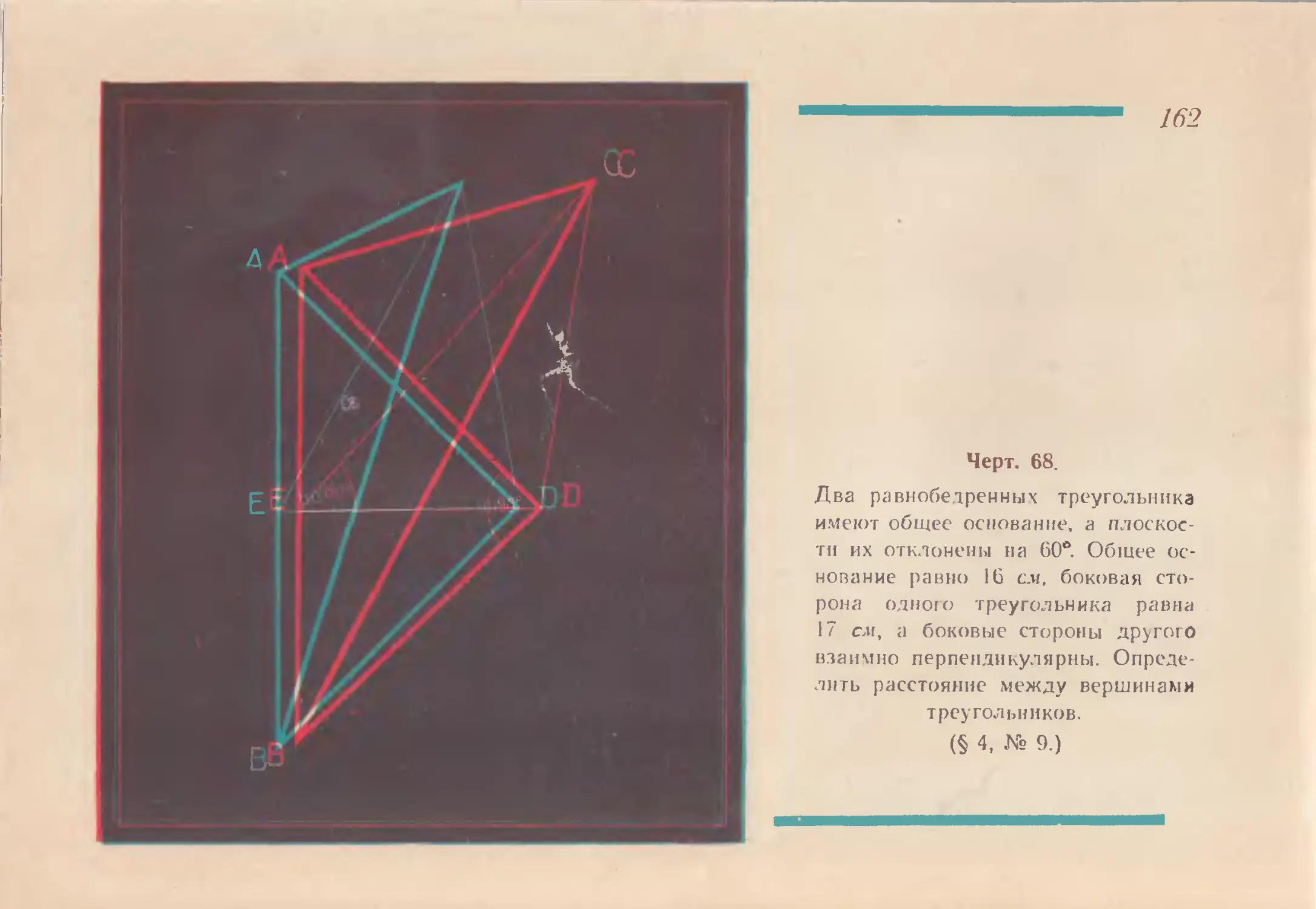
Черт. 68.
Два равнобедренных треугольника
имеют общее основание, а плоскос-
ти их отклонены на 60°. Общее ос-
нование равно 16 см, боковая сто-
рона одною треугольника равна
17 с.и, а боковые стороны другого
взаимно перпендикулярны. Опреде-
лить расстояние между вершинами
треугольников.
(§ 4, № 9.)
163
Черт. 69
Дан треугольник АВС со сторона-
ми: АВ = 9\ ВС— 6 и АС —5. Через
сторону АС проходит плоскость М,
составляющая с плоскостью тре-
угольника угол в 45°. Найти рас-
стояние между плоскостью М и вер-
шиной В.
(§ 4, № 102.)


164
Черт. 70.
Прямая АВ параллельна плоскости
М и отстоит от нее на а; через АВ
проходит плоскость Р, образующая
с плоскостью М угол в 45°; в плос-
кости Р проведена прямая линия
под углом 45° к АВ. Определить ее
отрезок между АВ и плоскостью М.
(§ 4, № И.)
11.	Сгереочер j .
165
Черт. 71.
АВ и CD — параллельные прямые,
лежащие на двух пересекающихся
плоскостях, образующих угол в 60°.
Точки А и D удалены от линии пе-
ресечения «плоскостей на 8 см и
6,3 см. Найти расстояние между
АВ и CD.
(§ 4, № 12.)


166
Черт. 72.
Отрезок АВ упирается своими кон-
цами в грани прямого двугранного
угла PMNQ-, концы отрезка нахо-
дятся на одинаковых расстояниях
от ребра MN двугранного угла.
Найти отношение углов, под кото-
рыми отрезок наклонен к граням.
(§ 4, № 13.)
167
Черт. 73.
АВ — прямая пересечения двух вза-
имно перпендикулярных плоскостей
М и Р\ CD — отрезок в плоскости
М, проведенный параллельно АВ на
расстоянии 60 см от нее; Е — точка
в плоскости Р на расстоянии 91 см
от АВ. Найти расстояние от Е
до CD.
(§ 4. № 16.)


168
Черт. 74.
Прямая АВ соединяет точки А и В,
лежащие на двух взаимно перпен-
дикулярных плоскостях. Перпенди-
куляры, опущенные из точек А и В
на линию пересечения плоскостей,
соответственно равны а и Ь, а рас-
стояние между их основаниями рав-
но с. Определить длину отрезка АВ
и длину его проекций на данные
плоскости.
(§ 4, № 17,.)
169
Черт. 75.
В правильной четырехугольной пи-
рамиде провести плоскость через
сторону основания перпендикулярно
к противолежащей боковой грани.
Сторона основания а=30 см, а вы-
сота пирамиды А = 20 см. Опреде-
лить площадь полученного сечения.
(§ 4, № 19.)


170
5. МНОГОГРАННЫЕ УГЛЫ
(черт. 76—80)
Черт. 76.
Каждый плоский угол трехгранного
угла равен 60°; на одном из ребер
отложен от вершины отрезок, рав-
ный 3, и из конца его опушен пер-
пендикуляр на противолежащую
грань. Найти длину перпендику-
ляра.
(§ 5, № 4.)
у
171
Черт. 77.
В трехграпиом углу два плоских
угла по 45°; двугранный угол меж-
ду ними прямой. Найти третий
плоский угол.
(§ 5, № 7.)
172
Черт. 78.
В трехгранном углу два плоских
угла по 45°; третий плоский угол
60°. Найти двугранный угол, проти-
волежащий третьему плоскому углу.
(§ 5, № 8.)
173
Черт. 79.
В трехгранном углу два плоских уг-
ла по 60°, третий — прямой. Найгп
угол между плоскостью прямого уг
ла и противолежащим ребром.
(§ 5, № 9.)

174
Черт. 80.
В трехгранном углу ребра взаимно
перпендикулярны. Внутри него из
вершины проведен отрезок, проек-
ция которого на каждое из ребер
равна 1. Напги его проекции на
грани. Сделать чертеж.
(§ 5, № 10.)
СОДЕРЖАНИЕ
От издательства.................. .	.....	3
Введение................................................................ 5
1. Методические указания .	...........	5
2. Как рассматривать стереочертежи................................. 9
ЧАСТЬ ПЕРВАЯ.
Стереочертежи к учебнику А. П. Киселева «Геометрия, ч. II»
1.	Прямые и плоскости (черт. 1—29)	.	.	.	13
2.	Ортогональные проекции точки, отрезка и фигуры (черт. 30 39)	12
3.	Многогранники (черт. 40—63)
4.	Круглые тела (черт 64—74)	.6
5.	Приложение (черт. 75—НО)	87
Ч Л С Г |> ВТОРА Я.
Стереочертежн к сборнику задач по стереометрии II. Рыбкина
I Перпендикуляр п наклонные к плогкосш (черт I 17)	'•
2.	Угол прямой линии	с плоскостью	(чер| IH 27)	II '
3.	Параллельные прямые н плоскости	(черт 28 ьО)	I"
4.	Двугранные углы и	перпендикулярные плоско, ш (чср| >! .'>)	I 
5.	Miioi игранные углы	(черт. 76 80|	...	1<<<
Метод анаглифической печати офсетным
способом освоен в производственных условиях
Московской фабрикой офсетной печати
Министерства культуры РСФСР
Григорий Алексеевич Владимирский
СТЕРЕОСКОПИЧЕСКИЕ ЧЕРТЕЖИ ПО ГЕОМЕТРИИ
*
Редактор В. Г. Долгополое
Художественно-технический редактор С. Гуревич
Переплет работы С. Гуревича и художника Ю- М. Сигова
Графические работы художника С. В. Филипповича
Корректоры Р. Н. Макарова и Н. Н. Петровская
*
Сдано в набор 30|111-1У61 г.
Печ. л. II. (Усл.
Тираж
Подп. к печ. 9/ГХ-1961 г. Форм. бум. 90x70 в Ч1в
л. 12,87) Уч.-пзд. л 9,14. Зак. № 130.	1
150 000 экз. (1 завод 1-50 000)
МНВКВМНМ Цена
Учпедгиз. Москва. И-18. 3-й проезд Марьиной рощи, II
Набрано в типографии Угдетехиздата
Отпечатано на Московской фабрике офсетной печати
Москва, И-345, Осташковское шоссе 78

Школьные учебники (((Р
SHEBA.SPB.&U/SHKOLA