Статистические методы в физике ядерных реакторов - Уриг Р.

Автор: Уриг Р.

Теги: общее машиностроение технология машиностроения физика теплофизика ядерная физика переводная литература издательство атомиздат

Год: 1974

Похожие

Ядерная физика и ядерные реакторы

Групповые константы для ядерных реакторов

Ядерные реакторы

Ядерные энергетические реакторы

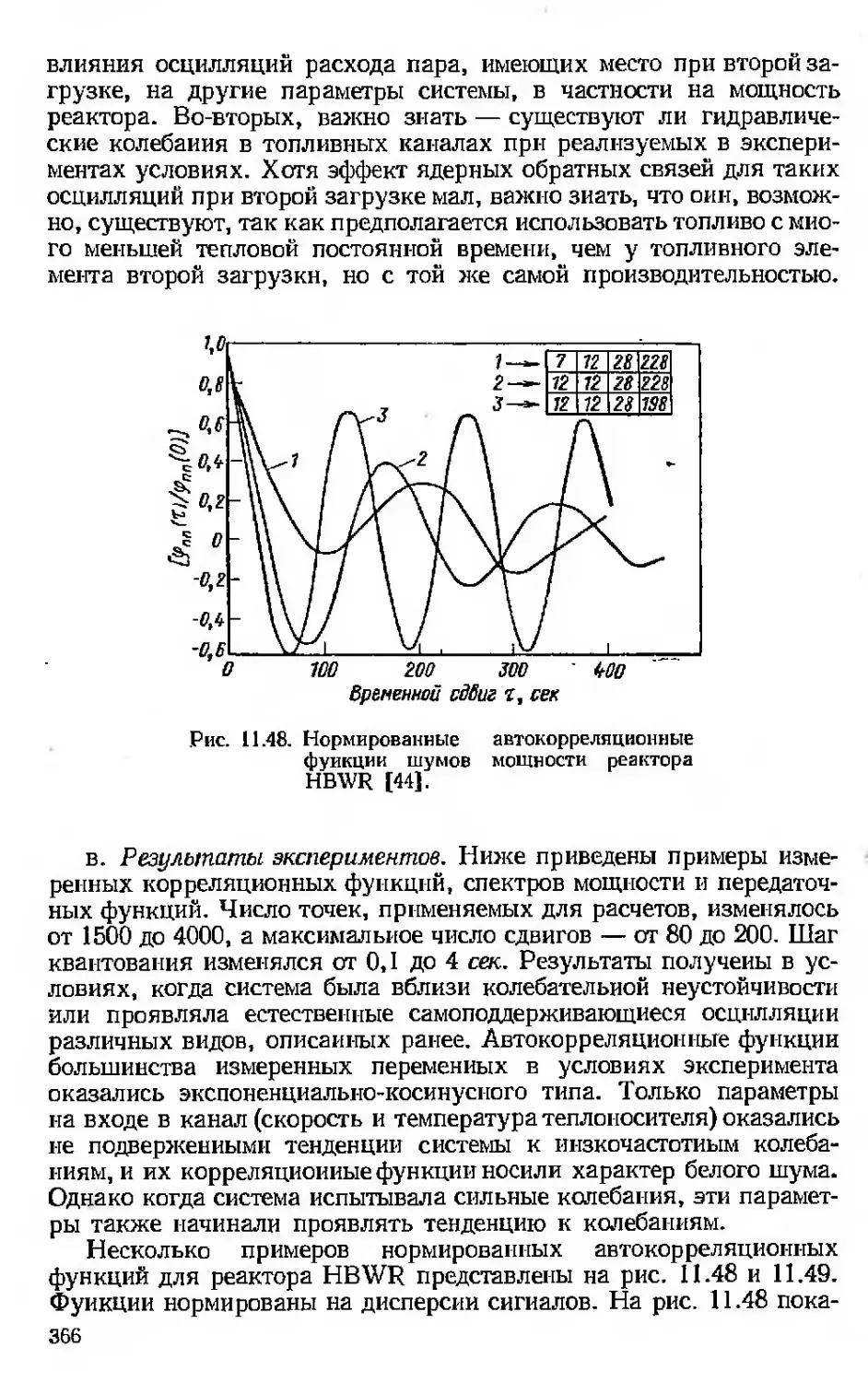
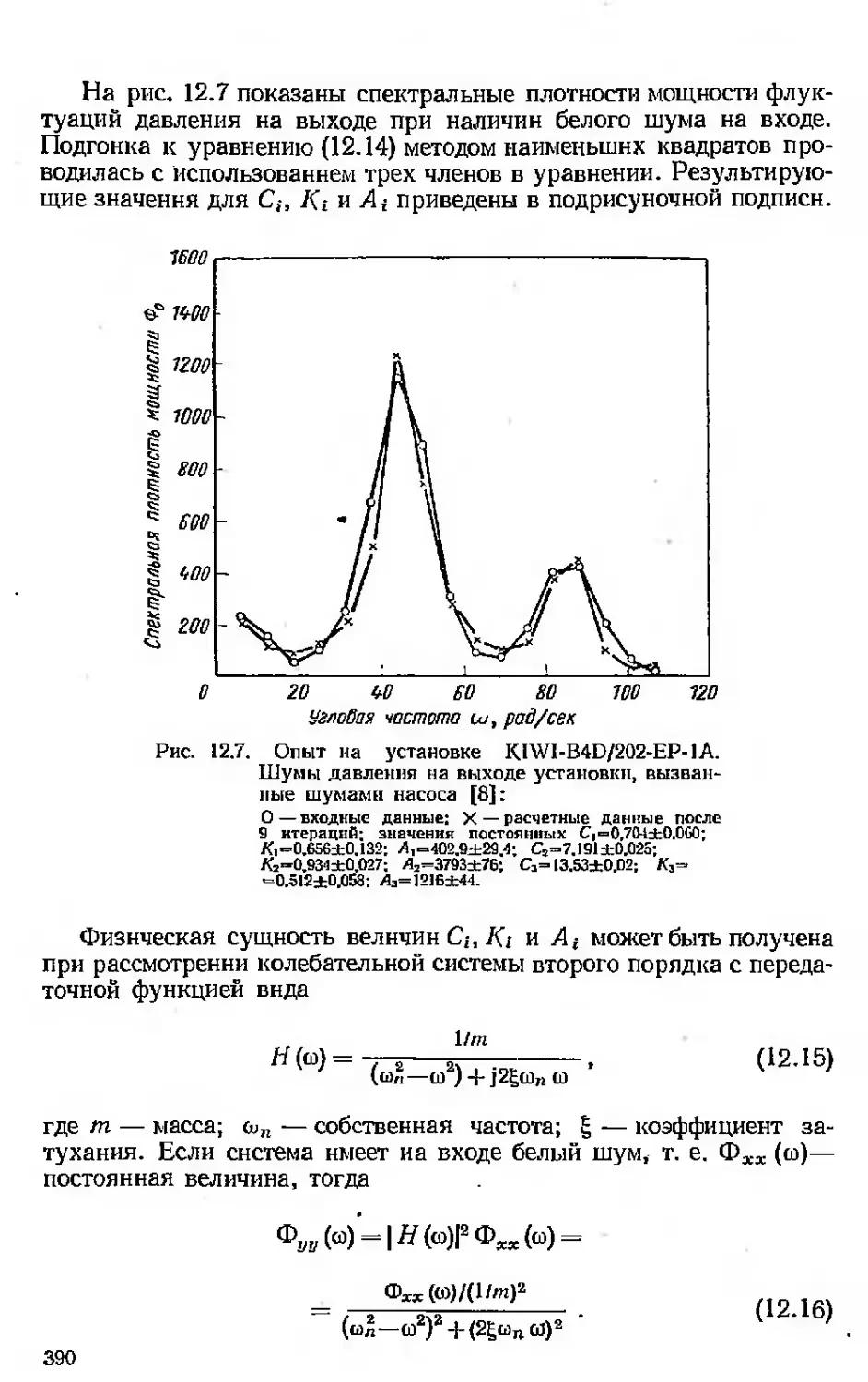
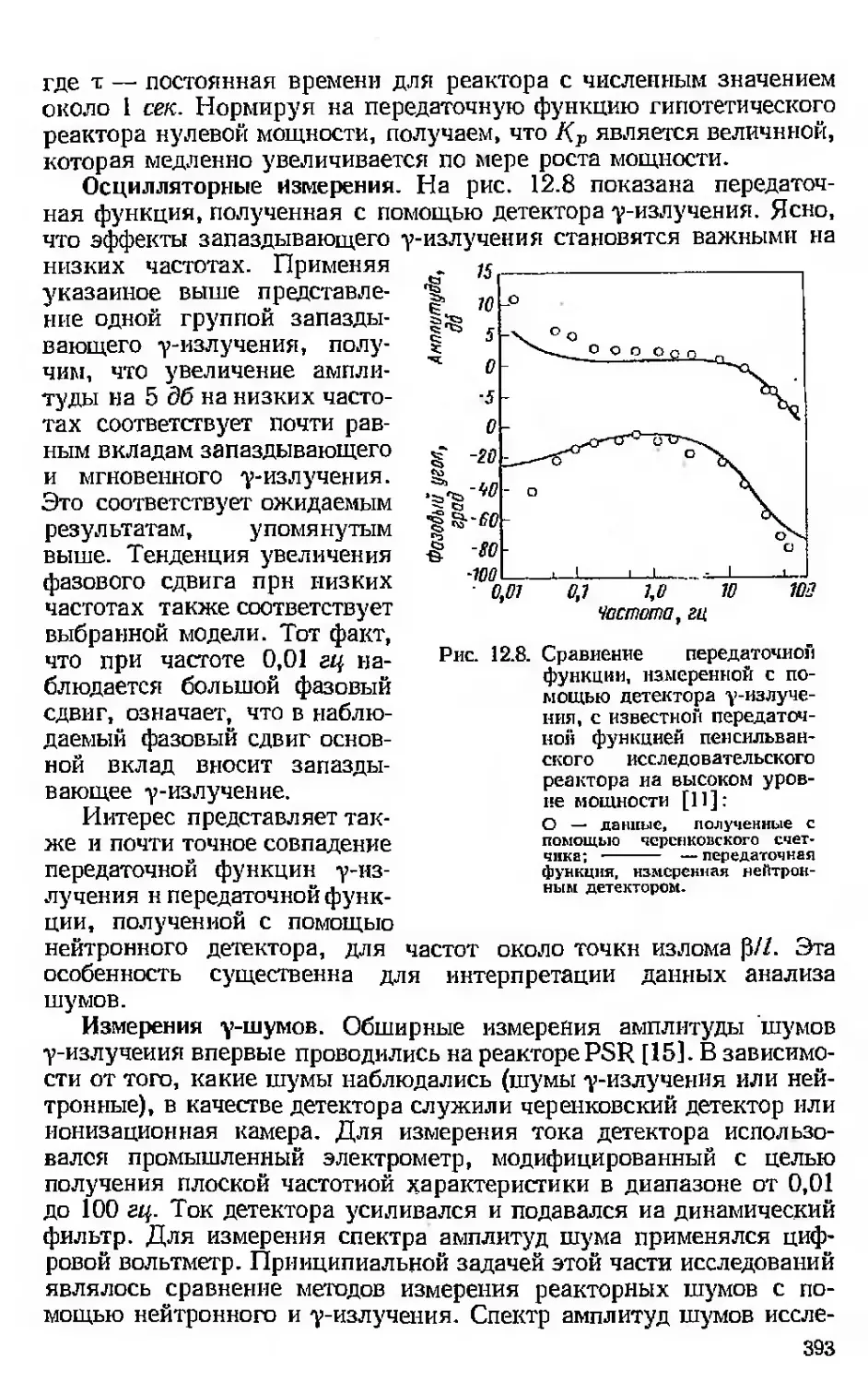
Текст

Р-УРИГ
СТАТИСТИЧЕСКИЕ
МЕТОДЫ
В ФИЗИКЕ
ЯДЕРНЫХ
РЕАКТОРОВ
Р • УРИ г
СТАТИСТИЧЕСКИЕ
МЕТОДЫ
В ФИЗИКЕ
ЯДЕРНЫХ
РЕАКТОРОВ
Перевод с английского
А. И. Ефанова, В. И. Пушкарева, А. П. Снротинна
Под редакцией доктора физико-математических
наук А. И. Могильнера
МОСКВА АТОМИЗДАТ 1974
УДК 621.039.584.2
НАУ
!{АЯ1
HW
RANDOM NOISE TECHNIQUES
in
NUCLEAR REACTOR SYSTEMS
ROBERT E. UHRIG
UNIVERSITY OF FLORIDA
Prepared under the auspices of the United States
Atomic Energy Commission
THE RONALD PRESS COMPANY • NEW YORK
У p и г P. Статистические методы в физике ядер вых реак-
торов. Пер. с англ. Под род. д-ра фнз.-мат. наук А. И. Мо-
гильнера. М., Атомиздат, 1974, 400 с.
Книга посвящена одному из развивающихся в последнее
время экспериментальных реакторных методов — анализу
случайных шумов, который позволяет определять важнейшие
динамические характеристики реакторной системы. Это пер-
вая монография, в которой систематизирован материал по
применению этого метода. В иен изложены методы регистра-
ции и обработки случайных процессов с использованием ма-
тематического аппарата теории вероятностен н современной
вычислительной техники; приведены методологические осно-
вы теории случайных шумов, которые могут быть применены
не только для реакторных процессов, но и для исследования
широкого круга технических и физических проблем в таких
областях, как океанография, медицина, связь, теория ин-
формации.
20408 — 044
У 034(01) —74
44—74
ПРЕДИСЛОВИЕ К ПЕРЕВОДУ
Ядерные реакторы в настоящее время стали одним из важ-
ных источников энергии. Расширяется область их примене-
ния. Для современного реакторостроения характерны тенденции
к постепенному вводу ранее не использовавшихся резервов, к дости-
жению предельных параметров ядерно-энергетической установки.
Реализация этих тенденций требует знания все более тонких свойств
реакторной системы. Значительная информация общереакторного
характера может быть получена путем исследования статистиче-
скими методами явлений временного нарушения равновесия различ-
ных внутриреакторных процессов, называемых реакторными шу-
мами.
Пионерами изучения реакторных шумов были Росси и Фейн-
ман. Основы теории реакторных шумов заложены в фундаменталь-
ных работах Пала. В настоящее время анализ реакторных шумов
стал одним из распространенных высокоэффективных и высокочув-
ствительных методов определения свойств реакторной системы:
как характеристик цепной реакции, так и технологических характе-
ристик ядерно-энергетическон установки.
Несмотря на возрастающее значение реакторных шумов как эк-
спериментального метода, в мировой литературе нет практических
руководств по экспериментальным приложениям этого метода. От-
сутствуют такие руководства и в отечественной технической лите-"
ратуре. Предлагаемая советскому читателю книга известного аме-
риканского специалиста в области прикладных вопросов реактор-
ных шумов Р. Урига в определенной степени восполняет этот пробел.
Автор книги сыграл значительную роль в популяризации и развитии
статистических методов исследования реакторных систем. По его
инициативе были проведены три международных симпозиума по ре-
акторным шумам, способствовавших распространению статисти-
ческих методов.
В книге Р. Урига изложены основные теоретические сведения
о многообразных методах изучения реакторных шумов, рассматри-
ваются вопросы технического обеспечения экспериментальных ис-
з
следований, передачи и обработки экспериментальной информации,
приводится описание типовых результатов экспериментальных ис-
следований реакторных шумов. Понимание и усвоение названного
материала не требует привлечения специального математического
аппарата, выходящего за пределы программы вуза.
Для’экспериментатор а, занимающегося физикой реакторов, цен-
ным в книге явится систематизация рассмотрения практически всего
арсенала современных экспериментальных методов изучения цеп-
ной реакции. Несколько менее систематизированы методы и резуль-
таты исследований технологических шумов энергетических реак-
торов, что в сущности отражает фактическое состояние проблемы
в настоящее время.
При переводе были выполнены сокращения в основном при изло-
жении общих неспецифических вопросов, хорошо освещенных в оте-
чественной литературе.
Простота и доступность, практическая направленность книги
и внимание к деталям выполнения статистических экспериментов
позволяют надеяться, что предлагаемая читателю монография
Р. Урига будет способствовать широкому проникновению статисти-
ческих методов в практику инженерно-физического эксперимента
при исследованиях ядерно-энергетических установок.
А. И. Могильнер
ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
Перевод этой книги на русский язык отражает- общность
интересов в научной и технической деятельности. Использование
ядерной энергии на благо человечества является возможно одной из
наиболее важных технических задач XX в. В связи с ограниченными
ресурсами доступных источников энергии все большие усилия при-
лагаются для широкого применения энергии ядерного деления
в производстве электроэнергии. Автор надеется, что данная книга
послужит вкладом в дело достижения этой цели.
Со времени окончания работы иад рукописью книги были дости-
гнуты значительные успехи в применении методов случайных шумов
к ядерным энергетическим реакторам. Такие шумовые методы могут
использоваться для контроля реактора во время нормальной эк-
сплуатации, для получения данных о конструкции и, может быть,
самое важное — для обеспечения безопасности эксплуатации реак-
тора. Действительно, одной из причин применения анализа
шумов ядерных энергетических реакторов является использование
этого метода как средства расширения стандартного эксплуатацион-
ного обслуживания ядерной энергетической установки для качест-
венного выполнения программ разработки конструкции реактора
и предэксплуатационных испытаний. Разумно ожидать, что методы
контроля в режиме on-line смогут в течение всей эксплуатации
установки обеспечить сохранение безопасных пределов, заложенных
в конструкции.
Автор надеется, что материал, представленный в книге, будет
полезен для ознакомления молодых научных работников и инжене-
ров с основами теории случайных шумов и ее применением к ядер-
ным реакторам. Несмотря иа то, что были предприняты усилия,
чтобы охватить весь необходимый материал, новые разработки не-
избежно будут сдвигать акценты на рассмотренных вопросах. На-
пример, быстрое преобразование Фурье стало сейчас широко рас-
пространенным средством анализа данных, так как эта процедура
может быть выполнена очень быстро на цифровой машине. Следо-
вательно, экспериментальные данные обрабытываютбя в реальном
5
масштабе времени, и поэтому результаты представляются почти
мгновенно. Недавно появились сообщения о том, что некоторые из
новых алгоритмов скоростного счета, которые легко реализуются
на малых цифровых вычислительных машинах, могут заменить бы-
строе преобразование Фурье как более предпочтительный метод
анализа данных. Хотя такие изменения в технике и аппаратуре важ-
ны, оии не меняют основ теории, представленной в настоящей книге.
По-видимому, ученые и инженеры, овладевшие теорией, смогут про-
должить развитие новых н лучших средств ее применения к техни-
ческим проблемам.
Автор признателен научному редактору книги А. И. Могильие-
ру за его помощь при переводе,’особенно в связи с такими трудностя-
ми, как отсутствие общепринятой терминологии, и уверен, что со-
держание книги при переводе не пострадало. Автор также благода-
рен Атомиздату за предоставление возможности публикации рус-
ского перевода и Комиссии по атомной энергии США за поддержку
при подготовке рукописи этой книги.
РОБЕРТ Е. У РИГ. ГЕИНСВИЛЛ. ФЛОРИДА 1973 г.
ГЛАВА 1.
ОБЩАЯ ХАРАКТЕРИСТИКА
СЛУЧАЙНЫХ ПРОЦЕССОВ
В ЯДЕРНЫХ РЕАКТОРАХ
§ 1.1. Случайные процессы в ядерных реакторах
В декабре 1942 г. на корте под трибунами стадиона Чикаг-
ского университета Энрико Ферми и его сотрудниками на «ядер-
иом котле» из графита и урана осуществлен первый эксперимент,
в котором была реализована контролируемая самоподдерживающая-
ся цепная реакция деления-. Основываясь на расчетах вероятностей
(называемых нейтронными сечениями) взаимодействия между нейт-
ронами и составляющими котел материалами, Ферми утверждал, что
при соответствующем расположении материалов можно достичь кри-
тичности. Вероятности различных типов взаимодействия, а именно
рассеяния, радиационного захвата и деления были измерены в серии
экспериментов, проведенных в предшествующие месяцы. Однако
уже в первые дни была отмечена вероятностная природа фунда-
ментальных процессов, которую успешно использовали в расче-
тах и экспериментах, позволивших осуществить первую в мире
самоподдерживающуюся цепную ядерную реакцию.
При приближении к критичности реакторной системы имеют
место флуктуации в уровне мощности, которые фиксируются систе-
мой нейтронных детекторов, регистрирующих мощность. Для кон-
троля цепной реакции в подкритическом реакторе обычно разме-
щается искусственный источник нейтронов. Чаще всего этот источ-
ник представляет собой композицию нз плутония и бериллия илн
полония и бериллия, в которой распад «-активного плутония нли
полония происходит случайно, т. е. каждый распад является со-
бытием, не зависящим от предыдущих и последующих распадов.
Следовательно, нейтроны, образующиеся при (а, л.)-реакцин, гене-
рируются случайно. Хотя часто говорят о среднем числе нейтро-
нов, испускаемых в единицу времени данным источником, число
нейтронов, испускаемых в следующие один за другим интервалы
времени, является случайно меняющейся величиной. Нейтро-
ны, попадая в ядерную систему, участвуют в различных типах вза-
имодействий. Например, нейтрон, образовавшийся при делении,
претерпевает ряд рассеивающих столкновений с материалом замед-
лителя или теплоносителя до возможного поглощения или утечки из
7
реактора. Каждый шаг в жизни нейтрона (который сильно зависит
от количества, ядерных сечений и геометрического расположения
материалов) может быть описан вероятностным образом. В случае,
когда происходит деление ядра, число образующихся нейтронов так-
же есть вероятностная величина, меняющаяся в пределах от 0 до
приблизительно 6, при среднем значении, равном ~ 2,5 при деле-
нии 23би.
Хотя поведение реакторной системы управляется микроскопи-
ческими характеристиками взаимодействий, практические наблю-
дения обычно ведутся за макроскопическими величинами. Когда
мы рассматриваем процессы, происходящие в подкритическом ре-
акторе, с точки зрения микроскопических величин, то обнаружи-
ваем, что система возмущается случайным явлением: эмиссией отдель-
ных нейтронов из постороннего нейтронного источника. Такие ней-
троны могут начать очень длинную цепочку делений, но в конечном
счете, если реактор подкритический, она должна оборваться. Одна-
ко каждая из цепочек деления, инициированная внешними нейтро-
нами , дает свой вклад в число нейтронов реактора, которое непосред-
ствен ио связывается с уровнем мощности. Ясно, что при большом
числе индивидуальных цепных реакций, происходящих одновремен-
но в реакторе и инициированных независимо излучаемыми нейтро-
нами от внешнего источника, общее число нейтронов увеличивается
или уменьшается стохастическим или случайным образом. Когда
реактор глубоко подкритичен, нейтронные цепочки очень коротки
и флуктуации относительно малы. Однако, если реактор прибли-
жается к критическому состоянию, средняя длина цепочек увели-
чивается. Например, если реактор имеет эффективный коэффициент
размножения 0,98, то каждый нейтрон, введенный в систему от внеш-
него постороннего источника, образует в среднем 50 дополнительных
нейтронов прежде чем цепочка оборвется. Это значит, что в типичной
урановой системе для генерации этих 50 нейтронов должно про-
изойти около 20 делений. Поскольку некоторые цепочки относитель-
но коротки, другие должны быть значительно длиннее, чтобы под-
держать эту среднюю величину.
Во .многих ситуациях геометрическое расположение, количество
или эффективное сечение материалов может меняться со временем,
и это изменение приводит к изменению числа нейтронов. Класси-
ческий эксперимент с котловым осциллятором является примером,
в котором поглотитель нейтронов, перемещаясь с помощью ротора
из одного положения в другое определенным образом, тем самым
меняет геометрическое расположение материала, поглощающего
нейтроны, а также и его эффективное сечение вследствие эффекта
самоэкранировки. В этом случае входной сигнал (движение мате-
риала и изменение эффективного сечения) будет неслучайным.
На практике этим методом часто пользуются в экспериментах
для создания детерминированного сигнала. Обычно реактивность
меняется синусоидальным образом (по крайней мере в первом при-
ближении) с помощью соответствующего перемещения поглотителя.
8
Следовательно, входное возмущение является периодическим и ско-
рее детерминированным, чем случайным. Однако выходной сигнал
иногда может столь сильно зависеть от статистических процессов
в реакторе, что детерминированная компонента (в данном случае
синусоидальная) будет практически полностью искажена случайной
компонентой.
Динамические характеристики системы исследуются с помощью
анализа выходных переменных как функции входных переменных
и времени. В отдельных ситуациях рассматриваемое явление появ-
ляется случайно в том смысле, что наблюдаемые флуктуации про-
являются как результат внутреннего или внешнего случайного воз-
буждения, которое не может полностью контролироваться. В других
случаях имеется вероятность того, что наблюдаемые переменные
флуктуируют случайным образом, даже если входной сигнал детер-
минирован. Обычно экспериментатор воздействует на систему либо
случайным, либо детерминированным входным сигналом, для того
чтобы изменить выходной сигнал, который анализируется отдельно
илн совместно с входным сигналом. В большинстве ситуаций на си-
стему влияет одновременно более чем одно из этих условий, т. е.
подкритическая система может быть возбуждена как внутренним
локальным источником нейтронов, так н нейтронным генератором,
чей выходной сигнал контролируется программным образом.
§ 1.2. Обоснование методов случайных шумов
в измерениях на ядерных реакторах
Доводами в пользу применения методов случайных шумов в из-
мерениях на реакторных системах могут быть следующие:
1. Измерение динамического поведения или контроль состояния
ядериой системы с минимальным возмущением илн влиянием на нор-
мальную работу.
2. Использование естественно возникающих флуктуаций числа
нейтронов для оценки параметров системы.
3. Использование специальной техники илн оборудования,
облегчающего проведение эксперимента н получение данных о про-
исходящих процессах.
4. Нанлучшее описание н объяснение природы происходящих
флуктуаций.
5. Использование теории флуктуаций для оценки погрешностей
эксперимента.
Автор не преподносит методы случайных шумов как универсаль-
ное средство для всех исследований в области динамики реакторов.
Скорее методы шумов дополняют классические методы исследования
динамики, такие, как эксперименты с реакторным осциллятором,
эксперименты с мгновенным изменением параметров, эксперименты
с импульсным источником нейтронов, и другие более или менее обыч-
ные способы, используемые при измерении параметров ядерных
систем.
9
Микроскопические методы шумов. Изучение шумов в реактор-
ных системах может вестись либо на микроскопическом, либо на мак-
роскопическом уровне. На микроскопическом уровне детектируются
индивидуальные цепочки, которые образуются в ядерном реакторе,
и изучение проводится с помощью статистических методов. Ранние
теоретические работы в этой области, выполненные Фейнманом
[1, 2], Ферми 12] и Хофманом [1—4] в Лос-Аламосе в 1947 г.,
привели к экспериментам россн-альфа на быстрой критической
сборке, описанным позже Орндоффом [51. Другие микроскопические
методы были развиты Фейнманом [1, 2], Могильнером и Золотухи-
ным [61, Беннетом [7], Палом [8, 9], Пачилио [101 и др. [11—14].
Некоторые из этих методов используют отклонение статистического
распределения от пуассоновского, другие непосредственно свя-
заны с определением вероятности детектируемого события. Во всех
случаях существо математической обработки зависит от типа эк-
спериментального оборудования и от того, какое событие, приводя-
щее к утечке нейтронов из системы, детектируется.
Макроскопические измерения шумов. Макроскопический подход
к измерению реакторных шумов был предложен Муром [15, 16]
и проверен экспериментально Коном [17, 18] спустя примерно 10 лет
после начала работ по микроскопическим исследованиям шумов.
Применение Муром к реакторным шумам метода Ланжевена осно-
вано на ранних работах по броуновскому движению, согласно ко-
торым шум в системе рассматривался как реакция системы на слу-
чайную или стохастическую возмущающую функцию, т. е. шум яв-
ляется реакцией системы на входной сигнал, носящий статистиче-
ский характер по отношению к последующему процессу. Если дина-
мические характеристики системы известны, можно установить кор-
реляцию или провести измерение спектральной плотности для пара-
метров системы.
Возмущающая функция может быть случайной флуктуацией
либо одной из переменных, либо одного из параметров системы.
Например, возмущением, приводящим к флуктуациям плотности
нейтронов в подкритическом реакторе, могут быть флуктуации в ско-
рости испускания нейтронов посторонним источником, иными сло-
вами, одна из переменных системы. С другой стороны, возмущающее
воздействие, приводящее к флуктуациям в реакторе нулевой мощ-
ности, может быть вызвано изменением доли запаздывающих нейт-
ронов, числа нейтронов, испускаемых при делении, эффективного
времени жизни нейтронов, т. е. параметрами системы. В отдельных
системах присутствуют иногда возмущающие функции обоих типов,
и все они должны учитываться. Однако в большинстве практических
ситуаций доминируют одна или две. возмущающие функции, всеми
остальными можно пренебречь. Например, такая переменная, как
реактивность, может преднамеренно изменяться произвольным
образом со среднеквадратической амплитудой от 10 до 100 раз
большей, чем следующая, наиболее значительная возмущающая
функция.
10
Применимость этих методов зависит от правильности понимания
динамического поведения исследуемой системы, т. е. от того, на-
сколько рассматриваемые процессы адекватно описываются мате-
матическими моделями. От случая к случаю степень упрощения
модели процесса меняется в зависимости от целей, преследуемых ис-
следователем. Часто оказывается достаточным описать передаточную
функцию, используя односкоростное представление с сосредоточен-
ным параметром и пренебрегая запаздывающими нейтронами. В дру-
гих случаях оказывается недостаточным использование модели, ос-
нованной на трехмерном транспортном уравнении Больцмана с вре-
менной зависимостью, описывающей поведение нейтронов в 30-груп-
повом приближении при разбиении реактора на 100 зон. Эффекты
обратной связи и другие нелинейности могут быть введены в ма-
тематическую модель н линеаризованы, поскольку среднеквадрати-
ческая амплитуда возмущающих функций случайных шумов обычно
настолько мала, что линеаризация допустима.
§ 1.3. Случайные процессы и переменные
Рассмотрим явления, происходящие в ядерных системах.
Поведение системы обычно контролируется измерением некоторых
«наблюдаемых» параметров (давлений, температур, уровня мощ-
ности и т. д.).Эти характеристики, измеряемые датчиками или пре-
образователями, которые превращают измеряемый параметр в фи-
зическую величину (электрический ток, механическое перемещение
и т. д.), легко осмысливаются экспериментатором, записываются
регистрирующей системой. Таким образом, временное изменение
представленного явления может быть изучено. Следовательно, к
входному и выходному сигналам системы уместно относиться как
к переменным величинам и определять их как случайные или детер-
минированные в соответствии с их природой. Вообще явление клас-
сифицируется как случайное, если его поведение описывается толь-
ко статистическими параметрами.
Рассмотрим временные диаграммы параметра системы (мощ-
ности атомной станции, работающей на комплекс промышленной
и бытовой нагрузки), показанные на рис. 1.1. Эти индивидуаль-
ные диаграммы (постоянные составляющие отброшены) можно
представить как нагрузочные" характеристики для нескольких (не
обязательно последовательных) 24-часовых периодов. Такой ряд
диаграмм назовем ансамблем сигналов, а каждую диаграмму—от-
дельным (выборочным) сигналом. Совокупность всех возможных от-
дельных сигналов, обусловленных случайными рассматриваемыми
явлениями, называется стохастическим процессом. Термин «про-
цесс» означает совокупность отдельных сигналов, достаточно боль-
ших, чтобы недвусмысленно установить статистические свойства
измеряемой величины.
Такой ансамбль сигналов, который представлен на рис. 1.1,
может быть получен путем индивидуальных измерений или разде-
11
лением одиночного сигнала на произвольное число частей. В боль-
шинстве практических случаев разница в значениях между терми-
нами «процесс» и «переменная величина» весьма мала. В последую-
щем термин «процесс» будем использовать при рассмотрении ансамб-
ля отдельных сигналов. Поскольку большая часть результатов тео-
рии случайных шумов основана на предположении эргодичности или,
по крайней мере, стационарности (оба понятия будут определены
позже), которые могут быть установлены только при наличии ансамб-
Рис. 1.1. Ансамбль записей сигналов во времени.
ля отдельных сигналов, более правильно использовать термин
«процесс». Однако в практике обычно приступают к анализу данных,
будучи уверенными только в автостациоиарности процесса, которая
относится только к отдельному сигналу. Следовательно, термин «пе-
ременная величина» также может применяться в этой ситуации. По-
стараемся сохранить различие между этими двумя терминами, хотя
в некоторых ситуациях выбор термина может быть совершенно про-
извольным.
Классификация процессов и переменных на детерминированные
или случайные в общем проста. Если переменная величина вос-
производима или ее дальнейшее поведение можно предсказать
(т. е. если она может быть представлена с разумной точностью четки-
ми математическими соотношениями), она классифицируется как де-
терминированная. Например, реактивность ядериого реактора при
12
работе синусоидального котлового осциллятора—переменная ве-
личина, описываемая математически как функция времени. С дру-
гой стороны, положение отдельного нейтрона по мере его перемеще-
ния в активной зоне реактора и с учетом его времени жизни непред-
сказуемо и, следовательно, должно классифицироваться как случай-
ная переменная величина. В лучшем случае мы можем оценить сред-
нее расстояние, проходимое всеми нейтронами в реакторе. Вообще,
последующее поведение случайных переменных описывается только
в терминах вероятностных и статистических величин.
Заняв экстремальную позицию, можно привести доводы в поль-
зу того, что нет такого понятия, как детерминированная перемен-
ная величина, т. е. иа «достаточно микроскопическом» уровне вся-
кое явление дает отсчет, который классифицируется как случайная
переменная величина. Можно найти также аргументы в пользу опи-
сания многих случайных переменных величин математическими от-
ношениями и предсказание их дальнейшего поведения, если рассмат-
риваемое явление достаточно хорошо понятно. Признавая возмож-
ность этих крайних интерпретаций, в большинстве практических
случаев легко удается различать детерминированные и случайные
переменные величины. Позже будут описаны методы математиче-
ского определения для ситуаций, в которых такая дифференциация
невозможна.
§ 1.4. Стационарные и эргодические процессы
Стационарные процессы. Функция х (Z) называется случай-
ной переменной, если ее значение в любой отрезок времени
может быть определено только с помощью статистических пара-
метров. Принципиальная классификация случайных переменных
состоит в определении их стационарности илн нестационарности.
Случайная переменная называется стационарной, если ее стати-
стические характеристики не изменяются со временем. Предполо-
жение стационарности обычно оправдывается для систем, в кото-
рых основные механизмы, приводящие к возникновению флуктуа-
ций, инвариантны во времени в течение достаточного периода.
Особенностью статистических' характеристик, которые должны
оставаться постоянными во времени, чтобы, служить доказатель-
ством стационарности процесса или переменной, является наличие
постоянной составляющей, определяющей стационарность процесса
нли переменной. Некоторые авторы (ошибочно) указывают, что для
установления стационарности достаточно показать, что среднее
значение для ансамбля сигналов и среднеквадратическое значение
остаются постоянными во времени. Другие [19] считают, что для до-
казательства слабой стационарности или стационарности в общем
смысле необходимо показать, что среднее значение для ансамбля
сигналов и автокорреляционная функция должны быть постоянными
функциями времени. Кроме того, они утверждают, что для случай-
ного процесса необходимо найти бесконечное множество моментов
13
высшего порядка и присоединенных моментов, чтобы установить
полное семейство функций распределения вероятности, описыва-
ющих процесс, и что в отдельных случаях, когда всевозможные мо-
менты н присоединенные моменты инвариантны во времени, случай-
ный процесс может быть определен как сильно стационарный или
стационарный в точном смысле. Однако они также указывают, что
в большинстве практических случаев установление слабой стацио-
нарности оправдывает допущение сильной стационарности.
Ясно, что даже в наиболее идеальных ситуациях сложно проде-
монстрировать сильную стационарность. Затруднительно даже на-
глядное представление слабой стационарности. Следовательно,
для среднего значения и среднеквадратического значения, или авто-
корреляционной функции, должен быть установлен диапазон зна-
чений, которые могут быть приемлемы для сигнала конечной дли-
тельности*.
Эргодические процессы. Все стационарные процессы могут быть
подразделены на эргодические н неэргодическне. Это свойство
иллюстрируется серией графиков, представленных на рис. 1.1.
Рассмотрим среднее значение по ансамблю для ряда сигналов
в данное время t\. Среднее по ансамблю, обозначаемое как <х (А)>»
рассчитывается по формуле:
.2 (1.!)
< х(О>= lim ------------
N-t-co N
Среднее по ансамблю в другие моменты (/2, /3 н т. д.) может быть рас-
считано подобным образом. Если процесс стационарный, то каждая
из этих средних по ансамблю должна быть той же самой, т. е. сред-
ние величины остаются постоя иными независимо от времени.
Рассмотрим теперь среднее по времени значение для отдельного
единичного сигнала х, (Z).
= f (1.2)
2T J
Если отдельные сигналы, представленные на рис. 1.1, описывают
стационарный процесс, то средняя по времени величина должна
* В американской литературе по приложениям теории случайных процес-
сов отсутствует общепринятое определение стационарности. Согласно приня-
тому в советской научной литературе определению, процесс является стацио-
нарным в широком смысле, если математическое ожидание соответствующей
случайной функции постоянно, а второй момент (корреляционная функция)
зависит только от разности временных аргументов. Процесс называется ста-
ционарным в узком смысле, если л-мериый закон распределения описываю-
щей его случайной функции при любом п зависит только от разности времен-
ных аргументов и не зависит от положения этих интервалов в области измене-
ния аргумента. В приложениях обычно имеет значение стационарность в ши-
роком смысле. Очевидно, что в случае нормальных случайных процессов оба
понятия совпадают. — Прим. ред.
14
быть той же самой. Если процесс является эргодическим, то сред-
нее по ансамблю в любое время <х (/)) должно быть равно средне-
му по времени значению для сигнала (f). С другой стороны, полу-
чение тождества численных величии невозможно в данной практи-
ческой ситуации, и, следовательно, для таких величин должны
быть установлены приемлемые значения отклонений. Необходимо
также, чтобы автокорреляционная функция и другие параметры,
связанные с усреднением по времени, сравнивались с соответствую-
щими характеристиками, зависящими от средних по ансамблю.
Случайные эргодические процессы являются важным классом
процессов, так как все их свойства могут быть определены путем
временного усреднения отдельных сигналов. В реальных условиях
случайные переменные, характеризующие стационарное физическое
явление, часто, к счастью, оказываются эргодическими. Поэтому
характеристики стационарных случайных процессов могут, вообще
говоря, удовлетворительно измеряться по одному наблюдаемому
сигналу достаточной длительности.
Автостационарность. Иногда говорят, что индивидуальные вре-
менные отсчеты случайной переменной стационарны. Это означает,
что свойства, определяемые в пределах относительно коротких вре-
менных интервалов по выбранному временному сигналу, от интер-
вала к интервалу, отличаются незначительно. Однако этн отлнчия
больше, чем можно обычно ожидать вследствие статистического раз-
броса отдельных реализаций. Такой тнп стационарности иногда на-
зывают автостационарностью, чтобы исключить путаницу с класси-
ческим определением.
Отдельный сигнал, получаемый при эргодическом случайном про-
цессе, является автостациоиарным. Кроме того, отдельные сигналы
для большинства физически интересных нестационарных случай-
ных процессов также являются автостационар ними. Беидат и Пир-
сон указывают, что если применимо предположение об эргодичности,
что справедливо для большинства стационарных физических яв-
лений, проверка автостациоиарности для отдельного единичного
сигнала эффективно подтверждает предположение об эргодичности
случайного процесса, из которого получен выбранный сигнал. Мы
будем пользоваться теорией, которая, строго говоря, справедлива
только для эргодических процессов, но которая применима к пере-
менным процессам, являющимся автостационарными.
СПИСОК ЛИТЕРАТУРЫ
1. Feynman R., de Hoffman F., Serber R. «J. Nucl. Energy», 1956, v. 3, p.64.
2. Fermi E., Feynman R. P., de Hoffman F- Theory of the Criticality of the
Water Boiler and the Determination of the Number of Delayed Neutrons.—
USAEC Report MDDC-383 (LADC-269), Los Alamos Scientific Laboratory,
December 1944. '
3. De Hoffman F. Intensity Fluctuations of a Neutron Chain Reactor. —
USAEC Report MDDC-382 (LADC-256), Los Alamos Scientific. Laboratory,
October 1946.
15
4. De Hoffman F. Statistical Aspects of Pile Theory. — In: The Science and
Engineering of Nuclear Power, CD. Goodman (Ed.), v. 11, p. 116. Addison-
Wesley Publishing Company, Inc., Reading, Mass., 1949.
5. Orndoff J. D. Prompt Neutron Periods of Metal Critical Assemblies. —
Nucl. Sci. Engng., 1957, v. 2, p. 450—460.
6- Mogilner A. I., Zolotukhin V. G. Measuring the Characteristics of Kinetics
of a Reactor by the Statistical p-Melbod.—«Atomic Energy» (USSR), 1961,
v. 10, N 4, p. 377—379. (См. Могильнер А. И., Золотухин В. Г. Измере-
ние характеристик кинетики реактора статистическим p-методом. «Атом-
ная энергия», апрель, 1961, т. 10, вып. 4).
7. Bennett Е. F. The Rice Formulation of Pile Noise. —«Nucl. Sci. Engng»,
1960, v. 8, p. 53—61.
8. Pal L. Determination of the Prompt Neutron Period from the Fluctuations
of the Number of Neutrons in a Reactor. — Central Research Institute of
Physics, Hungarian Academy of Sciences, Budapest, 1962.
9. Pal L. Statistical Fluctuations of Neutron Multiplicaton. — In: Procee-
dings of the Second United Nations International Conference on the Peace-
ful Uses of Atomic Energy, Geneva, 1958. v. 16, p- 687: United Nations,
N. Y., 1959.
10. Pacilio N. Short Time Variance Method for Prompt Neutron Lifetime Mea-
surements. — «Nucl. Sci. Engng», 1965, v. 22, p. 266.
II. Matthes W. Statistical Fluctuations and Their Correlation in Reactor Neut-
ron Distribution. — «Nukleonik», 1962, v. 4, p. 213.
12. Harris D. R. The Sampling Estimate of the Parameter Variance/Mean in
Reactor Fluctuation Measurements.—USAEC Report WAPD-TM-157,
Westinghouse Electric Corp., Bettis Plant, August 1958.
13. Bryce D. H. Measurement of Reactiving and Power Through Neutron De-
tection Probabilities. — In: Noise Analysis in Nuclear Systems. Gaines-
ville, Fla., Nov. 4—6, 1963, Uhrig R. E. (Coordinator); AEC Symposium
Series, 1964, N 4 (TID-7679).
14. Furuchashi A-, Izumi S. A Proposal on Data Treatment in the Feynman
Alpha Experiment. — «J. Nucl. Sci. Tech.», Tokyo, 1967, v. 4, p. 99.
15. Moore M. N. The Determination of Reactor Transfer Functions from Measu-
rements at Steady Operation. — «Nucl. Sci. Engng», 1958, v. 3, p. 387—
394.
16. Moore M. N. The Power Noise Transfer Function of a Reactor. — «Nucl.
Sci. Engng», 1959, v. 6, p. 448—452.
17. Cohn С. E. Determination of Reactor Kinetic Parameters by Pile Noise
Analysis. —«Nucl. Sci. Engng», 1959, v. 5, p. 331—335.
18. Cohn С. E. A Simplified Theory of Pile Noise. —«Nucl. Sci. Engng», 1960,
v. 7, p. 472.
19. Bendat J., Piersol A. Measurement and Analysis of Random Data. John
Wiley and Sons, Inc., N. Y., 1966. (См. Бендат Дж., Пирсол А. Измерение
и анализ случайных процессов. Пер. с англ. М-, «Мир», 1974.)
ГЛАВА 2.
СТАТИСТИЧЕСКИЕ МЕТОДЫ,
ПРИМЕНЯЕМЫЕ ПРИ АНАЛИЗЕ
СЛУЧАЙНЫХ ШУМОВ
§ 2.1. Введение
Анализ случайных шумов основывается на статистических
методах. Действительно, чтобы понять, как теория случайных
шумов используется для анализа динамических систем, необходимо
знание фундаментальных концепций статистических методов. По-
скольку по статистическим методам! существует обширная литера-
тура, в настоящей главе рассматриваются вопросы, только непосред-
ственно относящиеся к анализу случайных шумов, приводится не-
обходимая в дальнейшем терминология и не делается попыток при-
водить строгие математические выводы.
§ 2.2. Средние значения и моменты вероятности
Термин «среднее значение» обычно используется для обозначе-
ния средней величины или первого момента функции плотности
вероятности. Однако он может использоваться н для представле-
ния других средних величин, таких, как среднеквадратическое зна-
чение (второй момент функции плотности вероятности) нли другой
функции, взвешиваемой с плотностью распределения, например ха-
рактеристической функции, имеющей экспоненциальный весовой
множитель перед функцией плотности вероятности.
Для дискретной переменной первый и второй моменты (среднее
и среднеквадратнческое значения) соответственно при функции плот-
ности вероятности р (хг-) равны:
N
2 Xi р (лг) N
= —= (2-1)
J] pU,) ?So
i = 0
н -
N
2 x? p (Xi) N
= -^7--------= У xfP M E (*)> <2-2)
2 p(*i)
i=0
ГСС. ПУБЛИЧНАЯ 17
НАУЧ. !O-T 'ХвИЧЕСКЗД
где Е (х) и Е (х£) — математические ожидания х и х2 соответственно.
Знаменатель равен единице, поскольку 7V — полное число событий
в дискретном случайном процессе. Подобные выражения могут быть
написаны для моментов высших порядков х8, х% х6 и т. д. Эти соот-
ношения для и (так же, как. и для высших моментов) справед-
ливы только для больших величин N, т. е. среднестатистическая
величина и математическое ожидание сходятся только при 7У->со.
Подобные выражения для средней и среднеквадратической вели-
чины для непрерывной переменной записываются соответственно:
f хр (х) dx
Р-Х——J хр (х) с/х = Е (х)
J р (%) dx. —со
(2-3)
F x2(jtfdx
««^=7—-—
J р (х) dx
J x-p(x)dx — £(х2).
(2.4)
Значения квадратного корня из среднеквадратической величины ipl,
дисперсии о* и среднеквадратического отклонения сх могут быть
получены как
(2.5)
= Их*.
^ = «--^)1/2. (2.6)
Другое статистическое усреднение, которое полезно применять
в теории случайных шумов, основано на методе использования ха-
рактеристической функции Мх (jo), которая представляет собой
экспоненту с комплексным показателем, взвешиваемую функцией
плотности вероятности непрерывной случайной величины:
J е,йг р (х) dx <ю
Л4к(]о) = —--------------= f ei®«p(x)dx,
J р (х) dx —со
(2.7)
где j — мнимая единица, v — действительная величина. Посколь-
ку уравнение (2.7) имеет вид интеграла Фурье*, при соответствую-
* Обычный вид интеграла Фурье может быть получен путем замены v на т
к х на со.
18
щих обстоятельствах можно применить обратное преобразование
Фурье для получения плотности вероятности
p(x) = -J- Т MK(jt>)e-J“dti. (2.8)
ZJI
—ос
При дискретных значениях случайной переменной х уравнение
(2.7) имеет вид:
Mx(jtO=2Wm)eI'”'“- (2-9)
т
Если взять производную от характеристической функции по о
g[^^)] =. J xel^p(x)dx (2.10)
и определить обе части при v = 0, то интеграл получается равным
среднему значению
(2.11)
dv |d=d
Видно, что первый момент случайной переменной х может быть по-
лучен дифференцированием характеристической функции по v
с последующей подстановкой в результат v = 0. Высшие моменты
случайной переменной определятся путем последовательного диффе-
ренцирования характеристической функции по о и вычислении ре-
зультата при v = 0:
^п_^. j)n Ап (М* (ji>)] I ^2 |2)
dvn |о=0
Такой процесс обычно называется генерацией моментов.
Для двух случайных переменных совместная характеристиче-
ская функция совместного распределения вероятностей непрерыв-
ных случайных переменных х и у имеет вид:
Ж (j^i, jo2) = eU°i ** ») р (х, у) dxdy. (2.13)
По аналогии с одномерным случаем, используя двумерное преоб-
разование Фурье, можно получить плотность совместного распре-
деления вероятности двух случайных переменных по их совместной
характеристической функции М (j vlt jog), т. е.

p(x.y) = -z~ f f Af(jtii,jo2)
(2jl) J J
e—j»t *—jf.«/ dvt dvz. -
(2.14)
19
§ 2.3. Вероятностные распределения
при радиоактивном распаде
Биномиальное распределение. Явление радиоактивного рас-
пада можно проанализировать с помощью элементарной теории
вероятностей. К тому же радиоактивный распад позволяет наглядно
показать вероятностные распределения: биномиальное, Пуассона
н Гаусса (нормальное) [1].
Если имеется большое число радиоактивных атомов с вероят-
ностью распада р, то может быть оценена вероятность распада т
атомов за время t. Рассмотрим в данный момент только т атомов
из No. Вероятность того, что первый из этих т атомов распадается,
равна р; что распадается первый и второй—ра; что распадается пер-
вый, второй и третий — р3 и т. д. Вероятность того, что распадутся
все т атомов, равнорт. Если ровно т атомов распадаются, то остав-
шиеся (Л?о— т) атомов не должны распасться. Вероятность этого
равна (1 — p)A'o—'n, так как вероятность избежать распада равна
1 — р. Следовательно, для данной группы из т атомов вероятность
точного распада т атомов за время t равна рт • (1 — p)w®—т. Од-
нако именно эта группа нз т атомов является не единственной груп-
пой атомов, которая может распадаться. Первым из распадающихся
атомов, входящих в число т атомов, может быть любой из 7VC ато-
мов, вторым—любой из Nq—1 атомов и т. д., т-м — любой из
No— т + 1 атомов. Произведение этих выражений
т— 1 AZ 1
"t,(.V0-l)(W0-2)...(A'0-m+l)= П (Л?о-1) = "°- „ (2.15)
I = 0 у* о in) I
дает общее число схем, по которым могут распасться т атомов из
No за время t. Поскольку произведение включает также порядок
выбора т атомов, необходимо его разделить на число перестановок
из т атомов, равное ml Следовательно, вероятность р (т) того, что
т атомов нз NQ распадутся за время t, равна
р"С (2-16)
L(/Vo— ту. ml J
Это выражение для р (т) обычно называют биномиальным распре-
делением вероятности, так как коэффициент в квадратных скоб-
ках является коэффициентом перед величиной хт в биномиальном
разложении (1 + х)Л'°- Вероятность 1 — р того, что атом не распа-
дается за время t, определяется отношением числа нераспавшихся
атомов N к начальному числу атомов No:
N/No = 1 — р — q, (2.17)
где q — вероятность того, что атом не распадается за время t.
20
Скорость распада ядер в момент времени t пропорциональна
числу остающихся ядер:
dNldt = —hN, (2.18)
где — коэффициент пропорциональности, являющийся характер-
ной константой распада для радиоактивного материала. Решение
уравнения (2.18) дает
Af//Vo = e-4 (2.19)
Комбинируя уравнения (2.16), (2.17) и (2.18), получим
р = 1 — N/No = 1—е-^ = 1 —9, (2.20)
' Р Ю = L %-т! =
L(W0—m)!m!j
Г---W(2.21)
а. Средняя скорость распада. Математическое ожидание скорости
распада радиоактивного материала может быть получено с помощью
закона биномиального распределения. Подставив уравнение (2.21)
в (2.1), получим среднее значение т, среднее число распадов за
время t:
Д т₽(т)=ДЧ(^«] рт^~т'- (2-22)
Это выражение можно вычислить, используя биномиальное разло-
жение выражения (px-J-?)Wo:
(px + q)N° = 2 Г,., ,1 P'n?<W|'~"1)= у (2.23)
,„=о1(Л'г,-"')!ти „.=о
Дифференцирование его по х дает
Wo
No р (px+q)N°—x = 2 тхт~1 р (т). (2.24)
т—О
Для х = 1, что приводит уравнение (2.23) к разложению единицы,
w0
^оР(Р + ?)"“-,=^оР = 2 '"P(m) = ll,«- (2.25)
т= 0
Используя уравнение (2.20), получим среднее число распадов за
время t:
^ = NoP = No(l~e-^. (2.26)
21
При рассмотрении времен, коротких по сравнению с периодом
полураспада радиоактивного материала, применимо приближение
е-м~1— и, (2.27)
тогда
= (2.28)
При рассмотрении времен, больших, чем одна сотая периода
полураспада, должно использоваться уравнение (2.26).
б. Среднеквадратическое отклонение измерений скорости счета.
Среднеквадратическое отклонение н дисперсия числа распадов за
время t могут быть получены из биномиального разложения урав-
нения (2.23) путем определения второй производной по х:
Л'ДМд —I)pa(/2x+<7)'v«»-2— у т(т— 1)л"1-2р(/п), (2.29)
т = 0
которое для х = 1 переходит в выражение
Л^о (Л\) — 1) ра = У, т(т—l)p(m)= V, m2p(m)— у, тр(т).
т=0 т=0 т=0
(2.30)
Используя уравнения (2.1) и (2.2), выражение (2.29) можно
привести к виду
Л'0(^-1)р2=^-рт. (2.31)
Дисперсия, определяемая уравнением (2.6):
= (2-32)
получается путем комбинации уравнении (2.26) и (2.31):
= ЛГС (М,— 1) Р2 + pm—Цт =
= NcP<) — = = Р) = М- (2-33)
Для радиоактивного распада, для которого р дается уравнением
(2.20), уравнение (2.33) преобразуется к виду
<й = 1*„е-« (2.34)
Если время наблюдения мало по сравнению с периодом полурас-
пада, т. е. мало, уравнение (2.34) переходит в
Cm = |.i„„ (2.35)
нли
<’т = УРт. (2-36)
т. е. среднеквадратическое отклонение числа рвспвдов за время t рав-
но корню квадратному из среднего числа распадов, которые про-
исходят за данный интервал времени.
22
Распределение Пуассона. Биномиальное распределение, опи-
сываемое уравнением (2.21), упрощается при наложении следующих
ограничений:
(2.37)
М,»1; (2.38)
и приближении 1, (2.39)
е««1+М; (2.40)
(2лх)‘/2 е~*х1: (формула Стирлинга); (2-41)
е Ne J No J (2.42)
pra«W0(l-e-») = W„W. (2.43)
В результате получаем выражение
m e— p(m)=±2L- , ml (2.44)
известное как распределение Пуассона, которое справедливо для
NOt больших 200, и X/, меньших 0,01. Это распределение почти сим-
метрично вблизи р/д, если исключить значения пг, удаленные от рт,
н становится все более симметричным при возрастании р/(1. Основное
преимущество распределения Пуассона состоит в том, что оно пол-
ностью определяется с помощью единственного параметра р„г
Гауссово, или нормальное, распределение. Если наложить до-
полнительные ограничения
ш>200, (2.45)
II-1™- (2.46)
и использовать приближение
In / 1 [ Нтп т___(р™ т)2 ^2 47)
\ т / т 2m2
уравнение (2.44), описывающее распределение Пуассона, сведется к
р(т) = (2л|.1т)“1/2 ехр [—(цт—т)а/2р„]. (2.48)
Это распределение называется нормальным распределением, или
распределением Гаусса, и является симметричным относительно
среднего значения рт.
а. Центральная предельная теорема. Важность нормального
распределения для большинства физических задач непосредственно
связана с использованием центральной предельной теоремы, которая
гласит, что сумма независимых случайных переменных при доста-
точно общих условиях подчиняется примерно нормальному распре-
23
делению независимо от исходных распределений переменных. По-
скольку многие наблюдаемые физические явления—результат вза-
имодействия многочисленных переменных, нормальное распреде-
ление представляет хорошее приближение для многих обычно встре-
чающихся функций распределения. Эта теорема бывает весьма по-
лезной во многих практических случаях. Например, в ядерном ре-
акторе результирующая плотность нейтронов в данной точке может
обусловливаться нейтронами, которые родились в результате цепо-
чек распадов, фактически не коррелируемых.
Ряс. 2.1. Гауссово (нормальное) распределение
вероятности.
б. Среднеквадратическое отклонение. Для больших значений
среднеквадратическое отклонение определяется по формуле, анало-
гичной уравнению (2.36) для биномиального распределения:
“rs; (2.49)
Подстановка уравнения (2.49) в (2.48) дает наиболее привычную
форму записи нормального распределения:
₽(m)='TV5Sexp [-^^1- (2-5°)
Кривая нормального распределения полностью определяется сред-
ним значением и среднеквадратнческнм отклонением от слу-
чайной переменной т. Кривые распределения по нормальному за-
кону для больших и малых значений дисперсии представлены на
рис. 2.1. Надо иметь в виду, что площадь под кривой функции плот-
ности вероятности равна единице независимо от величины диспер-
сии. Если среднее значение р.т равно нулю, кривые нормального рас-
пределения (см. рис.1 2.1) симметричны относительно точки т — 0.
Интегрирование функции плотности вероятности от — а до +
+ а дает вероятность того, что m будет лежать вблизи на рассто-
24
янии в пределах [ а |. На рис. 2.1 интеграл представлен заштрихо-
ванной площадью. Величина а, при которой интеграл
Ищ+в
р (tri) dm (2-51)
равен 1/2, называется вероятной ошибкой, т. е. половина экспери-
ментальных данных будет попадать в интервал около среднего зна-
чения плюс или минус вероятная ошибка. Можно показать, что для
нормального распределения вероятная ошибка и среднеквадрати-
ческое отклонение связаны между собой соотношением
вероятная ошибка = 0,6745 сгто (2.52)
и что с вероятностью 68,27% экспериментальные данные будут по-
падать в интервал возле среднего значения
Интеграл от р (tri), определяющий функцию распределения ве-
роятности Р (т) для нормального распределения, не вычисляется
аналитически. Однако подстановкой
|im—т = У 2а и (2.53)
интеграл сводится к функции ошибок, определяемой как
erf н — %- Г е-du, (2.54)
Vn J
о
которая может быть вычислена по таблицам математических
функций.
§ 2.4. Корреляционные функции
Корреляция—одно из важнейших понятий в анализе случайных
шумов. Корреляция устанавливает количественное и (или) качест-
венное отношение переменной к самой себе, к другой переменной
или нескольким переменным в зависимости от времени или с изме-
нением времени. Чтобы показать статистическую основу этого поня-
тия, оно будет введено здесь с использованием некоторых статисти-
ческих отношений, полученных ранее в этой главе.
Рассмотрим степень зависимости между двумя действительными
случайными переменными хну. Если построить диаграмму рассея-
ния для дискретных значений Хг и yt случайных величин так,
как’показано на рис. 2.2, то можно, применив метод наименьших
квадратов, провести по данным точкам прямую. Если все точки по-
падут на эту прямую, можно сказать, что случайные переменные х
и у являются линейно зависимыми или полностью коррелирован-
ными. Если точки так широко рассеяны, что они не выделяют ка-
кую-либо отдельную прямую, переменные х и у, вероятно, являются
независимыми нли некоррелированными. Для случая, представлен-
25
кого на рис. 2.2, где данные, по-видимому, выделяют прямую, не-
смотря на большое количество разбросов, х и у являются частично
зависимыми или частично коррелированными.
Воспользуемся методом наименьших квадратов для определения
по данным точкам прямой:
ур = а + Ьх, (2.55)
где ур — предсказываемое значение у, а и Ь — постоянные пересе-
чения и наклона прямой соответственно.
Среднеквадратическую ошибку es можно определить как:
е, ~Е 1{у~УрП ~Е{[у~ (а + МН- (2.56)
Рис. 2.2. Диаграмма рассеяния для случайных пе-
ременных х и у.
(2.57)
(2.58)
(2.59)
(2.60)
Дифференцирование по а и b и приравнивание результатов
нулю дает выражения:
де^да = — 2£ (у) + 2ft + 2ЬЕ (х) = О,
dtjdb = — 2£ (ху) + 2п£ (х) + ЧЬЕ (1Л) = О,
откуда
^_£(лу)—£(>:)£ (у) £(ху)—£(>.)£ (у)
В (z2)-(£ (x)F
с „ £ (ху) £ (х)-Е (у) Е (х-) £ (ху) Е(х)~~Е(у)Е (хя)
(£(хя)—[£(х)]я)£(х) о‘Е(х)
Уравнение (2.55) использовалось для получения линии
сии у от х. Столь же обоснованно рассмотреть линию регрессии х
от у путем подгонки точек к прямой
хр = а' + Ь'у,
(2-61)
26
где хр — предсказываемая величина и а’ и Ь' являются соответст-
венно пересечением оси х и наклоном (по отношению к оси у). Кон-
станты а' и Ъ’ определяются из уравнений:
у — & Е & (&Y ^2 62)
°у
Е (ху) Е (у) —Е (х) Е (у2) ъ
а----------Fpfo) •
Если х и у полностью коррелирбваны, регрессии, полученные при
подгонке прямой х от у и у от х, должны быть идентичными, т. е.
две линии на рис. 2.2 должны совпадать. Отсюда получаются отно-
шения:
а = — аЧЪ't или ав' = — а', (2.64)
н
b = 1/У, или bb' = 1. (2.65)
Нормированный коэффициент корреляции. Если х и у не пол-
ностью коррелированы, можно определить степень корреляции по
отклонению от уравнения (2.65). Нормированный коэффициент кор-
реляции определяется как корень квадратный из произведения двух
коэффициентов наклона b и Ь':
р = [до»]1 /2 _ Г [£ (*#)—£(*)£(*/)]211 /г _ ГЕ &у}—Е (х) Е (у)] (2.66)
I / I <bc<ty I
Используя неравенство Шварца, можно показать, что
|£(%i/)|^|£(x)| |£(//)|. (2.67)
В случае, когда х и у некоррелнрованны (линейно независимы), слу-
чайные переменные
Е (ху) = Е (х) Е (у) (2.68)
и, следовательно, р = 0. Из этих уравнений видно, что абсолют-
ное значение нормированного коэффициента корреляции меняется
от нуля для некоррелированных переменных до единицы для пол-
ностью коррелированных переменных, т. е.
0<1р1<1. (2.69)
Ковариационная функция. Определим ковариацию Cxv между
х и у как числитель уравнения (2.66):
Сху = Е (ху) — £ (х) £ (у). (2.70)
Алгебраические преобразования уравнения (2.70) дают
= f К*—Ра)(4/—Ну)] = § f(*— pjte—pg)p(x,y)dxdy. (2.71)
27
В частном случае для одной переменной, когда х = у,
Схх = Е [(х— Кх)2] = о*. ( 2.72)
Понятия линейно независимые переменные и некоррелирован-
ные переменные не идентичны. Независимые случайные перемен-
ные некоррелированны. Обратное утверждение, т. е. что некор-
релированные переменные независимы, не справедливо в общем
случае, так как при Сху и ржу равных нулю переменные х и у
могут быть связаны нелинейной зависимостью.
В общем случае средние значения отдельных случайных пере-
менных х и у не остаются постоянными во времени и должны опре-
деляться в различные моменты времени. В моменты и где = t,
a = t 4- т, ковариация х (4) и у (/2) равна:
Еху 01’ ^s) “ Сxll (Е 4“ т) = Сху (т) =
= Е {(х 0)—|хЛ- 0)1 [у 0 4-т) — (/+?)]}. (2.73)
Подобные выражения могут быть написаны для Схх (/, t 4- т) и
Суу 0» 4- т). В том случае, когда т = 0, уравнение (2.73) перехо-
дит в уравнение (2.72).
Корреляционные функции. Взаимная кор-реляционная функция
определяется как
(т) == Е [х (/) у (I 4- т)]. (2.74)
Сравнение уравнений (2.74) и (2.73) показывает, что ковариация
является частным случаем взаимнокорреляционных функций, из
которых вычитаются средние значения. Для стационарных процес-
сов уравнение (2.73) записывается
Сху (т) = Е [х (/) у (1-\- т)] - (т) — (2.75)
Для одной переменной, когда х = у, получаем автокорреляционную
функцию
<₽хх (?) = Е [х (/) х (t + т)]. (2.76)
Корреляционные функции выражаются через функции плотности
совместной вероятности как
<М^= $ $ x(ii)y(tjp[x(tjy№]dxdy. (2.77)
Для частного случая, при т = 0:
Ч>« (0) = Е [х (0 у (/)], (2.78)
(0) = Е {[х (/)]“} = < (2.79)
28
С помощью неравенства Шварца можно показать, что
|фхДг)|2<Ф.тх(0)ф9В(°).
(0)Сви(0)
|Фхх(т)Кф«х(0)='Ф1.
|Схх(г)|<Сю(0) = ад.
(2,80)
(2.81)
(2.82)
(2.83)
Используя уравнение (2.66), переопределим нормированную взаим-
нокорреляционную функцию (нормированную взаимноковариацион-
ную функцию) как
р,„(т) =-------------- (2.84)
(Сх, (0) Сто (0)]1 /2
которая удовлетворяет условию
|р«„(т)|<1. (2.85)
Функция Pxj/(t) показывает степень линейной зависимости между
x(t) и y(t) при изменении времени иа т.
СПИСОК ЛИТЕРАТУРЫ
1. Evans R. D. The Atomic Nuclear, McOraw-Hill Book Company, Inc., N. ¥.,
1955.
2. Jahnke E., Emde F. Table of Functions, 4th ed., Dover Publications, N.'Y.,
1945. (См. Янке E., Эмде Ф. Таблицы функций с формулами и кривыми.
Изд. 3-е. Пер. с англ. М., Гос. изд-во физ.-мат. лит., 1959.)
3. Bendat J. S., Piersol A. G. Measurement and Analysis of Random Data.
John Wiley and Sons, Inc., N. Y., 1966. (См. Беидат Дж., Пирсол А. Из-
мерение и анализ случайных процессов. Пер. с англ. М.,«Мир», 1971.)
ГЛАВА 3.
СТАТИСТИЧЕСКИЕ
ДИСКРЕТНЫЕ МЕТОДЫ
В РЕАКТОРНЫХ
СИСТЕМАХ
§ 3.1. Введение
Методы измерения шумов могут быть разделены в основном
на микроскопические методы (которые основываются на стати-
стике изменения числа нейтронов) и макроскопические методы (ко-
торые основаны на изучении интегрального поведения системы).
В этой главе будут рассматриваться микроскопические методы,
включающие вероятность регистрации нейтронов, отклонение плот-
ности вероятности от распределения Гаусса или Пуассона, отно-
шение дисперсии к среднему распределению временных интервалов
между отсчетами и другие подобные явления.
Большинство статистических методов было развито для крити-
ческих реакторов нулевой мощности. В последних работах предла-
гаются некоторые методы, которые могут быть распространены на
энергетические реакторы л подкритические системы. Некоторые
методы наиболее пригодны для тепловых реакторов, другие — для
быстрых реакторов. Иногда определяющим фактором в выборе ме-
тодики является имеющееся в наличии оборудование.
Природа цепной реакции ядерных процессов в реакторе обуслов-
ливает отклонение детектируемых отсчетов от нормального распре-
деления, поскольку отдельные отсчеты зависят от других нейтро-
нов в цепочке. Следовательно, статистические характеристики ре-
зультата счета зависят от динамических характеристик ядерной
системы.
Имеется несколько экспериментальных методов, основанных на
счете нейтронов, при которых по эффективности детектора и росси-
альфа-константе распада мгновенных нейтронов, определяемой
ниже, может быть найдена мощность реактора. Одним из первых
экспериментальных методов, разработанных для этой цели, был
метод росси-альфа 11], состоящий в измерении условной вероятно-
сти отсчета в интервале времени А при времени t вслед за отсчетом
при t — 0. Относительная дисперсия счета нейтронов, регистрируе-
мых в определенном временном интервале, была изучена Фейнманом
и др. [2]. Другой метод определения [3//— метод нулевой вероят-
ности, предложенный Могильнером н Золотухиным 13], заключает-
ся в измерении вероятности отсутствия счета в определенном вре-
зе
менном интервале. Все эти методы рассмотрены в работе [4] и пред-
ставлены в сокращенной форме в этой главе.
Исследование Бабала I5J показывает, что все эти методы лех'ко
могут быть получены нз теории Колмогорова о ветвящихся
процессах [6]. Курант и Валлейс [7] изучали флуктуации числа ней-
тронов в реакторе, используя уравнение Фоккера — Планка, полу-
ченное на основании вероятностно-балансного рассмотрения, и вы-
вели формулу для дисперсии счета нейтронов. Пал [8] использовал
метод первого соударения’для вывода уравнений нулевой вероят-
ности, дисперсии и корреляционной функции, которые имеют не-
посредственное отношение к условной вероятности классического
росси-альфа-эксперимента.
В этой главе предполагается, что реакторная система описы-
вается моделью с сосредоточенными параметрами, если это не ого-
варивается особо. Такое предположение обычно считается обосно-
ванным при исследовании динамики реактора, если характерные
физические-размеры активной зоны не превышают нескольких длин
миграции.
В критических с нулевой мощностью или слегка подкритическнх
реакторных системах одним из наиболее важных параметров яв-
ляется константа спада мгновенных нейтронов, известная как кон-
станта* росси-альфа и определяемая
l-fe(l-P)
I I Л '
где все символы имеют значения,обычно используемые в теории ре-
акторов [9, 10].
Для системы критической на запаздывающих нейтронах это урав-
нение переходит в
ас = № = ₽/Л, (3.2)
поскольку в этом случае Z и Л равны. Отсюда можно выразить а
через ас:
°=т (1 ~ f)=“Ц1 - у) = “о П-р (3.3)
где р (долл) — реактивность, выраженная в долларах.
§ 3.2. Вероятностное распределение
нейтронов деления
Основной причиной статистических флуктуаций числа нейтро-
нов в большинстве реакторных систем нулевой мощности является
различие в числе нейтронов, образующихся прн каждом делении.
Выход нейтронов на деление определяется вероятностными про-
* Первоначально константа Росси определялась как отрицательная ве-
личина, однако представленное определение сейчас более употребительно.
31
цессамн, которые в свою очередь связаны с конкурирующими про-
цессами, происходящими при делении. Например, рассмотрим вы-
ход нейтронов при делении 2S5U. Вероятность выхода vp нейтронов,
где vp равно целому числу от нуля до шести, и соответствующая
функция распределения вероятности приводятся в табл. 3.1.
Таблица 3.1
Вероятность выхода v нейтронов при делении 233 U
V Р (V) /»(v) V р (V) V* р (V)
0 0,03 0,03 0 0
1 0,16 0,19 0,16 0,16
2 0,33 0,52 0,66 1,32
3 0,30 0,82 0,90 2,70
4 0,15 0,97 0,60 2,40
5 0,03 1,00 0,15 0,75
6 ~0 1,00 0 0
5 = 1,00 v=2,47 •v2=7,33
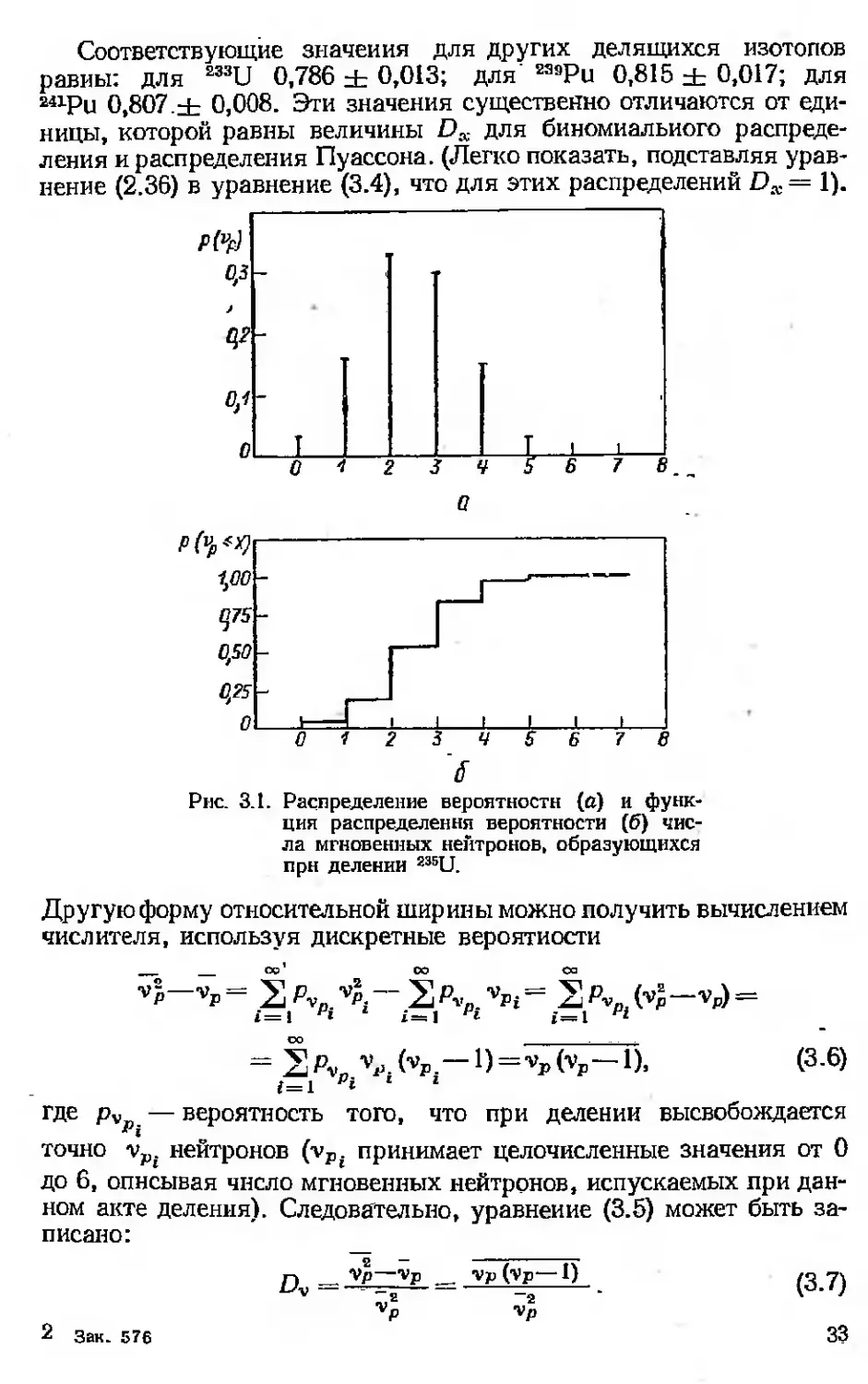
График распределения вероятности н функции распределения
вероятности представлен на рнс. 3.1. Из рис. 3.1, а следует, что рас-
пределение вероятности для ур не является распределением Пуас-
сона, хотя огибающая этих дискретных величин имеет колоколооб-
разную форму. Отклонение распределения vp от пуассоновского
(или биномиального) распределения является одной из его отличи-
тельных и полезных характеристик.
Относительная ширина Dx распределения вероятности опреде-
ляется как
Z\ =
11Х
Нх
(3.4)
Дайвеном и др. 1111 было показано, что относительная ширина DVi
иногда называемая параметром Дайвеиа, соответствует нормализо-
ванному среднему значению для числа мгновенных нейтронов на
деление:
<у^ —Г' ( ’
В литературе обычно используется последняя система обозначений.
Используя значения, приведенные в табл. 3.1, для 2S6U, можно
получить:
Dv = (72-vp)/v2 = (7,33-2,47)/(2,47)2 = 0,796,
что хорошо согласуется с значением 0,795 ± 0,007, полученным
Дайвеном и др. [11].
32
Соответствующие значения для других делящихся изотопов
равны: для 233U 0,786 ± 0,013; для 23sPu 0,815 ± 0,017; для
241Ри 0,807.± 0,008. Эти значения существенно отличаются от еди-
ницы, которой равны величины О:, для биномиального распреде-
ления и распределения Пуассона. (Легко показать, подставляя урав-
нение (2.36) в уравнение (3.4), что для этих распределений Dx = 1).
Р(Ч)
V
V
V
al Т __I__j_1__
0 <2 Ч5 67 8
Рис. 3.1. Распределение вероятности (а) н функ-
ция распределения вероятности (б) чис-
ла мгновенных нейтронов, образующихся
прн делении 235U.
Другую форму относительной ширины можно получить вычислением
числителя, используя дискретные вероятности
=°=1}* (3-6)
где pVp — вероятность того, что при делении высвобождается
точно vp. нейтронов (vp. принимает целочисленные значения от 0
до 6, описывая число мгновенных нейтронов, испускаемых при дан-
ном акте деления). Следовательно, уравнение (3.5) может быть за-
писано:
о, = = ур^р-п . (3.7)
Vp
33
2 Зак. 576
§ 3.3. Метод росси-альфа
Метод росси-альфа был впервые предложен Росси, а ста-
тистическая теория нейтронных цепочек эвристически развита Фейн-
маном, Хофманом и Сервером [2]. Их выводы излагаются в этой гла-
ве. Более строгие математические выводы выполнены Матесом [12],
Боргвалвдом и Стегеманом ИЗ], Бабала [5] и Айияма [14]. Этот ме-
тод первоначально был разработан для реакторных систем и а быст-
рых нейтронах, где число нейтронных цепочек, существующих в
Рис. 3.2. Структурная схема анализатора Орндоф-
фа [1].
ядерной системе, в любой момент невелико н распад нейтронной це-
почки происходит очень быстро из-за очень короткого времени жиз-
ни нейтрона. Последние модификации этого метода, с применением
другой аппаратуры, позволяют использовать его для реакторных
систем на тепловых нейтронах, где цепочки значительно перекры-
ваются и их распад является более медленным нз-за большего вре-
мени жизни нейтрона.
В первоначальных экспериментах росси-альфа Орндоффом была
использована счетная система, соответствующая той, которая пред-
ставлена на рис. 3.2. Система может работать с одним детектором,
обеспечивающим два входа / и 2. Могут быть использованы и раз-
дельные детекторы, так как теоретический вывод зависит только
от регистраций, связанных с цепочкой распада. Использование двух
34
детекторов делает менее критической проблему синхронизации ап-
паратуры. Принцип заключается в определении вероятности того,
что нейтрон будет зарегистрирован во временном интервале А спу-
стя время t вслед за регистрацией нейтрона при t — О, в то время
как исходное деление произошло при t0. Если рассматривать умно-
жение для подкритической размножающей системы, данное Мэр-
реем [9] только для мгновенных нейтронов, то число мгновенных
нейтронов в системе определяется как
S S
пи =--------- —-- >
где S — мощность нейтронного источника в реакторе. Число мгно-
венных нейтронов н, следовательно, число нейтронных цепочек в си-
стеме обратно пропорциональны а при данной мощности источ-
ника S. В быстрой сборке при очень слабом источнике нейтронов S
вполне возможно, что все нейтроны в околокритической системе бу-
дут членами единичной нейтронной цепочки. Следовательно, чув-
ствительный детектор часто может регистрировать два или более
нейтронов одной и той же цепочки. •
Теоретическое рассмотрение. Если первый счет нейтрона данной
цепочки происходит в момент t = 0, то имеется определенная ве-
роятность того, что детектор спустя время t зарегистрирует либо
случайный нейтрон (т. е один из нейтронов другой цепочки), либо
родственный (т. е. один из нейтронов той же цепочки, отсчет которой
был произведен в момент t — 0). Вероятность регистрации случай-
ного нейтрона равна А А, где А — средняя скорость счета детекто-
ра, а А — временной интервал измерения, т. е. временная ширина
одного канала анализатора. Поскольку число мгновенных нейтро-
нов в среднем должно уменьшаться экспоненциально, вероятность
фиксации родственного нейтрона уменьшается как ехр (—af). От-
сюда общая вероятность регистрации нейтрона (как случайного,
так и родственного) во временном интервале А определяется как
р(/) А = А А + В exp (—at) А, (3.9)
где коэффициент В, выведенный Фейнманом, Хофманом и Серве-
ром [2] с участием ОрндоффаИ], определяется следующим образом.
Вероятность того, что деление произойдет в момент t0, в интервале
Ао илн dt0 есть:
p(t0) dt0 = F dt0, (3.10)
где F — средняя скорость делений в системе. Вероятность регистра-
ции в интервале Ai в момент tlt где tt > t0, происходящей вследст-
вие деления в момент t0, равна:
(3.11)
где в — эффективность детектора в отсчетах на деление, vp — дей-
ствительное число мгновенных нейтронов, испускаемых при деле-
нии в момент t0‘, v—скорость тепловых нейтронов; Ху—макроско-
2* 35
пическое сечение деления; nSj — средняя скорость делений на еди-
ничную нейтронную плотность.
Подобным образом определяется вероятность отсчета родствен-
ного нейтрона в интервале Д2 в момент /21 где > tlt следующем
за отсчетом при /j:
р (z2) Д2 = е (vp— 1) е—1'1-'”’ Д2, (3.12)
где коэффициент (ур — 1) учитывает тот факт, что нейтрон, зареги-
стрированный в момент 4, выбыл из цепочки деления. Эти три ве-
роятности Fdt0, р (Zi)Ai, р (/2)Д2> будучи независимыми, должны быть
перемножены, чтобы можно было получить совместную вероятность
деления в момент 4 с последующим отсчетом в интервале Ду в момент
и другим отсчетом в интервале Д2 в момент /2, при которой детек-
тируемые нейтроны являются частью цепочки, возникшей при де-
лении в момент tQ. Следовательно, полная вероятность предшеству-
ющего ряда происходящих событий и обусловливающих связанные
по цепочке отсчеты является интегралом от произведения трех
вероятностей по всем моментам t0 (от — оо до 4), в которые могло
произойти исходное деление, т. е.
t,
₽с(Д-^)Д1Л2= J =
= 1)е-'‘('’ + '1“2'",Д1Д.,(|/11 =
= Fb- vp (vp-1) д, Д,
(3.13)
Следует отметить, что vp(vp—1) указывает на соответствующее
осреднение распределения мгновенных нейтронов, испускаемых на
деление, определяемое уравнением (3.6). Уравнение (3.13) можно
написать в более простой форме, используя тождество
~ = (3.14)
р Sf SfVl ' ’
н определение а из уравнения (3.1):
₽с (6 Q Д.Д, = F^ ’> -4т7 Д,Д2. (3.15)
Вероятность случайной пары отсчетов в интервалах Д2 и Д2 опре-
деляется как
PR (h At Д3= Я e2 Ai A2. (3.16)
36
Таким образом, полная вероятность пары отсчетов в интервалах Дх
и Д2 представляет собой сумму случайной и связанной по цепочке
вероятностей:
Р(ht2)Д,Д, = еаД, Д2+F& Д,Д. =
=^К+^м/е_а<'г_'‘1д4 (ЗЛ7)
где ЕеЛ — вероятность того, что отсчет произойдет в интервале Д,
и Dv — параметр Да иве на, определяемый уравнением (3.7). Если
положить ЕеДх равным I, тем самым требуя, чтобы в момент прои-
зошел отсчет, то в таком случае ЕеД2 представляет вероятность слу-
чайного отсчета в интервале Л2» а второй член в квадратных скоб-
ках уравнения (3.17) представляет вероятность связанного по це-
почке отсчета в момент /2, следующего за отсчетом в момент /х.
Это заключение может быть распространено для определения
вероятности связанного по цепочке отсчета, происходящего через tt
вслед за отсчетом в момент t — 0:
РеЙД =
ЩЕ^-е—Д
2 (1—кр) I
(3.18)
Оридофф показал, что это выражение при использовании детек-
тора из делящегося вещества должно быть уточнено для вероятности
отсчета, производимого в момент t, в результате деления и про-
цесса регистрации в момент t = 0 заменой выражения vp(vp — 1)
на
vp(vp-l) + 2vpl-^6,
ир
где б — эффективное число нейтронов, образующихся при делении
и детектируемых в момент t = 0. Поскольку б зависит от характе-
ристики и места размещения детектора, она должна оцениваться
для каждой экспериментальной установки. Обычно эта поправка
мала (около 1 %) и ею часто пренебрегают.
Полная вероятность отсчета в интервале Д через время
вслед за отсчетом в момент /=0, определяется выражением
Р(*)Д =Р««Д + Ре(0Д =
= Т-еД I E^vp Ь'Р—1)_+2'',Р I1—М kp ali /3 [Q\
2v”(l-kp)l ’ V '
которое имеет форму уравнения (3.9):
р(;)Д = ЛД+Ве-“'Д, (3.20)
где
Л = Ге (3.21)
37
является средней скоростью счета и
q = Е (vp— 1) + 2у?> (1—kp) fykp] kp ~ eDy kp .3 g
2vp(l— kP)l ~2(l—kP)l' 1 '
Уравнение (3.20) является результатом, полученным нз экспери-
ментов россн-альфа, где выражение Л А представляет фон некорре-
лированных отсчетов и может быть исключено, с тем чтобы оставить
один экспоненциальный член, по которому может быть вычислена
константа затухания а. Следует отметить, что некоррелированный
член зависит от плотности делений (т. е. от уровня мощности в кри-
тическом реакторе или мощности источника в подкритической си-
стеме), в то время как связанный по цепочке или коррелированный
член не зависит от уровня мощности. Таким образом, уменьшение
плотности делений будет увеличивать в измерениях отношение по-
лезного сигнала к шуму.
Экспериментальные измерения. Независимо от того, использует-
ся один или два детектора, аппаратура, представленная на рис. 3.2,
служит главным образом часами, которые измеряют временной ин-
тервал между пусковым и последующими импульсами. Если обес-
печиваются достаточные задержка и число каналов совпадения, то
некоторые нейтроны могут быть зарегистрированы после каждого
пускового импульса. Поскольку этот комплекс оборудования яв-
ляется дорогостоящим, то желательно использовать коммерчески
более доступные многоканальные анализаторы. При этом должны
быть приняты несколько отличные методы, зависящие от требуемой
для экспериментов временной разрешающей способности, которая
в свою очередь определяется порядком величины времени жизни
нейтрона (доли микросекунды, либо несколько микросекунд, либо
несколько сотен микросекунд).
Методика эксперимента подобна той, которую применил Орн-
дофф, включая использование многоканального анализатора как
универсальной пересчетной схемы. Первый импульс запускает внут-
ренние часы, детектируемые импульсы регистрируются соответ-
ствующим временным каналом. Коммерчески доступные универсаль-
ные пересчетные схемы обеспечивают ширину канала <Z Ю мксек
с временем нечувствительности после каждого зарегистрированного
импульса в несколько микросекунд. Специальная система, разрабо-
танная Дайзом и Урнгом [15], включает цифровую вычислительную
машину в качестве универсальной пересчетной схемы с целью обес-
печить ширину каналов ~ 3 мксек и попеременную систему ввода
информации, чтобы не принимать во внимание мертвое время (т. е.
один входной канал ведет отсчет(ы), в то время как другие хранят
отсчет(ы), сделанный в предыдущее время). Если скорость счета низ-
ка (<1000 импульсов в секунду), может быть применен многоканаль-
ный анализатор в схеме, использующей принцип времени пролета
для обеспечения ширины канала < 0,1 мксек, однако за каждым им-
пульсом следует некоторый интервал нечувствительности аиализа-
38
тора (обычно 10 мксек). Специальное оборудование, использующее
буферную память для временного запоминания импульсов до конца
цикла, обеспечивает очень узкую ширину каналов (<0,01 мксек)
в отсутствие мертвого времени.
Несколько модифицированная методика, предложенная Браисо-
ном и др. [16], использует универсальную пересчетную схему, в ко-
торой импульс от первого детектора пускает часы и импульс от вто-
ричной системы останавливает их. Вторичная система запоминает
импульс в соответствующей ячейке памяти н восстанавливает преж-
нее состояние анализатора. Такой метод действительно измеряет
время между двумя детектируемыми событиями, но в этом случае
предпочтительно измерение более коротких временных интервалов.
Авторы работы [16] указывают, что откорректированная вероят-
ность регистрации нейтрона в п-м канале равна
Рп = спI (с0 + 2 ct ). (3.23)
где Ct и сп — число отсчетов в i-м и п-м каналах соответственно;
с0 — число циклов, в течение которых не происходило регистрации;
N — общее число каналов анализатора. Эта методика будет рассмот-
рена в § 3.7.
Михалчо [17] усовершенствовал метод, описанный в работе [16]
путем введения изменяющейся временной задержки между детек-
тором 2 и анализатором. В этом случае импульсы в детекторе 2,
которым предшествовал пусковой импульс в детекторе 1, накаплива-
ются. Вероятность р (/), определяемая уравнением (3.20), теперь
запишется в следующем виде:
р (/') Д = АД + ВД ехр (—а/')» (3.24)
где t' — t — ta < 0. Символом td обозначается время задержки,
другие обозначения те же самые, что и в уравнении (3.9). Этот ме-
тод, который аналогичен корреляции последовательности импуль-
сов, обеспечивает двукратное измерение а при одной серии опытов.
Результаты экспериментальных измерений росси-альфа обра-
батываются с помощью метода наименьших квадратов и уравнения
(3.9), откуда и определяются параметры А, В на. Затем уравнения
А = Ге (3.25)
В = SVjJ (Vp-(3 26)
2vJ(l — kp)l 2alz V '
могут быть использованы для получения любых двух из пяти вели-
чин Г, е, DVt kp или /, если другие три известны.
Карэм [18] отметил, что во многих случаях, особенно когда
имеется отражатель, экспериментальные данные согласуются с
уравнением
р (t)& — A& + ВД ехр (—ос/) -Б В'А. ехр (—af t), (3.27)
39
где а' > а, за исключением случая быстрых реакторов с замедля-
ющим отражателем. Этот случай широко рассматривался в работе
[19], но полностью удовлетворительного объяснения в ией не было
даио. Наблюдаются также некоторые пространственные эффекты,
хотя они недостаточно хорошо изучены.
Соотношение между а и р, описываемое уравнением (3.1), и оп-
ределение а не являются справедливыми для быстрых сборок с от-
ражателем. Коэн [20] высказал предположение, что это связано с фи-
зическим смыслом а и а', Ясно, что модель с сосредоточенными па-
раметрами непригодна для систем с отражателем, особенно когда
отражатель значительно отличается по составу от активной зоны.
§ 3.4. Метод, использующий отношение дисперсии
к среднему (метод Фейнмана)
Теоретическое рассмотрение. Другим статистическим методом,
близким к методу росси-альфа, является метод Фейнмана [2], в ко-
тором определяется отношение дисперсии к среднему числу отсче-
тов, производимых за фиксированный временной интервал. При
неоднократном измерении числа отсчетов, происходящих в ядерной
системе за данный временной интервал, можно связать параметры
ядерной системы с отношением дисперсии к среднему числу отсче-
тов s3/c, т. е.
?/с = (с*—са)/с, (3.28)
где с — среднее число отсчетов за интервал времени Т. Число пар
отсчетов за этот интервал дается выражением
—£1 „ СЛС^1) (3.29)
(с—2)!2! 2 7
так как число двойных -комбинаций из ряда с событий равно
с!/2[(с—2)1. Следовательно, среднее число пар отсчетов в интер-
вале Т равно
\ р (h, Q dtlt dte,
(3.30)
где p(tlf &>)—полная вероятность пары отсчетов в интервалы
dtx и Использовав дифференциальную форму уравнения (3.17)
Для p(ti, /2), получим:
С(С~1> = j j Рейх рей, +
Еп ь2е-а«.-*.>
-------------.dt;
2(i—ад/
F2 е2 Т2 , fe'D. крТ / 1—е~°'Л
2 2(1 — ад2 \ аТ )
(3.31)
40
Поскольку
c—FeT,
(3.32)
можно преобразовать уравнение (3.31) и" получить
=S=14- —""у
Z 1 '(I—w
(3.33)
где
(3.34)
и рр является «мгновенной реактивностью»*, определяемой как
(3.35)
Уравнение (3.33) приводится к виду
(с2—Э)/с—с/с=s^{c— sh/c = У,
(3.36)
где Saz — дисперсия распределения Пуассона. Следовательно, -зна-
чение Y может быть интерпретировано как разность между относи-
тельной (или приведенной) дисперсией s2/c переменной, связанной
по цепочке, и пуассоновской случайной переменной. Поскольку для
случайных пуассоновских флуктуаций V равно нулю, оно является
мерой дополнительных флуктуаций (превышающих чисто случай-
ные), которые существуют для событий, связанных по цепочке.
Этот метод первоначально был использован Фейнманом и др. [21
для определения дисперсии числа нейтронов, образующихся при
тепловом делении 235U, путем вычисления V для Т 1/а, т. е.
когда член в скобках в уравнении (3.33) примерно равен единице.
Если известны эффективность счетчика и коэффициент размножения
на мгновенных нейтронах, может быть вычислено.
Во многих реакторных экспериментах пренебрежение запазды-
вающими нейтронами обеспечивает хорошее приближение, посколь-
ку они фактически дают постоянный вклад для тех временных интер-
валов, в течение которых ведется эксперимент. Однако для тепловых
и промежуточных систем необходимо учитывать влияние запаздыва-
ющих нейтронов. Беннет [21] получил выражение, учитывающее
* Мгновенная реактивность рр — термин, определяемый аналогично
реактивности р. Эти две реактивности связаны между соотношением рр =
41
запаздывающие нейтроны. В этом случае уравнение (3.33) прини-
мает вид:
г2__? пл. / —а- Т\
~ = 1 + У — Н„ (а,) (1 -). (3.37)
с ai \ щТ /
где Ai и определяются через передаточную функцию
мощности
нулевой
(3.38)
Бениет [21] вычислил значения Ait а, и Но (а*) для | р | < (3/10
и I <Z 5 • IO-4 сек, для критического или слабо подкритического
реактора. Эти значения приведены в табл. 3.2. Запаздывающие ней-
троны вносят другой нежелательный эффект. Как отметил Пал [8],
последующие временные интервалы измерений являются коррели-
рованными (взаимозависимыми) п уравнение (3.33) должно быть
исправлено также с учетом этой корреляции. Пал предложил ввести
время выдержки 0 между последующими временными интервалами
измерений для уменьшения этой зависимости, но не дал какой-
либо корректирующей формулы. Бабала [51 указал, что эффект та-
кой корреляции становится малым при увеличении числа наблю-
дений. Пачилио [22], однако, отметил, что экспериментально он не
обнаружил этой корреляции.
Экспериментальные методики. Эксперимент для определения от-
ношения дисперсии к среднему достаточно прост: измеряется число
отсчетов достаточно много раз в течение временного интервала
и рассчитывается дисперсия. Измерения повторяются для других
временных интервалов Т различной продолжительности. Из графика,
представляющего зависимость дисперсии от Т, можно определить а,
используя метод наименьших квадратов и уравнение (3.33).
Обычно для счета событий, детектируемых в течение временного
интервала Т, применяется пересчетная схема с блоком пропускания,
управляемая точным таймером; выходной сигнал печатается иа лен-
те или пробивается на картах. Операция вывода данных обычно пре-
рывает эксперимент и вводит мертвое время между последователь-
ными наблюдениями. Погрешность нз-за мертвого времени может
быть уменьшена при использовании усовершенствованного много-
канального анализатора, в качестве универсальной пересчетной схе-
мы, имеющей от 1000 до 4000 каналов. Мертвое время в такой схеме не
превышает 10—20 мксек. Хотя для одновременного накапливания
и запоминания данных и тем самым исключения мертвого времени
должно создаваться специальное оборудование, различные методы,
описываемые ниже, являются наиболее общими в настоящее время.
42
Помимо проблемы мертвого времени предшествующие методы
связаны с накоплением большого количества данных. В методе,
впервые предложенном Стегеманом [23], используется многоканаль-
ный анализатор, в котором детектируемые импульсы поочередно рас-
пределяются по каналам. По окончании интервала Т в память ана-
лизатора дополнительно подается единичный импульс, направля-
емый в очередной адрес и одновременно в канал, возвращающий
систему в исходное положение. (Например, если за интервал Т де-
тектируется 341 событие, единичный отсчет (импульс) направляется
в 342 ячейку памяти. Последний адрес всегда на единицу больше
числа отсчетов, так как адрес отсчета, возвращающего схему в исход-
ное положение, является первым адресом.) Этот метод дает дискрет-
ную функцию вероятности, и, модифицируя уравнения (2.38, 2.39),
можно рассчитать среднее и среднеквадратическое значения и, сле-
довательно, дисперсию и отношение дисперсии к среднему:
м
°-2 (‘--1) <3-39>
S(.--i)
i= I
М
2 Л)
? 2 (3-40)
2(<-о
i=l
где М — число запоминающих каналов (ячеек памяти) в анализа-
торе; —число отсчетов, накопленных в t-м канале. Должны быть
приняты меры предосторожности для того, чтобы число отсчетов за
временной интервал не превышало числа каналов, имеющихся в ана-
лизаторе или специальном оборудовании, таком, например, как вспо-
могательная цифропечатающая система.
Оба приема имеют существенные недостатки, связываемые со
стационарностью изучаемой системы. Поэтому существует общий
прием записи в течение достаточно длительного времени выходного
сигнала детектора на магнитную ленту и повторной обработки это-
го временного сигнала до получения необходимой информации
(см. [24, 251). Такие записи позволяют также сравнивать между
собой результаты, получаемые различными методами. Следующий
метод, примененный Турканом и Драгтом [26], заключается в исполь-
зовании очень короткого базового временного интервала, так что
последующие испытания могут быть сложены для того, чтобы
образовать более длительные временные интервалы, ' кратные
базовому.
Измерения параметров. Из уравнений (3.33) и (3.37) видно, что
имеется несколько параметров, которые можно вычислить при изме^
43
рениях отношения дисперсии к среднему (например, константа спа-
да мгновенных нейтронов а, дисперсия числа нейтронов, испуска-
емых при делении, реактивность подкритической системы, уровень
мощности критической системы). Очевидно, не все из ннх вычисля-
ются независимо. Кроме того, тип изучаемой системы (быстрая,
промежуточная нли тепловая) также определяет, какие параметры
могут быть вычислены. Пачнлио [27] выразил ограничения для ис-
пользования уравнения (3.33) в терминах о^Т: оно применимо до
тех пор, пока справедливо неравенство
сс2Т < 1. (3.41)
Физически это значит, что интервал Т должен быть достаточно
коротким, чтобы эффект запаздывающих нейтронов был незначитель-
ным, т. е. T<Z5® мксек для критических или околокрнтнческнх си-
стем. Однако влияние запаздывающих нейтронов становится ме-
нее важным, если реактор становится более подкритическнм.
Пачилио [28] установил, что число счетных интервалов N влияет
иа точность измерений, хотя онн не входят в уравнения (3.33) илн
(3.37) в явном виде. Он также вывел отношение для относительного
стандартного отклонения, где последующие события рассматрива-
ются как некоррелированные:
где Y определяется уравнением (3.34). Он провел параметрическое
изучение уравнений (3.37) н (3.42) и заключил, что:
1) большое число коротких временных интервалов в опытах пред-
почтительнее малого числа длительных интервалов;
2) зависимость У от а возникает для аТ <Z 1, но затем исчезает
при возрастании Т;
3) измерение отношения дисперсии к среднему по Фейнману
требует: а) очень низкой мощности; б) высокой эффективности детек-
тора (10_3— 10~4для урановых систем); с) большого числа корот-
ких измерений.
Если ограничить Т диапазоном
1/а<7«1/а2, (3.43)
уравнение (3.33) можно привести к виду:
1 1 -j-У (для подкритических систем), (3.44)
С Рр
g8~«1 -}- e£?v —— = 1 4-Уцрит (для критических систем). (3.45)
с р2
Условия (3.43) могут не удовлетворяться в графитовых и тяжеловод-
ных системах. Но даже в этом случае выражения (3.43), (3.44) нс-
44
пользовались Фейнманом и др. (2] и Курусина [291 для измерения
DVf Мак-Каллохом [30] для измерения р в плутониевой системе
и Линдеманом, и Руби [31] для измерения подкритичности. Подкри-
тические измерения основываются на отношении
Укри, = [^(1-Р)в]/Ря = Р>(«—РГ
У еО,/Р? ₽!

(3-46)
Этот метод не требует постоянства времени генерации для измене-
ний реактивности, но требует, чтобы эффективность детектора оста-
валась постоянной. Представленные результаты хорошо согласу-
ются с экспериментами с импульсным нейтронным источником
вплоть до подкритичности, равной 3,5 долл [32]. Эффективность е
может быть рассчитана по уравнению (3.28), если реактивность оп-
ределяется из измерений а и ас, а р из расчета. Абсолютная ско-
рость деления в системе определяется так:
F = Л/е, (3.47)
где А — средняя скорость счета в эксперименте.
§ 3.5. Метод дисперсии Беннета
При достижении критичности на запаздывающих нейтронах
приведенная дисперсия, рассчитываемая по уравнению (3.37), рас-
ходится («_, стремится к 0, поскольку а7 = — р/11,6). Чтобы из-
бежать этой трудности, Беннет [21] предложил альтернативный ме-
тод, который не дает расхождения при достижении критичности на
запаздывающих нейтронах, а именно: измерение второго момента
разности отсчетов для последовательных интервалов времени (диф-
ференциальный метод). С точки зрения нейтронной статистики,
реактор в таком случае ведет себя как подкритическая система.
Беннет вывел соотношение
<(Cfe+i—Cft)a> _11_V н (cufl_________3/2 +1 /2 ехР (~ 2gir) —2 exp (—а,7)\
2<cft> Л af7 J*
(3-48)
где сй — число отсчетов в Л-м временном интервале продолжитель-
ностью Tt другие символы имеют свой прежний смысл. Серия усред-
нений выполняется по N временным интервалам. Если выполняется
условие a2T <£ 1, уравнение (3.48) приближенно может быть пред-
ставлено выражением:
<(Он-1~__
2<с*>
__। / 1 ___, 3/2~Ь 1/2 ехр ( 2аТ) 2ехр (- аТ) \___j Ц7 49)
45
где
8^v /j 3/2 Ч-1 /2 exp (—2aT) —2 exp (—aT)
7Г ‘
(3.50)
По аналогии co значением величины У в эксперименте Фейн-
мана по определению отношения дисперсии к среднему W представ-
ляет увеличение флуктуаций вследствие зависимости (коррелирован-
ности) появления нейтронных цепочек по отношению к флуктуа-
циям, которые имелись бы, если бы они были полностью случай-
ными. Однако меньшее значение по сравнению с У показывает, что
коррелируемость между разностями в числе отсчетов для после-
дующих интервалов меньше, чем коррелируемость между числом
отсчетов. При малых Т как так и У стремятся к нулю, при увели-
чении Т W и У стремятся асимптотически к величине e.Dv/р*, но не
одинаковым образом.
В этих экспериментах могут быть использованы те же пропуска-
ющие схемы, что и для экспериментов по методу Фейнмана, но про-
цедура анализа данных должна быть другой. Мертвое время между
циклами, особенно для очень коротких интервалов, так же сущест-
венно, как и для метода Фейнмана. Вероятностный анализатор Сте-
гемана, применяемый для экспериментов Фейнмана, не может быть
использован в этом методе. Следовательно, необходимо иметь дело
с большим количеством данных и экспериментальная погрешность
будет большей, чем в дисперсионных измерениях.
§ 3.6. Методы определения вероятности
Существует несколько методов измерения параметров реактор-
ных систем, которые основаны на определении р-, (Д), вероятности
счета i импульсов за временной интервал Д. Когда имеются связанные
на цепочке отсчеты, pt (Д) является функцией с (среднего чис-
ла отсчетов за интервал Д) и коррелирующего члена У, описываю-
щего дополнительные (по отношению к чисто случайным) флуктуа-
ции, которые происходят при наличии связанных по цепочке собы-
тий. Для некоррелированных случайных событий pt (Д) является
только функцией с.
Экспериментальные измерения включают измерение частот
fi (Д), или частотного распределения, и сравнения его с pt (Д) —
распределением вероятности. Полученные таким образом вероят-
ности затем используются для определения отношения дисперсии
к среднему, из которого могут быть определены параметры системы
с помощью метода Фейнмана, т. е. с помощью уравнения (3.33).
И, наоборот, вероятность pi (Д) может быть выражена через пара-
метры ядернон системы.
Метод нулевой вероятности (метод Могильнера). Метод .нулевой
вероятности был впервые предложен Могильнером и Золотухиным
13] в 1961 г. Для серии испытаний, в которых Д варьируется в шнро-
46
ком диапазоне, измеряется средняя доля пустых каналов (т. е. ка-
налов с нулевыми отсчетами за интервал Д) при использовании М
каналов анализатора. Могильнер и Золотухин применили вероят-
ностные производящие функции для расчета распределения вероят-
ности дискретной случайной переменной, определяемого уравне-
нием (2.47), в связи с легкостью расчетов вероятностей и моментов.
Однако их первоначальное решение было основано на предполагае-
мом отрицательном биномиальном распределении отсчетов нейт-
ронов
F(A,z)= 2’е'гр;(Д) = [1+(1-ег)УГ7/1', (3.51)
1 = 0
где z — вспомогательная переменная; с — среднее число отсчетов
за интервал времени Д и У — корреляционный параметр, определя-
емый уравнением (3.34). Если число отсчетов I = 0, вспомогатель-
ная переменная стремится к — сю , и нулевая вероятность опре-
деляется как
1пр0(Д) = Г(Д, -_оо)=-у1п(Н-У), (3.52)
или
р0(Д)==(14-Ю~'/1'- .(3.53)
Из экспериментальных значений р0(Д) можно получить Y и, следо-
вательно, а.
Пал [81 дал теоретическое обоснование для нулевой вероятности,
используя более точную теорию, и вывел выражение:
1пр0(Д) = -----2—in +
' Т+1 1 (т-1)ад L J/’3
где
а все другие величины определены выше в этой главе.
Пал [33] отметил, что первые два члена разложения уравне-
ния (3.54) в степенной ряд по ePv/p₽ дают то же выражение для
1пр0 (Д), что и уравнение (3.52). Такое разложение в степенной ряд
возможно только для eDv/pp < 1, что означает, что дисперсия от-
счетов едва ли отличается от распределения Пуассона. Однако а
намного легче определяется для случая, когда 1, т. е.
когда дисперсия отсчетов совершенно отлична от распределения Пу-
ассона. Пал рекомендует пользоваться более точным уравнением
(3.54), поскольку его работа показала, что приближения, использо-
ванные Могильнером, справедливы для Д < 3 мксек.
Баба лэ [51 вывел уравнение (3.54), применив трехинтервал ьную
производящую функцию вероятности, и разделяет рекомендации
Пала*. Однако Пачилио считает, что экспериментальное согласие
между результатами, полученными с помощью уравнений (3.53)
и (3.54), распространяется на диапазон, более широкий, чем ожи-
дается .
Для эксперимента такого типа используется вероятностный ана-
лизатор, описанный в § 3.4, который в качестве выходного сигнала
дает дискретные вероятности pi (Д). Необходимыми для этих экспе-
риментов являются только значения р0 (Д) и с, причем
Ро (А) = Ж (3.56)
где А/о — число отсчетов в первом канале (нулевые отсчеты в течение
времени Д) и М — полное число отсчетов по всем каналам. Среднее
число отсчетов с может быть получено мониторным счетчиком. При-
менение метода наименьших квадратов при определении р0 (Д) в за-
висимости от Д дает значения а. и Пачилио [34] использовал
этот метод для измерения абсолютного уровня мощности, а Линде-
ман и Руби [31] для измерения подкритической реактивности.
Метод нулевой вероятности обычно применяется на тепловых
реакторах при очень низком уровне мощности, так как должно быть
значительное число интервалов с отсутствием отсчетов, чтобы этот
метод был пригоден.
Метод модели Пойя. Метод модели Пойя представляет собой раз-
витие метода Могил ьиер а, в котором все величины pi (Д), аппрок-
симированные вероятностным распределением Пойя [35], сравни-
ваются с частотным распределением отсчетов, т. е. рядом групп Д-
каналов с i отсчетами.
Распределение Пойя является действительным отрицательным
биномиальным распределением. Выражение для pt (Д) получает-
ся с помощью последующего дифференцирования вероятностной
производящей функции.
Результат дает рекуррентное соотношение:
₽г(Д)==щттрг₽‘-1(Д)’ (3-57)
где последний член ряда
р0(Д) = (1-|-У)-“с/г (3.58)
является нулевой вероятностью в методе Могильиера.
Для определения частотного распределения отсчетов для различ-
ных значений временного интервала Д в эксперименте используется
вероятностный анализатор. Проблема мертвого времени для корот-
ких временных интервалов остается столь же существенной, как и
* Еще раньше формула (3.54) была получена в работе [42]. — Прим. ред.
48
для метода Фейнмана. Для получения оптимальных значений вели-
чине и У применяется метод наименьших квадратов. Приближение,,
предложенное Могильнером и Золотухиным [3], включает миними-
зацию величины
Х3= у , (3 59)
Ср.
£=0
где Ci — действительное число отсчетов, накопленное в t-м канале,
и cPi — ожидаемое число отсчетов, получаемое из теоретических
отношений распределения вероятностн по уравнениям (3.57) и
(3.58). Пачилио 134] предложил другой метод, в котором минимизи-
руется величина
й- 3 ^(ft-W. (3.60)
- i=0
где Wi —- весовая функция, обычно полагаемая равной единице,
a bi н определяются так:
Pf-Pj-I = с-(»+П (3.6!)
Pf-i i(l+V)
В. = . (3.62)
н £(1 + У)
Если величина с определяется монитором, то можно показать, что
отношение дисперсии к среднему будет описываться выражением
где М — число значений i, используемых в суммах. Этот метод об-
работки данных дает хорошее согласие с методом дисперсии Фейн-
мана.
§ 3.7. Метод распределения интервалов
(метод Бабала)
Работа Бабала [5], использующая распределение длин интерва-
лов между отсчетами, по-виднмому, имеет ряд преимуществ по срав-
нению с другими методами счета. В случае последовательности некор-
релированных отсчетов, распределение интервалов определяется
вероятностью отсутствия счета во временном интервале умножен-
49
ной на вероятность счета в бесконечно малом временном интервале
dt, откуда непосредственно следует
р (0 dt = р0 (/) рс (di) = exp ( — FeZ) Fedt. (3.64)
Поскольку в этом случае отсчеты не зависят один от другого, урав-
нение (3.64) представляет распределение вероятности интервалов
времени между отсчетами. Более строго оно должно быть записано
следующим образом:
р (fl dt = Рс (dnp^ Р . (3-65)
где dt' — бесконечно малый временной интервал, непосредственно
предшествующий интервалу t. Знаменатель в уравнении (3.65) дол-
жен удовлетворять условию нормализации:
$Р(/)Л=1.
о
Уравнение (3.64) дает вероятность того, что после начального мо-
мента t = 0, выбранного произвольно, первый отсчет произойдет
в интервале dt спустя время t. Уравнение (3.65) дает вероятность
того, что после отсчета при t = 0 следующий отсчет произойдет в ин-
тервале dt спустя время t. Для коррелированной последовательности
отсчетов эти вероятности отличаются друг от друга. По терминоло-
гии Бабала, уравнения (3.64) и (3.65) называются соответственно
распределением случайно начатых (RO) интервалов и распределе-
нием счетно-счетных (СС) интервалов, а вероятности обозначаются
как
Pro (Z) и pec (Z)-
Распределение счетно-счетных интервалов. Бабала [5] вывел
выражение для распределения счетно-счетных интервалов, исполь-
зуя трехинтервальную производящую функцию, полагая первый
п третий интервалы стремящимися к нулю. В результате ои получил,
что
Pec Ю di = С1 W dt + W ехР dt, (3.66)
где
С,(/) = 4fePo(/) Г (v+l) + (T-l)exp(-aW) Г (3.67)
v I (f + 1)2—(v — 1)2ехр(— ayt) J
С2 (f)=^------8^P4(0_g--------. (3.68)
a[(V+D2-(V-1)2 exp (-av)]<2
Величина о, эквивалентная мощности источника нейтронов, равна
(7 = -^^- или о = —(3.69)
Dv aDv
Параметр у определяется равенством (3.55), а значение por{t) (вероят-
ность отсутствия счета в интервале от 0 до t) — уравнением (3.54)
50
при Д — t. Величина S является мощностью нейтронного источника
в подкрнтической системе. Два вида уравнений (3.69) записаны для
подкритической и критической систем соответствеиио.
Уравнение (3.66) имеет некоторые особенности, представляющие
интерес. Если положить & <£ рр, т. е. у —1, и увеличить мощность
источника S так, что С3 0, то в результате получится выра-
жение
рсс = Fz ехр (— Fe/) dt, (3.70)
которое идентично уравнению (3.64) для пуассоновского распре-
деления отсчетов, т. е. некоррелнруемого процесса.
Вероятность рсс (0 зависит как от уровня мощности (мощности
источника), так н от эффективности детектора, но ее использование
имеет преимущества перед другими статистическими методами.
При высоких уровнях мощности, когда метод росси-альфа неприме-
ним для измерения параметров, С2—>- 0, получаем выражение
Рсс {t)dt = Сг (Z) dt, (3.71)
которое может быть использовано для измерений параметров.
Если эффективность детектора очень низка (т. е. в <С Р₽ и у —> 1)
все методы счета слабых интенсивностей непригодны. Однако, если
2eDv/P₽ <С уравнение (3.65) записывается в виде
Рсс (0 == ехр (—Fel) LFe + (е£\>/2Лр) ехр (—а/)] =
= ехр (—At) [А 4- В ехр (—а/)], (3.72)
которое, исключая член ехр (—FeZ) сопоставимо с выражением рос-
си-альфа. Для быстрых реакторов, когда эффективность детекторов
низка, низка скорость счета и временные интервалы коротки, эк-
споненциальный член ехр (—Fet) примерно равен единице н урав-
нение (3.72) переходит в уравнение
Рсс (Z) dt == (А + В ехр (—at))dt, (3.73)
идентичное уравнению (3.20) для эксперимента росси-альфа. Эго
объясняет успешное применение метода росси-альфа Брансоном
и др. 1161, когда они фактически измеряли счетно-счетные времена.
Экспериментальная методика была описана в § 3.3. Первый им-
пульс запускает анализатор, каналы которого подключаются пре-
цизионным таймером (отметчиком времени). Второй отсчет останав-
ливает анализатор, отсчет помещается в ячейку памяти соответст-
вующего канала, иа котором анализатор был остановлен, и систе-
ма восстанавливается для следующего отсчета. Такое устройство
регистрирует только половину данных, т. е. интервал времени меж-
ду двумя разными импульсами. Если анализатор автоматически за-
пускается схемой остановки и восстановления, то могут быть за-
регистрированы все данные. Однако этот прием укорачивает интер-
вал времени на величину, равную мертвому времени (на время, не-
обходимое для остановки анализатора, запоминания отсчета, вос-
51
становления и пуска анализатора). В современных анализаторах это
мертвое время может быть очень коротким, однако, как обычно,
необходимо сделать соответствующую поправку.
Метод распределения случайно начатых интервалов. Метод рас-
пределения случайно начатых интервалов близок методу распре-
деления счетно-счетных интервалов. Главное отлнчие его состоит
в том, что начало интервала выбирается случайно процессом, ко-
торый не коррелирует с изучаемым ядерным явлением. Бабала 151
получил выражение для вероятности распределения случайно нача-
тых интервалов:
Pro W А = 2FePa W [ (т-+1)+-(т—1)ехр( ~ку<) 1 dt, (3.74)
Vro^ (TH-1)=—(т —1)«ехр(—«тО J 1
где у и ро (/) определяются уравнениями (3.69) и (3.54) соответст-
венно. Как и в случае распределения счетно-счетных интервалов,
процесс становится пуассоновским и
Pro (/) d/ = Fe exp (—Ге/) d/, (3.75)
когда у 1 из-за уменьшения эффективности е или значительной
лодкритичности системы.
Пачилио [321 отметил, что J р«о(/) dt представляет вероятность
о
того, что после времени t — 0, выбранного случайно, первый им-
пульс придет в интервале от 0 до /. Поскольку рс (/) есть вероят-
ность того, что то же самое событие произойдет в интервале между /
и бесконечностью, то получается выражение
PoW+$P№W'f<=1- <3'76)
О
нз которого следует, что
Pro = — дРо (0 IBI. (3.77)
Мы также можем считать pRo(t) вероятностью того, что после
импульса, пришедшего в интервале между произвольным началом
и dt последует пустой интервал. Эта вероятность может быть выраже-
на как произведение вероятности одного отсчета между 0 и dt и веро-
ятности следующего отсчета, происходящего за пределами времени,
большего /. Отсюда
Pro (f) dt = (FedF> [1 — $ Рсс W dt ]’ (3-78)
L о -*
где интеграл дает вероятность того, что после отсчета при t = О
следующий отсчет произойдет в интервале между 0 и /. Следова-
тельно,
п (/) = - аРдо(/- = — 52 Ро (-}- . (3.79)
рсс W FЕ dt Fz V '
52
Экспериментальный подход по существу тот же, что и в методе рас-
пределения счетно-счетиого интервала, за исключением того, что
диализатор после восстановления запускается случайным импуль-
сом. Этот .метод эффективен при изучении систем с тепловыми ней-
тронами, но имеет существенные ограничения и не может применять-
ся при изучении систем иа быстрых нейтроиах. Остин и др. [361
использовали этот метод, который они назвали «выжидающий вре-
менной альфа-метод», и получили хорошее согласие с измерениями
росси-альфа и измерениями с импульсным нейтронным источником.
§ 3.8. Метод мертвого времени
(метод Сринивасам а)
Другой метод измерения а был предложен в работе Срииива-
сана 137]. Он основывается на том факте, что при введеиии искусст-
венно изменяемого мертвого времени в измерительную аппаратуру
оно оказывает влияние на корреляцию между отсчетами. Обсудим
это влияние для случая нечувствительности прибора, определенной
Срииивасаном следующим образом. Предположим, что последова-
тельность входных импульсов (реальных отсчетов) от нейтронного
детектора поступает в прибор, который дает последовательность
выходных импульсов (выходных отсчетов). Если прибор передал
реальный отсчет на выход, то появляется запрет на второй выходной
сигнал, если прошел временной интервал, меньший d (мертвого вре-
мени) между двумя последующими реальными отсчетами. Таким
образом, этот прибор регистрирует число интервалов длиннее, чем d
между реальными отсчетами.
Для некоррелированных отсчетов отношение между скоростью
счета Cd иа выходе нечувствительного прибора и реальной скоростью
С дается формулой
Cd = С exp (—Cd), (3.80)
где экспоненциальная функция является просто вероятностью того»
что интервал между двумя реальными отсчетами будет больше»
чем d. Дисперсия выходных отсчетов за время А для такой системы
при пуассоновском распределении входных импульсов по Срини-
васану определяется следующим образом:
откуда сг = с + с2 (A—d)>o. (3.81)
где (3.82)
c = CdA. (3.83) 53
Для коррелированных отсчетов, т. е. таких, которые проис-
ходят в ядерном реакторе нулевой мощности, дисперсия отсчетов
для выключающегося прибора равна
<3-84’-
где для мертвых времен короткой продолжительности
В=1— Crf Г1 Т—(3.85>
Преобразование уравнения (3.84) дает
с I \ Л ' J К
+^Pco(d)Bexp(-ad).^ll- (3.86}
где pco(d)—вероятность того, что интервал между двумя отсче-
тами будет1 больше, чем
рс0 (d) = 2р„ (d) [ (V +11 +-(V~ ° -ехр (--^>-1, (3.87).
0V ZL (т+*)=—(v—t)=exp (—ceTd) J’
причем p0 (d) вычисляется по формуле (3.54) при A = d, а .остальные
обозначении прежние.
Уравнение (3.86) является довольно сложным для практического
определения а при вариации мертвого времени d. Однако оно может
быть использовано для оценки влияния мертвого времени прибора
на дисперсию. Легко увидеть, например, что влияние мертвого вре-
мени может быть незначительным, если Cd 1, tzd 1 и А.
Подобный анализ в.случае невыключающегося прибора является
более сложным и здесь не приводится.
§ 3.9. Методы корреляционного анализа
Взаимная корреляционная функция стационарного процесса
Фх» (т)» частным случаем которой является автокорреляционная
функция (рхх (т) при х = у, определяется уравнениями (2.74) и
(2-77):
Ч-а|, = Е[х (/) y(t+т)] = (j (j х (h) у (t2) р [х (<i), У (/2)] dxdy, (3.88>
54
где р [х (4), у (4)1 — функция совместной вероятности наступления
события х в момент времени 4 и события у в момент /2 при определен-
ном
т = 4 — 4. (3.89)
Если событие х — регистрация нейтрона детектором 1 и у — де-
тектором 2 (или детектором 1 в частном случае, когда х = у), то
легко показать, что корреляционная функция будет вероятностью
пары отсчетов, происходящих в интервале Аг при tr и Д2 при 4> т. е.
происходящих с интервалом т. Эта же величина исследовалась
в § 3.3 прн обсуждении метода росси-альфа. Отсюда
4>M>(T) = P(/i. О = РС (6. U)+pR(h, i2). (3.90)
где р (4> 4) — вероятность отсчета в момент 4, за которым следует
отсчет прн 41 индексы С и R относятся к коррелированным и случай-
ным событиям. Если используется одни детектор, то уравнение (3.90)
становится подобным уравнению (3.17) при условии, если исключить
дельта-функцию Дирака при т = 0:
Ч>.™ W = f1 + ре2 2 (flip), ехр (— ат) + Fe6 (т) =
= A2 -}- АВ ехр (—ат) J- А6 (т) == А [Я -ф В ехр (—ат)] Л6 (т), (3.91)
где А и В определяются уравнениями (3.25) и (3.26). Этот подход
известен как метод автокорреляционного анализа. С теоретической
точки зрения, метод по существу является методом россн-альфа,
однако методика измерения совершенно другая. Следует отметить,
что случайные или фоновые величины зависят от квадрата скорости
делений/72 (нлн мощности), в то время как амплитуда перед экспо-
нентой зависит только от В. Следовательно, этот метод ограничивает-
ся очень низкими скоростями делений. Член с дельта-фувкцвей Ди-
рака отсутствует в экспериментах росси-альфа вследствие запазды-
вания по фронту первого канала совпадений (см. рис. 3.2).
При использовании двух детекторов одинаковой эффективности 8
накапливаемые случайные отсчеты независимы и, следовательно,
некоррелнрованны, так как детектируемые нейтроны поглощаются,
и уравнение (3.91) принимает вид:
Г) k ~~
Фад W=Р2 + „„ /т; ехр (—ат) = Л2 + АВ ехр (—ат) =
z (1 —tip) I
= А (А -ф В ехр (—ат)), (3.92)
Этот метод известен как метод взаимно-кор реляционного анализа.
Исключение члена с дельта-функцией Дирака в уравнении (3.92)
является принципиальным отличием при использовании метода вза-
имной корреляции во времени с двумя детекторами. Как будет по-
казано ниже, это соответствует исключению постоянного фона в ча-
стотной области и позволяет проводить измерения детекторами с от-
55
носительно низкой эффективностью. Поскольку предшествующий
вывод основывается на модели реактора с сосредоточенными парамет-
рами, детекторы обычно располагаются достаточно близко друг к
другу. Реактор должен быть достаточно малым, чтобы пространст-
венные эффекты были незначительны.
Типичный корреляционный эксперимент при получении импуль-
сов от детектора проводится с записью импульсов от одного или двух
детекторов и с повторением записи для каждого значения т. Обычно
число отсчетов х и у для малых временных интервалов А определяет-
ся как скорость счета в интервале А и обработка данных .ведется со-
гласно уравнению
1 N—k
(М) = S х [/ + И1 у [/ + (£ + k) А], (3.93)
где полный интервал представляет суммарное число временных ин-
тервалов А:
т = ЛА. (3.94)
Расчеты, связанные с использованием уравнения (3.92), требуют
много времени и обычно выполняются с помощью ЭВМ. Часто более
удобно использовать метод росси-альфа, чем проводить автокорре-
ляционные измерения. Иногда импульсы преобразуются в аналого-
вую переменную или применяется детектор типа ионизационной ка-
меры, чтобы получать аналоговые переменные, которые могут быть
обработаны коррелятором аналогового типа. Соотношение (3.92)
применимо только для реакторов достаточно малых размеров, ко-
торые могут быть представлены сосредоточенными параметрами.
Специфические пространственные эффекты, если они соответственно
не учитываются или не распознаются, могут исказить результаты.
§ ЗЛО. Ковариационные измерения
Ковариация, определяемая уравнением (2.70):
Сху = Е (ху) — Е (х) Е (у) (3.95)
представляет собой разность между средним значением произведе-
ния переменных и произведением их средних значений. Если эта
разность исчезающе мала, две переменные не коррелируют, в про-
тивном случае она является мерой корреляции между ними. Если
получено большое число отсчетов сг (А) н с2 (А) двух нейтронных
детекторов во временном интервале А, то ковариация может быть
рассчитана следующим образом:
Си(Д) = <(с1—(сгЖсг—<с.))> = <с1с2> — <е,> <с2). (3.96)
Коэн [38] указал, что, если применимо -приближение для мгно-
венных нейтронов
|а2А[<£1, (3.97)
56
выражение Фейнмана для отношения дисперсии к среднему можно
модифицировать и получить другие (но эквивалентные) выраже-
ния: С12(А) <с1> Г р? L . 1—ехр(—аД) 1 (3.98)
аД ]
и Ci. (А) ElCv[ , 1—ехр(—аД) 1 (3.99)
<с2> Р? L аД ] ’
Если приближение мгновенных нейтронов неприменимо, уравне-
ния (3.98) и (3.99) принимают вид:
(ЗЛ00>
= (<х,) [1 - (3.101)
где Ai, Но (аг-) н аг те же, что и в уравнении (3.36), н приводятся
в табл. 3.2. Следует отметить, что единица в уравнении (3.33), ко-
торая представляет собой случайный шум (в действительности, от-
носительную дисперсию пуассоновского распределения), может быть
исключена введением взаимной корреляции в этот процесс.
Т аблица 3.2
Постоянные передаточной функции для реактора на запаздывающих
нейтронах нулевой мощности с горючим 235 U
вблизи критичности [21]
₽ = 0.0064; Л<5-10 4 сек- 1 р 1<0,1 р
1 Cb£ сек-1 Д- сек™1 «о «Ч>
I (₽—р)/А (1-Й/А (1—Р)/2(Р—Р)
2 2,89 29 164
3 1,02 20 186
4 0,195 11,2 237
5 0,068 6,1 284
6 0,0143 1,2 343
7 —р/11,6 11,6 4,5—-J- 2р
Ковариационный метод удобнее обычного метода Фейнмана,
поскольку он частично исключает эффекты смещения измерений в те-
чение конечного времени, которые присущи описанным выше ме-
тодам (в которых предполагалось, что относительная дисперсия пуас-
соновского распределения равна единице, в то время как при изме-
рении в течение конечного времени она может несколько отличаться
от единицы).
57
§3.11. Метод эндогенного
пульсирующего источника*
При проведении эксперимента росси-альфа для измерений при-
меняется многоканальный анализатор как универсальная пересчет-
пая схема. Первый нмпульс запускает анализатор, а последующие
импульсы регистрируются в соответствующих каналах, при этом не
принимается во внимание увеличивается ли, уменьшается ли нейт-
ронная плотность или остается постоянной. Эндогенный импульсный
метод использует запускающий импульс, который возникает, когда
флуктуация нейтронной плотности достигает выше среднего и предва-
рительно выбранного уровня. Спонтанные всплески до величин,
значительно превышающих средний уровень, могут рассматриваться
как следствие изменений в скорости делений, спад к низшему уров-
ню характеризуется фундаментальной константой спада а. Преиму-
щество этого метода по сравнению с обычными росси-альфа измере-
ниями, использующими универсальную пересчетиую схему, обуслов-
лено предварительным отбором измеряемых моментов в период спа-
да нейтронной плотности. Это обеспечивает увеличение отношения
снгнал/фон, поскольку анализируются только цепочки распадв
значительной амплитуды. Этот метод имеет некоторые черты, свой-
ственные измерениям с импульсным источником нейтронов, оста-
ваясь простым, экономичным и удобным, как обычный метод росси-
альфа. Уменьшение времени, необходимого для метода эндогенного
пульсирующего источника, по сравнению с обычным измерением
*росск-альфа, таково, что он применим на тепловых реакторах. По-
добные преимущества можно ожидать и в отношении быстрых реак-
торов.
Теоретическое рассмотрение. Плотность нейтронов может быть
описана с помощью отсчетов, детектируемых в интервале А:
с(/) = соехр(—а/)4-с, (3.102)
где с -— средняя величина фона, определяемая для критического
реактора уравнением (3.32) как
c = FeA. (3.103)
Для подкритической системы
c = SeA/-v(1 — k). (3.104)
Амплитуда спонтанных всплесков с0 над средней величиной равна
c0^cS/B, (3.105)
где S/B — отношение сигнал/фон.
Пачилио [391 отметил, что этот'метод эквивалентен методу им-
пульсного источника с интенсивностью (над установившимся уров-
* Этот метод иногда называется методом собственного пульсирующего
источника.
58
нем), определяемой уравнением (3.105), и частотой импульсов, оп-
ределяемой как
к = f Pi- (3106)
где Pi — вероятность счета i импульсов в интервале времени Д,
если с есть среднее число отсчетов в интервале Д. Пачилио [39] про-
табулпровал величины с0 и 7? для различных экспериментальных
условий и рассчитал время, необходимое для набора данного числа
всплесков в подобных измерениях на системах с тепловыми реак-
торами. Результат имел значительно лучшую статистическую точ-
ность и меньшее время измерений в сравнении с обычным методом
росси-альфа. Хотя это изучение предусматривает установку де-
тектора в активную зону для обоих типов измерений, последние
работы Пачилио [22] показали, что такие измерения могут быть
выполнены с детекторами, размещаемыми в отражателе.
Экспериментальные измерения. Экспериментальная установка,
за исключением специального предварительного селектора и пуско-
вого устройства, по существу та же, что и используемая в экспери-
менте росси-альфа с одним детектором. Было использовано несколь-
ко схем:
1. Пачилио 139] использовал быстродействующий измеритель
скорости счета. Измерительная система включалась при достижении
предварительно выбранного .порогового уровня. Этот уровень
регулировался в соответствии с уровнем мощности и эффективно-
стью детектора.
2. Другой метод, нспользованиый Пачилио [39], заключался
в счете числа импульсов за определенный временной интервал Д.
Анализатор запускался, когда число импульсов достигало выбран-
ного уровня.
3. Хващевскнй и др. [40] применяли два измерителя скорости
счета: один с большой постоянной времени ts, другой с малой Tf.
Когда происходил всплеск, на него реагировал измеритель с малой
постоянной времени, в то время как другой не реагировал, тем са-
мым запуская измерительную схему. Этот метод имеет жесткое
ограничение:
ту<1/а<т5. (3.107)
4. Боргвальд [41] и Пачилио [39] использовали простой триггер
трех совпадений следующим образом. Импульс от детектора отпи-
рал схему совпадений на время, обратно пропорциональное вы-
бранной скорости счета. Если в этот интервал времени приходили
от детектора еще два импульса, проводилось измерение. Очевидно,
что возможны другие схемы.
Экспериментальные данные обычно подгоняются к уравнению
(3.102), чтобы получить величину а- как меру измеряемой реак-
тивности.
59
Хващевский и др. [40] установили соответствие этих результатов
в пределах ±2% с обычными экспериментами с импульсным нейтрон-
ным источником в диапазоне изменения реактивности —0,05 4-
-=---0,35 долл для обогащенных систем с водо-графитовым замед-
лителем. Пачилио [39] провел измерения по методу эндогенного
пульсирующего источника в диапазоне изменения реактивности от
критичности до —13 долл на обогащенной системе с органическим
замедлителем. Эти результаты находятся в хорошем согласии
с экспериментами с импульсным источником нейтронов.
СПИСОК ЛИТЕРАТУРЫ
1. Orndoff J. D. Prompt Neutron Periods of Metal Critical /Assemblies. —
«Nucl. Sci. Engng», July 1957, v. 2, p. 450.
2. Feynman R. P., de Hoffman F., Serber R. Dispersion of the Neutron Emis-
sion in U-235 Fission. — «J. Nucl. Energy», 1956, v. 3, p. 64.
3. Mogilner A. I., Zolotukhin V. G. The Statistical r-Method of Measuring the
Kinetic Parameters of a Reactor. — «Atomic Energy» (USSR), 1961, N 10,
p. 377. (См. Могильнер А. И., Золотухин В. Г. Измерение характеристик
кинетики реактора статистическим р-методом. — «Атомная энергия»,
1961, т. 10, вып- 4, с. 377-)
4. Thie J. A. Reactor Noise. — Rowman and Littlefield, Inc., N. Y., 1963.
5- Babala D. Neutron Counting Statistics in Nuclear Reactors. —Norwegian*
Report KR-114, November 1966.
6. Kolmogorov A. N., Dmitriev N. A. Theory cl Branching Processes. —
«Dokl. Akad. Nauk USSR», 1947, v. 56, p. 7 (См. Колмогоров A. H., Дмит-
риев H. А. Теория ветвящихся процессов. — «Дохл. АН СССР», М.—Л.,
Изд-во АН СССР, 1947, т. 56, № 1, с. 7.)
7. Courant Е. D., Wallace Р. R. Fluctuations of the Number of Neutrons in
Pile. — «Phys. Rev.», 1947, v. 72, p. 1038.
8. Pal L. 1. Statistical Fluctuations of Neutron Multiplication. — In: Pro-
ceedings of the Second United Nations International Conference on the Pea-
ceful Uses of Atomic Energy. Geneva, 1958, v- 16, p. 687; United Nations,
N. Y., 1959.
9. Murray R. L. Nuclear Reactor Theory. — Printice Hall, Inc., Englewood
Cliffs., N. J., 1957. (См. Меррей P. Физика ядерных реакторов. Пер. с англ.
М., Атомиздат, 1959.)
10. Glasstone S., Edlund М. С. The Elements of Nuclear Reactor Theory. —
D. Van Nostrand Co., Inc., N. Y., 1952. (См. ГлесстонС., Эдлунд M. Осно-
вы теории ядерных реакторов. Пер. с англ. М., Изд-во иностр, лит.,
1954.)
II. Diven В. С., Martin Н. С., Tascbek R. F-, Terrell J. Multiplicities of Fission
Neutrons. — «Phys. Rev.», 1956, v- 101, p. 1012.
12. Matthes W. Statistical Fluctuations and Their Correlation in Reactor Neut-
ron Distribution. — «Nukleonik», 1962, v. 4, p. 213.
13. Borgwaldt HL, Stegemann D. A Common Theory for Neutronic Noise Ana-
lysis Experiments in Nuclear Reactors. — «Nukleonik», 1965, v. 7, p. 313.
14. lijima T- Remark on Rossi-Alpha Experiment.—«Nukleonik», 1967. v. 10,
p. 93.
15. Diaz H_, Uhrig R. E. A Digital Computer Controlled Data Acquisition and
Processing System for Nuclear Experiments. —«Trans. Amer. Nucl. Soc.»,
November 1965, v- 8, p. 588.
16. Brunson G. S., Curran R. N., Gas id Io J. M., Huber R. J. A Survey of
Prompt—Neutron Lifetemes in Fast Critical Systems. — USAEC Report
ANL-6681, Argonne National Laboratory, August 1963.
17. Mihakzo J. T. Prompt — Neutron Lifetime in Critical Enriched—Uranium
Metal Cylinders and Annuli. — «Nucl. Sci., Engng», 1964, v. 20, p. 60.
60
18. Karam R. A. Measurements of Rossi-Alpha in Reflected Reactors. —
«Trans. Amer. Nucl. Soc.», June 1964, v. 7, p. 283. '
19. Suwalski W-. NORA First HaO Core Noise Measurements. Part I. Rossi-
Alpha Method. — Norwegian Report NORA-Memo-112, 1965.
20. Cohn С. E. Reflected Reactor Kinetics. —«Nucl. Sci. Engng», 1962, v. 13,
N. 1, p.12.
21. Bennett E. F. The Rice Formulation of Reactor Noise. — «Nucl. Sci. Engng»,
1960, v. 8, N. 1, p. 53.
22. Pacilio N. Comitato Nazionale per I’Energia Nucleate, personal communi-
cation, 1968.
23. Stegemann D. Die Analyse des Neutronenravschens in Reaktoren. —
German Report INR-4/66-1, 1966
24. Albrecht R. W. The Measurement of Dynamic Nuclear Reactor Parameters
Using the Variance of the Number of Neutrons Detected. — «Nucl. Sci.
Engng», 1962, v. 14, N. 2, p. 153.
25. Johnson R. L. A Statistical Determination of the Reduced Prompt Gene-
ration Time in the SPERT IV Reactor. — USAEC Report I DO-16903, Phil-
lips Petroleum Company, August 1963.
26. Turkcan Е.» Dragt J. B. Experimental Study of Different Techniques for
Analyzing Reactor Noise Measured by a Neutron Counter. — Dutch Report
RCN-1NT-75, 1967.
27. Pacilio N. Review of Statistical Methods for Reactor Parameter Measu-
rement Developed at C. S. N. Casaccia. — Italian Report RT/FI 66—37,
1966.
28. Pacilio N. Short Time Variance Method for Prompt—Neutron Lifetime-
Measurements. — «Nucl. Sci. Engng», 1965, v. 22, N. 2, p. 266.
29. Kurusyna K- Analysis of Nuclear Reactor Noise. — «Genshiryoku -Kogyo»,
1962, v. 8. p. 49.
30. McCulloch D. B. An Absolute Measurement of the Effectiwe Delayed Neut-
ron Fraction in the Fast Reactor ZEPHYR. — British Report AERE-R/M-
176, July 1958.
31. Lindeman A. J., Ruby L. Subcritical Reactivity from Neutron Statistics.—
«Nucl. Sci. Engng», 1967, v. 28, No. 2, p. 308.
32. Pacilio N. Reactor—Noise Analysis in the Time Domain. — USAEC Criti-
cal Review Series. USAEC Report TID-24512, April 1969.
33. Pal L. 1. Statistical Theory of Neutron Chain Reactors. — In: Proceedings,
of the Third United Nations International Conference on the Peaceful Uses-
of Atomic Energy. Geneva, 1964, v. 2, p. 218—224; United Nations, N. Y.,.
1965.
34. Pacilio N. The Polya Model and the Distribution of Neutrons in a Steady
State Reactor- — «Nucl. Sci. Engng.», 1966, v. 26, N. 4, p. 565-
35. Polya G., Eggenberger F. Uber die Statistik Verketterer Vorgange. —
«Z. Angew. Match. Meeh.», 1923, b. 3, s. 279.
36. Austin D. T. e. a. Comparison of the Waiting-Time Alpha with the Rossi-
Alpha. — «Trans. Amer. Nucl. Soc.», 1967, v. 10, No. 2, p. 591.
37. Srinivasan M-, Sahni D. A Modified Statistical Technigue for the Measu-
rement of a in Fast and Intermediate Reactor Assemblies. — «Nukleonik»,.
1967, v. 9, N. 3, p. 155—157.
38. Cohn С. E. Argonne National Laboratory, personal communication, 1968.
39. Pacilio N. Neutron Statistics Techniques Applied to the ROSPO Reactor. —
In: Proceedings of the Karlsruhe EAES Symposium III, European Atomic-
Energy Society, 1966, p. 9.
40. Chwaszchewski S. e. a- Improved Methods for Prompt—Neutron Period’
Measurements. —«Nucl. Sci. Engng», 1966» v. 25» N. 2, p. 201-
41. Borgwaldt H. Karlsruhe Nuclear Research Center, personal communication.
1966.
42. Золотухин В. Г., Могильнер А. И. К распределению числа отсчетов ней-
тронного детектора, помещенного в реактор. —«Атомная энергия», 1963,.
т. 15, вып. 1, с. 11—16.
ГЛАВА 4
ОСНОВНЫЕ
СООТНОШЕНИЯ
ТЕОРИИ
СЛУЧАЙНЫХ шумов
§ 4.1. Введение
Вероятность того, что именно атом 23БП в системе поглотит ней-
трон и произойдет деление, зависит от его положения, окружающих
материалов и их сечений взаимодействия, энергии нейтрона, отно-
сительного движения нейтрона и атома 235U. Эти факторы обуслов-
ливают статистические изменения во времени между делениями
в системе. Поскольку вероятность деления определяется характе-
ристиками ядерной системы, некоторые из них могут быть найдены
с помощью анализа их статистических изменений. Как показано
в гл. 3, наличие коррелированных событий, обусловленных цепоч-
ками делений, увеличивает величину флуктуаций по сравнению с
флуктуациями, которые могут происходить в других случаях.
§ 4.2. Автокорреляционная функция
Автокорреляционная функция является расширением понятия
среднеквадратнческого значения и включает в себя временную за-
висимость. Тогда как среднеквадратическое значение представляет
собой средний квадрат величины функции в данное время, автокор-
реляционная функция фдае (т) есть среднее произведение двух зна-
чений переменной, разделенных временным интервалом т. В момент
tk автокорреляционная функция процесса х (/), показанного на
рис. 1.1, будет иметь следующий вид:
N
2 xi Wk) XI (Oi-Ьт)
<Pxx(th, T)=.lim-^--------------(4.1)
Л’-со /V
Если процесс стационарен во времени, определяемая функция ста-
новится не зависимой от времени:
2 мп (<+т)
Ф« W = ------------
Л'-со /V
(4-2)
62
Основной прием при вычислении корреляции состоит в смеще-
нии во времени одной переменной по отношению к другой, умно-
жении смещенной переменной на первоначальную н усреднении по
бесконечному интервалу времени или числу сигналов. Для эргодиче-
ского процесса усреднение по числу сигналов можно заменить усред-
нением по времени и автокорреляционная функция примет вид:
т
4>.xm СО = lim -Ь С X; (/) Xi а +т) dt = Е [хг (/) xt (t + т)], (4.3)
1 1 т->^2Т J
—т
где Xt (/) — любая кривая, представляющая запись отдельного сиг-
нала. Если х, (t) — непериодическая величина, то пределы для Т
необходимо устремлять к бесконечности. Для частных случаев, ко-
гда временной сдвиг равен нулю, автокорреляционная функция ста-
новится равной величине:
т
4>xW(0) = lim-b С [х;(/)]гЛ = £[х?(/)]=1Й (4.4)
1 1 Т'ЧХ> J 1
—Т
которая, по определению, является среднеквадрэтическим значени-
ем х (/).
Если функция х (/) стационарна во времени, то ее можно рассмат-
ривать как сумму флуктуирующей составляющей х' (/) и-постоянной
составляющей, имеющей среднее значение ря, т. е.
• X р) = рж + х’ (/). (4.5)
Подстановка уравнения (4.5) в уравнение (4.4) дает
Ф®.®(0) = £ [р=] + £ [2рЛУ (01 + £ lx' (0sJ, (4.6}
где последнее слагаемое является дисперсией: о® (квадратом стан-
дартного отклонения), первое — квадратом среднего: pj. Второе
слагаемое равно нулю:
£ [2рях' (01 = 2рх£ [х' (0] = 2ржрЛ' — 0, (4.7}
поскольку рЛ* равно нулю по определению У. Следовательно, урав-
нение (4.6) переходит в уравнение
(0) = -F Р£. (4.8)
Автокорреляционная функция фз^. (т) также содержит некоторую
информацию, касающуюся частотного распределения случайного
сигнала х (0- Если ФЛ.ж(т) быстро меняется с изменением т, то преоб-
ладают высокие частоты, если ф^ (т) с изменением т меняется очень,
медленно, преобладают очень низкие частоты.
Можно легко показать, что автокорреляционная функция
(т) является четной функцией и; следовательно, она симметрнч-
63
на относительно вертикальной оси. Эта симметрия может быть вы-
ражена при помощи равенства
ф.-с.т (т) = (—т). (4.9)
Кроме того, Фяа:(т) никогда не превосходит фжж (0), т. е. срхж (т)г^
=Сфа.-я(0) Для всех т. Это вытекает из неравенства
[X (/) ± х (t + т)]а > 0. (4.10)
Разложение в ряд этого выражения, перестановка членов, интегри-
рование от — Т до -+- Ту деление на 27 и переход к пределу при 7,
•стремящемся к бесконечности, дает
I ф.™ (т) | < < = 4W (0) (4.11)
для случая, если применимы определения, представленные урав-
нениями (4.3) и (4.4), для стационарной во времени переменной.
Перегруппировка этого выражения дает отношение
I 'Рта (т) | /'Р.т.т (0) < 1, (4.12)
которое часто называется нормированной автокорреляционной функ-
цией при учете знака и всегда имеет значение по модулю меньше
единицы, кроме случая, когда т — 0.
Если х (/) содержит периодическую компоненту, фхя (т) также
•будет содержать периодическую компоненту с тем же самым перио-
дом, но фхх (т) не дает информации о фазе периодической компо-
ненты. Однако, если х (/) содержит только случайные компоненты
и р.ж равно нулю, фжж(т) стремится к нулю при т, стремящемся к бес-
конечности. Значение х (t + т) становится некоррелированным
со значением х (/) при т, стремящемся к бесконечности.
Если две некоррелируемые случайные переменные хх и ха имеют
нулевые средние значения и автокорреляционные функции фи (т)
и ф22 (т), то автокорреляционная функция от х1 + х2 выражается
как фп (т) 4- ф22 (т). Это может быть показано с помощью подста-
новки в уравнение (4.3) значения х = хх + х2.
§ 4.3. Автоковариационная функция
Во многих практических приложениях среднее значение вели-
чины равняется нулю и предшествующие соотношения упроща-
ются. Действительно, часто необходимо (и это является стандарт-
ным приемом) исключить среднее значение величины из эксперимен-
тальных данных, прежде чем проводить их дальнейшую обработку.
Таким образом, автокорреляционную функцию переменной, сред-
нее значение которой равно нулю, удобно определить как автоко-
вариационную функцию в обозначить ее символом Схх (т). Связь
между автокорреляционной и автоковариационной функциями мо-
лкет быть установлена с помощью подстановки уравнения (4.5)
64
в (4.3) и использования уравнения (4.8). Исходя из определения сред-
него значения величины, среднеквадратнческого значения, дис-
персии и стандартного отклонения, можно получить:
<Рх« fr) = фх' X- И + Р, Их- + Их Их' + Их =
= фх- х' (т) + Рх = Схх (т) + р.;, (4.13)
так как по определению, равна нулю.
Автоковариациоиная функция Схх (т) идентична автокорреля-
ционной функции, если среднее значение величины равно нулю или
если среднее значение исключается. Эффект присутствия среднего
значения рх в переменной х (Z) приводит к смещению автокорреля-
ционной функции на величину р®. (Этот факт будет обсужден ннже,
когда будет рассматриваться влияние присутствия постоянной
составляющей.)
Во многих практических ситуациях среднее значение переменной
равно нулю и уравнение (4.13) переходит в уравнение
фхх ('С) = фх-х- (т) — Схх (т). (4.14)
В большинстве случаев при анализе экспериментальных данных
среднее значение х исключается из выбранной записи сигнала,
прежде чем эти данные будут обрабатываться. Следовательно, не
существует различия между автоковариационной и автокорреляци-
онной функциями приведенной переменной при условии, что среднее
значение реализации изучаемого сигнала равно среднему значению
величины х (/). В дальнейшем понятие автокорреляционной функ-
ции будет использоваться тогда, когда ие будет необходимости тре-
бовать, чтобы среднее значение величины было равно нулю. Необ-
ходимость такого требования будем специально отмечать или будем
использовать автоковариациоиную функцию Схх (т). Иными сло-
вами, в дальнейшем будем применять терминологию, свойственную
области случайных шумов, хотя разница между корреляционной
и ковариационной функциями сохраняется.
§ 4.4. Спектральная плотность мощности
При определении автокорреляционной функции в одном случае
приходится иметь дело с поведением функции во времени и, следо-
вательно, работать во временной области. Другой подход связан
с работой в частотной области с разложением сигнала по его частот-
ным составляющим. Для непериодической функции для того, чтобы
перевести ее в частотную область, обычно необходимо применять
фурье-преобразование функции, так как при этом обеспечивается
непрерывная совокупность представляемых частот. Однако в случае
стационарного случайного или стохастического процесса х (/) не мо-
жет быть произвольно малой для больших /, поскольку статистиче-
ские характеристики должны оставаться постоянными во времени.
3 Зак. 576 65
co
Следовательно, J |x (t) | dt не сходится и фурье-преобразование
неприменимо.
Эту трудность можно преодолеть, введя новую функцию, назы-
ваемую спектральной плотностью мощности, обозначаемую симво-
лом Ф (со), как фурье-преобразование автокорреляционной функ-
ции, т. е.
фях(»)=^[ф!«е(т)] = $ ФЛЖ(т)е-1®Мт.
(4.15)
Поскольку фжж (г) стремится к нулю прит —> ± со, то J ] фжж (т) | di
существует н определение (4.15) справедливо.
Сущность спектральной плотности мощности может быть пока-
зана путем подстановки в уравнение (4.15) определения фа.ж (т):
Ф«х(°>)= f=
со I т -1
f f fWfU+i'jdt e-i»TdTj
J I T-*-00 J I
—co L — T J
(4.16)
где / (/) определяется как случайная функция, стационарная во
времени, равная х(£) в интервале— Т t Т и нулю для | / | >
> Т, как показано на рис. 4.1 (он б), т. е.
/(0 = х(/),
(—Т < t < Т);
/W=o, (id>n-
(4-17)
Поскольку J | f (/) | dt существует, то существует его фурье-
преобразование F (ю). Порядок интегрирования и предельный пере-
ход могут быть переставлены местами, так как в этих двух опера-
циях участвуют различные переменные. Следовательно,
оо т
©»:(“)= limf f /(/)/(Z+T)e-J“TdfdT. (4.18)
Т->са £1 J J ,
—co —T
Подставив
r' = t + T
(4.19)
66
в уравнение (4.18) и разбив его на два интеграла, получим
Г се
Ф«х (и) = Пт -±- Г f (/) ej dt Г f (т') <*' dx' =
Т-*-со ЯТ J J
— Т —со
= Hm -L[F(W)’F(q)]= lim (4.20)
Т -*• DO 7'—>03
где звездочкой помечено сопряженное значение. Равенство (4.20)
дает другое определение функции спектральной плотности мощности.
Рис. 4.1. Случайная переменная х(1) (а) и усеченная слу-
чайная переменная f(Z) (б).
Величины Фхж (со) и <рЛЛ (т) фактически содержат одну и ту же
информацию относительно статистических свойств х (/). Кроме
того, преобразование уравнения (4.15) является обратимым*, так
как Фхж (со) -> 0 при со -> ± со , н автокорреляционная функция
и спектральная плотность мощности представляют парное фурье-
преобразование, т. е.
ФЖх(“)= $
<Рхх (t) = (“) е,ют du>.
(4-21)
(4.22)
* Как будет рассмотрено ниже, исключение составляет физически не-
реализуемый случай белого шума.
3* 67
Эти уравнения известны как соотношения Винера — Хинчина,
названные так в честь двух математиков, которые первыми указали
на эквивалентность автокорреляционной функции и спектральной
плотности. Поскольку <рхж (т) и Фжж (со) симметричны, отношения
Винера — Хинчина можно выразить, используя косинусоидальное
преобразование. В этом случае уравнения (4.21) и (4.22) примут
вид:
Флгв (tt) = 5 C0S
1 с
(т) =------- \ ф (to) COS tOTtfoj.
2л J
(4.23)
(4.24)
Удачной аналогией, которая действительно приводит к понятию
спектральной плотности мощности применительно к Фжз: (to), яв-
ляется представление х (?) в качестве напряжения, прилагаемого
к сопротивлению в 1 ом. Тогда ф® является средней рассеиваемой
мощностью, а Фжж (со) — средней мощностью на единичную часто-
ту, вычисленную для данной частоты. Такое представление может
быть продемонстрировано при рассмотрении равенства (4.22) для
частного случая, когда т = 0, т. е.
4>xx(0)=^ = V- \
2Л «•’
— со
(4-25)
Для линейной частоты / уравнение (4.25) переходит в
<Р.та(О) = Ф?= «WX
(4.26)
Это значит, что среднеквадратическое значение х (/), которое, как
было показано равенством (4.8), эквивалентно <ржж (0), определяется
площадью под кривой спектральной плотности мощности Фжж (/).
§ 4.5. Специальные автокорреляционные функции
и спектральные пло-рности мощности
Имеется ряд автокорреляционных функций и спектральных
плотностей мощности, которые неоднократно встречаются в практи-
ческих ситуациях, поэтому знать эти специальные случаи важно
для понимания проводимых измерений. Кроме того, автокорреля-
ционные функции и спектральные плотности мощности могут быть
представлены как линейные функции, и применен принцип супер-
68
позиции, если переменные независимы и имеют нулевые средние
значения:
Фхх (Т) = Ф11 СО + <р23 (т) + ... + <Pj ; (т) +
+ +<PWW W = 3 <Рп W. (4-27)
/=1
где ж (Z) = Xi (Z) + xs (£) 4-... 4-(/) 4-... 4-Хд,(£) = x^t) (4.28)
1=1
и все переменные Xt (/) независимы. Преобразование Фурье урав-
нения (4.27) дает эквивалентное выражение в частотной области:
Ф«Л«)==Фн(со)+Ф23И4-...4-Ф^(со)= f Фн (со). (4.29)

——
О
Рис. 4.2. Графики функций (рхя (т) и Фяя (to) для постоянной
Следовательно, появляется возможность определять переменную
как сумму нескольких простых переменных, находя индивидуаль-
ные компоненты автокорреляционной функции или спектральной
плотности мощности или вместе и то и другое.
Постоянная. Постоянная может рассматриваться как переменная,
которая не имеет частотной составляющей кроме <о = 0 и всюду кор-
релирует сама с собой. Если константа имеет значение (амплитуду)
а, то
Ч’х.т (т) = Е [°-а] == «2.
(ю) = § о2 е— j •" dr = 2та2 6 (со).
(4.30)
(4.31)
Ha рис. 4.2. изображены функции <рях. (т) и Фж, (со) для постоян-
ной.
Синусоида. Для синусоиды
х (/) = A sin <л01 (4.32)
автокорреляционная функция имеет вид
Фхх <т) = ~ cos ц, т. (4.33)
69
Поскольку рассматривается процесс стационарный во времени,
положение начала произвольно. Следовательно, наличие фазового
угла в уравнении (4.32), даже равного 90° (что может изменить си-
нус на косинус), не повлияет на результаты, представляемые урав-
нением (4.33). Важность этого процесса состоит в том, что амплитуда
автокорреляции не стремится к нулю с возрастанием т, как в случае
непериодических изменений. Следовательно, используя большие
значения т, можно установить наличие периодических составляю-
щих в шуме.
Рис. 4.3. Графики функций фях (т) и Фжж (to) для синусоиды.
Спектральная плотность мощности для синусоиды должна вы-
ражаться, как это интуитивно чувствуется, дельта-функциями Ди-
рака, существующими при ±<оо. Это легко показать:
/з 'р
Фд.Л. (со) = — i cos <оо т cos сот dr —
ТТ Д2
= ~ Iй (“ + ч) + 6 (“—Ч) I
(4.34)
Автокорреляционная функция и спектральная плотность мощности
синусоиды приведены на рис. 4.3.
Белый шум. Белый шум определяется как случайная перемен-
ная, имеющая постоянную функцию спектральной плотности мощ-
ности для частот от минус бесконечности до плюс бесконечности.
Такая функция должна содержать все частоты в равных количест-
вах, но, поскольку это подразумевает бесконечную мощность, та-
кой функции ие существует. Термин белый шум появился по анало-
гии с термином белый свет, который имеет постоянную спектраль-
ную плотность мощности в широком диапазоне частот. Рассмотрим
случай, когда спектральная плотность мощности имеет постоянную
амплитуду а, т. е.
Фхж(о) — а.
(4.35)
70
Автокорреляционная функция при этом имеет вид
ФЛя;(т)=-^— J СОЗСОТСЙО = П<5 (т),
(4.36)
что означает, что функция л (/) полностью некоррелирована, кроме
точки т = 0, т. е. функция полностью случайна. Графики функций
Фа-.г- СО и Фхк (w) приведены на рис. 4.4.
Рис. 4.4. Графики функций <рхх (т) и Фях (со) для бе-
лого шума.
а. Низкочастотный белый шум. Во многих практических слу-
чаях понятие «белый шум» используется, чтобы показать, что пере-
менная имеет постоянную спектральную плотность мощности во всем
диапазоне интересующих частот. Если Фжж (со) постоянна в интер-
вале частот от нуля до точки излома частотной характеристики при-
меняемой системы, то предположение о белом шуме является обыч-
ным приемом, упрощающим математическую обработку. В конкрет-
ном случае, когда Фжа; (со) постоянна вплоть до соо, т. е.
Фх» = 0,
(|и|>и„),
(4.37)
корреляционная функция имеет вид
<РетМ=Д- f Фет И е1
J
Йо
axdti) = —— ( coscordco —
Src J
— <д0
3TT 3T COo %
(4.38)
Графики (т) и Фаж (со) для низкочастотного белого шума пред-
ставлены на рис. 4.5.
б. Белый шум в заданной полосе пропускания. Обычно сущест-
вует как верхний, так и нижний предел области частот, имеющихся
в сигнале. Нижний предел может обусловливаться связью системы
по переменному току, тогда как верхний предел существует во всех
физически реализуемых системах. Кроме того, белый шум в преде-
лах полосы пропускания может быть получен при прохождении
широкополосного случайного шума через узкополосный фильтр.
71
Белый шум в пределах полосы пропускания с идеальными харак-
теристиками имеет спектральную плотность:
= [(“е--v) <1“1< (“е+-Т-)] • <4-39)
Фжх(<о) = О (за пределами полосы пропускания),
где А со — ширина полосы п <ос — центральная частота полосы про-
пускания. При этом, конечно, предполагается, что Асо/2< сдс. Тогда
ь)с4-Дс<>/2
<Р.,,М = ^- J ocos^^cosvf^^lp]. (4.40)
Сйс—Дсо/2
Рис. 4.5. Графики функции <ржх (т) и Фжж (со) Для низкочастотно-
го белого шума.
Анализ этого выражения показывает, что оно представляет высоко-
частотную косинусоиду cos ел с т, амплитуда которой модулируется
Рис. 4.6. Графики функций <ржя (т) и Фх® (со) для белого шума в поло-
се пропускания Лео.
от значения (оАсо/л) при т = 0 в соответствии с изменением члена
в квадратных скобках. Графики функций <pKA. (?) и Ф^. (со) пред-
ставлены и а рис. 4.6.
Случайный шум с экспоненциальной автокорреляционной функ-
цией. Большинство переменных имеют автокорреляционные функ-
ции, уменьшающиеся с возрастанием корреляционного интервала т.
Часто такие автокорреляционные функции могут быть аппрокси-
72
мированы с разумной степенью точности, экспоненциальной функ-
цией вида
<р(т) = с2 ехр (—₽|г|),
(4.41)
представленной на рис. 4.7. Использование в качестве амплитуды
о2 согласуется с уравнением (4.8), когда рх = 0. Стационарные во
времени процессы, автокорреляционные функции которых экспо-
ненциальны, называются марковскими случайными процессами.
Рис. 4.7 Графики фхж (т) и Фхх (со) для случайного шума, имею-
щего экспоненциальную автокорреляционную функцию.
Спектральная плотность мощности такой переменной определяет-
ся следующим образом:
°'2 с—fi 1 т । е—1шт dr =

--2ой е—₽Tcos<ordT =
—о
(4.42)
Графики фЛХ (т) и Фхх (со) приведены на рнс. 4.7.
Случайный шум с экспоненциально-косинусоидальной авто-
корреляционной функцией. Имеется большое число процессов, ко-
торые при возбуждении входным сигналом, носящим характер бе-
лого шума, воспроизводят случайный шум с экспоненциально-коси-
нусоидальной автокорреляционной функцией. Примеры этому, при-
водимые Бендатом [ 1J, включают тепловой шум в электрических це-
пях, броуновское движение, атмосферные возмущения, модулиро-
вание синусоиды с произвольной амплитудой и фазой, дробовой
эффект, тепловые шумы в линейных системах и другие. Рассмотрим
переменную, имеющую автокорреляционную функцию в виде
(т) = о2 ехр (—р I т I) cos т, (4.43)
которая представлена на рис. 4.8. Отметим, что выражение
о2ехр (—₽|т|) дает огибающую функции. Спектральная плотность
мощности записывается следующим образом:
73
Фжзс(со) = cr2e“P|Tl со5©(|те”^<0Тг/т =
— 2с2 J e—₽T cos co0 т cos сот dr =
о
------₽--------H-------2------1 =
L (o +<o„)a + ₽a - (o-o„)2 +₽2 J
__ 2Bo2 f______033 (fl" + ^o)______1
L co4 + 2a)2 (P°— cog) + (P* +<Dg)- J '
(4.44)
Рис. 4.8. Экспоненциально-косинусоидальная автокорре-
ляционная функция.
Хотя это выражение кажется сложным, некоторые свойства его лег-
ко установить. При со -> оо Фхх (со) 0. Для со = 0
<4Л5>
Эти асимптотические значения полезны при построении зависимости
(и)-
Взяв производную и приравняв ее нулю, можно определить на-
личие и местоположение максимума или минимума (со):
аФхх(С0) = -ЙО [Ш< +2 (р»+(0g) (О* + (F-2p2(0g-3(0«)] (4 46
dco [co<4-2^(pa-co§)+(₽a+cog)2]3
Рассмотрение этого выражения показывает, что оно непрерывно
для любых действительных значений со. Приравняв это выражение
нулю, найдем частоты со1? при которых Фжа: (со) достигает максималь-
ного или минимального значения:
0*-b2(p2+co2)G)2 + (f/—2р2со2—Зсо^) = О. (4.47)
Решая квадратное уравнение и извлекая квадратный корень, полу-
чаем частоту
COj = ± (₽2 +со2) /< [2со0_(р+ g)2)'/2]I/2, (4.48)
74
которая является действительной только при
3wJ >РЕ. (4.49)
Если это условие выполняется, максимальные значения получаются
при значениях определяемых уравнением (4.48). Это макси-
мальное значение находится путем подстановки ±<*>1. в уравнение
(4.44), решая которое, получаем
Рнс. 4.9. Спектральные плотности мощности для переменных, имеющих
экспоненциально-косинусоидальную автокорреляционную функ-
цию (а — 3(OoZ>pz; б~3<Оо<Р2).
График функции Фд-д. (св) показан на рнс. 4.9а. Если условие (4.49)
не выполняется, т. е. если
3^<₽2, (4.51)
уравнение (4.47) не имеет действительных корней и, следователь-
но, Фжж (со) не имеет максимумов, кроме ’ максимума при со = 0.
Это значит, что Фжж (со) монотонно уменьшается при со-> со. Этот
случай показан на рис. 4.9 б.
§ 4.6. Взаимная корреляционная функция
Метод, использованный для автокорреляционной функции, по-
добным же образом можно применить для определения взаимной
корреляционной функции между любыми двумя выбранными сиг-
налами xt (Z) и yi (/) (рис. 4.10), взятыми из двух эргодических про-
75
цессов х (f) и у if) соответственно. Эта взаимная корреляционная
функция имеет вид:
т
фад (т) = lim ~ [ xt (/) yt (I +т) * = £ [X; (/) yt « +т)]. (4.52)
T~>CO Z/ J
Взаимная корреляционная функция является действительной функ-
цией как для положительных, так и для отрицательных значений т.
Однако в отличие от автокорреляционной функции, она не симмет-
рична по отношению к вертикальной оси, и ее максимальное значе-
ние обычно достигается не прн к = 0. Для- отрицательного сдвига
получаем
<₽№ (—t) = -Е U (/) у (t — т)]. (4.53)
Рис. 4.10. Определение взаимной корреляционной функции отдель-
ных сигналов xt (t) и yt (I).
Вводя перенос начала па временной оси
V = / — т (4.54)
в уравнение (4.53), получаем
<РЗД (—т) = Е [х (/' + т) у (/')). (4.55)
Поскольку рассматриваются стационарные во времени процессы,
то штрих у ? в уравнении (4.55) может быть опущен:
Ч’и (—4 = Е [х (Z + т) у (/)] =
= Е ly (f) х (I + т)] = <р„ (г). (4.56)
Важно отметить, что следует обращать внимание на то, какая пере-
менная смещается относительно другой, поскольку взаимная корре-
ляционная функция не является четной функцией и, следовательно,
не одинакова, для положительных и отрицательных т. Другим вы-
76
ражением для. взаимной корреляционной функции уху (т) является
выражение
Ч-i» (т) = Е [х (t — т)у (QJ, (4.57)
где смещение х по отношению к у делается в том же направлении,
что и в уравнении (4.53). Хотя <ржу (т) может превышать (р ху (0),
можно показать, что верхним пределом для <рх£/ (т) будет выражение
I <Рад СО I + %„(())]. (4.58)
Другое полезное соотношение получается с помощью неравенства
Шварца, которое применительно к переменным х (/) и у (t 4- т) уста-
навливает:
В{[х (О]2} Е{[у (t 4- т)]2} > Е{[х (Z) у (t 4- т)Р). (4.59)
Поскольку у (0 стационарна,
Е {(л/(/ + t)F) = Е {[^ (01й). (4.60)
Следовательно, выражение (4.59) преобразуется в
<р15: (0) (0) > [<рзд (т)]2 = I <рзд (т) I2, (4.61)
которое можно переписать в виде отношение:
|-<Рвд fr) ls/<Pxx (0) <Р„ (0) < 1. (4.62)
часто называемого нормированной взаимной корреляционной функ-
цией (если учитывается знак <рк!/), всегда имеющей значение, равное
или меньшее, единицы.
§ 4.7. Взаимная ковариационная функция
Способом, подобным тому, который использовался при рассмот-
рении автокорреляционных функций, определим взаимную ковариа-
ционную функцию двух переменных как взаимную корреляционную
функцию для случая,.когда средние значения этих переменных рав-
ны нулю.
Рассматривая переменные
х (0 = х' (f) 4- (4.63)
У W = У' Ю + 1-4/. (4.64)
где х' (/) и у' (/) — флуктуации около средних значений и
соответственно, и подставляя их в уравнения, определяющие вза-
имную корреляционную функцию, получаем:
Чад СО = Е [х (;) у (I+т)] = Е {[х' (/) + иJ [{/'(* 4- О 4- н„]} =
= Е [х' (/) у' (I+01 + P.J, Е [х' (/)] + |.ix Е [у' (<)] 4- p.s . (4.65)
По определению х’ (?) и у'(t), средние значения Е[х' (/)] и
Е {у' (t-Нт)] равны нулю, и уравнение (4.65) переходит в уравнение
4W (*) = Фх' У <г) -ЬМя И/ = Cw (т) + М* hr» (4-66)
где CX1J (т) является взаимной ковариацией переменных х (?) и у (/).
В соответствии с методом, используемым для автоковариации,
символ СХу (т) будет использоваться для взаимной ковариационной
функции х (?) и у (?) для случая, когда р..х или ру должны быть равны
нулю. Если это условие не выполняется, будет использоваться обо-
значение (Рд.р (т) для взаимной корреляционной функции.
§ 4.8. Взаимная спектральная плотность
Аналогичным же образом, который использовался для спект-
ральной плотности мощности, определяется взаимная спектральная
плотность Ф.ху((о) двух переменных х (?) и у (t) как интегральное пре-
образование Фурье взаимной корреляционной функции, т. е.
<Т\„ (и>) = $ Фет (т)е ~J A.
(4-67)
Столь же справедливо и обратное преобразование:
фад (Т) = ^7 J И Е’ d“-
(4.68)
Эти уравнения представляют пару преобразований Фурье, ко-
торая в точности аналогична отношению между автокорреляцион-
ной функцией и спектральной плотностью мощности. Однако вза-
имная спектральная плотность не имеет физической интерпретации,
аналогичной интерпретации функции спектральной плотности мощ-
ности.
Поскольку взаимная корреляционная функция не является чет-
ной, в комплексном экспоненциальном преобразовании уравнений
(4.67) и (4.68) нельзя использовать косинусоиду. Следовательно,
взаимная спектральная плотность представляет собой комплексную
величину, имеющую как действительную, так и мнимую часть (или
амплитуду и фазовый угол).
Чтобы проиллюстрировать сущность взаимной спектральной
плотности, подставим в уравнение (4.67) выражение (4.52) для вза-
имной корреляционной функции:
П7 —,
Дт J-V (/) У (Z + т) Л (4.69)
—т -J
78
Определим усеченные переменные А (Z) и А (Z) как.
A«) = x(Z)>(|Z|<7’); АЙ = 0,(|/|>7) (4.70)
/2(0 = !/(^(1Л<Т); /2(0 = 0, (1Л>П (4.71)
что обеспечивает возможность применить теперь преобразование
Фурье. Если использовать предельный переход при Т со, то
А (/) и /2 (<0 будут стремиться к х (£) и у (t) соответственно. Подста-
новка этих усеченных переменных в уравнение (4.69) и изменение
порядка интегрирования дают:
фта(“)= 1™ -Г- f А(0* f А(Н~т)е-1'«йт. (4.72)
T-t-ca 41
Замена переменной
g = т + t (4.73)
приводит к уравнению:
Ф„(В)=Нп11 F A(£)e-l««dE. (4.74)
T-> oa 41 J , J
— T —co
Пределы первого интеграла могут быть заменены на ± со, так как
А (О = вне пределов интервала ±7, что приводит к сопряжен-
ному преобразованию Фурье, где — со заменено на со. Уравнение
(4.74) переходит в уравнение
Ф^(“У= Вт -^ГЙ1(-“)^3(“)]= Вт ~ if; (ra)F2(o)]. (4.75)
У—>оз Zi У—>оя 41
Используя неравенство (4.61)
1фад (т)]2 = I Фх, (т) I2 < Фхх(0) <рта (0), (4.76)
можно получить эквивалентное соотношение в частотной области
|Фад(Ш)|»<<Ьс>)Фи>). (4.77)
которое преобразуется в отношение
|Фх„(“)|2/Ф«хЙ)ФтоЙ)<1- (4.78)
Это отношение в последующем изложении будет называться коге-
рентной функцией*.
* Левая часть неравенства (4.78) часто называется в литературе квадра-
том когерентной функции. — (Трим. ред.
79
§ 4.9. Соотношения между входными
и выходными сигналами
Временная область— автокорреляционные функции. Для уста-
новления отношения между шумовыми характеристиками входного
н выходного сигналов линейной динамической системы рассмотрим
линейную систему, имеющую импульсную характеристику h (t)
и получающую входной сигнал х (t). Выходной сигнал системы у (I)
определяется интегралом свертки:
!/(/)= $ A(X)x(/-7.)dX, (4.79)
где 1 — временная переменная интегрирования.
Подставив уравнение (4.79) в автокорреляционную функцию
фу» (т) = Е [у (/) у (t + т)1, (4.80)
получим
4>вв(т)=£ ft(k)x(/-k)A $ ft©x(/ + T-|)d|], (4.81)
где £ — переменная интегрирования по времени для второго инте-
грала. Математическое ожидание дает среднее значение только
в отношении переменной t, следовательно, уравнение (4.81) может
быть преобразовано:
Фуу('г)= $ ^(X)Zi(^)£[x(Z-l)x(z+-r-|)]^dK (4.82)
По определению автокорреляционной функции,
Фхж (т — £ -Ь X) = Е U (/ — Ц х (I + т — |)] (4.83)
и уравнение (4.82) переходит в уравнение:
<Р„„(т) = $ $й(7.)Л©^(г-| + Х)^Л. (4.84)
Это" выражение показывает связь между автокорреляционной функ-
цией входного сигнала х и выходного сигнала у. Хотя это соотно-
шение представляется сложным, в некоторых ситуациях оно может
быть очень полезно.
Рассмотрим тот особый случай, представляющий значительный
интерес, когда подкритическая система имеет следующую импульс-
ную характеристику:
п (t) = А ехр (—at), (t 0);
Л(0 = 0, (/<0). (4.85)
80
Подстановка уравнения (4.85) в (4.84) дает:
(т) = f е-" №+5) Фхх (т—g+Л.) d£ dZ.
О о
(4.86)
Нижннй предел интегралов равен нулю, поскольку импульсная ха-
рактеристика равна нулю при отрицательном времени. Введя за-
мену переменной
Ц = £ - А (4.87)
и исключив | из уравнения (4.86), получим:
<$Уу (т) = (j Л2 е—сХ е—“ фЛ.ж (т—ц) d[i d%=
о о
= Л2 J фд-д. (т— ц) е—е~2оХ d%=
о о
/2 г
=— \ Фях ft— Р) е~ам (4.88)
ZCC J :
Если на входе системы действует белый шум, автокорреляционная
функция этого входного сигнала пропорциональна дельта-функции
Дирака, т. е.
<Р,г (т — р) = К 6 (т — р). (4.89)
Поскольку дельта-функцня Дирака равна нулю везде, кроме точки
т, равного р, можно заменить член ехр (—ар.) на выражение
ехр (—ат) и вынести его за знак интеграла, т. е. '
<Р„„ (т)=ехр (—ах) § 6 (т—р) dp =
О
=—— ехр (—ат) = К' ехр (—ат),
(4.90)
поскольку интеграл в выражении (4.90) равен единице по определе-
нию дельта-функции Дирака (К' — коэффициент пропорциональ-
ности). Это выражение показывает, что автокорреляционная функ-
ция выходного сигнала системы, имеющей экспоненциальную им-
пульсную характеристику, пропорциональна ехр (—ат), из которой
легко определить величину а.
Частотная область — спектральные плотности мощности. При
рассмотрении связи вход — выход в частотной области, применив
81
к уравнению (4.84) интегральное преобразование Фурье, можно
получить много полезных выражений:
ФИ,(“)= f 'f-ra(T)e-J'“v/T =
оо Г со со л
= S S f /гW©(Px.t(т~g-l->)</£ A e-i“TdT. (4.91)
—оо | —оо —оо I
Подставив новую переменную
Н — т — % -|- К
(4.92)
и исключив переменную т, получим выражение
СО оо оо
%» = $ $ $ AWA®q>s0((p)e-l‘»<M+B-MdEdXdn =
со со ео
= jj li (l)e+<“^dX J J (pI>.([x)e-l“>1dp.=
—-К ~tx> —co
= H* (w) H (w) (co) = I H (co) I2 Фта (co), (4.93)
которое весьма удобно при рассмотрении широкого круга проблем.
Из уравнения (4.93) следует, что связь между Фхх (со) и ФЙУ (со)
зависит только от амплитуды передаточной функции Н (со) реактора
и что никакой информации относительно фазового угла получить
нельзя.
Если входной сигнал можно рассматривать как белый шум, т. е.
имеющий спектральную плотность мощности, равную постоянной К
во всем интервале интересующей нас частотной области, то урав-
нение (4.93) можно переписать в виде
= (4.94)
Временная область — взаимные корреляционные функции. Рас-
смотрим взаимную корреляционную функцию между входным сиг-
налом х (Z) и выходным сигналом у (/) системы, имеющей импульсную
характеристику h (/) Подставив интеграл свертки, определяемый
уравнением (4.79), для у (Z), получим
ФЯ1/ СО = £ I* (*—О У =
— Е (t—т) h (X) х (t — X) dX
(4.95)
82
Поскольку усреднение по времени, определяемое оператором
математического ожидания, производится только по переменной /,
уравнение (4.95) может быть преобразовано к виду
Ч’здМ= § h(K)E [*(/—K)x(t—
$ Л(Х)<рях(т—X)dX.
(4.96)
Видно, что уравнение (4.96) представляет собой интеграл типа ин-
теграла свертки, т. е. взаимная корреляция между входным и вы-
ходным сигналом динамической системы определяется как свертка
импульсной характеристики и автокорреляции входного канала.
Интересно отметить, что если переменная на входе х (/) представ-
ляет собой белый шум, автокорреляционная функция которого про-
порциональна дельта-функции Дирака с коэффициентом пропорцио-
нальности К, то, применив подход, использованный при выводе
уравнения (4.90), получим:
<рад(т) = К $ Л(Х)6(т—K)dK=Kh(z) J 6(т—4dX=J<*(T),(4.97)
т. е. взаимная корреляция между входным и выходным сигналом
динамической системы, когда выходной сигнал представляет собой
белый шум, пропорциональна импульсной характеристике.
Частотная область—взаимные спектральные плотности. Взаим-
ная спектральная плотность между входным и выходным сигналом
динамической системы может быть получена с помощью преобразо-
вания Фурье уравнения (4.96):
Фед(<о)= S —A) е~(4.98)
Подстановка
р = т — X (4.99)
в уравнение (4.98) и исключение т приводят к уравнению
$ $ Л(^)(рЯ4;(р)е-^^+х)^^ =
-= $ /i(X)e-i^dX J фях(н)е-'мМр==Я(ю)Фжя(©), (4.100)
т. е. взаимная спектральная плотность между входным и выходным
сигналами равна передаточной функции, умноженной на спектраль-
ную плотность мощности входного сигнала.
83
§ 4.10. Практическое рассмотрение
Теория случайных шумов, представленная в предыдущих пара-
графах этой главы, дает математический аппарат для анализа дан-
ных, получаемых в экспериментах самого широкого профиля. Од-
нако, в большинстве практических случаев приходится принимать
в расчет поведение физически реализуемой системы. Например,
спектральные плотности мощности и взаимные спектральные плот-
ности предполагаются существующими во всем диапазоне час гот от
— оо до + оо. В физически реализуемых системах можно измерить
эти спектральные плотности в диапазоне частот от нуля до опреде-
ленной граничной частоты соо. Практический выход из этого огра-
ничения состоит в том, что должен быть введен видоизмененный тип
спектральных плотностей, называемых односторонними спектраль-
ными плотностями.
В предыдущих параграфах все интегралы, включающие свертку
переменной и импульсной характеристики, имели пределы от — оо
до + оо. Однако реализуемая импульсная характеристика по не-
обходимости должна быть равной нулю для t < 0, поскольку си-
стема не может реагировать на импульс до его прихода. Следова-
тельно, нижний предел этих интегралов должен быть равен нулю.
И верхний предел, равный бесконечности, как для интегралов сверт-
ки, так и для преобразования Фурье, не достижим в физически
реализуемых условиях, поэтому интегрирование должно быть ог-
раничено конечным временем. Если к этому времени интегрируе-
мые величины стремятся к нулю, то полученные выше соотноше-
ния являются хорошим приближением. В противном случае при
обработке экспериментов, длящихся ограниченное время, возни-
кают погрешности. Значения этих погрешностей рассматриваются
ниже.
Интегрированию по диапазонам частот присущи те же ограниче-
ния, т. е. существует реальный верхний предел частоты, до кото-
рой могут быть измерены спектральная плотность мощности и вза-
имная спектральная плотность. Если эти спектральные плотности
не стремятся к нулю при верхней частоте (d0> то из-за отсутствия из-
мерений за пределами частоты юс в результаты могут быть внесены
ошибки. Из математических преобразований очевидно, что при об-
работке экспериментов как во временной, так и частотной области
может быть получена одна и та же информация, т. е. проведение об-
ратного преобразования Фурье не дает какого-либо пути изменить
количество информации, которое теоретически может быть извлече-
но из данного эксперимента. Однако существует множество ситуаций,
при которых более удобно проводить измерение в какой-либо одной
области, чем в другой, вследствие приспособленности специального
оборудования или устройства обработки данных. Кроме того, про-
стота входных-выходных связей линейных систем в частотной об-
ласти дает возможность исследователю лучше «чувствовать», что
84
происходит в системе. Это особенно справедливо в том случае, если
исследователь имеет дело с измерениями в частотной области, что
является обычным для большинства инженеров и многих научных
работников.
§ 4.11. Односторонняя спектральная плотность
Выше было установлено, что спектральная плотность мощности
и взаимная спектральная плотность связаны соответственно с авто-
корреляционной и взаимной корреляционной функциями преобра-
зованиями Фурье. Можно легко измерить корреляционные функции
и провести обратное преобразование Фурье, если необходимо по-
лучить двусторонние спектральные плотности (т. е. спектральные
плотности, которые существуют во всем диапазоне частот от—оо
до 4- оо). Это несложно, так как можно измерить корреляционные
функции как для положительных, так и для отрицательных значе-
ний т. Действительно, значения автокорреляционной функции для
положительных и отрицательных т одни и те же, так как она яв-
ляется четной н, следовательно, симметричной.
Спектральная плотность мощности и взаимная спектральная плот-
ность могут быть также измерены при использовании узкополосной
фильтрующей системы, которая подробно обсуждается ниже. Оче-
видно, что измерения частотного типа можно проводить только для
положительных частот, так как отрицательные частоты не имеют
смысла в физически реализуемой системе.
Односторонняя спектральная плотность мощности. Чтобы по- -
казать связь между односторонней (охватывающей диапазон от О
до + оо ) и двусторонней (охватывающей диапазон частот от — оо
до + с») спектральными плотностями, рассмотрим сначала спект-
ральную плотность мощности, которая является более простой
нз этих двух функций. Ранее было определено, что двусторонняя
спектральная плотность мощности является преобразованием Фурье
автокорреляционной функции. Легко видеть, что спектральная плот-
ность мощности является также симметричной функцией относи-
тельно нулевой частоты, как показано на рис. 4.11. Определим те-
перь новую одностороннюю спектральную плотность мощности
(ю)> которая существует только в области частот от 0 до + оо,
таким образом, чтобы площадь под кривой Фяя: (со) от — со до 4- оо
[равная среднеквадратнческому значению х (/)! была равна пло-
щади под кривой Gxx (со) от 0 до 4- оо, т. е.
= Gxx(a)da. (4.101)
—са 0
Отсюда
^«(ю) = 2Ф».х(ю). (0<<0<оо);
G3[J<o) = Ox.;[(«), (<о==О);
е„(а) = 0, (—СО<И<0). (4.102)
85
Эта связь показана на рис. 4.11. Физически реализуемая односторон-
няя спектральная плотность мощности Gxx (со) может быть измерена
прямыми методами, использующими прием фильтра, т. е. такими
методами, которые применяются в электротехнике много лет, то-
гда как двусторонняя спектральная плотность мощности ФЛ.К (со)
получается с помощью математических преобразований автокорре-
ляционной функции, которая может быть либо измерена, либо рас-
считана.
Рис. 4.11. Односторонняя [G«« (©)] и двусто-
ронняя [Фхж (со) 1 спектральные
плотности мощности.
Проведя преобразование Фурье, комплексный экспоненциальный
член можно представить в виде синуса и косинуса, используя соот-
ношение Эйлера:
е±Ют — cos сот ± j sin сот. (4.103)
Отсюда
Фхх(ео)= § срхх (т) cos сот dr—j J <pvx(t) sin cord?. (4.104)
—00 —oo
Последний интеграл равен нулю, поскольку фхзс (т) симметрична,
и уравнение (4.104) переходит в равенство
Фжх(ш)= $ фЛХ(т)coscoxdT—2 Jj фЯЛ.(т)cosспdr, (4.105)
—со О
а односторонняя спектральная плотность мощности теперь выражает-
ся следующим образом:
^«(“) = 2®xx(“) = 4 f <p^(T)coswrdT. (4.106)
О
Обратным преобразованием уравнения (4.106) можно получить, что
Ч\.г(т) = 4~ $ 01,(o)eJ‘“d(0=3_$20;eI(o)el“ldco =
=—(4.107)
2л 0
86
Следовательно, уравнения (4.106) и (4.107) можно рассматривать
как пару .преобразований, которая во многих отношениях подоб-
на паре преобразований Лапласа, в которых переменная s замене-
на на jco.
Особая ситуация может возникнуть, когда переменные содержат
постоянные составляющие, приводящие к появлению дельта-функ-
цни односторонней спектральной плотности в начале координат.
Б этом случае необходимо приближаться к нижнему пределу интег-
рирования—нулю — снизу, чтобы учитывать влияние этой дельта-
функции. _
Односторонняя взаимная спектральная плотность. Определение
функции односторонней взаимной спектральной плотности Gsy (со),
где со меняется только от 0 до + оо, более сложно, поскольку взаим-
ная корреляционная функция несимметрична. Используя подход,
аналогичный примененному при выводе уравнения (4.102), опреде-
лим физически реализуемые функции односторонней взаимной спект-
ральной плотности Gxy (со) и Gvx (со) следующим образом:
бху(со)=2ФхДсо) = 2 Фху (т) e-i“T (со>0),
Сад(и) = Фч,(0) (Ш=О),
Gxl/(a) = 0 (<в<0) (4.108)
и
G1»(“) = 2®wc(o>) = 2 J <psa. (т) е—(ш>0),
0№(Ю) = Ф₽(0) (и-0).
С,я(<в) = 0 (со<О). (4.109)
Отметим, что Gxll (ш), Gsx (<о), (<о) и Ф (ш) являются комплекс-
ными величинами, поскольку взаимная корреляционная функция
<ржу несимметрична. Действительную и мнимую части Gxy (со)
и буж (со) определим как
0зщ(<в) = Сч,(ш)—^(ш), (4.110)
0!/ж(ш) = С!,а;(ш)—^(ш), (4.111)
где Cxv (со) и Сух (со) — действительные части, Qxy (со) и Qvx (со) —
мнимые части соответственно.
\ Подставив уравнение^. ПО) в (4.108), получим:
Оа.;,(ш) = Сх1/(со)—j<23;„(w) = 2 $ Ч.:,„(т)е”.1'«Л^
= 2 $ Фад(т)е-1“тс1т+2 $ (4.112)
87
Посколькут — переменная интегрирования, то, введя замену в пер-
вом интеграле
т = — т' (4.113)
и опустив штрих, получим
(о) = 2 (—т) е,<и Л 1-2 §<pw (т) е~ *« dr. (4.114)
СО О
Используя равенство, даваемое уравнением (4.56)
т) = срвз1(т), (4.115)
и меняя пределы интегрирования в первом интеграле, можно по-
лучить, что
°х!/ (®) = 2 ГФ„« <т) eimT А+2 \ <р.т„ (т) е-<“т dr. (4.116)
о о
Подстановка соотношения Эйлера для комплексной экспоненты
(4.103) в уравнение (4.116) приводит к уравнению:
°н/ (“) = cxv (“)— j<2TO И = 2 S Ф//» (т) (cos ат+j sin от) dr +
о
+2 5ч>х9(т) (cosшт—j sin сот) А =
о
= 2 $ [fine (т) + Фи/ <т)1 cos шт dr—
с
—i2 5 (Фи/ (т)—<РВ1 (т)1 sin шт А, (4.117)
о
из которого могут быть выделены действительная и мнимая части:
(“) = 2 S (ф«/ (т) + Ф(/х (т)] cos шт dr (4.118)
о
и
Qx.j (а) = 2 $ [фад (т)~Фи: (т)1 sin шт А. (4.119)
о
Из этих выражений видно, что Сху (со) — действительная четная
функция частоты, в то время как Qxy(to)—действительная нечет-
ная функция частоты. Следовательно,
схв (ш) = С„, (-<>) = С„х (ш) = С„х (-ш) (4.120)
и
Qxy Н = — Qxs (—©) = — QpxM=Q,JX(—со). (4.121)
88
Поскольку функция GX1J (со) комплексна, она может быть записана
в полярных координатах:
GI>) = |Gw(o>)|e,e»»(M’ (0 <ш<оо), (4.122)
где |Gxy (со) | — амплитуда и 6Я£/ (со) — фазовый угол могут быть
выражены через мнимую и вещественную составляющие, а именно:
| (со) | = (со) + (&у (со)] М2 (4.123)
и
%(“)= arctg (4.124)
[ Сху (®) J
В практике используются два приема для измерения взаимной
спектральной плотности. Первый заключается в измерении взаим-
ных корреляционных функций <ра.у (?) и ф&ж (т), расчете действитель-
ной и мнимой составляющих по уравнениям (4.118), (4.119) и опре-
делении взаимного спектра и его фазового угла по уравнениям
(4.123) и (4.124). Другой метод заключается в непосредственном из-
мерении вещественной и мнимой составляющих с помощью частотно-
полосного оборудования и определении амплитуды и фазы взаим-
ного спектра по уравнениям (4.123) и (4.124).
Взаимные корреляционные функции могут быть рассчитаны по
С (со)- и Q (со)-спектрам с помощью следующих соотношений:
Фм'(Т)=2? J Фад(“)е'и'йш=:-^ J Фч,(и)е*«Ло+
со со со
+— f Ф (ra)el“Tdra=— Г ю Ю) el“T cfo)=
2л J 2л J 2 2л J 2
0 0 о
= “ J -у 1С„Л (ш)—jQi,s (“)] [cos шт—j sin шт] dm' +
о
+4- f 4- И' -jQvz (“)] [cosrar +j sin шт] da =
J z
0
= J Кад (“) + Cyx (Ш)] cos шт +
0
+4" [СадlClMss(B)l sin ифи +
+ j J {ф [Qq, (“) + Q»» (“)] COS ШТ +
0
+ 4" lCyx (M) ~cXy (“)] sin co-г} dco. (4.125)
89
Используя равенства (4.120) и (4.121), соотношение (4.125) можно
упростить и привести к виду:
<РхИ W = f 1СЧ, (co) COSCOT +<2^, (со) sin сот] da. (4.126)
*0
Связь между входным и выходным сигналами. Связь между вход-
ным и выходным сигналами, описанная в § 4.9, может быть выражена
через односторонние спектральные плотности. Уравнение (4.93),
включающее спектральную плотность мощности, записывается при
этом следующим образом:
Gyy (со) =Я* (со)Н (со) Gxx(со) = |Н (со) |я Схх (со), (4.127)
а уравнение (4.100), включающее взаимную спектральную плотность,
как
Gxy (со) = И (со) Gxx (со). (4,128)
§ 4.12. Зависимость корреляционных функций
и спектральных плотностей
от среднего значения
Автокорреляционная функция. Рассмотрим случайную перемен-
ную, имеющую среднее значение рж. Автокорреляция определяется
в соответствии с выражением
Фхх (т) = Е U (0 х (/ + Т)1 (4.129)
и показана на рис. 4.12. График автокорреляционной функции сим-
метричен относительно вертикальной оси, а максимальное значение,
равное среднеквадратическому значению находится при г =
~ О.-При стремлении т к ± оо <рла. (т) стремится к р;, т. е. автокорре-
ляционная функция смещается по вертикали на величину р! из-за
того, что х (t) имеет среднее значение рж, что и показано на рис. 4.12.
Поскольку случайная переменная x(t), имеющая среднее значение р,
может рассматриваться как сумма
x(t) = х' (0 + рж, (4.130)
где х' (Z) — та же переменная с нулевым средним значением, авто-
корреляционная функция х (/) может быть выражена как сумма ав-
токорреляционных функций л/ (/) и рж, т. е.
Ф«М = Ф*'«'(т)+р.Г
(4.131)
Легко показать, что дисперсия равна разности между значением
автокорреляционной функции при т = 0 и смещением горизон-
тальной оси.
90
Спектральная плотность мощности. Двусторонняя спектраль-
ная плотность мощности может быть получена с помощью преобра-
зования Фурье автокорреляционной функции. Применив преобра-
зование Фурье к уравнению (4.131), получим:
(<•>) — Ф*'*' (со) + 2ярх 6 (со),
(4.132)
т. е. наличие среднего значения, отличного от нуля, добавляет дель-
та-функцию Дирака в начале координат, как показано на рис. 4.13.

Рис. 4.12. Автокорреляционная функция случайной
переменной, имеющей среднее значение
^¥=0.
Рассмотрим связь между односторонней н двусторонней спек-
тральной плотностью мощности, определяемую уравнением (4.101):
ф>-
2- J®„(a>)da> = AJ GJnt(a>)da>,
(4.133)
где обозначение нижнего предела символом 0~ означает, что нижний
предел должен стремиться к нулю снизу, для того чтобы включить
дельта-функцню Днрака, находящуюся в начале координат. Это
согласуется с уравнениями
Ога(<о) = 2Фта(<о), (и>0);
Оие(а>) = Фага(0) = 2я^, (<о = О);
0^(0)= 0,
(ю<0)
(4.134)
и показано на рис. 4.13.
Из вышеизложенного следует, что графики автокорреляционной
функции и спектральной плотности мощности дают одну и ту же ин-
формацию и различаются только видом. Сравнение значений
и о®, по этим двум графикам дает полное соответствие при согласован-
ности преобразования. Исходя из определения спектральной плот-
ности мощности как квадрата средней амплитуды на единицу ча-
стоты, можно показать, что среднеквадратическое значение полу-
91
чается путем определения площади под кривой спектральной плот-
ности мощности от нуля до бесконечное™, т. е.
=-Л f G„(a)da = aj4-К-
(4.135)
Если в это интегрирование не включать начало координат или если
среднее значение равно нулю, площадь под кривой равна диспер-
сии а|.
Рис. 4.13. Спектральная плотность мощности пере-
менной, имеющей среднее значение
К?* О-
Рис. 4.14. Взаимная корреляционная функция
дпух переменных, каждая из которых-
имеет свое среднее значение.
Взаимная корреляционная функция. В случае взаимной корре-
ляции наличие постоянных составляющих и в переменных
х (/) н у (/) приводит к кривой взаимной корреляции, показанной
на рис. 4.14, т. е. взаимная корреляционная функция смещается по
вертикали на величину одьу. Математически это выражается как
И = 4W И + Ив. (4 • 136)
где х' и у" — переменные со средними значениями, равными нулю.
Взаимная спектральная плотность. Двусторонняя спектраль-
ная плотность определяется с помощью преобразования Фурье урав-
нения (4.136):
ФХ!/ (со) = Фх'!/' (со) + 26 (со), (4.137)
92
а односторонняя спектральная плотность с помощью уравнения
(4.103):
<Ззд(“) = 2Фвд(и), (и>0);
Сад(<о)=Фи,(О), (о = 0);
Сет(<о) = 0, (о<0).
(4.138)
Графики этих функций представлены на рис. 4.15.
Рис. 4.15. Взаимная спектральная плотность двух
переменных для случая, когда обе име-
ют средние значения.
§ 4.13. Когерентные функции
Наличие постороннего шума илн других входных переменных
может отрицательно влиять на качество измерений. Другими факто-
рами, ухудшающими измерения, являются отклонения от предпола-
гаемой линейности системы и конечное время измерения. Обычным
показателем качества измерения для отдельной системы вход —
выход является когерентная функция, которая может рассматри-
ваться как показатель внутренней согласованности измерений.
Рассмотрим динамическую систему без учета каких-либо практи-
ческих ограничений в частотной области, в которой могут проводить-
ся измерения. В § 4.11 были получены соотношения, связывающие
сигналы вход — выход:
сЙ’=|Яр(о)|гс«хМ
<3«Д®) = ^с(“)С,;с(ш).
(4.139)
(4.140)
Индексы рис введены для указания того, что амплитуда передаточ-
ной функции определяется при использовании либо спектральной
плотности мощности, либо взаимной спектральной плотности.
93
Определим новую переменную у3 (со), называемую когерентной
функцией, как отношение квадратов амплитуд передаточной функ-
ции, которые измеряются этими двумя способами, т. е.
в, . 1^(со)Р 1бад(со)1М?хИй)2 |бад(со)12 ......
I Нр (со) р Gyy (co)/Gxx (со) GKX (со) Gyy (со)
Когерентная функция может быть также определена через дву-
сторонние спектральные плотности:
Т2 И = | Фж9 (со) |8/Фях (со) Фо (со). (4.142)
Если все предположения, использованные при выводе уравнений
(4.139) и (4.140), справедливы, то когерентная функция равна еди-
нице. С помощью неравенства (4.78) можно показать, что когерент-
ная функция удовлетворяет неравенству
„ |Фя1/(С0)Г2
у2 ((0) = 1, (4.143)
Фхх(С0)Ф.о(С0)
т. е. когерентная функция всегда меньше или равна единице.
Когерентная функция может иногда рассматриваться как мера
линейности связи между входным и выходным сигналами. Если ко-
герентная функция меньше единицы, одной из возможных причин
(но необязательно единственной причиной или даже наиболее важ-
ной) является неполностью линейная зависимость между входным
и выходным сигналами. В сложных системах для двух переменных
возможна ситуация, когда невозможно установить ошибочную вза-
имную коррелированность, что и выявляется с помощью значения
когерентности вблизи нуля. В практических случаях иногда значение
когерентной функции получается больше единицы, однако это обыч-
но означает неточность в измерениях, сбой в вычислительной ма-
шине и тому подобное.
§ 4.14. Корреляция при использовании двух детекторов
и измерение спектральной плотности
Взаимная корреляция выходных сигналов двух детекторов. Рас-
смотрим систему, показанную на рис. 4.16, где Н (со) символизирует
ядерный реактор, в который поступает возмущение I (/). Выход-
ной сигнал—нейтронная плотность—измеряется двумя регистриру-
ющими системами, расположенными рядом, с передаточными функ-
циями Hi (со) и Я2 (со). Выходные сигналы детекторов уг (/) и yz (/)
искажаются детекторными шумами тх (Z) и ш2 (0 соответственно.
Применив интеграл свертки, получим, что выходной сигнал реак-
тора должен описываться выражением
п (!) = $ h (X) i (Z—X) dX. (4.144)
94
Входные сигналы детекторных систем имеют вид
Xj (0 = тг (t) -Ь п (0 (4.145)
и
х2 (0 = т2 (t) -Ь п (t). (4.146)
С помощью интеграла свертки и уравнений (4.145) и (4.146) выход-
ные сигналы у± (/) и у2 (t) описываются следующими выражениями:
Рис. 4.16. Структурная схема корреляционного экспе-
римента с двумя детекторами, имеющими
собственные шумы.
лИ= $ Л1(ц)л-1(г—ц)ф= н)+«(«—
оо со оо
= 5 J J ftiСи)Л(й.)»(#—ц—X)dXd|i, (4.147)

+ f 5 n)dT)d£.
(4.148)
Отметим, что р, X, £ и q являются переменными интегрирования
по времени. Взаимная корреляционная функция между у± (t) и
у2 (t) определяется как
<Pi£ СО = фук у, (т) =^Е [&. W У2 V 4-т)]• (4.149)
95
Если подставить соотношения (4.147) н (4.148) в уравнение
(4.149), используя соответствующие определения корреляционной
функции, то получим
<р12(т)= J J (р,) А2(£) <р,И1 г„, (тгЧ-р.—
+SS hi W А2 ® А 1’1) "₽« ‘ <т+Р—Е—’1) dp (Ч Л] 4-
+ ® Ai И Аз <Э А W ч>«. i (t+1-'—s+X) dp &, +
оз
+ ® А1 (W Ла (I)Л (Мll (’ll <Рн (т+н—Е+—ч)dpdj dldi], (4 150)
—оо
Поскольку шумы /пх (/) и т2 W по предположению не коррели-
руют друг с другом и с входным сигналом I (/), взаимные корре-
ляционные функции фт1<а (т), (т), <pWbt- (т) равны нулю н пер-
вые три члена в (4.150) исчезнут. При этом получим:
<г1г(т)=
= Й А1 (н)hs(t,)h (X)h (т|) <pi( (т-J-ц—E +X—Т|)dpdEdXdtp (4.151)
Это выражение настолько сложно, что использовать его целесооб-
разно только в некоторых специальных случаях. Если рассматри-
ваются две идентичные детекторные системы, т. е.
Лх (0 = /1, (0.
то, введя замену переменных
с = Е—14
р = 11—
и исключив т] и %, можно получить:
сс со Г оо “I
ЧЧг (Т)= § Н MlOMo + lOdp X
---СО ОО L—со J
X j h(X)Л(р + %)dXj <p;i(T—о—p)dpda =
= J $ ‘If.,/„ (о) Ч'м, (P) <Fii (t—°— p)dpdo.
S6
(4.152)
(4.153)
(4.154)
(4.155)
= А ехр (—а/), (/>0);
Л (0 = 0, (7<0);
Л1(/) = Вехр(—Р0, (/>0);
МО=о,
Тогда
Флл(т) = —-е_“|т|.
2a
Фл.ь.(т:) = ^е_р|х|
zp
и уравнение (4.158) перейдет в уравнение
Ф12(т)=Х С — е—“'“I — e-eix-airfo=!
' J 2a 2₽
Г e_„|a|_6|T_a|^0
Для входного сигнала, имеющего характер белого шума,
ф«(т—р)=Х6(т—о—р), (4.156)
где X—константа, 6—дельта-функция Дирака. Введя новую за-
мену переменной
е = р+а (4.157)
и исключив р из уравнения .(4.155), получим
Ф12(т)= S фЛ1(1>(а)фЛЛ(е—а)К8(т—6)<forfe =
= К^ фь1|1,(а)ф№(6—a)da J 6(т—6)dB =
=Х $ Ф/1,/1, (о) Фм (t— a) da, (4.158)
поскольку J 8 (г—6) de равен 1 и 6(т—6) отлично от нуля толь-
ко при т=В. Предположим, что импульсные характеристики k(t)
и h^f) имеют вид:
(4.159)
(4.160)
(4.161)
(4.162)
(4.163)
Если интеграл разбить на три части при а = 0 и a = т if под-
ставить (о — т) вместо j т — a ] и — а вместо | а | для областей ии-
4 Зак. 576 97
тегрировання, в которых знаки величин должны быть отрицатель-
ными, как показано на рис. 4.17, можно получить, что
еао—₽ (т—о) е—аа-Р (т—о) (fo-f-
С е-ао+р (т-n) fa =-KAW-----(ре-ат _ ае-Вт) =
J 2сф(Р2 — С1г) '
=К1е-<^—К2е-^, (4.164)
где Ki н Ко—постоянные. Поэтому взаимная корреляционная функ-
ция выходных сигналов двух детекторов, когда импульсные харак-
теристики системы н аппаратуры экспоненциальны, представляет
собой разность двух экспонент, одна из которых имеет характери-
стическую постоянную реакторной системы а, а другая — характе-
ристическую постоянную аппаратуры р. Если
(4.165)
т. е. если аппаратура имеет широкий диапазон пропускания частот
(что является разумным предположением, если надлежащим об-
разом измерять передаточную функцию системы), эксперименталь-
ные данные могут быть обработаны с помощью уравнения (4.164)
и метода наименьших квадратов, что позволяет вычислить постоян-
ные а и ₽.
Если частотная характеристика аппаратуры постоянна во всем
диапазоне частот, представляющем интерес, то во всех случаях для
практических целей можно предполагать, что
ht (Z) = ВЪ (t) (4.166)
и
фЛ1Лх ft) = (т). , (4,167)-
98
При этом уравнение (4.164) перейдет в
(т) =К Се~“° В2б(т—<j) do =
У 2а
= КАгГ [e~°Il6(T—°)do= •
О
КА& Въ „-Се, X. КЛ2Ва „т ..
—-------е—а. 1 б (т—о) do =---------е~ат, (4.168)
2а J 2а
о
поскольку б (г — о) отлично от нуля только при о = х. Следова-
тельно, взаимная корреляционная функция выходных сигналов двух
детекторов, расположенных рядом, является экспоненциальной
функцией т.
Взаимная спектральная плотность выходных сигналов двух де-
текторов. Преобразование Фурье взаимной корреляционной функ-
ции определяет взаимную спектральную плотность':
Ф,2(<0) = 5 <Т) е -i“' dT = Л1 W Л2 © h (Ч h (’I) X
X <р1г-(т + р + Л—Tj) е—dp, dfc, d% dr] dx. (4.169)
Произведя замену переменных
= (4.170)
в уравнении (4.169) и исключив т, получим:
Ф12(со) = jj hi (р) e+w dp, J hz (g) e-i“s dg x
—CO —00
X J h (Z,) eJtoZ dZ. Л (i]) e^^di] Tii(Qe“^d£ =
= m (<o) я2 (CD) (co) H (GJ) Фн (co) =
- Щ (co) Я2 (co) IH (co)|2 Ofi (CD). (4.171)
Если два детектора идентичны н каждый имеет импульсную. ха-
рактеристику Aj(Z) н передаточную функцию ^(со), то
Ф12 (CD) = I Нг (CD) I21И (со)|2 Фн (CD). (4.172)
Следует отметить, что все члены уравнения (4.172) действительны
и, следовательно, взаимная спектральная плотность действительна.
Это просто показывает, что для идентичных детекторов методика,
4* 99
представленная на рис. 4.16, является по существу эквивалентной
измерению автокорреляции или спектральной плотности мощности
при отсутствии шума детектора.
Уравнения (4.170) и (4.171) равно применимы и для односторон-
ней спектральной плотности, т. е.
G12 (со) = Щ (со) (со) Я* (со) Н (со) Gif (со) =
= т (со) Н2 (co) IН (со) |2 GH (со), (4.173)
G12 (со) = | Нг (со) |2 | Н (со) |2 G-f (со). (4.174)
§4.15. Многоканальные по входу
линейные системы*
Во многих практических системах выходной сигнал может быть
суммой реакций на несколько входных сигналов. Это иллюстри-
руется рис. 4.18, где (Т), й2 (Т), hN (/) — импульсные харак-
теристики индивидуальных подсистем; хг (I), х3 (/) ... xN (Т) —
входные сигналы; yt (/), yz (Т), yN(f) — соответствующие вы-
ходные сигналы, которые суммируются в результирующий выход-
ной сигнал:
N
y(t)= 2 а. И-
i=l
(4.175)
Рассмотрим выходной сигнал yi (/), получающийся в t-м канале
при входном сигнале х, (/), для случая, когда остальные вход-
ные сигналы равны нулю. Функции hi (/) и Я, (/), определяемые со-
ответственно как импульсная характеристика (или весовая функция}
и передаточная функция, связывают входной Xi(t) и выходной
yt (/) сигналы. Связь входного и выходного сигналов во временной
области н в частотной области является такой же, как и для любой
другой системы:
!/,(/) = йг.(1)х£(/—
(4.176)
Yi (со) = Hi (со) Xi (со). (4.177)
Суммарный выходной сигнал во временной и частотной областях
определяется как
N N со
в(0=2 в(«)= 2 $ (4.178)
Y (ш) = 2 Yi (“) = 2 Hl (“) (о).
(4.179)
Этот раздел основан на работах [2, 3].
100
Предположим, что различные входные сигналы xt (I) являются вы-
деленными функциями различных стационарных случайных про-
цессов, имеющих средние значения т. е.
= (/)].
В этом случае среднее значение у определится как

(4.180)
(4.181)
Поскольку оператор математического ожидания Е показывает, что
усреднение производится только по времени уравнение (4.181)
можно переписать:
N со N со
ц„= 2 5 h,WElxi(l—Ч1^= 2 5 (4.182)
Поскольку для стационарного- во времени процесса является по-
стоянной, ее можно вынести за знак интеграла:
р®=21ч $ л<(А.)<а.
(4.183)
Видно, что если каждое среднее значение щ равно нулю, то среднее
значение выходного сигнала ру также равно нулю. В этом разделе
далее предполагается, что все средние значения равны нулю.
101
Автокорреляционная функция. Автокорреляционная функция
может быть рассчитана также и для стационарного во времени про-
цесса по формуле:
'Р,,,,(т) = Е [у (/) у (/ -К)1 =
= Е [2 yt (t) 2 ук(t +?)] . (4.184)
где i и k — индексы двух различных суммирований. Подстановка
уравнения (4.176) в (4.184) приводит к выражению:
[N N со
X $ МВ +*-1)^1- (4.185)
Поскольку усреднение проводится только по временной переменной,
уравнение (4.185) можно преобразовать к виду:
<Piw(t)=2 2 К й^)М£)£-Ка-*.)л'Ж+т—E)]dXd£=
f=I Л=1
--00
N N со
= 2 2 (4.186)
t=i 22^
где <p£ft (т) определяется как
<fih (т) = 'Г.,; (Т) = £ [X; (0 хк (Z + т)], (4.187)
Выражение для автокорреляционной функции выходного сигнала,
описываемого уравнением (4.186), является общим и применимо для
коррелированных входных сигналов. Если предположить, что сред-
ние значения всех входных сигналов равны нулю и сигналы взаимно
не коррелируют, то
Ч’,л(т) = <Гн(т), (<=й);
<Ргл(т) —0, (i#=A). (4.188)
и уравнение (4.186) может быть упрощено:
N оо —
Ч>й,ГО = .2 (4.189)
Спектральная плотность мощности. Соотношения для спектраль-
ной плотности мощности системы с многоканальным входом могут
быть также получены из основных формул. Для стационарного во
102
времени процесса функция спектральной плотности мощности полу-
чается с помощью преобразования Фурье автокорреляционной функ-
ции, определяемой уравнением (4.186):
©„,» = $ ег-,И1 [.2 2 Ц Л;^)Аь(Е)-<Р,„(^-Е+т)^^1 dx.
(4.190)
Подставив в уравнение (4.190) тождество
ехр [—jw (Ь—£)1 ехр [ -j- jo(Ь-£)] = 1, (4.191)
изменив порядок интегрирования и суммирования и введя
замену переменной
Н = Ь~Е4-т, (4.192)
можно получить, что
©и» =2 2 л„©х
z=ife=i_Jo J
Xe^MdfC ф№(р.)е-^41= 2 2 Я? (и) Я,» Фо», (4.193)
J ё=1 fe=i
—оо
где (а) представляет функцию взаимной спектральной плот-
ности между входными сигналами хг- (/) и xh (/), так как
Ф„» = ФЧ!Ч1 (<>). (4.194)
Кроме того, уравнение (4.193) справедливо для случая, когда вход-
ные сигналы не коррелируют. В этом случае, а также, когда все сред-
ние значения равны нулю, уравнение (4.193) может быть упрощено:
Фто И = 2 НЦи) Н, (со) Ф„ (и) = 2 IН, (0))|2 ф„ (со). (4.195)
f=l t=l
Взаимная корреляционная функция. Взаимная корреляция и
взаимные спектральные отношения системы, представленной на
рис. 4.18, могут быть получены таким же образом, как и автокорре-
ляция и спектральная плотность мощности в предыдущем пара-
графе. Взаимная корреляционная функция между выходным сиг-
налом у н любым входным сигналом xt (Z) определяется выражением:
4i„ = £(^i(/)y(M-'t)] =
= £
N <»
xt (t) S xk (t 4-T— hk ОТ db
ft=i J
103
= 2 h,,(/.')E[xi (/)х(1(<+т—X]dl =
A=l J
= 2 \ Лл(Х)<р(„(т—A)d7.,
A=4 J
(4.196)
которое справедливо для коррелированных входных сигналов. Если
входные сигналы взаимно не коррелируют и имеют средние значе-
ния, равные нулю, уравнение (4.196) переходит в равенство
^iy (т) — Л* (X) <рг-,- (т—1)
(4.197)
которое представляет свертку импульсной характеристики г-го
входного сигнала. Это значит, что, если входные сигналы некор-
релированы, взаимная корреляция между любым выбранным вход-
ным сигналом и выходным сигналом будет такой же, как если бы
данный входной сигнал был единственным в системе.
Взаимная спектральная плотность. Вывод выражения для вза-
имной спектральной плотности аналогичен выводу соотношений для
спектральной плотности мощности. Взаимная спектральная плот-
ность между любым входным сигналом xt и выходным сигналом у
находится с помощью преобразования Фурье взаимной корреля-
ционной функции, определяемой уравнением (4.196), т. е.
ф1»(“)= § § МЧ<Рн.(*—l.)dzj tfr =
N <x>
= 2 Ц (44><i.(T—^e-'^dldr. (4.198)
Введя замену' переменной
р. = т —1 (4.199)
и перегруппировав члены, получим
фгЛ“)=2 ? ? <р№ (р) е-dp =
A=I
= 2 Нк(а)Ф1к(^, (4.200)
А=1
которое справедливо для коррелируемых входных сигналов. Если
входные сигналы не коррелируют и имеют средние значения, рав-
ные нулю, уравнение (4.200) можно упростить:
фг,(и) = //г(<0)Ф„(<0). (4.201)
104
Зависимости, определяемые уравнениями (4.197) и (4.201), озна-
чают, что, если входные сигналы являются взаимно независимыми,
взаимная корреляция и взаимная спектральная плотность между
данным входным сигналом и выходным сигналом определяются точ-
но так же, как если бы все другие входные сигналы были бы равны
нулю.
В математическом смысле, однако, как будет показано ниже,
наличие других входных сигналов, так же как и присутствие посто-
роннего шума, приводит к интерференции при измерении передаточ-
ной функции Hi (со). В результате этой интерференции уменьшается
точность измерений.
Рис. 4.19. Структурная схема системы с двумя вхо-
дами.
Частный случай системы с двумя входными сигналами. Линей-
ные системы с двумя входами .очень часто используются в практи-
ческих случаях и являются удачной иллюстрацией соотношений,
полученных в предыдущих параграфах. Рассмотрим систему с двумя
входами, представленную на рис. 4.19. Если применительно к этой
системе переписать уравнение (4.200), то получим
(ю) — Hi (^ОФи (со) + Н2 (со) Ф12 (со) (4.202)
и
Ф2у (со) = Нх (со) Ф21 (со) + Н2 (со) Ф22 (со). (4.203)
Если исключить случай, когда и х2 заведомо коррелируют (т. е.
когда существует функциональная зависимость между лу и х2), то
можно решить уравнения (4.202) и (4.203) относительно Нг (со)
иЯ2(со):
^1(“)=Ф1Л“)ГX
" L ®22 (со) Ф1В (со) ] /
х Г j _ ®iz (ю) ®2i (со)~1
L Фи (со) Фгг (со) J
Я2(со) = Фад
(со) Г1 — - м (со) Фцс(т)] / ф . (со) X
1 4 ®„(co)®2„(co)J/ 22(}

___®21 (СО) Ф12 (со)1
Фц (о) Фгг (со)].
(4.204)
(4.205)
105
Для случая, когда корреляции между лу и хг нет и оба средних зна-
чения равны нулю, эти уравнения сводятся к обычным соотноше-
ниям:
(и) = Ф1„ (о)/Фи (to) (4.206)
и
Н2 (<о) - Ф2„ (со)/Ф22 (со), (4.207)
что и показывает уравнение (4.201).
Для случая, когда между входными переменными и х2 суще-
ствует определенная связь, как показано на рис. 4.20, рассмотрим
функциональную зависимость вида:
ха (£) = J А3 (&) (jf—X) dX,
(4.208)
т. е. хт и х2 являются, соответственно, входным и выходным сигна-
лами системы, имеющей передаточную функцию Я8(со). Это просто
означает, что хг в действительности приходит двумя путями к вы-
ходному сигналу у. Единая передаточная функция Н (со), устанав-
ливающая связъ выходного сигнала с входным, имеет вид:
Н (со) == Нг (со) 4- Нъ («) Н3 (со). (4.209)
Односторонние спектральные плотности. Хотя выражения для
многоканальных по входу линейных систем были получены с исполь-
зованием двусторонних спектральных плотностей Фгг (со) и (со),
их можно заменить физически реализуемыми односторонними спект-
ральными плотностями Ga (со) и Оц (со) соответственно, для поло-
жительных величин со сократив двойку как общий множитель. Сле-
довательно, уравнения (4.193) и (4.200) в общем случае, когда вход-
ные переменные могут быть коррелированными, имеют вид:
<to(“)=2j«(®№W«>) (4.210)
106
и
GiB(®)= 3 Hh(a)Gth(u>).
(4.211)
Для двух входных сигналов эти уравнения можно записать
следующим образом:
Gm И = Hi (га) Н2 (га) Сц (га) + Н* (га) Н2 (га) GIS (га) +
+Hl (га) Н2 (га) Си (га)+HI (га) Н2 (га) С22 (га); (4.212)
Gi„ И = (“) <?п (“) + Н2 (га) С12 (га); (4.213)
(a)=Ht (га) G21 (га)+Н2 (га) С2, (га). (4.214)
Последние два уравнения можно решить относительно передаточ-
ных функций /7х(со) и Н2(со):
И = Glv(га) Г1-^S-Ml / С11 (га) X
L 022 (СО) о1у (СО) J /
хГ1_О12(й)О21(га)-| (4.215)
L 312 (со) G22 (со) J
И
Н2 (га) = GZy (га) Г14^’1 / Gu (га) X
L о u ((0) U2y (СО) J /
хГ1_С12(га)С21(га)1 (4.216)
L Gii(«)G22(ra)J '
В случае, если между двумя входными сигналами нет корреляции
и оба средних значения равны нулю, уравнения (4.215) и (4.216)
принимают вид:
Hi (со) = GltJ (co)/Gu (со) (4.217)
и
Н2 (со) = G2!/ (<o)/G29 (со). (4.218)
Для линейной системы с двумя входами, когда входные сигналы
могут быть коррелированными, может быть получена обычная коге-
рентная функция:
V?» = IG1V (ra)|2/Gu (го) Gm (га), (4.219)
где G,,, (га) и GI(i, (га) определяются уравнениями (4.213) и (4.212)
соответственно. Подобное выражение может быть найдено для
?2i/ («•) путем замены индекса 1 на 2 в уравнении (4.219). В особом
случае, когда входные переменные (I) и х2 (f) имеют нулевые
средние значения и не коррелируют, т. е.
G12 (cd) = G21 (cd). = 0,- (4.220)
107
уравнение (4.219) перепишется в виде:
(“) = I Hi WF Он (®)/| Я, « Gu (<>) +1 Hs (< Ga3 (Ю). (4.221)
Подобным образом
yly (со) = I Н2 (со)|2 G22 (со)/| « Gu (со) +1Н2 (со)|2 G3S (со). (4.222)
Сложение уравнений (4.221) и (4.222) дает
(4.223)
что указывает на то, что каждая из этих когерентных функций долж-
на быть меньше единицы, если другая не равна нулю.
Условные спектры. Сравнение уравнений (4,2.15) — (4.218)
показывает, что выражение в квадратных скобках уравнений (4.215)
и (4.216) представляют собой поправочные коэффициенты, которые
необходимо учитывать, если имеется некоторая корреляция между
двумя входными сигналами. Кроме того, очевидно, что знаменатели
этих коэффициентов одинаковы и равны:
Гj_ 012 (и) 021 (Ш)1 = Г[---IGiztrn)!8 1 _ 2 (ю)] (4.224)
L 0ц (со) G22 (со) J I 0ц (со) 02Е (co)J
где 712 (со) — обычная когерентная функция. Числители и знамена-
тели (4.215) и (4.216), представляющие спектральные плотности
и поправочные коэффициенты, являются условными спектрами
(иногда называемыми остаточными спектрами), т. е. числитель урав-
нения (4.215) представляет взаимную спектральную плотность
между переменными х2 (/) и у (/) при условии исключения влияния
переменной х2 (/) на у (/). Общепринятое обозначение для такого
условного спектра Gly_2 (со). Подобным образом знаменатель этого
уравнения представляет спектральную плотность мощности хх (/)
при условии исключения влияния переменной х2 (/). Она обозна-
чается как Gu_3 (со). Следовательно, уравнения (4.215) и (4.216)
могут быть записаны следующим образом:
Н.(ц>)= (4.225)
Сц.г(Ю)
И
Я, (<>) = . (4.226)
C22.1 (СО)
Парциальные когерентные функции. Для многоканальной по
входу системы с коррелированными входными сигналами обычная
когерентная функция не является показателем качества измерения,
так как корреляция между любыми двумя входными сигналами вли?
яет (уменьшает или увеличивает, в зависимости от конкретной си-
туации) на обычную когерентную функцию между одним из входных
108
сигналов и выходным сигналом. Следовательно, необходимо опре-
делить парциальную когерентную функцию через условный спектр.
По аналогии парциальная когерентная функция между г-м
входным сигналом (t) и выходным сигналом у (Z) после исключе-
ния влияния k-ro входного сигнала определяется как
Уи.к (го) = (и) б,,,.;, (го)/6,(.„ (го) X
X 6^.,, (ш) = | GiBjl (го)|г/С,7.„ (ш) 6п.к (го). (4.227)
Поскольку ytv.k (со) является когерентной функцией, она удовлет-
воряет неравенству
(4.228)
Величина (®) интерпретируется как когерентная функция
между (/) и разностью, получаемой вычитанием из у (/) предска-
зываемого вклада xk (/), полученного с помощью метода наимень-
ших квадратов. Парциальный коэффициент корреляции в класси-
ческой статистике интерпретируется как коэффициент корреляции
между двумя переменными, когда влияние третьей переменной ис-
ключено и ложные корреляции подавлены. Энохсои [2] отметил, что
аналогичная интерпретация применима к парциальным когерент-
ным функциям. Обычно высокая когерентность между двумя про-
цессами указывает на линейную связь по каналу вход — выход
между двумя процессами, но в действительности это может быть
ложным выводом вследствие корреляции выбранной входной пере-
менной с другой входной переменной. Если парциальная когерент-
ная функция рассчитывается, то часто наиболее близкой к действи-
тельности оказывается меньшая величина.
Может иметь место и противоположный эффект, когда два раз-
ветвленных входных сигнала проходят через линейные системы и
суммируются для получения одного выходного сигнала, как это
показано на рис. 4.20. При этом вследствие линейных зависимостей
парциальная когерентная функция между любым входным сигналом
и выходным сигналом должна быть равна единице, но обычно коге-
рентная функция получается меньше единицы. Причина этого в
том, что каждый входной сигнал дает вклад в выходной сигнал, а
это не учитывается в расчете обычной когерентной функции между
выходным сигналом и отдельным входным сигналом.
Входной сигнал, наиболее сильно влияющий на выходной, будет
иметь большую когерентность с выходным сигналом. В случае кор-
релированных входных сигналов не существует столь большого раз-
личия, как в случае некоррелированных входных сигналов, и урав-
нение (4.223) неприменимо. Этого и следовало ожидать, поскольку
существует относительно большая корреляция между двумя вход-
ными сигналами. Основная когерентная функция может оказаться
большей, чем она должна быть из-за того, что, даже если нет ли-
нейной зависимости между одним иэ рассматриваемых входных
109
сигналов и выходным сигналом, второй вход/юй сигнал, который мо-
жет быть существенно коррелированным с первым входным сигналом,
может линейно влиять на выходной сигнал. В этом случае парци-
альная когерентная функция должна быть много меньше, чем обыч-
ная когерентная функция.
СПИСОК ЛИТЕРАТУРЫ
1. Bendat J. S. Principles and Applications of Random Noise Theory. John
Willey and Sons, Inc., N. Y., 1958. (См. Бендат Дж. Основы теории слу-
чайных шумов и ее применение. Пер. с англ. М., «Наука», 1965.)
2. Enochson L. D. Frequency Response Fnnctions and Coherence Functions for
Multiple Input Linear Systems. — Report NASA-CR-32, April 1964.
3. Bendat J. S., Pierso! A. G. Measurement and Analysis of Random Data. —
John Wiley and Sons, Inc., N. Y., 1966. (См. Бендат Дж., Пирсол А. Изме-
рение н анализ случайных процессов. Изд. 2-е. Пер. с англ. М., «Мнр»,
1974.)
ГЛАВА 5.
ЭЛЕМЕНТАРНАЯ
ТЕОРИЯ
РЕАКТОРНЫХ
ШУМОВ
§5.1. Введение
В третьей главе были рассмотрены вопросы детектирования нейт-
ронов от нейтронных цепочек, которые и определяют число нейтро-
нов в ядерной системе. Рассматривая регистрацию отдельных нейт-
ронов как непрерывный процесс, о флуктуации числа нейтронов
в процессе регистрации мы судим по флуктуациям тока детектора
или выходного напряжения ннтенсиметра. Рассмотрим теперь эти
флуктуации выходного тока или напряжения как случайный про-
цесс с помощью методик, описанных в четвертой главе.
§ 5.2. Источник эквивалентного шума*
В большинстве работ по физике реакторов нейтроны трактуются
как непрерывная среда, в то время как они являются дискретными
частицами. Дискретность нейтронов и статистическая природа цеп-
ной реакции приводят к случайным флуктуациям числа нейтронов,
которые называются шумом реактора.
Шум реактора можно представить как результат действия слу-
чайного нейтронного источника эквивалентного шума, помещаемого
в реактор, который создает флуктуации числа нейтронов в реакто-
ре вследствие естественных статистических флуктуаций скорости
деления и поглощения нейтронов. В любой момент этот источник мо-
жет быть либо положительным, либо отрицательным, обусловливая
соответственно избыток или дефицит по отношению к среднему зна-
чению. Характеристики источника можно легко рассчитать с по-
мощью обычной теории случайных шумов, а затем провести измере-
ние результирующего реакторного шума с использованием пере-
даточной функции источника.
Для упрощения расчетов предположим, что флуктуации числа
нейтронов в реакторе по отношению к среднему малы и что доля за-
паздывающих нейтронов р пренебрежимо мала по сравнению с еди-
ницей. Генерация, поглощение и утечка нейтронов в реакторе могут
* Понятое нейтронного источника, эквивалентного шуму, было впервые
введено Коэном [1]. • '
111
быть рассмотрены через их время жизни, по аналогии со случайным,
потоком электронов в диоде, идущих от эмиттера к коллектору. По-
скольку все эти процессы подчиняются распределению Пуассона,
мощность источника эквивалентного шума может быть определена
из формулы Шоткн [2], которая первоначально была получена для
описания шума в электронном диоде с ограниченной температурой.
Обычно она записывается так:
Gn (о) = < | /12 > = 2е3ш, (5.1)
где G// (<о)—спектральная плотность мощности шумового тока диода,
а2-сек; е-—заряд электрона, k; т — среднее число электронов, про-
текающих в секунду.
Аналогичная формула для расчета нейтронного источника экви-
валентного шума имеет вид
G„ И = <| So |!> = 2 з й,-, (5.2)
i
где Gss (со) — спектральная плотность мощности источника экви-
валентного шума, нейтрон?/сек; qi-—дополнительное число нейтро-
нов, получаемое в результате единичной ядер ной реакции типа i;
— среднее число реакций типа i, происходящих в реакторе в се-
кунду. Суммирование проводится по всевозможным типам ядерных
реакций, которые могут происходить в реакторе. Отметим, что спект-
ральная плотность мощности источника эквивалентного шума пред-
полагается независимой от частоты и, значит, шум источника являет-
ся белым. Это предположение справедливо вплоть до частот порядка
обратной величины времени жизни возбужденного ядра, которое
составляет менее чем 10-20сек при условии, если не рассматриваются
запаздывающие нейтроны. Среднее время запаздывания i-й группы
запаздывающих нейтронов составляет 1/Х^ и представляет собой
критерий, который может сделать несправедливым предположение
белого шума для запаздывающих нейтронов Однако на практике
несоответствие, возникающее при использовании этого предположе-
ния, как было показано Шеффом и Альбрехтом 13], приводит к по-
явлению малых членов, имеющих значение порядка р по отношению
к основному результату. Таким образом, значение поправочных чле-
нов настолько мало, что имн почти всегда можно пренебречь [41.
В настоящей главе теория реакторных шумов рассматривается
на основе одногрупповой модели реактора с сосредоточенными па-
раметрами. В табл. 5.1 перечисляются конкретные реакции, обус-
ловливающие существование источника эквивалентного шума. Рас-
сматриваются только реакции непродуктивного поглощения, деле-
ния и утечка. Дополнительные реакции (включающие генерацию
и распад предшественников запаздывающих нейтронов), дают вклад,
измеряемый долями р, т. е. меньше, чем другие реакции, и поэтому
не учитываются. Принятые здесь обозначения следующие: А —
полное макроскопическое сечение непродуктивного поглощения,
112
включая и утечку; F — макроскопическое сечение деления; п —
полное- число нейтронов в реакторе; I — время жизни мгновенных
нейтронов.
Таблица 5.1
Составляющие источника реакторного шума [1]
Характер процесса Средняя скорость протекания процесса Полное число производимых нейтронов в результате единичного процесса
Непродуктивное по- глощение, включая утеч- Деление, приводящее к образованию /V мгно- венных иептронов П А ~Т’ A+F 1 А + РР» — 1 N— 1
Величины F и А подчиняются условию критичности
vF/(A+F)= 1,
(5-3)
где *v — среднее число нейтронов (как мгновенных, так и запазды-
вающих), получаемых на деление. есть вероятность того, что при
делении будет получено 7V мгновенных нейтронов, и подчиняется
следующим условиям:
2Р« = 1 (5.4)
и
2tfP„=(l—₽)v«v. (5.5)
Л=0
Подстановка величии из табл. 5.1 в уравнение (5.2) определяет
спектральную плотность мощности для источника эквивалентного
шума:
Gss (CD) = <| So |2> Г А + F 2 (TV— I)2 Р J . (5.6)
Используя равенства (5.3)—(5.5), получаем
где
Gss (о) = <1 «о |2>=~- , (5.7)
I V
Vs = £Л’%. (5.8)
Л'=1
113
Спектральная плотность мощности эквивалентных флуктуаций реак-
тивности находится из выражения:
6Рр (а>) = <| р Р> = ( -Т)2 <| S„ р>, (5.9)
поскольку малые флуктуации реактивности могут рассматриваться
как введение в критический реактор источника мощностью р/г/Л
нейтронов в секунду на такое время, пока результирующая флуктуа-
ция полного числа нейтронов п остается малой. Комбинация урав-
нений (5.7) и (5.9) дает выражение
Opp (<о)=<| Р |»г> = . (5.10)
п V
Поскольку шум реактора, чтобы быть изученным, должен фикси-
роваться, должен быть рассмотрен и процесс регистрации, которая
обычно ведется с помощью детектора (такого, как ионизационная
камера, которая, поглощая некоторое количество нейтронов в реак-
торе, выдает электрический сигнал). Будем считать, что этот детек-
тор собирает часть всех нейтронов, поглощаемых в реакторе. Сред-
ний ток, проходящий через камеру, будет определяться выраже-
нием
7=eQn/lt (5.11)
где Q — заряд, возникающий при поглощении нейтрона. На этот
установившийся ток будут налагаться флуктуирующие токи, кото-
рые образуются по двум причинам. Во-первых, флуктуации тока вы-
зываются шумовыми флуктуациями числа нейтронов реактора, воз-
действию которых и подвергается камера. Эти флуктуации описы-
ваются следующим образом:
G,p ,р «о) = <| 1Р (ю) |*> = <| п (Ю)Р > =
= -^ О„п («>) = -^ (Ю) | Н„ (ю) р =
где (со) — передаточная функция реактивности реактора. Во-
вторых, поскольку установившийся ток / в камере создается многи-
ми импульсами тока, образующимися при регистрации отдельных
нейтронов, то, вследствие статистического характера процесса ре-
гистрации, появляется компонента, имеющая характер белого шума.
Ее спектральная плотность может быть получена с помощью урав-
нения (5 1)
Ч = <3 4«> = 2<22еп//- (5.13)
114
Поскольку эти две компоненты шума в первом приближении
являются некоррелированными (если е 1), их просуммированные
спектральные плотности определяют шум полного тока иа выходе
камеры:
<| I (<> = <] 1Р (со) |2> +<] 1С(<о)р>. (5.14)
Следовательно,
С„(и) = <|/(со)|г> =
I In V
(5.15)
Передаточная функция реактивности критического на всех нейт-
ронах реактора без специального учета влияния запаздывающих
нейтронов определяется как
Нр(и)=^=—
Др (и) )ш + (₽/1)
и уравнение (5.15) принимает вид
G//(cd) = <]Z((d)P> =
2Q2 er? / s -v2—v\
I \ +со3/2+₽-3 ’ V J'
(5.16)
(5.17)
Таким образом, отношение реакторного шума к белому шуму на
выходе камеры зависит от эффективности камеры е.
Для того чтобы шум камеры не был ограничивающим фактором,
т. е. чтобы компонента-реакторного шума могла наблюдаться, эф-
фективность детектора е в частотной области, где детектор является
чувствительным, должна быть больше, чем со2/2 4- ₽2. Это означает,
что эффективность камеры должна быть порядка 5- 10_ъ (не менее).
Нет необходимости, чтобы эффективность камеры превышала это
требование во много раз, поскольку наличие члена со второй сте-
пенью очень быстро снижает вклад меньшей компоненты.
Тип спектра шума, описываемого уравнением (5.17), экспери-
ментально наблюдался на ряде реакторов [5]. Уравнение (5.17)
содержит полное описание шума реактора*. Оно точно эквивалент-
но выражениям, полученным в других работах 161, в которых ис-
пользовались другие, совершенно различные методы. Оно может
использоваться для объяснения появления шумов других типов
и статистических экспериментов на реакторах 17—91.
* Фактически описывает шум цепной реакции, включая процесс его
регистрации. — Прим. ред.
115.
§ 5.3. Метод Ланжевена — модель
с сосредоточенными параметрами
Переходя к рассмотрению уравнений кинетики реактора, следует
иметь в виду, что переменные и соотношения между переменными
являются стохастическими или случайными функциями времени.
Уравнения реактора с сосредоточенными параметрами могут быть
записаны в операторной форме:
+ = (5-18)
(D+MCiW = T-«(0 (*=1.2.........6), (5.19)
Л
где Л, pi и К} — рассматриваемые постоянные параметры и D — опе-
ратор производной по времени. Эти уравнения описывают кине-
тику идеального (без шумов) реактора при произвольном изме-
нении реактивности. Если реактивность поддерживать постоянной,
то не должно быть решений, которые имели бы характер шума.
Но это не согласуется с поведением реакторов, и, следовательно, эти
уравнения необходимо расширить для того, чтобы они учитывали
наблюдаемый шум.
Мур [11, 12] отметил, что эти параметры в действительности
являются усредненными по времени величинами, получаемыми при
макроскопических наблюдениях. Если, например, измеряются мгно-
венные значения X, то должен быть определен ряд значений ХЛ,
математическое ожидание которого является тем значением X, ко-
торое входит в уравнения (5.18) и (5.19).
Одно из наблюдаемых значений можно записать:
к (0 = (/), (5.20)
где 6 X,- (Z) — случайная флуктуация, имеющая нулевое математи-
ческое ожидание, т. е.
Е [6Хг (/)] = 0, (5.21)
откуда
Е (/)] = X. (5.22)
Поэтому равенства (5.18) и (5.19) можно рассматривать как форму
записи математического ожидания другого ряда дифференциальных
уравнений, которые могут быть названы макростохастическими
уравнениями системы. Параметры в уравнениях (5.18) и (5.19) яв-
ляются математическими ожиданиями стохастических параметров,
а переменные — математическими ожиданиями стохастических пе-
ременных.
Прежде чем перейти к макростохастическим уравнениям, уста-
новим, какие именно из параметров в уравнениях (5.18) и (5.19)
стохастические. Рассмотрим невозмущенный реактор, описываемый
116
уравнениями (5.18) и (5.19) с одной группой запаздывающих нейт-
ронов. В этом случае эти уравнения перейдут в равенства:
О+-^₽),1(/) = Хс(/),
(£>+%) с (/) = -£-«».
Л
(5.23)
(5.24)
агогорые можно привести к виду
[О2+ £>(-£=£ 4-Х) + ^р1(/) = 0. (5.25)
Можно показать, что для того, чтобы система имела стационарно-
эргодический шум (который для наших целей является типичным
щумом, представляющим интерес), достаточным условием является
неинвариантность оператора, определяющего систему, по отноше-
нию к изменению хода времени [12]. Оператор в уравнении (5.25)
удовлетворяет этому требованию. Кроме того, можно также показать,
что, если имеются стохастические параметры, которые создают ста-
ционарный шум, они не могут быть фундаментально связаны с
производными высшего порядка в системе, определяющей оператор.
Это рассмотрение наводит на мысль, что для того, чтобы найти пара-
метры, достаточные для создания стационарно-эргодического шума,
необходимо, рассмотрев только уравнение (5.25), определить, ка-
кие параметры при исключении из системы оставляют результирую-
щее уравнение инвариантным к изменению времени. Это удовлетво-
ряется при условии, что производная высшего порядка системы
остается в результирующем инвариантном уравнении. Такое рас-
смотрение показывает, что исключение параметров X и р/Л приводит
уравнение (5.25) к виду
{П2)/г (/) = 0, (5.26)
в котором сохранился оператор D2 и которое инвариантно к измене-
нию хода времени. Следует подчеркнуть, что эти аргументы лишь
устанавливают достаточный ряд стохастических параметров и дают
максимум того, что можно ожидать от макроскопической теории.
Микроскопическая стохастическая теория кинетики реактора, хотя
и является очень сложной, определяет необходимые и достаточные
параметры и их средиеквадратические значения. Этн последние
определяют относительный вклад каждого источника шума в сум-
марный шум. Рассмотрим параметры X н р/Л, представленные
в общем случае в виде
X (/) = 4- М (0 (5.27)
и
= <5-28)
Л \ Л /о Л
117
Подставив эти соотношения в уравнения (5.23) и (5.24) и выде-
лив изменяющиеся члены, получим:
''w [D+(“д Vi]+1-Л] с w=
=[-4 й]вй+|6?- (/>] с <5-29>
L л j
«(О [-(тф]+ ID + Х«1сW= I67- ю]«(0+1—6А(Z)]с(Z), (5.30).
где выражения в правых частях уравнений (5.29) и (5.30) представ-
ляет собой макростохастические возмущающие функции реактор-
ной системы. Прибегнув к вычислению математического ожидания
величин, уравнения (5.29) и (5.30) можно свести к уравнениям (5.23}
и (5.24), если
£[— б-L (Z)n(z) + 6Xft) с (/)] = 0, (5.31).
т. е. если математические ожидания макростохастических возмуща-
ющих функций в уравнениях (5.29) и (5.30) равны нулю. Как отме-
тил Мур [12], р, Л и К могут считаться флуктуирующими при рас-
смотрении, ограниченном только макроскопическими условиямиу
тогда как п (Z) и с (/) являются функциями, ограничиваемыми микро-
скопической системой, и средние значения результатов умножения
6Х (Z) и б [₽/Л (/)] на п (/) и с (/) должны быть исчезающе малы. Сле-
довательно, уравнение (5.31) удовлетворяется.
Уравнения (5.29) и (5.30) могут быть названы уравнениями Лан-
жёвена, поскольку операторы в квадратных скобках уравнений
(5.29) и (5.30) являются функциями дифференциального оператора
одной переменной.
В рассматриваемом примере реактор был «невозмущен», т. е.
флуктуации реактивности и мощности нейтронного источника были
запрещены. Во многих реакторах такие флуктуации очень сущест-
венны и иногда полностью определяют динамическое поведение ре-
акторной системы. Часто флуктуации реактивности в энергетическом
реакторе зависят от уровня мощности. Флуктуации мощности источ-
ника могут быть обусловлены присутствием постороннего источника
(либо искусственных источников, таких, как Ри — Be, Sb —- Be,
Ra — Be и т. д., либо нейтронных генераторов ускорительного типа)
или внутреннего источника (спонтанное деление горючего, реакции
(у, п) на замедлителе). За исключением случаев применения нейтрон-
ного генератора и перемещения регулирующих устройств, статисти-
ческие характеристики (включая спектральную плотность мощности)
входных флуктуаций либо в мощности источника, либо в реактнв-
118
пости не могут быть проконтролированы. Точнее, эти характерис-
тики зависят от природы рассматриваемых процессов. Часто для
таких входных флуктуаций принимается предположение об их белом
спектре, но такое предположение должно быть обосновано.
§ 5.4. Пространственно-зависимый
реакторный шум*
Общая теоретическая модель. Теория пространственно-зависи-
мых стохастических флуктуаций, разработанная Шеффом и Аль-
брехтом [3,4], является достаточно общей, так что к конкретной мо-
дели реактора может быть применен любой подход, в котором на-
ходится соответствующая функция Грина для уравнения средней
нейтронной плотности рассматриваемой системы. Здесь использует-
ся приближение, основанное на методе Ланжевеиа, целью которо-
го в первую очередь является получение взаимной корреляционной
функции нейтронной плотности или вообще выходного сигнала в за-
висимости от корреляционной функции входного сигнала и системы
функций Грина для рассматриваемого уравнения. Эта процедура
затем обобщается для того, чтобы установить корреляционные
функции скорости счета в точке. Функции спектральной плотности
получаются с помощью преобразования Фурье, либо результирую-
щей корреляционной функции, либо основного уравнения. Это дает
возможность получить взаимную корреляционную функцию как
результат двойной свертки по двум функциям Грина и корреля-
ционную функцию эквивалентных «источников шума», находящихся
в системе. Свойство этих источников шума довольно детально ис-
следовано, чтобы можно было выявить основные физические взаимо-
связи, необходимые для получения расчетного метода н конкретных
формул.
Модель, используемая для расчета взаимной и автокорреляцион-
ных функций, основывается иа функции Грина или весовой функции
решения линейной системы. Хорошо известно, что-плотность нейт-
ронов может быть получена при помощи интеграла свертки, если из-
вестно распределение источников и функция Грииа. Теперь пред-
положим, что источник или входной сигнал флуктуирует стохасти-
ческим образом. Тогда нейтронная плотность или выходной сигнал
также имеет стохастические флуктуации. Физический смысл члена
флуктуирующего источника или входного сигнала может быть полу-
чен путем обобщения метода Ланжевена, данного Муром [12]. По-
скольку свертка включает интегрирование, выходной сигнал систе-
мы является менее случайным, чем входной, из-за «сглаживания»,
производимого при интегрировании. С точки зреиня физики процес-
са, флуктуации во входном сигнале зависят от характерных длин
и времен, связанных с индивидуальными столкновениями, в то вре-
мя как пространственное и временное изменение выходного сигнала
* § 5.4'— 5.7 представляют обзор работ [3, 4].
119
должно оставаться значительно более медленным, чтобы гаранти-
ровать применимость приближения о непрерывной плотности нейт-
ронов. Свертка включает интегрирование как по объему, так и по
времени и имеет вид:
У (г, I) = 55 h (г', г, т) х (г', t —т) d3 г', dr,
(5.32)
где h (г', г, т) — функция Грина. Как у (г, /), так и х (г, t) флук-
туируют и связаны друг с другом выражением
У (г, /) = х (г,/)/Г (г, Z),
(5.33)
где Г (г, £) — дифференциальный оператор:
Г (г, t) — + Dr -}-a2 + Dr Ч-... Ч-СоЧ-Cj Dt 4-c2 Dt 4-... (5.34)
Когда оператор Г (г, £) является функцией дифференциальных опера-
торов одной переменной, уравнение (5.33) называется уравнением
Ланжевеиа.
Уравнения кинетики реактора, включающие временные и про-
странственные эффекты, для средних значений (средний входной
сигнал равен нулю) записываются в следующем виде:
Г (г, t)y(r, /) = 0,
(5.35)
но коэффициенты с0, а1г аъ ... и с0, с2 ... в операторе представляют
средние значения величин, которые в действительности флуктуи-
руют стохастическим образом, т. е.
°2(0 = лг4-6аг(0,
аг(г) = ... н т. д.
Ci(i) = ci+ &!(«),
с2(/) = сг+&г(С,
сг (/) = ... и т. д.
(5.36)
(5.37)
а. Взаимная корреляционная функция нейтронной плотности.
Проведем конкретный расчет взаимной корреляционной функции
нейтронной плотности для двух точех гх и г2 и двух моментов вре-
мени 4 и /2. Рассмотрим произведение
!/1(Г1, /1)!/2(г2, /2)= 5 5Mr;. ri, Ti)dsr;dT1 5 $ r2. т2) X
X J.'i(r;, t—t—т2)сРг^т2.
(5.38)
120
Уравнение (5.38) усредняется по ансамблю сигналов или, в пред-
положении эргодичности процесса, по времени. Взаимная корреля-
ционная функция выходного сигнала определяется как
4>л».(гт. г2, т) = lim -L. (У1(г„ /1)1/..(r2, tI+r)dtt, (5.39)
T— ОЭ 21 J
где сделана подстановка + т. Взаимная корреляционная
функция входного сигнала выражается подобным же образом. При
таких определениях усреднение по времени уравнения (5.38) дает
взаимную корреляционную функцию выходного сигнала для левой
части уравнения (5.38). Изменяя порядок интегрирования, легко
показать, что правая часть содержит взаимную корреляционную
функцию входного сигнала. Результатом этого является:
<Рйй(Г1. r2, Т) ft(rj, r„TjJcPrJdTi^ J h(r'2, r2, r2) x
Or' Or'
1 1 2
Xtpi.zjr;, rJ.-t+tj—T2)d3r'dT2. (5.40)
Уравнение (5.40) является общим, поскольку еще не ограничивается
физическими условиями, которые будут введены в дальнейшем. Од-
иако прежде чем получить нужные результаты на основании уравне-
ния (5.40), необходимо знать корреляционную функцию входного
сигнала. Часто ее значение не бывает точно известно, но точно из-
вестно ее значение при т = 0. В этом случае чаще всего предпола-
гается, что она соответствует белому шуму, т. е. корреляция вход-
ного сигнала принимается пропорциональной дельта-функции Дира-
ка. Это предположение ограничивает обоснованность (достоверность)
корреляционной функции выходного сигнала значительно больше
по сравнению с действительной «шириной» пика корреляционной
функции входного сигнала. Часто предположение о белом шуме
делается тогда, когда известна автокорреляционная функция вход-
ного сигнала и когда его использование оправдывается упрощением
решения и соответствующими требованиями для получения резуль-
тата. Взаимная корреляционная функция входного сигнала, имею-
щего характер белого шума, в общем случае описывается следую-
щим образом:
<₽«,*>(G, г;, t+tj—т2)=л(г;)б(г;—т2). (5.41)
-Уравнение (5.41) указывает на то, что корреляция существует толь-
ко для идентичных точек по объему и при т == т2 — Часто велн-
121
чина корреляции является функцией пространственных перемен-
ных. Подстановка уравнения (5.41) в (5.40) дает:
fa» г3»т) =
= h (г', гъ -г) h (г’, Го, tH-Tj) А (г') d3 г' dxlt (5.42)
* Ч
где £ «== 0, если т положительно, и £ ~ [г], если оно отрицательно.
Эти ограничения вызваны тем, что функция Грина при отрицатель-
ном аргументе равна нулю. Автокорреляционная функция получит-
ся приравниванием гх — г2.
Поскольку фактически показано, что флуктуирующий член
в уравнении (5.35) имеет среднее значение, равное нулю, то это за-
ключение содержит в себе предположение, что процесс накладывает-
ся на среднюю нейтронную плотность. Таким образом, автокорре-
ляционная функция содержит подлежащий вычитанию квадрат сред-
него значения, а взаимная корреляционная функция •— подлежащее
вычитанию произведение двух средних значений. Более правильно
эти функции называть авто- и взаимными ковариационными функ-
циями .
б. Функция взаимной спектральной плотности. Важно рассмот-
реть и другую форму уравнения (5.42) в зависимости от функций
взаимной спектральной плотности, поскольку этот результат в неко-
торых случаях будет более удобен. Коэффициент во взаимной корре-
ляционной функции белого шума А (г) так же, как и обоснование
и ограничения, связанные с предположением белого шума, может
быть более легко получен при изучении поведения функции спект-
ральной плотности.
Преобразование Фурье уравнения (5.40) приводит к следующему
СООТНОШеНИЮ ВХОДНОЙ (г[, Гд, со) и выходной ФУ1,Л 01, г2, со)
функций взаимной спектральной плотности:
ф»..й(г1. г2. “)= S #*(>;. Г1. j“)d3r; х
х 5 н (г;, г2> jco) фх, , х. (г;, г;,«), (5.43)
где Н (г{, г1, jbi) — частотная характеристика для единичного то-
чечного источника, расположенного в точке г{, которая получается
преобразованием Лапласа функции Грина с заменой s на Jco. По от-
ношению к переменной Лапласа s она является передаточной функ-
цией. Отметим, что по отношению к пространственным переменным
она остается функцией Грина и что она может быть также использо-
вана для получения передаточных функций для более сложных рас-
пределений источников. Звездочка указывает на комплексно, со-
пряженную переменную.
122
Преобразование Фурье взаимной корреляционной функции бело-
го шума, описываемой уравнением (5.41), приводит к выражению
Фх,», о-;, т;>=а «) 6 (г;—rj). (5.44)
Таким образом, функция взаимной спектральной плотности имеет
вид
Фи и. <Г1' Г2’ “) = S Д (Й. j “) W (Г1. г2- j И) А Ю d3 ri- (5-45)
’’1
-а функция спектральной плотности мощности
0^1 (гъ со) = IН (г', гъ j to) [2 А (г') d3 г], (5.46)
где \Н (rj, rlf j и |2 —квадрат модуля передаточной функции.
В частности, //(rj, гь s) является плотностью нейтронов в точке гх,
•определяемой передаточной функцией источника в точке г', т. е.
представляет собой отношение преобразования Лапласа плотности
нейтронов в точке гх к преобразованию Лапласа единичного
источника в точке г'. Отметим, что Н (г[, гх, s) является функцией
Грина по отношению к переменным гх и г'. _
в. Коэффициент A (гх) источника шума входного сигнала. Преж-
де чем применять уравнение- (5.42), нужно найти выражение для
А (гг). Это может быть сделано для одной из нескольких возможных
моделей, которые описывают реакторную систему. Использование
хорошо известной пространственно независимой модели, -включая
запаздывающие нейтроны, дает лишь приближенно правильные ре-
зультаты.-Неточность является прямым следствием предположения
о том, что источник шума имеет характер белого шума, ио в единицах
частоты погрешность незначительна из-за малого объема области
источника шума.
Выражение для А (rj выводится ниже с помощью обобщения
пространственно независимого метода, предложенного Коэном [1].
Величина А (гх) представляет собой входную или эквивалентную
спектральную плотность мощности источника на единицу объема
около точки гх. Как результат предположения о белом шуме оиа яв-
ляется постоянной по отношению к частоте со. Затем для вычисления
этого постоянного спектра используется формула Шотки [2]. Гово-
ря более точно, поскольку формула Шотки аппроксимирует реаль-
ный спектр его значением при нулевой частоте, приближение спра-
ведливо вплоть до частот порядка обратной величины среднего вре-
мени корреляции (т. е. среднего времени, в течение которого реаль-
ный процесс сильно коррелирован). Коэн отметил, что для простран-
ственно независимого случая это среднее время должно быть поряд-
ка времени, требуемого для перехода нейтрона из связанного в не-
связанное квантовое состояние, которое меньше, чем 10~-°сек. Такая
оценка полностью приемлема здесь..
123
Для расчета коэффициента источника шума пли, иначе, спект-
ральной плотности мощности реакторного источника эквивалент-
ного шума, формула Шотки записывается в следующем виде:
>1(г) = 39?т1,
(5-47}
где А (г) имеет размерность нейтрон2/(см3-сек); — полное число
нейтронов, образующихся при одной ядерной реакции типа t, —
среднее число реакций типа i, происходящих в кубическом санти-
метре. Неявно эта формула предполагает, что все реакции незави-
симы. Различные реакции, приравниваемые к эквивалентному ис-
точнику, приводятся в табл. 5.2. Здесь р (vp) — вероятность непус-
та б л в ц а 5.2
Отдельные составляющие для эквивалентного источника [3]
Характер процесса Средняя скорость протекания процесса Результирую- щее ЧИСЛО генерируемых нейтронов
Поглощение без деления Деление с выходом vp мгновенных нейтронов Распад предшественников t-го типа запаздывающих ней- тронов Нейтрон источника Полная утечка нз элемента объема около точки г [п (г)//] [S„,/£o] [п (г)//) [Sy/S„] р (vy) MCi S(r) [-£=/(] [V2n(rJ] —1 Vp—1 1 1 —1
кання при данном делении мгновенных нейтронов; —
макроскопическое сечение поглощения без деления; I — время
жизни теплового нейтрона, равное 1/п2с; остальные обозначения
имеют свой обычный смысл. Применение уравнения (5.47) к про-
цессам, перечисленным в табл. 5.2, приводит к следующему выра-
жению для Л (г):
л(г)=^ га. V (v,~ wp (v„)+ +
' L" vp J
+ V Z, сг + S (г) — V2 п (г). (5.48)
Поскольку система стационарна,
2 \ Ct (г) = 2 -у- « W = -у- п (г). (5.49)
124
где в зонах, в которых k = v ^f/^a равно нулю, с, (г), конечно, тоже
равны нулю и
Sp(vp)=l (5.50)
vp
и
3vpp(vp) = (l-₽)v. (5.51)
Необходимо найти выражение для среднего квадрата числа мгновен-
ных нейтронов, которое может быть получено несколькими путями.
Предположим на мгновение, что 0 — константа, а не средняя флук-
туирующая величина, т. е. 0 — условная вероятность того, что если
нейтрон испускается, то он с вероятностью 0 будет запаздывающим
нейтроном, а (1 — 0) — условная вероятность испускания мгновен-
ного нейтрона. Тогда
v? = (l — 0)7. (5.52)
Подставляя уравнения (5.49)—(5.52) в уравнение (5.48), по-
лучаем:
(Г)=-4й- [(1 - ₽) (^- 2 v)] +1 + *₽} +
+S(r)----И ^п(г) +
I I L 'V
+6/г+2Лр]+S(r) — ¥-у*п(г). (5.53}
Найдем также соотношение между п (г) и S (г) для подкритического,
случая, которое для несложного распределения источников является
очень простым. Например, для бесконечного гомогенного реактора:
с равномерным распределением источников средняя нейтронная
плотность связана с плотностью источника соотношением
п = S//6/2. (5.54)
В этом случае уравнение (5.53) имеет вид:
А=— 0(1 — Р)^^- + 2(^+А₽)1. (5.55}
*V J
Предположение о постоянстве 0 можно легко исключить, но сна-
чала надо оценить предположение о том, что источник шума имеет
характер белого шума. Использование предположения о белом шуме
в случае пространственно независимой модели, включая запазды-
вающие нейтроны, несколько не согласуется с тем, что было получено-
Беннетом и др. 113]. Различия имеют величину порядка 0. Действи-
тельно, величина несоответствия достаточно мала, так что этим почти
всегда- можно пренебречь.
125.
Приложение к скорости счета детектора. Для анализа результа-
тов экспериментальных измерений проведем некоторую модифика-
цию предшествующих результатов, связанных с нейтронной плот-
ностью. Скорость счета детектора определяется как
с (г, /) = и (AVSd)n (г, /),
(5.56)
где Sd — макроскопическое сечение детектирования. Это значение
является математическим пределом скорости счета, измеряемой на
интервале Г, когда Т -> 0. Исторически величина AVSd была заме-.
нена на bS^ или e0Sc, где е и е0 представляют эффективности детек-
тора (т. е. отношение числа отсчетов в детекторе либо к скорости де-
ления в единице объема, либо к скорости поглощения в единице
объема). Хотя флуктуации скорости счета пропорциональны флук-
туациям нейтронной плотности, если величина v (A VSd) постоянна,
из этого не следует, что автокорреляционная или взаимная корреля-
ционная функция скорости счета пропорциональна нейтронной
плотности. Это различие объясняется тем, что счетчик при детекти-
ровании нейтронов поглощает их. Таким образом, корреляция в ней-
тронной плотности, которая будет следствием присутствия одного
нейтрона в системе в начальный момент времени t и присутствия того
же нейтрона или дочернего в конечный момент времени £ + т, долж-
на быть исключена из корреляционной функции скорости счета. Од-
нако корреляция единичного нейтрона вносит вклад в автокорреля-
ционную функцию при т = 0 или в дисперсию скорости счета.
§ 5.5. Пространственно-зависимый шум
в бесконечной среде
Взаимная корреляция в бесконечной среде. Для получения взаим-
ной корреляционной функции нейтронной плотности между двумя
точками наблюдения гх и г2 в однородной гомогенной бесконечной
среде Шефф и Альбрехт [3,4] использовали функцию Грнна в общем
уравнении (5.42):
Г=- Т) =
= S S Г2> T-riaH(i\)d3ridTj. (5.57)
S г)
Сделав эту подстановку, отметив, что коэффициент входного шума
А — константа, и выполнив указанное интегрирование, получим
взаимную корреляционную функцию:
АЕ
ехр (—21 гг —
гЕ| 1 а£)| 14-11—2« (|-г|— 1 / £]гх—г2|
126
---д^ехр (21 г, — г.,| /ЛГ) х
X Г |~—,ат+ Е(Г1~^-+2|Г1—rJpTFll. (5.58)
L 2 I'd JJ
где
Е=1Щ* (5.59)
и u(t—а) является единичной ступенчатой функцией. Выражение
для автокорреляционной функции для выбранной точки наблю-
дения можно легко получить из уравнения (5.58), приравняв г2
к га:
=wrr(4- «i-о- <=»>
Подстановка значения константы А, определяемой уравнением
(5.55), в соотношения (5.58) и (5.60) дает взаимную-и автокорреля-
ционную функции соответственно для нейтронной плотности. Одна-
ко корреляционные функции скорости счета отличаются от корреля-
ционных функций нейтронной плотности, так как детектор при ре-
гистрации поглощает нейтрон. Поскольку измеряется именно ско-
рость счета, детекторная корреляция является наиболее интересной.
Шефф и Альбрехт [3,4] получили автокорреляционную функцию ско-
рости счета:
₽> (^)+
+2(6й+ед ДУ6(т)^ Г (-Ь, а|т| J. (5.61)
Детектор имеет объем ДУ, сечение Ed, среднюю скорость счета с —
= иДУЕдП. Следовательно, размерность корреляционной функции
скорости счета сак-2. Автокорреляционная функция, описываемая
уравнением (5.61), является пространственно-независимой, но она
существенно отличается от функции для модели реактора с сосредо-
точенными параметрами, которая представляет собой простую экспо-
ненту:
ф(т)р* = Д'ехр (—а|т|). (5.62)
Автокорреляционная функция в точке для бесконечного реактора
отличается от корреляции для реактора с сосредоточенными пара-
127
метрами из-за того, что все деления в точечном реакторе имеют рав-
ную вероятность регистрации, в то время как в системе конечных
размеров большую вероятность регистрации имеют деления, про-
исходящие ближе к детектору.
Существенное различие между корреляцией в точке для беско-
нечной среды и корреляционной функцией реактора с сосредоточен-
Рис. 5.L Сравнение пространственно-независимой
автокорреляционной функции и автокор-
реляционной функции скорости счета то-
чечного детектора, размещенного в бес-
конечном гомогенном реакторе [4];
----— —пространственно независимая, нор-
мированная, в критическом реакторе;
---- —реактор критический.
мымн параметрами показано на рнс. 5.1.Верхняя кривая соответст-
вует уравнению (5.62). Нижняя группа кривых соответствует урав-
нению (5.61) для нескольких значений подкритичности.
Взаимная корреляционная функция между двумя точечными де-
текторами в бесконечной среде зависит только от расстояния между
ними и времени корреляции Т. Взаимная корреляционная функция
скорости счета между двумя точками в бесконечном гомогенном реак-
-128
торе в одногрупповом приближении получается подстановкой коэф-
фициента источника шума входного сигнала в уравнение (5.58):
г3,г)=1^?[2(в/г+ед^г(-Ш,а|т|)6(т)6г1Г₽ +
-₽) ^ Г(--^1^-1-^ х
“v lri—Гг1 ]_\ \ £ //
х(^+[1-2и(1т1-^т)]х
х{( +
—ехр ~^aL l^1~rg| j Г |-Г,а|т[+-
'+-4^+Ш|ГГг| ]]} (563>
Уравнение (5.63) оценено, и результаты представлены на рис.5.2.
На графике показана взаимная корреляционная функция в зависи-
мости от времени корреляции т и от расстояния между точками в ка-
честве параметра в критической бесконечной системе. Как и следо-
вало ожидать, величина корреляции уменьшается прн удалении де-
текторов друг от друга. В этой модели взаимная корреляционная
функция при стремлении т к пулю стремится к конечному значению,
в то время как автокорреляционная функция становится беско-
нечной.
В области плато или близкой к плато взаимная корреляционная
функция скорости счета приближенно записывается:
со" (г г у)
фу. у. И1>Г2> Ч — Л " Л . ~
liJ~ 8jtL21Г1—гв | “V
exp^ ~V-x<|r,-r,|
(к/т)|/2
/(Г1—Гд)а
4L31 т |
X ехр [ —а | т |
/|Г1-Г2|а\
4Да [ т | /
(5.64)
L
Частный случай уравнения (5.64) при т — С был также получен
Нателсоном н др. 114]. Действительно, известно, что взаимная кор-
реляционная функция должна стремиться к нулю при т, стремящемся
к нулю, потому что время распространения нейтронов конечно.
В диффузионной теории этого результата не получается, так как
только в транспортной теории, как в приближении более высокого
порядка, по сравнению с диффузионной теорией, проявляется ко-
нечная скорость распространения нейтронов.
5 Зак. 576 129
Влияние подкритичности системы на взаимную корреляционную
функцию показано на рис. 5.3. Значение взаимной корреляции
уменьшается с уменьшением реактивности, как и следовало ожидать.
Три группы кривых представляют автокорреляционную функцию
Рис. 5.2. Зависимость взаимной корреляционной функ-
ции скорости счета двух точечных детекто-
ров, размещенных в бесконечном гомогенном
критическом реакторе, от расстояния между
детекторами [4]. (Числа у кривых означа-
ют расстояние между детекторами в диффу-
зионных длинах.)
критического реактора и взаимные корреляционные функции для
расстояний между детекторами в 4 и 10 длин диффузии.
Функции спектральной плотности мощности и взаимной спект-
ральной плотности в бесконечной среде. Функция взаимной спект-
ральной плотности получается из взаимной корреляционной функ-
ции с помощью преобразования Фурье. Преобразование Фурье
130
уравнения (5.58) дает следующее выражение для функции взаим-
ной спектральной плотности нейтронной мощности:
(г1* Г2» Ы) = д-Та! Г“
4лД2 I п—Г210)
X ехр(—[(°8+а>в)1 + а]}*/2 *n~Гг * ) X
Рис. 5.3. Влияние под критичности на взаимную
корреляцию скорости счета двух точеч-
ных детекторов, расположенных в беско-
нечном гомогенном критическом реакто-
ре [4J:
—-----— реактор критический; •—-—--------
реактор подкрнтический. (Первые числа у кри-
вых означают расстояние между детекторами
в диффузионных длинах.)
В пределе при ri = r3 уравнение (5.65) выражает функцию спек-
тральной плотности мощности:
5*
. . = (Л/21г)(/,2^)~3/2
[(a’+fifl'/' + a]1'2
(5.66)
131
Ф
&1 У1
С другой стороны, спектральная плотность мощности нейтронной
плотности получается подстановкой значения коэффициента источ-
ника шума входного сигнала из уравнения (5.55).
Функция взаимной спектральной плотности между двумя точка-
ми в бесконечной среде с учетом запаздывающих нейтронов была
Рис. 5.4. Сравнение функции спектральной
плотности мощности единичного то-
чечного детектора с функцией взаим-
ной спектральной плотности скорости
счета от двух точечных детекторов,
размещенных в бесконечном критиче-
ском реакторе [4]. (Числа у кривых
означают расстояние в диффузионных
длинах.)
получена Шеффом и Альбрехтом 14] путем обобщения уравнения
(5.65):
Г2,и)=^|£™..±=£х
Lraln—ra I V
х 11 х
X sin^/ -^-{[аа+<оЕ],/2 — а})17’ * Г1~Гг* j • (5.67)
На рис. 5.4 даны графики уравнения (5.67) для трех раз-
личных расстояний между детекторами (в диффузионных длинах).
Из рис. 5.4 видны следующие важные характеристики взаимной
спектральной плотности: 1) значение взаимной спектральной плот-
ности уменьшается с увеличением расстояния между детектора-
ми и 2) крутизна наклона при высоких частотах увеличивается
с ростом расстояния между детекторами.
132
§ 5.6. Влияние границ на корреляцию
Точечный детектор в бесконечной среде дает менее коррелирован-
ную функцию, чем бесконечный детектор в бесконечной среде. Если
детектор конечного объема поместить в бесконечную гомогенную
среду, автокорреляционная функция такого конечного детектора
(предполагается отсутствие возмущений) должна быть интегралом
взаимной корреляционной функции по объему детектора.
Такой расчет был выполнен Шеффом и Альбрехтом [4] для куби-
ческого детектора со стороной 2а. Результат для большей нагляд-
ности можно представить как результат для точечного детектора
плюс поправочные члены на конечный объем детектора. «Лучшее
приближение в этой области получается путем интегрирования
уравнения (5.64) по объему детектора:
4>м (т) ~ Г f -——т |ехр А
8jiL2 J J | rj—га [ ] \
V V I '
Val |rt—г2|
L
------------------------ехр Г — а | т | — г, d3 г2. (5.68)
1/- [ I . Z(ri-rzp-| Ч 11 4L2[t[ ] 7
1/11 Г|Т|- 4£*|-r| J J
На рис. 5.5 представлен график автокорреляционной функции
в бесконечной среде в зависимости от времени запаздывания т, где
объем детектора является параметром.
Зависимость, получаемая для идеального детектора конечных
размеров, ведет себя почти таким же образом, как и взаимная корре-
ляционная функция, но уменьшается с увеличением объема детек-
тора. Этот эффект вызывается усреднением, т. е. кррреляцноииая
функция идеального детектора конечных размеров является средним
по всем взаимным корреляциям внутри детектора. Сглаживание
кривых, являясь таким же общим эффектом, рассмотренным выше,
также указывает на то, что спектр прн преобразовании Фурье,
подобно взаимному спектру, должен быть более выраженным при
со = 0.
Расчеты по уравнению (5.68) были выполнены для идеального
невозмущающего детектора. Если детектор вносит возмущение, то
его эффективный объем должен приниматься большим, чем его фи-
зический объем, тогда можно ожидать, что результаты для точечного
реактора будут более соответствовать реальным возмущающим
детекторам.
Расчеты автокорреляционной и взаимной корреляционной функ-
ций в одномерной геометрии для реакторов, имеющих границу (та-
ких, как бесконечное полупространство и бесконечная пластина),
для точечных детекторов были выполнены Шеффом и Альбрехтом
[4]. Результаты показывают, что эффект приближения границы при-
водит к более белому спектру, что н наблюдалось экспериментально.
Вдали от границы для бесконечного полупространства спектр при-
133
ближается к спектру точечного детектора в бесконечной среде. В ог-
раниченных системах спектр меньше изменяется на осях симметрии,
но не становится даже приближенно подобным результату в точеч-
ном реакторе до тех пор, пока имеются все шесть границ параллеле-
пипеда (или их эквивалентов в других геометриях).
Рис. 5.5. Влияние размера детектора на автокорреля-
ционную функцию скорости счета в беско-
нечном гомогенном критическом реакторе
[4]. (Числа у кривых означают размер де-
тектора в диффузионных длинах.)
Детектор конечных размеров в бесконечной среде дает результа-
ты, которые приближаются к результатам для реактора с сосредото-
ченными параметрами. Результаты, полученные для ограниченной
среды, показывают, как и ожидалось, что автокорреляционная функ-
ция основной собственной функции даже для точечного детектора рав-
на результату, полученному для реактора с сосредоточенными пара-
метрами. Таким образом, рассмотрение детектора конечных размеров
134
б реакторе конечных размеров дает хорошее приближение к авто-
корреляционной функции реактора с сосредоточенными параметра-
ми. С другой стороны, расчеты Шеффа и Альбрехта [4] выявили про-
странственные эффекты, которые оказались более явно выраженны-
ми, в реальной системе реактора без отражателя. Одна нз причин
этого — использование функции Грина применительно к односко-
ростной диффузионной теории. Интуитивно можно ожидать, что
включение зависимостей от энергии, так же как и эффектов переноса,
должно привести к уменьшению влияния высших пространственных
гармоник в определении корреляционных функций и (или) функций
спектральной плотности.
§ 5.7. Пространственно-зависимый шум
в параллелепипеде без отражателя
Корреляционные функции. Взаимная корреляционная функция
в параллелепипеде без отражателя между двумя точками с коорди-
натами гх и г2 получается с помощью функции Грина в общем урав-
нении для взаимной корреляционной функции. Необходимо выбрать
распределение внешних источников нейтронов и найти соответст-
вующий коэффициент взаимной корреляции входного сигнала.
Наиболее интересной и реальной формой для выбора распреде-
ления источника и, следовательно, коэффициента источника входно-
го сигнала является распределение по критической собственной функ-
ции. Прн желании легко перейти к распределению точечных источ-
ников.
Результирующей взаимной корреляционной функцией скорости
счета для бесконечного времени запаздывания является выраже-
ние:
Фв. 1а(Г1. г2. г) =
ехр i 8*“г)
(г1>(гг) • Л в- (5-69)
2 abd О/гБь+ feghP
где
Л = [2 (6Й, + /г, ₽) 6г, г, 6 (г) + XLzZ I; (5.70)
h ] 4 v9 J
G — константы; 7?g (/-J и Rh(rz) — трехмерные собственные функ-
ции; g и h — индексы тройного суммирования; е' — отношение чис-
ла отсчетов в единице объема детектора к числу делений в единице
объема реактора при детекторах, размещенных в реакторе. Величина
эквивалентна отношению е/Д V, где ДV — объем детектора.
Функции спектральной плотности. Функция взаимной спектраль-
ной плотности в реакторе формы параллелепипеда без отражателя
легко получается с помощью преобразования Фурье уравнения(5.69).
135
Функция спектральной плотности мощности в таком реакторе яв-
ляется просто частным случаем при гх = г2. Действуя подобным об-
разом и затем включая влияние запаздывающих нейтронов в члены,
зависящие от частоты, получаем:
Фй /. (Гр W) с» М': v GE R* (г,) -ffli+MW. +
+ 2 SGB>’ У,) +
. “g (6ЛВ1>+ *г₽вь)/'С|.
+еТАу|1_]-и v_Pi_Pg=Zy -----------------------н
' ' —1 jcod-Xf] VS [а|+(7й“)2]
а« ' ah
“1+(W «iWh“)2
! V с8ьде(г1) ^h(ri)
gll
. (5.71)
'gh
Результат существенны?/! образом перегруппирован для того, что-
бы подчеркнуть тот факт, что он дает действительную величину
(т. е. корреляционная функция является симметричной относитель-
но т = 0). Первые две строчки спектральной плотности [см. урав-
нение (5.71)] независимы от частоты и соответствуют членам белого
шума в пространственно независимой функции спектральной плот-
ности. Основная составляющая (мода), т. е. член для g (g, т, р =
= 1, 1, 1), запишется как
Фв. (Гр И) - с„ ДУ G, RI (г,) X
1
«t + (Yi со)3
(5-72)
Величина в квадратных скобках идентична результату для про-
странственно независимого случая, исключая в', которое равно
& = VA№f = v£dnlv£fii (5.73)
и дает отношение отсчетов на единицу объема детектора к числу деле-
ний в единице объема. Определение, более часто используемое в про-
странственно независимой теории, представляет собой отношение
полного числа отсчетов в детекторе к полному числу делений в реак-
торе.
Очень интересный факт, появляющийся при численном решении
уравнения (5.71), состоит в том, что преобладание пространственно
независимой формы или главного члена ряда происходит не столько
из-за быстрой сходимости, сколько из-за значительного взаимного
сокращения членов более высокого порядка. Таким образом, в ку-
136
бическом реакторе без отражателя не наблюдается исчезновение
отдельных членов высокого порядка, а отклонение от основного чле-
на является результатом суммирования многих членов.
Поскольку функция спектральной плотности мощности обычно
более часто используется в измерениях реакторного шума, Шефф и
Альбрехт [3, 4] представили несколько графических расчетов в од-
носкоростном диффузионном приближении, чтобы проиллюстриро-
вать влияние изменения расположения детектора в критическом
10~' 1 10 10s 103 10ч
Частота cj, рад[сек
Рис. 5.6. Сравнение функций спектральной плотности
мощности скорости счета для точечного де-
тектора, размещенного в центре гомогенных
кубических реакторов без отражателя [4].
и подкритнческом реакторах кубической формы без отражателя. Осо-
бый интерес в этих данных представляет влияние изменения безраз-
мерного параметра L2BS при изменении объема реактора. Вместо
того чтобы уменьшаться прн увеличении объема реактора, он воз-
растает, и, следовательно, в геометрически малых системах наблю-
даются наибольшие пространственно зависимые эффекты.
С помощью уравнения (5.71) были сделаны численные расчеты
спектральной плотности для куба со стороной s как включая, так
и исключая белый шум (нлн независимую от частоты часть), т. е.
первые две строчки уравнения (5.71). В представленных кривых бе-
лый шум исключен, поэтому легко выявляются пространственно
зависимые эффекты. На рис. 5.6 изображена спектральная плот-
ность мощности, включая член белого шума, для детектора, распо-
ложенного в геометрическом центре куба, т. е. х = у = z = 0, а
поверхности куба находятся на расстоянии ±s/2. Все рассматривае-
мые реакторы критические, и асимптотическое поведение для про-
странственно независимого случая показано пунктирными линиями
137
в области со — р// (где I — время жизни мгновенных нейтронов в ко-
нечной среде и записываемое выше как lt основной составляющей).
На рис. 5.6 видно, что для наибольшего значения £2В2 = 0,3031
или для наименьшего реактора в единицах диффузионной длины (но
наибольшего по физическим размерам) пространственно зависимые
эффекты почти отсутствуют. Эти эффекты имеют место лишь при вы-
соких частотах и низких амплитудах, когда становятся неизмеряе-
мыми. Высокочастотная пространстаенно независимая постоянная
составляющая по форме пропорциональная со2 является обоснован-
Рис. 5.7. Функции спектральной плотности мощности
для скорости счета точечного детектора,
размещенного в точке с координатами
*=I/=z=s/4 в критических кубических ре-
акторах без отражения.
ной вплоть до частот около 300 рад!сек и амплитуд на 3 декады
(60 56) ниже плато. Прн переходе к меньшим значениям L2B2 про-
странственно зависимые эффекты становятся более явно выражен-
ными. Для наименьшего значения LPB2 = 0,0197 функция спектраль-
ной плотности хуже аппроксимируется с помощью пространствен-
но независимой формы для всех частот, много больших, чем частота
излома, равная 267 рад!сек.
На рис. 5.7 представлены графики спектральной плотности мощ-
ности тех же критических реакторов для детектора, смещенного
относительно центра куба к углу и имеющего координаты х = у =
= z = s/4. В этом случае для наибольшего значения £2В2 =
= 0,3031 пространственно независимая форма еще до некоторой сте-
пени является преобладающей, это приближение является справед-
ливым вплоть до частоты, равной примерно 80 рад!сек, и амплитуд,
138
на 1,5 декады. (30 дб) меньших амплитуды плато. Для случая малых
значений £2В2 пространственно независимая составляющая пол-
ностью отсутствует для частот порядка р// и выше. Действительно г
асимптотический ход зависимости для частот, больших о = p/Zr
более близок к результату, получаемому для точечного детектора
в бесконечной среде, имеющему асимптотический ход, пропорцио-
Рнс. 5.8. Влияние подкритпчности на функции
спектральной плотности мощности скоро-
сти счета для точечного детектора, раз-
мещенного в центре гомогенных кубиче-
ских реакторов без отражателя [4]:
---------под критичность 6 Р; ----• ------- — ПОД-
критичность 3 р.
нальный со1/2. В общем, эффект приближения к границам увеличи-
вает составляющую белого шума в спектре и уменьшает амплитуду.
В пределе, на поверхности реактора, спектр становится плоским,
нли белым, с нулевой амплитудой.
На рнс. 5.8 показано влияние подкритичности в 3 и 6 р (долла-
ров) на спектральную плотность детектора, расположенного в цент-
ре куба, х — у = z = 0. Пунктирные линии при больших частотах
представляют результаты машинного расчета, которые являются
139
более точными, но требуют чрезвычайно много машинного времени.
Зона с малым значением £2Б2 плохо аппроксимируется пространст-
венно независимой составляющей.
Все расчеты, представленные для кубического реактора без от-
ражателя, выполнены в предположении точечного детектора. Для
отдельно рассмотренного случая было отмечено, что реакторы с боль-
шим Б2 проявляю'!* более сильное изменение спектральной плот-
ности, чем реакторы с малой величиной В2. Это условие может не
выполняться при рассмотрении детектора конечных размеров.
В этом случае меньший (по размерам) реактор будет, вероятно, более
подходящим для размещения относительно большого детектора
(в длинах диффузии), чем большой реактор. В меньшем реакторе
это будет приводить к уменьшению пространственной зависимости
спектральной плотности. Как указывалось выше, влияние конечных
размеров детектора, размещаемого в бесконечной среде, приводит
к тому, что спектральная плотность приближается к результату,
получаемому для реактора с сосредоточенными параметрами. Мож-
но показать, что эффект незначителен для детекторов малых разме-
ров порядка нескольких диффузионных длин или меньше. Однако
на практике детекторы часто имеют значительно большие размеры,
по крайней мере в одном измерении. Следовательно, детектор конеч-
ных размеров в кубическом реакторе без отражателя должен иметь
спектральную плотность, описываемую лучше всего основной со-
ставляющей (собственной функцией).
§ 5.8. Заключение
Расчеты, сделанные Шеффом и Альбрехтом, иллюстрируют не-
сколько интересных аспектов, касающихся явлений реакторного шу-
ма, которые проявляются, только когда используется пространствен-
но зависимая теория. Средн них наиболее важны следующие:
1. Обычно применяемая точечная модель реактора эквивалентна
размещению бесконечного однородного детектора в бесконечной раз-
множающей среде. Точечный детектор в бесконечной среде не дает
согласия с результатами для точечного реактора.
2. Функции взаимной корреляции и спектральной плотности
в бесконечной среде были получены в явном виде, и были установле-
ны свойства, зависящие как от расстояния между детекторами в дли-
нах диффузии, так и от времени или частоты.
3. Эффект приближения детектора к границе состоит в том, что
спектр смещается в сторону белого шума. Этот вывод согласуется с
влиянием эффективности детектора в пространственно независимой
теории.
4. Размер детекторов, когда детектор становится большим, при-
водит к результатам пространственно независимой или точечной мо-
дели.
5. В прямоугольном параллелепипеде без отражателя взаимная
корреляционная функция в общем случае не является четной функ-
140
цней относительно значения т = 0, а функция взаимной спектраль-
ной плотности является комплексной. Хотя можно полагать, что
для большинства случаев размещения детекторов результаты будут
подобными тем, которые описываются пространственно независимой
теорией, прн интерпретации измерений спектра и корреляции двух
детекторов в понятиях пространственно независимой теории должна
быть проявлена значительная осторожность.
6. Функция спектральной плотности мощности даже в кубе без
отражателя имеет четкую пространственную зависимость. Эта зави-
симость может быть сильно уменьшена тщательным размещением
детектора на одной, двух или более осях симметрии системы.
СПИСОК ЛИТЕРАТУРЫ
1. Cohn G. Е. A Simplified Theory of Pile Noise.—«Nucl. Sci. Engng», 1960,
v. 7, N 5, p. 472.
2. Goldman S. Frequency Analysis Modulation and Noise. McGraw-Hill Book
Company, Inc., N. Y., 1948, p. 355.
3. Sheff J. R., Albrecht R. W. The Space Dependence of Reactor Noise,
I-Theory. —• «Nucl. Sci. Engng», 1966, v. 24, N 3, p. 246.
4. Sheff J. R., Albrecht R. W. The Space Dependence of Reactor Noise,
Il-Calculations. —«Nucl. Sci. Engng», 1966, v. 26, N 2, p. 207.
5. Cohn С. E. Determination of Reactor Kinetic Parameters by Pile
Noise Analysis. — «Nucl. Sci. Engng», 1959, v- 5, N 5, p. 331.
6. Courant F. C., Wallace P. R. Fluctuations of the Number of Neutrons in
a Pile. —«Phys. Rev.», 1957, v. 72, p. 1038.
7. Orndoff J. D. Prompt Neutron Periods of Metal Critical Assemblies. —
«Nucl. Sci. Engng», July 1957, v. 2, p. 450.
8. Feynman R. P., de Hoffman F., Serber R. Dispersion of the Neutron Emission
in D-235 Fission. — «J. Nucl. Energy», 1956, v. 3, p. 64.
9. Badgley R. W., Uhrig R. E. Power Spectral Density Measurements in a
Subcritical Nuclear Reactor. —«Nucl. Sci. Engng», 1964, v. 19, N 2, p. 158.
10. Schultz M. S. Control of Nuclear Reactors and Power Plants. McGraw-Hill
Book Company, Inc., N- Y., 2nd ed., 1961. (См. Шульц M. А. Регулирова-
ние энергетических ядерных реакторов. Пер. с аигл. М., Изд-во иностр,
лит., 1957.)
11. Moore М. N. Role of the Dispersion Low in Space-Dependent Kinetics in
Reactor Kinetics and Control. — Tucson, Ariz., March 25—27, 1963,
Weaver L. (Coordinator); AEC Symposium Series, 1964, N 2 (TID-7662),
p. 169—178.
12. Moore M. N. The Determination of Reactor Transfer Function from Mea-
surements at Steady Operation. — «Nucl. Sci. Engng», 1958, v. 3, N 4,
p. 387.
13. Bennett E. F. The Rice Formulation of Reactor Noise.—«Nucl. Sci. Engng»,
1960, v. 8, N 1, p. 53.
14. Natelson M., Osborn R. K., Shure F. Recent Developments in the Analysis
of Neutron Noise Experiments. — In: Neutron Noise, Waves and Pulse
Propogation. Gainesville, Fla., Feb. 14—16, 1966» Uhrig R. E. (Coordina-
tor); AEC Symposium Series, 1966, N 9 (TID-7679), p. 669—688.
ГЛАВА 6.
МЕТОДЫ
лнллизл
ШУМОВ
§ 6.1. Введение
Измерения шумов проводятся в ядерных реакторных системах
в критическом и подкритическом состояниях. Шумы были измерены
также в реакторах в надкритическом состоянии, ио ограничения вре-
мени таких измерений очевидны. Для поддержания нейтронного по-
тока и а квазистатическом уровне в подкритической реакторной си-
стеме необходим искусственный источник нейтронов. Этим внешним
источником может быть смесь Ри — Бе или Ро — Be, которая ис-
пускает нейтроны в случайные интервалы времени при радиоактив-
ном а-распаде плутония или полония. Такие нейтроны получаются
в результате (а, п)-реакцни а-частиц с бериллием. Внешние нейт-
роны могут быть обусловлены также (у, п)-реакцией высокоэнер-
гетических у-квантов, испускаемых продуктами деления, распреде-
ленными по активной зоне, причем реакция происходит на бериллии
или дейтерии в активной зоне или отражателе. Третьей возмож-
ностью производства внешних нейтронов является спонтанное деле-
ние 238П или Ри.
Предположим, что ядерные параметры подкритической системы
ие зависят от времени, а флуктуации параметров на выходе обуслов-
лены флуктуациями на входе. В этом случае реакторную систему
можно описать соотношениями, полученными в гл. 4. Обычным мето-
дом является измерение спектральной плотности мощности входного
и выходного процессов или взаимной спектральной плотности меж-
ду входом и выходом, из которых может быть получена передаточная
функция реакторной системы. Параметры системы затем опреде-
ляются из передаточной функции.
Особые проблемы возникают в подкритических системах, в кото-
рых нейтронная плотность довольно низка. Последнее означает, что
требуются высокоэффективные детекторы. Получить полезную ин-
формацию из флуктуаций нейтронной плотности трудно, так как мно-
гие приборы очень инерционны при работе на нижних диапазонах.
Методы преодоления этих трудностей обсуждаются в следующих па-
раграфах.
Присутствие внешнего нейтронного источника в близкой к кри-
тическому состоянию системе создает нежелательный высокий фон,
142
который может вызвать искажение измеряемой величины. В крити-
ческом реакторе, но и а нулевом уровне мощности нейтронная плот-
ность существенно флуктуирует относительно средней величины.
Однако при увеличении мощности эти флуктуации становятся
больше по абсолютной величине, но они незначительны по сравне-
нию со средним уровнем нейтронной плотности. Эти флуктуации
обусловлены статистической природой процесса деления (т. е. числа
нейтронов, возникающих в одном акте деления), геометрическим
распределением различных материалов в сборке, их сечениями,
энергией отдельных нейтронов в зависимости от координат и дру-
гих параметров. Когда мощность увеличивается, наиболее сущест-
венные флуктуации вызываются возмущениями реактивности, воз-
никающими в результате движения регулирующего стержня или
изменения положения отражателя. Иногда такие возмущения реак-
тивности могут быть вызваны флуктуациями скорости теплоносите-
ля, вибрацией и т. д. В других случаях, чтобы провести измерения
шумов, необходимо умышленно ввести в систему возмущение.
Методы измерений и тип детектирующей системы очень тесно
связаны с уровнем мощности. В подкритическую и почти критиче-
скую системы наиболее целесообразно помещать импульсные детекто-
ры и проводить импульсные измерения, описанные в гл. 3.
Когда мощность реактора становится значительной, для измере-
ний шумов чаще всего в качестве первичной величины используется
ток ионизационной камеры. В этом случае применимы стандартные
методики корреляционного и спектрального анализа. Когда мощ-
ность достигает уровня, иа котором наблюдаются существенные теп-
ловые эффекты, шумовые методы могут использоваться для детекти-
рования нестабильностей потока теплоносителя, вибрации компо-
нент активной зоны, а также значительных объемов пара. Некото-
рыми экспериментаторами сообщалось о детектировании шумовыми
методами начала кипения в активной зоне, однако публиковались
также сообщения об отсутствии возможности такого детектирования.
Методика получения параметров из шумовых измерений заклю-
чается в определении передаточной функции илн импульсной функ-
ции системы. Передаточная функция критического реактора нулевой
мощности имеет верхнюю частоту излома, равную р//, и нижние ча-
стоты излома, зависящие от постоянных распада Хг- и долей запазды-
вающих нейтронов Поскольку постоянные распада и доли за-
паздывающих нейтронов изменяются в зависимости от содержания
плутония и урана в топливе, путем измерения нижних частот излома
передаточной функции можно оценить величину выгорания в реак-
торе.
Одним из наиболее важных измерений в подкритических систе-
мах является измерение степени подкритичкости, илн реактивности.
В действительности реактивность в ядерной системе не может быть
измерена непосредственно; легче определять р/0, £// или другие ве-
личины, которые являются комбинацией р£, р и I. Обычно для опре-
деления реактивности измеряется росси-альфа-постоянная.
143
Серьезной проблемой, связанной с измерениями в подкритнче-
ских системах, является требование высокой эффективности детек-
тора. Однако недавние эксперименты с взаимной корреляцией сиг-
налов двух детекторов показали преимущества метода и возможность
использования менее эффективной детектирующей системы. Это по-
зволяет располагать во многих случаях детектор вне активной зоны
и, следовательно, поместить детектор вне корпуса энергетического
реактора. Двухдетекториый метод подробно обсуждается в настоя-
щей главе.
§ 6.2. Корреляционные измерения
В гл. 4 были описаны основные соотношения теории случайных
шумов. Применяя этн соотношения к реакторным системам, можно
получить большое количество информации об этих системах при усло-
вии, что имеется адекватная модель (передаточная функция или им-
пульсная функция) реакторной системы.
Основные уравнения во временной области, приведенные в гл. 4:
+ (6.1)
и
ФадСО= $ й(А) (₽хд.(т—X)dA (6.2)
полезны только при определенных условиях. Некоторые из этих
условий обсуждаются ниже.
Белый шум на входе. Если входной сигнал может быть представ-
лен белым шумом, то автокорреляционная функция входного сиг-
нала пропорциональна дельта-функции Дирака 6 (т) и уравнение
(6.1) имеет вид
Фи,(*)= f $ /1(Л)Л©/6(т-| + Х)Й^Л, (6.3)
где А — постоянная пропорциональности. Если мы заменим пере-
менные
Н = (6.4)
и используем тот факт, что функция 6 (т — р,) не равна нулю только
при т — р и интеграл от дельта-функцни равен единице, то получим
+ W $ /6(т-р)dV.=A4,llh(T). (6.5)
— со — со
.144
Соотношение (6.5) полезно только в некоторых случаях, когда h (/)
представляет собой простую функцию. Например, если h (t) являет-
ся экспоненциальной функцией, то (phh (т) также будет экспонен-
циальной функцией, и коэффициент ослабления системы оценивается
в соответствии с соотношением (4.90).
Детектирование периодических компонент. Одним из наиболее
полезных аспектов измерения автокорреляционной функции яв-
ляется обнаружение существования периодических компонент на
выходе системы. Когда функция имеет периодическую компоненту,
ее автокорреляционная функция (исключая область вблизи нуля)
также является периодической функцией с тем же самым периодом.
Если периодическая компонента теряется в случайных шумах, не-
обходимо провести автокорреляционный анализ для больших времен-
ных сдвигов, пока не обнаружится периодическая компонента. Если
периодический характер автокорреляционной функции совершенно
ясен, то для идентификации наиболее существенных частотных ком-
понент можно использовать фурье-анализ. В некоторых случаях час-
тотные компоненты связаны с физическими явлениями в реактор-
ной системе. Очевидно, что эти частотные компоненты находятся
путем спектрального анализа, если сигнал не искажен другими
флуктуациями. Автокорреляционная функция очень эффективна для
определения периодических компонент в присутствии больших фо-
новых шумов.
Взаимные корреляционные функции. Соотношение между взаим-
ной корреляционной функцией входа и выхода линейной системы
(6.2) может быть упрощено, если сигнал на входе является белым
шумом. Тогда автокорреляционная функция входного сигнала про-
порциональна дельта-функции Дирака и уравнение (6.2) принимает
вид:
Фад(т)= $ й(Х)Аб(т—X)dX = A/i(t) $ 6(т—Х)б/Х = АА(т). (6.6)
Следовательно, взаимная корреляционная функция входного и вы-
ходного сигналов пропорциональна импульсной переходной функ-
ции. Это соотношение особенно удобно применять в тех случаях,
когда спектральная плотность мощности входного сигнала постоян-
на в интересующем нас диапазоне частот. Соотношение (6.2)
между Фар (г) и фЛА: (т) полезно также, если функция (рхх (т) из-
вестна или может быть измерена.
Автокорреляция корреляционной функции. Извлечение информа-
ции изданных, неточных из-за присутствия шумов, часто проводится
путем подгонки экспериментальных данных методом наименьших
квадратов к выбранной модели. В работе 11 ] использовался другой ме-
тод, заключающийся в оценке импульсной переходной функции
взаимным корреляционным методом [соотношение (6.2)]. Вместо
оценки действительных ошибок взаимной корреляционной функции
4>ху (т) исключалось, насколько это возможно, их влияние путем
145
рассмотрения флуктуаций корреляционной функции как шума
и использования метода автокорреляции для фильтрации этих
флуктуаций. Другими словами, определялась автокорреляция
взаимной корреляционной функции.
Эта методика применима как для автокорреляционной функции,
так и для взаимной корреляционной функции. Пусть измеренная кор-
реляционная функция состоит из истинной корреляционной функции
Ф (т) и функции ошибок е (т):
ф(т) = ф(т) + е(т). (6.7)
Автокорреляционная функция <р (т) есть
Т'ф ф (и) = Е [ф (т) ф (т + и)] = Е {[<р (т) + е (т)] [<р (т + р) + е (т + р)]} =
=Фте (р) + <йр. (|0 + (Н)+Фи (р). (6.8)
Если ошибка случайная, последний член в (6.8) является дель-
та-функцией Дирака. Даже если ошибка не случайна, этот член
быстро стремится к нулю. Взаимные корреляционные члены (р)
11 Фгф (р-) равны нулю, так как нет корреляции между функцией оши-
бок и истинной корреляционной функцией. Следовательно, преоб-
ладает первый член фф(р (р). Для важного случая, когда корреляцион-
ная функция экспоненциальна, ффф (р) также является экспонен-
циальной функцией. В работе [11 показано, что эта методика умень-
шает вариацию ординат измеренной взаимной корреляционной функ-
ции в два раза, а вероятность данной ошибки — в шесть раз, если
импульсная переходная функция (которая пропорциональна взаим-
ной корреляционной функции при входном сигнале в виде белого
шума) была экспоненциальной. Предполагалось, что импульсы де-
тектора, собираемые в каждом канале временного анализатора, под-
чиняются распределению Пуассона и что скорости счета в соседних
каналах отличаются незначительно.
§ 6.3. Измерения спектральной плотности
Соотношения (4.93) и (4.100) между спектральными плотностями,
важные для измерений в ядерных реакторах, запишем как
(to) = |/7 (to) [2 Фхх (to), (6.9)
®x„(to) = tf(to)®xx(to), (6.10)
а аналогичные соотношения, включающие односторонние спектраль-
ные плотности, в виде
(6.11)
Gxy(^^H(^Gxx^). (6.12)
146
Спектральные плотности мощности процесса можно рассматривать
как линейные функции и записать в соответствии с уравнением
(4.29) как
6„И = 2 G4.,.(o),
(6.13)
где
х(0= f
i=l
(6.14)
Применение этих соотношений к ядер ним реакторам будет проде-
монстрировано ниже.
Рис. 6.1. Структурная схема системы детектирования
нейтронов в реакторе.
На измерения нейтронной плотности или потока в ядерном реак-
торе оказывают влияние шумы детектора, так как детектирование
нейтронов происходит в результате возникающих взаимодействий
поглощения или рассеяния отдельных нейтронов. Обычно выход си-
стемы детектирования нейтронов состоит нз двух компонент: одной—
обусловленной флуктуациями в системе, другой — обусловленной
шумами детектора.
Рассмотрим систему, изображенную на рис. 6.1, где Я (cd) н
#1 (со) — передаточные функции реактора и аппаратуры соответ-
ственно. Входные сигналы х (?) н п (?) представляют собой возмуще-
ния в реакторе (либо мощности источника, либо реактивности)
и шумы детектора соответственно. Применив соотношения (6.11)
и (6.13) в этой системе, получим
GB„ (<о) = Gnn (<о) | (и) [’+(и) | Я, (о) |2 |Я (о) р, (6.15)
которое может быть преобразовано к виду
Gly = Gyv (co)/j Нг (CD) р = G№X (cd) I Я (CD) p-|-Gnn (CD), (6.16)
где Gyy — «скорректированная» спектральная плотность мощности.
В общем случае шумы детектора молено рассматривать как белый
шум в интересующем нас диапазоне частот, н, следовательно, Gnn (w)
считать постоянной величиной.
Если функция х (?) по своей природе случайна (например, вход
есть эквивалентный источник шума) или может быть сделана слу-
147
чайной (например, возмущением реактивности), СжЖ(со) будет по-
тоянной величиной. Следовательно, (6.16) примет вид:
С^ = Л|Я(со)|2 + В,
(6.17)
где А нВ — постоянные, представляющие соответственно Gxx (со)
ч Gnn (^)*
Во многих простых реакторных системах передаточную функцию
можно представить инерционным звеном первого порядка, т. е.
(6.18)
Н (to) = 1/ (jсо + а),
Рис. 6.2. График скорректированной спектральной
плотности мощности для инерционной
системы первого порядка.
тогда (6.17) запишется как
G'yy (со) = Л/(щ2 + а2) + В. (6.19)
Это соотношение, показанное на рис. 6.2, удобно для измерения вели-
чины росси-альфа подкрнтической и критической ядерных систем.
Основной проблемой в этой методике является малое отношение кор-
релированных шумов к некоррелированным шумам (А1а?)/В.
Это отношение, которое можно рассматривать как отношение сиг-
иал/шум, очень мало для низкоэффективных детекторов даже в слу-
чае высокой скорости счета. Два асимптотических уровня в .соот-
ношении (6.2) становятся почти равными, и оценка постоянной а
из этих измерений бывает затруднительной. Для успешных измере-
ний требуется эффективность детектора около 10-4, т. е. один нейт-
рон детектируется на каждые 10 000.
Из рис. 6.1 видно, что измерительную аппаратуру можно рас-
сматривать как систему с двумя входами, т. е. входами измеритель-
ной аппаратуры являются шумы детектора п (Z) и выход реактора
z (t). Как показано соотношением (4.206), когда два входа независи-
мы, взаимная спектральная плотность между одним входом и выхо-
дом не подвержена влиянию другого входа. Следовательно,
GzV (to) = (co)Gzz (to).
(6.20)
148
Однако для наблюдения доступны только х (/) и у Поэтому,
преобразовав систему, как показано на рис. 6.3, и применив урав-
нение (4.201), получим
(6.21)
Gxy («) = Gxx (<d).
Piic. 6.3. Альтернативная структурная схема де-
тектирования нейтронов в реакторе.
Так как Н1 (о) определяется путем калибровки аппаратуры, Н (со)
находится из соотношения
Н (со) = Gxy (со)/6жя (со)/7х (со). (6.22)
Для случая, когда функция Gxx (со) неизвестна и не может быть из-
мерена, ниже описан метод взаимной корреляции двух детекторов.
§ 6.4. Измерения передаточных функций
Существуют несколько методов измерения передаточной функции
ядерной системы. В общем случае измеряется реакция системы на
введение известного входного сигнала (периодического, переходного
н меняющегося случайно). Сигналы, изменяющиеся случайным
образом, либо специально подаются на вход системы, либо возни-
кают в результате внешних возмущений, не контролируемых ис-
следователем. Необходимо быть уверенным в том, что частотное со-
держание случайных сигналов находится в интересующем нас диа-
пазоне и их амплитуда достаточно велика для проведения измерений.
Переходные н периодические сигналы являются по своей приро-
де детерминированными, поэтому с их помощью можно получить не-
обходимые амплитудные и частотные характеристики. В общем слу-
чае периодические сигналы более удобны, хотя иногда переходные
сигналы имеют определенное преимущество [2]. В качестве перио-
дических могут применяться сигналы синусоидальные и прямоуголь-
ной формы, сигналы, содержащие много частот, ряды импульсов
и большое многообразие волн сложных форм. Использование чисто
синусоидального сигнала имеет некоторое преимущество по сравне-
нию с другими периодическими сигналами, заключающееся в том,
что вся мощность такого сигнала сконцентрирована на одной частоте
и, следовательно, частотная реакция системы может быть определена
149
при относительно низком отношении сигнал/шум. Если входной
сигнал достаточно велик по амплитуде, для ограничения помех
удобно использовать узкополосный фильтр.
Многокомпонентный периодический сигнал одновременно содер-
жит информацию о нескольких частотах. Отношение сигнал/шум
на этих частотах может поддерживаться на приемлемом уровне, если
мощность входного сигнала сконцентрирована на этих выделенных
частотах. Образованные таким образом периодические сигналы из-
вестны как псевдослучайные сигналы. Как и случайные сигналы,
многокомпонентные периодические сигналы должны охватывать инте-
ресующий частотный диапазон, кроме того, как на высших частотах,
так и на низших должна быть сконцентрирована достаточная мощ-
ность сигнала. Например, принципиальным недостатком сигналов
прямоугольной формы является то, что амплитуда /г-й гармоники
сигнала составляет 1/п амплитуды основной гармоники. Следова-
тельно, если охватываются шесть октав частоты (т. е. отношение
высшей частоты к низшей равно 27, нлн 128), отношение амплитуд
высшей и низшей частотных компонент будет 1/128, или менее 1%.
Если входной сигнал линейной системы без обратной связи яв-
ляется чистой синусоидой, выходной сигнал будет также синусои-
дой, которая отличается от входной только по амплитуде н фазовому
углу. Этн изменения определяют реакцию для отдельной частоты.
Реакция на входной сигнал может быть определена для ряда частот
и таким образом оценена передаточная функция.
Процедура становится более сложной, когда возмущающий сиг-
нал содержит несколько частот одновременно. Теоретически фурье-
анализ входного и выходного сигналов дает точное значение ампли-
туды и фазы каждой частотной компоненты, которое, в свою очередь,
позволяет определить передаточную функцию. Однако практически
точно ее измерить таким путем нельзя, можно только оценить пере-
даточную функцию, так как шумы и нелинейности приводят к ошиб-
кам. Качество этой оценки зависит от типа возмущающего сигнала
и метода его анализа.
Выходной сигнал ядерной системы состоит из двух компонент: ре-
акции на возмущающий сигнал и случайного сигнала, который в об-
щем случае не связан с возмущающим. Теоретически можно исклю-
чить некоррелированные шумы, но только для бесконечно длинной
реализации. На практике имеют дело с реализациями конечной дли-
ны, поэтому шумы вносят неопределенность в результаты. Посколь-
ку величина ошибок, вызванная шумами, является функцией отно-
шения сигнал/шум, в общем случае результаты можно улучшить,
увеличивая амплитуду сигналов. Однако когда система нелинейна
или ее нельзя представить дифференциальными уравнениями с по-
стоянными коэффициентами, увеличение амплитуды может вызвать
искажение сигналов.
Из-за случайной природы шумов частотный анализ часто дает
статистический разброс данных. Последний можно уменьшить, при-
менив один из методов сглаживания. Сглаживание проводится путем
150
усреднения по группам частот, когда частотные зависимости полу-
чены из фурье-анализа входного и выходного сигналов, или приме-
нением «весовой функции» к корреляционной функции сигнала с по-
следующим фурье-преобразоваиием модифицированной корреляци-
онной функции. Хотя последний метод кажется более сложным,
в общем случае он удобнее для обработки. После появления алгорит-
мов быстрого фурье-преобразовання этот метод при использовании
ЦВМ для обработки данных требует меньших затрат времени, чем
фурье-аиализ.
§ 6.6. Прямой гармонический анализ
Когда шум присутствует между входом и выходом системы, он
обычно появляется и в выходном сигнале. Если ко входу системы
приложен пробный сигнал любого типа, то выходной сигнал содер-
жит две составляющие: одну — вызванную входным сигналом, вто-
рую — шумами самой системы. При бесконечно длительной ре-
гистрации входного и выходного сигналов в принципе возможно отде-
лить шумы от выходного сигнала и точно измерить реакцию системы
на входной сигнал (при условии отсутствия в шумах периодических
компонент, связанных с входным сигналом). В общем случае прово-
дится гармонический анализ для выделения отдельных частотных
составляющих, с помощью которых строятся диаграммы Боде (за-
висимости амплитуды и фазы передаточной функции от частоты).
Выделение отдельных частот путем прямого фурье-анализа — наи-
более общий и простейший метод с аналитической точки зрения.
Одиако когда отношение сигиал/шум мало для выделения отдельных
частот и длительность регистрации коротка для обеспечения удов-
летворительной погрешности, корреляционные методы имеют су-
щественные преимущества.
Метод выделения дискретных частот, описанный в настоящем
•параграфе, был предложен в работе [3]. Рассмотрим, каким образом
шумы влияют на обработку данных и вызывают погрешности, завися-
щие от амплитуды сигнала и времени наблюдения, в тех случаях,
когда методом гармонического анализа [21 выделяются отдельные час-
тоты (в действительности узкая полоса частот А/). Пусть входной сиг-
нал системы, показанной на рис. 6.4, есть х (/), а выходной — у (/),
причем выходной сигнал состоит из шумового сигнала w (t) и полез-
ного сигнала v (£), т. е.
У Й - И [t) 4- w (t). (6.23)
Поскольку входной сигнал предполагается периодической функци-
ей, v (t) также будет периодической функцией и функция у (t) мо-
жет быть выражена с помощью разложения функции v (t) в ряд
Фурье плюс шумы w (t):
y(t) = 3 (a„cosco„/4-b„sinw„/) 1 +®(Z). (6.24)’
151
При этом предполагается, что шумы не имеют периодических ком-
понент и представляют собой стационарный процесс с нулевым сред-
ним значением. Коэффициенты ряда Фурье ап и Ьп полезного сигнала
v (t) есть
тР
ап= $ и(/)cos(Ипtdt, (6.25)
о
тР
bn = J Ц (t) sin G>n tdt, (6.26)
о
где Р — период основной гармоники сигнала; п — порядковый
номер гармоники; т— число периодов за время регистрации. Та-
Рис. 6.4. Динамическая система с шумами только
на выходе системы.
ким образом, величина тР представляет собой длительность ре-
гистрации. Коэффициенты ряда Фурье ап и Ь'п выходного сигнала
у (/) есть
тР
ап = ап-р J w(£)costdt (6.27)
о
и
bn=bn-P jj w (/) sin con tdt. (6.28)
о
Сравнение уравнений (6.24) — (6.28) показывает, что шумы дают
ошибки в коэффициентах за целое число т циклов:
Уеа-ь“е|,
где индекс п — номер гармоники,
тР
еа-- 5 w (0 cos ®n tdt
о
и
тР
еь= J w (Z) sin /d/.
о
(6.29)
(6.30)
(6.31)
152
Видно, что ошибка зависит от длительности регистрации тР,
ио не зависит от номера гармоники п.
Вследствие случайного, характера шумов ошибки епт имеют оп-
ределенный разброс. Например, ошибки будут разными для различ-
ных п в данной регистрации, и это вызывает разброс точек в спектре
амплитуд. Если рассматривать большое число величин ет, можно
получить функцию плотности вероятностей р (е,п). Вклад в интегралы
в соотношениях (6.30) и (6.31) для одного цикла (в этом случае
рассматривается f-й цикл для /г-й гармоники) есть
12
+
$ w (t) sin con t г
(6.32)
Следовательно, для tn циклов
1 1
епт = ~т 2 ет= (6.33)
z=i
где каждое значение еПт имеет свою функцию плотности вероятности
р (ет) н дисперсию s2 (еПга).
Если шумы являются гауссовскими, их дисперсия есть
S4e„m) = ^(^enl)+^(AeiJ+...+
+ S2(ie„m'|= 2 s'(4re"')- <6'34’
Поскольку все еП1- имеют одну и ту же плотность вероятности, не
зависящую от г, соотношение (6.34) принимает вид
ss(e„) = ms2^ е„У
(6.35)
О &пт
Рнс. 6.5. Плотность вероятности оши-
бок в гармоническом анали-
зе для трех длительностей
реализации [3].
где индекс т опущен. Следова-
тельно, стандартное отклонение
ошибки n-й гармоники есть
(6.36)
Видно, что стандартное отклоне-
ние обратно пропорционально
корню квадратному из числа циклов, т. е. корню квадратному из дли-
тельности наблюдения. Это показано на рис. 6.5. Поэтому можно
сделать’вывод, что ошибка, вызванная шумами, пропорциональна
амплитуде сигнала и корню квадратному из длительности наблю-
дения.
153
Для экспериментального определения передаточной функции
существует несколько методов, основанных на выделении дискрет-
ных частот. Они отличаются главным образом способом, которым
производится фурье-анализ. После определения коэффициентов
ряда Фурье для входного н выходного сигналов находят частотные
характеристики из отношения амплитуд и фазового угла. Отноше-
ние амплитуд при частоте пы1 есть
I Н (»«i) I = I + Ь;,х), (6.37)
и фазовый сдвиг при частоте «со, равен
6 (/г<й1) = [ardg (fc„B/ons)—arctg (блх/сиа.)], (6.38)
где а„ и Ь„ — коэффициенты при синусах п косинусах для n-й гар-
моники; <01 — основная частота (индексы хи у относятся к входному
и выходному сигналам соответственно).
§ 6.6. Конечная длительность реализации
Если входной сигнал системы — периодическая функция, пере-
даточная функция системы может быть получена либо прямым гар-
моническим анализом, либо измерением спектральных плотностей
входного и выходного сигналов. В любом случае длительность реали-
зации должна быть равна целому числу циклов. Если используются
методы измерения спектральных плотностей, частоты, при которых
определяются эти плотности, должны быть кратными основной гар-
монике входного сигнала. Можно показать, что автокорреляционная
функция периодического сигнала содержит ту же самую периоди-
ческую составляющую с соответствующей амплитудой. При этом
в спектральной плотности мощности сигнала содержатся острые пи-
ки.
В работе 12] показано, что если длительность реализации не
равна целому числу циклов (периодов), можно получить сущест-
венную ошибку. Если фурье-аналнз случайного процесса прово-
дится в течение конечного интервала времени, то этот процесс дол-
жен рассматриваться как периодический с периодом, равным дли-
тельности наблюдения Т. В противном случае можно получить оши-
бочную интерпретацию результатов.
Если анализируемый процесс свободен от внешних шумов, то
применение корреляционных методов не имеет преимуществ по
сравнению с прямым гармоническим анализом. Однако когда вы-
ходные сигналы содержат шумы (как это бывает на практике), можно
получить улучшение, применив сглаживание спектральных плот-
ностей Сглаживание обычно проводится путем умножения корреля-
ционных функций на «весовую» функцию с последующим фурье-
преобразованием модифицированных корреляционных функций.
Сглаживание можно применить и к спектральным плотностям в
частотной области.
154
Здесь уместно рассмотреть проблемы использования реализаций
конечной длины для вычисления корреляционных функций. Опреде-
ления, данные в гл. 4, требуют, чтобы временные функции рассматри-
вались за бесконечно долгое время. Поскольку в действительности
это условие невыполнимо, мы получаем только оценку корреляцион-
ной функции. Оценка не может быть сделана для временных сдви-
гов т, больших длительности реализации. Обычно желательно ис-
пользовать временные сдвиги не более некоторой (5—10%) части от
длительности реализации, за исключением случая периодического
процесса, где временной сдвиг корреляционной функции может
превосходить длительность реализации. Вместо корреляционной
функции в общем виде
<M^)=}im^; Jj (6.39)
используется оценочная корреляционная функция в виде
<₽;«(•")= Г \ x(t)y(t+r)dl. (640)
где Т — длительность регистрации, тп1 — максимальный временной
сдвиг.
§ 6.7. Временные и спектральные «окна»
Концепция временных и спектральных «окон» была развита в
работе 14] и затем обобщена Хэннингом 13]. В рассмотрении этого
вопроса мы будем следовать работе [3]
Покажем, что оценки спектральных плотностей определяются
из некоторой модифицированной корреляционной функции, полу-
ченной путем умножения (т) на окно, которое представляет собой
соответствующую четную функцию т. Модифицированная оценоч-
ная корреляционная функция часто является плохой оценкой ис-
тинной корреляционной функции, тогда как фурье-преобразова-
нне модифицированной оценочной корреляционной функции в боль-
шинстве случаев может быть очень приемлемой сглаженной оценкой
истинной спектральной плотности.
Пусть временное окно w (т) сеть четная функция т, удовлетворяю-
щая следующим условиям:
и/ (0) = 1;
w (г) = 0 ’(|т| >тт) (6.41)
Тогда модифицированная оценочная корреляционная функция есть
q>w (т) -= w (т) (т), (6 42)
155
где <рд.</ (т) определена только в диапазоне | г | т„р а (т) —
для всех т. Поэтому существует фурье-преобразованне Ф" (to). Соот-
ношение (6.42) можно переписать следующим образом:
(®) = «7 ((й)фФ^ (со), (6.43)
где W (со) —фурье-преббразованне временного окна w (т), а звез-
дочка означает операцию свертки. Спектральная плотность Ф' (to)
не может быть определена, так как функция ср' (т) не определена для
| т J тто. Однако можно показать, что среднее от большего числа
функций <р" (т) будет достигать истинной корреляционной функции
<₽ (т), т. е.
£|Ч-'ч(т:)^са(т)<р„,(т). (6.44)
Следовательно,
£ [ФлГ/ (со)] — W (со)*фху (со), (6.4 5)
где Фхр (со) — истинный мощностный спектр. Соответствующее
точное соотношение
£ [Ф*'р (coj] = J со)Флр(со)сйй (6.46)
дает среднее значение Ф*р (со) как сглаживание истинного спектра
Ф xv (coj) вблизи частоты coj с «весами», пропорциональными W (со2—
— со). Таким образом, Ф" (соь) является выражением истинного
мощностного спектра, пропущенного через окно W (cot — со).
Функция W (со) часто называется спектральным окном, соответст-
вующим временному окну w (т). Каждое временное окно w (т) имеет
соответствующее спектральное окно W (со), и их часто называют па-
рой окон. Поскольку выбор временного окна ограничен условия-
ми (6.41), спектральное окно всегда имеет одну основную полосу око-
ло со = 0 и несколько боковых полос пропускания с уменьшающи-
мися по мере увеличения частоты амплитудами. В общем случае
спектральные окна выбираются таким образом, чтобы боковые по-
лосы пропускания имели как можно меньшие амплитуды.
Обычно используются четыре пары окон. Это — «усеченная»
оценка, сглаживание по Бартлетту, сглаживание по Хэннингу и сгла-
живание по Хэммингу. Ниже эти временные и спектральные окна
обозначены индексами 0, 1, 2, 3 соответственно.
Усеченная оценка. В усеченной оценке корреляционная функция
не ослабляется для | т [ тт и приравнивается нулю для больших
значений т, т. е. временное окно определяется выражением
O’o(t)=l, (|t|<T,„);
(т) = О, (lTl>Tm) (6.47)
и соответствующее спектральное окно есть
(“) = 2vm sin сотт/сотт. (6.48)
Эти окна показаны на рис. 6.6.
156
Сглаживание по Бартлетту. В сглаживании по Бартлетту кор-
реляционная функция ослабляется линейно в интервале |т|^тт>
т. е. временное окно имеет вид
Рис. 6.6. Временное и
ной оценки.
спектральное окна для усечен-
и соответствующее спектральное окно есть
(6-50)
Эти окна для сглаживания по Бартлетту показаны на рис. 6.7.
Рис. 6.7. Временное п спектральное окна для сглажи-
вания по Бартлетту.
Сглаживание по Хэннингу. Временное окно для сглаживания
по Хэнниигу определяется выражением
^(4=4-[1 + c°s^], (|г|<гга); (6 51)
ги2(г) = 0, . (|т|>тга)
и соответствующее спектральное окно есть
И73(М) =4- И7О(Ю) +4 W„ ( «+ -2L) + -±-W„ f <0- -2Д (6.52)
2 4 \ тт/4 \ тт/
157
где №0 (со) дано соотношением (6.48). Эти окна для сглаживания по
Хэннингу показаны на рис. 6.8.
Сглаживание по Хэммингу. Временное окно для сглаживания
по Хэммингу определяется выражением вида
ги3(т) = 0,54 + 0,46 cos (|т|<т,„);
Рис. 6.8. Временное и спектральное окна для сглажива-
ния но Хэннингу.
и соответствующее спектральное окно есть
Г3 (ш) = 0,54 №„ (со) + 0,23 Го (ш + -^-) + 0.23 We (ш— -Л-), (6.54)
где (со) дано формулой (6.48). Эти окна для сглаживания по
Хэммингу показаны на рис. 6.9.
Рис. 6.9. Временное и спектральное окна для сглажива-
ния по Хэммингу.
Из рис. 6.8 и 6.9 видно, что сглаживающие пары «Хэннинг» и
«Хэмминг» дают лучшую фильтрацию с минимальным искажением.
«Весовая» функция Бартлетта легко применяется во временной об-
ласти и в общем случае обеспечивает удовлетворительное сглажи-
вание. Усеченная оценка обычно не позволяет получить удовлетвори-
тельного сглаживания и приводит к большим флуктуациям.
158
§ 6.8. Анализ спектральной плотности
Структурный описательный анализ спектральной плотности.
В работе [5] предложено различать в измерениях спектральных плот-
ностей структурный описательный спектральный анализ и сравни-
тельный спектральный анализ. Целью структурного спектрального
анализа является обеспечение высокого разрешения частотных ком-
понент процесса. В этом анализе большее внимание уделяется час-
тотному разрешению, чем статистической точности. Поэтому про-
водится детальное исследование частотного спектра в малых час-
тотных интервалах. Упор на разрешение, а не на точность является
особенностью, отличающей структурный спектральный анализ от
сравнительного спектрального анализа.
При структурном спектральном анализе выбор интервала наблю-
дения Т определяется низшей частотной компонентой процесса.
Практически достаточна выборка, равная трем или четырем перио-
дам низшей частоты, которая нас интересует. Однако очень низкие
частоты искажают вычисленный спектр вследствие тренда («плава-
ния» или дрейфа), который может быть определен как вклад частот,
меньших 1/2Т, т. е. дрейф относится к тем частотным компонентам
х (/), у которых половина периода больше Т. Поскольку спектраль-
ный анализ проводится для стационарных процессов (т. е. средний
уровень сигнала не меняется во времени), необходимо до начала
спектральных вычислений исключить дрейф. Это можно выполнить
подгонкой по экспериментальным данным соответствующей функции
методом наименьших квадратов и последующим вычитанием нз х(/)
расчетных значений. Методы выявления дрейфа н его исключения
подробно рассматривались в работе [61.
Разрешение высоких частот — основная цель структурного опи-
сательного спектрального анализа. В этой связи требуется возможно
большее число оценок спектральной плотности на выделенном диа-
пазоне частот. Чем больше это число, тем более подробно описы-
ваются пики и пологие участки спектра. Наиболее простой путь
выделения числа частотных интервалов пг заключается в определе-
нии диапазона частот, в котором измеряется спектральная плот-
ность, а затем в делении этого диапазона на полосы шириной А/.
Полосу частот А/ следует выбирать достаточно узкой с тем, чтобы
получить по крайней мере три-четыре оценки спектральной плот-
ности в любой области, где ожидается пик спектральной плотности.
Сравнительный анализ спектральной плотности. Описание спект-
ральной плотности с высоким разрешением часто является лишь
начальной фазой более точного анализа спектральной плотности
в выделенном диапазоне частот. Например, необходимо количест-
венно сравнить спектральную плотность мощности на данной часто-
те нз двух или более опытов. Такой сравнительный анализ важен,
в частности, при исследовании динамического поведения в данном
частотном диапазоне перед и после изменений компонент (таких, как
регулирующая система) ядерных реакторов. Необходимое требование
159
сравнительного спектрального анализа — высокая статистическая
достоверность во всех операциях, даже если это приводит к ухуд-
шению структурного разрешения. В действительности требования
высокой статистической точности и высокого разрешения частот
практически несовместимы.
При реальном спектральном анализе случайного сигнала дли-
тельность реализации конечна, следовательно, мы получаем оценку
спектральной плотности. Поскольку параметры случайного процес-
са на конечной длине реализации лишь оцениваются, определить
точность спектральных оценок можно только статистически. Дли-
тельность реализации Т и полоса частот Д/(или До)* являются важ-
ными параметрами. Когда Д/ уменьшается для улучшения разреше-
ния, доля информации, содержащаяся в реализации, которая исполь-
зуется в расчете оценки спектральной плотности, уменьшается,
и поэтому статистическая точность оценки также уменьшается.
§ 6.9. Статистические степени свободы
Концепция статистических степеней свободы в спектральном ана-
лизе основывается на математических представлениях характерис-
тик распределения отдельных оценок спектральной плотности [7].
Рассмотрим диапазон частот от —/0 до +/0 (f0 — максимальная ин-
тересующая нас частота) и разделим этот диапазон на m интервалов.'
Для непрерывной переменной число статистических степеней свобо-
да на частотный интервал есть (Д/Т), где Т — время в секундах,
в течение которого проводится измерение, и Д/— полоса частот в
герцах, полученная путем деления диапазона частот от —/0 до +/0 на
m интервалов, т. е.
Д/ = 2/0//п. (6.55
Для дискретной переменной число степеней свободы на частотный
интервал есть Nhn, где N — число дискретных точек в измерении.
Чтобы получить надежную оценку спектральной плотности на
данной частоте, мы должны сгладить каждую из (m -|- 1) оценок, ис-
пользуя оценки спектральной плотности в соседних частотах. Если
предположить, что истинная спектральная плотность имеет пики,
которые шире, чем разрешение Д/, то можно показать, что этот
процесс сглаживания эквивалентен усреднению каждой оценки по
двум из m частотных полос. Таким образом, каждая сглаженная
оценка спектральной плотности имеет около 2Tkf или 2Nlm степе-
ней свободы для непрерывной и дискретной переменных соответ-
ственно. Можно показать, что эффективное среднее число статисты-
* Угловая частота [ и циклическая частота <о связаны соотношением <о =
= 2л£.
160
ческих степеней свободы k для непрерывной и дискретной перемен-
ных соответственно есть
k = [277V — Al » 2T&f, (6.56)
(6.57)
Практически корректирующий член 3/2 неважен, так как в боль-
шинстве случаев получение приемлемой точности требует большого
числа степеней свободы н вычитание этого члена не имеет сущест-
венного значения.
Соотношение между числом статистических степеней свободы
н достоверностью параметров спектра основывается на статистичес-
ком распределении спектральных оценок. При определенных пред-
положениях о случайном процессе отношения таких оценок к истин-
ным величинам имеют ^-распределение с Л степенями свободы. До-
верительные интервалы каждой спектральной оценки могут быть
определены из свойств ^-распределения. Соотношение между сте-
пенями свободы и отклонениями от истинного значения табулировано
в стандартных статистических таблицах.
Теоретическая плотность распределения спектральных оценок
случайного сигнала с гауссовым распределением амплитуд и оди-
наковой спектральной плотностью в пределах полосы пропускания
фильтра является ^-распределением с /г степенями свободы. Сле-
довательно, доверительные пределы 1 — tx для оценки спектраль-
ной плотности Gxx (со), соответствующей доверительному уровню tx,
есть
°”(ю) к- < G™ (<о) < -А? (ФА (6.58)
Пй/г! Р[Й-о/2]
где Gxx (со) — истинная спектральная плотность; (лхх (со) — ее
экспериментальная оценка; Plxa/sl п /’[Х® — функции %2-
распределения для процентилей гх/2 и (1 -— tx/2), связанных с верх-
ним и нижним доверительными пределами соответственно.
На рис. 6.10 показаны отклонения от истинного значения в за-
висимости от числа степеней свободы для нескольких доверительных
пределов [81. Используя эти данные, можно определить необходимое
число степеней свободы в тех случаях, когда нужная достоверность
выражается через минимальное и максимальное отношения оценок
спектральной плотности к истинным значениям.
Поскольку основная цель сравнительного спектрального анали-
за — сравнение спектральной плотности в иесколькнх частотных
полосах одного или нескольких спектров, целесообразно выделить
необходимое число степеней свободы для сравнений с некоторой ста-
тистической достоверностью. Наиболее подходящей для проведения
£ “Зак. 576 161
таких сравнений является классическая таблица значений F, где
в данном случае F есть отношение %2-параметров для двух полос час-
тот в предположении, что полосы частот одинаковы. Степени сво-
боды для каждой из двух полос представляют собой соответствующие
параметры, связанные с F. Сравнение оценок спектральных плот-
ностей лучше делать при одинаковом числе степеней свободы, хотя
это и необязательно.
Таким образом, достаточно определить диагональные члены лю-
бой стандартной таблицы значений F, чтобы найти критические от-
ношения спектральных плотностей с необходимыми доверитель-
Рис. 6.10. Соотношение между числом степеней свободы и отно-
шением оценок спектральной плотности к истинному
значению спектральной плотности для нескольких зна-
чений доверительных пределов [8].
ними пределами. В качестве примера в табл. 6.1 указаны диагональ-
ные члены стандартной таблицы F для трех доверительных пределов
(по данным работы [5]). Видно, что отношение оценок спектраль-
ных плотностей [Ci ((в)/С2 (w)l (dj (оз) > С2 (со)), каждая из которых
вычислена с 50 степенями свободы, больше 1,6 для 5% случаев, в
то время как истинные спектральные плотности в каждой из двух
полос частот одинаковы. Измеренное отношение, превышающее
1,6 с 90%-ным доверительным пределом, может рассматриваться как
признак существенной разницы в спектральной плотности. Если
выбран 80 %-доверительный предел, то критическое отношение рав-
но 1,44 прн том же числе степеней свободы. В этом случае сущест-
вует 10%-ная вероятность того, что измеренное отношение, большее
1,44, не представляет истинной разницы в спектральной плотности.
Это критическое отношение быстро растет с уменьшением числа
162
степеней свободы. Так, например, при 90%-ном доверительном пре-
деле, когда обе оценки деваются с 10 степенями свободы, критичес-
кое отношение равно 2,32.
Таблица 6.1
Критические значения F для сравнения оценок спектральной плотности [5J
Число степеней свободы /с Довери- тельный 80%-ный предел (1 — а) Довери- тельный 90%-ный предел (1—а) Довери- тельный 95%-ный предел (1-а) Число степеней свободы К Довери- тельный 80%-ный предел (1—а) Довери- тельный 90%-иый предел (1-а) Довери- тельный 95%-иый предел (1-а)
5 3,45 5,05 7,15 35 1,55 1,76 1,96
6 3,05 4,28 5,82 40 1,51 1,69 1,88
7 2,78 3,79 4,99 45 1,48 1,64 1,81
8 2,59 3,44 4,43 50 1 ,44 1,60 1,75
9 2,44 3,18 4,03 ' 60 1,40 1,53 1,61
10 2,32 2,98 3,72 70 1,37 1,49 1,61
12 2,15 2,69 3,28 80 1,34 1,45 1,55
14 2,03 2,48 2,98 100 1,29 1,39 1,48
16 1,93 2,33 2,76 200 1,20 1,26 1,32
18 1,86 2,22 2,60 300 1,17 1,22 1,26
20 1,79 2,12 2,46 400 1,15 1,19 1,23
25 30 1,69 1,61 1,96 1,84 2,23 2,07 500 1,12 1,16 1,19
§ 6.10. Влияние некоррелированных шумов
на измерения передаточной функции
Большое влияние оказывают дополнительные шумы входа или
выхода на измерение передаточной функции ядерной реакторной
системы. Шумы могут возникать при детектировании дискретных
событий (шумы детектора) из-за помех, связанных с влиянием элект-
рических систем (особенно в диапазоне промышленной частоты
50 гф), или из-за присутствия других внешних или внутренних не-
коррелированных шумов. Эта общая проблема была провнализиро-
ваиа в работе [9] и описанный в ней метод рассматривается в этом
параграфе.
Шумы на входе и выходе. В наиболее общем случае некоррели-
рованные шумы присутствуют на входе и выходе измерительного
устройства (рнс. 6.11). Измеряемые входной и выходной сигналы
состоят из двух сигналов и (?) н v (f), и двух шумовых компонент
т (/) и п (/) соответственно, т. е.
х (/) = и (/) 4- т (7) (6.59)
= v (t) 4- П (/). (6.60)
Соотношения для спектральных плотностей следующие:
Ста(а>)=С„„И+С™л(“). (6.61)
GW (“) = °™ М + Сп„ (Ш). (6.62)
Оад(со) = С„с(ш). (6.63)
6* 163
Соотношение (6,63) для взаимной спектральной плотности справед-
ливо для большинства экспериментов, поставленных надлежащим
образом. Истинная функция когерентности системы есть
yiv (го) = | Guc (го) |=/G„„ (го) С„о (со),
(6.64)
тогда как измеренная функция когерентности входного процесса
х (£) и выходного процесса у (t) есть
тЛ (о>) = | Gxll (го) |2/G„ (co) Gm (го) =
= I С„г (го) |2/[С„„ (го) + Gmm (го)] [Gc„ (го) + G„„ (го)]. (6.65)
Рис. 6.11. Динамическая система с шумами на входе и
выходе.
Разделив числитель и знаменатель этого выражения нз
Gull i®)Gvv (го) использовав определение (6.64), получим
(®)=тг» (го) Г1 + с,п"(ю) + + д™™(ю)с""(го)-1 -1 (6 66)
L Сии (to) GyC (to) GKlt (to) Gco (ГО) J
Из соотношения (6.66) ясно, что измеренная в присутствии п (/)
или m (/) функция когерентности меньше, чем истинная функция:
(6.67)
Следовательно, присутствие шума на входе или выходе системы
ухудшает качество измерений.
Метод взаимной спектральной плотности. Для иллюстрации
вышеизложенного рассмотрим измерение амплитуды передаточной
функции взаимнокор реляционным методом, т. е.
| я (го) | = 1 1 — *Guv * =
Gxx (го) (®) + tnm (го)
__ IСuv (ГО) (ГО) _ | Нс (и) [ ,g gg.
I + (Gmm (ro)/GuK (ГО)) 1 4- [Gmm (to)/GHli (to)]
После преобразования получим
|//с(го)| = |Д(го)| [1 + (6.69)
L Сии (Го) J
т. е. истинная амплитуда передаточной функции равна измеренной
амплитуде, умноженной на коэффициент, который показывает, что
164
присутствие шумов т (/) на входе системы и измерительного устрой-
ства дает смещенную оценку амплитуды передаточной функции.
а. Только выходные шумы. Соотношение (6.69) не включает в себя
шумы, которые могут присутствовать и а выходе системы, и требова-
ние несмещенной оценки амплитуды передаточной функции взаимно-
корреляционным методом заключается в том, чтобы на входе систе-
мы отсутствовали шумы т (/).
Для случая, когда шумы присутствуют только в выходном сигна-
ле, истинная функция когерентности, как это видно из соотношения
(6.66), равна
ТМ*) = [1 +Gnn (cd)/Gou (cd)]. (6.70)
Оценка функции когерентности может быть несмещенной только
в случае, когда шумы, поступающие на устройства, измеряющие
входной и выходной сигналы, равны нулю. Как будет показано ниже,
точность измерения связана с функцией когерентности, поэтому
можно сделать вывод, что присутствие шума в устройстве, измеряю-
щем выходной сигнал системы, не будет смещать оценки передаточ-
ной функции, хотя и неблагоприятно скажется на точности.
б. Только входные шумы. Присутствие шумов в устройстве, изме-
ряющем входной сигнал системы-, будет давать смещенные оценки
передаточной функции, а также неблагоприятно влиять на точность.
Величина смещения, как видно из соотношения (6.69), прямо про-
порциональна отношению спектральных плотностей шума т (t)
и входного сигнала и (f).
Метод спектральных плотностей. Положение существенно хуже
при оценках амплитуды передаточной функции методом измерения
спектральных плотностей, т. е.
L Gxx (СО)
IV2 = Г Сот(СР) + Gnn (СР) В/2
L Guu (cd) +Gmm (со) J
[ Нр (CD) |2 + [Gnn (CD)/CKH (CD)] U/2
1 +[Gmm (b))/Guu (CD)] J
(6-71)
После преобразования соотношения (6.71) получим
//„(<□) = (6.72}
I L GKW (CD) J Guu (CD) J
Из соотношения (6.72) ясно, что несмещенную оценку амплитуды
передаточной функции можно получить из измерения спектраль-
ных плотностей только при отсутствии шумов в устройстве, измеряю-
щем входной и выходной сигналы*. Конечно, величина смещения
зависит от соотношения спектральных плотностей шумов п (/),
т (f) и входного сигнала и (/). Часто оценки амплитуды передаточ-
* Исключение представляет система с передаточной функцией первого
порядка.
165
ной функции получают измерением спектральных плотностей, а
влиянием шумов т {£) и п (f) пренебрегают. В этом случае присутст-
вие шумов т (/) дает заниженную оценку амплитуды передаточной
функции, тогда как присутствие шумов п (f) приводит к завышенной
оценке. Несмотря на то, что смещение, обусловленное шумами на
входе измерительного устройства, стремятся скомпенсировать иа вы-
ходе измерительного устройства, истинная оценка в конечном ре-
зультате получается довольно редко.
Шумы только на входе или только на выходе. Если шумы при-
сутствуют только в измерениях входного сигнала или только вы-
ходного, можно получить выражения для коррекции смещения, ко-
торое обсуждалось выше, в зависимости от измеряемой функции ко-
герентности 7.^ (со). Вначале рассмотрим случай, когда шумы при-
сутствуют только при измерениях входного сигнала. Из определе-
ния функции когерентности и соотношений между спектральными
плотностями входного и выходного сигналов получим
у~ху (со) I Нр (со) Iй = |Сзд(№)1а . =
Gxx (со) Gvv (to) Gxx (со)
Сии (со) [ Н (со) |2 zg
Gb(co)
откуда можно получить квадрат истинной амплитуды передаточ-
ной функции:
I Н (“) I2 = й,1 (со) |*. (6.74)
Gtw (со)
После упрощения выражения (6.74) с помощью равенства (6.66)
для п (/) = 0 получаем
= ytv (га) Г---(и) [. (6.75)
L GUII (Го) + Gmm (со) ] l GXx (со) J
Для случая, когда
у2в(со)л;1, (6.76)
путем комбинации соотношений (6.74) и (6.75) получаем
|77(со)р = [^(<о)|2[^(со)]-1. (6.77)
Легко показать, что истинная амплитуда передаточной функции,
измеренной методом взаимной корреляции, в случае наличия шумов
только во входном сигнале дается выражением
I //(со) |= |Hc(co)|[TlH“)]-]. (6.78)
166
Если шумы присутствуют только при измерениях выходного сигна-
ла, соотношение (6.74) переходит в формулу
|Я((о)|2 = |ЯР(«)|2^(“), (6.79)
на которую не накладывается ограничение (6.76). Как указывалось
выше, при измерении взаимной спектральной плотности оценка ам-
плитуды передаточной функции является несмещенной, т. е.
Е [|Я(ш)|] = |Яс(ш) |. (6.80)
Ясно, что присутствие шума входного сигнала больше влияет на
оценку такого параметра, как функция когерентности и точность,
чем присутствие шума при измерении выходного сигнала.
§ 6.11. Точность измерений передаточной функции*
Передаточная функция физической системы, определенная путем
анализа случайного входного и выходного сигналов, представляет
собой лишь приближение истинной передаточной функции, так как
измеренные спектральная н взаимная спектральная плотности яв-
ляются только оценками истинных значений. Можно определить
статистическую точность этих экспериментальных оценок.
Когерентность Уху («) дает прямое указание на погрешность
в оценке Я (оз), вызванную шумами. Если значение уД&'(С0) мало,
Доля полной мощности в ответном сигнале у (t), обусловленная вход-
ным сигналом х (f), мала и величина Н (оз) может быть получена с
существенной погрешностью. И наоборот, значение у^у (®), близкое
к единице, указывает на большую надежность оценки. Таким обра-
зом, анализ, основанный на статистических представлениях, 'тре-
бует определения точности экспериментальной оценки передаточной
функции.
Исследование погрешностей, связанных с измерениями переда-
точной функции, было проведено Гудменом [101. Первый разработан-
ный им метод основывался на предположении, что измерение дает
несмещенную оценку с дисперсией около истинного значения. Стро-
го говоря, это несправедливо для оценки погрешностей, связанных
с экспериментальными данными, хотя и часто используется с этой
целью. Рассмотрим передаточную функцию, полученную методом
измерения взаимной спектральной плотности, т. е.
Я(а>)=|&ч,(а>)|/6ет(а>), (6.81)
ен(®) =еСку (ю). (6.82)
Функция когерентности определяется как
(®) = I Gxy И |3/СЯЯ (<й) Суу И. (6.83)
* Эта часть основывается на работе [10]. Подробный анализ дан Бенда-
том и Пирсоном [11].
167
В работе [10] найдено выражение для вероятности Ртого, что по-
грешности определения амплитуды и фазы передаточной функции
будут меньше некоторого значения, т. е.
Р — Prob
|Я|-1 Я|
|Я|
<sine н |6— 6|<е|«
i—уад
< 2 2
1 — уху COS 8
(6.84)
/Можно преобразовать выражение (6.84), чтобы получить число сте-
пеней свободы
/г =
21п(1—Р)
(6.85)
1 — Тад cos2 в
которое очень полезно для планирования эксперимента. К сожале-
нию, необходимо предположить известным значение функции коге-
рентности уху (со), так как она непосредственно связана с качест-
вом измерения. Обычно выбирается низкая оценка чтобы до-
стигнуть требуемой точности измерения.
Можно найти погрешность в подстановкой тригонометрического
равенства
C0S2 е = 1 —• sin2 Е (6.86)
в выражение (6.34) и решением его относительно е, т. е.
Е ~ sinH»[1 -
(6.87)
Это означает, что с вероятностью Р справедливы три неравенства
(смысл всех неравенств один и тот же):
11й|—|/У| | <|/У|sine,
| Я | (1 —sin е) < | Н | < | Н | (1 + sin е);
1-bsin е 1—sine
(6.88)
(6.89)
(6.90)
|е-е|<[ё|<|е-|-Е|.
(6.91)
Эти соотношения графически изображены на рис. 6.12, где с вероят-
ностью Р оценки Н (со) попадают в заштрихованную область. Для
значений е < 0,2 в выражениях (6.88), (6.89) и (6.90) можно исполь-
зовать
sin £ Ж E.
(6.92)
168
Рис. 6.12. Оценка статистической погреш-
ности в измерениях передаточ-
ной функции [11].
В работах [12] и [13] также исследовались погрешности как откло-
нения от экспериментальных значений. Опять предполагалось,
что измеренная величина несмещенная. Для общности рассматрива-
лась система с многими независимыми и коррелированными входами.
Мы рассмотрим общее выражение для погрешности и ограничимся
случаями одного и двух входов.
Рассмотрим систему, изображенную на рис. 4.18 с q входами, где
передаточные функции Яг- (со) даны взаимнокорреляционным соот-
ношением из уравнения
(4.211)
(6.93)
для случая, когда входы
коррелированы. Для случая,
когда входы иекогерентны,
соотношение (6.93) можно
упростить и привести к виду
= (6.94)
Для обоих случаев (1 —
—а)—процентные доверитель -
ные пределы для истинной
амплитуды | Hi (со) | и истинного фазового угла 6г (со) — для каж-
дой частоты / и каждой системы (i = 1, 2, ... q) даются в виде
[| Й, (ш) | -Д,(и)] < | Яг (и) | < [| Й( (<>) 1+ А, (в)],
[ёг(а)—8,(о>)] [ёг(а>) +«,(<!>)],
(6.95)
(6.96)
где выражения для погрешности определения амплитуды (радиаль-
ной) Д? (со) и фазы (со) даются для каждого рассматриваемого слу-
чая. Эти соотношения показаны схематично на рис. 6.13, где с (1 —
— ct) — доверительной вероятностью значения Hi (со) нахо-
дятся внутри круга.
Множество некогерентиых входов. Для случая, когда все входы
некоррелированные, Дг (со) и 6i (со) даются в виде
Si(<0)=[-2-(F„1.„,.n) [1-й,(<в)]^М1,/2. (6.97)
[Я— 2 Сц (со) ]
б£ (со) = arc sin [Д £ (to)/1 Ht (со) I], (6.98)
где k — число статистических степеней свободы для каждой оцен-
ки спектральной плотности; (ГП1, П1. „) —100%-ныеточки F-pacnpe-
деления сп1 = 2 и n2 = k — 2 степенями свободы; Gn (со), Gyy (со)—
169
измеренные спектральные плотности i-ro входного и выходного сиг-
налов соответственно; yh — измеренное значение функции, коге-
рентности между выходом у (/) и i-м входом xt- (t), т.е.
ТЛ (“) = I (“) Г/Gu (“) Gw (“)• (6.99)
Для этого случая точность увеличивается с ростом числа степе-
ней свободы для каждой спектральной оценки, увеличением (при-
ближением к единице) фактора когерентности (со) и увеличением
отношения G,,,, (a)IGti (со), которое представляет собой квадрат ам-
плитуды передаточной функции Ht (со).
Рис. 6.13. Статистические ошибки в измерениях пере-
даточной функции с многими входными
сигналами.
Один вход. Для случая, когда имеется только один входной сиг-
нал, все соотношения (6.94)—(6.99) применимы с подстановкой ин-
декса i=l.
Множество когерентных входов. Когда входные сигналы корре-
лированы, оценка статистических ошибок усложняется. Выраже-
ния (6.95) и (6.96) остаются справедливыми, за исключением того,
что величина Дг (со) имеет вид
Л/x I 2? т , 1 ~ Т^-*<С0) От(а)]Ч2 ,K1nm
Ai(u>)= -----г о) :—4—— • . (6-100)
[п— 2q I — Yf.jeUo) Gu (со) J
где q— число входов. Степени свободы /^-распределения даны при
— 2q и = п — 2q; уу.х (со) — измеряемая величина много-
канальной функции когерентности между выходом у (/) и всеми
измеренными входами; yf.x—измеряемая величина многоканаль-
ной функции когерентности между входом х (f) и другими измеряе-
мыми входами, исключая Xt (/). Множество функций когерентности
дается выражением
ylх (со) = 1 - [Cfi (со) G£J “ ’, (6.101)
170
где Glx обозначает i-ю диагональ обратной матрицы [Gxse (ш)]-1
и матрица ОЛХ (ш) дается выражением
G„» =
(6.102)
Gn(“) CJ2(ш) ... Glq(a)
621(ш) С22(ш) ... С2? (ш)
_651(ш) С,2(ш) ... GgQ(o)_
Множество функций когерентности уу.х (со) между выходом у (I)
и всеми входами дается в виде
Ъ.х (Ш) = 1 — [GBI( (ш) G?„ (ш)] -(6.103)
где G$xx (со) есть t-ый диагональный элемент обратной расширенной
матрицы iG^-x (со)]’1. Расширенная матрица G ужх (со) имеет вид
Gvy М GJZ1 (“) G{/2 (“)•• GVg И "
G1V (“) G11 (®) gi2(®) • Gi« (“)
с!,хх(<п) = G21 (М) G22 (М) (“) (6.104)
-G«» G^) Gg^)-Ggq(-
Выражение для (co) то же, что и в соотношении (6.98).
Два когерентных входа. Если входные сигналы системы с двумя
входами коррелированы, то матрица (6.102) превращается в матрицу
G>)=K G12!m!l <6Л05>
[G21(co) G2a (со) ]
и обратная матрица есть
[Ста(<0)]--=-1-Г (6106)
A (—G2I(o>) Gn(<»))
где Д — детерминант матрицы Окж (со)
A=lrU^ =[С11(“)С2гИ-|G1SM|21. (6.107)
|С21(ш) С22(ш)|
Следовательно, первый и второй диагональные элементы обратной
матрицы [GIX (ш)1-1 суть
G«xi (®) = ,
Д Си (о) С22 (ш) - I Gls (ш) |« ’
G„s (о) = £11^ =------------Сц<т)---------
А 6ц(ш)С2,,(ш)—|012(ш)|!
(6.108)
(6.109)
171
и множество функций когерентности из уравнения (6.107) можно
записать в виде соотношения
Тьл (<о) = 1 —[ОИ&1Х]—1 =
|____. Oil (to) 628 (Ю) — | Gjg (fo) |g = |б18 (ГО)|В _ ^2^ (6 110)
6ц (co) G-22 (го) 6ц(<о)С 22 (го)
которое теперь является обычной функцией когерентности (го).
Аналогично получим
Y2-Л- (го) = IС21 (го) Р /6Ц (со) Gas (со) = vl t (го). (6. Ш )
Чтобы найтн //-й диагональный элемент [О^жж(го)] обратной расширен-
ной матрицы [Gvaa- (со)]-1 для двух входов, рассмотрим расширен-
ную матрицу
Чу И
1Ч«ж С05)] — G 1У (w)
G^ (го)
GWi (co) G4SS (co)
Gu И G12 <ro)
Gai (to) Ggo (co)
(6.112)
Ее обратная матрица есть
[G„xx (и)] 1
C.F.(G„„)
C.F.(GIa)
C.F.(GW)
C.F.(G„J
C.F.(Gn)
C.F.(Ga)
C.F.(G„2-) 1
C.F.(G12)
C.F.(G22)
(6.113)
где C.F. (,Gyy) означает адъюнкт
матрицы G„„ (и) и детерминант
Д' =
Gyy (со)
GiS (со)
G2y (со)
Gpi (со) Gy2 ((о)
Оц(со) 012(со)
G21(co) Ge2(co)
(6.114)
Диагональные jc-e члены обратной расширенной матрицы (6.113)
имеют вид
^(и)=с^ад=^|
Gji (to) G12 (со) I
G2l(co) G22(ro) |
[Gix Go2~*G12 Ggi]
[Ggi/ G11622 + Gyi G12 Ozy 4- Gr/2 Giy 621—Gym Gn Gzy —
—Gyy 612 G2i—Gyi Giy G22I
172
Следовательно, множество функций когерентности между выходом
у (/) и всеми входами есть
Уу-Х ~ 1 --[Gyy Gyxx\~ 1 —
[Cgg Ои G^s. + Gyi 612 G^y + Gyz (iiy Got—Gyo Gn C2y —
__ j_______________—Gflt/ Gi2 G2i —Gfli Giy G22] __________
Gn G22--Gyy G12 Ggl]
_ Gy» Gn Ggy + Gyi Giy G22—Ggi &is G»y—Gg2 Gig &2i 116)
Gyy Gn 622 — Gyy G12 G2i
Поскольку многие члены в соотношении (6.116) весьма сложны
для расчета, для оценки точности измерений передаточной функции
необходимо применение ЦВМ.
СПИСОК ЛИТЕРАТУРЫ
I. Valat J. Reactivity Measurements Using Source Excitation and Correla-
tion Techniques. — In: Noise Analysis in Nuclear Systems. Gainesville,
Fla., N 4—6, 1963, Uhrig R. E. (Coordinator): AEC Symposium Series,
1964, N 4 (TID-7619).
2. Kerlin T. W. The Pseudo-Random Binary Signal for Frequency Response
Testing. — USAEC Report ORNL-TM-1662, Oak Ridge National Labora-
tory, September 1966.
3. Hennig T. Testing for Plant Transfer Functions in the Presence of Noise
and Non-linearity: II. Getting Dynamics from Noise Signals. — Control
Engng, 1967, II, N 9, p. 119.
4. Blackman R. B., Tukey J. W. The Measurement of Power Spectra. — Dover
Publications. N- Y., 1958.
5. Zimmerman S M. The Rocket dyne Spectral Analysis Computer Program. —•
Research Report 60—11, Rocketdyne Division of North American Aviation,
Inc., 1960.
6. Zimmerman J. M. Correlation and Spectral Analysis of Time Varying Da-
ta. — Research Report R-882, Rocketdyne Division of North American
Aviation, Inc., 1958.
7. Spadaro F. D. Numerical Filters and Their Application to the Characteri-
zation of Dynamic Systems. — Research Report 60—8, Rocketdyne Divi-
sion of North American Aviation, Inc., 1960.
8. Schiesser W. E. Statistical Uncertainly of Power Spectral Estimates. —
Bulletin 711-C1, Weston — Boonshaft and Fuchs, 1966.
9. Enochson L. D. Frequency Response Functions and Coherense Functions
for Multiple Input Linear Systems. — Report NASA-CR-32, April 1964.
10. Goodman N. R. On the Joint Estimation of Specrta, Со-spectrum and Quad-
rature Spectrum of a Two-Dimensional Stationary Gaussians Process. —
«Scientific Paper», .N 10, Engineering Statistics Laboratory, New York
University, 1957.
11. Bendat J. S., Piersol A. G. Measurement and Analysis of Random Data.
John Wiley and Sons, Inc., N. Y., 1966. (См. Бендат Дж., Пор co л А. Из-
мерение и анализ случайных процессов. Пер. с англ. М., «Мир», 1974.)
12. Goodnan N. R. Simultaneous Confidence Bands For Matrix Frequency
Response Functions and Related Results. — Research Memorandum
RM-972-351, Rocketdyne Division of North American Aviation Corp., 1963.
13. Goodman N. R. Measurement of Matrix Frequency Response Functions. —
Report AFFDL-TR-65-56, Air Force Flight Dynamics Laboratory, June
1965.
ГЛАВА 7.
МЕТОДЫ
ИЗМЕРЕНИЯ
ШУМОВ
И АППАРАТУРА
§ 7.1. Аппаратура для измерений реакторных шумов
Измерение параметров ядерных реакторов шумовыми методами
может быть проведено с помощью либо специально разработанной
аппаратуры, либо аппаратуры общего типа, имеющейся обычно в
исследовательских лабораториях. Эти измерения могут быть выпол-
нены также путем обработки данных на ЦВМ, либо в режиме on-line,
если ЦВМ непосредственно связана с экспериментальным оборудо-
ванием (возможно, на основе разделения по времени), либо в режиме
off-line, если данные могут быть предварительно зарегистрированы
(обычно на магнитной ленте). Выбор каждого из этих методов обра-
ботки сильно зависит от цели эксперимента, природы эксперимента,
типа имеющегося оборудования и стоимости недостающего оборудо-
вания.
Однако можно выдвинуть некоторые общие требования, справед-
ливые для многих случаев.
Если измерения проводятся для проверки принципа или возмож-
ности данного исследования, часто преимущества имеет использо-
вание широкодоступной аппаратуры, чтобы минимизировать финан-
совые вложения в специализированную аппаратуру для детального
эксперимента.
Если измерения составляют часть обширной программы, тре-
бующей множества измерений в течение длительного периода вре-
мени, целесообразна закупка или разработка специализированного
оборудования и возможна в некоторой степени автоматизация про-
цесса измерений.
Когда измерения проводятся с очень сложной системой, вклю-
чающей в себя десятки или сотни переменных, которые необхо-
димо анализировать, или система включает в себя много входов,
то для обработки данных используются цифровые методы. Сдругой
стороны, большое количество оборудования, требуемого для нако-
пления и обработки данных, а также для подготовки, отработки и
проверки программ ЦВМ, связанных с обработкой данных, обычно
не оправдано для отдельных экспериментов, пока они не являют-
ся основным направлением лаборатории.
174
§ 7.2. Методы непрерывного анализа данных
с помощью аналоговых ЭВМ*
Основная цель применения аналоговой вычислительной машины—
анализ непрерывных (аналоговых) данных в экспериментах на ядер-
пых реакторных системах. Обсуждаемые методы включают в себя
измерение среднего значения переменной, среднеквадратических
и стандартных отклонений, автокорреляционной функции, спект-
ральной плотности мощности, фурье-анализ, исключение дрейфа.
Методы измерения средних значений, дисперсии, стандартного
отклонения н исключения дрейфа могут быть реализованы в режиме
оп-Нпе, в то время как методы вычисления корреляций и спектраль-
ных плотностей могут быть применены в этом режиме только для
отдельных значений т и со. Однако эту трудность можно избежать-
применнв несколько раздельных
параллельных каналов для от- . .
дельных значений т и со, в ре- ——Q——J __________________-дЦ]
зультате чего одновременно вы- 1
чнсляются много точек корреля-
ЦИОННЫХ функций И спектральных р11С. 7.1. Схема усреднения,
плотностей.
Описываемая ниже методика имеет дело с «экспоненциально
распределенным прошлым» (ЭРП) Ш функции на временном интер-
вале Т.
Чтобы ввести понятие экспоненциально распределенного прош-
лого переменной, рассмотрим аналоговую схему, изображенную на
рис. 7.1, которая имеет на выходе сигнал
У V) = V 1 т *1 * (fl dt = Их- (7.1)
Величина сигнала равна средней величине где переменная
х {1} усредняется за период от 7\ до Tz. Очевидно, проблемой яв-
ляется выбор интервала — 7\ таким, чтобы усилитель за время
интегрирования не перегружался, т. е. интегрирование должно про-
водиться за конечный период времени. По окончании интегрирования
интегратор должен быть возвращен к своим начальным условиям,
и новая величина вычисляется за интервал времени от Tz до Т3.
В результате получается серия средних значений которые су-
щественно не зависят друг от друга. Для эргодического процесса
эти значения будут одинаковы при условии, что интервал интегри-
рования достаточно велик.
Из этого рассмотрения видно, что прошлая информация стано-
вится ненужной после того, как интегратор возвращается к началь-
ным условиям. В работе [1] показано, что прошлая информация
должна становиться ненужной постепенно, а не внезапно, и пред-
* Описанные здесь методы предложены в работах [1] н [2] и обобщены
в работе [3J.
175
ложено использовать экспоненциальную весовую функцию, чтобы
подчеркнуть недавнюю прошлую информацию и ослабить далекое
прошлое. Рассмотрим систему с экспоненциальной весовой функцией
h (/) = ехр (—сс/). (7.2)
Выходной сигнал системы представляет собой свертку весовой функ-
ции н входного сигнала х (/), т. е.
у (/) — х (к} ехр I — со (t—A.)] dkt (7.3)
где % —временная переменная интегрирования. Интегрирование
в соотношении (7.3) может рассматриваться как процесс усреднения
за временной интервал от-—оо до Т, следовательно, соотношение
(7.3) принимает вид
y(t) = х(Х)ехр[—сс(Т—X)]dX. (7.4)
Эта замена необходима, так как данные будущего процесса недо-
ступны для обработки в режиме on-line. Отметим, что выходной сиг-
нал у (0 является средней величиной х (I), но он также изменяется
в зависимости от машинного времени Т, т. е.
y(t)~E[x(T)]= х(Х)ехр[—<х(Т—A)]dA =
= ехр (— аТ) х (к) ехр (ак) dk. (7.5)
Среднее значение. Чтобы реализовать это соотношение на ана-
логовой машине, продифференцируем уравнение (7.5) относительно
машинного времени Т и, используя правило Лейбница, получим:
jg_(O = d£[x(O] =_де_а7-Г x(?b)e<Atl?b +
dT dT Л,
+ е-‘1Т [х (Т) е“П = х (Г)—аЕ [х (0]. (7.6)
Это уравнение легко моделируется на аналоговой машине, как
показано на рис. 7.2, и является уравнением фильтра первого по-
рядка, или системы с запаздыванием первого порядка с постоянной
времени 1/сс, которая показывает, как быстро прошлая информация
становится ненужной. Эта постоянная времени произвольно выби-
рается достаточно большой, чтобы фильтровать случайные флук-
туации, и достаточно малой, чтобы исключить влияние продолжи-
тельного дрейфа.
176
Рис. 7.2. Схема усреднения с экспо-
ненциально распределенным
прошлым.
Если х (Г) изменяется резко, то у (f) изменяется постепенно (на
99% за 5 постоянных времени, т. е. 5/а). Другими словами, интегра-
тор «забывает» 99% информации, существовавшей перед скачкооб-
разным изменением, следовательно, ЭРП-усреднение является ус-
реднением по временному интервалу, приблизительно равному 51а.
Очевидно, что начальное условие интегратора влияет на усред-
ненное значение в начале изме-
рений. Это значение должно
представлять хорошую оценку
среднего для получения разум-
ного усреднения в начале изме-
рений. В противном случае тре-
буется около пяти временных
интервалов, равных постоянной
времени фильтра, чтобы достичь
разумной величины.
Дисперсия и стандартное отклонение. Аналогично определению
среднего значения Оттерманн [1] определил ЭРП-дисперсию как
о3 (Г) =5 {х (X) - Е [х (7)}3 ехр [—(7—Х)1 dX, (7.7)
которую можно представить как экспоненциально взвешенное усред-
нение квадрата отклонений переменной от ее среднего. Это выраже-
Рпс. 7.3. Схема измерения среднего квадрата величины
с экспоненциально распределенным прошлым.
иие легко реализуется на аналоговой машине следующими ступенями:
вычисление среднего по схеме, изображенной на рис» 7.2, вычитание
этого среднего из входной функции, возведение в квадрат разности,
усреднение квадрата с помощью второй схемы усреднения. Такое
устройство показано на рис. 7.3. Снова необходимы хорошие на-
чальные условия в обоих интеграторах, или мы должны выжидать
около пяти временных интервалов, равных постоянным времени
фильтров, чтобы получить разумно надежные показания. Если необ-
ходимо получить стандартное отклонение, схема, изображенная на
рис. 7.3, дополняется схемой извлечения квадратного корня.
Корреляционные функции. ЭРП взаимная корреляционная
функция <рЖу (т) может быть определена как
<Рк»(т)- jj [х(Х)^(Х-|-т)]ехр[—а(7—(7.8)
177
Это выражение также легко может быть реализовано на анало-
говой машине следующими ступенями: одна из переменных, в дан-
ном случае у, поступает на блок запаздывания на время г, затем
умножается на х (/), и произведение усредняется с помощью схемы,
изображенной на рис. 7.2. Структурная схема вычислительной ма-
шины для взаимной корреляции показана иа рис. 7.4. При автокор-
реляции одна и та же переменная используется на обоих входах.
Рис. 7.4. Схема измерения взаимной корреляции
с экспоненциально распределенным про-
шлым.
Временное запаздывание —одна из наиболее трудных величин
для реализации в физических системах. Устройства для временных
запаздываний описаны в следующем параграфе. На аналоговой вы-
числительной машине наиболее общим методом является использо-
вание схемы Паде. На рис. 7.5 показана схема запаздывания на
время т с помощью приближения Паде четвертого порядка. Погреш-
Рис. 7.5. Схема аппроксимации Паде четвертого порядка.
ностъ схемы не превышает одного градуса фазового сдвига для час-
тот во входном сигнале х (/), при которых произведение максималь-
ной частоты сигнала на временную задержку меньше 6,5 рад, т. е.
™мако<6.5 (7-9)
Преобразование Фурье и спектральная плотность мощности. ЭРП
преобразования Фурье х (/) можно определить как
Л(со)= I х (%) 6-^^% =
178

т
= [cos coT—j sin шт] JJ x (X) e—a <r-N x
X [cosco (T—X) +j sin co (T—X)] dX.
(7.10)
Поскольку соотношение (4.20) показывает, что спектральная
плотность мощности равна квадрату амплитуды преобразования
Фурье, имеем
Рис. 7.6. Схема измерения спектральной плотности с
экспоненциально распределенным прошлым.
Ф(о) = Um [ X(со) |2 — lim [X(со)X (—со)] — lim [cos2<яТ-р sin2соТ]х
7'—оо Т-'Оа
Хц Jj х(Х)е— atT~cos со (Т—X)dX
sin со (Г—X)dX
(7.10
Структурная схема расчета ЭРП спектральной плотности мощ-
ности дана на рис. 7.6. Схема, состоящая из усилителей 1, 2 и 3,
образует генератор синусоидальных колебаний. Усреднение функции
производится путем обратной связи в усилителе 1. Поскольку вы-
ходной сигнал усилителя 2 сдвинут на 90° по отношению к выходному
сигналу усилителя 7, ясно, что выходные сигналы Zx н Z2 представ-
лены в квадратных скобках в уравнении (7.11). Обоснованность
этой схемы можно доказать, определив передаточные функции
Zi (s)/X (s) и Z2 (s)/X (s), которые имеют внд:
Zi (s)/X (s) = (s + a)/l(s -p a)2 + <o2], (7.12)
Zs (s)/X (s) = co/[(s -I- a)2 + ©21. (7.13)
179
Обратные преобразования Фурье (7.12) и (7.13) дают импульсные
функции, которые имеют затухающие осцилляторные члены, сдви-
нутые по фазе на 90°.
Исключение дрейфа. Дрейф можно рассматривать как состав-
ляющую, содержащую очень низкочастотные компоненты. Следо-
вательно, для устранения этих компонент необходимо установить
фильтр, пропускающий
высокие частоты с относн-
о Г пх. ° I тельно низкой нижней ча-
—।—o-LJ стотой среза. Аналоговая
I______________I схема, показанная на
1 рис. 7.7 и имеющая пере-
Рис. 7.7. Схема высокочастотного фнльт- Даточную функцию
ра первого порядка. у (s)/X (s) = s/(s + сос),
(7.14)
приемлема для исключения дрейфа, состоящего нз частот ниже час-
тоты среза сос. Более острые срезы могут быть получены при использо-
вании передаточных функций более высокого порядка, таких, как
квадрат или куб передаточной функции, определяемой уравнением
Рис. 7.8. Схема высокочастотного фильтра вто-
рого порядка.
(7.14). Рассмотрим, например, передаточную функцию второго по-
рядка, которая является квадратом выражения (7.14), т. е.
y(S)/X(S)U-_A_l;
L(s+cdc)J
(7.15)
которая реализуется на аналоговой вычислительной машине по схе-
ме, показанной иа рис. 7.8. Эта процедура существенно улучшается
путем усовершенствований и использования более сложных схем
и методик.
§ 7.3. Измерение плотности вероятности
Метод измерения. Для получения лучшего представления о плот-
ности вероятности и ее физической сущности рассмотрим случай-
ную переменную х (/). Из флуктуаций переменной, показанных на
рис. 7.9, видно, что переменная некоторое время находится в ин-
тервале амплитуд между х и х + Ах.. Этот интервал определя-
ет отрезок кривой, и в общем случае проекция этого отрезка на
180
временную ось дает временной интервал. Для каждого значения х
временные интервалы, в пределах которых переменная х находится
в диапазоне Дх, суммируются, и отношение суммы этих временных
интервалов к полному времени Т представляет собой вероятность
сигналу находиться в интервале Дх при значении х. Эта вероятность
Р (х, Дх) = (х, Дх)/7 (7-16)
есть безразмерная величина, так как является отношением суммы
временных интервалов к другому временному интервалу. Одна-
ко имеются два аргумента вероятности — амплитуда х и ин-
тервал Дх. Интуитивно ясно, что вероятность возникновения
события в малом интервале в общем случае пропорциональна вели-
чине этого интервала. Поэтому разумно предположить, что когда
интервал очень мал, то делением на интервал Дх можно получить
величину, которая больше не зависит от этого интервала, а зависит
только от амплитуды. Эта величина определяется как плотность
вероятности. К сожалению, она зависит от длительности наблюде-
ния флуктуирующей переменной, но по мере увеличения длитель-
ности наблюдения становится более независимой от Т. Из выраже-
ния (7.16) вероятность должна быть всегда меньше единицы. Однако
плотность вероятности, которая может быть получена более точно
как
St£ (х, Дх)
тКх
.... Р (х, Дх)
р (х) = Iim х ' = lim
Дж-0 Дх Лл-0
Г—со У—со
(7.17)
принимает положительное или нулевое значение. Можно сделать
плотность вероятности безразмерной величиной умножением
ее на бесконечно малую величину dx н заменой суммы интегралом,
т. е.
р(х)= lim -
Дя-0
Р (х, Дх)
Дх
= lim — ГМхМх
г-оо Т J Дх
о
(7.18)
181
В результате плотность вероятности будет всегда меньше или равна-
единице.
Строгое измерение плотности вероятности требует, чтобы Дх
становилась бесконечно малой величиной, а временной интервал
Т и диапазон значений х бесконечно большими. Следовательно, из-
мерение плотности вероятности является оценкой временной вели-
чины. В общем случае эта оценка дает ответ на вопрос, каково от-
личие от истинного значения из-за конечной длительности реали-
зации и конечного интервала Дх. Эта разница является ошибкой.,
которую нужно минимизировать в практических измерениях.
Применение многоканального амплитудного анализатора для
измерений плотности вероятности. Другой метод измерения рас-
Ркс. 7.10. Структурная схема измерения плотности вероят-
ности.
пределения плотности вероятности, предложенный в работе 15], за-
ключается в применении многоканального амплитудного анализато-
ра, имеющегося во многих ядерных лабораториях. Структурная схе-
ма измерений с помощью такого анализатора показана на рис. 7.10.
Процедура измерений заключается в том, что флуктуирующая пере-
менная х (/) подается на сравнивающее входное устройство многока-
нального амплитудного импульсного анализатора и затем на обыч-
ный импульсный пороговый вход подключается импульсный гене-
ратор. Импульсы генератора должны иметь одну и ту же высоту,
а их ширина согласоваться с характеристиками анализатора. По-
скольку показание канала, в котором регистрируются импульсы,
зависит от разницы напряжений входа сравнивающего устройства
и импульсного входа, таким способом эффективно выбираются зна-
чения флуктуирующей переменной х (/), причем в каждый момент
времени имеется импульс от генератора, который направляется
в канал анализатора, номер которого пропорционален значению
флуктуирующей переменной. Следует отметить, что может оказаться
необходимым суммировать флуктуирующее напряжение с напряже-
нием смещения н выбрать коэффициент усиления суммирующего
усилителя для согласования напряжения на входе сравнивающего
устройства с характеристиками многоканального анализатора.
182
§ 7.4. Измерение корреляционных функций
Измерение корреляционной и взаимной корреляционной функций
аналоговыми приборами проводится относительно прямыми спосо-
бами. Процесс измерения корреляции включает трн существенные
стадии: временное смещение одной переменной относительно другой
.(наиболее трудная стадия), умножение этих двух переменных и ус-
реднение за достаточно длинный период времени. Обычно время за-
паздывания изменяется дискретным образом для получения достаточ-
ного количества точек кривой корреляционной функции. Можно
изменять сдвиг непрерывно, если это делается сравнительно медлен-
Головка воспроизве-
дения
Рис. 7.11. Устройство магнитной записи для измере-
ния корреляции.
но, чтобы время усреднения, в то время как т изменяется в узком
диапазоне, было сравнительно велико. Возникающая здесь пробле-
ма аналогична проблеме изменения средней частоты полосового
фильтра при спектральном анализе, которая обсуждается ниже. Су-
ществует множество способов умножения и усреднения, и может быть
получена любая желаемая точность этих операций, если выбрана
соответствующая аппаратура. Однако проблема создания временной
.задержки более сложна. Если задержка не слишком длинна или мак-
симальная частота слишком высока, иногда используется схема Паде,
показанная на рис. 7.5, но применение этой схемы ограничено соот-
ношением (7.9). Более общим методом создания задержки является
запись на магнитную ленту с последующим воспроизведением. Та-
кое типичное устройство показано иа рис. 7.11. Обычное устройство
магнитной записи видоизменено таким образом, чтобы магнитная
лента сматывалась с барабана 1, проходила мимо головки записи
и воспроизведения А, вокруг направляющего шкива, мимо головки
записи и воспроизведения В н наматывалась на барабан 2. Сущест-
ва
вуют несколько способов, которые часто используются для создания
запаздывания. Один из них заключается в записи переменной х (Z)
с головки А на одной дорожке и снятии сигнала с головки В, при
этом создается запаздывание
t = L/V, (7.19)
где L — длина ленты между головками А и В, а V — скорость,
с которой лента движется мимо этих головок. Имеются определенные
ограничения такого типа записи, одним из которых является мини-
мальная величина сдвига, который может быть получен, так как
длина ленты, проходящей вокруг направляющего шкива, конечна,
и нет возможности приблизить шкив как угодно близко к головкам.
Эту трудность можно преодолеть установкой третьей подвижной
головки записи и воспроизведения С, следовательно, запаздывание
становится ограниченным со стороны нулевого значения только раз-
мерами головок записи и воспроизведения и скоростями ленты.
Другая широко используемая процедура записи, когда т мало,
заключается в записи данных на две дорожки магнитной ленты с по-
мощью двух отдельных головок записи А и В. Пусть с головки А
ведется запись на дорожку Дас головки В — на дорожку 2. Если
данные вначале записывались при расположении направляющего
шкива в середине диапазона своего перемещения, то движение шкива
в одном направлении будет давать положительные временные сдви-
ги, тогда как движение в другом направлении — отрицательные
временные сдвиги. Данные могут быть записаны при минимальной
длине ленты между головками А и В, и затем отрицательные вре-
менные сдвиги могут быть получены воспроизведением записи на
дорожке 1 через головку В и записи на дорожке 2 через головку А.
Здесь минимально возможный отрицательныйвременной сдвиг равен
т = L/V. (7.20)
Умножив и затем усреднив выходной сигнал с головки Л, запи-
санной на дорожку 1, с выходным сигналом с головки В, записан-
ным на дорожку 2, и выходной сигнал, записанный на дорожке 2
с головки А, с выходным сигналом, записанным на дорожке 7 с го-
ловки В, можно определить взаимную корреляцию двух перемен-
ных (которые являются одинаковыми для автокорреляции), запи-
санных на две дорожки. Значения для обоих сдвигов -J-t и —т из-
меряются одновременно. Размещение нескольких головок вдоль маг-
нитной ленты позволяет измерять несколько точек одновременно.
Однако из-за высокой стоимости устройства с несколькими голов-
ками используются в корреляционных измерениях редко.
Магнитная память также может быть очень эффективным уст-
ройством задержки при наличии соответствующих аналого-цифро-
вых и цифро-аналоговых преобразований. Такие устройства обык-
новенно используются в лабораториях, оборудованных гибридны-
ми вычислительными машинами. Входной аналоговый сигнал кван-
туется со скоростью, соответствующей частотному содержанию сиг-
184
нала, оцифровывается и вводится в магнитную память. Величина
задержки определяется числом точек, накопленных в памяти, преж-
де чем она будет приведена в исходное состояние, скоростью цифро-
аналогового преобразователя и обращением к корреляционной
системе. Рассмотрим, например, сигнал, у которого верхняя частота
ограничена 20 гц. Приемлемая скорость квантования может быть 50
точек в секунду; таким образом, накопление 10 точек в магнитной
памяти будет давать задержку, равную 1/5 сек, накопление 200
точек обеспечивает задержку 4 сек н т. д.
§ 7.5. Измерения спектральной плотности
Существуют в основном две методики оценки спектральной
и взаимной- спектральной плотности. Первая из них заключается
в измерении автокорреляционной или взаимной корреляционной
функции и последующем преобразовании Фурье корреляционных
функций. В этой классической методике для расчетов используются
ЦВМ. Другая методика заключается в фильтрации: сигнал или сиг-
налы пропускаются через полосовой фильтр и выделяется доля сиг-
нала в данном частотном диапазоне. В случае измерения спектраль-
ной плотности мощности сигнал возводится в квадрат и затем делит-
ся на ширину полосы частот для получения среднего квадрата вели-
чины иа единицу частоты, который по определению является спек-
тральной плотностью мощности. В случае измерения взаимной
спектральной плотности два сигнала после фильтрации перемножа-
ются и усредняются, затем делятся на ширину полосы пропускания
фильтра для получения действительной составляющей. Та же самая
процедура используется для получения мнимой составляющей, за
исключением того, что один из сигналов после фильтрации сдви-
гается на 90° по фазе. Амплитуда взаимной спектральной плотности
является корнем квадратным из суммы квадратов действительной
и мнимой составляющих, а фазовый угол — арктангенсом отноше-
ния мнимой составляющей к действительной.
Чтобы вывести эти соотношения, рассмотрим определение авто-
корреляционной функции переменной величины х (/):
<Рях (т) = Е [х (f)x (t 4- т)]. (7.21)
Автокорреляционная функция есть также обратное преобразо-
вание Фурье спектральной плотности мощности, т. е.
<Р.та (т) = 7- f (®) =Т- С (и) ei^da. (7.22)
2Л J 2л J
—со Q
Если временной сдвиг т равен нулю, то, приравняв соотношения
(7.22) и (7.23), получим
£ I-1 (t) х (t +t)J = Е [хв (/)] = ^- С G„: (01) dm. (7.23)
2л J
о
185
Если теперь пропустить переменную х (?) через идеальный
фильтр, который пропускает частоты только в диапазоне Ай, то
соотношение (7.23) превратится в соотношение
©с4-А©/2
£[х!(/. Ли)] = -~ [
сос—Д«/2
С»х(®е. Дю)
(7.24)
где йс -— центральная частота полосы пропускания. В очень узкой
полосе частот Ай не будет существенных изменений спектральной
плотности мощности GKJC (со), и, таким образом, она может быть вы-
Полосовой фильтр Квадротор Сгема усреднения “Д? I
Рис. 7.12. Структурная схема измерения спектральном плотно-
сти мощности.
несена за знак интеграла. Уравнение (7.24) тогда превращается
в равенство
ос4-(Д<и/2)
Е [х- (/, Асе)] — — Gxx Ай) f dffl = — (йс, Асо) Ай, (7.25)
2я •' 2я
Ыс — (Ды/2)
которое преобразуется к виду
Gxx (®с» = ЗлЕ [х2 (А Ай)]/Ай. (7.26)
Для линейной частотной полосы* А/, соответствующей угловой
полосе частот Ай, аналогичное соотношение имеет внд
Gxx (fc, Af) = (А А/)]/АД (7.27)
Спектральная плотность мощности без труда может быть измере-
на путем выполнения соотношения (7.27). Переменная х (/) про-
пускается через полосовой фильтр с центральной частотой /с и ши-
риной полосы А/. Отфильтрованный сигнал затем возводится в квад-
рат, усредняется и делится на АД чтобы получить спектральную плот-
ность мощности. Структурная схема таких измерений показана на
рис. 7.12. Для практического применения этой схемы необходимо
ввести фильтры высокой частоты перед н после полосового фильтра,
чтобы удалить постоянные составляющие. Высшая частота среза двух
высокочастотных фильтров определяет самую низкую частоту, при
которой может быть измерена спектральная плотность мощности.
Процедура измерения взаимной спектральной плотности во многих
отношениях аналогична, но более сложна из-за комплексности ве-
личин. Рассмотрим определение взаимной корреляционной функции
186
’Фяу fr) величин х (/) и у (/) (которое является обратным преобразо-
ванием Фурье взаимной спектральной плотности):
<pss (т) = Е [х и х (I 4- т)] = еи‘т (7.28)
Однако мы должны оперировать с односторонней спектральной
плотностью Gxy (со) и ее действительной и мнимой составляющими
Еху (ш) и Qxy (ш):
С^(ш) = Ся.„(ш)—jQx„(u), (729)
так как двусторонняя спектральная плотность содержит компонен-
ты в отрицательном частотном диапазоне, которые физически не
могут быть измерены. Уравнение (4.126) дает связь Сху (со) и-^ж{/ (со)
с корреляционной функцией <рЖ|/ (т) в вид
1 00
(Рад (Т) = 'С'-“ C°S “Т+ 5‘П dV>' (73°)
О
При т = 0 соотношение (7.30) превращается в выражение
1
<pw(O) = E[x(f)S(/)] = ЛГ С*»*». (7.31)
ZJt J
о
Если мы пропустим переменные х (I) и у (/) через идентичные
идеальные фильтры с полосой пропускания А со, то в результате по-
лучим
СЙ0-НДЮ/2)
Е I.V (/, Дш) у (I, Дш)] = — \ СхУ (шс, Дш) dm =
ZJT J
w0— (Aco/S*
<ов+ (До/2)
= — Сху (шс, Дш) f da = — Сху (шс, Дш) Дш, (7.32)
2л ’ J 2л
о0—(До/2)
или после преобразования
Сху («с, Асо) — 2лЕ [х (/, Асо)^/ (/, Асо)]/Асо. (7.33)
Мнимая составляющая Qxv (со) может быть получена при рас-
смотрении случая, где
т == л/2сос. (7.34)
Подстановка этого значения т в соотношение (7.30) дает
<ред (п/2ие) = Е [X (f) у (t +-^-)1 = 4" f ICw (“) cos +
\ 2Юс 'J J z0)c
О
4-<2зд(ш) sin-^1 du. (7.35)
2СОс J
187
Если х (z) и у (Z) пропустить через идентичные идеальные фильтры
с полосой пропускания Дю, то в результате будем иметь соотноше-
ние
йс-РДС0/2
Ли')] = 4' Г [См)К. M cosv +
\ ^С®с J V L “
<ЙС —ДИ/2
«с4-(Д(й/2)
+ QXB (4, Лю) sin у] da = Т- QXIJ (<о„ До) J do =
<ос—(Дй>/2)
= V- Q.XI1 (“е. Ди) Ди. (7.36)
ZJL
которое можно преобразовать к виду
Qxy Ao) = 2лЕjx (/, Дсо) у (/ -р, ДсоДсо. (7.37)
Запаздывание в соотношении (7.37) может быть достигнуто
с помощью любого устройства запаздывания, описанного в §7.4,
но часто удобнее использовать тот факт, что это запаздывание
Рис. 7.13. Структурная схема измерения взаимной спектральной плот-
ности.
соответствует фазовом)7 сдвигу на 90° при центральной частоте сос.
Поскольку переменные сигналы пропускаются через узкополосные
фильтры, достаточно ввести фазовый сдвиг на 90° для центральной
частоты сос в одном из отфильтрованных сигналов. Амплитуда
и фазовые углы взаимной спектральной плотности на частоте сое
в диапазоне Дсо определяются соотношениями
| Gw (о, Дю) | = V [Сга (и. Дю)]2 + [QxS (ю, Дш)]« (7.38)
И
еА (о, До) = arctg [ Qt" (ю’ Am)-1. (7.39)
L Сху (о. Дю) j ’
Структурная схема измерения взаимной спектральной плот-
ности показана на рис. 7.13. Применяемые приборы и методы под-
робно обсуждаются в следующих двух параграфах.
188
Схему, показанную на рис. 7.13, можно применить для измерения
спектральной плотности прн подаче одного и того же сигнала на оба
входа. В этом случае мнимая компонента Qxy (<о) должна быть равна
нулю (этот факт используется для контроля при соответствующей
калибровке системы). Однако более удобно в этом случае приме-
нять один полосовой фильтр. Тогда по схеме, изображенной на
рис. 7.12, измеряется все, что необходимо.
§ 7.6. Методы фильтрации при измерениях
спектральной плотности
Существуют три различных метода фильтрации, которые исполь-
зуются при измерениях спектральных плотностей. Первый из них
заключается в применении группы фильтров со смежными полосами
пропускания. Преимуществом метода является возможность одно-
временного измерения на многих частотах. Если диапазоны фильт-
ров выбраны надлежащим образом, можно получить измерения
спектральной плотности мощности в режиме on-line. Второй метод
заключается в применении настроенного полосового фильтра, подоб-
ного рассмотренному в § 7.7, в котором для фильтрации используются
активные и пассивные цепочки. Принципиальный недостаток обоих
методов в том, что такие фильтры не обладают прямоугольными час-
тотными характеристиками, которые необходимы для реализации
соотношений, полученных в § 7.5. В таком фильтре амплитуда вход-
ных сигналов ослабляется на 24 или самое большее на 36 дб на
октаву. Через фильтр этого типа может проходить сигнал гораздо
большей мощности, чем через фильтр с идеальными характеристи-
ками- Серьезным недостатком такого фильтра является тот факт,
что с ростом частоты он все больше отличается от идеального. Сле-
довательно, если входной сигнал является шумом, измерение мощ-
ности в диапазоне от 8 до 12 гц должно было бы давать тот же резуль-
тат, что и измерение мощности в диапазоне от 48 до 52 гц. К сожале-
нию, это не выполняется и может привести к очень серьезным по-
грешностям в измерениях спектральной плотности, как видно из
рис. 7.14 и 7.15. На рис. 7.14 показаны частотные характеристики
идеального и обычного фильтров, имеющие наклон 24 дб на октаву
для двух диапазонов от 8 до 12 гц и от48до52г1{. Площадь под кри-
вой представляет собой корень квадратный из мощности сигнала,
пропускаемого фильтром. Площадь под кривой в правой части
рис. 7.15 примерно в 3,1 раза больше площади под кривой в левой
части рисунка, поэтому измерение спектральной плотности мощности
при помощи фильтра в правой части дает результат, примерно в 10
раз превышающий результат измерения при помощи фильтра в ле-
вой части, хотя результаты должны быть одинаковыми. Ясно, что
эффективная полоса пропускания правого фильтра больше, чем
левого, и больше полосы 4 гц идеального фильтра.
При корректных измерениях, в которых применяется этот тип
фильтра, необходимо, чтобы эффективная ширина полосы пропуска-
189
ния была равна ширине действительной частотной характеристики
между точками, в которых значение амплитуды равно 0,707 значе-
ния в центральной точке или ослабление равно—3 дб. Даже если ис-
пользуются эффективные ширины полос, прохождение сигнала вне
Частоте, ец
Рис. 7.14. Ослабление сигнала полосовыми фильтрами
(полулога рифм пческая шкала).
полосы пропускания искажает измерение. Следовательно, необходи-
мо установить ширину полосы пропускания фильтра так, чтобы ве-
личина Q фильтра, выраженная формулой
Q = /С/Д/ = со с/Дез,
(7-40)
оставалась постоянной во всем частотном диапазоне измерения.
Рис. 7.15. Ослабление сигнала полосовы-
ми фильтрами (линейная
шкала).
В общем случае величи-
на Q определяет качество
фильтра и показывает,
насколько он близок к
идеальному. Ясно, что для
идеального фильтра вели-
чина Q должна быть беско-
нечной. Значения Q, до-
стигающие 2, иногда ис-
пользуются в измерениях
спектральной плотности,
но качество таких измере-
ний обычно бывает плохим.
Во многих приборах, вы-
пускаемых промышлен-
ностью, значение Q для не-
которых типов кварцевых
•фильтров > 30 000. Это обеспечивает очень резкое ослабление
сигнала по обе стороны от полосы пропускания. Значения Q для
двух фильтров, показанных на рис. 7.15, равны 1,79 и 3,97.
Метод гетеродинной фильтрации. Наиболее общим методом,
используемым для фильтрации в измерении спектральных плотно-
го
стей, является гетеродинный метод. Фильтры, в которых приме-
няются кварцевые кристаллы, обеспечивают очень высокие значения
Q. Однако эти фильтры имеют высокие значения центральной час-
тоты, обычно в области 100 кгц, поэтому для исследований в области
более низких частот необходимо переместить центральную частоту
полосы пропускания и использовать преимущество высоких значе-
ний Q.
Рис. 7.16. Анализатор спектра с полосовым фильтром
гетеродинного типа.
Гетеродинная система показана на рис. 7.16.- Она состоит из вы-
сокочастотного генератора, модулятора и фильтра. Модулятор ум-
ножает входную функцию х (f) на выходной сигнал высокочастот-
ного генератора, который имеет вид
f (Z) = A cos соо/, (7.41)
где <л0 •— несущая частота генератора. Тогда выходной сигнал мо-
дулятора есть
z (/) = f (t)x (/), (7.42)
который после преобразования Фурье дает
Z (со) = J ехр(—jco/) х (t) A cos соо tdt. (7.43)
Применяя формулу Эйлера
cos u>„ t = -Г [ехр (jo„ t) + ехр (—/)]
в уравнении (7.43), получаем
z(“) = y J ехр[—j(co—coo)z]x(z)dz+
(7.44)
+ у J ехР I—J (“>+%)*]* W* = у [X(о—%) + X(<» + о0)], (7.45)
191
где X — преобразование Фурье х (/) для указанных частот. Это пе-
ремещение частотного распределения начальной функции симмет-
рично относительно несущей частоты оказалось возможным благо-
даря гетеродинной системе. Когда выходной сигнал модулятора про-
пускается через полосовой фильтр с шириной полосы А со, у которого
средняя частота сос отличается от несущей частоты ш0 на величину
сох, т. е.
coi = сос — соо, (7.46)
тогда любые частотные составляющие, лежащие между ш0 — —
— Acd/2 и соо — сох J- Дсо/2, будут пропускаться через фильтр.
Поскольку величина является мерой смещения центральной час-
тоты фильтра сос относительно несущей частоты сох, установка не-
сущей частоты обеспечивает перемещение спектра входного сигна-
ла к частотному диапазону фильтра. Таким образом, проблема при-
ближения частоты фильтра к спектру входного сигнала исключает-
ся путем перемещения спектра относительно частоты фильтра.
Обычн о это выполняется сканированием частоты генератора через
равные интервалы, начиная с частоты ниже центральной частоты
фильтра до частоты выше центральной частоты таким образом, что-
бы пройденный частотный диапазон был равен ширине полосы час-
тот анализируемого сигнала. Если скорость сканирования слишком
высока, полезная информация на данной частоте не успевает анали-
зироваться фильтром и статистическая неопределенность оценки
поэтому увеличивается. Кроме того, узкие полосовые фильтры не
могут полностью реагировать на резкие изменения спектра сигнала.
Фазовый сдвиг на 90° при взаимном спектральном анализе легко
выполняется в гетеродинной системе фильтрации путем использо-
вания сигнала вида cos со0 t с выхода генератора для модуляции од-
ного входного сигнала и сигнала вида sin соо t с выхода генератора
для модуляции другого входного сигнала. Поскольку несущая час-
тота может быть в 50—100 раз больше высшей частоты анализируе-
мого сигнала, применение в модуляторе синусоидального сигнала
вместо косинусоидального эффективно дает фазовый сдвиг 90°,
необходимый для взаимного спектрального анализа.
Переменные электронные фильтры. Характеристики пассивных
фильтров обычно не удовлетворяют требованиям измерения спект-
ральных плотностей, так как создают нагрузку при подсоединении
к схеме измерения и влияют на устройства, связанные с ними. По-
этому необходимы фильтры, включающие в себя операционные уси-
лители, чтобы обеспечить высокий входной импеданс для предотвра-
щения перегрузки и низкий выходной импеданс для подключения
регистрирующего или другого измерительного оборудования. Ис-
пользуются два типа фильтров (либо отдельно, либо в комбинации):
высокочастотный фильтр, который пропускает все частоты выше не-
которой частоты, и низкочастотный фильтр, который пропускает все
частоты ниже некоторой частоты. Высокочастотный и низкочастот-
ный фильтры могут быть соединены последовательно для получения
192
полосового фильтра или параллельно для получения полосового за-
градительного фильтра. Последний часто применяется для исклю-
чения преобладающей частоты, которая не представляет интереса для
исследователя, например для исключения сетевой иаводки 50 гц.
Такой фильтр может также использоваться в обратной связи опера-
ционного усилителя, чтобы получить систему с определенной поло-
сой пропускания.
Рассмотрим теперь работу низкочастотного и высокочастотного
фильтров. Простейшая структурная схема низкочастотного фильтра
показана на рис. 7.17. В обычной установке две или три таких схемы
могут быть соединены последовательно для обеспечения соответст-
Чсиление - 1 Усиление = 1
Рис. 7.17 Упрощенная схема низкочастотного
фильтра [6].
вующего ослабления высших частот и пропускания низких частот.
Низкочастотный фильтр состоит из трех операционных усилителей,
два из которых имеют коэффициенты усиления, равные единице, и
третий — коэффициент усиления k. Часть выходного сигнала kE.2
через обратную связь подается на емкость Сх. Если обе емкости и
оба сопротивления равны, передаточная функция фильтра есть
п 13) =------—----------------------, V )
Ei ($) (5/соо)а 4- (2—k) (s/coo) +1
где частота среза
соо = IIRC. (7.48)
Коэффициент усиления схемы при частоте со0 равен
|Е3 (соо)/Ех (соо)| = 1/(2 — А) = 1/2А, (7.49)
где коэффициент максимума
А = 1 — А/2. (7.50)
Максимум частотной характеристики для трех различных зна-
чений коэффициента максимума показан на рис. 7.18.
Структурная схема высокочастотного фильтра показана на
рис. 7.19. Сигнал обратной связи kEz подается на вход первого уси-
лителя через сопротивление Ry. Если обе емкости и оба сопротивле-
ния равны, передаточная функция фильтра имеет вид
=-------------------------(7.51)
E,(s) (s/<o0)2 + (2—Л)(я/{о„) +1
7 Зак. 576
193
При частоте среза (ос коэффициент усиления снова становится рав-
ным 1/(2 —k), в соответствии с формулой (7.50). Частотные характе-
ристики высокочастотного фильтра аналогичны характеристикам,
приведенным иа рис. 7.1, если повернуть кривые вокруг оси (n/jRC =
= 1. В обычных промышленных фильтрах коэффициент максимума
приблизительно равен 0,6 при коэффициенте усиления около —
1,5 дб на частоте среза, а спад коэффициента усиления составляет
12 дб иа октаву для отдельной низкочастотной или высокочастотной
схемы. Две схемы, соединенные последовательно, дают коэффициент
Рис. 7.18. Эффект углового пика в схеме низкочастотно-
го фильтра [6].
ослабления — 3 дб иа частоте среза и спад коэффициента ослабле-
ния 24 дб иа октаву или 80 дб иа декаду. Передаточная-функция (от-
ношение выходного напряжения к входному) фильтра, использую-
щего две схемы, для четырех случаев может быть выражена следую-
щим образом:
Н (s) = 2А +1]2 ; (пропускание низких частот),
(7-52)
Я (s) -----------------------; (пропускание высоких частот).
[(s/<DL)£ + 2>l(s/CDL)4- lf V Р 3 h
(7.53)
Н (s)= 77~,———------------( -----7---------------; (пропускание
[(s/<ow)2+2^(s/G5w) + ip[(s/coL)2+2X(s/coL) + l]s
полосы частот), (7.54)
194
[(s/0>„)2 + 2?l(s/ro„)+ip
(s/COr)4
-----------------------: (полосовой заградительный фильтр),
I(s/®L)a+2Z(s/®L)+IF
(7.55)
где ©£ и со я — низкая и высокая частоты среза высокочастотного
н низкочастотного фильтров соответственно. Они определяются соот-
ношениями
(7.56)
о)я = 1/Т?£,Оь (7.57)
где/?н н Сн — сопротивление и емкость, используемые в высоко-
частотном фильтре, a /?l и Cl — сопротивление и емкость, исполь-
Рис. 7.19. Упрощенная схема высокочастотного
фильтра [6].
зуемые в низкочастотном фильтре. Коэффициент Л, который обычно
одинаков для составных фильтров независимо от значений сопро-
тивления и емкости, устанавливается приблизительно равным 0,6.
Это дает коэффициент усиления в максимуме около 0,75 дб и умень-
шает ослабление на частоте среза по сравнению с ослаблением
фильтра, у которого коэффициент максимума равен единице. Регу-
лировка ширины полосы пропускания для различных способов ра-
боты иллюстрируется рис. 7.20. Полосы пропускания для четырех
различных ширин показаны кривыми /—4.
Коэффициенты усиления иа средней частоте изменяются слабо
при различных частотах среза. Наклон приблизительно 12 дб на
октаву, или 80 дб на декаду для всех кривых. Минимальная полоса
пропускания получена путем выбора двух равных частот среза; это
приводит к падению коэффициента усиления при выбранной частоте
на 6 дб, н спад еще на 3 дб соответствует частотам, равным 0,77 и 1,3
этой частоты.
Фильтрация с настроенными магнитными головками. Усовер-
шенствование настроенных магнитных головок, о котором сообща-
лось в работе [7], привело к новому методу анализа спектральной
195
плотности сигнала в диапазоне 0,06—10 000 гц с применением толь-
ко одной скорости записи. В отличие от электронных фильтров
настроенные магнитные головки не имеют дрейфа и обладают
плоской частотной характеристикой во всем диапазоне от инфраниз-
ких до звуковых частот. Анализируемый сигнал регистрируется на
магнитной ленте, затем лента протягивается около одной или не-
скольких специально настроенных магнитных головок, чувствитель-
ных только к отдельной длине волны сигнала, записанного на лен-
те. Выход настроенной магнитной головки дает непосредственно ам-
плитуду каждой компоненты сигнала, поэтому исключается необхо-
Рлс. 7.20. Нормированная частотная характери-
стика фильтра:
1 — OOOft: 2 — fn— 100/Д: 3 — f№
4~~fu(f/i—высокая частота среза,
—низкая частота среза).
димость в настроенных фильтрах. Частотная характеристика
настроенной магнитной головки определяется механической кон-
струкцией и не зависит от времени. Поскольку эти головки избира-
тельны к длине волны, детектирование не зависит от скорости про-
тяжки.
Чтобы представить принцип действия настроенной магнитной
головки, рассмотрим несколько обычных магнитных головок, у кото-
рых обмотки соединены последовательно, как показано на рис. 7.21.
Когда ступенчатый сигнал на ленте проходит около головок, сосед-
ние обмотки дают выходное напряжение обратной полярности. Если
головки сдвинуты так близко, что расстояние между ними сравнимо
с зазором в головке, реакция на ступенчатый сигнал на магнитной
ленте является сигналом знакопеременным. Одним из путей получе-
ния головки с большим количеством зазоров является бифилярная
намотка проволоки на изолятор, где каждый виток проволоки пред-
ставляет собой отдельную головку, соединенную в противоположной
полярности с соседним витком. Такое устройство показано на
рис. 7.22. Если на ленте зарегистрирован синусоидальный сигнал
с длиной волны, равной шагу бифилярной намотки, напряжения,
196
индуцированные во всех витках, находятся в фазе, и в результате на
выходе получается большой сигнал. Для любой другой длины волны
зарегистрированного сигнала напряжения, индуцированные в сле-
дующих один за другим витках, находятся не в фазе, и поэтому сум-
Рис. 7.21. Ряд обычных магнитных головок вос-
произведения с обмотками, соединенны-
ми в обратной полярности [7].
мирный выходной сигнал сильно уменьшается. Таким образом, маг-
нитная головка действует как селективный фильтр и его острота,
или коэффициент Q зависит исключительно от числа витков в на-
мотке. Если число витков удваивается, величина резонансного сиг-
нала также удваивается, а полоса пропускания уменьшается вдвое.
Рис. 7.22. Бнфиляриая намотка проволоки на изо-
лятор [7].
Когда на магнитной ленте регистрируется сигнал сложной фор-
мы, каждая частотная составляющая дает циклическое намагничи-
вание с длиной волны
X - V//, (7.58)
где f — частота, Vr — скорость записи. Если теперь лента протя-
гивается около настроенной головки с шагом намотки Хо, выходной
сигнал, снимаемый с головки, пропорционален амплитуде сигнала,
записанного на частоте
f = (7.59/
Выходные сигналы, соответствующие различным частотным ком-
понентам записанного сигнала, получаются путем протяжки
197
ленты около нескольких головок с различными шагами намотки.
Сигнал может быть зарегистрирован при различных скоростях
записи, тогда определенная длина волны будет соответствовать при
протяжке ленты около одной головки некоторому диапазону час-
тоты записанного сигнала. Чтобы расширить еще больше диапазон
частот, можно объединить два метода, в которых ряд записей, по-
лученных при различных скоростях, воспроизводится с помощью
нескольких головок. Увеличение скорости воспроизведения увели-
чивает скорость изменения магнитного потока в головке, а следо-
вательно, и выходной сигнал на всех длинах волн. Поэтому обычно
используется высокая скорость воспроизведения.
Применение настроенных магнитных головок для спектрального
анализа рассматривается в работе [7]. Настроенные головки изго-
товлялись для экспериментальной установки и имели обмотки с ко-
личеством двойных витков в диапазоне от 6 до 96 на 2,5 см длины.
При обычной скорости записи 18,75 см!сек они настроены на частоты
от 45 до 720 гц. В установке возможно изменение скорости протяж-
ки в широком диапазоне от 0,025 до 250 см!сек. Для этого диапазона
головки будут настроены на частоты от 0,06 до 9600 гц. Для записи
используются стандартная магнитная лента и обычная головка,
питаемая постоянным током с высокочастотным напряжением сме-
щения. Это устройство дает плоскую частотную характеристику за-
писи в диапазоне от постоянного тока до 10 кгц.
§ 7.7. Выбор частотного интервала
спектральной плотности
При измерении спектральной плотности необходимо определить,
как близко должны быть произведены оценки спектральной плот-
ности в интересующем нас частотном диапазоне. Ясно, что прн слиш-
ком близком расположении измеренных точек результаты будут
сильно коррелированы. С другой стороны, если точки расположены
на слишком далеком расстоянии, может быть потеряна полезная ин-
формация. Для идеальных узких полосовых фильтров минимальное
разрешение равно ширине полосы пропускания А/. Поскольку
реальные фильтры не имеют резких границ, обычно в качестве оцен-
ки разрешения для измерений с помощью таких фильтров прини-
мается величина 2А/. Эту величину необходимо также использовать
и для того, чтобы уменьшить смещение в измерениях спектральной
плотности. Однако для уменьшения дисперсии нли стандартного от-
клонения оценок ширина полосы пропускания А/ должна выби-
раться как можно большей, так как дисперсия обратно пропорцио-
нальна произведению ТАД где Т —длительность реализации. Если
длительность реализации не ограничена, можно получить произволь-
но высокое разрешение и малое смещение, просто увеличив дли-
тельность опыта Т.
Величина k, равная 2ТА/, представляет собой число статистиче-
ских степеней свободы, связанных с переменным значением длитель-
198
ности реализации Т и ограниченных полосой пропускания А/ в том
смысле, что реализация может быть восстановлена из отдельных от-
резков длительностью 1/2 АД Следовательно, 2ТА/ отрезков пол-
ностью определяют такую реализацию.
Рассмотрим фильтр, у которого величина
Q = Д/Д/ (7.60)
является постоянной Когда центральная частота увеличивается,
полоса пропускания А/должна также увеличиваться, чтобы Q оста-
валась постоянной. Как было показано выше, спектральное разре-
шение пропорционально величине А/. Следовательно, относительное
разрешение для различных центральных частот пропорциональ-
но значению А/7Д, которое равно обратной величине Q. При постоян-
ной полосе пропускания фильтра относительное разрешение умень-
шается с увеличением центральной частоты, однако для фильтра
с постоянным значением Q относительное разрешение не изменяется
при увеличении/с, недействительное спектральное разрешение ста-
новится хуже. Для такого фильтра средний квадрат ошибки е2 есть
е2 = 1/ТАД (7.61)
и, таким образом, эта^ошибка уменьшается при увеличении цент-
ральной частоты при постоянных значениях Q и Т.
Теперь рассмотрим пь фильтров, которые имеют постоянную по-
лосу пропускания А/ и занимают частотный диапазон от Д до Д, т.е.
'И ;? ,7И
ГДС Д — минимальная интересующая нас частота; Д — максималь-
ная частота. Приближение, полученное в уравнении (7.62), спра-
ведливо при Д большем, чем примерно ЗОД. Например, если частота
Д = 500 гц, fi — 10 гц и А/ — 2 гц, то число полос, необходимых
для всего диапазоне, должно быть равно 245.
Теперь рассмотрим случай, когда используется фильтр с постоян-
ной Q. Максимальная скорость сканирования (С.С.) для центральной
частоты есть
С.С. = dfjdt = fc/QT. (7.63)
После интегрирования
<7-64>
ft °
получим
МТ = In Д/Д. (7.65)
Если желательно сохранять максимальную скорость сканиро-
вания, частотный диапазон должен сканироваться по (логарифми-
199
ческому закону, т. е. медленно прн низких частотах, где величина
А/мала, и быстро при высоких частотах, где А/ велика.
Если Q 1 и Д fi, в рассматриваемом случае требуется около
20 фильтров, чтобы охватить диапазон от 10 до 500 гц. Таким обра-
зом, для анализа требуется значительно меньше фильтров. Следует
отметить, что фильтрация с постоянной Q дает распределение час-
тотных диапазонов, для которых центральные частоты равномерно
распределены по логарифмической шкале. Такая фильтрация совер-
шенно необходима для анализа систем, где рассматриваются харак-
теристики системы в широком логарифмическом диапазоне. Однако
в этом нет необходимости при анализе резонансов илн мощности
сигнала в данном частотном диапазоне.
При применении электронных фильтров типичное ослабление
амплитуды составляет 80 или 120 дб на декаду. Несмотря на то что
это является резким ослаблением, нельзя пренебрегать пропуска-
нием сигнала вне полосы А/. Однако при использовании методики
фильтрования с постоянной Q эффект этого пропускания для каж-
дого измерения тот же самый, следовательно, он не влияет на отно-
сительные измерения.
§ 7.8. Анализ периодических процессов
Любой периодический процесс может быть полностью описан
(за исключением информации о фазе) спектром дискретных частот,
которым дает амплитуду и частоту всех гармонических компонент.
Каждая гармоническая компонента сигнала представлена в спектре
линией, не имеющей ширины. Однако прн измерении спектра всегда
получается конечная ширина полосы, которая определяется полосой
пропускания фильтров анализатора, т. е. каждая гармоническая ком-
понента является пиком, ширина которого равна ширине полосы про-
пускания анализатора. Для получения соответствующего разреше-
ния требуется ширина полосы пропускания, по крайней мере равная
частотному интервалу между компонентами анализируемого сигнала.
Однако при определенных обстоятельствах желательно иметь поло-
су пропускания, включающую в себя несколько гармонических ком-
понент.
В общем случае результатом анализа периодического процесса
является амплитудный спектр. Амплитудный спектр можно предста-
вить несколькими способами, например, через средние, абсолют-
ные, среднеквадратнческие или средние квадраты значений отдель-
ных компонент. Для большинства инженерных приложений пред-
ставляет интерес среднеквадратйческое значение сигнала, так как
амплитудный спектр есть корень квадратный из спектральной плот-
ности мощности.
На рис. 7.23 показана структурная схема анализатора, применяв-
шегося в работе [8] для измерения взаимной спектральной плот-
ности, в котором используется гетеродинный метод фильтрации» Этот
анализатор пригоден для анализа периодических или случайных
200
Рис. 7.23. Анализатор взаимной спектральной плотности.
процессов. Генератор имеет два выхода — синусоидальный и коси-
нусоидальный, которые обеспечивают соответствующее фазовое соот-
ношение. Выходными сигналами системы являются спектральные
плотности входного сигнала х (/) и выходного сигнала £/(/), а также
взаимные спектры этих двух переменных. Используя эти выходные
сигналы, можно получить на основании соотношений (4.122) и (4.123)
амплитуду н фазу взаимной спектральной плотности, а также ам-
плитуду и фазу передаточной функции системы на основании соот-
Рнс. 7.24. Структурная схема вычисления передаточной функции и функ-
ции когерентности.
ношений (4.128) и (4.124). Кроме того, рассчитывается функция коге-
рентности для оценки статистической погрешности измерений ам-
плитуды и фазы передаточной функции На рис. 7.24 показана струк-
турная схема системы для расчета амплитуды и фазового угла пере-
даточной функции и функции когерентности на основании выходных
данных системы, изображенной на рис. 7.23.
§ 7.9. Анализ спектров переходных процессов
Переходные процессы, применяемые для анализа систем, можно
рассматривать как возмущения, энергия которых распределена в не-
прерывной полосе частот, в отличие от периодических процессов,
в которых энергия сконцентрирована при дискретных значениях
частоты-. Переходные процессы очень часто используются в экспе-
риментах на ядерных реакторах. Если известны частотный спектр
и величина сигналов, вызвавших переходные процессы, экспери-
мент, проводимый при этих переходных процессах, может быть про-
анализирован путем сравнения спектров входного и выходного сиг-
налов.
202
Поскольку переходные процессы непериодические, их спектр
представляется преобразованием Фурье. Однако практически ана-
лиз переходных процессов проводится с помощью их искусствен-
ного повторения, поэтому спектр таких процессов является рядом
дискретных компонент, т. е. может быть представлен в виде ряда
Фурье. Свертка этого ряда есть интеграл Фурье. Сделав интервал
между переходными процессами большим по сравнению с длитель-
ностью переходных процессов, можно получить достаточное число
коэффициентов Фурье для определения преобразования Фурье.
Рис. 7.25. Анализатор спектра импульсов [8].
Для изучения переходных процессов необходим специальный
частотный анализатор- На рис. 7.25 показана упрощенная струк-
турная схема анализатора переходных процессов [8], основанного
иа применении метода гетеродинной фильтрации. Один из фильтров
выделяет синусные составляющие, другой — ортогональные им,
или косинусные, составляющие. Среднее от суммы квадратов этих
двух компонент пропорционально спектральной плотности мощг
ности импульса.
Измерения взаимной спектральной плотности и передаточной
функции аналогичны измерениям с синусоидальными и случайны-
ми сигналами. Структурная схема системы, производящей измере-
ния взаимной спектральной плотности, показана на рис. 7.26.
Здесь снова используются два ряда фильтров для анализа входных
и выходных сигналов. Относительные синусные и косинусные
компоненты двух сигналов должны рассматриваться вместе со всеми
взаимными произведениями, что до известной степени аналогично
действиям с комплексными числами. Такие операции эффективно
выполняются устройством, показанным на рис. 7.26, в котором
203
частоты на регистрирующее
устройство (ось к)
Рис. 7.26. Анализатор взаимного спектра импульсов [8J.

вычисляются действительная и мнимая компоненты взаимной спект-
ральной плотности. Передаточная функция системы может быть по-
лучена из данных переходного процесса, так же как из анализа
случайных процессов, или может быть вычислена с применением
системы, изображенной на рис. 7.24.
СПИСОК ЛИТЕРАТУРЫ
1 Otterman J. The Properties and Methods for Computation of Exponential-
ly Mapped Past Statistical Variables. —«IRE» (Inst. Radio Engrs.) Trans.
Auto. Control, I960, v. AC-5, N I, p. 11—17.
2. Levine L. Methods for Solving Engineering Problems Using Analog Compu-
ters. — McGraw-Hill Book Company, Inc., N. Y., 1964.
3. Electronic Associates, Continuous Analysis with Analog Computers Using
Statistical and Regression Techniques, Bulletin N ALAC-62023.
4. Deusen B. D. Van. Data Acquisition and Statistical Analysis Using Ana-
log Computers Techniques- — «SAE Transactions», 1963, v. 71, p. 350.
5. Krouse S. Technical Measurements Corporation, personal communication,
1965.
6. Instruction Manual for Ultra Low Frequency Band-pass Filter, Model 330A
Manual, Krohn-Hite Corp., 1963.
7. Douce J. L., Parr P. J. Use of Tuned Heads for Spectrum Analysis. —
«Control Engng», 1964, v. 11, N 8, p. 63.
8. Randall R. L., Pekrul P. J. Application of Analog Time and Frequency
Correlation Computers to Reactor System Analysis. — In: Neutron Noise,
Waves and Pulse Propagation. Gainesville, Fla., Uhrig R. E. (Coordina-
tor): AEC Symposium Series, 1967, N 4 (CONF-660206), p. 357—380.
ГЛАВА 8.
СБОР,
ПЕРЕДАЧА
И ЗАПИСЬ
ДАННЫХ
§ 8.1. Введение
До появления программ разработки энергетических реакторов
экспериментальные измерения в реакторных системах проводились
небольшими группами экспериментаторов, которые использовали
относительно простые системы приборов, размещенные рядом с ре-
актором или, для незащищенных сборок, в соседних комнатах,
в которых обеспечивалась необходимая радиационная защита.
Особое внимание обычно обращалось на простоту всей системы в це-
лом, хотя отдельные приборы часто были весьма сложны; относи-
тельно мало усилий прилагалось для облегчения проведения обыч-
ных экспериментов, таких, как калибровка регулирующих стержней
и измерение периодов.
В программах разработки энергетических реакторов, в част-
ности, при исследованиях, связанных с реакторами KIWI, PLUTO
н NERVA, предназначенных для космических аппаратов, для
получения данных пришлось использовать более сложные системы.
Исследуя энергетические реакторы, экспериментаторы разработали
оснащенные большим количеством детекторов топливные сборки,
подобные тем, которые используются в настоящее время в Хал-
дейском реакторе с кипящей водой. Потребовалось также измерять
миогне переменные, которые влияют на общие характеристики ре-
акторной системы, как, например: давление, температура, фазо-
вое состояние (газ нли жидкость) теплоносителя или замедлите-
ля, скорость теплоносителя, расход, уровень мощности, положе-
ние устройств контроля реактивности, вибрации, ускорения, пере-
мещения. Часто такие измерения делаются во многих точках по
всей реакторной системе. Полученные данные необходимо записать
для последующего анализа, поскольку экспериментаторы не в сос-
тоянии проанализировать большое количество поступающей ин-
формации во время эксперимента.
Из предыдущего обсуждения очевидно, что использование циф-
ровых вычислительных машин даже для таких обычных операций,
как калибровка регулирующих стержней и измерение периода,
может быть очень выгодной с точки зрения экономии времени н ра-
206
бочей силы. Применение цифровых вычислительных машин для
анализа характеристик реактора и особенно результатов динами-
ческих исследований стало почти обязательным. Измерение функ-
ций корреляции и спектральной плотности можно осуществлять
специализированными приборами, подобными тем, которые рассмот-
рены в гл. 7. Действительно, очень многие полезные работы были
выполнены с помощью таких приборов; но при изучении сложной
реакторной системы в целом, которая может иметь много входных
функций, необязательно зависящих друг от друга, но влияющих
на данную выходную функцию, обычно нет иного выбора, кроме
цифровых методов.
Решение вопроса о применении цифровой вычислительной маши-
ны для обработки данных в режиме on-line или простой записи
данных на магнитную ленту для последующей обработки обычно
зависит от индивидуальных особенностей установки и характера
эксперимента. Вообще говоря, большинство экспериментальных
данных записываются и анализируются после эксперимента.
Большинство экспериментальных реакторных систем оснаще-
ны приборами, предназначенными только для проведения экспери-
ментов. Такие системы могут также включать цифровую вычисли-
тельную машину, которая используется для обработки в режиме
on-line н для текущего контроля эксперимента, выполняя функ-
ции либо регулирующего устройства с обратной связью, либо ав-
томатического программного устройства, либо и того и другого
одновременно.
Определенные эксперименты, такие, как исследования KIWI
и NERVA, должны выполняться дистанционно; сигналы от детек-
тора должны передаваться на расстояние около километра, прежде
чем они будут записаны. Кроме того, запись данных ведется по 100
или 200 каналам, имеющим свои собственные обозначения, диапа-
зон изменения, калибровку и частотную характеристику, что явля-
ется сложным делом, требующим тщательного и систематического
подхода.
§ 8.2. Получение данных
В подкритических сборках или сборках с нулевой мощностью
основными используемыми приборами являются нейтронные детек-
торы, которые могут представлять собой камеры импульсного или
токового типа в зависимости от режима работы и имеющихся при-
боров. Выходным сигналом ионизационной камеры является очень
слабый электрический ток, генерируемый при движении заряженных
частиц, рожденных при взаимодействии с нейтронами, к централь-
ному электроду. Число взаимодействий в детекторе должно быть
достаточно большим, чтобы выходной сигнал являлся непрерывной
переменной, т. е. могла быть обоснованно применена центральная
предельная теорема. Этот очень слабый ток затем должен быть усилен
до величины, достаточной для передачи сигнала к приборам, кото-
207
рые находятся на расстояниях от нескольких метров до нескольких
километров.
Ядерные приборы могут также работать в импульсном режиме
и накапливать импульсы, используя различные приборы. В ряде
экспериментов используются многоканальные временные анализа-
торы для записи количества импульсов от отдельных нейтронных
взаимодействий и хранения этой величины в ячейках памяти на
магнитных сердечниках. Такая система обычно применяется при
исследовании повторяющихся явлений в ядерных системах, созда-
ваемых, например, импульсными и псевдослучайными входными
сигналами. Можно также использовать схемы измерения скорости
счета, например схемы с диодными цепочками, которые дают непре-
рывную (аналоговую) мгновенную скорость появления импульсов.
В действительности устройства измерения скорости счета дают сред-
нее показание за конечный период времени, н если скорость счета
падает, то, чтобы избежать значительных флуктуаций (т. е. чтобы
была применима центральная предельная теорема), постоянная
времени прибора должна быть увеличена.
Выбор того, записываются ли импульсы в цифровом виде отдель-
ными импульсами или в виде непрерывного сигнала от схемы измере-
ния скорости импульсов, обычно определяется имеющимися в рас-
поряжении приборами, скоростью появления импульсов и характе-
ром выполняемого эксперимента. Сбор отдельных импульсов в мно-
гоканальном временном анализаторе является простым процессом
и обычно не создает серьезных проблем. С другой стороны, запись
импульсов в аналоговом или цифровом виде на ленту крайне не-
эффективно использует записывающую систему. Например, типич-
ная система прямой записи имеет верхний частотный предел около
100 кгц.
Если учесть флуктуации скорости импульсов и время вос-
становления, требуемое записывающему устройству для разделения
двух соседних импульсов, практически верхний предел средней
скорости импульсов может составлять 10 000 имп!сек. Запись им-
пульсов с помощью метода частотной модуляции допускает макси-
мальную среднюю скорость импульсов от 5000 до 10 000 имп!сек.
Цифровая запись ограничена скоростью записи и количеством дво-
ичных единиц на единицу длины. Например, цифровая лента
средней плотности, допускающая 222 дв.ед./см, при скорости
280 см!сек ограничена 62 550 имп1сек, распределенными равно-
мерно. Следовательно, максимальная средняя скорость импульсов
для случайного распределения может составить 10 000 имп!сек.
Во всех трех случаях используется полная ширина полосы частот
одного записывающего канала для записи относительно небольшого
количества информации. Более эффективные методы записи данных
обсуждаются ниже в этой главе.
Для реакторов, которые имеют заметный уровень мощности
и требуют наличия теплоносителя обычно приходится проводить
дополнительные измерения, например, температуры и давления
208
в различных точках реактора, расхода теплоносителя и вибра-
ций. При проведении разного рода динамических экспериментов
с автоматическим регулятором или без него обычно очень жела-
тельно записывать положение стержня регулирования, сигналы
обратной связи и большое число других связанных сигналов, не-
обходимых для правильного анализа динамических характеристик
различных компонент системы регулирования и для отделения
характеристик регулятора от динамического поведения самого ре-
актора. В большинстве случаев для измерения температуры исполь-
зуются термопары или термометры сопротивления, для измерения
давления и вибрации используются различные типы датчиков давле-
ния и измерителей ускорения. Почти все эти приборы имеют вы-
ходной сигнал, который является непрерывной переменной (ана-
логовый сигнал); верхний частотный предел сигналов относитель-
но низок — несколько герц при изменении температуры, несколь-
ко десятков герц для флуктуаций давления и несколько сотен
герц для вибрации.
§ 8.3. Запись непрерывной информации
Информация, полученная в экспериментах на ядерных реакто-
рах, может быть записана различными методами. Выбор лучшего
метода записи в данном эксперименте во многом зависит от характе-
ра эксперимента. Часто результатом эксперимента является после-
довательность импульсов, которые накапливаются в пересчетной
схеме или многоканальном анализаторе; выходные сигналы этих
приборов могут Сыть отпечатаны или пробиты на бумажной ленте
или записаны на магнитной ленте для последующей обработки. Во
многих экспериментах может оказаться очень эффективным исполь-
зование специальных приборов (в частности, при записи плотности
нейтронов, представленной импульсами от ядерного детектора).
В более сложных экспериментах, однако, имеется много пере-
менных, таких, как температура, давление, мощность, расход, поло-
жение регулирующих стержней и т. д., которые обычно представ-
ляются аналоговыми напряжениями и которые должны быть записа-
ны. Запись таких данных на магнитную леиту таким образом, чтобы
они могли быть сосчитаны спустя некоторое время и соответствую-
щим образом обработаны, является обычной процедурой. На практи-
ке во многих ситуациях данные одновременно записываются иа само-
писец, чтобы можно было визуально наблюдать, что происходит во
время выполнения эксперимента. Применение самописцев также
очень удобно для экспериментатора, когда он позже хочет выбрать
специфические области эксперимента для подробного анализа. Оче-
видно, что при этом необходимо проводить соответствующее вре-
менное кодирование, которое должно быть записано как на маг-
нитную, так и на бумажную леиту.
Обычно используются три метода записи непрерывных сигналов:
прямая запись, частотная модуляция и цифровая запись. Эти
209
методы подробно описаны Вебером [1], а здесь представлен
только их краткий обзор.
Система прямой записи. В этой системе имеется усилитель для
нормализации данных; которые должны быть записаны; для ком-
пенсации неоднородности частотных характеристик записывающей
головки и окисного покрытия магнитной ленты применяется высоко-
частотное напряжение смещения. Усилитель прямого воспроизведе-
ния состоит из входного предусилителя, схемы выравнивания
частот и выходного усилителя. Схема выравнивания частот изменя-
ется для различных скоростей ленты и используется для компенса-
ции нелинейностей в головке, ленте и усилителе, давая постоянную
частотную характеристику в широком диапазоне частот. При пря-
мой записи сигнал смешивается с высокочастотным напряжением
смещения и поступает прямо на записывающую головку в виде
изменяющегося электрического тока. Схематические диаграммы
записывающей н воспроизводящей головок показаны на рис. 8.1.
Головки состоят из магнитных сердечников в виде замкнутых колец,
имеющих узкие немагнитные зазоры, расположенные последова-
тельно с магнитными линиями сердечника. Магнитная поверхность
ленты взаимодействует с записывающей головкой в зазоре, шунти-
руя зазор и замыкая магнитные линии в сердечнике головки. Ток
сигнала проходит через обмотку, которая находится на магнитном
сердечнике, и создает магнитный поток яр, величина которого про-
порциональна записываемому току i:
яр = Xt, (8.1)
где Л — коэффициент пропорциональности. Любой участок маг-
нитной ленты, прошедшей через, зазор, сохраняет остаточную
намагниченность, которая пропорциональна потоку в тот момент,
когда участок проходит через зазор. Следовательно, истинная за-
пись имеет место на заднем крае зазора.
210
При записи синусоиды интенсивность намагниченности ленты
изменяется синусоидально вдоль ленты. Длина волны записывае-
мого сигнала вдоль ленты соответствует каждой завершенной поло-
вине периода входного электрического сигнала. Длина волны X
прямо пропорциональна скорости ленты v н обратно пропорцио-
нальна частоте f записываемого сигнала:
= v/f. (8.2)
Бо время считывания намагниченная поверхность ленты проходит
через зазор считывающей -головки. Участок ленты, находящийся
в контакте с зазором, замыкает магнитный сердечник считывающей
головки; при этом магнитные силовые линии проходят через сер-
дечник. Величина магнитного потока является функцией средней
намагниченности участка ленты, действительно перекрываемого
зазором в данный момент. Когда лента проходит через считываю-
щий зазор, поток в сердечнике, зависящий от намагниченности
ленты, генерирует в обмотке ЭДС, величина которой пропорциональ-
на не величине потока, а скорости его изменения, т. е.
е=К'^. (8.3)
Следовательно, напряжение на концах обмоткн считывающей го-
ловки зависит от частоты, как показано на рис. 8.2. Для получе-
ния амплитудной характеристики, не зависящей от частоты, не-
обходимо, чтобы выходной усилитель имел обратную частотную
характеристику. Это обычно достигается использованием выравни-
вающих контуров в выходном усилителе. В некоторых записываю-
щих устройствах выравнивание автоматически изменяется при по-
вороте переключателя диапазона скоростей. В других устройствах
211
при изменении скорости считывания приходится извлекать один
контур и заменять его другим.
Частотная характеристика магнитной записывающей системы
ограничена как верхней, так и нижней частотой. Для очень низких
частот выходное напряжение при считывании меньше, чем уровень
шумов записывающей системы, и поэтому полезный выходной сиг-
нал отсутствует. В области высоких частот частота падает, когда
длина волны записываемого сигнала приближается к размеру
зазора считывающей головки. Выходной сигнал близок к нулю,
когда X приближается к размеру зазора, так как выходное напря-
жение пропорционально среднему значению намагниченности лен-
ты под зазором.
Поскольку магнитные материалы характеризуются нелиней-
ным соотношением между силой магнитного поля Я, приложенного
к ним, и результирующей намагниченностью В, необходимо вводить
высокочастотное напряжение смещения с величиной достаточно
большой (обычно в несколько раз превышающей входной сигнал),
чтобы магнитная головка работала на линейном участке кривой ВН.
Современные магнитофоны могут записывать 14 дорожек на
магнитной ленте шириной 25,4 мм, некоторые последние модели
записывают даже 28 дорожек на ленте шириной 25,4 мм. Чтобы
обеспечить минимальное взаимодействие между соседними голов-
ками, используются два набора головок и прослаивание дорожек.
Ширина дорожек 1,27 мм, расстояния между центрами дорожек
1,78 мм, расстояние между любыми данными наборами головок
3,56 мм с учетом прослаивания. Типичные зазоры в записывающей
и считывающей головках соответственно равны 0,0127 и 0,00203 мм.
Частотная характеристика записывающей системы сильно за-
висит от скорости леиты. Скорости ленты, обычно используемые
в настоящее время в Соединенных Штатах для записи аналоговых
данных, 'равны 152; 76; 38; 19; 9,5; 4,75 и 2,38 см!сек. Ухудшение
характеристик является следствием изменения зазора головки,
насыщения ленты, изменения скорости ленты и увеличения эффекта
перекоса и детонации. Интервалы частотных характеристик маг-
нитофонов с прямой записью даны в табл. 8.1.
Таблица 8.1.
Частотные характеристики типовых систем магнитной записи
Скорость ленты, см/сек Интервал частот Скорость ленты, см/сек Интервал частот
нижняя частота, гц верхняя частота,как нижняя частота» ец верхняя частота,кгц
2,38 30 3,75 38 50 60
4,75 30 7,5 76 70 120
9,5 35 15 152 120 240
19 40 30
212
Запись с частотной модуляцией. При частотной модуляции (ЧМ)
некоторая частота принимается за среднюю, или несущую частоту,
соответствующую нулевому входному сигналу. Сигнал, который
должен быть записан, модулирует эту несущую частоту. Модулиро-
ванный сигнал записывается методом прямой записи, описанным
в предыдущем разделе. Девиация частоты модулированного сигнала
обычно ограничена величиной 7,5% несущей частоты, хотя может
использоваться девиация до 40%. Следовательно, наименьшая
частота, которая может быть записана даже при большом отрица-
тельном входном сигнале магнитофона, значительно выше нижнего
частотного предела системы прямой записи. Это означает, что могут
быть легко записаны постоянные и очень низкочастотные сигналы.
Однако верхний частотный предел для ЧМ-записи гораздо ниже
верхнего предела при прямой записи. Это связано с двумя факто-
рами: обычным ограничением 7,5% (или 15%) несущей частоты
для уменьшения искажения н необходимостью использования фильт-
ра низких частот с частотой обрезания около 1/5 несущей частоты.
Частотные характеристики типовых ЧМ-магннтофонов для стан-
дартного и расширенного интервалов (7,5 и 15% соответственно)
приведены в табл. 8.2.
Таблица 8.2
Частотные характеристики типовых записывающих систем с
частотной модуляцией
Скорость ленты. см{сек Верхний частотный предел
Стандарт Расширенный диапазон
2,38 156,25 гц 312,5 гц
4,75 312,5 гц 625 гц
9,5 625 гц 1,25 кгц
19 1,25 кгц 2,5 кгц
38 2,5 кгц 5,0 кгц
! 76 5,0 кгц 10,0 кгц
152 10,0 кгц 20,0 кгц
Поскольку частота генератора регулируется амплитудой инфор-
мационного сигнала, ЧМ-система очень чувствительна и удобна для
записи сигналов переходных процессов. ЧМ-воспроизводящий уси-
литель состоит из предусилителя, ограничителя, дискриминатора
и выходного фильтра, который изменяется в зависимости от скорости
ленты, давая частотную характеристику ±1/2 дб во всем интервале.
Большая часть информации, записываемой во время эксперименталь-
ных исследований на ядерном реакторе, состоит из сигналов, в ко-
торых максимальная частота относительно низка, и для записи
данных на ленту применяется многоканальная передача, чтобы
более эффективно использовать имеющуюся .полосу пропускания
213
записывающей системы. В типичном испытании 14 каналов данных
записываются на магнитную ленту шириной 25,4 мм. Один из этих
каналов обычно используется для временного кодирования, а дру-
гой — для высокочастотного синхронизирующего сигнала, который
служит для компенсации натяжения ленты, перекоса, детонации
и т. д. Применение системы многоканальной передачи с двойной
частотной модуляцией (ЧМ—ЧМ) по стандартам МГТ* позволяет
на каждой из оставшихся 12 дорожках обрабатывать сигналы от 18
датчиков, получая всего 216 записей данных, при условии, что час-
тота сигналов не превышает стандартные, допустимые МГТ зна-
чения. Система многоканальной передачи с тройной ЧМ позволяет
0 1001 10001
Цифровая запись ВС
а
О 100110001
Цифровая запись Вк
Цифровая запись Б8ВИ
б
Рис. 8.3. Системы цифровой записи [I].
Цифровая запись БВнО
г
еще больше увеличить число информационных дорожек, записы-
ваемых на одну ленту, если частота данных достаточно низка.
Система записи с однополосной и частотной модуляцией (ОМ—ЧМ)
может быть также применена при записи на магнитную ленту,
если частотное содержание сигнала укладывается в интервал за-
писи 30—3000 гц ОМ—ЧМ-системы.
Цифровая запись. Цифровая запись на магнитную ленту широко
используется в системах обработки информации и в цифровых вы-
числительных машинах. Цифровые (или буквенные) данные запи-
сываются в двоичном виде с помощью нулей и единиц.
Цифровая запись производится намагничиванием ленты до на-
сыщения в любом из двух возможных направлений (+ или —)
в дискретных позициях вдоль длины ленты. Четыре обычно исполь-
зуемых метода записи нулей и единиц описаны Вебером 11].
1. Метод с возвратом к с м е щ е н и ю (ВС). Лента
намагничивается до насыщения в одном направлении прн записи
нуля и в противоположном направлении при записи единицы
(рис. 8.3, а).
* МГТ — Межведомственная группа по телеметрии — организация
в США, занимающаяся вопросами телеметрии. — Прим, персе.
214
2. Метод с возвратом к нулю (ВН). Лента в нор-
мальном состоянии находится в ненамагниченном состоянии. Еди-
ницы записываются намагничиванием ленты в одном направлении
н нули записываются намагничиванием ленты в противоположном
направлении. Лента возвращается к ненамагниченному состоянию
после записи каждой двоичной единицы информации единицы или
нуля (рис. 8.3, б).
3. Метод без возврата к нулю с изменением
(БВНИ). Лента всегда находится в состоянии насыщения в одном
нли другом направлении, н изменение этого
состояния происходит только прн измене?
нии от единицы к нулю или наоборот
(рис. 8.3, в).
4. Метод без возврата к
и у л ю с отметкой (БВНО). Лента
всегда находится в состоянии насыщения
в том или другом направлении, н изме-
нение состояния происходит только при
записи единиц (рис. 8.3, г).
Наиболее широко в цифровой записи
используется метод БВНО, так как он
позволяет получить наилучший компро-
мисс между точностью, простотой, осу-
ществимостью и совместимостью. Как
видно из рис. 8.3, эта система содержит
наименьшее число перевертываний потока.
Однако метод требует использования вну-
тренней синхронизации, ио это также
необходимо и для методов БВНИ и ВС.
Только метод ВН обладает свойством само-
синхронизации.
Цифровые значения представляются
комбинацией двоичных единиц информа-
Таблица 8.3
Четырехразрядное дво-
ичное представление
чисел
Десятич- ное число Двоичное представление
0 0000
1 0001
2 0010
3 ООН
4 0100
5 0101
6 оно
7 0111
8 1000
9 1001
10 1010
И 1011
12 1100
13 1101
14 1110
15 НН
цин. n-Разрядное двоичное число может представлять числа
от 0 до 2" — 1. Обычно применяемое четырехразрядное пред-
ставление чисел от Одо 15 в качестве примера даио в табл. 8.3.
Например, число 17369 в двоично-десятичном коде выражается как
0001 0111 ООН ОНО 1001, требуя для записи 20 двоичных единиц.
В двоичной форме оио должно быть представлено 15-разрядным
двоичным числом, так как 215 — 1 ~ 32767. Следовательно, 17369
в двоичной форме есть 100001111011001. Двоичное представление
более эффективно для записи информации в том смысле, что данное
число может быть представлено меньшим числом двоичных разрядов
и требует меньше места на магнитной лейте.
Если число содержит десятые доли, необходимо вводить масштаб-
ный коэффициент. Масштабный коэффициент обычно также нужно
записывать, если только он не является постоянным и может быть
учтен при обработке информации. Например, если выходной сигнал
215
датчика изменяется в интерваде от 0 до 1,023 g и имеет погрешность
около 0,001 в, можно представить это напряжение в виде 10-раэряд-
ного числа, так как 210-— 1 = 1023. Следовательно, масштабный ко-
эффициент равен 1000. В другом случае можно предположить, что
максимальный сигнал равен 1023 мв, что может быть непосред-
ственно представлено 10-разрядным числом. При этом необходимость
в масштабном коэффициенте снимается введением меньшей единицы
измерения. Поскольку цифровые данные имеют погрешность только
± 1/2 последнего значащего разряда, использование 10-разряд-
ного представления дало бы погрешность ±1/2 мв.
Погрешность информации около милливольта, поэтому 10-раз-
рядное представление достаточно точно. Если переменная может
быть как положительной, так и отрицательной, для обозначения
знака используется дополнительный разряд.
Лента с цифровой записью содержит малые области, которые
намагничены в том или другом направлении, поэтому качество за-
писи может быть относительно невысоким по сравнению с лентой,
на которой записаны аналоговые величины (при ЧМ- или прямой
записи), но запись является четкой. Наличие значительного уровня
шумов до 10% сигнала, требуемого для насыщения, не ухудшает
качества выходного сигнала цифровой записи. «Взаимные помехи»
между соседними каналами обычно не представляют каких-либо
проблем, и на ленту шириной 12,7 мм обычно записываются до
7 дорожек без расположения головок в шахматном порядке, как это
делается при записи аналоговых сигналов.
При записи на магнитную леиту плотность записи обычно сос-
тавляет 79, 219 и 315 двоичных единиц (или символов) на сантиметр
при скорости ленты до 381 см!сек. Скорости 190 и 287 см!сек исполь-
зуются наиболее часто, но в ряде систем приняты скорости 76,
114 и 152 см!сек. В некоторых последних моделях записываются
более 400 двоичных разрядов иа сантиметр при скорости
287 см!сек с помощью девятидорожечиой записи на ленту шириной
25,4 мм.
Поскольку потеря единственного двоичного разряда в соответ-
ствующем месте может изменить знак или значение, то для обеспе-
чения точности записи в цифровой системе одна дорожка обычно
служит для контроля четности. В типичном случае на семидорожеч-
ной ленте для информации отведены только 6 дорожек, а иа седьмую
дорожку заносится четность.
Рассмотрим семидорожечную цифровую ленту с использова-
нием отрицательной четности. 6 двоичных единиц из 6 информа-
ционных дорожек суммируются. Если сумма четная (0, 2, 4
или 6), генерируется двоичная единица четности (единица) и за-
писывается иа дорожку контроля четности, в результате чего сум-
ма всех двоичных единиц нечетная. Если число двоичных еди-
ниц нечетное, т. е. 1,3 или 5, тогда иа дорожку контроля четности
записывается нуль. При желании может быть использована по-
ложительная четность.
216
Типичная схема семидорожечиой ленты показана на рис. 8.4.
Приведенная на рисунке одна выборка информации состоит из двух
символов; причем каждый символ в свою очередь состоит из семи
разрядов, любой из которых может быть единицей или нулем. Один
разряд в каждом символе служит для контроля четности, а осталь-
ные шесть обычно используются для записи данных. Обычно на сан-
тиметр ленты приходится не менее 80 символов. Рассмотрим 12-раз-
рядное представление, включая знак выходного сигнала датчика.
Это означает, что будут использоваться по крайней мере 2 символа
- Разряд знака
- Наибольший значащий разряд
х Разряд четности
Направление движения ленты
Ширина
ленты
Й,7лн
-I к-Одна выборка данных
Рис. 8.4. Выборка данных, представленная 12-разрядной
цифровом записью на семидорожечную магнитную
ленту шириной 12,7 мм.
в секунду. При плотности 315 символов на сантиметр и скорости
ленты 381 см! сек можно записать 60 000 дискретных данных в се-
кунду. Это значительно превышает любые потребности в записи при
экспериментах с шумами в ядерных системах, и поэтому обычно
применяется многоканальная передача (с разделением повремени)
различных переменных.
§ 8.4. Аналого-цифровое преобразование
При подготовке информации, записанной в аналоговой форме,
для цифровой обработки основным этапом является цифрование
информации, т. е. преобразование ее из аналоговой в цифровую
форму. Сюда включаются выборка из аналоговых данных за очень
короткие интервалы времени (называемые апертурой), преобразо-
вание напряжения в число (обычно двоичное) и передача числа в со-
ответствующей форме иа последующие этапы обработки. Апертура
выборки должна быть достаточно мала, чтобы не происходило за-
метного изменения переменной. Такая выборка называется иногда
импульсной выборкой. Типичная апертура выборки может состав-
лять 0,1 мксек, если применяется усилитель типа «выборка н хра-
нение». Часто используются два таких усилителя попеременно,
чтобы избежать взаимодействия между последовательными выбор-
ками. Один усилитель производит выборку данных, а другой задер-
живает предыдущую выборку, пока она преобразуется в число.
Преобразователи с последовательным приближением. Анало-
го-цифровое преобразование (АЦП) производится путем сравнения
217
неизвестного напряжения, выдаваемого выбирающим и задержи-
вающим усилителем, с эталонным. Это сравнение может выполнять-
ся различными способами, каждый из которых имеет свои преи-
мущества и недостатки в отношении скорости, осуществимости
и стоимости. Обычно используются преобразователи с последова-
тельным приближением, так как они обладают высоким быстродей-
ствием для широкого интервала приложений при разумных стоимо-
стях. Преобразователь последовательно делит эталонное напряже-
данных Время
6
Рис. 8.5. Преобразователь с последовательным приближением [2].
ние пополам. Например, при преобразовании напряжения в число
с четырьмя значащими двоичными разрядами последовательные
приближения происходят по этапам, показанным иа рис. 8.5, а.
Сначала преобразователь сравнивает половину полного диапазона
(1000). Затем сравнивается либо четверть полного диапазона (0100),
либо три четверти полного диапазона (1100) в зависимости от того,
было ли предыдущее приближение больше или меньше выборки.
После четырех приближений получается четырехразрядное число.
Этот метод требует только одного шага на разряд для преобразова-
ния любой величины. Последовательные шаги, возможные при ра-
боте четырехразрядного преобразователя, показаны на рис. 8.6;
полученная в результате дискретная переменная — на рис. 8.5, б.
218
Скорость последовательных приближений АЦП может быть
увеличена различными методами, в частности методом подынтер-
валов. Метод подынтервалов состоит в делении интервала сигнала
на ряд равных подынтервалов н выборе такого подынтервала, в ко-
торый попадает входное напряжение, причем одновременно сравни-
вается входной сигнал с границами выбранных подынтервалов.
Подынтервал, в котором оказывается входное напряжение, в даль-
.0111
^0101
. s Jon
(10)^
KW01
✓ 1111
1101
ООП
^0001
(1s<1110
1101
m<1100
1011
1010
_ ’001
ts)< woo
. 0111'
(?0110
.0101
0100
.0011
«<0010
^0001
т~~*~оооо
05)
(W
(13)
аг)
(id
(10)
(3)
(8)
(7)
(Б)
(5)
М
(3)
(г)
(D
(о)
Рис. 8.6. Иллюстрация метода последовательных приближений
аналого-цифрового преобразования переменной с точ-
ностью 4 разряда (десятичные эквиваленты приведе-
ны в скобках).
нейшем еще делится на подподыитервалы и сравнивается с входной
переменной. Процесс продолжается до тех пор, пока не достигается
требуемая точность преобразования. Использование четырех по-
дынтервалов почти в четыре раза увеличивает скорость преобразо-
вания, ио может удвоить или утроить стоимость.
Из предыдущего обсуждения очевидно, что скорость преобра-
зования зависит от точности, с которой должно быть получено
цифровое значение переменной. Поскольку АЦП требуется значи-
тельно большее время для определения частного значения при очень
высокой точности (например, 13 или 14 разрядов), чем при низкой
точности (8 или 10 разрядов), существует оптимальное соотношение
между скоростью и точностью для данного типа АЦП. Кроме того,
имеются чрезвычайно быстрые методы преобразования такие, как
219
мгновенный АЦП, но количество необходимых сравнивающих уст-
ройств равно 2"—1, где п— число разрядов для требуемой
точности. Такое устройство может быть выгодным для 8-разряд-
ного преобразователя, требующего 255 сравнивающих устройств,
ио очень невыгодным для 13-разрядного преобразователя, в кото-
ром понадобилось бы 8191 сравнивающее устройство.
Масштабное соотношение между входным напряжением и циф-
ровым значением зависит от эталонного напряжения, подаваемого
Рис. 8.7. Погрешности цифрового представления пе-
ременных. Цифровая переменная (а). Вы-
ходной сигнал выбирающего и задержива-
ющего усилителя (6).
иа преобразователь. Например, в 10-разрядном преобразователе
в качестве эталонного подается напряжение 10,24 в. Преобразова-
тель делит эталонное напряжение на 210, или 1024, равных интерва-
лов на каждый разряд. Следовательно, каждый разряд соответст-
вует 10,24/1024 = 0,01 в.
Погрешности АЦП. При преобразовании непрерывного (анало-
гового) сигнала в цифровую форму возникает погрешность, которая
может быть равна значению наименьшего кванта, обычно равного
наименьшему значащему разряду (НЗР). Поскольку погрешность
квантования центрирована, она равна ±1/2 НЗР. На рис. 8.7, а
в качестве примера показана погрешность, которая возникает при
преобразовании аналоговой переменной в цифровую форму с рав-
номерными интервалами по времени. Уменьшение НЗР, очевидно,
уменьшит расхождение между аналоговой кривой и цифровыми
значениями. (Заметим, что выборки из аналоговой кривой, пред-
220
ставленные точками на концах отрезков, • воспроизводятся АЦП
только до ближайшего дискретного уровня, т. е. ±1/2 НЗР.)
На рис. 8.7, б показан выходной сигнал выбирающего и задержи-
вающего усилителя, в котором цифровое значение задерживается иа
дискретном уровне, пока оно не заменяется следующим значением
выборки.
Чтобы показать важность погрешности преобразования, предпо-
ложим, что погрешность имеет равномерное распределение вероят-
ности, равное единице на единичном интервале квантования (т. е.
1 НЗР) и нулю во всей остальной области:
р (х) = 1
р W = О
(—0,5 < х < 0,5),
(в остальных случаях). (8.4)
Поскольку среднее значение рх из-за симметрии равно нулю, сред-
неквадратическое отклонение
Г со 11/2 | 0.5 1 1/2
= И x3p(x)rfx = j хМх =0,288 НЗР. (8.5)
| —со J I—0,5 J
Для 10-разрядного АЦП, имеющего полный интервал 1023 разря-
да, отношение среднеквадратического шума сигнала к сигналу равно
0,000281, т. е. погрешность составляет менеё~0;03% полного диапа-
зона. Этого достаточно для обработки данных.
Погрешности из-за наложения частот. Данные в цифровой форме,
показанной на рис. 8.7, а, могут быть представлены как
X(t)=x(f) 2 6(/ —пД),
(8-6)
где X (/) — переменная в цифровой форме; х (Z) — аналоговая пе-
ременная; А — интервал выборки; о (t — /?Д) — дельта-функция
Дирака при t = /?Д; п — целое число.
Эта последовательность нмпульсов может быть записана в виде
ряда Фурье:
2 6(/-/1Д) = 2С„ехр[-^],
(8.7)

где

(8.8)
—Д/2 —СО
Выполнив преобразование Фурье уравнения (8.6), получим:
1 1
Х(ю) = Т 2 2 X[j(<0-0>„)]. (8.9)
221
Это уравнение показывает, что частотный спектр X (со) дискретного
сигнала есть сумма первоначального спектра и первоначального
спектра, сдвинутого иа где Д и юв — частота выборки
и соответствующая ей угловая частота, равная
Л = cos/2n= 1/Д. (8.10)
Это явление (известное как наложение частоты) ведет к кажуще-
муся увеличению энергии низких частот за счет присутствующих
1W
-f0 о f0 f
а
ixiw)
Х(со)
1Х(со)
•f -^fs 0 fs 2fs f
г
Рис. 8.8. Спектры аналоговых, соответствующих им
дискретных н содержащих эффект наложе-
ния частот цифровых данных:
а—аналоговые данные; б — цифровые данные
прн правильной выборке; в — компоненты под-
вергшихся эффекту наложения цифровых данных;
г — содержащие эффект наложения частот циф-
ровые данные.
в первоначальном сигнале высоких частот. Рассмотрим частотный
спектр, который становится равным нулю при частоте Д, часто на-
зываемой частотой среза, как показано на рис. 8.8, а. Отрица-
тельиый^спектр показан для математической полноты, хотя он
222
не существует в физически реальных системах. Если частота выбор-
ки fs более чем вдвое превышает частоту среза, спектр дискретной
переменной, который повторяется через частотный интервал Д,
имеет вид, показанный на рис. 8.8, б. В интервале между —Д и /0
спектр тот же, что и на рис. 8.8, с, а вне интервала fQ спектр нева-
жен, так как данные не обрабатываются за пределами этой частоты.
Если частота выборки < 2/0, спектр дискретной переменной имеет
вид, показанный на рис. 8.8, в, а результирующий спектр — на
рнс. 8.8, а, где посторонний спектр, возникающий при выборке,
искажает спектр внутри интервала —Д и 4-Д. Наложение частот
может быть основным источником погрешности систем с дискрет-
ным представлением данных, если его не исключить.
Погрешность из-за наложения частот также имеет место в кри-
вых взаимной спектральной плотности и спектральной плотности
мощности, если не приняты соответствующие меры предосторож-
ности. Имеются несколько методов для исключения эффекта на-
ложения. Один из методов состоит в том, чтобы выборки произво-
дились при скорости, более чем вдвое превышающей максимальную
частоту, присутствующую в сигнале. Это невыгодно с точки зрения
возможностей АЦП, стоимости обработки данных, требуемой точ-
ности и т. д. В действительности частотное содержание сигнала
может не быть известным заранее. Другой обычно используемый
метод состоит в постановке фильтра низких частот между входным
сигналом и АЦП и выбором такой частоты среза фильтра, при которой
все частотные компоненты в аналоговом сигнале, большие половины
требуемой скорости выборки, исключаются. Обычно частота среза
фильтра низких частот составляет одну четверть частоты выборки,
что обеспечивает пренебрежимо малую величину эффекта наложе-
ния частот. Если выборка уже проведена, единственно, что может
быть сделано для удаления высокочастотных компонент, это исполь-
зование методов цифровой фильтрации, которые будут обсуждены
в дальнейшем.
Существуют и другие методы выборки, которые позволяют из-
бежать наложения частот, хотя онн применяются не так широко,
как изложенный метод равномерной выборки. Одним из наиболее
очевидных методов является прямой ввод переменной в интегратор
и получение средних значений за интервал выборки делением интег-
рала на временной интервал. Любая флуктуация, которая происхо-
дит в течение интервала выборки, просто изменяет значение, полу-
ченное в процессе интегрирования. Аналогичный метод используется
в цифровых вольтметрах интегрирующего типа, в которых входная
переменная эффективно выбирается фиксированное число раз за
интервал выборки и выходной сигнал получается как среднее (нли
сумма) всех отдельных выборок.
Другой метод исключения эффекта наложения частот состоит
в выборке переменной со случайным интервалом. Преимущество
этого метода состоит в том, что существует конечная вероятность
регистрации любого события или серии событий, которые могут
223
произойти за равномерные интервалы между выборками. Однако
обычно качество данных, полученных этим методом невысоко, так
как прн больших интервалах выборки могут быть потеряны нёкото-
рые составляющие сигнала.
§ 8.5. Многоканальная передача:
распределение времени работы оборудования
В типичных экспериментальных ситуациях могут оказаться не-
сколько переменных, которые обрабатываются нлн записываются
на одну и ту же цифровую ленту. Последнее достигается простым
распределением времени записывающего цифрового устройства
или анализатора. Цифровые записывающие устройства не позволяют
записывать данные по нескольким каналам одновременно, потому
что все дорожки (обычно семь илн девять) используются для записи
данных от одного входа. Распределения времени работы магнитофона
можно достичь, если для каждого датчика применить свой аналого-
цифровой преобразователь, которые работают последовательно.
Однако поскольку преобразователи весьма дорогн, а каждый нз них
функционирует только часть времени (1/п, где п — число записы-
ваемых каналов), оказывается необходимым распределение времени
всей преобразующей, формирующей и записывающей системы в це-
лом. Это достигается применением многоканального модулятора,
который либо последовательно, либо программированным образом
выбирает различные информационные сигналы, представляемые
для записи или обработки. В типичной ситуации экспериментатор
имеет 50 переменных, которые необходимо выбирать через равные
интервалы времени, что может быть сделано, используя последова-
тельную многоканальную модуляцию. В другой ситуации экспе-
риментатору требуется выбирать 10 переменных в 20 раз быстрее,
чем выбираются остальные 40 переменных. Тогда необходима зара-
нее запрограммированная последовательность многоканальных
модуляторов.
Очевидно, что при прямой выборке данных последовательным
методом, происходит некоторый сдвнг данных. Рассмотрим, напри-
мер, 50-канальный модулятор, способный производить 10 000 вы-
борок в секунду. Это означает, что выборка производится каждые
100 мксек н для выборки всех 50 записей данных требуется 5 мсек.
Выборка из последней записи данных будет сделана 5 мсек спустя
после первой записи, и поэтому между этими двумя записями будет
сдвиг в 5 мсек. Если многоканальный модулятор работает непрерыв-
но без какого-либо разрыва между выборкой нз последнего н перво-
го каналов, максимальный сдвиг данных составляет 21/2 мсек
из-за циклического характера выборки. Сдвиг может быть скомпен-
сирован соответствующей обработкой данных, если характер его
влияния на результат известен. Однако в некоторых ситуациях его
влияние неизвестно н попытка скомпенсировать сдвиг вводит еще
большую погрешность, чем дает сам сдвнг. Чтобы избежать сдвига
224
полностью, используются выбирающие и задерживающие усилители.
По команде из многоканального модулятора все усилители одно-
временно выбирают записи входных данных и задерживают полу-
ченное напряжение, пока все данные не преобразуются в цифровую
форму и из многоканального модулятора не поступит следующая
команда на выборку данных.
Существуют два обычно используемых типа многоканальных
модуляторов: многоканальные модуляторы с высоким уровнем
и с низким уровнем. Многоканальные модуляторы с высоким уров-
нем имеют возможный интервал рабочих напряжений ±10 в, а у мо-
дуляторов с низким уровнем возможный рабочий интервал ±50 мв.
Преимущество многоканальных модуляторов с низким уровнем
состоит в том, что они могут обрабатывать сигналы, приходящие
непосредственно от датчиков, без предварительного усиления,
в то время как модулятор с высоким уровнем обычно требует исполь-
зования дополнительного усилителя постоянного тока для увели-
чения сигнала датчика до рабочего интервала напряжений. Много-
канальные модуляторы с низким уровнем обычно несколько более
сложны и в прошлом были более чувствительны к шумам датчика
и. менее надежны, чем установки с высоким уровнем. Однако в на-
стоящее время разработаны удовлетворительные модели многока-
нальных модуляторов с низким уровнем, но они значительно доро-
же модуляторов с высоким уровнем, имеющих ту же скорость преоб-
разования. Выбор типа многоканального модулятора обычно де-
лается из соображений экономичности, т. е. с учетом стоимости мно-
гих усилителей постоянного тока по сравнению с повышенной
стоимостью многоканального модулятора с низким уровнем.
§ 8.6. Система сбора цифровой информации
Чтобы показать степень сложности этого вопроса, рассмотрим
две системы. Первая представляет собой простейшее устройство,
которое может быть успешно использовано для аналого-цифрового
преобразования. Эта система была введена в действие в Отделе
ядерной техники во Флоридском университете в 1962 г. и соот-
ветствовала состоянию технологии того времени.
Структурная схема отдельных компонент этой системы SEL-600
представлена на рис. 8.9. Система состоит из 8-канального модуля-
тора (с возможным расширением до 48 каналов) без выбирающего
и задерживающего усилителя и работает с,двумя скоростями
15 000 и 28 571 выборок в секунду. Нижний предел используется
при Записи данных иа ленту низкой плотности (79 двоичных еди-
ниц на 1 см), а высокая скорость — при записи иа ленту средней
(нестандартной) плотности (151 двоичная единица на 1 см). Ана-
лого-цифровой преобразователь имеет 12-разрядное устройство,
которое производит ll-разрядные величины и знак. Интервал вход-
ного напряжения от —4,096 до ±4,096 в. Наименьший значащий
8 Зак. Б76 225
разряд соответствует 0,002 в. Если входное напряжение превышает
этот интервал, его необходимо ослабить; если оно значительно
меньше, требуются усилители для увеличения входного напряжения
до значения, при котором точность отдельных выборок данных
удовлетворительна. АЦП имеет частоту выборки 400 кгц, что огра-
ничивает скорость выборки (в настоящее время обычно используются
гораздо большие скорости преобразования). Устройство контроля
формата используется для приведения цифровых значений в соот-
Входной
аналоговый сигнал
Рис. 8.9. Структурная схема системы.
ветствующую форму, генерирует четность и записывает ее на цифро-
вой магнитофон. Устройство контроля формата, кроме того, обеспечи-
вает запись либо в разреженной, либо в уплотиеииой форме. Однако
поскольку устройство не имеет блока памяти для хранения данных
во время пробела, часть данных теряется, если используется разре-
женная форма записи. Устройство контроля формата обеспечивает
введение идентифицирующего числа в начале каждого опыта или,
для разреженной формы записи, в начале каждого массива данных.
Идентифицирующее число является 12-разрядиым числом, которое
определяется положением 12 индивидуальных тумблеров иа перед-
ней панели. Введение идентифицирующего числа в начале каждого
опыта очень важно, так как иначе невозможно определить, где иа
цифровой ленте расположены данные. Управление системой осу-
ществляется вручную, хотя могут быть установлены устройства
226
для пуска и остановки цифровой записи по дистанционным сигналам,
записанным непрерывным ЧМ-методом на магнитофон вместе с экс-
периментальными данными.
Система проста, дешева, но не гибка. Постоянная скорость выбор-
ки является, возможно, наиболее сильным ограничением системы,
так как время записи ~3,5 мин. Рассматриваемая установка не
имеет «читающей» электроники и не проводит контроля четности
перед тем, как информационная лента ставится на магнитофон
цифровой вычислительной, машины. Поскольку употребление раз-
реженной формы записи связано с потерей данных, она обычно не
применяется. Могут быть использованы дополнительные устройства
«читающей» электроники, контроля четности и памяти для хранения
данных в течение промежутка записи, но по экономическим сооб-
ражениям они не применяются, так как не существенны для работы
оборудования.
Противоположностью этой системы является система обработки
информации, установленная в Ядерно-космической лаборатории
Вестингауза для обработки данных, полученных в экспериментах
на ядерном ракетном реакторе NERVA, которые проводятся на Ядер-
ной ракетной испытательной станции (штат Невада). Эксперимен-
тальные данные записываются в ЧМ—ЧМ-многоканальной модули-
рованной форме на 14-дорожечные аналоговые магнитофоны, в ко-
торых одна из дорожек используется исключительно для сигнала
временного кода, а другая дорожка — для сигнала синхронизации
скорости с частотой 100 кгц. Данные записываются по каналам
МГТ с номерами от 14 до 18; таким образом, пять записей данных
могут быть сделаны на каждой из оставшихся 12 дорожках, или
всего 60 информационных дорожек на магнитную ленту. Многока-
нальный модулятор имеет возможность обработки. до 60 каналов
данных одновременно и записи их в разреженном или уплотненном
формате на цифровую ленту. Буферная память предотвращает потерю
данных при использовании разреженного формата.
Система оборудована установкой автоматического контроля,
которая осуществляет поиск любой части данных простым набором
начального и конечного времени на наборном кольце, находящемся
на передней панели. Машина считывает временной код, подводит
ленту к начальной точке, записывает данные и останавливается в
заданное время. Система имеет дискриминаторы, позволяющие обра-
батывать любую из 60 информационных дорожек аналоговой ленты.
Схема пропускания импульсов позволяет вести запись при ско-
ростях 16 000, 8000, 4000, 2000, 1000, 500 и 250 выборок в секунду.
Установка оснащена системой памяти, в которой блоки информации
хранятся н затем записываются целыми блоками на цифровую маг-
нитную ленту. Цифровой магнитофон работает только во время за-
писи этих блоков информации, и, таким образом, продолжительность
эксперимента, которая может быть записана прн скорости 250 вы-
борок в секунду, в 64 раза больше, чем при скорости 16 000 выборок
в секунду.
8* 227
Система также оснащена фильтром низких частот, через который
могут быть пропущены данные, чтобы исключить высокочастотные
компоненты и избежать ошибок наложения частот. Частота среза
фильтра задается в цифровом виде, и результаты поэтому могут
быть воспроизведены.
Хотя в настоящее время существуют гораздо более сложные сис-
темы, две рассмотренные системы являются типичными примерами
систем, которые используются в экспериментах на ядерных реак-
торах.
СПИСОК ЛИТЕРАТУРЫ
1. Analog-Digital Conversion Handbook. Digital Equipment Corp., Maynard,
Mass., 1964.
2. Systems Engineering Laboratory. — Fort Lauderdale, Fla., personal com-
munication, 1962.
ГЛАВА 9.
МЕТОДЫ ГЕНЕРАЦИИ
ПСЕВДОСЛУЧАЙНЫХ
ШУМОВ
И ИХ ПРИМЕНЕНИЕ
§ 9.1. Введение
Для измерения параметров ядерных систем часто необходимо
вводить случайное возмущение для возбуждения системы в спе-
цифическом интервале частот. Использование случайных перемен-
ных оправдывается тем, что возмущение системы, как правило,
достаточно мало, так что анализ может проводиться в линейном
приближении. Кроме того, во многих случаях условия опыта не поз-
воляют вводить большие возмущеиня в систему, например, по
соображениям безопасности или просто из-за того, что режим ра-
боты системы не допускает значительных возмущений. Несомненное
преимущество заключается также в том, что случайные шумы со-
держат широкий интервал частот и поэтому могут быть сделаны
одновременные измерения во всем интервале частот.
Большую пользу принесли исследования со случайными шумами,
автокорреляционной функцией которых является дельта-функция
Дирака. К сожалению, последнее справедливо, если переменная —
результат дискретных независимых событий и имеет ограниченную
продолжительность. Первое условие может быть удовлетворено
с высокой точностью прн использовании термоионных диодов или
радиоактивных источников в качестве источника получения слу-
чайных шумов. Однако отрезок времени, в течение которого прово-
дится эксперимент с источником случайных шумов, должен быть
конечным, поэтому автокорреляционная функция такого случай-
ного шума конечной длительности имеет боковые полосы, т. е. авто-
корреляционная функция флуктуирует относительно временной
осн случайным и непредвиденным образом, как показано на рнс. 9.1.
Среднеквадратическая амплитуда случайных флуктуаций автокорре-
ляционной функции относительно временной осн, например, в ин-
тервале от а до b (см. рис. 9.1) относительно мала и составляет не
более 1 % максимального значения. При увеличении длительности
эксперимента эта величина уменьшается. Однако амплитуда боко-
вых полос в любой момент времени совершенно непредсказуема
и может составлять до 10% (и выше) максимума. Такие флуктуации
вызывают значительные погрешности измерений, если считать, что
229
автокорреляционная функция представляет собой дельта-функцию.
Например, в гл. 4 было получено соотношение
4>я/(г)= $ (9.1)
Если принять, что автокорреляционная функция входного сигнала
х (/) эквивалентна дельта-функции, то уравнение (9.1) упрощается
ДО
Ч>1!( (т) = Kh (т), (9.2)
т. е. взаимная корреляция между входным и выходным сигналами
пропорциональна импульсной переходной функции. Это чрезвы-
чайно полезное и удобное соотношение, но, к сожалению, предполо-

Рис. 9.1. Автокорреляционная функция случайной перемен-
ной конечной длительности, у которой фжж (т) не
достигает нуля.
жения, сделанные при переходе от уравнения (9.1) к уравнению
(9.2), просто неприменимы, если автокорреляционная функция
входного сигнала имеет форму, показанную на рис. 9.1. Исполь-
зование соотношения (9.2) может привести к серьезным погрешно-
стям. С другой стороны, при достаточно большой продолжитель-
ности эксперимента боковые полосы, показанные на рис. 9.1, имеют
тенденцию к уменьшению, и погрешность, связанная с использо-
ванием уравнения (9.2), становится менее значительной.
Для преодоления некоторых трудностей, вызываемых действи-
тельно случайными переменными, экспериментаторы обратились к пе-
риодическим сигналам, статистические характеристики которых во
многом похожи илн почти совпадают со статистическими характе-
ристиками случайных переменных. Это не лишено оснований, по-
скольку любая случайная переменная конечна по длительности
и часто используется при обработке данных так, как если бы она
была периодической функцией с периодом, равным длительности
эксперимента. Кроме того, физически невозможно иметь действи-
тельно случайную переменную, автокорреляционная функция ко-
торой является дельта-функцией Дирака, так как это означает, что
переменная должна иметь постоянную для всех частот спектральную
плотность мощности. Такая функция физически бессмысленна, так
230
как процесс имел бы бесконечную среднюю энергию. Существует,
однако, большое число физически реальных типов возмущений, ко-
торые могут с достаточной степенью аппроксимировать это свойство
в рассматриваемом частотном диапазоне.
§ 9.2. Входные переменные для взаимной корреляции
Синусоидальная входная функция. Рассмотрим входную функ-
цию в виде синусоидального сигнала
х (t) — A sin (со/ + 6), (9.3)
для которого автокорреляционная функция равна
Д2
COS шт. (9.4)
Подставив ее в уравнение (9Л), получим
Фя!/(т)==~' (^)C0S о)(т—(9.5)
откуда видно, что взаимная корреляционная функция соответствует
в этом случае реакции системы на косинусоидальный сигнал с ампли-
тудой Л2/2 н частотой о>. Таким образом, полный график передаточ-
ной функции системы может быть получен повторением измерений
на различных частотах. В известной степени эта процедура экви-
валентна классическому измерению частотных характеристик с од-
ним дополнением, что шум, присутствующий в выходном сигнале,
подвергается взаимной корреляции, конечно, при условии, что шум
не коррелирован с синусоидальной входном функцией. В данном
случае взаимная корреляция в основном выполняет функции уз-
кополосного фильтра со средней частотой cd, который отделяет
у (I) от посторонних шумов п (f). Такая процедура может быть ис-
пользована в реакторных осцилляторных экспериментах, в кото-
рых случайные флуктуации, возникающие из-за статистической при-
роды ядерных процессов, столь велики, что затемняют синусои-
дальный сигнал, вводимый либо осциллятором реактивности, либо
нейтронным генератором с синусоидально модулированным выхо-
дом. Поскольку в .любых измерениях частотных характеристик при
наличии значительных шумов требуется определенная фильтрация,
очевидно, что взаимная корреляция является одним из наиболее
эффективных средств осуществления такой фильтрации.
Существуют и другие доводы для использования детерминиро-
ванного и периодического входного возмущения системы (извест-
ный частотный состав, известная амплитуда сигнала, простота реали-
зации). Для измерения передаточной функции в заданном частотном
интервале входная переменная исследуемой системы должна со-
держать частотные компоненты в рассматриваемом интервале. При
правильно сконструированном псевдослучайном входном сигнале
231
можно получить сигналы в рассматриваемом диапазоне частот, амп-
литуда которых в любой точке не превышает заданного уровня.
Кроме того, большинство псевдослучайных переменных представляет
собой функцию, значения которой быстро изменяются от одного
уровня к другому с последующей задержкой на этих частных уров-
нях, т. е. являются прямоугольной волной, в которой продолжитель-
ности дискретных уровней варьируют в относительно широком диа-
пазоне. Такая входная функция легко осуществима в большинстве
встречающихся на практике систем.
Периодические импульсы. Поскольку большинство псевдослу-
чайных сигналов имеют прямоугольную форму, рассмотрим серию
прямоугольных импульсов в качестве входной функции системы. Для
Рнс. 9.2. Периодические импульсы (скважность импуль-
сов b = w/P) [1].
оценки динамических характеристик этой системы должна быть
составлена взаимная корреляционная функция выходного сигнала
с входной функцией. Рассмотрим серию периодических импульсов,
показанных на рис. 9.2, а. Ширина импульса равна w, период—Р.
Серия построена таким образом, что площадь импульсов над гори-
зонтальной осью равна площади под горизонтальной осью между
импульсами; скважность импульсов определяется как
b = w/P. (9.6)
Автокорреляционная функция этой переменной получена авто-
ром работы [1] и, как показано на рис. 9.2, в, представляет собой
ряд треугольников с периодом Р, таким же, что и у периодических
импульсов. Максимальное значение автокорреляционной функции
равно bSz (1 — b), ширина треугольника 2w. Кроме того, автокорре-
ляционная функция между двумя треугольниками отрицательна
и ее величина равна bwS2 (I — b). Очевидно, что автокорреляцией'
ная функция имеет сходство с импульсной функцией, или дельта-
функцией Дирака, только если ширина треугольника 2w достаточ-
но мала, а значения функции между пиками (часто называемые бо-
ковыми полосами) малы. Кроме того, пики автокорреляционной
функции должны достаточно далеко отстоять друг от друга, чтобы
в процессе свертки, описываемом уравнением (9.1), можно было
232
рассматривать только один пик. Это означает, что период входной
переменной х (Z) и, следовательно, автокорреляционной функции
должен быть больше, чем время, требуемое для спада до нуля или
равновесного значения импульсной переходной функции. При рас-
смотрении системы с запаздыванием первого порядка, импульсная
переходная функция которой является экспоненциальной, т. е.
h(t) = Aexp 0);|
/!(/) = о, 0),/
необходимо, чтобы
aw < 1 (т. е. w < 1/а)
(9-7)
(9-8)
(9.9)
1 (т. е. 1/а),
с б
Рис. 9.3. Случайные импульсы (средняя скорость импуль-
сов т и скважность b = тио) [| J.
где 1/а — постоянная времени системы. К сожалению, высокая
разрешающая способность, даваемая соотношением (9.8), приоб-
ретается ценой низкой статистической точности из-за больших
периодов, требуемых для исключения частично перекрывающихся
характеристик последовательных импульсов. Для рассматриваемого
случая взаимная корреляционная функция между входным сигна-
лом, представляющим собой серию периодических импульсов, и вы-
ходным сигналом имеет вид:
4W (т) = bwSzh (т), (9.10)
где b — скважность возмущающих импульсов. Эта процедура
позволяет непосредственно измерять импульсную переходную функ-
цию и является реальным методом, используемым в традиционных
импульсных нейтронных экспериментах, в которых многоканальный
временной анализатор играет роль взаимного коррелятора.
Случайные импульсы. Если теперь предположить, что импульсы,
показанные на рис. 9.2, а, возникают со случайными, а не с перио-
дическими интервалами при средней скорости импульсов т, как
показано на рис. 9.3, а,, то результирующая автокорреляционная
функция, полученная в работе [1], будет иметь вид, показанный на
рис. 9.3, б. Она очень похожа на автокорреляционную функцию
на рис. 9.2, б за исключением того, что имеется только однн тре-
233
угольник вместо многих и отсутствуют боковые полосы. Поскольку
переменная ие является более периодической, то ограничения,
даваемые соотношением (9.7), отсутствуют и остаются лишь ограни-
чения соотношения (9.8). Взаимная корреляция между входной
функцией (в данном случае серией случайно расположенных диск-
ретных импульсов) н выходной функцией дается уравнением (9.10),
таким же, как и для периодических импульсов. На практике может
Рис. 9.4. Случайная прямоугольная волна (средняя
скорость нулевых значений равна £ значе-
ний в секунду) [1].
оказаться желательным свести до минимума вероятность того, что
два импульса будут перекрываться. Это достигается при условии,
что скважность импульсов очень мала, т. е.
b 1 или w 11т. (9-11)
Случайная прямоугольная волна. На рис. 9.4, а показана еще
одна случайная волна с импульсами прямоугольной формы, в ко-
торой нулевые значения (моменты пересечения оси абсцисс) удалены
друг от друга на случайные интервалы согласно закону распределе-
ния Пуассона со средней скоростью £ нулевых значений в секунду.
Ее автокор реляционная функция приведена на рис. 9.4, б. Для
высокой временной разрешающей способности необходимо, чтобы
а/g < 1 или а < . (9.12)
Автокорреляционная функция, показанная на рис. 9.46, опре-
деляется выражением
<РхЛЧ = -^е-26|т|. (9.13)
и, следовательно, взаимная корреляционная функция между вход-
ным и выходным сигналами равна
(9.14)
Псевдослучайные прямоугольные волны. По многим практи-
ческим причинам часто желательно аппроксимировать случайную
234
прямоугольную волну, приведенную на рис. 9.4, а, псевдослучай -
ной прямоугольной последовательностью, т. е. прямоугольной
волной, которая казалась бы случайной, но не являлась такой. Та-
кая форма волны показана на рис. 9.5, а, где нулевые значения
могут иметь место только в моменты, кратные некоторому' элемен-
тарному' интервалу А сек. Вероятность появления нулевого значе-
Рпс. 9.5. Псевдослучайная прямоугольная волна
(средняя скорость пересечения нулевой
линии равна Д/2) [1].
ния в конце каждого интервала примерно 1/2, и автокорреляционная
функция для этого случая представлена на рис. 9.5, б. Требование
высокой разрешающей способности выглядит как
аА < 1. (9.15)
Взаимная корреляция между входным н выходным сигналами
в этом случае дается выражением
'Р«»(Ч = -^'»(Т)- (9-16)
Псевдослучайная двоичная периодическая переменная. Четыре
рассмотренных выше прямоугольных входных сигнала могут быть
использованы для получения информации о поведении системы во
времени. В каждом случае имеется параметр, связанный с возмуще-
нием, который определяет временную разрешающую способность,
полученную в данном измерении. Вообще этот параметр должен быть
фиксированным, чтобы обеспечить равную разрешающую способ-
ность. Например, если импульсы или прямоугольные волны округ-
ляются из-за конечного времени нарастания и спада в генераторе
импульсов, эти эффекты будут несущественны прн условии, что их
временной масштаб мал по сравнению с постоянной времени системы
1/а. Преимущество прямоугольной волны состоит в том, что имеется
множество физических систем, которые могут быть легко возбуждены
таким образом. Кроме того, удобство псевдослучайной прямоуголь-
ной волны состоит в доступности приборов, которые необходимы
для измерений взаимной корреляции, поскольку нулевые значения
имеют место только при временах, кратных основному временному
интервалу А. Если псевдослучайная переменная является периодн-
235
ческой, то можно синхронизировать входную функцию с каналами
многоканального временного анализатора, который обычно исполь-
зуется для измерений в реакторных экспериментах. Если перемен-
ная непериодическая, она имеет очень небольшие (если они вообще
есть) практические преимущества перед формой волны, показанной
на рис. 9.4, а.
На рис. 9.5, б приведена автокорреляционная функция псевдо-
случайной переменной с постоянными боковыми полосами; она будет
периодической с периодом Р, если псевдослучайная прямоугольная
волна является периодической- Такое условие выполняется для трех
общих типов псевдослучайных переменных. Первый тип — макси-
мальная последовательность линейного регистра сдвига, второй —
последовательность остатков квадрата (оба типа подробно описаны
ниже). Третий тип — последовательность сдвоенных простых чисел,
описанная Голомбом и др. [2] (здесь не рассматривается).
Другая важная характеристика различных сигналов — функция
спектральной плотности мощности. Если переменная периодиче-
ская, как в случае периодических импульсов, показанных
на рис. 9.2, й, так и в случае периодических псевдослучайных пря-
моугольных волн, спектральная плотность мощности представляет
серию дискретных импульсов (линейчатый спектр), равноудаленных
друг от друга на интервал, равный основной частоте Д. С другой
стороны, если входная переменная является случайной, как напри-
мер, случайные импульсы на рис. 9.3, а или случайная прямоуголь-
ная волна на рнс. 9.4, й, то спектральная плотность мощности пред-
ставляет собой непрерывную функцию. Если автокорреляционная
функция имеет треугольную форму» как в случаях, приведенных
на рис. 9.2,6, 9.36, 9.56, спектральная плотность мощности (илн
ее огибающая, если спектр дискретный) пропорциональна функции
следующего вида:
Gxx (со) = К [(sin А)1А2], (9.17)
где А — функция со, которая зависит от формы волны, а Д' — кон-
станта. На рис. 9.6 графически показано уравнение (9.17). Для
автокорреляционной функции экспоненциальной формы, представ-
ленной на рис. 9.4, б, спектральная плотность мощности описыва-
ется уравнением
(со) = 2g/(coa + 4|2), (9.18)
показанным на рис. 9.7; здесь £ — число нулевых значений в секунду.
Псевдослучайная переменная может быть определена как пере-
менная, которая детерминирована по своей природе, но с любой
разумной степенью аппроксимации схожа со случайной переменной.
Вообще это означает, что псевдослучайная переменная является
по своему характеру периодической, хотя могут быть и исключения.
Двоичные сигналы обычно определяются как сигналы, которые могут
принимать только два значения при чрезвычайно быстром пере-
236
ходе, между этими двумя значениями. Случайная телеграфная вол-
на, показанная на рис. 9.4, а, в которой сигналы изменяются от
одного значения до другого со случайными интервалами, —
хороший пример случайной двоичной переменной, так как время,
при котором переменная переходит от одного уровня к другому,
определяется тем или иным случайным процессом (например, распа-
дом радиоактивного источника или эмиссией электронов в термо-
ионном диоде, или нулевым значением генератора случайных
шумов).
Использование псевдослучайных переменных в измерениях па-
раметров системы — относительно новый метод, который был широко
разработан в ядерных исследованиях [3—7]. Псевдослучайная
О U)o 2а>0 со
Рис. 9.6. Спектральная плотность
мощности переменной,
имеющей треугольную
автокорреляционную
функцию.
Рис. 9.7. Спектральная плотность
мощности переменной,
имеющей экспоненциаль-
ную автокорреляционную
функцию.
переменная обычно может рассматриваться как детерминированная
переменная, как правило, периодическая, статистические характе-
ристики которой при хорошей аппроксимации эквивалентны ха-
рактеристикам истинно случайной переменной. Доводом в пользу
использования псевдослучайных переменных является трудность
генерации истинно случайной переменной и подачи ее на вход физи-
ческой системы, в то время как генерация псевдослучайных сигналов
и их применение относительно просты. Например, типичный гене-
ратор белых шумов использует свойство диода или радиоактивного
источника давать на выходе случайный сигнал. Можно оценить
среднеквадратическое отклонение этой переменной от среднего зна-
чения, ио нельзя точно предсказать максимальное значение, которое
будет иметь место в течение заданного временного интервала. Если
усиление на входе системы отрегулировано для установки ожидае-
мого максимального значения, имеется большая вероятность, что
амплитуда большинства флуктуаций будет слишком мала, чтобы
эффективно возмущать исследуемую систему. С другой стороны, если
усиление достаточно велико, чтобы большинство случайных сигна-
лов вносили эффективное возмущение, то максимальные сигналы,
237
которые появляются время от времени, могут вывести систему
в нелинейный режим нли в режим ограничения нли насыщения.
Типичным псевдослучайным сигналом является двоичный (с дву-
мя уровнями) периодический сигнал, амплитуда которого известна
точно, а переход от одного состояния к другому происходит при вре-
мени, кратном основному временному интервалу Д. Частотный сос-
тав этого сигнала определяется выбором периода и задающей частоты,
которая численно равна 1/Д. Таким образом, псевдослучайный сиг-
нал может быть легко получен, отвечая любым заданным требова-
ниям.
Поскольку псевдослучайная переменная является периоди-
ческой и детерминированной, она может быть использована в изме-
рительных системах, в которых производится обычный гармони-
ческий анализ входной н выходной функций системы. Однако обыч-
но можно многое выбирать обработкой псевдослучайных перемен-
ных как частного случая случайных переменных. Возникает боль-
шое число ситуаций, в которых использование псевдослучайной
переменной в качестве входной функции системы имеет определен-
ные преимущества перед использованием чисто случайных или
обычных детерминированных сигналов.
§ 9.3. Максимальная последовательность линейного
регистра сдвига (т-последовательность)
сдвига представляет
В значительном большинстве обычно применяемых методов гене-
рации псевдослучайных двоичных периодических сигналов исполь-
зуется регистр сдвига с соответствующими обратными связями,
дающий так называемую максимальную последовательность линей-
ного регистра сдвига, или просто m-последовательность. Регистр
бой ряд триггеров*, соединенных в каскад
таким образом, что при поступлении ко-
мандного сигнала состояние (либо 0, либо 1)
каждого каскада регистра сдвига передает-
ся в следующий каскад последователь-
ности. Входной сигнал первого каскада
регистра сдвига обычно представляет собой
выходной сигнал устройства, суммирую-
щего по модулю 2, иногда называемого
полусумматором.
Устройство, суммирующее по модулю
2, вырабатывает сумму любых двух дво-
ичных выходных функций А и В сог-
ласно таблице соответствия (табл. 9.1).
Если обе входные функции А и В имеют одно и то же значение
(либо 0, либо I), выходная функция равна 0. Если две вход-
ные функции имеют различные значения, выходная функция
Таблица 9.1
Таблица соответствия
Подробно см. в работе [8].
238
равна 1. Суммирование по модулю 2 может логически произ-
водиться с помощью полусуммирующего контура. Регистр сдвига
состоит из объединенных в каскад триггеров, запускаемых с необ-
ходимой скоростью импульсами от внутренних часов. Выходы опре-
деленных триггеров, выбранных таким образом, чтобы давать т-
последовательность, суммируются по модулю 2, и их сумма подается
в качестве обратной связи на вход первого каскада регистра сдвига.
На рис. 9.8, а показана структурная схема четырех каскадного
регистра сдвига, в котором выходы разрядов 3 и 4 суммируются
Сдвиг Сдвиг
импульсов 1111 импульсов
Сдвиг
' импульсов 1111
0111
0071
оса]
1000
0100
OD7C
70S]
1100
0113
1011
0101
1010
1101
1170
1111
а
'—[®ь-
'1111
0111
0011
1001
ПВО
1110
1111
)д
ни
от
1011
0101
1010
1101
оно
ООН
1001
OWO
0010
0001
1000
1100
то
mi
в
- Рис. 9.8. Выходные функции трех возможных вариантов четы-
рехкаскадного регистра сдвига. Четырехразрядные
двоичные числа представляют значения, принимаемые
четырьмя каскадами регистра сдвига при прохожде-
нии цикла (-1—сумматор по модулю 2).
в полусумматоре и результирующий выходной сигнал подается на
первый каскад регистра сдвига. Если в начальном состоянии все
разряды каскада сдвига имеют единичное значение, последующие
состояния каждого разряда регистра показаны внизу под рис 9.8, а.
Очевидно, что после 15 изменений состояния на регистре сдвига
вновь появится начальное состояние, представленное как 1111,
и последовательность повторится с периодом в 15 сдвигов. Можно
показать, что число сдвигов в одном периоде максимальной после-
довательности дается выражением
Z = 2₽~l, (9.19)
где р — число каскадов в регистре сдвига. Следовательно, для
четырехкаскадного регистра сдвига должно произойти 15 сдвигов,
прежде чем последовательность повторится. Если используется уст-
239
ройство собственной обратной связи через полусумматор, длина пос-
ледовательности, выходящей из регистра сдвига, дается уравнением
(9.19).
На рис. 9.8, б показан случай, в котором генерируемая после-
довательность не максимальна. Выходные сигналы каскадов 2 и 4
поступают через полусумматор снова на вход. В последовательности,
показанной под рис. 9.8, б, процесс повторяется всего через шесть
этапов. Такая последовательность не является максимальной после-
довательностью для четырехкаскадного регистра сдвига. Следует
указать, что выходная функция регистра сдвига (в данном случае
выходной сигнал четвертого каскада) определяется правыми циф-
рами четырехзначных двоичных чисел иа рис. 9.8, а.
Рис. 9.9. Выходная функция четвертого каскада
регистра сдвига, показанного на
рис. 9.8, а.
На рис. 9.9 показана псевдослучайная двоичная переменная,
которая генерируется с использованием выходного сигнала чет-
вертого каскада. Два уровня обозначены как 0 н 1, но они могут
представлять два любых уровня сигнала. Выходная функция.каскада
остается постоянной в течение интервала времени между сдвигом
импульсов, которые отстоят друг от друга на Д сек. Следовательно,
частота сдвига Д равна обратной величине интервала времени Д.
Период волны, как показано на рис. 9.9, равен ZA.
Во многих случаях имеется несколько комбинаций обратных
связей через полусумматор, которые дают последовательность мак-
симальной длины. На рис. 9.8, в показана такая схема, в которой
получаемая последовательность проходит 15 этапов, прежде чем она
повторится. Тщательное изучение последовательности, выходящей
из этого регистра сдвига, показывает, что она идентична последова-
тельности регистра сдвига} показанного на рис. 9.8, а, только имеет
обратный порядок, т. е. результирующая переменная обращена
во времени по сравнению с выходным сигналом схемы на рис. 9.8, а.
Это не изменяет ее статистических свойств.
В максимальной последовательности число единиц в каждом
периоде превышает число нулей иа. единицу. Кроме того, в каждом
периоде имеется в два раза больше последовательностей, или серий,
состоящих из единиц или нулей, длиной К, чем серий длиной К-+ 1.
Рассмотрим, например, десятиразрядную двоичную последователь-
ность линейного регистра сдвига. Количество серий с единицами
и нулями показано в табл. 9.2. Из таблицы видно, что эта величина
240
является геометрической прогрессией как для единиц, так и для
нулей, за исключением двух наиболее длинных последовательностей:
по одной для единиц и для нулей. Если помножить общее число
серий на длину серии и просуммировать все эти произведения для
всей последовательности, то окажется, что сумма равна 1023, т. е.
согласуется с результатом, который получается из уравнения (9.19)
для р, равного 10.
Таблица 9.2
Число серий*
Длина серии (число интервалов А) Из единиц Из нулей Всего Произведение числа серий на длину серий
10 9 8 7 - 6 5 ! 4 3 2 1 1 0 1 2 4 8 16 32 64 128 0 1 1 2 4 8 16 32 64 128 1 1 2 4 8 16 32 64 128 256 10 9 16 28 48 80 128 192 256 256
Всего . . . 1023 * Общий интервал времени без изменения уровня.
Другая важная характеристика двоичных максимальных после-
довательностей — свойство «сдвига н суммирования», которое заклю-
чается в следующем: если любую максимальную последовательность
сместить на целое число временных периодов и затем сложить по мо-
дулю 2 с первоначальной последовательностью, возникает третья
идентичная последовательность, смещенная по отношению к первым
двум. Это свойство может оказаться очень полезным при разработке
генератора двоичных псевдослучайных шумов, а также при ис-
следовании в режиме реального времени корреляции с другими
переменными.
Математический метод получения т-последовательности. Ма-
тематический метод для получения максимальной последователь-
ности разработан Голомбом [9], Бердсоллом и Ристенбаттом [10)
и Рое [11]. В этом методе каждый разряд р-разрядного регистра сдви-
га рассматривается как р-мерный вектор, а система с регистром
сдвига (с обратной связью) — как линейный оператор, формирую-
щий последовательные состояния р-мерного вектора. Такая операция
может быть представлена квадратной матрицей X, Первая строка
этой матрицы соответствует первому разряду регистра, вторая стро-
241
ка—второму разряду и т. д. Это же верно и для р-го столбца, т. е.
первый столбец представляет первый разряд, второй столбец —
второй разряд и т. д. Каждый элемент матрицы равен или 1, или 0.
1 в любом месте указывает, что состояние триггера, соответствующего
номеру столбца, задает состояние триггера, соответствующего опре-
деленной строке; в противном случае на этом месте находится 0.
Рассмотрим генератор, изображенный на рис. 9.8, а. Составим
матрицу X, отмечая, что на первый разряд подается сигнал с третье-
го и четвертого разрядов, поэтому в первой строке 1 войдет в столбцы
3 и 4. На второй разряд подается сигнал с первого разряда, поэтому
во второй строке 1 поместим в столбец 1. На третий разряд подается
сигнал только от второго разряда, поэтому поместим 1 в столбец
2 третьей строки. На четвертый разряд подается сигнал только от
третьего разряда, поэтому 1 поместим в столбец 3 четвертой строки.
Матрица имеет вид:
х = -001 1- 10 0 0 0 10 0 _0010_
(9.20)
Аналогично матрица для генератора, изображенного иа рис. 9.8, е,
выглядит так:
х = -1001- 10 0 0 0 10 0 (9.21)
_0 0 1 0_
Следует заметить, что диагональ ниже главной диагонали будет
всегда состоять из единиц, а первая строка матрицы представляет
коэффициенты обратной связи. В общем виде матрица X для р
разрядов записывается следующим образом:
С1 С2 С3 С;
1 0 0 0 . 0 0
0 1 0 . 0 . о. 0
х= 0 0 1 . 0 . 0 0 , (9-22)
0 0 . 0 . 1 0
где Ci — коэффициенты обратной связи (0 или 1).
.242
Построение обратной связи, необходимое для генерирования
последовательности максимальной длины, было рассмотрено для
широкого диапазона последовательностей. В некоторых случаях мо-
гут быть использованы несколько различных обратных связей,
в других случаях может оказаться необходимым применять несколь-
ко полусумматоров для генерирования последовательности.
В табл. 9.3 приведены обратные связи, которые требуют наличия
только одного полусумматора для генерирования последователь-
ностей с количеством разрядов р до 33.
Одна из схем, не включенная в табл. 9.3, ио весьма полезная
в экспериментах с ядерными системами, состоит из 8-разрядиого
регистра сдвига, дающего последовательность с максимальной дли*
Сдвиг
импульсов

®—I Hg |——|
Рнс. 9.10. Восьмиразрядный регистр сдвига.
ной 255Д временных интервалов. Оиа не представлена в табл. 9.3,
поскольку не может быть выполнена с одной обратной связью.
Одна из возможных схем для генерации такой последовательности
представлена на рис. 9.10. Матрица для этой конфигурации имеет
вид:
х=
“0 1 0 0 0 0 Ol-
io о о о о о О
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 1
0 0 0 0 0 1 0 0
_0 0 0'0 0 0 1 0_
(9.23)
Схемы с 12-, 13-, 14-, 16- и 19-разрядиыми регистрами сдвига
возможны, однако они требуют более одного сумматора по модулю 2.
17- и 20-разрядиые генераторы, использующие только один полу-
сумматор, обычно столь же полезны, как и 16- и 19-разрядные
регистры сдвига, которые работают с несколькими полусуммато-
рами. 8-разрядиый регистр сдвига упомянут здесь потому, что ои
очень удобен при проведении экспериментов на ядерных системах,
243
Таблица 9.3
Обратные связи для генерации /^-последовательности с р
до 33 при использовании только одного полусумматора
р Z Суммируемые разряды
2 3 1 и 2
3 7 1 и 3, 2 и 3
4 15 1 и 4, 3 и 4
5 31 2 н 5, 3 и 5
6 63 1 и 6, 5 и 6
7 12? 1 и 7, 6 и 7
9 511 4 и 9, 5 и 9
10 1023 3 и 10,7 и 10
Н 2 047 2 н I1, 9 п 11
15 32 767 I и 15, 14 и 15
17 131 071 3 и 17, 14 и 17
18 262 143 7 и 18, 11 и 18
20 1 043 575 3 и 20, 17 и 20
21 2 097 151 2 и 21, 19 и 21
22 4 194 303 1 и 22, 21 и 22
23 8 388 607 5 и 23, 18 и 23
25 33 554431 3 к 25, 22 и 25
28 268 435 455 3 и 28, 25 и 28
31 2 157 473 647 3 и 31, 28 к 31
33 8 629 894 591 13 и 33, 20 н 33
в которых информация в виде импульсов от детекторов накапли-
вается в многоканальном анализаторе, имеющем 256 каналов, или
в которых проводятся 2 или 4 выборки на каждый сдвиг соответст-
венно в 512- или 1024-канальных временных анализаторах.
Автокорреляционная функция ///-последовательности. Одно из
наиболее важных свойств максимальной последовательности регист-
ра сдвига состоит в том, что ее автокорреляционная функция до-
статочно близка к дельта-функцни, а боковые полосы постоянны.
Это постоянство позволяет учесть ' корреляцию боковых полос,
если это оправдано условиями эксперимента. Автокорреляционная
функция получена скорее путем рассуждений, чем математическим
путем. Рассмотрим ^-разрядный регистр сдвига с одной обратной
.связью, который генерирует максимальную последовательность
(m-последовательность), имеющую период ZA, где Z определено
уравнением (9.19)'. Поскольку каждый разряд регистра сдвига
просто пересылает входной сигнал от предыдущего разряда, выход-
ные сигналы любых двух разрядов одинаковы, за исключением того
что один выходной сигнал сдвинут на ЛА, где k — число разрядов
между двумя выходными функциями. Воспользовавшись свойством
сдвига и суммирования m-последовательностн, получим, что выход-
ной сигнал полусумматора, который подается на вход регистра
244
сдвига и, следовательно, на выходы всех разрядов, является также
т-последовательностью.
Если положить, что в псевдослучайной переменной два уровня
m-прследовательности равны +1 и-—1, среднее значение перемен-
ной будет равнозЬ причем знак определяется тем, какой уровень
имеет больший временной интервал. Например, последовательность
со 127 сдвигами с 63 положительными интервалами и 64 отрицатель-
ными интервалами имеет среднее значение— 1/127. Если среднее
значение принять равным нулю, значения двух уровней в этом при-
мере должны быть равны +128/127 и —126/127.
Для иллюстрации автокорреляционной функции рассмотрим
/n-последовательность с уровнями +1 и -—1. Автокор реляционная
функция имеет вид:
Ч>ю(йД)=-у (9-24)
где х,1 — значение m-последовательности иа г-м интервале. Так как
Xi и xi+h имеют значения Н или —1, корреляционный процесс,
согласно уравнению (9-24), превращается
в определение числа интервалов, при ко-
торых Xt и хг+ь имеют одинаковый знак
(положительный или отрицательный), и
числа интервалов, в которых знаки раз-
личны. Табл. 9.4 представляет собой
таблицу соответствия для перемножения
+ 1 или —1. Полное совпадение с таблицей
соответствия для сложения по модулю 2,
приведенной в табл. 9.2, оказывается
очень полезным при оценке автокорреля-
ционной функции.
Процедура оценки автокорреляционной
функции с помощью уравнения (9.24), когда
xi и xi+h имеют значения +1 или —1, ока-
зывается такой же, как и суммирование подмодулю 2 двух последо-
вательностей, которые сдвинуты на /г А по отношению друг к другу.
Поскольку результатом сдвига и суммирования является другая
последовательность, у которой число интервалов одного уровня пре-
вышает число интервалов другого уровня на единицу, то число ин-
тервалов, в которых Xi и xi+h имеют одинаковый знак, на единицу
меньше, чем число интервалов, имеющих различные знаки. Тогда
уравнение (9.24) принимает вид:
<ра.я(ЛД) = —Л (й¥=0, Z, 2Z, 3Z,...). (9.25)
Для k = О, Z, 2Z, ... фХ!К = 1, так как две последовательности Xi
и xi+h идентичны. Если4придать k нецелочисленные значения в пре-
делах ^А из k = О, Z, 2Z, .... то фж{е (йА) оказывается линейной
I 245
Т а блица 9.4
Таблица соответствия
для умножения
+ 1 и—1
комбинацией двух значений 1 н —1/Z. Следовательно, автокорреля-
ция m-лоследовательности описывается выражением
4’I.xW=l—(0<|т|<Д);
= (0<|x|<(Z- 1)Д). (9.26)
Поскольку псевдослучайная последовательность является перио-
дической с периодом ZA, автокорреляционная функция также по-
вторяется с периодом ZA. Автокорреляционная функция псевдо-
случайной двоичной переменной показана иа рис. 9.11*.
Рис. 9.11. Автокорреляционная функция псевдослучайной двоич-
ной переменной.
Основное требование в отношении длины последовательности
регистра сдвига состоит в том, чтобы период Z был достаточно боль-
шим и последовательные пики автокорреляционной функции не
препятствовали свертыванию автокорреляционной функции с им-
пульсной переходной функцией. Это означает, что период должен
быть больше, чем время, необходимое для затухания импульсной
переходной функции до нуля. Применение 20- или 25-р азрядных
регистров сдвига для получения очень больших периодов приводит
к тому, что боковые полосы —1/Z становятся крайне малыми.
Однако их присутствие необходимо при обработке информации для
целого числа циклов, если используется специфическое свойство
псевдослучайных двоичных последовательностей — свойство по- *
стояиства боковых полос. Все это требует обработки огромного
количества информации. ’Однако по разным причинам многие ис-
следователи предпочитают обрабатывать не целое число циклов, а не-
большую часть длинного цикла для многих циклов. В некоторых
* Если амплитуды двух уровней псевдослучайной двоичной последо-
вательности равны +Z и —А, то правую часть уравнений (9.26) следует ум-
ножить на Л®.
246
случаях количество получаемой информации при этом оказывается
настолько ограниченным, что потеря информации, связанная
с рассмотрением целого числа циклов, была бы недопустимой. В дру-
гих случаях используются очень длинные последовательности, по-
тому что величина боковых полос мала и ими можно пренебречь,
не вводя какой-либо значительной ошибки. Вообще можно сказать,
что отказ от целого числа циклов приводит .к отклонению боковых
полос от идеала, показанного на рис. 9.11, но это отклонение
уменьшается при увеличении числа циклов. Если при обработке
информации рассматривается только часть одного цикла, ошибка
гораздо больше, чем при использовании значительного, но не цело-
го количества циклов.
Спектральная плотность мощности /«-последовательности*. Из
теоремы Винера—Хинчина известно, что спектральная плотность
мощности функции представляет собой преобразование Фурье ав-
токорреляционной функции, т. е.
Фга(со) = 5 Ф™С)ехр(—]0)T)dT. (9.27)
Поскольку (т) — периодическая величина с периодом Р, воз-
можно комплексное представление ряда Фурье для автокорреля-
ционной функции:
4>та(т) = 2 (9.28)
п= —со
где
F/2
Яп=-Г j 4>„(r)e-'“"’dT (9.29)
—Р/2
И
ron = ntOj = = 2пп!Р. (9.30)
Тогда
Фга(о)= \ 2 Л„е)ю»те“1,иДг. (9.31)
__________п= —со
Порядок интегрирования и суммирования можно изменить, так как
ряд Фурье для автокорреляционной функции сходится равномерно:
©»(»)= 2 Лр“"’е~**=
П=—со —со
= 2 А„ $ е—1 (“-“>•)Ttfr = 2 Х„6(со—га„). (9.32)
П=—со —со П=в—СО
* Этот метод в основном аналогичен методу, использованному Хэмптоном
247
Подставив уравнение (9.29) в (9.32), получим
” Г 1 Т 1
ф.™(“) = 2 7" J '₽.™(т)ехР(—/“t)dT 6(ш—ш„) =
п= — со [ г —Р/2 J
Р/2 со
= — J fcWe-J^dT V 6(со—соп) =
—Р/2 п=~оо
=-£<(<•) 2 в («-«„), (э.зз)
* 11=— со
где
р/2
Ф;*(а)= $ <рхх(т)е-^б/т (9.34)
—Р/2
представляет собой преобразование Фурье автокорреляционной
функции, определенное на интервале в один период. Подстановка
уравнения (9.26) в уравнение (9.34) в интервале от —Р/2 до +Р/2
дает:
ф- (со) = P(Z +Л. Г sin («>f/^) Р —L Г sin <mPg) 1 (9 35)
z- L coP/2Z J Z [ сйР/2 J ’ V '
Подставив это уравнение в уравнение (9.33), получим:
Ф fa)=J- У fP<Z+l) [sin(con P/2ZH2
} P n=^a>\ Za L COnP/2Z J
>-
Задающая частота fc равна
fc = Zfn = Zasjil^st = n^iZl^si, (9.37)
а период определяется как
P = гд = Z!fc = 1/Д = 2л/(0ь (9.38)
следовательно, равенство (9.36) можно представить в следующем
виде:
Ф«х(/)=-^6(/) +
+ 2 g±L[sin(n^;Z)]86p_.. (9.39)
248
Уравнение (9.39) показывает, что спектральная плотность мощ-
ности периодической псевдослучайной двоичной последователь-
ности определяется амплитудными коэффициентами Фурье при гар-
монических частотах, кратных основной частоте которая в свою
очередь равна обратной величине периода.
Характеристики /^-последовательности. Рассмотрим 9-разряд-
ный регистр сдвига. Согласно уравнению (9.19), Z — 511 временным
приращениям за один период. Предположим, что регистр сдвига
Частота., гц
Рис. 9.12. Спектральная плотность мощности псевдослучайной
двоичной переменной.
работает на частоте сдвига, или задающей частоте /с, равной 1 кгц,
тогда приращение времени А равно 1 мсек. При этом период
Р = ZA = Z!fc (9.40)
и в нашем случае равен 0,511 сек. Основная частота этой периоди-
ческой переменной тогда равна
А = 1/Р = 1/ZA = fc!Z, (9.41)
что б нашем случае составляет 1,958 гц или 12,33 рад!сек. Ниже
будет показано, что частотный спектр сигнала доходит до нуля при
частоте сдвигов /с, но практически верхний предел полезного частот-
ного интервала равен половине частоты сдвигов. Следовательно,
полезный интервал частот рассматриваемого псевдослучайного
двоичного сигнала лежит в пределах от 1,958 до 500 гц.
Если задающую частоту удвоить, т. е. если принять fc=2000 a/j,
полезный интервал частот составит 3,92ч-1000 гц- Удваивается
как верхний, так и иижиий частотный предел. Нарнс. 9.12 показана
спектральная плотность мощности этого сигнала в нормализованном
масштабе в зависимости от частоты, выраженной как в номере гар-
моники, так и в долях задающей частоты.
249
Используя 10-разрядный регистр сдвига вместо 9-разрядного,
получим Z = 1023 сдвигов на цикл и период 1,023 сек для задающей
частоты 1 кгц. Полезный интервал частот при этом становится рав-
ным 0,978—500 гц. Удвоение задающей частоты до 2 кгц дает интер-
вал частот 1,9564-1000 гц. Из этих примеров видно, что существу-
ет относительно немного ограничений на интервал частот, который
может генерироваться таким устройством. Однако на выбор разрядов
и задающей частоты могут повлиять другие соображения, в част-
ности, при использовании цифровой обработки информации.
Спектральные плотности мощности псевдослучайных последо-
вательностей с одинаковым периодом Р, но разным числом сдви-
гов на последовательность, имеют одинаковую частоту гармоник,
но различное распределение энергии. Для коротких последователь-
ностей энергия сигнала сконцентрирована в низкочастотном диапа-
зоне, в то время как для более длинных последовательностей ампли-
туда меньше меняется от гармоники к гармонике, однако низко-
частотные амплитуды гораздо меньше соответствующих величин
для более коротких последовательностей. Керл ин [7] указал, что
номер гармоники nh, при котором амплитуда гармоники уменьша-
ется вдвое по сравнению с амплитудой первой гармоники, для
Z > 20 равен
nh « 0,44Z. (9.42)
Кроме того, он показал, что энергия, содержащаяся в гармониках,
которые не более чем вдвое превышают основную, составляет
—/71% общей энергии сигнала и что средняя амплитуда этих гармо-
ник примерно равна
Р1/2 « 0,71/0,44Z « 1,6/Z. (9.43)
Это также показывает, что энергия сигнала сконцентрирована
в нескольких гармониках для коротких последовательностей
и распределена по многим гармоникам для более длинных последо-
вательностей, что отражено на рис. 9.13.
Керл ин [7] рассмотрел погрешность, связанную с численной
оценкой частотной характеристики системы, нспользуя для исследо-
вания периодические псевдослучайные двоичные сигналы. Хорошо
известно, что гармонический анализ периодических сигналов приме-
ним только для расчета гармонических частот. Керл ином были изу-
чены результаты оценки спектральной плотности мощности ш-после-
довательности при произвольных частотах и при гармонических
частотах с помощью анализа как полного цикла, так и полуцикла.
Погрешности, возникающие при рассмотрении полного цикла и
произвольных частот, действительно оказались драматическими.
Например, Керлин показал, что отклонение в 1% от гармонической
частоты дает 50%-ную погрешность в расчетной амплитуде десятой
гармонической компоненты. Следует, однако, отметить, что эта
процедура включает в себя использование эффективной полосы про-
пускания, которая почти равна расстоянию между гармониками
250
(т. е. равна основной частоте), что увеличивает разницу между ре-
зультатами расчетов, выполненных для гармонических частот,
и расчетов', выполненных для негармонических частот. Если эф-
фективная полоса пропускания фильтра, связанного с преобразо-
ванием Фурье, включает несколько гармоник, разница между
этими результатами будет существенно уменьшена. Керлин [7],
однако, показал, что анализ половины цикла значительно умень-
шает погрешности, связанные с негармоническими частотами, осо-
бенно для гармоник выше четвертого порядка.
Керлин также изучал погрешности при прямых измерениях
спектральной плотности мощности (как мощности, приходящейся
В
| 0,10
t
X о, OS
i
g 0,06
§
I qw
i-aa?
S
18-разрхдная последовательность
63-разрядная последовательность
251-разрядная последовательность
a zo w so eo m m №) ко iso zoo
л-ионео галноники
Рис. 9.13. Спектральная плотность мощности m-последова-
телыюстен различной длины [7].
на единицу интервала частоты) с помощью полосовых фильтров
и пришел к следующим выводам.
1. Если фильтр имеет полосу пропускания много меньшую, чем
частотное расстояние между гармониками, при измерении вход-
ного спектра мощности могут быть получены хорошие результаты,
если средняя частота фильтра близка к гармонической частоте.
2. Если полоса пропускания фильтра много меньше, чем частот-
ное расстояние между гармониками, и средняя частота 'фильтра
не близка к гармонической частоте, будет получена ошибочная спект-
ральная плотность мощности, но получить приблизительно пра-
вильные значения частотных характеристик н передаточной функ-
ции еще возможно при условии, что спектральная плотность мощ-
ности входного сигнала и взаимная спектральная плотность между
входным и выходным сигналами измерены при совершенно одинако-
вых частотах. Кроме того, полагается, что средняя частота фильтра
гораздо ближе к одной гармонике, чем к другой, и что все другие
гармоники достаточно далеко удалены и оказывают очень слабое
влияние.
3. Если фильтр имеет полосу пропускания, которая велика по
сравнению с частотным расстоянием между гармониками, то можно
251
получить хорошие частотные характеристики, если все гармоники
в полосе пропускания имеют примерно одинаковую амплитуду и
если спектр мощности выходного сигнала слабо изменяется около
средней частоты.
Это показывает, что можно получить хорошие результаты по
частотным характеристикам в некоторых случаях, когда спектр
мощности входного сигнала и взаимный спектр порознь не являются
подходящими. Однако, полагаясь на такого рода компенсированное
поведение, необходимо проявить предельную осторожность.
§ 9.4. Псевдослучайная переменная типа
остатков квадрата
Максимальная последовательность линейного регистра сдвига
благодаря простоте ее получения обычно используется в эксперимен-
тах с псевдослучайными шумами, однако исторически раньше была
рассмотрена другая последовательность, имеющая те же функции
автокорреляции и спектральной плотности мощности. Речь идет о по-
следовательности «остатков квадрата». В качестве примера ее гене-
рации рассмотрим простое число в виде
Q = 4р — 1. (9.44)
Пусть р=5, тогда Q = 19. Числа от 1 до 19 запишем в порядке, ука-
занном в табл. 9.5, и обозначим х. Во втором столбце приведем х2—
Рис. 9.14. Псевдослучайная двоичная последовательность
остатков квадрата.
квадрат этих чисел. В третьем столбце поместим tn — наибольшее
целое число, включая 0, которое при вычитании mQ из х2дает
положительный остаток, кроме 0, меньший, чем Q. Например,
для х2 = 49, т = 2; это означает, что из 49 можно вычесть 2 X 19,
и в остатке получить 11. (Интересно отметить симметрию остатков
относительно горизонтальной линии, проведенной между х = 9
и х = 10, если исключить х = 19.) Теперь псевдослучайная после-
довательность может быть получена следующим образом: отложим
на временной оси 19 равных интервалов, как показано на рис.9.14.
Затем припишем амплитуду одного из дискретных уровней тем ин-
тервалам, номера которых соответствуют числам в столбце остатков
квадрата табл. 9.5, включая последний номер 19. Для рассматри-
ваемого примера значение +1 приписывается временным интерва-
252
Таблица 9-5
Последовательность остатков квадрата
X X* т Остаток (x=~m Q)
1 1 0 1
2 4 0 4
3 9 0 9
4 16 0 16
5 25 1 6
6 36 1 17
7 49 2 11
8 64 3 7
9 81 4 5
10 100 5 5
11 121 6 7
12 144 7 11
13 169 8 17
14 196 10 6
15 225 11 16
16 256 13 9
17 289 15 4
18 324 17 1
19 361 18* 19
* Это значение может быть равно 19, тогда остаток будет равен 0; следователь-
но. интервалы должны быть пронумерованы от 0 до 18, а не от 1 до 19, как сделано
на рис. 9.14.
лам, помещенным в последнем столбце табл, 9.5 (т. е. интервалам
1, 4, 5, 6, 7, 9, II, 16, 17, 19) и значение 1 приписывается остальным
временным интервалам (т. е. интервалам 2, 3, 8, 10, 12, 13, 14, 15
и 18). Результирующий сигнал показан на рис. 9.14.
§ 9.5. Многочастотные двоичные входные сигналы
Частотные характеристики реакторной системы о’бычно могут
быть представлены с достаточной точностью ограниченным коли-
чеством точек при условии, что точки .выбраны с необходимой
точностью и разумно удалены друг от друга. Семь или восемь точек,
удаленных друг от друга на одну октаву, обычно хорошо перекры-
вают ширину полосы в две декады. Если эти две декады выбраны ра-
зумно, динамические свойства системы описываются достаточно-
хорошо. Исключение, конечно, представляют острые резонансы,
когда для описания поведения системы требуется большое коли-
чество точек на кривой частотной характеристики. Вообще точки
измерения на кривой частотной характеристики выбраны достаточно
эффективно, если они представляют арифметическую прогрессию
и нанесены на логарифмическую частотную шкалу.
253-
Метод обработки информации, при котором частотные характе-
ристики измеряются от точки к точке, называется прямым. Однако
по многим причинам часто используются методы, которые дают ре-
зультаты измерений сразу на нескольких частотах, хотя при этом
требуется сложная аппаратура, проведение многочисленных проб-
ных опытов для выполнения правильной регулировки всех прибо-
ров, что вносит в реализацию такой системы дополнительные труд-
ности. Часто характеристики системы изменяются во времени, в ре-
зультате чего время для проведения измерений от точки к точке ока-
зывается ограниченным. Если измерения выполняются для всех
частот одновременно, эффект нестационарное™ пренебрежимо мал
нли может быть выделен во время обработки полученных данных.
Иногда крайне желательно определить изменение характеристик
системы в зависимости от времени.
Если в качестве входного сигнала системы используется белый
шумовой сигнал, который проходит через фильтр нижних частот, то
такой входной сигнал обычно и труден для генерации и не очень
эффективен для целей измерения. Если, например, ширина полосы
шумового сигнала равна 100 гц и анвлизнруются только семь илн
восемь частот, распределенных геометрически, причем анализ
проводится одинаково для всех частот, т. е. при одинаковой полосе
•фильтрации, полоса пропускания фильтра должна составлять
1 гц или меньше. В этом случае в измерении используются только
7 или 8% энергии сигнала. С другой стороны, если полоса пропус-
кания фильтра возрастает по мере увеличения частоты (т. е. если
применяется фильтр с постоянным «Q»), измерительный процесс
гораздо более эффективен в том отношении, что большая доля энер-
гии сигнала используется для измерений. Однако при этом измере-
ние осреднено по широкому диапазону частот н может быть непра-
вильным для отдельной частоты в этом интервале.
Если требуется информация только для ограниченного числа час-
тот, наиболее эффективным является сигнал, состоящий нз смеси
только этих частот. Полезная энергия сигнала в этом случае макси-
мально возможна, а искажения от нежелательных компонент сиг-
нала минимальны. Кроме того, очень удобно выбрать частоты та-
ким образом, чтобы выходной сигнал был периодическим; семь
частот, расположенных в геометрической прогрессии от основной
частоты Д до 64Д, рассмотрены Дженсеном 1141. Для иллюстрации
рассмотрим многочастотный сигнал, представляющий сумму этих
семи частот, т. е.
X (0 = COS C1V + COS +
+ а4 cos -40^ ~F as cos 8сох/ +
+ ale cos 16©^ + а32 cos 32(Bj/ + ссй cos 64сог/. (9.45)
Сначала рассмотрим случай/ когда все коэффициенты-равны 1, т. е.
== — 6Zjc = С32 = ^64 ~ 1- (9.46)
254
к сожалению, максимальное значение временной функции очень
-велико н функция амплитудного распределения незначительно от-
личается от соответствующего сигнала белого шума. Поэтому вве-
дем новую функцию:
х' (t) = х (t)/ I X (t) I, (9.47)
которая имеет те же нулевые значения, что и х (I), но амплитуда
ее равна +1 или —I в зависимости от знака х (I). При соответст-
вующем усилении и смещении можно получить сигнал, изменяю-
а
б
Рис. 9.15. Многочастотные двоичные сигналы [14]:
а — Хд‘. й|=йг=О4=Ов=Я|б“ва2=Об«—1; б — х^: в,=
="G<"=Oi6=C(h'= I, й2—сз=йэ2™ —1; в •— л-jgi о, =0,5,
а2=at =1,0, 0=1,2, Oie=Gas“l.B, fiM=2,0.
щийся между двумя любыми уровнями. Кроме того, x'(f) гораздо
легче получить-с помощью какого-либо генератора н ввести в ис-
следуемую систему.
Дженсен 114) исследовал три сигнала такого типа. В первом,
рнгнале, обозначенном ха (/), все коэффициенты равны единице,
как показано в уравнении (9.46) и на рнс. 9.15, а. На рисунке
приведена только половина цикла и сигнал можно рассматривать
как симметричный по отношению к любой вертикальной пунктир-
ной линии. Дженсен исследовал также два других сигнала. Сигнал,
обозначенный Хб (/), имеет амплитудные коэффициенты
tZi — lj
az — ав ~ = — 1»
(9.48)
25&
а сигнал, обозначенный лв(/), имеет амплитудные коэффициенты
= 0,5;
«а = «л = ЬО;
а8 = 1,’2; (9.49)
^•16 = ^Э2 = 1 >8>
пс4 = 2,0.
Амплитуды семи рассматриваемых частотных компонент этих
трех сигналов, полученные при разложении в ряд Фурье, даны
в табл. 9.6. Эффективность сигналов т], которая может быть опре-
делена как процент мощности в семи исследуемых частотах:
сумма квадратов амплитуд семи рассматриваемых компонент Фурье
1] = 100
сумма квадратов амплитуд всех компонент Фурье
(9.50)
представлена для сигналов ха, х'б, х'в в табл. 9.7.
Таблица 9.6
Коэффициенты разложения Фурье
Гармоника 4 ХБ хв Г армоника 4 4 ХВ
1 25,0 18,2 10,8 16 22,5 25,7 20,3
2 19,3 22,7 13,7 32 18,9 21,3 28,7
4 8 21,6 18,7 23,6 22,1 15,6 17.8 64 21,6 18,3 30,3
Мощность составляющих сигнала, не входящих в семь рассмат-
риваемых частот, распределена среди остальных составляющих
в результате ограничения амплитуд. Процент мощности в нерас-
сматриваемых гармониках для М <1 100 и для N > 100 (где N —
номер гармоники) приведен в табл. 9.7.
Таблица 9.7
Распределение мощности по гармоникам
Сигнал Эффективность (мощность семи рассматриваемых частот). % Мощность лерассматри- ваемых частот, %
W-C100 №>100
64,8 26,9 8,3
ХБ 71,2 21,6 7,2
ХВ 63,2 21,2 15,6
256
Амплитуда x'B ft) Амплитуда xB(t) Амплитуда х'Аft)
Рис. 9.16. Спектр амплитуд хД, х& х'в [14].
9 Зак. 576
Спектр амплитуд трех двоичных переменных, показанный на
рис. 9.16, и распределение мощности по гармоникам, представлен-
ное в табл. 9.7, очень удобны при сравнении трех двоичных сигна-
лов. Сигнал хб (t) наиболее эффективен и имеет наиболее однород-
ные амплитуды для рассматриваемых компонент. Однако для систем,
которые сильно ослабляют высокие частоты, более подходящим
является сигнал х'в.
Должны существовать и другие комбинации коэффициентов,
которые давали бы более эффективные двоичные сигналы, но ни-
каких попыток получить их не было сделано. Вообще лвобой из
трех сигналов может быть использован для исследования реактор-
ных систем; сигнал х'Б (Z) широко использовался при испытаниях
Халдейского кипящего реактора [15].
§ 9.6. Псевдослучайная двоичная переменная
с обратным повторением
Существуют н другие средства для исключения коррекции бо-
ковых полос автокорреляционной функции входного сигнала, кото-
рые заключаются в использовании специальной формы псевдо-
случайной двоичной переменной, называемой последовательностью
Рис. 9.17. Псевдослучайная двоичная перемен-
ная с Р=7Д (а) и соответствующая
переменная с обратным повторением
с Р = 14Д (б).
с обратным повторением, которая описана Годфри [16]. Для ее
генерации знак псевдослучайной двоичной переменной прн каждом
последующем приращении Д изменяется на обратный. Поскольку
Z нечетное, период последовательности с обратным повторением
равен 2ZA. На рис. 9.17 показана последовательность с обратным
повторением, полученная нз псевдослучайной двоичной перемен-
ной с Z = 7. Важно, что среднее значение равно нулю и что длина
358
наиболее длинной серии равна 4А по сравнению с ЗА для псевдо-
случайной двоичной переменной.
Легко показать, что автокорреляционная функция последова-
тельности с обратным повторением в момент iA (i — целое число)
получается умножением автокорреляционной функции псевдослу-
чайной двоичной последовательности ср (t'A) на (—1)*. Это означает,
Рис. 9.18. Автокорреляционная функция псевдослучай-
ной переменной с Р = 7Д (а) и автокорреля-
ционная функция соответствующей переменной
с обратным повторением с Р = 14Д (б).
что треугольные положительные пики будут иметь место при
i = 0,'2Z, 4Z, ..., а треугольные отрицательные пики — при i = Z,
3Z, ... Боковые полосы пилообразно изменяются между —1/Z
и 4-1/Z. На рис. 9.18 показаны автокорреляционные функции
псевдослучайной переменной и соответствующей последователь-
ности с обратным повторением. Поскольку площадь между кривой
(т) н осью абсцисс определяет влияние боковых полос иа изме-
рение,ч последовательность с обратным повторением привлекательна
для измерений взаимной корреляции..
9* 259
§ 9.7. Использование псевдослучайных переменных
в качестве заменителя случайных шумов
Распределение вероятности амплитуд. Использование псевдо-
случайных переменных в качестве случайных шумов может быть
вполне удовлетворительным в одних случаях, но неудовлетвори-
тельным в других случаях. Наиболее существенная разница имеется
в графиках плотностей вероятности амплитуд, что показано на
рис. 9.19, на котором сравниваются плотности вероятности ампли-
туд гауссовых случайных шумов и псевдослучайной переменной.
В ситуациях, в которых важна плотность или распределение вероят-
(а — гауссова случайная
переменная; б — псевдо-
случайная переменная).
заны отношения равные
ности амплитуды, такая разница
может помешать использованию
псевдослучайной переменной вместо
гауссовой переменной. Можно от-
фильтровать псевдослучайную пе-
ременную до точки, где ее плотность
вероятности похожа на плотность
вероятности гауссовой случайной
переменной. Это иллюстрируется
рис. 9.20, на котором показана
15-разрядная псевдослучайная дво-
ичная переменная, отфильтрован-
ная фильтром Баттерворда второго
порядка с частотой среза fb. Ча
стота среза изменялась, давая
несколько различных отношений
fjfb (/с — задающая частота псев-
дослучайной переменной). Пока-
S, 7, 10, 12, 15, 20, 40, 60 н 80. Кли-
нообразный характер плотности вероятности еще виден для отно-
шения, равного 3, но исчезает по мере увеличения задающей часто-
ты. Для отношения, равного 20, плотность вероятности близка
к гауссовой. Однако уже для отношений 7 и 10 становится заметной
небольшая асимметрия, которая делается совершенно явной при
отношениях 60 и 80. Эта асимметрия является в основном следстви-
ем распределения длин серий (см. табл. 9.2). Поскольку каждая
псевдослучайная последовательность имеет нечетное число сдвигов
на период, самую длинную серию имеет одно состояние н вторую
по длине серию имеет другое состояние. Кроме того, эти две серии
обычно в цикле далеко разделены во времени. Эта разница хотя
и кажется небольшой, но создает эффект асимметрии, отмеченный
на рис. 9.20. Этот эффект можно ликвидировать суммированием
двух псевдослучайных переменных различной длины с образова-
нием третьей псевдослучайной переменной. Такая процедура мо-
жет быть использована в зависимости от характера эксперимента.
Корреляционные эксперименты. При проведении экспериментов
по кинетике реакторных систем основное требование состоит в том,
260
чтобы частотный состав псевдослучайного входного сигнала был
совместим с динамическими характеристиками компонент иссле-
дуемой системы. Если исследуется постоянная времени быстрого
затухания подкритической .системы, рассматриваемый интервал
частот совершенно другой, чем при изучении ксеноновых или тем-
пературных флуктуаций в энергетических реакторах. Очевидно,
что частотный состав псевдослучайных двоичных сигналов может
быть легко изменен выбором частоты и периода сдвига (длиной по-
Рнс. 9.20. Плотность вероятности фильтрованной псевдо-
случайной переменной, использующей Пораз-
рядный регистр и фильтр Баттерворда второго
порядка [17].
следовательиости). Ниже будут обсуждаться практические соображе-
ния выбора параметров этих последовательностей в конкретных
экспериментах.
В гл. 4 показано, что определенные упрощенные соотношения,
включающие корреляционные функции и спектральные плотности
входных и выходных сигналов, справедливы, если автокорреляцион-
ная функция входа есть дельта-функция Дирака и ее спектральная
плотность мощности постоянна на всех частотах. Такие идеальные
условия никогда не выполняются для действительных переменных,
но могут быть хорошо аппроксимированы рядом псевдослучайных
переменных, как показано выше в этой главе. Действительная
автокорреляционная функция любой истинно случайной двоичной
переменной (см. рнс. 9.3 и 9.4) не будет асимптотически прибли-
жаться к нулю на бесконечности, так как сигналы имеют конечную
длину. Флуктуации автокорреляционной функции около временной
оси (боковые полосы) имеют тенденцию к уменьшению по амплитуде
по мере увеличения длительности сигнала, но нет никаких осно-
ваний утверждать, что амплитуда боковых полос будет меньше
261
любого заданного значения. Последовательность максимальной
длины и последовательность остатков квадрата имеет автокорре-
ляционные функции, которые полностью определены, как показано
на рис. 9.11. Прн увеличении периода последовательности ZA мак-
симальные значения становятся более разнесенными и боковые поло-
сы уменьшаются. По мере увеличения частоты основание треуголь-
ников становится меньше. Следовательно, комбинация большого
периода и высокой задающей частоты дала бы автокорреляционную
функцию, которая хорошо аппроксимирует дельта-функцию Ди-
рака. Спектральная плотность мощности такой переменной, как
показано на рис. 9.12, имеет близко расположенные гармоники
и полезную амплитуду до /с/2, которая может быть очень
высокой.
К сожалению, во многих случаях неудобно, а иногда н невоз-
можно, использовать высокую задающую частоту н (или) длинные
периоды. В этих случаях необходимо вводить поправку на конеч-
ные размеры треугольников и наличие боковых полос. Последнее
выполнимо, так как автокорреляция определена.
В некоторых типах корреляционных'экспериментов достаточно
возбудить систему широкополосным входным сигналом. Для этого
пригоден любой двоичный сигнал, описанный выше в этой главе,
например случайный двоичный сигнал, который включает и выклю-
чает нейтронный генератор ускорительного типа, возмущающий
подкритическую ядерную систему. Поскольку эта система линей-
на, амплитуды возмущений могут быть сделаны очень большими,
а влияние сопровождающих шумов малым. Автокорреляционная
функция выхода высокоэффективного детектора, размещенного
в подкрнтической системе, дает хорошие измерения методом рос-
си-альфа. В экспериментах с взаимной корреляцией получаются
хорошие результаты, если известны и учтены статистические харак-
теристики входной переменной. Только в некоторых специальных
случаях допустимо предположение, что входной сигнал является
белым, и можно использовать особые свойства белых шумов для
анализа эксперимента. Однако вся тяжесть доказательства такого
предположения ложится иа исследователя, который это делает.
§ 9.8. Взаимная корреляция с псевдослучайными
двоичными сигналами
В гл. 4 показано, что с помощью функции корреляции и спек-
тральной плотности вход-выходные соотношения для линейных
систем определяются следующими выражениями:
Фм(т)= S (9.51)
Фю(«>) = Н(ш) ©„(«>); (9.52)
Свд(й>)=Н(ш)Сзя(ш). (9.53)
262
Применение двух последних выражений для оценки Н (со)
не представляет каких-либо проблем, если могут быть получены
достаточно точные прямые измерения Gxy (со) и Gxx (со) или Фж9 (со)
и Фд-д, (со). Однако иногда целесообразно или даже необходимо из-за
имеющегося оборудования использовать временное соотношение,
описываемое уравнением (9.51). Процедура очень проста, если вход-
ная функция х (£) является белым щумом, имеющим автокорреля-
ционную функцию в виде дельта-функции Дирака. Как следует
из уравнения (4.97), уравнение (9.51) преобразуется в
Ф«И^ = ^(т), - (9.54)
где К — коэффициент пропорциональности между функцией
Фки СО взаимной корреляции и импульсной переходной функцией
h (т). Как указано выше, часто нельзя получить приближение бе-
лых шумов, что затрудняет проведение оценки h (т) по уравнению
(9.51), еслн фдз; (т) известна. Однако можно использовать псевдослу-
чайную двоичную входную функцию, имеющую автокорреляцион-
ную функцию, показанную на рнс. 9.11, в следующих случаях.
1. Период ZA больше, чем время спада импульсной характе-
ристики до равновесного значения, т. е. постоянная времени систе-
мы значительно меньше, чем период входной переменной.
2. Импульсная переходная функция незначительно изменяется
в течение одного интервала А (средней ширины треугольного шага).
3. Треугольный пик 2А настолько узок, и амплитуда боковых
полос столь мала, что ими можно пренебречь.
Если эти условия не выполняются, для преодоления упомяну-
тых трудностей используется детерминированная (и известная)
форма автокорреляционной функции.
Обычно выполнение первого условия с псевдослучайной двоич-
ной переменной не представляет никаких затруднений, а второе
условие удовлетворяется, за исключением начального участка им-
пульсной переходной функции, где h (т) изменяется очень быстро.
Последнее обстоятельство может исказить измерения h (т) в этой
области и во многих случаях сместить максимальное значение.
Указанный эффект уменьшают оптимальным подбором частоты ре-
гистра сдвига и количества выборок за интервал А задающей ча-
стоты. При этом предполагается, что псевдослучайный двоичный
сигнал почти эквивалентен белому шуму. Однако, как видно
из графика спектральной плотности мощности, спектр является
дискретным и амплитуды отдельных компонент спадают в соответ-
ствии с соотношением типа (sin х/х)2, достигая нуля в первый раз
на частоте, равной задающей частоте.
Выше примерно 1/10 задающей частоты имеется частотный ин-
тервал, для которого амплитуды дискретных частотных компонент
почти постоянны. Это соответствует интервалу, где sin х примерно
равен х. Если задающая частота достаточно высока, так что рассмат-
риваемый интервал частот меньше, чем V10 задающей частоты,
263
допустимо предположение о том, что спектральная плотность мощ-
ности входного сигнала постоянна во всем интервале частот. Сле-
довательно, при этих условиях справедливо, что амплитуда переда-
точной функции пропорциональна амплитуде взаимной спектраль-
ной плотности между входом и выходом. Кроме того, при этих
предположениях справедливо аналогичное соотношение во вре-
менной области (т. е. что импульсная переходная функция пропор-
циональна взаимной корреляции между входом и выходом).
Система on-line взаимной корреляции с использованием псевдо-
случайной двоичной входной функции. Непосредственная взаим-
ная корреляция с использованием псевдослучайных двоичных
Рис. 9.21. Система взаимной корреляции.
входных сигналов производилась авторами работ [3, 4, - 18].
У всех этих экспериментаторов были почти одинаковые методы с
незначительными вариациями. Сущность процедуры показана иа
рис. 9.21, где на вход подается псевдослучайная двоичная перемен-
ная, генерируемая любым описанным выше методом. Следующий
этап — генерация точно такой же псевдослучайной двоичной пере-
менной, но запаздывающей на временной интервал /гД. Это запазды-
вание может осуществляться самыми разнообразными способами.
Запаздывающая псевдослучайная переменная затем умножается
на выходную функцию системы для получения взаимной корреляции
между входом и выходом. Поскольку запаздывающая входная пере-
менная является псевдослучайным двоичным сигналом и обычно
смещена так, что двоичные уровни равны, но противоположны по
знаку» операция умножения легко выполняется переключающими
либо электронными, либо механическими устройствами. Усредне-
ние выполняется интеграторами, ЯС-контурами или операционными
усилителями.
Коррекция боковых полос псевдослучайной двоичной перемен-
ной. Чтобы определить истинную импульсную переходную функ-
цию, следует уточнить влияние отрицательных боковых полос.
Это можно сделать довольно просто, так как псевдослучайный
сигнал и его автокорреляционная функция являются детерминиро-
ванными.
264
Рассмотрим импульсную переходную функцию h (А), которая
равна 0 для к 0. Нормализованная автокорреляционная функция
может быть лредставлена следующим образом:
<раж(т—Л) = —1/Z,
fe(T_X)=l+£±L(^j,
^(т—Х) = —1/Z,
[0<Х<(т-Д)];
[(т—Д)<Л<т];
[т<Х<(т—Д)];
(9.55)
[(т + Д)<^<гД].
Подстановка уравнения (9.55) в уравнение (9.51) дает:
I ’ *+* ]
<Рм(т)=Тд' j ОД(х.—r)ta— /i(x)(x—T)dx +
Lt”А ' t J
T-FA ГA/А т+д . 1
+ Jj Л(Я.)«а,-----!- J /i(X)dk— jj й(Х)А , (9.56)
т—д l О т—A J
где последний член представляет собой вклад боковых полос в ав-
токорреляционную функцию.
Если Д мало, так что h (Л.) можно считать постоянной в интервале
т — Д X-Ь Д, уравнение (9.56) сокращается до
<М (т) = (14- 1/Z) Л (т) Д—ЛД, (9.57)
а импульсная переходная функция определяется выражением
A[1+(1/Z)J ’ ' '
где h — среднее значение Л(>.) за один период псевдослучайной пос-
ледовательности. Поскольку Л (т) = 0 для т < 0,
<Рм,(—Т) = —ЛД, (9.59)
то окончательно
,, <Р«К W —<Ред(—Т) фздМ -фед/—Т)
А(Т)- A[l+(./Z)] =-------С-------’ (9‘6°)
где С — константа, равная
С = Д (1 + 1/Z) (9.61)
и постоянная для данной последовательности регистра сдвига и за-
дающей частоты. Поскольку <рК1/ (—т) отрицательна, то процедура
получения истинной импульсной переходной функции эквивалент-
на сложению коэффициента корреляции (—т) |/С с измеренной
импульсной переходной функцией.
265
Следует отметить, что импульсная переходная функция h (т)
не обязательно стремится к 0 при верхнем пределе интеграла NA,
а может достигать постоянного фонового значения. В эксперимен-
тальной ситуации это соответствует фону запаздывающих нейтронов
и (или) какому-либо другому фону, например отражению в комнате.
Поэтому, когда измеренная импульсная переходная функция кор-
ректируется указанным образом, необходимо, как предложено
Гарелисом 119], проанализировать результаты по kfi/L Важно по-
лучить достаточное количество данных, что произведенная коррек-
ция сделана с наибольшей точностью.
Модифицированная взаимная корреляционная функция. В урав-
нении (9.57) для взаимной корреляционной функции
фхэ (т) = (1 4- 1/Z) А (т) А—ЛА (9.62)
член А А представляет собой смещение. Вместо проведения описан-
ной коррекции можно использовать модифицированную взаимную
корреляционную функцию, предложенную независимо авторами
работ [20] и [19] в немного различающейся форме. Введем новую
переменную
/(/)== 1 + х (/), (9.63)
где %(/) изменяется от —I до 4-1 псевдослучайным образом, как вид-
но из рнс. 9.9. Как указано в табл. 9.2, всегда существует еще одно
приращение А, имеющее на одно состояние больше, чем другое.
Если принять, что имеется больше значений 4-1, то среднее значе-
ние х (/) равно
x=l/Z. (9.64)
Выходной сигнал системы для постоянного входного сигнала х
равен
“ хд
у= Л(Х)х(/—X)dX = x h (tydh — xhZb.. (9.65)
—со О
Подставив уравнение (9.64) в (9.65), получим
£=ЛД. (9.66)
Модифицированная переменная х' (/), описываемая уравнением
(9.63), изменяется от 0 до 2 и имеет среднее значение
x' = l + l/Z = (Z+l)/Z. (9.67)
Результирующее среднее значение у' для входного сигнала х из
уравнения (9.65) равно
F = (l + l/Z)ftZ& = (Z+l)M. (9.68)
S66
Когда переменные взаимной корреляционной функции имеют
отличные от доля средние значения, результат, как следует иа
уравнения (4.136), равен
Фа® (т) = ЧЧ ио <т) + ХУ> (9 69)
где х0 и у0 — переменные, имеющие нулевые средние значения.
Поскольку х (f) и у (t) имеют средние значения соответственно
1/Z н /тА, можно воспользоваться уравнением (9.69) и получить
Ф*.».('') = Ф«М—х»=ф«(т)—hMZ. (9.70)
Подстановка уравнения (9.57) в уравнение (9.70) дает
ф«0 М=(1 + i/z) Л(т) a-/7a-m/z=(1 + i/z) л [Л(т)-Л].
(9.71)
Теперь произведем взаимную корреляцию г/ (/) и х (f) [не х' (/)[.
Используя уравнение (9.69), получаем
Фвд - (т) = Ф». (т)+х у' =
=(1 + т)Л [/! +~т (1 +т)=
= (1+-J-) л [Л(т)~h+Ti] = (1 +-Ь) дл (Т) = СЛ(Т). (9.72)
где С — коэффициент пропорциональности, определяемый уравне-
нием (9.61).
Эта процедура позволяет отказаться от поправок благодаря
простому приему взаимной корреляции между выходом при смеще-
нии входного сигнала х* (f) и первоначальным сигналом х (Z). В боль-
шинстве ядерных систем входной сигнал должен быть смещен (на-
пример, нейтронный источник не может быть отрицательным). Кроме
того, для взаимной корреляции обычно применяется первоначальный
псевдослучайный двоичный сигнал х (/) генератора псевдослучайных
шумов.
Влияние конечности ширины полосы псевдослучайного входного
сигнала. В общем случае коррекция спада в области высоких частот
входного сигнала проводится с помощью расчета частотной харак-
теристики, эквивалентной измеренной функции взаимной корреля-
ции, коррекция частотной характеристики на спад входного спектра
и последующего определения истинной импульсной переходной
функции из откорректированной частотной характеристики. Дру-
гой метод оценки влияния конечности ширины полосы входной
переменной на импульсную переходную функцию был разработан
Камминсом [21]. Разлагая характеристики системы в бесконечный
267
ряд и обрывая его после двух членов, он показал, что погрешность
в импульсной переходной функции равна
д (9-73)
6А(т) = у/1'(0), (т = 0).
Расчеты Балкомба [22] для систем с сосредоточенными парамет-
рами показали, что максимальная погрешность имеет место в на-
чале координат. Следовательно, уравнение (9.73) для т = 0 пригод-
но для определения погрешности импульсной переходной функции,
если обеспечено хорошее представление производных. К сожале-
нию, такого представления обычно не бывает и приходится исполь-
зовать итерационный метод, например, описанный Камминсом [21].
Влияние входных и выходных характеристик датчиков на изме-
рения взаимной корреляции- Если вход или выход системы датчи-
ков имеет полосу пропускания, которая значительно превышает
полосу пропускания системы, исследуемой методом взаимной кор-
реляции, они не оказывают на измерения какого-либо заметного
влияния. Однако системы датчиков обычно состоят из относительно
инерционных механических или пневматических компонент. В таком
случае системы датчиков можно считать состоящими из отдельных
систем, соединенных последовательно с исследуемой системой. Для
этого, конечно, необходимо, чтобы импульсная характеристика
или передаточная функция датчиков была известна илн могла быть
измерена.
В случае использования двоичного сигнала с основным времен-
ным интервалом А желательно, чтобы время изменения переменной
от одного уровня до другого было меньше, чем А/10. В работе [21]
показано, что если принять, что это время составляет 3 постоянных
времени (произвольно определенной как время, за которое пере-
менная достигает около 68% своего стационарного значения), по-
грешность в амплитуде передаточной функции составляет менее
1%, а погрешность в фазовом угле равна примерно 6 град при пере-
ходном времени менее А/10.
Авторы работы [231 подробно исследовали погрешности входа
датчика в экспериментах с двоичной взаимной корреляцией. Они
пришли jc заключению, что, когда переход от одного уровня к дру-
гому полностью завершается внутри интервала А и переходы явля-
ются обратимыми (т. е. переход от состояния 4-1 в состояние—1
происходит таким же образом, как от состояния —1 в состояние
4-1), основной эффект запаздывания перехода состоит в умень-
шении ширины полосы входного сигнала.
Годфри [24] сравнил погрешности, связанные с экспоненциаль-
ным переходным процессом н равномерно ускоренным переходным
процессом между двумя уровнями, и "обнаружил, что погрешность
обратимого экспоненциального переходного процесса значительно
268
меньше. Для систем первого порядка с аД<0,1 погрешность в им-
пульсной переходной функции составляет менее 2,5%, если посто-
янная времени переходного процесса равна Д/5 и менее 0,16% при
постоянной времени Д/50. В одном эксперименте Годфри [25] обна-
ружил, что хотя время перехода сигнала от уровня к уровню было
значительно больше основного интервала Д, тем не менее была по-
лучена достаточная точность измерения взаимной корреляционной
функции.
§ 9.9. Использование псевдослучайных
троичных переменных
для исследования нелинейных систем
Псевдослучайная переменная, имеющая три уровня (—1, 0,+1),
была получена в работах [26, 27] в качестве входного сигнала
системы взаимной корреляции для измерения ядер нелинейной
системы. Винер [28] показал, что выходной сигнал широкого класса
нелинейных систем может быть представлен в виде бесконечной
суммы ортогональных неоднородных функционалов случайного вход-
ного сигнала и что ядра этих функционалов характеризуют нели-
нейную систему таким же образом, как импульсные характеристики
описывают линейную систему. Для уменьшения времени, требуемо-
го для проведения взаимной корреляции Винера для нелинейных
систем, были разработаны троичные переменные. Такие переменные
удобны также при определении характеристик линейных систем при
наличии нелинейностей.
Гифтопулос и Хупер [26, 27] описали процедуру построения
троичной переменной следующим образом:
1. В любой момент времени сигнал может принимать только
одно из трех возможных (нормализованных) значений: +1,0 нлн —1.
2. Сигнал является прерывным и может изменять значение
только через постоянные временные интервалы Д.
3. Сигнал является периодическим с периодом
Р = ХД, (9.74)
где
Z = 1. (9.75)
4. Z-й бит Ct переменной генерируется согласно линейной ре-
курсивной формуле
Ct = «г- + а2 С^2 + ...+арС^ (9.76)
где правая часть уравнения (9.76) определяется суммированием
по модулю 3, так что Ci удовлетворяет правилу 1. Коэффициенты
а* являются целыми числами, выбранными из трех значений: +1,
0, —1 или, что то же самое, +2, +1,0. Некоторые наборы-коэффи-
циентов а1г аа, ..., ар, которые дают последовательности длины Z,
приведены в табл. 9.8. Типичная троичная периодическая перемен-
269
ная для р = 3, Z — 26, ar = 1, а2 = а3 = 2 показана на рис. 9.22,
и ее автокорреляционная функция представлена на рис. 9.23.
Таблица 9.8
Некоторые типичные рекурсивные коэффициенты [27] для
троичных последовательностей длиной Зр—1
р N С1 а» fls °4 ав «П а?
3 3 4 4 5 5 6 6 7 7 8 8 26 26 80 80 242 242 728 728 2186 2186 6560 6560 I 1 2 1 0 2 1 1 2 . 2 2 0 2 0 1 0 2 0 1 0 1 1 I 0 2 2 1 0 1 2 1 1 1 1 2 1 1 1 1 2 0 0 1 2 1 0 2 2 1 0 1 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1
Основное требование при генерации троичных сигналов состоит
в том, чтобы корреляционная функция за конечный временной ин-
тервал и до некоторого порядка k примерно равнялась корреляци-
онной функции гауссова белого шума. Корреляционная функция
А-го порядка периодической переменной с периодом Р есть перио-
дическая функция с тем же периодом, определяемая соотношением
J х (t)х х {t + di- (9-77)
270
Для троичной периодической переменной корреляционная функ-
ция первого порядка в интервале 0 <2 А <2 Р/2 примерно равна
соответствующей корреляционной функции гауссова белого шума
[2]. Корреляционные функции четных порядков, как и для гауссова
белого шума, равны 0 [2]. Корреляционная функция третьего по-
рядка для A* =jb А2 Ф А3 равна нулю всюду, кроме относительно не-
большого числа «аномальных» областей [26], и имеет максимальное
значение прн Ai = Ав — А3 = 0. Поскольку троичная периодическая
переменная имеет корреляционные функции первого, второго
и третьего порядков, которые примерно совпадают с соответству-
ющими функциями для белого шума, онн применимы для измерения
ядер нелинейных систем, которые могут быть охарактеризованы
только первыми тремя функционалами Винера. Следовательно, эта
переменная применима для измерения ядер ht (А) и Л2 (А^, А2) нели-
нейных систем, описываемых вход-выходным соотношением Воль-
терры:
t
У (/) = hx (х) х (/—
п
—$ рг2 (X,, М х (t—XJ X (t—Х2) dX, dK,
о о
(9.78)
где х (?) — входной и у (7) — выходной сигналы.
271
На рис. 9.24 показана нелинейная система, в которой произво-
дится взаимная корреляция. Лишь одна задержка позволяет оценить
линейное ядро h (А) почти так же, как и двоичная переменная;
троичная переменная, однако, позволяет минимизировать нелиней-
Рнс. 9.24. Система взаимной корреляции, использующая в каче-
стве входного сигнала псевдослучайную троичную пе-
ременную [27]
ные эффекты. Использование обеих задержек позволяет оценить
нелинейное ядро h (Aj, А2). В работе [26] рассмотрены ограничения
метода н приведены несколько примеров, иллюстрирующих метод.
СПИСОК ЛИТЕРАТУРЫ
1. Stern Т. Е. Reactor Impulse Response Using Random Source Excitation
and Cross Correlation. — In: Noise Analysis in Nuclear Systems. Gaines-
ville, Fla., Uhrig R. E. (Coordinator); AEC Symposium Series, June 1964,
N 4 (TID-7679), p. 203—218.
2. Golomb S. W., Baum er t L. D., Easterling M. F., Stiffler J. J., Viberbi A. J.
Digital Communications. Prentice-Hall Book Company, Englewood Cliffs,
N. Y., 1964.
3. Balcomb J. D., Demuth H. D., Gyftopoulos E. P. A Cross-Correlation Met-
hod for Measuring the Impulse Response of Reactor Systems.—«Nucl.
Sci. Engng», 1962, v. 12, N 2, p. 218.
4. Stern T. E-, Blaquiere A., Valat J. Reactivity Measurement Using Pseudo —
Random Source Excitation. — «Reactor Sci. Technol.», 1962, v. 16, p. 499.
5. Uhrig R. E. The Impulse Response of an Exponential Assembly. — Expo-
nentianal and Critical Experiments. Symposium Proceedings, Amster--
dam, 1963, v.3, p. 205; International Atomic Energy Agency, Vienna, 1964
(STI/PUB/79).
6. Uhrig R. E. Techniques Closely Related to Pulsed Neutron Research. — In:
Pulsed Neutron Research, Symposium Proceedings, Karlsruhe, 1965, v. 2,
p. 657; International Atomic Energy Agency, Vienna, 1965 (STI/PUB/104).
7. Kerlin T. W. The Pseudo — Random Binary Signal for Frequency Respon-
se Testing. — USA EC Report ORNL—TM-1662. Oak Ridge National
Laboratory, September 1966.
8. The Digital Logic Handbook. Digital Equipment Corp., 1968.
9. Golomb S. W. Sequences with Random Properties. — Report for Contract
N 639489, Glenn L. Martin Company, June 1965.
272
10. Birdsall T. G., Ristenbatt M. P. Introduction to Linear Shift Register Gene-
rated Sequences. — Technical Report N 90, University of Michigan Re-
search Institute, October 1968-
11. Roe G. M. Pseudo-Random Sequences for the Determination of System
Response Characteristics: Sampled Data Systems. — Report 63-RL-3341E,
General Electric Research Laboratory, June 1963.
12. Hampton R. L. T. A Hybrid Analog-Digital Pseudo-Random Noise Gene-
rator. —• «Simulation», 1965, v. 4, N 3, p. 179.
13. Cooper G. Purdue University, personal communication, 1963.
• 14. Jensen J. R. «Notes on Measurement of Dynamic Characteristics of Linear
System», Part III, Servoteknisk forskningslaboratorium, Dan marks,
Tekniske Hojskole, Copenhagen, Denmark, 1959.
15. Fishman J. Pseudo-Random Reactivity Perturbation Experiments with the
HBWR Second Fuel Charge. — Norwegian Report HPR-50, Halden Boi-
ling Water Reactor, Halden, Norway, 1964.
16. Godfrey K. R. Dynamic Analysis of Data from a Zero-Power Nuclear Reac-
tor. — National Physical Laboratory, British Report Auto—TM (67), p. 6,
December 1967.
17. Howe R. University of Michigan, personal communication, 1965.
18. Meyer P., Garelis E. Use of a Pseudorandom Source Input in the Measure-
ment of Impulse-Response Functions. — In: Neutron Noise, Waves and
Pulse Propagation- Gainesville, Fla., Uhrig R. E. (Coordinator); AEC
Symposium Series, 1966, N 9 (CONF-660206), p. 333—342.
19. Garelis E. Consideration of Finite Correlation Times in Pseudo-Random
Impulse Response Methods. «Trans. Amer. Nucl. Soc.», 1965, v- 8,
N 2, p. 435.
20. Nara M., Suda N. Some Investigations into the Application of Pseudo-
Random Binary Signals to Reactor Dynamics Measurements. — In:
Neutron Noise, Waves and Pulse Propagation. Gainesville, Fla.,
Uhrig R. E. (Coordinator); AEC Symposium Series, 1966, N 9
(CCNF-660206), p. 247—270.
21. Cummins J. D. A Note on Errors and Signal to Noise Ratio of Binary
Cross-Correlation Measurements of System Impulse Response. — British
Report AEEW-R-329, February 1964.
22. Balconib J. D. A Cross-Correlation Method for Measuring the Impulse
Response of Reactor Systems. — Ph. D. Thesis, Massachusetts Institute
of Technology, June 1961.
23. Godfrey K. R-, Murgatroyd W. Input-Transducer Errors in Binary
Cross-Correlation Experiments.—«Proc. IEEE», 1965, v. 112, N 3,
p. 575—583.
24. Godfrey K- R- Input-Transducer Errors in Binary Cross-Correlation
Experiments — 2.—«Proc. IEEE», 1966, v. 113, N I, p. 185—189.
25. Godfrey K. R. Input—Transducer Errors in Binary • Cross-Correlation
Experiments — 3.—«Proc. IEEE», 1966, v. 113, N 6, p. 1095—1102.
26. Gyftopoulos E. P-, Hooper R. J. .Signals for Transfer-Function Measu-
rements in Nonlinear Systems. — In: Noise Analysis in Nuclear Systems.
Gainesville, Fla., Uhrig R. E. (Coordinator); AEC Symposium Series».
June 1964, N 4 (TID-7679), p. 335—345.
27. Hooper R. J., Gyftopoulos E. P. On the Measurement of Characteristic
Kernels of a Class of Nonlinear Systems. — In: Neutron Noise, Waves
and Pulse Propagation. Gainesville, Fla., Uhrig R. E. (Coordinator);
AEC Symposium Series, May 1967, N 9 (CONF-660206), p. 343—356.
28. Wiener N. Nonlinear Problems in Random Theory. —Technology Press —
Wiley, 1958. (См. Винер H. Нелинейные задачи в теории случайных
процессов. Пер. с англ. М., Изд-во иностр, лит., 1961).
273
ГЛАВА 10,
ОБРАБОТКА
ДАННЫХ
НА ЦИФРОВЫХ
МАШИНАХ
§ 10.1. Введение
Основной целью перевода экспериментальных данных в цифро-
вую форму является приведение их к виду, удобному для обработки
на цифровых вычислительных машинах или в других специализиро-
ванных цифровых системах обработки данных. Данные из системы,
Первая запись серии испытании Вторая запись серии испытаний
Рис. 10.1. Формат магнитной ленты.
состоящей из многоканального модулятора и цифрового преобра-
зователя, могут непосредственно вводиться в цифровую вычисли-
тельную машину или записываться на магнитную ленту в цифровом
виде, а затем спустя некоторое время воспроизводиться в вычисли-
тельной машине или системе обработки данных. При непосредст-
венном вводе данных в вычислительную машину на машине имеют-
ся входные шины, через которые данные могут передаваться либо
поразрядно от цифрового преобразователя нли по одной или не-
274
сколько выборок одновременно из промежуточного буфера. Фор-
мирование и обработка данных обычно управляются программой
вычислительной машины.
Для цифровых данных, записанных на ленту, обработка оказы-
вается более громоздкой. Большинство цифровых ленточных записы-
вающих устройств используют либо семь, либо девять дорожек,
образуя 7- или 8-разрядный символ, один из разрядов которого
обычно предназначен для записи четности, обеспечивающей точную
запись данных. Поскольку представление данных 6 или 8 разряда-
ми обычно неточно, для каждой величины должны быть отведены
два или три символа. Практически все цифровые вычислительные
машины имеют стандартные форматы ленты, которая применяется
в этих случаях. На рис. 10.1 показан формат ИБМ, предназначен-
ный для 12-разрядного информационного слова (II разрядов и 1 раз-
ряд знака), записываемого на ленту с семью дорожками.
§ 10.2. Исключение регулярной составляющей
Обычно распределение вероятности амплитуд случайной шумо-
вой переменной имеет нормальную, или гауссову, плотность вероят-
ности. Кроме того, обычно предполагается, что случайная перемен-
ная является стационарной и эргодической. При этом подразуме-
вают, что ее статистические свойства не изменяются во времени
и любые две выборки записи, взятые с одной непрерывной записи
функции, должны быть статистически эквивалентны. Эргодичность
означает, что несколько выборок, на которые можно разбить одну
непрерывную запись функции, должны быть статистически экви-,
валентны полной записи функции. При наличии стационарности
и эргодичности средние свойства любого участка всей записи экви-
валентны и не изменяются во времени. Это позволяет использовать
величины средние по времени, а не средние по одной или нескольким
выборкам.
Многие статистические свойства случайных переменных, с кото-
рыми сталкиваются при исследовании переходных .процессов, из-
меняются со временем и не являются ни стационарными, ни эрго-
дическими. Однако такие временные записи иногда удается разде-
лить на несколько более коротких выборок временной записи,
в которых функция практически стационарна. Когда длина более'
короткой выборки записи не очень.велика по сравнению с времен’
ным периодом самой низкой имеющейся частоты, можно ожидать
большие расхождения между результатами экспериментальных
серий при разных временах, поскольку длина выборки недо-
статочно велика, чтобы дать правильную оценку статистических,
свойств.
Стационарность случайных процессов предполагает, по опреде-
лению, что всеми начальными переходными эффектами можно пре-
небречь и чисто статистические свойства процессов не изменяются,
т. е. считается, что они начались при t — — со. Точные статисти-
275
ческме свойства случайных процессов имеют место, только если
размер выборки записи бесконечен. Практически это невыполнимо,
и достаточно точные результаты получают из конечных, но боль-
ших выборок записи.
В большинстве случайных процессов, которые имеют физическую
природу, существует некоторая степень нестационарности, поэто-
му свойства многих выборок часто используются для определения
их статистических свойств. Однако такой подход имеет ряд недо-
статков: ввиду трудностей, которые возникают при воспроизводстве
любого данного случайного процесса, количество данных, доступ-
ных для статистического анализа, часто оказывается недостаточ-
ным и имеет ограниченную точность. Даже если записи многочис-
ленны ц (или) длительны, они могут содержать ложную информа-
цию, вызванную влиянием посторонних случайных или неслучай-
ных физических процессов. Наконец, при наличии достаточного
числа точных выборок записи обработка данных — очень обремени-
тельная и трудоемкая задача. Следовательно, для выполнения хо-
рошего статистического анализа необходимы быстродействующие
цифровые вычислительные машины.
Желательно использовать простые статистические соотноше-
ния, справедливые для стационарных и эргодических процессов.
Данные, которые в основном нестационарны, можно сделать ста-
ционарными, исключив регулярную составляющую, которая может
либо являться линейной функцией, либо состоять нз одной или
нескольких очень низких частот. Обычно применяемая процедура
для исключения регулярной составляющей заключается в подгонке
экспериментальных данных к полиномиальной функции
у (/) = а0 + aj + a2tz + a3t* + af + ... (10.1)
методом наименьших квадратов и последующим вычитанием зна-
чений, полученных по подогнанной полиномиальной кривой, из
отдельных экспериментальных значений. Как правило, выделения
полиномов третьего н четвертого порядков достаточно, чтобы данные
стали стационарными. Очевидно, что член ай представляет стацио-
нарное, или среднее, значение, а коэффициент сц — наклон прямой
линии, проведенной через данные. Если для обработки экспери-
ментальных данных использовать полином второго порядка
у (/) = а0 + att + fls/2, (10.2)
который представляет собой параболу, то при хорошей аппроксима-
ции это эквивалентно подгонке данных к половине синусоидальной
волны и, следовательно, исключению частотных компонент, длина
волны которых вдвое- превышает длину записи. Например, выделе-
ние параболы из 10-секундной записи почти равноценно исключению
частотной компоненты 0,05 гц. Случайная переменная с регулярной
составляющей, соответствующей кривой второго порядка, показа-
на на рис. 10.2. Подобным образом выделение кубического уравне-
ния из данных почти эквивалентно исключению компонент, дли-
276
на волны которых равна длине записи (т. е. в указанном примере
это эквивалентно исключению частотной компоненты 0,1 гц).
Другой достаточно часто применяемый метод исключения
регулярной составляющей состоит в обработке данных фильтром
высокой частоты. Это может быть сделано аналоговой фильтрацией
при получении данных в аналоговой форме. (Простейший пример —
использование емкостной связи для исключения постоянной илн
Рис. 10.2. Наличие сильной регулярной составляющей второго
порядка в сигнале у (/).
стационарной составляющей.) Однако большинство аналоговых
фильтров не пригодны для фильтрации высоких частот из-за низ-
кой частоты среза, поэтому чаще используется цифровая фильтра-
ция, описанная ниже.
§ 10.3. Цифровая обработка периодических данных
Существуют две общие категории переменных, с которыми обыч-
но имеют дело, — случайные и детерминированные. Однако для
обработки данных более удобно разделить переменные на периоди-
ческие и непериодические, при этом случайные переменные входят
как подкласс в непериодические переменные. Для периодических
переменных можно накапливать данные по многим циклам и затем
обрабатывать их так, как если бы это были данные по одному циклу.
Преимущество этого метода — уменьшение количества обрабатьь
ваемых данных и в то же время достижение точности, соответст-
вующей большим периодам. Этот метод обычно применяется в тех
случаях, когда для сбора данных используются многоканальные
временные анализаторы, либо при проведении периодических экспе-
риментов (например, исследовании нейтронных волн), либо в пере-
ходных экспериментах (например, экспериментах с повторяющи-
мися нейтронными импульсами). В качестве примера, который
в дальнейшем будет рассмотрен подробно, можно привести псевдо-
случайный импульс, у которого входной псевдослучайный сигнал
по своей, природе действительно периодический и, следовательно,
реакция любой системы, возмущенной этим входным сигналом,
является периодической.
277
Метод применим, если данные, полученные из периодических
сигналов и записанные на магнитную ленту, должны быть подверг-
нуты заданному числу выборок в каждом цикле и затем усреднены
по всем циклам для каждой точки. Это значит, что выборки должны
быть сделаны в одинаковые относительные временные моменты
каждого цикла. Суть проблемы синхронизации можно проиллюст-
Рис. 10.3 Цифровое накопление периодических данных.
рировать следующим примером. Рассмотрим систему с линейным
запаздыванием, которая возмущена смещенным псевдослучайным
сигналом, показанным на рис. 10.3, а. Для простоты рассмотрим
трехразрядную последовательность, имеющую только 7 сдвигов
в периоде; скорость выборки равна одной выборке на сдвиг. Выход-
ной сигнал трехразрядного регистра сдвига, который смещен та-
ким образом, чтобы давать нулевое значение для одного из двух
278
уровней, показан на рис. 10.3, а (это может быть выход нейтронного
генератора, который запускается и выключается псевдослучайным
сигналом). Идеализированный выходной сигнал системы с линейным
запаздыванием, например, подкритической ядерной системы, в ко-
торой запаздывающими нейтронами можно пренебречь, возмущен-
ный псевдослучайной переменной, показан на рис. 10.3, б.
Если выходная переменная подвергается выборке через равно-
мерные временные интервалы (показано точками), результатом
является дискретная перемен-
ная, представленная на рис.
10.3, е, где предполагается, что
выборочное значение постоянно
в течение всего интервала. По-
скольку истинные выходные
экспериментальные данные не-
сомненно будут содержать ста-
тистические флуктуации, более
реалистично непрерывный вы-
ходной сигнал ядерной системы
может быть представлен рис.
10.3, г, а соответствующие дис-
кретные значения переменной
показаны на рис. 10.3, д. Оче-
видно, что дискретные данные,
номер отсчета
Рис. 10.4. Суммарная амплитуда
для пяти циклов.
полученные в каждом из пяти
циклов (см. рис. 10.3, д'), суще-
ственно различны, в то время
как дискретная переменная (см.
рис. 10.3, в), полученная без шу-
мового фона, имеет строго одну
и ту же форму в каждом цикле.
На рис. 10.4 показаны суммарная амплитуда и среднее значение,
полученные суммированием дискретных значений, определенных
в соответствующие временные интервалы в каждом нз пяти циклов
рис. 10.3, г. Если число циклов, использованных для осреднения,
достаточно велико, средняя амплитуда для шумовой переменной
почти совпадает с величиной в отсутствие шума, показанной на
рис. 10.3, в. Кроме того, средняя амплитуда сигнала может обраба-
тываться как циклическая величина с применением только того ко-
личества точек, которое содержится в одном цикле, но прн этом
точность будет соответствовать данным, полученным по пяти
циклам.
Для правильной обработки данных необходимо иметь какие-
либо указания, когда заканчивается один цикл н начинается сле-
дующий. Можно просто иметь машинный счетчик числа выборок
и начинать новое накопление данных после получения соответст-
вующего количества выборок. Недостаток метода в том, что един-
ственная ошибка счетчика может привести к ошибочности всех
оставшихся данных. Более удачным способом было бы введение
279
сигнала, например такого, как показано на рнс. 10.3, е, в допол-
нительный информационный канал и использование изменения
знака этой переменной как признака начала нового цикла.
§ 10.4. Цифровая фильтрация
Общие соображения. Цифровая фильтрация применяется для
подавления определенных частот в информации, которая выражена
в цифровой форме. Ее преимущество перед чаще используемой ана-
логовой'фильтрацией в том, что вырезаемая частота может быть
сделана как угодно узкой простым выбором соответствующего ме-
тода счета. Раньше принципиальным недостатком метода было не-
обходимое большее счетное время. Во многих случаях был неболь-
шой выбор данных, уже записанных в цифровой форме и содержа-
щих частотные составляющие, которые должны быть подавлены,
чтобы избежать наложения частот. Однако разработанные недавно
рекурсивные методы, включающие обратную связь, значительно
сократили потребление машинного времени.
Процесс фильтрации, или сглаживания, основан на предполо-
жении, что требуемая информация может быть отделена от нежела-
тельных шумов на основе частотной днекрнмннацин. Поскольку
предполагается, что информация состоит в основном из низкочастот-
ных компонент записанного сигнала, а шум, напротив, состав-
ляет высокочастотные компоненты сигнала, сглаживание тре-
бует разработки соответствующих фильтров низкой частоты. Не-
достаточно, чтобы временная зависимость выходных последова-
тельностей сглаживающего фильтра выглядела гладкой. Например,
выходные временные последовательности, представляющие нейт-
ронный поток в ядерном реакторе, нужно дифференцировать, чтобы
получить реактивность реактора. В процессе дифференцирования
усиливаются высокочастотные шумы. Таким образом, реактивность,
полученная расчетом, использующим дифференцирование кажу-
щихся гладкими временных выходных последовательностей, пред-
ставляющих нейтронный поток, может содержать большое коли-
чество шумов. Поэтому, если результирующие измерения должны
быть плавными, фильтр’, который сглаживает данные, соответст-
вующие нейтронному потоку, должен сильно ослаблять высоко-
частотный шум, не искажая низкочастотную информацию.
Цифровая фильтрация временных последовательностей. Для
лучшего понимания фундаментальных процессов, составляющих
цифровую фильтрацию, рассмотрим фильтр, структурная схема
которого показана на рис. 10.5, где х (Z) — нефильтрованный
входной сигнал, у (Z) — фильтрованный выходной сигнал, h (/) —
импульсная переходная функция фильтра. Фильтрованный вы-
ходной сигнал может быть получен с помощью интеграла свертки:
y(i)^ J h{t}x{t~l)dk (10.3)
280
Для простоты обсуждения иа рис, 10.6 представлена характе-
ристика идеального фильтра (усиление равно I в интервале частот
от —<о0 до +<оо и 0 при | со | > ш0). Рассмотрение отрицательных
частот удобно математически, хотя они ие имеют физического
смысла в любой реальной системе. Соответствующая импульсная
переходная функция (возможно, в данном случае более удачным
Рис. 10.5. Структурная схема филь- Рис. 10.6. Частотная характе-
рна, ристина идеального
фильтра.
термином является весовая функция) h.(t) определяется интегра-
лом Фурье функции, показанной на рис. 10.6, т. е.
Л(;) = -Г ? H(m)exp(jm/)do). (10.4)
2jl ~'оо
Поскольку Н (и) равна 0 всюду, кроме интервала от —соо до +ш0,
где функция равна 1, уравнение (10,4) можно записать в следу-
ющем виде:
/г(;)=— [ (l)exp(jmZ)do). (10.5)
2л J
Используя равенство Эйлера
exp (jtitf) = cos со/ + j sin at (Ю.б)
и учитывая, что Н (со) симметрична (поэтому исключено влияние
члена j sin и/), можно преобразовать уравнение (10.5) к виду:
h (t) = — f 2 cos a>t da = — sin a>t I = —. sin<a" , (Ю.7)
2л .1 nt I al Cl>0 t
0 °
представленному на рис. 10.7. Весовая функция определена от —оо
до оо во временной области, поэтому нужно обрезать ряд иа
конечном времени.
Для цифровой фильтрации необходимо свернуть импульсную
переходную функцию, определяемую уравнением (10.7) с входными
данными, согласно теореме, выраженной уравнением (10.3). По-
скольку весовая функция распространяется от — оо до + оо, дли-
на записи должна быть бесконечной. Однако физически это не имеет
смысла, поэтому идеальный фильтр, показанный на рис. 10.6
281

Рис. 10.7. Переходная характеристика иде-
ального фильтра.
(иногда называемый фильтром типа «товарного вагона»), также
физически нереален.
Цифровая фильтрация осуществляется преобразованием сверт-
ки в уравнении (10.3) в цифровой форме. Если информация состоит
из цифровых выборок, разделенных друг от друга Д секундами,
а весовая функция фильтра из дискретных точек, также отстоящих
иа Д секунд, преобразование свертки может быть выражено урав-
нением
м
y(i&)= 2 h(k&)x[(i—k)&], (10.8)
ft = — м
где М — число точек в положительной или отрицательной полу-
плоскости. Процедура фильтрации иллюстрируется рис. 10.8. На
рис. 10.8, а показаны вы-
борки амплитуд сигнала
<*ерез дискретные интерва-
лы Д секунд, а на рис.
10.8, б — импульсная пе-
реходная функция, выра-
женная уравнением (10.7)
и представленная всего
25 точками (Л4 = 12). Из
графиков видно, что пер-
вой точкой сигнала, кото-
рая может быть отфильтро-
вана, является М + 1-я
точка, при условии, что к результирующим значениям применено
соответствующее взвешивание. Поэтому первые М точек записи ин-
формации обычно отбрасываются. Это относится также и к послед-
ним М точкам. Если первоначальная запись состоит из N точек,
в фильтрованной записи оказывается только N — 2М точек. (На-
пример, если в начальной записи имеется 1000 точек и весовая функ-
ция представлена в каждой полуплоскости 50 точками, то в фильт-
рованной записи будет только 900 точек.) Очевидно, что существует
оптимальное отношение N к М в любой данной ситуации, так как
точность измеренных в опыте параметров непосредственно связана
с длительностью опыта, в то время как качество фильтрации зави-
сит от длины весовой функции.
Резкий обрыв весовой функции при некотором произвольном
максимальном времени /ИД или количестве точек, как показано на
рис. 10.8, б, неблагоприятно отражается на ослаблении некоторых
частотных компонент ниже со0 и ведет к пропусканию некоторых
частотных компонент выше <л0._ Хотя полностью искажения избе-
жать нельзя, его можно уменьшить правильным выбором и ис-
пользованием второй весовой функции й2 (/), как показано на
рис. 10.9. Назначение второй весовой функции — усилить пер-
вую. Эта функция спадает до нуля при некотором максимальном вре-
282
мени tm. Поскольку требования к Л3 (/) почти те же, что и к окнам
запаздывания, применяемым при расчете спектра мощности (т. е.
преобразование Фурье Я3 (со) должно быть очень малым вне за-
-*------------ATZJ
Рис. 10.8. Дискретная переменная и весовая функ-
ция:
а — дискретная переменная хц б — дискрет-
ная весовая функция (/И=>12).
данного интервала частот), Балкомбом Ill было предложено исполь-
зовать окна Хениинга:
•* \ гт /
Л.«) = 0, (|f|>im).
(10.9)
х(ш) x(t) Фильтр 7 Y(co) y(t) Нг(ы),1>гП) Фильтр 2 Z(a>) lit)
Рис. 10.9. Последовательное соединение двух
фильтров.
где tm — произвольный временной предел, выбранный так, чтобы
уменьшить ту часть h2 (/), которая должна быть отброшена. Преоб-
разование Фурье hz (/) дает передаточную функцию второго фильтра:
W /гл\ 4 sin .з .. sintofm »1 р <
И = tm —--------tm © ——-------— , (10.10)
CO/m (t0aZ?n—Л®)
которая эквивалентна уравнению (6.52) и показана на рис. 10.10.
Поскольку две весовые функции hx и h2 умножаются друг на друга
28з
во временной области, две импульсные переходные функции, пред-
ставленные на рис. 10.6 и 10.10, должны быть свернуты, давая функ-
цию частотной характеристики или функцию фильтра, показанную
на рис. 10.11. Из этого рисунка видно, что для частот, меиьших
соо— (л/2/пг), информационный сигнал почти не нарушен, в то
время как для частот, больших + (л/2/пг), частотные составляю-
щие сильно ослаблены. В промежуточной области величина ослаб-
ления зависит от частоты, как показано на рнс. 10.11. Определим
со/, и как
<*L = Ч- (*/2Лп) = 2^Ь (10.11)
II
Ин = и0 + (л/2/т) = 2л/н. (10.12)
Суммируя и вычитая эти уравнения, получаем:
Ц>=(о>1.+к>и)/2;
/о = (Ы“/н)/2,
(10.13)
*т=л/2(<0н—а>д) =
= Wffn-Ц (10.14)
Когда рассмотренная филь-
Рис. 10.10. Частотная характеристика
для сглаживания по Хен-
нингу.
этим все частоты, большие /н, так
иие фильтра почти равно нулю. Ес
скорости выборки, коэффициент
трующая система применяет-
ся для предотвращения на-
ложения частот, /у/ можно
принять равной половине
скорости выборки, исключая
как при этой частоте пропуска-
ли принять fn равной половине
г, рассчитываемый по формуле
r—fdfn
(10.15)
определяет используемую долю теоретической полосы частот. По
мере приближения г к 1, требуемое число точек весовой функции
стремится к бесконечности, так как это означает бесконечно длинную
весовую функцию. Действительное число точек весовой функции
М [предел суммирования в уравнении (10.8)], определенное Бал-
комбом [1], равно
м=— =__________1 ]//"
д 4Д((н-/д) 4Д(1-г)
(10.16)
Однако поскольку принято, что fH равно 1/2Д, уравнение (10.16)
превращается в
1И=1/2(1-г). (10.17)
Нетрудно видеть, что существует оптимальное значение г, так как
машинное время пропорционально Л1, в то время как полученная
284
информация пропорциональна коэффициенту г. Таким образом, ин-
формация, полученная на единицу машинного времени, пропор-
циональна величине г (1 — г), Эта функция имеет максимум при
г — 1/2, т. е.
fL-hi/2. (10.18)
Значения г, использованные для фильтрации, могут изменяться
в большую или меньшую сторону от оптимального значения, рав-
ного 1/2, в зависимости от того, делается ли больший упор на
максимум получаемой информации или на уменьшение требуемого
машинного времени.
В предыдущем обсуждении полагалось, что фильтрованная функ-
ция имеет количество выборок в единицу времени то же, что и исход-
ная функция. Если это не так, расчеты, представленные уравнением
(10.8), выполняются для каждой q-й точки, где q — отношение ин-
тервала выборки фильтрованных данных к интервалу выборки
исходных данных. Следует отметить, однако, что частотное содер-
жание дискретного сигнала не должно превышать половины
от скорости выборки фильтрованного сигнала. Таким образом,
н fa и ft в q раз меньше идентичных скоростей выборки. Однако
весовые функции из-за содержащихся низких частот должны рас-
пространяться на длительный период времени и точки весовой функ-
ции должны быть расположены с интервалом времени ^А.
Расчет цифрового фильтра. Описанный выше метод взвешивания
прост и имеет много применений, но часто оказываются необходи-
мыми очень резкие фильтры или фильтры специальной формы.
Тогда применяются более сложные процедуры. Общий подход,
разработанный Ормсби [2], для расчета цифровых фильтров обоб-
щен здесь для нескольких частных случаев, представляющих
интерес.
Разработка линейных операций с точки зрения дискретной во
времени весовой функции фильтра основана на подгонке соответ-
ствующей функции частотной характеристики фильтра к предпо-
285
лягаемой форме; при этом используется предположение, что спектры
больших и практически длинных желательных и нежелательных
сигналов не перекрываются. Это предположение делает операцию
сглаживания частью классической проблемы создания фильтра,
пропускающего определенную частоту. Для бесконечного вре-
менного предела частотная функция Я (со) н непрерывная нли диск-
ретная весовая функция h (t) образуют пару преобразований Фурье.
Для конечных временных пределов выбирается конечный ряд весов
/гп, частотная функция которого подгоняется методом наименьших
квадратов к предполагаемой частотной функции. При этом полу-
чается система совместных интегральных уравнений, решением
Рнс. 10.12. Спектральная функция для класса ли-
нейных фильтров:
— (угловая) частота среза, равная 2 л f0:
(оду — предельная частота пропускания [SJ.
которой является зависящее от времени обратное преобразование
Фурье предполагаемой частотной функции. Получаемая частотная
функция, связанная с конечным рядом весов, в этом случае имеет
минимальную среднеквадратическую ошибку по отношению к
предполагаемой частотной функции.
Получены различные формулы, описывающие веса, в зависи-
мости от формы спада частотной функции. Общие полиномиальные
формы среза дают весовые функции, обеспечивающие высокую
степень ослабления. Для фильтров, имеющих передаточную функ-
цию Н (со), спектральная или частотная функция с единичным
усилением и нулевым фазовым углом в полосе пропускания пред-
ставляет кривую ослабления р-ге порядка между полосами про-
пускания н подавления и показана на рис. 10.12, где од и co#—
частота среза и предельная частота пропускания соответственно.
Математически это можно выразить следующим образом:
0
1
7?(<о) =
(| <jj| > ан),
(|q|<Ql),
( ——<aL),
(10.19)
(q£.^o<qh).
286
Для частного случая, в котором р == 1, кривые участки рис. 10.12
становятся прямыми линиями, что указывает на линейный спад
амплитуды с частотой. Для этого случая импульсная переходная
функция, или весовая функция фильтра, полученная преобразо-
ванием Фурье уравнения (10.19) при р = 1, равна:
cosoDr t—cos со« i .
Л(0 =--“------<10.20)
Весовая функция может быть легко найдена с помощью равно-
удаленной выборки. Оценка с использованием весов Фурье дает
минимальную среднеквадратнческую ошибку между передаточной
функцией фильтра с конечным числом весов и предполагаемой пере-
даточной функцией в- интервале | со | между 0 и половиной частоты
выборки. Определим нормированную частотную переменную
X = <о/<оя =(10.21)
где <ов — эффективная угловая частота выборки н Д — частота
выборки данных. Затем можно найти X/. и Кн'.
K^d^fdh (10.22)
— = (10.23)
и, кроме того, определить Хд как разницу между Хя и Х£, т. е.
Хд — —fa = (©я —со£)/cos = (fa —(10.24)
Дискретная весовая функция в соответствии с уравнением (10.20)
теперь имеет вид
. , , cos2jtnX) —cos2sv?Xrr
№)=---------— • (|0-25)
где п — 0, ±1, ±2, ...,
Величина Х£, которая определяет крутизну спада (чем меньше
XD, тем круче спад), вместе с числом весов N указывает на резуль-
тирующую точность Н (<о). Точность уменьшается для меньших
значений Х£ и (или) меньших N.
Результаты, полученные Ормсби [21, типичные для эффектив-
ности такого рода фильтров, показаны на рис. 10.13, где XD = 0,02,
TV = 50 и Х£ = 0,10. Прн этом максимальная погрешность пропус-
кания < 0,25% до значения X — 0,081, а максимальная погрепы
иость подавления (по отношению к единице) < 0,25% для X >
> 0,139. Эффективное значение Х£ с учетом этих погрешностей
равно 0,058. При максимальных погрешностях пропускания и по-
давления < 0,5% получим эффективное значение Хд, равное 0,038,
т. -е. полоса пропускания до X = 0,091 и полоса подавления для
X свыше 0,129. График характеристики фильтра этой конструкции
дан на рис. 10.13 сплошной линией.
287
Расчет фильтра с р = 1 предполагает разрывы производной
Н (со) при «£ И со#. Наибольшие погрешности в полосах пропуска-
ния и подавления имеют место около этих точек. Модификация
принятой спектральной функции между со£ и сон для удаления раз-
рывов производной позволяет уменьшить погрешность подгонки
или увеличить крутизну спада при той же погрешности. Это мо-
жет быть сделано путем параболического сглаживания в окрест-
ностях со£ и соя, как показано на рис. 10.14. Параметр k позво-
Рис. 10.13. Частотная характеристика фильтра
с Р= 1 [2].
ляет семейством парабол охватить различные значения интервала
со/у — W£. Входящие в уравнения параметры о, с и е могут быть вы-
ражены через k, чтобы удовлетворить условиям рис. 10.14.
Кривая I:
Я (со) = 1—а (со—(0£)2, (со£^со^со£+/гЛсо). (10.26)
Кривая 2:
Н (со) = ссо -р е, (со£-рЛДю ^со^сон—АДсо). (10.27)
Кривая 3:
Н (со) = £Х(С0—С0/у)2, (<0/у— АДСО (0 ^СО/у),
(10.28)
где
Дсо = СО/у—С0£.
(10.29)
288
Параметры а, с и е равны
й = —1/2£(1—Л)(Дсо)\
с — —1/(1 — k) Дсо,
е = [2со_ь + (2 — k) Дсо]/2 (1 — k) Дю.
(10.30)
(10.31)
(10.32)
Из этих соотношений можно получить выражение для дискретных
весовых функций модифицированных фильтров с р = 1:
h (пД) — {sin 2пп [XL+ (1 —- /г) М 4- sin 2л/г 4- k^D) —
—sin2railfl—sin2nn?iL}/4/e(l—/г)^Ь (л/г)8. (10.33)
Рис. 10.14. Спектральная функция модифицирован-
ного фильтра с р = ! [2].
Эти фильтры являются фазовыми фильтрами низких частот.
Кроме того, существуют квадратурные фильтры (которые произ-
водят постоянный фазовый сдвиг на ±90°), полосовые фильтры
и фильтры высоких частот, удобные во многих применениях.
Простая схема для получения эффекта пропускания высоких частот
состоит в вычитании дискретного выходного сигнала фильтра из
дискретного входного сигнала; полосовой эффект может быть полу-
чен вычитанием выходных сигналов двух фильтров низких частот
с различной полосой среза. На практике используется единствен-
ный фильтр, который имеет весовую функцию вида
h (п&) = hx (nA) — h2 (пД), (10.34)
где hx (nA) и (пД) — веса двух фильтров низких частот, име-
ющих частоты среза соответственно. и Квадра-
турные фильтры могут быть рассчитаны подобным же образом,
только для получения весовой функции из импульсной переходной
функции по уравнению (10.19) используется синусоидальное пре-
образование Фурье.
10 Зак 5 76 289
Фильтр на 1/3 октавы. Фильтр, составленный из двух резони-
рующих систем второго порядка, удаленных друг от друга на
выбранную частоту, образуя полосовой фильтр с шириной полосы
частот на уровне — 3 дб, равной 1/3 октавы, называется фильтром
на 1/3 октавы. Негрон 13] провел спектральный анализ, исполь-
зуя цифровую форму фильтра на 1/3 октавы.
Уравнение фильтра в s-об ласти имеет вид
H(s) = -----------------“1^---------------------, (10.35)
(s’ -I- s -I- co?) (sa -I- 2gcoE s + CO?)
где
<0j = 2sifc(l —Д//2);
co3—2stfc (1 + Д//2);
(10.36)
(10.37)
£— декремент затухания; fc — средняя частота полосы пропуска-
ния; Д/-—ширина полосы пропускания. Значения £ — 0,05 и
и Д/ = 0,170 гц были получены эмпирически для фильтра.на 1/3
октавы. Подставив s — jco, усиление передаточной функция урав-
нения (10.35) можно записать так:
|//(И)1 {1(оЛ-О?)2-|- С,Л+ (2i;cWl}1/2’ (10'38)
Относительный минимум имеет место прн среднегеометрической
частоте:
с» л? Усох (о2, (10.39)
где амплитуда
-------2г---------(10.40)
1 (сос-со-Г-М^со,
Относительные максимумы имеют место при о = <лх н со — <л2>
и в обоих случаях амплитуды равны
17^1)1=1^)^ о f. 2 ”1 „ о 2Н/2- (10.41)
2g [(col—“J) + 4£ col coil1/2
Амплитуда нормируется на 1 делением на среднее геометриче-
ское максимума и минимума, определяемых уравнениями (10.40)
н (10.41), т. е. уравнение (10.38) делится на
л = ]/ I Н (]/Ш1й2) I |Я(ё>оТ =
со.)г+ 4^0!со.] [(col—со?)2 + 4g2 со? со?]112 ’ (10-42)
290
Следовательно, нормированная амплитуда передаточной функции
становится равной
I ГГ / \ 1 I Н (®) I __
| н (со) |w = —- —
_. g [(Ш1— ш2)в + [(<>? — Ш1)а + РЕВ Ш| <»гЛ1 /г 0О 43)
ш? {((с,Л - ш2)2 + №>хС»)2] [(to? - ш2)2 + McWl}1'2
Это выражение было реализовано на цифровой вычислительной ма-
шине Негроном [3], графики усиления фильтра и фазового угла
Рис. 10.15. Амплитуда и фаза фильтра в 1/3 ок-
тавы [3].

приведены на рис. 10.15. Для реализации расчета фильтра был ис-
пользован рекурсивный метод, изложенный в следующем пункте.
Выбор фильтра на 1/3 октавы оказался удобным из-за подобия его
фильтрам аналогового типа. Цифровые фильтры с более плоскими
и более острыми частотными характеристиками могут быть построе-
ны рекурсивными методами.
Рекурсивные фильтры. Рекурсивные фильтры (иногда называе-
мые фильтрами обратной связи, потому что часть выходных данных
подается на вход и усредняется с входными данными) гораздо более
эффективны, чем обычные цифровые фильтры при проведении сгла-
живания или фильтрации данных, так как обычно для достижения
заданной степени фильтрации требуется меньше времени. Типичное
10* 291
выражение для метода цифровой рекурсивной фильтрации имеет
ВИД
р <1
Уь = 2 <\хк_I + s biyk-t, (10.44)
/=0 х = 1
где аг и bi — весовые коэффициенты. Уравнение (10.44) представ-
ляет собой преобразованный вариант обычного выражения цифро-
вой фильтрации:
Й,= 2 Л, (**+< + **-«). (10.45)
1=0
где h-i — дискретные значения конечной импульсной переходной
функции
fc
С Н (со) ехр (jcof)rfco. (10.46)
zjt, J
0
Одним из простейших рекурсивных фильтров является линей-
ный фильтр с одной степенью свободы вида
У г = Xi + ayt-i + %* (10.47)
который легко реализуется на цифровой вычислительной машине.
Может оказаться необходимым экспериментально определить соот-
ветствующие значения коэффициента а, чтобы достичь требуемой
фильтрации.
Еще одним цифровым фильтром, который бывает полезным в оп-
ределенных приложениях, является гамма-фильтр, разработанный
Корнелльской авиационной лабораторией [41. Уравнение фильтра
имеет вид
У1 = (1 ~У) Уг-х + (1 -Т/2) (Xi-x^ (10.48)
где у — характеристическая постоянная фильтра.
Метод рекурсивной фильтрации, использованный Негроном I3J,
применительно к фильтру иа 1/3 октавы описывается уравнением
—ЕУп-1—Руп-г—Gyn-S—Hy„-t, (16.49)
где коэффициенты А—Н являются коэффициентами, выраженными
в величинах Z в /-преобразовании передаточной функции нормиро-
ванного фильтра уравнения (10.43) после того, как оно приведено
к рациональной полиномиальной форме, даваемой выражением
H(Z)=Y(Z)IX(Z) =
= (AZa+BZ-1 + С/-2 + DZ-3)/(Z°+EZ-1+FZ~2+GZ~S+HZ-1).
(10.50)
292
§ 10.5. Статистический анализ
Цифровой статистический анализ временных последователь-
ностей, получающихся ври цифровом преобразовании эксперимен-
тальных данных, является простой процедурой. В библиотеке
программ имеется ряд соответствующих программ общего назначе-
ния для вычислительных машин; еще большее число специальных
программ используется в отдельных установках. Не будем подробно
описывать эти программы, так как они изменяются в зависимости
от специфики программы и установки, а приведем описание мате-
матических соотношений, выраженных в цифровой форме, которые
используются в этих расчетах.
Данные могут быть получены непосредственно из эксперимента
или записаны на магнитную ленту и воспроизведены. Они преобра-
зуются в цифровую форму, как описано в гл. 8, и передаются в циф-
ровую вычислительную машину с помощью перфокарт, магнитных
лент, магнитных барабанов или бумажной ленты илн вводятся через
дистанционный пульт управления. Результаты используются в виде
временных последовательностей, полученных при выборке данных,
производимой, как правило, через постоянные интервалы времени
Д сек. Ниже описаны последующие операции, производимые в ти-
пичных программах статистического анализа, таких, как RAVAN
[5], MAC/RAN [61 или VAC [71. Более обширный обзор дан Бен-
датом и Пирсолом [8].
Статистические моменты. Среднее значение выборки рассчиты-
вается из данных по выражению
*= Ц- 2 Xi, (10.51)
где N — количество выборок данных, at — индекс каждой выборки
(i = 1, 2, .... N), соответствующий временному интервалу выборки.
Среднее значение выборки вычитается из каждого значения выборки
= —х, (10.52)
и среднеквадратическое отклонение S выборки, или второй цен-
тральный момент, получается из выражения
5= у 2 г?/(А1 — 1) или S2= 2г?/(JV-1), (10.53)
где S2 — дисперсия выборки. Показатель асимметрии Св рассчи-
тывается из соотношения
N
С„ = 2 ^JNSs. (10.54)
293
Для нормального распределения показатель асимметрии равен 0.
Эксцесс С к определяется как
Сл= 2 zl/WS4 (10.55)
1 = 1
и для нормального распределения равен 3.
Плотность вероятности и функция распределения. Плотность
вероятности р (х) есть
р (х) = &Р (х)/Дх, (10.56)
где Р (х) —• функция распределения вероятности и Дх — ширина
классифицируемого интервала.
Число наблюдений и количество данных в каждом классифици-
руемом интервале рассчитывается следующим образом:
1. Из наблюдаемой функции / (/) рассчитывается максимальная
амплитуда (/?s) и минимальная амплитуда (/Д).
2. Оценивается К — число классифицируемых интервалов по
выражению
К = In Л7ДД, (10.57)
где 1/Д •— скорость выборки; Д -г- наивысшая частотная составляю-
щая в наблюдаемой функции х (/); 0<Д^Д и fc — частота
Найквиста, равная
Д = 1/2Д. (10.58)
3. Рассчитывается длина классифицируемого интервала С:
C = (RZ — RM, (10.59)
откуда
к
х,= 2 Kj + iC. (10.60)
»= 1
4. Табулируется число наблюдений и количество данных
в каждом классифицируемом интервале Xj. Предполагается, что
функция распределения вероятности равна
Р(х)== p(x)dx. (10.61)
В дискретной форме функция выражается так:
к
Р(х)= 2 фг, (10.62)
i = 1
где — количество наблюдений на классифицируемый интервал.
294
Гауссовы функции вероятности. Гауссова (нормальная) функция
плотности вероятности имеет вид
в«<=^Йехр[-т]- (1063)
Где х. — среднее значение по классифицируемому интервалу;
х— средняя расчетная величина по наблюдаемым популяциям;
S — среднеквадратическое отклонение; i = 1, 2, 3, ... Д.
Гауссова функция распределения вероятности определяется как
G(x)=2g(x), (10.64)
4=1
где g (x)i — количество наблюдений на классифицируемый интер-
вал из уравнения (10.63):
Функции вероятности Рэлея. Функция плотности вероятности
Рэлея представлена выражением:
'•Wi| = ^-exp(-^r). (10.65)
где Xi — среднее значение по каждому классифицируемому интер-
валу и i = 1, 2, 3, ... Д.
Функция распределения вероятности Рэлея имеет вид
Я(х) = 2 r(x)i, (10-66)
/=[
где Д — количество классифицируемых интервалов и г (х), —
функция плотности вероятности Рэлея.
Измерения «хи-квадрат». Измерения «хн-квадрат» (%2) исполь-
зуются для определения «добротности гауссовой кривой». Эта ве-
личина определяется как
х2= 2 (°‘7ег)а ’ (10.67)
где Of — измеренная плотность вероятности; — ожидаемая гаус-
сова плотность каждого классифицируемого интервала; Д — число
классифицируемых интервалов.
Нет никаких оснований считать .аномальным, если х2 меньше
или равно ожидаемому табличному значению %2 в 5% точек. Если
%2 больше ожидаемого табличного значения в 5% точек, распреде-
ление, возможно, ие является нормальным.
Исследование стационарности. Для исследования стационар-
ности рассмотрим запись выборки длиной Т, как показано на-
рис. 10.16, полученную из случайной записи х (?). Запись длиной Т
295
делится на много приращений, обозначенных Д&, где k = 1, 2, 3, ...
Дисперсия оценивается по следующей формуле:
(10.68)
где N — количество выборок данных за временные интервалы Д;
х — величина амплитуды х (/); k — 1, 2, 3, ...» К; К — общее коли-
чество подразделений записи.
Рнс. 10.16. Исследование стационарности.
Затем рассчитывается нормированная дисперсия этих дисперсий
из уравнения
(10.69)
Ожидаемая нормированная дисперсия для чисто случайной и ста-
ционарной переменной равна
S2 = 1/ГДд
(10.70)
где Т — интервал времени и Д/ — общая ширина полосы частот
записи.
296
§ 10.6. Представление в виде рядов Фурье
(классический метод)
Как было указано б § 6.5, периодические переменные могут быть
представлены во временной области рядами Фурье:
xW=-y + -|- 2 (“nCosncOjZ + ^sinncOi/), (10.71)
п= 1
где коэффициенты ап и Ъп определяются как
р
ап= [ х(/)coswntdt, (10.72)
b
p
bn — j x (/) sin G)n tdt. (10.73)
о
Здесь P —• период переменной и <on — n-я гармоника основной
частоты o)lt определяемая как
<ол = п»! — 2зшД = 2stn!P. (10.74)
Если переменная х (t) дискретна и имеет N равноудаленных
на А сек значений, х (0 можно представить последовательностью
точек xf.
Xi^x (г'Д), (t = 1, 2, 3, TV). (10.75)
Это, конечно, справедливо только в том случае, если принятая ско-
рость выборки fs соответствует достаточно высокой частоте среза
Д, чтобы избежать наложения частот, т. е.
Л > 2Д- (10.76)
Предположим, что
Д = 1/Д = 2Д. (10.77)
Поскольку основная частота Д равна
Д = 1/р = 1/ДТД, (10.78)
наивысшая гармоника, которая присутствует в данных при исполь-
зовании N выборок, равна
Следовательно, окончательный вид ряда Фурье по уравнению
(10.71), проходящего через N точек, содержит только N/2 гармоник:
М/2
2 + • -U0.80)
297
где ап и Ьп, определенные по уравнениям (10.72) и (10.73), можно
оценить интегрированием по формуле трапеций. Результат полу-
чается равным
А ( 1 п хч 2ллг .
ап=—Кч+2 2d *ic°s—+**
N— 1 о .
2 2ти
X£S,n —
i-I
(10.81)
(10.82)
Для частных случаев i — 0 и i = N члены, содержащие косинусы,
равны 1, а члены с синусами равны 0. Заметим, что первый член
в уравнения (10.80), с/МД, представляет собой среднее значение
х, которое равно нулю, если нз данных исключена регулярная
составляющая (включая стационарный член). Коэффициенты ап
и Ьп рассчитываются на основе данных по одному периоду и затем
подставляются в уравнение (10.80) для представления в виде ряда
Фурье.
Уравнение (10.80) может быть упрощено до следующего вида:
9
л'('Л) = 7т2 Cn&w",
П=1
(10.83)
(10.84)
где
N
с„ = 2 Х1 .
Эти два уравнения составляют пару преобразования Фурье.
Случайные величины -можно также представить рядами Фурье,
если предположить, что они периодические с периодом, равным
длине записи. Это очень важное предположение, так как бесконечно
длинных записей, требуемых для интегрального представления
Фурье, не существует.
§ 10.7. Функции корреляции
и спектральные плотности
Вычисления в цифровой форме корреляционных функций, и
спектральных плотностей из временных выборок данных просты
и не создают математических проблем. Принципиальным вопросом
является лишь подбор соответствующих значений скорости выбор-
ки, количества задержек, частотного интервала и полосы пропуска-
ния, чтобы получать имеющие смысл и правильные результаты,
которые могут быть полезными при оценке характеристик иссле-
дуемой системы.
298
Автокорреляционные и взаимные корреляционные функции.
Рассмотрим сначала взаимную корреляцию двух переменных (авто-
корреляционная функция которых является частным случаем, когда
переменные одинаковы). В дискретной форме взаимная корреля-
ционная функция имеет вид
фзд (/гЛ) = X х № у № + =
* =1
= (* = 0, 1,2, (10.85)
где k — текущее число задержек; т — максимальное число задер-
жек и (&А) — оценка взаимной корреляционной функции
х (i'A) и у (i А) для смещения &А.
Очень удобны значения корреляционных функций для нулевых
задержек:
'р«ло)=4г 2х2(,’д)=£(л:2’ (10-86)
i= 1
И
'М°)=^Г ^х(1Е)у(1Е)^Е(ху). (10.87)
f= 1
Максимальная задержка mA определяет эквивалентное разре-
шение частотной полосы пропускания для оценок спектральной
плотности в интервале частот 0 f /с, где fc — частота среза.
Предположим, что скорость выборки fs вдвое превышает частоту
среза; т. е.
Л = 2Д, (10.88)
В соответствии с уравнением (6.55) примем, что диапазон частот
от —/с до -h/c разделен на т частотных интервалов, т. е.
A/=2/=c/m = fB/m = l/mA = l/TMaHC. (10.89)
Можно предположить и то, что эквивалентная полоса пропускания
А/ вдвое превышает интервал, полученный делением диапазона час-
тот от 0 до /с на m равных интервалов, т. е. что эквивалентная по-
лоса пропускания вдвое превышает истинную полосу пропускания.
Следовательно, при известном fs можно подобрать А/ выбором т.
Ниже это обсуждается подробнее.
Спектральная плотность мощности. Автокорреляционная функ-
ция симметрична н поэтому преобразование Фурье, дающее спект-
ральную плотность мощности, представляет собой функцию с дей-
ствительными значениями. Этот случай гораздо проще, чем несим--
метричная функция взаимной корреляции, поэтому рассмотрим его
отдельно. Симметрия позволяет использовать разложение по коси-
299
нусам по уравнению (10.81), так как члены с синусами равны нулю.
Б результате получаем:
Используя соотношения, приведенные в гл. 4, из уравнения (10.90)
можно получить одностороннюю спектральную плотность мощности
(мА/).
Значения Фх.а. (мА/) и Gxx (нА/) должны быть рассчитаны только
для т 1 отдельных дискретных частот, равных
/ = лД/m (п = 0, 1, 2, т). (10.91)
При этом получим т/2 независимых спектральных оценок, так как
значения, отстоящие иа 2fjm друг от друга, будут коррелирова-
ны. Для этих частот спектральная плотность мощности равна
ф.гх(«/с/т) =-Н<й> + 2 У <р,со8 — +(—1)пФт1. (10.92)
2 I tn
где индекс п — номер гармоники.
Предварительную оценку можно сгладить разного рода фильт-
рацией. Удобно использовать для сглаживания автокорреляцион-
ной функции метод Хеннинга. Для этого окна Хеннинга
D(i&) = — (1 + cos—Y (/=0,1,2,...,™); (10.93)
2 \ m )
умножаются на автокорреляционную функцию.
Поскольку D (0) = 1 н D (/мА) = 0, комбинация уравнений
(10.93) и (10.92) дает
ф.та„ = ф(«/с/т) =
[т—' . . 1
Ч>«. + У 0 + cos—) q> cos — . (10.94)
• _! \ т } 1 tn I
В других случаях сглаживание может быть произведено в час-
тотной области, где соответствующие соотношения имеют вид:
Фо = 0,50 Фо + 0,50 Фх; (10.95)
Ф„ = 0,25 Фп_,+0,50 Ф„ + 0,25 Ф„+1; (10.96)
Фт = 0,50Фт_г+0,50Фт. (10,97)
300
Из соотношений между односторонней и двусторонней спектраль-
ными плотностями очевидно,что аналогичные соотношения для оце-
нок односторонней спектральной плотности мощности будут иметь
вид:
Go = 0,50 Go+0,50 Gb
(10.98)
Gn = 0,25 6„_! + 0,50 Gn+ 0,25 Gn+1; (10.99)
Gm = 0,50 Gm_x + 0,50Gm. [(10.100)
Сглаживание предварительных оценок необходимо, так как пе-
риодограмма, определяемая уравнением (10.94), основана на диск-
ретной автокорреляционной функции, являющейся частным слу-
чаем уравнения (10.85), в котором обе переменные одинаковы.
Хотя оценка отдельного значения (цД) достаточно точна,
оценка всех точек автокорреляционной функции одновременно
не является хорошей.
Если предварительные значения спектральной плотности изме-
рены прямыми полосовыми методами, то сглаживание Хеннинга
по уравнениям (10.95)—(10.100) может оказаться излишним. В этих
случаях необходимость сглаживания зависит непосредственно
от используемого метода.
Взаимная спектральная плотность. Ввиду отсутствия симметрии
у взаимной корреляционной функции анализ взаимной спектральной
плотности более сложен. Как и в гл. 4, рассмотрим вещественную
CxlJ (f) и мнимую Qx!I (f) составляющие взаимной спектраль-
ной плотности, описываемые уравнениями (4.118) и (4.119):
J^W + ^jTjlcosZnfTd-c, (10.101)
О
Q„, (/) = 2 J 1'1’зд (г) — ч>вх (г)] sin 2 л/т dr, (10.102)
О
где (рлу (?) и .<рИх (г) — взаимные корреляционные ’функции для
х 0. и
6,„ (/) = сад (/) - (/) = 2Фта (/) =
= | G„, (/) | ехр [j евд (/)], (/ > 0); (10.103)
I (f) I =[«,(/) + (&, (/)I'L2; (Ю.-104)
ex„ (/) = arctg (-Q^ (/)). (Ю.105)
301
Используя правило трапеций для интегрирования (10.101) и (10.102)
(если ч>кУ (т) и фйгс (т) представлены конечным числом N дискретных
равноудаленных значений), получаем:
(пД/) = А (0) +2 £ (<‘Д)cos +
+ Фгса (Л1Д) COS T +
+ 2 2' Ч>,Л<Д)сов(^) + ф„а;(тД)со8 (=^)] =
" ~ +(0) + (0) + cos ()[ч>™(тЛ)+(тЛ)1 +
+ 2cos ) I ,2 [Ч>ад(ВД+ q>„,(<Д)]|). (10.106)
Аналогично
<2IS,(nAf) = Afsin [ф^ДтД)—ф^тД)]-!-
L 'с
+ 2sin2^-("е РМ/Д)-ф„я(гД)]|]. (10.107)
Эти величины нужно оценить только для гармонических частот
уравнения (10.91):
Cn = Cxs (nfjm) = А С <р{р (0) + (0) + (— 1)" [фад (тД) +
+ ф,,(тЛ)] + 2со8?А |“е [(М/й)+ Ч>„Л«Л)]^, (10.108)
<2„ = Qx,,W./m)= А^1п^.|т2 (10.109)
Как и для спектральной плотности мощности, необходимо сгла-
дить вещественную и мнимую компоненты, применив сглаживание
Хеннинга. В частотной области выражения, использованные для
т 4- 1 гармонических частот, имеют вид:
60 = 0,560+0,5^; (10.110)
$0 = 0,5(20 + 0,5(2!; (10.111)
Сп = 0,25 6П_!+0,56п + 0,256п+1; (10.112)
Qn = 0,25<2n_! + 0,5<2п + 0,25<2п+1; (10.113)
302
Cm = 0,5Cm_1+0,5C„l; (10.114)
QTO = 0,5Qm_1 + 0,5Qm. (10.115)
Двустороннюю спектральную плотность можно также оценить
с помощью соотношений:
фта (0 = (0/2 = (0~/<2ад (01/2, (f > 0) (10.116)
И
%Un = ^(~D = ^K(f)/2==[C?/x(f)-fQsx(f)]/2, (f>0). (10.117)
§ 10.8. Передаточные функции
и функции когерентности
Передаточная функция может быть оценена либо из спектраль-
ной плотности мощности, либо из взаимной спектральной плотности
входного х (t) и выходного у (£) сигналов. Соотношения, приведен-
ные в гл. 4, имеют вид
I н (01 = [Ф™ (0/Ф.™ № = [0„ (О / о» (7)11/2 (10.118)
I н (01 =--1 Ф,,„ (01/Ф™ (0 = I оэд (01 /сга (f) =
= 1С$„ (7)+Qi, (7)]1'5/G„ (f), (10.119)
6 (7) = arctg [Q^, (0/C^ (7)]. (10.120)
Для дискретных гармонических частот
f — nfjm (n = 0, 1, 2, m) (10.121)
и предыдущие соотношения приобретают вид:
I н„ | = IЙ („7е/т) I = [Фга (лА7)/Фга («А01'/2 =
= [Ои, («А7)/С,.т (nAF)] > /2 (10.122)
И
|Нп1 = |Н(п7с/т)| = |Ф;с,,(пД7)|/ФяДпА7);= |Озд(пА7)|/Оте(пД7) =
= lG„ (nAf)+Qlu (nAf)]/Gxx (nAf), (10.123)
On = 0 Шт) = arctg [—(?„, (nA7)/Cw (nAf)]. (10.124)
Функция когерентности находится из выражения.
(0 = I Фад (014/Ф«, (0 ф„ (f) = I (f )|2/Ста (7) С„„ (7) = .
= [С,» (О + QI, (f)VGxx (f) G„ (7). (10.125)
Для дискретных гармонических частот она равна
Уп = Тад (ПАТ) = [CJ„ (fiA7) + (hAf)]/Gxx (nAf) Gm (nAf). (10.126)
303
§ 10.9. Выбор параметров реакторных исследований
Одно из основных ограничений большинства цифровых про-
грамм взаимной корреляции состоит в том, что число точек, для
которых должна быть вычислена функция взаимной корреляции,
не превышает некоторого числа, например 2000. Кроме того, объем
экспериментальных данных, получаемых из некоторых реактор-
ных экспериментов, ограничен несколькими минутами для данной
серин условий. С точки зрения получения наилучших результатов,
как правило, желательно использовать максимальное число дан-
ных и проводить нх анализ из самого длительного опыта. Конечно,
должны быть учтены и другие условия, например частотное содер-
жание сигнала, интересующий интервал частот, требуемое разре-
шение и т. д.
Рассмотрим опыт длительностью 50 сек, результаты которого
преобразуются в цифровую форму со скоростью 40 выборок в се-
кунду (т. е. всего 2000 точек). Наибольшая частота, которая может
быть представлена в сигнале, равна х/8 скорости выборки fst т. е.
20 выборкам в секунду. Это означает, что входные данные должны
быть отфильтрованы, чтобы удалить все частотные компоненты,
более высокие, чем 20 гц. Единственной альтернативой такой филь-
трации является цифровая фильтрация данных после перевода нх
в цифровую форму для исключения наложения частот. Последняя
процедура является дорогостоящей в смысле затрат машинного
времени, но она позволяет в определенных случаях избежать необ-
ходимости повторного цифрового преобразования.
Скорость выборки автоматически устанавливает временное при-
ращение Д для корреляционной функции. Следовательно, следу-
ющий шаг — определение количества задержек, которые должны
быть использованы в процессе корреляции, так как число задержек
прямо пропорционально разрешению и обратно пропорционально
точности илн доверительному уровню результата. Выбор числа
задержек также влияет на обращение Фурье, применяемое для рас-
чета взаимной и спектральной плотностей и передаточной функции,
так как определяет интервал между частотными компонентами.
Поскольку число приращений частоты равно числу задержек т,
приращение частоты Д/ равно обратной величине произведения
удвоенного временного приращения и количества задержек т, т. е.
Д/ = 1/2 т&. (10.127)
Например, если /s равно 40 выборкам в ^секунду, Д = 0,025 сек
и т = 100, то, согласно уравнению (10.127), Д/ = 0,2 гц. Таким
оказывается приращение частоты (или разрешение) для вычислений
взаимной спектральной плотности и плотности мощности, а также
и передаточной функции. Для 100 приращений (по 0,1 гц каждое)
максимальная расчетная частота равна 20 гц, что, очевидно, равно
максимальной частоте, которая может/быть исследована прн ско-
рости 40 выборок в секунду,
304
Увеличение числа, задержек до 200 дает разрешение / = 0,1 гц,
но максимальная частота, которая может быть исследована, снова
равна 20 гц, как и в предыдущем случае. Однако общее время кор-
реляции в первом случае равно 0,025 X 100 = 2,5 сек, в то время
как во втором случае оно в два раза больше. Кроме того, как будет
показано в дальнейшем, увеличение числа задержек уменьшает
точность или качество отдельных измерений.
При ограничении по числу точек, которые могут быть обработа-
ны, существует оптимум между длительностью опыта и максималь-
ной исследуемой частотой, т. е. если представляют интерес вы-
сокие частоты (например, 100 гц), требуется скорость выборки
200 выборок в секунду, причем максимальная длительность опыта
равна 10 сек. Как показано ниже, уменьшение длительности обра-
батываемого опыта также ухудшает точность данных. Однако при
рассмотрении высоких частот нет никакого другого выбора кроме
обработки нескольких «временных отрезков» одной я той же
записи и простого осреднения результатов. Обычно при обработке
экспериментальных данных эта проблема не возникает, поскольку
представляющие интерес данные имеют низкую частоту.
Другим важным моментом при выборе числа временных задер-
жек является условие, чтобы автокорреляционная функция дости-
гала нуля за выбранное время корреляции (т. е. за время тД).
Для 100 задержек с Д = 0,025 сек время корреляции составит 2,5 сек.
Если автокорреляционная функция достигает нуля и осциллирует
относительно горизонтальной осн в течение этого интервала вре-
мени, сглаживав ня Хеннинга было бы вполне достаточно для
любых отклонений, когда последние значения автокорреляцион-
ной функции не равны нулю. С другой стороны, если принять
только 20 задержек, время корреляция составит 20 X 0,025 =
= 0,5 сек; возможно, что автокорреляционная функция не достиг-
нет горизонтальной осн н в общем случае сглаживание Хеннинга,
несомненно, внесет некоторые искажения в спектральную плотность
мощности- Количественная оценка такого эффекта крайне сложна
и, к сожалению, перед обработкой данных нельзя предсказать,
достигнет лн автокорреляционная функция нуля за выбранное
время корреляции. Поэтому для данных, полученных на новой
исследуемой системе, может оказаться необходимым провести^один
или два пробных корреляционных опыта, прежде чем выбрать оп-
тимальные параметры обработки данных.
Функция когерентности является величиной, которая^ может
быть использована как мера достоверности, вводимая в результаты
измерения передаточной функции. Функция когерентности у2 оп-
ределяется как отношение выражения для | Н (f) | s, полученного
из измерений взаимной спектральной плотности, к этой же величине,
полученной нз измерений спектральной плотности мощности:
\ _ (I Gxy (f) UGxx (f))s _ I Gxy (f)ls (10 128)
Gyy(f)/Gxx(f) GxxWGyytI)'
305
Функция рассчитывается для каждого экспериментального зна-
чения передаточной функции. Из-за нелинейности исследуемой
системы, повышенного уровня шумов в записях входного и выход-
ного сигналов или из-за слишком малой амплитуды у^у (со) от-
личается от единицы и достоверность соответствующих экспери-
ментальных точек переходных характеристик снижается. Однако
при наличии, многочисленных входов система становится очень
сложной, и может оказаться возможным получение высококаче-
ственных данных, даже если функция когерентности между двумя
переменными, определенная уравнением (10.128), имеет небольшие
значения.
Соотношение между функцией когерентности и точностью или
качеством амплитуды Н (/) и фазового угла 0 (/) передаточной функ-
ции можно получить из выражений, определенных Гудменом [9].
С хорошим приближением он показал, что P-вероятность того, что
выполняются соотношения
|.W(fl (Wtf)|<sint. (10129)
|ё(П-е(П|<е, (Ю.130)
определяется выражением
р«1—Г—Lziwtf?—1*/2, (Ю.131)
[ 1—7x^(f)cos2e j
где символ «*» означает измеренное значение (величина без «а»
является истинным значением); к—число статистических степеней
свободы; е — заданная мера погрешности и у^у — функция коге-
рентности между двумя переменными х и у.
Рассмотрим 40-секундный отрезок записи при 50 выборках
в секунду, что дает 2000 выборок. Если использовать предположе-
ние Бендата и Пирсола 181, что т <1 0,1 N, количество задержек
в последующей корреляции и расчетах спектральной плотности
должно составлять 200. Число статистических степеней свободы,
даваемое уравнением (6.57), равно
~ (дЛя больших k), (10.132)
L т 2 | т
где N •— общее число точек, ат — число задержек. Для 1000 за-
держек число статистических степеней свободы k — 20. Уравнение
(10.131) показывает, что эта величина низка и, следовательно, точ-
ность. мала. Нетрудно видеть, что для достижения разумной точ-
ности при этих условиях необходимо иметь значение функции ко-
герентности максимально’близким к единице.
Для улучшения ситуации число статистических степеней свободы
должно быть увеличено. Из уравнения (10.132) видно, что этого
306
можно достигнуть только увеличением числа выборок или умень-
шением числа задержек. Поскольку указанное число выборок
уже равно максимальному числу, которое может быть обработано,
единственной возможностью является уменьшение числа задержек.
Рассмотрим пример, для которого число задержек уменьшено с 200
до 100, до 50 и затем до 25, что увеличивает число статистических
степеней свободы соответственно с 20 до 40, до 80 н затем до 160.
Уравнение (10.131) показывает, что для того, чтобы с 90%-ной до-
стоверностью погрешность была меньше, чем постоянная е, равная
0,1, необходимо иметь функции когерентности, равные примерно
0,96; 0,92; 0,84 н 0,72 соответственно, но при этом полоса разре-
шения А/ возрастает (т. е. ухудшается) отх/8 до х/4, до 1/2 и до 1 гц.
В обратном случае при постоянной функции когерентности, рав-
ной, например, у2 = 0,9, величина погрешности уменьшается с 0,170
до 0,117, до 0,080, до 0,057. Улучшение качества данных ухудшает
разрешение, а также уменьшает число точек на кривой переда-
точной функции.
Можно провести ряд исследований, связывающих функцию ко-
герентности с числом задержек, которое должно быть использовано,
чтобы достичь заданной точности; возможно, здесь нужно провести
некоторую оптимизацию. Однако функцию когерентности нельзя
определить, пока не известны все спектральные плотности, и в ре-
зультате нельзя определить заранее, сколько задержек должно быть
использовано. Как правило, число задержек составляет от 5 до 10%
общего числа выборок. Очевидно, может сложиться ситуация, при
которой указанное соотношение не будет лучшим, и данные следует
обработать еще раз с учетом результатов, полученных в первом
приближении. Для циклических данных, суммированных по не-
скольким циклам, число задержек может быть равно числу выборок
данных в цикле.
Функция когерентности в основном определяется первоначаль-
ными данными и слабо зависит от выбранного числа задержек.
Следовательно, если измерение выполнено, то ничем нельзя уве-
личить количество содержащейся в ием информации или уменьшить
число посторонних флуктуаций, т. е. увеличить отношение сигнал/
шум. В лучшем случае можно надеяться, что удастся упростить
обработку данных наиболее благоприятным образом, возможным
при имеющихся обстоятельствах.
§ 10.10. Быстрое преобразование Фурье
Преобразования рядов Фурье. В классическом, или прямом,
методе оценки преобразований Фурье, описываемом уравнениями
(10.83) или (10.84), должно быть сделано приблизительно № вы-
числительных операций. Существует другой метод, называемый
быстрым преобразованием Фурье, который недавно был предложен
в работе [101 и обобщен в работах [1Г1 — [131. В действительности
метод был впервые предложен в 1942 г. [141 для решения некото-
307 ~
рых задач рассеяния рентгеновского Излучения. Этот метод осуще-
ствляет преобразование Фурье, выполняя N logB N математичес-
ких операций. Метод использует рекурсивную формулу, кото-
рая определяет преобразование Фурье через несколько более
коротких преобразований. Обычно более короткие преобразования
содержат только два или четыре члена ряда, так что эти операции
могут быть сделаны только сложением и вычитанием. При рассмот-
рении большого числа экспериментальных точек экономия машин-
ного времени оказывается значительной. Отношение числа опе-
раций, выполняемых в двух методах, равно:
R = A/2//V log2 Л/ = A71og2 Лг. (10.133)
Например, для N, равного 4096 экспериментальным точкам, R рав-
но 341,3. Следовательно, быстрое преобразование Фурье сокращает
истинное арифметическое время счета примерно в 340 раз. С учетом
всех операций полное время в этом примере может уменьшиться
примерно в 100 раз. Этот фактор, определяющий уменьшение за-
траченных усилий, обусловлен использованием арифметических
операций.
Дискретные преобразования Фурье. Под дискретным преобразо-
ванием Фурье понимается преобразование временных последова-
тельностей, свойства которого близки к преобразованию Фурье
непрерывной переменной, которая представлена в дискретной
форме в виде временной последовательности. Преобразование про-
изводится по своим правилам и обладает очень полезным свойством
обратимости преобразования, которое аналогично свойствам ин-
тегрального преобразования Фурье. Преобразование определяет
спектр временных последовательностей, и перемножение преобразо-
вания двух временных последовательностей соответствует процессу
свертки временных последовательностей.
В работе [15] были указаны следующие полезные свойства дис-
кретного преобразования Фурье.
1. Свертка обратного дискретного преобразования Фурье про-
изведения двух дискретных преобразований Фурье есть периоди-
ческая средняя свертка двух первоначальных временных после-
довательностей.
2. Дискретное преобразование Фурье временной последова-
тельности, циклически сдвинутой иа А, есть дискретное преобразо-
вание Фурье временной ’ последовательности, умноженной на
ехр (— 2 зг jnA/JV).
3. Дискретное преобразование Фурье суммы двух функций
есть сумма дискретных преобразований Фурье этих двух функций-
Кокран и др. [111 отметили, что метод может быть применен для:
1) расчета спектральной плотности мощности и автокорреля-
ционных функций дискретных данных;
2) моделирования фильтров;
3) распознавания образов с использованием двумерной формы
дискретного преобразования Фурье;
308
4) расчета взаимных спектральных плотностей (включая веще-
ственную и мнимую компоненты) и функций взаимной ковариации
и корреляции;
5) разложения свернутых функций.
Дискретная форма преобразования Фурье в комплексной
экспоненциальной (а не тригонометрической) форме имеет вид
^п = Л2Хгехр(—2л]ш/М, (п = 0,1,...,М—1), (10.134)
f=0
где — n-й коэффициент дискретного преобразования Фурье
и Xi — i-я выборка из временной последовательности, содержащей
N выборок. Индекс/г представляет собой гармонику преобразования.
Обратное дискретное преобразование Фурье имеет очень про-
стую форму:
jv-t
Х; = — S Апехр (2л]‘ш7й/), (г = 0,1,..., М —1). (10.135)
N п=о
Следовательно, процедура вычисления преобразования уравнения
(10.134) может быть использована для расчета его обратного преоб-
разования по уравнению (10.135) простым переобозначением Ап и
Xf, введением масштабного коэффициента UN н изменением знака
у показателя экспоненты.
В быстром преобразовании Фурье производится последователь-
ное объединение постепенно возрастающих весовых сумм выборок
данных, умноженных на коэффициенты н Xi. Подробности рас-
четной процедуры приведены в [10—13].
Свертка. Метод быстрого преобразования Фурье также чрезвы-
чайно удобен прн свертке двух временных последовательностей.
Свертка X (/Д) и У (г'Д) выполняется перемножением двух вре-
менных последовательностей, сдвинутых по отношению друг
к другу:
W-1
х (г'Д)» у й'Д) =— S [я (£Д) у —/гД)], (10.136)
N Л=о
где знак * означает свертку. Прямой расчет свертки во временной
области -требует N арифметических операций на каждую точку.
Однако если вместо умножения двух временных последователь-
ностей рассчитать преобразование Фурье х (г'Д) и у (г‘Д) методом
быстрого преобразования Фурье, перемножить их в частотной
области и затем обратить по Фурье результат снова во временную
область, можно достичь значительной экономии машинного вре-
мени. Математически это можно выразить так:
х (Z Д) * у (£Д) =F~i {F [х (гД)] F [у (*Д)]}, (10.137)
где F н представляют прямое и обратное дискретные преоб-
разования Фурье. Эта процедура аналогична использованию ло-
гарифмов для выполнения умножения.
309
Корреляционные функции и спектральные плотности. Взаим-
ная корреляционная функция, частным случаем которой является-
автокорреляционная функция, подобна выражению свертки, да-
ваемому уравнением (10.136), за исключением того, что знак члена'
запаздывания изменен на обратный:
. Л—I
<РВД(ЙД)=4- 2 Xа&)!/((&+/гД), (10.138).
/V Z=D
и спектральная плотность равна преобразованию Фурье:
Фяу (nAf) = F (АД)]. (10.139>
Другой возможностью определения взаимной спектральной плот-
ности является использование дискретной формьт уравнения (4.75),.
т. е.
Фхв (лДП = Л_[Х (—nAf) Y (nAf) =
= {F*U (<А)1 F W (£А)]>, (10.140)
где F* означает сопряженное дискретное преобразование Фурье-
Эти операции выполняются гораздо проще методом быстрого преоб-
разования Фурье, чем с помощью уравнений (10.138) и (10.139)-
Корреляциоииая функция получается из уравнения
ФхУ (АД) = F-i [Фяи (пДГ)] = F-i {F* [х (iA)l F [у (iA)]}, (10.141)
которое может быть решено с помощью быстрого преобразования
Фурье.
Предыдущие формулы для взаимной корреляционной функции
и взаимной спектральной плотности применимы к автокорреляци-
онной функции и спектральной плотности мощности, если предпо-
ложить, что у (ZA) = х (£Д). Односторонние спектральные плот-
ности Gxv (nAf) и Gxx (nAf) можно также получить из Фкр (nAf)
и Фа:к(пД/), используя уравнения (4.106), (4.108) и (4.109).
Цифровая фильтрация. Цифровая фильтрация временных по-
следовательностей представлена в § 10.4 как процесс свертки между
временными последовательностями и дискретными весовыми функ-
циями. Уравнение (10.8) дает фильтрованную переменную у (1А),
равную:
y(iA) = h(iA)*x(iA) =
м
= 2 {A(AA)x[(i—ft) А]}, (10.142)
k=—м
810
где М—количество временных приращений в половине /?(1Д). Сле-
довательно, цифровую фильтрацию можно провести, используя
уравнение (10.137):
у (IД) = h (ib)*x (i Д) = F1 {F [h (iA)] F [x (i Д)1}. (10. 143)
Фильтр может иметь любые характеристики, рассмотренные
в-§ 10.4 и представленные соответствующим образом функцией
Экономия времени при использовании быстрого преобразования
Фурье. Временные преимущества быстрого преобразования Фурье
перед прямым преобразованием определены Кокраном и др. [11]
и представлены в табл. 10.1, где М — число выборок во временной
последовательности. Таблица дает количество использованных
умножений и относительный выигрыш для быстрого преобразова-
ния Фурье' временных последовательностей с 8192 выборками,
определяемый отношением числа умножений для двух методов.
Таблица 10.1
Сравнение числа умножений, требуемых для прямого н
быстрого преобразований Фурье
Операция Примерное число умножений Соотношение прямого и быстрого умножений для 8182 выборок
прямое быстрое
Дискретное преобра- зование Фурье № 2Mlog2M 315
Свертка или фильтра- № ЗМ logs ЛГ 210
ция N f ЛГ \
Функция корреляции т(т+3) 3MIogoAf 39
Спектральная плот- ность* т(т+3)+л 2ЛГ log2 N 354
* В работе [11] не рассмотрена.
СПИСОК ЛИТЕРАТУРЫ
1. Balcomb J. D. Los Alamos Scientific Laboratory, personal communica-
tion, 1964.
2. Ormsby J. F. A. Design of Numerical Filters with Applications to Mis-
sile Data Processing.—«Commun. ACM» (Ass. Comput. Mach) 1961,
v. 8, p. 440—466.
3. Negron C. D. Digital One-Third Octave Power Spectral Analysis. —
Engr. Paper 3693, Douglas Aircraft Co., Missile and Space Systems Divi-
sion, 1966.
4. Notess С. B. A Study of the Atmospheric Turbulence Based upon Flight
Measurements of Gust Velocity Components. — Report VC-99I-F-I
(WADD-TR-51-259), Cornell Aeronautical Laboratory.
5. Marshall Space Flight Center. RAVAN. Digital Computer Code for Random
Vibration Analysis, 1962.
311
6. Measurement Analysis Corp., MAC/RAN. Digital Computer Code for
Analysis of Random Data, 1967.
7. Springer T. Los Alamos Scientific Laboratory, personal communication,
8. Bendat J. S., Piersol A. G. Measurement and Analysis of Random Data.
John Wiley and Sons, Inc., N. Y., 1966. (См. Бендат Дж., Пирсол А. Из-
мерение и анализ случайных процессов. Пер. с англ. М., «Мир», 1974.)
9. Goodman N. R. On the Joint Estimation of the Spectra, Co-Spectrum
and Quadrature Spectrum of a Two-Dimensional Gaussian Process. —
Scientific Paper, N 10, Engineering Statistics Laboratory, New York
University, 1957.
10. Cooley J. W., Tukey J. W. An Algorithm for the Machine «Calculation
of Complex Fourier Series.—«Math. Comput.», April 1965, v. 19, p. 297—301.
11. Cochran W. T. e. a. What is the Fast Fourier Transform? — «Proc. IEEE»
(Inst. Elec. Electron. Eng.), October 1967, v. 55, N 10, p. 1664—1677.
12. Singleton R. C. On Computing the Fast Fourier Transform. — Логотип.
АСМ» (Ass. Comput. Mach.), October 1967, v. 10, N 10, p. 647—654.
13. Brigham E. O., Morrow R.‘ E. The Fast Fourier Transform. — «IEEE»
(Inst. Elec. Electron Eng.), Spectrum, December 1967, p. 63—70.
14. Danielson G. C., Lanczos C. Some Improvements in Practical Fourier
Analysis and Their Application to X-Ray Scattering from Liquids. —
«J. Franklin Inst.», April 1942, v. 233, p. 365—380, 435—452.
15. Gentllmen W. M., Sande G. Fast Fourier Transforms for Fun and Profit. —
Fall Joint Computer Conference, AFIPS Proceedings, American Federa-
tion of Information Processing Societies, 1966, v. 29, p. 563—578.
ГЛАВА 11.
ИЗМЕРЕНИЕ
ШУМОВ
В ЯДЕРНЫХ
РЕАКТОРАХ
§ 11.1. Введение
В этой главе описаны примеры измерений шумов, которые были
выполнены на ядерных реакторах за последние несколько лет.
О некоторых из них подробно сообщалось на двух симпозиумах,
организованных Комиссией по атомной энергии США во Флориде
в 1963 [11 и 1966 12] годах.
Выделенные в этой главе примеры выбирались с целью полу-
чить широкий спектр типичных шумовых экспериментов, которые
могут быть проведены на ядерных реакторах. К сожалению, объем
книги не позволил представить изящные работы многих авторов,
внесших вклад в область измерения реакторных шумов.
§ 11.2. Эксперименты по счету
нейтронных импульсов
Эксперименты по счету импульсов от нейтронов были первыми
статистическими, нлн шумовыми экспериментами, проведенными на
ядерных реакторах [3]. Простота этих экспериментов и доступность
многоканальных анализаторов общего н специального назначения
делают этот тип экспериментов легко выполнимым. Первоначально
эти эксперименты проводились только на быстрых реакторах, в ко-
торых время жизни нейтронов мало, поэтому могут детектироваться
отдельные цепочки нейтронов. Затем подобные эксперименты были
распространены на реакторные системы на тепловых и промежуточ-
ных нейтронах. В общем случае один или более методов счета им-
пульсов полностью конкурируют с другими методами измерения па-
раметров под критической системы или реактора нулевой мощности.
Выбор методов счета импульсов. В нескольких проведенных
исследованиях сравнивались различные методы счета импульсов
на ряде данных, полученных из серий опытов на одном реакторе.
Одно из наиболее исчерпывающих исследований было выпол-
нено Пачнлно [4—6], который обобщил результаты этого исследо-
вания и, последующей работы в моногрвфин 17]. В аналогичном
исследовании на реакторе NORA [8] сравнивались метод распре-
деления вероятностных интервалов [9, 10] с методами росси-альфа
н фейнмана-альфа. В работе [11] описан ряд подобных экспери-
313
ментов, выполненных на реакторе типа «Argonaut» в реакторном
центре в Петтене (Нидерланды).
В основном цель этих исследований заключалась в сравнении
методов при идентичных условиях. Как и следовало ожидать, ни
один из методов не дал серьезного отличия от другого, поэтому
выбор метода часто диктуется главным образом имеющимся в на-
личии оборудованием и соответствующими программами обработки
экспериментов на ЦВМ, опытом исследователя и другими обстоя-
тельствами. Однако некоторые методы ограничены уровнем мощ-
ности (т. е. мощность должна поддерживаться на возможно низ-
ком уровне,' чтобы обеспечить удовлетворительное отношение
сигнал/фон), тогда как другие методы ограничены эффективностью
детектора. Обычно методы, требующие высокой эффективности
детектора, пригодны только для систем на тепловых нейтронах,
а методы, требующие низкого уровня мощности для получения
приемлемого отношения сигиал/фон, находят применение в систе-
мах на быстрых нейтронах. Несколько из этих методов пригодны
как для систем на быстрых, так и на тепловых нейтронах.
Исторически первыми методами счета импульсов были клас-
сический метод россн-альфа для быстрых реакторных систем и
метод Фейнмана для реакторных систем на тепловых нейтронах,
заключающийся в определении отношения дисперсии к среднему
значению. Из-за простоты метода россн-альфа многие исследова-
тели пытались применить его к системам на тепловых нейтронах.
Эти усилия стимулировались доступностью многоканальных ана-
лизаторов и цифровых логических модулей, нз которых могут быть
собраны сложные схемы, управляющие работой анализатора. Од-
нако анализаторы не могли работать подобно анализатору совпаде-
ний Орндоффа [3], и часто результаты метода россн-альфа расходи-
лись с другими методами измерений. Система регистрировала кор-
реляции между отдельными импульсами, возникающими в- одном
цикле, и импульсами триггера, разделенными по крайней мере од-
ним циклом времени. Это делает непригодным выражение (11.1)
для данного измерения. Однако во многих случаях можно получить
правильное значение а путем анализа экспоненциального участка
кривой р (t) в зависимости от t.
С помощью двух детекторов и импульсов триггера в геометрии
с низкой эффективностью детектора в работах [12], [13] в системах
на тепловых нейтронах получены экспериментальные результаты,
согласующиеся с другими методами. Бабала [8] развил методы из-
мерений величины росси-альфа в системах иа быстрых и тепловых
нейтронах и разделил их на методы росси-альфа I типа и росси-
альфа II типа. Он показал теоретически, что в пределе при нулевой
эффективности вероятность р (t) в методе росси-альфа II типа равна
р (/) в методе росси-альфа I типа*.
* Эта классификация не является общепринятой, хотя разница двух ти-
пов экспериментов ясно установлена.
314
В работе [14] предложен оригинальный метод уменьшения эф-
фективности запускающего детектора путем введения прерывателя
в линии,- ведущей к триггеру анализатора. Последующие экспери-
менты [15] показали, что такой подход оправдан, когда эффективное
время работы прерывателя мало, и для этого случая было получе-
но выражение для вероятности р (t).
Введение специальных характеристик в многоканальные ана-
лизаторы в работах [14] и [13] привело к новым типам эксперимен-
тов, которые фундаментально отличались от метода росси-альфа.
К ним Относятся методы временных интервалов от случайного на-
чала, мертвого времени, распределения интервалов и спонтанного
импульсного источника.
Метод временных интервалов от случайного начала, часто назы-
ваемый методом случайного начала, ограничен эффективностью
детектора и, таким образом, пригоден только для систем на тепло-
вых нейтронах.
Метод спонтанного импульсного источника является модифици-
рованным методом росси-альфа, в котором триггерные устройства
порогового типа позволяют выделять предпочтительно данные
с высоким отношением сигнал/фон. Следовательно, этот метод
пригоден для систем как на тепловых, так и на быстрых ней-
тронах.
Метод интервала от импульса до импульса, развитый Бабала
18], имеет ряд решающих преимуществ перед другими методами.
Пачилио отметил, что ои столь же эффективен, как метод росси-
альфа для быстрых систем и намного превосходит его для тепловых
систем. Он также указал, что этот метод в отличие от большинства
других статистических методов не ограничен чрезвычайно низкой
эффективностью детектора и (или) высоким уровнем мощности и
что фактически даже в предельных случаях окончательная формула
еще содержит существенную информацию о необходимых реактор-
ных параметрах [7].
Все дисперсионные методы, включая метод Фейимаиа (метод
определения отношения дисперсии к среднему) и разностный метод
Бениета, ограничены эффективностью детектора и, следовательно,
могут применяться только в системах иа тепловых нейтронах.
Единственным исключением является ковариационный метод, в ко-
тором используются выходные сигналы двух детекторов и перед
обработкой данных удаляются средние значения. Наличие двух де-
текторов допускает применение детекторов с более низкой эффек-
тивностью, и, следовательно, этот метод пригоден для систем на бы-
стрых нейтронах. Различные вероятностные методы (методы нуле-
вого отсчета, единичного й нулевого отсчета, четного или нечетного
счета) в общем случае ограничены эффективностью детекторов и,
следовательно, применимы только для систем иа тепловых нейтро-
нах. Метод временных интервалов от случайного начала можёт рас-
сматриваться как вероятностный метод и подвержен тем же самым
ограничениям.
315
Классические измерения росси-альфа. Эксперимент по опреде-
лению росси-альфа (первый из техники счета нейтронов) был про-
веден Росси, который предположил, что ядерные системы самомо-
дулированы из-за присутствия длинных цепочек и что время жизни
мгновенных нейтронов может быть получено измерением усреднен-
ного по времени распределения нейтронов, связанных общим пред-
шественником. Этот метод основывается на том факте, что возник-
новение деления в сборке является неслучайным процессом из-за
временной корреляции
между нейтронами, ко-
торые имеют общего
предшественника. Для
обеспечения фиксации
коррелированных во
времени импульсов на
фоне случайных импуль-
сов скорость делений
должна поддерживаться
достаточно низкой, что-
бы предотвратить суще-
ственное перекрытие
отдельных цепочек в
сборке. Это требование
фактически не дает воз-
можности использовать
метод в его классичес-
Рис. 11.1 Типичные результаты определения ком виДё ДЛЯ систем на
величины а на реакторе «Godiva» тепловых нейтронах,
прн различных реактивностях [3]. Теория измерений рос-
си-альфа дана в гл. 3.
Орндофф [3] сообщил о серии экспериментов, выполненных
на быстрых сборках без отражателя «Godiva» и «Jezebel». Резуль-
таты экспериментов, приведенные на рнс. 11.1 и 11.2, подтверж-
дают соотношение [данное ранее как уравнение (3.9)]:
р (/) А = ДА + В ехр (-а/) А. (11.1)
Измерения были выполнены с анализатором специального на-
значения, показанным на рис. 3.2.
Использование двух детекторов делает менее строгими требова-
ния к разрешающему времени усилителей, чем при работе с одним
детектором. При работе одного канала, ко входу которого подсо-
единены вместе детекторы 1 и 2, необходимы задержка около
0,5 мксек для предотвращения совпадения отсчета самого с собой
и исключения тех отсчетов, которые возникают в пределах времени
восстановления усилителя.
Измерения на сборке из 235 И «Godiva», результаты которых
показаны на рис. 11.1, проводились для величии реактивности,
316
изменяющихся от критического состояния на запаздывающих ней-
тронах до почти критического состояния на мгновенных нейтронах
(р = 86,6 10-2 Р). После каждого цикла измерений осуществля-
лось раздвижение отдельных частей сборки для снижения фоновой
плотности нейтронов до начала нового цикла.
Рис. 11.2. Результаты опытов на реакторе
«Jezebel» при различных реактив-
ностях [3]:
Номер
подкритического
состояния
2
3
4
6
7
8
На рис. 11.3 показана зависимость величины росси-альфа от
реактивности. Из значения <zc = [3/Z при критичности на запазды-
вающих нейтронах и определенной независимо величины р най*
дено, что эффективное время жизни нейтронов в сборке «Godiva»
равно 0,66 * IO-8 сек,.
317
Измерения на сборке «Jezebel» были ограничены подкрнтн-
ческим состоянием, так как нейтроны спонтанного деления 238 Ри
затрудняли регистрацию нейтронов цепной реакции. Однако кривая
зависимости величины росси-альфа от числа одинаковых плуто-
ниевых дисков (которые непосредственно определяют реактив-
ность), подобная изображенной на рис. 11.3, может быть экстрапо-
лирована к критичности иа запаздывающих и мгновенных нейтро-
нах, и, следовательно, для этих условий определена масса урана.
Измерения росси-альфа в системах на тепловых нейтронах.
Как указано в предыдущих разделах, метод росси-альфа применим
в системах на тепловых нейтронах. В методике, описанной в § 3.3,
Рис. 11.3. Зависимость росси-альфа от реак-
тивности, полученная на реакто-
ре «Godiva» [3].
произвольный импульс от детектора запускает таймер импульсного
генератора, который открывает каналы многоканального времен-
ного анализатора, и последующие импульсы (исключая пусковой)
регистрируются анализатором. По окончании цикла анализатор
ожидает ближайший импульс для пуска нового цикла.
Схема, использованная в экспериментах Бабала [8], описана
в работе [131 и показана на рнс. 11.4. Эта схема позволяет опреде-
лять корреляцию между запускающим импульсом от одного детек-
тора и импульсами, непосредственно следующими от друге го детек-
тора. Специальная управляющая схема работает от стандартного
многоканального анализатора времени пролета. Переключатель
•Si выбирает детектор, который выдает импульсы для запуска ана-
лизатора, а переключатель S3 — детектор, импульсы которого ана-
лизируются. Импульс, запускающий анализатор, открывал его пер-
вый канал, и задерживался на 2,5 мксек. Импульс с выхода схемы
задержки закрывает первый канал и запускает импульсный гене-
ратор, открывающий каналы анализатора, ширина которых может
быть выбрана от 17 до 200 мксек. Схема задержки тг останавливает
счетчнк по истечении времени, соответствующего обычно 100 кана-
лам, и запускает схему задержки т2, которая выдает импульс на
остановку анализатора. Схема задержки т2 открывает схему «И»1,
и анализатор ожидает пусковой импульс для начала нового цикла.
318
Результаты измерений на реакторе NORA, где пусковые и кор-
релированные импульсы поступали от одного детектора, располо-
женного в центре активной зоны, показаны на рис. 11.5. Когда
пусковые импульсы поступали от детектора, находящегося в центре
активной зоны., а коррелированные импульсы — от детектора, рас-
положенного на краю топливной области, результаты были хуже,
чем полученные для одного детектора. Однако результаты улучша-
лись, когда запускающий детектор помещался в положение с мень-
шей эффективностью, а детектор, выдающий коррелированные
Детектор 7г------
1\№сили-
||J7?g/№
Временной
анализатор
Оста-р^
новка
Блок управления
Детектор 2г
Высокое
напряжение
Высокое
напряжение
11™/7 .
। ^каналов
I Импульс
\от
"{детектора'
ныи ге- —'
нератор
17-200 мксек
Рис. 11.4. Схема для измерений росси-альфа [13].

[Номер ce/wJ] [Лерфопечать]
импульсы, располагался в центре активной зоны. Из этих экспери-
ментов был сделан вывод, что отношение сигнал/шум улучшается
при уменьшении эффективности запускающего детектора.
В работе [14] предложен метод «прерывания» последовательно-
сти импульсов, поступающих на пусковой канал, путем использо-
вания внешнего периодического сигнала,-который не связан с им-
пульсами детектора. Этот метод позволяет оставлять детектор в по-
ложении высокой эффективности и в то же время обеспечивать лю-
бую требуемую эффективность. В работе [15] проведена серия из
трех экспериментов, заключающихся в 20-мин утнбй записи им-
пульсов на магнитной ленте. При использовании обычного времен-
ного анализа экспоненциальный спад обнаружить не удалось.
Лишь применив метод прерывания с коротким временем пропуска-
ния, получили заметный экспоненциальный член. Хотя большая
часть запускающих импульсов в этом методе теряется, оставшаяся
часть эффективно используется. В работе [15] описано экспери-
ментальное оборудование, которое позволяет измерять полную
корреляционную функцию и получить четкий экспоненциальный
член плюс фон с коэффициентами, данными Оридоффом [3].
319
Итак, корректное отношение сигнал/фон, данное Орндоффом,
можно получить в том случае, если аппаратура действительно изме-
ряет полную корреляцию последовательности импульсов детектора.
Однако обычный временной анализатор в действительности изме-
ряет корреляционную функцию между запускающими импульсами
и следующей за ними последовательностью коррелированных им-
Рис. 11.5. Данные для определения росси-альфа,
накопленные с помощью детектора 1,
приводимого в действие детектором 1.
(Уровень воды—’65,0 см, критический
уровень воды — 77,3 см, ширина канала
анализатора — 5 мксек, реактор NORA
[13]). Измеренное значение cto =
= 64,2 сек~х, вычисленные значения из
графика а = 1003 сек~1, ctj = 459 сект1.
пульсов. Если чувствительность детектора.или скорость счета высо-
ка, некоторые импульсы будут просчитываться, что неблагоприятно
влияет на отношение сигнал/фон и может привести к неудовлетво-
рительным результатам.
Измерения отношения дисперсии к среднему (метод Фейнмана).
Отношение дисперсии к среднему числу отсчетов за время Т
{см. уравнение (3.33)1 есть
сг—с- = д /1 1—ехр(—ссГ)
с \ аТ
(Н-2)
320
где
д sDv _ e(vp—Vp)fep
Pp " v^P-M3 '
(11.3)
Это соотношение справедливо для счетных интервалов порядка
0,1 сек,, так как рассматриваются только мгновенные нейтроны.
Более того, при выводе этого соотношения предполагалось, что
корреляция между различными измеряемыми величинами с в дан-
ном интервале Т отсутствует. Пал и др. [17] полагали, что время вы-
держки между интервалами должно быть > 3 сек. Однако Бабала
[8] утверждает, что эффект корреляции пренебрежимо мал даже для
Рис. 11.7. Определение р// из данных,
полученных методом Фейн-
мана иа реакторе NORA
[13] (<zc == 214 сек-’).
Рис. 11.6. Данные, полученные мето-
дом Фейнмана на реакторе
NORA и соответствующие
уравнению (11.2). Времена
выдержки: □—0 сек, О —
1 сек; А — 3 сек. Уровень
воды 77,25 см-, а, —
= 232 сек-1.
нулевого времени выдержки между выборками, если число отсче-
тов в интервале велико. Эта точка зрения еще дискутируется.
На рис'. 11.6 показаны экспериментальные результаты, при-
веденные в работе [13], для реактора NORA, на основании которых
можно вычислить величины а и А. Подобные зависимости величин а
н А были получены при других значениях реактивности. Эти резуль-
таты показаны на рис. 11.7, где реактивность выражена как отно-
шение критического уровня воды к действительному уровню {hjh).
На рис. 11.8 дан график величины А в зависимости от 1/а2, кото-
рый описывается линейным законом. Легко показать, что
(пл,
Рр рр \ vp J \ -vp / L Л2 J а2
Следовательно, наклон прямой линии, изображенной на рис. 11.8,
еСТЬ cpg-уухг(1—A (Ц.5)
k V? Л . Л3 J 1/а3 '
321
И Зак. 576
из которого может быть вычислена эффективность детектора е,
если другие коэффициенты известны или могут быть измерены
независимо. Затем абсолютная скорость делений может быть опре-
делена из скорости счета импульсов как
F = cte. (11.6)
Техника измерения распределения вероятности для метода
Фейнмана. Техника измерения распределения вероятности, о кото-
Рис. 11.8. Определение эффек-
тивности счетчика из
рой сообщалось в работе [18], опи-
сывалась в § 3.4. Отношение диспер-
сии к среднему можно вычислить нз
измеренного распределения вероят-
ности и затем для получения пара-
метров ядерной системы использо-
вать метод Фейнмана. Специальный
анализатор плотности вероятности
для прямых измерений вероятностей
р (Т), где п изменяется от 0 до 127,
схематически показан на рис. 11.9.
Принцип его действия следующий.
Импульсы от детектора поступают на
вход А быстродействующей электрон-
ной схемы переключения, которая
переключается на одно положение от
каждого приходящего импульса. Им-
пульсы от таймера, определяющего
данных, полученных
методом Фейнмана
на реакторе NORA
[13] (е=1,9-10-3
отсчет/деление).
длительность временного интервала
Т, поступают на вход В. Согласно
положению электронного переключа-
теля вход открыт для импульса вре-
мени, который дает сигнал на счетчик,
связанный с этим выходом. Если,
например, 10 импульсов приходят в течение интервала, выход 10-го
переключателя открывает вход 10, так что импульс от таймера пере-
дает сигнал в счетчик 10. Это означает, что 10 импульсов поступили
в течение этого временного интервала. Переключатель возвра-
щается в исходное положение, и анализатор плотности вероятности
открыт для нового цикла. В конце опыта для одного значения Т
вероятность р (Т) получается непосредственно делением числа от-
счетов в счетчике i, Nt иа число отсчетов в счетчике интервала вре-
мени Nr:
Pi = N-jNT. (11.7)
Характеристики анализатора контролируются импульсным счет-
чиком-монитором, так как равенство
127
(11.8)
j=0
322
должно выполняться для числа отсчетов в счетчике-мониторе Np
•Дополнительный контроль ведется по соотношению
127
1Уг=£?/г. (11.9)
Эксперимент обычно ставится следующим образом. Согласно
характеристикам исследуемой сборки и величине реактивности,
программируются ‘последовательность, величины и число времен-
ных интервалов. Обычно измерение с одной величиной Т повто-
рно. 11.9. Структурная схема анализатора распределе-
ния вероятности [18].
ряется несколько раз, чтобы определить и исключить эффекты
дрейфа реактора и аппаратуры. Время измерения за один интервал
зависит от скорости счета н требуемой статистической точности.
Для каждой величины Т измеряется полное распределение вероят-
ности. Все данные эксперимента собираются и направляются на
ЦВМ‘для вычислений согласно уравнениям (3.33), (3.39) и (3.40).
Чтобы получить постоянную спада мгновенных нейтронов, исполь-
зуется метод наименьших квадратов. Величина Y определяется
соотношением (3.34).
Для дальнейшего объяснения метода рассмотрим несколько ти-
пичных результатов измерений распределения вероятности, вы-
полненных на реакторе STARK. На рис. 11.10 показаны измерен-
ные для пяти различных значений временных интервалов Т рас-
пределения вероятности (сплошные линии), для сравнения указаны
также эквивалентные распределения Пуассона (пунктирные линии).
Распределения были взяты из эксперимента, в котором использо-
П* 32S
вался высокоэффективный детектор. Величина Y из выражения
(3.34), которая дает максимальное отношение коррелированных
импульсов к некоррелированным импульсам детектора, была равна
Рис. 11.10. Измеренные распределения вероятности
(------------------) и эквивалентные распределения
Пуассона (———).
1,64, и величина а равна 139 сект1. Вследствие больших значений
У отклонение от распределения Пуассона существенно, причем это
отклонение увеличивается с увеличением значения Т. Полученные
параметры реактора хорошо согласуются с результатами других
методов.
324
Другим способом оценки реакторных параметров является
использование модифицированной формы уравнения (3.33), т. е.
р y__EPvT1 1-ехр(-аТ)1 (1110)
С С рр [ аТ J
В качестве примера на рис. 11.11 показано экспериментально
найденное отклонение от дисперсии распределения Пуассона в за-
висимости от длительности интервала Т [13]. В этом эксперименте
эффективность детектора была значительно ниже, чем в предыду-
щем, и поэтому величина Y была равна 0,34. Последнее означает,
что в выходном сигнале де-
тектора только 34% (макси-
мально) коррелированных
импульсов. За время 7, ука-
занное на рнс. 11.11, анали-
зировалось около 105 импуль-
сов детектора. На реакторе
STARK были проведены дру-
гие эксперименты при раз-
личных условиях для опреде-
ления диапазона примени-
мости метода распределения
вероятности.
Наиболее важным выво-
Рис. 11.11. Отклонение от модифициро-
ванной дисперсии распределе-
ния Пуассона в зависимости
от длины интервала. !
дом нз экспериментов, выпол-
ненных на реакторе STARK, является то, что даже при значе-
ниях Y 0,3 возможно точное (в пределах 2—3%) определение
постоянной спада мгновенных нейтронов. На основе этого резуль-
тата были оценены все необходимые параметры быстрой сборки
с плутониевым топливом [13].
При Y = 0,35 были вычислены следующие параметры в диапазоне
изменения реактивности от 0,1 р до 4 [3: скорость деления F,
мощность реактора Р, минимальная эффективность детектора е,
средняя скорость счета детектора Fe, порядок длительности времен-
ного интервала Т, средняя скорость счета детектора на интервал
ct. Оказалось возможным осуществить измерения а при изменении
реактивности в пределах 0,2 р — 3(3. При критичности на запазды-
вающих нейтронах измерение нельзя было выполнить из-за отно-
сительно высокого уровня мощности. Поэтому постоянные спада
мгновенных нейтронов прн критичности на запаздывающих ней-
тронах должны были определяться экстраполяцией. Из-за высокой
скорости счета время, необходимое для измерения одного значения
а, не превышало 20 мин. Вывод, сделанный в работе [181, заклю-
чался в том, что метод анализа распределения вероятности может
использоваться для определения физических параметров в быстрых
сборках с плутониевым и урановым топливом.
Метод распределения интервалов (метод Бабала). Серия экс-
периментов, выполненных на реакторе NORA, анализировалась
325
Бабала [8] с целью сравнения метода распределения интервалов
с другими методами измерения постоянной спада мгновенных ней-
тронов а. Измерялись несколько отрицательных реактивностей для
однородной квадратной решетки из стержней UO2 3%-ного обога-
щения с замедлителем Н2О и «бесконечным» радиальным отражате-
лем Н2О. Изменения реактивности достигались путем изменения
уровня воды.
Рис. 11.12. Упрощенная схема для измерения распределения интер-
валов [8].
Упрощенная структурная схема для измерения распределения
интервалов дана на рис. 11.12. Импульсы после усиления и формиро-
вания подаются на 400-канальный- анализатор. Для обеспечения
требуемого режима работы анализатора собраны дополнительные
блоки. После включения анализатора иа каналы подаются импуль-
сы от импульсного генератора,пока первый импульс от детектора
не зарегистрируется в соответствующем канале. Одновременно
Рлс. 11.13. Упрощенная схема вероятностного анализатора,
применявшегося в измерениях на реакторе NORA
[8]-
анализатор автоматически возвращается в исходное состояние,
и начинается новый цикл. В случае отсутствия отсчета в течение
цикла следующий цикл запускался первым поступающим импуль-
сом. С помощью этого же анализатора, работающего по принципу,
описанному в предыдущем разделе, были получены данные для опре-
деления распределения вероятности и отношения дисперсии к сред-
нему. Упрощенная структурная схема этой системы показана на
рис. 11.13. Здесь отсутствует время выжидания между следующими
326
друг за другом временными интервалами. После определения крити-
ческой высоты (hc~78,82 см) были сделаны измерения в диапазоне
изменения h от 77,5 см до 69,6 см с шагом 1 см.
Распределение интервалов, полученное в работе [13], обрабаты-
валось Бабала [8] методом наименьших квадратов в соответствии
с уравнением (3-66) для получения величии Fe, а, у н о. «Веса» от-
дельно измеренных величин брались обратно пропорциональными
числу набранных отсчетов в каналах анализаторов. Проверка со-
ответствия результатов с помощью распределения %2 подтверждает
правильность выбора «весов».
Рис.- 11.14. Постоянная спада мгновенных нейтронов
н обратная скорость счета в зависимости
от реактивности для реактора NORA [8].
Для гомогенного реактора без отражателя реактивность являет-
ся линейной функцией 1/Л2 и величина с обратно пропорциональна
реактивности. График зависимости 1/с от 1/Л2, приведенный на
рис. 11.14, показывает, что эта модель применима для описания
результатов измерений. Из графика зависимости а от 1/Л2, изо-
браженного иа рис. 11.14, определялись величины ас — р/Л н от-
рицательная реактивность на мгновенных нейтронах в долларах:
р₽ = p/р = а/ас. (11.11)
Величина
р/|.'ёЙ^ = [2/(у2—1)],/2, (11.12)
где =
D, = (v?-vp)/^, (11.13)
показана в зависимости от реактивности на рис. 11.15.
Если использовать значение DVt равное 0,795 [191, то можно
оценить отношение е/р. Подставляя теоретическое значение р,
равное 0,0079, имеем, что эффективность счетчика, полученная
методом распределения интервалов, равна 0,00289. Это значение
разумно согласуется со значением 0,00252, полученным методом
Фейнмана. Зависимости 1/с (см. рис. 11.14) и р/}^e.Dv (см. рис. 11.15),
327
полученные методом распределения интервалов, не экстраполи-
руются точно к нулю при критичности на запаздывающих и мгновен-
ных нейтронах, однако отклонения лежат в пределах ошибок.
Результаты измерений методом распределения интервалов яв-
ляются более точными, чем результаты метода измерения отношения
дисперсии к среднему (метод Фейнмана). Каждое измерение распре-
деления интервалов для первых трех значений реактивности про-
должалось 15 мин; измерение для последних шести значений реак-
тивности длилось 20 мин. Длительность измерения вероятностей,
Рис. 11.15. Величина p/V,eDv в зависимости от
реактивности (8], полученная мето-
дом Фейнмана (-----------------—) и методом
распределения интервалов (------).
используемых для определения дисперсии, изменяется от 70 до
116 мин для различных значений реактивности. При анализе вероят-
ности отсчета наиболее длинные времена при соответствующих
условиях были 47 мин и 116 мин.
Времена, требуемые для измерений методами Фейнмана и Мо-
гильнера, можно уменьшить, а точность определения параметров
улучшить надлежащим выбором длительностей временных интерва-
лов, ио сравнение этих методов тем не менее заставляет отдать пред-
почтение методу измерения временных интервалов.
§ 11.3. Измерения шумов в критических реакторах
В предыдущем параграфе рассматривалась статистика отдель-
ных импульсов детекторов. В настоящем параграфе мы будем иметь
дело с выходными сигналами детектора, которые являются флук-
туирующей переменной величиной. В общем случае это означает,
что применяется ионизационная камера и анализируются флук-
туации ее тока.
Однако импульсы, поступающие от детектора, можно преобра-
зовать с помощью измерителя скорости счета (обычно с этой целью
используется схема с диодом) так, чтобы выходной сигнал пред-
328
ставлял собой флуктуирующее напряжение. Временное поведение
сигнала с выхода измерителя скорости счета и сигнала ионизацион-
ной камеры аналогично в том смысле, что обе системы реагируют
на возникновение отдельного импульса с характеристическими по-
стоянными времени, которые обусловлены электрическими харак-
теристиками камеры и схемы измерения скорости счета. Преиму-
щество схемы измерения скорости счета в том, что постоянная вре-
мени изменяется путем подбора электрических параметров схемы
без изменения чувствительности или эффективности детектора.
Кроме того, передавать без искажения на большое расстояние им-
пульсы проще, чем слабые токи. Однако в обоих случаях необхо-
димо иметь достаточно большое число детектируемых нейтронов,
чтобы выполнялась центральная предельная теорема и выходной
сигнал мог считаться непрерывной величиной.
Измерения отношения $/1. Первые измерения шумов, проведен-
ные Коэном [20], включали в себя измерения отношения p/Z, кото-
рое является величиной росси-альфа для критического реактора.
Измерения были выполнены способом, описанным в § 6.3. Пере-
даточная функция реактивности для критического реактора с хо-
рошим приближением может быть представлена следующим образом:
Я(о)= l/(j<o +ас)= l/(jco 4- p/Z), (ИЛ4)
Спектральная плотность мощности выходного сигнала нейтрон-
ной плотности есть
G' (<о) = с™(0)>.^—^-=-+В, (11.15)
' Яасо)!2 <ва + а? ' ’
где Л и В — постоянные; GvtJ (со) — измеряемая спектральная
плотность мощности; (со) — передаточная функция прибора;
СУу (ь>) — спектральная плотность мощности с поправкой на влия-
ние прибора.
Предположение о том, что величина А постоянна, означает,
что спектральная плотность мощности флуктуаций реактивности
является постоянной в интересующем нас диапазоне частот. Это
предположение подтверждено экспериментально. Типичные резуль-
таты экспериментов на реакторе NORA показаны на рис. 11.16.
Величина р// получена подгонкой методом наименьших квадратов
к экспериментальным данным расчетной кривой в соответствии
с уравнением (11.15). Видно, что с детекторами, имеющими доста-
точно высокую эффективность, можно получить удовлетворитель-
ные результаты измерения р//.
Метод двух детекторов. Когда эффективность детектора умень-
шается, отношение сигнал/фон также уменьшается и результаты
измерений становятся хуже. Это затруднение преодолевается путем
использования метода двух детекторов, в котором измеряется взаим-
ная корреляция выходных сигналов двух детекторов. Теорети-
ческие основы этого метода изложены в § 4.14.
329
Обширные серии экспериментов, выполненных на реакторе
STARK в Карлсруэ с применением метода двух детекторов, опи-
саны в работе [21]. Два детектора располагались в трех разных
рядах графитового отражателя и тепловой колонны. Когда они
удалялись друг от друга, отношение сигнал/шум уменьшалось.
На рис. 11.17—11.19 показаны графики спектральных плотностей
выходных сигналов отдельных детекторов и графики взаим-
ной спектральной плотности выходных сигналов двух детекторов.
Рис. 11.16. Сравнение спектральной плотности
шумов мощности реактора NORA
с результатами эксперимента мето-
дом осциллирующего стержня (ре-
актор иа уровне мощности 5 вт, ка-
мера или осциллятор в центре); О —
данные спектра шумов; Д—-данные
осцплляторного метода;----------------г- кри-
вая, полученная методом наимень-
ших квадратов по результатам шу-
мового эксперимента.
Показанная величина QMaKC является максимальным отношением
коррелированных и некоррелированных шумовых компонент, ко-
торое имеет место при низких частотах.
Все эксперименты проводились на мощности 10 ent. Сечение реак-
тора схематично показано в углу каждого графика спектральной
плотности. Реактор состоит в основном из цилиндрической быстрой
сборки (средний диаметр 37 см, высота 61 см), которая окружена
кольцевой зоной реактора типа «Argonaut», и большого графитового
отражателя. Быстрая сборка собрана из 37 вертикальных труб
из нержавеющей стали, наполненных исследуемым материалом ак-
тивной зоны. В этой загрузке обогащение в «быстрой» зоне
составляло 7%235U (45,25 кг). Быстрая активная зона окружена
буферной зоной средней толщиной 5 см из естественного урана для
поглощения тепловых нейтронов, поступающих извне. Тепловая зона
состояла из 332 топливных пластин типа «Argonaut» (6,92 кг 23BU),
разбитых на 24 группы, с расстоянием между пластинами 6,2 мм.
Замедлителем являлась обычная вода с температурой 80° С. Со-
ззо
гласно измерениям с камерой деления, доля мощности, выделяемой
в быстрой зоне, составляет 9%, в буферной зоне из естественного
урана — 11% ив тепловой зоне — 80%. Для измерений спектраль-
ной и взаимной спектральной плотностей мощности две содержа-
щих нзотоп WB гамма-компенсированные камеры располагались
в различных положениях в отражателе.
Серии опытов были выполнены для исследования зависимости
результатов измерений спектральной и взаимной спектральной плот-
ностей мощности от отношения фйгакс и определения минимального
Рис. 11.17. Спектральная и взаимная спектральная плот-
ности мощности в тепловой зоне в зависимо-
сти от частоты [21].
значения этой величины в методе взаимной спектральной плотности.
Методика измерений заключалась в изменении отношения QMaKC пу-
тем удаления камер из внутренней области и расположения их во
внешней области отражателя. Вначале спектральная плотность
была измерена для каждой камеры в положениях и указан-
ных на рис. 11.17. Отношение QMaKC в этих измерениях можно
получить делением постоянного значения спектральной плотности
при частоте около 1 гц (коррелированные плюс некоррелированные
шумы) на постоянное значение спектральной плотности при высо-
ких частотах (некоррелированные шумы), т. е.
(U + Q/U = 1 + C/U = I + QMBKC, (11.16)
где U и С — некоррелироваииая и коррелированная компоненты
шума соответственно.
Для одинаковых камер в положениях и отношение QMaKC
больше для камеры в положении так как она ближе к тепловой
331
зоне. Частотный состав взаимной спектральной' плотности для двух
камер в положениях и также показан на рис. 11.17. Затем
камера из положения Вг была переставлена в положение В 2 так, что
средний ток камеры в положении В2 составлял 25% от. тока камеры
в положении В±. Камера, находившаяся в положении была по-
мещена в точку Кг» где ее средний ток равен току камеры в поло-
жении В2. Поскольку эффективности камер в положениях Bz и
К2 равны, то для определения -Смаке измерялась только спектраль-
ная плотность мощности. Этот результат и взаимная спектральная
плотность для положений и ^2 показаны на рис. 11.18. Умень-
Рис. 11.18. Спектральная и взаимная спектральная плот-
ности мощности (СПМ и ВСПМ) в тепловой
зоне в зависимости от частоты [21].
шение Смаке ДО 0,5 заметно влияет на автокорреляционные изме-
рения. В последних двух опытах камеры удалялись в положения
/С3 и В3, где их средние токи были равны между собой и составляли
20% от тока в положениях ЛгиВй соответственно (см. рис. 11.19).
Кривая спектральной плотности на рис. 11.19 почти плоская, и
отношение фмакс падает до 0,1. В том случае, когда получить по-
лезную информацию из автокорреляционных экспериментов нельзя,
дает еще надежные результаты двухдетекторный взаимный кор-
реляционный метод, как это видно из распределения взаимной спе-
ктральной плотности на рис. 11.19. Однако необходимо отметить,
что время, требуемое для анализа, с уменьшением Смаке увеличи-
вается.
Из результатов экспериментов можно сделать вывод, что для
автокорреляционного измерения с помощью одного детектора от-
ношение Смаке должно равняться по крайней мере 2, чтобы полу-
чить правильную постоянную спада мгновенных нейтронов. ДвуХ-
332
детекторные взаимные корреляционные измерения могут быть про-
ведены для значений Q„nKC, снижающихся до величины 0,1. В этом
случае результаты получаются вполне удовлетворительными, а эф-
фективность детектора уменьшается примерно в 20 раз.
Измерение 09ф в реакторе с циркулирующим топливом. Об
интересном применении шумовых методов для измерения величины
раф в реакторе с циркулирующим и стационарным топливом сооб-
щалось недавно в работе [22]. Измерения проводились на экспе-
риментальном реакторе с топливом' в виде раствора соли урана
(MSRE). Реактор MSRE является реактором с графитовым замед-
лителем и жидким топливом, тепловая мощность которого 10 Мет.
Циркулирующее топливо находится внутри активной зоны 9 сек
и вне активной зоны в контуре теплоносителя около 16 сек. Стан-
дартные измерения спектральной плотности проводились на мощ-
ности 10 вт в критическом состоянии реактора с циркуляцией теп-
лоносителя и без циркуляции. Экспериментальные данные аппрок-
симировались методом наименьших квадратов выражением вида
(11.15), в котором в передаточную функцию реактора был включен
вклад запаздывающих нейтронов.
Экспериментальные данные и аппроксимирующие их теоретиче-
ские кривые показаны на рис. 11.20, а, где кривая А соответствует
случаю циркулирующего топлива, а кривая В случаю стационар-
ного топлива. На рис. 11.20, б и 11.20, в показаны спектры после
вычитания фона, вызванного шумами детектора. В обоих случаях
время генерации нейтронов равно 290 мксек, а значения рэф для
случаев циркулирующего и статического топлива 0,00428 и 0,00678
333
0,1 0,2 0,5 1 2 5 10 20 50
, Частота, гц
а
Рис. 11.20. Измеренные спектры ней-
тронной мощности, норми-
рованные на постоянный
ток ионизационной камеры
для реактора MSRE при
мощности 10 вт [22]:
а — спектры до вычитания
шумов детектирования (Л —
циркулирующее топливо. В—
неподвижное топливо): б—
спектр за вычетом шумов де-
тектирования с циркуляцией
топлива (--------------------расчетная
кривая, для которой Л=
=2,9-10—* сек; fW - 0,00428,
Х=0,87 €₽«-’; е — спектр за
вычетом шумов детектирова-
ния для неподвижного топли-
ва (---------— расчетная кри-
вая, для которой Л=2,9Х
Х10-* сек, Рпф =0,00678.
=0,87 сек-*).
334
соответственно. Хотя погрешности этих измерений довольно вели-
ки, доказана принципиальная возможность применения шумового
метода для измерения 0яф. Точность можно повысить с помощью
двухдетекторного метода, рассмотренного в § 4.14.
Автокорреляцйонный метод. В § 4.9 мы получили соотношение
для автокорреляционной функции выходного сигнала системы,
у которой импульсная переходная функция описывается экспонен-
Рпс. 11.21. Горизонтальное сечение реактора LFR, пока-
зывающее положения детектора [23].
той и на входе которой имеется сигнал в виде белого шума. В этом
случае автокорреляционная функция имеет вид
flw (*) = К1 ехр ( —от), (11.17)
где — постоянная, сс — постоянная спада в системе.
Если система содержит фоновые шумы (шумы детектора), кото-
рые не зависят от входного сигнала, можно использовать принцип
суперпозиции для автокорреляционных функций, данный уравне-
нием (4.27), откуда
4W W = М ехр (—от) + <рп„ (т), (11.18)
где фпп (т) — автокорреляционная функция фоновой компоненты.
Если фоновый шум белый, то
(т) = Ki ехР ( — ат) 4-/<2б (т) (11.19)
и фоновые шумы не влияют на измерение постоянной спада экс-
поненты. Если фоновый шум не является белым, то функция <рпп (т)
обычно быстро стремится к нулю с увеличением т и в автокорреля-
ционной функции остается один экспоненциальный член. Следова-
тельно, можно измерить величину росси-альфа реактора. Примером
такого типа экспериментов является измерение на низкопоточном
реакторе LFR [23]. На рис. 11.21 показаны активная зона реак-
тора LFR и четыре положения детектора в этом эксперименте.
На рнс. 11.22 приведены автокорреляционные функции, получен-
ные в этих четырех положениях детектора. Для всех четырех слу-
335
чаев наклоны экспонент совпадают, но качество данных заметно
ухудшается с уменьшением эффективности детектора, так как
отношение сигнал/фон уменьшается.
Рис. 11.22. Автокорреляционные функции, из-
меренные при различных положе-
ниях детектора в критическом реак-
торе [23].
Генератор случайного сигнала Система возмущения реактивности
Рис. И.23. Схема случайного возмущения реактивности [24].
Метод взаимной корреляции. В § 4.9 было показано, что взаим-
ная корреляционная функция системы пропорциональна импульс-
ной переходной функции, если входной сигнал является белым шу-
мом. На практике это соотношение считается справедливым, ^если
336
р(Р,отн.ед, <p(t),imn.ed.
Рнс. 11.24. Автокорреляционная н взаимная
корреляционная функции для слу-
чайного возмущения реактивности
со среднеквадратической амплиту-
дой рср.кв=1»Ь-10-
а — непосредственно из зарегистриро-
ванных сигналов; б — нз сигналов, про-
пущенных через простой низкочастот-
ный фильтр с частотой среза 20 расЦсеК--,
е —из сигналов. пропущенных через
простой низкочастотный фильтр с часто-
той среза 2 рад/сек J34].
337
cneicif альная плотность мощности входного сигнала постоянна в ин-
тересующем нас диапазоне частот. В работе [24] этот метод приме-
нялся для измерения импульсной переходной функции реактора
в Брукхейвене. Радиоактивный источник создавал случайные флук-
Рнс. 11.25. Передаточная функция
реактора:
а — амплитуда; б — фаза;
О — экспериментальные
данные при рср.кв. =
= 1.5- I0-* сек; А — экс-
периментальные данные
при рср.кп s 3,0-10-*;
---------расчетные кри-
вые при Д=200-10“Б сек,
₽эф=0.ББ I0-- [241.
туации, которые усиливались
и затем подавались для управ-
ления электромеханическим ос-
циллятором случайной реак-
тивности. Эта система показана
на рис. 11.23.
На рис. 11.24 показаны авто-
корреляционная функция вход-
ного сигнала и взаимная корре-
ляционная функция между флук-
туациями внешней реактивности
и выходным сигналом флуктуа-
ций плотности нейтронного по-
тока. Поскольку входной сиг-
нал ие является белым шумом,
необходимо использовать интег-
рал свертки для получения ис-
тинной импульсной переходной
функция. Однако обычно при-
меняют преобразование Фурье
автокорреляционной функции
входного сигнала и взаимной
корреляционной' функции вход-
ного и выходного сигналов и
цию нз отношения взаимной
получают передаточную функ-
спектральной плотности к спект-
ральной плотности мощности входного сигнала. Результаты такого
измерения на брукхейвенском реакторе показаны на рис. 11.25.
§ 11.4. Измерения реактивности
Метод измерения спектральной плотности мощности. Об изме-
рениях реактивности в заглушенных ядерных реакторах с приме-
нением шумовых методов впервые сообщалось в работе [25]. Факти-
чески это были измерения величины росси-альфа, которые могли
интерпретироваться в терминах реактивности, если эффективное
время жизни нейтронов и эффективная доля запаздывающих ней-
тронов известны из расчетов нлн других экспериментов. Эти изме-
рения были выполнены на учебном реакторе Флоридского универ-
ситета, который является реактором типа Argonaut, с плутоннево-
бериллиевым источником нейтронов, расположенным близко к од-
ной из двух топливных зои. Высокоэффективный детектор распола-
гался в центре замедлителя между двумя топливными зонами. Тех-
ника измерений аналогична применявшейся Коэном [201 дляопреде-
338
ления р// в критических системах, только возмущением системы
являлись флуктуации мощности источника вместо флуктуаций
реактивности. Теория этого метода подробно рассматривалась
в § 6.3. Система описывалась передаточной функцией одноточеч-
ного реактора, которая с хорошим приближением может быть
представлена в виде
H(w) = l/(j w + a), (11.20)
где а определяет частоту излома. Росси-альфа-постояиная равна
а = [1 — k (1 — £)]// = (₽ — р)/Л. (11-21)
Измерялась спект-
ральная плотность мощ-
ности выходного сигна-
ла. Затем вводились
необходимые поправки
на динамические харак-
теристики аппаратуры
и методом наименьших
квадратов теоретическая
модель подгонялась к
экспериментальным дан-
ным. Таким образом,
оценивалось значение а
Рис. 11.26. Калибровка измерительной аппа-
ратуры [25].
в соответствии с уравнением (6.16). Для скорректированной
спектральной плотности можно записать
ей (о) = °т (ю) = —— +в,
|#1(0»|3 Ш2+и=
(11.22)
где А и В — постоянные; GVIi (со) — измеренная спектральная
плотность; Gys/ (со) — спектральная плотность мощности после кор-
рекции иа динамические характеристики аппаратуры Н2 (со).
Частотные характеристики аппаратуры определялись калиб-
ровкой системы с помощью нейтронного генератора, выход которого
изменялся по синусоидальному закону. Результаты калибровки
показаны на рис. 11.26. Измеренная спектральная плотность дели-
лась на величину | (со) |2 для получения скорректированной
спектральной плотности G1jy (<о)/| (со) |2. Затем минимизирова-
лась сумма
----в-----А_
|^i(<o)|3 с^+а3’ k '
где каждая точка бралась с одинаковым весом. Параметрами, кото-
рые варьировались для лучшей.подгонки, были Л, В и а. Расчет
выполнялся и а ЦВМ.
На рис. 11.27 показаны четыре скорректированные кривые спек-
тральной плотности мощности, пронормированные при частоте
339
2000 гцу полученные для одной загрузки. Кривые описываются
приведенными выше уравнениями, и уровни при низкой и высоких
частотах хорошо определяются.
Хотя представленные измерения были по сегодняшним стан-
дартам относительно грубыми, они привели к разработке усовер-
шенствованных методов измерения реактивности (фактически а)
путем использования шумов. Одним из основных ограничений этого
метода являлась необходимость применения высокоэффективного
детектора. Когда подкрптичность (фактически <х) увеличивается,
качество измерения ухудшается, так как отношение сигнал/фон
{А!о?)!В = QMaKC уменьшается пропорционально 1/а2.
Рис. 11.27. Измерения спектральной плотности мощности
для четырех конфигураций реактора. Все дан-
ные нормированы па значение прн частоте
2000 гц [25]:
• .— опыт А. волн залита, стержни 2 и 3 извлечены;
Д—опыт В, вода залита, стержень 3 извлечен;
А—опыт С, вода залита, все стержни введены;
О — опыт Д, вода слита, все стержни введены.
Одна из проблем анализа реакторных шумов — уменьшение
содержания паразитных шумов, особенно шумов детектора и ап-
паратурных шумов. В соответствии с уравнением (11.22) компонента
шумов детектора В пропорциональна эффективности детектора
е, тогда как величина А пропорциональна е2. На рис. 11.28 показаны
идеальные спектры мощности, содержащие постоянный фон [26].
При высоких частотах составляющая реакторных шумов становится
меньше, чем составляющая шумов камеры, так что в конечном итоге
наблюдаются только последние шумы. Высокие эффективности де-
тектора, очевидно, могли бы позволить наблюдать реакторные шумы
при высоких частотах, но шумы камеры остаются помехой, особен-
но при анализе шумов в подкритическом состоянии. Даже в низко-
частотной области реакторные шумы становятся меньше, чем шумы
камеры для глубокого подкритического состояния системы. Чтобы
получить высокую эффективность детектора, его целесообразнее
помещать в активную зону и соединять несколько детекторов па рал-
340
лелыю. Этими методами можно усилить сигнал камеры, но шумовая
компонента полностью не подавляется.
В работе [26] предложен другой метод измерения реактивности.
Этот метод иллюстрируется рис. 11.29. Кривые спектральных плот-
ностей построены с учетом запаздывающих нейтронов, хотя обычно
желательно ограничиться измерениями в области высоких частот,
где справедливо упрощенное представление передаточной функции
в соответствии с уравнением (11.22). Если измерения ограничены
частотным диапазоном, в котором спектральная плотность мощности
входного сигнала постоянна, отношение спектральных плотностей
Рис. 11.28. Теоретические спектры шумов реактора (с фо-
ном) [26]:
--------- с постоянной спектральной плотностью
фона; ---— —без фона.
выходного сигнала при частотах и fs, как показано на рис. 11.29,
можно использовать для определения реактивности- Это отношение
определенное как
= Gyll (f^Gyy (fj = A‘„ (f„)/A*„ (fj, (11.24)
где A}jV представляет квадрат амплитуд при и f2, связано с ре-
активностью соотношением
Значения частот и /2 подбираются так, чтобы усилить зави-
симость р от R. Кроме того, должна, на ходиться в плоской части
кривой, изображенной на рис. 11.29, тогда как должна выби-
раться больше частоты излома, определяемой а. -Ширина полос
пропускания для двух измерений на частотах и должна быть
одинаковой, но поскольку шкала частот на рис. 11.28 логарифмн-
341
ческая, полосы частот кажутся разными. Однако в некоторых слу-
чаях необходимо, чтобы значения Q фильтров были равны, т. е.
Q = Л/Д Л = ЛУД h, (И.26)
особенно в случаях, когда фильтры сильно отличаются от идеаль-
ного.
На рнс. 11.29 представлены идеальные условия измерения, когда
существует очень высокое отношение сигнал/шум. На самом деле
фон, обусловленный шумами детектора, усилителя и некоррелиро-
ванными с шумами реактора, будет изменять спектры, как показано
на рис. 11.28. При этих условиях на выбор частот накладывается
Рис. 11.29. Теоретические спектры шумов реактора
(без фона) [26]:
G(fi)/G(f8)=8.0 (критическое состояние);
Gtfi)/G(fs)“2.9 (Р“—1Р); -1.8
(р= -2₽).
дополнительное ограничение в том смысле, что они должны быть
низкими, чтобы отношение сигнал/фон было приемлемым. Это огра-
ничение можно преодолеть в значительной степени применением
двухдетекторного метода, который обсуждается ниже.
Влияние выбора частот было показано Шульцем [27] в ряде экс-
периментов, выполненных на чистой критической сборке CES.
Результаты приведены на рис. 11.30, где6(100)/6 (10) представляет
отношение корня квадратного из среднего квадрата амплитуды
выходного сигнала полосового фильтра с центральной частотой
100 гц к корню квадратному из среднего квадрата амплитуды выход-
ного сигнала идентичного полосового фильтра с центральной часто-
той 10 гц. Следовательно, мы можем определить отношение амплитуд
(11.27)
которое соответствует определению (11.24). Экспериментальные
результаты на рнс. 11.30 согласуются с теоретическими расчетами*
основанными на передаточной функции реактора CES.
342
На рис. 11.31 показана экс-
перимента льная зависимость,
полученная для критического
и подкритического состояний
сборки CES.’Видно, что от-
ношение G (600) IG (10) не из-
меняется с изменением уровня
мощности критического реак-
тора н существенно меняется
с изменением реактивности
подкритического реактора.
Некоторую вариацию это-
го метода использовал Шульц
[27] для измерения реактивно-
сти. В этом эксперименте сиг-
нал нейтронного детектора де-
лился на две частотные обла-
сти, высокую и низкую, про-
пусканием сигнала через вы-
сокочастотный и низкочастот-
ный фильтры, соединенные
параллельно. Отношение ам-
плитуд взято вместо отноше-
ния спектральных плотностей
____I___J----J-----1---1----1----0,10
-7 -6 -5 -4 -3 ~2 -1 0
Степень подкритичности лк, %
Рис. 11.30. Экспериментальные за-
висимости отношения
спектральных плотно-
стей от Дк. "*
0/ -
0,2
0,1
0
40 ~8 -4 -2 0 20 40 60 80 100120
Степень подкритич- Мощность, От
ности &/(,%
§
Рис. 11.31. Отношение спек-
тральных плотностей
|G(600) |/|G(10) | в
зависимости от мощ-
ности Л/г н от-
ношение спектраль-
ных плотностей
|G(600)[/|G(10)] в
зависимости от мощ-
ности при Д/г=О.
полученные на реак-
торе CES [27] .
мощности. Принципиальное преимущество такого метода заключает-
ся в том, что амплитуды двух выходных сигналов много больше,
чем в случае применения узкополосных фильтров, и, следовательно,
точность для данного времени измерения выше. Для каждой конфи-
гурации реактора эту систем)? необходимо калибровать экспери-
ментально. Кроме того, она очень чувствительна к флуктуациям
уровня фоновых шумов.
Метод взаимной спектральной плотности. Принципиальные
недостатки метода измерения спектральной плотности мощности,
основными из которых являются требование высокой эффективности
детектора и высокий уровень фона, были преодолены в методе, пред-
ложенном практически одновременно в Японии и ФРГ [28, 29].
343
В этом методе два детектора помещены рядом и измеряется взаимная
спектральная плотность двух выходных сигналов. Метод по сущест-
ву эквивалентен автокорреляционному методу, описанному выше.
Однако тот факт, что плотность нейтронов измеряется путем погло-
щения нейтронов в отдельных детекторах, приводит к тому, что
шумы регистрации этих двух детекторов иекоррелированы. Следо-
вательно, метод измерения взаимной спектральной плотности эф-
фективно устраняет нежелательный высокий фон путем умножения
и интегрирования. Таким образом, постоянная спада может быть
измерена детекторами, имеющими много меньшую эффективность.
Основная теория двухдетекторных взаимных корреляционных из--
Рнс. 11.32. Структурная схема, применявшаяся в работе
[30] для измерения спектральной плотности
шумов мощности реактора.
мерений дана в § 4.14. В качестве примера рассмотрим работу [30]„
которая иллюстрирует применение двухдетекторного метода для
измерения реактивности.
Структурная схема, применявшаяся для измерения спектраль-
ной плотности мощности реактора, показана на рнс. 11.32. Чтобы
получить высокий уровень нейтронного потока в подкритическом
состоянии и исключить пространственную зависимость, присущую
обычному источнику нейтронов, шумы подкритического реактора
бассейнового типа TTR-1 (учебный реактор в Тошиба) измерялись
при введении стержня, когда мощность реактора медленно умень-
шалась с постоянным периодом, определяемым постоянной спада
запаздывающих нейтронов. В этом случае источником нейтронов
был предшественник запаздывающих нейтронов, который распа-
дался с наименьшей постоянной спада. Строго говоря, рассматри-
ваемый процесс является нестационарным. Однако определение ос
связано с анализом поведения мгновенных нейтронов, наблюдаемо-
го за очень короткий период времени (или в области высоких
частот спектральной плотности). В области высоких частот выпол-
няется предположение, что входные сигналы стационарны. В этом
344
эксперименте сигналы детекторов преобразовывались из флуктуаций
тока во флуктуации напряжения и записывались в течение 40—
50 сек. Затем выходные сигналы записывающего устройства отдельно
усиливались и подавались на полосовые фильтры, опять усилива-
лись и перемножались на электронном множителе. Выходной сигнал
миожителя интегрировался в течение времени записи.
На рис. 11.33 показаны измеренные спектральные плотности вы-
ходных сигналов двух детекторов, расположенных симметрично на
краю активной зоны реактора TTR-1. Измерения проводились
в критическом состоянии и для четырех положений стержня регу-
лирования, а также при полностью введенном стержне аварийной
Рис. 11.33. Спектральная плотность мощности выходного
сигнала детектора № 1, нормированная на уро-
вень шумов камеры [30]:
О — критическое состояние, о — стержень регулиро-
вания введен на 300 ям; □—стержень регулировании
введен на 400 *—стержень регулирования вве-
ден на 500 Д — стержень регулирования введен
на 800 мм; А—стержень аварийной защиты введен
на 800 мм.
защиты. Видно, что компонента реакторных шумов уменьшается
при увеличении подкритичности. В частности, в случае введения
стержня аварийной защиты никакой информации нельзя получить,
так как кривая спектральной плотности почти плоская. Кривые,
показанные на рис. 11.34, были получены корреляционным методом
с применением аппаратуры, структурная схема которой приведена
на рис. 11.32. Ясно, что шумовая компонента камеры [член В в урав-
нении (11.22)] исключена и можно получить информацию для
глубокого подкритического состояния. Форма кривой распределе-
ния взаимной спектральной плотности описывается выражением
^^М = Л/(й2+а2)> (11.28)
где А — постоянная спектральная плотность белого шума входного
сигнала.
345
Время жизни нейтронов было найдено из соотношения ас —
для критического состояния и оказалось равным 8,12 • 10-6 сек.
при р = 0,00785. Реактивности в различных состояниях подкритич-
ности определялись из соотношения p/р = (ас—а)/ас.
Рис. 11.34. Взаимная спектральная плотность [30]:
О — критическое состояние; о — стержень регу-
лирования введен на 400 juh; • —стержень регу-
лирования введен па 500 мм; А — стержень регу-
лирования введен на 800 лш; А —стержень ава-
рийной защиты введен на 800 мм.
В табл. 11.1 приведены величины а и реактивности для несколь-
ких состояний подкритичности, определенные методом анализа реак-
торных шумов, и для сравнения —- методом положительного
периода.
Таблица 11.1
Значения а и реактивности, измеренные на реакторе TTR-1
Состояние подкритичностн а, сек""1 Реактивность. рэф
Метод реакторных шумов Метод реакторных шумов Метод положитель- ного периода
Критическое состояние Стержень регулирования введен на 300 мм Стержень регулирования нведен на 400 мм Стержень регулирования введен на 500 мм Стержень регулирования введен на 800 мм Стержень аварийной защиты вве- ден на 800 мм 96,3±0,9 129,24-1,4 145,2±1,7 155,0± 1,8 168,8±2,3 448,0±9»5 0.341 0,507 0,610 0,753 3,651 (Г, 345 0,530 0,680 0,762
346
Автокорреляционная функция. В § 11.3 была описана серия
экспериментов, выполненных на реакторе LFR [31]. С помощью
той же самой методики были проведены измерения на реакторе
LFR -для четырех подкритическнх состояний. Для интерпретации
этих измерений применялись уравнения (11.18) й (11.19).
На рис. 11.35 показаны четыре автокорреляционные функции,
переходящие в экспоненты примерно через 6 мсек. Как и раньше,
качество измерений ухудшается, когда с увеличением подкритич'
ности отношение сигнал/фон уменьшается.
Рис. 11.35. Автокорреляционные функции шумов
реактора LFR в подкрнтических со-
стояниях [23].
Метод взаимной корреляции. Измерение взаимной корреляции
между входным и выходным сигналами для определения функции
отклика системы было впервые применено к ядерным реакторам
в работе [32], где измерялись импульсная переходная функция
н передаточная функция реактора — прототипа ядерных ракет-
ных двигателей (KIWI-A-1). Применение этого метода для измере-
ния реактивности подкритическнх систем было предложено неза-
висимо Уригом [33] и Штерном и др. [34]. Метод включает в себя
использование псевдослучайной двоичной последовательности,
автокорреляционная функция которой та же, что у гауссова слу-
347
чайного шума. Эта последовательность импульсов создается ней-
тронным генератором, расположенным в подкритическом реакторе.
Измеряется взаимная корреляция между выходным сигналом детек-
тора, расположенного в подкритическом реакторе, и псевдослу-
чайным входным сигналом. В результате получается импульсная
переходная функция системы, которая затем подвергается фурье-
анализу для определения передаточной функции. Импульсная пе-
реходная функция системы с сосредоточенными параметрами опи-
сывается экспонентой вида ехр (•— ссГ), где а является росси-
Рис. 11.36. Структурная схема псевдослучайной импульсной си-
стемы [34].
альфа-постоянной системы. Следовательно, можно определить из
импульсной переходной функции значение». Обширное эксперимен-
тальное исследование этого метода выполнено в работе [35].
Строго говоря, нет необходимости применять псевдослучайную
последовательность импульсов для измерения реактивности в под-
критической системе, но преимущества этого метода намного превы-
шают его недостатки, даже в том случае, когда отличительные ха-
рактеристики псевдослучайной двоичной последовательности не
используются. Характеристики псевдослучайных величин обсуж-
дались подробно в гл. 9.
На рис. 11.36 показана структурная схема экспериментального
оборудования с одним детектором. Система обработки данных соз-
дана на базе 1024-каиальиого полупроводникового анализатора
348
с подсоединенным к нему блоком логики. Блок логики дает возмож-
ность анализатору работать как системе с последовательно откры-
вающимися счетчиками, каждый из которых принимает импульсы
в течение заранее определенной длительности времени. Мини-
мально допустимая ширина канала, когда блок логики работает
как внешнее распределительное устройство, составляет 100 мксек,
которая включает в себя 20 мксек мертвого времени, необходимого
для передачи данных в память. В дополнение к входному сигналу
от детектирующей системы на многоканальный блок логики подают-
ся даа других сигнала: команда на внешнее распределительное
устройство и сигнал триггера, который служит в качестве команды
на восстановление начальных условий. Когда накапливаются дан-
ные в 1024 каналах (256 или 512 каналах, если используется */4
или % часть памяти), система останавливается, пока не приходит
вторая команда от триггера. Особенностью схемы является то, что
многоканальный счетчик не принимает следующую команду на
возврат в исходное состояние, пока не закончит цикл через все
1024 канала. Следовательно, данные регистрируются только в тече-
ние каждого цикла. Хотя это увеличивает время эксперимента и
может вызвать трудности в интерпретации результатов измерения
величины кр//, следует указать, что эта проблема разрешима. Схему
многоканального анализатора можно модифицировать для исклю-
чения описанных выше трудностей-
Детектирующая система и связанные с ней электронные устрой-
ства были обычными и собирались из стандартных блоков. В за-
висимости от вида измерений использовались два типа детекторов.
Для измерения импульсной переходной функции сборки при различ-
ных геометрических параметрах применялся гелиевый детектор
длиной 30 см с внешним диаметром 2,5 см, расположенный вне сбор-
ки. Для измерений распространения импульса специально скон-
струированная камера деления в форме плоского диска диаметром
7,5 см и толщиной 0,6 см располагалась между отдельными топлив-
ными пластинами системы. Основой системы был генератор псев-
дослучайной двоичной последовательности импульсов, который
состоял из регистра сдвига на много ячеек с соответствующей об-
ратной связью, обеспечивающей получение последовательности
импульсов максимальной длины. Для большинства обсуждаемых
экспериментов использовался регистр сдвига с восемью ячейками,
который управлялся кварцевым генератором на 10 кгц через дели-
тель частоты, дающий частоты сдвига 10 кгц, 5 кгц, 2,5 кгц и т. д.
Выходной сигнал каждой нз восьми ячеек подавался иа схему «И»
с восемью входами. В конце последовательности выходные напря-
жения всех восьми ячеек находились в состоянии «I», и схема «И»
выдавала импульс, который затем использовался для синхрониза-
ции триггера, дающего команду на возвращение в исходное состоя-
ние на вход блока логики. Выходной сигнал последней ячейки
регистра сдвига управляет через триггеры Шмитта работой
импульсной системы нейтронного генератора.
349
Для правильного накопления данных важно, чтобы генератор
псевдослучайной двоичной последовательности и система накопления
данных были синхронизированы. Это достигается путем использова-
ния импульса триггера из схемы «И» регистра сдвига в качестве
команды на возврат в исходное состояние и сигнала генерато-
ра, управляющего работой регистра сдвига в качестве внешнего
пускового канала многоканального счетчика блока логики. Таким
образом, поддерживается синхронизация между i-м каналом много-
канального счетчика и ячейкой регистра сдвига. Поскольку бы-
стродействие системы накопления данных в два или более раз боль-
ше быстродействия регистра сдвига, можно распределять по два
или более каналов для каждого сдвига регистра. При этом улуч-
шается временное разрешение, но требуется более длительное время
измерения, чтобы не ухудшалась точность измерения в отдельной
точке.
В некоторых экспериментах применялся ускоритель Ваи-де-
Граафа на 4 Мэв (модель KN-4000), дающий ток 300 мка. Однако
средний ток пучка на мишень был обычно 20—50 мка. Энергия па-
дающих частиц поддерживалась в пределах ± 2 кэв в диапазоне от
1 до 4 Мэв. Таким образом, возможны выбор мишеней и, в свою
очередь, широкий выбор энергий нейтронов. Для описанных
здесь экспериментов использовалась литиевая мишень, которая
давала нейтроны с энергией ~ 300 кэв. Ускоритель монтировался
вертикально, как показано на рис. 11.37, и пучок направлялся вниз,
где с помощью магнита он заворачивался в горизонтальную плос-
кость и проходил через фокусирующий магнит иа мишень, произ-
водящую нейтроны, которая располагвлась рядом со сборкой, на
которой проводились опыты. Блок импульсов высокого напряжения
нейтронного генератора управлялся регистром сдвига через триг-
гер Шмитта. Эта схема дифференцирует прямоугольный импульс
случайной ширины, поступающий от регистра сдвига, и выдает на-
чальный и конечный импульсы, которые управляют отклоняющи-
ми пластинами, расположенными сразу же после фокусирующего
магнита. Блок импульсного высокого напряжения и отклоняющие
пластины позволяют получать импульсы шириной от нескольких
микросекунд до нескольких миллисекунд. Этот диапазон достато-
чен для псевдослучайных импульсных экспериментов.
В экспериментах использовалась подкритическая импульсная
-сборка Флоридского университета UFAPA, показанная иа
рнс. 11.38. Эта сборка является размножающей системой с замедли-
телем (обычной водой) и высокообогащенным топливом. Она по-
ставлялась как подкритическая система с максимально возможным
значением /гаф = 0,98. Однако с применением обычного импульс-
ного метода было, найдено, что максимальное значение /гэф для
сборки без отражателя равно 0,952.
Теоретически сборка может рассматриваться как «голая» систе-
ма. Изменение реактивности осуществляется только изменением
.уровня замедлителя, вытекающего через два слива треугольной
350
формы, расположенные в одном конце сборки, как показано на
рис. 11.38. Скорость наполнения бака водой регулируется клапа-
ном, управляемым системой автоматического регулирования. Ава-
рийная остановка обеспечивается двумя управляемыми с помощью
соленоидов клапанами, которые нормально закрыты. Во время экспе-
риментов сборка UFAPA закрывалась со всех сторон кадмием тол-
щиной 0,1 см для уменьшения влияния нейтронов, отраженных
от стен зала.
Рис. 11.37. План расположения импульсного нейтронного гене-
ратора Ван-де-Граафа [34]:
1 — кирпичная облицовка; 2— ускоритель Ван-де-Граафа;
3— двери: 4— крышка люка; 5 —кирпичная облицовка;
б —щели для пучка ускорителя; 7 — реактор UFAPA;
В — отклоняющий магнит; 5 — поворотный базис.
Полученные данные вначале корректировались на соответству-
ющее мертвое время анализатора путем линейного увеличения чис-
ла импульсов в каждом канале. Затем вычиталось среднее значение
скорости счета и вычислялись необходимые корреляционные функ-
ции. Так же вычислялись корреляционные функции для отрицатель-
ных временных сдвигов. Описанным выше методом был выполнен'
ряд экспериментов на сборке UFAPA для определения импульсной,
переходной функции и характеристик распространения импульса.
Измерения проводились с помощью ускорителя Ван-де-Граафа с.ли-
351.
тиевой мишенью, которая являлась источником нейтронов с энер-
гией 300 кэв.
В типичном эксперименте ускоритель модулировался псевдо-
случайным сигналом, полученным от регистра сдвига с 8 ячейками,
Рис. 11.38. Схема сборки UFAPA [34]:
/ — две коробки для уплотнения винтов, скрепля-
ющих основание; 2 — дно слива; 3— вертикальная
пластина, регулирующая слив (диапазон переме-
щения 125 лыс); 4 — основание из алюминиевого
бруска толщиной 12,5 лиг; 5 — входной трубопро-
вод; 6 —прорези для расположения отдельной
топливной пластины: 7— топливные пластины с
ураном 93%-ного обогащения в алюминиевой оче-
хловке (5 рядов с 49 пластинами на ряд); В—поло-
жение направляющих шпилек; 9—верхняя рама
(AI) с прорезями шириной 10 лиг, /0—бруски, рас-
ставленные с промежутком (AI); И — перекрыва-
ющиеся площади бака и пластины для скрепления
и герметизации; Й—два слива треугольной фор-
мы с углом наклона 30°; 13 — открытая верхняя
часть устройства для слива; 14 — два свинцовых
винта для регулирования высоты в диапазоне
125 Л1м; 15 — гибкая дренажная труба для слива;
15 — два клапана сброса воды диаметром 37 лиг,
приводимые в действие соленоидом (нормально
открытые); 17— аварийный слив воды из бака.
дающего 5000 сдвигов в секунду. Для этих экспериментов детек-
тор малых размеров размещался в различных положениях внутри
сборки. Использовались 4 выборки иа сдвиг, причем максималь-
ный счет в любом канале составлял 216. Результаты показаны на
рис. 11.39.
352
Импульсная переходная функция сборки была получена для
различных уровней воды, соответствующих различным подкритич-
ностям, с применением большого детектора, расположенного вдоль
одной стороны сборки. При проведении этих измерении нейтрон-
Рис. 11.39. Экспериментальные результаты, полученные на
сборке UFAPA псевдослучайным импульсным мето-
дом при двух уровнях воды (5000 сдвигов в секун-
ду, две выборки на сдвиг) [34]:
О—уровень воды 410 лыс, а=Ш5 сею-1; А —уровень во-
ды 440 мм. Ц“1065 сек-'; □—уровень воды 460 мм,
а=908 сек-’; © — уровень воды 490 мм, а-=830 сек-’;
А — уровень воды 515 мм, а”710 сек-1.
ный источник (в данном случае ускоритель Кокрофта — Уолтона на
150 кэв, использующий для производства нейтронов с энергией
14,7 Мэв реакцию D — Т ) располагался в центре, в средней точке
между дном сборки и уровнем воды. После введения соответствую-
щих поправок на фон и отрицательные боковые полосы автокор-
12 Зак. 576 353
реляционной функции входного сигнала были получены результаты,
показанные на рис. 11.40.
Чтобы измерения были правильными, необходимо иметь времен-
ные постоянные системы много меньшие, чем период последователь-
ности импульсов входного сигнала (в 5 или более число раз). Кроме
Рис. 11.40. Экспериментальные результаты, полученные иа
сборке UFAPA методом псевдослучайных им-
пульсов (высота воды 500 мм; 5000 сдвигов в
секунду; 4 выборки if а сдвиг; регистр сдвига
иа 8 положений; детектор—•плоская камера де-
ления— располагался между топливными пла-
стинами) [34].
Расстояние от мишени до сборки: О—300 -n.it, * —
515 мм.
того, импульсная переходная функция не должна существенно
изменяться за интервал Д, который является средней шириной
входной автокорреляционной функции треугольной формы. Очень
часто невозможно удовлетворить указанное требование на началь-
ном участке импульсной переходной функции, где функция очень
быстро возрастает. В общем случае это будет вносить искажение и
354
вызывать смещение максимума импульсной переходной функции.
Эффект минимизируется путем оптимального выбора частоты реги-
стра сдвига и числа выборок на интервал А регистра сдвига. Для
удовлетворения перечисленных выше условий необходимо, чтобы
выполнялось соотношение
А<7<(2« —1) А, (11.29)
где Т — постоянная времени исследуемой системы.
Другой метод получения данных с помощью псевдослучайных
двоичных флуктуаций интенсивности нейтронного источника для
измерения реактивности подкритической системы был предложен
Рис. 11.41. Система для измерения взаимной корреляции.
в работе [34]. Усовершенствованный вариант этого метода исполь-
зовался в работе [36]. Структурная схема показана иа рис. 11.41.
Корреляционная функция определялась путем применения псев-
дослучайной двоичной последовательности, воздействующей с за-
паздыванием на время iA (i — 1, 2, ... 2rt-1) и а электронные «воро-
та», управляющие потоком импульсов от детектирующей системы
к ряду счетчиков. «Ворота» служат в качестве множителя запазды-
вающей псевдослучайной переменной (которая принимает значения
нуль и единица, как обсуждалось в § 9.7) на выходной сигнал реак-
тора, представленный импульсами детектора. Интегрирование осу-
ществляется счетчиками, которые служат в качестве сумматора.
Каждый из счетчиков М (£Д) получает импульс с (?) только тогда,
когда его «ворота» открыты. «Ворота» открываются, когда соот-
ветствующий сигнал s (t — tA), открывающий «ворота», положитель-
ный. Для символической записи работы этого устройства примем,
что Л4+ (?А) — полное число импульсов, полученных за время Т
12* 35Б
(зарегистрированных счетчиком М (г'Д) 1, когда s (t — iti) — поло-
жительная величина; М- (ZA) — полное число импульсов, полу-
ченных за время Т, когда s (t — iA) — отрицательная величина.
Следовательно, полисе число импульсов, полученных за время Т
(зарегистрированных счетчиком М 0), есть
7И0 = ЛД (г А)+М_ (с А). (11.30)
Тогда, обозначив оценку функции <psn (т) при т = t'A, как
<PSn (*А)> получим
(iA) =[Л4+(1Д)-Л4_(1Д)]-^-, (11.31)
где е — эффективность детектора; р — среднее время жизни ней-
трона в реакторе; s—амплитуда флуктуирующей компоненты ней-
тронного источника. Комбинация уравнений (11.30), (11.31) дает
(1Д) = [2Л4+(»Д)-Л4О]-^-. (11.32)
ег
Таким образом, каждый счетчик М (ZA) используется для оценки
<psn (т) при определенной величине т.
Более совершенный вариант схемы приведен в работе [361.
В нейТимелись показывающие устройства с линейной и логарифми-
ческой шкалами, устройство для выбора любой необходимой псевдо-
случайной последовательности, переменная частота сдвига от 100 гц
до 2 Мгц. Разрешающее время системы 100 нсек. Измеритель реак-
тивности в режиме on-line., основанный на двухдетекторном методе
измерения спектральной плотности, был предложен в работе [371
для контроля реактивности при подходе к критическому состоянию
во время загрузки. Для модели реактора с сосредоточенными пара-
метрами можно показать, что реактивность в долларах есть
-₽-=1 — ,1133)
₽ «с V Сад(Ш1)
где ссс — постоянная спада мгновенных нейтронов при критичности
на запаздывающих нейтронах (ас = p/Z); Gxl/ (<dx), GXff (<о2) —
измеряемые взаимные спектральные плотности на частотах и
со 2 соответственно, как показано на рис. 11.42.
Структурная схема для реализации этого измерения приведена
на рис. 11.43- Выходные токи двух ионизационных детекторов уси-
ливаются, и определяется взаимная корреляционная функция иа
двух частотах <ох и со2- Специальные схемы проводят операции деле-
ния, извлечения квадратного корня, умножения и вычитания в со-
ответствии с уравнением (11.33).
Ограничения, накладываемые на величины Wj н <о2, суть
М (11.34)
со 2 ct. (11.35)
356
Влияние больших у-полей на измерения реактивности. В реак-
торах большой мощности измерения реактивности остановленного
реактора серьезно затрудняются из-за большого и переменного
фона,- вызванного у-излучением продуктов деления. По соображе-
ниям эффективности размещение детектора подкрнтйческой реак-
тивности ограничено областью активной зоны или областью в не-
посредственной близости к активной зоне, где уровень у-излучения
может быть велик ( ~ 10е р/ч), а уровень нейтронного потока низок
[ ~ 104 нейтрон/'(см2 сек)]. Опытным путем установлено, что
Рис. 11.42. График взаимной спектральной плотности для
подкритического реактора [37]. (Частота из-
лома передаточной функции реактора Юо=
_ 1 -к(1 -0) j
импульсы от у-излучеиия накладываются и дают отсчет, несмотря
на то что уровень дискриминации установлен чуть ниже.порогового
значения для импульсов, производимых нейтронами. Результаты
общего решения этой проблемы сообщались Шульцем [38].
Первый подход для исключения влияния у-излучеиия, пред-
принятый в работе [39], заключался в использовании большого^чне-
ла малых детекторов, соединенных параллельно. Каждый малый
детектор имел свой собственный предусилитель, усилитель и дис-
криминатор, и выходы всех систем складывались после дискримина-
торов. Каждый детектор относительно нечувствителен к у-излуче-
нию из-за своего размера, и, следовательно, вероятность наложения
импульсов от у-фоиа мала. Однако выходной сигнал, обусловлен-
ный регистрацией нейтронов батареей детекторов, является суммой
выходов отдельных детекторов. В работе [39] показано, что улучше-
ние в дискриминации у-изл учения для четырех детекторов в 10Б раз
больше по сравнению со случаем, когда выходные сигналы четырех
детекторов складываются перед дискриминацией н усилением.
Принципиальный недостаток этой широкополосной системы в том,
357
что собственная чувствительность ограничивает диапазон измерений
двумя декадами от уровня потока остановленного реактора н, сле-
довательно, ограничивает диапазон измерения реактивности оста-
новленного реактора. Кроме того, экспериментально было найдено,
что этот метод должен включать в себя другие усовершенствования,
чтобы даже частично реализовать свои потенциальные преимущества.
Второй подход заключался в применении быстродействующих
электронных схем для улучшения характеристик обычных детекто-
ров, работающих в высоком 7-поле. Об этом методе сообщалось
в работе [40]. Он имеет дополнительное преимущество, заклю-
Рис. 11.43. Структурная схема измерителя реактивности
[37].
чающееся в увеличении диапазона реактивности, в котором может
быть измерен запас подкрнтичности. В работе [40] использовались
электронные схемы с разрешающим временем около 50 нсек при
уровнях у-излучения до 10е р/ч и камера деления, в которой в от-
личие от детектора, наполненного газом BF3, не возникала проблема
пространственного заряда при газовом усилении. Однако для про-
ведения измерений реактивности остановленного реактора необхо-
димо применение также быстродействующих электронных схем.
Преимущества быстродействующих схем ясно вИдны нз результатов
одной из серии опытов, выполненных Шульцем [38], которые пред-
ставлены на рис. 11.44. В опытах использовались детекторы, на-
полненные газом BF3. С применением быстродействующей электро-
ники оказалось возможным измерение нейтронных потоков при уров-
не 7-излучения 3000 р/ч. Когда детектор был помещен в свинцовую
защиту толщиной около 1,5 см, надежные измерения нейтронного
потока были сделаны при уровнях 7-излучения до 2-104 р/ч.
Третий подход заключался в конструировании детектора спе-
циально для измерений в остановленном реакторе. Основные тре-
бования к нему — высокая эффективность, высокая чувствитель-
ность и минимальный объем газа. Конструкция камеры деления
позволяет получить хорошую дискриминацию у-излучения, но ей
358
не хватает чувствительности, и она становится постепенно ра-
диоактивной, когда находится даже в небольших нейтронных по-
токах. Хотя пропорциональный счетчик с покрытием 10В чувст-
вителен к у-изл учению, он может быть сделан высокочувствитель-
ным к нейтронам н, следовательно, очень эффективным. Конструк-
ция Шульца обеспечивала максимальную поверхность покрытия
10В при минимальном газовом объеме. Она представляла собой боль-
шое число (99) малых детекторов (диаметром 5,5 мм, длиной 375 /и),
соединенных параллельно и образующих трубку с диаметром 75 мм
и длиной около 950 мм. Общая площадь покрытия толщиной
Рис. 11.44. Ослабление скорости счета в зависимо-
сти от у-поля для установки с порого-
вой дискриминацией амплитуды им-
пульса [38]:
--------электронная схема с узкой поло-
сой пропускания; ———- —электронная
схема с широкой полосой пропускания.
0,8 мг/см2 изотопом 10В 92% обогащения составляла 3700 см2
Детектор мог работать как импульсный счетчнк или как иониза-
ционная камера переменного тока, и каждый элемент имел чувст-
вительность 0,6 имп/сек на единицу потока (ширина полосы 1 кгц).
Сборка нз 99 элементов показана на рис. 11.45. Она имела чувстви-
тельность 33 имп!сек на единичный поток. Средняя высота импульса
на аноде была 80 мв с максимальным разрешающим временем 40 нсек
при работе с нагрузкой 70 ом. Сборка имела протяженность плато
в 50 в с наклоном 3%/в при коэффициенте усиления импульсного
усилителя, равном 2500. Общая емкость была 750 пф, и сопротивле-
ние утечки превышало 1012 ом.
При сочетании трех рассмотренных выше подходов оказывается
возможным создание отвечающих необходимым требованиям, но
дорогих систем для измерения реактивности в остановленном
реакторе с высоким уровнем у-из лучения.
Распространение импульса. Метод псевдослучайных импульсов
и взаимная корреляционная техника применялись для исследования
359
характеристик распространения импульса в ядерных системах.
Преимущество этого метода изучения распространения импульса
заключается в том, что он позволяет следить за возмущением, вве-
денным на одном конце системы, намного дальше внутри сборки
Рис, 11.45. Специальный детектор, разработанный для измерений шумов* в
остановленном реакторе [37]:
а — элемент детектора, покрытый бором; б —элементы в сборе
(99 элементов).
посредством исключения из данных некоррелированных шумов
фона. Смещение пика взаимной корреляции дает время распростра-
нения возмущения, а форма импульсной переходной функции
определяется взаимной корреляционной функцией.
§ 11.5. Шумовые измерения
в энергетических реакторах
В энергетическом реакторе флуктуации нейтронной плотности,
обусловленные статистической природой процесса деления или ва-
риациями интенсивности источника, несущественны по сравнению
с флуктуациями нейтронной плотности, связанными с флуктуация-
ми реактивности. Основная причина этого явления видна из
сравнения передаточных функций. Для модели с сосредоточенными
параметрами передаточная функция источника идентична передаточ-
360
ной функции реактивности, за исключением члена лв/Л в числителе
последней- Следовательно, передаточная функция реактивности за-
висит от мощности, т. е. флуктуации мощности или нейтронной плот-
ности для данной величины возмущения реактивности прямо пропор-
циональны мощности. Следовательно, передаточная функция и свя-
занные с ней параметры могут быть измерены путем случайного
возмущения реактивности и определения спектральной плотности
мощности между флуктуациями реактивности и мощности. Резуль-
тирующая передаточная функция включает в себя влияние всех
механизмов обратной связи, таких, как температурные коэффициен-
ты, кипение, вибрация, возмущения потока теплоносителя и си-
стемы регулирования.
Другие измерения шумов включают в себя контроль реактора
с точки зрения нежелательных или опасных явлений. Причинами
флуктуаций реактивности, вызывающих флуктуации мощности,
могут быть вибрации механизмов регулирования, нестабильности
потока теплоносителя, кипение, случайные электрические переход-
ные процессы, изменения скорости теплоносителя и т. д. Устанавли-
вают причину эффекта обычно измерением взаимной корреляции
двух переменных систем. Для сложных систем, имеющих много
входов, необходимо применение описанного в гл. 4 метода частных
и составных функций когерентности. Искусственное введение флук-
туаций мощности путем введения возмущения реактивности и ско-
рости теплоносителя становится общепринятым в программах ис-
следования ядерных ракетных двигателей реакторных систем
KIWI, «Phoebus» и NERVA. Метод псевдослучайного возмущения
успешно использовался во многих этих опытах.
Детектирование кипения в энергетических реакторах. Одной
нз проблем в реакторах с водой под давлением является детектиро-
вание кипения, особенно если конструкция реактора не приспо-
соблена для работы с кипением теплоносителя. Очень важно детек-
тировать пузырьковое кипение, чтобы предотвратить кипение в боль-
ших размерах, которое могло бы привести к разрушениям твэлов.
В работе [24] сообщалось об успешном детектировании кипения
в активной зоне энергетического реактора «Saxton» путем измерения
спектральной плотности флуктуаций нейтронного потока в активной
зоне. Утверждалось, что шумовой анализ является простым, полез-
ным и эффективным средством обнаружения пузырькового кипения
в действующих энергетических установках. В распределении спек-
тральной плотности мощности наблюдался хорошо выраженный
резонанс, и исследование резонанса при различных условиях ра-
боты показало, что ои определенно относится к пузырьковому кипе-
нию. Влияние мощности на резонанс в реакторе «Saxton» показано
на рис. 11.46- Аналогичные измерения при других рабочих .усло-
виях в других реакторах и сравнение площади резонанса с анали-
тически вычисленной степенью пузырькового кипения позволи-
ли установить соотношение между резонансом и пузырьковым
кипением.
361
Измерение выгорания в энергетическом реакторе. Большинство
энергетических реакторов сейчас используют низкое обогащение
(от 2 до 4 % 235U) топлива, в котором выгорает 2S6U и образуется
23SPu. Поскольку доли запаздывающих нейтронов хорошо извест-
ны для 236U и 23БРи и, кроме того, они сильно отличаются, можно
Рис. 11.46. Влияние мощности реактора на ре-
зонанс в спектре сигнала компенси-
рованной ионизационной камеры,
установленной на энергетической
установке «Saxton»:
•-------200 кет, 275е С: 0 — 7 Мет,
275° С; Д —18 Мвт. 275° С; V —
22,3 Мвт. 275’С; -Н — 23,3 Мвт, 275° С.
экспериментально определить долю 2SSPu путем измерения р. От-
ношение р// легко определяется при помощи измерения флуктуаций
-нейтронной плотности, так как верхняя частота излома передаточ-
ной функции, обусловленная мгновенными нейтронами, есть р//.
Теоретически для определения этой величины может использоваться
362
любой тип шумовых измерений, но практические соображения дик-
туют применение техники взаимной корреляции или взаимной спек-
тральной плотности с двумя детекторами для подавления фоновых
шумов, вызванных у-излучением и реакцией (у, п). Если время
жизни- нейтронов известно, можно оценить |3. Тогда Ери—доля
мощности, производимой плутонием, — вычисляется из соотношения
Р == р0 (I -ьрРи Fpu = 0,0064 (1 —Fpu) 4-0,0021 ЕРи, (11.36)
где р мощность, производимая 230 Ри щ
Ри мощность, производимая 235 U, 4-
-4-мощность, производимая 23DPu
При необходимости можно
ввести различные поправки,
такие, как поправки, обус-
ловленные утечкой запазды-
вающих нейтронов, или мощ-
ность, производимую деления-
ми S38U. Затем можно решить
уравнение (11.36) относитель-
но Ери для различных времен
кампании. Из данных уровня
мощности и макроскопичес-
кого сечения деления вычис-
ляется количество плутония.
На рис. 11.47 показан гра-
фик амплитуды передаточной
функции, определенной шу-
мовым методом, который по-
казывает, как к концу кам-
пании сдвигается верхняя
частота излома к более низ-
ким значениям. Уже сообща-
лось [43], что точность опре-
деления £// шумовыми мето-
дами достигает ± 1/2%. Это
Рис. 11.47. Определение доли мощности
(Д), выделяемой в 2S9Pu, из
передаточных функций в на-
чале п конце кампании мето-
дом измерения шумов [43]
(частота излома меняется в
9,3/12,7 раза. В начале кам-
пании величина р равна
0,0064, в конце кампании—
0,0047, откуда F = 0,04).
означает, что значение Ери могло
бы быть определено с погрешностью ± 0,01, а отношение числа
атомов 2S9Pu к числу атомов 285U с погрешностью ± 0,005.
Хотя эта точность недостаточна для определения содержания 238Ри
для экономических целей, такое измерение может оказаться полез-
ной индикацией продолжительности остающейся кампании, так как
содержание плутония легко определяется без выгрузки активной
зоны и проведения химического анализа.
Измерения собственных шумов энергетических реакторов. Мно-
гие измерения выполнены с использованием собственных шумов
в реакторе, вызываемых одним или несколькими источниками. Пре-
363
имущество таких измерений в том, что наблюдение за поведением
системы совершается непосредственно и нет необходимости прибе-
гать к внешним возмущениям. Таким образом, выполнение экспе-
римента становится относительно простым, я на первый взгляд
кажется, что шумовой метод настолько хорош, что даже лучше,
чем другие методы исследования динамики систем. Это было бы
справедливо, если бы не существовало ограничений, наиболее серь-
езные из которых перечислены ниже [44].
1. Шумы, генерируемые датчиком, электронным и регистриру-
ющим оборудованием, ухудшают истинный измеряемый сигнал.
Фактически из-за низких уровней истинного шума по сравнению
с помехами (низкое отношение сигнал/шум) шумовые методы
ие всегда удобны.
2. Источники шума не всегда ианлучшнм образом расположены
в системе.
3. Часто нельзя измерить точно поведение сигнала источника
и связать его с откликом системы.
4. Частотное содержание сигнала, генерируемого источником,
может не охватывать весь диапазон, -представляющий интерес для
динамических исследований. Одивко шумовые сигналы обычно со-
держат частоты, к которым система динамически чувствительна.
5. Основные предположения, сделанные для упрощения прак-
тического применения шумовой техники, могут быть нестрого
справедливыми или вообще несправедливыми, т. е. могут иметь
место нелинейности и иестациоиариости.
Шумы в реакторах возникают различным образом. В реакторах
«нулевой» мощности вклад во флуктуации сигнала детектора дает
статистическая природа цепной реакции. В энергетических реакто-
рах шум может вызываться флуктуациями в системе входных вели-
чии, в плотности замедлителя или теплоносителя, в расположении
топлива или поглотителя и в образовании потока пузырьков пара.
Кипящие реакторы проявляют более сильные шумы в сигналах мощ-
ности, потока теплоносителя и температуры. Таким образом, имеет-
ся больше возможностей извлечения посредством шумовых методов
информации о динамическом поведении таких систем, чем во многих
других реакторах.
а. Цель шумовых измерений. В общем случае цель таких измере-
ний заключается в получении информации, дополнительной к той,
которая может быть получена посредством других типов измерений
динамических характеристик системы. Это достигается решением
нескольких отдельных задач, наиболее важные из которых сформу-
лированы в работе [44].
1. Определение общих статистических свойств флуктуаций н
через эти свойства — определенных параметров системы (например,
времени жизни нейтронов).
2. Определение передаточных функций между различными пере-
менными системы и через передаточные функции — также опреде-
ленных параметров системы.
364
3. Изучение пространственной зависимости отдельных вели-
чин (например, потока теплоносителя, температур и нейтронных
потоков).
4. Измерение явных и скрытых периодичностей в системе. Под
скрытыми периодичностями мы понимаем периодические осцил-
ляции с низкой амплитудой, которые нельзя детектировать с по-
мощью простого визуального наблюдения реализации сигналов.
Однако такие периодичности проявляются ясно как осцилляции
автокорреляционных функций и как пики в спектрах мощности
сигналов. Когда осцилляции существуют, шумовые методы дают
также количественное измерение их свойств.
5. Измерение состояния системы при эксплуатации и полу-
чение, таким образом, основы для системы детектирования по-
вреждения компонент системы. Отклонение от установленной моде-
ли могло бы быть индикацией повреждения компонент системы.
6. Оценка начальных условий нестабильности для различных
параметрических изменений.
7. Различение источников шума для понимания динамического
поведения. Для различения источников шума иногда требуется,
чтобы была хорошо определена динамическая модель, описывающая
систему. Знание источников шумов может служить возможным
указанием на то, где в системе имеются динамически чувствитель-
ные места для того, чтобы ослабить их влияние и, если необходимо,
улучшить их динамическое описание.
б. Измерения шумов кипящего водяного реактора. Как пример
использования собственных шумов для измерений в энергетических
реакторах, рассмотрим шумовые измерения, сделанные на кипящем
водяном реакторе HBWR со второй топливной загрузкой [441.
Измерения проводились только на высоких уровнях мощности, и
условия экспериментов были такими же, как и при других типах
динамических экспериментов. Особое значение придавалось иссле-
дованиям динамики активной зоны и наиболее неясных вопросов,
хотя исследовались и некоторые из переменных параметров конту-
ров теплоносителя.
Наибольшие изменения в уровнях шумов как функции условий
эксплуатации наблюдались для макроскопических параметров, та-
ких, как мощность, давление, начальный расход пара. Изменения
уровней шума других сигналов (локальных температур и расходов)
в общем случае менее чувствительны к изменениям условий. Наи-
менее чувствительной к вариациям рабочих условий (в исследуемом
диапазоне) является скорость теплоносителя на входе в канал. Учи-
тывая низкочастотные осцилляции во временном поведении системы
н важность низкочастотного диапазона для динамики системы, в шу-
мовых измерениях большое внимание уделялось частотному диа-
пазону от 0,001 до 0,2 гц. Для того чтобы избежать ошибок, приме-
няли соответствующую низкочастотную фильтрацию. Были прове-
дены также исследования на высоких частотах (до 5 гц) по двум
основным причинам. Во-первых, представляло интерес изучение
365
влияния осцилляций расхода пара, имеющих место при второй за-
грузке, на другие параметры системы, в частности на мощность
реактора. Во-вторых, важно знать — существуют ли гидравличе-
ские колебания в топливных каналах прн реализуемых в экспери-
ментах условиях. Хотя эффект ядерных обратных связей для таких
осцилляций при второй загрузке мал, важно зиать, что оин, возмож-
но, существуют, так как предполагается использовать топливо с мно-
го меньшей тепловой постоянной времени, чем у топливного эле-
мента второй загрузки, но с той же самой производительностью.
Рис. 11.48. Нормированные автокорреляционные
функции шумов мощности реактора
HBWR [44].
в. Результаты экспериментов. Ниже приведены примеры изме-
ренных корреляционных функций, спектров мощности и передаточ-
ных функций. Число точек, применяемых для расчетов, изменялось
от 1500 до 4000, а максимальное число сдвигов — от 80 до 200. Шаг
квантования изменялся от 0,1 до 4 сек. Результаты получены в ус-
ловиях, когда система была вблизи колебательной неустойчивости
или проявляла естественные самоподдерживающиеся осцилляции
различных видов, описанных ранее. Автокорреляционные функции
большинства измеренных переменных в условиях эксперимента
оказались экспоненциально-косинусного типа. Только параметры
на входе в канал (скорость и температура теплоносителя) оказались
не подверженными тенденции системы к низкочастотным колеба-
ниям, и их корреляционные функции носили характер белого шума.
Однако когда система испытывала сильные колебания, эти парамет-
ры также начинали проявлять тенденцию к колебаниям.
Несколько примеров нормированных автокорреляционных
функций для реактора HBWR представлены на рис. 11.48 и 11.49.
Функции нормированы на дисперсии сигналов. На рис. 11.48 пока-
366
зано влияние условий работы реактора на шумы мощности*. Как
видно, система слегка осциллирует уже при мощности 7 Мвт и
осцилляции увеличиваются при повышении мощности. В действи-
тельности в опыте 3 наблюдается очень большая синусоидальная
компонента, которая не затухает со временем- На рис. 11.49 дана
автокорреляционная функция скорости теплоносителя на входе
в канал, которая является типичной корреляционной функцией
белого шума с острым пиком при нулевом времени корреляции.
Однако в этой функции имеется также периодичность с периодом
Рис. 11.49. Нормированная автокорреляционная
функция шумов скорости теплоноси-
теля реактора HBWR [44].
На рис. 11.50 приведена взаимная корреляционная функция
между реактивностью и мощностью реактора для опыта 3, резуль-
таты которого показаны на рис. 11.48. На рис. 11.51—11.53 показаны
соответствующие взаимные спектральные плотности, спектральная
плотность между реактивностью и мощностью. Были также изме-
рены спектры мощности шумов различных параметров, включая
мощность реактора, уровень замедлителя, теплосъем и скорость
теплоносителя в топливных сборках. В общем, результаты наблю-
дений, обобщенные в работе [44], следующие:
1. В л и я и’и е уровня мощности реактора на
спектральную плотность мощности шумов
мощности реактора. На уровне мощности 15 Мвт сис-
тема проявляет сильные самоподдерживающиеся колебания в час-
тотном диапазоне (около 0,007 гц), где функция взаимной спектраль-
ной плотности от реактивности к мощности также имеет пик. С умейь-
* Таблицы из четырех чисел иа графиках рис. 11.48—11.53 дают значе-
ния мощности (в тепловых мегаваттах), мощности, уносимой теплоносителем
(в процентах от полной мощности), давления пара (в атмосферах) и уровней
воды (в сантиметрах).
367
шением мощности колебания становятся меньше и сдвигаются в об-
ласть более низких частот. Уровень шумов увеличивается с ростом
мощности реактора, и флуктуации больше концентрируются около
о, 8
0,6
о,ь
£ 0,2
& о
•0,2
-0,6
-МО -200 0 200 ООО
Временной сдвиг т, сек
Рис. 11.50. Взаимная корреляционная функция ме-
жду реактивностью и мощностью реак-
тора HBWR [44].
отдельной частоты. Наконец, при достаточно большой мощности
система становится нестабильной (амплитуда колебаний на этой
частоте нарастает).
Рис. 11.51. Взаимиая спектральная плотность шумов ре-
активности и мощности реактора HBWR [44].
2. Влияние уровня замедлителя на флук-
туации мощности реактора. Система является бо-
лее колебательной при высоком уровне замедлителя. Этот резуль-
тат согласуется с измерениями методом осциллятора реактивности.
368
Формы спектров показывают, что амплитуда колебаний при низком
уровне замедлителя меньше, чем при среднем уровне, и повышение
уровня замедлителя приводит к появлению высокого, но узкого
пика. Это становится ясным из рассмотрения автокорреляционных
функций на рис.-11.48. Частота колебаний увеличивается с умень-
шением уровня замедлителя.
3. Увеличение теплосъема. Система стабилизи-
руется с ростом теплосъема, и этот результат снова соответствует
результатам осцилляторных измерений.
-32-------------------------------------------
-зе - Г\ \п |gg]гг»|
:: / ч
-56 -
-60 У--1 1 I 1 ’ I 1 '!_1 L. I I I.J 11!-1 1 1 i И >11
10~3 Ю~2 Ю'1 1
Частота, гц
Рис. 11.52. Спектральная плотность мощности шумов
реактивности в реакторе HBWR [44].
4. Спектры мощности шумов расхода теп-
лоносителя на входе в высокочастотной
области. Как и в случае зависимости шумов мощности реактора
от уровня замедлителя, шумы расхода имеют пик вблизи 1,2 гц.
Взаимная корреляция между расходами в топливном элементе и
вблизи границы активной зоны указывает, что они ие осциллируют
в фазе, но полностью не отличаются по фазе друг от друга. Во
всех случаях имеется также пик в диапазоне от 1,8 до 2,7 гц. Дру-
гой пик около 4,5 гц вызывается, вероятно, пульсациями, создавае-
мыми турбиной из-за неодинаковых расстояний между лопатками
турбины.
5. Поведение шумов температуры’ замед-
лителя на различной высоте. Уровень температуры
замедлителя в наибольшей степени связан с объемом пара, и его
поведение подобно поведению уровня шумов давления в корпусе.
Уровень шумов наиболее низок на дне бака, где с большей вероят-
ностью наблюдаются различные гармоники основного резонанса.
Измерение температуры в нижней точке, таким образом, позволяет
более отчетливо выделить эти -гармоники. Сигнал термопары, рас-
13 Зак. 576 . 369
положенной в центре, дает среднюю частоту уровня шумов более
высокую (от 0,01 до 0,05 гц), чем частоты, которые могут обусловли-
ваться турбулентностью, вызванной нагреванием замедлителя.
Из вышесказанного ясно, что шумы температур замедлителя
могут дать достаточно полезную информацию о поведении замедли-
теля, если провести нх тщательное исследование в зависимости от
координат и условий работы реактора.
г. Пределы стабильности. Аккасу [45] установил, что исследо-
вание зависимости среднего квадрата флуктуаций соответствую-
щим образом выбранных величин от наиболее важных параметров
Рис. /1.53. Передаточная функция между реактивностью
и мощностью реактора HBWR [44].
(мощности, давления, теплосъема и т. д.) позволяет определить
пределы стабильности изучаемых систем. На основе полученной
зависимости строится график обратной величины соответствующего
среднего квадрата как функции выделенного параметра. Точка,
где экстраполированная кривая пересекает абсциссу, указывает
значение, при котором средний квадрат флуктуаций становится
расходящимся. В работе [45] указывалось также, что предел ста-
бильности в среднеквадратическом значении может отличаться от
предела стабильности в значении средней величины.
По-видимому, этот метод дает не совсем правильные пределы
стабильности в случае флуктуаций, наблюдавшихся на реакторе
HBWR, где проявляются большие нелинейности. Тем не менее на
рнс. 11.54 приводится пример предсказания предела стабильности
мощности по четырем точкам. График показывает начало нестабиль-
ности при 16 Мвт. Этот результат хорошо подтвержден экспери-
ментом. Хотя в эксперименте мощность не превышала 15 Мвт,
даже небольшое уменьшение теплосъема приводило к расходящимся
370
колебаниям мощности, указывая на то, что предел стабильности
находится немного выше 15 Мет.
д. Источники шума в реакторе HBWR. Проблеме источника
шума уделялось большое внимание обычно для того, чтобы устранить
некоторые из упомянутых выше ограничений. В немногих случаях
источник шума локализуется определенно, но большей частью
полученные результаты приводят только к указанию направления,
где можно искать источник шума. Часто исследователи пытаются
локализовать параметр, у которого флуктуации проявляют в ин-
тересующей частотной области признаки белого шума и принимают
его за детерминированный шум. На реакторе HBWR эта проблема
Мощность, МВт
Рис. 11.54. Обратная величина дисперсии мощности
в зависимости -от уровня мощности реак-
тора HBWR (мощность 1,4 Мет, темпера-
тура замедлителя 230° С, уровень замед-
лителя 228 сл!) [44].
не была решена, в частности, из-за сложности системы. Однако с до-
статочно высокой достоверностью установлено, что периодические
колебания в контуре теплоносителя не являются причиной флук-
туации параметров реактора. Также определено, что шумы полной
реактивности не являются белыми. Следуя принципу отыскания
источников белого шума и основывая его доказательство на наблю-
дениях поведения величин иа входе в канал, можно полагать, что
источником шума является либо контур теплоносителя, либо за-
медлитель.
е. Основные выводы относительно измерений шумов реактора
HBWR. Основываясь на опыте, полученном на реакторе HBWR,
можно сказать следующее об использовании внутренних шумов [44]:
1. Это очень полезное дополнительное к другим экспери-
ментальным методам средство исследования динамики систе-
мы. Одиако оно не такое мощное в определенных областях,
как методы, использующие внесение известного возмущения.
2. Оно дает информацию о тенденции системы к осцилляциям
и, таким образом, может использоваться для предсказания
начальных условий осцилляций.
13*
371
3. Оно дает количественную меру природы осцилляций в тер-
минах величины и частотной полосы.
4. Оно может использоваться для получений первой прибли-
женной оценки пределов стабильности в зависимости от из-
менений различных параметров.
5. Необходимо проявлять осторожность при применении ме-
тода в исследовании динамики систем в терминах передаточ-
ных функций, если ожидается любой тип нелинейностей.
В линейных стационарных системах могут быть получены не-
плохие результаты при измерениях передаточных функций
с относительно малым количеством данных.
Рис. И.55. Упрощенная схема ядерной установки для ракетного
двигателя с охлаждением жидким водородом [45]:
АРК — автоматический регулируемый клапан; БК —
блокирующий клапан;’ А С — аварийный сброс; ПН —
питательный насос.
Измерения шумов в реакторах ядерных ракетных двигателей
с возмущениями на входе. Введение входных возмущений реактив-
ности для измерения динамических характеристик ядерного реакто-
ра высокой мощности было впервые выполнено при экспериментах
на реакторе KIWI-A-3. Входной сигнал выбирался в виде псевдо-
случайной двоичной последовательности, которая использовалась
для возмущения реактивности путем введения сигнала в схему ре-
гулирования. Этот тип опытов был выполнен последовательно на
ядерных ракетных реакторах NERVA, KIWI и «Phoebus» [45, 46].
Задавались возмущения реактивности и скорости потока жидкого
водорода, являющегося теплоносителем.
О результатах экспериментальных измерений динамических ха-
рактеристик реактора «Phoebus-1 А», в которых применялись воз-
мущения скорости потока водорода, сообщалось в работе [46].
Псевдослучайный шумовой сигнал вводился в схему регулирования
расхода, и на магнитной ленте регистрировались температуры, дав-
ления, расход, мощность и скорость турбонасоса. Обработка прово-
дилась после опыта. На рис. 11.55 показано оборудование реактора
«Phoebus-1 А», который охлаждается жидким водородом, прокачи-
ваемым через реактор. Жидкий водород накапливается в дьюарах
и прокачивается через трубопровод, находящийся в вакуумной ру-
башке, длиной около 60 м в реактор. Поток теплоносителя посту-
пает во впускное отверстие сборки, проходит через выпускное от-
372
верстие охлаждающих каналов, через отражатель, через активную
зону и выходит через выпускное отверстие. Скорость потока водо-
рода контролируется замкнутым контуром системы регулирования.
Необходимая скорость потока достигается путем сравнения вычис-
ленной скорости потока с требуемой и использования полученной
разности для образования необходимого сигнала скорости турбона-
соса. Этот требуемый сигнал затем сравнивается со скоростью
турбонасоса, и сигнал ошибки обеспечивает необходимый сигнал
регулирования клапана. Из-за взаимодействия двух контуров для
обеспечения шумового входного сигнала необходимы заданное пре-
рывание потока (чтобы обеспечить низкочастотную составляющую
в реакции системы) и заданное модулирование скорости (чтобы обес-
печить высокочастотную составляющую в реакции системы). Шу-
мовой входной сигнал для требуемого модулирования скорости по-
давался через фильтр, выделяющий частотную полосу для измерения
реакции системы в диапазоне до 10 гц.
Псевдослучайный сигнал, используемый в качестве входного
сигнала, представлял собой последовательность регистра сдвига на
9 положений со скоростью 100 сдвигов в секунду, дающую А о-
= 0,01 сек, Z — 511 сдвигов на цикл и период Р — 5,11 сек. П=
скольку целью эксперимента было получение передаточной функции
реактора по давлению в частотном диапазоне от 0,5 до 10 гц, упомя-
нутый выше сложный метод введения шумового сигнала был необ-
ходим для обеспечения требуемого спектра шумов на входе впуск-
ного отверстия сборки. Флуктуации давления измерялись акусти-
ческим датчиком давления.
Флуктуации давления на всем протяжении системы показаны
иа рис. 11.56. Легко заметить корреляцию между флуктуациями по
мере движения теплоносителя на всем протяжении системы. Из гру-
бой оценки данных очевидно, что содержание высоких частот
в тестовом сигнале на входе трубок теплоносителя недостаточно.
Уровни наблюдаемых сигналов даны в табл. 11.2. Данные обраба-
тывались с помощью метода взаимной спектральной плотности
и процедуры анализа ошибок, описанной в гл. 4.
Таблица’ 11.2
Характеристика флуктуаций давления в опыте иа реакторе
Расположение точек замера давления Размах сигнала от пика до пика, атм Среднеквадра- твческое значение сигнала, атм Среднее давление. атм
Вход выпускного отверстия тру- бопровода 17,5 5,7 890
Вход в отражатель 7,0 2,6 750
Вход в активную зону 9,0 2,7 648
Выход из активной зоны 6,6 2,2 545
373
На рис. 11.57 показана передаточная функция по давлению
реактора, а на рис. 11.58 — передаточная функция от выпускного
отверстия трубок теплоносителя, которая незначительно отличается
от передаточной функции всего реактора. Передаточные функции
давления в отражателе и активной зоне не имеют частот излома ниже
10 гц. Таким образом, основной вклад в форму передаточной функ-
Рис. 11.56. Возмущения давления в реакторе «Phoebus-IA» [45]:
а — возмущения давления па входе выпускного отверстия; б — возмущения
давления на входе в отражатель; в — возмущения лавчення на входе
в активную зону; г—возмущения давления па выходе из активной зоны.
На рис. 11.59 даны функция когерентности и ошибка, вычислен-
ные по формулам (6.82) и (6.86). Функция когерентности и ошибка
дают статистическую меру ожидаемой погрешности в измерении
передаточной функции, вызванной шумами системы и конечной дли-
тельностью эксперимента. Таким образом, можно оценить с 70 %-ной
доверительной вероятностью, что для частот до 8 гц погрешность
измерения амплитуды не больше, чем 0,72 дб, и ошибка фазы
не больше, чем 5,2°. Ожидаемые ошибки меньше для всех частот,
исключая 4 гц.
Результаты шумового эксперимента показывают, что можно
измерять передаточные функции давления в реакторе с флуктуа-
циями давления 1—2% от средней величины. Таким образом, этот
тип шумовых экспериментов можно проводить, не создавая помех
другим задачам испытания.
Измерения шумов и безопасность энергетического реактора.
Общее соотношение между измерениями шумов и безопасностью
374
реактора рассматривалось в работе [47]. Очевидно, что измерение
степени подкритичности, как уже отмечалось в этой главе, важно
для безопасности любого реактора. Однако в этом разделе кратко
даются выводы применительно только к безопасности энергети-
ческого реактора.
Энергетическим реакторам присущи большие трудности при ана-
лизе шумов, чем реакторам нулевой мощности, так как сложные
условия работы на высоких уровнях мощности создают, много типов
шумов и требуют более тщательного экспериментального исследова-
Рис. 11.57. Передаточная функция от
давления на входе выпу-
скного отверстия к давле-
нию на выходе теплоноси-
теля из активной зоны при
работе реактора «Phoe-
bus-1 А» на полкой мощно-
сти [45].
Рис. 11.58. Передаточная функция от
давления на входе выпуск-
ного отверстия к давлению
на входе теплоносителя в
отражатель при работе
реактора «Phoebus-1А» па
полной мощности [45].
иия и наблюдения за поведением реактора. До сих пор больше про-
водится специальных исследований во время пуска реактора, чем
при эксплуатации на полной мощности. Основной причиной, про-
ведения шумовых опытов является помощь в исследованиях ста-
бильности- Однако повышение безопасности путем непосредствен-
ного исследования динамических характеристик реактора также
представляет благоприятную возможность анализа шумов.
В работе [48] показано, что случайные эффекты реактивности,
вызванные флуктуациями температуры или плотности замедлителя,
являются доминирующей причиной шумов нейтронного потока.
Среднеквадратическое значение реактивности, обусловленное таки-
ми источниками, обычно много больше, чем от других источников.
В частности, флуктуации мощности реактора, вызванные этими флук-
туациями реактивности, должны превышать собственные флуктуа-
375
ции детектора, вызванные дискретным характером регистрации
отдельных нейтронов. Ситуация, отличная от той, которая наблю-
дается в реакторах нулевой мощности, где источником шума служат
случайные события в цепной реакции. По этим причинам для боль-
шинства исследований шумов в энергетических реакторах не тре-
буются высокоэффективные детекторы в активной зоне.
Возможность детектирования спектральных резонансов, кото-
рые могут неожиданно стать большими, — еще одно достоинство
Рис. 11.39. Функция когерент-
ности н ошибка при
измерении переда-
точной функции от
давления теплоноси-
теля на входе вы-
пускного отверстия
к давлению на вы-
ходе из активной
зоны при работе ре-
актора «Phoebus-1 А»
па полной мощно-
сти [45].
методов шумового анализа в энерге-
тических реакторах. С точки зрения
безопасности, это может оказаться
наиболее существенным применением
шумов для эксплуатации реактора.
В’ работе [49] удачно применен
на реакторе Atomics International
дисплей, на котором проявлялся
спектр шумов и, следовательно, ре-
зонансы или другие аномалии спект-
ра могли, как и другие параметры
реактора, непрерывно наблюдаться
на пульте оператора. Для многократ-
ной регистрации спектра G (со) на
самописце с узкой лентой фирмой
«Мнллетрон» создана промышленная
установка, названная вычислителем
передаточной функции. Удобство
монитора, работающего в режиме
on-line, отмечалась в недавнем вы-
пуске «Nuclear Safety». Вопрос о
применении шумовых методов в ка-
честве монитора безопасности зависит
от того, в какой степени нвблюдения
оператора за флуктуациями мощности
могут быть заменены более привычны-
ми мониторами, имеющими более низ-
кие пороги детектирования аномалий. Отличный пример применения
шумов нейтронного потока в качестве монитора аномального пове-
дения был дан недавно на опытном реакторе General Electric [52].
Увеличение амплитуды шумов в течение четырех дней послужило
причиной остановки реактора с целью проверки активной зоны.
Некоторые металлоконструкции имели повреждения и допускали
движение компонент активной зоны под действием потока тепло-
носителя.
Установлено, что взаимные корреляционные методы являются
мощным средством определения расстояния, на котором переменная
величина х (такая, например, как температура теплоносителя на
входе) влияет на другую переменную величину у (такую, как нейт-
ронный поток) с запаздыванием по времени т [52, 54]. На реакторе
376
для испытания материалов в Даунри, являющимся исследователь-
ским реактором с охлаждением тяжелой водой, сильная корреляция
между изменением температуры, измеряемой термопарой на входе
теплоносителя в активную зону, и нейтронным потоком указала ис-
точник шума мощности. Недавно в работе [54] получены экспе-
риментальные данные о взаимной корреляционной функции вход-
ной температуры натрий-калиевого теплоносителя и мощности
(нейтронного потока) быстрого реактора в Даунри. Флуктуации
мощности реактора зависели от флуктуаций температуры теплоноси-
теля, измеренной термопарой, применявшейся в испытаниях.
В работе [53] описан отличный пример использования взаимной
корреляции для слежения за основным источником шума в энерге-
тическом реакторе небольших размеров. Случайные переходные
процессы в электрических цепях, возникшие в результате переклю-
чений, вызывали флуктуации расхода на выходе электромагнит-
ного насоса, которые в свою очередь приводили к флуктуациям
температуры теплоносителя и шумам реактивности.
По мере строительства больших энергетических реакторов более
распространенной становится внутризонная аппаратура и увели-
чивается интерес к пространственной зависимости шумов. Большие
реакторы чувствительны к ксеноновым колебаниям, которые доста-
точно хорошо изучены. Однако, если распределение потока меняется,
можно ожидать тенденции к нестабильности с периодом порядка
секунд, для исследования которой шумовые методы могут быть
полезным средством.
Примеры таких применений шумовых методов можно найти в ки-
пящих водяных реакторах. Возможно, что этот тип реакторов дол-
жен иметь пространственную нестабильность, обусловленную пусто-
тами в объеме активной зоны, аналогичную ксеноновой нестабильно-
сти для активных зон до некоторой степени больших, чем реактор
«Дрезден». Спектральный анализ шумов внутризоииых ионизацион-
ных камер в сочетании с опытами по осцилляции регулирующего
стержня подтвердил стабильность этого реактора. Более систе-
матическое исследование было проведено на реакторе VBWR [56],
для которого было обнаружено, что внутризонная ионизацион-
ная камера имеет более высокие частотные компоненты фурье-
спектра по сравнению с внезонной камерой. Тем не менее, из-за
малых размеров этого реактора взаимная корреляционная функ-
ция при нулевом временном сдвиге между этими камерами была
очень большая
СПИСОК ЛИТЕРАТУРЫ
1. Uhrig R. Е. (Coordinator) Noise Analysis in Nuclear Systems. Gainesvil-
le, Fla., Nov. 4—6, 1963; AEC Symposium Series, 1964, N 4. (TID-7679).
2. Uhrig R. E. (Coordinator) Neutron Noise, Waves and Pulse Propagation.
Gainesville, Fla., Feb. 14—16, 1966; AEC Symposium Series, 1967,
N 9 (CONF-660206).
3. Orndoff J. D. Promt Neutron Periods of Metal Critical Assemblies.—«Nucl.
Sci. Engng», 1957, v. 2, p. 450.
377
4. Pacilio N. Review of Statistical Methods for Reactor Parameter Measu-
rements Developed at C. S. N. Casaccia. Italian Report RT/FI-(66) 37,
1966-
6. Pacilio N. Short Time Variance Method for Promt Neutron Lifetime
Measurements. —«Nucl. Sci. Engng», 1965, v. 22, N 2, p. 266.
6. Pacilio N. Statistical and Pulsed Experiments in Organic Moderated
and Reflected Assemblies.—«Energ. Nucl»., 1968, v. 15, N 2, p. 129.
7. Pacilio N. Reactor-Noise Analysis in the Time Domain- AEC Critical
Review Series. USAEC Report TID-24512, April 1969-
8. Babala D. Neutron Counting Statistics in Nuclear Reactors. Norwegian
Report KR-114, November 1966.
9. Babala D. Interval Distributions in Neutron Counting Statistics.—«Nucl.
Sci. Engng», 1967, v. 28, N 2, p. 243.
10. Babala D., Ogrin R. Measurement of the Promt Neutron Decay Consta-
nt of the NORA Reactor by the Interval Distribution Technique.—«Nucl.
Sci. Engng», 1967, v. 29, N 3, p. 367.
11. Turckan E., Dragt J. B. Experimental Study of Different Techniques
for Analyzing Reactor Noise Measured by a Neutron Counter. Dutch Re-
port RCN Int. 75, 1967.
. 12- Striber T. Neutronen Lebensdauer und Reaktivitaet Measungen an
tbermische Reaktaren mit Hilfe der Rossi-alpha-Methode. — «Nukleonik»,
1963, в. 5, s. 170.
13. Christensen H. e. a. A Review of NORA Project. Noise Experiments. —
In: Neutron Noise, Waves and Pulse Propagation. Gainesville, Fla.,
1966, Uhrig R. E. (Coordinator); AEC Symposium Series, 1967, N 9
(CONF-660206).
14. Borgwaldt H. Comment on Rossi-alpha Experiments Performed with Spect-
ral Time Analyzers. German Report INR'— Notiz N 152/66, 1966.
15. Edelmann M. e. a. Pulsed Sourse and Noise Measurements of the STARK
Reactor at Karlsruhe. — In: Pulsed Neutron Research, Symposium Proce-
edings, Karlsruhe, 1965; International Atomic Energy Agency, Vienna,
1965 (STI/RUB/104).
16. Brunson G. S., Gurran R. N., Gasidlo J. M-, Huber R. J. A Survey of Promt
Neutron Lifetimes in Fast Critical Systems. USAEC Report ANL-6681,
Argonne National Laboratory, August 1963.
17. Pal L. e. a. Experimental Determination of the Ratio p// on the ZR-1
Critical Assembly. —«J. Nucl. Energy», 1963, v. 17, p. 473.
18. Bayer A., Seufert H., Stegemann D. Special Experimental Techniques
Developed Recently for Application in Fast Zero-Power Assemblies. —
In: Proceedings of the International Conference of Fast Critical Experiments
and Their Analysis. Argonne. Ill, Oct. 10—13, 1966; USAEC Report
ANL-7320, Argonne National Laboratory.
19. Diven В. C., Martin H.C., Taschek R. F., Terrell J. Multiplicities of Fission
Neutrons. —«Phys. Rev-», 1956, v. 101, p. 1012.
20. Cohn С. E. Determination of Reactor Kinetic Parameters by Pile Noise
Analysis. —«Nucl. Sci. Engng», 1959, v. 5, p. 331.
21. Seifritz W., Stegemann D., Vath W. Two-Detector Cross-Correlation Experi-
ments in Fast-Thermal Argonaut Reactor (STARK). — In: Neutron
Noise, Waves and Pulse Propagation. Gainesville, Fla., 1966, Uhrig R. E.
(Coordinator); AEC Symposium Series, 1967, N 9 (CONF-660206).
22. Fry D. N. e. a. Neutron Fluctuation Measurements at Оак Ridge National
Laboratory. — In: Neutron Noise, Waves and Pulse Propagation. Gaines-
ville, Fla., Uhrig R. E. (Coordinator); AEC Symposium Series, 1967,
N 9 (CONF-660206).
23. Dragt J. R. Accurate Reactor Noise Measurement in a Low-Power Critical
Reactors. — «Nukleonik», 1966, v. 8, N 4, p. 188. . .
24. Rajagopal V. Determination of Reactor Transfer Functions by Statistical
Correlation Methods. — «Nucl. Sci. Engng», 1962, v. 12, p. 218.
25. Badgley R. W-, Uhrig R. E. Power Spectral Density Measurements in a Sub-
critical Nuclear Reactor.—«Nucl. Sci. Engng», 1964, v. 19, N 2, p. 158.
378
26. Ricker C. W. e. a. Investigation of Negative Reactivity Measurement by
Neutron Fluctuation Analysis. — In: Noise Analysis in Nuclear Systems.
Gainsville, Fla., 1963, Uhrig R. E. (Coordinator); AEC Symposium Series,
1964, N 4 (TID-7679).
27. Schultz M. A. Shutdown Reactivity Measurements Using Noise Techni-
ques. — In: Noise Analysis in Nuclear Systems. Gainesville, Fla., 1963;
Uhrig R. E. (Coordinator); AEC Symposium Series, 1964, N4 (TID—7679).
28. Nomura T. Improvement in S/N Ratio of Reactor Noise Spectral Den-
sity.—«J- Nucl. Sci. Technol.», Tokyo, February 1965, v. 2, N’2, p. 76.
29. Borgwaldt H., Stegemann D. A Common Theory for Neutronic Noise
Analysis Experiments in Nuclear Reactors. — «Nukleonik», 1965, v. 7,
N 6, p. 313.
30. Nomura T., Gotoh S., Vamaki K. Reactivity Measurements by the Two—
Detector Cross-Correlation Method and Supercritical Reactor Noise Ana-
lysis. — In: Neutron Noise, Waves and Pulse Propagation. Gainesville,
Fla., 1966, Uhrig R. E. (Coordinator); AEC Symposium Series, 1967,
N 9 (CONF-660206).
31. Dragt J. B. Analysis of Power Reactor Noise Measured in a Zero-Power
Reactor and Calculations on Its Accuracy, — In: Neutron Noise, Waves
and Pulse Propagation. Gainesville, Fla., 1966, Uhrig R. E. (Coordina-
tor); AEC Symposium Series, 1967, N 9 (CONF-660206), p. 591—621.
32. BalcombJ. D., Demuth H. B., Gyftopoulos E. P. A Cross-Correlation Method
for Measuring the Impulse Response of Reactor Systems.—«Nucl. Sci.
Engng», 1961, v. 11, N 2, p. 159.
33. Uhrig R. E. Impulse Response of an Exponential Assembly. — In:
Exponential and Critical Experiments. Symposium Proceedings, Am-
sterdam, 1963; International Atomic Energy Agency, Vienna, 1964
(STI/PUB/79).
34. Stern T. E., Blaquiere A., Valat J. Reactivity Measurement Using Pseu-
do-Random Source Excitation. —«J. Nucl. Energy», 1962, Parts A and
B, v. 16, p. 449.
35. Uhrig R. E., Ohanian M. J. Pseudorandom Pulsing of Subcritical Sys-
tems. — In: Neutron Noise, Waves and Pulse Propagation. Gainesville,
Fla., 1966, Uhrig R. E. (Coordinator); AEC Symposium Series, 1967, N 9
(CONF-660206).
36. Meyer P., Garelis E. Use of a Pseudorandom Source Input in the Meas-
urement of Impulse-Response Functions. — In: Neutron Noise, Waves
and Pulse Propagation- Gainesville, Fla., 1966, Uhrig R. E. (Coordinator);
AEC Symposium Series, 1967, N 9 (CONF-660206).
37. Seifritz W., Stegemann D. An On-line Reactivity Meter Using the Two
Detector Crosscorrelation Technique for Shutdown Reactivity Measure-
ments. •—«Trans. Amer. Nucl. Soc»., 1967, v. 10, N 1, p. 283.
38. Schultz M. A. Measurement of Shutdown Reactivity in Large Gamma
Fields. — In: Neutron Noise, Waves and Pulse Propagation. Gaines-
ville, Fla., 1966, Uhrig R. E. (Coordinator); AEC Symposium Series, 1967,
N 9 (CONF-660206).
39. Yang R. Milletron Corp., personal communication, 1966.
40. Furet J., Pupponi J. Some Particular Aspects of Control in Nuclear Po-
wer Reactors. — In: Proceedings of the Third International Conference
on the Peaceful Uses of Atomic Energy Geneva, 1964, v. 4, p. 213, Uni-
ted Nations, New York, 1965.
41. Booth R. S., Perez R. B. Excitation of Neutron Waves by Modulate and
Pulsed Sources. — In: Pulsed Neutron Research. Symposium Proceedings,
Karlsruhe, 1965, p. 701; International Atomic Energy Agency, Vienna
1965 (TID/PUB/104).
42. Rajagopal V. Reactor Noise Measurement on Saxton Reactor. — In:
Noise Analysis in Nuclear Systems. Gainesville, Fla., 1963, Uhrig R. E.
(Coordinator); AEC Symposium Series, 1964, N 4 (TID-7679), p. 427—447.
43. Thie J. A. Milletron, Inc., personal communication, 1965.
379
44. Eurola T. Noise Experiments with the HBWR Second Fuel Charge.
Norwegian Report HPR-53, December 1964.
45. Akcasu A. Z. Mean Square Instability in Boiling Reactors. — «Nucl.
Sci. Engng», 1961, v. 10, N 4, p. 337.
46. Johnson J. A. Measurement of Pressure—to—Pressure Transfer Functi-
ons Through the Phoebus—1A Nuclear Reactor. — In: Neutron Noise, Wa-
ves and Pulse Propagation- Gainesville, Fla., 1966, Uhrig R. E. (Coor-
dinator); AEC Symposium Series, 1967, N 9 (CGNF-660206).
47. Thie J. A. Noise Analysis in Reactor Safety.—«Nucl. Safety», 1966, v. 7,
N 3, p. 271.
48. Thie J. A. Noise Sources in Power Reactor. — In: Noise Analysis in
Nuclear Systems. Gainesville, Fla., 1963, Uhrig R. E. (Coordinator);
AEC Symposium Series, 1964, N 4 (TID-7679), p. 357—368.
49. Randall R. L. On-Line Reactor-Safety Monitor for Rapid Detection
and Diagnosis on Reactor System Instabilities. — «Trans. Amer. Nucl.
Soc.», 1963, v. 6, N 1, p. 74—75.
50. McLeod N. B., Schultz M. A. The Performance and Characteristics of
the Milletron Transfer Function Computer. USAEC Report NYO-2483
Nuclear Utilities Services, Inc. and Milletron, Inc., May 1963.
51. Haubenreich P. N. Power Reactor Stability.—«Nucl. Safety», 1964, v. s,
N 4, p. 354—356.
52. Larson H. J., Stratton K- The Evaluation and Measurement of Reactor
Safety Performance. —«Nucl. Applications», 1965, v. I, N 3, p. 225—229.
53. Randall R. L., Griffin C. W. Application of Power Spectra to Reactor
System Analysis. — In: Noise Analysis in Nuclear Systems. Gainesville,
Fla, 1963, Uhrig R. E. (Coordinator); AEC Symposium Series, 1964, N 4
(TID-7679), p. 104—134.
54. Boardman F. D. Noise Measurements in the Dounreay Fast Reactor. —
In: Noise Analysis in Nuclear Systems. Gainesville, Fla., 1963.
Uhrig R. E. (Coordinator); AEC Symposium Series, 1964, N4 (TID-7679),
p. 469—500.
55. Eurola T. Reactor-Noise Experiments on Halden Boiling Water Re-
actor. — In; Noise Analysis in Nuclear Systems. Gainesville, Fla., 1963,
Uhrig R. E. (Coordinator); AEC Symposium Series, 1964, N 4 (TID-7679),
p. 449—468.
56. Pluta P. R. VBWR Noise Analysis. Report APED-4285, Genaral Elect-
ric Company, Atomic Power Equipment Dept., March 30, 1964.
ГЛАВА 12.
СПЕЦИАЛЬНЫЕ
СТАТИСТИЧЕСКИЕ МЕТОДЫ
И ИХ ПРИМЕНЕНИЕ
В ЯДЕРНЫХ РЕАКТОРАХ
§ 12.1. Введение
В этой главе представлены некоторые из специальных шумовых
методов и нх применения, которые логически не связаны с вопро-
сами, обсуждаемыми в других главах книги. Однако их расположе-
ние в конце книги отнюдь не имеет отношения к их важности и по-
лезности. Применение многих из этих методов' не ограничивает-
ся ядерными реакторами.
§ 12.2. Оптическое наблюдение корреляции
В работе [1] доказана возможность применения оптического
метода для детектирования корреляции между двумя сигналами.
Присутствие некоррелированных и коррелированных событий в цеп-
ной реакции может выражаться в поведении выходных сигналов
при визуальном наблюдении. В двухдетекториом корреляционном
эксперименте, где детектируются независимые события, не ожи-
дается подобия двух выходных сигналов. Такой случай изображен
на рис. 12.1, где показаны выходные сигналы для двух каналов в за-
висимости от времени. Центральная частота fc равна 1 гц, и ширина
полосы А/ равна 0,95 гц. Сигналы не проявляют общих характерис-
тик. Иная картина имеет место в присутствии коррелированных со-
бытий, обусловленных ветвящимися процессами цепной реакции.
Если периоды наблюдения достаточно велики, коррелированные
события цепной реакции будут проявляться в сигналах. Поэтому
корреляция между сигналами должна выражаться в подобии ам-
плитуд и в пересечениях нулевой линии в эквивалентных точках на
временной оси. Подобие выходных сигналов двух фильтров должно
быть более отчетливым, когда увеличивается вклад коррелирован-
ных шумов. Это явление ясно видно иа рнс. 12.2. Здесь показаны
выходные сигналы фильтров (f = 1 гц и А/ = 0,95 гц) для камер,
расположенных рядом с активной зоной реактор а.
Корреляция сигналов в двухдетекториом эксперименте наблю-
дается оптически более четко, если выходной сигнал одного фильтра
подается и а пластины осциллоскопа, отклоняющие луч в направле-
нии оси х, а выходной сигнал другого фильтра на пластины, откло-
381
Рис. 12.1 Некоррелированные выходные сигналы фильтров в двух-
детекторном взаимном корреляционном эксперимен-
те [1].
Рис. 12.2. Частично коррелированные выходные сигналы фильтров
в двухдетекторном взаимном корреляционном экспери-
менте [1].
ияющне луч в направлении оси у, и результирующий сигнал на эк-
ране фотографируется в течение времени, достаточного для получе-
ния геометрических фигур, показанных на рис. 12.3. Другой экс-
Рис. 12.3. Оптическое наблюдение
корреляции [1]:
а—некоррелированные сиг-
налы; б — частично кор-
релированные сигналы
(/=40 гц)-, в — частично
коррелированные сигналы
({=• 15 гц); г — частично
коррелированные сигналы
(/=1 гц); д— автокорре-
ляционные сигналы.
тремальный случай — автокорреляционный эксперимент с двумя
идентичными сигналами, который дает прямую линию под углом
45° к. осям х и у (см. рис. 12.3). Отношение доли коррелированных
к некоррелированным шумам Q увеличивается на рис. 12,3, б, в, г
из-за изменения центральной частоты от высоких к более низким
383
величинам. Таким образом, величина корреляции сигналов опреде-
ляется непосредственно из оптического наблюдения.
В предположении, что распределения амплитуд коррелированных
и некоррелированных частей в сигналах х и у близки к гауссовому,
кривые постоянной интенсивности света являются эллипсами. Для
случая, в котором основные оси эллипса наклонены под углом 45°
к осям х и у, получено следующее соотношение:
nW = (b+I)/(L-l), (12.1)
где а и b — большая и малая полуоси эллипса и
L = l/'(l + Qr2/3)(l+Qr2/s)- (12.2)
Уравнение (12.1) проверено в работе [1] при измерениях на
реакторе STAR К, и получено совпадение в пределах ±20%.
Если коэффициент передачи в х-м канале At выбран таким, что
A-JAz = ех/е2, некоррелированные сигналы дают круг, и мы имеем
простое соотношение:
(afb)* = 1+QV3 И + И- (12.3)
§ 12.3. Анализ реакторных шумов с применением
знаковой корреляции
Использование знака переменной величины в дискретные интер-
валы времени вместо ее численных значений в то же самое время
Рис. 12.4. Распределение вероятно-
сти [3].
эквивалентно оцифровке перемен-
ной с помощью одного значащего
бита. Этот метод был предложен
в работе [2] и усовершенствован
Драгтом [3].
Предположим, что х (/) = 0. За-
меним автокорреляционную функ-
цию знаковой автокорреляцион-
ной функцией фр (т):
<?Гхх ft) = sign lx И1 sign [х (t + т)].
(J2.4)
В работе [2] показано, что если
шумы являются гауссовыми, то
справедливо соотношение
sin Г— Фр (т)1 = 2е£?. (12.5)
L 2 fe(0)
Этот метод проверялся для ана-
лиза реакторных шумов путем
применения цифрового оборудования в измерениях шумов на реак-
торе LFR [31. Эксперимент проводился следующим образом. Ток
ионизационной камеры в реакторе с небольшой подкритичностью
384
квантовался по времени со скоростью 1000 выборок в секунду,
оцифровывался (9 уровней) и вводился в память ЦВМ. Здесь под-
считывалась функция срЛХ (т) путем усреднения по времени. Затем
все числа заменялись их знаками ( 4- 1 или — 1) относительно
средней величины к (0 и опять рассчитывалась автокорреляцион-
ная функция в соответствии с уравнением (12.4). От второй функ-
ции находились синусоидальные значения в соответствии с уравне-
нием (12.5), затем обе функции сравнивались. Эксперимент был
Рис. 12.5. Сравнение непосредственной и знаковой автокорреляционных функ-
ций шумов реактора LFR [3].
повторен для восьми выборок шумов, измеренных при идентичных
условиях,’ каждая из которых содержала 1'0 000 точек. Таким обра-
зом можно было получить средние значения и стандартные откло-
нения для корреляционных функций и их разностей. Кроме того,
было, определено и сравнено с гауссовым одномерное частотное
распределение точек.
Результат показан на рис. 12.4 в виде графика распределения
вероятности. Теоретически гауссово распределение реакторных
шумов может быть подтверждено посредством применения цент-
ральной предельной теоремы для случая подкритического реактора
на достаточно высоком уровне мощности.
Результат сравнения между обычной’и знаковой автокорреля-
ционными функциями дан на рис. 12.5, где кружками показано
385
отношение фяа: (т)/фжж (0). Разница между этой функцией и функ-
цией sin фрлл. (t)J показана в увеличенном в десять раз масштабе
(черные кружки) вместе со стандартными отклонениями. Между
этими функциями не было обнаружено существенной разницы.
В верхней части рисунка показано отношение стандартных откло-
нений функций sin фрж^| и ухх (т)/фхх (0). Удивительно, что
знаковая корреляционная функция имеет погрешность только приб-
лизительно в 1,5 раза больше, чем обычная корреляционная функ-
ция. Определение корреляционных функций для [sign х (/)] вместо
х (Z) может рассматриваться как измерение х (/) с точностью до
одного бита. Поскольку задержка, умножение и суммирование чи-
сел, представленных в виде одного бита, очень легко выполняются
электронными схемами, метод знаковой корреляции представляет
интересные возможности для прямого анализа реакторных шумов
в режиме on-line.
§ 12.4. Внутр и реакторные измерения скорости
теплоносителя и вибрации с помощью
внутризонных электродов и взаимной корреляции
В работе [4] сообщалось о методе измерения локальных скоро-
стей теплоносителя н распределения расходов в гидравлических мо-
делях реакторных активных зон с целью оптимизации теплопередачи
и относительных характеристик потока теплоносителя. Проводящие
электроды, смонтированные на стенках внутризонных каналов теп-
лоносителя, использовались для измерения изменений проводимости
без нарушения потока теплоносителя. Изменения проводимости
индуцировались путем инжекции малых количеств раствора соли
в поток, входящий в модель активной зоны. Взаимные корреляцион-
ные измерения дают время запаздывания между сигналами двух
детекторов.
Основой для измерений профиля потока является дальнейшее
распространение рассмотренного выше метода, в котором раствор
соли инжектируется против течения в секции, где проводится испы-
тание, и измеряются изменения сопротивлений в этой секции с по-
мощью проводящих элементов. Корреляционный метод включает
в себя инжекцию раствора соли при медленной постоянной скоро-
сти. Гидравлическая турбулентность превращает концентрирован-
ный раствор соли в малые вихревые образования, которые распро-
страняются через систему и проявляются вблизи электродов как
случайные изменения проводимости. Основная проблема заключает-
ся в измерении запаздывания переноса изменении проводимости
между двумя электродами вдоль одного и того же канала теплоно-
сителя. Поскольку взаимная корреляционная функция между дву-
мя случайными когерентными сигналами имеет максимальную
положительную величину при временном сдвиге, соответствующем
386
временному запаздыванию менаду двумя сигналами, можно исполь-
зовать взаимное корреляционное измерение для точного определе-
ния этого времени. Типичная взаимная корреляционная функция,
полученная в таких измерениях, показана на рис. 12.6.
Затем определяется средняя скорость жидкости:
у___ постоянная X расстояние
(12-6)
где постоянная является масштабным коэффициентом, относящим
время запаздывания измеренной скорости потока к средней скорости
потока. Этот масштабный коэффициент определяется опытным путем
для отдельного канала и является функцией числа Рейнольдса.
случайными сигналами
о Максимум коэффициента
о корреляции
О 0,1 0,2 0,3 Ofi 0,5 0,6 0,7 0,8 0,3 1,0
Время запаздывания, мсек
Рис. 12.6. График взаимной корреляции сигналов датчиков рас-
хода в трубопроводе [4].
Датчиком проводимости [5] служит изолированный электрод,
показывающий направление потока теплоносителя. Проводящим
путем является расстояние от этого электрода через лоток теплоно-
сителя к противоположной стенке канала. Локальное время пере-
носа находится по корреляции сигналов от двух электродов, рас-
положенных вдоль одного и того же канала. Профиль потока в пол-
ной сборке получается с помощью большого количества каналов из-
мерения во многих точках по высоте н проведения соответствую-
щих записей при требуемых скоростях потока. Применение уравне-
ния (12.6) дает полный профиль потока.
Перемешивание и пересечение струй потока находят из уравне-
ния баланса объема, примененного к профилю аксиального потока.
Пути пересечений струй в потоке определяются с помощью расчет-
ной программы, описанной в работе (6]. Непосредственно пересече-
ние может быть получено в двойном канале. Инжекция раствора
в один канал и наблюдение коэффициента корреляции в другом
канале будут давать прямое измерение пересечения потоков в зазоре
между каналами. Полученные результаты затем можно распростра-
нить на опыт с многими каналами.
387
О применении спектральной плотности мощности для измерения
гидравлической вибрации в модели активной зоны с использованием
тех же самых электродов и постоянного сопротивления раствора упо-
миналось в работе [4]. Движения элементов активной зоны приводят
к изменениям проводимости, которые измеряются анализатором
спектра. В этих измерениях электроды располагались близко к топ-
ливному стержню, а не в канале и раствор соли не инжектировался.
Соотношение между сопротивлением и величиной зазора для малых
изменений около номинального зазора есть
Д7? = рДА/2п (г-ф А)2, (12.7)
где Д/? — изменение сопротивления; h — величина . зазора;
г — радиус электрода; р — удельное сопротивление зазора.
Полное сопротивление зазора дается выражением
Амплитуда вибраций находится путем подстановки величины
измеренного сигнала, коэффициенты передачи регистрирующего
устройства и анализатора спектра, масштабных коэффициентов
в основное соотношение (12.7). Эти коэффициенты передачи и масш-
табные коэффициенты получают предварительной калибровкой
используемого оборудования. Выражение для ДА теперь принимает
вид
&h = 2lllr+hrkKkc&V, (12.9)
р
где kR — масштабный коэффициент перехода от сопротивления
к напряжению; Кс—коэффициент усиления регистрирующего уст-
ройства и анализатора спектра; ДУ—зарегистрированное изменение
напряжения.
Постоянные р и Кс, переменная величина ДУ измеряются в опы-
те. Вибрационное смещение в зависимости от частоты определяется
из соответствующим образом пронормированного измерения средне-
квадратического значения спектральной плотности мощности запи^-
санного сигнала, снимаемого с электрода. Аппаратурные шумы,
электрические помехи и т. п. определяются из сравнения вибра-
ционного спектра с фоновым спектром.
§ 12.5. Применение экспоненциально-косинусных
автокорреляционных функций в обработке данных,
полученных в опытах на ядерных системах
Многие экспериментаторы сообщали об обнаружении экспонен-
циально-косинусных автокорреляционных функций в теоретиче-
ских исследованиях случайных процессов, и это подтверждалось
наблюдениями таких явлений, как шумы вакуумных электронных
ламп, затухание радиолокационных волн, явление турбулентности
388
в атмосфере, броуновское движение в газах, выходной сигнал резо-
нансной схемы, к входу которой приложен широкополосный сигнал
[7]. Для автокорреляционной функции вида
<рхх (т) = А ехр (—К | т |) cos Ст
(12.10)
соответствующая спектральная плотность мощности дается урав-
нением (4.44), т. е.
(ш) = Г-------^+^+с=)--------
' л 1ш4+2(№—C“)a>’+(№+<?)».
(12.11)
Свойства спектральной плотности мощности обсуждались в § 4.8, •
и здесь рассматриваются только обобщенные свойства.
Когда со стремится к бесконечности, Ф (со) стремится к нулю.
Если 3 С2< К2 (случай 1), не существует максимумов спектральной
плотности и она монотонно уменьшается до нуля по мере стремле-
ния со к бесконечности. Если 3 С2 > № (случай 2), единственный
максимум спектральной плотности проявляется при
Ш1 = (К2 + C2)V4 [2С — (№ + С2)1'2]1/2 (12.12)
и величина этого максимума есть
1с [ (№+с2)‘'2-с]’
(12.13)
Практически комбинация двух или более случаев I и (или)
случаев 2 дает адекватное представление большинства типов спект-
ральной плотности мощности, т. е.
Ф (со) — Ф^ (со) -р Фг (®) 4“ • • • 4~ Фм (®) =
_ у Г (08+(Kf+cf) 1 (12 14)
[^+2(кГ-сПсо2+(я?+сГ)г]'
Этот метод использовался Уригом для анализа шумовых измере-
ний выходного давления водорода в «холодном» опыте на установке
KIWI-B4D/202-EP-1A.
Сигнал, управляющий скоростью насоса, возмущался гауссовым
«случайным» шумом. Данные опыта обрабатывались с применением
программы VAC [9] для автокорреляционной функции н спектраль-
ной плотности мощности, после чего проводилась обработка нели-
нейным методом наименьших квадратов в соответствии с уравнением
(12.14) [10]. Для ускорения сходимости применялось «взвешивание»
вида 1/Ф. Выбор числа членов уравнения (12.14), используемых
в процессе подгонки к экспериментальным данным, определялся
формой кривой. (Например, если имелись три существенных пика,
использовались три члена.)
389
На рис. 12.7 показаны спектральные плотности мощности флук-
туаций давления на выходе при наличии белого шума на входе.
Подгонка к уравнению (12.14) методом наименьших квадратов про-
водилась с использованием трех членов в уравнении. Результирую-
щие значения для Ch IQ и приведены в подрисуночной подписи.
1600
& 1W0
I
ё 1200
I
* 1000
8
§ 800
§
I Б0°
1 ^оо
s'
§ 200
О 20 УО 60 80 100 120
Угловая чостото ш,рад/сек
Рис. 12.7. Опыт на установке KIWI-B4D/202-EP-1A.
Шумы давления на выходе установки, вызван-
ные шумами насоса [8]:
О — входные данные: X — расчетные данные после
9 итераций; значения постоянных С|=0,704±0.060;
Ki=0.656*0.132; ^,=402.9*29.4; Cs=-7.191*0.025;
Кг=0.93-1 ±0.027: -3793*76; С3= 13.53*0,02; Кэ=
=0.512*0.058: А,=1216±44.
Физическая сущность величин С,, ZQ и может быть получена
при рассмотрении колебательной системы второго порядка с переда-
точной функцией вида
Н (со) =
1/т
—со2) 4* j2£c0n со
(12.15)
где т — масса; <ип — собственная частота; £ — коэффициент за-
тухания. Если система имеет иа входе белый шум, т. е. Фхх (со)—
постоянная величина, тогда
Ф^(о) = |Я«Фях(ш) =
390
Фхх(ОЗ)/(1/7П)2
(и2—со2)2-Р(2^п со)2
(12.16)
Если мы применим фурье-преобразование спектральной плотно-
сти мощности, то получим автокорреляционную функцию:
,п М _ яФже ехр (—&0п I X I) v
™ х
x[cosco„/l—г+ )ЛТ|-р sinro„yi—ф (12.17)
Когда коэффициент затухания мал (т. е. £ *<0,1) и система пол-
ностью недемпфи рована, синусным членом можно пренебречь и
уравнение (12.17) принимает вид
(т)=Вехр(—^<о„ |г |)cos<o„ ]/l—g2r. (12.18)
Сравнение с уравнением (12.10) показывает, что Сг являются
собственными частотвми затухания (соп]/"1 — i®), a At—коэф-
фициентами затухания. Следовательно, модель системы охлаждения
установки KIWI-B4D/202 может рассматриваться как состоящая
нз трех независимых недемпфированных колебательных систем.
§ 12.6. Анализ шумов ядерных реакторов
с применением у-излучения
Применение у-излучения в качестве средства исследования ди-
намики реактора успешно показано в работах [11, 121. Особый
интерес к исследоввниям у-излучения, описанным в этом параграфе,
возник из-за необходимости оценки источников помех прн анализе
нейтронных шумов в реакторах большой мощности. Практическое
применение борных ионизационных камер, расположенных вблизи
активной зоны (где отношение ионизации, обусловленной нейтро-
нами, к ионизации, обусловленной у-квантами, может быть небла-
гоприятным), зависит от шумов у-квантов, спектральные характе-
ристики которых обычно считаются «плоскими». В работе [11]
показано, что это ие так.
Чтобы оценить роль, которую играют у-кванты в анализе шумов,
были проведены четыре основных эксперимента. В первом выполня-
лись обычные осцилляторные измерения амплитуды и фазы переда-
точной функции исследовательского реактора PSR иа низком н вы-
соком уровнях мощности. Во втором повторялись осцилляторные
измерения, но ионизационная камера, использовавшаяся в первом
эксперименте, заменялась системой детектирования у-квантов.
В следующем эксперименте проводились измерения спектральной
плотности мощности шумов на низком и высоком уровнях мощности
обычной борной ионизационной камерой.’ В заключение была выпол-
нена серия экспериментов с детектором у-излучения вместо иониза-
ционной камеры. Для измерений флуктуаций нейтронного н у-из-
лучений электронное оборудование оставалось тем же самым,
только изменялись детекторы.
391
Детектирование у-излучсния и измерения. Сигналы у-излучения
измерялись по черепковскому излучению оптической системы,
состоящей из светонепроницаемой, заполненной водой трубы диа-
метром 75 /л/л, протянувшейся от активной зоны до поверхности бака
реактора. В этом устройстве вода является средой для генерации
света в результате эффекта Вавилова — Черенкова (как оптичес-
кий канал, идущий к поверхности фотоумножителя). Из прямого
расчета по формулам квантовой механики видно, что электрон
должен иметь по крайней мере энергию 0,265 Мэв, прежде чем
начнет проявляться эффект Вавилова — Черенкова. При взаимо-
действии с водой у-квантов в интересующем нас диапазоне энер-
гий комптон-эффект будет преобладать над фотоэффектом как
метод преобразования у-кваитов в высокоскоростные электроны.
Для комптон-эффекта требуется энергия у-кваитов около 0,7 Мэв,
прежде чем начнется эффективное черепковское излучение. С уве-
личением энергии выход иа один фотон повышается.
По сравнению с ионизационной камерой детектор Черенкова
имеет хорошую дискриминацию иизкоэиергетических у-кваитов про-
дуктов деления. Однако более важно отсутствие в детекторе Черен-
кова любого эффекта ограничения или насыщения, когда измерение
ведется в непосредственной близости от реактора, работающего иа
полной мощности. Миниатюрная ионизационная камера, испытан-
ная во время этой работы, показала некоторую нелинейность в этих
полях (15-10® р'ч).
Предполагалось, что запаздывающие у-кв анты будут преобладать
при низких частотах. При высоких частотах мгновенные у-кванты
должны давать основной вклад. Опубликованные данные говорят
о том, что около половины полного у-нзлучення и а деление является
мгновенным {131. Остающаяся запаздывающая часть распределена
в большом -интервале времени. Точное временное распределение
у-нзлучения после деления широко исследовано, и соответствующее
представление временного запаздывания у-излучения дано Вейнбер-
гом и В игнером [14].
В работе [111 отмечается, что вклад от мгновенных и запазды-
вающих компонент может быть представлен моделью, имеющей пере-
даточную функцию вида:
5!Д = (/( 4-----+ + + G (S). (12.19)
А К ($) \ р 1 + ту s 1 + s 1 -F-Tn s )
Уравнение (12.19) дает изменение интенсивности у-излучения
для данного малого изменения реактивности. (Здесь G/? (s) —
обычная передаточная функция реактора; /(„ •— доля мгновенного
у-изл учения; Kz... К.п—доли запаздывающего у-из л учения.)
Для иллюстрации возьмем одну группу запаздывающих у-кваитов.
Тогда уравнение (12.19) упрощается и принимает вид
392
где т — постоянная времени для реактора с численным значением
около 1 сек. Нормируя на передаточную функцию гипотетического
реактора нулевой мощности, получаем, что КР является величиной,
которая медленно увеличивается по мере роста мощности.
Осцилляторные измерения. На рис. 12.8 показана передаточ-
ная функция, полученная с помощью детектора у-излучения. Ясно,
что эффекты запаздывающего у-излучения становятся важными на
низких частотах. Применяя
указанное выше представле-
ние одной группой запазды-
вающего у-излучения, полу-
чим, что увеличение ампли-
туды на 5 дб на низких часто-
тах соответствует почти рав-
ным вкладам запаздывающего
и мгновенного у-излучения.
Это соответствует ожидаемым
результатам, упомянутым
выше. Тенденция увеличения
фазового сдвига прн низких
частотах также соответствует
выбранной модели. Тот факт,
что при частоте 0,01 гц на-
блюдается большой фазовый
сдвиг, означает, что в наблю-
даемый фазовый сдвиг основ-
ной вклад вносит запазды-
вающее у-излучение.
Интерес представляет так-
же и почти точное совпадение
передаточной функции у-из-
лучения н передаточной функ-
ции, полученной с помощью
нейтронного детектора, для
особенность существенна для интерпретации данных
шумов.
Измерения у-шумов. Обширные измерения амплитуды 'шумов
у-излучеиия впервые проводились на реакторе PSR [15]. В зависимо-
сти от того, какие шумы наблюдались (шумы у-излучения или ней-
тронные), в качестве детектора служили черепковский детектор или
ионизационная камера. Для измерения тока детектора использо-
вался промышленный электрометр, модифицированный с целью
получения плоской частотной характеристики в диапазоне от 0,01
до 100 гц. Ток детектора усиливался и подавался иа динамический
фильтр. Для измерения спектра амплитуд шума применялся циф-
ровой вольтметр. Принципиальной задачей этой части исследований
являлось сравнение методов измерения реакторных шумов с по-
мощью нейтронного и у-излучения. Спектр амплитуд шумов иссле-
Рис. 12.8. Сравнение передаточной
функции, намеренной с по-
мощью детектора ^’-излуче-
ния, с известной передаточ-
ной функцией пенсильван-
ского исследовательского
реактора иа высоком уров-
не мощности [И]:
О — данные,
ПОМОЩЬЮ ----------------
чнкв; — —г.
функция, измеренная
ным детектором.
полученные с
черепковского счет-
— — передаточная
нейтрок-
частот около точки излома
|3/Z. Эта
анализа
393
давался в зависимости от уровня мощности и расстояния детектора
от активной зоны реактора.
На рис. 12.9 показаны принципиальные результаты измерения
шумов у-излучения. В осцилляторных экспериментах можно было
получать информацию, начиная с уровня мощности около 2 кет.
В шумовых экспериментах необходимо было достичь уровня мощ-
ности 100 кет, чтобы получить ясные и повторяющиеся спектральные
характеристики. На уровнях мощности 100 и 200 кет не наблю-
далось существенной разницы в частотных характеристиках. Инте-
ресио отметить, что при уда-
лении детектора у-излучеиия
от активной зоны не было оче-
видных изменений в частот-
ных характеристиках на рас-
стояниях до 35 см. Начиная
с этого расстояния уровень
черенковского свечения ста-
новился настолько низким,
что дальнейшие измерения
были невозможны. Во всех
случаях, когда могли быть
получены воспроизводимые
результаты, частота излома
для у-нзлучения была равна
4 гц.
Рис. 12.9. Спектры шумов у-квантов на
поверхности активной зоны
(•) и на расстоянии 30 см от
активной зоны (О) [И].
Интерпретация измерений у-шумов. Из измерений передаточной
функции совершенно ясно, что запаздывающее у-излучение не ока-
зывает заметного влияния в частотном диапазоне свыше 1 гц.
Можно было ожидать, что в этом диапазоне будет хорошее согласие
между измерениями у-шумов и нейтронных шумов. Эта гипотеза
была подтверждена представленной здесь экспериментальной ра-
ботой, в которой можно было сделать прямые сравнения.
Данные измерений шумов у-излучения и нейтронов указывают,
что в спектре шумов реактора PSR могут быть изменения при уве-
личении уровня мощности. Такое поведение шумов наблюдалось
раньше [111, хотя причина не была выяснена. Осцнлляторные из-
мерения указывают, что реакторные кинетические характеристики
существенно не меняются с изменением уровня мощности.
Как отмечалось выше, воспроизводимые данные спектра шумов
не могли быть получены ниже уровня мощности реактора 100 кет
с помощью детектора у-излучеиия, хотя осцнлляторный снгиал мог
детектироваться по крайней мере на уровне мощности 2 кет. Эта
ситуация, по-видимому, была вызвана очень большим у-фоном от
предшествующих продуктов деления в реакторе во время измерений.
Вероятно,-полезные флуктуации у-излучеиия терялись на фоне не-
коррелированных шумов. Отношение фона к интенсивности изме-
ряемых у-квантов могло достигать величины от 1 до 20. Поэтому
пока флуктуации не создавались на существенном уровне мощности,
394
их было трудно наблюдать большим детектором у-излучения. Однако
детектор, чувствительный к у-квантам с энергиями выше 6 Мэв,
мог бы, вероятно, улучшить положение путем почти полного исклю-
чения фона.
Когда брали данные для больших расстояний от реактора, не
предполагали, что сигналы от регистрации у-квантов будут1 заметно
изменять свою способность передавать информацию от активной
зоны к детектору. С практически мгновенным временем пролета и
практически не измеримым временем замедления без потери времени
на диффузию у-кванты при прохождении расстояния между актив-
ной зоной и детектором должны подвергаться только ослаблению
и не должны заметно терять временную информацию. Данные изме-
рения шумов у-излучения в зависимости от расстояния, о которых
сообщалось в работе [13], подтвердили эту гипотезу.
Наблюдения шумов у-излучения ясно показывают существова-
ние амплитудного распределения в спектре шумов. Измерения пере-
даточной функции подтвердили, что при частотах выше 1 гц резуль-
таты, полученные с детектором у-излучеиия, должны быть практи-
чески те же самые, что и результаты с нейтронным детектором.
Наблюдения спектров шумов нейтронного и у-излучения иа высоких
уровнях мощности для больших расстояний от активной зоны об-
наруживают их подобие около частоты излома 4 гц. Следовательно,
эти шумы представляют флуктуации мощности реактора, а не эф-
фекты детектора или удаленности детектора от активной зоны.
Далее этот факт подтверждается независимостью спектрального
распределения амплитуд шума от расстояния до активной зоны для
измерений у-излучения.
В результате измерений, выполненных в работе [11], видно,
что анализ шумов у-излучения может быть полезным средством изу-
чения кинетики реактора. Более того, эффекты запаздывающего и
мгновенного у-излучения достаточно просто связаны с передаточной
функцией и, следовательно, наблюдение за временным поведением
у-квантов может служить дополнительным средством исследования
физики продуктов деления.
§ 12.7. Измерения акустических шумов
в ядерных реакторах
О применении шумовых методов для анализа акустических сиг-
налов с целью исследования характеристик Окриджского исследо-
вательского реактора сообщалось в работе [16]. Отмечалось, что
характеристики акустического фона зависят от расхода теплоноси-
теля, но относительно нечувствительны к изменениям нейтронного
потока. Эта зависимость от расхода теплоносителя приписывалась
шумам кавитации, и предполагалось, что кавитация может вызы-
вать модуляции потока посредством образования пустотелых пузырь-
ков. О детектировании пузырькового кипения с помощью измерений
нейтронных шумов на реакторе «Saxton» сообщалось в работе [17].
395
Однако в работе [18] указывалось, что нельзя детектировать пузырь-
ковое кипение в Окриджском исследовательском реакторе, и пред-
полагалось, что индуцированные потоком теплоносителя флук-
туации нейтронной плотности (по крайней мере для Окриджского
исследовательского реактора) будут всегда маскировать флуктуации,
обусловленные пузырьковым кипением. В работе [19] отмечалось,
что возможность детектирования кипения с помощью измерений ней-
тронных шумов прн любом уровне кипения увеличивается с ростом
уровня мощности, но делалось также предположение, что возрас-
тающий уровень шума, индуцированного потоком теплоносителя,
п связанный с увеличением расхода теплоносителя, требующегося
для удаления тепла, отрицательно сказывается иа чувствительно-
сти. Далее автор указал, что измерения акустических шумов яв-
ляются более чувствительным средством обнаружения кипения, чем
измерения нейтронных шумов, по крайней мере в 1000 раз в боль-
шинстве случаев. Автор и его помощники продолжают развивать
акустические методы в качестве средств детектирования пузырько-
вого кипения и определения количества возникающего пара.
СПИСОК ЛИТЕРАТУРЫ
1. Seifritz W., Stegemann D., Vath W. Two-Detector Cross-Correlation
Experiments in Fast-Thermal Argonaut Reactor STARK. — In: Neutron
Noise, Waves and Pulse Propagation, Gainesville, Fla., 1966, Uhrig R. E.
(Coordinator); AEC Symposium Series, 1967, N 9 (CONF-660206).
2. Veltman В. P. Th., Kwakernaak V. H. Regelungstechnik, 1961, в. 9,
s. 357.
3. Dragt J. B. Reactor Noise Analysis by Means of Polarity Correlation. —
«Nukleonik», 1966, v. 8, N 4, p. 225.
4. Randall R. L., Pekrul P. J. Application of Analog Time and Frequency
Correlation Computers to Reactor Systems Analysis. — In: Neutron
Noise, Waves and Pulse Propagation. Gainesville, Fla., 1966, Uhrig R. E.
(Coordinator); AEC Symposium Series, 1967, N 9 (CONF-660206).
5. Randall R. L., Pekrul P. J., Grayban G. R. Development of Noise Ana-
lysis Techniques for Measuring Reactor Coolant Velocities. — USAEC
Report NAA-SR-11193, Atomics International, February 1966.
6. Elliot R. D. Thermal Analysis Program (TAP-3), Preliminary User’s Ma-
nual, Atomics International Program, April 1964.
7. Bendat J. S. Principles and Applications of Random Noise Theory. John
Wiley and Sons, Inc., N. Y., 1958. (См. Бендат Дж. Основы теории случай-
ных процессов и ее применения. Пер. с англ. М., «Наука», 1965).
8. Uhrig R. Е. Use of Exponential Cosine Autocorrelation Functions in
Processing Nuclear-System Test Data. — «Trans. Amer. Nucl. Soc.»,
1965, v. 8, N 2, p. 586.
9. Springer T. Los Alamos Scientific Laboratory, personal communication,
1964.
10. Cockrell R. G. University of Florida, personal communication, 1964.
11. Kenney E. S. Noise Analysis of Nuclear Reactors with the Use of Gamma
Radiation. — Im Neutron Noise, Waves and Pulse Propagation- Gaines-
ville, Fla., 1966, Uhrig R. E. (Coordinator); AEC Symposium Series, 1967,
N 9 (CONF-660206).
12. Lehto W. K. Measurement of Dynamic Reactor Parameters by Photon
Observation. Ph. D. Dissertation, University of Michigan, November
1967.
396
13. Rockwell T. Reactor Shielding Design Manual. D. Van Nostrand Com
рапу, Inc., Princeton, N. Y., 1956. (См. Защита ядерных реакторов. Пер"
с англ. Под ред. С. Г. Цыпина. М., Изд-во иностр лит., 1958.)
14. Weinberg А. М., Wigner Е. Р. The Physical Theory of Neutron Chain
Reactors. The University of Chicago Press, Chicago, 1958. (См. Вейнберг A.,
Вигнер E. Физическая теория ядерных реакторов. Пер. с англ. Под
ред. Я- В. Шевелева. М., Изд-во иностр, лит., 1961.)
15- Shen С. Н. Noise Analysis of the Pennsylvania State University Reactor.
M. S. Thesis, The Pensylvania State. University, December 1965.
16. Saxe R. F. Acoustic Characteristics of the Oak Ridge Research Reactor. —
In: Neutron Noise, Waves and Pulse Propagation. Gainesville, Fla.,
1966, Uhrig R. E. (Coordinator); AEC Symposium Series, 1967, N 9
(CONF-660206), p. 475—485.
17. Rajagopal V., Gallagher J. M. Some Applications of Dynamic (Noise)
Measurements in Pressurized—Water—Reactor Nuclear Power Plants..—
In: Neutron Noise, Waves and Pulse Propagation. Gainesville, Fla,
1966, Uhrig R. E. (Coordinator); AEC Symposium Series, 1967, N 9
(CONF-660206), p. 487—501.-
18. Fry D. N., Roux D. P., Ricker C. W., Stephenson S. E., Hanauer S. H.,
Trinko J. R. Neutron—Fluctuation Measurements at Oak Ridge National
Laboratory. •— In: Neutron Noise, Waves and Pulse Propagation. Gai-
nesville, Fla., 1966, Uhrig R. E. (Coordinator); AEC Symposium Series,
1967, N 9 (CONF-660206), p. 462—474.
19. Saxe R. F. North Carolina State University, personal communication,
1969.
ОГЛАВЛЕНИЕ
Предисловие к переводу.................... ........... 3
Предисловие автора к русскому изданию . ................... 5
Глава 1. Общая характеристика случайных процессов в ядерных
реакторах................................................ 7
§ 1.1. Случайные процессы в ядерных реакторах .... 7
§ 1.2. Обоснование методов случайных шумов в изме-
рениях на ядерных реакторах...................... 9
§ 1.3. Случайные процессы и переменные...........11
§ 1.4. Стационарные н эргодические процессы.....13
Список литературы..........................................15
Г л а в а 2. Статистические методы, применяемые при анализе слу-
чайных шумов...............................................17
§ 2.1. Введение..................................17
§ 2.2. Средние значения и моменты вероятности ..... 17
§ 2.3. Вероятностные распределения при радиоактив-
ном распаде......................................20
§ 2.4. Корреляционные функции . •................25
Список литературы................................. - • . • 29
Г л а в а 3. Статистические дискретные методы в реакторных систе-
мах ..........................................................30
§ 3.1. Введение.................................. 30
§ 3.2. Вероятностное распределение нейтронов деления 31
§ 3.3. Метод росси—альфа......................... - 34
§ 3.4. Метод, использующий отношение дисперсии
к среднему (метод Фейнмана)...................40
§ 3.5. Метод дисперсии Беннета.....................45
§ 3.6. Методы определения вероятности .............46
§ 3.7. Метод распределения интервалов (метод Бабала) 49
§ 3.8. Метод мертвого времени (метод Сриннвасаиа) . . 53
§ 3.9. Методы корреляционного анализа..........54
§ 3.10. Ковариационные измерения...............56
§3.11. Метод эндогенного пульсирующего источника 58
Список литературы....................................60
Глава 4. Основные соотношения теории случайных шумов ... 62
§4-1. Введение.................................62
§ 4.2. Автокорреляционная функция............’. . . 62
§ 4.3. Автоковарнацноиная функция.............64
§ 4.4. Спектральная плотность мощности ........ 65
§ 4.5. Специальные автокорреляционные функции
и спектральные плотности мощности.............68
§ 4.6. Взаимная корреляционная функция.............75
§ 4.7. Взаимная ковариационная функция.............77
§ 4.8. Взаимная спектральная плотность.............78
§ 4.9. Соотношения между входными и выходными сиг-
налами ............................................80
§ 4.10. Практическое рассмотрение ............... 84
§ 4.11. Односторонняя спектральная плотность....85
§ 4.12. Зависимость корреляционных функций и спект-
ральных плотностей от среднего значения .... 90
§ 4.13. Когерентные функции.......................93
§ 4.14. Корреляция при использовании двух детекторов
и измерение спектральной плотности..........94
§ 4.15. Многоканальные по входу линейные системы - . 100
Список литературы................................... . . . .110
Г л а в а 5. Элементарнаи теория реакторных шумов............111
§ 5.1. Введение....................................Ш
§ 5.2. Источник эквивалентного шума..............111
398
§ 5.3. Метод Ланжевена — модель с сосредоточенными
параметрами 11b 119 126 133 135 140
§ 5.4. Пространственио-зависнмый реакторный шум . .
§ 5.5. Пространственно-зависимый шум в бесконечной
среде
§ 5.6. Влияние границ на корреляцию . . .
§ 5.7. Пространственно-зависимый шум в паралле-
лепипеде без отражателя
§ 5.8. Заключение . . - - -
С п н сок литературы 141
Г л а в а 6. Методы анализа шумов ....... § 6.1. Введение § 6.2. Корреляционные измерения § 6.3. Измерения спектральной плотности § 6.4. Измерения передаточных функций § 6.5. Прямой гармонический анализ § 6.6. Конечная длительность реализации § 6.7. Временные и спектральные «окна» § 6.8. Анализ спектральной плотности § 6.9. Статистические степени свободы § 6.10. Влияние некоррелированных шумов на изме- рения передаточной функции § 6.11. Точность измерений передаточной функции . . 142 142 144 146 149 151 154 155 159 160 163 167
Спи сок литературы - - 173
Г л а в а 7. Методы измерения шумов и аппаратура § 7.1. Аппаратура для измерений реакторных шумов § 7.2. Методы непрерывного анализа данных с помощью аналоговых ЭВМ . . . 174 174 175
§ 7.3. Измерение плотности вероятности........... . 180
§7.4. Измерение корреляционных функций.......... .183
§ 7.5. Измерения спектральной плотности..........185
§ 7.6. Методы фильтрации прк измерениях спектральной
плотности........................................189
§ 7.7. Выбор частотного интервала спектральной плот-
ности ...........................................198
§ 7.8. Анализ периодических процессов ........ 200
§ 7.9. Анализ спектров переходных процессов......202
Список литературы.......................... ................205
Глава 8. Сбор, передача и запись данных .................. 206
§ 8.1. Введение..................................206
§ 8.2. Получение данных..........................207
§ 8.3. Запись непрерывной информации ......... 209
§ 8.4. Аналого-цифровое преобразование...........217
§ 8.5. Многоканальная передача: распределение вре-
мени работы оборудования ......... 224
§ 8.6. Система сбора цифровой информации.........225
Список литературы...........................................228
Глава 9. Методы генерации псевдослучайных шумов и их приме-
нение ......................................................229
§ 9.1. Введение..................................229
§ 9.2. Входные переменные для взаимной корреляции 231
§ 9.3. Максимальная последовательность линейного
регистра сдвига (т—последовательность) ... 238
§ 9.4. Псевдослучайная переменная типа остатков квад-
рата ............................................252
§ 9.5. Многочастотные двоичные входные сигналы .... 253
§ 9.6. Певдослучайная двоичная переменная с обрат-
ным повторением................................ 258
§ 9.7. Использование псевдослучайных переменных в ка-
честве заменителя случайных шумов................260
399
§ 9.8. Взаимная корреляция с псевдослучайными двоич-
ными сигналами ............................ ..... 262
§ 9.9. Использование псевдослучайных троичных перемен-
ных для исследования нелинейных систем .... 269
Список литературы..........................................272
Глава 10. Обработка данных на цифровых машинах..........j . 274
§ 10.1. Введение.............................. 274
§ 10.2. Исключение регулярной составлиющей........275
§ 10.3. Цифровая обработка периодических данных . . 277
§ 10.4. Цифровая фильтрация.....................280
§ 10.5. Статистический анализ...................293
§ 10.6. Представление в виде ридов Фурье (классиче-
ский метод).................................... 297
§ 10.7. Функции корреляции и спектральные плотности 298
§ 10.8. Передаточные функции к функции когерентности 303
§ 10.9. Выбор параметров реакторных исследований . . 304
§ 10.10. Быстрое преобразование Фурье..........307
Список литературы..........................................311
Глава 11. Измерение шумов в ядерных реакторах......... 313
§ 11.1. Введение...............................313
§ 11.2. Эксперименты по счету нейтронных импульсов 313.
§ 11.3. Измерение шумов в критических реакторах - - . 328
§ 11.4. Измерение реактивности............... 338
§ 11.5. Шумовые измерении в энергетических реакто-
рах ............................................360
Список литературы.....................................377
Глава 12. Специальные статистические методы и их применение
в ядериых реакторах........................................381
§ 12.1. Введение................................381
§ 12.2. Оптическое наблюдение корреляции........381
§ 12.3. Анализ реакторных шумов с применением зна-
ковой корреляции................................384
§ 12.4. Внутриреакторные измерения скорости тепло-
носителя и вибрации с помощью внутркзонных
электродов и взаимной корреляции................386
§ 12.5. Применение экспоиепциально-носииусных авто-
корреляционных функций в обработке данных,
полученных в опытах на ядерных системах .... 388
§ 12.6. Анализ шумов ядерных реакторов с применением
у-излучении.....................................391
§ 12.7. Измерения акустических шумов в ядерных ре-
акторах .... ..................................395
Список литературы.................................... - 396
Роберт Ури г
СТАТИСТИЧЕСКИЕ МЕТОДЫ В ФИЗИКЕ ЯДЕРНЫХ РЕАКТОРОВ
Редактор Г. п. Паршина
Художественный редактор А. Т, Кирьянов
Переплет художника А. И. Шаварда
Технический редактор Н. А. Власова
Корректоры JH. А. Жарикова, Л. С. Тимохова
Сдано в набор 13/XI 1973 г. Подписано к печати 8/V 1974 г.
Формат 60X90/16. Бумага типографская № 2- Усл.-печ. л. 25,0 Уч.-изд. л. 25,16
Тираж 1 460 экэ. Зак. изд. 71366 Зак. тип. 576 Цена 2 р. 76 к.
Атомиздат, 103031, Москва, К-31, ул, Жданова, 5
Московская типография Кв 4 Союзполиграфпрома при Государственном комитете
Совета Министров СССР по делам издательств, полиграфии и книжной торговли
Москва. И-41. Б. Переяславская ул., дом К» 46
. ж , •