ВЫСШЕЕ
ЭКОНОМИЧЕСКОЕ
ОБРАЗОВАНИЕ
В.А. Малугин
Математика для экономистов
ЛИНЕЙНАЯ АЛГЕБРА
Курс лекций
Допущено УМО по классическому университетскому образованию
в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению 080100 «Экономика»
Москва
2006
Эксмо!
УДК 512
ББК 22.143
М 18
Об авторе:
Малугин В.А. — кандидат физико-математических наук, доцент
кафедры «Математические методы анализа экономики» эконо-
мического факультета МГУ им. М.В. Ломоносова
Рецензенты:
Черемных Ю.Н. — доктор экономических наук, профессор кафедры
«Математические методы анализа экономики» экономического
факультета МГУ им. М.В. Ломоносова
Гаврилец Ю.Н. — доктор экономических наук, профессор, заведую-
щий лабораторией математической социологии ЦЭМИ РАН
Малугин В.А.
М 18 Математика для экономистов: Линейная алгебра. Курс лекций. —
М.: Эксмо, 2006. — 224 с. — (Высшее экономическое образование).
ISBN 5-699-12627-9
Книга входит в состав учебного комплекса «Математика для экономистов», спе-
циально созданного для экономических вузов страны экономическим факультетом
МГУ им. М.В. Ломоносова. Ее цель — в ясной и удобной для восприятия форме дать
студенту-экономисту весь объем необходимых ему математических знаний в части
линейной алгебры. При этом студент четко сориентирован, для чего и когда ему
будет полезно знание тех или иных разделов дисциплины: для решения каких эконо-
мических задач нужна матричная алгебра, как с помощью систем линейных уравнений
можно построить модель многоотраслевой экономики, какие методы оптимизации по-
зволяют решить задачу максимизации прибыли и т.д.
Издание предназначено для студентов и преподавателей экономических факуль-
тетов и вузов.
УДК 512
ББК 22.143
ISBN 5-699-12627-9
© В.А. Малугин, 2006
© ООО «Издательство «Эксмо», 2006
Содержание
Предисловие................................................ 9
ГЛАВА 1. МАТРИЧНАЯ АЛГЕБРА................................ 11
§1.1	. Матрицы............................................ 11
Основные сведения о матрицах.......................... 11
Виды матриц........................................... 12
§1.2	. Операции над матрицами............................. 14
Умножение числа на матрицу............................ 14
Сложение матриц одинакового размера................... 14
Вычитание матриц одинакового размера.................. 14
Умножение матрицы на матрицу.......................... 15
Возведение матрицы в целую положительную степень...... 16
Транспонирование матрицы.............................. 16
Свойства транспонирования матрицы..................... 17
§1.3	. Определители квадратных матриц..................... 17
Введение определителя................................. 17
Свойства определителей..........:..................... 22
Вычисление определителя............................... 26
§1.4	. Обратная матрица................................... 28
Теорема о существовании обратной матрицы.............. 28
Свойства обратных матриц ............................. 30
§	1.5. Матрицы элементарных преобразований .............. 33
Типы матриц элементарных преобразований............... 33
3
Элементарные преобразования матрицы.................... 34
Способ построения обратной матрицы..................... 39
§ 1.6.	Ранг матрицы........................................ 41
Определение ранга матрицы.............................. 41
Ранг матрицы при элементарных преобразованиях.......... 43
Линейные комбинации строк или столбцов................. 45
Связь ранга с числом независимых строк (столбцов)...... 47
Строка матрицы как линейная комбинация независимых
строк матрицы.......................................... 48
Вопросы для повторения..................................... 49
ГЛАВА 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ........................ 51
§2.1. Общие понятия системы линейных уравнений............. 51
§2.2. Нахождение единственного решения системы
линейных уравнений......................................... 52
Метод обратной матрицы................................. 52
Метод с использованием расширенной матрицы............. 54
Метод с использованием формул Крамера.................. 55
§ 2.3.	Общий подход к решению систем уравнений............. 58
Равносильность систем линейных уравнений при
элементарных преобразованиях........................... 58
Метод Гаусса........................................... 59
Теорема Кронекера — Капелли............................ 63
Схема решений системы уравнений........................ 64
§ 2.4.	Базисные решения системы уравнений.................. 65
§ 2.5.	Однородные системы линейных уравнений............... 66
Свойства однородной системы линейных уравнений......... 67
Фундаментальные решения................................ 68
§ 2.6.	Общее решение системы неоднородных
линейных уравнений......................................... 73
§ 2.7.	Модель Леонтьева многоотраслевой экономики.......... 75
Вопросы для повторения..................................... 78
4
ГЛАВА 3. ВЕКТОРНАЯ АЛГЕБРА................................. 80
§ ЗЛ. Векторы на плоскости и в пространстве
(геометрические векторы)............................... 80
Линейные операции над векторами........................ 81
Координаты вектора..................................... 82
Скалярное произведение векторов........................ 82
Свойства скалярного произведения....................... 84
Векторы в трехмерном пространстве...................... 84
§ 3.2.	Линейные векторные пространства..................... 86
Понятие линейного векторного пространства.............. 86
Вектор в и-мерном пространстве......................... 87
Линейная зависимость и независимость векторов.......... 88
Свойства линейной зависимости векторов................. 89
§ 3.3.	Размерность. Базис векторного пространства.......... 91
Размерность векторного пространства.................... 91
Базис векторного пространства.......................... 92
Разложение вектора по базису........................... 93
Дополнение до базиса................................... 96
§ 3.4.	Переход к новому базису............................. 99
Матриц	а перехода к новому базису.................... 99
Свойст	ва матрицы перехода...........................100
§ 3.5.	Линейные подпространства............................102
Линейные подпространства................................ 102
Сумма и пересечение линейных подпространств............. 103
Свойства суммы и пересечения подпространств.............104
Линейная оболочка.......................................104
Свойства линейной оболочки.............................. 105
§ 3.6.	Евклидовы пространства............................. 105
Евклидовы пространства................................ 105
Свойства длины вектора................................ 107
Ортонормированная система векторов ................... 108
Ортогональное дополнение.............................. 112
Свойства ортогонального дополнения...................... 113
Вопросы для повторения...................................... 116
5
ГЛАВА 4. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ......................... 117
§4.1.	Общие сведения о линейных отображениях......... 117
Отображения....................................... 117
Образ, ранг, ядро, дефект отображения............. 118
Отображение базиса................................ 119
§ 4.2.	Линейные операторы ............................ 121
Линейные операторы и их свойства.................. 121
Структура линейного оператора......................122
Матрицы оператора в разных базисах.................125
Определитель оператора в разных базисах............126
§ 4.3.	Собственные векторы и собственные значения
линейного оператора....................................127
Собственные векторы и собственные значения.........127
Независимость собственных векторов.................129
§ 4.4.	Симметричный оператор.......................... 131
Симметричный оператор..............................131
Ортогональность собственных векторов...............132
§ 4.5.	Квадратичные формы............................. 133
Понятие квадратичной формы........................ 133
Связь между квадратичной формой и оператором.......136
Приведение квадратичной формы к каноническому виду ... 137
Свойства канонических форм........................ 139
Критерий Сильвестра .............................. 140
Вопросы для повторения................................ 145
ГЛАВА 5. ВЕКТОРНЫЕ ФУНКЦИИ.............................146
§ 5.1.	Векторные функции скалярного ар!умента..........146
Определение векторной функции скалярного аргумента .... 146
Предел и непрерывность векторной функции скалярного
аргумента......................................... 147
Дифференцирование векторной функции скалярного
аргумента......................................... 148
Свойства производной векторной функции скалярного
аргумента......................................... 149
6
Правила дифференцирования векторной функции
скалярного аргумента............................... 149
§ 5.2.	Векторные функции векторного аргумента...........150
Определение векторной функции векторного аргумента..150
Потенциальное поле вектора......................... 152
Дифференцирование векторной функции
векторного аргумента................................155
Вопросы для повторения..................................156
ГЛАВА 6. КЛАССИЧЕСКИЕ МЕТОДЫ ОПТИМИЗАЦИИ............... 157
§6.1.	Локальный экстремум............................. 157
Определение локального экстремума.................. 157
Необходимые условия локального экстремума ..........158
Достаточные условия локального экстремума.......... 161
Использование квадратичных форм.................... 163
§ 6.2.	Условный экстремум.............................. 168
Определение условного экстремума................... 168
Первый метод нахождения условного экстремума ...... 170
Второй метод нахождения условного экстремума
(метод Лагранжа)................................... 173
Геометрическая интерпретация необходимых условий
для условного экстремума........................... 174
Окаймленный гессиан................................ 175
Последовательность действий при отыскании условных
экстремумов функции двух переменных................ 178
§ 6.3.	Экстремум неявной функции....................... 183
§ 6.4.	Бюбальный экстремум............................. 187
§6.5.	Экстремум в системах функций......................190
§6.6.	Экстремум в системах неравенств .................194
§ 6.7.	Оптимизация потребительского поведения
(функция спроса)........................................198
7
§6.8.	Максимизация прибыли в проектном анализе.........200
§ 6.9.	Глобальный экстремум в задачах
математического программирования.......................206
Вопросы для повторения.................................210
СПИСОК ЛИТЕРАТУРЫ......................................211
ТЕМАТИЧЕСКИЙ УКАЗАТЕЛЬ.................................212
Предисловие
Учебник создан в помощь студентам-экономистам и допол-
нен сборником задач и упражнений по линейной алгебре. Автору,
в течение ряда лет ведущему математические курсы на экономи-
ческом факультете, пришлось столкнуться с проблемами, связан-
ными с отсутствием математических учебников и задачников,
адаптированных к требованиям современной математизирован-
ной экономической науки.
Рекомендуемые студентам пособия (выпуска 60-х годов про-
шлого века) стали устаревать. Современная же математическая
литература ориентирована в основном на студентов математичес-
ких специальностей. В созданных специально для студентов-эко-
номистов учебниках высшая математика дается на элементарном
уровне, недостаточном для полноценного освоения специаль-
ных экономических дисциплин. В связи с этим назрела потреб-
ность в обновлении учебной экономико-математической литера-
туры для студентов экономических отделений университетов.
Учебник написан в рамках требований университетского об-
щеобразовательного стандарта в области математики. Он базиру-
ется на работах [1—7], при этом автор использовал наиболее ин-
тересные педагогические находки по изложению материала в
доходчивой форме, а также наиболее удачные примеры и иллюс-
трации.
В связи с последовательным изучением математического ана-
лиза и линейной алгебры на многих экономических отделениях
вузов раздел функций нескольких переменных (ФНП) разбит на
две части. Первую часть составляет собственно инструментарий
ФНП. Этот материал включен в учебник по математическому
9
анализу. Вторую часть составляют методы оптимизации, содер-
жащие исследования на экстремум. Эти методы используют как
инструменты математического анализа, так и аппарат линейной
алгебры. Поэтому данный материал изложен в учебнике по ли-
нейной алгебре. Он заканчивается понятием глобального экстре-
мума в задачах линейного и нелинейного программирования, что
составляет предмет следующего изучаемого математического
курса — «Исследование операций».
Начало и конец доказательства основных утверждений и тео-
рем выделены в учебнике значками ◄ и ►.
Матричная алгебра
§1.1. Матрицы
> Основные сведения о матрицах
> Виды матриц
Матричная алгебра является важным элементом экономи-
ческих расчетов. Многие экономико-математические модели
рассматриваются и решаются в матричной форме.
Основные сведения о матрицах
Определение. Матрицей с размерами тхп называется
прямоугольная таблица чисел, содержащая т строк и п столбцов.
Числа, составляющие матрицу, называются элементами матри-
цы. Матрицы обычно обозначают заглавными буквами латин-
ского алфавита, например А, В, С,..., а для обозначения элемен-
тов матрицы используются строчные буквы с двойной индекса-
цией: ау, где i — номер строки, j — номер столбца. Числа i и j
определяют расположение элемента ач в матрице А и играют роль
координат этого элемента в прямоугольной таблице чисел.
Например, матрица
а\1	•••	а\п
аП	•••	а2п
<ат\ ат1	amnj
имеет т строк и п столбцов.
11
Линейная алгебра. Курс лекций
Набор
ап,..., ain)
называется z-й строкой матрицы А, а набор
называется j-м столбцом матрицы А. Любые строки и столбцы
матрицы А, в свою очередь, являются матрицами.
Две матрицы А и В одинакового размера называются равны-
ми, если они совпадают поэлементно. Равенство записывается
как А = В.
Виды матриц
Матрица произвольного размера, все элементы которой рав-
ны нулю, называется нулевой и обозначается О.
Матрица, состоящая из одной строки А - (аИ, а12,..., а1п), на-
зывается матрицей-строкой или вектором.
Матрица, состоящая из одного столбца А -
, называется
матрицей-столбцом или также вектором.
Матрица называется квадратной п-ro порядка, если число ее
строк равно числу столбцов и равно п.
Элементы квадратной матрицы av, у которых номер строки
совпадает с номером столбца, называются диагональными и обра-
зуют главную диагональ.
Если все недиагональные элементы квадратной матрицы рав-
ны нулю, то матрица называется диагональной. Например,
(2
О
1
О
А =
О
О
О'
О
— диагональная матрица третьего порядка.
12
Глава 1. Матричная алгебра
Квадратная матрица, на главной диагонали которой стоят
единицы, а все остальные элементы равны нулю, называется еди-
ничной и обозначается Е. Например, матрица
Е =
4 О О О'
0 10 0
0 0 10
.0 0 0 1,
является единичной матрицей четвертого порядка.
Квадратная матрица, у которой все элементы выше или ниже
главной диагонали равны нулю, называется треугольной.
Произвольная матрица вида С - (А | В), составленная из двух
матриц, разделенных вертикальной чертой, называется расши-
ренной. Например, матрица
fl 2
3
6
9
4 5
7 8
С =
1 0 0
0 1 0
0 0 1;
является расширенной. Она составлена из квадратной матрицы
третьего порядка и единичной матрицы третьего порядка.
Матрица может содержать своими элементами другие матри-
цы. Например, матрица
А =
си
°21
может быть записана в виде А =
, где ах, а2, ..., ап — матри-
цы-строки исходной матрицы.
Квадратная матрица А п-го порядка называется симметрич-
ной, если ее элементы подчиняются следующему равенству:
где/,у= 1,2,..., п.
13
Линейная алгебра. Курс лекций
§1.2. Операции над матрицами
>	Умножение числа на матрицу
>	Сложение матриц одинакового размера
>	Вычитание матриц одинакового размера
>	Умножение матрицы на матрицу
>	Возведение матрицы в целую положительную степень
>	Транспонирование матрицы
>	Свойства транспонирования матрицы
Над матрицами возможно проведение некоторых арифмети-
ческих операций.
Умножение числа на матрицу
Эта операция производится по следующему правилу: число
умножается на каждый элемент матрицы.
Произведением числа на матрицу А = (а^ называется матрица
В= (bfJ) такая, что В- X • А.
Элементы матрицы В вычисляются по формуле btj, = X atj, где
i- 1, 2,..., т, j= 1, 2,..., п.
Замечание. Общий множитель всех элементов матрицы
можно выносить за знак матрицы.
Сложение матриц одинакового размера
Соответствующие элементы матриц складываются.
Суммой матриц А = (ау) и В- (by) называется матрица С = (с,у)
такая, что С= А + В. Элементы матрицы С вычисляются по фор-
муле Су=ау + by, где i= 1, 2,..., т, j= 1, 2,..., п.
Вычитание матриц одинакового размера
Соответствующие элементы матриц вычитаются.
Разностью матриц А = (йу) и В - (by) называется матрица
С= (су) такая, что С- А + (— 1) х В. Элементы матрицы С вычисля-
ются по формуле Су=ау—Ьу, где i= 1, 2,..., m,j- 1, 2,..., п.
14
Глава 1. Матричная алгебра
Умножение матрицы на матрицу
Элемент новой матрицы, стоящий на пересечении z-й строки
и /-го столбца, равен сумме произведений элементов z-й строки
первой матрицы на соответствующие элементы /-го столбца
второй матрицы. Операция определена при условии, что число
столбцов первой матрицы равно числу строк второй.
Произведением матрицы А = (ai}) на матрицу В= (Ь,,) называется
матрица С- (с#) такая, что С=А • В. Элементы матрицы Свычис-
ляются по формуле
-anby + al2b2J +... + ainb„j.	(1)
ПРИМЕР.
l O+O l+HJ-p) 1-(-1)+O O+(-1)-2A (2 -3)
2 0+11+0-(-2)	2-(-1)+1-0+0-2	-2/
Замечание 1. Используя знак сокращенного суммирова-
ния, формулу (1) можно записать в виде
си = &*Ьц, i = 1,2,..., т, j = 1,2,..., п.
к^\
Замечание 2. Введем обозначение матрицы в виде , оз-
начающее, что матрица содержит т строк и п столбцов. Тогда
произведение матриц можно записать следующим образом:
А В= С .
тхк кхп тхп
Замечание 3. Порядок матриц-сомножителей существен.
Поэтому говорят об умножении матрицы А на матрицу В справа
или слева.
Если произведение матриц А  В существует, то произведение
матриц В  А может не существовать.
Если существуют произведения матриц А • В и В • А, они мо-
гут быть матрицами разных размеров.
Если матрицы А и В квадратные, то их произведения А  В
иВ-А существуют и имеют одинаковый порядок, но в общем слу-
чае А  В* В-А.
15
Линейная алгебра. Курс лекций
Замечание 4. Умножение единичной матрицы Ена квад-
ратную матрицу А не изменяет последней: Е • А - А  Е= А.
Замечание 5. Произведение двух ненулевых матриц мо-
жет дать нулевую матрицу О, например:
О (А
о о]
= 0.
Возведение матрицы
в целую положительную степень
Возведение матрицы в целую положительную степень к сво-
дится к произведению к одинаковых матриц:
Ак=АА-А.
к
Дополнительно определим А° = Е, А'= А.
Замечание 1. Возведение в степень матрицы может при-
вести к нулевой матрице. Например:
fi XY 1 П f1 n_f° °)
[-1 -ij "[-i -U 1° oJ
Замечание 2. Операция возведения в степень определена
только для квадратных матриц.
Транспонирование матрицы
(переход к матрице, у которой строки и столбцы меняются
местами).
Матрица
Оц о2, ... от1
а12 о22 ... ат2
а, а. ... а
\1л 2п	тп /
называется транспонированной по отношению к матрице
°i2	а\п
а1\ ап  а2п
ат1 "• amnj
16
Глава 1. Матричная алгебра
и обозначается Лг.
Замечание. Из определения следует, что если матрица
А имеет размер т х п, то транспонированная матрица АГ имеет
размер п х т.
Операции транспонирования, а также операции сложения и
умножения матриц обладают легко проверяемыми свойствами.
Свойства транспонирования матрицы
1)	(АТ)Т=А.
2)	(а • А)т=Ат + В?, где а — число.
3)	(Л + В)Т~АТ + ВТ.
4)	(А В)Т=ВТАТ.
Свойства операций сложения и умножения:
1)	А+В=В+А.
2)	(А +В) +С=А+(В + С).
3)	а (А + В) = осЛ + аВ.
4)	А (В +С) = АВ +АС.
5)	(А+В)С-АС + ВС.
6)	С (АВ) = (СА) В.
7)	а(АВ) = (аЛ)В = А(аВ).
§1.3. Определители квадратных матриц
>	Введение определителя
>	Свойства определителей
>	Вычисление определителя
Введение определителя
Свяжем с каждой квадратной матрицей А некоторое число,
вводимое по определенному правилу. Назовем это число опреде-
лителем матрицы и обозначим его |Л |.
Определителем матрицы первого порядка Л = (д,,) назовем число
И = («.,)
Определителем матрицы второго порядка
17
Линейная алгебра. Курс лекций
назовем число, равное
И=
«И
«21
«!2
«22
«12
«22
— йпЛ/п О\2Мп,
где Му (индекс J равен 1 или 2) — определитель матрицы первого
порядка, полученный вычеркиванием из матрицы /11-й строки и
у-го столбца.
Например, определитель Мх, получен из матрицы А вычерки-
ванием 1-й строки и 1-го столбца. Следовательно, величина опре-
делителя Мн равна а22:
1 — «22-
Тогда
«11
Определителем матрицы третьего порядка А - о21
<«3i
«12	«13
«22	«23
«32	«33 >
назовем число, равное
(2)
где M}J (индекс j равен 1, 2 или 3) — определитель матрицы вто-
рого порядка, полученный вычеркиванием из матрицы Л 1-й
строки и у’-го столбца. Например, определитель Ми получен из
матрицы А вычеркиванием 1-й строки и 1-го столбца:
^.=
«22
«32
«23
«33
— о22«33	«23«32 ,
М12 =
«21
«3!
«23
«33
— о2|«33	«23«31 ’
18
Глава 1. Матричная алгебра

«2!
«3!
«22
«32
— о2,о32 «22«з1 .
Подставим полученные соотношения в (2):
«и
И = о2|
«3!
«12	«13
«22 а23
«32	«33
— Ои(д2203з О23О32) «|2(«21«33 «23«31) +
(3)
+ 0,3 (о21«32	«22«31)~ «11«22«33 + «12«23«31 +
+ O2|#32fl13	«13«22«И а\ 1«32«23	«21«12«13 •
Из структуры формулы видно, что в каждое слагаемое в пра-
вой части равенства входит по одному элементу из каждой строки
и каждого столбца матрицы. Формулу (3) несложно запомнить,
если воспользоваться правилом треугольников (рис. 1.1). Берутся
произведения элементов, соединенных линиями. На рисунке
слева линиями указаны произведения элементов, которые следу-
ет взять со знаком «+», справа — со знаком «—».
Рис. 1.1
Например, величина определителя матрицы
О -Г
1 О
1 з,
1
равна |л|= 2
-2
О -1
1 О
1 3
= 11-3+0-0(-2)+2-1-(-1)-
-(-2)-1-(-1)-1-1-0-0-2-3 = -1.
Предположим, что определители матриц, порядок которых
меньше п, введены. Определителем квадратной матрицы и-го по-
рядка
19
Линейная алгебра. Курс лекций
«п	а12	...	а)и
«21	«22	•••	а2п
<ап\	ап2	•••	annj
назовем число
где Му — определитель матрицы (и — 1)-го порядка, полученной
из матрицы А вычеркиванием 1-й строки и у-го столбца.
Введем понятия минора и алгебраического дополнения.
Минором Ми элемента ау матрицы А п-ro порядка называется
определитель (и — 1)-го порядка, полученный из матрицы А вы-
черкиванием z-й строки и у'-го столбца. Например, минор М2,
элемента а23 матрицы третьего порядка получается вычеркива-
нием из матрицы 2-й строки и 3-го столбца:
«и
«12
М23 =
«я о32
«И
«з!
«12
«32
~«11«32	«12«31 .
Алгебраическим дополнением Ау элемента ау матрицы А п-го
порядка называется минор Му, взятый со знаком (—V)'+J:
Л=(-1)'+У
Используя понятие алгебраического дополнения, формулу
(4) можно записать в виде
И =аиМи -а12М12 + ...+(-1)"+1а1яМ1и =
“«1|Д|+«12-^12 + -" + «1л-^1п •	(5)
Замечание 1. Рассмотренные нами выше определители
Му, М12,... есть миноры соответствующих элементов матрицы.
Замечание 2. Формула (5) допускает сокращенную запись:
И = ЕНГ' аммч	
2=1	2=1
20
Глава 1. Матричная алгебра
Иными словами, определитель квадратной матрицы равен
сумме произведений элементов 1-й строки на их алгебраические
дополнения.
Замечание 3. Формула (5) называется разложением опре-
делителя по 1-й строке.
Замечание 4. Величина алгебраического дополнения А,9
элемента ау зависит только от положения этого элемента (/, J)
в матрице А. При замене элемента ау матрицы на другое число ве-
личина алгебраического дополнения Ау не изменяется.
ТЕОРЕМА
(о величине определителя квадратной матрицы)
Определитель квахрятной матрицы равен сумме произведений элемен-
тов любой строки или любого столбца на их алгебраические дополнения:
И = Z(-1)+У aijMij , где j = 1,2,..., п,
>1 >1
=Х«Л > гда>= t 2> •••’ «
/=1	1=1
◄ При доказательстве ограничимся для простоты рассмотре-
нием матрицы третьего порядка. Мы получили формулу разло-
жения определителя по 1-й строке (2). Разложим теперь опреде-
литель, например, по 2-му столбцу:
Икстолбеч - «12^12 + «22^22	«32^32'
Каждый минор М12 (»= 1, 2, 3) является определителем второ-
го порядка:
М12 =
«12
«я
«23
«33
— «12«33	«31«23>
Л/22 =
«п
«31
«13
«33
- «11«33	«31«13 ’
м32=
— «ц«23 fl2l«l3 
Подставим эти выражения в формулу (6), раскроем скобки и
соберем положительные слагаемые, затем отрицательные. Полу-
чим
21
Линейная алгебра. Курс лекций
MLamwfcn “ й12 («21«33	«31 «23)+ «22 («I I «33	«31«1з)
—<Т32 («; |«2 з — а21а1з) = а11^22^33 + «12«23«31 + «21«32«13 —
—«13«22«31 — «11«32«23 ~ «21«|2«33 •
Сравнивая правые части соотношений (3) и (7), убеждаемся в
ТОМ, ЧТО |Л| = И2столбец-
Подобным образом проверяются и другие равенства, получа-
емые разложением определителя по определенной строке или
столбцу. ►
ПРИМЕР. Вычислить
п -го порядка
определитель треугольной матрицы
«п
О
«12	«13	•••	«1л
«22	«23	"•	«2 л
О	«33	-	«Зл
о о о - «т,
Решение. Имеем
”«11 «22-"«on '
Мы убедились, что определитель треугольной матрицы равен
произведению ее диагональных элементов.
Свойства определителей
1)	Определитель с нулевой строкой или нулевым столбцом
равен нулю.
Для доказательства этого свойства достаточно разложить оп-
ределитель по нулевой строке или по нулевому столбцу.
2)	Умножение определителя на число равносильно умноже- <
нию какой-либо строки или столбца определителя на это число.
Умножим любую строку или столбец исходного определите-
ля на число, разложим определитель по этой строке или столбцу,
22
Глава 1. Матричная алгебра
14 =
вынесем это число за скобки и свернем оставшееся в скобках вы-
ражение в исходный определитель.
3)	При транспонировании матрицы величина ее определите-
ля не изменяется: Не-
разложим определитель И по 1-й строке, транспонируем его.
Разложим полученный определитель [Л7] по 1-му столбцу. Из до-
казанной выше теоремы следует, что результат будет одинаков.
4)	При перестановке двух строк или столбцов определитель
меняет знак.
В определителе
О|2 ...
°21	°22	•" а2п
йп\ ап2	апп
переставим, например, первую и вторую строки. Получим
°2i а21 ... а1п
а,, а,-, ... а,
11	v*|2
а, а. ... а
к! п2	пп
Разложим определитель |Я|, по второй строке, а определитель
|Л|2 — по первой. Получим
14 =— а2\^2\ +^22^22 +--- + (—1)	°2п^2п^
14 = а2хМ2х —а22М22 + ... + (—1) а2„М2п,
откуда следует 14=44-
Теперь переставим i-ю строку с (i + к)-й. Для этого сместим
1-ю строку на к строк вниз. Определитель изменит знак к раз.
Строка с номером i + к окажется при этом на (i + к — 1)-м месте.
Переставим эту строку на место i-й строки, для чего поднимем ее
на к — 1 строк вверх. Определитель изменит знак к — 1 раз. В ре-
зультате процедуры определитель изменит знак нечетное число
раз: к + к — 1-2к— 1, т.е. знак определителя при любой пере-
становке строк изменится.
5)	Определитель матрицы с двумя одинаковыми строками
(столбцами) равен нулю.
23
Линейная алгебра. Курс лекций
При перестановке двух строк определитель изменит знак.
Переставим местами одинаковые строки. Определитель останет-
ся таким же. Значит, —|Л| = |Л|. Отсюда следует, что |Л| = 0.
6)	Определитель, содержащий две пропорциональные строки
(столбца), равен нулю.
Вынесем коэффициент пропорциональности за знак опреде-
лителя. В нем образуются две одинаковые строки. Поэтому такой
определитель равен нулю.
7)	Определитель можно разложить на сумму определителей.
Представим элементы z-й строки определителя в виде суммы
двух слагаемых. Получим
flll ... ZZ,„
а^+рс, ... а/»„+рс„
О„1	•"
где а, р — некоторые коэффициенты, равные в частном случае
единице. Разложим определитель |Л| по z-й строке, используя
алгебраические дополнения, преобразуем полученную сумму.
Тогда
И = X(aZ>, +рс7)4	+1>Л = а£М/ + р£сЛ =
у=1	7=1	7=1	7=1	7=1
= а-|Л|1+Р-|4,
где
8)	Определитель матрицы не изменится, если к элементам
одной строки прибавить элементы другой строки, умноженные
на одно и то же число.
Полученный определитель можно разложить на сумму двух
определителей. Один из них является исходным. Другой содер-
жит две пропорциональные строки и, следовательно, равен нулю.
24
Глава 1. Матричная алгебра
9)	Сумма произведений произвольных чисел Ьх, Ь2, Ьп на
алгебраические дополнения элементов любой строки (столбца)
равна определителю матрицы, полученной из данной заменой
элементов этой строки (столбца) на числа />,, Ь2,Ьп.
Свойство вытекает из замечания 4 к алгебраическим допол-
нениям и доказанной теоремы.
10)	Сумма произведений элементов одной строки матрицы
на алгебраические дополнения к элементам другой строки этой
матрицы равна нулю.
Умножим элементы z-й строки исходной матрицы на алгеб-
раические дополнения кj-й строке и составим сумму:
41^yl +fli?A2 + -" + 4иАл	•
|UI
Подобная сумма получается из матрицы, у которой на месте
j-й строки стоит Z-я строка:
«11	42	4в		
4.	4з -	4„	<-/-я	строка
41	4г -	4«	<-У-я	строка
411	412 -			
Эта матрица имеет две одинаковые строки, поэтому вели-
чина ее определителя равна нулю.
11)	Определитель произведения квадратных матриц равен
произведению определителей этих матриц, т.е.
1-МЧ4И-
В силу громоздкости преобразований ограничимся рассмот-
рением матриц второго порядка. Пусть А = (а> ^1, 1«з 4, J Тогда АВ = (а' fl2W' \4 41/ \4 47	вАь‘ Ч ^4 7 (ахЬх +а2Ь3 ахЬ2 + а2Ь. \а3Ьх + а.Ь3 а3Ь2 + а4Ь^ ,
25
Линейная алгебра. Курс лекций
Рассчитаем величины определителей трех матриц, а также ве-
личину |Л • |Б|:
I А\ = а, а4 - о2а3, |Б| =	- Ь2Ь3,
1^1 = (а/», + о2/>3)(a3b2 + a4b4)-{a}b2 +a2b4)(a3fy + а4Ь3)=
= axa3bxb2 + axaAbxb^ +a1a3b2b3 + a2a4b3b4 ~axa3bxb2 -axa^b2b3 -
^2 ^3^1 ^4	^2^4 ^3^4 ’
|Л|-|Б| = (а,а4-a^bfo-bj^a^b,-ata4b2b3 -
~а2а3Ь^Ь4 + a2a3b2b3.
После сокращения подобных (они подчеркнуты) получаем
справа одинаковые выражения для | АZ?| и \А | • |Б|.
Вычисление определителя
Существует несколько способов вычисления величины опре-
делителя. Выбор способа диктуется видом и порядком определи-
теля. Удачно выбранный способ позволяет существенно сокра-
тить вычисления. Рассмотрим их на примере определителя мат-
рицы третьего порядка.
ПРИМЕР. Вычислить определитель матрицы
1-й способ. Использование теоремы о разложении определи-
теля по любой строке или столбцу.
Разложим определитель, например, по 3-му столбцу:
= _(_4 _ 8) _ (_4+4)+2(-8 - 4) = -12.
26
Глава 1. Матричная алгебра
2-й способ. Использование правила треугольников:
2
2
-2
2 -1
-А 1 = 2-(-4)-2+2-1-(-2)+2-(-2)-(-1)-(-1)-(-4)-(-2)-
-2 2
-2-2-2-(-2)1-2 = -16-4+4+8-8+4 = -12.
3-й способ. Использование свойств определителя для преоб-
разования его к виду, когда он содержит строку или столбец с
максимальным количеством нулей. Разложение определителя по
этой строке (столбцу):
О
2
2
-2
2
-4
-2
-1
1
2
- {прибавим к 1-й строке 3-ю} -
О
2
-2
-2
1
1
2
{разложим определитель по 1-й строке} -
= 1(-1)'+3
2 -4
-2 -2
= -4-8 = -12.
4-й способ. Использование свойств определителя для преоб-
разования его к треугольному виду. Величина определителя вы-
числяется как произведение элементов, стоящих на главной диа-
гонали:
2 2-1
2
1 = {1-ю строку умножим на —1 и сложим со 2-й
-2 -2 2
строкой, поместив результат на месте 2-й строки} =
2 2-1
О -6
-2 -2
2 = {1-ю строку сложим с 3-й и поместим результат на
2
2
2 -1
месте 3-й строки} = О
-6 2 = {перемножим элементы главной
О 1
О
диагонали} =—12.
27
Линейная алгебра. Курс лекций
§1.4. Обратная матрица
> Теорема о существовании обратной матрицы
> Свойства обратных матриц
Теорема о существовании обратной матрицы
Матрица А называется невырожденной, если ее определитель
отличен от нуля, т.е. |Я| * 0. В противном случае она называется
вырожденной.
Определение. Матрица А~' называется обратной по от-
ношению к квадратной матрице А, если выполняется равенство
А-'А=АА-' = Е.	(8)
Следующая теорема устанавливает условия существования
обратной матрицы.
ТЕОРЕМА
(о существовании обратной матрицы)
Обратная матрица А'1 существует и единственна тогда и только
тогда, когда исходная матрица невырожденна.
◄ Необходимость. Пусть матрица Л имеет обратную матрицу
А~Тогда А• А=А • А~' = Е . Используя свойство 11 определителя,
получаем |Л| • |Л_||=|£| = 1, откуда вытекает |Л“' I = Д-. Следователь-
1 1 И1
но, И * 0. Матрица А является невырожденной. ►
◄ Достаточность. Пусть матрица А является невырожденной:
И * 0. Матрицу А транспонируем и на основе транспонирован-
ной матрицы АТ построим новую матрицу Ар, элементами которой
являются алгебраические дополнения элементов матрицы Ат. На-
зовем матрицу Ар присоединенной. Итак,
28
Глава 1. Матричная алгебра
Запишем новую матрицу В как произведение матриц Ар и А:
В=Ар • А. Она имеет вид
«12
«22
ат2
«2л
«тл>
Элементы матрицы Б вычислим по отдельности и воспользу-
емся равенством ДТ = Д., которое легко проверяется.
А. = Д\-ап + Д2 -с21 +.-+4г„ап1 =Х4> ’«л =Z4i-аР =
7=1	7=1
=Z«7i 41 =14 ’
>=|
^21 = 41 '«II + 4г2’«21 + — + 4л'«и1 = ^4/’«/1 = Л4/2’°71 =
7=1	7=1
=£Оу1-д2=0.
7=1
Продолжая вычисления, обратим внимание на то, что отлич-
ными от нуля окажутся только диагональные элементы матри-
цы В:
Ьу = ДТ1 %+ДТ2 %++ДТИ	=	% =
Jt=l
п
= ^Да 'akj ~
*=1
|Л|, если i = j,
О, если i j.
Поэтому матрица В имеет вид
Линейная алгебра. Курс лекций
Следовательно,
АР-А-\А\Е.
Аналогично можно доказать, что
Рассмотрим соотношение
ЛРЛ = ЛЛР=|Л|£.
Разделив его на |Л| ф 0, получим
АГ л-л AF -к
И	И
Ар
Поскольку для матрицы	выполнено равенство (8), эта
И1
матрица является обратной по определению:
◄	Единственность обратной матрицы. Пусть, кроме обрат-
ной матрицы А~' к матрице А, существует еще одна обратная мат-
рицаХф А '. Тогда выполняется равенство X- А = Е. Умножим это
равенство справа на А~1. Получим X • А • А~1 = Е • А~1, откуда X- Е=
=Е  А~1 или Х-А'. Таким образом, не существует обратной мат-
рицы Л, отличной от Ат'. Аналогично доказывается, что равенство
А  Y = Евыполняется в том единственном случае, когда Y- А ►
Свойства обратных матриц
◄	Умножим обе части равенства слева на Л1:
А~'(АхУ^А-'-А.
Слева стоит произведение матрицы А~' на обратную ей (А ') 1,
которое равно единичной матрице, справа — произведение об-
ратной матрицы на исходную, также равное единичной матрице.
Следовательно, равенство верно. ►
30
Глава 1. Матричная алгебра
2)	(Л')Г =(ЛГ) '.
◄	Умножим обе части равенства слева на А Т:
лг(л')г=лг(лг)'.
Далее воспользуемся свойством 4 транспонирования матри-
цы и перепишем левую часть соотношения так: (А~1 • А)т. Правая
часть равенства есть произведение матрицы Ат на обратную ей.
Получаем Ет-Е. Откуда следует тождество Е=Е. ►
-(<•
◄	Умножим равенство слева на Л"':
Ат(А')т^Ат(Ату'.
Левую часть равенства представим в виде произведения 2т
сомножителей:
А А-.А^А^ А"'... А~1 = Ап  (Ап
£
Левая часть равенства свертывается до матрицы Е, правая
часть равенства есть произведение матрицы Ат на обратную ей.
Следовательно, равенство обращается в тождество Е-Е. ►
4)	И
◄ Для равенства А~' • А = Евоспользуемся свойством 11 опре-
делителей. Получим |Д-' • Л| = |Е\, откуда следует |Л"' | • |А\ -|£| = 1.
Поэтому |Л“' ! = -!-.►
1 1 И
5)	(АВ)1 = В 'А '.
◄ Умножим равенство слева на матрицу В:
В(АВ)~' = В-В1 А1.
Правая часть соотношения примет вид Е А~1 или А~1. Итак,
В(АВ)~1 = А~'.
31
Линейная алгебра. Курс лекций
Умножим последнее равенство слева на А. Получим
А В (АВ)~1 =А А '.
Слева стоит произведение матрицы АВ на обратную ей (АВ)~\
справа — произведение матрицы А на обратную ей Л-1. Следова-
тельно, Е=Е. Свойство 5 доказано. ►
Доказанная теорема дает способ вычисления обратной мат-
рицы.
ПРИМЕР. Найти матрицу, обратную данной
Решение. Обратную матрицу будем искать, делая последова-
тельно следующие шаги:
1)	Находим определитель матрицы А. Его величина |Л| = —1.
Следовательно, обратная матрица существует.
2)	Находим транспонированную к А матрицу А':
' 1 2 -2'
2 -1 -2
-1 1
3)	Находим алгебраические дополнения к элементам матри-
цы Ат:
4=Н)“‘
Записываем присоединенную матрицу:
Ар
' 1 О
-4 -1
ч-6 -2
Г
-3
-5,
4)	Вычисляем обратную матрицу:
32
Глава 1. Матричная алгебра
' 1 о г
-4 -1 -3
-6 -2 -5,
Г-1
-Г
3
5,
О
1
2
Другой способ вычисления обратной матрицы дает метод
Жордана. Но вначале познакомимся с матрицами элементарных
преобразований, на использовании которых основан этот метод.
§1.5. Матрицы элементарных преобразований
> Типы матриц элементарных преобразований
> Элементарные преобразования матрицы
> Способ построения обратной матрицы
Типы матриц элементарных преобразований
Матрицами элементарных преобразований называются мат-
рицы следующих трех типов.
1-й тип. Матрицей элементарных преобразований 1-го типа
называется любая матрица, полученная из единичной матрицы
перестановкой каких-либо двух строк или столбцов. Например,
если в единичной матрице пятого порядка
Тооо
0 10 0
Е =	0 0 10
0 0 0 1
1,0 о о о
(Г
о
о
о
1,
переставить местами вторую и третью строки, получается матри-
ца элементарных преобразований 1-го типа:
fl О
V0 О
О О
О
1
О
О 0 О'
1 о о
ООО
О 1 о
о о 1?
В матрице /23 все элементы вне главной диагонали равны
нулю, за исключением тех, которые стоят в позициях (2,3) и (3, 2).
33
Линейная алгебра. Курс лекций
2-й тип. Матрицей элементарных преобразований 2-го типа
называется любая матрица, полученная из единичной заменой
диагонального элемента на любое действительное число, не рав-
ное нулю. Например, матрицей элементарных преобразований
2-го типа является матрица
Vo о
О О О'
ООО
1 о о
О а О
0 0 1,
II« =
О
О
О
О
1
о
о
у которой в позиции (4,4) находится число а * 0.
3-й тип. Матрицей элементарных преобразований 3-го типа на-
зывается любая матрица, отличающаяся от единичной наличием
одного внедиагонального элемента, не равного нулю. Например,
Ш24“
1
О
о
о
.0
О
1
О
О
о
О
О
1
О
О
о
ь
о
1
о
(Г
о
о
о
1,
является матрицей элементарных преобразований 3-го типа. У нее
в позиции (2,4) стоит не равное нулю число Ь.
Элементарные преобразования матрицы
Назовем элементарными преобразованиями матрицы А такие
изменения в ее строках и столбцах, которые возникают при умно-
жении матрицы А на матрицы элементарных преобразований
слева или справа.
1.	Умножение матрицы А на матрицу 4 слева переставляет
строки с номерами i и j. Например,
34
Глава 1. Матричная алгебра
%	«12	«13	«14	«15
«31	«32	«зз	«34	«35
«21	«22	«23	«24	«25
«41	«42	«43	«44	«45
,«51	«52	«53	«54	«55
переставляет 2-ю и 3-ю строки местами.
2.	Умножение матрицы А на матрицу IIV слева равносильно
умножению i-й строки матрицы А на число а.
Например,
умножает 4-ю строку на число а.
3.	Умножение матрицы А на матрицу Шу слева равносильно
прибавлению к /-й строке матрицы А ее j-й строки, предвари-
тельно умноженной на Ь. Например,
	1 0 0 0 о'		«II «12	«13	«14	«15	
	0 1 0 b 0		«21	«22	«23	«24	«25	
/я24	0 0 10 0		«31	«32	«33	«34	«35	=
	0 0 0 1 0		«41	«42	«43	«44	«45	
	0 0 0 0 1		«51	«52	«53	«54	«55	
	к	>		k	/	
«II	«12	«	3	«14	«15	
«21 +^’«4|	«22 + ’ «42	«23	К Ь • (2^	O24	’ ^44	^25	' ^45		
«31	«32	а	3	«34	«35	
«41	«42	а.	13	«44	«45	
<	«51	«52	ai	3	«54	«55	>	
35
Линейная алгебра. Курс лекций
прибавляет ко 2-й строке матрицы А ее 4-ю строку с коэффици-
ентом Ь.
Легко проверяются преобразования со столбцами матрицы А.
4.	Умножение матрицы А на матрицу /;/ справа переставляет
столбцы с номерами i и J.
5.	Умножение матрицы А на матрицу IIV справа равносиль-
но умножению i-го столбца матрицы А на число а.
6.	Умножение матрицы А на матрицу Шу справа равносиль-
но прибавлению к i-му столбцу матрицы А ее ./’-го столбца.
Замечание 1. Элементарные матрицы всех трех типов яв-
ляются невырожденными. Элементарные матрицы второго и
третьего типов не вырождены, поскольку они имеют треугольный
вид. Элементарная матрица первого типа не вырождена, так как
при разложении определителя элементарной матрицы первого
типа по любой строке (столбцу) образуется определитель единич-
ной матрицы с ненулевым коэффициентом. Разложим, напри-
мер, определитель матрицы /23 по 1-й строке:
1
О
О
О
О
О О
О 1
1 О
О О
О О
О О
1 0=-1.
О 1
Замечание 2. Ни одно из элементарных преобразований
не может превратить невырожденную матрицу в вырожденную.
Следовательно, умножение исходной матрицы на матрицу эле-
ментарных преобразований, меняя в большинстве случаев вели-
чину определителя матрицы, не приводит к его обнулению.
ТЕОРЕМА
(об умножении матрицы на матрицы элементарных преобразо-
ваний)
Любая невырожденная матрица А путем умножения на матрицы
элементарных преобразований Ех, Ег,Ек может быть сведена к еди-
ничной, т.е. найдутся такие матрицы элементарных преобразований Et,
Ег,..., Ек, последовательное умножение которых на матрицу А слева пре-
образует исходную матрицу А в единичную:
Ек-... E2 Ei А = Е.
36
Глава 1. Матричная алгебра
◄ Пусть матрица А невырожденная. Сведем матрицу А с по-
мощью элементарных преобразований к матрице треугольного
вида. Поскольку матрица А невырожденная, она ненулевая. Най-
дем в 1-м столбце ненулевой элемент и, меняя строки местами,
поставим этот элемент в позицию (1,1), если ранее там стоял ну-
левой элемент. Итак, а * 0. Прибавим ко 2-й строке матрицы 1-ю
строку, предварительно умноженную на -л2|/ап. В позиции
(2,1) появляется нуль. Прибавим к 3-й строке матрицы 1-ю стро-
ку, предварительно умноженную на -а3| /оп . Тогда в позиции
(3, 1) также появится нуль. Продолжив эти элементарные преоб-
разования (л — 1) раз, получим матрицу
«и	а12	...	а1п
0	а22	...	л2п
< 0	ап2	«лл >
В дальнейших преобразованиях 1 -я строка не участвует. Най-
дем во 2-м столбце ненулевой элемент и, меняя строки местами,
поставим этот элемент в позицию (2, 2), если ранее там стоял ну-
левой элемент. Имеем л22 . Прибавим к 3-й строке матрицы 2-ю
строку, предварительно умноженную на -а32 /а22. В позиции
(3, 2) появляется нуль. Продолжив эти элементарные преобразо-
вания (л — 1) раз, получим матрицу
Теперь в дальнейших преобразованиях уже не участвуют 1-я
и 2-я строки. Продолжив этот процесс (совершив t раз элемен-
тарные преобразования), придем к треугольной матрице
«п
0
0
«12	«13	—	«1л
«22	«23	•"	«2 л
0	«зз	-	«з"
10	0	0 ... а")
37
Линейная алгебра. Курс лекций
На главной диагонали стоят элементы, отличные от нуля.
Приведение матрицы к треугольному виду с ненулевыми элемен-
тами на главной диагонали всегда возможно, так как в противном
случае (если бы не нашлось ни одного не равного нулю элемента
в каждом столбце) определитель матрицы оказался бы равным
нулю.
Элементарные преобразования строк матрицы равносильны
умножению этой матрицы слева на соответствующие матрицы
элементарных преобразований. Поэтому процесс преобразова-
ния матрицы к треугольному виду можно представить в виде пос-
ледовательного умножения t раз слева исходной матрицы на
матрицы элементарных преобразований
Е1-...Е2Е1А = А1.
Продолжим элементарные преобразования матрицы Аг Ум-
, , 1
ножив 1-ю строку матрицы А. на число —, получим в позиции
(1,1) единицу. Аналогичными элементарными преобразования-
ми (преобразования 2-го типа) получим единицы во всех пози-
циях главной диагонали. Матрица Л, приводится к следующему
виду:
1	«|2	«|3	...	«|„_|	«|„
О	1	«23	•"	®2, л-1	^2п
д _ О	О	1	•"	^3,л1	^Зл
О	0	0	...	1
,0 О О ... О 1 ,
Следующий, последний, шаг — получить нули во всех пози-
циях выше главной диагонали. Опираемся на последнюю строку.
Последовательно прибавляя к первым п — 1 строкам последнюю,
умноженную соответственно на -«,„, -а2„, ..., -«„_,„ , приходим
к матрице, у которой первые п — 1 элементов последнего столбца
равны нулю. Действуя аналогичным образом, опираясь на пред-
последнюю строку, получаем в первых п — 2 позициях предпос-
леднего столбца нули. Продолжая совершать подобные элемен-
тарные преобразования, окончательно получаем
38
Глава 1. Матричная алгебра
А^Е=
'1 О
О 1
О о
о о
<° 0
О	...	(Г
о	...	о
1	...	о
о	...	о
о	...	t
Таким образом, совершив к элементарных преобразований
в матрице А, мы привели ее к единичной. Используя матрицы
элементарных преобразований, запишем результат в матричной
форме:
Ек ’"Ем Е/-Eltl Et Ех А-Е
или
Ек-...Е2ЕХ А = Е.
(9)
Теорема доказана. ►
Способ построения обратной матрицы
Умножим обе части равенства (9) на матрицу Л-1 справа. Тогда
Ек-...Е2ЕХАА'=ЕА~'.
После преобразований получим
Ек -... Е2 ЕХ=А ' 
(Ю)
Это равенство лежит в основе способа построения обратной
матрицы. Пусть А — невырожденная матрица «-го порядка. Со-
ставим новую матрицу, которую назовем расширенной: (А[Е).
Пусть единичная матрица Е имеет также порядок «. Будем
последовательно совершать с расширенной матрицей такие эле-
ментарные преобразования, которые равносильны умножению
этой матрицы слева на матрицы элементарных преобразований
Ех, £2Еп. Получим
(Ек:..-Е2.ЕхА\Ек:..Е2-Ех-Е).
Подставив (9) и (10) в полученную расширенную матрицу,
будем иметь
(Ек ...Е2Ех .А\Ек.....Е2Ех.Е) = (Е\А-').
39
Линейная алгебра. Курс лекций
Таким образом, если путем элементарных преобразований
с расширенной матрицей слева от черты получить единичную
матрицу, то справа от черты образуется обратная матрица.
Замечание. Применяя элементарные преобразования к
расширенной матрице (Л|Б), можно получить матрицу (£14~1 • В).
Матрица А• В широко используется при решении систем ли-
нейных уравнений. Для получения этой матрицы следует прово-
дить элементарные преобразования только со строками расши-
ренной матрицы, так как эти действия равносильны умножению
матриц элементарных преобразований слева на расширенную
матрицу.
ПРИМЕР. Найти матрицу, обратную матрице
О Г
-1 О
1
Решение. Составим расширенную матрицу:
'2	0	1	1	0	0"
1-10 0 10
0	1	1	0	0	1,
Поменяем местами 1-ю и 2-ю строки:
1-10 0 10"
2 0 110 0
0 1 1 0 0 1>
Прибавим ко 2-й строке 1-ю строку, умноженную на —2:
1-10 0	10"
0 2 11-20
0	110 0 1у
Умножим 3-ю строку на —2 и сложим со 2-й:
-1 0 0	2 1 J)	0 -1	0	1	0" 1 -2 0 1 -2 -2,
40
Глава 1. Матричная алгебра
Ниже главной диагонали получили треугольник нулей. Обра-
зуем теперь нули выше главной диагонали, для чего ко 2-й строке
прибавим 3-ю:
rl -1 О О 1 О'
О 2 0 2 -4 -2.
0 0-11 -2 -2,
Умножим 1-ю строку на 2 и сложим со 2-й:
2 0	0 0 2	0 0 0-1	2 -2 -2 2-4-2 1 -2 -2
Умножим 1-ю и 2-ю строки на 0,5, 3-ю строку — на —1:
Г1 0 0 1-1 -Г
0 10 1-2-1
J) 0 1 -1 2 2,
Слева от черты получена единичная матрица, значит, спра-
ва — обратная матрица А_|:
' 1
Л-’= 1
(-1
-1 -Г
-2 -1
2 2,
§ 1.6. Ранг матрицы
>	Определение ранга матрицы
>	Ранг матрицы при элементарных преобразованиях
>	Линейные комбинации строк или столбцов
>	Связь ранга с числом независимых строк (столбцов)
>	Строка матрицы как линейная комбинация независимых
строк матрицы
Определение ранга матрицы
Понятие ранга матрицы — одно из фундаментальных
в линейной алгебре. В матрице А размером т х п вычеркиванием
каких-либо строк или столбцов можно образовать квадратную
41
Линейная алгебра. Курс лекций
матрицу k-ro порядка (кх к). Определитель Мктакой матрицы на-
зывается минором к-го порядка. У матрицы размера т х п есть ми-
норы первого порядка, второго порядка и так далее до к-ro поряд-
ка, где к = min(m, и). Например, у матрицы А имеются миноры
5x3
первого, второго и третьего порядков.
Определение. Рангом матрицы А называется наивыс-
тхп
ший порядок отличных от нуля миноров этой матрицы.
Обозначение: rang А или г(А).
Свойства ранга:
1)	Ранг нулевой матрицы считается равным нулю.
2)	r(A)<min(m, п).
3)	г(Л) = п у матрицы и-го порядка тогда и только тогда, когда
И* о.
ПРИМЕР. Вычислить ранг матрицы
	А	0	1 О'
А =	1	0	1 0
3x4	<о	1	° °>
Решение. Для матрицы Л ранг г(Л)<пйп(3, 4) = 3. Чтобы
проверить, может ли ранг быть равным 3, вычислим все миноры
3-го порядка, которые можно образовать из матрицы вычеркива-
нием одного столбца:
л/3(|) =	1 0 1 1 0 1 0 1 0	= 0, м<2) =	1 0 0		= 0,	=	1 1 0 1 1 0 ООО	= 0,
			1 0 0 1	0 0			
			0 1	0			
		л/<4) =	0 1	0	= 0.		
			1 0	0			
Следовательно, ранг не может быть более 2. Легко найти ми-
нор 2-го порядка, отличный от нуля. Например, М2 =	= 1.
Но тогда г(А)-2.	0 1
Поиск ранга матрицы большого порядка перебором миноров
является трудоемкой задачей. Развиты эффективные методы оп-
ределения ранга матрицы.
42
Глава 1. Матричная алгебра
К введенным ранее трем типам элементарных преобразова-
ний матрицы добавим еще два:
4-й тип. Отбрасывание нулевой строки или столбца.
5-й тип. Транспонирование матрицы.
Ранг матрицы при элементарных преобразованиях
ТЕОРЕМА
(о ранге матрицы при элементарных преобразованиях)
Элементарные преобразования не изменяют ранга матрицы.
◄ Рассмотрим последовательно все типы элементарных пре-
образований матрицы.
Элементарные преобразования 1-го типа меняют строки или
столбцы в матрице. В этом случае определитель матрицы меняет
знак, но не может обратиться в нуль.
Элементарные преобразования 2-го типа умножают строку
или столбец на не равное нулю число. Но тогда определитель
матрицы умножится на это число, что не может привести к его
обнулению.
Элементарные преобразования 3-го типа приводят к при-
бавлению к z-й строке матрицы А ее у-й строки, что не меняет
величины определителя.
Элементарные преобразования 4-го типа позволяют отбро-
сить все миноры к-го порядка, равные нулю, и перейти к рас-
смотрению миноров к— 1 порядка. На величине ранга это, оче-
видно, не отразится.
Элементарные преобразования 5-го типа транспонируют
матрицу, отчего величина ее определителя, как известно (свой-
ство 3 определителей), не изменяется.
Мы установили, что при элементарных преобразованиях
матриц их определители либо сохраняются, либо изменяют свою
величину, не обращаясь при этом в нуль. В результате сохраняет-
ся наивысший порядок отличных от нуля миноров исходной
матрицы, т.е. ее ранг не изменяется. ►
Теорема дает возможность посредством элементарных пре-
образований привести матрицу к определенному виду, когда ее
ранг вычисляется без труда. Рассмотрим задачу эффективного
вычисления ранга подробнее.
43
Линейная алгебра. Курс лекций
Матрица А называется матрицей ступенчатого вида или сту-
пенчатой матрицей, если она имеет вид
«11	«12	•••	«1г	•••	«1/
41		«12	—	«1г	-	«q	0	«22	•	••	«2г	-	«2л
	0	«22	•"	«2г	-	«2л	...	...		•	
А =	0	0 ...	«Зг	«з„ или А =	0	0 .	°гг	... ат
	...						0	0 .	.. 0	... 0
	<0	0 ...	«„ 	ат)		...			
					<0	0 .	.. 0	... 0
где аа эь 0; i = 1, 2,г; г < k = и). Ранг ступенчатой мат-
рицы равен г, так как существует минор порядка г, отличный от
нуля:
«п
0
0
«12	—	«1г
«22	•"	«2г
0	...	а„
= «1Г«22-«^*°-
Таким образом, произвольную матрицу А» следует привести
к ступенчатому виду! Число ненулевых строк матрицы будет рав-
но ее рангу. Если квадратная матрица А примет треугольный вид,
ее ранг будет равен п. При проведении элементарных преобразо-
ваний с матрицей знак равенства ставиться не может (матрицы не
равны), ставится обычно знак тильды « ~ » .
ПРИМЕР. Найти ранг матрицы
'2 -1 3
4-2 5
2 -1 1
-2 4'
1 7
8 2>
Решение. Ко 2-й строке прибавим 1-ю, предварительно умно-
женную на — 2, к 3-й строке прибавим 1-ю, предварительно умно-
женную на — 1. Получим
'2 -1 3
4-2 5
2 -1 1
-2
1
8
4'
7
2.
'2
0
0
-1
0
0
3 -2 4'
-1 5 -1
-2 10 -2
44
Глава 1. Матричная алгебра
К 3-й строке прибавим 2-ю, предварительно умноженную
на — 2. Получим
r2 -1 3 —2
0 0-15
,0 0 —2 10
4А р -1 3
-1 ~ 0 0-1
-2J (0 0 0
—2
5
О
-1 3
О -1
-2
4
-1
5
Число ненулевых строк равно 2. Тогда г(А)=2. При ином
обосновании выделим из матрицы минор максимального поряд-
ка, не равный нулю. Это, например, М2 =
г(Л)=2.
Тогда
Линейные комбинации строк или столбцов
Познакомимся с понятием линейной зависимости строк или
столбцов. В матрице
'«11	«12	-	«1/
а21 а22 ... а2г1
А-
а , а ...а
K wl m2 •” тп /
введем обозначения строк:
в| — (оц а12 ... а|и)
е2 = («21	«22	«2и)
®m—(«ml «m2	— «тп)
Эти строки в], е2, ... ет являются и-мерными и представ-
ляют собой матрицы размерностью 1 хи. В новых обозначениях
исходная матрица записывается в виде
*1
е2
е
Строка e = (Z>! b2 ... Ьп), определяемая равенством
е = Л. jCj +Х2е2 +...+^.mem,
(И)
45
Линейная алгебра. Курс лекций
называется линейной комбинацией строк е|5 е2, ет, где
X,, X2 ... Хт — любые действительные числа.
В развернутом матричном виде последнее равенство выгля-
дит так:
(А А ... bn) = \(an ai2 ... c,„)+X2-(c2l а22 ... о2и)+...+
+	ат2 — Отп)-
Для элементов строки е имеем систему уравнений
= X|<7H + Х2а21 +-"+^-1й<и1’
£>2 — Х1а12 + Х2а22 +---+Хтлт2,	(12)
...................  9
А = Мп + А>°2п + — + ААп-
Строки е15 е2, ..., еи называются линейно зависимыми,
если существуют такие Х„ Х^,,..., Х„, не равные нулю одновремен-
но, что линейная комбинация этих строк равна нулевой строке
Х| в, + 'К2С2+ А1®т — о.
Строки ер е2, ..., ет называются линейно независимыми,
если линейная комбинация этих строк равна нулевой строке толь-
копри X, = Х2 =... Хи = 0.
ТЕОРЕМА
(о линейной комбинации строк матрицы)
Если строки матрицы линейно зависимы, то одна из них является
линейной комбинацией остальных.
◄ Пусть строки ер е2, ..., еи линейно зависимы. Тогда
найдутся числа X,, Х2,..., Х„, не все равные нулю одновременно и
такие, что
X]+ Х2е2+... + Х„е„ - о.
Пусть, например, Х„ *0. Перенесем первые т-1 слагаемых
направо и разделим равенство на Хт * 0.
X1 X 2	X П1-1
е =—-е,—-е, —...——е ,
т 1	1	2	'1	/п-1
ИЛИ
46
Глава 1. Матричная алгебра
ет ~ ^Iei +^2е2 +-" + ^m-iem-l >
где Х;=-—, /= 1,2,/и-1. ►
^-т
Замечание 1. Верно и обратное утверждение: если одна из
строк является линейной комбинацией остальных, то эти строки
линейно зависимы.
Замечание 2. Аналогичными свойствами обладает мно-
жество /я-мерных столбцов.
Связь ранга с числом независимых строк (столбцов)
ТЕОРЕМА
(о связи ранга с числом независимых строк)
Ранг матрицы равен числу ее независимых строк (столбцов).
◄ Пусть матрица А имеет ранг г. По определению ранга
матрицы, существует минор порядка г, отличный от нуля. Пусть
для определенности это минор
*0.
Тогда строки е„ е2, ..., ег линейно независимы. Предполо-
жим противное. Например, строка с номером г есть линейная
комбинация остальных строк. В этом случае
er +Х2е2+...+Хг_,ег_| .
Проведем элементарные преобразования, не изменяющие
величину определителя. Прибавим к этой строке 1-ю строку,
предварительно умноженную на - X,, 2-ю строку, умноженную
на -Х2 , и т. д., наконец, (г-1)-ю строку, умноженную на -Хг_| .
Получим на месте строки с номером г последовательно строку
er —XjCi
ег Х|в| Х2е2
ег Х]С| Х2е2 ... ХГ_|СГ_|
47
Линейная алгебра. Курс лекций
Последняя строка теперь будет состоять из одних нулей. Но
тогда Мг = 0 , что невозможно. Наше предположение о том, что
строки еи е2, ..., ег линейно зависимы, неверно. ►
Строка матрицы как линейная комбинация
независимых строк матрицы
ТЕОРЕМА
(о представлении строки в виде линейной комбинации независи-
мых строк)
Каждая строка матрицы А может быть представлена в ваде линей-
ной комбинации независимых строк матрицы.
◄ Пусть матрица А имеет ранг г. По определению ранга
тхп
матрицы, существует минор порядка г, отличный от нуля. Пусть
для определенности это минор
а, а з ... а
rl г2	гг
Рассмотрим минор (г+1)-го порядка матрицы А, который
можно получить, добавив к минору Мг i-ю строку и J-й столбец
матрицы (г<i<т, r<j<n):
Этот минор Л/г1| равен нулю, как минор более высокого по-
рядка, чем г. Разложим его по последнему столбцу:
а1/47+ОИ27+- + йа4+^-	•	(13)
Разделим равенство на Мг * 0 и введем обозначения:
48
Глава 1. Матричная алгебра
^kj
(~l)i+JMr к’
где к= 1, 2,г.
Перепишем равенство в следующем виде:
^ = Х1а|у + Х2а2у + -+М5-,	(14)
где J = r+ 1,т .
Это равенство верно также и для 7=1,2,..., г. Действитель-
но, если добавить к минору Мг j-й столбец матрицы с одним из
номеров j = 1, 2, ..., г, новый минор Л/г+| будет содержать два
одинаковых столбца. Следовательно, его величина также равна
нулю, и равенство (13) будет иметь место. Перепишем соотноше-
ние (14) в виде столбца равенств для всех у= 1, 2,..., п:
ап =Х|Оц +Х2п2| +...+%ror|,
о(2 = ^|О|2 +А.2о22 +...+Хгог2,
ai„=K<h,+^a2n + ...+krarn.
Мы получили систему уравнений длй нахождения элементов
/-й строки, подобную (12). Запишем систему в матричном
виде (см. (12)-» (11))
в,. =Xjej+X2e2+...+Хгвг .	(15)
Равенство (15) дает представление i-й строки как линейной
комбинации независимых строк е1; е2, ..., ег. Поскольку /-я
строка выбрана произвольно, заключаем, что каждая строка
матрицы может быть представлена в виде линейной комби-
нации независимых строк матрицы. ►
Замечание 1. Все рассуждения в отношении строк спра-
ведливы также и для столбцов.
Замечание 2. Задача определения числа независимых
строк или столбцов матрицы сводится к нахождению ее ранга.
Вопросы для повторения
1. Привести определение матрицы. Перечислить виды матриц.
2. Сформулировать арифметические операции над матрицами.
З.	Что означает транспонирование матрицы? Привести свойства транс-
понирования.
49
Линейная алгебра. Курс лекций
4.	Сформулировать понятие определителя квадратной матрицы любого
порядка.
5.	Чем алгебраическое дополнение элемента atj матрицы отличается от
минора того же элемента?
6.	Как найти величину определителя?
7.	Перечислить свойства определителей.
8.	Дать определение обратной матрицы. Привести ее свойства.
9.	Что такое матрицы элементарных преобразований? Что называют
элементарными преобразованиями матрицы?
10.	Объяснить способ построения обратной матрицы, основанный на ис-
пользовании расширенной матрицы.
11.	Сформулировать определение ранга матрицы.
12.	Какие строки матрицы называются линейно независимыми?
Системы линейных уравнений
Решение многих экономических задач сводится к исследова-
нию и решению систем линейных уравнений.
§ 2.1. Общие понятия системы линейных уравнений
Система т линейных уравнений с п переменными имеет вид
о|1х1+а1Л+...+о|Л=/>|,
а21Х1 +а22Х2 +-- + а2пХп =^2’	Ц)
.........................9
а.х, +а„,х, +...+ах„ = Ьт,
т 1 I /и/ z	тп п т7
или в сокращенной записи
^а^ -bi} i = 1,2,tn.
7=1
Здесь роль переменных, подлежащих определению, играют
величины Xj, называемые неизвестными. Параметрами являются
переменные atj и />„ которые могут принимать любые действи-
тельные значения. Все afj называются коэффициентами при пере-
менных, все bj — свободными членами уравнений.
Решением системы называется упорядоченная совокуп-
ность чисел а,, а2,..., а„, которая при подстановке в систему об-
ращает каждое уравнение в тождество. Линейная система урав-
нений называется совместной, если она имеет хотя бы одно ре-
шение, и несовместной, если она не имеет решений. Совместная
система уравнений называется определенной, если она имеет
единственное решение, и неопределенной, если она имеет более
51
Линейная алгебра. Курс лекций
одного решения. Две системы уравнений называются равно-
сильными, если они имеют одно и то же множество решений.
Системы уравнений удобно решать в матричной форме. За-
пишем систему (1) в виде матричного уравнения. Введем обозна-
чения:
где А — матрица коэффициентов при переменных, или матрица
системы; X — матрица-столбец неизвестных; В — матрица-стол-
бец свободных членов. Тогда система уравнений может быть
представлена в матричном виде
или в компактной матричной форме
А Х=В.
§ 2.2. Нахождение единственного решения системы
линейных уравнений
>	Метод обратной матрицы
>	Метод с использованием расширенной матрицы
>	Метод с использованием формул Крамера
Рассмотрим вначале частные случаи решения системы ли-
нейных уравнений.
Метод обратной матрицы
Решим это уравнение в случае т = п и |Л| ф 0. Для матрицы А
существует обратная матрица А'. Умножим слева обе части мат-
ричного уравнения на А"1:
52
Глава 2. Системы линейных уравнений
A~'AX = A~'B
или
Х = А~'-В.
Уравнение в матричном виде решено. Для нахождения эле-
ментов матрицы неизвестных ЛГследует найти обратную матрицу
коэффициентов и умножить ее на столбец свободных членов В.
ПРИМЕР. Решить систему уравнений
х{-х2+ 2х3 = 1,
• -2Х| +х2 + х3 = 2,	(2)
х, -х2 +х3 =-1.
Решение. Запишем систему в матричном виде
' 1 -12'
-2 1 1
.1-11,
' Г
2
-1,
Матрица коэффициентов
не вырождена (ее определитель |Л| = 1). Поэтому существует об-
ратная матрица, которая легко может быть найдена одним из рас-
смотренных в гл. 1 способов:
-1 -У
-1 -5
О -1,
Находим далее произведение
'1
А'В= 3
1
Матрица неизвестных равна
53
Линейная алгебра. Курс лекций
Х =
= А~'В =
'S'
6
1*з J	I2 J
*i = з,'
Ответ можно записать также в виде *2=6,
<*з = 2->
Метод с использованием расширенной матрицы
Более эффективный способ решения системы из п уравнений
с п неизвестными можно осуществить с помощью расширенной
матрицы (см. Замечание к разделу «Способ построения обратной
матрицы», гл. 1, § 1.5).
Составим расширенную матрицу
(Л|Я).
Элементарными преобразованиями строк расширенной мат-
рицы приведем матрицу А к единичной. Тогда матрица В обра-
тится в матрицу
Ат1  В.
Расширенная матрица примет вид
(Е\А~1 • В).
Извлекая из расширенной матрицы матричное произведение
А~1 • В и приравнивая его к матрице неизвестных, получаем для
неизвестных равенство
f*>)
х2 =А'В.
<*з>
ПРИМЕР. Решить систему уравнений (2) с помощью расши-
ренной матрицы.
Решение. Составим расширенную матрицу
' 1 -12 1
(Л|Б)= -2112
Приведем вначале матрицу А к треугольному виду:
54
Глава 2. Системы линейных уравнений
'1 -1 2 Г
0-1 5 4
0 О -1 -2,
Далее образуем треугольник нулей выше главной диагонали:
1 -1
0 -1
0 О
Наконец, получим единицы на главной диагонали:
'1 0 0 3'
0 1 06
J) ° 12
Следовательно,
Метод с использованием формул Крамера
Третий способ решения системы из п уравнений с п неиз-
вестными дает теорема швейцарского математика Габриэля
Крамера (1704-1752).
ТЕОРЕМА КРАМЕРА
(о решении системы уравнений с помощью определителей)
Пусть у кнадратной матрицы коэффициентов при неизвестных в сис-
теме из п линейных уравнений с п неизвестными определитель |Л| * 0.
Пусть | A\j — определитель матрицы, получаемой из матрицы А заменой
j-го столбца столбцом свободных членов. Тогда система содержит единст-
венное решение, имеющее вад
55
Линейная алгебра. Курс лекций
|4|	_ |4|
“ИГ 2"ИГ
'ИГ
◄ Развернем матричное уравнение Х= А~1  В и запишем об-
ратную матрицу через алгебраические дополнения:
Перемножив матрицы, получим
4iA + 4А +"-Дп^и
42Л + -^22^2 +—Ai2^n
4Л+4Л+-4Д )
Сумма Д^ +ДД +... + ДД представляет собой произведе-
ние чисел Ьх, Ь2, Ь„ на алгебраические дополнения элементов
1-го столбца. Она равна определителю матрицы, полученной из
данной заменой элементов этого столбца на числа Ь„ Ъг, Ь„
(свойство 9 определителей). Следовательно,
Аналогично сумма Ai2bl+A22b2+...+An2bn есть произведение
чисел Ьх, b2,..., Ь„ на алгебраические дополнения элементов 2-го
столбца. Тогда
56
Глава 2. Системы линейных уравнений
Продолжив вычисления, окончательно получим
141 г_14|
“И’ *’ИГ
Способ решения системы линейных уравнений, основанный
на формулах Крамера, получил название метода или правила
Крамера.
ПРИМЕР. Решить систему уравнений (2) методом Крамера.
Решение. Условия, при которых правило Крамера работает
(т = п, |Л| * 0), выполнены. Воспользуемся формулами Крамера
1 -1 2
2 1 1
-1 -1 1
1 -1 2
-2 1 1
1 -1 1
1 1 2
-2 2 1
3 = 3-х.-Ш-_1	1
1	’ ’ ИГ 1-1 2
-2 1 1
1-11
Замечание. Перечисленные методы решения систем ли-
нейных уравнений становятся трудоемкими при ручном счете
57
Линейная алгебра. Курс лекций
уже при п>4. Однако они удобны при решении задач на ком-
пьютере.
Рассмотренные методы являются решением систем частного
вида, для которых выполняются условия т = п, |Л| * 0. Перейдем
к рассмотрению решения линейных систем общего вида. В даль-
нейшем будем оперировать понятиями матричной алгебры.
§ 2.3. Общий подход к решению систем уравнений
>	Равносильность систем линейных уравнений
при элементарных преобразованиях
>	Метод Гаусса
>	Теорема Кронекера — Капелли
>	Схема решений системы уравнений
Равносильность систем линейных уравнений
при элементарных преобразованиях
ТЕОРЕМА
(о равносильности систем при элементарных преобразованиях)
При элементарных преобразованиях строк первых четырех типов
линейные системы остаются равносильными.
◄ Рассмотрим элементарные преобразования каждого типа
по отдельности.
1.	Если система линейных уравнений получена из исходной
системы элементарными преобразованиями 1-го типа, т.е. изме-
нен порядок уравнений в системе, то решения системы не изме-
нятся.
2.	Если система линейных уравнений получена из исходной
системы элементарными преобразованиями 2-го типа, т.е. одно
из уравнений умножено на число а ф 0, это не приведет к измене-
нию решений системы.
3.	Если система линейных уравнений получена из исходной
системы элементарными преобразованиями 3-го типа, т.е. одно
из уравнений представляет собой сумму двух уравнений, одно из
которых предварительно умножено на число А, это также не при-
ведет к изменению решений системы.
58
Глава 2. Системы линейных уравнений
Действительно, пусть xf,x°,...,x° — решение системы урав-
нений. Тогда уравнения с произвольными номерами i и j
anXi+-+ai„x„^bl ,
пу1х1+...+пуЛ=Оу
при подстановке чисел х°,Х2,...,х° обратятся в тождества. Сло-
жим оба уравнения, предварительно умножив первое из них на
число А:
k(aiiXi +...+а1пхп-bl)+(aJlixl +...+aJnxn-Ь}) = 0 •
Подставив сюда числа х”, х°,..., х°, получим А  0 + 0 — 0.
4.	Если система линейных уравнений получена из исходной
системы элементарными преобразованиями 4-го типа, т.е. одно
из уравнений, содержащее нулевые коэффициенты и нулевой
свободный член, вычеркнуто, это, очевидно, не изменит решений
системы. ►
Применение элементарных преобразований при решении
систем линейных уравнений приводит к мощному методу реше-
ния произвольных линейных систем — методу немецкого мате-
матика и физика, профессора Геттингенского университета Кар-
ла Фридриха Гаусса (1777—1855).
Метод Гаусса
Метод Гаусса заключается в последовательном исключении
неизвестных с помощью элементарных преобразований.
Для системы уравнений (1) образуем расширенную матрицу:
'«11	«12	’	 «1„	41
«21	«22	‘	”	«2л	4
Ai	«m2	•	" «тп	
Посредством элементарных преобразований приведем рас-
ширенную матрицу к ступенчатому виду
59
Линейная алгебра. Курс лекций
«1 । fl12
О й22
О О
О О
О О
<0 О
%
«2л
О
О
О
«1л
«2л
О
о
о
А л
А
о J
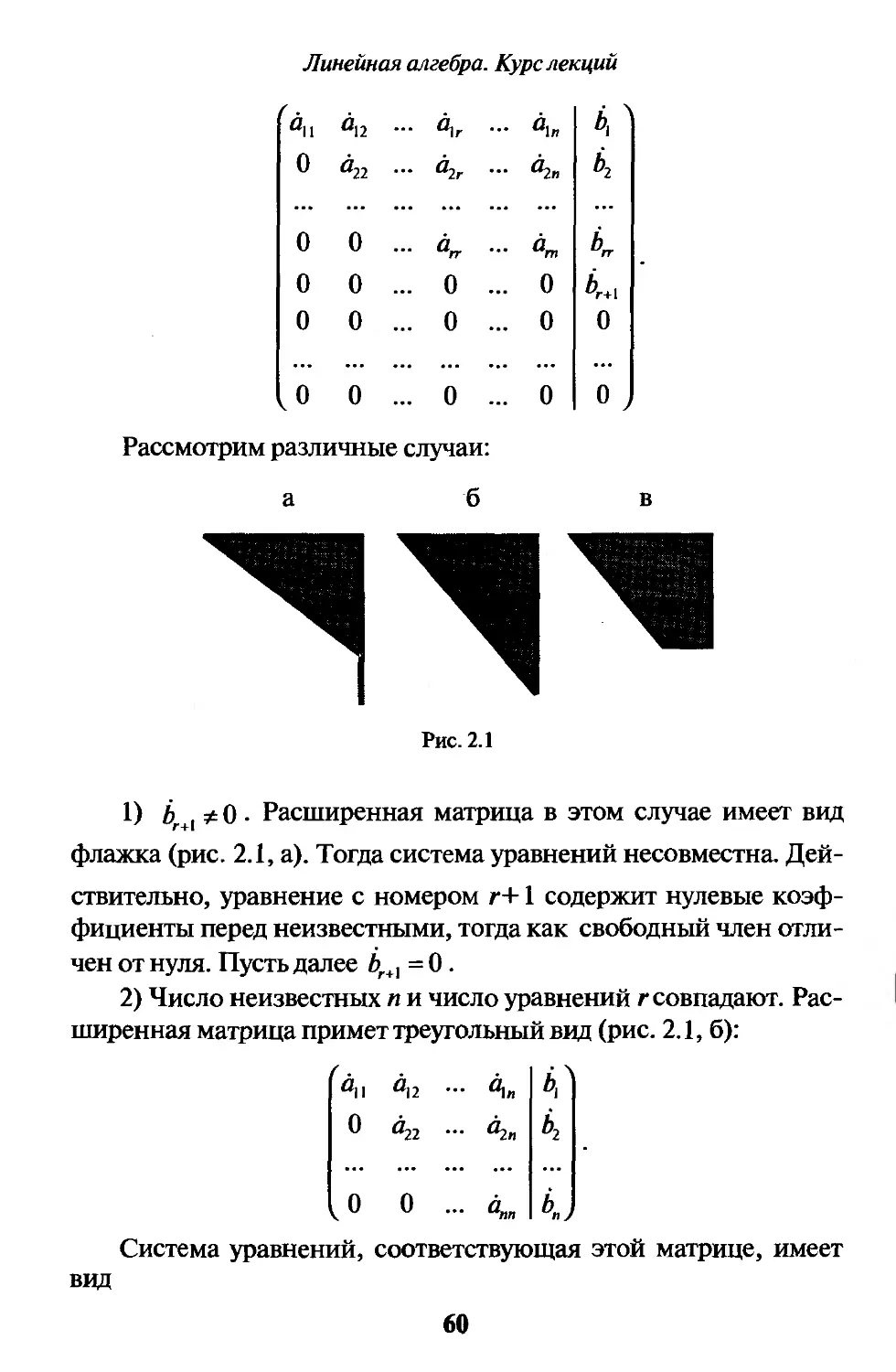
Рассмотрим различные случаи:
а
в
Рис. 2.1
1)	br+i * 0 • Расширенная матрица в этом случае имеет вид
флажка (рис. 2.1, а). Тогда система уравнений несовместна. Дей-
ствительно, уравнение с номером r+1 содержит нулевые коэф-
фициенты перед неизвестными, тогда как свободный член отли-
чен от нуля. Пусть далее 4+| = 0.
2)	Число неизвестных п и число уравнений г совпадают. Рас-
ширенная матрица примет треугольный вид (рис. 2.1, б):
Система уравнений, соответствующая этой матрице, имеет
вид
60
Глава 2. Системы линейных уравнений
alixl+al2x2+...+alnxn=bl,
^22Х2 +'" + ^2пХп = ^2’
........5
а х — b .
L ял Л Л 
Из последнего уравнения определяется неизвестная величи-
на хп. Подставляем ее в предыдущее уравнение с номером п—1
и находим х„„Р Продолжая этот процесс, находим неизвестные со
все меньшими номерами. Наконец, подставив найденные значе-
ния неизвестных х2, х3,хп в первое уравнение, найдем величи-
ну хг Итак, при п = г система определена и имеет единственное
решение.
3)	Число неизвестных п больше числа уравнений г. Вид рас-
ширенной матрицы — трапеция (рис. 2.1, в). Последнее уравне-
ние содержит переменные xr, хг+1,х„. Выразим в этом уравне-
нии переменную хг через остальные неизвестные и подставим в
уравнение с номером г— 1. Найдем переменную хг_15 которая бу-
дет выражена через те же неизвестные х15 х^, ..., х„. Результат
подставим в уравнение с номером г — 2 и т. д. Таким образом, мы
можем определить значения переменных хг, хг-1,..., Xj через неиз-
вестные хг+1, хг+2,..., хи:
*1 = Й1.г+1*г+1 +4,г+2*г+2 +- + 4Л +*1>
Х2 ~ ^2,г+\ Xr+1 + ^2,г+2Хг+2 + — + *hnXn + ^2 »	ц
...................................9
х = а ,х ,+а ,х n+...+й х +Ь.
"г **г,г+1лг+1 '	г,г+2 г+2. глл г
Придавая неизвестным хг+1, хп произвольные значения,
получаем бесконечное множество решений системы уравнений.
ПРИМЕР. Решить систему линейных уравнений
Зх, - 2х2 + 5х3 + 4х4 = 2,
• 6х, - 4xj + 4х3 + Зх4 = 3,	(3)
9Xj - 6х2 + Зх3 + 2х4 = 4.
Решение. Составим расширенную матрицу системы
61
Линейная алгебра. Курс лекций
'3 -2 5 4 2'
6—4 4 3 3
,9-632 4>
С помощью элементарных преобразований приведем ее к
ступенчатому виду
(3 -2	5	4	2^	.	„
П 1 1 т" 0 'о -6 -5 -1 '	<4)
(О о	о	о	oj	v	7
Исходная система эквивалентна следующей системе уравне-
ний:
Зх, - 2х2 + 5х3 + 4х4 = 2,
-6х3 -5х4 =-1.
Выразим из второго уравнения х3 через х4 и подставим в пер-
вое уравнение системы. Тогда
*i=A(12x2+x4+7),
1О
х3=|(-5х4+1).
Придавая произвольные значения неизвестным
х2 = а и х4 = Ь,
получаем общее решение системы уравнений
х,=1(12а+*+7),
1О
х2 =а9
х3-|(-5б+1),
о
х4 — Ь.
Решение методом Гаусса представляет собой кропотливый
и часто длительный процесс. Когда в конце пути может оказаться,
что система не имеет решения, наступает разочарование. Столько
сделано работы — и как ничтожен итог. В середине XIX в. Лео-
польдом Кронекером (1823—1891), профессором Берлинского
университета, была найдена та «лакмусовая бумажка», по реак-
ции которой можно судить о наличии или отсутствии решений
системы линейных уравнений. Ею оказался ранг.
62
Глава 2. Системы линейных уравнений
Теорема Кронекера — Капелли
ТЕОРЕМА
(о совместности системы уравнений)
Линейная система совместна тогда и только тогда, когда ранг мат-
рицы системы равен рангу расширенной матрицы этой системы.
◄ В системе линейных уравнений (1) введем обозначения
матрицы коэффициентов
ч
А-
«12
«22
"•	«1л
"•	«2л
@тп >
<«ml
и расширенной матрицы
Ч
Af -
ат2
«12
«22
«1л
«2л
<ат\
а .
m2
а
тп
Ь.
а также обозначения столбцов, составленных из коэффициентов

Xi«i + х2а2 +...+хпап = Ь.
Необходимость. Пусть система совместна, т.е. сущест-
вуют Ар А2,..., А„ такие, что выполняется равенство
А,«! +А2«2, + ... + А„«й — Ь.
Из него следует, что столбец b есть линейная комбинация ос-
тальных столбцов матрицы системы. Следовательно, добавление
в матрицу коэффициентов при неизвестных столбцах свободных
членов ранга не меняет: г(Л) = г(Лр). ►
63
Линейная алгебра. Курс лекций
◄ Достаточность. Пусть матрицы Л и Л7> имеютодинако-
вый ранг г(Л)=г(Лр). Тогда г столбцов матрицы (пусть это, на-
пример, будут первые г столбцов) линейно независимы. Остальные
п — г столбцов, а именно:	,...,ап, Ь — являются линейными ком-
бинациями первых г столбцов. В частности, найдутся такие
Х2, ...,ХГ, не все равные нулю одновременно, что
X.] flj + Х2в2> + + Хгвг =
Расширим это равенство за счет добавления в него слагаемых
с коэффициентами Хж = 0,..., :
+ Х2«2 +... + \ar + Хг+1«г+1 +... + Х„«и = Ь.
Но это и означает, что исходная система имеет решения
Х| =Х|, х2 =:Х2, ..., хг =ХГ, хг+1 = Хг+) = 0, ..., хп=Х„ = 0.^
Схема решений системы уравнений
Доказанная теорема позволяет в компактном виде предста-
вить схему решений системы из т линейных уравнений с п пере-
менными (рис. 2.2).
Рассмотрим более подробно случай бесконечного множества
решений. Оказывается, оно может быть определенным образом
структурировано.
64
Глава 2. Системы линейных уравнений
§ 2.4. Базисные решения системы уравнений
Пусть число линейно независимых уравнений меньше числа
переменных, а значит, г < п. Назовем г переменных основными или
базисными, если определитель матрицы из коэффициентов при
них отличен от нуля. Предположим, что это переменные х,, х2,...,
хг. Тогда переменные хи х2, —,хг выражаются через переменные
хг+1, х^2, ..., х„ (см. п. 3 метода Гаусса) с помощью соотноше-
ний (2). Назовем последние переменные неосновными или свобод-
ными. Количество этих переменных равно п — г.
Определение. Решение системы (1), в котором все и — г
свободных переменных полагаются равными нулю, называется
базисным. В системе (Г) базисным решением является
х2 = Ь2,
........>
 xr = 'br,
Хг+1 - О’
х„ = 0
или в матричной форме
'К
ь2
ьг
о
<0,
(5)
В сокращенной матричной форме базисное решение выгля-
дит так:
х = Ь.	(5')
Базисное решение является частным решением системы (1).
В качестве основных переменных могут быть выбраны и дру-
гие переменные. Количество способов выбора г переменных из
их общего числа п не может быть больше числа сочетаний из
п элементов по г. Эта величина описывается формулой теории ве-
роятностей
" г!(и-г)!
Пример (3) содержит 3 уравнения с четырьмя переменными.
Ранги исходной и расширенной матриц равны и составляют ве-
личину, равную 2. Следовательно, две переменные в системе
65
Линейная алгебра. Курс лекций
можно выразить через оставшиеся две переменные. Формула чис-
ла сочетаний дает общее число способов выбора двух переменных
из четырех:
Г2 _ 4!
4 2! 2!	’
Возможны следующие наборы основных переменных:
менных
= 0. Любой из других наборов переменных можно
Х} X,	Xj	х2	х2	х3,
Хз’ Х4	Хз’ Х<’ Х4‘
Однако набор переменных хи х2 не может быть основным,
так как определитель матрицы из коэффициентов при этих пере-
3 -2
О О
сделать основным. Таким образом, число базисных решений рав-
но 5. В решенном примере (3) в качестве основных были выбраны
переменные хи х3, а переменные х2, х4 объявлены свободными.
Если принять их равными нулю, получим одно из базисных ре-
шений системы (3):
7 п 1 п
xi=7V’ Х2=0’ Хз=7> х4=°-
1о	О
Подведем итог. При г < п совместная система т линейных
уравнений с п переменными имеет бесконечное множество реше-
ний, среди которых имеются базисные решения. Их число конеч-
но и не превышает величины С'.
§ 2.5. Однородные системы линейных уравнений
> Свойства однородной системы линейных уравнений
> Фундаментальные решения
Система линейных уравнений называется однородной, если
все свободные члены системы равны нулю:
«11*1 + «!2*2 +- + « =0>
«21*1 +fl22-*2 + ••• + а2пХп =0>	(ф
......................•.....9
,ат1Х1 +ат2Х2 +"‘ + атпХп =
66
Глава 2. Системы линейных уравнений
В матричном виде систему можно записать следующим об-
разом:
где
«II
«21
«12	•"	«1л
«22	«2л
х2
"О'
о
<«т|
«m2	" «тл>
х.
; о=
о
Свойства однородной системы линейных уравнений
1) Однородная система всегда совместна, так как всегда име-
ет, по крайней мере, нулевое решение.
2) Для существования ненулевых решений ранг матрицы ко-
эффициентов должен быть меньше числа переменных г < п, т.е
число линейно независимых уравнений должно быть меньше
числа переменных. В этом случае |Л| = 0.
( х,Л
3) Если матрица-столбец (вектор) е =
темы (6), то и столбец е'=ке =
А,Хц
Хх2|
х21
х.
есть решение сис-
также является решением

системы.
Пусть е — решение системы. Тогда матричное уравнение при
подстановке Х= е’ обращается в тождество А • е' = 0.
Действительно, найдем произведение матриц А и А  е:
Л-(1в)=Л-(Л-в)= 1-0 = 0.
Отсюда столбец е' = 1 • е также является решением матрично-
го уравнения.
4) Если матрицы-столбцы et =
есть решения
67
Линейная алгебра. Курс лекций
системы (6), т.е. А • et = О и А • е2 = О, то и столбец «=!)«! +Х2е2,
где Xj, 12 — произвольные числа, также является решением систе-
мыЛ  е = О.
Для доказательства перемножим матрицы Аие = к1е1 + Х2е2 :
А-+А.2е2) = Л-(Л.|в|)+A(k2e2)=kt (A el)+k2 (А е2)~
= A,j О + Х2 0 — 0.
Следовательно, всякая линейная комбинация решений од-
нородной системы линейных уравнений также является решени-
ем этой системы.
Заметим, что среди решений однородной системы выделяют-
ся решения, которые можно назвать главными решениями. Через
них выражаются другие решения. Попробуем разобраться в этом
и найти эти выделяющиеся, фундаментальные, решения.
Фундаментальные решения
Решения е2,..., ер однородной системы называются линейно
независимыми, если линейная комбинация этих решений
+Х2е2 + ...+'Крер равна нулевому столбцу только при условии
=0  Построим матрицу решений, расположив
матрицы-столбцы решений по столбцам новой матрицы. В соот-
ветствии с теоремой о ранге матрицы ранг новой матрицы будет
численно равен числу столбцов новой матрицы т.е. числу линей-
но независимых решений системы.
Определение. Совокупность линейно независимых ре-
шений е15 е2, ..., ер однородной системы уравнений называется
фундаментальной, если общее решение системы является линей-
ной комбинацией решений «„ е2,..., ер.
ТЕОРЕМА
(о фундаментальных решениях однородной системы)
Если ранг г матрицы коэффициентов при переменных однородной
системы уравнений меньше числа переменных п, то:
1)	существует совокупность линейно независимых решений системы;
2)	число линейно независимых решений равно п — г;
3)	любое решение системы можно представить в ваде совокупности этих
независимых решений, т.е. в виаде линейной комбинации фундамен-
тального набора решений.
68
Глава 2. Системы линейных уравнений
◄ Решим систему (6) в общем виде. Выпишем матрицу ко-
эффициентов и приведем ее элементарными преобразованиями
к ступенчатому виду:
о12	...	а1г	...
О	а22	...	...	о2п
<°	0	^rr	-	anj
Базисными возьмем переменные х,, х2, хг, тогда свободны-
ми переменными станут , хг, 2,..., х„. Если в процессе приведения
матрицы коэффициентов к ступенчатому виду пришлось поме-
нять столбцы, можно перенумеровать переменные. Для свобод-
ных переменных введем обозначения хг1|= с,, хг,2=с2,..., хп=с„_г.
Далее, действуя по методу Гаусса, из последнего уравнения
с номером г найдем величину хг, которую подставим в преды-
дущее уравнение с номером г— 1. Из уравнения с номером г— 1
найдем величину хг1, которую подставим в уравнение с номером
г—2, и т. д. В результате получим решение системы в общем
виде:
X] = X] ] С] + х12с2 +... + х^_гсп_г,
Х2 = *21C1 + Х22С2 + ”• + Х2л-гСп-г’
 Хг = ХгА + Хг2С2 + ••• + Хгл-гС„-г>
X = С .
Л ПГ
Здесь коэффициенты ху получены в результате преобразова-
ний, i=l, ..., г, j=l, ..., п—г. Запишем решения в матричной
форме:
Х1'		Хц		%'			'Хх^	
х2		х21		х22			Х2л-г	
хг	= А	Хг>	+ с2	Хг2	+ .	 + С„-Г	Хг,„-г	(7)
*г+|		1		0			0	
х„ >		<0,		<0,			< 1 >	
				69				
Линейная алгебра. Курс лекций
или в сокращенной матричной форме:
х = с|е| +с2е2+...+сгег ,	(7')
где х, «„ е2, ег — соответствующие матрицы-столбцы (векто-
ры). Величины с„ с2, с„_г могут принимать любые действи-
тельные значения. Примем с, = 1, с2 = 0,..., с„_г = 0. Тогда частное
решение системы будет выглядеть так:
		
х2		х21
хг		xrl
		1
		<0,
Придавая величинам с2,..., сп_г другие значения, убедим-
ся, что матрицы-столбцы	^а я		\„-г' Х2.п-г
	хг2		Хг,п-г
	0		0
	<0,		< 1 ,
также являются решениями системы однородных уравнений.
Число этих столбцов равно п — г. Составим из них матрицу,
записав более подробно последние п — г строк:
хг1 хг2
1	0
0	1
0	0
< о	о
Хг,„-г
о
о
о
1 >
70
Глава 2. Системы линейных уравнений
Матрица содержит минор М„, порядка я—г, по главной диа-
гонали которого стоят единицы, остальные элементы равны ну-
лю. Очевидно, М,.= 1. Следовательно, ранг матрицы равен п—г.
Но тогда эти столбцы линейно независимы.
Мы доказали, что матрицы-столбцы, стоящие в правой части
выражения (7), являются решениями однородной системы, они
линейно независимы. Их число равно п—г. Общее решение (7)
однородной системы получено в виде линейной комбинации этих
независимых решений. Теорема доказана. ►
Замечание 1. Базисными переменными мы выбрали не-
известные Х|,х;, ...,хг. В качестве базисных можно выбрать любой
набор из г переменных при условии, что определитель матрицы
из коэффициентов при них отличен от нуля. Количество спосо-
бов выбора таких г переменных из их общего числа п не превы-
шает величины
С =____—___.
" г!(я-г)!
Отсюда следует, что число фундаментальных наборов реше-
ний (ФНР) ограниченно.
Замечание 2. Для нахождения множества решений одно-
родной системы достаточно найти какой-нибудь ФНР системы
и составить его линейную комбинацию.
Замечание 3. Любая однородная система уравнений, име-
ющая ненулевые решения, обладает ФНР.
Замечание 4. Если матрицы-столбцы в (7) не содержат
иррациональностей, подбором коэффициентов с,, с2,сп, всег-
да можно создать ФНР, все элементы которого будут целыми
числами.
ПРИМЕР. Решить систему однородных уравнений, выделив
какой-либо ФНР,
2х, -х2 + х3 -х4 =0,
 X) + 2х2 - 2х3 +3х4 = 0,
Зх, + х2 — х3 +2х4 = 0.
Запишем матрицу коэффициентов и, совершив элементарные
преобразования со строками, приведем ее к ступенчатому виду:
71
Линейная алгебра. Курс лекций
'2 -1
1 2
<3 1
1
-2
-1
-1А р
3 ~ 2
2 -2 ЗА р 2
-1 1 -1 ~ 0 -5
1 -1 2) Ц) -5
-2 ЗА
5 -V
2J V3
1 2 -2 ЗА
О -5 5 -1)
Ранг матрицы г = 2. Вернемся от матрицы к системе уравне-
ний
(8)
х, + 2х2 - 2х3 + Зх4 = О,
-5х2 +5х3 -7х4 =0.
Возьмем базисными переменными х,, х2, тогда свободными
останутся х3, х4. Найдем х,, х2 и запишем решения в удобной для
дальнейшей записи форме:
1
X] =0х3--х4,
,	7
Х2 =1-Х3~^Х4,
х3 = 1х3 +0х4,
х4 =Ох3 + 1х4.
В матричном виде решение системы можно записать так:
Обозначим коэффициенты перед столбцами в правой части
х4
Х3 ~ С1 ’	5 — С2
и запишем общее решение системы еще раз:
(9)
72
Глава 2. Системы линейных уравнений
Задавая коэффициентам с„ с2 произвольные значения, полу-
( П
чаем совокупность всех решений системы. Столбцы и
линейно независимы и представляют набор из двух фундамен-
тальных решений (ФНР), через которые выражаются все осталь-
ные решения системы.
Другой подход к форме записи заключается в составлении
таблицы для системы (8):
2
5
Заполняем таблицу, задавая значения свободным перемен-
ным х3, хА. Рассчитываем значения переменных х., х2. Подбираем
коэффициенты а,, а2 так, чтобы при умножении их на элементы
соответствующей строки получались целые числа. Пусть а, = 1,
а2 = —5. Решение системы запишем в виде (9).
§ 2.6. Общее решение системы неоднородных
линейных уравнений
ТЕОРЕМА
(об общем решении системы неоднородных уравнений)
Общее решение системы линейных уравнений с п переменными равно
сумме общего решения соответствующей ей системы однородных ли-
нейных уравнений и некоторого частного решения исходной системы.
◄ Для системы т линейных уравнений с п переменными
оиХ1 + о12х2 +...+а1пхп -Ь{,
а2\Х\ + а22Хг + ••• + а1пХп =	’
аш1х + ат->х? + -• + ат„х„ - Ь„,
mi 1 m2 2	тп п т>
запишем расширенную матрицу
73
Линейная алгебра. Курс лекций
Используя элементарные преобразования, приведем ее к сту-
пенчатому виду:
	4г .	• 4г •	• 4«	А '
0	4г .	 4г •	• 4„	4
0	0 .	• < •	• 4,	4
0	0 .	. о .	. 0	i>r+l
0	0 .	. о .	. 0	0
<0	0 .	. о .	. 0	0,
Убедившись, что система имеет решения, методом Гаусса
найдем последовательно переменные xr,xr_l,...,xl, выраженные
через свободные переменные хг+1,хг+2,...,хп. Для свободных
переменных введем обозначения xril=cl, хг+2=с2, х„=сп_г.
В результате получим решение системы в общем виде:
X, = X,,с, + х}2с2 +... + х, „_гс„г + 4,
х2 —x2lct +х22с2 + +x2fI^rcfir +Ь2,
...................................9
xr = xr,c,+xr2c2 +...+xr„_rc„_r+br,
хг+| =Ср
X„=C„_r-
Коэффициенты xv, b, получены в результате преобразова-
ний, / = 1,..., г, j= 1,..., п — г. Величины с,, с2,..., с„_г могут при-
нимать любые действительные значения. Запишем решения в
матричной форме:
74
Глава 2. Системы линейных уравнений
или в сокращенной матричной форме:
х = c}et + c2e2+... + crer+b,
где х, et,e2,..., er, b — соответствующие матрицы-столбцы
(векторы). Линейная комбинация + с2е2 +... + сгег есть общее
решение (7) системы однородных линейных уравнений, век-
тор Ь — частное решение (5) исходной системы. В сокращен-
ной матричной форме эти решения представлены формулами
(7') и (У). ►
Таким образом, бесконечное множество решений — это не
случайные наборы чисел, а бесконечное множество определен-
ным образом структурированных совокупностей.
В заключение главы рассмотрим задачу балансового анали-
за — одну из экономико-математических моделей «затраты — вы-
пуск», которые разрабатывал экономист, русский по происхож-
дению, закончивший Ленинградский госуниверситет и эмигри-
ровавший в 1931 г. в США, Василий Леонтьев. За цикл этих работ
он в 1971 г. получил Нобелевскую премию.
§ 2.7. Модель Леонтьева
многоотраслевой экономики
Многоотраслевое хозяйство требует баланса между отдель-
ными отраслями. Каждая отрасль является, с одной стороны,
производителем одного определенного набора видов продук-
ции, а с другой — потребителем другого набора видов продук-
ции. Возникает сложная задача: согласовать объемы производ-
ства каждой из отраслей, чтобы удовлетворить все потребности
в продукте каждой отрасли. Эта задача может быть сформули-
75
Линейная алгебра. Курс лекций
рована в виде экономико-математической модели межотрасле-
вого баланса (модели Леонтьева), требующей привлечения ап-
парата матричной алгебры.
Рассмотрим для определенности производственную сферу
из п отраслей, каждая из которых производит один (свой) про-
дукт. Выделим определенный период времени, например год,
в течение которого все коэффициенты остаются постоянными.
Пусть
х, — общий (валовой) выпуск /-й отрасли (х, > 0), i = 1,2,..., п;
xv — объем продукции /-й отрасли, поставляемой для у-й от-
расли в процессе производства;
у, — конечный спрос на продукцию i-й отрасли (у, > 0). Сюда
относятся личное потребление граждан, содержание государ-
ственных и общественных институтов, чистый экспорт, произ-
водственное накопление и т.д. Тогда балансовые соотношения
примут вид
Х|-Х1|+Х|2+... + Х,я+У1,
х2=х21+х22+...+х2„ + у2,	(10)
x„=xni+x„2+... + xm+y„.
х„
Введем коэффициенты прямых затрат а, = — >0; /, у—1,
х,.
2,..., п, показывающие затраты i-й отрасли на выпуск одной еди-
ницы продукции дляу-й отрасли. Заменив в (10) х^ = о^х7, получим
систему п линейных уравнений с п переменными:
х, = л,,х, +aI2x2 + ...+о1„х„ + у1,
х2 = а21х, + а,2х2 +...+а2„х„ + у2,
|х„ = а,,^ + а„2х2 +... + атх„ + у„
или в матричной форме
X = AX + Y,	(11)
где X— матрица (вектор) выпусков отраслей;
А —матрица прямых затрат;
Y— матрица (вектор) конечного спроса.
76
Глава 2. Системы линейных уравнений
Упрощенная экономико-математическая модель межотрас-
левого баланса составлена. Это матричное уравнение может быть
решено. Из (11) следует, что
(E—A)X=Y.	(12)
Матрица (Е — А) не вырождена, что можно доказать, исходя
из экономических соображений. Тогда
Х= (E—A)~lY.
Матрица S = (Е — А) 1 называется матрицей полных затрат.
Ее коэффициенты имеют четкий экономический смысл. Зададим
конечный спрос, например, в виде вектора Y} =
, т.е. требуется
обеспечить конечный спрос на одну единицу продукции 1-й от-
расли. Матрица (вектор) выпусков отраслей будет иметь вид
Следовательно, каждый элементу,, /= 1, 2,..., л матрицы пол-
ных затрат S есть выпуск продукции каждой из отраслей для обес-
печения единицы конечного спроса на продукцию 1-й отрасли.
Рассмотрим применение модели на примере.
ПРИМЕР. В таблице приведены данные по балансу между
двумя отраслями за некоторый период. Найти необходимый объ-
ем валового выпуска каждой отрасли, если конечное потребление
1-й отрасли увеличится вдвое.
Отрасль		Потребление		Конечный продукт	Валовой продукт
		1	2		
Производство	1	Х|1 = 11	х,2= 12	У, =77	х, = 100
	2	*21 = 21	*22 = 22	,2 = 157	х2 = 200
77
Линейная алгебра. Курс лекций
Решение. Находим матрицу прямых затрат:
*11	*12
°п	*i	*2	fO,ll	0,06
а21 а21}	*21	*22	(0,21	0,11
< *1	*2	>
Матрица полных затрат:
0,89 -0,06Y' f 1,14 0,08А
-0,21 0,89 ) (о,27 1,14)
S = (E-A),=
По условию вектор конечного продукта должен быть равен
г=(1541
(157J
Найдем вектор валового выпуска:
X = (E-A)~'Y =
1,14 0,08А Г154А
0,27 1,14 J (157J
188,12
220,56
Следовательно, валовой выпуск в 1-й отрасли необходимо
увеличить на 88,12 усл. ед., а во 2-й отрасли — на 20,56 усл. ед.
Данные по балансу между двумя отраслями за следующий пе-
риод:
Отрасль		Потребление		Конечный продукт	Валовой продукт
		1	2		
Производство	1	хн = 20,69	х12 = 13,23	У1 = 154	х, = 188,12
	2	х21 = 39,5	х22 = 24,26	,2=157	х2 = 220,56
Расчеты проводились с точностью до 2-й значащей цифры
после запятой, поэтому возникла погрешность в десятых долях.
Вопросы для повторения
1.	В чем заключается метод обратной матрицы решения системы линей-
ных уравнений?
2.	Объяснить, как работает метод расширенной матрицы при решении
системы уравнений.
3.	Привести формулы Крамера и решить систему уравнений, используя
эти формулы.
78
Глава 2. Системы линейных уравнений
4.	В чем заключается метод Гаусса?
5.	Сформулировать условие совместности системы линейных уравне-
ний.
6.	Что такое базисные решения системы?
7.	Какие решения системы уравнений называются фундаментальными?
8.	Из каких решений складывается общее решение неоднородной сис-
темы линейных уравнений?
9.	На произвольном примере рассмотреть модель Леонтьева многоот-
раслевой экономики.
Векторная алгебра
§ 3.1. Векторы на плоскости и в пространстве
(геометрические векторы)
>	Линейные операции над векторами
>	Координаты вектора
>	Скалярное произведение векторов
> Свойства скалярного произведения
>	Векторы в трехмерном пространстве
Определение. Вектором на плоскости или в простран-
стве называется направленный отрезок, имеющий начальную и
конечную точки. Обычно вектор обозначается строчной бук-
вой с чертой а (либо буква выделяется жирным шрифтом а)
или же двумязаглавными буквами, означающими начало и ко-
нец вектора АВ. Мы будем рассматривать так называемые сво-
бодные векторы, начальную точку которых можно выбирать
произвольно. Такие векторы можно произвольно переносить
параллельно самим себе.
Определение. Длиной или модулем |«| вектора называет-
ся число, равное длине направленного отрезка. Вектор, длина ко-
торого равна единице, называется единичным вектором, или ор-
том. Вектор, начало и конец которого совпадают, называется ну-
левым и обозначается о. Векторы, лежащие на параллельных
прямых, называются коллинеарными.
80
Глава 3. Векторная алгебра
Линейные операции над векторами
1.	Суммой векторов а и b называется вектор с = а+b, начало
которого совпадает с началом вектора а, а конец — с концом
вектора b (рис. 3.1). Этот способ построения суммы векторов
называется правилом треугольника.
Если на векторах в и как на сторонах, построить паралле-
лограмм, то большая диагональ параллелограмма будет суммой
векторов в и А. Этот способ построения суммы векторов называ-
ется правилом параллелограмма (рис.3.2).
2.	Произведением числа X на вектор а называется вектор Ь,
имеющий длину |А| = |Х||а|. Направление вектора b совпадает с на-
правлением а, если А > 0, и противоположно по направлению,
если X < 0.
3.	Разностью двух векторов а и b называется вектор
с = в + (-1)Л = а-А. На рис. 3.2 вектор —Ь изображен пунктиром.
Сумма векторов ан—Ь также изображена пунктиром. Легко ви-
деть, что а — b есть меньшая диагональ параллелограмма.
Укажем основные свойства линейных операций над векто-
рами:
\)	a + b = b+a ; 2)в + (А+с)=(в + А) + с ; 3)а + о = а;
4) a(a + b)-aa+ab‘, 5)а-о = о.
81
Линейная алгебра. Курс лекций
Координаты вектора
Координатами вектора а в декартовой системе координат на-
зываются координаты его конечной точки при условии, что на-
чальная точка вектора лежит в начале координат. В дальнейшем

по умолчанию будем считать, что
все векторы отложены от начала ко-
ординат. На рис. 3.3 координатами
вектора а на плоскости ОХУ явля-
ются два числа х, и у,, что обычно
записывается в виде а = (х,, у,).
Запишем линейные операции
над векторами в координатах.
Пусть заданы векторы а = (х15 у,) и
Ь = {х2,у2).
2) а±Л = (х1±х2,у1±у2);
3) X  а = (Axj, Ху,).
Скалярное произведение векторов
Определение. Скалярным произведением двух векторов
называется произведение модулей этих векторов, умноженное на
косинус угла между векторами и обозначаемое («, Ь):
(а, д) = |л| • |Л| • cos ф.	(1)
Найдем скалярное произведение, выраженное через коорди-
наты векторов. На координатной плоскос-
ти построим векторы а=(х,, yt), b = (х2, у2) и
с = а — b = (х, — Хг, у, — у2). Они образуют тре-
угольник, изображенный на рис. 3.4. По
теореме косинусов найдем длину стороны,
образуемой вектором с:
|с|2 = |а|2 +1 й|2 - 2 |а| |й| cos ф.
Отсюда следует
|a||A|cos<p
82
Глава 3. Векторная алгебра
Выразим векторы через их координаты:
|«Г = *!2 + Ух , |*Г = Х22 + У2 , кГ =	- Х2 )2 + (у, - У2 )2.
Тогда
|в| |Л| cos <р = Х'+	+	+	~	~ *2)- ~	~ Уг •
Раскроем скобки и приведем подобные. Получим
(о, *) = |а11*| cos <р = ххх2 + уху2,	(2)
т.е. скалярное произведение двух векторов равно сумме произве-
дений соответствующих координат этих векторов.
Рассмотрим некоторые следствия формулы (2).
1)	В скалярном произведении положим а = Ь. Тогда
(в, Л) = (в, в) = |в| |«| cos 0° = |в|2 = х2 + у2,
т.е. скалярный квадрат вектора равен квадрату его длины.
2)	Найдем из равенства (1) величину cos <р:
cos<p =
(д,Л) _	х^+у^
ИН
3)	Пусть вектор b направлен вдоль оси ОХм имеет единичную
длину |й| = 1, т.е. b = (1, 0). Тогда для всякого вектора а = (х15 х2) ве-
личина
cosa =
(в, b) _ хх • 1 + ух • 0 _ хх
1вН*1	1в1	+ у2
описывает косинус угла между вектором а и положительным на-
правлением оси ОХ. Точно так же при направлении единичного
вектора b вдоль оси ОУ(Ь = (0,1)) величина
COS0 =
Ух
у1хх+Ух
описывает косинус угла между век-
тором а и положительным направле-
нием оси ОУ (рис. 3.5); cos а и cos р
называются направляющими косину-
сами вектора а.
Рис. 3.5
83
Линейная алгебра. Курс лекций
Свойства скалярного произведения
1)(а,й) = (й,«).
Справедливость свойства вытекает из формулы (1), если
учесть четность функции cos <р.
2) (в + Ь, с) = (в, с) + (Ь, с).
Пусть векторы а, Ь, с заданы своими координатами а = (х,, у2),
b = (х2, у2), с = (х3, у3). Запишем скалярное произведение (в + Ь, с) в
координатах:
(в + Ь, С ) = (х, + х2 ) х3 + (у, + у2 ) Уз =
= (*Л + У1Уз)+(*2*з + Л'зХ'з )•
Выражения, представленные в скобках, есть соответственно
скалярные произведения (а, с) и (А, с). Отсюда следует свойство 2.
3) (Х-а, Л) = (в, Х-А) = Х-(в, А).
Действительно,
(X а, Ь) = |Х • а| |Л| cos <р = |Х| |а| |б| cos ф],
(«, х*)=|«1М cos ф = |Х| |e| |Z»| cos ф2,
Х-(в, Ь) = Х-|в||б|со8ф.
При X > 0 имеем |Х| = X, <pt = <р2 = <р. Правые части трех равенств
равны X |а||б совф.
При X < 0 имеем |Х| = —X, <р( = <р2 = тс — q>, cos<pj = cos<p2 = —coscp,
т.е. опять получаем равенство правых частей.
При X = 0 свойство 3 очевидно.
Векторы в трехмерном пространстве
В трехмерном пространстве вектор задается тремя числами:
а = (х„ у,, z,). Линейные операции над векторами а = (х„ у„ z,) и
Ь = (х25 У1> г2) в пространстве аналогичны операциям над вектора-
ми на плоскости:
1) |в|=7х2+у2+Z12;
2) а± b = (х, ±х2, У| ±у2, zt ±Z2);
3)X-e = (Xx15 Хур XzJ;
84
Глава 3. Векторная алгебра
4) (а, b) = |«||A|cos<p = х,х2 + у,у2 + z,Z2;
5) cos<p=
(a,b)	Xlx2 + yty2 + zLZ2 .
I«M	у/xf + yf + zf
6) направляющие косинусы векто-
ра а равны:
xi
cos а = г--	— ।-----
y]xf + ух + z2 y]xl+ yl+zl
у,	zi
cosR=-T=	cos у =-7=
yjxl+y^+z^	yjxj+yt+zt
где а, p, у — углы между вектором а и положительными направле-
ниями осей Ох, Оу, Oz соответственно (рис. 3.6), причем
cos2 а+cos2 Р + cos2 у = 1 •
Замечание. Пусть вектор а = (xt, yt, ) является единич-
ным, т.е. ^xf+yf + zf = 1 • В этом случае cos а = х,, cos Р = yt, cos у = zx.
Следовательно, единичный вектор полностью задается своими
направляющими косинусами а = (cos a, cosp, cosy).
Пусть заданы векторы единичной длины i,j, к, направленные
вдоль осей х, у, z соответственно (рис. 3.6). Они обладают следую-
щими свойствами.
1)	Заданные в координатах, они имеют вид i = (1, 0, 0), j =
= (0,1,0),Л = (0,0,1).
2)	Матрица, составленная из координат векторов
0 10,
имеет ранг, равный 3. Отскуй сОед^ут, что строки линейно неза-
висимы. На этом основании будем считать геометрические век-
торы i, j, к линейно независимыми.
3)	Векторы i,j, к перпендикулярны друг к другу (взаимно ор-
тогональны).
4)	Пусть задан произвольный вектор а = (х„ у„ z,)- Векторы
xi », У1Г Zt к лежат на соответствующих координатных осях, а их
сумма по правилу параллелограмма равна
x}i+yj+ztk = a.
85
Линейная алгебра. Курс лекций
Тройка векторов, обладающих перечисленными свойствами,
называется ортонормированием базисом (ортобазисом). Всякий
вектор может быть разложен по ортонормированному базису. Фор-
мула (3) называется разложением вектора а по векторам i,J, к.
ПРИМЕР. Найти скалярное произведение двух векторов
а - xxi+yj+ ztknb = x2i+y2j+ z2k.
Решение. Запишем скалярное произведение векторов в и А:
(в, b) = (xli + yj+ztk, x2i + y2j + z2k)-
Пользуясь вторым свойством скалярного произведения, на-
ходим
(в, i) = x1x2(t, i)+ypc2(j, i)+zxx2(k, i)+xxy2(i, j) +
Ъ'лСл J)+Ziy2(k’ J)+\z2{h к) + ухг2а, k)+
+ztz2(k, k).
Учитывая, что
(». 0 = (J, J) = (к, к) = 1, (j, i) = {к, i) = (к, j) = 0,
получаем (a, b) = xtx2 + yty2 + ztz2 
§ 3.2. Линейные векторные пространства
>	Понятие линейного векторного пространства
>	Вектор в /7-мерном пространстве
>	Линейная зависимость и независимость векторов
>	Свойства линейной зависимости векторов
Понятие линейного векторного пространства
Для дальнейшего изучения векторного анализа нам понадо-
бится понятие векторного пространства.
Определение. Множество W элементов х, у, z,... назы-
вается линейным пространством, если по некоторому правилу:
1. Любым двум элементам х и у из W поставлен в соитьстствие
элемент из W, обозначаемый х+у и называемый суммой элемен-
тов хиу.
2. Любому элементу х из И7 и каждому числу X поставлен в со-
ответствие элемент из И7, обозначаемый X • х и называемый про-
86
Глава 3. Векторная алгебра
изведением числа X на элемент х, причем справедливы следую-
щие аксиомы:
1)х+у=у + х;
2) (х+у) + z=x+(у + z);
3)Х- (х+у) = Х-х+Х-у;
4)	(Х + Ц)  х=Х-х+Х-х;
5)	X  (ц  х) - (X • ц) • х;
6)	1 Х=Л",
7)	существует нулевой элемент 0 такой, что х + 0 = х для
любого хе W;
8)	для каждого элемента х существует противоположный
элемент — х такой, что х+ (—х) = 0.
Элементы любой природы, удовлетворяющие двум правилам
и восьми аксиомам, по определению, образуют линейное про-
странство. Например, совокупность любых матриц размера пг х п
образует линейное пространство, поскольку для них выполнены
оба правила и все аксиомы. Легко проверить, что совокупность
геометрических векторов, например трехмерного пространства,
также является линейным пространством.
Линейное пространство называется пустым, если оно состо-
ит из нулевого элемента.
Вектор в /7-мерном пространстве
Определение, п-мерным вектором называется математи-
ческий объект, который состоит из упорядоченной совокупности
действительных чисел, называемых компонентами вектора, и за-
писывается в виде х = (Xj, Хг,..., х„). Название ««-мерный вектор»
связано с тем, что при п = 2 или п = 3 совокупность чисел можно
интерпретировать как совокупность координат вектора на плос-
кости или в пространстве.
Два л-мерных вектора х = (xt, х2, ..., х„) и у = (у„ у2, ..., у„)
называются равными, если равны все компоненты векторов, т.е.
х, = у-, где i= 1,2,..., и.
Пусть для и-мерных векторов выполнены правила сложения
и умножения на число, удовлетворяющие аксиомам линейного
пространства. Тогда множество всех л-мерных векторов называ-
ется линейным векторным пространством и обозначается W.
87
Линейная алгебра. Курс лекций
Декларируя правила сложения и умножения для «-мерных
векторов, мы должны уточнить, как следует производить эти
действия над совокупностями п действительных чисел. Иначе го-
воря, введем операции над «-мерными векторами.
Суммой двух векторов х = (хр х2,..., х„) и у = (yt,y2, , У„) на-
зовем вектор z = x+y такой, что
z = (z,, z2,	z„) = (Xj + Ji, Xj + у2,..., х„ + у„).
Произведением действительного числа Л на вектор х назовем
вектор у = X  х такой, что
J = (Ji> Уг> •••> к) = (Ч> Ч« •••> Ч)-
Замечание. Введенные согласно определению операции
над «-мерными векторами аналогичны операциям над прямо-
угольными матрицами. Поэтому «-мерные векторы можно рас-
сматривать как матрицы-строки X = (xt, х2, ..., х„) или как
матрицы-столбцы X =
и совершать над векторами матрич-
ные операции.
Линейная зависимость и независимость векторов
Пусть каждый из векторов в наборе х, at, а2, ..., ат есть
«-мерный вектор.
Определение. Вектор х называется линейной комбинацией
векторов а2,ат, если найдутся такие действительные числа
Ч Х2,..., Л.и, что
x = X1e1 + X2a2+...+Xmam.
Векторы вр а2,ат называются линейно зависимыми, если
существуют такие числа А,, Х2,..., Лт, не все одновременно рав-
ные нулю, что
A1«1 + A2e2+...+Amam = o.
(4)
88
Глава 3. Векторная алгебра
Если равенство (4) выполняется только при At = А2 =...= Ат = О,
то векторы называются линейно независимыми.
ПРИМЕР. Даны два неколлинеарных вектора. Доказать, что
они линейно независимы.
Решение. Предположим иное: векторы л., а2 линейно зависи-
мы. Тогда существуют не равные одновременно нулю числа Ар А2,
такие, что А,^ + А2о2 = о. Пусть для определенности А * 0. Разделив
Х2в2
обе части равенства на А, 0, получаем ах = —-— . Значит, векто-
л,
ры коллинеарны, что противоречит условию.
Свойства линейной зависимости векторов
1)	Если среди нескольких векторов (набора векторов) один из
них есть линейная комбинация части остальных, то весь набор
векторов линейно зависим.
Пусть имеются векторы х, а,, а2 ат, причем вектор
х = Atat + Х2в2 +... + ХАаА, где k<tn. Перенесем все члены в одну
часть и дополним слагаемыми 0 • ahl,..., 0 • ат. Получим линей-
ную комбинацию
+ Х2в2 +... + \ак + 0 e*+i +... + 0  ат + (-1)х= о,
в которой нашлись А15 А2, ..., Ат, не все одновременно равные
нулю. Значит, векторы х, at, а2,..., ат линейно зависимы.
2)	Если среди набора векторов at, а2, ..., ат имеется нулевой
вектор, то весь набор векторов линейно зависим.
Пусть, например, нулевым является вектор ах. Тогда равен-
ство (4) останется справедливым при А, = 1, А2 = А3 =...=А.т = 0.
3)	Если векторы at, а2,..., ат линейно независимы и существу-
ет вектор х, являющийся линейной комбинацией а}, а2,..., ат, т.е.
х = Xjflj + А,о2 +... + ‘ктат, то коэффициенты Ар А2,..., Ат опреде-
ляются по вектору х единственным образом.
Пусть вектор х можно представить как две линейные комби-
нации с различными коэффициентами:
х = Х1«1+Х2в2 + ... + ХЛвЛ и х = р1в1+|12а2+... + |1л.
89
Линейная алгебра. Курс лекций
Тогда
х =	+ Х,в2 +... + \ак -	+ ц2а2 +... +	,
откуда
(X, - р,)«, + (Х2 - ц2 )а2 +...+(kt - цА К = 0.
Из линейной независимости векторов at, а2,ат вытека-
ет, что
(Х1-ц,) = (Х2-ц2) = ... = (ХЛ-ц*) = 0,
а значит,
^-|=Ир ^-2=Й2> —’	= М-* •
ПРИМЕР. Являются ли векторы at = (1, —1, 2, 2),
e2 = (—1 —2 3 0),в3 = (2,1,-1, 2), в4 = (1,0,—2, —1) линейно зави-
симыми? Если да, найти всю совокупность значений коэффици-
ентов, реализующих линейную зависимость.
Решение. Составим векторное равенство
Равенство (5) есть система линейных однородных уравнений
с четырьмя переменными. Составим матрицу из коэффициентов
и определим ее ранг:
' 1 -1
-1 -2
2	3
. 2 0
2 ИГ1-1
3	0	0 -3
-1-2	0 5
2 -1J |о 2
2
3
-5
—2
-1 2 Г
-3 3	1
0 0-7
0 0 -7,
'1 -1 2 Г
0-331
0	0	0	1
,0 0 0 0,
90
Глава 3. Векторная алгебра
Очевидно, ранг матрицы равен 3. Система (5) имеет, кроме
нулевого решения А, = Х2 =...=Ат = 0, бесконечное множество ре-
шений. Следовательно, векторы ах, а2, а3, а4 линейно зависимы.
Далее найдем структуру бесконечного множества решений, для
чего продолжим элементарные преобразования со строками мат-
рицы по методу Гаусса — Жордана:
Отсюда следует
, где се R.
(6)
Решение (6) представляет всю совокупность значений коэф-
фициентов Ар А2, А3, А4, реализующих линейную зависимость век-
торов в2> вз, вд-
Замечание. Как видно из примера, вопрос о линейной за-
висимости векторов сводится к исследованию существования не-
нулевого решения у линейной однородной системы уравнений.
§ 3.3. Размерность.
Базис векторного пространства
>	Размерность векторного пространства
>	Базис векторного пространства
>	Разложение вектора по базису
>	Дополнение до базиса
Размерность векторного пространства
Определение. Векторное пространство называется п-мер-
ным, если среди множества его векторов найдутся п линейно неза-
висимых векторов, а любые п+1 векторов уже окажутся зависимы-
ми. Число п называется размерностью векторного пространства.
Например, среди бесконечного множества векторов, распо-
ложенных в одной плоскости, любые два неколлинеарных векго-
91
Линейная алгебра. Курс лекций
ра являются линейно независимыми. Выберем какие-либо два
неколлинеарных вектора = (х„ и а2 = (yt, у2). Добавление тре-
тьего вектора e3 = (z„ z2) к выбранным двум делает их линейно за-
висимыми. Действительно, система уравнений, полученная из
векторного равенства ytat + Х2а2 +Х3а3 = о, будет иметь вид
Матрица коэффициентов I Х| Z* I имеет ранг, равный
1*2 Уг Ъ)
двум, откуда следует, что один из трех столбцов есть линейная
комбинация двух других. Следовательно, размерность такого ли-
нейного векторного пространства равна двум.
Базис векторного пространства
Определение. Упорядоченная совокупность п линейно
независимых векторов «-мерного векторного пространства назы-
вается базисом этого пространства.
Выбранные нами в рассмотренном выше примере в опреде-
ленном порядке два неколлинеарных вектора составляют базис в
двухмерном пространстве. Если векторы поменять местами, они
также составят базис этого пространства, но другой. Если выбрать
два других неколлинеарных вектора в определенном порядке, на
них можно построить свой базис.
В общем случае пусть в «-мерном векторном пространстве
содержится т векторов (т > п). Количество способов выбора п
линейно независимых векторов из общего числа т не превышает
величины
Сп =
т п\(т-п)\
Кроме того, выбрав п векторов, можно построить и! упорядо-
ченных совокупностей. Тогда количество базисов в таком «-мер-
ном векторном пространстве может достигать величины
.. т' । т'
N =---------П:	—-----
п\(т-п)\	(т-п)1
Если в векторном пространстве определен базис, другие век-
торы могут быть выражены через этот базис.
92
Глава 3. Векторная алгебра
Разложение вектора по базису
ТЕОРЕМА
(о разложении вектора по базису)
Каждый вектор линейного пространства можно представить, и
притом единственным образом, в виде линейной комбинации векторов
базиса.
◄ Пусть векторы ах, а2,ап образуют базис. Возьмем произ-
вольный вектор х. Тогда совокупность векторов at, а2, ..., ап, х
линейно зависима, т.е. найдутся такие не равные одновременно
нулю числа Х„ ..., X„, X, что
+ h2a2 +...+Аплп + Ах = о,
причем X 0. Если бы выполнялось равенство X = 0, то хотя бы
один из коэффициентов Х15 Х2, ..., Х„ обязан быть не равным
нулю. Но это противоречит определению линейной независи-
мости векторов ах, а2,ап.
Разделим обе части уравнения на X 0. Получим
ЛЛ	Л
Равенство (7) есть линейная комбинация векторов базиса
X = х,ах + Х>й2 +... + х„а„ = '^х1а1,	(7')
;=|
X, - , п
гдех,. = --±, 1 = 1,2,..., п.
К
Представление вектора х в виде линейной комбинации (7')
является единственным в силу свойства 3 линейной зависимости
векторов. ►
Замечание. Равенство (7') называется разложением век-
тора х по базису ах, а2,..., ап, а числа хх, х2,..., хп — координатами
вектора х в этом базисе. Считая компоненты вектора его коорди-
натами, можно представить вектор х набором своих координат
х = (Х], х2, ..., х„) . Таким образом, упорядоченная совокупность
действительных чисел (так определяется «-мерный вектор) есть
набор координат в определенном базисе некоторого «-мерного
вектора.
93
Линейная алгебра. Курс лекций
ПРИМЕР. Векторы «(, а2, а3, а4, а5, аь заданы совокупностями
действительных чисел
в1=(1,0), в2 = (0,1), а3 =(1,1), «4 = (2,1),
й5 = (1,2), в6 = (2,2).
1.	Найти размерность и базис линейного пространства, в ко-
тором заданы векторы.
2.	Сколько базисов можно построить на данных векторах?
3.	Задав базис, разложить остальные векторы по этому базису.
Решение. Составим матрицу из координат всех векторов:
1 0 1 2 1 2Л
О 1 1 1 2 2)‘
1.	Ранг матрицы равен двум. Только два линейно независимых
столбца содержатся в этой матрице. Остальные столбцы могут быть
представлены как линейные комбинации двух выбранных линей-
но независимых столбцов. Следовательно, размерность пространс-
тва равна двум. Базисными векторами можно выбрать векторы
aj = (l, 1),в2 = (0,1), расположив их в следующем порядке: ах,а2.
2.	Число базисов, которые можно построить, не превышает
величины
т\ _ 6! 1-2-3-4-5-6
(ш-и)!"4!	1-2-34
На самом деле их меньше. На векторах «3 = (1, 1), а6 = (2, 2)
построить базис невозможно. Они коллинеарны и, следователь-
но, линейно зависимы: —2а1 +at = о. Число возможных базисов
равно 28.
3.	Разложим векторы в3=(1,1),в4=(2,1),в5=(1,2), в6=(2,2) по
выбранному базису в,, at.
Начнем с векторов в3 и а4:
а3 = х,а, + х2а2 , а4 = у,а, + у2аг .
Представим векторы равенства как матрицы-столбцы:
fl) fl) fO) f2) fl) fO)
94
Глава 3. Векторная алгебра
В матричной форме
f 1 О V X] А
[б 1
Йр оу.рЛ (2А
’Io wJ“IJ
или в сокращенной матричной форме
А Х=В
решение матричного уравнения имеет вид
или
|х2)_[о 1) \1J11J’ bJ4° 1J
Следовательно,
a j — а । "Ь л 2 , а д — 2й । ч* а 2 .
Действуя аналогично, для векторов й5 и й6 получаем разло-
жения й5 = й] + 2й2 , й6 = 2й] + 2й2 .
Замечание. Рассмотрим однородную линейную систему
т уравнений с п переменными
a11x1+ai2x2+... + ai„x„ = 0,
агххх+а2гхг+...+аг„хп = Ъ,
......................9
ат^+ат2х2+...+атпхп=0,
имеющую ненулевые решения. Пусть ранг системы равен г. Она
обладает фундаментальным набором решений (ФНР) (см. гл. 2,
§ 2.5 «Однородные системы уравнений»)
95
Линейная алгебра. Курс лекций
которые линейно независимы. Эти независимые решения, яв-
ляющиеся совокупностями из п чисел, можно представить как
«-мерные линейно независимые векторы. Любое решение систе-
мы представляется в виде линейной комбинации ФНР. Если взять
векторы в], е2, ...» еи_г в качестве базиса некоторого линейного
векторного пространства, то все множество решений однородной
системы и будет этим векторным пространством, называемым
пространством решений однородной системы. Размерность про-
странства равна числу независимых векторов, т.е. п — г.
Вопрос о нахождении базиса «-мерного линейного векторно-
го пространства сводится к перебору наборов из п произвольных
векторов этого пространства и изучению ранга матрицы, состав-
ленной из координат выбранных векторов. При нахождении мат-
рицы с величиной ранга г = п соответствующие векторы можно
брать как базис векторного пространства.
Если уже имеются к линейно независимых векторов {к < п),
возникают вопросы:
1. Можно ли создать базис в рассматриваемом векторном
пространстве, опираясь на имеющиеся к векторов и дополняя их
другими п —к векторами?
2. Если можно, то как это сделать?
Ответ на первый вопрос дает следующая теорема.
Дополнение до базиса
ТЕОРЕМА
(о дополнении до базиса)
Пусть векторы ах, а2, ..., ак линейного пространства W раз-
мерности п линейно независимы, причем к < п. Тогда в простран-
стве Ж найдутся векторы et+l, et+2, ..., а„ такие, что совокуп-
ность п векторов в], в2, ..., ак, ак+х, ак+г, ..., ап составит
базис этого пространства.
◄ Пусть х — произвольный вектор линейного векторного
пространства W. Представить любой вектор х в виде линейной
комбинации векторов ах, а2, ..., ак нельзя, так как в противном
случае совокупность векторов ах, а2,..., ак была бы базисом. Од-
нако в силу условия к < п это невозможно. Поэтому должен су-
96
Глава 3. Векторная алгебра
шествовать вектор et+l е W такой, что дополненная система век-
торов ак, ак+х, будет линейно независимой.
Если к + 1 = п, то эта система является базисом пространст-
ва W.
Если к + 1 < п, следует повторить рассуждения с векторами
®1» •••, ак, ак+х.
Следовательно, любая заданная совокупность линейно неза-
висимых векторов может быть дополнена до базиса векторного
пространства. ►
Перейдем к методу дополнения А: линейно независимых век-
торов до базиса. Пусть даны векторы ах = (хи,..., хх„),..., ак = (хкх,
..., хЛи). Составим из координат векторов матрицу, расположив
для удобства координаты векторов по строкам:
% - V
Л1 ... хкп>
Поскольку векторы линейно независимы и к < п, элементар-
ными преобразованиями строк матрица приводится к ступенчато-
му виду. Дополним полученную матрицу п — к строками вида
(О, ..., 1, ..., 0) так, чтобы ранг новой матрицы, например такой:
хн .	•• Х\к		••	V
0 .	 Хкк		" Хк,п-\	Хкп
0 .	.. 0	1	0	0
0 .	.. 0	0	1	0
< 0 •	. 0	0 .	. 0	1,
стал равен п. Тогда векторы ах = (хп, ..., х1и), ..., ак = (хкх, ..., хкп)
вместе с векторами аА(1, ..., ап, координаты которых располо-
жены в последних п — к строках матрицы, составят базис «-мер-
ного линейного векторного пространства.
Замечание. Дополнение векторов ах = (хп,..., х|л),..., ак -
= (хкх,..., хкп) до базиса произвольными векторами ам, ак+2, а„
97
Линейная алгебра. Курс лекций
соответствующей размерности может не дать п линейно незави-
симых векторов.
ПРИМЕР. Дополнить набор векторов л,=(1 2 -1 0),
й2 = (-1 1 -2 1) четырехмерного векторного пространства до
базиса этого пространства.
Решение. Если выбирать векторы с произвольными коорди-
натами, дополняя базис, среди них могут оказаться векторы,
являющиеся линейными комбинациями данных векторов. На-
пример, вектором й3=(2 1 1 -1) нельзя дополнить базис,
поскольку в3 =й, -в2. Составим матрицу из координат данных
векторов, приведем ее к ступенчатому виду и дополним ее дву-
мя строками, чтобы она приняла вид
2 -1 О'
0 3-31
0 0	1 0
,0 0 0 1,
Векторыв|=(1 2 -1 0),й2 = (-1 1 -2 1),й3=(0 0 1 0),
й4 = (0 0 0 1) линейно независимы и составляют базис четы-
рехмерного пространства.
В векторном пространстве не всегда удобно работать с уже
заданным базисом. Например, если вектор х = (х(, х2) задан в бази-
се flt, а2 (рис. 3.7), имеет смысл перейти к другому базису, elt е2,
составленному из единичных и взаимно перпендикулярных век-
торов. В новом базисе вектор имеет координаты х = (xf, х2). Воз-
никает вопрос: как, зная координаты вектора в старом базисе и вза-
имное расположение векторов старого и нового базисов, вычислить
координаты вектора в новом базисе?
98
Глава 3. Векторная алгебра
§ 3.4. Переход к новому базису
>	Матрица перехода к новому базису
>	Свойства матрицы перехода
Матрица перехода к новому базису
Пусть В= (е1; е2,е„) и В' = (е[, е2,	е') — старый и новый
базисы линейного «-мерного векторного пространства W. Каж-
дый из векторов нового базиса можно выразить через векторы
старого базиса:
«21*2 + •••+«„ А»
е2 = апех+а22е2+... + ап2еп,
е,„ = а1пе1+а2пе2+,„+а„пеп,
а также представить в матричной форме:
'«и а12 ... а,/
(8)
k«»i «„2 - a„J
или в сокращенной матричной форме:
В' = В Т.
Матрица
'«11	«12	-	«In'
у, _ «21	«22	•••	«2л
<«л1	«л2	—	«ли у
называется матрицей перехода от старого базиса е к новому бази-
су е’.
Замечание. Следует обратить внимание на то, что коор-
динаты разложения векторов нового базиса по старому базису
располагаются в матрице перехода по столбцам.
99
Линейная алгебра. Курс лекций
Свойства матрицы перехода
1) Матрица перехода является невырожденной, т.е. |7'| ф 0.
Действительно, из равенства |Т| = 0 следует, что один из столб-
цов матрицы Т является линейной комбинацией остальных
столбцов. Тогда один из векторов есть линейная комбинация
других векторов этого базиса, что невозможно.
2) Матрица перехода от нового базиса к старому имеет вид Т1.
Умножив равенство (8) на Т 1 справа, получим
°11	°12	•"
<аи1 ап2 ••• ат;
Найдем зависимость между координатами вектора в разных
базисах. Пусть некоторый вектор х имеет координаты (хп х2, ...,
х„) в старом базисе и координаты (xf, х2, х'п) в новом базисе.
Тогда
х = ххех + х2е2 +... + хпеп = х'хе'х + х'2е'2 +... + х'пе'п.
Подставив в это выражение разложения векторов (ех, е2,
..., е') по базису (ех, е2, ..., с,), получим
Х|в| + х2е2 +... + х„е„ — Xj (й| хех + о21^г •••+) + х2 (^12^1 ^22^2 +
+а2„е„ ) + - + *„(°1 Л1 + «2 1*2 + - + anngn )•
Перенесем все влево и сгруппируем слагаемые с одинаковы-
ми сомножителями е':
(Х] —Х|Оц — х2аХ2 —... — хпаХп) ех + (х2 —хха2Х — х2а22 —
~Xna2n) е2 + -+(*„ - *141 - Х2а„2 ~	~ Х'пат) е„= 0
Это равенство выполняется при условии, что все коэффици-
енты перед е' равны нулю. Следовательно,
х, =х1/а11+х2а12+...+ х'а1п,
х2 — Х|П2| + х2а22 +... + х„о2„,
...........................
Х„ = Х1Ч1 + х2аг,2 + -+<«„„•
100
Глава 3. Векторная алгебра
В матричной форме
Координаты вектора в новом базисе выражаются через коор-
динаты вектора в старом базисе:
В развернутой матричной форме
ПРИМЕР. Векторы х = (1, 3, -2), < = (1, 1, 0), е2 = (1, 0, 1),
<?' = ((), 1, 1) заданы своими координатами в старом базисе е15е2>
е3. Выразить координаты векторах в новом базисе е{, е2, е'3:
Решение. Матрица перехода от старого базиса к новому базису
имеет вид
Г1
Т= 1
<0
1 (Г
о 1
1 L
Вычисляется обратная матрица:
7”1
Координаты вектора в новом базисе:
101
Линейная алгебра. Курс лекций
§ 3.5. Линейные подпространства
>	Линейные подпространства
>	Сумма и пересечение линейных подпространств
>	Свойства суммы и пересечения линейных подпространств
>	Линейная оболочка
>	Свойства линейной оболочки
Линейные подпространства
Из множества векторов линейного пространства W выберем
некоторую совокупность векторов и обозначим ее V. Пусть для
любых векторов х и у из Ки любого числа Хе R выполняются сле-
дующие условия:
1)х+уеГ; 2)Х-*еГ.
Тогда множество векторов V называется линейным подпро-
странством пространства W.
Примеры линейных подпространств:
1.	Каждое линейное пространство обладает двумя подпро-
странствами: нулевым подпространством и самим пространством.
Эти подпространства называют тривиальными.
2.	Линейное пространство Wx векторов на прямой, проходя-
щей через начало координат, имеет два тривиальных подпро-
странства.
3.	Линейное пространство W2 векторов на плоскости
(рис. 3.8) имеет, кроме двух тривиальных подпространств, беско-
Рис. 3.8
102
Глава 3. Векторная алгебра
нечное множество подпространств Vx, V2,.... Каждое из них со-
стоит из векторов, которые лежат на прямой, проходящей через
начало координат (предполагается, что все векторы отложены от
начала координат).
4.	В геометрическом пространстве W3 векторов пространства
каждая прямая и каждая плоскость, проходящие через начало ко-
ординат, определяют линейное подпространство.
Сумма и пересечение линейных подпространств
Суммой VY + V2 линейных подпространств и V2 линейного
пространства W называется совокупность всех векторов а е W,
которые можно представить в виде (разложить)
а=х+у, где хе V{, ye V2.
Если для каждого вектора а это разложение единственное,
сумма линейных подпространств V{ и V2 называется прямой и за-
писывается в виде Vx © V2.
Пересечением линейных подпространств V\ и ^ли-
нейного пространства W называется совокупность всех векторов
Ь, которые принадлежат одновременно подпространствам Vx и V2.
На рис. 3.9 пересечению подпространств V} и V2 геометрического
пространства W3 принадлежат векторы Ьх и Ь2.
Рис. 3.9
103
Линейная алгебра. Курс лекций
Свойства суммы и пересечения линейных подпространств
1) Сумма и пересечение линейных подпространств являются
линейными подпространствами.
2) Размерность суммы линейных подпространств равна сум-
ме размерностей подпространств минус размерность их пересе-
чения.
Линейная оболочка
Определение. Линейной оболочкой Цх}, х2) двух векторов
X! и х2, принадлежащих линейному пространству W, называется
совокупность всех линейных комбинаций этих векторов
а = а- х( + р- х2, где а, р е R
Иначе говоря, линейная оболочка состоит из бесконечного
множества векторов а, представимых в виде линейных комби-
наций векторов х, и х2. На рис. 3.10 построены векторы Xj и х2, а
также приведено несколько их линейных комбинаций ..., а5.
В общем случае линейной оболочкой множества X векторов,
принадлежащих линейному пространству W, называется сово-
купность всех линейных комбинаций этих векторов
Z(Jf) = -!e = ^X,x, |х, е X, Х, е/?, и = 1,2,... >.
Рис. 3.10
104
Глава 3. Векторная алгебра
Свойства линейной оболочки
1) Линейная оболочка содержит само множество X
2) Если линейное пространство ^содержит множество X, то:
а) пространство ^содержит и его линейную оболочку ДА);
б) ЦХ) — линейное подпространство пространства W.
ПРИМЕР. Н айти линейную оболочку множества решений
системы уравнений
х, + хг - х4 = О,
х3 +х4 =0.
Решение. Ранг матрицы коэффициентов системы уравнений
равен 2. Выберем свободными переменными х2 и х4. Тогда общее
Векторы £,=(—1, 1, 0, 0}ит|=(1, 0, -1, 1) образуют фун-
даментальный набор решений однородной системы. Любое ре-
шение системы является их линейной комбинацией. Значит, ли-
нейная оболочка векторов £ и т| и есть множество решений одно-
родной системы уравнений, т.е. L (£,, т|) = + с2т] >гдс с\ >	
§ 3.6. Евклидовы пространства
>	Евклидовы пространства
>	Свойства длины вектора
>	Ортонормированная система векторов
>	Ортогональное дополнение
>	Свойства ортогонального дополнения
Евклидовы пространства
Введенное нами линейное векторное пространство не содер-
жит информации о том, как измерять длины и углы в этом про-
странстве. Иначе говоря, оно не содержит метрики. Неожидан-
на
Линейная алгебра. Курс лекций
ной на первый взгляд является возможность решить этот вопрос,
если ввести понятие скалярного произведения.
Определение. Линейное векторное пространство Wна-
зывается евклидовым, если любым двум векторам х и у из W ста-
вится в соответствие число, обозначаемое как (х, у), причем вы-
полняются следующие условия:
1)	(х, у) = (у, х);
2)	(х+у, z) = (х, z) + (у, z);
3)	(А • х, у) = А (х, у), где А е R;
4)	(х, х) > 0, если х — ненулевой вектор; (х, х) = 0, если
х — нулевой вектор.
Евклидовым линейное пространство названо по имени древ-
негреческого математика Евклида, создавшего в 3 в. до н. э. Евк-
лидову геометрию — «первое приближение для описания струк-
туры реального физического пространства» (БСЭ).
Определение. Число (х, у) называется скалярным произве-
дением векторов х и у. Поскольку векторы задаются набором сво-
их координат, надо определить, какие действия следует совер-
шить с координатами векторов, чтобы получить число (х, у). Оп-
ределим скалярное произведение векторов х = (х,, х2, ..., х„)
иу = (У], У2,	у„) формулой
(х, y) = x,y,+x2y2+...+x„y„.
Заданное таким образом скалярное произведение «-мерных
векторов для случая п = 2 или п = 3 обращается в рассмотренное
ранее скалярное произведение геометрических векторов. Теперь
появляется возможность определить длины и углы в простран-
стве.
Замечание. Очевидно, что из равенствах = у следует ра-
венство (х, z) = (у, z). Переход от равенства векторов к равенству
скалярных произведений назовем скалярным умножением.
Определение. Длиной (нормой) вектора х в евклидовом
пространстве называется величина
|х| = ^(х, х) = 7xi2+x2+-+х„2 
В двух- или трехмерном евклидовом пространстве длина век-
тора имеет ясный геометрический смысл. Однако в четырех-,
пяти- или «-мерном евклидовом пространстве смысл длины век-
тора теряется. Поэтому вместо длины вектора часто вводят поня-
тие нормы вектора.
106
Глава 3. Векторная алгебра
Определение. Углом между ненулевыми векторами х и у
евклидова пространства называется число <р, определяемое из ра-
венства
(х, j)
cosq>= \	, гдеО<<р<л.	(9)
М-и
(х, j)
Определение требует доказательства того, что -1 < \ .   < 1
И-И
для любых пар ненулевых векторов х и у, о чем речь пойдет ниже.
Свойства длины вектора
1)	Если вектор х нулевой, т.е. х = (0, ..., 0), то его длина
|х| = у](х, х) = ^O+... + О = 0, и обратно: если |х| = 0, то вектор х ну-
левой.
2)	|Хх| = |Х|-|х|, гдеХеЛ
Действительно,
|Хх| = ^(Хх,)2 +(Хх2)2 + ... + (Ххп)2 = |Х|-^х2 +х2 + ... + Х2 = |Х|-|х|-
3)	|(х, у )| < |х| • |у | — неравенство Коши — Буняковского.
Для доказательства введем параметр t&R. По определению
скалярного произведения, неравенство
(tx-y, tx-y)>0
верно для любых векторов х и у. Преобразуем неравенство к квад-
ратному относительно t:
Z2(x, x)-2z(x, у)+(у, у)>0.
При Ze Л неравенство верно. Следовательно, дискриминант
квадратного трехчлена должен быть меньше либо равен нулю:
Z) = (x, у)2-(х, х)(у, у)<0.
Отсюда
(х, у)2<(х, х)(у, у) или |(х, у)|<|х|-|у|.
Замечание. Из неравенства Коши — Буняковского еле-
(х, у)
дует-1<~-	/<1 . Определение угла в (9) становится коррект-
4И
ным.
107
Линейная алгебра. Курс лекций
4)	|х +у | < |х|+|у | — неравенство треугольника.
С одной стороны,
(х+у, х+у) = |х+у|2.
С другой стороны,
(х+у, х+у) = (х, х) + 2(х, у)+(у, у) = |х|2 + 2(х, у)+|у|2-
Воспользуемся неравенством
2(х, у)<2|(х, у)| <2|х|-|у|
Тогда
|х|2+2(х, у)+|у|2 < |х|2+2|х|-|у|+|у|2=(|х|+|у|)2.
Значит,
|х+у|2<(|х| + |у|)2.
Извлечем квадратный корень и в результате получим нера-
венство треугольника.
Определившись с длинами и углами, используем новые от-
крывающиеся возможности в развитии векторной алгебры.
Два ненулевых вектора х и у называются ортогональными,
если их скалярное произведение равно нулю, т. е. (х, у) = 0. Из
равенства (х, у) = |х| • |у| • coscp = 0 следует, что cos<p - 0 или угол
л
S’ - . Для двух- или трехмерного пространства ортогональность
векторов означает, что они взаимно перпендикулярны.
Для ортогональных векторов неравенство в свойстве 4 за-
меняется равенством
|х+у| = |х|2+|у|2.
Ортонормированная система векторов
Система векторов et, е2, ..., еп называется ортогональной,
если (е(, Cj) = 0 при i*j,u нормированной, если |е,| = 1 для всех
1= 1, 2,..., п. Если векторы системы ортогональны и нормиро-
ваны, они называются ортонормированными.
108
Глава 3. Векторная алгебра
Замечание. Чтобы нормировать ненулевой вектор, необ-
ходимо разделить его на норму. Пусть задан вектор х = (1, —1, 2,0).
Его норма |х| = у/12 +(-1)2 +22 = Тб. Нормированный вектор имеет
х ( 1	-1	2	А
вид е = —7 = 1-^,	—j=, О I. Его длина |е| = 1.
|х|	л/6	V6	)
ТЕОРЕМА
(о независимости ортонормированной системы векторов)
Ортонормированная система векторов линейно независима.
◄	Докажем, что ортогональные и нормированные векторы
Ср е2,еп линейно независимы, т.е. докажем, что равенство
Х|в| + ^2^2 + +	= ®
справедливо лишь при X, = Х2 = ... = = 0. Умножив обе части ра-
венства скалярно на вектор ех получим
eJ+M*., «2)+- + Mei> е»)=(вр °)
илих1.1+х2.о+...+хп.о = о •
Отсюда следует X, = 0. Умножая последовательно равенство
скалярно на е2, е3,еп, будем иметь Х2 - ... = Тп = 0 • ►
ТЕОРЕМА
(о существовании ортобазиса)
Во всяком «-мерном евклидовом пространстве существует ортонор-
мированный базис.
◄	Доказательство теоремы представляет собой алгоритм по-
следовательного построения ортонормированного базиса по за-
данному базису fx,f2,	, названный методом ортогонализации.
Положим вектор = fx и нормируем его: е -	, получив
l*il
первый вектор ортонормированного базиса. Построим вектор
g2=f2-al-el	(10)
так, чтобы он был ортогонален вектору ех. Должно выполняться
условие (g2, ех) = 0. Из этого условия найдем аР Умножив скаляр-
но равенство (10) на е{, получим
109
Линейная алгебра. Курс лекций
(g2, e,) = (f2-al e„ e,) = (f2, ej-a^e,, e,) = 0,
откуда ct j = (/’2, e,). Тем самым вектор g2 = f2 ~{f2, «i)«, станет
ортогональным вектору Тогда вторым вектором ортонормиро-
ванного базиса станет вектор е2 = рЦ .
Ift I
Пользуясь найденными векторами elt е2 и заданным векто-
ром f3, построим вектор
gi =fi ~ Piei — Ргез >	(И)
ортогональный единичным векторам е, и е2, для чего умножим
скалярно равенство (11) последовательно на е} и е2 и приравняем
к нулю:
{gi, в|) = (А-Р1«1-Р2«2. ft) = (A> «|)-Р|(«и «1)“
~Р2(г2> ei)~D’
{gi, е2)={/3-^ех-^2е2, e2) = {f3,	е2)~
-Р2(е2, е2) = 0.
Поскольку(е2, е1) = 0,(е|, е1) = (е2, е2) = 1 ,получим
Pi ~{fi, ei)’P2 ~(fi, ег)'
Теперь вычислим вектор:
gi=fi~(fi, ft )<>-&, е2)е2-
Затем нормируем его, сделав третьим вектором ортонорми-
рованного базиса е3 -	. Продолжая процесс ортогонализации,
Ift I
по заданному базису /(, f2, fn построим ортонормированный
базис (или ортобазис) в„ е2,..., е„. ►
Замечание. Если векторы х и у разложены по произволь-
ному базису (7'):
х = х,а, + х2а2 +...+х„а„ = ^х^, у = у,а, + у2а2 +...+у„а„ =	,
1=1 1=1
то скалярное произведение векторов, имея п2 слагаемых, выгля-
дит довольно громоздко:
ПО
Глава 3. Векторная алгебра
(*, .У) = 1ХхА’	"/) •
\»=1	(=1	/	1=1 7=1
В ортонормированием базисе е15 е2,еп скалярное произ-
ведение векторов вычисляется просто:
(х» y) = [ixiei>	=	е>) = ±хЛ -
\ <=1	<=1 J >=1 7=1	>=1
В частности,
Тогда длина вектора равна

ПРИМЕР. Методом ортогонализации построить ортонор-
мированный базис по базису евклидова пространства fx = (1,1),
/=(1,2).
Решение. Положим вектор -f\ и нормируем его:
Построим вектор g2 =f2 - а- ех так, чтобы выполнялось усло-
вие , е!) = 0 • Получим
(«2, e,) = (4-ae„ е,)-(/2, е,)-а(е,, е,) = 0,
откуда
Вычислим вектор g2.
f л 3 (1 И ( 1 П
е, =/> - а е. =(1, 2)-~i= =	— •
V21V2 у/2) 12 2)
Нормируем вектор g2:
111
Линейная алгебра. Курс лекций
Векторы et и е2 образуют ортонормированный базис евклидо-
ва пространства.
Проверка:
U Hi 1 о
^2 I л/2 J V2 V2
Ортогональное дополнение
Пусть задано евклидово пространство W и пусть V= — неко-
торое линейное подпространство евклидова пространства W.
Определение. Совокупность Vх векторов у простран-
ства W, обладающих свойством
(у,х) = 0,
где х — произвольный вектор из И=, называется ортогональным
дополнением к подпространству V. На рис. 3.11 изображено трех-
мерное евклидово пространство. В нем стрелками указаны
векторы, из которых состоит ортогональное дополнение Vх и ко-
торые ортогональны всем векторам из линейного подпростран-
ства V=. В изображении векторов мы отказались от соглашения
об откладывании всех векторов от начала координат.
112
Глава 3. Векторная алгебра
Свойства ортогонального дополнения
1) Ортогональное дополнение И1 есть линейное подпро-
странство евклидова пространства W.
Пусть векторы j! иу2 принадлежат К1, векторх — произволь-
ный вектор из Тогда (у(, х)=(у2, х) = 0- Сложив скалярные
произведения, получим
(j'n X)+(J2»	*) = 0-
Следовательно, у, +у2 е И ‘ .
Если (у, х) = 0 , то и (ау, х) = 0, где а е R, т.е из уеИх
следует ауеИх.
2) Линейное пространство IF есть прямая сумма подпро-
странств и И1, т.е. не содержит пересечений и Г1.
Пусть «„ е2,..., ек — ортонормированный базис V": е,, ем,...,
ер — ортонормированный базис V\ Среди системы векторов
е2, ..., ек, еь е/+1,..., нет одинаковых, и эта система ортонорми-
рование, следовательно, линейно независима. Докажем, что она
образует базис «-мерного евклидова пространства. Предполо-
жим, что это не так, что число (1 + 2 + ... + &)+(/+(/+!)+...+ р)<п.
Тогда существует вектор х пространства, такой, что система век-
торов ех, е2,..., ек, eh el+i, ер, х линейно независима. Применим
к этой системе процесс ортогонализации. Построенный на осно-
ве х вектор , будет ортогонален в„ е2,..., ек, значит, ер.х е
С другой стороны, вектор ортогонален eh е1+х, ер, значит,
, ± F*. Таким свойством обладает только нулевой вектор. Поэ-
тому = о. Отсюда вытекает линейная зависимость ех, е2,...,
е/5 е1+1, ер, х, что противоречит допущению. Таким образом,
система векторов	еь ei+i, --^р является базисом «-мер-
ного евклидова пространства, т.е. 1 + 2+... + & + / + (/ + !)+.,. + р = п.
Из свойства 2 следует, что любой вектор пространства W
можно представить, причем единственным образом, в виде сум-
мы векторов из Г и V\
а = х+у.
Свойство 2 в общем виде можно записать так:
W = V=®V±.
113
Линейная алгебра. Курс лекций
Вектор х е Г называется ортогональной проекцией вектора
а на линейное подпространство а вектор у е И1 — его орто-
гональной составляющей (рис. 3.11).
Если задан вектор а и известен ортонормированный базис et,
е2,..., ек подпространства то могут быть найдены ортогональ-
ная проекция и ортогональная составляющая вектора а. Разло-
жим искомый вектор хе К по базису е„ е2,..., ек с неизвестными
пока коэффициентами разложения X,, А2,Кк'.
х = А,] в] + А2 е2 + ... + Ал еп.
Представим вектор а в виде суммы ортогональной проекции
х и ортогональной составляющей у:
а = х+у или e = A] ei + 'k2e2 + ... + к„еп+ у.
Умножим обе части последнего равенства скалярно на вектор et:
(«1, в) = Х1(е|, е,) + Х2(е1, е2) + ...+Хя(в„ ел) + (е,, у),
откуда первый коэффициент разложения А] = (a, et). Повторив
действия с векторами ех, е2,ек, получим остальные коэффици-
енты А2 = (в, е2),..., Ал = (в, е„). Следовательно, искомый вектор
хе Гпредставляется как
х=(а,	£>, + («, е2)е2 + ... + (в, еп)еп,	(12)
а вектор у е К1 — как
у = а-х = а-(а, ei)el-(a, е2)е2-...-(а, е„)е„.
Аналогично решается задача нахождения ортогональной
проекции и ортогональной составляющей вектора а при задан-
ном векторе а и известном ортонормированном базисе ех, е2,
ек, подпространства Vх.
ПРИМЕР. Подпространство V" линейного четырехмерного
пространства ^задано системой уравнений
х, + х4 - О,
х2 + х3 = 0.
Найти ортогональную проекцию вектора а = (1, —2, —1, 0)
на подпространство и его ортогональную составляющую.
114
Глава 3. Векторная алгебра
Решение. Найдем ортонормированный базис подпростран-
ства V", для чего определим набор фундаментальных решений
системы. Общее решение однородной системы:
Векторыо = (0, —1, 1, 0) и а = (—1, 0, 0, 1) образуют фунда-
ментальный набор решений и, следовательно, базис подпро-
странства Г. Векторы ортогональны. Их нормы |в, | = >/2 и |в21 = V2.
Поэтому ортонормированный базис подпространства :
Найдем скалярные произведения (a, et), 1=1, 2:
Ортогональная проекция вектора а
(см. формулу (12))
х = (в, «,)<>,+(«, е2)е2=-^=(°,
на подпространство Р
Проверка:
/ ч 1 1
(*, у ) = --
2 2
1
+ -
2
2) 2’2
Векторы х и у ортогональны.
115
Линейная алгебра. Курс лекций
Вопросы для повторения
1.	Сформулировать определение геометрического вектора и перечис-
лить линейные операции над векторами.
2.	Определить скалярное произведение векторов и перечислить свой-
ства скалярного произведения.
3.	Дать определение линейного векторного пространства.
4.	Что такое «-мерный вектор? Перечислить операции над «-мерными
векторами.
5.	Какие векторы называются линейно зависимыми?
6.	Сформулировать определение размерности и базиса векторного про-
странства.
7.	Как разложить произвольный вектор линейного пространства по ба-
зису?
8.	В чем заключается идея дополнения линейно независимых векторов
до базиса?
9.	Как перейти от одного базиса векторного пространства к другому?
Ю.Что называется линейным подпространством векторного простран-
ства?
11.	Сформулировать определения суммы и пересечения линейных под-
пространств.
12.	Какое векторное пространство называется евклидовым?
13.	Что такое норма вектора?
14.	Какой базис называется ортонормированным?
15.	В чем суть метода ортогонализации?
16.	Какие векторы составляют ортогональное дополнение?
Линейные отображения
§ 4.1. Общие сведения о линейных
отображениях
> Отображения
>	Образ, ранг, ядро, дефект отображения
>	Отображение базиса
Отображения
Пусть R" и /?'" — линейные пространства размерности «и/и.
Определение. Отображением линейного пространства
R" в линейное пространство R™ называется правило Р , по кото-
рому каждому элементу хеЛ," ставится в соответствие един-
ственный элемент у еК'". Запишем отображение в виде
у = Р(х).
Под элементом пространства будем понимать не обязатель-
но вектор. Это может быть скалярный элемент, матрица и т.д.
Частным случаем отображения является функция у = /(х), по-
скольку каждому значению аргумента х ставится в соответствии
по определенному правилу единственный элемент у. Например,
у = sin(x).
Отображение называется линейным, если для любого элемен-
та х, пространства и любого числа А. выполняются соотношения:
1) Р(х,+х2) = Р(х,)+Р(х2);
2) Р(Хх)=АР(х).
117
Линейная алгебра. Курс лекций
Примеры линейных отображений.
1. Если каждому векторух е R" ставится в соответствие вектор
у = а • х е R”, где а * 0, то говорят, что задано отображение (преоб-
разование) подобия. Процесс отображения представляет собой
умножение каждого вектора на число.
2. Если каждой матрице-столбцу Xразмерности п х 1 из про-
странства матриц /?"*' ставится в соответствие матрица-столбец Y
размерности znxl из пространства матриц Rm*\ то задано отоб-
ражение пространства столбцов X в пространство столбцов Y.
Процесс отображения представляет собой умножение матрицы
Р на столбцы X:
тхп	их!
Y = РХ.
mxl тхп их1
Равными называются линейные отображения Р} и Р2, если
для любого элементах е Rm выполняется равенство
/?(хМ(х)-
Образ, ранг, ядро, дефект отображения
Образом irnP линейного отображения Р называется мно-
жество всех элементов пространства у е Rm, для каждого из кото-
рых найдется элементх е Rn, такой, что Р(х) = у .
Рангом линейного отображения называется размерность об-
раза этого отображения.
Ядром кегР линейного отображения Р называется множе-
ство всех элементов пространства хе/?'', каждый из которых отоб-
ражение Р переводит в нулевой элементу = 0 пространства R™.
Дефектом def Р линейного отображения называется размер-
ность ядра этого отображения.
ТЕОРЕМА
(об образе и ядре)
Образ и ядро линейного отображения являются линейными подпро-
странствами соответственно пространств R™ и R".
118
Глава 4. Линейные отображения
◄ Пусть j] и у2 — элементы образа линейного отображе-
ния Р. Тогда существуют такие элементы х, и х2 из Л"» что
у1 = Р(х1) и у2=Р(х2). Найдем линейную комбинацию +
+ \1У2-
Mi + М2 = *-1 ^(* * xi) + ХгЛх2) = ЛХГ xi) +
+Р(А2 • х2) = Р(А,х, + А2х2 ) •
Из равенства следует, что для элемента у =	из R%
нашелся элемент х =	из R". Следовательно, произволь-
ная линейная комбинация + к2у2 также лежит в imP,T-e. образ
линейного отображения является линейным подпространством
пространства R™.
Пусть теперь х, и х2 - элементы ядра линейного отображе-
ния Р. Тогда справедливы равенства
Р(х,)=0,Р(х2)=0.
Составим линейную комбинацию А,х, + к^ и проведем опе-
рацию линейного отображения:
Р(к}х1 + А2х2)-А,Р(х1)+А2Р(х2) = А1 0 + А, 0=0.
Следовательно, отображение Р переводит линейную комби-
нацию А]*] + А2х2 в нулевой элементу = 0. Значит, ядро линейного
отображения является линейным подпространством. ►
Отображение базиса
ТЕОРЕМА
(об отображении базиса)
Пусть е — (е, е2, еп) — произвольный базис пространства /?”.
Тогда, каким бы ни был набор элементов а — (at, в2,в„) линейного
пространства R", существует отображение Р, переводящее векто-
ры e^R^' в векторы a^R", где i = 1, 2, п, т.е. Р(е,)=а,,
i = 1,2,п. Это отображение линейно и является единственным.
◄ Разложим произвольный элемент х из пространства R{‘ по
базису е:
х = xte} + х2е2 +... + хпеп .
119
Линейная алгебра. Курс лекций
Построим элемент а е по следующему правилу:
а = х,а, + х2в2 +...+хпап.
Введем отображение Р:
в = Р(х).
Запишем равенство в развернутой форме:
Р(х,е, + х2е2 +... + хпеп) = х1в1 + х2в2 +... + хпап,
или
х,Р(е,)+х2Р(е2)+... + хпР(еп) = х,в, + х2а2 +... + х„в„.
Перенесем все слагаемые влево и сгруппируем их:
Х1 (Л«1)-«1 ) + Х2 (Р(е2)-«2) + -+х„	) - «л)=О-
Равенство справедливо для произвольных х1,х2,...,хп при ус-
ловии
Р(в1) = в1, Р(е2) = а2, ..., Р(еп) = ап.*
Линейность. ◄ Воспользуемся сокращенной формой записи.
п	п
Пусть х = ^х(е(., у =	Составим линейную комбинацию
;=1	/=1
этих элементов и найдем ее отображение:
Р(Хх + р.у) = £(Хх, + ру,)а, = Х£х,л; + l^yiai = ХР(х)+ цР(у).
М	М	1=1
Условие линейности отображения выполнено. ►
Единственность. ◄ Предположим существование еще одного
отображения Q, такого, что
£>(в;) = в,., где i = 1, 2,..., п.
Тогда
р(х)=ixi°i=ixiQ(ei)=±хЛ. ]=Q(x) 
»=i	i=i	\ i=i )
Значит, отображения Р и Q совпадают. ►
120
Глава 4. Линейные отображения
Следствие. Линейное отображение из пространства в про-
странство R" ъюжвг быть определено преобразованием векторов
базиса (действием линейного отображения на векторы базиса).
◄ Действительно, если задать линейное отображение систе-
мой уравнений	P(e,) = «i,
	Р(е2) = «2, ^(еп) = ®„>
то действие линейного отображения на произвольный элемент х,
разложенный по базису е = (е,, е2,..., е„), будет существовать. ►
§ 4.2. Линейные операторы
>	Линейные операторы и их свойства
>	Структура линейного оператора
>	Матрицы оператора в разных базисах
>	Определитель оператора в разных базисах
Линейные операторы и их свойства
Определение. Будем рассматривать линейные отображе-
ния, действующие из векторного пространства R" в это же про-
странство R". Подобные отображения называются линейными
операторами.
Введем арифметические операции с линейными операторами.
1.	Суммой операторов Дч Р2 называется оператор Р- j> + Р2,
который действует по следующему правилу: Р(х) = Р} (х)+Р2 (х).
2.	Произведением оператора Рх на число А. называется опера-
тор Р2 = X j\, действующий по правилу: Р2 (х) = X Р{ (х) •
3.	Произведением оператора Р2 на оператор Г\ называется
оператор Р - Р21\, определяемый из равенства: Р(х) - Р2 (х)}.
Оператор Е называется тождественными^ единичным, если
Ё[х) = х.
121
Линейная алгебра. Курс лекций
Все введенные операторы являются линейными. Докажем,
например, что оператор произведения линеен:
Р2(^(Лх+цу)) = Р2(^(Лх)+^(цу)) = Р2(^М+^(^) =
= ХР2(^(х))+цР2(^(у))=ХР(х)+цР(у)-
Структура линейного оператора
Пусть в пространстве R" задан базис е,, е2,	е„. Произволь-
ный вектор х может быть разложен по этому базису:
x = xlev+x2e2+... + xne„.
Подействуем на вектор х оператором Р :
P(x) = P(x]ev+x2e2+...+xnen) = x]P(e])+x2P(e2)+...+xnP(en) .
Величины Pfe,), Р(е2),..., Р(е„) являются векторами из/?" и
поэтому могут быть разложены по базису в,, е2,..., еп:
Р(е,i) = aue}+a2ie2 + ...+anie„.
Тогда
Р(х) = х, (о, ,е, + о21е2 +... +оп1е„)+х2 (а12е, + а22е2 +...+ап2еп)+... +
+х„(а]пе} +а2пе2 +...+оп„е„) = (о11х1 +о12х2 +...+а1пх„)е, +
+(о2,Х1 +а22х2 +...+а2пхп)е2 +...+(оя1х, +оп2х2 +...+а„лхп)е„.
С другой стороны, Р(х) есть некоторый вектор у е R", кото-
рый может быть разложен по заданному базису:
Р(х) - у = у,е,. + у2е2 +...+упеп.
Разложение вектора у по базису единственно. Поэтому
y^a^+a^+...+а^,
y2=a2ix}+a22x2+...+a2nxn,
........................................
Уп=апЛ+ап2х2+...+атх„.
Система уравнений в развернутой матричной форме имеет вид
122
Глава 4. Линейные отображения
или в сокращенной матричной форме
Y=PX.
Таким образом, действие линейного оператора на вектор х
сводится к умножению некоторой матрицы Р= (а,у) на матрицу-
столбец X, составленный из координат векторах. Матрица Рна-
зывается матрицей линейного оператора Р в базисе et, е2, —,еп.
Исследуем ранг линейного оператора Р. Оператор Р , явля-
ясь частным случаем линейного отображения, имеет ранг, рав-
ный размерности образа imP этого отображения, а следователь-
но, размерности соответствующего подпространства. Подпро-
странство составлено из векторов P(et), Р(е2), Р(еп) и их
линейных комбинаций. Число линейно независимых векторов
среди них составляет размерность подпространства. Координаты
векторов P(et), Р(е2), Р(еп) образуют столбцы матрицы Р.
Поэтому число линейно независимых столбцов матрицы Р (им
соответствуют линейно независимые векторы) и есть ранг опера-
тора Р . Вывод: ранг матрицы Р линейного оператора Р равен
рангу оператора.
В том случае, когда ранг г линейного оператора равен п
(г— п, т.е. матрица оператора не вырождена (|Р| * 0), только нуле-
вой вектор преобразуется оператором в нулевой вектор. Действи-
тельно, матричное уравнение Y= Р  Xимеет единственное реше-
ние, что обеспечивает взаимно-однозначное соответствие между
векторами х и у, причем нулевому вектору соответствует нулевой
вектор.
Если матрица линейного оператора является вырожденной
(г < л), некоторые векторы, отличные от нулевого, такой оператор
переводит в нулевые векторы. Возникает дефект линейного опе-
ратора. Соответствующее подпространство ядра оператора пере-
стает быть нулевым. По виду матрицы оператора можно найти
ядро, а именно базис ядра и размер дефекта.
123
Линейная алгебра. Курс лекций
ПРИМЕР.			Линейный оператор Р задан матрицей
	' 1 -1	2'	
Р=	-2 1	1	в некотором базисе векторного пространства R3.
	<-1 о	з,	
Найти базис ядра и размер дефекта оператора.
Решение. Пусть вектор х = (х,, х2, х3) принад лежит ядру линей-
ного оператора Р , т.е. оператор переводит вектор х в нулевой
вектор Р[х)-О- Поскольку Р(х) = Р Х, запишем матричное
уравнение Р- Х= О в развернутом виде:
' 1 -12'
-2 1 1
<-1	о з,
'О'
о
Я
Найдем решение системы, для чего матрицу коэффициентов
приведем к ступенчатому виду:
' 1 -1 2А Г1
-2 1 1 ~ О
k-i оз] [о
-1 2'
-1 5
0 °,
Отсюда следует решение системы:
Совокупность векторов х составляет подпространство решений
уравнения Р[х)-О, а следовательно, ядро оператора Р . Базисом
подпространства можно выбрать вектор а = (7, 5, 1), размерность
подпространства или размер дефекта оператора равны единице.
Продолжим обсуждение задачи и выясним, что представляет
собой подпространство, в которое оператор Р переводит векто-
ры пространства 7?3. Пусть е{, е2, е3 — базис пространства 7?3, в ко-
тором задана матрица оператора Р . Образ imР есть линейное
подпространство, построенное на векторах Р{е}), Р(е2), Р(е3)
(можно сказать: линейная оболочка, натянутая на векторы
P(et), Р(е2), Р(е3)).Тогда
124
Глава 4. Линейные отображения
P(ei)=ei-«2+2«3>
Р{е2) = -2ех+е2+е^,
Р(е3) = -е} + Зе3.
Ранг матрицы
' 1 -2 -Г
-1 1 О
<213,
коэффициентов полученной системы равен двум. Тем самым
только два вектора из трех Р(е}), Р(е2), Р(е3) являются линейно
независимыми, например: P(et), Р(е2). Значит, базис образа
imP оператора Р равен двум. Следовательно, оператор Р , имея
дефект, равный единице, переводит векторы из пространства R3
(dim/? = 2) в подпространство R2 (dim/? = 2). Вообще, для любого
линейного отображения справедлива формула
rang Р+defectP = dim R.
Матрицы оператора в разных базисах
Перейдем к вопросу о поведении линейного оператора при
замене базиса. При переходе от старого базиса к новому в про-
странстве R" матрица Р линейного оператора Р изменяется, од-
нако определитель матрицы оператора сохраняет свою величину.
ТЕОРЕМА
(о связи матриц оператора в разных базисах)
Матрицы Р и Р' линейного оператора Р в старом базисе et,
е2, е„ и новом базисе ef, е2, ..., е'п связаны соотношением
Р' = Т~' Р Т, где Т — матрица перехода от старого базиса к новому.
◄ Пусть в пространстве R” заданы два базиса: ех, е2, е„
иг', е2, ..., е'п. Воздействие оператора Р на вектор х порож-
дает вектор у. В старом базисе имеем Y = Р • X, в новом ба-
зисе — К = Р' • X’. Пусть Т — матрица перехода от старого базиса
к новому. Тогда X = Т- X’, Y=TY.
125
Линейная алгебра. Курс лекций
Умножим равенство X - Т  X слева на матрицу Р\ Р Х =
=Р-X, Y— Т- X или Y=P- Т- X. Умножим обе части последнего
равенства на Г-1: Г-1 Y = Т ' РТХ' или Y' = T~' РТХ'.
Сравнив полученное равенство с X = Т  X, получим
Определитель оператора в разных базисах
ТЕОРЕМА
(об определителе оператора в разных базисах)
Определитель матрицы линейного оператора не зависит от выбора
базиса.
◄ Вычислим определитель матрицы Р', используя свойство
определителя произведения матриц, а также свойство определи-
телей обратных матриц:
|/>-|»|Гч Р Т|=|Т'|| |РНТ|=|7”|| ]Т| |Р|=|Е| |Р|=|Р|. ►
Следствие. Ранг матрицы линейного оператора не зависит от
выбора базиса.
ПРИМЕР. В базисе е,, е2, е3 линейный оператор задан матри-
(2 -1 -П
цей Р= 1	2-2
<3 0 -1,
Найти матрицу оператора в новом базисе
е'}, е2, е'3 , связанном со старым базисом матрицей перехода
Т =
' 1 -10
-2 1 0
-1 -2 1
Решение. Найдем матрицу, обратную матрице перехода:
Матрица линейного оператора в новом базисе будет иметь
вид
126
Глава 4. Линейные отображения
Проверка показывает, что |Р| = |Р'| = 7, т.е. определитель мат-
рицы оператора не изменился при переходе к другому базису.
§ 4.3. Собственные векторы и собственные
значения линейного оператора
> Собственные векторы и собственные значения
> Независимость собственных векторов
Собственные векторы и собственные значения
Определение. Ненулевой векторхназывается собствен-
ным вектором линейного оператора Р, если найдется такое число
X, называемое собственным значением линейного оператора, что
Р(х)=Х-х.	(1)
Равенство (1) означает, что вектор х, подвергнутый действию
линейного оператора, умножается на число Л. Появляется колли-
неарный вектор. Среди векторов линейного векторного про-
странства могут существовать такие, воздействие оператора на
которые переводит эти векторы в коллинеарные самим себе. Если
на таких векторах построить базис, преобразования линейной ал-
гебры значительно упростятся.
Не всякий линейный оператор обладает собственными век-
торами. Например, в геометрической плоскости R2 оператор по-
ворота на угол, не кратный п, не имеет ни одного собственного
вектора, поскольку ни один ненулевой вектор после поворота не
останется коллинеарным самому себе.
Решим задачу нахождения собственных векторов оператора.
Запишем равенство (1) в матричной форме:
Р Х=Х Х.
127
Линейная алгебра. Курс лекций
Преобразуем матричное уравнение:
Р Х-Х Х=О или (Р-кЕ)Х=О.
Матричное уравнение всегда имеет нулевое решение:
io;
Для существования ненулевых решений ранг матрицы ко-
эффициентов должен быть меньше числа переменных г < п, т.е.
число линейно независимых уравнений должно быть меньше
числа переменных. В этом случае должно быть выполнено усло-
вие
|Р-ХЕ| = 0.	(2)
Расписав уравнение (2) относительно X подробнее, получим
Раскрыв определитель, получим уравнение n-й степени от-
носительно А:
(-1)" X" + а„_, X""1 +...+а]Х+а0 = 0 ,
которое называется характеристическим уравнением оператора
Р . Корни уравнения называются характеристическими или соб-
ственными числами оператора. Множество всех собственных чи-
сел оператора Р называется спектром этого оператора. Много-
член левой части уравнения называется характеристическим
многочленом.
Решив характеристическое уравнение, получаем собствен-
ные числа X,, Х2,..., Х„. Для каждого найденного собственного зна-
чения найдем ненулевые векторы ядра оператора Р — \ Е.
Именно они будут собственными векторами, соответствующими
собственному значению X,. Другими словами, необходимо решить
однородную систему уравнений (Р — X, • Е) Х= О. Ее общее реше-
ние дает всю совокупность собственных векторов, отвечающих А,.
128
Глава 4. Линейные отображения
Общее решение однородной системы, как известно, структу-
рировано. Оно представляет собой линейную комбинацию фун-
даментального набора линейно независимых решений (векто-
ров). Число линейно независимых векторов в фундаментальном
наборе называется геометрической кратностью собственного
значения X,. Вводится также алгебраическая кратность — крат-
ность Л, как корня характеристического многочлена.
Независимость собственных векторов
Существование линейно независимых векторов среди соб-
ственных, отвечающих различным собственным числам Х15 Х2,
определяется следующей теоремой.
ТЕОРЕМА
(о независимости собственных векторов)
Собственные векторы х15 х2,..., хп оператора, отвечающие различным
собственным значениям X,, Х2,линейно независимы.
Не останавливаясь на доказательстве теоремы, укажем на
важное следствие теоремы. На п линейно независимых собствен-
ных векторах можно построить базис «-мерного линейного век-
торного пространства.
Замечание. Определитель матрицы Р — Л.  Е (соответ-
ственно характеристический многочлен) не зависит от выбора
базиса.
◄ Действительно,
|Р'- Х-Е| = |7’“| -Р-7’-ХЕ| = |Т’4 РТ-ХТ' -Е-Т| =
= |£-1 Р-I E 7’| = |7’“||-| Р-ХЕ 1-17’1 = 1 Р-Х-Е|-
Следовательно, при переходе к новому базису собственные
числа сохраняются. ►
ПРИМЕР. Найти собственные значения и собственные век-
торы линейного оператора Р , заданного матрицей Р =
в пространстве R2.
Решение. Составим характеристическое уравнение:
3 -2^
-1 2)
129
Линейная алгебра. Курс лекций

-2
2-Х
= Х2-5Х+4 = 0.
Из квадратного уравнения найдем собственные значения ли-
нейного оператора X, = 1, = 4. Чтобы найти собственные векто-
ры, решим матричные уравнения:
(Р- Xj Е)Х= О и (Р- Х2 Е)Х= О.
В развернутом виде
2 -2Y х.	(О А (-1 -2Y х. 1 (О А
111 = 1	и	1 = 1	.
-1 1 дх2) (oj (-1 -2j[x2) (oj
Соответствующие однородные системы:
2х, - 2х2 = 0, 1-х, - 2х2  О,
-х, + х2 = О, [-х, - 2х2 = 0.
Общие решения систем:
х. (А (X. (-2^
= с,1 и =с2 , , гдес„с2еЛ.
*2) 4U 1*2) Ч Ь
Таким образом, множество собственных векторов, отвечаю-
41J’
где сп с2 g R. Векторы af = (1, 1), а2 = (—2, 1), например,
щих собственным значениям X, = 1 и Х2 = 4, имеет вид ct
Г-2А
1Г
с2
являются линейно независимыми. Они могут быть приняты в ка-
честве нового базиса в пространстве R2.
Пусть elfe2,	— собственные векторы линейного операто-
ра Р в пространстве R", которые примем в качестве базиса. Тогда
разложение векторов Pfa), Р(е2) > —, Р(еп) по базисувр е2,..., е„
примет вид
^(«1) = С11е1 +«21*2 +- + вя1«л = V1»
Р(е2) = ц2е, + а22е2 +... + ап2еп = Х2е2,
Л«л)=°1л«1 +«2Я«2 +-+оляе„ =Хле„.
130
Глава 4. Линейные отображения
Отсюда следует, что	если i =j и = 0, если ij. Поэто-
му в базисе, составленном из собственных векторов, матрица
оператора будет иметь диагональный вид:
	'й\\	«12	•	.. о, 'I		'К	0 .	.. о5
р=	«21	«22	•	.. а. 2п	—	0	Х2 .	.. 0
	...	...			0	0 .	.. 0
	<«Л1	«л2	•	* >			0 .	•• ч,
§ 4.4. Симметричный оператор
>	Симметричный оператор
>	Ортогональность собственных векторов
Симметричный оператор
Определение. Линейный оператор Р в евклидовом про-
странстве R” называется симметричным, если для любых векторов
х и у из пространства R” выполняется равенство
(Р(х), j) = (x, Р(у)).
ТЕОРЕМА
(об условии симметричности оператора)
Для того чтобы линейный оператор был симметричен, необхо-
димо и достаточно, чтобы его матрица в ортонормированном базисе
была симметрична.
◄ Рассмотрим для простоты евклидово пространство R2.
Пусть в ортобазисе et, е2 заданы векторы х - (х,, х2), у = (у,, у2).
Линейные операторы Pt и Р2 определены своими матрицами:
Р\ _1 «п «12 | и р2 =| 11	12 I. Вычислим векторы ^(х) и P2(j):
1«21 «22/	1«21 «22/
ОцХ| +о]2х2
«21^1 + «22^2
131
Линейная алгебра. Курс лекций
pl (^11 ^12 ( У1 (^цУ1 +ЬпУ1
к ^21	^22/ W 4^21^1 + ^22^2 7
Найдем скалярные произведения (Р(х), у) и (х, P(y)j:
(/•(х), у) = (а1]х1 +о12х2)^ ч-^х, + а22х2)у2 =
— ацУ1Х1 +а12У1Х2 +а21У2Х\ +а22УгХ2 •>
(Х> Л (у)) = (М + ЬпУ2 )*| + (Ь21У1 + Ь22У2 )^2 =
= А1Х1У1 + ЬПХ\Уг +Ь21Х2У1 +Ь22Х2У2-
Найдем разность скалярных произведений:
(^04 У)“(Х>2 ^(У)) = (Ц|-*||)^У1+(Й21-*12)Х1У2 +
+(°12 ~^21)Х2У1 + (°22 ~^22)ХгУ2.
Если для любых векторов х и у из пространства R2 равенство
(^(х), у)-(х,2 Р(у)) = 0	(3)
выполнено (необходимость), то верна система
°п ~
»г.=А,.	(4)
°12 — ®21 >
а22 = ^22 
И обратно: если условия (4) соблюдены для любых векторов
х и у, то равенство (3) выполнено (достаточность). Система ра-
венств (4) означает, что Pt = Р2 = Р. ►
Ортогональность собственных векторов
ТЕОРЕМА
(об ортогональности собственных векторов)
Собственные векторы симметричного линейного оператора, соот-
ветствующие различным собственным числам, взаимно ортогональны.
132
Глава 4. Линейные отображения
◄ Пусть х и у — собственные векторы оператора Р , соот-
ветствующие собственным числам X, и Х^ причем X] По
определению симметричного оператора,
(Р{х), у) = (х, Р(У)\
Подставив сюда правые части равенства {Р{х^ = 7.хх ,
(Р(у)) = Х2у , получим (Х^, у) = (х, Х2у) • Вынесем числа X, и 7^
за знак скалярного произведения, перенесем слагаемые влево и
разложим на множители: (X, — 7^)  (х, у) = 0.
Поскольку X, * 7^, получаем (х, у) = 0, что и означает взаим-
ную ортогональность векторов х и у. ►
Отметим другие важные свойства симметричного оператора.
1)	Характеристическое уравнение симметричного оператора
имеет только действительные корни.
2)	Если в евклидовом пространстве R” задан симметричный
оператор Р, то в R” существует ортонормированный базис et,
е2,..., е„, составленный из собственных векторов Р .
3)	Если все собственные числа X,, 7^, ..., Х„ симметричного
оператора положительны, то (Р(х), х)>0 для любого ненулево-
го вектора х.
§ 4.5. Квадратичные формы
>	Понятие квадратичной формы
>	Связь между квадратичной формой и оператором
>	Приведение квадратичной формы к каноническому виду
> Свойства канонических форм
>	Критерий Сильвестра
Понятие квадратичной формы
Пусть L = (ау) — симметричная матрица и-го порядка, т.е.
а — а -
у
Определение. Выражение
л п п
(5)
,=| >1
133
Линейная алгебра. Курс лекций
называется квадратичной формой переменныхх15 х2,хп. Выра-
жение (5) есть сумма всех квадратов переменных плюс сумма всех
удвоенных произведений разных переменных, причем каждый
член суммы взят с некоторым коэффициентом. Матрица L назы-
вается матрицей квадратичной формы.
Построим квадратичную форму. Введем матрицу-столбец
переменных X =
, матрицу-строку этих переменных ХГ =
= (х15 х2,..., х„) и найдем произведение матриц:
ап ап
а, о,
\ л1 к2
' ” А
п
п
После перемножения получим
л	л	л	л л
YaijXlXJ+Y^JX2XJ +- + LfllAX> = YYaijXiXJ •
/=1	j=l	j=l	<=1 7=1
Следовательно, в матричной форме квадратичная форма мо-
жет быть представлена в виде
Матрице-столбцу переменных можно поставить в соот-
ветствие вектор х, координатами которого в ортобазисе е,, е2,
..., еп будут элементы матрицы-столбца. Тогда выражение (5)
можно интерпретировать как числовую функцию векторного
аргумента х: £(х).
ПРИМЕР. Найти матрицу квадратичной формы
£(х) = -х2 +6х,х2 -Зх(х3 +4х2х3 +х22 -Зх3 •
Решение. Общий вид заданной квадратичной формы
134
Глава 4. Линейные отображения
L(x) = Оу + 2о]2х|х2 + 2«l3x,x3 + 2а23х2х3 +а22х2 +а33х3.
Поэтому
«Н
О] 2
<°13
°12	°13
°22	°23
°23	°33 >
£ =
' -1 3 -1,5'
3	1	2
-1,5 2 -3 >
Пусть оператор Р переводит вектор у в вектор х. Поскольку
действие линейного оператора Р на вектору сводится к умноже-
нию некоторой матрицы Р = (o(J) на матрицу-столбец Y, состав-
ленную из координат вектора у, запишем линейное преобра-
зование в матричном виде: X = Р • Y. Выясним, как изменяется
матрица квадратичной формы при линейном преобразовании
векторов х—>у:
£(х) = ХТЦX = (PY)T L, (PY) = YT (PTLlP)Y = YT^Y ,
где Д’=РГ1»Р.
Пусть дополнительно выполняется условие невырожденнос-
ти матрицы оператора |Р| * 0, а квадратичная форма является чис-
ловой функцией вектора у: Z(y)=YTL2Y. Найдем, какизменяется
матрица квадратичной формы при линейном преобразовании
векторов у -> х. Решим матричное уравнение X— Р- Y, умножив
обе части равенства слева на Р-1: У= РХ.
Тогда
Z(y) = YTL,Y = (Р-'Х^ЦР-'Х = Хт ((Р' )%Р-') X = ХТ£,Х,
где Д =(P ,)rZ2p-'.
ПРИМЕР. Как изменится матрица квадратичной формы
£(х) = -х2 + 2x^2 + Зх^
при линейном преобразовании векторов
х^З^-гуз, х2=у|+2у2 ?
Решение. Матрица заданной квадратичной формы равна
-1 1
1 3
£ =
.матрица линейного оператора Р при линейном пре-
135
Линейная алгебра. Курс лекций
образовании векторов х = Р(у) имеет вид Р =
-2)
2J
. Под дей-
ствием линейного оператора матрица квадратичной формы ста-
нет равной
, „г , Р(3 ПН пр -2)=f о
(-2 2Д 1 з) (1 2) (16 о)’
а квадратичная форма примет более простой вид:
Z(y) = 32y1y2 .
Связь между квадратичной формой и оператором
В линейной алгебре часто возникает необходимость приведе-
ния квадратичной формы к наиболее простому виду. Хотя в разо-
бранном примере квадратичная форма стала проще (одно слагае-
мое вместо трех), в общем случае таким видом является диаго-
нальный вид квадратичной формы.
Определение. Квадратичная форма называется канони-
ческой, если все коэффициенты при произведениях различных
переменных равны нулю, т.е. о,7 = 0 при i*j'.
L(x) = aux1i+a11x}+...+amx1n =	.
i=i
Матрица канонической квадратичной формы является диа-
гональной:
raiX	0	...	О'
О	а22	...	О
О	0	...	О	'
о •••
ТЕОРЕМА
(о связи между формой и оператором)
Пусть матрицы симметричного линейного оператора и квадратич-
ной формы, заданные в ортонормированном базисе, совпадают. Тогда
квадратичная форма связана с оператором в евклидовом пространстве
формулой
£(х) = (Р(х), х).	(6)
136
Глава 4. Линейные отображения
◄ Определим в евклидовом пространстве ортонормирован-
ный базис е}, е2,	е„, в котором симметричный оператор Р
имеет матрицу Р = (а^), произвольный вектор х — координаты
х = (х1? х2,х„). Тогда
Р(х) = р( Yxiei ] = Zx/^(e<) •
v f=i	7 /=1
Найдем скалярное произведение векторов Р(х) их:
(Р(х), х) = Ср(£х,е,1	=
V \/=1	7 7=1 J
= £хЛ«Д lv/]=Hx/xy(^(e/)’ е>)-
V 1=1	У=1	)	1=1 7=1
Вычислим (Р(е,), ej. Вектор Р(е,) разложим по базису
е„е2, ..., е„:
~ п
Р(е<) = Рие1 +Рне2 +-+Рщеп = ^Рк1ек .
к=\
Тогда
/л	\
(Р(е,.), еу)= ХЛЛ, е} =р„.
7
Следовательно,
££х,Х,(Р(в,), e7) = LL^/X7X/ = Дх)-
1=1 j=\	/=1 j=\
Таким образом, если матрица симметричного оператора сов-
падает с матрицей квадратичной формы, то симметричный ли-
нейный оператор связан с квадратичной формой в евклидовом
пространстве посредством скалярного произведения (6). ►
Приведение квадратичной формы к каноническому виду
ТЕОРЕМА
(о приведении квадратичной формы к каноническому виду)
Любая квадратичная форма, заданная в евклидовом пространстве,
может быть приведена к каноническому виду.
137
Линейная алгебра. Курс лекций
◄ Пусть матрица симметричного оператора Р в евклидовом
пространстве совпадает с матрицей квадратичной формы и задан
ортонормированный базис е,, е2, е„, состоящий из собственных
векторов линейного симметричного оператора Р (в силу одного
из свойств симметричного оператора это всегда возможно):
Р(е, ) = Х,.е,. .
Скалярное произведение запишем в виде
Разложим произвольный вектор х по этому базису х = '^xiel
f=I
и найдем скалярное произведение (Р(х), х):
(Р(х), х) = Цх,х.(р(е,.),	=
Ы >1	<=1
Отсюда
Д*)=(^(х)’ Х) = ЕМ? ,
1=1
что означает канонический вид (диагональность) матрицы квад-
ратичной формы:
%	0	...	О'
т О	х2	...	О
"о	О	...	О
<0	о	...	хи>
ПРИМЕР. Квадратичную форму
£(х) = -х2 - х2 - х2 + 2х,х2 + 2xtx3 - 2х2х3 привести к диаго-
нальному виду.
Решение. Вектор х задан в некотором ортобазисе своими ко-
ординатамих = (х1; х2, х3). Введем симметричный оператор Р(х),
матрицу которого примем равной матрице квадратичной формы
-1 1 Г
1 -1 -1 .
< 1 -1 -1>
138
Глава 4. Линейные отображения
Составим характеристическое уравнение
-1-Х	1	1
1	-1-Х	-1
1	-1	-1-Х
=-зх2- х3=о.
Корни уравнения X! = —3, Х^ = 0. В новом ортобазисе, со-
ставленном из собственных векторов матрицы, вектор х имеет ко-
ординаты х = (хр х2, х3). Поэтому
/_(х) = -Зх2 + 0х22 + Ох2 = -Зх2.
Замечание. Канонический вид квадратичной формы не
является однозначно определенным. Например, заданную квад-
ратичную форму легко преобразовать без использования симмет-
ричного оператора:
£(х) =
—(х2 + х2 + х2 - 2Х]Х2 - 2х,х3 + 2х3х3 ) =
= —(Xj -х2 +Х3)2 .
Линейное преобразование х{ =х{ -х2 +х3 приводит квадра-
тичную форму к каноническому виду £(х) = -х2. Однако в этом
случае вектор х = (х]5 х2, х3) уже не является разложенным по
ортобазису, составленному из собственных векторов матрицы.
Свойства канонических форм
Полученные разными способами канонические формы обла-
дают некоторыми общими свойствами.
1) Закон инерции: число положительных, число отрицатель-
ных и число нулевых коэффициентов при квадратах переменных
в канонической форме не зависит от способа приведения квадра-
тичной формы к этому виду.
2) Свойство ранга: ранг матрицы квадратичной формы равен
числу отличных от нуля коэффициентов канонической формы и
не изменяется при линейных преобразованиях.
Определение. Квадратичная форма Цх) называется по-
ложительно определенной, или знакоположительной, если для лю-
бого ненулевого векторах выполняется неравенство £(х) > 0.
139
Линейная алгебра. Курс лекций
Определение. Квадратичная форма Цх) называется не-
отрицательно определенной, или положительно полуопределенной,
если для любого ненулевого вектора х выполняется неравенство
Цх) > 0.
Аналогично определяются отрицательно определенная и непо-
ложительно определенная (отрицательно полуопределенная) квад-
ратичная форма.
Определение. Миноры, примыкающие к левому верхне-
му углу матрицы, называются угловыми.
Определение. Миноры, имеющие своей диагональю
главную диагональ матрицы, называются главными.
ТЕОРЕМА
(об определении знака формы по собственным числам)
Для того чтобы квадратичная форма была положительно (отрица-
тельно) определенной, необходимо и достаточно, чтобы все собственные
числа матрицы квадратичной формы были положительными (отрица-
тельными).
◄ Пусть для определенности квадратичная форма положи-
тельно определена. Представим квадратичную форму в канони-
ческом виде Цх) = \х1 +К2х^ +... + Цх^ >0 . Здесь X,, Х2, ..., Х„ —
собственные числа матрицы в базисе ех,е2,..., е„.
Необходимость. ◄ Пусть £(х)>0 . Квадратичная форма свя-
зана с оператором: £(х) = (Р(х), х) •
В частности, L(ei) = (Р(е,), е,.) = (Х,е,., е,.) = X,-, где i = 1, 2,..., п.
Из условия Це,) > 0 вытекает X,- > 0. ►
Достаточность. ◄ Если все Х1? Х2, ..., Х„ положительны, то
£(х) = Х1х]2 +Х2х2 + ...+Хях2 >0 . ►
Критерий Сильвестра
Иногда при исследовании знакоопределенности квадратич-
ной формы более удобным становится применение критерия ан-
глийского математика, профессора Оксфордского университета
Джеймса Джозефа Сильвестра (1814—1897).
140
Глава 4. Линейные отображения
ТЕОРЕМА
(об определении знака формы по угловым минорам)
Для того чтобы квадратичная форма с матрицей
Ч	0,2	•• V
О|2	°22	•	”	«2„
	«2„	•	.. а пп /
была положительно (отрицательно) определенной, необходимо и доста-
точно, определив знаки угловых миноров ее матрицы
		°|2	аХп
М.=а,. , М2= "	12 ,..., М =	О|2	°22	•	ai„
ап а22	...			
		°2л	•	•• опп
руководствоваться следующим:
1)если все угловые миноры положительны, квадратичная форма бу-
дет положительно определенной;
2) если миноры чередуют знаки, начиная с отрицательного, квадра-
тичная форма будет отрицательно определенной.
◄ Из четырех сформулированных в критерии утверждений
докажем, например, что при £(х)>0 угловые миноры Мх > О,
М2 > 0,..., Мп > 0. Пусть положительно определенная квадратич-
ная форма задана в базисе ех, е2,..., е„. Рассмотрим подпространс-
тво Vk, построенное на базисе ег, е2,ек, где 1 < к< п, и квадратич-
ную форму £(х), которая на подпространстве Vk примет вид
Lk(x) . Квадратичная форма Д (х) > 0 для любого ненулевого век-
торах = (х1; х2,..., хк) из подпространства Vk. и тем самым все собс-
твенные числа X], к2, ..., X* положительны. Отсюда определитель
матрицы квадратичной формы
0
0
<0
о	...	о	'
х2	...	о
о	...	о
0	...	кк>
141
Линейная алгебра. Курс лекций
также положителен: |ZJ > 0. Но |ZJ = Mk. Значит, Mk > 0. Пере-
бирая все k= 1, 2,..., п, придем к неравенствам Мх >0,М2> 0,
М„>0.к
В заключение приведем таблицу оценки знакоопределеннос-
ти квадратичной формы.
Форма Положительно определенная	Обозна- чение Цх) > 0	Оценка знакоопределенности формы	
		по минорам матрицы L	по собственным значениям X матрицы L Если все собственные значения X положительны
		Если все угловые миноры положительны: Aff >0,то Х=1,2,..., п	
Отрицательно определенная	Цх) < 0	Если в угловых минорах чередуются знаки, причем JWj < 0: (-1)‘МГ>0,то к = 1, 2,..., п	Если все собственные значения X отрицательны
Положительно полуопределенная	ОД>0	Если все главные миноры неотрицательны: М” >0,то fc=l,2, —, и	Если все собственные значения X неотрицательны
Отрицательно полуопределенная	ад<о	Если в главных минорах чередуются знаки, причем A/" <0 : (-1/А/" >0, к= 1, 2,..., п	Если все собственные значения X неположительны
Неопределенная	Цх) < 0		Если собственные значения X имеют разные знаки
Равная нулю	од=о		Если все собственные значения X равны нулю
ПРИМЕР. Квадратичную форму
£(х) = 7х2 +8х22 +х32 +6х,х2 -4х,х3 исследовать на знакоопре-
деленность.
142
Глава 4. Линейные отображения
Решение.
1-й способ. Составим характеристическое уравнение для мат-
рицы квадратичной формы:
7-Х	3	-2
3	8-Х	О
-2 О 1-Х
= -Х3+16Х2-58Х + 15 = 0.
Решая уравнение 3-й степени, получаемХ, =5, X,, =
!	’	2,3	2
Собственные числа матрицы положительны, квадратичная фор-
ма является положительно определенной.
2-й способ. Найдем угловые миноры матрицы квадратичной
Г 7 3 -2>
3
8
формы L-
L-2 О
О
1,
= 7, М2 =
= 47, М3 =
7 3
3 8
-2 О
-2
0=15.
7 3
3 8
Все угловые миноры положительны. По критерию Сильвест-
ра имеем знакоположительную квадратичную форму.
3-й способ. Приведем квадратичную форму к каноническому
виду с помощью алгебраических преобразований:
£(х) = 7х2 + 8х2 + х3 +6х,х2-4х,х3 =
+(3х2 + 6х, х2 + Зх2)+5х2 + (4х2 - 4х,х3 + х2) =
= 3(х, + х2 )2 + 5х2 + (2х, - х3 )2.
Выражение представляет собой сумму квадратов и обращает-
ся в нуль только при х, = х2 = х3 = 0 . Тем самым для любого нену-
левого вектора х выполняется неравенство £(х) > 0. Форма поло-
жительно определена.
4-й способ заключается также в проведении алгебраических
преобразований. Группировку 3-го способа трудно угадать. Но
можно делать целенаправленные и последовательные алгебраи-
143
Линейная алгебра. Курс лекций
ческие преобразования, используя метод выделения полного квад-
рата.
Выпишем сначала все слагаемые, содержащие переменную
X], и преобразуем алгебраическую сумму:
I2 9 2 4 2
I -^хг2--х}
3	2
= 71х,+-х2-у
х3
Положим
3	2
у, = X) + - х2 - - х3, у2 = у2, у3 = у3.
Получим
£(х) = 7у,2 -уу2 — ~у3 +8у2 +у2.
Выражение
9 2 4 2 с 2	2
-уУ2-уУ3 +8у22 + у32
является квадратичной формой, зависящей от меньшего числа
переменных. При необходимости вновь выделяем полный квад-
рат и т. д. В данном случае требуется привести только подобные
члены:
£(х) = 7у2+уу22+уу32.
Очевидно, что форма положительно определена.
Если все коэффициенты при квадратах равны нулю, то
следует начинать преобразование с введения новых перемен-
ных:
Ъ = У, +У2’
Х2=У!-У2,
хк=Ук, к = 3,...,п.
Тогда образуются квадраты, и мы перейдем к обычному ва-
рианту.
144
Глава 4. Линейные отображения
Вопросы для повторения
1.	Привести определение отображения линейного пространства.
2.	Что такое образ, ранг, ядро, дефект отображения?
3.	Сформулировать определение линейного оператора и привести его
свойства.
4.	В чем заключается действие линейного оператора на вектор?
5.	Как связаны матрицы линейных операторов в разных базисах?
6.	Что такое собственные векторы и собственные значения линейного
оператора?
7.	Дать определение симметричного оператора и привести условие его
симметричности.
8.	Какова связь между квадратичной формой и линейным оператором,
имеющими одинаковые матрицы?
9.	Как определить знак квадратичной формы по собственным числам ее
матрицы?
10.	Как определить знак квадратичной формы по угловым минорам ее
матрицы?
ГЛАВА 5
";"'Г'’'7	:.-?т
Векторные функции
§ 5.1. Векторные функции скалярного аргумента
>	Определение векторной функции скалярного аргумента
>	Предел и непрерывность векторной функции скалярного
аргумента
>	Дифференцирование векторной функции скалярного
аргумента
>	Свойства производной векторной функции скалярного
аргумента
>	Правила дифференцирования векторной функции
скалярного аргумента
Определение векторной функции
скалярного аргумента
Предположим, что каждому значению скалярного аргумен-
та х ставится в соответствие п функций у,(х), у2(х),	у„(х).
Набор этих функций положим координатами вектора у
у(х) = (у,(х), у2(х),	у„(х))
и будем считать, что задана векторная функция (вектор-функция)
у скалярного аргумента х.
Если вектор-функцию у(х) представить как радиус-вектор
г(х), начало которого помещено в начало координат, то конец ра-
диуса-вектора г(х) будет описывать некоторую кривую, называе-
мую годографом векторной функции. На рис. 5.1 для евклидова
146
Глава 5. Векторные функции
векторного пространства с размерностью, равной трем, построе-
на векторная функция
, , (sin6x cos6x
г(х)= -----, ------, X
\ X	X
где хе [0,1; 2л]. Перед нами пример годографа, изображающе-
го спираль. Для четырех последовательных значений аргумента
/0 < г, < /2 < t3 показаны радиусы-векторы, выходящие из начала
координат.
Пусть е,, е2, еп — базис «-мерного векторного простран-
ства. Разложим вектор-функцию по векторам базиса:
у W=у, (х)е> + Уг (х)е2 + • • •+у„ (*К •
Предел и непрерывность векторной функции
скалярного аргумента
Вектор-функция у(х) называется ограниченной, если сущест-
вует такое число М, что для всех значений аргумента х из облас-
ти определения справедливо неравенство |у(х) | < М. Из опреде-
ления ограниченности функции у(х) следует ограниченность ее
координат у, (х),у2(х),...,ул(х). Действительно, из неравенства
147
Линейная алгебра. Курс лекций
|у(х)| = л/у2 (х)+у2 (х)+... +У2п (*)5 yjn-y^x) < М
следует
|у I < —т= = М. <
Iz maxi /	1
\1П
Вектор а = (а1, а2,а„) называется пределом векторной функ-
ции при х -> х0, если для любого сколь угодно малого числа е > О
существует такое число 5 > 0, что для всех значений аргумента х из
области 0 < |х — х0| < 5 справедливо неравенство |у(х) — в| < е.
Математическая запись lim у(х) - а .
х~>хо
Если предел limy(x) существует, то
Х~*ХО
limy(x) = e. limy.(x)+e2 lim у2(х) + ...+
X—>-*0	К—X—
+е„ limy„(x) = olel +а2е2+...+а„е1.
Векторная функция у(х) называется непрерывной в точке х0,
если
limy(x) = y(x0).
*->*0
Последнее равенство следует понимать так:
limyl(x) = y1(jq)), limy2(x) = y2(x0),	limy„(x)-y„(x0).
X-^Xf)	x~>xo	X->X(I
Дифференцирование векторной функции
скалярного аргумента
Пусть для векторной функции у(х) существует предел:
у(х0+Дх)-у(х0) Ду
п m —ь---------------------—- = li m —.
Лх->0 Дх	Дл^° Дх
Он называется производной оту(х) по переменной х в точке
Л
х0 и обозначается —. Для координат вектора у(х) это означает,
ах
по определению, что
х) Ду Ду,(х) Ду2	Дул'
—= |hm	lv hm^-1, ..., limb-
ic	Дх I Дх->0 Дх Лх->о Дх	Лх->о Дх
= (К(Х)’ У1(х)’	к'(*))-
148
Глава 5. Векторные функции
Свойства производной векторной функции
скалярного аргумента
1)	Производная -^^- = у'(х) является вектором (вектор-
ах
производной) с координатами
(Х(*)> Уг(х)> — К'(*))-
v, dy(x)
2)	Вектор —лежит на каса-
ах
тельной к кривой у(х). В частности,
dir(x)
dx
для вектора г(х) вектор
сов-
падает с касательной к годографу в
точке М(рис. 5.2).
3)	Скалярное произведение
вектор-функции на вектор-произ-
водную равно нулю:
Это непосредственно следует из свойства 2.
4)	Из условия |у(х)| = const не следует равенство нулю век-
тор-производной, поскольку при изменении аргумента х век-
торная функция может менять только направление. Например,
радиус-вектор описывает сферу, радиус которой — величина
постоянная, а направление радиуса-вектора от точки к точке на
сфере меняется.
Правила дифференцирования векторной функции
скалярного аргумента
J Ф(*)+Ф))_Ф(х) । dz(x)
dx dx dx
d(k(x)-y(x)) d'k(x) .	, .dy(x\ .
2	\ к >—j (x) + (x) —v-2 , где X(x) — скалярная
dx dx	dx
функция.
149
Линейная алгебра. Курс лекций
ах ах	dx
4 dy(u(x))^dy du
dx du dx
§ 5.2. Векторные функции векторного аргумента
>	Определение векторной функции векторного аргумента
>	Потенциальное поле вектора
>	Дифференцирование векторной функции векторного
аргумента
Определение векторной функции векторного аргумента
Пусть в некоторой области D заданы п функций от т пере-
менных:
У, = У,(хи х2, хт), у2 = у2(х„ х2, хт),
У„ = УЛХ'> хт)-	(О
Другими словами, пусть заданы п функций от векторного ар-
гумента х = (х15 х2,..., хт):
У1=У1(*)> У2=Уг(*)> > У„ = У„(Х)-
Набор переменных ylt у2,уп можно представить как коор-
динаты некоторого нового вектора у:
У=(У1,У2> ->Ул)-
Тогда будем говорить, что задана п-мерная векторная функция
у от т-мерного вектор-аргумента х:
J’=J’(«)=(y1(x), у2(х),..., у„(х)).
Если в каждой точке М(хх, х2) евклидова векторного про-
странства R2 определена векторная величина
у = у (М) = у, (х,, х2) • е, + у2 (х,, х2) • е2,
то говорят, что задано векторное поле у. Координаты уДхр х2),
у2(Х|, х2) образуют две скалярные функции.
150
Глава 5. Векторные функции
Рис. 5.3
Пример векторного поля векторной функции
у = y(A/) = sin(xl)el + cos(x2)e2
изображен на рис. 5.3. В каждой точке М с координатами
(Хр х2), где 0 < х, < 2 л, 0 < х2 < 2л, вычисляются sinX] и cosx2, кото-
рые являются координатами вектора у(М). Направления стре-
лок на рисунке указывают направления векторов в каждой точ-
ке. Длина стрелки пропорциональна величине вектора в данной
точке (коэффициент пропорциональности равен 0,25).
Линейная алгебра. Курс лекций
Для геометрической характеристики векторного поля служат
векторные линии. Векторной линией называется кривая, касатель-
ная к которой в любой точке М имеет то же направление, что и
вектор поля у в этой точке. На рис. 5.4 пунктиром изображена
векторная линия на плоскости.
Потенциальное поле вектора
Векторное поле вектора у(М) называется потенциальным,
если существует скалярная функция и(М) такая, что
grad и = у.	(2)
При этом функция и(М) называется потенциалом поля, а ее
поверхности уровня в евклидовом пространстве R' — эквипотен-
циальными поверхностями. Для евклидова векторного простран-
ства R2 вместо поверхностей вводятся линии уровня, называемые
эквипотенциальными линиями. Пусть
У = У|(х],Х2)в|+у2(х|,Х2)е2.
По определению градиента,
, ди ди
gradn = —в] +— е2.
Эх, дх2
Поэтому соотношение (2) равносильно следующим скаляр-
ным равенствам:
Эи /	\ Эи /	\
=	^ = УЛХ^Х2)-
ПРИМЕР 1. Для функции Кобба — Дугласа и-а{х} -1)“х2р
найти вектор-функцию.
Решение.
= у, (х, ,х2) = оа(х, - Ip' хр,
— = у2 (х, ,х2) = о₽(х, -1)“ xf.
Вектор-функция у векторного аргумента х(хР х2), разложенная
по векторам базиса, имеет вид
у = у, (х, ,х2 )е, + у2 (xj ,х2 )е2 = аа(х, - if xfe, +
+оР(х. -1)“х2 'е2 = и| а е, +— е2
'	^Х| -1 х2
(3)
152
Глава 5. Векторные функции
Рис. 5.5
Она называется градиентом функции и. Модуль вектора [у|
функции и указывает величину изменения потенциала и(х) и
позволяет на графике функции и(х) найти участки с наибольшей
скоростью ее изменения. На рис. 5.5 приведен график модуля
функции (3) jy(x)j примера 1, изображенный в первом октанте
системы координат при а — 1, а = 0 = 0,5, в области 1 < х < 5,
0,01 < у < 4. На стенках поверхности, указанных светлыми стрел-
ками, происходит наибольшее изменение векторной функции.
Они обрезаны сверху на уровне |у(х)| = 5, чтобы выявить характер-
ные особенности нижней части поверхности. Темная стрелка
указывает место минимального изменения модуля векторной
функции на графике.
Градиент функции Кобба — Дугласа является полноценной
векторной функцией векторного аргумента. Градиент функции
и(х,, х^)=х|/^х^
имеет вид
grad и =
Векторное поле градиента представлено на рис. 5.6. Длина
стрелки пропорциональна величине вектора в данной точке (ко-
эффициент пропорциональности равен 0,25). Пунктиром изоб-
ражены векторные линии, сплошной линией — эквипотенциаль-
ные поверхности (линии уровня).
153
Линейная алгебра. Курс лекций
Скалярные функции у^х^х^, y2(xt,x2) определяют у(г) —
векторную функцию векторного аргумента, где г = г(Х], х2) —
вектор с началом в начале координат и концом в точке М.
ПРИМЕР 2. Найти потенциал векторного поля радиуса-век-
тора г(Х], х2) и эквипотенциальные линии поля.
Решение.
г = XjC, + х2е2 = grad и,
где «(хр х2) — скалярная функция, производные которой по X] и
х2 равны соответственно Xj и х2.
Очевидно,что и(х1,х2)=Х' *Хг .
„	, х2+х2	.г2
Следовательно, r = xlel +х2е2 =grad 1	- = grad—.
z	z
г2	г2
Линии уровня функции и=— можно найти из равенства —=С,
где С — константа. Линиями уровня, или эквипотенциальными
линиями, будут концентрические окружности с радиусами у/2С .
154
Глава 5. Векторные функции
Дифференцирование векторной функции
векторного аргумента
Предположим, что все функции дифференцируемы в об-
ласти D. Производной вектор-функции у по вектор-аргумен-
ах
ту х в точке х0 называется предел
у(х0+Дх)-у(х0) Ду
lim — -------------------------—- - lim —.
Дх—>0	Дх	Дх—>0 Дх
Для координат вектора у(х) это означает, по определению,
что
В свою очередь, производная скалярной функции векторного
аргумента определяется так:
.. &ук (&yk Ду*	.. Ду* А
lim ..., lim—^-1,
дх-»о Дх |л*|-»оДх, л^-’ОДХз	Дх»->°Дхт1
где k= 1,2,..., п.
Таким образом, производной оту (х) по переменной х являет-
ся матрица размерностью пхт, составленная из частных произ-
водных функций по следующему правилу:
	"Эу,		
	Эх,	Эх2	Эхт
	дУ2	ду2	Эу2
ЧУ =	Эх.	Эх,	Эх„
dx	1	Z	т
		дУп	ЭУ„
	^х.	Эх2	Эх„ ,
Эта матрица получила название матрицы Якоби.
155
Линейная алгебра. Курс лекций
ПРИМЕР. Найти матрицу Якоби вектор-функции
у(х) = (2х, + Зх3, -х2 + 2х3, 5х,-х2).
Решение.
	Эх,	Эх2	Эу/ Эх,	
	ду2	fo2	ЭУ2	Z и j = 0-12
dx	Эх.	Эх,	Эх,	
	1			5 -1
	дУз	дУз	ЭУз	X	/
	^х,	Эх2	Эх3>	
Укажем важное свойство дифференцирования сложной век-
тор-функции. Если задана «-мерная дифференцируемая вектор-
функция у от /«-мерного вектор-аргумента и, а вектор-аргумент,
в свою очередь, является дифференцируемой вектор-функцией
от ^-мерного вектор-аргумента х, то
(4)
Ф(И(Х))_Ф du
dx du dx
dy
Равенство (4) есть произведение матриц Якоби — размер-
Л	/и
ностью п х т и — размерностью т х к. В результате получим
dx
матрицу размерностью п*.к.
Вопросы для повторения
1.	Сформулировать определение векторной функции скалярного аргу-
мента.
2.	Что такое годограф векторной функции?
3.	Как берется производная векторной функции скалярного аргумента?
4.	Перечислить свойства производной вектор-функции.
5.	Сформулировать определение векторной функции векторного аргу-
мента.
6.	Что такое потенциальное поле вектора?
7.	Как берется производная векторной функции векторного аргумента?
ттг'Л.
Классические методы оптимизации
Классические методы оптимизации построены на использо-
вании как инструментов математического анализа (теория функ-
ций нескольких переменных), так и на аппарате линейной алгебры
(матричная алгебра, векторная алгебра, квадратичные формы).
§6.1. Локальный экстремум
>	Определение локального экстремума
>	Необходимые условия локального экстремума
>	Достаточные условия локального экстремума
>	Использование квадратичных форм
Определение локального экстремума
Пусть функция z = (х, у) существует в некоторой области,
и точка М(х0, х0) — внутренняя точка этой области.
Определение. Точка М(х0, х0) называется точкой локаль-
ного максимума (минимума) функции z = (х, у), если существует
окрестность точки М{х0, х0) такая, что для всех точек М(х, у) из
этой окрестности z(x0,y0)>z(x,y) (z(x0,y0)<z(x,y)).
Определение можно интерпретировать в терминах прираще-
ний. Если приращение функции &z = z(x0 + Дх,у0 + Ду)-г(х0,у0),
соответствующее приращению аргументов Ах и Ду, в некоторой
окрестности точки М(х0, х0) сохраняет знак, то точка М(х0, х0) яв-
ляется точкой локального максимума (минимума).
Значение функции в точке М(х0, х0) называется локальным
максимумом или локальным минимумом функции. Точки максиму-
157
Линейная алгебра. Курс лекций
кис. б.1
ма и точки минимума функции называются точками экстремума
функции, а сами максимумы и минимумы функции — ее экстре-
мумами.
Будем различать строгий экстремум (его условие
z(x0,y0)>z(x,y) или z(x0,y0)< z(x, у))vi нестрогий экстремум (ус-
ловие z(x0,y0)>z(x,y) или z(xQ,y0)<z(x,y)). Например, функ-
ция z = yjx2 + У2 имеет в точке (0,0) строгий локальный минимум,
равный нулю (рис. 6.1), а функция х=]х—у\ — нестрогий локаль-
ный минимум, равный нулю на линии у = х (рис. 6.2).
Необходимые условия локального экстремума
ТЕОРЕМА
(о необходимом условии экстремума)
Если М(х0, х() — точка экстремума функции, то все частные произ-
водные в этой точке равны нулю либо не существуют.
◄ Пусть в точке М(х0, х0) функция z = z(x, у) имеет экстремум.
Зафиксируем переменную у, придав ей значение у = у0. Тогда
функция z = z(x, у0) будет функцией одной переменной по х. Пос-
кольку она имеет экстремум в точке х0, ее производная по х, рав-
158
Глава 6. Классические методы оптимизации
Рис. 6.2
ная —-
дх
, обратится в нуль или не будет существовать. Подоб- '
(*Ъ.Го)
ным образом убеждаемся, что также равна нулю или не
оу, >
J (Wo)
существует. ►
Следствие. Если М(х0, х0) — точка экстремума функции
Z = z(x, у), то первый дифференциал функции равен нулю.
Следствие вытекает из определения дифференциала
dz = z х dx+zу dy = 0  dx+0 dy = 0.
Если частные производные обращаются в нуль в точке
Л/(х0, х0), она может и не оказаться точкой экстремума. Напри-
dz
мер, функция z = х2 — у2 имеет частные производные —- 2х и
Эх
— = -2 у , которые в точке (0,0) равны нулю. Из графика (рис. 6.3)
оу
видно, что в точке (0,0), указанной стрелкой, минимума или мак-
симума нет. Таким образом, необходимые условия не оказыва-
ются достаточными.
159
Линейная алгебра. Курс лекций
Точки, в которых производные — = 0, — = 0 либо они не су-
дх ду
шествуют, называются критическими точками функции. Те из
dz n dz п
критических точек, в которых — = 0, — = 0, называются стаци-
дх dy
опарными. Среди стационарных точек есть точки, в которых экс-
тремум функции не достигается. Они называются седловыми точ-
ками, или точками минимакса. На рис. 6.3 стрелкой указана по-
добная точка. На рис. 6.4 приведены возможные варианты
критических точек.
Рис. 6.3
Рис. 6.4
160
Глава 6. Классические методы оптимизации
Достаточные условия локального экстремума
Достаточные условия рассмотрим вначале для функции двух
переменных, затем перейдем к общему случаю.
ТЕОРЕМА
(об исследовании на экстремум по угловым минорам)
Пусть всюду в окрестности точки (х0, у0):
1) определена функция z. - z(x, у);
2)ZX, z'y непрерывны,причем z'(x0,y0) = 0,£'(х^,уо) = О;
3)z", Zxy, z"y непрерывны.
В этом случае угловые миноры

*£(*о>Ро) CCWo)
z"(x0,y0) z"(x0,y0)
матрицы
С(хо,уо) С(хо,УоУ|
z"(x0,y0) z”(x0,y0)J
определяют поведение функции z = z(x, у) в точке (х0, у0), причем:
1)	если угловые миноры М} > О, М2> 0, функция z = z(x, у) имеет в
точке (х0, у0) минимум;
2)	если угловые миноры < О, М2> 0, функция z = z(x, у) имеет в
точке (х0, у0) максимум;
3)	если угловой минор М2 < 0, функция z = z(x, у) не имеет в точке
(х0, у0) экстремума.
◄ Разложим приращение функции в точке (х0, у0) в ряд Тей-
лора до второго дифференциала включительно:
Д?|,	'+±:d2z	+о(р2)
МЛ МЛ 91	,	, v >
Л».Л
В точке (х0, у0) первый дифференциал = 0. Поведение
функции (ее приращение) определяется вторым дифференциа-
лом. Слагаемое о(р2) является бесконечно малым по отношению
—d2z
2! <
Поэтому можно выбрать столь малую окрестность
161
Линейная алгебра. Курс лекций
точки (х0, у0) , что знак Az будет определяться знаком d2z в этой
точке. Итак, если d2z|,	> 0, то Azl . > 0, т.е. при выходе из
'(Wo)	«Л)
точки (х0, у0) функция возрастает. В противном случае при
d2zl , < 0 будем иметь Azl , < 0. Функция будет убывать при
K-Wo)	Vo-W
движении из точки (х0, у0).
Раскроем второй дифференциал:
d2z = z"dx2 + 2z" dxdy+z"dy2
dx
и вынесем dy за скобки, обозначив — через t. При вариации dx и
dy
,	_ dx
dy в произвольных пределах переменная t - — изменяется от —
dy
до +«. Тогда
d2z=dy2(z^+^t+z;y}.	(1)
Выражение (1) представляет собой квадратный трехчлен,
описывающий параболу. Поведение параболы определяется ее
коэффициентом при квадрате неизвестной и знаком дискрими-
нанта D. Проведем это исследование.
1.	При z">0 и D = (z") -z"z"<0 квадратный трехчлен
описывает параболу, направленную ветвями вверх и всю лежа-
щую выше оси абсцисс. Это означает, что при —«=</< +«> второй
дифференциал d2 z > 0, следовательно, Az > 0. Функция имеет в
точке (х0, у0) минимум.
2.	При z"<0 и D = (z") ~z"z'y<0 квадратный трехчлен
описывает параболу, направленную ветвями вниз и всю лежа-
щую ниже оси абсцисс. Это означает, что при — «= < t < +°° второй
дифференциал d2z < 0, следовательно, Az < 0. Функция имеет в
точке (х0, у0) максимум.
3.	При выполнении условия D = (z" )2 - z" z" > 0 в некотором
интервале изменения t часть параболы расположена выше оси
абсцисс, для других значений t часть параболы расположена
ниже оси. Соответственно при движении из точки (х0, у0) в на-
162
Глава 6. Классические методы оптимизации
правлениях, для которых t > 0, т.е. дифференциалы dx и dy имеют
одинаковый знак, будем иметь один знак Аг. При движении в дру-
гих направлениях, по которым t < 0, а значит, дифференциалы dx
и dy имеют разные знаки, получим другой знак Аг Экстремума
нет.
Из вторых производных составим матрицу
CCWo) г"(х0,у0)
,C(wo) 4Cwo).
Условия г">0и D = [z'^ -z^z^, <0 означают, что угловые
миноры > 0, М2 > 0. В точке (х0, у0) наблюдается минимум.
Условия z"<0 и D = (z"}2 -z"z" <0, соответствующие макси-
муму, приводят к неравенствам Мх <0, М2 > 0. Наконец, условие
D - (z'^ - z'^z”y > 0 приводит к неравенству М2 < 0, означающему
отсутствие экстремума. Теорема доказана. ►
Использование квадратичных форм
Для рассмотрения общего случая привлечем теорию квад-
ратичных форм. Второй дифференциал функции нескольких
переменных можно рассматривать как симметричную квадра-
тичную форму относительно дифференциалов переменных. Ее
частным случаем является второй дифференциал от функции
двух переменных, рассмотренный выше. Второй дифференци-
ал функции п переменных и = и(х1г х2,..., х„) имеет вид
d2u = l—dx.A----dx7 + ...+—dxn \ и.
^Эх, Эх2	Эхя )
Матрица этой квадратичной формы, составленная из вторых
частных производных функции ы = г/(х1, л^, ..., х„), называется
матрицей Гессе*.
* В действительности, рассматривая теорию алгебраических линий на
плоскости и алгебраических поверхностей, профессор Гессе ввел понятие оп-
ределителя подобной матрицы, названного позднее гессианом.
163
Линейная алгебра. Курс лекций
Как и в случае двух переменных, приращение функции Ди в
точке возможного экстремума Мй(х^ ,х®,...,хйп} разложим в ряд
Тейлора:
+о(р2)-
_п	'	М,!
Знак приращения Az|w при непрерывности частных произ-
водных до второго порядка включительно в точке Л/о и ее некото-
рой окрестности будет определяться знаком второго дифферен-
циала, являющегося квадратичной формой. Условия знакоопре-
деленности квадратичной формы известны как критерий
Сильвестра. Напомним, что критерий Сильвестра основан на
изучении знаков угловых миноров матрицы квадратичной фор-
мы. На основе этих рассуждений сформулируем теорему.
ТЕОРЕМА
(об исследовании на экстремум по второму дифференциалу)
Пусть всюду в окрестности точки Мо (х,',хх,','):
1)	определена функция и = и (х,, х^,хи);
2)	все частные производные первого порядка их , где i = 1,п,
непрерывны, причем и' | = 0;
3)	все частные производные второго порядка ихх , где i,j = 1,п,
непрерывны;
4)	второй дифференциал d2 и в точке Мо является знакоопределен-
ной квадратичной формой.
Тогда функция и = и(х,, х^,хл) имеет в точке Л/о локальный экс-
тремум, причем:
а)	при d2u > 0 — локальный минимум,
б)	при d2u < 0 — локальный максимум.
164
Глава 6. Классические методы оптимизации
Если же d2u является знакопеременной квадратичной формой в
точке Мо, то функция и = u(xlf х2,хп) не имеет локального экстре-
мума.
Дадим еще одну формулировку достаточных условий локаль-
ного экстремума, удобную в использовании.
ТЕОРЕМА
(об исследовании на экстремум по угловым минорам)
Пусть всюду в окрестности точки Мо (х®, х2,..., х°):
1)	определена функция и = i/(xt, л^,хл);
2)	все частные производные первого порядка и' , где i = 1, п,
непрерывны, причем и' | = 0 ;
3)	все частные производные второго порядка и"х , где i,j = 1,п,
непрерывны.
В этом случае угловые миноры М{, М2, ..., М„ матрицы Гессе Н
определяют поведение функции в точке Мй, причем:
а)	если все угловые миноры положительны, функция и = и(х{, х2,
хп) имеет в точке Мй минимум;
б)	если знаки миноров чередуются, начиная с отрицательного,
функция и = w(x,,	..., х„) имеет в точке Л/о максимум.
Замечание. Теорема дает достаточные условия локально-
го экстремума. Интересно отметить, что эти достаточные условия
не являются необходимыми. Например, функция и = х4 + у4 име-
ет в точке (0, 0) строгий минимум, хотя d2u > 0 не выполнено в
силу равенства нулю в этой точке всех вторых производных. Для
этой функции при любых dx и dy имеет место d2u = 0. Одну из
идей нахождения экстремума в таких случаях рассмотрим ниже.
ПРИМЕР 1. Функцию z = х3 - у3 - Зху исследовать на локаль-
ный экстремум.
Решение. Найдем критические точки функции
z'x = 3х2 -Зу-О,
z;=-3y2-3x=o.
165
Линейная алгебра. Курс лекций
Решениями системы являются координаты двух точек:
х. =0,	[х, = -1,
[у2=1
Найдем вторые частные производные:
С=6х, z" =-3, z"
и составим из них матрицу Гессе:
1. Точка (0,0).
М2 =
6х
-3
-3
-бу
= -36ху-9|(ооГ-9.
Экстремума нет.
2. Точка (—1,1).
-3 _бу 36лу 9к 'л> 27’
Рис. 6.5
166
Глава 6. Классические методы оптимизации
Экстремум есть; Мх = 6х|(| = -6. Следовательно, в точке (—1, 1)
функция имеет локальный максимум zmax = (х3 - у3 -Зху)|( ( = 1.
На рис. 6.5 приведен график функции z = х3 - у3 - Злу. Тем-
ной стрелкой указано положение максимума функции, светлой
стрелкой — седловая точка (точка минимакса).
ПРИМЕР 2. Функцию z = х4 + у4 исследовать на локальный
экстремум.
Решение. Эту функцию мы уже рассматривали в Замечании к
теореме и обнаружили, что все вторые частные производные
в стационарной точке (0,0) равны нулю.
Обратимся непосредственно к приращению функции
Д4„.Л)=(*о +д*)4 +U+ду)4 -W+<
которое в точке (0,0) имеет вид
Цо.оГ^)44’^)4-
Рис. 6.6
167
Линейная алгебра. Курс лекций
Очевидно, что при любых значениях Дх и Ду, таких, что
(Дх)2 + (Ду)2 * 0 , приращение
А4о.о) -(Ах)4+(Ду)4>°.
По определению, функция z = х4 + у4 имеет в точке (0, 0) ми-
нимум. На рис. 6.6 представлен график функции z - х4 + у4, на
котором выделена точка минимума и стрелкой указано местона-
хождение этой точки.
§ 6.2. Условный экстремум
>	Определение условного экстремума
>	Первый метод нахождения условного экстремума
>	Второй метод нахождения условного экстремума (метод
Лагранжа)
>	Геометрическая интерпретация необходимых условий
для условного экстремума
>	Окаймленный гессиан
>	Последовательность действий при отыскании условных
экстремумов функции двух переменных
Определение условного экстремума
Определение. Условным экстремумом функции z= г(х,у)
называется максимум или минимум функции, достигнутый при ус-
ловии, что ее аргументы связаны некоторым уравнением g(x, у) = 0:
z = z(x,y),
g(x,y)=0.
В дальнейшем экстремумы, не являющиеся условными, бу-
дем называть безусловными.
При нахождении условных экстремумов функции z=z&,y)
аргументы х и у уже нельзя рассматривать как независимые пере-
менные. Они связаны между собой соотношением g(x, у) - 0, ко-
торое называется уравнением связи.
168
Глава 6. Классические методы оптимизации
Для пояснения различия между локальным (безусловным)
и условным экстремумом рассмотрим функцию
Z=z(x,y) = x1+y1.
Она описывает так называемый параболоид вращения и
имеет безусловный минимум в точке, указанной темной стрел-
кой. Добавим уравнение связи (ограничение в виде равенства)
g(x,y) = y-x,
описывающее плоскость. Задача формулируется теперь так:
найти экстремум функции z=x2+y2, рассматривая среди всех
значений (х,у) только те, которые в совокупности образуют
плоскость Р. Другими словами, экстремум следует искать сре-
ди точек, принадлежащих одновременно обеим поверхностям,
изображенным на рис. 6.7. Эти точки образуют белую линию.
Минимальное значение (условный минимум) достигается в
точке, указанной светлой стрелкой.
Замечание. Условный экстремум может существовать не
в одной точке. В частном случае это может быть линия, как
представлено на рис. 6.8. Здесь стрелкой указан достигаемый на
отрезке прямой условный минимум функции z = max(|x|,|y|) при
дополнительном условии связи g(x,y) = 2y-3 = 0. Локальный
Рис. 6.7
169
Линейная алгебра. Курс лекций
Рис. 6.8
минимум функции z= max(|x|,|y|) также существует. Он находит-
ся в точке с координатами (0, 0).
Опишем два метода поиска условного экстремума.
Первый метод нахождения условного экстремума
Пусть уравнение связи g(x, у) = 0 может быть разрешено от-
носительно зависимой переменной: у = /(х). Подставим функ-
цию у = f(x) в исследуемую на экстремум функцию z.=z(x, у). По-
лучим функцию одного аргумента
z = z[x,f(x)) = z(x),
в которой учтено условие связи. Далее надо исследовать функцию
z = z(x) на локальный экстремум, который будет являться д ля фун-
кции z=z(x, у) условным экстремумом.
ПРИМЕР 1. Исследовать на условный экстремум функцию
Z=х. у при условии X — у +1 = 0.
Решение. Из уравнения связи найдем у=х+1 и подставим
в исследуемую функцию:
Z-x(x+ 1).
Исследуем ее на экстремум:
z' = 2х +1 = 0 .
170
Глава 6. Классические методы оптимизации
Рис. 6.9
Критическая точка л;,----. Вторая производная z" = 2>0.
Поэтомувточке х0 =-^ существует минимум функции z=x(x+ 1),
2 1 1
соответственно в точке с координатами х0 = --, у0= — — услов-
ный минимум функции z-xy. Его значение z0 =~  На рис. 6.9
представлены описываемые обеими функциями поверхности,
пересекающиеся по белой линии. На точку условного минимума
указывает стрелка.
ПРИМЕР 2. Исследовать на условный экстремум функцию
z = min(|x|, |у|) при условии у + 1 = 0.
Решение. Подставим в исследуемую функцию величину у=—1
из уравнения связи. Получим z = min(|x|, 1).
1. Если |х| < 1, то Zi - |х|.
2. Если 1 <|х|, то z2= 1, причем значение z2- 1 больше либо
равно значению в любой точке х при условии |х| < 1. Следова-
тельно, 1 будет максимальным значением функции z = min(|x|, |у|),
аргументы которой связаны уравнением у+1=0, т.е. Zmax=l.
Поверхность z = min(|x|, |у|) и плоскость у + 1 = 0 представлены на
171
Линейная алгебра. Курс лекций
Рис. 6.10

рис. 6.10. Линии их пересечения, где функция z достигает макси-
мального значения, выделены белым цветом.
Непосредственная подстановка используется в простейших
случаях. Часто подобная подстановка приводит к громоздким
выражениям для исследуемой функции или бывает невозмож-
но решить уравнение связи относительно зависимой перемен-
ной. В этих случаях используется эффективный метод, предло-
женный французским математиком Жозефом Луи Лагранжем
(1736-1813).
Замечание. Рассмотренная нами в последнем примере
функция является обобщением двухфакторной (зависящей от
двух переменных) производственной функции Леонтьева, кото-
рая имеет вид
. (х, х7
y = min —— .
^2 J
Здесь переменные хи х2 полагаются неотрицательными и
обозначают соответственно затраты капитала и затраты труда,
параметры а2 являются положительными и отвечают соот-
ветственно за фондоемкость продукции и трудоемкость про-
дукции.
172
Глава 6. Классические методы оптимизации
Второй метод нахождения условного экстремума
(метод Лагранжа)
Уравнение связи g(x, у) = 0 определяет величину у как функ-
цию у - у(х) от переменной х. При подстановке у=у (х) в исследу-
емую функцию z- z(x, у) получим функцию одной переменной
(z = z(x, у(х)), производная которой в точке возможного услов-
ного экстремума М0(х0, у0) равна нулю, или, что равносильно
этому, должен быть равен нулю дифференциал функции:
^м1)=С\м^+<\м^=0.	(2)
Из уравнения связи g(x, у) = 0 соотношение между дифферен-
циалами аргумента и функции в любой точке, а следовательно, и
в точке Мо определяется равенством
^L„^ + ^L/7 = O.	(3)
Умножим равенство (3) на некоторое число X (множитель
Лагранжа), которое определим ниже, и сложим с равенством (2):
(z'x +xg; )Мо dx+(z;+xg;	dy=о.	(4)
Слева в равенстве (4) стоит дифференциал dL(x, у) функции
Z(x,y) = z(x,y)+Xg(x,y) , которую называют функцией Лагран-
жа. Равенство dL(x, у) = 0 при изучении нами локального экс-
тремума получалось исходя из того, что L'x = 0, L'y = 0 . Это дава-
ло необходимые условия локального экстремума. В рамках ло-
гической цепочки рассуждений о локальном экстремуме
функции Цх, у) потребуем выполнения условий Ц - О, Ц = 0 в
точке Мо. С этой целью выберем множитель X так, чтобы было вы-
полнено равенство
А'к=«+^)«.=°-	<5)
Тогда из соотношения (z'+Xg')^ dx = 0 получим
Теперь можно сказать, что равенства (5) и (6) выражают необ-
ходимые условия локального экстремума в точке М0(х0, у0) функ-
173
Линейная алгебра. Курс лекций
ции Лагранжа L(x,y) = z(x,y)+Kg(x,y). Иногда говорят, что сис-
тема
Ц = ^у+^'у = 0у
L' = z'x+^g'x=0,
g(x,y) = 0
определяет условия первого порядка при нахождении условного
экстремума.
Геометрическая интерпретация необходимых условий
для условного экстремума
Интересна геометрическая интерпретация решений систе-
мы. Введем векторы grad z(x, у) = [z.x, z') и grad g(x, у) = (g', g').
Из системы легко получить равенство
gy g'x ’
откуда следует коллинеарность векторов grad z(x, у) и gradg(x, у).
Построим фрагмент карты линий уровня функции z=z(x,y)
(рис. 6.11). Пунктиром обозначен график функции g(x,y) = 0.
Линии уровня Z]
gradz(xpy1)

Рис. 6.11
174
X
Глава 6. Классические методы оптимизации
Градиенты grad z(x0, у0) и grad z(xl,yl) перпендикулярны к лини-
ям уровня функции z-z(x, у) в точках Мо и Мх соответственно.
Векторы gradg(x0, у0) и gradz(x}, ух) перпендикулярны к линии
g(x, у) = 0 также в точках ЛГ0 и Мх. При движении справа налево
вдоль кривой g(x, у) = 0 пересекаются линии уровня функции
Z=z(x,y) , причем каждое следующее пересечение происходит с
линией более низкого уровня. Градиенты grad z и grad g в каждой
точке направлены под разными углами, как это имеет место, на-
пример, в точке Мх. Коллинеарность векторов grad z и grad g воз-
никает в точке Мо. Следовательно, в этой точке выполнены необ-
ходимые условия локального экстремума функции Лагранжа. При
дальнейшем движении вдоль кривой уравнения связи g(x, у) - О
пересекаются линии более высокого уровня. Можно заключить,
что в точке Мо имеется минимум. Если бы кривая уравнения свя-
зи, выйдя из точки Мо, продолжала пересекать линии все более
низкого уровня, точка Мо оказалась бы седловой (или точкой ми-
нимакса).
Окаймленный гессиан
Для функции Лагранжа L(x, у) получены необходимые усло-
вия локального экстремума. Теорема о достаточных условиях ло-
кального экстремума функции Цх, у) подобна ранее сформули-
рованной теореме о достаточных условиях локального экстрему-
ма для функции и=и(хх,хг, ...,х„), но между ними существуют
отличия.
ТЕОРЕМА
(об исследовании на экстремум по окаймленному гессиану)
Пусть всюду в окрестности точки Л/0(х0,у0):
1)	определена функция L(x,y)=z(x, у) + ^g(x,y);
2)	обе частные производные первого порядка L', £' непрерывны,
причем £'1 =0, £'| =0;
г	х|«о	У|л/0
3)	все частные производные второго порядка L", L", L" непре-
рывны;
4)	дифференциалы dx и dy связаны между собой соотношением
g'xdx+g'dy = 0, причем g'\ * 0;
175
Линейная алгебра. Курс лекций
5)	второй дифференциал d2L в точке Мо является знакоопределен-
ной квадратичной формой.
Тогда функция Цх, у) имеет в точке Мо локальный экстремум, а
функция z=z(x, у) — условный экстремум:
а)	при d2L > 0 — локальный минимум;
б)	при d2L<0 — локальный максимум.
◄ Доказательство теоремы заключается в обосновании ис-
пользования в данной теореме выводов ранее рассмотренной
теоремы о достаточных условиях для функции и = и(х{, х2,хп)
при исследовании на локальный экстремум.
Уравнение связи g(x, у) = 0 приводит к существованию зави-
симости между дифференциалами dxwdy. Как известно, второй
дифференциал не обладает инвариантностью формы. Поэтому
выражение для d2L требует уточнения. Найдем дифференциал
от дифференциала dL = Lxdx + Lydy в точке Мо, считая у зави-
симой переменной:
d2L = d(dL) = d{Lxdx+Lydy] = dx^L'^dx + Lxydy}+
+(Z" Jx + L£dy)dy + Ly  d2y.
Здесь Z" = L" в силу непрерывности вторых производных,
Z' = 0 в стационарной точке Мо. Поэтому второй дифференциал
функции Лагранжа в точке Мо будет совпадать со вторым диффе-
ренциалом функции Лагранжа двух независимых переменных:
d2L - L" dx2 + IL’^dxdy + Lyydy2.
Следовательно, можно воспользоваться выводами о знакооп-
ределенности d2L и соответственно знаке AZ по знакам угловых
миноров матрицы Гессе:
1) если М] > О, М2 > 0, функция Цх, у) имеет в точке Мо мини-
мум;
2) если М] <0, М2> 0, функция Цх, у) имеет в точке Мо мак-
симум.
Если сделать вывод о наличии экстремума при произвольных
dx и dy невозможно, найдем dy из равенства g'xdx + g'ydy - 0 и под-
ставим в d2L:
176
Глава 6. Классические методы оптимизации
-^dx
< Sy ,
d2L = L"dx2+2L"dx -^dx +L"
Л-А	ху	~г	уу
Sy
Вынесем за скобки множитель-----у
(«;)
d2L = -
d2x
И
(-fe)2 + 2g'xg'yL^ -(£)2 Z").
Эта формула может быть приведена к удобному для исполь-
зования виду. Второй сомножитель в произведении вычисляется
как определитель матрицы в точке (х0, у0):
( О
Н = g'
s'x
L"
S^
4
Sy
L"
Матрица //называется окаймленной матрицей Гессе, а опре-
делитель |Я] — окаймленным гессианом. Если гессиан	> > 0,
то d2L < 0, что указывает на безусловный максимум функции
Цх, у) и условный максимум функции z-z(x, у). Если |Я|(л	< 0,
то d2L > 0. Это соответствует безусловному минимуму функции
Z(x, у) и условному максимуму функции z=^(x, у). Если |/7|(л у j-0,
метод не работает. Обоснование закончено. ►
Замечание 1. Метод Лагранжа не указывает условий, при
которых условный экстремум отсутствует.
Замечание 2. При составлении функции Лагранжа мож-
но брать неопределенный множитель с любым знаком. Выбор оп-
ределяется соображениями удобства.
Замечание 3. Вычисляемый неопределенный множитель
Т может оказаться любым действительным числом, включая ир-
рациональное число. В частном случае при X = 0 условный экстре-
мум исследуемой функции совпадает с ее локальным экстремумом,
если таковой существует. На рис. 6.12 представлено графичес-
кое решение задачи на условный экстремум функции z = 1 - х2 - у2
177
Линейная алгебра. Курс лекций
Рис. 6.12
с уравнением связи g(x,y) = у - х = 0. Линия пересечения выделе-
на темным цветом. Стрелкой указан условный экстремум функ-
ции z = 1 - х2 - у2, совпадающий с ее локальным максимумом.
Вычисленное значение множителя X = 0.
Последовательность действий при отыскании условных
экстремумов функции двух переменных
Задача. Найти условный экстремум функции z=z(x,y) при
наличии уравнения связи g(x, у) = 0. Краткая формулировка:
z = z(x,y)-*extr,
g(x,y) = 0.
(7)
Решение.
1)	Составляем функцию Лагранжа Z(x,y) = z(x,y)+Xg(.x,у) •
2)	Находим производные функции Цх, у) и приравниваем их
к нулю. Присоединяем уравнение связи, получая систему из трех
уравнений для определения координат возможных точек экстре-
мума (х0, у0) и множителя Лагранжа X.
3)	Строим окаймленную матрицу Гессе, вычисляем окайм-
ленный гессиан в точке (х0, у0) и делаем вывод о наличии услов-
178
Глава 6. Классические методы оптимизации
ного экстремума. Находим значение функции z = z(x, у) в точке
условного экстремума.
ПРИМЕР. Провести исследование на условный экстремум
Z = x2 + 12xy + y2 -textr,
4х2+у2 =25.
Решение. Составим функцию Лагранжа:
£(х, у) = х2 +12ху + у2- а(4х2 + у2 - 25)
и запишем систему уравнений из первых производных и уравне-
ния связи:
L' = 2х+12у-8Ах = 0,
L' = 12x+4y-2Kx = 0,	(8)
4х2 + у2 = 25.
Из первых двух уравнений получаем
(1-4А)х = -6у,
6х = (1 -2)у.
(9)
Очевидно, что точка с координатами (0,0) является реше-
нием системы (9), но не удовлетворяет последнему уравнению
системы (8). Полагая теперь х* 0, у * 0, разделим первое уравне-
ние системы (9) на второе
1-4А	6
6 " А-2
и решим полученное уравнение. Корни уравнения А, = -2, А 2 =
17
4
Подставив А, = —2 в первое или во второе уравнения системы (8),
2 „
найдем связь между переменными х и у: х = —у. Подстановка
2
выражения х = -—у в третье уравнение системы (8) даету=±3.
17	3
Соответственно х = +2. Для А, =— получим у = ±4, х = ±-.
4	2
Итак, получены четыре стационарные точки (х,-, у,, k,), i= 1,..., 4:
179
Линейная алгебра. Курс лекций
4 (1-3-2)
4(-2,з,-2),	44~4’7)
Найдем все вторые производные функции Лагранжа:
£"=2-8Х, z;=i2, z;=4-2A.
Составим матрицу Гессе из вторых производных:
2-8Х 12 12р-4х 6 1
12 4-2xJ' ( 6 2-xJ ’
Подстановка любого значения множителя из X = -2, X •> = —
-	4
приводит к равенству нулю минора М2. Поэтому обратимся к
окаймленной матрице Гессе
g*
ДХ
gy
L"
Lyy ;
r0 8x 2y '
8x 2-8X	12
2y 12	4-2X,
= 2 4x
4x у
1-4X	6
6	2-X,
Рассмотрим последовательно четыре стационарные точки.
1)4(2, -3,-2).
О
|Я| = 2 8
-3
-3
6
4
— —1250<0.
В точке 4(2, —3, —2) достигается условный минимум = -50.
2)4(-2,3,-2).
-8
9
6
=-1250<0.
8
9
6
3
6
4
Здесь условный минимум	= —50.
180
Глава 6. Классические методы оптимизации
|Я| = 2 6 -16
6 =1250>0.
В точке
425
z = —.
^тах а
достигается условный максимум
-16
= 1250>0.
О 6
Здесь условный максимум zmax =	.
На рис. 6.13 и 6.14 представлено графическое решение задачи
на условный экстремум.
Пересечения поверхностей изображены с двух точек обзора,
отличающихся приблизительно на 90°. Стрелками показан один
из минимумов (рис. 6.13) и один из максимумов (рис. 6.14).
Метод неопределенных множителей Лагранжа может быть
перенесен на случай функции от любого числа аргументов. Пусть
требуется определить условный экстремум функции п перемен-
ных z = z(xl,x2,...,xn) при наличии туравнений связи
gI(xI,x2,...,x„)=0,
ft(x,,x2,...,x„) = 0,
gm(x„x2,...,x„)=0,
181
Линейная, алгебра. Курс лекций
Рис. 6.14
Глава 6. Классические методы оптимизации
где т<п. Составляем функцию Лагранжа, используя т множи-
телей Лагранжа X,, Х2,...,	:
£(х1, х2,х„)=z(x,, х2,xJ+X^i (х,, х2,..., х„)+
+k2g2(xi,x2,...,xn)+...+'Kmgm(xi,x2,...,xn).
Приравняв к нулю все частные производные первого поряд-
ка, получим систему из п + т уравнений для определения множи-
телей Xj,X2,...,Xm и координат Х|,х2,...,х„ возможных точек ус-
ловного экстремума. Если матрица Гессе не показывает наличие
экстремума, находим дифференциалы всех уравнений связи
dg, = gfdx, + g{dx2 +...+g{dxn = О,
dg2 = g2dxx + g2dx2 +... +g[dxn = 0,
dgn - g’„dx, + g'dx-, +... + g'dx„ = 0.
Решаем систему из m уравнений с п переменными dxf, dx2,...,
dx„. Предполагая, что ранг г матрицы системы г= т, находим т
переменных, которые выражены через свободные п — т перемен-
ных. Подставим их в квадратичную форму d2L и составим квад-
ратную матрицу размера (л-/и)х(л-/п) квадратичной формы.
Далее, применив критерий Сильвестра, сделаем вывод о наличии
экстремума.
§ 6.3. Экстремум неявной функции
Пусть функция z=z(x, у) определяется уравнением
Дх, у, z) = 0. Потребуем, чтобы функция z=z(x, у) была дважды
непрерывно дифференцируема и Г'# 0.
Первый дифференциал в стационарной точке равен нулю:
F' F'
dz--~=;dx—^-(fy=Q,
F F
что может иметь место в силу независимости дифференциалов dx
и dy только при
(Ю)
183
Линейная алгебра. Курс лекций
Уравнения (10) выражают необходимые условия существова-
ния экстремума, определяя точку (х0, у0) возможного экстремума.
Для нахождения достаточных условий найдем второй дифферен-
циал в стационарной точке (х0, у0):
d2z = d(dz) = dl
I Fz
( F'\	( F'}
= -dx dl — - dydl — .
Lf'J	Lf'J
\ z /	\ Z /
(11)
Найдем отдельно каждое из слагаемых в правой части равенс-
тва (11):
' F"F'~ F'F"
xx z х zx
. J
dxdy.
В стационарной точке Г/ - 0 , поэтому равенство значитель-
но упростится:
(F'\ ( F"\	(F"\
dx dj ~ = -=7 dx2 + dxdy.
Аналогично можно доказать, что
&dxdy+(%)dy2
Подставим полученные равенства в (11) и преобразуем квад-
ратичную форму, используя F" = F^:
( F',y\	(F"}	(F"\
d2z --I1 dx2-21 ~ I dxdy-I dy2. (12)
Матрица Гессе для квадратичной формы (12) примет вид
184
Глава 6. Классические методы оптимизации
z W«)
Применяя критерий Сильвестра к найденной матрице, ис-
следуем знакоопределенность квадратичной формы d2z и сделаем
вывод о существовании экстремума неявной функции.
ПРИМЕР. Найти локальный экстремум неявной функции
F(x,y,z)-z2 -2z-x3 -у3-Зху-З-0 в области считая
Z=z(x,y).
Решение. Найдем частные производные функции F(x,y,z) по
всем переменным:
Fx' = -3x2-3y,
F; = -3y2-3x,
F^-2z+2.
Чтобы определить стационарные точки, решим систему урав-
нений:
Д'=-Зх2-Зу = 0,
f;=- 3y2-3x=o.
Выразим переменную у из первого уравнения и подставим во
второе
Получим критические точки Р} с координатами х1 = 0, у1 = 0 и
Р2 с координатами х2 - — 1, у2 = — 1. Подстановка этих значений ар-
гументов в уравнение Г(х, у, г) = 0 с учетом z>0 даст значения
Zi = 1 и z2 = л/5-1.Итак,имеемРг-(0,0,1)и Д (-1,-1,-J5-1).
Найдем вторые частные производные: F" = -6х, F" = -бу,
F" = -3 и составим матрицу Гессе квадратичной формы для не-
явной функции:
185
Линейная алгебра. Курс лекций
		F"\ ху	—6x	-3	
н=		f; _	2z + 2	2z + 2		
	F4	*'4	-3	-6y	
					
	1 Л'	F:)	I 2z + 2	2z+2,	
	Зх	3 A	( x	1 A	
	 				
	z + l	2z+2	, Z + l	2z+2	
	3	Ь	1	У	
	2z + 2	z + l )	\2z + 2	z + l >	
Обращаем внимание на следующее: из матрицы можно вы-
_ 1
нести множитель 3, но нельзя вынести множитель---, так как
z+l
нужна информация о знаке первого углового минора Мх. Рас-
смотрим вначале точку Р21-1, -1, >/5 -1).
1. Р2 (-1,-1, >/5-1).
Здесь Mt - —- = -Д < 0, Мг - 3——= > 0 . В этой точ-
Z+1 45	(z+l)	20
ке достигается локальный максимум, равный 45 -1.
Рис. 6.15
186
Глава 6. Классические методы оптимизации
2. Pj(O, О, 1). Здесь Л/, =
второму дифференциалу:
—— = -/= = 0. Поэтому обратимся ко
3	3
d2 F = 0 • dx1 + 2-dxdy + 0 dy2 = —dxdy.
2z + 2	2
Очевидно, d2Fne является знакоопределенной квадратичной
формой. Поэтому в данной точке экстремума нет. На рис. 6.15
приведен фрагмент поверхности заданной неявной функции.
Стрелками указаны точки Р} и Р2.
§6.4. Глобальный экстремум
Глобальным экстремумом называются наибольшее и на-
именьшее значения функции в замкнутой ограниченной об-
ласти D. Пусть функция z=x(x, у) непрерывна в этой области.
Тогда найдется точка (х0, у0), в которой функция принимает на-
ибольшее (наименьшее) значение. Если точка (х0, у0) лежит
внутри области D, она является стационарной, и в ней может
достигаться локальный максимум или минимум. Наибольшее
или наименьшее значение функция может принимать также
на границе области. Следовательно, задачу исследования функ-
ции z=x(x, у) на глобальный (global) экстремум в области
g(x, у) < 0 можно сформулировать так:
Z-z(x,y)-^gl. extr,
g(x,y)<0.
Решение задачи разбивается на две части:
1) исследование функции z=x(x, у) на локальный (local) экс-
тремум в областных, у) < 0:
Z=z(x,y)-+loc. extr,
g(x,y)<0.
2) исследование функции z=x(x, у) на условный (conditional)
экстремум на границе области g(x, у) = 0:
Z = z(x,y)—> cond. extr,
g(x,y) = 0.
187
Линейная алгебра. Курс лекций
Наибольшее (наименьшее) из всех этих чисел и будет иско-
мым наибольшим (наименьшим) значением функции z=x(x, у) в
области D.
ПРИМЕР. Исследовать на глобальный экстремум функцию
Z = 2-x2 -у2 в области х1 + у2 >1, И <2, [у| <2.
Решение. Для решения задачи
Z —2-х2-у1 —> gl. extr,
 х2 + у2 > 1,
надо рассмотреть несколько случаев:
Z = 2 - х2 - у1 —> loc. extr,
1) {х2 +у2 >1,
|х|<2, |у|<2.
Находим стационарные точки: z'=-2x = 0, z'=-2y = 0.
Единственная стационарная точка (0, 0) не входит в рассматри-
ваемую область.
Z - 2 - х2 - у1 —> cond. extr,
2) ]х2 + у2 = 1,
|х|<2, |у|<2.
Подставим выражение х2+у2=1 в исследуемую функцию.
Получаем z = 2-(x2+y2) = 2-l = l. Во всех точках окружности
функция принимает одно и то же постоянное значение z= 1.
Z = 2 - х2 - у2 —> cond. extr,
х2 +у2 >1.
В силу симметрии задачи из двух случаев достаточно рас-
смотреть один, например х=2. Подставим х=2 в функцию z.
z = 2-4-y2 = -2-у2. Это парабола с ветвями, направленными
вниз. Критическая точка у = 0, в которой функция принимает
значение, равное z= —2. На концах отрезка [—2, 2] функция равна
z=-6.
188
Глава 6. Классические методы оптимизации
!Z = 2-x2 -у1 —> cond. extr,
|х|<2, |у| = 2,
х1 + у2 >1.
Система рассматривается аналогично случаю 3. Собираем все
полученные значения функции z-
Z\x! +у2 =1 ~
z(2,0) - z(-2,0) - z(0,2) = z(0, - 2)=-2,
z(2,2) = z(-2, - 2) = z(2, -2)-z(-2,2) = -6.
Выбираем наибольшее и наименьшее значения из всех этих
чисел:
^gl. max — 1 ’ **gl. min ~ 6.
График функции z-2-x2-y2 в области х2+у2>1, |х| < 2,
|у < 2| приведен на рис. 6.16.
Замечание. При исследовании функции на глобальный
экстремум можно ограничиться отысканием значения функции
в критических точках. Достаточные условия обычно не исполь-
зуют.
Рис. 6.16
189
Линейная алгебра. Курс лекций
В математическом анализе существует класс так называемых
выпуклых функций, примерами которых могут служить функции,
представленные на рис. 6.6—6.8 и 6.12. Они широко применяются
в экономике и в дальнейшем будут нами изучаться. Выпуклая
функция не имеет сед ловых точек. Поэтому равенство ее частных
производных нулю является не только необходимым, но и доста-
точным условием локального экстремума. Локальный экстремум
выпуклой функции является также и глобальным, т.е. наиболь-
шим значением функции в случае, когда функция выпукла вверх,
и наименьшим, когда она выпукла вниз.
§ 6.5. Экстремум в системах функций
Изучение экстремумов математических объектов, задаваемых
несколькими функциями, является значительно более сложной за-
дачей. В общем случае задачу можно сформулировать так: найти
экстремум функции z=z(x, у), заданной системой функций
Поиск решения начнем с нахождения множества таких точек
на координатной плоскости Оху, в которых значения функций
системы равны
f(x,y)=g(x,y).
Решение этого уравнения у - у(х) подставим в одну из функ-
ций z = f(x,y(x)) = z(x) и исследуем на экстремум функцию
z - z(x). Критическая точка х0 для функции z=z(x) задает стацио-
нарную точку (х0, у0) на плоскости Оху, в которой возможен экс-
тремум 4х(Г -f{xa, у0). Геометрически это означает, что в про-
странстве разыскивается совокупность линий пересечения по-
верхностей, описываемых заданными функциями. На линиях
пересечения находим наибольшее или наименьшее значение z^-
Получим необходимые условия экстремума системы функ-
ций. Считая в системе (13) переменные хи у функциями перемен-
ной z, продифференцируем оба уравнения по Z'-
f'x'z+f'y'z=i,
g'xx' + g'yy'z = l.
190
Глава 6. Классические методы оптимизации
Вычтем из первого уравнения второе:
и, полагая, что х' * 0 и {f' - g') * 0, разделим обе части равенства
на эти величины. Получим
X
fy-Sy X'z 
dy
Очевидно, - = ^- = ^- = у'х-
х, ах dx
dz
Поскольку z = f(x,y(x)), найдем производную по х, которая
в критической точке Zq будет равна нулю:
Х|х_х = Л'+Л'Х = 0-
,х~х0	Л
Отсюда при условии f' * 0 получим
Х=-£.
г
Jy
Подставим в уравнение
fy Sy
производную
г
Jy
и после несложных преобразований, считая f' * 0 , получим
ПРИМЕР. Исследовать на экстремум функцию z=z(x, у), за-
данную системой уравнений
Z = y]x2+y2,
Z = |y-x|.
191
Линейная алгебра. Курс лекций
I
Рис. 6.17
Решение. Область значений функции z>0. Найдем корни
уравнения
у^+у1 =|У-Х|,
для чего возведем его в квадрат:
х2 + у2 = у2 -2ху + х2.
После сокращения уравнение примет вид ху-0. Следова-
тельно, х=0 или у=0. При х - 0 получим z - Jy2 = |у| • Очевидно,
минимальное значение z равно 4lin = 0 при у=0 и х=0. Другой
случай (у=0) приводит к тому же результату. Отметим, что
4^(0, 0) = 0 представляет собой глобальный минимум функции z-
На рис. 6.17 изображены графики функций z-yjx2 +у2 и
z=|у — х|, пересекающиеся по плоскостям у - 0 и х - 0. Линии пе-
ресечения поверхностей указаны белым цветом.
Некоторые из функций системы могут быть заданы в неяв-
ном или параметрическом виде.
ПРИМЕР. Исследовать на экстремум функцию z=z(x, у), за-
данную системой уравнений
х2 + у2 + Z2 = 1,
X + y-Z = 0.
192
Глава 6. Классические методы оптимизации
Решение. Подставим z - х+у в первое уравнение:
х2 +у2 + (х+у)2 = 2.
Представим уравнение как квадратное относительно у:
Его решение
у2 + ху+х2 -1 = 0.
-х+^4-Зх2
у- у
подставим во второе уравнение системы. Получим
z=
x + \l4-3x2
2
Исследуем функцию z(x) на экстремум с помощью производ-
ной
3
,	1	1	~4Х	_
z ,=-±--F====0.
2 2
Рис. 6.18
193
Линейная алгебра. Курс лекций
h 3 2  3 п	1
Уравнение ^1-—х = ±—х ПРИХ-0 имеет решение х1 
При х < О решение х, = —L. Исследование знаков производной
V3
1	2
показывает, что в точке х, - -j= достигается максимум zmax =	>
1	2
в точке х2 =	— минимум zrnin =
Окончательно получаем
Графики обеих функций представлены на рис. 6.18. Стрел-
ками указаны минимум и максимум функции z- (х, у), причем
минимум хорошо виден, а максимум скрыт под поверхностью
сферы. Для улучшения обзора из сферы удалена часть поверх-
ности.
§ 6.6.	Экстремум в системах неравенств
Математическими объектами, задаваемыми системами не-
равенств, в трехмерном случае являются объемные геометри-
ческие фигуры, границы которых описываются некоторыми
функциями. Формулировка задачи выглядит следующим об-
разом: найти экстремум функции z= z(x, у), заданной системой
неравенств
F(x,y,z)<0,
G(x,y,z)^0.
Задача отыскания подобного экстремума математического
объекта сводится к решению нескольких систем
1.	Исследование функции z=z(x, у), определяемой из уравне-
ния F(x, у, z) = 0, на локальный экстремум при условии справед-
ливости неравенства G(x, у, z) < 0, т. е.
F(x,y,z)=0-> z = z(x,y)-yfoc. extr,
G(x,y,z)<G.
194
Глава 6. Классические методы оптимизации
2.	Исследование функции z=z(x,y), определяемой из урав-
нения G(x, у, z) = 0, на локальный экстремум при условии спра-
ведливости неравенства F(x, у, z) < 0, т. е.
G(x,y,z) = 0-> z = z(x,y)->toc. extr,
F(x,y,z)<0.
3.	Исследование функции z-z(x,y), определяемой из урав-
нения F(x, у, z) = G(x, у, z), описывающего линию пересечения
поверхностей.
ПРИМЕР. Исследовать на экстремум функцию z=z(x, у), за-
данную системой неравенств
3x2 + 3y2 + z2 <1,
х2 + у2 <z2.
Решение. Первая из систем
|г| = 71-3(х2 + у2),
2	2	2
X + у < z
позволяет найти максимальное значение |г|тах=1 при условии
х2 + у2 = 0, что не противоречит условию х2+у2 <
Рис. 6.19
195
Линейная алгебра. Курс лекций
Из второй системы
Зх2 + Зу2 + z2 < 1,
\z\=>!x2 + y2
можно сделать вывод о росте функции z с ростом х2 + у2. Ограни-
чения на х2 + у2 следуют из неравенства х2 + у2 <  Следователь-
но,
На границе, являющейся пересечением поверхностей, вы-
полняется равенство
Z2=l-3x2-3y2=x2 + y2,
откуда следует х2 + у2 =	. В точках на этой окружности функ-
ция \z\ = ^2- Следовательно, наибольшее значение функции
^.max(0,0)= 1, наименьшее значение функции ^glmax(0,0) = -1.
На рис. 6.19 приведена область, ограниченная данными нера-
венствами. Стрелками указаны точки, в которых функция
z=x(x, у) принимает наибольшее и наименьшее значения.
ПРИМЕР. Исследовать на экстремум функцию z=x(x, у), за-
данную системой неравенств
Iz^x2 —ху+у2,
[z^x+y+1.
Решение. 1. Исследуем функцию z-x2 -ху + у2 на локальный
экстремум в области z<x + у+1 ,т. е. рассмотрим систему
jz = x2-ху + у2,
|z<x+y+l.
Необходимые условия
z'=2x-y = 0,
,	_	„ дают стационарную
z'y = -x+2y = 0
точку Р, с координатами х} = 0, у, = 0, в которой zx - 0. Неравен-
ство z<x + у +1 в стационарной точке выполнено.
2. Функция z = х+у+1 не имеет локального экстремума, по-
этому система
196
Глава 6. Классические методы оптимизации
Z>x2-ху + у2,
z=x+y+l
не дает решений при исследовании на локальный экстремум.
3. Рассмотрим поведение функции z на пересечении поверх-
ностей. Решим систему
z = x2-ху+у2,
Z = X + y + l.
Выразив переменную у из второго уравнения как у = z - х -1,
подставим ее в первое уравнение. Тогда
Z = x2-x(z-X-l) + (z-X-l)2.
После преобразования получим функцию z=z(x) в неявном
виде:
F(x,z) = z2 -3z- 3xz+ Зх2 + Зх+1 = 0.
Приравняв к нулю производную неявной функции z- z(x)
Рис. 6.20
197
Линейная алгебра. Курс лекций
получим: F' - 0 при z = 2х + 1. Из системы уравнений
Z = 2x + 1,
Z2 -3z-3xz + 3x2 + 3x + l = 0,
а также из равенства у=z — х — 1 найдем стационарную точку Р2 с
координатами
х2-1 + у[2, у2 = 1 + >/2, z2 = 3+2-J2
и стационарную точку Р3 с координатами
х3=1->/2, у3 = 1-у[2, z3 = 3~2y/2.
Выбирая из zr, z2, z3 наибольшее и наименьшее значения,
окончательно получим zgL max(l + V2, 1 + V2j = 3 + 2^2, £gkmax(0,
0) = 0. На рис. 6.20 построены области z^x2 -ху + у2 иг<х+у+1.
Стрелками указаны полученные точки Pt, Р2, Р3.
§ 6.7. Оптимизация потребительского поведения
(функция спроса)
Рассмотрим задачу зависимости объема личного потребле-
ния или спроса от доходов, цен и социально-демографических
факторов. Пусть С7(х) — целевая функция потребления, харак-
теризующая предпочтения потребителя, х= (х15 х2,..., х„) — век-
тор объемов потребления благ х;, п — количество рассматрива-
емых благ. Покупая для личного потребления товары х, по
ценам Pj, покупатель ограничен размером своего дохода I.
Ставится задача оптимизации потребительского поведения с
бюджетным ограничением
{/(х)->тах,
Хр,л=/.
.<=1
Решением задачи потребительского выбора является функция
спроса — вектор х° =х° (/>,/) = (Х|'(/>,/), х°(р,/), ..., х“ (/>,/)).
каждая координата которого зависит от вектора цен
Р = (Рр Р2, • Р„) и дохода/.
198
Глава 6. Классические методы оптимизации
Рассмотрим задачу на условный экстремум для функции двух
переменных	Ц (х)=х^ шах, Pi х, + р2х2 — I.
Целевая функция является выпуклой. Поэтому, как указы-
валось ранее, при исследовании функции на экстремум доста-
точные условия можно не использовать. Составим функцию
Лагранжа:
£(хрх?) =
-ifoxj + p^-Z)
и запишем систему уравнений из первых производных и уравне-
ния связи:
Ц =	= кР\,
 Ly = -х^х2 = Тр2,
р}Х}+р2Х2 = 1.
Разделив первое уравнение на второе, придем к системе
 х, р2
Р}Х'+р2Х2=1,
решением которой являются
В стационарной точке (х“, х“) выпуклая функция U(х) мак-
симальна. Векторная функция спроса имеет вид
/ )
2pJ'
Следовательно, количество приобретаемого товара прямо
пропорционально доходу и обратно пропорционально цене то-
вара.
199
Линейная алгебра. Курс лекций
§ 6.8. Максимизация прибыли
в проектном анализе
В процессе принятия инвестиционных решений приходит-
ся решать задачу максимизации планируемой прибыли. Одна
из функций, с помощью которой в проектном анализе прини-
мается инвестиционное решение (критерий), называется чис-
тым дисконтированным доходом NPV (Net Present Value). Эко-
номический смысл этой функции состоит в максимизации раз-
ности между всеми проектными доходами и затратами, т.е.
прибыли. Однако, следуя теории проектного анализа, в этом
расчете необходимо учитывать время произведения затрат и
время получения доходов, а также процентную ставку. Все это
находит отражение в критерии 2VWблагодаря применению те-
ории изменения ценности денег во времени.
Кладя деньги в банк, мы рассчитываем на денежный прирост.
Он определяется по формуле сложных процентов
x(')=x(°)(i+^L
где ДО) — первоначальный вклад, положенный в банк на t лет
под г годовых процентов. Поставим теперь задачу следующим
образом. Какую сумму надо положить в банк под г % в год, что-
бы через Глет получить Д/) денежных единиц? Другими слова-
ми, найти стоимость суммы денег, полученной через t лет, но
приведенной к настоящему времени. Очевидно, она равна
(1+йо)
Величину г можно назвать ставкой дисконта, отражающей
изменение стоимости денег во времени.
Предположим, рассчитывается проект, который принесет
через год доход в размере 6(1) денежных единиц, через два го-
да — b (2) денежных единиц и т.д. Тогда, пересчитанный к насто-
ящему времени, он составит в течение /лет величину, равную
Ь(1)	&(2)
^enejits	Г f
1+юо (1+1Оо)
200
Глава 6. Классические методы оптимизации
Реализация проекта потребует затрат в каждом году жиз-
ненного цикла проекта е(1), е(2), ..., e(t). Пересчитанные к на-
стоящему времени ежегодные затраты составят величину

100
Рассчитаем чистый дисконтированный доход NPV (Net
Present Value), составляющий, как уже указывалось, разность
между приведенными к настоящему времени будущими потока-
ми доходов и затрат с учетом инвестиции Imesmenl в начальный мо-
мент. Получим
NPV--J +В -Е
1 ’Л '	Л nvesment 1 enefits Expenses
Чистый дисконтированный доход NPV, как уже говорилось,
характеризует эффективность проекта и является одним из ос-
новных критериев при выборе проекта. Рассмотрим Л'РИподроб-
нее. Он представляет собой функцию двух переменных: ставки
дисконта г и времени жизни проекта (или горизонта его плани-
рования) t. Время жизни проекта оказывается конечной величи-
ной, обычно равной 5—10 годам, после чего требуется радикаль-
ная реорганизация, новое инвестирование или ликвидация про-
екта. В противном случае проект начнет приносить убытки.
Функция чистого дохода (прибыли) PnJU =b(n)-e(n) (дохо-
ды минус затраты) для каждого проекта индивидуальна. Одна-
ко некоторые свойства функции являются общими для реаль-
ных проектов: первоначальный рост, достижение максимума и
последующий спад.
Несколько конкретизируем немного проект. Пусть он рас-
считан на 10 лет. Рассмотрим два различных случая, отличающих-
ся различным поведением на заключительной стадии проекта.
1. В начале стадии убывания чистого дохода менеджеры под-
держивают проект различными мерами, добиваясь превыше-
ния доходов над затратами. Пусть функция прибыли имеет вид
(рис. 6.21)
/> = 0,8я2еЧ)’8".
201
Линейная алгебра. Курс лекций
В начале проекта прибыль растет медленно, в течение трех
лет выходит на максимум. Затем в течение последующих 7 лет она
падает по экспоненте до 10 % от своей максимальной величины.
202
Глава 6. Классические методы оптимизации
Зависимость функции NPVот ставки дисконта г в пределах
5—50 % и времени развития проекта п по годам приведена на
рис. 6.22. Плоскость на рисунке проведена на уровне NPV = 0 и
отсекает участки с NPV> 0. Для каждого года проекта можно
определить величину г (норму дисконта IRR), при которой за-
траты на проект окупятся. Для г= 44 % это произойдет только в
конце проекта (NPV станет больше нуля). При г > 44 % проект
станет убыточным. На рис. 6.22. красная линия отсекает ставку
процента г= 44 %. Если ставка процента равна, например, 27 %,
проект окупится к четвертому году (дисконтированный пери-
од окупаемости — критерий DPBP=3). Светлой стрелкой на
рис. 6.22 указана точка на поверхности, соответствующая
7ЛК=27%и/)РРР=3.
2. Проект не поддерживается новыми идеями, инвестиция-
ми, живет за счет внутренних ресурсов. Вся прибыль извлекает-
ся из проекта. Или в проекте обнаружились проблемы, которые
привели во второй половине жизненного цикла проекта к пре-
вышению расходов над доходами Пусть в этом случае функция
прибыли имеет вид (рис. 6.23)
Р = 0,2л2 (1-0,17л).
В начале проекта прибыль растет медленно, в течение четы-
рех лет она выходит на максимум. Затем в течение последующих
двух лет прибыль падает до нуля. Расходы продолжают расти.
Линейная алгебра. Курс лекций
t
Рис. 6.24
Зависимость в этом случае функции NPVот ставки дисконта
г в пределах 5—50 % и времени развития проекта п по годам при-
ведена на рис. 6.24. По-прежнему плоскость на рисунке проходит
через ординату со значением NPV= 0. В первые годы проект раз-
вивается благополучно. При невысокой ставке процента прибыль
появляется на четвертом году реализации и на 5—6-м году дости-
гает максимальных значений. Однако последние три года могут
развиться катастрофические события. Что на первый взгляд уди-
вительно, катастрофа возникает при малых ставках дисконта, в то
время как при больших ставках проект затухает медленно. Это
видно из рис. 6.25. Причина этого явления состоит в том, что при
низкой процентной ставке деньги с течением времени остаются
«дорогими». Потери денежных средств на 7—10-м году проекта
весьма чувствительны. При высокой ставке процента деньги на
7—10-м году проекта становятся «дешевыми». Их потеря не столь
чувствительна.
Действительно, доход, полученный от проекта на и-м году
жизненного цикла, пересчитанный к началу проекта, равен
2>{и)-с(и)
204
Глава 6. Классические методы оптимизации
Отношение прибылей, а в данном случае — убытков при
низкой ставке t\ и высокой ставке г2 составит величину
Ь(п)-е(п)
Z	/	\ л
I /* / I
Убытки (rt) Ц + /100 J
Убытки (г2)	6(и)-е(и)
100+г2Т
100 + Г] J ‘
Для г, = 5 % и г2 = 50% на 7-м году жизни проекта будем
иметь
100 + r2Y
100 + /J
150%у
105% J
= 12,14.
Это означает, что потери составят при низкой процентной
ставке в 12 раз большую величину, чем при высокой. Отсюда
вывод: при низкой ставке процента следует более зорко следить
за прибылями—убытками. По достижении максимума прибыли
и вначале спада следует принимать решительные меры, ибо
Рис. 6.25
205
Линейная алгебра. Курс лекций
«промедление смерти подобно». Проект при низкой процент-
ной ставке и неблагоприятном стечении обстоятельств может
быть потерян для инвестора с большими убытками.
§ 6.9.	Глобальный экстремум в задачах
математического программирования
В общем виде задача математического программирования
для двух переменных записывается следующим образом:
1)	z = /(х,у)->шах, &(х,у)<0,	z=f(x,y)-+ min, g,(x,y)>0,
	’	или 2) • g„(x,y)<0, х>0, у>0.	g„(x,y)>0, x>0, y>0,
где f(x, у) — целевая функция, не имеющая локальных экстре-
мумов, g/x, у), ..., g„(x, у) — функции, ограничивающие поиск
решения. Ограничения х > 0, у > 0 указывают на поиск реше-
ния только в первой четверти координатной плоскости. Точка
(х0, у0) называется оптимальным решением системы уравнений и
неравенств, если в этой точке целевая функция достигает мак-
симального значения в первом случае и минимального — во
втором. Максимум или минимум целевой функции являются
глобальными экстремумами. В этом отличие задачи математи-
ческого программирования от задач на условный или локаль-
ный и даже на глобальный экстремум, который может дости-
гаться как на границе области, так и во внутренних точках. За-
дачи 1 и 2 называются сопряженными и образуют двойственную
пару.
К необходимости решать задачу математического програм-
мирования (ЗМП) приводят:
1.	Проблема планирования производства, т. е. планирование
производства определенных видов продукции так, чтобы было
обеспечено наиболее рациональное использование материаль-
ных, финансовых и других ресурсов. Должен быть достигнут
максимум или минимум (в экономике — оптимум) некоторой
функции, описывающей прибыль, объем производства и т.д.
206
Глава 6. Классические методы оптимизации
2.	Проблема оптимального смешения. Требуется выбрать
количество каждого из исходных ингредиентов для составле-
ния смеси, если известна стоимость единицы ингредиента.
Смесь надо получить с заданными свойствами, причем с на-
именьшими затратами. Такие задачи оптимального смешения
возникают в металлургии, сельском хозяйстве, пищевой про-
мышленности и т.д.
3.	Транспортная задача перевозки произведенного продук-
та от различных производителей нескольким потребителям.
Поставки должны осуществляться таким образом, чтобы изде-
ржки на транспортировку были минимальными.
4.	Проблема оптимального планирования финансов и др.
Если все функции, входящие в задачу математического
программирования, линейны, имеем задачу линейного про-
граммирования (ЗЛП). В случае же нелинейности хотя бы од-
ной из функций имеем дело с задачей нелинейного программи-
рования (ЗНП). Приведем примеры нескольких задач мате-
матического программирования, обратив внимание на их
геометрическую интерпретацию.
На рис. 6.26—6.28 в трехмерной системе координат постро-
ены модели следующих видов.
Модель ЗЛП (рис. 6.26):
ах+£у + g=z->max,
онх+о12у + ^ <0,
a21x+Oj2 + b2 <0,
a3ix+a32y + b3 <0,
х>0,
у>0.
Модель ЗНП (рис. 6.27):
(х — а)2 +(у- р)2 + у=z -> max,
ЯцХ+ОиУ+А] <0,
я2|х + д22 +Ь2 <0,
а31х + а32у+Ь3 <0,
х>0,
у>0.
207
Рис. 6.26
Рис. 6.27
Глава 6. Классические методы оптимизации
Рис. 6.28
Модель ЗНП (рис. 6.28):
Jax+Py + g->max,
[ах2 +by2 -с<0.
На рис. 6.26 представлена геометрическая интерпретация
ЗЛП, в которой требуется найти максимальное значение линей-
ной функции г=ах+ру + у, изображающей плоскость, ограни-
ченную линейными неравенствами, также изображающими плос-
кости, расположенные вертикально.
На рис. 6.27 дана геометрическая интерпретация ЗНП, в ко-
торой нелинейной частью является исследуемая на максимум
функция, представляющая собой параболоид вращения
Z = (x-a)2 +(у-р)2 + у 
Наконец, на рис. 6.28 нелинейность ЗНП представлена функ-
цией ограничения ах2 + by2 - с < 0. Это цилиндроид с плоскостью
внутри, на которой требуется обнаружить максимальное значе-
ние г,11ах. Часть цилиндроида вырезана для улучшения обзора.
Визуально глобальный максимум на каждой из исследуемых
поверхностей легко определяется. Максимальное значение отме-
чено темной точкой.
209
Линейная алгебра. Курс лекций
Разработаны различные методы решения ЗМП, например
симплекс-метод. Их изучением занимается экономико-матема-
тическая дисциплина «Исследование операций», которая полно-
стью опирается на пройденный материал.
Вопросы для повторения
1.	Сформулировать определение экстремума функции нескольких пере-
менных.
2.	Привести необходимые условия локального экстремума.
3.	Сформулировать теорему об исследовании на локальный экстремум
по угловым минорам.
4.	Дать определение условного экстремума.
5.	Дать геометрическую интерпретацию необходимых условий условно-
го экстремума.
6.	Описать метод Лагранжа по исследованию функции на условный экс-
тремум.
7.	Что такое окаймленный гессиан?
8.	Записать достаточные условия при исследовании неявной функции
на экстремум.
9.	Описать схему исследования функции на глобальный экстремум.
Список литературы
1.	Краснов М. Л., Киселев А. И., Макаренко Г. И. и др. Высшая ма-
тематика. Т. 1. М.: Эдиториал УРСС, 2000.
2.	Красс М. С. Математика для экономических специальностей.
М.: Дело, 2002.
3.	Пискунов Н. С. Дифференциальное и интегральное исчисле-
ние. Т.1. М.: Наука, 1985.
4.	Высшая математика для экономистов/Под ред. проф.
Н. Ш. Кремера. М.: Банки и биржи, изд. Объединение
“ЮНИТИ”, 1998.
5.	Задачи и упражнения по математическому анализу/Под ред.
Б. П. Демидовича. М.: Интеграл-пресс, 1997.
6.	Ильин В. А., Ким Г. Д. Линейная алгебра и аналитическая гео-
метрия. М.: Изд-во Моск, ун-та, 1998.
7.	Ильин В. А., Позняк Э. Г. Линейная алгебра. М.: Наука, 1999.
Тематический указатель
Б
Базис векторного пространства 92
Базисные решения системы уравнений 65
В
Введение определителя 17
Вектор в «-мерном пространстве 90
Векторы в трехмерном пространстве 87
Виды матриц 12
Возведение матрицы в целую положительную степень 16
Второй метод нахождения условного экстремума (метод Лаг-
ранжа) 175
Вычисление определителя 26
Вычитание матриц одинакового размера 14
Г
Геометрическая интерпретация необходимых условий для ус-
ловного экстремума 174
Глобальный экстремум 187
Глобальный экстремум в задачах математического программи-
рования 206
д
Дефект отображения 118
Дифференцирование векторной функции векторного аргу-
мента 155
212
Дифференцирование векторной функции скалярного аргу-
мента 148
Дополнение до базиса 96
Достаточные условия локального экстремума 161
Е
Евклидовы пространства 105
И
Использование квадратичных форм 163
К
Координаты вектора 82
Критерий Сильвестра 140
Л
Линейная зависимость и независимость векторов 88
Линейная оболочка 104
Линейные комбинации строк или столбцов 45
Линейные операторы и их свойства 121
Линейные операции над векторами 81
Линейные подпространства 102
м
Максимизация прибыли в проектном анализе 200
Матрица перехода к новому базису 99
Матрицы оператора в разных базисах 125
Метод Гаусса 59
Метод обратной матрицы 52
Метод с использованием расширенной матрицы 54
Метод с использованием формул Крамера 55
Модель Леонтьева многоотраслевой экономики 75
н
Независимость собственных векторов 129
Необходимые условия локального экстремума 158
213
о
Образ отображения 118
Общее решение системы неоднородных линейных уравне-
ний 73
Окаймленный гессиан 175
Определение локального экстремума 157
Определение ранга матрицы 41
Определитель оператора в разных базисах 126
Оптимализация потребительского поведения (функция спро-
са) 198
Ортогональное дополнение 112
Ортогональность собственных векторов 132
Ортонормированная система векторов 108
Определение векторной функции скалярного аргумента 146
Определение векторной функции векторного аргумента 150
Определение условного экстремума 168
Основные сведения о матрицах 11
Отображение базиса 119
Отображения 117
Первый метод нахождения условного экстремума 170
Понятие квадратичной формы 133
Понятие линейного векторного пространства 86
Последовательность действий при отыскании условных экстре-
мумов функции двух переменных 178
Потенциальное поле вектора 152
Правила дифференцирования векторной функции скалярного
аргумента 149
Предел и непрерывность векторной функции скалярного аргу-
мента 147
Приведение квадратичной формы к каноническому виду 137
Р
Равносильность систем линейных уравнений при элементар-
ных преобразованиях 58
Разложение вектора по базису 93
Размерность векторного пространства 91
Ранг матрицы при элементарных преобразованиях 43
Ранг отображения 118
214
с
Свойства длины вектора 107
Свойства канонических форм 139
Свойства линейной зависимости векторов 89
Свойства линейной оболочки 105
Свойства матрицы перехода к новому базису 100
Свойства обратных матриц 30
Свойства однородной системы линейных уравнений 67
Свойства определителей 22
Свойства ортогонального дополнения 113
Свойства производной векторной функции скалярного аргу-
мента 149
Свойства скалярного произведения 84
Свойства суммы и пересечения подпространств 104
Свойства транспонирования матрицы 17
Связь между квадратичной формой и оператором 136
Связь ранга с числом независимых строк (столбцов) 47
Симметричный оператор 131
Скалярное произведение векторов 82
Сложение матриц одинакового размера 14
Собственные векторы и собственные значения 127
Способ построения обратной матрицы 39
Строка матрицы как линейная комбинация независимых строк
матрицы 48
Структура линейного оператора 122
Сумма и пересечение линейных подпространств 103
Схема решения системы уравнений 64
т
Теорема Кронекера — Капелли 63
Теорема о существовании обратной матрицы 28
Типы матриц элементарных преобразований 33
Транспонирование матрицы 16
Умножение матрицы на матрицу 15
Умножение числа на матрицу 14
215
ф
Фундаментальные решения 68
Экстремум в системах неравенств 194
Экстремум в системах функций 190
Экстремум неявной функции 183
Элементарные преобразования матрицы 34
Я
Ядро отображения 118
Малугин Виталий Александрович
МАТЕМАТИКА ДЛЯ ЭКОНОМИСТОВ:
ЛИНЕЙНАЯ АЛГЕБРА
Курс лекций
Ответственный редактор И. Ескевич
Редакторы Т. Косолапова, В. Зеленько
Художественный редактор Е Брынчик
Технический редактор Н. Тростянская
Компьютерная верстка А. Мусаев
Корректор Н. Боровая
ООО «Издательство «Эксмо»
127299, Москва, ул. Клары Цеткин, д. 18/5. Тел.: 411-68-86,956-39-21.
Home раде: www.eksmo.ru E-mell: lnfoeeksmo.ru
Подписано в печать 28.10.2005
Формат 60x90 '/16- Гарнитура «Таймс». Печать офсетная.
Бумага тип. Усл. печ. л. 14,0.
Тираж 4000 экз. Заказ 6238
Отпечатано во ФГУП ИПК «Ульяновский Дом печати»
432980, г. Ульяновск, ул. Гончарова,14