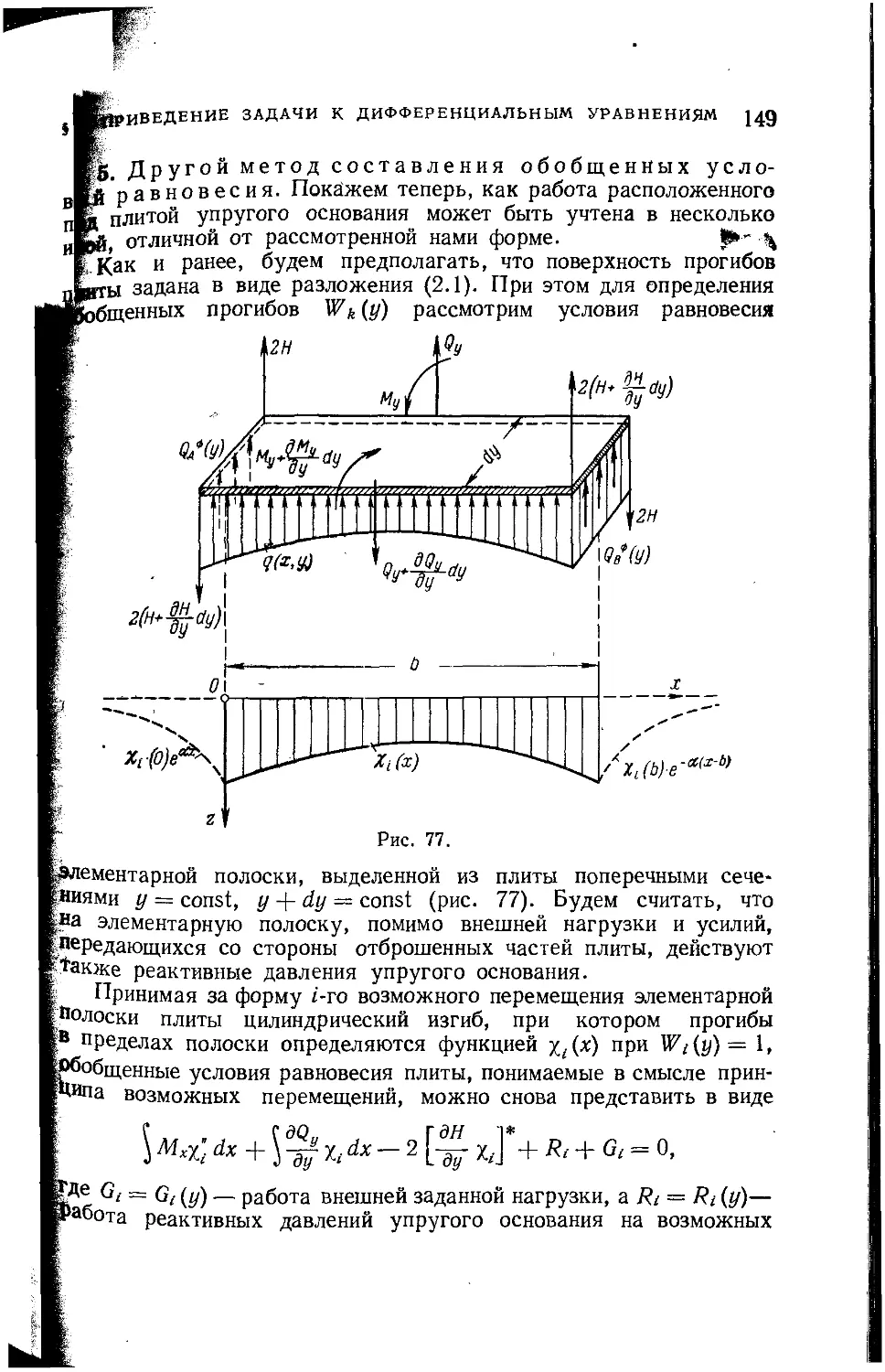
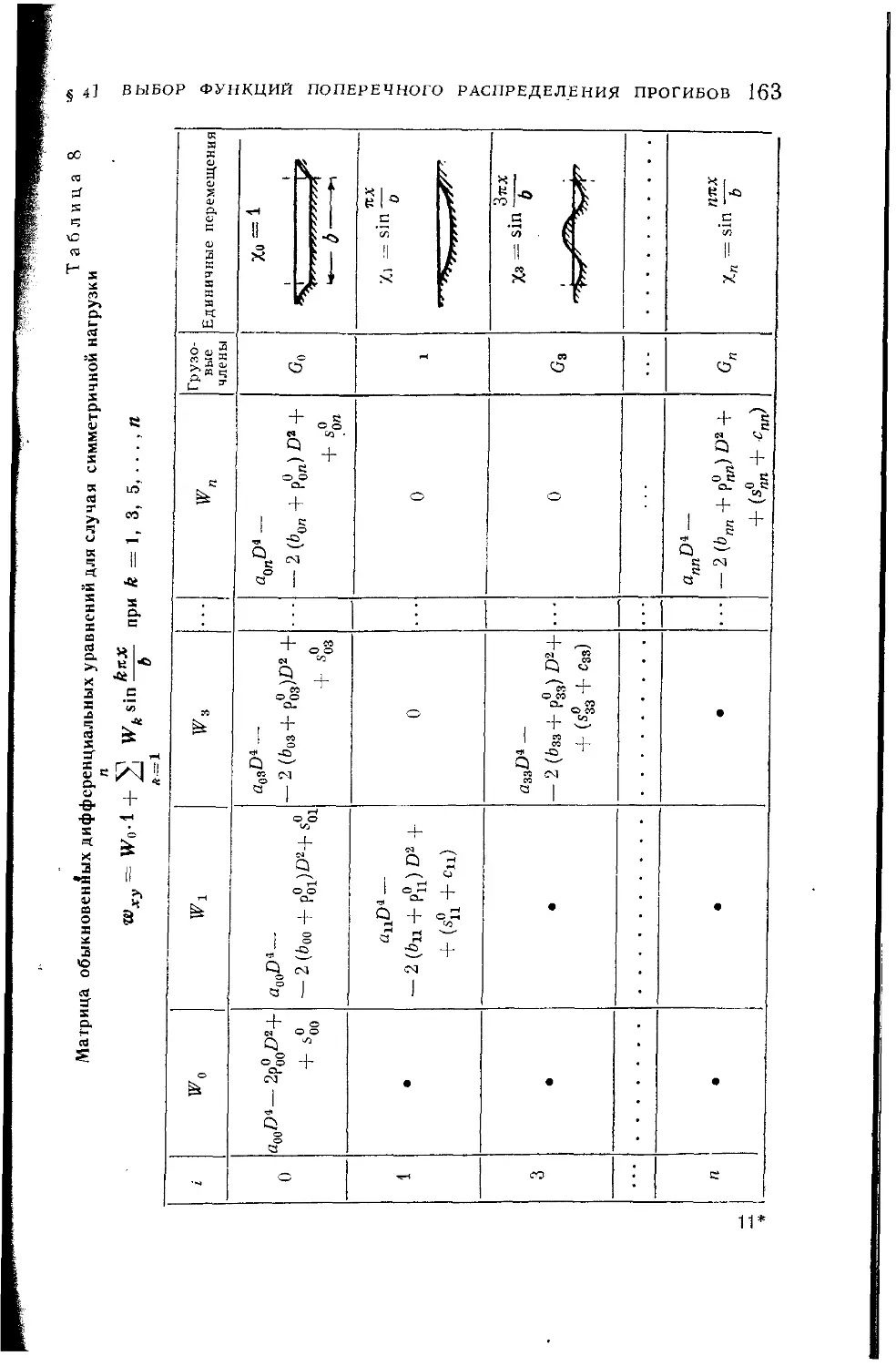
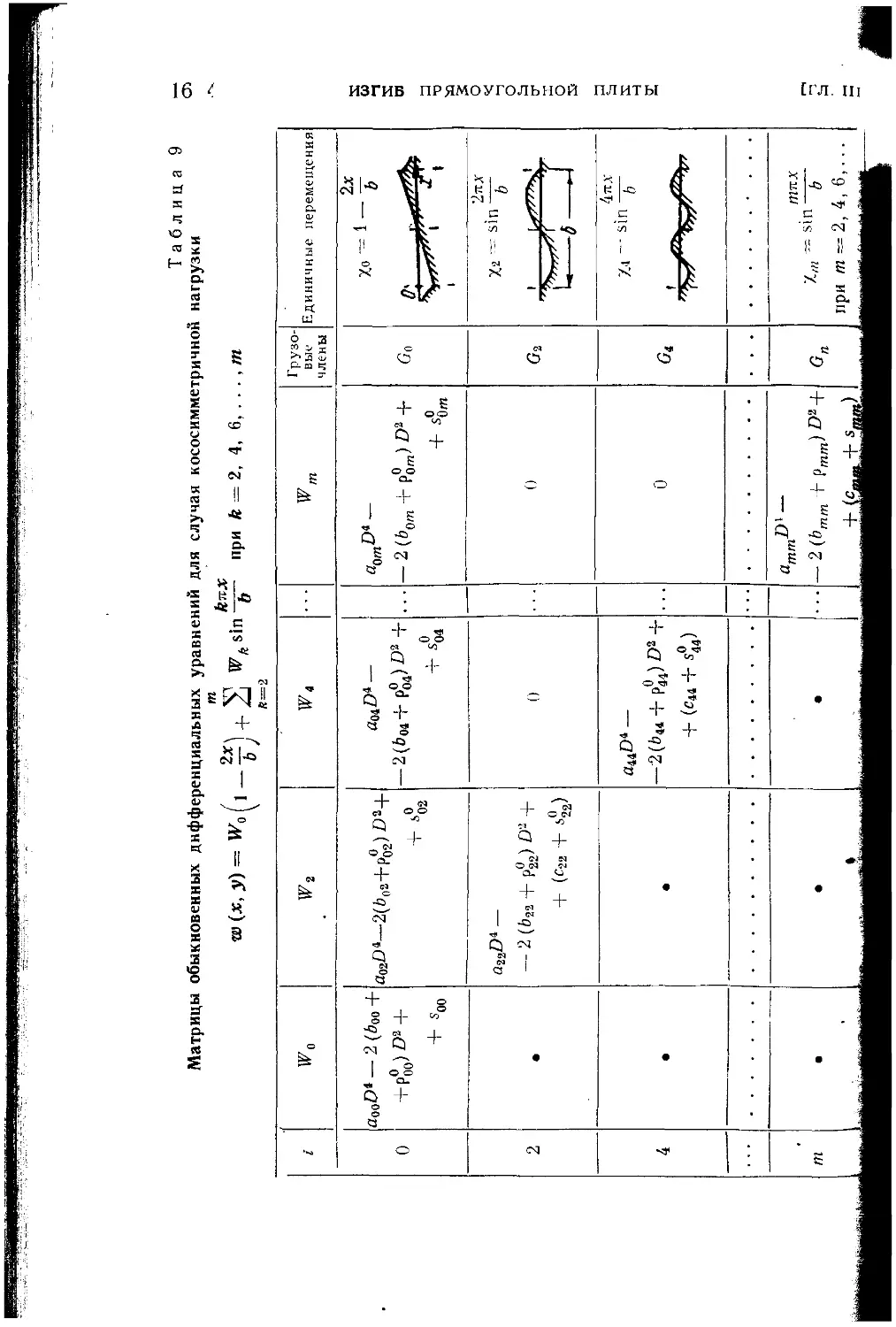
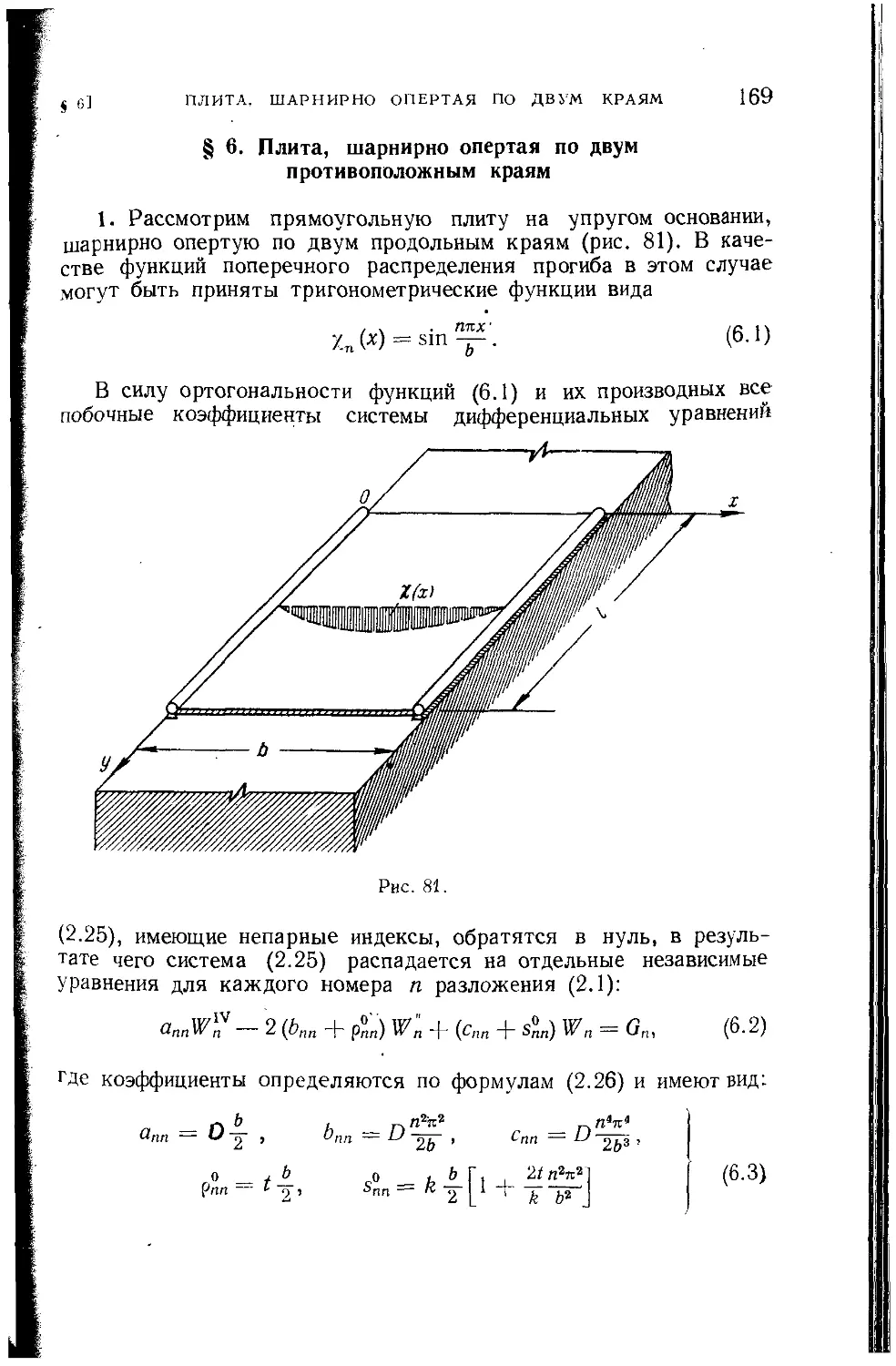
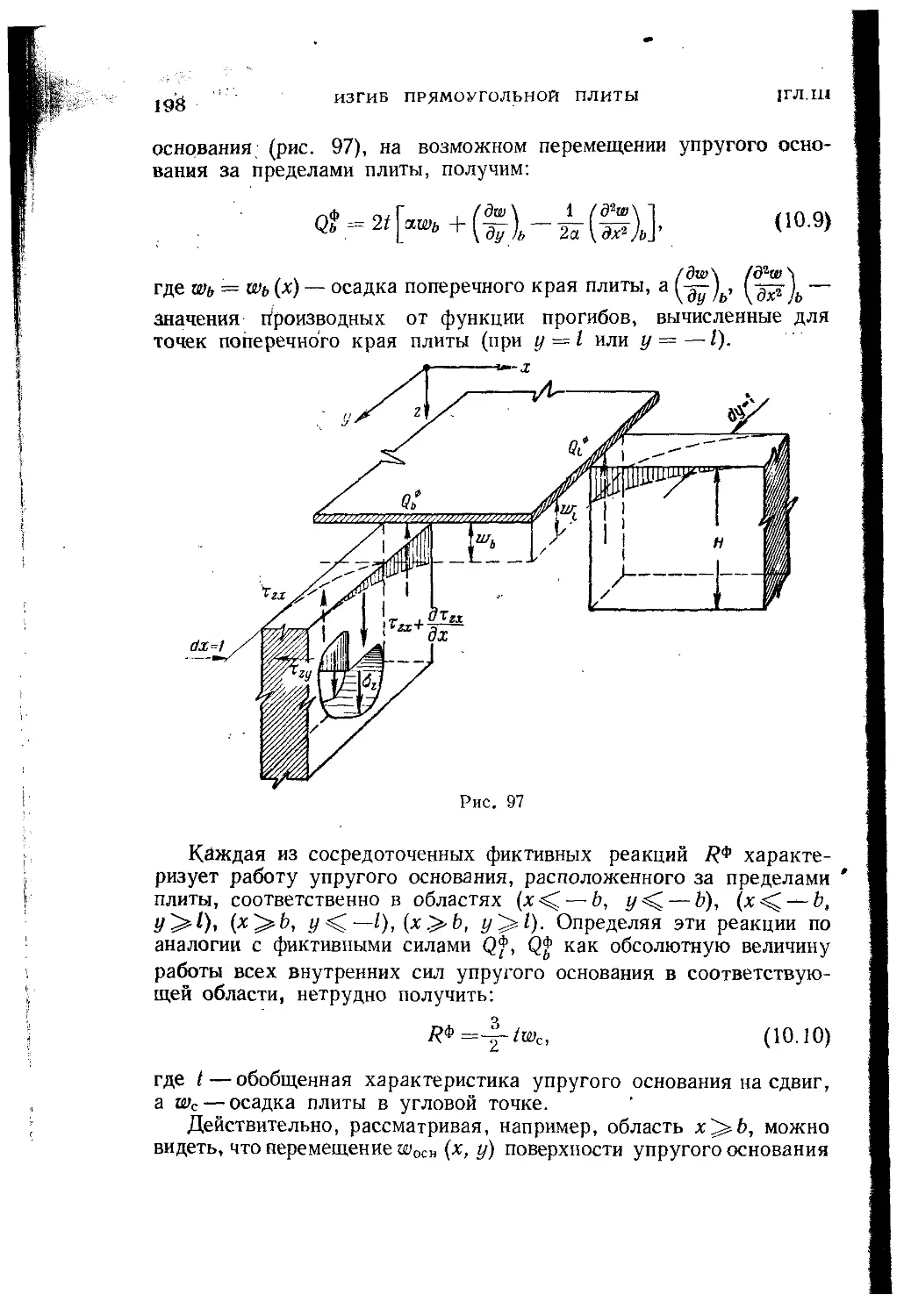
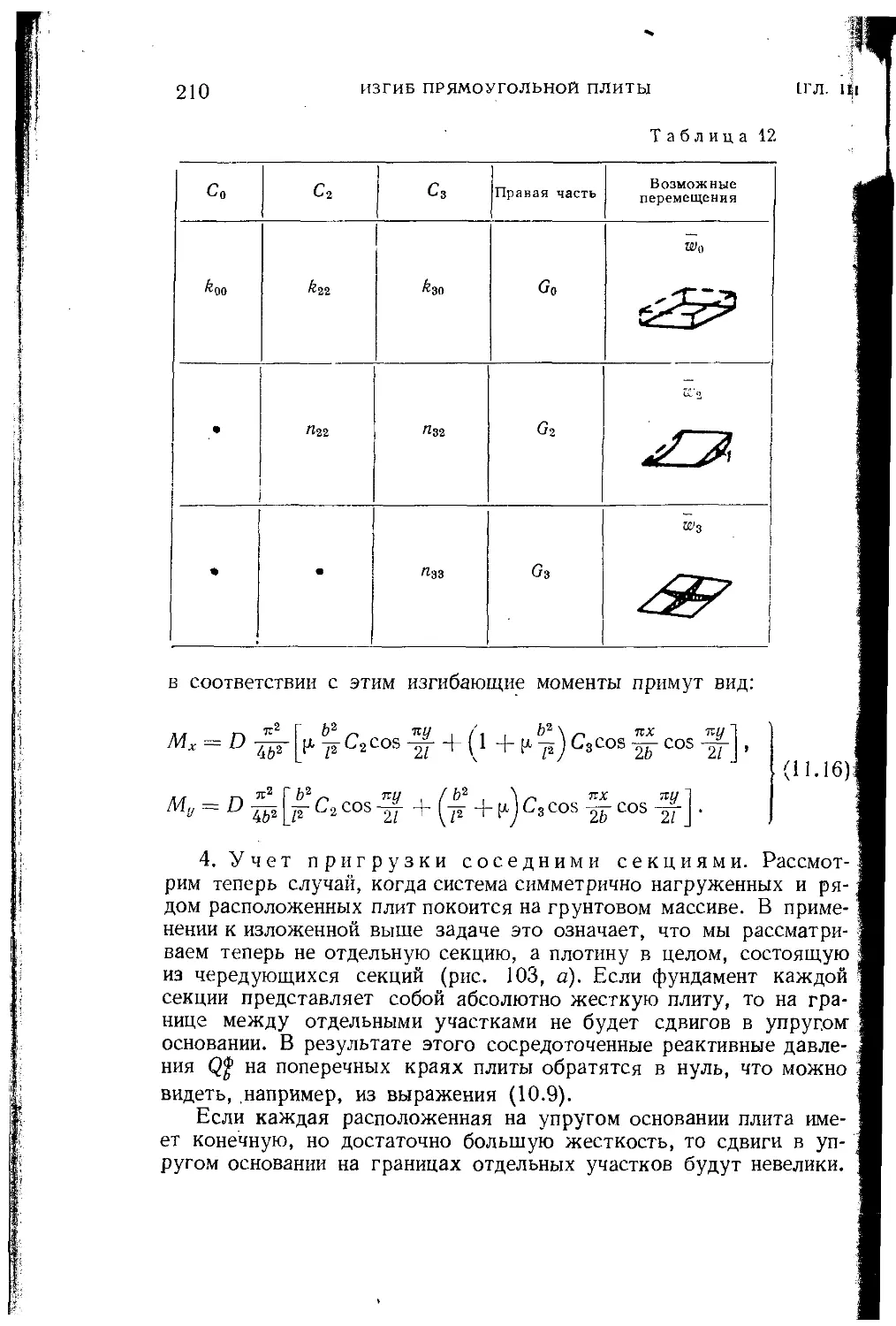
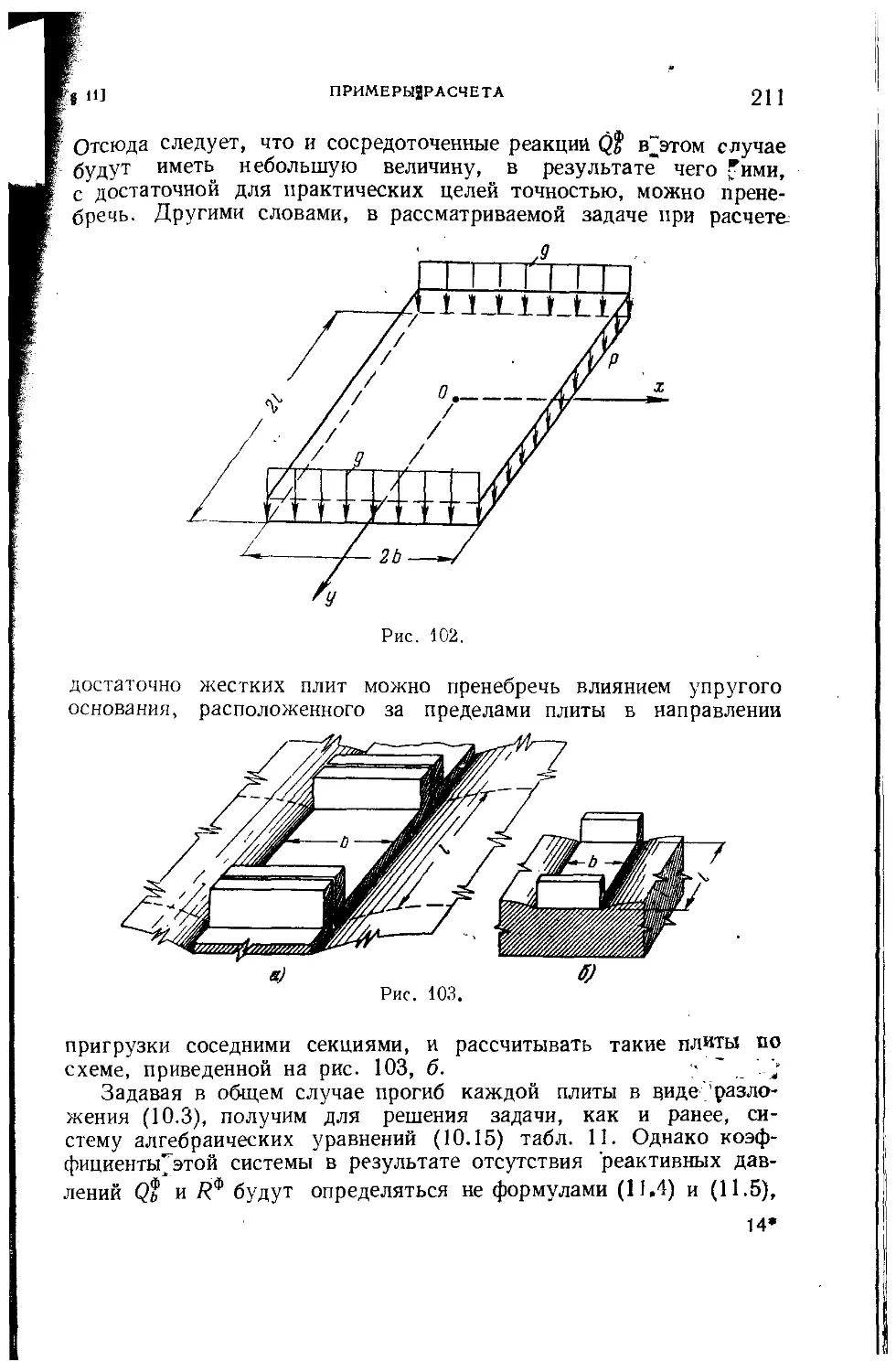
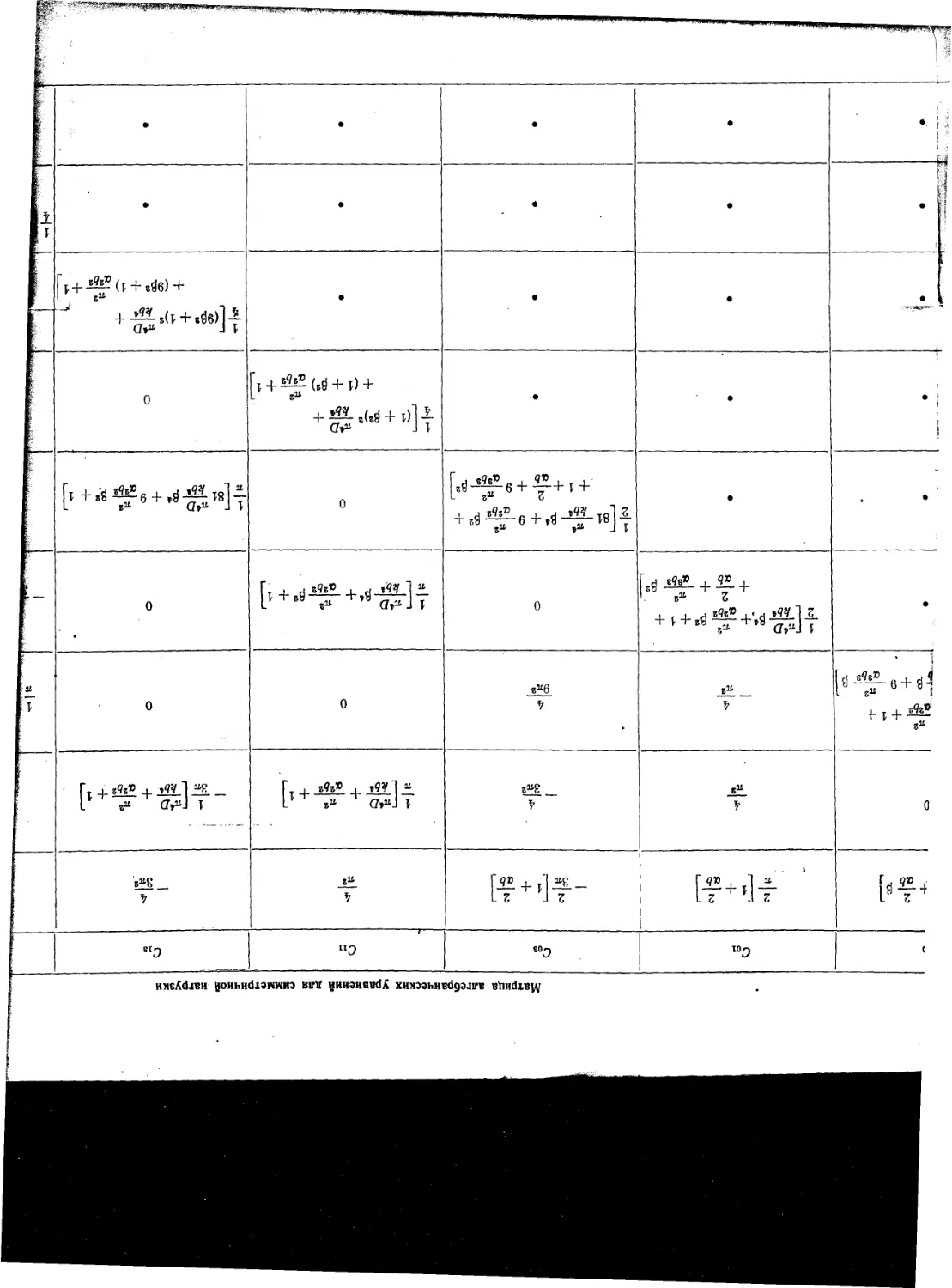
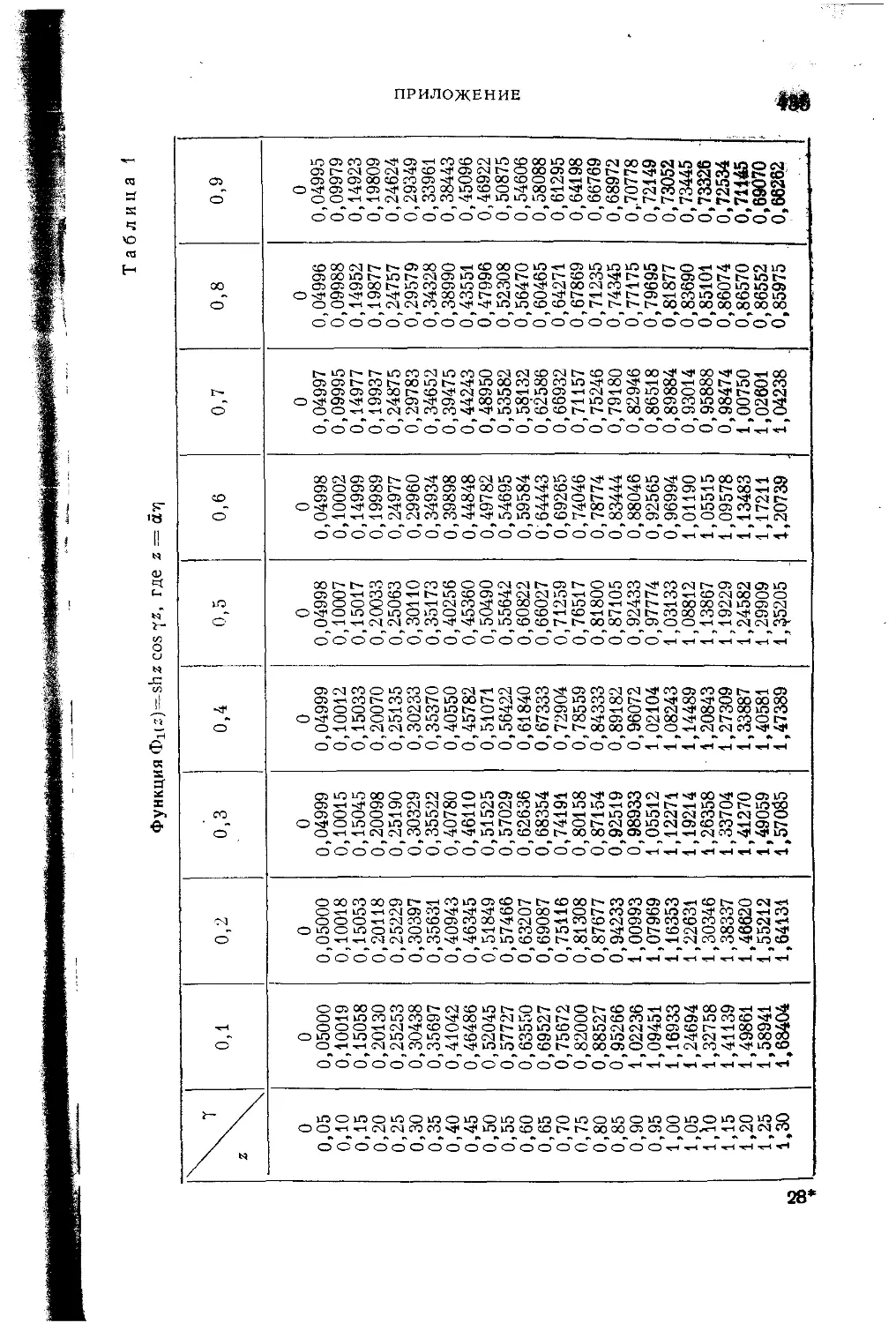
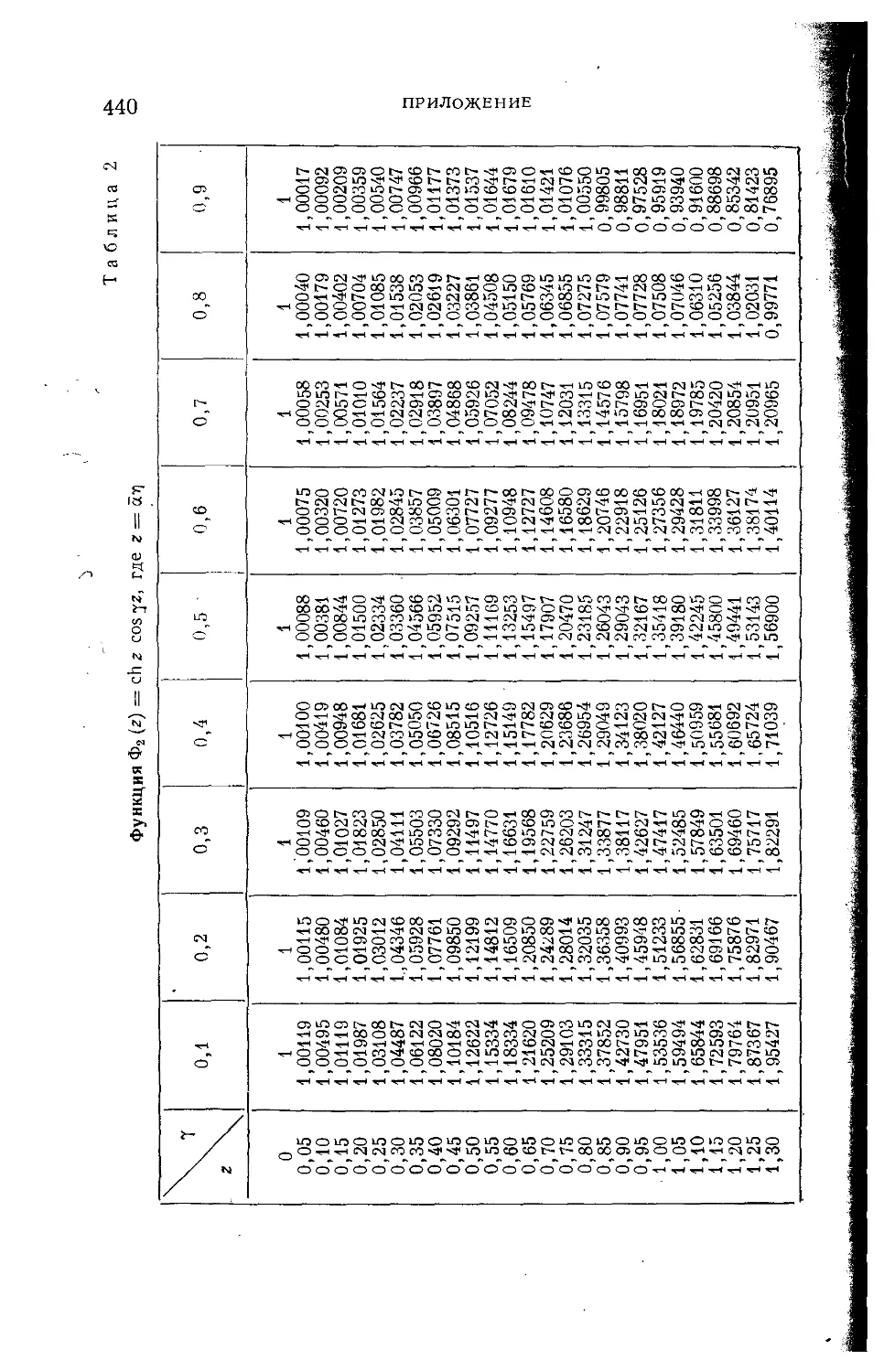
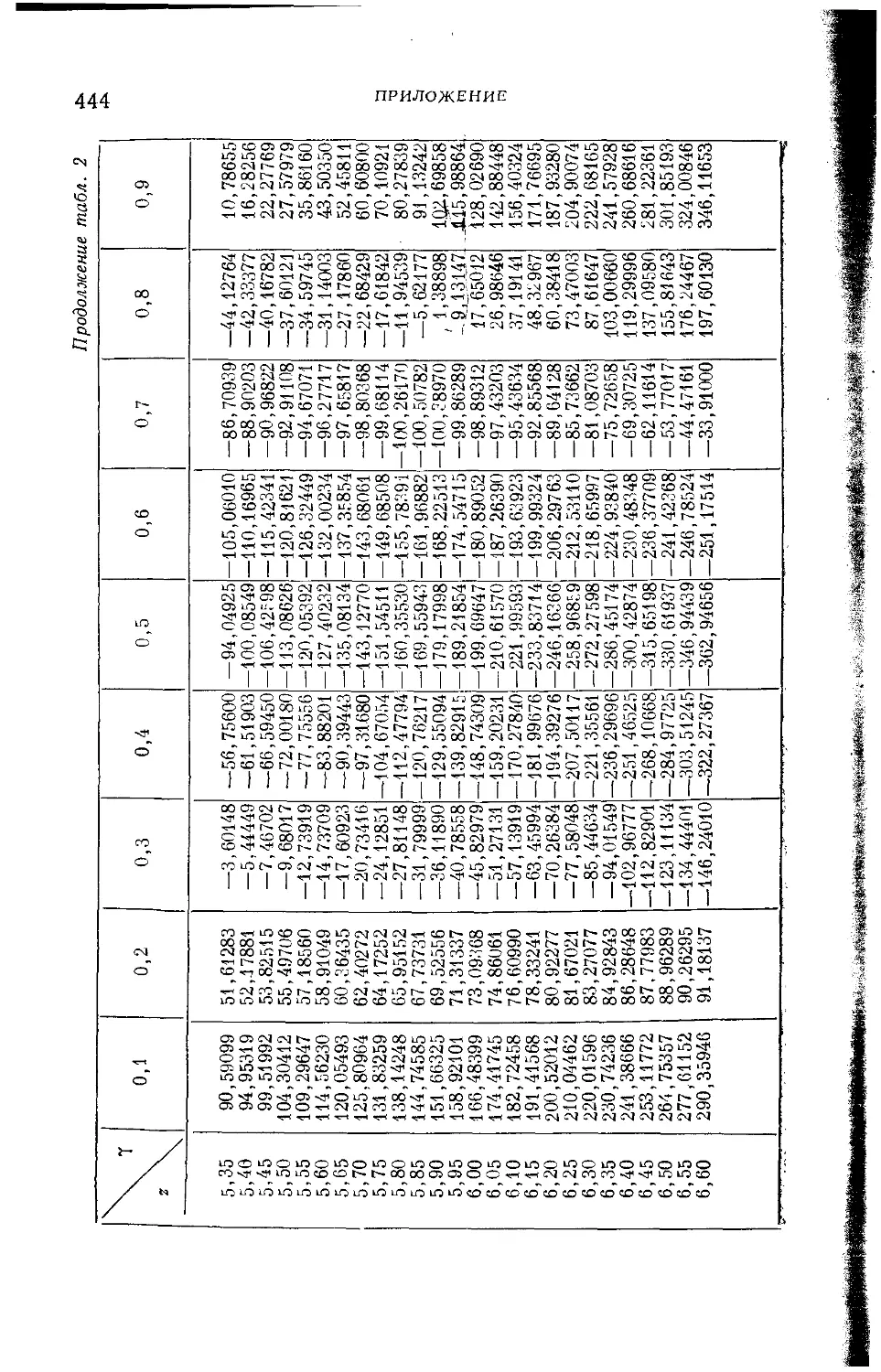
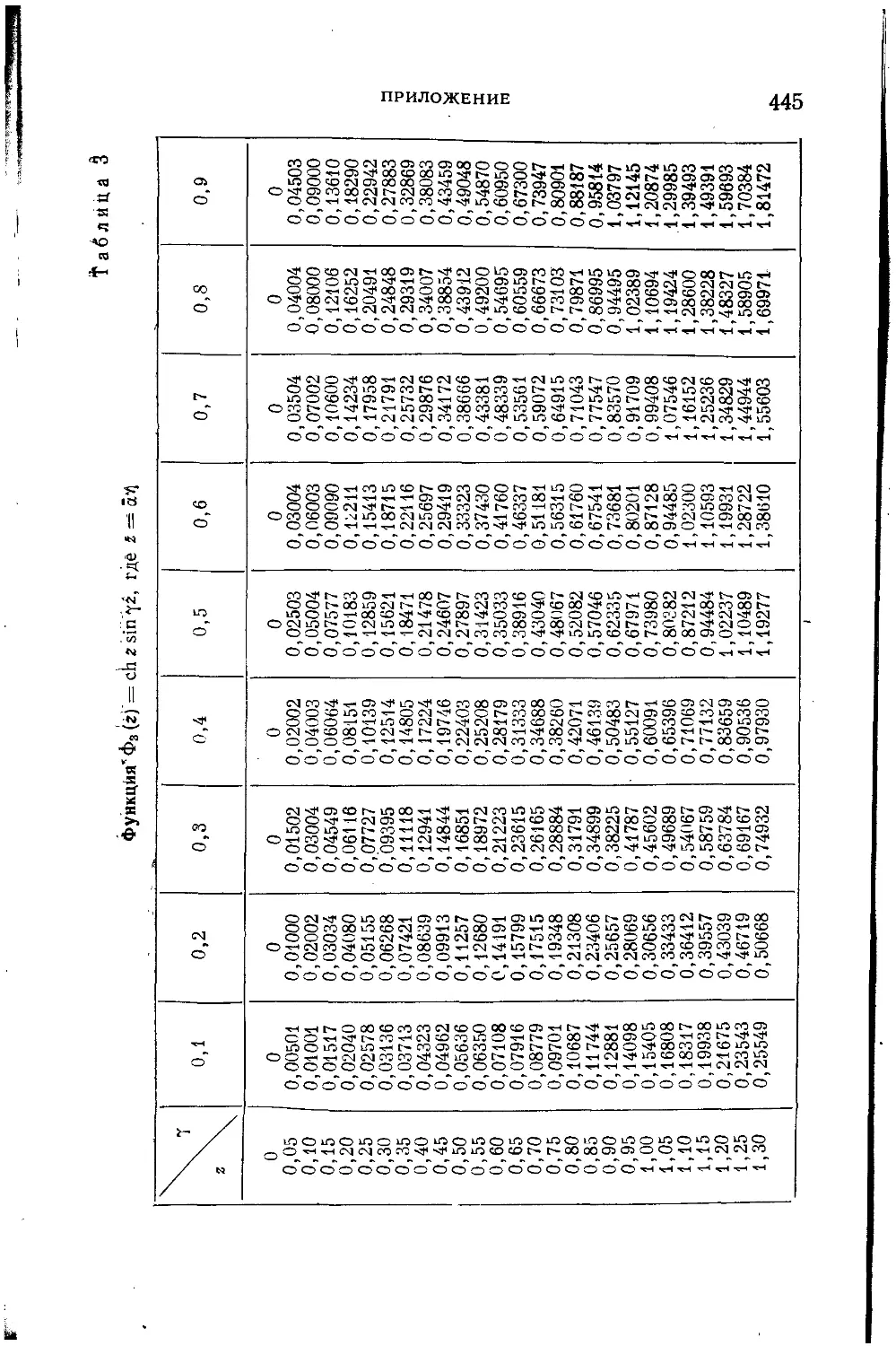
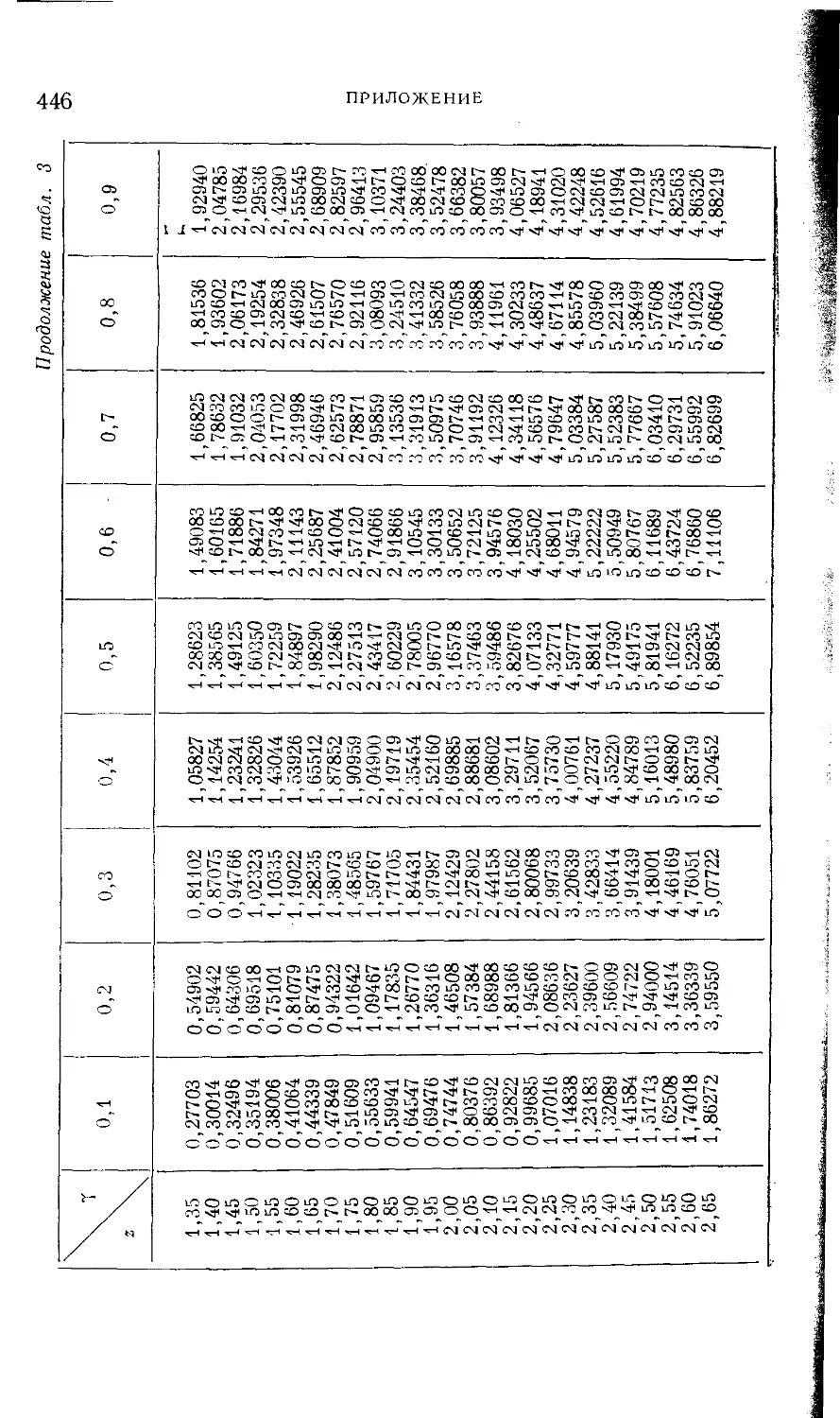
Текст
В. 3. ВЛАСОВ и Н. Н. ЛЕОНТЬЕВ
Q2A.O^
fe 5S(
БАЛКИ, ПЛИТЫ И ОБОЛОЧКИ
НА УПРУГОМ ОСНОВАНИИ
Пермский рпвнарюз
&«(Т|1ЯЬМИ Н 3J ЧН 8-Т I III 1 Hill
Б И Ь Л И О Т Е К А
г. йе>мь, ул. газеты «Звезда», J6 17*
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1960
* ;♦
ОГЛАВЛЕНИЕ
Предисловие ........................................................ >
Глава I. Приложение общего вариационного метода к теории упругого
основания .................................................. И
§ 1. Основы вариационного метода приведения сложных двумер-
ных проблем теории упругости к одномерным.............. 11
§ 2. Определение деформаций упругого основания в условиях
плоской задачи. Расчетные схемы упругого основания ... 21
§ 3. Плоская модель упругого основания с двумя характеристиками 28
§ 4. Однослойное основание с переменным упругим параметром 40
§ 5. Двуслойное упругое основание........................... 43
§ 6. Определение деформаций упругого основания в пространствен-
ных условиях................................................ 50
§ 7. Пространственная модель упругого основания с двумя харак-
теристиками ................................................ 55
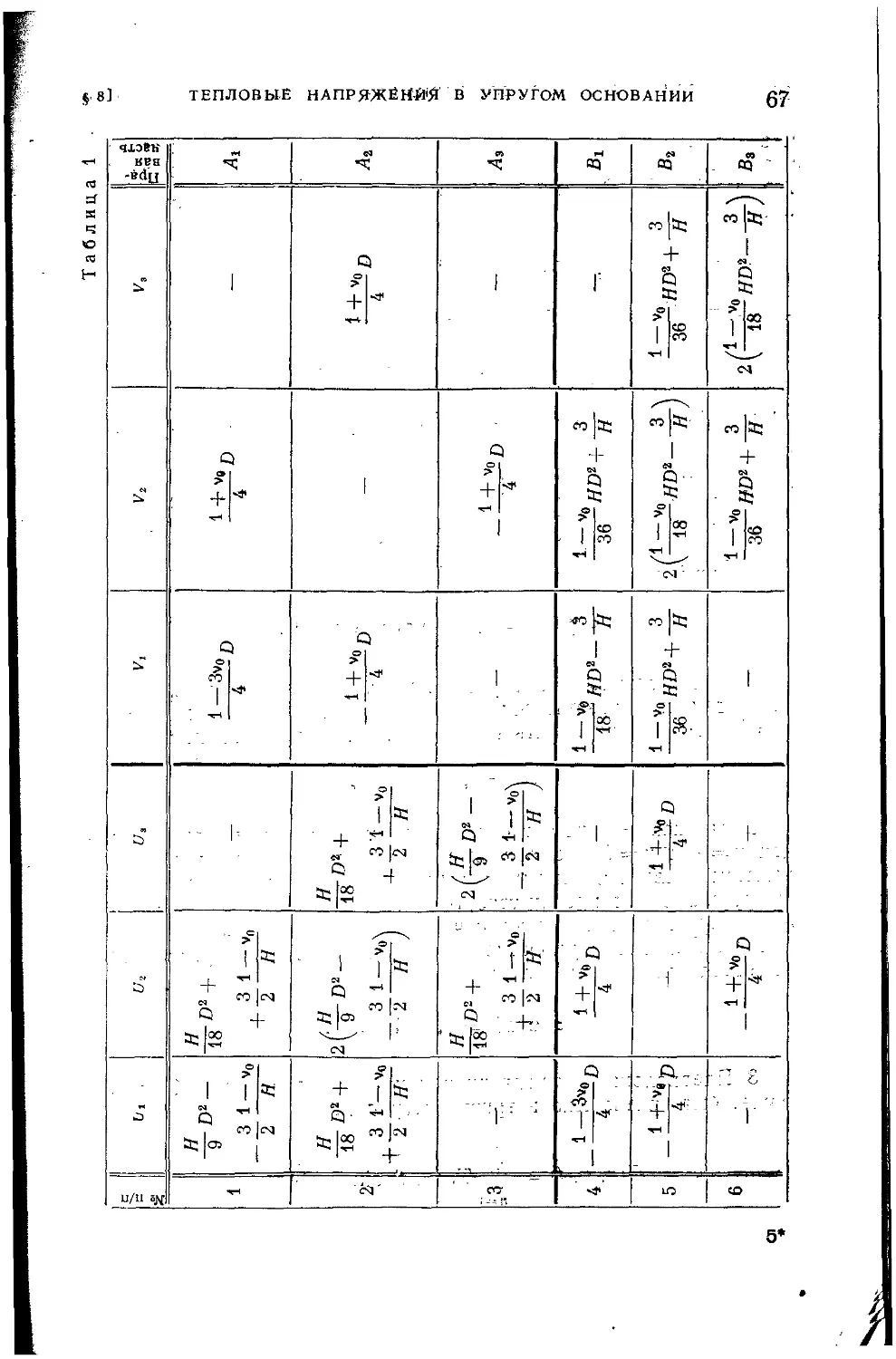
§ 8. Тепловые напряжения в упругом основании................ 63
Глава II. Изгиб балки иа упругом основании..................... 73
’ § 1. Дифференциальное уравнение изгиба балки на упругом основа-
нии с двумя характеристиками................................. 73
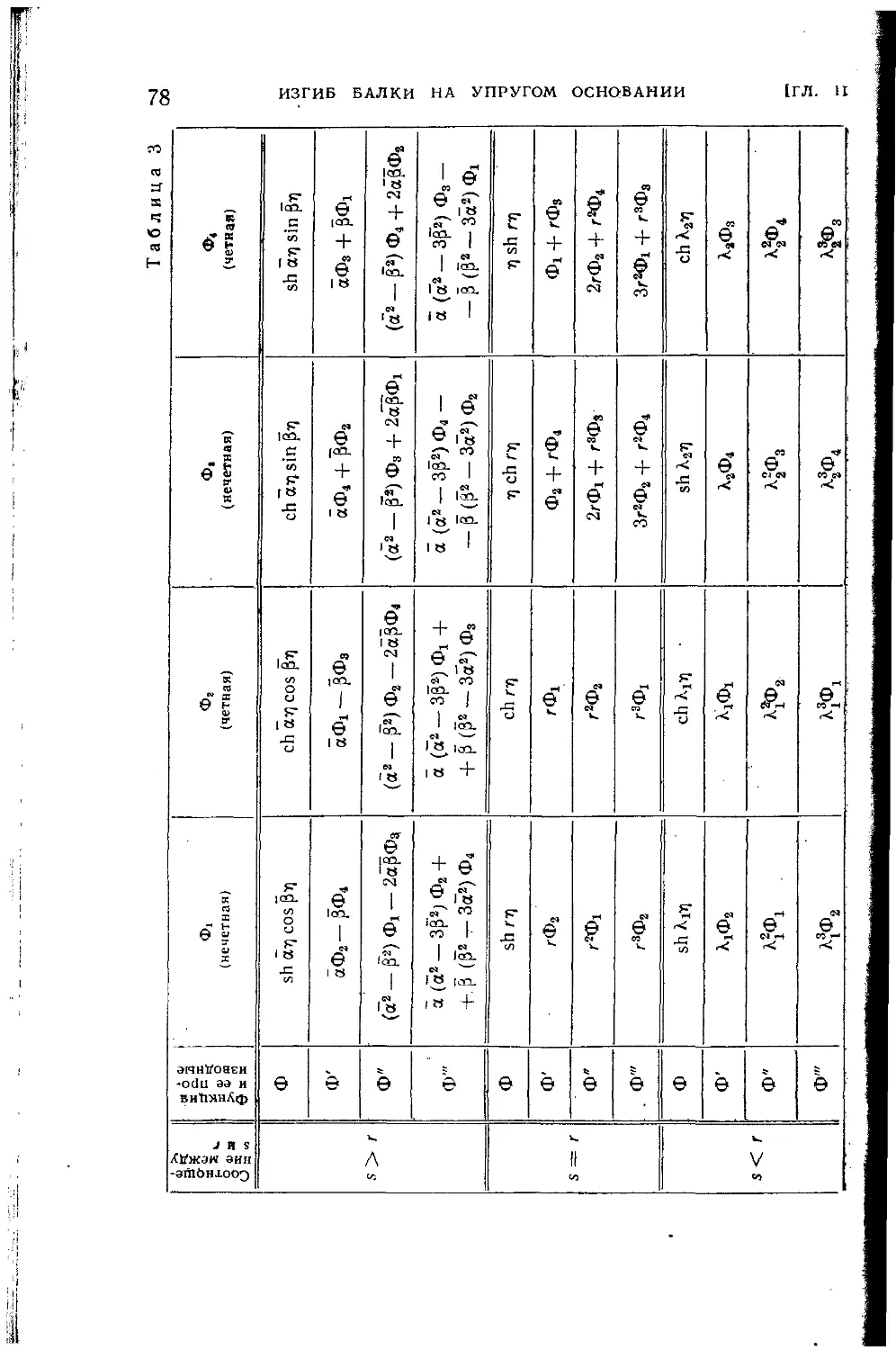
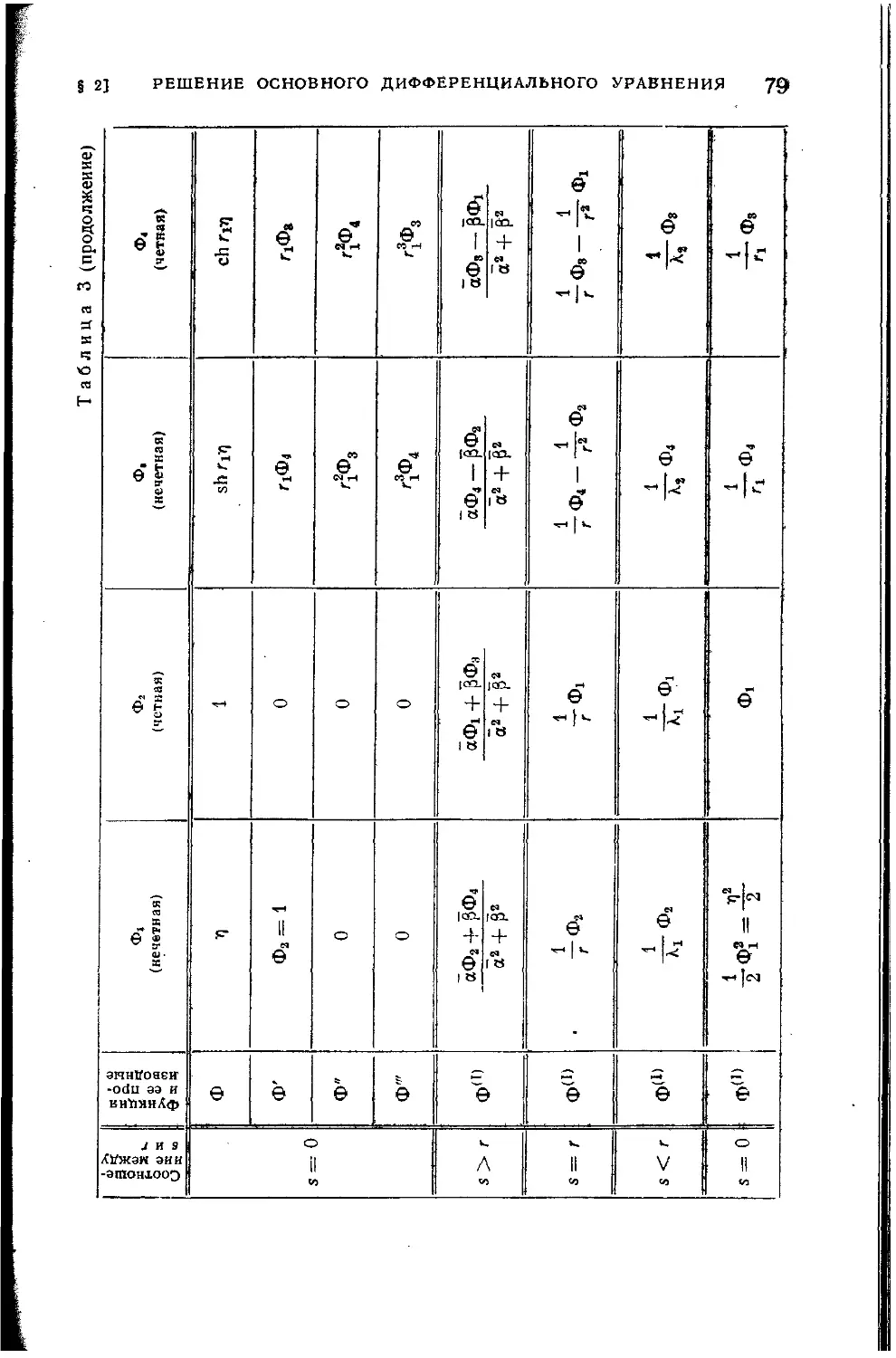
§ 2. Решение основного дифференциального уравнения при помощи
частных интегралов.......................................... 77
§ 3. Решение по методу начальных параметров................. 81
§ 4. Бесконечно длинная балка............................. 90
§ 5. Жесткая балка.......................................... 98
§ 6. Упругая балка конечной длины.......................... 111
§ 7. Влияние боковой пригрузки............................. 119
§ 8. Балка на упругом двуслойном основании................. 130
Глава III. Изгиб прямоугольной плиты на упругом однослойном ос-
новании..................................................... 137
§ 1. Постановка задачи. Дифференциальное уравнение изгиба пли-
ты на однослойном основании.............................. 137
§ 2. Приведение задачи об изгибе плиты на упругом основании к
обыкновенным дифференциальным уравнениям ....... 141
§ 3. Обобщенные внутренние силы. Граничные условия на Попе-
речных краях плиты......................................... 153
4 ОГЛАВЛЕНИЕ
§ 4. Выбор функций поперечного распределения прогибов. Границ-
ные условия на продольных краях............................ 155
§ 5. Выбор функций поперечного распределения прогибов стати-
ческим методом .............................................. 166
§ 6. Плита, шарнирно опертая по двум противоположным краям 169
§ 7. Решение дифференциального уравнения изгиба плиты по методу
начальных параметров......................................... 171
§ 8. Определение начальных параметров. Вычисление моментов
и поперечных сил............................................. 176
§ 9. Цилиндрический изгиб и кручение узкой плиты. О рас-
чете балок в пространственных условиях....................... 184
§ 10. Приближенный расчет плиты со свободными краями на сим-
метричную нагрузку............................................ 194 ^^Ви
§ 11. Примеры расчета........................................ 204
§ 12. Общий случай загруження плиты со свободными краями . . . 213 ^^ВВ
§ 13. Общие уравнения толстых плит на упругом однослойном ос-
нованин....................................................... 220 ^^В|
Глава IV. Осесимметричная деформация круглых плит иа упругом од-
нослойном основании................................................ 226 ^^В|
§ 1. Постановка задачи. Основные дифференциальные зависн-
мости...................................................... 226
§ 2. Общий интеграл дифференциального уравнения круглой плиты
на однослойном основании..................................... 229
§ 3. Абсолютно жесткая плита (круглый штамп)................. 235
§ 4. Кольцевой штамп......................................... 241
§ 5. Бесконечная плнта под действием сосредоточенной силы . . . 243
§ 6. Упругая плита конечных размеров..................... 247
Глава V. Осесимметричная деформация пологой сферической оболоч-
ки иа упругом однослойном основании . ....................... 254
§ 1. Основные дифференциальные зависимости теории пологой
сферической оболочки.......................................... 254 ^В~
§ 2. Дифференциальное уравнение сферической оболочки на упругом
однослойном, основании........................................ 258 ^В
§ 3. Общее решение основных дифференциальных уравнений в
случае осесимметричной деформации............................. 260 ^В
§ 4. Пологая сферическая оболочка под действием равномерно рас- ^В
пределенной нагрузки...................................... 265 ^В
§ 5. Пологая сферическая оболочка под действием контурной на- ^В
грузки.................................................... 270 -^В
§ 6. Приближенный расчет пологой сферической оболочки на ^В
упругом основании......................................... 274 ^В
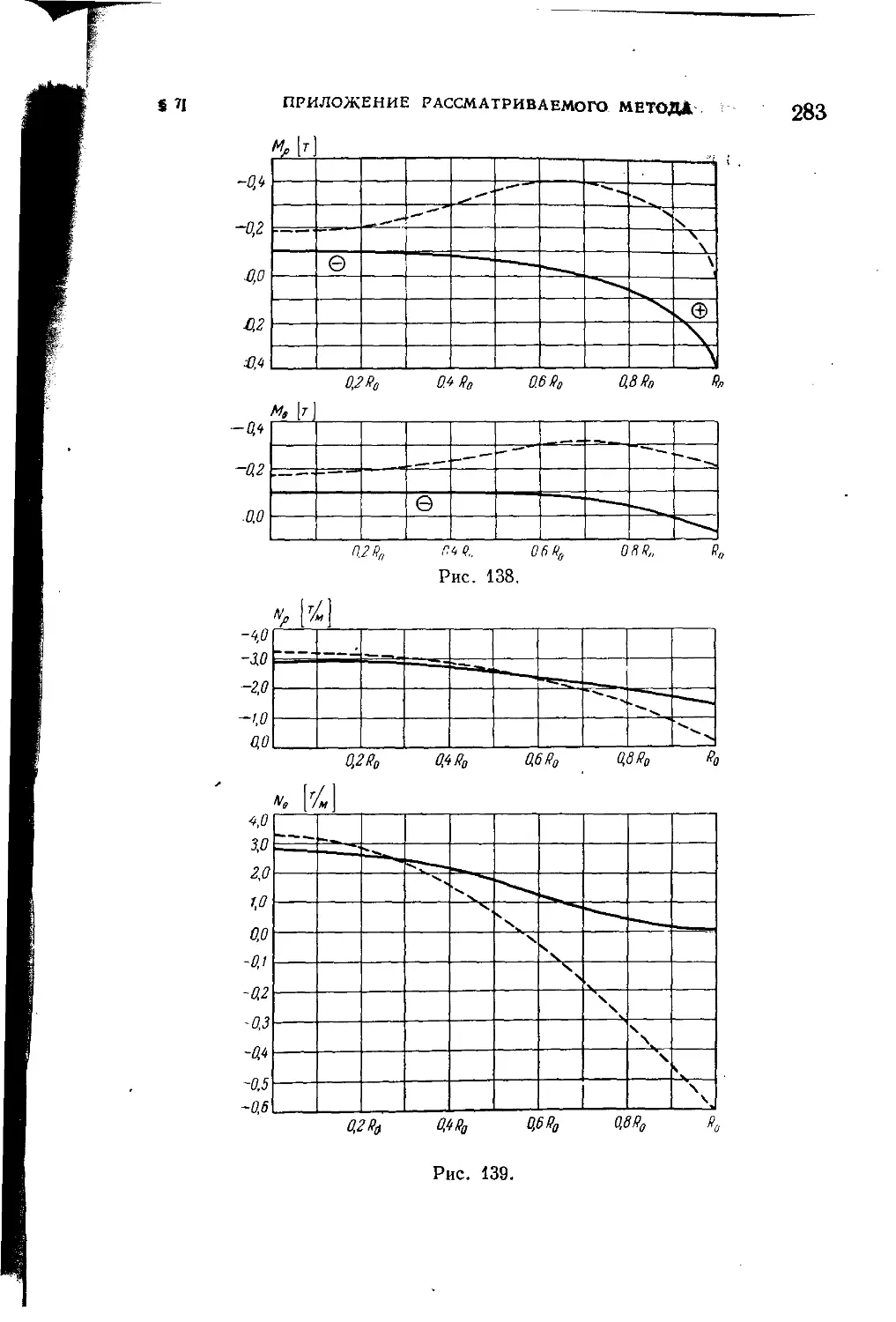
§ 7. Приложение рассматриваемого метода к расчету днищ цилин-
дрнческнх резервуаров......................................... 281 •
ОГЛАВЛЕНИЕ
5
Г л а в а VI Динамика и устойчивость балок и плит на упругом основании 288
' § 1. Дифференциальное уравнение колебаний балки на упругом од-
нослойном основании.............................................. 288
§ 2. Свободные колебания балки........................... 290
§ 3. Действие мгновенного импульса.......................... 299
§ 4. Вынужденные колебания балки............................ 303
§ 5. Динамический расчет балок как систем с конечным числом
степеней свободы............................................ 305
§ 6. Дифференциальное уравнение колебаний плиты на упругом
однослойном основании ...................................... 312
§ 7. Приближенный расчет безграничной плиты на сосредоточен-
ный удар.................................................... 314
§ 8. Плита, шарнирно опертая по контуру..................... 323
§ 9. Колебании плиты со свободными от закреплений краями . . 326
§ 10; Устойчивость прямоугольной плиты на упругом однослойном
основании при сжатии в одном направлении.................... 340
§ 11, Устойчивость узкой плиты на упругом однослойном осно-
вании ....................................................... 344
§ 12. Устойчивость предварительно напряженной плиты на упру-
гом основании............................................... 351
Глава VII. Метод начальных функций. Приложение метода к теории
толстых плит и теории упругого основания..................... 355
§ 1. Общее решение пространственной задачи теории упру-
гости ....................................................... 355
§ 2. Решение уравнений теории упругости методом начальных
функций..................................................... 357
§'3. Основные свойства матрицы линейного преобразования по
методу начальных функций.................................... 368
§ 4. Общий метод приведения трехмерной задачи теории упру-
гости к двумерной........................................... 371
§ 5. Толстая плита, находящаяся под действием нагрузки,
расположенной симметрично относительно ее срединной
плоскости................................................... 373
§ 6. Толстая плита, находящаяся под действием нагрузки, рас-
положенной антисимметрично относительно срединной плос-
кости .......................................................377
§ 7. Деформация упругого основания под нагрузкой, приложенной
к его поверхности........................................... 380
§ 8. Контактная задача по расчету плиты на упругом осно-
вании ...................................................... 383
§ 9. Теория плнт-оболочек переменной толщины, находящихся под
действием произвольно заданных поверхностных нагру-
зок ... . .................................................. 385
§ 10. Общее решение плоской задачи теории упругости.......... 388
6
ОГЛАВЛЕНИЕ
§ 11. Изгиб толстой плиты в условиях плоской деформации. По-
строение приближенного решения......................... 395
§ 12. Применение тригонометрических рядов для решения плоской
задачи...................................................... 400
§ 13. Построение точного решения для прямоугольной полосы при
произвольных граничных условиях на поперечных и однород-
ных граничных условиях на продольных краях.................. 409
§ 14. Другой вид однородных граничных условий смешанного типа
на продольных краях полосы........................... 415
§ 15. Пространственная и плоская задачи теории толстых много-
слойных плит.................................................420
§ 16. Многослойное упругое основание........................430
Приложение ..................................................... 433
Литература........................................................ 484
Предметный указатель ............................................ 488
ПРЕДИСЛОВИЕ
< - 'Теория балок и плит, лежащих на упругом основании, пред-
ставляет собой весьма обширный раздел современной строительной
механики. В этой области выполнено огромное количество работ,
многие из которых содержат ценные практические методы расчета
балок и плит на упругом основании.
Однако существующие методы расчета еще далеко не совершен-
ны и не: дают ответа на множество разнообразных вопросов, вы-
двигаемых строительной практикой. Большая часть этих методов
носит слишком* сложный для практических вычислений характер;
не могут считаться совершенными и те гипотезы, которые принима-
ются для работы естественного грунта. Имеющиеся методы не по-
зволяют рассчитывать сложные пространственные системы на упру-
гом основании. Так, гипотеза коэффициента постели, рассматрива-
ющая упругое основание как систему отдельных, не связанных
между собой пружин и позволяющая вследствие этого достаточно
просто производить расчет конструкций на упругом основании,
в. ряде случаев приводит к результатам, резко расходящимся с
действительностью.
Гипотеза упругого изотропного полупространства, согласно со-
временному грунтоведению, достаточно полно отражает физические
свойства естественного основания. Однако методы расчета, бази-
рующиеся на этой гипотезе, очень сложны, в результате чего
практически приемлемые решения получены здесь только для
весьма ограниченного круга задач.
Таким образом, перед современной теорией расчета фундаментов
иа упругом основании стоит ряд серьезных проблем, наиболее важ-
ными из которых являются: 1) уточнение расчетных схем основания,
в смысле сближения их с действительностью; 2) разработка методов
расчета сложных пространственных конструкций с учетом упругой
8
ПРЕДИСЛОВИЕ
податливости грунта; 3) упрощение методов расчета сооружений
на упругом основании в целях более широкого внедрения их в ин-
женерную практику.
В отношении уточнения расчетов можно полагать, что учет упру-
го-пластической работы грунта основания позволит в дальнейшем
приблизиться к действительной работе конструкций.
Вопросы расчета сложных пространственных конструкций на
упругом основании, которые стоят перед инженерной практикой,
могут быть, очевидно, наиболее эффективно решены при помощи
приближенных методов. Эти же методы дают возможность упро-
стить расчетные выражения.
В настоящей работе предлагается новая техническая теория рас-
чета конструкций на упругом основании, в основу которой положен
общий вариационный метод В. 3. Власова. Эта теория является более
точной, чем известная теория Винклера—Циммермана, и одновре-
менно более простой, чем теория упругого полупространства.
Согласно предлагаемой технической теории упругое и в общем
случае неоднородное основание рассматривается как однослойная
или многослойная модель, свойства которой описываются двумя
или несколькими обобщенными упругими характеристиками. Эта
модель была предложена в 1949 г. В. 3. Власовым в его монографии
«Строительная механика тонкостенных пространственных систем».
В дальнейшем теория однослойного основания развивалась в рабо-
тах Н. Н. Леонтьева [11], [55], В. П. Ручкина [68], Л. В. Косабь-
яна [45], А. А. Чече [81], [82] и др.
Следует отметить, что основное дифференциальное уравнение,
характеризующее работу однослойного основания, совпадает по
виду с решением, полученным М. М. Филоненко-Бородичем [75],
[76], а также с решением Вигхарта. Таким образом, модели Виг-
харта и М. М. ФиЛоненко-Бородича в математическом отношении
эквивалентны рассматриваемой нами модели однослойного основа-
ния. Отметим также, что упругое основание, аналогичное одно-
слойной модели, было рассмотрено П. Л. Пастернаком [62].
Предлагаемая техническая теория позволяет сводить решение
различного рода практически важных задач к решению обыкновен-
ных дифференциальных уравнений, которые хорошо изучены и
интегрируются в известных табулированных функциях. Простота
математических приемов и четкость расчетной схемы делают рас-
ПРЕДИСЛОВИЕ
9
сматриваемую теорию весьма гибкой и позволяют решать не только
основные задачи по расчету балок и плит на упругом основании,
но и ряд более сложных вопросов. Сюда относятся, например, воп-
росы расчета оболочек, вопросы учета боковой пригрузки и подсти-
лающего слоя, вопросы динамики и устойчивости сооружений на
упругом основании. Предлагаемая теория с успехом может быть
применена и в горном деле при решении задач, относящихся к опре-
делению напряжений и деформаций в однослойных и многослойных
пластах горных выработок, имеющих горизонтальное или наклон-
ное расположение.
Авторы не претендуют в настоящей книге на полноту освещения
всех интересных для практики вопросов и не считают, что предла-
гаемые ими методы универсальны. Многие задачи освещаются в этой
работе впервые, вследствие чего разработка их не доведена еще до
готовых формул и таблиц. Однако накопившийся к настоящему
времени обширный материал по расчету конструкций на упругом
однослойном основании делает необходимым выпуск подобной ра-
боты, которая, как авторы надеются, окажется полезной и для ин-
женерной практики, и для дальнейших исследований.
Книга состоит из семи глав. В первых шести главах излагаются
вопросы расчета балок, плит и сферических оболочек на упругом
основании, а также некоторые задачи, связанные с динамикой и
устойчивостью этих конструкций. Материалом для I, II и III глав
послужила в основном диссертационная работа Н. Н. Леонтьева
[55]. В главах IV и V использованы результаты исследований
В. П. Ручкина [68], любезно предоставленные им авторам на-
стоящей книги. В заключительной, VII главе освещается новый
подход к решению контактных задач. Здесь изложен метод началь-
ных функций [10, 13, 14], позволяющий сводить сложные трехмер-
ные задачи теории упругости к двумерным, а также рассмотрены
некоторые примеры, иллюстрирующие этот метод. В конце книги
приведен список основных литературных источников, которые в
разной степени были использованы авторами в процессе работы над
книгой. Этот список, конечно, не является полным. Для того чтобы
читатель имел возможность более подробно ознакомиться с имею-
щимися работами в области расчета конструкций на упругом ос-
новании, в списке литературы указаны источники [42, 50, 64],
содержащие библиографию по рассматриваемому вопросу.
10
ПРЕДИСЛОВИЕ
При подготовке книги авторы стремились сделать ее доступной
не только для научных работников и аспирантов, но и для инжене-
ров, работающих в конструкторских бюро и проектных организа-
циях. В целях облегчения практических вычислений книга снаб-
жена таблицами, безразмерными эпюрами и примерами расчета.
Однако основная задача книги заключается в том, чтобы вооружить
инженера знанием эффективного вариационного метода, который
позволит ему в каждом конкретном случае проектирования самому
выбрать ту или иную расчетную схему, построить соответствую-
щую модель упругого основания и решить задачу достаточно прос-
тыми и доступными математическими средствами.
Между авторами труд распределен следующим образом: главы
I, II, III, IV, V и VI книги написаны Н. Н. Леонтьевым, глава
VII — В. 3. Власовым. Общая редакция книги осуществлена
В. 3. Власовым.
Авторы считают своим приятным долгом выразить признатель-
ность В. П. Ручкину, В. В. Власову, Е. И. Силкину, А. Н. Елпать-
евскому и Л. В. Косабьяну за помощь, оказанную ими в работе над
рукописью, а также В. В. Петрову и Д. Н. Соболеву за большую
работу по подготовке рукописи к печати.
В. 3. Власов , Н. Н. Леонтьев
ГЛАВА I
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
К ТЕОРИИ УПРУГОГО ОСНОВАНИЯ
§ 1. Основы вариационного метода приведения сложных
двумерных проблем теории упругости к одномерным
1. Рассмотрим тонкую прямоугольную пластинку, нагруженную
силами, действующими в плоскости этой пластинки (рис. 1,а).
Предположим, что деформация пластинки происходит без искрив-
ления, в результате чего напряженное состояние пластинки харак-
Рис. 1.
теризуется лишь нормальными напряжениями <зх, <зи и касатель-
ными напряжениями хху, хуХ. При этом напряжения <зх, ау, хху, хух
не зависят от координаты г, так как толщина пластинки 8 прини-
мается достаточно малой. Такая задача в теории упругости носит
название задачи о плоском напряженном состоянии пластинки.
Задача о плоском напряженном состоянии представляет собой
двумерную проблему теории упругости, поскольку перемещения,
деформации и напряжения являются здесь функциями двух коорди-
нат: х и у. Для решения этой задачи теория упругости распола-
гает двумя основными методами: методом напряжений и методом
12
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
перемещений. По первому методу за основные неизвестные при-
нимаются напряжения ал(х, у), аУ(х, у), тху(х, у), ~ух(х, у), которые
разыскиваются из условий неразрывности деформаций рассматри-
ваемой системы. Этот метод аналогичен методу сил, широко при-
меняемому в строительной механике статически неопределимых
стержневых систем. В качестве основных неизвестных второго
метода принимаются перемещения и (х, у), v (х, у), определяемые
из статических условий равновесия упругой системы. Этому методу
в строительной механике соответствует метод деформаций.
В дальнейшем для решения поставленной задачи мы восполь-
зуемся методом перемещений, приняв за основные неизвестные
перемещения и (х, у) п v (х, у) некоторой точки М (х, у) пластинки.
Условимся различать для рассматриваемой пластинки два направ-
ления: продольное, совпадающее с направлением оси Ох, и попе-
речное, совпадающее с направлением оси Оу. В соответствии с этим
мы будем называть в дальнейшем и (х, у) продольным, a v (х, у) —
поперечным перемещением. Перемещения и (х, у) и v (х, у) будем
считать положительными, если их направления совпадают с поло-
жительными направлениями координатных осей.
Напомним, что связь между напряжениями и деформациями
в условиях плоской задачи теории упругости устанавливается сле-
дующими зависимостями:
Е
Сх = I-—+ ^уу)>
£
Qy — 1_;г (s<w + ™хх},
_ Е
ТхУ = tyx — 2 (1 + v) *xv> .
(1-1)
где E — модуль упругости, a v — коэффициент Пуассона материала
пластинки, гхх = гхх (х, у) и = syy (х, у) — относительные удли-
нения соответственно в продольном и поперечном направлениях,
вху = ехг, (х, у) — деформация сдвига.
Деформации пластинки sxx, гуу, sxy, входящие в уравнения (1.1),
могут быть выражены через искомые перемещения и и и в сле-
дующем виде:
ди ди ди . dv ,.
г*х~дх' + <1,2'
Таким образом, по определении перемещений и и v рассма-
триваемая задача может считаться полностью решенной, поскольку
напряженное и деформированное состояние пластинки характе-
ризуются формулами (1.1) и (1.2).
2. Для получения достаточно простого приближенного решения
представим искомые функции и (х, у) и v (х, у) двух переменных
S 1]
ПРИВЕДЕНИЕ ДВУМЕРНЫХ ПРОБЛЕМ К ОДНОМЕРНЫМ
13
в виде следующих конечных разложений:
и (х, У) = 2 Ui W (/ = 1, 2, 3,..., пг),
(Е3)
v (х, у) = 2 Vk (х) (у) (k= 1,2,3,..., п),
А=1
из которых первое содержит пг, а второе — п слагаемых. Функции
U£(x), Vk(x) будем считать искомыми, а функции <р,(у), ф* (у) —
заданными. Для ряда задач функции (р£(у), &г(у) удобно прини-
мать безразмерными, а функции U£ (х), Vk (х) — имеющими размер-
ность перемещения.
Согласно размерностям и физическому смыслу выражений (1.3)
функции Ui(x), Vk(x) могут быть названы обобщенными переме-
щениями. Действительно, каждая из т функций U£ (х), вычисленная
для определенного сечения х = const пластинки, обобщенно харак-
теризует в этом сечении величину продольного перемещения и,(х, у).
Аналогично каждая из п функций V*(x) в целом для всего сече-
ния х = const определяет величину поперечного перемещения
vk(x, у). Распределение же продольных и поперечных перемещений
по сечениям х = const характеризуется соответственно функциями
?z(y) и ф* (у). В результате этого функции <р£(у) и Фа (.у) могут
быть названы функциями поперечного распределения перемещений.
Функции <$i (у) и Фа (у), аппроксимирующие деформированное
состояние пластинки в поперечном направлении, могут быть вы-
браны различными способами при условии, чтобы эти функции были
линейно независимыми и отвечали физическому содержанию задачи.
Для пояснения сказанного приведем несколько примеров.
Рассмотрим задачу об изгибе узкой пластинки (балки) со сво-
бодными от закреплений продольными краями. Принимая для такой
пластинки гипотезу плоских сечений и считая, что деформации
[ Удлинений пластинки в направлении ее ширины равны нулю, можно
представить искомые перемещения и (х, у), v (х, у) в виде
«(х, y) = t/i(x)^(i/) = U1(x)-y, 1
' о(х,^) = У1(х)ф1(у) = УДх)-! / (-)
(начало координаты у выбрано в средней точке поперечного сечения).
Таким образом, в этой задаче для функций поперечного распре-
деления перемещений нами выбраны выражения
?1(У)=У, Ф1(х)=1,
а Остальные функции, <рг-(у) и <f>k(y) (при i > 1 и k > 1), положены
равными нулю.
14 ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ. I
Из выражений (1.4) следует, что обобщенное перемещение Ux (х)
представляет собой угол поворота, а обобщенное перемещение
Vi(x)— прогиб пластинки.
Желая несколько уточнить элементарное решение сопротивле-
ния материалов в случае изгиба достаточно высокой пластинки,
Рис. 2.
находящейся под действием кососимметричной (относительно оси Ох)
нагрузки (рис. 2), можно принять разложение (1.3) в виде
и (х, у) = Ux (х) у + U2 (х) sin ]
(1-5)
v (х, у) = Vx (х) 1 + V2 (х) cos ~, ]
т. е. выбрать для функций у, (у), <1>&(у) выражения
<Р1(У) = У> ЫУ) = sin^f.
Ф1(у) = 1> <My) = C0S^-
Первыми членами в формулах (1.5) представлены перемещения,
относящиеся к закону плоских сечений; вторые слагаемые этих
формул характеризуют дополнительные перемещения, которыми
учитывается отклонение от гипотезы плоских сечений и от гипотезы
о равенстве нулю поперечных удлинений.
Уточненное решение для высокой пластинки (балки-стенки)
можно получить и другим путем. Можно, например, мысленно
разбить пластинку по высоте на ряд горизонтальных полосок
и принять, что в пределах каждой полоски остается справедливым
закон плоских сечений. Для всего же поперечного сечения пла-
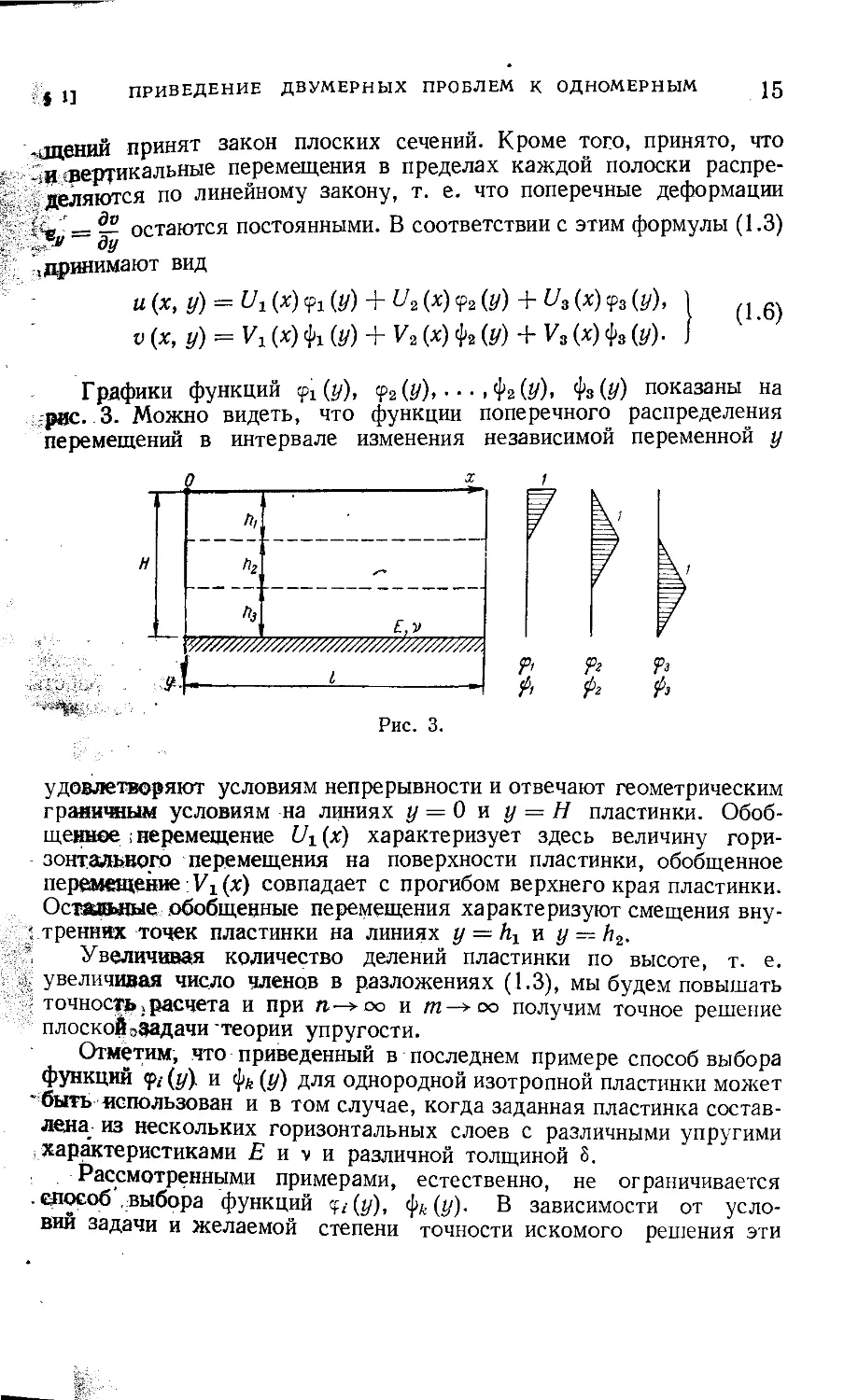
стинки этот закон уже не будет иметь места. В качестве примера
на рис. 3 приведена пластинка со свободным верхним и жестко
закрепленным от горизонтальных и вертикальных перемещений
нижним краем. По высоте эта пластинка разделена на три части,
причем в пределах каждой полоски для горизонтальных переме-
ПРИВЕДЕНИЕ ДВУМЕРНЫХ ПРОБЛЕМ К ОДНОМЕРНЫМ jg
'' э * J
. тений принят закон плоских сечений. Кроме того, принято, что
и вертикальные перемещения в пределах каждой полоски распре-
деляются по линейному закону, т. е. что поперечные деформации
остаются постоянными. В соответствии с этим формулы (1.3)
.^ч " ду
Принимают вид
и(х, у) == Ui(x)<p1(y) + U2(x)tf>2(y) + U3(x)tf>3(y), | (16)
v (x, у) — Vi (x) фх (у) + V2 (x) ф2 (y) + V3 (x) ф3 (у). J
Графики функций <pi (//), <р2 (г/), . • • , фг (у), Фз (.У) показаны на
рис. 3. Можно видеть, что функции поперечного распределения
перемещений в интервале изменения независимой переменной у
удовлетворяют условиям непрерывности и отвечают геометрическим
граничным условиям на линиях у = 0 и у = Н пластинки. Обоб-
щенное , перемещение £А(х) характеризует здесь величину гори-
зонтального перемещения на поверхности пластинки, обобщенное
перемещение; Vi (х) совпадает с прогибом верхнего края пластинки.
Остальные обобщенные перемещения характеризуют смещения вну-
: тренних точек пластинки на линиях у = hr и у = h2.
’ Увеличивая количество делений пластинки по высоте, т. е.
увеличивая число членов в разложениях (1.3), мы будем повышать
точность, расчета и при п—>оо и т—-> оо получим точное решение
плоской --задачи -теории упругости.
Отметим, что приведенный в последнем примере способ выбора
функций <р, (уу и фй (у) для однородной изотропной пластинки может
' быть использован и в том случае, когда заданная пластинка состав-
лена из нескольких горизонтальных слоев с различными упругими
характеристиками Е и у и различной толщиной 8.
Рассмотренными примерами, естественно, не ограничивается
.способ выбора функций ?z(z/), ф*(г/). В зависимости от усло-
вии задачи и желаемой степени точности искомого решения эти
16
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. 1
функции могут быть заданы бесконечным множеством других спо-
собов, как линейно независимые и непрерывные функции коорди-
наты у.
Представление искомых перемещений в виде разложения (1.3)
при конечных числах т и п означает сведение пластинки к системе
с конечным числом степеней свободы в поперечном направлении
при сохранении бесконечного числа степеней свободы в продоль-
ном направлении. Такие системы могут быть названы дискретно-
континуальными в отличие от двумерных расчетных моделей пла-
стинок, описываемых дифференциальными уравнениями в частных
производных и, следовательно, мыслимых как двумерные деформи-
руемые тела, обладающие бесконечным числом степеней свободы
по обеим переменным х и у.
Из разложения (1.3) следует также, что двумерная задача
теории упругости приведена нами к одномерной, ибо по розыскании
всех т функций Ui(x) и п функций VA(x) (функций одного пере-
менного) продольные и поперечные перемещения и (х, у), v (х, у)
пластинки будут определены с известной степенью точности.
3. Для определения функций Ut (х) и Vk (х) используем условия
равновесия элементарной полоски шириной dx = 1, выделенной из
пластинки сечениями х = const и х 4- dx = const (рис. 1,6). Под
условиями равновесия будем понимать согласно принципу возмож-
ных перемещений Лагранжа равенство нулю суммарной работы
всех внешних и внутренних сил этой полоски на любом возможном [
для нее перемещении. I
Возможными продольными перемещениями элементарной полоски 1
при условиях (1.3) являются перемещения Uj — ^j(y) при Uj— 1, !
где j может принимать любое значение из т возможных._Возмож- 1
ные поперечные перемещения полоски определяются в виде пА = фА(у) 1
при Vh = 1, где индекс h обозначает любое из п возможных пере- |
мещений. Таким образом, выделенная вертикальная полоска, к ч 1
деформируемый элемент пластинки, обладает (т 4- п) степенями |
свободы в плоскости пластинки. Из этих степеней свободы т 1
относятся к продольным перемещениям (параллельным оси Ox), I
ап — к поперечным перемещениям (параллельным оси Оу).
По отношению к выделенной полоске роль внешних сил играют
<Эах
увеличенные в 8 раз нормальные напряжения ах, ах 4- dx и ка-
, ^УХ ,
сательные напряжения тух, тух 4- dx, возникающие от взаимо-
действия полоски с отброшенными частями пластинки, а также
заданная нагрузка, компоненты которой в направлении осей Ох ,
и Оу составляют соответственно р(х, у) и q(x,y). Внутренними
силами полоски являются нормальные напряжения <зу и касатель- ?
ные напряжения тху, также увеличенные в 8 раз. |
§ 1] ПРИВЕДЕНИЕ ДВУМЕРНЫХ ПРОБЛЕМ К ОДНОМЕРНЫМ jy
Составляя выражения для работы всех внешних и внутренних
сил полоски на возможных для нее т + п перемещениях, получим:
[r^'.dF + \р(х, y)^jdy = 0 (/=1,2, 3,. .., tri), (1.7)
J v$hdF + J q (x, y)tyh dy= 0 2, 3---ri), (1.8)
где dF = 8 dy — дифференциал площади поперечного сечения пла-
стинки, 8 — толщина пластинки.
Каждое из уравнений (1.7) выражает собой равенство нулю
суммы работ всех внешних и внутренних сил элементарной полоски
при деформациях в продольном направлении. Первым членом здесь
характеризуется работа внешних по отношению к полоске сил
<Эа„
-^-8. Средним членом представлена работа внутренних сдвигающих
сил тхг/8 на деформациях сдвига, которые при равенствах (1.2),
(1.3) и Uj— 1 определяются производной (г/) от функции <р/(г/).
Каждое из уравнений (1.8) получено путем приравнивания нулю
суммарной работы всех сил элементарной полоски на соответствую-
щих перемещениях при изменении деформированного состояния
пластинки в поперечном направлении. Как и в выражении (1.7),
первым членом здесь представлена работа внешних по отношению
^^ух г
к полоске сил средним членом — работа внутренних нор-
мальных сил <зуЪ на поперечных деформациях фА.
Последние члены в уравнениях (1.7), (1.8) относятся к вир-
туальной работе заданной нагрузки р (х, у) и q(х, у).
Внося в формулы (1.1) разложения (1.3) получим выражения
нормальных и касательных напряжений:
m п
°* = г=Ы2 +7 3 v^'k] >
/=1 k=l
п т
Й=1 Z=1
Р гп п
2 (1 + v)[2 + 2
(1-9)
Подставляя теперь в уравнения (1.7) и (1.8) выражения для
искомых напряжений, представленных формулами (1.9), получим
окончательно систему обыкновенных дифференциальных уравнений
относительно искомых функций Ut (х) и Vk (х), состоящую из т
Уравнений, соответствующих пг степеням свободы перемещений
2 В. 3. Власов, Н. Н. Леонтьев
Г“”” ’ , -л, ••«‘Лгц.гоз I
I БИБЛИОТЕКА I
1 у Ве;ш>, У-т <• Звезда»,_
18
ПРИЛОЖЕНИЕ ОБЩЕГО^ ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
полоски в продольном направлении и п уравнений, соответствую-
щих п степеням свободы перемещений этой полоски в поперечном
направлении. Эта система в сокращенной записи имеет следующий
вид:
т 1 т П / 1 . , „
Z=1 i=l k=l
(/= 1,2, 3, ...,т),
- 3 chi) и- + Ц- 2 -
z=i
п 4 __v2
+ (Л = 1, 2, 3,... . n).
А=1
Коэффициенты уравнений (1.10) при выбранных функциях <у,-(р),
/ = 1.2, 3........т), фй(у), фл(г/) (k, h = 1, 2, 3.nj и,
следовательно, известных производных от этих функций <р' (у),
q>'(p), ф^(р), ty’h(ti) определяются как своего рода обобщенные
моменты инерции по формулам:
ал = ац = J <у;ср,- dF,
Ьл = Ьц= ^wftdF,
Cik = dF,
tjk ~ Т/Ф* dF’
fhk = г kh = j фаф/; dF,
Shk = Skh = $ M/i dF,
Chi = фаф/ dF,
thk = dF.
(1.11)
В этих формулах интегралы распространяются на всю длину
полоски (т. е. на ширину заданной прямоугольной пластинки),
dF = c>dy—дифференциал площади поперечного сечения пластинки,
5 = 8 (//) — толщина пластинки, которая в общем случае может
быть и переменной в направлении оси Оу.
Коэффициенты (1.11) могут быть легко вычислены графоанали-
тическими приемами строительной механики при помощи предва-
рительно построенных эпюр для функций <р/(«/), $ь(у) и произ-
водных от них <?!(//), ^(р).
Свободные члены р, = р; (х) (] = 1,2,3,... , tri), qh = qh (x)j
(h = 1,2, 3,..., ri) уравнений (1.10) при заданных нагрузках р (х, у),.
q(x, у) вычисляются, как обобщенные продольные и поперечные]
погонные (отнесенные к единице длины) сллы по формулам:
Р!= \р(х, y)tf>jdy, qh=\q(x,y)$hdy. (1.12)j
§ i] ПРИВЕДЕНИЕ ДВУМЕРНЫХ ПРОБЛЕМ К ОДНОМЕРНЫМ J9
Положительные направления сил р (х, у) и q (х, у) приняты совпа-
дающими с положительными направлениями координатных осей.
В общем случае в формулах (1.12) предполагается, что силы
у) и У У) распределены по высоте пластинки по какому-
либо произвольно заданному закону от координаты у. В частности,
формулы (1-12) распространяются также и на внешнюю нагрузку,
приложенную на продольных краях пластинки и состоящую в общем
случае из заданных на этих краях сдвигающих и нормальных сил.
В этом случае интегралы в формулах (1.12), в соответствии с фи-
зическим смыслом определяемых по этим формулам величин (воз-
можная работа заданной нагрузки), следует вычислять с учетом
сосредоточенных факторов. Так, например, если, кроме массовых
сил р(х,у) и <7 (х, у), по верхнему краю пластинки действуют
сдвигающие и нормальные силы р(х, 0), <7 (х, 0), то формулы (1.12)
в развернутом виде запишутся следующим образом:
Р/= р (х) (0) + J р (х, y)tf>j(y)dy, |
( (1 •1
Ун = У (х) фа (0) + ) у (х, у) фл (у) dy, J
где <р/(0), фа (0) — значения функций (р3-(р) и фа (у) при у — 0, т. е.
на верхнем крае пластинки. Такие интегралы, учитывающие
в интервале интегрирования как распределенные, так и сосредо-
точенные факторы, носят название интегралов Стилтъеса.
4. Из современных методов интегрирования симметричной
системы обыкновенных дифференциальных уравнений с постоян-
ными коэффициентами наиболее эффективным является метод
А. Н. Крылова, позволяющий привести эту систему наиболее
быстро к одному эквивалентному ей дифференциальному уравне-
нию. В нашем случае это уравнение будет порядка 2 (т + п).
Отсюда следует, что искомые функции (7/(х), V& (х), удовлетво-
ряющие системе уравнений (1.10), будут определены с точностью
до 2(т + п) произвольных постоянных интегрирования. Число
этих постоянных находится в полном соответствии с числом
независимых геометрических условий, которые могут быть заданы
для крайних сечений пластинки х = 0 и х — I (I — длина пластинки
fe продольном направлении).
Действительно, положение всех точек любого из сечений х = const
после деформации характеризуется т + п независимыми величинами,
из которых т величин Ui (х) определяют положение этих точек
® продольном направлении (из плоскости х = const), а п величин
К* (х) в плоскости поперечного сечения. Мы можем, таким образом,
для.одного крайнего сечения пластинки произвольно задаться т + п
величинами. Для двух сечений х = 0 и х = /, ограничивающих данную
пластинку по ее длине, число независимых условий равно 2(т + п),
что соответствует числу произвольных постоянных интегрирования.
2*
20
Приложение общего вариационного метода
[гл. I
Распоряжаясь этими постоянными, мы можем получить решение
для данной пластинки при самых разнообразных геометрических
граничных условиях, заданных относительно продольных и попе-
речных перемещений. Рассмотрим задачу о пластинке, для кото-
рой граничные условия в сечениях х = 0 и х = I заданы в усилиях
или, в случае смешанной краевой задачи, частью в перемещениях.
Заметим, что напряжения сх и хух по сечению х = const при
выбранных функциях («/) и ф* (//) могут быть выражены
через т + п независимых обобщенных статических величин. Исходя
из понятия о виртуальной работе нормальных и сдвигающих сил
ах3 и т^З поперечного сечения пластинки на каждом из т + п
возможных перемещений точек этого сечения, получим для обоб-
щенных статических величин формулы:
Т} (*) = j dF (/= 1, 2, 3,, т),
(1-14)
Sh (х) = j dF (h = 1,2, 3, . . . , n),
где dF = 8 dy.
В формулах (1.14) интегралы распространяются на все попе-
речное сечение пластинки. Величины Т, (х) и Sh (х) представляют
собой обобщенные продольные и поперечные силы в сечении х = const
пластинки. Рассматривая эти величины как внутренние силы пла-
стинки, выразим их через основные функции Ui (х) и Vk(x). На
основании выражений (1.9), (1.11) и (1.14) будем иметь:
т
TI(x) = E^aliUi
i=l
sh(x) = g(2 2
3 Z=1 А=1
т
(z, j = 1, 2, 3,’. . m),
(1-15)
(h, k = 1,2, 3, . ..,«). I
Выражения (1.15) и позволяют поставить на поперечных краях
пластинки х = 0 и х = I 2(т + п) обобщенных граничных условия,
если последние заданы в напряжениях.
Действительно, пусть по какому-либо краю х = х0 пластинки
действует заданная система погонных нормальных усилий р° (х0, у)
и сдвигающих усилий <7° (х0, у), которые, как функции от у, заданы
совершенно произвольно (рис. 4).
Выделяя у края пластинки элементарную полоску dx и рассма-
тривая, как и ранее, условия равновесия этой полоски в смысле
принципа возможных перемещений, получим:
(<?о8 — р°) ip dy = 0
J (т°х8— ф>) tyhdy = 0
(/ = Г, 2, 3..........т),
(/г = 1, 2, 3, .. ., п).
(1-16)
S 21
ДЕФОРМАЦИИ УПРУГОГО ОСНОВАНИЯ В ПЛОСКОЙ ЗАДАЧЕ 2J
Сопоставляя выражения (1.14) и (1.16), будем иметь:
Sh (х) = j qo^ dy. T^x) = \p°^dy, (1.17)
Таким образом равенства (1.17) устанавливают зависимость
между обобщенными силами (1.15) и заданными внешними нагруз-
ками в сечении х = х0.
Имея общий интеграл дифференциальных уравнений (1.10)
и пользуясь формулами (1.17) и (1.15), можно определить дефор-
мации и напряжения пластинки при самых разнообразных гра-
ничных условиях в сечениях х = 0 и х—1, заданных в уси-
лиях, в перемещениях или частью в усилиях, а частью в пере-
мещениях.
2. Определение деформаций упругого основания в^условиях
плоской задачи. Расчетные схемы упругого основания
Рассмотрим теперь второй случай плоской задачи, по внешней
форме противоположный первому. В качестве примера возьмем
упругое основание, представляющее собой сжимаемый слой толщи-
ной Н, расположенный на бесконечно жестком основании (рис. 5).
Будем предполагать, что размеры сжимаемого слоя хотя бы в одном
направлении, например в направлении оси z, очень велики, а внеш-
няя нагрузка не зависит от координаты z и лежит в плоскостях,
параллельных плоскости хОу. Кроме того, будем считать, что
толщина упругого основания, условия его опирания, значения упру-
гих характеристик и все прочие условия остаются в направлении
оси z постоянными. Подобный случай в теории упругости носит
название плоской деформации, поскольку перемещения всех точек
тела происходят в плоскостях, перпендикулярных к оси г.
Выделим из упругого основания двумя плоскостями, параллель-
ными плоскости хОу, узкую пластинку толщиной 3 (рис. 5). Заметим,
ЧТР каждая такая пластинка находится в одинаковых условиях
с любой соседней. Напряжения ах, ау, txy, хух, деформации гхх,
ъХу и перемещения и и v такой пластинки являются функциями
22
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
только двух координат. Как и в рассматриваемой ранее задаче
о плоском напряженном состоянии, связь между этими напряже-
ниями, деформациями и перемещениями устанавливается уравне-
ниями (1.1) и (1.2). Различие заключается лишь в значении
упругих постоянных, входящих в уравнения (1.1). В случае плоской
деформации вместо характеристик Е и v в выражения (1.1)
следует подставить величины Ео и v0, определяемые по формулам
F м
Ео = -^-, >0 = ^, (2.1)
1 - % 1 _ ГГ>
где Егр и vrp — соответственно модуль упругости и коэффициент
Пуассона материала основания (грунта).
Для определения деформированного и напряженного состояния
выделенной пластинки снова воспользуемся методом перемещений,
для чего искомые перемещения и (х, у) и v (х, у) представим в виде
разложений (1.3). Составляя условия равновесия элементарной
полоски шириной dx =1 (см. рис. 1) подобно тому, как это было
сделано в § 1, мы получим систему (т + п) обыкновенных диф-
ференциальных уравнений относительно одномерных функций U; (х)
и К (*):
m т п
3 ayU- - Цр 3 + 2 ^tik - Цр Cik) Vk +
Z=1 1 = 1 J=1
1 — v2
+ ~~p—~ Pi ~ 6 (/’ = 1, 2, 3, . . . , tn),
m , , , n n
- 2 ~ ЧгМ 2 - 2+
k=i k=i
1 - v2
+ —~qh = 0 (h= 1,2,3, . . . ,n).
^0
(2.2)
^2] ДЕФОРМАЦИИ УПРУГОГО ОСНОВАНИЯ в ПЛОСКОЙ ЗАДАЧЕ 23
Можно видеть, что дифференциальные уравнения (2.2) отли-
чаются от аналогичных уравнений (ЕЮ) предыдущего параграфа
только величиной упругих постоянных Е и v. Коэффициенты же
о /л/этих уравнений определяются, как и ранее, по
формулам (1.11) и зависят только от вида функций <рг(г/) и фА(у).
Свободные члены р. и qh уравнений (2.2) представляют собой
работу заданных горизонтальной р (х, у) и вертикальной q (х, у)
нагрузок соответственно на перемещениях <р;. (у) и (у) и вычи-
сляются в общем случае по формулам (1.13).
При рассмотрении работы упругого основания массовые силы,
распределенные в толще основания, чаще всего не учитываются.
Обычно предполагается, что упругое основание работает только
под нагрузкой, приложенной к его поверхности. В этом случае
грузовые члены уравнений (2.2) определяются в виде:
Р^Р^-ъ-т. | (23)
<7Й = <7(*МЛ(°)> I
где р (х) и q (х) — соответственно сдвигающие и нормальные по-
•верхностные силы, a (0) и (0) — значения функций у. (у) и
фл (у) на поверхности основания (при у = 0).
По определении функций Ui (х) и Vk (х) из системы уравне-
ний (2.2) и соответствующих граничных условий перемещения и (х, у)
и v (х, у) в упругом основании могут быть найдены по форму-
лам (1.3), а напряжения ах, ау, тху — по общим формулам (1.9),
в которых значения упругих постоянных следует принять со-
гласно (2.1).
Таким образом, система обыкновенных дифференциальных урав-
нений (2.2) позволяет определять напряженное и деформированное
состояние упругого основания, принимаемого за линейно деформи-
руемую среду конечной толщины Н, в условиях плоской дефор-
мации. При ограниченном числе членов, принятом в разложениях
(1.3), решение (2.2) можно расценивать как известное приближение
к точному решению теории упругости. Вместе с тем можно считать,
что дифференциальными уравнениями (2.2) характеризуется неко-
торая обобщенная модель упругого основания, построенная на базе
общего вариационного метода. Действительно, выбирая для огра-
ниченного числа функций <рДг/) и ф/г (у) различные выражения,
мы будем получать ряд моделей упругого основания, приближен-
ных с точки зрения теории упругости, но достаточно точных с точки
зрерия практических приложений. Увеличивая количество членов
в формулах (1.3), мы будем все более совершенствовать исходную
модель упругого основания и тем самым увеличивать точность
решения.
24
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
Следует отметить, что увеличение числа членов в разложениях
(1.3) является нежелательным, так как оно влечет за собой повы-
шение порядка системы дифференциальных уравнений (2.2) и вслед-
ствие этого приводит к более сложным вычислениям. Повысить
точность решения можно другим путем, а именно — более удачным
выбором функций <pz(t/) и Ранее уже отмечалось, что в рас-
сматриваемом методе функции <pz (у) и ф/г (у) должны выбираться
в соответствии с конкретным содержанием задачи и с нашими
представлениями о возможном характере распределения переме-
щений по высоте основания. Если функции <рДу) и (у) задать
по некоторому закону, являющемуся результатом либо опытных
данных, либо более точных теоретических исследований, то при
минимальном числе членов, принятых в разложениях (1.3), можно
получить решения, достаточно верно отражающие действительность.
Покажем на нескольких примерах возможные способы выбора
функций (?. (у) и (у) при рассмотрении работы упругого основания.
Другими словами, приведем некоторые возможные расчетные модели
упругого основания, построенные на основе изложенного вариа-
ционного метода.
Предположим, что рассматривается упругое основание, в котором*
горизонтальные перемещения или отсутствуют, или малы настолько,
что ими можно пренебречь. В этом случае можно принять:
и (х, у) = 0, ।
v(x,y) = 3 П(х)ФИУ). | (2'4)
k=l '
При этом система дифференциальных уравнений (2.2) будет
содержать только уравнения второй группы и запишется в виде
. П П 1 — V2
з - 3= °’ (2-5)
k=l k=l
где
= J Ш dF> Shk = J ФЖ dF'
Можно считать, что дифференциальные уравнения (2.5) описы-
вают определенную модель упругого основания, в основу которой
положена гипотеза о том, что горизонтальные перемещения в основа-
нии отсутствуют. Такая модель способна «распределять» нагрузку,
т. е. способна вследствие связности работать и за пределами при-
ложения нагрузки. Схематически модель, описываемая дифферен-.
циальными уравнениями (2.5), может быть представлена как система
упругих элементарных столбиков (пружин), между которыми возни-
Рис. 6.
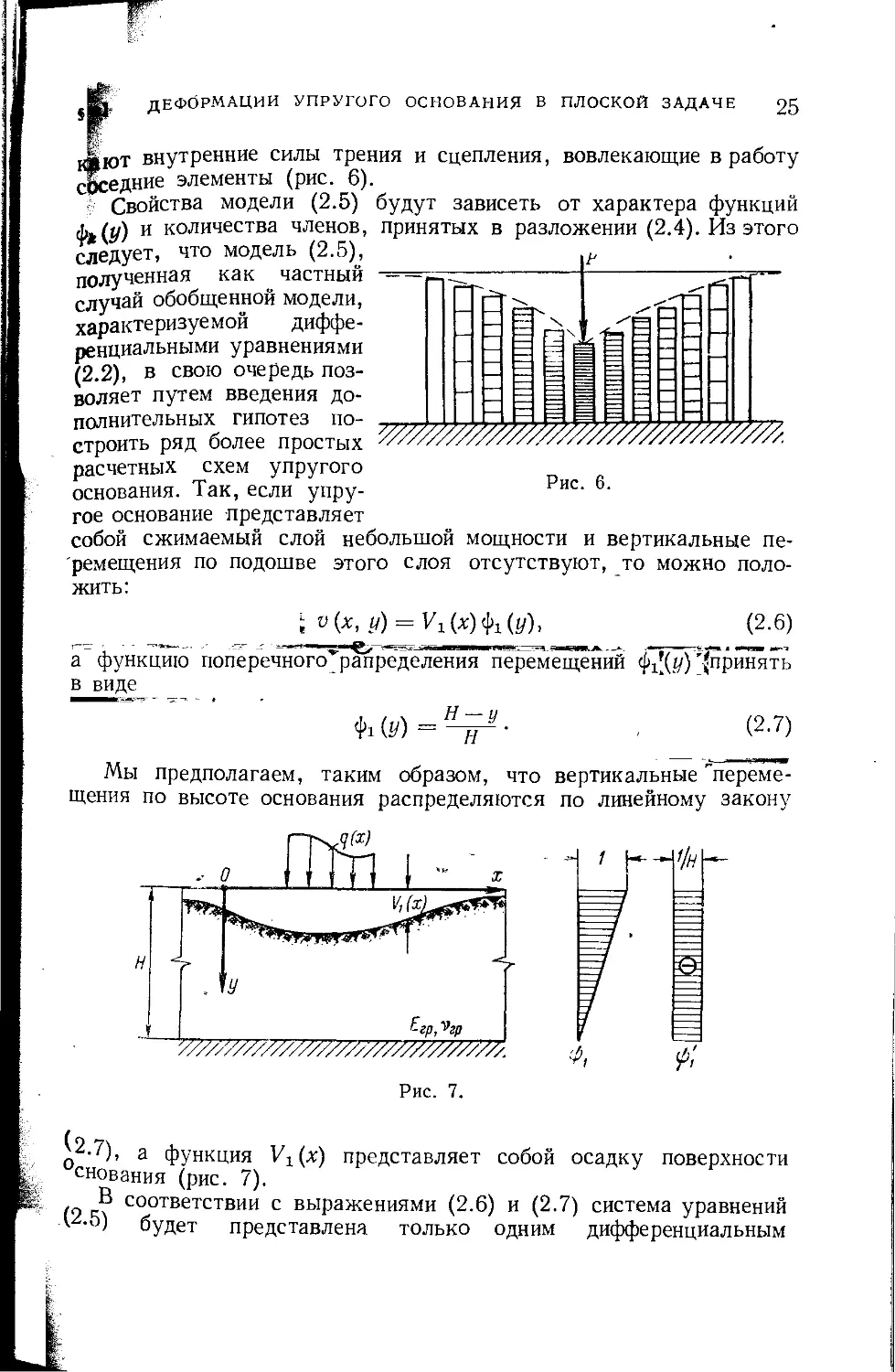
ДЕФОРМАЦИИ УПРУГОГО ОСНОВАНИЯ в ПЛОСКОЙ ЗАДАЧЕ 25
к»ют внутренние силы трения и сцепления, вовлекающие в работу
соседние элементы (рис. 6).
' Свойства модели (2.5) будут зависеть от характера функций
ф. (у) и количества членов,
следует, что модель (2.5),
полученная как частный
случай обобщенной модели,
характеризуемой диффе-
ренциальными уравнениями
(2.2), в свою очередь поз-
воляет путем введения до-
полнительных гипотез по-
строить ряд более простых
расчетных схем упругого
основания. Так, если упру-
гое основание представляет
собой сжимаемый слой небольшой мощности и вертикальные пе-
ремещения по подошве этого слоя отсутствуют, то можно поло-
жить:
^о(х, г/) = У1(х)ф1(у), (2.6)
а функцию поперечного’ршгределения перемещений (^(у)'(принять
в виде
Ф1(У)=^‘ , (2-7)
Мы предполагаем, таким образом, что вертикальные "переме-
щения по высоте основания распределяются по линейному закону
q2-7), а функция Vx(x) представляет собой осадку поверхности
снования (рис. 7).
, соответствии с выражениями (2.6) и (2.7) система уравнений
U-5) будет представлена только одним дифференциальным
26
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
(ГЛ. 1
уравнением
—2—— sijVi Ч----------px-^-q1=Q, (2.8)
£о
где
ги =\ ^dF = ^-,
J * о
Н (2.9)
8ц = j Ф? dF = J .
О J
Если считать, что внешняя нагрузка q (х) приложена только
к поверхности основания, грузовой член дх определится по формуле
(2.3) и будет совпадать по величине с этой нагрузкой:
71 = 9(х).
Модель упругого основания, характеризуемая уравнением (2.8)
может быть названа моделью с двумя характеристиками или, для
краткости, однослойной моделью (см. [11]).
Напряжения в однослойной модели вычисляются приближенно
по общим формулам (1.9) подстановкой в них выражений (2.4),
(2.6) и (2.7):
м; =
Во
(1 - $ Н
Хух — 'ху
Ео
(2.10)
VxW,
1
I
I
Можно видеть, что нормальные напряжения ау в однослойной
модели остаются постоянными по высоте основания, а касательные
напряжения меняются по линейному закону.
В случае, если толщина И сжимаемого слоя достаточно велика,
выбор функции фх по линейному закону (2.7) будет весьма схема-
тически характеризовать работу упругого основания, так как в этом
случае уже нельзя считать, что напряжения ау по всей высоте
слоя сохраняют постоянную величину Для того чтобы уточнить
расчетную схему, не увеличивая количества членов в разложении
(2.6), функцию фх следует выбрать так, чтобы она более пра-
вильно отражала естественный закон затухания осадок и напря-
жений по глубине основания. Например, можно положить (рис. 8)
ф = shy (Я-у) 2 Н)
где т — некоторый постоянный коэффициент, характеризующий
быстроту затухания осадок по глубине основания. Решение задачи
§ 2]
ДЕФОРМАЦИИ УПРУГОГО ОСНОВАНИЯ В ПЛОСКОЙ ЗАДАЧЕ 27
пои этом будет описываться дифференциальным уравнением (2.8),
однако коэффициенты ru и su этого уравнения должны опреде-
ляться с_ учетом выражения (2.11).
Рис. 8.
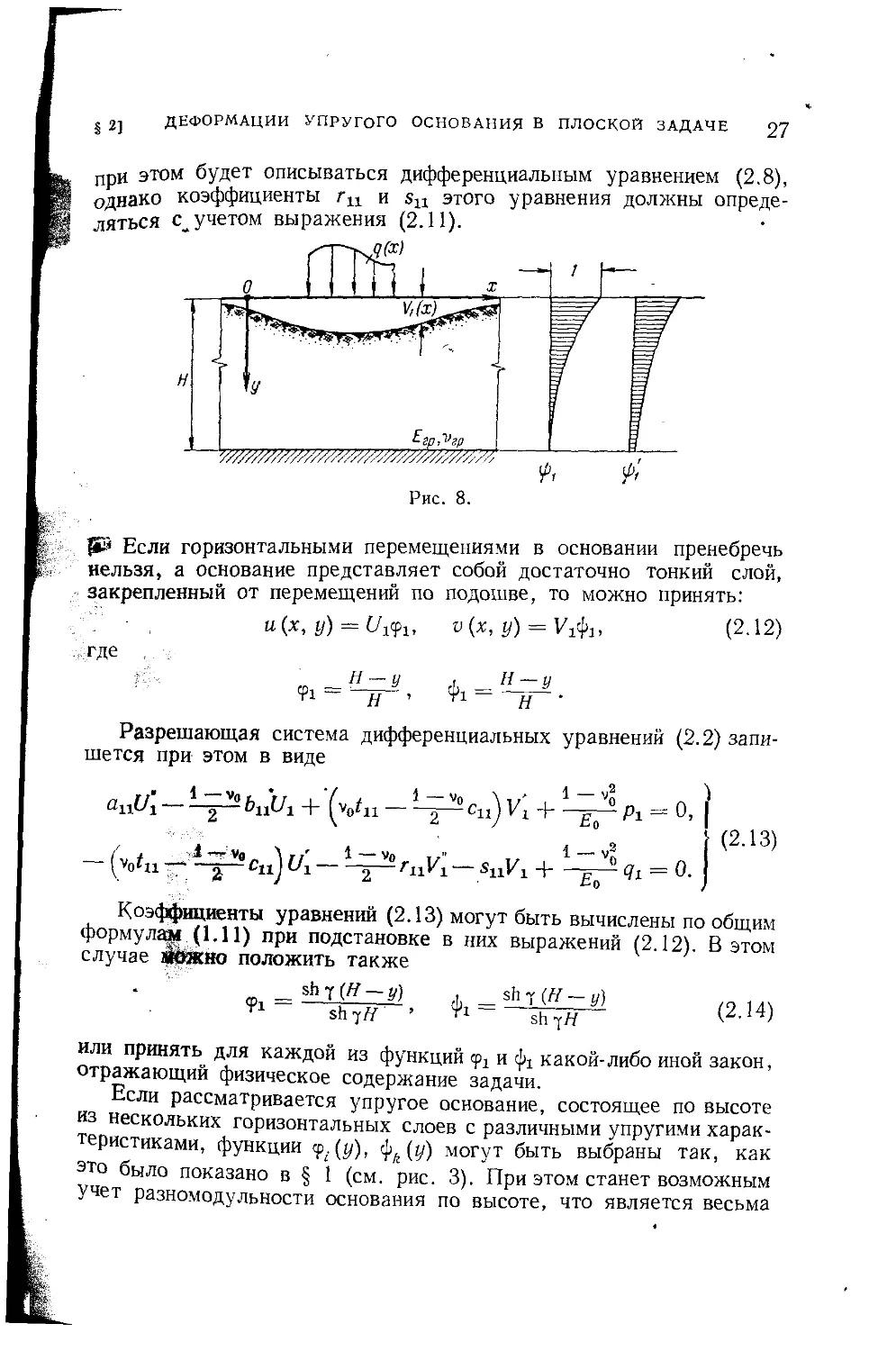
{83 Если горизонтальными перемещениями в основании пренебречь
нельзя, а основание представляет собой достаточно тонкий слой,
закрепленный от перемещений по подошве, то можно принять:
, и(х, у) = о(х, р) = У1ф1, (2.12)
где .
Разрешающая система дифференциальных уравнений (2.2) запи-
шется при этом в виде
ап^1-------------------------2—"I |
°2 (2-13)
[v(Ai Hi-----2~^riiVi — siiVi H-7i = o. j
Коэффициенты уравнений (2.13) могут быть вычислены по общим
формула^ (1.11) при подстановке в них выражений (2.12). В этом
случае можно положить также
r sh?# ’ т1 sh^
или принять для каждой из функций <р2 и фх какой-либо иной закон,
отражающий физическое содержание задачи.
Если рассматривается упругое основание, состоящее по высоте
из нескольких горизонтальных слоев с различными упругими харак-
теристиками, функции <pz(y), ф/; (у) могут быть выбраны так, как
это было показано в § 1 (см. рис. 3). При этом станет возможным
учет разномодульности основания по высоте, что является весьма
28
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. 1
существенным при решении целого ряда задач. Полученную таким
образом модель упругого основания можно назвать многослойной
моделью. Отметим, что многослойная модель, может быть принята
и при рассмотрении работы однородного упругого основания, тол-
щина которого Н достаточно велика. В этом случае по сравнению,
например, с однослойной схемой, описываемой уравнением (2.8)
или системой двух уравнений (2.13), многослойная модель позволит
значительно повысить точность решения.
Таким образом, плоская обобщенная модель упру-
гого основания, свойства которой описываются дифферен-
циальными уравнениями (2.2), позволяет путем того или иного
выбора функций <р;. (у) и (у) получать бесчисленное множество
различных схем упругого основания, достаточно верно отражающих
ту или иную конкретную задачу. Поскольку важнейшей особен-
ностью расчета конструкций на упругом основании является пра-
вильное моделирование самого упругого основания, общий вариа-
ционный метод в этом смысле представляет широкие возможности.
Большинство из тех расчетных моделей упругого основания,
которые могут быть получены на базе общего вариационного метода,
оказываются более простыми, чем схема упругой полуплоскости,
положенная, например, в основу известных методов Б. Н. Же-
мочкина и М. И. Горбунова-Посадова. В результате этого стано-
вится возможным расчет сложных конструкций с учетом упругой
податливости оснований.
В дальнейшем мы будем в основном рассматривать лишь наибо-
лее простую расчетную схему упругого основания — модель с двумя
упругими характеристиками. Уже эта простая модель позволяет
более правильно учесть упругие свойства грунта, чем например,
известная модель Винклера — Циммермана. Вместе с тем модель
упругого основания с двумя характеристиками дает возможность
при помощи простого математического аппарата производить расчет
как балок и плит, так и более сложных систем на упругом осно-
вании.
§ 3. Плоская модель упругого основания с двумя
характеристиками
1. Основные дифференциальные зависимости.
Пусть упругим основанием служит сжимаемый слой толщиной Н
(рис. 9). Предположим, что перемещения в этом слое, вызванные
действием поверхностной нагрузки, могут быть приближенно пред-
ставлены в виде
и(х, y) = Q, v(xt y) = V1(x)^1(y), (3.1)
где ф1 («/) — функция координаты у, выбираемая в зависимости от
условий задачи.
ПЛОСКАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
29
§ ж
Вивыбор перемещений в виде (3.1) предполагает, что основную
EL в работе упругого основания играют вертикальные переме-
щении v(x, у)- Горизонтальные
Др перемещения и (х, у) счита-
ются настолько малыми, что ими
можно пренебречь.
Заданным перемещениям
(3 1) в упругом основании соот-
ветствуют деформации
= Vi(x)cpi(t/), >
гху = К(х) фх (у), J (3-2)
гхх = О, j
где £хх и sw — линейные деформации соответственно в направле-
нии осей Ох и Оу, а еху — деформация сдвига.
Нормальные и касательные напряжения вычисляются по общим
формулам (1.9) и имеют вид
= )
‘ (3.3)
Д-г = 2 (1 4 vo) 1
Для задачи о плоской деформации упругого основания постоян-
ные Ео и v0 определяются формулами
где £гр и vrp — соответственно модуль упругости и коэффициент
Пуассона материала основания.
Вследствие того, что из всех перемещений сохраняется только
одно обобщенное перемещение Vj. (х), система дифференциальных
уравнений (2.2), как уже было показано в предыдущем параграфе,
будет состоять здесь только из одного уравнения второй группы,
соответствующего одной заданной функции фх(у):
+ (3.5)
~ со
Грузовой член уравнения (3.5) представляет собой работу
заданной поверхностной нагрузки q (х) и определяется по формуле
<71 W = ?МФ1(0)> (3.6)
еде фх (0)'— значение функции фх (у) у поверхности основания
(при у = 0).
30
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. 1
Коэффициенты уравнения (3.5) имеют следующий вид:
Гц = J ф?(г/) dF, I °„ 2 (з.7) 8ц = J (y)dF, 0 )
где dF = о dy. После почленного Ео ,, умножения на величину дифферен-
циальное уравнение (3.5) может быть представлено в виде
2/Vi — kVi + q^ = 0, (3.8)
где г £qSii ) ~ 1 - V2 p 0 1 M j Eprlt | 4 (1 + v0) )
Дифференциальным уравнением (3.8) выражена зависимость
между вертикальными перемещениями (осадками) основания и на-
грузкой, приложенной к его поверхности. От известной зависимости,
вытекающей из гипотезы прямой пропорциональности {гипотеза
коэффициента постели), уравнение (3.8) отличается наличием члена
со второй производной от обобщенного перемещения Ki. Этим членом
при коэффициенте 2/ учитывается влияние касательных напряже-
ний, возникающих в упругом основании.
Таким образом, рассматриваемая модель упругого основания
принципиально отличается от модели Винклера — Фусса*). В ре-
зультате учета касательных напряжений эта модель способна «рас-
пределять» нагрузку. Это означает, что рассматриваемая схема
упругого основания получает осадки не только непосредственно
под местом приложения нагрузки, но и за пределами последней
(см. рис. 6).
Свойства упругого основания, описываемого дифференциальным
уравнением (3.8), зависят от величины двух интегральных харак-
теристик (3.9). Первая характеристика k определяет работу упру-
гого основания на сжатие. В этом смысле коэффициент k анало-
гичен коэффициенту постели. Вторая характеристика t определяет
* Гипотеза коэффициента постели, обычно называемая в технической
литературе гипотезой Винклера, предложена впервые русским академиком
Н. И. Фуссом в 1801 г.
ПЛОСКАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
31
паботу упругого основания на сдвиг (срез), т. е. определяет «рас-
пределяющую» способность основания *).
Для решения дифференциального уравнения (3.8) необходимо
пассмотреть граничные условия задачи, которые, как отмечалось
аыше, должны быть поставлены в интегральной форме: в обоб-
щенных усилиях или перемещениях.
В соответствии с формулами (3.1) и (3.3) обобщенные силы
упругого основания (1.10) принимают вид:
Sx =
(3.10)
[2 (1 + v0)
2. Выбор функции поперечного распределения
перемещений. Распределение перемещений и нормальных на-
пряжений по высоте Н рассматриваемого упругого основания,
а следовательно, и основные свойства этого основания определяются
функцией ср! (г/). В предыдущем параграфе уже было сделано
несколько замечаний 6 возможном выборе функции фт(у). Так,
было отмечено, что для достаточно тонкого сжимаемого слоя,
в пределах которого нормальные напряжения ау остаются постоян-
ными, можно принять
<Ш=^. (З.Н)
Функция (3.11) соответствует неподвижному закреплению сжи-
маемого слоя по его подошве (см. рис. 7), постоянной деформа-
ции удлинения в направлении оси Оу
*уу = ~У1 (х) -Jj-
и постоянной величине нормальных напряжений по высоте слоя
(3.12)
Н-у
Vi (х)-
Я(1-у02) м ’
Коэффициенты (3.7) определятся при этом в форме
н
Г t 2 j г? ЪН
гп= =-3-,
О
Sn = ф!2 dF = ,
_______________ о
*) Следует отметить, что П. Л. Пастернак предложил называть характери-
стики k и t двумя коэффициентами постели и в соответствии с этим одно-
слойную модель упругого основания — моделью с двумя коэффициентами по-
стели [62]. Отметим также, что дифференциальное уравнение (3.8) совпадает по
виду с решением, полученным М. М. Филоненко-Бородичем для его простей-
шей модели упругого основания [76], а также с решением Вигхарта.
а
(3.13)
32
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
а упругие постоянные дифференциального уравнения (3.9) при-
мут вид
k = £°5
, _ ЕОЪН
12(14- v0) •
Для обобщенной поперечной силы упругого основания (3.10)
получим выражение
(3.15)
Формулы (3.14) и (3.15) характеризуют работу упругого осно-
вания, осадки которого в поперечном направлении определяются
Рис. 10.
линейным законом (3.11). Следует, однако, отметить, что при
расчете конструкций на упругом основании формулы (3.14) и со-
ответствующий им закон распределения осадок (3.11) могут быть
приняты и тогда, когда упругое основание имеет достаточно
большую толщину, состоит из ряда сжимаемых слоев с различ-
ными коэффициентами упругости и, в частности, представляет
собой упругую полуплоскость. В этом случае под величиной И,
входящей в формулы (3.11) и (3.14), следует понимать высоту
некоторого расчетного слоя, эквивалентного в смысле своей ра-
боты заданному упругому основанию.
Заменяя реальное упругое основание эквивалентным слоем,
в пределах которого нормальные напряжения аи принимаются по-
стоянными (рис- Ю), можно определить толщину Н этого слоя,
например, из сопоставления относительны/ осадок поверхности
основания, характеризуемых уравнением (3.8), с теми, которые
имеют место в действительности.
Если по каким-либо соображениям нежелательно вводить по-
нятие об эквивалентном расчетном слое, а упругое основание
имеет достаточно большую толщину, функция поперечного распре-
S 3]
ПЛОСКАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
33
деления осадок фх (у) может быть принята в виде
<3-16)
где И — глубина залегания материкового слоя (для упругой полу-
плоскости Н—>оо), а у— коэффициент, зависящий от упругих
свойств материала основания и характеризующий быстроту зату-
хания осадок по глубине основания.
В соответствии с выражением (3.16) нормальные напряжения
в основании определяются формулой
(3-17)
°и =
Ео7 у ch? (Я-у)
Я(1-^) 1 ’ &уН
а упругие постоянные дифференциального уравнения (3.9) примут
вид: k = —ф*, t = ЕоЪН Я(1-м»)Т’ “ 12 (1 + м0) (3.18)
где у Я sh yff ch у И -4- уН Ук 2 зЬ8ТЯ (3.19)
3 1 sh уН ch уН — уН 2 уН sh2yfi '
Для обобщенной поперечной силы основания получим, как и
ранее, формулу
н
S1==\^1dF = 2tV'1(x), (3.20)
о
где характеристика t определяется вторым из выражений (3.18).
Можно видеть, что нормальные напряжения на этот раз не
остаются постоянными, а меняются по закону гиперболического
косинуса (см. рис. 8 и рис. 14). Характеристики упругого осно-
вания (3.18) отличаются от полученных ранее характеристик (3.14)
постоянными коэффициентами ф* и ф/, которые позволяют более
точно учесть упругие свойства грунта.
Отметим также, что характеристики (3.14) при увеличении
толщины деформируемого слоя И получают либо бесконечно ма-
лые, либо бесконечно большие значения, в то время как характе-
ристики k и t, определяемые формулами (3.18), в пределе при
Н —> ос имеют конечную величину. Это означает, что формулы
(3.16) и (3.18) применимы в том случае, когда толщина упругого
слоя весьма велика и практически ее можно положить равной
бесконечности. Другими словами, функция (3.16) может быть
рекомендована для приближенного расчета конструкций на упру-
гой полуплоскости.
3 В. 3. Власов, Н. Н. Леонтьев
34 ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ. I
Аналогичные результаты могут быть получены и в том случае,
когда в качестве функции фх {у) принята показательная функция
W = (3.21)
также достаточно хорошо соответствующая нашим представле-
ниям о характере затухания перемещений и напряжений по глу-
бине упругого основания.
Естественно, что выбор функций поперечного распределения
осадок ф1 (у) в виде (3.11), (3.16) и (3.21) не является единственно
возможным. В зависимости от условий задачи эти функции могут
быть представлены в виде различных аналитических выражений,
соответствующих либо решениям теории упругости, либо экспери-
ментальным данным.
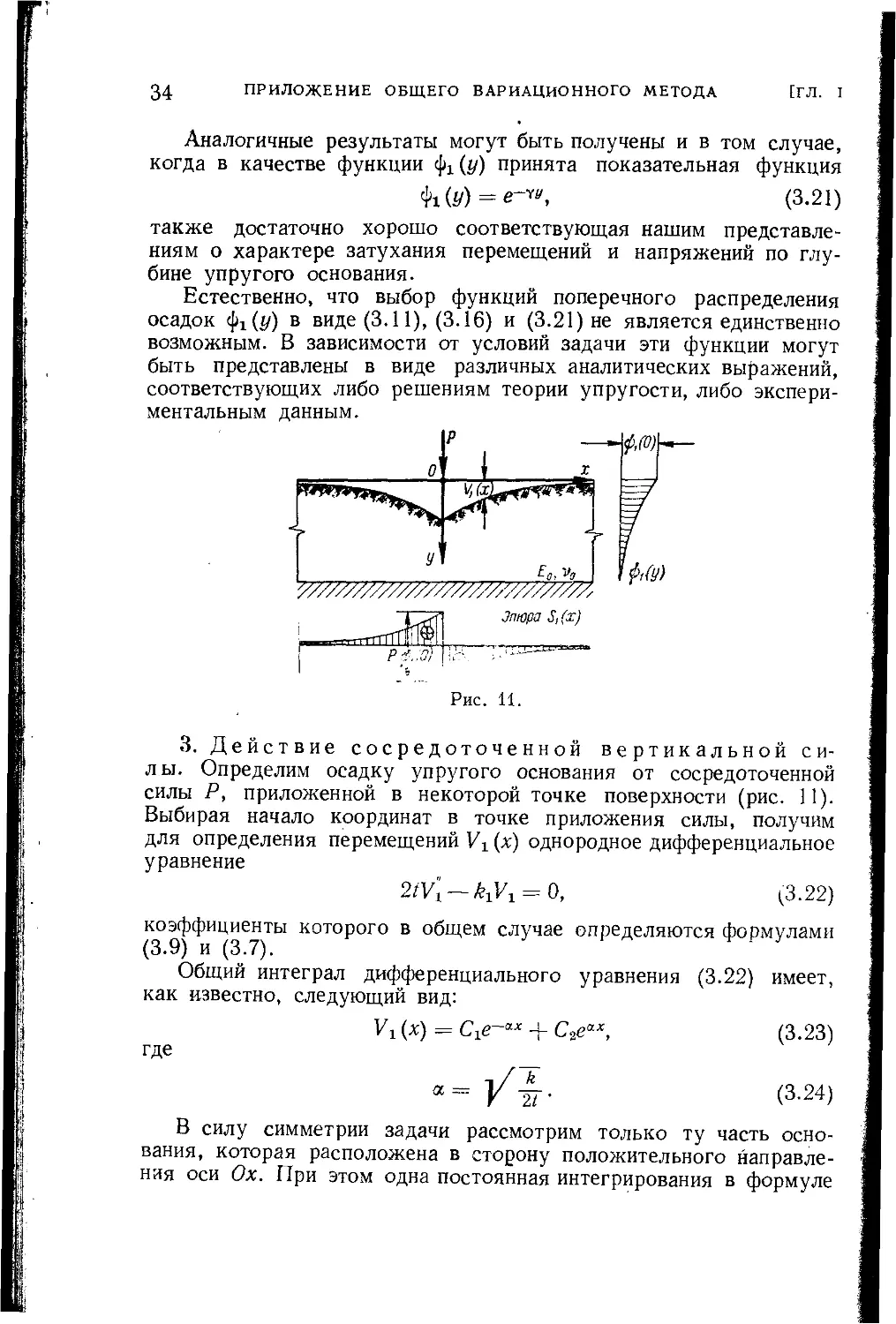
Рис. 11.
3. Действие сосредоточенной вертикальной си-
лы. Определим осадку упругого основания от сосредоточенной
силы Р, приложенной в некоторой точке поверхности (рис. 11).
Выбирая начало координат в точке приложения силы, получим
для определения перемещений (х) однородное дифференциальное
уравнение
2iV\ —= 0, (3.22)
коэффициенты которого в общем случае определяются формулами
(3.9) и (3.7).
Общий интеграл дифференциального уравнения (3.22) имеет,
как известно, следующий вид:
Vi (х) = Суг~ах + С2еах, (3.23)
где _
«=/4- <3-24)
В силу симметрии задачи рассмотрим только ту часть осно-
вания, которая расположена в сторону положительного направле-
ния оси Ох. При этом одна постоянная интегрирования в формуле
5 з] ПЛОСКАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
35
(3.23) определится из того условия, что осадки основания в точ-
ках, бесконечно удаленных от места приложения нагрузки, равны
нулю:
прих—>оо V1(x)->0. (3.25)
Из условия (3.25) следует, что
С2 = 0.
Для определения второй произвольной постоянной рассмотрим
статические условия, заданные в сечении х = 0.
Согласно своему физическому смыслу обобщенная поперечная
сила упругого основания Si (х), характеризующая работу всех
сил сечения х = const на единичном возможном перемещении
ц1(х, у) = 1 • epi (у) при Уг(х)= 1, терпит разрый в тех сечениях,
где к поверхности упругого основания приложены сосредоточен-
ные силы (см. рис. 11).
Исходя из этого и учитывая симметрию задачи, для опреде-
ления второй постоянной интегрирования С\ получим условие:
при х = 0 5^0) = — 4~Ф1(0), (3.26)
где <pi(0) — значение функции фДу) у поверхности основания.
Замечая, что обобщенная поперечная сила определяется
формулой (3.10), а вертикальные перемещения основания форму-
лой (3.23), условие (3.26) можно переписать в виде
2а/С1 = -^-ф1 (°>-
откуда
. _ р Фх (0)
1 4 at
(3.27)
Перемещение любой точки упругого основания может быть
теперь представлено в форме
ц(х,у) = Р^е—фДу), (3.28)
где
k ь E°s^ t = Е°гп
It ’ 1 — ч0 ’ ' 4 (1 + v°) ’
и и
Гц = 8 5 Ф1 (у) dy, su = 8 J Ф12 (у) dy.
о о
(3.29)
Если функция поперечного распределения перемещений выбра-
на в виде линейной зависимости (3.11), то формула (3.28) пере-
пишется следующим образом:
и (х, у) =
3 (1 ~$ Р е-а_хн-у
/6 (1 — v0) Е1‘ Н
(3.30)
3!
36
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
где
l/A._____1 Уб(1—v0)
а ~ V 2t n (1 - v0)
В качестве примера на рис. 12 приведена безразмерная эпюра
осадок поверхности упругого основания V(х), рассчитанная по
формуле (3.30) для несколь-
ких значений аргумента х/Н
при v0 = 0.
Величины действительных
осадок поверхности основания
определяются при этом по
формуле
Из приведенного графика
можно видеть, что затухание
осадок в стороны от места
приложения нагрузки проис-
ходит в однослойном основа-
нии сравнительно быстро,
согласно (3.16) формула (3.28),
перемещения в упругом основании,
о,о
0,2
Ofi
0,6
0,8
КО
1,2
2.
Эпюра V(x)
о________х/н
'V(x)
Рис. 12.
При выборе функции фг (у)
характеризующая вертикальные
будет иметь следующий вид:
, ч 3(1
V Кб (1 -v0)
1 Р е~ах
shy И
(3.31)
где
а
т/ А _ * Уб<1—у0) ,
V 2t ~ Н (1-vo)
3 1 shyH chyH—уН
ТуН shtyH ’
(3.32)
ф = Н 1 / 1 gh7tfehT//+T//
‘ V 3 shTtfchTtf-Ttf’
Переписывая формулу (3.31) в виде
(3.33)
нетрудно для безразмерной эпюры осадок поверхности упругого
основания
Г7(У) *
|/6 (1 — v0> Ф/Ф<
(3.34)
S 3]
ПЛОСКАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
37
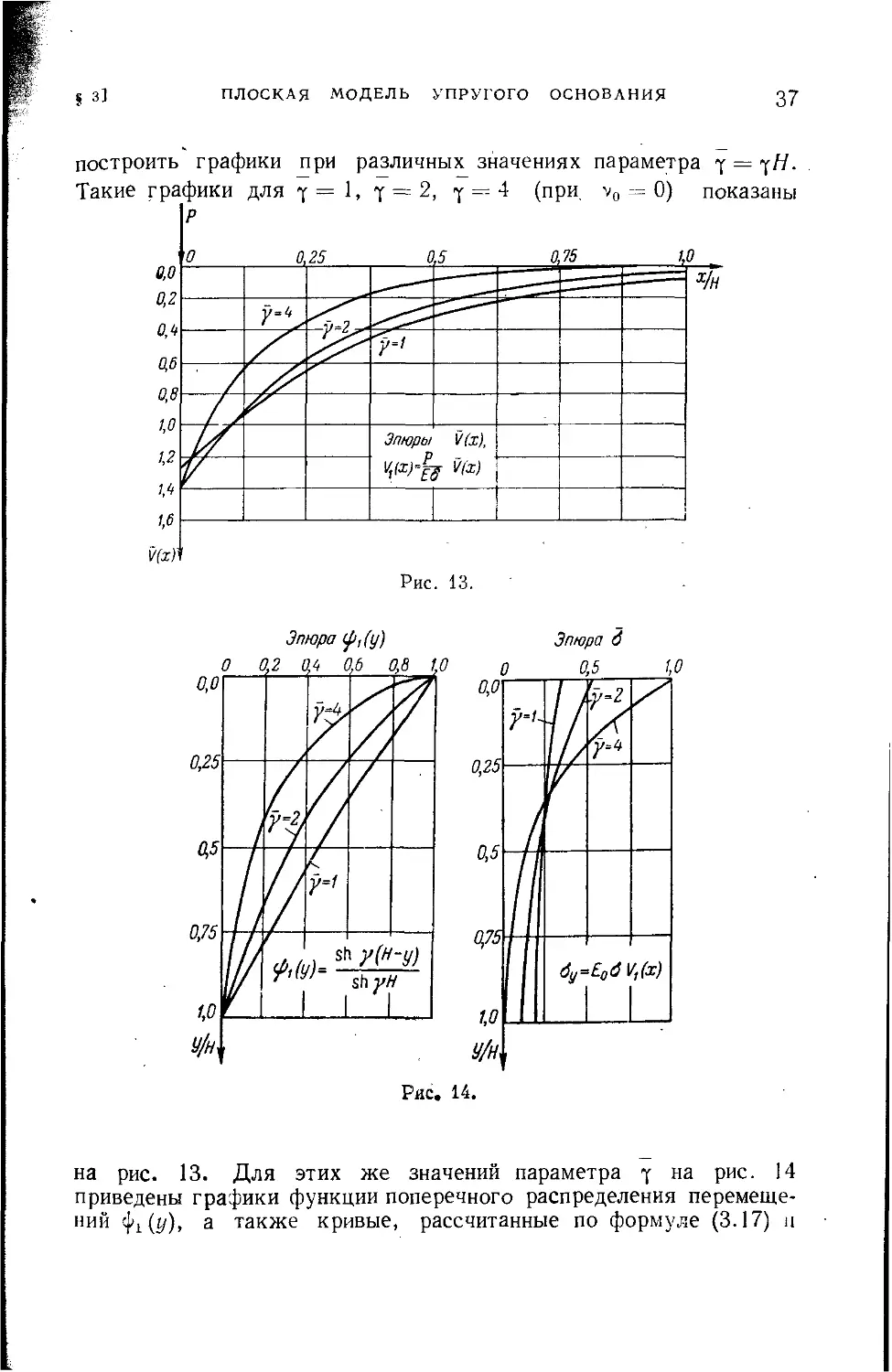
построить графики при различных значениях параметра у =
Такие графики для т=1, Т = 2, у = 4 (при v0 = 0) показаны
на рис. 13. Для этих же значений параметра у на рис. 14
приведены графики функции поперечного распределения перемеще-
ний 4ц (у), а также кривые, рассчитанные по формуле (3.17) п
38
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
ГЛ. [I
характеризующие распределение нормальных напряжений зу по
высоте основания.
Приведенные графики показывают, что увеличение параметра
Y вызывает все большую концентрацию осадок и нормальных
напряжений вблизи приложения силы и более быстрое затухание
этих величин по толщине основания.
Из рассмотрения эпюры нормальных напряжений можно видеть
и известную схематичность предлагаемой модели упругого осно-
вания, заключающуюся в том, что на поверхности основания,
свободной от нагрузки, нормальные напряжения су отличны от
нуля. Это обстоятельство объясняется тем, что для решения
задачи нами применялся вари-
ационный метод, учитывающий
условия равновесия в интеграль-
ной форме и не обеспечивающий
выполнения всех условий равно-
весия в каждой точке рассмат-
риваемой системы.
Следует отметить, однако,
что в дальнейшем нас будут
интересовать лишь вопросы рас-
чета фундаментов, расположен-
ных на упругом основании, а не
напряженное состояние упругого
основания как такового. Поэто-
му с отмеченным недостатком, не оказывающим непосредственного
влияния на напряженное состояние фундамента, можно вполне
примириться.
4. Расчет на распределенную нагрузку. Для опре- '
деления перемещений упругого основания от нагрузки, распреде-
ленной на его поверхности по некоторому закону q(х), наиболее
просто воспользоваться формулой (3.28), которая при у = 0 харак-
теризует кривую осадок упругого основания в случае действия
сосредоточенной силы. Можно видеть, что эта кривая при Р = 1
обладает свойством инфлюэнтной линии и позволяет, таким обра-
зом, определить осадку любой точки поверхности основания при
произвольном загружении.
Считая, что внешняя нагрузка q (?) является известной функ-
цией ? расстояния от начала координат, для осадки основания
в точке К (рис. 15) получим выражения:
при а <1 х < h
х b
V; (х) = С1 | \q (?) е- d% + \q (?) </?] ; (3.35)
а . .х
«3]
ПЛОСКАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
39
при х > b
ь
(х) = Сх j q (J) е~а- (3.36)
а
при х < а
ь
V1 (х) = Ст J q (?) е“ d%. (3.37)
а
Здесь, как и ранее,
с, - М . (3.38)
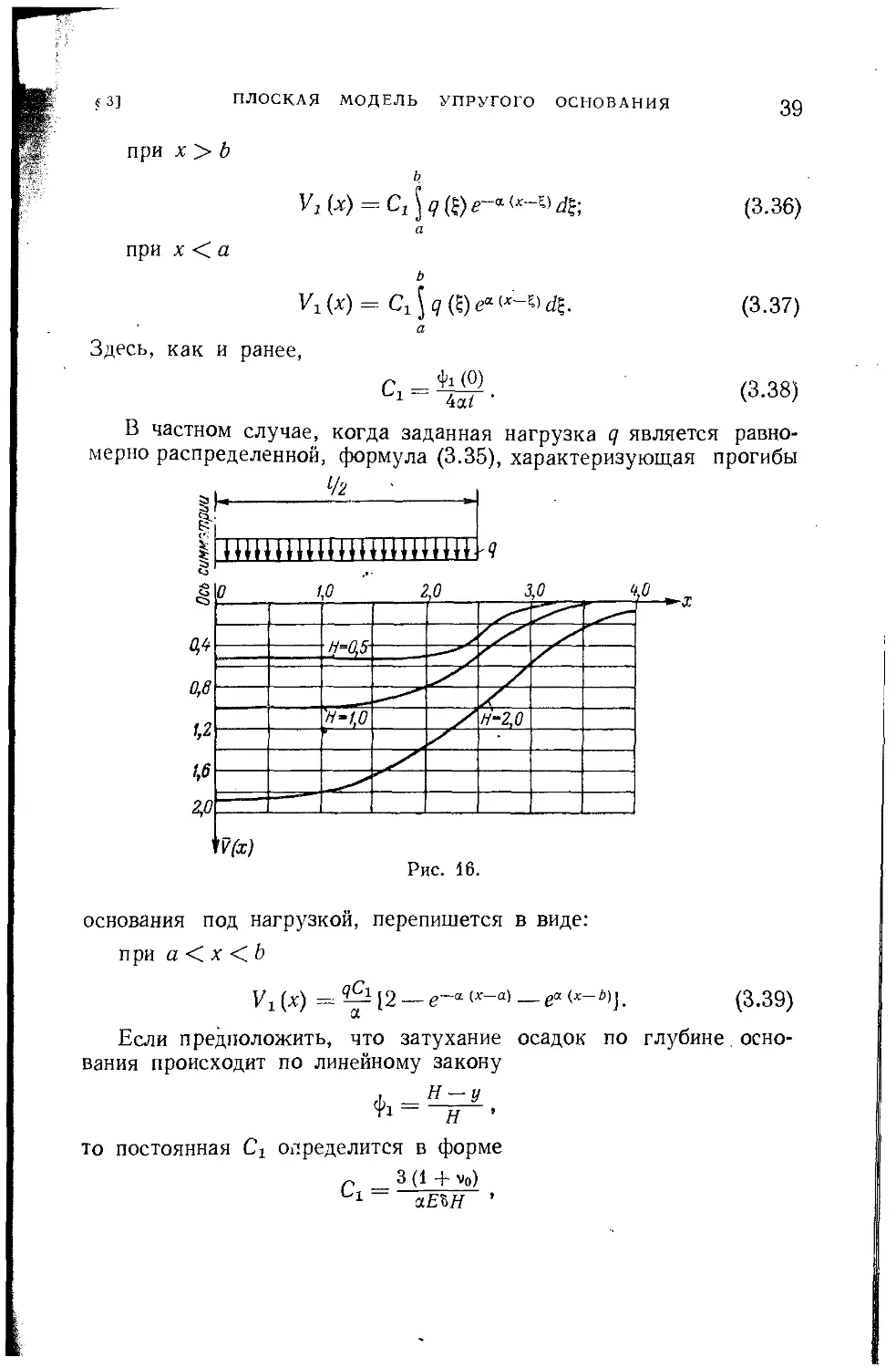
В частном случае, когда заданная нагрузка q является равно-
мерно распределенной, формула (3.35), характеризующая прогибы
основания под нагрузкой, перепишется в виде:
при а < х < b
У, (х) = [2 — <А'-а> — еа <*-*>]. (3.39)
Если предположить, что затухание осадок по глубине осно-
вания происходит по линейному закону
то постоянная Ci определится в форме
р _________________________3 (1 + Vo)
1 - аЕЪН ’
40
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
а выражение (3.39) примет вид
(х) = [2 — е~“ <*-а> — е“ <*-*)], (3.40)
где
, £8
k =--------5— .
7? (1 — v§)
На рис. 16 показаны эпюры осадок V (х), рассчитанные по
формуле (3.40) для некоторых значений параметра И (при v0= 0).
При этом величины действительных осадок определяются выра-
жением
Приведенные графики показывают, что с уменьшением пара-
метра Н рассматриваемое основание по характеру своей работы
приближается к винклеровской схеме. При увеличении И кривая
осадок становится более плавной, а абсолютные величины осадок
возрастают.
§ 4. Однослойное основание с переменным упругим параметром
1. В том случае, когда упругие характеристики основания
изменяются в направлении осей Ох или Оу по какому-либо извест-
ному закону, определение деформированного и напряженного
состояния упругого основания под нагрузкой значительно услож-
няется. Однако и здесь для решения задачи может быть исполь-
зован изложенный выше метод.
Рассмотрим, например, упругое основание, толщина которого
Н в направлении оси Ох меняется по линейному закону (рис. 17).
Для перемещений некоторой точки М (х, у) основания выберем,
как и ранее, следующие приближенные выражения:
u (х, z/) = 0, и(х, //) = Р1(х)ф1(х, у), (4.1)
4 ОДНОСЛОЙНОЕ ОСНОВАНИЕ С ПЕРЕМЕННЫМ ПАРАМЕТРОМ
41
Будем предполагать, что функция поперечного распределения
перемещений (х, у) определяется линейным законом
(х, у) = , (4.2)
где
д = д0 —еох, (4.3)
а %— тангенс угла, характеризующего изменение толщины сжи-
маемого слоя в направлении оси Ох (рис. 17).
Интегральные условия равновесия элементарной полоски dx = 1,
выделенной из основания, в соответствии с общими уравнениями
(1.7), (1.8) и принятыми выражениями (4.1) — (4.3) без труда
могут быть представлены в форме следующего дифференциального
уравнения с переменными коэффициентами:
1 17" — v° ХА I/' ® Г1 । 1 ту I Vo п р
—^ЬН(х)У--------g-8e0V - —[1 +-------------JV + -—<7 = 0.
(4-4)
Дифференциальным уравнением (4.4) в общем виде устанавли-
вается зависимость между осадками упругого основания V (х) и
внешней нагрузкой q (х), распределенной на его поверхности. Для
решения конкретных задач к этому уравнению следует присоеди-
нить еще граничные условия, сформулированные в обобщенной
форме.
Согласно выражениям (4.1) обобщенная поперечная сила упру-
гого основания, характеризующая работу всех сил сечения х =
— const на виртуальном перемещении v (х, у) = 1 • фх (х, у) при
Vi(x)= 1, определится формулой
н
S^x^dF. (4.5)
о
Внося (4.1) и (4.2) в последнее из выражений (1.1), получим:
_________Fg dv Ер Г у' Н у __Q0y у "I /д
ух~ 2(l + v0) дх_______________________________2(l+vo) L 1 Н № К1]’ 1 ’
где Н = Но — 0ох.
Подставляя теперь (4.6) и (4.2) в формулу (4.5) и производя
интегрирование, получим выражение для обобщенной поперечной
силы упругого основания
s* = i2<nk>I2"wvi--e”v'‘|- (<7>
2. Рассмотрим частный случай, когда к поверхности упругого
основания приложена сосредоточенная сила Р (рис. 18). Выбирая
42 ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ.
начало координат в загруженном сечении, получим для решения
задачи однородное дифференциальное уравнение
+ (4.8)
Можно видеть, что уравнение (4.8) является дифференциаль-
ным уравнением эйлеровского типа. Действительно, произведя
Рис. 18.
сокращения и умножив каж-
дый член на Н (х), получим:
№ (х) К + пН (х)
(4-9)
где
п = — 6о> т = — (°о + vy) •
Известной подстановкой
Н = ег, г = In Н, дифферен-
циальное уравнение (4.8) приводится к уравнению с постоянными
коэффициентами
Ci (п — 1)^1 4“ nN 1 = 0. (4.10)
Составляя характеристическое уравнение
Х2 + (н — 1)Х + т = 0,
получим для его корней формулу
(4.11)
Поскольку величина т в рассматриваемой задаче не может
быть положительной, оба корня (4.11) будут вещественными
числами
= Х2 = г2. (4.12)
В соответствии со значениями (4.12) общий интеграл диффе-
ренциального уравнения (4.8) запишется в виде
V, = Ct (Но - 90x)-ri + С2 (Но - 0ох)\ (4.13)
Исходя из условия, что в точках, бесконечно удаленных от
места приложения нагрузки, перемещения в основании равны
нулю, можно видеть, что постоянная С2 на участке слева от силы
§ 5]
ДВУСЛОЙНОЕ УПРУГОЕ ОСНОВАНИЕ
43
и постоянная Сх справа от силы обращаются в нуль. Таким обра-
зом, будем иметь:
Vn = C2(Ho-0ox)r\ (4.14)
В формулах (4.14) через и 7ц обозначены перемещения
поверхности упругого основания соответственно слева и справа
от места приложения силы (рис. 18).
Для определения произвольных постоянных интегрирования
6?i и С2 в начальном сечении согласно физическому содержанию
задачи могут быть поставлены условия:
при х = 0 Vi = Vii, Si — 8ц = Р, (4.15)
где Si и SXI — значения обобщенных поперечных сил соответст-
венно слева и справа от начального сечения.
Подставляя выражения (4.14) в формулу (4.7), будем иметь:
£05 (2гх-1)0о с
12.(1 + у0) /Г1 1
5ц =
£05 (2г2 - 1) НГг0о
12 (1 + v0)
(4-16)
Раскрывая условия (4.15) при помощи формул (4.14) и (4.16),
получим выражения для произвольных постоянных интегрирования:
= 6(1+уп)^ 6(1+уп)Я^
1 £'o4’0o(''i + гг) 2 £о*0о(Г1 + г2)
(4-17)
Формулы (4.1), (4.14) и (4.17) позволяют представить верти-
кальные перемещения любой точки упругого основания в следую-
щем виде:
при х < О
v (х, у)
при х> О
V (х, у)
6 (1 + Ур) Рр1 Г1 , . Н(х) — у .
£р80о('1 + '2) W ЖЙ ’
6 (1.+ Уо) Рр 2 ррр2 /д-\ Р (-*-) У
£oS0o (Г1 + г2)
где г у и г2 — корни характеристического уравнения, определяемые
по формуле (4.11), а Я(х) — толщина сжимаемого слоя в попе-
речном сечении х = const.
§ 5. Двуслойное упругое основание
1. Рассмотрим упругое основание толщиной Н == Лх + h2, рабо-
тающее в условиях плоской задачи теории упругости (рис. 19).
Будем предполагать, что основание состоит из двух слоев, имею-
щих различные модули упругости и коэффициенты Пуассона.
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ. I
Подставляя выражения (5.2) в формулы (5.4) и произведя не-
сложные преобразования, можно уравнения (5.3) представить в
более наглядной форме:
2/iV1 + ^iV2 q = 0, 1
GK + Ш + 2 (^ + t2) V2 - (fej + k2} V2 = 0, I
где Ь — Е1Ъ i EihiZ (5-7)
«1 Ы1-^) ’ 1 ~ 12(1 vi) ’
k% = — фь Ы1~*22) * , Е2И2Ъ , 2 12(1 + v2)^’ (5-8)
причем величины ф/; и ф/ определяются формулами (3.19).
Отметим, что коэффициенты (5.7) и (5.8) дифференциальных
уравнений (5.6), как и в случае упругого основания с двумя
характеристиками, имеют четкий физический смысл: коэффициенты
k± и k2 характеризуют соответственно работу верхнего и нижнего
слоев основания на сжатие, коэффициенты F и t2 — на сдвиг.
Для решения системы дифференциальных уравнений (5.6) введем
в рассмотрение новую функцию Fixy Выразим через эту функцию
и ее производные искомые перемещения V, (х) и Й2 (х) так, чтобы
второе уравнение системы (5.6) удовлетворялось тождественно
при любом выборе функции Fix}. Исходя из этого, получим:
(х) ikx + k2} F(x)-2 (у + t2} F" (x), 1
V2ix} = klFix} + t1F"ix}. J
Непосредственно подстановкой формул (5.9) в уравнения (5.6)
убеждаемся, что второе уравнение обращается в тождество,
а первое принимает вид
/1 (3^ + 4^) FIV — 2 (З^х + i±k2 ф t2k±} F" + k1k2F = q(x}. (5.10)
Дифференциальным уравнением (5.10) полностью описывается
напряженное и деформированное состояние двуслойного упругого-
основания. Для решения конкретных задач к этому уравнению
необходимо присоединить еще соответствующие граничные условия.
Поскольку граничные условия в настоящем методе формули-
руются в обобщенной форме, введем в рассмотрение обобщенные
внутренние силы, соответствующие обобщенным перемещениям
V± (х) и V2(x) упругого основания. Имея в виду, что элементар-
ная поперечная полоска, выделенная из основания, обладает двумя
S 5]
ДВУСЛОЙНОЕ УПРУГОЕ ОСНОВАНИЕ
47
степенями свободы в своей плоскости, согласно (1.14) получим:
Si — \ Тухфх dF,
о
н
52 = $ tyxtyzdF,
о
(5.Н)
где dF =; 8 dy.
Для касательных напряжений тех упругого основания в силу
формул (5.1) и (5.2) будем иметь выражения:
при
при > (5.12)
т _ Е2 v' sh 7 (Н - у)
~2(1+уг) shTA2 ’ >
Подставив (5.12) в формулы (5.11) и произведя интегрирова-
ние по всей высоте упругого основания, представим обобщенные
силы в виде
s1 = /1(2v; + K),
S2 = Wi + 2 (/х + t2) V's.
(5.13)
Если учесть теперь зависимости (5.9), то обобщенные силы
и S2 можно выразить также и через разрешающую функцию
Е(х):
51 = И [(3fi + 4/2) Е'"+(3^1 + 2ke) F'l,
52 — + /1^2 Ф 2/2^j) F'. I
2. Описанная нами двуслойная модель упругого основания
может быть названа основанием с четырьмя упругими характери-
стиками. Подобная модель является более совершенной, чем
однослойная, свойства которой определяются лишь двумя незави-
симыми параметрами k и t (см. § 3).
Выбирая так или иначе характеристики klt k2, tx и t2, мож-
но получить ряд различных расчетных схем упругого основания.
В дальнейшем мы остановимся на рассмотрении лишь одной
такой схемы, представляющей собой частный случай двуслойного
основания.
Из формул (5.7) можно видеть, что если толщина верхнего
слоя уменьшается и при этом уменьшается модуль упругости
Elt то коэффициент /х стремится к нулю, а коэффициент со-
храняет конечную величину. Таким образом, если принять, что
48 ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ. I
тонкий сжимаемый слой грунта, расположенный Вблизи поверх-
ности упругого основания, имеет значительно меньший модуль
упругости, чем нижележащие слои, то для параметров первого
слоя можно приближенно принять
71==0, (5.15)
где К— некоторый коэффициент, аналогичный коэффициенту по-
стели и зависящий только от свойств упругого основания вблизи
поверхности.
В результате такого выбора упругих постоянных двуслойное
основание будет представлять собой среду, верхний слой которой
работает только на сжатие {t1 = 0) и в этом смысле аналогичен
винклеровскому основанию, а нижний — как на сжатие, так и
на сдвиг.
Полагая в уравнениях (5.9), (5.13) и (5.14) = 0, =
получим: !
^ = (/(+^-2^, = (5.16)
О, S2 = S .! (5.17)
Основное дифференциальное уравнение задачи (5.10) перепи-
шется при этом в виде
— 2/2F" + k2F = '1^. (5.18)
Уравнение (5.18) в отличие от дифференциального уравнения
(5.10) позволяет рассмотреть задачу о работе двуслойного осно-
вания с верхним винклеровским ело
ем. Отметим, что под термином «дву-
слойное основание» мы будем пони-
мать в дальнейшем именно этот
частный случай двуслойной модели.
3. Предположим, что в некоторой
точке поверхности к упругому осно-
ванию приложена сосредоточенная
сила Р (рис. 21). Выбирая начало
координат в загруженном сечении,
получим для определения разрешаю-
щей функции F(х) однородное дифференциальное уравнение J
— 2t2F" + ksF = 0. (5.19)
Уравнение (5.19) в точности совпадает с уравнением (3.22),
решение которого было рассмотрено в § 3. Путем аналогичных
рассуждений (см. (3.23), (3.27), (3.31)) нетрудно получить:
3(1—v«) i р
1 V6 (1 -v2) Ма
(5.20)
51
ДВУСЛОЙНОЕ УПРУГОЕ ОСНОВАНИЕ
49
где
а2
1 Уб(1-у2)
1 — v2
фа
(5.21)
а величины ф, и ф«г определяются формулами (3.32).
Внося (5.20) во второе из уравнений (5.16), будем иметь
^ = Т6д4) Ж <5-22>
Можно видеть, что формула (5.22) является’ точным повторе-
нием решения (3.31). Подстановкой выражения^ (5.20) в первое
из уравнений (5.16) нетрудно убе-
диться в том, что вне точки при-
ложения силы
4. При действии на двуслойное
основание равномерно распределен-
ной нагрузки q (рис. 22) решение
задачи можно наиболее просто по-
лучить, если воспользоваться функ-
цией (5.20), которая при Р = 1
обладает свойством линии влияния.
решением (см. § 3 и § 4)
По аналогии с рассмотренным ранее
получим:
при
при х > b
р = 9_ [2 — е~а* — еа^~ь)]';
р = -7А— [g-a,(x-b)_ e-a2x] .
ZA «2
(5.23)
Подставляя (5.23) в уравнения (5.16), будем иметь:
при
при х > b
Л = (е-агх + ga.U-b)) ,
1\к<ъ 4к2
V2 = -%--------оТТ (e~a‘x -+- ё’Их-Ь)) ;
Ух = = -9- (е^-Ь) _ е-агх).
(5.24)
(5.25)
Из выражений (5.24), (5.25) можно "видеть, что на незагру-
женных участках основания поверхностный слой не (работает
4 В. 3. Власов, Н. Н. Леонтьев
50
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
(что соответствует гипотезе коэффициента постели), вследствие чего
здесь Vi = V2. В пределах нагрузки за счет обжатия верхнего
Ч
Рис. 23.
слоя перемещения отличаются от V2 на величину
W = V1_V2 = JL. (5.26)
При этом функция V2 всюду непрерывна, а претерпевает
разрыв в сечениях, соответствующих концам нагрузки (рис. 23).
§ 6. Определение деформаций упругого основания
в пространственных условиях
Рассмотрим теперь трехмерное упругое основание толщиной /7,
расположенное на несжимаемом подстилающем слое (рис. 24)
Будем предполагать, что на это основание действует внешня5
нагрузка, компонента
которой в направленщ
осей Ох, Оу и Oz состав
ляют соответствен^
Р (х, у, z), g (х, у, z) 1
Ч (х, у, z).
Как и в случае плос
кой задачи, для опреде
ления напряженного 1
деформированного со
стояния упругого осно
вания применим мето,
перемещений, приняв :
Рис. 24. основные неизвестнь
перемещение и(х, у, z
ц(х, у, z), w(x, у, z) произвольной точки М (х, у, z) основани!
Эти перемещения будем считать положительными в том случа
когда их направления совпадают с положительными направлен!
ями соответствующих координатных осей.
j 6] ДЕФОРМАЦИИ ОСНОВАНИЯ В ПРОСТРАНСТВЕННЫХ УСЛОВИЯХ 51
Строя решение пространственной задачи по аналогии с рас-
смотренным ранее двумерным решением, представим искомы^
перемещения и, v, w в форме следующих конечных разложений:
т и (х, у, г) = 2 «Z (х, у) <pz (z) 1=1 (/ = 1, 2, 3, • • > щ),
1 V (X, у, z) = 2 vg (х> у) xg (х) S=1 п (?= 1, 2, з,. (6.1)
w (х, у, г) = 2 Wk (Х, у) фА (z) й=1 (£ = 1, 2, з,. .п).
Можно видеть, что функции <pz(z), *g(z), фй (z) разложений
(6.1) характеризуют собой распределение горизонтальных и верти-
кальных перемещений по высоте основания. Эти функции выби-
раются заранее как безразмерные линейно независимые функции
и в этом смысле считаются заданными. Функции щ(х, у), vg(x, у),
wk (х, у), имеющие размерность прогиба, считаются искомыми.
Согласно физическому смыслу эти функции будем называть
обобщенными перемещениями.
Нормальные и касательные напряжения упругого основания в
случае пространственной задачи определяются известными форму-
лами:
(6.2)
где
4»
(6-3)
причем £гр и мГр—соответственно модуль упругости и коэффи-
циент Пуассона упругого основания.
4*
52
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
Внося разложения (6.1) в формулы (6.2), выразим напряже-
ния упругого основания через обобщенные перемещения в виде:
6.4
(6-5)
Для определения функций щ(х, у), vg(x, у), Wk(x, у) выде-
лим из основания элементарный столбик высотой Н со сторонами
dx — 1, dy = 1 (рис. 24 и рис. 25). Такой столбик, как дефор-
мируемый элемент рассматриваемой системы при условиях (6.1),
обладает (т +1 -Т п) степенями свободы в направлении осей х,
у и г. В соответствии с этим числом степеней свободы обобщен-
ные условия равновесия элементарного столбика, понимаемые в
смысле принципа возможных перемещений Лагранжа, могут быть
представлены в виде:
\~l£vidz — \'хг dz + S V dz + $ p^‘dz = 0
(/' = 1, 2, 3.....m),
*fdz dz + dz -f- q-*f dz = 0 (6.6)
(f = 1, 2, 3....../),
f Г f (•
J'dF'M2- ^^hdz + ^-^-tyhdz + ^qtyhdz = 0
(h = 1, 2, 3......«).
Каждое из уравнений (6.6) ' выражает собой равенство нулю
s 6] ДЕФОРМАЦИИ ОСНОВАНИЯ В ПРОСТРАНСТВЕННЫХ УСЛОВИЯХ 53
суммарной работы всех внешних и внутренних сил элементарного
столбика на соответствующем виртуальном перемещении:
й/(х, у, z) = <p/(z),
у, z) = *f(z),
wh (х, у, z) = фп (z)
при
U/ (*> у) = 1>
Vf (*, у) = 1. wh (X, у) = 1 •
Члены, перед которыми стоит знак
минус, относятся к работе внутрен-
них сил. Остальные члены характе-
ризуют работу внешних (по отноше-
нию к выделенному столбику) сил.
Подставляя в уравнения (6.6) фор-
мулы (6.4), (6.5), получим относи-
Рис. 25.
тельно искомых функций иДх, у), vg(x, у), wk(x, у) систему
дифференциальных уравнений в частных производных, которая
в сокращенной записи имеет следующий вид:
т
2
ду2
, 1+уо у z
-г 2 Ate дхду
£=1
V ( -JL '
l+v0^,
2 1‘дхду
/ = 1
dwk , l-»20n n
*=1, - Z dx Ea Pl °
(/=1, 2, 3, . . . , m),
1-Vo d2vg V_ 1-vo V „ ,
- - - “ ~2— Zl nr& VB I
g=i
i-v \ dwk 1-v*
2, 3, .. . , /),
2 дхг
п
k
1
(6.7)
А=1
(/=1,
VI / , 1-Vo ) ди,
2j\vodw 2 Ckij дх
= 1
, I-Vpy (d2wk ,
> 2 A rhkl дх2 -r
А=1
g=i
-5Ц2 I — 2jshkWk +
(й = 1, 2, 3,..., п).
1-VOA, ,
2 ду +
1 — Va
&0
54
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
Коэффициенты уравнений (6.7) определяются по формулам:
<2/7 — ац — ’ x^x^y dz j
Ьц = Ьц = <pz<pz dz, nfg ~ ngf ~ 5 xfxS ’
с jk = \<pjtykdz, kfk = 5 dz,
dik = Ф/Ф* dz , hk = 5 х$* dz,
rhk = \<M>kdz, см = j фл?г dz, (6-8)
$hk = Skh=\ флф/г dz, dhi = $ фйф/ dz,
khe; ” dz j tfi~ j y.f(fidz,
dz > ф y-g dz .
В . этих формулах интегралы (определенные) распространяются
на всю высоту И упругого основания.
Свободные члены уравнений (6.7) характеризуют работу задан-
ной внешней нагрузки на соответствующих виртуальных переме-
щениях и вычисляются по формулам:
Pi = 5 Р (х, у, z) (z) dz , j
gf = }g(x, У, z)*f(z)dz,
gh = \q (X, y, z) фл (z) dz .
(6-9)
При наличии внешней нагрузки, приложенной к поверхности
упругого основания, интегралы (6.9) следует рассматривать как
интегралы Стилтьеса (см. пояснения к формулам (1.12), (1.13)).
Так, например, если массовые силы р(х, у, z), g(x, у, z),
<j(x, у, z) отсутствуют и внешняя нагрузка представлена только
поверхностными силами р (х, у), g(x, у), q(x, у), то формулы
(6.9) перепишутся в виде:
Р/ = р (х, у) (0),
gf = g (х, у) >.f (0),
qh = q (X, у) фи(О) , .
(6.10)
где <р/(0), xf(0), фА (0) — значения функций <pz-(z), x/(z), фА(г) на
поверхности рассматриваемого массива (при z = 0).
Дифференциальные уравнения в частных производных (6.7)
полностью описывают работу упругого основания конечной тол-
щины Н. При этом упругое основание рассматривается как бес-
ПРОСТРАНСТВЕННАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
55
§ 7J
конечная толстая плита, соответствующим образом закрепленная
по опорной поверхности и способная воспринимать нормальные и
тангенциальные нагрузки.
С точки зрения теории упругости система дифференциальных
уравнений (6.7) дает приближенное решение для толстой изотроп-
ной плиты. Это решение будет тем более точным, чем большее
количество членов принято в разложениях (6.1). Вместе с тем
можно считать, что дифференциальными уравнениями (6.7) опре-
деляется некоторая обобщенная пространственная модель упругого
основания, свойства которой зависят от количества членов в раз-
ложениях (6.1) и характера функций (z), xg(z), фд(г). Выбирая
для ограниченного числа функций <р6 xg, различные выражения,
мы будем получать различные расчетные схемы упругого основа-
ния, в большей или меньшей степени отвечающие действительности.
Вопрос о выборе функций поперечного распределения переме-
щений <pz, xg, ф* был рассмотрен нами достаточно подробно в § 2
при описании работы упругого основания в условиях плоской за-
дачи. Здесь мы только отметим еще раз, что функции <рг, xg, фй
следует вводить в соответствии с конкретными условиями рассма-
триваемой задачи, например, по закону, являющемуся результа-
том экспериментальных исследований. При этом уже простейшие
модели упругого основания, получаемые при минимальном коли-
честве функций <pz, xg, ф^, будут более верно отражать действи-
тельность, чем известное упругое основание, построенное на ги-
потезе коэффициента постели.
§ 7. Пространственная модель упругого основания
с двумя характеристиками
1. Рассматривая упругое основание ограниченной толщины /7
(рис. 26), предположим, что горизонтальные перемещения в осно-
вании всюду равны нулю:;
и(х, у, z) = О, v (х, у, z) = О, (7.1)
а вертикальные перемещения определяются формулой *)
ш(х, у, z) = w(x, у)ф(г), (7.2)
где ф (г) — функция поперечного распределения перемещений,
выбираемая заранее в соответствии с физическими условиями
задачи.
Согласно выражениям (7.1) и (7.2) разрешающая система диф-
ференциальных уравнений (6.7) будет состоять только из одно-
го уравнения третьей группы. Это уравнение может быть
*) В целях краткости написания индекс 1 при функциях w (х, д) и ф (г)
®десь и в дальнейшем опускается.
56
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
(ГЛ. I
представлено в виде
. __ <у2
-4p4uVMx, у) — snw(x, у) 4- —~ qY = 0, (7.3)
Z CQ
где
/ ч д2ш(х, у) , d2w(x, у)
V2U) (х, у) =-----+ LJ-a- -• - <7-4)
я
ru = ^2(z)dz,
оз
Свободный член уравнения
боту заданной нагрузки q (х,
У,
Рис. 26.
я
sii = Ф'2к(2) dz (7’5)
о
(7.3) характеризует собой ра-
z) на виртуальном переме-
щении w (х, у, z) = ф (z) при
w (х, у) = 1 и вычисляется
по формуле
я
= ф, y,^z)^(z)dz.
О
(7-6)
Если ' внешняя нагрузка
состоит только из поверхно-
стных сил q (х, у), формула
(7.6) принимает вид:
>1=<7(х, У)Ф(О). (7.7)
где ф (0) — значение ^функции
ф(г) у поверхности упругого основания (при z = 0).
Несложные преобразования позволяют переписать дифферен-
циальное уравнение (7.3) в более наглядной^форме:
2/V2m (х, у) — kw(x, у) + q± = 0.
(7-8)
Коэффициенты полученного уравнения имеют вид:
г,__ EpSn 1
к ~ 1 — м2 ’
1 v0
*ЕрГц
4(1+ *о) '
(7-9)
Можно видеть, что коэффициент k определяет работу упруго-
го основания на сжатие и в этом смысле аналогичен коэффициен-
ту постели, а коэффициент t характеризует работу упругого осно-
вания на сдвиг.
Таким образом, дифференциальное уравнение в частных произ-
водных (7.8) отличается от известной зависимости, вытекающей
из гипотезы коэффициента постели, наличием члена
2/Т2да(х, у),
| 7]
ПРОСТРАНСТВЕННАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
57
которым учитывается влияние касательных напряжений'на дефор-
мированное состояние упругого основания. Для определения коэф-
фициентов (7.9) следует задаться функцией поперечного распреде-
ления перемещений ф(г). Предположим, что эта функция в соот-
ветствии с условиями задачи может быть выбрана в виде
= <7Л0)
где «у — некоторый коэффициент, характеризующий быстроту за-
тухания осадок на глубине основания.
Внося (7.10) в выражения (7.9), получим:
k ==-----ф* ,
. Е0Н ,
12(1-Но)
где
ЧН Г sh 4Н ch у И 4- тЯ 1
~ 2 L ;sha чН J ’
3 1 Г sh уН ch 4Н — чН
~ ~2~ЧЁГ[ S&4H
(7.11)
(7.12)
Упругие постоянные основания £0 и v0 определяются форму-
лами (6.3) и имеют вид:"
(7-13)
Рис. 27.
2. Вычислим осадку упругого основания от сосредоточенной
силы Р, приложенной в некоторой точке его поверхности (рис. 27).
Для решения этой задачи перейдем к полярной системе коор-
динат (9, р). Помещая начало от-
счета в точку приложения силы,
получим однородное дифференци-
альное уравнение
V2№ — а2Г = 0, (7.14)
где
“=/Т- (7лб
Поскольку рассматриваемая
нагрузка симметрична относитель-
но начала координат, обобщенные вертикальные перемещения не
будут зависеть от полярного угла 9. В этом случае оператор
58] ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ. I
Лапласа, входящий в уравнение (7.14), определится в виде
VW (р) = ~ • (7.16)
ар* 2 ,Р Ф
Введением новой переменной
? — /ар (7.17)
однородное уравнение задачи (7.14) нетрудно привести к диффе-
ренциальному уравнению типа Бесселя мнимого аргумента
d^W 1 dW । цу n /7 1
-d^+Z~dZ+W = °- . (7 8)
Общее решение дифференциального уравнения (7.18), как из-
вестно *), может быть представлено через модифицированные
функции:
117 = С!/0(ар)+С2/С0(ар). (7-19)
где 10 (ар) и Ко (ар) — модифицированные функции Бесселя нуле-
вого порядка соответственно первого и второго рода, Сг и С2—
произвольные постоянные интегрирования. На рис. 28 приведены
графики функций /0(ар), Ко (ар) для некоторых значений аргумен-
та (ар). Можно видеть, что поведение этих функций аналогично
поведению показательных функций.
Поскольку модифицированные функции 10 (ар), Ко (ар) действи-
тельны во всей области измерения независимой переменной р,
*) См., [например, Ватсон Дж. Н., Теория бесселевых функций, ч. 1,
2, 1949.
§ 7]
ПРОСТРАНСТВЕННАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ
59
постоянные интегрирования Сх и С3 будут также действительны-
ми величинами. Для вычисления этих постоянных необходимо
рассмотреть физическую сторону поставленной задачи. Условие
затухания осадок упругого основания вдали от места приложения
нагрузки позволяет записать:
при р —> ОО
(7.20)
Так как функция /0 с возрастанием переменной р стремится
к бесконечности, условие (7.20) дает нулевое значение для одной
из постоянных интегрирования:
С1 = 0. (7 21)
Для определения второй постоянной С2
следует рассмотреть статические условия
задачи. Выделим из упругого основания вбли-
зи места приложения силы элементарный
цилиндр радиуса р = е при г 0 (рис. 27 и 29).
Условие равновесия этого цилиндра, в смыс-
ле изложенного выше вариационного метода
может быть представлено в виде
2п Н
тгрф(2) dz+Рф (0) = 0. (7.22)
о о
Уравнение (7.22) характеризует работу
Рис. 29.
касательных напряжений т2р, распределенных
по боковой поверхности цилиндра, и внешней силы Р на виртуаль-
ном перемещении w (р, г) = ф (z) при W (р) = 1.
Согласно разложению (7.2), касательные напряжения т2р в
цилиндрической системе координат (г, р) определяются по фор-
муле
'zp
__hСр), л /2)
2(1+v0) d?
(7.23)
Подставляя (7.23) в уравнение (7.22), а также учитывая выра*
жения (7.19) и (7.21), получим:
га/СгКх (ар) р d9 = Рф (0), (7 24)
о
где функция Ki(ap) может быть вычислена по асимптотической
формуле
достаточно верной при малых значениях аргумента ар(ар< 1).
6Q ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ. I
Раскрывая условие (7.24), получим следующее выражение для
постоянной интегрирования С2:
Со _ Рф(0) 4л/ ’ (7.25)
где, как и ранее, н
j Eof 11 “ 4(1 +v0) ’ Гц = 5 dz • 0 (7.26)
На основании формул (7.21), (7.25) и (7.2) вертикальное пе-
ремещение любой точки упругого основания может быть пред-
ставлено в виде
^(Р. г)=Г^-К0(аР)ф(г). (7.27)
Если, например, функция поперечного распределения переме-
щений ф(г) выбрана в форме (7.10), выражение (7.27) позволяет
получить:
w (р, г) = ЗР^+/о)- Ко (ар)’ (7- 28)
где , ___
а V 21 H 1 - v„ ’
. 3-1. Г sh ch 1 (7 29)
2 y//L sh27tf .1’ >
ф _ 7/7 Ch +
га 3 V 3 sh7H ch — 7H '
При выборе ф (2) по закону показательной функции
ф(г) = е~тг (7.30)
для упругого полупространства (7/—> ос) будем иметь:
®(p, Z) = l2p^+-^ КоЫе~^, (7.31)
где
У2(1-у0У
1 — Vo
а у — некоторый коэффициент, имеющий размерность [ 1./ м] и
характеризующий затухание осадок по глубине основания.
р
На рис. 30 в качестве примера приведены графики —
кратных осадок поверхности упругого основания, рассчитанные
по формуле (7.31) при z = 0 и v0 = 0. Для сравнения здесь же
приведена кривая Буссинеска для v0 = 0. Из приведенных графи-
ков следует, что с увеличением параметра у связность упругого
основания уменьшается, в результате чего рассматриваемое осно-
§ 7] ПРОСТРАНСТВЕННАЯ МОДЕЛЬ УПРУГОГО ОСНОВАНИЯ 61
ва'1ие'"по своим свойствам приближается к винклеровской схеме.
Напротив, уменьшение этого параметра позволяет получить более
ссязное упругое основание, обладающее большей распределитель-
ной способностью.
3. Рассмотрим теперь упругое основание под действием на-
грузки, равномерно распределенной внутри круга радиуса /?
(рис. 31).
В этом случае мы будем иметь две области и два дифферен-
циальных уравнения, которые соответствуют этим областям:
при 8 р R
при р < 00
1 dIFi _ q
dp2 + р dP. aW/i- IF’
+ 1 _ а2№ = о .
dp2 1 р dp 2
! (7.32)
I
62
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. 1
Решение дифференциальных уравнений (7.32) может быть пред-
ставлено в виде:
Гх = (ар)+ С2К0 (ар) f-|,
W2 = С310 (ар) + СЛо (ар)
(7.33)
где коэффициент k определяется первой из формул (7.9).
Исходя из физического содержания задачи, для определения
постоянных интегрирования Clt С2, С3, С4 получим следующие
граничные условия:
при р — 0 при р —> ОС -^ = 0, dp r2 = o, (7.34)
при P~R Wi = w2, dWi _ dp dp (7.35)
Условия (7.34) позволяют непосредственно получить:
С2 = С3 = 0 .
Остальные два условия по подстановке в них
(7.33) принимают вид:
С1/о(а/?)-СЛо(а/?) = -|,
СХЛ (а/?) + CtKi (<*R) = 0 ,
(7.36)
выражений
(7.37)
где /х, Ki — соответствующие модифицированные функции перво-
го порядка.
Решая систему двух алгебраических уравнений (7.37) относи-
тельно постоянных Сх и С4, получим:
р __ q_______________Ki («Ю_____________
1 k l0{aR) Ki(aR) + Ii(aR) Ко (.aR) ’
r = J7 ______________li(aR)__________
4 k Io(aR)Ki(a.R) + h(aR) Ko(aR) '
(7.38)
Формулы (7.38) и являются решением рассмотренной задачи,
поскольку поверхности оседания соответственно для внутренней
и внешней областей круга R определяются формулами:
1Г1(р) = С1/.(«р) + |. I (7 39)
Г2(р) = СЛ0(аР). I
S 8]
ТЕПЛОВЫЕ НАПРЯЖЕНИЯ В. УПРУГОМ ОСНОВАНИИ
63
Отметим, что рассмотренная задача жет быть решена и не-
сколько иначе, а именно при помощи выражения (7.27), которое при
z = 0 и Р = 1 характеризует поверхность влияния для осадок.
Исходя из этого, для осадки в центре круга можно, например,
получить:
2П н
№(°)=^^К°(ар)рсИ0 = (7.40)
о о
где ф (0) — значение функции ф (г) при г = 0.
§ 8. Тепловые напряжения в упругом основании
1. При проектировании оснований под массивные фундаменты
может возникнуть вопрос об определении напряжений и дефор-
маций, являющихся результатом температурных воздействий.
С этой задачей приходится сталкиваться также и при расчете
толстых плит и блоков, расположенных на жестком или упругом
основаниях.
В качестве примера рассмотрим упругий слой, расположен-
ный на жестком основании (см. рис. 5) и находящийся в услови-
ях плоско-деформированного состояния, вызванного плоским темпе-
ратурным полем. Будем считать, что температурное изменение за-
дано в общем случае как функция координат х, у и времени t:
Т = Т(х, у, t).
Для приближенного решения поставленной задачи вновь вос-
пользуемся изложенным выше вариационным методом, для чего ис-
комые перемещения и (х, у, Г), v (х, у, /) представим в виде ко-
нечных рядов:
пг
и (х, у, t) = 2 (*, 0 ?< (у)
1
п
V (х, у, t) = 2 (X, t) фА (у)
*=1
(z = 1, 2, 3, . . ., m),
(k = 1, 2, 3, . . ,,n),
(8-1)
где функции (J, (х, /), V* (х, t) будем считать искомыми, а функ-
ции <pz(y), фл(у) — выбираемыми заранее в соответствии с условия-
ми задачи.
Рассматривая обобщенные условия равновесия элементарного
столбика высотой Н и размерами в плане 1 X S и принимая, что
поверхностные и объемные силы в упругом основании отсутству-
64
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
(ГЛ. I
ют, получим, как и ранее (см, выражения (1.7) и (1.8)), ^'систему
щ + п уравнений:
j ~дГ VidF ~ j dF = 0
(/= 1,£2, 3,..., т),
(h = 1, 2, 3,..., га),
(8-2)
где dF = 8 dy.
В отличие от приведенных ранее уравнений (1.1) связь между
напряжениями <зх, <зи, 'ху и деформациями
__ди _dv _ ди
+
в случае температурной задачи и при условиях плоско-деформи-
рованного состояния осуществляется уравнениями:
Ев (ди . dv\ аЕ0Т
0 * = ----z -г + v<> т- ~ 1’
1 — у‘\дх ду) 1 — v0
Еп (dv , ди\ аЕ0Т
5 I Т । ^0 ~ '« /
1 — Vg \ ду дх( 1 — Vo (
_ Ео (ди diA j
'^“2(1+v0) \ду + дх)> )
(8-3)
где а — коэффициент линейного расширения; Т = Т (х, у, t) —
температура в точке (х, у) в момент времени t' Ео и v0 — постоян-
ные, связанные с модулем'упругости слоя формулами (2.1).
Подставив ряды (8.1) в уравнения (8.3) и внеся найденные та-
ким образом выражения в (8.2), мы получим систему ш + п обык-
новенных дифференциальных уравнений относительно искомых функ-
ций U, (х, f), Vk (х, /):
2 ay и7- Цр 2 by ui + 2 Цр c/AJ) V'k -
i=l 7=1 4=1
— oc (1 + vo) Xit = 0
(j = 1, 2, 3, . . ., m),
m
- 3 - pp cw) U'{ + 3 rhkV"k -
Z=1
n
— 3 Shk Vk + a (1 -V ^o)Yhr = 0
.4=1
(ft= 1, 2, 3, . . ., n).
’(8.4)
§ 81
ТЕПЛОВЫЕ НАПРЯЖЕНИЯ В УПРУГОМ ОСНОВАНИИ
65
Коэффициенты ац , Ьц ,..г^, Shk уравнений (8.4) определя-
ются, как и ранее, формулами (1.11) и зависят только от вида
функций ср, (у), Фа (у)- Свободные члены Х/г и Унт вычисляются
по формулам:
Х/т^^ф/dF, YhT = \T^hdF. (8.5)
Рис. 32.
Дифференциальными уравнениями (8.4) при соответствующих
граничных условиях полностью описывается задача о температур-
ном равновесии слоя конечной
толщины Н в условиях плос-
ко-деформированного состоя-
ния. Заметим, что изложен-
ный здесь метод применим
также к расчету упругих ос-
нований и толстых плит, на-
ходящихся в условиях прост-
ранственного напряженного
состояния. В этом случае трех-
мерная задача термоупруго-
сти может быть приведена к
двумерной подобно тому, как
это было сделано нами в § 6,
при рассмотрении работы упругого основания под нагрузкой.
2. Для иллюстрации изложенного метода рассмотрим частный
случай. Будем предполагать, что упругий слой, находящийся в
условиях плоского деформированного состояния, имеет ограничен-
ную длину в направлении оси х (рис. 32). Кроме того, примем,
что по своей подошве этот слой жестко защемлен, в результате
чего отсутствуют перемещения и (х, у) и v (х, у) на плоскости кон-
такта с основанием.
Ограничимся в разложениях (8.1) приближенно тремя первы-
ми членами, положив:
и (х, у, 0 = иг (х, t) (у)+U2 (х, t) <р2 (у) + U3 (х, t) <р3 (у), 1
v (х, у, 0 = V. (х, f) фх (у) + У2 (х, t) ф2 (у) + Уз (х, 0 ф3 (У)- I ' '
При этом в качестве функций <рх (у), <р2(у). ?з (у), фх (у), фа(у),
ф3 (у) выберем функции, приведенные на рис. 33. Заметим, что
в зависимости от условий каждой конкретной задачи и желаемой
степени точности искомого решения в разложениях (8.6) может
быть взято большее или меньшее количество членов. При этом тру-
доемкость вычислений будет соответственно повышаться или по-
нижаться.
Пользуясь формулами (1.11) и графиками функций <pz (у), ф* (у),
а также графиками их первых производных <р;(у), Фа(у)
6 В. 3. Власов, Н. Н. Леонтьев
gg ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА (ГЛ. 1
(см. рис. 33), получим для коэффициентов дифференциальных
уравнений (8.4) значения:
ън
&11 — Г11 — -g-1
_ _ ън
а12 ~ а21 ~ Г12 — Г21 — а23 — а32 — ^23 — Г32 — jg i
ais = а31 = r13 = r3i = 0,
_ 2ЪН
aS2 — азз — ~g~ »
, 35
bn — S11 — -jj-,
, , _ 35 (8.7)
fcj2 = &21 = Sj2 — S21 — ^23 — П32 — S2s — S32 — ,
^13 — &31 — S13 ~ S31 = 0,
. — A _ 65
D22 - O33 - yy ,
, __ . _ _ . _ 5
C11 — c12 — ^11 — r21 — C23 — r32 — 2“ 5
C13 ~ ^13 = C22 = ^22 = C31 — ^31 ~ C33 ~ ^33 ~ 0,
C21 = ^12 ~ C32 ~ ^23 = ~2 '
Внося эти значения в (8.4), можно систему шести дифференци-
альных уравнений относительно шести искомых функций t/j, t/2,
&з, У1, У2i V3 представить в виде, приведенном в табл. 1. В этой
таблице символами £)2 и D обозначены соответственно двукратная
ТЕПЛОВЫЕ НАПРЯЖЕНИЯ В УПРУГОМ ОСНОВАНИИ
67
Таблица
ЧХЭВН BBS -Bdu "Ч <1 » =а О? а со - 03 '
1 с о + 1 г со с- с а е т тч 36 nLJ н со # £ к. е Г ГЧ С . 3 с 00 ГЧ <1
' °л + т «|за + ем । h° 1 со СО о С к, е т тч 'С I Э-- ta 00 тч q СО е С о тч за ' е: SS со
С е & 1 тЧ с о + , - ' 1 е> с а ' т ГЧ за 1 е. оо со « . с ' а о т тч * а с - Я. 1
-- h - н Л8В2+ , , 3 1-vo за см 1 ем Q За 1® CSJ -. 3 Т—v0\ : 2 Н } 1 * с - 4- ГЧ а
н -TsD + с ? тч СО - аа СМ - - 1 ем Q Ц;|с5 CSJ О со tc + с» о 'ф Q Г тч СО и«л + 1 L^d } - -1 с 4 ^ч
м Q За |оа 3 1 — v0 CSJ + СЧ Q. ф , з Г-vfl CN Г : С О cS ‘ т 1 1 - . . £ . + тч •4С - - Г
U/U оДО тч сМ' со U0 со
5*
68
ПРИЛОЖЕНИЕ ОБЩЕГО БАРИАЦИОННОГО МЕТОДА
[ГЛ I
и'-однократная операции дифференцирования над функциями, по-
мещенными в верхней строке таблицы. Температурные члены Л1;
Л2, Л3, Bi, В2, В3, отнесенные в правую часть уравнении, имеют
вид:
Л1 = а(1 ,
Д2 — а (1 + ''о) <j?2 dy >
Л3 = а (1 + vo) Фз dy ,
Bi = — а(1 4- v0) \Tq>'idy, j
S2 = -a(l +^T^2dy, j (8.8)
B3 = — а (1 -j- ''о) Т'Фз dy •
Дифференциальные уравнения табл. 1 при заданной функции
Т — Т (х, у, /) могут быть проинтегрированы известными метода-
ми математического анализа. При этом граничные условия на тор-
цах х = 0 и х = I в соответствии с изложенным вариационным
Методом должны быть поставлены в обобщенной форме. Так, в
случае свободных торцов граничные условия могут быть сфор-
мулированы в следующем виде (см. (1.14)):
ax<fj dF = О, xxytyh dF = 0. (8.9)
При полном защемлении торцов, препятствующем как вертикаль-
ным, так и горизонтальным перемещениям в сечениях х — 0 и
х — I, следует приравнять нулю обобщенные перемещения:
И; 0, ' lZfe = 0.
(8.10)
В дальнейшем мы остановимся на том случае, когда на тор-
цах х = 0 и х — I рассматриваемого массива имеются диафрагмы,
жесткие в своей плоскости и гибкие из своей плоскости. Такие
диафрагмы будут препятствовать только ^вертикальным перемеще-
ниям. При этом в торцовых сечениях напряжения ах обращаются
в нуль. Подобные граничные условия в обобщенной форме запи-
сываются следующим образом:
<зх <?i dF = 0,
14 = 0.
(8.П)
3. Предположим, что заданная температурная функция Т (х, у, t)
может быть разложена в тригонометрический ряд:
К-! (2п — 1)ях
у-у = 2 Tri^yt ty sin —J-—. - (8.12)
. n =1 . .
§ 8] ТЕПЛОВЫЕ НАПРЯЖЕНИЯ в УПРУГОМ основании gg
Коэффициенты Фурье Тп (у, t) этого ряда определяются в виде
i
Тп {у, (X, у, t) sin (2-л-^^dx. (8.13)
О
Будем считать также, что граничные условия задачи характери-
зуются равенствами (8.11). В этом случае приближенное решение
дифференциальных уравнений табл. 1 можно получить при помо-
щи тригонометрических рядов. Для этого искомые функции
Ui (х, t), Vk (х, t) следует представить в форме:
0° \
Ui (х, 0 = 2 и in (0 cos ,
7 (8.14)
Vk (х, 0=2 Vkn (0 sin
Л—1
Нетрудно видеть, что выражения (8.14) удовлетворяют условиям
(8.11).
Подставляя разложения (8.12), (8.14) в уравнения табл. 1, мы
получим систему алгебраических уравнений для определения неиз-
вестных коэффициентов Uin (t), Ул„(/) рядов (8.14). Для каждого но-
мера п разложений (8.12), (8.14) эта система будет состоять из
шести уравнений относительно шести коэффициентов: Uln, U2n, U3n,
Vln, V2n, V3n (табл. 2). Грузовые члены этих уравнений вычисля-
ются по формулам:
н
Агп = (2п— 1) 7t (1 -|-Vo) <х\тп (у, 0<f>i dy
О
н
Bkn = — (1 + v0)aZ Тп(у, t)^'kdy
о
(z = 1, 2, 3),
(k= 1, 2, 3).
(8.15)
Решение рассмотренной температурной задачи сведено нами
таким образом, к решению системы алгебраических уравнений.
Заметим, что эту систему следует решать в общем виде, посколь-
ку свободные члены А/п, Bkn уравнений табл. 2 представляют со-
бой функции времени t.
По определении коэффициентов Uin (/), U2n (/)> Usn (/), Vln (О»
Viri (/), V3n (0 из уравнений табл. 2 перемещения в упругом слое
в любой момент времени могут быть найдены при помощи формул
(8.14), (8.6). Для определения напряжений следует использовать
уравнения (8.3). Внося в эти уравнения формулы (8.6) и (8.14),
мы определим нормальные и касательные напряжения упругого
70 ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА [ГЛ. 1
№ п/п У1П - - USn
1 _ Г(2п - 1)2я2 Н [ . 9 1 + 3’ 1 I + у (1 - Vo) ] Г (2га —I)2 я2 Н _ L w 1 2 (1 — Уо) н J —
2 Г (2га — l)2r.2 Н L 18 1 3 11 2 (1 —vo) н J _2р^я + ,3 1 1 + у(1 -v0) Г (2n — I)2 я2 Н [18 Z 3 И
3 — Г(2га — 1)2я2 И L 18 1 3 1 1 -у(1-Уо)-я] _2р-^4+ , 3 11 + y(l-v0)-^J
.4 у (2га — 1) (1 —3v0) (3” — 1) (1 + vo) —
5 у (2га— 1) (1 + vq) — j" (2га — 1) (1 + vo)
6 — у (2га — 1) (1 + v0) Г
§ 81
ТЕПЛОВЫЕ НАПРЯЖЕНИЯ В УПРУГОМ ОСНОВАНИИ
71
Таблица 2
Vln V2n V^n Правая часть
J(2n-l)(l-3v0) jr(2n— 1)(1 + vo) — ^ln
'J' (2” — 1) (1 + vo) — (2n — 1) (1 4- v0) ^2П
— "4 (2« —1) (1 + vo) — ^3n
Гя2 (2n — I)2 (1—vp) L 18 X H I I x t +3 Гя2С2п—1)2(1—vo) L 36 x , H z 1 X I 3 Я J — Bin
[я2 (2n — I)2 (1—v0) п [я2(2п-1)2(1-^о) v fw2(2n-l)2(l-v0) _
[ 36 " H „ I 1 X I ~3 H J 1 18 X H „ 1 1 X z +3 я] L 36 H „ Z 1 X I ~3 tfj В in
Гя2(2п—l)2(l-^»o) v Гп2(2ц—1)2(1—vo) v
— L 36 H n I 1 X I ~3 HJ L 18 ’ x н „ z 1 X Z +3 /7 J В zn
72
ПРИЛОЖЕНИЕ ОБЩЕГО ВАРИАЦИОННОГО МЕТОДА
[ГЛ. I
3
(2л — 1) лх
слоя в следующем виде:
00
ах = -^~ У
3
+ Vo S Vkn (0 фй (,У)—а (1 + Vo) Тп (у, f) sin
k—i
OG г 3 3
= —2 S тиу)^о^4^Ж(о<рЛ*/)-
* vo n=jLfe=i i=l
- а (1 + v0) Ta (y, o] sin
co p 3
(8.16)
- Е° У У I
^-2(1 + vo)
, (2л-
3
7^ Е v'kn (0 фй (у) COS
‘ л=1
(2л — 1) т.х
т
Формулы (8.16) дают возможность проследить изменение напря-
жений б любом сечении упругого слоя в течение всего периода
колебания температуры при условии, что температурная функция
известна. Так, например, при помощи этих формул может быть
произведен расчет бетонного блока на изменение температуры, про-
исходящее в процессе схватывания и твердения бетона, или на
усадку бетона, если известно аналитическое выражение закона
усадки *).
*) Примеры расчета бетонного блока на температурные воздействия см.
в работах А. А. Чече [81], [82].
fjjkBA II
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
§ I-
Дифференциальное
основании с
уравнение изгиба балки
двумя характеристиками
на упругом
Предположим, что на поверхности упругого Однослойного ос-
нования покоится балка, несущая произвольну закон
ку р(х) (рис. 34). Для бая»;
плоских сечении. Трением, возникающим и ду
будем пренебрегать. В этом Дифференциальное уравнение
изгиба балки может быть представлено в вид
£jpv(x) = р(х) — Q(x), (1л?
где q (х)——реактивные давления упругого основания (нагрузка на
0СН°па^е)’ а У(х)“пр0Гибда?иЛеКП D содержит две неизвестные
Дифференциальное уравнение ц.г; а Р „ дтявне-
(bvHKTTMM I/ И Л(г\ Ппя определения этих функции к уравне-
ниюН 1/с!.едует присоединить дополнительное условие, выража-
ц.1) следует присоед на 0СН0Вание и его осадкой,
ющее зависимость между нагрУзкои v rnvHTV
а также контактное условие о плотном при е
74
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
Ранее было показано, что дифференциальное уравнение равно-
весия однослойного основания имеет вид*):
— 2/V" + &V = ? (х) ф (0), (1-2)
где f ? k=7^-2\¥4y)dy, 1 — J
° 0 Н (1-3)
t = . Д Ф2(у)Л/. 4(1 + v0) J ° 0
По условиям задачи функцию поперечного распределения пе-
ремещений ф(у) удобнее выбрать так, чтобы ф(0) = 1. При этом
обобщенное перемещение V (х) будет представлять собой осадку
поверхности упругого основания, а уравнение (1.2) перепишется
в виде
— 2tV" + kV = g(x), (1.4)
где q (х) — нагрузка на основание.
Вследствие того, что прогиб балки совпадает с осадкой поверх-
ности упругого основания, уравнения (1.1) и (1.4) могут быть рас-
смотрены совместно:
— 2tV” + kV = q (х), 1
EJVIV = p (x) — q (x). |
Исключая из системы (1:5) функцию q(x), получим основное
дифференциальное уравнение задачи, выражающее зависимость меж-
ду нагрузкой на балку и ее прогибом:
- EJV1V — 2tV" + kV = р (х). (1.6)
Отметим, что дифференциальное уравнение (1.6) отличается от
известного уравнения, вытекающего из гипотезы коэффициента по-
стели, тем, что в нем имеется дополнительный член со второй про-
изводной от прогиба балки. Этим членом учитывается влияние ка-
сательных напряжений, возникающих в упругом основании.
Для большинства задач при решении дифференциального урав-
нения (1.6) удобнее перейти от действительной координаты х к при-
веденной координате т; = Д-, где L — некоторая величина, име-
ющая размерность длины. Величину L можно, например, принять
равной
(1.7)
У
*) Индекс 1 при функциях V (у) н ф (у) в дальнейшем всюду опускаем.
$ 1] УРАВНЕНИЕ ИЗГИБА БАЛКИ НА УПРУГОМ ОСНОВАНИИ 75
в соответствии с чем она может быть названа упругой характе-
ристикой балки*).
Дифференциальное уравнение (1.6) перепишется при этом в виде
dy;4 drf ' EJ
(1-8)
Здесь г2 и s4 — безразмерные упругие характеристики, вычисляе-
мые по формулам:
н
2 tl? q 1 — Vp Г , 2 ,
г =ЁТ =2~1Г\
о
н
si = k~ET=ZL\ &dy.
(1-9)
Необходимо отметить, что дифференциальное уравнение (1.8)
характеризует собой обобщенные условия равновесия слоя грун-
та, рассмотренного совместно с балкой, расположенной на его по-
верхности. Вследствие этого функция V (у) по принятой ранее
терминологии представляет собой обобщенное вертикальное пере-
мещение.
Обобщенному прогибу V (у) и обобщенному углу поворота
cp(vj) = -j- V (т;) (в данном случае эти величины совпадают с действи-
тельным прогибом и углом поворота балки) соответствует обобщен-
ная поперечная сила, характеризующая состояние касательных на-
пряжений в сечении х = const рассматриваемой системы. В отли-
чие от балочной поперечной силы Q для обобщенной силы введем
новое буквенное обозначение. Согласно основной идее рассматри-
ваемого вариационного метода эта сила определится в следующем
виде (см. вторую из общих формул (1.10) гл. I):
N Ь) = -14 [V" (v) ~ 2/-V' (7))]. (1.10)
Выражение (1.10) .необходимо учесть при постановке граничных
условий, которые, как отмечалось в гл. I,' должны быть зада-
ны в интегральной форме.
По определении функции V (?]) реакции упругого основания q (vj)
могут быть найдены из уравнения (1-4), а изгибающие моменты и
поперечные силы балки — по известным формулам сопротивления
* Аналогичное выражение для упругой характеристики L принято в мето-
де М. И. Горбунова-Посадова в случае расчета бесконечно длинной балки
125], [26].
[гл. II
(1.11)
(1-12)
7Q ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
материалов:
.. CTd2V EJ (PV
М = — EJ ---------1
dx2 L1 dr? ’
_ p,W=_ EJ_d^
dx3 ~ L3 d-t? •
Рассмотренное решение относится к работе балки в условиях плос-
кой задачи теории упругости. Это означает, что дифференциальное
уравнение (1.6) [или (1.8)] одина-
ково справедливо как для балок,
лежащих на узком вертикальном
слое, ширина которого равна
ширине балки 8 (рис. 35), так
и для полос шириной 8, выде-
ленных в поперечном направле-
нии из длинных плит (рис. 36),
лежащих’на упругом основании.
Первая задача, как известно,
характеризуется условиями пло-
Рис- 35. ского напряженного состояния,
вторая — условиями плоского деформированного состояния.
При -расчете балок (полос) в условиях плоского деформирован-
ного состояния упругие характеристики основания Е и v0, входя-
Рис. 36.
щие в выражения (1.3) и (1.7), следует вычислять по формулам:
Ё v
Ео=^Г, = U-13)
1 — % 1 vrp
где £гр, vrp — соответственно модуль упругости и коэффициент
Пуассона упругого основания.
Кроме того, в формулах (1.11) и (1.12) характеристику жест-
кости полосы J следует положить равной
J ~ 12 (1 — р2) •
где р, — коэффициент Пуассона материала полосы.
j 21 РЕШЕНИЕ ОСНОВНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 77
§ 2. Решение основного дифференциального уравнения
при помощи частных интегралов
1. Для решения дифференциального уравнения (1.8) предвари-
тельно должен быть найден общий интеграл соответствующего од-
нородного уравнения
^-2r2^- + s4K = 0. (2.1)
ат]4 ат]2 ' 4 '
Как известно, общий интеграл однородного дифференциально-
го уравнения четвертого порядка имеет вид:
V (tj) = СХФХ + С2Ф2 4- С3Ф3 + С4Ф4, (2.2)
где Clt С3, С3, — произвольные постоянные интегрирования, Фь
Ф2, Ф3, Ф4—некоторые известные функции, определяемые в за-
висимости от вида корней характеристического уравнения
&4 — 2r2&2 + s4 = 0] (2.3)
и, следовательно, в зависимости от соотношения между величина-
ми s и г.
Замечая, что характеристики s и г не могут быть отрицатель-
ными, рассмотрим три возможных случая соотношений между ве-
личинами s и г. Корни характеристического уравнения (2.3) опре-
деляются при этом в следующем виде:
1) при s > г
k = + а + ₽Л
где а и р — действительные положительные числа, равные
2) при s — г
ki — k3 — г,
k3 = kt — — r\
(2-4)
(2.5)
(2-6)
(2.7)
при-
трех
В соответствии с формулами (2.4), (2.6) и (2.7) в табл. 3
ведены выражения для функций Фх, Ф2, Ф3, Ф4, а также их
последовательных производных Ф', Ф", Ф'". Эти производные вы-
ражаются линейно через функции Фх, Ф2, Ф3, Ф4, что облегчает
Дифференцирование выражения (2.2). Кроме того, в табл. 3
Таблица 3
Соотнесе- ние между s и г Функция и ее про- изводные Ф1 (нечетная) Ф2 (четная) ф, (нечетная) Ф4 (четная)
s > г ф sh ат; cos рт; ch ат; cos рт) ch ат) sin Вт) sh ат) sin |3т)
ф' аФ2 — рф4 аФ1 — рФз (хФ^ ^Фг аФ3 + рФх
ф" (а2 — р2) Фх — 2а|ЗФа (а2 — р2) Ф2—2арФ4 (а2 — р2) Ф3 + 2аЗФ! (а2 — З2) Ф4 + 2аЗФ2
ф'" а (а2 - Зр2) Ф2 + +.р (Р2н-За2)Ф4 а (а2 - Зр2) Фх + + Р (Р2 - За2) Ф3 а (а2 — Зр2) Ф4 — — £ (<32 — За2) Ф2 а (а2 — ЗЗ2) Ф8 — -Р (₽2 —За2) Фг
S = Г ф sh гт) ch гт) т) ch гт; Т) sh ГТ)
ф' гФ2 Г<£>! Фз 4~ ^*Ф1 Ф1 4" гФ3
ф" Г2Ф1 г2Ф2 2гФ1 + г8Ф« 2гФ2 + г2Ф4
ф'" г3Ф2 Г?ФХ Зг2Ф2 + г2Ф4 Зг2Ф1 + г3Ф3
s < г ф sh Ajt; ch Ajt; sh Х2т) ch Х2т;
ф' Л2Ф4 Х2Фз
ф" ^Ф2 Фз
ф'" МФ2 ХЗФ1 ^Ф4 Цфз
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ. II
§ 2] РЕШЕНИЕ ОСНОВНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 79
Таблица 3 (продолжение)
ф4 (четная) £ к. л и ее © К. ё* се к. Г3фл 13 ё ICQ. 1 со © 1 в d |ЙХ + d 1 а 1 1 ~ Фз — Ф1 Т~ Фз со ©
ф, (нечетная) кЪ qs © к. ео © се «н к. ©” СО «н аФ4 —ЗФ3 се |<ЗХ + се 1 в d © j |се^ 1 © ч> © -к ©
Ф2 (четная) О О О © |OCL + © । а о» iqcl + се 1 в © 1 Т7Ф> ©
Ф, (нечетная) II d © О О © |СО- 4- d © ।« d fax + d i а d © d © II « ©
аннКояеи -осШ зэ и вийянАф © © ё © © © % ©
J И 9 ХНжак эи и -этонхооэ О II со А со II со v со О II со
82
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
через функции Ki, К2, Кз, Ki и их производные, образовали еди-
ничную матрицу, т. е. приняли следующие значения:
i V (0) = /С (0) <р(0) = ^кло) М(0)= Р г п -^Kt(O) У(0) = (0)]
1 1 0 0 0
2 0 1 0 0
3 0 0 1 0
4 0 0 0 1
Из общего решения (3.1) и свойств единичной матрицы следу-
ет, что постоянные Съ С2, С3, совпадают с начальными пара-
метрами, а именно с обобщенными усилиями и перемещениями в
сечении = 0, т. е.
Ci = Vo, = <р0, С3 — 34О, Ci = No,
а функции К2, Кз, Kt выражают влияние начальных парамет-
ров, равных единице, на прогиб в сечении с координатой т;, т е.
являются коэффициентами влияния. Обозначая
Ki=Kvv K2 = Kv<t, Кз — KvM, Kt = Kvn,
получим:
V (т() = V0Kyy + ^aKV9 + МоКум + N0Kvn- (3.2)
Производя над выражением (3.2) линейные дифференциальные
операции, определяемые формулами (1.10), (1.11), нетрудно вы-
разить величины <р, М, .¥ в сечении с координатой как функ-
ции начальных параметров и соответствующих коэффициентов влия-
ния. Совместно с формулой (3.2) получим при этом систему:
V (т() = V0Kvv + <Po-Kvq> + M0KvM + К0Kvn,
<р (Ti) = V0/(cpv + <?OKW + М0К?м + KoKtfNt
Л4(т]) = VqKmv 4~ 4" М0Кмм 4- KqKmni
N (ij) = V0Knv 4" <?oKnv 4" M0Knm 4- К0Knn-
(3.3)
Совокупность 16 функций ВЛИЯНИЯ Kw , Knn, вхо-
дящих в выражения (3.3), образует матрицу прямого линейного
преобразования величин Vo, <р0, Л40, No в V„, <рч, Mr,, N^. По опре-
делении начальных параметров задача может считаться решенной.
Отметим, что за начальное сечение может быть принято вооб-
ще любое сечение т; = t, в котором величины V/, <ft, Mt, Nf счи-
§ 3] РЕШЕНИЕ ПО МЕТОДУ НАЧАЛЬНЫХ ПАРАМЕТРОВ gg
таются известными. При этом значения Vv, ср^, MTl, в сечении,
отстоящем от начального на расстоянии т; — t, определяются при
помощи тех же функций влияния, если на участке между этими
сечениями справедливо однородное дифференциальное уравнение
изгиба (2.1). Таким образом, можно записать:
Уц = VtKvv + + MiKvm + NtKyN,
= VtK<tv + <Р/Кфч> + + N .
M-n = V(Kmv + + MiKmm + NtKMNt (
Nr, = ViKnv 4“ <ptKN!f 4" NtKNN. .
Функции ВЛИЯНИЯ Kw,---, К NN вычисляются здесь как функ-
ции аргумента Д— Z), для чего достаточно определить функции
Фх,..., Ф4 как функции Фх CG — О,---, Ф4(т]— О-
Одним из важнейших свойств матриц (3.4) или (3.3) является
их симметричная структура, вследствие которой из 16 функций
влияния только 10 являются различными. Четыре функции, рас-
положенные на восходящей диагонали, не повторяются. Осталь-
ные 12 функций, расположенные симметрично относительно этой
диагонали, попарно равны, т. е.
К мм = К w, К фЛ1 = Кум,
Kmn — Куу, = KMv,
&MN = Куч, |
K-NM = К^у. f
(3-5)
Отмеченное свойство является следствием теоремы Бетти
о взаимности работ*).
2. Учет внешней нагрузки. Общий интеграл не-
однородного уравнения. Рассмотрим пример, приведенный
на рис. 38. Балка конечной длины Z нагружена сосредото-
ченными силами Рх, Р2,..., Рп. Точки приложения сил определены
безразмерными координатами tlt tn.
Можно видеть, что на первом участке 0 < т] < tr все кинема-
тические и статические факторы определяются через начальные
параметры и функции влияния по уже известным формулам:
V h) = VoKw Д) + 'PcKv.p Cg) + MCKVM (rt) + NcKvn Cg), )
Ф (tj) = УоЛфг Cg) 4- (r;) 4- (r() 4- NqK^n (g), J <3
M (Д = VcKmv (g) + <рсКм9 (r() 4- МсКмм (g) 4- NcKmn (g), j
N (g) = V0^л’v (v]) 4- ФсКл’ф (t() 4- M0Knm (rt) + NqKnn (t;). /
*) Более подробно о свойствах функций влияния, составляющих матрицы
прямого и обратного преобразования, см. в монографиях В. 3. Власова:
’Тонкостенные упругие стержни», Гсстехиздат, 1940, и «Строительная меха-
ника тонкостенных пространственных систем», Стройиздат, 1949.
6*
84
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
Выражения (3.6) остаются справедливыми до тех пор,
пока справедливо однородное дифференциальное уравнение (2.1),
т. е. пока функции V (у), <р (•*)), М (ig), N (tj) остаются непре-
рывными.
Если в какой-либо точке балки с координатой т] = tk задан
разрыв одной из этих функций на определенную величину, т. е.
приложена внешняя сосредоточенная нагрузка, то, пользуясь
принципом наложения, вытекающим из линейности преобразова-
ния (3.6), следует для сечений с координатой т] > tk прибавить
влияние этого разрыва. Оно будет равно произведению величины
разрыва на соответствующую функцию влияния, вычисленную для
координаты (•*) — tk).
Так, например, в каждой точке, где действует сосредоточенная
сила Pi, функции V (т)) ср (f)), М (тд) остаются непрерывными и
только jV (tj) получает приращение на величину (— Pi). Поэтому
для участка < у < t2 (рис. 38) можно записать:
И (т]) = V0Kvv (т;) + (р0/<уф (ц) + M0Kvm 0*]) + N0Kvn h) —
— — tl),
<p C*l) = oKvv (*)) + ?оКфф СФ + M0Kvm (ri) + ('*]) —
PlK<pN (ig t j),
= VoKmv С*)) + ТоКмф ('Ф + M0Kmm (•*)) + (•*))—
— PiKmn{ti — ti),
li ж V<iKnv (n) + <РоКуф (ri) + M0Knm (*)) + NoKnn^) —
— PiKnn (fl — ti).
РЕШЕНИЕ ПО МЕТОДУ НАЧАЛЬНЫХ ПАРАМЕТРОВ
85
§ з]
На произвольном участке /,• < tj < ti+1 будем иметь:
V (»]) = VoKvv (tj) + <f>oKv9 (tj) + M0KVM (»]) -f- N0Kvn (fj) —
i
- 2 PkKvN C*i—tk),
k—1
<P (t/) = (Y/) + Фо^фф (Y/) + MqK^m (tj) + NoK<?n (tj) —
i
--2 ЛгХф/Дт)— tk),
k=1 (3.8)
M (ri) — V0Km\’ (я) + Фо^Мф (Y/) + MqKmm (v) + N0Kmn (tj) —
I
-- 2 P kKuN (TJ tk),
k—1
N (tj) — V0Knv (tj) + То^аф (*)) + M0Knm (tj) + N0Knn (tj) —
i
— 2 Pk^NN^—tk)-
A=1
В случае распределенной нагрузки р (/) (рис. 39), которую
можно рассматривать как совокупность сосредоточенных элемен-
тарных сил, для загруженного участка получим:
У (т;) = V0Kvv (т() + cp0KVip (т() + M0Kvm (?]) +
+ N0Kvn (О KVN (т)- t) dt,
а
? (*)) = V0K<?v (7]) + <Р(Лфф (Т() + MQK<fM (7]) 4
+ N0K,n (ti)-\P (0 KvN (7) - t) dt,
a
M (t))= V0Kmv (t;) + %Км<р (т;) + MqKmm (fl) +
+ N0Kmn (ri)-\p (t) К MN (7J - t) dt,
N (tj) = VuKnv (t;) + <Р(Даф (t;) + M0Knm (t;) +
4- N0Knn (tj)— p (t) К NN (tj — t) dt.
a
(3.9)
При одновременном действии распределенных и сосредоточенных
сил интегралы в формулах (3.9) следует понимать в смысле
8g ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ (ГЛ. II
Стилтьеса, т. е. надо присоединять к ним последние члены (сум-
мы) выражений (3.8).
Для случая произвольных внешних воздействий, т. е. в са-
мом общем виде, решение неоднородного дифференциального
Рис. 39.
уравнения (1.8) может быть представлено следующим образом:
V7 (v]) = V0Kvv + <?oKv<f + — Fv,
ср (-ф = 1/0/(фУ 4“ ‘PoXqxp 4“ -М0/С(>м 4“ Ру, ।
М ('ф = V0/Gw 4- <p0^Mtp 4" М0Кмм + N0Kmn — Fm,
N ('ф = V0Knv + VoKnv 4- M^Knm + NqKnn — Fn,
где под Fv, Fq, Fm, Fn следует понимать некоторые известные
функции, определяемые в зависимости от вида нагрузки и ее
расположения на балке. При этом заметим, что «нагрузка» может
состоять не только из вертикальных сил и моментов: заданными
внешними воздействиями могут являться также и сосредоточенные
прогибы, и углы поворота (переломы) балки.
РЕШЕНИЕ ПО МЕТОДУ НАЧАЛЬНЫХ ПАРАМЕТРОВ
87
§ 31
Например, для случая, представленного на рис. 40, функции
Fv и FM определяются в виде:
при 0< CiG < *1 Fv = FM = 0;
при С ^G < ^2 Fv — PKvn Cg — ^1), Fm = PKmn ('G — ^1);
при ^2 ' < G < h Fv = PKvn Cg — ^1) — MKvm (“G — *2) Fm= PKmn Cg — ^1) — МКмм ("G — ^2)
при К < G < *4
Fv = PKvn — tj — MKvm (i)— tz)~ bVKvv^ — ts), (3‘H>
Fm= PKmn (tj — /i) — МКмм (tj — t2) — AVKmv ('G — /3);
при Z4 < т)
Fv = PKvn Cg — ti) — MKvm (tj — — KVKvv (g — t3) —
— Д<р/<Кф(тд —/4),
FM= PKMN (tj — t,) — МКмм (tj — t2) — ДУХми ("G — is) —
— Д<р/<Мф(7) —^)-
Начальные параметры Vo, <p0, Mo, No, с точностью до кото-
рых определены искомые расчетные величины в общих формулах
(3.10), вычисляются в изложенном методе чрезвычайно просто,
поскольку за начало отсчета может быть принято любое сечение
балки. Так, выбирая один из концов балки за начальное сечение
(т] = 0), мы тем самым сразу определяем два параметра из четы-
рех. При этом два других начальных параметра могут быть
всегда найдены из системы только двух уравнений (при любой
«нагрузке»), составленных относительно противоположного конца
балки.
Например, если в сечениях = 0 и tj = -j- имеется свободное
опирание, то известно, что
уо = о, Л1О = °; (3.12)
V = 0, М (-{-) = °- <з. 13)
Раскрывая условия (3.13) при помощи общих формул (3.10),
а также учитывая (3.12), для определения параметров <р0 и Мо,
88 ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ. II
получим систему двух алгебраических уравнений:
V = «РоКуф + NqKvn — Fy = О,
М = <PqFmv + F0Kmn — Fm — О,
где Kv9, Kvn, Км9, Kmn, Fv, Fm — величины соответствующих
функций при аргументе tj = (х = /).
3. Вычисление функций влияния. Записывая общее
решение неоднородного дифференциального уравнения изгиба
балки на упругом основании в виде формул (3.10), мы предпола-
гали функции Kvv, Knn известными. Покажем теперь,
как определяются эти функции для наиболее характерного случая,
когда s > г.
Напомним, что при выводе основных формул настоящего ме-
тода мы исходили из однородного дифференциального уравнения
(2.1), общий интеграл которого характеризует величину обобщен-
ного прогиба V (tj) и имеет вид:
V (т)) = СХФХ + С2Ф2 + С3Ф3 + С4Ф4. (3.14)
Остальные кинематические и статические факторы опреде-
ляются при этом посредством линейных дифференциальных опе-
раций над функцией (3.14):
<р с*1) = 4-г,
Л1(7]) = Л7П Д2 V > (3.15)
У(7]) = — — 2г2Г].
Внося выражение (3.14) в формулы (3.15), а также замечая,
что в начальном сечении (?) = 0)
Ф2=1, фх = ф3 = ф4 = 0,
V = V0, ф = М = М0, N = N0,
после несложных вычислений получим для произвольных постоян-
ных Сх, С2, С3, С4 следующие значения:
Сх = Г s2BL®„+ 3 L
2а £s2 L r Г EJ /vo J ’
с2 = Уо,
(3.16)
S 3]
РЕШЕНИЕ ПО МЕТОДУ НАЧАЛЬНЫХ ПАРАМЕТРОВ
89
СО
S
СО
Коэффициенты влияния
о (£Ф1—аФ8) ь. ь; II % !> X 0- II аг К i£ II §
«0 •Ч 5 N СО |0О. 1 « СМ
II <
€ е '+ ,е? 1«
о N •Ч ^3 1 « см |0£Х । СМ 9’ 9’ 9-
1 5 ь. S II 5 5< II 5 5 sc II
о 9- СО > 3 F [ ч> в ei.l<» 1 «0 1 в 1 )« 1 ® |СО- 52- 'со “ч ial Лу Ч 1 « '-2-
|CD- 1 » СМ + о» е с. ! в
Ь. 1 9- II 9- 9- К II 1°°- 9- е7""' |СО- * 1 II
о ч> е „ 1,сО- U 1« 1 N в II ""л в 1 8 1 в lea. ся jloQ. <* | в 1 см II ЬсГ в ч> со N -J 5 i'S- <N II 5< со е 1 8 1 Ч? % “ N СО <0 Т в « Т М * 1
F 57 е- р 5 F
90
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
Подставляя теперь найденные значения (3.16) в формулы (3.14)
и (3.15), мы выразим величины V (?]), ?(т[), Л4 (?]), N (т)) через
начальные параметры Уо, <р0, Мо, No и функции влияния Kvv,
Knn- Для рассмотренного случая (s > г) матрица коэф-
фициентов влияния приведена в табл. 4.
Аналогичным образом могут быть определены коэффициенты
влияния и для двух других случаев соотношения между харак-
теристиками s и г:
s = г и s < г.
§ 4. Бесконечно длинная балка
1. Рассмотрим балку бесконечной длины, загруженную сосре-
доточенной силой Р (рис. 41). Выбирая начало координат в точке
р
} \“ I }
I ______________________________________
Рис. 41.
приложения силы, получим для
решения задачи однородное диф-
ференциальное уравнение
d*V
drf
— 2r*~ + s4V = 0.
(4.1)
Останавливаясь на случае
s > г, запишем общий интеграл
уравнения (4.1) в форме
V (т)) = sin рт) + С2е~cos рт] + Сйеат‘ sin р?] + C4<?a71cos p-yj, (4.2)
где величины а и р определяются выражениями (2.5).
В силу симметрии'ограничимся рассмотрением правой части
балки. При этом, исходя из условия:
При 7] —> ОО
получим:
V->0,
С3 = С4 = 0.
(4-3)
Общее решение (4.2) примет теперь следующий вид:
Vfr^C^ + C^, (4.4)
где
Fi = ег~sin рт], ) (4 5)
Fz = е~а1) cos рт]. J
Постоянные интегрирования Сх и С2 могут быть определены из
§ 4]
БЕСКОНЕЧНО ДЛИННАЯ БАЛКА
91
условий в начальном сечении:
при т) = О <Р (0) = 4 4 = °’
^(0) = -#^-2г2Я = -4-
' ' Ls L^7! dr\ J 2
(4.6)
где ф (0) — угол поворота, a N (0) — обобщенная поперечная сила
в сечении т; = 0 *).
Раскрывая условия (4.6) при помощи формулы (4.4), будем
иметь:
СЛ(0) + СХ(0) = 0,
pi9 (4-7)
C^'(0) + C2F2'(0)= .
Решение системы алгебраических уравнений (4.7) дает для
искомых постоянных интегрирования следующие выражения:
с _ PL3 _____________(°)____________
1 ~ 2£J р(0) f (0) - г; (0) г; (0) ’
(4.8)
с = PL3______________F' (0)_________
2 2£J р’’’ (0)7/ (0)-F’" (0)^(0) ’
где Fx(0), Fi (0), F2(0), F2 (0) — значения первых и третьих
производных от функций Fj и f 2 в сечении с кобрдинатой tj = 0.
Внося выражения (4.8) в формулу (4.4), а также учитывая
формулы (1.7), (1.9) и (2.5), можно теперь представить функцию
прогибов балки окончательно в виде
V(71) = —-% [«F1 (7]) + ₽F2 (7))]. (4.9)
Выражения для изгибающих моментов и поперечных сил балки
«а основании формул (1.11) и (1.12) примут вид:
мм , (4.10)
Ч а В J
Q 01) =-4 ~ • (4J1)
L 2а р J
*) Обобщенным условиям (4.6) в данном
граничные условия:
при т; = 0
случае соответствуют обычные
1 dV г.
<Р (0) = -=— -V- = о,
L ат;
Q (0) = -
£J d?V_ = _ Р_
La di)3 2
92
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
Реактивные давления упругого основания согласно уравнению
(1.4) определятся выражением
q (?1) = l^(S2 + 2f2) F2 (?i) + “ (®2 “ 2/"2) F1 ’ (4J2)
Полученные нами расчетные формулы (4.9)—(4.12) имеют про-
стую структуру и могут быть поэтому без труда использованы
для определения напряженного и деформированного состояния
бесконечной балки.
По аналогии с имеющимися для бесконечной балки решениями
(см., например, [25]) формулы (4.9)—(4.12) могут быть перепи-
саны также в следующей сокращенной форме:
Р (i — v2) _
Q0) = -FQ(t]),
Л4 (tj) = PLtn (tj),
<?('»)) =Z_g(7j).
(4.13)
Входящие в выражения (4.13) безразмерные функции приве-
денной координаты определяются в виде:
у 0) - й 2 0) + Ш za ps4 4 L а £ J
<7(т))= - [р (s2 4- 2г2) F2 (т))+ а (s2 2r2) Fj (к))]. 4(Х р (4.14)
По своему геометрическому смыслу функции (4.14) представ-
ляют собой безразмерные эпюры соответствующих расчетных
величин. Нетрудно показать, что между этими функциями суще-
ствуют соотношения:
= | (4.!5)
<р' h) = «Cg). Q' 0) = — <J ("ti- •*
— i
*) <Р (ч) =_____Fi (>]) — безразмерная эпюра
4а р
тельное значение которого вычисляется по формуле
P(l-V2)
<₽(•>')) <₽(•>!)•
угла поворота, действи-
4] БЕСКОНЕЧНО ДЛИННАЯ БАЛКА 93
2. Отметим, что расчетные формулы (4.9)—(4.12) или (4.13)
носят общий характер и остаются справедливыми при любом вы-
боре функции поперечного распределения перемещений ф(у),
с точностью до которой определены упругие постоянные k, t, s2,
г8, a. ₽•
Далее, в качестве примера рассмотрим случай, когда функ-
ция ф(у) выбрана в виде
Ф(г/) =-----тЛ-, (4.16)
sh7"
где L — упругая характеристика балки, определяемая формулой
(1.7), а 7 — некоторый коэффициент, зависящий от свойств упру-
гого основания.
Для постоянных, входящих в формулы (4.9)—(4.12), получим
при этом следующие выражения:
k = —g°5
s‘ = 2-^,
— -» / S2 + г2
а - у —2
t=
12(14- v0)
_1_7#
2 L
sh^chl^+1"
L L L
sh2!^
L
(4-17)
shI^chl^-2^
• о L L L L
L
Если упругое основание представляет собой полуплоскость,
т. е. Н—*<х>, то формулы (4.17) принимают вид:
ь— Е°5 Т
2(l-v2) L ’
jL
~~ 8(1 4- v0) 7 1
(4.18)
s4 = 7,
-2 — 1~V°
47
94 ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ. В
_ _На_рис._42, 43, 44 и 45 приведены безразмерные эпюры
Эти эпюры дают возможность j определять расчетные ординаты
для сечений балки, находящихся на приведенных расстояниях
7!=.^- = 0; 0,2; 0,4;...; 4,0
от начала координат. Действительные расстояния до этих сечений
будут:
х = rtL = 0,0/,; 0,2/,; 0,4/,;...; 4,0/. [л].
§ 4]
БЕСКОНЕЧНО ДЛИННАЯЛБАЛКА
На приведенных графиках безразмерные эпюры показаны
только для положительных значений iq (для части балки, находя-
щейся справа от загруженного сечения). Для отрицательных зна-
чений т] величины ординат v, tn, Q, q остаются такими же, и только
знак при Q меняется на обратный. Заметим, что переход от
Рис. 45.
безразмерных эпюр к действительным эпюрам V, М, Q, q осу-
ществляется по формулам (4.13).
Можно видеть, что увеличение параметра у приводит к умень-
шению изгибающего момента в нагруженном сечении, что объяс-
няется повышением концентрации реактивных давлений вблизи
96
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
точки приложения силы. При этом и абсолютные осадки балки
в значительной степени уменьшаются.
Для сравнения на рис. 43, 44 и 45 нанесены безразмерные
эпюры соответствующих величин, полученные Н. М. Герсевановым
и Я. А. Мачеретом (см. [21] и [25]) для бесконечной балки, рас-
положенной на упругой полуплоскости *), а также показаны без-
размерные эпюры, полученные из расчета по методу коэффициента
постели. При этом коэффициент постели принимался равным пер-
вому из коэффициентов (4.18) и рассчитывался по формуле
k = ЕоЪ -3_
2(1—vg) L
(4.19)
для следующих значений:
т = 1,5; v. = 0.3, L =
Сравнение с расчетом, основанным на гипотезе коэффициента
постели, показывает (см. на рис. 44 кривую, построенную при
7 = 1,5), что учет работы упругого основания на сдвиг сказы-
вается на уменьшении макси-
мальных изгибающих моментов
А^Мо мальных изгибающих моментов
________________________xfy), под нагрузкой. Однако для рас-
W/ЖЖ смотренного значения 7 различие
результатов незначительно и со-
ставляет примерно 4%.
Из приведенных графиков
И
Рис. 46.
можно видеть также, что при вы-
боре функции ф(1/) в виде (4.16) и при значениях параметра
7 = 1,0 и 7 = 1,5 предлагаемая теория дает меньшие значения
для максимальных положительных моментов, чем расчет в усло-
виях плоской задачи теории упругости (разница в моментах со-
ставляет примерно 15—20%). При этом уменьшение параметра
7 сближает результаты обоих методов.
3. Рассмотрим случай, когда бесконечная балка загружена
в некотором сечении сосредоточенным моментом Мо (рис. 46),
положительное направление которого будем считать совпадающим
с ходом часовой стрелки. Покажем, что эта задача может быть
легко решена при помощи формул, полученных нами выше для
случая загружения балки сосредоточенной силой.
Будем предполагать, что в точках О и К, расположенных
друг от друга на расстоянии ds, к балке приложены две равные
и противоположно направленные силы Р (рис. 47). Рассмотрим,
•) На рис. 42 такой сравнительной эпюры привести нельзя, так как
в условияхл1лоской задачи теории упругости осадки не могут быть определены.
§ 4]
БЕСКОНЕЧНО ДЛИННАЯ БАЛКА
97
например, вопрос о том, какова будет величина прогиба балки
в некоторой точке п (т;) от совместного действия сил Ро и Рк.
На основании первой из формул (4.13) получим:
Vpo С7!) =-----------v
Суммарный прогиб балки в точке п (т;) будет равен
V (?i) - Vp0 + VPk = - [v (rt + ds) - v (Ti)]. (4.20)
Предположим теперь, что ds стремится к нулю, а Р — к беско-
нечности, но при этом произведение Pds = Мо остается конечной
Л
cfs |—
к_______То
п(7р г)
Р,
_____7
Рис. 47.
и - постоянной величиной. Умножив и разделив правую часть
последнего равенства на ds, в пределе будем иметь:
Мо(1—v®) - Л4о(1—v®) -
V W =--------v <4-21>
Аналогичным образом, при помощи выражений (4.13) для рас-
сматриваемой задачи могут быть получены формулы и для других
расчетных величин:
Mo(l-v2o) _
£0Ы3 4м
М (tj) = — Л40щ' (?;) = Л40тл[ (т;),
Q (ij) = Q' = —
7 (тд)> — ZT Q'C'l) = рг ЯМ (Т().
[ (4.22)
7 В, 3. Власов, Н. И. Леонтьев
98
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. Ц
Принимая во внимание зависимости (4.18), можно записать:
йм Сд) = <Р Gg), tnM (тд) = Q Cg), 1
фм (тд) = т (-yj), Qm (тд) = q (тд). J
Таким образом, безразмерные эпюры прогиба vM, угла пово-
рота <рл1, изгибающего момента тм, поперечной силы Qm для слу-
чая действия момента Мо совпадают соответственно с безразмер«
ными эпюрами ср, m, Q и q, полученными для случая загружения
балки сосредоточенной силой Р.
Дифференцируя один раз последнее из выражений (4.17) и
производя несложные преобразования, для безразмерной эпюры
9м (т;) будем иметь:
9м Cg) = r*F2 (*д) + Л (7J). (4.24)
4а 3
§ 5. Жесткая балка
Из балок конечной длины можно выделить один частный,
но весьма важный случай, когда балку практически можно счи-
тать бесконечно жесткой. Расчет таких балок сводится к опре-
делению реактивных давлений q (х): остальные искомые величины
могут быть найдены при помощи обычных уравнений статики.
При расчете жестких балок заданную внешнюю нагрузке
удобно раскладывать на симметричную и кососимметричную сов
ставляющие, производя вычисления для каждого из этих видом
нагрузки в отдельности. Окончательный результат может бытйВ
получен при этом суммированием результатов симметричного Л
кососимметричного расчетов. I
1. Случай симметричного загружения. При дейст-Я
вии симметричной нагрузки _ осадка жесткой балки постоянна,
т. е. I
И(х)=С0. (5.1)1
Поскольку в пределах длины балки осадка поверхности упру-Я
гого основания будет также постоянной величиной, формула (1.4),Я
выражающая зависимость между нагрузкой на основание и егоЯ
перемещениями, позволяет получить
q (х) = kC0. (5.2и
Можно видеть, таким образом, что реакции упругого основа-Я
ния по длине балки постоянны и определяются аналогично винЛ
клеровскому расчету. |
ЖЕСТКАЯ БАЛКА
99
ej
I Однако в рассматриваемом случае функция осадки основания
(х) не должна претерпевать разрыва у концов балки, как это
Предопределяется гипотезой коэффициента постели. Другими сло-
вами, однослойное упругое основание включается в работу !>не
только в пределах конструкции, но и за пределами последней
А -----------------2.------------------- В X
Рис. 48,
(рис. 48). Это обстоятельство имеет существенное значение и
может быть учтено следующим образом.
Ранее было отмечено (см. § 3 гл. I), что обобщенная попе-
речная сила основания
н
S (х) = (р) dF = 2tV' (х) (5.3)
о
терпит разрыв в тех сечениях х = const, где к поверхности упру-
гого основания приложена сосредоточенная сила.
Если рассмотреть эпюру S (х) для балки, приведенной на
рис. 48, то можно увидеть, что под балкой обобщенная попереч-
ная сила S согласно (5.1) равна нулю. За пределами балки эта
сила отлична от нуля, в результате чего в сечениях х = — I и
х == / в эпюре S (х) имеются разрывы. Отсюда следует, что по
концам балки действуют сосредоточенные реактивные давления
Q , которыми учитывается работа упругого основания за преде-
лами конструкции.
Наличие сосредоточенных реактивных давлений Q* можно
' Установить также, исходя и из других соображений. Так напри-
! мер, если мы предположим, что по подошве жесткой балки дей-
ствуют только распределенные реакции (5.2), то сразу получим
| противоречие: осадка поверхности однослойного основания под
• Равномерно распределенной нагрузкой не будет постоянной (см.
t § 3 гл. I). Для того чтобы в пределах балки удовлетворялось
1 7*
jqq ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ.
условие (5.1), по концам балки следует приложить сосредоточен-)
ные силы, дающие дополнительные прогибы поверхности основа--
ния (заштрихованная часть эпюры осадок на рис. 49).
Величина сосредоточенных реактивных давлений Q* опре-;
деляется в общем случае как разность значений обобщенных!
Рис. 49.
поперечных сил S, вычисленных слева и справа от конца балки:)
q* = s0(-/)-s6(-/), 1 (54)
Qb = 8б (/) — 80 (/), f
где 8Й — обобщенная поперечная сила, относящаяся к участку
свободного основания, а Зф— к участку основания, расположен-
ного под балкой.
Знак сосредоточенных давлений Q* устанавливается так же^
как знак распределенных реактивных давлений q (х): реакция,
действующая на балку снизу вверх, считается положительной.
Работа упругого основания за пределами балки описывается
однородным дифференциальным уравнением
— 2tV" + kV = 0. (5.5)
Решение уравнения (5.5) позволяет получить для осадок сво*
бедного основания следующие выражения:
при х — I Pj — Сое^х+1~>' |
при х^1 Уц = Сое-а(х_б. | (5-6)
Учитывая формулы (5.1), (5.6) и (5.3) и исходя из равенств
(5.4), в рассматриваемом случае получим:
Qi = Qb = 2а/С0, (5.71
'где )
4. (5.q
i5]
ЖЕСТКАЯ БАЛКА
101
Для определения осадки Со используем условие равновесия
балки, для чего приравняем нулю проекцию всех сил на верти-
каль- Учитывая, что на балку, кроме заданной внешней нагрузки
р будут действовать реактивные давления, представленные
равномерным отпором q и двумя силами Q* и Q1, получим:
с» = WT25F • ' <5-9>
Внося значение (5.9) в формулы (5.2) и (5.7), определим реак-
тивные давления:
______*_____
4 21 1 + 2Д1’-
kt
пФ — пФ _ Ро 1
Qa-Qb~ -2-—лг
1+2Й
(5.10)
(5.И)
В формулах (5.10), (5.11) через Ро обозначена величина сум-
марной вертикальной нагрузки.
Отметим, что для определения постоянной Со можно исполь-
зовать также обобщенное условие равновесия рассматриваемой
системы (балка 4- упругое основание), понимаемое в смысле изло-
женного выше вариационного метода. Это условие, характери-
зующее собой равенство нулю суммарной работы всех внешних и
внутренних сил системы на виртуальном перемещении и (х, у) —
= 1-ф(у), запишется в виде
+х,Н
— cv^'(y)dFdx+ Poty(O) = °> (5-12)
—30 О
где dF — 8dy, а а;/ — нормальные напряжения, определяемые пер-
вой из формул (3.3) гл. I.
Внося в уравнение (5.12) выражение (3.2) гл. I, учитывая
формулы (1.3), (5.1), (5.6) и замечая, что мы приняли ранее
Ф(0) = 1, будем иметь:
—/ -f-1 Оэ
С°/г^ еа(х+» dx-]- dx + e-a<x_Z) dx] = Ро, (5.12')
—со —I I
или
С„!г [2/ -I- -?-] = 2С0 \kl 4- 2аД = Ро, (5.12")
откуда для постоянной Со снова получим выражение (5.9).
Сравнивая выражения (5.12') и (5.12") с формулой (5.7), мож-
но видеть, что в рассмотренном случае каждая из фиктивных
JQ2 ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. и
реакций Q* пропорциональна по своей величине k — кратному объему
соответствующей осадочной лунки, возникающей в упругом осно-
вании за пределами балки, т. е.
—i
Qa = k Сое“(х+/) dx = 2а/С0,
-°0 '
00
Qb = k Сое—dx =’>2а^С0.
(5.7')
К аналогичному (выводу можно прийти и в том случае, если
за виртуальное перемещение рассматриваемой системы принять
Рис. 50.
перемещение, определяемое формулами (5.1) и (5.6) при Со =,1.
В отличие от выражения (5.12) работа внутренних сил будет
складываться здесь из работы нормальных напряжений аи и ка-
сательных напряжений хух. Однако окончательный результат снова
запишется в виде (5.12").
2. Случай кососимметричного загружения. При
действии на жесткую балку кососимметричной нагрузки осадка
балки определяется равенством
К(х) = 0ох, (5.13)
где 0О = tg <р0 — тангенс угла наклона балки к горизонту
(рис. 50).
Как и ранее, формула (1.4), выражающая зависимость между
нагрузкой на основание и его осадкой, позволяет получить:
q’t(x) = ktiox. (5.14)
Для определения сосредоточенных реактивных давлений Q*
вычислим величину обобщенных поперечных сил упругого основа-
L 5] ЖЕСТКАЯ БАЛКА
ния S (%) на участках свободного основания и в пределах
балки.
Исходя из общей формулы’(5.3) и замечая, что осадка
вания за пределами балки равна:
при х < — I VT = — 0o/ea(x+z> ; 1
при х>1 Vn ='^ole~|
103
длины
осно-
(5.15)
получим следующие выражения для обобщенных поперечных сил:
при — I
при — I < х < I
при х^ I
S = — 2<х£90/езс<*+г)
S = 2/90;
S = — 2а/%/е-“<*-0.
(5.16)
Формулы (5.4) позволяют определить сосредоточенные реакции
на краях балки:
где
-Qi=Ql = 2/(l +а/)90,
(5.17)
т / k
Л ~ V 21 '
Используя условие равновесия балки, а именно, приравнивая
нулю суммарный момент всех действующих на балку сил отно-
сительно середины балки, получим:
а _ ______ЗМ0_____
0 21 [kP +6/(Ц- а/)] '
(5,18)
Подставляя (5.18) в формулы (5.14) и (5.17), получим выра-
жения для реактивных давлений упругого основания:
(5.19)
(5.20)
где Мо — суммарный момент внешних сил относительно начала
координат, характеризующий заданную кососимметричную на-
грузку.
Формулами (5.10), (5.11) для случая симметричного загруже-
ния и (5.19), (5.20) для кососимметричного загружения полностью
104
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
решается задача расчета жесткой балки, поскольку после опре-
деления реактивных давлений могут быть найдены обычными спо-
собами сопротивления материалов эпюры изгибающих моментов и
поперечных сил.
3. Примеры расчета. Анализ полученных ре-
зультатов. Известное точное решение задачи о плоском сим-
метрично загруженном штампе, полученное Садовским, имеет вид:
q (т) =-----------—=
'v " те/ /1 — д
(5.21)
где т] = у--абсцисса, приведенная к полудлине балки I.
На рис. 51 показана эпюра реактивных давлении, соответствую-
щая решению (5.21). Можно видеть, что характерной особенно-
Сосредоточенные реактивные
стью этой эпюры является воз-
растание ординат у концов бал-
ки. При этом на концах
реактивные давления q (nj) име-
ют бесконечно большие зна-
чения.
Вследствие того, что в пред-
лагаемом методе упругим осно-
ванием является не упругая по-
луплоскость, а однослойная мо-
дель, свойства которой опреде-
ляются двумя параметрами: k и
t, бесконечно большим ордина-
там q (т() точного решения в на-
шем методе соответствуют сос-
редоточенные силы Q$.
давления Q* нельзя рассматри-
вать. конечно, как реальные силы, действующие в упругом осно-
вании по концам балки. Возникновение реакций обусловли-
вается работой упругого основания за пределами конструкции.
В результате этого сосредоточенные реакции следует по-
нимать как фиктивные силы, которыми характеризуется влияние
свободного от нагрузки основания на напряженное состояние
балки.
Ранее было отмечено, что основные свойства рассматриваемого
упругого основания зависят от характера функции поперечного
распределения перемещений ср (у), которая выбирается заранее в
соответствии с конкретными условиями задачи. Полученные нами
формулы (5.10), (5.11), (5.19) и (5.20) носят общий характер и
позволяют определять реактивные давления упругого основания
при любом выборе функции ср (у).
§ 51
ЖЕСТКАЯ БАЛКА
105
Рассмотрим теперь в качестве примера случай, когда функция
поперечного распределения перемещений выбрана в виде
, Н — у
sh 7 —
Ш =(5.22)
sh —
где I — полудлина балки, а у — некоторый коэффициент, характе-
ризующий быстроту затухания осадок по глубине основания.
В соответствии с формулами (1.3) и (5.22) упругие параметры
основания определяются в виде:
ВрВ
/__ Е0ЪН ,
12 (1 + v0)
(5.23)
где
(5.24)
/' , 7я , 7я 7я
л - 7я | 1 _ / / _+ /
Z 1/ 3 7/7 , 7Й 7//'
Г shT-chT'“T'
Внося выражения (5.23) в общие формулы (5.10), (5.11), (5.19)
н (5.20), получим:
для симметричной нагрузки
Q = ------------------ ---------
4 21 Г уН , 7/7 7/7
1 + | / Sh z С z ~ z
27 I/ уН уН уН
Т shVchJT + ¥
ПФ = fo____________1 - ---
2 Г уН уН уН
1 + 2у 1 / sh~Fch~r+ I
чо) |/ к 7я7я 7я
Г sh—ch—- —
(5.25)
106
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
(ГЛ. И
для кососимметричном
Л-!,,
<7 = -/Г
нагрузки
1
sh^ch^+^
, уН , уН уН
sh —— сп —г-—
. уН , у/У уЯ
!Lz i ~ i ^20=^)
sh^ch^+2± Y
2 (1—Vo)
1 —Vfl
sh^ch^+^
sh^ch^r^
(5.26)
ОФ = ____________________
-2Z sh^chYH+^ -----------.
. , £ У___I___I __£ , > 2 (1—v0)
‘Г3 l-’>.6hrHchYH_ Y_H ' ' 1-v»
.уН ~ у Н
СП —--f- ——
. уН , уН уН
sh—ch— -v
Рассмотрим случай симметричного загружения, которому со-
ответствуют безразмерные графики q и Q<t, приведенные на рис. 52
и ,53. Этими графиками характеризуются величины реактивных
давлений при трех значениях параметра 7 (7= 1,0; 7= 1,5; 7=2,0)
и v0 — 0,3. Переход к действительным реакциям q и Q* осущест-
вляется здесь по формулам^
Q* = y°Q*. , (5.27)
Из приведенных графиков можно видеть, что для принятых
значений 7, уже начиная с отношения 1,5 н-2,0, величина
реакций остается практически постоянной. Отсюда следует, что при:
$ 5)
ЖЕСТКАЯ БАЛКА
107
относительной мощности сжимаемого слоя j > 1,5-ь 2,0 упругое
основание начинает работать, как упругая полуплоскость (Н = оо).
Можно видеть также, что при увеличении параметра у концентра-
ции "реактивных давлений по краям фундамента уменьшаются и
основание^по своей работе приближается к винклеровской схеме.
Для сравнения полученного нами решения (5.25) с точным
решением теории упругости определим изгибающий момент в
центре балки т0, возникающий от воздействия только одних ре-
активных давлений q и 0ф:
'”»“? + «ф/ = ТнФё7- <5-28>
Внося_в формулу (5.28) выражения (5.23), (5.24), будем иметь:
w _ Pol 3? + ]/6(l —v0) sh 7 ch 7 + 7
/71о — о /--------=---- ’
_______1 / 3sh у ch у— у
67 4- уФ (1 — v0) г sh 7 ch 7 -|- 7
гДе 7 = Т у
В случае упругой полуплоскости = оо) формула
репишется в виде
т0 = Р01т0,
~ 1 T+F2(l-v0)
2 27 +]/2(1-v0)
(5.29)
(5.29) пе-
(5.30)
(5.31)
108
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
На рис. 54 показан безразмерный график т0, построенный
при помощи формулы (5.31) для некоторых значений параметра
у при v0 = 0,3. Нетрудно видеть, что при у=1,5 тп = 0.32, что
совпадает с решением М. И. Горбунова-Посадова для жесткой
балки [26]. С увеличением параметра у кривая, характеризующая
Рис. 55.
т0, асимптотически приближается к значению 0,25, соответствую-
щему гипотезе коэффициента постели.
Таким образом, если принять у — 1,5, то эпюра реактивных дав-
лений (7, Q*), полученная при помощи предлагаемого метода,
будет эквивалентна эпюре д(т]), полученной в результате пло-
§ 5}
ЖЕСТКАЯ балка
109
ского расчета (см. (5.21)) по тем моментам, которые эти давле-
ния дают в средней части балки. А так как эпюра q для жест-
кой балки определяется однозначно при действии симметричной
нагрузки любого вида и зависит только от Ро и I, то и 'эпюры
М (х), полученные предлагаемым методом, при любой нагрузке
будут близки к эпюрам,
найденным при
плоского расчета теории
упругости.
В качестве примера на
рис. 55 и 56 приведены
эпюры М и Q жесткой
балки, вычисленные для
трех важнейших случаев
нагрузки при у = 1,5. Срав-
нение с соответствующими
данными точного решения *)
(пунктирные кривые и циф-
ры в скобках) показывает,
что различие в результатах
помощи
наблюдается только вблизи концов
балки.
При сопоставлении кососимметричного расчета с точным реше-
нием теории упругости (рис. 57) можно также убедиться в том,
что результаты в обоих случаях при у= 1,5 весьма близки.
4. Учет пластических деформаций под краями
фундамента. В рассмотренных решениях для жесткой балки
предполагалось, что осадка поверхности упругого основания V (х)
представляет собой непрерывную функцию. В результате этого
под краями фундамента была выявлена концентрация реактивных
давлений, представленная фиктивными силами Q*.
*) См. монографию М. И. Горбунова-Посадова «Расчет конструкций на
упругом основании» , Госстройиздат, 1953, ч. 1, гл. 1, §6.
110 ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ 1ГЛ. 1
В естественных условиях возникновение резко повышенных
давлений вызовет под концами балки сдвиги частиц грунта (пла-
стические деформации), вносящие существенные изменения в об-
щую картину напряженного состояния основания и фундамента.
В этом случае к грунту уже не
применимы методы теории упру-
гости; здесь должна быть исполь-
зована специальная, достаточно
сложная теория, учитывающая
упруго-пластические деформа-
ции основания.
Однако предлагаемый при-
ближенный метод позволяет весь-
ма просто учесть отмеченное
обстоятельство. П редположим,
что под краями симметрично на«
груженной балки в упругом основании произошли сдвиги, вслед-
ствие чего функция осадки V (х) в сечениях х = 1 и х =—1
терпит разрыв на величину
с = (1 — р)С0, (5.32)
где р — некоторый коэффициент, характеризующий осадочность
упру!ого основания (рис. 58).
Эпюра реактивных давлений будет представлена здесь, как и
ранее, равномерным отпором q и фиктивными силами Q*. Равно-
мерный отпор определяется формулой (4.2) и равен
q = kCa. (5.33)
Фиктивные давления Q* в силу формул (5.3) и (5.4) будут
равны
Q* = Q* = 2а^С0 (5.34)
Используя условие равновесия балки, получим выражение для
постоянной Со:
Рв
(5.35)
Внося (5.35)
для реактивных
Са 2 (kl + 2сф/) *
в формулы (5.33) и (5.34), получим выражения
давлений q и Q*:
« = £»____1'
q 21 , , ’ I
0*--^—7
(5.36
1 +2сф/
$ “1
УПРУГАЯ БАЛКА КОНЕЧНОЙ ДЛИНЫ
! !1
Из полученных выражений можно видеть, что при fj = 0 упру-
гое основание за пределами конструкции не работает и мы имеем
винклеровскую расчетную схему. При р — 1 решение (5.35) сов-
падает, естественно, с рассмотренным ранее решением (5.9).
Аналогичные рассуждения могут быть проведены и для случая
кососимметричного загружения балки.
§ 6. Упругая балка конечной длины
1. Представим дифференциальное уравнение изгиба балки на
однослойном упругом основании (см. § 1 настоящей главы) в виде
'drf drf “t~
s«|7 _ £L4
bv EJ
(6-1)
Здесь 7] = ~— приведенная координата, a L — упругая харак-
теристика балки (характеристическая длина), (определяемая по
формуле
г _17
где 8 — ширина балки.
Коэффициенты уравнения (6.1) имеют вид:
Г2 = dy,
О
и !
s4 = 2L dy. *
о J
(6.2)
(6.3)
Раннее было отмечено, что общий интеграл неоднородного
дифференциального уравнения (6.1) для балок конечной длины
проще всего определяется по методу начальных параметров, из-
ложение которого дано в §3. Применяя этот метод, общее реше-
ние задачи можно представить в виде:
V (т;) = 1Л)Кж+ + М„Кум + N nKvN — Fv,
? C»l) = VoKq,V,+ <PoK”+ + N0Kvn — F?,
А1(т])= V 0Kmv + <р()Кл<'5 + М0Кмм + N 0Kmn — Fm
N (t;) = VqKnv + 9()K.v, + MqKnm + — Fn,
где Kvv, Kyr,, . . • , Knm, Knn — функции влияния, приведенные
в табл. 2; Fy, F^, Fm, Fn — функции, зависящие от характера
и величины внешней нагрузки [см., например, (3.11)]. . ..
112
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
2. Для определения начальных параметров Vn, <р0, Л40, No не-
обходимо рассмотреть граничные условия, заданные на концах
балки.
> Если балка имеет закрепленные от перемещений концы, то
краевые условия могут быть поставлены обычнЫм образом:
а) при шарнирном опирании конца
Е = 0, М = 0; (6.5')
б) при жестком защемлении конца
V = 0, 9 = 0. (6.5")
Для балки со свободными от закреплений концами при поста-
новке граничных условий должны быть учтены условия совмест-
ной работы балки и упругого основания. На свободных участках
основания (/) и (//) (рис. 59) осадка V(х) определяется с точно-
стью до одной произвольной постоянной /ф или D2, а на участке
основания под балкой (III)— с точностью до четырех произволь-
ных постоянных Cj, С2, С3, Ci [см. формулу (2.9)]. Очевидно,-
что для определения этих постоянных на границе рассмотренных
участков (т. е. по концам балки) должно быть поставлено шесть
независимых условий (по три на каждом конце балки).
Естественным условием для каждого конца, свободного от на-
грузки, является:
1) М = 0. (6.6')
Два других условия, учитывающих неразрывность функции >
V (х), могут быть записаны в следующем виде: ]
2) Vo = V6; (6.6")
3) S = N при х = 0 (или х = 21), j
где Vo— осадка основания, Еб— осадка балки, a S и N — обоб-l
щепные поперечные силы соответственно для свободных участковj
основания (/, //) и участка под балкой (HI). 1
§ 6]
УПРУГАЯ БАЛКА КОНЕЧНОЙ ДЛИНЫ
113
Отметим, что условия (6.6") соответствуют рассмотренным
раннее условиям (4.4) для жесткой балки и предопределяют, та-
ким образом, возникновение фиктивных реакций Q* по концам
упругой балки.
Опуская случаи (6.5') и (6.5"), мы рассмотрим в дальнейшем
лишь вопросы расчета балок со свободными от закреплений кон-
цами, как представляющие наибольший практический интерес и
вместе с тем являющиеся наиболее сложными.
' 3 . Выбирая начало координат на левом конце балки (рис. 59),
получим в соответствии с условиями (6.6) и формулой (5.3) выра-
жения для двух начальных параметров:
Л40 = О, No = S (0) = 2WV0. (6.7)
Решение (6.4) может быть теперь представлено в виде:
V (т;) = (Kvv + 2a£Kwv) Vo + Kw фо — Fv , )
Ф Cq) “ (^C<pv “Ь 2ос(Кфдг) Vq Ч- Кф<₽ 9о ^<р, I
М (ц) = (Kmv + Vo + Км^0 - FM, (6,8)
N Cg) = (Kjvv + 2uIKnn) Vo + Км9<ро — Fn . ,
Используя условия, заданные на другом конце балки:
21
при Tj = -J-
м ® = °’ Л? ®= “ 2aZV ® ’ (6.9)
нетрудно определить два других начальных параметра Vo и ср0
следующим образом:
Коэффициенты выражений (6.10) вычисляются по формулам:
Oi =
а2
(6.Н)
as = KNv (^).+ (j) + (2«02 ’
8 В. 3. Власов, Н. Н. Леонтьев
114
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
Величины Kmv , Kmn (у) , • • •, FM , Fv 0^), входящие
в формулы (6.10) и (6.11), представляют собой значения соответ-
Рис. 60.
ствующих функций в сечении
2/
с координатой т] =.
Формулы (6.8) и (6.10) да-
ют полное решение задачи об
изгибе балки конечной длины
на упругом основании• под
действием произвольной внеш-
ней нагрузки.
В случае достаточно длин-
ных балок для повышения ;
точности вычислений начало;
координат целесообразно вы-!
брать в середине балки, пред-
варительно разложив заданную (
нагрузку на симметричную и j
(рис. 60). Решение в этом случае 1
на основании рассуждений, ан а-
кососимметричную составляющие
может быть без труда получено
логичных приведенным выше.
Расчетные формулы принимают вид:
а) при симметричной нагрузке
V (т]) — KvvV0 + ЛумЛ10 — Fy,
ф С»1) = KvvV0 + Кчм — Fv, 1
Л1 (tj) = KmvV0 + КммМ0 — FM, [
N (t]) = KnvV0 + KnmM0 — Fn, )
где
_ biFM + 2a^v ]
K° = - 626s !
_ — ь«[гм(г) + 2gZfv]
° bybi — b<2,b%
б) при кососимметричной нагрузке
И (tj) = Ал/Ф<р0 + KvnN о — Fv, ]
<Р (Т)) = Kw<p0 + K,tN N0~F^, I
M (т() = + KmnN0 — Fm, 1
(71) = F^NVtf>0 + KnnNo — Fn , )
(6.12)
(6.131
f61'
УПРУГАЯ БАЛКА КОНЕЧНОЙ ДЛИНЫ
115
ь^м (д)-
— Z?2^5 ’
b=FM (cLj~bt + ^atFv fд)]
fci&e — b%b&
Коэффициенты выражений (6.12) и (6.13) определяются фор*
мулами:
bi = Knm G;) + ^Kvm
bg Kmm ^д^ ’
b3 = Knv + 2atKvv
l\
LJ ’
Отметим; что в формулах (6.12) и (6.13) должна учитываться
только та нагрузка, которая расположена справа (или слева) от
начала отсчета. При этом Kvm(^), ..., ,
fv^-0 — величины соответствующих функций при аргументе
/
^д-
В полученных нами решениях (6.8), (6.12) и (6.13) точно вы-
полняются условия равновесия балки, контактное условие о плот-
ном прилегании балки к грунту и условие непрерывности осадки
основания. Статические граничные условия удовлетворяются
при этом приближенно: при равенстве нулю изгибающих моментов
М балочные поперечные силы Q по концам балки в общем слу-
чае отличны от нуля. Это обстоятельство объясняется особенно-
стями принятой нами модели упругого основания, свойства кото-
рой характеризуются двумя обобщенными параметрами k и t.
4. Анализ приведенных формул показывает, что упругие свой-
ства балки и грунта могут быть охарактеризованы совместно
одной сводной величиной
Х = 1 (6.15)
1л
которая представляет собой приведенную полудлину балки.
В методах расчета, основанных на решении плоской задачи
теории упругости (например, в методе М. И. Горбунова-Посадова),
в качестве основной упругой характеристики принимается обычно
величина, называемая показателем гибкости балки.
8*
116
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ. II/
Показатель гибкости вычисляется по формуле
__ rc£0S/8
“ 4(1-^)£7’
(6.16);
где I — полудлина балки, а 8 — ее ширина.
Сопоставляя формулы (6.2), (6.15) и (6.16) можно видеть, что
характеристики Хи/ связаны между собой соотношением
* = (6.17)
Рассмотрим несколько примеров, показывающих, как влияет
приведенная полудлина балки К на расчетные результаты. Будем;
предполагать при этом, что упругое основание представляет собой
полуплоскость (Н — оо), а функция поперечного распределения;
перемещений ф(г/) выбрана в виде (4.16). '
На рис. 61 и 62 приведены безразмерные эпюры реактивных;
давлений q и изгибающих моментов т, рассчитанные по форму-
лам (6.12) для двух балок, загруженных в центре сосредоточен-
ными силами Р. Упругие характеристики X этих балок соответ-
ственно равны: Х = 1,24 (/ = 3,0) и X = 1,64 (/ = 7,0). Вычисли
ния проводились для двух значений параметра г (7= 1,0 и т= 1,5)
§ 6J
УПРУГАЯ БАЛКА КОНЕЧНОЙ ДЛИНЫ
117
при >0 — 0 и Н = оо. На этих же графиках для .сравнения нане-
сены безразмерные эпюры (сплошные линии), построенные по дан-
ным М. И. Горбунова-Посадова [26] для балки с показателями
гибкости t — 3,0 и t = 7,0. Действительные значения реакций
Реактивные давления q
Рис. 62.
упругого основания и изгибающих моментов определяются во всех
случаях при помощи следующих переходных формул:
q = qj , М. — mPl.
Нетрудно видеть, что с уменьшением приведенной полудлины
балки X концентрации реактивных давлений Q* на концах балки
возрастают, что влечет за собой увеличение изгибающих моментов.
Это проявляется тем резче, чем меньше величина параметра 7.
Напротив, чем более гибка или длинна балка, т. е. чем больше
приведенная полудлина X, тем больше реактивные давления кон-
центрируются возле точки приложения нагрузки, вызывая этим
уменьшение изгибающего момента в центре балки.
Безразмерные эпюры реактивных давлений q, полученные по
методу М. И. Горбунова-Посадова, по всей длине балки, за
исключением участков, близких к концам балки, хорошо согла-
суются с эпюрами q, рассчитанными при 7= 1,0 и 7= 1,5. Это
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ. Ц
приводит к достаточно хорошему согласованию и между соответ!
ствукмцими эпюрами изгибающих моментов. ]
Можно видеть, что как для упругих балок конечной длины, так
и для бесконечных балок величины, изгибающих моментов при
у = 1,5 оказываются несколько меньшими, чем соответствующие
значения, найденные из расчета в условиях плоской задачи тео-
рии упругости.
На рис. 63 показаны безразмерные эпюры прогибов и изгибаю-
щих моментов для жесткой балки (пунктирные линии и цифры
в’ скобках) и упругой балки с приведенной полудлиной X = 0,86
(/=1), рассчитанные при у = 1,5, v0 = 0,3, Н = оо. Сравнение
этих эпюр показывает, что для балок с приведеннной полудли-
ной 0 < X < 0,86 можно при расчете пользоваться формулами
(5.23), т, е. приближенно принимать эти балки за абсолютно
жесткие.
Аналогичным образом, сопоставляя результаты расчета упру-
гой балки, нагруженной сосредоточенной силой, с соответствую-
щими результатами, полученными для бесконечной балки (пунк-
тирные линии и цифры в скобках на рис. 64), можно убедиться
в том, что уже при Х= 1,85 (/ — 10) эти результаты практике-'
ски совпадают: разница в максимальных моментах составляет
здесь около 5% *).
Таким образом, решение, полученное для упругой балки
конечной длины, позволяет установить границы перехода от схемы
конечной балки к схемам жесткой и бесконечно длинной балок.
*) Как и ранее, сравнение в этом случае проводилось при у = 1,5, Н =
= оо, vo = 0,3,
SV] \ ВЛИЯНИЕ БОКОВОЙ ПРИГРУЗКИ 119
Эти (границы, в случае загружения балки сосредоточенной силой
определяются в следующем виде:
X < 0,86 — жесткие балки,
0,86 < X < 1,85 — конечные балки,
X > 1,85 — бесконечные балки.
Отметим, что указанные границы расчетных категорий балок
совпадают с теми, которые определяются методами теории упру-
гости и, в частности, методом М. И. Горбунова-Посадова.
§ 7. Влияние боковой пригрузки
1. Изложенный метод позволяет рассмотреть ряд специальных
вопросов, относящихся к теории балок на упругом основании. Од-
ним из таких вопросов является расчет балок с учетом нагрузки,
приложенной к упругому основанию за пределами фундамента.
Рассмотрим, например, задачу об осадке и напряженном
состоянии жесткой балки, в стороне от которой на расстоянии а
к упругому основанию приложена сосредоточенная сила G (рис. 65).
120
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. Ii
Исходя из рассмотренных ранее решений (см. § 3 гл. I и
§5 гл. II) для осадок поверхности упругого основания на участ-
ках I, II, III и IV (рис. 65), получим выражения:
Vj =
V а — Со + бох,
= D2ea<1-*) + Dae~a^-X\
Vtv = О^‘+а~х},
(7.1)
где a = j/".
Решение поставленной задачи сводится, таким образом, к оп-
ределению шести произвольных постоянных: Dt, D2, D?„ D.^
Co и 0O.
По исходным данным поверхность упругого основания предпо-
лагается всюду непрерывной. В результате этого на границах
участков I, II, III и IV могут быть поставлены четыре незави-
симых условия:
при х - — 1 Vi = Vn,
при х = 1 Vii = Via, (7.2)
при х = 1 + а V in = ViV,
Shi — Siv = G,
где Sin и Siv — обобщенные поперечные силы упругого основания
соответственно на участках III и IV*).
Раскрывая условия (7.2) при помощи формул (7.1) и (4.3),
получим:
r>i с0—0oz, j
П2 + Ds = Со Ц- 0О/, I
+ D3eM — Di = 0, | (7.3)
+ Dae^a+Di = ^-i. j
*) Последним из выражений (7.2) выражено условие, что обобщенная по-
перечная сила S (х) в сечении х = l + а претерпевает разрыв на величину G.
Как и ранее (см. § 1 гл. II), здесь предполагается, что ф(0) = 1.
§ 7] ВЛИЯНИЕ БОКОВОЙ ПРИГРУЗКИ 121
Уравнения (7.3) позволяют вычислить постоянные Dlt D%, D3,
Di через параметры Со и 0О в виде:
/?1 = с0-е0/,
iate
(7-4)
о. = (с. + ВДе-“ + щ-5-^
Для определения величин Со и 0О следует рассмотреть условия
равновесия балки, находящейся под совместным действием задан-
ной внешней нагрузки и реактивных давлений упругого основания
q(x) и Q4.
Реактивные давления q(x), распределенные по подошве балки,
в соответствии с (1.4) и (7.1 в) имеют вид:
q = k(C0 + еох). (7.5)
Для сосредоточенных реакций Q* формулы (5.4) позволяют
записать:
Q* =S/(-/)-S//(-/), |
(7.6)
Ql = 5n(/)-S/n(/). J
Вычисляя обобщенные поперечные силы по формуле (5.3) с
учетом выражений (7.1) и (7.4) и подставляя затем их значения
в (7.6), получим окончательные выражения для сосредоточенных
реакций Q* и Q*:
Q*=2/[aC0 —(1 +а/)60], |
Q* = 2HaCo + (l+a/)0o]-.A. (7-7)
Условия равновесия балки, представляющие собой равенство
нулю суммарной проекции всех сил на вертикаль и равенство
нулю суммарного момента относительно центра балки, позволяют
теперь получить для постоянных Со и 0О следующие формулы:
г* ________е I
0 2(kl + 2al) ’ I
з(м. + ^)
о 21 [kP + 6 t (1 + a/)] • )
(7.8)
122
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
4гл.
Нетрудно видеть, что формулы
ных ранее формул (5.9) и (5.18)
члена, содержащего величину G.
(7.8) отличаются от получен-
только наличием в числителе
Этим членом и учитывается
влияние пригрузки.
Анализируя выражения (7.7), можно видеть также, что при-
грузка снижает концентрацию
балки и тем самым несколько
реактивных давлений
на концах
изменяет картину напряженного
Рис. 66.
состояния фундамента. При этом влияние пригрузки сосредото-
ченной силой G быстро уменьшается с увеличением расстояния а
до силы. Отметим, что аналогичным образом влияние пригрузкй
может быть учтено и в том случае, когда на некотором расстоя-
нии от балки к упругому основанию приложена не сосредоточен-
ная сила, а произвольного вида нагрузка р(х). Для этого в каж-
дом частном случае следует составить граничные условия, подоб-
ные условиям (7.2), и рассмотреть статические условия равнове-
сия балки. При этом задача будет всегда сводиться к решению
системы алгебраических уравнений с тем или иным количеством
неизвестных.
2. Рассмотрим две жесткие балки длиной 21г и 2/2, располо-
женные рядом и нагруженные каждая произвольной внешней
нагрузкой. Будем предполагать, что под действием нагрузки балкй
получили перемещения, показанные на рис. 66.
За положительные направления углов поворота 0!, 02 и внеш-
них моментов Мг
вращением часовой
систему координат,
и М2 примем направления,
стрелки. Для каждой балки
поместив начало отсчета в
совпадающие с
выберем
свою
балки.
центре каждой
J 7] ВЛИЯНИЕ БОКОВОЙ ПРИГРУЗКИ 123
Для определения основных неизвестных С1г 0Ь С2 и 02 восполь-
зуемся результатами предыдущего примера. На основании изло-
женного выше можно видеть, что распределенные реакции 7i(x)
и ?2 (х), возникающие соответственно на участках первой и второй
балки, равны:
qi (х) = (Сх + 0хх) k, |
7а (х) = (С2 + 02х) k. /
Нетрудно также определить сосредоточенные реакции Q* и Qb-
=12/[аСх —(1+aZ) 6Х], |
Q| = 2ПаС2 + (1 +а/)62], )
где а =‘/4’
Решение поставленной задачи сводится, таким образом, к вы-
числению шести постоянных величин: С1г 0Х, С2, 02, Q£x и Q^,
для чего требуется составить систему шести алгебраических урав-
нений. В соответствии с принятыми на рис. 66 обозначениями
эта система может быть представлена в виде табл. 5.
Первые четыре уравнения таблицы характеризуют собой усло-
вия равновесия каждой балки в отдельности; последние два —
условия непрерывности осадки основания в месте примыкания
балок
при х± = (х2 = Vi = В2, = $2.
Мы не приводим решения полученной системы в общем
виде, полагая, что в каждом частном случае удобнее произ-
водить расчеты при помощи непосредственной подстановки чисел
в уравнения.
В дальнейшем ограничимся рассмотрением лишь частного слу-
чая, когда обе балки имеют одинаковую длину 21 и нагружены
каждая симметричной нагрузкой Ро (рис. 67).
124
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
лица
Правая часть Р1 Ml СО а. со о О
•e-G* О' 1 1 1 1
&С О' •ен 1 1 1 7
СО Ф 1 1 2/ (1 + ah) со со 1 3 Iго + '"со а + со СЧ « сч 1
Ф - 2/ (1 + а/,) 1 Г й/21 2/1 |~(1 + ah) i + ~д- 1 ся
с2 1 1 а 4- еч t>4 С4 1 1
и 0» + т/2/) Z а СЧ 1 1 | 1
Ms п/п t>4 со со
$ 7]
ВЛИЯНИЕ БОКОВОЙ ПРИГРУЗКИ
125
Используя условия симметрии и исходя из общих уравнений
табл. 5 и формул (7.10), в этом случае будем иметь:
9о =
/ kp
2kl\zT +
Qct = Qt =-----г
fe/2 4aZ at \
3T + ~ + z~kT + z)
aPp______________
4al at \
“ + 2 17 + 2)
________atPp_______
kP ial at
"ЗГ +___+ Z~kT
(7.H)
Q*a = Ql -
at\~3T + 1)P»
kP 4al „ a
ЗГ + ~ + 2 ~k.
Предположим теперь, что функция поперечного распределе-
ния перемещений ф(у) выбрана в виде (5.22). Характеристики
упругого основания k, t и а определятся при этом формула-
ми (5.23), (5.24). Если принять также, что упругое основание пред-
ставляет собой полуплоскость и Н —> оо, то формулы (5.23) примут
126
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
вид:
, _ Еоъ г
Z (1 — vg) 2
4__ ЕрЪ1 3
12(l-v0)27 ’
T /2 (l-v„)
7 l-v0 '
(7-12)
Подставляя выражения (7.12) в формулы (7.11), получим:
Т2 + у т /2 (1 — v0) + у (1 — v0)
7 ^72 + 7 /2 (1 — vo) + "gy (1 — v0) /2 (1 — vo) + у (1 — v0)]
x _______________ 3/2(1-vo)_________________________,
4 [/ + T /2 (1 — v0) + gy (1 — vo) /2 (1 — vo) + у (1 — v0)J
<& = <$.=
Po3(l-v0) /2(1-v0)
= г _______ 3 _______ 3 -i ’
16? [/+7 /2 (1 — Vo) + "8/ (*—’0) /2 (1 — Vo) + у (1 — Vo) J
(7-13)
Q* = Qb =
; p0/2(1-v0) [/+4(i-v»)]
4T ^2 + 7 /2 (1 — v0) + -Jy (1 — vo) /2(1 — vo) + у (1 — vo)] J
Для реактивных давлений упругого основания <?i(x) будем
иметь:
Ра / + 47^2(l-vo)+y(l-vo) + -|-Tr2 (1 -v0)y
71 (*) — ~2l ~ 3 ~ 3 •
/ + 7 /2 (1 — Vo) + gy (1 — Vo) /2 (1 — Vo) + у (1 — Vo)
(7.14)
На рис. 68 приведены безразмерные эпюры изгибающих момен-
тов и поперечных сил левой балки, рассчитанные по формулам
§7]
ВЛИЯНИЕ БОКОВОЙ ПРИГРУЗКИ
127
(7.13), (7.14) при 7=1,5, v0 = 0,3 для того случая, когда обе
балки нагружены равномерно распределенной нагрузкой интен-
сивности р. Переходные формулы для вычисления действительных
значений моментов и поперечных сил имеют вид:
М = pl2m, Q = plQ. (7.15)
Для сравнения на этих же графиках показаны (пунктирными
линиями и цифрами в скобках) результаты расчетов, проведенных
по формулам (5.25) без учета боковой пригрузки. Можно видеть,
что в рассмотренном случае пригрузка вносит существенные изме-
нения в характер расчетных эпюр и вместе с тем значительно
снижает величины положительных изгибающих моментов и попе-
речных сил.
3. Аналогичным образом может быть решена задача о влиянии
пригрузки и для упругих балок конечной длины 2/. В качестве
примера рассмотрим две конечные балки с характеристиками
Хх = и Х2 = , расположенные рядом на упругом основании
L1
(рис. 69).
Решая задачу по методу начальных параметров (см. § 2 и § 6),
выберем для каждой балки начало отсчета на ее левом конце.
При этом в соответствии с выражениями (6.7) граничные условия
примут вид:
при ^1 = 0
а) Мо = 0 b) Nl0 = 2aZVj;
При (ТГ)2=О)
с) Mld = М» = 0; d) Vj=V"; е) М</= М"; ’ (7J6)
ПРИ TJ2 = -^
f) M'd = 0; g) Nd = — 2ctiVd,
128
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. II
где
_ 7 2£1J1(1-^)
L1 ~ У ЕаЪ
У 2£3/3(1—vg)
У £»s
а индексы I и II показывают, к первой или второй балке отно-
сится данная величина.
Нетрудно видеть, что кинематические и статические факторы
первой балки будут определены с точностью до двух параметров:
Vo и <ро, а второй — с точностью до трех параметров: У”, ф”, Al”.
Поскольку параметры У" и Al” могут быть выражены через
величины У(' и фо [см. условия (7.16d, е). а также (7.17), (7.18)],
то задача в конечном счете сводится к определению только
трех начальных параметров: Vf', фо, фо*- Граничные условия
(7.16с, f, g) позволяют составить для определения этих параметров
систему трех алгебраических уравнений.
Эта система приведена в табл. 6, где в целях сокращения
записи приняты следующие обозначения:
К” = Knv — 2atKvv,
Kn = Кш- 2xtKvN,
К" = Kn\ — 2atKv\,
а индексы I и II, как и ранее, показывают соответственно, к пер-
вой или второй балке относится данная величина.
По определении начальных параметров из уравнений табл. 6
расчетные формулы могут быть представлены в следующем виде:
для первой балки
У (71) — (Kvv "Г 2%tKvN) Го "Г Wo — Гу,
ф1 (71) = + 2аП<ф/у) Уо + К^фо — Г?,
7И1 (т;) = (Kmv + 2^Kmn) Уо + Км^0 - FlM, |
AI (т]) = (Кд-у Ч~ 2aZ/C,vA') Уо Kn-^o— Fд-; )
для второй балки
у11 (rj = K”vy” + к” ф” + KvnN" - г"
ф" (ч) = Cv-y" + к” Фо1 + - F",
м11 (у) = К^уУ" + кХф" + KmnN" - г”,
А/11 (7]) = KnvV" + + K"vA/” - Г". .
§ 7] ВЛИЯНИЕ БОКОВОЙ ПРИГРУЗКИ
Таблица 6
Правая часть 4- ffl -а 2 2 > X -i s. =? * =5 < ~ < — е + + t - X 2- X s * * 1 г? + +
! ^3
“с? (,'р) &1Ь{ Куф (^1) ^MV "+ + KMN^ Q1 _Г * * X? 2 > -Г
> X + . <м -и 2- 2, 2- < -ь. ~У « + 5 -|- <м < 43 -G -s « * X 4 G S, 2, « “ 43 СМ 4- Л < М •—1 <, х; 2 К " - 1 ~4 х +
Граничное условие н-*?3 ii ^43 « СМ н
№ п/п СМ со
9 В. 3. Власов, Н. Н. Леонтьев
I3Q ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ. II
Мы не приводим примеров расчета по формулам (7.1*7), (7.18),
однако нетрудно убедиться в том, что здесь, как и в случае
жестких балок, боковая пригрузка снижает концентрацию реак-
тивных давлений на концах балки, в результате чего картина
напряженного состояния балки в значительной степени изменяется.
§ 8. Балка на упругом двуслойном основании
1. Рассмотрим жесткую балку длиной 2/ и шириной 8, рас-
положенную на двуслойном основании и несущую произвольную
внешнюю нагрузку (рис. 70). Будем предполагать при этом, что
для упругого основания справедливы гипотезы (5.1) и (5.15)
гл. I. Это означает, что мы рассматриваем упругое основание
с верхним винклеровским слоем, свойства которого описываются =
дифференциальными уравнениями (5.16) и (5.18) гл. I. j
В отличие от выражений (5.2) гл. I для функции поперечного:
распределения перемещений ф2 (У) по всей высоте основания примем
линейный закон изменения (см. рис. 70) *). При этом, исходя из
общих формул (5.4) гл. I и учитывая зависимости (5.15) гл. I,
получим формулы для основных характеристик упругого осно-
вания:
Zi = 0,
__ е2ъ
__ E2^h2
12 (1 4- v2)
(8.1)
*) Приводимые ниже выкладки остаются справедливыми и при любом
другом выборе функции ф2(</), поскольку этой функцией характеризуются
лишь величины коэффициентов k2 и t«.
« 8]
БАЛКА НА УПРУГОМ ДВУСЛОЙНОМ ОСНОВАНИИ
131
Вследствие того, что прогиб жесткой балки равен нулю, пе-
ремещение поверхности упругого основания под балкой (участок III
на рис. 71) в общем случае будет задано в виде
Vi = Со + 90х, (8.2)
где Со — осадка центра балки, а 90— тангенс угла наклона балки
к горизонту.
Рис. 71.
В соответствии с первым из уравнений (5.16) гл. I зависи-
мость (8.2) накладывает на основную функцию F (х) следующее
условие:
— Zt^F" (/С 4- ^2) F = со 4* 0ох. (8-3)
Условие (8.3) представляет собой основное дифференциальное
уравнение рассматриваемой задачи. Общий интеграл этого урав-
нения может быть представлен в виде
F (х) = С, ch $х + С2 sh ?>х 4- , (8.4)
где
?" • <8-5»
Для определения постоянных интегрирования Ci и С2 нужно
использовать условия, заданные на концах балки, или точнее, на
границах участков, отмеченных на рис. 71.
Согласно физическому содержанию задачи этими условиями
будут:
при х = —I V2 = V", S‘ —- S2n; (8.6)
при x = I V'" = V2’, S2H = S2‘, (8.7)
9*
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
1ГЛ. II
132
где индексы I, II, III показывают, к какому участку относится
соответствующая величина.
Исходя из полученного ранее решения (5.22) гл. I, осадку
основания за пределами балки можно представить в виде:
у' = D1e“2(x+Z)
V" = D2e““2(v-
(8.8)
где
Формула (5.17) гл. I позволяет получить для обобщенных
сил S2 следующие выражения:
S2 = 2а2^2Д1е“^<л+/\
S"1 = О sh px 1 C2p ch px].
Раскрывая граничные условия (8.6), (8.7) при помощи фор-
мул (8.4), (8.8) и (8.9), получим для определения постоянных;
интегрирования систему четырех алгебраических уравнений:
-C1chpi + C2Shp/ + 4-Di=
-C1Sh8/ + C2shp/ —
Т с+», <8-к
-C1chp/-C2shp/ + 4-D2=
‘ Л Л -г «2
— C1Shp/ + C2ch p/ + -^D2 = 0,
‘ рЛ
где
Г Z/2 Г £1%
.• Уравнения (8.10) позволяют вычислить постоянные
D1 и D2 с точностью до величин Сп и 90. Для определения осадк
центра балки Со и угла поворота 90 должны быть использован
еще не принятые нами во внимание условия равновесия балки: '
Решая систему (8.10) и используя также условия равновеси
нетрудно получить для основных расчетных величин следующ
J 81 балка на упругом двуслойном основании 133
выражения:
1
~ г пГз7
IKk-, ch 8/1 л + Bj
г__________________________1___________________ и,
- . [А /' th В/\ В2 ] 2 ’
l-Kki. ch 3/1 у- — a)[ j + -y j
------- Co i '
K (CU-0O.')[th2?z 3- 2/1 + лth 3/ + ij - - ch2^
/J‘ = К + k2 ZB^Bs ’
r----- Co — QqI
K (Co + Oo/) [th2 3/ + 2 Kl+A th 3/ + 1] — - ch2
D- ' К + k2 2BA
K + k.2 Bx PB
IKk, .th?/ , D 2 ’
л -r Bi
/л _ К + k2 B2 MB
° ~ r-Kk2 >. / th 3/ • B2 2 ’
?/’V з/ Г'г з
(8.11)
где Po — суммарная вертикальная нагрузка; Мо — суммарный
момент всех сил, взятый относительно центра балки и считаю-
щийся положительным в том случае, когда его направление
совпадает с направлением вращения часовой стрелки; В1? В2, В?
и X — коэффициенты, вычисляемые по формулам:
В1= 1 +К1 +Xthp/,
В2 = +х + th ₽/,
(8.121
По определении постоянных (8.11) обобщенные перемещения
Vj, V2 и разрешающая функция F могут быть найдены по фор-
мулам (5.16) гл. I, (8.2) и (8.4) гл. II, а реактивные давления упругого
основания — по формуле (5.18) гл. I*). Внося в эту последнюю
формулу выражение (8.4), получим:
q (х) = К (Со -С W - (Сг ch ₽х + С2 sh ₽х)1. (8.13)
L А “г J
*) Заметим, что изгибающие моменты и поперечные силы жесткой балки
при известной эпюре q (г) рассчитываются обычными способами сопротивления
материалов.
J 34 ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ [ГЛ. II
Необходимо отметить, что в рассмотренном решении выпол-
няются не только условия равновесия балки и условие о плотном
прилегании балки к грунту, но и статические граничные усло-
вия: например, на концах балки, свободных от закреплений
и нагрузок, изгибающие моменты и поперечные силы будут
равны нулю. Это объясняется тем, что сосредоточенные реак-
тивные давления Q*, свойственные однослойному основанию, в
двуслойной модели упругого основания отсутствуют.
2. Рассмотрим более подробно случай симметричного загруже-
ния жесткой балки. Полагая в формулах (8.11) 7И0
соответствует симметричному загружению, и исходя из общей;
формулы (8.13), получим выражения для реактивных давлений
д (х) упругого основания:
,------ ch Вх
q W — 21 .----- n th 3/ ’
(8.14)
где
<815t
Если функция поперечного распределения перемещений ф2 (У
задана по линейному закону (см. рис. 70), то коэффициенты k
и t2 определяются равенствами (8.1). Внося выражения (8.1
в (8.15), получим для реактивных давлений q (х) окончательж
следующее выражение:
q(x) = 4t^w, (sis:
где
?(х) =
(8.1
На рис. 72 представлены графики безразмерных функций д(х)-
вычисленные при = I и v0 = 0 для нескольких значений napal
1 К
метра X = — .
1
§ 8] БАЛКА НА УПРУГОМ ДВУСЛОЙНОМ ОСНОВАНИИ 135
Можно видеть, что во всех случаях интенсивность реактивных
давлений возрастает от середины к краям балки, причем на самих
краях балки реакции упругого основания имеют конечную вели-
чину. Уменьшение параметра X приводит к уменьшению краевых
давлений: при X = 0 (&2 = оо) двуслойное основание вырождается
в винклеровское упругое основание. Напротив, при увеличении
параметра X (X—> оо) двуслойная модель приближается по своей
работе к упругой полуплоскости.
3. При расчете упругой балки конечной длины дифференциаль-
ное: уравнение изгиба балки
EJV™ = p — q (8-18)
следует рассматривать совместно с дифференциальными уравне-
ниями (5.16) и (5.18) гл. I, характеризующими работу двуслой-
ного упругого основания. Вследствие того, что прогиб балки по
условию задачи совпадает с осадкой поверхности упругого осно-
вания первое из выражений (5.16) гл. I может быть внесено
в уравнение (8.18). Для определения основной функции F (х)
нетрудно получить при этом систему двух дифференциальных
Уравнений:
EJ [- 2t2Fvl + (К + k2) FIV] = р - q,
— 2Kt2.F" + Kk2F = q.
(8.19)
136
ИЗГИБ БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. П;
Исключая из уравнений (8.19) функцию q(x), будем иметь:
-EJ^-Fvl + EJ-^4^FiV — 2t2Fu + k2F = ^, (8.20)
А А А
Можно видеть, что основное уравнение задачи (8.20) пред-
ставляет собой обыкновенное дифференциальное уравнение шестого
порядка с постоянными коэффициентами. Уравнение (8.20) инте-
грируется в элементарных функциях, поэтому решение его не
может вызвать особых затруднений. Граничными условиями на
свободных от закреплений и нагрузки краях будут условия (8.6),;
(8.7), а также обычные статические условия: М = 0, Q = 0.
На каждом конце балки может быть поставлено, таким образом,
по четыре независимых условия, что соответствует общему числу
произвольных постоянных интегрирования *).
После определения функции F (х) из уравнения (8.20) и соот-
ветствующих граничных условий прогиб балки и реакции упругого
основания можно рассчитать по формулам (5.16) и (5.18) гл. I,
а изгибающие моменты и поперечные силы — по известным фор-
мулам (1.11), (1.12) гл. II.
*) Основная функция F (х) определяется с точностью до шести пронзволь-!
ных постоянных на участке длины балки, что соответствует порядку уран-
нения (8.20), и с точностью до двух постоянных за пределами балки (см.,
например, (8.8)). •
ГЛ ABA 111
ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ НА УПРУГОМ
ОДНОСЛОЙНОМ ОСНОВАНИИ
§ 1. Постановка задачи.
Дифференциальное уравнение изгиба плиты
на однослойном основании-
Рассмотрим прямоугольную плиту, расположенную на упругом
основании, свойства которого описываются дифференциальным
уравнением в частных производных (7.8) гл. I (рис. 73). В отно-
шении плиты будем считать справедливыми гипотезы, принимаемые
Рис. 73.
обычно в теории изгиба пластинок. Кроме того, будем предпо-
лагать, что силы трения и сцепления между плитой и поверх-
ностью упругого основания отсутствуют.
При этих предположениях дифференциальное уравнение изгиба
плиты, записанное в прямоугольной системе координат, имеет,
138 ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ [гл.II
как известно, следующий вид:
V2V2u> (•*, У) = ' (1-Г
В этом уравнении символом V2V2 обозначен двойной лапласо!
оператор второго порядка. Раскрывая этот оператор, можно пред
ставить уравнение (1.1) в форме
(Pw , о <Pw , d4w _________ р”
~дР + Z дх2 ду2 —
(1.2
*
где w = w (х, и) — поверхность прогибов плиты, р = р (х, у) —
Eh3
приходящаяся на плиту нагрузка, D = ---цилиндриче-
(1 — р. J
ская жесткость плиты.
Уравнение (1.2) называется уравнением изгиба тонких плит,
однако оно применимо для расчета подавляющего большинства
прямоугольных плит, встречающихся в инженерной практике.
Как Показал акад. Б. Г. Галеркин [17], уравнение (1.2) может
быть использовано даже в том случае, когда отношение толщины:
плиты к наименьшему размеру ее в плане составляет 1:3.
Дифференциальным уравнением в частных производных (1.2):
устанавливается зависимость между искомой поверхностью про-
гибов плиты w(x, у) и приходящейся на плиту внешней нагрузкой:
р* (х, у). Поскольку рассматриваемая плита покоится на упругом:
основании, внешняя нагрузка р* (х, у) состоит из заданных поверх-
ностных сил р(х, у) и реактивных давлений упругого основания
Ч(х,у)-.
P* (х, у) = р(х, y) — q(x, у). (1.3)
Реактивные давления представляют собой неизвестную функцию
координат х, у. Отсюда следует, что рассматриваемая задача по;
расчету плиты на упругом основании состоит в том, что требуется:
определить поверхность прогибов плиты w (х, у) и закон распре-^
деления реакций упругого основания q (х, у) по ее опорной поверх--
ности. При этом, естественно, должны быть выполнены статические;
условия равновесия плиты, а также контактное условие о плотном:
прилегании плиты к поверхности упругого основания.
Ранее было установлено (см. гл. I, § 7), что работа одно--
слойного основания под нагрузкой, распределенной по его поверх-;
ности, характеризуется дифференциальным уравнением следующего;
вида:
— 2tV2w (х, у) + kw(x, у) = q (х, у) ф (0),
(1.4)
ПОСТАНОВКА ЗАДАЧИ. УРАВНЕНИЕ ИЗГИБА ПЛИТЫ
139
оператор Лапласа.
Л =
1
ф2(/г— упругие характеристики одно-
слойного основания,
до до
где V2 =
1 vo 0J
н
t =----(
4 (1 + v0) j
0
ф(г)— функция поперечного распределения перемещений.
По условиям задачи прогиб плиты и осадка поверхности одно-
слойного основания, расположенного под плитой, совпадают. Кроме
того, нагрузка на основание q (х, у) по отношению к плите пред-
ставляет собой реактивные давления основания. Отсюда следует,
что дифференциальные уравнения (1.2) и (1.4) могут быть рас-
смотрены совместно.
Для упрощения выкладок мы будем в дальнейшем предпола-
гать, что функция поперечного распределения перемещений ф (z)
выбрана так, что ф(0)=1. Внося значение q(x, у) из уравне-
ния (1.4) в дифференциальное уравнение изгиба плиты (1.2),
получим:
(1-5)
2 _____________________________
(1.6)
V2V2U) — 2r2V2u> + s4u) = ~ ,
где г2 и s4 — обобщенные упругие характеристики плиты и осно-
вания, определяемые по формулам:
4 (1 + v0) D = ’
О
Еа- -fcp'2(z)dz =А,
о
a D — цилиндрическая жесткость плиты. Входящие в формулы
(1.6) характеристики основания Ео и v0 в рассматриваемом случае
пространственной задачи определяются
Д — —р
S4 =
(1-^)0
выражениями:
Vrp
(1.7)
. 2 ’
1 — \Г
гр
где Егр и vrp—соответственно модуль упругости и коэффициент
Пуассона материала основания (грунта).
Полученное нами дифференциальное уравнение (1.5), характе-
ризующее изгиб плиты на упругом однослойном основании, является
основным уравнением рассматриваемой задачи. Оно отличается
от известного уравнения, вытекающего из гипотезы Винклера —
Циммермана, тем, что в нем имеется дополнительный член при
1 — V
гр
140
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
(ГЛЙ!
коэффициенте г2, которым учитывается влияние касательно
напряжений, возникающих в упругом основании.
По определении функции прогибов плиты w (х, у) из ди<|
ференциального уравнения (1.5) и заданных для плиты границ
ных условий реакции основания q (х, у) могут быть найден!
Рис. 74.
из уравнения (1.4), а моменты и поперечные силы
известным формулам теории изгиба пластинок:
(рис. 74) — по
.. ,, ( d2w d2w \
\ дх2 ‘ оу2 )
d2w . d2w
И
» = + I1»)
N,= -D±(^ + ^), -
дх \ ох‘ ду2j
,, n d / d-w . d2w \
у ду \ дх2 ' ду2 ;
Отметим, что поперечные силы Nx, Ny и крутящие моменты Н.
на краях пластинки обычно заменяются, по Кирхгофу, эквива-
лентными им приведенными поперечными силами Qx и Qy. Этй
силы для пластинки с прямоугольным контуром могут быть
вычислены по формулам:
- DL^3 r (2 Ох ду2 J ’ i
L ду3 v ‘ 7 дх2 ду J
№] ПРИВЕДЕНИЕ ЗАДАЧИ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ]4]
I § 2. Приведение задачи об изгибе плиты на упругом
I основании -к обыкновенным дифференциальным уравнениям
* 1. Общие соображения. Проблема изгиба плит на упру-
гом основании, как и родственная ей проблема изгиба пластинок,
представляет собой одну из сложнейших задач математической
теории упругости. Поэтому решение ее в замкнутой аналитиче-
ской форме удается получить только для сравнительно небольшого
числа краевых задач. В большинстве же случаев решение основ-
ного дифференциального уравнения (1.5) в замкнутой аналитиче-
ской форме, т. е. в такой форме, когда функция прогибов w(x, у)
выражается конечной формулой от переменных х и у, при совре-
менном состоянии прикладной математики не может быть получено.
Объясняется это тем, что аппарат функций, которыми располагает
прикладная математика и значения которых вычисляются при
помощи тех или иных элементарных действий и таблиц (полиномы
различных порядков, тригонометрические функции, гиперболические
функции, бесселевы функции и др.), несмотря на свое много-
образие, не в состоянии охватить всевозможных задач по изгибу
даже одной только прямоугольной пластинки.
Поэтому при решении более или менее сложных задач по тео-
рии изгиба пластинок или плит используют обычно приближенные
методы, основанные на применении рядов. Одним из таких мето-
дов является, например, метод тригонометрических рядов оди-
нарных (задача Мориса Леви) или двойных (задача Навье).
Однако метод тригонометрических рядов, достаточно простой
и удобный для практических вычислений, пригоден только для
некоторых частных случаев граничных условий. Поэтому здесь
при решении поставленной задачи мы используем более общий
метод, а именно метод приведения к обыкновенным дифференци-
альным уравнениям.
Общий вариационный метод приведения к обыкновенным диф-
ференциальным уравнениям в применении к задаче об изгибе
прямоугольной пластинки с достаточной полнотой изложен в мо-
нографии В. 3. Власова «Строительная механика тонкостенных
пространственных систем», 1949 г. Здесь же мы дадим приложе-
ние этого метода к расчету пластинки, или, что то же самое,
тонкой плиты, расположенной на упругом основании. При этом
будем предполагать, что рассматриваемая плита может иметь
любые граничные условия на поперечных и продольных краях,
а также может иметь переменную толщину, изменяющуюся в од-
ном или двух направлениях по ступенчатому закону.
2. Приведение двумерной задачи к одномерной.
Условимся различать для плиты два направления — поперечное,
совпадающее с направлением оси Ох, и продольное, совпадающее
с направлением оси Оу (рис. 75).
142
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ.ПГ
Искомую поверхность прогибов плиты, т. е. функцию двух
переменных w (х, у), представим в виде следующего конечного
разложения:
Щх, у) = S (2-О
k =1
Будем считать при этом, что система безразмерных функций
/_А (х), аппроксимирующих прогиб плиты в поперечном направлении,,
выбрана заранее, а функции Wk(y), имеющие размерность проги-
ба, подлежат определению. В соответствии с их физическим
Рис. 75.
смыслом функции Wk(y) могут быть названы обобщенными проги-
бами, а функции (.х) — функциями поперечного распределения
прогиба.
Отметим, что функции поперечного распределения прогиба
у (х) могут быть выбраны самыми различными способами, но так,,
чтобы они были линейно независимы и удовлетворяли геометри-
ческим граничным условиям на продольных краях плиты. Про-
стейшим примером такой системы, удовлетворяющей геометриче-
ским граничным условиям
и (0) = Х,(^) = 0,
является ряд, составленный из тригонометрических функций
kr.x ,
sin -у-, если k принимает все последовательные значения от
единицы до п.
Представление поверхности прогибов в виде разложения (2.1}
цри конечном числе п означает сведение рассматриваемой плиты.
$ 21 ПРИВЕДЕНИЕ ЗАДАЧИ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ 143
к системе с конечным числом степеней свободы в поперечном
направлении при сохранении бесконечного числа степеней свободы
в продольном направлении. Это означает также приведение дву-
мерной задачи теории упругости к одномерной, ибо после разы-
скания всех п функций Wk(y) (функций одного переменного)
значения прогибов и>(х, у) будут определены с известной степенью
точности.
Для определения искомых функций Wk(y) используем условия
равновесия элементарной пластинки, выделенной из рассматривае-
Рис. 76.
мой системы (плита -ф упругое основание) поперечными сечениями
у = const и у -ф dy = const (рис. 75 и рис. 76). При этом под
условиями равновесия будем понимать, согласно принципу воз-
можных перемещений Лагранжа, равенство нулю суммарной ра-
боты всех внешних и внутренних сил этой пластинки на всяком
возможном для нее перемещении.
За форму г-го возможного перемещения элементарной пластин-
ки примем цилиндрический изгиб в вертикальной плоскости, при
котором прогибы верхней грани в пределах расположения
плиты определяются одной из функций (х) при соответствующем
обобщенном прогибе Wt(y) = 1. Поскольку все возможные пере-
мещения пластинки характеризуются при этом совокупностью п
линейно независимых функций /_Дх), нетрудно будет составить п
независимых условий равновесия, из которых и определятся все
п ИСКОМЫХ функций Wk (j/)-
3. Обобщенные условия равновесия элементар-
ной пластинки. Выделенная из рассматриваемой системы
элементарная пластинка включает в себя сжимаемый слой
144 ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты [ГЛ. ш|
упругого основания высоты Н и полоску плиты, расположенную;
на поверхности упругого основания (рис. 76).
Для составления обобщенных условий равновесия рассмотрим
в отдельности те силы, которые приходятся на полоску плиты
и элемент упругого основания, заключенный между сечениями
у = const и у + dy = const.
Помимо заданной внешней нагрузки на элементарную полоску
плиты, со стороны отброшенных частей плиты будут действовать
дМи д$и
усилия Му, Qy по сечению у = const и Му-\- -^dy, Qy+~~dy
по сечению у + dy — const. Кроме того, в угловых точках
полоски будут действовать сосредоточенные вертикальные силы j
2Н и 2^Н ~г dtj) , происходящие от приведения (по Кирхго- 1
Фу) крутящих моментов к статически эквивалентным им допол- J
нительным поперечным силам. .
Все перечисленные усилия (положительные направления этих ;
усилий показаны на рис. 76) представляют собой по отношению ;
к рассматриваемой полоске плиты внешние силы. Внутренние ,
усилия полоски создаются напряжениями, возникающими в про-
дольных сечениях х — const и приводящимися к изгибающим
моментам Мх и приведенным поперечным силам Q..
Роль внешних сил по отношению к сжимаемому слою упругого j
основания играют нормальные и касательные напряжения, дейст- J
вующие на вертикальных гранях у = const и у dy = const рас- i
сматриваемой элементарной пластинки. Внутренние силы упругого ?
основания создаются нормальными напряжениями ах, и каса-
тельными напряжениями и тхг.
Составляя обобщенные условия равновесия рассматриваемой ;
системы, понимаемые в смысле принципа возможных перемещений, 1
подсчитаем теперь работу каждого из названных усилий в отдель-
ности.
Работа внутренних сил, действующих на полоску плиты, :
определяется работой изгибающих моментов Мх и поперечных i
сил Qx на соответствующих деформациях полоски. При этом ра-
бота поперечных сил Qx в силу основной геометрической гипо-
тезы, принимаемой в теории изгиба пластинок, равна нулю, a s
работа изгибающих моментов, отнесенная к элементу dy,- равна
$ Mx7J‘ dx. (2.2) j
Интеграл, входящий в формулу (2.2), распространяется по :
всей длине выделенной полоски в пределах от 0 до Ь.
Работа внешних сил, действующих на элементарную полоску j
плиты (отнесенная к dy), складывается из следующих составных |
§ 2] ПРИВЕДЕНИЕ ЗАДАЧИ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ 145
- а) Работа внешней заданной нагрузки, которая определяется
выражением
Gi = $ Р (х, у) Xi W dx, , (2.3)
где интеграл распространяется не только на распределенную на-
грузку р (х, у), но также и на сосредоточенные поперечные силы
и моменты и понимается в смысле интеграла Стилтьеса. Формула
(2.3) может быть представлена поэтому в следующем разверну^
том виде:
Gi = 5 Р (х, у) Xi (х) dx + ^pc (у) х£ (с) -г 2 (У) х£ (с), (2.4)
где рс(у) и тс(у) — поперечные вертикальные нагрузки и моменты,
сосредоточенные на линиях х = хс, а (с)> X,- (с) — значения соот-
ветствующих функций в сечениях х = хс.
Отметим, что к числу сосредоточенных усилий относятся также
приведенные поперечные силы (0), (Ь) и изгибающие моменты
7И% (0), МХ(Ь), действующие по концам полоски.
Суммы в формуле (2.4) охватывают все поперечные нагрузки
и моменты, сосредоточенные на линиях х = хс, а интеграл распро-
страняется на всю ширину пластинки и относится к распределен-
ной поперечной нагрузке р(х, у).
б) Работа приведенных поперечных сил Qy
и Qy + -^- dy-
\d^^dx-
(2-5)
в) Работа сосредоточенных поперечных сил 2Н и 2 (7/ + dy):
-2 [<*']• (2-6>
Здесь, как и в дальнейшем, прямые скобки со звездочкой
будем понимать как подстановку, означающую разность стоящих
в скобках величин, определенных для крайних точек полоски.
Отметим, что работа продольных изгибающих моментов Му
на принятых для полоски возможных перемещениях (х) при
Wt (у) — 1 равна нулю.
Работа внутренних и внешних сил, действующих на элементар-
ную пластинку, выделенную из упругого основания, в силу ос-
новных гипотез, принятых для однослойного основания
и (х, у, г) = 0, и (х, у, г) = 0,
определяется работой нормальных напряжений и касательных
напряжений соответственна на деформациях сжатия и сдвига,
W В. 3. Власов, Н. Н. Леонтьев
146
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
11
а также работой касательных напряжении хгу и тгу -}-
распределенных на гранях у — const и у + dy = const пластик
Обозначим эту работу через Ri(y). |
Суммируя работу всех внешних и внутренних сил, действую^
на рассматриваемую элементарную пластинку, можно представ
интегральное условие равновесия этой пластинки, соответствуй
какому-либо из п возможных перемещений xz. в следующем н|
X
г
е
^M^dx+^^dx-2^^ + Ri + G = 0 (1)
(z = 1, 2, 3, ... , n).
4. Работа внешних и внутренних сил упрурДо
основания. Рассмотрим вначале наиболее важный в праИ-
ческом отношении случай, когда оба продольных края шЖ1
свободны от закреплений.
Исходя из условия, что функция w(x, у), характеризукйИя
осадку поверхности упругого основания, непрерывна и, в <яВ'-
ности, не имеет разрывов на продольных краях плиты, предстгДи
приближенно осадку основания за пределами плиты в ф<Де
разложения Я
w(x, у) = 3 ^(У)ХОА(Х)- («)
А —1
Входящие в разложение (2.8) функции Wk(y) представл)
собой, как и ранее, обобщенные прогибы, а безразмерные функ
ХоА (х) определяются выражениями: j
1
слева от плиты при х 0 = х* (0)
справа от плиты при x'^t-b ^ok = xk(b)e~a^x~b'i,
где а = , k и t — обобщенные характеристики упругого
нования (см. (1.14)), (0) и хА(й) — значения функции nonej
ного распределения прогиба ХА(Х) на продольных краях пай
(при х = 0 и х = b). i
Мы предположили, таким образом, что выделенная из уируА
основания элементарная пластинка шириной dy и высотой Н
тает точно так же, как рассмотренная нами ранее плоская ’(Я
слойная модель: затухание осадки поверхности основания пройй
дит здесь по экспоненциальному закону е~ах. При этом кажд|
виртуальному перемещению полоски плиты я
wi{x, у) = I-/.(х) 1
ПРИВЕДЕНИЕ ЗАДАЧИ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ 147.
о
о
б
У
ветствует вполне определенное перемещение поверхности упру-
основания за пределами конструкции.
Зереходя к вычислению возможной работы внешних и внутрен-
сил выделенной из упругого основания элементарной пластинки,
йтим, что перемещения точек упругого однослойного основания,
деляются формулой (7.2) гл. I. Вследствие этого виртуаль-
перемещениям поверхности упругого основания
ш/(х, у) = 1-хДх)
(2.10)
'гу И Tzy +
ут соответствовать следующие виртуальные перемещения точек
'ругого основания:
Wi(x, у, г) = 1-х(*)Ф(2).
Работа (отнесенная к dy) касательных напряжений т;
^^-dy, распределенных на гранях у = const и у ф- dy = const
астинки, на виртуальном перемещении (2.10) равна
V0 г аг
) dx\
—оо 0
(2.11)
Работа внутренних напряжений аг и т2Х на деформациях пла-
тки, отвечающих виртуальному перемещению (2.10), соответ-
1енно равна
-f-oo Н |
— 5 dx \ а^(х)Ф'(z)dz> I
Z н | (2-12)
— \ dx T„X/ (х) ф (г) dz.
—ОО о '
Согласно формулам (6.4), (6.5), (7.1) и (7.2) гл. I и формуле
'•1) входящие в выражения (2.11) и (2.12) напряжения опреде-
иотся в виде:
V0 k=l
xzy — 2(l+v0) 2 k(y')T.k^x')’ fc=l (2.13)
=271755'Кг) i
10*
148
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
irjj?
Отметим, что формулы (2.13) позволяют вычислять напряжения
в упругом основании только в области, расположенной непосред-
ственно под плитой. Для определения нормальных и касательных
напряжений за пределами плиты на основании разложения (2.8)
в формулах (2.13) следует заменить функции х*(х) и х^ (х) соотве-
тственно на xofe (х) и х^(х).
Внося формулы (2.13) в выражения (2.11) и (2.12) и произ
интегрирование в указанных пределах, получим выражение
работы внешних и внутренних сил упругого основания:
п
Ri {у) = 2 {2Л хлdx + Пхл]П} w"k —
k=i1 J J
n , „
где
н
1 — v00
H
t = — * Д A’(z)d
4(1 + v0) J ‘ v '
о
1 /~ k
a ~ Г 2Г"
k’
по
Интегралы, входящие в формулу (2.14), вычисляются
ширине плиты в пределах от 0 до Ь. Двойные прямые ск
[[ ]] здесь и в дальнейшем будем понимать как сумму стоя
в скобках величин, определенных для краев плиты (при х >
Ь = 0).
В том случае, когда продольные края плиты шарнирно о
или жестко защемлены и, таким образом, не могут иметь ве
кальных смещений (хх(0) = х*(6) = 0), упругое основание за!
делами плиты не работает. Формула (2.14) в этом Случае уН
щается и принимает вид:
Rt (У) = Д {2^ ХЛ- dx W"k - (k J ХЛ dx +?t J ХЛ- dx) Wk}
Как частный случай общей формулы (2.14) получаем реши
когда один из продольных краев Плиты свободен, а другой
креплен от вертикальных перемещений.
«ПРИВЕДЕНИЕ ЗАДАЧИ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ 149
fg. Другой метод составления обобщенных усло-
|й равно вес и я. Покажем теперь, как работа расположенного
L плитой упругого основания может быть учтена в несколько
Ед( отличной от рассмотренной нами форме.
ЕКак и ранее, будем предполагать, что поверхность прогибов
»ты задана в виде разложения (2.1). При этом для определения
{общенных прогибов Wk(y) рассмотрим условия равновесия
,.2Н
2(н^ау)
Рис. 77.
^.Элементарной полоски, выделенной из плиты поперечными сече-
|ниями у = const, у + dy = const (рис. 77). Будем считать, что
|На элементарную полоску, помимо внешней нагрузки и усилий,
^передающихся со стороны отброшенных частей плиты, действуют
;+акже реактивные давления упругого основания.
[ Принимая за форму /-го возможного перемещения элементарной
|Полоски плиты цилиндрический изгиб, при котором прогибы
|в пределах полоски определяются функцией хг (х) при W£(y)= 1,
[Обобщенные условия равновесия плиты, понимаемые в смысле прин-
ципа возможных перемещений, можно снова представить в виде
I Г г дО ГдН 1*
I \M^dx +\-^x£dx — +tfz + Gz = O,
L Де Gz = Q{ (y) — работа внешней заданной нагрузки, a Ri = Ri (у)—
[Работа реактивных давлений упругого основания на возможных
150
ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ
[ГЛ. III
перемещениях полоски
Wi(xt у) = 1 •£,(*).
Реакции упругого основания для выделенной из плиты полоски,
как и в случае балки, работающей в условиях плоской задачи,
будут состоять из распределенных давлений q(x, у) и фиктивных
сил Q*(z/), приложенных на концах полоски (рис. 77)*).
Согласно разложению (2.1) и формуле (1.4), выражающей зави-
симость между нагрузкой на основание и его осадкой, получим
выражение для определения реактивных давлений q(x, у):
п п п
q(xt y) = k 2 WkXk-2t 5 WkX’k-2t 2 W’kXk, (2.17)
k=l h=l k=l
где упругие характеристики k и t вычисляются по форму-
лам (2.15).
Работа распределенных реакций (2.17) на перемещении Xz мо-
жет быть теперь представлена в виде
1 п
— У)х^х = 2 2 —
h=l
- S (А dx + 2t\ dx - 2t [x;x;j *) wk . (2.18)
Я==1
Сосредоточенными фиктивными силами Q* учитывается влияние
свободного от нагрузки основания, расположенного за преде-
лами плиты, на напряженное состояние конструкции. Другими
словами, эти силы являются результатом работы всех сил, дей-
ствующих на выделенную из основания элементарную пластинку,
на возможных для основания перемещениях XoZ за пределами
плиты.
Определяя сосредоточенные реакции Q* как некоторый экви-
валент работы напряжений упругого основания, расположенного
за пределами плиты, на виртуальных перемещениях Xoz, получим:
Л
Q* = - 2t 2 {wk [Х; (0) - aXfc (0)1 + A.Xft (0) W"A ,
V (2.19)
Q.B=2t 2 {Wk [X; (6) + aXft (6)] - ±-Xfc (0 1H .
*) Отметим, что фиктивные реакции Q* (у) представляют собой погонные
силы, отнесенные к единице длины продольного края плиты.
§2] ПРИВЕДЕНИЕ ЗАДАЧИ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ 151
Работа этих реакций на возможных перемещениях полоски Zz
равна
-[Q^-(O) + q*z.(6)] =
п
= - 3 {(2ЦхЛ-1* + 2^[[ХЛ.]])Га-4 [1хЛ]]И. (2.20)
А = 1 1
Суммируя выражения (2.18) и (2.20), для работы реактивных
давлений упругого основания получим:
Ri (У) = 2 М вд, dx + [[ад.]] } W'k—
— {k<\^dx + 2t\/k/.dx + 2<x.t [[x*Xz]l} Wk. (2.21)
Формула (2.21), естественно, в точности совпадает с полученной
ранее формулой (2.14).
6. Разрешающая система обыкновенных диффе-
ренциальных уравнений. На основании выражений (1.8),
(1.9) и (2.1) силовые факторы Мх, Н, и их производные, вхо-
дящие в уравнение (2.7), определяются в следующем виде:
Mx = —D 2 ^W"kXk+ Wk/k),
k=l
*=i
y *=1
Qy = -D 2 {^Xa+(2-H)W.
k=i
^ = _оЗ(Ц7Л4+(2-и)117И.
y k=l
(2.22)
Подставляя выражения (2.22) в уравнение (2.7), получим
2 w^\XkXldx+ 2 r;(2-p)j4z/x-
4 =1 k=l
- 2 2 r; (1 - p) [Z;Z/] + 2 J z,z;.dx +
*=i *=i
+ (2-23>
k=l
152 ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
1ГЛ. III
Производя в выражении (2.23) интегрирование по частям:
\x"Adx= IXaXJ* —
(2.24)
5 хл dx = — J z;z; dx,
и подставляя формулы (2.24), (2.21) в уравнение (2.23), нетрудно
привести последнее к виду
S агк№? - 2 S (bik + p«J W"k + S + s»ft) Wk - Gz = 0 (2.25)
A = 1 A=1 A=1
(i = 1,2, 3,..., n);
здесь
aik = 3 D $ dx>
bn = 2 D Ц x'a'i dx~ у [ZAXz + XhXil * } .
Cik = S £> $ xlxj dx<
(2.26)
Pm = t\ КЛdx + Пхл-П.
sm = k Ц W-idx + IT 5 dx+^~ IlZfeX,-]]}
где D = -|2_ p-y — цилиндрическая жесткость плиты; p — коэф-
E v
фициент Пуассона материала плиты; Ео = —, v0 = ——
1 Vrp 1 vrp
— упругие характеристики, причем Егр, vrp— соответственно мо-
дуль упругости и коэффициент Пуассона материала основания-
Формулы (2.26) относятся к случаю, когда пластинка имеет тол-
щину, изменяющуюся по ступенчатому закону в направлении оси Ох.
При этом интегралы вычисляются по каждому участку, имеющему
постоянную жесткость £)=const; выражение в квадратных скобках
со звездочкой означает разность значений (/д' + ХЛ) на концах
каждого участка; знак 3 охватывает все такие участки по ши-
рине выделенной полоски.
Можно видеть, что коэффициенты уравнения (2.25) определяются
в основном только выбранной системой функций -//г (х). При этом
они обладают свойством взаимности, или переместительности, т. е.
Oik = @ki, bik — bki> Cik = Ckii p®^ = p®z-, = S®^, (2.27)
что является выражением теоремы Бетти о взаимности работ сил
одного состояния на перемещениях другого состояния.
§ 3] ОБОБЩЕННЫЕ ВНУТРЕННИЕ СИЛЫ. ГРАНИЧНЫЕ УСЛОВИЯ 153
Свободный член уравнения (2.25) также зависит от выбранной
формы поперечного перемещения; функция Gz(y) вычисляется по
формуле (2.4) и представляет собой обобщенную погонную на-
грузку, соответствующую форме возможного перемещения /Дх).
Давая индексу i различные значения от 1 до п, мы получим
для определения п неизвестных функций Wk полную систему п
обыкновенных дифференциальных уравнений с постоянными коэф-
фициентами, которая в силу формул (2.27) будет иметь симмет-
ричную структуру. Все уравнения при этом будут четвертого'
порядка относительно каждой искомой функции.
7. Определение моменто.в и поперечных сил. Решив;
тем или иным способом систему уравнений (2.25) при заданных
граничных условиях на поперечных краях плиты, мы найдем вы-
ражения для всех функций Wk (у) и тем самым на основании
разложения (2.1) определим функцию прогибов w(x, у).
Формулы для определения моментов и поперечных сил плиты
(1.8) и (1.9) получат при этом вид:
мх = --D s k=l n (a)
-o2 + k=l n (b)
н = Hx = —Hy=—D 2 (1 - p) W’k-ik, n (c)
Мх — k=l (d) (2.28)
Ny = -о 2 (r;zs + r;z;). n (e)
Qx = -o 2 (Р-ЛИ'Х + 'ГлТ (f)
Qy = -OSd’A + P-f)’'*). k=l (g) j
§ 3. Обобщенные внутренние силы.
Граничные условия на поперечных краях плиты
Как уже отмечалось ранее, функция W:(y) является обобщен-
ным прогибом пластинки, соответствующим возможному перемеще-
нию /г. (х) элементарной полоски. В соответствии с этим производ-
ная от обобщенного прогиба W't (у) представляет собой обобщенный
угол поворота <pz(y). Как и в теории изгиба балок, геометрическим
154
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ III
величинам ITZ (у) и <pz (у) соответствуют статические величины,
представляющие собой обобщенные изгибающие моменты Mi (у) и
обобщенные поперечные силы N^y). Необходимость введения этих
величин обусловлена тем, что в рассматриваемом вариационном ме-
тоде граничные условия, как и условия равновесия, должны фор-
мулироваться в интегральной форме, т. е. через обобщенные
геометрические величины W t, <pz и статические величины Mi, Nt.
Согласно физическому содержанию метода под обобщенным
моментом Mt мы будем понимать работу всех изгибающих момен-
тов Му сечения у = const на соответствующих им возможных
dwi
перемещениях = <pzxz при = 1;
под обобщенной поперечной
•силой Ni — суммарную работу поперечных сил N и, крутящих
моментов И, а также касательных напряжений в основании хги
для сечения [у ='const на возможных перемещениях wt = W
при Wi= 1.
Отметим, что касательные напряжения хгу, действующие в се-
чениях у = const упругого основания, в силу формул (6.5), (7.2)
гл. I й (2.1) гл. III, определяются в виде
(3.1)
Работа этих напряжений на возможных для упругого основа-
ния перемещениях должна быть подсчитана по всему поперечному
сечению у = const, т. е. в направлении оси х, от — оо до 4 30
и по высоте основания от 0 до Н.
Поскольку z-е возможное перемещение любой точки М (х, у, z)
однослойного основания определяется выражением
Wi (х, у, z) = Wi (у) Xi W Ф М" (3-2).
при Wi(y) = 1, виртуальная работа касательных напряжений хгу
может быть представлена в виде
МФ (г) dxdz.
(3.3)
Замечая что перемещения поверхности упругого основания
за пределами плиты определяются формулами (2.8), (2.9), внося
зависимость (3.1) в формулу (3.3) и выполняя указанное интегри-
рование, получим для возможной работы касательных напряжений
5 4]
ВЫБОР ФУНКЦИЙ ПОПЕРЕЧНОГО РАСПРЕДЕЛЕНИЯ ПРОГИБОВ 155
поперечного сечения у = const следующее выражение:
п
2 {2t\^idx + 4 пх*х/П}
(3-4)
Исходя из определения и используя формулы (2.1), (2.28)
и (3.4), нетрудно теперь представить обобщенные моменты и по-
перечные силы сечения у = const в виде:
м- = - 2 {(S D $ \rk - и 2 D (J z;z;.dx- [Z;zj *) wk}
k—l
(3.5)
N<=- 2 (SdSxaXz^J w"k +
k=l
+ 2 {(2 — и) 2 ° ( J ХЛ dx - [Z;Zz] *) + 2/ J ХЛ dx +
A=1
®".' (3.6)
(z = 1, 2, ... , ri),
Выражения (3.5) и (3.6), устанавливающие зависимость между
обобщенными перемещениями и обобщенными силами, позволяют
задать на поперечных краях плиты граничные условия в инте-
гральной форме.
Вследствие того, что общий порядок разрешающей системы
(2.25) равен 4п, функции Wk будут найдены с точностью до 4п
произвольных постоянных. Для получения определенного решения
к уравнениям (2.25) должно быть присоединено 4п граничных
условий. Из выражений (2.1), (3.5), (3.6) нетрудно видеть, что
на каждом из поперечных краев плиты у = 0, у = I может быть
задано по 2п граничных условий. При полной заделке граничные
условия задаются в обобщенных перемещениях; для свободного
края — в обобщенных усилиях; при свободном опирании — частью
в усилиях, частью в перемещениях.
§ 4. Выбор функций поперечного распределения прогибов.
Граничные условия на продольных краях
Функции Xk (х)> представляющие деформированное состояние
пластинки по координате х, могут быть ^выбраны различными
способами при условии, что эти функции удовлетворяют геоме-
трическим граничным условиям на продольных краях плиты и
линейно независимы. Рассмотрим некоторые способы выбора
функций Xk и связанные с этим свойства матрицы уравнений (2.25).
156
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. I
1. Фундаментальные функции поперечных к
лебаний балки. За функции xfe(x) могут быть приняты фу
даментальные функции поперечных колебаний балки постоянно:
сечения при граничных условиях, аналогичных тем, котор;
заданы на продольных краях плиты.
Приведем некоторые сведения из теории фундаментальнь
функций, необходимые для дальнейшего изложения*). Напомни:
что при рассмотрении задачи о свободных колебаниях однопр
летной весомой балки длиной b исходят из дифференциально:
уравнения
<4J
где Х= X (х) — прогиб оси балки в точке с абсциссой х, ар— некс
торый параметр, характеризующий частоту собственных колебани:
балки.
Общий интеграл однородного дифференциального уравнена
(4.1) может быть представлен в виде
X (х) = Сх sin + С2 cos + С3 sh + Ci ch . (4.2
Произвольные постоянные Сх, С2, С3, С4 и параметр р, вхо-
дящие в формулу (4.2), определяются из граничных условий*
заданных на концах балки х = 0 и х — Ь. Следовательно, в зави-
симости от этих условий функция прогибов X (х) будет иметь
тот или иной вид.
Рассмотрим некоторые частные случаи граничных условий.
1. Оба края балки шарнирно оперты.
В этом случае граничные условия для функции А (х) запи-
шутся в виде:
при х= О Х(0) = Х"(0) = 0, 1 «
при х = b X(b) = X" (Ь) = 0. /
Раскрывая условия (4.3) при помощи формулы (4.2), получим;
С2 С4 — 0, j
—с2 + с4 = о, I (4 4 j
sin р-4-С2 cos р-ф С3 sh рС4 ch р = 0, |
— Cxsinp — С2 cos р + С3 sh р Ц-С4 ch р = 0. I
*) Более полно этот вопрос рассмотрен в монографии В. 3. Власов:
«Строительная механика тонкостенных пространственных систем», 194&-
См. также § 2 гл. VI.
s 4] ВЫБОР ФУНКЦИЙ ПОПЕРЕЧНОГО РАСПРЕДЕЛЕНИЯ ПРОГИБОВ 157
Из первых двух уравнений имеем С2 — Ct = 0. Остальные два
уравнения
принимают при этом вид:
Су sin р. + С3 sh р. = О,
— Сх sin р + С3 sh р = 0.
1 (4-5)
Так как все произвольные постоянные одновременно не будут
равны нулю (в этом случае мы будем иметь неинтересное для
нас нулевое решение), то определитель полученной системы
однородных уравнений (4.5) должен быть равен нулю. Отсюда
для параметра р нетрудно получить трансцендентное характери-
стическое уравнение
sinp = 0,
дающее бесконечное множество действительных корней рт
(т = 1, 2, 3, ...). Эти корни будут:
ге, 2тг, Зя.....mit. (4.6)
В соответствии с корнями (4.6) мы будем иметь полную сис-
тему фундаментальных фунлций:
Хт (х) = sin—у (т = 1, 2, 3, . ..),
определяющих бесконечное число форм собственных колебаний
однопролетной свободно опертой балки и удовлетворяющих
граничным условиям (4.3).
2. Оба конца балки имеют жесткую заделку. В этом случае
граничные условия определятся в виде:
при х = 0
при х — b
X (0) = X' (0) = 0,1
X (Ь) = X' (б) = 0. J
(4-7)
Раскрывая условия (4.7) при помощи формулы (4.2), получим,
как и ранее, однородную систему алгебраических уравнений
относительно постоянных интегрирования Сх, С2, С3, С4. Прирав-
нивание нулю определителя этой системы позволяет получить для
р. характеристическое уравнение
cos (л ch (л = 1,
корни которого (т = 0, 1, 2, ..., оо) будут:
0; 4,730; 7,853; 10,996; . . .; (4.8)
Фундаментальные функции Хт (х), определяемые корнями (4.8},
158 изгиб прямоугольной плиты [гл. и:
для рассматриваемого случая принимают вид:
Хт (х) = sin —---sh -у — am I cos — ch -y ) ,
где
sin vm - sh
a =---------г---.
cos — ch Hm
He останавливаясь далее на рассмотрении других частных
случаев, отметим, что таким же путем, исходя из уравнения
(4.2) и заданных граничных условий задачи, можно выявить фун-
даментальные функции Хт (х) не только для однопролетной балки
при всевозможных граничных условиях, но и для многопролетных
неразрезных балок, имеющих, помимо крайних опор, также и
промежуточные опоры. При этом в каждом частном случае для
определения нужного нам числа независимых произвольных
постоянных мы будем иметь систему однородных уравнений;
Приравнивая нулю определитель этой системы, получим для
параметра р. характеристическое уравнение, дающее бесчислен,
ное множество действительных корней. Этими корнями и гранич-
ными условиями будут определены все фундаментальные функция
рассматриваемой задачи.
В табл. 7 приведены фундаментальные функции для шести
основных случаев граничных условий однопролетной балки. Здесь
же показаны соответствующие этим функциям характеристичен
ские уравнения, а также значения первых четырех корней этих-
уравнений. •
Для удобства практического пользования фундаментальными
функциями в приложении (см. табл. 5—10) даны вычисленный
значения самих функций Хт (х) и величин, пропорциональных:
первой, второй и третьей производным от этих функций
-4(6)ЛХДХ), 7^(х), !
V-m V-m
для девяти промежуточных сечений балки вдоль пролета и двух)
крайних сечений х = 0 и х = Ь; при этом введена относительная!
координата £ = — . Таблицы дают значения фундаментальных!
функций и их производных для сечений с относительными!
координатами £ = 0; 0,1; 0,2;...; 0,9; 1,0. Значения этих:
функций даны в таблицах для первых четырех корней характер
ристического уравнения рх, р2, р3, р4, т. е., по существу, для*
первых четырех членов разложения в ряд по фундаментальным!
функциям. ]
Заметим, что фундаментальные функции, определенные изло-1
женным выше способом, обладают рядом свойств, весьма важных!
s 4] ВЫБОР ФУНКЦИЙ ПОПЕРЕЧНОГО РАСПРЕДЕЛЕНИЯ ПРОГИБОВ 159
Корни характеристического уравнения 1 общая формула Для (п>4) е е ^ч + е см К СМ ^ч Ч- е см К см *4 1 CM CM -b к -h e к
к СМ СО см СО ^ч U0 U0 CO co о о CM U0 CO о uo co - CO
к сО СО ю о о о СО ио со аь О 00 uo 00 O S о eq О
Л К СМ см СО ио 00 см со ио 00 о co uo 00 CO о 00 CO о
£ го II * К СО II о о со о со ^4 U0 00 ^4 co CO CM a co co CO CM о co
Характе- ристиче- ское уравне- ние sin у. = 0 ЦТ сл О О 1Т СЛ 3 *Q СЛ О CJ 1 II II J- 11 II i- :i.:S 11
Коэффициент а 1 Ci- 45 сл А _с сл т 5- СЛ О sin у — sh у cos p. — ch p. । i 4 qs Ц- 4 uys 4 ЦЭ 4- ri SOO й- .E ’сл X 5- c 'ел "v5
Фундамен- тальная функ- ция X (£) и/ i. .S *СЛ sin yg — — sh yg — —a (cos yg— — ch ц£) sin yg 4- 4- sh yg — — a(cosyg+ + ch yg) sin yg— 1 — shyg — — a (cos yg— — ch yg) sin yg — — a sh yg sin yg 4- । 4- a sh yg
Граничные условия я р. 1 с ч О О IIJI X X о о II J1 X X о о X X о о J1 X X о ° 11 II X X о о JI J1 XX _
№ с* 2. и С н о ° II J1 X X о ° II J1 X X о о J1 о ° II II X X о ° II J' X X о ° II J' X X
Различные случаи граничных условий на поперечных краях т4$ * Яч 1 4
№ п/п ^ч СМ CO uo CO
160 ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ (гл. ш
с точки зрения практических приложений. Прежде всего, эти
функции по всей длине балки ортогональны. Это означает, что
определенный интеграл от произведения двух функций Хт (х\
и Х„(х), взятый по всей длине балки, при m=j=n равен нулю:
ь
§ Хт (х) Хп (х) dx = 0.
о
Свойством ортогональности обладают также и вторые произ-
водные от фундаментальных фун ций, а следовательно, в силу
основного дифференциального уравнения (4.1) и все четные про-
изводные от этих функций. Если т=]=п, то
ь
5 Хт (х) Хп (х) dx = 0. ;
о
Интеграл же из квадрата фундаментальной" функции Хт (х),
как и из квадрата второй производной от этой функции, независима
от номера ее т всегда отличен от нуля. При этом величина?
интеграла \X2mdx не зависит от граничных условий на краю x=Qi
° I
и может быть выражена только через значение самой функций
и ее производных на краю х = Ь:
ь 4
^X2m(x)dx =|[X2m-2X'mx; + (Xk)2W- I
о 1
Переходя к вопросу расчета плиты на упругом основании,?
рассмотрим случай, когда в качестве функций поперечного рас-?
пределения прогиба (х) приняты фундаментальные функции X*(x)J
Прежде всего, можно видеть, что в этом случае граничные
условия, заданные на продольных краях плиты, всегда будут
удовлетворены, если функции = Xk выбраны в соответствии;
с этими условиями.
Далее нужно отметить, что разрешающая система дифферен-з
циальных уравнений (2.25) при несколько упрощаете^!
Так, для симметричных задач (когда поперечное сечение плиты
соответствует схемам 1, 2, 3 табл. 7) система уравнений (2.2Я
распадается на две независимые системы, содержащие каждая
только четные или только нечетные члены разложения (2.1)1
В случаях 4, 5 и 6 (табл. 7) система уравнений (2.25) остается
единой. I
Кроме того, в силу ортогональности фундаментальных фунм
ций и их вторых производных обращаются в нуль коэффициент»
§ 4] ВЫБОР ФУНКЦИЙ ПОПЕРЕЧНОГО РАСПРЕДЕЛЕНИЯ ПРОГИБОВ 161
ацг, Gib, ptk при i=f=k, что, естественно, облегчает проведение рас-
четов.
2. Тригонометрические функции. Рассматриваемая
задача решается наиболее просто в том случае, когда продоль-
ные края плиты имеют шарнирное опирание (схема 1 в табл. 7).
Здесь фундаментальные функции вырождаются в тригонометриче-
. • k~X
ские функции sin у которых все последовательные производ-
ные ортогональны. Вследствие этого, а также вследствие того,
что функции = sin ~ на продольных краях плиты (при х = О
и х = Ь) обращаются в нуль, все коэффициенты (2.26) при i=f=k
будут равны нулю. При этом система дифференциальных уравне-
ний (2.25) полностью распадается на отдельные независимые
уравнения, каждое из которых будет четвертого порядка относи-
тельно искомой функции Wk(y).
Однако тригонометрические функции могут быть использованы
и тогда, когда плита имеет свободные от закреплений продольные
края или когда один продольный край шарнирно оперт, а другой
не имеет закреплений (случаи 3 и 6 табл. 7). В этом случае
можно аппроксимировать упругую линию поперечной полоски при
помощи ряда, составленного из первых (линейных) членов соот-
ветствующего ряда фундаментальных функций и из тригонометри-
ческих функций sin ~ .
Так, для плиты со свободными краями (случай 3) функция
прогибов w(x, у) может быть представлена в следующем виде:
при симметричной нагрузке
w(x, y) = W0(y)\ + W1(y)sm^+W3(y)sm3^ + ...- (4.9)
при обратносимметричной нагрузке
ю(х, у) = ^0 (у)(1 - - у) + W2(y) sin Ws(y)sin^+... (4.10)
Для плиты, шарнирно опертой на одном из краев (случай 6),
получим:
ш (х, у) = Wo (у) у Д ИД (У) sin у Д (у) sin Д ... (4.11)
Ранее уже было отмечено, что в случае 3 система дифферен-
циальных уравнений (2.25) распадается на .две независимые си-
стемы. При этом в силу ортогональности тригонометрических
функций каждая из систем значительно упростится. Напри-
мер, для плиты постоянной жесткости (D = const) при выборе
Функций %k(x) согласно (4.9) и (4.10) разрешающая система
р в. 3. Власов, Н. Н. Леонтьев
162
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
(ГЛ. III
обыкновенных дифференциальных уравнений (2.25) соответственно
для симметричной и кососимметричной нагрузок может быть пред-
ставлена в виде табл. 8 и 9.
Можно видеть, что матрица каждой из приведенных систем
будет содержать ненулевые члены только по главной диагонали,
в первой строке и первом столбце. Все остальные члены будут
при этом равны нулю.
В приведенных таблицах Di и D2 — дифференциальные опера-
торы, которые обозначают, что от указанных в заглавной строке
функций берется четвертая или вторая производная. Коэффициен-
ты а00, poo, Soo, aoi, s°nn вычисляются по формулам (2.26)
подстановкой в них выражений:
для симметричной нагрузки
/.о 1 > /.„ sin (при п = 1, 3, 5, 7, ...);
для кососимметричной нагрузки
у = 1-----г-, sin —г- (при т = 2, 4, 6, ...).
А-0 £ * Ли £ \ Г 1 1 1 /
Грузовые члены, стоящие в правых частях приведенных урав-
нений, представляют собой работу згданной нагрузки на соответ-
ствующем перемещении Wпри W, = 1.
Приведенные примеры выбора функций
поперечного
распреде-
ления прогиба xk показывают, что для получения полного в ма-
тематическом смысле решения изложенный метод приводит к
необходимости решать бесконечную систему обыкновенных диф-
ференциальных уравнений.
Однако вследствие хорошей сходимости рядов, составленных
из фундаментальных или тригонометрических функций, при про-
ведении практических расчетов в разложении (2.1) достаточно
брать весьма ограниченное число членов и, следовательно, решать
систему не столь высокого порядка. Так например, в том слу-
чае, когда заданная нагрузка хотя бы в одном направлении (по
оси х) близка к равномерно распределенной, в разложениях (4.9)
и (4.10) можно ограничиться двумя, максимум — тремя членами
и при этом получить вполне достаточную для целей практики
точность вычислений. В равной степени это относится и к другим
рассмотренным выше случаям опорных закреплений плиты.
Заметим, что при ограниченном числе членов, принятом в раз-
ложении (2.1), изгибающие моменты Мх и поперечные силы \'х
и действующие в поперечных сечениях х — const, для повы--
шения точности вычислений могут быть определены не по форму-
лам (2.28), а непосредственно из условий равновесия подобно
Таблица?
Матрица обыкновенных дифференциальных уравнений для случая симметричной нагрузки
п
Wxy= РК0-1 + 2 W'feSin^. при k =1, 3, 5, ...,п
Л—1
L ^0 w3 • • К Грузо- вые члены Единичные перемещения
0 а<ю^— 2Роор2+ 4- s° йоо а00^4“ — 2 (boo + Poi)^2+ soi а0зО4 — -2(Ьйз+р°03)^ + + S03 а0п^~ _2(bon + p°o„)D* + + Son Go Zo = 1
1 • ЦцО4 -2(bu + P?1)D* + + (3?! + Пт) 0 0 1 nx
3 • • ЧззО4 - -2(Ьзз+Р°33)О2 + + (s33 + сзз) 0 Оз 3itx X« = sin "у
п j • • annDl~ ~2(bm + ^nn)D- + + (sm + cnn> G„ nnx xn = sin T
ВЫБОР ФУНКЦИЙ ПОПЕРЕЧНОГО РАСПРЕДЕЛЕНИЯ ПРОГИБОВ 163
Таблица 9
Матрицы обыкновенных дифференциальных уравнений для случая кососимметричной нагрузки
т
W (», У) =
k~x
при k = 2, 4, 6, . . . , т
п=:2
1 ^0 w2 wt Грузо- вые члены Единичные перемещения
0 aQQD* — 2 (#оо 4“ + pSo)°3 + + soo a02Di—2(6o2+p°2) Да+ + ь° b02 aolDi — — 2(6o«+ P04) D2 + + S04 aom^>i -2^0m + P?m)O3 + + s0m Go 4 2X Xo “= 1 - у »
2 • — 2 (b22 + P22) + + (C‘22 + *22) 0 0 G3 2 их /2 = Sin -y 1 "fcO
4 • • aiiDi — -2(644+ P^)Oa + + (c44 + s°4) 0 Gt 4лх Z4 - sin -y
т • • • am,nD'‘~ -2(bmm + ?mm) D* + + (cmm. + smm) Gn mnx при m = 2, 4, 6,. . .
ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ [ГЛ. III
j 4] ВЫБОР ФУНКЦИЙ ПОПЕРЕЧНОГО РАСПРЕДЕЛЕНИЯ ПРОГИБОВ Jgg
тому, как это делается в сопротивлении материалов при опреде-
лении касательных напряжений в балке.
3. Выполнение статических условий на про-
дольных краях. Как уже отмечалось выше, система функ-
ций /А(х) в предлагаемом методе может быть выбрана только
в соответствии с геометрическими
ными на продольных краях плиты.
граничными условиями, задан;
Вопрос о том, будут ли удов-
летворены при этом статические условия, зависит от типа гра-
ничных условий задачи и вида функций /^(х). Как правило, ста-
тические условия выполняются только приближенно, что, однако,
не вносит существенных погрешностей в расчеты.
Статические условия на линиях х = О и х = b являются част-
ными случаями условий равновесия, которые, вообще говоря,
должны выполняться не только на этих линиях, но и на всех
линиях х — const. Между тем условия равновесия учитываются
нами только в интегральной форме при составлении уравнений
Лагранжа (2.25). При таком решении, как и всегда при решении
вариационными методами, отклонение от точного решения и от
точного соблюденья условий равновесия в среднем получается
небольшим, но в отдельных точках и, в частности, на граничных
линиях х = 0, х = 6 условия равновесия могут не выполняться.
Поясним сказанное следующими примерами.
а) При свободном крае х = 0 пластинки в качестве функций
/л(х) могут быть выбраны фундаментальные функции Xk(x), от-
вечающие условиям:
при х = О
X" (С) = X'" = О, Х(0)=/=0, Х'(0)=/=0.
Тогда из выражений (2.28а) и (2.28f) нетрудно получить:
Л4Д0) = -П S fzWx/..,
qz(o) = -o S
k=1
(4.12)
Эти равенства при заданных = Х^ и найденных Wk совпа-
дают со статическими граничными условиями только при вполне
определенных граничных значениях Мх и Qx; со всякими другими
значениями и, в частности, с однородными граничными условиями
МД0) = 0, Qx(0) = 0 (4.13)
они не совпадают. Следовательно, статические граничные условия
на свободных краях в общем случае выполняются только при-
ближенно, с точностью, зависящей от числа членов ряда.
166 ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ [ГЛ. ш
б) В случае шарнирного опирания пластинки на линии х = О
фундаментальные функции удовлетворяют условию
Х(0) = о, х"(0) = 0.
Тогда из выражения (2.28а) получаем равенство
МД0)-0. (4.14)
Следовательно, при шарнирном опирании однородное гранич-
ное условие, заданное в виде (4.14), удовлетворяется автомати-
чески. Если же на контуре задан внешний момент, отличный от
нуля, то такое неоднородное граничное условие не удовлетворяется
ни при каком числе членов разложения.
Противоречивость полученного в этом случае решения будет
однако чисто формальной, так как она относится только к гра-
ничному сечению х = 0. В соседнем сечении, сколь угодно близ-
ком к граничному, мы можем подойти весьма близко к действи-
тельному значению момента Мх, взяв достаточное число членов
ряда.
В § 5 будет показано, как путем другого выбора или расши-
рения системы функций yk (х) можно близко подойти к заданным
статическим условиям на продольных краях при минимальном
числе членов ряда.
§ 5. Выбор функций поперечного распределения
прогибов статическим методом
Выбор функций ХдДх) не ограничивается фундаментальными;
или тригонометрическими функциями. Функции поперечного рас-
пределения прогиба можно построить также и статическим (
методом. ;
Для этого нужно рассматривать элементарную полоску плиты;
dy как обыкновенную балку и определить для этой балки’
в соответствии с заданными граничными условиями упругую линию J
т. е. линию прогибов от той или иной поперечной нагрузки. Давая)
различные виды этой нагрузке, мы будем иметь различные формы)
изгиба балки, т. е. различные функции хА(х). Так, например,]
загружая балку-полоску сосредоточенной силой и давая различ-|
ные точки приложения этой силе по длине балки, мы будем!
получать различные формы прогибов, которые могут быть приняты!
за функции хА(х) (рис. 78). В этом случае функции будут,!
очевидно, выражаться кривыми третьего порядка (разными для|
каждого участка балки). ч
Точно так же, загружая балку-полоску распределенной на^|
грузкой и давая этой нагрузке по длине балки разные закон»
§ 5] ВЫБОР ФУНКЦИЙ СТАТИЧЕСКИМ МЕТОДОМ 167
изменения, мы можем элементарными приемами строительно
механики получить из известного дифференциального уравнения
yiv _
'k EJ
и граничных условий различные виды функций Каждом} виду
сплошной нагрузки будет соответствовать своя функция прогибов
балки В случае равномерно
распределенной нагрузки, имею-
щей на разных участках балки
разную интенсивность (положи-
Рис. 78.
Рис. 79.
тельную или отрицательную) (рис. 79), прогибы балки на каж-
дом участке будут выражаться (при постоянной для этого участка
жесткости EJ) параболами четвертого порядка. Так как функции
yk (х) и их производные на отдельных участках элементарной
поперечной полоски могут иметь различные аналитические выра-
жения, мы в дальнейшем будем понимать интегралы в правой части
формул (2.26) как сумму интегралов по всем этим участкам.
Статический метод является более общим и поэтому более
гибким, чем метод фундаментальных функций. Его общность вы-
168
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
Ггл. HI
текает из следующего свойства фундаментальных функций:
XIV (*) = Ч (*)•
В частном случае, когда закон изменения нагрузки подобен са-
мой линии прогибов, фундаментальные функции также являются
линиями прогибов.
Далее, при наличии на свободном крае х = 0 заданной попе-
речной нагрузки Q (х) =/= 0 или при наличии на свободном или
шарнирно опертом крае заданного момента Мх=/=0 мы можем
включить в число функций /.Дх) упругие линии балки-полоскй
от краевых нагрузок Qx(0) = 1 и соответственно от МДО) = 1,
При этом мы сразу получим на свободном крае х = 0 и вблизи
него лучшее приближение к точному решению, чем то, кото-
рое может дать конечное число членов ряда фундаментальных
функций.
Отметим также, что при расчете сложных конструкций стати-
ческий метод проще, чем метод фундаментальных функций, на-
пример, при расчете неразрезных плит и плит переменной толщи-
Рис. 80.
г(х.
ны, жесткость которых меняется в направлении оси х по ступен-
чатому закону.
В этом случае элементарную полоску dy такой конструк-
ции следует рассматривать в зависимости от вида этой конст-
рукции в сечении у = const как ступенчатую или как неразрез-
ную балку. Загружая
такую балку какой-либс
внешней нагрузкой, мь
можем для нее извест
ными методами строи*
тельной механики полу;
чить функцию прогибо|
хД*)- 1
Варьируя внешнюю
нагрузку, будем полу
чать различные вид|
функций yk (х), аппроЙ
симирующих измене™
прогибов w (х) в сечен»
у = const. На рис. S
показаны графики функций /Дх), полученные как прогибы w
разрезной балки от трех видов нагрузки, аппроксимирующей пд
гибы неразрезной плиты, заделанной по краюх —0 и имеющей Я
линиям х = щ, х = аг 4~ ^2 и х = щ 4- Щ> + а3 "жесткие опори
параллельные оси Оу. Я
*з(х)
S 61
ПЛИТА. ШАРНИРНО ОПЕРТАЯ ПО ДВУМ КРАЯМ
169
§ 6. Плита, шарнирно опертая по двум
противоположным краям
1. Рассмотрим прямоугольную плиту на упругом основании,
шарнирно опертую по двум продольным краям (рис. 81). В каче-
стве функций поперечного распределения прогиба в этом случае
могут быть приняты тригонометрические функции вида
Zn(x) = Sin^’. (6.1)
В силу ортогональности функций (6.1) и их производных все
побочные коэффициенты системы дифференциальных уравнений
Рис. 81.
(2.25), имеющие непарные индексы, обратятся в нуль, в резуль-
тате чего система (2.25) распадается на отдельные независимые
уравнения для каждого номера п разложения (2.1):
annW^ - 2 (bnn + р°п) W“n + (спп + s°„) Wn = Gn, (6.2)
где коэффициенты определяются по формулам (2.26) и имеют вид:
n b
@пп — О ~2 j
bnn — D-^- ,
спп — и ,
о — / b
упп ' 2 ’
S° - Ь — Г1 -г- -
inn - К 2 i k b2 J
(6.3)
170
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
Ггл. in
В дальнейшем в целях краткости написания индекс п. будет
нами опускаться. Однако нужно помнить, что каждый коэффи-
циент а, Ь, . .., s° и функция W относятся к определенному
числу разложения п.
2. Для проведения практических вычислений уравнение (6.2)
удобнее записать в безразмерных координатах. Вводя новую
ц
переменную v; = у и замечая, что
d№ j_dW d2W _ 1
17 — T17 ’ dy2 ~ I2 dr2 и т- Д-’
перепишем уравнение (6.2) в виде
W™— 2r2W"+ s*W = -^-G, (6.4)
где
/-2 — /2 )
Внося в выражения (6.5) значения (6.3), получим для коэффи-
циентов уравнения (6.4) следующие значения:
г //D
где L = 1/ у----относительная характеристика жесткости кон-
струкции, I — длина, b — ширина плиты, а — /
В дальнейшем для коэффициента г2 мы примем сокращенное 1
обозначение: |
„2 _ „2, 2 1
' ~ ' 1 Л’ ' 0, j
ГДе I
(6-7)
Дифференциальным уравнением (6.4), коэффициенты которого!
определяются по формулам (6.6), полностью описывается рассмот-1
ренная задача об изгибе, плиты, имеющей шарнирное опирание|
по двум противоположным краям. При этом решение может быть!
получено с любой степенью точности, поскольку уравнение (6.4),|
как отмечалось выше, справедливо для каждого члена разложена
ния с индексом п. I
§ 7] РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ИЗГИБА ПЛИТЫ 171
Нетрудно видеть, что полученное уравнение совпадает по виду
с рассмотренным ранее дифференциальным уравнением изгиба
балки (1.8) гл. II и отличается от последнего только величиной
упругих постоянных г2 и s4. Отсюда следует, что для решения
этого уравнения могут быть использованы методы, аналогичные
тем, которые применялись нами при расчете балок в условиях
плоской задачи (см. §§ 2, 3, 6 гл. II)..
§ 7. Решение дифференциального уравнения изгиба плиты
по методу начальных параметров
В случае действия произвольной внешней нагрузки интегриро-
вание основного дифференциального уравнения задачи (6.4) может
быть произведено наиболее просто по методу начальных параметров.
Общее решение запишется при этом в форме:
IF (т]) = K^iHF0 •+• /С^ф<р0 J- КюьМ, KwnN0— Fw, ]
<Р (71) — 0 + + K^nN0 — F,,, J
Л4 (т;) = + Кмср'Ро + КммЛ40 -f- Kmn^’o — Fм, |
N (71) = К№ф<р0 + КлгмМ0 + KnnNо — Fn- )
где Kww, К\с~- • • •, Knn— коэффициенты влияния; 1FO, <р0, ;И0,
jV0 — соответственно величины обобщенного прогиба и угла пово-
рота, а также обобщенного момента и поперечной силы в сечении,
принятом за начало отсчета; Fw, • • ., Fn— функции, учитываю-
щие внешнюю заданную нагрузку.
Для вычисления коэффициентов влияния, входящих в выраже-
ния (7.1), необходимо знать решение однородного дифференциаль-
ного уравнения, соответствующего уравнению (6.4). Это решение,
как известно, может быть представлено в виде
W (т]) =- СхФх + С2Ф2 -Ь С3Ф3 С4Ф4, (7.2)
где С4, С2, . . ., С4 — произвольные постоянные интегрирования;
Ф4, . . ., Ф4— функции, зависящие от вида корней характеристиче-
ского уравнения, т. е. от значения коэффициентов г2 и s4.
В рассматриваемой вадаче, как и в случае изгиба балки на
упругом основании, наиболее характерным является следующее
соотношение между коэффициентами ths:
s > г.
При этом функции Ф4, . . ., Ф4 представляет собой гиперболе-
172
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ.111
тригонометрические функции вида (см. табл. 3)
Ф4 — sh ат; cos Рц, Ф2 = ch ац cos р-ф | (7.3)
Ф3 = chai]sin Рц, Ф4 = shaT] sin p-q, /
1 / s2 4- г2 а — |/ 2 , (7.3')
Поскольку искомая функция IF является функцией безразмер-
ной координаты Т| = —, обобщенный угол поворота <р определится
в виде
? = Ж = (7-4)
Lay 1
Для обобщенного момента М и обобщенной поперечной силы
У на основании выражений (3.5), (3.6) и (6.1) получим формулы:
= * (7'5)
где р— коэффициент Пуассона материала плиты, а а, b и р°—
коэффициенты, определяемые формулами (6.3).
Учитывая равенства (6.3) и (6.7), перепишем формулы (7.5)
в следующем виде:
М = I (?в)
N =- |(Г--((2-|л)г; + 2г?|1Г>. (
В силу выражений (7.2), (7.4), (7.6) прогиб, угол поворота,
обобщенные моменты и поперечные силы определятся в виде:
1F = б?1Ф1 ф- С2Ф2 ~Ь С3Ф3 + С4Ф4, 1
/ср = С4 (<хФ2 рФ4) + С2(аФ4 — РФз) Ф ^з(а^4 4* рФа)4
+ С4 («Ф3 + рФД,
—/И— С7г{[(1- р) г1 ф- Го] Ф1 — 2арФ3} — С2{[(1 -—р) г4 +
+ г?] Ф2 - 2арФ4} - С3 {[(1 - р) d + го] Ф3 + 1 (7-7)'
+ 24Ф,} - С4 {[(1 - р) г? + rg] Ф4 2арФ2}.
l— N = Ci {а [s2 — pri] Ф2 + 3 [s2 + рг4] Ф4} ф
4~ С2 {а [s2 рг4] Ф4 ф- р [s2 ф- рг4] Ф3}—С3 {р [s2 ф- рг4] Ф2—
- а [s2 - рг?] Ф4} - С4 {р [s2 + рг?] Ф4 - а [s2 - рг?] Ф3}.
§ 7] РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ИЗГИБА ПЛИТЫ 173
В начальном сечении (принятом за начало отсчета), т. е. при
т( = 0, учитывая формулы (7.7), найдем:
№0 = С2, j
/<р0 = аС4 + [ЗС3, j
~ Ма = - С2 [(1 - ft) г? 4- г02] - 2аЗС4,
А/о = С& [s2 — Jiri] — Сзр [s2 4- [Аг?].
(7-8)
Решая уравнения (7.8) относительно постоянных Сп С2, С3, С4,
нетрудно получить:
С, = ^Г(з* 4- ;xr?)pz<po + ₽ 4^1 ’
2aps21- fl J
c2 - WQ,
C3 = 1 ~ aZ<Po — a 4Г N° I ’
2aps21. a .j
C4 ---------==- jl(l fi)rj4-r0] ^7o + yy^o} .
2ao l “ J
(7-9)
где величины a и определяются формулами (7.3'), а обобщенные
характеристики s, гг и г0 — выражениями (6.6) и (6.7).
Внося теперь значения (7.9) в формулы (7.7), можно пред-
ставить решение однородного уравнения, соответствующего урав-
нению (6.4), в виде (7.1), т. е. при помощи начальных параметров
и коэффициентов влияния (функции Fw, . .Fn при этом не будут
входить в полученные выражения). В соответствии с равенствами
(7.7) и (7.9) коэффициенты влияния определятся в форме, приве-
денной в табл. 10.
Для учета правой части уравнения (6.4), т. е. для учета за-
данной нагрузки, к полученным выражениям следует добавить
со знаком минус функции Fw, . . . , F зависящие от вида внеш-
ней нагрузки и ее расположения на плите. Вопрос о характере
этих функций в зависимости от заданных внешних воздействий
был рассмотрен нами ранее на примере расчета балки конечной
длины (см. § 3, гл. II). Поэтому для пояснения сказанного мы
здесь ограничимся лишь одним частным примером.
Пусть на плиту действует нагрузка, приведенная на рис. 82.
Можно видеть, что на участие 0 < т] < И задача характеризуется
однородным дифференциальным уравнением, в результате чего все
искомые величины определяются здесь лишь через значения
Таблица 10
Г о Фо м. N о
* -п ^uzuz = 2др ^аРФз — К1 ~ ?) ri + + rol + (s2 — р-rp аФз] I2 KwM ; /3 KwN- 2а^2>< . Х(£Ф1 — аФ3)
к^ = Ж[(52 + к^Ф1~ — (s2 — ^ф аФ3] 2><2^Ф2 + + [(1 — н)4+ фом K<fAf 2аа₽ Х X (аФз + ₽Ф) = тл
Кми/ •= гЙу{s4 ~ ?Г1[(2 ~ ?) ri+ + 2фФ4 Км* =~2^[^ + 1<}Х X [(1 + н) 4+ Ф + + (S2 — fir2) [s3 + г2]} Фх + + a {(s2 — jxr2) [(1 — (л) г2 + + Го1(s2 + нф [s2 ~ И) Фз] ММ ~~ ^<₽г ^MN ~^W<f
Knw' 2а|1® ^i(S" + f2)(s2“ ;ЛФ+ + [(1 — и) г? + ''ol <s2 + ^ri)i ф1 + + a [(s2 - г2) (s2 + иф - -1(1-И) 4+ ф (s2 ~нф] Фз> Nv K-mw K-NM ~^<(W
начальных параметров:
IF (tj) = Kww(v) ^'o+Kw'v (tj) ®04-7CirM (tj) Mo^ Kwn (tj) No,
q> (tj) = Кфцгфт;) 1FO + /(w (tj) ?o + KqM (tj) Mo + /СфД’ (tj) No,
M (tj) — ^о+^Мф (tj) "po ' L Kmm (tj) Mo4-Kmn (tj) No,
X (tj) = Knai(tj) IFo+Kn,^) cp0 + Knm{^ Mq + Knn (tj) A1o.
(7.10)
На участке плиты tY < tj < i2 из выражений (7.10) следует
соответственно вычесть функции Fw, Fv, FЛ1, Fn следующего
вида:
Fw — G)Kw>; (tj — li),
F^ = (tj — Ij),
Fm = GiKuN.iyi — li).
Fn = G^a'n (tj — li);
(7-11)
здесь
Gi = S pc'f. (c) = PiX (И) + P2X (c2),
где x (c) — значение функции поперечного распределения прогиба
в месте приложения сосредоточенной силы.
На следующем участке (12 < rt < t3) грузовые функции опре-.
делятся в форме:
Fw = GyKwN (Tj—t-i) -f- G3Kwn (tj I2),
Fф = G^K^x; (tj li) т GsKyN (tj 12), (712)
Fm = G-lKmn (tj — Л) + G3Kmn (ri I2),
Fff = GxKnn (t) — li) 4~ (tj la), 1
где
Gj — P3y, (c3).
176 ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ [ГЛ. 1Ц
На участке распределенной нагрузки (t3 < < 1) грузовые
функции будут иметь следующий вид:
Fw = GlKwn (т) — Л) + GsKwn (») — G) +
+ (/) Kwn^ — t)dt,
F4 = G^n (т) - M + G3K-iN G) +
+ JG4 (v-t)dt,
FM = G^Kmx (K-tJ + G.Kmn h - t2) + <7-13)
+ Ga (/) (tj — t)dt,
Fn = GjKnn C*i — H) + G3Nnn (t( — ^2) +
-Г J G4 (/) Knn - /) dt,
0
где °
Gt = \)P (x, t;) x (x) dx.
0
§ 8. Определение начальных параметров. Вычисление моментов
и поперечных сил
Поскольку за начало отсчета может быть принято любое по-
перечное сечение плиты, два из четырех начальных параметров
IFO, ф0, Ма, No, входящих в основные уравнения (7.1), опреде-
ляются обычно сразу из условий задачи (см. §§ 3, 6 гл. II). При
этом два других параметра независимо от характера внешней
нагрузки могут быть найдены решением системы только двух
уравнений, составленных относительно другого поперечного сече-
ния (7j = const) плиты. Покажем это на некоторых частных при-
мерах.
Поперечные края плиты шарнирно оперты. В це-
лях упрощения числовых расчетов представим внешнюю нагрузку
ц
в направлении оси т; = -у в виде симметричной и кососимметрич-
ной составляющих. При этом за начало координат примем сред-
нее сечение плиты (рис. 83).
Рассматривая вначале случай симметричного загружения
(рис. 83, а), получим:
при -ц = ~ = 0 ^=0, No = 0. (8.1)
§8] ОПРЕДЕЛЕНИЕ НАЧАЛЬНЫХ ПАРАМЕТРОВ 177
Согласно условиям (8.1) общее решение задачи запишется
U7 (т;) = (ч) + M0Kwm (^) — Fw О?),
9 (Ti) = (“П) + Мо/<фм И — F9 (tj),
7И (г() = (у) + М0Кмм ('<) — ^м(^)>
N (71) == W0KNw (у) + M0Knm (?;) — Fn (/;).
Отметим, что в уравнениях (8.2) функциями Fw, . . . , FN учи-
тывается внешняя нагрузка, расположенная только по одну сто-
рон\дот начала координат. Оставшиеся неизвестными параметры
Рис. 83.
1Р’О и ТИО определим из
по поперечному краю:
условия шарнирного опирания плиты
ПРИ L’7! = у("Ч =~у)“ W = 0, М = 0. (8.3)
Раскрывая условия (8.3), получим:
W = W0Кww (д) + — Fw — 0, 'l
М (д) = IV'oKmif (д) + М0Кмм (д) — Fm — 0- (
(8.4)
Решение системы уравнений (8.4) позволяет найти:
12 В. 3. Власов, Н. Н. Леонтьев
178
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. III
где Кмм (у), ..., Кмг(у), Fw (4)’ Fm (т) “ значение соответ-
ствующих функций влияния и грузовых функций в сечении
1
7]=-2-.
В случае кососимметричной нагрузки (рис. 83, б) в начальном
сечении могут быть поставлены условия:
при 7] = = О
Г о = 0, 7И0 = 0.
(8-6)
Общее решение запишется при этом в форме:
№ С*]) = (т]) + N0Kwn Cg) — Fw (tj), |
ф (т;) = сроКфФ (i)) + Л/оКфл/ (т]) — F<f (т)), ।
M O']) = (tj) + NqKmn Cg) — Fm Cg)> I
N Cg) = Cg) + N0Knn (tq) — Fn (tj), )
где, как и ранее, функциями Fw (tj), . . . , Fn Cq) учитывается
нагрузка, расположенная только справа (или слева) от начала
координат.
Исходя из условий (8.3) по поперечному краю, получим:
W (уу — сро^ГФ (у у + N0Kwn (уу —Fw (уу = 0,
М fy^ = сроКм? (у) + NoKmn (у) — Fm (у) = 0,
(8-8)
откуда
Поперечные края плиты жестко защемлены. При:
жестком защемлении поперечных краев плиты (рис. 84) условия?
в среднем сечении tq = 0 в случаях симметричного и кососиммет-
ричного загружений запишутся, как и ранее, соответственнс
в виде (8.1) или (8.6). При этом решение задачи в случае сим
метричной нагрузки будет представлено формулами (8.2); пр!
кососимметричном загружении — формулами (8.7).
§ 8]
ОПРЕДЕЛЕНИЕ НАЧАЛЬНЫХ ПАРАМЕТРОВ
179
Условия на поперечных, защемленных краях плиты имеют вид:
при 'G =-j- (11 = —у) <р = 0. (8.10)
Исходя из условий (8.10) и формул (8.2) и (8.7), нетрудно
определить значения начальных параметров:
при симметричном загружении
(8.11)
при кососимметричном загружении
~ f<^wn
(8.12)
где K<fM, Kwm, • • , Kw, K<?n, Fw, F^ —значения соответствую-
щих функций при аргументе = -g-.
Поперечные края плиты свободны от закрепле-
ний. На поперечном, свободном от закреплений крае плиты
(рис. 85) граничные усло-
вия могут быть записаны
в форме:
№(j-) = №OCH,
N (т) = 5осн’ ’
м(1) = о, j
(8.13)
где 1ИОсн — осадка основа-
У 1
ния в сечении т]= -у- =~^,
Рис. 84
*$осн —обобщенная попереч-
ная сила основания в том
же сеченИи.
Первое из условий (8.13) носит чисто геометрический харак-
тер и выражает собой мысль о том, что осадка поверхности осно-
вания непрерывна. Второе и третье условия, имеющие статический
12*
180
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. III
характер, аналогичны соответствующим условиям для свободного
конца балки конечной длины, расположенной на упругом однослой-
ном основании (см. § 6 гл. II).
Осадка свободного основания за пределами плиты в направле-
нии оси у может быть приближенно принята затухающей по за-
кону показательной функции, как это ранее принималось в отно-
шении осадок в направлении оси х (см. § 2). В этом случае
будем иметь (рис. 85):
даосн = IFoch(I/)x W = (*) е 2^’ (8-14)
где о, = |/^- , а х (х) — функция поперечного распределения про-
гиба, определяемая формулой (6.1). Отметим, что выбор функции
Рис. 8.5.
осадок основания за пределами плиты в виде (8.14) непосред
ственно удовлетворяет первому из граничных условий (8.13).
Обобщенная поперечная сила на участке свободного основани
характеризующая работу касательных напряжений тгг/
5осн,
в с
чении у = const упругого основания на возможных для него пер
мещениях, определяется формулой (3.4). Замечая, что в наци
случае функция поперечного распределения прогиба х (*) отлич
от нуля только в пределах полосы шириной Ь, из формулы (3.
получим:
П • г
*^ОСН “ 2/ 2 IFqch ^XfcX,^-
-А i *
(8.1
S 8]
ОПРЕДЕЛЕНИЕ НАЧАЛЬНЫХ ПАРАМЕТРОВ
181
Внося в выражение (8.15) значение (6.1) и учитывая выраже-
ние (8.14), получим для обобщенной поперечной силы упругого
основания, расположенного за пределами плиты (в сторону поло-
жительного направления оси у)-.
Soch = - е~а (8.16)
Значение этой силы у края плиты, т. ’е. в сечении у = ~
“ л
1 \
у; — у), равно
SOcH = -attFOCH(4.).
Замечая, что
г (1)=«/<,„ (4),
можно представить граничные условия (8.13) в виде:
м (I) _ 0.
(8.17)
В случае симметричного загружения плиты общее решение,
как и ранее (см. (8.2)), запишется в следующем виде:
W (т;) — W0Kww ('q) + M.0Kwm (т]) — Fw (-q),
ср (т() = W0K„w 0]) + М0К.м (у) — F* 01), /8 18ч
М (cq) = W^Kmw 0]) + М0Кмм 0]) — Fм 01),
N (iq) = FqKauz (т() + M0Knm 0i) — Fn (cq).
Раскрывая условия (8.17) при помощи выражений (8.18), не-
трудно определить начальные параметры Wo и Мо:
vff — ^nm + аН’Ку'м') Fm ~ КМм + <*tbFw)
0 К mw (Knm + ail)KWM^ ~ К мм
д . ^Fn + atbFw) — {KN^ + «^МСц/ц?) Fм
0 KMw (KNm + a(bKWM^ ~ Кмм (%nw+ atbKwvF)
При кососимметричной нагрузке решение задачи имеет вид:
01) = (т*1) + N$vn 01) — Fw ("q),
<р (eq) = <Ро-^фф 01) H- N0K<fN (tj) Ftp (?;), (8.20)
Л4 (iq) = cp0^M<p 01) + N0Kmn 0]) — FM 0])-
A/’ (tj) = VoKn* fa) + N»Knn O() — F .
182
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[гл. in
Условия (8.17) позволяют в этом случае получить:
^Мф ^NN + aibKwx) FMN(KN<f + ’
д, _ ^Мф (F N + at^ Fw) — ^Ыч> + FM I
° Km<p ^NN + aZ^lFJv) — KM{A«N9 + а^^ЦГф)
(8.21)
Входящие в формулы (8.19) и (8.21) величины Knn, • • •, Kw<n
Fw, , Fn представляют собой значения соответствующих функ-
ций при аргументе 71 = 4- (y = -L-\ Упругие постоянные ан/
определяются, как и ранее, по формулам:
___ н н
а=1/ t = r<ri- (8-22)
* u (1 — v2) J T 4 (1 + v0) J *
0 о 0
где
Условия на поперечных краях различны. Если
плита в направлении оси у не имеет оси симметрии, т. е. гранич-
ные условия, заданные на ее поперечных краях, различны, то целе-
сообразно принять за начальное сечение один из краев плиты
(рис. 86). При этом определение начальных параметров может
быть произведено совершенно аналогично тому, как это было по-
казано на примерах расчета симметричных плит. Так, для плиты,
показанной на рис. 86, начало координат можно поместить, н
пример, на краю, свободном от закреплений. В соответствии
условиями (8.13) два начальных параметра сразу определять
§ 8] ОПРЕДЕЛЕНИЕ НАЧАЛЬНЫХ ПАРАМЕТРОВ 183
в виде:
Мо = 0, No = a«IF0. (8.23)
На основании выражений (8.23) решение задачи запишется
в форме:
(Т1) — (Kww + utbFwN) Wo + — Fw, )
ф Cg) ~ (Kvw 4” ай/С<рл/) Wo -j- фо Ftp, । .g эд
44 (tj) = (Fmw + oMKmn) IF0 + Лмрфо — Fm, ।
N (?]) — (Knm + иЛЬКым) Wo + Лмф% — Fn- J
Значения параметров IF0 и <p0 можно теперь определить, исходя
из граничных условий, заданных на другом краю плиты при
у; = 1 (у = /). Так, если этот край имеет шарнирное опирание,
то граничные условия будут иметь вид:
при у; = 1 1F = 0, М = 0. (8.25)
Раскрывая условия (8.25), получим:
,ту __________KMr-P w — Р м_____________
0 ^Мф 4- atbKWN“) — KW9 (Кmw + а(ЬКмы> ' ?g 25)
_ + atbKWN) Pм ~ (FMW + atbKMN) ?w
Fm^(Fww 4- 4tbKWN) — Km^FmwF aibKMN)
Отметим, что в решении (8.26) функции Км?, Kw?, • • • , Fw, Fm
вычисляются для аргумента т; = 1 (у = /). При этом грузовые
функции Fw, Fm в отличие от рассмотренных ранее примеров
учитывают всю нагрузку, приходящуюся на плиту, от т; = 0 до
4=1-
Вычисление моментов и поперечных сил. По опре-
делении обобщенного прогиба плиты W (т;) действительные мо-
менты и поперечные силы могут быть рассчитаны по общим фор-
мулам (2.28). Замечая, что W (т;) является функцией безразмерной
координаты т] = -у- , а также учитывая равенство (6.1), можно
представить формулы (2.28) для каждого члена п разложения (2.1)
в виде:
Мх = - D [%- IF" (т]) - W (tj)] sin ,
Му = - D [± W" (т;) - у (^)2 W (ti)] sin ,
И = Нх = — Ну = — пЦ^-^1Г(71)со5^,
(8.27)
Nx = - D Г" (ti) - (Т-)8 W (ti)] cos ,
Ny = - D [A W'" (ti) - 4 (-v)’ W (7))] sin n-f.
184
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. Ill
§ 9. Цилиндрический изгиб и кручение узкой плиты.
О расчете балок в пространственных условиях
I. Рассмотрим узкую прямоугольную плиту, нагруженную
симметричной относительно оси у нагрузкой (рис. 87).
Если предположить, что поперечное сечение такой плиты,
имеющее в общем случае участки различной толщины, не дефор-
мируется, то из всех возможных перемещений элементарной
Рис. 87.
поперечной полоски dy = 1 останется только одно поступательное
перемещение
Хо=1. (9.1)
При этом коэффициенты (2.26) ’основной системы дифферен-
циальных уравнений (2.25) определяются в виде:
^00 —' 3 ВщЬт,
^оо — ^оо — 9»
Sgo == kb—j—4ocZ,
(9.2)
Г. Ehm
где Dm = |2 — цилиндрическая жесткость плиты на участю
поперечного сечения длиной Ьт (рис. 88).
ЦИЛИНДРИЧЕСКИЙ ИЗГИБ И КРУЧЕНИЕ УЗКОЙ ПЛИТЫ 185,
§ 9]
Принимая во внимание, что
и ь — EJm
Um°m “ 1-|л2 ’
получим для первого коэффициента выражение
а00 = ! _ р.2 3 = 1 — [*2 ’ (9-3)
где J — суммарный момент
ты относительно оси Ох.
На основании выраже-
ний (9.2) и (9.3) дифферен-
циальное уравнение задачи
может быть представлено
в виде
WlN — 2r2№" + s4№ =
= (9.4)
инерции поперечного сечения пли-
Свободный член G, ха- Рис- 88•
рактеризующий обобщен-
ную нагрузку, совпадает в данном случае с действительной погон-
ной нагрузкой, что можно видеть из формул (2.4) и (9.1).
Следует отметить, что дифференциальное уравнение цилиндри-
ческого изгиба плиты (9.4) имеет такой же вид, что и уравнение
(1.8) гл. II изгиба балки в условиях плоской задачи, и отличается
от него только наличием коэффициента Пуассона р., а также ве-
личиной коэффициентов s4 и г2. Дополнительные члены - 4а/,.
tLJ
1 — ;i2 t
~EJ ~<Г ’ вх°Дяи1ие в эти коэффициенты, учитывают наличие
фиктивных реакций Q*, распределенных по продольным краям,
плиты, т. е. учитывают пространственную работу упругого осно-
вания.
186
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. Ill
Из формул (3.5) и (3.6) для обобщенного момента М и обоб-
щенной поперечной силы N можно получить выражения:
М=— )
1 р I (9.6)
w = — АА w" + 2tb (1 + AW'-
1 — Р2 1 \ 1 ab } >
Выражения (9.6) должны быть учтены при постановке гранич-
ных условий на поперечных краях плиты.
Интегрирование дифференциального уравнения (9.4) может
быть проведено при помощи изложенных выше методов (см. § 2
Рис. 89.
и § 3 гл. II). По определении обобщенного прогиба плиты действ»
тельные продольные моменты Му и поперечные силы N у вычис
ляются по формулам (2.28 Ь, е), которые в данном случае имею’
вид:
Му = — DW", Ny = — DW'". (9/
Из формул (9.7) очевидно, что моменты Му и поперечные сил
Ny распределяются в поперечном сечении пропорционально жес
костям Ьт (рис. 89).
§ 9] ЦИЛИНДРИЧЕСКИЙ ИЗГИБ И КРУЧЕНИЕ УЗКОЙ ПЛИТЫ JgJ
2. Рассматривая ту же плиту под действием кососимметричной
нагрузки (рис. 89), примем функцию поперечного распределения
прогиба в виде:
= %'(х) = 1. (9.8)
В отличие от рассмотренных ранее примеров функция Xi (х)
имеет здесь размерность прогиба (длины). В результате этого
обобщенный прогиб
XV/ = w г/)
представляет собой безразмерную величину, а именно угол закру*
чивания плиты
6 = 6(//).
Обобщенная нагрузка на основании выражения (9.8) опреде-
ляется формулой
G = р (х, у) х dx 4- 2 РсХс = т [у) (9.9)
и представляет собой интенсивность внешнего крутящего момен-
та т(у).
Коэффициенты основного дифференциального уравнения могут
быть вычислены по общим формулам (2.26) и представлены
в форме:
«и = 2 Dm 5х' dx = Р2’
Ьц = (1 и) 2
«и =
(9.10)
Р?1 = ^<1 + ^ 12 ab J
S?1 12 \ ~ a2*2 abj'
где а = у ; k и t — постоянные, характеризующие работу
упругого основания соответственно на сжатие и сдвиг; J — сум-
марный момент инерции поперечного сечения плиты; р— радиус
инерции эпюры жесткостей (рис. 89), определяемый по формуле
2 iW^M
<‘=-ПГ------ЁОА--------------------- <9J1)
гг » 2 Ь2
Для плиты постоянной ТОЛЩИНЫ р2 = .
Дифференциальное уравнение задачи принимает вид:
au6IV - 2 (b1± + р?3) 9" + 8^6 - т = 0. (9.12)
188
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
Егл. in
Обобщенный момент М и поперечная сила N определяются
формулами:
'М-~гДгР!9", (9.13)
+ + <9J4>
где р2— радиус инерции эпюры жесткостей (9.11).
Действительные продольные моменты Му, крутящие моменты И
и поперечные силы Nu могут быть представлены в виде:
Му = — 0x6", j
И = — 0(1 —р.)9', (9.15)
Ny = — Dx®"'. ) •
Формулы (9.15) показывают, что эпюры распределения Му и
Ny по поперечному сечению плиты подобны произведению эпюры
Xi = х на эпюру жесткости О, а распределение крутящих момен-
тов И пропорционально жесткостям От (рис. 89).
Дифференциальное уравнение (9.12) вместе с выражениями
(9.13), (9.14) определяет состояние стесненного кручения плиты,
которое характеризуется тем, что в плите, помимо крутящих мо-
ментов И, возникают также и изгибающие моменты Му.
Обобщенный момент (9.13) в данном случае представляет собой
бимомент, т. е. совокупность продольных нормальных напряжений
в сечении у = const, статически эквивалентную нулю. Обобщенная по
перечная сила характеризует собой полный крутящий момент в се-
чении у =const, состоящий из крутящего момента от поперечных сил
Ny (первый член формулы (9.14)) и крутящего момента от реактив-
ных давлений упругого основания (второй член формулы (9.14)).
3. Отметим, что дифференциальное уравнение цилиндрического
изгиба плиты (9.4) может быть использовано при расчете балки
в условиях пространственной задачи. Для этого следует положить
[х = 0, a EJ считать обычной балочной жесткостью. Грузовой
член G будет представлять собой при этом заданную погонную
нагрузку.
Как и в случае плоской задачи (см. гл. II), балки в зависи-
мости от приведенной характеристики жесткости могут быть раз-
делены на три категории: длинные, короткие и жесткие.
При расчете длинных балок на действие сосредоточенной сил1
и момента может быть использована методика, изложенная
§ 4 гл. II. Следует, однако, учесть (при постановке граничны:
условий), что обобщенная поперечная сила N в пространственны;
условиях определяется второй из формул (9.6), а упругие ха рак
теристики.г2 и s4— формулами (9.5).
§ 9] ЦИЛИНДРИЧЕСКИЙ ИЗГИБ И КРУЧЕНИЕ УЗКОЙ ПЛИТЫ JgQ
Расчет коротких балок на произвольную внешнюю нагрузку
проще всего производится по методу начальных параметров, изло-
жение которого применительно к расчету балок дано в § 3 гл. II
и применительно к расчету плит — в § 7 настоящей главы. Коэф-
фициенты влияния, приведенные в табл. 4, при решении уравне-
ния (9.4) должны быть пересчитаны в соответствии с выражениями
(9.5) и (9.6). Начальные параметры определяются из граничных
условий, поставленных в обобщенной форме. Так, например, если
концы балки свободны от закреплений, граничные условия могут
быть записаны в форме (8.13).
При расчете жестких балок можно исходить не из диффе-
ренциального уравнения (9.4), а непосредственно из условий
равновесия балки, находящейся под совместным действием заданной
внешней нагрузки и реактивных давлений упругого основания
(см. § 5 гл. II).
Например, при расчете жесткой балки на симметричную нагрузку
можно положить
W(y) = C0. (9.16)
Реактивные давления упругого основания будут состоять из
распределенных по опорной поверхности сооружения реакций q,
погонных реакций Q* и сосредоточенных реактивных сил Тф, при-
ложенных на концах балки (рис. 90). Возникновение сосредоточен-
ных реакций Тф обусловливается тем, что упругое основание
деформируется за пределами конструкции. Эти силы следует рас-
сматривать, таким образом, как фиктивные силы, которыми учиты-
вается влияние свободного основания, расположенного за пределами
балки (в областях у < 0, у > /), на напряженное состояние балки.
В соответствии с формулами (2.17), (2.19) и (9.16) реакции
q и Q* определяются в виде:
q = kC0,
Q? = 2а/С„.
(9.17)
190
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ III
Для вычисления сосредоточенных реакций Тф примем, что осад-
ка поверхности упругого основания в областях у < 0 и у > I
Рис. 91
происходит по закону убывающей ' показательной функции. Так,
например, в области у < 0 (рис. 91) будем иметь:
b )
при ---------g-
а (х ' —)
w (х, у) = С.е ' г 2' е7-'7,
ь , ь
при —
• (9.18)
w (х, у) = Сое^,
при
г ь\
w (х, у) = Сое ' - е^.
Полагая, что работа реакции Тф на единичном перемещении
Со = 1 равна работе всех внутренних усилий упругого основания;
в области у < 0 на возможных перемещениях (9.18) при Со= 1,|
т. е. определяя фиктивную силу Т* как возможную работу нор-
мальных и сдвигающих напряжений а2, ~гх, tzy упругого основанш
в области г/'< 0, получим:
Тф =C0(2affe + 3/).
(9.1
Отметим, что сосредоточенные реакции Т*, строго говоря
складываются из распределенных по поперечному краю балЮ
реакций Q* и сосредоточенных угловых реакций /? * (см. далее)
9] ЦИЛИНДРИЧЕСКИЙ ИЗГИБ И КРУЧЕНИЕ узкой плиты 191
§ 10). Однако при расчете балки, т. е. конструкции, которая
в поперечном направлении принята неизгибаемой, это обстоятель-
ство не имеет значения, в результате чего реактивные давления
на конце балки могут быть представлены суммарной сосредото-
ченной силой .
Используя условие равновесия балки, т. е. приравнивая нулю
вертикальную проекцию всех сил, действующих на балку, а также
учитывая выражения (9.17) и (9.19), получим уравнение для опре-
деления постоянной Со:
[kbl 4~ 4а// + 4а/Ь -ф 6/] Со = Ро,
откуда
С° = '[kbl + 4а/ (° + &) + 6/] ’ (9,20>
где Ро — суммарная вертикальная нагрузка, действующая на балку;
I — длина, а b — ширина балки.
По вычислении осадки Со реактивные давления основания опре-
деляются формулами (9.17) и (9.19), а изгибающие моменты и по-
перечные силы вычисляются по известным методам сопротивления
материалов.
Аналогичным образом может быть проведен расчет жесткой
балки и на кососимметричную нагрузку. Если начало координат
помещено в центре балки, то осадка характеризуется формулой
W(y) = eoy,
где 90 — тангенс угла наклона балки к горизонту. Значение по-
стоянной 60 можно определить, исходя, например, из условия
равенства нулю моментов всех сил, действующих на балку, отно-
сительно начала координат:
2Ч = о
(см. § 5 гл. II).
4. Рассмотрим пример расчета симметрично нагруженной же-
сткой балки в предположении, что функция поперечного распре-
деления перемещений ф(г) выбрана в виде
. н~г
shT—й—
ф(?) =------jj—. (9.21)
sh7T
192
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ.III
Внося формулу (9.20) в выражения (9.17) и (9.19), получим
выражение для реактивных давлений упругого основания:
(9.22)
При выборе функции ф(х) в виде (9.21) выражение для коэф-
фициента а = у/', то входящего в формулы (9.22), примет вид
(см., например, формулы (5.23), (5.24) гл. II):
(9.23J
Если однослойное основание представляет собой упругое полу-
пространство —> оо^, то формула (9.23) упрощается и выраже-
ния (9.22) принимают следующий вид:
На рис. 92 и рис. 93 приведены безразмерные эпюры изгиба-
ющих моментов М, рассчитанные по формулам (9.24) при у = 1,5;
у0 = 0,3; -у = 5 и -у == 10 для двух случаев загружения балки.
Для сравнения на этих же графиках нанесены безразмерные эпю-
ры изгибающих моментов по данным М. И. Горбунова-Посадова
s, 9]
ЦИЛИНДРИЧЕСКИЙ ИЗГИБГИ КРУЧЕНИЕ УЗКОЙ ПЛИТЫ
193
для плоского и пространственного (при — = 1(f) расчета жесткой
балки.
Переход от безразмерных эпюр к действительным значениям
моментов осуществляется здесь по формулам:
при равномерно распределенной нагрузке
М = МрР,
при действии сосредоточенной силы
М - МР1.
Из [рассмотрения приведенных графиков можно видеть, что
различие в эпюрах моментов плоского и пространственного
Рис. 92.
расчетов очень велико. Так, при действии на балку равномерно
распределенной нагрузки и при отношении — 10 максимальный
момент, полученный по плоскому расчету, почти в 3,5 раза
превышает максимальный момент полученный по пространствен-
ному расчету.
Можно видеть также, что с уменьшением отношения -у изги-
бающие моменты балки возрастают: чем~шире балка, тем ближе
результаты пространственного и плоского расчетов.
13 в. 3. Власов, Н. Н. Леонтьев
194 ИЗГИБ ПРЯМОУГОЛЬНОЙ ПЛИТЫ [ГЛ. III
Сравнение результов предлагаемого метода с данными М. И. Гор-
бунова-Посадова ^при -у = ю) показывает, что в рассмотрен-
ном случае различие в максимальных изгибающих моментах
сравнительно невелико и составляет около 15% при загружения
балки равномерно распределенной нагрузкой и около 1,5% при
загружении сосредоточенной силой.
§ 10. Приближенный расчет плиты со свободными краями
на симметричную нагрузку
1. Рассмотрим прямоугольную плиту, нагруженную симметрич-
ной нагрузкой р(х, у) и расположенную на однослойном упругом
основании (рис. 94). Будем предполагать, что края плиты свобод-
ны от закреплений. Начало координат поместим в центре плиты.
Дифференциальное уравнение изгиба плиты на упругом однослой-
ном основании имеет вид:
DV1 2 * * * *V2sy — 2t\2w + kw = р (х, у), (Ю.1)
где w(x, у) — искомая функция прогибов плиты, a k и t — обоб-
щенные характеристики упругого основания, определяемые по
формулам:
н н
k = -^4- ф'2 dz, t = ф2 dz (10.2)
(1 — v?) J т 4 (1 4- v0) J т v '
°7 о о
$ 10] ПРИБЛИЖЕННЫЙ РАСЧЕТ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ 195
Предположим, что заданная внешняя нагрузка близка к рав-
номерно распределенной. В этом случае для получения простого
приближенного решения представим искомую поверхность проги-
бов w (х, у) в виде разложения
w (х у) = Со 4- С, cos ~ 4- С2 cos Ц- 4- С3 cos cos (10.3)
где Со, Си С2, С3 — постоянные коэффициенты, имеющие раз-
мерность прогиба.
Можно видеть, что формула (10.3) удовлетворяет геометри-
ческим условиям задачи. Первым членом здесь определяется
Рис. 94,
осадка плиты как жесткого штампа; вторым и третьим членами —
цилиндрический изгиб плиты соответственно в направлении осей
х и у. Третий член формулы (10.3) определяет изгиб плиты в
двух направлениях.
Для вычисления коэффициентов Сг, входящих в формулу (10.3), .
используем вариационный метод Бубнова — Галеркина, который бу-
дем трактовать как способ приближенного применения начал#
возможных перемещений. Другими словами, для определения этих
коэффициентов рассмотрим условия равновесия, понимаемые р
смысле равенства нулю суммарной работы всех внешних и внутг
ренних сил плиты на возможных для нее единичных перемещениях:
^о = 1>
— пх
t^cos^,
W2 = COS“2P
— 7C.V KU
w3 = cos cos
(Ю.4)
2. Определение реактивных давлений упругого
основания. Анализируя основное уравйение (10.1), нетрудно
видеть, что первый член характеризует состояние внутренних сил
13»
196
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. иг
плиты; члены при коэффициентах k и t — реактивные давления
упругого основания, распределенные по опорной поверхности плиты
и возникающие в результате работы упругого основания на сжа-
тие и сдвиг.
Нужно учесть, однако, что, кроме этих сил и внешней нагруз-
ки р(х, у), на плиту будут действовать также дополнительные
реакции Q*, распределенные по краям плиты. Этими [реакциями,
как уже неоднократно отмечалось, учитывается пространственная
работа упругого основания за пределами конструкции. В случае
2D
К
Qt(x)
Рис. 95.
ПлйТ прямоугольного или полигонального очертания, помимо рас- ;
предвоенных реакций, в углах плиты появятся еще и сосредото-
ченные' реакции R& (рис. 95). Для того чтобы учесть реакции Q*
и в общем выражении работы всех внешних и внутренних сил
йлиты, определим их величину, исходя из следующих соображений.
будем предполагать, что осадка юосн поверхности упругого
Основания за пределами плиты характеризуется следующим зако-
ном (рис.96)*):
' в направлении положительной оси х
йУосн (х, у) ^Wt {у) е~а <*-*>;
в направлении положительной оси у
и>осн (х, у) = wb (х) <»-»,
(10.5)
(10.6)
' । V И н.у—
! ! Привс(дийые ниже формулы носят приближенный характер, поскольку
в- прост.ранетренных условиях осадка, основания, за, пределами конструкция
будет происходить по более сложному закону (см., например, § 7 гл. I).
j 1в ПРИБЛИЖЕННЫЙ РАСЧЕТ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ }Q7
где а = |/ wt(y)— прогиб продольного, а ау*(х)— прогиб
поперечного края плиты. В квадранте, заключенном между этими
направлениями, осадку основания будем принимать в виде
аУосн (х, у) =. аус е~ “ е~аи-п , (10.7)
где ©с —значение прогиба в угловой точке плиты (рис. . 96). .
Ранее было показано (см. § 2 гл. Ш), что если за пределами
плиты распределение осадки основания происходит по, закону
Рис. 96.
(10.5), то фиктивные реакции на продольном крае плиты Qt вы-
числяются по формулам (2.19). Для рассматриваемой задачи эти
» формулы могут быть представлены в виде
Qt — 2t + \дх 2а (.ду* }
(Ю.-8)
Индекс I в выражении (10.8) показывает, что значения функ-
ции прогибов плиты w (х, у) и ее производных должны вычислять-
ся здесь для точек продольного края плиты (при х = — b или
х = Ь).
Аналогичным образом может быть получено выражение и для
фиктивных реакций Q*, распределенных по поперечному краю
плиты. Определяя эти реакции как абсолютную величину работы
всех сил элементарной полоски dx = 1, выделенной из упругого
19Й
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
1ГЛ.Ш
основания (рис. 97), на возможном перемещении упругого осно-
вания за пределами плиты, получим:
Оъ = 2t +
да/ \ 1 / д-и> \ I
ду )ь 2а V дх2 )ьJ’
(10.9)
/dw\ /дга>\
где Wb — wb(х) — осадка поперечного края плиты, а )ь —
значения производных от функции прогибов, вычисленные для
точек поперечного края плиты (при у = 1 или у = —/).
Рис. 97
Каждая из сосредоточенных фиктивных реакций характе-
ризует работу упругого основания, расположенного за пределами
плиты, соответственно в областях (х<С — — &), (х<^ — Ь,
У^1), (х~^Ь, у —/), y^l). Определяя эти реакции по
аналогии с фиктивными силами Q*, Q* как обсолютную величину
работы всех внутренних сил упругого основания в соответствую-
щей области, нетрудно получить:
(10.10)
где /—-обобщенная характеристика упругого основания на сдвиг,
a wc — осадка плиты в угловой точке.
Действительно, рассматривая, например, область х~^Ь, можно
видеть, что перемещение ®осн (х, у) поверхности упругого основания
j 10 ПРИБЛИЖЕННЫЙ РАСЧЕТ ПЛИТЫ CO СВОБОДНЫМИ КРАЯМИ
199
в этой области определяется формулой (10.7). В соответствии с
этим, возможное перемещение точек упругого основания характе-
ризуется здесь выражением
w (х, у, z) = шосн (х, у) ф (z) = 1 -е~а е~°- ф (г). (10.11)
Внутренними силами упругого основания являются напряже-
ния а2, х2х, хгу, определяемые формулами:
£
° г = —т^Ф'(г)даосн (х, у),
д%сн(*. У)
ду
(10.12)
"гх
= 2ДЫ(2>
д^ОС11(*. У)
дх
Абсолютная величина работы этих напряжений на возможном
перемещении (10.11) по всей области х^Ь, у>>1 равна
оо со И — —
7?ф = (о2^оси Ф' + тгх ф + x2y-^~^dxdydz, (10.13)
ь i о
где
г^оси (х, у) = е~“ е—а (у-Ч,
Внося в выражение (10.13) формулы (10.12) и выполняя ин-
тегрирование в указанных пределах, получим для реакций /?*
формулу (10.10).
Следует отметить, что реакции 7?ф, определяемые формулой
(10.10), имеют сравнительно небольшую величину и их влияние
на общую работу плиты будет невелико. Кроме того, в реальных
условиях вследствие возникновения концентрированных давлений
вблизи углов плиты появятся пластические деформации. Эти обсто-
ятельства говорят о том, что в практических расчетах реактивны-
ми давлениями 7?* в углах плиты можно пренебречь.
3. Вариационные уравнения равновесия. Состав-
ляя выражения для работы всех внешних и внутренних сил пли-
ты на возможных для нее единичных перемещениях (10.4), полу-
чим систему четырех алгебраических уравнений относительно че-
тырех постоянных коэффициентов разложения (10.3). Эта система
200
ИЗГИБ ПРЯМОУГОЛЬНОЙ: плиты
(ГЛ. Ill
может быть представлена в виде:
[kw — р] dxdy + 2 + 2^Q* dy A- 4R* = О,
[D “ 2/ S + kw - p] cos Tb dx dy +
+ 2 Qftcos dx = 0,
П1° ~2t w+kw ~~ dcos dx dy+
+ 2 Q/cos ^-dy = Q,
СГГп/д4® । о ^*'a) d*w\ „,/<Э2и> 32a>\ ,
jjL wx< ' дх2ду2' dy4) \dx2 dy2)
+ kw — p cos cos dx dy = 0,
r | Zb 21 1
(10.14)
где w— функция прогибов плиты, определяемая выражением (10.3);
р = р(х, у) — внешняя заданная нагрузка; Q*, Q*, — реакции
упругого основания, распределенные по краям и в углах плиты.
Интегралы, входящие в уравнения (10.14), определенные и вычис-
ляются в следующих пределах: по переменнойхот (—/>)до(4-6),
по переменной у от (—/) до (4-0- При наличии сосредоточенных
внешних нагрузок эти интегралы следует понимать в смысле инте-
гралов Стилтьеса.
Первое уравнение системы (10.14) характеризует работу всех
внешних по отношению к плите сил на единичном вертикальном
перемещении w0 = 1. Членом при коэффициенте k здесь учитыва-
ется работа упругого основания на сжатие.
Второе уравнение системы (10.14) относится к работе всех сил
при цилиндрическом изгибе плиты в направлении оси х. Членом
с коэффициентом D здесь учитывается работа изгибающих момен-
тов Мх; членом с коэффициентом t — работа упругого основания
под плитой при сдвигах в направлении оси х.
Аналогичные заключения можно сделать и в отношении треть-
его уравнения, характеризующего работу всех сил плиты при
цилиндрическом изгибе в направлении оси у. Из внутренних сил
плиты здесь будут совершать работу лишь изгибающие моменты
Му. Членом при коэффициенте t учитывается работа упругого
основания при сдвигах по оси у.
Последнее уравнение системы (10.14) характеризует изгиб
плиты в двух направлениях, аналогичный изгибу плиты, шарнир-
но опертой по контуру. Работа внутренних сил’ в этом случае
складывается из работы изгибающих моментов Мх и Му и крутя-
щих моментов Н.
§ Ю] ПРИБЛИЖЕННЫЙ РАСЧЕТ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ 201
Внося в выражения (10.14) формулы (10.3), (10.8),
(10.9), (10.10) и производя несложные вычисления, получим для
определения коэффициентов Со, Съ С2, С3 окончательно систему
алгебраических уравнений (10.15), приведенную в табл. 11.
Таблица 11
Со Ci С2 С8 Правая часть Возможные перемещения
^00 &10 &20 &зо Go ®0
• «и «21 «31 . Gi W1
• • «22 «32 Gt
• • • «33 Gt 103
Коэффициенты уравнений (10.15) определяются по формулам:
kQ0 = 4[lbk + 2а/ (/ + &) +
k10 — — [Ibk + 2а/5],
/г20 + 2а//],
kM = ^lbk-,
(10 16)
202
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
£ГЛ. Ill
»п = 2 + -f т ‘ i D + 2«,6 +
18
«21 = lbk,
тс
«31 — — + — ь + Тб" Ь3 Dy
п22 = 2 [ibk + 44 Z + HD + 2а// + JA-],
4 Г... . л2 Ь , . л4 Ь ГЛ
”32 ~ 4Г + ТТ^ + IlTF DJ’
«33-^+^-( v ' t? ' i6 D If + ib + к?
тде D = 12 (i _ p2j — цилиндрическая жесткость плиты, a k и t —
обобщенные характеристики упругого основания, определяемые
формулами (10.2).
Можно видеть, что коэффициенты (10.16) характеризуют ра-
боту реактивных давлений упругого основания, а коэффициенты
(10.17) — работу как реактивных давлений, так и внутренних сил
плиты. При этом коэффициенты с симметричными индексами об-
.ладают свойством взаимности или переместительности, т. е.
^io — ^01>
«12 = «21,
&20 — &02,
«13 = «31,
^30 — ^03,
«23 = «32,
(10.18)
что является выражением теоремы Бетти о взаимности работ сил
одного состояния на перемещениях другого состояния.
В силу зависимостей (10.18) матрица алгебраических уравне-
ний (10.15) обладает симметричной структурой, что значительно
облегчает определение искомых постоянных в том случае, когда
в разложении (10.3) для повышения точности вычислений взято
не четыре, а большее количество членов.
Грузовые члены, стоящие в правой части уравнений (10.15)
табл. 11, представляют собой работу заданной внешней нагрузки
на соответствующих единичных перемещениях (10.4) и определя-
ются в виде
Gz = р (х, у) Wi dx dy.
(10.19)
4. Заметим, что систему алгебраических уравнений (10.15)
можно было получить, не вводя понятия о фиктивных реакциях
Q*, Q*, /?*• В этом случае при составлении вариационных
уравнений равновесия рассматриваемой системы (плита ф- упругое
основание) следовало бы учесть работу всех внутренних сил не
§ 101 ПРИБЛИЖЕННЫЙ РАСЧЕТ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ
203
только в пределах расположения плиты, но и за ее пределами,
подобно тому как это было сделано нами в § 2 при выводе обоб-
щенных условий равновесия элементарной полоски dy. Естествен-
но, что. в конечном счете- мы получили бы здесь совершенно тот
же результат, поскольку фиктивные силы Q*, Q*, ДФ определя-
ются нами как работа всех внутренних сил, действующих на
упругое основание, расположенное за пределами плиты. Таким
образом, понятие о фиктивных силах Q*, Q*, /?Ф, представляющих
собой некоторый эквивалент работы внутренних сил упругого
основания, введено лишь в целях сокращения записи и большей
наглядности изложения.
5. После определения из системы уравнений (10.15) постоян-
ных Со, Clt С2, С3 могут быть вычислены прогибы плиты по фор-
муле (10.3), моменты и поперечные силы — по формулам (1.8)’.
Внося в эти формулы разложение (10.3), получим, например, для
изгибающих моментов следующие выражения:
Г р. ге2’Г £>2 „ "У I гех .
= DC2cos 2j- + cos +
/ - , \ „ rex Tty 1
+ (J +H7rJC3COS 2b COS-^-J,
< = D ~ C2 COS Д U G cos +
\ „ rex reyT
+ (7^ + P-J C3 COS 2b cos -2г}
(10.20)
Отметим, что система уравнений (10.15) позволяет также по-
лучить (как частные случаи) приближенные решения
для плиты, шарнирно опертой по контуру, а также плиты,
имеющей шарнирное опирание только на поперечных или только
на продольных краях. Для этого в разложении (10.3) нужно
соответственно положить Со = Сг = С-, = 0 или Со = = 0
(Со = С2 = О).
Для случая, когда внешняя нагрузка резко отличается от
равномерно распределенной, а также для получения более точно-
го решения при расчете на равномерную нагрузку, в разложении
(10.3) следует взять большее количество членов (см. § 12). За-
дача при этом сведется к определению постоянных коэффици-
ентов системы алгебраических уравнений, аналогичных уравнениям
(10.15). Каждое уравнение полученной системы будет иметь чет-
кий физический смысл, характеризуя суммарную работу всех
внешних и внутренних сил плиты на соответствующем единичном
перемещении.
204
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. Ill
§ 11. Примеры расчета
1. Рассмотрим расчет прямоугольной плиты в предположении,
что функция поперечного распределения перемещений ф (z) выбрана
в виде
Н — г
shy—г—
ф(*)=—4-. (н-i)
sh —
где у — некоторый коэффициент, зависящий от упругих свойств
основания, а b — полуширина плиты.
Обобщенные характеристики упругого основания определяются
при этом в следующем виде;
/г- £от
2b (1-vg)
1/ Sh~rchv + ~T
Г sh^
(11.2)
,уН уН уЯ
2 shTch~r + T
— Vo . уН уЯ у Я ’
sh —j— ch—-------г-
b b о
где
(11.3)
(£гр и vrp,— как и ранее, соответственно модуль упругости и
коэффициент Пуассона упругого основания).
Внося выражения (11.2) в формулы (10.16) и (10.17), умножая
1 —
левую и правую часть уравнений (10,15) на величину F , 0 и про-
изводя несложные преобразования, получим значения коэффициен-
Ill
ПРИМЕРЫ РАСЧЕТА
205
тов алгебраических уравнений табл. И:
feoo=4[тттА+4(i+4-)v6d-vo)/n(/n-+
, 3 1— Ур 1
+ Т7Г 5 mt ’ 16 у J
кю = v [-у- у"тк + У6 1 — у») т‘ та\’
^20 = -у [“Г Т тк + 'TT^6(1”V«) т‘
, 16 Y 1
Лз° ~ ^’Т b тк’
(Н.4)
„ Г 1 1 । «п = + "2 1 - Ур /. т , 16г \ Ь }
16 у b 1
+4-уб(1 - v0) mt та (1-Уо)М «Г
32 у: ‘/6(1- у0) т«.
16 у 1 = ж2 2 b тк' п k Г 7 1 if- 1 — > *0 «, 1 / 1 \»1 16г \ ь) ]’
Пз1 ~ я L 2 Ь тк^ 1 16 у b mt 4
«22 = 2 [4 Т 4- 1 — Ур 16 у * у mt 4- ж® Ь 16г / 4-
(И-5)
4 /- — -—— / тг2
+ -у/б(1—>0);у/П, /Ма+з^
___(1 - Ур)2 nlt Ь I
у2 У 6 (1-у0) ™а 1 Г
«32 —
/п* 4-
ж2 1 — yn b . ж5 b 1
-Тд----------Т~ tflf 4--Тд----Г I,
16 у I ' 16г I J
Г у I я21 —
'1зз^[4-у^ + -б —
где
(11.6)
- / в "<н . Y^ , fH
1/ 1 sllTch^T + V
та Г -з УН уН тН
г sh-r^-r---r
206
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
(гл. ш
Входящая в формулы (11.5) величина г характеризует относи-
тельную жесткость плиты и упругого основания. Эта величина,
определяется по формуле
г==_2^ь (П7)
£>(1 —vg)
и носит название показателя гибкости плиты *).
Для грузовых членов уравнений (10.15) будем иметь:
.. Ci = y)dxdy>
С2 = И р (х, у) cos ^dxdy,
° (11.8$
С3 = Ц^^р(х, р) cos ^-dxdy,
С4 = -ЦрИр(х, у) cos-g-cos dx dy.
плиты на равномерно
В качестве первого примера
2. Приближенный расчет
распределенную нагрузку.
рассмотрим прямоугольную плиту, находящуюся под действием
равномерно распределенной нагрузки интенсивности р (рис. 98).
Размеры плиты в плане и характеристики жесткости примем рав-
ными:
/ = 25, 7=1,5, г =1,0, v0 = 0,4. (11.9)
Будем считать, что плита расположена на упругом основании
бесконечной толщины, т. е. примем Н = оо.
*) Аналогичное значение показателя гибкости г принимается в работах
М. И. Горбунова-Посадова [25J, [26].
11 ]
ПРИМЕРЫ РАСЧЕТА
207
Подставив величинь (11.9) в формулы (11.4) и (11.5), получим:
йОо = 9,58, Иц = 310,4, п22 = 23,50, 1
kw = 4,51, «21 = 2,44, «32 = 14,22, 1
^20 — 5,23, п31= 197,8; n33 = 241,l. | (П.10>
^зо — 2,44;
Грузовые члены (11.8) при р — const примут вид:
С) С8 С8 О Св to м о 1! II II а а и а оо hi | гч | ts | | ° < о 1 О 1 о 1 © ТЗ ’ (11.11)
Внося значения (11.10) и (11.11) в уравнения (10.15) и решая
эти уравнения относительно постоянных Со, Съ С2, Cs, получим:
1 — V2
Со = 4О8-\О'а—^р1,
^0
1 - V2
С1 = 2,37-10“3-=-°р/,
1 — V2
С2= 17,4-10~3 —=^р/,
1 — V2
С3 = 0,4-Ю~3 —^pl.
Функция прогибов плиты определится, таким образом, в виде
w(x, у) = £408 + 2,37cos+ 17,4cos —
— 0,4cos~cos^j^~^--10-3. (11.13)
На рис. 99 и рис. 100 приведены безразмерные эпюры изгиба-
ющих моментов Мх и Му, рассчитанные при помощи формул
(10.20), (11.12) при у, = 0 соответственно для сечений х = 0 и
у = 0 плиты. Действительные значения моментов определяются
здесь следующими переходными выражениями:
Мх = МхрЬ\ Му = Мур12.
208
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
(ГЛ. III
Для сравнения на этих же графиках нанесены значения моментов,
полученные изложенным выше методом при г = 5, а также дан-
ные метода М. И. Горбунова-Посадова для жесткой плиты (пунк-
тирная линия) *).
Безразмерные зпюры
Зля сеч. у-0
Учитывая приближенность изложенного метода, а также то
обстоятельство, что, по М. И. Горбунову-Посадову к категории
жестких относятся плиты с показателем гибкости
,, 8
/4’
можно заключить, что результаты расчетов в рассмотренном слу-
чае достаточно хорошо совпадают.
3. Приближенный расчет фундаментной плиты
водосливной плотины. На рис. 101 приведен возможный
вариант решения одной из секций водосливной плотины облегченной
*) См. М. И. Горбунов-Посадов, Расчет конструкций на упругом
основании, 1953, стр. 457.
§ nJ
ПРИМЕРЫ РАСЧЕТА
209
конструкции. Фундамент такой секции представляет собой
прямоугольную бетонную плиту постоянной жесткости, на попереч-
ных краях которой расположены бычки. Одной из наиболее опас-
ных стадий расчета фундаментной плиты является та, которая
относится к периоду постройки плотины, а именно к тому време-
ни, когда плита и бычки возведены, а водослив отсутствует. На
рассмотрении этого случая мы и остановимся.
Рис. 101.
Вследствие того, что бычки имеют весьма большую жесткость
в своей плоскости, поперечные края плиты могут быть приняты
неизгибаемыми. При этом связь плиты с бычками при рассмотре-
нии работы плиты можно считать аналогичной шарнирному опира-
нию. Принимая для поверхности прогибов плиты приближенное
выражение (10.3), в силу высказанных соображений мы должны
положить Ci = 0. При этом алгебраические уравнения (10.15)
примут вид табл. 12.
Коэффициенты системы алгебраических уравнений табл. 12 опре-
деляются, как и ранее, формулами (11.4), (11.5). Грузовые члены,
в предположении, что нагрузки на плиту складываются из равно-
мерно распределенной по всей плите нагрузки р и погонной на-
грузки g (рис. 102), вычисляются по формулам:
С0 = 4(р/4-й)1ТЛо,
с2=4-р'ЦР-
Х-<0
После определения постоянных Сп, С2, С9 из системы
ний табл. 12 получим выражения для прогибов плиты:
(11.14)
уравне-
w(x, у) = Со + C2cos-|y- + C3cos~ cos -^-; (11.15)
14 В. 3. Власов, Н. Н. Леонтьев
210
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
1ГЛ.
Таблица 12
Со с2 Сз Правая часть Возможные перемещения
&оо ^22 &зо Go Wo
• «22 ^32 g2 А
• • Пзз G3 W3
в соответствии с этим изгибающие моменты примут вид:
М.
2 | 62 ny 1 /, b2 \ „ nx nu~l
^-^TT^cos^ + p +[L^jCsCOS-^-COS -27-J ,
(11.16)
ЛХ ПЦ
C3cos g^COS^
4. Учет пригрузки соседними секциями. Рассмот-
рим теперь случай, когда система симметрично нагруженных и ря-
дом расположенных плит покоится на грунтовом массиве. В приме-
нении к изложенной выше задаче это означает, что мы рассматри-
ваем теперь не отдельную секцию, а плотину в целом, состоящую
из чередующихся секций (рис. 103, а). Если фундамент каждой
секции представляет собой абсолютно жесткую плиту, то на гра-
нице между отдельными участками не будет сдвигов в упругом’
основании. В результате этого сосредоточенные реактивные давле-
ния на поперечных краях плиты обратятся в нуль, что можно
видеть, например, из выражения (10.9).
Если каждая расположенная на упругом основании плита име-
ет конечную, но достаточно большую жесткость, то сдвиги в уп-
ругом основании на границах отдельных участков будут невелики.
h 'Ч
ПРИМЕРЫ^РАСЧЕТА
211
Отсюда следует, что и сосредоточенные реакций в"этом случае
будут иметь небольшую величину, в результате чего ’ими,
с достаточной для практических целей точностью, можно прене-
бречь. Другими словами, в рассматриваемой задаче при расчете
достаточно жестких плит можно пренебречь влиянием упругого
основания, расположенного за пределами плиты в направлении
пригрузки соседними секциями, и рассчитывать такие плиты по
схеме, приведенной на рис. 103, б. ' ' j'
Задавая в общем случае прогиб каждой плиты в виде ’разло-
жения (10.3), получим для решения задачи, как и ранее, си-
стему алгебраических уравнений (10.15) табл. 11. Однако коэф-
фициентыГэтой системы в результате отсутствия реактивных дав-
лений Qf и 7?ф будут определяться не формулами (11.4) и (11.5),
14;
212
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
1ГЛ. III
а следующими выражениями:
&оо= 4 [уу7”* +т|^6(1 — v0)m,/na],
kw = у [у у ,
kio = у у mk + у у Кб(1 — >0) mtma\ ,
. 16 у I
kso тг3 2 b mk’
«и --= 2 I у Y mk -г -Jg- — у rnt , уу (у j J ,
16 у I
п^ = ~^±Тт>-
4 Г 7 / , л3 1 — Vo Z . тг5 ( I \з 1
n^=n\i^mk+^^r~bmt + wr[-b) |>
о Г Т I . л3 1 — v0 b , л5 Ь .
«га - 2 |у у mk + yr — -j- mt + уу у +
. 1 г-------- I 7Г2 1 — Vo mt Ь
+ 6(1 -VO) jmt ma + (1 _Voj TJ’
4 Г 7 I . л3 1 — vo b , jt561
”32 = 77 [т У mft + 16" 1 mt + 167 7 J ’
Г 7 Z я3 1 — vo /, , I2 \ b
Пза - Lt T mk + Тб ~+ / 7 +
+ TLfi ,П 4
16r \ b2 J I J ’
где величины mk, mt, ma и г вычисляются по формулам (11.6),
(H-7).
Для грузовых членов по-прежнему будем иметь:
Ci = y^Widxdy- (11.19)
Если предположить, что поперечные края плиты вследствие
наличия абсолютно жестких бычков не изгибаются, поверхность
прогибов следует принять в виде (11.15). В этом случае для оп-
ределения постоянных Со, С2, С3, как и в рассмотренном выше
примере, получим систему алгебраических уравнений табл. 12
коэффициенты которой будут характеризоваться на этот раз вы-
ражениями (11.17) и (11.18).
Отметим, что учет пригрузки соседними секциями может ска-
заться в значительном снижении положительных и увеличении
отрицательных моментов Му и изменении общего характера рабо-
ты плиты.
f g j2] ОБЩИЙ СЛУЧАЙ ЗАГРУЖЕНИЯ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ 213
§ 12. Общий случай загружения плиты со свободными краями
1. Метод решения. Рассмотрим общий случай загружения
прямоугольной плиты, свободно лежащей на упругом основайии.
При этом будем предполагать, что внешняя нагрузка состоит из
сосредоточенных вертикальных сил Р и сил, распределенных на
плите по некоторому закону р(х, у).
Известно, что решение задачи об изгибе плиты заключается в
определении функции прогибов w (х, у) из основного дифференци-
ального уравнения (10.1) при заданных для плиты граничных усло-
виях. Если принять, что края плиты свободны от закреплений и
внешней нагрузки, то граничные условия, носящие статический
характер, запишутся в следующем виде:
. b г. f d2w d2w \ n
при х = + г = — £)(—+|Л—j = o,
। /о >. dsw "I „ф I (12.1)
При у = + -д- Му = — D -s-г + и, = 0,
r J —- 2 у \ ду2 k дх2/
Q = _ D + (2 - (X) -^1 = Q*,
у Ldt/8 ' ' дх2ду\
(12.2)
где величины Q?, Qb, характеризующие работу упругого основа-
ния за пределами плиты, определяются по формулам (10.8) и (10.9).
Для решения рассматриваемой задачи снова воспользуемся ва-
риационным методом Бубнова-—Галеркина. Существо этого мето-
да состоит в том, что функция прогибов w(x, у) выбирается в виде
ряда, каждый член которого удовлетворяет заданным граничным
условиям. Можно, например, положить:
т п
W (х, у) = 22с тп'утп (х, у), (12.3)
1 1
где (f>mn (х, у) — заранее выбираемые функции, а Стп — подлежа-
щие определению постоянные параметры.
Заметим, что аппроксимирующие функции сртп могут быть выб-
раны любыми способами при условии, что эти функции линейно
независимы и удовлетворяют геометрическим граничным условиям
задачи. Точное выполнение статических условий в рассматривае-
мом методе необязательно, поскольку условия равновесия при
214 ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты (ГЛ. 111
составлении уравнений Лагранжа учитываются приближенно не
только на граничных линиях, но и во всех точках плиты.
В дальнейшем в качестве функций сртп будем принимать три-
гонометрические функции в комбинации с линейными членами, ха-
рактеризующими перемещения плиты как жесткого диска. Такой
выбор функций сртп удовлетворяет геометрическим граничным усло-
виям (на краях плиты w=/=0, ^-=£0), а также первым из ста-
тических условий (12.1) и (12.2) при р. = 0. Остальные статичес-
кие условия выполняются при этом приближенно.
Исходя из принципа возможных перемещений Лагранжа, для
определения постоянных коэффициентов Стп ряда (12.3) нетрудно
составить систему алгебраических уравнений, каждое из которых
показывает, что суммарная работа всех внешних и внутренних
сил плиты на возможных для нее перемещениях равна нулю.
Эта система может быть представлена в следующем виде:
т п
2 2 [OV2V2<pm„ — 2/V2<pm„ + ktf>mn — р] qik dx dy +
1 1
+ ф lQmn (s) + Q$(s)]<prt(s)dsj- =0 (12.4)
(i = 1, 2, 3,.. ., tn; k = 1, 2, 3, . . ., n),
где cpmn (s), tfik (s) — значения аппроксимирующих функций на
контуре.
В уравнениях (12.4) членами, стоящими под знаком двойно-
го интеграла, выражается работа внутренних сил плиты (изгиба-
ющих и крутящих моментов), работа упругого основания на сдвиг
и сжатие под плитой, и, наконец, работа внешней нагрузки. Кон-
турным интегралом определяется работа поперечных сил, прило-
женных к контуру плиты, на возможных перемещениях контура.
Первый член характеризует работу приведенных по Кирхгофу до-
полнительных поперечных сил (см. формулы (1.9)), возникающих
на краях плиты в результате приближенного выполнения стати-
ческих условий (12.1), (12.2). Вторым членом учитывается работа
реактивных давлений (10.8), (10.9), приложенных к контуру пли-
ты и характеризующих деформацию упругого основания за пре-
делами конструкции.
Выше было отмечено, что влиянием сосредоточенных реактив-
ных давлений, действующих в углах плиты и определяемых фор-
мулой (10.10), в практических расчетах можно пренебречь. По- 1
этому работа реакций /?ф в уравнениях (12.4) не учитывается1.
Интегралы, входящие в уравнения (12.4), вычисляются по всей
площади и всему контуру плиты. При наличии сосредоточенных
факторов, например в случае сосредоточенных внешних нагрузок,
§ 12] ОБЩИЙ СЛУЧАЙ ЗАГРУЖЕНИЯ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ 215
эти интегралы должны пониматься в смысле интегралов Стилтьеса.
Так, для конечного числа сосредоточенных сил вместо интеграла
следует взять сумму произведений из величины каждой силы на
значение функции «р,* в том месте, где эта сила приложена.
После несложных преобразований алгебраические уравнения
(12.4) могут быть представлены в следующей канонической форме:
^00,00 Соо 4* Oqo.IO Сю 4* • • 4* ^оо.тпСтп — Д00,
^Ю.ОоСоо + 81О,1оС1о 4~ • • - 4~ Со,тпСтп = Д10>
8/А.00 Соо + 8/*,1()С10 4- ... 4- ^ik.mnCmn — &ik,
^тп,OQ^qo ^mn.loCio 4“ • • • 4“ $тп,тп ~ ^тп •
Коэффициенты уравнений (12.5) имеют вид:
$ik,tnn = J [DV2V2<pm„ - 2/V2<pтп 4~ ktfmn ] ffik dx dy 4*
4- ф [Qmn (s) 4 Q*(s)]<pz*(s)ds. (12.6)
(12.5)
Следует отметить, что при определении коэффициентов кано-
нических уравнений (12.5) нельзя формально относиться к вычис-
лению интегралов формулы (12.6), которые в общем виде характери-
зуют виртуальную работу сил. одного состояния на перемещениях
другого состояния. Согласно теореме Бетти эти коэффици-
енты обладают свойством взаимности, или переместительности
(^ik.mn = в результате чего матрица уравнений (12.5) име-
ет симметричную структуру.
Свободные члены канонических уравнений (12.5) вычисляются
по формуле
А/* = р (х, у) dxdy (12.7)
и представляет собой работу заданной внешней нагрузки на воз-
можных перемещениях.
При решении практических задач заданную нагрузку общего
вида бывает удобнее представить в виде четырех отдельных сим-
метричных и кососимметричных составляющих. Например, сосредо-
точенная сила, приложенная в произвольной точке с координата-
ми х = а, у = с, может быть разложена на четыре отдельные на-
грузки по схеме, приведенной на рис. 104.
Производя в дальнейшем расчет на каждый компонент нагруз-
ки в отдельности, мы значительно сократим вычислительную
работу. Расчетные формулы при этом также упростятся.
216
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[гл. III
2. Расчет на симметричную нагрузку. В случае
нагрузки, симметричной относительно обеих осей (рис. 104, б),
выражение (12.2), аппроксимирующее функцию прогибов плиты,
может быть представлено в виде
т п
W (х, у) = Соо +2 Сто COS + 2 COS +
1 1
т п
+ 22C™cos^cos^ (12.8)
1 1
(m, п = 1, 3, 5, 7, . . ., (2k — 1)).
Формула (12.8) является обобщением формулы (10.3), принятой
нами ранее для приближенного расчета плиты.
Рис. 104.
Составляя выражения для работы всех сил плиты на возмож-
ных перемещениях, или, другими словами, вычисляя коэффициенты
(12.6), получим систему алгебраических уравнений (12.5) относи-
тельно неизвестных параметров Соо, Ст0, СОп, Стп.
§ 12] ОБЩИЙ СЛУЧАЙ ЗАГРУЖЕНИИ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ 217
В табл. 13 приведена матрица алгебраических уравнений для
случая, когда в формуле (12.8) принято девять членов (т = 3,
п = 3), соответствующих девяти возможным перемещениям плиты:
осадке плиты как жесткого штампа; четырем перемещениям, ха-
рактеризующим цилиндрический изгиб в направлении осей Ох и
Оу, и четырем перемещениям, аналогичным прогибам свободно
опертой по контуру плиты.
Можно видеть, что приведенная матрица симметрична ’отно-
сительно главной диагонали. Для составления ее необходимо вы-
числить 29 безразмерных коэффициентов, имеющих достаточно
простую структуру.
Входящие в эти коэффициенты величины а, k, t и D опре-
деляются по формулам:
о
и
(12.9)
Здесь I и b — соответственно длина и ширина плиты;’ D —
цилиндрическая жесткость плиты; k и t — обобщенные характе-
ристики упругого основания; ф = ф (z) — функция, характеризующая
распределение перемещений по толщине упругого основания; £0
и v0 — величины, определяемые через модуль деформации Егр и
коэффициент Пуассона vrp упругого основания по формулам:
Грузовые члены A,k приведенных уравнений имеют вид:
1 ГС
Aik = ~МЬ \\ Р у>> dx dy-
(12.11)
При наличии сосредоточенных нагрузок интегралы формулы
(12.11) должны пониматься в смысле интегралов Стилтьеса.
3. Расчет на нагрузку, симметричную относи-
тельно одной из осей и кососимметричную отно-
сительно другой оси. Если внешняя нагрузка симметрична
относительно оси Ох и кососимметрична относительно оси Оу
(рис. 104, в), то функция прогибов плиты может быть представлена &
Таблица 13
as C31 c88 Правая часть Возможные единичные перемещения
4 Зя2 4 3л2 4 9я2 +<i
x*!""* 7-я
,'\S .'у? ^00 = 1 </
it2 ] + ^2ь2 + 1] • 0 0 t Тж/С- . ПХ X s X ^10 ’= COS ~7~ • 0
0 1 г s’c , „ л2 n я I81 Ab4" + 9 a2b2 + jJ 1 Г , я40 , n я2 1 Зя L81 Ab4 + 9 a2b2 + 1 J ^30 -X у!' - — Зях S Wso = cos ~~b~
0 84+ --в2 +1] Зя LAb4 P + oWP + J 0 ^41)1 .'/ /' “.'/ — тсу 'Уч w°l = cos ~T~
+9^₽.8+d 0 1 Г я40 . Зя L81 Ab4 p + Я2 "I + 9 a^b2 + ^4 03 J / /f— Ъки wos = cos -J—
0 0 0 j4 11 — ’tJC] t^y a,u = cos i cosк»
l^+ Ab4 + ^+1)^5- + 1] 0 0 Л13 -y^rniiiiwitfwwmB^^ — 3^1J ✓ _ cos cos _ у S b I
• 1 Г я4£> , 4[(9 + P2)8 Tb' + + (9+P*)^ + (| 0 31 ^п~ — Зях яц WS1 = c°s -^- cos -J-
• > • 1 Г тт4£) tl81 (1 + и2-^г + + 9(1+ ₽2)^ + 1] A 33 jiiL. ’ Зях Зяи a)88 = cosCOS -p
Матрица алгебраических уравнений для симметричной нагрузки
a Cm Cos Си Cis
-b+41 it L aft J 2 Г 2 1 “ 3л j.1 + ab J 4 Л2 Зла __
0 4 4 3л2 1 Гтг4£> 7ta ] tt L kb* + a*b* + J 1 pt4D tta 1 Зтг [ Ab4 + aab2 + 1J
7C2 № + 14 p+9^ и t __4_ ita 4 9ла 0 0 г П i
• 1 Г’С*1) Й4Д__^!_ йа J- 1 -4- 2 L Afe4 P ,+ aaba + 1 + 2 , ла i + чЬ + a3&3 M 0 1 Г i^D tr [ kb* 1 aafca ₽ + 1J 0 i j
• • 4 Г wf4 ТЕ® 2 L81 kb* P + 9 aW P + +1 + «0 +9 «V H 0 1 Г ti*D „ na 1 '
5 i i t • • • ' 1 r l[(l+₽V^ + it2 .1 + (1 + ₽a) + 1J 0 -
1 —auH^WtJ^- • • • 1 Г T^D Т[(9?» + 1)а^+ r + (9P* +1)^ + 1] :3
i • • • • • ' 1 4
!- ’ ' • • • •
^^^*^™>M*M*Ml***f,‘Mri'1"tllllllll'*a**iiHMttiil.i ll , li .-^.^..,а..„..^A... .... , — и,,г «тМ|ИТ,tltwt' ,«®
Матрица алгебраическ
Соо Сю Сзо С о1 Соз
9 + т=г(1 + £) cto л [ ab -Ь+41 л L «ь J 2 Г 2 1 “ Зл L1 + ЛЬ J
• £Г2^ + л!_ + 1 + 2 L kb* а2Ь2 + 43+5б4) 0 / 4 __4_ Зл2 -
• • Им^+9^+1+ 2 1 + ^ + 9^И _ 4 л2 4 9л2
• • • 1 Vit&D А 7 в* -I- —- В2 4- 1 + 2 L kb1 р <х2&2 р Г + А + j£_ ва ’1 г ab + а3й8 р J 0 я
• • • • Ц81 «• ₽‘+9.’6.₽’+ +1+«2»+9«’». f]
• • • • • I! i
• • • • •
• • • • *
• • • • • 1
Власов, Н. Н. Леонтьев
Матрица алге
с„„ С га С10 Coi
0—0 12 1 + a2b2J 1 Г, 2 1 Тр + ab 2 Г. , 6 , 12 1 ™| 1 + ab ‘h а2&2|
2-0 • 1 Г „ %‘D , . тг2 , 2 [16 kb* 1 ‘ а2й2 + + 1,4 2^ з] + 1 ab' ‘ a3ft3 1J 0 2 —.
4-0 • • 1 Г KlD Ап те2 2-[256Ъг'Н6^ + 1 + 2 я2 1 + ab В + 16 а3Ь3 1_ гс2 1 3i 9
0-1 • • • ₽4+^зг+1+ + 12(2~Н)^>+^ + + 22 , 3^-В21 ’ а2й2 а3Ь3 р .
0-3 • • • • + 1 + 108 (2 ,_1 + Л аЬ а2Ь2
2-1. • • • •
2-3 • • • •
4-1 • • • •
4-3 • • • •
Матрица алгебраических уравнений для нагрузки, кососимметричной относительно оси Оу
с08 С21 С23 С41
111 а2Ь2| 2 Г 6 12 1 9л а.Ь + aaJ’i , 2 Зга2 л2
_ JL Зтг2 1 Г „ n4D л2 ) л [16 kb* + 4 a2ft2 + J 1 Г л«О , Л2 ,3 ~+Н16 kb* + ' а2^2 + и 0
1 Зл2 1) 0 4f256 ~ +16^ + 1] л 1 kb оРо1 J -i[256 /
! + 1 + З^Гд32| a368 J 0 _1_Г21Р. 344- 32 л. 11 2л | № р + a2b2 р ' J 0 1 1 x*D оа л2 1 4л 1 kb* + а2,?® + *]
1 Г n4D л2 ТI81Ibr^ + 9oW'32 + Л2£) + 1 + 108 (2-[А)-^-З2 + + Л + 4^- + 27 -й» Н ab а?Ь- aab® J О 1 Г n*D л2 1 2^[811М ₽’+9^3г+1_| 0 1 Г л -zd8li
• 1 Г n*D zL(4+62)2feM + + (4+^)^2 +1] 0 0
1 Г... Л4О ,
• • T|^-F9H--^r + + + 932) 0
• • • 1 Г Tt*D zL<16+^2^- + (16 + ₽2) ~ +1]
• • • • 4[(1б+яз2: + (i
гричиой относительно оси Оу •
Саз Си
~ Зл2
I Г n*D . п2 ,1 “ЗИ16^4- + J 0
0
f 0 1 1 л4О п- ~^hH4+^2+'j
1 Г л*£> • ’ п2 "1 2л" L81 йМ” Р4 + 9 а2^ Р® + 1J 0
, 0 1 0
1 Г(44-дв-^ л2 1 + (^ + «З2) ^з + 1] 0
• 1 Г лф zL<16+^if + ТС2 + (16 + (В2) ^г- +
Таблица 1
С 43 Правая часть Возможные единичные перемещения
218
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. III
виде
т п
, . 2х . vi „ . т-х , 2х VI „ пт.у
w (-С У) — ^оо —F 2j Сто sln "-у—I—4" 2j Con cos ——|-
2 1
m n
i ITlTtX mvy /1 n t r»\
+ 22 Cmn sin fj COS 7 (12.12)
2 1
(m = 2, 4, 6,. ..; n = 1, 3, 5,. ..). J
Нетрудно видеть, что выражение (12.12) удовлетворяет фи-
зическому содержанию задачи. Первым членом здесь определяете^
поворот плиты как жесткого диска вокруг оси Оу. Одинарным^
рядами характеризуется цилиндрический изгиб в направлении оси
Ох и деформация продольных краев плиты. Двойным рядом оп-1
ределяются перемещения, соответствующие свободному опираникй
плиты. Учитывая выражение (12.12), по формуле (12.6) нетрудна
вычислить все коэффициенты разрешающей системы алгебраически»
уравнений (12.5). Как и в случае симметричного загружения, огра!
ничиваясь, например, девятью членами разложения (12.12) (т =2; 41
п=1;3), получим систему девяти алгебраических уравнений!
приведенную в табл. 14. Грузовые члены этих уравнений харакя
теризуют собой работу заданной внешней нагрузки на соответст!
вующих виртуальных перемещениях и вычисляются по формул®
(12.11). Величины а,, р, k и D, входящие в выражения для коэф!
фициентов табл. 14, определяются формулами (12.9). 1
Аналогично при нагрузке, симметричной относительно оси О®
и кососимметричной относительно оси Ох (рис. 104, г), функции
прогибов может быть принята в виде J
т
W (%, У) = соо -f + -у 2 Сто COS -^-4-
1 fl
п т п
Пли . \п v-i тп* ппц /1О
4- 2j Con Sin — + 2j 2cm«c°s ~r sin— (I2- ‘W
2 12 ,;Я
(tn = 1, 3, 5,. . .; n = 2f 4, 6,...).
Матрица алгебраических уравнений для этого случая (i*Rl
-//2=1; 3; п = 2; 4) приведена в табл. 15.
4. Расчет на кососимметричную нагрузку. При на-
грузке, кососимметричной относительно обеих осей (рис. 104,^),
«функцию Прогибов можно составить из нечетных функций в йИДе
I g 12] ОБЩИЙ СЛУЧАЙ ЗАГРУЖЕНИЯ ПЛИТЫ CO СВОБОДНЫМИ КРАЯМИ 219
следующего ряда:
W (х, У) = СОО-^ +-f 2j Ст0 sin ~y~ +
2
п т п
+ ^SC0.sin= + 22c„.Sin=Sm^ (12-14)
2 2 2
(т, п = 2, 4, 6, 8, . . .).
Первым членом здесь выражается деформация плиты по ги-
перболическому закону с сохранением прямолинейности краев.
Две одинарные суммы характеризуют деформации краев плиты.
Двойной суммой определяются перемещения, соответствующие
свободному опиранию плиты по контуру.
Как и в рассмотренных случаях, коэффициенты основной си-
стемы алгебраических уравнений вычисляются здесь по формуле
(12.6), а грузовые члены— по формуле (12.7). В табл. 16 приве-
дена матрица уравнений, соответствующая первым девяти членам
разложения (12.14). Как и ранее, все основные величины, состав-
ляющие эту матрицу, определяются выражениями (12.9), а гру-
зовые члены — выражением (12.11). Уравнения, приведенные в
таблицах 13—16, позволяют производить приближенный расчет
прямоугольной плиты на произвольную внешнюю нагрузку.
Можно видеть, что в общем случае для этой цели требуется
решить четыре системы алгебраических уравнений, каждая из ко-
торых содержит по девяти неизвестных и имеет одинаковое строе-
ние с системой канонических уравнений теории рам. В качестве
способа, позволяющего достаточно просто производить решение
приведенных уравнений, может быть рекомендован, например,
способ Гаусса, обеспечивающий необходимые контрольные проверки.
После определения прогибов плиты из выражений (12.8),
(12.12), (12.13) и (12.14) внутренние усилия плиты, т. е. моменты
и поперечные силы, определяются по формулам (1.8) и (1.9). Точ-
ность полученных решений будет зависеть от характера заданной
нагрузки и числа членов, принятых в разложениях (12.8), (12.12),
(12.13) и (12.14). Известно, что при нагрузках, близких к равно-
мерно распределенным, сходимость тригонометрических рядов до-
пета точно высока. В приведенных решениях мы ограничились треть-
ем приближением, приняв в каждом из рядов, аппроксимирующих
I Функцию прогибов, по девяти членов. Можно думать поэтому,
1Что принятая точность вычислений будет вполне удовлетворять
практическим целям, если внешняя нагрузка распределена по не-
которой части площади плиты. При необходимости получения
большей точности приведенные решения на основании выражений
V*2.5) и (12.6) могут быть без труда развиты дальше. Напротив,
«3 удДуУ ^^sf^ejsfefc«r’J«r-V'-W’S-- C22
_A[i + A+2£| 6- L ab a2*2 J 1 7C2 _ 2_ 2л2
1 2л2 1 Г 7Z4P , П* Ъ— 16 Т/Л + ~2TT “b 1 2n L kb4 a2b2 1 Г , тс2 .1 5— 1 16 '~t~T~A—h 4 2k2 -j- 1 2tc L «Ь4 a2d2 J
1 4л2 0 0
0 1 Г л4£> л2 2л L16 kb* + 4 a263 + j 0
f n4D л2 |2561^^+1б^^ + :^d b 1 + 192(2-И)^г02 + 6 12 л2 I + ab + a2fe2 + 48 a3&8 “J 0 1 Г л4£) ^[256^^ + л2 J + 16^^+ 1]
• 1 Г ^iD 4 [16<1 + ^2)21^ + + 4(l + 32)^ + 1] 0
c • 1 Г w4-» 4[16(1 + W^r + л2 1 + 4(1 +4₽2) -^+ 1]
• e •
• • •
Таб
C it Си Правая часть та Возможные единичные пе^
1 2я2 1 4я2 ^00 ж-. 1
0 0 . А 20 — 2у 2пх ^20 = у Sin -у S
1 Г re4D , .„, л2 , .1 2л j256 kb* + 16а2Ь2 + 1] __1_ 4л Г n*D тс2 1 [256 + 16 + 1] Лао — 2у 1 ®40 = У sin "У- |
1 Г, л4О |2л L16 kb* + + 4^i^+i] 1 0 Ло2 — 2% 2пу 1 ^02 = £~sin — |
0 _ 1 4л Г л42Э |2561F 34+ л2 "] +16^2 +1] А 04 — 2х 4пу I шо4 == у S1’n ~i~ 1
0 % j i 0 А 22 — . 2тсх 2лу 1 ®22 = Sltl —у Sin —у 1
0 i 0 Ага — . 2лх 4тгл/ ®24 = sm —у Sin —у
1 Г л4О Т|16(4+32)2^- + 7С2 1 + 4 (4 4- Р2) 'а2р “Ь J 0 А 42 - . 4ях 2т а>а = sin —у sin —у
• 1 Г те4П И25б(1+^2^+ 7С2 3 +16 (1 + ₽2)yj2+1] А44 — 4тсх 4тсг/ — sin —sin ——
S3 S3 CJ 1 Г re4D , . n* 2n [16 kb1 + a262 ' о 164 « Го K 1 а + ** CD. к 1*^ CO -и о 1 Г TtW 416(1+ 32)2-^ + 7Г2 + 4(l + 32)-^ •
k 4 О Q __1_ L ,A, a_l 6n L r ab r a262 J 164 Im 1 1 4те2 c + , i 1 91 ' ] CD. °°- + 1» Iе1 O’ ~ "e S> Q к e ”« 1 « Ъ P§ 00 T ^ + + 1 1*4 2L ’ eq о eq, rjj Q !’* ea . г |s 2 + s + Ч» + и» + • и
<я © : CJ [ , <?» . ,1 L Zl 9 J T 4* Ж _ I + , , t—4 64 , co- Г + « “ &- K 1 8 4 T + 1 164 + 7 eq o Sx 1 1» 1 _1_ ” kS 00 1 rC“ о •§ CO 4“ t j 4" ^l«= • • •
3? О 1 Гл 6 o , 12 1 ft— “b A P H 2A2~ 32 1 бтс L .ad a2b2 H J о 1 Г TC^D 7Г2 -d256-^ +16^+1 + + 192(2-|л)^г₽2 + 6 „ 12 л2 I + ~£b 3 + ^₽2+48^f N • • • •
о 64 <2> 1 Сч" Д CD. [64 2 k? 1« + CD. 501« l г“ Z\ + гй-^(г!^ (7г“ + l + ^f + - s“ • • • • •
M-T J V Ил4 6 L16 + 48 (2
о © <2> g ^288 (1 P-) ££4 |32 + 1 + 6 + (l+?)^+ 12 I + (1 + 0®) a262 J • • • • • •
0-0 2—0 4—0 0-2 1 2-2
Сю Cso C„2
Зп L + ab p f a№ J . _ J£ Г]..._ JL 5 4- -l2- вз! 9n L ab ;ta2&2 p J 1 Г, , 2-1 I +
1 [tc4D n2 6" [~kb* + rfb2 p3 + 1 + n2D 6 „ + 12(2-h)-^ + -^ + 12 л2 1 + afb2 P2 + 3 a?b2 J !) 2 rt2
1 Г n*D n'“ 4 81t^ + 9-^+1 + 6 |_ kb* a2b2 7г2Г) r + 108(2-4)-^.S2+^ + , 12 n2 D 1 + aW + 27 as&3 J 2 Зтг2
• • 1 Г л4В n2 TL16w^ + 4^^ + 1+ ++4 d
• • »
* • •
аачхноэц- -н
.S^’+
г ?04 С12 с 14
: 1_ 2тс [1+^] 2 л 7Г2 -
Г 1 тсг _±Г^ + 2^- + 1] 2л 1 kb4 + агЬ2 J — 4гс [ № + aW +1]
1 Зпа 0 0
0 1 Г n4D ла 1 vL16^^ + 4^^+1J и
1 Г л4О Т L256 4-1 + -~т CLO + ‘8aV?S + + 16 -Йз- И a3b9 r J 0 1 Г Л4О -[256 ^^ -Ь 16- I
г С • 1 Г n4D т [<1 + Т&- + + (1 + 4?2)^2 + 1] 0 1 1
1 • • 1 Г "4о zld + lW-^4 + (1 + 1632) тс2 1 2Е и 1 ab2 + J
г 1 • 1 • •
• • •
т
м ---
t-32 ’-'84 часть —
2 Зтт2 1 3it2 ^00
(I 0 Лю / г / ~ ty / / / “'IO = TCOSV
1 Г TC4D 7Г2 1 —81-^r + 9^ + 4 4л [ kb^ asb2 j Лзо / 4 / — 2у Зп ~7~ ““so = ~ cos
7t2 1 + 4 аЧЛ P2 + *] 0 Лоа 4-4- - 2- / / ^3 = 311! —
(1 1 Г n“D -•d256 i^4+ 7Г2 1 + 16 Wfp + lj Л(>4 —— — 4тег/ 4 .S К’О4 = sin ~
0 0 Ли 4“^^ _ пх 2' -Г- 7 /“ WI2 = cos ь sin
0 0 Л14 %rrn1llpiuna»/ _ я/ 4 f~~W / Wu ~ cos ~y sin “
1 Г rcW t[(9+4₽2)2if + П2 "1 + 0 + 4^) ^+1| 0 Лзз - Зте% / 4 / Wvt=cos 'vsin
• 1 Г n4D Т|(9 + 16Л2-^ + + <9 + m -^ +1] Л 34 — 3mc 4 / ~7~ 1^34 = cos -y sin -
220
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. II
если требуется невысокая точность вычислений, то в матрицах ал|
гебраических уравнений таблиц 13—16 можно ограничиться мень|
шим числом членов, как это было показано в § 10 настоящей
главы. 1
Отметим, что в качестве аппроксимирующих функций сртп мо|
гут быть рассмотрены не только тригонометрические функции, на
и ряд других функций, удовлетворяющих граничным условиям
задачи. Так, например, высокую точность решения при ограни^
ченном числе членов ряда (12.3) можно получить, если в качестве
функций сртп принять выражения, построенные при помощи фун4
даментальных функций поперечных колебаний балки (см. табл. 7)3
В качестве функций сртп могут быть приняты также и различные
степенные полиномы *). ;
§13. Общие уравнения толстых плит на упругом
однослойном основании
Рассмотрим работу толстой плиты на однослойном упруго
основании в условиях пространственной задачи теории упругое#
(рис. 105). !
Решая поставленную задачу методом перемещений,
вим согласно изложенному ранее общему вариационному
проста'
м#одУ
*) Некоторые вопросы расчета прямоугольных плит на упругом осивЙанШ’
рассмотрены в работе Л. В. Косабьяна [45]. I
i «j
общие уравнения толстых плит
221
искомые перемещения 'плиты и основания в виде следующих конеч-
ных разложений:
и(х, у, z) = Ui'(X, t/)<Pi.(z),
у, z) = V1(x, y)<Pi (z), ц3 р
О)(х, у, z) = w1(x, у) Ф1 (г) + w2 (х, y)<p2(z),
где Ui(x, у), v1(x, у), w1(x, у), w2(x, у)—искомые функции двух
переменных; <pi(z), (z), ф-2 (z) — функции, зависящие только от
Рис. 106.
одной координаты z и выбранные в соответствии с условиями
рассматриваемой задачи в следующем виде (рис. 106):
при z < h
при z > h
Ф1 (z) = Ц- , ф2 (z) = 1;
?i (z) = 0,
<Mz)=0, ф2 (z) =H + ft~’
(13.2)
Из рис. 106 и равенств (13.2) можно видеть, что функции (z)
и ф1 (z) характеризуют деформацию плиты на абсолютно жест-
ком основании. При этом предполагается, что поверхность
основания идеально гладкая, т. е. между плитой и основанием
не возникает сил трения и сцепления. Кроме того, можно видеть,
что в отличие от обычного расчета тонкой плиты здесь при помо-
щи функции (z) учитывается поперечное обжатие конструкции.
Функция ф2 (z) позволяет учесть податливость основания и
характеризует основание как однослойную модель, которая рабо-
тает как на нормальные напряжения аг (характерные для винкле-
ровского основания), так и на сдвигающие напряжения т2Х, тгу.
'Следует отметить, что функция ф2 (z) на участке z > h может быть
222
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. Ill
задана не только по закону прямой линии, как это предопреде-
ляется последней из формул (13.2), но и по любому другому за-
кону. В частности, для функции ф2 (z) при 2 > h можно принять
закон убывающей показательной функции или гиперболического
синуса, как это было показано ранее в § 11.
Таким образом, предполагаемое решение, с точки зрения стро-
гой математической теории упругости, носит приближенный харак-
тер: рассматриваемая система наделяется в направлении оси Ог
конечным числом степеней свободы, и, кроме того, мы не учиты-
ваем горизонтальных перемещений в упругом основании. Вместе
с тем это решение позволяет существенно уточнить известный
расчет плиты на упругом винклеровском основании как в части
работы самой плиты, так и в части работы упругого основания.
Для определения искомых функций (х, у), vt{x, у), wr(x, у),
ш2 (х, у) рассмотрим обобщенные условия равновесия элементарно-
го столбика dx = 1, dy = 1, выделенного из плиты и упругого
основания (рис. 105). Под условиями равновесия будем понимать
равенство нулю суммарной работы всех внешних и внутренних
сил этого столбика на возможных для него единичных перемеще-
ниях: .
«1(х, у, Z) = фДг),
у, z) = фДг),
при
th(X, у) = 1,
W1(X у) = 1,
£1(х, У, Z) = ^(z),j
W2 (X, у, 2) = ф2 (2) I
1>1 (х, у) = 1, I
(Х, I/) = 1. j
(13.3)
В общем виде эти условия равновесия могут быть представле
ны, как и ранее, системой дифференциальных уравнений (6.6) гл.1 .
При наличии выражений (13.1) и (13.3) уравнения (6.6) гл. I при
мут вид:
Г дах С , Г dt С
?! dz+ Уф 1 dz + }PC?LdZ=2 0>
Г д°и С ' f д^их С
}-~<pidz — J dz + ) dz + № dz = 0,
dz-\Q^dz+\d~^-^dz ^idz = o,
'^2 dz - ~'dy dZ dZ=^'
(13.4)
Интегралы в уравнениях (13.4) вычисляются по всей высоте
элементарного столбика в пределах от 0 до h + Н. Входящие в
эти уравнения напряжения <зх, ау, iXz, Хуг, ~ху могут быть
определены при помощи общих формул (6.2) гл. I подстановкой
в последние выражений (13.1). Отметим, что при вычислении на-
§ 131
ОБЩИЕ УРАВНЕНИЯ ТОЛСТЫХ ПЛИТ
223-
пряжений следует учитывать двуслойность элементарного столбика,
упругие постоянные которого при z < h характеризуются величи-
нами Е и v, а при z^h—величинами Ео, v0.
В дальнейшем мы будем предполагать, что объемные силы в
плите и упругом основании отсутствуют, а на плиту действует
только вертикальная поверхностная нагрузка q (х, у). В этом
случае грузовые члены уравнений (13.4) примут вид:
#1 dz = (0) = q, $ б/ф2 dz = дф2 (0) = q •
(13.5>
Внося в уравнения (13.4) выражения для нормальных и ка-
сательных напряжений, а также учитывая зависимости (13.5),
получим систему дифференциальных уравнений толстой плиты на
упругом однослойном основании:
d2Ui , 1 — v d2«i
f
1 — v 1 -J- v d2Vi ____
dy2 1711 2 U1 ' 011 2 dx dy
1 — v dw-i 1 — v dw2 n
— £11 й— —5-------------£12 о ~л :=
11 2 dx 2 dx
i — v d2ui , d2vj 1 1 — v
1 — v dw-i 1 — v dw2 n
— £ц ——з--------------£12 —о— ~д —
11 2 dy 2 2 dy
2
1 + v d2ut
2 dx ду
di^
, E
/1 — v , \ dus . /1 — v j \ dvj ,
i C11—' —4“ C11 — v“ll “a h
\ 2 11 LLJ dx ' \ 2 11 11,/ dx
1 — v d2Wi . 1 — v Э2И1) .
~2ГГ11~д^~ snwi +
, 1 — v d2w2 , 1 — v d2w2 ,1 — v2 n
~2~ ~dW' + ~~2~ E^^-0’
Г E E л ] d«i , [ E „ E Idvi ,
I 9 /1 _l_ -Й C12 1 _ „2Й12 I 9 (1 _|_ v) C12 1—v2C(12]_^y +
Э2о>1 , E v d2Wi
2 (1 + v) '12 ~dE2~^ 2(1 + v) Г12 "Эу2
£ „ , Г E ,.| Eo _o 1 d2w2 ,
~ S12“’1 "Г L ^(1 +*)'f22 + 2 (1 + v0) Г22 J ~dxr
E । Eo о I d2w2 Eo 0
2(1 + v) Г22' 2 (1 + v0) f22 J dy2 i _v2 S22W2 -|- q — 0,
(13.6)
где и1 = и1(х, у), v1 = v1(x, у), w1 = w1(x, у), w2 = w2(x, у);
Е, v, Ео, v0 — соответственно модули упругости и коэффициенты
Пуассона материала плиты и упругого основания; q = q (х, у) —
действующая на плиту вертикальная нагрузка.
224
ИЗГИБ ПРЯМОУГОЛЬНОЙ плиты
[ГЛ. III
Правая часть
о -ь •ST +
С 1 5й Q + сч |Csl (1+l^lizpo2 + \ 2 £ 1 + у0 А / х , Ер 1+У //А;й 1 \. 2 Е 1 + v0 h ) и о Ео 1 4- v 1 “ Е 1 + v0 Hh
С 1 -г-( ГС -С 1 еч Ь-, + еч И -С Г С- еч 4- н 3 и
Яхп 7, 6 (1 — у) А2 |сч 1 й) Q 1
(л — I) 9 — la —+ Iff л — i -С ст н’ + ч Q * Q
cq ГО j
§ 13]
ОБЩИЕ УРАВНЕНИЯ ТОЛСТЫХ ПЛИТ
225
Коэффициенты уравнений (13.6) в соответствии с формулами
(13.2) определяются в виде:
°11 = f 2 , А3 \^dz=-^, «и -= ^lYdz =
feu = (<рх)2 dz — h, Si2 = <M>2 dz = 0
S22 = CP2)2 dz =
С11 = dz = — J , f* . n fa
Гц dz = J , (13.7)
С12 ~ dz = — h, ^12 = J Ф1Ф2 dz =- ,
ft
du ~ <Р1ф1 dz = 0, ^22 = 5 Ф2 dz = h, 0
ft4-H
diz = <pi<f>2^z= 0, 0 C . 2 j H Г22 — \ г 2 • ft
Подставив значения коэффициентов (13.7) в (13.6) и произведя
несложные преобразования, можно записать дифференциальные
уравнения (13.6) в окончательном виде, приведенном в табл. 17.
В этой таблице через Dx, Dy, D2X, D2 обозначены дифферен-
циальные операторы, указывающие, что от функций, выписанных
в верхней строке, должны быть взяты соответственно первая или
вторая производные по координате х или у.
Системой четырех дифференциальных уравнений табл. 17, со-
ставленных относительно четырех искомых функций нх, vlt wu
w2, полностью описывается рассмотренная задача об изгибе тол-
стой плиты на упругом основании, поскольку, по определении этих
функций, перемещения и напряжения в плите и упругом основа-
нии могут быть вычислены по общим формулам (13.1) и (6.2) гл. I.
15 В. 3. Власов, Н. Н. Леонтьев
ГЛАВА IV
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ
НА УПРУГОМ ОДНОСЛОЙНОМ ОСНОВАНИИ
§ 1. Постановка задачи. Основные дифференциальные
зависимости
Рассмотрим
круглую плиту постоянной толщины
ложенную на упругом основании с двумя характеристика»
(рис. 107). Будем предполагать, что внешняя нагрузка действу
симметрично относительно центра плиты, в результате чего пли’
находится в условиях осесимметричной деформации. Отн<
плиту полярной системе координат (9, р). Начало коо]
нат поместим в центре плиты, а расстояние от центра до
сматриваемой точки будем обозначать. через р. В поля{
системе координат дифференциальное уравнение изгиба пЛ
на упругом однослойном основании (см. § 1 гл. Ill) запит
в виде
V₽V> — 2r2VpU7 + s4U7 = 4
ПОСТАНОВКА ЗАДАЧИ. ОСНОВНЫЕ ЗАВИСИМОСТИ
227
где
£о
4 (1 + VO) D
ф2 (z) dz,
Еу
(1 — vg)Z>
ф'2 (z) dz,
(1-2)
a D = i2~(f_~2y — цилиндрическая жесткость плиты.
Поскольку рассматриваемая задача характеризуется осевой
симметрией и прогибы плиты W = W (р) не зависят от полярного
угла 6, оператору Лапласа, входящий в уравнение (1.1) опреде-
лится в форме
= . (1.3)
k dp2 р dp '
Обыкновенным дифференциальным уравнением (1.1) при соот-
ветствующих граничных
об изгибе круглой пли-
ты на упругом основа-
нии с двумя характе-
ристиками. Это уравне-
ние отличается от из-
вестного уравнения из-
гиба круглой плиты на
упругом винклеровском
основании наличием чле-
на (—2r2VplV'), которым
учитывается работа ка-
сательных напряжений,
возникающих в одно-
слойной модели.
угловиях полностью описывается задача
Рис. 108.
2. При осесимметричном изгибе в кольцевых сечениях плиты
Р = const будут возникать радиальные изгибающие моменты 7ИР и
поперечные силы Qp (рис. 108). В радиальных сечениях 6 = const
возникнут только изгибающие моменты Мв. Зная уравнение
упругой поверхности плиты и ее цилиндрическую жесткость,
можно эти радиальные и кольцевые усилия вычислить по извест-
ным формулам:
ц. «т =
р dp ) ~
v>— -—
. Р dp
.г , 1 —мл
М, = — 4-
р \ dp2 1
п( d2W
Ме = —D и -~г
v ср2
Q₽ = — D = - D -±- v>.
dp \ dp2 1 р dp д dp и
( (1-4)
15*
228
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ.
Отметим, что поперечные силы Qp принимаются положите^]
ными, если на площадках с положительной внешней нормали]
направление этих сил совпадает с положительным направление]
оси Oz. Изгибающие моменты Л1Р и Л40, вызывающие растяжешИ
в нижней части плиты, также считаются положительными. fl
3. Наряду со статическими величинами (1.4) введем в pafl
смотрение обобщенную поперечную силу, характеризующую cfl
стояние касательных напряжений плиты и упругого основанв
в кольцевых сечениях р = const при р<}7?. Исходя из основнД
идеи изложенного вариационного метода, можно для обобщеннД«
поперечной силы, отнесенной к единице длины, получить следуй]}
щую формулу (сравни с формулой (1.10) гл.II): fll
W₽ = — — (1.Я
\ Ф dp / ' fl|
где flj
и I
r2 = D = 4 (1 +°vo) D dz- fl
О Ж;
Отметим, что правило знаков для силы ,NP совпадает с npai
лом, установленным ранее для поперечных сил.
На участке свободного основания, расположенного за пред<
лами плиты (р }>./?), для обобщенной поперечной силы в отлич!
связанных с расчетом конечных
от Мр примем новое обозн!
чение 5'р. Исходя из форм|
лы (1.5) (см. также формуя
(3.10)гл. I), получим для эта
силы выражение |
Формулы (1.5) и (l.q
должны учитываться при рая
основании.
смотрении краевых зад:
плит на упругом однослойн
Рассмотрим, например, плиту, края которой свободны от i
реплений и нагрузки (рис. 109). Граничные условия в сече
р = R этой плиты запишутся в виде:
Л4р(Р) = 0, WAR) = WAR), Rp(R)=Sp(R), (11
где IFj и И?2 — прогибы плиты и осадки поверхности упруго!
основания соответственно для областей р^СР и p^R, a
ОБЩИЙ ИНТЕГРАЛ ДИФФ. УРАВНЕНИЯ КРУГЛОЙ ПЛИТЫ 229
> __обобщенные поперечные силы, определяемые формулами (1.5)
|Г(1.6).
f Двумя последними из условий (1.7) характеризуется непре-
Ррывность деформированной поверхности упругого основания. Дру-
гими словами, этими условиями учитывается t работа упругого
"основания за пределами конструкции.
Раскрывая последнее из выражений (1.7) при помощи формул
(1.5) и (1.6), получим:
— D + 27 = 2t .
dp ₽ 1 1 dp dp
Сравнение полученного выражения с последней из формул
(1.4) позволяет представить рассматриваемое граничное условие
в виде
Q₽(/?) = _D^-V>1 = 2Z(^-^-). (1.8)
Можно видеть, таким образом, что на свободном от нагрузки
и закреплений крае плиты возникает фиктивная контурная сила
Q* = Qp (7?). Как и в рассмотренных ранее задачах по расчету
балок и прямоугольных плит, возникновение фиктивной силы
Q* обусловливается связностью однослойного основания и способ-
ностью последнего воспринимать сдвигающие усилия.
Заметим, что выражение (1.8) может быть также переписано
в виде*)
Q* = S₽!-S₽1, (1.9)
где SPi и Sp2 — обобщенные поперечные силы упругого основания,
вычисленные соответственно для сечений R— в и Я + в прие—>0.
§ 2. Общий интеграл дифференциального уравнения круглой
плиты на однослойном основании
1. Введем вместо р безразмерную координату g = Величи-
ну Lo определим в виде
• L.= (2.1)
н
где k = _—__( ф'2 (z) dz — коэффициент, характеризующий работу
1 — Vq Q
грунта на сжатие; D — цилиндрическая жесткость плиты.
*) Подобное определение фиктивных сил Q* давалось ранее при рассмо-
трении балок (см. гл. II, § 5).
230 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [гл. fw
Основное дифференциальное уравнение задачи (1.1) можм
теперь представить в форме
V|V|r - , (2.J
где 1
а2 р , ? I
° ~ D ~ 4 (1 + v0) D J & dz' (2'Ч
0 3
Под символом V| в уравнении (2.2) обозначен оператор Лам
ласа, приведенный к безразмерной координате: и
= (2.J
dt2 1 $ dE, ' Я
2. При отсутствии заданной поверхностной нагрузки диффе!
ренциальное уравнение (2.2) становится однородным: 1
— 2г?7|Г + W = 0. (2.5|
Это уравнение может быть приведено к системе эквивалентный
ему двух дифференциальных, уравнений второго порядка. Дей
ствительно, пусть W = W (£) представляет собой какое-либа
частное решение однородного уравнения (2.5)-, удовлетворяющей
в то же время дифференциальному уравнению 1
+ = 0, (2.6)
где через X обозначена некоторая постоянная величина, подлежа-
щая определению.
Исходя из уравнения (2.6) будем иметь:
= \2w. } v'
Подставив теперь выражения (2.7) в исходное уравнение (2.5),
получим относительно X характеристическое уравнение
X2 + 2г^ + 1 = 0. [(2.8)
Значения корней Xi и Х2 характеристического уравнения (2.
определяются формулами: .
х1 = — fo + K(ro2)2— 1 , j (2;
Х2 = — Го — V(r20)2~ 1. J
Следует отметить, что для реальных грунтов значения инте
ральной характеристики г2 находятся в интервале
0<r?< 1. (24
t-г] ОБЩИЙ ИНТЕГРАЛ ДИФФ. УРАВНЕНИЯ КРУГЛОЙ ПЛИТЫ 231
| Случай Го =?= О является предельным и, с точки зрения
впаботы упругого основания, предполагает отсутствие сил сдвига
в упругом основании (/ = 0).
Таким образом, корни характеристического уравнения (2.8)
следует рассматривать как комплексно сопряженные величины:
== — Ci + Ьа,1
, , . } (2.11)
К2 = а — —at— brt, f '
где _________
ах = rl bt =У j _ (r2)2.
Заметим, что комплексные величины (2.11) расположены в
областях (рис. 110)
гс > arg а у,
— тс
(2.12)
и равны по модулю, согласно тео-
реме Виета, свободному члену ха-
рактеристического уравнения (2.8),
т. е. равны единице:
|а| = 1 |а| = 1. (2.13)
Исходя из уравнения (2.6), мож-
но видеть, что двум комплексно
сопряженным корням (2.11) соот-
ветствуют два независимых дифференциальных уравнения второго
порядка:
+ aWt = 0,
dt?
l^. + auz2 = o.
5 de,
(2-14)
arg а < — у
dt? +
1 dWr
5
3. Общий интеграл основного дифференциального уравнения
(2.2) может быть теперь представлен в виде
w = Wt + W2 + Wp, (2.15)
где Wt и W2— фундаментальная система частных интегралов,
Удовлетворяющая дифференциальным уравнениям (2.14), a Wp —
частный интеграл, соответствующий неоднородному уравнению (2.2).
Введением новых переменных по формулам:
и = Уа^, v = ya^, (2.16)
232
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ. IV
нетрудно преобразовать уравнения (2.14) к уравнениям Бесселя
нулевого порядка:
du2
d2W2
dv2
1 dWi
и du
1 dW2
v dv
+ ^i=0,
+ w2 = 0.
(2-17)
Решение системы (2.17), как это следует из теории бесселе-
вых функций*), можно записать в виде:
W, (?) = ВЛ (/«!) + В2Н? (YaJ), 1
Г2(?) = B3J0 (Va~i) + ВЛН™ (Vai), J
где Jo (Va?) и Jq (Va I) —функции Бесселя первого рода, нулевого
порядка, аргументов Vai и Vai; #0° (Vai) и ft'02> (Vai) — фун-
кции Ганкеля первого и второго рода, нулевого порядка от тех
же аргументов.
Используя решение (2.18), перепишем общий интеграл (2.15)
окончательно в форме
г=влоЛГ?)+ в,н"> (Vai) +
+ B3J0(^i)+B4B(02>(Vai)+WP. (2.19)
Отметим, что для решения практических задач аргумент ци-
линдрических функций, входящих в выражение (2.19), удобнее
представить в показательной или тригонометрической форме:
Va = ei<9 = cos® г sin ср, ]
. . . (2-20)
V а = а-'4’ = cos ср — i sm ср, )
где <p = yarga, а модуль комплексных чисел Ya и Vа в соот-
ветствии с (2.13) положен равным единице.
Из выражений (2.12) и (2.20) можно видеть, что функции
htVai), H^(Vai), h(Vai), H^(Vai)
определены в областях
*) Теория бесселевых функций изложена, например, в книге Р. О. Кузь-
мина [51]. Наиболее подробное изложение см. в книге Д. Н. Ватсона [4].
(2.23)
§ 2] ОБЩИЙ ИНТЕГРАЛ ДИФФ. УРАВНЕНИЯ КРУГЛОЙ ПЛИТЫ 233
В частном случае, когда характеристика упругого основания
на сдвиг t равна нулю (г3 = 0), эти функции определяются вдоль
прямой, наклоненной к действительной оси под углом <р = ~ .
4. Так как функции Jo (У al), Н(о1} (/a?), Jo (У а ?), Н(2}(Уа£),
являются комплексными, а функция прогибов плиты W должна
быть действительной, то, очевидно, постоянные Сх, С2, С3, С4
также должны быть комплексными числами. Для того чтобы вы-
разить решение задачи через действительные функции, перепишем
интеграл (2.19) в другой форме:
W = С1Мо (?) + С2ц0 (?) + C3f0 (?) + Cigo (?) + Wp, (2.22)
где, как и ранее, Wp— частный интеграл неоднородного уравне-
ния (2.2).
Здесь введены следующие обозначения:
«о (?) = Re Jo (Уа ?) = ./»^) + /о(Ка?) ,
v0 (?) = Im Jo У а ?) = /о(Г^)^/о(^) ,
/—, (/а?) + //<2) (/а?)
fo (?) = Re И™ У al) = -° -- —р-°—----- >
£о (I) = Im Hq (V al)=-------'
Из выражений (2.23) следует, что функции u0(?), f0(?) пред-
ставляют собой действительные, а функции v0(l), g0(l)— мнимые
части функций Бесселя и Ганкеля нулевого порядка. Так как
эти функции действительны, то действительными будут и произ-
вольные постоянные С2, С3, С4. По своему поведению
функции ии (?) и v0 (?) несколько напоминают функции cos ?,
£5 sin? теории балок на упругом винклеровском основании:
при ?—>0 они остаются конечными, а при ?—>оо стремятся
к бесконечности.
Функция f0 (?) при ? —> 0 имеет особенность типа ?21п ?, а функ-
ция g0 (?) при ?-^0 обращается в бесконечность. Обе эти функции
при ?—> оо стремятся к нулю и этим несколько напоминают функ-
ции e_^cos?, e-'sin?.
5. Внося полученное нами общее решение (2.22) в формулы
(1.4) и используя известные правила дифференцирования цилин-
дрических функций, можно получить выражения для девиации,
234
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ. IV
изгибающих моментов и поперечных сил плиты:
- 4 [С1М) + с2е2 (е) + с3о3 (?) + (?) - ,
м9 = {сх (?) - (1 - J1) М1 (?)] + С2 [М2 (?) -
- (1 - р9 Ж (I)] + С3 [Мз (?) - (1 - |Х) мз (?)] +
+ с4 [М4 (?) - (1 - и) я (?)] - к2- 41 wp\,
L S J J
{C1 [!1Л11 (9 + (1 - [9 Ж (91 + ^2 (?) +
H- (1 — p.) Ж2 (?)] + C3 [piMs (?) + (1 - [X) M3 (?)] +
+C4 [piM4 (?)+ (1- pOM4 (?)] - [piV? + Цр—]Wp} ’
Q₽= - ^[ciQ1 (?) + C2Q2 (?)+C3Q3 (?) + C4Q4 (?) +^VlWP]'
В формулах (2.24) приняты следующие обозначения:
ei (9 = «1 (9 cos ? ~ Vi (9 sin <р,
б2 (9 = «1 (9sin ? + (9cos <р>
0з (?) = fl (9 c°s ? — gi (?) sin <P,
e4 (9 = fl (9 sin ? + Si (9 COS <p;
(2.25)
All (9 = «0 (9 cos 2<p — v0 (?) sin 2<p,
M2 (?) = u0 (?) sin 2<p + v0 (?) cos 2cp,
Al3 (9 = f 0 (9 cos 2cp — g0 (?) sin 2<P,
Al4 (?) = f0 (?) sin 2<p + g0 (?) cos 2ep;
Ali(?) = l«i (?) cos <p — w1(?)sin<p],
— 1
Al2 (?) = [Hi (?) sin + w4 (?) cos cpl,
AI3 (9 = у [fl (9 cos cp — g! (?) sin <pl,
AI4 (9 = у [fi (?) sin <p + g! (?) cos <p];
Qi (?) = «1 (?) cos 3cp — Vi (?) sin 3cp,
Q2 (?) = «1 (?) sin 3cp 4- w4 (£) cos 3cp,
Q3 (?) = fi (?) cos 3<p — g4 (B) sin 3<p,
Qi (?) = fi (?) sin 3cp 4- (I) cos 3<p,
(2.26)
(2.27)
(2.28)
§ 31
АБСОЛЮТНО ЖЕСТКАЯ ПЛИТА (КРУГЛЫЙ ШТАМП)
235
где
1
? = 2 arS а>
(2.29)
а комплексное число а определяется формулами (2.11).
Входящие в выражения (2.25) — (2.28) функции их(|), vx (g)
представляют собой действительные, а функции fx(|), £i(|) —
мнимые части функций Бесселя и Ганкеля первого порядка. Эти
функции определяются через функции Jx(]/a£)> -Л (У<%),
Ях2> (УаЕ) п0 формулам, аналогичным формулам (2.23).
6. Выражения (2.22) и (2.24) дают общее решение задачи об
осессиметричной деформации круглой плиты на однослойном осно-
вании. Входящие в эти выражения произвольные постоянные ин-
тегрирования Сх, С2, С3, С4 подлежат определению из соответ-
ствующих граничных условий. В классических случаях опирания
плиты (шарнирное опирание или защемление по контуру) поста-
новка граничных условий не встречает затруднений и выполняется
обычным образом:
при шарнирном опирании на контуре
М. (4) = 0;
при защемлении на контуре
IF = (А) = 0,
\ ьо /
= о
\ dp / при
(2.31)
Если плита свободно покоится на упругом основании, то, вслед-
ствие связности грунта и возможности его работы за пределами
приложения нагрузки, необходимо рассматривать бесконечную
область, лежащую вне пределов плиты.. Как было показано в § 1
настоящей главы, влияние этой области сказывается в том, что
по контуру плиты возникает фиктивная контурная поперечная
сила Q*, которая и учитывается в соответствующем граничном
условии.
§ 3. Абсолютно жесткая плита (круглый штамп)
Рассмотрим круглую плиту под действием осесимметричной
нагрузки, равнодействующая которой равна Ро. Будем предпола-
гать, что плита имеет настолько большую жесткость, что дефор-
мациями ее можно пренебречь и рассматривать плиту как круг-
лый штамп, осадка которого составляет IFX = Со (рис. 111).
236
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ. IV
Деформированное и напряженное состояние упругого основания
за пределами плиты при R р < оо определяется в общем случае
дифференциальным уравнением (7.8) гл. I. При отсутствии по-
Рис. 111.
верхностной нагрузки в пределах рассматриваемой области, это
уравнение становится однородным и принимает вид:
+ =0, (3.1)
где a = а W2 = W2 (р) — функция, характеризующая осадки
основания за пределами плиты.
Решение дифференциального уравнения (3.1) (см. гл. I, § 7)
имеет форму:
r2 = C1Z0(ap) + C2R0(ap). (3.2)
Таким образом, рассматриваемая задача сводится к определе-
нию постоянных интегрирования Си С2 и осадки плиты Со из со-
ответствующих граничных условий и условий равновесия плиты.
Поскольку деформированная поверхность упругого основания
предполагается непрерывной, а осадки основания на бесконечно-
сти — равными нулю, граничные условия, определяющие постоянные
Сг и С2, могут быть сформулированы следующим образом:
при р~ R
при р —> ОО
(3.3)
Исходя из второго условия (3.3) и учитывая поведение функ-
ции /д (ар) на бесконечности, получим:
Сх = 0. (3.4)
Значение произвольной постоянной С2 определится из первого
условия (3.3):
/-» _ бо
2“ K0(aR)
(3.5>;
§ 3] АБСОЛЮТНО ЖЕСТКАЯ ПЛИТА (КРУГЛЫЙ ЩТАМП) 237
Для определения осадки штампа Со составим теперь условие
равновесия рассматриваемой системы (плита + упругое основание),
понимаемое в смысле изложенного вариационного метода. Это
условие, характеризующее равенство нулю суммарной работы всех
внешних и внутренних сил системы на виртуальном перемещении
ау(р, z) = 1 - ср (z),
может быть записано в следующем виде:
— В 5 5 M'(z)pdpd9dz + ^ J м' (2) Р dP dz ] +
ООО о о R
+ Л4(0) = 0, (3.6)
где aZl и сгг—нормальные напряжения, возникающие в упругом
основании соответственно под плитой и за ее пределами. Согласно
общим формулам (6.4) гл. I эти напряжения определяются в виде:
^^-^0^(2),
1—vo
Fn (3.7)
1 vo
Внося формулы (3.7) в уравнение (3.6) и выполняя интегриро-
вание в указанных пределах, получим:
tC0[^ + 2^ XgR) ] = />„,
или окончательно
где, как и ранее,
Ki(aR) I
aRKo (aR) J
(3.8)
[1+2
н
(3.9)
Реактивные давления упругого основания могут быть получены
из общей формулы (7.8) гл. I подстановкой в нее выражения
W, = Со:
Ро
Я — —
П/+11 +2
Ki(aR) 1
aRKo(aR) J
(З.Ю)
Кроме распределенных давлений (3.10), по контуру круглой
плиты будут действовать также фиктивные реакции Q*,
238
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ. IV
имеющие размерность кг/см или т/м (рис. 112). Эти погонные
силы возникают в результате работы упругого основания за пре-
делами плиты и соответствуют тем бесконечно большим давлениям,
которые выявляются под краями круглого штампа точными мето-
Рис. 112.
дами теории упругости.
Значение фиктивных реакций
Q* может быть определено при
помощи общей формулы (1.8), в
которой следует положить ФЛ1=СО.
Таким образом, будем иметь:
Q* = 2/
(3.11)
Подставляя (3.2) в формулу (3.11) и учитывая (3.4), (3.5) и
(3.8), получим выражение для фиктивной реакции Q*:
,Ф =___________Ро____________К1(а/?)
_Г, , „ Ki(aP) ] аРКо(аР)
"Я1 +2
(3.12)
Отметим, что реактивные давления упругого основания, вы-
численные по формулам (3.10), (3.12), удовлетворяют статическо-
му условию равновесия щлиты 2z — 0. Действительно, нетрудно
убедиться в том, что
nR2q + 2лД(/ = Ро. (3.13)
Заметим также, что это решение справедливо при любом вы-
боре функции поперечного распределения перемещений ф(г),
с точностью до которой определена характеристика
(3.14)
При рассмотрении ряда -практических задач функцию ф (z)
удобно принять по линейному закону (2.7) гл. I или в виде
[sh п
(Ф(*)= Д Ь (3-15)
sll R
где Н —толщина сжимаемого слоя грунта, R — радиус плиты,
у—некоторый безразмерный коэффициент, зависящий от упругих
свойств основания. Например, при выборе функции ф(а) в фор-
ме (3.15) интегральные характеристики упругого основания
§ 31
АБСОЛЮТНО ЖЕСТКАЯ ПЛИТА (КРУГЛЫЙ ШТАМП)
определятся следующим образом:
(1 — vg) Zf 1
< . Е0Н л
1 12 (1 + уо)
где
3__R_
2 уН
чН ~<н -
sh R ch R + R
sh’V J
hilL hl!L ~
Щ R Ch R - R
Sh^
s R J
, 7^ ~<H ~tH
i_ sh~R~ch~R~ + R
3 u Tff u 7Z/
sh r ch r — r
R
239
(3.16)
(3.17)
Рис. ИЗ.
2 R
ф; =
основания q в зависимости от приведенной толщины сжимае-
мого слоя . Такие графики, вычисленные при v0 = 0,4 и у = 1,0,
7 = 1,5, приведены на рис. 113. При этом значения q показаны в
процентном отношении к соответствующим значениям реактивных.
1
240 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТЗ [гл. IV
давлений, рассчитанных по Винклеру. Можно видеть, что Г
реактивные давления однослойного основания q, действующие по1
подошве штампа, меньше винклеровских. Это объясняется тем, ]
что по контуру штампа возникают фиктивные силы Q*, характери- 1Й
зующие работу однослойного основания за пределами плиты и Я
эквивалентные бесконечным пикам напряжений точного решения Я
теории упругости.
Приведенные графики показывают также, что при значениях
тТ
75-, больших чем 2-г-2,5, реактивные давления практически оста-
К
ются постоянными. В результате этого деформируемое основание
уже при ^-> 2,5 может рассматриваться как упругое полупро-
странство (//= оо). С уменьшением приведенной толщины упру.
(5-<1,0+2,5)
того слоя
однослойное основание приближается
по своей работе к винклеровской схеме: реактивные давления q
увеличиваются за счет уменьшения величины краевых концентра- >
ций Q*. )
По определении реакций упругого основания изгибающие мо- j
менты и поперечные силы жесткой плиты могут быть рассчитаны 1
известными методами теории осесимметрично загруженных круглых
пластинок. При этом под внешней нагрузкой следует понимать
как активную заданную нагрузку, так и реактивные давления
упругого основания.
В качестве примера приведем формулы, определяющие значе-
ния радиальных изгибающих моментов в центре плиты от воздей-
ствия распределенных реактивных давлений q и кольцевых сил
Q* в отдельности. При обозначениях, принятых в формулах (3.10),
(3.12), будем иметь:
где
М9 (0) = qR2Mq (0), . MQ (0) = PRMq (0),
(3.18)
MQ (0) = —
M (0\ - +|a)^q(^)
" K1(aR) '
8L1 +2 aRKo(aR) j
3 + ц____
Kt (aR)
aR'K0(aR)
(3.19)
Считая, что функция поперечного распределения перемещений
4(2) выбрана в виде (3.15), а упругие постоянные основания
определены формулами (3.16), (3.17), нетрудно построить гра-
фики, характеризующие изменение величин Mq (0) и Л1о(0) в за-
висимости от приведенной толщины упругого слоя . Такой гра-
§ и
КОЛЬЦЕВОЙ ШТАМП
241
фик для Mq (0) показан на рис. 11Ф для двух значений пара-
метра у (у = 1,0 и у = 1,5) при v0 = 0,4; р. = 1/6.
Можно видеть, что по мере увеличения глубины упругого
слоя значения радиальных моментов в центре плиты увеличи-
с решением теории упругого полупространства, а при у = 1,0
отклоняется от последнего на 20 — 25 %.
§ 4. Кольцевой штамп
Рассмотрим теперь кольцевой штамп под действием осесим-
метричной погонной нагрузки Р (рис. 115), равнодействующая
которой равна
Ро = 2*RP.
Внутренний радиус кольца обозначим через Rlf внешний —
через Т?2- Для осадки поверхности упругого основания примем
следующие обозначения:
IF] (р) — осадка основания
внутри кольца, IF2 = Со—
осадка под подошвой штам-
па, Г3 (р) — осадка свобод-
ного основания за преде-
лами кольца.
Как и в предыдущей
задаче, для областей
0<Р<Я1 и R2 р < 00
циальное уравнение (3.1),
имеет место однородное дифферен-
в результате чего осадка основания
16 В. 3. Власов, Н. Н. Леонтьев
242
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ
[ГЛ. IV
определяется здесь выражениями:
^i(p) = C1/o(ap) + C2Ko(ap), 1
^з (р) = С3/0 (ар) + С,К0 (ар). j <4-1 >
Исходя из физического содержания задачи, гдля1 определения
произвольных постоянных интегрирования Съ С2,|С3, СДможно
записать следующие условия:
при р = 0 при р = Ry ^=0; dp ^1 = С0; (4-2)
при р = R2 W2 = Со;
при р^-ОО W2 = 0.
Внося выражения (4.1) в (4.2), получим:
С____ £°
1 /0(а/?1)’
С2 = С3 = О,
р ____ Ср
4 - ко (а/?2)
(4-3)
Таким образом, осадка основания для различных областей
будет представлена формулами:
'«'“Л '
W2 (Р) = Со,
W^ = K^K^-
(4-4)
Для определения осадки штампа Со составим теперь условие
равновесия рассматриваемой системы, понимаемое в смысле прин-
ципа возможных перемещений Лагранжа. По аналогии с (3.6)
это условие может быть представлено в виде
'Н 2т: Rt Н 2т: Rs
5 5 (г) р dp dO dz + <зг2ф' (2) р dp d9 dz +
. 0 0 0 0 0 fl.
Н 2т: оо
+ 5 И (г) ? dP d® dz + роф1 (°) = °-
(4.5)
§ 5]
БЕСКОНЕЧНАЯ ПЛИТА ПОД ДЕЙСТВИЕМ СИЛЫ 243
В уравнении (4.5) знак минус перед квадратными скобками
поставлен потому, что этим членом определяется работа внут-
ренних сил.
Подставляя в уравнение (4.5)
значения нормальных напряжений,
величина которых определяется
формулами, подобными форму-
лам (3.7), и интегрируя в указан-
ных пределах, нетрудно получить
выражение для осадки штампа:
Рис. 116.
Ро
Со =
.2 2 n, W) Я • (4'6)
2 + +2п/?2ко(0[/?2)а/?2]
Общие формулы (7.8) гл. I и (1.9) гл. IV при значениях (4.4)
и (4.6) позволяют определить реактивные давления упругого ос-
нования в виде:
РВ
7 =--------
"(^2-^)
Ri A (afli) Rl Ki(aR2)
R% — R*aRiIo<aPi) + Rl~R[ aRzKotaRz)
Qt=---------
^(Rf-Ri)
p Rt.
°K1 aRiI0(aRi)
I Ri
1 + 2 \ #2-^1
li(aRi) Rz Ki(aRz)
a/?i/0(a/?i) + p>2_ R2 a/?2K0(a/?2)-
_ Ki(aRz)
0<2 aRzKolaRz)
\ R22~ R1 aRir<>(aRl) +
Rl Ki(aRz) \
Rz aRzKoiaRrf j
где под Q* и Q* следует понимать фиктивные контурные силы,
действующие соответственно на внутреннем и внешнем контурах
штампа (рис. 116).
§ 5. Бесконечная плита под действием сосредоточенной силы
Рассмотрим бесконечную плиту, загруженную сосредоточен
ной силой Р (рис. 117). Начало координат поместим в точку
приложения силы, в результате чего будем иметь осесимметрич-
ную однородную задачу, для которой справедливо дифференци-
альное уравнение
- 2ttfW + kW = 0. (5.1)
16*
244
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ
[ГЛ. IV
Решение уравнения (5.1), как это было показано в § 2 на-
стоящей главы, может быть представлено в виде
W = C1Uo (?) + C2v0 (?) + C3f, (?) + Cigo (?), (5.2)
где
4
Расчет плиты сводится, таким образом, к определению по-
стоянных интегрирования Clt С2, С-, Ci.
Рис. 117.
По условиям задачи при
?-» оо все усилия и перемещения
плиты должны обращаться в
нуль. Так как функции и0(%)
и и0 (?) при ? —> оа стремятся к
бесконечности, то очевидно
Ci = С2 = 0. (5.3)
прогиб плиты должен оставаться
при ?—>0 представляет собой
В начале координат (? = 0)
конечным. Так как функция f0(?)
конечную величину, а g0(?)
стремится к бесконечности, то коэффициент при g'o (?) должен рав-
няться нулю и, следовательно, С4 = 0.
Таким образом, будем иметь:
r-C3f0(?). (54
Для определения постоянной С3 рассмотрим условие равной!
сия элементарного цилиндра (р-^0), выделенного из плит
и упругого основания в начале координат (рис. 118), В смыс.
изложенного вариационного метода это условие может бы'
§5] БЕСКОНЕЧНАЯ ПЛИТА ПОД ДЕЙСТВИЕМ СИЛЫ 245
представлено в виде
jw₽pd0 + P = O, (5.5)
о
где — обобщенная поперечная сила, определяемая формулой
(1.5).
Заметим что обобщенное условие (5.5). может быть записано и
в обычной форме:
J Qp9d0 + P= 0, (5.6)
о
поскольку по условиям задачи в начале координат девиация
равна нулю:
при р = 0 ^ = 0. (5.7)
На основании последней из формул (2.24) получим выраже-
ние для поперечной силы:
Г'о
Внося выражение
указанных пределах,
ную Cs в виде
(5.8) в уравнение (5.6) и интегрируя в
можно определить произвольную постоян-
PL3
С = °
3 ' 4Osin2<p
(5-9)
Формулы (5.4) и (2.24) позволяют теперь получить оконча-
тельные выражения для перемещений и усилий бесконечной плиты:
IF = 40 sin 2<р W’
dW
dp ~ 4Osin2<p SW’
p —y
мр =
м0 = 1р-адчч1-!А)лм)],
Q₽ = p 4£0sin2<p
(5.10)
где функции 63, М3, М3, Q3 определяются общими формулами
246 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ плит I
(2.25) — (2.28) или в раскрытом виде следующими рядами:
ОО
«>®=0-Ю 2 4^4Г‘^2<'"+'4-
т — О
оо
-жч з аг+-2 <»+>?+
т=0
оо
+ ?iSin2T + A s
2п г 1 тс т\ (т Н- 1)!
tn = 1
X (т)2Ш + 'sin2(m + 1)<р(1 + у 4- . • • + ^),
оо
лма = (|-2-’) 2 bff-(4)”sin2(ra+i).f-
4 т = о v '
оо
tn — о ' ' Х
оо
-4 з t^(4)"s1n2(m + I)9(i+i+
+т + •••*• s) > I
«•«Н>-24) 3 Sfew®“»s2<m+^-
--0"т + 4 3 -тЬ^®”=1п2(т+ 1)? +
тс \ 2 1 / о т\ (т + 1)! \ 2/ v 1 / г ।
-L Sin2(P I 1 У Y
‘ 7Г r It ml(m + l)lA
tn ~ 1 v '
/ £ \ 2m . _ , , A d\
x (y) sm 2(m+ l)<pp + 2-+... + —) ,
oo
<Ы0 = (‘-г) 3 У4(4)" + *соз2(т + 2)т_
m — 0
co
-K'4+4 2 ^&©“+1='"2<'" + 2)t-
tn = о
---1 sin 2<p — y- sin 4cp 4- — 5] x
"5 r 2те г n (m-j-1)! л
X (у)2"1 +1 sin 2 (m + 2) <p (j 4- j 4- . . . + 1?).
$ 6J УПРУГАЯ ПЛИТА КОНЕЧНЫХ РАЗМЕРОВ ' 247
Удерживая в рядах (5.11) ограниченное число членов, можно с
достаточной для практических целей точностью вычислить пере-
мещения и усилия плиты в наиболее загруженных сечениях при
значениях р, близких к нулю.
Отметим, что при ср — 45°, т. е. при отсутствии сил сдвига в
упругом основании, полученное решение в точности совпадает с
решением Герца для бесконечной плиты на упругом винклеров-
ском основании.
§ 6. Упругая плита конечных размеров
Общее решение задачи о круглой плите на упругом основа-
нии изложено нами в § 2 настоящей главы. Здесь мы рассмот-
рим только несколько частных примеров, поясняющих общую
теорию.
Для возможности проведения практических расчетов, в при-
ложении (см. табл. 12) приведены таблицы функций Бесселя
1-го рода комплексного аргумента, а также таблицы функций
t>i (ё), 6г(*)> Мг(£), Л42 (S), Mi (;), TW2(S), определяющих деформи-
рованное и напряженное состояние плиты. Таблицы составлены
через 1° в области 45°<С‘Р<С65° и дают значения соответствую-
щих функций для сечений с относительными координатами
? = = 0; 0,05; 0,10; 0,15; ... ; 1,0.
Ьо
Для расчета плит, геометрические размеры и физические свой-
ства которых таковы, что аргумент £ соответствующих функций
превосходит предел приведенных таблиц, следует обратиться к
монографиям [4], [86], позволяющим вычислять функции Бесселя
1-го рода нулевого и первого порядков. При этом переход к
функциям 61 (£), 62 (|), . . . , ТИ2(В), которыми определяются девиа-
ция, изгибающий момент и поперечная сила плиты, может быть
произведен на основании зависимостей (2.25) — (2.28). ♦
Кроме того, для возможности бестабличного расчета плит при
р
Sr = f- > 1,0 в рассмотренных ниже примерах приведены ряды,
которыми определяются все необходимые расчетные величины.
1. Круглая плита под действием равномерно рас-
пределенной нагрузки. Рассмотрим расположенную на уп-
ругом однослойном основании круглую плиту радиуса R, находя-
щуюся под действием равномерно распределенной нагрузки интен-
сивности р (рис. 119).
Дифференциальное уравнение изгиба такой плиты может быть
записано в следующем виде:
- 2r^lW! + Wi = , (6.1)
248 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ. IV
где ? = у---приведенная координата, a ri и Lo — обобщенные ха-
рактеристики плиты и упругого основания, определяемые по фор-
мулам:
/£2 4 ,—
Для области,
внешней по отношению к плите, справедливо
Рис. 119.
однородное дифференциальное уравнение, которое в безразмер-
ных координатах имеет вид:
v|№2 — 4r2 = 0, (6.3)
где
4 = ^ = -2/. (6.4)
Входящий в уравнения (6.1) и (6.3) оператор Лапласа опре-
деляется в форме
2 _ d2 1 d _
V5 d^+S,dE,' t6,5)
Ранее было показано, что общее решение дифференциальных
уравнений (6.1) и (6.3) может быть представлено в виде:
= C1Uo (?) + C2v0 (?) + Csf0 (?) + CigQ (?) + f, (6.6)
W% = Cs/0 (<x0?) -j- C6K0 (<Xq?), (6.7)
где — частный интеграл неоднородного дифференциального урав-
нения (6.1); /0(а0?), Ко(ао?) — модифицированные бесселевы фун-
кции первого и второго рода нулевого порядка аргумента а0?;
Ci, . . . , С6 — произвольные постоянные интегрирования.
Таким образом, решение задачи об изгибе плиты, свободно
лежащей на однослойном упругом основании, определяется с точ-
ностью до шести постоянных интегрирования. Исходя из физиче-
j 6] УПРУГАЯ ПЛИТА КОНЕЧНЫХ РАЗМЕРОВ g49
ского содержания задачи, для вычисления этих постоянных можно
поставить шесть независимых граничных условий:
при р = 0 (5 = 0) ^ = 0, $QpPd6=0; 0 (6.8)
при р = R Мр = 0, (6-9)
при р —> ОО (£-> °°) 1*Мр) = о. (6.10)
Условия (6.8) характеризуют равенство нулю девиации и по-
перечной силы в центре плиты, условие (6.10) — затухание осадок
упругого основания на бесконечности. Выражениями (6.9) опре-
деляются граничные условия на свободном от закреплений и на-
грузки крае плиты при р = R. При этом второе условие (6.9)
учитывает влияние свободного основания, расположенного за
пределами плиты, на напряженное состояние последней
[см. (1.8)]
На основании соображений, изложенных в § 3 и § 5 ]см.,
например, (3.4) и (5.4)] и относящихся к условиям (6.8) и (6.10),
постоянные Cs, Ct и С6 следует положить равными нулю:
С3 = С4 = С6 = 0, (6.11)
после чего прогибы плиты и осадка поверхности свободного
основания определятся в виде:
W1 = C1u0(l) + C2v0^+ ‘ (6.12)
й72 = СЛоЫ)- (6.13)
Исходя из третьего условия (6.9), нетрудно получить выраже-
ние для постоянной С6:
СпМ^ + С^о «д) + -|
Св = Ко («о?#)
t к
где b .
Оставшиеся произвольные постоянные С± и С2 можно опреде-
лить теперь из не использованных еще пеовог-о и второго усло-
вий (6.9). Раскрывая эти условия при помощи общих формул (1.4),
(6-14)
250 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ. IV
получим:
‘2И7 1 — dFt п \
------ГЧг -°’
d 2 2iLl\dW1_dW1l (6.15)
^75^1 =-----'D~l-d5 d? J ’ f
Подставляя (6.12) и (6.13) в выражения (6.15) и используя
известные правила дифференцирования цилиндрических функций,
будем иметь:
т1С1 + т2С2 = 0, 1
п1С1 + п2С2 = Gp, |
где
mi = Mi(?^)-(l-!x)M1(?«),
/и2 = М2 fa) — (1 — [х) М2 (?«),
п ,е , , Ki(ao^)
«1 Qife)+ 2 — “о (Вд) аоко (Ио5 ),
0 ’ (6.17)
„ -О (Р 1 -4- 02(^ v(t\Kl^ '
"2~Q2fo)+—2-------
р _Р_ (а°*к)
р k аоКо (aojfl)
Решение системы алгебраических уравнений (6.16) позволяет
получить для постоянных интегрирования Сг и С2 следующие
выражения:
_ GPnh
— т2щ
Gpmi
^1П2 — т2П1 ’
(6.18)
По определении произвольных постоянных, деформации и усилия
круглой плиты могут быть рассчитаны по известным формулам:
CiU0 (?) 4- C2v0 (?) + >
^ = -^[СЛЮ + с2е2(?)],
m₽=^[CA(I) + c2l2(?)],
Lo . - (6.19)
Me = ^tc1r1(?) + c2r2(?)],
Z-o-
Q₽ = -73[C1Q1(?) + C2Q2(?)].
5 6]
УПРУГАЯ ПЛИТА КОНЕЧНЫХ РАЗМЕРОВ
251
Входящие в выражения (6.19) функции u0(g), ^о(Е), • • • » Qa(^)
определяются рядами:
«о (9= 3 дыг(4Гсо52гасР’
т — о
•’•©= 3 W“© sm2nf’
tn = о
°° (_ I) m \гт + 1
<Ш = 3 (т!)(т"+1)ГЫ COS 2 (/и + 1)<р,
m = о
“ (— I)"1 /£\2m + l
M?) = 3 ml (m + 1)1 \2J sin 2(tn 4- l)<p,
m — о
Mi(E)= zj W'j) cos 2 (tn + 1) cp,
m = 0
7 (—l)m /?\2m
Mi(£) = 3 (ml)2 \2/ sin 2 (tn + 1) <p,
m = 0
— 1м (—1)OT f %A2m
ад = | 3 cos2(/n + i)?.
m = 0
— 1 V (— i)m (z,\-m
^2(^)=y3 ml (in +l)l Ы sin 2 (/n+1)?,
m = о
(—I)"1 + 1
Qi®- 3 m\(m+l)l W COS 2 (tn + 2) cp,
m = 0
°° (_ j)"1 /? \zm + 1
3 m!(m + l)! Ш Sin 2 (tn + 2) cp, .
m = 0
м® = ад- (i - и) 5
ад = ад-(1-[х)ад,
ад = !*ад + (1-р0ад),
a2($) = + (i - n)M2(i).
(6.20)
2. Круглая плита под действием равномерно
распределенной контурной нагрузки. Если круглая
плита находится под действием контурной нагрузки Pk (рис. 120),
то основное дифференциальное уравнение (6.1), устанавливающее
зависимость между внешней нагрузкой и прогибами плиты, стано-
вится однородным. Общее решение рассматриваемой задачи может
'252 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ КРУГЛЫХ ПЛИТ [ГЛ. IV
быть представлено поэтому в виде:
Г i = C1Uo (?) + C2v0 (?) + C3f0 (?) + CiSa (?), 1
^2 = C5I0 (а0?) + СйК. (а0?). )
Как и в первом примере, граничные условия запишутся здесь
в форме (6.8) — (6.10), за исключением второго условия (6.9),
Рис. 120.
вместо которого следует записать:
при Р = R Q₽ = 2/ + Р1г. (6.22)
На основании рассуждений, совершенно аналогичных тем, ко-
торые были приведены выше, нетрудно получить:
с, = с„ = с. = о, с. = + , (6.23)
после чего прогибы плиты Wr и осадка свободного основания W2
в области р > R определятся в виде:
Wi = C1Uo (?) + C2v0 (?), W2 = СвК0 (а0?). (6.24)
Раскрывая не использованные еще граничное условие
первое из условий (6.9), будем иметь:
v 1 £ d; j
d 2ZLo (dw* dw'\ I PkL° П I
(6.22) и
(6.25)
Подставляя теперь выражения (6.24) в (6.25), получим, как и
ранее, систему двух алгебраических уравнений относительно по-
стоянных и С2.
т2С2 — 0, njCj -р п2С2 —
(6.26)
Входящие в уравнения (6.26) коэффициенты т2, пь п2
определяются формулами (6.17), а свободный член Gpk, характе-
ризующий внешнюю нагрузку, имеет вид:
Р L3
(6-27>
§ 6]
УПРУГАЯ ПЛИТА КОНЕЧНЫХ РАЗМЕРОВ
253
Таким образом, постоянные интегрирования CL и С2 могут
быть снова рассчитаны по формулам (6.18), в которых следует
заменить только Gp на Gpk. При этом прогиб плиты определяется
первой из формул (6.24), а девиация,
перечные силы — по формулам (6.19).
3. Круглая плита под дей-
ствием распределенных по
контуру моментов. Рассматри-
вая плиту, представленную на рис. 121,
можно видеть, что для решения по-
добной задачи остаются справедливы-
изгибающие моменты и по-
ми все приведенные выше выкладки.
Действительно, для областей О «Д
и «С I < оо общее решение задачи
может быть записано в виде (6.21), причем,
но получить:
С3 = С4 = С5 = О,
_ Сщо (5Л) + С2»о (5Л)
Сб = АДТДРД
Рис. 121.
как и ранее, нетруд^
(6.28)
Значения ^постоянных интегрирования С± и С2 определятся из
граничных условий:
при р = R (5 = h) М^Мк, Q = (6.29)
Раскрывая эти условия при помощи общих формул (1.4) и
(6.21), а также учитывая (6.28), получим:
trijCi —р nuCR — Gу, —р ц2С2 — 0.
(6.30)
Коэффициенты системы (6.30) рассчитываются, как и ранее,
по формулам (6.17), а свободный член Gm имеет вид:
= (6.31)
Для произвольных постоянных CL и С2, определяющих реше-
ние задачи, будем, таким образом, иметь:
_m2G^ -----
1 Ш1П2— П1/«2 ^1^2 — ^1^2 х
ГЛАВА V
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ПОЛОГОЙ
СФЕРИЧЕСКОЙ ОБОЛОЧКИ НА УПРУГОМ ОДНОСЛОЙНОМ
ОСНОВАНИИ
§ 1. Основные дифференциальные зависимости теории пологой
сферической оболочки
1. Тонкостенные пространственные конструкции, очерченные
по части некоторой поверхности и имеющие малый подъем по
сравнению с размерами конструкции в плане, называются пологими
оболочками. Исследования показывают, что оболочка, подъем
которой не превышает х/6 наименьшего размера Zmin в плане, может
быть отнесена к категории пологих оболочек.
Так как при < 4- кривизны оболочки весьма малы, пред-
Zmin b
ставляется возможным отождествить внутреннюю геометрию сре-
динной поверхности пологой оболочки с евклидовой геометрией
на плоскости. Геометрический смысл этого весьма важного для
пологих оболочек допущения состоит в том, что первая квадра-
тичная форма поверхности пологой оболочки заменяется соответ-
ствующей квадратичной формой для плоскости. Это означает
также, что’ гауссова кривизна, определяемая формулой
К = kik2 == ,
для пологих оболочек весьма мала и может быть приближенно
принята равной нулю.
Помимо отмеченных допущений, при рассмотрении общих урав-
нений равновесия пологой оболочки принимаются во внимание
только главные моментные члены, не содержащие в качестве мно-
жителей кривйзны поверхности и производные от этих кривизн.
Все остальные моментные члены, как весьма малые и не оказывающие
существенного влияния на внутренние силы и изгибающие моменты
оболочки, отбрасываются *).
*) Общая теория пологих оболочек предложена впервые В. 3. Власовым.;
Подробное изложение этой теории дано в монографии В. 3. Власова [8]. ;
ОСНОВНЫЕ ЗАВИСИМОСТИ ТЕОРИИ ОБОЛОЧКИ
255
2. Рассмотрим пологую оболочку, имеющую форму части сфе-
рической поверхности радиуса Р (рис. 122). Пусть р и 9 —полярные
координаты точки горизонтальной плоскости, над которой возвы-
шается оболочка. Будем считать, что полюс оболочки при проек-
тировании его на эту плоскость совпадает с полюсом полярных
координат р, 9. При этом в силу геометрических гипотез, ле-
жащих в основе общей теории пологих оболочек, незави-
симые переменные р и 9 будут также
и координатами точек, лежащих на
срединной поверхности оболочки.
Предположим, что рассматривае-
мая оболочка находится под дейст-
вием одной только нормальной наг-
рузки Z, положительное направление
которой совпадает с направлением
внешней нормали (рис. 122). В этом
случае все статические и геометри-
ческие уравнения, характеризующие
напряженное и деформированное со-
стояние пологой сферической оболоч-
ки, могут быть сведены к следующей
системе двух дифференциальных урав-
нений:
Я V2V2O _ w =0
Eh ’
_L V2<D + DV2V2ay — Z = 0,
I\
Рис. 122.
где w = w (p, 9) — нормальное перемещение оболочки (это переме-
щение принимается положительным, если оно направлено по внешней
нормали), а Ф = Ф(р, 9) — функция напряжений, определяющая
внутренние тангенциальные силы оболочки по формулам:
М 1 дф 1 д2Ф
₽ р др ' р2 д02 ’
.. д2Ф
~ др2 ’
1 д2Ф 1 дФ
5 — др дб + р2 дб •
(1-2)
Под символом V2 в уравнениях (1.1) понимается дифферен-
циальный оператор второго порядка:-
= (L3>
256 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ.
Величины h и D представляют собой соответственно толщину
оболочки и ее цилиндрическую жесткость:
D = 12 (1 — [г2) ’
В соответствии с физическим смыслом первое уравнение (1.1)
может быть названо геометрическим, поскольку оно выражает
собой условие неразрывности деформаций, а второе уравнение —
статическим, поскольку это уравнение характеризует условие
равновесия оболочки в направлении нормали.
Если ввести новую скалярную функцию F = F (р, 9) так, чтобы w
и Ф согласно первому из уравнений (1.1) определялись через эту
функцию по формулам:
w = V2V2F,
Q==^_w,
(1-5)
то второе уравнение (1.1) примет следующий вид:
£)V2V2V2V2f +^aV2V2F — Z = 0. (1.6),
Заменив теперь в этом уравнении V2V2E на w, получим:
DV2W + — Z = 0. (1.7)
Можно видеть, таким образом, что нормальные перемещения w
сферической оболочки определяются дифференциальным уравнением
четвертого порядка (1.7), имеющим точно такую же структуру,
что и уравнение изгиба пластинки на упругом винклеровском
основании с коэффициентом постели k, равным
, Eh
k —
Отсюда следует, что в отношении деформаций, определяемых
одними только прогибами w, имеется полная аналогия между
пологой сферической оболочкой и надлежащим образом закреп-
ленной на контуре круглой пластинкой, лежащей на упругом
основании. Как и в случае изгиба круглой пластинки, деформации
изгиба хр, хе и кручения t определяются здесь формулами:
§ 1] ОСНОВНЫЕ ЗАВИСИМОСТИ ТЕОРИИ ОБОЛОЧКИ
257
3. Внутренние усилия в пологой сферической оболочке, дей-
ствующие в сечениях р = const, 6 = const, могут быть разделены
на две группы: осевые (тангенциальные) силы jVp, Ne, S, соответ-
ствующие безмоментному состоянию оболочки, и изгибающие
и крутящие моменты Мр, Мв, И и
поперечные силы Qp, Q8, соответ-
ствующие ее изгибному состоянию.
Положительные направления этих
внутренних усилий на площадках с
положительными внешними норма-
лями показаны на рис. 123.
Рис. 123.
Рис. 124.
Как было отмечено выше, первая группа сил определяется ,
функцией напряжений Ф = Ф(р, 0) по формулам (1.2). Вторую
группу сил характеризует функция перемещений ш=ш(р, 0). В силу
отмеченной выше аналогии эти силы вычисляются точно так же,
как и в случае изгиба круглой пластинки:
Мр = — D (х„ + р.хв),
Мв = — D (х8 + [лхр),
Н = D (1 — [л) т,
(1.9)'
1 а (МО>
где хр, х8, т определяются по формулам (1.8), а дифференциальный
оператор V2 — по формуле (1.3).
Для нахождения тангенциальных перемещений оболочки и (р, 0),
и v (р, 0), направленных по касательным к координатным линиям
р= const, 0 = const (рис. 124), следует рассмотреть физические,
зависимости, устанавливающие связь между усилиями безмоментного
17 В. 3. Власов, Н. Н. Леонтьев
258 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V
состояния Мр, Л19, S и деформациями оболочки:
= (1 —р.2) (е₽+ Иее)> ^9 = (1 _ р.2) (е +Ие₽), 5 = 2^1р) ы>
(1.11)
где sp, е9, w — соответственно деформации растяжения (сжатия) и
сдвига.
В случае пологой сферической оболочки деформации sp, s9, ы,
входящие в выражения (1.11), определяются через перемещения
и, v и w по формулам:
ди . w ,
е'=т +
1 ди и , w j
Ее = Тй0+т + т’ н1-12)
____ 1 ди . dv v I
W ~ р <30 dp Р ' !
Таким образом, после определения функции напряжений Ф
и нормального перемещения w из системы (1.1) и при наличии
формул (1-2) и (1.11) тангенциальные перемещения оболочки и
\ и v могут быть найдены из диф-
/: ференциальных уравнений (1.12),
/ I в которых величины w, ер, г0 и
Ч j w следует считать известными.
j Ч § 2. Дифференциальное
уравнение сферической оболочки
на упругом однослойном
основании
Допустим, что пологая сфе-
рическая оболочка расположена
на упругом основании, свойства
которого описываются дифферен-
циальным уравнением вида
2/V2to — kw + q = 0, (2.1)
оператор, определяемый формулой
характеристики упругого основания;
Поскольку нормальные перемещения оболочки w и осадки
упругого основания совпадают по всей поверхност контакта
оболочки с основанием (рис. 125), дифференциальные уравнения .
(1.7) и (2.1) могут быть рассмотрены совместно:
DV2V2w + ~ w — Z = 0, — kw+",q = 0- (2.2)
Рис. 125.
где V2 — дифференциальный
(1.3), k и t — обобщенные
q — нагрузка на основание.
§2] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ОБОЛОЧКИ 259
Замечая, что внешняя по отношению к оболочке нагрузка
состоит из заданных сил р и реактивных давлений основания q:
Z = p—q, (2.3)
и исключая из (2.2) величину q, получим:
D^2w — 2tV2w + (k+-^w = p. (2.4)
Дифференциальное уравнение (2.4) характеризует состояние
изгибной деформации сферической оболочки на упругом однослой-
ном основании. Можно видеть, что это уравнение совпадает по
виду с уравнением изгиба пластинки на однослойном основании
(см., например, (1.1) гл. IV). Отличается только коэффициент
при w, который в данном случае состоит из двух частей, т. е.
увеличен по сравнению с соответствующим коэффициентом уравне-
ния (1.1) гл. IV на величину Eh/ R2.
Таким образом, все статические и кинематические факторы
рассматриваемой сферической оболочки, соответствующие [состоя-
нию ее изгибной деформации, определяются так же, как и в случае
изгиба круглой пластинки на упругом основании, который был
рассмотрен в главе IV.
Для определения напряжений и перемещений безмоментного
состояния оболочки следует рассмотреть первое из уравнений
системы (1.1):
JLv2V2O=V2w. (2.5)
Уравнение (2.5) может рассматриваться как неоднородное
бигармоническоё уравнение, поскольку функция w, представляющая
собой решение уравнения (2.4), считается здесь заданной. Определив
функцию Ф из уравнения (2.5) и соответствующих граничных
условий, найдем тангенциальные усилия, деформациши переме-
щения сферической оболочки по формулам (1.2), (1.11), (1.12).
Если задача о расчете пологой сферической оболочки может
быть отнесена к категории осесимметричных, то в разрешающих
уравнениях (2.4), (2.5), а также ео всех других зависимостях,
связанных с определением напряженного и деформированного
состояния оболочки, следует отбросить производные по 0. При
этом оператор Лапласа примет более простую форму:
Л2 1 d
V2 = (2.6)
. dp2 р dp . ' '
Значительно упростятся также и все остальные расчетные
выражения.
17*
260 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V
Так, на основании формул (1.8), (1.9), (1.10) для моментов
и поперечных сил оболочки будем иметь:
Л4Р = —Di'v2^ —Д ,
р I р dp J ’
= + (27)
Qp = — d4~ V2IV,
p dp ’
Qo = н = 0.
На основании формул (1.2) и (1.12) получим:
1 4® »r d2® О А /А О\
Vp =------j— , N& = —j j-, S = 0; (2.8)
p p dp ’ dp2 ’ ’ ' ’
du W и W n ,o n,
= S« = r + -R’ W = 0- (2-9)
В выражениях (2.7)—(2.9) функции W = W (p), Ф = Ф(р),
и = и (p) являются функциями одной независимой переменной р.
§ 3. Общее решение основных дифференциальных уравнений
в случае осесимметричной деформации
1. Изгибное напряженное состояние оболочки.
Как и в случае изгиба пластинки, введем вместо р безразмерную
координату ?= , где
' ‘ <3-»
Дифференциальное уравнение (2.4) преобразуется при этом
к виду
- 2r^fW + W = , (3.2)
где
= ТГ - (з.з)
„2 _ d2 1 d zo .
V’ di + ? d^ ’ (3’4)
Общий интеграл дифференциального уравнения (3.2) по аналогии
с интегралом (2.2) гл. IV может быть представлен в форме
Г = C1Ua (?) + C2v0 (?) + C3f0 (?) + Cigo (?) + Wv, (3.5)
§ 3J ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ ДИФФ. УРАВНЕНИЙ 261
где и0 (?), v0 (?), f0 (?),jt0 (?) — соответственно действительные и мни-
мые части функций Бесселя и Ганкеля нулевого порядка, а
WP — частный интеграл уравнения (3.2). На основании общего
решения (3.4) все статические и кинематические факторы оболочки,
соответствующие ее изгибному состоянию, определятся -формулами
(2.24) гл. IV, в которых под Lo следует понимать величину (3.1).
2. Безмоментное напряженное состояние оболоч-
к и. Для отыскания функции напряжений Ф — Ф (р) рассмотрим
дифференциальное уравнение (2.5). Заменив переменную р на
безразмерную координату £ = р / Lo, где величина Lo определяется
формулой (3.1), перепишем уравнение (2.5) в виде
Ehl?
7|7|Ф =V|IV. (3.6)
Входящая в уравнение (3.6) функция W = W (?) определяется
формулой (3.5), а дифференциальный оператор — формулой (3.4).
Общее решение дифференциального уравнения (3.6) может быть
представлено в форме
ф==__А(фо + ф^), (3.7)
где Фо = Фо (?) — общее решение однородного бигармонического
уравнения, соответствующего уравнению (3.6); Ф«г = Ф^(?)— ча-
стный интеграл неоднородного уравнения
= V|U7. (3.8)
Решение однородной бигармонической задачи в осесимметричной
постановке хорошо известно. Это решение имеет следующий вид:
Фо = С5 + С6?2 + С7?2 In ? + С8 In ?, (3.9)
где С6, Св, С7, С8 — постоянные интегрирования.
Частный интеграл неоднородного бигармонического уравне-
ния (3.8) может быть представлен в виде
Фде- = — (?) -|- С2^>2 (?) Ч- Сзфз (?) Ч- (?)] 4- Фр, (3.10)
где Фр — частный интеграл, соответствующий частному интег-
ралу Wр решения (3.5), а функции cpi, %>2, ?з, 9а определяются
формулами:
91 (?) = «о (?) cos 2ср + v0 (?) sin 2ср,
?2 © = — w0 (?) sin 2<p + v0 (?) cos 2<p,
?3 (?) = fo & cos 2<p + go (?) sin 2?,
?4 (?) = - fo (?) sin 2cp + go (?) cos 2<p;
(З.И)
262 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V 1
I
здесь, как и ранее, J
• <? = arg(Ka) =4'аг§а>
где а — комплексное число, определяемое формулами (2.11) гл. IV
в соответствии с выражениями (3.3) и (3.1).
Непосредственной подстановкой нетрудно убедиться, что реше-
ние (3.10) действительно удовлетворяет неоднородному уравне-
нию (3.8).
Таким образом, общий интеграл дифференциального уравне-
ния (3.6) в соответствии с полученными решениями (3.9) и (3.10)
может быть записан в виде
EhL2n
ф = —1— Ст (В) — С2ср2 (?) — С3ср3 (?) — С4ср4 (?) +
+ съ + св?2 + с7?2 in ? + с8 in ? + <dpj. (з. i 2)
На основании выражений (2.8) получим выражения для нор-
мальных усилий:
VP = [С1П1 (?) + С2/г2 (?) + С3п3 (?) + C,nt (?) +
+ 2С6 + С7(1 + 21п^) + С8^ + ^-^], (3.13)
N, = ~ [и0 (?) - «1 (?)] + С2 [Оо (?) - «2 (?)] +
+ с3 [f0 (?) - п3 (?)] + С4 [g0 (?) - п4 (£)] 4- 2С6 +
1 <*2Ф„ 1
С7 (3 + 2 In ?) - С8 А- + -^} • (3.14)
Входящие в выражения (3.13), (3.14) функции пу, п2, п3, пА
определяются формулами:
«1 (?) = y l«i (?) cos «Р Hi (?) sin ср],
п2 (?) = А[— Ы1 (В) sin ср, + о4(?) cos ср],
«з (?) = у [h (?) c°s <Р + gi (?) sin ср],
«4 (?) = у [— f • (?) sin <p + gj (?) cos cp],
'3.15)
где, как и ранее, ul? vt, fL, gL — соответственно действи-
тельные и мнимые части функций Бесселя и Ганкеля первого
порядка.
§ 3] ОБЩЕЕ РЕШЕНИЕ ОСНОВНЫХ .ДИФФ. УРАВНЕНИЙ 263
Рассмотрим теперь деформированное состояние оболочки.
В безразмерных координатах дифференциальные уравнения (2.9),
устанавливающие зависимость между деформациями и перемеще-
ниями оболочки, примут вид:
Т1 U . W до.ю;
80 “ Lo Ц + R '
В соответствии с физическими уравнениями (1.11) и выраже-
ниями (3.16) нетрудно получить:
v i л/ Eh , . . Eh Г 1 (du . и \ . 2W1 ,7.
& + ее) = [-ц + т) + -r-J • (3.17)
С другой стороны, исходя, из выражений (2.8), записанных
в безразмерных координатах, и формулы (3.7), получим выражение
для суммы нормальных усилий Np и Ne:
(Фо + Фг). • (3.18)
Lo
Учитывая соотношение
?|ФК, = 1С, (3.19)
вытекающее из дифференциального уравнения (3.8), перепишем
выражение (3.18) в виде
Я + Л^О = + W). (3.20)
Сопоставляя (3.17) и (3.20), получим:
После несложных преобразований выражение (3.21) может быть
представлено в виде
+ А = И)?|ФО- (1 + р)Г]. (3.22)
£ R
Полученным дифференциальным уравнением (3.22) устанавли-
вается связь между искомым тангенциальным перемещением и
и известными функциями Фо и W. Внося (3.9) и (3.5) в уравне-
ние (3.22), получим окончательно:
~ + = 2а {(1 _ И) [4С6 + 4С, (In I + 1)] -
-- (1 + и) [ClU0 (0 + (?) Csfo (?) + (?) + И7р]}. (3.23)
264 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V
Общее решение дифференциального уравнения (3.23) имеет вид:
м = {- (h’+ И) [CiXi (?) + С2Х2 (В) + СзХз (?) + QX4 (В) +
+ + (1 — [Л) [2Ceg + с7(261п^ + £)] +uP}, (3.24)
. Lo (1 + u) 1
где —A в ~s----------интеграл однородного уравнения, опреде-
« « Lo (1 + р)
ленный с точностью до постоянной величины —; ир — ча-
стный интеграл, соответствующий функции Wp; ^функции JX1 (|),
Хг(?), Хз(?)> Х«(?)> определяются формулами:
Xi (?) = “г (?) c°s <р + th (?) sin
Ха(?) = — u4(?) sin 9 +^(^cos 9,
Хз (?) = fi (?) cos 9 + gt (В) sin 9,
X4 (?) = — fi (?) sin 9 + (?) cos 9.
Отметим, что при выводе дифференциального уравнения (3.23),
вследствие сложения нормальных усилий (3.13) и (3.14), выпадает
из поля зрения константа С8. Между тем в формуле (3.24), опре-
деляющей тангенциальное перемещение и, появилась новая постоян-
ная Др Нетрудно убедиться, что постоянные С8 и Д4 тождественны
между собой. Действительно, подставляя, например, решение
= _ М1+Е2 (3.26)
с
очевидную для пологой сферической оболочки зависимость
* г Eih Г 1 / du । и \ । , ч > х "| . г, 0*74
— 1 — [77\+ ( 1 (3-27)
получим для той части радиального усилия, которая определяется
только перемещением и0, т. е. первым членом формулы (3.17),
№==^-Л-^-. (3.28)
Сравнивая эту величину с величиной радиального усилия, харак-
теризуемого членом при постоянной С8 в формуле (3.13), можно
видеть, что
Д1 = Се.
Приведенные выкладки показывают, что проблема расчета
пологой сферической оболочки сводится к определению восьми
произвольных постоянных интегрирования, количество которых
в точности соответствует порядку исходной системы дифферен-
циальных уравнений (1.1). Из этих постоянных первые четыре
(С11вС2, Сз, Ci) соответствуют изгибному состоянию и последние
четыре (Св, С6, С7, С8)— безмоментному состоянию оболочки.
4] ПОЛОГАЯ ОБОЛОЧКА ПРИ РАВНОМЕРНОЙ НАГРУЗКЕ 265
Заметим, что произвольная постоянная С6 не влияет на деформи-
рованное и напряженное состояние оболочки, следовательно, она
может быть отброшена, как несущественная. Следует отбросить
также решение, представленное в формулах (3.13), (3.14), (3.24)
логарифмической функцией, так как логарифмическая функция
в случае двусвязной области (каковой может являться оболочка)
многозначна и не удовлетворяет условию единственности решения.
Для этого нужно постоянную С7 при логарифмической функции
положить равной нулю.
Можно видеть, таким образом, что общее решение для пологой
сферической оболочки определяется окончательно с точностью до
шести произвольных постоянных. Отсюда следует, что на каждом
крае оболочки возможна постановка трех граничных условий, два
из которых будут относиться к состоянию изгибной деформации,
а одно — к безмоментному состоянию.
Граничные условия, соответствующие состоянию изгибной дефор-
мации, могут быть заданы либо в перемещениях W, W' (геомет-
рические усилия), либо в усилиях Мр, Qp (статические условия),
либо частью в усилиях, а частью в перемещениях (смешанные
условия). *
Граничные условия безмоментного состояния определяются либо
через значение тангенциального перемещения и, либо через значение
радиальной силы Np.
§ 4. Пологая сферическая оболочка под действием
равномерно распределенной нагрузки
1. Рассмотрим пологую сферическую оболочку на упругом
основании, находящуюся под действием равномерно распределенной
Рис. 126.
нагрузки р (рис. 126). Будем предполагать, что края оболочки
свободны от закреплений в результате чего возможна деформа-
ция упругого основания за пределами конструкции. ^Нормальные
266 ОСЕСИММЕТРИЧНАЯ/ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ}; [ГЛ. V
перемещения оболочки в соответствии с (3.5) определятся в
виде
= Схи0 (В) + C2v0 (?) + C3f0 (?) + Cigo (?) + Wp, (4.1) ;
pR2 '
где Wp — Eh'+'kR2—частный интеграл дифференциального уравне-
ния (3.2).
Для области, внешней по отношению к оболочке, имеет место I
дифференциальное уравнение |
V|TT2-a^2 = 0, (4.2) 1
общий интеграл которого может быть представлен в форме I
IF2 = 5x/o(ao?) +ДЛоЫ), (4.3) I
где I
a= = a=p_j!£» j f44' j
0 a Lo 2t ' ~ V Eh + kR2 ' I
Под величинами Br, B2 выражения (4.3) следует понимать 1
произвольные постоянные интегрирования; /0 (<хоё), /<0 (а0?) пред- |
ставляют собой модифицированные функции Бесселя и Ганкеля I
нулевого порядка аргумента а0?. |
Можно видеть, таким образом, что состояние нормальной 1
деформации оболочки со свободными от закреплений краями опре- |
деляется с точностью до шести произвольных постоянных интег- |
рирования. Для определения этих постоянных, как и в случае |
изгиба круглой пластинки (см. (6.8) — (6.10) гл. IV), могут быть |
сформулированы следующие граничные условия: I
при р=0 (? =0) а) ^1 = 0, б) Qppd9 = 0; 1
0 |
при р = До Г? = в)7Ир=0, I
V (4.5) I
. „ о . dW2 dWt\ 0 I
Г) )C0Sp, • 1
д) ИМЯо) = «ЫДо); I
при р-»оо (?—>оо) е) IV2(p) = 0. ‘ 1
Отметим, что четвертое из граничных уравнений (4.5)' отличается 1
от соответствующего условия (6.9) гл. IV наличием коэффициента 1
cos (3, где р — центральный угол оболочки. Это объясняется тем, 1
что фиктивная поперечная сила оболочки равна проекции фиктивной Я
поперечной силы круглой плиты на нормаль к срединной поверхности Я
оболочки в точках контура. я
§ 4J
ПОЛОГАЯ ОБОЛОЧКА ПРИ РАВНОМЕРНОЙ НАГРУЗКЕ
267
Исходя из первого, второго и шестого условий, нетрудно
получить:
С3 = С4 = В1=.О, (4.6)
после чего нормальные перемещения оболочки определятся в виде
= C1Uo © + C2v0 (g) + • (4-7)
Пятое из условий (4.5) позволяет определить постоянную В2:
2 Ко (<Хо5д)
(4.8)
F- Ко
где ;R = -f .
Подставляя в оставшиеся неиспользованными третье и четвер-
тое условия выражения (2.7) для Мр и Qp, получим:
1 — н dUH
при р = Ro 0
К 4
5 d£
dWil
-dricos
(4-9)
Раскрывая выражения (4.9) при помощи формул (4.3), (4.6),
(4.7) и (4.8), получим для определения постоянных и С2 си-
стему двух алгебраических уравнений:
aiCi +а2С2 = О, + b2C2 = Gp,
где
а^лмад-о-ролмад,
а2 = м2 (BR)-(1 -Р)М2 (ад,
, ( 2tL2 Г Ki(a0SR) аос°§ ₽ ~||
— |Qi(b?) + (ад cos р п0 (ад (ао^) j j
, I 2/Z,® Г Ki (<Xo5ff) «о cos ₽
^2 = (Q3 (^) + -ЁГ [ 02 (^) cos ₽ - v0 (ад-Ko(aoQ-] f
Р __ pR2 Ki(aoSR)
Up~ Eh + kR2 Ко(аоад '
Входящие в выражения (4.11) значения функций
Мъ М2, М2, Qn Q2, 9ь 02
(4.Ю)
(4.11)
(4.12)
могут быть вычислены по формулам (2.25) — (2.28) гл. IV или
при помощи соответствующих рядов (6.16) гл. IV.
268 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ) СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V
Решение системы (4.10) позволяет получить:
°ра2 Q _ Gpal
Я1&2 — «2&1 ’ 2 ЩЬ2 — а2&1 *
(4.13)
После определения нормальных перемещений оболочки в виде
(4.7) девиация, моменты и поперечные силы оболочки могут быть
рассчитаны по формулам:
^ = -1[СА© + с2е2(е)],
Ьо
л1Р = ^[С1А1(е) + с2А2(е)],
Lo
Ms = [CiZi (В) + c2Z2 (?)], (4,14)
Lo
Qp = -r3lCiQi© + C2Q2®]-
Lo
Входящие в эти формулы функции 6Х (£),..., Q2(B) опреде-
ляются рядами (6.20) гл. IV или выражениями (2.25) — (2.28)
гл. IV.
2. Рассмотрим плоское напряженное состояние пологой
оболочки. Для функции напряжений Ф, определяемой форму-
лой (3.12), в соответствии с (4.7) нетрудно получить выражение
ф=-¥ [-® ®+
+ C^2lne+Csln| + -^^g. (4.15)
Входящие в выражение (4.15) функции <рх (В), ф2 (В) определяют-
ся зависимостями (3.11) или соответствующими этим зависимостям
рядами:
ОО \
<Р1 (?) = 3 fep (|р cos 2 (m — 1) <Р, I
т~0 V •/ 4 / I
оо (
?2(В)= S 7^2-(Ip sin 2 (m— l)<p. '
m==0 ' ’ ' ' /
(4-16)
Как было отмечено ранее, постоянные С5 и С7 в фор-
муле (4.15) должны быть приняты равными нулю, в результате
чего эта формула перепишется в виде
ф = [“ ® ~ ® + С8 in т] •
(4.17)
§ 4] ПОЛОГАЯ ОБОЛОЧКА ПРИ РАВНОМЕРНОЙ НАГРУЗКЕ
269
Согласно формуле (4.17) и общим выражениям (3.13), (3-14),
получим формулы для нормальных усилий оболочки Np и Ne:
ХР = ™[С1П1® + С2п2(В) + 2Св+ С8 1 + , {4,18)
{Сх [и0 (В) - П1 ($)] + С2 [п0 (В) - п2 (В)] +
+ 2Св-С8| + |^^}, (4.19)
где nx(B), п2(В)— функции, определяемые формулами (3.15) или
тождественными этим формулам рядами:
СО
1 X? (—l)m / £ \2tn
П1 W = т 2j Ы cos 2mcP’
m=0 ' 7
„ 1 V (—4)'" /$\2m • о
2 (В) — 2 m! (m + ip ( 2 J Sin 2т?‘
(4.20)
Тангенциальное перемещение оболочки и, определяемое фор-
мулой (3.24), на основании (4.17) — (4.19) примет вид:
и — (1 + И) [С1Х1 (В) + С2/2 (В) + Cg-^- -f-
+ 1г*ТКгЕ] + 2с«('-1# (4'2|>
где Хг(В)> Ха (В) — функции, определяемые соотношениями
или следующими рядами:
® = 2j «!(«+!)! \2) C0S2/n<P’
m=o
co '
V (-4)m /B\2m+1 • о
X2(B)- 2lo-ffi?(w + 1-), Sin2m?. j
(3.25)
(4.22)
В полученных нами решениях (4.17), (4.18), (4.19), (4.21) по-
стоянные Ci и С2 определяются формулами (4.14), а постоянные
С6 и С8 подлежат определению из граничных условий, соответ-
ствующих состоянию тангенциальной деформации.
В рассматриваемой задаче эти условия могут быть представ-
лены в виде:
при р=0 (В=0) и = 0; |
n ft Яо\ (4.23)
при р = Ro ^В = 1
Np = — (2Фзтр = — f-o[W’2 — W\]sinB. J
270 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V
Первое граничное условие (4.23) характеризует равенство ну-
лю тангенциальных перемещений в полюсе оболочки, что является
следствием осевой симметрии. Второе условие (4.23) учитывает
наличие на контуре оболочки фиктивных сил
TV* == — Q* sin р, (4.24)
равных по своей величине проекции фиктивных поперечных сил
круглой плиты на касательную к срединной поверхности оболочки
в точках контура. Знак минус поставлен здесь потому, что со-
гласно принятому правилу знаков положительной поперечной кон-
турной силе соответствует отрицательная величина радиального
контурного усилия N*.
Из первого условия (4.23) можно видеть, что
С8 = 0.
(4.25)
Второе условие позволяет определить постоянную С6 в виде
= 4 [ тг - - т ’ (4 26)
где
AZ* = _?£ sin р х
^0
Сх«о (^>) + С2и0 (?R) + -g- P^rR2-
----------------/ГгГГГ №)
Ao (<Xosft)
(4-27)
Таким образом, напряжения и перемещения состояния танген-
циальной деформации оболочки определяются формулами (4.18),
(4.19), (4.21) при значениях постоянных Св и С8, характеризуемых
формулами (4.25) и (4.26).
§ 5. Пологая сферическая оболочка под
действием контурной
нагрузки
1. Предположим, что расположенная на упругом основании
оболочка находится под действием вертикальной контурной на-
грузки (рис. 127).
В этом случае дифференциальное уравнение (3.2), характери-
зующее состояние нормальной деформации оболочки, будет одно-
родным и решение его запишется в виде
= C1Uo (Е) + C2v0 (Е) + C3fо (Е) + Cigo (Е) (5.1).
Для области, внешней по отношению к оболочке (₽0^P^°°)>
как и ранее, будем иметь:
V72 = (а0Е) + В2К0 (^о^)., (5.2),
§ 5]
ПОЛОГАЯ ОБОЛОЧКА ПРИ КОНТУРНОЙ НАГРУЗКЕ
271
Произвольные постоянные, входящие в выражения (5.1) и (5.2),
определяются из граничных условий. Эти условия, как и в преды-
дущей задаче, могут быть представлены в виде (4.5), за исклю-
чением четвертого условия, которое следует заменить тождест-
венным ему по смыслу граничным условием:
при Р = Ro = у2)
\ ^0/
dW2 dWA , n "I D
—-dd + p*Jcos₽’
(5.3)
где Pk — распределенная по
Удовлетворяя первому,
второму, пятому и шесто-
му из граничных условий
(4.5), нетрудно получить:
Сз = ^4 = Bi — 0,
Ci«o (Zr) + C2v0 (ij^)
Ко(ао^) •
(5-4)
Раскрывая с помощью
решений (5.1), (5.2) и об-
щих выражений (4.9) пунк-
ты в) и г) условий (4.5) и
контуру вертикальная нагрузка.
учитывая значения посто-
янных (5.4), получим для определения С± и С2 систему двух ал-
гебраических уравнений:
—|— CI2C2 — б,
b±Ci -j-- ^2^2 = Gp-
Решение системы (5.5) позволяет получить: 4
браг q _ GPai
aih2 — a2&i ’ 2 0J&2 — a2bi '
(5-5)
(5.6)
В выражениях (5.5) и (5.6) под а1; а2, и Ь2 следует пони-
мать величины, определяемые формулами (4.11). Значение грузо-
вого члена 6р вычисляется здесь по формуле
р Is
GP =------^-°cos₽. (5.7)
Таким образом, в рассматриваемом случае нормальные пере-
мещения оболочки могут быть представлены выражением
UZj = С±и0 + СаМО, (5.8)
а девиация, моменты и поперечные силы — формулами (4.14).
Входящие в эти формулы постоянные Сх и С2 рассчитываются по
формулам (5.6).
Безмоментное состояние оболочки характеризуется наличием
тангенциальных усилий
^=^[c1n1(?) + C2n2(g) + 2Ce + C8l], |
{G [уо (0 — fh (5)] + С2 [ио (5) — пг (5)] + 2С6 — С8 ]
и перемещений
и = f1 + И) [ ciXi (5) + С2Х2 (I) + G {]+ 2С6 (1 - (л) е}. (5.10)
Граничные условия безмоментного состояния для рассматри-
ваемой задачи имеют вид:
u(0) = 0, NP(RO) — N$ — P*sin₽, (5.11)
где Af* — тангенциальная контурная фиктивная сила (4.24), опре-
деляемая в данном случае по формуле
. ,Ф 2/ г„ 0 г д . с1“о (5/?) + с2°о (5#) „ . . ] . _
N -------Ко (ао?Л)--ао^1(аоВя) sm Р-
(5.12)
Первое граничное условие (5.11) позволяет получить:
С8 = 0. (5.13)
Из второго условия (5.11) следует:
1 Г (к® — Рь)sin 3
С»=Т ---------ЁГ-----С1П1(^)-С2П2(^) . (5.14) 2
2. Если к контуру оболочки приложена горизонтальная на-
грузка Nk (рис. 128), то задача решается совершенно аналогич-
но предыдущей. Отличаться будет только граничное условие (5.3),
которое запишется здесь в виде
Q₽ (7?о) = 2/ cos ₽ - Nk sin p. (5.15)
При этом постоянные интегрирования Сг и С2 будут опреде-
лены формулами (5.6), в которых грузовой член Gp следует за-
менить новым грузовым членом GN, определяемым по формуле
Gn = —^-sinp. (5.16)
§ 5] ПОЛОГАЯ ОБОЛОЧКА ПРИ КОНТУРНОЙ НАГРУЗКЕ 273
Безмоментное состояние оболочки будет характеризоваться,
как и ранее, усилиями (5.9) и перемещениями (5.10). Соответ-
ствующие этому состоянию граничные условия примут кип;
u(0) = 0, Np (7?0) = — Nk cos р. (5.17)
Условия (5.17) позволяют получить для постоянных интегри-
рования Се и С8 следующие значения:
С8 = 0, • 1
r _ 1 Г (N^-Nkcos^R -I | (5.18)
С6— 2 C^j (В#) — С2п2 (В#) J , I
где У* — фиктивная контурная сила, определяемая формулой
(5.12).
3. Предположим, что оболочка находится под действием мо-
ментов Mk, расположенных по ее контуру (рис. 129).
Нетрудно видеть, что решение этой задачи можно снова пред-
ставить в форме (5.1) и (5.2). Граничные условия запишутся
в виде (4.5), за исключе-
нием пункта в), вместо ко-
торого следует принять:
Mp(R0) = Mk. (5.19)
Раскрывая граничные
условия, получим:
С3 = С4 = Bi = 0,
„ ___ СЩо (5Я) + C2Vo (Jig)
2~ Ко(ао^)
(5.20)
При этом для опреде-
ления постоянных Ci и С2 будем иметь следующую систему двух
алгебраических уравнений:
GiCi ~Г а2С2 — Gm,
biCi Ь2С2 = 0,
(5.21)
где величины а2, bL и Ь2 определяются выражениями (4.11), а
грузовой член Gm имеет вид:
Gm =
MkL20
D
(5.22)
18 В. 3. Власов, Н. Н. Леонтьев
274
ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОГО БОЛОЧКИ [ГЛ. V
Решение системы (5.21) позволяет получить:
______GMb* С __________°мЬ1
1 a-ibi — a2&i ’ 2 Я1&2 — аЛ
(5.23)
Для вычисления усилий и перемещений безмоментного состоя-
ния снова будем иметь формулы (5.9) и (5.10),£в которых посто-
янную С8 следует отбросить (С8 = 0), а величину С6 определять
по формуле
И^~С1"1(ад~С2"2М • (5,24)
§ 6. Приближенный расчет пологой сферической оболочки
на упругом основании
1. Учитывая малую деформируемость ‘ пологой оболочки из
плоскости срединной поверхности, можно предположить, что по
отношению к упругому основанию оболочка ведет себя, как жест-
кий штамп.
Реактивные давления упругого основания определяются при
этом по формулам (3.10) и (3.12) гл. IV, полученным
лого штампа радиуса 7?0 (рис. 130, а):
q =---- Р<>
для круг-
Ki(aRo) Г
Ко(аЯо) аЯо]
Ро Ki(aRo)
(6.1)
Оф =__________________________________
4 пР Г1+2 Ki(a-Ro) 1 Ko(aRo) а#о ’
°L K0(aR0)aR0]
(6.2)
где Ро’— равнодействующая заданной вертикальной нагрузки.
Расчет оболочки на упругом основании будет сведен, таким
образом, к определению деформаций и напряжений оболочки от
действия уравновешенной нагрузки, представленной, с одной ст0.
Eg б] / ПРИБЛИЖЕННЫЙ РАСЧЕТ ПОЛОГОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ 275
|роны, заданными внешними силами и, с другой — реакциями упру-
[ гого основания q и Q*. Для случая загружения оболочки равно-
е мерно распределенной нагрузкой р расчетная схема показана
на рис. 130,6. На этой схеме
p' = p — q, (6.3)
а фиктивные силы Q* равны
= = (6-4)
2. Ранее было показано (см. § 1
настоящей главы), что решение задачи
о пологой сферической оболочке, на-
ходящейся под действием вертикаль-
ной нагрузки р*, сводится к интегри-
рованию двух дифференциальных
уравнений:
D^W + ^W-p’ = 0, ]
„ <6‘5)
^v2v2o-v2if = o,
из которых первое позволяет определить функцию перемещений
IF, а второе — функцию напряжений Ф.
В безразмерных координатах
где ____
, У DR2
L° ~ |/ Eh ’
и уравнения (6.5) перепишутся в виде:
+ IF = —у-
, EhL?
vfvfo = —V|IF.
(6-6)
(6-7)
(6-8)
Входящий в выражения (6.7) и (6.8) оператор Лапласа в, слу-
чае осесимметричной задачи имеет форму:
3. Однородное уравнение, которое получается, если в уравне-
нии (6.7) положить р* = 0, может быть приведено к системе двух
18*
276 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V
эквивалентных ему уравнений второго порядка:
1 dW , .1V7 л
-d^-^T^+iW = 0’
d2W . 1 dW .1V7 n
(6.10)
Общий интеграл системы (6.10) имеет вид:
IV
(6.Н)
где Jo (5 У Г) и Jo (g J/— z) — функции Бесселя первого рода нуле-
вого порядка аргументов (?У i) и (?]/—z); Н{01} (% ]/ z) и
^o2)(B|Z—z)— функции Ганкеля первого и второго рода нулевого
порядка от тех же аргументов.
Сравнивая решение (6.11) с решением (2.19) гл. IV, можно
видеть, что различие здесь состоит только в том, что аргументы
рассматриваемых функций различны. При этом интеграл (6.11)
представляет собой частный случай более общего решения (2.19)
гл. IV, поскольку прямая, вдоль которой определены входящие
в решение (6.11) функции Бесселя и Ганкеля, в плоскости ком-
плексной переменной наклонена к действительной оси под углом
в сорок пять градусов:
<р = arg У i = 45°, )
ср = arg У-— z = — 45°. I
Отсюда следует, что все решения, полученные нами ранее при
рассмотрении оболочки на упругом основании, будут справедливы
й в настоящем случае.
4. Решение (6.11) удобнее, как и ранее, выразить посредством
действительных функций:
+ + + (6.13)
Где
u0(e) = Rej0(r/e), fo(e) = Re <(//?), \
t>0(|) = ImJ0(|/re), g0® = ImT/'2)(/=7?). I
Из общих выражений (2.26) гл. IV и (6.12) следует, что меж-
ду функциями (6.14) существуют следующие зависимости*):
; Ди0 = ц0, Av0 = — u0, Afo = go, Ag0 = — f0. (6.15)
.*) Функции (6.14) носят в литературе название функций Томсона. Таб-
лицы этих функций и их производных приведены в приложении (табл. 11)-
§ 6] ПРИБЛИЖЕННЫЙ РАСЧЕТ ПОЛОГОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ 277
В соответствии с (6.13) общий интеграл неоднородного урав-
нения (6.7) может быть представлен в виде
= C1Wo (|) 4- С2о0 (|) 4- C3f0 ® 4- CiSo ® + Wp, (6.16)
где Wp — частный интеграл уравнения (6.7).
Рассматривая, например, случай, когда р* = const, будем иметь:
= (6.17)
Отметим, что пункты а) и б) граничных условий (4.5) позво-
ляют получить:
C3 = Ct = 0. (6.18)
В результате этого решение (6.16) можно окончательно пред-
ставить в форме
w = c1Wo(a)4-c2Me) + ^. (6Л9)
Исходя из общих формул (2.7) и используя зависимости (6.15)
и (6.19), получим для всех кинематических и статических факто-
ров изгибного состояния оболочки при р* = const следующие выра-
жения:
" ==4tc1U;® + c!0;ffli,
D ( Г и' (5) 1
= п0(?)-(!-|Т)Л12 +
Ьо k L 4 j
4- С2 [-и0(?)-(1 -у)
(6.20)
~ “41 I +
ьо
+ с2[-рш0(а) + (1-^)^]},
qp=-4-[c^©-csuo®j-
Выражения (6.20) могут быть получены и из общих формул
(4.14) подстановкой в последние зависимостей (2.25) — (2.28)
гл. IV при значениях (6.12).
Безмоментное состояние оболочки характеризуется, как и ра-
нее, общими формулами (4.17) — (4.19), (4.21) при значении (4.25).
В рассматриваемом случае эти формулы можно представит!»
278 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ.
1
в следующем виде:
ф = [- (?) + С2и0 (?) + + У-2, (6.21
Eh Г r vo (5) I л “о(^) I пр 1 1 пп,
^₽=T[-Ci —+ С2 —+ 2C6+T^j, (6.22
«о & "
5 .
лг0 =
2
и = {- (! + и) I- <4 (?) + с2«; (?)] +
+ 2С6 (1 — ;л) |
5 J -Г ^в+ 2 Eh)
(6.22
<6-23)
Формулы (6.19) — (6.23) определяют напряжения и деформа-
ции пологой оболочки с точностью до трех постоянных интегри-
рования. Эти постоянные подлежат определению из граничных ус-
ловий, заданных на контуре оболочки. При этом два из возможных?
граничных условий будут относиться к состоянию нормальной
деформации оболочки и одно — к ее безмоментному состоянию.
5. Рассмотрим числовой пример расчета пологой сферической
h-0,4Mj"WM
Рис. 131.
оболочки, представленной на
рис. 131.
Для геометрических и фи-
зических характеристик обо-
лочки и упругого основания
примем следующие значения*):’
R = 13,5 м,
ft = 0,46 м,
Ro = 5,1 м,
£гр = 4-103 т/м\
>гР = 0,4,
H/Ro= 1,0,
f =1,0 м,
Е = 2-106 щ/л2,
{л = 0,167,
7= 1,55,
Р — 1,0 щ/м,
D = 16,2-104 т/м.
(6.24)
функция ф (?)
*) Предполагается, что
щеиий в упругом основании выбрана в виде (3.15) гл. IV.
поперечного распределения переме>
§ 61 ПРИБЛИЖЕННЫЙ РАСЧЕТ ПОЛОГОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ 279
В соответствии с формулами (3.16), (3.17) гл. IV обобщенные
характеристики упругого основания имеют следующий вид:
й= 1,6.10s m/м3, 2/= 1,85-103 т/л, i
а = 0,93 1/м, а/?0=4,72. / (6-25)
Формулы (6.1) й (6.2) позволяют получить для реакций уп-
ругого основания величины:
6^=0,269 т/м2, Q* = 0,315 т/м,,
в результате чего из формулы (6.3) получим:
р* = — 0,269 т / м2.
Внося в выражение (6.6) значения (6.24), получим:
£0= 1,34 м, 5д=^ = 3,8.
^0
(6.26)
(6.27)
(6.28)
Функции, входящие в расчетные формулы (6.19) — (6.23), при
£#=3,8 равны:
и0 = — 1,967,
v0 — — 2,345,
= —0,742,
и0 = — 2,822,
vQ = 0,0526
V
^ = 0,138.
^R
(6.29)
Граничные условия для определения постоянных С1г С2, С6 в
рассматриваемом случае принимают вид:
при р = /?0(ел = ^) < = о,
Qp=(P-Q*)cos₽, \
Np=— (Р — Q*)sinp. J
Раскрывая эти условия, будем иметь:
1
, Z3 (Р — 0ф) cos В
<4&г) - Czu0 (Ь)>---5----------
(6.30)
(6.31)
п (?«) , ко , 1 P*R2 _
— С1 ~Ц~ + С2 + 2С«+ 2 “Ё/Г -
280 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ. [ГЛ. V
§ 71 ПРИЛОЖЕНИЕ РАССМАТРИВАЕМОГО МЕТОДА 281
Внося в выражения (6.31) полученные ранее значения (6.26),.
(6.28), (6.29), нетрудно найти постоянные интегрирования:
Ci=—3,68-16^ м, Са = —3,26-16*8 м, С6 = —0,948-IG^jw.
(6.32)
На рис. 132, 133, 134, 135 приведены эпюры радиальных'и кольце-
вых моментов Мр, Мв, а также усилий Np и No, рассчитанные
по формулам (6.20), (6.22) при значениях постоянных ((6.32).
Кроме того, на рис. 132, 133 показаны значения моментов Мр,.
и Л40) рассчитанные для круглой пластинки радиуса R = 7?0 при
тех же значениях характеристик упругого основания и конструк-
ции. Расчеты эти проводились при помощи трех различных ме-
тодов: методр, изложенного в гл. IV настоящей книги (при.
Н/ Ro = 1, ' у = 1,55), метода упругого полупространства [26] и
метода коэффициента постели при значении коэффициента’ постели
k = 1,6« 10s ml м3.
Сравнение приведенных графиков показывает, что величины
изгибающих моментов Л4Р и Л4е пологой сферической^'оболочки
значительно меньше тех, которые характеризуют напряженное
состояние круглой плиты.
§ 7. Приложение рассматриваемого метода к расчету днищ
цилиндрических резервуаров
В предыдущих параграфах нами были рассмотрены некоторые
задачи, относящиеся к расчету пологой сферической оболочки,
расположенной в упругом основании. При этом предполагалось,,
что оболочка имеет свободные от закреплений края и загружена
282 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ
либо равномерно распределенной, либо контурной нагрузкой
(рис. 126—129). '
Рассмотрим теперь случай, когда сферическая оболочка пред*
ставляет собой днище цилиндрического резервуара, опирающего*
ся на упругое основание (рис. 136).
1. Если учесть, что место сопряжения днища и цилиндра укреп*
ляется обычно опорным кольцом, то в первом приближении можно
считать, что днище резервуара
представляет собой сферическую
оболочку, защемленную по конту-
ру. Другими словами, сфериче-
ская оболочка может быть рассчитана здесь вне зависимости от
остальных частей конструкции по схеме, представленной на
рис. 137. Контурными силами Р на этой схеме обозначена на-
грузка, которая передается на оболочку от стенок резервуара;:
равномерно распределенная нагрузка р представляет собой дав-:
ление наполняющей резервуар жид ости. Реакции упругого ос-:
нования q и рассчитываются по формулам (6.1), (6.2) в пред-
положении, что по отношению к упругому основанию оболочка
ведет себя, как жесткий штамп.
Напряжения и деформации оболочки определяются здесь, как
и ранее, формулами (6.19) — (6.23) с точностью до трех посто-
янных интегрирования Clt С2, С6. Для отыскания этих постоян-
ных могут быть сформулированы следующие граничные условия:
при р = ₽0 (е = ^)
U7 = О, 0, и = 0.
(7.1)
Рис. 139.
283
284 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ [ГЛ. V
Раскрывая условия (7.1), получим:
CiW0 (£я) + Czvo (Вя) = >
Ciuo (Ы + C2vq (В«) = О,
- (1 + И) I- Civ'o fa) + Czu0 (^)l + 2С6 (1 - [№ -
где р* = p — q.
Уравнения (7.2) позволяют определить постоянные интегри-
рования в следующем виде:
с =vo (^)рЧР
(М^)Мад-М^ММ Eh ’ i
с, =------(7.3)
(мадмад-мадмад] Eh
Г = + Iх) / 21цр2 (S^) + (^)J_. \p*R*
6 ^-н) [«о(s«)^(^)—«;(^)^(^)j ’
В качестве примера на рис. 138 и 139 приведены эпюры
изгибающих моментов Мр, и усилий Np, N9, рассчитанные
Рис. 140.
по формулам (7.3), (6.20), (6.22) для случая, когда днище резер-
вуара загружено одной контурной нагрузкой Р. Значения упругих
5 71
ПРИЛОЖЕНИЕ РАССМАТРИВАЕМОГО МЕТОДА
285
постоянных грунта и конструкции приняты здесь согласно (6.24).
На этих же графиках нанесены (пунктиром) полученные ранее
данные расчета оболочки со свободными от закреплений краями.
Можно видеть, что усиление оболочки по контуру жестким
кольцом, препятствующим радиальному перемещению и углу
поворота, приводит к некоторому уменьшению величин Мр, Mq,
Np и значительному уменьшению растягивающего усилия Nq на
контуре оболочки. Последнее обстоятельство для оболочки, пред-
ставляющей собой днище резервуара, имеет весьма существенное
значение.
2. Если опорное кольцо препятствует только радиальному
перемещению, то расчетная схема оболочки может быть принята
согласно рис. 140.
Рис. 141.
Граничные условия запишутся здесь в следующем виде:
при р = Ro (% = ц)
W = Q, Мр = 0, и = 0. (7.4)
Раскрывая эти условия, будем иметь:
D*
C1Uq(Ir) + С2У0(^д) = ££ >
(7.5)
— (1 + I- c1V'o (^) + с2«; (ед)] +
+ 2св(1-р)е/?-Ц^^ел= о.
286 ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ СФЕРИЧЕСКОЙ;) ОБОЛОЧКИ [ГЛ. V
В соответствии с уравнениями (7.5) нетрудно определить по-
стоянные интегрирования:
где
р____________Ki P*R2
1 “ [«о(5д)К1+»о(адад Eh •
г____________Кз_______Р*К2
2~ [«o(^)Ki+fo(^)K2] Eh ’
с (1 + и) Г ।
К1 = «о(Ы + (1-р)^а)-
Sr
Ъ = v0 (?«)+(!-P)
Sr
(7-6)
3. Для получения более точного решения рассматриваемой
задачи необходимо учесть совместную работу днища и цилинд-
рического резервуара, другими словами, учесть влияние, которое
оказывает цилиндрическая оболочка на работу днища. Для это-
го можно воспользоваться известными в строительной механике
методами расчета статически неопределимых систем: методом сил
или методом перемещений (деформаций).
Применяя, например, метод сил, следует провести разрез в
зоне примыкания днища к цилиндрическому резервуару и вместо
отброшенных связей приложить соответствующие неизвестные уси-
лия (рис. 141). Согласно принятым направлениям неизвестных
усилий канонические уравнения этого метода, выражающие собой
условия неразрывности деформаций, примут вид:
(Дц + А*) Хг + (Дс12- Д«) Х2 - ДХ9 + Д«р- Д«р = 0, )
(Д21 "Ь Дм) Xi 4- (Д22 + Д22) Х2 — Аг? + Дгр + Дгн = 0. J
Первое уравнение (7.7) характеризует равенство нулю взаим-
ного угла поворота в месте разреза, а второе — отсутствие вза-
имного смещения в направлении неизвестной Х2.
Коэффициенты и грузовые члены уравнений (7.7) представля-
ют собой абсолютные величины соответствующих перемещений.
Первый индекс показывает, в каком месте и по какому направ-
лению возникает перемещение, второй индекс — причину возник-
новения перемещения. Коэффициенты с индексом «с» относятся
к перемещениям стенки резервуара, с индексом «д»—к переме-
щениям днища.
§ 7] ПРИЛОЖЕНИЕ РАССМАТРИВАЕМОГО МЕТОДА 287
Грузовые члены Д19, Д^, Д^р, Д2р характеризуют абсолют-
ные величины перемещений от внешних нагрузок q и р; грузовые
члены Д«р, Д«р —от контурной нагрузки Р, передающейся на
днище со стенки резервуара.
Нетрудно видеть, что все коэффициенты и грузовые члены
с индексом «д» могут быть рассчитаны при помощи общих выра-
жений (6.19), (6.20), (6.23), полученных ранее при рассмотрении
пологой сферической оболочки.
Для вычисления коэффициентов с индексом «с» следует рас-
смотреть задачу об осесимметричной деформации цилиндрической
оболочки, загруженной как внешней радиальной нагрузкой q, так
и контурными силами и Х2- Эта задача, как известно, сво-
дится к решению простого дифференциального уравнения четвер-
того порядка, в точности совпадающего по виду с дифференци-
альным уравнением изгиба балки на упругом винклеровском ос-
новании.
Поскольку расчет цилиндрической оболочки на осесимметрич-
ную нагрузку хорошо изучен и подробно изложен в ряде
монографий *), вычисление коэффициентов с индексом «с», характе-
ризующих перемещения стенки, не может вызвать каких-либо
затруднений.
Отметим, что все сказанное выше будет справедливо и в том
случае, когда днище резервуара представляет собой не сфериче-
скую оболочку, а круглую плиту. При этом коэффициенты урав-
нений (7.J), содержащие индекс «д», могут быть вычислены с по-
мощью расчетных формул, приведенных в §3 и §6 гл. IV.
*) См., например, [8].
ГЛАВА VI
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
НА УПРУГОМ ОСНОВАНИИ
§ 1. Дифференциальное уравнение колебаний балки
на упругом однослойном основании
Рассмотрим балку шириной 8, расположенную на поверхности
упругого основания и загруженную произвольной внешней на-
грузкой р(х, t) (рис. 142).
Предположим, что нагрузка
является функцией времени
t, т. е. представляет собой
динамическую нагрузку, при
действии которой силы инер-
ции деформируемой системы
приобретают существенное
значение.
Рис. 142.
Дифференциальное уравне-
ние движения балки может быть представлено в виде
EJVW (х, t) — р (х, t) —т-х —q (х, t), (1.1)
с г л г 5Й8
где EJ — жесткость балки, </ — , тг— погонная масса
балки, q (х, /) — реакции упругого основания, создаваемые силами
упругости и силами инерции грунта.
Для определения реакций q(х, t) выделим из упругого основа-
ния элементарный столбик (см. § 2 и §3 гл. I) и рассмотрим ус-
ловия равновесия этого столбика, понимаемые в смысле принципа
возможных перемещений Лагранжа. Предполагая, как и ранее, что
горизонтальные перемещения в однослойном основании отсут-
ствуют, а вертикальные перемещения характеризуются функцией
Ф(у), получим выражение для виртуальной работы всех внешних
$ ]] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ КОЛЕБАНИЙ БАЛКИ 289
и внутренних сил, действующих на этот столбик:
н н
2<& 5 * ”Ш d'J V' ~ 5 v~
' 0 ° 0
н
— mob^^y)dy^ + q(x,t)==Q, (1.2)
0
где q (x, f) — погонная нагрузка, приложенная к поверхности уп-
ругого основания (реакция основания); т0= — масса единицы
объема (т0—объемный вес грунта, g — ускорение силы тяжести);
Ео и v0 — характеристики упругого основания, определяемые фор-
мулами:
Е
р _ 1Р_
1 —v2
х vrp
vo =
Vrp
vrp
(1-3)
где Егр и vrp — соответственно модуль деформации и коэффици-
ент Пуассона, упругого основания.
Вводя сокращенные обозначения для коэффициентов:
н
k=^\V4y)dy,
° о
н
t = > , Л?5 , Ф2(у)^У,
4 (1 -f- v0) j т J ’
о
Н
т0=т^ ty\y)dy,
О
можно переписать уравнение (1.2) в виде
2tV"~ kV-m^ + q (х, i) =0.
(1-4)
(1-5)
Уравнение (1.5) представляет собой дифференциальное урав-
нение колебаний однослойного основания под нагрузкой q(x,t).
Рассматривая уравнения (1.1) и (1.5) совместно, исключая из них
функцию q (х, I) и производя некоторые преобразования, получим:
yiv _ 2ггУ'+ s4V + от* , (1.6)
- Ul L-td
19 В. 3. Власов, Н. Н. Леонтьев
290
где
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. VI
Н
~ =—Ф'2(*/ш
£J(l-v2)Jr
н
р = 4т= , —Д ф2(^)^>
EJ kEJ (1 + v0) J т V£7/
о
\ 1
EJ \ g g J т а I EJ
(1-7)
(у и уо — соответственно объемные веса материала балки и упру-
гого основания).
Дифференциальным уравнением в частных производных (1.6)
характеризуются колебания балки на упругом однослойном осно-
вании. Из этого уравнения можно видеть, что в колебательном
движении участвует не только масса балки, но и обобщенная мас-
са упругого основания т0. Таким образом, полученное уравнение
в отличие от часто встречающихся в литературе аналогичных
уравнений описывает движение балки с присоединенной к ней мас-
сой упругого основания.
§ 2. Свободные колебания балки
1. Предположим, что внешняя возмущающая нагрузка р(х, t)
отсутствует. Дифференциальное уравнение движения (1.6) перепи-
шется при этом в виде
yiv_2r2V''+s4V = — m*^-. (2.1)
Уравнение (2.1) описывает свободные колебания балки, т. е.
колебания балки, которая каким-либо образом выведена из состоя-
ния равновесия, а затем предоставлена самой себе.
Решение этого дифференциального уравнения можно искать в
виде произведения двух функций, из которых одна зависит толь-
ко от абсциссы х, а другая — только от времени t, т. е. в виде
У = Х(х)Т(0. (2.2)
Подставляя (2.2) в уравнение (2.1), получим:
XIV—2r2X"+s4X т*Т"
--------------= —- Т . (2.3)
Нетрудно заметить, что левая часть полученного равенства
зависит только от переменной х, а правая — только от перемен-
ной t. Вследствие этого равенство (2.3) будет справедливо при
« 21
СВОБОДНЫЕ КОЛЕБАНИЯ БАЛКИ
291
любых значениях х и t только в том случае, если обе его части
равны постоянному числу. Обозначая это число через т*(а2, бу-
дем иметь:
Т"+ <а2Т = 0, (2.4)
Xiv __ 2г2Х"+ (s4 — т*<о2) X - 0. (2.5)
Таким образом, решение дифференциального уравнения в част-
ных производных (2.1) сводится к интегрированию двух обыкно-
венных дифференциальных уравнений (2.4) и (2.5).
Можно видеть, что дифференциальное уравнение (2.4) имеет
такую же форму, как и уравнение свободных колебаний системы
с одной степенью свободы; оно выражает простое гармоническое
колебание с частотой о>. Решение этого уравнения имеет следую-
щий вид: £
Т ='А sin tot -ф В cos (at, (2.6)
где А и В — произвольные постоянные интегрирования, определя-
емые из начальных условий задачи.
Дифференциальным уравнением (2.5), записанным относительно
функции прогибов Х(х), определяется форма свободных' колеба-
ний балки. Переходя к интегрированию этого уравнения, перепи-
шем его в виде
XIV —2r2X'—(X4—г4)Х = 0, (2.7)
где X4— некоторый параметр, зависящий от частоты колебаний
системы «о и вычисляемый по формуле
Х4= г4— s4+ mW. (2.8)
Общий интеграл уравнения (2.7) может быть представлен в
форме ы
X (х) = Сх sh ах -ф С2 ch ах -ф С3 sin fix -ф С4 cos fix, 1
где Ci — произвольные постоянные, а и р— коэффициенты
аргументов гиперболических и тригонометрических функций, свя-
занные с относительной упругой характеристикой г2 и параметром
X2 зависимостями:
а2= X2 -ф г2, р2= X2 — г2. (2.9)
Так как частота колебаний остается пока неизвестной, то и
параметр X2, от которого зависят величины аир, будет пока не-
определенным.
Общее решение уравнения (2.7) записано, таким образом,
с точностью до пяти произвольных величин: четырех постоянных
интегрирования С4 и неопределенного параметра X. Для
отыскания этих величин следует рассмотреть граничные условия,
заданные на краях~балки. Эти условия могут быть, как известно,
19*
292
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. VI
статического, кинематического или смешанного типа. При этом
на каждом конце балки может быть поставлено только два соот-
ветствующих условия. Заметим, что во всех случаях граничные
условия при отсутствии внешних сил представляются однородны-
ми равенствами, т. е. равенствами, содержащими значение иско-
мой функции X (х) или ее производных в точках х = О и х = I.
Раскрывая граничные условия, заданные на краях балки х =0
и х = /, при помощи формул
X (х) = С4 sh ах -ф С2 ch ах -ф С3 sin fix -ф С4 cos fix,
X' (х) = С4а ch ах -ф С2а sh ах -ф С3° cos fix —С4р sin fix,
X" (х) = Сха2 sh ах-ф С2а2 ch ах— C3fi2sinfix— C4fi2 cos fix, | ^-Ю)
X'" (x) = С4а3 ch ах -ф С2а3 sh ах — C$s cos fix -ф C4fi3 sin fix, j
получим в каждом частном случае систему четырех линейных
уравнений относительно четырех постоянных интегрирования
Сх,...,С4. Так как граничные условия выражаются однородными
равенствами, то линейные уравнения, составленные по этим усло-
виям, будут однородными.
Эти уравнения в общем случае могут быть записаны в следу-
ющей форме:
аи (^) Ci -ф ai2 (^) + #1з (X) С3-ф а14 (X) С4 = 0,
«21 (X) Сх+ CZ22 (X) С2 + Паз (^) Сз -ф a2t (^) С4 = 0,
азх (^) Ci4~ аз2 (^) С2 -ф а33 (X) С3 -ф а34 (X) С4 = 0,
п41 (X) Сх4~ п42 (X) С2 -ф ais (X) С3 -ф а44 (X) С4 = 0,
(2.U)
где «^(Х) (г, k= 1,2, 3,4) — коэффициенты, зависящие, как не-
трудно видеть, от параметра X дифференциального уравнения (2.7).
Приравнивая нулю определитель системы уравнений (2.11), полу-
чим уравнение относительно искомого параметра:
Д(Х) = Яц(Х) а12(Х) а13 (^) а14 (^) °23 О') °24 (^) = 0.
«21 О') азх (^) °22 (^) П32 О’)
азз О') п34 (X)
а4Х (X) П42 (X) «43 О') «44 (^) •
(2-12)
Уравнение (2.12) носит название характеристического уравне-
ния однородной краевой задачи, т. е. задачи, представленной од-
нородным дифференциальным уравнением (2.7) с неопределенным
параметром X и однородными граничными условиями (2.11). По-
скольку параметр X в рассматриваемом нами случае колебаний
системы связан с частотой колебаний ю,уравнение (2.12) представляет
собой также и уравнение частот собственных колебаний системы.
Так как параметр X2 входит согласно формулам (2.9) и (2.10)
в состав аргументов гиперболических и тригонометрических функ-
j2] СВОБОДНЫЕ КОЛЕБАНИЯ БАЛКИ • 293
ций, то характеристическое уравнение (2.12) относительно иско-
мого параметра X будет трансцендентным. Это уравнение дает для
Х.2 бесконечное множество значений. Нетрудно показать, что все
корни уравнения (2.12) независимо от того, к какой краевой за-
даче это уравнение относится, будут действительными.
Параметры Х£ (п = 1,2,3,...), определяемые характеристиче-
ским уравнением (2.12), могут быть названы фундаментальными
числами однородной краевой задачи.
Таким образом, определяя изложенным здесь методом пара-
метр X3, мы получим бесконечное множество фундаментальных
чисел Xi, Х|, Xg,..., причем все эти числа будут действительными.
Каждому фундаментальному числу Х£ будет соответствовать со-
гласно формуле (2.8) определенная частота колебаний. Бесконеч-
ному множеству фундаментальных чисел Х„ (и = 1,2,3,...) соот-
ветствует, таким образом, бесконечное множество частот собст-
венных колебаний.
Из уравнения (2.8) нетрудно получить выражение частот:
Точно так же каждому фундаментальному числу Х^ соответ-
ствует согласно формулам (2.9) пара чисел а„ и рп. определяю-
щих функцию Хп(х). Мы получаем, таким образом, бесконечное
множество функций Хп(х) (п= 1,2,3,...), удовлетворяющих всем
условиям данной однородной краевой задачи. Эти функции назы-
ваются фундаментальными функциями (см. §4 гл. III).
Так как произвольные постоянные Сх,...,^ при каком-либо
значении фундаментального числа X определяются однородными
уравнениями (2.11) с точностью до одного общего множителя, то
каждая из фундаментальных функций Хп (х) определится также
с точностью до множителя.
2. Известно, что функции собственных колебаний любой упру-
гой линейно-деформируемой системы взаимно ортогональны, т. е.
при i=j=k
I
^XiXkdx = 0. (2.14)
о
В рассматриваемой задаче отмеченное свойство взаимной орто-
гональности функций Xi и Xk можно доказать следующим образом.
Функции Х, и Xk являются решениями дифференциального
уравнения (2.7), откуда следует:
(Xe_^)Xz = X]v-2r2X- 1
. (Х1-М)Х,- = ХГ-2г3Х;, I }
294 ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ Ггл. VI
где 1* и А* — фундаментальные числа, соответствующие фунда-
ментальным функциям Xi и Хк.
Умножая первое из равенств (2.15) на Xk, второе — на X/,
вычитая почленно одно равенство из другого и интегрируя полу-
ченное равенство в пределах от х = 0 до х — I, найдем
1
(M-Xl)$X(X*dx =
О
I I II
= $ XiVXk dx — J X’vXi dx — 2rB (J X'i Xkdx — J Х’кХс dx). (2.16)
0 0 0 0
Применяя к правой части равенства (2.16) формулу интегриро-
вания по частям^ получим
i
(x?-xl)$x,x*dx =
О
= [X7xft - X'kXi - X'iX'k + X’kX'i - 2r* (X'iXk - X'kXi)]lQ, (2.17)
где символом [ ]o обозначена разность значений стоящей в скобках
величины при х = I и х = 0.
Нетрудно видеть, что правая часть равенства (2.17), представ-
ляющая собой величину, пропорциональную работе граничных
обобщенных сил М и Q состояния I на соответствующих им пе-
ремещениях другого состояния k, в случае однородных граничных
условий независимо от вида закрепления равна нулю. На этом
основании мы можем написать
i
(X? —Xl) \XiXkdx = Q.
О
Так как при i=j=k фундаментальные числа X; и X2 будут раз-
личными, то
Х^Х| = О
и, следовательно,
i
j XiXk dx = О,
о
что доказывает теорему об ортогональности фундаментальных
функций.
Заметим, что, как и в рассмотренном ранее случае колебаний
простой балки (см. § 4 гл. III), свойством ортогональности будут
обладать не только функции Х£ и Xk, но и все четные производ-
ные от этих функций. Обозначая через Хг-2от) и Х^т) четные про-
§ 21 СВОБОДНЫЕ КОЛЕБАНИЯ БАЛКИ gQg
изводные 2/п-го порядка (т = 1, 2, 3,...), мы можем это свой-
ство представить в виде
i
\x(r}X(r}dx = ^. (2.18)
О
Свойство (2.18) может быть доказано для любого значения т
тем же способом, что и свойство ортогональности функций.
3. Рассмотрим несколько примеров на построение фундамен-
тальных функций и определение частот собственных колебаний
балки, расположенной на упругом однослойном основании.
а) Пусть балка имеет шарнирное опирание по концам. Гранич-
ные условия в этом случае запишутся в виде:
при х = 0 и х = I X = X" = 0. (2.19)
Раскрывая эти условия при помощи формул (2.11), получим
для определения произвольных постоянных Сг, ..., С4 следующие
уравнения:
. С2 = 0,
а2С2 — р2С4 = 0,
Ci sh aZ + С2 ch aZ + С3 sin pZ + С4 cos pZ = 0,
С4а2 sh aZ + C2a2 ch aZ — C3p2 sin pZ — C4p2 cos pZ = 0.
Первые два уравнения дают:
С2 = С4 = 0.
Остальные два приводятся к виду:
sh aZCx + sin pZC3 = 0, >
a2shaZCi — p2sinpZC3 = 0. J (2.20)
Приравнивая нулю определитель системы уравнений, получим
характеристическое уравнение
(a2 -р р2) sh cd sin pZ = 0
или
sinpZ = O. (2.21)
Корни этого уравнения будут:
Р„ = т- <2-22>
If
Подставляя рп во вторую из формул (2.9), найдем все фундамен-
тальные числа данной задачи:
, Х’=^+г*. (2.23)
296
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. VI
Этими фундаментальными числами определяются согласно фор-
муле (2.13) все частоты собственных колебаний системы при за-
данных граничных условиях:
= V^К+2г’(т)’+(т)‘] (2.24)
Полученная формула носит достаточно общий характер. По-
лагая, например, в формуле (2.24) характеристики s4 и г8 рав-
ными нулю, мы получим как частный случай известную формулу
для частот собственных колебаний простой однопролетной балки.
Принимая равной нулю только одну характеристику г2, мы полу-
чим значения частот для балки, опирающейся на винклеровское
основание с коэффициентом постели k.
Определив фундаментальные числа X2 и частоты колебаний
w„, мы можем найти фундаментальные функции Хп- Согласно
характеристическому уравнению
sin р/ = 0.
В результате этого из уравнений (2.20) следует:
Сх = 0.
Значит, в нашем случае обращаются в нуль три константы:
Сх = С2 = С4 = 0. (2.25)
Константа С3 остается, таким образом, не определенной.
Подставляя значения (2.25) в первую из формул (2.10), полу-
чим фундаментальные функции Хп (х), определенные каждая с
точностью до одного множителя. Принимая этот множитель за
единицу, получим:
А1 = 5Шу, Л2 = SIH —, A3 = sin—,... (2.26)
б) Если край балки, принятый за начальное сечение, имеет
шарнирное опирание, а другой край — жесткую заделку, то гра-
ничные условия примут вид:;
при х = О X = X" = 0, 1
при x = l Х = Х' = 0. j 1 '
Эти условия приводят к уравнениям:
Са + — 0,
а2С2 — р2С4 = 0,
sh a/Ci ф- ch а/С2 ф- sin р/С3 ф- cos р/С4 = 0,
а ch а/Ci ф- а sh а/С2 ф- р cos р/С3 — р sin р/С4 = 0.
(2.28)
§ 21
СВОБОДНЫЕ КОЛЕБАНИЯ .БАЛКИ .
297
Отсюда получаем:
С2 = С4 = 0, '
sh a/Ci + sin $ICS = 0, .
a ch a/Ci + p cos p/C3 = 0.
Характеристическое уравнение принимает вид:
р sh a/ cos р/ — a ch а/ sin р/ = 0.
Подставляя в уравнение (2.30) значения
(2.29)
(2.30)
а=|<Х2 + г2, р = |<Х2 — г2,
представим уравнение (2.30) в следующем виде:
/х2 —r2thJ/X2 +г2/== /Х2 +r2tg/x2 —г2/. (2.31)
Трансцендентное уравнение (2.31) при заданной относительной
характеристике г2 определяет все фундаментальные числа X2, Х|,
Х|, ... рассматриваемой здесь краевой задачи. Зная эти числа,
найдем по формуле (2.13) все частоты юь ю2, ыз, . .. собственных
колебаний балки, имеющей шарнирное закрепление на одном
конце и жесткую задатку на другом.
Фундаментальные функции Хп (х), определяемые фундаменталь-
ными числами X2 и условиями (2.27), могут быть представлены
в виде
Хп (х) = sin р^Х2 — г2 / sh 1^X2 ф- г2х — sh V^2n + r2/sin фО.2 — г2 x
(n =1, 2, 3, . . .).
(2.32)
Нетрудно убедиться, что функции Хп, определяемые форму-
лой (2.32), удовлетворяют граничным условиям (2.27).
Найденные здесь фундаментальные функции Хп (х) зависят
также от параметра г, представляющего собой в нашем случае
относительную упругую характеристику. Давая этому параметру
различные значения, мы будем каждый раз получать новые се-
мейства фундаментальных функций Хп(х) со своими фундамен-
тальными числами X2, определяемыми при заданном параметре г2
уравнением (2.21), причем все эти функции при любом значении
параметра г2 обладают свойством ортогональности. Мы можем,
таким образом, задаваясь частными значениями параметра г2,
построить ряд новых ортогональных функций. При г2 = О
эти функции переходят в известные функции колебаний простой
балки с одним, заделанным и другим шарнирно опертым концом
(см. § 4 гл. III).
298
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
(ГЛ. V
в) При жестком закреплении обоих концов балки граничные 3
условия будут иметь вид:
при х = О X = О, X' = 0; |
при х = I X = 0, X' = 0. j
Раскрывая эти условия, подобно тому как было сделано в пре-
дыдущих примерах, и приравнивая нулю определитель полученной
системы уравнений при произвольных постоянных Clt С2, С3, С4,
получим характеристическое уравнение для определения фунда-
ментальных чисел X2. Это уравнение имеет вид:
cos К2 — г2 /ch)А2 + г2/ — /'2—f2/sh)/\24-r2/= 1.
(2.34)
Фундаментальные функции определятся в форме
Хп (х) = (ch — cos р„/) (ап sh апх — sin рпх) —
— (а„ shа„/ — sin р„/) (ch а„х — cos i3„x), (2.35)
где ______ ________________
<х„=Г^ + А pn=/x2-r2.
Полагая г — 0, получим характеристическое уравнение и фун-
даментальные функции, встречающиеся в задаче о колебаниях
простой балки, имеющей на концах жесткие заделки.
Мы рассмотрели только несколько примеров вычисления фун-
даментальных чисел и фундаментальных функций, определяющих
соответственно частоты и формы собственных колебаний балки,
расположенной на упругом однослойном основании. Пользуясь
изложенным здесь методом, можно найти частоты, а следовательно,
и формы колебаний балки и при других граничных условиях.
4. Исходя из свойств общего интеграла однородного линейного
дифференциального уравнения, можно записать общее выражение
для свободных колебаний балки на упругом однослойном основании
в следующем виде:
У(х, 0 = § Хптп= § X„(HnsinwnZ + B„cosw„0, (2.36)
П=1 п—1
где Ап и В а — произвольные постоянные интегрирования.
Выражение (2.36) может быть также представлено в другой,
эквивалентной ему форме:
V (х, /) = 2 СпХп sin <лп (t — фп), (2.37)
п=1
где роль постоянных Ап и Вп играют коэффициент Сп и величина
<|>п, характеризующая сдвиг фаз.
З) ДЕЙСТВИЕ МГНОВЕННОГО ИМПУЛЬСА 299
Из формулы (2.36) следует, что упругая линия балки, совер-
шающей свободные колебания, представляет собой геометрическую
сумму бесконечного множества кривых вида^
Хп (Ап sin <£>nt + Вп cos wnt),
которые могут быть названы собственными или главными формами
поперечных колеба'ний балки. Каждая из этих кривых сохраняет
форму кривой Хп и колеблется со своей частотой юп, в резуль-
тате чего изогнутая ось балки V (х, t) не имеет постоянной Формы,
непрерывно изменяя свое очертание.
После определения прогибов балки в виде (2.36) вычисляем
скорость движения в каждой точке по формуле
^=2 Х„<оп(Л„со5<оп/ —B„sinwn0- (2.38)
п=1
Для изгибающих моментов и поперечных сил балки будем
иметь выражения:
М(х, t) = — EJ S Хп (/InSinaV + Bncoswn0> (2.39)
n—1
Q (x, t) = — EJ S X"n (Дп sin <£>nt + Bn cos <ant). (2.40)
n=l
Графики этих величин, так же как и график У(х, /), непре-
рывно изменяют свое очертание. При этом естественно, что наи-
большие значения ординат этих графиков получаются в разных
сечениях балки и в различное время.
§ 3. Действие мгновенного импульса
Пусть на упругую балку длиной I, расположенную на однослой-
ном основании, действует нагрузка, интенсивность которой на по-
гонную единицу длины равна р(х). Будем считать, что продол-
жительность действия этой нагрузки бесконечно мала, 3 резуль-
тате чего в момент ее исчезновения перемещения точек балки еще
бесконечно малы, но скорости уже имеют определенные конечные
значения.
После удаления нагрузки балка придет в состояние движения,
т. е. будет совершать свободные колебания, определяемые фор-
мулой
* V (х, t) = S Хп(Ап sin<o„/ + Bncos<anf). (3.1)
п—1
300 ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ [ГЛ. VI
Предположим, что формы собственных колебаний стержня Хп
и соответствующие этим формам частоты шп уже определены нами
из рассмотрения краевых условий задачи. Для вычисления входя-
щих в выражение (3.1) коэффициентов Ап и Вп рассмотрим на-
чальные условия.
Приведенная характеристика нагрузки р(х) позволяет для на-
чального момента времени t = 0 записать следующие уравнения:
V (х, 0) = 0,
аи (х, 0) _
dt ~ °’
(3.2)
где v0 — начальная скорость.
Из первого условия (3.2) следует, что постоянная Вп в выра-
жении (3.1) должна быть принята равной нулю. Для того чтобы
раскрыть второе условие, выразим начальную скорость любого,
элемента dx балки в виде
v
- _ Р (*)
0 — т
(3.3)
где т — приведенная масса системы, определяемая на основании
последней из формул (1.7) в виде
R
т = Ш1 + mQ = Й + 2^ $ (г/) dy.
о
Поскольку скорости балки при Вп = 0 определяются формулой
ОО
== j ХпАп(*п cos ,
п=1
второе условие (3.2) можно представить в виде
оо
- 2
п=1
(3.4)
Таким образом, вычисление коэффициентов лп сводится к раз-
ложению функции в ряд по функциям собственных колебаний
балки Хп.
Умножим обе части равенства (3,4) на одну из собственных
функций и проинтегрируем это произведение по всей длине балки:
1 Г хп Г
~ j Р Xk ~ j Xnxk dx. (3.5)
О П=1 о
§ 3]
ДЕЙСТВИЕ МГНОВЕННОГО ИМПУЛЬСА
301
В силу ортогональности фундаментальных функций пе» ицтрг-
ралы в правой части уравнения (3.5) при n=/=k обращаются
в нуль.
Отличным от нуля останется только один интеграл
i
o>kAk Х% dx. (3.6)
о
В результате этого уравнение (3.5) примет вид:
i i
~ р (х) Xk dx = mkAk Xl dx,
о о
откуда
i
р (x) Xk dx
Ak=°-------1-----. (3.7)
m<ok dx
о
Исходя из формул (3.1) и (3.7), можно представить решение
задачи окончательно в виде
i
оо <\jP(.x)Xndx
V (х, 0 = ~ 2 °—i---------Хп sin vnt. (3.8)
х2п dx
о
Для изгибающих моментов и поперечных сил балки будем
иметь выражения:
оо \p(x)Xndx
M(x,i) = — ^X ---j----Х'пsin
т "=1 ^X2ndx
О
I
оо \p(x)Xndx
Q (х, /) = — ^ 2 5—у—-Хтп sin <ont
' 'П n=l ^X\dx
(3.9)
о
3Q2 ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК и ПЛИТ [ГЛ. VI
Полученные формулы показывают, что каждая составляющая
импульса
рп (х) = тАпыпХп
вызывает простое гармоническое колебание по форме Хп с часто-
той wn и амплитудой, равной + АпХп.
Отметим, что ряд (3.8), выражающий прогиб, сходится срав-
нительно медленно. Еще медленее сходятся ряды (3.9), характе-
ризующие моменты и поперечные силы. Это обстоятельство может
внести значительные трудности в
< I -] I । -/i—। -j практические расчеты. Однако
__нужно иметь в виду, что в по-
лученных формулах (3.8) и (3.9)
{ не учитывается затухание сво-
Рис. 143. бодных колебаний, которое в
действительности имеет сущест-
венное значение. Колебания вы-
соких тонов затухают значительно быстрее, чем колебания малой
частоты; к тому времени, когда прогиб, отвечающий основной фор-
ме, достигает максимума, большинство колебаний высших тонов
успевает затухнуть.
В результате этого в рядах (3.8) и (3.9) для получения доста-
точной точности вычислений можно ограничиться лишь первыми
членами.
В качестве примера рассмотрим однопролетную балку, распо-
ложенную на упругом основании и имеющую шарнирное опирание
на концах (рис. 143). Пусть на балку действует мгновенный им-
пульс интенсивности р, равномерно распределенный по пролету.
Как было показано ранее, фундаментальные функции в этом
случае определяются формулами (2.26), а частота собственных
колебаний балки — формулой (2.24). Для определения коэффици-
ентов Ап внесем выражения (2.26) в формулу (3.7). После неслож-
ных вычислений
получим:
i
Г пп
р \ sin — х dx
о
4р
П7С/П(0л
Ап
(3.10)
т<оп \ sin2— х dx
о
примет вид:
1 . п~ . ,
----sm -г- х sin (лп1 =
Пып 1
и решение (3.8)
оо
v(x, о =
v ’ 1
n=i
^ьр Г1 * itX • I I 1 • ЗтсХ • , . "1 /п 1 1 v
— — — Sin -г sin (01Г + 5— Sin -5- Sin (03/ + ... . (3.11)
пт L<O1 / 3(D3 I J
S 41
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ БАЛКИ
303
Отметим, что в формуле (3.11) для п приняты лишь нечетные
значения вследствие того, что симметричный импульс будет вызы-
вать только симметричные колебания балки.
§ 4. Вынужденные колебания балки
Рассмотрим случай, когда на балку расположенную на упру-
гом основании, действует внешняя нагрузка, определяемая фор-
мулой
р(х,/) = р(х)Н0- (4-1)
Выражение (4.1) показывает, что нагрузка р(х, t) изменяется
во времени на всей длине балки по одному и тому же произволь-
ному закону f(t). Будем предполагать, что изменение внешней
нагрузки не сопровождается заметными изменениями массы системы,
т. е. примем, что величина т останется в процессе движения
постоянной.
Ранее было показано, что задача о колебаниях балки на упру-
гом основании сводится к интегрированию неоднородного дифферен-
циального уравнения (2.6). Решение этого уравнения, как известно,
складывается из общего решения соответствующего однородного
уравнения и некоторого частного интеграла уравнения (1.6).
Общее решение однородного уравнения имеет форму:
Гоо
V(x, t) = 2 Xn(Xnsin<on/ + Вп cos ant). (4.2)
n=l
Произвольные постоянные An и Bn входящие в это решение,
определяются путем разложения заданных начальных значений
дУ
для V и в ряд по собственным функциям Хп. Это было по-
казано нами в предыдущем параграфе при рассмотрении расчета
балки на мгновенный импульс.
Для определения частного решения уравнения (1.6), характе-
ризующего вынужденные колебания балки, разложим нагрузку
р(х) также в ряд по собственным функциям Хп, т. е. представим
нагрузку р(х) в виде
р(х) = 2С„Хл. (4.3)
п=1
Коэффициенты Сп ряда (4.3) можно определить, умножив ле-
вую и правую части равенства (4.3) на X* и проинтегрировав
полученное выражение по всей длине балки. Принимая во внимание
304 ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И плит [ГЛ. VI
свойство ортогональности функций X (х), получим:
Z
Р (х) Xk dx
Сп = Ц----------. (4.4)
о
Если среди внешних нагрузок р(х) имеются также и сосредо-
точенные силы Р, то верхний интеграл, входящий в формулу (4.4),
следует понимать в смысле Стилтьеса. Выражение (4.4) может
быть поэтому переписано в виде
i
§ Р (х) Xk dx + 2 PXk
сп = °------г, (4.5)
dx
о
где Xk — значения функций Xk в точках приложения силы Р.
Заметим, что каждая из функций Хп может рассматриваться
как упругая линия, вызванная статическим действием распреде-
ленной нагрузки интенсивности ьРтХп. Очевидно, что статиче-
ская нагрузка СпХп вызовет упругую линию, ординаты которой
С
будут равны —-— Хп. Так как динамическая нагрузка вызывает
тпт
перемещения, определяемые известной формулой*):
t
V (х, t) = со VCT (u) sin <о (t — u)du, (4.6)
о
то в рассматриваемом случае, когда эта нагрузка равна CnXnf(t),
прогибы балки определяются выражением
С г
Vn (х, о = хп f (u) sin <оп (t — и) du, (4.7)
п о
где во избежание путаницы через и обозначено время, которое
изменяется в пределах от 0 до t.
Ввиду того, что внешняя нагрузка представлена рядом (4.3),
окончательное выражение для вынужденных колебаний балки,
*) См., например, Рабинович И. М., Курс строительной механики,
ч. II, 1954.
‘ДИНАМИЧЕСКИЙ РАСЧЕТ БАЛОК
вызванных этой нагрузкой, запишется в виде
00 с *
v (х, о = 2 («)sin (z—«)du-
n=l " *
305
(4-8)
Суммируя выражения (4.2) и (4.8), можно общее решение не-
однородного дифференциального уравнения (1.6), учитывающее
как свободные, так и вынуженные колебания балки, представить
в форме
ОО
V (х, 0 = 2 Ап sin 6)nt + Вп cos <i)nt +
n==l L
Cn t 1
— \f (w)sinw„ (/ — u)du .
n J
0
(4.9)
По определении прогибов балки V (х, t) рассматриваемая задача
может считаться полностью решенной, поскольку изгибающие мо-
менты и поперечные силы балки вычисляются при помощи извест-
ных формул сопротивления материалов, а скорость движения оп-
ределяется дифференцированием выражения (4.9) по параметру t:
M = ~Ejd5’ * = (4-10)
00 r-
v = = 2 Ллыл cos <0nt — Bnton sin +
n=l *-
c ‘ 1
+ (и) cos <an(t — u) du J . (4.11)
о
§ 5. Динамический расчет балок как систем с конечным
числом степеней свободы
С точки зрения динамики сооружений рассмотренные нами
балки представляют собой системы с бесконечным числом степеней
свободы. При всевозможных статических и динамических воздейст-
виях деформированная осьтакихсистем может принимать бесконечное
множество различных очертаний. В результате этого точный дина-
мический расчет упругих балок, позволяющий вычислить весь
спектр частот, приводит обычно к бесконечному ряду, составлен-
ному из собственных функций данной краевой задачи.
В ряде случаев, однако, можно считать, что рассматриваемая
балка обладает конечным числом степеней свободы. Так, например,
20 В. 3, Власов, Н. Н. Леонтьев
306
ДИНАМИКА НЕУСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ.
если предположить, что балка, расположенная на упругом осно-5
вании, достаточно жестка и не испытывает изгибных деформаций,5
то расчет ее следует проводить, как для системы с двумя степе-
нями свободы. Упругие балки также можно приближенно рассчи-
тывать, как системы с конечным числом степеней свободы. В этом
случае из бесчисленного множества форм, которые может прини-
мать упругая линия балки, выбирают несколько основных форм,
Рис. 144.
которые и рассматриваются в процессе расчета. При этом за воз-
можные формы колебаний могут быть приняты любые функции,
близкие к кривой изгиба балки и отвечающие геометрическим
граничным условиям. Такой подход значительно упрощает решение
динамической задачи и вместе с тем оказывается во многих слу-
чаях вполне приемлемым для практических целей.
1. В качестве первого примера рассмотрим симметричные коле-
бания жесткой балки, расположенной на упругом однослойном
основании (рис. 144). Для вычисления частоты собственных коле-
баний предположим, что перемещения балки определяются в виде
V = CT(t). (5.1)
Составим уравнение равновесия балки, под. которым будем
понимать равенство нулю суммарной работы всех сил, действую-
щих на балку, на возможном для нее единичном поступательном
перемещении V = 1. Силы инерции одного погонного метра балки
определяются формулой
^ = ^ = /^7". (5.2)
Кроме этих сил, на балку действуют еще реактивные давле-
ния упругого основания q и Q*.
В общем случае распределенные реакции q, вычисленные с
учетом инерционных сил основания, определяются формулой (1.5)
в виде
Q = — 2^ + kV + m0 . (5.3)
§51 ДИНАМИЧЕСКИЙ РАСЧЕТ БАЛОК 307
Внося в выражение (5.3) зависимость (5.1), получим: '- !' *
q — kCT + т(1СТ*. - (5.4)
Для определения фиктивных реакций Q* следует подсчитать
работу нормальных и касательных напряжений, а также работу
инерционных сил упругого основания, расположенного за; преде-
лами балки. При этом за возможное единичное перемещение (наг
пример, справа от балки) здесь нужно принять перемещение
Vo =’е-а^~1К
Произведя несложные вычисления, найдем реактивные давле-
ния Q*:
Q* = (МТ + т0^Т"> С = (2а/Т + Т') С, (5.5)
где
«=^-1 Г («-)</». ° j! •
7/ A №(y)dy, 4 (1 -|- vo) J т v / y (5.6)
Отметим, что формула (5.5), позволяющая вычислить сосре-
доточенные реакции Q*, в случае динамической задачу, отлича-
ется от формулы (5.7) гл. II наличием второго члена, которым учи-
тывается возникновение инерционных сил в упругом основании.
Суммируя работу всех сил, действующих на балку, и прирав-
нивая эту работу нулю, получим дифференциальное уравнение
следующего вида:
(2/Jfe + 4aZ) Т + (2/m0 + 21тг2тй^} Т" = 0. , 5.7)
Перепишем уравнение (5.7) в форме
‘(*+4)
mg 1 \
mi 2aZ /
Т = 0.
(5.8)
-4+5+
Можно видеть, таким образом, что жесткая балка на упру-
гом основании совершает простые гармонические колебания с
частотой
k 1+
/П! /По ОТо 1
1 + mi *" тг 2а1
(5.9)
20*
308 ДИНАМИКА И УСТОЙЧИВОСТЬ ВАЛОК и плит [ГЛ.У|
Осадка балки в произвольный момент времени равна
V = CiSin cat + C2cos<o/, (5.10]
где Сх и С2 — постоянные, определяемые в соответствии с началь-
ными условиями рассматриваемой задачи. )
2. В качестве второго примера рассмотрим задачу о свобод-'
ных колебаниях упругой балки конечной длины 21, свободно^
I
0
Рис. 145.
ЗЛ1
тг
лежащей на однослойном основании (рис. 145). Предположим
опять, что эта балка совершает симметричные колебания. В этом
случае форма упругой линии балки приближенно может быть
представлена в следующем виде:
X(x) = 3A-cos-^ (/ = 0, 1, 3, 5.........п). (5.11)
1=0
Первый член суммы (5.11) (при i — 0) определяет перемеще-
ние балки как жесткого диска, остальные члены этой суммы при
нечетных значениях i характеризуют ее симметричный изгиб. Мож-
но видеть, что функция X (х) удовлетворяет геометрическим ус-
ловиям задачи и одному из статических граничных условий (при
x = +l М = 0). Второе граничное условие (прих = +/ Q — 0)
при этом не выполняется.
Для нахождения частот собственных колебаний балки, со-
ответствующих формам (5.11), составим условие равновесия бал-
ки, понимаемое в смысле принципа возможных перемещений. Диф-
ференциальное уравнение изгиба (2.5) с учетом выражений (1.7)
может быть переписано в виде
EJXIV — 2tX’ + (k — mo2) X = 0. (5.12)
Bg^
№ f 5] ДИНАМИЧЕСКИЙ РАСЧЕТ БАЛОК 309
И| Подставим в уравнение (5.12) значение (5.11):
aAeJ Ш + 2t Ш + (k-’ma^cos^. (5.13)
Me i=o l \ / \ z j
В' Рассмотрим полученную формулу. Первым членом здесь ха-
В растеризуется состояние внутренних сил балки при изгибе по-
к следней по закону (5.11); вторым и третьим членами при коэффи-
f циентах t и k — состояние реакций упругого основания, распреде-
| ленных по опорной поверхности балки; последним членом — вели-
! чина инерционных сил.
| Кроме этих нагрузок, на балку будут действовать еще сосре-
доточенные реакции Q*, возникающие на концах балки при по-
гружении ее в грунт как жесткого диска. В рассматриваемом
случае величина этих реакций может быть определена при помо-
щи формулы (5.5)*):
<2Ф = (2^--^-<о2)Ло.
(5-14)
Подсчитывая работу всех перечисленных выше сил на каждом
из возможных перемещений балки, получим следующую систему
алгебраических уравнений:
г п
j 2 — т(°2) A-i cos^ dx + 2Q* = О,
—I 1=0
\ 2 \EJ +2/ (W +k - т<*2 ] х
J AmJ |_ \4,4 / \ «ь / J
—I 1=0
<5.15)
5 2[£Л'5-)‘+2<Ух
—11=0
. 1ТСХ Птсх , п
X Ai COS -gy- COS -7>j- dx = О
(/ = 0, 1, 3, 5, 7.n).
*) Предполагается, что упругое основание за пределами балки совершает
гармонические колебания с частотой <о.
ЗЮ ДИНАМИКА И УСТОЙЧИВОСТЬ ВАЛОК и ПЛИТ [гл. VI
Вычисляя интегралы, входящие в формулы (5.15), можно эту
систему представить окончательно в виде:
[Ч1 + - (mi + + mo i) A° +
+ — mu2)(—1) 2 = 0,
i =
+ 2t + Д1==0,
1) 2 Ло +
1 /„.n4re4 o nV . , ™ Л n
H—2“\EJ 16K + — m(a ) An — 0
(z = 1, 3, 5, 7..n).
(5.16)
Система однородных алгебраических уравнений (5.16) тож-
дественно удовлетворяется при Ло = = А3 = ... = Ап = 0. Од-
нако это тривиальное решение отвечает случаю, когда балка не
испытывает \ колебаний. Для получения интересующего нас нену-
левого решения следует приравнять нулю определитель этой сис-
темы, состоящий из коэффициентов при постоянных А/. Раскрывая
п + 3
этот определитель, мы получим уравнение степени —относи-
тельно неизвестных ь>2, из которого и определим все частоты соб-
ственных колебаний балки <+, соответствующие формам колеба-
ний (5.11).
Как частный случай отсюда может быть получена частота ко-
лебний жесткой балки w0, которая ранее была определена нами
в виде (5.9). Приведенное решение позволяет также отыскать
частоты собственных колебаний шарнирно опертой балки. Для
этого в разложении (5.11) следует опустить первый член с индек-
сом / = 0 и соответствующие члены в уравнениях (5.16). Посколь-
ку для практических целей чаще всего необходимо знать только
наименьшие частоты, то в общем случае свободно лежащей балки в
разложении (5.11) можно ограничиться только первыми двумя-
тремя членами. В соответствии с этим для определения низших
частот необходимо будет решить квадратное или кубическое урав-
нение.
§ 5]
ДИНАМИЧЕСКИЙ РАСЧЕТ БАЛОК
311
В рассмотренных примерах предполагалось, что балка совер-
шает симметричные колебания. В общем случае в силу ортого-
нальности симметричных и кососимметричных форм колебаний за-
дача распадается на две отдельные части: о симметричных и о
кососимметричных колебаниях балки. При этом для определения
частот, соответствующих кососимметричным формам колебаний,
может быть использован метод, аналогичный рассмотренному выше.
3. Пусть балка со свободными от закреплений краями подвер-
жена действию симметричного мгновенного импульса, интенсив-
ность которого на погонную единицу длины балки равна р (х).
Начальные условия в момент времени t — 0 имеют вид:
V (х, 0) = 0,
дУ (х, 0) _ р (х)
dt т
(5.17)
Исходя из первого условия (5.17) и формулы (5.11), можно
функцию прогибов балки приближенно представить в виде
п
V (х, f) = 2 A- cos-^- sin w;7, (5.18)
z=o
где частота колебаний <oz определяется системой алгебраических
уравнений (5.16).
Второе условие (5.17) позволяет записать:
р (х) v л 1ТСХ
Z—о
(5.19)
Из выражения (5.19) следует, что для определения коэффи-
циентов At заданную функцию нужно разложить в ряд по
cos^(t = 0, 1, 3, 5,...). Умножая левую и правую части фор-
мулы (5.19) на каждый член этого ряда и интегрируя полученные
выражения по всей длине балки, получим:
п 2 — 1 Г
Ло&*о Ч- 2 А‘ыг 1) = ~т[ j ? ^Х’
i=i о
I
к . < 2 С , . тех ,
— Л0<о0 Ч" } Р W cos 2i dx’ (5.20)
п—1 I
^Л0ы0(—1) 2 + 4„(o„ = ^p(x)cos—р dx
о
(i = 1, 3, 5, 7, ...pi).
312 ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ [ГЛ.VI
Система уравнений (5.20) позволяет вычислить все коэффици-
енты At выражения (5.18).
По определении прогибов балки в виде (5.18) можно изгиба-
ющие моменты и поперечные силы, соответствующие членам раз-
ложения (5.18) с индексом 1>1, рассчитать при помощи извест-
ных формул (4.10). Для вычисления усилий балки, соответствую-
щих первому члену ряда (5.18), следует предварительно опреде-
лить реактивные давления упругого основания. Поскольку первым
членом характеризуются колебания балки как жесткого диска,
то реакции основания при известном коэффициенте Ао можно найти,
используя формулы (5.4) и (5.5). Изгибающие моменты и попе-
речные силы балки могут быть вычислены затем известными ме-
тодами сопротивления материалов.
§ 6. Дифференциальное уравнение колебаний плиты
на упругом однослойном основании
Изгибные колебания плиты, расположенной на упругом осно-
вании, можно рассматривать как состояние статического рав-
новесия изогнутой плиты, к элементам которой, помимо нагрузки
Р (х, у, t), приложены еще силы инерции I—° резуль-
тате этого дифференциальное уравнение колебаний плиты может
быть получено из уравнения изгиба (1.1) гл. III в виде
(*> У, t) = Р* (х, у, /) — т± , (6.1)
где тг— масса, приходящаяся на единицу квадратной поверх-
ности плиты; р* (х, у, t) — внешняя нагрузка, состоящая из за-
данных сил р (х, у, t) и реактивных давлений упругого основания
q(x, у, /) и вычисляемая по формуле
р* (х, у, t) = p (х, у, f) — q (х, у, t). (6.2)
В отличие от рассмотренной нами ранее статической задачи
величина реактивных давлений р (х, у, t) должна быть определена
с учетом инерционных сил, возникающих в упругом основании при
его движении.
Для определения реакций q(x, у, t) снова выделим из упру-
гого основания элементарный столбик с основанием dx — 1, dy = 1
и рассмотрим условия равновесия этого столбика, понимаемые в
смысле принципа возможных перемещений Лагранжа (см. § 6 гл. I).
$ 6]
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ КОЛЕБАНИЙ ПЛИТЫ 3131
Предположим, что горизонтальные перемещения в упругом ос-
новании отсутствуют, а вертикальные перемещения характеризу-
ются только одной функцией ф (г) *):
и (х, у, г, 0 = 0,
V (X, у, 2, t) = 0,
w (х, у, г, t) = w (х, у, t) ф (г).
(6.3)
Учитывая инерционнные силы упругого основания, можно пред-
ставить обобщенные условия равновесия элементарного столбика в.
виде
\ \ фйг—
о 0 0
— J /«о d2w ^2dz + q (х, у, t) = 0, (6.4)
о
где q (х, у, t) — нагрузка, приложенная к поверхности упругого'
основания; т0 = —— масса, приходящаяся на единицу объема уп-
ругого основания, То — объемный вес грунта, g—ускорение силы
тяжести; Н— толщина сжимаемого слоя.
Подставляя в уравнение (6.4) величины нормальных и каса-
тельных напряжений упругого основания а2, тгх, хгу, которые при
наличии соотношений (6.3) могут быть вычислены по общим фор-
мулам (6.2) гл. I, и производя над этим уравнением несложные
преобразования, получим:
— 2tv2ay (х, у, t) + kw (х, у, t) + тп = q (х, у, t),
где
н .
о
н
t = / ггт.—; Ф2 (z) dz,
4 (1 + v0) 2 т v '
о
(6.5)
(6.6)
н
т0 = т0^ ф2 (z) dz.
о
•) Как и ранее, будем считать, что функция ф (z) выбрана таким образом,
что ф (0) = 1.
314
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. VI
Дифференциальное уравнение в частных производных (6.5) ха-
рактеризует колебания упругого основания под нагрузкой q (х, у, t).
Это уравнение может быть рассмотрено совместно с основ-
ным дифференциальным уравнением (6.1), поскольку прогибы пли-
ты и осадки поверхности упругого основания, расположенного
под плитой, совпадают и, кроме того, нагрузка на основание
q(x, У> t) по отношению к плите представляет собой реактивные
давления упругого основания.
Исключая из уравнений (6.1) и (6.5) функцию q (х, у, t), по-
лучим дифференциальное уравнение вынужденных колебаний плиты
на упругом однослойном основании. Это уравнение может быть
представлено окончательно в виде
V2V2ay — 2r2V2uy + 84щ/ + т* , (6.7)
где
s4 = -А- =--\ Ф'2 (z) dz,
D (1 —v2)DJT
v О' о
о
m* = = р j,? г (z)d2V
D ' Я s J т J D f
(6-8)
D — цилиндрическая жесткость плиты, т и т0 — объемные веса
соответственно материала плиты и упругого основания, h — тол-
щина плиты, g — ускорение силы тяжести, Ео и v0 — характери-
стики упругого основания, определяемые формулами:
Е — £гр
----- Л 9 >
1 — v
vrp
При рассмотрении свободных
сутствии внешней возмущающей
(6.7) несколько упрощается и принимает вид:
V2V2tei — 2г2?2щ/ + 84щ/ = — т* .
1 о/2
vrp
1 vrp
колебаний плиты, т.
нагрузки р(х, у, t),
(6.9)
е. при от-
уравнение
(6.10)
§ 7. Приближенный расчет безграничной плиты *
на сосредоточенный удар *)
Рассмотрим бесконечную плиту, расположенную на упругом
однослойном основании (рис. 146). Пусть в некоторой точке этой
плиты внезапно приложена внешняя сосредоточенная сила Р (/),
•) Приводимый в настоящем параграфе пример расчета выполнен в Ин-
ституте механики АН СССР Е. И. Силкиным.
ПРИБЛИЖЕННЫЙ РАСЧЕТ БЕЗГРАНИЧНОЙ ПЛИТЫ
315
§ 71
изменение которой во времени происходит согласно графику,
представленному на рис. 147.
В результате внезапного приложения внешней нагрузки плита
приходит в колебательное движение. Задача заключается в
определении напряженного и деформированного состояния плиты
в период действия ударной силы (0 t -с), а также в после-
дующий период свободных колебаний плиты
(г t < оо). р
Применяя полярную систему коорди-
нат, выберем начало отсчета в точке при- ________________
ложения силы P{t). Можно видеть, что
прогибы плиты будут зависеть здесь толь- (
ко от одной пространственной координаты —————х —
Р и времени t, т. е.
г 1 . Рис. 147.
W = W (р, t).
Основное дифференциальное уравнение задачи, характеризую-
щее свободные колебания плиты, в полярных координатах может
быть представлено в виде
VpVpQy — 2г27рШ + = — т* , (7.1)
где
V2_ Л + JLJ-
V ₽ ~ Эр2 ф р др ’
_1_ А.
vpvp ар4 р др3 р2 др2 ~ Р3 др
1. Решение основного дифференциального урав-
нения. Представим решение однородного уравнения (7.1) в виде
ш(р, /) = №(р)Т7), (7.3)
316
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
1гл. vr
(7-5)
(7.8) 3
(7.13)
(7.6)
(7.7)
где W (р)— функция, зависящая только от переменной р, а Т (t)
только от времени t.
Подставляя выражение (7.3) в дифференциальное уравнение3
(7.1), получим:
m*T" + s4T
--------w---------------т-----• (7-4)
Нетрудно видеть, что дифференциальное уравнение (7.4) мо-
жет быть удовлетворено при всех значениях р и t только в том
случае, если обе его части будут представлять собой постоянные
числа. Другими словами,
V2V2U7 2r2V2U7
m*T" + s4T
№ — r -'' ’
где X4 — параметр, подлежащий определению.
Из соотношения (7.5) следует:
+ (s4 + к4) Т = 0,
V2V2U7 _ 2r2V2U7 — VW7 = 0.
Введем обозначение:
S4 + к4 2
---J-- = W ,
т*
тогда уравнение (7.6) примет следующий вид:
Т" + со2Г = 0.
Решение этого уравнения может быть записано в форме
Т = £>i sin (at -j- cos (at, (7.1C)
где £>i и D2— произвольные постоянные интегрирования.
Дифференциальным уравнением (7.7), записанным для функции
прогибов W (р), определяется форма свободных колебаний плиты.
Решение этого уравнения будем искать в виде
V2W = nW. (7.11)
Внося выражение (7.11) в уравнение (7.7), получим для опре-
деления параметра п характеристическое уравнение
п2 — 2г2п — к4 = 0,
откуда
Л==Г2±|/Г4 + Х4. (7.12)
На основании выражений (7.11) и (7.12) можно видеть, что
дифференциальное уравнение четвертого порядка (7.7) эквивалент-
но двум дифференциальным уравнениям второго порядка:
W4(/r44-k4- r^W = 0, 1
V2r — (/r4 + k4 4- г2) W = 0. J
$ 71 ПРИБЛИЖЕННЫЙ РАСЧЕТ БЕЗГРАНИЧНОЙ ПЛИТЫ 317
Производя замену переменной в уравнениях (7.13), т. е. при-
яимая в первом уравнении
х =р J^r4 + X4 — г®
Щ и во втором уравнении
х=гр|Л|/г4 + X4 + г2,
В получим:
I С?- + —? + ^ = 0- (7.14)
f dx* 1 х dx 1 ' '
В Таким образом, дифференциальные уравнения (7.13) приводятся
к уравнениям Бесселя нулевого порядка действительного и мни-
Е мого аргументов.
В Переходя обратно к переменной р, можно решение исходного
I дифференциального уравнения (7.7) представить в функциях Бес-
| селя первого и второго родов от действительного и мнимого ар-
[ гументов *):
г (р) = ЛЛ (р V/д+^-г2) + л 2у0 (р J/V^T^-r2) +
+ АЛ (р К/^Т>? + г2) + ЛЛо (р К/^+^+г2). (7.15)
где 70, Уо— бесселевы функции от действительного аргумента
соответственно первого и второго рода, /0, До— бесселевы функ-
ции первого и второго рода от мнимого аргумента (модифициро-
ванные бесселевы функции), Alt Л2, А3, At—произвольные посто-
янные интегрирования.
В соответствии с выражениями (7.3), (7.10) и (7.15) общее ре-
шение основного дифференциального уравнения задачи (7.1) мо-
жет быть записано в форме
® (р> 0 ~ [T^i sin a>t + £>2 cos <о£] [ A±Jо A2Yо 4* Л37о ДлКоЬ
(7-16)
2. Определение произвольных постоянных ин-
тегрирования из начальных и краевых условий.
Для определения шести произвольных постоянных интегрирования,
входящих в выражение (7.16), необходимо рассмотреть заданные
для плиты начальные и граничные условия. Исходя из физичес-
кого содержания задачи, функцию прогибов w(p, t) следует под-
чинить следующим граничным условиям:
при р-> 0 w=/= со; | ? 17.
при р—> оо w —>0. J
*) Отметим, что в § 2 гл. IV решение аналогичного уравнения было
представлено в несколько иной форме. См. также решения, приведенные в
§ 7 гл. I и § 6 гл. V.
318
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК1И ПЛИТ
[гл. VI
Так как при р — 0 функции Yo и Ко стремятся к бесконеч-
ности, а при роо функция 10 принимает бесконечно
значения (см. рис. 28, 148 и 149), то постоянные А
должны быть положены равными нулю:
2, Дз, ^4
^2 — Д3 — Д4 — О,
(7-18)
Предположим, что до момента удара прогибы плиты отсутст-
вовали, т. е.
при t = 0 w — 0. (7.19)
Отсюда следует, что £>2 — 0- На основании изложенного об-
щее решение (7.16) можно представить в виде
Рис. 148.
аДр, t) = Csinw/-J0 (р]/Уг4 + Х4 — г2), (7.20)
где С — некоторая новая произвольная постоянная. Для опреде-
ления этой постоянной при-
мем, что ударная масса М в
момент соударения с плитой
(при t = 0) имеет скорость Ео.
Если жесткость плиты неве-
лика, то условие для вычис-
ления постоянной С может
быть приближенно сформули-
ровано в следующем виде:
при t = 0 и р = 0
5- = V0. (7.21)
равенство скоростей ударной
массы и плиты в точке соприкосновения в начальный момент
времени.
Так как
= Са cos o)t • Jo (р ]/”У г4 + —г2)
и
Jo(0)= 1,
то условие (7.21) можно переписать следующим образом:
Сео = Уо,
откуда
С = (7.22)
$ 7] ПРИБЛИЖЕННЫЙ РАСЧЕТ БЕЗГРАНИЧНОЙ
Внося выражение (7.22) в решение (7.20), получим выражение
для прогибов тонкой плиты:
да(р, /) = —sin <0/*</q (р j/'K/'4 + ^4—гг) • (7.23)
В случае массивной плиты коэффициент С может быть опре-
делен из условия равенства количества движения ударной массы
и плиты в момент соударения:
Wl = _Lc«cos«/-J0(0) I +
g g V ' I <=o
Pi ____________
2~mC<’> cos tot • Jo (p]/V '4+Х4-''2)р<Ц=0+
0
+„=! \ 2remC<o cos co/ • Jo(p V Уг* + К— r2)p dp |<=o f (7.24)
где tn—обобщенная масса плиты и упругого основания, опре-
деляемая при помощи последней из формул (6.8) в виде
н
т = tn*D = 4- ЗИ (Z) dz; (7.25)
о б J
о
Р1, Иг....Рп —корни (нули) функции Jo (рУ уг^ — ^—г2^, гра-
фик которой представлен на рис. 149.
Отметим, что в выражении (7.24) необходимо брать абсолют-
ные значения интегралов.
Знак суммы в последнем
члене распространяется по
всем полуволнам функции
расположенным в пределах
той зоны плиты, которая
приходит в движение, т. е.
получает начальную ско-
рость в момент удара. Эта
зона может быть опреде-
лена экспериментально. В
качестве первого прибли-
жения примем, что радиус действия ударного импульса определя-
ется лишь первой полуволной функции Jo- При этом выражение
(7.24) (при t = 0) перепишется в виде
И1
= _L Coj + 2пСат J pJn (р j/y^ + ^^r2) dp.
О
(7.26)
320
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ.
Заметим, что
Ul _______________ Hi
J р^о( Р КУ> + ^4 - Г2) dp = —xJ0 (х) dx =
о о
— xJ1 W
(V г1 + А1 — г®)
Поскольку первый корень функции Jo (х) равен [-ч = 2,4048, а
A (Pi) = 0,5191, то для интеграла формулы (7.26) получим значе-
ние
U1 __________________
Формула (7.26) позволяет теперь определить постоянную С в
виде
г_ РИо(Уг4 + Х4—г*)
(о [Р (У г4 + — г2) + 2,5топ§]
(7.27)
Внося (7.27) в общее выражение (7.20), получим формулу для
прогибов массивной плиты:
w(p,
РУо (V г* + М- г2)
<0 [Р — г2) + 2,5remg]
sin o>t- Jo (p ]/~+ X4—r2}.
(7.28)
3. Определение параметра X, связанного с часто-
той колебаний плиты со. В формулах (7.23) и (7.28), ха-
рактеризующих прогиб плиты в
период действия ударной нагруз-
ки, содержится параметр X, свя-
занный с частотой колебаний
плиты со зависимостью (7.8).
Для определения этого парамет-
ра рассмотрим условие равно-
весия элемента плиты, выделен-
Рис- 150- ного вблизи места приложения
нагрузки (рис. 150).
Пренебрегая реакциями основания и инерционными силами,
можно приближенно представить условие равновесия этого эле-
мента в виде
2k/?Q =
Р д2ш
7
(7.29)
If 7] ПРИБЛИЖЕННЫЙ РАСЧЕТ БЕЗГРАНИЧНОЙ ПЛИТЫ 321
где 2? — радиус выделенного элемента, a Q — поперечная сила
плиты, определяемая формулой
C = + (7'30>
Преобразуем несколько выражение (7.30), произведя в нем
замену переменной. Введем новую координату по формуле
R = р К/г‘ + А4 (7.31)
Формула (7.30) перепишется при этом в виде
Л— л ^/~т~т~ч л 1 ди> 1 d2w \
Q ()/ г4 + X —г2) R2 dR + R dR2 j • (7.32)
Подставив в (7.32) значение (7.20), получим:
Q = — D (/г*4-Х4 — г2)’л С sin cat [j0"' (R) —
- ^4' (/?)]• (7.33)
Замечая, что функция Jo (R) и производные от этой функции
по независимой переменной R связаны соотношениями:
' г ____ т т if __________ J1 т т m__________________в R Ri J 1 J1 । j
0 Jli J 0 Jot J0 R2 ^2 "Г " 0>
можно переписать выражение (7.33) в виде
Q = — D (]/г* 4- Х* — г2)’/г С sin wt (R). (7.34)
График функции (R) представлен на рис. 151. Из этого
графика следует, что формула (7.34) дает неверное значение
перерезывающей силы Q при р = 0. Поэтому определим параметр
X, задаваясь условием, что зона R = 1,8 исключается из рас-
смотрения. Формула (7.34) перепишется при этом в виде
Q = — 0,582 D г* 4- Х* — г2)73 С sin <ot. (7.35)
Подставив (7.35) и (7.20) в выражение (7.29) и учитывая
формулы (6.8), получим уравнение
(/^-rf ------------------P(s‘+ff--------• (7-36)
19,4 руЛ + То <i>2(z)dz]
Вычислив из уравнения (7.36) параметр X4, можно определить
по формуле (7.8) частоту колебаний плиты в период действия
удара.
21 В. 3. Власов, Н. Н. Леонтьев
322
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. V;
4. Свободные колебания плиты. По окончании действия
ударной нагрузки плита продолжает совершать свободные
Рис. 151.
колебания, получив к этому
времени известные переме-
щения и скорости. Эти пере-
мещения и скорости, харак-
теризующие начальные усло-
вия для свободных колебаний
плиты, определяются при по-
мощи формулы (7.20) в виде
w = С sin ют70,
57- = Сю cos ют- Jn.
nt и
(7.37)
Учитывая краевые условия в начале координат и на беско-
нечности, представим, решение основного дифференциального
уравнения (7.1), как и ранее, в форме
w (р, t) = [ГФ sin ю* (t — т) -|- D2 cos ю’ (t — т)] Д Jo* =
= [Cj sin ю’ (t — т) + C2 cos ю* (t — t)] Jo*. (7.38)
Величины ю* и X* (величиной X* определяется аргумент функ-
ции 70‘) в отличие от вычисленных ранее параметров ю и X ха-
рактеризуют частоту свободных колебаний плиты. Для определе-
ния постоянных С1 и С2 рассмотрим начальные условия. Поло-
жив в формуле (7.38) t — т, получим:
щ о, I
dw ,rr> | (7.39)
аГ = ® CiJ0. ) v
Решая уравнения (7.37) и (7.39) относительно постоянных С\
и С2, получим:
Ci = С -Т- COS (ОТ —
Х <0* /*
С2 = С sin ют -4°,
Jo
(7.40)
где коэффициент С в случае гибкой плиты определяется форму-
лой (7.22), а в случае жесткой плиты — формулой (7.27).
Подставляя значения постоянных Сх и С2 в решение (7.38),
получим окончательно:
w (р, t) — |^- cos ют sin ю* (t — т) -ф sin ют cos ю* (t — т)] CJ0. (7.41)
Для определения параметра ю‘, входящего в формулу (7.41),
вновь рассмотрим исходное дифференциальное уравнение (7.1).
§ 81 ПЛИТА, ШАРНИРНО ОПЕРТАЯ ПО КОНТУРУ 32З
Будем искать теперь решение этого уравнения в виде . ' . = aw, ’ (7.42)
где а — некоторый неопределенный параметр.
Внося (7.42) в уравнение (7.1), получим:
а2&у—2r2a.w + s4w = —т*^ (7.43)
Подставим выражение (7.41), определяющее прогибы плиты w
в процессе ее свободных колебаний, в (7.43). В результате та-
кой подстановки получим:
а2 — 2г2а + s4 = mV2. (7.44)
В выражении (7.44) величина w* должна рассматриваться как
функция параметра а. Экстремальные свойства этой функции
позволяют составить условие:
у = °- (7.45)
Раскрывая условие (7.45):
dm*__ а — г2 _
— 2г2а + s4 ’
V т*
можно видеть, что это условие выполняется, если параметр а
имеет величину
а = г2.
Выражение (7.44) позволяет теперь получить для частоты
собственных колебаний плиты следующую формулу:
Здесь приведенная масса плиты и упругого основания т*
определяется, как и ранее, в виде
§ 8. Плита, шарнирно опертая по контуру
1. При рассмотрении свободных колебаний плиты, расположен -
ной на упругом основании и шарнирно опертой по контуру
(рис. 152), будем предполагать, что прогиб плиты в каждый мо-
мент времени определяется выражением
W (х, у, t) = w (х, у)Т (/). (8.1)
21
324 ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ [гл. Vf
Дифференциальное уравнение, характеризующее форму изогну
той поверхности плиты, запишется при этом, как и ранее, в виде
V2V2^ — 2г2^2ш + (s4 — tn w2) w = 0. (8.2)
Решение уравнения (8.2) представим в форме бесконечного
ряда:
ОО 00
®(м) = 2 2 Ain cos V cos <8'3)
1=1 П=1
Можно видеть, что каждый член этого ряда удовлетворяет
граничным условиям, заданным на контуре плиты:
, Ь „ 52пу г,
при % = +-=- w = 0, -гтг = 0;
— 2 дх2
, I „ d2w „
при i/ = ±y ш = 0, ^ = 0.
Для определения частот w собственных колебаний плиты под-
ставим ряд (8.3) в дифференциальное уравнение (8.2), умножим
l~x hnx . ,
это уравнение на cos cos —, где / и h — произвольные целые
числа, и проинтегрируем полученное выражение по всей поверх-
ности плиты:
ь I
X cos cos cos cos dx dy = 0. (8.4)
Уравнением (8.4) характеризуется работа всех обобщенных
сил плиты и упругого основания на возможных для плиты еди-
ничных перемещениях. Вследствие ортогональности тригонометри-
ческих функций все интегралы при i ф j и п ф h обратятся в
5 g] ПЛИТА, ШАРНИРНО ОПЕРТАЯ ПО КОНТУРУ J25
нуль. Уравнение (8.4) можно представить поэтому в виде
®12те2 , п2те2\2 . „ „/{2тс2 , п2те2\ . . . ,1
F ~р~) + 2г (-у- + -р—) + 8 — Ш <0 j X
X cos2^cos2^dxdy = 0. (8.5)
При Ain = 0 мы будем иметь тривиальное решение, соответ-
ствующее случаю, когда деформации плиты отсутствуют. Отсю-
да следует, что
(^+^y + 2r»(« + ^) + S‘-m-»- = 0,
а частоты свободных колебаний плиты определяются формулой
•)/" 1 Г/12ге2 . П2ге2 \2 о »/(2ге2 И2л2 \ /I ,о
ы‘п ~~ V пё К'б2’ "1“ ) + 2r (д2- + ~1Г) + s J ' (8>6)
Давая числам i и п всевозможные целые значения, мы полу-
чим весь спектр частот плиты. Соответствующие этим частотам
главные формы колебаний имеют вид:
. i~x П~у /о ~
wln = Ain COS -у- cos -р . (8.7)
Если плита испытывает симметричные или обратносимметрич-
ные относительно оси х колебания, то числа i будут иметь со-
ответственно только нечетные или четные значения; случаям
прямой или обратной симметрии колебаний относительно оси у
будут соответствовать нечетные или четные значения чисел п.
2. Для вычисления коэффициентов /!,« следует рассмотреть
начальные условия задачи. Пусть на плиту действует мгновенный
импульс, интенсивность которого, отнесенная к единице поверх-
ности плиты, равна р(х, у). В начальный момент времени пере-
мещения в плите отсутствуют и функцию прогибов w(x, у, t)
можно представить в виде
W (х, y,t) = 2 2 Aln cos 7Г cos 7^ s5n (8-8)
(=1 n=l
При этом скорости плиты определяются следующим образом:
— = 3 2 Atn OJ-COS ¥cos njrcos M
£=1 n=
Начальная скорость в момент t = 0 равна
®,=, = 2 2 A"»-” cos'Scos7 = ^. (8.10)
1^1
326
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ.VI
Раскладывая функцию р(х,у) в двойной ряд по косинусам,
l^X /тли
т. е. умножая равенство (8.10) на произведение cos —cos —
и интегрируя полученное выражение по всей поверхности плиты,
в силу ортогональности тригонометрических функций получим:
ь/а . Щ
. Г „ iitx 9 птсу , ,
Ain o>ni \ \ cos2 -г- cos2 -j—dxdy =
-b/2 -1/2
b/2 1/2
1 Г Г , \ inx nny dx du.
= — \ \ p (x, y) cos — COS
m J J'' ’ь I
—b/2 —1/2
откуда
b/2 1/2
4 \ \ p (x, y) cos^ dx dy
& —b/2—1/2_____________Ь 1 (8.H)
гп “>intb
, Функция прогибов плиты в любой момент времени t может
быть теперь представлена следующей окончательной форму-
лой:
Ь:2 1/2
Г С , . ^Х птсу . ,
\ \ р (х, у) COS —Г~ cos ~т~ ах аУ
оо оо j J О I
w У’ V = ----------------------
2==1 П=1
X cos ~ cos sin (0Z„ t. (8.12)
Внося формулу (8.12) в общие выражения для изгибающих
моментов и поперечных сил (1.8) гл. III, мы определим усилия,
возникающие в плите от действия мгновенного импульса р{х, у).
§ 9. Колебания плиты со свободными от закреплений краями
1. Определим частоты собственных колебаний плиты, свобод-
но лежащей на упругом основании (рис. 153). Применяя для
решения основного уравнения (6.10) метод разделения пере-
менных, получим дифференциальные уравнения следующего
вида:
Г' + (о2Г = 0, (9.1)
— 2t^zw + (k — mod) w --- 0. (9.2)
S 9]
КОЛЕБАНИЯ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ gg^
г Форму деформированной поверхности плиты w (х, у) . предста-
вим в виде ряда -
w (х, у) = 3 3 Стп Чтп (х' У')’ (9.3)
1 1
где <ртп (х, у) — линейно независимые функции, выбираемые за-
ранее в соответствии с геометрическими граничными условиями
задачи, а^Стп — постоянные коэффициенты. В дальнейшем в ка-
честве функций <fmn мы примем тригонометрические функции в
комбинации с линейными членами, характеризующими перемеще-
ния плиты как жесткого диска.
Для определения частот колебаний плиты, соответствующих
формам колебаний (9.3), составим условия равновесия, исходя из
принципа возможных перемещений Лагранжа. Для этого подсчи-
таем работу всех внешних и внутренних сил плиты на каждом
из возможных для нее единичных перемещений, как это было
сделано нами, например, в § 12 гл. III.
Внося разложение (9.3) в уравнение (9.2), можно условия
равновесия плиты представить в виде следующей системы алгеб-
раических уравнений:
т п ( е е
2 2 2/v2^+.(^ — m^<fmn]<fikdxdy +
+ |[<2 тп (s) + Q*(s)]<pifeds}}==0
(г= 1,2, 3, k = 1, 2, 3,.. ., n), (9.4)
где <pmn(s), (ptk (s) — значения функций <p(x, у) на контуре
плиты.*
328
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. VJ’
В уравнениях (9.4) членами, стоящими под знаком двойного^
интеграла, характеризуется работа внутренних сил плиты, реак-5
тивных давлений упругого основания и инерционных сил, возни-
кающих в плите и упругом основании. Контурным интегралом ’
определяется работа поперечных сил, приложенных к контуру
плиты. Первый член определяет работу приведенных по Кирх-
гофу дополнительных поперечных сил (см. формулы (1.9) гл. III),
которые возникают на краях плиты в результате приближенного
удовлетворения статических условий функциями <р (х, у). Вторым
членом учитывается работа реактивных давлений, распределен-
ных на контуре плиты и характеризующих деформацию свобод-
ного от нагрузки упругого основания. Исходя из общих формул
(10.8) и (10.9) гл. III, а также учитывая работу инерционных
сил упругого основания, расположенного за пределами плиты
[см., например, формулы (5.5) и (5.14)], для этих реакций будем
иметь:
|_\ 0 4а/7 1 ‘ \дх Ji 2a\dy2//J
(9-5)
L\ 0 4aZy ° 1 \ду ;ь 2a\5xa/Z>J
где индексы l и b показывают, что сила Q* относится соответ-
ственно к продольному (х = + &) или поперечному (у = +1)
краю.
Отметим, что уравнения (9.4) будут справедливы и в том
случае, если рассматриваемая плита расположена на основании,
упругом в смысле гипотезы коэффициента постели. При этом в
уравнениях (9.4) следует отбросить члены, содержащие величи-
ну Q* и коэффициент I, а также считать характеристику k равной
коэффициенту постели.
Уравнения (9.4) могут быть переписаны в следующей разверну-
той форме:
3qo, 00 ^00 4' ^00. 1о Сц. + • • • + ^00. тп Стп — 0,
310. 00 Qo 4“ 310, 10 Сю 4" • • • 4" S10, тп Стп = 0.
00 Соо 10 С10 4-...4- ^ik, тп Сщп
(9.6)
^тп, оо
'тп,
тп.тпСтп — 0»
где
^ik.rnn = \\ PVV5?™ — 2t^mn + (k — /П(О2) <fmn ]<pikdxdy +
+ ^[Qmn{s) + Q*(s)]c?ik(s)ds. (9.7)
j g] КОЛЕБАНИЯ ПЛИТЫ CO СВОБОДНЫМИ КРАЯМИ
329
Интегралы, входящие в формулу (9.7), вычисляются по всей
площади и всему контуру плиты. При этом нужно иметь в виду,
что интегралами (9.7) характеризуется виртуальная работа сил
одного состояния рассматриваемой системы на перемещениях
другого состояния. В результате этого коэффициенты (9.7) обла-
дают свойством взаимности (8<ft> тп = Ьтп.гь), а матрица уравнений
(9.6) — симметричной структурой.
Система однородных алгебраических уравнений (9.6) имеет
отличное от нуля решение, если определитель этой системы, со-
стоящий из коэффициентов при СгА, равен нулю:
^00, 00 ^10. 00 °00, 10 • ^10, 10 • ^00, П1П $10, mn = 0. (9-8)
00 $mn, 10 • mn*
Раскрывая определитель (9.8), мы получим уравнение
(пг ф- п)-й степени относительно квадратов частот <оа, из которо-
го и найдем все т 4- п частот, соответствующих формам колеба-
ний (9.3). При этом собственные колебания плиты будут опре-
деляться формулой
И* (х, У> О = 2 2 Стп фтп (X, У) Sin <0mn (t фтп), (9-9)
1 1
где фтп—постоянная, характеризующая сдвиг фаз.
Заметим, что в том случае, когда деформированная поверх-
ность плиты представлена тригонометрическими функциями, общая
задача о движении плиты на упругом основании, в силу ортого-
нальности этих функций, распадается на четыре независимые за-
дачи о симметричных и кососимметричных (относительно одной или
двух координатных осей) колебаниях плиты. В дальнейшем мы
рассмотрим каждую из этих задач в отдельности.
2. При рассмотрении симметричных колебаний выражение (9.3)
может быть представлено в виде
т n ft 1
w(x, у) — Qo 4- 2 cos ~ь 2 cos ~~i
1 1
tn n
4-22c^cosZFcos^r- <9-10>
1 1 .
(tn. n — 1,3, 5,..., (2k — 1)).
33Q ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ [ГЛ» 4
Это означает, что в качестве функций <ртп нами принят
следующие функции:
, trntx
?00 — 1, ?т0 — COS ,
ппи тпх tint!
*роп — COS , tymn — COS “ COS —j— ,
где т.п— нечетные целые числа.
Подставляя (9.11) в формулу (9.7), нетрудно вычислить все
коэффициенты уравнений (9.6). В качестве примера в табл. 18
приведена матрица алгебраических уравнений для случая, когда
в формуле (9.10) приняты четыре члена (т = 1, n = 1), соответ-
ствующих четырем возможным формам колебаний плиты. Можно
видеть, что приведенная матрица симметрична относительно
главной диагонали. Для составления ее необходимо вычислить
10 безразмерных коэффициентов, имеющих достаточно простую
структуру.
Входящие в эти коэффициенты величины а, р, k, D и tn0
вычисляются по формулам:
о
О
_______ н
т0 = тп^ ф2 (z) dz,
(9.12)
где I и Ъ — соответственно длина и ширина плиты, D — цилин-
дрическая жесткость плиты, т0 — приведенная масса упругого
основания, k и t — обобщенные характеристики упругого основа-
ния, ф — ф (I) — функция, характеризующая распределение пере-
мещений по толщине упругого основания.
Приравнивая нулю определитель этой матрицы, мы получим
алгебраическое уравнение четвертой степени относительно пара-
метра <о2. Это уравнение и позволит вычислить четыре частоты
собственных колебаний плиты, соответствующие четырем выбран-
ным формам колебаний.
Если предположить, что рассматриваемая плита является
абсолютно жесткой, то в разложении (9.10) следует ограничиться
§ 91
КОЛЕБАНИЯ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ
,331
одним первым членом. При этом, используя табл. 18, получим:
1+и<1+₽)-+(! +
^ + l+£V = o
т0 ' ab J
или
(1)
. i+4(i + в)
k ab' 1
т0 ! + mi + 1 + j
т0 ab
(9.13)
3. Останавливаясь на рассмотрении случая кососимметричных
колебаний, можно функцию прогибов плиты принять в следующем
_ виде:
а) при колебаниях, симметричных относительно оси х и косо-
симметричных относительно оси у,
т п
w(x, у) = С004 + У Cm0 sin У Соп cos +
Ь 1 b b I
2 1
т п
+ У у.Стп sin^cos^L' (9.14)
I) I
2 1
(tn = 2, 4,6,. . . ; n = 1, 3, 5, . . .);
б) при колебаниях, кососимметричных относительно оси х и
симметричных относительно оси у,
tn п
w(x,y) = C00 CmQ cos^+ 2 Соп sin^ +
1 2
т п
+ 22C^ cos^sin^ (9.15)
1 2
(т= 1,3,5,...; п = 2,4,6,...);
в) при колебаниях, кососимметричных относительно обеих
осей,
т
w (X, у) = Соо + у Сто sin +
ID I D
2
п ГП п
+ ^у C^sin^ + yyc^sin^sin^ (9.16)
2 2 2
(п, т — 2, 4,6, 8,...).
s
9]
КОЛЕБАНИЯ ПЛИТЫ СО СВОБОДНЫМИ -КРАЯМИ
333
Таблица 18
mi + т0
k
1 (ге4Д> тс2
те [kb1 + a2b2 1
mi + т0 1
~ k “ j
Г „ те2 -»
rLl^^+a2*2^ +
2 rfl
+ 1 + Tb + cW ~
1 Г те’О те2
те[ТьГ^ + ^Р2 +
+ 1-^ф^2]
1 Г %4D
т|(1 + 32)2Ъг +
+ (1 + £2) -^2 + 1 —
mi + т0 ,
k “ .
334
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[гл,
£"00 Сга
0-0 1 Г 6 / 12 3 L1 + ab I1 + 3 ) + а2Ь2 ~ , 3 + 21 k Д + та + ab j J М'+^о-
2-0 • 1 Г 'Ч) 7Г2 2 ¥ I16 kb4 + 4 а2*2 + 1 + ab + те2 т0 / mi 8 \ + 4 с№~ Т?+7^+ ab )" J
0-1 • •
2—1 • •
336
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. |
Соо £ю 1
0-0 1 Г 6 / 1 \ 12 з" L1 + ль + З"J + а3*2 — /По Л , /Hi , ЗР + !\ J k \ + т0 ab / j 2 Г 6 12 I 3^ L1 + аЬ + а3^2 ~ 1 то Л , mi , Л k \ + т0 + ab} J
1—0 • 1 Г tc4D тс2 6 L kb11 + а3Ь3 + + TT3D 6 + 12 (2 — ц) kf)l З2 + а6 3 + 12 „ л2 + а2/>2 Р + 3 a3b3 Р — f. , mi , 31\ Л \ то J
0—2 • •
1—2 • •
и
КОЛЕБАНИЯ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ
337
Таблица 20
f 0)2 С11 Возможные перемещения
1 Г. 2 т0 VI1 + ab~ k х . х (1 + — + -у) ш21 А \ 1 т0 ' ab] J А - 2у wm = — & г
V k “) 1 Гтг4Л , тс2 2^ L kb* +:а2Ь2 + 1 — _ЕЦГ?ои3] - 2у тех №10 = у cos у /X
1 Г rc4D Т[16 kb* + + 4 Р2’-+ 1 + 2 тс2 + + 4 —575 ?2 — ' ab ~ а3Ь3 f + ^J-V| k \ ' mOj±ab/ .) 1 Г n*D TL16I^^ + + 4 aV Р2 +*1:“ _^. + — 2icy wa2 = sin — У?
• 1 Г , it4D t[(v+ kb^ + 7Т2 4- (1 + 4р3) 4-1" k “ J _ - tzx. *. 2iti/ 0У12 = cos у sin- yr
22 В. 3. Власов. Н. Н. Леонтьев
33g ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ [ГЛ. Vll
Coo I С20 J 1
0—0 -i-1288(1 -^-^^ + 1 + 6 12 + ^(1+3) + ^(1+Р2)- тв (t пц 3(1 + Р)\ J k \ Ио «& ) J 1 Г 6 12 L1 + ab 0 + а2*2 02 ~ ^о / "Ч 38 \ ]
2—0 • 1 Г тс4О тс2 б- L16 'Ж + 4 а2*2 + 1 + ТГ2Р 6 + 48(2-!x)w82 + -5F8 + 12 те2 + а2*2 + 12 а3Ь3 Р ~ m0 f mi 3£\ 1 “ k V + т0 + ab ) “ J
0—2 • •
2—2 • •
КОЛЕБАНИЯ ПЛИТЫ СО СВОБОДНЫМИ КРАЯМИ
339
Таблица 21
с 02 С 22 Возможные перемещения
1 Г 6 12 Зл + ай + а2й2 X Л , Ш1 , 3 \ 2 k \ "* ти "* ай/03. 1 / Ш1 + то Л т> к1 “ k “J — ixy woo^7b
1 ( *'D 7Г3 2ГО \16 ~kb* + 4 а2й2 + + 1__тЦт1и2) — 2у . 2тсл ^20 — "J” Sin fy 1
4~ 1 jli 1 сл_ v 1 'з «13, х + 31 Is «о 1-5 « |3, 1 1 1* Ч? + .+ S 7 3 l'g|g° ах оо со. . 1, С О Н Ci Н "Г” 4" +§|5 ..is, + * ~'В 5Н |со 1 1 / 7C4D 7С3 7>— ( . д З4 4~ 4 —215-4- 2tz \ kb4 * “ а2Ь2“ mi + mQ \ . + 1 k . > _ 2х . 2ку 0*02 = "J" sln 1 ’ 1 - ‘ ч‘ "1 л \
• 1 г ^“D -4-[16(1+^)21бГ + п2 + 4 (1 + Р2) ^2 + 1 - mi 4~ тр 1 - k “ J 2яХ . 2пу at>22 = sin sin —
22*
340
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. VI
Как и в рассмотренном раннее случае симметричных колеба-
ний, коэффициенты уравнений (9.6) вычисляются здесь по фор-
муле (9.7).
Ограничиваясь в разложениях (9.14), (9.15) и (9.16) только
первыми четырьмя членами, можно уравнения (9.6) соответствен-
но для случаев а), б) и в) представить в виде матриц, приведен-
ных в табл. 19, 20 и 21. Входящие в эти матрицы величины а,
[J, k, D и т0 определяются, как и ранее, формулами (9.12).
Приравнивай детерминанты полученных матриц нулю, мы будем
иметь'алгебраические уравнения четвертой степени относительно
«о2 для каждого из рассматриваемых случаев колебаний. Эти урав-
нения позволят вычислить по четыре частоты собственных коле-
баний плиты для каждого пз случаев а), б), в).
; Ограничиваясь в разложениях (9.14) и (9.15) первыми линей-
ными членами, нетрудно при помощи табл. 19 и 20 определить
частоты колебаний жесткой плиты в следующем виде:
при кососимметричных колебаниях относительно оси у
при кососимметричных колебаниях относительно оси х
моо
. 1 + И+ЦтН2
k ab \ 3 / a2b2
«О 1 -I -I 1 +^~
тд ab
(9.18)
Первое приближение для случая кососимметричных колебаний
по двум направлениям (табл. 21) дает:
j Л 2SS (Г - И) + Г + 6 (i + 3) + -gy (1 + З2)
/ к Rtr ао а£Ьл
V 1 I W1 4 1+33
r тв ab
(9.19)
। ,§ 10. Устойчивость прямоугольной плиты на упругом
j однослойном основании при сжатии в одном направлении
Рассмотрим прямоугольную плиту, расположенную на упру
; гом однослойном основании и нагруженную продольными сжимаю
; щими силами N (х) (рис. 154).
§ 10J устойчивость прямоугольной плиты
341
Дифференциальное уравнение устойчивости такой плиты имеет
следующий вид:
Dy2y2w— 2ty2w + kw = — N(x)^, (10.1)
где D—>цилиндрическая жесткость плиты, a k Kt — обобщенные
характеристики упругого основания. Отметим, что сжимающие
силы в уравнении (10.1) считаются положительными.
Задавая поверхность прогибов плиты в форме конечного разло-
жения
w (*> У} = 3 Wk (у) и {х) (10.2)
fe=i
и предполагая, как и ранее (см. § 2 гл. III), функции (х)
известными, а функции Wk (у) подлежащими определению, можно
дифференциальное уравнение в частных производных (10,1) при-
вести к виду
3 a,k WkV — 3 I2 — Nik] Wk + 3 ^Cik + s"dWlt = °,
k-i fe=i *=i -
(/= 1,2,3, ... ,n). (IO-3)
Коэффициенты aik, bik, cik, ?°ik, 4 уравнения (10-3)
ляются только выбранной системой функций xH*) и величинами-
342
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ. VI
упругих постоянных плиты и основания:
aik = ZD Х‘ dx,
blk = ED | dx — lx* Xi + Xh X/I*J >
Cik =5 ED \'/k X‘ dx, (10 4)
p°fc = Xfe Xi dx + [[Xk xdh
Sik = k {jx* Xi dx + J^Xk Xidx + ~ [ [х/г Xi] 1} •
Коэффициенты Nih, зависящие от величины сжимающей нагруз-
ки N (х), рассчитываются по формуле
Nik = (x)Y.iXkdx. (10.5)
Если заданная нагрузка является равномерно распределенной,
т. е. ;V(x) = const, то уравнение (10.3) может быть записано в
в форме
aik 2 I 2 (bih + W"h +
k=i *=11 J
+ 2^ + ^)^ = °’ <10-6)
A=1
где P — полная величина сжимающей нагрузки, а b — ширина
плиты.
Давая индексу i последовательно все значения от 1 до п, по-
лучим из уравнений (10.6) или (10.3) полную систему однородных
обыкновенных дифференциальных уравнений относительно искомых
функций Wk (у) (k = 1,2,..., п). Эти уравнения при выбранных функ-
циях Xk[x){k~ 1, 2,..., п) будут известны с точностью до пара-
метра Р (в общем случае N), представляющего собой искомую
критическую силу. Присоединяя к уравнениям (10.6) однородные
граничные условия, заданные для функций Wk (у) на крайних
сечениях у = 0 и у — I, мы из условий существования решений,
отличных от нуля, получим для Р бесконечное множество значе-
ний. Так как система дифференциальных уравнений (10.6) имеет
симметричную структуру, то характеристические числа в описы-
ваемой здесь однородной краевой задаче всегда будут иметь дей-
ствительные значения.
Ранее было отмечено, что из существующих методов решения
системы обыкновенных дифференциальных уравнений с постоянными
коэффициентами наиболее эффективным является метод Крылова,
§ io] устойчивость прямоугольной: пЛитй 343
разработанный им применительно к задаче о малых колебаниях
систем со многими степенями свободы.
Для достаточно длинной пластинки решение уравнений (10.6)
может быть представлено в форме
Wk(y) = Ckshr% (k = 1,2,3,..., п), -(Ю.7)
где Ck — произвольные постоянные, а X — длина полуволны сину-
соиды, определяющей форму потери устойчивости в направлении
координаты у.
Подставляя выражение (10.7) в уравнения (10.6) и приравни-
вая нулю определитель системы, образованный из коэффициентов
при Ck, получим характеристическое уравнение, порядок которого
относительно Р равен п. Уравнение это будет вековое, и, следо-
вательно, корни его будут действительны. Вследствие того, что
характеристическим уравнением при конечном числе п в алгебраи-
ческой форме связаны две неизвестные величины — сила Р и длина
полуволны X, то для определения этих величин должно быть еще
использовано условие экстремума
При решении практических задач в разложении (10.6) можно
иногда ограничиться одним только первым членом. При этом
форма потери устойчивости плиты в направлении ее ширины будет
представлена одной только функцией / (х), а дифференциальное
уравнение устойчивости примет вид:
4rIV + ^n — 2B)W" + CW = 0, (10.8)
где W = W (у) — искомый обобщенный прогиб; А, В, С, —
коэффициенты, вычисляемые по формулам:
A = £>Jz2dx,
B = d{ Jx'2 dx-y dt + I lx2n,
p Г P 9/ P 9л/ 1 (10.9)
C= D^^x + k^dx+^^dx+^l^]]},
А1ц = \N(x)x*dx.
Рассматривая далее именно этот случай и, кроме того, пред-
полагая, что плита достаточно длинна представим реше-
ние уравнения (10.8) в форме (10.7). При этом получим:
Л®4-^-2В)©г+С = 0- (10,10)
344
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[гл. VI
Из формулы (10.10) можно видеть, что обобщенная сжимающая
сила есть функция параметра X. Поэтому для определения
наименьшего значения этой силы, которое и будет критическим,
необходимо продифференцировать выражение (10.10) по X и при-
равнять производную^!-1 нулю. Выполняя указанное, найдем:
4 __
X = (10.11)
Теперь нетрудно определить критическое значение силы АГП:
Nn == 2 (В 4- У АС). (Ю.12)
Если сжимающие силы распределены в поперечных сечениях
плиты равномерно (М (х) = const), то выражение (10.12) может быть
переписано в форме
Р = (В + У АС), (10.13)
где Р — полная величина сжимающей нагрузки.
Вводя обобщенные геометрические характеристики:
можно формулы (10.11) и (10.13) представить также в виде:
где F — площадь всего поперечного сечения плиты, h — толщина,
а I — длина плиты. Если размер плиты в направлении оси у соиз-
мерим с шириной b и длина волны X, полученная по форму-
ле (10.11), превышает этот размер, то для пластинки нужно принять
величину I за длину волны и по формуле (10.10) определить сжи-
мающую критическую силу. Если же длина волны меньше I и
в длине I укладывается п раз с некоторым остатком, то необходи-
мо взять X равным - и и найти для этих значений по фор-
муле (10.10) соответствующие величины N^. Меньшее значение
Nu и будет являться критическим.
§11. Устойчивость узкой плиты на упругом однослойном
основании
Наиболее простое решение дифференциальных уравнений устой-
чивости (10.3) может быть получено в том случае, когда попе-
речное сечение плиты можно считать недеформируемым. Такое
предположение будет справедливо для достаточно длинных плит,
«»»J
УСТОЙЧИВОСТЬ УЗКОЙ ПЛИТЫ
345
имеющих свободные края (рис. 154) или один шарнирно опертый
край (рис. 156), а также в ряде других случаев, когда элемен-
тарная поперечная полоска dy, выделенная из плиты, оказывается
геометрически изменяемой (см., например, рис. 155). За функции
yk (х) в этом случае естественно
принять перемещения полоски,
Рис. 155.1 Рис. 156.
Рассмотрим некоторые частные примеры.
1. Прямоугольная плита, шарнирно опертая по
продольному краю. Рассмотрим прямоугольную пластинку
постоянной толщины h, загруженную центрально приложенной
сжимающей силой Р = Nb (рис. 156). За форму возможного пере-
мещения в направлении оси х примем поворот этой пластинки
как жесткого диска относительно закрепленного края:
Х = х.
В этом случае задача будет характеризоваться дифференциаль-
ным уравнением (10.8), для коэффициентов которого нетрудно
получить выражения:
В = Db(l -|Л) + Z|3(l +2I5),
(11.1)
346 ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ [ГД. |
Уравнение устойчивости запишется при этом в виде
^!V + \wh~So—:л)—S'1 + АУН + 51"1 + Af1+АЖ =
1 Ь2К к ' D\ ' ab/ | ' D L ab\ ' ab/J
(11.:
Будем считать, что на поперечных краях у = 0 и у = I пли'
имеет шарнирное опирание. Решение уравнения (11.1) может бы
представлено поэтому в форме
W7 —С sin у. (11,3)
Отметим, что для плит, поперечное сечение которых не дефор-!
мируется, потеря устойчивости всегда происходит по одной полу-'
волне, т. е. параметр X формулы (10.7) всегда равен длине пла-
стинки I.
Внося (11.3) в уравнение (11.2) и сокращая на отличный от
„ . г. у
нуля множитель С sin у, получим:
Г-Р 6 /1 ' 2/л > ЧК , k fi > 3 А । Ml л
\_Db Ь2 ( D v + ab)]/2 + о[ + ab\ + aJj °’
откуда
„ n3EJ . 6EJ , о.. А , 3 \ , ОТГ. , ЗА. 1
РУр — /2(1 — ^) + ^(l + p.) 1 2th (1 + ab) + п2 I 1 + аД + aj] ’
(11.4)
T bh3
где J = — момент инерции поперечного сечения плиты.
Можно видеть, что первый член формулы (11.4) при р = 0
совпадает по величине с эйлеровской критической силой для цен-
трально загруженного стержня. Вторым членом этой формулы
характеризуется увеличение критической силы, вызванное закреп-
лением продольного края пластинки. Последние члены формулы
(11.4) учитывают поддерживающее влияние упругого основания.
Если рассматриваемая плита расположена на основании, упру-
гом в смысле гипотезы коэффициента постели, то для определе-
ния величины критической силы Ркр в формуле (11.4) следует
отбросить члены, содержащие характеристики t и а, при помощи
которых учитывается работа упругого основания на сдвиг. При
этом для критической силы получим следующее выражение:
гЭД 6£/ kbl*
^кр —/2 (1 _ р.) + ft2 (1 4-р.) + n2 >
где k — коэффициент постели упругого основания.
2. Прямоугольная плита со свободными от за-
креплений продольными краями. Рассмотрим прямо-
>5 jj] УСТОЙЧИВОСТЬ УЗКОЙ ПЛИТЫ 347
угольную плиту, загруженную продольными усилиями, распре-
деленными в сечениях у = const по заданному линейному закону
м(х) (рис. 157). Эти усилия могут быть приведены к цен-
тральной сжимающей силе Р (сжатие принято со знаком 4-) и
изгибающему моменту М, действу-
ющему в плоскости плиты. Будем
предполагать, что плита состав-
лена из участков различной тол-
щины и в общем случае не имеет
продольной оси симметрии.
За возможное перемещение вы-
деленной из плиты поперечной
полоски примем поступательное
перемещение /д = 1 и поворот
у* = х относительно оси, прохо-
дящей через центр тяжести по-
перечного сечения пластинки
(рис. 158).
Поверхность прогибов плиты
определится при этом в виде
Рис. 158.
w(x, у)= 1F1Z1+ W. +W2x,
(Н-6)
где и Ц72 — обобщенные перемещения. Функция Wi, имеющая
размерность прогиба, характеризует цилиндрический изгиб плиты
в продольном направлении; безразмерная функция определяет
угол поворота относительно центральной оси. Таким образом,
348
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
(ГЛ.
предполагается, что плита может потерять устойчивость в изгиб]
крутильной форме.
Разрешающая система дифференциальных уравнений устой’
вости в рассматриваемой задаче запишется в форме:
012^2 +1^11 ----2(Й114-рц)] ф- [Л\2
— 2 (612 + р12)] W'z + (Сц + s°j) + (с12 + s12) W2 = О,
+ a22Wl2v + I^2i - 2 (621 + pgj] г; + \NM - I
--2(^22 + f22)] ^2 + (C21 + S21) + (C22 + .S22) ^2=0.1
Коэффициенты уравнений (11.7) вычисляются по формулам
(10.4) и имеют вид:
Он = 2 Dmbm, а12 = ,
&22 = %т)(Хт Ч~
~ ^12 “ ^22 = S Dmbm,
Сц “ С12 = С22 = О,
Р1°1 = ^(1 + ^)> Р?2 = | (С2— С21)(1 + (П,8)
Р22 = [з- (с? + с2 — с1сг) + 2^ь ’
Sh = kb (1 + , S?2 = (с22 — cl) (1 + ,
S22 = ^[3 (С1 + с2 — CtC2) + (С1 + с2) .
В выражениях (11.8) знак суммы охватывает все участки
с различной жесткостью (различной толщиной /г); индекс т ука-
Eh3
зывает номер соответствующего участка; D = 12 (1 — у.2)—цилин-
дрическая жесткость; b — полная ширина плиты; k и t — соответ-
ственно характеристики упругого основания на сжатие и сдвиг.
Коэффициенты уравнений (11.7), зависящие от величины сжи-
мающей нагрузки, согласно формуле (10.5) равны:
Nil = j N (х) х? dx, j
Ni2= \N (x)zix2rfx, ?
N22 = (x) y?2dx. I
(H.9)
5 л] устойчивость узкой плиты 349
Входящие в выражения (11.9) продольные силы N (х) могут
быть представлены в виде
ЛГ(х) = и(х)Л, (11.10)
где п(х)— заданные нормальные напряжения, определяемые по
формуле
п(х) = £- + ^х. (11.11)
В формуле (11.11) F и J2 = — соответственно площадь
и момент инерции поперечного сечения плиты; М— Рех, где ех —
эксцентриситет приложения сжимающей силы Р.
Внося выражения (11.10) и (11.11) в (11.9) и замечая, что
7Д = 1, а /г = х, получим:
где
Nll = ^nhdx=P,
ДГ1а = nxh dx= М,
w22 = J nx2h dx= -J- + -Ц-,
J3 = ^x3dF, dF — hdx.
(И-12)
(11.13)
Подставив значения коэффициентов (11.8) и (11.12) в уравне-
ния (11.7), будем иметь окончательно:
<Хи^Г+ (Р - 2&)W[ + + (М- 2Р?2) г; +
+ S^ = °’ (11.14)
+ (Л1 — 2Р^) W[ + 5^ + 022^+ [
+ -- 2 (Ь22 + p22)J 1^2 + 2 = 0./
Системой двух однородных дифференциальных уравнений (11.14)
характеризуется устойчивость внецентренно сжатой прямоуголь-
ной плиты на упругом основании с переменной жесткостью попе-
речного сечения. Решение этих уравнений не вызывает особых
затруднений и позволяет достаточно просто определять критиче-
ские значения сжимающих нагрузок. Покажем это на частных при-
мерах.
3. Прямоугольная плита постоянного сечения.
Если. прямоугольная плита со свободными продольными краями
имеет постоянную толщину h и загружена центральной сжимающей
350
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ.
силой Р (рис. 159), коэффициенты (11.8) и (11.12) принимают вид:
Пц — Db — . fl12 — Ь11 — ^12 — С11 — С12 — С22 — О,
о j,/, , 1\ 0 „0 Л 0 /&3/, . 3 \
pH - tb (1 + , Р12 -- «12 - 0, р22 - + -ь) ,
О ььЛ , 2 \ о _ А I 6 I 12 \
SU - kb (1 4- ~b) , s22 - уД1 -b + ,
Nn=P, A/12=0, /V22 = ^ = ^..
i L4
(11.15)
Система (11.14) распадается при этом на два независимых
уравнения:
aulF}v + (Р - 2&) Г; + - О,
(11.16)
4- |>п - 2 (&22 + р?2)] W", 4- s°22r2 = 0. (11.17)
Дифференциальное уравнение (11.16) характеризует изгибную,
Предположим, что на поперечных краях плита имеет шарнир-
ное опирание. Полагая
r^CiSiny, r2 = C2siny (11.18)
§ 12J
УСТОЙЧИВОСТЬ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ ПЛИТЬЦ 35£
и внося (11.18) в уравнения (11.16) и (11.17), получим значения,
критических сил:
р>=₽(ё^+2"'(* 1 + а) + ‘^(1 + а). Щ.и»
‘ + И1 + й) + к SO + s +
(11.20),
Можно видеть, что в случае центрального сжатия критическая
сила (11.19), соответствующая изгибной форме потери устойчивости,
всегда является наименьшей, другими словами, симметричная:
плита не может потерять устойчивость в форме закручивания.
Рассмотрим эту же плиту под действием моментной нагрузки
М (рис. 160). При вычислении коэффициентов (11.15) заметим,
что отличие будет состоять только в определении величин Nik'.
NY1 = Q, М12 = М, N22=M?
(11.21).
Поскольку для симметричной плитымомент инерции J3 — ^х3 dF
равен нулю и, следовательно, Д022 — 0, система уравнений устой-
чивости (11.14) примет вид:
йцГГ—+ + Air; = 0,
2 (622 + р22Ж+ з22Г2 = 0. (*1 ’22)
При шарнирном опирании поперечных краев решение системы
(11.22) может быть снова представлено в форме (11.18).
Подставив (11.18) в уравнения (11.22), получим формулу для
вычисления критического момента:
М = (йи + 2рп + Sn ^0 [а22 + 2 (Ь22 -р Р°г)^2 + s22
(11.23)
Отметим, что в этом случае плита теряет устойчивость в сме-
шанной, изгибно-крутильной форме.
§ 12. Устойчивость предварительно напряженной плиты
на упругом основании
1. Рассмотрим предварительно напряженную прямоугольную
плиту, сжатую арматурным стержнем, расположенным в продоль-
ном сечении х = ех (рис. 161). Естественно, что сам стержень при
этом растянут некоторой силой R — n2&F, где ДЕ — площадь,
поперечного сечения стержня.
352 И ДИНАМИКА 1И1УСТОЙЧИВОСТЬ2БАЛОК’И1.ПЛИТ j 1ГЛ.
(12.1
Эпюра нормальных напряжений по поперечному сечению плит
у = const для этого случая будет иметь характер, показаний
на рис. 161. Можно видеть, что нормальные напряжения всюд
за исключением точки расположения стержня, распределяются j
закону внецентренного сжатия:
R ^ех
П1~ f ~Г х’
где R — натяжение арматурного стержня.
Таким образом, в рассматриваемой задаче напряженное состо
яние характеризуется тем, что плита загружена уравновешенно!
(статически эквивалентной нулю) системой сил, т. е.
ьл ь:
yn(x)dF = Р = 0, п (х) xdF М — 0.
о о
02.2»
Если предположить, что поперечное сечение плиты не дефор-
мируется, то решение этой задачи будет описываться, как и
Рис. 161.
ранее, системой дифференциальных уравнений (11.14). Для плиты
постоянной толщины коэффициенты этих уравнений, не зависящие
от величины сжимающей нагрузки, определяются формулами (11.15).
Коэффициенты, содержащие параметр внешней нагрузки, вычи-
сляются по формулам (11.9), где интегралы в данном случае дол-
жны пониматься в смысле Стилгьеса. Произведя интегрирование,
_ ,1 12] УСТОЙЧИВОСТЬ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ ПЛИТЫ 353
И? получим:
Hf Nii — \n(x')dF==\n1dF—n2&F=O, )
В J J 1
В Nit = ( n (x) x dF = ( thx dF — n2 &Fex = 0,
J , (12.3)
К N22 = \n(x)x2dF = ^ + J^-Re2x,
Ий J Г J 2
I где Jz = ^x2dF, Js = ^xadF, dF = hdx.
* Внося значения (11.15) и (12.3) в уравнения устойчивости (11.14),
будем иметь:
- 2Р?ж+8®^= oq
<222^2 Ч~ [Af22 2 (Ь22 + Р22)] W2 Ц- 822^2 = 0, J .
где в случае плиты постоянной толщины
ЛГ22-^(п-4). (12.5)
Первое из уравнений (12.4) не содержит параметра нагрузки,
вследствие чего
= 0.
Таким образом, устойчивость плиты характеризуется вторым
из уравнений (12.4), записанным относительно функции IF2. По-
скольку обобщенное перемещение IF2 представляет собой угол
поворота, можно видеть, что в рассматриваемом случае плита
теряет устойчивость в форме закручивания. Отсюда следует, что
для предварительно напряженной плиты изгибная форма потери
устойчивости вообще невозможна.
Предполагая, что поперечные края плиты имеют шарнирное
опирание, представим решение второго из уравнений (12.4) в
форме
IF2 = Csiny. (12.6)
Внося выражение (12.6) во второе из уравнений (12.4), полу-
чим значение критической силы:
RKp = £2---- [а22 /г + 2 (522 + Р22) + S22 , (12.7)
12
где [коэффициенты а22, b22, p°2, S22 рассчитываются по форму-
лам (11.15).
23 В. 3. Власов, Н. Н. Леонтьев
354
ДИНАМИКА И УСТОЙЧИВОСТЬ БАЛОК И ПЛИТ
[ГЛ.
2. Рассмотрим предварительно напряженную плиту постоянна
толщины при действии на нее внешней сжимающей нагрузки, пр;
ложенной с некоторым эксцентриситетом ер (рис. 162).
Дифференциальные уравнения устойчивости в этом общем сл;
чае, совмещающем в себе две рассмотренные ранее задачи, запи
шутся в виде:
+ (Р - 2р?!) PepWz = О,
PePW[ + a22IF2IV + [(P + P)|g - Rez - 2 (bzz + р2°2)]^ +
+ s22IF2 = 0.
(12.8;
Заметим, что в частном случае, когда внешняя нагрузка не
имеет эксцентриситета (ер = 0), система уравнений (12.8) распада-
ется на два независимых урав-
нения, из которых первое опре-
деляет чисто изгибную форму
х потери устойчивости,а второе —
" потерю устойчивости плиты в
форме закручивания.
3. Во всех приведенных вы-
ше примерах предполагалось,
что плита имеет шарнирное опи-
рание на поперечных краях
у = 0 и у = I. При ином закреп-
лении этих краев (жесткая за-
делка, свободный край и т. д.)
для определения критической
силы необходимо найти общий
интеграл соответствующего ли-
нейного однородного дифферен-
Рис. 162. циального уравнения и подчи-
нить его граничным условиям.
Это даст систему однородных алгебраических уравнений отно-
сительно произвольных постоянных интегрирования, поскольку
граничные условия в задачах устойчивости также являются
однородными. Исходя из условия равенства нулю определителя
этой системы (разыскивается нетривиальное решение), нетрудно
получить некоторое трансцендентное уравнение относительно пара-
метра, характеризующего сжимающую нагрузку. Это уравнение
имеет бесчисленное множество корней, наименьший из которых
позволяет установить критическое значение сжимающих сил.
ГЛАВА Vll
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ.
ПРИЛОЖЕНИЕ МЕТОДА К ТЕОРИИ ТОЛСТЫХ ПЛИТ
И ТЕОРИИ УПРУГОГО ОСНОВАНИЯ
§ 1. Общее решение пространственной задачи теории упругости
1. Общая задача о равновесии твердого изотропного упругого
тела, испытывающего малые деформации, описывается в прямо-
угольной системе прямолинейных координат х, у, z известными
дифференциальными уравнениями:
dsx . дхху , ^хг
дх ' ду ' дг
д°у , д^уг , дхух-
ду ' дг ' дх
до, дх дх
дг ' дх ду '
(1.1)
(1.2)
где ах, хуг> ххг—составляющие тензора напряжений; и, и,
w — составляющие вектора перемещения точки; а, Ь, с — составля-
ющие вектора интенсивности объемной силы в данной точке;
23*
356
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VII
„ Е
G = 2 (1 + v) — М°ДУЛЬ упругости материала
фициент Пуассона*).
при сдвиге; v — коэф-
2. Ранее уже отмечалось, что в теории упругости различают
два метода решения общей задачи — метод перемещений и метод
напряжений. По первому методу за основные функции принима-
ются перемещения и = и (х, у, z), v = v (х, у, z), w = w (x, у, z).
Этим методом мы и пользовались в предыдущих главах при рассмо-
трении работы упругого основания в условиях плоской и простран-
ственной задач. По второму методу за основные функции прини-
маются напряжения ах=ах(х, у, z),..., xxz = xxz (х, у, z).
Помимо этих общеизвестных методов, к решению многих задач
может быть применен и смешанный метод. Этим методом мы и
воспользуемся теперь при решении общей пространственной задачи
теории упругости.
За основные искомые функции примем: перемещения и —
= и(х, у, z), v = v(x, у, z), w = w(x, у, z) и напряжения
ог. Составляющие и, v и w вектора полного перемещения будем
считать положительными, если они совпадают с направлением
координатных осей х, у, z.
Аналогично, составляющие туг, аг вектора полного напря-
жения, действующего на площадке с внешней нормалью, направ-
ленной по оси z, будем принимать положительными, если они
соответственно совпадают с направлением осей координат х, у, z.
В дальнейшем, в целях упрощения записи, вместо перемещений
и, v, w будем рассматривать пропорциональные им величины U, V,
W, определяемые формулами:
и = Gu, V = Gv, W = Gw.
(1-3)
Эти новые величины назовем для краткости также перемеще-
ниями.
Для искомых напряжений также введем более простые обозна-
чения :
xxz = X, xyz = Y, qz = Z. (1.4)
Исключая из уравнений (1.1), (1.2) напряжения <зх, ау, хху = тух,
получим систему шести основных дифференциальных уравнений
смешанного метода. Эти уравнения в новых обозначениях (1.3),
*) Отметим, что уравнения (1.2) были приведены нами ранее, в § 6 гл. I.
При этом в качестве упругих псстоянных трехмерного массива (упругого осно-
вания) нами принимались несколько иные величины, а именно £0 и v0, опре-
деляемые через модуль упругости Е и коэффициент Пуассона v формулами
(6.3) гл. I.
§ 2] РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ НАЧАЛЕНЫХ фЙНЬий
(1.4) будут иметь следующий вид:
dU dW , v
дг ~ дх + А’
dV dW у
дг ~ ду ' Y'
dW __________у (dU а|/ \ . 1 — 2у ?
дг 1 — v \ дх ' ду ) ' 2 (1 — v) ’
dZ = дХ дУ
дг дх ду С’
дУ __ 1 + у d2U /д2У_2 д2И \_______у dZ
дг 1 — м дх ду дх2 ' 1 — v д</2) 1 — v ду
дХ_ _ _ 1 +_у &V _ /d2U_2 d2U \_______у dZ_
дг 1 — у дх ду \ дуг ' 1 — v дх2 J 1 — у дх
(1-5)
Для остальных напряжений ах, ау, тху будем иметь формулы:
(1-6)
Полученными основными дифференциальными уравнениями (1.5)
и присоединенными к ним граничными условиями определяются
тесть искомых геометрических и статических величин, характери-
зующих деформированное и напряженное состояние тела.
3. Отметим, что смешанный метод представления общих урав-
нений равновесия упругого изотропного тела можно применять
также и к динамическим задачам теории упругости. В этом слу-
чае искомые функции U, V, W, X, Y, Z будут зависеть от пере-
менных х, у, z,t, а в уравнения (1.5) нужно ввести дополнительно
выражения инерционных сил:
т dW _ m d2V т дгУ
G дР ’ Д а/2 ’ G дР
(1-7)
§ 2. Решение уравнений
теории упругости методом начальных
функций
1. Отметим в теле две плоскости: начальную 2 = 0 и параллель-
ную ей z = const. Часть тела, заключенная между этими плоско-
стями, представляет собой слой произвольно фиксированной тол-
щины 2 = const. Искомые основные величины уравнений (1.5) при
358
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VII
фиксированном значении координаты z зависят только от двух
переменных х, у, определяющих положение точки на плоскости
z = cqnst. Так, величины U, V, W, X, Y, Z определяют векторы
полного перемещения и полного напряжения, действующие в какой-
либо Точке (х, у) фиксированной плоскости z = const. Величины
t/0, Vb, Хо, Yo, Zo, относящиеся к начальной координатной
плоскости z=0, будем в дальнейшем называть начальными основны-
ми функциями, соответственно геометрическими и статическими.
' На рис. 163 показаны направления положительных перемеще-
ний ‘ и | напряжений, относящихся к точкам нижней плоскости
z = const и к точкам верхней начальной плоскости 2 = 0 (ось z
направлена сверху вниз).
’.За положительные геометрические и статические величины в
точках какой-либо фиксированной плоскости z = const принимают-
ся составляющие соответствующих векторов, действующие по
направлению осей координат. Это же правило сохраняется и для
составляющих £/0, геометрического вектора начальной пло-
скости 2 = 0. Составляющие же Хо, Уо, Zo статического вектора,
относящиеся к начальной плоскости 2 = 0, при положительных
значениях действуют против направлений соответствующих осей
координат.
2. Общее решение уравнений (1.5) будем искать в виде рядов
Маклорена по переменной z:
§ 2] РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ НАЧАЛЬНЫХ ФУНКЦИЙ 359
в целях упрощения записи для частных производны* от какой-
либо функции F = г (х, у, z) примем обозначения:
df с 3F -dT=aF’ ~w = ^F> dF г -dT = rF’
dx2 ’ ду* ~ Р Г ’ = r2p- dz^ r r' (2.2)
dnF пТ; dnF .пС = арр _ апр дхп ду'1' дПЬ ПГ = rnF dzn
и вообще
ЬА-Щ+т р fr , „ = afr”F. dxkdyldzm ‘
Эти обозначения соответствуют так называемому символическому
методу, позволяющему операции дифференцирования и линейных
преобразований исходных уравнений производить методами линей-
ной алгебры.
Уравнения (1.5) в новых обозначениях принимают вид:
rU=— alF-фХ,
rV = —plF + У,
rl = — aX — py — c,
rY=- W ~ (fV + H ~ - b, '
rX = -a₽V _ (JW + a.
(2-3)
В дальнейшем объемные силы а, b, с будем считать равными
нулю.
Умножая равенства (2.3) на л и исключая затем при помощи
тех же равенств (2.3) члены, содержащие rU, rV,.. .,гХ, получим
общие формулы для вторых производных ПО 2 от искомых функ-
ций. Эти формулы в принятых обозначениях (2.2) будут иметь
следующий вид:
rv=-T±-va₽y-(2rE-:?s + «s)r-2-(r^₽z, М
г,®’-Г^(«, + ₽’)»7-2(Г=^“Х-2(Г^₽Г’ I
360
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
(ГЛ. vii
гЧ = гД; (“2 + П °^+ 1Л (“2 + Н 1^; (*2+₽2)4
= dh, (*2 + ?2) R - r^-v “Р* - (fe Р2 + y,
rzX = 1~ (“2 + Я *2 + ₽2) X - а₽У:
(2-4)
Для получения общих формул для частных производных третьего
порядка по переменной г следует равенства (2.4) помножить на г
и затем при помощи формул (2.3) исключить члены, содержащие
rU, rV,..гХ. Производные более высоких порядков получаются
аналогичным образом.
3. Формулы (2.3), (2.4) справедливы при любых значениях
независимых переменных х, у, z. Полагая в них 2 = 0, получим
формулы для частных производных правых частей равенств (2.1).
Исключая эти производные и выполняя необходимые преобразова-
ния, связанные с группировкой дифференциальных операций над
одноименными функциями {70, Vo, . . ., Хо, получим общие формулы,
позволяющие выразить искомые функции U, V,.... X через началь-
ные функции Uо, V0,.-..,X0 и их частные производные.
Запишем эти формулы в следующем виде:
И = LuuU0 LuvV0 4- ... 4- LuxX0,
V = LvuU0 LwVо 4- ... 4- LvxX0,
(2.5)
X = LXuU0 4- Lxi/Vо + • • • + LxxX0,
где Luu, Luv,---,Lxx — линейные дифференциальные опера-
торы, относящиеся к начальным функциям Uo (х, у), Vo (х, у), .. .
.. ., Хо (х, у), зависящие от переменной г и содержащие частные про-
изводные по переменным х, у начальной плоскости г = 0.
Эти операторы, в соответствии с излагаемым здесь методом,
представим в виде следующих бесконечных рядов:
= 1 _ ^=4 - 4 р+г«’+
+4тг - ,44^ + •
г г । г® (2 — v) 2 г5 (3 — v) . .
uwt— Lzx az 4- 6(1_v) T a— 120 v) 7 a +
Z7(4-y)
5040 (1 —v) 1 + ’
Luz-Lwx- 4(1_v)=t + 24(1_v)Tr2a- 480 (1 — v) I “ ' 20 160(1 — v) T a + ’ • • o>3 9*5 _
^-Мл- 12(1 — v) 120 (l-v)TaP l3360 (1 — v) T a₽ + ’ • Z3 (3 — 2v) 2 23 Q2 i Z5 (2—v) 2 2 1 Lux — Z 12(1— v) a 6^ ’ 120(1—v) T a + I XL y2R2 _ f T4a2 ?L_ „4D2 _|_ + 120^P 10080(1—v)‘ 5040 ‘ p ' ' ' Lvu — LXy — 2(i _ V)a₽ + 12(1 _ч) T a₽ 9>6 240 (1 - v) 4 • L„ - L„ - 1 \ J P \ + ‘2i^} 1V +
+ 24 ->V 720720"
+ « op- 1 1 + + 1 1 Sx s + 1 8 ~ i— >— CM ?— 1 1 С' 1 > .S' S" 1 1 1 T 1 s 2 X 1 Xi л 3 1 о) -H 1 + I 4- 1 N 3 ~ % - G, - A « ~ 1 co - S I 'гН7* г— >- N О Г * - ~ + 71 ~ Г s- 10 s-%- i «^§ij< + +ii II +^^50^0^— J- ~ V oq ax N w X” s* T * 4" T j + " J "i V J § =7 । "IJ, -Ц ”N § 'I 1 + 1 1 ii n -2 и и N & * £ -JO M -J II II И II II t Ъ i. Л -X -X & & (2.6)
362
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. V
! J 1 ! -2 г4 (1 +V)1 v4 I
L**’ = Lzz - 1 + 2(1_vj I —24 (1 - V) T +
+ 21Й+?)...Т6_
'720 (1 — v) *
I _ г U - 2v> I г3у „2 _ +2v) 4 _
bwz ~ 2(1 -v) ^6(1 — v)4 240(1 —v) 4
z7(l+v) vB
5040(1 — v) 1
Lzu = Lxw = — +
+ 120(1 — v) T6a - • •
= l„ = - e7!iOy T<? + 7<p_...
I г3 4 . z5 e г7 8
-bzw — — 3(i _V)T +зо(1—V)T 840(1 —v) T +’
, , г (1 — v) _ i г3 (3 + v) 2 „
Lyv = Lxu =----j _ v a₽ + vj' T a₽ —
г5 (5 + v) 4 q । г7 (7 + v) 6
120 (1 — v) a₽ + 5040 (1 — v) ? aP
Ly,= -^~^ + 3-(^ 1T + TT’"’-
э>5 5»5 5>7 ,7
__ _______ -1- ———__—— Y^B^ —1— ___
20(1— vpP 1201 ^ 630(1—v) 7 P ^ 5040 7
LXU^-^- г₽2 + 3-^TV + 4 vV-
~~ 20 (1—v) 'Г4'*2 —’ 120 ^P2 + 630(1—v) 'Г'’0'’2 + 5040 T6₽2 ~ • • •
(2.6)
В этих формулах символами у2, у4,. . .,у2п обозначены двумер-
ные на плоскости переменных х, у дифференциальные операторы:
гармонический, бигармонический и полигармонический кратности п.
Эти операторы связаны с одночленными операторами
а2 = -д-- В2----—
дхг ’ Р — ду2
соотношениями:
у2 = а2 + р2, у4 = (а2 + р2)2, . . Т2« = (а2 + р2)\
4. Обращаясь со всеми дифференциальными операторами
а, а2, р, р2, ар, у2, у4, . . ., у2п
4, 21 РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ НАЧАЛЬНЫХ ФУНКЦИЙ 363
правых частей равенств (2.6), как с алгебраическими величинами,
над которыми можно, в смысле излагаемого здесь символйческого
метода дифференцирования и интегрирования, производить дейст-
вия сложения, вычитания, умножения и деления, и применяя к
бесконечным рядам (2.6) методы суммирования, можно операторы
Luu, Luv, Luw, • • •, Lxy, LXx общего решения (2.5) записать в замк-
нутой аналитической форме, содержащей тригонометрические
а. ’
функции операционного аргумента yz = z у
Суммирование бесконечных операционных рядов (2.6) осущест-
вляется просто, если воспользоваться разложениями тригономет-
рических функций по степеням их аргумента:
Sincp = 9 3! + I 1 , . . <pa y(sm<p —c?cos<p) = -3r 1 , . . у (sin cos <p) = cp - i <pa । <p4 cos9=l-y + y- 2<p5 3<p7 5! 7! ' ' 2<p3 3<p5 31 1 5!
1 у (<p sin cp + 2cos cp) — 1 - 9* . 2<pe З98 4! ' 6! 8!
у (3sin<p — <p cos >p) = <p — 95 . 2q>7 З9’ 5! । 7! 9! + • • •
Полагая в этих разложениях ср = yz и производя суммирование
операционных рядов (2.6), получим:
Lxx = Luu = cos yz — 2(/_у) sin I2-
, r 1 aBz .
Lyx = Luv = — ~j T 'Sin yz,
Lzx = Luw = — 2(11__v) у K1 — 2v) sin T2 + I2 cos T2L
T r 1 az .
Lwx = Luz = — 4-(1 _ vj — sin yz,
Lvx = Luy = — 4 yr (sin Tz — I2 cos T2)> . (2 7)
Lux = -y sin yz — 4Y~-vj Y(sin yz — yZ COS TZ)’
г r 1 aBz .
Lxy = Lvu = — 2-(1 _ v) — sin yz,
, т 1 B2z .
Lyy = Lvv = cos yz — 2(1_v) -y- sin yz,
Lzy = L'/w = — 2(/_v)y- [(1 — 2v)sinTz + yzcos yz],
364
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ.
r г 1 Рг .
= Lvz = - 4(1_vjsmyz,
Lxz = Lwu = 2(1^) T K1 “ 2v>sin yZ — yZC0S yz]’
Lyz = Lwv = -y [(1 — 2v) sin Y2 — Y2 cos %z],
Lzz = Lww = — t (sin yz — yz cos yz),
= 4(/_y -y 1(3 — 4v) sin yz — Y2 cos 72],
Lxw = Lzu = sln T2>
Z-yuz = Lzv = sin ^z’
Lzw = — 7 (sin T2 — T2 cos T2)>
Lxv = Lyu = — (vsin Y2 4- 72cos 7г),
1 в3
- -у- (sin yz + yz cos 7г),
1 a2
(2.7)
а2 .
Lyv =------— sin yz
Lxu = — -у- sin yz — — (sin yz + yz cos yz).
Таким образом, для дифференциальных операторов Luu, Luv,
...,Lxx мы имеем две формы представления: одну — чисто диф-
ференциальную, записанную в виде бесконечных операционных '
рядов (2.6), и другую — интегро-дифференциальную, представ-
ленную трансцендентными операционными формулами (2.7), содер-
жащими операторы вида:
7 = («2 + = (£ 4 • у = (а2 + fJ2)
А =(а2 + ₽2)-’/!.
Здесь, как и ранее,
а2 I R2 _ JL I JL
+ P gx2 4- gy2
5. Выразив величины U(x,y,z), V(x,y,z)......X(x,y,z) no
формулам (2.5) и (2.6) через основные начальные функции Uo (х, у),
Vo(.x, у), . .Х0(х, у), частные производные этих функций и пере- :
менную г, можно затем по общим формулам (1.6) определить и
остальные напряжения ~х, °у и тху = хух, действующие на площад-
ках, параллельных оси z. Формулы для этих напряжений прини-
$ 2] РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ НАЧАЛЬНЫХ ФУНКЦИЙ
365
мают следующий вид:
= Аиио ~г ЛуУ0 4- • • + АхХ0,
Су — B(jUо + ByVo + • • • +
~ху — ~ух — CuUо -f- CyVo + • • • + CxX0,
(2-8)
где A<j, Ay, . .Ax, By, By,. .,, Bx, Cu,Cy,...,Cx— дифферен-
циальные операторы, определяемые бесконечными рядами по
формулам:
„ 2 22
A(J = 4--ос — ----
и 1 — v 1 — v
2«
(2а2 + ₽2) а + (За2+ р2)Т2а-
-зб0(^(4а2 + ^^+---’
г4
^=T^₽-r^l(l+v)a2 + v₽2]₽4-w^J^
X [(2 + v) а2 + мр2] Т2р - w~-y- l(3+v)a2+ v₽2^₽+...,
41Г = - ^ (а2 + vp2) + зЛТ|-_ (2а2 + v₽2) т2 -
- 60(Г=4 (3“2 + V₽2) + 2-520^) <4*2 +>₽2)Т6----
= 1^-2^) К* + v)a2 + vP*] + X
х [(2 + v) а2 + v₽2J Т2 - 71^—у[(3 + v)a2 + v₽2]^+...,
г8
г5
^=T^P-67^[(l+v)a2 + v₽2]p + w^.
X [(2 + v)a2 + vp2]T2p_—[(3+v)a2+v№^+...)
= 2-TZ~ «- 67TZV) 1(3 - >) a2 + (2 - v) p2) a +
+ 120(Г24У 1(4~v)a2 + (2- v) ₽2JT2a-
-56W=^l(5->)«2 + (2->)₽2]T4a-...,
= “-dh^2 + (l+v)p]a+ir^X
X [va2 + (2 + v) P2] 72a—jy [va2+(3+v)p2h4a+...,
P - ~ (*2 + 2p2) P + (a2 + 3p2)T2p-
- 36of=4<a2 + 4₽2)^+ • • -
(2.9)
366
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
Bv? = - (™2 + ₽2) + з(Г?Г7) + 2₽2) Ч2 ~
- № + 3.02) Ч2 + 2520^) (-2 + 4₽2) "Г6 - • • ’
в? = r^-2-(T^j -2(Т^) ^2 + 0 + ₽21 +
+ 24 (1 — v) tV0t2 + (2 + Р21 ~~ 720 (1 — v) Х
X [W2 + (3 + v) р2] у4 + . . .,
42^r₽-6(rU)^2-v)a2 + (3-v)₽2J₽ +
+ 120 (1 - v) К2 ~ ч) а2 + (4 - V) р2] f р -
- 5040^7) «2 - °? + <5 - Т4₽ + • • • •
= г^а-6(1^)[у7'2 + (! +у)₽21а + IW^T х
X [va2 + (2 + v) р2] у2а — [va2 + (3+v)p2]T4a+...,
с„ - ₽ - 4 + Ф + X + р") T=f> -
а = а—уу + Уу)« + ^-(«’ + ^у).(!а-
~ет(012 + г^1)!)т,а + ---
С. = - 2жР + f 4 -+
+ 25204(Г2»),('а|)~""
С‘ = - Г(Г^)01₽+ 12(1'-,)^- ЙО(Г-»)Ч‘1,Р+
СУ = 2Х - 4 у + ^2 р j а + jJ у + ^2 у _
... — ЗО4о(“а + П2'У)11а +
сА = ^~4(^«г+р’)р+Й(?Е-У’+рУ’р-
- 5W »! + ?’) т‘?4-
[ГЛ.
§ 21 [РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ НАЧАЛЬНЫХ ФУНКЦИЙ
Применяя к этим рядам правила суммирования и используя.
в соответствии с этим формулы (2.7), получим для операторов,
правых частей равенств (2.9) другое представление в замкнутой;
трансцендентной символической форме:
2 га3
Аи = Д----а COS yZ----т,—г Sin yZ,
1 и 1 — V 1 у( 1----у) 1 ’
„ (а2 + 2у32) га2
Д1Г = - * (1Lvh sin tz - —vcos ?z-
Xv = ₽ cos yz — sin yz,
Az = ^ cos yz - -2-(T-Iv)T a2 sin yz,
. p / a2 v . . za2B
Ay = —7Г- , 4 — -5-5- Sin yZ + yy, V-» COS YZ,
’ 7(1 — v) \ 2y2 ) * 1 2(1—v) 72 * ’
. za3 1 а Г/с, \ a2 7 .
A* = 2(1 —v)y2 COS + (T^T7 [<2 - V) - "Sy2”J Sln
D 2v zaB2
By = -----a cos yz — T,—sin yz,
1 -- V * (1 — v) 7 1 ’
D 2va2 + 32 . zB2
=----., - sin yz — cos yz,
(1 — v) 7 * 1--V * ’
D 2B Z£S
Bv = COS yz - sin yz,
B2 = cos yz - 2(11V)T ?2 sin yz,
n В Ггп ч В2 7 . zB3
By = YTfcj I (2 - v) - 2^-1 Sin yz + 2(1_pv)72 c°s 72,
D a / P2 \ • 1 z^2
Bx = (у - sin yz + cosTz,
a zo(2?
Си = В cos 7Z--T-.----— sin 7Z,
г 1 (i—v) 7 * ’
ctB
Cqy == — (1 _V) 7 U1 — 2^) sin yz + yz cos Tz],
<> zaB2
Gy = a cos yz--r.—sin yz,
* (1 —'/) 7 *
Cy — sin yz — 2 (1 _ v) (sin yz — yz cos yz),
n aBz
Cz = -^Tbr7Sln^'
CX = Y sin yz — (sin yz — yz cos yz).
(2.10>
Эти формулы могут быть получены и непосредственно из фор«-
мул (1-5), (2.5) и (3.7).
368
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VI
§ 3. Основные свойства матрицы линейного преобразования
по методу начальных функций
1. Формулами (2.5) дается общее решение рассматриваемой^
пространственной задачи теории упругости. Этими формулами при i
операторах Luu, Ьиу, Lxx, определяемых либо бесконечными
рядами (2.6), либо эквивалентными им тригонометрическими опе-
рационными формулами (2.7), устанавливается однозначное соот-
ветствие между шестью начальными функциями Uo (х, у), Vo (х, у),...
...,Х0(х,у), относящимися к точкам начальной координатной
плоскости 2=0, и шестью искомыми функциями U (х, у), V (х, у), . . .
. ..,Х(х, у), относящимися к точкам какой-либо произвольно
фиксированной плоскости г — const. 4
Итак, формулами (2.5) представлен общий закон преобразова- 1
ния начальных функций в искомые. Как известно, матрица, реали-
зующая тождественное преобразование, имеет единичную главную
диагональ и нулевые побочные члены. Это свойство матрицы выте-
кает также и из наших общих формул (2.7).
Таблица 22
и V w Z У X
и Вии Luv ВцУ Buz Buy В их
V Вуи Byy Byw Byz By у Вух
W Вуи Byy Byy Byz Byy Вух
г Bzu Lzv Bzy Bzz Bzy Bzx
у . Вуи Byy Byy Byz Byy Вух
j X LXU В XV Bxw Bxz B\Y Lxx
°х Au Av Ay Az Ay Ах
| Ви By By to N By вх
cu Cy Cy B^z Cy Сх 1
j 3] СВОЙСТВА МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ 369
Назовем преобразование начальных функций в искомые прямым
преобразованием. Совокупность 36 операторов Luu, Luv,..Lxx
(2.9) и (2.10) образует матрицу этого прямого линейного преоб-
разования. Такая матрица выписана в виде табл. 22 и 23. Если
в формулах (2.5) считать U, V,..., X заданными, a Uo, Уо. • •Хо
искомыми, то будем иметь обратное преобразование. В этом случае
задача приводится к интегрированию системы шести совместных
дифференциальных уравнений в частных производных бесконечно
высокого порядка в пределе.
Эта на первый взгляд сложная проблема разрешается весьма
просто, если исходить из физического смысла метода начальных
функций. Принимая какую-либо плоскость z = const за начальную,
функции U, V, . . ., X— за заданные (преобразуемые), а функции
Uo, Уо> • • •> Хо — за искомые (преобразованные), давая в соответст-
вии с этим в формулах (2.5) координате z отрицательное значение
и принимая во внимание, что в этом случае операторы Luu,
Luv, , Lxx, как четные функции от z, сохраняют прежние зна-
ки, а остальные операторы Luw, Luv, ., LXy, как нечетные
функции от z, меняют свои знаки на обратные, получим:
Uo — LuuU + jt-c/vV — LuwW -]- LuzZ — LuyY — LuxX,
V0 = LvuU + LvvV — LywW -]- LyzZ — LyyY — LyxX,
Wo = — LwuU — LwvY -}-LwwW — LwzZ-VLwyY -\-LwxX,
Zo = LzuU + LzvY — LzwW + LzzZ — LzyY — LzxX,
Yo = — LyuU — LyvV 4~ LywW — LyzZ -]- LyyY-]- LyxX,
Xo = — LxuU — LxvV + Lxw — LxzZ — LxyY+LxxX.
(3,1)
Этими формулами представлено обратное преобразование.
2. Подставляя функции Un, Vn, • • • > Хо, определяемые форму-
лами обратного преобразования (3.1), в правые части равенств
прямого преобразования (2.5), получим в результате двукратного
взаимно-обратного преобразования тождественные соотношения.
Отсюда следует, что преобразования (2.5) и (3.1) обладают
свойством ортогональности. Это свойство, отмеченное в задачах,
относящихся к теории тонкостенных стержней и оболочек, а также
и к методу начальных параметров А. Н. Крылова по расчету
балок на упругом основании, состоит в том, что сумма попарных,
в смысле символического дифференцирования, произведений из
элементов строки прямого преобразования (2.5) и столбца обратного
преобразования (3.1) равна единице, если строка и столбец имеют
разные номера (наименования).
Определитель, составленный из операторов преобразования (2.5)
или (3.1), равен единице. Это положение, как и свойство
24 В. 3. Власов, Н. Н. Леонтьев
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ (ГЛ. VH
(zlsoozl + zluts)x x 1)_ ** 1 — zl uts — X
(zlsoozl + zluis)X 1 (ft — T) _ 1 — zl uts — г» (zl SOO zl + + zl uts л) X 1 (A - r) X ЙЮ A
(zitns—zlsoozl) x zl uis AZZJ. zl^ zl UIS Л г!ю Z
[zl soozl — — zlutS(A1> —g)] X x —Pfr I [zl SOO (л — j) г — —zluts zl] T [zlsoozl— zluts X x (лг — т)] x x И* — т) г Й T [zl soo zl — — zl Uts (Ag—T)] X X AI1ZL1L? to ;
(zl SOO zl — — zl uts) 5^. X гЙ х(л P V— г! uts— T ' T zl uts X x 1(л —т) v__ zd [zl soozl + zluts x x (лг— т)1 x X Х<л~ T) Z — 3 zl uts X X — zlsoo zs^ zl utsfcPZ- z^to Л
(zlsOOzl — zl Uts) X у 81 (*—l)V_ »® I 1 L — гъ uts — T (zlsoozl — zluts) X X _P1 — zl uts X x — T)v_ ZX) [zlsoo zl + zl uts x x («г — т)1 x x — т)г_ i L zl uis x ' z0to X<i-PE- T zl uts x zEB X — г! soo V ft
X A Z Л Л n
ЕЕ в XI и 1Г 9 в 1
5 4] ПРИВЕДЕНИЕ ТРЕХМЕРНОЙ-ЗАДАЧИ К ДВУМЕРНОЙ 371
ортогональности преобразований (2.5) и (3.1), строго соблюдается
в предельном случае, когда операторы Luu, Luv,..., Lxx опре-
деляются трансцендентными операционными формулами (2.7).
Помимо отмеченных свойств, операторы преобразования (2.5)
подчиняются закону взаимности:
Lyu = Lxy, Luv = Lyx и т.' д. (3.2)
В силу равенств (3.2), выражающих, по существу, теорему
о взаимности работ внешних сил для двух каких-либо различных
состояний равновесия упругого тела, матрица каждого из преоб-
разований (2.5) и (3.1) имеет симметричную структуру с диаго-
налью симметрии, идущей из левого нижнего угла матрицы
в правый верхний.
Взаимность операторов Lvu и Luv и симметричных с ними
операторов Lxy и Lyx преобразований (2.5) и (3.1) обусловливается
изотропностью упругого тела относительно оси z. Мы получаем,
таким образом, для операторов как прямого (2.5) так и обратного
(3.1) преобразований следующие соотношения:
Lyu — Lxy, Lzu — Lxw, Lwu = Lxz, Lvu = Lxy> Lg g
Luu = Lxx, Lw = Lyx, Luw = Lzx, Luz = Lwx, Luy = Lyx-]
§ 4. Общий метод приведения трехмерной задачи теории
упругости к двумерной
Начальные функции Uo (х, у), Vo (х, у).....Хо (х> У) в изла*
гаемом методе играют роль шести произвольных двумерных
функций, получающихся при интегрировании основных дифферен-
циальных уравнений (1.5) методом разложения искомых функций
по степеням z. Начальные функции задаются граничными усло-
виями на плоскостях z = 0 и z = h — const или, в более общем
случае, z = h(x, у). На каждой из плоскостей определяются три
функции.
Как уже отмечалось, граничные условия могут быть чисто
статическими, чисто геометрическими или, наконец, Смешанного
типа.
В случае статических условий в точках граничной поверхности
задаются три компонента вектора полного напряжений. Искомыми
функциями в этом случае будут компоненты U0(x, у), Vo (х, У),
W0 (х, у) вектора перемещения начальной плоскости. Для этих
компонентов получим из статических условий, заданных на ниж-
ней поверхности z = h(x, у), систему трех дифференциальных
уравнений.
В случае чисто геометрических условий заданными величинами
будут компоненты перемещений, а искомыми — напряжения
372
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ.
Ха(х, У)> Yo(x, у), Z0(x, у). Для этих трех искомых статически^
начальных функций также получим из геометрических условий^
задаваемых на граничной поверхности z = h(x, у), систему тре:
линейных дифференциальных двумерных уравнений.
В случае смешанной задачи граничные
условия, относящиеся
к точкам начальной плоскости 2 = 0, задаются частью в переме-
щениях, а частью в напряжениях. Всего для каждой точки пло-;
скости 2 = 0 будем иметь три условия. Для остальных трех искомых,
функций получим из трех условий, задаваемых на поверхности !
g = h(x, у), систему трех также двумерных дифференциальных|
уравнений.
Раскрывая при помощи изложенного общего метода начальных
функций граничные условия, задаваемые на плоскости z = 0 и на
поверхности z = h{x, у), мы всегда можем привести трехмерную
проблему теории упругости к двумерной задаче, описываемой -
системой трех линейных дифференциальных уравнений для трех !
искомых начальных функций от переменных х, у *).
Для упругого слоя переменной толщины h = h (х, у) эти
уравнения будут с переменными коэффициентами. В случае слоя
тостоянной толщины h = const дифференциальные уравнения
эудут с постоянными коэффициентами.
Порядок дифференциальных уравнений, как вытекает из сущ-
ности излагаемого здесь метода, зависит от числа членов разло-
жения по степеням г, удерживаемых в формулах (2.6) для диффе-
ренциалоных операторов общего линейного преобразования (2.5).
Граничные условия, задаваемые на плоскости z = 0 и на
поверхности z = h{x, у), точно удовлетворяются непосредственно
в процессе приведения трехмерной задачи к двумерной. Гранич-
ные условия на боковой цилиндрической поверхности выполняются
при интегрировании двумерных дифференциальных уравнений. Эти
условия удовлетворяются с точностью до тех членов общих
разложений (2.6), которые в данной задаче отбрасываются.
Если в разложениях (2.6) ограничиться для перемещений
линейными членами относительно г, для касательных напряжений
X, Y — членами, содержащими z2, и для нормального напряже-
ния Z — первыми членами по z3 включительно, то мы будем
иметь решение, позволяющее удовлетворить граничным условиям
на боковой поверхности только в смысле Сен-Венана.
В этом случае мы будем иметь общую моментную теорию
толстых плит, свободную от гипотезы Кирхгофа — Лява. Если
же в разложениях (2.6) удержать члены и более высоких поряд-
ков, то мы получим более точную теорию толстых плит. В этом
случае в точках боковой поверхности, помимо осевых сил и
*) Аналогичный метод, но в несколько иной постановке, предложен
А. Н. Лурье [56].
§ 5] ПЛИТА ПОД ДЕЙСТВИЕМ СИММЕТРИЧНОЙ НАГРУЗКИ 373
моментов, рассматриваемых в задачах о плоском напряженном
состоянии плиты и об изгибе плиты, возникает система самоурав-
новешенных напряжений, приводящаяся к обобщенным силам той
же природы, что и бимоменты.
Таким образом, исходя из метода начальных функций, можно
построить общую бимоментную теорию толстых плит и оболочек,
свободную от гипотезы Кирхгофа — Лява и позволяющую разре-
шить краевую задачу с любой наперед заданной степенью
точности.
§ 5. Толстая плита, находящаяся под действием нагрузки,
расположенной симметрично относительно ее срединной
плоскости
1. Пусть плита, имеющая постоянную толщину 2/г, находится
под действием поверхностных, в общем случае нормальных и
касательных нагрузок, приложенных в плоскостях г = +Л
и имеющих симметричное расположение относительно срединной
плоскости плиты (рис. 164).
За начальную координатную плоскость примем срединную
плоскость плиты, ось z направим сверху вниз, ось х — слева
направо, а ось у — по правилу правовинтовой системы координат.
В рассматриваемом случае загружения плиты в точках ее сре-
динной плоскости по условиям симметрии задачи отсутствуют
вертикальные перемещения и касательные напряжения; поэтому
из шести начальных функций Uo, Уо,..., Хо следует положить
равными нулю Wo, Хо, Yo.
Искомыми функциями будут два тангенциальных перемещения
- U0(x, y),V0(x, у) и одно нормальное напряжение Z0(x, у).
374
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
1ГЛ VII
Полагая в формулах (2.5) IVO = Хо = Уо = 0, получим:
U = Luu Uо + Luv Vo + LuzZq,
V = Lyu Uq + Lyy Vo + Lyz Zo,
IV = LwuUo + Lwy Vo + LwzZq,
Z — Lzu Uo + Lzv Vo + Lzz Zo,
У = Lyu Uo + Lyy Vo + Lyz Zo,
2C = LxuUo + Lxv Vo + Lxz Zo.
Для определения искомых функций Uo (х, у), Vo (х, у), Za (х, у)
имеем систему трех дифференциальных уравнений, получающихся
из уравнений (5.1) путем приравнивания компонентов напряжений
К, У, Z при z — h заданным функциям Zh (х, у), Ун (х, у), Xh (х, у):
Lzu (A) t/0 4” Lzv (A)V0 + Lzz (h)Z0 = Zh.
Lyu (Л) t/0 + Lyy (A)V0 + Lyz (h)Z0 — Yh, J
Lxu (h) Uo + Lxv (h) Vn + Lxz (h) Zo = Xh, .
(5-2)
где Lzu (h), LZy (h), . . . , LXz (h) — дифференциальные операторы,
определяемые по соответствующим формулам (2.6) при z — h.
Уравнения (5.2) при заданных функциях Xh, Yh, Zh образуют
систему совместных линейных дифференциальных уравнений
в частных производных по двум независимым переменным х, у.
2. Рассмотрим более подробно задачу о равновесии плиты,
находящейся под действием одной только нормальной нагрузки
Zh (х, у), расположенной симметрично относительно срединной
плоскости. В этом случае два последних уравнения (5.2) при
Xh — Yh = 0 будут однородными. Эти уравнения будут удовлет-
воряться, если ввести в рассмотрение новую функцию F = F (х, у)
по формулам:
Uo= (Lxv Lyz — LyyLxz)hF, 1
Vo = —(Lxu Lyz — LyuLxz)hF, ? (5.3)
Zo = (Lxu LyV — LyuLxv)hF, '
в которых указанные в скобках дифференциальные операторы
составляются по правилам символического дифференцирования на
плоскости z — h. Подставляя (5.3) в первое уравнение (5.2),
получим для основной искомой функции F = F (х, у) одно раз-
решающее уравнение:
(Lzu (Lxv Lyz— Lyy Lxz) — Lzv (Lxu Lyz — Lyu Lxz) +
+ Lzz(Lxu Lyy — Lyu Lxy)lh F — Zh, (5.4)
j 5] , ПЛИТА ПОД ДЕЙСТВИЕМ СИММЕТРИЧНОЙ НАГРУЗКИ
375
где дифференциальный оператор над функцией F, стоящий в квад-
ратных скобках, определяется приближенно по формулам (2.6) и
точно — по формулам (2.7). В этих формулах следует считать z = h.
Порядок основного разрешающего уравнения зависит от числа
членов разложения (2.6), которое устанавливается в зависимости
от относительной толщины плиты и от желаемой точности реше-
ния задачи. Так, ограничиваясь для плиты средней толщины
в разложениях (2.6) лишь первыми членами, мы получим прибли-
женную техническую теорию равновесия симметрично нагруженной
плиты.
Для получения точной теории в уравнение (5.4) следует под-
ставить точные значения для дифференциальных операторов,
определяемые при z = h трансцендентными формулами (2.7).
В этом случае для основной функции F будем иметь трансцен-
дентное дифференциальное уравнение, в котором частные произ-
водные от функции F по переменным х, у входят в аргументы
тригонометрических выражений. Это уравнение может быть
представлено в виде
sin [sin уА cos уА + уй] F = Zh. (5.5)
Для искомых функций Uo, Vo, Zo получим следующие формулы:
t/o = 2иШ'^ К1 ~ 2v)sin — cos ТЛ1 F >
К = 27T~\S К1 — 2v)sin — cos F’
ZQ = 7^П-7/г (sin у/г + TfA cos y/z) F.
(5-6)
Порядок уравнения (5.5) можно понизить, если ввести в рас-
смотрение новую разрешающую функцию
ф = (5.7)
1 -- V ' '
Уравнения (5.5) и (5.6) перепишутся при этом в виде:
т[й+=
ий = у- [(1 — 2v) — h cos %h ] Ф,
70 = | [(1 — 2v)s-^ — h cos у/г ] Ф,
Zo = у [sin %h + %h cos %h] Ф.
(5.8)
(5-9)
376 МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ (ГЛ. VII I
Если воспользоваться разложением входящих в формулы (5.8н
(5.9) тригонометрических функций по степеням их аргумента, та
трансцендентное дифференциальное уравнение задачи (5.8) можн4
представить в обычной дифференциальной форме. Переходя5
к общепринятому обозначению ?2 = а2 + р2 = V2, получим:
[2AV2 — | /i3V2v2 + /i5V2V2V2 —...] Ф = Zhf
Выражения (5.9) перепишутся при этом в виде:
Uo = аЛ Г— v + ЛV — ^±2 ^V2V2 + .. .1Ф,
L О 1ZU J
Уо = РЛ [- V + Цр Л2?2 - /z4V2V2 + • •.] ф,
ZQ = k Гг— -|-/i2V2 4- l/i4V2V2 — ...1 72Ф.
L о “V j
(5.10>
(5.И)
Уравнениями (5.8) или (5.10) представлено точное решение
рассматриваемой задачи о деформированном и напряженном
состоянии симметрично загруженной толстой плиты. После опре-
деления функции Ф из этих уравнений и соответствующих гра-
ничных условий, задаваемых в точках боковой поверхности плиты,
можно вычислить начальные функции Uo, Vo, Zo по формулам
(5.11), а перемещения U, V, W и напряжения Z, Y, X плиты —
по формулам (5.1). Для определения остальных напряжений
°х, Эд, ^хд следует использовать общие выражения (2.8).
Как уже отмечалось выше, для получения приближенного
решения в уравнениях (5.10), (5.11) или, что то же самое, в раз-
ложениях (2.6) следует ограничиться определенным количеством
членов. Так, например, сохраняя в уравнении (5.10) два первых
члена, получим:
72У2Ф_^72Ф = -^7л. (5.12)
Для искомых начальных функций получим при этом следующие
формулы:
Ц> = -^у, = Zo = 2Й72Ф. (5.13)
Заметим, что в том случае, когда плита находится под дейст-
вием осесимметричной нагрузки, для решения задачи как в точной,
так и в приближенной постановке мы будем иметь обыкновенное
дифференциальное уравнение, записанное в полярных координатах.
i| 6] ПЛИТА ПОД ДЕЙСТВИЕМ АНТИСИММЕТРИЧНОЙ НАГРУЗКИ 377
§ 6. Толстая плита, находящаяся под действием нагрузки,
расположенной£антисимметрично относительно срединной
плоскости
1. Если на плиту толщиной 2h действует нагрузка, состоящая
из нормальных и касательных напряжений (рис. 165), приложенных
в точках граничных плоскостей z = + h антисимметрично относи-
тельно срединной плоскости z = 0, то в точках срединной пло-
скости обращаются в нуль тангенциальные перемещения и нор-
мальное напряжение. Принимая за начальную плоскость z = 0 п
полагая в общих формулах (2.5) Un — Vo = Zo = 0, будем иметь:
О’ = L[/]yjWo-j-LuyYo-^LuxXo,
V—Lyw W0-}-LyyY0+£vxX0,
W = LwwWo+LwyYo+LhzxX0,
Z,=LzwW o+^-zy Y0-{-LzxX0,
Y = LyvzW0-1t-LyYiY0-YL'YxX0,
X = LxwW о+Lxy Y о+LxxX0.
(6.1)
Искомыми начальными функциями в данной задаче являются
одно перемещение Wo = Wo (х, у) и два напряжения Хо = Х0(х, у),
Уо = Уо (х, у), относящиеся к точкам срединной плоскости.
Для этих трех искомых функций получим из статических
граничных условий систему трех дифференциальных уравнений:
Lxw Wo + LxxX0 + LxyY0 = X*,
Lyw Wo + LyxX0 + Lyy Ya — Yh, ?
Lzw Lzx Xo + LzyY0 = Z/,,.
(6.2)
где в операторах Lxw, Lxx, . • • , Lzy следует положить z = h.
Если на плиту действует одна только вертикальная нагрузка-
Zh = Zh(x, у), то два первых уравнения системы (6.2) будут
378
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VH
однородными. Этим уравнениям мы удовлетворим, введя функцию]
F = F (х, у) по формулам: <
Wo = {Lxx Lyy — Lyx Lxy)h F,
Xo =—(LxwLyy — LywLxyfhF,
Г„ = (Lxw Lyx — LywLxxhP,
(6-3)
где индексом h отмечается, что дифференциальные операторы,
стоящие в скобках, вычисляются при z = h.
Третье уравнение системы (6.2) по подстановке в него (6.3)
принимает вид:
{Lzw {Lxx Lyy— Lyx Lxy) — Lzx {Lxw Lyy — Lyw Lxy) +
+ Lzy{Lxw Lyx — Lyw Lxw)]h F = Zh. (6.4)
2. Порядок уравнения (6.4), как и порядок дифференциальных
выражений (6.3), определяющих через основную функцию F (х, у)
искомые величины, зависит от степени точности, с которой мы
желаем решить данную задачу.
Раскрывая дифференциальные операторы (6.3) по общим
формулам (2.6) и полагая в этих формулах z = h, получим:
VjZ — [1_(11?_51 \72 _u Hl?_51 V2V2_ 1 p
L 2(1— y) ^24(1 — y) •••jr,
x« = [-r^! + ^>V!V!-4“F'
(6.5)
Здесь в соответствии с принятой символикой
V* = 4^ + X , = F - ₽F = • (6.6)
дх2 ду2 дх “ ду ' '
Для функции F получаем дифференциальное уравнение
[__?Н_________?Н___v2 _!_____
1.3(1-у) 15(1 —у) ^315(1 —у)
2/?9 1
- 2835(1-.) ^ + -]т = г.. (6.7)
3. Дифференциальное уравнение (6.7), определяющее функцию
F = F(х, у), является для данной задачи основным разрешающим
уравнением. Порядок этого уравнения, так же как и порядок
дифференциальных выражейЬй (6.5), определяющих через основную
функцию F {х, у) искомые величины срединной плоскости, зависит
' $ 6,1 ПЛИТА ПОД ДЕЙСТВИЕМ АНТИСИММЕТРИЧНОЯ НАГРУЗКИ очл
от степени точности, с которой мы желаем решить данну»аадачу
Это уравнение является основным уравнением бимоментнд^ <еорий
изгиба толстых плит, находящихся под действием антисимметрич-
ной нагрузки Zh = Zh(x, у).
Для получения приближенного решения удержим в форму-
лах (6.5) и в уравнении (6.7) по одному только первому члену.
При этом получим:
т-^-V2^, Yo = — у-— V2^,
1 — v дх ' ° 1 — v ду *
V2V2F = 3Л~~)9
W h'
Го = F, Хо =
(6.8)
Полагая согласно принятым обозначениям (1.3)
®'«=2<гЬг“’'
где w == w (х, у) — действительное вертикальное перемещение
точки срединной плоскости, и исключая из уравнений (6.8) функцию
F (х, у), получим:
X Eh* V Eh2 ™dw
°” 2 (1 — vs) V dx ’ 2(1-V2) V dy ' ,ftcn
Результат, представленный формулами (6.9) и уравнениями (6.8),
относится к моментной теории изгиба плиты.
Таким образом, моментная теория изгиба упругих плит является
частным случаем изложенной выше общей бимоментной теории,
свободной от гипотезы Кирхгофа — Лява, и соблюдается для до-
статочно тонких плит и в случае действия антисимметричных
сплошных, а не сосредоточенных нагрузок. Если толщина плиты
по сравнению с ее другими размерами представляет собой не
малую величину и плита находится под действием местных (со-
средоточенных) нагрузок, то для решения такой задачи следует
исходить из более точной теории, описываемой уравнением (6.7).
В уравнении (6.7) можно для плиты средней толщины ограничиться
первыми двумя или тремя членами, в зависимости от характера
задачи и от степени точности решения. Заметим, что основная
функция F = F (х, у) инвариантна относительно координат.
Уравнения (6.4) и (6.7) в точной трансцендентной форме
имеют вид
[у/г — sin у/г cos у/г] F = Zh. (6.10)
380
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
ггл,
Искомые .функции Ц701 Уо, Хо определяются при этом
формулам:
^[cos^-^^sin^jF, |
L ' ' J } (6.11
уо= — rr^sin^F, Хо = — jTzViri'r/iF. J
§ 7. Деформация упругого основания под нагрузкой,
приложенной к его поверхности
1. Рассмотрим упругий слой конечной толщины Н, располо-
женный на несжимаемом массиве и находящийся под действием
поверхностных нормальных и касательных нагрузок Zh, Xh, Yh
Рис. 166.
(рис. 166). Будем предполагать, что на плоскости контакта этого
слоя с материком отсутствуют касательные напряжения X и Y,
а также равны нулю вертикальные перемещения W. Это означает,
что рассматриваемый упругий слой может свободно скользить
по контактной плоскости, что схематически показано на рис. 166.
Принимая за начальную координатную поверхность плоскость
контакта, мы снова получим для перемещений и напряжений
упругого слоя выражения (5.1). Таким образом, рассматриваемая
задача в точности совпадает с задачей расчета толстой плиты на
симметричную нагрузку.
В общем случае действия поверхностных сил ZH, Хн, YH
система разрешающих дифференциальных уравнений запишется
в виде (5.2). При отсутствии касательных нагрузок (Хя = Уя = 0)
основное уравнение принимает вид
\Lzu (LxvLyz— LyyLxz) — Lzv {Lxu Lyz— Lyu Lxz) +
+ Lzz{Lxu Lyy — Lyu Lxv)]h F — — Zh (7.1)
S 71
или
ДЕФОРМАЦИЯ УПРУГОГО ОСНОВАНИЯ
381
2//V2— -j- tf3V2V2 + 1 WW — . . .1 ф = _ ZH, (7.2)
Сохраняя в уравнении (7.2) только первые члены, получим
основное дифференциальное уравнение приближенной технической
теории упругого основания конечной толщины Н:
v-v’®-iv’® + 3i-z„ = o, v> = ^.+^. (7.3)
Отметим, что основание, описываемое дифференциальным
уравнением (7.3), будет более правильно отражать действительную
работу упругого слоя, чем рассмотренная ранее однослойная
модель, поскольку в этом основании учитывается наличие не
только вертикальных, но и горизонтальных перемещений.
Рис. 167.
2. Предположим, что упругий слой, находящийся под действием
поверхностных нагрузок ZH, Хн, Ун, неподвижно закреплен по
начальной плоскости z = 0 (рис. 167). В этом случае из шести
начальных функций Uo, Vo,. .. ,Хп следует положить равными
нулю Un, Va, Wo. Искомыми функциями будут нормальные
и касательные напряжения Zo, Vo, Хо»
Исходя из уравнений (2.5), получим:
U = Luz 20 + Ьцу Yo + ^их Хо,
V — Lyz Zo + Lyy Vo Lyx XQ,
W = LwzZ<\ + ЬнгуУд + 4)
Z = Lzz Zo 4* bzr Vo 4- Lzx X^,
Y — Lyz Zo 4* byy Vo 4* Lyx Xn,
X = Lxz Zo 4- Lxy Vo 4- ^xx Xo.
382
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VII
Для определения функций Z0(x, у), Ya(x, у), Х0(х, у) при!
равняем напряжения Z, Y, X при z — h заданным функциям
ZH (х, у), Yh(x, у), Хн(х, у): 1
Lzz(H)Z0 + Lzy(H)Y0 + Lzx(H)X0 = -ZH, j ’
LyZ (Н) Zo + Lyy (H)Y0 +Lyx (И) Хо — YH, (7.5)
Lxz (H) Zo + Lxy (tf) Yo + LXx (FT) Xo = Xu. J
Полученная система трех дифференциальных уравнений в част-
ных производных по двум независимым переменным х, у является
разрешающей системой рассматриваемой задачи.
В частном случае, когда упругий слой находится только под
действием нормальной поверхностной нагрузки Zu (Хи = Yu = 0),
для решения системы (7.5) можно ввести новую функцию
F = F (х, у), определяемую формулами:
А = (LXyLyX — Lyy Lxx)n F,
Yо = — (Lxz LyX — LyZ Lxx)h F,
Xo= (Lxz Lyy — LyZLxy)hF.
(7-6)
Подставляя выражения (7.6) в уравнения (7.5), нетрудно убе-
диться, что два последних уравнения системы (7.5) тождественно
удовлетворяются, а первое уравнение приводится к виду
\LZZ (LXy Lyx — Lyy Lxx) — LZy (Lxz LyX — Lyz Lxx) +
+ Lzx (Lxz Lyy — LyZ LXy)\h F — —Zh. (7.7)
Дифференциальным уравнением (7.7) описывается напряженное
и деформированное состояние основания, неподвижно закрепленного
по плоскости z = 0. Порядок этого уравнения будет зависеть от
числа членов, взятых в выражениях (2.6). Внося в уравнение (7.7)
точные значения дифференциальных операторов, определяемые
при z = Н трансцендентными формулами (2.7), можно основное
уравнение (7.7) представить в другой, эквивалентной уравнению
(7.7) форме:
[-4(1^,/ Т2 - cos2 sin2 Т и ] F = - (7.8)
При этом получим формулы для искомых функций Zo, Уо, Хо
za = cos Sin уН — cos у//] F,
Yo = 2yC(°iSj-\) cos - (1 - 2v) sin чН] F,
%o= 2Y(1-^) ((1 ~ 2v) sin 7Я ~ cosy//] F. j
(7-9)
§ 81
КОНТАКТНАЯ ЗАДАЧА РАСЧЕТА ПЛИТЫ
§ 8. Контактная задача по расчету плиты на упругом
основании
Рассмотрим плиту, находящуюся под действием нагрузки
р(х, у) и расположенную на поверхности упругого основания,
представляющего собой сжимаемый слой конечной толщины Н
(рис. 168).
Рис. 168.
За начальную координатную плоскость примем, как и ранее,
плоскость, по которой упругий слой опирается на подстилающий
его массив. Будем считать, что перемещения на начальной пло-
скости отсутствуют, т. е. Uo = Vo — Wo =0.
При этом напряженное и деформированное
состояние упругого основания будет опи-
сываться уравнениями (7.4).
Для определения функций Zo, Yo, Хо
рассмотрим граничные условия, заданные
на плоскости z = Н. Считая, что между
плитой и упругим основанием не возникает
сил трения и сцепления, получим:
XH = YH=0. (8.1)
Дифференциальное уравнение изгиба
плйты на упругом основании имеет вид:
£)V2V2ay(x, у) = р (х, y) — q(x, у), (8.2) Рис.. 169.
где р (х, у) — внешняя заданная нагрузка, a q (х, у) — реактив-
ные давления упругого основания.
По условиям данной задачи прогибы плиты и)(х, у) и
нормальные перемещения поверхности упругого основания
384 МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ [ГЛ, О
1
wH (х, у) = -q-Wh (х, у) совпадают. Отсюда следует, что Wh = (я|
(положительные направления для перемещения поверхности осн®
вания и прогибов плиты показаны на рис. 169). Кроме того, реам
тивные давления q (х, у) по отношению к упругому основании
представляют собой поверхностную нагрузку Zh(x, у) (рис. 169)|
Учитывая принятое ранее правило знаков, можно записать слей
дующее выражение для нормальных напряжений, возникающих'
на поверхности упругого основания:
ZH(x,.y) = -^-^2WH(x, у)-р(х, у). (8.3),
Раскрывая граничные условия (8.1) и (8.3) при помощи фор-
мул (7.4), получим:
Lzz (Н) Zo + Lzy (Н) Уо + Lzx (Я) Хо =
= —^\72\72[Lwz(H)Z0+LWy(H}Y0+LWx(H)X0]-P, (g
Lyz (Я) Zo + Lyy (Н) Yo + Lrx (H) Xo = О,
LXz (H) Zo + LXy (H) Yo + Lxx (H) Xo = 0.
Выражения (8.4) могут быть переписаны также в другой
форме:
[lzz(H) + ^Lwz (Я)] Zo +[£zr(//)+|TUw (Я)] Уо +
+ [Lzx (И) + -f- ^Lwx (tf)] Xo = - p, I (8.5)
Lyz(H) Z0 + Lyy(H)Y0 + Lyx(H)X0 = 0, j
Lxz (H) Zo + Lxy(H) y0 + Lxx (H) Xo = 0.]
Дифференциальными уравнениями в частных производных (8.5)
описывается сложная контактная проблема расчета плиты на уп-
ругом основании. В этих уравнениях, как и ранее, символами
LZZ(H}, LWZ(H), . . . , Lxx (FT) обозначены дифференциальные
операторы, определяемые по формулам (2.6) или (2.7) при z=H.
Введением новой функции F (х. у) система трех уравнений
(8.5) может быть приведена к одному разрешающему уравнению.
Определяя функцию F выражениями (7.6), получим:
[(^zz + -Q-'f’Aw'z) (LxyLyx — LyyLxx} —
— ( Lzy ^Lwy^ (LxzLyx — LyzLxx) +
+ {lZx + -^'fLwx) (LxzLyy — LyzLXy}]hF = —p. (8.6)
§ 9]
ТЕОРИЯ ПЛИТ-ОБОЛОЧЕК ПЕРЕМЕННОЙ ТОЛЩИНЫ
385
Дифференциальное уравнение (8.6) представляет собой точное
уравнение изгиба плиты на упругом основании, которое рассмат-
ривается как изотропный упругий слой конечной толщины И.
Принимая в выражениях для дифференциальных операторов (2.6)
ограниченное число членов, мы будем получать приближенные
решения. При этом порядок уравнения (8.6) будет зависеть от
принятого числа членов, т. е. от требуемой точности решения.
§ 9. Теория плит-оболочек переменной толщины,
находящихся под действием произвольно заданных
поверхностных нагрузок
Рассмотрим общую задачу о равновесии плиты, имеющей пе-
ременную толщину h = h(x, у). Эта задача имеет большое прак-
тическое значение при проектиро-
вании покрытий типа пологих
оболочек переменной толщины с
верхним плоским основанием
(рис. 170).
Выбирая плоскость верхнего
основания за начальную координат-
ную плоскость z = 0 и считая по-
верхностную нагрузку в точках
этой плоскости заданной, мы должны в уравнениях (2.5) рас-
сматривать компоненты напряжений Хо, Уо, Zo как заданные
функции от х, у. Искомыми начальными функциями в этой об-
ласти будут все три перемещения:
Uo = Uo (х, У), Vo = Vo (х, у), Wo = W (х, у).
Таким образом, все перемещения
U = U (х, у, z), V = V (х, у, z), IV = IV (х, у, г)
и все напряжения
X — X (х, у, г),
= &х (х> у, а),
Y = Y (х, у, z), Z = Z (х, у, г),
Sy = ау (х, у, z), тХу = sxy (х, у, г)
определяются для любой точки х, у, z с точностью до трех иско-
мых начальных функций £70(х, у), V0(x, у), lV0(x, у). Полагая в
этом общем решении z = h(x, у), мы получим формулы для всех
трех компонентов вектора перемещения и всех шести компонен-
тов тензора напряжения, относящихся к точкам поверхности
/г = /г(х, у), ограничивающей плиту-оболочку снизу. Напряжения
X, Y, Z, ах, ау, тху при z = h(x, у) должны „находиться в рав-
новесии с заданной поверхностной нагрузкой, приложенной в
точках нижней граничной поверхности h = h(x, у).
25 В. 3. Власов, Н. Н. Леонтьев
386
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VI
(9-3)
Обозначая компоненты этой заданной поверхностной нагрузки'
в осях неподвижной системы прямоугольных координат х, у, г’
через Xv, Yv, Zv, мы можем условия равновесия элементарного
тетраэдра с косой площадкой, относящейся к заданной граничной'
поверхности h = h(x, у), записать в следующем виде:
X,, = cos (v, х) хху cos (v, у) ф- X cos (v, z) (x, у, z), (9.1);
где cos (v, x), cos (v, y), cos (v, z) — косинусы углов между внеш-
ней нормалью к площадке, лежащей на поверхности h = h{xy\
и соответственно осями координат х, у, z. Эти косинусы опреде- '
ляются формулами:
, , dh
C°s(v, х)=^
1
!
, , dh
COS (v, y) = 5-
v dy
1
(9-2) i
cos (v, z) =
1
Уравнения (9.1), относящиеся к точкам граничной поверхности
h = h (х, у) и являющиеся статическими условиями для этой по-
верхности, принимают следующий вид:
Xv = 1 —.-------
-/ /д/Л2 /dhY
V \7TyI + (“/ы ) + 1
2
Z, =
dh [ dh °X^Y 1 - X
dh ''ух dx 1 dh p
dh 'zx дх *’ dh T2yd^~ z).
1
Подставляя в уравнения (9.3) напряжения из общих формул
(2.5), (2.8) и считая в этих формулах начальные статические
величины Хо, Yo, Zo заданными, получим для искомых функций
U0(x, у), V0(x, у), W'0(x, у) систему трех линейных двумерных
дифференциальных уравнений в частных производных с перемен-
ными коэффициентами. Порядок каждого из этих уравнений зави-
сит, как неоднократно отмечалось ранее, от числа членов, кото-
рые удерживаются в общих операционных разложениях (2.6).
Рассмотрим более подробно моментную теорию плит-оболочек
переменной толщины h = h(x, у). В этом случае мы должны ис-
§ 9]
ТЕОРИЯ ПЛИТ-ОБОЛОЧЕК ПЕРЕМЕННОЙ ТОЛЩИНЫ
387
ходить из предположения, что перемещение W остается постоян-
ным по толщине оболочки (не зависит от координаты z), переме-
щения U и V меняются по линейному закону, касательные напря-
жения X и У — по закону квадратной параболы, нормальное
напряжение Z — по закону кубической параболы. В соответствии
с этой гипотезой из общих формул (2.5) и (2.8) получаем для
перемещений и напряжений следующие приближенные формулы:
U = - z^ + zW0, V = V0-zd-^ + zY0,W = W0,
v /2 d2U0 , d2U0\ 1 + v „
— v dx2 ' dy2 ) 1—v dxdy
2 - v _2 52Xo z2 d2X0 1 d2Yо ,
2 (1 —v) Z dx2 2 dy2 2 (1 —v) 2 dx dy
+ i-^-Z2V2 + Xo—-7-— Z
1 — v dx ' u 1 — v dx
i +v d2U0 _ / 2 d2V0 _
1 — v 2 dx dy 2 \1 — v dy2 1 dx2 )
2-v 2py0 __ z2 д2У0_ 1 2
2(1 — v) dy2 2 dx2 2(1—v) 2
+-z^— z2V2^+y0
1 1 — v dy ' u
d2X0
dx dy '
_____ az0
1 — v 2 dy ’
— 1-- Hv2 (dU° I \____________i____zsV2 V2U7 -
_ z v { dx + dy J з (1 _ v) z v v w о
— z + Zo + V2Zo +
\ dx 1 dy J 1 u 1 2 (1 — v) u '
(9-4)
2 ~ v ,3y2 (dX0 . dY0 \
6 (1 -v) \ dx ду Г
+v ITz + "if) +
2— v axo v aY0 , V- - 7
+ ттг\;z + rr-v z + i _Vo
2 ( dUo . аи0\ 2 / d2W0 ,d2W0\,
= —V(v — + z(vL-^- + +
______ dUo ] dVo ____________n d2Wо . I'dXr, . dYa \
xy ~ dy ' dx Z dx dy^~ \ dy ' dx J
Легко видеть, что напряжения, определяемые формулами (9.4),
удовлетворяют общим дифференциальным уравнениям равновесия
(1.1). Подставляя эти напряжения в уравнения (9.3), получим
25*
388
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ, Vi
систему дифференциальных уравнений для определения искомы:
функций (70(х, у), У0(д, у),. W0(x, у).
Уравнениями (9.3) и формулами -(9.4) описывается общая мс
ментная теория равновесия плиты-оболочки переменной толщин!
h
h(x, у). Эта теория, построенная
на предположения х
общего характера, чем теория Кирхгофа — Лява, т, е. свободная;
от гипотезы об ортогональности линейного элемента к срединной?
поверхности,
позволяет
определить напряжения
деформации
плиты-оболочки при произвольном законе изменения толщины
h = h(x, у), т. е. при произвольно заданном очертании поверх-
ности h = h(x, у), ограничивающей оболочку снизу. К уравнениям
(9.3) в каждом частном случае краевой задачи следует присоеди-
нить граничные условия, заданные для искомых функций (70, Уо,
Wo в соответствии с принятой расчетной моделью.
Точное решение этой краевой задачи для плит произвольно задан-
ной переменной толщины h = h (х, у) представляет весьма слож-
ную и едва ли разрешимую при современных средствах матема-
тического анализа проблему. Заметим, что из существующих
методов приближенного интегрирования уравнений с переменными
коэффициентами наиболее эффективным является вариационный
метод Бубнова — Галеркина.
§10. Общее решение плоской задачи теории упругости
Выше было показано, что решение общей пространственной
задачи теории упругости методом начальных функций сводится к
Рис. 171.
определению шести двумерных
функций Uo, Vo, Fo, Хо, Уо, Zo,
называемых начальными. Пос-
кольку рассматриваемая теперь
плоская задача теории упругости
представляет собой частный слу-
чай пространственной, то для
определения деформированного и
напряженного состояния тела
здесь необходимо знать только
четыре начальные функции: пе-
ремещения и0(х), v0(x) и напряжения t°xy(x), на начальной
плоскости у = 0 (рис. 171). В этом можно убедиться, если для
решения плоской задачи вновь применить смешанный метод, при-
няв за основные неизвестные перемещения и(х, у), v(x, у) и нап-
ряжения хху (х у), ву(х, у), и представить затем искомые вели-
чины в виде бесконечных рядов по степеням координаты у.
- Действительно, уравнения равновесия упругого изотропного
тела (1.1) в случае плоской задачи и при отсутствии объемных
§ 10]
ОБЩЕЕ РЕШЕНИЕ ПЛОСКОЙ ЗАДАЧИ
389
сил принимают вид:
0в" д-t п да ’ Зт -------------- -
тг+тг-°- т^ + тг- = °- (101!
Связь между напряжениями и перемещениями, например^ для
случая плоской деформации устанавливается зависимостями: ;
2(1 Г/, х ди . ах = (1 — v) д- + v д- , 1 — 2v Lv ' дх ' ду\ ’ 26 rzi \ dv х ди“| о ц — . _ (1 v) -ч -4- v -j 1, у 1 — 2м ' ду dxj (ди , dv\ ~Хух - G ’ (10.2)
где Г - Е 2 (1 4-м) • . ,
Вводя для сокращения записи обозначения:
U = Gu, V = Gv,
X = тху, Y = ау,
д д а
д- = а, ч- = В,
дх ду г
можно уравнения (10.1) и (10.2) относительно
переписать в виде:
= — aV + X,
8V = — а(7 + к1." —. Y,
‘ 1 — v 1 2 (1 — м) ’
= — аХ,
(Ю.зУ
искомых величий
(10.4)
8Х = — a?U — аУ.
" 1 — V 1 — V
Напряжение а х определится при этом по формуле
^^[(l->)at/ + v3H. (Ю.5)
Представляя по аналогии с (2.1) искомые величины в виде
рядов Маклорена по переменной у, получим решение основных
уравнений (10.4) в форме:
{7= LuijU0 LuVV0 ф- LvyYй + LuxX0,
V= LyvU0 4- LyvVo 4* LvyY0 4- LvxX0, . (10.6)
Y = L yuUq 4* AkvV0 4* LyyY0 4- LyxX0,
X = LxuU0 + ‘H ^xyYй 4- LxxXq,
где через Luu, Luv, . . . , Lxy, LXx, как и ранее, обозна-
чены относящиеся к начальным функциям U0(x), V0(x), ^o(*)»
Хо (х) линейные дифференциальные операторы, зависящие от
390
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
1ГЛ.
и0 Ио 1
и у3 (2 — V) . LUU ~ 1 — 2 (1 — v) а + , У4 (3 - у) 4 У9 (4 - у) , т 24 (1 — v) Л 720 (1 - v) а 4 ' ' ' у3 (2 — v) 1 Luv~ —У<*+ 6(1 —v) a — , г/6(3 —v) 120(1 —v)a + , -У7/4- V)... g7_ + 5040(1 —v) a
V Z/V у9 (1 + V) LVU = ~ 1—v а+ 6(1— v) а3 — _^(2±v)_ 120(1—v)a + + 5040 (1 — v) а y2^ Lvv — 1 + 2 (j _ v) a — У4 (1 + y) . , 24 (1—v) a + , У' <2 + v) 0 + 720 (1 — v) a “ ' ' ’
Y t/2 yi LYU - 1_V а 6(1—v)a + г/’ + 120 (1 — v) a’ ~ ' У3 3(1— v)a + + 30(l —v)a — У1 8 . 840 (1 — v) a + ' ’ ’
X 2г/ „ W LXU~ 1— v a +3(1—V)a г/5 6 , У1 . 20(1 —v) a + 630 (1 - v)a ^XV = YU
л 2 2z/2 лг/ — 1 _ v a — 1 _ v “3 + . У4 . У9 4 , + 4(l-v)a 90(1—v) a + ••• II + to 1 tc5 Oi < i + 1 1 w < ft ^-4 s» + 1 1 A Й : Г 4
ОБЩЕЕ РЕШЕНИЕ ПЛОСКОЙ ЗАДАЧИ
391
§ 101
Таблица 24
Го Xo
г/2 у* з luy~ 4(1 — v) а + 24(1 — v) а у* 480(1 —v)a + , У8 _ y3(3-2v) LUX — У 12 (1 — v) a + ^(2-v^ + 120(1 —v) a y^5-2^ a. .
+ 20160 (1—v)a 10080(1 — v) <*+•••
у (1 — 2v) z/sv LVY~ 2(1—v) +б (l-v)a - Vi (1 + 2v) 240(1 —v)a + y~ (1 + v) 6 + 5040 (1 — v) a ~ Lvx = luy
LYY ^ Lvv Lyx = Lw
Lxy~ Lvu Lxx = Luu
1—v 2(1—v) a + , У4(2 + у) ai_ + 24 (1 - v) a У6 (3 + v) 6 720 (1 — v) a + ‘ ‘ ’ 4 У (2-v) У3(3 —v) Ax- i_v“a 6(1—v) a + У5(4-у) . + 120(1—v)a y7(5-v,)._a7 + — 5040(1 — v) a +
Таблица 25
Uo Yo Xo
и Luu аУ ~ ау 2(T-i)'sln^ , 1 — 2v Luv — — 2 __ v) sin ay — a у 2 (1 - V) cos аУ luy~ 4 (i __ v) '‘n 1 ^ux — a sin ~ 1 1 4(1 — v) a x X (sin ay — ay cos ay)
Sx 1 * 1 Lyu “ 2 (1 — v)sin аУ ~ ау 2(l-v)cos аУ ay lVV-2(1-v) x X sin ay + cos ay 3 — 4v LVY- 4(i_-vjSsin^- У -4(l-v)cos^ ^vx = ^uy
а?у . LYU~ 1 - V S’n^ . a lyv — i _ v x X (sin ay — ay cos ay) Lyy = Lvv Lyx = Lvv
а LXU — 1 — у Х X (sin ay + ay cos ay) Lxv — Lyu Lxy=Lvv ^xx~Luu
°х 2a Au~ i _v cos аг/- ua2 ТТГ7sin аУ a Ay i _ v X X (sin ay 4- ya cos ay) Ay- i __v cosay — ya 2(1-V)sin^ ya AX - 2 (1 - v) cos ay + 3 —2v + '2(ij-V)s'na:L
392 МЕТОД начальных функций [гл.
S VOl ОБЩЕЕ РЕШЕНИЕ ПЛОСКОЙ ЗАДАЧИ 39$
переменной у и содержащие производные по ггерю^нной х. Эти
операторы могут быть представлены либо в форме бесконечных
рядов (табл. 24), либо в трансцендентной форме операционного
метода (табл. 25). В последней строке табл. 24 и табл. 25 при-
ведены выражения для операторов, полученных при помощи фор-
мулы (10.5) и позволяющих вычислять напряжение "ах. через
известные н ачальные функции в следующей форме:
ах — AuU0 ~h ~h АуУ0 -j- АхХ0. (10.7)
u Заметим, что формулы (10.2) — (10.5) и табл. 24, 25 относятся
к случаю плоско-деформированного состояния. Для того чтобы
этими формулами можно было пользоваться и при решении задач
о плоском напряженном состоянии тела, в них достаточно заме-
нить модуль упругости Е и коэффициент Пуассона v соответст-
Е (1 4- 2v) 1 v гт
венно на величины - и • Произведя, например,
такую замену в табл. 25, можно ' матрицу линейного преобразо-
вания величин П0(х), V0(x), ¥0(х), Х0(х) в величины Щх, у),
V (х, у), Y (х, у), Х(х, у) для случая плоского напряженного-
состояния представить в виде табл. 26.
Формулами (10.6), представляющими общий закон преобразо-
вания начальных функций в искомые, дается общее решение
рассматриваемой здесь плоской задачи теории упругости. Эти
формулы симметричны относительно восходящей диагонали:
Luy = Lyx, Luv = £ух, Lvv = Lyy , Luu = Lxx,
Lyu — Lxy, Lyy = Lxv,
что является по существу следствием закона о взаимности работ
внешних сил для двух каких-либо различных состояний равнове-
сия упругого тела.
Начальные функции (70 Уо, Уо, Хо, входящие в-формулы
(10.6), играют роль четырех произвольных функций,, получаю-
щихся при интегрировании основных уравнений (10.4). Эти функции
задаются граничными условиями на плоскостях у = 0 и у — h —
= const. При этом на каждой плоскости у = const может быть
задано по две функции.
Поскольку две из четырех начальных функций всегда бывают
известны с самого начала, то решение плоской задачи теории
упругости сводится к определению двух начальных функций из
граничных условий, заданных на плоскости у — h. Раскрывая эти
условия, будем иметь систему двух обыкновенных дифференциаль-
ных уравнений, вообще говоря, бесконечно высокого порядка.
При приближенном решении задачи порядок этих уравнений бу-
дет зависеть от числа членов, удерживаемых в разложениях для
операторов, приведенных в табл. 24.
Таблица 26
Vo Yo Xo
и Luu = cosay — 1 + V — —2— ay Sln ay 1 L uv = — T K1 ~ v) S1 n ay+ + (!+*) ay cos ay] 1 + 4 luy- ysmay 3 — v Lux - 4a 81паУ + 1 + V + 4 у cos ay
V 1 Lvu = у К1 —,J) sin аг/ — — (1 + v) ay cos ay] 1 + v Lvv = -2~ avsina(/ + + cos ay lvy = ^uv ^VX—Lyy
Y Lyu = (1 +v) a2//sin ay Lyy .= (!+*) ax X (аг/'cos ay — sin ay) Lyy — Lvv Lyx= Luv
X Lxu= — (1 +v) a X X (sin ay + ay cos ay) L xv = Lyu Lxy = Lvu Lxx=
°х Av — (i A- v) a X X (2 cos ay — ay sin ay) Av — (1 + v) a X X (sin ay + ay cos ay) A у = v cos ay — 1 + 4 —* —2— аУ sln &У Ax — у [(1 + v) ay cos ay,+ + (3 + v) sin ayj
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
§ и] изгиб плиты в условиях плоской деформации 3g5
§ 11. Изгиб толстой плиты в условиях ПЛОСКОЙ дефпрЫЯЦИИ.
Построение приближенного решения
В*качестве иллюстрации изложенного метода рассмотрим изгиб
толстой плиты, работающей в условиях плоско-деформированного
£ШЬ
л
о
х
л
I
I
1/’’
Рис. 172.
состояния (рис. 172). Пусть внешняя нагрузка состоит только из
нормальных сил р(х), расположенных кососимметрично относи-
тельно срединной плоскости у = 0.
Принимая за начальную плоскость у = 0, получим для двух
начальных функций нулевые значения:
f/t) = yo=0. (11.1)
Общие формулы (10.6) и (10.7), определяющие перемещения и
напряжения в плите, перепишутся при этом в виде:
- U = LuvVo + LvxX0, j
V = LvvV0 + T-vx^'o, I /11 o\
Y = LyvV0 + LyxX0, [
X = LxvV0 + Z-xxXo- J
Раскрывая граничные условия, заданные на плоскости y = h
(при у = h, Yh = р (х), Хй = 0), получим для определения началь-
ных функций Уо и Хо систему двух обыкновенных дифференциаль-
ных уравнений:
LyV (й) Vo -р Lyx(h) Хо = р, )
Lxv(h)Vo + Lxx(h)Xo = 0. f (
396
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[гл.
(11.4
(И.6) 5
можно
(11.7) :
(П-8)
(П-9)
по сте-
в обыч-
Введением разрешающей функции F по формулам:
Lxv\h)F-
t0,
мы тождественно удовлетворим второе из уравнений (11.3). П
этом первое уравнение (11.3) примет следующий вид:
(Lyv Lxx — LyxLxv)hF — р. (11.5)j
Для решения поставленной задачи необходимо основное урав-
нение (11.5) представить либо в обычной дифференциальной фор-
ме, для чего входящие в это уравнение операторы следует рас-|
крыть при помощи табл. 24, либо в точной трансцендентной
форме.
В последнем Случае выражения для дифференциальных операто-
ров нужно записать в соответствии с табл. 25. Заметим, что вто-
рой путь более удобен, поскольку от трансцендентной интегро- |
дифференциальной формы нетрудно, перейти и к обычной дифферен- !
циальной форме записи.
Раскрывая дифференциальные операторы уравнения (11.5) при
помощи табл. 25, получим:
! [ah — sin ah cos ah] F = p.
Выражения (11.4), определяющие начальные
представить при этом в виде:
Vo = Feos ah-=-77-^—r ah sin ahi F,
L 2(1 —v) J
j
Xo =----j—a2h sin ah-F.
функции,
функций
Пользуясь разложением тригонометрических
пеням их аргумента, перепишем уравнения (11.6) и (11.7)
ной дифференциальной форме:
2Л3 . Г. й2 о , 2Л4 д Л« в , -] „
тп—г a4 1------а2 + тлт а4 — тлт-а® + • • • И = Р>
3 (1—v) L 5 1 105 945 1 J '
г» = [1 - А*“‘ ~
4-v
720 (1 — v)
/г2 о Г< Л2 . 2 , Л4 , № 6 . 1г.
а |! 6 а + 120 “ 5040 а +"-у *
1 -V
Уравнениями (11.6) и (11.8) представлено точное решение рас-
сматриваемой задачи. Для получения приближенных решений бу-
§ 113 ИЗГИБ ПЛИТЫ В УСЛОВИЯХ ПЛОСКОЙ ДЕФОРМАЦИИ 397
дем ограничивать уравнение (11.8) и выражения дай дифферен-
циальных операторов табл. 24 определенным количеством членов
Оставляя, например, в уравнениях (11.8) и (11.9) лишь первые
члены, будем иметь: н
3<^)'Г,У=₽. (11.10)
V() = F, 1
Y (lU1>
X« = -T^vf •
Из выражений (11.11) можно видеть, что в первом прибли-
жении разрешающая функция F совпадает с функцией 1/0, кото-
рой характеризуются вертикальные перемещения средней линии
плиты, а уравнение (11.10) представляет собой обычное урав-
нение изгиба балки, работающей в условиях плоской дефор-
мации. Таким образом, в первом приближении мы получили эле-
ментарное решение сопротивления материалов, соответствующее
гипотезе плоских сечений. Матрица начальных функций, или,
что то же самое, уравнения (11.2), перепишется при этом в виде
табл. 27.
Таблица 27
Vo Хо
и —уа
V 1 —
Y У2 4 — 3(1 — V) а —уа
X СО 8 - 7 । 1
°- — т а2 1~v —
Из табл. 27 следует, что для горизонтальных перемещений
принят линейный закон распределения по высоте плиты; верти-
кальные перемещения считаются постоянными; для нормальных
напряжений as = У и касательных напряжений Т-Ху — X принят
соответственно закон кубической и квадратной параболы.
398
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
Подставляя в табл. 27 соотношения (11.11), получим:
дифференциального
[гл. у
(11.12
(11.13)
(11.14)
(11.16>
^T = -X, v = v0,
(l-v)K = f (3/z2-y2)Viv,
= (y2-/F) Vo
(1-v) ax = -2y4
Функция прогибов Vo определяется здесь из
уравнения (11.10) и граничных условий, заданных на краях плиты
х = +/. На каждом крае может быть поставлено при этом по
два условия, что согласуется с выражениями (11.12) и уравне- )
нием (11.10). Заметим, что на свободном от закреплений и на- ?
грузки крае плиты приведенное решение позволяет снять напря-
жения только в смысле Сен-Венана, т. е. путем приравнивания i
нулю момента и поперечной силы (Ко = 0, Ко =0).
Для уточнения полученного нами элементарного решения со-
противления материалов сохраним в уравнении (11.8) и выраже-
ниях (11.9) по два первых члена. При этом будем иметь:
Jp(l-V),
Vo = F--^-=-^-h2F",
0 2 (1 — v) ’
Xo = - h2F"' + «7^—,
u 1 — v b (1 — v)
Й4Л;
Как и в первом приближении, примем, что перемещение оста-
ется по толщине плиты постоянным:
К = (11.15)
Внося (11.14) и (11.1) в табл. 24 и оставляя в соответствии .
с порядком разрешающего уравнения (11.13) в полученном вы-
ражении для U члены, содержащие F' и F'", в выражении для
Y — члены, содержащие FIV, FVI, для X— члены, содержащие F'",
Fv, и для ах — члены, содержащие F", Flv, представим искомые-
перемещения и напряжения плиты в виде:
U = - yF' + , у \у2 + h2] F'",
(1 — v) Y = f (3/i2 — y2) F1V — (5A4 — y4) FVI,
(1 _V)X = (y2 — h2)F'" — yi~hi Fv,
(1-v) °x = -2y F" + |y8FIv.
j и] изгиб плиты в условиях плоской деформации 394
Первые члены выражений (11.16) в точности совпадают с по-
лученным ранее решением (11.12). Дополнительные члены этих
выражений, учитывающие отклонение от гипотезы плоских сече-
ний, вносят уточнение в элементарное решение.
Общий интеграл дифференциального уравнения (11.13) имеет
форму:
F = Сг ф- С2х + С3х2 4- С4х3 4- С8 sh х + С6 ch х 4- G,
(11.17)
где G — частный интеграл уравнения (11.13), зависящий от
вида заданной внешней нагрузки, а С1( ...,С6—произвольные по-
стоянные.
Для определения шести постоянных интегрирования, входящих
в выражение (11.17), на каждом поперечном крае плиты должны
быть сформулированы по три граничных условия. В случае пол-
ного защемления края (V = О, U = 0) формулы (11.14), (11.15) и
(11.16) позволяют записать эти условия в виде:
р— = °. ]
} (11.18>
F' = 0, F'" = 0. j
Если на краю имеется жесткая в своей плоскости и гибкая из:
плоскости диафрагма (Е = 0, ах = 0), то граничные условия при-
мут вид:
F = 0, F" = 0, FIV = 0. (11.19)
При свободном от закреплений и нагрузки крае (ах = 0, тХ4, = 0)
граничные условия имеют вид:
F" = 0, FIV = 0, .
?г u*-h* 1 J (11.20),
[(г/2 — h2) F'" - v—^~ Fv] dy = 0. I
0
Таким образом, расчет плиты во втором приближении может
быть проведен при любых граничных условиях, заданных на по-
перечных краях плиты х = +1. Определив произвольные постоян-
ные интегрирования из этих условий, а затем функцию F по фор-
муле (11.17), получим для вычисления перемещений и напряжений
в плите формулы (11.16). При помощи этих формул может быть
произведен расчет достаточно толстых плит, для которых от-
клонение от закона плоских сечений весьма существенно,. Следует
отметить, что если в формулах (11.16) мы заменим коэффициент
Пуассона v на величину , то получим решение задачи об
400 МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ [ГЛ. vj|
изгибе высокой балки (балки-стенки), работающей в условиях плсЦ
ского напряженного состояния. я
Увеличивая количество членов в основном дифференциальном
уравнении задачи до трех, мы еще более повысим точность выя
числений. Этот процесс может быть продлен и далее. Нужно|
иметь в виду, однако, что повышение точности расчетов связано!
с повышением порядка основного дифференциального уравнения 1
и, следовательно, с увеличением трудоемкости вычислений. Вме-
сте с тем для практических целей уже второе приближение дает
весьма удовлетворительные результаты.
В настоящем параграфе мы рассмотрели только задачу об из-
гибе толстой плиты при произвольных граничных условиях, задан-
ных на ее поперечных краях х = +/, и наметили порядок пост-
роения приближенного решения этой задачи. Заметим, что ана-
логичным образом может быть рассмотрен и ряд других задач по
расчету массивных конструкций, работающих в условиях плоской
задачи теории упругости, например тех, которые были приведены
нами в §§ 5, 6, 7 и 8. Во всех этих случаях из граничных условий,
заданных на продольных краях плиты, следует получить основ-
ное разрешающее уравнение задачи и затем, удерживая в этом
уравнении и операторах табл. 24 определенное количество чле-
нов, строить приближенное решение с наперед заданной степенью
точности.
§ 12. Применение тригонометрических рядов для решения
плоской задачи *)
1. Остановимся теперь на рассмотрении достаточно широкого
класса задач по теории пластинок и плит прямоугольного очерта-
ния, характеризующихся такими граничными условиями, которые
допускают применение тригонометрических рядов. Пусть, напри-
мер, края плиты х = 0 и х = I (рис. 173) жестко соединены с тон-
кими листами-диафрагмами, абсолютно жесткими в отношении
перемещений в своей плоскости и допускающими свободные пере-
мещения из плоскости. Подобные граничные условия формулиру-
ются в следующем виде:
при х —- 0 и x = l V=Y’ = cJr = O. (12.1)
Из условий (12.1) и общих уравнений (10.1), (10.2) следует,
что изменение основных расчетных величин по координате х
*) В настоящем параграфе, а также в §§ 13,14, 15 и 16 использованы не
которые материалы кандидатской диссертации В. В. Власова «Метод началь
ных функций в плоской задаче теории упругости», 1958 г., а также материа
лы из его работ [13], [14].
$ 121
ПРИМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
401
может быть задано в виде:
U (х, у) = 2 fm (У) cos апх,
П=1
V (х, у) = f2„ (у) sin а„х,
п=1
бж (х, у) = 2 fin {у) sin а„х,
П=1
У (х, у) = 2 fan (у) sin апХ,
П=1
X (X, у) = fin (у) COS апх,
П=1
(12.2)
гт ,
где а„ = -j~ , / — длина плиты в направлении оси х.
Как известно из теории упругости, выражения (12.2) соответ-
ствуют решению Файлона. Аналогичным образом, задаваясь пере-
мещением U и напряжением X в виде ряда по синусам, а пере-
мещением V и напряжениями Y и ах в виде ряда по косинусам,
придем к выражениям, соответствующим решению Рибьера, кото-
рое характеризуется граничными условиями:
при х = 0 и х = I U = X = 0.
(12.3)
Рассматривая в дальнейшем решение (12.2), будем считать,
что на начальной плоскости плиты при у = 0 известны все на-
чальные функции U„,V0,XQ и Yg, заданные в виде тригонометри-
ческих рядов с постоянными коэффициентами:
Uo = 2 ип cos а„х,
п=1
Ко = 2 vn sin а„х,
П=1
Ко = 2 ^sina„x,
П=1
хо = 2 Хп cos а"х-
п=1
(12.4)
Подставляя (12.4) в общие интегралы перемещений и напря-
жений, записанные в виде табл. 25, и производя необходимые пре-
образования, мы выразим напряженное и деформирдванное со-
стояние плиты через начальные функции при граничных условиях
(12.1). Покажем, например, как преобразуется первое слагаемое
в формуле для перемещения U:
cos ТУ — --ТУ sin ту) Uo (х) =
V V f(a^)2'n4-1 + ''M2'"+2lcosax-
= 2 «п 2 + ~2~(2^+Х)Г J COSOtrtX -
/2=1 т=0
00
= 2 ип (ch а„у + Цр <хпу sh а?! у ) cos апх.
п=1 V
26 В. 3. Власов, Н. Н. Леонтьев
402
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[гл. v:
Таким же образом преобразуются и остальные члены матр!
цы, приведенной в табл. 25. В окончательном виде интегралы,
определяющие напряжения и перемещения плоско-деформироваН'
ной плиты, принимают вид:
00
= р^у 2 Г(1—v)cha„y+ у a„ysha„y
П=1 1
v 1
— у [(1 — 2v) sh a„y + а„у ch а„ у\ — у упу sh а„ у 4
+ [-уу- sh а.пу + у ch апу| J cos anx,
У = -Л-2 J^[a„r/cha„y —(1 — 2v)sha„y] +
1 — v 12
n=i
Г 1 I У
+ v„ (1 — v) ch a„ г/— у any sh any J + у
3—4v ,
—— sh a„ [/—
- an
к U 1 •
— r/ch ctny + у xnysn an ypin anx,
У = узу 2j [“n^y sh any + v„a„ (sh a„y — an у ch a„y) +
n=l 1
4- Ун |"( 1 — '>) ch a„ (/ — у sh a„yl + у [(1 —2v)sh any4
(12.5)
4- any ch any 1 sin an x,
X = y^y 2 {и«ап (sh а«У + апУ ch a„y) — vna.n у sh a„y +
n=l 1
+ У [(1 — 2v) sh any — a„y cha„yJ4-
4- xn [(1 — v) ch a„y 4- у a„y sh a„y]| cos a„ x,
oo
= узу 2 1— u^n (2ch a„y 4- a„y sh a„y) 4-
n=l 1
4- n„a„ (sh a„y 4- a„y ch a„y) 4- yn (v ch a„y 4-
. 4-ysha„y 1 — у((3—2v) sha„'y4-a„ychany]j-sina„x.
§ 121
ПРИМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ
403
Формулы (12.5) носят общий характер и остаются-Енраведжи*
выми при любых граничных условиях, заданных на пропл^ну^
краях плиты у = 0 и у = h, '
А
Изменив в этих формулах коэффициент Пуассона v на — г
мы получим общее решение для пластинки, находящейся В-уело
виях плоско-напряженного со-
стояния при граничных усло-
виях (12.1).
Заметим, что аналогичные
формулы могут быть получены
и для задач, характеризующих-
ся граничнымиусловиями(12.3).
Рассмотрим теперь некото-
рые частные примеры.
2. Предположим, что в пря-
моугольную плиту (рис. 173) по
граничной плоскости у = h вдавливается плоский штамп. Будем
считать, что нормальные перемещения плиты под штампом явля-
ются известной функцией от х, а на другой границе плиты, при
у = 0, равны нулю. Кроме того, будем считать, что на краях пли-
ты у — 0 и у = h отсутствуют касательцые напряжения X.
В соответствии с (12.2) положим:
У
h
О
777.
----------- I ---------~
Рис. 173.
при у =h
ОО
V (х) = 2 sn sin “я х'
п=1
Таким образом, получим следующие граничные условия:
при у = 0
при у = h
Ко = Хо = 0;
(12.6)
ОО
V — 2 8 л sin осдХ. Х = 0.
п=1
Начальные функции Uo и Уо определяются из граничных усло-
вий, заданных на краю у ~h. Полагая в формулах (12.5) соглас-
но (12.6) vn и хп равными нулю, приравняем выражения для V й
X при y — h граничным значениям (12.6). Для каждого члена
ряда получим при этом систему двух уравнений относительно
26*
404
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ.
неизвестных ип и уп: Я
2 [р„ ch р„ - (1 - 2v) sh р„] ип + h (5-=^ shp„-chp„)z/„ = fl
= 4^(1—v)8n, I
2 Pn (sh pn pn ch pn) un + h [(1 2v) sh pn pn ch p„] yn = 0, 1
n nnh I
где pn = — . A
Определив из этих уравнений неизвестные ип, уп и пользуясь!
выражениями (12.5), можно перемещения и напряжения плиты оп-|
ределить в виде: 1
U = - 2 5п9°аМ {К1 - 2v) sh pn - p„ ch p„] ch pn1J +
n—1 11 l
-J- pn sh pn (tq sh pnT])|,
V = 2 {[2(1- V) sh p^ + p„ ch p„J sh p„’ 7] -
: n—1 n
— pnshpn(7)Chp„7j)|,
00
Y = 2 { (Sh P„ + P„ ch p„) ch pn7] - pn sh P„ X
n=l n
X hshp„iq)|,
V X' C0S ^П^ [ L n , Q , Q [ . Q
X = 2j -------Гл--1ch Pn sh Pn vt — sh pn (Т] sh p„ iqH,
n=1 ,шп i )
(12.7)
v M„sinM
— 2j ЙД
n=l n
|(sh pn — pn ch p„) ch pn t] +
+ Pn Sh P„ (iq Sh P„ 7])},
где nJ == -у, | — безразмерные координаты, Ди = (1 — v) sh2 p„. j
В выражения для напряжений Y, X, ах величина (1—v), за-1
висящая от коэффициента Пуассона, входит лишь как множитель, j
который можносвынести за знак суммы. Если же мы предположим, I
что при р = 0 и y = h равны нулю не напряжения X, а переме-|
щения U, то придем к более сложным выражениям для напряже-1
ний;и перемещений. В этом случае в формулах для напряжений]
уже нельзя будет вынести за знак суммы коэффициент Пуассона.1
Таким: .образом, при граничных условиях смешанного типа (12.6)1
подучаем своеобразное обобщение теоремы Мориса Леви для пря-*|
моугольной плиты. |
§ 12] ПРИМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ 4Q5
3. В качестве второго примера рассмотрим двуслойную плиту,
на которую действует вертикальная нагрузка
ОО
р = 2 pnsinanx.
П=1
Обозначим упругие характеристики и толщины верхнего и ниж-
него слоев соответственно через Glt vx, hr и G, v, h и выберем на-
правление осей координат, как показано на рис. 173. Будем счи-
тать, что верхний, тонкий слой плиты работает как пластинка.
Для нижнего слоя примем следующие граничные условия:
при у = О Уо = Хо = 0; .
D } (12.8)
при у = h X = 0, "1К+У=_р, /
где D — цилиндрическая жесткость пластинки.
Последним из условий (12.8) выражен тот факт, что посколь-
ку верхний слой работает как пластинка, то на нижний слой пет
редается нагрузка, определяемая из уравнения цилиндрического
изгиба пластинки. Раскрывая условия (12.8), найдем ^неизвест-
ные коэффициенты ип И уп разложений (12.4).
Формулы для перемещений и напряжений могут быть записа-
ны в следующем виде:
U = - 2 ch - (1 - 2v) sh ₽„] ch M -
n=l Pn n 1 .
— pnsh pn (iq sh pniq)|,
l/ = -S^^{[2(l-v)shpn + p chpjshM-
— sh pn (iq ch tj)|,
Y = — 2 Pn T {(sh ch pn) ch —
n=l n 1
— pnshpn (7]ShpnT])|>
(!2.9)
X = 2 ~"^"д (ch pn sh pnT] — sh pn (tj ch pnT])},
n=l n
00 -de
°x = — 2 P" T n {(shpn — pn ch P„) ch pnT] +
n=l n l
+ sh (t; sh pn
406 МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ [ГЛ. vfl|
где Д„ принимает значение .Я
Дга = {3n + A sh 2{3„ + (1 ~/3} ° $ sh2р,;. (12.юЯ
4. Решение в тригонометрических рядах можно получить и не-я
сколько иным путем. Для этого следует исходить не из общих!
разложений (12.2), (12.4), а непосредственно из основного диффе-1
ренциального уравнения задачи. Покажем это на рассмотренной!
ранее задаче об изгибе толстой плиты (см. § 11). 1
Основное уравнение, записанное относительно разрешающей 1
функции F, имеет в этом случае вид: 1
1 [<хА — sina/z cosa/г] F = р(х). (12.11) |
Для сокращения выкладок рассмотрим только случай дейст- 1
вия симметричной относительно оси Оу нагрузки. I
При граничных условиях (12.1) и начале координат, располо- 1
женном в центре плиты, будем искать решение уравнения (12.11) 1
в форме
F=2xncos^ (п= 1,3,5, ...,(2/п—1)). (12.12) '
1
Разложим заданную нагрузку р(х) в ряд по косинусам:
00
Р(х) = 2j P"cos 2Г
п==1
где
рп=4 \ р (х) c°s тгах'
О
Подставляя выражение (12.12) в левую часть, а (12.13) — в
правую часть уравнения (12.11), пол'учим для коэффициентов раз-
ложения (12.12):
1/2
4(1 — v) f р (х) cos Л х dx
Ап =____________о____________, (12.14)
пте ^nh — 4 sh 2ЛП h]
где
' (п = 1,3, 5,... ,(2/п—1)).
(77 = 1,3, 5,...,(2/77— 1)), (12.13)
1/2.
§ 12]
ПРИМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ 4Q7
Формулы (11.7) и (12.12) позволяют определить
функции Vo и Хо в виде:
°° К h
Vo = 2 Л „ fch Х„/г + 2 ” sh X„ft 1 со% Кх,
п= 1 L ' ' J
оо A
Xo = — 5 j—^x^shX„ftsinX„x.
n=l
начальные
(12.15)
Внося (12.15) в табл. 25 и производя необходимые преобразова-
ния, получим выражения для перемещений и напряжений симмет-
рично изгибаемой плиты:
ОО
= 271=77) 2 Л„[(1 — 2v)chX„/zshX„z/ —
' } п=1
— \nh sh \nh sh \ny + КгУ ch \nh ch X„z/] sin X„x,
00
V = 271=7) 2 Л„[2(1 —v)ch Х„Лch Ky—Kych X„ftshX„i/+
' ' n=l
+ \nh sh \nh ch X„z/] cos X„x,
00 Д x
Y = 2 l\ih sh \ny sh \nh + ch Xn/z sh \ny —
n=l
— \ny ch Xnft ch X„r/] cos Xnx,
” A ,2
X = 2 1У sh Ky ch \nh — h ch \ny sh Xn/i] sin X„x,
n=l
00 Д X
°x = 2 гЕт; tsh M ch M + Ky ch \ny ch Xn h —
n=l
— Xn/i sh Xnz/ sh Xn h ] cos Xnx.
(12.16)
5. Приведем еще точное решение в тригонометрических рядах
для плиты, находящейся под действием нагрузки, симметричной
как относительно оси Ох, так и относительно оси Оу (рис. 174).
Разрешающее уравнение имеет в этом случае следующий вид:
«Га/г + Я р = _ р (х)>
1 — v L J
(12.17)
где
д
а == д-
дх
408 МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
(ГЛ. VI
Решение этого уравнения будем искать в форме
ОО
Г=ЗЛ„СО8^- (п= 1,3,5, ...,(2/тг—1)).
и=1
Раскладывая заданную нагрузку в ряд по cos^A,
(12.1
ПОЛуЧ!
выражения для коэффициентов Ап разложения (12.18):
1/2
4(1 — м) р (х) cos Кпх dx
(12.19)
где
= J (п= 1,3, 5,...,(2/п—1)).
Для начальных функций Yo и Uo будем иметь:
ОО
1А> = — 271-V) 2 sin 1
' Л=1 I
ОО I
П = 4 ; 2 Gn COS ХИХ, j
П=1
где
(12.20)
Вп = Ап [(1 — 2v) sh \nh — \nh ch \/th],
Cn = AnK [sh \nh 4- \nh ch \nh].
(12.21)
§ 13]
ТОЧНОЕ РЕШЕНИЕ ДЛЯ ПРЯМОУГОЛЬНОЙ ПОЛОСЫ
409
Напряжения и перемещения плиты примут вид;
00
и = — 2(/_ . 2 (Bnchkny+
V 7 П=1
+ sh \nh sh X„z/) sin
°° Г x у
V = 2 shx„/ishx„z/— 2-^~-chX„/ishX„z/+
n=l '
к у 1
+ 2'(1 _--V) sh ^nh ch M] cos X„x,
CO
(1 — v)y = 2 [Лпк2пу sh knh sh kny — Cn ch kny} cos knx,
n=^l
00
(1 —v)X = 2 W*shX„ у—z/shXrtftchX„z/)sinX„x?
H=1
co
(1 — V) Or = 2 An^n (—sh knh ch kny + \nh ch \nh ch kny—
П=1
— X„z/ sh knh sh kn y) cos l„x.
(12.22)
§ 13. Построение точного решения для прямоугольной полосы
при произвольных граничных условиях на поперечных
и однородных граничных условиях на продольных краях
В предыдущем параграфе мы рассматривали вопросы, связан-
ные с построением точных решений для прямоугольной ‘пластинки.
(плоско-деформированной пли-
ты), имеющей на поперечных
краях граничные условия, допу-
скающие применение тригоно-
метрических рядов. Теперь мы
остановимся на вопросе получе-
ния точных решений для прямо-
угольной полосы при произволь-
ных граничных условиях на кра-
ях х = 0 и х = 1 (рис. 175) и
Рис. 175.
однородных граничных условиях
на линиях у = 0 и y = h.
Рассмотрим вначале случай однородных граничных условий
смешанного типа, т. е. предположим, что на краях у — 0 и y=h
имеем:
и = ”у = 0.
(13.1)
410
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
1ГЛ. VI
Условия (13.1) означают, что на краях у = 0 и y — h полоса!
усилена жесткими в своей плоскости и гибкими из своей плоско-1
сти диафрагмами. В этом случае начальные функции Uo и Уо|
равны нулю. 1
Раскрывая условия (13.1) при помощи общих формул табл. 26, |
получим систему двух дифференциальных уравнений беско-1
нечно высокого порядка относительно двух искомых начальных ;
функций Уо и Хо:
— [(1 — v) sina/i + (1 + v) a/i cos а/г] Vo +
+ у p3 a v sin ah -j- (1 -j- v) h cos ah j Xo = 0,
2 (1 + v) a (a/i cos a/i — sin a/i) Vo —
— [(1 —v)sina/i + (14- v)a/icosa/i] Xo = 0.
Введением разрешающей функции F(x) по формулам:
Vo = — (! , sin ah + a/i cos ah) F,
\1 + V ' /
XQ = — 2a (ah cos ah — sin ah) F,
(13.2)
(13.3)
второе уравнение (13.2) будет тождественно удовлетворено, а
первое после некоторых преобразований примет следующий вид:
(sin2 т/г) F = 0. (13.4)
Решение уравнения (13.4) будем искать в виде
F — Cekx. (13.5)
Подставляя выражение (13.5) в (13.4), получим относительно k
характеристическое уравнение бесконечно высокого порядка:
sin2&/i = 0. (13.6)
Корни этого уравнения определяются в виде
k - —
Rn~ h ’
где п — любое целое положительное число.
Общее решение уравнения (13.4) определится, таким образом,
в форме
ОО
F = 2 Anchknx + Bnshknx+ Cnxchknx+ Dnxshknx, (13.7)
n=0
где An, Bn, Cn и Dn — произвольные постоянные.
Подставляя общий интеграл (13.7) в соотношения (13.3), по-
лучим окончательные выражения для начальных функций Уо и Хо.
Внося далее найденные значения для Vo и Хо в общие формулы
§ 13] ТОЧНОЕ РЕШЕНИЕ ДЛЯ ПРЯМОУГОЛЬНОЙ ПОЛОСЫ
табл. 26, получим соотношения для напряжений и Перемещений
пластинки в случае граничных условий (13.1). Заметим, что с
точки зрения практических вычислений для получения этих соот-
ношений удобнее сначала подставить выражения (13.3) в ук
упростить полученные результаты, а затем уже. воспользо-
ваться зависимостью (13.7). Проведя указанные операции, можно
представить перемещения и напряжения пластинки в следующем
виде:
СО
U = 2 (— 1)" h lknAn ch knX + knBn sh knX +
[1 — v *1
1 । v sh knx knx ch knx] Cn -J-
г 1 ~ v ”11
4-1 — chknx 4- knxsh knx I Dn\sinkny,
oo
V = 2 (- l)nhlknAnshknx 4- knBnch£nx4-
n=l 1
+ (np;ch knX +knX sh knX)Cn +
/2 \ 1
4- (sh knx 4- knx ch knx J DA cos kny,
“ , (13.8)
У = — 2 2 (—i)nknhknAn{shknx + knBnchknx +
n~l
4- (2 ch knx 4- knx sh knx) Cn 4-
4- (2 sh knx 4- knx ch kn x) Dn} sin kny,
OO
X = 2 2 (— 1 )nkn. h{knAn ch knx 4- knBn sh knx 4-
4- (sh knx 4- knx ch xnk) Cn 4-
4- (ch knx 4- knx sh knx) Dn} cos kny,
OO
ax = 2 2 (— 1)" {knAn sh knx 4- knBn ch knx 4-
4~ knXCn sh kn x 4~ knXDn ch knX } sin kny•
Заметим, что из общего решения (13.8) выпало элементарное
решение в полиномах, отвечающее нулевым корням уравнения
(13.6), в результате чего формулы (13.8) представляют собой
неполные выражения для перемещений и напряжений. Это эле-
ментарное решение нельзя получить в общей форме посредством
412 МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ [ГЛ. VI»
введения разрешающей функции F, так как функции Vo и Хо вы-
ражаются через F с помощью операций дифференцирования, вслед-
ствие чего часть решения в полиномах выпадает.
Для того чтобы найти элементарное решение, перейдем от
символической формы записи дифференциальных уравнений (13.2)
к действительной форме в виде бесконечных рядов. Выделяя из
этих уравнений лишь первые члены, получим систему двух диф-
ференциальных уравнений, каждое из которых будет уравнением
первого порядка относительно искомых функций Vo и
— aVo + X0 = 0, aX0 = 0. (13.9)
Из уравнений (13.9) найдем;
Х0 = А0, Vq = Aox+Bo. (13.10)
Подставляя значения (13.10) в общие формулы (10.6), полу-
чим:
U = Y — ах = 0, V = АохBCl, X = Ао. (13.11)
Решение (13.11) отвечает состоянию чистого сдвига пластинки.
При этом постоянная Во характеризует жесткое смещение пла-
стинки в направлении оси у.
Складывая выражения (13.8) и (13.11), мы найдем общее ре-
шение для перемещений и напряжений полосы. Каждому номеру
п этого решения отвечает свое элементарное напряженное и де-
формированное состояние. В совокупности бесконечное число этих
элементарных состояний образует точное решение задачи при гра-
ничных условиях (13.1). При этом все элементарные состояния
ортогональны между собой.
Полученное решение содержит 4п -ф 2 произвольные постоян-
ные, которые необходимо определить из граничных условий на
краях полосы х = 0 и х = I. На каждом крае может быть за-
дано по два граничных условия. Раскладывая заданные на этих
краях статические или геометрические величины в ряды Фурье на
отрезке (0, h) по синусам или косинусам в соответствии с фор-
мулами (13.8) и (13.11) и приравнивая выражения для соответ-
ствующих перемещений и напряжений (13.8) при х = 0 и х = I
этим разложениям, получим для каждого номера п=/=0 систему
четырех алгебраических уравнений для определения неизвестных
постоянных Ап, Вп, Сп и Dn. По определении этих постоянных
задача отыскания напряжений и деформаций полосы будет пол-
ностью решена.
В ряде случаев удобнее перейти от постоянных Ап, Вп, СПГ
Dn к другим произвольным постоянным, имеющим более четкий
физический смысл. Для этого примем за начальную плоскость
полосы плоскость х = 0, считая по-прежнему, что на краях у=О
и у = h выполняются граничные условия (13.1). В этом случае
$ 13] ТОЧНОЕ РЕШЕНИЕ ДЛЯ1ПРЯМОУГОЛЬНОЙ ПОЛОСЫ
413
начальными будут функции:
U‘ = U(O,y), V = V(O,y), Х* — Х(0,у), о; = Ох(0,у).
Для новых начальных функций, как это следует из (13.8)
и (13.11), должны выполняться соотношения:
ОО 00
U* = 2' ип sin kny, V* = 2 cos kny,
T (13.12)
X* = 2 < cos kny, < = 2 <sin к"У- .
n=0 n—1
В этих формулах коэффициенты «*, v*n, х”п, а*п являются коэф-
фициентами Фурье тригонометрических рядов для начальных функ-
ций. Выразим коэффициенты Ап Вп, Сп и £)„ через коэффициен-
ты v*n, х*п, а*. Для этого положим в формулах (13.8) и (13.11)
х — 0 и приравняем полученные результаты соответствующим вы-
ражениям (13.12). Получим:
<=(-1)«/1(йлДл-4ч^О„), 1
4 =Х 1)"Л (knBn + 1 .j. v Ci) ,
х; = (-1)«2М(^лл + ол),
< = (-1)«2^Ж,
(13.13)
B0 = v*, До = 4 (13.14)
Из_соотношений (13.13) будем иметь:
Ап~( ])" 1мп (2ы» +
1-V Хп\
1 + V kn ) ’
Сп =(<— 1)л (у'п 2^—) ,
(13.15)
Подставляя зависимости (13.14) и (13.15) в формулы
(13.8) и (13.11), получим общие выражения для напряжений и
414
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VII-
ф перемещений:
V = 2 (Г К1 + v) knx ch knx — (1 — v) sh knx] -h
+ u* (ch knx— knx sh knx^ xn*sh knx +
«
у [-y— sh ^nX — 0 + v) x ch knx sin kny,
V = v’ -f x’x + 2 (ch knx + knx sh knx) —
n=l
— у [(1 — v)shM 4- (1 M) M ch Mlу рЦ— X
]1 I - V ")
-----4— °'nx sh knx> cos kny,
00 f
Y = 2 I (1 “h v) v“nkn (2 ch k"X + knX sh knx) +
n~ 1
-h (1 v) u*nkn (sh knx + k~nx ch knx) —
---у [(3 4-v) sh fe„x -h (1 -hv)fenxchfenxl +
(13.16)
00
x = xo + S {0 + v) v'nkn (sh knX -h Meh knx) —
n—1
— (1 v) u*nk2nx sh knx + x*n (ch knx + Цг~ knx sh knx J 4-
+-y [(1 —v)shM—(1 H~v)Mch МП cos Ma
00
Ox = 2 {о + v) ^nk2nx sh M + (1 + v) unkn (sh м —
n=l
X
— knxchknx) + ~y 1(1 —v)sh£nx + (1 + v)fertxch^x]-h
"h °n (— M~~ ^nX sh ^nX "h ch knx)| sin ^"У‘
14]
ДРУГОЙ ВИД ГРАНИЧНЫХ УСЛОВИЙ НА КРАЯХ ПОЛОСЫ
415-
Выражения (13.16) позволяют определить напряжения и де-
формации полосы в условиях плоского напряженного со-
стояния при произвольных статических, геометрических или
смешанных граничных условиях на краях х = 0 и х = I.
В этом смысле решение в тригонометрических рядах (13.16>
является обобщением известного в теории упругости решения.
Файлона.
Отметим, что выражения (13.16) можно получить и дру-
гим, более простым путем: непосредственной подстановкой за-
висимостей для начальных функций (13.12) в общие формулы
табл. 26. При этом следует предположить, что формулы табл. 26-
записаны для случая разложения по координате х с начальной плос-
костью х=0.
Заметим также, что при получении общего решения (13.16) из
решения (13.8) мы применили метод, представляющий собой не-
которое обобщение известного метода начальных параметров Ко-
ши—Крылова.
§ 14. Другой вид однородных граничных условий
смешанного типа на продольных краях полосы
Рассмотрим теперь другой вид однородных граничных условий
смешанного типа (рис. 176). Будем считать, что при у —0 и y=h
V=r^ = 0. (14.1>
В этом случае для двух начальных функций будем иметь:
Ко = Хо = 0.
Удовлетворяя граничным условиям при у = h, получим систе-
му двух дифференциальных уравнений бесконечно высокого поряд-
ка относительно искомых начальных функций Uo и
[(1—v) sin ah— (1 4-v) a/zcosa/i] По+
+ 4[(3-v)s-^--(l+v)/icosaA]y0 = 0, (H 2)
— 2(1 + v) a (sin ah -f- ah cos ah) Uo +
+ 1(1 — v) sin ah — (1 + v) ah cos ah] Yo = 0.
Введением разрешающей функции F (x) по формулам:
= sina/i —a/icos ah 'j F, 1 (14.3)
Yo = 2a (sin ah 4- ah cos ah) F, J
416
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VI
мы удовлетворим второму уравнению системы (14.2). При
этом первое уравнение может быть снова приведено к виду
(13.4).
Поскольку разрешающие уравнения для задач (13.1) и (14.1)
одинаковы, то при построении общего решения в рассматриваемом
Рис. 176.
случае могут быть повторены рассуждения предыдущего пара-
графа. При этом для разрешающей функции F снова получим
выражение (13.7).
Для определения общих интегралов перемещений и напряже-
ний необходимо, как и ранее, получить элементарное решение в
полиномах. Для этого нужно исходить из системы двух диффе-
ренциальных уравнений:
— 2vat/0 + (1 — >)^о = 0, 1
2(1 +y)a.2U0 + ^a.Y0'= 0, J
(14.4)
полученных из уравнений (14.2) посредством сохранения в них
лишь первых членов.
Из уравнений (14.4) будем иметь:
Un = Цр Вох + До, Y0 = vB0. (14.5)
Внося выражения (14.5) в общие формулы (10.6), получим:
U = ^Вох + Ао, Y = vB0, ах = В0. (14.6)
Выражениями (14.6) представлено элементарное решение, со-
ответствующее растяжению полосы равномерно распределен-
ной нагрузкой ах = Во. Постоянная До не влияет на напряжен-
ное и деформированное состояние пластинки: этой постоянной
характеризуется жесткое смещение полосы в направлении
оси х.
$ 14] ДРУГОЙ ВИД ГРАНИЧНЫХ УСЛОВИЙ НА КРАЯХ полосы 417
Используя зависимости (14.5), (14.3), (13.7) и (10.6), получим:
U = Ао + -- v- Вох — 2 (— 1)"А \kn shknxAn +
+ kn ch knxBn + (ylp-7 ch knX + knX sh knX) Cn +
+ sh k'lX ^nX ch ^nX ) cos ^y,
00
V = 2 (— l)n/i {&n ch knxAn + kn sh knxBn +
+ [rTv sh ^nX ^nX ch ^nX ] Cn ~*~
+ [1 + V ch &пХ + sh knx J D„| sin kny,
Y = vB0 + 2 2 (— 1 )n knh [kn ch knxAn + kn sh knxBtl +
n=l
+ (3 sh knx + knx ch knx) Cn +
+ (3 ch knx + knx sh knx) Dn} cos kny,
(14.7)
X = 2 2 (~ tynknh [kn sh knxAn + kn ch knxBn +
n=l
+ (2 ch knx + knx sh knx) Cn +
4- (2 sh knx + knx ch knx) D 1 sin kny,
sA- = Bo — 2 2 (— y)nknh [kn ch knxAn + kn sh knxBn +
n=l
+ (sh k x + &«xch knx) Cn +
+ (ch knx + knx sh knx) cos kny. .
Как и в случае, рассмотренном в предыдущем параграфе, об-
щее решение (14.7) представляет собой бесконечную совокупность
ортогональных элементарных состояний. С помощью произвольных
постоянных Ао, Во, Ап, Bn, Сп, Dn (м=1, 2,..., оо) можно
удовлетворить любым граничным условиям на краях х = 0 и
х = 1. При этом можно снова перейти от этих постоянных к дру-
гим, имеющим более четкий механический смысл. Для этого сле-
дует принять плоскость х = 0 за начальную и считать U (0, у) =U*,
V (0, у) = V, X (0, у) = X’, ах (0, у) = а* новыми начальными
функциями.
27 В. 3. Власов, Н. Н. Леонтьев
МЕТОД НАЧАЛЬНЫХ
ФУНКЦИЙ
[ГЛ. VII
418
Из формул (14.7) следует, что
вий (14.1) новые начальные функции
U* = 2 и*п cos kny,
П=0
в случае граничных . усло-i
можно представить в виде: ;
ОО
х* = 3 х*п sin м»
. V* = s v* Sin kny,
Приравнивая выражения
зависимостям (14.8), мы получим алгебраические соотношения, из
которых определим постоянные:
n—0
(14.7) при x = 0 соответствующим
^ = -(-ir4?
3 + v °л 'I
4 (1 + v) kn J ’
_______*_______
2 (1 + v) kn
С _ (____1 \п 1 ~г v / п
1 2h \2kn
п
. До = «;, Во = а;
О’
Подставляя формулы (14.9) в (14.7), получим выражения для j
напряжений и перемещений через начальные функции (14.8), ана-
логичные соотношениям (13.16):
и = ио + V
п=1
•пХ j
V
— [ (1 — v) sh knx — (1 -j- v) knx ch knx] —
— X* X sh knx +
sh k„x , ,
—-----—(1 +v) x ch knx
[(1 — v) sh knx + (1 + v) knx ch knx] +
n=l
2
(14.8) ;
I (14.9)
’ (14.10).
§ 14] ДРУГОЙ ВИД ГРАНИЧНЫХ УСЛОВИЙ НА КРАЯХ полосы 4]9
+ v[3fe~V + (1 + V)xchfenXJ +
+ % x sh knx | sin kny,
00 f
У = VGq +2 [0 + v) M* kn (sh knX + knx ch knx) +
n=l
+ (1 + v) v*n kn (2 ch knx + knx sh knx) +
+ -y [(3 + v) sh^x + (1 + \)knx<AiknX] +
+ a* ( vchknx + 11~v knx sh&nx)!- cos kny, (14.10)
x = S {o + v)u* ^xshM + (1 H-v)n*Msh£nX +
П~1
+ knxch k x) + x’ (ch knx^^ v knx sh knx —
°n 1
—-у [(1 — v) sh&nX — (1 + v) knxchknx] 1 sin kny,
co
Зд = a* + 2 ((1 + v) Un kn (sh knx - knx ch knx) —
n=l
*
— (1 + xshfe„x---------^[(1 — v)sh£nx +
+ (1 + v)knxchknx\ +
+ a* ( ch knx — kn sh &nx^| cos kny.
ri \ , Zi /1
Формулами (13.16) й (14.10) представлены общие решения
плоской задачи теории упругости в тригонометрических рядах-
Эти решения являются обобщениями известных решений Файлона
и Рибьера, поскольку решения Рибьера и Файлона не содержат
непосредственно общих интегралов для перемещений, ‘ в то время
как решения (13.16) и (14.10) определяют как напряженное, так
и деформированное состояние полосы. Пользуясь интегралами
(13.16) или (14.10), мы можем поэтому получить решение для
задач (13.1) и (14.1) не только при статических граничных усло-
виях’ на краях х-0их = /, нои при геометрических условиях
и различных условиях смешанного типа. . : 1
Заметим, что приведенными примерами не; огрщшчивазтёя
класс задач по теории прямоугольных пластинок, который может
27»
420
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. V
быть решен точными методами математического анализа. Анал!
гичным образом точные решения могут быть получены, наприме
при однородных статических граничных условиях, заданных а
продольных краях полосы (см. [15]), а также при других вида:
граничных условий. На основе этих однородных решений нетруд
но получить достаточно простые приближенные формулы, позво
ляющие производить расчет прямоугольных пластинок (плоско-де
формированных плит) вообще при произвольных граничных уело-]
виях, заданных на всех четырех сторонах пластинки. Таким же
способом могут быть найдены решения и в случае действия
мас->
совых сил, а также при различных температурных воздействиях.]
§15. Пространственная и плоская задачи теории толстых
многослойных плит
1. Рассмотрим толстую плиту, состоящую из ряда горизон- ]
тальных слоев с различными
упругими характеристиками:
(рис. 177). Обозначим тол-!
щину всей плиты через h, \
а толщины и упругие пос- j
F тоянные слоев — соответст-
венно через hm, vm, Gm,
где т — номер слоя, и нап- J
равим оси координат так,
как показано на рис. 177. ;
Будем предполагать, что
при переходе через плос- ]
кость контакта слоев век- J
торы перемещений и напря-
жений изменяются непре-
В
целях сокращения записи введем
рывно.
для искомых величин
&Z) ^XZ) tyzj
в отличие от (1.3) и (1.4) новые обозначения:
и (х, у, г) = иъ v(x,y,z) = U2, w(x,y,z) = Ua, \
az(x,y,z) = Uif ихг(х,у,г) = U5, tyz(x,y,z) = Ua. I I15-1)
Начальные функции u0, v0, w0, Zo, Xn, Yo определятся при]
этом в виде:
u0 (х, z/) = t/J, v0 (х, у) = t/o, w0 (х, у) = £7®, 1
2o(x,t/) = f/o, Xo(x,t/) = f/o, y0(x,t/) = t/». J (15'2)
В новых обозначениях и при отсутствии массовых сил
общие интегралы пространственной задачи (2.5) могут быть
§ 151 ПРОСТРАНСТВЕННАЯ И ПЛОСКАЯ ЗАДАЧИ ТЕОРИИ ПЛИТ 421
представлены в форме
= 3 Lik(z}Uak (i = 1,2, . . . ,6). (15.3)
k=i
Полагая в выражении (15.3) v — v1( G= Glt z^ht, получим
формулы, определяющие перемещения и напряжения первого слоя
плиты. Заметим, что эти формулы будут содержать только три
из шести начальных функций (15.2), поскольку три начальные
функции всегда известны с самого начала из граничных условий,
заданных на плоскости z = 0. Для определения искомых величин
второго слоя найдем вначале величины перемещений и напряже-
ний на плоскости контакта первого и второго слоев при z = hr.
Эти величины будут являться начальными функциями для второ-
го слоя. Полагая теперь в выражении (15.3) v = v2, G = G2 и
подставляя сюда выражения для начальных функций второго слоя,
получим формулы, определяющие перемещения и напряжения во
втором слое плиты:
в
^1=3^(Z)^° (/=1,2,...,6), (15.4)
4=1
где
в
(г) = 2 Ай (г) А$ (ЙО (й, < z < й3). (15.5)
/=1
В выражении (15.5) через Ай (й1) и Ай (z) обозначены опера-
торы Lik соотношений (15.3), взятые с упругими характеристика-
ми первого слоя при z = йх и с упругими характеристиками вто-
рого слоя при произвольном значении z, т. е.
Ай (ЙО = Lik(^1,G1,h1'), 1
L<2)(z) = A;7(v2,G2,z) (й^г^йО. / 1 '
Можно видеть, что матрица || L*k (z) || определяется формально
как произведение матрицы || Ай (2) || на матрицу Ц Ай (й2) ||. При этом
в матрицу || L*k (z) || будут вновь входить только три начальные
функции, относящиеся к плоскости z = 0. Аналогичным образом
матрица || L*k (z) || для перемещений и напряжений т-го слоя пли-
ты формально представляет собой произведение матриц
ИА$ (йу) || (/ = 1, 2.т - 1) и \\Ь№ (г) || (йт_, < z <йт). .
Составляя при помощи указанного метода выражения для пе-
ремещений и напряжений, относящиеся к нижней плоскости плиты
z = й, и используя граничные условия, заданные на этой пло-
скости, мы получим систему основных дифференциальных
422
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ.
уравнений рассматриваемой пространственной задачи, позволяющую
разыскать три неизвестные начальные функции и, следовательн<
напряженное и деформированное состояние многослойной плиты.
2. Рассмотрим случай плоской деформации многослойной плит
(рис. 178). Примем новые обозначения:
u(x, y) = Uu v(x,y)=U2, I (15,
°!/ (х, у) = U3, txy (х, у) = Ut, ах (х, у) = U5, j
u0(x) = Ui, v0(x) = U°2, | (15 {
r0(x) = t/s°, XoW-^4- t
В этих обозначениях общее решение (10.6) может быть пред-
ставлено в виде
Ut = 2 Llk(y)U*k 0 =1.2, 3,4).
k=i
(15.9)
Как и в случае пространственной задачи, для перемещений и
напряжений в m-м слое плиты будем иметь:
4
0=1-2, 3,4), (15.10)
k=i
где матрица || L*k (у) || формально представляет собой произведение
матриц
(/= 1, 2, ..., /п-1) и ||^Г)(р)|| (/гт_1<т/</гт).
Заметим, что выражение (15.10) содержит только две началь-
ные функции из четырех, поскольку две начальные функции опре-
деляются непосредственно из
граничных условий, заданных на
плоскости у = 0.
Раскрывая при помощи (15.9)
граничные условия, заданные
на плоскости у = h, и удовлет-
воряя этим условиям, получим
для определения оставшихся
начальных функций систему
двух обыкновенных дифферен-
циальных уравнений с постоян-
ными коэффициентами бесконеч-
Рис. 178.
но высокого порядка.
Остановимся более подробно на том классе задач, для кото-
рого на поперечных краях плиты при х = 0 и х — I выполняются
вполне определенные граничные условия. Будем считать, что на-
чальные функции могут быть представлены в виде следующих
$ 15] ПРОСТРАНСТВЕННАЯ И ПЛОСКАЯ ЗАДАЧИ ТЕОРИИ ПЛ;
423
рядов с постоянными коэффициентами:
= 2 u°ln sin се'пХ'
п= 1
Us = 2 “зп COS апх,
п=0
(15.11)
^4 = X и$п sin апх,
л=1
^2=2 U°n C0S a"X’
, л=0
tilt
где an = —.
Разложениям (15.11) на краях плиты х = 0 и х — 1
следующие условия:
и1 = и4 = 0 (и — хху = 0).
отвечают
(15.12)
Такие условия имеют место, например, в каждом пролете
многопролетной плиты, опирающейся на бесконечное количество
одинаковых опор, постав-
ленных на равных расстоя-
ниях друг от друга, при
действии нагрузки, сим-
метричной относительно
концов каждого пролета
(рис. 179).
Ранее уже отмечалось
(см. § 12), что представле-
ние начальных функций в
виде (15.1 ^ соответствует
известному в теории упру-
гости решению Рибьера.
При замене же в рядах
(15.11) синусов на косинусы
рассмотренное в § 12 решение Файлона,
условиям на краях:
Рис. 179.
и косинусов
на синусы мы получим
отвечающее следующим
(15.13)
Подставим разложения (15.11) в формулы (15.9). Раскрывая
при помощи табл. 25 выражения для операторов L/k и свертывая
получаемые при этом двойные ряды в одинарные, будем иметь:
U2 = Us = 0.
л=1:
1 1
2(l-7)a^shan^J +
u°
и2п
2(1—v)
X [(1 —2v) sh а,пу + а,пу ch апу] -|-
i/shanr/4-
(15.14)
u°in ГЗ —2
4G(1— v) L а„
sin а„х,
424
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
t^g — U20 —
“3°o(l-2v)
2(1-*)
У +
°° ( и°
+ 2 127ГГ7) К1 — 2v) sh апУ — <*пУ ch а„у] +
П=1
1 1 “°
+ Ugn [ch апу — 27137^) а"У sh ^У] + 4G (Г~) х
X (^7-^ sh апу —у ch апу^— У sh апУ] cos а«х’
Us = и“о + 2 {“ T~v лпУ sh а"У +
П=1
и0 G
+ {~,ап <sh ХпУ ~ *пУ ch ап#) +
+ и°зп (ch апу — 2ТГ~) а«У sh а^) —
— ?~7Г11 GS [(1— 2v) sh апу + апу ch anJl cos а„х,
Ut = 2 {r=hа" <sh ХпУ +ХпУ ch + т^> sh ХпУ ~
п—1
и3п
— 271^7) К1—2v)sh *пУ ~~ ЛпУ ch а«^ +
+ u’n [ch а.пу + 27j4tV) х“У sh а"#]} sin а«х>
и® v ( u®G
u6 = + 2j an (2 ch ЬпУ + a„r/sh a„r/) +
n~l
U2n°
+ j-zr; a" (sh Щ Щ ch ^пУ) +
+ т~; (v ch <*пУ + у Щsh лпУ) +
1
2(1—';) К3 — 2v) sh <*пУ + <*пу ch апг/]| cos а.пх.
§ 15] ПРОСТРАНСТВЕННАЯ И ПЛОСКАЯ ЗАДАЧИ ТЕОРИИ ПЛИТ
Формулами (15.14) при v = v1( G = G± характеризуется Наря-
женное и деформированное состояние первого слоя плиты. Коэф-
фициенты unin этих формул представляют собой неизвестные вели-
чины, определяемые из граничных условий на плоскостях у = О
и y — h.
Подставив разложения (15.11) в выражения для перемещений
и напряжений произвольного /n-го слоя плиты (15.10), получим
формулы для перемещений и напряжений в этом слое. Заметим,
что при определении перемещений и напряжений в m-м слое плиты
через начальные функции (15.11) можно также воспользоваться
другим, более простым способом. Каждый член любого ряда (15.11)
ортогонален на отрезке (0, Г) всем остальным членам этого ряда.
Поэтому формулы (15.14) можно трактовать как совокупность
бесконечно большого числа независимых и ортогональных друг
другу напряженных и деформированных состояний плиты. Следо-
вательно, коэффициенты для перемещений и напряжений в т-м
слое плиты от n-х членов рядов (15.11) согласно (15.14) найдутся
по формулам:
4
2 4?‘(r/)uL (z — 1, 2, . . . , 5). (15.15)
*=1
Здесь матрица || а$* (у) || определяется как произведение матриц
Wa^^Gj, Л/)|| (/= 1, 2, ..., т-1) и \\а® (vm, Gm, z/)||.
В качестве примера рассмотрим задачу о равновесии двуслой-
ной плиты под действием вертикальной равномерно распределенной
нагрузки интенсивности р, приложенной по верхней плоскости
плиты (см. рис. 179). Обозначим ширину опоры плиты через 2с,
расстояние между опорами — через I и выберем систему коор-
динат, как показано на рис. 179.
Будем считать, что в опорах под действием внешней нагрузки
возникают одни лишь нормальные напряжения Us, распределенные
по ширине опоры равномерно. В этом случае эпюра напряжений U8
при у— h принимает на опорах постоянное значение (— а меж*
ду опорами тождественно равна нулю.
Из граничных условий на верхней, начальной, плоскости плиты
следует, что
(7° = и°0 = -р, (7’=0.
Разложим нормальную нагрузку, действующую на нижней пло-
скости плиты, в ряд Фурье на отрезке (0, /):
/ 00 2 \
U3(x, h) = — pH + 2 — s>n <х„с cos а„х). (15.16)
П=2, 4. 6 ”
426 МЕТОДТНАЧАЛЬНЫХ ФУНКЦИЙ [ГЛ. VI»*
Первым членом этого ряда представлена нагрузка U30 (ft) = — р.
Совместное действие этой нагрузки и нагрузки U30 = — р вызывает
равномерное сжатие плиты. Нагрузки, представляемые остальными
членами ряда, на отрезке (0, /) статически эквивалентны нулю.
Эпюра бх Эпюра
Удовлетворяя граничным условиям при у = h и применяя фор-
мулы (15.15) и (15.16), получим:
<‘^ + °S,’C = -z<siria^ I (1517)
«Г^ + ^4%^0’
где
«Й’’ = 2 4/’ (v2, G2, Л2) аЙ’ (vi, Gb hj. (15.18)
/=1
Из уравнений (15.17) определим все неизвестные коэффициенты
н«п и н°п (п = 2, 4, 6,.. .). Зная коэффициенты разложений на-
чальных функций, найдем напряженное и деформированное состоя-
ние плиты.
На рис. 180 приведены эпюры нормальных напряжений U3 =
j
и U6 = ах по среднему сечению пролета х = у I. Размеры плиты
и упругие характеристики следующие:
Aj = Л2 = "т h б2 = 10 Glt Vj = v2 = 0,3.
На диаграммах приведено по два графика. Один график (сплош-
ная линия) соответствует сумме трех членов ряда (15.16), а другой
(пунктирная линия) соответствует двум членам ряда. Из эпюр
§ 15] ПРОСТРАНСТВЕННАЯ И ПЛОСКАЯ ЗАДАЧИ ТЕОРИИ ПЛИТ 427
видно, что нормальное напряжение ах терпит разрыв непрерыв-
ности на плоскости контакта слоев.
В рассмотренном примере предполагалось, что на плоскости
контакта слоев отсутствуют взаимные перемещения точек нижнего
и верхнего слоев. Приведем теперь решение для случая, когда
плоскость контакта идеально гладка, в результате чего на этой
плоскости касательные напряжения С/4 = txy равны нулю, а пе-
ремещение иг = и терпит разрыв непрерывности. При этом пере-
мещение. U2 = v и нормальные напряжения [73 — <зу изменяются
непрерывно.
Принимая для начальной функции нижнего слоя плиты разло-
жение в ряд
Ui (х) = у w°„sina„x, (15.19)
п=2, 4, в
получим для определения неизвестных коэффициентов разложений
Uin, и£п и и°п начальных функций U[, и следующие выра-
жения:
(V1J Gil h-l) Uln + &421 (Vl» Gj, /ij) ll^n — 0,
+ Ода’и’л + Оз? (Ч, Gi, h2) = — Sina„c,
(15.20)
°4i? Win a42* ~i' <4? (''г, G2, hs) u^n — 0,
где коэффициенты afM* определяются по формуле (15.18).
Первым и третьим уравнениями системы (15.20) выражено
Условие отсутствия напряжений [74 на плоскости контакта слоев
и на нижней граничной плоскости плиты Вторым уравнением —
условие равновесия для напряжений U3 на нижней плоскости пли-
ты. Этих уравнений достаточно для определения напряженного
и деформированного состояния плиты в рассматриваемом случае.
На рис. 181 приведены графики напряжений 0а = су и U6 — ax
по среднему сечению плиты. Размеры и упругие характеристики
взяты те же, что и в предыдущем примере. Эпюры получены для
суммы двух членов ряда (15.16). Нормальные напряжения по
среднему сечению для каждого из слоев практически меняются
по линейному закону. Эпюра <зх терпит разрыв непрерывности на
плоскости контакта слоев.
3. Метод тригонометрических рядов может быть применен и
к решению пространственной задачи, если на противоположных
поперечных краях плиты выполняется одно из условий: 1) каса-
тельные напряжения на плоскости края равны нулю, и перемеще-
ние из плоскости края равно нулю; 2) нормальное напряжение
на плоскости края равно нулю, и тангенциальные перемещения
428
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VII
в плоскости края равны нулю. Граничные условия первого вида
соответствуют условиям (15.12), а второго — условиям (15.13)
плоской задачи.
В случае граничных условий первого типа на всех поперечных
краях плиты (х = 0, к — а, у = 0, у — Ь) начальные функции могут
Зпюра бх Эпюра бу
быть представлены в следующем виде:
^i = 2 sin a"x cos $тУ' = S S u°inm cos a,1X cos $тУ’
n=l m~Q n=om=o
u°2=2 2 u°2nm cos ЛпХ sin $my' =2 2 w°nm cos ЛпХsin $тУ'
n==0 m=i n=0
00 co co co
^3 = 22 w"nm cos anX cos $тУ’ = 2 S u°nm sin a'iX cos РтУ>
n=o zn=o n—1 m—o
(15.21)
где
mt n mn
Если на всех поперечных краях выполняются граничные усло-
вия второго типа, то в разложениях (15.21) везде необходимо
изменить синусы на косинусы и косинусы на синусы. Если на двух
противоположных поперечных краях выполняются условия пер-
вого типа, а на двух других — условия второго типа, то тригоно-
метрические функции одного аргумента необходимо оставить без
изменений, а в функциях другого аргумента изменить синусы на
косинусы и косинусы на синусы.
§ 15] ПРОСТРАНСТВЕННАЯ И ПЛОСКАЯ ЗАДАЧИ ТЕОРИИ ПЛИТ
Поступая таким же образом, как и в случае плоской яедуУИ»
нетрудно определить напряженное и деформированное состояние
многослойной плиты, находящейся в условиях пространственной
задачи. Неизвестные коэффициенты разложений начальных функ-
ций (15.21) должны быть найдены из граничных условий плиты
на плоскостях z = 0 и z — h.
Напряженное и деформированное состояние плиты, отвечающее
разложениям (15.21), можно представить следующим образом.
Рис. 182.
Рассмотрим многослойную плиту, опирающуюся на большое число
рядов колонн. Ряды колонн поставлены в двух взаимно ортого-
нальных направлениях (рис. 182). Колонны одинаково располо-
жены, в направлении рядов имеют плоскости симметрии, и рас-
стояние между центрами соседних колонн постоянно и равно а
для одного направления рядов и b — для другого.
Плоскости, проходящие через центры колонн в направлении
их рядов, образуют два семейства взаимно ортогональных пло-
скостей симметрии всей конструкции в целом. Если на плиту
действует внешняя нагрузка, симметричная относительно обоих
семейств плоскостей симметрии конструкции, то в силу симметрии
задачи все отдельные элементы многоопорной плиты, представ-
ляющие собой прямоугольные плиты, опирающиеся на четыре
соседние колонны, будут находиться в одинаковых условиях. Для
каждой такой плиты на поперечных краях выполняются граничные
условия первого типа, и, следовательно, начальные функции, опре-
деляющие напряженное и деформированное состояние плиты, будут
430 МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ - [ГЛ. V1K 1
представлены в форме разложений (15.21). Если на плиту дей-
ствует нагрузка, обратносимметричная относительно обоих семейств
плоскостей симметрии конструкции, то для каждого элемента
многоопорной плиты на поперечных краях выполняются граничные
условия второго типа, и, следовательно, начальные функции будут
представлены разложениями, получающимися из (15.21) заменой
всех синусов на косинусы и косинусов на синусы. И наконец, если
плита нагружена симметрично относительно одного из семейств
плоскостей симметрии и кососиммметрично относительно другого,
то мы будем иметь задачу смешанного типа: в разложениях (15.21)
функции одного аргумента остаются без изменения, а в функциях
другого аргумента меняются местами синусы и косинусы. Таким
образом, в общем случае загружения многоопорной плиты произ-
вольной внешней нагрузкой полное решение задачи может быть
воставлено из четырех отдельных решений, соответствующих наз-
санным типам симметричных и кососимметричных нагрузок.
§ 16. Многослойное упругое основание
Изложенная выше теория толстых многослойных плит целиком
применима к определению деформаций и напряжений, возникающих
в упругом многослойном
основании под действием
приложенной к его поверх-
ности внешней нагрузки
(рис. 183).
Исходя из этой теории,
перемещения и напряжения
в первом слое упругого
основания, работающего в
условиях плоско-деформи-
рованного состояния, могут быть представлены в виде
4 оо
Ui = 2 (.У’ а) fi (х, а) «° (а) + Bik (у, а) gi (х, а) и*’ (а)] da
k=l
(t = 1, 2, . .., 5), (16.1)
где fi(x, а) = sin ах при 1 = 1,4 и fz(x, а) — cosax при i = 2, 3, 5:
gt (х, а) = cosax при г = 1,4 и gi (х, а) = sin ах при / = 2,3,5;
через Aik обозначены известные функции, входящие в выражения
(15.14):
л at/shat/
Л11“СЬаг/+2(1_^ ,
л23 = 4ёТГ=^) (Цг1 sh “ Уch *у)
§ 16] МНОГОСЛОЙНОЕ УПРУГОЕ ОСНОВАНИЕ
И Т. д.; функции В1к определяются, так
из выражений, аналогичных соотношениям (15.14), но отвечающих
другому представлению начальных функций (форма Файлрна). >
Напряжения и перемещения в произвольном /rt-м слоенеогра-
ниченной плиты, в случае непрерывности векторов перемещений
и напряжений при переходе через плоскость контакта слоев, опре-
деляются по формулам ‘ •
Ui = \ [A/kfiUk ~Ь Bikgiifk 1 da. (16.2)
1 —СО
Здесь, как и ранее, матрицы || A*k || и || Bik || представляют собой
соответственно произведение матриц
\\A^[a,hh v/( Gz)|| ||Л^(а, у, vm,Gm)„
и матриц
||Bi4)(a)/i/,v/,G;)|| ||<’(а, у, vm,Gm) ||
(/=-- 1, 2,. .т— 1), (/im_1<r/</im)-
Неизвестные функции u°k и очевидно, должны быть найдены
из граничных условий на плоскостях плиты у = 0 и у = h.
Рассмотрим в качестве примера бесконечно простирающееся
упругое основание, на которое в некоторой ограниченной области
действует внешняя нагрузка (см. рис. 183). Будем считать, что
это основание расположено на жестком материке, причем между
основанием и материком отсутствует трение. В этом случае на
начальной плоскости у = 0 перемещение U2 и касательное напря-
жение Ui тождественно равны нулю, и, следовательно, в форму-
лах (16.2) необходимо положить = и°* = и° = и°* — 0. Для опре-
деления неизвестных функций и“, и°, воспользуемся
статическими граничными условиями на верхней плоскости у = h.
Будем считать, что на плоскости у = h приложена одна лишь
нормальная нагрузка р (х), отличная от нуля на интервале
Oi<Cx<Ca2 (рис. 183). Представим р(х) в виде интеграла Фурье:
р(х) = -^- da. р (К) cos а (X — х) А. (16.3)
—СО 01
Приравнивая выражения для напряжений U3 и из (16.2)
на граничной плоскости у = h соответственно граничному значе-
нию (16.3) и нулю, получим следующую систему алгебраических
432
МЕТОД НАЧАЛЬНЫХ ФУНКЦИЙ
[ГЛ. VII
уравнений для определения искомых неизвестных функций:
2 A*i (а/z) w? = — Р W cos 2 №) м? = 0;
г=1. 3 ai i=I, 3
2 B*31(ah) и°* ~ р (У) sin oikdk; 2 (a/z) wf = 0.
/=1, з £ /=1, з
(16.4)
Определив из (16.4) функции «9 и u°* (i — 1,3), по формулам
(16.2) найдем напряженное и деформированное состояние рассмат-
риваемой плиты. Заметим, что выражения для перемещений и на-
пряжений в конечной форме не могут быть получены, поскольку
интегралы (16.2) не выражаются в элементарных функциях. Зна-
чения всех расчетных величин могут быть найдены посредством
численного интегрирования.
Аналогичным образом может быть рассмотрена пространствен-
ная задача равновесия многослойного основания, бесконечно про-
стирающегося в двух направлениях. В этом случае необходимо
исходить из суммы представлений четырех типов для начальных
функций, одно из которых есть (15.21), а другие получаются из
(15.21) соответствующей заменой синусов на косинусы и косину-
сов на синусы. Для удовлетворения граничных условий упругого
основания на граничной плоскости z — h необходимо воспользо-
ваться двойным интегралом Фурье.
ПРИЛОЖЕНИЕ
28 В. 3. Власов, Н. Н. Леонтьев
Функция O^-’j - shz cos 72, где z = ат;
Таблица 1
7 z 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0 0 0 0 0 0 0 0 0 0
0,05 0,05000 0,05000 0,04999 0,04999 0,04998 0,04998 0,04997 0,04996 0,04995
о,ю 0,10019 0,10018 0,10015 0,10012 0,10007 0,10002 0,09995 0,09988 0,09979
0,15 0,15058 0,15053 0,15045 0,15033 0,15017 0,14999 0,14977 0,14952 0,14923
0^20 0,20130 0,20118 0,20098 0,20070 0,20033 0,19989 0,19937 0,19877 0,19809
6,25 0,25253 0,25229 0,25190 0,25135 0,25063 0,24977 0,24875 0,24757 0,24624
0,30 0,30438 0,30397 0,30329 0,30233 0,30110 0,29960 0,29783 0,29579 0,29349
0,35 0,35697 0,35631 0,35522 0,35370 0,35173 0,34934 0,34652 0,34328 0,33961
0,40 0,41042 0,40943 0,40780 0,40550 0,40256 0,39898 0,39475 0,38990 0,38443
0,45 0,46486 0,46345 0,46110 0,45782 0,45360 0,44848 0,44243 0,43551 0,45096
0,50 0,52045 0,51849 0,51525 0,51071 0,50490 0,49782 0,48950 0,47996 0,46922
о;55 0,57727 0,57466 0,57029 0,56422 0,55642 0,54695 0,53582 0,52308 0,50875
0,60 О;63550 0,63207 0,62636 0,61840 0,60822 0,59584 0,58132 0,56470 0,54606
0,65 0,69527 0,69087 0,68354 0,67333 0,66027 0,64443 0,62586 0,60465 0,58088
0J0 0,75672 0,75116 0,74191 0,72904 0,71259 0,69265 0,66932 0,64271 0,61295
0,75 0’82000 0,81308 0,80158 0,78559 0,76517 0,74046 0,71157 0,67869 0,64198
0,80 0,88527 0,87677 0,87154 0,84333 0,81800 0,78774 0,75246 0,71235 0,66769
0,85 0,95266 0,94233 0,92519 0,89182 0,87105 0,83444 0,79180 0,74345 0,68972
0,90 1,02236 1,00993 0,98933 0,96072 0,92433 0,88046 0,82946 0,77175 0,.70778
0,95 1,09451 1,07969 1,05512 1,02104 0,97774 0,92565 0,86518 0,79695 0,72149
1 ;оо 1; 16933 1,16353 1,12271 1,08243 1,03133 0,96994 0,89884 0,81877 0,73052
1,05 lj24694 1,22631 1,19214 1,14489 1,08812 1,01190 0,93014 0,83690 0,73445
1,10 Г, 327 58 1,30346 1,26358 1,20843 1,13867 1,05515 0,95888 0,85101 0,73326
1,15 i;4U39 1,38337 1,33704 1,27309 1,19229 1,09578 0,98474 0,86074 0,72534
1,20 i;49861 1,46620 1,41270 1,33887 1,24582 1,13483 1,00750 0,86570 0,71145
1,25 1,58941 1^55212 1,49059 1,40581 1,29909 1,17211 1,02601 0,86552 0,69070
1,30 1,68404 1,64131 1,57085 1,47389 1,^5205 1,20739 1,04238 0,85975 0,66262
приложение
Продолжение табл. 7'
Z \ 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 а, 9
1,35 1,78270 1,73391 1,65538 1,54310 1,40455 1,24047 1,05380 0,84796 0,62669
1,40 1,88568 1,83015 1,73880 1,61344 1,45648 1,27104 1,06073 0,82966 0,58237
1,45 1,99310 1,93015 1,82666 1,68486 1,50766 1,29886 1,06277 0,80438 6,52911
1,50 2,10537 2,03419 1,91731 1,75738 1,55795 1,32858 1,05947 0,77157 0,46633
1,55 2,22261 2,09738 2,01072 1,83091 1,60714 1,34488 1,05036 0,73067 0,39343
1,60 2,34721 2,25688 2,10888 1,90705 1,65648 1,36358 1,03586 0,68170 0,31008
1,65 2,47338 2,37216 2,20646 1,98087 1,70144 1,37582 1,01281 0,62230 0,21486
1 ;?о 2,60748 2,49417 2,30895 2,05716 1,74606 1,38464 0,98327 0,55357 0,10791
1J5 2,74774 2,62123 2,40064 2,13422 1,78862 1,38834 0,94578 0,47429 —0,01172
1,80 2,89286 2,75358 2,52353 2,21195 1,82888 1,38673 0,89977 0,38372 —0,14470
1,85 3,04832 2,89142 2,63575 2,29021 1,86642 1,37902 0,84451 0,28119 —0,29171
1,90 3,20933 3,03501 2,75146 2,35889 1,90102 1,36475 0,77939 0,16592 —0,45346
1 ;э5 3,37793 3,18466 2,87060 2,44781 1,93219 1,34337 0,70358 0,03719 —0,63066
2,00 3,55458 3,34055 2,99339 2,52687 1,95959 1,31423 0,61646 —0,10590 —0,82402
2,05 3,73956 3,50301 3,10058 2,60579 1,98274 1,27666 0,51709 —0,26412 —1,03427
2,10 3,93350 3,67232 3,24978 2,68443 2,00116 1,22996 0,40472 —0,43834 —1,26210
2,15 4,13668 3,84875 3,38350 2,76255 2,01429 1,17338 0,27840 —0,62941 —1,50822
2> 4,34969 4,03257 3,52107 2,83985 2,02174 1,10616 0,13723 —0,83829 —1,77339
2,25 4,57290 4',22416 3,66240 2,91607 2,02269 1,02741 —0,01970 —1,06583 -2,05820
2,30 4'80697 4,42376 3,80763 2,99091 2,01670 0,93624 —0,19348 —1,31303 —2,36347
2,35 5,05016 4; 63179 3 95659 3,06402 2,00292 0 83173 —0,38516 —1,58087 —2,68966
2,40 5,30957 4,84849 4 10957 3,13499 1,98074 0,71290 —0,59576 —1,87027 —3,03758
2,45 5,57919 5,07431 4,26623 3,20344 1,94925 0,57873 —0,82642 —2,18223 —3,40766
2,50 5,86210 5,30953 4 42687 3,26892 1,90775 0 42799 —1,07845 —2,51779 -3,80055
2,55 6Д 5862 5,55456 4 59123 3,33099 1,85525 0 25961 —1,35284 —2,87790 —4,21674
2,60 6,46972 5,80982 4’75935 3,38901 1,79084 0 07230 —1,65112 —3,26355 —4,65659
2,65 6,79584 6,07564 4 93115 3,44247 1,71345 —0,13520 —1,97442 -3,67583 —5,12050
приложение
Продолжение табл. 1
7 z 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
2,70 7,13793 6,35242 5,10662 3,49079 1,62204 —0,36424 —2,32416 —4,11566 —5,60891
2,75 7,49655 6,64058 5,28546 3,53325 1,51534 —0,61629 —2,70189 —4,58103 —6,12180
2,80 7,87293 6,94069 5,46778 3,56906 1,39238 —0,81092 —3,10842 —5,08194 —6,65962
2,85 8,26730 7,25289 5,65319 3,59750 1,25157 —1,19532 —3,54581 -5,61029 —7,22196
2,90 8,68123 7,57796 5,84188 3,61784 1,09168 —1,52563 —4,01547 —6,17010 —7,80934
2,95 9,11516 7,91621 6,03314 3,62895 0,91124 —1,88526 —4,51876 —6,76203 —8,42094
3,00 9,57047 8,26815 6,22721 ’ 3,63007 0,70866 —2,27606 —5,05752 —7,38707 -9,05686
3,05 10,04774 8,63418 6,42342 3,62000 0,48225 —2,69997 —5,63294 —8,04607 —9,71624
3,10 10,54843 9,01490 6,62183 3,59763 0,23028 —3,15889 —6,24701 —8,73943 —10,39890
3,15 11,07336 9,41081 6,81606 3,56177 —0,04892 —3,65482 —6,90096 —9,46811 —11,10341
3,20 11,62428 9,82242 7,02326 3,51114 —0,35758 —4,18993 —7,59685 —10,23253 —11,82927
3,25 12,20160 10,25015 7,22537 3,44427 —0,69761 —4,76636 —8,33604 —11,03313 —12,57552
3,30 12,80738 10,69479 7,42810 3,35983 —1,07112 —5,36645 —9,12047 —11,87028 —13,33901
3,35 13,44242 11,15675 7,36047 3,25599 —1,48060 —6,05250 —9,95143 —12,74411 —14,11966
3,40 14,10859 11,63661 7,83242 3,13135 —1,92814 —6,76704 —10,83103 —13,65199 —14,91552
3,45 14,80615 12,13509 8,03268 2,98386 —2,41663 —7,53249 —11,76030 —14,60255 —15,72362
3,50 15,53965 12,65246 8,23112 2,81175 —2,94872 -8,35155 —12,74163 —15,58680 -16,54197
3,55 16,30772 13,18962 8,42657 2,61284 —3,52681 —9,22679 —13,77574 —16,60721 -17,36725
3,60 17,11336 13,74719 8,61848 2,38479 —4,15446 —10,16123 —14,86516 —17,66339 —18,19696
3,65 17,95784 14,32540 8,80552 2,12563 —4,83434 —11,15761 —16,01041 —18,75430 —19,02671
3,70 18,84359 14,92543 8,98715 1,83256 —5,57003 —12,21873 —17,21375 —19,87902 —19,85355
3,75 19,77199 15,54752 9,16184 1,50314 —6,36465 —13,34785 —18,47581 —21,03608 —20,67251
3,80 20,74572 16,19250 9,32871 1,13417 —7,22211 —14,54809 —19,79852 —22,22414 -21,47912
3,85 21,76625 16,86075 9,48736 0,72313 -8,14585 —15,82244 —21,18216 —23,41778 —22,26815
3,90 22,83704 17,55315 9,63323 0,26665 —9,14015 —17,17414 —22,62890 —24,68542 —23,03433
3,9Ь 23,95877 18,27058 9,76776 —0,23881 —10,20878 —18,60674 —24,13866 -25,95365 —23,77083
4,00 25,13565 19,01316 9,88877 —0,79686 —11,35670 —20,12331 —25,71311 -27,24325 —24,47251
приложение
Продолжение табл. 1
Z X 0,1 0,2 о,з °,4 0,5 0,6 0,7 0,8 0,9
4,05 26,38305 19,78177 9,99392 —1,41098 —12,58750 —21,72760 —27,35201 —28,55126 —25,13082
4,10 27,66204 20,57702 10,08130 —2,08569 -13,90673 —23,42279 —29,05613 —29,87351 —25,73892
4,15 29,01701 21,39985 10,14882 —2,82496 —15,31867 —25,21255 —30,82539 —31,20590 —26,12927
4,20 30,43847 22,25023 10,19471 —3,63325 —16,82951 —27,10023 —32,66062 —32,54361 —26,77021
4,25 31,92756 23,12937 10,21578 —4,51527 —18,44307 —29,08957 —34,55984 —33,88206 —27,17503
4,30 33,48928 24,03792 10,20996 —5,47673 —20,16644 —31,18438 -36,52442 —35,21501 —27,49380
4,35 35,12521 24,97606 10,17433 —6,52260 —22,00409 —33,38766 -38,55151 —36,53586 —27,71408
4,40 36,84079 25,94430 10,10571 —7,65848 —23,96331 —35,70350 —40,64193 —37,83841 —27,82675
4,45 38,63817 26,94355 10,00072 —8,89029 —26,04930 —38,13518 —42,79222 -39,11504 —27,81811
4,50 40,52296 27,97432 9,85611 —10,22468 —28,26954 —40,68587 -45,00121 —40,35690 —27,67685
4,55 42,49703 29,03708 9,66751 —11,66829 -30,63003 —43,35951 -47,26550 -41,55555 —27,38829
4,60 44,56695 30,13175 9,43215 —13,22809 —33,13885 —46,15954 -49,58444 —42,70082 —26,93962
4,65 46,73528 31,25916 9,14460 —14,91193 —35,80139 —49,08927 —51,95098 —43,78207 —26,31484
4,70 49,00875 32,42019 8,80054 —16,72708 —38,62729 —52,15078 —54,46493 —44,78877 —25,50014
4,75 51,38955 33,61402 8,39541 —18,68222 -41,62283 —55,34860 —56,81814 —45,70843 -24,47719
4,80 53,88572 34,84139 7,92303 -20,78564 —44,79654 —58,68340 —59,30666 —46,52672 —23,23084
4,85 56,49994 36,10361 7,37911 -23,04742 —48,15772 —62,16105 -61,82639 —47,23167 —21,74264
4,90 59,24067 37,39897 6,75641 -25,47672 —51,71414 —65,78156 —64,36824 —47,80653 —19,99464
4,95 62,11104 38,72870 6,04834 —28,08394 —55,47333 —69,54706 —66,92416 —48,23565 —17,96785
5,00 65,11925 40,09199 5,24913 —30,87966 —59,44716 —73,46043 -69,48834 —48,50219 -15,64204
5,05 68,26951 41,48935 4,34973 —33,87499 —63,64207 —77,52282 —72,04822 —48,58808 —12,99692
5,10 71,57158 42,92048 3,34510 —37,08234 —68,07066 —81,73482 —74,59685 —48,47241 —10,01152
5,15 75,02932 44,38410 2,22343 —40,51314 —72,13951 —86,09819 —77,11912 —48,13608 —6,66598
5,20 78,65344 45,88042 0,97884 —44,18195 —77,66282 —90,61251 —79,60781 —47,55714 —2,93471
5,25 82,44813 47,40872 —0,40018 -48,10236 —82,84640 —95,27670 —82,04319 —46,71222 1,20149
5,30 86,42415 48,96811 —1,92318 —52,28761 —88,30426 —100,09179 —84,41582 —45,57649 5,76755
43g приложение
Продолжение табл. 1
7 Z 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
5 35 90 58638 50,55720 —3,60130 —56,75312 —94,04447 -105,05476 —86,70498 —44,12540 10,78600
5,40 94,94931 52,17668 -5,44427 —61,51652 —100,08141 —110,16516 —88,89840 -42,33204 16,28189
5 45 99’51624 53,82317 —7,46674 —66,59204 —106,42205 —115,41915 —90,96486 —40,16633 22,27687
5,50 104 30064 55,49520 —9,67985 —71,99940 —113,08248 —120,82217 —92,90797 —37,59996 28,79731
5,55 109,31016 57,19076 —12,74078 —77,75530 —120,06896 —126,34031 —94,68256 —34,60179 35,86609
б'бО 114’55917 58,90888 —14,73790 —83,87971 —127,33884 —131,99873 —96,27454 —31,13917 43,50831
5,65 120'05195 60,36286 —17,60880 —90,39219 —135,07799 -137,35514 —97,66570 —27,17793 52,45681
5',70 125^80683 62,40132 —20,73369 —97,31462 —143,12450 —143,67740 —98,80147 —22,68378 60,60664
5,75 131’82992 64,17122 —24,12803 -104,66842 -151,54265 —149,68205 —99,67912 —17,61806 70,10779
5’80 138’13992 65,95031 —27,81097 —112,47588 —160,35236 —155,78106 —100,25986 —11,94517 80,27692
5^85 144i74345 67,73618 -31,79946 —120,76017 -169,55661 -161,96613 —100,50616 —5,62168 92,02674
5,90 151,66098 69,52451 —36,11836 -129,54900 —179,17729 —168,22260 —100,38820 —1,38896 102,69704
5,95 158^91886 71,31240 -40,78503 —138,86788 —189,21598 -174,53559 —99,86154 9,13135 114^870^
6,00 166,48194 73,09278 —45,82923 —148,74127 —199,69451 —180,88829 —98,89189 17,64990 128,02532
6,05 174,41552 74’, 85978 —51,27074 -159,20055 -210,61336 —187,26183 —97,43095 26,98616 142,88289
6,10 182,72274 76,60912 —57,13861 —170,27668 —221,99369 —193,63728 —95,43537 37,71910 156,40166
6,15 191^41393 78,33169 —63,45936 —181,99510 —233,83501 —199,99143 —92,85484 48,30579 171,65394
6^20 200^51847 80,02212 —70,26326 —194,39116 —246,15164 —206,29593 —89,64054 60,38368 187,93125
6’25 210,04306 81,66960 —77,57990 —207,49963 —258,96660 —212,63320 -85,73602 73,46949 204,89921
6j30 220,01447 83,27021 -85,44577 —221,35412 —272,27414 —218,65849 —81,08648 87,61488 222,68014
6,35 230,73290 84,91484 —94,01163 —236,28727 —286,45433 -224,92918 —75,72347 103,00238 241,56937
б’4О 241^36929 86,28027 —102,96036 —251,44715 —300,40710 —230,46689 —69,30226 119,29138 260,66739
6,45 253,10847 87,77662 —112,82488 -268,09688 -315,64004 ^236,36844 —62,11387 137,09078 281,21333
6 ’ 50 264,75237 88,96249 —123,11078 -284,97596 —330,61787 -241,42258 —53,76993 155,81572 301,85056
6^55 277,61038 90,26258 -134,44346 —303,51120 —346,94296 —246,78423 —44,47143 176,24394 324,00713
6,60 290,35838 91,21779 -146,23956 —322,27248 -362,94522 —251,17421 —33,90988 197,60057 346,11525
ПРИЛОЖЕНИЕ
3
Таблица 2
Функция Ф2 (z) — ch г cos jz, где г = ат;
7 2 0,1 0,2 0,3 0,4 0,5 ' 0,6 0,7 0,8 0,9
0 1 1 1 1 1 1 1 1 1
0,05 1,00119 1,00115 1,00109 1,00100 1,00088 1,00075 1,00058 1,00040 1,00017
0,10 1,00495 1,00480 1,00460 1,00419 1,00381 1,00320 1,00253 1,00179 1,00092
0,15 1,01119 1,01084 1,01027 1,00948 1,00844 1,00720 1,00571 1,00402 1,00209
0,20 1,01987 1,01925 1,01823 1,01681 1,01500 1,01273 1,01010 1,00704 1,00359
0,25 1,03108 1,03012 1,02850 1,02625 1,02334 1,01982 1,01564 1,01085 1,00540
0,30 1,04487 1,04346 1,04111 1,03782 1,03360 1,02845 1,02237 1,01538 1,00747
0,35 1,06122 1,05928 1,05503 1,05050 1,04566 1,03857 1,02918 1,02053 1,00966
0,40 1,08020 1,07761 1,07330 1,06726 1,05952 1,05009 1,03897 1,02619 1,01177
0,45 1,10184 1,09850 1,09292 1,08515 1,07515 1,06301 1,04868 1,03227 1,01373
0,50 1,12622 1,12199 1,11497 1,10516 1,09257 1,07727 1,05926 1,03861 1,01537
0,55 1,15334 1,14812 1,14770 1,12726 1,11169 1,09277 1,07052 1,04508 1,01644
0,60 1,18334 1,16509 1,16631 1,15149 1,13253 1,10948 1,08244 1,05150 1,01679
0,65 1,21620 1,20850 1,19568 1,17782 1,15497 1,12727 1,09478 1,05769 1,01610
0,70 1,25209 1,24289 1,22759 1,20629 1,17907 1,14608 1,10747 1,06345 1,01421
0,75 1,29103 1,28014 1,26203 1,23686 1,20470 1,16580 1,12031 1,06855 1,01076
0,80 1,33315 1,32035 1,31247 1,26954 1,23185 1,18629 1,13315 1,07275 1,00550
0,85 1,37852 1,36358 1,33877 1,29049 1,26043 1,20746 1,14576 1,07579 0,99805
0,90 1,42730 1,40993 1,38117 1,34123 1,29043 1,22918 1,15798 1,07741 0,98811
0,95 1,47951 1,45948 1,42627 1,38020 1,32167 1,25126 1,16951 1,07728 0,97528
1,00 1,53536 1,51233 1,47417 1,42127 1 35418 1,27356 1,18021 1,07508 0,95919
1,05 1,59494 1,56855 1,52485 1,46440 1,39180 1,29428 1,18972 1,07046 0,93940
1,10 1,65844 1,62831 1,57849 1,50959 1,42245 1,31811 1,19785 1,06310 0,91600
1,15 1,72593 1,69166 1,63501 1,55681 1,45800 1,33998 1,20420 1,05256 0,88698
1,20 1,79764 1,75876 1,69460 1,60692 1,49441 1,36127 1,20854 1,03844 0,85342
1,25 1,87367 1,82971 1,75717 1,65724 1,53143 1,38174 1,20951 1,02031 0,81423
1,30 1,95427 1,90467 1,82291 1,71039 1,56900 1,40114 1,20965 0,99771 0,76895 .
44Q приложение
Продолжение табл. 2
z 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
1,35 2,03958 1,98376 1,89185 1,76545 1,60694 1,41922 1,20564 0,97015 0,71760
1,40 2,12986 2,06714 1,96396 1,82237 1,64509 1,43564 1,19809 0,93710 0,65779
1,45 2,22520 2,15493 2,03938 1,88106 1,68323 1,45012 1,18653 0,89805 0,59072
1,50 2,32599 2,24735 2,11823 1,94154 1,72109 1,46228 1,17049 0,85242 0,51520
1,55 2,43232 2,34450 2,20043 2,00266 1,75278 1,47177 1,14947 0,79961 0,43050
1,60 2,54455 2,44663 2,28618 2,06738 1,79574 1,47822 1,12295 0 73901 0,33615
1,65 2,66282 2,55384 2,37546 2,13259 1,83175 1,48119 1,09039 0,66996 0,23132
1,70 2,78754 2,66640 2,46339 2,19922 1,86663 1,48026 1,05117 0 59180 0,11537
1,75 2,91887 2,78447 2,55015 2,26707 1,90002 1,47480 1,00468 0,50353 —0,01245
1,80 3,05725 2,90828 2,66531 2,33592 1,93163 1,46464 0,95033 0,40528 —0,15283
1,85 3,20288 3,03803 2,76939 2,40633 1,96105 1,44894 0,88733 0,29545 —0,30650
1,90 3,35621 3,17391 2,87739 2,47731 1,98802 1,42721 0,81506 0,17352 —0,47421
1,95 3,51750 3,31625 2,91750 2,54892 2,01203 1,39887 0,73266 0,03872 -0,65672
2,00 3,68722 3,46521 3,10509 2,62116 2,03272 1,36327 0,63946 —0,10986 —0,85477
2,05 3,86738 3,62108 3,20509 2,69362 2,04957 1,31969 0,53452 —0,27303 —1,06913
2,10 4,05326 3,78413 3,34873 2,76616 2,06208 1,26741 0,41704 —0,45169 —1,30053
2,15 4,25047 3,95463 3,47658 2,83855 2,06970 1,20566 0,28606 —0,64673 —1,54971
2,20 4,45782 4,13282 3,60860 2,91044 2,07200 1,13366 0,14065 —0,85913 —1,81748
2,25 4,67565 4,31907 3,74468 2,98160 2,06814 1,05050. —0,04029 —1,08978 —2,10445
2,30 4,90460 4,51360 3,88496 3,05165 2,05765 0,95526 —0,19741 —1,33970 -2,41147
2,35 5,14503 4,71682 4,02922 3,12027 2,03969 0,84700 —0,39224 —1,60989 -2.73904
2,40 5,39769 4,92896 4,17777 3,18702 2,01362 0,72474 —0,60565 -1,'90131 —3,08800
2,45 5,66290 5,15044 4,33024 3,25150 1,97850 0,58741 —0,83882 —2,21497 -3,45879
2,50 5,94163 5,38157 4,48693 3,31327 1,93363 0,43380 —1,09308 -2,55195 —3,85212
2,55 6,23417 5,62271 4,64756 3,37186 1,87801 0,26279 —1,36944 -2,91321 —4,26847
2,-60 6,54150 5,87428 4,81216 3,42661 1,81071 0,07311 —1,66944 -3,29976 -4,70825
2,65 6,86398 6,13660 4,98063 3,47701 1,73065 i —0,13656 —1,99423 -3,71271 —5,17188
приложение 441
Продолжение табл. 2
т z \. 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
5,35 90,59099 51,61283 —3,60148 —56,75600 —94,04925 —105,06010 —86,70939 —44,12764 10,78655
5,40 94,95319 52,47881 -5,44 449 —61,51903 —100,08549 —110,16965 —88,90203 —42,33377 16,28256
5,45 99,51992 53,82515 -7,46702 —66,59450 —106,42598 -115,42341 —90,96822 —40,16782 22,27769
5,50 104,30412 55,49706 —9,68017 —72,00180 —113,08626 —120,81621 —92,91108 —37,60121 27,57979
5,55 109,29647 57,18560 —12,73919 —77,75556 —120,05392 -126,32449 —94,67071 —34,59745 35,86160
5,60 114,56230 58,91049 —14,73709 —83,88201 —127,40232 —132,00234 —96,27717 —31,14003 43,50350
5,65 120,05493 60,36435 —17,60923 —90,39443 —135,08134 —137,35854 -97,65817 —27,17860 52,45811
5,70 125,80964 62,40272 —20,73416 —97,31680 —143,12770 —143,68061 —98,80368 —22,68429 60,60800
5,75 131,83259 64,17252 —24,12851 —104,67054 —151,54511 —149,68508 —99,68114 —17,61842 70,10921
5,80 138,14248 65,95152 —27,81148 -112,47794 —160,35530 —155,78391 —100,26170 —11,94539 80,27839
5,85 144,74585 67,73731 —31,79999 — 120,76217 —169,55943 —161,96882 —100,50782 —5,62177 91,13242
5,90 151,66325 69,52556 —36,11890 —129,55094 —179,17998 —168,22513 —100,38970 , 1,38898 102,69858
5,95 158,92101 71,31337 —40,78558 —139,82915 —189,21854 —174,54715 —99,86289 -.^13147 ^4115,98864
6,00 166,48399 73,09368 —45,82979 —148,74309 —199,69647 —180,89052 —98,89312 17,65012 128,02690
6,05 174,41745 74,86061 —51,27131 —159,20231 —210,61570 —187,26390 —97,43203 26,98646 142,88448
6,10 182,72458 76,60990 —57,13919 —170,27840 —221,99593 —193,63923 —95,43634 37,19141 156,40324
6,15 191,41568 78,33241 —63,45994 —181,99676 —233,83714 -199,99324 —92,85568 48,32967 171,76695
6,20 200,52012 80,92277 —70,26384 —194,39276 —246,16366 —206,29763 —89,64128 60,38418 187,93280
6,25 210,04462 81,67021 -77,58048 —207,50117 —258,96859 —212,53110 —85,73662 73,47003 204,90074
6,30 220,01596 83,27077 —85,44634 —221,35561 —272,27598 —218,65997 —81,08703 87,61647 222,68165
6,35 230,74236 84,92843 —94,01549 —236,29696 —286,45174 -224,93840 —75,72658 103,00660 241,57928
6,40 241,38666 86,28648 —102,96777 —251,46525 —300,42874 —230,48348 —69,30725 119,29996 260,68616
6,45 253,11772 87,77983 —112,82901 —268,10668 —315,65198 —236,37709 —62,11614 137,09580 281,22361
6,50 264,75357 88,96289 —123,11134 —284,97725 —330,61937 -241,42368 — 53,77017 155,81643 301,85193
6,55 277,61152 90,26295 —134,44401 —303,51245 —346,94439 —246,78524 —44,47161 176,24467 324,00846
6,60 290,35946 91,18137 —146,24010 —322,27367 —362,94656 —251,17514 —33,91000 197,60130 346,11653
444 приложение
Таблица 3
Функция'<t>3 (г) = ch г sin 72, где l = а1»!
7 Z 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0 0 0 0 0 0 0 0 0 0
0,05 0,00501 0,01000 0,01502 0,02002 0,02503 0,03004 0,03504 0,04004 0,04503
0,10 0,01001 0,02002 0,03004 0,04003 0,05004 0,06003 0,07002 0,08000 0,09000
0,15 0,01517 0,03034 0,04549 0,06064 0,07577 0,09090 0,10600 0,12106 0,13610
0,20 0,02040 0,04080 0,06116 0,08151 0,10183 0,12211 0,14234 0,16252 0,18290
0,25 0,02578 0,05155 0,07727 0,10139 0,12859 0,15413 0,17958 0,20491 0,22942
0,30 0,03136 0,06268 0,09395 0,12514 0,15621 0,18715 0,21791 0,24848 0,27883
0,35 0,03713 0,07421 0,11118 0,14805 0,18471 0,22116 0,25732 0,29319 0,32869
0,40 0,04323 0,08639 0,12941 0,17224 0,21478 0,25697 0,29876 0,34007 0,38083
0,45 0,04962 0,09913 0,14844 0,19746 0,24607 0,29419 0,34172 0,38854 0,43459
0,50 0,05636 0,11257 0,16851 0,22403 0,27897 0,33323 0,38666 0,43912 0,49048
0,55 0,06350 0,12680 0,18972 0,25208 0,31423 0,37430 0,43381 0,49200 0,54870
0,60 0,07108 0,14191 0,21223 0,28179 0,35033 0,41760 0,48339 0,54695 0,60950
0,65 0,07916 0,15799 0,23615 0,31333 0,38916 0,46337 0,53561 0,60559 0,67300
0,70 0,08779 0,17515 0,26165 0,34688 0,43040 0,51181 0,59072 0,66673 0,73947
0,75 0,09701 0,19348 0,28884 0,38260 0,48067 0,56315 0,64915 0,73103 0,80901
0,80 0,10687 0,21308 0,31791 0,42071 0,52082 0,61760 0,71043 0,79871 0,88187
0,85 0,11744 0,23406 0,34899 0,46139 0,57046 0,67541 0,77547 0,86995 0,95814
0,90 0,12881 0,25657 0,38225 0,50483 0,62335 0,73681 0,83570 0,94495 1,03797
0,95 0,14098 0,28069 0,41787 0,55127 0,67971 0,80201 0,91709 1,02389 1,12145
1,00 0,15405 0,30656 0,45602 0,60091 0,73980 0,87128 0,99408 1,10694 1,20874
1,05 0,16808 0,33433 0,49689 0,65396 0,80382 0,94485 1,07546 1,19424 1,29985
1,10 0,18317 0,36412 0,54067 0,71069 0,87212 1,02300 1,16152 1,28600 1,39493
1,15 0,19938 0,39557 0,58759 0,77132 0,94484 1,10593 1,25236 1,38228 1,49391
1,20 0,21675 0,43039 0,63784 0,83659 1,02237 1,19931 1,34829 1,48327 1,59693
1,25 0,23543 0,46719 0,69167 0,90536 1,10489 1,28722 1,44944 1,58905 1,70384
1,30 0,25549 0,50668 0,74932 0,97930 1,19277 1,38610 1,55603 1,69971 1,81472
Продолжение табл. 3
2 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
1,35 0,27703 0,54902 0,81102 1,05827 1,28623 1,49083 1,66825 1,81536 1,92940
1,40 0,30014 0,59442 0,87075 1,14254 1,38565 1,60165 1,78632 1,93602 2^04785
1,45 0,32496 0,64306 0,94766 1,23241 1,49125 1,71886 1,91032 2,06173 2,16984
1,50 0,35194 0,69518 1,02323 1,32826 1,60350 1,84271 2,04053 2,19254 2,29536
1,55 0,38006 0,75101 1,10335 1,43044 1,72259 1,97348 2,17702 2,32838 2,42390
1,60 0,41064 0,81079 1,19022 1,53926 1,84897 2,11143 2,31998 2,46926 2,55545
1,65 0,44339 0,87475 1,28235 1,65512 1,98290 2,25687 2,46946 2,61507 2'68909
1,70 0,47849 0,94322 1,38073 1,87852 2,12486 2,41004 2,62573 2,76570 2'82597
1,75 0,51609 1,01642 1,48565 1,90959 2,27513 2,57120 2,78871 2,92116 2,96413
1,80 0,55633 1,09467 1,59767 2,04900 2,43417 2,74066 2,95859 3,08093 3,10371
1,85 0,59941 1,17835 1,71705 2,19719 2,60229 2,91866 3,13536 ,3; 24510 3,24403
1,90 0,64547 1,2677 0 1,84431 2,35454 2,78005 3,10545 3,31913 з;41332 3,38468
1,95 0,69476 1,36316 1,97987 2,52160 2,96770 3,30133 3,50975 3,58526 3,52478
2,00 0,74744 1,46508 2,12429 2,69885 3,16578 3,50652 3,70746 3,76058 3,66382
2,05 0,80376 1,57384 2,27802 2,88681 3,37463 3,72125 3,91192 3,93888 3,80057
2,10 0,86392 1,68988 2,44158 3,08602 3,59486 3,94576 4,12326 4,11961 З’93498
2,15 0,92822 1,81366 2,61562 3,29711 3,82676 4,18030 4,34118 4,30233 4'06527
2,20 0,99685 1,94566 2,80068 3,52067 4,07133 4,25502 4,56576 4,48637 4,18941
2,25 1,07016 2,08636 2,99733 3,75730 4,32771 4,68011 4,79647 4,67114 4,31020
2,30 1,14838 2,23627 3,20639 4,00761 4,59777 4,94579 5,03384 4,85578 4,42248
2,35 1,23183 2,39600 3,42833 4,27237 4,88141 5,22222 5,27587 5,03960 4,52616
2,40 1,32089 2,56609 3,66414 4,55220 5,17930 5,50949 5,52383 5,22139 4^61994
2,45 1,41584 2,74722 3,91439 4,84789 5,49175 5,80767 5,77667 5,38499 4,70219
2,50 1,51713 2,94000 4,18001 5,16013 5,81941 6,11689 6,03410 5,57608 4,77235
2,55 1,62508 3,14514 4,46169 5,48980 6,16272 6,43724 6,29731 5,74634 4^82563
2,60 1,74018 3,36339 4,76051 5,83759 6,52235 6,76860 6,55992 5,91023 4j86326
2,65 1,86272 3,59550 5,07722 6,20452 6,89854 7,11106 6,82699 6,06640 4'88219
446 приложение
Продолжение табл. 3
7 z \ 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
2,70 1,99340 3,84241 5,41296 6,59130 7,29201 7,46443 7,09596 6,21329 4,88047
2,75 2,13248 4,10483 5,76855 6,99892 7,70313 7,82870 7,36575 6,34938 4,85568
2,80 2,28072 4;38377 6,14531 7,42828 8,13265 8,20354 7,63550 6,42419 4,80581
2,85 2,43845 4,68011 6,54416 7,88038 8,58070 8,58894 7,90405 6,58162 4,72807
2,90 - 2,60631 4,99497 7,01212 8,35625 9,04813 8,98442 8,17040 6,67944 4,62027
2',95 2,78504 5,32946 7,41330 8,85698 9,53509 9,38967 8,43291 6,74765 4,47931
3,00 2,97519 5;68460 7,88630 9,38346 10,04239 9,80439 8,69050 6,80030 4,30279
3,05 3,17747 6,06174 8,40741 9,93695 10,57013 10,22730 8,94124 6,82963 4,08726
ЗЛО 3,39272 6,46204 8,91522 10,51849 11,11905 10,65962 9,18402 6,83272 3,83013
3,15 3,62280 6,88673 9,47419 11,12942 11,68923 11,09903 9,41633 6,80712 . 3,52800
3'20 3,86501 7,33759 10,06510 11,77086 12,28137 11,54515 9,63667 6,74979 3,17757
3,25 4,12362 7,81576 10,68938 12,44395 12,89545 11,99711 9,84244 6,65746 2,76630
з;зо 4,39876 8,32296 11,34891 13,15014 13,53227 12,45403 10,03188 6,52702 2,31789
3,35 4,69105 8,86085 12,04510 13,89050 14,19129 12,91464 10,20170 6,35494 1,80145
зло 5,01693 9,43106 12,78058 14,66666 14,87365 13,37783 10,35018 6,13763 1,22240
3,45 5,33208 10',03573 13,55646 15,47992 15,57878 13,84198 10,47372 5,87128 0,57672
3,50 5,68282 10,67654 14,37560 16,33169 16,30749 14,30582 10,56948 5,55173 0,13938
3,55 6,05520 11,35554 15,23956 17,22329 17,05884 14,76745 10,63396 5,17474 —0,92993
3^0 6,45104 12,07508 16,14931 18,15639 17,83390 15,22488 10,66408 4,73605 —1,79923
3,65 6,87121 12,83747 17,11200 19,13232 18,63143 15,67631 10,65544 4,23084 —2,75126
3,70 7,31775 13,64494 18,12539 20,15263 19 45247 16,11940 10,60448 3,65462 -3,79000
3,75 7,79141 14,52132 19,19315 21,21891 20 29548 16,55134 10,50681 3,00195 -4,92028
3,80 8,29413 15,40548 20,31858 22,33293 21,15715 16,96991 10,35775 2,26793 —6,14546
3,85 8^82835 16,36428 21,50389 23,40209 22,04784 17,37203 10,15251 1,44687 -7,47058
3,90 9,39500 17,37900 22,75298 24,70987 22 95586 17,75412 9,88627 0,53352 —8,89930
3,95 9,99607 18,45298 24,06772 25 97627 23 88354 18,11346 9,55316 —0,47824 —10,43586
4,00 10,62437 19,58983 25,45236 27,29649 24’83137 18,44562 9,14798 —1,59398 —12,08444
ПРИЛОЖЕНИЕ 447
Продолжение табл. 3
\ 7 Z X. 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
4,05 11,31131 20,79251 26,90921 28,67270 25,79651 18,74711 8,66419 —2;82051 —13,84876 15 73292
4,10 12,02942 22,06496 28,44287 30,10630 26,77913 19,01332 8,09597 —4,16372
4,15 12,79100 23,41074 30,05552 31,59861 27,77640 19,23955 7,43599 —5,62999 17 73992
4,20 13,59906 24,83423 31,75283 33,15189 28,78862 19,42109 6,67780 —7,22642 19 8743?
4,25 14,45965 26,34727 33,54641 34,77736 29,82023 19,55775 5,81528 —8,96175 —22,14415 —24,53475 -27,06657 —29,73649 —32,54482 —35,49498 —38,58500 41 81798
4,30 15,36444 27,93147 35,41337 36,44720 30,84535 19,62729 4,83596 —10,83586
4,35 16,32743 29,61448 37,38454 38,19239 31,88537 19,64163 3,73663 —12,86318
4,41) 17,34920 31,39345 39,45749 40,00451 32,93147 19,58455 2,50703 —15,04787
4,45 18,43200 33,27360 41,63407 41,88585 33,97798 19,45324 1,13856 —17,39791
4,50 19,57979 35,26091 43,92118 43,83700 35,02414 19,23813 —0,37857 —19,91965
4,55 20,79590 37,36032 46,32206 45,85973 36,06181 18,93191 —2,05375 —22,62109
4,Ь0 22,08526 39,57886 , 48,84427 47,95529 37,09697 18,52585 —3,89670 —25,50886
4,65 23,45114 41,92254 51,49085 50,12536 38,11425 18,10657 —5,91796 —28,59039 —45,19112 —48,70458 —52,35493 —56,14161 —60,05827 —64,06083 —68,26434 —72,54245 —76,92302 —81,40054 —85,95998 —90,59175 —95,27623 —100,00462
4,70 24,89904 44,39814 54,26891 52,37107 39,11529 17,37749 -8,12907 —31,87302
4,75 26,43264 47,01280 57,18267 54,69280 40,09226 16,61533 —10,54092 —35,36335
4,80 28,05744 49,77343 60,24044 57,09250 41,04049 15,71358 —13,16533 —39,06824
4,85 29,77811 52,68911 63,44551 59,56963 41,95315 14,66102 —16,01324 —42,99430
4,90 31,60168 55,76609 66,80650 62,12564 42,82406 13,41497 —19,10081 —47,14769
4,95 33,53285 59,01621 70,33054 64,76305 43,64643 12,05342 —22,43383 —51,53568
5,00 35,57848 62,44545 74,02368 67,47911 44,41243 10,47251 —26,03137 —56,16209
5,05 37,74339 66,06497 77,89192 70,27463 45,11185 8,68769 —29,90528 —61,03382
5,10 40,03759 69,88495 81,94593 73,15075 45,73757 6,68414 —34,07026 —66,15413
5,15 42,46527 73,91524 85,18846 76,10606 46,27788 4,44630 —38,53973 —71,52785
5,20 45,03665 78,16697 90,63344 79,13952 46,72434 1,95689 —43,32810 —77,15816
5,25 47,75722 82,65277 95,28385 82,25162 47,06354 —0,80135 —48,49664 —83,04916
5,30 50,63939 87,38509 100,15287 85,43977 47,28367 —3,84656 —53,92099 —89,20018
448 приложение
Продолжение табл. 3
7 z 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
5,35 53,68948 92,37488 105,24334 88,70284 47,37108 —7,19770 —59,75513 —95,61516 —104,75155
5,40 56,91811 97,63780 110,57152 92,03831 47,31330 —10,87681 —65'97160 —102;29185 —109;50210
5,45 60,33435 103,18709 116,14032 95,44425 47,09250 —14,90262 —72'57999 —109;22960 —114;22818
5,50 63,95008 109,03777 121,96506 98,91837 46,69534 —19,30040 —79',60328 —116; 42637 —118;91003
5,55 67,76486 115,18706 128,02845 102,43947 46,09436 —24,21423 —87,03568 —123; 85921 —123;49784
5,60. 71,82488 161,70706 134,40917 106,05187 45,29569 —29,29840 —94,94125 —131;58047 —128; 02296
5,65 76,10719 128,55961 141,05011 109,70232 44,53431 —34,94838 —103'28721 —139,52487 —132 ,'39191
5,70 80,63981 135,78146 147,99033 113,40351 42,95968 —41,06783 —112Д1090 —147; 70341 —136; 59289
5,75 85,43245 143,39178 155,23061 117,14874 41,38561 —47,68520 —121,42021 —156,10564 —140;66144
5,80 90,50621 151,41070 162,79293 120,92873 39,51245 —54,82858 —131Д0694 —164;б5584 —144;32736
5,85 95,87047 159,85935 170,67927 124,73804 37,31064 —62,52528 —141Д6516 —173;52835 —147; 77376
5,90 101,54688 168,75991 178,90985 128,56898 34,75548 —70,80867 -152; 43166 —182; 51462 —150;88572
5,95 107,54760 178,13375 187,49164 132,40923 31,81720 —79,70995 —163,84076 —191;66148 —33SU602151
6,00 113,86041 188,00704 196,44078 136,25085 28,46611 —89,26320 —175,81132 —200;94105 —155,87778
6,05 120,60903 127,70091 198,40542 205,76382 140,08107 24,66655 —99,50171 —188; 34540 —210;33366 —157; 64792
6,10 209,35357 215,70485 143,88794 20,38918 —110,46182 —201;46854 —219;80676 —158; 85069
6,15 135,00903 220,88173 225,60174 147,65368 15,59430 -122,17877 —215; 17741 —229,32805 —159;43494
6,20 14$ ,15404 233,01706 236,14356 151,36574 10,24429 —134,69104 —229;48896 —238; 86109 —159,31874
6,25 6,30 151,54263 245,79282 247,11376 155,00815 4,29693 —148,03825 —244,40454 —248; 36736 —158 ,'42968
160,41509 259,24161 258,53366 158,56081 —2,28993 —162,26119 —259;93321 —257; 80393 —156 ,'69565
6,35 170,01148 273,74609 270,75383 162,21269 —9,57294 —177,61825 —276,42594 —264; 60020 —154;22759 :
6,40 179,72337 288,30975 282,78142 165,32624 —17,56606 —193,50657 —292,85399 —276; 28706 —150,36333
6.45 6,50 6,55, 190,43458 304,35324 296,07320 168,68285 —26,38906 —210,85911 —310,60286 —285,55051 —145,75911 i
201,26899 213,24250 320,45266 308,94568 171,44064 —35,98424 —228,73275 —328; 19493 —292; 81035 —139.60024
333,22089 323,20682 174,42085 -46,56147 —248,27300 —347; 21743 —302,45527 —132,49076 >
6,60 225,35119 З&в,U6136 337,20348 176,72456 —57,98074 —268,33229 —365; 98986 —309;91302 —123,67632 :
ПРИЛОЖЕНИЕ
Функция Ф4 (z) = sh z sin yz, где г = й г)
Таблица 4
I Z 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0 0 0 0 0 0 0 0 0 0
0,05 0,00025 0,00050 0,00075 0,00100 0,00125 0,00150 0,00175 0,00200 0,00225
0,10 0,00100 0,00200 0,00301 0,00401 0,00501 0,00601 0,00701 0,00801 0,00901
0,15 0,00226 0,00452 0,00677 0,00903 0,01128 0,01354 0,01578 0,01808 0,02027
0,20 0,00403 0,00805 0,01207 0,01609 0,02010 0,02410 0,02809 0,03208 0,03601
0,25 0,00631 0,01262 0,01892 0,02522 0,03149 0,03775 0,04398 0,05019 0,05636
0,30 0,00913 0,01826 0,02737 0,03645 0,04551 0,05452 0,06348 0,07238 0,08122
0,35 0,01250 0,02498 0,03743 0,04984 0,06219 0,07446 0,08664 0,09871 0,11066
0,40 0,01643 0,03282 0,04917 0,06544 0,08160 0,09763 0,11351 0,12921 0,14469
0,45 0,02093 0,04182 0,06262 0,08331 0,10382 0,12412 0,14417 0,16392 0,18335
0,50 0,02604 0,05202 0,07787 0,10353 0,12892 0,15399 0,17868 0,20293 0,22666
0,55 0,03178 0,06347 0,09496 0,12617 0,15728 0,18734 0,21713 0,24626 0,27464
0,60 0,03817 0,07621 0,11398 0,15133 0,18814 0,22427 0,25960 0,29399 0,32733
0,65 0,04525 0,09032 0,13500 0,17912 0,22247 0,26559 0,30619 0,34620 0,38474
0,70 0,05305 0,10586 0,15813 0,20964 0,26012 0,30932 0,35701 0,40295 0,44691
0,75 0,06162 0,12289 0,18346 0,24301 0,30530 0,35768 0,41231 0,46431 0,51384
0,80 0,07097 0,14149 0,21110 0,27937 0,34585 0,41011 0,47175 0,53038 0,58560
0,85 0,08116 0,16176 0,24117 0,31886 0,39423 0,46676 0,53590 0,60120 0,66214
0,90 0,09226 0,18378 0,27380 0,36161 0,44650 0,52777 0,60476 0,67687 0,74350
0,95 0,10430 0,20765 0,30913 0,40782 0,50284 0,59331 0,67844 0,75745 0,82962
-4,00 0,11732 0,23348. _ 0,34729 0,45765 0,56343 0,66356 0,75709 0,84304 0,92057
1,05 0,13140 0,26138 0,38847 0,51127 0,62843 0,73870 0,84081 0,93367 1,01624
1,10 0,14663 0,29148 0,43280 0,56891 0,69813 0,81891 0,92980 1,02944 1,11664
1,15 0,16305 0,32401 0,48051 0,63075 0,77265 0,90433 1,02413 1,13037 1,25307
1,20 0,18070 0,35880 0,53174 0,69704 0,85230 0,99531 1,12400 1,23653 1,33128
1,25 0,19971 0,39631 0,58673 0,76801 0,93727 1,09193 1,22954 1,34797 1,44553
1,30 0,22016 0,43662 0,64571 0,84389 1,02784 1,19444 1,34087 1,46468 1,56378
450 приложение
Продолжение табл. 4
z 'к 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
1,35 0,24214 0,47987 0,70888 0,92498 1,12423 1,30306 1,45814 1,58672 1,68639
1,40 0,26573 0,52627 0,77650 1,01154 1,22679 1,41802 1,58152 1,71406 1,81306
1,45 0,29106 0,57598 0,84881 1,10386 1,33570 1,53957 1,71106 1,84668 1,94351
1,50 0,31820 0,62904 0,92617 1,20228 1,45140 1,66793 1,84698 1,98457 2,07764
1,55 0,34729 0,68627 1,00877 1,30711 1,57407 1,80333 1,98933 2,12764 2,23753
1,60 0,37879 0,74791 1,09791 1,41988 1,70557 1,94768 2,14005 2,27776 2,35726
1,65 0,41185 0,81252 1,19112 1,53737 1,84183 2,09631 2,29377 2,42903 2,49778
1,70 0,44759 0,88229 1,29154 1,66355 1,98761 2,25437 2,45612 2,58706 2,64343
1,75 0,48584 0,95683 1,39855 1,79764 2,14175 2,42046 2,62522 2,74981 2,79035
1,80 0,52674 1,03635 1,51269 1,94001 2,30469 2,59488 2,80121 2,91704 2,93861
1,85 0,57048 1,12149 1,63419 2,09117 2,47672 2,77782 2,98406 3,08851 3,08749
1,90 0,61722 1,21222 1,76360 2,25150 2,65839 2,96955 3,17387 3,26394 3,23656
1,95 0,66719 1,30907 1,90131 2,42154 2,84994 3,17033 3,37049 3,44300 3,38492
2,00 0,72055 1,41237 2,04787 2,60176 3,05189 3,38038 3,57409 3,62530 3,53202
2,05 0,77755 1,52252 2,20374 2,79268 3,26459 3,59992 3,78436 3,81045 3,67665
2,10 0,83840 1,63995 2,36944 2,99484 3,48864 3,82917 4,00143 3,99789 3,81872
2,15 0,90336 1,76511 2,54559 3,20884 3,72431 4,06838 4,22496 4,18715 3,95643
2,20 0,97267 1,89846 2,73274 3,43527 3,97258 4,31769 4,45501 4,37755 4,08779
2,25 1,04665 2,04052 2,93146 3,67473 4'23261 4,57727 4,69108 4,56849 4,21548
2,30 1,12552 2,19176 3,14257 3,92784 4,50626 4,84735 4,93316 4,75913 4,33445
2,35 •1,20963 2,35281 3,36653 4,19535 4,79341 5,12808 5,18076 4,94875 4,44456
2,40 1,29982 2,46953 3,60432 4,47788 5,09474 5,41955 5,43365 5,13634 4,54451
2,45 1,39491 2,70661 3,85652 4,77623 5,41057 5,72181 5,69128 5,30538 4,63268
2,50 1,49683 2,90065 4,12406 5,09106 5,74152 6,03501 5,95334 5,50145 4,70748
2,55 1,60538 3,10703 4,40761 5,42326 6,08803 6,35923 6,22099 5,67670 4,76714
2,60 1,72108 3,32648 4,70827 5,77353 6,45077 6,69433 6,48793 5,84537 4,80989
2,65 1,84422 3,55978 5,02678 6,14289 6,83001 7,04041 6,75917 6,00613 4,88369
ПРИЛОЖЕНИЕ
Продолжение табл. 4
7 2 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
2,70 2,75 2,80 2,85 2,90 2,95 3,00 3,05 3,10 3,15 3,20 3,25 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 3,75 3,80 3,85 3,90 3,95 4,00 1,97547 3,80785 5,36428 6,53202 7,22644 7,39730 7,03217 6,15742 4,83650
2Д1512 4,07141 5,72159 6,94195 7,64042 7,76497 7,30579 6,29769 4,81615
2,26392 4,35147 6,10003 7,37355 8,07273 8,14310 7,57925 6,42509 4,77040
2^42217 4,64886 6,50047 7,82777 8,52342 8,53160 7,85128 6,53768 4,69650
2^59058 4,96482 6,92449 8,30580 8,99352 8,93019 8,13014 6,63368 4,59238
2,76982 5,30034 7,37280 8,80858 9,48297 9,33837 8,38683 6,71078 4,45483
2,96048 5,65649 7,84730 9,33705 9,99272 9,75590 8,64752 6,76666 4,28144
3,16325 6i03461 8,36978 9,89247 10,52282 10,18152 8,90122 6,79906 4,06896
3'37898 6,43586 8,87910 10,47588 11,07401 10,61644 9,14682 6,80504 3,81462
З;60835 6,86148 9,43946 11,08862 11,64638 11,05834 9,38181 6,78217 3,51506
3,85219 7,31324 10,03170 11,73180 12,24061 11,50684 9,60469 6,72740 3,16703
4,11124 7,79229 10,65728 12,40659 12,85672 11,96108 9,81289 6,63746 2,76700
4,38681 8,'30034 11,31807 13,11441 13,49551 12,42019 10,00463 6,50928 2,31159
4',67951 8,83906 12,01548 13,85634 14,15639 12,88289 10,17661 6,33932 1,79702
5,00576 9,41007 12,75213 14,63403 14,84065 13,34805 10,32715 6,12397 1,21968
5,'32135 10,01552 13,52915 15,44874 15,54740 13,81410 10,45262 5,85946 0,57556
5,67247 10,65709 14,34941 16,30193 16,27778 14,27976 10,55023 5,54161 — 0,13912
6,'04522 11,33682 15,21444 17,19490 17,03071 14,74310 10,61643 5,16621 — 0,92840
6'44142 12*05707 16,12704 18,12930 17,80729 15,20216 10,64817 4,72899 — 1,79655
6,86193 12^82013 17,08890 19,10649 18,60628 15,65515 10,64106 4,22512 — 2,74754
7;30881 13,62827 18,10325 20,12802 19,42871 16,09971 10,59152 3,65016 — 3,78537
7;78279 14^8402 19,17192 21,19544 20,27304 16,53304 10,49520 2,99863 — 4,91484
8,28613 15,39007 20,29826 22,31059 21,13598 16,95293 10,34739 2,26566 — 6,13962
8;82036 16,34947 21,48442 23,47485 22,02788 17,35631 10,14332 1,44556 — 7,46382
9'38731 17^36476 22,73933 24,68969 22,93704 17,73957 9,87817 0,53308 — 8,89201
9,98866 18,43931 24,04988 25,95702 23,86584 18,10004 9,54608 —0,47789 —10,42813
10,62724 19'57670 25,43530 27,27818 24,81472 18,43325 9,14185 —1,59291 —12,07633
Х7 Z 0,1 0,2 0,3 0,4
4,05 11,30444 20,77989 26,89297 28,65540
4,10 12,02282 22,05284 28,42725 30,08977
4,15 12,78480 23,39911 30,04059 31,6g292
4,20 13,59295 24,82307 31,73856 33,1'3699
4,25 14,44964 26,32903 33,52319 34,75329
4,30 15,35879 27,92118 35,40033 36,43378
4,35 16,32199 29,60462 37,37210 38,17967
4,40 17,34398 31,38399 39,44560 39,99246
4,45 18,42697 33,26452 41,62271 41,87442
4,50 19,57496 35,25221 43,91034 43,82618
4,55 20,79078 37,35197 46,31171 45,84948
4,60 22,08080 39,57086 48,83440 47,94560
4,65 23,44685 41,91487 51,48143 50,11620
4,70 24,89493 44,39080 54,25994 52,36241
4,75 26,42868 47,00577 57,17411 54,68461
4,80 28,05318 49,76587 60,23129 57,08332
4,85 29,77446 52,68266 63,43774 59,56233
4,90 31,59865 55,76074 66,80009 62,11968
4,95 33,53372 59,01029 70,32348 64,75653
5,00 35,57524 62,43977 74,01696 67,47298
5,05 37,74028 66,05954 77,88556 70,26885
5,10 40,03462 69,87976 81,93984 73,14581
5,15 42,46241 73,91028 86,18268 76,10094
5,20 45,03390 78,16221 90,62792 79,13470
5,25 47,75459 82,64822 95,27860 82,24709
5,30 50,63687 87,38073 100,14788 85,43551 ।
Продолжение табл. 4
°,5 0,6 0,7 0,8 0,9
25,78094 18,73579 8,65896 — 2,81880 -13,84040
26,76443 19,00288 8,09152 — 4,16143 —15,72428
27,76260 19,22999 7,43230 — 5,62710 —17,73110
28,77568 19,41236 6,67480 — 7,22317 —19,86539
29,79960 19,54421 5,81126 — 8,95554 —22,12882
30,83400 19,62006 4,83418 —10,83187 —24,52572
31,87475 19,63404 3,73539 —12,85889 —27,05756
32,92155 19,57865 2,50627 —15,04334 —29,72753 я
33,96871 19,44793 1,13825 —17,39317 —32,53594
35,01549 19,23339 — 0,37847 —19,91473 —35,48622
36,05376 18,92768 — 2,05329 —22,61694 —38,57638 о
37,08947 18,52211 — 3,89591 —25,50371 —41,80953 * ъ rfl > J
38,10728 18,00736 — 5,91688 —28,58517 —45,18286 X '
39,10882 17,37461 — 8,12772 —31,86775 —48,69652 S
40,08625 16,61284 —10,53934 —35,35806 —52,34710
41,03426 15,71119 —13,16333 —39,06232 —56,13309 ' £i z** <
41,94801 14,65923 —16,01128 —42,98903 —60,05091
42,81995 13,44368 —19,09696 —47,14317 —64,09497
43,64205 12,05221 —22,43158 —51,53051 -68,25749
44,40839 10,47156 —26,02900 —56,15699 —72,61007
45,10814 8,68697 —29,90282 —61,02880 -,-76,91670
45,73417 6,68364 —34,06773 —66,14922 -81,39449
46,27475 4,44600 —38,53714 —71,52304 —85,95421.,
46,72150 1,95677 —43,32546 —77,15346 -90,580^1
47,06095 — 0,80131 —48,49397 -83,04459 -95,2ЙИ
47,28131 — 3,84637 —53,91831 —89,19574 —99,99ЙИ
ф- J"
*
Продолжение табл. 4
\’ г X 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
5,35 53,68675 92,37019 105,23799 88,69833 47,36868 — 7,19733 — 59,75210 — 95,61030 —104,74623
5,40 56,91579 97,63381 110,59670 92,03456 47,31137 — 10,87637 — 65,96891 —102,28768 -109; 49763
5,45 60,33213 103,18328 116,13603 95,44072 47,09076 — 14,90206 — 72,57731 —109,22556 —114; 22396
5,50 63,94794 109,03412 121,96098 98,91506 46,69378 — 19,29975 — 80,82406 —116,42247 —118; 90605
5,55 67,51612 115,20209 128,04446 102,45231 46,10013 — 24,08865 — 87,04658 —123,87473 —123,51331
5,60 71,82292 121,70374 134,40549 106,04897 45,29445 — 29,29760 — 94,93865 —131,57687 —128;01946
5,65 76,10530 128,55643 141,04662 109,69961 44,33370 — 34,94752 —103,28465 —139,52141 —132,38863
5,70 80,63800 135,77843 147,98702 113,40098 42,93872 — 41,06691 —112,10839 —147,70011 —136; 60478
5,75 85,27362 143,38889 155,22747 117,14637 41,38177 — 47,68423 —121,41775 —156,10248 —140;65859
5,80 90,50455 151,40793 162,78995 120,92652 39,51172 — 54,82757 —131,19874 —164,71558 —144; 32472
5,85 95,86888 159,85670 170,67644 124,73597 37,31002 — 62,52424 —141,56281 —173,52547 —147,77131
5,90 101,54536 <t68,75738b 178,90717 128,56705 34,75496 — 70,82586 —152,42937 —182,51188 —150,88345
5,95 107,54614 Т78,1313Г .187.48910 132,40744 31,81677 — 79,70877 —163,83854 —191,65855 -Яйалооо?
6,00 113,85901 188,00473 196,43836 136,24917 28,46576 — 89,26211 —175,80916 —200,93858 —155,87586
6,05 120,60860 198,40322 205,76154 140,07952 24,66628 — 99,50061 —188,34331 —210,33133 —157,64618
6,10 127,70862 209,35145 215,47974 143,88649 20,38897 —110,46070 —201,46650 —219,80454 —158,85600
6,15 135,09780 220,87972 225,59969 147,65234 15,59415 —122,17766 —215,17546 —229,32597 —159,43350
6,20 143,15286 233,01514 236,14162 151,36449 10,24421 -134,68993 —229,48707 —238,85912 —159,34743
6,25 151,54150 245,79099 247,11192 155,00699 4,27100 —148,03721 —244,40282 —248,36551 —158,42845
6,30 160,41400 259,23985 258,53191 158,55974 — 7,73562 —162,26010 —258,84232 —257,80219 —156,69459
6,35 170,00452 273,73487 270,74273 162,20604 — 9,57255 —177,61097 —276,41461 —267,45539 —154,22127
6,40 179,71043 288,28900 282,76107 165,31433 —17,56480 —193,49264 —292,83290 —276,26717 —150,35251
6,45 190,42762 304,34211 296,06237 168,67668 —26,38810 —210,85140 —310,59151 —285,54008 —145,75378
6,50 201,26807 320,45121 308,94428 171,43987 —35,98408 —228,73171 —328,19344 —293,80902 —139,59961
6,55 213,24162 338,21950 323,20549 174,42014 —46,56128 —248,27198 —347,21600 —302,45053 —132,49713
6,60 225,35036 356,05004 337,20224 176,72390 —57,98052 —268,33130 —365,98851 —309,91188 —123,67586
ПРИЛОЖЕНИЕ
ПРИЛОЖЕНИЕ
455
Таблица 5
Фундаментальная функция X (%) = sin у.?.
Оба края балки свободно оперты (случай 1)
di = 3,1416 Первый член разложения Р-г = 6,2832 Второй член разложения
I хГП 1 II с-1 к f b V Х = - — х" \ Р-i 7 b /'Ь\' X х=-(~) X" \Р-2/ "т" и *15
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,3090 0,5878 0,8090 0,9511 1,0000 0,9511 0,8090 0,5878 0,3090 0,0000 1,0000 0,9511 0,8090 0,5878 0,3090 0,0000 —0,3090 —0,5878 —0,8090 —0,9511 —1,0000 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,5878 0,9511 0,9511 0,5878 0,0000 —0,5878 —0,9511 —0,9511 —0,5878 0,0000 1,0000 0,8090 0,3090 —0,3090 —0,8090 —1,0000 —0,8090 —0,3090 0,3090 0,8090 1,0000
Из = 9,4248 Третий член разложения и* = 12,5664 Четвертый член разложения
II 1ХР Х = -СТХ" b (Ъ\‘, ГзХ' = -УХ X /6 V х=-(-) X'
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,8090 0,9511 0,3090 —0,5878 —1,0000 —0,5878 0,3090 0,9511 0,8090 0,0000 1,0000 0,5878 —0,3090 —0,9511 —0,8090 0,0000 0,8090. 0,9511 0,3090 —0,5878 —1,0000 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,9511 0,5878 —0,5878 —0,9511 0,0000 0,9511 0,5878 —0,5878 —0,9511 0,0000 1,0000 0,3090 —0,8090 —0,8090 0,3090 1,0000 0,3090 —0,8090 —0,8090 0,3090 1,0000
456
ПРИЛОЖЕНИЕ
Фундаментальная функция
Оба края
Ui — 4,7300 Первый член разложения (а = 1,01781)
х |л II X ь \Н1) / b v — х'" \?1/
0,0 0,1 0,2 о,з 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,1925 0,6304 1,1155 1,4814 1,6164 1,4814 1,1155 0,6304 0,1925 0,0000 0,0000 0,7395 1,0416 0,9494 0,5570 0,0000 —0,5570 —0,9494 —1,0416 -0,7395 0,0000 2,0356 1,0934 0,1989 —0,5536 —1,0591 —1,2372 —1,0591 —0,5536 0,1989 1,0934 2,0356 —2,0000 —1,9682 —1,7792 —1,3636 -0,7431 0,0000 0,7431 1,3636 1,7792 1,9682 2,0000
Мз = 10,9960 Третий член разложения (а3 =- 1,000034)
X ? = Т X b / b \2 (к) а-
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,7705 1,5080 0,8671 —0,6306 —1,4060 —0,6306 0,8671 1,5080 0,7705 0,0000 0,0000 1,0120 0,1094 —1,1817 —1,2699 0,0000 1,2699 1,1817 —0,1094 —1,0120 0,0000 2,0000 —0,1047 —1,2861 —0,7924 —0,6579 1,4224 0,6579 —0,7924 —1,2861 -0,1047 2,0000 —2,0000 —1,6777 —1,3307 1,1088 1,2481 0,0000 —1,2481 -1,1088 1,3307 1,5777 2,0000
ПРИЛОЖЕНИЕ
457
X (5) = sin р.5 —- ch р' — a (cos pH — ch pij).
заделаны (случай 2)
Таблица 6»'
Второй Ми = 7,8532 член разложения (а2 = 0,999223)
X ~ ь X ь — X' р.2 / ь v (— X" \н«/ [ b \3 (—) х"' \ На /
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,4551 1,2053 1,5044 1,0351 0,0000 —1,0351 —1,5044 — 1,2053 —0,4551 0,0000 0,0000 0,9569 0,7902 —0,0978 —1,0506 —1,4530 —1,0506 —0,0978 0,7902 0,9569 0,0000 1,9984 0,4551 —0,7931 —1,3229 —0,9665 0,0000 0,9665 1,3229 0,7931 —0,4551 —1,9984 —2,0000 —1,8705 —1,2099 —0,1001 0,9462 1,3742 0,9462 —0,1001 —1,2099 —1,8705 —2,0000
" ‘1 " 1 — \ = 14,1370 Четвертый член разложения (а4 = 0,99999)
X S = т X — X’ / Ь \® и*
0,0 0,1 о,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 1,0711 1,3244 —0,4075 —1,3966 0,0000 1,3966 0,4075 —1,3244 —1,0711 0,0000 0,0000 0,9031 —0,6923 —1,3644 0,1967 1,4123 0,1967 -1,3644 —0,6923 0,9031 0,0000 2,00001 —0,5829 —1,2052 0,4365 1,4033 0,0000 —1,4033 ‘ -0,4365 1,2052 0,5829 -2,0000 —2,0000 —1.39ДЗ 0,5730 1,3352 —0,2042 —1,4156 —0,2042 1,3352 0,5730 —1,3913 —2,0000
458
ПРИЛОЖЕНИЕ
Фундаментальная функция
Оба края балки
ц, = 4,7300 Первый член разложения (ах = 1,01781)
м X b — X’ Pi / Ь А2 X" \91/ / ь V — X'” \91 /
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 —2,0356 —1,0934 —0,1989 0,5536 1,0591 1,2372 1,0591 0,5536 —0,1989 —1,0934 —2,0356 2,0000 1,9682 1,7792 , 1,3636 0,7431 0,0000 —0,7431 —1,3636 —1,7792 —1,9682 —2,0000 0,0000 —0,1925 —0,6304 —1,1155 —1,4814 -1,6164 —1,4814 —1,1155 —0,6304 —0,1925 0,0000 0,0000 —0,7395 —1,0416 —0,9494 —0,5570 0,0000 0,5570 0,9494 1,0416 0,7395 0,0000
1Х8 = 10,996 Третий член разложения (а3 = 1,000034)
Н |-е II иг X b — X' Из ( b \2 — X" \9з/
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 —2,0000 0,1047 1,2861 0,7924 —0,6579 —1,4224 —0,6579 0,7924 1,2861 0,1047 —2,0000 2,0000 1,6777 0,3307 —1,1088 —1,2481 0,0000 1,2481 1,1088 —0,3307 —1,6777 —2,0000 0,0000 —0,7705 —1,5080 —0,8671 0,6306 1,4060 0,6306 —0,8671 —1,5080 —0,7705 0,0000 0,0000 —1,0120 —0,1094 1,1817 1,2699 0,0000 —1,2699 —1,1817 0,1094 1,0120 0,0000
ПРИЛОЖЕНИЕ
459
X (?) — sin 9$ + ch 95 — a (cos у.? + ch уЛ).
свободны (случай 3)
Таблица 7
Второй U2 == 7,8532 член разложения (а2 = 0,999223)
II <3*1 X ь — X' 92 / ь v Ы х" / b \8 (—) X1" \ 92 /
0,0 0,1 0,2 0,3 О’, 4 0,5 0,6 0,7 0,8 0,9 1,0 —1,9984 —0,4551 0,7931 1,3229 0,9665 0,0000 —0,9665 —1,3229 —0,7931 0,4551 1,9984 2,0000 1,8705 1,2099 0,1001 —0,9462 —1,3742 —0,9462 0,1001 1,2009 1,8705 2,0000 0,0000 —0,4551 —1,2053 —1,5044 —1,0351 0,0000 1,0351 1,5044 1,2053 0,4551 0,0000 0,0000 —0,9569 —0,7902 0,0978 1,0506 1,4530 1,0506 0,0978 —0,7902 —0,9569 0,0000
= 14,137 Четвертый член разложения (а4 = 0,999999)
X — X' 9* О’*-
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 —2,0000 0,5829 1,2052 -0,4365 -1,4033 0,0000 1,4033 0,4365 —1,2052 —0,5829 2,0000 2,0000 1,3913 —0,5730 —1,3352 0,2042 1,4156 0,2042 —1,3352 —0,5730 1,3913 2,0000 0,0000 —1,0711 —1,3244 0,4075 1,3966 0,0000 —1,3966 —0,4075 1,3244 1,0711 0,0000 0,0000 -0,9031 0,6923 1,3644 —0,1967 —1,4123 —0,1967 1,3644 0,6923 —0,9031 0,0000
460
ПРИЛОЖЕНИЕ
Фундаментальная функция
Один край балки заделан,
Ui = l,8751 Первый член разложения (ах = 1,362223)
X X b — X' 91 1 ь V Ы х“ / b V —) \ 91 /
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,4560 0,1740 0,3712 0,6262 0,9250 1,2563 1,6107 1,9764 2,3504 2,7244 0,0000 0,4747 0,8813 1,2665 1,4857 1,6898 1,8347 1,9276 1,9777 1,9971 2,0000 2,7244 2,3504 1,9764 1,6107 1,2563 0,9250 0,6262 0,3712 0,1740 0,0456 0,0000 —2,0000 —1,9971 —1,9777 —1,9276 —1,8347 —1,6898 —1,4857 —1,2665 —0,8813 —0,4747 0,0000
из = 7,8548 Третий член разложения (а а == 1,00078)
X X b — X' Рз / Ь \2 — X" \Рз/ \рз/
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,4560 1,2100 1,5137 1,0547 0,0395 —0,9501 —1,3158 —0,7904 0,4583 2,0016 0,0000 0,9593 0,7945 —0,0899 —1,0327 —1,4147 —0,9641 0,0916 1,2066 1,8702 2,0000 2,0016 0,4583 —0,7904 —1,3158 —0,9501 0,0395 1,0547 1,5137 1,2100 0,4560 0,0000 —2,0000 —1,8702 —1,2066 —0,0916 0,9541 1,4147 1,0327 0,0899 —0,7945 —0,9593 0,0000
ПРИЛОЖЕНИЕ
461
X (5) = sin p.ij — ch [л? — a (cos [Д — ch
другой свободен (случай 4)
Таблица 8
ц2 = 4,6941 Второй член разложения (а2 = 0,981863)
X X b — X' Р*2 Н2Х"
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,1816 0,5914 1,0330 1,3423 1,4014 1,1579 0,6223 —0,1372 —1,0293 —1,9637 0,0000 0,7014 0,9728 0,8515 0,4227 —0,1895 —0,8443 —1,4104 —1,7936 —1,9703 —2,0000 1,9637 1,0293 0,1372 —0,6223 —1,1579 —1,4014 —1,3423 — 1,0330 —0,5914 —0,1816 ’ 0,0000 —2,0000 —1,9703 —1,7936 —1,4104 —0,8443 —0,1895 0,4227 0,3515 0,9723 0,7014 0,0000
Ц4 = 10,9956 Четвертый член разложения («< = 0,999967)
’ b X b [ b V Ых" / b V ( —) X”
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,7704 1,5076 0,8661 —0,6334 —1,4141 —0,6552 0,7933 1,2863 0,1048 —1,9999 0,0000 1,0119 0,1090 —1,1826 —1,2725 —0,0081 1,2453 1,1079 —0,3309 —1,6777 —2,0000 1,9999 —0,1048 —1,2863 ' —0,7933 0,6552 1,4141 0,6334 —0,8661 —1,5076 —0,7704 0,0000 —2,0000 —1,6777 —0,3309 1,1079 1,2453 —0,0081 —1,2725 —1,1826 0,1090 1,0119 0,0000
462
ПРИЛОЖЕНИЕ
Фундаментальная функция
Один край балки заделан,
= 3,9266 Первый член разложения (ах = —0,0278749)
X ^-ь X — X' Pi 1 b V X' \ Н1/
0,0 0,0000 1,0279 0,0000 —0,9721
0,1 0,3939 0,9539 —0,3714 —0,8938
0,2 0,7310 0,7443 —0,6826 —0,6705
0,3 0,9648 0,4323 —0,8829 —0,3332
0,4 1,0642 0,0698 —0,9358 —0,0702
0^5 1,0214 —0,2810 —0,8268 0,4834
0,6 О;8529 —0,5586 —0,5615 0,8553
0,7 0,5995 —0,7052 —0,1657 1,1426
0,8 0,3230 —0,6774 0,3198 1,3226
0,9 0,0965 —0,4495 0,8539 1,4015
1,0 0,0000 0,0000 1,4136 1,4147
ПРИЛОЖЕНИЕ
463
г
а 9
X (?) = sin — a ch
другой свободно оперт (случай 5)
ц2 7,0685 Второй член разложения (а2 == 0,00122285) [
X X b — X' р2 / ь V — X" \Р2 1 / b \» i f 1 VW ! \ / Л
0,0 0,0000 0,9988 0,0000 —1,0012
0,1 0,6496 0,7588 —0,6505 —0,7618
0,2 0,9854 0,1535 —0,9901 —0,1588 1
0,3 0,8475 —0,5279 —0,8574 0,5178 :
0,4 0,2991 —0,9613 —0,3197 0,9406 i
0,5 —0,3996 —0,9464 0,3579 0,9046 ;
0,6 —0,9323 —0,4968 0,8487 0,4132
0,7 —1,0569 0,1504 0,8869 —0,3204 !
0,8 —0,7555 0,6323 0,4179 —0,9800
0,9 —0,2714 0,6489 —0,4249 —1,3452
1,0 0,0000 0,0000 —1,4141 —1,4143
!_ 1 pt, = 10.2102 Третий член разложения (a3 = = 0,0000520346)
X l = -b X b — X' Из ( b \2 X" \Нз/ / b \3 (—) \Нз/
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1.0 0,0000 0,8527 0,8912 0,0821 —0,8051 —0,9193 —0,1406 0,7954 1,0424 0,4876 0,0000 1,0000 0,5226 —0,4537 —0,9961 —0,5895 0,3869 1,0002 0,6804 —0,2188 —0,7176 0,0000 0,0000 —0,8525 —0,8908 —0,0809 0,8082 0,9279 0,1645 —0,7291 —0,8586 0,0223 1,4142 —1,0000 —0,5224 0,4542 0,9972 0,5926 —0,3783 —0,9763 —0,6141 0,4027 1,2275 1,4142
= 13,3520 Четвертый член разложения (а4 = 0,00000224861)
X $ = Т X b X' 94 / ь V — X’ \ 94/ Н’х'" :
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,9723 0,4543 —0,7634 —0,8096 0,3856 0,9845 0,0618 —1,0004 —0,7064 0,0000 1,0000 0,2336 —0,8908 —0,6461 0,5870 0,9214 —0,1588 —1,0101 —0,3601 0,6676 0,0000 0,0000 —0,9723 —0,4543 0,7632 0,8092 —0,3874 —0,9912 —0,0876 0,9009 0,3328 —1,4145 —1,0000 [ —0,2336 0,8908 0,6459 —0,5874 —0,9232 0,1520 0,9843 ' 0,2606 —1,0412 —1,4139
464
ПРИЛОЖЕНИЕ
Фундаментальная функция
Одни край балки свободно оперт,
Ui = 3,9266 Первый член разложения (at = 0,0278749) *
X X b X' 91 / Ь V — ТС" \91/ ( Ь V —) ТС'" \ 91 /
0,0 од 0,2 0,3 ОД 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,3714 0,6826 0,8829 0,9358 0,8268 0,5615 0,1657 —0,3198 —0,8539 —1,4136 0,9721 0,8938 0,6705 0,3332 —0,0702 —0,4834 —0,8553 —1,1426 —1,3226 —1,4015 —1,4147 0,0000 —0,3939 —0,7310 —0,9648 —1,0642 —1,0214 —0,8529 —0,5995 —0,3230 —0,0965 0,0000 —1,0279 —0,9539 —0,7443 —0,4323 —0,0698 0,2810 0,5586 0,7052 0,6774 0,4495 0,0000
Третий член Ех3 ~ 10,2102 разложения (а, = — 0,0000520346)
X ^-ь X ь — X' Из / ь v ) ТС" \9з/ а-
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,8525 0,8908 0,0809 —0,8082 —0,9279 —0,1645 0,7291 0,8586 —0,0223 —1,4142 1,0000 -0,5224 —0,4542 —0,9272 —0,5926 0,3783 0,9763 0,6141 —0,4027 —1,2275 , —1,4142 0,0000 —0,8527 —0,8912 —0,0821 0,8051 0,9193 0,1406 —0,7954 —1,0424 —0,4876 0,0000 —1,0000 —0,5226 0,4537 0,9961 0,5895 —0,3869 —1,0002 —0,6804 0,2188 0,7176 0,0000
«Наложение
461
X(?) = sin 9? +ash р£.
другой свободен (случай 6)
Таблица 10
Второй р,2 = 7,0685 член разложения а2 = 0,00122285)
X X ь — X' 92 ( ь v — X" \ 92 / / b \а —) X" \ 92 /
0,0 о,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,6505 0,9901 0,8574 0,3197 —0,3579 —0,8487 —0,8869 —0,4179 0,4249 1,4141 1,0012 0,7618 0,1588 —0,5178 —0,9406 —0,9046 —0,4132 0,3204 0,9800 1,3452 1,4143 0,0000 —0,6486 —0,9854 —0,8475 —0,2991 0,3996 0,9323 1,0569 0,7555 0,2714 0,0000 -0,9988 —0,7588 —0,1535 0,5279 0,9613 0,9464 0,4968 —0,1504 —0,6323 —0,6489 0,0000
= 13,3520 Четвертый член разложения (а4 = 0,00000224861}
X ^-ь X Ь — X’ 94 ( ь V — \ 94/ ( b \8 X'" \ 94 /
0,0 0,1 0,2 о,з 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,0000 0,9723 0,4543 —0,7632 —0,8092 0,3874 0,9912 0,0876 —0,9009 —0,3328 1,4145 1,0000 0,2326 —0,8908 —0,6459 0,5874 0,9232 —0,1520 —0,9843 —0,2606 1,0412 1,4139 0,0000 —0,9723 —0,4543 0,7634 0,8096 —0,2856 —0,9845 —0,0618 1,0004 0,7064 0,0000 —1,0000 —0,2336 0,8908 0,6461 —0,5870 —0,9214 0,1588 1,0101 0,3601 —0,6676 0,0000
30 В. 3. Власов, Н. Н. Леонтьев
466
ПРИЛОЖЕНИЕ
ПРИЛОЖЕНИЕ
Таблица 11
Функции Томсона
«0 (5) f<, (Q 4Го(5)
Продолжение табл .11
С «о (С) ые) М?) go (5)
1 1
0 00 1,0000 —0,0000 0,5000 — 00
002 1,0000 —0,0001 0,4997 —2,5643
004 1,0000 —0,0004 0,4989 —2,1232
0 06 1,0000 —0,0009 0,4978 —1,8653
0 08 1,0000 —0,0016 0,4963 —1,6825
0,10 1,0000 —0,0025 0,4946 —1,5409
0,12 1,0000 —0,0036 0,4926 — 1,4254
0,14 1,0000 —0,0049 0,4904 —1,3279
0,16 1,0000 —0,0064 0,4880 —1,2436
0,18 1,0000 —0,0081 0,4854 —1,1695
0,20 toooo —0,0100 0,4826 —1,1033
0 22 1,0000 —0,0121 0,4797 —1,0437
0 24 0,9999 —0,0144 0,4767 —0,9894
0 26 0*9999 —0,0169 0,4735 —0,9397
0 28 0,9999 —0,0196 0,4701 —0,8938
0^30 0/9999 —0,0225 0,4667 • —0,8513
0 32 0,9998 —0,0256 0,4632 —0,8117
0 34 0,9998 —0,0289 0,4595 —0,7747
036 Oj9997 —0,0324 0,4558 —0,7400
0 38 0,9997 —0,0361 0,4520 —0,7073
0,40 0,9996 —0,0400 0,4480 —0,6/65
0 42 0,9995 —0,0441 0,4441 -0,6473
0 44 0,9994 —0,0484 0,4400 —0,6198
o’46 0,9993 —0,0529 0,4359 —0,5935
0 48 0/9992 —0,0576 0,4318 —0,5686
0^50 0,9990 —0,0625 0,4275 —0,5449
0 52 0,9989 —0,0676 0,4233 —0,5223
О* 54 0,9987 —0,0729 0,4190 —0,5( )06
056 0,9985 —0,0784 0,4146 —0,4800
058 0*9982 —0,0841 0,4102 —0,4602
O’60 0,9980 —0,0900 0,4058 —0,4413
0 62 0,9977 —0,0961 0,4014 -0,4231
o’64 0,9974 —0,1024 0,3969 —0,405/
o’66 O”9970 —0,1089 0,3924 —0,3889
0 68 0^9967 —0,1156 0,3879 —0,3729
0^70 0,9962 —0,1224 0,3834 —0,3574
0 72 0,9958 —0,1295 0,3788 —0,3425
o’74 0^9953 —0,1368 0,3743 —0,3282
076 0^9948 —0,1443 0,3697 —0,3144
078 0*9942 —0,1520 0,3651 —0,3011
0^80 0,9936 —0,1599 0,3606 —0,2883
0,82 0,84 0,86 0,88 0,90 0,9929 0,9922 0,9915 0,9906 0,9898 —0,1680 —0,1762 —0,1847 —0,1934 —0,2023 0,3560 0,3514 0,3469 0,3423 0,3377 —0,2760 —0,2641 —0,2526 —0,2415 —0,2308
0,92 0,9888 —0,2113 0,3332 —0,2205
0,94 0,9878 —0,2206 0,3286 —0,2105
0,96 0,9867 —0,2301 .0,3241 -0,2008
0,98 0,9856 —0,2397 0,3196 —0,1915
1,00 0,9844 —0,2496 0,3151 —0,1825
1,10 0,9771 —0,3017 0,2929 —0,1419
1,20 0,9676 —0,3587 0,2713 —0,1076
1,30 0,9554 —0,4204 0,2504 —0,0786
1,40 0,9401 —0,4867 0,2302 —0,0542
1,50 0,9211 —0,5576 0,2110 —0,0337
1,60 0,8979 —0,6327 0,1926 —0,0166
1,70 0,8700 —0,7120 0,1752 —0,0023
1,80 0,8367 —0,7953 0,1588 0,0094
1,90 0,7975 —0,8821 0,1433 0,0189
2,00 0,7517 —0,9723 0,1289 0,0265 _
2,20 0,6377 —1,1610 0,1026 0,0371
2,4 0,4890 —1,3575 0,0804 0,0429
2,6 0,3001 —1,5569 0,0614 0,0446
2,8 0,0651 —1,7529 0,0455 0,0447
3,0 —0,2214 —1,9376 0,0326 0,0427
3,2 —0,5644 —2,1016 0,0220 0,0394
3,4 —0,9680 —2,2334 0,0137 0,0356
3,6 —1,4353 —2,3199 0,0072 0,0314
3,8 —1,9674 —2,3454 0,0022 0,0260
4,0 —2,5634 -2,2927 —0,0014 0,0230
4,2 —3,2195 —2,1422 —0,0039 0,0192
4,4 —3,9283 —1,8726 —0,0056 0,0156
4,6 —4,6784 —1,4610 —0,0066 0,0125
4,8 —5,4531 —0,8837 —0,0071 0,0097
5,0 —6,2301 —0,1160 —0,0071 0,0073
5,2 —6,9803 0,8658 —0,0069 0,0053
5,4 —7,6674 2,0845 —0,0065 0,0037
5,6 —8,2466 3,5597 —0,0059 0,0023
5,'8 —8,6644 5,3068 —0,0053 0,0012
6,0 —8,8583 7,3347 —0,0046 0,0004
Таблица 12
Кинематические и силовые факторы для круглой плиты оо
5 «о(5) fo(5) ' 01(5) 02(?) A7i(5) А12(5) М-2 (5) 7И1(5) Qi (5) Q2 (5)
9 = 46°
0,00 1,0000 0,0000 0,0000 0,0000 —0,0349 0,9994 —0,0174 0,4947 0,0000 0,0000
0,05 1,0000 —0,0006 —0,0009 0,0250 —0,0343 0,9995 —0,0172 0,4997 —0,0249 —0,0017
0,10 1,0000 —0,0024 —0,0016 0,0500 —0,0324 0,9996 —0,0168 0,4997 —0,0499 —0,0034
0,15 1,0002 —0,0056 —0,0024 0,0749 —0,0293 0,9998 —0,0160 0,4998 —0,0748 —0,0050
0,20 1,0003 —0,0100 —0,0030 0,0999 —0,0249 1,0001 —0,0149 0,4999 —0,0998 —0,0065
0,25 1,0005 —0,0156 —0,0034 0,1249 —0,0193 1,0004 —0,0155 0,5000 —0,1248 —0,0077
0,30 1,0007 —0,0225 —0,0035 0,1500 —0,0125 1,0009 —0,0118 0,5001 —0,1498 —0,0088
0,35 1,0009 —0,0306 —0,0034 0,1751 —0,0044 1,0013 —0,0098 0,5002 —0,1748 —0,0095
0,40 1,0010 —0,0400 —0,0030 0,2002 0,0050 1,0018 —0,0074 0,5003 —0,1999 —0,0100
0,45 1,0012 —0,0506 —0,0021 0,2253 0,0157 1,0023 —0,0018 0,5005 —0,2250 —0,0100
0,50 1,0012 —0,0626 —0,0009 0,2504 0,0275 1,0029 —0,0018 0,5006 —0,2501 —0,0097
0,55 1,0012 —0,0770 0,0008 0,2754 0,0406 1,0033 0,0015 0,5008 —0,2753 —0,0089
0,60 1,0011 —0,0900 0,0030 0,3005 0,0551 1,0037 0,0050 0,5009 —0,3004 —0,0065
0,65 1,0011 —0,1058 0,0058 0,3257 0,0708 1,0040 0,0089 0,5010 —0,3257 —0,0056
0,70 1,0006 —0,1227 0,0092 0,3509 0,0877 1,0042 0,0133 0,5012 —0,3510 —0,0030
0,75 1,0000 —0,1404 0,0132 0,3760 0,1058 1,0043 0,0178 0,5013 —0,3762 0,0001
0,80 0,9992 —0,1602 0,0180 0,4012 0,1253 1,0044 0,0227 0,5014 —0,4015 0,0040
0,85 0,9982 —0,1810 0,0236 0,4263 0,1459 1,0039 0,0277 0,5015 —0,4269 0,0089
0,90 0,9969 —0,2029 0,0300 0,4514 0,1680 1,0033 0,0333 0,5015 —0,4522 0,0141
0,95 0,9951 —0,2261 0,0371 0,4764 0,1912 1,0025 0,0391 0,5015 —0,4778 0,0204
1,00 0,9932 —0,2504 0,0453 0,5015 0,2151 1,0012 0,0452 0,5015 —0,4923 0,0276
<₽ =47
0,00 1,0000 0,0000 0,0000 0,0000 —0,0698 0,9976 —0,0349 0,4988 0,0000 0,0000
0,05 1,0000 0,0006 —0,0017 0,0249 —0,0692 0,9977 —0,0347 0,4988 —0,0247 —0,0035
0,10 1,0001 0,0024 —0,0034 0,0499 —0,0673 0,9979 —0,0343 0,4989 —0,0495 —0,0069
0,15 1,0004 0,0056 —0,0050 0,0748 —0,0642 0,9984 —0,0335 0,4990 —0,0743 —0,0102
0,20 1,0007 0,0100 —0,0065 0,0999 —0,0599 •0,9990 —0,0324 0,4991 —0,0991 —0,0134
ПРИЛОЖЕНИЕ
Продолжение табл. 12
5 «о (9 «о (5) 6i (5) 62 (5) Мг (5) (5) Л12© Qi(Q
0,25 1,0011 0,0156 —0,0077 0,1248 —0,0543 0,9997 —0,0310 0,4993 —0,1240 —0,0165
0,30 1,0016 0,0224 —0,0088 0,1498 —0,0475 1,0006 —0,0293 0,4996 —0,1488 —0,0193
0,35 1,0021 0,0305 —0,0096 0,1750 —0,0395 1,0017 —0,0273 0,4999 —0,1738 -0,0218
0,40 1,0026 0,0399 —0,0100 0,2000 —0,0301 1,0028 —0,0250 0,5001 —0,1989 -0,0239
0,45 1,0029 0,0506 —0,0101 0,2253 —0,0196 1,0040 —0,0224 0,5005 —0,2239 —0,0257
0,50 1,0034 0,0624 —0,0098 0,2504 —0,0077 1,0053 —0,0194 0,5008 -0,2490 —0,0272
0,55 1,0039 0,0756 —0,0089 0,2756 0,0054 1,0067 —0,0162 0,5012 —0,2744 —0,0281
0,60 1,0043 0,0901 —0,0075 0,3010 0,0197 1,0081 -0,0127 0,5016 —0,2997 —0,0286
0,65 1,0048 0,1058 —0,0056 0,3263 0,0354 1,0095 —0,0087 0,5020 -0,3251 —0,0283
0,70 1,0048 0,1227 —0,0031 0,3518 0,0523 1,0109 —0,0045 0,5025 —0,3506 —0,0276
0,75 1,0049 0,1409 0,0000 0,3772 0,0703 1,0124 0,0001 0,5029 —0,3763 —0,0262
0,80 1,0049 0,1604 0,0040 0,4027 0,0898 1,0136 0,0049 0,5034 —0,4019 —0,0242
0,85 1,0045 0,1811 0,0087 0,4283 0,1107 1,0147 0,0101 0,5038 —0,4276 —0,0213
0,90 1,0040 0,2032 0,0140 0,4538 0,1326 1,0157 0,0156 0,5041 —0,4537 —0,0156
0,95 1,0030 0,2265 0,0203 0,4796 0,1559 1,0165 0,0214 0,5045 —0,4796 —0,0131
1,00 1,0018 0,2511 0,0275 0,5052 0,1810 1,0170 0,0265 0,5050 —0,5056 —0,0078
<р = 48°
0,00 1,0000 0,0000 0,0000 0,0000 —0,1045 0,9945 —0,0522 0,4977 0,0000 0,0000
0,05 1,0000 0,0006 —0,0026 0,0249 —0,1039 0,9946 —0,0520 0,4977 —0,0244 —0,0052
0,10 1,0002 0,0024 —0,0051 0,0497 —0,1021 0,9950 —0,0516 0,4978 —0,0489 —0,0103
0,15 1,0006 0,0506 —0,0076 0,0746 —0,0990 0,9957 —0,0508 0,4980 —0,0734 —0,0154
0,20 1,0010 0,0099 —0,0100 0,0996 —0,0947 0,9966 —0,0498 0,4982 —0,0979 —0,0203
0,25 1,0016 0,0155 —0,0122 0,1245 —0,0892 0,9977 —0,0484 0,4985 -0,1225 —0,0251
0,30 1,0022 0,0224 —0,0139 0,1495 —0,0825 0,9991 —0,0467 0,4989 —0,1472 -0,0296
0,35 1,0030 0,0304 —0,0157 0,1746 -0,0745 1,0007 —0,0447 0,4993 —0,1720 —0,0339
0,40 1,0038 0,0399 —0,0170 0,1997 —0,0653 1,0024 —0,0424 0,4997 —0,1968 —0,0378
0,45 1,0047 0,0504 —0,0179 0,2250 —0,0548 1,0044 —0,0398 0,5001 —0,2218 —0,0414
ПРИЛОЖЕНИЕ
Продолжение табл. 12
и «о (?) (?) 0i(?) о2(?) (?) АЫ?) М\ (Q Л12(?) Qi(?) Q2(?)
0,50 1,0056 0,0623 —0,0185 0,2501 —0,0431 1,0066 —0,0369 0,5007 —0,2468 —0,0446
0,55 1,0065 0,0755 —0,0185 0,2756 —0,0301 1,0089 —0,0336 0,5014 —0,2721 —0,0473
0,60 1,0074 0,0899 —0,0182 0,3009 —0,0159 1,0113 —0,0301 0,5021 —0,2975 —0,0495
0,65 1,0083 0,1056 —0,0171 0,3265 —0,0003 1,0148 —0,0263 0,5028 —0,3229 —0,0512
0,70 1,0091 0,1226 —0,0155 0,3522 0,0164 1,0164 —0,0220 0,5035 —0,3485 —0,0522
0,75 1,0099 0,1407 —0,0132 0,3778 0,0344 1,0190 —0,0176 0,5042 —0,3743 —0,0527
0,80 1,0105 0,1603 —0,0102 0,4036 0,0539 1,0217 —0,0128 0,5050 —0,4003 —0,0524
0,85 1,0109 0,1812 —0,0064 0,4229 0,0746 1,0242 —0,0076 0,5058 —0,4265 —0,0514
0,90 1,0111 0,2033 0,0001 0,4555 0,0966 1,0268 —0,0022 0,5065 —0,4528 —0,0496
0,95 1,0111 0,2267 0,0035 0,4876 0,1198 1,0293 0,0006 0,5074 —0,4793 —0,0470
1,00 1,0107 0,2514 0,0097 0,5077 0,1444 1,0314 0,0097 0,5082 —0,5059 —0,0435
<₽ = 49°
0,00 1,0000 0,0000 0,0000 0,0000 —0,1392 0,9903 —0,0696 0,4951 0,0000 0,0000
0,05 1,0000 —0,0006 —0,0035 0,0248 —0,1386 0,9905 —0,0695 0,4951 —0,0240 —0,0068
0,10 1,0003 —0,0024 —0,0069 0,0495 —0,1368 0,9910 —0,0690 0,4953 —0,0480 —0,0138
0,15 1,0007 —0,0056 —0,0102 0,0743 —0,1338 0,9918 —0,0682 0,4955 —0,0722 —0,0205
0,20 1,0013 —0,0099 —0,0134 0,0991 —0,1296 0,9930 —0,0672 0,4958 —0,0963 —0,0272
0,25 1,0021 —0,0155 —0,0165 0,1241 —0,1242 0,9946 —0,0658 0,4962 —0,1206 —0,0337
0,30 1,0028 —0,0223 —0,0198 0,1491 —0,1176 0,9964 —0,0642 0,4966 —0,1449 —0,0338
0,35 1,0038 —0,0304 —0,0218 0,1740 —0,1079 0,9985 —0,0622 0,4972 —0,1693 —0,0468
0,40 1,0049 —0,0397 —0,0240 0,1992 —0,1006 1,0009 —0,0600 0,4977 —0,1935 —0,0515
0,45 1,0061 —0,0503 —0,0258 0,2245 —0,0902 1,0036 —0,0574 0,4985 —0,2186 —0,0568
0,50 1,0073 —0,0622 —0,0273 0,2496 —0,0787 1,0066 —0,0545 0,4993 —0,2434 —0,0618
0,55 1,0087 —0,0753 —0,0283 0,2752 —0,0656 1,0098 —0,0513 0,5001 —0,2684 —0,0662
0,60 1,0100 —0,0896 —0,0287 0,3006 —0,0519 1,0133 —0,0479 0,5010 —0,2937 —0,0703
0,65 1,0112 —0,1054 —0,0286 0,3263 —0,0366 1,0169 —0,0440 0,5020 —0,3192 —0,0737
0,70 1,0125 —0,1213 —0,0279 0,3552 —0,0200 1,0207 —0,0400 0,5029 —0,3447 —0,0767
0,75 1,0138 —0,1406 —0,0267 0,3781 —0,0020 1,0245 —0,0355 0,5040 —0,3707 —0,0790
ПРИЛОЖЕНИЕ
Продолжение табл. 1'2
М5) «о (5) 01(5) ©2(5) Mi (5) Mi (^ Ah (!) Qi(5) Q2(O
0,80 1,0149 —0,1602 -0,0246 0,4042 0,0171 1,0285 —0,0308 0,5051 —0,3968 —0,0805
0,85 1,0160 —0,1810 —0,0219 0,4306 0,0376 1,0326 —0,0257 0,5063 -0,4231 —0,0814
0,90 1,0168 —0,2032 —0,0182 0,4568 0,0594 1,0367 —0,0202 0,5074 —0,4498 -0,0815
0,95 1,0174 —0,2266 —0,0140 0,4835 0,0826 1,0407 —0,0145 0,5087 —0,4757 —0,0809
1,00 1,0178 -0,2515 —0,0085 0,5100 0,1070 <р = 50° 1,0447 —0,0084 0,5099 —0,5038 —0,0795
0,00 1,0000 0,0000 0,0000 0,0000 —0,1736 0,9848 —0,0868 0,4924 0,0000 0,0000
0,05 1,0001 —0,0006 —0,0043 0,0245 —0,1730 0,9850 —0,0867 0,4924 —0,0233 —0,0085
0,10 1,0004 —0,0024 —0,0087 0,0491 —0,1713 0 9856 —0,0862 0,4926 —0,0469 —0,0170
0,15 1,0010 —0,0055 —0,0129 0,0738 —0,1683 0,9866 —0,0855 0,4929 —0,0705 -0,0255
0,20 1,0017 —0,0098 —0,0168 0,0986 -0,1643 0,9881 —0,0845 0,4932 —0,0941 —0,0338
0,25 1,0026 —0,0154 —0,0208 0,1233 —0,1588 0,9829 —0,0831 0,4937 —0,1178 —0,0418
0,30 1,0038 —0,0222 —0,0248 0,1485 —0,1524 0,9922 • —0,0815 0,4943 —0,1419 —0,0502
0,35 1,0051 —0,0302 —0,0278 0,1731 —0,1448 0,9994 —0,0796 0,4950 —0,1658 —0,0575
0,40 1,0066 —0,0395 —0,0309 0,1939 —0,1358 0,9980 —0,0774 0,4957 —0,1899 —0,0648
0,45 1,0082 —0,0501 —0,0336 0,2241 —0,1258 1,0014 —0,0749 0,4966 -0,2141 —0,0719
0,50 1,0099 —0,0619 —0,0360 0,2494 —0,1144 1,0052 —0,0721 0,4976 —0,2386 —0,0783
0,55 1,0118 —0,0749 —0,0379 0,2748 —0,1019 1,0093 —0,0690 0,4987 —0,2633 —0,0849
0,60 1,0137 —0,0893 —0,0392 0,3004 —0,0881 1,0138 —0,0655 0,4999 —0,2883 —0,0907
0,65 1,0157 —0,1049 —0,0399 0,3262 —0,0730 1,0184 —0,0618 0,5010 —0,3135 —0,0960
0,70 1,0177 —0,1218 —0,0404 0,3521 —0,0567 1,0228 -0,0577 0,5024 —0,3390 -0,1008
0,75 1,0197 —0,1401 —0,0402 0,3784 —0,0391 1,0285 —0,0534 0,5037 —0,3648 —0,1050
0,80 1,0217 —0,1596 —0,0389 0,4047 —0,0203 1,0338 —0,0487 0,5052 —0,3911 —0,1071
0,85 1,0236 —0,1805 -0,0371 0,4306 1,0393 —0,0437 0,5066 —0,4176 -0,1113
0,90 1,0254 —0,2027 —0,0345 0,4572 1,0450 —0,0385 0,5082 —0,4443 -0,1135
0,95 1,0271 —0,2263 —0,0311 0,4843 1,0507 —0,0328 0,5099 —0,4714 —0,1147
1,00 1,0285 -0,2511 -0,0267 0,5114 1,0565 —0,0268 0,5116 —0,4990 -0,1153
ПРИЛОЖЕНИЕ
Продолжение табл. 12
5 М?) «0 (?) 01 (5) (?) Л41(?) лм?) Мг (?) М2 (5) Qi (?) <Ы?)
0,00 1,0000 0,0000 0,0000 0,0000 <р = 51° —0,2079 0,9781 —0,1039 0,4890 —0,0000 0,0000
0,05 1,0001 0,0006 —0,0052 0,0244 —0,2073 0,9783 —0,1038 0,4891 —0,0228 —0,0102
0,10 1,0005 0,0024 —0,0104 0,0489 —0,2056 0,9791 —0,1033 0,4892 -0,0457 —0,0203
0Д5 1,0012 0,0055 —0,0154 0,0733 —0,2028 0,9804 —0,1026 0,4896 —0,0686 —0,0303
0,20 1,0021 0,0098 —0,0204 0,0980 —0,1988 0,9832 —0,1016 0,4900 —0,0916 —0,0405
0,25 1,0032 0,0153 —0,0259 0,1227 —0,1936 0,9844 —0,1003 0,4906 —0,1147 —0,0500
0,30 1,0046 0,0220 —0,0297 0,1474 —0,1873 0,9871 —0,0987 0,4913 —0,1380 —0,0596
о;з5 1,0062 0,0300 —0,0340 0,1723 —0,1798 0,9913 —0,0969 0,4921 —0,1614 —0,0690
0,40 1,0080 0,0393 —0,0380 0,1972 —о,1712 0,9947 —0,0948 0,4931 -0,1850 —0,0776
0,45 1,0100 0,0498 —0,0416 0,2224 —0,1613 0,9992 —0,0922 0,4940 —0,2088 —0,0869
0,50 1,0121 0,0615 —0,0449 0,2476 -0,1502 1,0027 —0,0895 0,4952 —0,2330 —0,1008
0,55 1,0144 0,0745 —0,0476 0,2731 —0,1380 1,0087 —0,0865 0,4965 —0,2572 —0,1033
0,60 1,0169 0,0888 —0,0500 0,2987 —0,1245 1,0141 —0,0832 0,4978 —0,2818 —0,11(9
0,65 1,0194 0,1044 -0,0517 0,3247 —0,1098 1,0188 —0,0795 0,4993 —0,3069 —0,1181
0,70 1,0221 0,1213 —0,0529 0,3507 —0,0938 1,0259 —0,0755 0,5009 —0,3320 —0,1247
0,75 1,0247 0,1394 —0,0535 0,3770 —0,0766 1,0322 —0,0713 0,5026 —0,3577 -0,1308
0,80 1,0274 0,1590 —0,0534 0,4035 —0,0581 1,0383 —0,0668 0,5044 —0,3836 —0,1362
0,85 1,0300 0,1799 —0,0526 0,4304 —0,0382 1,0448 —0,0619 0,5063 —0,4100 —0,1410
0^90 1,0326 0,2021 —0,0509 0,4509 —0,0170 1,0519 —0,0567 0,5082 —0,4369 —0,1451
0,95 1,0351 0,2256 —0,0486 0,4848 —0,0055 1,0593 -0,0536 0,5102 —0,4641 —0,1484
1,00 1,0433 0,2505 —0,0454 0,5123 —0,0004 1,0668 —0,0453 0,5123 —0,4917 —0,1509
0,00 1,0000 0,0000 0,0000 0,0000 ср = 52° —0,2419 0,9703 —0,1209 0,4851 0,0000 0,0000
0,05 1,0001 0,0006 —0,0060 0,0242 -0,2414 0,9705 —0,1208 0,4852 —0,0200 -0,0117
ОДО 1,0006 0,0024 —0,0120 0,0485 -0,2398 0,9714 —0,1204 0,4854 —0,0441 —0,0235
0,15 1,0013 0,0054 —0,0179 0,0729 —0,2369 0,9729 —0,1197 0,4858 —0,0601 —0,0350
472 ПРИЛОЖЕНИЕ
Продолжение табл.
5 «о (5) «о ($) 01 (С) 02© ЛМ5) Mi ($) ЛМ5) Qi(5) Q2(5)
0,20 1,0024 0,0153 —0,0238 0,0972 —0,2331 0,9753 —0,1187 0,4863 —0,0886 —0,0466
0,25 1,0038 0,0207 —0,0293 0,1218 —0,2281 0,9775 —0,1175 0,4869 —0,1106 —0,0580
0,30 1,0053 0,0218 —0,0348 0,1463 —0,2219 0,9808 —0,1159 0,4877 —0,1335 —0,0692
0,35 1,0072 0,0298 —0,0399 0,1713 —0,2148 0,9845 —0,1142 0,4887 —0,1518 —0,0802
0,40 1,0093 0,0400 —0,0449 0,1960 —0,2063 0,9888 —0,1121 0,4898 —0,1793 —0,0909
0,45 1,0117 0,0494 —0,0494 0,2210 —0,1968 0,9936 —0,1096 0,4909 -0,2000 —0,1014
0,50 1,0142 0,0610 —0,0536 0,2463 —0,1861 0,9989 —0,1070 0,4923 —0,2259 —0,1115
0,55 1,0169 0,0742 —0,0572 0,2716 —0,1742 1,0051 —0,1040 0,4938 —0,2468 —0,1213
0,60 1,0199 0,0892 —0,0606 0,2973 —0,1612 1,0110 —0,1008 0,4955 —0,2738 —0,1307
0,65 1,0229 0,1038 —0,0633 0,3231 -0,1468 1,0178 —0,0973 0,4972 —0,3013 —0,1369
0,70 1,0262 0,1206 —0,0654 0,3494 —0,1313 1,0250 —0,0935 0,4990 —0,3231 —0,1480
0,75 1,0294 0,1387 —0,0670 0,3758 —0,1145 1,0325 —0,0894 0,5010 —0,3473 —0,1560
0,80 1,0328 0,1582 —0,0680 0,4025 —0,0964 1,0406 —0,0849 0,5031 -0,3741 —0,1633
0,85 1,0362 0,1790 —0,0671 0,4295 —0,0771 1,0489 -0,0801 0,5053 —0,3951 —0,1699
0,90 1,0395 0,2011 —0,0677 0,4569 —0,0464 1,0576 —0,0751 0,5076 —0,4270 —0,1761
0,95 1,0429 0,2247 —0,0663 0,4845 —0,0344 1,0663 —0,0697 0,5100 —0,4547 -0,1814
1,00 1,0477 0,2496 —0,0640 0,5125 -0,0110 1,0756 —0,0640 0,5125 —0,4818 —0,1861
? = 53°
0,00 1,0000 0,0000 0,0000 0,0000 —0,2756 0,9613 —0,1378 0,4806 0,0000 0,0000
0,05 1,0002 0,0006 —0,0069 0,0240 —0,2751 0,9616 -0,1377 0,4807 —0,0200 -0,0132
0,10 1,0007 0,0024 —0,0138 0,0481 —0,2735 0,9626 —0,1373 0,4809 —0,0424 —0,0265
0,15 1,0015 0,0054 —0,0205 0,0722 —0,2708 0,9643 —0,1366 0,4813 —0,0602 —0,0396
0,20 1,0027 0,0096 —0,0272 0,0964 —0,2671 0,9666 —0,1357 0,4819 —0,0852 —0,0527
0,25 1,0043 0,0150 —0,0336 0,1207 —0,2623 0,9696 —0,1345 0,4827 —0,1107 -0,0656
0,30 1,0061 0,0216 —0,0399 0,1451 —0,2564 0,9731 —0,1330 0,4836 —0,1284 —0,0784
0,35 1,0082 0,0295 —0,0459 0,1696 —0,2496 0,9774 —0,1313 0,4846 —0,1520 —0,0909
0,40 1,0107 0,0386 -0,0517 0,1944 —0,2414 0,9822 —0,1293 0,4859 —0,1726 —0,1033
0,45 1,0134 0,0490 —0,0572 0,2193 —0,2322 0,9877 —0,1270 0,4872 —0,1942 —0,1154
ПРИЛОЖЕНИЕ
Продолжение табл. 12 *t
5 «о (5) «о (5) МО MS) Mt (?) М2 (5) All (?) AM?) Qi(?) QH?)
0,50 1,0164 0,0606 —0,0622 0,2444 —0,2219 0,9938 —0,1245 0,4888 —0,2178 —0,1272
0,55 1,0196 0,0735 —0,0669 0,2697 —0,2142 1,0005 —0,1216 0,4904 —0^2377 —0Д387
0,60 1,0213 0,0876 —0,0712 0,2954 —0,1978 1,0077 —0,1185 0,4923 —0,2643 —01498
0,65 1,0267 0,1030 -0,0749 0,3213 —0,1839 1,0153 —0*1151 О;4943 —0^2826 —0,1604
0,70 1,0305 0,1197 —0,0790 0,3475 —0,1689 1,0237 —0,1113 0,4965 —0^3124 —0 1708
0,75 1,0344 0,1378 —0,0804 0,3741 —0,1527 1,0324 —0,1074 0j4987 —0^3393 —0’1805
0,80 1,0385 0,1571 —0,0824 0,4008 —0,1352 1,0417 —0,1031 0,5011 —0,3626 —0,1898
0,85 1,0427 0,1778 —0,0837 0,4100 —0,1164 1,0515 —0,0986 0,5036 —0,3881 —0'1985
0,90 1,0468 0,1998 —0,0843 0,4557 —0,0964 1,0616 —0,0936 0,5063 —0*4148 —0 2066
0,95 1,0511 0,2234 —0,0840 0,4857 —0,0748 1,0720 —0,0884 О;5091 —0,4390 —0 2141
1,00 1,0553 0,2482 —0,0829 0,5120 —0,0522 1,0829 —0,0829 О;5120 —О;4693 —0^2208
9 = 54°
0,00 1 0000 0,0000 0,0000 0,0000 —0,3090 0,9511 —0,1545 0,4755 0,0000 0,0000
0,05 1,0002 0,0006 —0,0077 0,0238 —0,3085 0,9515 —0,1544 0,4756 —0,0202 —0,0149
0,10 1,0008 0,0023 —0,0154 0,0475 —0,3070 0,9525 —0,1540 0,4759 —0,0404 —0,0299
0,15 1,0017 0,0053 —0,0230 0,0714 —0,3045 0,9544 —0,1534 0,4763 —0,0609 —0,0447
0,20 1,0031 0,0095 —0,0305 0,0954 —0,3009 0,9570 —0,1525 0,4770 —0,0813 —0,0595
0,25 1,0048 0,0148 —0,0378 0,1195 —0,2964 0,9603 -0,1513 0,4778 —0,1019 —0,0741
0,30 1,0068 0,0215 —0,0449 0,1437 —0,2907 0,9642 —0,1500 0,4788 -0,1227 —О;0887
0,35 1,0093 0,0292 —0,0519 0,1680 —0,2840 0,9690 —0,1483 0,4800 —0,1438 —0,1020
0,40 1,0121 0,0382 —0,0581 0,1925 —0,2763 0,9744 —0,1464 0,4814 —0,1655 —0,1173
0,45 1,0151 0,0485 —0,0649 0,2173 —0,2676 0,9804 —0,1442 0,4828 —0,1866 —0,1312
0,50 1,0185 0,0600 —0,0703 0,2424 —0,2576 0,9872 —0,1418 0,4846 —0,2090 —О', 1448
0,55 1,0223 0,0727 —0,0765 0,2675 —0,2467 0,9947 —0,1388 0,4865 —0,2309 —0,1584
0,60 1,0262 0,0868 —0,0816 0,2931 —0,2346 1,0028 —0,1362 0,4885 —0,2536 —0,1712
0,65 1,0304 0,1021 —0,0863 0,3191 —0,2214 1,0116 —0,1327 0,4907 —0,2767 —О; 1838
0,70 1,0348 0,1187 —0,0905 0,3452 —0,2069 1,0208 —0,1292 0,4931 —0,3003 —0,1962
0,75 1,0393 0,1367 —0,0941 0,3718 —0,1912 i;0307 -0,1254 0,4957 —0,3245 —О;2081
приложение
Продолжение табл. Г2
5 «о (5) »о(5) 61(E) Mi (8) М3(8) Mi (5) ма(О Qi(S)
0,80 1,0441 0,1559 —0,0970 0,3987 —0,1744 1,0412 —0,1213 0,4984 —0,3492 —0,2195
0,85 1,0491 0,1765 —0,0994 0,4261 —0,1563 1,0521 —0,1169 0,5012 —0,3745 —0,2304
0,90 1,0541 0,1985 —0,1010 0,4539 -0,1370 1,0639 —0,1123 0,5042 —0,4003 —0,2407
0,95 1,0591 0,2219 -0,1019 0,4821 —0,1163 1,0759 -0,1072 0,5074 —0,4270 —0,2506
1,00 1,0643 0,2466 —0,1019 0,5108 —0,0943 1,0884 -0,1018 0,5107 —0,4542 —О; 2597
ср = 55е
0,00 1,0000 0,0000 0,0000 0,0000 -0,3420 0,9397 —0,1710 0,4698- 0,0000 0,0000
0,05 1,0002 —0,0006 —0,0085 0,0234 —0,3415 0,9401 —0,1709 0,4699 —0,0191 —0,0160
0,10 1,0008 —0,0023 -0,0170 0,0470 —0,3401 0,9412 -0,1705 0,4702 —0,0383 —0,0321
0,15 1,0019 —0,0053 -0,0255 0,0706 —0,3376 0,9433 —0,1699 0,4707 —0,0586 —0,0481
0,20 1,0034 —0,0094 —0,0339 0,0942 —0,3344 0,9461 —0,1691 0,4714 —0,0770 —0,0641
0,25 1,0053 —0,0147 -0,0420 0,1181 —0,3300 0,9496 -0,1680 0,4723 —0,0965 —0,0798
0,30 1,0076 —0,0212 —0,0500 0,1420 —0,3247 0,9539 —0,1667 0,4732 —0,1164 —0,0955
0,35 1,0103 —0,0289 —0,0577 0,1662 —0,3183 0,9592 —0,1652 0,4747 —0,1304 —0,1111
0,40 1,0134 —0,0378 —0,0654 0,1905 —0,3110 0,9651 -0,1634 0,4762 -0,1566 —0,1265
0,45 1,0168 —0,0480 —0,0725 0,2151 —0,3026 0,9719 -0,1613 0,4779 —0,1773 —0,1418
0,50 1,0206 —0,0593 —0,0795 0,2407 —0,2933 0,9794 —0,1590 0,4797 —0,1981 —0,1578
0,55 1,0247 —0,0720 —0,0860 0,2651 —0,2827 0,9875 —0,1563 0,4818 —0,2197 -0,1714
0,60 1,0292 —0,0859 —0,0920 0,2904 —0,2713 0,9965 —0,1535 0,4841 —0,2414 —0,1858
0,65 1,0340 —0,1010 —0,0977 0,3162 —0,2587 1,0061 —0,1504 0,4866 —0,2637 —0,2000
0,70 1,0390 —0,1175 —0,1029 0,3424 —0,2449 1,0165 —0,1471 0,4892 —0,2865 —0,2138
0,75 1,0442 —0,1353 —0,1075 0,3690 —0,2300 1,0275 —0,1434 0,4990 —0,3100 —0,2268
0,80 1,0497 —0,1544 —0,1115 0,3960 —0,2139 1,0392 —0,1395 0,4950 —0,3339 —о;2402
0,85 1,0554 —0,1749 —0,1150 0,4234 —0,1965 1,0516 —0,1353 0,4981 —0,3585 —0,2528
0,90 1,0612 —0,1967 —0,1171 0,4513 —0,1781 1,0645 —0,1308 0,5015 —0,3838 —0,2649
0,95 1,0671 —0,2200 —0,1232 0,4826 —0,1582 1,0780 —0,1261 0,5050 —0,4110 -0,2814
1,00 1,0732 —0,2447 —0,1203 0,5087 —0,1380 1,0922 —0,1210 0,5087 —0,4366 —0,2876
ПРИЛОЖЕНИЕ
Продолжение табл. 12
5 «о (5) MS) 91(5) 92(5) (5) Ма(5) ЛМ?) AM?) Qi (Q Q2(5)
0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 1,00 0,00 0,05 0,10 0,15 1,0000 1,0002 1,0009 1,0021 1,0037 1,0058 1,0083 1,0113 1,0147 1,0185 1,0227 1,0273 1,0323 1,0376 1,0428 1,0491 1,0552 1,0617 1,0682 1,0751 1,0820 1,0000 1,0002 1,0010 1,0023 0,0000 -0,0006 —0,0023 —0,0052 -0,0093 —0,0145 —0,0210 —0,0285 —0,0374 —0,0473 —0,0587 —0,0711 —0,0848 —0,0998 -0,1162 —0,1338 —0,1527 —0,1732 —0,1947 —0,2179 —0,2424 0,0000 -0,0006 —0,0022 —0,0051 0,0000 —0,0094 —0,0188 —0,0281 —0,0373 —0,0463 —0,0553 —0,0640 -0,0724 —0,0806 —0,0884 —0,0959 -0,1030 —0,1097 —0,1159 -0,1215 —0,1268 —0,1314 —0,1352 —0,1385 —0,1409 0,0000 —0,0102 —0,0203 —0,0304 0,0000 0,0232 0,0464 0,0696 0,0930 0,1162 0,1403 0,1642 0,1882 0,2125 0,2372 0,2622 0,2875 0,3131 0,3392 0,3658 0,3928 0,4204 0,4482 0,4768 0,5060 0,0000 0,0228 0,0457 0,0686 <Р = 56° —0,3764 —0,3760 —0,3746 —0,3724 —0,3692 — 0,3652 -0,3601 —0,3542 —0,3472 —0,3394 —0,3306 —0,3207 —0,3099 -0,2979 -0,2849 —0,2708 —0,2555 —0,2391 —0,2215 —0,2025 —0,1823 <р = 57° —0,4067 —0,4063 —0,4050 —0,4030 0,9272 0,9276 0,9289 0,9311 0,9341 0,9380 0,9428 0,9484 0,9548 0,9721 0,9702 0,9791 0,9889 1,0095 1,0108 1,0328 1,0356 1,0592 1,0635 1,0884 1,0942 0,9135 0,9140 0,9154 0,9177 -0,1873 —0,1872 —0,1869 —0,1863 —0,1855 —0,1845 —0,1833 —0,1818 —0,1800 —0,1781 -0,1760 —0,1735 —0,1709 —0,1680 — 0,1647 —0,1613 —0,1576 -0,1537 —0,1494 —0,1449 —0,1400 —0,2033 —0,2032 —0,2029 —0,2024 0,4636 0,4636 0,4640 0,4646 0,4653 0,4'.63 0,4675 0,4689 0,4705 0,4726 0,4743 0,4766 0,4791 0,4818 0,4847 0,4877 0,4910 0,4945 0,4981 0,5019 0,5059 0,4567 0,4568 0,4572 ' 0,4577 0,0000 —0,0180 —0,0359 —0,0541 —0,0723 —0,0907 —0,1094 —0,1282 -0,1475 —0,1670 —0,1859 —0,2073 —0,2280 —0,2494 —0,2713 -0,2938 —0,3170 -0,3408 —0,3653 —0,3906 —0,4155 0,0000 —0,0167 —0,0335 —0,0503 0,0000 —0,0174 —0,0347 —0,0520 —0,0693 —0,0864 —0,1035 —0,1205 —0,1376 —0,1540 —0,1704 —0,1867 —0,2027 —0,2185 —0,2340 —0,2492 —0,2640 —0,2784 —0,2926 —0,3062 —0,3199 0,0000 —0,0186 —0,0373 —0,0558
476 ПРИЛОЖЕНИЕ
Продолжение табл. 12
Власов, Н. Н. Леонтьев
С «о(5) МО 01 (5) 02(5) Alj (5) Мг (?) Л4Н?) ЛМО <21(0 (МО
0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 1,00 1,0041 —0,0091 —0,0404 0,0917 —0,4000 0,9209 —0,2016 0,4585 —0,0674 —0,0743
1,0063 —0,0143 —0,0502 0,1189 —0,3963 0,9251 -0,2007 0,4596 —0,0845 —0,0928
1,0090 —0,0206 -0,0599 0,1382 —0,3916 0,9302 —0,1996 0,4609 —0,1019 —0J113
1,0122 —0,0282 —0,0694 0,1619 —0,3860 0,9362 —0,1982 0,4624 —0,1195 —0J296
1,0161 —0, U«5l й —0,0786 0,1857 —0,3795 0,9431 —0,1965 0,4641 —0,1376 —0J478
1,0202 —0,0467 —0,0877 0,2037 —0,3722 0,9509 —0,1948 0,4661 —0J559 —0,1659
1,0247 —0,0578 —0,0964 0,2342 —0,3640 0,9596 —0,1927 0,4683 —0,1746 —0,1838
1,0297 —0,0702 —0,1048 0,2589 -0,3548 0,9693 —0,1905 0,4706 —О'1939 —Q 2016
1,0352 —0,0837 -0,1126 0,2840 —0,3446 0,9798 —0,1880 0,4733 —0^2135 —0,2191
1,0410 —0,0986 —0,1204 0,3095 —0,3334 0,9911 —0,1853 0,4762 —0,2337 —0,2365
1,0473 —0,1147 —0,1276 0,3355 —0,3211 1,0034 —0,1823 0,4792 —О'2546 —0,2538
1, (|5, 8 —0,1322 —0,1343 0,3620 —0,3079 1,0164 —0,1790 0,4826 —0,2761 —0^2707
1,0607 —0,1509 —0,1405 0,3889 —0,2936 1,0303 —0,1756 0,4863 —0^2982 —0^2873
1,0677 —0,1711 —0,1460 0,4164 —0,2782 1,0450 —0,1719 0,4898 —0^3210 —О’3037
1,0757 —0,1926 —0,1510 0,4444 —0,2615 1,0606 —0,1679 0,4938 —0^3447 —0,3197
1,0829 —0,2154 —0,1555 0,4731 —0,2436 1,0770 —0,1637 0,4980 —0,3690 —0^3353
1,0908 —0,2399 —0,1590 0,5023 —0,2245 1,0941 —0,1591 0,5023 —0,3942 —0'3506
<₽ = 58°
0,00 0,05 0,10 1,0000 0,0000 0,0000 0,0000 —0,4384 0,8988 —0,2192 0,4494 0,0000 0,0000
1 ,о< оз —0,0006 —0,0110 0,0225 —0,4380 0,8993 —0,2191 0,4495 —0,'0153 —0^0197-
1,0010 —0,0022 -0,0219 0,0449 —0,4369 0,9007 —0,2188 0,4499 —0,0309 —0’0395
0,15 0,20 1,0025 —0,0050 —0,0328 0,0676 —0,4349 0,9032 —0,2183 0,4505 —0^0463 —0^0592
1,0044 —0,0090 —0,0435 0,0903 —0,4323 0,9067 —0,2177 0,4514 —0/1621 —О'0789-
0,25 1,0068 —0,0140 —0,0542 0,1131 —0,4287 0,9111 —0,2168 0,4545 —0^0778 —0,0986 ’
0,30 1,0098 —0,0203 —0,0648 0,1361 —0,4245 0,9165 —0,2158 0,4538 —0,0939 —0’1180
0,35 1,0133 —0,0277 —0,0751 0,1594 —0,4194 0,9229 —0,2145 0,4554 -О; 1103 —0'1375
0,40 1,0173 —0,0362 —0,0852 0,1829 —0,4134 0,9302 -0;2130 0,4573 —О; 1270 —0,1570
0,45 1,0218 —0,0460 —0,0951 0,2067 —0,4066 0,9386 —0,2113 0,4594 —О; 1441 -0Л763 f
478
ПРИЛОЖЕНИЕ
Продолжение табл. 12
*te
’ »-*• О О О О О О О О О О О О О О О О 0.0 О О 1-^00 0 0 i Оѩѩ00 00*4*<1СЭС»елСЛ4>«А*ОООЭЬ5№'-л>±00 о О С© 00 00 1 Otn ОСл ОСл ОСЯ о ОЮСлОСлОСЛ ОСл ОСЛ О ОСяОСЛО |Г«
кА.^00000000000'00000000 — о о о о о со оо -J О Сл ел Us 03 03 ЬЗ — •-*. О О О О О О О со со СО-q 1 о сэ ел о о -q со и*- us -q о ел с© ел <-*• -q ел ьз — о о сссооо^ , -J •-*. СО кА. -q оо 03 US о -J О 00 № КЗ 00 О 00 № 03 О 03 ©3 03 СЛ о 3
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 II 1 1 1 ООооооооооооооооооооо ооооо Kobe — ♦—ь-ы-^^ьОООООООООООООО ЬЗ ЬЗ — — — ОЗ ООО о Л» КЗ О С© *4 О ел US 03 ЬЗ — н- Q О О О О 03000©*. ос:*с>«озл*сгсоозес>ослА*елсэсоозООкй*ьеоо оз со -q сз Со О USK3 СЛ — — 03СО~-4~-4О>£*-О~-400С0~-4СО№СЛО ОО *3 03 ЬЗ ©3 <2 о S
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ооооооооооооооооооооо JO О JO о о оо о о оо ** — — — — ' к*, о о со оо **q оо ел us оз ьз О с© оо -q о us оз ьз — о с© с© со ~q ©? , аооооьеозееозозозкз — с©*зсоА»ьес©*зсл№0 -q — us со с© — 03 со 1— КЗ 03 03 ел О № о оо с© ЬЗ кА. о 00 US о ел о N3003CO —
ООоооооооооооооооооос ооооо USUsusUS03Ce03b3b3b3b3i-A.— ООООО rfs US US us оз Оо ел be о-q us ьз co-q us ьз c©-q ел оз о оо сз us ьз о «©сзозо-q -q -q с© — Us -q — сосс*лозсо0оознА.с©*зслОЗ^О ЬЗ оз rfs ©j с© о сз о ьз©з ел ьз оо — ьеоосл-еьеоооьзсэо с© оз с© с© оз ф ю
111111111 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 о о о о о о о о о о о о о о о о о о О О О -6 ооооо СО 03 ceus^usrf^usa^ususususjsusususus^^tn II 03 03 03 03 оз ел ~q со о — ьеози>«елаоао*з*лоооос©с©с©с©с©о >-*03usao-q с© us оо — оз оо ел us оо о us с© оз оо ьз ел -q оо ел о tfsocoooo sa оз us ел ел -q о us о -q оо о со с© аз — о оз оо -q о g оаэоозоо лме)
кА. кА. t— t— кА. О О о о О о о О О О О О О о о о >-а. НА. НА. 1— О О О О О С© С© е© С© С© С© С© С© 00 00 00 00 00 00 00 00 ООООО , оо оз us ьз о оо-~q ел us се ьз о о с© оо ~q-q ~q оз аз ©з со ©j us се — ЬЗ — — b3US«qhA.-q03,-AOC©ObeCnC©USOOOa>0 00 00 С© — US кА. 1— ОЬЗС>ЭОС©ОзООЛ*0*<1Сли>*С>ЭСл5СлООО>₽'0 кА. ©3 СЛ *4 *4 £ ю S
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ооооооооооооооооооооо ооооо ьеьзьзьзьзьзкзьзьзьзьзьзьзьзьзьзкзьзьзьзье на. ьэ ь»э ь»э ь»э кА. кА. КЗ ЬЗ КЗ 03 03 оз оз US US us US US us us us us us ел соооо — C:e©o3ooo»-A.rfsa3ooob0o3usc3“qooooc©c©c©o -q — us оо — ЬООООкА.О-<1кА.СЛСли>-ООС©ЬОЬО>-А'ОООЗ^С©0 03 ЬЗ 00 ЬЗ 03 £( 3
ооооооооооооооооооооо ооооо US Us US Us US >(>. Us js Us us us us us js us us js >£> * 3* *. *• 0oco~q-qcn>c:eлcлeлususususc<зoзoзoзoзc-зoзo: c©oooo-q-q -q — азьз^с<зюсльзс©ооз1-А.с©^азсл1£-г-0Озоз be-qcooorfs kA.ooookA.ci»P'Cnoocnuschc©ojoco>₽'b3b3CnkA. о e©c©be-qus I1 J'n
1111111(1(1111111111 1(1(1 о ojo ojo oooooooooooooooo ооооо СА?ЬЗЬ©ЬЗЬзЬЭкА.|-А. — ^кА^к^оООООООО 03 03 ьз ьз ьз »—с©-еслозкА.с0-есэЛ'*сек*Осомоепозьэк*о uskA.c©-qin «о м
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Ооооооооооооооооооооо ооооо Ь5 b5kA.kA.hA. ^^^^^^000 ОООООО О £* 03 03 03 03 к*. О С© 00-q О СЛ US Ь5 к* О С© 00 <1 СЭ ел 03 Ь5 »-к Q Oooousb© ел US 03 ЬЭ Ь5 кА. О СО с© 00-q CJ СЛ us >₽• 03 Ь5 ьь О О СЛОО<1-<1 . оз *q кА. сл оо кА. оз ел оо о ьз us ел -q с© >-а. оз us о оо о аэ оз оо ьз ел о ю S
Продолжение табл. 12
6Zf
аинажоЕиаи
Продолжение табл. 12
5 М5) vo (5) 01 (?) М?) ЛМО м2 (?) М, (?) М2(?) . <21(?) <Ы£)
0,20 1,0053 —0,0083 —0,0527 0,0834 —0,5555 0,8383 —0,2787 0,4168 —0,0380 —0,0928
0,25 1,0083 —0,0129 —0,0658 0,1045 —0,5533 0,8435 -0,2782 0,4181 —0,0477 -0,1161
0,30 1,0119 —0,0187 —0,0788 0,1259 —0,5507 0,8499 —0,2775 0,4197 —0,0578 —0,1394
0,35 1,0161 —0,0256 —0,0916 0,1476 —0,5475 0,8574 —0,2768 0,4216 -0,0682 —0,1629
0,40 1,0211 —0,0336 —0,1043 0,1695 —0,5438 0,8662 —0,2758 0,4238 —0,0788 —0,1862
0,45 1,0266 —0,0426 —0,1169 0,1918 —0,5396 0,8760 —0,2748 0,4262 —0,0899 —0,2098
0,50 1,0327 —0,0527 —0,1363 0,2144 -0,5348 0,8871 —0,2736 0,4290 —0,1013 —0,2334
0,55 1,0395 —0,0640 —0,1415 0,2376 —0,5295 0,8994 —0,2724 0,4320 -0,1133 —0,2571
0,60 1,0468 —0,0765 —0,1535 0,2612 —0,5235 0,9128 —0,2709 0,4355 —0,1257 —0,2809
0,65 1,0549 —0,0902 —0,1653 0,2854 —0,5169 0,9275 —0,2693 0,4391 —0,1387 -0,3047
0,70 1,0634 —0,1050 —0,1768 0,3103 —0,5096 0,9434 -0,2676 0,4430 -0,1524 -0,3287
0,75 1,0725 —0,1212 -0,1881 0,3354 —0,5017 0,9604 —0,2657 0,4473 —0,1667 —0,3528
о;во 1,0822 —0,1385 —0,1989 0,3615 —0,4931 0,9785 —0,2637 0,4518 —0,1817 -0,3770
0,85 1,0924 —0,1572 —0,2094 0,3881 —0,4835 0,9981 —0,2615 0,4567 —0,1976 —0,4013
о;эо 1,1031 —0,1774 —0,2195 0,4155 —0,4732 1,0186 -0,2590 0,4618 —0,2163 —0,4256
о;э5 1,1143 —0,1987 —0,2293 0,4439 —0,4621 1,0406 —0,2565 0,4672 -0,2318 —0,4501
1,00 1,1261 —0,2216 —0,2387 0,4729 —0,4500 1,0637 —0,2538 0,4729 —0,2503 —0,4748
<₽ = 63°
0,00 1,0000 0,0000 0,0000 0,0000 —0,5878 0,8090 —0,2939 0,4045 0,0000 0,0000
0,05 1,0004 —0,0005 —0,0147 0,0202 —0,5876 0,8096 —0,2939 0,4046 —0,0077 —0,0238
0,10 1,0014 —0,0020 —0,0294 0,0405 —0,5870 0,8114 —0,2937 0,4051 —0,0156 —0,0475
0,15 1,0033 —0,0045 —0,0440 0,0609 —0,5861 0,8143 —0,2935 0,4058 —0,0234 —0,0714
0,20 1,0059 —0,0081 —0,0586 0,0814 —0,5847 0,8185 —0,2931 0,4069 —0,0315 —0,0953
0,25 1,0092 -0,0126 —0,0732 0,1020 —0,5830 0,8238 —0,2927 0,4082 —0,0396 —0,1192
0,30 1,0132 —0,0183 —0,0877 0,1229 —0,5808 0,8304 —0,2922' 0,4098 —0,0480 —0,1432
0,35 1,0179 —0,0250 —0,1021 0,1441 —0,5783 0,8382 —0,2916 0,4118 —0,0567 —0,1672
0,40 1,0234 —0,0328 —0,1162 0,1656 —0,5754 0,8471 —0,2907 0,4140 —0,0657 —0,1924
0,45 1,0295 —0,0415 —0,1305 0,1874 —0,5720 0,8573 —0,2899 0,4165 -0,0751 -0,2158
ПРИЛОЖЕНИЕ
Продолжение табл. 12
t5
5 "о (5) '^(Х) 61(5) е2 (5) All (5) Л4а(5) All (5) ЛМ5) Qi(5)
0,50 1,0364 —0,0515 —0,1414 0,2096 —0,5684 0,8687 —0,2889 0,4194 —0,0849 —0,2402
0,55 1,0440 —0,0625 —0,1583 0,2324 —0,5643 0,8813 —0,2879 0,4226 —0,0951 —0,2646
0,60 1,0523 —0,0747 —0,1719 0,2555 —0,5597 0,8952 —0,2867 0,4260 —ОД 059 —0,2894
0,65 1,0612 —0,0880 —0,1853 0,2793 —0,5548 0,9103 —0,2854 0,4297 —0,1171 —0,3143
0,70 1,0709 —0,1072 —0,1987 0,3036 —0,5495 0,9266 —0,2839 0,4338 —0,1291 —0^3392
0,75 1,0810 —0,1185 —0,2117 0,3287 —0,5437 0,9442 —0,2823 0,4381 —0,1417 —0,3644
0,80 1,0919 —0,1355 —0,2244 0,3543 —0,5376 0,9681 —0,2806 0,4428 —ОД 550 —0^3898
0,85 1,1035 —0,1538 —0,2368 0,3807 —0,5310 0,9882 —0,2787 0,4478 —0,1691 —0Д154
0,90 1,1156 —0,1735 —0,2489 0,4078 —0,5239 1,0047 —0,2767 0,4531 —0,1839 —0,4412
0,95 1,1284 —0,1945 —0,2607 0,4359 —0,5165 1,0273 —0,2746 0,4587 —ОД 997 —0,4672
1,00 1,1417 —0,2169 —0,2721 0,4647 —0,5085 <р = 64 е 1,0513 —0,2722 0,4647 —0,2163 —0,4933
0,00 1,0000 —0,0000 —0,0000 0,0000 —0,6157 0,7880 - —0,3078 0,3940 0,0000 0,0000
0,05 1,0004 —0,0005 —0,0154 0,0197 —0,6156 0,7886 —0,3078 0,3941 —0,0060 —0^0242
0,10 1,0015 —0,0019 —0,0308 0,0395 —0,6145 0,7904 —0,3077 0,3946 —0,0121 —0'0485
0,15 1,0035 —0,0044 —0,0461 0,0593 —0,6143 0,7934 —0,3075 О;3954 —0^0183 —0^0729
0,20 1,0061 —0,0079 —0,0615 0,0793 —0,6133 0,7977 —0,3072 0,3964 —0,0246 —0’0972
0,25 1,0096 —0,0123 —0,0768 0,0994 —0,6119 0,8032 —0,3069 О;3978 —0^0310 —0Д217
0,30 1,0138 —0,0178 —0,0919 0,1198 -0,6103 0,8098 —0,3065 0,3994 —0,0378 —ОД 662
0,35 1,0188 —0,0243 —0,1071 0,1405 —0,6083 0,8178 —0,3060 0,4014 —0,0447 —0Д709
0,40 1,0245 —0,0319 —0,1221 0,1615 —0,6060 0,8270 —0,3054 0,4037 —0'0520 —ОД 957
0,45 1,0310 —0,0405 —0,1371 0,1828 —0,6034 0,8374 —0,3047 0,4063 —0'0596 —0^2206
0,50 1,0383 —0,0501 —0,1519 0,2046 —0,6006 0,8490 —0,3040 0,4093 —0,0677 —0^2458
0,55 1,0463 —0,0610 —0,1667 0,2268 . —0,5974 0,8620 —0,3031 0,4124 —0,0761 —О', 2709
0,60 1,0549 —0,0729 —0,1812 0,2496 —0,5937 0,8761 —0,3021 0Д159 —0,0851 —0^2965
0,65 1,0643 —0,0859 —0,1956 0,2728 —0,5899 0,8916 —0,3011 0,4198 —0,0946 —О', 3222
0,70 1,0745 —0,1001 —0,2099 0,2968 —0,5858 0,9083 —0,2999 0,4239 —0,1047 —0^3481
0,75 1,0853 —0,1156 —0,2239 0,3213 —0,5811 0,9254 —0,2986 0,4284 —0,1153 —0,3743
ПРИЛОЖЕНИЕ
приложение
483
Продолжение табл. 12
UP О’ £i£?2J22£2 S43£24&5££J£$S2**S<3a*-«iocsicsicoojeQoco S3i2S2£ О О ф^чг^чг^чт* ч-f СЧ 04
isj* О’ 00 Ф Ф Г*- 04 ОСОГ'*04Г’ч*4Г'чГ'чСОЮСОч^<^0040ч^С©1П*-«чг»« ^oO'TJHSSs Ф*3’оосог’ч04юо|1П^Г’ч*з<^с»Г'-Ю101пё5с5 04 £2 1ГЭ со оо ооо^^счмл ?:^><МЛОФ^ОООс^СмУ *1’*1*1**4 *“• ООООООООООООООООО*н-₽и*4*-< <?с?с?с?с? ооооооооооооооооооооо 1 1 1 1 1 11 Illi II 111 11111111}
и? 15 °?? ^ooio io сою ю сч ю со сч £2 22 \2 ^3 42 £2£0с0«5<>;0с000001юо0чгнюст5со000100с001л со со чр lq оо оо со оо со со оо ф ф ф ф о о о *4 *4 oi oi со со •*< СОСОСОСОСОСОСОСОсОСОСОч^ч^чРчРчРчРч^чРч^ч^ О о о о о ооооооооооооооооооооо
UP |< eq X о со со чРчрсосчог^чр-тмсо-^соо^сччрсососочр-^соч^ Ю-^СЧО ’-|'Нти«г<тиоООФФСОГ'Г'СОЮ^СОСЧ’^СОО ффффф oicqoioqoicqcqc>q-^4r-«^-₽4-₽4'T-<«₽M-^*^4r-«^oo eq eq eq eq 04 cococococococococococococococococococococo 00000 ооооооооооооооооооооо 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
($.1 zw CO о О ОЮ^ЮСС*С^<Х1Ю«НС^ФС4,-?С0ФС0С0С'000 lq co 00 eq со Осооо-^и’Эчгноосо^эсооо-^ю-^оосоФГ’чО'^Ф ЧГ CO 00 *4 СО ФОСО^Ь-ХСОФО^М'СЮ^ХОМ^Ь-С’П О О Ф О О Г*Г*Г-Г*1>«0«1>-1>«ОСООООООООООООФФФФФО ОООти-и О О О О О О О О О О О О О О О О О О О О чН
(5) W о со eq со х> со lQ oQ^oouoococooor^^r^ococqcoootfo-tf-crr^o СО Ю Ф со 00 00 V-со *<Р cq <О Ю чН V-ю Ф cq ЧР со со Ю СО чгч Ь-Г'СЮЮ (I ЮьО1ЛМ0и0Ю-<Г-<Г'СРС0С0О4'^'^ОФ00[>СОЮ'СР ю ю юю ю II c^c^cqcqcqcqcqcqcqcqcqcqcqcqoq-^*^^^^^ 00000 ооооооооооооооооооооо 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
UP еч Ф ООСЮО^ЮСОтиОЙФСЭОЛ^СОФЮООО LQ LQ О ООООС’чС’чС’чСССОС'чООС^ОСОСОСТ’СОООСОФС’чиО СССМФГч-Ю Оч^С-ЭЮГ-ОчгнеОЮГчОС^чСНСООО’^СОСОООчНчР sr b-ФМЮ ОООООО^’^'Н'^ЙЙММ^^ОЮЛ^'^ со СО СО <1< «. - - - ~ - - * ооооооооооооооооооооо ооооо 1 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
UP ф Ст> со о- СО СО 0'^СЧ'^ФОО'гИ'^ФОСОООСООФФ001-ООСОСО о-чтн^оо осос'1ооючг-«сс>с'1Г'-соф«<5<01-оою0100«<5<оо со Ю со Г- Ф О’^Ю'^^О^О’^М^’ЮЬ-ФОМЮЮСОСОФО cqcqcqoqcq ооооооо’Н’^’^’^’П’^^м^^ммйл ООООО ООООООООООООООООООООО 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
UP о О cocqcqoo оюфсог'О^Г'О^ссюо^ооо^^соЮ'Н С^ОФОчгн 00-^-<Г1>«С\10«СОчгнСТ>ООФОСОО«С^ООС01Л>ЮС^ СО LQ со Ф ООООО-^чгнС^С0С0’0*1ГЭ0«С0Ф'^СЧ'СГС0С0О ,_( см о о О О О О О О О О О О О О О ч-< чгн ч-< чгн 04 ооооо ооооооооооооооооооооо 1 1 1 1 1 IIIIII 1 1 1 II II II 11 II 1
UP о 3 Ю'но^со о^сосо^с^фсО'СсюЮ'СО^союйюсо СОО1С4ЮФ ООчгнсОСООчСГФ^СЧ^ООГ^ГчООФ-^^ООСЧГч о> о eq со чр ооооО’^’^’^йсосо^юог'ХО’г-'М'С^ о OOOOOOOOOOOOOOOO*^^-^^^
UP СЮО^О О^>О^ОЮО1^О^ОЮОЮОЮОЮОЮО 00 00 Ф Ф О ООчНчгчСМС^СОСО*е,«<5<ЮЮСОСОЬчО«СОСОФФО ОООО*ч 0 0 00 0 0 00 0 00 00 00 0 0 00 0*4
ЛИТЕРАТУРА
1. Антоневич П. Г., К расчету балок и плит, опирающихся на упругое
основание, Изв. Томского политехи, ин-та, № 76, 1954.
2. Ахша румов Р. Т., Об одном методе расчета прямоугольных пластин
на упругом основании, Сб. трудов Ереванского политехи, ин-та, № 4,
1950.
3. Безухов Н. И., Теория упругости и пластичности, М., Гостехиздат,
1953.
4. В а т с о н Д. Н., Теория бесселевых функций, ч. 1—2, М., ИЛ, 1949.
5. В и к с н е В. П., О колебаниях балок, лежащих на упруго-массивном ос-
новании, Сб. «Вопросы динамики и динамической прочности», № 2, Изд,
АН ЛатвССР, Рига, 1953.
6. Винокуров Л. И., Определение отпоров упругого полупространства
под нагруженным фундаментом при учете совместной работы нескольких
фундаментов и образования участков пластических отпоров, Труды Харь-
ковского инж.-строит, ин-та, вып. 5, 1957.
7. В л'а со в В. 3., Некоторые новые задачи по теории тонкостенных кон-
струкций, Сб. статей под ред. В. В. Бургмана, вып. 1, М., 1948.
8. В л а с о в В. 3., Общая теория оболочек и ее приложение в технике, Гос-
техиздат, М.—Л., 1949.
9. В л а с о в В. 3., Пространственные конструктивные облегченные формы
гидротехнических сооружений и методы их расчета, Изв. АН СССР, Отд.
техн, наук, № 10, 1951.
10. В л а со в В. 3., Метод начальных функций в задачах теории упругости,
Изв. АН СССР, Отд. техн, наук, № 7, 1955.
11. Власов В. 3., Леонтьев Н. Н., Техническая теория расчета фун-
даментов на упругом основании, Труды Московского инж.-стронт. ин-та,
сб. № 14, 1956.
12. В л а с о в В. 3., Тонкостенные пространственные системы, Госстройиздат,
М., 1958.
13. Власов В. В., Метод начальных функций в плоской задаче теории упру-
гости, Изв. МВО СССР, № 2, 1958.
14. Власов В. В., Метод начальных функций в задачах равновесия толстых
многослойных плит. Изв. АН СССР, Отд. техн, наук, № 7, 1958.
15. В л а с о в В. В., Метод начальных функций в плоской задаче теории упру-
гости, канд. диссертация, М., 1958.
16. Г а л е р к и н Б. Г., Упругие прямоугольные и треугольные свободно опер-
тые толстые плиты, подверженные изгибу. Доклады АН СССР, № 10, 1931.
17. Г а лер кин Б. Г., Напряженное ссстояние при изгибе прямоугольной
плиты по теории толстых плит и теории плит тонких, Труды Ленинград-
ского ин-та сооружений, вып. 2, 1935.
18. Галин Л. А., О гипотезе Циммермана—Винклера для балок, Прикл.матем.
и мех., т. 7, вып. 4, 1943.
ЛИТЕРАТУРА
485
19. Г а л и н Л. А., Контактные задачи теории упругости, Гостехиздат, М.,
1953.
20. Г а с т е в В. А., Расчет тонких пластинок иа упругом основании, нагру-
женных по прямоугольным площадкам, Труды Ленинградского ии-та ин-
женеров промышленного строительства, № 1, 1934.
21. Г ер с еванов Н. М.и Мачерет Я. А., К вопросу о бесконечно длин-
ной балке на упругой почве, нагруженной силой, Гидротехническое строи-
тельство, № 10, 1935.
22. Г и л ь м а н Л. С., К вопросу об определении напряжений на поверхности
упругой среды, Труды Ленинградского ин-та инженеров промышленного
строительства, вып. 1, 1934.
23. Г о р б у и о в -П о с а д о в М. И., Плиты на упругом основании, Строй-
издат, М., 1941.
24. Горбунов-Посадов М. И., Осадки фундаментов на слое грунта,
подстилаемом скальным основанием, Стройиздат, М., 1946.
25. Горбунов-Посадов М. И., Балки и плиты на упругом основании,
Стройиздат, М., 1949.
26. Горбунов-Посадов М. И., Расчет конструкций на упругом основа-
нии, Гос. изд. литературы по строительству и архитектуре, М., 1953.
27. Д и д о в Б. В., Разработка метода расчета плиты на упругом основании
по Циммерману, Сб. трудов лаборатории оснований и фундаментов
ВОДГЕО. № 9, 1938.
28. Д н н и и к А. Н., Круглая пластинка на упругом основании, Изв. Киев-
ского политехи, ин-та, 1910.
29. Д и н н и к А. Н„ Приложение функций Бесселя к задачам теории упру-
гости, ч. 1, Киев, 1913.
30. Е г о р о в К- Е., Распределение напряжений и перемещений в двухслой-
ном основании ленточного фундамента, Сб. трудов научно-иссл. сектора трес-
та глубинных работ, № 10, 1939.
31. ЖемочкинБ. Н., 1) Плоская задача расчета бесконечно длинной балки
на упругом основании; 2) Расчет балок на упругом полупространстве и
полуплоскости. Изд. ВИА, М., 1937.
32. Жемочкнн Б. Н. иСиницын А. П., Практические методы расчета
фундаментных балок н плит на упругом основании (без гипотезы Винкле-
ра), Стройиздат, М., 1947.
33. 3 а в р и е в К- С., Свободные колебания балок на упругом основании,
Сообщения АН ГрузССР, 1945.
34. И ш к о в а А. Г., Точное решение задачи об изгибе круглой пластинки, ле-
жащей на упругом полупространстве, под действием симметричной равно-
мерно распределенной нагрузки, Доклады АН СССР, т. 4, № 2, 1947.
35. Канторович Л. В. иКрылов В. И., Приближенные методы высшего
анализа, Гостехиздат, М.—Л., 1950.
36. Киселев В. А., Развитие метода деформаций на рамы на сплошном упру-
гом основании, Проект и стандарт, № 10, 1933.
37. К н^с е л е в В. А., Балки и рамы на упругом основании, ОНТИ, М.—Л..
38. Клейн Г.' К., Учет неоднородности, разрывности деформаций н других
механических свойств грунта при расчете сооружений на сплошном основа-
нии, Труды Московского инж.-строит, ин-та, сб. № 14, 1956.
39. Клишевич Г. В., Расчет балок на упругом основании в применение
его к расчетам гидротехнических сооружений, Госэнергоиздат, Л.—М.,
1932.
40. К л у б и и П. И., О расчете днищ шлюзов-и доков, Изв. АН СССР, Отд.
техн, наук, № 3, 1953.
41. Коренев Б- Г., Об изгибе неограиидениэй плиты, лежащей на упругом
основании, Доклады АН СССР, т. 79, -вып. 8, 1951.
486 ЛИТЕРАТУРА
42. к op е и е в Б. Г., Вопросы расчета балок и плит на упругом основании,
Госстройиздат, М., 1954.
43. К о р е и е в Б. Г., Конструкции, лежащие на упругом основании, Строитель-
ная механика в СССР 1917—1957, М., 1957.
44. К о р н е в и ц Э. Ф. и Эндер Г. В., Расчет сплошных днищ сухих до-
ков, Госстройиздат, М., 1940.
45. К о с а б ь я и Л. В., Расчет прямоугольных плит на упругом однослойном
основании, канд. диссертация, 1956.
46. К речме р В. Б., Расчеты и проектирование плоских железобетонных
фундаментов, ч. 1, ОНТИ, М.—Л., 1936.
47. Крылов А. Н., О расчете балок, лежащих на упругом основании.
Изд. АН СССР, М„ 1930.
48. Крылов А. Н., Вибрация судов, Изд. АН СССР, М.—Л., 1936.
49. К у з н е цо в В. И., Упругое основание, Гос. изд. литературы по строи-
тельству и архитектуре, М., 1952.
50. К у з н е ц о в В. И., Работы советских ученых в области теории расчета
конструкций иа упругом основании, Труды Института истории техники
АН СССР, № 8, 1954.
51. Кузьмин Р. О., Бесселевы функции, ОНТИ, М—Л., 1935.
52. Л е о н о в М. Я-, К теории расчета упругих оснований, Прикл. матем. и
мех., т. 3, вып. 2, 1939.
53. Леонов М. Я-, К расчету фундаментных плит, Прикл. матем. и мех.,
т. 4, вып. 3, 1940.
54. Леонтьев Н. Н., Практический метод расчета тонкостенной цилиндри-
ческой трубы на упругом основании, Труды Московского йнж.-етриит. ин-тй,
сб. № 27", 1957.
55. Л е о и т ь е в Н. Н., Приложение вариационного метода В. 3. Власова к
расчету фундаментов гидротехнических сооружений, канд. диссертация, 1952.
56. Л у р ь е А. И., Пространственные задачи теории упругости, Гостехиздат,
М, 1955.
57. Л я в А., Математическая теория упругости, ОНТИ, М.—Л., 1935.
58. М а л и е в Л. С., Балки.на упругом основании с переменным по их длине
коэффициентом постели, Труды Ленинградского ин-та инженеров промыш-
ленного строительства, вып. 6, ГОНТИ, Л., 1938.
59. Мусхелишвили А. И., Некоторые основные задачи математической
теории упругости, изд. 3-е, Изд. АН СССР, М., 1949.
60. Никольский А. И., Универсальный метод расчета сооружений на сжи-
маемых грунтах, сб. Свирьстроя, XIII—XIV, 1937.
61. Пастернак П. Л., Статическая теория гибких балок и плит на упругом
основании, Бетон и сталь, № 9—10, Берлин, 1926.
62. Пастернак П. Л., Основы нового метода расчета фундаментов на упру-
гом основании при помощи двух коэффициентов постели, Гос. изд. литера-
туры по строительству и архитектуре, М —Л., 1954.
63. Пузыревский Н. П., Фундаменты, Госстройиздат, М., 1944.
64. Рабинович И. М., Достижения строительной механики стержневых
систем в СССР, Изд. Акад. арх. СССР, М., 1949.
65. Р а б и и о в и ч И. М., Курс строительной механики, ч. II, -,Гос. изд. лите-
ратуры по строительству и архитектуре, М., 1954.
66. Руднев В. И., Новейшие методы расчета балок иа сплошном упругом
основании, Труды ВИОС, Основания и фундаменты, сб. № 2, Стройиздат,
1934.
67. Р у д и е в В. И.,Приближенный метод расчета балки на сплошном упругом
основании без гипотезы Винклера, Сб. НИС Фундаментстроя, № 8, 1937.
68. Р у ч к и и В. П., Расчет днищ резервуаров на сплошном упругом основа-
нии, канд. диссертация, 1956.
69. С и м в у л и д и И. А., Расчет балок, лежащих иа сплошном упругом ос-
новании, без гипотезы Винклера, Метрострой, № 5, 1936.
ЛИТЕРАТУРА
487
70. С н и т ко Н. К., Расчет балок на упругом основании переменного сечения,
Вестннк инженеров и техников, № 8, 1935.
71. Тимо ш е и к о С. П., Теория упругости, над. 2-е, ОНТИ, М.—Л., Главная
ред. техи.-теоретической литературы, 1937.
72. У ма иски й А. А., О расчете балок на упругом основании, Стройиздат
М„ 1933.
73. Уманский А. А., Специальный курс строительной механики, ч. 1,
Госстройиздат, М.—Л., 1935.
74. УрбанИ. В., Температурные напряжения в балке, лежащей на сплош-
ном упругом основании, Труды Московского ин-та инженеров транспорта,
вып. 54, Трансжелдориздат, 1937.
75. Филоненко-Бородич М. М., Некоторые приближенные теории
упругого основания, Ученые записки МГУ, вып. 46, 1940.
76. Филоненко-Бородич М. М., Простейшая модель упругого осно-
вания, способная распределять нагрузку, Сб. трудов Московского электро-
мех. ии-та инженеров транспорта, вып. 53, Трансжелдориздат, 1945.
77. Филоненко-Бородич М. М., Теория упругости, изд. 4-е, Физ-
матгиз, М., 1959.
78. Флорин В. А., Определение реакций полуплоскости посредством при-
менении строки Маклорена, Сб. Гидроэнергопроекта, вып. 2, 1937.
79. Ф л о р и и В. А., Расчеты оснований гидротехнических сооружений, Строй-
издат, М., 1948.
80. Ц ы т о в и ч Н. А., Механика грунтов, изд. 3-е, Стройиздат, М., 1951.
81. Ч е ч е А. А., Применение вариационного метода В. 3. Власова к решению
некоторых практических задач термоупругости, кавд. диссертация, 1952.
82. Ч е ч е А. А., Расчет бетонных блоков и массивных плит иа жестком и упру»
гом основаниях от температурных воздействий с применением метода проф
В. 3. Власова, Сб. научных работ Белорусского политехи, ин-та, вып. 54,
Минск, 1956.
83. Ш а п и р о Г. С., Изгиб полубесконечной плиты, лежащей на упругом основа-
нии, Прикл. матем. н мех., т. 7, вып. 4, 1943.
84. Шехтер О. Я-, О влиянии мощности слоя на распределение напряжений
в фундаментной балке, Сб. трудов НИС треста глубинных работ, № 10, 1939.
85. Ш е х т е р О. Я., Расчет бесконечной плиты, лежащей на упругом основании
конечной и бесконечной мощности и нагруженной сосредоточенной силой,
Сб. трудов НИС Фундаментстроя, № 10. 1939.
86. Ш п и л ь р е й н Я. Н., Таблицы специальных функций, 1933.
87. Штаерма н И. Я., Контактные задачи теории упругости, Гостехиздат,
М.—Л., 1949.
88. ШтаерманИ. Я-, Распределение давления под фундаментом при нали-
чии пластической зоны, Труды Московского инж.-строит, ин-та, сб. № 14,
1956.
89. Янке Е. и Эмде Ф., Таблицы функций с формулами и кривыми Гос-
технздат, М.—Л., 1959.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аргумент операционный 363
Балка бесконечная 90, 119
— длинная 188
— жесткая 98, 119, 130, 188, 307
— конечная И, 119, 135
— короткая 188
Бесселя уравнение 58
— функции 232
---модифицированные 58, 226
Бимомент 373
Бубнова—Галеркина метод 195, 213, 388
Вектор геометрический 388
— статический 358
Виета тесрема 231
Винклера гипотеза 30
Винклера—Циммермана гипотеза 139
--- модель 28
Вигхарта решение 31
Власова задача 141
Ганкеля функции 232
----- модифицированные 266
Гипотеза Винклера 30
— Винклера—Циммермана 139
— Кирхгсфа—Лява 372, 379
— коэффициента постели 30
— о равенстве нулю поперечных удли-
нений 14
— плоских сечений 13
Горбунова-Пссадова метод 108, 119
Давление реактивное 92, 100, 104, 307
Девиация 272
Деформация изгиба 256
— кручения 256
— осесимметричная 260
— пластическая 109
— плоская 21
— поперечная 17
— растяжения 257
— сдвига 12, 257
Деформация сжатия 257
— температурная 64
— удлинения 12
Длина характеристическая 111
Днище резервуара цилиндрического 281
Жесткость конструкции 170
— плиты цилиндрическая 138
— полосы 76
Загружение кососимметричное 102
— симметричное 98
Задача бигармоническая 261
— Власова 141
— контактная 384
— Леви 141
— Навье 141
— плеская 12, 388
— пространственная 355
— симметричная 159, 243
— температурная 64
Закон взаимности операторов преобра-
зования 371
— внецентренного сжатия 352
— затухания осадок 26
Затухание осадок 39
Изгиб балки 13
— осесимметричный 227
— плиты на однослойном основании 139
— — толстой 395, 406
— стенки 14
— цилиндрический 184, 188
Импульс мгновенный 299, 302, 311
Интеграл Стилтьеса 19, 54
Кирхгсфа—Лява гипотеза 372, 379
Колебание простое гармоническое 291
Колебания балки 288, 290, 308
---вынужденные 303
— — жесткой ЗС5
— — упругой 308
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
489
Колебания основания 289
— плиты 312
--- бесконечной 314
---главные 325
---кососимметричные 331, 340
— свободные 322
---симметричные 329
Кольцо спорное 282, 284
Концентрация реактивных давлений
107, 109
Коэффициент влияния 82
— постели 31, 96
— Пуассона 12
— сжатия грунта 229
Коэффициенты Фурье 413
Кривизна гауссова 254
Кручение плиты узкой 184
Лагранжа принцип 143
— уравнение 165
Лапласа оператор 58, 227
--- двойной 138
Леви задача 141
— теорема 407
Линия прогибов 167
— упругая 304
Маклорена ряд 358
Масса системы обобщенная 319
--- приведенная 300
Матрица единичная 82
— коэффициентов влияния 90
— преобразования 84
— прямого преобразования 82, 84, 369
Метод Бубнова—Галеркина 195, 210,
388
— Горбунова-Пссадова 108, 119
— деформаций 286
— Коши — Крылова 415
— коэффициента постели 96, 281
— Крылова 19, 342
— напряжений 356
— начальных параметров 81, 111, 171
--- функций 357
— перемещений 12, 286, 356
— Пузыревского—Крылова 81
— сил 286
— символический 359
— смешанный 356
— статический 167
— тригонометрических рядов 161,
427
— упругого полупространства 281
— фундаментальных функций 167
Модель Винклера—Фусса 30
— Винклера—Циммермана 28
— упругого основания двумерная 16
Модель упругого основания двуслой-
ная 47
-------многослойная 28
-------обобщенная плоская 23, 28
-------однослойная 26, 31
-------с двумя коэффициентами по-
стели 31
-------с двумя характеристиками
26, 28, 55
Модуль упругости 12
Момент изгибающий 91, 140, 193
— инерции 346, 349
— — обобщенный 18
— критический 351
— крутящий 140
— обобщенный 154
Навье теорема 141
Нагрузка 86
— кососимметричная 14, 102, 162, 176,
218
— симметричная 98, 162, 176, 194,
216, 356, 365
Напряжения 52
— касательные 15, 17, 51, 154
— нормальные 15, 17, 51
— тепловые (температурные) 63
Натяжение арматурного стержня 352
Оболочка сферическая полегая 254
— цилиндрическая 286, 287
Оператор Лапласа 58, 227
— — двойной 138
— однозначный 362
Операторы дифференциальные 162, 360,
393
— — бигармонические 362
---гармонические 362
•--полигармонические 362
Ортогональность преобразований 369
— фундаментальных функций 159, 294
Осадка поверхности основания 25, 36,
НО
Основание с двумя характеристиками
55
— с четырьмя характеристиками 47
— упругое двуслойное 43, 130
— — многослойное 430
— — однослойное 137
---трехмерное 50
Отпор равномерный 101, НО
Параметры начальные 82, 84, 87, 112,
176
Перемещение 12, 51, 356
— виртуальное 177
— возможное 16
490
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Перемещение динамическое 304
— обсбщенное 13, 14, 51, 75, 82
— оболочки нормальное 255
---тангенциальное 257
— поперечное 12
— продольное 12
Пластинка ступенчатая 152
Плита бесконечная 243
— водосливной плотины 208
— двуслойная 404, 425
— жесткая 235
__ конечная 247
— круглая 226, 229, 235, 251, 253
— многопролетная 423
— многослойная 420, 429
— плоско-деформнрованная 402
---напряженная 403
— прямоугольная 169, 345 , 349, 400,
403
— толстая 220
Плита-сболочка 385
Плоскость контактная 380, 427
Поверхность плиты изогнутой 324, 329
— прогибов плиты 142, 195, 341, 347
Показатель гибкости балки 115, 116
---плиты 206, 208
Полоса прямоугольная 409
Полудлнна балки приведенная 115, 117
Потеря устойчивости изгибная 350
--- крутильная 350
Преобразование обратное 369
— прямее 369
Приведение двумерной задачи к одно-
мерной 141, 143
— трехмерной задачи к двумерной 371
Пригрузка боковая 119, 122, 210
Принцип возможных перемещений 20
— Лагранжа 143
Прогиб балки .97
— обобщенный 75, 142, 154
— пластинки 14
Пуассона коэффициент 12
Пузыревского—Крылова метод 81
Работа виртуальная 17, 20, 154
— напряжений 56, 59, 147, 199
— однослойного основания 138, 149,
200
— сил 17, 52
---внешних 56, 144, 146, 200
--- внутренних 144, 146, 200
Реакции фиктивные 113, 198, 202
Решение Внгхарта 31
— Рибьера 401, 419, 423
— Садовского 104
— Файлона 415, 419, 423
— Филоненко-Бородича 31
Рибьера решение 401, 419, 425 .
Ряд Маклорена 358
— Фурье 425, 431
Ряды операционные 364
Садовского решение 104
Сила внешняя 16
— внутренняя 16
— критическая 342, 344 , 346, 350
----Эйлера 346
— обобщенная 47
---- внутренняя 153
---- поперечная 20, 41, 75, 91, 99,
140, 154
----- продольная 20
---------- сжимающая 344
— ударная 315
— фиктивная 150, 272
Силы внутренние нормальные 17
------сдвигающие 17
— инерционные 306, 312, 357
— массовые 23
— поверхностные 23
Симметричность матриц 83
Система дискретно-континуальная 16
— функций фундаментальная 81, 157
Слой упругий конечной толщины 380
----переменной толщины 372
----постоянной толщины 372
Составляющие вектора интенсивности.
355
----перемещения 355
— тензора напряжений 355
Состояние деформированное 17, 22
— — плоское 21, 76, 393
— напряженное 21, 22
----плоское 11, 76, 393
---- пространственное 366
— оболочки безмоментное 257,259, 261,
272
---- изгибное 257, 260
----плоское напряженное 268
Стилтьеса интеграл 19, 54
Теорема Беттн 153
— Виета 231
— Леви 404
— о взаимности работ 371
Теория плит бимоментная 373, 379
----моментная 372, 379
----сблочек моментная 386.
----приближенная 375
---- точная 375
Томсона функции 276
Угол поворота 14, 93
----обобщенный 75, 154
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Удлинение относительное 12
Уравнение Бесселя 58
— вековое 343
— геометрическое оболочки 256
— изгиба балки 73
---- плиты 226
----тонких плит 138, 139
— колебаний балки 156
— Лагранжа 165
— статическое оболочек 256
— сферической оболочки 258
— характеристическое краевой зада-
чи 292
Усилия в оболочке 257
— кольцевые 227
— обобщенные 82
— радиальные 227
Условие контактное 138
Условия граничные геометрнческне372
---- кинематические 292
----смешанные 292, 372
----статические 292, 371
— неразрывности деформаций 256
— равновесия 16, 52, 195
---- вариационные 199
----обобщенные 75, 143, 149
Устойчивость плиты 340, 343, 346
----внецентренно сжатой 349
----предварительно напряженной
353
----узкой 344
Факторы кинематические 84, 88
— силовые 151
— статические 84, 88
Файлона решение 415, 419, 423
Фнлоненко-Бороднча решение 31
Форма операторов Дифференциальная
364, 396
----интегро-дифференциальная 364,
396
Формулы операционные трансцендент-
ные 364
Формы колебаний главные 299
Функции Бесселя 232
----модифицированные 58, 266
Функции влияния 83, 88 ЧИ
— Ганкеля 232 «Ц
---- модифицированные 266
— колебаний собственных 293
— начальные 388
----основные геометрические 358.
— — статические 358
— Томсона 276
— тригонометрические 161
— фундаментальные 293, 297
----колебания балкн 155, 159
Функция гиперболо-тригонометриче-
ская 172
— изгиба балки на упругом основании;
80
— осадки основания (прогибов) 99
— поперечного распределения пере-
мещений 13, 15, 31, 92, 104
-------- прогиба 142
— прогибов балкн 80, 91
Фурье коэффициенты 413
— ряд 425, 431
Характеристика балкн упругая 75, 11Ё
— упругого основания 32, 33, 45
Характеристики основания интеграла
ные 30, 56
— упругие 22, 45, 76, 77
----однослойного основания '139
----основания (обобщенные) 139
----плиты (обобщенные) 139
Частота колебаний 157, 310
— свободных колебаний плиты 322„
325
— собственных колебаний 293, 296
-------- балкн 156
Числа фундаментальные 293
Число степеней свободы 16, 52
Штамп кольцевой 241
— круглый 235
— симметричный 104 ]
Эйлера сила критическая 346