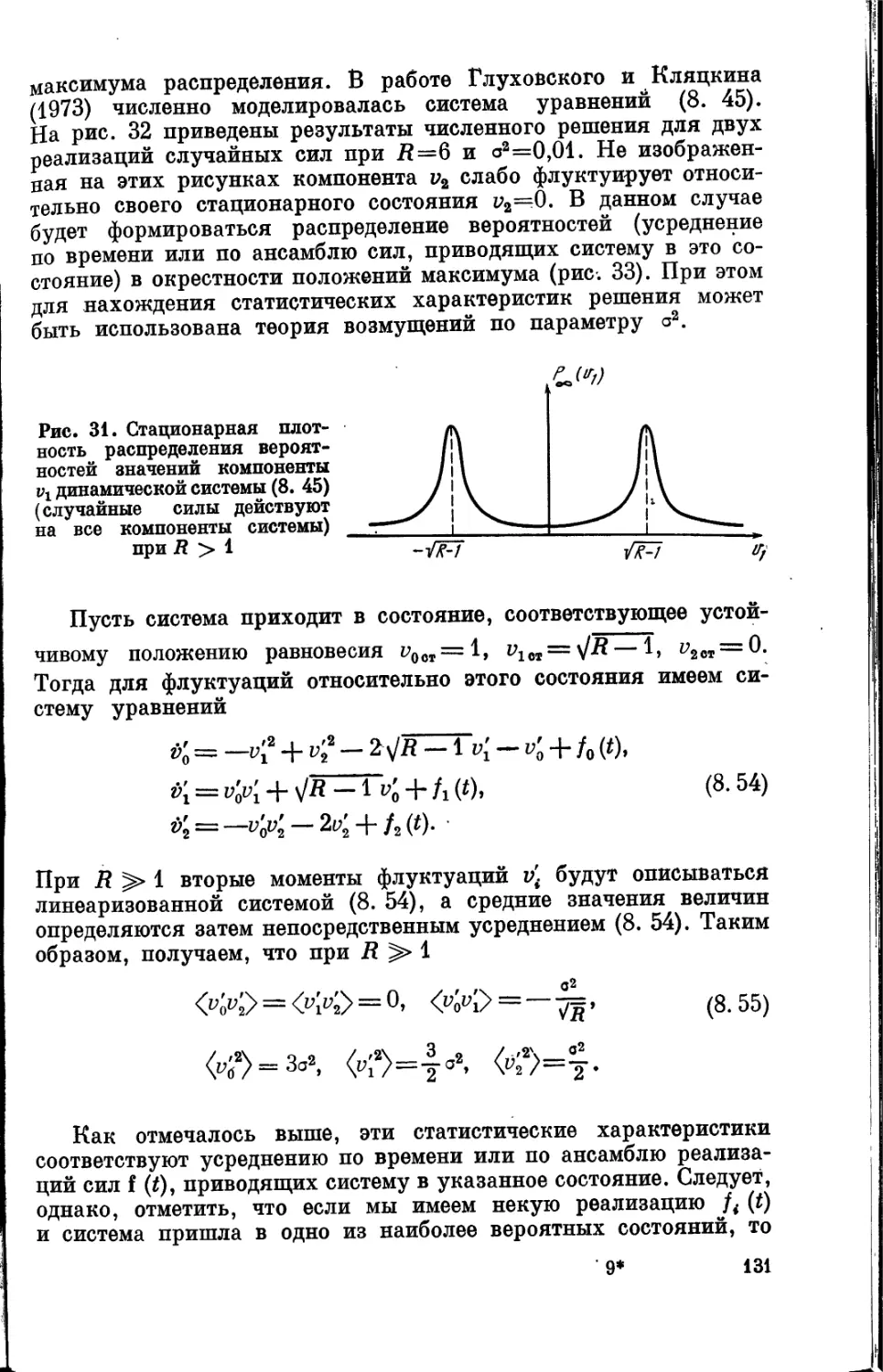
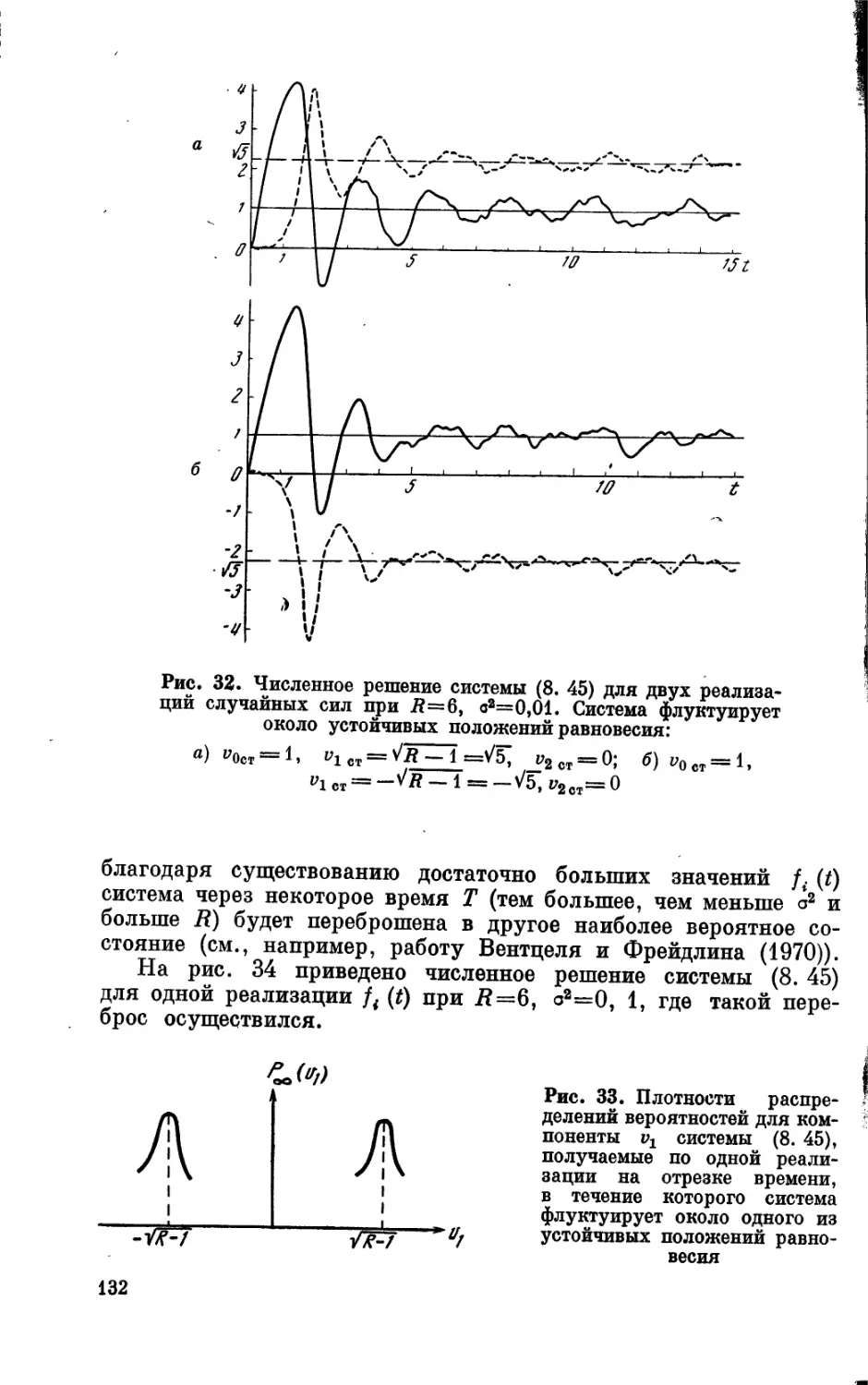
Текст
НЕЛИНЕЙНЫЕ
СИСТЕМЫ
ГИДРОДИНАМИЧЕСКОГО
ТИПА
I
/
академия наук ссср
ИНСТИТУТ ФИЗИКИ АТМОСФЕРЫ
НЕЛИНЕЙНЫЕ
СИСТЕМЫ
ГИДРОДИНАМИЧЕСКОГО
ТИПА
ИЗДАТЕЛЬСТВО «НАУКА»
МОСКВ А 1974
УДК 55.511.32
Нелинейные системы гидродинамического типа. Должан-
ский Ф. В., Кляцкин В» И., Обухов А, М,, Чусов М. А. М.,
«Наука», 1974.
В монографии излагается теория систем гидродинамиче-
ского типа с применением ее к расчету простейших явлений,
важных для геофизики: конвективных процессов, каскадного
преобразования энергии в развитом турбулентном потоке,
а также к проблеме количественного учета различного рода
«шумов» в нелинейных системах, моделирующих процессы
в атмосфере.
Сформулированы общие критерии, которым должны удов-
летворять модели, претендующие на описание реальных гидро-
динамических процессов. Уравнения движения таких моделей,
названных системами гидродинамического типа, обладают
важнейшими свойствами исходной системы уравнений гидро-
динамики. Результаты могут быть применены к теории моде-
лирования естественных гидродинамических процессов как
в лабораторных условиях, так и с помощью ЭВМ.
Монография рассчитана на специалистов, работающих
в области динамики атмосферы и океана, прикладной гидро-
динамики, а также на аспирантов и студентов старших кур-
сов, обладающих достаточной математической подготовкой.
Ответственный редактор
академик
А. М. ОБУХОВ
тт 20807-0194 _ _ _
Н 042(1)-1974 Б3"81"73
© Издательство «Наука», 1974 г.
ПРЕДИСЛОВИЕ РЕДАКТОРА
При теоретическом изучении таких крупных естественных объек-
тов, как атмосфера Земли в целом или Мировой океан, в настоящее
время широко используются гидродинамические модели. Это поз-
воляет объяснить и предсказать многие геофизические процессы
на основе решения уравнений гидромеханики. Решение послед-
них, когда они применяются к решению геофизических задач,
развивается по двум взаимно дополняющим друг друга направле-
ниям.
Первое направление основано на линеаризации исходных урав-
нений относительно некоторого известного стационарного решения.
Напомним, что это направление ведет свое начало по крайней мере
с динамической теории приливов, созданной Лапласом в 1774—
1776 гг. (Лаплас (1799); см. также Дарвин (1898)). Работа Гельм-
гольца (1886), также выполненная в русле этого направления и
посвященная динамике перемещения атмосферных масс, стала клас-
сической для теоретической динамики атмосферы.
Линеаризация с успехом применяется для изучения распростра-
нения волн в атмосфере и океане (внутренние волны, волны Рос-
сби—Блиновой, акустические и гравитационныв/Волны). Развитие
линейной теории позволило за последние 20—30 лет дать общую
классификацию динамических процессов в атмосфере и выяснить
механизм «адаптации» барического поля. Наиболее полный и со-
временный обзор этих результатов содержится в монографии Ди-
кого (1969).
Однако для решения важнейших практических задач, например,
численного прогноза погоды, исследования основных механизмов
преобразования энергии в атмосфере, построения теории океа-
нической циркуляции, линейная теория оказалась совершенно
недостаточной. Это явилось причиной разработки второго направ-
ления, основная особенность которого — построение упрощенных
моделей, описываемых ограниченным числом параметров, т. е.
использование в качестве модели системы с ограниченным коли-
чеством степеней свободы. Уравнения движения этих систем ока-
зываются уже существенно нелинейными. Решаются они обычно
численно с использованием ЭВМ; иногда их удается исследовать
качественно методами нелинейной механики. Это направление
3
необходимо для изучения геофизических объектов (атмосфера,
Мировой океан) в целом, и поэтому оно бурно развивается сейчас
как в СССР, так и за рубежом.
В связи с этим возникают общие вопросы: что это за упрощен-
ные модели; как их строить и каким общим требованиям они
должны удовлетворять; какие важные свойства изучаемого объекта
должны быть обязательно сохранены в «хорошей» модели; как их
конкретно сформулировать. Авторы настоящей монографии и по-
пытались четко сформулировать указанные вопросы и по воз-
можности дать на них ответ.
Заметим, что значение рассматриваемых в монографии проблем
выходит за рамки изучения только геофизических объектов; они
важны и в физике всякий раз, когда исследователь сталкивается
с необходимостью учета нелинейных эффектов, например, в физике
плазмы (Кадомцев и Карпман (1971)), для решения задач которой
уже созданы методы исследования нелинейных процессов в непре-
рывных средах.
Рассмотрение широкого класса нелинейных моделей, эффек-
тивно используемых в динамической метеорологии, в частности
в численном прогнозе погоды и теории общей циркуляции атмо-
сферы, показывает, что, как правило, соответствующие задачи
решаются с учетом нелинейности «во втором порядке», т. е. в боль-
шинстве важнейших геофизических приложений применение квад-
ратично-нелинейных уравнений оказывается уже достаточным.
Очень существенно при изучении крупных геофизических объек-
тов использование интегралов движения, например энергии, мо-
мента количества движения, потенциального вихря. Очевидно, что
в «хороших» моделях должны существовать аналоги соответствую-
щих интегралов движения, в противном случае общий физический
анализ результатов становится затруднительным или практически
невозможным.
При анализе и «конструировании» гидродинамических моделей
представляется весьма полезным общее понятие «система гидро-
динамического типа», введенное одним из авторов монографии
(Обухов, 1969). Так называется система, у которой общие свойства
уравнений с точки зрения характера нелинейности и законов
сохранения такие же, как и у изучаемого гидродинамического
объекта, но которая имеет конечное число степеней свободы.
Более точное определение и описание свойств систем гидро-
динамического типа дается в главе II после краткого изложения
в предшествующей главе основных методов аппроксимации урав-
нений гидродинамики.
В книге рассматриваются конкретные интерпретации простей-
ших систем гидродинамического типа. При этом удается исследо-
вать вопросы, важные для изучения любой нелинейной модели,
например, существование стационарных решений, их устойчивость,,
обмен энергией между основными степенями свободы (модами).
4
В монографии изложены результаты лабораторного экспери-
мента, в котором простейшая трехмодовая модель была реализо-
вана в виде «жидкого вращения» ртути в трехосном эллипсоиде.
Внешнее возбуждение, имитирующее бароклинные силы в реаль-
ных геофизических системах, в лабораторном эксперименте осу-
ществлялось с помощью вращающегося магнитного поля.
На основе изложенных в книге общих методов анализа нелиней-
ных гидродинамических систем исследована модель конвекции и
установлены критерии устойчивости. При этом оказалось возмож-
ным включить в рассмотрение влияние силы Кориолиса, что явля-
ется характерным для геофизических задач.
Вряд ли здесь уместно более подробно излагать содержание
книги — общее представление об этом дает оглавление. Хотелось
бы отметить только, что в книге, написанной коллективом ав-
торов — сотрудниками теоретического отдела Института физики
атмосферы АН СССР, имеется некоторое разнообразие стилей,
причем главы, излагающие вопросы общего характера, переме-
жаются с материалом, относящимся к решению конкретных
гидродинамических задач. Нам казалось, что такое построение
может облегчить чтение, делая его менее утомительным. Оконча-
тельное суждение предстоит высказать читателю.
В известном смысле предлагаемая книга является введением
в «анатомию» сложных квадратично-нелинейных гидродинами-
ческих систем. Возникающие при этом простейшие «блоки», об-
ладающие небольшим числом степеней свободы, исследуются
вполне конкретно на примере систем, представляющих самостоя-
тельный интерес.
Написанию книги значительно способствовали дискуссии
с Л. А. Диким, любезно согласившимся дать дополнительные за-
мечания к общему определению систем гидродинамического типа
(приложение I). В подготовке материала принимали активное
участие сотрудники теоретического отдела ИФА АН СССР и прежде
всего А. Б. Глуховский и Е. Б. Гледзер. В оформлении иллюстра-
тивного материала большую* помощь оказала И. Б. Казицкая.
Всем этим лицам авторывыражают свою искреннюю благодарность.
Авторы будут весьма признательны читателям за критические
замечания.
А, М. Обухов
ВВЕДЕНИЕ
Одна из основных трудностей получения конкретных выводов
(не только количественного, но и качественного характера) о дви-
жении жидкости вызвана бесконечностью числа степеней свободы
гидродинамических объектов, которая сочетается с нелинейностью
уравнений гидродинамики. Одним из возможных путей ее преодо-
ления является замена объекта с бесконечным числом степеней
свободы системой с конечным числом степеней свободы, но описы-
ваемой нелинейными уравнениями, аналогичными уравнениям
гидродинамики. При реализации этой возможности сразу возни-
кает вопрос: а какое минимальное число степеней свободы должно
быть у этой системы для того, чтобы она отражала наиболее су-
щественные черты процесса? Дать общий ответ на этот вопрос
весьма трудно, так как очень большое значение имеет конкретная
постановка задачи.
Вопросы математического обоснования такой редукции в на-
стоящее время еще мало разработаны и связаны с решением очень
трудных проблем, которым посвящена, например, монография
Ладыженской (1970).
В связи с этим естественно обратиться к неоднократно опи-
санным в литературе гидродинамическим экспериментам, указы-
вающим на эффективность использования правильно выбранной
нелинейной модели с малым числом параметров. При интерпрета-
ции этих экспериментов основную роль играет теория подобия,
позволяющая выделить важнейшие безразмерные параметры (кри-
терии подобия), от которых зависит характер изучаемого процесса.
В таких экспериментах некоторые «фазовые характеристики»
исследуемого движения могут зависеть от всегда задаваемого с не-
которой неопределенностью начального состояния, и в этом смысле
можно говорить о многозначности решений данной гидродинами- .
ческой задачи. Она может проявляться как неопределенность '
установления в системе того или иного режима движения, опре-
деляемого в основном внешними параметрами. После этого началь-
ные возмущения несущественны и, как правило, «забываются»
системой в процессе ее эволюции. Зачастую некоторое весьма
простое частное решение фактически вообще не реализуется, так
как оказывается неустойчивым.
5
Как известно, основными безразмерными критериями явля-
ются, например, число Рейнольдса для динамики несжимаемой
вязкой жидкости, число Тейлора для динамики вращающейся
жидкости, числа Рэлея и Прандтля для конвективных движений.
На неединственность решений уравнений гидродинамики указы-
вают классические эксперименты Тейлора (1923) и Бенара (1901),
показавшие возможность существования различных режимов жид-
кости. На рис. 1 последовательно представлены фотографии тече-
ния между вращающимися цилиндрами при различных числах
Тейлора, а рис. 2 иллюстрирует характер изменения ячеек Бенара
при изменении числа Рэлея.
Не вдаваясь в детали теоретических исследований указанных
течений, являющихся предметом многих монографий (см., на-
пример, Шлихтинг (1959), Гринспэн (1968)), можно сформулиро-
вать основной их вывод: при определенных условиях жидкость
ведет себя как динамическая система со сравнительно небольшим
числом эффективных степеней свободы.
С математической точки зрения качественное изменение ха-
рактера течений при изменении внешних параметров свидетель-
ствует о том, что само течение становится неустойчивым относи-
тельно возмущений, которые всегда существуют в природе. Это при-
водит к установлению нового динамического режима (так называе-
мая бифуркация решения). Новый динамический режим часто ока-
зывается уже устойчивым в определенном диапазоне изменения па-
раметров. Однако здесь возможны различные ситуации. Так, на-
пример, устойчивость в целом всегда имеет место, если жидкость
движется как твердое тело. С другой стороны, имеются течения,
которые, по-видимому, сразу переходят в турбулентные, когда
число Рейнольдса превосходит критическое значение. Для наибо-
лее изученного движения вязкой жидкости в круглой трубе даже
при закритических числах Рейнольдса необходим некоторый ма-
лый, но конечный «толчок» для перевода системы в турбулентное
состояние. Об этом говорит известное явление «затягивания» ла-
минарного режима (Монин и Яглом (1965)).
Имеющиеся данные и опыт теоретических исследований гидро-
динамической устойчивости указывают на чрезвычайную слож-
ность этой проблемы. Внимание многочисленных исследователей
сосредоточено на изучении отдельных примеров и сравнительно
узких классов течений типа упомянутых выше. Однако в ряде слу-
чаев в нелинейной постановке задачи все же удается доказать
устойчивость определенного типа при заданных параметрах и до-
статочно общей постановке задачи (Арнольд (1965), Дикий (1965а, б;
1967), Юдович (1965)).
В связи с этим можно отметить, что в развитии нелинейной
теории устойчивости, тесно связанной с проблемой возникновения
турбулентности, в настоящее время определилось два основных
направления:
Рис. 1. Вихри между двумя концентрическими цилиндрами при различных
числах Тейлора (Гринспэн (1968))
Рис. 2. Ячеистая структура
в слое жидкости, подогревае-
мой снизу (Шлихтинг (1959))
а — толщина слоя 4 мм, течение
ламинарное;
б <— толщина слоя 10 мм, течение
ламинарное;
в — толщина слоя 20 мм. течение
турбулентное
1. Аппроксимация уравнений гидродинамики конечномерной
системой обыкновенных дифференциальных уравнений (метод
Галеркина).
2. Развитие и обоснование теоретических соображений Ландау
(1944) (см. также Ландау и Лифшиц (1953), Монин и Яглом (1965)
и работу Рюэля и Такенса (1971), посвященную переходу ламинар-
ного течения в турбулентное).
Первое направление основано на разложении решений уравне-
ний гидродинамики в конечные ряды по системе координатных
функций и соответствует проектированию бесконечномерного фа-
зового пространства решений уравнений гидродинамики на конеч-
номерное подпространство. Далее в первой главе мы подробцее
остановимся на этом методе, так как он представляется наиболее
перспективным с точки зрения дальнейшего развития теории.
Второе направление связано с соображениями Ландау о раз-
витии турбулентности в результате роста малых возмущений.
Согласно Ландау при переходе числа Рейнольдса (или какого-
либо иного параметра, характеризующего течение) через крити-
ческое значение стационарное течение теряет устойчивость, и уста-
навливается новый, вообще говоря, периодический автоколебатель-
ный режим (вторичное течение), который, в свою очередь, устой-
чив только в определенном интервале значений параметра. Далее
он снова теряет устойчивость и т. д. Предполагается, что по мере
того как параметр увеличивается могут последовательно появ-
ляться новые виды возмущений и при этом будут возникать ус-
ловно-периодические движения со все большим числом частот.
Поэтому при достаточно большом значении параметра течение
будет столь сильно возбуждено, что его можно считать турбулент-
ным. При этом значение параметра, при котором происходит смена
режимов, и характер неустойчивости можно определять, лине-
аризируя уравнения гидродинамики относительно соответствую-
щего решения. Описание гидродинамической неустойчивости в
линейной постановке задачи можно найти в классических моногра-
фиях Линя (1955) и Чандрасекара (1961). Отметим, что последова-
тельная реализация общей схемы Ландау представляет в настоящее
время непреодолимую задачу. Более того, даже осуществление
первого шага в схеме Ландау для простейших течений натал-
кивается на серьезные трудности. В связи с этим Стюартом и дру-
гими (см. обзорные работы Стюарта (1971а, б)) была предложена
относительно простая приближенная процедура расчета вторичных
течений вблизи порога потери устойчивости ламинарного течения.
Однако их метод требует знания тех собственных функций (век-
торов), которым отвечают растущие возмущения (по линейной тео-
рии). Эта задача уже сама по себе достаточно сложна, и решается
она главным образом путем использования метода Галеркина для
выделения основных неустойчивых мод. Таким образом, указан-
ные выше два направления отнюдь не являются взаимоисключаю-
щими, и уже сейчас намечаются пути их синтеза.
9
В’предлагаемой читателю книге сделана попытка систематизи-
ровать различные подходы к разработке и анализу нелинейных
моделей гидродинамических процессов, включая простейшие мо-
дели, допускающие непосредственное аналитическое исследование.
При этом имелись в виду возможности применения предлагаемых
методов анализа и конструирования нелинейных моделей к гео-
физическим задачам.
После первой главы, где дается краткое изложение общих прин-
ципов аппроксимации гидродинамических уравнений, в главе II
излагается теория систем обыкновенных дифференциальных урав-
нений, получаемых в результате такой аппроксимации. Основным
здесь является понятие «система гидродинамического типа».
В главе III дается физическая интерпретация простейшей си-
стемы гидродинамического типа на примере задачи о движении
жидкости в трехосном эллипсоиде. Основные вопросы, такие, как
устойчивость движения и стационарные режимы, исследовались
не только теоретически, но и экспериментально на лабораторной
установке в Институте физики атмосферы АН СССР.
В главе IV общие методы анализа систем гидродинамического
типа применяются к вопросу о нелинейных взаимодействиях
в задаче о конвекции. С помощью достаточно простой модели уда-
ется выяснить специфику нелинейных процессов в явлениях кон-
векции, представляющих большой интерес для геофизических
приложений. Это относится, в частности, к одновременному
учету нелинейных свойств системы и влияния силы Кориолиса.
С помощью простейших трехмодовых систем (триплетов) ока-
зывается возможным строить более сложный системы с большим
числом степеней свободы. Такой метод применяется в главе V
для моделирования каскадного процесса преобразования энергии
в турбулентном потоке. С помощью моделей, имеющих вид нелиней-
ных цепочек, удается получить известные законы распределения
энергии в спектре турбулентного потока.
В главе VI показано, каким способом сформулированные ра-
нее методы могут быть применены к изучению взаимодействия ко-
лебаний (волн), например, волн Россби—Блиновой. При этом
оказывается полезным обобщение построенных систем гидроди-
намического типа на случай комплексных координат в фазовом
пространстве системы. Глава VII носит более математический ха-
рактер и посвящена разработке вопросов, относящихся к струк-
туре простейших систем гидродинамического типа.
Последняя VIII глава посвящена краткому изложению не-
которых вопросов, связанных со статистическим описанием про-
цессов в нелинейных системах, моделирующих гидродинамические
явления. Эта глава носит как бы «заявочный» характер, поскольку
сама тема является очень широкой и выходит за рамки монографии.
Глава полезна для ознакомления читателя с общей постановкой про-
блемы. Материал,^предъявляющий несколько повышенные требова-
ния к математической подготовке читателя, выделен в приложениях.
Глава I
КОНЕЧНОМЕРНЫЕ АППРОКСИМАЦИИ
УРАВНЕНИЙ ГИДРОДИНАМИКИ
§ 1. Аппроксимация уравнений гидродинамики
по методу Галеркина
Метод Галеркина, а точнее метод Бубнова—Галеркина является
одним из наиболее универсальных методов решения краевых
задач для дифференциальных уравнений, обыкновенных или
в частных производных, линейных или нелинейных. Впервые этот
метод был применен в 1913 г. для решения задач теории упругости
И. Г. Бубновым (Бубнов, 1913), а в более общей форме в 1915 г.
Б. Г. Галеркиным (Галеркин, 1915). Изложение указанного ме-
тода приводится во многих руководствах по приближенным ме-
тодам вычислений (см., например, монографии Михлина (1957,
1966), Красносельского, Вайникко и др. (1969)). Сущность метода
заключается в следующем.
Пусть неизвестная функция и (Р), заданная в некоторой об-
ласти V координат Р, удовлетворяет неоднородному оператор-
ному уравнению
Lu = ?(P) (1.1)
и некоторым однородным линейным краевым условиям. Оператор
L будем считать пока линейным оператором. Далее, пусть имеется
полная система координатных функций срх (Р),. . ., cpn (Р),. . .
(так называемая координатная последовательность), которые
нужное число раз (в соответствии с требованиями задачи) диффе-
ренцируемы и которые удовлетворяют всем краевым условиям
нашей задачи. Ввиду того, что Lu — f есть нулевой элемент про-
странства, он ортогонален ко всем уп, т. е.
(Lu— /, cpfc) = O, со, (1-2)
гДе (а, Ь) — соответствующим образом введенное скалярное про-
изведение *. Метод Галеркина состоит в том, что приближенное
* В задачах гидродинамики скалярное произведение полей естественно
определять, используя соответствующее выражение для кинетической
энергии.
11
решение уравнения (1. 1) ищется в виде линейной комбинации
координатных функций
гая(Р)=2зд^) (!-3)
к=1 ;
с неопределенными коэффициентами аЛ, которые затем определя-
ются из условий ортогональности невязки Lun—f первым п эле-
ментам координатной последовательности
(Lun — f, Ю=°> * = 1, п. (1.4)
Эти условия приводят к следующей системе п линейных уравнений
относительно коэффициентов ак:
п
= 7 = 1, и. (1.5)
к~1
ЗдесьЛ — матрица с элементами A Jk=(L^k, fy), a=(a1? а2,. .ап),
a tj—kf' ?/)• В силу линейности краевых условий функция
(1. 3) им, очевидно, удовлетворяет. Таким образом, метод Галер-
кина сводит неоднородную краевую задачу (1. 1) к неоднородной
системе линейных уравнений (1. 5), решение которой определяет
коэффициенты линейной комбинации (1. 3). В сущности он эк-
вивалентен одному из проекционных методов приближенного ре-
шения операторного уравнения (1. 1) (см., например, монографию
Красносельского, Вайникко и др. (1969)). В том случае, если
L (и) — нелинейный оператор, указанная выше процедура также
может быть выполнена, но в левой части (1. 5) мы будем иметь век-
тор, зависящий от коэффициентов разложения . ., ап уже
нелинейным образом. Следует отметить, что первоначально в ка-
честве условия применимости метода Бубнов сформулировал тре-
бование ортогональности координатных функций, которое на са-
мом деле необязательно, однако, приводит к значительному со-
кращению выкладок.
Аналогичным образом решается задача и о нахождении соб-
ственных значений для уравнения Ьи=Уи.
Метод Галеркина уже давно широко применяется для практи-
ческого решения самых разнообразных прикладных задач, в том
числе весьма успешно и к решению нелинейных задач, хотя
обоснование его оказывается сравнительно трудным. Поскольку
вопросам, связанным с обоснованием указанного метода, посвя-
щена обширная математическая литература, мы не будем под-
робно останавливаться на них.
Вследствие того, что метод Галеркина достаточно универсален
и эффективен, он занимает весьма важное место среди других
прямых методов, используемых в гидродинамике. В качестве при-
мера рассмотрим следующую краевую задачу с начальными зна-
чениями для уравнений Навье—Стокса, описывающих движение
несжимаемой жидкости в ограниченной области V пространства;
12
^+L(v) = ^ + (v.V)v-vAv = -lvP + f, (1.6)
Uh UU f-'
div v = 0,
v|s = 0, v(x, 0) = a(x). (1.7)
Здесь v (x) — поле скорости, v — кинематическая вязкость, f —
массовая сила, давление р определяется, как обычно, из условия
несжимаемости, на границе S области V поставлены условия
прилипания.
Решение этой задачи ищется в соответствующем пространстве
векторных функций и (х)=^{и1 (х), и2 (х), и3 (х)}, х£7, квадра-
тично интегрируемых по области V, причем скалярное произве-
дение в этом функциональном пространстве определяется равен-
ством
(u, v) = j (и • v) d3x. (1. 8)
У
Здесь интеграл распространяется по всей области V, занятой
жидкостью, а точка означает обычное скалярное произведение
двух векторов.
С помощью метода Галеркина решение задачи (1. 6) сводится
к решению конечной системы обыкновенных дифференциальных
уравнений. Для этого, следуя Ладыженской (1970) и Брушлинской
(1964), будем искать приближенное решение задачи (1. 6) в виде
V„ (X, t) = 2 Ч (0 Ф* (х), (! • 9)
к=1
причем в качестве координатной последовательности {фа (х)}
берется полная в V система ортонормированных собственных век-
торных функций следующей ^^1ейной задачи:
= —Mfc + (!•10)
dMfc = 0, = 0 (1.10а)
и, кроме того,
(Ф1^=1. (1.11)
У
Свойства оператора, соответствующего этой задаче, описаны в мо-
нографии Ладыженской (1970), обозначениями которой мы и поль-
зуемся.
Подставляя (1. 9) в (1. 6) и умножая обе части получающегося
равенства скалярно на получим
dz л / \ л
2Г+ 5 (Ь (0 ф, (х) • фй(х)М3х = J (f • ф*) d3x, (1.12)
к — 1, п.
13
Здесь член, отвечающий силам давления, опускается в силу того,
что из (1. 10а) следует, что i
( (Vp . фй) J3X = Xр (n. ^}dS = 0, (1.13)
У 8 1
где п означает единичный вектор нормали к поверхности S.
Легко убедиться, что соотношения (1. 12) эквивалентны сле-
дующей галеркинской системе п обыкновенных дифференциальных
уравнений:
4 = — —+ (1.14)
h »»=1
где
Тия = ПФ*ЧФг?)Ф».)^ (1.15)
а свободные члены в (1. 14) суть коэффициенты Фурье массовых
сил
Д=$(ЬФЙ)^ (1.16)
У
(точка, стоящая над символом и, означает дифференцирование по
времени).
Таким образом, искомые амплитудные функции zk (t) находятся
из уравнений (1. 14) и начальных условий
= *=ТГ^ ' (1.17)
где в силу (1. 11)
z^) — j (а(х) • ф^ (я))-й3я, к—1,п. (1.18)
Коэффициенты ~{к1т удовлетворяют соотношению
п
2 4klmZkZlZm = (1.19)
fc, Z, «п=1
которое выражает, очевидно, закон сохранения кинетической
энергии жидкости при отсутствии массовых сил (1=0) и вязкости
(v=0), поскольку в этом случае, ввиду ортогональности ф*и (1.11),
из (1. 14) получим
У fc=l
Метод Галеркина широко применяется в прикладных задачах
гидродинамики. Он оказывается весьма полезным при исследова-
нии устойчивости различных гидродинамических течений (см., на-
пример, работы Ди Прима (1955), Брушлинской (1965) и (1968),
14
Стюарта (1960), Уотсона (1960), Кувабара (1966), Бириха (1965),
Пекериса и Школлера (1967) и (1969), Доуэлла (1969), Джорджа
и Хелламса (1972)) и, в частности, при исследовании устойчивости
конвективных течений (Гершуни и Жуховицкий (1972)). Приве-
денный перечень работ, конечно, не является полным.
В следующем параграфе мы рассмотрим один характерный
пример эффективного применения метода Галеркина к свободному
движению идеальной жидкости, заключенной в эллипсоидальную
полость. Этот вид течения имеет большое значение, так как в ряде
частных случаев он поддается точному теоретическому анализу
и в то же время сохраняет все те характерные особенности, ко-
торые присущи многим реальным течениям в силу нелинейности
уравнений гидродинамики. В третьем параграфе мы рассмотрим
применение метода Галеркина уже к неидеальной жидкости, на
примере задачи о плоском движении вязкой жидкости под дейст-
вием периодической силы.
§ 2. Жидкий гироскоп как иллюстрация
применения метода Галеркина
к исследованию движения идеальной несжимаемой
жидкости
Рассмотрим задачу о вихревом свободном движении идеальной
несжимаемой жидкости, ограниченной поверхностыогэллипсоида,
уравнение которого имеет вид
S(z, у, z)^g+g+^-l = O. (1.21)
Эта задача является в известном смысле классической и рассматри-
валась в трудах Гринхилла (1879), Хафа (1895) и Пуанкаре (1910),
а также Жуковского (1885).
Для решения задачи естественно использовать известное урав-
нение Гельмгольца (см., например, книгу Кочина, Кибеля и Розе
(1963))
^=^4-(v.V)a=(fi.V)v, Q = rotv, (1.22)
принимая во внимание уравнение неразрывности
divv = 0 (1-23)
й граничное условие на поверхности 5=0
y» = (v-n)|g=0, (1.24)
I
которое можно также записать в виде
(V- V)5=0 (1.24а)
при 5=0.
15
Здесь п означает единичный вектор нормали к поверхности.
Существует частный вид движения жидкости, в котором уравне-
ния Гельмгольца (1. 22) допускают точное решение, а именно од-
нородное вихревое движение жидкости, при котором вектор Й=
=rot v остается постоянным в каждый момент времени и одинаковым
для всех частиц жидкости. Далее будет показано, что имеются три
линейно независимые поля скорости, каждое из которых описывает
стационарное однородное «эллиптическое» вращение жидкости
вокруг какой-либо из трех главных осей эллипсоида. Эти стацио-
нарные бездивергентные векторные поля скорости, которые, оче-
видно, линейно зависят от координат, представляют точные ре-
шения уравнения Гельмгольца (1. 22) и удовлетворяют граничному
условию (1. 24), т. е. являются касательными к границе области.
С помощью таких полей, которые мы будем далее называть опор-
ными, может быть описан и более общий класс движений жидкости
в эллипсоидальной полости, при которых скорости частиц жид-
кости зависят от времени, но по-прежнему являются линейными
функциями их координат. Для этого полезно воспользоваться
методом Галеркина, причем в качестве координатных функций ис-
пользовать указанные опорные поля.
Уравнения движения несжимаемой жидкости в эллипсоидаль-
ной полости для случая, когда скорости являются линейными
функциями координат, можно найти, например, в монографиях
Ламба (1947) или Моисеева и Румянцева (1965), где показывается,
что указанные уравнения по своей форме полностью эквивалентны
уравнениям Эйлера для свободного движения твердого тела,
имеющего неподвижную точку (гироскопа). Мы воспроизводим
этот вывод в удобных для нас обозначениях.
В качестве опорных (координатных) полей выберем три без-
дивергентных поля, линейные по координатам и удовлетворяющие
граничному условию (wt.*V) 5=0 на поверхностях 5=const
w1 = -4zj + fyk,
w2 = —ужк+yzi, (1.25)
а . . b . ,
X
Эти поля ортогональны в том смысле, что j wt. • wfcd3x = 0 при
г
Поля скоростей представим в форме
v(r, i) = “i(0w1(r) + <i)2(i)w2(r) + <o3(i)w3(r). (1.26)
Величины (Oj, ш2, и о)8 называются параметрами Пуанкаре. Эти па-
раметры просто связаны с соответствующими компонентами
16
вихря 2=rot v. Вычисляя компоненты вихря, получаем
~ dw dv b2 + с2
1 ду dz be n
n du dw (ft eft ,,
2 dz dx ca 2 v 7
o dv du eft 4- fe2
Wq = 3--r~ =------4-(Do.
л dx dy ab л
Пользуясь уравнениями движения задачи, легко проверить,
что каждое опорное поле wx, w2 или w3 определяет одно из трех
стационарных решений задачи:
MjWp <o2w8, w3w3, (1.28)
которые получаются из (1. 26) как частные случаи при
а>2 = (D3 = 0, = const, (DT — (D3 = О, (02 = const
И (Dx = (D2 = 0, (D3 — Const.
Из доказанного следует, что идеальная несжимаемая жидкость,
заключенная в эллипсоидальную полость, может совершать сво-
бодное стационарное однородное вращение вокруг любой из глав-
ных осей эллипсоида, т. е. такое движение, при котором ротор ско-
рости не зависит ют времени, остается постоянным в пространстве
и направлен вдоль какой-либо из главных осей эллипсоида.
В общем случае поле скорости v(x, Z), представленное равен-
ством (1. 26), является нестационарным. Динамические уравне-
ния для параметров сох, ш2 и со3 получаются в результате под-
становки представления (1. 26) в уравнение Гельмгольца (1. 22),
которое в данном случае имеет следующий вид:
. fi = (Q.V)v. (1.29)
Записывая уравнение (1. 29) в проекциях на ось х, получим
21 = (Q. V)u, (1.30)
где Йх, й2 и й3 определяются формулами (1. 27), а компонента
скорости и задается следующим выражением:
з
M = 2<eft(Wft’i)=T'l°2Z“T<,)3?/- (1-31)
fc=l
Подставляя в (1.30) й8, Q3 и и, получим
й (.»+>)-<.+.»> (1,32)
ос 1 ОС 2 '
2 Нелинейные системы
17
Умножая обе части получившегося соотношения (1. 32) на Ъс и
вводя новые обозначения
/х = Ь2 + с2
/2 = с2 + а2, (1.33)
/З = а2 + Ь2,
мы придем к динамическому уравнению для о)х, из которого осталь-
ные уравнения для <о2 и <о3 получаются циклической перестановкой
индексов (12 3). Окончательно будем иметь следующую дина-
мическую систему уравнений:
М1 = (4 — Д>2®з»
^2^2 ~ (Л Л) Ш3Ю1» (1 • 34)
/3<Ь3 = (А —
которую также можно записать более компактно в векторном
виде
M = wxM. (1.35)
Здесь
<*> = Wji + ш2 j + <o3k, (1.36)
вектор М имеет компоненты
= (/,* = 1,2,3). (1.37)
1.к — диагональная матрица, элементы которой равны
/и = Д, Z22 = Z2, Z33 = Z3, (1. 37a)
a 12 и I3 определяются формулами (1. 33).
Таким образом, формулы (1. 26) и (1. 25), где о)х, о>2 и
находятся путем решения уравнений движения (1.34), имеющих
точно такой же вид, как и уравнения движения обычного механи-
ческого гироскопа (уравнения Эйлера), дают точное решение за-
дачи о свободном нестационарном движении идеальной жидкости
внутри эллипсоидальной полости, характеризующимся линейным
полем скорости. Поэтому естественно назвать эту систему «гидро-
динамическим гироскопом».
Известно, что уравнения (1. 34) допускают аналитические
решения, выражающиеся через эллиптические функции (см., на-
пример, книгу Ландау и Лифшица (1958)).
Остановимся кратко на тех выводах, касающихся общего ха-
рактера движений изучаемой динамической системы, которые
могут быть получены путем анализа интегралов движения. Легко
убедиться в том, что система (1. 34) обладает двумя квадратичными
интегралами движения:
Е=у (71W1 + Ё = °, (1 • 38)
J = Ц&1 + /2о>2 + 7=0, (1.39)
18
причем первый из них с точностью до постоянного множителя сов-
падает с кинетической энергией жидкости гироскопа, которая
имеет вид
(iAPz:—#, (1. 38а)
Z J о
V
где т=^13 каЪс р — масса всей жидкости, заключенной внутри
эллипсоидальной полости. Второй инвариант соответствует, однако,
не квадрату момента количества движения, как это имеет место
для механического волчка*, а представляет сумму квадратов
циркуляций Г1? Г2 и Г3 по главным сечениям эллипсоида
7=1(Г? + Ц+Г|), (1.39а)
. где
1\ — Г2 = tocS2, Г3 =
Равенства (1. 38) и (1. 39), выраженные через компоненты
введенного выше вектора М, записываются следующим образом:
МуЦ + муц + Myi. = 2Е | (1.40)
Ml + Ml + Ml = M2 = 1 J. (1.41)
Для определенности будем считать, что
A>72>J3. (1.42)
Пользуясь законами сохранения, записанными в форме (1. 40)
и (1. 41), можно сделать некоторые заключения относительно
устойчивости движения жидкого гироскопа. Для этого прежде
всего заметим, что (1. 40) и (1. 41) представляют собой (в осях
Л£1? М2 и М3) соответственно уравнения поверхностей эллипсоида
с полуосями ах, а2 и а3, определяемыми выражениями
а2==\/2ЕЦ, а3 = ^2ЁГ3, (1.43)
и сферы с радиусом М. При перемещении вектора М его конец
движется вдоль линии пересечения указанных поверхностей.
Сам факт пересечения обеспечивается очевидными неравенствами
а2 < М2 < ,
геометрически означающими, что радиус сферы (1. 41) лежит
между наименьшей и наибольшей из полуосей эллипсоида (1. 40).
В случаях М=а± или М=а3 происходит касание сферы эллип-
соидом энергии в точках большой или малой оси, причем точки
касания являются точками максимума или минимума энергии
При движении идеальной жидкости внутри трехосного эллипсоида меха-
нический момент жидкости не сохраняется, и возникают реакции, которые
могут быть измерены (см. гл. III).
2*
19
}
Рис. 3. Фазовые траектории в случае вращения вокруг малой (а)
и большой (б) осей
соответственно, и им отвечают стационарные устойчивые вращения
жидкого гироскопа вокруг осей Мг и М3, соответствующих наи-
большему и наименьшему значениям 1Х и Z3. В самом деле, при
малых отклонениях от этих состояний будут выполняться равен-
ства: М=а34-8 или М—а^—Ъ^ где 8—некоторый малый параметр и
траектории движения имеют вид замкнутых кривых, окружающих
ff=Z,M; C=Z, C=Z,
a)
J) (fcO)
5
Рис. 4. Фазовые траек-
тории в случае враще-
ния вокруг средней оси
а — М > №ЁТ2, б — М < \/2ЕТг
a
ось М3 или Мг вблизи соответствующих полюсов эллипсоида, как
это показано на рис. 3, а и б. Поэтому движение устойчиво.
В случае если М=а2, геометрическим местом точек пересече-
ния эллипсоида энергии со сферой является две плоские кривые
(окружности), пересекающиеся друг с другом в полюсах эллип-
соида на оси М2, которые будут, очевидно, седловыми точками.
20
Этому случаю отвечает неустойчивое вращение жидкого гироскопа
вокруг средней оси М2. Действительно, при малом отклонении
от указанного состояния, траектории, проходящие вблизи полю-
сов на оси М2, удаляются на большие расстояния от этих точек.
Картина траекторий вблизи седловой точки показана на рис. 4,
а и б.
Таким образом, качественно мы показали справедливость
следующего признака устойчивости движения. Для того чтобы
стационарное движение было устойчивым, необходимо и доста-
точно, чтобы энергия имела максимум или минимум на поверх-
ности J=const.
§ 3. Плоское движение под действием периодической
силы
х, у не-
(1.44)
Рассмотрим теперь двумерное движение в плоскости
сжимаемой вязкой жидкости, возбуждаемое периодической в про-
странстве силой, направленной по оси х и равной у sin ру (у > 0).
Это движение описывается системой уравнений
ди , ди% . дии 1 дР . А .
зг + зг- + -т-=----3- + vAh + y sin ру,
dt 1 дх 1 ду р дх 1 11
ди , дии . ди* 1 дР . А
— J- —=--------—UvAy,
dt 1 дх 1 ду р ду 1 ’
du । ди_q
дх ' ду
Здесь и и и}— проекции скорости на оси х и у, Р — давление,
Р — плотность, v — кинематическая вязкость.
Система уравнений Навье—Стокса и неразрывности (1. 44)
имеет стационарное решение, соответствующее ламинарному те-
чению вдоль оси х при постоянном давлении, следующего вида:
S=-X^sinpi/, v — 0, Р — const. (1.45)
Вводя^масштабы длины р"1, скорости и времени pvy"1
и переходя к безразмерным переменным, приведем систему (1. 44)
к виду
ди . ди* . дии дР , 1 А .1
-S7-+-5 Ь-З—= 3- + -Б- Sin У,
dt 1 дх 1 ду дх 1 R 1 R 99
ди , дии i du2_ дР ! 1 .
^“г дх ly+'R^9
________л
дх ’ ду *
Стационарное решение в этих переменных имеет вид
й = sin у, v = О, Р = const,
(1.46)
(1. 45а)
21
Здесь R=^lylp9 — число Рейнольдса. Вводя функцию тока ф
с помощью соотношения
получаем, что она удовлетворяет уравнению вида
___-cos и а 47\
Я/™ дх ду ' ду дх~ R С0 У' С1-47)
ф = —cos у.
Стационарное решение (1.45), соответствующее ламинарному
течению, как показано в работах Мешалкина, Синая (1961) и
Юдовича (1965, 1966), в линейной постановке задачи неустойчиво
относительно малых возмущений при определенных значениях
параметра R. Эти возмущения быстро растут во времени, черпая
энергию из энергии течения (1. 45), благодаря чему растут напря-
жения Рейнольдса, описываемые нелинейными членами в (1. 47),
что приводит к уменьшению амплитуды ламинарного течения,
пока не установится некоторое новое равновесное течение (обычно
называемое «вторичным течением»).
Представим гидродинамические поля в виде
и == U {у, t) -|- и' (х, у, t), v = v' (х, у, t),
Р = Р0 + Р'У, t), ф=Т(у, 0 + Ф' (®, У> О-
Здесь U (у, t) — новый профиль равновесного течения, подлежа-
щий определению наряду с равновесными напряжениями Рейнольд-
са, штрихом обозначены соответствующие конечные возмущения.
Будем считать, следуя цитированным выше работам, возмущения
гармоническими по х с длиной волны 2 л/а (а >0). Новый про-
филь течения U (у, t) есть результат усреднения и по х на расстоя-
нии длины волны.
Легко видеть, что при а 1 ламинарное течение (1. 45) един-
ственно и устойчиво при всех/? (Юдович (1965)), а неустойчивость
может проявляться только для возмущений с а <1.
В соответствии с линейной теорией устойчивости будем на пер-
вом этапе учитывать только нелинейное взаимодействие первой
гармоники возмущений со средним потоком, пренебрегая генера-
цией высших гармоник и их взаимодействием как между собой,
так и со средним потоком.
Представим все возмущения в виде
<р'(я, у, £) = <р(1)(у, 0 ехР (iax) + £)ехр(—tax),
vf, Pf, ф'), (1.48)
где величина ср(~Х) комплексно сопряжена к <р(1). Тогда из системы
(1. 46) получаем систему уравнений для среднего потока и воз-
22
Мущений рш (после исключения величин Р' и U') (Кляцкин
(1972))
V д тт > i I (П^Н)\ 1 W , 1 .
ли+-(” —;=т«+т“г'>'
(s-4)to"’+4l74o'”_‘'">^1=(>- (1'49>
При этом второе уравнение системы (1. 49) является обычным
уравнением Орра—Зоммерфельда. Аналогичную систему можно
получить и для функции тока.
Для исследования устойчивости ламинарного режима (1. 45)
следует считать во втором уравнении системы (1. 49)
U (у) = sin у.
В этом случае получаем
ta s*n + Д]у<1> = 0- (!• 50)
Представим возмущения г/11 в виде
1/0= 2 pWexpfof + Iny}. (1.51)
w=— со
Подставляя (1. 51) в (1. 50), получаем систему уравнений для
А (Я2 + П2) [0 + V(D + [Я2 - 1 + (п - 1)»] -
— уяй[а2—1 + (n + I)2] — п =—оо, 4“°°* (1.52)
Изучение системы (1. 52) (Мешалкин и Синай (1961), Юдович
(1965)) показало, что при некоторых ограничениях на волновое
число а и число R существуют вещественные положительные зна-
чения а, т. е. решения неустойчивы. Дисперсионное уравнение
для а имеет при этом вид бесконечной цепной дроби, и критиче-
ским числом Рейнольдса является 2?кр=\/2 для а ->0. Иначе
говоря, наиболее неустойчивыми являются длинноволновые воз-
мущения в направлении действующей силы. Поэтому можно
считать, что в рассматриваемой задаче существует малый пара-
метр а, что позволяет асимптотически проинтегрировать уравне-
ние Орра—Зоммерфельда (Юдович (1966)). Мы не будем подробно
останавливаться на этом. Отметим только, что компоненты соб-
ственного вектора (г?*1)} задачи (1.52) имеют разный порядок
по а. Так, все компоненты вектора {р^}, начиная с п= +2 и бо-
лее мелкомасштабные, будут по крайней мере порядка а4. Поэтому
можно ограничиться при рассмотрении только наиболее суще-
ственными гармониками с п=0, ±1, что по существу является
применением метода Галеркина с тригонометрическими коорди-
натными функциями. В этом случае
U {у, t) ~ U (t) sin у, (1. 53)
23
а уравнение для принимает вид
If) Лу(1> +iaU sin у ^(1> + Лг;(1Ч = °- (*• 54)
Подставляя в (1.49) разложение
п<1’= 2 vj» (t)exp(lny], w=—1
получаем для функций
z0 = p(n, z+ = ^) + p£y, г_ = (^-р£Ж U(t) (1.55)
систему уравнений
d гт . 4 1 1 тт dt a Z0Z~— R R d тт (X2 Ttz0 — a.Uz_ — — -jZ0, (1.56) d а -г г 1 dt Z~~~2 Uz<> ~~~RZ~' Lz dt + ~ R
Уравнение для величины z+ отщепляется от остальных уравне-
ний, и, следовательно, возмущения, соответствующие величине
2+, могут только затухать со временем. Оставшиеся три уравне-
ния образуют простейшую трехкомпонентную систему гидроди-
намического типа (см. следующие главы). Эта система уравнений
эквивалентна динамическому описанию движения гироскопа с ани-
зотропным трением, возбуждаемого моментом внешних сил отно-
сительно неустойчивой оси. Анализ системы (1. 56) показывает,
что при R < 7?кр — \)2 устанавливается ламинарный режим с U — 1,
zi = 0. При R^>\/2 этот режим становится неустойчивым и
устанавливается новый режим, соответствующий профилю сред-
него потока и равновесным напряжениям Рейнольдса (вторич-
ное течение)
тт ^2 4 R — v'F п
~Z0Z- — —& ’ z+—°’
= R>^' (1-57)
или, переходя к размерным величинам, получаем
и (у) = \J2vp sin ру, <u’v!y —-1 R~r^ COS py. (1. 58)
Отметим, что амплитуда установившегося равновесного среднего
течения не зависит от амплитуды возбуждающей силы. Кроме
того, величина может быть как положительной, так и отри-
24
Рис. 5. Профиль средней скорости (а) и линии тока вторичного
течения (5), R = 2RSS = 2 /2 (Vo > 0)
дательной в зависимости от знаков амплитуд начальных малых
возмущений.
Функция тока установившегося равновесного течения имеет
ВИД
<|)j =--A cos у — у [\/2а sin у cos ах + sin аж]. (1. 59)
На рис. 5 изображены линии тока, соответствующие течению
(1.58) при R=27?кр=2\/2 (i#> >0), уравнение которых
a cos у + \j2a sin у cos ах -|- sin ах = С. (1. 60)
На этом же рисунке также дано схематическое изображение про-
филя среднего потока. В этом случае, в отличие от ламинарного
течения (1. 45), возникают системы вихрей, периодически распо-
ложенных в пространстве, наклон больших осей которых опре-
деляется знаком производной по у профиля среднего потока.
Течение (1. 58) было получено, как указывалось выше, в пред-
положении, что нелинейное взаимодействие гармоник возмуще-
ния не существенно по сравнению с их взаимодействием со сред-
ним потоком. Это будет справедливым, если течение (1. 58) устой-
чиво, в свою очередь, относительно малых возмущений. Проверку
устойчивости можно провести обычным путем, линеаризуя урав-
нение для функции тока (1. 47) относительно течения (1. 58)
(Кляцкин (1972)). При этом оказывается, что течение (1. 58)
устойчиво, если ограничиться гармониками того же вида, что
и решение (1. 58). Имеются указания на то, что оно является
неустойчивым относительно мелкомасштабных возмущений
\СМ. также работу Юдовцча (1973)),
г
Глава II
СИСТЕМЫ
ГИДРОДИНАМИЧЕСКОГО ТИПА
§ 1. Квадратично-нелинейные системы,
интегралы движения
В гл. I было показано, что конечномерная аппроксимация уравне-
ний гидродинамики является весьма эффективным методом опи-
сания того или иного течения жидкости. В практических расчетах
на ЭВМ, например, при численном прогнозе погоды, всегда рас-
сматривается некоторая «модель» системы, состояние которой
описывается конечным числом параметров, а применяемые чис-
ленные схемы, являющиеся аппроксимацией уравнений в частных
производных (уравнения гидродинамики), можно трактовать как
уравнения движения для выбранной модели.
Очевидно, модели могут быть «хорошими», если они отражают
некоторые основные свойства исходной системы уравнений гидро-'
динамики и обладают достаточной точностью или, в противном
случае, могут оказаться неудовлетворительными с физической
точки зрения. В связи с этим имеет смысл разобраться более
детально в конечномерных аппроксимациях уравнений гидроди-
намики и, в частности, выяснить те требования, которые должны
предъявляться к «хорошим» моделям.
Каковы же те общие черты схематизированных уравнений
гидродинамики, о которых может идти речь в связи с обсуждае-
мым кругом вопросов? Это прежде всего характер нелинейности
уравнений, определяющих эволюцию системы во времени. Будем
считать, что ux, и2, . . ., ип — параметры, определяющие состоя-
ние системы в рамках выбранной модели, являются линейными
функционалами от поля скоростей жидкости. Такими парамет-
рами могут быть, например, значения компонент скорости потока,
усредненные по некоторой области в окрестности точек, принад-
лежащей заданной сетке, или коэффициенты разложения функций
тока в ряд по шаровым функциям (до некоторого фиксированного
номера) для определенных выбранных уровней (разумеется,
в конечном числе), как это делается в спектральных моделях ат-
мосферы. Используя для величин некоторое естественное на-
чало отсчета, систему уравнений движения (уравнения прогноза)
26
модели, содержащей п параметров, можно записать в следующей
форме: 1
“. = 2Л<Л-+т52Г<>^и>М4’ (2-
J з к
где члены, стоящие в правой части, сгруппированы по степеням
параметров ик. Матрица коэффициентов Л.у, характеризующая
влияние членов первой степени определяет линейную часть
прогностического оператора, набор коэффициентов Г.>л опреде-
ляет влияние членов второй степени, т. е. квадратичную часть
оператора прогноза, и т. д. Старшая степень членов, учитываемых
в прогностическом уравнении для п., определяет характер нели-
нейности системы. Уравнения гидродинамики идеальной несжи-
маемой жидкости являются квадратично нелинейными. Сохране-
ние только линейных членов в общих уравнениях динамики ат-
мосферы позволяет исследовать лишь качественный характер
атмосферных процессов и полезно при решении некоторых спе-
циальных задач о малых колебаниях атмосферы (наиболее совре-
менное изложение этих вопросов имеется в монографии Л. А. Ди-
кого (1969)). Вместе с тем для задачи прогноза погоды и изучения
закономерностей обмена энергией в атмосфере необходимо учи-
тывать квадратичные члены и, по-видимому, нет существенной
необходимости привлекать члены более высокого порядка. Таким
образом, большинство задач динамической метеорологии, решае-
мых, в частности, на ЭВМ, использует динамические уравнения
с квадратичной нелинейностью.
Любопытно, что это свойство уравнений динамической метеоро-
логии роднит их с уравнениями, описывающими процессы в био-
ценозах, привлекающие большое внимание биологов в связи с ре-
шением экологических проблем. Известно простейшее уравнение
биоценоза в системе, состоящей из особей двух типов (травоядные
и хищники) при наличии неограниченного запаса зеленого корма
(Вольтерра (1931)). Обозначим через Nr численность популяции
травоядных, N % — число хищников и запишем соответствующее
уравнение биоценоза в квадратичном приближении
N1 — aN1 — ^N1N2,
с(2. 2)
N2 = — тА2-ЗА\А2.
Это и есть уравнения Вольтерра, в которых а, (3, у и 8 — поло-
жительные коэффициенты, описывающие «динамику» данной си-
стемы. Интересно, что эта система допускает «интеграл движения»
силу уравнений динамики
системы dHldt~Q. Выведенная из состояния равновесия (если,
например, выловить половину всех хищников) такая система
УДет совершать колебания. В силу нелинейности системы период
этих колебаний зависит от амплитуды, а форма заметно отли-
ается от синусоидальной. Анализ соответствующих колебаний
27
имеется в книге А. А. Андронова и др. (1959), а также в курсов
Арнольда (1971). I
В отсутствие внешних сил и диссипации движение жидкости,!
как и любой другой механической системы, сопровождается со-!
хранением энергии (квадратичного функционала от поля скоростей).!
Наряду с характером нелинейности существование такого ин-1
теграла движения является второй важнейшей особенностью урав- I
нений гидродинамики, которую необходимо учитывать при по-1
строении конечномерных динамических моделей, претендующих!
на описание реальных гидродинамических систем. Вообще нужно !
стремиться к тому, чтобы в рамках упрощенной модели существо-1
вали аналоги общих интегралов движения, которыми обладают 1
исходные уравнения движения. Так, например, уравнения дви-1
жения баротропной атмосферы, состояние которой описывается I
функцией тока ф, с учетом сжимаемости имеют вид (см., например, I
Монин (1970)) 1
ft = 2»,w (2.3)1
с дополнительным условием на границе области ф lL =0. В этом 1
случае полная энергия выражается интегралом 1
ё S S [(grad +мч dxdy- (2-4> I
R I
Существует также и второй квадратичный интеграл, связанный I
с сохранением потенциального вихря I
J = ^(^-kl^dxdy. (2.5)1
R I
Фазовые координаты для такой модели атмосферы вводятся разло- !
жением по некоторой опорной системе ортогональных функций 1
(Xi (#, У)} и аппроксимацией ряда конечным числом членов ф= I
п л
= 5й»Хг В качестве Xt. удЬбно выбрать собственные функции 1
1 Я
оператора А |
дх< = — *?Хр хЛ=°- |
Полученная таким образом упрощенная система уравнений дви- Я
жения также обладает двумя квадратичными интегралами дви- 1
жения. Следует, однако, подчеркнуть, что если существование -Я
интеграла энергии является общим свойством всех гидродинами- Л
ческих систем, то наличие других инвариантов связано с их ин- !
дивидуальными особенностями, которые уже не носят столь Я
универсального характера и могут иметь различный физический Я
смысл. В только что рассмотренном примере существование вто- Я
рого квадратичного интеграла движения (2. 5) оказывается пря- I
28
следствием двумерности течения жидкости, тогда как трех-
мыоВОе течение идеальной жидкости, вообще говоря, сопровож-
дается лишь сохранением энергии.
д Рассмотрим теперь в качестве простейшего примера систему
сего лишь с двумя степенями свободы квадратично-нелинейного
вида, обладающего квадратичным интегралом движения (энергия),
заданным в виде
(2.6)
2Е = х2 + х1
Уравнения движения такой системы в общем случае имеют вид
; I, [t,k=i, 2
' Х2= ^ikXiXk J
(по одинаковымаийдексам предполагается суммирование). Из тре-
бования сохранения «энергии» следует, что а11=Ь22=0,2а12-|-Ь11=0,
а224-2&12=0» и уравнения движения можно записать в следующем
виде:
xi = (a*i + ₽*2) Х2>
^2 = —(а^1 + ₽ж2) xi-
Вводя новое время т = \/а2 + $4 и делая преобразование поворота
Р а
• Va2+p2 у'аЗ+рз
а $
У = г- ...~ Х1 + / - ' #<>,
^2+^2 1 Va2-|-p2 -
приведем уравнения движения (2. 6) к виду
dX а
—=у2,
dt у '
(2. 6а)
(2.7)
(2. 66)
dy
—ХУ*
dt
Решение при соответствующем выборе начала отсчета времени
имеет вид
х = a th (ат),
У = ±ach-1 (ат), (2. 8)
где а?—х2 Знак у зависит от начальных условий и сохраняется
а процессе движения (рис. 6).
Как видно из рис. 6, построенная система является суще-
ственно апериодической. Координата х возрастает монотонно,
а координата у совершает единичный всплеск, после чего затухает.
Можно привести пример диссипативной системы, поведение ко-
торой описывается уравнениями (2. 66). Рассмотрим движение
язкого газа в теплоизолированном сосуде.
29
...
Вязкость газа представим в виде v= Хос, где л0 — средняя длин?
свободного пробега (постоянная величина), с — величина, про
порциональная скорости звука.
Рассматривается простейшее движение в виде плоской попе
речной волны с волновым числом к и амплитудой скорости и
Рис. 6. Движение квадратично-нелинейной системы с двумя
степенями свободы
Полагая внутреннюю энергию пропорциональной с2, полную эне]
гию системы запишем в форме
Я==(с2 + и2)М/4, (2.9}
при этом dEldt—Q.
Принимая во внимание закон сохранения энергии, а также,
что
dufdt = —vA:2zz,
получаем окончательно
dujdt = —реи,
dc/dt — ри2, ‘ (2.10)
где p = X0fc2 — параметр системы, имеющий размерность обратной
длины. Эта система совпадает с приведенной выше канонической
формой (2. 66) (достаточно положить х~рс, у=ри).
Заметим, что физический смысл имеет только часть траекто-
рии, отвечающая положительной вязкости: v=Xoc >0. Рассмотрен-
ная система имеет явно диссипативный характер: энергия «актив-
ной» компоненты постепенно уменьшается, переходя во внутрен-
нюю энергию, с чем связано увеличение вязкости.
§ 2. Понятие регулярности и определение систем
гидродинамического типа
Важной характеристикой квадратично-нелинейной системы
является дивергенция фазового потока
D = ^duk!duk, (2.11)
(А:)
где йк определяются из уравнений движения.
30
Для рассмотренной выше простейшей системы (2. 66) D —
т. е. дивергенция фазового потока отлична от нуля.
Именно с этим связан монотонный характер движения (см. рис. 6).
Напомним, что в статистической^физике ограничиваются рас-
смотрением гамильтоновых систем, для которых дивергенция
базового потока всегда равна нулю. В дальнейшем динамические
системы, сохраняющие в процессе движения фазовый объем, т. е
такие системы, у которых Z)=0, будем называть регулярными.
Как было только что показано, для квадратично-нелинейных
систем с двумя степенями свободы существование квадратичного
интеграла энергии несовместно с требованием регулярности.
Примером регулярной системы является гироскоп, в чем нетрудно
убедиться непосредственным вычислением, используя уравнения
Эйлера (1. 34), приведенные в предшествующей главе.
Введем теперь формальное определение систем гидродинамиче-
ского типа (СГТ). Этот класс регулярных систем выделяется сле-
дующими условиями:
(1) фазовым пространством СГТ является линейное векторное
пространство п измерений (п — порядок системы);
(2) их уравнения движения квадратично-нелинейны;
(3) существует по крайней мере один (с точностью до постоян-
ного множителя) квадратичный положительно определенный ин-
теграл движения (энергия).
Обозначим компоненты вектора, характеризующего динамиче-
ское состояние СГТ, через и* (f=l, 2, . . ., п). В силу условия (2)
уравнения движения системы можно записать в следующей форме;
' (2.12)
(по одинаковым индексам проводится суммирование). «Ко-
эффициенты взаимодействия» ГД образует тензор третьего ранга
(динамический тензор), который естественно считать симметрич-
ным по нижним индексам
Г^ = Пу. (2.13)
Упомянутую в определении энергию системы можно представить
в виде
2£ = g,^V, (2.14)
гд;е — положительно определенный тензор второго ранга.
Требование сохранения энергии dEldt^Q в силу уравнений дви-
^ЯИя (2. 12) налагает на динамический тензор следующее усло-
Гсл + Г^ + Г.^О, (2.15)
пр6 динамический тензор с опущенным первым ин-
В ксом. Тензор g.k будет употребляться для опускания индексов,
аимный тензор g*\ определяемый как совокупность элементов
31
матрицы, обратной по отношению к матрице |]ga||, удовлетворяет
условию
( 1 при 1 — к,
Л»=Ч = {0 „„„ t¥.„. <216>
С помощью gik осуществляется операция поднятия индексов*.
В дальнейшем удобно иметь дело с таким представлением (будем
называть его энергетическим) уравнений движения (2. 12), в ко-
тором удвоенная энергия задается суммой квадратов компонент
вектора состояния. В этом случае
{1 i__к
О 1=£к, (2Л7)
и, следовательно, не имеет смысла различать верхние и нижние
индексы тензорных величин.
{^Энергетическое представление уравнений движенияуотвечает
выбору некоторой ортогональной системы координат фазового
пространства. Переход от одного энергетического представления
к другому осуществляется с помощью ортогонального преобразо-
вания. Напомним, что число параметров, определяющих полную
группу ортогональных преобразований в n-мерном пространстве,
равно п (п—1)/2. .
В гидродинамике полную энергию обычно относят к единице
массы (масса системы сохраняется при всех обстоятельствах).
В этом случае Е имеет размерность квадрата скорости, «энерге-
тические параметры» динамического состояния и* — размерность
скорости, а коэффициенты взаимодействия Г*.Л — размерность об-
ратной длины (волнового числа).
Условие регулярности означает, что
Отсюда следует, что для регулярных систем ковариантный век-
тор
Ъ = ГХЧ = О. (2.18)
Системы гидродинамического типа естественно возникают при
конечномерной аппроксимации уравнений гидродинамики невяз-
кой жидкости по методу Галеркина. На выполнение теоремы Лиу-
вилля (условие регулярности) при аппроксимации уравнений
гидродинамики рядами Фурье указал Ли (1952). Это условие по
существу выделяет определенный класс динамических систем ин-
вариантным способом (независимо от конкретного выбора системы
координат, поскольку условие формулируется в тензорной форме).
Л. А. Дикий показал, что других дополнительных условий, фор-
♦ С основными понятиями тензорного анализа и их применениями в меха-
нике читатель может ознакомиться по книге Сокольникова (1951).
32
мулируемыхТинвариантным способом с помощью уравнений,
линейных относительно компонент динамического тензора, просто
не существует (см. приложение I). Вместе с тем свойство регуляр-
ности оказывается очень существенным при статистическом опи-
сании гидродинамических систем (Обухов, 1969).
§ 3. Эквивалентность триплета классическому гироскопу
Опираясь на общее определение систем гидродинамического
типа, мы можем теперь сказать, что уравнения движения Эйлера
для гироскопа являются примером СГТ третьего порядка. Такую
систему будем называть триплетом. Гидродинамической интер-
претацией триплета является течение идеальной несжимаемой
жидкости внутри трехосного эллипсоида с линейным распределе-
нием скорости, исследованное в предыдущей главе.
Покажем, что триплет — простейшая нетривиальная СГТ.
Это следует уже из того факта, что нетривиальных СГТ при тг=2
не существует, о чем говорилось выше. Можно воспользоваться
также общей формулой для числа независимых компонент дина-
мического тензора СГТ. При этом опорную систему координат
будем предполагать декартовой и уравнения движения СГТ будут
заданы в энергетическом представлении.
Общее число компонент тензора I\. который симметричен
по паре индексов, 7\Г0=п2 (п-|-1)/2. Таково общее число коэффи-
циентов в любой квадратично нелинейной системе с п степенями
свободы. Закон сохранения энергии (2. 15) эквивалентен тожде-
ственному обращению в нуль некоторой кубической формы и
дает п^п линейных связей между коэффициентами Г6
Условие регулярности дает дополнительно п связей. Считая упо-
мянутые условия независимыми (это обстоятельство можно про-
верить), получим следующее число независимых компонент ди-
намического тензора:
2V = ZV0—"(n + 1)(re + 2)_ п =
=^(Зп2_|_зп_п2_3п_2 — (2.19)
Легко видеть, что N принимает положительное целое значение,
начиная с п=3, которому соответствует 7V=5.
Таким образом, в общем случае уравнения движения триплета
в некоторой ортогональной системе координат зависят от пяти
параметров. Обозначив фазовые координаты через г2 и р3,
Уравнения движения триплета можно представить в виде
— РО 2 3 + Z (^2 — |) + ™ А — nVlV^
™ (vl — t’l) + nv2v3 — lv2vv (2- 20)
v3 = + n (Pi — + lv3vi — Wr
3 Нелинейные системы 33
Причем
Pq + <7о + ro = (2*21)
в остальном коэффициенты произвольны.
Нетрудно проверить, что является интегралом
движения и
dv1/dv1 + дд2/ди2 + 5Йз/Зр3 = О,
т. е. выполняются закон сохранения энергии и условие регуляр-
ности.
Покажем, что система уравнений (2. 20) эквивалентна урав-
нениям Эйлера из теории гироскопа, которые в энергетических
переменных имеют следующий вид:
Ui = pa2u3,
u2 = gtt3uv (2.22)
й3==гиги2,
при p+q+r-=0.
Наше утверждение в более точной формулировке означает,
что всегда можно выбрать новые переменные являющиеся
линейными функциями «старых» переменных vv v2i v8, так, чтобы
w?+ua+w3 = и ПРИ этом уравнения движения в новых
переменных будут иметь форму (2. 22).
Основная идея ? доказательства этой теоремы заключается
в том, что тензор в любой системе координат определяется
пятью независимыми’ параметрами и при ортогональных преоб-
разованиях координат новые значения параметров линейно вы-
ражаются через старые. Такими же свойствами обладает симмет-
ричный тензор второго ранга 4а,*для которого Sp4=0 (А=
=||4а|| матрица коэффициентов). Если нам удастся инвариант-
ным способом установить взаимно однозначное соответствие между
компонентами тензора Г. ^к и симметричными матрицами А с
Sp4=0, то, опираясь на теорему о приводимости симметричных
матриц к диагональному виду, мы тем самым приведем ^к к не-
которой канонической форме.
ч Искомый изоморфизм устанавливается с помощью единичного
полностью антисимметричного тензора третьего ранга &^к
А'j>uc (2.23)
(как всегда, по одинаковым индексам производится суммирование).
Напомним, что компоненты е^к отличны от нуля, только если все
индексы различны и в любой системе координат
®123 ~ ®231 = ®312 = “М > ®132 = ®321 = ®213 =-• (2. 24)
Подставляя в (2. 23) элементы тензора Т<^к, которые задаются
34
коэффициентами уравнений (2. 20), получим следующее представ-
ление для матрицы А:
А =
Яо — Го
Зп
Зт
Зп
Го — Ро
31
Зт
31
Ро 9о
(2.25)
Осуществляя ортогональное преобразование, которое приводит
матрицу А к диагональному виду
А'п 0 О
О А'п О
О О А'
«га
(2.25а)
и учитывая, что новы© коэффициенты д, г также должны удов-
летворять условию (2. 21), получим
Р “§* С^зз ^22)’
<7=4Ип-^з)’ (2-26)
Г==’3‘(-^22 ^и)-
Остальные параметры обращаются в нуль.
Таким образом, в новых переменных и2, иа уравнения дви-
жения приобретают форму (2. 22), и теорема об эквивалентности
произвольного триплета классическому гироскопу доказана.
В качестве примера рассмотрим систему, описываемую уравнени-
ями:
О
О
О
v2 — —lVjV2, А —
о
о
31
О
31
о
2>3 = ^iy3>
При ортогональном преобразовании (па, t>3)
У2 = (»2 + Пз)> V3 = -Jf («3 — »2)>
матрица А преобразуется в диагональную матрицу
ООО
О — 31 О
0 0 3/
3*
35
и уравнения движения приводятся к виду
Т72 = —lu^i^
u3 =
что легко проверить непосредственным вычислением.
Поставим теперь вопрос о том, каким образом из сложной
регулярной системы получить более простую систему, также регу-
лярную и удовлетворяющую закону сохранения энергии.
Практически для упрощения системы используется метод
«замораживания» части фазовых координат и переход к «укоро-
ченной» системе, описываемой уже меньшим числом уравнений.
Вопрос о законности такой операции решается обычно на основе
физических соображений, позволяющих оценить, насколько воз-
буждены «лишние» степени свободы, которые теоретик склонен
«заморозить» ради упрощения задачи.
Пусть исходная система обладает п степенями свободы, где
п достаточно велико. Если система задана в ортогональном базисе,
т. е. энергия выражается через сумму энергий каждой отдельной
степени свободы, то при замораживании некоторого числа степеней
свободы закон сохранения не нарушается и энергия также
представляется суммой квадратов оставшихся компонент. В са-
мом деле, замораживание означает введение таких сил реакции,
что, начиная с некоторого номера nz+l, тг/-|-2, . . ., п, правые
части уравнений движения тождественно обращаются в 0:
= + Л = 0 Для i~nf (2.27)
Тогда при условии, что и. (0)—0, эти составляющие никогда не
будут возбуждаться, сохранение энергии следует из уравнения
баланса
поскольку
f. — Q для 7 = 1, п',
и.~0 для l = nf + l, п.
Доказательство сохранения энергии для «укороченной» си-
стемы следует также из равенства (2. 15), справедливого для всех
7, у, А = 1, 2, .. ., тг, а следовательно, и для 7, у, Л=1, тг7,
поскольку замораживание эквивалентно отбрасыванию тг—тг' урав-
нений и «лишних» переменных. Однако полученная таким обра-
зом новая система совсем не обязательно будет регулярной.
В частности, при переходе от тг=3, к п—2 нельзя получить ре-
гулярную нетривиальную систему, как это было выяснено выше.
Чтобы условия регулярности для укороченной системы вы-
полнялись, достаточно замораживать те степени свободы, которым
соответствуют уравнения с правыми частями, не содержащими
таких степеней свободы, т. е. dvk/dvk =0 (для некоторого фикси-
рованного к).
36
Можно выделить класс систем, для которых существует орто-
гональный базис, образованный стационарными состояниями си-
стемы. В таком базисе коэффициенты взаимодействия от-
личны от нуля, только если все индексы г, /, к различны* Такие
системы мы будем называть вполне регулярными. В этом случае
при использовании естественного базиса любая подсистема, полу-
ченная замораживанием любых переменных, будет регулярной.
Нетрудно показать, что система обязательно будет вполне
регулярной, если существует два существенно различных ква-
дратичных интеграла (один из них — энергия), причем все соб-
ственные значения второй квадратичной формы должны быть
различны (нет кратных корней в энергетическом представлении).
Примером вполне регулярной системы может служить баро-
тропная атмосфера, движение которой описывается уравнением
(Обухов (1969))
^=Д-1[Дф, Н ф|£ = 0, (2.28)
где Д-1 — оператор Грина для данной краевой задачи.
Очевидно, любое решение уравнения
Дф + &2ф=0 (2.29)
является стационарным решением уравнения (2. 28) и в сово-
купности образует полную систему «опорных функций» (базис).
Можно привести пример регулярной, но не вполне регулярной
системы (при п=4)
dxlldt = —x1x2 — y1yi,
dy1/dt = —x1y^x2y1,
dxjdt = х\ — у{. (2. 30)
dyjdt = 2^,
+ д^дхъ + дх2)дх2 + ду2)ду2 = 0,
2E^x^+y\+xl+yl — интеграл движения. Однако у этой системы
не существует ортогонального базиса, образованного стационар-
ными состояниями.
§ 4. Конструирование сложных систем
путем суперпозиции триплетов
В начале этой главы было выяснено, что простейшей системой
гидродинамического типа является триплет. Оказывается, что
триплет можно рассматривать как основной элемент при построе-
нии сложных гидродинамических систем с большим числом сте-
пеней свободы. Конструирование таких сложных систем из про-
стейших триплетных «блоков» опирается на важное понятие
суперпозиции СГТ*
37
Пусть имеются два тензора третьего ранга и удов-
летворяющие условиям
=0, а = 1, 2, (2. 31)
ПГ = о.
Очевидно, теми же свойствами будет обладать и сумма
Г,-,л = П?л + Г‘Гл. (2.32)
Соответствующую динамическую систему, определенную динами*
ческим тензором Г. ,fc, будем называть суперпозицией систем
(1) и (2).
Приведенный выше пример системы (2. 30) является суперпо-
зицией двух триплетов (хъ yv х2) и (xv yv у2). Это видно из при*
веденной выше записи
dXi dt —У1У2
dt У1х2 —У2Х1
dx2 dt №-у1) *
dy2_ dt * 2®1У1
Первый триплет (я^, у19 х2) дан в «косом» представлении, второй —
(хх, уъ у2) в «прямом» (каноническом) представлении. Аналогично
можно строить системы, являющиеся суперпозицией любого
числа триплетов.
Принцип суперпозиции триплетов позволяет «конструировать»
сложные многомодовые модели с «заданными свойствами».
Ниже, в гл. VII, будет показано, как таким способом построить
«многоуровенные» модели для описания процесса каскадного пре-
образования энергии в развитом турбулентном потоке.
§ 5. Некоторые общие замечания о применении СГТ
в геофизике
Общее определение систем гидродинамического типа охваты-
вает широкий класс задач, в которых (при надлежащей параме-
тризации полей) уравнения гидродинамики решаются в квадра-
тичном приближении. Сюда входят не только задачи, использу-
ющие модель несжимаемой жидкости, но и вопросы, трактуемые
в рамках модели слабо-Сжимаемой среды, когда для медленных
(вихревых) гидродинамических процессов сжимаемость учитыва-
ется квазистатически, а быстрые волновые процессы имеют ма-
38
jo амплитуду и не оказывают обратного влияния на медленные
процессы, которые, в свою очередь, являются для волновых
процессов некоторым заданным фоном. Именно так дело обстоит
в задачах динамической метеорологии. Следует, однако, предо-
стеречь читателя, что для исследования существенно нелинейных
волновых процессов квадратично-нелинейное приближение может
оказаться недостаточным и в уравнениях движения потребуется
учет кубических членов.
Трудная проблема энергетического взаимодействия вихревого
поля (турбулентность) и звуковых волн, по-видимому, относится
к этому классу задач, выходящих за рамки развитой выше теории
систем гидродинамического типа.
Для простейших случаев такие системы допускают вполне
конкретное исследование. На них удается промоделировать такое,
вообще говоря, весьма сложное явление, как гидродинамическая
неустойчивость, выяснить роль нелинейности в явлениях кон-
векции, построить системы типа цепочек, поясняющие каскадный
механизм преобразования энергии (Обухов, 19716).
Приводимые примеры в последующих главах в значительной
степени имеют иллюстративный характер, однако, как можно
думать, окажутся полезными при анализе реальных динамических
процессов в атмосфере и в Мировом океане.
Основная трудность при этом — отыскание подходящей «си-
стемы координат» (опорных функций), при пользовании которой
гидродинамические процессы допускают приближенные описания
в рамках рассмотренных в этой книге схем. Тем самым речь идет
об отыскании некоторых наиболее удобных для исследования
спектральных моделей.
Представляется, что самый эффективный путь раскрытия за-
кономерностей в динамике земной атмосферы, рассматриваемой
как единая физическая система, состоит в правильном сочетании
общих методов нелинейной механики с конкретными расчетами на
электронно-вычислительных машинах.
Для построения наиболее «экономных» координатных систем
в фазовом пространстве при описании реальных геофизических
объектов может оказаться полезным также метод разложения
полей по естественным ортогональным составляющим (Багров
(1959), Обухов (I960)). Этот метод уже сейчас получил опреде-
ленное развитие в применении к исследованию вертикальной
структуры атмосферы, а также к изучению синоптических про-
цессов над значительной частью Северного полушария (Мещерская
и другие (1970)). Построение соответствующих естественных со-
ставляющих метеорологических полей для глобального анализа
динамических процессов в атмосфере и сопоставление их с си-
стемами функций, получаемых из динамических соображений,
окажется возможным, когда исследователи получат в свое распо-
ряжение достаточно полный материал наблюдений о метеорологи-
ческих процессах в масштабе всего земного шара.
Глава III
ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
ГИДРОДИНАМИЧЕСКОЙ СИСТЕМЫ
ТИПА ТРИПЛЕТ
§ 1. Предварительные замечания
Настоящая глава посвящена исследованию особенностей вынуж-
денного движения триплета, которые, как будет показано ниже,
нетрудно воспроизвести с помощью лабораторного эксперимента.
Такой динамической системе уделяется особое внимание по двум
причинам. Во-первых, как простейшая СГТ, она доступна анали-
тическим методам описания и, следовательно, позволяет детально
разобраться в механизме нелинейного взаимодействия на при-
мере трех мод. Во-вторых, в ряде случаев течение реальной
жидкости управляется динамическим уравнениями триплета, что
дает возможность применять их для решения некоторых кон-
кретных задач гидродинамики. Например, задача о свободном
жидком вращении внутри эллипсоида (гл. I) нашла свое приме-
нение в теории приливов и рассматривалась в трудах Гринхилла
(1879), Хафа (1895) и Пуанкаре (1910), посвященных исследова-
нию колебаний самогрквитирующей жидкости, вращающейся
с постоянной угловой скоростью вокруг неподвижной оси. Весьма
полезной она оказалась и при изучении динамики тел с полостями,
заполненными жидкостью (Моисеев и Румянцев (1965)), начало
которому было положено Жуковским (1885). К примерам ее
применения относятся также резонансное взаимодействие пла-
нетарных волн (Лонге-Хиггинс, Гилл (1967)), плоское течение
жидкости под действием периодической силы (гл. I) и некоторые
другие, о которых речь пойдет ниже. Вообще согласно теореме,
сформулированной в гл. I, исследование любого течения, в кото-
ром возбуждено не более трех степеней свободы (т. е. при его
описании можно ограничиться тремя членами разложения по
методу Галеркина), сводится к классической задаче о движении
механического гироскопа, как это сделано, например, в работе
Лоренца (1960) при выводе максимально упрощенных уравнений
динамики баротропной атмосферы.
Движение триплета при отсутствии внешних и вязких сил
достаточно подробно рассмотрено в гл. I, а кроме того, в гл. V
будет дано аффинно-инвариантное его описание с помощью ха-
рактеристической квадратичной формы. Здесь нас будет интере-
40
совать динамика вынужденного движения триплета, рассмотрение
которого позволит проиллюстрировать известное в гидродинамике
явление, когда под влиянием незначительного изменения внепттгих
условии в системе происходит скачкообразный переход из одного
состояния в качественно новое состояние, причем последнее не
всегда устанавливается однозначно. В связи с этим уместно
вспомнить предложенную Бюргерсом (1939) математическую мо-
дель одномерного турбулентного течения жидкости, задава-
емую следующими уравнениями:
dUfdt=F — и2 — vt7,
(3.1)
dujdt — Uu — vu,
где jj ~ скорость основного потока, и — амплитуда пульсаций,
F — внешняя сила, v — диссипативный параметр, причем за
единицу длины выбран характерный размер потока.
Замечательное свойство модели Бюргерса состоит в том, что
она действительно описывает (хотя и не полностью) поведение
реальной гидродинамической системы, поскольку, как будет
показано в следующем параграфе, множество всех решений си-
стемы (3. 1) совпадает с подмножеством решений уравнений вы-
нужденного движения триплета.
Для наглядности дальнейшего изложения воспользуемся гид-
родинамической интерпретацией вынужденного движения три-
плета, имея в виду течение вязкой жидкости внутри эллипсоида
под действием внешних сил.
§ 2. Вынужденное движение жидкости внутри эллипсоида
Единственное предположение о линейности по пространству
поля скоростей, на котором основывался в гл. I вывод упрощен-
ных уравнений движения идеальной жидкости внутри эллипсо-
ида, для вязкой жидксти, строго говоря, не выполняется, хотя бы
из-за условий прилипания на стенках и возникновения вблизи
них пограничного слоя. Можно, однако, ожидать, и это дейст-
вительно согласуется с результатами эксперимента (см. § 3),
что влияние указанных факторов, по крайней мере для жидкостей
с малой вязкостью, не распространяется в глубь жидкости, а сво-
дится к эффективному торможению жидкого ядра, поле скоростей
в котором уже незначительно отличается от линейного.
Предполагая далее, что такое торможение пропорционально
угловой скорости вращения жидкого ядра, уравнения его движения
можно представить в следующем виде:
М-XM + F, (3.2)
dt
гДе компоненты вектора М{=1(кшк (см. гл. I), Iik— диаго-
нальная матрица, элементы которой равны /и=/(1)=Ь2+с2
41
1м=1.ъ=а*+с3, I33 = I(3,=a2+b*, a, b и (Г-главные полуосц
эллипсоида, поверхность которого задается уравнением
(x-Ja)2 + (ж2/Ь)2 + (ж3/с)2 = 1.
Для определенности положим, что а > Ь > с. Параметры
характеризующие угловые скорости вращения вокруг главных
осей эллипсоида, связаны с компонентами ротора скорости Q со-
отношениями
Ш1— &2 _|_ с2 21> ад2— аг+С2 22> Ш3 — 2з- (3-3);
F есть момент внешних сил, приложенный к единице массы;
жидкости, а X — эффективный коэффициент трения, которое ради
простоты предполагается изотропным. Учет анизотропии сид
трения не представляет труда, если ввести вместо X тензор коэф-;
фициентов трения
Наибольший интерес представляет случай, когда момент
внешних сил действует в направлении наиболее неустойчивого
вращения, т. е. вдоль средней оси. Поэтому в дальнейшем пред-
полагается, что F=(0, F, 0). Для облегчения анализа удобно5
воспользоваться несущественным ограничением; а именно Z(2)=;
= (Z(1)+Z(3))/2, и ввести новые зависимые переменные J
С7==и2, = (»! + »3)/\/2, р2 = (»3 — u^ls/2, (3.4)
где — (суммирование не подразумевается).
В новых переменных уравнение (3. 2) эквивалентно следующей
системе:
Z7=p(^-^)-Xt7 + /, ;
v1 = pUv1 — Xvu (3.5)’
г>2 = ——Xz?2.
Здесь f = параметр р, имеющий размерность обратной
длины, характеризует динамический масштаб системы L—Hp и
определяется равенством
Р = (а2 - с2)/2 [(а2 + Ь2) (Ь2 + с2) (с2 + а2)]7«. (3. 6)
Полагая равными нулю левые части (3. 5), легко убедиться, что
полученная таким образом система алгебраических уравнений
имеет три решения, которыми исчерпываются все стационарные
режимы жидкого вращения:
A) U = f/\, ^ = ^ = 0,
при f > 0 (3.7);
В, В') и = \1Р, р1=±/£-^, Р2 = О, ]
42 ।
при f
а
О в режимах В и В1, напротив, ^=0,
2
Исследование на устойчивость по отношению к бесконечно
малым возмущениям, которое при желании читатель без труда
выполнит самостоятельно, показывает, что режим А оказывается
устойчивым, если В = |/р/Х2| 1. Безразмерный параметр R
можно трактовать как число Рейнольдса, определенное по на-
пору- В противном случае, когда R > 1, сколь угодно малое
возмущение «опрокинет» гидродинамический волчок в одно из
двух состояний — В или В', которые с точки зрения устойчивости
Рис. 7. Зависимость относи-
тельной кинетической энергии
жидкого вращения от
= | /р/Х21. Ео — кинетическая
энергия при Л=1
совершенно равноправны, и выбор одного из них зависит от знака
начального возмущения.
Из рис. 7, на котором приведена зависимость относительной
полной кинетической энергии жидкого вращения от R для ре-
жимов А, В иВ'9 видно, что при фиксированном R устойчивым
состояниям соответствует минимальная энергия.
Следует подчеркнуть, что в рамках использованных при-
ближений явление опрокидывания наблюдается только при за-
кручивании жидкости вокруг средней оси, поскольку в противном
случае уравнение (3. 2) допускает единственный стационарный
режим А. Заметим также, что область устойчивости режимов В
и В1 совпадает с областью их математического существования
R 1, причем в случае режимы А, В и В' тождественны.
Чтобы получить более полное представление о поведении рас-
сматриваемой гидродинамической системы, попытаемся постро-
ить в пространстве параметров (U, v19 v2) фазовые кривые, кото-
рые, вообще говоря, трехмерны. Однако, как видно, из (3. 5)
и (3. 7), при / > 0 компонента у2, равная нулю в начальный мо-
мент, остается таковой в течение всего времени движения, кото-
рое описывается в этом случае первыми двумя уравнениями си-
стемы (3. 5), в точности совпадающими с уравнениями (3. 1).
Этим попутно устанавливается непосредственная связь жидкого
гироскопа с моделью Бюргерса, недостаток которой состоит в том,
что она несимметрична по отношению к изменению знака внешних
43
Рис. 8. Фазовые траектории жид-
кого гироскопа при 0 < R < 1
dvx
di
сил, а поэтому не дает полного,
описания движения гидродина-
мической системы.
При отрицательных внешних
силах «замороженной» оказыва-
ется и, следовательно, исклю-
чению подлежит второе урав-
нение (3. 5). Таким образом,
соблюдая указанные ограниче-
ния, фазовые кривые можно
строить в фазовой плоскости
(U, pj либо (U, z>2), в зависи-
мости от знака возбуждающей
силы. Положим для определен-
ности / О, р2=0 и введем
безразмерные переменные U =
=pU/X и v1=pp1/X. Будем те-
перь считать U и такими без-
размерными переменными и
перепишем два уравнения (3.5)
в следующем виде:
(3.8)
где Стационарные решения изображаются в фазовой пло-
скости (U, vj точками с координатами
. A) U = R, ^ = 0,
В, Bf) C7 = l, ^1=±V^=T (3,7а)
которые являются особыми точками системы уравнений (3. 8).
Заметим, что А расположена на вершине параболы U==B —•
а В и В! — на пересечениях ее с горизонтальной прямой U=l.
Траектории, по которым фазовые точки устремляются к стацио-
нарному состоянию, схематически изображены на рис. 8 и 9 для
различных областей изменения R. Точно воспроизвести фазовые
кривые без численного интегрирования невозможно, поскольку
общее решение системы (3. 8) не представимо в аналитическом
виде. Поэтому для их построения удобно воспользоваться сле-
дующими соображениями (см. также Бюргерс (1939)).
Наклон касательной в любой точке фазовой кривой, за исклю-
чением особых точек, определяется равенством
/3 9)
dv± У1(С7 —1) •
Отсюда видно, что в точках, где фазовая кривая пересекает пара-
болу U=R — и горизонтальную прямую U=l, касательная
44
Рис. 9. Фазовые траектории жидкого гироскопа при 1 < R < 9/8 (а)
и R > 9/8 (б)
имеет горизонтальное и вертикальное направления соответственно.
Кроме того, при vx ->0 \dU!dv^ -> оо. В этом случае асимпто-
тическое поведение фазовой кривой легко получить, интегрируя
(3. 9) и пренебрегая последним слагаемым числителя правой
части. Тогда получим
। ^мо) ।=| гг=4 Г”Е) ехр (£Z°_ (3-10)
где (U09 р?) — фиксированная точка, достаточно удаленная от
особых точек, причем i?J<^l. Согдасно (3.10) фазовая кривая
при -> 0 асимптотически приближается к положительной полу-
оси ординат, пересечение с которой возможно только в особой
точке (ось ординат сама является фазовой траекторией).
Наконец, поведение фазовых траекторий в окрестностях осот
бых точек нетрудно исследовать, линеаризируя систему (3. 8)
относительно одного из стационарных состояний Л, В или В'.
Поступая таким образом в отношении режима А, получим, что
вблизи него при R <Z 1
= (3.11)
где (t7*, v*) — фиксированная точка, причем |CZ* — 7?|, |z?*| R.
Из (3. 11) следует, что точка А — узел, в котором все фазовые
кривые, исключая ось ординат, имеют общую горизонтальную
касательную (рис. 8).
45
Уравнения движения, линеаризованные относительно режима
В, принимают вид
^i = v/7?_ 1 £7\ U> = U — 1, 14 = ^ —Vfl — i. (3.12a)
Исключая v'v получим уравнение колебаний маятника с трением
^4-^.4.2 (R 1) W = О,
dx' ‘ dt 1 v ' ’
(3.126)
корни характеристического многочлена которого
к —~1 8Д /3 13\
В интервале 1 < 7? <1 ®78 оба корня отрицательны, и мы вновь
получаем узел, наклон общей касательной в котором задается^
равенством
1 — ^9 — 8В
du I
dfi [в
(3. И)
। I y/g_g jo
Единственная кривая с наклоном dU/dz;1[£ =-------' 1— делит
полуплоскость i>i>0 на две области (см. рис. 9, а), в одной из ко-
торых фазовые траектории приближаются к точке В справа, в дру-
гой — слева.
При R > % (рис. 9, б) согласно (3. 13) корни оказываются
комплексно-сопряженными с отрицательной вещественной частью,
т. е. в этом случае точка В является устойчивым фокусом (см.,
например, Арнольд (1971)).
Из рис. 8, 9 хорошо видно, как меняется характер вынужден-
ного движения триплета с увеличением величины внешнего воз-
буждения. Если при В < 1 все фазовые траектории устремляются
в точку А, то при R > 1 происходит бифуркация, фазовые тра-
ектории, напротив, отталкиваются от нее и притягиваются к точ-
кам В либо Вг в зависимости от знака начального значения vv
Отсюда следует, что два тождественных триплета при одинаковых
внешних воздействиях могут находится в различных динамически
равновесных состояниях.
Интересно также отметить, что точки В и В1 на рис. 9, а тополо-
гически эквивалентны точке А на рис. 8, т. е. при переходе через
критическое значение /?=1 в характере стационирования не происхо-
дит качественных изменений, пока R <?/8. При 2?>9/8 узлы в точ-
ках В и В1 сменяются фокусами, в результате чего вместо моно-
тонного приближения к стационарному состоянию система совер-
шает нелинейные затухающие колебания.
Полученные до сих пор выводы о свойствах движения вязкой
жидкости внутри эллипсоида основываются, как мы видели, на
46
нескольких упрощающих предположениях, справедливость кото-
вых можно доказать только экспериментально. С этой целью был
выполнен лабораторный эксперимент, описанию которого посвя-
щен следующий параграф.
§ 3. Лабораторный эксперимент
Основной результат теоретического анализа состоит в том, что
вынужденное жидкое вращение вокруг средней оси эллипсоида
при R > 1 становится неустойчивым и любое случайное возму-
щение опрокинет систему в новое стационарное состояние: В
либо В1. Как следует из (3. 7), при R >> 1 кинетическая энергия
движения сосредоточивается в тех составляющих движения, на
которые внешние силы не оказывают прямого воздействия. Реа-
лизация такого явления и была целью первого этапа экспери-
мента (Должанский (1972))<
Предварительно отметим, что ось жидкого вращения в режимах
В и В1 образует с плоскостью (ях, я3), перпендикулярной вектору
момента внешних сил F=(0, F, 0), угол (тт/2 — р), который, как
легко показать с помощью (3. 3), (3. 4) и (3. 7), определяется
равенством
Ip. __ Q2-------1 Ь2 (а2 4- с2) / 2 /о
a^ + 2a^ + b^\R-i) ’ ’ 1 '
Отсюда следует, что при В >* 1 указанная ось расположена почти
перпендикулярно (§ = тс/2) к направлению момента внешних
сил. Угол а, который образует проекция оси жидкого вращения
с большой осью эллипсоида х19 зависит только от геометрии эл-
липсоида, что видно из следующего равенства:
tga = _^=_sgn(/)_(_J_) f (3.16)
тде положительйые значения а отсчитываются в направлении
против часовой стрелки, если смотреть со стороны положительной
полуоси х2. Согласно (3. 15) при изменении знака внешних сил
проекция оси жидкого вращения на плоскости (х19 х3) поворачи-
вается на угол 2 а или 2a+ тг. Важно то обстоятельство, что при
В >> 1 векторы скорости течения в точках плоскости (х^ х2), до-
статочно удаленных от оси х19 образуют с последней угол — а,
т. е. они почти параллельны оси жидкого вращения, которое
устанавливается при изменении знака момента внешних сил.
Это легко показать, если воспользоваться разложением поля
скорости по параментам со., введенным в гл. I.
Указанная особенность режимов В и В1 использовалась для
их регистрации при лабораторном моделировании течения жидко-
сти внутри эллипсоида, которое было выполнено следующим об-
разом. Во вращающееся магнитное поле, создаваемое трехфазным
47
током, вводилась капсула из плексигласа, внутренняя полость
которой имеет форму трехосного эллипсоида с главными полу-
осями а=30 мм, 6=24 мм и е=15 мм. Напряженность магнитного
поля достигала максимальной величины при 2500 ампер-витках
на каждую фазу.
Капсула с эллипсоидальной полостью и общий вид экспери-'
ментальной установки изображены на рис. 10.
Для регистрации направления вращения жидкости внутрь
полости на одинаковых расстояниях от центра эллипсоида были
введены маленькие флюгеры с осями, расположенными в плоскости1
(^i, х2) параллельно оси вращения магнитного поля. Глубина
погружения лопаток флюгеров составляла приблизительно чет-
вертую часть от максимальной. Выведенный наружу верхний
конец оси флюгера был снабжен стрелкой, укрепленной парад-j
дельно плоскости лопатки флюгера. Оси, стрелки и лопатки
флюгеров были изготовлены из немагнитного материала.
Заметим, что параметры установки обеспечивают соблюдение
условий гальванического приближения магнитной гидродинамики
(см. Брагинский (1959)), при которых магнитные силовые линии
не увлекаются жидкостью. Поэтому движение жидкости не могло
оказать сколько-нибудь заметного влияния на величину крутиль-
ного момента пондеромоторных сил, определяемых напряжен-
ностью магнитного поля.
Слабая чувствительность флюгеров, обусловленная трением |
в опорах, не позволяла зарегистрировать режим А при закру-
чивании ртути вокруг средней оси х2, поскольку потеря его
устойчивости из-за малой вязкости ртути наступает при очены
малых значениях момента внешних сил /=Х2/р. Поэтому, чтобы
иметь возможность сравнить картины всех трех видов течений,
закручивание ртути осуществлялось двумя способами: а) вокруг
короткой оси х3, когда согласно теории режим А всегда устойчив,
и б) вокруг средней оси х2, причем оси флюгеров в каждом случае
располагались параллельно оси вращения магнитного поля. Для
этого были изготовлены две капсулы с одинаковыми по размерам
эллипсоидальными полостями, отличающиеся различной ориен-
тацией осей флюгеров.
Стационарный режим движения жидкости устанавливался
в течение 5—12 сек после включении магнитного поля, в зави-
симости от величины крутящего момента. Это регистрировалось
с помощью стрелок, которые в конечном итоге принимали опре-
деленное положение. Ориентация стрелок в случаях «а» и «б»
показана соответственно на рис. 11, а и б, причем картинка,
приведенная справа, имеет место для всех |/| > 0,4 /тах(/тах опре-
деляется возможностями установки).
Как видно из рисунков, картины движения в обоих случаях
существенно различны. Если в первом случае вектор угловой
скорости вращения, жидкости совпадает по направлению с мо-
ментом внешних сил, то во втором случае вращение жидкости
48
Рис. 10. Капсула с эллипсоидальной полостью (а) и общий вид эксперимен-
талыюй установки (о)
4 Нелинейные системы
происходит вокруг оси, расположенной почти в горизонтальной
плоскости под углом |а| 35° (ошибка измерения +5°) к боль-
шой оси эллипсоида. Дрейф вокруг средней оси х2 столь незна-
чителен, что флюгерами не регистрируется. В противном случае
стрелки оказались бы непараллельными. Из рисунка видно также,
что при изменении направления вращения магнитного поля на
противоположное флюгеры поворачиваются в плоскости (х^ х3)
на угол 2|а| «70°. Многократным повторением эксперимента
в случае «б» при фиксированных величине и направлении враще-
ния магнитного поля удавалось получить две возможные ориен-
тации стрелок: аналогичную рис. 11, б и противоположную*
Рис. 11. Ориентация стрелок в режиме А при вращении магнитного поля
вокруг короткой оси эллипсоида (а). На рисунке (б) дана ориентация стре-
лок и осей жидкого вращения Qt+) и Q(~J в режиме В' при закручивании жид-
кости вокруг средней оси х2. При вращении магнитного поля против часовой
стрелки (/ > 0) флюгеры устанавливаются в направлении заштрихованных
стрелок, а жидкое вращение происходит вокруг оси Q(+J. В режиме В стрелки
и векторы вращения СК-’ и имеют противоположную ориецтацию
Сопоставляя результаты эксперимента с выводами теоретиче-
ского анализа, нетрудно убедиться, что картина движения на
рис. 11, б соответствует режиму В', а значение а согласуется
с равенством (3. 16). Таким образом, теоретически ожидаемые
эффекты получили экспериментальное подтверждение.
Задача следующего этапа лабораторного моделирования со-
стояла в проведении количественных измерений характеристик
движения рассматриваемой гидродинамической системы, на ос-
нове которых делаются окончательные выводы о степени спра-
ведливости развитой выше теории. Для этого нет необходимости
непосредственно измерять скорости течения ртути внутри по-
лости, что связано с рядом технических трудностей. Принци-
пиальная схема эксперимента, подробное описание которого
содержится в работе Гледзера и Новикова (1973), выглядит сле-
дующим образом.
; Внутрь магнитной системы помещается заполненная ртутью
капсула, закрепленная на упругом подвесе так, что средняя
ось эллипсоида вертикальна и снабжена емкостным датчиком
для регистрации углов поворота с помощью специальной элек-
50
тронной аппаратуры, которая включает в себя записывающее
устройство. Любое изменение величины магнитного поля приво-
дит к возникновению в системе нелинейных крутильных коле-
баний, которыми сопровождается переходный процесс от одного
стационарного состояния к другому, причем характер таких
колебаний определяется движением жидкости внутри эллипсои-
дальной полости. На рис. 12 показана типичная форма экспери-
ментальных кривых переходных процессов при включении
(рис. 12, а) и выключении (рис. 12, б) магнитного поля. Чув-
ствительность аппаратуры не позволила проводить измерения
вблизи критических значений R. Поэтому во всех экспериментах
Рис. 12. Типичная форма экс-
периментальных кривых пере-
ходных процессов при вклю-
чении (а) и выключении (б)
магнитного поля
величина магнитного поля соответствовала значениям R >> 1.
В связи с этим уместно отметить, что возникновение затухающих
колебаний при таких значениях R было предсказано в § 2 и про-
иллюстрировано на рис. 9, а.
Кривые переходных процессов были получены затем числен-
ным интегрированием системы (3. 2) совместно с уравнением кру-
тильных колебаний капсулы
(3.17)
где IQ — момент инерции системы, состоящей из капсулы с ртутью
и датчика; к — упругость подвеса; v — коэффициент трения
демпфирующего устройства, предназначенного для гашения соб-
ственных колебаний системы, L — момент сил, создаваемый маг-
нитным нолем, М^ 2/5аст — вертикальная составляющая
момента количества движения, т — масса ртути.
Сопоставление целого ряда расчетных и экспериментальных
кривых показало вполне удовлетворительное согласие между
ними, и, кроме того, в итоге их совместной обработки удалось,
в частности, рассчитать величину эффективного коэффициента
трения X, входящего в (3. 2).
Процессы гидродинамической неустойчивости внутри трех-
осного эллипсоида можно наблюдать и непосредственно с помощью
иного типа экспериментов, методика которых также была разра-
ботана в Институте физики атмосферы АН СССР (Обухов А. М.,
4*
51
(1973); Гледзер Е. Б., Новиков Ю. В., Обухов А. М., Чусов М. А.
(1974)). С этой целью был изготовлен прозрачный полый блок
из органического стекла, внутренняя поверхность которого
представляет собою трехосный эллипсоид с осями с=70 мм,
Ь = 120 мм и <2=150 мм. Полость заполняется соленой водой
со взвешенными в ней шариками из синтетической смолы с плот-
ностью 1,025 г/см\ Диаметр шариков 2,5 мм.
При наблюдениях применяется следующая методика. Блок,
укрепленный на планшайбе двигателя постоянного тока, приво-
дится во вращение со скоростью 500 об!мин. Вращение продол-
жается несколько минут, в результате чего жидкость и стенки
полости начинают вращаться как единое твердое тело. Далее
следует быстрая полная остановка блока, а движение жидкости
продолжается по инерции. Дальнейшее протекание гидродинами-
ческих процессов определяется взаимной ориентацией осей эллип-
соида относительно оси вращения при предварительном раз-
гоне.
Таким методом быстрые процессы установления движения
жидкости удается наблюдать непосредственно, а также фикси-
ровать с помощью кинокамеры. Для подробного изучения про-
цессы фотографировались со скоростями от 5 до 64 кадров в се-
кунду. Исследуемая область внутри полости освещалась плоским
тонким лучом света, плоскость которого ориентировалась перпен-
дикулярно оптической оси объектива кинокамеры.
Возможны три основных положения полости при предваритель-
ном разгоне жидкости.
1. Полость вращается вокруг короткой оси эллипсоида, как
это показано на рис. 13,а. После остановки блока жидкость
продолжает вращение в первоначальном направлении. Движение
является устойчивым и продолжается весьма долго. На рис. 13, б
показаны первые шесть снятых одна за другой фотографий про-
цесса (слева направо), непосредственно следующих за моментом
остановки полости (снято сверху).
2. Полость вращается вокруг средней оси (рис. 14, а). Тотчас
после остановки полости жидкость вращается в направлении
разгона (первая фотография рис. 14, б). Затем происходит «опро-
кидывание» оси вращения потока почти на 90°, после чего жид-
кость продолжает вращение уже в плоскостях, параллельных плос-
кости, проходящей через большую и среднюю оси. Далее
на рис. 14, б даны фотографии ряда последовательных моментов
процесса опрокидывания потока в полости и его конечная форма.
Направление опрокидывания произвольно.
Устойчивость жидкого вращения вокруг короткой оси и не-
устойчивость при «закрутке» вокруг средней оси следуют из про-
стой «трехмодовой» теории движения жидкости внутри эллипсоида,
рассмотренной выше.
3. Несколько неожиданный результат получен при осуще-
ствлении «закрутки» вокруг длинной оси (рис. 15).
52
Рис. 13. Эксперимент с вращением эллипсоида вокруг короткой оси
Рис. 14, Эксперимент с вращением эллипсоида вокруг средней оси
Рис. 13. Эксперимент с вращением эллипсоида вокруг длинной оси
Непосредственно за моментом остановки следует образование
двух вихревых потоков вблизи «полюсов». Начинается сложный
и быстрый процесс опрокидывания, вызванный принципиальной
неустойчивостью течения жидкости в направлении разгона.
В процессе опрокидывания в полости возникают три движения
жидкости: экваториальное в направлении разгона и два вихревых,
являющиеся к нему касательными. Развитие касательных вихрей
идет за счет увеличения их диаметров и поворота плоскостей
вращения. Одновременно уменьшаются объем и мощность эква-
ториального потока. Завершение процесса опрокидывания насту-
пает приблизительно через 0,8 сек после его начала в момент,
когда вихревые движения захватывают весь объем полости и со-
прикасаются между собой. Экваториальное движение в этот
момент уже не существует. Поскольку последнее являлось носи-
телем энергии, запасенной при разгоне, а вихревые движения
существовали за счет ее расходования, то с момента его исчезно-
вения вихревые движения быстро разрушаются. Движение жид-
кости начинает носить хаотический характер *.
^(Результат последнего эксперимента, очевидно, не укладывается
в трехмодовую теорию, согласно которой вращение вокруг длинной
♦ Описанный эффект впервые обнаружил Ю. В. Новиков,
54
оси должно быть устойчивым, и требует для своего объяснения
привлечения дополнительных степеней свободы. К настоящему
времени законченная теория такого явления еще не построена.
Некоторые предварительные соображения будут высказаны ниже.
Картина движения, изображенная на рис. 15, б, симметрична
относительно плоскости, проходящей через центр инерции эллип-
соида перпендикулярно большой оси, и указывает на существова-
ние вихревых течений в каждой половине полости. Попыт емся
теперь, основываясь на упомянутой симметрии, отыскать конеч-
ную систему ортогональных бездивергентных векторных функ-
ций W/, которыми можно было бы ограничиться в разложении
скорости течения по методу Галеркина для описания уже извест-
ной нам картины движения. Такую систему легко получить линей-
ной комбинацией из тороидальных полей для сферы (сферический
вихрь Хилла, см., например, Кочин, Кибель, Розе (1963)) при де-
формации сферы до данного эллипсоида и однородных линейных
и квадратичных векторных полей, касательных к семейству
эллипсоидов (х/а)2 -\-{zlc)2= о 1. Она имеет следую-
щий вид:
*=—Pl+fl*,
».=?Ч45+4&:+5-1)]* <3-18>
причем ортогональность векторов (i=l, 2, 3) следует понимать
в том смысле, что
-у J w<.w/3x = 8y, (3.19)
У
где V — объем, занимаемый соответствующей
лости, — символ Кронекера. По-прежнему
что а > b > с. Тогда вектор скорости течения
вить в виде
у = о»! (i) W1 + <о2 (i)w2 + <1)3 (0 w3.
половиной по-
предполагается,
можно предста-
. (3.20)
Заметим, что в таком представлении нормальная составляющая
скорости течения на поверхности эллипсоида обращается в ноль.
Случай и о)2= (о3=0 соответствует квазитвердому вращению
вокруг большой оси х.
Умножая левую и правую части уравнения Эйлера
J+(v-V)v=—igradp (3.21)
на w., пользуясь представлением (3. 20) и определением скаляр-
ного произведения (3. 19), получим следующую систему уравнений
55
Рис. 16. Области неустойчи-
вости при движении жидкости
вокруг длинной оси эллипсои-
дальной полости
относительно параметров <о., ко-
торая описывает движение жид-
кости в каждой из выделенных
половин эллипсоида:
з (62 _ с2)
1 7 (о2 + с2) 2
й2 = 5 +1з^У' ®1юз> (3- 22)
(b3 =
(7а2 — 15d2)
5 (а2 + 362)
Вводя энергетические переменные
/ J2 + С2 V/
5 / 0)1
и2=[^ + 3ст]'1^2,
и3 = [(а2362)/35]*/« <о3,
систему (3. 22) можно переписать в виде
й1 = ри2и3.
u2=qasult (3.22а)
где р, q иг удовлетворяют условиюр+?+г=0 и имеют следующие
выражения:
п________15_________(d2 — с2)________
Р ~ V5* \/(&2 + с2) (в2 + 3С2) (О2 4-362) ’
(О. ли)
__1___________(7а2 — 15 с2)_____
9 ~ \^(62 + с2) (а2 + Зс2) (а2 + 3d2) ’
г________1__________(7а2 — 15d2)_____
~ V5 ^(d2 + с2) (а2 + Зс2) (а2 + 3d2) ’
Таким образом, мы вновь приходим к уравнениям Эйлера теории
гироскопа, согласно которой вращение вокруг оси х будет не-
устойчивым, если
р<0, ?>0, г>0. (3.24)
Отсюда следует, что полуоси эллипсоида а, Ъ и с должны удовлет-
ворять неравенствам
J/r-^-c<[a<Z ]/-у- Ъ. (3. 24а)
56
На рис. 16 область неустойчивости, задаваемая неравенствами
(3. 24а), ограничена треугольником, изображенным пунктиром.
Более детальное исследование (также без учета вязкости)
жидкого вращения вокруг длинной оси было выполнено Глед-
зером, который получил следующие условия неустойчивости:
<3.25)
На рис. 16 неравенству (3. 25) соответствует область, заклю-
ченная внутри треугольника, изображенного жирными сплошными
линиями. Звездочкой обозначена точка, которая отвечает исполь-
зованному в эксперименте эллипсоиду с полуосями а=150 мм,
Ь=120 мм, с=70 мм. Из рисунка видно, что полученные области
неустойчивости в значительной степени перекрываются.
Более поздние эксперименты Ю. В. Новикова по вращению
эллипсоида с отношением осей 0,84:1:1,17 указали на устойчи-
вость эллиптического вращения вокруг длинной оси, что согла-
суется с приведенной схемой областей неустойчивости (рис. 16).
Глава IV
НЕЛИНЕЙНЫЕ ВЗАИМОДЕЙСТВИЯ
В ЗАДАЧЕ О КОНВЕКЦИИ
§ 1. Общие замечания к построению
малопараметрической модели конвекции
Нелинейные взаимодействия играют первостепенную роль в фор-
мировании конвективных течений. Общий вывод эксперименталь-
ных и теоретических исследований конвекции жидкости, начало
которым положено еще Бенаром (1901) и Рэлеем (1916), состоит
в том, что с увеличением интенсивности внешних источников тепла
конвективный процесс претерпевает на определенном этапе ка-
чественные изменения или, как в таких случаях говорят, происхо-
дит переход от одного режима конвекции к другому. Такое явление
обычно объясняют так называемой бароклинной неустойчивостью
первичного конвективного течения, которая возникает благодаря
тому, что в жидкости создается избыток потенциальной энергии
за счет внешнего нагревания. Под влиянием случайных возмуще-
ний потенциальная энергия преобразуется в кинетическую энер-
гию отдельных мод движения, в том числе и тех из них, которые
вначале оставались невозбужденными. В результате число мод,
участвующих в формировании конвективного течения, возрастав!
и, кроме того, происходит перераспределение энергии между ними,
что и приводит в конечном итоге к переходу конвекции в каче-
ственно новое состояние. В таких случаях число Рэлея — без-
размерный критерий, которым обычно характеризуют конвек-
цию, превосходит некоторое критическое значение завися-
щее от конкретных условий задачи.
Для геофизики особый интерес представляет термическая кон*
векция вращающейся жидкости, которой за последнее времь
уделяется большое внимание в связи с изучением механизмов
ответственных за формирование общей циркуляции земной атмо
сферы. Трудности, возникающие при изучении столь сложно!
гидродинамической системы, как атмосфера, заставили специа
листов обратиться к исследованию менее сложных, но родствен
ных гидродинамических систем типа вращающихся кольцевые
сосудов с жидкостью, главное преимущество которых состоя'
в том, что их сравнительно легко воспроизвести в лабораторные
условиях. Это позволяет получить зависимость свойств движение
58
жидкости от ее физических и внешних параметров, строго контро-
лируемых в эксперименте.
1 Впервые лабораторные эксперименты по конвекции вращаю-
пихся жидкостей были выполнены Фульцем (1951) и Хайдом
Н953), впоследствии неоднократно воспроизведенные и суще-
ственно дополненные исследованиями ряда других авторов, ле-
тальное обсуждение результатов которых можно найти, например,
в обзоре Хайда (1970). Для нас важным является то общее, что при-
суще всем лабораторным экспериментам и что состоит в следующем.
Сосуды имеют форму цилиндрических или кольцевых каналов;
внешнее нагревание жидкости неоднородно по горизонтали, а вра-
щение ее осуществляется вокруг вертикальной оси симметрии.
Поведение жидкости в таких сосудах определяется главным
1дЯо,
Рис. 17. В ПЛОСКОСТИ (оГ<г, Л»)
схематически изображена кри-
вая устойчивости осесиммет-
ричного течения (режим Гад-
лея) в кольцевых сосудах
„ верхний ”
осесимметричный режим
I осесимметричный режим
1g Та
образом двумя безразмерными критериями подобия: числами
Россби и Тейлора ^===4d*QQ/hv^ где Ли d —
соответственно вертикальный и горизонтальный размер сосуда,
g — ускорение силы тяжести, р — коэффициент теплового расши-
рения, Qo — угловая скорость вращения сосуда и v — кинема-
тическая вязкость жидкости.
При малых числах Тейлора в канале устанавливается осесим-
метричное течение, экспериментальная кривая устойчивости ко-
торого схематически изображена на рис. 17 в фазовой плоскости *
(оТ"сЖО- В области, расположенной справа от кривой, устойчивым
является один из трех видов несимметричных течений, объеди-
няемых под общим названием режимов Россби, подробное опи-
сание которых содержится в книгах Лоренца (1967) и Старра (1968).
Из рис. 17 видно, что фактор вращения при определенных
условиях приводит к появлению качественно новых особенностей
конвективного процесса, характерных исключительно для вращаю-
щихся жидкостей. Режимы Россби вообще не существуют при ма-
лых < оГ«кр, когда влияние вращения практически еще не ска-
зывается. Осесимметричный режим, устанавливающийся при ма-
* По аналогии с пространством скоростей пространство безразмерных кри-
териев подобия мы также будем называть фазовым.
59
лых (2%* и разрушающийся под влиянием их возрастания, вновь
оказывается устойчивым, если при фиксированном
внешнее неоднородное нагревание становится достаточно интен-
сивным. В таких случаях говорят, что «нижний» осесимметричный
режим переходит в «верхний», фазовая точка которого располо^
жена над критической кривой (см. рис. 17).
Теоретическое объяснение взаимного преобразования режимов.
Гадлея и Россби дано в работе Лоренца (1962), которая представ-
ляет замечательный пример аналитического исследования нелиней-
ной конвекции, выполненного с помощью малопараметрической
математической модели. Надо сказать, что при изучении конвек-
тивных процессов, как правило, приходится прибегать к громозд-
кому численному интегрированию гидродинамических уравнений,
тогда как аналитическими методами к настоящему времени уда-1
лось получить только отдельные результаты, относящиеся преиму-
щественно к конвекции жидкости, подогреваемой снизу (см., на-
пример, Сорокин (1954), Горьков (1957), Малкус и Веронис (1958)
и некоторые другие работы, обсуждаемые в упомянутой книге
Монина и Яглома). Однако для понимания механизма бароклин-
ной неустойчивости имеют большое значение задачи, доступные;
теоретическому анализу, поскольку именно они дают представле-
ние о зависимости свойств движения жидкости от ее физических
и внешних параметров. Уже работа Лоренца (1962) показывает,
сколь полезными могут оказаться малопараметрические модели
для изучения реальных процессов в жидкости. В гл. II были
сформулированы определенные требования, которые должны предъ-
являться к малопараметрическим моделям, претендующим на опи-
сание гидродинамических систем. Естественно попытаться
на основе обобщения указанных требований на случай конвек-
ции применить общий подход, развитый в гл. II, к построению
простейшей модели бароклинного течения, пригодной, в частности,
для исследования конвекции, возникающей в условиях гори-
зонтально неоднородного разогрева и вращения.
Обобщение должно содержать требование существования до-
полнительных инвариантов, соответствующих сохранению энтро-
пии и потенциального вихря, которым сопровождается свободное
течение бароклинной жидкости, и, кроме того, в интеграл энергии
должны входить члены, ответственные за доступную потенциаль-
ную энергию.
Модель такого типа можно построить (см. Должанский
(1973а, б)) с помощью рассмотренных выше уравнений Эйлера
теории гироскопа, если учесть архимедовы силы и ввести уравне-
ние переноса тепла. Для достижения цели вновь удобно восполь-
зоваться гидродинамической интерпретацией уравнений триплета,
подразумевая движение жидкости внутри эллипсоида с линейным
полем скорости. В этом случае задачу удается свести к изучению
квадратично-нелинейной динамической системы с шестью стене-
60
яями свободы, с помощью которой мы Выделим важнейшие свойства
конвективного процесса, кратко описанные выше.
Отметим, что в отличие от движения жидкости под действием
магнитного поля, рассмотренного в предшествующей главе, кон-
вективное течение оказывает уже существенное влияние на ве-
личину и направление внешнего возбуждения, хотя в обоих слу-
чаях приложенные силы имеют вихревой характер. Такой эффект
обратной связи учитывается в предлагаемой ниже модели.
§ 2. Модельные уравнения и интегралы движения
В общем виде физическая постановка задачи выглядит сле-
дующим образом. Вязкая несжимаемая жидкость, заключенная
внутри эллипсоида, уравнение поверхности которого
8 (х) = (xJa)2 + (xjbf + (жз/с)2 = 1,
(а>&>с),
находится в условиях стационарного неоднородного внешнего
нагрева. Эллипсоид вместе с источниками тепла приведен в со-
стояние равномерного вращения вокруг оси, проходящей через
его центр инерции, параллельно вектору силы тяжести с угловой
скоростью 20, которая предполагается не слишком большой,
чтобы влиянием центробежных сил по сравнению с силой тяжести
можно было пренебречь.
Поведение такой системы, вообще говоря, описывается уравне-
ниями гидродинамики в приближении Буссинеска
^+(v.V)v + 2fi0Xv = -|gradp-₽gT + f, (4.1)
. V) Т = е/С/), div v = 0, (4. 2)
где v — вектор скорости течения, р и р — средняя плотность
и коэффициент объемного расширения жидкости соответственно,
g — ускорение силы тяжести, которое в системе координат,
связанной с вращающимся эллипсоидом, остается постоянным
как вектор, коллинеарный вектору Йо (dg/<fr-'gXfio=O)> Т —
отклонение температуры от некоторого постоянного значения Zo,
определяемого конкретными условиями задачи, f — внутренние
вязкие силы, для которых rot f^O, е — приток тепла к единице
массы жидкости за счет внешнего нагрева и теплопроводности,
который в дальнейшем будем предполагать линейной функцией
пространственных координат (х±, х3), с?— удельная теплоем-
кость при постоянном давлении.
Движение реальной жидкости внутри эллипсоида, как было
показано в гл. III. при определенных условиях хорошо описы-
61
йается линейным нолём скоростей. Поэтому, применяя метод,
аналогичный тому, который был использован в гл. II при выводе
динамических уравнений триплета из уравнений гидродинамики,
решение системы (4. 1) и (4. 2) будем искать в классе функций,
удовлетворяющих условиям
д2и./дху-дхк = 0, д2Т1дх^дхк = О, (4. 3)
что эквивалентно сохранению только первых членов в разложе-
нии полей v и Т по опорным функциям (см. гл. I). В результате
получим следующую упрощенную систему уравнений конвекции:
-^=(0 X (М + 2М0) + ₽g (1X q) - хм, (4.4)
lT=®Xq + Q,
(4.5)
где компоненты вектора <о в системе координат с осями хъ х21 х^
совпадающими с главными осями эллипсоида, выражаются через
компоненты Q=rot v, уже знакомые нам по гл. I соотноше-
ниями (1. 27). Как и раньше, М£=1.ки>к, Iik=0 при i^k
и Z11=71=b24-c2, 722=Z2=a2+c2, Z33=Z3=a2-]-b2, причем предпо-
лагается, что главные полуоси эллипсоида удовлетворяют не-
равенству а > Ъ > с, MQi=Iik <*>ок,
Ш01 ~ С2 ^01> Ш02 ~ ~а2 С2 ^02» Ш03 ~ ~а2 &2 ^03’ 6)
Составляющие векторов q и — соответственно разности
температур и притоков тепла на главных полуосях эллипсоида, т. е.
г дТ Ъ — —
& дхг 9 дх% 9 С дх3,
(4. 7)
1 = (a cos Тр b cos у2, с cos у3),
где cos суть направляющие косинусы силы тяжести. Последним
членом в правой части (4. 4) учитывается диссипация.
Рассмотрим некоторые особенности упрощенных уравнений
конвекции. Умножая скалярно левые и правые части уравне-
ний (4. 4) и (4. 5) соответственно на со и |3gl и складывая, получим
уравнение баланса полной энергии Е
(4.8)
62
Умножая затем (4. 4) на q, а (4. 5) на (М-|-2М0) и вновь складывая,
придем к так называемому уравнению трансформации потенциаль-
ного вихря (см. Обухов (1962))
#= (М + 2М0). Q - kq • М. (4.9)
Здесь
JSrxzyM • to + gpi* q, (4.10)
/ = (M + 2M0).q,
которые при отсутствии внешнего нагрева и трения (е=0, Х=0)
являются аналогами хорошо известных гидродинамических инва-
риантов. Понятие потенциального вихря впервые было введено
Эртелем (1942) и часто используется в метеорологии (см., напри-
мер, Монин (1970)).
Следует заметить также, что первое слагаемое в первом ра-
венстве (4. 10) соответствует кинетической энергии свободного
жидкого вращения, а второе является мерой так называемой
доступной потенциальной энергии (Лоренц (1955)), которая дости-
гает минимального отрицательного значения при устойчивой тем-
пературной стратификации, когда grad Т имеет направление,
противоположное силе тяжести.
Кроме того, как непосредственно следует из уравнения (4. 5),
согласно которому вектор q при Q=0 вращается с угловой ско-
ростью со, рассматриваемая гидродинамическая система обладает
еще одним интегралом движения q—|q|. В принятых нами прибли-
жениях он соответствует сохранению энтропии замкнутой системы.
Используя это обстоятельство, полную энергию можно опреде-
лить как
£' = уМ. w + g₽ (/<? + !• q); (4.10')
она уже не принимает отрицательных значений, а ее минимум
равен нулю.
При ®=0 система (4. 4), (4. 5) допускает стационарное решение,
которое отвечает состоянию механического равновесия (е>=0)
с отличным от нуля вертикальным градиентом температуры.
В этом случае q коллинеарен вектору 1. При устойчивой стратифи-
кации (grad T’g <0) малые отклонения от механического рав-
новесия приводят в отсутствие вязкости к возникновению гармо-
нических колебаний с частотами Брента—Вяйсаля (см., напри-
мер, Эккарт (I960)), которые зависят от ориентации эллипсоида,
свойств заполняющей среды и величины grad Т, Например,
в случае, когда малая ось х3 направлена вверх, %(i^3) колеб-
лются с частотами $gdT/dx3)\ если дТ!дх3 > 0.
Таким образом, упрощенные уравнения конвекции, исследо-
ванием которых мы займемся в следующих параграфах, сохраняют
63
важнейшие свойства исходных гидродинамических уравнений.
Введение дополнительных ограничений очевидно привело бы к
несохранению указанных свойств, а поэтому систему (4. 4), (4. 5)
в которой учтено влияние архимедовых сил и процессов переноса
тепла, можно рассматривать как простейшую модель бароклин-
ного течения жидкости.
Заканчивая постановку задачи, заметим, что в рамках исполь-
зованных приближений нетрудно вывести явное выражение
для поля давления р. В самом деле, подставим в уравнение (4. 1)
разложения Т и v соответственно по параметрам q. и ох (см. гл. I
(1. 26)) и проинтегрируем его правую и левую части вдоль не-
которой кривой, выходящей из начала координат, где положим
_р=0, исключая тем самым гидростатическую составляющую
давления. Тогда, принимая во внимание, что удовлетворяют,
векторному уравнению (4. 4), получим
Р (х, О/p — + SiQ{ + Ri^ (4- 11)
где Ру — элементы симметричной матрицы, выражения для ко-:
торых имеют вид
Рц — (Х2 4" ^з)/2» ^12 = а2 £2 Х1Х2> Лз = а2 [ с2 ^1^3» (4. 12)
^22 = (Х1 4” Хз)1%> ^23 = ^2 С2“ Х2Ж3> ^33 — (Х1 +
(™s Т1 cos Т2 + a cos Тз , (4.13)
R1 = х1 4“ Т* ^01 2 а2 ^^2^02 2 а2 с2 (4.14)
a S. и R. (i=2, 3) легко получаются из (4. 13) и (4. 14) круговой
перестановкой индексов (123) и (afee). Первое слагаемое в (4. И)
соответствует реакциям связи, второе имеет термодинамическое
происхождение, а последнее обусловлено силами Кориолиса.
Полезно отметить, что выражение (4. 11) строго выполняется
лишь для невязкой жидкости. В противном случае его следует
рассматривать как приближенное, поскольку из-за прилипания
жидкости на стенках линейные поля скорости и температуры
в вязкой жидкости не могут сформироваться. Однако движение
внутренних слоев жидкости, как было показано в гл. III, доста-
точно хорошо аппроксимируется такими полями.
/
§ 3. Стационарная конвекция в покоящемся эллипсоиде
Ограничимся на первом этапе исследованием конвекции в по-
коящемся эллипсоиде (2о=0). Такая задача представляет само-
стоятельный интерес, и, кроме того, она поможет нам в дальней-
64
ем лучше разобраться во влиянии сил Кориолиса на формйро-
ше_\ие бароклинных течений. Поступление энергии от внешних
источников тепла к жидкости проще всего учесть, задав е фор-
мулой Ньютона
е/ср = р(Т — Т), (4.15)
е — эффективный коэффициент теплопроводности, обратная
величина которого определяет характерное время затухания
в неподвижной среде отклонений от равновесной температуры Т.
Последняя предполагается заданной линейной функцией простран-
ственных координат, и, кроме того, р может учитывать как моле-
кулярный, так и радиационный механизм передачи тепла.
Как было показано в гл. III, неустойчивость циркуляции
внутри полости при движении, характеризующемся линейным
полем скорости, можно наблюдать при условии, если закручи-
вание жидкости происходит вокруг средней оси эллипсоида.
Поэтому дальнейшее рассмотрение проводится в предположении,
что малая ось эллипсоида х3 направлена вверх, а внешние источ-
ники тепла создают grad Т в положительном направлении большой
оси хг Введем новые безразмерные зависимые переменные Wi
и 0г, согласно следующим равенствам:
W.=:WJX, 0. = -^.-^. (4.16)
Вновь удобно ограничиться случаем I2=(/14-73)/2. Последнее
ограничение, как уже указывалось в гл. III, несущественно.
Тогда, принимая во внимание ориентацию эллипсоида по отно-
шению к силе тяжести и внешним источникам тепла, уравнения
конвекции (4. 4) и (4. 5) можно представить в следующем виде:
W, = - W. + Рг'1 А 02)
•*2
Ж2 = —2Г.Ж3Ж, — W2 — Рг"1©,, (4.17)
0Х = -Ж302 + 1Р20з + Рг1 (Ra - ©х),
0 = JP3©X — И\08 — Рг’1©,, (4.18)
©з=— и7,©! + w,e2—Рг-^з,
где Г.=(/3—/х)/2^ (j=l, 2, 3), причем Гх > Г2 > Г3,
Г2=2ГхГ3/(Гх4-Г3). В дальнейшем мы будем часто использовать
указанные соотношения. Точкой обозначена операция дифферен-
цирования по безразмерному времени т=Х£. Pr=X/fi,
/2 ¥ ’
ДУ — разность равновесных температур, созда-
ваемая в неподвижной среде внешними источниками тепла на боль-
шой полуоси эллипсоида.
5 Нелинейные системы
65
В применений к данной гидродинамической системе безраз-
мерные параметры Ra и Рг естественно называть числами Рэлея
и Прандтля соответственно. Следует, однако, подчеркнуть, что они
определяются не молекулярными, а эффективными коэффициен-
тами вязкости и теплопроводности, которые, как уже указыва-
лось, могут учитывать влияние пограничного слоя, внутреннего
трения и лучистого теплообмена.
' Легко убедиться, что одно из стационарных решений си-
стемы (4. 17), (4. 18) имеет вид
Ж1=И73 = 0, W2 = W20== — (4-19)
102 УЗ (о \ 2 J)
е1=_Ргж20, 02==о, е3 = Рг2иг,
причем Ж20 является единственным действительным корнем куби-
ческого уравнения:
W* + Pr~W2 + Pr3 Ra = 0. (4. 20)
Движение, определяемое равенствами (4. 19), соответствует
обычной регулярной конвекции с восходящими течениями в нагре-
тых областях и нисходящими течениями в холодных. Такой
режим конвекции в применении к атмосфере и лабораторным
экспериментам принято называть гадлеевским, по имени одного
из первых исследователей общей циркуляции земной атмосферы.
Мы также будем придерживаться этой терминологии и обозначать
его буквой Н (Hadley). Заметим, что в режиме Н момент бароклин-
ных сил (F =0glxq, выраженный членом Буссинеска в правой
части (4. 4) и (4. 17), действует вдоль средней оси эллипсоида
(0Х > 0, 02=О), т. е. его направление совпадает с направлением
жидкого вращения со.
Наложим на стационарный режим Н малые возмущения и ли-
неаризуем систему (4. 17), (4. 18) относительно такого состояния,
пренебрегая членами второго порядка малости. Матрица со-
ставленная из коэффициентов правой части линеаризованных
уравнений, имеет вид
/ —1 0 Wo 0 Гх/(Г2Рг) 0 \
/ 0 —1 0 Рг'1 0 0 \
„ / r.JKn 0 —1 0 0 о 1 ,
е^=| \20 (4.21)
1 ° PrW20 0 —Pr’1 0 w „ 1 УУ 20 1
\ — PrW20 0 -Рг^20 0 —Рг-1 0 /
\ 0 Рг^20 0 0 —Рг1/
В силу специфики структуры матрицы (4. 21) соответствующий
ей характеристический многочлен ||е^ — а 1|| (1 — единичная
66
матрица) можно представить в виде произведения двух полиномов
третьей степени от а
о3 + (1 + 2Рг-1) о2 + [Рг~2 + 2Рг-1 + (1 + Рг) Ж20] а +
+ (Рг-2 + ЗР720),
(4. 22)
°3 + (2 + Рг’1) о2 + [1 + 2Рг-1 + (Рг - Г2Г3) Ж20] о +
+[Рг-1 + 77 (Рг + Гз - ГЛPr-1) WQ •
Применяя для исследования корней многочленов (4. 22) извест-
ный критерий Льенара—Шипара (см., например, Гантмахер
(1966)), получим следующее необходимое и достаточное условие
устойчивости режима Гадлея:
О < £- (Г2Г3 - Г3 Рг - Рг2) Ж20 < 1, (4. 23)
т. е. в этом случае все корни указанных многочленов имеют отри-
цательную действительную часть. Полезно отметить, что действи-
тельные части корней первого многочлена (4. 22) отрицательны
при любых значениях, входящих в него параметров, а (4. 23)
есть условие положительности свободного члена второго куби-
ческого полинома (4. 22), которое, как нетрудно показать, влечет
за собой выполнение остальных неравенств критерия Льенара—
Шипара.
Условие (4. 23) с помощью третьего равенства (4. 19) можно
записать в явном виде
Ra < RaKp -= sh 13 Arsh 3 pr ——-----------
— Рг — 2 (х + 1) Рг2]’72)}, (4.24)
где х=Г1/Г3=73/71 — безразмерный геометрический параметр,
значения которого могут изменяться в пределах 1 х 3.
Параметр х характеризует степень сплюснутости эллипсоида,
причем х=1 соответствует сфере, а при с —>0 х ->3.
На рис. 18 изображена зависимость критического числа Рэлея
RaKp от Рг при различных значениях х. Области устойчивости ре-
жима Н лежат справа от кривых. Каждая кривая имеет вертикаль-
ную асимптоту, определяемую значением
<4-25>
что следует из (4.24).
Таким образом, полученный критерий устойчивости указывает
на весьма интересную особенность циркуляции вокруг средней
5*
67
оси. Потеря устойчивости Такого течения: при возрастании Йа
наступает только при условии, если эффективный Рг < Рг0,
причем максимально неустойчивым по отношению к режиму Н
оказывается наиболее сплюснутый эллипсоид (х=3).
Задача о нахождении стационарных решений системы (4. 17),
(4. 18), соответствующих другим не гадлеевским типам циркуля-
ции, сводится к вычислению корней алгебраических уравнений
степени выше четвертой, и поэтому такие решения не представимы
явными аналитическими выражениями. Однако для дальнейшего
исследования в них нет необходимости, достаточно ограничиться
асимптотическими разложениями.
Рг
Z7.7 0,2 0,0
Рис. 18. Критические кривые
режима Н для различных зна-
чений параметра х
Полагая в (4. 17), (4. 18) левые части равными нулю, выразим
сначала 0- через динамические параметры W.
©i = (i + PrWf) 8, е2 = Рг (Рт/г3 +1)
e3 = (PrWJP3 —Рг1Г2)8, (4-26)
где 8=Ra/(l-[-PrW2), W2==W^Вместо последнего ра-
венства (4. 26) удобнее пользоваться выражением для 03, которое
легко получить из уравнения баланса энергии (4. 8)
03 = Рг2(-Ь-Ж| + 1Г2+Аж2). (4.26а)
Отсюда, в частности, видно, что во всех стационарных режимах
конвекции при заданном способе внешнего разогрева устанавли-
вается устойчивая вертикальная стратификация (03>О).
Подставляя (4. 26) в (4. 17), получим следующую систему
уравнений для определения стационарных значений динамических
параметров W.:
1\Ж2Ж, - W, + Ь- (Рг/Г3 +1) 8Ж3 = О,
*2
2Г2ИЛ1И/3 + Рг 8И^ + Ж2 = —Pr'ig, (4. 27)
ГзИ7!^ — Ж3 = 0.
Хотя 8 зависит от решения, введение его существенно облегчает
анализ, поскольку, как будет показано ниже, при больших
68
числах Рэлея в качестве малого параметра можно взять 8-1.
Режим Н приобретает теперь простой вид
Н) ИЛ1 = ИЛ3 = 0, W2 = — Рг^З. (4.28)
При других режимах конвекции все W^=0. Поэтому для того,
чтобы однородная относительно WT и ТУ3 система, состоящая
из первого и третьего уравнений (4. 27), имела ненулевые решения,
необходимо потребовать равенства нулю ее определителя, вычис-
ление которого приводит к следующему квадратному уравнению:
Ж* + ^^-1/^ = 0, И 29)
где Рг=Рг-|-Г3.
Исключая W3 из второго и третьего уравнений (4. 27), получим
выражение для Wr
W2----- ^2 + Рг-1 5 М 30\
уу 1 — 2Г2Г31Г2 + Рг в ’
из которого следует, что W2 не может быть положительным корнем
уравнения (4. 29). Выбирая отрицательный корень, с помощью
(4. 30), получим, что система (4. 27) имеет два дополнительных
решения С и С", которыми совместно с Н исчерпываются все ста-
ционарные режимы конвекции в покоящемся эллипсоиде:
С) Wr = W^
C'}WX = ~W1<S,
^3 = Г3ТГ1О^2)
рг10= К1 “ ? (8))/Рг (2 й ? (8) “ Рг)Г ’ (4-32)
? (3) =4(1 + /1+-^(2Г2/М2).
Из требования неотрицательности числителя дроби первого ра-
венства (4. 32) следует, что область существования режимов С
и С’ определяется неравенством
А (Г2Г3 - Г3 Рг - Рг2)3(3/Рг)2 >'1, (4. 33)
а2
причем в случае равенства все три режима Я, С и С совпадают.
Сопоставляя (4. 33) с (4. 23) и третьим равенством (4. 28), легко
видеть, что область неустойчивости режима Н полностью совпадает
с областью математического существования режимов С и С'. Таким
образом, становится понятным, почему для жидкостей с Рг > Рг0
циркуляция вокруг средней оси не теряет устойчивости.
69
Рис. 19. Векторная диаграмма: (а) течение жидкости, находящейся под
действием неоднородного внешнего нагрева внутри эллипсоида; (б) жид-
кость приводится в движение механическим моментом внешних сил F (гл. III)
Используя (4. 31), (4. 32) и определение 8, нетрудно показать,
что при Ra -> оо 8 ~ Ra1/3-H? (1). Поэтому для Ra/RaKP >> 1
8"1 является малым параметром, по которому можно разлагать
решения С и С". В этом случае согласно второму равенству (4. 32)
<р(8) = 1 + О(8~2); отсюда следует
с, С) И\ = ±Ж10) = + 0(3-1),
1213
жз= + ж1о + 0(8-1), (4.31а)
1 2
= [(! - - Рг)? + 0 (8“2)- (4- 32а)
Здесь мы не приводим выражений для 0^, которые легко получить
с помощью (4. 26) и (4. 26'). Отметим только, что ~ 8, а 02
и е3 - 82.
Отличительная особенность режимов С и С' состоит в том,
что оси их жидкого вращения не совпадают с направлением
момента бароклинных сил JT. Более того, угол между ними при воз-
растании Ra стремится к тг/2.Всамом деле, поскольку 0г/02 ~ З*"1,
момент бароклинных сил при Ra >> 1 становится почти парал-
лельным большой оси эллипсоида хг. Однако, как следует
из (4. 31а), вектор to стремится занять перпендикулярное положе-
ние параллельно плоскости (#2, #3), так как W\c ростом Ra не раз-
вивается. Причина такого поведения жидкости становится понят-
ной, если учесть, что циркуляция вокруг оси х^ параллельной
grad Т, не осуществляет теплообмен между источниками и стоками
тепла.
70
На рис. 19, а приведена векторная диаграмма, иллюстрирую-
щая состояние конвекции в режимах Н, С и С.
Исследование, выполненное таким же методом, как в случае
режима Гадлея, показывает, что по крайней мере для Ra >> 1
оба режима С и С" устойчивы по отношению к малым возмущениям.
Это означает, что в одинаковых условиях внешнего нагревания
конвекция может находиться в одном из двух существенно раз-
личных состояний, которое устанавливается в зависимости от знака
начального возмущения. Аналогичным свойством, как мы видели
в гл. III, обладает движение электропроводящей жидкости внутри
эллипсоида, возбуждаемое не нагревом, а вращающимся магнит-
ным полем. Существенное отличие, однако, состоит в том, что
в случае нагрева явление опрокидывания сопровождается изме-
нением величины и направления вектора крутящего момента.
Это проиллюстрировано векторной диаграммой на рис. 19, а,
а для сравнения на рис. 19, б приведена векторная диаграмма
стационарных состояний течения жидкости, закручиваемой маг-
нитным полем вокруг средней оси х2.
Перейдем теперь к исследованию конвекции во вращающемся
эллипсоиде, течение жидкости в котором приобретает качественно
новые черты.
§ 4. О влиянии сил Кориолиса на формирование
конвективных течений
внутри вращающегося эллипсоида
Сохраняя ориентацию эллипсоида по отношению к силе тяжести
и внешним источникам тепла, приведем его в состояние равномер-
ного вращения вокруг малой оси х3 (Qo=(O,O, Qo)). В этом случае
мы уже имеем дело с гидродинамической системой, родственной
геофизическим в том смысле, что в ней присутствует два свойст-
венных им определяющих фактора: горизонтальный неоднород-
ный нагрев и вращение вокруг вертикальной оси. Для определен-
ности будем предполагать, что й0 > 0, т. е. вращение происходит
против часовой стрелки, если смотреть с положительного напра-
вления оси х3. Уравнения конвекции, соответствующие указан-
ной постановке задачи, можно представить в следующем безраз-
мерном виде:
W, = IWP3 - W. + i-Ta w2 4- -И Ь.'
W2 = — 2Г2Ж3ТУ1 - W, - Та W. - ©,/Рг, (4. 34)
w3=r3WjW2—w3,
= —W302 + W2e3 + Рг-1 (Ra - ej,
Й^Жз^-ЖА-Рг-^, (4.35)
63 = — W& + Wfi, - Pr-1 ©3,
71
где Та2 = 2^/к2— число Тейлора, которое с точностью!
до величины порядка единицы определяется как квадрат отно-
шения сил Кориолиса к силам трения (см., например, Лоренц
(1967)). Совокупностью параметров Ra, Та обычно и характери-
зуют конвекцию вращающихся жидкостей.
Чтобы исследовать свойства стационарных режимов конвекции,
приведем систему (4. 34), (4. 35) к виду, удобному для отыскания
асимптотических решений, поскольку точные значения искомых
величин являются корнями алгебраических уравнений степени
выше четвертой (ср. § 3). Поскольку (4. 18) и (4. 35) совпадают,
подставим выражения (4. 26) в систему (4. 34), левые части ко-
торой положим равными нулю. Исключая из полученной таким
образом системы алгебраических уравнений W± и Ж3, приходим
к следующему уравнению пятой степени относительно W2:
(W, + 8/Рг) (ц/| + sty, - (wi -
+ = (4'36>
Из первого и третьего стационарных уравнений (4. 34) и второго
равенства (4. 26) следует, что
W. = -Та Ж2/[Г2Г3 (w* + W2 - А-)]. (4. 37)
Важно отметить, что последнее выражение в отличие от (4. 30)
для покоящегося эллипсоида уже не требует отрицательности ТУ2,
а поэтому любой действительный корень уравнения (4. 36) отве-
чает некоторому стационарному режиму конвекции. Это наводит
на мысль о возможности размножения стационарных решений
уравнений конвекции, вызванного исключительно влиянием сил
Кориолиса. Используя (4. 36) и (4. 37), попытаемся теперь иссле-
довать асимптотическое поведение стационарных решений системы
уравнений (4. 34) и (4. 35) при движении в фазовой плоскости
(Та, Ra) вдоль кривой Та=/ (Ra), где / (Ra) монотонно возрастаю-
щая функция, заданная на полуоси Ra 0. Определенная труд-
ность состоит в том, что левая часть (4. 36) и выражение (4. 37)
зависят не только от ТГ2, но и от остальных динамических перемен-
ных из-за входящего в них параметра В. Поэтому выясним сначала
некоторые общие свойства таких решений.
Из уравнения баланса энергии (4. 8), записанного в форме
(4. 26а), следует, что при Ra -> оо W. (f=l, 2,3) возрастают не бы-
стрее RaVs, поскольку неравенство Q. < Ra согласно второму
началу термодинамики выполняется для любого режима конвек-
ции. Параметр 8 при этом по крайней мере не убывает. Рассмот-
рим один частный, но важный для нас случай фазовых траекторий
Ra=a Та4-о (Та), a=const>0. Принимая во внимание ука-
72
данные ограничения и сопоставляя главные члены уравнения
(4. 36), приходим к выводу, что вдоль таких траекторий параметр
3=0 (Ra) для всех стационарных решений системы (4. 34), (4. 35),
за исключением, быть может, случая, когда W2 убывает быстрее,
чем 8 возрастает. Но такого типа решений, как легко показать
с помощью (4. 37) и третьего равенства (4. 34), вдоль рассматри-
ваемых траекторий вообще не существует. Поскольку о — Ra,
то либо W2=0 (1), лйи) W2 —> О при Ra ->оо.
Нетрудно теперь убедиться в том, что любое стационарное
решение системы (4. 34), (4. 35) вдоль траектории Ra= а Та 4~о (Та)
характеризуется одним из двух видов асимптотического пове-
дения:
Ж1 = 0(1),
Н) v
01 = O(Ra),
R) '
= O(Ra),
JV2 = O(Ra^),
©2 = 0(1),
Ж2 = 0(1),
02=O(Ra),
Ж3 = 0 (Ra-1),
©3 = 0(1),
W3 = O(1),
©3 = 0(1).
(4.38)
(4.39)
По причинам, указанным ниже, стационарные режимы конвекции,
соответствующие (4. 38) и (4. 39), будем обозначать буквами Н и R.
Пользуясь аналогичными соображениями, можно также по-
казать, что вдоль других фазовых траекторий Ra=a Та” +о (Та”)
характер асимптотики стационарных решений имеет вид
1<тг<2
W, ~ Ra1"1/», W2 ~ Ra1"2/», W3 ~ Ra2-3'», 2 п $4 3
Н) Wj ~ Ra-1+3/«, H^—Ra1-2'», W3 ~ Ra1/», п 3
W, ~ Ra1/»-1/», W9 ~ Ra1/», W3 ~ Ra1/», 1 7 4 'О 7 1 ^п^З
R) = W^ — RaC»-1)'2»,
71 3
С)^=0(1), W2~Ra4
W3 ~ Ra<”-1)/2»,
K's ~ Ra*/.,
(4. 40a)
(4. 406)
(4. 40b)
(4.41)
(4.42)
Асимптотическое поведение (i = l, 2, 3) непосредственно следует
из определения 8, (4. 26) и (4. 26а).
Для решений типа С при п > 3 члены уравнений (4. 34),
содержащие Та, не являются главными по порядку величины,
а поэтому ими в первом приближении можно пренебречь. Отсюда
следует, что в этом слуцае при Ra 1 конвективные режимы типа
С по существу не отличаются от соответствующих режимов в по-
коящемся эллипсоиде, подробно исследованных в предшествующем
параграфе, а влияние сил Кориолиса приводит к незначительной
73
модификации таких течений. В дальнейшем мы убедимся в том,
что уравнения (4.34) и (4.35) вдоль траекторий Ra=O(Ta*j
с п > 3 не имеют решений, отличающихся от С, С' и Н.
Наибольшую трудность представляет исследование числа ста*
ционарных состояний конвекции вдоль траекторий Ra=O (Та3)
(п=3). Дело в том, что в этом случае, как следует из (4. 40b) —
(4. 42), все решения имеют одинаковый характер асимптотического
поведения и отличаются коэффициентами при главных членах раз-
ложения, удовлетворяющими системе алгебраических уравнений,
которая фактически не проще, чем исходная. Поэтому нам при-
дется прибегнуть к искусственному приему, смысл которого состоит
в следующем. Поскольку в рассматриваемом случае 8 и Та ~ Ra’\
каждому решению вдоль фиксированной кривой Ra=aTa3 +
о (Та3) отвечает в плоскости (Та, 8) луч 8=х Та + о (Та),
наклон которого зависит от решения, т. е. фиксированному зна-
чению а, вообще говоря, соответствует несколько значений
Если бы нам удалось установить такую многозначную зависимость,
можно было бы найти число стационарных решений.
Для этого положим в уравнении (4. 36) 8 известным параметром
и будем искать асимптотику его возврастающих (по модулю) кор-
ней вдоль луча 8=/Га + О (1), используя 8 в качестве параметра
разложения. Полученные таким способом выражения для W2
совместно с (4. 37) и третьим равенством (4. 34) используем для
восстановления упомянутой зависимости с помощью определения
8=Ra/(l + PrW2). Асимптотику растущих корней уравнения
(4.36) можно представить в виде
Ж2 = е8 + О (1), (4.43)
где е удовлетворяет следующему алгебраическому уравнению:
(е + Pr-i) (е + + (Г2Г3х2)-1 (* - I?) = 0. (4. 44)
Составляя дискриминант и находя его нули, нетрудно показать,
что уравнение (4. 44) имеет три действительных (отрицатель-
ных) решения при условии, если
Рг<Рг0, х-2<Х?2 = Д2Г3)-^(\/Г+1?-1). (4.45)
Здесь Mr + 2Г3) т=(Г2Г3 - Г3Рг - Рг2), т;=8/8 (3? + т)? -
— у2/2, а Рг0 задается равенством (4. 25) (см. § 3). Первое неравен-
ство (4. 45) получается из требования положительности у и сог-
ласно § 3 настоящей главы является необходимым условием суще-
ствования режимов С и С', которым отвечают два из упомянутых
корней уравнения (4. 36). На это указывает результат предель-
ного перехода в (4. 44) при х что соответствует лучу Та=0
(точнее, Ta=const, но это несущественно). Тогда один из корней
ех= — Рг-1, а два других — е2=е3=— Рг/Г2Г3, и главные члены
в разложении (4. 43) совпадают с полученными в § 3.
74
в случае х=Хо и Рг < Рг0 уравнение (4. 41) имеет единственный
действительный корень кратности три, т. е. луч 8=/0Та + О (1) есть
отображение в плоскости (Та, 8) границы области существования
режимов С и С', которая в фазовой плоскости (Та, Ra) ведет себя
как кубическая парабола Ra=O (Та?). На рис. 20 дано схематиче-
ское изображение указанной границы, пересекающей ось ординат
в точке со значением RaRP, выражение для которого получено выше
(см. § 3 (4. 24)). Из рис. 20, в частности, видно, что силы Кориолиса
препятствуют переходу в состояние С или С', оказывая в этом
смысле стабилизирующее влияние на конвективный процесс.
Дальнейшее исследование будем проводить в предположении,
что Рг > Pro, исключая тем самым режимы С и С' из рассмотре-
ния. Хотя в этом случае уравнение (4. 44) имеет единственный
Рис. 20. Граница области су-
ществования стационарных ре-
жимов С и С" в плоскости
(Та, Ra)
действительный корень по причинам, обсуждавшимся выше, мы
не можем еще утверждать, что при любом / ему отвечает режим Н.
С помощью (4. 37) и третьего равенства (4. 34) асимптотическое
разложение для динамических переменных Wt и ТГ3 можно пред-
ставить в виде
W1 = - [X (Г2Г3е + К)Г + о (Н,
Ws = —Г3е [X (Г2Г3е + § + О(1). (4. 46)
Тогда, пользуясь определением S, (4. 43), (4. 46), нетрудно найти
зависимость от х параметра а=а(х), определяющего фазовую
траекторию Ra= аТа8 + О (Та8), которая вместе с решением,
соответствующим корню е (х), отображается в луч 5=хТа 4- О (1).
Зависимость а=а(х), схематически изображенная на рис. 21,
имеет вид:
а = PrW Г1 Ч-------Г1 ~ . (4. 47)
Л1_ Г (Г2Г3е + Рг)’-J k ’
График на рис. 21 легко построить, принимая во внимание, что
при х > X* = \/Рг Г3/Рг единственный корень уравнения (4. 44)
е < 0 и при х -> 00 стремится к своему минимальному отрица-
тельному значению е=— Рг-1. При / причем е (х*)=0,
a e(0)=r2-4
75‘
Из рис. 21 видно, что в промежутке 0 < а <^ат каждому знд
чению а ставится в соответствие три значения /, которые otbJ
чают трем различным стационарным решениям системы (4. 34)
(4. 35) вдоль фазовой траектории Ra= аТа3 + оТа3. Область сущ&
ствования двух из них, для которых е > 0, в плоскости (Та, R^
ограничена сверху кубической параболой Ra=%Ta3 + о (Та3)*
Отрицательные корни соответствуют режиму Н, область математик
ческого существования которого неограниченна. Два новых ре-
жима, которые мы будет обозначать через 7?х и /?2, не имеют ана-
логов в покоящемся эллипсоиде, а поэтому их пояление вызвано
исключительно влиянием сил Кориолиса.
Чтобы лучше разобраться в характерных особенностях конвек-
тивного процесса внутри области, ограниченной упомянутой
Рис. 21. Графическая зави-
симость а= а (/), определяе-
мая равенством (4. 47)
L
кубической параболой, перейдем к исследованию асимптотических
решений системы (4. 34), (4. 35) вдоль лучей Ra— аТа + о (Та).|
Подставляя последовательно разложения (4. 38), (4. 39) в систему
уравнений (4. 34), (4. 35), левые части которых полагаются рав-|
ными нулю, получим две простых системы алгебраических урав-j
нений относительно коэффициентов при главных членах разло-:
жения. Опуская несложные выкладки, сформулируем основной
результат.
Асимптотическим поведением типа Н характеризуется един-
ственное стационарное решение
Я) °
01 = Ra + o(Ra), 02 = -^±^±|1+о(1), (4.48)
х 1 а ао
®з = Т^а2 + °(1)>
где а^ = Рг/Г3, a Ws =
Асимптотическое разложение типа R имеют два стационарных
решения:
1
W1 = - £ + о (1), W2 = + Pr-1 [a0 (a - a> + о (1),
7?! и Я2) р_ ?4 ао\
e^^LRa + ofRa), ©2 = _Z£ RZ2Ra + o(Ra),
причем через обозначен режим, в котором W2 < 0.
Остановимся на некоторых свойствах конвективных течений,
задаваемых равенствами (4.48) и (4.49). Во-первых, из сопостав-
ления членов уравнений (4. 34) по порядку величины легко ви-
деть, что бароклинные силы с точностью до главных членов раз-
ложения уравновешиваются силами Кориолиса. Иначе говоря,
Рис. 22. Область неустойчи-
вости режима Н ограничена
сплошной кривой. Пунктирная
кривая ограничивает область
существования режимов и
Т?2 сверху
рассматриваемые решения приближенно удовлетворяют равенству
2M0Xa)=gpiXq> которое по существу является хорошо известным
уравнением геострофического ветра, записанным в приближении
Буссинеска для линейных полей скорости и температуры. Как
непосредственно следует из (4. 48), (4. 49), геострофические тече-
ния в эллипсоиде характеризуются циркуляцией в плоскости,
почти перпендикулярной gradT, причем в режиме Н устанавлива-
ется температурная стратификация, близкая к равновесной.
Во-вторых, согласно второму равенству (4. 49) луч Ra= о^Та +
+ О (Та) ограничивает область математического существования
режимов и Т?2 снизу и совместно с кривой Ra= awTa3 + о (Та3),
изображенной на рис. 22 пунктиром, определяет в плоскости
(Та, Ra) асимптотику границы указанной области.
Еще одна важная особенность геострофических течений состоит
в том, что в режимах Л2 и Н при а > а0 ^2 > 0» т- е- циркуляция
в плоскости (^, х3) происходит в направлении, противоположном
естественной конвекции. В реальных гидродинамических систе-
мах, в частности в земной атмосфере и вращающихся кольцевых
ссудах с жидкостью, такое явление действительно наблюдается
и сопровождается так называемым эффектом «отрицательной вяз-
кости» (см. Старр (1968)). В связи с этим уместно отметить, что для
воспроизведения обратной ячейки циркуляции с помощью осред-
ненных уравнений гидродинамики приходится прибегать к необыч-
77
ной гипотезе замЬтканйя, отражающей активную роль напряжений
Рейнольдса в формировании среднего течения, которое компенсм
рует энергетические потери за счет энергии пульсаций (см. Виль-
ямс и Дэвис (1965); Должанский (1969, 1971)).
Не вдаваясь в детали исследования асимптотик стационарных
решений вдоль траекторий Ra= аТа” + о (Та”) при 1 < п 3,
укажем только, что вдоль любой из них режимы Н и Я2 характера
зуются обратной ячейкой циркуляции (Ж2 > 0) в сечении (хг, z3)t
тогда как в режиме R± Ж2<0. Однако, как было показано выше,
вдоль тракторий Ra=O (Та3) (п=3) прямая ячейка устанавлива-
ется в режиме Н, а оба режима Ях и Я2 оказываются «аномальными»
(Ж2 > 0). Это могло бы вызвать сомнение в правильности выб-
ранной классификации конвективных течений. В том, что режиму
Гадлея действительно соответствуют найденные выше решения,
проще всего убедиться, осуществляя предельный переход при х ->
->1. В этом случае эллипсоид стягивается в сферу, нелинейные
члены исчезают из динамических уравнений (4. 34) и конвективный
процесс описывается единственным стационарным решением
типа Я, тогда как корни, соответствующие режимам Rr и Я2,
уходят в оо.
Сравнивая теперь свойства всех найденных нами решений,
приходим к заключению, что внутри области математического
существования режимов R должна находиться кривая Ra=o (Та3),
на которой W2 в режиме Н меняет знак*, причем эта кривая возра-
стает быстрее Та” при любом п < 3. То же самое касается и ре-
жима Ях, хотя кривые, на которых происходит смена знака вели-
чины W2 для режимов Rt и Я, вообще говоря, могут не совпадать.
На рис. 22 область аномальных режимов Я ограничена сплошной
кривой, пунктиром изображена верхняя граница области сущест-
вования режимов Я.
Из-за отсутствия точных стационарных решений систему
(4. 34), (4. 35) исследование на устойчивость найденных режимов
конвекции представляет весьма трудоемкую задачу и требует
выполнения большого объема вычислений. Без значительных зат-
рат удается получить лишь необходимые условия устойчивости
режима Я, если воспользоваться его представлением в виде (4. 48)
для траекторий Ra= аТа + о (Та) и линеаризировать систему
(4. 34), (4. 35) относительно такого стационарного состояния,
пренебрегая членами второго порядка малости. Согласно крите-
рию Льенара—Шипара требование положительности коэффициен-
тов характеристического многочлена линеаризованных уравне-
ний, выражение для которого мы опускаем из-за его громоздкости,
приводит к необходимому условию устойчивости а < «^(Рг/Гз)1^.
Таким образом, как следует из второго равенства (4. 48), потен-
циально устойчивыми оказываются режимы Я с прямой ячейкой
♦ Точнее, речь идет о верхней границе области положительных значений W2
в режиме Н.
78
циркуляций в сечении (#п я3), а в области аномальных режимов Н
физически реализуется конвективное течение негадлеевского типа.
Вопрос о том, будет ли это режим Rx или Т?2 или даже нестационар-
ен конвекция, требует дополнительного исследования.
результаты численного интегрирования системы (4. 34),
(4. 35) показывают, что при определенных условиях оба режима
и Т?2> а также режим Н с прямой ячейкой циркуляции оказыва-
ются устойчивыми. Мы не будем останавливаться на этом подробно,
поскольку выполненный выше теоретический анализ уже позво-
ляет сделать некоторые существенные выводы.
§ 5. Обсуждение результатов
В связи с проблемой описания конвективных течений с помо-
щью малопараметрических моделей результаты исследования
§§ 2—4 заслуживают некоторого дополнительного обсуждения.
На примере простейшей модели бароклинного течения мы просле-
дили за хорошо известным в гидродинамике, но недостаточно изу-
ченным явлением потери устойчивости первичного конвективного
течения при достижении числом Рэлея некоторого критического
значения и образования вторичных течений, какими являются
здесь режимы С и С". При этом после возникновения вторичных
течений тождественные системы, находящиеся в одинаковых внеш-
них условиях, могут в дальнейшем пребывать в различных устой-
чивых состояниях.
Конвективный процесс, развивающийся внутри вращающегося
эллипсоида в условиях горизонтально неоднородного разогрева,
проявляет, как мы видели, характерные для типичных геофизи-
ческих систем свойства, в формировании которых при прочих рав-
ных условиях определяющая роль принадлежит силам Кориолиса.
Силы Кориолиса не только искажают или модифицируют стацио-
нарные режимы конвекции, свойственные покоящейся системе,
но могут привести к полному их разрушению и установлению
нового вида конвективного течения, которое условно по анало-
гии с геофизической терминологией назовем режимом Россби.
Область неустойчивости режима Н имеет определенное сходство
с областью существования режимов Россби, наблюдаемых в лабо-
раторных экспериментах с кольцевыми сосудами. Чтобы иметь
возможность сопоставить рис. 17 и 22, отобразим кривые, изобра-
женные на рис. 22 в фазовой плоскости (Та, Ra) в пространство па-
раметров (qT«, Ro), где /й“Та2, Ro — число Россби, которое в при-
менении к данной гидродинамической системе можно определить
как (ср. с выражением, приведенным на стр. 59)
Ro = — 3x2 + 2% — 1 Ra /д сq\
Но— QgZ2 — (х + 1)2 РгТа2 *
Тогда нижняя и верхняя ветви сплошной кривой, а также пунктир-
ная кривая на рис. 22 отобразятся на плоскости (еЛг, Ro) соответ-
79
ствейно в кривые Ro==O ((/'«г72), Ro=o (аГ^“1/2) и Ro=O (qA*1/2),
которые схематично изображены на рис. 23. Верхняя ветвь сплош-
ной кривой возрастает быстрее „ при любом к < V2.
Сплошные кривые на рис. 17 и 23 имеют довольно хорошее ка-
чественное сходство. Лоренц (1962) получил также область
неустойчивости режимов Россби в цилиндрических сосудах,
Рис. 23. Отображение кри-
вых, изображенных на рис. 22,
В ПЛОСКОСТЬ (qT'«г, Ro)
которой, как можно ожидать, соответствует на рис. 23 область
между сплошной и пунктирной кривой, поскольку в указанной
области или ее части режимы Rx и Т?2 являются аномальными.
Нельзя, однако, с полной уверенностью утверждать, что сплош-
ная кривая на рис. 23 есть критическая кривая режима Гадлея,
поскольку устойчивость режима Н здесь не доказана. Кроме того,
вершина кривой построена гипотетически и не исследовалась.
Наряду с дестабилизирующим влиянием силы Кориолиса ока-
зывают на конвективный процесс и обратное действие. Это видно
из рис. 20, согласно которому «опрокидывание» в один из режимов
С и С' должно происходить при больших значениях Ra, чем в по-
коящейся системе. Если зафиксировать скорость вращения, то для
жидкостей с эффективными Рг < Рг0 можно представить следую-
щие стадии изменения, которые будет претерпевать конвективный
процесс при увеличении интенсивности внешних источников тепла:
стационарный режим Гадлея, режим Россби, вновь режим Гад-
лея, переходящий в новое стационарное состояние С или С".
Существенно также, что стадии взаимных переходов «нижнего»
режима Гадлея и режима Россби должны осуществляться вблизи
геострофического баланса сил, который непременно соблюдается
во всех геофизических системах и положен в основу многих теоре-
тических исследований.
Заслуживает внимания зависимость числа возможных состоя-
ний конвекции от Рг, которая, по-видимому, имеет место и в
реальных гидродинамических системах. Результаты этой главы
основаны на феноменологическом учете вязкости и теплопровод-
ности. Это привело к появлению в уравнениях движения безраз-
мерных критериев подобия, определяемых не молекулярными,
а эффективными коэффициентами вязкости и теплопроводности,
которые, строго говоря, должны быть найдены экспериментальным
путем.
Глава V
МОДЕЛИРОВАНИЕ КАСКАДНОГО ПРОЦЕССА
ПЕРЕДАЧИ ЭНЕРГИИ
СИСТЕМАМИ ТИПА ЦЕПОЧЕК
§ 1. Модель с простым зацеплением
из подобных элементов
До сих пор в конкретных приложениях мы рассматривали дина-
мические системы с небольшим числом степеней свободы. Попыта-
емся теперь построить более сложные системы для моделирования
каскадного процесса преобразования энергии в рамках общей
схемы Ричардсона (1922), Колмогорова (1941), Ландау (1944).
Вообще говоря, уравнения гидродинамики, разложенные по
любому набору ортогональных опорных функций, приводят к си-
стемам гидродинамического типа, являющимися суперпозицией
простейших триплетов. При использовании стандартных разло-
жений, например рядов Фурье, характер «зацепления» отдельных
триплетов оказывается достаточно сложным. Можно надеяться,
однако, что для конкретных систем (с заданным способом возбуж-
дения) уравнения движения могут быть существенно упрощены,
если выбрана некоторая «естественная» система опорных функций,
и описание системы ограничивается только наиболее активными
степенями свободы, причем некоторые малоэффективные взаимодей-
ствия не учитываются.
Опираясь на эти общие соображения, рассмотрим схему из по-
добных триплетов различного масштаба (геометрический параметр
р.) с простым зацеплением, когда каждая устойчивая мода дан-
ного триплета жестко сцеплена с неустойчивой модой, принадле-
жащей триплету меньшего масштаба. Триплеты будем изображать
графически треугольником. При этом стрелка указывает направ-
ление возбуждения при возникновении неустойчивости. Урав-
нения такой «многоярусной» системы, схематически представлен-
ной на рис. 24, имеют вид
4г = Ро (4 — —хоуо + /о;
1. ^г= — ZWii + PiMi — ^2) — ХЛ1?
^=p0v0v12 + Рг Из — у|4) — \и12,
6 Нелинейные системы
81
Рис. 24. «Многоярусная» нелинейная модель. На рисунке изо-
бражены 4 яруса
+ Р2
= —РЛг^гз + Рг Н “ узв) ~ Х2У23;
2- ^SF = РАЛг + Рг (Н» — Ни) —
= РЛг^г* + Рг С17 ~ is) ~
* (5.1)
. ^-1 к
г—1. —LJdL
dt
... 1 <Р<2'-1.
При к нечетном (к~2р — 1)
. dvi, 2р-1 .
г- —di~ = PVi. 2p-l +
"4“ Pi (yi+l, 4p-3 yi+I, 4р-г) 2p-l>
При к четном (k = 2p)
dvi,2p ,
pVit 2p +
(yl+l, 4p-l y?+l, 4p)
\Vi, Zp>
\<к<2\
82
Первым индексом пронумерованы «ярусы», а вторым — компо-
ненты триплетов, расположенные на заданном ярусе.-Внешняя
сила /о действует только на основном уровне, через Х^ обозначены
диссипативные коэффициенты, которые возрастают с увеличением
номера. Можно положить Х.= a2vpp где v — кинематическая вяз-
кость среды, a — числовой множитель порядка единицы. Система
построена так, что выполняется закон сохранения энергии (при
/о=О, Х^=0), а в общем случае имеет место уравнение баланса
энергии
= (5.2)
Где Ф = 2 — диссипация, WQ = fQvQ — подводимая мощность.
it к
Картину возбуждения такой сложной системы можно предста-
вить следующим образом. Пусть к моменту включения внешней
силы в системе имеются малые случайные возмущения. Для про-
стоты можно принять У,&(0)= + е (знаки равновероятны). При
включении внешней силы определенного знака и достаточной вели-
чины начинает возрастать v0, причем возбуждается одна из компо-
нент первого уровня, а именно та, для которой четность индекса к
совпадает со знаком vQ (при v0 > 0 возбуждается р12). Развитие
возмущений одновременно сопровождается ростом одного из квад-
ратичных членов на предшествующем уровне, который моделирует
напряжение Рейнольдса. Знак «активной» компоненты определя-
ется знаком начальной «затравки» и тем самым указывается на-
правление дальнейшего возбуждения, когда интенсивность воз-
мущения на данном уровне превзойдет некоторое значение —-
|pJKP=Х/+1/д.. При достаточной величине внешней силы этот про-
цесс последовательного возбуждения все более высоких уровней
будет развиваться до тех пор, пока не возбудятся все уровни вплоть
до некоторого номера п. Этот уровень определяется тем условием,
что триплет более высокого яруса, опирающийся на данный уро-
вень, окажется уже устойчивым. Одна из таких возможных возбу-
жденных ветвей показана схематически на рис. 24; она изображена
сплошной линией.
Если знак внешней силы также считать случайным, то общее
число возбужденных ветвей составляет 2й, и все они равновероятны.
Рассмотрим одну такую типичную ветвь, причем изменим направ-
ление отсчета на некоторых уровнях так, чтобы все v- (второй ин-
декс не пишем, так как на каждом уровне имеется только одно
возбуждение) были положительны. Уравнения движения теперь
запишутся в форме простой цепи
^- = —Povi — V’o + /o- /0>°>
-^ = роРо^ ——\->0>
6*
83
= — Pi-^i — (5.3)
dui 9 1
P<-lVi-lVi — P&l — \+l»i+l,
—~ — p -p .p — k„L>,
at * n~i w"“^ n nt**
y«+i = °(e)—°-
Условие того, что возбуждение дошло до уровня п, можно записать
так:
Рп-?Рп-2 \г-1’ Рп-тУп-Л ~ Pnvn < \н-р (^*
Заметим, что если мы «заморозим» все компоненты возмуще-
ний, кроме первой (тг=1), то получим схему Бюргерса (1939)
(см. гл. III), а сама цепочка (5. 1) представляет суперпозицию
таких схем с простейшим способом зацепления.
Расчет стационарного режима и отвечающего ему распределе-
ния энергии был проведен для случая, когда структурные пара-
метры р. образуют геометрическую прогрессию со знаменателем
D—Pi+ilPv При сравнении результатов с экспериментом парциаль-
ные энергии Е^1%/2 следует рассматривать как величину энергии,
отнесенную к октаве (или ее определенной доле) с волновым чис-
лом к. ар..
При больших значениях параметра A?=|/0|/p^v2 (аналог числа
Рейнольдса по напору) для ограниченного числа ярусов получается
закон
V; = с (D) W^, Е( = , (5. 5)
С (£>)=£>’/.
и оценка верхней границы спектра
pB^(W0/v3)4 (5.6)
При знаменателе Р, близком к единице, в значительной части
спектра, включая большие частоты (но не доходя до границы спек-
тра), стационарное решение рассмотренной дискретной модели
хорошо аппроксимируется решением соответствующего дифферен-
циального уравнения по переменной |=ln plpQ. Это уравнение
в точности соответствует модели Коважного (1948). При небольшом
числе ярусов соответствующее дискретной модели разностное
уравнение приходится решать численно.
Результаты такого расчета для системы (5.3) при Z) = ^3 и
n=10 (значение D было выбрано в достаточной мере произвольно)
приведены на рис. 25 сплошной линией. На рисунке показана
кривая, отвечающая непрерывной схеме Коважного. Заметная
разница наблюдается только для трех высших уровней.
84
Таким образом, динамическая модель нелинейных взаимодей-
ствий в потоке несжимаемой жидкости, построенная с помощью
простейших цепочек триплетов, позволяет получить наглядную
картину энергетических процессов в развитом турбулентном потоке.
Рис. 25. Спектральное рас-
пределение амплитуд при п= 10
Для стационарного режима эта модель приводит к законам распре-
деления энергии, достаточно хорошо изученным как теоретически,
так и экспериментально.
Можно рассчитывать, что рассмотренная выше модель окажется
полезной также при изучении нестационарных эффектов, таких,
например, как перестройка спектра турбулентности при скачко-
образном изменении внешних условий или при модулированном ре-
жиме возбуждения. К сожалению, экспериментально эти вопросы
еще мало изучены.
§ 2. Модель с двойным зацеплением,
допускающая два квадратичных интеграла движения
Известно, что плоский поток идеальной жидкости имеет, кроме
интеграла энергии, еще и интеграл квадрата вихря. В ряде работ
(см., например, Крейчнан (1967)) для двумерной турбулентности
было показано, что, кроме колмогоровского закона, существует
также закон, связанный с передачей квадрата вихря по спектру.
В предыдущем параграфе рассматривалась система гидродинами-
ческого типа, допускающая в условиях самоподобия стационарное
решение, аналогичное колмогоровскому закону, описывающему
каскадный процесс передачи энергии в развитом турбулентном по-
токе. Эта система имеет простейший вид связи уравнений друг с дру-
ком: каждое уравнение связано с предыдущим и последующим.
Рассмотрим теперь систему с более сложным типом зацепле-
ния, когда каждое уравнение связано с двумя предыдущими и
двумя последующими. При этом на основании уравнения несжима-
емости в фазовом пространстве
85
будем считать, что в уравнение для Z-моды не входит соответ-
ствующая ей скорость. Тогда
+ /о>
г>1 = + с(2Чу2 + fl*
*>2 = C^V3Vi + C^VjV3 + C&'V'fr,
.................................... (5.7)
=41)у.-+л+2 + Ч-Л+i + c^vi-xvi-^
К = Фп-Л+2 + Ф»-Л-2 — ХЛ>
Уя+1 = с«+1У«Уя-1 — Ч+Л+1-
Здесь у. — скорость г-й моды, с. — параметры взаимодействия;
на достаточно высокие моды, начиная с n-й, действуют силы внут-
реннего трения, описываемые коэффициентами Хя; /0 и Д — внеш-
ние силы.
В системе (5. 7) выписаны лишь такие нелинейные члены, ко-
торых достаточно для выполнения в отсутствие внешних сил и
вязкости двух законов сохранения, выражаемых квадратичными
интегралами:
Е=2^
i
i
где к. — волновое число (1^=1/^ — масштаб i-й моды). Инте-
гралы Е и £Г являются аналогами интегралов энергии и квадрата
вихря для двумерного движения.
Для того, чтобы dEldt—Q и dQ/d£=O, необходимо выполнение
следующих условий:
<1) * * * V + ^Л + с^=о,
+*М?2=о, /=о, 1,....
Отсюда легко выразить все коэффициенты, например, через
c11Ie3c’ ^ = ^3=^, (5.9)
i = 1, 2, ... 1 = 2, 3, ...
И система (5. 7) примет вид
• Л?_1 — I
Vi--СЛ+1Р»+2 С<-1 Щ _ ^+1 У<-1У«+1 +
+ v<-^ - + А> (5.10)
i = 0,
86
где, по определению, можно считать, что
С-1 ~ С-2 ~СП~ ®П+1 = 0>
/,.=0, / = 2,3,4,...,
= О, i=0, 1, ..п — 1,
^>0, с,.>0, Л,.+1>ЛГ
Из (5. Ю) легко видно, что при возбуждении v{_t и v,_a возрастает
скорость v(.
Найдем стационарное решение системы (5. 10) при условии
самоподобия
(5-И)
Для 1*=2, 3, . . ., re — 1 имеем
с v v ______с &<-i ~ v v _i_c — v v —о
CiVMVi+2 Ci-1 kj — kj+i Vi-lVi+l^ Ci-2 kj^ — kl U<
Или, используя (5. 11),
р,6_1±«®(13+ 1 0.
‘ g3 v ‘ g4
Отсюда
1) |л = д~Ч ^~£уз,
2) v — q'1,
Рассмотрим потоки энергии We и квадрата вихря Иа
Жв = /оро + /Л, ^=We,
^0=^о+^л. зг=И7«-
Из (5. 7), (5. 10), (5. 11) имеем
ТУя = с0р5^[^—др3],
Ж0 = -с<Д^[др3-1]д2.
Таким образом, в случае 1) Ws=0, а для v( получим
„5 = Л7-'-,
в случае 2) Жв=0 и
„!=иг,
Мы нашли, что для системы (5. 7), сохраняющей два квадратич-
ных интеграла, существуют два стационарных режима. Первый
соответствует колмогоровскому закону, связанному с передачей
87
энергии по спектру. Второй режим связан с передачей квадрату
вихря по спектру. Ему соответствует известный «закон минус 3»
для энергетического спектра в плоском турбулентном потоке.
Пусть теперь, кроме сил /0 и /х, на моды j — 1, / и j 4- 1 с до-
статочно большим j действуют силы /у_х, /^, /у+1. Тогда для систему
(5. 7), (5. 9) нетрудно получить следующее стационарное решение;
у/,
(9г-1)*о/ ’
И7ж<0, Ж8=0,
^о3зАо у/,
И72>0, Wb = 0.
Таким образом, в области крупных масштабов поток энергии
идет от мелкомасштабных компонент (т. е. отрицателен), поток
квадрата вихря равен нулю, а спектр энергии совпадает с колмого-
ровским. В мелкомасштабной области осуществляется закон
«минус 3», причем поток квадрата вихря идет в мелкомасштаб-
ную область. Аналогичные результаты были получены и в числен-
ных экспериментах по плоской турбулентности (см., например,
Лилли (1972)).
Глава VI
СИСТЕМЫ
С КОМПЛЕКСНЫМИ ХАРАКТЕРИСТИКАМИ
И ЗАДАЧА О ВЗАИМОДЕЙСТВИИ КОЛЕБАНИЙ
§ 1. Комплексное расширение систем
гидродинамического типа
Для описания процессов нелинейного взаимодействия колебаний,
в частности волн, интересно обобщение понятия СГТ на случай
координат, представляемых комплексными числами.
Пусть S%m — некоторая квадратично-нелинейная система чет-
ного порядка, имеющая квадратичный интеграл. Мы будем го-
ворить, что система S2m допускает комплексное представление,
если при разбиении координат состояния на пары (xv i/x), (ж2,
z/2), . . ., (хт, ут) (вЪекоторой подходящей системе координат) и
введении комплексного вектора состояния
+ к=Л, 2,
уравнения движения могут быть записаны в форме
(6.1)
причем существует квадратичный интеграл движения, представ-
ляемый некоторой положительно определенной эрмитовой формой
E = ^gikzk),
gki=g<k- (6-2)
В силу существования квадратичного интеграла коэффициенты
взаимодействия (в общем случае комплексные числа) удовлетво-
ряют известным соотношениям
г,- л + Гу,ы + Г.и. = 0.
Совершенно очевидно, что далеко не всякая система четного
порядка допускает представление в комплексной форме. Это
следует из простого подсчета числа параметров (коэффициентов
взаимодействия) системы. Так, например, п=6, тп=3, число
вещественных параметров системы, допускающей комплексное
представление, равно 16 (удвоенное число параметров общего
триплета без требования регулярности), в то время как наиболь-
89
шее число независимых параметров СГТ шестого порядка (с уче
том регулярности системы) оказывается равным 64, т. е. в 4 рад.
больше.
При рассмотрении комплексных систем естественно ограни-
читься унитарными преобразованиями, оставляющими неизмен-
ным вид фундаментальной формы (zgz), которая в нормальной
системе координат выражается через сумму квадратов модуле!
комплексных координат.
Может оказаться, что при надлежащем выборе системы коорди,
нат коэффициенты взаимодействия будут выражаться веществен-
ными или чисто мнимыми числами. В этом случае естественно
ограничиться подгруппой унитарных преобразований, при кото-
рых это свойство коэффициентов сохраняется. Получаемую
при этом группу будем называть основной группой системы.
Если параметры системы в некотором представлении оказы-
ваются вещественными, то, задавая в начальный момент значе-
ния координат вещественными, мы будем получать в соответствии
с уравнениями движения вещественное значение для любого
момента времени. Таким образом, условие Imzt.=0 выделяет
инвариантное подпространство размерности тп, в котором мы
получаем подсистему размерности т. По отношению к ней исход-
ную систему мы будем называть комплексным расширением.
После этих общих определений переходим к построению кон-
кретных примеров, пользуясь методом комплексного расширения
систем, уже исследованных ранее.
Простейшая нетривиальная система S2 всегда может быть за-
писана в форме
. (6.3’
dt -КХ1-
Эта система имеет интеграл
Е = рх* + «2.
Переходим теперь к ее комплексному расширению, полагая
zi = Ж1 + 1У»
г2=Ж2 + ^2-
Уравнения движения получаем, пользуясь общей формулой
(6. 1)
и§- = —
> = (6.4)
где параметр к теперь, вообще говоря, уже комплексное число,
параметр р считаем вещественным. Заметим, что введение пара-
90
<eTPa P не наРУшает общности рассмотрения, так как, делая
замену переменных zr2=X222(X— вещественно), в новых
переменных получим |х' = Х2{л, и это значение может быть сделано
равным любому заданному числу (кроме естественного значения
единица может оказаться полезным значением р-=1/2, как это
будет показано ниже).
Наряду с системой уравнений (6. 4) следует иметь в виду
эквивалентную систему, получаемую операцией комплексного
сопряжения
РЦГ~ — kZ2Zl>
$ = (6.5)
Легко убедиться, что jE=(jiz1^1+22z2) является интегралом движе-
ния — фундаментальной формой.
Рассмотрим замену переменных
z\ = z2 = eiB*z2,
где фазы 0Х и 02 — вещественны. При такой подстановке система
сохраняет вид, при этом
Если &=|ф“<т, то, положив, например, 01=ср/3, 62=—2<р/3, можно
сделать к’ вещественным.
Таким образом, основной группой системы является совокуп-
ность таких преобразований, при которых фазы удовлетворяют
условию
26^=о. (6.6)
При этом условии коэффициент к остается вещественным, если
он был таковым. В дальнейшем, не нарушая общности, будем
считать Л==4.
Совокупность преобразований, которые оставляют неизменным
вид уравнений, мы будем называть группой автоморфизмов сис-
темы. В данном случае эта группа содержит один параметр —
фазовый угол для одной из компонент
е2=о, о1=-^.
В отличие от вещественного случая комплексная система допускает
еще один — кубический интеграл движения.
Умножим первое уравнение на 2zxz2, а второе — на pz\ и сложим.
Тогда получим вещественную величину
^(ф8)=-2|41-М1 + ик14.
Таким образом
Я = 1т(^2) (6.7)
91
является интегралом движения, который в развернутой форм!
имеет вид к -, 1
Н = (х1 — ^)у24-2®1у1 »ж2. (6.81
Уравнения движения (6. 4) также запишем в развернутой форм®
^dT=—+ УгУ» j
dy, i
at (6.9)
~3f— %х1Уг
Полученная система четвертого порядка оказывается регуляр-
ной, так как
। ду± дхъ . дуя ___ о
дх1'ду1'дх2'ду2~
Более того, при соответствующем выборе параметра р. (р-=1/2)
соответствующие уравнения движения можно записать в форме
Гамильтона. Чтобы убедиться в этом, вычислим производные
от кубической формы Н
|^=2 (хгу2 + х2у±), ^-=2(—У1у2 + хтх2),
S=2^’ f
Легкой видеть, что уравнения движения принимают гамильтонову
форму, если положить
*1 = Рр У1 = <11, *2=?2> */2=Р2»
& = dHldpv = дН)др2,
Pi = —dHjdq^ р2 = —dHjdq2\ (6.10)
в новых переменных Н имеет вид: Н~р2 (pl—qD+^p^q^ Таким
образом, подстановка z1-p1-\-iq1, z2—q2-{-ip2 приводит нас к си-
стеме, в которой функция Н является функцией Гамильтона.
Иногда бывает удобным рассматривать в качестве основной
переменной сопряженное значение второй координаты — w~z2.
Каноническая форма^ уравнений движения имеет вид
dzfdt = —2u>£,
dwjdt = z2.
Дифференцируя второе уравнение, получаем для w уравнение
второго порядка с переменным, но вещественным коэффициентом
92
^Idt^-\-^\dwldt\w=Q. Решив это уравнение при заданных йа-
чальных условиях w|;_o=wo, (dw/eft) к-о=^, находим, что
z = ±'\]dwldt‘
Квадратичный интеграл, выраженный через функцию w, имеет вид
£=|“’1а+Ж|.
а гамильтонова функция записывается в форме
Н = Im (wz2) = Im (w .
Полагая u?=pe<9, получим
dw dp I . »e d0 и т / _ dw\ 9 d0
dt dt 1 r dt* \ dt / r dt
Наличие двух интегралов движения позволяет получить реше-
ние в квадратурах *. , ’
Уравнения движения в новых переменных имеют вид
(О. 1Z)
п dp d6 . d20 л
2й7'й7 + р^=О-
Второе уравнение (6. 12) непосредственно интегрируется и при-
водит к интегралу #=const. Пользуясь этим интегралом, по-
лучаем __________
g-Aff,+4/^W=°. <б-1з>
Легко проверить, что «энергия»
£=pI + l.|/'№ + p>(4)s
действительно является интегралом уравнения (6. 13). Рассмотрим
частный случай Я=0, тогда
0, 6 = 90 = const.
Не нарушая общности, благодаря возможности фазовых преоб-
разований, будем считать 0о=О. Таким образом, система ока-
зывается вещественной, а для этого случая мы уже имеем общее
решение
w = th at,
Л
____. а 1
Z — ^2 °h dt ’
где а? = кЕ, причем рш1п=0- (6.14)
* Эти квадратуры выражаются через эллиптические интегралы.
93
Фаза 0 меняется скачком от —те до те при переходе через точку?;
t=0. Л
При H^=Q выберем начало отсчета времени в момент,1
когда р=р*, определяемому из кубического уравнения на основу
интеграла энергии при условии = О
Pl + <=Z-
Положим
Р. = ТГ* и A = -L-L, 0<r,<i-
Тогда
r3 — r, + 2h = O, 2Л = г,(1 —rj). (6.16)
Отсюда следует, что | Н | не может превзойти Нт„ = h*as/2, где
h* = 4^3—значение, соответствующее г¥ = 1Д/3, т. е.
ТТ __ а3
В этом случае drldt=Q, dtft/dt^O, и система совершает гармо-
нические колебания с частотой
ш=+^=±^.
“ Р* V3
Знак ш определяется знаком Н,
w = ae<wt, sign Н,
2 V3 ’ dt 3 s >
л-- /(Dt 7С\
2=1/^=+аДт+г).
Г dt — Уз
при Н > О,
I 12 I * I I ( 2 । 1 \ «2
^ = 1ш12+т|зг|=т(т+з-)=т-
Энергия распределяется в отношении 2 : 1 между w- и z-kom-
понентами.
При 0<С|Я|<Яшах ситуация показана на рис. 26.
Амплитуда р* меняется за один полу период в пределах от гх (А)
до г2 (А), являющихся корнями уравнения (6. 16). При этом
0<r1<l/v'3<r2<l.
Полупериод обмена энергией между компонентами выражается
интегралом
^2=Г2(А)
( -j—• (6-17)
2 2а (1 - у)2 - 4А2
^=r2(A)
94
L
Досле того как определено р (0 обращением интеграла
t=- ( у
2а J у (1 — у\ч — 4Л2 *
УГг2(Л) У V
изменение фазы находится дополнительной квадратурой
i
0 = (6.18)
О
При уменьшении h период системы возрастает, и при h—>0 оно
переходит в апериодический режим, рассмотренный выше.
Рис. 26. Графическое реше-
ние уравнения (6. 16) (г* как
функция h)
W ±. г? (h) г*
<3
Описанная модель может быть применена к задаче о колеба-
ниях двух параметрически связанных вибраторах, рассмотренной
в работах Цельмана (1970, 1971).
Рассмотрим теперь комплексное расширение триплета. Пара-
метры его будем считать вещественными и равными по абсолют-
ной величине единице. Это всегда можно сделать, выполнив масш-
табное преобразование.
Соответствующие уравнения движения запишутся в форме
dz-^ldt •— ^2^3’
dz^dt — z3zlt (6.19)
dz3/dt =—zrz2*
Эта система имеет два независимых интеграла движения
^=|(h1|2 + 2|Z2P+|Z3P)> (6.20)
$ = Ы2-Ы2-
Система не меняет своего вида при замене переменных z'1 = ei^z1,
z^ — e^z^ z3 = e^z3 при условии
61 + 92 + 93 = 0.
Проводя фазовое преобразование, можно добиться, чтобы в задан-
ный момент времени при £=0 z1=]z1|=pf°> и z3=p<°). Фаза «сред-
95
ней» координаты при этом определяется инвариантным способом!
Z2=p^. и
Легко^видеть, что функция i
Н = Im (z^Zq) = pjo)p£o)p£o) sin <р = const, (6. 21):
т. e. является интегралом движения, так как
d/dt (z^) = —| z2z312 + | z3zx |2 — | zxz212
вещественно. Пользуясь функцией Я, можно записать уравнения
движения в гамильтоновской форме. Для этого следует положить
zi = Pi + z2 = g2 + гр2, z3 = p3 + lq3,
(Р2Ч3 — №) + i (?2?3 + P2P3) = —Vs-
Другие уравнения проверяются аналогично.
Исследование различных типов движения комплексного трип-
лета целесообразно проводить, рассматривая прежде всего спе-
циальные случаи, которые эквивалентны анализируемым ранее
моделям.
1. Я=0. Это означает, что <р=0, т. е. можно выбрать систему
координат, в которой в некоторый момент времени все координаты
zx, z2, z3 вещественны. Поскольку параметры системы также веще-
ственны, то мы приходим к классической задаче движения гиро-:
скопа, решение которой можно найти в любом курсе механики
(см., например, книгу Ландау и Лифшица (1958)). При фиксиро--'
ванном Е и уменьшении S период возрастает. Случай S—0 от-
вечает апериодическому движению по сепаратрисе.
2. 5=0, Я7Й). В этом случае | zx | = | z31, выполнив соответству-
ющее фазовое преобразование, можно добиться того, чтобы
при £=0 zx—zz, а благодаря инвариантности уравнений движе-
ния при замене zr-+z3, z3-*zr это равенство сохраняется для лю-.
бого момента времени. __
Полагая z2=2u?, z1=z3=V2^> приходим к уже исследованному
уравнению (6. 11)
dw/dt = z2,
dzjdt ~—2wz.
В общем случае, когда 5=И=0, исследование проводится ана-
логично. Существует максимальное значение Я, зависящее от Е и
5, при котором все координаты меняются по чисто гармониче-
скому закону и обмена энергией при этом не происходит; частота
при этом максимальна. При уменьшении |Я| период увеличива-
ется и превращается в период колебания обычного гироскопа
при Я—>0.
Заметим, что энергии «крайних компонент» меняются син-
фазно и противофазно по отношению к энергии средней ком-
поненты z2.
96
L
Детальный анализ соответствующих колебаний имеется в статье
Цельмана (1971).
Связь рассмотренной выше системы с задачей о колебаниях
связанных осцилляторов становится очевидной, если рассмотреть
величины
и = z^^,
(6.22)
где <*>i, юз произвольны, а о>2 = -{-о>3 (все частоты положитель-
ные) и комплексные амплитуды удовлетворяют уравнению (6. 19),
то и, р, w подчиняются уравнению гармонических колебаний
с дополнительными членами, описывающими нелинейные воз-
действия (в квадратичном приближении)
^=ЧВ + Я(₽и’).
^=i<o3v + r(uw), (6.23)
M=ia2w + q(uv).
Если при этом рг>0, то возможен «распадный режим», когда
колебание с наибольшей частотой <о2 в течение длительного времени
(по отношению к периоду Т2—2tc/(d2) отдает свою энергию колеба-
ниям с меньшими частотами.
Основная задача при исследовании конкретных колебательных
процессов (включая волны) заключается в расчете параметров
р, г, описывающих нелинейность системы.
Конкретные примеры рассмотренных процессов обмена энер-
гии при нелинейном резонансе (со2== о^Ц-Юд), представляющих
интерес для геофизики, можно найти в сборнике переводных
статей «Нелинейная теория распространения волн» (см., напри-
мер, Филлипс (1967)), а также в статьях Бреховских (1966, 1968).
Заметим, что уравнение триплетного взаимодействия, по-види-
мому, раньше всего было использовано в задачах нелинейной
оптики (Бломберген (1966)) (см. также обзор Кадомцева и Карп-
мана (1971)).
В заключение естественно рассмотреть вопрос, при каких
условиях СГТ четвертого и соответственно шестого порядков
можно редуцировать к системам второго и третьего порядка
с комплексными координатами. Очевидно, что необходимым ус-
ловием является существование группы автоморфизмов, о кото-
рых говорилось выше. Можно показать, что эти условия явля-
ются и достаточными. Другими словами, если СГТ четвертого
порядка допускает однопараметрическую группу ортогональных
преобразований, оставляющих неизменными уравнения движения,
7 Нелинейные системы
97
то ее всегда можно преобразовать к виду (6. 9) и, следовательно,
записать в комплексной форме в виде системы второго порядка
с комплексными координатами. Наличие такой группы обычно
можно установить, исходя из условий физической задачи. Так,
например, оно имеется в задаче о движении жидкости в кольце-
вом канале и в других задачах с аксиальной симметрией.
Аналогичные условия имеют место и для систем шестого по-
рядка, только здесь речь идет уже о более «богатой группе», со-
держащей уже два параметра.
В качестве конкретного примера применения вышеизложенной
методики рассмотрим, следуя Лонге-Хиггинсу и Гиллу (1967),
резонансное взаимодействие планетарных волн (волн Россби—
Блиновой).
§ 2. Резонансное взаимодействие планетарных волн
«Планетарными волнами» или волнами Россби—Блиновой
(см. работы Россби (1939), Блиновой (1943)) называются гиро-
скопические волны, вызывающие глобальные движения, проис-
ходящие в слое жидкости или газа, покрывающей вращающийся
земной шар.
Пусть, (я, у) — координаты в касательной плоскости сферы,
причем х отсчитывается на восток, а у — на север. Основным
динамическим уравнением, описывающим планетарные волны,
является уравнение сохранения потенциального вихря
^[(Д-а*)ф] + р|±=О, (6.24)
где a?=f!gh, ^—df/dy, g и f обозначают соответственно ускорение
силы тяжести и параметр Кориолиса, h — средняя глубина
жидкости, ф — функция тока, а через DIDt обозначено дифферен-
цирование в системе, движущейся вместе с жидкостью.
Уравнение (6. 24) является приближенным, а именно, в нем
оставлены только наиболее важные нелинейные члены, которые
определяют горизонтальную адвекцию вихря. Полный вывод
динамического уравнения, выражающего сохранение потенциаль-
ного вихря, содержится, например, в работе Обухова (1962) и
монографии Кочина, Кибеля, Розе (1963).
При рассмотрении решений уравнения (6. 24) удобно перейти
к приближению p-плоскости, в котором аир принимаются по-
стоянными. Тогда, выбирая единицы измерения длины и времени
соответствующим образом, можно положить в (6.24) а=р=1 и
переписать уравнение в виде
^[(А-1)й+Й = О. (6.25)
98
Линеаризированное уравнение (6. 25) при этом имеет вид
А[(Д-1)+ц4* = 0. (6.26)
Это уравнение имеет гармоническое решение
ф = a exp {I (кх -\-1у — at)} (6. 27)
при условии, что а удовлетворяет дисперсионному соотношению:
а(к2 + 12+1) + & = 0. (6.28)
При этом компонента фазовой скорости в направлении с востока
на запад определяется соотношением
Так как выражение в правой части (6. 29) всегда отрицательно,
то волны всегда распространяются на запад. Эти волны и называ-
ются волнами Россби—Блиновой.
Рассмотрим три свободные планетарные волны, определяе-
мые в первом приближении выражением
'K=aKexP(i(V + ^/ — (« = 1, 2, 3). (6.30)
Для каждой волны удовлетворяется дисперсионное соотношение
(6. 28), т. е.
^(^ + /2й + 1) + ^ = 0, (п=1, 2, 3). (6.31)
Ддя резонансного взаимодействия этих волн необходимо, чтобы,
кроме того, выполнялись бы еще условия
+ ^2 + ^3 — 0,
Zi 1% Я” Z3===: о,
°i + °2 + аз= 0. (6. 32)
Отметим, что условий, накладываемых на девять величин ая,
кп, 1п, всего шесть. Поэтому имеется большой набор волн, для кото-
рых выполняются соотношения (6. 31), (6. 32). При заданном
волновом векторе, например k2={&2, Z2), подробный анализ вол-
новых векторов кх, к3, при которых имеется резонансное взаимо-
действие, содержится в цитированной выше работе Лонге-Хиг-
гинса и Гилла.
Рассмотрим теперь динамику взаимодействия этих волн. Рас-
крывая производную DIDt в явном виде, можно записать урав-
нение (6. 25)
+ + (6.33)
Уравнение (6. 33) имеет ряд интегралов движения. Это, во-первых
j dxdy [1 (g)2 + | g)2 +1 Ф2] =: const (6. 34}
7*
99
Интеграл энергии. Первые два члена подынтегрального выражёЛ
ния представляют собой плотность кинетической энергии, а треЛ
тий —- плотность потенциальной энергии (в безразмерной форме). |
Кроме того, имеются интеграл уравнения (6. 33), выражающий
закон сохранения потенциального вихря
j dxdy (Дф — ф) = const, (6. 35)
и интеграл, выражающий закон сохранения массы
j dxdyty = const. (6. 36)
Представим решение для слабо взаимодействующего триплета
волн в виде
ф = ах cos 9! + л2 c°s + % cos ®з» (6. 37)
где 9W обозначают фазы волны — (п==1> 2, 3),
а амплитуды ап (t) представляют собой медленно меняющиеся
функции одного только времени t. Подстановка (6. 37) в (6. 33)
приводит к уравнению
(xj +1) аг cos + (4 + 1) а2 cos 02 + (х| + 1) а3 cos 03 =
= Cja^ [cos (02 + 03) — cos.(62 — 03)] + С3а^ [cos (03 + 0Х) —
— cos (03 — 0Х)] + С^а3 [cos (0х + 02) — cos (0Х — 02)], (6. 38)
где хя=|&я|2=к* а через Сг, С3, С3 обозначены коэффициенты
взаимодействия, так, например,
ci =4 (х2— XD (z х М) и т. д.,
где z — единичный вектор, направленный по вертикали вверх.
Для волновых векторов, удовлетворяющих условию резонанса
(6. 32),
z • X Ь3] = Z • [k3 X k-jJ z • [kj X Ь2] = 26,
поэтому
С1 = Ь(х1-х|), с2 = 6(х|-х?), C3 = 6(x?-xf). (6.39)
Если, далее, фазы ея связаны соотношением
в1 + е2 + е3 = О,
то три члена в левой части (6. 38) уравниваются тремя членами
в правой части при условии, что
(1 -|- х|) = 6 (х| х|) а2а3,
(1 4- х!) «2=6 (хз — Х1) а3«1> (6- 4°)*
(1 + Хз) «3 = 6 (Х1 — х!) «!«*•
100
Остальные члены в правой части в общем случае не соответствуют
свободным волнам и поэтому не будут непосредственно участ-
вовать в резонансном переносе энергии. Уравнения (6. 40) можно
получить также следующим путем. Умножая, например, (6. 38)
на cos9x и усредняя по быстро меняющимся фазам, мы и прихо-
дим при условии (6. 32) для медленно меняющейся величины
аг к первому из уравнений системы (6. 40) и т. д. Система (6. 40)
представляет собой гидродинамический триплет, рассмотренный
в предыдущих главах. Система уравнений (6. 40) имеет два ин-
теграла движения:
(1 + X?) а| + (1 + х|) а* + (1 4- х2) а| = const, (6.41)
(1 + х^ а? + (1 + x|)2 al + (1 + х|)2 а| = const, (6.42)
аналогичные (6. 34), (6. 35) и представляющие собой законы со-
хранения энергии и потенциального вихря.
Если обозначить через Дп изменение величины в течение
времени от момента t() до момента то с помощью интегралов
(6. 41), (6. 42) получаем соотношения
(1+х?)Д1 + (1+х1)Д2 + (1+^)Д3 = 0, (6.43)
(1 + х*)* Дх + (1 + х*)* Д2 + (1 + 4)2 Аз = 0,
из которых следует:
! + *! л _±±21д _ * + л f6 дм
Пусть, например, х|<х8<х|. Тогда знак Д2 всегда противополо-
жен знакам Дх и Д3, т. е. поток энергии в сторону двух крайних
волновых чисел и х3 всегда имеет один и тот же знак, противо-
положный знаку потока энергии в сторону промежуточного
волнового числа х2. Однако что касается знака потока энергии,
например, в сторону волнового числа х, то он зависит не только
от знака величины аха2а3, но также от знака величины b (х^—
хз)-
Отметим, что в случае, когда два из волновых чисел хх, х2, х3
равны между собой, соответствующий коэффициент Ct обраща-
ется в нуль.
Уравнения гидродинамического триплета подробно обсужда-
лись в предыдущих главах, и поэтому мы не будем останавли-
ваться на их решении.
Отметим, что аналогичным образом можно рассматривать
резонансное взаимодействие волн Россби—Блиновой и на сфере.
В этом случае разложение следует проводить по сферическим
гармоникам. Таким же образом можно рассматривать и задачу,
представляющую большой интерес для метеорологов, о резонанс-
ном взаимодействии волн как между собой, так и об их взаимо-
действии с зональным потоком (Галин (1974)).
101
Отметим, однако, что в этих задачах в общем случае (при про-
извольном выборе начальных данных), мы приходим к комплекс-
ному триплету. В рассмотренной выше задаче, благодаря началь-
ному выбору фаз, кубическая форма Н (6. 21) равна нулю, и,
как было показано выше, комплексный триплет можно переписать
для действительных переменных в виде вещественного гидроди-
намического триплета.
В заключение отметим также, что аналогичным образом можно
рассматривать и другие волновые задачи, представляющие боль-
шой геофизический интерес, например, задачи взаимодействия
внутренних гравитационных волн (Филлипс (1967)), поверхност-
ных волн (Бреховских (1966)).
Глава VII
СТРУКТУРНЫЕ СВОЙСТВА
КВАДРАТИЧНО-НЕЛИНЕЙНЫХ СИСТЕМ
§ 1. Аффинные инварианты и критерий существования
квадратичного интеграла для систем второго порядка
В гл. II мы уже исследовали некоторые свойства простейших
квадратично-нелинейных систем при линейной замене переменных
Естественно ввести общие понятия эквивалентности квадратично-
нелинейных систем. Две такие системы называются эквивалент?
ными, если путем некоторой замены переменных, осуществляе-
мой с помощью обратимого линейного преобразования (детерми-
нант соответствующей матрицы отличен от нуля), можно* добиться
численного равенства компонентов взаимодействия Г*опреде-
ляющих уравнения движения этих систем. Мы будем говорить
также, что эквивалентные системы имеют одинаковую структуру.
Всякое структурное свойство является общим для всего класса
эквивалентных систем.
Регулярность и существование квадратичного интеграла
движения являются примером структурных свойств, с помощью
которых в гл. II был выделен специальный класс СГТ. Число
независимых линейных интегралов системы также является струк-
турным свойством. Мы будем называть это число индексом вы-
рождения системы. Если линейных интегралов движения вообще
не существует, то система называется невырожденной.
Примером однократно вырожденной системы является симме-
тричный гироскоп, для которого J^J^J и уравнения Эйлера
имеют вид
Js^=0. '
3 dt
Поскольку в этом случае существует интеграл момента, то <о3=
=const, и уравнения движения становятся фактически линейными.
103
В общем случае при наличии одного линейного интеграла J
движения соответствующую линейную форму можно принять *
за одну из координат состояния хп, и для оставшихся тг—1 пере-
менных мы получим смешанную систему I
+ /,00—1, (7. 2) |
где матрица А\~Т1п1г В силу постоянства хп А1к определяет линей-
ную часть прогностического оператора. Встречающиеся в при-
ложениях смешанные системы, уравнения движения которых
содержат линейную и квадратичную части, формально можно
рассматривать как чисто квадратичные нелинейные системы в про-
странстве состояний, размерность которого на единицу больше
порядка данной системы, но допускающие линейный интеграл.
Ранее при рассмотрении квадратично-нелинейных систем мы I
постулировали существование квадратичного интеграла, имея
в виду наличие интеграла энергии в конкретных физических
системах. При более общем подходе возникает естественный
вопрос о критериях существования квадратичных интегралов
движения. Если нам известны только уравнения движения си-
стемы
(7.3)
и мы хотим отыскать квадратичную форму S=42 aikx<xk, являю-
щуюся интегралом движения, т. е. такую, для которой dS!dt=Q,
то из уравнений движения для неизвестных коэффициентов aik
получаем систему линейных однородных уравнений
+aftmr« =0. (7.4)1
ТТ ° пт Ti ~Ь" 1 ) Н” 2)
Число таких уравнении N- —*—у—~а число неизвестных
М = гсе В частности, для небольших значений п получаем
следующие значения N и М: '
п 2 3 4 5
N 4 10 20 35
М 3 6 10 15
При п^2 число уравнений всегда больше числа неизвестных*
и условие совместности системы (7. 4) накладывает существенные
ограничения на коэффициенты взаимодействия rj.fc. Система
(7. 3) допускает положительно определенный интеграл только
при условии, что система (7. 4) оказывается совместной и среди
104
возможных решений удается отыскать такие, для которых форма
5 является положительно определенной. Следует заметить, что
такой прямой способ исследования приводит к крайне громозд-
ким вычислениям уже при тг=3.
Для простейших систем второго и третьего порядка можно,
однако, получить простые критерии путем исследования аффин-
Hbix инвариантов соответствующей системы дифференциальных
уравнений. Такое исследование представляет определенный
интерес, так как указывает путь получения интегралов движе-
ния, связанных непосредственно с уравнениями движения системы
инвариантным способом.
По уравнениям движения системы можно построить аффинор
Г (х), представляемый в любой системе координат матрицей
Г<(х) = ^ = Г^. (7.5)
OXJ
С помощью афинора Г (х) можно записать уравнения возмущен-
ного движения вблизи заданной траектории %* (t). Полагая
==£*(/) _[_у\ где удовлетворяет исходным уравнениям движе-
ния и пренебрегая квадратичным по у членом, получаем
У = Г(х)у. (7.6)
Отсюда следует, в частности, что собственные значения аффинора
Г (х) являются некоторыми скалярными функциями вектора х и
имеют размерность обратного времени.
Для квадратично-нелинейных систем характеристический аф-
финор зависит от векторного аргумента линейно. Условия сим-
метрии тензора по нижним индексам можно записать в следу-
ющей форме:
Г(х)у = Г(у)х. (7.7)
Линейное аффинорное поле Г (х) в фазовом пространстве, удов-
летворяющее условию (7. 7), взаимно однозначно связано с урав-
нениями движения системы. Вместо характеристических чисел
матрицы ||Г*|| (аффинора Г) можно рассматривать величины
—о (х) = Sp Г (х), х = Xs = SP Г2 (х)> X3 = spr3(x), ... (7.8)
являющиеся однородными формами различного порядка от век-
тора состояния с размерностью частоты в некоторой степени и
определяющие симметричные тензоры соответствующего порядка.
Среди этих форм функционально независимыми могут быть
не более чем п форм, так как Zw+1, Xw+2, . . . можно выразить
через формы Х2, . . . .,
Для регулярных систем Sp Г (х) = —о = 0.
Дифференцирование однородной формы порядка т при исполь-
зовании квадратично-нелинейных уравнений движения приводит
К однородной форме порядка (тп-|-1). Таким способом между раз-
личными характеристическими формами могут быть установлены
105
дифференциальные соотношения, вид которых, конечно, не зави-
сит от выбора системы координат. Поэтому для получения таких
соотношений, имеющих инвариантный характер, можно пользо-
ваться любой удобной системой координат.
После этих общих замечаний перейдем к рассмотрению про-
стейшего случая: квадратично-нелинейной системы при п=2.
Докажем следующую теорему: если эта система имеет интеграл
движения
то этот интеграл представим в форме
Если Е представляет энергию системы, то константа J имеет раз-
мерность момента инерции. Для доказательства этого положения
воспользуемся канонической системой координат, в которой
в качестве одной из координат выбран параметр а, а в качестве
другой — «дополнительный параметр» С такой, что сумма квад-
ратов — (о2-Ц2) с точностью до множителя совпадает с энергией
и, следовательно, является интегралом движения. Из геометри-
ческих соображений ясно, что построение такой системы коорди-
нат всегда возможно. Напишем теперь соответствующие уравне-
ния движения
J=4W2 + r2>44W>
где коэффициенты Г. jlc определяются из двух условий:
dt . да_
+ =
Отсюда следует, что
^i,u Г1>22 = Г212 = Г2 22 = 0, (7.10)
^1,12 ~ *2" ^2,11 = 1 •
Таким образом, в канонической системе координат
d, „ <711)
Ti="
10$
Следовательно, интеграл движения /Г=1/2 (+^2) может быть
записан в аффинно-инвариантной форме
-®=-И»! + ж)- <7Л2>
Величины о и d^ldt непосредственно вычисляются из уравнений
движения. Заметим, что любой другой квадратичный интеграл
может отличаться от Ё только постоянным множителем. Отсюда
получаем критерий того, что заданная квадратично-нелинейная
система дифференциальных уравнений имеет положительно опре-
деленный интеграл движения. Сначала по заданным уравнениям
движения находится величина а, а затем d^ldt и, соответственно,
£==V2 (°2+^<з/сЙ). Если при подстановке в уравнения движения
обнаружится, что dEldt ~ 0 и, кроме того, Е является положи-
тельно определенной формой, то тем самым искомый интеграл дви-
жения будет уже найден. Может оказаться, что dEldt 0, тогда
у системы нет квадратичных интегралов. Существует также сле-
дующая возможность: Е является интегралом движения, но не об-
ладает свойством положительной определенности. Ниже рас-
смотрены соответствующие случаи на конкретных примерах.
1. Пусть в некоторой системе координат уравнения движения
имеют вид
х — —6я2 — 1ху — 2у2,
у = 10х2 + Нху + Зу2. 1
Будем исследовать эту систему, пользуясь изложенным выше ме-
тодом. Находим прежде всего величину о
°=~(й+~12х+1у—11х ~~ Qy=х + у'
Вычислим теперь на основании уравнений движения производную
+ 'У = 4а:2 + ^ху + г/2 = (2а: + у)2 > 0.
Отсюда следует, что квадратичная форма
Е = т (°2 + й)=4 (5*2++2у2) > 0
положительно определенная. Проверим, является ли она интег-
ралом движения.
7F *+1Й = <5а: + 3jz) (~6ж2 ~lxy ~ +
+ (Зх + 2у) (1(Ъ2 + 1ixy + Зу2) = 0.
Таким образом, в данном примере Е есть квадратичный интеграл
движения.
107
2. Рассмотрим второй пример. Пусть имеется система
х = —х2 — Зг/2,
у = х2 + ^ху — у\
Для нее
а = 2(р —г),
г=4^ + ^
£=Н’!+Ю=4<1! + ’!»0'
Однако, как легко убедиться,
(ж2 + У2) = 2 (—Я3 + &у + ху3 — у3) 0.
Это означает, что система вообще не имеет квадратичных интегра-
лов.
3. Наконец, в случае системы
получаем
da 9
—Ц, ~т: = —X,
dt
-fsO.
Квадратичная форма Е этой системы является интегралом дви-
жения, но не является положительно определенной. Легко уста-
новить, что в этом случае существуют интегральные кривые, ухо-
дящие на бесконечность за конечное время.
§ 2. Условия существования алгебраических интегралов
для регулярной системы третьего порядка
Регулярная система третьего порядка определяется в произ-
вольной системе координат, как нетрудно подсчитать, пятнад-
цатью числовыми коэффициентами. Для исследования такой сис-
темы можно воспользоваться аффинно-инвариантными характерис-
тиками, которые могут быть найдены лишь из вида системы.
Если система в действительности принадлежит классу СГТ, то
между аффинными характеристиками возникают определенные
соотношения, которые можно проверить.
108
Для отыскания таких соотношений воспользуемся специальной
системой координат, в которой уравнения движения триплета
имеют канонический вид, указанный в гл. II
#2 = 2^1, (7.13)
х3 = гхтх29
причем p+q-\-r=O. Для определенности будем считать, что рг >
0, pq < 0, rq <С 0; это означает, что хг и х3 — устойчивые моды,
а х2 — неустойчивая. Построим для этой системы характеристи-
ческую матрицу (аффинор)
/ 0 рх3 рх2\
ГЯх)={^}= 0 • (7.14)
\гх2 гху 0 /
В силу регулярности Sp Г=0 и основной интерес приобретает
характеристическая функция (квадратичная форма) которая
по определению (7. 8) равна
X = Sp Г2 (х) = 2qrxj + 2грх2 + 2Р<№1 В(х). (7.15)
Если система не вырождена, то характеристическая квадратичная
форма также не вырождена и имеет два члена отрицательных
и один положительный, т. е. сигнатуру (--+). Для однократно
вырожденной системы (симметричный гироскоп) характеристи-
ческая форма содержит одно слагаемое, имеющее отрицательный
знак. Двукратно вырожденный триплет отвечает тривиальной
системе, у которой все коэффициенты равны нулю.
Если мы вычислим характеристическую форму для некоторой
системы третьего порядка и убедимся после соответствующего
исследования, что сигнатура формы отличается от (---+), это
будет означать, что система не является СГТ, так как для нее
не существует положительно определенного интеграла движения.
Если сигнатура получилась «правильной», то мы можем продол-
жить анализ, определив с помощью дифференцирования согласно
уравнениям движения величины dxJdt, d?yjdt2 и dfyJdP , являю-
щиеся соответственно формами третьего, четвертого и пятого
порядка (С, Z?, Е).
Выполним теперь соответствующие вычисления для СГТ, вос-
пользовавшись каноническим представлением. Дифференцируя
форму (7. 15), с учетом уравнений движения (7. 13) получаем
= i2pqrx1xzx3 = С (х), (7.16)
i2pqr + q ^i)2 + r fo^)2]sD (x)> (7• I7)
4^=-^=48pgra:1a:2a:3 (qrx\ + rpx% + pqx$ == E (x). (7.18)
109
Сравнение (7. 18) с (7. 16) и (7. 15) показывает, что выполняется
следующее фундаментальное соотношение:
Е(х) = 2В(х)С(х). (7.19)
Полученное соотношение носит аффинно-инвариантный характер
и поэтому справедливо для любой СГТ третьего порядка. Это
соотношение, выражающее форму пятого порядка через произве-
дение формы второго и третьего порядка, можно назвать условием
приводимости. Оно является необходимым условием существова-
ния квадратичного интеграла движения у регулярной системы
третьего порядка.
По существу, можно считать, что это соотношение при выпол-
нении некоторых дополнительных требований типа неравенств
является также достаточным условием того, что данная регуляр-
ная система принадлежит классу СГТ. Во всяком случае исполь-
зование афинно-инвариантного соотношения (7.19) приводит для
характеристической функции к дифференциальному уравнению
третьего порядка, которое эквивалентно системе трех уравнений
первого порядка, описывающих триплет в каноническом пред-
ставлении.
Из (7. 19) вытекает, что
dv
' (7.20)
Отсюда сразу получаем интеграл движения
I
§—Z2 = —^ = const, (7.21) J
где
W — B^ — D (7.22)
есть форма четвертого порядка, являющаяся интегралом движения.
Уравнение (7. 20) также легко интегрируется. После умноже-
ния обеих частей на d^ldt получаем
y=® = const- (7.23) i
Отсюда следует, что форма шестого порядка
Ф = |с2 + О- ^ = 4 53+ 4-С2 — BD (7-24)
является вторым интегралом движения, что легко проверить
непосредственно.
Полученное дифференциальное уравнение (7. 23) для харак-
теристической функции х, содержащее два параметра W и В
(постоянные вдоль траектории), является известным уравнением
110
Вейерштрасса и при замене переменных х = ^6(3, ^ = ^6т] приво-
дится к стандартной форме
(з|)2=4₽3-^-*з, <7.25)
где _
g2 = 23^6W9 g3 = — 2Ф. (7.25а)
Решением этого уравнения является эллиптическая ^-функция
Вейерштрасса (Бейтмен и Эрдейи (1967)).
В следующем параграфе будет показано, что из условия су-
ществования для исходной системы положительно определенного
квадратичного интеграла вытекает, что указанные выше формы
четвертого W и шестого Ф порядка для СГТ должны удовлетво-
рять неравенству
9ф2>о. (7.26)
Заметим при этом, что положительность W следует уже из того,
что по определению W = В2 — и вместе с тем она является
интегралом движения; поэтому после усреднения по траектории
получаем
0<1У = <£2>. (7.27)
§ 3. Интегрирование уравнений движения канонического
триплета
Как известно, уравнения движения триплета допускают два
независимых квадратичных интеграла, причем физический смысл
этих интегралов зависит от характера задачи. Так, например, для
эйлеровского гироскопа в качестве второго интеграла (наряду
с энергией) обычно используется квадрат момента, а в гидродина-
мической интерпретации триплета, указанной в первой главе, роль
второго интеграла играет сумма квадратов циркуляции по главным
сечениям.
При общем теоретическом анализе уравнений движения три-
плета целесообразно рассматривать некоторые «канонические»
интегралы, в выражения для которых входят только коэффици-
енты исходных уравнений. В связи с этим введем в рассмотрение
следующие три зависимых интеграла движения:
5',^-—S2 = il—21 53 = 21—21 (7.28)
1 g Г ’ 2Гр’ 6 Р Q V
связанные соотношением
51 + 52 + 53 = °, (7.28а)
11Г
или Эквивалентные им интегралы ех, й ёз
®1 = $2’ ®2 — 81 *^3’ £3 = ^2 $1* (Л 29)
Последние величины можно также записать в виде
2xf xl xl _________2x1 xl xl 2xl xl х% qn
1 р q г 9 2 q р г 9 6 г р q ' '
f ®1-®2 = З53» e2--®3 = 3^1> S3---®1 = 3i$2- • 30a)
Удобно также использовать другую нормировку для канони-
ческих интегралов, вводя инварианты
«1 =—(4)/’P?rei> —(4)/3^ге2> ез = — (j)l,P9re3< (731)1
которые, как следует из (7. 29), связаны соотношением I
ei + е2 + ез = 0- (7 32)
Выведем аналитическое выражение для В(х), задаваемой
(7. 15), воспользовавшись сначала для этой цели аналитическими
решениями уравнений (7.13). Известно, что решение (7. 13) вы-
ражается через эллиптические функции Якоби (см., например,
Ландау и Лифшиц (1958)). Непосредственной проверкой можно
убедиться, что если выбрать начало отсчета времени в момент,
когда #з=0, то «
д;1 = Л1с1пу^,
я2 = Л2спт£, (7.33)
х3 = A3sn yL
Здесь
спт = \/1—sn2x, dnt = \/l—&2sn2x, (7.33а)
д /®3 —д __ 1 /е8 —®2\У«
1 61/Д Qr / ’ 2 61/з\ рг ) ’
(7-33б)
^=2-^3 ’ (1.33в)
у = 6-1/’ \Je-i — е3 0,550 — е3.
(7. 33г)
Далее, используя (7. 15), (7. 33), (7. 336), а также следующую
формулу связи ^-функции Вейерштрасса с эллиптическими функ-
циями Якоби (см. Гурвиц и Курант (1968)):
1Р 1 [(е3 — dn2 {и \/в! — е3) + (е3— е2) сп2 (и \/е1 — е3) +
+ (е2 — е3) sn2 (a \Zex — е3}] (7.34)
получим
В (х) = б’Мб"7’* + ш') 1,817^(0,55 + ш'). (7. 35)
>112
Как известно, основными периодами ^-функции Вейерштрасса
являются 2(о и 2(о', т. е.
(и) = •$> (и; 2и), 2(о')
и
ei — "Й5(ю), е2 = + <*>')» вд = (а?)4
Поскольку мы рассматриваем только вещественные значения
ev е2 и е3, то, как следует из теории эллиптических функций, вто-
рой полупериод <о' является чисто мнимым и, если ev е2 и е3 дей-
ствительные и различные, а также
^1>в2>ез> - (7.36)
то величины, выражающиеся в виде интегралов
2о> = f ------- dz = 2KW ( (7. 37)
J V(t — ех) (т — е2) (t — е3) Vej — е3
«1
«3
2ш' = 1 f dz . . = 2iK (к'} , (7. 38)
J 'z(e1 — т) (е2 — т) (е3 — т) ^ех — е3
и будут основными периодами интересующей нас эллиптической
функции Вейерштрасса tp (и) (Бейтмен и Эрдейи (1967)).
Здесь К (А) — полный эллиптический интеграл 1-го рода
те/2
О
— № sin'2 <?
а к' — дополнительный модуль
к1 = yji—kh
^Выражение (7. 35) для характеристической формы В (х) можно
получить, не прибегая непосредственно к решению (7.33) и (7. 336)
исходной системы уравнений (7.13), если воспользоваться аффинно-
инвариантным методом описания, приводящим, как было показано
выше, к алгебраическому дифференциальному уравнению Вейер-
штрасса (7. 25), (7. 25а) для р. Указанный метод обладает несом-
ненным преимуществом, поскольку не требует использования
какой-либо специальной системы координат. Для того чтобы полу-
чить требуемую формулу, заметим, что общее решение уравнения
(7. 25) записывается с помощью эллиптической ^-функции Вейер-
штрасса в следующем виде:
р ft) = £(?] +С), (7.39)
где С — произвольная постоянная.
Далее, используя свойство (7. 32) и выражения для интегралов
движения W и Ф через канонические интегралы движения е1? 8
8 Нелинейные системы
113
Рис. 27. Аппроксимация решений
циями при
тригонометрическими функ-
е2 ие3, которые могут быть получены из определений (7. 22), (7. 24)
и (7 30), (7. 31), нетрудно показать, что инварианты е2 и е3
совпадают с корнями кубического уравнения
4z3 —g2z —g3 = 0, (7.40)';
соответствующего (7.25). Поэтому если предположить, что
е2 и е3 вещественны, то дискриминант А уравнения (7. 40) будет *
положителен
А = g* — 27g| = 12 (4W3 — 9Ф2) > 0, (7. 41)^
и мы получаем неравенство (7. 26). В этом случае из свойств,
^-функции Вейерштрасса следует, что существует такая пара при-1
митивных периодов 2«>, 2о/ чтоо> — вещественное число, а о/ —
мнимое, причем о> и о/ определяются из соотношений (7. 37)f
(7. 38) и (7. ЗЗв), в которых е19 е2 и е3 находятся как функции W
и Ф из решения кубического уравнения (7. 40), (7. 25а). Учитывая,!
что функция р (ограничена и при любых т] может принимать
лишь действительные значения, находим с помощью известных
свойств ^-функции Вейерштрасса (см., например, Бейтмен и Эр-
Рис. 28. Лемнискатический случай: &2=0,5 (представле-
ние через тэта-функции)
114
Рис. 29. Аппроксимация решений гиперболическими
функциями при&2=0,7 (a), Zc2=l—10~3 (б), &2=1— 0,74Х
X10"8 (в)
дейи (1967)), что константа С в (7. 39) должна быть равна о/е
откуда и следует полученное ранее другим способом выражени
(7. 35).
Связь W и Ф с е1ъ е2 и е3 находится путем использования формул
для симметрических функций корней алгебраического уравнения
8*
115
(7. 40), (7. 25а) (Бейтмен и Эрдейи (1967)), что приводит к следую-
щим соотношениям:
W = б-7’ (е* + еЦ- е|), (7.42)
Ф = —ге^вд. (7.43)
На рис. 27, 28, 29 представлены в безразмерном виде графи-
ческие зависимости решений /2 и Хз уравнений движения (7. 13)
и характеристической формы р от безразмерного параметра вре-
мени при значениях параметра А:2=0,4; 0,5; 0,7; 0,999 и А;2=1—
—0,74«10“8 соответственно, причем время отсчитывается в неко-
торых условных единицах, в которых период для решений
Хг и Хз оказывается равным четырем.
Из сравнения кривых, отвечающих данным типичным случаям,
видно, что при А:2, близких к нулю (практически в интервале
0 <^к2 < 0,5), кривые имеют синусоидальный вид. При значениях
А:2, приближающихся к единице, экстремумы кривых становятся
менее острыми и при значениях А:2, близких к единице (рис. 29, б
и в), они приобретают заметно выраженный ступенчатый характер.
Форму всех этих кривых удобно исследовать с помощью асимптоти-
ческих представлений эллиптических функций через тригонометри-
ческие функции (при малых к2) и гиперболические функции
(при А:2, близких к единице). Вывод соответствующих формул
приводится в приложении II.
Глава VIII
СТАТИСТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ
ГИДРОДИНАМИЧЕСКОГО ТИПА
§ 1. Стационарные гауссовские распределения
при отсутствии внешних воздействий
Применение статистических методов к изучению процессов в сис-
темах гидродинамического типа представляет интерес в связи
с проблемой турбулентности и оценкой влияния молекулярных
флуктуаций на гидродинамические процессы. Естественно, что
статистическое описание СГТ носит модельный характер, вместе
с тем оно существенно проще, чем применение статистики к исход-
ным уравнениям гидромеханики, и не требует сложного математи-
ческого аппарата.
Описать статистически динамическую систему — это значит
задать нормированную плотность вероятности f (u, t)9 %ля кото-
рой выполняется уравнение Лиувилля
= = (8.1)
которое с учетом (2.12) можно переписать в виде
ff+^Gr^“v/)=0- м
Если система регулярна, то (8. 2) эквивалентно условию
т. е. / является интегралом движения.
При этом наиболее интересным является случай, когда / явно
не зависит от времени. Таким образом, к СГТ применима известная
теорема статистической механики о том, что плотность стационар-
ного распределения является интегралом движения системы.
В связи с этим для любой системы гидродинамического типа
существует стационарное распределение Гаусса
f — Ce~9№, (8.3)
где а (и) — квадратичная форма, пропорциональная энергии
Такое распределение соответствует распределению Гиббса (Лан-
дау и Лифшиц (1964)). В тех случаях, когда в системе имеется
117
еще второй квадратичный интеграл, отличный от энергии, как,
например, в двумерной гидродинамической задаче, где сохраня-
ется также средний квадрат вихря, можно построить стационарные
гауссовские распределения, отличные от распределения Гиббса
и зависящие от двух параметров (Обухов (1969), Кляцкин (1969)).
Зная плотность распределения /, можно вычислять математи-
ческое ожидание физических величин — функций состояния
системы
<Ф>=5 <|»(u)/(u)du, (8.5)
где ф — некоторая функция состояния, а интеграл берется по
всему фазовому пространству, du=diA/iA . .dun — элемент объ-
ема фазового пространства.
В гидродинамике при изучении турбулентных движений ши-
роко используется метод моментов Фридмана и Келлера. Для
конечномерных моделей моменты представляются симметричными
тензорами различных порядков
и* = <>*>,
= (8.6)
Bijkl =<и^ики1у,
Используя уравнения движения системы, например, уравнения
(2. 12), можно построить для моментов цепочку уравнений —
известные в гидродинамике уравнения Фридмана — Келлера
(точнее, их конечномерный аналог)
К~У(1тВ1т,
Bij ~ Г‘1тВ'1т + у rimBilm, (8. 7)
Bijk=4 ГкВлг”+4 Г1'тВк“т + 4 ЛтВ^1т,
Бесконечная система обыкновенных дифференциальных уравне-
ний — уравнений Фридмана — Келлера, по существу, эквива-
лентна одному уравнению в частных производных — уравнению
Луивилля (8. 2).
Для того чтобы оборвать бесконечную цепочку уравнений
Фридмана — Келлера и получить замкнутую систему уравнений
для моментов первых трех порядков, М. Д. Миллионщиков (1941)
предложил известную гипотезу «замыкания» — так называемую
118
гипотезу четвертых моментов, которая сводится к применению
формулы (предполагается, что <V>=0)
Bijkl = BiJBkl + BikBjl + BilBkj. (8. Ь)
Это соотношение является точным для распределений Гаусса,
а в общем случае может рассматриваться как некоторое прибли-
жение.
Посмотрим теперь, как «работает» метод моментов в сочетании
с гипотезой Миллионщикова при отыскании характеристик ста-
тистически-стационарного режима в СГТ. Для простоты ограни-
чимся случаем канонического триплета, хотя аналогичные вычис-
ления можно было бы провести и в общем случае. Уравнения
движения системы имеют вид
dxjdt = pyz,
dy/dt = qzx, (8. 9)
dz/dt = rxy, p + q + r = 0.
Умножая обе части уравнений движения на соответствующие ве-
личины и осредняя, находим уравнения для моментов
d (x*y/dt = 2р (xyzy, (8.10)
d (хуУ/dt = p <y2zy + q (zx2y,
Другие уравнения для вторых моментов получаются циклической
подстановкой (#yz), (pqr). Вторые производные от вторых моментов
будут выражаться уже через моменты четвертого порядка
d2 <(x2y/dt2 = р2 <j/2z2> + РУ (z2x2y + рг (x2y2y,
d\xyyidt2 = kpq <z2yzy + pr (x?yy + qr <яу3>, (8.11)
Требуя равенства нулю вторых производных, что выполняется для
стационарных распределений, и пользуясь гипотезой Миллион-
щикова для вычисления моментов четвертого порядка, легко
убедиться, что получаемые при этом уравнения удовлетворяются,
если все недиагональные компоненты вторых моментов обраща-
ются в нуль
<ху> = <yz> = <za:> = 0, (8.12)
а главные моменты В^-^зру, -B22=<i/a>, 533=<z2> удовлетворяют
соотношению
p/B^q/B^r/B^O. (8.13)
Учитывая что р+?+г=0, последнее уравнение означает, что
квадратичная форма
_ 1 / Ж2 . у2 . 2 2 \
2 В%2 Bj
119
является интегралом движения, и, следовательно, функция Гаусса
полностью определяемая вторыми моментами, является точным
решением для стационарной задачи. Соотношения Миллионщи-
кова для четвертых моментов при этом выполняются автомати-
чески.
Таким образом, применение гипотезы Миллионщикова к сис- 1
темам гидродинамического типа при дополнительном требовании
обращения в нуль вторых производных по времени от моментов
второго порядка (слабая стационарность) приводит к некоторому
квадратичному интегралу движения, с помощью которого можно
построить стационарное распределение Гаусса. Если у системы
нет квадратичных интегралов, кроме энергии, то мы, естественно,
приходим к распределению Больцмана, для которого параметр
распределения (3 является аналогом обратной температуры.
Вычислим теперь среднее значение введенной в гл. V характе-
ристической формы <
Х = 8рг2(и),
пользуясь при этом стационарным распределением (8. 3) типа
Больцмана. Полагая 'X.=Ciku<uk, гДе С.&=Г"тГ”гя, получаем \
В энергетическом представлении с учетом (8. 4) имеем =2 8**713 '
и, следовательно, \
<X>=fsPC.
Вычислим также среднее значение энергии
<я>=4<£«»'»‘>==-И1>г«в"=р
откуда следуют известная формула Больцмана <7Г>/п=6=1/р. <
Отношение среднего значения характеристической формы / к УД~
военной средней энергии
<х> „ 1
2 <я> п
уже не зависит от распределения параметра р и может рассматри-
ваться как некоторая внутренняя характеристика системы, опре-
деляемая инвариантным способом.
Покажем теперь, что среднее значение / всегда отрицательно
и в любом энергетическом представлении инвариант — Sp С
выражается через сумму квадратов коэффициентов взаимодей-
ствия. Воспользуемся для этого основным циклическим соотно->
шецием (2. 15), выражающим закон сохранения энергии
гт, /fc + г/, ы + г&, = °-
SpC
120
Умножим это равенство на Г*’» л и проведем свертку. Заметим
при этом, что в энергетическом представлении различие между
верхними и нижними индексами пропадает и, следовательно,
2S — представляет собой существенно положительную
величину — сумму квадратов коэффициентов взаимодействия
(в силу свойств симметрии динамического тензора многие коэф-
фициенты при этом входят в сумму дважды). Выполняя соответ-
ствующие вычисления, получаем
2S = —(Г*- ЛТЛ ki + Г‘> „) = —2 Sp С.
Таким образом, в энергетическом представлении
5=„SpC= 2 п.а+т 2 п.„-
При фактическом пользовании этой формулой следует помнить, что
при ] =7^= к соответствующие коэффициенты взаимодействия непос-
редственно входят в правую часть уравнений движения, а компо-
ненты вида представляют соответственно удвоенные коэффи-
циенты при квадрате некоторой переменной. Отсюда следует пра-
вило — след характеристической матрицы, вычисленной в любой
декартовой системе координат (энергетическое представление),
взятый с обратным знаком, представляет собой сумму квадратов
коэффициентов, входящих в правую часть уравнений движения,
при этом квадраты коэффициентов при квадратах соответствую-
щих переменных берутся с двойным весом, т. е. считаются как бы
дважды.
Поясним сказанное на примере двух простейших эквивалент-
ных между собой систем:
dujdt — —pu2u3t
du2/dt = 2pu3uv (Л)
du3/dt = —
и dvjdt — —pv2vv
dv2/dt = pv{ — pvl, (B)
dv3/dt = pv2v3.
Как уже отмечалось ранее (гл. II, § 3), система В переходит
в систему А при ортогональном преобразовании: zz1 = (p1 4-р3)/\/2,
и2 = 1>2, и3 = (р1 —i?3)/V2.
Для системы А имеем
/ 0 — ри3 —рил
г(и)=^Г7=1 2рцз 0 2РИ1 Ь
3 \—Р«2 —•?«! 0 / ____
/ = (вСп) = Sp Г2 (и) == —4р2и2 — 2р2«2 — 4р2и2,
—SpC = 6p2.
121
Сумма квадратов коэффициентов очевидно равна как раз этой
величине р2+(2р)2+р2=6 р2. Во втором #случае (система В)
—ри2 —рих 0 \
0 -2^3),
О Pv2 /
% = (vC’v) = Spf/2 (р) = 2p2z?2 — 4р2г?2 — 4р2(?2,
—Sp С1 = 6р2.
Как и следовало ожидать, мы получили то же значение. Вычислим
теперь для системы р «сумму квадратов» коэффициентов (учиты-
вая правило весов)
Р2 + 2 (р2 + р2) + р2 = 6р2. |
Полученная выше инвариантная характеристика системы мо-
жет оказаться полезной при анализе сложных систем и их аппрок-
симации более простыми.
Отметим в заключение, что решение общего уравнения Лиу-
вилля в нестационарном случае, связанное с большими математи-
ческими трудностями, представляет определенный интерес и для
прогностических целей. В этом случае хотя сами уравнения
прогноза являются чисто динамическими (некоторая аппроксима-
ция уравнения гидродинамики), задача прогноза ставится ста-
тистически благодаря неполноте начальной информации (непол-
нота измерений, турбулентность и т. п.). Уравнением, описываю-
щим эволюцию функции распределения во времени, как раз и явля-
ется уравнение Лиувилля. Такой подход к задачам численного
прогноза метеорологических процессов описан в ряде работ,
опубликованных в последние годы (Обухов (1967), Татарский
(1969), Эпштейн (1969), Флеминг (1971)).
§ 2. Уравнение Эйнштейна — Фоккера для СГТ
при наличии диссипации и внешнего шума
Переходим теперь к рассмотрению систем гидродинамического
типа, находящихся под влиянием некоторого внешнего воздей-
ствия. При этом учитываются также диссипативные и флуктуа-
ционные силы. Конкретно рассматривается простейшая система
типа триплета.
Системы гидродинамического типа с учетом линейного трения
и внешнего шума можно описывать динамическими уравнениями *
^=F.(v)-k<% + O) (Z=l, N), (8.14)
♦ В общем случае диссипативный член имеет вид Однако всегда можно
выбрать систему координат, в которой две положительно определенные
квадратичные формы — энергия и диссипация — имеют диагональный вид,
что соответствует (8. 14).
122
где Х(Л — коэффициент трения для j-компоненты 7V-мерного век-
тора v, a (v) — квадратичная по v функция, обладающая свой-
ствами (см. гл. II)
a) p.F.(v) = 0, (8.15)
б) dFi (v)/dv. =0.
Здесь и ниже по повторяющимся индексам подразумевается сум-
мирование по i=l до N (за исключением тех случаев, когда один
из индексов заключен в круглые скобки, как, например, в (8.14)).
Сторонние случайные силы /. (t) можно считать гауссовскими
случайными функциями, дельта-коррелированными во времени
со средним значением, равным нулю, т. е.
</Л* + ^)>=Л8(х)- ' <8Л6)
Дельта-коррелированность («белый шум») обусловлена тем
обстоятельством, что временной радиус корреляции сторонних
сил т0 много меньше, чем характерное время изменения динамичес-
кой системы 7=1/X.
Пусть СГТ в момент времени t—О находилась в состоянии v (0).
Система уравнений (8. 14) является системой первого порядка
по времени, и ее решения в момент времени t > 0 определяются
величинами f .t' Q<^tf ноне зависят от них при t' >
> t, т. е.
= ° пРи t’>t, (8.17)
Для дальнейшего нам понадобится значение вариационной
производной bv. (t') при t'—t: Чтобы вычислить эту вели-
чину, проинтегрируем систему (8. 14) по t
t t
vt (0=^0) + j drf. (T) + j dr [Ft (v (x)) - (t)]. (8.18)
0 0
Подействуем теперь на (8. 18) оператором 8/8/^. (f) при t' <it.
Тогда с учетом (8. 17) получаем*
Устремляя затем t' получаем выражение
(8.20)
8/у(0 V V°- >
Введем в рассмотрение плотность вероятностей для решения
v (t) системы уравнений (8. 14), т. е. функцию
^(v) = <8(v(0-v)>. (8.21)
* Мы считаем, что начальные значения vi (0) не зависят от f.
123
(8.23)
(8. 22),
(8-24)
Здесь v (t) — решение системы (8. 14), соответствующее опреде^
ленной реализации f (2), а усреднение производится по множеству
всех реализаций f. Дифференцируя (8. 21) по t и используя (8.14),
получаем уравнение для Pf (v)
{^(у) - К“Ч] Pt} <f< (0 8 [V (0 - V]>. (8. 22)
Выражение, состоящее в (8. 22) под знаком усреднения, представ-
ляет собой среднее значение от произведения случайного про-
цесса f. (Z) и функции от решения системы (8. 14) v (0, которая
является функционалом от этого случайного процесса.
В приложении III выведена общая формула для вычисления
таких средних значений, которая для рассматриваемого случая
с учетом равенства (8. 20) принимает вид
где Ф* (v) — произвольная функция от v (t). Уравнение
следовательно, можно переписать в виде
dt
соответствующем уравнению Эйнштейна — Фоккера с постоянным
во времени тензором диффузии.
Начальным условием для (8. 24) является условие Ро (v) =
— 8 (v—v (0)) для детерминированных начальных данных — v (0)
или же условие более общего вида Ро (v)=Wr (v), если начальные
условия v (0) заданы статистически.
Уравнение (8. 24) является исходным уравнением для изучения
статистических свойств СГТ при наличии диссипации и внешнего
шума.
В качестве конкретного примера использования уравнения
(8. 24) рассмотрим задачу о равновесных тепловых флуктуациях
в СГТ (относительно состояния покоя v (0)=0), вызванных тепло-
вым движением молекул ♦.
Для равновесных тепловых флуктуаций стационарное решение
уравнения (8. 24), не зависящее от начальных данных, должно
иметь характер максвелловского распределения, соответствую-
щего закону равнораспределения энергии по степеням свободы
Р& (v) = const exp {—и*/2кТ}, (8. 25)
* Общая корреляционная теория равновесных гидродинамических флуктуа-
ций была построена в работе Ландау и Лифшица (1957) путем введения
«стороннего тензора напряжения» в уравнение Навье—Стокса и вектора
«стороннего теплового потока» в уравнение переноса тепла, обладающих
определенными статистическими свойствами, аналогичными формуле
(8. 16). На основе этой теории в работе Кляцкина (1971) изучались про-
странственно-временные корреляции равновесных гидродинамических по-
лей в идеальном газе, возбуждаемых тепловым движением молекул, и
обсуждалась область применимости макроскопической теории турбулент-
ности.
124
где к — постоянная Больцмана, а Т — равновесная температура.
' Подставляя (8. 25) в (8. 24), получаем для величин соотноше-
ния
pf.) = 2\(i)kTf (8.26)
являющиеся аналогом формулы Эйнштейна для коэффициента
диффузии броуновской частицы. При этом в силу условий (8. 15)
имеет место
5/^.{f/(v)Pco(v)}-0. (8.27)
Соотношения (8. 16) и (8. 26), таким образом, полностью опреде-
ляют статистику «сторонних сил», и нелинейные члены в уравне-
ниях (8. 14), в силу (8. 27), роли не играют. Эти факты хорошо
известны и представляют по своей сути приложение флуктуа-
ционно-диссипативной теоремы (см., например, приложение I
к книге Левина и Рытова (1967)) к СГТ.
Отметим, что динамическую систему (8.14) с соотношениями
(8. 16), (8. 26) можно рассматривать как уравнения Ланжевена,
описывающие броуновское движение СГТ. В простейшем случае
(83) система (8. 14) описывает броуновское вращательное движение
гироскопа (в пространстве скоростей), и величины при этом
представляют собой эффективные коэффициенты трения, опреде-
ляемые сопротивлением среды.
г Если случайные силы Д (t) вызваны не молекулярным движе-
нием, то соотношение (8. 26) не имеет места, и величины р% не за-
висят, вообще говоря, от Х(,). В этом случае стационарное распре-
деление вероятностей не является, вообще говоря, гауссовским
распределением. Однако если СГТ может быть описана системой
феноменологических уравнений (8. 14) с X(<) = X=const и р%~
= p.2=const, то стационарное распределение вероятностей для v
имеет вид, аналогичный распределению (8. 25)
(0 = const ехр (8.28)
I Г* J
§ 3. Шумы в СГТ при наличии регулярной
составляющей силы
Пусть теперь на СГТ помимо случайных сторонних сил дей-
ствует также регулярная сила g. Уравнения, описывающие ди-
намику СГТ, в этом случае примут вид
^L=Ff(v) + g<-k(%+ /,(#) (8.29)
с теми же «сторонними силами», что и в уравнении (8. 14). Если
случайные силы f (t) вызваны молекулярным движением, то теп-
ловые флуктуации могут и не быть равновесными. Однако из фи-
зических соображений естественно считать, что тепловые флук-
125
’гуации описываются уравнением (8. 29) и в этом случае. Когда
i(t) представляют влияние мелкомасштабных движений на дви-
жения более крупных масштабов, уравнение (8. 29) можно при-
нять за основу описания.
При отсутствии флуктуаций система (8. 29) имеет стационар-
ные решения, соответствующие решению системы алгебраических
уравнений
(8.30)
Следует отметить, что решение системы (8. 30) не единственно,
и при выборе определенных решений должна учитываться устой-
чивость их по отношению к бесконечно малым возмущениям.
Наличие нелинейных членов в (8. 29) приводит к тому, что
среднее движение (усреднение производится по ансамблю реали-
заций /) не совпадает с решением системы (8. 30) (поскольку воз-
никают напряжения Рейнольдса).
Так как уравнения (8. 29) описывают флуктуации макроско-
пической системы, в рассматриваемой задаче существует малый
параметр a2=jji2/Xp2iCT (отношение энергии шумов к кинетической
энергии макроскопического движения), малость которого позво-ч
ляет в ряде случаев существенно упростить задачу. В общем виде
задача, описываемая уравнением (8. 29), чрезвычайно сложна.
Однако наиболее важные общие черты поведения ее можно изу-
чить на примере простейшей системы (53).
Рассмотрим более подробно простейшую систему гидродина-
мического типа (53), уравнения для которой запишем в безраз-
мерном виде
^0 “ Г2 ~~ + =---^2—^2- (8.31)
Как отмечалось в третьей главе, эта система эквивалентна
динамическому описанию движения гироскопа с изотропным тре-
нием, возбуждаемого постоянным моментом внешних сил отно-
сительно неустойчивой оси. Стационарное решение этой системы
определяется параметром (числом .Рейнольдса) R. Критическим
параметром при этом является 7?кр=1. В случае R <С 1 имеется
стационарное решение, соответствующее «ламинарному» режиму
Ц)ст = Я, «’1 от = ст = 0. (8.32)
При R > 1 этот режим становится неустойчивым относительно
бесконечно малых возмущений и устанавливается новый стацио-
нарный режим («вторичное течение»)
'’оот-t <^=±^-1, ^от = 0. (8.33)
При этом в установившемся режиме уже имеется элемент случай-
ности, а именно, величина р1ст может быть как положительной,
так и отрицательной, в зависимости от знаков амплитуд малых
начальных возмущений.
126
Рассмотрим теперь воздействие случайных внешних сил на
эту динамическую систему. Пусть сначала случайная сила дей-
ствует только на компоненту vQ. В этом случае динамическая
система будет описываться уравнениями
— V1 — V0 + R + /о (0 >
г>1 = ЦА — t7l>
= — vQv2 — vt, (8. 34)
</о(Г+^)/о(0> = 2о2а(т).
При R < 1 компоненты и i?2 возбуждаться не будут, а стацио-
нарное распределение вероятностей для компоненты v0 будет
гауссовским
Poo (^о) = const ехР {—(t?o — )2/2а2}. (8. 35)
Если R > 1, то не будет возбуждаться компонента р2.Компоненты
же v0 и vx будут удовлетворять системе уравнений
»о = — — »о + R 4- /о (0, ^1 = ^1 — vi- (8-36)
Представим р0 в виде у0=1 -j-v'. Тогда система (8. 36) примет вид
г>; = — vl + (R — 1) — v'o + fo(t), t>j = v'ovv (8.37)
Отметим, что эволюция во времени компоненты vt определяется
ее начальным значением. Если (0) > 0, то в отсутствие случай-
ной силы (t) при £ -> оо стремится к своему стационарному
значению \JR — 1 • В «случае же щ (0) < 0, l\ (Z) -> — \jR — 1 при
00.
Пусть для определенности vr (0) > 0. Тогда, представляя vr
в виде рх=ехр {<р}, систему (8. 37) можно переписать в виде
? = Уо = —+
С7(т)=1е2’-(Я-1)?. (8.38)
Система уравнений (8. 38) аналогична уравнению Ланжевена
для описания броуновского движения частицы во внешнем поле
/7 (<р) — играет роль координаты частицы, a v0 — ее скорости).
Соответствующее уравнение Эйнштейна — Фоккера для со-
вместной плотности вероятностей ср и v'o имеет вид (см., например,
работы Уленбека (1971), Кляцкина и Татарского (1973))
+ + (8.39)
dt ди0 ду ’ ду ди^ 1 dv^ v 0 1 '
vr2
где H — + U (ср) — аналог функции Гамильтона. И, следова-
тельно, стационарное распределение вероятностей для решения
127
уравнения (8. 39) аналогично каноническому распределению Гиббса
Рсо^о’ <р) = constехр{—у#). (8.40)
Из распределения (8. 40) следует, что стационарное распределе-
ние для компоненты ид будет гауссовским
^o(yo)=constexp| — (8.41)
а распределение вероятностей для ср не является гауссовским, и
они не коррелируют между собой.
Рис. 30. Стационарные плот-
ности распределения вероят-
ностей для компоненты vr ди-
намической системы (8.37) и
для флуктуаций ц/ компо-
ненты VQ ОКОЛО Ц)ст=1 В СЛУ-
чае, когда R > 1, а случай-
ные силы действуют лишь на г0
Возвращаясь к переменной v19 получаем стационарное распре-
деление вероятностей для нее в виде
Рт (иг) — const
(8-42)
Распределения вероятностей (8. 41)—(8. 42) схематически изо-
бражены на рис. 30.
Отметим, что при критическом режиме (7?=1), как видно из
(8. 42), не существует стационарного распределения вероятностей
для компоненты иг. Аналогичное распределение вероятностей
можно получить и для случая vr (0) <0.
Отметим, что переход системы из начального состояния к ста-
ционарному, описываемому формулой (8. 40), происходит в две
стадии: сначала быстро устанавливается максвелловское распре-
деление по скоростям и после этого значительно медленнее про-
исходит установление распределения (8. 42) по координате ср.
Обсуждение этого вопроса см., например, в работе Уленбека
(1971). Вторая стадия описывается при этом уравнением Эйн-
штейна — Смолуховского
= Р, и + а^(у) (8. 43)
dt ду (дер t ' * '/ ' д<р2 ’ '
которое для переменной vx принимает вид
(“ И- (л - Ь» +
(8Л4'
128
Отметим, что уравнение (8* 44) является уравнением Эйнштейна-
Фоккера для стохастического динамического уравнения
г>1 = —[р? — (Я — 1)] + рх/0 (О,
которое можно получить и непосредственно путем усреднения
системы (8. 37) по соответствующему интервалу времени.
Рассмотрим теперь более сложный случай, когда на каждую
из компонент действуют случайные силы. При этом соответствую-
щая стохастическая задача описывается динамической системой
Л) = ^2 — у1 — уо + Я + /о (О»
г>1 = Vi —yi + /i(i), (8.45)
г>2 = —V2 — + /2 (0,
</< V + х) (*)> = 2с28м8 (г), <Д (t)> = 0 (а2 < 1).
Если jR=O, то, как указывалось выше, стационарное распределе-
ние вероятностей имеет вид
Рю (v) = const exp {—р|/2а2).
Пусть теперь Я=0 и R <1. Тогда для флуктуаций компонент
относительно их стационарных значений v't=vf—v.et получаем
систему уравнений
= — vi + v2 — v'<, + /о (0.
= + (8-46)
*>2 = -~v'ov2 ~ (! + + Л (0-
Для нахождения статистических характеристик решения системы
(8. 46) можно воспользоваться теорией возмущений по малому
параметру а2. Вторые моменты компонент будут описываться
при этом линеаризированной системой уравнений (8. 46), а сред-
ние значения можно получить затем уже непосредственным усред-
нением системы уравнений (8. 46). В этом приближении все ком-
поненты не коррелируют между собой, а дисперсии флуктуаций
и. имеют вид
W> = °!, <v;’>=r^s, (8.47)
Отметим, что формулы (8.47) применимы лишь при R 1.
При увеличении R увеличиваются как интенсивность, так и вре-
менной радиус корреляций для компоненты в то время как
интенсивность флуктуаций величины v2 уменьшается. При R ->1
увеличивается также как это следует из (8. 46). Максимум
флуктуаций для величины v[ при этом достигается при переходе
динамической системы через критический режим.
9 Нелинейные системы
129
При критическом режиме (т. е. при /?=1) уравнения для
флуктуаций принимают вид
#0 = ~Vl + V2 —v'o + fo (0.
^=Ф1 + /1(0» (8-48)
г>2 =—— 2р2 + Л (0-
Флуктуации компоненты v2 можно описывать линеаризирован-
ным уравнением (о2 <<; 1), и для их дисперсии получаем <Х8> =
= а212. Компоненты же и0 и v{ будут уже описываться нелинейной
системой уравнений
г>;=—у;2—р;+/о(О. ^=^X+/i(0. (8.49)
и линеаризация недопустима.
Усредняя (8. 49), получаем для стационарных флуктуаций
«^=0, «>=-<>;*>. (8.50)!
Кроме того, умножая первое уравнение (8. 49) на v'o, второе на.
v', складывая и усредняя, получаем выражение
Ю = 2з2. (8.51)
Как отмечалось выше, при критическом режиме усиливается *
интенсивность флуктуаций и[ и, следовательно, увеличивается <
величина (уоу, в то время как дисперсия флуктуаций vQ1 согласно -
(8. 51), существенно не изменяется. Поэтому ясно, что для оценки I
флуктуаций vQ и и\ можно заменить во втором уравнении системы
(8. 49) величину v'o на (v'Q> и, следовательно, рассматривать упро- 1
щенную систему
— —v'* — v'Q + f0 (t), = <ф v[ + Д (t). (8.52)
Откуда получаем для стационарных флуктуаций v'o и v[ выражения
<^> = -<^> = 3. (8.53)
Аналогично получаем, что временная корреляция компоненты
при критическом режиме имеет вид'
<& (< + т) yj(i)> = а ехр {—а | т |),
что дает для временного радиуса корреляции выражения — 1/о.
Рассмотрим теперь закритический режим (R >1). Стацио-
нарное распределение вероятностей для компоненты имеет вид,
схематически изображенный на рис. 31, с двумя максимумами:
в окрестности у1ст=+\/Я— 1, соответствующими устойчивым
стационарным состояниям; и минимум при ^=0, отвечающий
неустойчивому состоянию. Эта плотность соответствует усредне-
нию по ансамблю реализаций случайных сил f.
Если же имеется одна реализация, то система с вероятностью
1/2 придет в одно из положений, соответствующих окрестности
130
максимума распределения. В работе Глуховского и Кляцкина
(1973) численно моделировалась система уравнений (8. 45).
На рис. 32 приведены результаты численного решения для двух
реализаций случайных сил при 2?=6 и о2=0,01. Не изображен-
ная на этих рисунках компонента у2 слабо флуктуирует относи-
тельно своего стационарного состояния у2==0. В данном случае
будет формироваться распределение вероятностей (усреднение
по времени или по ансамблю сил, приводящих систему в это со-
стояние) в окрестности положений максимума (рис. 33). При этом
для нахождения статистических характеристик решения может
быть использована теория возмущений по параметру а2.
Рис. 31. Стационарная плот-
ность распределения вероят-
ностей значений компоненты
динамической системы (8. 45)
(случайные силы действуют
на все компоненты системы)
при R > 1
Пусть система приходит в состояние, соответствующее устой-
чивому положению равновесия z?0OT = 1, р1ст — у/И — 1, р2ст = 0.
Тогда для флуктуаций относительно этого состояния имеем си-
стему уравнений
«>о = —v'i И" vt — 2\/R —1vi — v'o + /о W>
= v'ov'i + \/R — ivo + fi (0» (8.54)
й2 = —+ Л (0- '
При R >> 1 вторые моменты флуктуаций будут описываться
линеаризованной системой (8. 54), а средние значения величин
определяются затем непосредственным усреднением (8. 54). Таким
образом, получаем, что при R >> 1
q2
<УХ>=<^2> = 0> <УХ>=—
(8.55)
«>=£.
Как отмечалось выше, эти статистические характеристики
соответствуют усреднению по времени или по ансамблю реализа-
ций сил f (Z), приводящих систему в указанное состояние. Следует,
однако, отметить, что если мы имеем некую реализацию (t)
и система пришла в одно из наиболее вероятных состояний, то
’ 9*
131
Рис. 32. Численное решение системы (8. 45) для двух реализа-
ций случайных сил при R=6, а2=0,01. Система флуктуирует
около устойчивых положений равновесия:
а) 00» = !» P1CT = vzB^l_=V/5; _г2ст = 0; б) 1'0ст = 1>
У1 ст = — — 1 = — V5,t>2oT= о
благодаря существованию достаточно больших значений (t)
система через некоторое время Т (тем большее, чем меньше а2 и
больше R) будет переброшена в другое наиболее вероятное со-
стояние (см., например, работу Вентцеля и Фрейдлина (1970)).
На рис. 34 приведено численное решение системы (8.45)
для одной реализации f{ (t) при 7?=6, а2=0, 1, где такой пере-
брос осуществился.
Т^-7 ~и1
Рис. 33. Плотности распре-
делений вероятностей для ком-
поненты v± системы (8. 45),
получаемые по одной реали-
зации на отрезке времени,
в течение которого система
флуктуирует около одного из
устойчивых положений равно-
весия
132
Рис. 34. Численное решение системы (8. 45), иллюстрирующее
явление «переброса», R=6, g2==0,1. Сплошной линией изобра-
жена у0, а пунктиром
Таким образом, если имеется только единственная реализация
f (t), то распределение вероятностей (усреднение по времени),
изображенное на рис. 31, будет формироваться только за время
t >> Т, иначе говоря, будет выполняться условие эргодичности.
В заключение приведем рис. 35, на котором показано поведение
при изменении R вторых моментов (нормированных на а2) флук-
туаций компонент решения системы (8. 45) относительно их ста-
ционарных значений.
Рис. 35. Зависимость от R
нормированных на о2 вторых
моментов флуктуаций компо-
нент динамической системы
(8. 45) относительно их ста-
ционарных значений
133
Таким образом, мы видели, что при учете влияния случайных
«шумов» на движение простейших систем гидродинамического
типа возникает не только слабое статистическое «размазывание»
устойчивых режимов, но и резкое усиление интенсивности флук-
туаций при переходе от одного режима к другому. Однако это
усиление происходит не всегда, а только в случаях, когда случай-
ные «шумы» действуют на неустойчивые моды. Кроме того, под
влиянием «шумов» появляется новый качественный эффект по
сравнению с детерминистической задачей, а именно явление
«переброса» между устойчивыми режимами. Осуществляемость
подобных явлений переброса в реальных системах представляет
большой геофизический интерес.
ПРИЛОЖЕНИЯ
Приложение I
К ОПРЕДЕЛЕНИЮ СИСТЕМЫ
ГИДРОДИНАМИЧЕСКОГО ТИПА
1. Обухов (1969) ввел определение класса систем гидродинами-
ческого типа (СГТ) как систем обыкновенных дифференциальных
уравненений с квадратическими нелинейностями
== /» ^==1, Л,
если для них выполняются условия сохранения энергии £=а^/2
и фазового объема (регулярность) dxJdx^Q (см. гл. II). Эти свой-
ства приводят к соотношениям для коэффициентов системы
Г<Л = Г,.^, (а) (П1.1)
Г<Л + ГЛ/ + Г** = 0’ (б) г«/ = °(в)-
(Везде принято соглашение о суммировании по дважды повторяю-
щемуся индексу.) Приведенное определение исходит из чисто
физических требований, и,ценность его зависит от того, насколько
богатым общими свойствами является определяемый класс си-
стем. Но в пользу такого определения говорит и некоторый чисто
математический аргумент, о котором пойдет речь в настоящем
приложении. Именно, будет выяснено следующее обстоятельство.
Соотношения (П 1.1) являются линейными относительно коэф-
фициентов и носят тензорный характер и, следовательно, не ме-
няют своего вида ни в какой ортогональной системе координат.
Тогда оказывается, что система соотношений (П 1.1) является мак-
симальной системой условий такого рода. Другими словами,
усилить ограничения типа (II 1.1) нельзя.
2. Формулировку последнего утверждения можно уточнить,
пользуясь терминологией теории представлений, знакомства с ко-
торой у читателя не предполагается (поскольку ниже приводится
минимум необходимых сведений*).
Тензоры третьего ранга образуют линейное подпростран-
ство, которое мы обозначим <^“. В качестве скалярного произведе-
ния в этом пространстве можно взять свертку тензоров (/, g)=
=fylegij1e. Каждому ортогональному преобразованию п-мерного
* Желающие углубиться в теорию представлений классических - групп мо-
гут прочитать книгу. Вейля (1939).
135
пространства с матрицей А = {а.*} соответствует ортогональное
преобразование в пространстве тензоров &
fijk — ai^aj^akyt^r (ПI. 2)
Это преобразование назовем Л(3). Элементарно проверяется, что
если матрице А соответствует Л(3), а В соответствует В(3), то
произведению этих матриц АВ соответствует произведение тен-
зорных преобразований Л(3)В(3), т. е. (ЛВ)(3)==Л(3)В(3). Это со-
ответствие называется представлением группы ортогональных
матриц линейными преобразованиями в тензорном пространстве
(ортогональными). В пространстве можно выделить линейные
подпространства, обладающие следующим свойством: если тензор
/ лежит в этом подпространстве, то и преобразованный тензор Л(3)/
также находится в этом подпространстве. Такие подпространства
будем называть инвариантными. Пример. Тензоры, симметричные
по всем индексам, образуют инвариантное подпространство. В
самом деле, пусть
Тогда
hji «Ру f ijk
и т. д. Второй пример. Тензоры, удовлетворяющие условиям
(П I. 1), назовем их СГТ-тензорами, также образуют линейное
инвариантное подпространство. Это проверяется точно так же.
Заметим, что подпространство СГТ-тензоров является частью
другого, состоящего из тензоров, все «следы» которых равны
нулю
f iik ~ f iji ~ fijj ~ О-
В самом деле, из (П I. 1) следует
/ iji — f aj = f ijj — fjij fjji — 0-
Подпространство тензоров с нулевыми следами назовем Го. Оно
инвариантно
f iik itfl itfhvftару ^a^kyfapf ^k^f aoqf
согласно свойствам ортогональных матриц.
Инвариантное подпространство назовем приводимым, если
в нем содержится другое инвариантное подпространство, отлич-
ное от нуля и от него самого. В противном случае оно называется
неприводимым. Если в каком-нибудь инвариантном пространстве
содержится инвариантное подпространство то совокупность
тензоров / £ ортогональных к тензорам из , также образует
инвариантное подпространство ' и представимо в виде орто-
гональной суммы
так как преобразования Л(3) сохраняют скалярное произведение,
а следовательно, и ортогональность тензоров. Если, в свою ОНО’
136
редь, одно из подпространств &п, &,п окажется приводимым,
то и его можно разложить. Продолжая этот процесс, разложим
все пространство & в ортогональную сумму неприводимых под-
пространств. Теперь мы можем сформулировать основную теорему:
подпространство СГТ-тензоров является неприводимым инвариант-
ным подпространством. Это и есть другая формулировка дока-
зываемого факта. Другими словами, если к условиям (П1.1)
добавить существенно новое тензорное условие, то тем самым
в подпространстве СГТ-тензоров выделится собственное инвари-
антное подпространство, которое, следовательно, должно быть
нулевым.
3. Введем еще три подпространства тензоров специального
вида
& 1 = {8оЛ Р fiijfk +
Ы - р м + ^f{ + W}> (П 1.3)
<^з— — р
где fi — вектор ft-мерного пространства, а константа р подобрана
таким образом, чтобы эти три подпространства были ортогональны
между собой
- р (8.-Д + • [W, - р + Ькё, + Wy)] =
= fkSk — Р (nfkgk + fkgk + Ш — Р (fkg* + nfkgk + fkgk) +
+ P2 (Wkgk + Vkgk) = fkgk [1 - 2 (n + 2) p + 3 (n + 2) p*] = 0
и т. д., t. e. p-1 — n-\-2 + \ln2 + ft — 2. Эти подпространства инва-
риантны
y P ? 4" a 4" \a/₽)] =
' = \jfk ~ P M M W (П L 4)
где В силу этого между тензорами такого специального
вида и векторами f. устанавливается линейное взаимно однознач-
ное соответствие, такое, что если тензору fijk соответствует вектор
Д, то A™fijk соответствует Иными словами, в подпростран-
ствах g^i, <^2, ^з представление равносильно действию группы
ортогональных матриц в своем собственном n-мерном простран-
стве. Отсюда следует неприводимость этих подпространств. Далее,
подпространства еГр <^з ортогональны к так как свертка тен-
зора с нулевыми следами с 8<у всегда дает нуль. Размерность под-
пространства о равна п3—Зп, а размерность каждого из под-
пространств^ х, зравна ft, поэтому мы можем сформулировать
следующую теорему: пространство тензоров третьего ранга раз-
лагается в ортогональную сумму инвариантных подпространств:
+ + (ПI. 5)
137
причем &2, <^з неприводимы. Нам осталось разложить <^~0
на неприводимые составляющие.
4. Каждому инвариантному подпространству можно поставить
в соответствие оператор ортогонального проектирования на это
подпространство. Данный оператор обладает свойством Р2=Р.
Для тензоров / из этого инвариантного подпространства имеем
Pf—f^ а для ортогональных к ним Р/=0. Из инвариантности под-
пространства следует перестановочность Р со всеми 4(3), Р4(3) =
=А(3)Р (достаточно проверить это равенство для тензоров под-
пространства и его ортогонального дополнения).
Обратно, всякий симметрический оператор, обладающий свой-
ством Р3—Р и перестановочный со всеми 4(3), определяет инва-
риантное подпространство тех тензоров /, для которых Pf=f.
Если инвариантное подпространство разлагается в ортогональную
сумму двух других, то и для соответствующих проекторов имеем
разложение
Лемма 1. Любой линейный оператсо, в подпространстве ^0,
перестановочный со всеми 4(3), есть линейная комбинация про-
стейших операторов, обладающих этим свойством, сводящихся
к перестановкам индексов тензора. Все такие операторы симмет-
ричны относительно введенного скалярного произведения.
Мы будем при доказательстве этой леммы опираться на недо-
казываемую нами, но широко известную основную теорему тео-
рии ортогональных инвариантов (см., например Вейль (1939)).
Будем называть ортогональным (полиномиальным) инвариантом
такой многочлен от координат системы векторов /, g, Л, который
не изменяется, если вместо координат этих векторов подста-
вить координаты векторов 4/, 4g, Ah, -где 4 — произвольная
ортогональная матрица.
.Основная теорема теории ортогональных инвариантов. Любой
полиномиальный инвариант от векторов f, g, h можно записать
в виде многочлена от попарных скалярных произведений этих
векторов. Иными словами, скалярные произведения образуют
базис системы инвариантов.
То же самое можно сформулировать так: любой тензор, по-
стоянный во всех системах координат, есть линейная комбинация
произведений тензоров 8^.. В самом деле, пусть pijkl — такой тен-
зор. Свернем его с произвольными векторами /, g, h, г:
Результатом свертки будет скаляр. Из постоянства тензора р
согласно приведенному выше определению следует, что это —-
инвариант. Значит его можно записать в виде суммы членов вида
c(fA)(g<r<). Так как векторы произвольны, то это значит, что
Рук1 есть сумма членов вида с .
138
Пусть теперь имеется линейное преобразование Г, переста-
новочное со всеми 4(8). Для его матрицы аРу имеем
^ijk, apyaara^8ayl = aiaa^ak^^, rsl
ИЛИ
tijk, тпр J^P'k‘flmr^'n8^'pl^o.^'(t гвГ
Иначе говоря, тпр есть постоянный тензор. Он есть сумма
членов вида]
cB4fcS. В . (П1.6)
Поскольку мы рассматриваем сейчас лишь тензоры с нулевыми
следами, то в случае, если в набор 8 в выражении (П I. 6) входит
8 с индексами из одной группы, например 8яр, применение такой
матрицы к тензору даст нуль, так как тензор нужно будет свер-
нуть по двум индексам. Значит, остаются лишь слагаемые вида
с 8^8^^ и т. п. Действие указанной матрицы на тензор сводится
к перестановке его индексов /<л=8<я 8^8^^=/^. Симметрия та-
кого оператора проверяется непосредственно
(Г/, g) = fj(kgtjk = ftjkgJik = (/, Tg).
Лемма 1 тем самым доказана.
5. Введем в рассмотрение группу подстановок индексов
/1 2 ЗХ
S=\l' 2' 3'j’
где через Г, 2', 3' обозначены те же индексы 1, 2, 3, но в другом
порядке. На примере напоминаем правило умножения подста-
новок
/1 2 ЗХ /1 2 ЗХ /1 2 ЗХ
\lf3 2/ \2^3И/ \2 1 3/‘
Каждой подстановке s соответствует линейный оператор в тензор-
ном пространстве^(или ^0), состоящий в соответствующей пере-
становке индексов; обозначим этот оператор через s. /'=s/ озна-
чает, что каждая компонента тензора /' равна некоторой компо-
ненте тензора / с теми же значениями индексов, но в другом
порядке, определяемом подстановкой. Именно, /м2г3=Л/г/г3'-
/1 2 ЗХ
Например, « = I 2 3 j /> /123 = /231» /312 = /123 и т- Д- Легко видеть,
что соответствие s—>5 обладает свойством s1s2 = S1s2, т. в- яв-
ляется представлением группы 53 линейными операторами в тен-
зорном пространстве.
Рассмотрим формальные линейные комбинации подстановок
e = 2e(s)s. (П1.7)
139
Их можно почленно складывать и умножать на вещественные
числа, т. е. они образуют векторное пространство, базисом кото-
рого являются элементы группы, т. е. 3!=6-мерное пространство.
Далее, их можно перемножать как многочлены, пользуясь зако-
ном умножения элементов группы
ab = ^ia(s)s^ib(t)t = ^ia(s)b (s) st = 2 (2 а (s^1) b (t)\ s.
st st s \ t /
Тогда это векторное пространство превращается в алгебру. Она
называется групповой алгеброй 21. Алгебра также представляется
линейными операторами в тензорном пространстве
а = 2 а ($) -> а = 2 а ($) 3.
S 8
Это линейное отображение, при котором сумме, произведению
на число и произведению двух элементов групповой алгебры со-
ответствуют сумма, произведение на число и произведение двух
операторов. При n 3 это представление является точным, т. е.
ненулевая линейная комбинация (II I. 7) дает ненулевой оператор.
Достаточно проверить действие этого оператора на тензоре, у ко-
торого лишь одна компонента, например /123, отлична от нуля.
Каждый член суммы 2а(5)5/ будет тензором, у которого одна
компонента отлична от нуля, причем эти компоненты разные, т. е.
сумма не может быть нулем.
Лемма 1, доказанная в предыдущем пункте, означает, что
проектором инвариантного относительно всех А(3) подпростран-
ства (^0 может быть лишь оператор а = 2 а (5)5 представления
8
групповой алегбры 21. Из того, что Р2=Р, и изтого, что представле-
ние является точным, следует, что соответствующий элемент груп-
повой алгебры также обладает свойством а2=а. Такие элементы
называются идемпотентными. Мы будет их обозначать всегда
буквой е с разными индексами. В частности, групповая единица е
также является идемпотентом.
Допустим, групповую единицу е удастся разложить в сумму
е = ^е{, (П1.8)
где е. — идемпотенты, причем
= е.еу = 0 (г =£j) (П I. 9)
или, как говорят, это ортогональная система идемпотентов.
Тогда соответствующие этим идемпотентам операторы ё. в тензор-
ном пространстве FQ являются проекторами на ортогональные
между собой инвариантные подпространства
^0 ~ 0’
Если какой-нибудь идемпотент ei далее неразложим на ортого-
нальные идемпотенты, то подпространство неприводимо отно-
сительно тензорного представления ортогональной группы.
140
Таким образом, асе свелось к разложению (П I. 8), т. е. к изу-
чению структуры групповой алгебры 21 группы 53. [Группа S3
имеет два образующих элемента:
Легко проверить, что все элементы группы имеют вид
е, о, о2, т, от, а2т. (П1. 11)
Очевидны соотношения от= та2, а2т=та, а3=т2=е.
Алгебра 21 представляет собой шестимерное векторное про-
странство с базисом (П I. 11). Если все элементы алгебры умно-
жить справа на один какой-нибудь элемент, то получится линей-
ное подпространство этого шестимерного пространства. Если
е. и ву — два взаимно ортогональных идемпотента, то и 21^.
не имеют общих элементов, кроме нулевого. В самом деле, если
aei — be^ то, умножая справа на е., будем иметь ae. — Q. Поэтому
если е. есть сумма ортогональных идемпотентов е' и е"., то 2let
разлагается в прямую сумму 21е'« и 21е[- и размерность простран-
ства 2te#- равна сумме размерностей 21^ и 2Ц-. Теперь напишем
следующие элементы алгебры 21:
ег (е + а + а2 + т + ат а2т),
e2 = "fr (е + ° + °2 — ~ — ох— с2т), (П1. 12)
е3 = ~ (2е — а — а2 + 2т — ат — а2т),
е4=-|- (2е — а — а2 — 2т -|- ^ + <&).
Без труда проверяются (П1. 8) и (П1. 9). Теперь докажем нераз-
ложимость этих идемпотентов. Легко видеть, что и тех пропор-
циональны elf или 21^— одномерное подпространство. То же самое
можно сказать о 21е2. Уже отсюда следует неразложимость е± и е2.
Можно проверить, что других идемпотентов, для которых 2Ц одно-
мерно, нет. Поэтому 2Ь3 и 21е4 по меньшей мере двумерны. Учи-
тывая, что сумма размерностей пространств 2tei, 21е2, 21е3, 21е4
равна шести, получим, что 2U3 и 2U4 в точности двумерны. Идем-
потент е3 неразложим, иначе 2к3 было бы разложено на одномер-
ные подпространства 21е3 и 2te3 а таких нет. Сказанное относится
и к е±. Искомое разложение е= ет + е2 + е3 + е4 получено.
Что представляют собой подпространства о» о? 0>
е4(^Г0? — это оператор симметрирования, ё2 — альтернирования,
т. е. —симметрические, ё2<^Г0 —- антисимметрические тензоры
со следом нуль.ё3®Г0 — этоСГТ-тензоры. В самом деле, проверим
(П1. 1). Свойство (а):
141
(ё—t) ё3^0 = -^- (ё — т) (2ё — а — а2 -|- 2т — ат—а2т) = (2ё — а —
— а2 -|- 2т — ат — а2т — 2т -|- ё2т -|- ат — 2ё + а2 + а) = 0.
Свойство (б) проверяется точно так же
(ё + а + а2)ё3(^о = О.
Пространство ё4<^0 состоит из тензоров, также удовлетворяющих
свойству (б), но вместо (а) имеет место антисимметрия по последним
индексам: (ё 4-т) ^о=О, назовем их квази СГТ-тензорами. Итак,
пространство тензоров со следами нуль представимо в виде орто-
гональной суммы четырех инвариантных неприводимых под-
пространств: а) симметрических тензоров, б) антисимметрических
тензоров, в) СГТ-тензоров, г) квази СГТ-тензоров. Теорема ил-
казана.
Приложение II
АСИМПТОТИЧЕСКИЕ ВЫРАЖЕНИЯ РЕШЕНИЙ
gH ХАРАКТЕРИСТИЧЕСКОЙ ФОРМЫ
ДЛЯ ДИНАМИЧЕСКОГО ТРИПЛЕТА
ЧЕРЕЗ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Поскольку динамические системы типа триплета весьма часто
встречаются в практических приложениях, полезно подробно
изучить их асимптотические свойства. С этой целью представим
решения (7. 33), (7. 336) уравнений движения (7. 13) в асимпто-
тической форме, воспользовавшись удобными аппроксимациями
рассматриваемых эллиптических функций, построенными с по-
мощью тригонометрических и гиперболических функций.
В дальнейшем без ограничения общности ради простоты будем
считать, что коэффициенты уравнения (7. 13) удовлетворяют усло-
виям
p = q = p0, г = —2р0. (ПИ. I)
Рассмотрим различные частные случаи.
а) «Тригонометрический» случай
А2<^1, ег = 2а — 8, е2 = — а+ 8, е3 =—а. (ПП.2)
С помощью формул (7. ЗЗв), (ПП. 2), (7.37) и (7. 38) получаются
следующие разложения для полупериодов о> и о/;
<0=-^, 2=|{1+4*2+^Л4 + О(Аб)}, (ПП.З)
142
iQ>
(ПП.4)
В данном случае полезно использовать аппроксимации основ-
ных характеристик триплета тригонометрическими функциями.
Для этого воспользуемся известными разложениями эллиптических
функций Якоби в ряды Фурье (см., например, Бейтмен и Эрдейи
(1967)), а также соотношениями (7. ЗЗв), (ПII. 2), после чего из
(7. 33), (7. 336) и (7. 33г) получим следующие приближенные вы-
ражения для решений уравнения (7. 13), справедливые с точностью
до величин второго порядка малости —Л4 включительно:
Z1 (т) = 1 — (1 + sin2 г) у+(3 + Sin4 г) у+о (Л6),
Х2 (t) = к cos ут {1 —(1
_(sin^8sin3^_3)^+O(fc«)}> (ПИ. 5)
Ъ W = —\/2*sin -р {1
Здесь
х<(г) = ^, Хо-...ч^, (/=1,2,3) (ПП.5а)
v 1 *о 0 6/s V2p0 v 1
(ПИ.56)
(ПИ.5в)
Аппроксимацию для характеристической формы (7. 35) можно
получить с помощью известной формулы связи ^-функции Вей-
ерштрасса с эллиптическими функциями Якоби (Бейтмен и Эр-
дейи (1967))
ЧР (и + 0)') = е3 + (е2 — е3)sn2 (и \Jer — е3}. (П И. 6)
которая часто встречается в приложениях. Получим
р (t) = —1 + ЗА2 sin2 Тт {1 - (1 — &+
+j-cos2 г (3 cos 2Г - 8) +1+ Q ' (ПП.7)
где
₽(г) = ^, = (ПИ. 7а)
143
В табл. 1 приведены результаты сравнения расчетов по ап-
проксимационным формулам (ПII. 5), (ПII. 7) и поточным фор-
мулам
х^=(1-у+|^)ап(^, к),
Х^ = /с(1-^+|^)сп(^, Л),
Х^т) = __к^2 (1 -I2+|к1') sn (Ki, к), (П И. 8)
р(т> = _1 + Зк2 (1 _ к2 £4) gll2 k)f
B = t/2, K(k)~K = f —dy
J Vl — Ar2 sin2 <p
о
Таблица 1. Сравнение аппроксимационных формул (ПП. 5) и (П II. 7)
с точными (П II. 8) при к2—0,4
Ьк Xi /2 -Хз -3
прибл. точн. прибл. точн. прибл. точн. прибл. точн.
0 0,860 0,860 0,544 0,544 0,000 0,000 1,000 1,000
0,1 0,855 0,855 0,536 0,535 0,134 0,138 0,973 0,971
0,2 0,841 0,839 0,511 0,510 0,263 0,269 0,895 0,889
0,3 0,820 0,816 0,472 0,472 0,382 0,383 0,779 0,774
0,4 0,793 0,788 0,422 0,420 0,487 0,489 0,640 0,632
0,5 0,765 0,757 0,362 0,359 0,576 0,578 0,496 0,486
0,6 0,738 0,727 0,295 0,292 0,647 0,650 0,361 0,351
0,7 0,714 0,702 0,224 0,220 0,701 0,705 0,246 0,237
0,8 0,695 0,683 0,151 0,150 0,739 0,740 0,160 0,157
0,9 0,684 0,670 0,076 0,075 0,762 0,753 0,106 0,104
1,0 0,680 0,667 0,000 0,000 0,769 0,770 0,088 0,088
в которых значения эллиптических функций брались из таблиц,
при &2=0,4 (см. табл. 1).
1 3
б) Лемнискатический [случай: к2= =— е3 = е2 = 0.
Прямоугольник периодов функции Вейерштрасса (z) В Z-
плоскости является в этом случае квадратом, а ее полупериоды ш
и со' выражаются следующим образом (Бейтмен и Эрдейи (1967)):
о =
'/За V3a
4 ' 4-ге1/»
~ 1,8541.
144
Выражения для х% и В> записанные в безразмерной форме,
имеют вид
XiW = dn^,
zJ,)=-^cn(r,^, (ПП.9)
Х3(т) = —sn(t, -^=),
₽ (т) = —3/1 (х) = — у СП2 •
Здесь Xi, Z25 Хз и ₽ определяются, как и ранее, выражениями
(ПП. 5а) и (ПП. 7а), ат — (ПП. 56). Для вычисления эллипти-
ческих функций Якоби, входящих в (ПП. 9), можно, как и в пре-
дыдущем случае, применить аппроксимации тригонометрическими
функциями, однако с целью повышения точности расчета удобно
воспользоваться выражениями эллиптических функций через
тэта-функции. Используя соответствующие приближенные выра-
жения для тэта-функций, можно получить удобные аппроксима-
ции для эллиптических функций Якоби, после чего из (ПП. 9)
будем иметь
Хх (т) = {1 4~ 4/г cos 2р + 8Л2 cos2 2 ус -|- 8Д3 cos3 2ут 4- О (№)},
/2 (т) = \/2/?4 cos р (1 + 2h cos 2ус + Д2[1 4соя2ут(1 — 4sin2ут)]—[—
-}- 2Л3 cos 2ус (1 — 4 sin2 р) 4- О (Л4)}, (ПII. 10)
Хз (т) = —25/<Л^sin ут{14- 2/icos2ут-[-А2[1 -4“ 4sin2yT(l — 4cos2yt)J4~
+ 2Л3 cos 2уи (1 — 4 cos2 ут) 4- О (Л4)},
Р (т)=—6Л1/г cos2ут {14-4А cos 2ут4~ 2/г2[2 cos 2^т (14~3cos 2ут)—1 ]4-
4- 8А3 cos 2ут (4 cos2jp cos 2р— 1) 4- О (А4)}.
Здесь Л = 6""= 0,04321, т = ,—0,847.. . (ПП. 10а)
2^(2 Л) . г
в) «Гиперболический» случай.
^ = «4^.8, е2 = а, е3 = —2а — 8. (ПП.И)
Разложения для полупериодов со и ш' имеют вид
f ;
- <пп-12)
+ (ПП.13)
10 Нелинейные системы
145
В этом случае оказываются полезными аппроксимации гипер^
б одическими функциями.
Следует отметить, что рассматриваемый случай фактически
сводится к случаю а), если воспользоваться формулами второго
главного унимодулярного преобразования для эллиптических
функций Якоби (Ахиезер (1970))
sn(p, fc)=Tcn(\B> к,>, cn(u, /с)= |
=_J_ dn(и, к) = ап.(.ц,4?ч , (ПП. 14)
cn(iu, к) ’ \ / сп(ш, к') ’ к м
поскольку дополнительный модуль к' 1. Таким путем с точ-
ностью до членов порядка (А/)4 включительно можно получить
следующие приближенные выражения, справедливые при малых
значениях аргумента т:
Xi(T)=^{1 + (ch2Ti: + 3)^2+
+ (7сЬ2Г4-25)^+О((Л')в)},
Х2 W {1 +(1 -1 sh2 г) (-^+
+ (75-19сЬ2Г)^+О((^)в)},
Z3(t) = -V2thr{l-|4(A:7 +
+ (75 - 2 ch2 г) +О ((*')’)}, (П П. 15)
Р (г) = (3 th2 Г - 2) [1 +1 (^)2]+[93~з2СЬ2г th2 Г - 2] х Я
Х3(к')* + О(т, |г|<|.
Здесь • 1
Т = 1 +| (Л')2+g (*')‘ + О т, (ПII. 15а)
a Xi, /2? Хз и ₽ имеют тот же смысл, что и в (ПII. 5а) и (ПII. 7а).
Вследствие экспоненциального возрастания гиперболических
функций, возникающих при разложении по степеням параметра i
(А/)2, полученные формулы оказываются применимыми лишь!
при достаточно малых значениях аргумента г, определяемых^
условием т << Q/2. Для получения формул, справедливых в не-d
которой окрестности 11—Q| <3 е, воспользуемся формулами из-|
менения аргумента эллиптических функций на четверть периода*
и половину периода (Бейтмен и Эрдейи (1967))
/ > \ СИ U / । \ •—- у / sn и
sn(K±u)=-^t =
(ПП.16)
а”(«±“)=а?г’
146
что приводи! к следующий аппроксимационным выражёнййм!
Xi (2 + г) = к’ ch ух {1 + (1 - (Л')2+
+p^gr-21) + 3J(F)4+0 {к, ,
Ъ. (2 -Н) =*' sh ух {1 +(1 (Л')24-
4-[ch2 Г <4g2r-27) 4- з] (^_|-o(fc'6)|, (ПП.17)
Ъ (2 + г) = -V2 {1 + (1 - sh2 ГО ф^+
+ [sh2 ух (sh2 ух — 4) + 7] +О (/с'8)},
Р (2 -с) = 1 — 3 (к1)2 sh2 ух + у sh2 ух X
X (sh2ух-3)(к')* + О((£')% |т|<2/2.
Соответствующие формулы, справедливые в некоторых окре-
стностях точек 2Q, 3Q и 4Q, получаются с помощью соотношений
симметрии
Xi (х + 22) = Х1 (х)> Xi (x+32)=Xi (х + s). Xi (х + 4S) = Xj (х)>
Хз (г + 22) = —х2 (х), Х2(х+32)=~Х1(х+ 2), Хг (х + 42) = Хз (х).
(П II. 18)
Хз (х + 22) ±= —х3 (х), Zs(x-]-32)=—х3(хЦ-2), Хз (х + 42) = Хз (х)>
₽(х + 22) = ₽(х), ₽ (х + 32) = ₽ (х + 2), р(х + 42)М(х),
которые нетрудно вывести из аналогичных формул симметрии
для эллиптических функций Якоби (Бейтмен и Эрдейи (1967)).
В табл. 2 и 3 приведены результаты сравнения аппроксима-
ционных формул с точными формулами
X^^fl + W+I^dn^, к).
Х1и)=[1+фЧ|(*')4]сп(^, к),
Х|М^_^2[1+^44(*')*]8П(/«( к), (ПП.19)
£<“> = —2 [14-2 (к1)2 4- 3 (*')♦]+
+ 3 [1 + (к1)2 + 2 (#)♦] sn2 (Ki, к)
при А;й=0,7 и 0,8 соответственно с использованием таблиц эллип-
тических функций (см. табл. 2 и 3)
!()♦
147
Таблица 2. Сравнение аппроксимационных формул (ПII. 15) и (П It. 17)
с точными (ПII. 19) при Л2=0,7
$к Xi “Хз 11 f-₽ .•
прибл. тонн. прибл. тонн. прибл. точн. прибл. точн.
0 1,44 1,44 1,23 1,23 0,00 0,00 3,44 3,44
0,1 1,42 1,41 1,20 1,20 0,36 0,36 3,27 3,25 .
0,2 1,37 1,35 1,14 1,13 0,69 0,69 2,80 2,73
0,3 1,29 1,27 1,04 1,02 0,98 0,97 2,04 2,05
0,4 1,18 1,165 0,91 0.89 1,22 1,21 1,26 1,28
0,5 1,05 1,06 0,76 0,73 1,40 1,40 0,48 0,56
0,6 0,97 0,97 0,59 0,58 1,55 1,53 —0,12 -0,03
0,7 0,89 0,89 0,46 0,43 1,64 1,63 —0,55 -0,46
0,8 0,83 0,83 0,28 0,28 1,69 1,69 —0,82 -0,76
0,9 0,80 0,80 0,14 0,14 1,72 1,72 -0,95 -0,94
1,0 0,79 0,79 0,00 0,00 1,74 1,74 -1,00 -1,00
Таблица 3. Сравнение аппроксимационных формул (ПП. 15) и (ПП. 17)
с точными (ПII. 19) при £а=0,8
Xi Ха -Xs -3
прибл. точн. прибл. точн. прибл. точн. прибл. точн.
0 1,26 1,26 1,14 1,14 0,00 ’ 0,00 2,84 2,84
0,1 1,23 1,23 1,11 1,10 0,36 0,36 2,65 2,64
0,2 1,67 1,67 1,04 1,03 0,68 0,68 2,16 2,15
0,3 1,07 1,06 0,92 Q,91 0,95 0,96 1,47 1,46
• 0,4 ' 0,96 0,95 0,78 0,78 1,18 1,17 0,80 0,79
0,5 . 0,85 0,84 0,64 0,63 1,34 1,33 -0,19 —0,18
,0,6 0,75 . 0,75 0,51 0,49 1,44 1,44 —0,28 —0,27
0,7 0,67 . 0,67 0,37 0,36 1,53 1,52 -0,63 -0,62
0,8 0,61 г 0,61 , 0,24 0,23 1,57 1,57 -0,85 -0,84
0,9 0,58 0,58 0,12 0,12 1,60 1,60 -0,97 -0,96
1,0 0,56 0,56 0,00 0,00 1,61 1,61 —1,00 -1,00
Приложение Ш
ОБЩИЙ МЕТОД ВЫЧИСЛЕНИЯ КОРРЕЛЯЦИЙ
ГАУССОВСКОГО СЛУЧАЙНОГО ПРОЦЕССА]
СО СВЯЗАННЫМ С НИМ ФУНКЦИОНАЛОМ
Пусть f{ (т) (г=1, .. . N, 0 ^7) —случайный процесс.
Статистические свойства этого процесса полностью описываются
его характеристическим функционалом
148
где v — произвольная детерминированная вектор-функция. Раз-
ложение Ф [v ] в функциональный ряд Тейлора определяет
поточечные моменты процесса f(^). Удобно ввести функционал
0 [v]=lnO[v], разложение которого определяет n-точечные ку-
мулянты (семиинварианты) процесса.
Введем также, следуя работе Кляцкина (1973), в рассмотре-
ние функционалы
2.[v(r), *'] =
fi («') exp
Ф[у(г)]
(1 = 1, (ПШ.2)
Используя понятие вариационной производной (см., например,
монографию Монина и Яглома (1967)), его можно представить
в виде
(ПШ.З)
Рассмотрим среднее от произведения <(fl (i')fl [f ('')+'»] (т)]>, где
компоненты у. (т) — детерминированные функции, a R — некий
функционал от случайного процесса. Это произведение можно
переписать в операторном виде, вводя оператор функционального
сдвига
или в виде
'6 /
= Н<Д[1(т) + ч(х)]>- <niIL4)
Полагая в (ПШ. 4) ц (т)=0, получаем окончательное выражение
<Л V') R [f (t)]> = (Qt [вд-, y\ R [f (trf}.
(ПШ.5)
149
Для гауссовского случайного процесса, рассматриваемого в вось-
мой главе
t
0[v(t)] = _^pw2(x)
О
и, следовательно,
где
0(г —£') =
1 при t V
1 /2 при t = t1
О при t <Z t1
В этом случае
</< («') R Р W]>=.о (t -1')
(ПШ.6)
(ПШ.7)
Формула (ПШ.7) для гауссовского 8-коррелированного во вре-
мени случайного процесса f (t) была получена впервые в работах
Фурутцу (1963), Новикова (1964) и Донскера (1964) (см. также
работу Кляцкина й Татарского (1973)).
ЛИТЕРАТУРА
Андронов А. А., Витт А. А. и Хайкин С. Э,
1959, Теория колебаний, 2 изд. М., Физматгиз.
Арнольд В. И.
1965, Вариационный принцип длят рехмерных стационарных течений
идеальной жидкости, Прикл. матем. и мех., 29, № 5, 846—851.
1971, Обыкновенные дифференциальные уравнения, М., «Наука».
1972, Лекции о бифуркациях и версальных семействах, Успехи матем.
наук, 27, № 5 (167), 119-184.
Ахиезер Н. И.
1970, Элементы теории эллиптических функций, 2 изд., М., «Наука».
Багров Н. Л.
1959, Аналитическое представ лениеТпоследовательности метеорологиче-
ских полей посредством естественных ортогональных составляющих,
Труды ЦИП, вып. 74, 3—24.
Бейтмен Эрдейи A. (Bateman Н., Erdelyi Л)
1955, The higher /transcendental functions, v. 3, N. Y. a. o.
(Русск. перевод: Высшие трансцендентные функции, т. 3, Эллиптиче-
ские и автоморфные функции, 1 изд., М., «Наука», 1967).
Бенар (Benard Н.)
1901, Les tourbillons cellulaires dans une nappe liquide transportant de
la chaleur par convection en regime permanent, Ann. de Chim. Phys.,
23, 62-114.
Бирих P. B.
1965, О спектре малых возмущений плоскопараллельного течения
Куэтта, Прикл. матем. и мех., 29, № 4, 798—800.
Блинова Е. Н.
1943, Гидродинамическая теория волн давления, температурных волн
и центров действия атмосферы, Докл. АН СССР, 39, № 7, 284—287.
1968, Решение нелинейной задачи о нестационарных атмосферных дви-
жениях планетарного масштаба, Докл. АН СССР, 183, № 2, 323—325.
Бломберген Н. (Bloembergen N.)
1965, Nonlinear optics. N. Y. — Amsterdam
(Русск. перевод: Нелинейная оптика, M., «Мир», 1966).
Брагинский С. И,
1959, К Fмагнитной гидродинамике слабопроводящих жидкостей,
Ж. экспер. и теор. физики, 37, № 5 (11), 1417—1430.
Бреховских Л. М.
1966, Звуковые волны под водой, обусловленные поверхностными вол-
нами в океане, Изв. АН СССР, сер. «Физика атмосферы и океана», 2,
№ 9, 970—980.
1968, Об излучении океанскими волнами инфразвука в атмосферу,
Изв. АН СССР, сер. «Физика атмосферы и океана», 4, № 4, 444—450.
Брушлинская Н. Н. .
1964, О предельных циклах уравнений движения твердого тела и галер-
кинских уравнениях гидродинамики, Докл. АН СССР, 157, № 5, 1017—
1020.
151
1965, О поведении решений уравнений гидродинамики при переходе
числа Рейнольдса через критическое значение, Докл. АН СССР, 162,
№ 4, 731—734.
1968, О рождении периодического течения и тора из ламинарного тече-
ния, «Некоторые вопросы механики горных пород», под ред. Л. В. Ер-
шова, М., МГИ, 57—79.
Бубнов И. Г.
1913, Отзыв о сочинениях проф. Тимошенко, удостоенных премии
Д. И. Журавского.
Сборник Ин-та инж. путей сообщения, вып. 81, СПб, 33—36; Избр.
труды, Госсудпромгиз, Л., 1956, 136—139.
Бюргерс (Burgers J. М.)
1939, Mathematical examples illustrating relations occuring in the theory
of turbulent fluid motion. Kon. Ned. Akad. Wet. (Eerste Sectie) DI.
XVII, N 2, 1-53.
Вейль Г, (Weyl H.)
1939, The classical groups, their invariants and representations,
(Русск. перевод: Классические группы, их инварианты и представления,
М., ИЛ, 1947).
Вейль И. Г. и Машкович С. 4.
1970, Численные эксперименты по изучению нелинейного взаимодействия
длинных волн и зональной циркуляции, Труды Гидрометцентра СССР,
вып. 71, 3—23.
Вентцель А. Д. и Фрейдлин М. И.
1970, О малых случайных возмущениях динамических систем, Успехи
матем. наук, 25, № 1 (151), 3—55.
Вильямс, Дэвис (Williams G. Р., Davies D. R.)
1965, A mean motion model of the general circulation, Quart. J. Roy.
Meteorol. Soc., 91, No 390, 471—489.
Волыперра (Volterra V.)
1931, Lemons sur la theorie mathematique de la lutte pour la vie, Paris.
Ворович И. И. и Юдович В. И.
1961, Стационарное течение вязкой несжимаемой жидкости, Матем. сб.,
53 (95), № 4, 393-428.
Галеркин Б, Г.
1915, Стержни и пластинки. Ряды в некоторых вопросах упругого равно-
весия стержней и пластинок. Вестник инженеров, т. I, № 19, 897—908;
Собр. соч., т. I, 169—195, М., Изд-во АН СССР, 1952.
Галин М, Б.
1974, К вопросу о нелинейном взаимодействии планетарных войн.
Изв. АН СССР, серия «Физика атмосферы и океана». 10, N 4.
Гантмахер Ф. Р.
1966, Лекции по- аналитической механике, 2 изд., М., «Наука».
Гельмгольц (Helmgoltz Н. L. F.)
1888, Ueber atmospharische Bewegungen, Sitzungsber. Akad. Wiss. Ber-
lin, 647—663; Wiss. Abh., Ill Band, Lpz. 1895, CXXVI, 289—308.
Гершуни Г. 3. и Жуховицкий Ё. М,
1972, Конвективная устойчивость несжимаемой жидкости, М., «Наука».
Гледзер Е. В,
1973а, Система гидродинамического типа, допускающая два квадратич-
ных интеграла движения, Докл. АН СССР, 209, № 5, 1046—1048.
Гледзер Е. Б» и Новиков Ю. В,
19736, Оценка характеристик нестационарного движения жидкости
в эллипсоидальной полости на основе измерения моментов сил,
Изв. АН СССР, сер. «Физика атмосферы и океана», 9, № 10, 1088—1090.
Гледзер Е. Б., Новиков Ю. В., Обухов А. М. и Чусов М. 4.
1974, Исследование устойчивости движения жидкости внутри трехосного
эллипсоида, Изв. АН СССР,, сер. «Физика атмосферы и океана». 10,
N 2 115—118.
152
Глуховский А. Б. и Кляцкин В, И,
1973, Случайные «шумы» в простейших нелинейных системах гидродина-
мического типа, Изв,. АН СССР, серия «Физика атмосферы и океана»,
9, № 7, 675—684.
Горьков Л. П.
1957, Стационарная конвекция в плоском слое жидкости вблизи крити-
ческого режима теплопередачи, Ж. экспер. и теор. физики, 33, № 2 (8),
402—411.
Гринспен (Greenspan Н. Р.)
1968, The theory of rotating fluids, Cambridge.
Гринхилл (Greenhill)
1879, On the rotation of a fluid ellipsoid about its mean axis, Proc. Camb»
Phil. Soc., Ill, 233.
Гурвиц и Курант (Hurwitz A., Cour ant R.)
1964, Vorlesungen fiber allgemeine Funktionentheorie und elliptische
Funktionen, Berlin u. a.
(Русск. перевод: Теория функций, М., «Наука», 1968).
Дарвин (Darwin G. Н.)
1898, The tides and kindred phenomena in the solar system, Boston; 2d
ed., San Francisco—London, 1962.
(Русск. перевод: Приливы и родственные им явления в солнечной системе,
М.—Пг., Госиздат, 1923; 2 изд., М., «Наука», 1965).
Джордж и Хелламс (George W. О., Heliums J, D.)
1972, Hydrodynamic stability in plane Poiseuille flow with finite amplitude
disturbances, J. Fluid Meeh., 51, 4, 687—704.
Ди Прима (Di Prima R. C.)
1955, Application of the Galerkin method to problems in hydrodynamic
stability, Quart. Appl. Math., 13, N 1, 55—62.
(Русск. перевод: Применение метода Галеркина к задачам устойчивости
в гидродинамике, «Механика», №^3 (37), 53—61, 1956).
Дикий Л. А.
1965а, К нелинейной теории гидродинамической устойчивости, Прикл.
матем. и мех., 29, № 5, 852—855.
19656, К нелинейной теории устойчивости зональных течений,
Изв. АН СССР, серия «Физика атмосферы и океана», 1, № 11, 1117—
1122.
1967, К нелинейной теории устойчивости зональных течений, «Динамика
крупномасштабных атмосферных процессов», под ред. А. С. Монина,
М., «Наука», 166—178.
1969, Теория колебаний земной атмосферы, Л., Гидрометиздат.
Доуэлл (Dowell Е. Н.)
1969, Non-linear theory of unstable plane Poiseuille flow, J. Fluid. Meeh.,
38, 401—414.
Должанский Ф. В.
1969, О расчете зональной циркуляции атмосферы, Изв. АН СССР,
серия «Физика атмосферы и океана», 5, № 7, 659—671.
1971, Численные эксперименты по моделированию зональной циркуля-
ции земной атмосферы, Изв. АН СССР, серия «Физика атмосферы и
океана», 7, № 1, 3—11.
1972, Лабораторное исследование устойчивости движения жидкости
в эллипсоидальной полости, Изв. АН СССР, серия «Физика атмосферы
и океана», 8, № 6, 661—664.
1973а, Вынужденная конвекция жидкости внутри эллипсоида, Изв.
АН СССР, серия «Физика атмосферы и океана»,: 9, № 6, 163—172.
19736, О влиянии сил Кориолиса на формирование конвективного про-
цесса внутри эллипсоида, Изв. АН СССР, серия «Физика атмосферы и
океана», 9, № 9, 908—918.
Донскер (Donsker М. D.)
1964, On function space integrals, Proc. Conf. Theory and Application
of Analysis in Functional Space, Cambridge (Mass.), 17—30. (Русск,
153
11
перевод: Об интегралах в функциональных пространствах, «Матема-
тика», 1967, 11, № 3, 128—138).
Жуковский Н.Е.
1885, О движении твердого тела, имеющего полости, наполненные одно-
родной капельной жидкостью, Журн. Русск. Физ.-Хим. Общ., ч. физ.,
т. 17, отд. I, № 6, 81—113; № 7, 145-199; № 8, 231—280; Собр. соч.,
т II, Гидродинамика, М.—Л., Гостехиздат, 1949, 152—309.
Кадомцев Б. Б. и Карпман В. И.
1971, Нелинейные волны, Успехи физ. наук, 103, № 2, 193—232.
Кляцкин В. И.
1969, К статистической теории двумерной турбулентности, Прикл. матем.
и мех., 33, № 5, 889—891.
1971, О равновесных гидродинамических флуктуациях^ идеальном газе,
Изв. АН СССР, серия «Физика атмосферы и океана», 7, № 5, 486—495.
1972, К нелинейной теории устойчивости периодических течений, Прикл.
матем. и мех., 36, № 2, 263—271.
1973, К статистической теории отражения света в случайно-неоднородной
среде, Ж. экспер. и теор. физики, 65, № 1 (7), 54—60.
Кляцкин В. И» и Татарский В. И»
1973а, Приближение диффузионного случайного процесса в некоторых
нестационарных статистических задачах физики, Успехи физ. наук,
110, N 4, 500-536.
19736, Статистические средние в динамических системах, Теор. и
мат. физ., 17, N 2, 273—282.
Коважный (Kovasznay L. S. G,)
1948, Spectrum of locally isotropic turbulence, J. Aeronaut. Sci., 15,
N 12, 745-753.
Колмогоров A. H.
1941, Локальная структура турбулентности в несжимаемой жидкости
при очень больших числах Рейнольдса, Докл. АН СССР, 30, № 4, 299—
303. > ; ^ 7 <
Кочин Н. Е., Кибелъ И. А. и Розе Н. В.
1963, Теоретическая гидромеханика, I, 3 изд., М., Физматгиз.
Красносельский М. А., Вайникко Г. М,, Забрейко П. П., Рутицкий Я. Б.,
Стаценко В. Я.
1969, Приближенное решение операторных уравнений, М., «Наука».
Крейчнан (Kraichnan R. Я.)
1967, Inertial ranges in two-dimensional turbulence, Phys. Fluids, 10,
N 7, 1417—1423.
Кувабара (Kuwabara S.)
1966, Nonlinear instability of the plane Couette flow, IUTAM—IUGG
Symposium on Boundary Layers and Turbulence (Including Geophysical
Applications), Kyoto, Japan, Phys. Fluids, 10, 1967, 115—116.
Ладыженская О, A.
1970, Математические вопросы динамики вязкой несжимаемой жидкости,
М., «Наука».
’ 1972, О динамической системе, порождаемой уравнениями Навье—Стокса,
Записки научных семинаров ЛОМИ, 27, № 6, Л., «Наука», 91—115.
Ламб (Lamb Я.)
1945, Hydrodynamics, 6th ed., New York.
(Русск. перевод: Гидродинамика, М.— Л., Гостехиздат, 1947).
Ландау Л. Д.
1944, К проблеме турбулентности, Докл. АН СССР, 44, № 8, 339—342.
Ландау Л. Д. и Лифшиц Е. М.
1953, Механика сплошных сред, 2 изд., М., Гостехиздат.
1957, О гидродинамических флуктуациях, Ж. экспер. и теор. физики,
32, № 3, 618-619.
1958, Механика, М., Физматгиз.
1964, Статистическая физика, 2 изд. М., «Наука».
154
Лаплас (Laplace Р. S.)
1799, Traite de Mecanique celeste, t. II, Livre IV, Des oscillations de la
mer et de I’atmosphere. Ch. I Th^orie du flux et du reflux de la mer, 171—
203.
Левин M. Л. и Рытое С. M.
1967, Теория равновесных тепловых флуктуаций в электродинамике,
Мм «Наука».
Ли (Lee Т. DJ
1952, On some statistical properties of hydrodynamical and magneto-
hydrodynamical fields, Quart. Appl. Math., 10, 1, 69—74.
Лилли (Lilly D. K.)
1972, Numerical simulation studies of two-dimensional turbulence, Geo-
phys. Fluid Dynam, 3, N 4, 289—319.
Линь (Lin С. C.)
1955, The theory of hydrodynamic stability, Cambridge.
(Русск. перевод: Теория гидродинамической устойчивости, М., ИЛ,
1958).
Лонге-Хиггинс и Гилл (Longuett-Higgins М. 5., Gill А. Е.)
1967, Resonant interactions between planetary waves, Proc. Roy. Soc.,
A299, № 1456, 120-140.
(Русск. перевод: Резонансное взаимодействие планетарных волн, Не-
линейная теория распространения волн, под ред. Г. И. Баренблатта,
М., «Мир», 1970, 161—187).
Лоренц (Lorenz Е. N.)
1955, Available potential energy and the maintenance of the general circu-
lation, Tellus, 7, 2, 151—167.
1960, Maximum simplification of the dynamical equations, Tellus, 12,
N 3, 243-254.
1962, Simplified dynamic equations applied to the rotating-basin experi-
ments, J. Atmosph. Sci., 19, N 1, 39—51.
1967, The nature and theory of the general circulation of the atmosphere,
Geneve.
(Русск. перевод: Природа и теория общей циркуляции атмосферы, Гидро-
метиздат, Л., 1970).
1972, Low order models representing realizations of turbulence, J. Fluid
Meeh., 55, №’3, 545—563.
Малкус и Веронис (Malkus W. V. R., Veronis G.)
1958, Finite amplitude cellular convection, J. Fluid Meeh., 4, N 3, 225—
260.
Маркушевич А. И,
1968, Теория аналитических функций, M., «Наука».
Мешалкин Л. Д. и Синай Я. Г.
1961, Исследование устойчивости стационарного решения одной системы
уравнений плоского движения несжимаемой вязкой жидкости, Прикл.
матем. и мех., 25, № 6, 1140—1143.
Мещерская А, В,^ Руховец Л, В., Юдин М. И. и Яковлева Н. И.
1970, Естественные составляющие метеорологических полей, Л., Гидро-
метиздат.
Миллионщиков М. Д. ,
1941а, К теории однородной изотропной турбулентности, Докл.
АН СССР, 32, № 9, 611—614.
19416, К теории однородной изотропной турбулентости. Изв. АН СССР,
серия «География и геофизика», 5, Кг 4—5, 433—446.
Михлин С. Г.
1957, Вариационные методы в математической физике, М., Гостехиздат.
1966, Численная реализация вариационных методов, М., «Наука».
Моисеев Н. Н. и Румянцев В. В.
1965, Динамика тела с полостями, содержащими жидкость, М., «Наука».
Монин А. С.
1970, Прогноз погоды как задача физики, М., «Наука»,
155
Монин А. С. и Яглом А. М,
1965, Статистическая гидромеханика, ч. 1, М., «Наука».
1967, Статистическая гидромеханика, ч. 2, М., «Наука».
Новиков Е. А.
1964, Функционалы и метод случайных сил в теории турбулентности,
Ж. экспер. и теор. физики, 47, № 5 (И), 1919—1926.
Обухов А. М.
1949, К вопросу о геострофическом ветре, Изв. АН СССР, серия «Гео*
графия и геофизика», 13, № 4, 281—306.
1960, О статистически ортогональных разложениях эмпирических функ*
ций, Изв. АН СССР, серия геофизич., № 3, 432—439.
1962, К динамике расслоенной жидкости, Докл. АН СССР, 145, № 6,
1239-1242.
1967, Weather and turbulence, Proc. Intern. Assoc. Meteor. Atm. Phys.,
Toronto, 1968, 102—107.
1969, Об интегральных инвариантах в системах гидродинамического
типа, Докл. АН СССР, 184, N 2, 309-312.
1971а, On invariant characteristics of systems of fluid mechanical type,
Fluid Dynam. Trans., 5, N 2, 193—199.
19716, О некоторых общих характеристиках уравнений динамики атмо-
сферы, Изв. АН СССР, серия «Физика атмосферы и океана», 7, № 7,
1973, О развитии возмущений при гидродинамической неустойчивости,
Численные методы механики сплошной среды (Новосибирск), 4, № 3,
121-125.
Пекерис и Школлер (Pekeris С. L., Shkoller В.)
1967, Stability of plane Poiseuille flow to periodic disturbances of finite
amplitude in the vicinity of the neutral curve, J. Fluid Meeh., 29, N 1,
31-38.
1969, Stability of plane Poiseuille flow to periodic disturbances of finite
amplitude, J. Fluid Meeh., 39, N 3, 611—627.
Пуанкаре (Poincare H.)
1910, Sur la precession des corps deformables, Bull. Astr. 27, 321—356.
Ричардсон (Richardson L. F.)
1922, Weather prediction by numerical process, Cambridge.
Россби (Rossby C. G.)
1939, Relation between variations in the intensity of the zonal circulation
of the atmosphere and the displacement of the semi-permanent centers
of action, J. Marine Res., 2, N 1, 38—55.
(Русск. перевод: Связь между колебаниями интенсивности зональной
циркуляции атмосферы и смещениями квазипостоянных центров дей-
ствия, «Вопросы предсказания погоды», под ред. Н. А. Багрова и
Г. И. Морского, Л., Гидрометиздат, 1958, 304—316.
Рэлей (Rayleigh)
1916, On convection currents in a horizontal layer of fluid when the higher
temperature is on the under side, Sci. Papers, Cambridge, 6, 432—443.
Рюэлъ и Такенс (Ruelle D., Takens F.)
1971, On the nature of turbulence, Communs. Math. Phys., 20, N 3, 167—
192. /
Сокольников (Sokolnikoff I. S.)
1951, Tensor Analysis, New York—London; 1964, 2d ed.
(Русск. перевод: Тензорный анализ, М., «Наука», 1971).
Сорокин В. С.
1954, О стационарных движениях жидкости, подогреваемой снизу,
Прикл. матем. и мех., 18, № 2, 197—204.
Старр (Starr V. Р.)
1968, Physics of negative viscosity phenomena, New York a. o.
(Русск. перевод: Физика явлений с отрицательной вязкостью, М., «Мир»,
156
Стюарт Дж. (Stuart j. Т.)
1958, On the non-linear mechanics of hydrodynamic stability, J. Fluid
Meeh., 4, N 1, 1—21.
(Русск. перевод: О нелинейной механике в теории гидродинамической
устойчивости, «Механика», № 3 (55), 19—38, 1959).
1960, On the non-linear mechanics of wave disturbances in stable and
unstable parallel flows, I. The basic behavior in plane Poiseuille flow,
J. Fluid Meeh., 9, N 3, 353—370.
1967, Hydrodynamic stability of fluid flows, Inaugural Lecture, Imperial
College of Science and Technology, London.
1971a, Nonlinear stability theory, Annual Rev. Fluid Meeh., 3, 347—370.
19716, Stability of laminar flows, Fluid Dynamics Transactions, 5, N 1,
267-287.
Татарский В. И.
1969, Использование динамических уравнений при вероятностном
прогнозе барического поля. Изв. АН СССР, серия «Физика атмосферы
и океана», 5, № 3, 293—297.
Томпсон (Thompson Р. D.)
1961, Numerical weather analysis and prediction, New York.
(Русск. перевод: Анализ и предсказание погоды численными методами,
под ред. Е. Н. Блиновой, М., ИЛ, 1962; Лекции по численным методам
краткосрочного прогноза погоды, Л., Гидрометиздат, 1969, 7—92).
Тэйлор (Taylor G. I.)
1923, Stability of a viscous liquid contained between two rotating cylin-
ders, Phil. Trans. Roy. Soc. London, A223, 289—343.
Уленбек Г.
1971, Фундаментальные проблемы статистической механики, Успехи
физ. наук, 103, № 2, 275—318.
Уотсон (Watson J.)
1960, On the non-linear mechanics of wave disturbances in stable and
unstable parallel flow, II. The development of solution for plane Poiseuille
and for plane Couette flow, J. Fluid Meeh., 9, N 3, 371—389.
Филлипс (Phillips О. M.)
1967, Theoretical and experimental studies of gravity wave interactions,
Proc. Roy. Soc., A299, N 1456, 104—119.
(Русск. перевод: Теоретические и экспериментальные исследования вза-
имодействия гравитационных волн, «Нелинейная теория распростране-
ния волн», под ред. Г. И. Баренблатта, «Мир», 1970, 141—160).
Флеминг (Fleming R. J.)
1971а, On stochastic dynamic prediction, I. The energetics of uncertainty
and the question of closure, Monthly Weather Review, 99, N 11, 851—
872.
19716, On stochastic dynamic prediction, II. Predictability and utility,
Monthly Weather Review, 99, N 12, 927—938.
Фуджита (Fujita H.)
1961, On the existence and regularity of the steady-state solutions oLNa-
vier—Stokes equations, J. Fac. Sci., Univ. Tokyo, 9, N 1, 59—102.
Фулъц (Fultz D.)
1951, Experimental analogies to atmospheric motion, Compendium Me-
teorol., Boston, 1235—1248.
Фурутцу (Furutsu К.)
1963, On the statistical theory of electromagnetic waves in a fluctuating
medium, J. Res. NBS, D. Radio Propagation, 67, N 3, 303—323.
1972, Statistical theory of wave propagation in a random medium and
the irradiance distribution function, J. Opt. Soc. Amer., 62, N 2, 240—
254.
Хайд (Hide R.)
1953, Some experiments on thermal convection in a rotating liquid, Quart.
J. Roy. Meteor. Soc., 79, N 339, 161.
1970, Some laboratory experiments on free thermal convection in a rotating
157
fluid subject to a horizontal temperature gradient and their relation to
the theory of the global atmospheric circulation, «The global circulation
of the atmosphere», ed. by G. A. Corby. London, 1970.
Каф (Hough S. S.)
1895, The oscillations of a rotating ellipsoidal shell containing fluid, Phil.
Trans. Roy. Soc. London, Al86, p. 1, 469—506.
Нелъман Ф. X,
1970, О перекачке энергии между нелинейно-связанными осцилляторами
в случае резонанса третьего порядка, Прикл. матем. и мех., 34, № 5,
957—962.
1971, О колебаниях системы связанных осцилляторов при одном резо-
нансе третьего порядка, Прикл; матем. и мех., 35, № 6, 1091—1096.
Чандрасекар (Chandrasekhar S.)
1961, Hydrodynamic and hydromagnetic stability, Oxford.
Шлихтпинг (Schlichting H.)
1959, Entstehung der Turbulenz, Berlin u. a.
(Русск. перевод: Возникновение турбулентности, М., ИЛ, 1962).
Эккартп (Eckart С.)
1960, Hydrodynamics of oceans and atmospheres, Oxford a. o.
(Русск. перевод: Гидродинамика океана и атмосферы, М., ИЛ, 1963).
Эпштейн (Epstein Е. 5.)
1969, Stochastic dynamic prediction, Tellus, 21, N 6, 739—759.
Эртель (Ertel H.)
1942, Ein neuer hydrodynamischer Wirbelsatz. Meteor. Zeitschrift, 59,
H. 9, 277—281.
Юдович В. И.
1965, Пример рождения вторичного стационарного или периодического
течения при потере устойчивости ламинарного течения вязкой несжимае-
мой жидкости, Прикл. матем. и мех., 29, № 3, 453—467.
1966, О неустойчивости параллельных течений вязкой несжимаемой
жидкости относительно пространственно-периодических возмущений,
«Численные методы решения задач математической физики», М., «Наука»,
242—249.
1973, Об автоколебаниях, возникающих при потере устойчивости парал-
лельных течений вязкой жидкости относительно длинноволновых перио-
дических возмущений, Изв. АН СССР, серия «Мех. жидк. и газа», № 1,
32-35.
Янке Е., Эмде Ф. и. Лёш Ф.
1968, Специальные функции. Формулы, графики, таблицы, М., «Наука».
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ РЕДАКТОРА ................................. . . 3
ВВЕДЕНИЕ 6
Глава I
КОНЕЧНОМЕРНЫЕ АППРОКСИМАЦИИ УРАВНЕНИЙ
ГИДРОДИНАМИКИ
§ 1. Аппроксимация уравнений гидродинамики по методу Галеркина И
§ 2. Жидкий гироскоп как иллюстрация применения метода Галеркина
к исследованию движения идеальной несжимаемой жидкости 15
§ 3. Плоское движение под действием периодической силы..................................................................... 21
г л а в а II
СИСТЕМЫ ГИДРОДИНАМИЧЕСКОГО ТИПА
§ 1. Квадратично-нелинейные системы, интегралы движения .... 26
§ 2. Понятие регулярности и определение систем гидродинамического
типа................................................... 30
§ 3. Эквивалентность триплета классическому гироскопу............ 33
§ 4. Конструирование сложных систем путем суперпозиции триплетов 37
§ 5. Некоторые общие замечания о применении СГТ в геофизике ... 38
Глава Ш
ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
ГИДРОДИНАМИЧЕСКОЙ СИСТЕМЫ ТИПА ТРИПЛЕТ
§ 1. Предварительные замечания............................................................................................. 40
§ 2. Вынужденное движение жидкости внутри эллипсоида....................................................................... 41
§ 3. Лабораторный эксперимент . . . ♦...................................................................................... 47
Глава IV
НЕЛИНЕЙНЫЕ ВЗАИМОДЕЙСТВИЯ
В ЗАДАЧЕ О КОНВЕКЦИИ
§ 1. Общие замечания к построению малопараметрической модели
конвекции.................................................. 58
§ 2. Модельные уравнения и интегралы движения.............................................................................. 61
§ 3. Стационарная конвекция в покоящемся эллипсоиде........................................................................ 64
§ 4. О влиянии сил Кориолиса на формирование конвективных течений
внутри вращающегося эллипсоида......................................................................................... 71
§ 5. Обсуждение результатов................................................................................................ 79
159
Глава V
МОДЕЛИРОВАНИЕ КАСКАДНОГО ПРОЦЕССА ПЕРЕДАЧИ ЭНЕРГИИ
СИСТЕМАМИ ТИПА ЦЕПОЧЕК
| 1. Модель с простым зацеплением из подобных элементов..... эд
§ 2. Модель с двойным зацеплением, допускающая два квадратичных
интеграла движения.......................................... 85
Глава VI
СИСТЕМЫ С КОМПЛЕКСНЫМИ ХАРАКТЕРИСТИКАМИ
И ЗАДАЧА О ВЗАИМОДЕЙСТВИИ КОЛЕБАНИЙ
§ 1. Комплексное расширение систем гидродинамического типа 89
§ 2. Резонансное взаимодействие планетарных волн............ 98
Глава VII
СТРУКТУРНЫЕ СВОЙСТВА
КВАДРАТИЧНО-НЕЛИНЕЙНЫХ СИСТЕМ
§ 1. Аффинные инварианты и критерий существования квадратич-
ного интеграла для систем второго порядка.................. 103
§ 2. Условия существования алгебраических интегралов для регуляр-
ной системы третьего порядка............................... 108
§ 3. Интегрирование уравнений движения канонического триплета 111
Глава VIII
СТАТИСТИЧЕСКОЕ ОПИСАНИЕ СИСТЕМ
ГИДРОДИНАМИЧЕСКОГО ТИПА
§ 1. Стационарные гауссовские распределения при отсутствии внеш-
них воздействий.......................................... 117
§ 2. Уравнение Эйнштейна—ФокДер а для СГТ при наличии диссипа-
ции и внешнего шума........................................ 122
§ 3. Шумы в СГТ при наличии регулярной составляющей силы ... 125
ПРИЛОЖЕНИЯ
Приложение 1. К определению системы гидродинамического типа . . 135
Приложение II. Асимптотические выражения решений и характери-
стической формы для динамического триплета через элементар-
ные функции............................................ 142
Приложение III. Общий метод вычисления корреляций гауссовского
случайного процесса со связанным с ним функционалом .... 148
ЛИТЕРАТУРА............................................... 151
Нелинейные системы гидродинамического типа
Утверждено к печати Институтом физики атмосферы
Редактор С. Ф. Шушурин. Художник В. В. Фирсова
Художественный редактор А. И. Жданов
Технические редакторы В. Д. Прилепская и Л. И. Куприянова
Сдано в набор 25/Х 1973 г. Подписано к печати 6/П 1974 г.
Формат бОхЭО1/^. Бумага № 1. Усл. печ. л.10.
Уч.-изд. л. 9,7. Тираж 1100. Т-02067. Тип. зак. 691.
Цена 68 коп.
Издательство «Наука»
103717 ГСП, Москва, К-62, Подсосенский пер., Д. 21
Ленинградское отделение издательства «Наука»
1-я типография издательства «Наука». 199034, Ленинград, В-34, 9 линий, д. 12
Опечатки
Стр. Строка Напечатано Должно быть
27 ф-ла (2. 2) -ИЛ +
54 22 сн. Рис. 13 Рис. 15
70 ф-ла (4. 31а) Рг Рг
РгРг /~ \/ РгРг \ /
70 ф-ла (4. 32а) Г2Г3 /Рг)/ Г2Г3 )/Рг
128 19 сн. "1 ехр ”1 ехр
Нелинейные системы
68 коп.