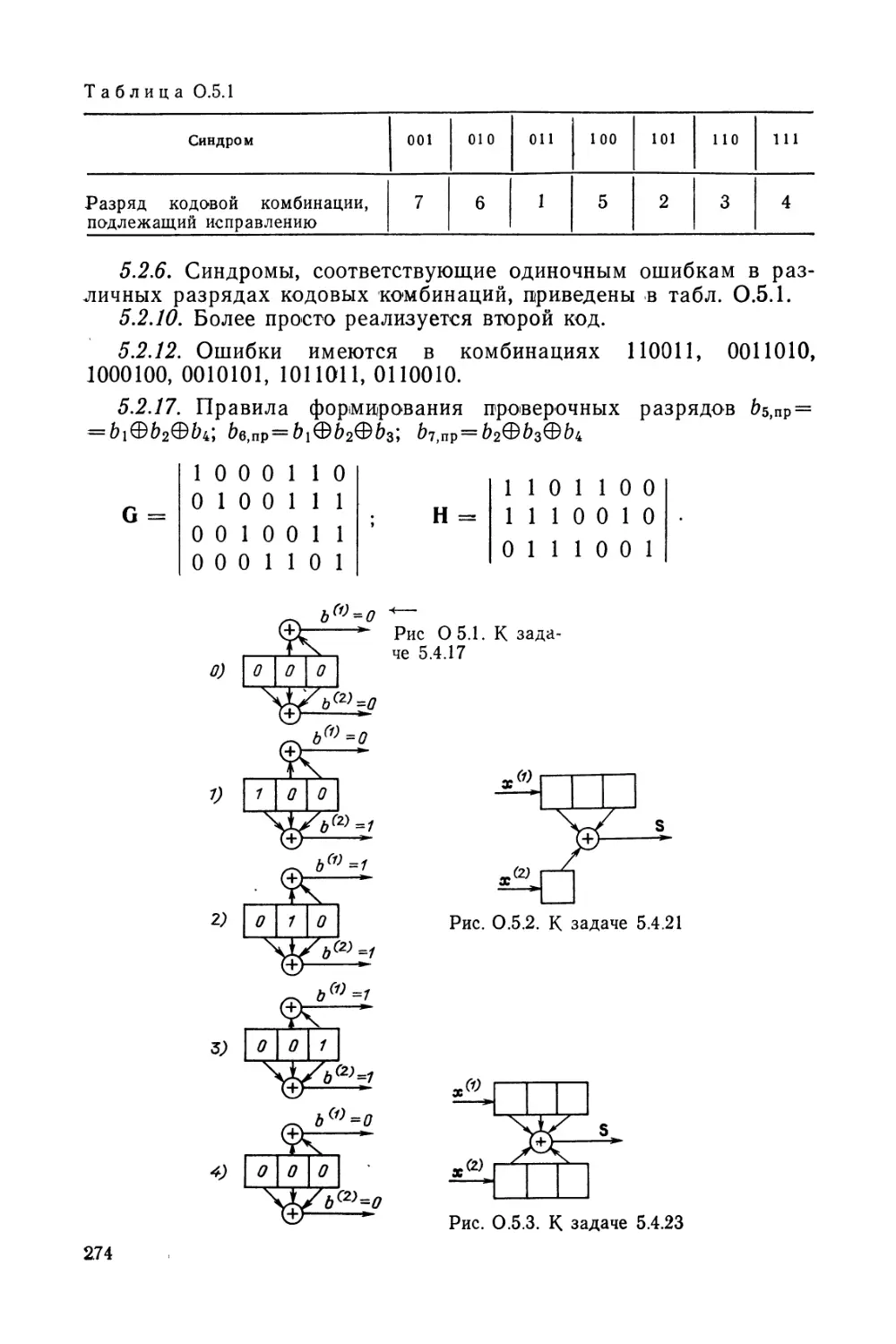
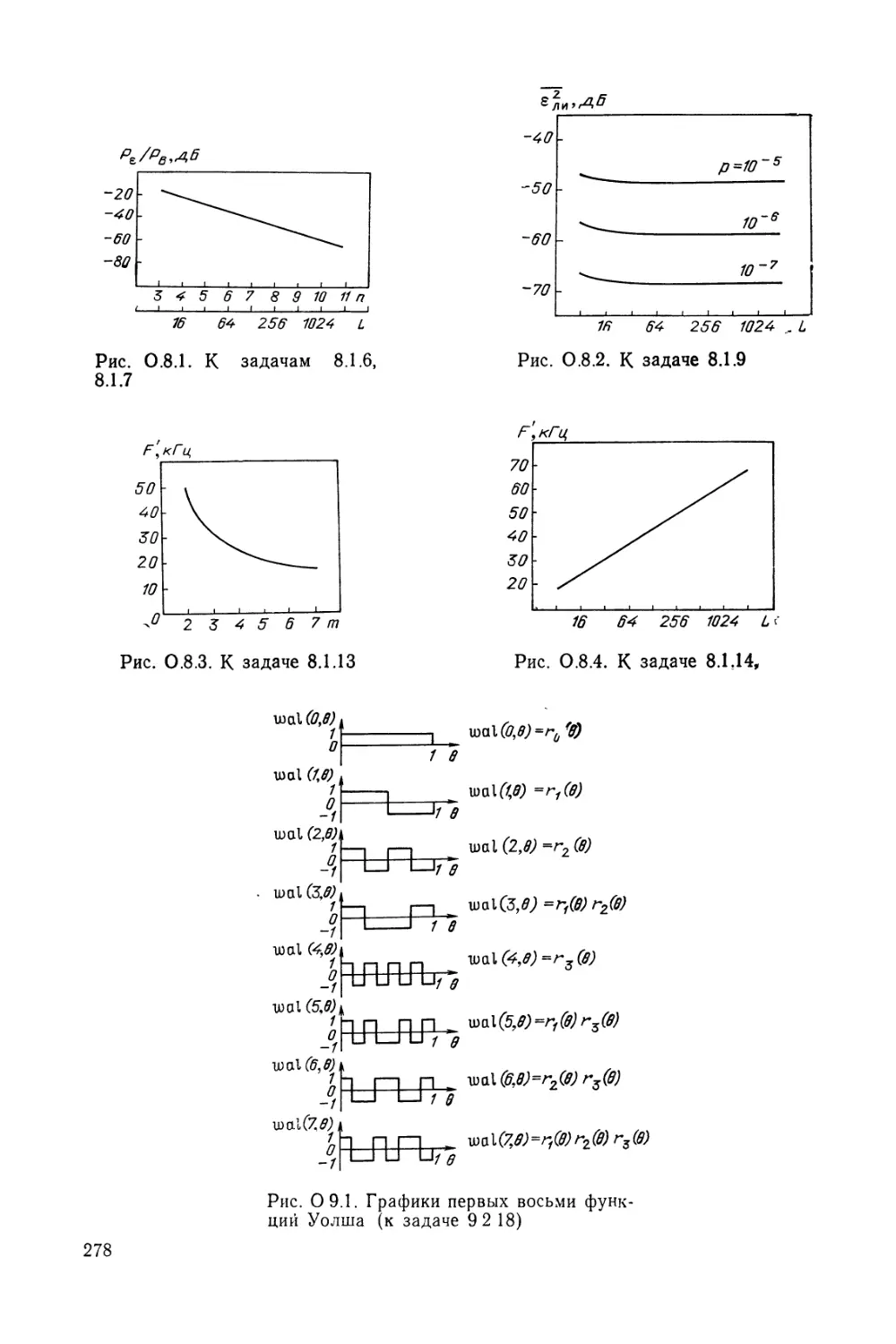
Автор: Кловский Д.Д. Шилкин В.А.
Теги: электротехника электрическая связь радиосвязь учебное пособие электросвязь
ISBN: 5-256-00675-4
Год: 1990
Текст
Д.Д.Кловский
В.А.Шипкин
ТЕОРИЯ
ЭЛЕКТРИЧЕСКОЙ
СВЯЗИ
Учебное
пособие
для высших
учебных
заведений
Д.Д.Кловский
В. А. Шилкин
ТЕОРИЯ
ЭЛЕКТРИЧЕСКОЙ
СВЯЗИ
Сборник
задач
и упражнений
Допущено Министерством связи СССР
в качестве учебного пособия
для студентов вузов связи,
обучающихся по специальностям
23.05 «Автоматическая электросвязь»,
23.06 «Многоканальная электросвязь»,
23.07 «Радиосвязь, радиовещание
и телевидение»
©Москва
«Радио и связь»
1990
Scan AAW
ББК 32.88
К50
УДК 621.312.01(076)
Рецензенты: кафедра теории электрической связи Одесского электротехни-
ческого института связи им. А. С. Попова (зав. кафедрой д-р
техн, наук (проф. А. Г. Зюко), д-р техн, наук пр оф. Л. Ф. Гри-
горовский
Редакция литературы по информатике и вычислительной технике
Кловский Д. Д., Шилкин В. А.
К 50 Теория электрической связи. Сб. задач и упражне-
ний: Учеб, пособие для вузов. — М.: Радио и связь,
1990. — 280 с.: ил.
ISBN 5-256-00675-4.
Приводятся задачи по основным разделам курса теории элек-
трической связи, в которых отражаются общие закономерности пе-
редачи информации по каналам связи. Отмечаются потенциальные
возможности различных способов передачи и приема сигналов.
В каждом разделе даются краткие теоретические сведения. Для
части задач приводятся подробные решения. Остальные задачи
сопровождаются указаниями к решению и ответами.
Для студентов вузов, обучающихся по специальностям «Авто-
матическая электросвязь», «Многоканальная электросвязь», «Радио-
связь, радиовещание и телевидение» и смежным специальностям.
К
2303020000-092
046(01)-90
ББК 32.88
Учебное издание
Кловский Даниил Давыдович
Шилкин Владимир Афанасьевич
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ.
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ
Учебное пособие
Заведующая редакцией Г. И. Козырева. Редактор В. И. Ченцова.
Переплет художника С. Ю. Архангельского. Художественный редактор А. В. Проценко
Технический редактор Т. Г. Родина. Корректор Т. В. Дземидович
ИБ № 1156
Сдано в набор 29.05.89 Подписано в печать 02.04.90
Формат 60X90716 Бумага типогр. № 2 Гарнитура литературная
Печать высокая Усл. печ. л. 17,5 Усл. кр.-отт. 17,5 Уч -изд. л. 18,51
Тираж 7000 экз. Изд. № 21142 Зак. № 53 Цена 95 к.
Издательство «Радио и связь», 101000 Москва, Почтамт, а/я 693
Типография издательства «Радио и связь», 101000 Москва, ул. Кирова, д. 40
ISBN 5-256-00675-4 © Кловский Д. Д., Шилкин В. А., 1990
ОГЛАВЛЕНИЕ
Предисловие......................................................... 5
Глава L системы связи и способы передачи сообщений 7
1.1. Сообщение и сигнал, система связи, канал связи ............... 7
1.2. Кодирование и декодирование....................................13
'1.3. Модуляция.....................................................15
Глав а 2. сообщения, сигналы, помехи..........................18
2Л. Сообщения, сигналы и помехи как случайные процессы .... 18
2.2. Спектры случайных процессов..........26
2.3. Огибающая, мгновенная фаза и частота узкополосного случайного
процесса............................................................27
2.4. Пространства сообщений и сигналов..............................31
2.5. Основы теории дискретизации функций непрерывного аргумента.
Теорема Котельникова................................................37
Глава 3. каналы связи...............................................40
3.1. Модели каналов связи и их математическое описание..............40
3.2. Изменения формы сигналов, обусловленные характеристиками непре-
рывного канала......................................................47
3.3. Аддитивные помехи в непрерывном канале связи...................51
3.4. Прохождение случайных воздействий через канал связи и его звенья 55
3.5. Уравнения состояния. Марковские модели каналов связи .... 59
Глава 4. основы теории передачи информации .... 63
4.1. Количественное определение информации. Энтропия и производитель-
ность дискретного источника сообщений...............................63
4.2. Количество и скорость передачи информации по дискретному каналу.
Пропускная способность дискретного канала. Теорема кодирования для
каналов с шумами....................................................67
4.3. Энтропия и производительность непрерывного источника сообщений 72
4.4. Количество и скорость передачи информации по непрерывному кана-
лу. Пропускная способность непрерывного канала......................76
Глава 5. основы теории помехоустойчивого кодирования 79
5.1. Принципы помехоустойчивого кодирования.........................79
5.2. Линейные двоичные блочные коды.................................81
5.3. Циклические коды...............................................87
5.4. Некоторые разновидности корректирующих кодов..................88
Глава 6. прием дискретных сообщений..........................94
6.1. Критерии оптимального приема. Алгоритмы оптимального приема при
точно известном сигнале.............................................94
6.2. Реализация алгоритма оптимального приема при точно известном сиг-
нале на основе согласованных фильтров...............................99
6.3. Помехоустойчивость (вероятность ошибки) оптимальных схем прие-
ма при точно известном сигнале......................................102
6.4. Алгоритм оптимального приема и помехоустойчивость при неопреде-
ленной фазе и амплитуде сигнала.....................................107
3
Глава 7. прием непрерывных сообщений................................ПО
7.1. Оптимальная оценка отдельных параметров сигнала................ПО
7.2. Оптимальная демодуляция непрерывных сообщений. Расчет помехо-
устойчивости аналоговых систем передачи...........................114
7.3. Оптимальная линейная фильтрация по критерию минимума среднего
квадрата ошибки...................................................118
Глава В. цифровые методы передачи непрерывных сооб-
щений ............................................................124
8.1. Характеристики качества передачи непрерывных сообщений в систе-
мах с импульсно^кодовой модуляцией..............................124
Глава 9. теория многоканальной передачи сообщений . 128
9.1. Основы теории разделения сигналов.............................128
9.2. Способы разделения сигналов...................................131
Глава 10. методы повышения эффективности систем пе-
редачи СООБЩЕНИЙ..................................................137
ЮЛ.. Предельная эффективность систем передачи сообщений . . . . 137
10.2. Эффективность аналоговых и цифровых систем.................141
10.3. Характеристики эффективности многоканальных систем .... 143
10.4. Эффективность избыточного кодирования и многопозиционных сиг-
налов ....................................................147
Решения и указания к решению задач главы 1......................150
Решения и указания к решению задач главы 2......................155
Решения и указания к решению задач главы 3......................172
Решения и указания к решению задач главы 4......................185
Решения и указания к решению задач главы 5......................199
Решения и указания к решению задач главы 6......................205
Решения и указания к решению задач главы 7......................230
Решения и указания к решению задач главы 8......................246
Решения и указания к решению задач главы 9......................247
Решения и указания к решению задач главы 10........................254
Ответы.............................................................266
Список литературы..................................................280
ПРЕДИСЛОВИЕ
Предлагаемая книга является первым учебным пособием по
курсу «Теория электрической связи» (ТЭС), изучение которого с
1988 г. предусмотрено учебными планами для специальностей «Ав-
томатическая электросвязь», «Многоканальная электросвязь»,
«Радиосвязь, радиовещание и телевидение» институтов связи.
При подготовке книги авторы использовали многолетний опыт
преподавания курса «Теория передачи сигналов» в Куйбышевском
электротехническом институте связи, а также опыт работы над
учебным пособием «Теория передачи сигналов в задачах», вы-
шедшим в издательстве «Связь» в 1978 г. и положенным в основу
настоящего издания.
Согласно программе курса ТЭС в данное учебное пособие, в
отличие от названного, включены задачи по таким разделам как
«Системы связи и способы передачи сообщений», «Уравнения со-
стояния. Марковские модели каналов связи», «Цифровые методы
передачи сообщений». В раздел «Пространства сообщений и сиг-
налов» введены задачи по ансамблям многомерных сигналов. Вы-
делен в отдельную главу и существенно дополнен материал по
методам повышения эффективности систем связи. Значительно пе-
реработаны главы «Теория многоканальной передачи сообщений»
и «Основы теории помехоустойчивого кодирования», в которую
включены новые задачи, в частности по сверточным кодам. Учеб-
ное пособие условно можно разделить на две части: в первой при-
водятся задачи, во второй — решения и ответы.
По содержанию, расположению материала и основным обоз-
начениям пособие соответствует учебнику [12], рекомендованному
для изучения курса ТЭС, и дополняет его.
Книга содержит 10 глав, в которых приведено около 600 за-
дач, иллюстрирующих общие закономерности передачи сообще-
ний по каналам связи, потенциальные возможности способов пе-
редачи и приема сигналов. Каждый раздел имеет краткое теоре-
тическое введение, в котором даны основные расчетные соотно-
шения.
В пособии приведены как простые, так и сложные задачи, ре-
шение которых может показаться затруднительным. В этих слу-
чаях потребуется квалифицированная помощь преподавателей.
В книгу не вошли традиционные задачи по расчету вероятностных
характеристик случайных величин и случайных процессов, кото-
рые содержатся, например, в |[3, 6]. При решении ряда задач воз-
никает необходимость использования микроЭВМ. В этом случае
5
можно воспользоваться прикладными программами из [1, 5, 9].
Многие вероятностные задачи расчета отдельных звеньев сис-
тем передачи сообщений, которые стоят перед современными ин-
женерами, занимающимися разработкой и эксплуатацией сис-
тем связи, требуют знаний, выходящих за пределы курсе ТЭС. В
этом случае следует обратиться к специальной литературе. Однако
при этом необходимо овладеть основными идеями и методами рас-
чета статистической теории связи. Именно с этой точки зрения
книга может оказаться полезной широкому кругу читателей, за-
нимающихся разработкой и эксплуатацией систем передачи со-
общений.
Глава1. СИСТЕМЫ СВЯЗИ И СПОСОБЫ
ПЕРЕДАЧИ СООБЩЕНИИ
1.1. СООБЩЕНИЕ И СИГНАЛ, СИСТЕМА
СВЯЗИ, КАНАЛ СВЯЗИ
Сообщением называют совокупность знаков (символов), содержащих те или
иные сведения (информацию).
Сообщения дискретного источника (текста телеграммы, данные с выхода
ЭВМ и другие) образуют счетные множества (эти символы можно пронумеро-
вать), в то время как сообщения непрерывного источника (речь, музыка, теле-
визионное изображение) образуют несчетные (континуальные) множества.
Физический процесс, отображающий (несущий) передаваемое сообщение по
времени, называют сигналом.
Если сигнал представляет собой функцию u(t), принимающую только ди-
скретные значения tik, его называют дискретным (точнее дискретным по состо-
яниям). Если сигнал может принимать любые значения в некотором интервале,
его называют непрерывным (по состояниям) или аналоговым.
Иногда сообщение (сигнал) задается не на всей оси времени, а только в
определенные моменты tk- Такие сообщения (сигналы) называют дискретными
по времени.
Совокупность технических средств, служащих для передачи сообщений от
источника к потребителю, называют системой связи.
Канал связи — это совокупность технических средств, обеспечивающих пере-
дачу сигнала от одной точки системы до другой. Точки входа и выхода ка-
нала определяются решаемой (исследуемой) задачей.
Канал является дискретным, если на его входе и выходе — дискретные (по
состояниям) сигналы, и непрерывным, если эти сигналы непрерывные. У ди-
скретно-непрерывного и непрерывно-дискретного канала на входе действуют ди-
скретные сигналы, а на выходе непрерывные и наоборот.
Емкостью (объемом) сигнала Ус называют произведение трех его физиче-
ских характеристик: длительности сигнала Тс, ширины спектра Fc и динамиче-
ского диапазона уровней сигнала (по мощности) Dc:
Ус — TcFcDc, (1-1)
pc=101g-^». (1.2)
г мин
В этом выражении Рмакс — максимальное (пиковое) значение мощности
сигнала; РМин — минимальное значение мощности сигнала.
7
Величина Vc чаще всего характеризует весь ансамбль используемых в дан-
ной системе связи сигналов. Иными словами, эта характеристика описывает сш-
нал как случайный процесс. В этом случае Тс — это средняя длительность сиг-
нала; Ро— ширина энергетического спектра, а Рмакс и РМИн при определении
Dc для ансамбля с неограниченным числом реализаций представляют собой
уровни мощности, которые соответственно превышаются и не превышаются с
какой-либо заданной малой вероятностью. Емкость сигнала — весьма важная
характеристика, позволяющая оценивать трудности, связанные с его передачей.
При наличии шумов в канале допустимый минимальный уровень мощно-
сти Рмин обычно определяется средней мощностью шумов в канале. Поэтому
можно записать
вс = 101g -”акс . (1.3)
Р ш
Максимальную мощность Рмакс иногда выражают через усредненную за
достаточно большой интервал времени мощность сигнала Рс. В этом случае
П2 Рс
(1.4)
где П2=РМакс/Рс—пик-фактор сигнала по мощности. Эта величина зависит
от статистики сигнала. Отношение средних мощностей сигнала и шума Рс/Ра
часто называют просто отношением сигнал-шум.
Аналогично емкости сигнала можно ввести характеристику, называемую
емкостью (объемом) канала,
VK = TKFKDK, (1.5)
где Тк — время использования канала; FK — полоса пропускаемых каналом час-
тот; DK — динамический диапазон уровней, пропускаемых каналом с допусти-
мыми искажениями.
Для передачи сигнала, имеющего объем Vc, с достаточно высоким каче-
ством должно выполняться неравенство
Vc^Vk. (1.6)
При этом необходимо согласование сигнала и канала по всем трем парамет-
рам, т. е.
Рс^Рк, РсСРк, De^DK. (1.7)
Выполнение этих условий означает, что для обеспечения удовлетворитель-
ного качества при передаче сигналов требуется, чтобы объем сигнала «вписы-
вался» в объем канала.
Естественно, что необходимо также согласование сигнала и канала в пре-
делах общих интервалов времени, частот и уровней.
Задачи
1.1.1. Дискретный источник выдает последовательность 3-сим-
вольных сообщений Au, Ai2f Агз (первый индекс показывает зна-
чение элемента, а второй — его номер в последовательности), вы-
бираемых из дискретного алфавита ai (г=0, К—1; К=8 — объ-
ем алфавита источника). Сколько различных сообщений N мо-
8
жет выдать такой источник? Выпишите реализации сообщений, у
которых два первых символа ап, а72-
1.1.2. Выпишите реализации сообщений источника, заданного
в задаче 1.1.1, у которых номера двух символов приведены в
табл. 1.1.
Таблица 1.1
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Н 1 1 8 7 - 4 1 7 7 __
*2 — 3 1 — 2 8 4 3 — 6 1
*3 2 — — 8 8 1 — 3 6 2 — 5
1.1.3. Данные из ЭВМ выдаются в двоичном коде (/п=2) ко-
довыми комбинациями, содержащими п=7 символов. Сколько
таких сообщений может выдать источник? Напишите две реали-
зации такого источника, принимая 1.
1.1.4. Решите задачу 1.1.3 для значений числа разрядов в ко-
довой комбинации п, заданных в табл. 1.2.
Таблица 1.2
Вариант 1 2 3 4 5 6 7 8 9 10 И 12 13 14 15
п 5 8 6 15 9 13 11 10 12 17 14 19 21 22 2
1.1.5. Дискретные источники А и В выдают двоичные симво-
лы Uik, bik^O, 1. Эти символы попарно отображаются (кодируют-
ся) новым символом Cik. Сколько реализаций принимает сим-
вол ^f/i?
1.1.6. Датчик температуры через дискретные интервалы вре-
мени Д/= 1 мин выдает значения температуры в пределах 16®...
... 36°. Сколькими уровнями К можно отобразить (квантовать)
шкалу температур, чтобы погрешность квантования б не превыси-
ла по модулю 0,5°? Сколько различных сообщений может выдать
такой дискретный во времени и квантованный по уровням источ-
ник, если длительность каждого сообщения Т=4 мин?
1.1.7. Решить задачу 1.1.6 для вариантов числовых значений
величин, заданных в табл. 1.3.
Таблица 1.3
Вариант 1 2 3 4 5 6 71 8 9 10 11 12
Д/, МИН б Т, мин 0,5 0,2 4 1 0,4 9 0,4 0,1 4 1 0,5 8 1 0,3 7 0,5 0,4 5 0,2 0,3 2 1 0,1 8 2 0,4 10 0,2 0,3 2 0,2 0,5 2 1 0,2 8
9
р,лБ
4
Рис. 1.1. Измене-
ние звукового дав-
ления
о 10 2 0 30 40 50 60 70 80 90 WO t,MC
1.1.8. Изменение давления, создаваемого говорящим у микро-
фона за время Т—100 мс, показано на рис. 1.1. Уровень давления,
измеряемый в децибелах, меняется в пределах 0,5... 3,5 дБ. Верх-
няя частота спектра сообщения Кмакс=4000 Гц. Сколькими реали-
зациями можно описать сообщения источника при дискретном
времени с шагом М= 1/(2ГмаКс) и квантовании уровней с шагом
ДР= 1 дБ?
1.1.9. Яркость точки плоского черно-белого изображения В(х, у)
меняется в пределах 0... 160 кд/м2 (кандела на квадратный метр).
Изображение имеет форму прямоугольника с размерами по вер-
тикали 625 мм и горизонтали 833 мм. Каким числом точек опре-
деляется кадр изображения, если различаются соседние точки на
расстоянии порядка 1 мм. Чему равно число различных кадров
изображения при квантовании яркости с шагом ДВ=10 кд/м2?
1.1.10. Три компоненты сигнала точки плоского цветного изоб-
ражения В(х, у), 7?(х, у), G(x, у) меняются независимо. Число
различимых точек кадра изображения М=0,75-(625)2=520000.
Чему равно число различных кадров изображения, если сигнал яр-
кости В(х, у) передавать с 16 градациями, а сигналы цветности
iR(x, у), G(x, у) с 8 градациями?
1.1.11. На рис. 1.2 показана реализация двоичного первичного
сигнала b(t) в системе передачи данных, отображающая 7 кодо-
вых посылок длительностью Т=10 мс. Каким числом реализаций
определяется такой сигнал на интервале ТН=7Т? Покажите, что
огибающая амплитудного спектра этого сигнала Sb(f)=hTX
' sin л / Т ’
nfT
максимум спектра соответствует нулевой часто-
X
те, а нули спектра соответствуют частотам fk=k[T, k = i, 2, 3,..
Какую полосу частот Fc занимает сигнал b(f), если ширина спек
. л. I sin л f т I
тра определяется тремя первыми лепестками функции --------— .
I «/Г I
1.1.12. На рис. 1.3 показана реализация напряжения нормиро-
ванного первичного сигнала b(t) в системе передачи речи с мак-
симальной частотой спектра Гмакс=4 кГц. С какой частотой ра-
ботает генератор стробирования (взятия отсчетов) речевого сиг-
нала, если шаг дискретизации во времени Д/= 1/(2Кмакс)? Каким
числом реализаций определяется речевой сигнал на интервале
Ю
b(t)
т .
Рис. 1.2. Реализация двоично-
Рис. 1.3. Реализация нормированного
го сигнала
речевого сигнала
Т=2 мс при дискретизации во времени и квантовании по уров-
ням с шагом Д&=0,02 В, если | b \ 1 В?
1.1.13. Решить задачу 1.1.12 для вариантов числовых значений
величин, приведенных в табл. 1.4.
Таблица 1.4
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
•^макс, кГц Т, мс ДЬ, В 1^1макс> В 4 4 0,01 1 5 4 0,02 2 6 2 0,02 3 2 6 3 6 0,06 0,01 3 2 9 10 0,02 4 10 9 0,07 7 8 1 0,08 4 1 2 0,01 3 4 9 0,04 2 9 5 0,04 2 1 3 0,05 5
1.1.14. Определить, во сколько раз емкость телевизионного сиг-
нала превосходит емкость радиовещательного сигнала (при оди-
наковой их длительности), если 7?тв = 6,5 МГц, и J7pB= 12 кГц. (Ди-
намические диапазоны телевизионного и радиовещательного сиг-
налов следует считать одинаковыми.)
1.1.15. Сравнить объемы двух сигналов, параметры которых
заданы в табл. 1.5.
Таблица 1.5
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Л. с Fi, кГц Dlt дБ Тг, с А. кГц О2> ДБ 4 8 70 3 4 50 5 1 70 7 10 90 3 8 20 5 3 80 7 3 80 6 4 100 9 3 50 1 3 20 4 9 30 5 8 20 6 3 50 9 1 70 4 4 10 6 10 80 10 4 90 8 2 60 1 9 90 8 3 40 1 5 20 9 6 20 5 7 100 3 1 10
1.1.16. Текст из ста букв передается по телефонному каналу
в течение 30 с. Тот же текст за то же время передается по телег-
рафному каналу пятизначным двоичным кодом. Приняв динами-
11
ческие диапазоны телефонного и телеграфного сигналов равны-
ми, определить, во сколько раз телеграфный сигнал экономичнее
телефонного.
1.1.17. Канал связи с полосой Гк=10 кГц предполагается ис-
пользовать в течение 10 с. В канале действует шум с равномер-
ной спектральной плотностью мощности Л/о=1О~4 мВт/Гц. Како-
ва предельная мощность сигнала, который может быть передан
по данному каналу, если объем канала Кк = Ю6?
1.1.18. Решить задачу 1.1.17. для вариантов числовых значений,
приведенных в табл. 1.6.
Таблица 1.6
Вариант 1 2 3 4 5 6 7 8 9 it И 12
Т’к, кГц 4 9 4 8 6 5 2 8 10 2 2 2
А/о, мВт/Гц 10“*! 10-9 10-5 IO”5 ю—4 10-5 10—4 10—6 ю—8 10-8 ю-4 ю—5
104 106 10е 106 105 106 10е 106 ю7 10» Ю5 106
Тк 1 с 7 7 20 8 5 30 5 10 7 9 9 20
1.1.19. Амплитудно-модулированный сигнал «ам(/) = £Лп(1 +
-\-т sin Q t)cos &ot предполагается передать по каналу с объемом
Кк=105 Найти допустимый коэффициент глубины модуляции т,
если полоса частот сигнала Fc= 100 Гц, а его длительность Тс=
= 10 с.
1.1.20. Решить задачу 1.1.19 для вариантов числовых значений,
приведенных в табл. 1.7.
Таблица 1.7
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Гк 4-104 3-104 104 9- Юз 8- 103 Ю4 5-103 4-104 З-Ю4 104 9-Ю3 5-103
Гс. Гц 400 400 900 500 700 700 800 100 900 400 600 200
Тс, с 6 3 7 8 9 5 4 9 5 8 3 3
1.1.21. По каналу связи, в котором действует шум с энергети-
ческим спектром go 0 = exp £ — j , передается
ЧМ-сигнал u4M(0 = t/mCos'[(oo/+'A® J/>(х)б?х-|-фо]- Полоса сиг-
о
нала Гс=100 кГц, длительность 70=10 с. Определить допустимую
амплитуду сигнала, если Кк=2-107; 0 = 1,13-105, средняя мощ-
йость шума Рш—10“2 Вт.
1.1.22. Амплитуда сигнала распределена по закону Релея:
w (А) = exp ( — = V А 0,
12
где А — мгновенное значение амплитуды сигнала; Л2 — средний
квадрат амплитуды.
Полоса частот сигнала Fc=4 кГц, а его длительность Тс=10с.
Найти объем сигнала, если за максимальный и минимальный уров-
ни мощности сигнала приняты такие значения, которые соответ-
ственно превышаются и не превышаются с вероятностью р=10~3.
1.1.23. Решить задачу 1.1.22 для числовых значений величин,
заданных в табл. 1.8.
Таблица 1.8
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Тс, кГц 5 3 4 6 9 1 2 4 10 2 7 6
Тс, с 15 17 14 18 19 17 14 15 17 10 12 17
Р 10—4 Ю-2 ю—2 10—6 ю—7 ю—5 ю-в 10—6 10—4 ю—6 ю-4 10—2
1.2. КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ
Кодирование (в узком смысле) —сопоставление дискретному сообщению
at(/=l,K) определенной последовательности кодовых символов, выбираемых
из конечного множества символов {6j} (/=l,m), называемого кодовым алфа-
витом. Если число разрядов во всех кодовых комбинациях п = const, то код
называется равномерным. Число кодовых комбинаций равномерного кода
(1.8)
где т— основание кода; п — число разрядов в кодовой комбинации.
Неравномерные коды характеризуются различным числом символов в кодо-
вых комбинациях. Примеры построения таких кодов будут приведены в гл. 4*
Каждую букву ансамбля {а$} с объемом К можно закодировать при
(1.9)
Если число кодовых комбинаций #=/<, то код называется простым (примитив-
ным). Число разрядов в кодовой комбинации равномерного примитивного кода
п = logTnK= log2K/log2m. (1.10)
Если же число кодовых комбинаций М>Л, то код называется корректирую-
щим. Принципы построения и свойства таких кодов будут рассмотрены в гл. 5.
При кодировании отдельным символам источника сообщений удобно по-
ставить в соответствие целые числа от 0 до К—1.
Любое целое число Л4 может быть представлено в системе счисления с ос-
нованием т:
М = Ьп-}Гпп-1 + Ьп-2^п~2+ ... +bim1 + bom0. (1.11>
Коэффициенты bi принимают значения от 0 до т—1. Их совокупность и есть
кодовая комбинация для символа а$, которому поставлен в соответствие но-
мер Мг:
Аг=>Л/г=>(/?Л_1Л Ьп— 2,..., bi, bo).
13
Декодирование состоит в восстановлении сообщения по принимаемым кодовым
символам.
Задачи
1.2.1. Источник сообщений выдает символы из ансамбля, име-
ющего объем К=8. Записать кодовые комбинации примитивного
равномерного двоичного кода, соответствующие символам данного
источника. Построить граф кода (кодовое дерево).
1.2.2. Какое число разрядов должен иметь равномерный при-
митивный код, предназначенный для кодирования 32-буквенного
алфавита, при основании кода т=2; 8; 16; 32?
1.2.3. Дискретный источник выдает символы из ансамбля {а<}
с объемом К=10. Какое минимальное число разрядов должны
иметь кодовые комбинации равномерного двоичного кода, предназ-
наченного для кодирования символов заданного ансамбля?
Записать кодовые комбинации. Будет ли полученный код прими-
тивным?
1.2.4. Первичный непрерывный сигнал путем дискретизации во
времени и квантования по уровню превращается в импульсную
последовательность с числом уровней К=128. Уровни квантован-
ного сигнала кодируются равномерным двоичным примитивным
кодом. Найти число разрядов в кодовой комбинации.
1.2.5. Какое наименьшее число разрядов должны иметь кодо-
вые комбинации двоичного и восьмеричного кодов, предназначен-
ных для кодирования сообщений алфавита, имеющего объем К=
= 16; 128; 57; 10; 432?
1.2.6. Закодировать двоичным кодом следующие числа: 5; 7;
17; 31; 32; 33; 127; 128; 129.
1.2.7. Сообщения, выбираемые из ансамблей, имеющих объем
К=8; 9; 16; 17; 32; 33; 256; 260, кодируются равномерным кодом
с основанием т=2; 3. В каких случаях величина n=log2/Klog^zn
будет точно выражать длину кодовой комбинации?
1.2.8. Чему должен быть равен объем алфавита К, который
можно закодировать равномерным примитивным кодом с осно-
ванием т=2; 3; 8 и п=2; 3; 5?
1.2.9. Технической скоростью передачи v называется количест-
во кодовых символов, передаваемых в единицу времени. Опреде-
лить техническую скорость передачи для стартстопного телеграф-
ного аппарата, передающего одну букву семью посылками: стар-
товой (20 мс), пятью кодовыми (20 мс каждая) и одной стопо-
вой (30 мс).
1.2.10. Кодовые символы передаются посылками постоянного
тока, имеющими длительность 5 мс. Чему равна техническая ско-
рость передачи?
1.2.11. Какую длительность должны иметь кодовые посылки
при технической скорости 50, 100, 200 Бод? (1 Бод соответствует
передаче одной посылки в секунду).
14
1.2.12. Буквам русского алфавита А, В, Е, К, О, М, С соответ-
ствуют следующие кодовые комбинации 5-разрядного двоичного
кода: 00000, 00011, 00101, 01001, 01011, 01100, 01111. Расшифруй-
те кодовые последовательности:
1) 011000101101111010010001100000;
2) 0111100101010010000001100;
3) 0110000000011110100100000.
1.3. МОДУЛЯЦИЯ
При модуляции параметр переносчика (несущей) f(k, меняется по
закону первичного сигнала b(t).
При гармонической несущей на практике применяется амплитудная моду-
ляция (АхМ). Сигнал AM.
Wam (0 == [UQ+kAb (0] cos (©о/+фо), (1.12)
где [/о, ©о, фо — амплитуда, частота и начальная фаза несущей; kA — крутизна
модуляционной характеристики.
Сигнал балансной модуляции (БМ-сигнал)
“БМ = *БМ 6 C0S + Фо) ’ <1ЛЗ>
Сигнал однополосной модуляции (ОМ-сигнал)
“ом (0 = Аом6 cos (“°z + фо) ± Аом ь (/) sin («о t + фо), (1 • 14)
где 5(0—сигнал, сопряженный с b(t) по Гильберту (у него все частотные
компоненты сдвинуты на 90°). Знак «—> в (1.14) соответствует системе ОМ с
верхней боковой полосой, знак «4~» — системе ОМ с нижней боковой полосой.
Сигнал фазовой модуляции (ФМ-сигнал)
“фм (О = и°cos [°0 * + ЛФМ 6 (0 + Фо1 • (1-15)
Сигнал частотной (интегральной) модуляции (ЧМ-сигнал)
“чм (0 = ^0 COS
t
«М + ^чи/^М^ + фо •
о
(1-16)
На практике применяются системы с двойной модуляцией, чаще всего системы
ОМ —AM, ФМ —AM, ЧМ —AM, ЧМ —ОМ, ОМ—ЧМ, ЧМ —ЧМ и др. Если
несущая модулируется дискретным сообщением, то говорят о дискретной моду-
ляции. Кроме дискретной AM, ФМ, ЧМ, используется система относительной фа-
зовой модуляции (ОФМ).
В отличие от ФМ при ОФМ фаза сигналов отсчитывается не от некоторого
эталона, а от фазы предыдущего элемента сигнала. При передаче двоичных со-
общений символ 0 передается, например, отрезком синусоиды е начальной фа-
зой предыдущего элемента сигнала, а символ 1—таким же отрезком с началь-
ной фазой, отличающейся от начальной фазы предшествующего элемента сиг-
нала на л.
В импульсных системах связи дискретные отсчеты b(kAt) непрерывного со-
общения передаются периодической последовательностью импульсов
со
/(.') = S <(ft, Т, Лт,( — kT),
k=—со
(117)
15
где v(t)—функция, определяющая форму импульсов (0^/^т); h — высота
(амплитуда) импульсов; т — длительность; Дт — отклонение импульса относи-
тельно тактовой точки; Т — период следования импульсов.
Задачи
1.3.1. Напишите выражение для сигнала в системе ОМ—ФМ
(в нижней ступени модуляции используется нижняя или верхняя
боковая полоса). Индексы 1 и 2 припишите параметрам соответ-
ственно первой и второй системы модуляции. Определите ширину
полосы сигнала, если первая поднесущая ^=100 кГц, верхняя ча-
стота сообщения FMaKc=4 кГц, а индекс модуляции во второй сис-
теме р2= 15.
1.3.2. Решить задачу 1.3.1 для числовых значений величин, за-
данных в табл. 1.9.
Таблица 1.9
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
/1, кГц 40 100 300 400 300 80 100 200 300 60 100 50
^макс, кГц 5 2 8 10 2 2 8 6 6 7 6 2
02 14 8 9 10 16 8 9 12 18 17 12 14
1.3.3. Напишите выражение для сигнала в системе ФМ—AM.
Определите ширину полосы частот сигнала, если /4= 100 кГц,
FMaKC=4 кГц, а индекс ФМ 01 = 15.
1.3.4. Решите задачу 1.3.3 по данным, приведенным в табл. 1.10.
1.3.5. Напишите выражение для сигнала в системе ЧМ—ОМ
(в верхней ступени используется нижняя боковая полоса). Опре-
делите ширину полосы частот сигнала, если Гмако=4 кГц, индекс
ЧМ равен 01= 15.
1.3.6. Напишите выражение для сигнала в системе ЧМ—ЧМ.
Определите ширину полосы частот сигнала, если индексы моду-
ляции 01=10, 02=15, fi = 100 кГц, Гмакс = 4 кГц.
1.3.7. Решить задачу 1.3.6 для вариантов числовых значений
величин, приведенных в табл. 1.10.
Таблица 1.10
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
01 9 * 8 7 5 8 10 8 6 6 7 6 5
02 7 7 8 9 9 10 9 9 8 7 9 8
h > «Гц 100 140 190 140 180 170 150 120 180 120 120 180
^макс> кГц 1 5 7 8 2 9 8 1 6 7 8 6
16
Рис. 1.4. Реализа-
ция сигнала дво-
ичной фазовой (от-
носительной фазо-
вой) модуляции
1.3.8. На рис. 1.4 дана реализация сигнала при двоичной ФМ,
содержащей 8 кодовых элементов. Напишите двоичный код, соот-
ветствующий этой реализации. Считаем, что первый элемент со-
ответствует символу 1.
• 1.3.9. Нарисуйте реализацию сигнала при двоичной AM с пас-
сивной паузой (символ 0 передается отсутствием излучения), со-
ответствующую коду 10111001.
1.3.10. Решить задачу 1.3.9 для следующих кодовых комби-
наций:
1) 10101101; 7) 00110011;
2) 11000101; 8) 01010101;
3) 10111011; 9) 00011100;
4) 11111000; Ю) 10000001;
5) 00011001; Н) 01111110;
6) 11110001; 12) 00111110.
1.3.11. Приняв, что на рис. 1.4 дана реализация сигнала при
двоичной ОФМ, восстановите код, соответствующий этому сигна-
лу, если: а) символ 1 передается сменой фазы предыдущего эле-
мента сигнала, а символ 0 — сигналом с той же фазой; б) символ
О передается сменой фазы предыдущего элемента сигнала, а сим-
вол 1 — сигналом с той же фазой.
1.3.12. Определите полосу частот, необходимую для передачи
сигнала при импульсной модуляции, если считать, что несущая
образована последовательностью прямоугольных импульсов дли-
тельностью т= 1 мкс, а ширина спектра определяется тремя пер-
. Isinix/T
выми лепестками функции -------— .
I л/т
1.3.13. Решите задачу 1.3.12 для значений т, приведенных в
табл. 1.11.
Таблица 1.11
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Т, МКС 5 2 10 8 20 40 90 60 30 70 6 4
1.3.14. Напишите выражение для сигнала АИМ—БМ. Какая
полоса частот требуется для его передачи, если ширину спектра
сигнала АИМ брать такую же, как в задаче 1.3.12?
17
1.3.15. Напишите выражение для сигнала ФИМ—БМ. Имеет-
ся ли различие в ширине спектра сигналов АИМ—БМ и ФИМ—БМ?
1.3.16. Найдите коэффициенты частотной избыточности для си-
стем ОМ, БМ, ФМ, ЧМ (при заданном индексе модуляции р и
Л<акс), АИМ и ФМ (при заданной длительности импульсов несу-
щей), ОМ—ЧМ и ЧМ—ЧМ.
Г л а в а 2. СООБЩЕНИЯ, СИГНАЛЫ, ПОМЕХИ
2.1. СООБЩЕНИЯ, СИГНАЛЫ И ПОМЕХИ
КАК СЛУЧАЙНЫЕ ПРОЦЕССЫ
Как сообщения, так и сигналы во многих случаях отображаются дискретными
(по уровням) процессами с дискретным временем (случайные последовательно-
сти). Их называют дискретными случайными процессами с элементами Д(/л),
которые могут принимать К различных значений аь ^2,...
Вероятность реализации отрезка (цепочки) дискретного случайного процес-
са с п элементами можно записать
P(a<i, ai2..щп)==Р(ац)Р(а^\ац)Р(а^\ац, ai2) ... Р(сцп\ац, аг2,...
... ,CLi(n— 1)) 1 (2,1)
где P(ain\azi, ai2, ацп-i)) — условная вероятность появления элемента atn в
момент tn при условии, что в предыдущие моменты tn-u ...,Л осуществлялась
реализация отрезка (цепочка) ап, а»2,, а<(п-п; A(th)=aib — реализация
символа в момент tk} i—значение элемента; k — момент времени (номер сим-
вола в цепочке).
Если отдельные символы цепочки появляются независимо (последователь-
ность Бернулли),
п
Р(ац,-, ain)= ПРШ, (2.2)
fc=i
где P(aik) —безусловная вероятность появления символа агк.
Важным видом случайной последовательности зависимых элементов являет-
ся цепь Маркова. Для простой цепи Маркова условная вероятность появления
некоторого элемента aih целиком определена, если известен предыдущий эле-
мент аг(л-1), т. е.
Р(ащ\ац,..., fli(ft-i)) = Р(0<fc|0i(fc-i)). (2.3)
Непрерывный случайный сигнал (процесс) X(t) с дискретным временем /а
полностью определен в п точках (сечениях), если известна л-мерная интеграль-
ная функция распределения:
Fn(xb х2,...,х„; f2,...,fn).=P{X(/i)^Xi,...,X(MCXn}, (2.4)
18
где Р{ } обозначает совместную вероятность событий, записанных в скобках,
X(th) представляет собой случайную величину и называется сечением случай-
ного процесса в момент th.
Частные производные функции распределения по всем Xh определяют п-
мерную плотность вероятности
. 4 \ Fn(xi> x2t...t хп; t19 t2,,.., tn)
X2.... tn)— дх1дх2...дхп
(2.5)
Марковская случайная последовательность обладает тем свойством, что при из-
вестном значении X(tk-i)=Xk-i вероятность значения X(tk) (6t>ffc-i) не за-
висит от значений процесса в любые более ранние моменты времени:
P(xkt 6i|xi, x2,... Л, t2t..., tk-i)=P(xk, tk\xk-i, th-i). (2.6)
Непрерывный и случайный процесс задан полностью, если для любого п и
любых моментов t2,..., tn в области его определения [О, Г] можно найти
функцию распределения. Математическое ожидание случайного процесса Х(/)
по ансамблю (или его среднее значение) определяется так:
оо
M{X(t)}^X(t) = tnx(t) = ^xw2(x, t)dx,
—со
(2-7)
где Wi(xt t)—одномерная плотность вероятности для сечения. Математическое
о ----
ожидание квадрата центрированного сигнала X(t)=X(t)—X(t) (дисперсия):
Л1{Ь(0} = Х2(0 = О{Х(/)} = <^(0= J[x-X(f)]2u>1(x. t)dx. (2.8)
—оо
Корреляционная функция случайного сигнала
Bx(ty, t2) = X(t1)X(t2) =
= J — ^K1)] [x2 — X(^)] w2 (Xi, x2; tlt t2)dx1dx2, (2.9)
—ool—oo
где w2(xi, x2-, fi, t2) —двумерная плотность вероятности для сечений X(t) в
моменты ti и t2. Иногда корреляционную функцию определяют без центрирова-
ния, тогда корреляционную функцию, определенную с центрированием, называют
функцией ковариации.
Случайный процесс, у которого математическое ожидание и дисперсия не
зависят от времени, а корреляционная функция зависит от разности t2—'Л=т,
но не от самих значений ti и t2, называется стационарным (в широком смысле).
Для стационарного случайного процесса |Вх(т) | ^а2х==Вх(0). Нормиро-
ванная корреляционная функция (коэффициент корреляции) стационарного про-
цесса 7?х(т) =Вх(т)/а2х. Интервал корреляции стационарного случайного процес-
са часто определяют по методу эквивалентного прямоугольника формулой
со
Тк = J|7?x(T)|dT. (2.10)
о
19
Для стационарных эргодических процессов с вероятностью, близкой к 1, ма-
тематическое ожидание по ансамблю равно среднему значению во времени од-
ной реализации процесса:
____ _______ 1 Т/2
mx = x(t)^x(t) = \im— Г x(t)dt; (2.11>
Т ->оо 1 _У/2
ё----- ё------ 1 П2 _
= №(/)« (/) = lim — f [x (t) - x (01® dt', (2.12>
Г-*» T -T/2
Bx (t) = X (0 X (t + T) « x (/) x (/ + r) =
1 T/2 ____ _______________
= lim— Г [x(t) - x(t)] [x(t + x)~ x(t)]dt. (2.13>
T->oo T _T/2
Для непрерывного (скалярного) марковского процесса диффузионного ти-
па двумерная плотность вероятности перехода w2(x, /|х0, /о) =w2(X(t) |Хр(/0))„
/>/о и одномерная безусловная плотность вероятности t^i(x, t) удовлетворяют
одному и тому же уравнению в частных производных Колмогорова — Фокке-
ра — Планка:
^2(х,'/|х0, /р) _ д [Л (х, /) ш2 (х, /|х0, /0)]
dt дх
, 1 д2[А2(х, t)w,(x, /|х0, /0)] _ с/ ч _
+ ~----------------—--------------; ау2(х, /|х0, /0) = 6(х — хв). (2.14>
2 дх2
Коэффициенты сноса Л1(х, /) и диффузии Л2(х, /) определяются как условные
математические ожидания:
A(x, /) = lim —^-[Х(/ + Д/)-Х(0|х(/)],
4' <2.1В>
Л2(х, /) = lim -{[Х(/ + A/) - X(t)]*\x(t)}.
д/->0 A t
Для стационарного марковского процесса коэффициенты сноса и диффузии не
зависят от времени:
Л!(х, /)=Xi(x), Л2(х, /)=Л2(х), (2.1G)
стационарная плотность
w (х) = lim w (х, /) (2.17)
/->оо
и может быть найдена согласно (2.14) из уравнения
“~“[Л2 (х) w (х)] = 2Ai (х) w (х) + cons/. (2.18)
Общее решение (2.18) содержит две произвольные постоянные, которые оп-
ределяются из условия нормировки J*a>(x)dX=l и граничного условия относи-
—оо
гельно w(x)t например
w(oo)=w(—оо)=0. (2.19)
Случайный процесс X(t) называется гауссовским, если его любая (при произ-
20
вольно выбранных сечениях) л-мерная плотность вероятности определяется фор-
мулой
™п(Х1> ХП> ^п) =
1 1 п п
= 1Z „ • exp — — S S vik (xt — mt) (xh — mk)
V (2л) D [ 2 z=i k=i
где vtk — элементы матрицы, обратной матрице корреляции
Вц (^i> ^i) В12 (/1, /2) • • tn)
В _ ^21(^2’ G) ^22(^2, ^2) • • «^2п(^2» ^п) .
Bni(tn, fj) Bn2(tnt t2) . . tn)
D — определитель матрицы В; тг = Х(/г).
(2.20)
Задачи
2.1.1. Дискретный двоичный источник выдает последователь-
ности из трех символов А (Л), Д(/2), A (t3). Возможные реализа-
ции источника имеют вероятности
Рх = Р (0х 02 03) = 0,1 ; Р5 = Р(010213) = 0,15;
Р2 = Р(0х 02 03) = 0,2; Рв = Р(0х1213) = 0,05;
Р3 = Р(1х0203) = 0,05; Р7 = Р (1х02 13) = 0,2;
Р4 = Р(111803) = 0,15; Р8 = Р (1Х 1213) = 0,1.
Найти: вероятности появления 2-символьных реализаций
P(cbi\ai2) и Р(йг2«гз); безусловные вероятности P(an), P(ai2)r
P(at3)\ условные вероятности переходов Р (ai31 анс^), Р(Яг10г2|
IОгз), р(ai31 ai2), Р(ai21аг1).
2.1.2. Решить задачу 2.1.1. для значений вероятностей 3-сим-
вольных реализаций, приведенных в табл. 2.1.
Таблица 2.1
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Рг 0,15 0,1 0,2 0,17 0,03 0,1 0,05 0,1 0,5 0,4 0,15 0,05
Р* 0,15 0,2 0,1 0,2 0,26 0,05 0,05 0,1 0,25 0,3 0,1 0,25
Рз 0,1 0,05 0,1 0,15 0,09 0,04 0,125 0,15 0,125 0,12 0,15 0,05
Р. 0,1 0,1 0,1 0,15 0,05 0,01 0,125 0,15 0,0625 0,06 0,2 0,2
Рь 0,15 0,2 0,3 0,1 0,16 0,2 0,175 0,2 0,0313 0,03 0,05 0,1
Рв 0,1 0,05 0,1 0,13 0,1 0,03 0,125 0,2 0,02 0,01 0,15 0,2
Р, 0,15 0,25 0,05 0,07 0,09 0,07 0,15 0,05 0,005 0,04 0,15 0,1
Р» 0,1 0,05 0,05 0,03 0,22 0,5 0,2 0,05 0,0062 0,04 0,05 0,05
2.1.3. Дискретный двоичный источник описывается простой
цепью Маркова с матрицей переходных вероятностей
|Р(1|1) Р(1|0)
|р(0|1) Р(0|0) ’
где Р (аг | а>) — вероятность символа аг при условии, что ему пред-
шествует символ а}.
21
Написать вероятности для всех 3-символьных реализаций ис-
точника.
2.1.4. Символы двоичного дискретного источника появляются
независимо от символов, ранее переданных (Р(аг|а;) =Р(аг)—
источник без памяти), причем Р(1)=0,8; Р(0)=0,2. Написать ве-
роятности для всех реализаций 3-символьных сочетаний источ-
ника.
2.1.5. Решить задачу 2.1.4 для значений вероятностей симво-
лов Р(1) и Р(0), приведенных в табл. 2.2.
Таблица 2.2
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Р(1) Р(0)' 0,75 0,7 0,62 0,4 0,35 0,41 0,5 0,8 0,36 0,17 0,25 0,38
0,25 0,3 0,38 0,6 0,65 0,59 0,5 0,2 0,63 0,83 0,75 0,62
2.1.6. Символы двоичного источника передаются с равной ве-
роятностью и независимо. Во сколько раз уменьшается вероят-
ность реализации цепочки из (п+2) символов по сравнению с ве-
роятностью реализации n-элементной цепочки?
2.1.7. Одномерная интегральная функция распределения ампли-
туды сигнала при замираниях определяется формулой F(U, t) =
= 1—exp (t72/t/2). Найти плотность вероятности амплитуды. Яв-
ляется ли процесс U (t) стационарным?
2.1.8. Интегральная функция совместного распределения ампли-
туд флуктуационной помехи в двух сечениях Л и t2 определяет-
ся выражением
Л (Ult и2; tlt i2) = {1 - exp [ - Ul/Ul (/)]} {1 -
- exp [ - U22/U22 (/)]}. > 0, U2 > 0.
Покажите, что F2(co, U2, t2)=Fi(U2, t2)\ F2(Ui, oo, ti) =
=Fi(Ui, t\). Найдите совместную плотность вероятности помехи
в двух сечениях. Покажите, что эти сечения независимы.
2.1.9. Совместная плотность вероятности мгновенных значений
шума в двух сечениях t\ и ^ = 6+т определяется гауссовским за-
коном:
w (nlt п2-,х)= ---- --. X
У(2Я)*О2(0о2 (т)]
1 Г ”1 (0 , п2 (0 _ 27? (т) n, (t) n2(t)
2 П - R2 (Т) ] [ О2 (0 + о2 (0 О1 (0 Оа (0
где /?(т) — нормированная корреляционная функция сечений;
<J2i(0, — соответственно дисперсии процесса в первом и
втором сечениях.
22
Покажите, что в каждом сечении распределение гауссовское
и при т=0 случайный процесс независим в двух сечениях.
2.1.10. Напишите совместную плотность двух сечений процес-
са Z(t)—s(t)+<N{t) (сигнал + шум) при условии, что сигнал де-
терминирован, а шум имеет гауссовское распределение.
2.1.11. Покажите, что для гауссовского процесса (см. задачу
2.1.9) распределение п2 при известном пх определяется гауссов-
ским законом:
/ О2 \2
t ( п2 — I
w (n»lni) — —======== ехр — А.---------
У2ло2(1-Яа(т)) |_ 2 11 - я» (т)]
Как модифицируется этот закон, если 7?(т)=0 и /?(т) = ±1?
Учесть одно из определений 6-функции:
_ / \ V 1 Г (х — в)2 ]
6 (х — а) = lim -т= exp I — --| .
' ’ а>_о 1/2ла2 Ч 2оа J
2.1.12. Полагая, что гауссовский процесс является марковским,
написать совместную плотность вероятности трех сечений про-
цесса.
2.1.13. Сечение дискретного случайного процесса при много-
уровневой модуляции принимает пять значений: Х\ =—2; Х2—1;
Хз=0; х4=1; х5=2 с вероятностями P(xi) =Р(хз) =0,1; Р(х2) =
= Р(х4)=0,2; Р(хз)=0,4. Найти математическое ожидание и дис-
персию сечения процесса.
2.1.14. Решить задачу 2.1.13 для распределений вероятностей,
приведенных в табл. 2.3.
2.1.15. Случайный узкополосный процесс определяется на ин-
тервале (—Т/2, Т/2) выражением Z(t) =.¥(/)cos©оН-У(Os*n®o^
где X(t), Y(t)—независимые стационарные гауссовские случай-
ные процессы с параметрами тх, ту, а2х, а2у, Рж(т) =Р«(т) =Р(т);
fo — средняя частота спектра; Р<С/о — граничная частота энер-
гетического спектра процессов X(t) и Y(t). Найти математическое
ожидание, дисперсию и корреляционную функцию процесса Z(t).
Доказать, что процесс Z(t) стационарен лишь при mx—my=Q,
о2х=о2у=о2-
2.1.16. В условиях стационарности процесса Z(t) из задачи
2.1.15 найти параметры mz, o2z, Pz(t) усреднением по времени
Таблица 2.3
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Pi 0,1 0,15 0,35 0,1 0,1 0,2 0,25 0,13 0,1 0,1 0,05 0,4
Р3 0,1 0,05 0,2 0,1 0,4 0,2 0,25 0,17 0,3 0,1 0,4 0,05
РА 0,2 0,25 0,25 0,1 0,4 0,2 0,1 0,15 0,1 0,5 0,4 0,4
рл 0,3 0,25 0,1 0,1 0,05 0,2 0,1 0,25 0,3 0,2 0,1 0,1
Рь 0,3 0,3 0,1 0,6 0,05 0,2 0,3 0,3 0,2 0,1 0,05 0,05
23
1- = nT~At
Рис. 2.1. Реализация случайного
хронного телеграфного сигнала
hx(t) и доказать, что они совпадают
со значениями, полученными ус-
реднением по ансамблю.
— 2.1.17. Найти корреляционную
_____________________________ функцию случайного синхронного
* телеграфного сигнала, реализа-
ции которого имеют случайный
равномерно распределенный
сдвиг Д/ относительно начала
координат (рис. 2.1), принимаю-
син' щего в дискретные моменты вре-
мени, кратные Т, значения ±h с
вероятностью 0,5 независимо от того, какое значение он имел на
предыдущем участке. Определить интервал корреляции этого про-
цесса.
2.1.18. Стационарный случайный сигнал имеет корреляционную
функцию В(т) = В(0)ехр(—р|т|), р=10~2 с-1. Найти интервал
корреляции Тк методом эквивалентного прямоугольника, а также
определив его как аргумент т, при котором В(т) =0,1В(0).
2.1.19. Решить задачу 2.1.18 для числовых значений величин,
заданных в табл. 2.4.
Таблица 2.4
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
₽, с-1 0,01 0,1 0,02 0,04 0,08 0,06 0,06 0,02 0,08 0,08 0,08 0,02
В(т)/В(0) 0,01 0,2 0,01 0,01 0,15 0,05 0,1 0,1 0,05 0,07 0,02 0,01
2.1.20. Неопределенный интеграл W(t)=^N(t)dt от стаци-
онарного процесса Af(/) с равномерным энергетическим спектром
(BN(ti, t2) = —Л)) и нулевым математическим ожиданием
называется процессом Винера. Докажите, что этот про-
цесс нестационарен и имеет математическое ожидание W(t)=0,
корреляционную функцию Bw(tlt t2) =Womiri[/i, /2]/2 и дисперсию
o2w(/1)=JV0/I/2.
2.1.21. Пользуясь тем, что корреляционная функция производ-
ной дифференцируемого (в среднеквадратическом) случайного
процесса X(t) равна B‘(tltt2)= , найти корреляционную
dti dtf
функцию производной винеровского процесса.
2.1.22. Стационарный случайный процесс имеет корреляцион-
ную функцию В (т)=В(0)ехр(—,р2т2), <р=10—2 с-2. Найти интер-
вал корреляции тк методом эквивалентного прямоугольника, оп-
ределив его как аргумент т, при котором В(т)=0,1 В(0).
2.1.23. Решить задачу 2.1.22 для числовых значений, заданных
в табл. 2.4.
24
2.1.24. Найти усредненную по времени корреляционную функ-
цию AM-сигнала иам(0 =)[£Ап+АамА(0]с08(®оН"<Ро)» если X(t) —
стационарный случайный процесс с корреляционной функцией
Bx{t).
2.1.25. Найти усредненную по времени корреляционную функ-
цию ОМ-сигнала «ом(0 =X(Z)cos(ooH--MOsin<W, где X(t)—со-
О о
пряжение по Гильберту от X(t)-, X(t) — стационарный случайный
процесс с корреляционной функцией Вх (т).
2.1.26. Найти усредненную по времени корреляционную функ-
О о
цию ФМ-сигнала иФМ(0 =^cos[(oo/+^om^(0], где ^(0—ста-
ционарный гауссовский случайный процесс с корреляционной функ-
цией
Вх(т) = Вя (0) Rx (т).
2.1.27. Показать, что для синхронного телеграфного сигнала
(рис. 2.1) математическое ожидание, дисперсия и корреляцион-
ная функция, найденные усреднением по времени, совпадают с
характеристиками, полученными в 2.1.17.
2.1.28. Показать, что нестационарная гауссовская плотность
вероятности случайного процесса x(t) с математическим ожида-
нием mx(t)=xoerat и дисперсией о2ж(/) = о2(1—er2at), а>0 удов-
летворяет уравнению Колмогорова — Фоккера — Планка (2.14)
при коэффициентах сноса Ai(/)=—amx(t) и диффузии Л2(/) =
= 2<i2/a.
2.1.29. В условиях предыдущей задачи, пользуясь уравнением
(2.18), показать, что стационарная плотность вероятности
1 / X2 \
w (х) = ,— ехр----------) .
V ’ 1/2лоа Н \ 2о’ /
2.1.30. Покажите, что гауссовская плотность вероятности пере-
хода ш(п2, //пн t—т) из задачи 2.1.9, в стационарном случае
(о21 = о22=о2) удовлетворяющая граничному условию а)(п2,
0/rti, 0)=6(п2—П1), удовлетворяет уравнению Фоккера — Планка
(2.14) с коэффициентом сноса Ai(t)=—amx(t) и диффузии
Л2(/) ==2о2/а только при выполнении условия
R' (т) = R (т) R' (0+), R (0) = 1, (2.21)
где J?'(0+) — значение производной R(x) при приближении к ну-
лю справа. Может ли существовать решение (может ли сущест-
вовать непрерывный стационарный марковский гауссовский про-
месс) в случае, когда нормированная корреляционная функция
R(x) непрерывна в точке т=0?
2.1.31. Докажите, что единственным решением уравнения (2.21)
является функция 7?(т)=ехр(—а|т|), а=— R'(0+), т. е. что ста-
ционарный гауссовский процесс с экспоненциальной корреляцион-
ной функцией является непрерывным марковским процессом.
25
2.2. СПЕКТРЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Спектральная плотность мощности G(f) (энергетический спектр) случайного
процесса определяет распределение средней мощности процесса по частоте. Од-
носторонняя спектральная плотность мощности, заданная при G0(f) =
=2G(f).
Средняя мощность процесса (дисперсия)
Рх = = ?G (/) df = JGO (/) df. (2.22)
—оо О
Спектральная плотность мощности центрированного стационарного случайного
о
процесса X(t) является преобразованием Фурье от корреляционной функции:
бх(Л= рх(т)е-'2я^т. (2.23)
—00
Отсюда
f Gx(f)^xdf. (2.24)
—оо
Пара преобразований Фурье связывает также усредненную по времени кор-
*
реляционную функцию нестационарного процесса Rx(x) и его усредненный
♦
энергетический спектр Gx(f). Ширину энергетического спектра часто определя-
ют по методу эквивалентного прямоугольника:
poWdf
О_____
Go мака
Вх(О)
Go макс
(2.25)
Произведение интервала корреляции тк и ширины энергетического спектра S
случайного процесса удовлетворяет соотношению
ТкГ9«1. (2.26)
Задачи
2.2.1. Найти энергетический спектр случайного синхронного те-
леграфного сигнала (см. задачу 2.1.17). Определить ширину энер-
гетического спектра F3 и убедиться, что ткГэ« 1.
2.2.2. Случайный стационарный процесс имеет равномерный
энергетический спектр G(f)=No/2 (белый шум). Показать, что
корреляционная функция этого процесса есть 6-функция, а его
дисперсия о2=В(0)=оо. Учесть соотношение Jexp(/2nfr)df=
=6(т).
2.2.3. Найти корреляционную функцию шума, имеющего рав-
номерную спектральную плотность, равную JVo/2 в полосе (—F,
4-tF) и нулю вне этой полосы. Показать, что сечения процесса,
26
разнесенные на интервал т, кратный величине 1/2F, не коррели-
рованы. Найти F3 и интервал корреляции тк.
2.2.4. Найти энергетический спектр стационарного марковского
гауссовского шума с экспоненциальной корреляционной функцией
В(т) =В(0)е~₽ |Т| . Найти ширину энергетического спектра F3
и оценить величину tKF3.
2.2.5. Найти энергетический спектр для стационарного случай-
ного процесса с гауссовской корреляционной функцией (задача
2.1.22) и его ширину F3. Оценить величину ткЛ.
2.2.6. Показать, что энергетический спектр случайного стаци-
онарного процесса Y(i) с корреляционной функцией Ву(т) =
=Вх(г)cosmqT определяется на положительных частотах при
fo^>F3 (F3 — ширина спектра процесса с корреляционной функ-
цией Bx(t)) соотношением
Gu(f)0 = Gx(f-f0),
где Gx (f) — энергетический спектр процесса X (I).
2.2.7. Найти усредненный энергетический спектр АМ-сигнала
(задача 2.1.24).
2.2.8. Найти усредненный энергетический спектр ОМ-сигнала
(задача 2.1.25).
2.2.9. Найти усредненный энергетический спектр ФМ-сигнала
(задача 2.1.26). Упростить это выражение при ^2фм^х (0)
2.2.10. Гармоническая несущая промодулирована по амплиту-
де двоичным случайным синхронным телеграфным сигналом (за-
дача 2.1.17). Найти усредненную во времени корреляционную
функцию и энергетический спектр АМ-сигнала.
2.2.11. Случайный синхронный телеграфный сигнал модулиру-
ет по частоте гармоническую несущую. Найти усредненную кор-
реляционную функцию и энергетический спектр, пользуясь пред-
ставлением сигнала двоичной ЧМ как суммы двух АМ-сигналов
(первый AM-сигнал имеет паузы при передаче символа 0, а вто-
рой— 1).
2.3. ОГИБАЮЩАЯ, МГНОВЕННАЯ ФАЗА
И ЧАСТОТА УЗКОПОЛОСНОГО СЛУЧАЙНОГО
ПРОЦЕССА
Узкополосный случайный процесс* Z(t) или любую его реализацию можно
представить в виде
z(Z)=r(/) со5ф(/), (2,27)
где ф(/) =соо/-Ьф(/) —мгновенная фаза; со0 = 2л/о — частота в полосе усредненно-
го, определенного на положительных частотах энергетического спектра процес-
са; r(t) и ф(0—огибающая и мгновенная начальная фаза, которые являются
медленно меняющимися по сравнению с cos (Hot функциями.
* Процесс называется узкополосным, если для него выполняется условие
(/о — средняя частота спектра).
27
Процесс (2.27) можно представить в виде
z(t) =x(/)cos a)Ot+y(t)sin (&ot, (2.28)
где x(t) и у (t) —квадратурные компоненты, определяемые соотношениями,
x(t) =r(t)cos qp(O; y(t) =r(Osin ф(0- (2.29)
Огибающую r(t) и фазу <р(0 можно определить по квадратурным компо-
нентам:
г(О = У^(0 + ^(О; <р (0 = arctg у (0/х (0. (2.30)
Квадратурные компоненты процесса z(t) можно представить как вещест-
венную и мнимую составляющие комплексной функции
Г V) = г (0 = X (0 + / у (t). (2.31)
Функция r(f) называется комплексной огибающей процесса. Комплексный
процесс z(t) можно представить следующим образом:
z (0 = г (0 е'2Я/» * = г (0 cos [<м + ф (01 + / Г (0 Sin [а>01 + <р (0] =
= г(0 + /Г(0, (2.32)
где z(t) —процесс, сопряженный процессу z(i).
Мгновенная частота процесса z(t) определяется соотношением
= = + (2.33)
Используя пару преобразований Гильберта
огибающую и мгновенную фазу сигнала можно определить так:
г(0 = ]Л2(О+Г2(О . t(0 = arctg-^-. (2.35)
При определении огибающей и фазы по Гильберту нет необходимости задавать
частоту процесса f0. Спектр по Фурье сопряженного сигнала Sz(/cd) связан со
спектром Sz(/co) соотношением
sJ(M _(/««»> »F« /<» (2.36)
ПР« />«•
Отсюда следует, что спектр комплексного сигнала z(t) существует только
на положительных частотах, причем
г (/) = 2jJs (/со) е/2я^ d/. (2.37)
о
Если узкополосный случайный процесс
Z(t) =X(t)cos cdq/+ Y(t)sin d)Qt=R(t)cos((dQt+^(t))
28
является гауссовским, а его квадратурные компоненты X(f) и Y(t) независи-
мы, то совместная плотность вероятности квадратурных компонент
, , 1 ( lx — mx(t)]2 [у— /п»(0]«)
w (х,и) =-------------exp J —1------- — ---------v п I. (2.38)
2яаж(0М0 Р( 2а2(0 2ст2(0 j 1
Здесь mv(t)—математические ожидания квадратурных компонент;
сг2х(0, <Л/(0 — дисперсии квадратурных компонент.
Поскольку
X(t)=R(t) cos Ф(0, Y(t)=R (0sin Ф (t),
можно перейти от декартовых координат х и у к полярным координатам г и
Ф и определить совместную плотность вероятности огибающей и фазы узко-
полосного случайного процесса
г ( (г cos ф — тх)9 (гsin ф — /п„)2 ]
(г, ф) =----------------exp J —-------1---------—--------1------— I.
2я аж (/) <3V (0 I 2а2 2q2 (0 J
(2.39)
Отсюда легко найти одномерные плотности вероятности огибающей W\(г) и
фазы о>1(ф).
Конкретный вид одномерных плотностей вероятности Wi(r) и Wi(q?) зави-
сит от соотношения между параметрами квадратурных компонент случайного
процесса.
Задачи
2.3.1. Найти огибающую, мгновенную фазу и мгновенную час-
тоту для БМ-сигнала
U (О = COS (w0 + Q) t + COS (w0 — Q)
Составить выражение для комплексного сигнала.
2.3.2. Найти огибающую, мгновенную фазу и мгновенную час-
тоту и составить выражение для комплексного сигнала, если про-
цесс описывается выражением
и (О = Vm COS (оо t-- р Um cos (соо + Q) t +
+ у ₽t/mcos (®0-&) t-
L
2.3.3. Дан сигнал z(t) = S (7zcos(coo/ + Qz)Z. Найти сопряжен-
i=i
ный сигнал z(t), а также огибающую, мгновенную фазу и час-
тоту.
2.3.4. Найти квадратурные компоненты АМ-сигнала
и (0 = Uo (1 + т cosQt) cos (aot + <р0)-
2.3.5. Дан сигнал u(t) = UiCOs ait ^U2cos vat. Найти огибаю-
щую и мгновенную фазу сигнала для случаев (о0=®1> ®о=
29
= (©i+<02)/2. Показать, что во втором случае огибающая совпада-
ет с огибающей по Гильберту.
2.3.6. Найти огибающую и мгновенную фазу ОМ-сигнала при
модуляции гармоническим колебанием sin Qt.
2.3.7. Показать, что сигналы, сопряженные по Гильберту с
сигналами zi (/) = t7mcostoo^ Z2(t) — UmsinG)ot (—рав-
ны zi (t) = t/msin W, z2(t) =—Umcosa0t лишь при T-+eo. Пока-
зать, что этот же результат следует из спектральных соотношений
Sz (]<>)) =—Sz(ja>) (при />0).
2.3.8. Найти огибающую и мгновенную фазу по Гильберту для
процесса z(t), имеющего спектральную плотность
I о
I 0 при
2.3.9. Найти одномерную плотность вероятности огибающей уз-
кополосного гауссовского случайного процесса, полагая, что ква-
дратурные компоненты симметричны (о2х=а22/=о2).
2.3.10. Найти одномерную плотность вероятности огибающей
узкополосного гауссовского случайного процесса, если квадра-
турные компоненты симметричны (о2х=а21/=п2) и mx=my=0.
2.3.11. Найти одномерную плотность вероятности огибающей
узкополосного гауссовского случайного процесса, если о2х=0,
mx=my=0.
2.3.12. Найти одномерную плотность вероятности фазы узко-
полосного гауссовского случайного процесса при условиях:
1) <*х = <^ = о2, тх = щу^ 0.
2) о2 = о2 = о2, тх = ту = 0.
2.3.13. Система фазовой автоподстройки частоты (ФАПЧ) эф-
фективно следит за фазой входного процесса, если она не превы-
шает величины л/n (и — целое число). Какова вероятность срыва
слежения, если на вход системы ФАПЧ поступает узкополосный
гауссовский шум, а и=2?
2.3.14. Показать, что при aP/5^> 1 обобщенное распределение
Рэлея можно приближенно представить в виде
и»х (И = W2лст2 ехр ( — (г2 + ap)/2a2)V^7ctp (1 + о2/8 ар г).
2.3.15. Найти плотность вероятности огибающей суммы гармо-
нического колебания с амплитудой Uo и узкополосного стационар-
ного гауссовского процесса с дисперсией о2. Построить графики
w(r) для /7о/<т=О; 1; 2; 3.
2.3.16. Найти среднее значение и дисперсию напряжения ынч
на выходе идеального ФНЧ, подключенного к линейному детекто-
ру с характеристикой преобразования
„ _ при ивх>0,
ивых ~ л ~
I 0 при ивх < 0,
30
если на вход детектора подается сумма гармонического сигнала
с амплитудой Um и узкополосного стационарного гауссовского шу-
ма с дисперсией о2.
2.4. ПРОСТРАНСТВА СООБЩЕНИЙ
И СИГНАЛОВ
Во многих вопросах, связанных с приемом и преобразованием сигналов,
весьма полезными оказываются геометрические представления различных функ-
ций (в дальнейшем будут рассматриваться только функции времени) в виде
векторов некоторого пространства.
Любую совокупность п вещественных чисел {хь х2, ..., *п} можно рассмат-
ривать как координаты точки в некотором л-мерном пространстве или коорди-
наты вектора xi = {хь ..., хп} в этом пространстве.
Сумма двух векторов х = {хь ... ,хп} и у= {уи ..., уп} дает вектор z=
= {zi,..., zn), координаты которого равны сумме одноименных координат век-
торов-слагаемых:
/=1,л. (2.40)
Если элементы Xi, уи Zi принадлежат одному и тому же пространству, то
это пространство относится к классу линейных.
Длина вектора в л-мерном пространстве (норма вектора) определяется со-
отношением
1|х|| = 1/ s х° . (2.41)
' 1=1
Расстояние между векторами х и у определяется как норма их разности
d (х, У) = ||х — у|| = р/ 2 (х, — .
(2.42)
Скалярное произведение х и у есть число
п
(ху)=5хгУг- (2.43)
fc=i
Если скалярное произведение двух векторов равно нулю, то такие векторы
называются ортогональными, а л-мерное пространство, в котором справедливы
соотношения (2.40) — (2.43), называется эвклидовым пространством и обозна-
чается Т?2.
Изложенные геометрические понятия используются в технике связи для на-
глядного представления сигналов и помех, которые характеризуются дискрет-
ной совокупностью координат. Такими координатами, в частности, могут быть
котельниковские отсчеты или коэффициенты ряда Фурье.
Если функции (сигналы и помехи) задаются на непрерывном интервале
(0, Г), то для их геометрического представления часто используют простран-
ство, которое называется гильбертовым и обозначается L2.
31
В пространстве L2 операции сложения и умножения задаются обычным об-
разом, а скалярное произведение определяется соотношением
1 т
(х (/) у (0) = — J X (0 у (0 dt. (2.44)
1 о
Норма вектора в пространстве задается следующим образом:
I ИХ (011 = у I х* (0 dt, (2.45)
а расстояние между векторами
d (х, у) = ||х (0 - у (ОН = ]/ -f-S (x(t)-у (t))*dt . (2.46)
Ансамбль сигналов {s<(/)} на интервале (0, Г) можно представить в виде
з,- (0 = 2 alf ср; (/), i =ТГМ. (2.47)
/=1
Здесь {<pt(0}—система ортонормированных базисных функций, удовлетворяю-
щих условию
т (0 при i j,
J<Pi(0<Pj(9<« = (2.48)
о 11 при i = j;
М —. число сигналов в ансамбле (при М = 2 — сигналы двоичные, при Л1>2 —
сигналы многопозиционные); п — число измерений (отсчетов) сигнала на ин-
тервале Т.
Коэффициенты разложения
т
Oo = j* МОфЯОЛ (2.49)
о
представляют собой проекции Z-го сигнала на j-ю базисную функцию.
Геометрически каждый сигнал ансамбля {si (/)} изображается точкой (век-
тором) в л-мерном пространстве с координатами (ап, а<2>т»а<я). При л=1
сигналы si(t) являются одномерными. Примером таких сигналов являются про-
тивоположные сигналы, которые изображаются двумя точками на одной пря-
мой.
Сигналы, удовлетворяющие условию
т
J s((t)Sj(t)dt=O, i^j, (2.50)
о
называются ортогональными.
Если сигналы удовлетворяют условиям
т
J si (0 si (0 dt = 0 при i ф j,
°т (2.51)
j si (0 SJ (0 dt = 0 при любых. i, /,
о
32
то они называются ортогональными в усиленном
смысле. Двоичные сигналы (ортогональные в уси-
ленном смысле) являются двумерными (л=2).
Они изображаются двумя ортогональными век-
торами на плоскости. Наиболее распространен-
ными многопозиционными сигналами являются
ортогональные, биортогональные и симплексные.
Биортогональные сигналы — совокупность сиг-
налов, содержащая ортогональные сигналы и
сигналы, противоположные им. Симплексные сиг-
налы характеризуются одинаковыми расстояния-
ми между собой. В л-мерном пространстве они
Рис. 2.2. Представление 3-
разрядных двоичных сиг-
налов в трехмерном про-
странстве
можно описать л-мерным
образуют правильный симплекс, число вершин
которого Л1=л+1.
Геометрическими представлениями можно
пользоваться и в том случае, когда сигналы
дискретны по уровням. Такие сигналы
вектором х = {xi,..., хп}> особенностью которого является то, что все его ко-
ординаты могут принимать лишь дискретные значения, которые обозначают О,
1, 2,...,т—1 (т — число дискретных состояний элемента сигнала). На рис. 2,2
в трехмерном пространстве показаны восемь векторов, соответствующих 3-раз-
рядным двоичным комбинациям ООО, 001, ..., ПО, 111.
Операция сложения элементов дискретного пространства вводится таким
образом, чтобы в итоге получились элементы, допустимые в данном простран-
стве. Для этого вводится операция сложения по модулю т. Например, при
т=2 правила суммирования
1®1=0; 1®0=1;
0®1 = 1; 0®0=0.
(2.52)
Расстояние между двоичными сигналами в л-мерных пространствах опре-
деляется чаще всего по Хеммингу:
п
rf(x, у)= (2.53)
1=1
т. е. его можно найти как результат сложения сумм по модулю 2 одноимен-
ных разрядов.
Геометрические представления справедливы и для случайных процессов с
той разницей, что их координаты в соответствующих пространствах следует
считать случайными числами, а сходимость сумм и интегралов понимается в
среднем.
3 адачи
2.4.1. Финитный сигнал длительности Т со спектром, ограни-
ченным полосой F, представляется усеченным рядом Фурье
s (0 = 2 ( V2 ак cos 6 — t+V2bK sin k — t
fe=l \ T T
2—53
33
причем L=FT. Найти норму вектора, представляющего сигнал
в 2£-мерном пространстве Эвклида. Дать физическое толкование
нормы этого вектора.
2А.2. По условию задачи 2.4.1 найти норму вектора, представ-
ляющего сигнал s(t) в 2Л-мерном пространстве Эвклида для ва-
риантов числовых значений, заданных в табл. 2.5.
наковые полосы частот F и длительности Г, дискретизированы по
Котельникову. Написать выражение для координат суммарного
сигнала в пространстве Эвклида. Найти норму суммарного сигна-
ла и выразить ее через нормы исходных сигналов в общем случае
и в случае равных норм исходных сигналов. Определить расстоя-
ние между сигналами.
2АА. Два сигнала, заданных на интервале Т, описываются вы-
ражениями
$i (/) = К2 ar cos у- t + 12 sin 1 + ]/2 а3 cos 3 t,
s2 (0 = /24?! cos у-1 + ]/2 b2 sin 2 у- t + ^2 b3 sin 3 у.1.
Определить координаты этих сигналов в пятимерном пространст-
ве Эвклида и вычислить скалярное произведение. Найти расстоя-
ние между сигналами Si (/) и $2 (О •
2.4.5. Решить задачу 2.4.4 для вариантов числовых значений,
заданных в табл. 2.6.
Таблица 2.6
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
7 7 2 8 5 3 5 1 7 9 9 2
а3 6 7 5 8 1 6 7 6 7 3 6 8
bi 7 1 1 1 5 9 8 1 6 6 4 3
ь9 10 6 4 1 4 5 2 8 5 2 1 1
h 7 1 8 6 8 3 4 5 3 4 6 9
34
2.4.6. В некоторой системе связи для передачи информации ис-
пользуются сигналы Si(Z) =acos(A©Z+<p) и Sz(f) = ocos(i©/ +
+<р+л/2) (k, I — целые числа), имеющие длительность Т. По-
казать, что данная система сигналов является ортогональной в
усиленном смысле. Найти расстояние между сигналами st(t) и
52 (0 в пространстве Гильберта.
2.4.7. Найти расстояние в пространстве Гильберта между сиг-
налами si (Z) =acos(fe©Z-|-<p), s2(f) =b cos(Z©H-<p+ji/2) для вари-
антов числовых значений, приведенных в табл. 2.7.
Таблица 2.7
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
a 4 10 3 3 8 4 2 4 7 7 7 8
b 3 6 2 7 2 7 2 10 5 3 10 7
k 3 10 4 5 8 4 9 2 10 7 6 2
I 4 1 5 3 2 3 10 10 5 7 5 3
2.4.8. Сигнал s\(t), имеющий длительность Т, задан рядом
Фурье
s (/) = at cos у- t + а2 cos 2 + а3 cos 3 у- t + bt siny-f-f-
+ fr2 sin 2 у-+ &3 sin 3 у-1
Найти координаты этого сигнала и показать, что норма сигнала,
вычисленная по этим координатам, равна норме в пространстве
Гильберта,
2.4.9. Показать, что в системе связи с широкополосными сиг-
налами, имеющими длительность 7’=20 мс и занимающими по-
лосу частот Г =10 кГц, можно создать:
а) ортогональную систему, содержащую 400 реализаций;
б) биортопональную систему — 800 реализаций;
в) ортогональную в усиленном смысле систему — 200 реализа-
ций.
2.4.10. Определить скалярное произведение сигналов $i(/) =
=Oi cos ©if и 52(Z) =02 cos ©г/, заданных на интервале Т, при усло-
вии Ш1+©2^>©1---©2=|Д©.
Найти нормы сигналов Si(f) и s2(t).
2.4.11. Решить задачу 2.4J10 для вариантов числовых значений,
заданных в табл. 2.8.
2.4.12. Показать, что расстояние между тремя произвольными
сигналами 5i (/), s2(f) и s3(Z), имеющими длительность Т, удовлет-
воряют условию
d(si, s3)^idl(52, s3) +rf(si, s2).
2*
35
Таблица 2.8
Вариант 1 2 3 4 5 6 7 8 9 10
ах, мВ 10 8 2 6 1 9 7 10 4 8
а2, мВ 5 10 5 3 10 5 9 3 9 3
©!» 10~*4, с—1 4,94 6,23 1,78 1,83 8,24 5,85 6,58 3,21 2,19 3,55
(02 е 10—*, С—1 4,87 6,15 1,79 1,75 8,37 5,95 6,61 3,31 2,17 3,49
Г, мс 40 90 40 80 70 50 20 80 100 20
2.4.13. На вход приемника поступают сигналы {яД/)}, задан-
ные на интервале (О, Т) в виде
si (0 = cos ср щ (t) + k sin ф Ui (/), i = 1, Л4,
где k — (произвольный коэффициент передачи; ф — фазовый сдвиг
в канале. Какими должны быть сигналы на передаче {ui(t)},
чтобы сигналы {МО} были ортогональными?______
2.4.14. По базисным функциям ф1 (t) = j/^E/Tcos со0/ и ф2(0 =
=—У2Е/Т$1п со о / составить -выражения сигналов биортогонально-
го ансамбля при 7И = 4. Изобразить полученные сигналы в виде
точек на плоскости. Найти расстояния между сигналами.
2.4.15. Заданы сигналы амплитудно-фазовой модуляции (АФМ-
сипналы) :
si (0 == У%Е1Т cos со0 /, $2 (/) = У 2 Е/Т cos (соо t + 2 л/3),
s3 (0 = У2Е1Т cos (сооt + 4 л/3), $4 (/) = 0.
Изобразить ансамбль АФМ-сигналов в виде точек на плоскости
•и 'определить расстояния между сигналами.
2.4.16. На рис. 2.3 изображен двумерный ансамбль симплекс-
ных сигналов (7И = п+1 =3). Найти расстояния между сигналами
ансамбля, полагая, что энергии всех сигналов одинаковы и рав-
ны Е.
2.4.17. По каналу связи передаются четыре 2-р<азрядные двоич-
ные комбинации, причем символу 0 соответствует первичный сиг-
нал А, а символу 1 — сигнал —h. Положим, что когда поэлемент-
Рис. 2.3 Двумер-
ный ансамбль сим-
плексных сигналов
ный приемник не может с большой надежно-
стью (из-за помех в канале) принять реше-
ние в пользу элементарного символа 1 или 0,
он регистрирует знак «?» (стирание), кото-
рый фиксируется нулевым уровнем. Изобра-
зить пространство первичных сигналов на
передаче и приеме.
2.4.18. Даны три 8-разрядные двоичные ко-
довые комбинации: bi = 01011001; b2 = 01000110;
Ьз“ 10110010. Показать, что расстояния
36
по Хэммингу между заданными комбинациями удовлетворяют
условию
d(bx, b3)^d(b1>b2) + d(b2, Ь3)
2.4.19. Решить задачу 2.4.18 для следующих вариантов 4-раз-
рядных двоичных комбинаций:
1) bl=0000 b2=llll b3=0010;
2) bl = 0001 b2=1110 b3=0011;
3) bi = 0010 b2=1101 b3=0101;
4) bi = 0011 b2=1100 b3=0111;
5) bj=0100 b2=1001 b3=1001;
6) b) = 0101 b2=1010 b3=0001;
7) bi = 0110 b2=1001 b3=0100;
8) bi = 0111 b2=1000 b3= 1000;
9) b!=1000 b2=01U b3=1011;
Ю) bi = 1001 b2=0110 b3=1110;
П) bi = 1010 b2=0101 ba=1100;
12) bj = 1011 b2=0100 b3=1010.
2.5. ОСНОВЫ ТЕОРИИ ДИСКРЕТИЗАЦИИ
ФУНКЦИЙ НЕПРЕРЫВНОГО АРГУМЕНТА.
ТЕОРЕМА КОТЕЛЬНИКОВА
В технике связи очень часто возникает необходимость представить детер-
минированные и случайные функции непрерывного аргумента (например, време-
ни или частоты) совокупностью их значений в дискретных точках (сечениях).
Такое представление называют дискретизацией функций по аргументу.
Очень часто дискретизацию осуществляют на основе теоремы В. А. Котель-
никова, согласно которой функция s(/), спектральная плотность которой отлична
от нуля только в полосе частот (—Т7, Г), полностью определяется своими зна-
чениями, отсчитанными в дискретных точках через интервал
М= 1/(2Г).
Значения функции s(t) в любой точке t выражаются формулой
s(/) = S s(W)
k=—co
sin 2nF (t — M0
2nF(/-W) ’
(2.54)
(2.55)
где s(kAt)—отсчеты непрерывной функции s(t) в дискретные моменты t=kAt.
Строго говоря, функция с ограниченным спектром не ограничена во времени
Хнефинитна) и, наоборот, финитная функция времени имеет неограниченный
спектр. Практический способ ограничения функции по спектру сводится к про-
37
пусканию сигнала через фильтр нижних частот (или полосовой фильтр). Отно-
сительная погрешность такого усечения спектра
____________ 7lS(/<o)|2df
6у - = F------------- (2.56)
s2(0 JlS(/<i))|2d/
О
в случае детерминированной функции s(t) и
lc(f)df
----------------- (2.57)
О
для случайного процесса,
Полагая, что одновременно ограничен спектр сигнала полосой F и его дли-
тельность интервалом Т, можно воспользоваться усеченным рядом Котельнико-
ва для приближенного представления сигнала:
£=1 2лг (* — кЫ)
В выражении (2.58) В=Т/Д/+1=2ЕГ+1—число отсчетов, приближенно
описывающих финитный сигнал $(/), или база сигнала. При 2ГТ^>1 можно
считать, что
В=2ГТ, (2.59)
Ряды (2.55) и (2.58) могут быть использованы и для представления слу-
чайных процессов. В этом случае коэффициенты указанных рядов являются
случайными величинами.
Если допустить, что воспроизведение процесса X(t) на приеме осуществля-
ется формированием ступенчатой функции Y(t) (рис. 2.4) с шагом Дг
У (0 = X (tt - Дг), ti<t< ti+1, (2.60)
то, полагая, что речь идет о стационарном случайном процессе, интервал оп-
ределения которого превосходит шаг воспроизведения Дг, можно найти средний
квадрат ошибки воспроизведения:
82 = [У (/) - X (/f)p = [X (/; - Дг) - X (/i)]2.
(2.61)
Осуществляя простые вычисления,
получаем относительную погрешность
воспроизведения
бв=82/Вх(0) =2[1-/?я(Дг)] , (2.62)
Рис. 2.4. К пояснению воспроиз-
ведения процесса X(t) путем фор-
мирования ступенчатой функции
38
где 7?х(Аг) —значение нормированной корреляционной функции процесса при
аргументе Ат.
Из (2.62) можно получить выражение для допустимой величины шага вос-
произведения Ат, исходя из заданной погрешности воспроизведения 6В:
ДГ=2?-1Ж(1—0,56в), (2.63)
где R~lx — функция, обратная нормированной корреляционной функции процесса.
Задачи
2.5.1. Определить относительную, погрешность бу при представ-
лении сигнала s(/)=aexp(—р2/2) (колокольный импульс) рядом
Котельникова, полагая, что полоса сигнала ограничивается в ре-
зультате пропускания через идеальный фильтр' нижних частот с
полосой F. Найти интервал дискретизации А/, полагая, что р=
= 20 с-1, бу=10%.
2.5.2. Найти относительную погрешность представления слу-
чайного синхронного двоичного сигнала рядом Котельникова при
произвольной граничной частоте. Определить величину бу, если
граничная частота выбрана равной и 2F3 (F3 — ширина энер-
гетического спектра, найденная по методу эквивалентного пря-
моугольника).
2.5.3. Решите задачу 2.5.1 для вариантов числовых значений,
заданных в табл. 2.9.
Таблица 2.9
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
₽, с-1 7 7 2 8 5 4 1 5 3 2 10 2
бу, % 6 9 5 6 3 4 3 5 8 2 8 2
2.5.4. Найти базу сигнала, представляющего собой последова-
тельность из п=15 элементарных прямоугольных двоичных им-
пульсов длительностью ти = 20 мс.
2.5.5. Решить задачу 2.5.4 для вариантов числовых значений,
заданных в табл. 2.10.
Таблица 2.10
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
л ти, мс 49 3 94 7 48 2 87 2 52 7 28 8 80 10 25 7 52 5 25 10 52 4 71 5
2.5.6. Случайный процесс с 'корреляционной функцией В (т) =
=В(0)ехр(—а|т|) дискретизирован с шагом А/. Найти погреш-
ность представления такого процесса рядом Котельникова в за-
висимости от параметров а и At
39
2.5.7. Решить задачу 2.5.6 для вариантов числовых значений,
заданных в табл. 2.11.
2.5.8. Нормированная корреляционная функция стационарного
случайного процесса, подлежащего дискретизации, =
= ехр(—а|т|). Найти шаг воспроизведения Дт, при котором отно-
сительная погрешность воспроизведения 6В равна 1%, а=0,1 с”1.
Сравнить полученную величину Дг с интервалом дискретиза-
ции по Котельникову Д/ (см. задачу 2.5.6), обеспечивающим та-
кую же погрешность 6У.
2.5.9. Для случайного процесса, имеющего нормированную кор-
реляционную функцию 7?х(т)=ехр>(—р2т2), найти шаг равномер-
ной дискретизации Дг, при котором обеспечивается заданная от-
носительная погрешность воспроизведения 6В.
2.5.10. Решить задачу 2.5.9 для вариантов числовых значений,
заданных в табл. 2.12.
Таблица 242
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
я - * 3 0,3 1 0,2 4 0,8 4 0,5 10 0,5 1 0,1 2 1 7 0,8 8 1 3 0,7 7 0,4 5 0,8 2
Г л а в а 3. КАНАЛЫ СВЯЗИ
3.1. МОДЕЛИ КАНАЛОВ СВЯЗИ И ИХ
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
Под каналом связи в широком смысле понимают совокупность средств, предна-
значенных для передачи сообщений и соответствующих им сигналов. Для при-
мера на рис. 3.1 представлена структурная схема канала связи при передаче
дискретных сообщений.
Классификацию каналов связи можно осуществлять по различным критери-
ям, в частности, по характеру сигналов на их входе и выходе. С этой точки
зрения различают три типа каналов.
40
Рис. 3.1. Структурная схема канала связи при передаче дискрет-
ных сообщений
Дискретные каналы. На входе и выходе таких каналов наблюдаются ди-
скретные сигналы (как по уровням, так и состояниям информационного пара-
метра во времени) или символы из конечномерного ансамбля. Примерами ди-
скретных каналов являются каналы, заданные между точками А—А, В—В, А—В,
В—А на (рис. 3.1.
Следует подчеркнуть, что дискретность или непрерывность канала опреде-
ляется только характером информационных параметров сигналов на его входе и
выходе.
Дискретный канал математически описан, если заданы алфавит кодовых сим-
волов на входе bi (i=l, m) вместе с их вероятностями P(bi)*, алфавит кодо-
вых символов на выходе (/’=1, m') и значения вероятностей переходов
P($j\bi) (t=l, /и; / = 1, т’), т. е. вероятностей того, что на выходе канала по-
явится символ 6j при условии, что на вход подан символ bi. (Если интересовать-
ся скоростью передачи информации по каналу, то следует также задать число
символов, подаваемых в среднем в единицу времени на вход канала. Однако эта
характеристика рассматриваться не будет.)
Совместная вероятность подачи символа bi на вход и появление символа ф
на выходе
P(bi, ^)=Р(Ь^Р(^\Ьг)=Р(^)Р(Ь^Ь^. (3.1)
Вероятность того, что на вход подан символ bi при условии, что на выходе
появится символ 6j (апостериорная вероятность)
Р (>,!>,)- —(3.2)
tn
2 Р(Ы)Р(ЬДЬ1)
f=i
(формула Байеса).
Дискретный канал называется однородным (стационарным) и без памяти, ес-
ли вероятности переходов P(tij\bi) для каждой пары i, j не меняются во времени
и не зависят от того, какие символы передавались ранее.
♦ Если источник имеет память, то должны быть заданы вероятности цепо-
чек символов или априорные и условные вероятности передачи символов.
41
Если эти вероятности зависят от времени, канал называется неоднородным
(нестационарным); если же они зависят от символов, переданных ранее, то ка-
нал называется каналом с памятью.
Если в однородном дискретном канале алфавиты на входе и выходе оди-
наковы (т=т') и для любой дары /=/=/ вероятности P(tij\bi)}=p0, а для пары
=q=l—(т—1)р0, то такой канал называют симметричным кана-
лом без стирания.
Если объем алфавита символов на выходе канала т' превышает объем алфа-
вита входных символов т, канал называют каналом со стиранием. Чаще всего
на практике встречаются дискретные каналы со стиранием, в которых m'=m+L
Для любой модели дискретного канала можно записать, пользуясь сложени-
ем в дискретном векторном пространстве (поразрядным, по модулю основания
кода т)
g[n] _ gtn] Е[п], (3.3)
где Btn] и ВСП] — случайные последовательности (кодовые комбинации) из п
символов на входе и выходе канала; ЕСП] — случайный вектор ошибки, который
в общем случае зависит от BlnJ. Различные модели отличаются распределени-
ем вероятностей вектора EtnJ.
При двоичном кодировании (т=2) компоненты (разряды) вектора ошиб-
ки принимают значения 0 и 1. Всякая 1 в векторе ошибки означает, что в соот-
ветствующем месте передаваемой последовательности символ принят ошибочно,
а 0 означает безошибочный прием. Число ненулевых символов в векторе ошибок
называется его весом. Он равен расстоянию по Хеммингу d(B(n], BtnJ) между
переданной и принятой кодовыми последовательностями.
Дискретно-непрерывные каналы. В таких каналах сигналы на входе ди-
скретны, а на выходе — непрерывны (по уровням) или наоборот. Примерами
таких каналов являются каналы, заданные между точками В—Z; А—Z±; Z—А
(см. рис. 3.1). Очень часто в технике связи определяют или обрабатывают не-
прерывные сигналы лишь в дискретных точках оси времени. В этом случае
говорят о сигнале или соответствующем канале с дискретным временем.
Будем для определенности в дальнейшем считать, что дискретно-непрерыв-
ный канал имеет дискретный вход и непрерывный выход. Дискретно-непрерыв-
ный канал математически описан, если заданы алфавит входных символов bi
вместе с их априорными вероятностями P(bi) и плотности переход-
ных вероятностей oj(z|6f) того, что на выходе канала появится реализация ко-
лебания z(t) при условии, что на вход поступил символ bi.
Эти плотности называют функцией правдоподобия того, что передан сим-
вол bi при условии, что фиксирована на выходе канала реализация колебания
z(Z).
Если z(t)=Si(f) +n(t) [st(/) — принимаемый на интервале анализа Т сиг-
нал, обусловленный подачей на вход канала символа n(t)—реализация ад*
дитивного (линейно складывающегося с сигналом) шума в канале], то в том
случае, когда сигнал Si(t) полностью детерминирован (его параметры извест-
ны точно в месте приема),
®(2|&<)=ш[5<(О+л(0|Ь<] =ол[п(0], (3-4)
т. е. функция правдоподобия определяется плотностью вероятности шума в ка-
нале.
42
При дискретном времени функция правдоподобия tw(z|6t)—это многомер-
ная (n-мерная) плотность вероятности. При п->оо можно получить функцию
правдоподобия (при непрерывном времени — функционал правдоподобия). Так,
если в канале действует гауссовский аддитивный белый шум N(t) со спект-
ральной плотностью NQt то
( 1 Т ч
W [2(01^1 = к exp - — J [z(0-st (0]« . (3.5)
I '''о о J
где X определяется условием нормирования *.
Вероятность того, что при заданном элементе принятого колебания z(t) был
передан символ bi (апостериорная вероятность), определяется формулой
Р (bi) w (z|M
P[6i|z(0]=K-LjZ-TLj2 . (3.6)
W(2)
m
где w(z) = S P(bi)w(z\bi)—плотность вероятности элемента сигнала z(t).
i=\
Если плотности вероятности w(z]bi) для любого сочетания z(f), bi оста-
ются постоянными во времени и не зависят от того, какие символы bt и эле-
менты z(t) фиксировались ранее, то дискретно-непрерывный канал называется
однородным (стационарным) и без памяти. Если плотности вероятности o>(z|6t)
зависят от времени, то канал неоднороден (нестационарен). Если они зависят
от предыдущих символов, то канал обладает памятью.
Непрерывные каналы. В таких каналах сигналы на входе и выходе непре-
рывны (по уровням).
Для математического описания непрерывного канала надо задать плотно-
сти вероятности входных сигналов w(u) и условные плотности вероятности пе-
рехода w(z]u).
Канал однороден (стационарен), если плотности вероятности переходов
w(z]u) не зависят от времени. Канал не имеет памяти, если значения выходно-
го сигнала z(t) в момент t зависят только от значения входного сигнала u(t)
в тот же момент времени. Если же значения сигнала z(t) в момент t зависят
от значений входных сигналов и в предшествующие моменты времени, то канал
имеет память.
3 .а д а ч л
3.1.1. На вход канала связи на интервале Т поступает сигнал
Ui(t) =acos(oo^+r2jn//n), где а — произвольная амплитуда; соо,
пг — постоянные; f=»l, m. С выхода канала снимается сигнал
Si(t) =&acos((W+<p), где ср — случайная фаза, равномерно рас-
пределенная на интервале (0, 2л). Показать, что по амплитуде
сигналов канал является непрерывным, а по параметру <р — диск-
р етно нн епр ер ывным.
3.1.2. На вход канала поступает периодическая последователь-
ность прямоугольных импульсов, про1модулированных по фазе не-
* В дальнейшем будем интересоваться н01р|МирО1вамными значениями функ-
ционалов правдоподобия w(z\bi)!K или их отношением. Поэтому вопросы схо-
димости коэффициента К. здесь рассматриваться не будут.
,43
Прерывным сообщением, а с выхода снимается аддитивная смесь
этого сигнала и флуктуационного шума. Показать, что по ампли-
тудам сигнала канал является дискретно-непрерывным, а по от-
ношению к фазам импульсов — непрерывным.
3.1.3. Показать, что вероятность того, что при передаче симво-
лов по двоичному однородному симметричному каналу без памяти
и стирания будет принято ошибочно q из п символов, определяет-
ся формулой
P(q)=Cinp4(l—ро)п~«.
3.1.4. Определить вероятность ошибочного приема q символов
в последовательности из п символов, передаваемой по двоичному
однородному симметричному каналу без памяти и стирания, если
вероятность ошибочного приема элементарного символа ро.
3.1.5. Решить задачу 3.1.4 для вариантов числовых значений,
заданных в табл. 3.1.
Таблица 3.1
Вариант 1 2 3 4 5 6
п 9 7 5 7 7 11
Я 3 2 2 4 5 2
Ро 4-10—5 9-10-5 4-10—5 5-10—5 2-10-8 2-10-3
Вариант 7 8 9 10 11 12
п 9 15 8 6 7 8
я 2 7 5 4 5 6
Ро 4*10—5 з. 10-5 3-10-8 5-10-5 7-10-3 5.10-3
3.1.6. Определить среднее число ошибок в цепочке из п симво-
лов в стационарном двоичном симметричном канале без памяти
и стирания, если вероятность ошибочного приема элементарного
символа ро. Упростить полученный результат для ро«^1.
3.1.7. Определить апостериорные вероятности передачи симво-
лов P(bi\6j), Р(&,|?) в дискретном однородном симметричном ка-
нале без памяти со стиранием, заданном вероятностями перехода
= 1—pi при t=/; P(#j|6i)=po при P(6m,\bi) =
=P(?\bi)=pc при pl=pz-\-(m—l)p0 (i=l, m; ? — сим-
вол стирания в месте приема, которому присвоен номер т'=т+
+ 1).
3.1.8. Вычислить апостериорные вероятности передачи симво-
лов в дискретном однородном симметричном двоичном канале со
стиранием для вариантов числовых значений, заданных в табл. 3.2.
3.1.9. Для дискретного однородного канала без памяти со сти-
ранием (m'=/n+l) найтй среднюю (безусловную) вероятность
правильного приема символов рщ>ав, безусловную вероятность оши-
44
Таблица 3.2
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Р1 0,99 0,9 0,6 0,8 0,7 0,8 0,9 0,9 0,6 0,7 0,9 0,75
Ро 0,005 — — — 0,2 0,15 0,09 — — — 0,06 0,22
Рс —. 0,06 0,35 о,1 — — —. 0,02 0,35 0,1 — —
Р&) 0,5 0,4 0,9 0,5 0,8 0,3 0,3 0,8 0,9 0,4 0,6 0,3
d (М 0,5 0,6 0,1 0,5 0,2 0,7 0,7 0,2 0,1 0,6 0,4 0,7
бочного приема символов рош, безусловную вероятность стирания
символов Рст, если известны условные вероятности правильных
переходов P(6j\bi), j—i, ошибочных переходов P(6j\bi), j=£i=£m',
и -стирания P(bm'\bi) =P(?\bi), и безусловные вероят-
ности передачи символов p(bi).
3.1.10. Показать, что характеристики однородного канала без
памяти со стиранием (пг' = пг+1) не зависят от априорных веро-
ятностей передачи символов и определяются только вероятностя-
ми переходов при.' условиях
= 1—ро—ре, P($j\bi)=pe, P(?\bi)=pc
(симметричный канал).
3.1.11. Двоичный однородный симметричный -канал со стирани-
ем характеризуется вероятностями переходов, заданными в табл.
3.3. Найти апостериорные вероятности передачи символов, безус-
ловную .вероятность ошибочного приема и безусловную вероят-
ность стирания. Априорные вероятности передачи символов счи-
тать одинаковыми:
Р(Ь1)=Р(Ь2)=0,5.
Таблица 3.3
Вариант 1 2 3 4 5 6 7 8 9 10 И 12
Ро 0,01 0,01 0,02 0,02 0,03 0,015 0,02 0,03
Р1 0,7 0,69 —- 0,75 0,8 —. 0,7 0,8 —. 0,7 0,65 0,9
Рс — 0,29 0,2 — 0,19 0,2 — 0,15 0,25 —• 0,3 —
3.1.12. Задан двоичный однородный канал без стирания и с па-
мятью, простирающейся на два соседних сим-вола. Пусть ошибки
в таком канале описываются простой цепью Маркова, причем ве-
роятность того, что данный символ будет принят ошибочно, рав-
на pi при условии, что предшествующий -символ принят верно, и
р2, если предшествующий символ -принят ошибочно. Найти для
такого капала безусловную (среднюю) вероятность ошибки и объ-
яснить, почему при заданной модели канала ошибки группируются
при p2>pi и рассредотачиваются .при pi>p2.
3.1.13. В дискретном канале переданная двоичная последова-
тельность В181= 11000111, а вектор ошибки £[’1= 1-0101010. Напи-
45
сать принимаемую последовательность ШЧ Чему равен вес век-
тора ошибки? Для какого канала характерен такой вектор ошиб-
ки: для канала с памятью (с группированием ошибок) или для
канала без памяти?
3.1.14. В дискретном канале переданная и принятая кодовые
комбинации равны В^81= 11000111, В[8^=11111111. Написать вектор
ошибки. Чему равен его вес? Для какого канала характерен та-
кой вектор ошибок: для симметричного или несимметричного ка-
нала, с памятью или без памяти?
3.1.15. Решить задачу 3.1.13 для следующих вариантов пар
принятых и переданных кодовых комбинаций:
1) B=10101 В=01010 2) В=Ш11 В =00011
3) В=00011 в = 11000 4) В = 00100 В =10001
5) В = 00111 в = 10000 6) В = 01010 В = 10011
7) В=010П В = 10100 8) В = 11100 В=00011
9) В= 10111 В = 01000 10) В=01111 В = 10000
Н) В=01001 в = 10110 12) В=110П В=00000
3.1.16. На вход дискретно-непрерывного канала на тактовом
интервале Т поступают двоичные сигналы Ui(t) = асоэ(<во^+фо)
или —асо5(<о<^+фо) (модуляция фазы на л). Колебание
на выходе канала на интервале анализа Т можно представить в
виде
2(/) +n(t), Si(t) — k(/)щ(/—r),
где k(t), т — коэффициент передачи канала и запаздывание сиг-
нала в канале; га(/) — реализация нормального флуктуационного
шума с равномерным энергетическим спектром.
Полагая, что все параметры сигнала известны точно в месте
приема (модель канала с постоянными параметрами), а колеба-
ние г(/) анализируется на интервале Т в дискретных сечениях 4.
кратных величине &t=l/(2F), написать выражения для функций
правдоподобия w(z|si) и w('z|s2).
3.1.17. По условию предыдущей задачи найти выражение функ-
ционала правдоподобия w('z[b{), полагая, что в канале действует
белый шум (F->-oo).
3.1.18. Показать, что в дискретно-непрерывном канале сравне-
ние величин апостериорных вероятностей передачи символов
p(bil'z) с различными номерами для выбора наибольшей сводится
к сравнению функций правдоподобия w(z|bi), умноженных на
P(bi).
3.1.19. При передаче узкополосных сигналов m(t) колебание
на выходе канала можно часто представить в виде z(f)=Sj(f) +
+«(/),. где Si(t) =&cos0K«i('O—ksmQKUi(t), Ui(t)—сопряженный
46
сигнал, a k ih 0к — коэффициент передачи /и фазовый сдвиг в ка-
нал е.
Полагая, что n(t) — реализация стационарного аддитивного
гауссовского белого шума со спектральной плотностью мощности
No, а фаза сигнала случайна и имеет равномерное распределение
на интервале —л, я (модель канала с неопределенной фазой),
найти функционал правдоподобия.
3.2. ИЗМЕНЕНИЯ ФОРМЫ СИГНАЛОВ,
ОБУСЛОВЛЕННЫЕ ХАРАКТЕРИСТИКАМИ
НЕПРЕРЫВНОГО КАНАЛА
Верность связи (степень соответствия переданного и принятого сообщений)
определяется главным образом искажениями сигналов в непрерывной части ка-
нала, а также присутствующими в канале аддитивными шумами*
Под искажениями понимают нежелательные изменения формы передавае-
мых сигналов, которые могут возникнуть как в линейных, так и нелинейных
звеньях канала *.
Сигнал s(t) в момент t на выходе произвольной физически осуществимой
линейной системы (канала) можно связать с сигналом на его входе u(f) ин-
тегралом Дюамеля
S(O= ]g(t, x)u{t-^)dx, (3.7)
О
где g(t, т) —импульсная переходная характеристика системы или реакция сис-
темы в момент t на б-импульс, поданный на вход в момент t—т.
Протяженность переходного процесса g(t, т) по переменной т называют
интервалом рассеяния во времени (или памятью) линейного канала. Обозначим
его через тр.
По методу равновеликого прямоугольника интервал рассеяния во времени
определяется соотношением
J |£(Лт)| dx
td= -—----------- • (3.8)
lg (f, т)Iмакс
Зависимость g(t, т) от аргумента t свидетельствует о том, что параметры
канала меняются во времени, что приводит к расширению спектра выходного
сигнала s(t) по сравнению со спектром входного сигнала. Это расширение
спектра (интервал рассеяния канала по частоте Гр) можно найти, если опре-
делить преобразование Фурье от s(t) или от g(t, т) (по переменной t, считая
т параметром), а затем и ширину (например, методом равновеликого прямо-
угольника) квадрата амплитудного спектра (спектра мощности).
* Следует заметить, что термин «искажения» относится к изменению формы
сигнала в тех звеньях канала, которые по своему назначению не должны это-
го делать. Вместе с тем следует иметь в виду, что ряд устройств (звеньев) ка-
нала связи выполняет целевые преобразования входных сигналов, немыслимые
без изменения их формы, например модуляция, демодуляция, интегрирование,
дифференцирование и др.
47
Коэффициент рассеяния
6p=TpFp (3.9)
является важной инженерной характеристикой любого канала связи.
Вместо системной характеристики линейной системы g(t, т) часто пользу-
ются характеристикой £(/<o, f)exp[j(p(co, /)], называемой передаточной
функцией системы. t
Характеристики g(tf т) и k(j®, t) связаны парой преобразований Фурье:
^(/со, 0 = J* g(/, т)е~/<оТ dr, (3.10)
—оо
g(t,t)= J kda.tjef^df. (3.11)
—со
В нелинейных звеньях канала связи выходной сигнал в момент t часто
можно связать с входным сигналом u(t) в тот же момент врейени некоторой
заранее известной (но не всегда взаимооднозначной) зависимостью (амплитуд-
ной характеристикой)
®(0=ф[«(0]. (3.12)
Такие нелинейные звенья называют неинерционными.
Задачи
3.2.1. Показать, что если параметры линейного канала не ме-
няются во времени (канал стационарен), его системные характе-
ристики удовлетворяют условиям:
g(t, т)=^(т); As(co, t)=k(a>).
3.2.2. Если сигналы на выходе и входе канала связаны соотно-
шением s(t)=>ku(l—тс), где k, Тс — известный ^коэффициент пере-
дачи и запаздывание в канале, то говорят, что отсутствуют иска-
жения формы сигнала. Показать, что в линейном канале искаже-
ния сигнала отсутствуют, если системные характеристики' канала
удовлетворяют условиям:
g(t, т) —тс); Ж (/со, 0 =Лехр(—}о>тс),
т. е. импульсная переходная характеристика имеет вид S-функции
(тР=0), амплитудно-частотная характеристика £(<о) не зависит
от частоты, а фазочастотная характеристи-
______R_________ ка <р(®) меняется линейно с частотой.
1—* 3.2.3. Пусть некоторый линейный канал
_|с с постоянными параметрми моделируется
и<™ — электрической схемой (четырехполюсни-
ком), показанной на рис. 3.2.
“ 1 Определить интервал временного рас-
Рис. 3.2. модель линей- сеяния (память) такого канала по мето-
ного канала с постоян- ДУ равновеликого прямоугольника, если
ными параметрами /? = 100 Ом и С=100 мкФ.
48
Таблица 3.4
Вариант 1 2 3 4 5 6 7 8 9 10 II 12
Rt Ом 100 90 75 150 200 170 300 150 120 500 50 75
С, мкФ 20 0,2 10 100 0,5 0,05 5 10 15 10 25 100
3.2.4. Решить задачу 3.2.3 для числовых значений R и С, задан-
ных в табл. 3.4.
3.2.5. Пусть передаточная функция некоторого линейного кана-
ла не зависит от частоты й(<в, t) =i&(/).
Показать, что в таком канале импульсная переходная харак-
теристика g(t, т) =Л(/)б(т), а сигнал на выходе s(rf) связан с сиг-
налом на входе соотношением s(/) =k(t)u(t), т. е. канал представ-
ляет собой безынерционный перемножителъ.
3.2.6. Для модели канала из предыдущей задачи найти интер-
вал рассеяния по частоте, полагая, что fe(/)=exp(—а/2).
3.2.7. Решить задачу 3.2.6 для вариантов значений а, заданных
в табл. 3.5.
Таблица 3.5
Вариант 1 2 3 4 5 6 7 8 9 10
а, с-2 10а 103 50 1,7-10s 10 5-Ю3 40 6-Ю2 5- 10а 101
3.2.8. Пусть некоторый линейный канал описывается импульс-
ной переходной характеристикой
g (t, т) = е~“*т е-0^, т О, t 0, ах > 0, а2 > 0.
Найти коэффициент рассеяния такого канала.
3.2.9. Найти коэффициент рассеяния канала из задачи 3.2.8
для числовых значений си и аг, заданных в табл. 3.6.
Таблица 3.6
Вариант 1 2 3 4 5 6 7 8 9 10
а1( с—1 0,01 0,02 0,05 0,04 0,4 0,45 0,61 0,17 0,015 0,15
«г, с-1 0,2 0,05 0,17 0,04 0,05 0,2 0,17 0,25 0,4 0,05
3.2.10. По линейному каналу с передаточной функцией k(j(a, t) =
=ife(co, t) exp [/<p(о, /)] передается узкополосный сигнал u(t) =
=A(l/)cos[to£+0 (/) ].
Показать, что огибающая выходного сигнала A'i(t) =k(<a, t)X
ХА(1), а его фаза 0'(/) =0i(rf) +<р(<в, t), т. e. канал вносит допол-
нительную модуляцию амплитуды и фазы.
49
Рис. 3.3. Модель многолуче-
вого канала
3.2.11. Некоторый линейный канал
моделируется неискажающей длинной
линией с отводами, создающими запаз-
дывание т<(0 и изменение уровня ki(t)
(модель многопутевого или многолуче-
вого распространения, рис. 3.3). Соста-
вить для заданной модели выражения
для системных характеристик g(t, т) в
k(a>, t). Записать соотношение для вы-
ходного сигнала s(/).
3.2.12. Предположим, что коэффи-
циент передачи линейного канала меня-
ется случайно соответственно по закону
Рэлея и односторонне-нормальному закону (см. § 2.3), а надеж-
ный прием на фоне шума обеспечивается, если амплитуда сигнала
в месте приема превышает пороговое значение A'nop—knopA=kUm>
£>1; иш — среднеквадратическое значение шума в канале.
Найти надежность связи в рэлеевском и односторонне-нормаль-
ном канале как вероятность выполнения неравенства
k i^nop — Л U ш!А.
3.2.13. Решить задачу 3.2.12 для вариантов числовых величин,
заданных в табл. 3.7.
Таблица 3.7
Вариант 1 2 3 4 5 6 7 8 9 10 И 12
А', мкВ 494 948 487 876 752 528 280 286 667 205 . 298 147
иш, мкВ 50 100 120 70 95 90 150 70 125 300 250 100
k 4,9 5,2 2,8 6,2 5,8 2,2 1,4 4,7 4,1 1,8 5,1 1,9
3.2.14. Пусть некоторый линейный канал с постоянными пара-
метрами, предназначенный для передачи сигналов в полосе час-
тот (0, 'Гмакс), имеет передаточную функцию
tfe (/о) = Ло e~A|“2e_-i(ai“+a2“;).
Напишите выражения для коэффициента передачи ^(/<в)кор линей-
ного четырехполюсника, обеспечивающего полную коррекцию ха-
рактеристик канала в заданной полосе частот.
3.2.15. Для канала из задачи 3.2.14 найдите коэффициент пере-
дачи корректирующего четырехполюсника и постройте графики
амплитудно-частотных и фазочастотных характеристик канала и
корректирующего четырехполюсника для вариантов числовых зна-
чений величин, заданных в табл. 3.8.
3.2.16. Пусть в некотором нелинейном звене канала связи сиг-
налы на выходе и входе связаны соотношением
is =0,1 и—0,Зы3.
50
Таблица 3.8
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
До 4ХХ, С А, са а2, с2 ^макс, Гц 0,07 2 10“7 ю-в 400 0,07 8 10-в 10“8 900 0,02’ 6 10“8 10“7 400 0,08 6 10—® 10“8 900 0,05 7 10“8 10“б 700 0,03 6 10—» 10“8 500 0,05 2 10—8 10“ « 200 0,01 1 10“7 10“7 900 0,07 5 10“8 ю-7 1000 0,09 8 ю—« 10“в 200 О) « « о 1 1 о - ООО о оо ' сч 0,02 7 10“в 10“в 800
Найти максимальный уровень (входного воздействия, при котором
относительное отклонение выходного сигнала от линейной зависи-
мости не превышает 3%.
3.2.17, Амплитудная характеристика канала удовлетворительно
аппроксимируется квадратичной зависимостью s(t) ==au2{t).
Найти амплитудную характеристику корректирующего четы-
рехполюсника.
3.3. АДДИТИВНЫЕ ПОМЕХИ
В НЕПРЕРЫВНОМ КАНАЛЕ СВЯЗИ
Аддитивные помехи в канале связи вызываются разными причинами и мо-
гут принимать самые различные формы. Тем не менее по их электрической и
статистической структурам такие помехи чаще всего разделяют на три основ-
ных класса:
1) флуктуационные или гладкие (распределенные по'частоте и времени);
2) сосредоточенные по частоте (гармонические);
3) сосредоточенные во времени (импульсные).
Флуктуационная помеха — это непрерывный во времени случайный процесс
(часто его полагают стационарным и эргодическим) с гауссовским распределе-
нием мгновенных значений и нулевым математическим ожиданием. Энергетиче-
ский спектр No такой помехи в пределах анализируемой полосы частот Г9 по-
лагают равномерным (помеха типа белого шума).
Плотность вероятности появления отрезка флуктуационной помехи длитель-
ностью Т
f \ т \
w (ит) = к ехр ( — — f и2 (/) dt] ,
\ ло о /
(3.13)
где К — постоянная, определяемая из условия нормировки (см. сноску на
стр. 43).
Гармоническая (сосредоточенная по частоте) помеха — это аддитивная по-
меха, энергетический спектр которой сосредоточен в сравнительно узкой полосе
частот, сопоставимой или даже существенно более узкой, чем полоса частот
сигнала.
Сосредоточенные помехи полагают равномерно распределенными в полосе
частот, т. е. вероятность рс.п появления сосредоточенной помехи в полосе F
пропорциональна этой полосе и зависит от среднего числа сосредоточенных по-
51
мех vc.n, превышающих пороговый уровень сигнала Р*пор, в единице полосы.
Импульсная помеха — аддитивная помеха, представляющая собой последо-
вательность импульсов, возбуждаемых кратковременными ЭДС апериодического
или колебательного характера.
Моменты появления импульсной помехи полагают равномерно распределен-
ными во времени. Это означает, что вероятность появления импульсной помехи
ри п в течение интервала Т пропорциональна длительности интервала, а также
среднему числу импульсных помех в единицу времени vH п, зависящему от до-
пустимого порогового уровня помехи.
Очень часто приемное устройство (а нередко и систему связи в целом)
строят оптимальным (или близким к оптимальному) по отношению с неизбеж-
ной в канале флуктуационной помехе, а в качестве радикального средства
борьбы с сосредоточенной и импульсной помехами используют такое построение
приемных устройств, при котором уменьшаются вероятности рс п и ри.п попа-
дания сосредоточенной и импульсной помех на решающую схему приемного
устройства. Такая задача успешно решается с помощью различных методов раз-
несенного приема, т. е. приема информации по параллельным независимым кана-
лам.
Задачи
3.3.1. Показать, что плотность вероятности реализации гаус-
совского флуктуационного шума с энергией Еш и спектральной
плотностью мощности No больше плотности вероятности реализа-
ции шума, имеющей нулевую энергию в ехр(—Еш/No) раз.
3.3.2. Найти отношение сигнал-шум р в полосе сигнала, полагая,
что сигнал — узкополосный процесс со средним квадратом значе-
ния огибающей А2, а флуктуационный шум порожден тепловым
движением электронов при абсолютной температуре проводни-
ка Т.
3.3.3. Решить задачу 3.3.2 для вариантов числовых значений
величин, заданных в табл. 3.9.
Таблица 3.9
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
f-io-*, Гц 4 9 4 8 7 5 2 8 10 2 2 8
А2, мкВт 4 6 3 1 7 8 4 8 10 3 8 6
Т, град 273 294 153 281 335 391 243 246 309 333 375 513
3.3.4. Узкополосный сигнал со средней мощностью Рс=100
мкВт принимается на фоне гауссовского стационарного шума, ко-
торый в полосе сигнала (/о—Af, fo+Af) имеет равномерный энер-
гетический спектр jVo=1O-8 Вт/Гц. Найти вероятность появления
* Пороговый уровень средней мощности сигнала Рпор различен для раз-
ных систем связи и определяется так,, что при превышении помехой этого по-
рога качество связи резко ухудшается,
52
флуктуационной помехи рф.п, средняя мощность которой превы-
шает пороговый уровень Рпор = 4Рс, при Af = 5 кГц.
3.3.5. Решить задачу 3.3.4 для числовых значений величин, при-
веденных в табл. 3.10.
Таблица 3.10
Вариант 1 2 3 4 5 6 7 8 9 10 п 12
Рс> мкВт 0,8 о,1 8 3 30 9 300 400 40 90 5 700
А/, кГц 5 7 7 8 1 9 4 6 2 1 9 10
Nq, Вт/Гц 10—8 IO-8 ю—8 ю-8 10-4 ю—6 ю—7 ю—6 ю—5 ю—8 ю—6 10-»
К 3 3 2 2 4 4 9 8 4 5 5 6
3.3.6. Найти отношение сигнал-шум, полагая, что сигнал такой
же, как в предыдущей задаче, а стационарный шум имеет энерге-
тический спектр G (/) =А ехр{—В (|/—/о)2],
В = (1,65/Д/)ас2, А = 7-10-9//2^ Вт/Гц.
3.3.7. При каком соотношении между пороговым уровнем и по-
лосой анализа сигнала F .вероятность появления сосредоточенной
помехи, превышающей порог, остается неизменной?
3.3.8. Некоторый источник выдает двоичные информационные
посылки со скоростью Г посылок/c. По каналу связи с полосой
FK эта информация может передаваться с помощью
параллельного модема: информация передается параллельно на
п независимых частотных поднесущих, причем каждая из них
обеспечивает скорость передачи 1'/п;
последовательного модема: информация передается короткими
посылками длительностью Т=1/Г на одной несущей (одноканаль-
ный вариант передачи).
Вероятность попадания сосредоточенной помехи со средней
мощностью Рс.п .в полосу канала связи близка к 1, в то время как
вероятность попадания двух или более таких помех очень мала.
Показать, что последовательный модем при той же средней мощ-
ности передатчика (Pnep=const) и эффективности использования
полосы (Y=/'/pK=const) обеспечивает в указанном канале боль-
шую ВерНОСТЬ, еСЛИ Рпер/Рс.п<1.
3.3.9. Пусть равновероятные символы А и Б двоичного источ-
ника для повышения качества передаются с помощью У=2£+1
независимых частотных каналов (частотно-разнесенная система
связи — 4PGC), причем при передаче символа А в каждом кана-
ле передается 1, а при передаче символа Б — 0. Вероятность по-
падания сосредоточенной помехи в одну ветвь разнесения рс.п =
=110-4
В месте приема символы А и Б регистрируются на основе ма-
жоритарного декодирования: если в большинстве частотных кана-
лов зарегистрированы 1, принимается решение в пользу символа
А, если же — 0, принимается решение в пользу Б. Найти вероят-
ность правильного декодирования д, если N = 5.
53
Таблица 3.11
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
N Рс. п 9 ю—1 7 10-2 5 0,5 7 0,05 5 0,4 7 0,09 11 0,04 5 0,08 7 0,07 3 0,2 9 0,08 11 10-3
3.3.10. Решить задачу 3.3.9 для вариантов числовых значений
величин, заданных в табл. 3.11.
3.3.11. Пусть прием информации в ЧРСС (задача 3.3.9) ведет-
ся только по n^N ветвям, свободным на данном интервале вре-
мени от сосредоточенной помехи, причем до принятия решения в
пользу символов А или Б сигналы отдельных ветвей складываются
так, что вероятность ошибочного приема символов равна рп-
Примем, что когда все ветви разнесения окажутся «забитыми»
сосредоточенной помехой, прекращается передача информации по
команде, переданной по каналу обратной связи.
Определить вероятность перерывов в передаче информации по
каналу, вероятность передачи информации по линии, среднюю ве-
роятность ошибочного приема символа.
3.3.12. Решить задачу 3.3.11 для числовых значений величин,
заданных в табл. 3.12.
Таблица 3.12
Вари- k ант ( 1 2 3 4 5 6 7 8 9 10 11 121
4 5 6 8 4 9 4 8 8 6 7 7
п 3 4 4 7 4 5 3 5 3 5 4 4
Рс.П 0,01 0,02 0,03 0,01 0,03 0,05 0,02 0,025 0,03 0,06 0,01 0,02
Рп 10~3 5.10“3 6-Ю"”3 2 • 10“"3 ю1-3 4 • 10“3 9 • 10~4 8-10“4 5.10""3 4-10‘~3 10~3 ю-“2
3.3.13. Пусть отрезок гармонического сигнала длительностью Т
и с амплитудой Um вместе с импульсной помехой после входного
блока с полосой Af подвергается двустороннему ограничению по
напряжению с уровнем Uo. Примем, что импульсная помеха не на-
рушает качество связи, если ее энергия на входе решающего блока
в 10 раз меньше энергии полезного сигнала: Ди.пСОЛ^с. Пока-
зать, что при Uo = Um качество связи не нарушается, если Af>
>10//.
3.3.14. Для борьбы с импульсной помехой при передаче двоич-
ных равновероятных символов источника 1 и 0 использовано их
Af-Кратное повторение (избыточное кодирование), а в месте прие-
ма — .мажоритарное декодирование. Полагая, что импульсные по-
мехи попадают независимо в отдельные тактовые интервалы с ве-
роятностью ри.п=0,01, вызывая при этом ошибочный переход, оп-
ределить вероятность ошибочного приема символа при числе вет-
54
вей разнесения W=3. Определить, во сколько раз уменьшилась
эта вероятность по сравнению с примитивным (безызбытонным)
кодированием.
3.4. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ
ВОЗДЕЙСТВИЙ ЧЕРЕЗ КАНАЛ СВЯЗИ
И ЕГО ЗВЕНЬЯ
Исследование преобразований случайных процессов при их прохождении
через линейные динамические системы (как с регулярными, так и случайно ме-
няющимися параметрами) связано с решением двух задач:
1) по данной корреляционной функции (энергетическому спектру) входно-
го воздействия X(t) найти корреляционную функцию (энергетический спектр)
отклика У (0 динамической системы, заданной ее характеристиками;
2) зная многомерные распределения входного воздействия X(t), найти мно-
гомерные распределения отклика Y(t) заданной динамической системы.
Вторая задача является более общей. Однако ее решение более сложно.
Поэтому здесь для линейных систем общего вида ограничимся лишь решением
первой задачи. Что касается прохождения случайных воздействий через нели-
нейные системы, то, рассматривая решение задач двух указанных выше типов,
ограничимся классом безынерционных детерминированных нелинейных систем,
Прохождение случайных процессов через линейные системы. Исчерпываю-
щей характеристикой линейной системы в общем виде (со случайно меняющи-
мися параметрами) является случайная импульсная переходная характеристика
G(t, т). С ней связана случайная комплексная передаточная функция
К(/<М) = J G ((, т) е-'шт 4т. (3.14)
—оо
Зная К (/со, /), обратным преобразованием Фурье получаем
G (/, т) = J К а<0, 0 е/<йТ df. (3.15)
— 00
Отклик системы на воздействие X(t) определяется интегралом Дюамеля (с уче-
том физической осуществимости)
Y(t) = ] G(t, (ЗД6)
О
Корреляционная функция отклика Y(i) линейной системы со случайной
характеристикой К(/со, /) на стационарное воздействие X(t) находится как
(/,< + ?) = j BK(f,t,T)Gx(f)^xdf, (3.17)
— 00
где Вк(/, /+т)=/С(—/со, /)/С(/(о, /+т)—корреляционная функция канала в об-
щем случае со случайно меняющимися параметрами; Gx(f) —энергетический
спектр воздействия.
55
Аналогично (3.17) определяется корреляционная функция отклика и при де-
терминированном воздействии, если под Gx(f) иметь в виду характеристику
Г /А Iim Is О'2”/)!2 /,
Gx(f) — hm ----------- , (3.18)
Т->оо 1
где |S(/2rcf) | — модуль спектральной плотности детерминированной функции.
Прохождение случайных процессов через нелинейные системы с детермини-
рованными параметрами. Функции распределения выходного процесса Y(t) той
или иной размерности при заданном распределении входного процесса X(t) и
заданной характеристике преобразования системы у==<р(х) могут быть получены
известными из теории вероятностей методами нахождения распределений функ-
ционально связанных случайных величин у и х.
Корреляционную функцию выходного процесса при известном двумерном
распределении входного процесса a>2(xi, х2; flt t2) можно определить по форму-
ле
1 1 [<P(X1)-*W][<P(*2)-
—оо — оо
— У (^2)] ^2 , х2; , /2) dx1 dx2, (3.19)
в то время как для определения математического ожидания выходного продук-
та достаточно знать одномерную плотность вероятности Wi(x; /):
my (/) = J* ф (х) «Ух (х ; t) dx. (3.20)
—00
Зада ч и
3.4.1. Показать, что отклик произвольной линейной системы
У(/) на случайное входное воздействие X(t) можно представить
суммой четырех независимых слагаемых
У (0 = У> (rf) + У2 (0 + Уз(0 + >
где Yi (t) — отклик детерминированной системы с характеристи-
кой g(t, r) = G(t, т) или fe(jco, /)=Х(/ю>, t) на детерминированное
воздействие m^(t) =X(t)-, Y2(t) — отклик системы с центрирован-
О О
ной хар актеристикой G(/, т) или К (jut, t) на детерминированное
воздействие тх((); Уз1 ('/) — отклик детерминированной системы с
характеристикой g(t, т) или fe(/o, t) на центрированное воздейст-
вие X(i); У4|(0 — отклик системы с центрированной характеристи-
о о
кой G(t, т) или Х(/чв, /) на центрированное воздействие X(t).
3.4.2. Показать, что для линейных систем, у которых переда-
точная функция не зависит от частоты K(j®, f)=K(t) (безынер-
ционные линейные системы), корреляционная функция отклика
связана с корреляционной функцией стационарного входного воз-
действия соотношением
Ву(/, t+т) = K(t)Ki(t+x)Вх(т).
56
3.4.3. Показать, что если параметры системы не меняются во
времени, т. е. К (/<>, /)=К(/<в), энергетический спектр отклика
Gv(f) связан с энергетическим спектром воздействия Gx(f) соотно-
шением
Gy(f)=G^f)K(^)K(-j^=GAf) 1К(» |2.
3.4.4. Последовательный колебательный контур с параметрами
2?, L, С находится под воздействием стационарного белого шума
с энергетическим спектром No. Найти энергетический спектр и
корреляционную функцию напряжения на емкости контура.
3.4.5. Решить задачу 3.4.4 для вариантов числовых значений
величин, приведенных в табл. 3.13.
Таблица 3.13
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
L, мкГн 700 700 200 800 500 300 500 100 700 900 300 400
/?, Ом 3 5 1 7 9 9 2 10 4 2 5 8
С, пФ 300 700 500 600 100 500 900 600 800 900 300 200
Nq-W, Вт/Гц 4 9 4 8 7 5 2 8 10 2 2 8
3.4.6. На вход канала с рассеянием во времени и по частоте с
корреляционной функцией
вя (f, Т) = а ехр ( -04 -1Я- -а2
\ /о то /
поступает гармонический сигнал с частотой f0 и случайной амп-
литудой.
Найти энергетический спектр и корреляционную функцию вы-
ходного процесса.
3.4.7. Стационарный белый шум со спектральной плотностью
мощности Л^о=10“6 Вт/Гц поступает на вход цепи, изображенной
на рис. 3.4. Найти энергетический спектр и корреляционную функ-
цию выходного процесса для числовых значений величин, задан-
ных в табл. 3.14.
Таблица 3.14
Вариант 1 2 3 4 5 6 7 8 9 10 и 12
L, Гн 0,01 0,04 0,07 0,04 0,01 0,08 0.05 0,01 0,09 0,01 0,07 0,08
Ом 7 7 2 8 5 3 5 10 9 9 9 2
Я2, Ом 6 3 7 8 9 5 4 9 5 8 3 3
3.4.8. На вход идеальной длинной ливни с линейно меняющей-
ся во времени задержкой поступает стационарный случайный про-
цесс с энергетическим спектром (?(/). Найти корреляционную
функцию и энергетический спектр выходного процесса.
57
3.4.9. На вход синхронного детек-.
тора (перемножитель, выходной про- >[
дукт которого подвергается низкочас-
тотной фильтрации) поступает случай-
ный процесс
Z (t) =ik/Mb (ff)cos (©of+<ро) +
L
+ Xn (f)'COS ®of + Уп (f) Sin ©olf,
Рис. 3.4. Схема линейной цепи
(к задаче 3.4.7)
который представляет собой аддитивную смесь БМ-сигнала и
флуктуационного шума*. Здесь ©0 — несущая частота; b(t) —
модулирующий сигнал с нулевым математическим ожиданием и
полосой частот Fc; Xn(t) и Уп(0 — независимые, квадратурные
компоненты гауссовского шума, у которых
тх = ту « 0; Вх (т) = Ву (т) = В (т) = No Fo .
Опорный сигнал ur(f) = JA-cos (©оН-фг) • Фильтр нижних час-
тот в полосе Fc будем считать идеальным с единичным коэффи-
циентом передачи. Определить:
одномерное распределение выходного продукта Y(t), его мате-
матическое ожидание my(t), дисперсию a2y(f);
корреляционную функцию и энергетический спектр для флук-
туирующей части K(f);
отношение сигнал-шум на входе рвх и выходе рвых детектора;
выигрыш в отношении сигнал-шум £=рВЫх/рВх.
3.4.10. На вход синхронного детектора поступает смесь сигна-
ла с угловой модуляцией и флуктуационного шума
Z (t) = t/n> cos (©о'^+О (f) +фо) + Xn(f)OOS ©of+
+ Уп(/) sin ©of,
где &(t) =&<pb(t) при ФМ; 0(f) =A©j* b(t)dt при ЧМ.
Определить те же характеристики, что и в задаче 3.4.9, пола-
гая, что при детектировании ЧМ-сигнала к синхронному детектору
подключается еще идеальная дифференцирующая цепь.
3.4.11. На вход безынерционного нелинейного устройства с ха-
рактеристикой у=х2 поступает стационарный гауссовский шум с
корреляционной функцией Вж(т) =о2®₽х(т) =ст2хе_“1т>.
Определить одномерную плотность вероятности выходного про-
дукта 7(f), математическое ожидание my(f), корреляционную
функцию By(t, f-H) и энергетический спектр Gv(f).
3.4.12. На вход линейного амплитудного детектора с характе-
ристикой
_ (kx при х 0,
10 при х < 0,
* Свойства шума считаются одинаковыми для всех нижеследующих задач
этого раздела,
58
поступает случайный процесс Z(Z) ='[Uri(A+rnb(t)) +ХП(/)] X
XoosW+yrrtOsiHtoo^, который представляет собой аддитивную
смесь АМ-оигнала и стационарного гауссовского .шума с равно-
мерным энергетическим спектром Nq в полосе частот канала FK =
= 2FC. Определить при b(t)=Q:
отношение сигнал-шум рВых на выходе идеального ФНЧ, под-
ключенного к линейному детектору;
отношение сигнал-шум на входе детектора рвх;
ВЫИГрЫШ В ОТНОШеНИИ СИГНаЛ-ШуМ g’ — рвых/рвх.
3.5. УРАВНЕНИЯ СОСТОЯНИЯ. МАРКОВСКИЕ
МОДЕЛИ КАНАЛОВ СВЯЗИ
Уравнения состояния X(t) и наблюдения Y(t) для л-мерной динамической
системы (канала) в матричном виде имеют вид
X(0=F[/, Х(/)]Х(0 + G[f, X(/)]U(0, ,
Y(0 = H[f, Х(0]Х(0, />/о, X(fo)=Xo, (3.21)
где X (0 = Х(0 = Xi(0 Х«(0 Л(0 А(0 х,(0 — вектор состояний со скалярными компонентами;
; U (0 = £/i(0 £М0 — вектор внешних воздействий;
Хп (0 ип (0
F, G, Н —матрицы, размерность которых согласована с размерностями X(t)t
U(t), характеризующие свойства системы (канала). Если внешнее воздействие
(порождающий процесс) случайный гауссовский процесс типа белого шума с
нулевым математическим ожиданием и корреляционной матрицей
В„(/, /+t) = U(0Ut(/+t)==Q6(t), (3.22)
где Т —- знак транспонирования матрицы; Q — симметричная, неотрицательно
определенная матрица, а функции (матрицы) F (/), G(/), H(Z) удовлетворяют
условиям непрерывности и ограниченности. Процессы X(t), X(t), Y(t), опреде-
ленные моделью (3.2’1), (3.2'2), являются марковскими. Их переходные плотно-
сти вероятности w(x, /|х0, tQ) и w(x, у, /|х0, уо, to) подчинены соответствую-
щим дифференциальным уравнениям в частных производных Колмогорова —
Фоккера — Планка (2.14).
Если гауссовский порождающий процесс воздействует на линейную цепь
(матрицы F, G, Н не зависят от X(t)), то и выходной процесс Y(t) будет га-
уссовским. Он будет также стационарным, если формирующая система являет-
ся линейной с постоянными параметрами (F, G, Н не зависят от X(t) и t). Рас-
пределение процесса будет негауесовским, если он сформирован нелинейной
системой.
Таким образом, метод переменных состояний позволяет представить случай-
ный процесс Y(t) его марковским приближением. Часто при использовании ме-
59
тода переменных состояний для моделирования процессов в каналах со случай-
но меняющимися параметрами уравнения наблюдения пишут в виде
Z(O = H[f, X(0]X(0 + N(0, (3.23)
где N(t)—аддитивный (обычно гауссовский) шум, сопровождающий наблюде-
ние. По заданному скалярному (одномерному) уравнению состояния (3.21) ко-
эффициенты сноса Л1(х, /) и диффузии А2(х, t), входящие в уравнение Кол-
могорова — Фоккера — Планка (2.14), определяются формулами
Л1(х,0 = Нт ту Л1{[х(< + Д/-х(0]|х(0}.
Д/-.0
Л2(х,0 = Нт + (3.24)
Д?->-0 Д‘
Задачи
S.5.I. Напряжение в цепи описывается при внешнем воздейст-
вии м(() = 1(() уравнением п-го порядка с -нулевыми начальными
условиями
ц(0) =«(0(0) =Ы(2)(О) = ... =м(п-П(0) =0.
Написать уравнения -состояния и наблюдения в скалярном и
матричном виде и схему аналогового вычислителя, -которая их реа-
лизует.
3.5.2. Случайные процессы на выходе двух каналов связи опи-
сываются уравнениями состояния и наблюдения
(0 = F, [/, X, (()] Хх (0 + G, [(, Хх (01U, (0;
= H1[f, XJOJX^O;
Х2 (/) = F2 [/, Х2 (0J х2 (f) + б2 [/, Х2 (/)] и2 (0;
Y2(/) = H2[/, Х2(/)]Х2(0; Х1(0) = Х10; Х2(0) = Х20.
Покажите, что эти случайные процессы
как выход векторного канала, описываемого
ния и наблюдения (3.21) с матрицами
можно представить
уравнением состоя-
0 .
о г2 ’
Сх 01 Х(0=К(0
gJ |х2(о
о
о н2
Н =
1^20
3.5.3. Линейная цепь n-го порядка с постоянными параметра-
ми определяется операторным коэффициентом передачи
К(р)
^•1РП ' ~Ь ^2 2Ч~-..~Ь^П _ L (р)
рП+^?1РП-1 + ... + ^п <№'
(3.25)
Напишите линейное скалярное уравнение n-го порядка с постоян-
ными коэффициентами, описывающее в установившемся режиме
60
случайный процесс на выходе системы К(/) с энергетическим
спектром
(j(f)= N° IК (i со) 12 = N° U <й^~‘ V a>)n~2 + ••• +
2 2 (/<o)" + ti(/®)"-1 + - + Фп
при воздействии на вход случайного стационарного белого гаус-
совского шума N(t) с энергетическим спектром N0/2 при нулевых
начальных условиях.
3.5.4. Покажите, что скалярное дифференциальное уравнение
л-го порядка, полученное в задаче (3.5.3), дается следующей ска-
лярной системой уравнений состояния и наблюдения:
Л) (t) =—Ф1-Х) (t) +Хг ('0 +Xi/i('f);
X? (0 =--фг-^2 (0 +Хз (/) +A.2/l(/) ;
Хп—1 (0 =—фп- iXn—1(0 +Xn(rf) +<Хп—1И(0> (3.26)
Яп (0 = фп^п (0 "Ь iXnW (0 J
У(0=^1(П.
Нарисуйте аналоговый вычислитель, реализующий уравнение
(3.26).
3.5.5. Покажите, что система (3.26) реализуется матричным
уравнением (3.21) с матрицами
3.5.6. Покажите, что стационарный гауссовский марковский
процесс S (0 с корреляционной функцией
Bs (t2, 0) = Рсexp (- а |0 -01) f Gs (f) = 2Pc”-. = — -----2'j
iV2’ v ° 1 v 12 x,/\ sv/ а2-|-4л2/2 а + /2л/ а )
можно при нулевых начальных условиях задать уравнением со-
стояния
S(t)-----а5(0 + /2аРёУ(0, S(-oo) = 0, (3.27)
V(t) — центрированный белый шум с единичной спектральной
плотностью. Воспользоваться методом перехода от изображения
К(р) =си/(р + а) * к оригиналу. Принять, что 2Рс/а — спектраль-
ная плотность порождающего- шума.
* Линейная цепь с постоянными параметрами (интегрирующая /?С-цепочка
с параметром а=1/7?С) с комплексным коэффициентом передачи /((/со) =a/(a+
+/2л/) или операторным коэффициентом передачи 7<(р) =a/(p+a) реализуема
(полюс лежит в левой полуплоскости переменного р), в то время как цепь с
операторным коэффициентом передачи 7<(р)— а/(р—а) нереализуема (полюс
лежит в правой полуплоскости).
61
3.5.7. Стохастическое дифференциальное
X(0 = f(x, t) + g(x, X(t0) = X0,
уравнение имеет вид
(3.28)
Покажите, что коэффициенты сноса и диффузии определяются
уравнениями
А(х,
4 OX Z
а стационарная плотность вероятности при нулевых граничных
условиях
w (х)----— exp ( — f dx \ (3.29)
3.5.8. Стохастическое дифференциальное уравнение определяет-
ся выражением (3.28) при х>0. При какой нелинейной функции
/(х) стационарная плотность w(x) определяется законом Рэлея:
w (х) = — ехр (— х2/2о2), х > 0.
1°2
3.5.9. Операторный коэффициент передачи (3.25) реализуемой
цепи разлагается на сумму простых дробей
Д’ (Р) = 2 ak/(p+Рк), <Xk = L (Pk)/Q (Ph)-
k=\
С учетом принципа наложения показать, что дифференциальное
уравнение цепи (уравнения состояния) с учетом нулевых началь-
ных условий имеет вид
^1(0=
Ха(0 = -Р2*2(0 + а2га(0
Xn(t)---ДЛп(0 + «пП(0
Y(t) = %Xk(t)
(3.30)
Построить «аналоговый вычислитель, (реализующий эти уравнения
состояния. Сравнить его схему со схемой вычислителя, получен-
ной в задаче (3.5.4) (рк — корни уравнения Q(p)=0).
3.5.10. Покажите, что система (3.30) реализуется матричными
уравнениями (3.21) и (3.22) с матрицами
62
Г л а в a 4. ОСНОВЫ ТЕОРИИ ПЕРЕДАЧИ
ИНФОРМАЦИИ
4.1. КОЛИЧЕСТВЕННОЕ ОПРЕДЕЛЕНИЕ
ИНФОРМАЦИИ. ЭНТРОПИЯ
И ПРОИЗВОДИТЕЛЬНОСТЬ ДИСКРЕТНОГО
ИСТОЧНИКА СООБЩЕНИЙ
Количество информации /(а»)*, содержащееся в символе а<, выбираемом из ан-
самбля {di} (j=l, 2,3,..., К, где К — объем алфавита) с вероятностью Р(а<),
К
причем 2 Р(аг-) = 1, определяется как
1=1
Z(ai)=-logP(a<). (4.1)
Основание логарифма в (4.1) может быть произвольным, оно определяет
лишь систему единиц измерения количества информации. Чаще всего
Z(ai)=-log2P(a<). (4.2)
При этом информация измеряется в двоичных единицах (битах). Одна дво-
ичная единица информации — это количество информации, содержащееся в од-
ном из двух выбираемых с равной вероятностью символов.
Среднее количество информации Я (Л), приходящееся на один символ, вы-
даваемый дискретным источником независимых сообщений с объемом алфавита
К, можно найти как математическое ожидание дискретной случайной величины
Z(at), определяющей количество информации, содержащееся в одном случайно
выбранном символе (знаке):
_____ К
Я (Л) = Z (аг)= - S P(ai)\ogP (at). (4.3)
i=*\
Эта величина называется энтропией источника независимых сообщений.
Одной из информационных характеристик дискретного источника является
избыточность
х=1~Я(Л)/ЯМакс(Л)= 1-Я(Л)/^/<. (4.4)
Избыточность источника зависит как от протяженности статистических свя-
зей между последовательно выбираемыми символами (памяти источника), так
и от степени неравновероятности отдельных символов. Если источник без памя-
ти (последовательно передаваемые символы независимы), все символы равно-
вероятны (р(а<) = 1/К), то Я(Л) =ЯмаКс(Л) и избыточность х=0.
* Эта характеристика определяет информативность выбора символа для
снеподготовленного» получателя и совершенно не учитывает как смысловое
содержание, так и субъективную ценность передаваемых сообщений.
63
Если в единицу времени источник выдает в среднем ци символов (скорость
источника ци), то среднее количество информации, создаваемое источником в
единицу времени,
Н'(А) =УиЯ(А)=Я|(А)/Тср, (4.5)
где Тер — средняя длительность одного символа.
Характеристику И'(А) называют производительностью дискретного источни-
ка. Источник называется стационарным, если описывающие его вероятностные
характеристики не меняются во времени*
3 а да чи
4.1.1. Источник сообщений выдает символы из ансамбля А =
= {аг} (здесь /=1, 2, 3, 4) с вероятностями P(ai)=0,2; Р(а2) =
= 0,3; Р(а3)=0,4; Р(а4)=0,1. Найти количество информации, со-
держащееся в каждом из символов источника при их независимом
выборе (источник без памяти). Вычислить энтропию и избыточ-
ность заданного источника.
4.1.2. Решить задачу 4.1.1 для источников сообщений, распре-
деления вероятностей которых приведены в табл. 4.1.
Таблица 4.1
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
Р(а,) 0,1 0,1 0,03 0,4 0,5 0,06 0,4 0,24 0,24 0,1 0,2 0,02
Р(а2) 0,25 0,05' 0,26 0,25 0,04 0,15 0,18 0,18 0,28 0,1 0,1 0,5
Р(а3) 0,15 0,04 0,09 0,05 0,03 0,15 0,1 0,38 0,05 0,1 0,3 0,03
Р(а4) 0,15 0,01 0,05 0,3 0,15 0,07 0,1 0,1 0,22 0,2 0,25 0,15
Р(а5\ 0,3 0,2 0,16 — 0,04 0,05 0,07 0,06 0,15 0,35 0,15 0,04
Р(а,) 0,05 0,03 0,1 — 0,12 0,29 0,06 0,02 0,06 0,15 — 0,12
Р(а7) — 0,07 0,09 —— 0,1 0,19 0,05 0,02 — — — 0,04
Р(аз) — 0,5 0,22 — 0,02 0,04 0,04 — — — — 0,1
4.1.3. Показать, что для источника без памяти с объемом ал-
фавита К энтропия Н(А) имеет максимальное значение //максИ) =
= log/C при равновероятных символах.
4.1.4. Показать, что при равных объемах алфавитов /С энтро-
пия дискретного источника с памятью //(Л/Д') не превышает энт-
ропию дискретного источника без памяти Н(А).
4.1.5. Память двоичного стационарного источника с символами
0 и 1 простирается лишь на два соседних символа и, следователь-
но, дискретная последовательность символов, выдаваемых источ-
ником, описывается простой цепью Маркова с матрицей переход-
ных вероятностей:
Р(1/1') Р(1/0')
Р(0/Г) Р(0/0') ’
где P(ai\a'j) — вероятность символа при условии, что ему
предшествует символ a'j.
64
Полагая, что Р(111') =0,9; Р(0|1')=0,1; Р(11О') =0,7, найти
энтропию источника и его избыточность. Найти энтропию и избы-
точность двоичного источника без памяти, но с теми же значе-
ниями вероятностей передачи символов.
4.1.6. Решить задачу 4.1.5 для дискретных стационарных ис-
точников, заданных матрицами переходных вероятностей:
1) 0,98 0,7/
0,02 0,3’
4) 0,8 0,7
0,2 0,3’
7) 0,35 0,35. 8)
0,65 0,65’
10) 0,97 0,82. 11)
0,03 0,18’
2) 0,75 0,4
0,25 0,6 ’
5) 11,65 0,65
‘0,35 0,35 ’
0,71 0,82
0,29 0,18 ’
0,59 0,5
0,41 0,5’
3) 0,6 0,5
0,4 0,5’
0,5 0,9
0,5 0,1 ’
0,7 0,56
0,3 0,44’
1 1
о О’
6)
9)
12)
4.1.7. Стационарный источник выдает за время 7’=106с дво-
ичными посылками длительности т=10 мс 107 бит информации.
За какое время и каким количеством двоичных посылок можно
передать тот же объем информации, если соответствующей обра-
боткой полностью устранить избыточность источника? Определить
избыточность источника.
4.1.8. Найти максимальное количество информации, которое со-
держится в квантованном телевизионном сигнале, соответствую-
щем одному телевизионному кадру при 625 строках разложения,
при условии, что сигнал, соответствующий одной строке изобра-
жения, представляет собой последовательность 833 (при отноше-
нии сторон кадра 4/3) статистически независимых случайных по
амплитуде импульсов, каждый из которых с равной вероятностью
принимает одно из 16 значений. Найти избыточность телевизи-
онного сигнала, если фактически кадр изображения с 16 града-
циями уровней содержит 9,37-105 бит информации.
4.1.9. Согласно экспериментальным данным безусловные веро-
ятности букв русского алфавита характеризуются табл. 4.2.
Найти энтропию источника, выдающего текст из этих букв,
при отсутствии статистических связей между буквами. Вычислить
избыточность источника, выдающего русский текст, обусловлен-
ную неравновероятностью выбора букв, а также и их статистиче-
скими связями (памятью источника), если по экспериментальным
данным энтропия источника Н(А) — 1 бит/символ.
4.1.10. Решить задачу 4.1.9 для источника, выдающего текст
из букв английского алфавита, безусловные вероятности которых
приведены в табл. 4.3.
При вычислении избыточности текста принять во внимание, что
с учетом 8-буквенных сочетаний энтропия Я (А) = 1,86 бит/символ.
4.1.11. Напряжение на выходе квантующего устройства может
принимать одно из 17 дискретных значений с шагом квантования
3—53 65
Таблица 4.2
Буква Вероятность Буква Вероятность Буква | Вероятность
Пробел 0,175 К 0,028 Ч 0,012
о 0,090 М 0,026 Й 0,010
е 0,072 Д 0,025 X 0,009
а 0,062 П 0,023 ж 0,007
и 0,062 у 0,021 ю 0,006
т 0,053 я 0,018 ш 0,006
н 0,053 ы 0,016 ц 0,004
с 0,045 3 0,016 щ 0,003
р 0,040 ь, ъ 0,014 э 0,002
в 0,038 б 0,014 ф 0,002
л 0,035 г 0,013
Таблица 4.3
Буква j Вероятность Буква Вероятность Буква Вероятность
Пробел 0,2 h 0,047 W 0,012
е 0,105 d 0,035 g 0,011
t 0,072 I 0,028 b 0,010
о 0,065 С 0,023 V 0,008
а 0,063 f 0,023 k 0,003
п 0,058 и 0,023 X 0,001
i 0,055 т 0,021 i 0,001
г 0,052 Р 0,018 q 0,001
S 0,052 У 0,012 z 0,001
Д. На вход квантующего устройства поступают независимые вре-
менные отсчеты (с интервалом Д/=0,Зс) сигнала с экспоненциаль-
ной .плотностью вероятности мгновенных значений
Wt (х) = (2а)-1 ехр» (— | х | i/а),
где а=0,5 В, хМакс=1,6 В, Д=0,2 В. Определить энтропию кванто-
ванного сигнала, его избыточность, скорость создания информа-
ции на выходе квантующего устройства (производительность).
4.1.12. Решить задачу 4.1.11 для сигнала с плотностью вероят-
ности мгновенных значений Wi(x) = (2ла)-0>5ехр{—х2/(2а)] для
вариантов числовых значений, заданных в табл. 4.4.
Таблица 4.4
Вариант 1 2 3 4 5 6 7 8 9 10 11 12
а, В2 0,5 0,2 0,5 0,2 0,5 0,2 0,9 0,7 0,7 0,3 0.8 0,2
Хмакс, В д, в 1,6 0,4 0,8 2,4 4,8 3,2 4 6,4 5,6 4,8 3,2 1,6
0,2 0,05 0,1 0,3 0,6 0,4 0,5 0,8 0,7 0,6 0,4 0,2
4.1.13. Для устранения статистических связей символов источ-
ника (их «декорреляции») в целях повышения эффективности свя-
66
зи 'иногда прибегают к перекодировке, которая сводится к сопос-
тавлению блока из п>\ символов первичного алфавита новому
символу «укрупненного» алфавита. Показать, что этот способ уст-
ранения связей символов не изменяет избыточность сообщений.
4.1.14. После устранения статистических связей символов
укрупненный алфавит характеризуется восемью символами, вероят-
ности которых даны в табл. 4.5. Показать, что использование не-
равномерного двоичного кода, указанного в табл. 4.5 (это эконом-
ный код Хаффмена, который более вероятным символам сопостав-
ляет более короткие кодовые комбинации), позволяет почти пол-
ностью устранить избыточность.
Таблица 4.5
Номер символа Вероятность Код ni
1 0,6 1 1
2 0,2 10 2
3 0,1 100 3
4 0,04 1000 4
5 0,025 10000 5
6 0,015 100000 6
7 0,01 1000000 7
8 0,01 10000000 8
4.2. КОЛИЧЕСТВО И СКОРОСТЬ ПЕРЕДАЧИ
ИНФОРМАЦИИ ПО ДИСКРЕТНОМУ КАНАЛУ.
ПРОПУСКНАЯ СПОСОБНОСТЬ ДИСКРЕТНОГО
КАНАЛА. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ
КАНАЛОВ С ШУМАМИ
Если на вход канала с шумами поступают символы bi (*=1, 2,... ,т), а
с выхода снимаются символы (/ = 1,2,...,/п'), то условные вероятности пере-
ходов а также и апостериорные вероятности P(bi\8j) удовлетворяют
соотношениям *:
0<m|dt) <1; 0<Р(Н^)<1. (4.6)
Это означает, что при фиксированном символе нельзя с полной определен-
ностью утверждать, какой символ bi передавался. Следовательно, часть инфор-
мации, содержащейся в символе 6», оказалась потерянной.
Среднее количество информации, теряемой при передаче произвольного
символа по каналу без памяти,
I (В|В) = Н (BIB) = - S 5 р (bilbj) Р (b}) log Р (bilbj) =
/=1 Г=1
/=1 f=l Р (bj)
* Для канала без шумов эти вероятности равны 0, если /У=/, и равны 1,
если j=i.
я*
Эта величина называется ненадежностью канала и показывает степень не-
определенности последовательности входных символов В при условии, что при-
нята последовательность В.
Средним количеством переданной по каналу информации на один символ
называется разность между количеством информации на входе канала 1(B) и
(количеством информации, потерянной в канале, 1(В\В).
Для источника и канала без памяти
1(В, В) = 1(В) — 1 (В\В) = Н (В) — Н (В\В) =
= “2 P(s„s,)log м
/=1 f=i Р (bi) Р (bj)
Это среднее количество информации на один символ, содержащееся в вы-
ходной последовательности В относительно входной последовательности В. По-
скольку 0^/7(В/В) ^Н(В) (условная энтропия никогда не превосходит безу-
словную), то 0^7 (В, В) 1(B). Количество информации 1(В, В)=0, если сим-
волы на входе и выходе независимы (очень сильные помехи или обрыв кана-
ла связи), и 1(В, В) = 1(B), если помехи отсутствуют.
Из (4.8) следует, что
ЦВ, В)=1(В, В)=Н(В)—Н(В/В). (4.9)
Величина
Н(В)=1(В) (4.10)
определяет информацию (энтропию) выходных символов канала. Часть этой
информации является полезной (информация о входных символах bi). Осталь-
ная часть информации является ложной (созданной помехами в канале). Вели-
чина Н(В\В) —1(В\В) определяет информацию, содержащуюся в последователь-
ности выходных символов В при известной последовательности входных симво-
лов В. Поскольку выходная последовательность отличается от входной исклю-
чительно из-за помех в канале, то Н(В\В) характеризует информацию имен-
но о помехах в канале или энтропию шума:
Я(В|В)=-£ P(bi,bj)logP(bj\bi). (4.11)
/=1 1=1
Если на вход дискретного канала поступает в среднем vK символов в еди-
ницу времени, то можно определить среднюю скорость передачи информации по
каналу с шумами:
Г (В, B)=vKI(B, В)=Н'(В) — Н'(В\В)=Н'(В)— Н'(В\В). (4.12)
Здесь Н'(В)—производительность источника на входе канала; Н'(В\В)—нена-
дежность канала в единицу времени; Н'(В) —производительность источника, об-
разованного выходом канала; Н'(В\В)—количество ложной информации, соз-
даваемой шумом в единицу времени.
Пропускной способностью канала называется предельная скорость переда-
чи информации при заданных свойствах канала (заданной помехе). Для ди-
скретного канала пропускная способность
C=vKmaxl(B, В), (4.13)
68
причем max ищется по всем возможным источникам входа при заданном vK и
объеме алфавита символов входа т*.
С понятием пропускной способности канала связана одна из важнейших
теорем теории информации — основная теорема К. Шеннона об оптимальном
кодировании. Применительно к дискретному источнику эта теорема гласит:
если производительность источника сообщений меньше пропускной способности
канала
Я'(4)<С, (4.14)
то существует способ оптимального кодирования и декодирования (преобразо-
вания сообщения в сигнал на передаче и обратного его преобразования в сооб-
щение на приеме), при котором вероятность ошибки может быть сделана как
угодно малой. Если #'(Д)>С, такого способа не существует.
Средняя вероятность ошибки при оптимальном кодировании определяется
соотношением
рот « (4.15)
где Т — длительность сигнала, соответствующего последовательности символов
источника достаточно большой длины л; С—Н'(А) —запас пропускной способ-
ности канала.
Для дискретного канала без шумов теорема оптимального кодирования
формулируется следующим образом: если производительность источника мень-
ше пропускной способности канала, то существуют способы кодирования, при
которых передача сообщений может осуществляться со скоростью
vc — vK/H{A)—e, (4.16)
где vK — скорость передачи двоичных кодовых символов; е — как угодно малая
положительная величина.
Из этой теоремы следует, что при оптимальном (по Шеннону) кодирова-
нии можно на один символ источника затратить
п«Я(А) (4.17)
кодовых символов.
Задачи
4.2.1. Найти .ненадежность Н(В\В) и энтропию шума двоич'Но-
го симметричного 'канала со стиранием (.рис. 4.1) с вероятностями
переходов Р(6|0) = Р(111) = 1—ро— ре, Р(?|0) = Р(?| 1) = ре,
Р(110) =Р(0| 1) =ро и априорными вероятностями символов Р(0)
и Р(1) = 1—Р(0).
4.2.2. Показать, что в симметричном m-ичном канале без па-
мяти и стираний энтропия шума определяется выражением
Я (В | В) =~р log[p/ (m— 1) ] —' (.1—р) log (1—р),
где р — суммарная вероятность ошибки.
* Строго говоря, С следует определить как наименьшую верхнюю границу
от ЦВ, В), так как одно единственное максимальное значение скорости по все-
возможным источникам входа может и не существовать.
69
Рис. 4.1. Граф двоичного
симметричного канала со
стиранием
4.2.3. Найти энтропию шума в двоич-
ном канале без памяти по заданной
энтропии источника на входе канала
Н(В), энтропии источника, образован-
ного выходом канала Н(В) и ненадеж-
ности канала Н(В\В) (значения Н(В),
И (В), Н(В\В) даны в табл. 4.6).
4.2.4. Показать, что при вероятнос-
ти ошибки, стремящейся к нулю, ско-
рость передачи информации по двоично-
му симметричному каналу со стиранием
(задача 4.2.1) определяется соотношением
1'(В, В) ==ик(1—рс)Н(В), где vK — число символов, поступаю-
щих на вход канала в единицу времени.
Таблица 4.6
Вариант 1 2 3 4 5 6 7 8 9 10
Я(В)-10“3, бит/сим- вол 1 4 9 4 8 7 5 2 8 10
Я(£)-10“3, бит/сим- вол 1 9 15 7 9 10 6 4 11 12
Н(В/£) • 10-3, бит/ символ 200 400 900 500 200 800 1000 290 200 800
4.2.5. На вход дискретного канала поступает И (В) бит/символ,
а по каналу в среднем передается ЦВ, В) бит/символ полезной
информации. Энтропия шума в канале Н(В\В) бит/символ.
Найти ненадежность канала и энтропию выходных символов.
Определить производительность источника на входе канала, нена-
дежность канала в единицу времени, среднюю скорость передачи
информации по каналу и скорость создания ложной информации
в канале, если на вход канала поступает в среднем vK символ/с
(значения Н(В), ЦВ, В), Н(В\В), vK даны в табл. 4.7).
Таблица 4.7
Вариант 1 2 3 4 5 6 7 8 9 £10
Ч(В) 20 40 90 40 80 70 50 80 200 60
'(в, В) 10 30 70 20 40 60 20 30 100 50
ЦВ/В) 40 60 120 60 120 100 80 90 300 90
50 40 90 70 60 100 100 75 100 80
4.2.6. Показать, что для /Пничного симметричного канала без
1а>мяти и стир-ания с вероятностями переходов
(1—р при j=i,
Р(МЬ{) = { р .^.
~ , П1ВИ
\т — 1
О
пропускная способность определяется соотношением
С = vK Г log m + (1 - р) log (1 - р) + р log —
t tn — 1
Упростить эту формулу для двоичного канала. Построить гра-
фик зависимости пропускной способности двоичного канала от ве-
роятности ошибки.
4.27. Найти пропускную способность m-ичного симметричного
канала без памяти и стирания по числовым значениям, приведен-
ным ,в табл. 4.8.
Таблица 4.8
Вариант 1 2 3 4 5 6 7 8 9 10
ик 700 700 200 800 500 300 500 1000 700 900
Ш 4 6 3 7 8 4 10 3 8 6
Р 0,1 0,01 0,2 0,02 0,15 0,015 0,01 0,01 0,02 0,003
4.2.8. Показать, что избыточность оптимального по Шеннону
кода определяется соотношением
Хк.мин=1—C/(yKlog/n) +е
(в — сколь угодно малая положительная величина).
Найти минимально (возможную избыточность оптимального ко-
да для двоичного канала при (вероятности ошибки р = 0 и 0,5.
4.2.9. Показать, что способы кодирования и декодирования,
обеспечивающие сколь угодно малую вероятность ошибки, суще-
ствуют лишь в случае, когда среднее число символов кода на один
символ источника удовлетворяет условию
- Я(Л)
0
.. и max ЦВ, В)
4.2.10. Какой запас пропускной способности С—И'(А) должен
иметь канал, чтобы при использовании оптимального кода с дли-
тельностью кодовой комбинации Т = 100 мс вероятность ошибки
не превысила величину Ю-6?
Во сколько раз изменится длительность кодовой комбинации
оптимального кода, если при неизменной вероятности ошибки за-
пас пропускной способности канала уменьшается в 2 раза?
4.2.11. Показать, что вероятность ошибки в канале с шумами
не может быть сколь угодно малой, если пропускная способность
канала С меньше производительности Н'(А).
4.2.12. Некоторый дискретный источник выдает символы из ан-
самбля {аг}, i=l, 9 с вероятностями, приведенными в табл. 4.9.
Закодировать символы данного ансамбля кодом Хаффмена. По-
строить граф кода и определить среднюю длину кодовой комби-
71
Таблица 4.9
Символ Qi aa а» ал я. а7 «8 а9
P(as) 0,2 0,15 0,15 0,12 0,1 0,1 0,08 0,06 0,04
нации. Сравнить полученный результат с минимальной длиной ко-
довой комбинации при кодировании равномерным двоичным ко-
дом. Показать, что код Хаффмена близок к оптимальному по Шен-
нону коду.
4.2.13. Закодировать кодом Хаффмена символы источника, по-
являющиеся с вероятноютями P(ai) =Р(а2) = 1/4, Р(а3)=Р(а4) =
= 1/8, Р(а5) =Р(а&) =Р(а7) = Р(а3) = 1|/16. Какую экономию в чис-
ле кодовых разрядов на один символ источника дает этот код по
•сравнению со случаем равномерного двоичного кода?
4.2.14. Построить код Хаффмена для шести сообщений Л, В, С,
D, Е, F, появляющихся с вероятностями 0,4; 0,25; 0,15; 0,1; 0,05;
0,05. Построить кодовое дерево, вычислить среднюю длину кодо-
вой комбинации и сравнить ее с энтропией сообщения.
4.2.15. Закодировать двоичным кодом Шеннона — Фано ан-
самбль сообщений {a?}, f=l,8, если вероятности символов имеют
следующие значения: P(ai) = Р(а2) = 1/4; Р(а3) =Р(а4) = 1/8;
Р(а5) =Р(а6) =Р(а7) = Р(а3) = 1/16. Найти среднее число разрядов
в кодовой комбинации. Показать, что такой код близок к опти-
мальному.
4.2.16. Построить код Шеннона — Фано для сообщений, задан-
ных в задаче 4.2.14. Вычислить среднюю длину кодовой комбина-
ции и сравнить ее с энтропией сообщения.
4.2.17. Построить код Шеннона — Фано для сообщений 4, В,
С, D, если они имеют вероятности а) 0,5; 0,25; 0,125; 0,125; б) 0,6;
0,2; 0,15; 0,05. Для обоих случаев сравнить среднюю длину кодо-
вой комбинации с энтропией сообщения.
4.3. ЭНТРОПИЯ И ПРОИЗВОДИТЕЛЬНОСТЬ
НЕПРЕРЫВНОГО ИСТОЧНИКА СООБЩЕНИЙ
Для описания информационных свойств непрерывного источника широко
используется понятие дифференциальной энтропии Л(Х):
А(Х)= — j* wx(x)\ogwx(x)dx. (4.18)
—оо
Это та часть энтропии непрерывного источника, которая зависит от функции
плотности вероятности сигнала Х(/), выдаваемого источником.
Наибольшее значение дифференциальной энтропии при независимых отсче-
тах и заданной дисперсии о2 имеет случайный процесс X(t) с гауссовским рас-
пределением мгновенных значений. В этом случае
Лмакс (X) =log ]/2лёа\ (4.19)
72
По аналогии с формулами для дискретного источника количество информа-
ции, содержащееся в одном непрерывном отсчете процесса У(/) относительно
отсчета процесса X(t), определяется формулой
'(х'Г) - 11 ”(4 20)
Здесь w2(x, у) —совместная плотность вероятности процессов X(t) и У(/).
Величину I (X, У) можно представить так:
/(X, У)=Л(Х)-/1(Х|У)=А(У)-Л(У|Х). (4.21)
Здесь Л(Х), Л (У)—соответственно дифференциальная энтропия на отсчет про-
цесса X(t) и У(0;
/г(Х|У)= — J J* w2(x, у) iogw1(x\y)dxdy (4.22)
— оо —оо
— условная дифференциальная энтропия отсчета X (t) при известном отсче-
те У(0;
Л(У|Х) = — J J w2(x,y)\ogwi(y\x)dxdy (4.23)
—оо —оо
— условная дифференциальная энтропия отсчета У(/) при известном отсче-
те X(t).
Эпсилон-энтропией Н г(Х) непрерывного источника, или собственной инфор-
мацией в одном отсчете процесса X(t), будем называть минимальное количест-
во информации, необходимое для воспроизведения сигнала X(t) по сигналу
X'(t) с допустимой дисперсией ошибки ог2п:
Яв (Х|Х') = min / (X, X') = ft (Х|Х') — log У2леап . (4.24)
Не(Х\Х') —это эпсилон-энтропия на один отсчет при условии, что отсчеты сиг-
нала фиксированы; Л(Х|Х') —дифференциальная энтропия отсчета сигнала при
условии, что отсчеты сигнала фиксированы.
Если источник выдает независимые отсчеты непрерывного сообщения ди-
скретно во времени, то его эпсилон-производительность
Ii'e(X\X')=vaHe(X\X') = оя [ft (X | X') — log 1/*2леа2] . (4.25)
где Vn — число отсчетов в единицу времени.
При непрерывном времени
я; (Х|Х') = 2 Fc [ft (Х| X') - log jAneo2] . (4.26)
Избыточность непрерывного стационарного источника
Хи = 1 ~Яе(Х|Х')/Я8 WMaKC. (4-27)
Задачи
4.3,1. Вычислить количество информации, содержащееся в од-
ном отсчете непрерывного сообщения, создаваемого стационарным
источником без памяти при абсолютно точном его воспроизведе-
нии.
73
4.3.2. Найта дифференциальную энтропию гауссовского слу-
чайного процесса с дисперсией о2.
4.3.3. Показать, что условная дифференциальная энтропия ста-
ционарного rayccOfBCKoro случайного процесса /i(X|Xnp), отсчет ко-
торого зависит только от одного предшествующего отсчета (мо-
дель марковского процесса с дискретным временем), определяется
формулой
h (Х|Хпр) = log/2лео2(1-Р2),
где R — нормированная корреляционная функция случайного про-
цесса.
4.3.4. Гауссовский случайный процесс с нулевым математиче-
ским ожиданием и дисперсией о2 проходит через линейный усили-
тель с коэффициентом усиления К. Определить приращение диф-
ференциальной энтропии выходного сигнала по сравнению с вход-
ным по данным, приведенным .в табл. 4.10.
Таблица 4.10
Вариант 1 2 3 4 5 6 7 8 9 10
<т2, мВт К 10 2 4 3 1 4 2 1 9 3
200 500 100 90 70 70 300 80 200 300
4.3.5. Сравнить дифференциальные энтропии гауссовского про-
цесса и процесса, равномерно распределенного на интервале (—а,
а), если их дисперсии одинаковы.
4.3.6. По каналу связи передается сигнал Х{1), представляющий
собой гауссовский случайный процесс с нулевым математическим
ожиданием и дисперсией <т2ж. В канале действует независимый
от сигнала гауссовский шум N(t) с нулевым математиче-
ским ожиданием и дисперсией о2п. Найти дифференциальную энт-
ропию входного и выходного сигналов, а также условные диффе-
ренциальные энтропии й(Х|У) и Л(У|Х) по данным, приведен-
ным в табл. 4.11.
Таблица 4.11
Вариант 1 2 3 4 5 6 7 8 9 10
а2х, мВт 4 9 8 7 2 7 20 8 6 6
а2Л, мВт 1 5 5 2 1 3 4 6 3 1
4.3.7. Определить эпсилон-энтропию непрерывного' источника
при фиксированной дисперсии шума воспроизведения.
4.3.8. Найти максимально возможное значение эпсилон-энтро-
пии при заданной средней мощности сигнала Рс и средней мощ-
ности шума воспроизведения (канала) Рш.
74
4.3,9. Показать, что при фиксированных средних мощностях
сигнала Рс и шума Рш максимально возможная эпсилон-произво-
дительность источника определяется соотношением Н' (Х)макс =
= yHlogp<p при дискретном времени и Н'ъ (X) макс=FZ log р при
непрерывном времени.
4.3.10. Непрерывный сигнал непрерывного времени Х(1) на вы-
ходе источника имеет равномерное распределение с дисперсией о2х.
Найти эпсилон-производительность источника, если полоса сигна-
ла FCi а дисперсия шума воспроизведения о2п. На сколько изме-
нится эпсилон-производительность источника, если он начнет вы-
давать сигнал с теми же параметрами, но с гауссовским распре-
делением? Числовые данные приведены в табл. 4.12.
Таблица 4.12
Вариант 1 2 3 4 5 6 7 8 9 10
а2ж, мВт 3 50 100 70 90 90 20 100 40 10
а2п, мВт 0,5 0,7 1 0,4 0,4 0,9 0,4 0,8 0,7 0,5
Fc-10"2, Гц 3,1 50 64 120 40 90 100 90 10 50
4.3.11. Найти избыточность источника, выдающего непрерывное
сообщение с равномерным распределением и независимыми от-
счетами, при мощности сигнала Рс и отношении сигнал-шум в ка-
нале р.
4.3.12. Решить задачу 4.3.11 для числовых данных, приведен-
ных в табл. 4.13.
Таблица 4.13
Вариант 1 2 3 4 5 6 7 8 9
Рс, мВт 10 60 90 40 40 80 90 30 50
Р 10 90 40 10 80 90 30 50 30
4.3.13. Определить избыточность непрерывного гауссовского ис-
точника с памятью при отношении сигнал-шум воспроизведения,
равном 10, и значениях нормированной корреляционной функции
случайного процесса, приведенных в табл. 4.14.
Таблица 4.14
Вариант 1 2 3 4 5 6 7 8 9 10
0,005 0,0075 0,01 0,025 0,05 0,1 0,2 0,4 0,5 0,6
75
4.4. КОЛИЧЕСТВО И СКОРОСТЬ ПЕРЕДАЧИ
ИНФОРМАЦИИ ПО НЕПРЕРЫВНОМУ
КАНАЛУ. ПРОПУСКНАЯ СПОСОБНОСТЬ
НЕПРЕРЫВНОГО КАНАЛА
Если на вход непрерывного канала поступил сигнал U(t), а в канале дей-
ствует аддитивная помеха N(t) так, что принимаемое колебание Z (/) = U (/) -г
+JV(/), то условная дифференциальная энтропия помехи h(Z\ U) =h(N). По-
этому
I(U, Z)=h(Z)—h(N). (4.28}
Скорость передачи информации по непрерывному каналу с дискретным вре-
менем
I'(U, Z)=v«[h(Z)—h(N)], (4 29)
где yK = 2FK—число отсчетов сигнала, передаваемое в одну секунду по кана-
лу с полосой Гк.
Пропускной способностью С непрерывного канала с заданным шумом и V»
будем называть предельное значение скорости передачи информации (4.29), до-
стигаемое при вариации всевозможных источников на входе.
При аддитивном шуме в канале
C=vK max[h (Z) —h (N) ]. (4.30)
Применительно к непрерывному источнику основную теорему оптимально-
го кодирования К. Шеннона можно сформулировать так: если эпсилон-произ-
водительность источника меньше пропускной способности канала Н'с(А) <С, то
существует способ кодирования и декодирования, при котором с вероятностью,
сколь угодно близкой к единице, средняя мощность шума воспроизведения
меньше заданной величины Рш. Если Н'е(А)>С, такого способа нет.
Максимальный объем информации, который может быть передан по непре-
рывному каналу с пропускной способностью С,
уик==ГкС> (4.31)
где Тк — время использования канала.
Задачи
4.4.1. По каналу связи передается сигнал £(/), представляющий
собой гауссовский случайный процесс с нулевым математическим
ожиданием, дисперсией о2 = 8 мВт, равномерным энергетическим
спектром No в полосе частот канала F = 3100 Гц. В канале дейст-
вует независимая от сигнала флуктуационная помеха типа белый
шум -с энергетическим спектром У0 = 3,22-1О~7 Вт/Гц, гауссовским
распределением и нулевым математическим ожиданием. Опреде-
лить среднее на один отсчет сигнала количество информации, пе-
реданное по каналу.
4.4.2. Решить задачу 4.4.1 для вариантов числовых значений
величин, приведенных в табл. 4.15.
4.4.3. С какой скоростью передается информация по каналу,
если на его вход поступает ук=Ю0 независимых отсчетов сигнала
76
Таблица 4.15
Вариант 1 2 3 4 5 6 7 8 9 10
а2, мВт No, мкВт/Гц F, кГц 8 0,3 7 10 0,7 2 4 0,2 8 5 °,2 7 8 0,2 5 9 0,7 3 2 0,8 9 ю 1 4 7 0,7 9 6 0,5 6
в секунду. Сигнал S(t) распределен по гауссовскому закону, ms =
= 0 и cr2s=2,8 Вт. В канале действует аддитивный гауссовский
шум с mn = 0 и о2п=0,4 Вт.
4.4.4. Решить задачу 4.4.3 для вариантов числовых значений
величин, приведенных в табл. 4.16.
Таблица 4.16
Вариант 1 2 3 4 5 6 7 8 9 10
Vk 200 900 400 800 1000 900 100 500 300 900
Л, Вт 4,6 3,1 1,1 2,9 1,8 5,8 2,0 3,0 1,3 3,3
а2п, Вт 0,3 0,6 0,1 0,2 0,3 0,5 0,2 0,5 1 0,6
4.4.5. Показать, что при заданном ансамбле входных сигналов
и 'фиксированной дисперсии помехи скорость передачи информа-
ции по непрерывному каналу будет иметь наименьшее значение
при гауссовском шуме в канале.
4.4.6. Найти пропускную способность гауссовского канала не-
прерывного времени, если F — полоса канала; Рс и Рш — фикси-
рованные федние мощности сигнала и шума в канале, которые
считаются .независимыми.
4.4.7. Найти пропускную способность гауссовского канала,
имеющего полосу Р=3,1 -йГц, если на вход канала поступает сиг-
нал, 'мощность которого Рс=1 мВт, а в канале действует белый
шум со спектральной плотностью мощности Мо=1О~7 Вт/Гц.
4.4.8. Решить задачу 4.4.7 для вариантов числовых значений
величин, заданных в табл. 4.47.
Таблица 4.17
Вариант 1 2 3 4 5 6 7 8 9 10
F, кГц 1 10 3 7 5 9 7 2 10 4
Рс, мВт No, мкВт/Гц 7 7 2 8 5 3 5 1 7 9
0,4 0,5 0,2 0,3 0,6 1 0,9 0,1 0,2 0,9
77
4.4.9. Определить максимально возможную величину пропуск-
ной способности гауссовского канала при неограниченной полосе.
4.4.10. Найти минимальную энергию сигнала, необходимую для
передачи одной единицы информации по каналу с шумами.
4.4.11. По гауссовскому каналу связи с полосой fo±0,5F пере-
дается сигнал s(f), имеющий спектральную плотность мощности
Go(/) =Д ех|Р [-чр2(/—/0)2] (Р=1,83-10“3 с, Л = 48-10~9 Вт/Гц, F=
= 3,1 • 103 Гц). В канале действует белый шум со спектральной
плотностью мощности Afo=lO-9 Вт/Гц.
Определить максимально возможный объем информации, ко-
торый может быть передан по данному каналу, если время ис-
пользования канала Тк=1 ч.
4.4.12. Решить задачу 4.4.11 для вариантов числовых значений
величин, приведенных в табл. 4.18.
Таблица 4.18
Вариант 1 2 3 4 5 6 7 8 9 10
₽. с-1 4 5 2 3 6 10 9 1 2 9
А, Вт/Гц 4 9 4 8 7 5 2 8 10 2
F, кГц 40 50 20 20 60 100 90 10 20 90
No, Вт/Гц 10-ю Ю-15 Ю-is 10-13 Ю-!9 10—17 10-ю Ю-15 ю—12 Ю-!8
4.4.13. Решить задачу 4.4.11, если передаваемый сигнал имеет
спектральную плотность мощности Go (f) = А ехр [—а | f—fo | ] по
числовым данным, приведенным в табл. 4.49.
Таблица 4.19
Вариант 1 2 3 4 5 6 7 8 9 10
А, Вт/Гц 1 10 9 9 8 3 7 6 5 1
а, с-1 1 2 1 3 8 3 5 1 4 6
F, кГц 7 7 2 8 5 3 5 I 7 9
No-10-9, Вт/Гц 1 2 1 3 8 3 5 1 4 6
4.4.14. Чему равна пропускная способность канала, если сред-
няя мощность сигнала 1 мкВт, а помехой является тепловой шум
приемного устройства с полосой 10 кГц. Приемник работает при
температуре 20 °C.
Таблица 4.20
Вариант 1 2 3 4 5 6 7 8 9 10
Рс, мкВт F, кГц 6 7 1 5 8 6 10 9 7 9
10 4 4 10 3 8 6 10 5 6
/, град 24 30 18 27 25 22 28 30 20 20
78
4.4.15. Решить задачу 4.4.14 для вариантов числовых значений
величин, заданных в табл. 4.20.
4.4.16. Определить величину отношения сигнал-шум в канале,
при котором по каналу можно передавать символы со скоростью
ии=2Г, если осуществляется оптимальное кодирование по Шен-
нону.
Г л а в а 5. ОСНОВЫ ТЕОРИИ
ПОМЕХОУСТОЙЧИВОГО
КОДИРОВАНИЯ
5.1. ПРИНЦИПЫ ПОМЕХОУСТОЙЧИВОГО
КОДИРОВАНИЯ
Корректирующими или избыточными кодами (см. § 1.2) называют коды, кото-
рые позволяют обнаруживать ошибки и исправлять ошибки и стирания, возни-
кающие при передаче дискретных сообщений. Для корректирующих кодов чис-
ло комбинаций N удовлетворяет неравенству
N=mn>K (5.1)
(в дальнейшем будем рассматривать только двоичные коды, для которых
т=2). При этом часть кодовых комбинаций используется для кодирования
(эти кодовые комбинации называются разрешенными, их число АГР=К), а
другая часть при кодировании не используется. Число неиспользованных при
кодировании комбинаций, называемых запрещенными, равно N—N? или W—К.
В л-разрядной кодовой комбинации корректирующего кода = log К сим-
волов являются информационными, г—п—k символов — проверочными (избы-
точными). Легко заметить, что число разрешенных кодовых комбинаций
7Vp=2ft. (5.2)
Избыточностью равномерного блочного кода является величина
Хк = 1—(log К) /(л log т), (5.3)
а относительной скоростью кода
Як =* (log К) / (л log т) = 1 —хк. (5.4)
При избыточном кодировании ошибки обнаруживаются, если переданная
разрешенная комбинация превращается в одну из запрещенных. Для декоди-
рования с обнаружением ошибок множество принимаемых кодовых комбина-
ций разбивается на К4-1 подмножества, из которых подмножества Вь В2 ...
..., В к содержат каждое по одной (разрешенной) кодовой комбинации, а под-
множество Вк+i—все остальные (запрещенные) комбинации.
При декодировании с исправлением ошибок множество В разбивается на
К неперекрывающихся подмножеств: Вь В2,..., Вк. Если принята кодовая
комбинация, принадлежащая подмножеству В,-, то считается, что передавалась
кодовая комбинация bt*. В подмножество Вг- следует включить те запрещенные
79
комбинации, которые наиболее вероятно могут образоваться из переданной раз-
решенной комбинации Ьг.
Если минимальное расстояние по Хеммингу (см. § 2.4) между разрешен-
ными кодовыми комбинациями б/МИн, то код позволяет обнаружить ошибку,
когда в кодовой комбинации число ошибочно принятых символов удовлетворя-
ет условию
q<d МИН' (5.5)
Следовательно, максимальная кратность обнаруживаемых ошибок <7о=^Мин—1.
Блочный корректирующий код исправляет ошибки, если их число
^^^мин/З. (5 6)
Максимальная кратность полностью исправляемых ошибок
_ J (^мин~ 0/2 при нечетном dMHH,
— > л /г> 1 .
“миц/2 — 1 при четном имин-
При декодировании с исправлением ошибок и стираний могут быть ис-
правлены ошибок и q^qc стираний, если их число удовлетворяет усло-
вию
q^<Z (с?мип—7с)/2.
В общем случае код с расстоянием dMHH исправляет произвольное число
q^qc стираний, q^qn ошибок и обнаруживает qu^q^qo ошибок при ус-
ловии, что 2<?и4-<7о + <7с<^мин.
Задачи
5.1.1. Сообщения источника, имеющего алфавит с объемом К =
=32, кодируются двоичным блочным кодом. Число разрядов в
каждой кодовой комбинации п=8. Какое число информационных
и проверочных символов содержится в каждой кодовой комбина-
ции? Сколько разрешенных и запрещенных комбинаций в ис-
пользуемом коде?
5.1.2, По условию задачи 5.1.1 определить избыточность и от-
носительную скорость кода.
5.1.3. Первичный непрерывный сигнал путем дискретизации во
времени и квантования по уровню превращается в импульсную
последовательность с числом уровней К =128. Каждый уровень
квантованного сигнала кодируется равномерным 10-разрядным
двоичным кодом*. Чему равна избыточность и относительная ско-
рость кода? Как изменяется избыточность и относительная ско-
рость кода, если число разрядов в кодовой комбинации уменьшить
на 2? Увеличить на 2?
5.1.4. Алфавит с объемом К=256 кодируется 15-разрядным
равномерным двоичным кодом. Чему равна избыточность и отно-
сительная скорость кода?
5.1.5. Комбинации n-разрядного двоичного блочного кода со-
* Такой способ кодирования непрерывных сигналов называется импульсно-
кодовой модуляцией (ИКМ). Более подробно ИКМ будет рассмотрена в гл. 8.
80
держат k информационных символов. Определите долю обнаружи-
ваемых таким кодом ошибок из всех возможных ошибок.
5.1.6. Для кода из предыдущей задачи определите долю исправ-
ляемых ошибок. При .каком условии код может применяться в
качестве исправляющего?
5.1.7. Определить избыточность и относительную скорость для
кодов по следующим данным:
1) т — 2, п = 7, К = 32; 2) т = 2, п=6, /( = 16;
3) ги = 3, п=4, /( = 27; 4) ги = 3, п = 5, /(=81.
5.1.8. Определить долю обнаруживаемых и исправляемых оши-
бок для двоичных кодов по следующим данным:
1) п=5, 6=4; 2) п=7, £=4; 3) лг= 15; £=11; 4) п=21, 6=10.
5.1.9. Определить долю обнаруживаемых ошибок для кода,
каждая комбинация которого содержит всего один избыточный
символ (п = £+'1).
5.1.10. Определить минимальное кодовое расстояние, необходи-
мое для обнаружения тройной ошибки.
5.1.11. Ошибки какой кратности может исправить код, для ко-
торого б/мин = 7?
5.1.12. Определить йМИн для кодов:
а) обнаруживающего тройную и исправляющего двойную
ошибки;
б) обнаруживающего пятикратную и исправляющего тройную
ошибки.
5.1.13. Показать, что код с расстоянием йМин позволяет обнару-
жить ^о^^мин—1 ошибок И исправить ^и^^мин/2—1 ошибок.
5.1.14. Каждые 100 символов двоичного источника кодируются
двоичной последовательностью, содержащей п= 125 кодовых сим-
волов. Определить избыточность кода хк. Найти вероятность пра-
вильного декодирования кодовой комбинации в канале с незави-
симыми ошибками, если йМИн = 6, вероятность ошибочной регист-
рации кодового символа р0 —0,05, а декодирование осуществляется
по минимуму расстояния по Хеммингу.
5.1.15. Символы двоичного источника А и В кодируются избы-
точным 3-разрядным двоичным кодом с йМИн = 3. Составить табли-
цу возможных состояний на выходе декодера при декодировании
по минимуму расстояния по Хеммингу в нестертых символах:
с исправлением стираний и обнаружением ошибок;
с исправлением ошибок и стираний;
с обнаружением ошибок и исправлением ошибок и стираний.
5.2. ЛИНЕЙНЫЕ ДВОИЧНЫЕ БЛОЧНЫЕ КОДЫ
Линейный двоичный код длины п — это код, для которого сумма по моду-
лю 2 любых разрешенных кодовых комбинаций также является разрешенной
кодовой комбинацией.
Если формирование кодовой комбинации осуществляется в два этапа, при-
чем на первом этапе образуются кодовые комбинации примитивного кода, а
81
затем по определенному правилу к ним добавляются избыточные (контроль-
ные, проверочные) символы, то код называется систематическим. Проверочные
символы &пр формируются по правилу
k
&ьпр= s (5-7)
/=1
где &-Ы; k — число информационных символов; г — число избыточных
символов. Суммирование в (5.7) осуществляется по модулю 2 для двоичного
кода *.
Коэффициент ущ равен 1, если информационный символ bi участвует в.
образовании проверочного символа £г,пр. В противном случае yi,i = 0. Сово-
купность коэффициентов yi,i удобно задать в виде матрицы размерности rxk
(г — строк, k — столбцов)
г = Vi.fe+1 71 ,k+2 ^2,k+l У2, k+2 Y3.J4-1 Тз,н-2 .. . Vfe,fe+1 . У/г, k+2 (5.8)
Vi.ft+r T2,fe4-r Тз.н-г • Vi.k+r
Проверочные символы в этом случае задаются соотношением
Vi.fe+1 •• • Tl.fc-R
Ьпр = = ЬуГ = |Мг— bkl V2,fe+1 .. . ?2,к+г • (5.9)
V/j.ft+i .. . ^k,k+r
Здесь b — матрица-строка заданной кодовой комбинации; уТ — транспониро-
ванная матрица коэффициентов уг,г. Линейный код можно получить линейным
суммированием по модулю 2 любых k линейно независимых кодовых комбина-
ций. Матрица, состоящая из k строк, образованных этими комбинациями, назы-
вается порождающей или производящей и имеет размерность kXn. В общем
случае порождающая матрица G записывается так:
^11 ^12 • • • bik
#21 ^22 ... b2k b2t fc-J-l ^2, • • • ^2, fe-f-r
bk, 1 bkt 2 • • • bkk bkt bkt k+2 . . . bkt
Здесь ba—j-й информационный символ i-й кодовой комбинации при j^k, или
/-й проверочный символ х-й кодовой комбинации при /^Л+1.
В качестве линейно независимых удобно использовать кодовые комбинации,
содержащие лишь один ненулевой символ. В этом случае порождающая мат-
рица G с учетом (5.9) принимает вид
G =
1 0 0. . .0 0 Ti,^4-2 •
0 1 0 ... 0 0 Т2, fe-H ^2, Н-2 •
° ° 1 ... 0 0 у3> y3t .
71, k+r
?2, fe-f-r
Тз, fe-f-r
(5.Н)
0 0 0 ... 0 1 Vk, k+2 • • • V/г, k+r
* Коды, у которых проверочные, символы формируются суммированием по
модулю 2, называются кодами с проверкой на четность.
82
где Ik — единичная матрица порядка k\ у — матрица коэффициентов ущ. Мно-
жество кодовых комбинаций кода, заданного порождающей матрицей (5.11),
является также множеством линейных комбинаций строк этой матрицы. Линей-
ный код длины п с k информационными символами и с г=п—k проверочны-
ми символами обозначается (n, k). Кодовую комбинацию такого кода можно
записать как
b = Ьг Ь2 • • ‘kk—2 ^k—i bk , пр ^/г+2, пр ’ * '^п, пр,
k r~n—k
где {Ьг}—информационные символы; {^;,пр}—проверочные символы.
Линейный (п, 6)-код можно задать проверочной матрицей Н, имеющей раз-
мерность гХп. Эта матрица имеет следующий вид:
Ti, я>4-1 ?2, М-1 • • • Yfe, Н-1 1 0 ’ ’ ’ 0
Н= Т1;А+2 ?2/+2 ; • • Ъ.*+201- • • 0 =||Т1Г||. (5.12)
Vl, k+r ?2, k+r • • • 4k, k+r 0 0... 1
В каждой строке проверочной матрицы на позициях информационных сим-
валов стоят коэффициенты а на позициях проверочных символов — единицы
и нули, причем единица указывает, какой именно проверочный символ соответ-
ствует совокупности коэффициентов данной строки.
Для каждой кодовой комбинации (л, 6)-кода матричное произведение
ЬНГ = О. (5.13)
Таким образом, совокупность кодовых комбинаций (л, 6)-кода—это мно-
жество всех последовательностей Ь, для которых выполняется условие (5.13).
Это соотношение лежит в основе процедуры декодирования линейных кодов.
Проверочная матрица (л, &)-кода является порождающей матрицей нового ли-
нейнюго (п, п—6)-кода, содержащего 2п~к комбинаций, т. е. Н(П,л) = О(П>п-а),
Такой (л, п—6)-код называется двойственным для исходного (л, 6)-кода.
Из (5.13) следует, что
G(n,fc)HT(n>fc) = G(n>b)Gr(n,n-fc) = 0. (5.14)
Это условие означает, что двойственные коды (л, k) и (л, п—k) являются ор-
тогональными.
Избыточность линейного двоичного кода
Хк = 1 —(log2ft)/n=l—kln=rln, (5.15)
где г=п—k—число проверочных символов.
«Оптимальным» является код (л, k), обеспечивающий наименьшую вероят-
ность ошибочного декодирования среди всех кодов той же длины п и избыточ-
ности rln.
Совершенные коды — это коды, которые свою избыточность расходуют на
исправление ошибок заданной кратности q. Квазисовершенным называется код,
который, кроме того, исправляет некоторую часть ошибок кратности ^+1.
83
Обнаружение ошибок при использовании линейных кодов основано на про-
верке соотношений (5.7): по принятой кодовой комбинации составляются конт-
рольные суммы по модулю 2
= 2 V/Jbt, i = k+1, k + r (5.16)
Z=1
(здесь 6i — l-й знак принятой кодовой комбинации Ь) и сопоставляется с про-
верочными символами принятой кодовой комбинации. Совокупность чисел
Cj_ft = Z?j>np®(6K0HTj,np для данной кодовой комбинации называется синдромом
с(б) =CiC2 ... Сг.
Декодирование принятой кодовой комбинации может быть осуществлено с
помощью проверочной матрицы Н. Если принята комбинация Ь, то синдром
с можно определить равенством с=ЬНг. Таким образом, синдром — это вектор-
строка (сь с2,... ,сг) с г компонентами (по одной для каждого проверочного
символа). Если b — переданная кодовая комбинация, а b — принятая, то сумма
их по модулю 2 b®b = Z называется шумовой последовательностью. При этом
с —ZHT.
При правильном приеме все элементы синдрома равны нулю. Отличие хо-
тя бы одного элемента синдрома от нуля означает, что произошла ошибка.
При декодировании с исправлением ошибок по виду синдрома можно оп-
ределить разряд кодовой комбинации, в котором произошла ошибка.
Задачи
5,2.1. Двоичный код, предназначенный для 1кодирования восьми
сообщений, содержит кодовые «комбинации:
bi=00000; b2=10011; Ь3 = 01010; Ь4=11001;
Ь5 = 00101; Ь6=10'110; Ь7 = 01111; b8= 11100.
Является ли данный код линейным? Найти избыточность кода и
б^МИН*
5.2.2. Построить систематический код (7, 4), предназначенный
для 'кодирования сообщений двоичного источника, имеющего объ-
ем К=24 символов. Показать, что ймин такого кода равно 3.
5.2.3. Для систематического кода (7, 4) из предыдущей задачи
построить производящую и проверочную матрицы.
5.2.4. Построить линейный код (7, 4) по заданной производя-
щей матрице
1 0 0 0 1 1 1!
0 10 0 110
°" 00 1 0 1 о Г
0 0 0 1 0 1 1
По производящей матрице составить правило формирования про-
верочных разрядов. Составить проверочную (Матрицу.
84
5.2.5. Линейный код (7, 4) построен по матрице
1 0 0 0 0 1 1
0 10 0 10 1
° 0 0 1 0 1 1 О'
0 0 0 1 1 1 1
Составить проверочную матрицу и показать процесс исправления
ошибок в произвольном разряде корректирующего кода, информа-
ционная часть которого представляет собой 4-разрядные комбина-
ции примитивного двоичного кода.
5.2.6. Для кода, заданного в задаче 5.2.4, составить таблицу
синдромов и показать, каким ошибочным разрядам они соответ-
ствуют.
5.2.7. Составить таблицу синдромов одиночных ошибок для ко-
да (7.4) из задачи 5.2.5 и показать, каким ошибочным разрядам
они соответствуют.
5.2.8. Убедиться в том, что в кодовых комбинациях 1000111,
0111010, 1101001, 0000000, принадлежащих коду из задачи 5.2.4,
может быть исправлена ошибка в любом информационном раз-
ряде.
5.2.9. Показать, что код, заданный производящей матрицей
1 0 0 0000000000 1 1
0 1 0 000000000 1 0 1
0 0 1 000000000 1 1 0
0 0 0 100000000 1 1 1
0 0 0 010000001 0 0 1
G = 0 0 0 001000001 0 1 0
0 0 0 000100001 0 1 1
0 0 0 000010001 1 0 0
0 0 0 000001001 1 0 1
0 0 0 000000101 1 1 0
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1
исправляет одиночные ошибки в произвольной кодовой комбина-
ции.
5.2.10. Сравнить с точки зрения способности исправления оди-
ночных ошибок линейные коды, заданные производящими матри-
цами
10000001 1 1 1 100000000 1 1
01000001 1 1 0 010000 0 0 1 0 1
00100001 1 0 1 001000 0 0 1 1 0
о II 00010001 0 1 I II с 000100 0 1 0 0 1
00001000 1 1 1 000010 0 1 0 1 1
00000101 0 0 1 000001 0 1 1 0 0
00000010 1 1 0 оооооо 1 0 1 1 0
Выяснить, какой из кодов реализуется более простыми средст-
вами.
85.
5.2.11. Решить задачу 5.2.10 для кодов, заданных производя-
щими матрицами
1 0 0 0 0 0 0 1 1 1 1 10000001 1 0 0
0 10 0 0 0 0 0 1 1 1 01000000 1 1 0
0 0 10 0 0 0 1 0 1 1 00100000 0 1 I
II гЧ С 0 0 0 1 0 0 0 1 1 0 1 о ьа II 00010001 0 1 0
0 0 0 0 1 0 0 1 1 1 0 00001000 1 0 1
0 0 0 0 0 1 0 1 0 0 1 00000101 0 0 1
0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 1 1 1 1 0
5.2.12. Определить, какие из приведенных кодовых комбинаций
линейного кода содержат ошибку:
МООШ, 0110101, 0011010, 0010110,
1000100, 1011011, 0010101, 0110010,
1100100, 0110101, 1001010, 0011011.
Код построен по матрице
G =
1000111
0 1 0 0 0 1 1
0010110
0001101
5.2.13. Для кода (7, 4) из задачи 5.2.2 достроить комбинации
двойственного иода (7,3).
5.2.14. Найти комбинации кода (7, 3), двойственного иоду
(7, 4), из задачи 5.2.4.
5.2.15. Найти комбинации кода (7, 3), двойственного коду
(7,4), заданного производящей матрицей в задаче 5.2.5.
5.2.16. В табл. 5.1 приведены 2-разрядиые двоичные информа-
ционные последовательности и соответствующие им кодовые ком-
бинации.
Показать, что полученный иод является систематическим кодом
с проверкой на четность, и выразить каждый разряд кодовой ком-
бинации в виде линейной комбинации информационных символов.
Найти для заданного кода порождающую и проверочную матри-
цы. Найти вероятность неправильного декодирования.
Таблица 5.1
Информационная последовательность Кодовая комбинация
00 00000
10 10111
01 01101
11 пою
Рис. 5.1. Схема формирования дво-
ичного кода
86
5.2.17. На рис. 5.1 показана схема формирования двоичного
кода при передаче по двоичному симметричному каналу с вероят-
ностью ошибочного перехода р0<0,5. Первоначально сдвиговый
регистр заполнен нулями; затем в регистр поступают четыре ин-
формационных символа и одновременно передаются по каналу.
После этого передаются три проверочных символа. Перед вычис-
лением проверочного символа все четыре информационных симво-
ла сдвигаются в регистре на одну позицию вправо-.
Найти проверочную матрицу, порождающую -матрицу, таблицу
декодирования и вероятность ошибочного декодирования для дан-
ного кода.
5.3. ЦИКЛИЧЕСКИЕ КОДЫ
Линейный двоичный код, которому принадлежат кодовые комбинации, по-
лученные путем циклической перестановки символов, называется циклическим.
Кодовый вектор b циклического кода представляют полиномом (п—4) сте-
пени: b(x) =ao+aix+a2x2+ +an-ixn-\ где коэффициенты а» принимают
значения 0 или 1. При таком представлении кодовый вектор, полученный из
b циклической перестановкой элементов, можно рассматривать как результат
умножения полинома Ь(х) на х, если считать, что хп = 1.
Полином наименьшей степени среди всех полиномов, соответствующих ко-
довым комбинациям циклического кода, называется порождающим полино-
мом g(x) = 1+yix+y2*2+ ... +УгХг. Коэффициенты yi равны 0 или 1. Степень
порождающего полинома определяет число проверочных символов в кодовой
комбинации. Число ненулевых членов полинома g(x) определяет предельное для
данного кода ^МИн.
Зная порождающий полином, можно построить все кодовые комбинации
циклического кода, а также устройства кодирования и декодирования. На по-
рождающий полином должен делиться без остатка двучлен хп±1. Полученный
результат определяет проверочный полином
А(х) = (х"~1)/я(х). (5.17)
Порождающий полином g(x) и проверочный полином h(x) являются орто-
гональными, так как при хп—1=0 они удовлетворяют условию
^(х)й(х)=0. (5.18>
При отсутствии ошибок в кодовой комбинации циклического кода должно вы-
полняться условие
^(х)А(х)=0. (5.19)
Невыполнение условия (5.19), т. е. ti(x)h(x) =/=(), является признаком ошибки.
Задачи
5.3.1. Записать кодовые комбинации циклического кода, полу-
ченные циклическим -сдвигом комбинации 110101.
87
5.3.2. Первые три комбинации циклического кода имеют вид
100001101, 110000110, 011000011. Построить остальные комбина-
ции этого кода.
5.3.3. Представить в виде многочленов заданные комбинации
некоторого циклического кода: 0111110, 0011111, 1001111.
5.3.4. Показать, что полином g'(x) = 1+х+х3 является порож-
дающим для циклического кода (7, 4). Составить кодовые комби-
нации циклического кода (7, 4).
5.3.5. Составить структурные схемы кодера и декодера для
циклического кода (7, 4), заданного порождающим полиномом
^г(х) = 1+х+х3. Пояснить процесс кодирования и декодирования
с исправлением ошибок.
5.3.6. Показать, что полином g(x) = 1 +х2+х3 является порож-
дающим для 7-разрядного циклического кода. Найти число1 инфор-
мационных и проверочных разрядов и б/МИн. Определить провероч-
ный полином.
5.3.7. Показать, что полином §(%) = 1+х + х2+%3 является по-
рождающим для 8-разрядного циклического кода. Найти число ин-
формационных и проверочных разрядов, б/Мин и определить прове-
рочный полином.
5.3.8. Какие комбинации циклического кода (7, 4), заданного
полиномом g(x) =14-%+х2, содержат ошибку: 1001000, 1111001,
0100101, 1111011, 0010111, 0011111, 0100011, 1000001, 1100110,
1111100.
5.3.9. Какие комбинации циклического кода (7, 4), заданного
полиномом g(x) = 1+х2+%3, содержат ошибку: 0001101, 0011110,
1001101, 1000110, 1100110, 0100011, 0110011, 1000011, 1010101,
1101000, 1101100, 0110100, 0110110.
5.3.10. Можно ли использовать полином g(x) = l+x2 + x5 в ка-
честве порождающего для построения циклического кода с кодо-
вым расстоянием д!мин = 5?
5.3.11. Какое максимальное число ошибок может исправить
циклический код, построенный с помощью порождающего полино-
ма g\x) = 1+х + х4?
5.3.12. Какое максимальное число ошибок могут исправить цик-
лические коды, построенные с помощью порождающих полиномов:
1) £(*) ==1+х2+х4; 2) g-(x) = 1+х2+х5; 3) g(x) = 1 +х+х3 + х6.
5.4. НЕКОТОРЫЕ РАЗНОВИДНОСТИ
КОРРЕКТИРУЮЩИХ КОДОВ
Итеративный код. Строится из двух линейных систематических кодов (ль
k\) и (п2, k2). Вначале сообщение кодируется кодом 1-й ступени (пь ki). Если
k2 комбинаций кода 1-й ступени записать в виде строк матрицы, то ее столбцы
содержат по k2 символов, которые являются информационными для кода 2-й
ступени (n2, k2). К столбцам этой матрицы необходимо добавить п2—k2 про-
-88
верочных символов. В результате получится матрица (niX/z2), содержащая
П\п2 символов, k\k2 из которых являются информационными:
Информацион- ные символы 2-й ступени 1 Информационные символы 1-й ступени ( Р1,1 ^1,2 •• • b\,kt 1 bk2t 1 bkz,2 • • • bk2, ki Проверочные символы 1-й ступени b\, fci-H • • • b\, nt bk2, k+l • • • bk„ n, (5.20)
Проверочные символы 2-й ступени ( • • • ^*.+1. *1 1 ( bn2, 1 • • • bn2, kx ЬП2, * • • bn2t
Минимальное кодовое расстояние двумерного итеративного кода
^мин—d\d2, (5.21)
где d2— минимальные кодовые расстояния кодов 1-й и 2-й ступени соот-
ветственно.
Код с постоянным весом — блочный код, каждая кодовая комбинация ко-
торого содержит одинаковое число единиц (одинаковый вес). Эти коды обозна-
чаются (k/l). Это означает, что комбинации n-разрядного кода с постоянным
весом содержат k единиц и / нулей (& + /=п).
Код с четным числом единиц — код, который образуется добавлением к
комбинации /г-разрядного кода одного знака, чтобы число всех единиц в новом
(и + 1)-разрядном коде было четным.
Код с числом единиц, кратным 3 — код, к каждой комбинации которого
добавляют два проверочных элемента, чтобы сумма всех элементов по модулю
3 была равной 0.
Повышение эффективности кода с обнаружением ошибок может быть до-
стигнуто введением определенных зависимостей между элементами кодовых
комбинаций Примером такого кода является корреляционный, в котором эле-
мент первичного кода преобразуется в два элемента: 1 преобразуется в 10, а
0—в 01.
В технике связи часто применяется инверсный код (код с повторением), в
основу построения которого положен метод повторения исходной кодовой ком-
бинации: при четном числе единиц кодовая комбинация просто повторяется, при
нечетном — повторяется в инвертированном виде.
Помимо блочных кодов, в настоящее время распространены рекуррентные
или цепные коды. В рекуррентном коде информационные символы чередуются с
проверочными, образуя последовательность
Z>iZ?12&2^23^3^34^4^45^5 • • ,
где bi—1-й информационный символ, являющийся 0 или 1 в соответствии с пе-
редаваемым сообщением, a frz,z+i — проверочный символ, определяемый урав-
нением
bi,i+i = bi+bi+i, (5 22]
причем суммирование осуществляется по модулю 2. Рекуррентный код, содер
жащий из п символов k информационных, обозначают (kin).
81
К рекуррентным кодам можно условно отнести относительный код, ис-
пользуемый в дискретных системах связи с относительной модуляцией фазы
(ОФМ).
Важной разновидностью рекуррентных кодов являются сверточные коды
(СК) [2, 11].
Кодер СК содержит регистры памяти для хранения определенного числа
информационных символов, преобразователь информационной последователь-
ности в кодовую (путем суммирования по модулю 2 выходов определенных
ячеек регистра), а также ключ, осуществляющий коммутацию через тактовый
интервал Т отдельных выходов кодера и канала. Процесс кодирования произ-
водится непрерывно. Если число информационных символов, одновременно по-
ступающих на вход кодера, обозначить через k, а через п—число соответствую-
щих им символов на выходе кодера, то скорость кода R=k!n. Длина кодирую-
щего регистра (ДКР), или память кода, определяется числом ячеек (разрядов)
регистра k. Термин «сверточный код» означает, что кодовая последовательность
может быть определена как свертка информационной последовательности и с
импульсным откликом кодера (откликом кодера на последовательность м=
= 1000 ...).
Структуру /-го (1^/^п) выхода кодера можно определить некоторым по-
рождающим полиномом
G(/) (D) = g</> + g{»D + 4'» D* + ... + g^Dv>
(5.23)
где Dr—’Оператор задержки на г тактов (разрядов), ^z(j) = l, если связь /-го
сумматора с /-й ячейкой регистра существует, и g№=0, если этой связи нет.
Наивысшая степень v в (5.23) называется длиной кодового ограничения (ДКО).
При 7? = 1/2 v = k—1.
Сверточный код можно задать порождающей матрицей
<?о Gi G2 • • • 6^—1 • • •
• • -Go Ci G2 • • • • • •
.....6o Gi 62 • • • 6^_i • • •
(5.24)
Строки матрицы (5.24) представляют собой сдвинутую на соответствующее
число разрядов базисную порождающую матрицу F= |GqGiG2 ... Ga-J (верхняя
строка матрицы (5.24)), определяемую импульсным откликом кодера и состав-
ленную из элементарных матриц Gi (f=0, k—1), содержащих k строк и п
столбцов. Для двоичных кодов элементами этих матриц являются символы 0
и 1.
Матрица символов на выходе кодера В определяется матричным произве-
дением
B = UG, (5.25)
где U — матрица входных информационных символов.
Сверточный код можно задать проверочной матрицей Н, удовлетворяющей
условию
GHr = 0. (5.26)
Здесь Т — знак транспонирования.
30
При декодировании СК декодером с числом входов, равным числу выходов
кодера, возможно формирование синдромов
S=XHT, (5.27)
где Х=В+Е (сигнал+шум в дискретном канале).
С учетом (5.26)
S=EHr, (528)
По виду последнего столбца матрицы Нт (читая его снизу вверх) можно оп-
ределить многочлены формирователя синдромов
Задачи
5.4.1. Построить кодовые комбинации итеративного кода, на 1-й
и 2-й ступенях которого использованы коды (7, 4).
5.4.2. Определить параметры двумерного итеративного кода п,
k и t/мин, если на 1-й и 2-й ступенях использованы коды (7, 4).
5.4.3. Определить параметры двумерного итеративного кода, в
котором на 1-й ступени использован код с проверкой на четность
(5, 4) с di = 2, а на 2-й ступени — код (7, 4) с d2=3.
5.4.4. Какой объем алфавита должен иметь дискретный источ-
ник, чтобы его символы можно было бы закодировать 7-разрядным
кодом с весом й = 3? Составить кодовые комбинации такого кода.
Найти избыточность кода.
5.4.5. Вероятность ошибочного приема элементарного символа
кодовой комбинации ро=1О-2. Чему будет равна вероятность не-
обнаруженной ошибки при использовании кода с постоянным ве-
сом (3/4)?
5.4.6. Решить задачу 5.4.5 для следующих значений вероят-
ности ошибочного приема элементарного символа: ро —10~3; 10-4;
ю-\
5.4.7. Решить задачу 5.4.5 для кодов (4/5), (3/8), (4/7), (5/6)
и значений ро=10-2; 10~3; 10~4; 10~5.
5.4.8. Составить кодовые комбинации кода с четным числом
единиц, построенного на основе 5-разрядного двоичного кода. Оп-
ределить избыточность полученного кода. Вычислить вероятность
необнаруженной ошибки, если вероятность ошибочного приема од-
ного знака кодовой комбинации ро=10~2.
5.4.9. Составить кодовые комбинации кода с четным числом
единиц на основе 6-разрядного двоичного кода. Определить избы-
точность полученного кода и вычислить вероятность необнару-
женной ошибки при ро= 10“2; IO-3; 10-4; 10-5.
5.4.10. Составить кодовые комбинации кода с числом единиц,
кратным 3, построенного на базе 5-разрядного двоичного кода, и
определить для него вероятность необнаруженной ошибки. Найти
избыточность полученного кода.
91
5.4.11. Полагая, что первичный код является 5-разрядным, най-
ти избыточность корреляционного кода. Определить вероятность
необнаруженной ошибки.
5.4.12. Определить вероятность необнаруженной ошибки для
инверсного кода, построенного па основе 5-разрядного двоичного
иода.
5.4.13. Двоичный источник информации выдает последователь-
ность символов 1001И1000110101. Найти контрольные символы и
записать кодовую последовательность рекуррентного кода (1/2).
Составить структурную схему кодирующего и декодирующего уст-
ройства для такого кода.
5.4.14. Показать, что кодирование в системе ОФМ является
рекуррентным.
5.4.15. Кодер СК с одним регистром и двумя выходами, кото-
рые поочередно коммутируются с трактом .передачи, показан на
рис. 5.2. Определите параметры R, k, v, а также порождающие
полиномы дли каждого из выходов G^(D), G(2>{D).
5.4.16. Кодер СК с двумя регистрами и тремя выходами пока-
зан на рис. 5.3. Определите параметр k для каждого регистра, а
также скорость кода R.
5.4.17. На вход кодера (рис. 5.2) подается единичная последо-
вательность «=1000.... Полагая, что начальное состояние регист-
ра нулевое (в дискретный момент 0), изобразите состояние кодера
в дискретные моменты 1, 2, 3, 4, ... (разнесенные на тактовый
интервал, равный Длительности информационного символа Т). На-
пишите двоичный импульсный отклик кодера. Найдите, пользуясь
принципом суперпозиции, двоичную последовательность на выхо-
де кодера, если информационная последовательность на входе и —
=11011.
5.4.18. Определить последовательность символов на выходе ко-
дера (рис. 5.2), если при подаче на вход кодера информационной
последовательности «=4101 базисная порождающая матрица, оп-
ределяемая импульсным откликом, найденным в задаче 5.4.17,
F=|G0, Gi, G2|, G0=0 1; Gt = l 1; G2=l 1.
Рис. 5.2. Сверточный кодер с
одним регистром
32
Рис. 5 3. Сверточный кодер с двумя
регистрами
5.4.19. Убедиться в том, что порождающая матрица
G =
1 1 0 0 0 1
110 0
1 1
соответствует 'кодеру, представленному на рис. 5.4 *.
5.4.20. Проверить, является ли матрица
1
0 1 1
0 0 0 1 1
проверочной для иода, формируемого кодером рис. 5.4.
5.4.21. По транспонированной проверочной матрице
Нг =
110 0 10
110 0
1 1
найти два многочлена, HSW(D) и Я8<2)(Л), определяющие форми-
рователь синдромов, и нарисовать схему, реализующую этот фор-
мирователь.
5.4.22. Шумовая последовательность в канале определяется
вектором-строкой Е=|101|. Найти синдром ошибок, если исполь-
зуется СК с порождающей матрицей, заданной в задаче 5.4.19.
5.4.23. Транспонированная проверочная матрица
Нг
1110 11
1110
1 1
Найти многочлены Hs(1) и //s<2) формирователя синдромов и нари-
совать схему, реализующую формирователь.
5.4.24. Найти синдром ошибок для шумовой последователь-
ности из задачи 5.4.22 по транспонированной проверочной матри-
це из задачи 5.4.23.
Рис. 5 4. Сверточный кодер
(к задаче 5.4.19)
* Отметим, что на выходе данного кодера образуется систематический СК,
для которого характерна передача в канал проверочного символа после каж-
дого информационного, тогда как во всех предыдущих задачах мы имели дело
с несистематическими СК, в которых информационные символы в явном виде
не присутствуют.
93
Г л а в a 6. ПРИЕМ ДИСКРЕТНЫХ СООБЩЕНИИ
6.1. КРИТЕРИИ ОПТИМАЛЬНОГО ПРИЕМА.
АЛГОРИТМЫ ОПТИМАЛЬНОГО ПРИЕМА ПРИ
ТОЧНО ИЗВЕСТНОМ СИГНАЛЕ
Здесь рассматриваются лишь синхронные системы связи (элементарные симво-
лы имеют неизменную длительность Т и начало отсчета фиксировано) и поэле-
ментные методы приема дискретных сообщений (последовательное вынесение
приемником решения об отдельных элементарных кодовых символах bk.i', k~
= 1,2, 3,... — номер последовательно передаваемого элементарного символа; /=
= 1,2,3,... — номер позиции кодового символа).
Одним из наиболее широко распространенных критериев оптимального при-
ема дискретных сообщений является критерий минимума средней вероятности
ошибки (критерий идеального наблюдателя).
Алгоритм работы приемника, оптимального по критерию идеального наблю-
дателя, можно записать так:
bk, 1 ________
P[bk4\z(t)] P[bk>i\z(t)], i*j, (6.1)
bk, j
или
bk, i
P(bkfi)w[z(t)lbkii] 55 P(bkti)W[z(t)\bktl], (6.2)
' bk, j
т. e. сводится к проверке системы из (m—1) неравенств: регистрируется номер
символа, который максимизирует сравниваемые величины. Здесь P[bk,i |z(t)] —
апостериорная вероятность передачи символа bk>1 при фиксации на интер-
вале анализа (О, Т&) реализации принимаемого колебания (сигнал + шум) ?(/);
w\z(/) | bk,<] — функция правдоподобия передачи символа bk,i при фиксации
z(t). При непрерывном времени эту функцию называют функционалом прав-
доподобия. (В задачах оптимальной обработки будем интересоваться отноше-
ниями функционалов правдоподобия, которое, в отличие от самого функциона-
ла, сходится во всех представляющих основной практический интерес ситуа-
циях) .
Приемник, работающий в соответствии с алгоритмом
bk, i
w[z(t)\bkti] * w[z(t)\bk-], (6.3)
bk, i
называют приемником, построенным по правилу максимального правдоподобия.
Очевидно, что, если все символы равновероятны, (6 3) следует из (6.2) и
этот алгоритм обеспечивает минимизацию средней вероятности ошибки. При
неизвестных априорных вероятностях Р(Ьк,г) оптимальный прием в системах
связи чаще всего осуществляют по алгоритму (6.3).
Логарифмируя левые и правые части (6.2), запишем этот алгоритм в эк-
вивалентном виде:
bk^ i
In w [г (/) I bk {]4-1пР(6д, г) 5? In w [z (01 71 + In(dft (6.4)
bk. i
94
Интервал анализа на приеме Га не всегда совпадает с тактовым интерва-
лом на передаче Т. Примем, что
Та=(1+£>)£, £>=0,1,2,.... (6.5)
Величину D называют фиксированной задержкой в принятии решения об
элементарном символе.
Если сигналы соседних символов перекрываются в месте приема (канал с
межсимвольной интерференцией, порожденной линейными искажениями (пере-
ходным процессом) или, как говорят, памятью канала), то при оптимальной
обработке и учете всей энергии принимаемого сигнала приходится брать £)>0.
Конкретная величина D связана с параметром £=тпер/7’=0,1,2— относитель-
ной памятью канала (тПер — практическая протяженность импульсной переход-
ной характеристики канала). При пренебрежении межсимвольной интерферен-
цией чаще всего берут Та = Г. Для каналов с межсимвольной интерференцией
(£>0) могут быть построены приемные устройства, когда D<zL (неполный
учет энергии принимаемых сигналов) и D^L (полный учет энергии принимае-
мых сигналов). При независимых и равных вероятностях передачи кодовых
символов
tn ш г (D)_i_nl
S S O’|z(0|B£(L)ZL, B*(D)X1], (6.6)
*<0=1 ft(D)=1
Г b(^)_1 h(O)_|.£) ]
где w [2(/)|Bft(L)_L , bkt j —функция правдоподобия того,
что при фиксации z(t) на интервале Та k-й символ имел номер i, до него пе-
редавались символы bk-ъ ..., bk-L, а после него — символы bk+it..., bk+D', mD —
число различных цепочек символов, которые могли быть переданы на интервале
анализа после &-го символа; mL — число различных цепочек символов,
последействия («хвосты») которых могут влиять на интервале анализа k-ro
символа.
Выражение (6.6) можно рассматривать как усредненную функцию правдо-
подобия (по символам, переданным до и после анализируемого). В условиях
достаточно надежной связи (которые и должны быть обеспечены в современ-
ных системах передачи дискретных сообщений) можно считать, что символы,
зафиксированные до анализируемого (&-го), действительно переданы по каналу
(с вероятностью, близкой к 1). Это означает, что на интервале анализа Т& поч-
ти точно восстановлен сигнал £Ост(0, порожденный «хвостами» предшествую-
щих символов, и вместо (6 6) можно написать
’ Г h<D>+D 1
a'[z(OI^,f]= S 4г(0-£ост№, г. Sfe(D)Xi ]• (6-7)
*<O=i
Обозначим через sr,i(t) (r= 1,..., m) r-ю реализацию принимаемого сигнала,
обусловленную на интервале Та Z-й позицией &-го символа, £ предшествующи-
ми символами и D последующими символами. Если сигналы sr,i(t) известны
точно в месте приема, а на интервале 7\ имеется реализация аддитивного ста-
ционарного шума с плотностью вероятности (в общем случае многомерной)
wfn(Z)], то
w[z(0|BftSzl,r • bfc.t, [n(0=z(0-srtl(01. (6.8)
95
Индекс г в левой части равенства означает, что берется цепочка символов до
и после анализируемого, порождающая сигнал
Задачи
6.1.1. По каналу связи без памяти передаются двоичные сим-
волы bi и Ь2 с вероятностями P(bi) =0,6; Р(62)=0,4, причем сим-
вол bi определяется в месте приема на интервале Т сигналом
Si(0'=0, а символ &2 — сигналом s2(t)=a (двоичная АИМ). В ка-
нале действует гауссовский стационарный шум с дисперсией о2 =
= 10—4 Вт. Сигналы Si (/) =0 и S2(0 = 10“2 В известны точно в мес-
те приема. Какой символ зарегистрирует приемник, оптимальный по
критерию минимума средней вероятности ошибки, принимающий ре-
шение по одному отсчету смеси z(t) = на интервале Т,
если в момент принятия решения z = 0,008 В? Изобразите струк-
турную схему этого приемника.
6.1.2. В условиях задачи 6.1.1. определить, какой символ будет
зарегистрирован при значениях величин, заданных в табл. 6.1.
Таблица 6.1
Вариант 1 2 3 4 5 6 7 8 9 10
P(bi) а2, Вт а, В z, в 0,5 10~4 10“3 8 • IO-3 • 5-0 О 1 О Lq 1 ьэ 1 СО СП 0,4 ю-6 5 • 10—3 5-Ю-3 0,55 5.10~6 6 - io—4 10“2 о о о ° 1 1 |м СО со О’ 0,42 2-10~4 2-10~3 2-10~3 00 4^00 н! Д. о ООО’ III01 СО СП о> Ш S Д. — Д- о ООО” 1 1 105 со ьэ ст> 0,65 2.10~5 1 о-2 3-10“3 из ео « 1 . О | О О — О *7 СО
6.1.3. Приемник по одному отсчету выносит решение в пользу
символа fti, если отсчет принимаемой реализации z(t) больше по-
рога (70; в противном случае выносится решение в пользу символа
Ь2. Определить пороговое значение UQ для приемника, оптимально-
го по критерию минимума средней вероятности ошибки, если пере-
даваемым двоичным символам bi и Ь2, имеющим априорные веро-
ятности P(bi) и Р(Ь2), соответствуют канальные сигналы S\ = a и
s2 = —а, а в канале без памяти имеется гауссовский стационарный
шум с дисперсией о2.
6.1.4. В условиях задачи 6.1.3 найти численные значения порога,
соответствующие числовым значениям величин, заданным в
табл. 6.2.
Таблица 62
Вариант 1 2 3 4 5 6 7 8 9 10
Р(Ь.) а2, Вт а, В 0,1 10—2 10-1 0,9 ю-2 10-1 0,2 ю-3 ю-2 0,8 IO-! Ю-з 0.3 ю-i 10—3 0,7 5-Ю-3. 10—1 0,4 5 10- з 10-1 0,6 Ю-з 10-2 0,15 5.10-4 10-2 0,85 5-IO-4 IO-2
96
6.1.5. Двоичные сигналы и канал те же, что в задаче 6.1.3. При-
емное устройство принимает решение о переданном символе по
трем независимым отсчетам zi, z2 и z3 принимаемой смеси (в точ-
ках /1 = Г/3, /2 = 2Т/3, /з = 7,)«
Найти алгоритм работы приемника, оптимального по критерию
минимума средней вероятности ошибки, и изобразить его струк-
турную схему. Чему равен оптимальный порог f/0 при равноверо-
ятных символах? _____
6.1.6. Символам bi с вероятностью P(bi) соответству-
ют известные точно в месте приема сигналы Si(t), определенные
на интервале (О, Т). В канале имеется стационарный белый шум
с энергетическим спектром NQ.
Показать, что при отсутствии межсимвольной интерференции и
анализе принимаемого колебания (сигнал + шум) на всем интер-
вале (О, Т) алгоритм работы приемника, минимизирующего сред-
нюю вероятность ошибки (приемника Котельникова), может быть
записан в виде
т ъ.
J* [2(О-^(ДО-^о1пР(^) ix
о Ь1
[z(t)-Sj(t)]*dt-NolnP(bt). (6.9)
О
Показать возможность реализации алгоритма (6.9) с помощью не-
линейной схемы, содержащей квадраторы.
6.1.7. Показать, что в условиях задачи 6.1.6 алгоритм оптималь-
ного приема может быть записан в виде
т ъг
J z (0 Sj (0 dt - [Et + No In P (bt)]/2 i
° T b} (6.Ю)
if z(t) Sj(I) dt- [E} + N0\nP(b})]/2,
bi°
T
где Ei = J* Si2dt — энергия сигнала и реализован с помощью
о
корреляционной схемы. Какие возможны упрощения в реализации
оптимального приемника, если реализации сигналов Si(t) имеют
равные энергии и равные вероятности?
6.1.8. Покажите, что если в условиях задачи 6.1.7 для передачи
используются двоичные символы 1 и 0 с вероятностями Р(1) и
Р(0), то алгоритм оптимального приема может быть записан так:
т 1
(6.11)
О о
1/0 = {Е1-Е2 + 1п[Р(0)/Р(1)]}/2
и реализуется одноканальной схемой. Чему равен оптимальный по-
рог Uo, если Р(1)=Р(0) и используются двоичные системы:
с пассивной паузой (AM);
4—53 97
с активной паузой {Ei~E2);
с активной паузой и противоположными сигналами =
= —S2CO (например, ФМ с изменением фазы на л)?
6.1.9. При заданной реализации принимаемой смеси z(t) (сиг-
нал-Ьшум) апостериорные вероятности передаваемых символов
1 и 0 P(l|z)=0,6 и P(0|z)=0,4. Какой символ зарегистрирует
приемник, оптимальный по критерию идеального наблюдателя?
6.1.10. Символам Ь\ и Ь2, имеющим априорные вероятности
Р(Ь{) и Р(Ь2), соответствуют на интервале (О, Г) принимаемые
сигналы si(t) и s2(t), заданные в виде точек si и s2 функциональ-
ного пространства с метрикой Гильберта. В этом же пространстве
точками z определены реализации принимаемой смеси z(t). Раз-
бить пространство сигналов на две непересекающиеся области
А1 и Л2, приписываемые решениям соответственно в пользу симво-
лов bi и Ь2 (собственные области) в предположении того, что сиг-
налы в месте приема известны точно, в канале без памяти имеет-
ся стационарный гауссовский белый шум с энергетическим спект-
ром No, принимаемое колебание анализируется на интервале
(О, Т) оптимальным приемником Котельникова, минимизирующим
среднюю вероятность ошибки. Как будет проходить граница меж-
ду собственными областями, если символы будут равновероятны?
6.1.11, На вход приемника поступает один из трех сигналов:
Si\t) =acos (dt, s2{t) = bsin(dt, s3(0==0 вместе с белым шумом. По-
скольку эти сигналы принадлежат двумерному пространству R2,
их можно изобразить векторами на плоскости. Покажите разбие-
ние пространства'сигналов на собственные области для двух слу-
чаев: а = Ь и Ь = 2а.
6.1,12. Покажите разбиение пространства сигналов на собствен-
ные области для четырех произвольных сигналов, принадлежащих
пространству R2.
6.1.13. Независимым и равновероятным двоичным символам 1
и 0 при ФМ с изменением фазы на л соответствуют в канале с па-
мятью (Л=1) ожидаемые элементарные сигналы
= s2(f) = -S1(0, (6.12)
где gi(t) —сигнал, определенный на интервале (О, Г); g2(t) —
сигнал, определенный на интервале (Т, 2Т) (рис. 6.1);
< f ч (1 при О^х^Т,
п (х) = 1 г
(О при х<0, х>Т.
Сигналы gi(t) и gz(t) известны точно в месте приема. Определить
алгоритм оптимального приема на интервале Тг = 2Т при флуктуа-
ционном шуме с энергетическим спектром NQ по критерию идеаль-
ного наблюдателя. Наметить структурную схему приемника, реа-
лизующего этот алгоритм.
6.1.14. Найти алгоритм оптимального приема в условиях задачи
6.1.13, полагая, что имеется «идеальная» обратная связь по реше-
нию (можно восстановить сигнал gQ^(t) по зарегистрированным
символам). Какова структурная схема приемного устройства?
98
IL, (t) A
Рис. 6.1. Сигналы ФМ на входе и выходе канала с памятью
6.1.15. Найти алгоритм оптимального приема в условиях задачи
6.1.14, полагая, что анализ принимаемой смеси г(/) ведется на ин-
тервале Га = Г (jD = O). Какой схемой можно его реализовать?
6.2. РЕАЛИЗАЦИЯ АЛГОРИТМА
ОПТИМАЛЬНОГО ПРИЕМА ПРИ ТОЧНО
ИЗВЕСТНОМ СИГНАЛЕ НА ОСНОВЕ
СОГЛАСОВАННЫХ ФИЛЬТРОВ
Линейным фильтром, согласованным с сигналом $<(/), называют фильтр
с постоянными параметрами и импульсной переходной характеристикой
g(t)^aSx(to-t)t (6.13)
т. е. форма последней зеркальна (относительно оси ординат, смещенной в топ-
ку t0) форме сигнала. Здесь а — произвольная постоянная.
Если длительность сигнала равна Г, то из условия физической реализуе-
мости следует, что
/о—7>0. (6.14)
На практике выбирают запаздывание to—Т.
Комплексный коэффициент передачи К (/со) согласованного фильтра
K(jto) = J* g(/)exp(—/coO^=aSt(/(o)exp(—/со/о), (6.15)
о
*
где Si (j(o) —комплексно-сопряженный спектр сигнала st(t).
4*
99
Согласованный фильтр в момент t0 при флуктуационной помехе типа «бе-
лый шум» обеспечивает на выходе максимально возможное отношение пиковой
мощности сигнала к средней мощности шума
Г2МЯКС =2Л2==2РсТ/^о=2ГГрвх. (6.16)
Если to=Tt то в произвольный момент времени сигнальную компоненту на
выходе согласованного фильтра можно найти как
t
Ус(1)=а$ Si(x)st(x+T—t)dt=aBs.(T—t), (6.17)
о 1
где —корреляционная функция сигнала
В момент окончания сигнала на входе фильтра t — T сигнал на выходе
согласованного фильтра достигает максимального значения
t
уе(Т)=а$ z(t)s,(t)dt, (6Л8)
О
которое совпадает с точностью до множителя а с сигналом на выходе корре-
лятора в момент окончания сигнала (см. алгоритмы оптимального приема, по-
лученные в задачах 6.1.5 — 6.1.6). Это позволяет в схеме оптимального прием-
ника для точно известного ансамбля сигналов заменить коррелятор, состоящий
из перемножителя и интегратора, согласованным фильтром.
Огибающая отклика согласованного фильтра, имеющего импульсную пере-
ходную характеристику g(t) на сигнал z(/), определяется соотношением
Г(О =
F г* 2 t ~
\z(t)g(t — x)dx .0 + J*z(/)g(/ — x)dx .0
(6.19)
Задачи
6.2.1. Сигнал s(t) задается функцией
... Г kt при 0^7<Т,
s (г) I
I 0 при t>T, КО.
Построить график импульсной переходной характеристики фильт-
ра, согласованного с сигналом s(t), при условии t0=T.
6.2.2. Построить графики импульсных переходных характерис-
тик фильтров, согласованных с заданными сигналами при условии
t$=T (Т —'длительность сигнала):
1) s(0 = Гаехр( — at) при O^f^T, lO при KO, T<_t‘,
2) s (/) = Гаехр( —fH2) при t 0 при KO, t>T;
3) s(0= 1 a [1 — exp ( — at) при t 0 при /<0, t>T-
4) s(0= f b [1 — exp ( — 0/2)] при to при КО, t>T;
5) s(t) = j ГЛ cos®/ при O^t^T, T’=20ji/®; [ 0 при КО, t>T.
100
6.2.3. Двоичные равновероятные символы передаются по каналу
без памяти сигналами Si (t) =А и s2 (/) =0 на тактовом интервале?.
В канале действует аддитивный стационарный белый шум. По-
строить структурную схему приемника на основе согласованного
фильтра.
6.2.4. Двоичные равновероятные символы передаются посредст-
вом ЧМ в канале без памяти. В месте приема на интервале ана-
лиза ?а = ? им соответствуют сигналы Si (/) =[7m COS (й)1^ + ф1) и
s2(/) = (7mCos((D2^+q)2). В канале действует стационарный белый
шум. Изобразить схему оптимального приемника на базе согласо-
ванных фильтров.
6.2.5. Показать, что согласованный фильтр для сигналов про-
извольной формы, в принципе, можно построить на основе неиска-
жающей линии задержки на время Т (Т — длительность сигнала).
6.2.6. Составить схему согласованного фильтра на базе длин-
ной линии с отводами для однополярного и двуполярного двоич-
ных сигналов, соответствующих последовательности символов
110010101. Нарисовать сигнал на выходе согласованного фильтра.
6.2.7. Составить схему согласованного фильтра на базе длин-
ной линии с отводами и построить графики импульсной переход-
ной характеристики и отклика для однополярного и двуполярного
сигналов, заданных следующими двоичными последовательнос-
тями:
1) 1010101; 2) 1110011; 3) 1101101;
4) 0110110; 5) 0001100; 6) 0010010;
7) 1111000; 8) 0001111; 9) 0001000;
10) 1110111; 11) 0100010; 12) 1100011;
13) 1000001; 14) 0111110; 15) 0011001.
6.2.8. Сравнить форму огибающих сигналов на выходе корре-
лятора и согласованного фильтра в случае подачи на их вход оди-
ночного прямоугольного видеоимпульса.
6.2.9. Показать, что результат (6.16) справедлив для любой ли-
нейной системы, для которой выходной процесс определяется со-
t
отношением //(/) = / s(x)z(x)dx.
о
6.2.10. Какой выигрыш в отношении сигнал-шум может дать
фильтр, согласованный с сигналом, имеющим длительность Т =
= 20 мс и полосу частот /7=10 кГц?
6.2.11. Определить, какой выигрыш в отношении сигнал-шум
могут дать фильтры, согласованные с сигналами, заданными сле-
дующими двоичными последовательностями:
1) 0101; 2) 1010; 3) 10101;
4) 01010; 5) 010101; 6) 101010;
7) 1010101; 8) 0101010; 9) 10111011;
Ю) 01000100; П) 11001100; 12) 01010101;
13) 1010101010; 14) 00001111; 15) 11110000.
101
Принять во всех последовательностях длительность элементарного
символа т=5 мс.
6.2.12, Показать, что огибающая отклика согласованного филь-
тра на сигнал z(t) = s(t) =&[cos 0Kw(O—sin0Ku(/)] (k, 0K — коэф-
фициент передачи и фазовый сдвиг канала) инвариантна к измене-
нию фазы 0К.
6.3. ПОМЕХОУСТОЙЧИВОСТЬ
(ВЕРОЯТНОСТЬ ОШИБКИ) ОПТИМАЛЬНЫХ
СХЕМ ПРИЕМА ПРИ ТОЧНО ИЗВЕСТНОМ
СИГНАЛЕ
При заданных системе сигналов, канале и способе анализа принимаемой
смеси сигнала и шума (по отдельным отсчетам или по континууму значений ка
тактовом интервале) оптимальный приемник обеспечивает минимальную вероят-
ность ошибки.
Вероятность ошибочного перехода P(6}\bi) (вероятность регистрации симво-
ла tij при условии передачи символа bi) определяется вероятностью невыполне-
ния системы неравенств, задаваемых алгоритмом приема. Средняя вероятность
ошибки для двоичной системы при произвольных значениях априорных вероят-
ностей передачи символов
2
Рош = S Р (bi) Р (bjlbi), j # i. (6.20)
Если априорные вероятности передачи символов одинаковы, то
1 2 -
Рош = “7“ S Р (bj\bi), j^i. (6.21)
2 Z=1
Для двоичного симметричного канала, в котором вероятность ошибочного
перехода не зависит от того, какой символ передавался,
pQm = P(bj\bi), i,j = T72, j*i. (6.22)
Из двоичных систем для неискажающего канала с белым гауссовским шу-
мом особый интерес представляет система с противоположными сигналами (на-
пример ФМ с изменением фазы на л). Однако ввиду реализационных трудно-
стей (случайного перескока фазы опорного колебания и появления «обратной
работы») на практике широко применяется двоичная система с ОФМ, в которой
информация закладывается в разность фаз соседних посылок. Платой за устра-
нение «обратной работы» является (в условиях надежной связи) удвоение ве-
роятности ошибки, обусловленной шумом в канале:
^ОШ0фМ ~2рОц]фм* (6.23)
Вероятность ошибки для многопозиционных систем в общем случае опре-
деляется сложнее, чем для двоичных. В области надежной связи вероятность
ошибочного приема многопозиционного символа рОш,т при использовании сис-
темы сигналов с активной паузой в симметричном канале
Рош,т~ (т—1)Рош, (6.24)
102
где рош—вероятность ошибочного приема двоичного символа в том же кана-
ле и при том же способе анализа смеси z(t).
Задачи
6.3.1. Определить среднюю вероятность ошибки для сигналов,
канала и приемника, рассмотренных в задаче 6.1.1.
Вычислить значения средней вероятности ошибки по данным,
приведенным в условиях задачи 6.1.2.
6.3.2. Определить среднюю вероятность ошибки для сигналов,
канала и приемника, рассмотренных в задаче 6.1.3 при P(&i) =
= Р(й2)=0,5.
6.3.3. Вычислить значения средней вероятности ошибки для
сигналов, канала и приемника, рассмотренных в задаче 6.1.3, по
данным, приведенным в табл. 6.2 (см. задачу 6.1.4).
6.3.4. Определить минимальную вероятность ошибки приемника
Котельникова при использовании m-позиционной системы ортого-
нальных на интервале (О, Т) сигналов с активной паузой в канале
без памяти с аддитивным стационарным гауссовским белым шу-
мом. Упростить результат для больших значений отношения сиг-
нал-шум.
6.3.5. Определить среднюю вероятность ошибки при оптималь-
ном приеме двоичных сигналов на фоне стационарного гауссовско-
го белого шума в канале без памяти и анализе на интервале
(О, Т) при P(bi)=7^P(b2). Записать выражение для средней веро-
ятности ошибки в системе AM (с пассивной паузой), ЧМ (с орто-
гональными сигналами) и ФМ (с противоположными сигна-
лами).
6.3.6. По результатам предыдущей задачи составить выражение
для средней вероятности ошибки в двоичных системах AM, ЧМ (с
ортогональными сигналами) и ФМ (с противоположными сигнала-
ми) при P(bi) = Р(Ь2) (передаваемые символы равновероятны).
Построить графики рдм, Рчль Р фм при изменении мощности пере-
даваемого сигнала от 1 до 100 Вт, полагая, что коэффициент пе-
редачи канала £=10~2, длительность сигнала Т=10 мс, спект-
ральная плотность мощности шума Мо=1О-7 Вт/Гц.
6.3.7. Показать, что при точно известном ансамбле двоичных
сигналов с заданной энергией и белым шумом в канале минималь-
но возможную вероятность ошибки обеспечивает система с проти-
воположными сигналами.
6.3.8. Показать, что при оптимальном приеме сигналов ОФМ
по методу сравнения полярностей вероятность ошибки можно оце-
нить по формуле (6.23). Вычислить вероятность ошибки, если сиг-
нал на передаче имеет среднюю мощность Рс = 0,5 Вт, коэффици-
ент передачи канала 6=10-2, длительность элементарной посылки
Т=10 мс, спектральная плотность мощности шума в канале No =
= 10~7 Вт/Гц.
103
6,3.9. Вычислить значения средней вероятности ошибки при оп-
тимальном приеме сигналов ОФМ по методу сравнения полярно-
стей для числовых значений величин, приведенных в табл. 6.3.
Таблица 6.3
Вариант 1 2 3 4 5 6 7 8 9 10
Рс, Вт 1 0,5 2 0,7 0,6 1,3 1,7 2,5 1,5 1
k 10—2 з*ю—* 1 2 410-3 * * ю—8 5-Ю-з ю—2 2-Ю-2 10-3 5-Ю-3 9-10—3
Т, мс 10 5 6 8 15 20 10 4 2 12
Wo Вт/Гц 10-7 510—7 10- « 440-е 9-Ю-8 10-’ 5 10—7 10-• 5-10-6 ю-8
6.3.10. Найти энергетический выигрыш по средней и пиковой
мощностям передатчика при переходе от системы AM к системам
ЧМ и ФМ и энергетический выигрыш перехода от системы ЧМ к
ФМ при оптимальном приеме точно известного ансамбля сигналов,
полагая вероятность ошибки неизменной.
6.3.11. Как и во сколько раз изменится вероятность ошибки при
оптимальном приеме точно известного ансамбля сигналов в случае:
1) перехода от системы AM к системе ЧМ при а) неизменной
пиковой мощности передатчика; б) неизменной средней мощности
передатчика; Л2ам=10;
2) перехода от системы AM к системе ФМ при а) неизменной
пиковой мощности передатчика; б) неизменной средней мощности
передатчика; Л2ам=10;
3) перехода от системы ЧМ к системе ФМ при неизменной пи-
ковой мощности передатчика; /i24M=10.
6.3.12. В системе двоичной ФМ использованы сигналы
s, (0= y^E/Tcos (®oz + (i- 1) л); 1=772;
где Е — энергия сигналов Т — длительность элементарной
посылки. Опорное колебание son(0, необходимое для работы кор-
реляционного приемника, имеет вид
«оп (0 = k У2 Е/Т cos (®о t + ф)>
где k — коэффициент пропорциональности; ф — фазовый сдвиг,
отличный от нуля. Определить вероятность ошибки, полагая, что в
канале действует стационарный белый шум со спектральной плот-
ностью мощности NQ) и оценить степень ухудшения помехоустойчи-
вости системы по сравнению с идеальным случаем (ф = 0).
Какую можно допустить фазовую расстройку ф, при которой
энергетический проигрыш ц не превысит значение 1,1 (потери мощ-
ности передатчика составляет 10%)? Построить графики зависи-
мости вероятности ошибки рош и энергетического проигрыша ц от
величины фазового сдвига ф при значениях h2 = 2; 4; 5; 8.
6.3.13. В системе двоичной ФМ, использующей сигналы Si(i)
из предыдущей задачи, опорное колебание формируется с помощью
104
высокодобротного избирательного контура, на вход которого воз-
действует аддитивная смесь гармонического колебания s (/) =
= ksi{t) и гауссовского стационарного белого шума n(t). Опорное
колебание при этом имеет вид
son (О = Ли (0 COS (®0 t + ф),
причем плотность вероятности фазы описывается соотношением
w (ф)= ехР (““ я2/2)/2л + a cos <р F {а х
X coscp) [exp ( — a2 sin2 <р)/2]/]Л2л
(а = ар/в — отношение регулярной и флуктуирующей компонент
входного колебания). Полагая, что амплитуда напряжения на вы-
ходе колебательного контура постоянна и равна Лоп(0 2Е/Т,
определить вероятность ошибки.
6.3.14. В системе двоичной ФМ для передачи информации ис-
пользованы сигналы
51 (О = V2 cos (о)о t + Фо), s2 (0 = — К2 Е/Т cos (coo t + фо).
Опорное колебание в корреляционном приемнике совпадает по
форме с сигналом Si(/): 5ОП(0==)/Л2£/Гсоз(соо^ + фо).
Полагая, что в канале действует гауссовский стационарный бе-
лый шум со спектральной плотностью мощности No, определить
вероятность ошибки и энергетический проигрыш, если из-за неточ-
ности работы системы синхронизации интервал интегрирования
сдвинут относительно начала посылки на величину т(|т|^Т/2).
Найти допустимую величину т, при которой энергетический
проигрыш не превышает величину г) = 1,1. Построить графики за-
висимости рош, т] от величины т при й2 = 2; 4,5; 8.
6.3.15. Полагая, что в системе ФМ использованы сигналы
$1(0 и $2 (0 из задачи 6.3.12, определить вероятность ошибки при
совместном учете как тактовой рассинхронизации на величину т,
так и несинфазности опорного и принимаемого колебаний на вели-
чину ср. Определить величину энергетического проигрыша. Пола-
гая, что допустимая величина энергетического проигрыша равна
1,1, найти допустимые значения величин т и ф.
6.3.16. Полагая, что опорные колебания формируются с ошибкой
по фазе на величину ф, а тактовая синхронизация дает ошибку т,
найти вероятность ошибки при оптимальном когерентном приеме
сигналов двоичной AM и ЧМ и величину энергетического проигры-
ша. Вычислить значения г] и рош для величин ф, т, приведенных в
табл. 6.4. Значения h2 принять равными 2; 4,5; 8.
Таблица 6.4
ф, град 1 2 5 10 15 20 25 30 40 50
т/Т 10—1 5-10—2 10“2 5-10—4 2-Ю-4 1,5-Ю—4 ю-4 5-Юб 2-105 1,5-10-5
105
6.3.17. Вывести выражение для вероятности ошибки и энерге-
тического проигрыша при оптимальном когерентном приеме сиг-
налов двоичной ФМ в канале с точно известными параметрами и
гауссовским стационарным белым шумом со спектральной плотно-
стью мощности Л/о, полагая, что для передачи информации исполь-
зованы сигналы
$1 (/) = У 2 Е/Т cos (ю01 + <р), s2 (t) = — У 2 Е/Т cos (ю0 t + ф),
а опорное колебание имеет расстройку по частоте
son (О = У % Е/Т cos [ (со0 + Дю) t + ф].
Какова допустимая расстройка Дю, при которой энергетический
проигрыш не превышает 1,1? Построить зависимость вероятности
ошибки рОш и т) от величины Дю, если Т = 20 мс, й2 = 4,5.
6.3.18. По условию предыдущей задачи найти вероятность
ошибки и энергетический проигрыш при оптимальном когерентном
приеме сигналов двоичной AM и ЧМ в условиях частотной расст-
ройки между опорным и ожидаемым колебаниями. Построить гра-
фики зависимости рОшдм и Рошчм, Лам, т] чм от величины Дю, если
Т= 10 мс, й2=8.
6.3.19. В канале с точно известными параметрами и гауссов-
ским стационарным белым шумом со спектральной плотностью
мощности АГ0 осуществляется прием двоичных сигналов ФМ:
а) корреляционным приемником; б) интегральным приемником.
Сравнить вероятности ошибок при данных способах приема и оп-
ределить энергетический выигрыш при переходе от интегрального
к корреляционному приему.
6.3.20. В системе двоичной ФМ для передачи информации ис-
пользованы сигналы.
ui (0 = V2 Е/Т cos ю0 t, u2(t) = — У2 Е/Т cos ю01
длительностью Т. Вследствие линейных искажений в канале на
вход приемника поступают сигналы
Si (0 = У2Ё/Т exp [-р2 (t-Т/2)2] cos ю01,
s2 (f) = — У2 E/T exp [ — Ра (/ — Т/2)2] cos ю0 t.
Полагая, что в канале действует гауссовский стационарный белый
шум со спектральной плотностью мощности Nq, определить ве-
роятность ошибки при корреляционном приеме, если опорное ко-
лебание имеет прямоугольную огибающую:
son (0 = V 2 Е/Т cos ю0 0 / 7\
Найти энергетический проигрыш по сравнению со случаем от-
сутствия линейных искажений. Построить графики зависимости
вероятности ошибки и энергетического проигрыша от величины
Гр при Л2 = 2; 4,5; 8.
6.3.21. Равновероятные символы 1 и 0 передаются посредством
сигналов: U\ (/) = Um sin юо/, u2(t)=—Um sin W, юо = 2л/7\
106
Канал не искажает сигналов и в нем имеется аддитивный стацио-
нарный гауссовский шум с энергетическим спектром Go (f) =
=2а/[(ш—й>о)2+«2]. Найти вероятности ошибки при оптимальном
приеме по правилу максимального правдоподобия, пользуясь мето-
дом приведения небелого шума к белому, полагая, что длитель-
ность переходного процесса на выходе «обеляющего» фильтра
Тпер<;Г. Найти энергетический проигрыш, связанный с наличием
небелого шума, по сравнению со случаем приема при наличии бе-
лого шума, имеющего в полосе (fo+Л fo—F) такую же среднюю
мощность.
6.4. АЛГОРИТМ ОПТИМАЛЬНОГО ПРИЕМА И
ПОМЕХОУСТОЙЧИВОСТЬ ПРИ
НЕОПРЕДЕЛЕННОЙ ФАЗЕ И АМПЛИТУДЕ
СИГНАЛА
Считаем, что межсимвольной интерференцией в месте приема можно пре-
небречь, интервал анализа 7\ = Т, передаваемые символы равновероятны, а ка-
нальные сигналы, соответствующие передаче i-го символа, узкополосные, т. е.
могут быть представлены в виде
s4(/)=^[cos0«i(O— sinOfij(f)], (6.25)
где 0 — фазовый сдвиг в канале; k — коэффициент передачи канала.
Если фаза сигнала 0 (а может быть также амплитуда и другие параметры
сигнала) неизвестна на интервале анализа, то приемное устройство должно быть
некогерентным * (не требовать знания фазовых соотношений для своей реализа-
ции). По правилу максимального правдоподобия алгоритм оптимального при-
емного устройства в этих условиях с учетом (6.3) можно определить так:
_____________bi _____________
аф(/)|^,А, 0....1 з»иф(/)|г>л й,0,...], (6.26)
bJ
где w(z(t)lb{> k, 0)—функция правдоподобия передачи символа bi при за-
данном z(t) и фиксированных значениях параметров k, 0; черта наверху —знак
усреднения по случайным (неизвестным точно) параметрам.
Задачи
6.4.1. Ансамбль сигналов в месте приема, соответствующий пе-
редаче tn символов, определяется согласно (6.25), причем фаза 0
случайна и равномерно распределена на интервале (—л, л). В
канале действует стационарный гауссовский белый шум с энерге-
тическим спектром Nq. Определить алгоритм оптимального прие-
ма при анализе принимаемой смеси на интервале Г, показать воз-
можность его реализации на базе корреляционной техники и на
основе согласованных фильтров.
* Анализируются оптимальные приемные устройства при неопределенной
фазе, принимающие решения на основе анализа z(t) на всем временном ин-
тервале (О, Т).
107
6.4.2, Показать, что если используется ансамбль сигналов с ак-
тивной паузой (Ei = const) в канале с белым стационарным гаус-
совским шумом, то при неопределенной равномерно распределен-
ной фазе алгоритм оптимального приема независимо от закона
распределения амплитуды сигнала выражается так:
bt
(6.27)
bj
где
/ z^u^dt * ,
о
—i-й сигнал на передаче и его сопряжение по Гиль-
берту.
6.4.3. Показать, что в каналах с неопределенной фазой и флук-
туационной помехой типа «белый шум» максимальную помехоус-
тойчивость имеет система с активной паузой и ортогональными в
усиленном смысле сигналами. Вычислить вероятность ошибки для
двоичной системы рош при F=1 кГц, 7V0= Ю—11 Вт/Гц, ^=10~8>
Рс=10 Вт. Каков энергетический проигрыш, связанный с незнани-
ем фазы сигнала?
6.4.4. Определить, при какой мощности сигнала Рс вероятность
ошибки в двоичной системе передачи сообщений с активной пау-
зой и ортогональными в усиленном смысле сигналами будет при-
нимать значения, приведенные в табл. 6.5, если F= \ кГц, ЛГ0 =
= 10"12 Вт/Гц, £2=10-8.
Таблица 6.5
Вариант 1 2 3 4 5 6 7 8 9 10
Рош 10“J 5-1 О'”6 2-10““6 Ю-6 5-10-6 2*10“6 10-в 5-10“7 2-10 “7 10“ 7
6.4.5. Вычислить полосу частот, при которой будут обеспечи-
ваться значения вероятности ошибки, заданные в табл. 6.5, если
Afo= 10~иВт/Гц, £2=10~7, а мощность сигнала Рс принимает зна-
чения, приведенные в табл. 6.6.
Таблица 6.6
Вариант 1 2 3 4 5 6 7 8 9 10
Рс, Вт 5 10 15 20 8 16 24 9 18 27
6.4.6. По данным задачи 6.4.3 найти вероятность ошибки рОшт
при оптимальном некогерентном приеме сигналов т-позиционной
системы с активной паузой, ортогональной в усиленном смысле.
Показать, что в области малых ошибок рОшт~'(т—1)рош.
108
6.4.7. Составить алгоритм работы оптимального приемника сиг-
налов двоичной ОФМ при неопределенной фазе сигнала и опреде-
лить вероятность ошибки. Каков энергетический проигрыш по
сравнению со случаем точно известного сигнала, если Рс=1 мВт,
Р = 500 Гц, Af0 = 5-10-7 Вт/Гц?
6.4.8. Вычислить вероятность ошибки оптимального приема сиг-
налов двоичной ОФМ при неопределенной фазе сигнала и найти
значения энергетического выигрыша по сравнению со случаем
точно известного сигнала для числовых значений величин, задан-
ных в табл. 6.7.
Таблица 6.7
Вариант 1 2 3 4 5 6 7 8 9 10
Рс, мВт F, Гц No, Вт/Гц 1 500 5-10й”7 1,5 450 4-10“7 2 550 ю-6 0,5 500 10“ 7 1,2 400 5-10“ 6 1,0 550 7-10-6 1,5 475 ю-7 2 600 10~7 2,4 350 5-10—7 2,7 400 2-10 - *
6.4.9. При неизвестных законах распределения фазы и ампли-
туды сигнала часто используется правило обобщенного максималь-
ного правдоподобия, сущность которого состоит в том, что из не-
скольких гипотез с неизвестными априорными вероятностями вы-
бирается та, для которой максимум функции правдоподобия
w(zlb,i) больше, чем для других гипотез, причем максимум берет-
ся по всем параметрам, определяющим плотность вероятности. По-
казать, что для систем с активной паузой алгоритм приемного уст-
ройства, соответствующий этому правилу, не отличается от (6.27).
6.4.10. Определить среднюю вероятность ошибки при оптималь-
ном некогерентном приеме сигналов двоичной ЧМ в канале с не-
определенной фазой и медленными замираниями в соответствии с
обобщенно-рэлеевским законом распределения. Каков энергети-
ческий проигрыш (требуемое превышение мощности передатчика)
при заданной вероятности ошибочного приема рОш=10~4, связан-
ный с замираниями по обобщенно-рэлеевскому закону по отноше-
нию к каналу с неопределенной фазой, но без замираний при зна-
чениях 92=а2р/о2 = 2; 4; 5; 15; 20; 25; 40; 50.
6.4.11. Решить задачу 6.4.10 для случая замираний сигнала по
закону Рэлея при вероятности ошибочного приема рОш=10-2; 10-3;
IO"4; IO”5; IO"6.
6.4.12. Решить задачу 6.4.10 для случая замираний по односто-
ронне-нормальному закону при вероятности ошибочного приема
рош= 10-2; 10-3; 10-4; 10~5; 10~6.
6.4.13. При приеме сигналов двоичной ЧМ распространена схе-
ма рис. 6.2, в которой ПФН и ПФ0 — полосовые фильтры, пропус-
кающие область частот F3 около частот нажатия и отжатия; Д —
амплитудный детектор. В определенный момент на интервале Т
выбирается тот или иной символ, в зависимости от того, в какой
ветви мгновенное значение огибающей окажется больше. Полагая,
109
Рис. 6.2. Схема неопти-
мального некогерентного
приема ЧМ-сигналов
что полоса фильтра F3=nlT (и>1, Т — длительность элемента
сигнала), а в канале действует гауссовский белый шум, найти ве-
роятность ошибки и сравнить ее с вероятностью ошибки при опти-
мальном некогерентном приеме.
6.4.14. В условиях задачи 6.4.13 построить график зависимости
энергетического проигрыша от параметра п при переходе от опти-
мального некогерентного приема к неоптимальному.
Г л а в а 7. ПРИЕМ НЕПРЕРЫВНЫХ СООБЩЕНИИ
7.1. ОПТИМАЛЬНАЯ ОЦЕНКА ОТДЕЛЬНЫХ
ПАРАМЕТРОВ СИГНАЛА
Задача оптимальной оценки (измерения) параметра сигнала состоит в определе-
нии некоторым наилучшим образом значения параметра b по принятой смеси сиг-
нала s(bt t), зависящего от этого параметра, и аддитивного шума
Z(t) = S(b, /) + ^(/),
Из-за наличия шума в канале и конечного интервала анализа оценка пара-
метра Ь отличается от истинного значения .параметра Ь, причем ошибка е=6—b
имеет случайный характер. Качество оценки проверяется обычно на выполнение
условий несмещенности, эффективности и состоятельности. Если среднее значе-
ние ошибки равно нулю (это означает, что среднее значение оценки равно ис-
тинному значению параметра), оценка называется несмещенной:
Л1[Е] = д —6 = 0 или b = b. (7.1)
Оценка называется эффективной, если дисперсия ошибки минимальна в
классе всех возможных оценок:
D [Е] = (Е — Е)2 = min. (7.2)
Оценка 6 называется состоятельной, если при увеличении интервала анализа
Т она сходится по вероятности к оцениваемому параметру
limP(|6 — 61 >е) = 0, (7.3)
Т->оо
при этом limD[E]=0.
Г->оо
ПО
Для нахождения оценок широко применяется правило максимального прав-
доподобия, в соответствии с которым в качестве оценки параметра принимает-
ся такое его значение #, которое максимизирует функцию отношения правдопо-
добия Z[z|s (&)], т. е. ti определяется из условия
dl Pls(fr)] _ д (аи [z[s (£>)] 1 _ Q
db db \ w (п) /
Полученная таким способом оценка называется максимально правдоподоб-
ной. Часто уравнение, определяющее максимально правдоподобную оценку
(уравнение правдоподобия), записывают в виде
ЦЫ№1>|11_,| (75)
db
Если существует несмещенная эффективная оценка максимального правдо-
подобия, то, как правило, уравнение правдоподобия имеет единственное реше-
ние, а полученная оценка состоятельна и асимптотически (при стремлении време-
ни анализа Т или объема выборки к бесконечности или же при ограниченном Т
при стремлении отношения сигнал-шум к бесконечности) эффективна и распре-
делена нормально.
Задачи
7,1.1. Принимаемый сигнал можно представить в виде s(ky t) =
= ku(t, 0), где k — коэффициент передачи канала; 0 — фазовый
сдвиг.
Найти максимально правдоподобную оценку коэффициента пе-
редачи канала, полагая, что сигнал u(t, 0) точно известен в месте
приема, а в канале действует гауссовский белый шум со спект-
ральной плотностью мощности No. Составить структурную схему
оптимального измерителя. Найти распределение ошибки измере-
ния, ее математическое ожидание и дисперсию.
7.1.2. На вход канала поступает сигнал u(t). Процесс на вы-
ходе канала на интервале анализа Т можно представить в виде
z(t) = ku(t) + и(/), где k — коэффициент передачи канала; n(t)—
реализация гауссовского шума. Спектральная плотность мощности
шума в полосе F равна No- Полагая, что параметры сигнала в
месте приема известны точно, a анализируется в дискретные
моменты ti, кратные величине Д£=1/(2Г), найти максимально
правдоподобную оценку коэффициента передачи канала.
7.1.3. По каналу передается сигнал u(t) =(/mcos((oo^+<po). В
канале действует гауссовский шум с равномерным энергетическим
спектром No в полосе F=l,l кГц. В результате наблюдения полу-
чено 11 независимых значений смеси сигнала и шума z(/):
2i = —2,203-IO"2 В; z2 = —1,104-10-1 В; г3 = 2,133-Ю"2 В; z4 =
= 1,746-10-1 В; 25 = 6,180-10"2 В; z6= 1,129-10’1 В; z7= 1,770-10"1 В;
z8=—1,285-10-1 В; z9 = 7,215-10"2 В; 2ю = —3,115-10“2 В; 2ц =
=—6,702-10-2 В.
Найти максимально правдоподобную оценку амплитуды сигна-
ла на выходе канала, если /0 = 47,1 кГц, <р0 = 0, Um=0,1 В, а первое
значение z(t) найдено при t = 0.
Ш
7,1.4. Решить задачу 7.1.3 для следующих вариантов числовых
значений величин:
a) Um = Q,2 В /о = 37,93 кГц Фо = 30°;
б) i/m = 0,3 В fo = 51,72 кГц Фо = 57°;
в) Um=0,4 В fo = 49,3 кГц Фо = 49°;
г) £/т = 0,45 В f0 = 27,2 кГц Фо =15°
7.1.5. По условиям задач 7.1.3 и 7.1.4 найти ошибку оценивания
амплитуды сигнала.
7.1.6. Найти максимально правдоподобную оценку коэффициен-
та передачи канала из задачи 7.1.1 при неопределенной фазе 0 и
составить структурную схему для оптимального измерителя.
7.1.7. На вход канала со случайно изменяющимся фазовым
сдвигом поступает сигнал u(t) = Um cos (coZ + cpo). В канале дейст-
вует гауссовский шум со спектральной плотностью Л/о в полосе
Г=1,7 кГц. В результате наблюдения получено 10 независимых
значений реализации смеси сигнала и шума z(t):
г1(/) = 1,05«10-2
24(0 = 1,15.10-2
z7(0 =7,18-IO-2
z10(0 = 1,16-10-2
г2(0=—9,01-Ю-3
25(/) = 1,19-10“3
28(0 =3,16-IO-2
23 (0 =8,15-IO"3
г6 (0 =—6,51 -10~3
г9(0=—2,10-Ю-3
отсчитанных в моменты /, кратные величине Д/=1/(2Г). Найти
максимально правдоподобную оценку коэффициента передачи ка-
нала k, если / = 47,1 кГц, <р0 = 45°, а первое значение z(t) найдено
при / = 0, 7\7О === 10—4 Вт/Гц.
7.1.8. Показать, что при больших отношениях сигнал-шум мак-
симально правдоподобная оценка амплитуды сигнала при неоп-
ределенной фазе является состоятельной, несмещенной, асимптоти-
чески эффективной, а ее качество такое же, как при определенной
фазе сигнала.
7.1.9 Найти максимально правдоподобную оценку фазы сигна-
ла в канале с флуктуационным белым шумом. Составить схему оп-
тимального измерителя. В области больших значений отношения
сигнал-шум найти распределение для ср, математическое ожидание
и дисперсию этой величины.
7.1.10. В результате измерения получено 10 независимых значе-
ний смеси сигнала и шума в дискретные моменты, кратные Д/ =
= 1/(2Г):
2! =0,201 В
25 = —0,292 В
29 = — 0,171 В
22 = 0,115 В
26 = 0,158 В
2ю = 0,158 В
23 = —0,082 В
27 = 0,092 В
24 = —0,126 В
28 = 0,0102 В
Известно, что z(t) =kUm cos (соЯ-ср), причем фаза имеет слу-
чайное значение, равномерно распределенное на интервале (0,2л);
n(t) — гауссовский шум с равномерным энергетическим спектром
No в полосе Г=1,5 кГц. Найти максимально правдоподобную
оценку фазы сигнала ср, если kUm = 0,2 В, / = 51,0 кГц.
112
Рис. 7.1. К определению
оптимальной оценки вре-
мени прихода сигнала
h (х) =
7.1.11. На вход приемника в пределах интервала анализа (О, Т)
поступает смесь гауссовского белого шума с энергетическим спек-
тром No и сигнал в виде радиоимпульса s(t)=a(t—t)cos(cd^+
+ cp)-/i(/—т) (рис. 7.1) с известной огибающей a(t—т), частотой
со, длительностью ти, случайным временем прихода и случайной
фазой,
1 при О^Х^Ти,
О при ти<х; 0>х.
Найти оптимальную по критерию максимума апостериорной ве-
роятности оценку времени прихода сигнала т, полагая, что этот
параметр равномерно распределен на интервале (О, Г), а случай-
ная фаза ф не зависит от т и равномерно распределена на интер-
вале (—л, л).
При большом отношении сигнал-шум найти распределение апо-
стериорной вероятности оцениваемого параметра, математическое
ожидание и дисперсию оценки.
7.1.12. На вход приемника в пределах интервала анализа (О,Г)
поступает смесь гауссовского белого шума и сигнала в виде пря-
моугольного радиоимпульса (см. задачу 7.1.11) с Ти = Г и извест-
ным временем прихода т = 0, со случайной равномерно распреде-
ленной фазой ф, известной амплитудой а и случайной частотой со.
Найти оптимальную по критерию максимума апостериорной веро-
ятности оценку частоты / = со/2л, полагая, что этот параметр имеет
равномерное распределение в пределах интервала (/мин, /макс). Па-
раметры ф и со считать независимыми. Наметить структурную схе-
му оптимального измерителя частоты. При большом отношении
сигнал-шум, /—foT^>l (fQ — истинное значение частоты
принимаемого сигнала) найти распределение апостериорной веро-
ятности оцениваемой частоты сигнала, математическое ожидание
и дисперсии оценки.
7.1.13. Прямоугольный радиоимпульс s(t, а) =а cos (со/Н-ф),
О</о^/^о+ти<Т принимается на фоне гауссовского стационар-
ного шума. Корреляционная функция шума В(т)=о2ехр(—а|т|).
Определить дисперсию оценки амплитуды а импульса, приняв ти =
ИЗ
= 10-2 c, fo = 2O кГц, а2 = 0,01 Вт, а=10-! с~!; 10~2 с"1; 10~3 с”1;
10-4 с-1.
7.1.14. Найти дисперсию оценки амплитуды А импульса гауссов-
ской формы
s (t, а) = А ехр [ - 2,8 (t - т0)2/т2], 0 < т0 < Т,
принимаемого на фоне гауссовского стационарного шума с экспо-
ненциальной корреляционной функцией В(т)=а2ехр(—а|т|).
7.1.15. Решить задачу 7.1.13 при условии, что сигнал (принима-
ется на фоне узкополосного шума с корреляционной функцией
В (т) = о2 ехр ( —а|т|) [cos (a sin cojt])/<oJ.
Упростить результат для случая g) = coi= соо + а2.
7.1.16. Найти дисперсию оценки временного положения т им-
пульса гауссовской формы
s (t, т0) = А ехр [ - 2,8 (т - т0) 2/т2],
принимаемого на фоне белого шума, если импульс практически
полностью располагается внутри интервала наблюдения.
7.1.17. Решить предыдущую задачу для случая, когда в канале
действует шум с корреляционной функцией В(т) = о2ехр(—а |т |).
7.2. ОПТИМАЛЬНАЯ ДЕМОДУЛЯЦИЯ
НЕПРЕРЫВНЫХ СООБЩЕНИЙ. РАСЧЕТ
ПОМЕХОУСТОЙЧИВОСТИ АНАЛОГОВЫХ
СИСТЕМ ПЕРЕДАЧИ
При передаче непрерывных сообщений принимаемое колебание z(t) на интер-
вале (0, Т) представляет собой аддитивную смесь сигнала известной формы
s[b(Z), /], зависящего от одного меняющегося во времени параметра b(t) (со-
общения), и аддитивного шума n(t):
z(t)=s\b(t), t]+n(t).
По принятому колебанию z(Z) необходимо наилучшим образом решить, ка-
кая реализация сообщения b(t) передавалась, т. е. в этом случае также можно
ставить вопрос об оптимальной в определенном смысле оценке 6(t). Оптималь-
ный прием меняющегося во времени параметра (непрерывного сообщения) мож-
но свести к задаче совместного оптимального приема многих параметров.
Если представить сообщение b(t) на интервале Т обобщенным рядом Фурье
вс
b(t}= SAft<pft(O, (7-6)
Л=1
(здесь {qpfe(/)}—система ортонормированных функций; Хлкоординаты (пара-
метры) непрерывного сообщения &(Z); Вс — база сообщения), то принимаемое
колебание
z(t) =s(X, t) +n(t),
где X={Xi, X2, ... Авс} —вектор параметров сообщения b(t).
114
Совместные максимально правдоподобные оценки координат сообщения оп-
ределяются из условия
д д
-тт-{/(г|Х)} = 0 или —— {In / (z|A)} = О, (7.7)
о Ла о Aft
где Z(z|A) —функционал отношения правдоподобия. При флуктуационном белом
шуме и известной форме сигнала s(A, t)
/ (z|A) == exp Г 2 т — р(0«(Ь, t)dt- о t)dt 2V0 о (7.8)
Зная оценки параметров Ал, можно найти оценку сообщения
вс И)= S йфНО- (7-9)
Ошибка е=#(/)—b(t) может рассматриваться как помеха (шум) на выходе
приемника (детектора).
Спектральная плотность мощности шума на выходе детектора при опти-
мальном приеме и больших значениях отношения сигнал-шум в канале опре-
деляется формулой
Свых (П = ^0 / I ~~ {s [6 (0, 0}Г. (7 • Ю)
/ Id Aft J
где Ал — координаты разложения b(t) в обычный ряд Фурье.
Качество непрерывных систем связи часто оценивают выигрышем модема в
отношении сигнал-шум
£ = Рвых/рвх. (7.11)
Здесь рвх= (Рс/Рш)вх— отношение средних мощностей сигнала и шума на
входе приемника;
___ / Fc
Рвых = Ь2 (0 / J* бВых (/) df
I 0
— отношение средних мощностей сигнала и шума на выходе приемника (детек-
тора). Величину рвых удобно выразить через пик-фактор сообщения
п= | b(t)|макс/ VW).
При | Ь (/) | макс = 1*
// ft \
Рвых = 1 / | П2 J бвых (f)df . (7.12)
/ \ о /
Очень часто качество непрерывных систем связи оценивают обобщенным
выигрышем
g'=pBuxFc/^F=gFc/F=g/at (7.13)
где Fc — полоса сообщения b(t)-t F — полоса сигнала s[6(0> fl; a=F/Fc.
В дальнейшем везде сообщение будем считать нормированным.
115
Обобщенный выигрыш систем с двойной модуляцией (при условии, что на
второй ступени используется прямая модуляция) *, может быть найден как
произведение обобщенных выигрышей
£,=£,н£,пн> (7.14)
где g'u —- обобщенный выигрыш при демодуляции несущего колебания; g'nH —
обобщенный выигрыш при демодуляции поднесущего колебания.
В широкополосных системах модуляции при некотором пороговом отноше-
нии сигнал-шум на входе приемника рпор качество связи резко падает (порого-
вый эффект). Пороговый эффект выражен тем резче, чем больше частотная из-
быточность сигнала, определяемая отношением ширины полосы сигнала и со-
общения а.
Задачи
7.2.1. Записать ортогональные разложения для ограниченного
интервалом Т сообщения b(t) на передаче, на приеме и по-
мехи в(/) на выходе приемника (детектора). Считать, что полоса
сообщения равна Fc. Выбрать в качестве базиса разло-
жения систему ортонормированных функций 1^2 cos(2knt/T) и
/Узт(2^л//Т).
7.2.2. Показать, что при слабом белом гауссовском шуме в ка-
нале и известной точно форме сигнала помеха на выходе оптималь-
ного приемника е(/)—стационарный гауссовский процесс с не-
коррелированными координатами и энергетическим спектром
овых (W.WW
7.2.3. Найти спектральную плотность мощности шума на выхо-
де детектора прямых систем модуляции при слабом флуктуацион-
ном шуме в канале и известной форме сигнала.
7.2.4. Вычислить спектральную плотность мощности шума на
выходе приемника сигналов амплитудной модуляции и построить
его зависимость от коэффициента глубины модуляции /п, от ам-
плитуды несущего колебания.
7.2.5. Вычислить спектральную плотность мощности шума на
выходе приемника ФМ-сигналов и построить ее зависимость от ин-
декса фазовой модуляции 0ФМ.
7.2.6. Показать, что ОМ нельзя строго отнести к прямым си-
стемам, а дисперсия произвольной координаты шума на выходе
оптимального приемника при «слабой» флуктуационной помехе в
канале определяется для этой системы формулой о2№
* Прямыми называются системы модуляции, в которых модулированный
сигнал $[&(/), Л в момент t зависит от значений сообщения в тот же момент
времени. Остальные системы модуляции относят к непрямым. В частности, не-
прямыми являются интегральные системы модуляции, в которых модулирован-
ный сигнал $[&(/), Л в момент t зависит от интеграла модулирующей функции.
К прямым системам модуляции можно отнести Дм, БМ, ФМ и т. п., к непря-
мым — ЧМ.
116
= Nof (2Tk2U2m) и, как для произвольной прямой системы, не за-
висит от частоты.
7,2.7, Найти предельные значения выигрыша и обобщенного вы-
игрыша в отношении сигнал-шум при известной форме сигнала и
слабом шуме в канале.
7.2.8. Найти общие выражения для предельных значений выиг-
рыша и обобщенного выигрыша прямых систем модуляции при
слабом шуме в канале.
7.2.9. Найти общие выражения для предельных значений выиг-
рыша интегральных систем модуляции при слабом шуме в канале
7.2.10. Определить выигрыш и обобщенный выигрыш для сис-
темы AM при слабом шуме в канале. Построить зависимость вы-
игрыша от коэффициента глубины модуляции.
7.2.11. Найти предельные значения выгрыша и обобщенного вы-
игрыша для системы БМ при слабом шуме в канале и показать,
что они реализуются при синхронном детектировании БМ-сигна-
лов.
7.2.12. Найти предельные значения выигрыша и обобщенного
выигрыша для системы ОМ.
7.2.13. Определить предельные значения выигрыша и обобщен-
ного выигрыша для системы ФМ при слабом шуме в канале. По-
строить зависимость выигрыша и обобщенного выигрыша от ин-
декса модуляции. Убедиться в том, что при слабом шуме в кана-
ле используемая на практике схема детектирования ФМ обеспе-
чивает предельную помехоустойчивость.
7.2.14. Найти энергетический спектр шума на выходе детекто-
ра интегральных систем модуляции при слабом флуктуационном
шуме в канале и известной форме сигнала.
7.2.15. Определить выигрыш и обобщенный выигрыш для систе-
мы ЧМ при слабом шуме в канале и построить зависимость их от
индекса частотной модуляции. Сравнить полученные зависимости
с соответствующими зависимостями в системе ФМ.
7.2.16. Показать, что при слабом шуме в канале распростра-
ненная схема частотного детектирования обеспечивает предельное
значение обобщенного выигрыша.
7.2.17. Показать, что для системы АИМ предельное значение
выигрыша дим = 1/(тн/7с), а обобщенного выигрыша £'аим = h
где ти — длительность импульса, Fc — ширина спектра сообщения.
7.2.18. Показать, что для системы ФИлМ предельные значения
выигрыша и обобщенного выигрыша определяются формулами
о,б / f \\ ' _ o,6 / г \2
5 ФИМ jp \ F J > SфИМ JJ2 у р, у *
где F — ширина спектра сигнала.
7.2.19. Найти значения обобщенного выигрыша для систем
двойной модуляции: ОМ—AM, ФМ—БМ, ЧМ—БМ, ОМ—ФМ,
AM—ФМ, БМ—ФМ, БМ—AM.
7.2.20. Используя соотношение для выигрыша идеальной сис-
темы связи и реальных систем, показать, что пороговый эффект
117
выражен тем резче, чем больше частотная избыточность каналь-
ного сигнала.
7.2,21, Определить пороговое отношение сигнал-шум для реаль-
ной системы ЧМ в канале с гауссовским белым шумом, полагая,
что качество этой системы резко падает, когда огибающая шума
превышает амплитуду сигнала.
7.2.22. Найти максимально возможное значение индекса моду-
ляции системы ЧМ, при котором обеспечивается работа выше по-
рога, найденного в 7.2.21, если требуется обеспечить отношение
сигнал-шум на выходе детектора рВых = 4600. Пик-фактор сообще-
ния П = 3.
7.3. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ
ФИЛЬТРАЦИЯ ПО КРИТЕРИЮ МИНИМУМА
СРЕДНЕГО КВАДРАТА ОШИБКИ
При непосредственной передаче сообщений B(t) (без модуляции) прини-
маемое колебание Z(t) (сигнал плюс шум)
Z(t)=S(t)+N(t), S(t)=B(t). (7.15)
Полагая, что S(t), —стационарные, несвязанные случайные процессы
с энергетическими спектрами Gs(f), GN(f), оценим качество передачи непрерыв-
ного сигнала S(t) (сообщения B(i)) средним квадратом ошибки
е2(0 = [$(* + т)-5(/)]2 , (7.16)
где S(/+t)—оценка сигнала в момент /+т; т —время запаздывания в уст-
ройстве оценки (фильтре).
В классе линейных фильтров * передаточная функция оптимального фильт-
ра Колмогорова — Винера (обеспечивающего е2мжн)
К(/2л/) =Gs(f)exp(_/2nfT)/(G8(f) + GW (f)),
а средний квадрат ошибки такого фильтра (достигаемый при т->-оо)
” Gs(f)GN(f)
1 Gs(f) + GN(f)
df.
Реализуемая часть K(/2nf), определяемого (7.17), дается формулой
ОО оо
К а 2л f) = Kt а 2л f) j f Ki (/ 2nv) Gs (0) e1Zn dvdf.
—co —co
(7.17)
(7.18)
(7.19)
Примем, что 1/[бв(/)+бя(/)]=К1(]’2л/)К*1(/л2/)—нереализуемая харак-
теристика обеляющего фильтра; Ki (р) — реализуемая передаточная функция (все
нули и полюса лежат в левой полуплоскости); Ki*(p)—нереализуемая переда-
точная функция **.
* Применение нелинейного фильтра не уменьшает е2, если s(t) и Аф) —га-
уссовские процессы.
** Нереализуем также фильтр с передаточной функцией K*i(/2nf)Gs(f).
118
Характеристики реализуемого линейного фильтра, обеспечивающего е2(/)мж»
(при несмещенности оценки е(/)=0) даже при т=0 и нестационарных процес-
сах S(t) и #(/) с корреляционными функциями Bs(fb f2), t2) можно
получить на основе метода стохастических дифференциальных уравнений.
Представим S(t) как первую компоненту многомерного марковского про-
цесса с уравнением состояния
k(O=f(Ox(O+g(Ov(n. (7.20>
где v(t) —порождающий гауссовский процесс с нулевым математическим ожи-
данием и единичной спектральной плотностью, матрицы f(/), g(t) определяются
корреляционной функцией процесса S(t).
Уравнение наблюдения
z(/) = G(Ox(/)+N(0. (721)
При G(0 = |10 ...0 ... 0| из (7.21) получим (7.15).
Фильтр Калмана, обеспечивающий минимум среднеквадратической ошибки
между x(t) и ее оценкой x(t) при подаче на вход (7.21), определяется уравне-
нием
х (0 = / (0 х (О + « (OGn' lz (0 — с (0 * (01. (7.22)
где Gn — спектральная плотность шума N(t), который считается белым. Вели-
чина K(t) =е2(г) ='[х(/)— х(/)]2 определяется дифференциальным уравнением
Риккати:
к (0 = f (0 кГ (0 + к (0 fт (0 - к (0 G~1 кг (0 + d (0 dT (0. (7.23)
Реализуемые схемы для оптимального приема (оценки) непрерывного со-
общения b(t), содержащегося в модулированном сигнале s(b(t), t), принимае-
мого на фоне аддитивного шума n(t) по критерию минимума среднего квадра-
та ошибки е2(/) — [#(/)—b(t)]2, можно получить на основе теории нелинейной
фильтрации.
Пусть сообщение b(t) описывается уравнением состояния
В(/).=—aB(/) + V(Z), (7.24)
где V(t) —стационарный белый шум с характеристиками
V(7j = 0; V(G)V(Z2) = -yGv6(<2-/1). (7.25)
Коэффициент сноса Ai(b, t) =—ab(t), диффузии A2(b, t) — Gv/2.
Принимаемое колебание Z(t) на интервале (0, Г) представляет собой сум-
му сигнала S(t, b) и стационарного белого шума N(t):
Z(t) = S[tt b(t)] + N^);
W) = 0; WJW^) = 6 (t2 - У0/2. (7.26}
Изменение во времени плотности вероятности ш [#(/), /] при данном z(t)
подчиняется уравнению Колмогорова — Фоккера — Планка, которое при доста-
119
Gs(f)= {
точно больших значениях отношения сигнал-шум и времени наблюдения приво-
дит к следующим уравнениям для оптимальной оценки и дисперсии ошибки:
; - dF(b, t)
b (/) = — a b (0 + к (0-,
db
d2F(b, t) 1
к (0= -2ак(0 + *2(0------+ , (7-27)
db2 2
d
где F\b(t), /] = —- In w(z\ b) —производная по времени к концу интервала об-
dr
работки логарифма функции правдоподобия. При белом шуме в канале с точ-
ностью до константы
F[ti(t), t]=—{z(t)—s[t, b\t)]}2INQ. (7.28)
Если b(t) является неэнергетическим параметром для s|7, 6(f)] (например,
при ФМ и ЧМ), то можно принять
F[6(t), fl=2z(0$[t ^(OJ/No. (7.29)
Задачи
7.3.1. Энергетические спектры сигнала и аддитивного шума оп-
ределены на положительных частотах соотношениями
Af/F при O^f^F,
0 при f>F,
A — Af!F при O^f^F,
0 при f>F.
Определить коэффициент передачи (модуль) оптимального
фильтра Колмогорова — Винера и найти энергетические спектры
ошибки, полезного сигнала и шума на выходе фильтра, средние
мощности трех этих компонент, а также параметр рвых (отношение
сигнал-шум).
7.3.2. Сигнал и шум, энергетические спектры которых даны в
предыдущей задаче, поступают на идеальный фильтр нижних час-
тот с амплитудно-частотной характеристикой
/Со<1 при O^f^F,
0 при 0>f, F<f.
Найти средний квадрат ошибки и отношение средних мощно-
стей сигнала и шума рвых = у2з/у2п на выходе этого фильтра. Сопо-
ставить эти параметры с соответствующими параметрами опти-
мального фильтра.
* 7.3.3. Заданы Gs(f) = 2aPs(a2 + co2)-1 и Gn(J)=O,5No. Найти
квадрат модуля коэффициента передачи нереализуемого (при
т = 0) обеляющего фильтра и показать, что его реализуемая часть
(/®) = l/Wo(l+/coa-1) ( /Т+Л+уша-1)-1; A=4Pca-W0-*. Най-
120
ти передаточную функцию оптимального реализуемого при т=0
фильтра Колмогорова — Винера.
7.3.4. Показать, что реализуемый оптимальный фильтр задачи
7.3.3 можно выполнить с помощью интегрирующей RC цепочки,
имеющей постоянную времени /?С = а-1(1-ЬЛ)-0’5, и каскада с ко-
эффициентом передачи (К1+Л—1)(1+Л)“0,5-
7.3.5. Показать, что передаточную функцию любого реализуемо-
го оптимального фильтра Fp(/(o) можно получить, используя ли-
нейную систему с обратной связью (рис. 7.2), если Я(/(о)=-
= /?р(/<о)[1—Показать, что если реализуема передаточ-
ная функция /’pG’o), то реализуем и фильтр с передаточной функ-
цией Н(]ы).
7.3.6. Показать, что реализуемый оптимальный фильтр задачи
7.3.5 можно выполнить по схеме с обратной связью (рис. 7.3), ес-
ли постоянная времени интегрирующей цепочки RC=l/a. Напи-
сать уравнения состояния, описывающие эту схему.
7.3.7. На вход фильтра Калмана подается колебание (7.15),
причем сигнал s(t) описывается уравнением состояния (7.20). По-
казать, что уравнение оптимальной фильтрации (относительно
s(t)) имеет вид
ds (t)/dt = — a s (0 + а (]Л1 + Л — 1) [z (t) — s (/)]
и совпадает с уравнением состояния задачи 7.3.6, а схема опти-
мального фильтра не отличается от схемы рис. 7.2.
7.3.8. Найти дисперсию ошибки фильтрации (задача 7.3.7) в
установившемся режиме.
7.3.9. Показать, что при прямой передаче (s[Z, b(f)]=ab(t),
b(t)—марковский гауссовский процесс, описываемый уравнениехм
(7.24)), уравнения (7.25) нелинейной фильтрации переходят в
уравнения линейной фильтрации:
b = — ab + a [z (t) — ab (ЭД/М),
к(0 = — 2ак(/) — к2 (t) a2/NQ + Gv/2'
7.3.10. Показать, что при балансной амплитудной модуляции
(s[Z, b(/)] =&БМ £(Qcos((oo^+cp), где b(t)—марковский гауссов-
Рис. 7.2. Линейная система с
обратной связью (к задаче
7.3.5)
Рис. 7.3. Линейная система с обрат-
ной связью (к задаче 7.3 6)
121
ский процесс, описываемый уравнением (7.24)), уравнения опти-
мальной фильтрации принимают вид
b (0 = — (а + £бм к Ь(1) + 2к (/) йБМz (f) cos (<o01 + <p0)/A/0,
к (/) = - 2 а к (0 - к2 (О^вм/М) + Gv/2.
7.3.11. Показать, что схема синхронного радиоприема (рис. 7.4)
реализует оптимальную фильтрацию [см. задачу (7.3.10)] в уста-
новившемся режиме (/—>оо), если выбрать постоянную интегриру-
ющей цепочки RC= 1/(а+к&2Бм/М>), а амплитуду местного гете-
родина мг=2к^бм /NoRC. При этом
K = aN0ksK[(\ + 0,5Gvklna-2No1)0-5- 1]-
7.3.12. Показать, что при ФМ ($[/, &(/)] = t/ocos(ci)/ +
+&фм МО+фо) b(t)—марковский гауссовский процесс, описывае-
мый (7.24)), уравнения оптимальной фильтрации принимают вид
Ь (/) = — а b (0 — £ФМ к (0 z (/) и0 sin [<о01 + &ФМ b (f) + <p0].W0>
к (t) = — 2а к (t) -J- Gv/2 — № (/) z (/) кФм. cos [со0 (/) + кфмЬ (/) + ф01 /Л/о
Нарисовать схемы аналоговых вычислителей с обратными связя-*
ми, реализующие эти уравнения.
7.3.13. Показать, что стационарная дисперсия ошибки для за-
дачи 7.3.12 при малом шуме в канале
к = 2а No [(1 -f- GvNok^No)°^ - 1] Uq1 k^.
7.3.14. Показать, что максимальное отношение пиковой мощно-
сти сигнала к средней мощности шума г2 на выходе линейного
фильтра с постоянными параметрами определяется соотношением
г2макс = рВх2/?Г при воздействии на его вход сигнала s(t) известной
формы с длительностью Т и полосой F и аддитивного белого шума
и обеспечивается согласованным фильтром. Здесь рвх — отношение
средних мощностей сигнала и шума на входе фильтра в полосе
сигнала.
7.3.15. Прямоугольный видеоимпульс s(t) длительности ти име-
ет случайную амплитуду а и случайное положение во времени А в
тактовом интервале (0, Т) (рис. 7.5,а), т. е. соответствует сигналу
АИМ или ФИМ. Сигнал s(t) принимается на фоне белого шума
Рис. 7.4. Схема синхронного Рис. 7.5. Прямоугольный импульс (а)
приемника и согласованный с ним фильтр (б)
122
N(t) с интенсивностью Nq так, что анализируемое колебание
z(t) =s(t) + n(t).
Показать, что а) согласованный с сигналом s(i) фильтр (СФ)
может быть реализован посредством линейной схемы, содержащей
три блока: интегратор, линию задержки на время ти и вычитаю-
щее устройство (рис. 7.5,6); б) оптимальная по критерию макси-
мального правдоподобия оценка амплитуды сигнала а может быть
получена по максимуму сигнала на выходе СФ независимо от зна-
чения Д^О, Д^Т—ти; в) оптимальная оценка положения фронта
импульса может быть получена по моменту времени достижения
максимума сигнала на выходе СФ независимо от значения ам-
плитуды; г) отношение пикового значения сигнала к средней мощ-
ности шума на выходе СФ г2=2а2ти/М)-
7.3.16. Показать, что фильтр согласованный с радиоимпульсом,
имеющим прямоугольную огибающую, частоту заполнения /о =
= соо/2л и длительность ти при /0=ти и (о0ти/2л = п (п — целое чи-
сло), имеет комплексный коэффициент передачи
К (/2л/) = а [1 -ехр ( —/сото)]// (со — ш0).
Как можно реализовать такой фильтр?
7.3.17. Найти отношение пиковой мощности сигнала к средней
мощности шума на выходе идеального полосового фильтра с по-
лосой Af=f2—fi, fi и f2 — граничные частоты полосы (рис. 7.6,а),
на вход которого поступают прямоугольный радиоимпульс с ам-
плитудой Um, длительностью тип частотой заполнения /0 = (/2+Л)/2
(рис. 7.6,6) и гауссовский белый шум с равномерной спектраль-
ной плотностью, и показать, что оно меньше, чем на выходе согла-
сованного фильтра, если Д/ти>1.
7.3.18. Определить полосу пропускания идеального полосового
фильтра (см. задачу 7.3.17), при которой достигается максимум
отношения пиковой мощности сигнала к средней мощности шума.
Показать, что выигрыш в отношении сигнал-шум, который обеспе-
чивает фильтр, согласованный с прямоугольным радиоимпульсом,
по сравнению с квазиоптимальным идеальным полосовым фильт-
ром равен при приеме одиночных импульсов всего лишь 0,86 дБ.
K&TCf/vQrtf)
Af/2
-------- К (2rtf)
Af/2
<p(27t-f)
а)
Рис. 7.6. Частотная характеристика идеального полосового фильт-
ра (а) и прямоугольный радиоимпульс (6)
123
Г л а в a 8- ЦИФРОВЫЕ МЕТОДЫ ПЕРЕДАЧИ
НЕПРЕРЫВНЫХ СООБЩЕНИЙ
8.1. ХАРАКТЕРИСТИКИ КАЧЕСТВА
ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
В СИСТЕМАХ С ИМПУЛЬСНО-КОДОВОЙ
МОДУЛЯЦИЕЙ
Для передачи непрерывных сообщений можно воспользоваться дискретным ка-
налом. При этом необходимо преобразовать непрерывное сообщение в цифро-
вой сигнал, т. е. в последовательность символов, сохранив содержащуюся в со-
общении существенную часть информации, определяемую его эпсилон-энтропи-
ей. Типичным примером цифровых систем передачи непрерывных сообщений
является система с импульсно-кодовой модуляцией (ИКМ).
Для преобразования непрерывного сообщения в цифровую форму исполь-
зуются операции дискретизации и квантования. Полученная таким образом по-
следовательность квантованных отсчетов кодируется и передается по дискретно-
му каналу, как всякое дискретное сообщение. На приемной стороне непрерыв-
ное сообщение после декодирования восстанавливается (с той или иной точ-
ностью) .
Основное техническое преимущество цифровых систем передачи перед не-
прерывными состоит в их высокой помехоустойчивости. Это преимущество на-
иболее сильно проявляется в системах передачи с многократной ретрансляци-
ей (переприемом) сигналов. Типичные системы этого класса — кабельные и ра-
диорелейные линии большой протяженности.
Если система состоит из k одинаковых звеньев, для обеспечения заданной
верности связи необходимо обеспечить на входе каждого ретранслятора отно-
шение сигнал-помеха в k раз больше, чем при передаче без ретрансляций. В
реальных системах число ретрансляций k может достигать нескольких десятков,
а иногда и сотен. В этих случаях накопление помех вдоль тракта передачи ста-
новится основным фактором, ограничивающим протяженность линии связи.
В цифровых системах передачи для ослабления эффекта накопления помех
при передаче с ретрансляциями наряду с усилением применяют регенерацию им-
пульсов, т. е. демодуляцию с восстановлением переданных кодовых символов
и повторную модуляцию на переприемном пункте.
Ошибочно принятые в одном регенераторе символы передаются и на сле-
дующие регенераторы, так что ошибки все же накапливаются. При использо-
вании k регенераторов и допустимой вероятности ошибки р<С1 необходимо в
демодуляторе каждого регенератора обеспечить вероятность ошибки
Pi^p/k. (81)
При цифровой передаче непрерывных сообщений можно, кроме того, по-
высить верность применением помехоустойчивого кодирования. Высокая поме-
хоустойчивость цифровых систем передачи позволяет осуществить практически
неограниченную по дальности связь при использовании каналов сравнительно
невысокого качества.
124
Другим существенным преимуществом цифровых систем передачи информа-
ции является широкое использование в аппаратуре преобразования сигналов
современной элементной базы цифровой вычислительной техники и микропро-
цессоров. Совокупность устройств, выполняющих преобразования входных циф-
ровых сигналов в выходные цифровые сигналы на основе заданного алгоритма
цифрового преобразования, называют цифровыми фильтрами. По существу,
цифровой фильтр является специализированной ЭВМ или микропроцессором.
Важнейшими элементами системы цифровой передачи непрерывных сооб-
щений являются аналого-цифровой преобразователь (АЦП), осуществляющий
преобразование непрерывного сообщения в цифровую форму на передающей
стороне, и устройство преобразования цифрового сигнала в непрерывный —
цифро-аналоговый преобразователь (ЦАП) на приемной стороне.
Преобразование аналог — цифра состоит из трех операций: сначала непре-
рывное сообщение подвергается дискретизации по времени через интервалы
А/; полученные отсчеты мгновенных значений Ь(Д/) квантуются; наконец, по-
лученная последовательность квантованных значений &кв(Д/) передаваемого
сообщения представляется посредством кодирования в виде последовательности
m-ичных кодовых комбинаций. Такое преобразование называется импульсно-ко-
довой модуляцией. Чаще всего кодирование здесь сводится к записи номера
уровня в двоичной системе счисления.
Полученный с выхода АЦП сигнал ИКМ поступает или непосредственно в
линию связи, или на вход передатчика (модулятора), где последовательность
двоичных импульсов преобразуется в радиоимпульсы.
На приемной стороне линии связи последовательность импульсов после
демодуляции и регенерации в приемнике поступает на ЦАП, назначение кото-
рого состоит в обратном преобразовании (восстановлении) непрерывного сооб-
щения по принятой последовательности кодовых комбинаций. В состав ЦАП
входят декодирующее устройство, предназначенное для преобразования кодовых
комбинаций в квантованную последовательность отсчетов, и сглаживающий
фильтр, восстанавливающий непрерывное сообщение по квантованным значени-
ям
Преобразование непрерывных сообщений в цифровую форму в системах
ИКМ сопровождается округлением мгновенных значений до ближайших раз-
решенных уровней квантования. Возникающая при этом погрешность пред-
ставления является неустранимой, но
контролируемой, так как не превы-
шает половины шага квантования
(рис. 8.1). Выбрав достаточно малый
шаг квантования, можно обеспечить
эквивалентность по заданному е-кри-
терию исходного и кв/антованного
сообщений. Погрешность (ошибку)
квантования, представляющую собой
разность между исходным сообще-
нием и сообщением, восстановленным
по квантованным отсчетам, называют
шумом квантования*
В системах ИКМ отличие приня-
того сообщения от переданного обус-
Рис. 8.1. К пояснению возникновения
ошибки квантования
125
ловлено наличием шума квантования и шума ложных импульсов, порождаемого
ошибками декодирования.
Можно показать, что при равномерном распределении шума квантование
на интервале между двумя соседними разрешенными уровнями, средняя мощ-
ность шума квантования
£?=(Д£)2/12, (8.2)
где ДЬ — шаг квантования.
Если положить, что сообщение B(t) нормировано, т. е. |В(/) |макс^1, то
отношение средних мощностей сообщения и шума квантования
Рв /Рл = = 12/[П2 * 4 * * (Д*)2] > (8.3)
где П — пик-фактор сообщения.
Шаг квантования ДЬ можно выразить либо через число уровней квантова-
ния L, либо через число символов двоичного безызбыточного кода п на один
отсчет сообщения:
ДЬ=2(А-1) =2/(2”—1). (8.4)
В этом случае
Рв/Р =3(£—1) 2/П2 = 3(2”—4) 2/П2. (8.5)
Определим теперь среднюю мощность шума ложных импульсов. Если веро-
ятность ошибочного приема одного кодового символа р, то для канала без па-
мяти вероятность ошибочного декодирования n-разрядной кодовой комбинации
рк=[1— (1—р)”]~пр при пр<^1. При декодировании каждый символ кодовой
комбинации, в зависимости от занимаемого им места, дает определенный
«вклад» в декодируемое сообщение. Если используется двоичный код, то ошиб-
ка в младшем разряде кодовой комбинации вызывает погрешность в выход-
ном сообщении, равную шагу квантования ДЬ; ошибка во втором символе при-
водит к появлению в выходном сообщении погрешности 2ДЬ и т. д. При этом
средняя мощность шума, обусловленного действием ложных импульсов,
2 2(г-»«р(Д^ s2(i-1)- (8.6)
п Х=1 1=1
При фиксированном значении n=log£ шум ложных импульсов зависит
только от вероятности ошибок р, которая, в свою очередь, определяется отно-
шением мощностей сигнала и помехи в канале и видом модуляции.
Шум квантования и шум ложных импульсов в системах ИКМ можно счи-
тать независимыми. Поэтому суммарный шум на выходе системы ИКМ имеет
среднюю мощность
4 = ®”2+8л.и- <8-7)
Задачи
8.1.1. Двоичные символы цифрового сигнала передаются по
гауссовскому каналу с помощью частотной модуляции. Какую ве-
личину h2 необходимо обеспечить при оптимальном некогерентном
126
приеме, если допустима вероятность ошибки в элементарном сим-
воле р= 10“5, а в системе использовано k регенераторов? Принять
k=\\ 10; 100; 1000.
8.1.2. Двоичные символы цифрового сигнала передаются по
гауссовскому каналу, используя относительную фазовую модуля-
цию. Какую величину h2 необходимо обеспечить при оптимальном
некогерентном приеме с использованием k регенераторов, если до-
пустимая вероятность ошибки р=10~6, а £=1; 10; 100; 1000?
8.1.3. Какую величину h2 необходимо обеспечить в гауссовском
канале, по которому двоичные символы цифрового сигнала пере-
даются, используя фазовую модуляцию, если допустимая вероят-
ность ошибки в элементарном символе р=10~5? Считать, что осу-
ществляется оптимальный когерентный прием с использованием
Л=1; 10; 100; 1000 ретрансляторов.
8.1.4. В системе ИКМ передается сообщение, имеющее равно-
мерное распределение мгновенных значений w(b) = l/2 и пик-фак-
тор П= У 3. Определить отношение средних мощностей сообщения
и шума квантования Рв!Ре, если число уровней квантования
Г = 128.
8.1.5. Определить отношение средних мощностей сообщения и
шума квантования в системе ИКМ, если сообщение имеет равно-
мерную плотность вероятности до(&) = 1/2, пик-фактор П = 3, а чис-
ло разрядов кода и = 8.
8.1.6. Построить зависимость относительной мощности шума
квантования Р&1Рв от числа уровней квантования L в системе
ИКМ при передаче сообщения с параметрами, заданными в зада-
че 8.1.4. Как меняется относительная мощность шума квантования
с увеличением числа уровней квантования в два раза?
8.1.7. Построить зависимость относительной мощности шума
квантования PJPb от числа разрядов кода п в системе ИКМ при
передаче сообщения с параметрами, заданными в задаче 8.1.4. Как
меняется относительная мощность шума квантования при увеличе-
нии числа разрядов кода на единицу?
8.1.8. Определить мощность шума ложных импульсов е2л.и в
системе ИКМ, если число разрядов кода п=7, а вероятность оши-
бочного приема одного разряда р=10-5; 10-6; 10“7.
8.1.9. Построить зависимость мощности шума ложных импуль-
сов от числа уровней квантования L при значении вероятности
ошибочного приема одиночного разряда р= 10~5; 10-6; 10-7.
8.1.10. Определить суммарную мощность шума квантования и
шума ложных импульсов Р% в системе ИКМ при вероятности
ошибки в одном разряде р=10-5 и числе разрядов кода п = 7. Най-
ти отношение средних мощностей сообщения и суммарного шума
Рв!Р^ если пик-фактор сообщения П= У 3, р=10-5; 10~6; 10“7.
8.1.11. Построить зависимость Рв1Р% от числа разрядов код£
(уровней квантования), если пик-фактор сообщения П=уг3,
р= IO"5; IO"6; IO"7.
127
8.1.12. Определить минимально необходимую полосу частот
сигнала ИКМ при основании кода т и полосе сообщения Fc. Че-
му равна полоса частот сигнала ИКМ при т = 2, Fc = 3,l кГц?
8.1.13. Построить зависимость полосы частот сигнала ИКМ от
основания кода т при полосе сообщения Fc = 3,l кГц.
8.1.14. Построить зависимость полосы сигнала ИКМ от числа
уровней квантования, приняв основание кода т = 2 и полосу со-
общений Fc = 3,l кГц.
8.1.15. Передача сигналов ИКМ по каналу связи осуществля-
ется с помощью двухполосной частотной модуляции (система
ИКМ—ЧМ). Какое отношение сигнал-шум в канале необходимо
обеспечить, чтобы при неоптимальном некогерентном приеме
(р = ехр(—р-вх/2) /2) можно было пренебречь ошибками в канале.
Передача ведется с k ретрансляциями.
8.1.16. Определить выигрыш g и обобщенный выигрыш g' в си-
стеме ИКМ—ЧМ, если число разрядов кода п = 1, пик-фактор со-
общения П = 3, число ретрансляций Л=1, полоса сообщения Fc~
= 3 кГц.
8.1.17. Определить выигрыш g и обобщенный выигрыш g' в си-
стеме ИКМ—ЧМ в условиях задачи 8.1.15, приняв число ретранс-
ляции &=10. Как изменяются g и g' по сравнению со случаем пе-
редачи без ретрансляций?
Г л а в а 9. ТЕОРИЯ МНОГОКАНАЛЬНОЙ
ПЕРЕДАЧИ СООБЩЕНИЙ
9.1. ОСНОВЫ ТЕОРИИ РАЗДЕЛЕНИЯ
СИГНАЛОВ
На рис. 9.1 приведена структурная схема, иллюстрирующая принцип построе-
ния систем’ многоканальной передачи сообщений. Сообщения ai(Z)> аг(0>.ч
... ,aN(t) в модуляторах Mi, М2,...,Мя преобразуются в канальные сигналы
«1(0.
Рис. 9.1. Структурная схема многоканальной системы связи
128
Сигнал &-го канала sh(t) = СЛф/1(/), где tyk(t) — функция пере-
носчика; Ch — некоторый коэффициент, отображающий передаваемое сообщение:
при непрерывном сообщении он представляет собой мгновенное значение функ-
ции сообщения, при дискретном сообщении — некоторое число, соответствующее
передаваемому символу.
В сумматоре S из совокупности канальных сигналов формируется группо-
вой сигнал s(Z), который затем в групповом модуляторе М. преобразуется в ли-
нейный сигнал $л(/). Этот сигнал поступает в линию связи ЛС. На приемном
конце линии связи линейный сигнал $л(/) в групповом приемнике П преобра-
зуется в групповой сигнал
s(t)= 2 Sk(t)= (91)
k—l
Из группового сигнала индивидуальные приемники Пь П2,..., П^- выделяют
канальные сигналы si(Z), s2(/), ..., sN(t) и из этих сигналов формируют сооб-
щения di(Z), d2(f), • ••, &n (0.
При отсутствии искажений и аддитивных шумов в канале однозначное вы-
деление канальных сигналов из группового сигнала (9.1) возможно лишь при
линейной независимости функций ансамбля {$&(/)}. Необходимым и доста-
точным условием этого является отличие от нуля определителя Грама:
Р11 Р12 • • • Pin
Р21 Р22 • • • Ргп
(9.2)
Pni Р»2 • • • Рпп
w Pki = ~ J* sh(f)si(t)dt.
1 о
Следует заметить, что при выполнении условия (9.2) групповой сигнал
(9.1) тождественно равен нулю только при нулевых значениях всех Ch.
Процедура выделения канальных сигналов из группового в месте приема
сводится к определению проекций вектора s на соответствующие координатные
оси. Эту операцию можно осуществить корреляционной обработкой:
1 т
L (S) = (st)) = — J’s (0 т)^ (t) dt = Ch,
1 0
(9.3)
где {т]ь(0}—система весовых функций (опорных сигналов), удовлетворяющих
условию
1 ( 0 при I k,
-7-J sft(0ni(O#=| (9.4)
1 о \ # 0 при I = k.
Для ортогонального ансамбля сигналов {$&(/)} базисные функции тр(О“
= Gsz(O, т. е. определяются тем же ансамблем. С учетом возможного взаимно-
го запаздывания сигналов в канале условие разделения (9.4) можно записать
для этих сигналов в виде
т
Bk, i(T) = J Sfe(0ru(' + r)dT = O; 0<т<7\
О
k, Z= I, N. (9.5)
5—53
129
Выполнение условия (9.5) позволяет строить несинхронную систему уплот-
нения (систему со свободным доступом каждого абонента в канал). Если же
система является синхронной (канальные сигналы имеют одинаковую длитель-
ность и начало отсчета), условие разделения (9.5) должно выполняться при
т=0.
Задачи
9.1.1. Можно ли построить многоканальную систему связи,
если в качестве канальных сигналов использовать сигналы биор-
тогональной системы {$&(/), —$&(/)}, &=1, N?
9.1.2. Можно ли построить многоканальную систему связи, если
в качестве канальных сигналов использовать функции {$&(/)}, ор-
тогональные на интервале (О, Т) при условии, что в составе систе-
мы {sft(/)}
а) имеются функции с нулевой энергией;
б) отсутствуют функции с нулевой энергией?
9.1.3. В двухканальной системе связи предполагается использо-
вать канальные сигналы $i (Z) =а\ cos (W + фо) и s2(t) = а2 cos(coo/ +
+фо+Дф), имеющие длительность Т>2л/(оо-
Найти величину Дф, при которой можно при отсутствии адди-
тивных шумов в канале осуществить однозначное выделение вы-
бранных канальных сигналов из группового сигнала:
s (/) = ks (0 = k \аг (/) + а2 s2 (/)].
9.1.4. Найти опорные сигналы (базисные функции) на приеме
т)1(0 и Л2(0» позволяющие осуществить разделение группового
сигнала s(t) =&[aiSi (t) 4-a2s2 (/)] двухканальной системы связи, в
которой использованы канальные сигналы Si(Z) =а} соэ((до/ + фо) и
s2(t) = а2 cos (соо^+фо + Дф), имеющие длительность 7'^>2л/(йо.
9.1.5. Выяснить, возможно ли однозначное разделение каналов
в трехканальной системе связи при отсутствии в канале искаже-
ний и аддитивных шумов, если в качестве канальных переносчи-
ков использованы сигналы si (t) —а^ cos (cooN-фо); s2 (/) =
= а2cos (юо^+фо+ДфО; s3(0 = а3соз((доН-фо+Дф2), имеющие оди-
наковую длительность Г»2л/юо.
9.1.6. Показать, что при гауссовском аддитивном стационарном
флуктуационном шуме в канале N(t) и ортогональном ансамбле
канальных сигналов {$k(t)}, известных точно в месте приема и
используемых для передачи равновероятных дискретных сообще-
ний, алгоритм разделения (9.3) можно назвать оптимальным по
критерию минимума средней вероятности ошибки.
9.1.7. Найти отношение сигнал-шум на выходе индивидуального
канала многоканальной системы, в которой использован ортого-
нальный ансамбль канальных сигналов (/)}, имеющих одинако-
вые энергии, полагая, что в канале действует гауссовский адди-
тивный стационарный флуктуационный шум и использован алго-
ритм разделения (9.3).
130
9.1.8. В многоканальной системе связи в качестве переносчиков
выбраны сигналы, последовательность которых образует степен-
ной ряд: ф4(/) = 1, ^2(t)=t, ф3(0=^> ••• Записать груп-
повой сигнал s(t), полагая что информация содержится в коэф-
фициентах Ct, С2, ..., CN.
9.1.9. Групповой сигнал двухканальной системы связи имеет
вид s = Si + S2 = Ci-1+С2-Л В приемном устройстве использованы
4 6
весовые функции вида т]1(0 = —Ф1(О —— ф2(0. Лг (0 =
Найти обобщение на выходе индивидуального приемника каж-
дого канала.
9.2. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
Частотное разделение. При таком способе разделения сигналы индивидуаль-
ных каналов можно записать в виде
Sk (t)=Ak (0 cos [со4- 0ft (/) ], (9.6)
причем информация закладывается в изменения огибающей 4а(/), фазы ОНО
или одновременно в изменении обоих этих параметров. Здесь соь — средняя час-
тота в спектре канального сигнала. Эти частоты выбираются так, чтобы инди-
видуальные сигналы практически не перекрывались по спектру.
Временное разделение. При таком способе разделения элементы канальных
сигналов передаются и принимаются последовательно во времени в общей по-
лосе частот, что обеспечивается импульсным модулятором и синхронно рабо-
тающими на передаче и приеме устройствами коммутации. Интервал следования
элементов индивидуального сигнала Ть чаще всего выбирается равным 1/(2Гс),
а частота импульсного генератора, осуществляющего дискретизацию во времени
сигналов индивидуальных источников, Fr=2Fcn, п— число каналов. В систе-
мах временного разделения канальные сигналы передаются по каналу после-
довательно. Такие системы иногда называют последовательными.
Разделение по фазе. При этом способе разделения в качестве индивидуаль-
ных сигналов на интервале Т выбирают сигналы е неизменной мгновенной
частотой:
Sk (О =А k (0 cos (<оо/+Фл). (9.7)
Коэффициенты Ak(t) зависят от передаваемой информации, а по различию
фаз фл осуществляется разделение. Систему разделения по фазе делают двухка-
нальной, так как только при п~2 сигналы (9.7) остаются линейно независи-
мыми при любой разности фаз Д<р=ф2—ф1=£л (см. задачу 9.1.5).
Разделение по форме. При таком способе разделения в качестве индиви-
дуальных сигналов используются сигналы различной формы, удовлетворяющие
условиям разделения и использующие общие полосы частот и интервалы вре-
мени. Как правило, это ансамбль ортогональных сигналов на интервале (О, Т).
В качестве канальных сигналов при разделении по форме часто используют по-
следовательные составные сигналы. В этом случае канальный сигнал длитель-
ностью Т формируется из последовательности N = T/th отрезков синусоидаль-
5* 131
ных колебаний длительностью ти (элементарные сигналы), которые могут раз-
личаться частотами, фазами и амплитудами. Когда элементарные сигналы раз-
личаются по частоте, то говорят, что последовательный составной сигнал коди-
руется в виде частотно-временной матрицы (ЧВМ). В качестве канальных сиг-
налов, разделяемых по форме, можно использовать и реализации шумового
процесса.
В связи с развитием цифровых методов разделения сигналов по форме в
качестве переносчиков индивидуальных сообщений используются дискретные ор-
тогональные последовательности, такие, как функции Радемахера, Уолша и др.
Функции Радемахера образуются из синусоидальных функций с помощью
Соотношения г* (0) = sign [sin (2*л0)], О^0<1, где 0 = t/T — безразмерное вре-
мя; Т — период функции; & = 0, 1,2,... — порядок функции.
Функции Уолша {wal(/n, 0)} образуются следующим образом. По опреде-
лению вводится функция wal(0, 0) = 1 при т = 0. При ш^1 необходимо
разложить m по модулю 2, т. е. представить суммой m=2,lx +2Ц2 + ... +2ЦР,
где p,i< р<2< ••• — положительные целые числа. Функция Уолша
wal(m, 6)=гД1+1 (е)гДг+1 (0) ...гДр+1 (6).
Комбинационное разделение. При таком способе, используемом для переда-
чи дискретных сообщений, одно значение модулируемого параметра группового
сигнала ставится в соответствие группе символов, выдаваемых индивидуаль-
ными источниками. Широко распространены системы комбинационного разделе-
ния двух двоичных источников: система двукратной частотной модуляции
ДЧМ, система двукратной фазовой (относительной фазовой) модуляции — ДФМ
[{ДОФМ). Эти системы являются четырехпозиционными.
Задачи
9.2.1. Усредненный энергетический спектр канального сигнала
при частотном разделении определяется выражением
Gk (/) = Л exp [ — 0* (со —<ofe)2]
(гармоническая несущая, модулированная по частоте или фазе га-
уссовским стационарным процессом).
Найти необходимый минимальный разнос между средними час-
тотами двух соседних каналов А/ = 2F\, полагая, что в полосе
сосредоточено 95% мощности индивидуального сигнала.
Найти отношение сигнал-переходная помеха на выходе раздели-
тельного полосового фильтра, считая, что ею частотная характе-
ристика (коэффициент передачи мощности) имеет форму трапе-
ции (рис. 9.2), причем в полосе fk + F2 сосредоточено 90% мощно-
сти канального сигнала. Коэффициент передачи фильтра
по мощности в пределах fk±F2 считать равным 1, а на ча-
стотах fk±Fi — равным 0,1. Принять р=1,23-10~4 с, А =
= 5-10—4 Вт/ Гц.
9.2.2. Показать, что система с частотным разделением исполь-
зует сигналы, удовлетворяющие условию (9.5), и, следовательно,
может работать в асинхронном режиме.
132
Рис. 9.2. к определению переходной
помехи и разнесения между каналь-
ными частотами многоканальной сис-
темы при трапецеидальных частотных
характеристиках разделительных
фильтров
Рис. 9.3. Реализация сигнала много-
канальной системы связи с ФИМ
9.2.3. Определить необходимую полосу Д/с для передачи десяти
независимых речевых сообщений (полоса каждого 0,3... 3,4 кГц)
с помощью однополосной модуляции на поднесущих и амплитуд-
ной модуляции общей несущей (система ОМ—AM) по линии свя-
зи с частотным разделением. Считать, что для уменьшения пере-
ходных помех между каналами разнос между поднесущими час-
тотами каналов возрастает (по сравнению с минимально не-
обходимой величиной) на величину защитного интервала Д/Защ,
составляющего 30% от Afft.
9.2.4. Решить задачу 9.2.3 для случая фазовой модуляции об-
щей несущей. Индекс фазовой модуляции рФМ =6.
9.2.5. В системе с временным разделением передаются незави-
симые речевые сообщения (полоса каждого 0,3 ... 3,4 кГц) с первич<
ной фазоимпульсной модуляцией и вторичной амплитудной моду-
ляцией общей несущей (система ФИМ—AM). Полагая, что линей-
ный сигнал занимает полосу 21,5 МГц, определить число каналов
п. Считать, что для уменьшения переходных помех оставляются за-
щитные промежутки Д/защ между тактовыми интервалами отдель-
ных каналов, составляющие 2% от интервала дискретизации пер-
вичного сигнала во времени (рис. 9.3), а максимальное время от-
клонения фронта импульса в тактовом интервале Д/макс=128ти
(ти — длительность элементарной посылки). Во сколько раз уве-
личится число каналов при том же отношении Д/макс/ти, если вслед-
ствие мер, принятых для компенсации переходного процесса в ка-
нале, можно будет отказаться от защитных промежутков между
тактовыми интервалами?
9.2.6. Определить необходимую полосу частот Afc для передачи
20 независимых речевых сообщений (полоса каждого 0,3... 3,4
кГц) с помощью системы ФИМ—AM (см. задачу 9.2.5).
9.2.7. Решить задачу 9.2.6 для системы ФИМ—ЧМ, полагая, что
Рчм = 10-
133
9.2.8. Групповой сигнал двухканальной системы фазового раз-
деления имеет вид
S (0 = %! (О cos (<оо t + Фо) + Х2 (0 sin (©01 + ф0),
где Xi(t) и Xi(t)—независимые стационарные модулирующие
процессы с одинаковыми дисперсиями. Прием осуществляется
двухканальной схемой (рис. 9.4), где опорные сигналы rji (/) =
= 2cos(ffloZ+ф), т]2(/) = 2sin(©o^+i|)), а фильтры нижних частот
предполагаются идентичными и неискажающими для модулирую-
о о
щих процессов Xi(/) и X2(t).
Найти отношение средней мощности переходной помехи (обус-
ловленной фазовой расстройкой А = ф—ер0) к средней мощности
сигнала в отдельном канале и определить расстройку, при кото-
рой это отношение не превышает 0,1.
9.2.9. Система связи с ФМ, использующая сигналы вида
Sk(t) =XfeCOs (сйьЛ-фь), может быть использована для передачи
по каналу с полосой 3,1 кГц сообщений от 20 дискретных источ-
ников, работающих синхронно со скоростью 120 бод (Тс = 8,333 мс).
Нарисовать амплитудные спектры канальных сигналов, убедить-
ся в том, что они существенно перекрываются, и определить интер-
вал анализа по алгоритму (9.3), на котором обеспечивается орто-
гональность канальных сигналов. Разнос Af=142 Гц.
9.2.10. Канальные сигналы длительностью Т асинхронно-адрес-
ной системы связи образованы одночастотными последовательны-
ми сигналами Sk(i) =X/l(Z)cos((Oo^+qpo), где Xktf) —двоичная дву-
полярная синхронная последовательность, содержащая N=T/x-]-1
посылок длительностью т.
Показать, что условия разделения этих сигналов (9.5) при
Т^>2л/о)о и /о^>1/то сводятся к требованию
Bktl(r) = f xft(0^a + ^)^=0, 0^т<Т,
О’
т. е. взаимной ортогональности двоичных последовательностей, об-
Рис. 9.4. Структурная схема
приемного устройства двухка-
нальной системы связи с фа-
зовым разделением
134
Рис. 9 5. Частотно-временная
матрица
разующих «адреса» отдельных каналов, при произвольном взаим-
ном сдвиге.
9.2.11. Канальные сигналы Sk(t) длительностью T = Nx (N= 17)
асинхронно-адресной системы связи образованы на основе частот-
но-временной матрицы (рис. 9.5).
Нарисуйте форму сигнала, полагая, что радиоимпульсы име-
ют неизменную амплитуду ft, и объясните, почему для его выде-
ления из группового сигнала может быть использована схема
(рис. 9.6), содержащая четыре полосовых фильтра ПФ, настроен-
ных на соответствующие рабочие частоты fi, f2, f3, ft; четыре ам-
плитудных детектора Д, четыре линии задержки ЛЗ с 17 отвода-
ми, в каждой линии задействован лишь один отвод, соответству-
ющий «адресу» данного канала (абонента); нелинейную схему
совпадений СС, на выходе которой появляется импульс сигнала,
несущий сообщение только при том условии, если задержанные
входные импульсы во всех ветвях совпадают во времени.
9.2.12. Определите возможное число одновременно работающих
каналов (число кодовых адресных комбинаций), которое можно об-
разовать на основе ЧВМ, реализация которой показана на рис. 9.5.
Незаштрихованные элементы ЧВМ соответствуют элементарным
сигналам, не используемым в данной адресной комбинации (эти
сигналы имеют нулевую амплитуду).
9.2.13. В отдельных каналах асинхронно-адресной системы с
сигналами, заданными в предыдущей задаче, передаются речевые
сообщения (полоса 0,3... 3,4 кГц). Первичная модуляция осуще-
ствляется по системе ФИМ, причем девиация фронта импульса
Д/макс = 128ти. Определить максимально возможную длительность
посылки Ти и полосу канального сигнала, имея в виду, что вторич-
ная модуляция — AM.
9.2.14. Решить задачу 9.2.13 в предположении, что вторичная
модуляция — ФМ, рФМ = 10.
9.2.15. Решить задачу 9.2.13 для системы АИМ—AM.
9.2.16. Построить графики первых шести функций Радемахера,
используемых в многоканальной системе связи с цифровым разде-
Рис. 9.6. Структур-
ная схема прием-
ного устройства
асинхронно - адрес-
ной системы связи
135
лением по форме. Определить полосу частот, требуемую для пере-
дачи сообщений в этой системе, если Г=20 мс.
9.2.17. Нарисовать графики функций Уолша, построенных по
первым четырем функциям Радемахера, и найти полосу частот,
необходимую для передачи сообщений в многоканальной системе
цифрового разделения по форме, в которой эти функции использо-
ваны в качестве канальных переносчиков, если Т = 20 мс.
9.2.18. В синхронной 4-позиционной системе комбинационного
разделения групповые символы передаются посредством частотной
модуляции синусоидальной несущей (система ДЧМ). Четырьмя
мгновенными частотами fi, /г, /з и f4 передаются значения двоич-
ных символов двух источников согласно табл. 9.1.
Таблица 9.1
Символ 1-го источника 1 1 0 0
Символ 2-го источника 1 0 1 0
Рабочая частота fl /г fs /4
Полагая, что параметры сигналов в месте приема известны с
точностью до фазы, а в непрерывном канале действует гауссовский
белый шум, определить вероятность ошибки в каждом двоичном
канале при оптимальном приеме (символы 0 и 1 передаются от
источников с равными вероятностями).
9.2.19. В синхронной 4-позиционной системе комбинационного
разделения групповые символы передаются посредством фазовой
модуляции синусоидальной несущей (система ДФМ). Четырьмя
значениями фазы фЬ <р2, <рз и <р4 передаются значения двоичных
символов двух источников согласно табл. 9.2.
Полагая, что параметры сигнала известны точно в месте прие-
ма, а в канале действует гауссовский белый шум, определить ве-
роятность ошибки в каждом двоичном канале при оптимальном
приеме и равной вероятности передачи символов 0 и 1.
Как изменится вероятность ошибки, если перейти от абсолют-
ной к относительной фазовой модуляции (система ДОФМ)?
Таблица 9.2
Символ Lro канала 1 1 0 0
Символ 2-го канала 1 0 1 0
Фаза сигнала ДФМ Л /2 /з Л
136
Г л а в a 10. МЕТОДЫ ПОВЫШЕНИЯ
ЭФФЕКТИВНОСТИ СИСТЕМ ПЕРЕДАЧИ
СООБЩЕНИЙ
10.1. ПРЕДЕЛЬНАЯ ЭФФЕКТИВНОСТЬ
СИСТЕМ ПЕРЕДАЧИ СООБЩЕНИЙ
Для оценки эффективности систем передачи сообщений часто употребляется
коэффициент использования канала по мощности р (энергетическая эффектив-
ность) и коэффициент использования канала по полосе частот у (частотная
эффективность)
Р=Ш> (10.1), (10.2)
где — скорость передачи информации, р0— отношение мощности сигнала
к спектральной плотности мощности шума No; F — полоса частот, занимаемая
сигналом. Коэффициенты р и у имеют смысл удельной скорости передачи ин-
формации
Обобщенной характеристикой эффективности систем передачи сообщений
является коэффициент использования канала по пропускной способности (ин-
формационная эффективность)
П=^/С. (10 3)
Если учесть формулу Шеннона для пропускной способности гауссовского
канала C=F log(p+1), где р = Рс/Рш, то
T]=Y[log(y/p+l)], у=рр.
(Ю.4)
Если положить т) = 1, что соответствует теореме Шеннона о кодировании для
каналов с шумами, то получается предельная зависимость между р и у:
Р=у/(2^1).
Эта зависимость отражает наилуч-
ший обмен между р и у в непрерыв-
ном канале. Если фиксировать ве-
роятность ошибки p=const, то, оп-
ределив зависимость Р = /(у), можно
сравнительно быстро найти системы,
удовлетворяющие заданным требова-
ниям по энергетической и частотной
эффективностям, а также выяснить,
насколько эти показатели для реаль-
ных систем близки к предельным.
Кривые предельной энергетической и
Рис. 10 1. Кривые предельной энер-
гетической и частотной эффективно-
сти систем передачи информации
-10 -8 ~б -4 -2 О 2 4 О рдб
137
частотной эффективности систем передачи сообщений для дискретных симмет-
ричных каналов (ДСК) и полунепрерывных каналов (ПНК) при основании
М=2 и 4 приведены на рис. 10.1. Здесь же приведены зависимости р(у) для
различных систем модуляции при р=10~5. На этом рисунке линии одинаковых
значений р представляют со-бой прямые под углом 45°.
Сравнительную эффективность систем передачи сообщений можно опреде-
лять по энергетическому выигрышу перехода ЭВ от ьй системы к /-й при фик-
сированной вероятности ошибки р = const и скорости передачи R = const:
3Bl7j = 10 lg(₽J₽j) = APi/j. (10.6)
Можно оценить выигрыш по частотной эффективности при переходе от f-й
системы к /-й:
Аугр = ю lg(Vi/Yz) = ю IgtRjFi/RiFi). (107>
Если R = const, то
Aytp—lOlg^/fj). (10.8>
Задачи
10.1.1. Определить наибольшее возможное значение энергетиче-
ской эффективности рмакс при передаче сообщений в канале с ад-
дитивным гауссовским белым шумом.
10.1.2. Найти предельно возможное значение частотной эффек-
тивности умакс при произвольном основании кода М.
10.1.3. Определить предельные частотную и энергетическую
эффективности для двоичного канала (Л4 = 2) с противоположны-
ми сигналами при 27?Т=1.
10.1.4. Как изменится частотная и энергетическая эффектив-
ность, если в предыдущей задаче принять М = 4?
10.1.5. Оценить выигрыш по частотной и энергетической эффек-
тивностям при переходе от 32-позиционной к 2-позиционной систе-
ме частотной модуляции при вероятности ошибки р=10-5.
10.1.6. Сравнить по информационной эффективности т] 2-позици-
онные системы AM, ФМ, ОФМ и ЧМ.
10.1.7. На сколько можно увеличить частотную и энергетичес-
кую эффективности, если осуществить переход от дискретного ка-
нала к каналу с непрерывным выходом при Л4 = 2 и Л4 = 4.
10.1.8. Определить энергетический выигрыш ДРг/j и выигрыш по
полосе Ауг/j при переходе от двоичной системы AM к двоичной
системе ЧМ и ФМ при одинаковой вероятности ошибки в случае
оптимального когерентного приема и фиксированной скорости пе-
редачи информации.
10.1.9. Найти эквивалентную вероятность ошибки для 10-пози-
ционной системы ЧМ и ФМ в случае оптимального когерентного
приема при Л2=12,8.
Определить выигрыш по эквивалентной вероятности ошибки
при переходе от системы ЧМ к системе ФМ.
138
10.1.10. Найти эквивалентную вероятность ошибки для случая
некогерентного оптимального приема 5-позиционной ЧМ при И2 —
= 16,5; 25; 32; 70; 100.
10.1.11. Найти энергетический выигрыш при переходе от 2-пози-
ционной системы ЧМ к 5-позиционной системе ЧМ в канале с не-
определенной фазой и флуктуационным шумом, полагая, что экви-
валентная вероятность ошибки р3= 10_2; 10-3; 10“4; 10-5. Скорость
передачи информации неизменна.
10.1.12. Найти величину коэффициента использования пропуск-
ной способности канала для 4-позиционной системы ЧМ, обеспе-
чивающей при неопределенной фазе и флуктуационном шуме экви-
валентную вероятность ошибки рэ= 10_4, полагая, что скорость пе-
редачи информации /? = 300 бит/с, а полоса частот системы F =
= 3,1 кГц.
10.1.13. Одним из способов повышения помехоустойчивости свя-
зи при наличии замираний является разнесенный прием, сущность
которого заключается в том, что переданное сообщение воспроиз-
водится по нескольким сигналам, несущим одну и ту же инфор-
мацию. Оценить вероятность ошибки в системе /г-кратного разне-
сения с автовыбором наиболее сильного сигнала (рис. 10.2) при
использовании двоичной системы с активной паузой, ортогональ-
ной в усиленном смысле (ЧМ), при медленных рэлеевских зами-
раниях в отдельных ветвях.
10.1.14. Найти энергетический выигрыш при переходе от одиноч-
ного к сдвоенному приему с автовыбором в канале с медленными
рэлеевскими независимыми замираниями в отдельных ветвях при
неизменной вероятности ошибки Р1=Р2 = Ю-4.
10.1.15. При проектировании передвижной приемопередающей
радиостанции, которая должна обеспечить двустороннюю передачу
двоичных символов, по экономическим соображениям, а также по
допустимым габаритным размерам возможно 3 варианта:
а) передатчик мощностью 800 Вт, одиночный прием, /г21 = 40;
Рис. 10.2. Схема раз-
несенного приема с
автовыбором ветви
с наиболее сильным
сигналом
139
б) передатчик мощностью 400 Вт, сдвоенный прием на разне-
сенные антенны, nz2 =20;
в) передатчик мощностью 200 Вт, строенный прием на разнесен-
ные антенны, /г23=10.
При каком варианте вероятность удовлетворительной связи
больше, если допустима вероятность ошибки 10~4? Изменится ли
результат, если допустить вероятность ошибки 10-2? (Принять, что
сигнал замирает по рэлеевскому закону, система с активной пау-
зой, ортогональная в усиленном смысле при автовыборе ветви с
наиболее сильным сигналом.)
10.1.16. Составной сигнал дискретной широкополосной системы
(В = 2/7Г»1) строится следующим образом: информационная по-
сылка длительностью Т разбивается на N двоичных элементов дли-
тельностью xq = T/N, а в качестве элементарного сигнала исполь-
зуются отрезки синусоидальных колебаний вида Um sin (tokt-'rtpk)
= £=1, N) длительностью то-
Полагая, что указанные сигналы использованы для передачи
двоичной информации в системе ЧМ, оценить вероятность ошибки
при оптимальном когерентном приеме и удельную скорость переда-
чи при 7V = 200, Т = 20 мс, если в канале действует стационарный
гауссовский белый шум со спектральной плотностью мощности
;V0= 10-6 Вт/Гц.
10.1.17. Показать, что при использовании широкополосных сиг-
налов с базой B = 2FT^> 1 влияние сосредоточенных по спектру по-
мех уменьшается пропорционально базе сигнала.
10.1.18. Определить энергетический выигрыш ЭВ при переходе
от параллельного метода передачи дискретной информации к пос-
ледовательному в однолучевом гауссовском канале без замираний,,
если число подканалов параллельной системы равно п и если при
этом переходе сохраняется: а) средняя мощность сигнала; б) пико-
вая мощность сигнала.
10.1.19. Известно, что в подрэлеевском канале связи при ап-
проксимации нормированной корреляционной функции компонент
канала функцией R(T) =ехр(—Г2/2(32) и ОФМ несократимая веро-
ятность ошибок
р = Т2 ехр (— <?2)/(4 (З2),
где р — средний период замираний; q2— превышение регулярной
части сигнала над флуктуирующей.
Определить выигрыш по вероятности ошибки при переходе от
параллельной системы с числом каналов и=12 к последователь-
ной системе передачи при скорости передачи 7?= 1200 бит/с, q2 = 5.
Р = 0,1 с.
10.1.20. В двухлучевом рэлеевском канале со взаимным запаз-
дыванием лучей Д/=2 мс длинные посылки (Ti = 5 мс) обрабаты-
ваются на интервале анализа 7\i = 7\—Д/, а короткие посылки
(Г2<2мс)— на интервале анализа Та2 = Т2-;-Д/. При этом закон
распределения энергии посылки на интервале анализа оказывается
различным.
140
Определить энергетический выигрыш по средней мощности npi
переходе от параллельной системы с я = 20 к последовательной npi
скорости передачи /?=1200 бит/с, если по обоим лучам распрост
ранения среднее превышение сигнал-шум одинаково и равнс
¥=20.
10.2. ЭФФЕКТИВНОСТЬ АНАЛОГОВЫХ
И ЦИФРОВЫХ СИСТЕМ
Если источник непрерывного сообщения является гауссовским, то скорост]
передачи R — Fc log рВЫх В этом случае информационная эффективность мо
жет быть записана в виде
т)= (logpBbix)/a log(pBbIx/g+l),
где g — выигрыш системы модуляции
Так же, как и для дискретных систем, непрерывные системы можно срав
нивать по кривым эффективности P = f(y), которые могут быть рассчитаны п<
формулам
Р— £ log Рвых/офвых; у — log Рвых/a.
(Ю.9)
Кривые частотной и энергетичес-
кой эффективности для аналоговых
и цифровых систем приведены на
рис. 10.3. Для аналоговых систем
цифры на кривых указывают значе-
ния a=F/Fc, а цифры в скобках —
значения рвых в децибелах. В облас-
ти порога кривые для ЧМ изображе-
ны штриховыми линиями. Для циф-
ровых систем расчеты производились
для канала, в котором устранены
межсимвольные помехи. Цифры на
кривых — это основание кода. Кри-
вые соответствуют вероятности
ошибки р=10-5, что соответствует
величине рВЫх~36 дБ при равенстве
мощностей шума квантования и шу-
ма ложных импульсов е2 = е2л.и.
При фиксированном отношении
сигнал-шум на выходе приемника
можно определить энергетический вы-
игрыш перехода от i-й системы к /-й:
ЭВг/j = 10 lg(pBx iRj/рвх jRi) ,
pBbix = COnst, (10.10)
Рис. 10 3. Кривые энергетической и час-
тотной эффективности аналоговых и
цифровых систем связи
где Яг—скорость ввода информации
в канал i-й системы.
141
Если фиксировать скорость ввода информации R, то ЭВгр можно выра-
зить через выигрыш системы модуляции g:
(10.11)
Выигрыш по частотной эффективности определяется так же, как и в сис-
темах передачи дискретных сообщений.
В условиях, когда рВых (а следовательно, и верность связи) меняется
случайно во времени, важной характеристикой качества системы связи является
ее надежность У, определяемая вероятностью (процентом времени для эргоди-
ческого процесса) того, что рВых превышает минимально допустимую (порого-
вую) рвыхпор величину, определяемую видом сообщения и особенностями его
получателя:
оо
/V = у (Овых) Рвых ’ (10.12)
р
вых. пор
где ^1(рвых) —одномерное распределение величины рВЫх. Эффективное сред-
ство повышения надежности связи — прием сигналов по независимым каналам.
Задачи
10.2.1. Рассчитать выигрыш g и информационную эффективность
т) для систем AM, БМ, ОМ, ФМ и ЧМ, полагая, что рВых = 40 дБ, и
во всех системах передается одно и то же сообщение с полосой Fc
и пик-фактором П = 3.
10.2.2. Решить задачу 10.2.1 для систем ФИМ—AM, ИКМ—AM,
ИКМ—ЧМ, ИКМ—ФМ."
10.2.3. Пользуясь графиками рис. 10.3, оценить величину выиг-
рыша по энергетической и частотной эффективности при переходе
от системы ИКМ—ЧМ при основании кода М = 4 к системе ИКМ —
ФМ с тем же основанием кода.
10.2.4. Найти выигрыш по частотной и энергетической эффек-
тивности при переходе от 10-позиционной к 5-позиционной систе-
ме ЧМ при рВых = 30 и 40 дБ.
10.2.5. На сколько ниже предела Шеннона частотная и энерге-
тическая эффективность 4-позиционной системы ИКМ—ФМ?
10.2.6. Найти энергетический выигрыш перехода от системы
AM, предназначенной для передачи речевого сообщения с пик-фак-
тором П = 3, т = 0,3 и Л = 3,1 кГц, к системе ФМ при Рфм = Ю-
10.2.7. Найти энергетический выигрыш перехода от системы
AM, предназначенной для передачи речевого сообщения с пик-фак-
тором П = 3, т = 0,3 и Fc = 3,l кГц, к системе ЧМ при рчм=15.
10.2.8. Найти энергетический выигрыш при переходе от системы
ФМ к системе ЧМ с той же полосой.
10.2.9. Найти значения энергетического выигрыша, выигрыша
ио удельной (на 1 Гц полосы частот) скорости передачи информа-
ции при переходе от системы передачи сообщения без модуляции
к системе AM, полагая, что в обеих системах передается речевое
сообщение с пик-фактором П = 3 и нормированной корреляционной
142
функцией 7?в=ехр[-^р|т|], р=103 Гц. Считать, что при ампли-
тудной модуляции несущей т = 0,4.
10.2.10. Решить (задачу 10.2.9 для случая перехода к систе-
ме БМ.
10.2.11. Решить радачу 10.2.9. для случая перехода к систе-
ме ОМ.
10.2.12. Решить задачу 10.2.9 для случая перехода к системе
ФМ, приняв 0ФМ =7;
10.2.13. Решить задачу 10.2.9 для случая перехода к системе
ФИМ—ОМ, приняв, что длительность импульса при ФИМ ти=
= 2,5-10"5 с.
10.2.14. Решить задачу 10.2.9. для случая перехода к системе
АИМ—ОМ, приняв длительность импульса ти = 2,5-10-5 с.
10.2.15. Определить надежность связи в процентах при переда-
че речевых сообщений, если Wi(pBbix) имеет рэлеевское распределе-
ние, а рПор/рвых = 0,01; 1; 10.
10.2.16. Во сколько раз увеличится надежность N2 связи, если
прием речевых сообщений вести по двум независимым каналам с
одинаковой статистикой при условии, что надежность одноканаль-
ного приема Л/\ = 0,1; 0,5; 0,8; 0,9; 0,99.
10.2.17. Во сколько раз изменится величина надежности 3-ка-
нальной системы разнесения по сравнению с 2-канальной N2,
если Д^ = 0,5.
10.2.18. Найти предельный коэффициент информационной эф-
фективности в системах AM, БМ, ОМ, ФМ, ФИМ—ОМ при рВых =
= 1000; 5000, если во всех системах передается речевое сообщение,
а параметры системы те же, что в задачах 10.2.9—10.2.14.
10.3. ХАРАКТЕРИСТИКИ ЭФФЕКТИВНОСТИ
МНОГОКАНАЛЬНЫХ СИСТЕМ
Имея в виду, что в канале действует флуктуационный шум с энергетиче-
ским спектром Nq, будем сравнивать две л-канальные системы, обеспечивающие
одинаковую верность и одинаковую суммарную скорость передачи информации
2?n = const по параметру эквивалентного отношения сигнал-шум:
Рэп = Рсп/(^п), (10.13)
где Рс п — средняя мощность канального сигнала в л-канальной системе.
Энергетический выигрыш перехода от i-й л-канальной системы к j-й в деци-
белах при фиксированной верности и скорости передачи информации
ЭВг7/=101£(рэ пг/Рэт) =10 lg(Pc«t/Pc nj). (10.14)
Энергетическая цена уплотнения
Ь(п)=Рс n/Pcl (10.15)
показывает, во сколько раз необходимо увеличить среднюю мощность сигнала в
л-канальной системе по сравнению с одноканальной, чтобы при той же спект-
143
ральной плотности мощности помех обеспечить неизменную верность приема в
каждом канале. Очевидно,
эв,/у = 101g Г |p(n)ip3il 1 = эвп//1 +101g yvK (10.16)
где ЭВг1/л—энергетический выигрыш перехода от t-й системы к /-й в однока-
нальном режиме при неизменных верности и скорости! передачи информации
7?i=const. 1
Если t-я и /-я системы отличаются только способом разделения сигналов, то
ЭВш=101^[Ь(л)^р(л)Л. (Ю.17)
Удельная скорость (коэффициент частотной эффективности) n-канальной систе-
мы определяется коэффициентом
yn = Rn/Fn — ^nRi/Fn = iinyi/ZF(n)i (1018)
где рп—коэффициент увеличения скорости передачи информации в п-канальной
системе по сравнению с одноканальной;
^(и)=Еп/Л (10 19)
— спектральная цена уплотнения, которая показывает, во сколько раз необхо-
димо увеличить занимаемую n-канальной системой полосу частот по сравнению с
одноканальной системой; yi — эффективность использования полосы частот одно-
канальной системы. Если для многоканальной системы pn = gF(n), то уп=Уь
Выигрыш г]р по эффективности использования полосы частот при переходе от
t-й системы к /-й определим отношением параметров уп в сравниваемых систе-
мах. Информационная эффективность многоканальной системы при передаче со-
общений по независимым каналам
т) = Сс/С2.= Sccft / VCfe. (10.20)
k=\ I £=1
Здесь Ck — пропускная способность k-ro канала при заданном способе разделе-
ния; CCk—пропускная способность расширенного &-го канала.
Разделение существующих каналов связи с заданной пропускной способ-
ностью С независимыми источниками приводит к существенному повышению эф-
фективности связи.
Задачи
10.3.1. В полосе стандартного телефонного канала шириной
/7 = 3100 Гц необходимо передавать информацию от независимых
двоичных источников без избыточности с производительностью
//'=1/7\=50 бит/с.
Сколько источников можно разделить по форме, если в каждом
канале используется частотная модуляция, а прием осуществляет-
ся согласованными фильтрами в указанной полосе при неопреде-
ленной фазе сигнала.
10.3.2. По условию задачи 10.3.1 определить число каналов при
частотном разделении (при использовании в месте приема полосо-
вых фильтров).
144
10.3.3. В условиях задачи 10.3.1 определить коэффициент ис-
пользования полосы частот двоичной ЧМ в однополосном режиме
Vi при приеме с помощью согласованного и полосового фильтров.
Определить также для обеих систем спектральную цену разделе-
ния gF(n), коэффициент увеличения скорости передачи информации
рп и коэффициент использования полосы частот уп.
10.3.4. Система с частотным разделением образуется путем од-
нополосной модуляции поднесущих и частотной модуляции общей
несущей (система ОМ—ЧМ). Будем считать системой А многока-
нальную систему ОМ—ЧМ, у которой девиация частоты Д/ не ме-
няется с изменением числа каналов /г, а системой Б — многока-
нальную систему ОМ—ЧМ, у которой Д/ растет пропорционально
числу каналов п.
Показать, что энергетический выигрыш перехода от системы А
к системе Б ЭВ д/б = 10 1g п2, что достигается ценой расширения
занимаемой полосы частот в п раз.
10.3.5. Определить энергетический проигрыш по отношению
сигнал-шум на выходе детектора индивидуального канала и спект-
ральный проигрыш перехода от 2-канальной системы фазового
разделения, рассмотренной в задаче 9.2.9 (при Д = 0), к 2-каналь-
ной системе частотного разделения с групповым сигналом
s (/) = Х± (/) cos ((Oi t + <рх) + X2 (t) cos (co21 + <p2)
при одинаковой пиковой мощности передатчика. Разнос между
средними частотами каналов считать равным удвоенной ширине
о
спектра модулирующего сигнала Хг(/). Пик-фактор модулирую-
щего сигнала П = 3.
10.3.6. Найти спектральный выигрыш перехода от асинхронной
системы частотного разделения ЧМ—ЧМ, предназначенной для
передачи N= 13440 независимых речевых сообщений, к асинхрон-
но-адресной АА системе на такое же число каналов, рассмотренной
в задаче 9.2.14. Считая, что обе системы работают при больших
отношениях сигнал-шум (выше пороговых) и обеспечивают одина-
ковую верность при одинаковом отношении сигнал-шум в канале,
определить энергетический проигрыш перехода от системы АА к
системе ЧМ—ЧМ.
10.3.7. Определить энергетический выигрыш и выигрыш по эф-
фективности использования полосы частот при переходе от 2-ка-
нальной системы частотного разделения с частотной модуляцией,
предназначенной для передачи независимых сообщений от двоич-
ных источников без избыточности, к системе ДЧМ. Считать, что пи-
ковая мощность передатчика фиксирована, в канале действует га-
уссовский белый шум, сигнал известен с точностью до фазы и осу-
ществляется оптимальный некогерентный прием.
10.3.8. Определить энергетический выигрыш и выигрыш по эф-
фективности использования полосы частот при переходе от 2-ка-
нальной системы частотного или временного разделения к системе
ДОФМ. Считать, что во всех сравниваемых системах передается
145
информация от двух независимых двоичных источников без избы-
точности, пиковая мощность передатчика фиксирована, в каждой
системе осуществляется ОФМ, в канале действует гауссовский
белый шум, сигнал известен точно в месте приема и осуществля-
ется оптимальный когерентный прием.
10.3.9. Определить пропускную способность 20-канальной сис-
темы частотного разделения с независимым гауссовским белым
шумом и интенсивностью, приведенной к входу передатчика,
Afo = 4,6-lO-4 Вт/Гц в отдельных каналах, полагая, что каждый ка-
нал занимает полосу частот 7> = 8000 Гц, переходная помеха а
каждом канале имеет характер гауссовского белого шума со сред-
ней мощностью, пропорциональной суммарной средней мощности
остальных каналов, в передатчике фиксирована пиковая мощность
Лиакс=Ю0 кВт и работает он в строго линейном режиме.
10.3.10. Определить пропускную способность 20-канальной сис-
темы временного разделения с теми же характеристиками канала
(в том числе по суммарной полосе частот F£=20FK) и передатчи-
ка, что в задаче 10.3.9. Сравнить значения пропускных способно-
стей, полученных в этих двух случаях.
10.3.11. Определить коэффициент эффективности 20-канальной
системы передачи независимых непрерывных гауссовских сообще-
ний, каждое из которых занимает полосу Гс = 4000 Гц и превышает
по средней мощности эквивалентный равномерный по полосе гаус-
совский шум на выходе канала в 7 раз. Сообщения передаются:
а) по каналу с частотным разделением (задача 10.3.9), когда мож-
но пренебречь переходным шумом; б) по каналу с временным раз-
делением (задача 10.3.10), когда можно пренебречь переходным
шумом.
10.3.12. Определить коэффициент эффективности 20-канальной
системы передачи независимых сообщений от дискретных источни-
ков без избыточности с производительностью //' = 4000 бит/с. Со-
общения передаются по двум разновидностям каналов, рассмот-
ренных в предыдущей задаче (ошибками в расширенном дискрет-
ном канале пренебречь).
10.3.13. Канал связи, имеющий большую протяженность, с об-
щей пропускной способностью 10000 бит/с используется при пере-
даче информации от 100 независимых источников с производитель-
ностью 50 бит/с каждый.
Показать, что стоимость передачи 1 бита информации в канале
с разделением в 25 раз меньше, чем при использовании для каждо-
го источника индивидуального канала с пропускной способностью
100 бит/с, если стоимость такого канала в 4 раза меньше стоимос-
ти одного канала с разделением.
146
10.4. ЭФФЕКТИВНОСТЬ ИЗБЫТОЧНОГО
КОДИРОВАНИЯ И МНОГОПОЗИЦИОННЫХ
СИГНАЛОВ
Параметром, по которому различные коды, а также различные системы пе-
редачи дискретных сообщений можно сравнивать между собой, является эквива-
лентная вероятность ошибки приема элементарного символа:
Рэ = 1—(1_Рк)1М (10.21)
где рк — вероятность ошибочного декодирования кодовой комбинации данного
кода; k — число информационных разрядов. Эквивалентная вероятность ошибки
определяет вероятность ошибки элементарного символа в двоичном симметрич-
ном стационарном канале без памяти, в котором система с примитивным коди-
рованием обеспечивает при передаче того же количества информации ту же веро-
ятность ошибочного декодирования кодовой комбинации рк, что и заданная сис-
тема с избыточным кодом.
Сравнение систем связи, использующих различные коды, по эквивалентной
вероятности ошибки рэ целесообразно проводить при неизменной средней ско-
рости передачи информации 7? = ук(1—Хк)=&/(пГс) и фиксированной средней
мощности сигнала Рс.
Очевидно, что корректирующий код целесообразно применять в случае, когда
рэ<Ро, где ро — вероятность ошибки, которая имела бы место при использова-
нии примитивного кода и неизменной скорости передачи информации. С другой
стороны из двух корректирующих кодов лучше тот, который обеспечивает мень-
шее значение рэ.
Рис. 10.4. Кривые энер-
гетической и частотной
эффективности систем с
многопозиционными сиг-
налами и корректирую-
щими кодами
147
Если фиксировать спектральную плотность мощности шума NQ и R, то па-
раметром сравнения можно сделать эквивалентное отношение сигнал-шум
Pd==pn/k = Pc/(N0R). (10 22}
Выигрыш по рэ при переходе от 7й к /-й системе
дг/3=Рэ ilpQj, Я = const, p9 = const. (10 23)
Эффективность системы кодирования можно оценить и по энергетическому
выигрышу перехода от i-й системы к /-й:
ЭВг/;= 10 lg(p3 г/рэ j), p3 = const (10 24)
На рис. 10.4 приведены Ру—диаграммы для некоторых ансамблей многопозици-
онных сигналов. Значения энергетической эффективности определялись по кри-
вым помехоустойчивости [7,11] p=f(h2) для вероятности ошибки р=10~5 (при
р<10~3 1/7, р=1//г2) При этом частотная эффективность
v==logM/(7F)==21ogM/ri. (10 25>
где М — объем ансамбля сигналов; п — его размерность (база).
Задачи
10.4.1. Найти эквивалентную вероятность ошибки в однород-
ном симметричном канале без памяти при применении «оптималь-
ного» совершенного кода (n, 1), использующего двоичные кодо-
вые комбинации
Ьх= 1 1 1... 1, Ь2 = 0 0 0...0,
п п
если декодирование с исправлением ошибок осуществляется по
минимуму расстояния по Хеммингу.
10.4.2. Показать, что эквивалентная вероятность ошибки при
использовании совершенного кода (3, 1) с кодовыми комбинаци-
ями 111 и 000 в однородном симметричном канале с независимы-
ми ошибками равна Зр20 (ро — вероятность ошибочной регистра-
ции элементарного символа).
10.4.3. Найти эквивалентную вероятность ошибки для линейно-
го кода (7,4). Определить выигрыш по эквивалентной вероятно-
сти ошибки при переходе от примитивного кодирования к коди-
рованию кодом ,(7, 4), если р0 = Ю~2; 10~4; 10~6.
10.4.4. Найти энергетический выигрыш перехода от системы с
примитивным кодированием к системе с кодом (7,4) в канале со
случайной фазой и ортогональными в усиленном смысле сигнала-
ми при 7? = const и р3= 10“2; IO-3; 10-4; 10-5; 10“6.
10.4.5. В канале с медленными рэлеевскими замираниями пе-
редача информации осуществляется примитивным кодом и кодом
‘<7,4). Какой выигрыш по эквивалентной вероятности ошибки да-
ет использование кода (7,4), если вероятность ошибки в регист-
рации одного символа (вероятность ошибочного перехода) ро~
= 10"2; 10-3; IO"4; 10"5; 10~6.
148
10.4.6. В условиях задачи 10.4.5 определить величину энерте-
тического выигрыша перехода от примитивного кодирования к
избыточному кодированию кодом (7, 4). Объяснить полученный ре-
зультат.
10.4.7. Код (7,4) используется для передачи информации в ка-
нале с быстрыми рэлеевскими замираниями при вероятности
ошибки в приеме элементарного символа р»= 10“2; 10-3; 10-4;
10-5; 10-6. Какой выигрыш по эквивалентной вероятности ошиб-
ки дает применение кода (7,4) по сравнению с примитивным ко-
дом?
10.4.8. В условиях задачи 10.4.7 определить величину энергети-
ческого выигрыша перехода от примитивного кодирования к ко-
дированию кодом (7,4). Объяснить полученный результат.
10.4.9. Для передачи информации в гауссовском канале с не-
определенной фазой и ортогональными в усиленном смысле сиг-
налами использован код (3, 1) с кодовыми комбинациями ООО и
111. Коэффициент передачи канала k. Вычислить выигрыш по эк-
вивалентной вероятности ошибки при переходе от поэлементного
приема к приему в целом.
10.4.10. В канале с постоянными параметрами при наличии ад-
дитивного стационарного гауссовского белого шума осуществля-
ется оптимальный когерентный прием двоичных сигналов ЧМ при
вероятности ошибки ро=О,5[1—Ф( j/^Zi2)]. В этих условиях пред-
полагается использовать корректирующий (/г, &)-код, исправля-
ющий ошибки максимальной кратности qn. Определить условия,
при которых такой код целесообразно использовать, полагая, что
Л2»1.
10.4.11. Циклический код (7,4) исправляет все одиночные
ошибки. Целесообразно ли применение этого кода при осуществ-
лении оптимального когерентного приема?
10.4.12. Целесообразно ли применение кода (3, 1), исправляю-
щего все одиночные ошибки, при поэлементном оптимальном коге-
рентном приеме?
10.4.13. Какую максимальную избыточность должен иметь кодг
исправляющий все одиночные ошибки, чтобы его целесообразно
было применять в условиях задачи 10.4.12?
10.4.14. Как меняются с ростом объема ансамбля М при фикси-
рованной размерности п удельная скорость у и энергетическая
эффективность р для систем многопозиционных сигналов ФМ и
АФМ?
10.4.15. Объяснить, почему в системах биортогональных, орто-
гональных и симплексных сигналов с ростом объема ансамбля М
возрастает энергетическая эффективность. Какова цена этого уве-
личения?
10.4.16. Определить частотную, энергетическую и информаци-
онную эффективности системы с сигналами 4-позиционной ФМ
(ФМ4), относящимися к классу биортогональных с М = 4.
14<>
10.4.17. Приняв за эталон систему ФМ4, разделить представ-
ленные на рис. 10.4 системы на следующие группы:
1) малоэффективные системы;
2) системы с высокой энергетической эффективностью;
3) системы с высокой частотной эффективностью;
4) высокоэффективные системы.
10.4.18. Какие сигналы необходимо применить в системе, обес-
печивающей энергетический выигрыш Др = 2,4 дБ и системы час-
тотной эффективности Ду=3 дБ по сравнению с системой ФМ4?
10.4.19. Пользуясь рис. 10.4, обосновать целесообразность пере-
хода в непрерывном канале с постоянными параметрами при р=
10“5 от системы ФМ2 без кодирования и оптимальном когерентном
приеме к системе с помехоустойчивым кодированием.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 1
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 1.1.
1.1.1. Поскольку каждый символ в 3-символьной последова-
тельности может принимать одно из восьми значений, источник
может выдать Af = 83 = 512 различных сообщений. Реализации со-
общений, у которых два первых символа аца72, выглядят следую-
щим образом:
1) Ф1#72#оз; 2) О,\ 1#7 2#1 з; 3) #11#72#23;
4) СС\ 1^7 2#33; 5) #11^72^43; 6) #11072^53;
7) аца72^бз’, 8) йцЯ72#7з-
1.1.3. Число всевозможных двоичных 7-разрядных кодовых ком-
бинаций М=27=128. Две возможных реализации сообщений за-
данного источника таковы: 1) 0111001; 2) 1010110.
1.1.5. Так как каждый символ пары принимает два возможных
значения: 0 или 1, то число всевозможных пар двоичных симво-
лов равно 22 = 4. Следовательно, символ Cik имеет четыре реали-
зации.
1.1.6. При заданной погрешности квантования 6 = 0,5° шаг
квантования Д=1°. При таком шаге квантования шкала темпера-
тур в интервале 18 ... 36° должна быть разбита на К=19 уровней.
Заданный источник может выдать Af=419 сообщений.
1.1.8. Число элементов сообщения при дискретном времени п =
= 71/)Д/ = 277максТ = 2-4000-0,1 =800. Каждый элемент может при-
нимать любое из 1 + (Рмакс—Рмин)/АР=3,5—0,54-1 = 4 значений
давления. Следовательно, число реализаций сообщения источни-
ка #=4800.
1.1.11. Число реализаций сигнала на интервале 7Т М=27 =
= 128. Огибающая амплитудного спектра такого сигнала будет
•соответствовать модулю комплексной спектральной плотности оди-
150
ночного прямоугольного импульса высотой h и длительностью Т:
т
S (ja) = J* h exp ( — j(dt) dt^ h [l//co — {1//co} exp ( — jcoT)] =
о
= hT sinJt/r exp (-0,5/®T).
n f T
Модуль комплексной спектральной плотности S (со) = hT
sin л f У I
nfT | ’
Sln- J . Нули спектра будут соответ-
на которых sin jrffe7’=0, или nfkT=kn (k=
Следовательно, Sb (co) = hT
ствовать частотам,
=0, 1, 2,...). Отсюда fk=k!T. Если ограничить спектр сигнала тре-
мя первыми лепестками функции | sin nfT/nfT |, то его ширина бу-
дет равна 3/Т=300 Гц.
1.1.12. Период следования стробирующих импульсов равен ша-
гу дискретизации &t=0,5/F. Следовательно, частота генератора
стробирования /Стр= l/At=2FKaKC=8 кГц. На интервале Т=2мс
при шаге Д^=0,5/ЕмаКс=1,25-10-4 с будет передано 16 отсчетов,
каждый из которых может принимать одно из 6/Д& = 50 значений.
Следовательно, заданный речевой сигнал при его дискретизации
и квантовании будет определяться У=5016 реализациями.
1.1.14. Очевидно, что при одинаковых длительностях и динами-
ческих диапазонах двух сигналов отношение их объемов будет
равно отношению их частотных полос:
Гтв/Грв=ГТв//:’рв= (6,5-106)/( 1,2-104) «540.
1.1.16. Как показано в решении задачи 1.1.14,
^ТЛф/^ТЛГ ~ ^ТЛф/Ртлг-
Для удовлетворительной передачи телефонного сообщения в спек-
тре речевого сигнала достаточно сохранить частотные составля-
ющие в полосе 300... 3400 Гц. Поэтому примем ГТЛф =3100 Гц.
Найдем полосу телеграфного сигнала. Эта величина зависит
от длительности элементарного импульса следующим образом:
^тлг =п/ти, где п — целое число порядка единицы. Определим ве-
личину ти. За 30 с по телеграфному каналу передается 100 букв,
каждой из которых соответствует кодовая комбинация, содержа-
щая пять элементарных импульсов. Следовательно, за 30 с будет
передано 500 импульсов, и длительность каждого импульса ти =
= 30/500=6-10-2 с. Поскольку для удовлетворительного воспро-
изведения обычно достаточно сохранить в спектре третью гармо-
нику частоты повторения импульсов, примем Гтлг=3/ти=50 Гц.
Отсюда КТЛФ/УТЛГ =3100/50=62, т. е. телеграфный сигнал эко-
номичнее телефонного в 62 раза.
1.1.17. По формуле (1.3) Dc=10\g(PMaKC/Pm). Величину дина-
мического диапазона сигнала, который может быть передан по за-
данному каналу, найдем по формуле (1.1): £>с= Кк/ГиГк. С уче-
151
том этого результата получаем РМакс=ЮРш. Найдем теперь мощ-
ность шума в канале с полосой FK= 10 кГц:
Pm=N0FK= Ю-4-104 = 1 мВт.
Отсюда РМакс=10 мВт.
1.1.19. Предполагая, что заданный сигнал и канал согласованы
по полосе, длительности использования, найдем допустимый дина-
мический диапазон АМ-сигнала, который можно передать без су-
щественных искажений по каналу с заданным объемом:
£с=ук/ТсРс=10.
Выразим теперь максимальную и минимальную мощности АМ-
сигнала (за период модулирующего процесса) через величину ко-
эффициента глубины модуляции: PMaKC=t/2m(l-|-m)2; Рмин =
= U2m(l-m)2.
Подставляя найденные значения Рмакс и РМИн в выражение для
Dc, получаем £>c=101gi[(l+m)2/(l—т)2] или (1+т)2/(1—т)2=
= 1001Dc. В данном случае РС=Ю и (1+/п)/(1—т) = У 10. От-
сюда получаем т = 0,53.
1.1.21. Если длительность и полоса сигнала согласованы с со-
ответствующими параметрами канала, то Dc= VKf(FcTc) =20.
Так как в соответствии с (1.3) DQ=lO\g(P„iKC/Pm), находим
Рмакс/Рш=Ю°-^С=100.
При ЧМ пиковая мощность сигнала Рмакс = ^2т. Найдем сред-
нюю мощность шума в канале и полосе сигнала:
fo+0,5Fc _ fo+0,5Fc
Рш = J* Go(/)df = (/«B(O)/₽) J ехр[ —л2(/ —
fo-0,5Fc fo-0,5Fc
— /о)2Ф2] df.
Вводя обозначение о=$/У2л2, получаем
_____ fo+0.5Fc
Рш = (Р(0)/Г2ло2) J ехр[ — (/—/0)2/2 a2]
fo-0.5 Fc
После замены переменной t=(f—fo)a имеем Рш=В(0)ФХ
X(0,5Fc/o), где Ф(х)—функция Крампа. Отсюда Рш=10-2ФХ
X (0,44)/ 2л) =9,5-10-3 Вт. С учетом этого результата имеем
t/m=lzPMaKc=)zT00PZ=0,975 В.
1.1.22. Вероятность того, что уровень мощности РМин=А2мин
ле будет превышен, равна вероятности того, что амплитуда зами-
рающего сигнала будет не больше Амин:
Р И < Амин) = Jмин(2 A/Т2) ехр (-А21А2) йА=\-ыр(- Д^н/Т2)
о
.152
Отсюда находим РМин=А2мин =—Л21п_[1—р(Л<Лмин)]_По условию
р(Л<Лмин) = 10-3. Поэтому Рмин—Л21п(0,999) « 10-3Л2. Аналогич-
но для Рмакс=Л2макс находим Рмакс = —Л2 In 10“3 = 6,9Л2. Динами-
ческий диапазон
Dc=101g(Pмакс /рмин ) —88,4 дБ.
По формуле (1.1) Ус=88,4-10-4-103 = 3,54-106.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 1.2
1.2.1. Согласно (1.10) 8=2П, откуда число разрядов
n=log28=3.
Процедура кодирования и кодовые комбинации приведены в
табл. Р.1.1. Граф кода приведен на рис. Р.1.1.
Таблица Р.1.1.
Сим- вол Число Разложение числа по модулю 2 Кодовая комби- нация
0 0-22-|-0-21 4-0-2° 000
1 0-22 + 0-2!+ 1-2° 001
«3 2 0-22+ 1-21 4-0-2« 010
а4 3 O.224-I.214- 1-20 011
^5 4 1-22 4-0-214-0-2» 100
5 1-22 4-0-214- 1-20 101
а7 6 1-22-|-1.214-0-20 по
7 1-22 4- 1.214- 1-20 111
1.2.3. Указание к решению. Учесть, что число разрядов в кодо-
вой комбинации не может быть дробным.
1.2.8. Согласно (1.9) К^.тп. Поэтому для пг=2 при п—2
при п=3 7<^8; при «=5 7(^32.
Для /и = 3 при п=2 К^9', при га=3 7С^27; при п=5 Аг<;243.
Для т—8 при п=2 /<^84; при п = 3 /<^512; при п = 5
^32768.
1.2.9. Одна кодовая комбинация стартстопного телеграфного
аппарата содержит п—7,5 посылок длительностью 7=20 мс каж-
дая. Общая длительность кодовой комбинации Тк=20-7,5= 150 мс.
Техническая скорость v=n/TK= \jT= 1/20=50 Бод.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 1.3.
1.3.1. Воспользуемся соотношением (1.14) для ОМ-сигнала.
Рассматривая его как модулирующий сигнал для системы ФМ, по
формуле (1.15) получим
«ом-фм (0 = c°s {®2 t + ^фм (*ом ь (0 со& X
X («! t + (pj т /гО!Л b (/) sin (tOj t + <₽!>]}.
153
Так как верхняя граничная частота в спектре ОМ-сигнала fi+
+FMaKc=104 кГц, полоса частот сигнала ОМ—ФМ Д/=202 (А+
+Л,акс) = 15-104= 1,56 МГц.
1.3.3. Используя формулы (1.15) и (1.12), получаем
«ФМ-АМ (0 = {^02 + *АМ COS [(Oj t +
+ ^ФМ b (0 + <Р1]} cos (®21 + ф2),
Так как верхняя граничная частота в спектре ФМ сигнала /макс =
==Р1^**макс4-/:1== 160 кГц, Д/фМ-АМ макс = 320 кГц.
1.3.5. Используя формулы (1.16) и (1.14), записываем
{✓ t
Ц)1 COS ((011 + £4M J* b (x) dx +
\ 0
+ <P1)| cos (co2 / + ф2) + £qm {^01 sin ^(011 +
f \1
+ £чм J b (*) dx + Ф1 I sin (°>21 + ф2)-
0 / J
Полоса частот сигнала ЧМ—ОМ будет равна полосе частот ЧМ-
сигнала:
А/чм-ом^ 2(3Чм ^макс= 120 кГц.
1.3.8. Так как первый элемент ФМ-сигнала, имеющий фазу,
равную нулю, соответствует символу 1, полагаем, что элемент сиг-
нала, имеющий фазу л, соответствует символу 0. Теперь легко
записать код, соответствующей заданной реализации сигнала:
11010011.
1.3.11. Так как информация о передаваемом кодовом символе
содержится в разности фаз двух соседних посылок сигнала, по-
лучаем для случая а) 0111010; б) 1000101.
1.3.12. Воспользовавшись результатом задачи 1.1.11, найдем
А/=3/х=3-106 Гц.
1.3.14. В системе АИМ в качестве переносчика используется
импульсная последовательность (рис. Р.1.2), которую при отсут-
ствии модуляции на интервале длительности сообщения Т можно
записать f(t)= S F(t—ЛГИ), где F(t) определяет форму
k=—0,5Т/ТИ
импульса; Тп==0,5/Ри^6,5/Рс — период следования импульсов.
Сигнал АИМ можно записать:
0,5Т/Ти
«АИМ (0 = 40/(0 = 40 2 F(t-kTB).
k=—0,5T/Ta
Сигнал АИМ—БМ:
0.5Т/Ги
«АИМ-БМ (0 = Ь (0 C0S (®0 + Фо) S F (t~ kTu).
k=-0,3T/Ta
154
Рие. Р.1.2. Импульсный пере-
носчик (а) и реализация сиг-
нала АИМ (б)
Рис. Р.1 3. Реализация сигнала
ФИМ
Полоса частот
А/аим-бм = 2 А /Аим = Ю6 Гц.
1.3.15. Сигнал ФИМ (рис. Р.1.3) можно записать в виде
0,5Т/Ти
Ифим (0 = 2 Р (4),
Л=—0,5Т/Ти
где tkt=—&Ги+Д6иаксЬ(6Ги)—временное положение модулируемо-
го импульса; Д/МаксЬ(&Ти) — мгновенное значение временного сдви-
га импульса от среднего положения; А/Макс — максимальное от-
клонение импульса, соответствующее &макс(0 = 1-
Сигнал ФИМ—БМ запишем в виде
ИфИМ-БМ (0 — Ифим (0 cos (юо t + фо) —
0.5Т/Ти
= cos (соо t + Фо) 2 Р (t - k Ти + Д /макс b (£ТИ)).
*=-0,5 77Ти
Нетрудно убедиться, что ширина спектра сигналов ФИМ—БМ и
АИМ—БМ одинакова.
1.3.16. Коэффициент частотной избыточности определим как
отношение полосы канального сигнала к полосе сообщения:
Kf = Рк/Рмакс• Тогда Кр = 1 ; /Ср бм = 2 ; Kf фм = 2 Рфм >
Kf чм = 2 Рчм ; Kf аим = Kf ФИМ ~ (Ти Рмакс)”"1 >
Аром-ЧМ = 2Рчм (fl+Pмакс) ^акс’ ^ЧМ-ЧМ =
= 2 Рчм2 (2 Рчм1 Рмакс + f 1) ^макс ’
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 2
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 2.1.
2.1.1. Возможные 2-символьные реализации вида ацаг2: 0102,
0112, li02, I1I2- Вероятность 2-символьной реализации 0i02 будет
155
Рис. Р.2.1. Граф дис-
кретного двоичного
канала
равна сумме вероятностей таких 3-символь-
ных реализаций, у которых два первых
символа — нули: P(0i02) =pi + ps = 0,25.
Аналогичным образом находятся вероят-
ности остальных 2-символьных реализаций:
P(0il2) =р2+рб = 0,25,
P(li02) —Р^~\~Р7=0,25,
P(lil2) =Р4+Р8 = О,25.
у которых первый символ а,ц:
Р (Ь) —Р2+Р4+Р6+Р8 — 0,5;
Р ( 1з) =Р5 + Рб+Р7 + Р8 = 0,5.
Безусловные вероятности вида Р(ац) равны сумме вероятно-
стей 3-символьных реализаций,
Р (01) =Р1Н~Р2 4"Р5Н-Рб=0,5.
Р (h) =РзН“Р4+Р7+Р8 = 0,5.
Аналогично
Р (02) =Р1+Рз+Р54~Р7 = 0,5;
Р(0з) =р1+р2+Рз+Р4 = 0,5;
Условные вероятности переходов находим согласно (2.1):
Р(02/01)=Р(0102)/Р(01)=0,5.
Аналогично найдем p(02/li) =0,5, P(l2/0i) =0,5, P(l2/li) =0,5.
Согласно (2.1)
р (03)0,02)= Р(О1 °а°3)
Р (01 02103) = --(°х °а°з)
= —^—=0,4
0,5-0,5
=0,2.
Р(03) 0,5
Аналогичным образом можно найти и остальные интересую-
щие нас вероятности.
2.1.3. Определим сначала безусловные вероятности Р(0) и
Р(1) символов цепи ^Маркова. Для этого воспользуемся графом
переходных вероятностей (рис. Р.2.1), на основе которого соста-
вим следующие уравнения:
Р(0)=Р(0)Р(0|0)+Р(1)Р(0|1);
Р(1)=Р(0)Р(1 |0)+Р(1)Р(1| 1).
Отсюда, учитывая, что Р(0)+Р(1) = 1, находим
1 - Р(110 _ Р(0|1)
Р(0| 1) + Р(1|0) ’
Р(1|0)
Р(1|0)+Р(0|1) •
Р(0) =
1 — Р (111)+Р (110)
Р(1)= 1 — Р(0|0)
' 7 1 -Р(0|0) + Р(0|1) •
156
Найдем вероятность Р(000). Согласно (2.1) с учетом (2.3) по-
лучаем Р (ООО) = Р (0) Р (010) Р (010) =
= 1 -Р(1| 1) р2 /0.0) = Р(0Ю)Р(0|0)Р(0|1)
1 — Р (111) 4-Р (110) ' Р(0|1) + Р(1|0)
Аналогично Р(001) = Р(0)Р(0|0)Р(1|0) =
= t -Р(1|1) р (010) Р (110) = ±МР^0|0)_Р(1|0)_ .
= 1 — р (111) 4-р (110) v 1 7 Р(0| 1) + р (110) ’
Р(0 1 1) = Р(0)Р(1|0)Р(1|1) = <°Ю^(И0)я(Ц_1) и т
v > v ' 1 ' р (0| 1) + Р (110)
2.1.4. Для решения задачи воспользуемся формулой (2.2).
Тогда
Р(000) = [Р(0)]3=8-10~3 Р(111) =i[P(l)]3 = 5,12-10-1;
Р(001) =Р (010) =Р(100) =P(l)i[P(0)]2 = 3,2-10-2;
Р (011) =Р(110) =Р(101) =Р(0)[Р (1)]2= 1,28-IO"1.
2.1.7. Плотность вероятности амплитуды найдем по формуле
(2.5):
п, .. dF(U,t) 2 U / U2 \
w (U, t) = ——— = -==- exp----------1 .
dU U2 (0 \ U2 (0 )
Нестационарность процесса U (/) вытекает из того, что одномер-
ная плотность вероятности является функцией времени.
2.1.8. Очевидно, что при [Л->оо
F2 (Ulf U2; f2) = 1 - exp (- U22/U22 (/)) = Fr (U2; Z2).
Из (2.5) следует, что
W1 (U2; t2) = exp ( — U2 lUTit)).
U22 (0
Точно так же при U2-+oo
F2 (Ult U2; tlt 4) = 1 - exp [ - = F. ; /x)
и W1 (Us, t2) = --4^- exp [ - t/2/77f(0] •
Pf (0
Согласно (2.5)
C/2; tlt Z2) = ^exp[-C/2/I72(0]=4^exp[-t/2/i72(0j=
^2)»
что доказывает независимость двух сечений помехи.
2.1.9. Указание к решению. Для определения плотности веро-
ятности в каждом сечении воспользуйтесь соотношением
и»1(л;)= 7о»2(/гг, r)dnfe.
157
При интегрировании по неинтересующей нас переменной допол-
нить показатель степени экспоненты до полного квадрата.
2.1.11. Указание к решению. Воспользуйтесь соотношением
ау(пь и2; т)=кУ1(И1)^(п2/П1; т).
2.1.13. Математическое ожидание дискретного случайного про-
п
цесса найдем по формуле Х= X j>iXi. В нашем случае X=ptXi-^
+Р2Х2+РзХз+Р4Х4+Р5^5 = 0. Дисперсию дискретного случайного
__________________________________ п
процесса находим по формуле (X—Х)2 = S Pi(xt—X)2.
В нашем случае
(X — X)2 = Pj Xi + р2 х% + Рз + р4 х% + р5 Ха = 1,2.
2.1.17. Найдем математическое ожидание процесса X(t) =
=—0,5/i+0,5/i=0. Следовательно, B.(t, Н-т) =X(t)X(t-{-x).
Зафиксируем произвольный момент t (см. рис. 2.1). Интервал,
отделяющий точку t от ближайшей точки, в которой может про-
изойти изменение знака процесса Х(1), распределен по условию
задачи равномерно в промежутке (О, Т):
Wl(bt) = l/T, O^Xt^T.
Рассмотрим сечение процесса X(i) в моменты t и /-|-т при т=И=
=/=0. Если то X(t)X(t-{-x)=h2. Если же т>А/, то
X(t)X(£-|-т) =0,5/i2—0,5/i2=0. Поэтому
В. (t, t + т) = р (т< Д t) h2 + р (т> Д t) 0 =
= Л’/и»1(Д0^(Д0 = Л2(1—^У
о V / /
Распространяя это выражение и на т<0, получаем В.(т) =
= Л2 (1 — По формуле (2.10) получим хк=Т/2.
2.1.18. Нормированная корреляционная функция заданного
сигнала Я(т)=ехр(—р|т|). По формуле (2.10) находим тк=
оо
= J ехр(—0T)d-r= 1/р= 100 с. Во втором случае тк находим из
о
условия 0,1=ехр(—ртк). Отсюда тк=—In0,1/рtv 141 с.
2.1.20. Указание к решению. При определении корреляционной
функции винеровского процесса воспользоваться фильтрующим
свойством б-функции:
J6 (х — a) f (х) dx = f (а).
—оо
158
2.1.24. Корреляционная функция АМ-сигнала
- ___________ Г Ъ о *1
Вам (t, t + х) = sAM (f) sAM (t + х) = Um 1 + X (/) X
L ит J
ХС08(®0^ + фо)^т И +4,— Х(/ + Т)1 COs[®0(Z + t)+ф0] =
L ит J
= Лдм В ° (х) cos (ю0 t + <р0) cos [<о0 (t + х) + <р0] +
+ U2m cos (®0 t + фо) cos [©0 (/ + х) + ф0].
Усредняя полученное выражение по t, находим
* k2 и2
ВАМ (Т) = —В » (х) COS ©о т н--— COS ©о т-
2 % 2
В этом выражении первое слагаемое представляет собой кор-
реляционную функцию случайной составляющей АМ-сигнала, а
второе — корреляционную функцию несущего колебания. .
2.1.25. Для заданного сигнала Som(0 определяем
Вомг(^> + т) = SOM (/) SOM (<4-т) =
= В»(х) cos (®о t + Фо)cos [®о (^ + т) + Фо] + В-?(т) sin (©01 + ф0) sin X
Х X
X [©о (t + т) + Фо] — В. т (х) cos (©о t + Фо) Sin ]©0 (t + х) 4- ф0] -
XX
— В^ . (х) sin (©014- ф0) [cos ©о (! + т) + Фо] •
X X
Осуществляя усреднение по времени, получаем
*
ВОм (х) = 0,5В о (х) cos ©о т + 0,5~(х) cos ю0 т —
Х X
— 0,5 В о - (х) sin ю0 т + 0,5В” „ (т) sin ©0 т.
XX XX
Приняв во внимание, что В”(т) = В0(т) и В„”(т)= — В~о(т), най-
X X XX XX
*
дем ВОм (х) = В о (х) cos ©0 х — В 0 ” (х) sin ©0 х.
Х XX
2.1.26. Представим ФМ-сигнал соотношением ВФМ (t) = Um cos X
Х[шо< + ЛФМХ(О].
Корреляционную функцию найдем как
Вфм (/, t + т) — 5ФМ (t) 5ФМ (/+т) =
U2m f о о
= —— {cos [2cd0 t + соо т + &ФМ X (t) + X (t + ^)] +
о о
+ cos [©о т — ЛфМ X (0 + ЛФМ X (t + х)]}.
15‘
Выполняя усреднение по времени, получаем
Яфм СО = 0.5 и2т лГ(соГ[й^ =
= 0,517^cos®0tA1 [cos0(Z, т)] +
+ 0,5 l/^sinw0TM [sin в (t, т)].
Здесь обозначено 0(/, т) =кф1Л [Х(/+т)—X (t) ].
Если одномерное распределение величины 0(/, т) является чет-
ной функцией, то
М [sin 0 (t, т)] = Jsin 0 (t, т) (0) d 0 = 0.
—оо
Поэтому при гауссовском модулирующем процессе усредненная
корреляционная функция ФМ-сигнала
ВФМ(т) = 0,5U2m Af[cos0(if, т)]cos®0т.
Поскольку величина 0(/, т) распределена по гауссовскому за-
кону как линейное преобразование модулирующего сигнала X(t),
для математического ожидания 0(/, т), используя [4], находим
оо 1 ОО / 02 \ / «Та \
f cos 0®! (0) d0 ---- fexp I----— cos 0 d 0 = exp----].
—oo —00 \ ' 2 '
Найдем дисперсию величины 0(/, т). Так как при фазовой моду-
ляции 0(/, т) =|£ФМ|[Х(£+т)—Х(/)], то
°е = [X (/ + т) - X (т)]2 = [X2 (t + т) +
+ X2 (0- 2Х (О X(t + т)] = 2^мВ.(0) [ 1 - Rо (т)].
В этом случае усредненная корреляционная функция модулиро-
ванного сигнала
5ФМ (*) = 0,5 U2m cos ®0 т exp { - ^2ФМВ$ (0) [ 1 - R° (т)]}.
2.1.28. Указание к решению. Для доказательства подставить в
(2.14) выражение для w(xi; t/xo; to) с учетом заданных значений
mx(t) и o2x(t).
2.1.29. Указание к решению. Решить уравнение (2.18), исполь-
зуя выражения A(/) и Л2(0 из задачи 2.1.28.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 2.2.
2.2.1. Подставив найденное в решении задачи 2.1.17 выражение
корреляционной функции случайного синхронного телеграфного
сигнала в (2.23), получим
160
G (f) =2/i2 f (1—t/T)cos otA.
о
Интегрируя, находим, что
G (f)=h2T (n/T) .
v ’ (af T)*
Ширину энергетического спектра найдем согласно (2.25), при-
няв во внимание, что Go(f)=2G(f):
Р = В (0) = № = 1
8 бомакс 2ft2 Т 2Т
Произведение
г 1 Т 1
га тк =------= — .
э к 2Т 2 4
Отметим, что на частотах, кратных значению 1/Т, энергетиче-
ский спектр синхронного случайного телеграфного сигнала имеет
нулевые значения.
2.2.2. В соответствии с (2.24) В (т) = — No J cos 2nfxdf. Так
2 „оо
как J соз2л/тЛ=б(т), для корреляционной функции белого шу-
ма получим В (т) =О,5Л^о6(т), о2 = В(0) = оо.
2.2.3. Указание к решению. За тк принять такое значение т,
при котором В (%) впервые становится равной нулю.
2.2.4. Указание к решению. Воспользоваться табличным интег-
ралом
J* exp (—£t)cos cordr = ₽/(₽2+4n2f2),
о
а также решением задачи 2.1.18.
2.2.6. Подставляя выражение Ву(%) в (2.23), получаем с уче-
том четности Ву (%)
Gy(f)=2§ Bx(t)cos coqTCos cotJt.
0
После простых преобразований получим
G^ (f) = J Bx (т) cos (со — со0) т d т + J Вх (т) cos (со +
о о
+o>0)TdT= 2_сх(/_/о)+2_Сж(/+/о).
На положительных частотах
Gy(f)0=Gx(f-f0).
6-53 161
2.2.8. Для энергетического спектра при ОМ имеем
Сом (f) = J В» (т) cos “от еЧот d т — J В о ~ (т) sin too т e-J<“T d т.
—00 —00 X X
После простых преобразований находим
Сом (/) = 0,5 [Go (f - f0) + G. (f + f0) + / G,~ (f - f0) - / G. y (f+f0)].
Здесь G ~(f) — взаимный энергетический спектр двух сопряжен-
X X
ных процессов. Известно, что
G (Л= I ПРИ f>0’
I /С;(Л при /<о.
С учетом этого
л /А (4-l2G; ^_М+2М+А>)] п₽и Ifl>IM-
[О при |f|<|fo|-
При определении спектра ОМ-сигнала только по положитель-
ным частотам
с;м0о=
2G>(f-f0) при f>f0,
О при f<f0.
2.2.9. Усредненной корреляционной функции ФМ-сигнала най-
денной в задаче 2.1.26, соответствует усредненный энергетичес-
кий спектр:
* U2 00
Сфм(/)= -^- J coso0Tcos(OTexp{-^MBo(0) [!-/?« (T)J}dx.
2 —00 х
Если &2ФМВ^(0)»1, то /?»(т) =В»(т)/В^(О) целесообразно раз-
ложить в ряд Маклорена:
/?(о2,(0)т2 /?(о4)(0)т1
------ + •
| оэ
Вторая производная R о (т) = -go J Go (f)cos<ordf при т=0 оп-
Х X ' —оо х
ределяется соотношением
^о2)(°)=--йт f Gо (f) f2df = — а2.
* (0) Да, *'
162
При &2ФМВ ° (0) 1 ненулевые значения
» и2
Вфм СО = v1 cos ш0т exp [ - k2K В<. (0) + к2фМ В. (т)]
/ Л Л
лежат в области, где 7?» (т),« 1, т. е. т«0.
X
Сохраняя поэтому только первые два члена разложения нор-
мированной корреляционной функции, находим
* и2
* z ч т
ВФМ (О = у cos ®отехр
^^(0)
2
0—2 00
аа= Г Go (f)f2df
Во(0)_< * v" '•
X
Корреляционной функции гауссовской формы
G(/)= 1/ у25----------ехр
Г 4М В (0) а2
соответствует энергетический спектр той же формы:
2 л2/2
4мВ(0)а2 _
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 2.3.
2.3.1. Приведем заданный сигнал и(/) к виду (2.28):
г (/) = . (cos <оо t cos Q t — sin со01 sin Q t + cos <o01 cos'Q t +
+ sin co01 sin Q t) = [Um cos Q't cos <o01.
В этом случае квадратурная компонента x(t) = Umcos-£lt, а
квадратурная компонента у(/)=0.
В соответствии с (2.30) имеем для огибающей г(/) = |х(/)| =
= Um | cos Qt | и для мгновенной начальной фазы <p(/) = arctgO=
= 0. Мгновенная фаза процесса «(/) ф(0 =<»о^+(р(О — W. Мгно-
венная частота <о(7) =—ф(/)=(1)о-
dt
Согласно (2.31) для комплексной огибающей получим
г (/) = г (t) = г (/) = Um |cos Q11.
Подставляя это выражение в (2.32), получаем для комплекс-
ного сигнала
и (t) = Um | cos Q11 cos coo t + j Um | cos Q11 sin coo L
2.3.2. Осуществив простые преобразования, приведем процесс
к следующему виду:
6* 163
и (f) = Um COS ©о i — cos й t COS (Do t +
+ sin Qi sin ©</ + cos Q t cos ®01 +
+ sin Ш sin <o0£= Um c.os®9t + $Um sin Ш sin <oo£
В соответствии e (2.29) имеем для квадратурных компонент
X{t)=Um\ y(f) —^UmSinQt.
По формулам (2.30) находим огибающую
г (t) = уи2т + р2 U2m sin2Qf = Um Vl+P2sin2Q/
и мгновенную начальную фазу <p(Z) =arctg(р sin Ш). Мгновенная
фаза ф(/) =<ooH-arctg(p sin Ш). Мгновенная частота
<о (0 = — ф (0 = ®0 + PQcosQ< .
' ’ dt 7 0 1 + (З2 sin2Q t
В соответствии с (2.32) комплексный сигнал
и (t) = Um V 1 + Р2 sin2 Q t cos [w01 + arctg (P sin Q /)] +
+ / V1 + P2 sin2 Q t sin [®01 + arctg (P sin Q /)].
2.3.3. Относительно частоты. <во сигнал
L L
Z(t) = 2 Ul COS (Ш0 + &z) t — COS coe t 5 MjCOsQjf —
Z=1 . 1=1
L
— sin (oo t 2 ui sin 1-
Z=1
Квадратурные компоненты сигнала z(t) определяются соотно-
шениями
L L
x (t)= 2 Ut cos ^z t; У (i) = S “z sin «z t-
Z=1 Z=1
Для огибающей по формуле (2.30) получим выражение
/7”ь v ~Г^ V
2 ui cos П + 2 “z sin Qj t) =
\z=i / \z=z /
= 1/ S «1+2 2 z/jMftcos(Qj-Qft)f, k^l.
У 1=1 1=1 k=l
Мгновенная начальная фаза
L
2 «z sin Qi t
<p (0 = arctg---------- •
5 ui cos Qi t
/=1
164
Мгновенная частота
(О (/) = (1)0 + [ф (01= ®о +
at
L L
2 s ul uh C°S (&l + ®k) t
I 1=1 fe=l_________________
2 S «/ uk cos (&l — Qfe) *
1=1 k=l
Сопряженный сигнал рассчитывается по формуле (2.32):
2(0 = 1/ S «1+ S S ai^cos^-QJ/x
У /=1 1=1 k=l
/ s ul sin Qf t \
X sin I coo/+arctg ----------- I •
\ S ui cos Qi t I
\ i=i /
2.3.7. Согласно (2.34) z^t)= — 7 С08<0»т , rfT.
л — 772 ‘ T
Введя переменную t—x=x, получим
zx (/) = ^2 cos<b0/ <+f/2 C0S(1>°* dx +
n t-T/2 X
+ ^n sinW/+f
Л ^У/2 X
При T->oo первый интеграл от нечетной функции в бесконеч-
ных пределах обращается в нуль, а второй равен л [4]. Следова-
тельно, Zi (0 = Um sin (dot при Т->оо. Аналогично можно показать,
что при Т->оо z2(t)=—t/mcos(oo^ Соотношение 5^(/со) =/Sz(/co)
при f>0 (см. формулу (2.36)) означает, что любую спектральную
составляющую сопряженного сигнала на положительной частоте
можно получить из соответствующей компоненты самого сигнала
путем фазового сдвига на л/2. Следовательно, при Т->оо
*1 (О = Um cos -у) = Um sin aot,
22(t) = Um sin (<b0= -t/rocosco0t
2.3.8. Заданному спектру соответствует согласно (2.37) комп-
лексный сигнал
г = 2 е/^ df sin °2 z sin 6)1 z — j cos °2 z ~ cos 01 z
p nt nt *
165
Согласно (2.32)
z (t) = Re z (0 = sin«»2*-sin<M . z (t) = Im z (/) =
nt
__ COS o2 t — COS C0x t
nt
Воспользовавшись (2.35), получим для огибающей и мгновенной
фазы:
г (t) = -Г- У (sin ®21 — sin <£>! f)2 + (cos ®21— c°s ®i 08 =
<o2 ~ <^i 2
Aw
sin— t
2
t
Ф (/) = arctg ~ <C0S(lV-C0SMi 0 = ®г + ®1 t
sin co21 — sin w21 2
2.3.9. При симметричных квадратурных компонентах, усредняя
(2.39) по <р, находим
W1 (г) = _2_ У ехр Г - ('c°s<P-^)2 _
1 V 7 2 лоа 5 Н [ 2о2
__ (г sin ф — ту)2 1 - - -
2 о2
Осуществив простые преобразования, получим
, . г / г* + т2 + т2- \
W-. (г) = ---- ехР-------------—— X
1 ’ 2 по2 к 2а2 /
0,
2n
X j* exp
о
„2 ।
4~ my
O2
cos(q> —<pp) </ф, r>0,
где фР = arctg .
тх _______
Введем переменную ы=ф—фр и обозначим Vт\-}-т\-а9.
В этом случае можно записать
2п
1 2п гп
— J* ехр cos (ф-фр) </ф =
= 2_2уреЭ-«аы = / (арг\
2" Jp °\o2J
Здесь Iq(z)—модифицированная функция Бесселя первого рода
нулевого порядка.
Таким образом,
/\ г ( r2 + ap\ 7 /aDr\
(г) = — ехР-------------5 Л Ь 0.
17 a2 F \ 2а2 / •0 \ а2 )
166
2.3.10. Указание к решению. Учесть, что /о(О) = 1.
2.3.11. Условие /пж=сг2ж=0 означает, что процесс Z(t) можно
представить в виде Z(/) = У(t)sin osot. Но тогда его огибающая сог-
ласно i(2.30) /?(0 = |У(0|. Поскольку ту=0, плотность вероят-
ности квадратурной компоненты У (t) имеет вид
О»! (У) =
1
V 2ла|
ехр
— оо < у < оо.
Уг \
Эта функция относительно у четная, поэтому конкретному значе-
нию модуля r=|t/|:>0 могут соответствовать значения y=ri и
у==—и, имеющие одинаковые плотности вероятности. С учетом
сказанного получаем искомое распределение для огибающей.
2.3.12, Двумерная плотность вероятности огибающей и фазы
узкополосного гауссовского случайного процесса при а2х=о21/=а2
и тх, ту^0 определяется соотношением (2.39), откуда
__ (г cos ф — тх)2 + (г sin ф — my)2 | &
2 о2 | ’
После простых преобразований получаем
/ \
। __ ар ।
/ \ еХР \ 2п2/<р Г г2 — 2 aD г cos (ф — фп) 1 f
«'х(ф) = -\—££_2_ J* г ехр----------р о w dr,
2 ла2 о L 2а J
где аР= V т2х-]-т2у и <рр= arctg .
тх
Дополняя показатель экспоненты в подынтегральной функции
до полного квадрата и вводя функцию Лапласа
Г(г)=-2— J ехр( —^\dt,
|/2Л -ОО \ 2 /
находим
/ \ 1 / otn \ , aD cos (® — фп) г,
(ф) = — ехр — -2- Ч-Е—4=—F х
1 2л 2 о2 ) '|/2лсг
ч, ГаР / Л ( а2 sin2 (<р - фр) \ .
X cos(<p —<pp)J ехр --------------) > 1ф-фр!<л
При тх—ту=0 следует равномерное распределение для фазы в
интервале (0, 2л): (ф) = 1/(2л).
2.3.14. Указание к решению. Воспользоваться асимптотикой
е2 1
/о(^) = -----И ...) и ограничиться двумя первыми слага-
емыми.
2.3.15. При ф—фр^л/60 можно считать cos(q)—<рР)~1,
sin (ф—фр) <рр. Если, кроме того, аР/о>3,тоехр{—а2Р/(2о2)]«
167
«О, а функция Лапласа F'[(aP/la)cos((p—<рр)] аг 1. В этих условиях
из результата задачи 2.3.12 следует
, ч ар „„„ / «р(Ф-Фр)2^
(ф) = ---7= еХР--------------- *
1VV/ сУ2л *4 2оа /
т. е. закон распределения фазы является гауссовским с матема-
тическим ожиданием <рр и дисперсией (a/aP)2.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 2.4.
2.4.1. Норму вектора s в n-мерном пространстве Эвклида най-
дем по формуле (2.41). В данном случае коэффициенты ряда
Фурье, представляющего сигнал s(t), есть не что иное, как коор-
динаты сигнала s(t) в пространстве, координатный базис которо-
го образован функциями вида У2cos(2knt/T) и У2sin(2knt/T),
Поэтому
Hs||= 1/ S (al + bl)-, ||s||2 = 2 +
Г k=l fc=l
где a2k и b2k — квадраты эффективных значений k-x членов разло-
жения сигнала s(t). Это есть средняя мощность соответствующих
слагаемых ряда. Сумма средних мощностей всех членов ряда да-
ет полную среднюю мощность сигнала s(t). Таким образом, квад-
рат нормы вектора имеет смысл средней мощности, а норма —
смысл эффективного значения сигнала.
2.4.3. Представим сигналы $1 (/) и s% (t) в виде
2nF(t - k Д t) '
2FT
s2(t) = 2 s2(k&t)
k=l
sin 2nF(t — kM)
2itF(t — kM)
r, - ( /As I sin 2л F (t — k Д t)
В координатном базисе {gft(0} = | 2~7р'(ГчГд0 /
координатами сигналов будут отсчеты s{k\t). В соответствии с
(2.40) находим s2 (t) =Si(M/)+s2(MZ).
Норма суммарного сигнала по формуле (2.41)
IISs 11=
2FT
2 И (kbt) + sl(k&t) + 2s1(k&t)si(kkt)].
А=1
2FT
Величина 2 Si(kAt)s2(k\t) есть скалярное произведение сиг-
ft=l
налов Si(t) и s2(t). Оно равно нулю, так как по условию задачи
сигналы ортогональны. Поэтому
l|ss||= Я Si ||2 + II s21|2.
168
Расстояние между сигналами по (2.46)
d (si, s2) = ||sx — s21| = 1/ 2 1% (kkt) — s2 (k ДОР = IIss||.
V fe=l
2.4.4. Указания к решению. Выбрать в качестве координатного
базиса совокупность функций
Ф1 (0 = /2 cos [(2 л/Т) fl ; <р2 (fl = /2 sin [(2 л/Т) fl ;
Фз (fl = /2 sin [(4 л/Т) fl ; ф4 (fl = /2 cos [(6 л/Т) fl ;
ф6(0= /2 sin [(6 л/Т) fl.
Воспользоваться формулами (2.46) и (2.43).
2.4.6. Проверим первое условие (2.51):
у- J а* cos
1 о
t + Ф1) c°s U 2-~ t + Ф1 + -у-1 dt =
— /------------ sin [(& + /) 2л + 2Ф1+ —1 —
2Т I (к + /) 2 л |? • V 2 J
—-----sin (2Ф1 + л/2) + -—-— sin [(k — I) 2 л — л/2] —
(k +1) 2л v (k — Z) 2л '
—----- sin л/2 I =0, k=^l .
(к — l) 2л )
Следовательно, сигналы S](Z) и Si(f) согласно (2.50) являются
ортогональными.
Теперь проверим второе условие (2.51):
1 т 1 Т ( о-. \
7 ?! (0 S1 (0^= J «2cos / + ф? X
2 о 1 о \ 1 /
/ 2л \
X sin I k — t + Ф1 j dt = 0-
Аналогично
vf %(ОМОЛ=0.
1 о
Следовательно, сигналы Si(t) и s2(t) являются ортогональными
в усиленном смысле.
Расстояние между сигналами Si(t) и s2(t) найдем по формуле
(2.46): J(sb s2) =а.
2.4.9. Указание к решению. Принять во внимание, что число
сигналов ортогональной системы равно ее базе В. Число возмож-
ных сигналов в биортогональной системе равно 2В, а в ортого-
нальной в усиленном смысле системе —В/2.
2.4.12. На рис. Р.2.2,а показаны сигналы Si (/), s2(t) и s3(0 в
виде точек некоторого пространства. Эти точки представляют со-
бой вершины некоторого треугольника АВС. ]\ля сторон треуголь-
169
Рис. Р.2.2. К решению задачи 2.4.12
s4t--------т8г
+
s3L--------Isz.
Рис. Р.2.3. Дву-
мерный ансамбль
биортогональных
сигналов
ника справедливо соотношение АС^.АВ-\-ВС (условие треуголь-
ника). Длина отрезка АС равна норме вектора разности сигна-
лов si (t) и s3 (0:
ДС = ||s1 S3II = d (sx, s3).
Аналогично AB=d(st, s2) и BC=d(s2, s3). Следовательно,
d(si, s3)<4/(si, s2)+d(s2, s3), причем равенство достигается толь-
ко в том случае, когда все три сигнала лежат на одной прямой
(рис. Р.2.2,б).
2.4.13. Указание к решению. Воспользоваться соотношениями
(2.51).
2.4.14. При М=.4 биортогональный ансамбль сигналов явля-
ется простейшим. Сигналы имеют одинаковые энергии и находят-
ся на одинаковом расстоянии от начала координат. При задан-
ных базисных функциях сигналы искомого ансамбля согласно
(2.47) имеют вид
st (/) = У 2 Е/Т cos (м01 + л/4); s2 (/) — ]/2 Е/Т cos (®01 — п/4) ;
s5 (/) = У 2 Е/Т cos (<о01 — 3 л/4); s4 (/) = У 2 Е/Т cos (®01 + 3 л/4).
Эти сигналы на плоскости образуют квадрат (рис. Р.2.3). Соглас-
но (2.46) расстояние между ближайшими сигналами этого ан-
самбля У 2Е/Т, а .между противоположными — 2 У Е/Т.
2.4.18. Найдем расстояния между заданными комбинациями
8
bi и Ь2 по формуле (2.53): rf(bi, b2) = S (хц®Хц) =5; d(bi, b3) =
= 6; rf(b2, Ь3)=5. <=1
Легко заметить, что d(bb b3)<d(bi, b2)+rf(b2, b3), так как,
6<5+5. Аналогично d(bb b2)<d(b2, b3)-|-d(bi, b3), так как 5<
<6+5, d(b2, b3) <d(bi, b2)+rf(bi, b3), так как 5<6+5.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 2.5.
2.5.1. Найдем сначала спектральную плотность колокольного
импульса
170
S (/о) = J s (0 dt= J a e-₽!'* e-w dt =
—oo —oo
= (a Ул/р) exp (—0,5co2/P2).
Поскольку полоса пропускания фильтра имеет величину F, опре-
делим по формуле (2.56) относительную погрешность представле-
ния колокольного импульса рядом Котельникова:
J ехр (— 0,5ш2/р2) df
бу= £------------------
J* ехр (— 0,5 ©2/Р2) df
о
Умножая числитель и знаменатель этого выражения на \fV2лр2
и принимая во внимание, что
..1 - f ехр (- 0,5 <о2/Р2) df = 0,25/л,
У2л02 о
находим
бу=2л[1—Ф(2лГ/р)],
где Ф(г) —функция Крампа.
Если 6у=10%, то из уравнения 0,1=2л[1—Ф(2лГ/р)] опре-
деляем по таблицам аргумент функции Крампа: 2лГ/р=2,4. При
Р=20 и Г=24/л Гц интервал дискретизации в соответствии с
(2.54) Д/=л/48=6,56-10-2 с.
2.5.2. С учетом решения задачи 2.2.1 по формуле (2.57) на-
ходим
„ 2 Г sin2(лFT) , а с с- zo г'гч!
Sv = — ------------—h 0,5 л — Si (2 л FT) ,
у л L л FT J
•О
где Si(x)= f smylydy — интегральный синус. При F=F3, учиты-
о
вая, что ГэГ=0,5, получаем
ду=2[2/л+0,5л—Si л] /л = 0,23.
Если то 6у=2(0,5л—Si2jt)/jT = 0,096.
2.5.6. Энергетический спектр этого случайного процесса
G(f)=2aB(0)/(a2+<D2).
При ограничении полосы такого спектра частотой F определим
погрешность усечения согласно (2.57):
dy= 1—(2/л) arctg (2л/7а).
Подставив сюда согласно (2.54) /7=0,5/Д/, найдем
6У = 1— (2/л) arctg (л/aAZ).
171
2.5.8. В соответствии с (2.63) при заданной нормированной кор-
реляционной функции
Дт = —101п(1—0,5бв).
Если бв = 0,01, то Ат = 0,05 с.
При дискретизации по Котельникову, используя результат за-
дачи 2.5.6, получаем
At= Юл/tg 0,5 (1—бу) л.
Для заданной величины бу = 0,01 Д/=0,523 с.
2.5.9. В соответствии с (2.62) можно написать уравнение
ехр(—р2Д2т) = 1—0,5бв,
откуда Дт = р-1/—In (1—0,5бв).
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 3
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 3.1.
3.1.4. Под ошибкой кратности q понимают событие, состоящее
в том, что какие-либо q символов из п переданных приняты оши-
бочно, а остальные п—q символов приняты правильно. Вероят-
ность такого события в рассматриваемом канале р9о(1—Po)n“g.
Так как q ошибок в цепочке из п символов могут появиться во
взаимно несовместимых случаях, по правилу сложения вероятно-
стей получаем P(q) = С?пр%(1—Po)n”g.
п
3.1.6. Используя результат задачи 3.1.4, находим q = 2 С%Х
«=1
Хр«о(1—po)n~4q. (Суммирование выполнено от <7=1, так как при
q=Q член суммы равен нулю).
Поскольку Cin = Cn-in/q, q=np0 2 Cnl'ipo’-1 (1—Po)n-1_(9-I)=
n—1 q=l
=npo 2 Crn-ipro(.l— Po)n~r-1.
r=0
Последняя сумма, представляющая собой сумму вероятностей
полной группы событий, равна единице. Следовательно, q=np&
и P(q) ж&прЧо, если принять (1—ро)п-9~1. Покажем, что при
яро<С1 это имеет место. Рассмотрим величину (1—ро)п- При
np0<^l (1—Po)n= (1—про/п)п = ехр(—про)^1. Поскольку n—q^.
^nt то и (1—p0)n“g~l.
3.1.7. Указание к решению. Воспользоваться формулой (3.2).
3.1.9. Указание к решению. Формулы для рправ, Рош и рст сле-
дуют из определения искомых характеристик, если принять, что
символу стирания на выходе канала «?» присвоен номер j—m', а
ошибка при передаче символов имеет место, если номера симво-
лов на передаче и приеме не совпадают (i=/=j=£m').
3.1.10. Указание к решению. Воспользоваться решением зада-
чи 3.1.9.
172
3.1.12. Если предшествующий символ принят ошибочно с веро-
ятностью рОш, то возникает ошибка с вероятностью рг. Если же
предшествующий символ принят правильно с вероятностью 1—рОш,
то возникает ошибка с вероятностью рь Таким образом, средняя
вероятность ошибки удовлетворяет уравнению рОш=рОшР2+
+ (1—Рош)Рь откуда Рош=Р1/(1+Р1—Р2).
Если р2>Рь то ошибочно принятые символы с большей веро-
ятностью предопределяют ошибочный прием следующего символа.
В этом случае рг>рОш<0,5 и ошибки в канале группируются.
Если же р2<Рь то после ошибочно принятого символа с боль-
шей вероятностью следующий символ будет принят правильно.
При этом рг<Рош, т. е. в канале происходит рассредоточение
ошибок.
3.1.16. Поскольку нормальный шум в анализируемых дискрет-
ных сечениях не коррелирован, а следовательно, и независим, то
его совместная (и=T!At=2FT)-мерная плотность вероятности
(«) = (1/К2лУ0 F)n ехр
где NoF=o2 — дисперсия шума. Поэтому функции правдоподобия
w (zlsi) — (2лМ0 F)~°’5n х
( п 1
^{г^-й^асоз^-т^ + фо]}2 I
хехр!--—---------------------------ь
I 2N0F )
w (zIsz) = (2л No F)-°-5n X
( n
{ S (г (ti) + k (ti) a cos [co0 (ti — T (ti) + <p0]}2
xexp
2N0F
3.1.18. Используя формулу Байеса (3.2), видим, что система
неравенств P(bi\z)>P(bj\z), равносильна другой системе не-
равенств: P(bi)w(z\bi) >P(xj)w(z\bj), i^j.
3.1.19. При точно известном сигнале с учетом (3.5) функционал
правдоподобия
w(z)Ui) = Кехр
1 т -]
— J* [z (/) — k cos 0 щ (i) + k sin 0 Ui(t)]2 dt =
^0 0
= /Cj exp f-^- (cos 0 Yt + sin 0 — 0,5 k2 Ef)l,
I No J
1 T
где /Ci = exp[-------f z2(t)dt] — константа, не зависящая от
Moi
Yt(t) = j z(t)ui(t)dt;Yi(t) = ]z(t)ui(t)di; u2(t)dt = f u2 (t)dt
0 0 0 0
173
— энергия элемента сигнала. Здесь учтено условие ортогональ -
ности сигналов Ui(t) и йг(1) на интервале (О, Т).
Усредняя w(z\ut) по 0, при w (0) =0,5/л, —л^0^л получаем
функционал правдоподобия при неопределенной фазе сигнала:
w (г| щ) =Л1ехр (—0,5№) Io (2kVi/Nq),
где
Vi =
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 3.2.
3.2.1. На рис. Р.3.1 показано несколько реализаций импульсной
переходной характеристики линейного канала с переменными па-
раметрами. Если свойства канала не меняются во времени (ка-
нал с постоянными параметрами), то реализации упомянутой ха-
рактеристики не должны зависеть от параметра t, т. е. g(t, т) =
=g(x). Это означает, что реакция канала с постоянными пара-
метрами на 6-импульс зависит лишь от интервала между момен-
том наблюдения t и моментом подачи сигнала на вход канала
t—т. Если g(t, x)=g(x), то, как следует из (3.10), передаточная
функция канала от времени не зависит.
3.2.2. Указание к решению. Подставив g(t, т) в формулу (3.6),
учесть фильтрующее свойство 6-функции.
3.2.3. Передаточная функция заданной модели канала (см.
рис. 3.2) К (/©)== (l+/2jifC7?)-1. Такой передаточной функции со-
ответствует переходная характеристика g(x) = (7?С)-1ехр(—x/RC),
т^О, что вытекает из (3.10).
По методу равновеликого прямоугольника (3.8) находим интер-
оо
вал рассеяния тР= f ехр(—xfRC)dx=RC, который в данном слу-
о
чае определяется постоянной времени цепи. Если 7?=100 Ом и
С=100 мкф, то Тр=10 мс.
Рис. РЗ 1. Реализации импуль-
сных переходных характерис-
тик линейного канала со слу-
чайно меняющимися парамет-
рами
174
3.2.5. Указание к решению. Воспользоваться известным опре-
делением 6-функции:
б(х) = (2л)-1 J ехр(/Х(о)Ао.
— оо
3.2.6. Заданной передаточной функции соответствует спектр
мощности
S2 (а>) = (4ла)~’ехр(—<в2/а2).
Пользуясь методом равновеликого прямоугольника, определяем
интервал частотного рассеяния
Fp = (2л)-1 Jexp (— ю2/а2) da> =
о
= —-------!----Г ехр (— 0,5(о2/а2) d<$.
Т/2л У2лая о
Отсюда, используя условие нормировки для гауссовского закона
распределения, находим /?р=0,5а/]'Л2л.
3.2.8. Интервал рассеяния во времени
со
тр= f ехр(—aix)dT=l/ai.
о
Функции е-а2* соответствует квадрат модуля амплитудного спек-
тра по Фурье (спектр мощности)
S2 (о) = (а22+(о2)-\
Интервал частотного рассеяния
FP= 1
О
После интегрирования получим Fp=0,25a2. Коэффициент рассея-
ния канала AP=rPFp=0,25a2/ai.
3.2.10. Запишем входной сигнал в комплексном виде u(t) =
= ите^9 где Um=Ume^.
Воспользовавшись (3.7) и (3.10), представим выходной сигнал
в комплексном виде:
S (/) == J* § (/, т)б/т==&((й, /) Um COS’[(o/-|-(p (<d, /) “Ьфо]
+/Й((О, /) t/m Sill [о/4”Ф ('®, 0+фо]-
Действительная часть этого выражения определяет выходной
сигнал:
s(/)=^((O, /) Um COS [<й)/-|-ф (<0, /) +фо] •
Заменив в соотношении для s(t) Um огибающей Л(0, а ф0 —
фазой 0(/), получим Л,(0=АЛ(0, 0,(О=©(О+ф-
175
3.2.11. Результат для g(t, т) следует из структуры многолуче-
вой модели (см. рис. 3.3).
Оуществив преобразование Фурье над заданной переходной ха-
рактеристикой g(t, т), с учетом фильтрующего свойства
п
б-функции получим K(ja, t) = S kt(f)exp(—Подставив
выражение для g(t, т) в (3.7), находим
8(0=
i=i
3.2.15. Указание к решению. Принять во внимание, что при
полной коррекции характеристик канала в заданной полосе час-
тот выполняется условие
кор — Воехр(—, 0 ^^Р'макс*
3,2.17. Очевидно, что максимальный уровень входного воздей-
ствия удовлетворяет уравнению
I$(цмакс) — 0*1 цмаксI _ 0,3 |ймакс18 =
0,1 1«макс1 0,1 |«макс!
Зкмакс13 = О,ОЗ.
Отсюда |«макс 1=0,1 В.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 3.3.
3.3.1. Согласно .(3.13) плотность вероятности реализации отрез-
ков флуктуационного шума с энергией Еш можно представить так:
Wi («г) =Лехр (—Еш/Мо). Если Еш=0, то Wi(ut) =К. Отношение
этих величин определяет искомый результат.
3.3.2. Средняя мощность теплового шума Pw==^kTFc, где k—
= 1,37-10~2^ Дж/град — постоянная Больцмана. Следовательно,
Рп 1 J2 -
™*=Л72.
3.3.4. Искомая вероятность рф.п определяется вероятностью вы-
полнения неравенства Лш>Лпор=рг4Рс. Огибающая шума Аш
имеет распределение Рэлея:
^1(ЛШ)=(ЛШ/РШ) ехр(—Л2Ш/(2РШ)), Рш=2Ш
Таким образом,
Рф.п = (ЛШ)^ЛШ - ехр (- РС/(МО Д 0) = 0,135.
3.3.7. Вероятность pc.n=^vc.nF, где k — коэффициент пропор-
циональности. Если среднее число сосредоточенных помех vc.n в
единичной полосе пропорционально РПор, то вероятность появления
сосредоточенной помехи рс.п, превышающей пороговый уровень,
остается неизменной, когда величина РПор обратно пропорциональ-
на полосе F.
176
3.3.8. Средняя вероятность ошибки параллельного модема
Рпар = 2 Pkt
k=l
где Pk — вероятность ошибки в каждом частотном канале. Сред-
няя же вероятность ошибки последовательного модема определя-
ется вероятностью ошибки элемента сигнала рПОсл = Ро. Вероятно-
сти ошибки pk и ро определяются отношением сигнал-сосредото-
ченная помеха в обоих модемах.
Для параллельного модема отношением сигнал-сосредоточен-
ная помеха в каждом частотном канале (Рс/Рс.п)пар=РперМРс.п,
в то время как (рс/рс.п)посл = Рпер/Рс.п. Попав в полосу £-го инди-
видуального канала параллельного модема при (Рс/Рс.п)пар< 1,
помеха обусловливает в этом канале значение pk~l/2 и, следова-
тельно, рпар~0,5, если даже по остальным частотным каналам ве-
роятность ошибки близка к нулю. В последовательном же модеме
помеха той же интенсивности обеспечивает значение (Рс/Рс.п)посл =
= п(Рс/Рсп) пар, которое при больших п может оказаться явно не-
достаточным для существенного понижения верности связи.
3.3.9. Вероятность ошибки р0 = 1—q= 2 7s* (/), где P(i) —
i=k+i
вероятность того, что помеха попадает в i из У каналов. С уче-
том биномиальной формулы (см. задачу 3.1.3)
<7=1-2 С^'.п(1-Рс.п)^.
i=fe+i
Если Af=2&+1=5, то k=2 и
q = 1 - [Cg pl.п (1 - рс.п)2 + Cl Рс.п (1 - Реп) + d Рс.п]•
При рс,п = 0,1 9 = 8,46-10-3.
3.3.11. Согласно биномиальной формуле вероятность переры-
вов в передаче pnep = P/N=pNcn. Вероятность наличия связи рСв =
= 1—pNc.n. Вероятность того, что при наличии связи прием ведет-
ся по n^N ветвям,
р (П) = Рс-П. (---Рс-п)
1-Реп
В этом выражении числитель определяет совместную вероят-
ность наличия связи и осуществления приема по п не забитым по-
мехой ветвям, а знаменатель определяет безусловную вероятность
связи. Средняя вероятность ошибочного приема символа в рас-
сматриваемой ЧРСС
N
Рош= 2 Р (fi) Рп.
П=1
3.3.13. Длительность импульсной помехи на входе (выходе) ог-
раничителя ти примерно обратно пропорциональна полосе пропус-
177
кания входного блока, т. е. энергия импульсной помехи после ог-
раничения Eu,n = U2Q/Af. С другой стороны, Ez=U2mTI2. При Um=
= и0 имеем Д/>10/Г.
3.3.14. Указание к решению.
Воспользоваться формулой для вероятности правильного деко-
дирования, полученной в решении задачи 3.3.9.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 3.4.
3.4.1. Произвольный случайный процесс X(t) можно записать
как сумму центрированного процесса X(t) и его математичес-
кого ожидания: X(t)=X(t)-\-mx(t). Аналогично представляются
и системные характеристики произвольной линейной системы:
G(Z, x) = G(t т) + £(/, т), где g(t, n) = G(t, т);
/С(/со, f) = /<(/co, t) + 6(/со, /), где ^(/ш, = t).
С учетом сказанного отклик произвольной линейной системы с
характеристикой G(t, т) или К (jay, t) на произвольное воздействие
X(t) может быть определен суммой У1 (/) + У2 (О + Уз (0 + У 4 (О
(рис. Р.3.2). Независимость откликов У1(/), У2 (0, ^з(0> У* (О
следует из статистической независимости детерминированной и
флуктуирующей частей любого случайного процесса, а также из
предположения независимости между входным воздействием X(t)
и свойствами системы, через которую это воздействие проходит.
а)
б)
Рис. Р.3.2. Прохождение слу-
чайных воздействий через ли-
нейную систему со случайно
меняющимися параметрами:
а— общая схема канала; б—пред-
ставление канала четырьмя парал-
лельными ветвями
3.4.4. Энергетический спектр от-
клика линейного четырехполюсника
с постоянными параметрами связан
с энергетическим спектром воздей-
ствия следующим соотношением:
Gv(f)=k2(2nf)Gx(f).
Модуль комплексного коэффи-
циента передачи колебательного
контура
k (2л f) = —, ° --------,
У (to2 — to2)2 + 4а2 <о2
где
&O=1/V~LC, a=0,5R/L.
Энергетический спектр выходно-
го процесса
Gv(f) =N0------------5--------.
(и2 — tog)2 + 4a2 to2
178
Совершая переход к корреляционной функции по (2.24), полу-
чаем
Bv (т) = No ©о а-1 ехр (— а|т|) [cos]/ю2 — а2 т +
+ а (©2 — а2)-015 sin ]/©2 — а2 |т| ].
Если (т. е. ©0>а), с учетом того, что ©2оа-1=2</?о/Ь,
(т) =2JVо<7?о£-1ехр (—а | т |) cos ©от.
3.4.6. Усредненный энергетический спектр входного сигнала
Gx(f) =0,5X26(f—/о).
Учитывая, что Bv(t, /-|-т) =Вк(т)Вх(т), получаем
By(t, / + т) = аехр( —а2|т|)-0,5Л2 Jexp^n/r —
—оо
-<*i1Л) 6 (f - /о) df = аехР (- а1 Ifol - а2 |т|) Л2 COS ©0 т.
3.4.8. Коэффициент передачи идеальной длинной линии с ли-
нейно меняющейся во времени задержкой
k (ja) = а ехр (—/W),
где а, I — константы. Корреляционная функция отклика
Ву (t, t + т) = a2 J*ехр (—/1 ast) ехр [—//©(/ + т)] Gx (f) ехр (/©т) df =
—оо
= а2Вх [(1 —/)т].
Такой корреляционной функции соответствует энергетический
спектр
G (/) = «2 рх [(1 - О Т1 ехР ( -/®т) dx =
—оо
= а2(!-/)-> Gx[f/(1 -/)].
Отсюда видно, что задержка процесса, пропорциональная вре-
мени, приводит к сдвигу средней частоты спектра на величину If о
(доплеровскому смещению частоты), к соответствующему расши-
рению (при 1—/<1) или сужению (при1— />1) его, а также к
изменению интенсивности в 1/(1—/) раз. Впрочем, в системах свя-
зи при |/|<1 в области достаточно высоких частот fo практиче-
ски во внимание следует брать только доплеровское смещение
частоты.
3.4.9. Перемножив Z(/) и u^(t) и выделив из произведения
только низкочастотный продукт, получим
Y (0 = --rgAM b (0 cos (ф0 - фг) +
+ 4" Хп (0 cos фР - 4" ur Yn sin фг.
179
Процесс Y(t) имеет гауссовское распределение с параметрами:
/иу (0 = UP-^ Ь (о COS (<р0 - фг); о2у (0 = -^U?FcN0.
Корреляционная функция для флуктуирующей части выходного
продукта
о / \ 1 г ?2 г sin 2Л Fc т
В« W = ~Т F с No о g ' ’
4 2л Fc т
а энергетический спектр равномерен в полосе частот Fc и равен
ад)=4^°-
4
Отношение сигнал-шум на выходе синхронного детектора
/р ip \ _ *ам^ОГсо52(Фо-Фг)
^с/^ш)вых о2 FoN<)
Отношение сигнал-шум на входе детектора в полосе канала
FK = 2FC
(PJP^-^- .
\ с/ ш/вх 2FgNq
Выигрыш модема
gBM=2cos2(<po—фг).
При фо=фг значение £БМ максимально и равно 2.
3.4.11. При квадратичном преобразовании случайной величи-
ны каждому значению У, которое всегда положительно, соответ-
ствуют два значения случайной величины X: Х\ = У У, X2=—V У.
Тогда в соответствии с методикой нахождения распределений
функционально связанных случайных величин получаем для од-
номерного распределения Wi (у) при условии,
что известно распределение w\(x) [10]:
= + y>0.
При гауссовском распределении входной величины
&У1 (у) = .—1--— ехр (---— Y
1/2яи^2Уу \ 2а2 J
Математическое ожидание выходного продукта согласно (3.20)
у = my = pc2 wx (x) dx = о2.
180
Двумерная плотность вероятности входного процесса [10]
&2(xi> хг)^
---------------ехр
2ла2"|/1 -R2
2о2 (1 - R2)
Х[х1 + х2 — лс2] |.
>
Корреляционная функция выходного процесса согласно (3.19)
Ву(х) = J °j(x2i — y)(x22 — y)w2(x1x2)dx1dx2.
—оо —оо
После несложных преобразований получим
Ву (т) = 2В2 (т) = 2о* Я2 (Т) = 2о4 е-2«1’ ।.
Такой корреляционной функции соответствует энергетический
спектр
ОИ/) = 4о4
2а______
4а2 + 4л2 /2
Обратим внимание на то, что хотя отклик и воздействие име-
ют различные распределения (выходной процесс не является га-
уссовским), форма корреляционной функции и энергетического
спектра флуктуаций на выходе системы такая же, как и на входе.
3.4.12. Огибающая входного процесса
R (0 = У [t/m (1 + /П& (0 + Хп (012 + У2 (0.
На выходе неискажающего ФНЧ с граничной частотой FC = FKI2
продукт линейного детектирования Унч (0 =KiR(t)9 где Ki — ко-
эффициент пропорциональности; примем далее Ki=l.
Процесс Унч(0 имеет обобщенное распределение Рэлея с ма-
тематическим ожиданием
тУнч (О = {(1 + 0,5а2 (0 0-2) 10 (0,25 а2 (/) а-2) +
+ [0,5а2 (0 о-2] 1г (0,25а2 0-2) ехр (_ 0,25 а2 (f) о-2)}
(o2=FKN0 — средняя мощность шума на входе детектора;
0,5a2p(/)=0,5t/2TO[14-m&(/)]2 — средняя за период высокой час-
тоты мощность AM-сигнала) и дисперсией
:°г„ч т - - чяч (»- 2’’+“S ю - Чнч <')
которую примем за среднюю за период высокой частоты мощность,
выходного шума.
Если величину rnVm(t) усреднить во времени, то получим пос-
тоянную составляющую выходного продукта, которая не несет ин-
формации. За полезную (сигнальную) составляющую выходного
продукта следует принять сигнал Ус (t) =ту нч (0—^нч(0-
18Е
Для упрощения анализа рассмотрим асимптотическое поведе-
ние тУНЧ(0 для двух крайних случаев: большое значение отноше-
ния сигнал-шум на входе рВх=0,5а2Р(/) /а2 1 и малое значение
отношения сигнал-шум на входе рвх<С1.
В первом случае, воспользовавшись асимптотикой,
Zn(x) = (2nx)-°’5(1+Vx)expx; Х=1/8
при п=0, Х=—3/8 при п=1,
получим
т»НЧ ® ~ аР ~
РШ вх «о2, g = Рвых/Рвх = 2m2 ОЙ 1 + т2 НО]-1 .
Во втором случае, воспользовавшись асимптотикой
/о (х) ж 14- (0,5х)2, h (х) «0,5х,
получим ^унч (/) = У 0,5no[l-]-0,5a2p(t)/o2]; Рс вых~®,5и4тт2лХ
Хб2(0/<?2;
Рш.вых « 0,43о2; g=3,7 • 2 • [о2 (1+m2H0) ] -'.
Обратим внимание на то, что в рассматриваемой нелинейной
схеме (линейном детекторе) сильная компонента на входе подав-
ляет слабую. Это сказывается, в частности, в том, что значение
параметра g при pBX<Sl уменьшается по сравнению с его значе-
нием при рВх>1 ва2/(3,7£72т)>1 раз.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 3.5.
3.5.1. Дифференциальное уравнение цепи запишем в виде
У™ (I) (/) + ... +а1У^+аоу= 1 (/).
Введем переменные состояния
X! (/) = у (0 ; х2 (0 =yW (/) ; ... ; Хп (/) ==^(п-1) (/) .
При замене переменных исходному дифференциальному уравне-
нию цепи n-го порядка будет соответствовать система дифферен-
циальных уравнений первого порядка:
4*1 4ха 4x„_j
ИГ = Х*’ = хз! -; —аГ=хп',
= — an-i хп — a„_2 x„_i — ... — а0+ 1 (/).
Эта система представляет собой скалярные уравнения состояния
заданной цепи.
Скалярное уравнение наблюдения для данной цепи
x\(t)=y(t).
182
Полученные уравнения состояния и наблюдения можно пред-
ставить в матричной форме:
AX(0 = FX(0 + Gln
Y(0 = HX(0.
С учетом правил векторно-матричных преобразований находим
Х(о = Хх (0 Х2 (0 ; F = 0 0 1 0 0 ... 1 ... 0 0
0 0 0 ... 1
*п(0 -а0 -«1 — а2 ... — Яп-1
0
g = 0 ; н - |1 0 0 1 ... 0|.
1(0
Схема аналогового вычислителя показана на рис. Р.3.3.
3.5.3. Нетрудно убедиться, что цепи с заданным операторным
коэффициентом передачи К(р) будет соответствовать оператор-
ное уравнение, связывающее между собой входное напряжение
u(t) и выходной процесс y(t):
Ъ Рп~' U (р) + Л2 U (р) + ... + Л„_, pU (р) +
+ *n UJ.P) = PnY (р) + рп~1 % Y (р) + ... +
+ ф„_1рУ(р) + фпУ(р).
Этому операторному уравнению соответствует скалярное линейное
дифференциальное уравнение n-го порядка с постоянными коэф-
фициентами:
У(П) (/) + y(n-l) (t) + ф2 у("-2) (/) + ... + у(1) (/) + -фп уп (0 =
= (0 + %2 U<"-2) (t) + «<*>(/) + М (О-
Рис. Р.3.3. Схема аналогового вычислителя (к решению задачи 3.5.1)
183
Представим это уравнение в виде
(0 = - % у{п~1' (0 - % у(л-2> (0 -
- -УпУ (0 + «(п-‘ ’ (0 + h (0 + ...
... +X„_i u^(t)+Knu(t).
Обозначим xn(t)=—^пУ (0 +Хп«(0.
Интегрируя с учетом этого обозначения уравнение для yw(t),
получаем
у(»-1 )(/)=- фх (0 - % г/<"-з) (0 - ... - у (0 +
+ хп (0 + и("-2> (0 + ... + А,„_! и (/).
Примем, что хп-1(0=—tyn-iy(t)-№n-iu(f). После интегрирования
уравнения для «/(п-1)(/) получим
y(n-2) (/) = _ 1|,1 у(п-З) ф _ у(п-4) (0 _ _ фп_2 у ф +
+ х„-1 (0 + и*"-3) (0 + ... + Л„_2 и (/).
Осуществив эту операцию п раз и приняв y(t)=Xi(t), получа-
ем систему уравнений состояния (3.25). Фрагмент схемы аналого-
вого вычислителя, реализующего эту систему, показан на рис.
Р.3.4.
3.5.6. Нетрудно показать, что при прохождении белого шума
N (t) через линейную цепь с операторным коэффициентом переда-
чи К(р) =а/(р-\-а) (интегрирующая 7?С-цепь) образуется гауссов-
ский процесс S (t) с корреляционной функцией
/2)=Рсехр(—а|/2—h|).
Рис. Р.3.4. Схема анало-
гового вычислителя (к
решению задачи 3 5.3)
184
Очевидно, что операторное уравнение для процесса S(t) мож-
но записать так:
S(p) =/^(p)Af (р) ==Af (р)а/(а+р)
или
pS(p)=-aS(p)+aN(p).
Такому операторному уравнению соответствует дифференциаль-
ное уравнение
Белый шум со спектральной плотностью мощности 2Рс/а можно
представить через белый шум V(t) с единичной мощностью:
N(t) = V2PjaV(t).
Поэтому
5(0=—aS (0 + V 2^V (0.
3.5.7. Указание к решению. Представить производную x(t) в
виде [х(Н~А0—х(0]/А^ и воспользоваться соотношениями (3.24).
3.5.8. Указание к решению. Сопоставьте закон Рэлея w(x) —
= — ехр —^7 j со стационарной плотностью вероятности из
задачи (3.5.7).
3.5.9. Указание к решению. Используйте методику решения за-
дачи (3.5.4).
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 4
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 4.1.
4.1.3. Воспользуемся вспомогательным неравенством —1,
которое следует из того факта, что линия и=1пх касается пря-
мой v=x—1 в точке х= 1 (рис. Р.4.1). Рассмотрим разность
х
Я(Л) —log/( = - 2P(at)logP(at)~
i=i
к XI ]
- S P (at) log К = 2 P (a.) log ' x
f=i i=i KP(at)
К
Полагая х=1/7<Р(аг), можно записать Н(А)—logK^ 2 Р(а,)Х
1=1
к
X[l/KP(ai)]\oge или Н(А)— logK< 2 [ 1/К—Р(at)]logе. Лег-
1=1
к
ко убедиться, что 2 [1//С—Р(а,)]=0. Следовательно, Н(Л) —
—log/C^O. Знак равенства будет только тогда, когда х=1//СР(а») =
185
Рис. P.4.1 К пояснению
неравенства —1
W(X)
-1,2 ~О,8 -о,4 О 0,4 0,8 1,2
Рис. Р.4.2. К определению вероятностей появления
уровней квантованного сигнала
= 1, поскольку при этом 1пх=х—1. Поэтому /f(X)=logK при
Р(а{) = 1,/К.
4.1.5. Прежде всего найдем безусловные вероятности передачи
символов из соотношения Р(0) =Р(0)Р(0|0')-р[1—Р(0)]Р(0|Г).
При заданных значениях переходных вероятностей Р(0) =0,125;
Р(1) =0,875. Можно убедиться в справедливости соотношения
Р(1) =Р(0)Р(110')+'[1—Р(0)]Р(11 Г).
Энтропия источника
Н (Л | А') = - Р (0) [Р (01О') log2 Р(0|0') +
+ P(l|0')log2P(l|0')]-P(l)(P(0|l')log2P(0|l') +
+ Р (11 Г) log2 Р (11 Г)] = 0,51 бит/символ.
Избыточность источника хи=1—Н(А | Л')//7Макс(Л) =0,49. Для
источника без памяти при тех же безусловных вероятностях пере-
дачи символов
Н (А) = — Р (1) log Р (1) — Р (0) log Р (0) = 0,541 бит/символ,
%и=0,459.
4.1.7. Заданный объем информации источник передает n=Tfx=
= 108 посылками. Средняя информация на символ Н=1/п=
= 107/108 = 0,1. Если избыточность полностью устранена, то каж-
дый символ двоичного источника несет в себе ЯМакс=1 бит ин-
формации и заданный объем передается пй=11Н№акс—107 посыл-
ками, или за время 7’о=тПо = 1О5 с. Избыточность источника
хи (п—По) /п= 1—п0/п= 1—То/Т = 1—7//Ямакс=0,9.
Обратим внимание на то, что сокращение избыточности источника
позволило бы на 90% экономичнее использовать во времени ка-
нал связи.
186
4.1.8. Количество информации, содержащееся в одном элемен-
те сигнала ЯМакс(Л)=1о£216=4 бит/символ. Число элементов изо-
бражения в одном кадре N=833-625=520625. Количество инфор-
мации в одном кадре /=7УЯмакс=4-520625=2,083-106 бит. Энтро-
пия реального телевизионного изображения при 16 градациях яр-
кости
Н(А) »9,37-105/5,21 • 105= 1,8 бит/символ.
Избыточность реального телевизионного сигнала хи=1—Н(А)/
Н (Л) „акс =0,55.
4.1.11. Вероятности появления уровней квантованного сигнала
определим по приближенной формуле P(Xi) =u>i (х,)Д=0,2Х
Хехр(—|хг-|/0,5), которая иллюстрируется рис.Р.4.2. Результаты
расчета сведены в табл. Р.4.1 .
Таблица Р.4.1
1 xi Р(х.) 1 xi
— 8 — 1,6 8-10—8 1 0,2 1,34-10-1
—- 7 — 1,4 1,2-lQ-» 2 0,4 9-Ю-»
— 6 — 1,2 1.8-10-» 3 0,6 6-10-2
— 5 — 1,0 2,8-10—2 4 0,8 4,0-10-2
— 4 — 0,8 4,0-10-2 5 1,0 2,8-10-2
-3 — 0,6 6,0-10-2 6 1,2 1,8-10-2
— 2 -0,4 9,0-10-2 7 1,4 1,2-10-2
— 1 — 0,2 1,34-10—1 8 1,6 8,0-10—3
0 0 2,0-10—1
По формуле (4.3) находим энтропию
Н = — 2 Р (xi) bg Р (хг) = 3,46 бит/отсчет.
i=—оо
Избыточность находим по формуле (4.4):
хи = 1 — 3,46/log217 = 0,159.
Скорость создания информации на выходе квантующего уст-
ройства согласно (4.5) Н' (А) =Н (А)Тср.
В данном случае Тср равно интервалу между двумя соседними
отсчетами входного сигнала: Н'(А) =3,46/0,3=11,53 бит/с.
4.1.13. Энтропия символа укрупненного алфавита Ну = пН(Л),
где Н(А)—энтропия первичного алфавита с объемом К. Объем
укрупненного алфавита Ку=Кп, поэтому Яу.Макс=1о§Кп=
=п/7макс(Л). Избыточность источника с укрупненным алфавитом
согласно (4.4)
х -1 1 пН(А) -и
И? "у маке пЯмаксМ)" ”’
где хи — избыточность первичного алфавита.
Поскольку избыточность осталась неизменной, но устранены
связи символов, приходится констатировать, что в укрупненном
187
алфавите отдельные символы более значительно отличаются сво-
ими априорными вероятностями.
Устранение избыточности сообщения укрупненного алфавита
возможно при неравномерном кодировании (см. решение задачи
4.1.14).
4.1.14. Обозначим источник восьмеричных символов через 4,
а источник, создающий двоичные символы неравномерного кода,
через В. Энтропия источника А: Н(А)=—2pi log2Pi = 1,781 бит/
i
символ. Избыточность источника В согласно (4.4)
хи(В) = 1
Я (В) = J _ vb н (в)
log2 2 vB
»в=1/7'срв — число символов источника В в единицу времени;
ТСр в — средняя длительность символа источника.
Чтобы не было потерь информации при кодировании, надо по-
требовать равенства производительностей источников А и В, т. е.
vbH(B)—vaH(A). Тогда
VB п
где n=vB/vA = TCpA/TCpB — среднее
точника В на один символ источника
В соответствии с табл. 4.5
число двоичных символов ис-
л.
n='2pini = 1,825 и хи(В) =
i
= 1—1,781/1,825. Избыточность составляет всего 2,4%.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 4.2.
4.2.1. В двочином симметричном канале со стиранием объем
алфавита на входе т=2, а объем алфавита на выходе т'=3. Эн-
тропия шума согласно (4.11)
« 3 2
Н(В\В) =- S ^P(bi)P(bj\bi)\ogP(bj\bl) =
/=1 z=i
= -Р(0)(1 -p0-pc)log(l-p0-pc)-P(l)p0logp0-
— Р (0) Ро logp0 - Р (1) (1 - р0 - д.) log (1 - р0 - рс) -
— Р (0) ро log Ро - Р (1) Ре log Рс =
= (1 - Ро - Рс) 10g (1 - Рр - Ро) ~ Ро 10g Ро ~ Рс 10g Ро.
Отметим, что ненадежность рассматриваемого канала не зависит
от априорных вероятностей входных символов. Перейдем к нахож-
дению энтропии шума.
В соответствии с формулой Байеса находим апостериорные ве-
роятности:
Р (01 б) =__? .
/>(0)(1 —р0 —
188
р (1 I 1) = _Р 0) Р<> Ро)___•
Р(1)(1-ро-рс) + Р(О)ро’
Р (011) =-------;
' р(1)(1_р0-рс) + Р(0)ро’
Р (11 б) =------;
V 1 Р(0)(1 — ро-Рс) + Р(1)Ро
Р(0|?) = Р(0); Р(1|?) = Р(1).
Совместные вероятности символов входа и выхода:
Р (0, б) = Р(0) (1 —/?0 —рс); Р(0, 1)Р(О)ро;
Р(1, 1) = Р(1) (1 — р0 —рс); Р(1, б)Р(1)>0;
Р(0, ?) = Р(0)рс; Р(1, ?) = Р(1)рс.
Подставив найденные совместные и апостериорные вероятнос-
ти в (4.7), получим для ненадежности двоичного симметричного
канала со стиранием
Н(5|В)= -P(0);(l-Po-Pc)log—;л'0)Г=п°С^тТ~
Р (0) (1 — Ро — Рс) + Р (1) Ро
Р(1)р»
-P(l)p0log
v ,И Р(1)(1-Ро-Рс) + />(О)РО
“ P <°> Po10g Pm д.р,тн----7 “P (W1 “ Po - PJ X
P(l)Po + P(O)(l—Po —Pc)
X log рпнТ'ТЛ-----------P <°> P° ,og P (°) - P <1 )>c10g P (1)•
P (1) (1 — Po~Pc) + p(0) Po
Если p0—>0, TO — P(0)pc logP(O)— P(l)pc logP(l) =
=рсЯ(В).
Ненадежность канала зависит как от вероятности стирания, так
и энтропии источника на входе канала.
4.2.2. Суммарная вероятность ошибки р — это вероятность то-
го, что при передаче фиксированного символа bi будет принят лю-
бой символ, кроме символа Hi. Поскольку всего может произойти
т—1 ошибочных переходов при фиксации символа bi на переда-
че, а канал симметричен, то вероятность приема фиксированного
символа 8j при передаче символа bi будет равна рЦт—1). Следо-
вательно, в /п-ичном симметричном канале вероятности переходов
удовлетворяют условиям
пр" / = f’
lp/(m-l) при /#=i.
Подставляя эти вероятности в выражение (4.11), находим эн-
тропию шума
Я(В|В)= - 2 2 p^p^bi^p^bi).
189
Выделяя из этой суммы слагаемые с номером /=/, получаем
Я(В|В)= - 5р(6г)(1-р)1оё(1-р)-
1=1
mm п п
- 2 2 P(bt) -^-log-^- =
/=1 т—\ т — 1
= - (1 - р) log (1 - р) - Р log —£—.
tn — 1
4.2.4. Согласно формуле (4.12) находим скорость передачи ин-
формации
I'{B, B)=vKI(B, B) = vK[H(B)-H(B\B)].
Как показано в решении задачи 4.2.1, ненадежность двоичного
симметричного канала со стиранием при ро->О Н(В\В) —рсН(В).
Следовательно, скорость передачи информации в таком канале
Г (В, B) = v^[H(B)-pcH(B)]=vKH(B) (1-Рс).
Чем больше вероятность стирания рс, тем надежнее отождест-
вляются символы 1 и 0 в месте приема, однако одновременно па-
дает скорость передачи информации по каналу. Следовательно,
имеет место обмен между верностью (качеством) и количест-
вом переданной информации.
4.2.6. Согласно (4.13) пропускная способность канала
С= Ок шах [Я (5)— Я(В|В)].
Как показано в решении задачи 4.2.2, энтропия шума /п-ично-
го симметричного канала без памяти и без стирания равна
Я(В|В)= -(l-p)log(l-p)-plog—.
т— 1
С учетом этого имеем
С = vK[max#(В) + (1 -p)log (1 —p) + plog—1.
Очевидно, что max Н (В) = log т. Следовательно,
C = o„[log/n + (l — р) log (1 -p) + plog—1.
Для двоичного симметричного канала без памяти и стирания
(т=т'=2)
С=vK [ 1 +р log р+ (1—р) log (1—р) ].
График величины C/vK в зависимости от р показан на рис. Р.4.3.
Пропускная способность канала равна нулю, когда вероятности
дерехода Р(0| 1) =Р(110) =0,5. (В этом случае символы на входе
и выходе оказываются независимыми.)
4.2.8. Избыточность кода (вторичного алфавита) можно опре-
делить по (4.4):
Хк=^1-Я(В)/Ямакс (5),
190
C/v
“ °>5
Рис. P.4.3. Зависимость
нормированной пропуск-
ной способности двоич-
ного симметричного ка-
нала без памяти от ве-
роятности ошибочного
приема символа
где Н(В) — энтропия ансамбля кодовых
символов. Очевидно, что при объеме ан-
самбля кодовых символов т Нмакс(В) =
= logm. Следовательно,
log т vK log т
где Я'(В) =икЯ(В); ик — число кодовых
символов, поступающих на вход канала в
единицу времени. Поскольку при кодиро-
вании должны отсутствовать потери инфор-
мации, то Н' (В) =Н'(А) где
vH — число символов, создаваемых источни-
ком сообщения в единицу времени; Н(А)
— энтропия источника. С учетом этого
1 уяща)
Кк 1 •
ик log т
Согласно теореме Шеннона лишь при
оптимальный способ кодирования. Следовательно, избыточность
кода не может быть меньше величины
ХК.МИН = 1 j + 8>
vK log т
где в — сколь угодно малая положительная величина.
Для двоичного симметричного канала без памяти и стирания
согласно решению задачи 4.2.6. C=vK[l +р logp+ (1—p)log(l—р)].
Подставляя эту величину в выражение хк.мин и учитывая, что т=
—2, получаем
v 1 Ml +plogp + (l — р) log(l — р)] ,
Кк.мин 1 , “Г Ь —
v„H(A)<zC существует
«к l°g2 2
= — plogp —(1 -p)log(l — p) + 8.
Если р=0 (в канале нет ошибок), то хк.мин = 8->0. Если р —
= 0,01, то Хк мин ~ 0,067, т. е. при не очень сильных помехах в ка-
нале избыточность оптимального кода невелика.
4.2.9. Способы кодирования и декодирования, обеспечивающие
сколь угодно малую вероятность ошибки, согласно теореме Шен-
нона, существуют лишь при H'(A)<zC. Если источник информации
выдает в единицу времени vn символов, а его энтропия Н(А), то
Н'(А) =ииН(А). Пропускная способность канала по определению
равна C=vKmaxI(B, В). Следовательно, можно записать, что
оптимальное кодирование по Шеннону возможно лишь при
vKH(A) сектах 1(В, В) или п= — >-------------. Здесь п —
Va max/(В, В)
среднее число символов кода на один символ источника.
4.2.10. Из (4.15) получаем запас пропускной способности
С - Н’ (Л) = - ^-Рош- = -log210~6- = 90,96 бит/с.
Т 200-10-3
191
Подчеркнем, что чем больше запас пропускной способности,
тем легче реализуется система связи, но одновременно падает ее
эффективность. Очевидно, что Т = —с (Л)~
Поэтому при сохранении вероятности ошибки (качества связи)
неизменной уменьшение запаса пропускной способности в 2 раза
(рост эффективности системы) влечет за собой увеличение дли-
тельности кодовой комбинации в 2 раза, что приводит к усложне-
нию системы (в частности, из-за усложнения устройств памяти на
передаче и приеме).
4.2.11. Предположим, что можно закодировать некоторый ис-
точник с производительностью H'(A)=C-j-2e, s>0 так, что не-
надежность канала Н'(Л|А) ^8. Тогда оказывается, что скорость
передачи информации в системе связи /(А, А) =Н'(А)—Н'(А|А) >
>С4-8, т. е. будет больше пропускной способности канала, что
противоречит ее определению. Противоречия не будет, если до-
пустить, что при Я'(Л)>-С сообщение передается с отличной от
нуля ненадежностью Я/(А|А)>8.
4.2.12. При кодировании по методу Хаффмена все символы ис-
точника располагают в порядке убывания вероятностей. Если не-
сколько букв имеют одинаковые вероятности, их располагают ря-
дом в произвольном порядке. Затем выбирают две буквы с наи-
меньшими вероятностями, и одной из них в качестве первого сим-
вола двоичного кода приписывают символ 0, а другой — символ 1.
Выбранные буквы объединяют в «промежуточную» букву, имею-
щую вероятность, • равную сумме вероятностей выбранных букв.
Затем в ансамбле оставшихся букв (вместе с промежуточной)
вновь находят две с наименьшими вероятностями и поступают
так же, как и на первом шаге. Эту процедуру осуществляют до тех
пор, пока не будет исчерпан весь алфавит.
Процесс кодирования показан в табл. Р.4.2. Средняя длина ко-
9
довой комбинации данного кода n= S ЛгР»=3,08. Минимальная
1=1
длина кодовой комбинации примитивного кода, которым можно
закодировать данный алфавит,
nMHH.n=log K/log m=4.
При оптимальном двоичном кодировании в канале без шумов
9
Пмин.о=НИ)!\ogm=H(Д)=— 2 Pilogpi = 3,04.
Средняя длина кодовой комбинации кода Хаффмена отличает-
ся от средней длины оптимального кода на
?.>.98_-..3’04 .1 оо % = 1,32 %,
3,04
что позволяет считать код Хаффмена близким к оптимальному.
4,2,15, Кодирование по методу Шеннона — Фано осуществля-
ется следующим образом. Все буквы записываются в порядке
192
Таблица Р.4.2
убывания их вероятностей. Затем вся совокупность букв разбива-
ется на две примерно равновероятные группы. Всем буквам верх-
ней группы приписывается первый кодовый символ 1, а буквам
нижней группы — символ 0.
Затем каждая группа аналогичным образом разбивается на
подгруппы по возможности с одинаковыми вероятностями, при-
чем верхним подгруппам в обеих группах приписывается символ 1
(второй кодовый символ), а нижним — символ 0. Эта процедура
осуществляется до тех пор, пока в каждой подгруппе не останет-
ся по одной букве. Процесс кодирования по Шеннону — Фано ил-
люстрируется табл. Р.4.3.
Средняя длина кодовой комбинации
_ 8
и= 5 ^^ = 2,75.
i=l
При оптимальном двоичном кодировании
— 8
п0 = Н (А) = — 2 Pi log Pi = 2,75.
Z=1
Таблица P.4.3
буква Pi Разбиение Кодовая комбинация
az a* as Off o7 o8 1/4 1/4 1/8 1/8 1/16 1/16 1/16 1/16 -4 pv }z . J •! }o 11 1 О 011 01 0 0 011 0 01 0 0 0 01 00 00
7—53
193
Следовательно, в данном случае код Шеннона — Фано является
оптимальным.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 4.3.
4.3.1. Рассмотрим сечение случайного процесса X(t), предпо-
ложив, что процесс в этом сечении имеет плотность вероятности
a?i(x). Разделим область изменений X на дискретные уровни Xi
с малым интервалом Дх между ними. Вероятность того, что зна-
чение X лежит в интервале (х,-, Xi+Дх), приближенно равна pi=
=а>1(хг)Дх. Будем считать, что отдельные отсчеты случайного сиг-
нала Х(1) независимы, а их распределение не зависит от времени
(стационарный источник без памяти). Тогда согласно (4.3) мож-
но записать выражение для энтропии на один отсчет квантован-
ного сигнала:
н&.х (х) = — S wi (xt) Д х log № Д х] =
I
= — s (Xi) \х log (xf)J — S ayx (хг) Дх log Дх.
i i
Чтобы непрерывный отсчет воспроизвести абсолютно точно, не-
обходимо, чтобы Дх—>0. Заменив тогда суммы соответствующими
интегралами, найдем энтропию одного отсчета непрерывного сиг-
нала
Н (X) = — (х) log о^(х) dx — lim log Дх Г(х) dx =
—оо — ОО
= — f&yx (х) log (х) dx ~ lim log Дх.
_оо Ах-*0
Так как lim logAx=—оо, Н(Х)=ео. Полученный результат оз-
Дх-*0
начает, что один непрерывный отсчет сигнала мог бы перенести
бесконечно много информации, если была бы возможность воспро-
извести его абсолютно точно. К сожалению, в реальных каналах
этой возможности нет.
4.3.2. Подставим в (4.16) выражение плотности вероятности
гауссовского случайного процесса:
h (X) = - 7 —---------ехр [ - (х~ОТж)21 log —L=^- X
1/2лаа L 2a2 J У 2 ла2
xexp
(x — mx)2 ~
2a2
_ (*—«хР |og n
2a2 J
_4__еХрГ_(±Г2М11 x
У 2ло2 L 2a2 ]
£ — log У 2no2
Вводя новую переменную (x—тх)1<з и интегрируя, получаем
h (X) = log Y 2лео2.
Следовательно, величина h(X) не зависит от тх.
194
4.3.3. Условная дифференциальная энтропия может быть опре
делена по формуле
Л(Х|Хпр) = J* (^> ^пр) log ^1 (^'1^'пр)
—сю —сю
Согласно [3]
(х|х”- ) - у2то. (.-«ч ир Г - (х -*« *>’]•
”’(х’ х°»>-гто.у!-«.
Подставляя эти выражения в соотношение для условной диф
ференциальной энтропии, получаем
ft(X|Xnp)=---------J jexp[->, + ^-2fa--1x
' пр/ 2ло2(1 — R2)_i_„ 1 2а2 (1 —fl2) J
X Г - log/2ло2 (1 - #») - -• -1 (х - хпрЯ)2 log el dxdxnp.
*- ZG£ (1 1\) J
После простых преобразований имеем
h (Х|Хпр) = log /2л ео2(1—У?2).
Обратим внимание на то, что с ростом нормированной корре
ляционной функции условная дифференциальная энтропия умень
шается.
4.3.6. Указание к решению. Принять во внимание, что выход
ной сигнал Y(t) =X(t)+N (t) при гауссовских и независимых про
цессах X(t) и N(t) будет иметь гауссовское распределение и дис
версию (У2у=(У2х+о2п- При вычислении условной дифференциаль
ной энтропии учесть, что
(х) Wt (у\х) dx = w1 (у).
—сю
4.3.7. По определению
Яе (X) = min / (X, X) = h(X)-maxh(X\X).
Поскольку X(t)=X(t)—N(t), то условная дифференциальна?
энтропия Л(Х|Х) при заданном сигнале X(t) полностью определи
ется шумом воспроизведения (канала) N(t). Поэтому max/i(X|X) =
—maxh(U). Если шум воспроизведения N(t) имеет фиксирован
ную дисперсию а2п, то шах/ЦХ) достигается при гауссовском рас
пределении случайной величины N:
max h (N) = log /2л е о2.
Следовательно, Н&(Х) —h(X)—log/2лео2п.
4.3.8. Максимум эпсилон-энтропии непрерывного сигнала бу-
дет достигаться при max/i(X). При заданной средней мощности
7* 195
сигнала Рс=о2ж max h(X) =log /2леРс и достигается при гаус-
совском распределении сигнала X(t).
Следовательно,
Нъ (Х)макс = logV2^Р~С - \OgV2^P~ = 4-log
где Рш=п2п — средняя мощность шума воспроизведения.
4.3.9. Согласно (4.23) при дискретном времени (с шагом кван-
тования во времени Д/=1/ии) эпсилон-производительность
Н'ъ (X) = va [h (X) - log /2л е а2].
Очевидно, что Н'а (X) будет максимальной, когда ft(X) макси-
мальна. Но при заданной дисперсии (средней мощности Рс) это
достигается при гауссовском распределении процесса X(t) (см. ре-
шение задачи 4.3.8).
С учетом (4.17) имеем
2
Н'г (Х)макс = vu 4 log 4- = 4-log 4-.
При непрерывном времени, полагая, что vH=2Fc, можно поль-
зоваться формулой
Н'е (Х)макс = Fc log
' ш
где Fc — полоса частот сигнала.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 4.4
4.4.1. Поскольку спектр равномерный, то отсчеты входного сиг-
нала и помехи, а следовательно, и сигнала на выходе независимы.
Согласно (4.28) 7(5, Z) =h(Z) — h(Z\S) = h(S)~h(S\Z).
Подставив сюда выражения для h(S), h(S\Z), ft(Z), h(Z\S)
из решения задачи 4.3.6, получим /(S, Z) =0,51og(l+<j2s/a2n) = 1,58
бит/отсчет.
4.4.3. В соответствии с (4.27) /(S, Z)=vKI(S, Z). Подставив
сюда выражение /(S, Z) из решения задачи 4.4.1, получим
Г (S, Z) = vK —log f 1 + = 1500 бит/с.
2 \ °п /
4.4.5. Согласно (4.29) при аддитивном шуме в канале
I'(S, Z)=vK[h(Z)-h(N)].
Очевидно, что минимальная скорость передачи информации бу-
дет определяться соотношением min/'(S,Z) = uKmin[ft(Z)—h(N)].
Если ансамбль входных сигналов фиксирован, то min [h(Z) —
—h(N)J будет иметь место при max ft (X). Если дисперсия шума
196
фиксирована, то гпах/ЦМ) будет при гауссовском распределении
шума, причем max /ЦМ) = logp<2neo2n. Следовательно, при ука-
занных условиях скорость передачи информации будет наимень-
шей и равной
/'(S, Z) = vK[h (Z) —log V 2леа2п].
4.4.6. Согласно (4.30) С=шах/ (S, Z). Как показано в реше-
нии задачи 4.4.5 для гауссовского канала, /'(S, Z)=vK[h(Z)—
—log К2леРш].
Отсюда следует, что пропускная способность гауссовского ка-
нала
С=уктах[Л (Z)— log 2леРш].
Если дисперсия шума фиксирована, то
C=yK[max/i(Z)—log'K 2леРш].
Дисперсия выходного сигнала o2z=Pc4-Pin, так как сигнал и
шум считаются независимыми. При фиксированной дисперсии
o2z max/i(Z) будет иметь место при гауссовском распределении
процесса Z=S\-N, а следовательно, при гауссовском распределе-
нии входного сигнала S(t). В этом случае
C = vK (log ]/2neoJ - log log (1+ Pc/Pm).
2
Полагая vK = 2F (в соответствии с теоремой Котельникова),
можно написать выражение для пропускной способности гауссов-
ского канала непрерывного времени
C=riog(l+Pc/Pm).
4.4.9. Воспользуемся формулой для пропускной способности га-
уссовского канала, полученной в решении задачи 4.4.6. Полагая,
что РШ=РЛГО, можно записать
C = Flog('l+-£-\ = Flogeln( 1 + -£Д
\ FNo ) \ FN0 ]
Найдем предел С при F->oo
С» = lim C = loge lim Fin ( 1 + -^2-Y
Поскольку ln(l+e)«e при e->oo, можем записать, что
C00 = logeF-^-=^loge.
FNq No
Легко показать, что пропускная способность гауссовского ка-
нала монотонно растет при расширении полосы канала F и асим-
птотически стремится к величине Соо.
4.4.10. Допустим, что сообщение передавалось в течение вре-
мени Т. Так как скорость передачи информации по каналу с лю-
бой полосой не больше, чем Соо, можем записать, что количество
197
переданной по каналу информации удовлетворяет неравенству
TI'(S, Z)^.TCOO или, с учетом результата задачи 4.4.9,
TI'(S, Z)^logeTPcfN0.
Отсюда следует, что для передачи TI'(S, Z) = l бит информа-
ции необходимо, чтобы сигнал имел энергию РСТ, удовлетворяю-
щую условию
E=PcT^N0/\og2e=N01п2=0,69М).
4.4.11. Средняя мощность заданного сигнала
/о+0.5Г
Ре = A J ехр [ - ₽2 (/ - /0)2] df = 46,5 • 10^’Вт.
f«—0.5F
Средняя мощность шума в канале PIU=/’WO=3,1 • 10-6 Вт. Про-
пускная способность канала
C=Flog2(l+Pc/Pm) = 1,24 • 104 бит/с.
Теперь по формуле (4.31) находим
уик= СТК = 1,24 • 104 • 3,6 • 103 = 4,46 • 107 бит.
4.4.14. Мощность теплового шума может быть определена по
формуле Pm=4kTF, где Т — абсолютная температура приемного
устройства; k — постоянная Больцмана, равная 1,37-10-23 Дж/град.
В данном случае F=10 кГц, 7’=273-Н°С=293°. Следователь-
но, Рш=4-1,37-10-23-293л; 1,64-10-16 Вт. При средней мощности
сигнала 10-6 Вт
С= 104log(l + 1010/l,64) ^3,26-105 бит/с.
4.4.16. Из условия основной теоремы кодирования Шеннона
H'(A)<zC следует, что в гауссовском канале оптимальное коди-
рование возможно только тогда, когда источник сообщения выда-
ет за одну секунду
Vn<.F\og2(lA-Pc/Pm)IH(A) символов.
Если источник выдает двоичные равновероятные и независи-
мые символы, то
ии<riog2 (1 +Рс/Рш) •
Очевидно, что условие v„<z2F может быть выполнено при
Рс/Рш<3. Если же Рс/Рш>3, то скорость выдачи символов источ-
ником можно сделать значительно больше 2FK, т. е. при Рс/Рш^З
предел Найквиста можно превысить. Следует, однако, отметить,
что на практике этот результат пока не достигнут.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 5
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 5.1.
5.1.1. Число информационных символов согласно (5.2) k—
= log2^p=log2K = log232=5. Число проверочных символов г=
=п—k=3. Используемый код содержит NP=K=32 разрешенных
кодовых комбинаций и N—Х=28—32=96 запрещенных кодовых
комбинаций.
5.1.2. Согласно (5.3) хк=1—(log 32)/8= 3/8. Согласно (5.4)
#к = 1—3/8=5/8.
5.1.5. Код содержит Np=2h разрешенных комбинаций из об-
щего числа М=2П комбинаций. Поскольку из-за ошибок при пе-
редаче любая из 2fe разрешенных комбинаций может превратить-
ся в любую из 2П комбинаций, всего имеется NpN—2h+n перехо-
дов, включающих Np=2h случаев безошибочных переходов. При
передаче разрешенных комбинаций происходят NP(NP—1) =
—2k(2h—1) переходов в другие разрешенные комбинации, что со-
ответствует необнаруживаемым ошибкам. Переходы в запрещен-
ные комбинации, число которых NP(N—Np)=2h(2n—2к), соответ-
ствуют обнаруживаемым ошибкам.
Следовательно, доля обнаруживаемых ошибок NP(N—NP)/NPN=
= 1— NpfiN= 1—2ft-n.
5.1.6. Если принятая запрещенная комбинация принадлежит
подмножеству В,, считается, что передана комбинация Ь«. Ошиб-
ка будет исправлена в тех случаях, когда принятая комбинация
действительно образовалась из bj. Таким образом, ошибки исправ-
ляются в (N—Мр) случаях. Доля исправляемых ошибок (2V—NP)f
NP(N—JVp)=l/JVp. Любой код может применяться в качестве ис-
правляющего при условии Np<zN.
5.1.13. Если при передаче .некоторой разрешенной кодовой ком-
бинации 'произошло q ошибок, то расстояние по Хеммиигу между
принятой и переданной комбина-
циями d=q. Так как между лю-
быми двумя разрешенными кодо-
выми комбинациями расстояние
по Хеммингу не меньше dмин, ТО
кодовая комбинация, отличаю-
щаяся от переданной в q =
= ^мин—1 разрядах, является за-
прещенной, и ошибки будут об-
наружены. Сказанное поясняется
на рис. Р.5.1,а.
Для доказательства того, что
Ь/pajp b2₽°W
4МИН ~ । ^МИН ~ /
____________Д^мин ___________т
Т)
код с расстоянием йМИн может ис-
править ?и^0,5б/мин—1 ошибок,
достаточно убедиться, что среди
Рис. Р5.1. К оценке обнаруживаю-
щей (а) и исправляющей (б) способ-
ности корректирующего кода
199
разрешенных кодовых комбинаций имеется только одна, которая
могла бы превратиться в принятую запрещенную комбинацию.
Допустим, что существуют две разрешенные кодовые комби-
нации bi и Ь2, которые при искажении 0,&/Мин—1 символов прев-
ращаются в одну и ту же запрещенную кодовую комбинацию Ь.
Это означает, что d(bh b) =0,&/МИн—1<0,54ин и d(b2, b) =
— О,5б/мин 1 <^0,5^/мИН«
Для того чтобы из комбинации bi получить комбинацию Ь2
необходимо изменить не более d(bb b)+rf(b2, b) символов, так
как выполняется условие d(bb b)+</(b2, b)^d(bi, b2) (см.
§ 2.4). Поскольку при сделанном допущении rf(b4, Ь)<0,5г/мин и
d(b2, Ь) <О,5б/Мин, имеем t/(bi, Ь2)<С^£/мин, что противоречит опре-
делению danH. Следовательно, при числе ошибок <7И=£^О,54/Мин'—1
принятой запрещенной комбинации может соответствовать лишь
одна разрешенная комбинация. Но это означает, что все qa оши-
бок могут быть исправлены. Правило декодирования в этом слу-
чае можно сформулировать так: если принята запрещенная ком-
бинация, то считается переданной ближайшая к ней разрешенная
комбинация. Сказанное поясняется рис. Р.5.1,6.
5.1.14. Указание к решению. Учесть, что кодовая комбинация в
данном случае декодируется правильно, если число ошибок в ней
не более двух.
5.1.15. Из восьми комбинаций заданного кода выбираем в ка-
честве разрешенных комбинаций ООО и 111. Из-за ошибок (пере-
ход 0 в 1 и 1 в 0) и стираний (появление на приеме третьего
символа «?») принятая комбинация отличается от переданной.
Из 27 комбинаций на приеме 25 являются запрещенными и, сле-
довательно, позволяют обнаружить некоторые ошибки и стирания,
Таблица Р.5.1
Состояния источника, канала и способ декодирования Состояние
1 1 2 | 3 1 |4 1 1 5 1 6 7 8
Символ источника А В в Л Л В Л В
Переданная кодовая комбина- ция ООО 1 1 1 111 ООО ООО 1 1 1 ООО 1 1 1
Принятая кодовая комбинация ООО ? 1 1 0 1 0 0 ? ? ? 10 ООО 1 ? ? ? ? ?
Расстояние по Хеммингу по нестертым символам 0 0 2 0 1 3 1 —
Декодирование с исправлением стираний и обнаружением ошибок А В л ? Л (ош) В (ош)
Декодирование с исправлением ошибок и стираний А В Л(ош) л Л или В (ош) Л (ош) В (ош) В или Л (ош)
Декодирование с исправлением стираний и ошибок, обнаруже- нием ошибок А В Л(ош) л ? Л (ош) В (ош) ?
200
а часть из них исправить. Возможные ситуации на выходе деко-
дера для различных состояний кодера, канала и способов декоди-
рования приведены в табл. Р.5.1.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 5.2.
5.2.2. Сначала необходимо образовать примитивный ^разряд-
ный код. Число кодовых комбинаций такого кода 1V=7<=24=16.
Одной ив комбинаций такого кода будет Ь=0101. Для получения
кодовой комбинации искомого кода необходимо к комбинации при-
митивного кода добавить три проверочных символа, определяемых,
например матрицей
¥15= 1
V= Yie = O
¥17= 1
¥25= 1
¥гв — 1
¥27= 1
¥35 =0 ¥45 = 1
¥зв =1 ¥46 = 1
¥37 = 1 ¥47 = 0
Согласно (5.9) получим
Ь5,пр='Ь1Ф&2®^4; Ьб,пр = ,^2®1’з®Ь4; Ь?,пр = ^1®&2®Ь3
(суммирование по модулю 2). В данном случае &5,пр = 0, 6б,пр = 0,
b?,np= 1. Кодовая комбинация кода (7, 4) — 0101'001. Аналогично
находятся и остальные комбинации кода (7, 4). Определив все
комбинации, нетрудно показать, что с?Мин = 3, приняв во внимание,
что dMHH равно минимальному весу полученных кодовых комбина-
ций, не содержащих нули во всех разрядах [14].
5.2.3. Указания к решению. Использовать матрицу коэффици-
ентов yi,i из задачи 5.2.2, а также (5.11) и (5.12).
5.2.4. Указание к решению. Для построения кодовых комбина-
ций необходимо перемножить вектор-строку примитивного 4-раз-
рядного кода с производящей матрицей.
5.2.5. Согласно (5?11) и (5.12)
о
о
1
1 1
0 1
1 о
1
1
1
1 о о
0 1 о
0 0 1
Н =
Допустим, что была передана комбинация Ь=| 10000011. Если
ошибок в ней нет, то выполняется соотношение (5.13). Если в ка-
ком-либо разряде происходит ошибка, то (5.13) не выполняется.
По виду результата в этом случае .можно указать разряд, в ко-
тором произошла ошибка. Например, при ошибке в первом раз-
ряде для ЬНТ получаем результат 001 для любой кодовой комби-
нации.
5.2.8. Указание к решению. Последовательно вводя ошибку в
каждый информационный разряд, убедиться, что (5.13) не вы-
полняется.
5.2.10. Осуществляя проверки по (5.13), легко убедиться, что
оба кода исправляют одиночные ошибки. Правила формирования
проверочных разрядов:
201
для первого кода
Ьй, пр — ^1®^2®^3®^4®Ьв’, йд, пр = Й1®Й2ф&3ф68ф67;
&ю, пР = ^1фЬ2фй4ф68фй7; &ц, пр = ^1ФЬ3ф&4ф&8фй6;
для второго кода
^8,fnp — ^4Ф ^>Ф ^в> ^9, пр — ^2® ^3® ^в® ^7>
^10, пр — ^1®йзф68ф&7; Ьц, пр = ^i®^2®bi®bb
Сравнение этих правил для первого и второго кодов показы-
вает, что во втором случае необходимо иметь меньшее число сум-
маторов по модулю 2.
5.2.13. Производящая матрица для двойственного кода (7.3)
1 1
G= 0 1
,1 1
0 110 0
110 10
1 0 0 0 1
Используя ее, можно для любой 3-разрядной информационной
последовательности построить кодовую комбинацию. Например,
для последовательности 111 имеем
Аналогично можно получить остальные комбинации.
5.2.16. Нетрудно заметить, что во всех кодовых комбинациях
bs=b\®b2’, bi—bi; bs = bi®b2.
Так как все кодовые символы являются линейными комбинациями
bi и Ь2, код является систематическим с проверкой на четность.
1
о
о
1
1 1
1 о
1
1
Порождающая матрица G =
проверочная
матрица
1
Н= 1
1
110 0
0 0 10
10 0 1
Вероятность ошибочного декодирования
Р=1—(1-р0)5-5р0(1-ро)4-2р02.(1-Ро)з.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 5.3.
5.3.4. Указание к решению. Проверить выполнение соотношения
(5.17).
5.3.8. Указание к решению. Проверить выполнение соотноше-
ния (5.19).
5.3.10. Так как число ненулевых членов порождающего много-
члена равно 3, б/мин не может быть больше 3. Следовательно, код
с б/мин = 5 построен быть не может.
202
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 5.4.
5.4.2. Для заданного кода п=П1П2 = 7-7=49; й = й1^2 = 4-4= 16.
Согласно (5.21) dUnH=did2=3-3 = 9.
5.4.5. Код (3/4) обнаруживает ошибки любой кратности, при-
водящие к изменению числа единиц. Не обнаруживаются лишь
ошибки смещения, при которых некоторое число единиц переходит
в нули, а такое же число нулей — в единицы. С учетом этого
рн.0 = СЧрО ( 1—Ро) 2С*4ро (1— ро) 3 + С23р20 (1—Ро) С24р20 X
X (1—ро)2 + С3зР3оС34>( 1—ро)•
5.4.8. В рассматриваемом коде из общего числа комбинаций
Л1 = 64 разрешенными являются К=32. Следовательно,
хк= 1—log2 K/log2A£=0,168.
Вероятность обнаруживаемой ошибки равна сумме вероятнос-
тей появления ошибок нечетной кратности: р0.о = С1бРо(1—Ро) +
+ С36р3о(1—Ро)3 + С56р5о(1—ро) «С16ро(1—Ро)5. Вероятность необ-
наруженной ошибки рн.о=1—(1—Ро)6—6ро('1—Ро)5.
5.4.13. Контрольные символы рекуррентного кода (1/2) найдем
согласно условию (5.21):
£>1,2=1; &2,з = 0; &з,4= 1; £>4,5; £>5,6=0;
£>6,7 = 1; £>7,8=0; £>8,9=0; £>9,10 = 1; £>ю,и = 0;
£>п,12=4; £>12,13 = 1; £>13,14= 1; £>14,15=1.
Кодовая последовательность кода (1/2) для данного случая
1100011010110000011011011'1011. Структурная схема кодера для
этого кода показана на рис. Р.5.2,а; структурная схема декоде-
ра — на рис. Р.5.2,б. Алгоритм декодирования кода (1/2) можно
сформулировать так: если условие (5.22) не выполняется для
двух соседних проверочных символов, то необходимо изменить
находящийся между ними информационный символ.
Синхронный
5) °)
Рис. Р.5.2. Структурные схемы коде-
ра (а) и декодера (б) для рекур-
рентного кода (1/2)
канала
^ионные
символы
Рис. Р 5 3. Структурные схемы коде
да (а) и декодера (б) для относи
тельного кода
203
5.4.14. Кодирование двоичной информации для передачи по
методу ОФМ осуществляется устройством, схема которого пред-
ставлена на рис. Р.5.3,а.
В этой схеме каждый символ с выхода сумматора по модулю
2 задерживается на один такт и затем суммируется по модулю 2
со следующим символом входной последовательности. В начале
работы на сумматор необходимо подать вспомогательный символ
О или 1. Например, если на вход кодера поступает последователь-
ность 01010101010101..., последовательность на его выходе имеет
вид 0011001100110011...
Декодирование осуществляется в схеме рис. Р.5.3,б. Здесь
входные символы задерживаются на один такт и суммируются с
последующими. В результате восстанавливается исходная комби-
нация
0О11ОО11ОО11ОО
\/\AAAAAAAA/VW
0101010101010
5.4.15. Так как на вход кодера рис. 5.2 одновременно поступа-
ет один информационный символ, k=l. За время, равное длитель-
ности одного символа на входе, образуются два символа на вы-
ходе. Поэтому п = 2. Скорость кода 7? = 1/2. Длина кодирующего
регистра k = 3. При /? = 1/2 v=k—1 = 2. Кодер рис. 5.2 характери-
зуется порождающими полиномами согласно (5.23) G^(D)=D +
+D2; G(2>(D) = 1+Z>+D2. Записывая последовательность коэффи-
циентов в виде двоичных комбинаций, получаем G<1) = 011; G(2> =
= 111.
5.4.18. Представим порождающую матрицу кодера согласно
(5.24) в виде
0 1 1 1 1 1 0 0 0 0 0 0...
0 1 1 1 1 1 0 0 0 0...
0 111110 0... ’
0 1 1 1 1 1...
Записывая информационную последовательность в виде векто-
ра-строки U = 11101... |, согласно (5.25) находим
0 1111
B = UG = |1 1 0 1... |
1 0 0 0 0...
1110 о...
1111 1...
0 11 1...
0 1...
= |0 1
1 0 0 0 1 0... |.
0 1 1
о
5.4.19. Указание к решению. Рассмотреть прохождение единич-
ной последовательности и =1000... через кодер и составить после-
довательность символов №> и Ь(2>, образующих импульсный отк-
лик h.
5.4.20. Указание к решению. Проверить выполнение условия
(5.26).
204
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 6
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 6.1.
6.1.1. Функции правдоподобия передачи символов Ьх и Ь2 при
заданном отсчете z(Z) определяются одномерными плотностями
вероятности:
(z| bj) = ехр (— z2l2a2)iyr2ло2,
(г| Ь2) = ехр (— (г — а)2/2о2)/Г 2ло2.
В условиях задачи алгоритм (6.3) можно записать так:
Р (bj) ехр (— z2/2o2) %Р (b2) ехр (— (z — а)2/2о2). (Р-6.1)
ь«
Подставляя сюда значения P(&i), P(b2), z, а, а2, находим
Р(&1)ехр(—z2/2o2) =0,435; Р(Ь2)ехр(—(2—а)2/2а2) =0,392.
Следовательно, приемник примет решение в пользу символа &i и
зарегистрирует его.
После логарифмирования соотношение (Р.6.1) можно записать
так:
Ьх
- z2/2o2 + In Р (\)^ - (z - а)2/2о2 + In Р (62). (Р.6.2)
ь2
После элементарных преобразований алгоритм приема примет
вид
z I2 UQ, (Р.6.3)
Ьх
где Uо — пороговый уровень, при превышении которого отсчетом
z(t) регистрируется символ &2, а в противном случае — Ьг, UQ~
а Р (Ьг) 2
Структурная схема приемника, реализующего алгоритм (Р.6.3),
показана на рис. Р.6.1. Она содержит следующие блоки: Г —
генератор очень коротких тактовых импульсов с частотой следова-
ния li/T, которые осуществляют выборку отсчетов входной смеси
z(t)\ К — ключ, осуществляющий квантование во времени вход-
Рис. Р.6.1. Структурная схема оп-
тимального приемника по одному
отсчету при точно известном сиг-
нале
Рис. Р.6 2. Структурная схема оп-
тимального приемника по трем от-
счетам при точно известном сиг-
нале
205
ной смеси; ССВ — схема сравнения с порогом UQ и выбора реше-
ния (если z>Uq регистрируется символ Ьг, ® противном слу-
чае — bi); УП — устройство памяти (хранения) регистрируемых
элементарных символов; Дек — декодирующее устройство.
6,1.3. Аналогично (Р.6.2) интересующий нас алгоритм приема
можно записать в виде
- (? - а)2/2о2 + In Р (bj - (г + а)2/2о2 + In Р (Ь2)
ь2
или, после тождественных преобразований,
Аи0, Е/О=^1П^-.
Ь. ° ° 2а Р^)
Если вероятности передачи символов равны, то оптимальный
порог для ан а лиз иру ем ых сигналов UQ = 0.
6.1.5. Функции правдоподобия передачи символов bi и Ь2 при
заданных отсчетах Zi, z2
ностями вероятности:
(1 \3
W) ир
и z3 определяются трехмерными плот-
(?i — а)2 __ (z2 — а)2 __ (z3 —^)2 1.
2аа 2а2 2а2 J
(?i + а)2 _ (г2 + а)2 _ (г8 + о)2 1
2а2 2о2 2а2 j
Согласно (6.3) и после элементарных преобразований алгоритм
приема запишем в виде
zx + z2 + z3 =?U0, Uo = In Р .
1 2 3 ь, ° ° 2а Р (bi)
При равновероятных символах порог Uo = O. Схема приемника
будет отличаться от схемы рис. Р.6.1 наличием блока суммирова-
ния (интегрирования) отсчетов входного сигнала * (рис. Р.6.2).
Генератор Г должен выдавать короткие импульсы с частотой сле-
дования 3/7\
6.1.6. Функционал правдоподобия передачи символа bi при
фиксации z(t) с учетом (3.5) и (6.8) можно записать в виде
го (г|&г) = К ехр - j* [z (t) - st (Z)]2 dt .
^0 о
Тогда согласно (6.4) следует алгоритм приема (6.9). На рис.
Р.6.3 показана схема, реализующая этот алгоритм. Она содержит:
т генераторов Г опорных сигналов Si(t)\ т вычитающих уст-
ройств ВУ; т квадраторов Кв, на выходе которых в момент t на-
пряжение равно [z (t)—Si (О]2’» fn интеграторов ** «j*»; схему срав-
нения и выбора решения ССВ; устройство памяти кодовых сим-
(Р.6.4)
* После принятия решения сумматор надо привести к нулевым начальным
условиям.
** После вынесения решения интегрирующие устройства в оптимальной схе-
ме должны быть приведены к нулевым начальным условиям.
206
Рис. Р.6.3. Реализация оптимального
приемного устройства по правилу
максимального правдоподобия при
точно известном ансамбле сигналов
Рис. Р 6 4. Структурная схема кор-
реляционного приемника при точно
известном ансамбле сигналов
волов УП; декодер. Если все символы имеют равные вероятности,
то алгоритм приема
т ь. т
J* [z(0-si(0]2d^ j> [z(/)-s,(/)]2dt (Р.6.5)
О Ь] о
и нет необходимости в вычитающих устройствах с опорными сиг-
налами No In Р.(Ь{).
6.1.7. Раскрыв в (6.9) квадратные скобки и выполнив элемен-
тарные преобразования, получим алгоритм (6.10), который реа-
лизуется с помощью схемы, называемой корреляционной, посколь-
ку основные операции над входным сигналом сводятся к опреде-
т
левию интегралов J z(t)si(t)dt (корреляционные функции между
о
z(t) И Si(t)).
Схема содержит: m генераторов Г сигналов Si(t)\ tn перемно-
жителей «X»; tn интеграторов «j»; ш вычитающих устройств ВУ
с опорными сигналами Oi=[E,—No In P(bi)]/2; схему сравнения
с пороговым уровнем и выбора решения ССВ; устройство памяти
УП; декодер Дек (рис. Р.6.4). Если символы равновероятны, а
сигналы Si(t) имеют равные энергии, то отпадает необходимость
в устройствах вычитания ВУ.
6.1.8. Если число символов равно двум, то из (гп—1) нера-
венств, определяющих алгоритм (6.10), остается лишь одно нера-
венство, которое после элементарных преобразований сводится к
(6.11). Алгоритм (6.11) реализуется одноканальной схемой (рис.
Рис. Р.6.5. Структурная схема
корреляционного приемника
для двоичных сигналов
207
Р.6.5), содержащей: генератор Г опорного сигнала $ол(0=51(0—
—$2(0‘, перемножитель «X»; интегратор « j »; схему сравнения с
пороговым уровнем Uq = -^- £ Ei—E2 + N0\n J и выбора ре-
шения ССВ. Если Р(0)=Р(1), то t/o= (£,i—Е2)!2. Для двоичной
системы с пассивной паузой $2(/)=0, £2=0, J7o = O,5£i и алгоритм
приема будет иметь вид
Для двоичной системы с активной паузой t/o = 0. Для системы
с противоположными сигналами алгоритм приема будет иметь вид
(P.6.6)
J
о °
6.1.10. Учитывая алгоритм (6.2), найдем границу между собст-
венными областями Л1 и Л2 из условия P(&i)a»(z|&i) = P(b2) X
Xw (z| b2). Подставив сюда выражения для функционалов w(zpf),
согласно (Р.6.4) получим
Р (Ьг) к ехр [ - -j- $[z (0 - S1 (О]2 л) =
l^o J
= P(b2)K ехр I -j- J [z(/)-s2(/)m4-
I ^0 о J
Логарифмируя, приводим это равенство к виду
1п Р (bj - J- f [z (0 - S1 (OF dt = In P (b2) - -2- f [z (0 - s2 (012 dt
No о Ко о
ИЛИ
f [z (t) - sx (0]2 dt - /[z (0 - s2 (OF dt = No In
0 0 r \O2)
T
Величина j* [z(0—Si(t)]2dt определяет в пространстве Гильберта
о
квадрат расстояния между точками пространства, соответствующи-
ми принятой реализации z(t) и сигналу Si(t) (см. § 2.4). Следова-
тельно, уравнение границы между собственными областями сигна-
лов согласно критерию минимума средней вероятности ошибки
можно записать
||z—Si||2—||z—s2||2 = Л/о In(Р(&i)/.P(Ь2)),
откуда следует, что граница между собственными областями сиг-
налов — это линия, являющаяся геометрическим местом точек,
разность квадратов расстояний которых до точек сигналов имеет
постоянную величину NQ 1пф(&1)|/Р(&2)]. Нетрудно убедиться в том,
что это перпендикуляр, проходящий через отрезок, соединяющий
точки Si и s2 (рис. Р.6.6).
208
Рис. Р.6 6. К оптимальному раз-
биению пространства двух сигна-
лов по критерию идеального на-
блюдателя
Рис. Р 6 7. Структурная схема оптималь-
ного приемника для канала с памятью
Найдем расстояния от основания перпендикуляра (точка z0)
до точек Si и s2. Очевидно, ||z0—Sill2—||z0—s2||2 = A/o ln[P(&i)/
P(i>2)]. С другой стороны, ||zo—Si|| + ||z0—S2|| = ||si—s2||. Поделив
первое равенство на второе, получим
ЛГ01п-^-
Iko - Sill - ||z0 - s2|| = ——.
I|S1 — s2||
Теперь нетрудно получить:
2 2 ||si — Sall
I|z. - SJI _ -L ||S1 - sj| - — N,
2 1 21 2 " ||s,-i,||
Очевидно, что при P(bt) =P(b2) граница между собственными
областями Al и Лг будет представлять собой перпендикуляр, про-
ходящий через середину отрезка, соединяющего сигнальные точки.
6.1.13. В данном случае D = L=\ (перекрываться могут только
сигналы, соответствующие соседним кодовым посылкам). На ин-
тервале анализа Т& = 2Т имеется всего 2D+b+1 реализаций сигналов
$г,<(/), соответствующих передаче 1 или 0 до анализируемого сиг-
нала и 1 или 0 после анализируемого. Реализация Si(t) =sni(t) =
=g2(i)h(t) +gi(t)h(t) +g2(t—T)h(t—T) +g^t—T)h(t—T) соответ-
ствует передаче 1 анализируемым сигналом, а также 1 до и после
него;
S. (О = SO11 (0 = - g2 (0 h (t) + gl (f) h (t)+g2(t-T)h(t-T) +
+ gi(t-T)h(t-Ty, s3(0 = Soio(0= -g2(t)h(t) +
+ gl (0h (0 + g2 (t-T) h{t-T)-gl(t-T)h{t-ту
209
«4 (0 = S11O (0 = Ё2 (О h (t) + gx (t) h (0 +
+ gz(t-T)h(t-T)-gl(t-T)h(t-T)-,
$5 (0 “ S000 (0 = S1 (0» S6 (0 = S001 (0 ~ S4 (0'«
S? (0 ~ S100 (0 = S2 (0> S8 (0 = S101 (0 = S3 (0-
Согласно (6.3) с учетом (6.6) и (6.8) получаем при белом ста-
ционарном шуме алгоритм оптимального приема
4 ( 1 2T 1 1 8 ( 1 2Т 1
2 ехр --f[z(0-sr(0Mk Sexp J[z(0-sr(0]2ctf ,
r=i l Л^о о ) о ,=5 ( JV0 oJ J
(Р.6.7)
или
4 Г о 2Т 1 1 8 Г 2 27
SexP — t z(t)sr(t)dt-ET/2 Ь= £ехр $ z(f)sT(t)dt — Ет/2 ,
г=1 |Л° о Jo г=5 о
(Р.6.8)
2Т
гцеЕг=$ s2r(t)dt.
о
На рис. Р.6.7 показана структурная схема приемника, реали-
зующего алгоритм (Р.6.7). Она содержит: блок измерения харак-
теристик канала и формирования из принимаемой смеси z(t) не-
обходимых для функционирования приемника сигналов синхро-
низации и восьми опорных сигналов sr(t) БИФ; вычитающие уст-
ройства ВУ; квадраторы К»в, интеграторы «J», нелинейные уст-
ройства с экспоненциальной характеристикой «ехр»; сумматоры
« + »; схему сравнения с пороговым уровнем и выбора решения
ССВ; устройство памяти УП; декодер Дек. Сравнивая (Р.6.5)
и (Р.6.7), отмечаем, что в отличие от канала без памяти для реа-
лизации оптимального приема в канале с межсимвольной интер-
ференцией требуется знание энергетического спектра шума в кана-
ле. При этом строго оптимальная схема в таком канале непре-
менно содержит нелинейные блоки..
6.1.14. Если имеется «идеальная» обратная связь по решению
(по зарегистрированным символам можно точно восстановить сиг-
нал «хвоста» g’ocT(0 от предшествующих символов), то можно
подвергнуть анализу колебания Za(O=0(O—gocr(t)- При D=1
(Та = 2Т) на интервале анализа могут быть образованы четыре
реализации: si(l) =Sn(t) =gi\t)h(t) +g2(t—Tyii(t—T) +gv(t—T) X
Xh(t—T), что соответствует передаче 1 анализируемым сигналом
и I после него;
S2 (0 = s10- (0 = gi (0 h (/) +£2I(t-T) h (t-T) -gi (t-T) h (t-T);
5з(О=5о1(О=— 52 (0; S4(O=5oo(O =—$1 (t).
Согласно (6.3) с учетом (6.7) и (6.8) получаем при белом стацио-
нарном шуме алгоритм оптимального приема
s ехр -—J* [zAt)-sAt)]2dt\ * £ехр L-L J [га (/) - sr (Z)]2 dH.
r=l ( о Jo г=з Ио й J
(Р.6.9)
210
Рис. Р.6.8. Структурная
схема приемника с об-
ратной связью по реше-
нию
Рис. Р 6.9 Структурная
схема оптимального при-
емника двоичных сигна-
лов для канала с па-
мятью
Я®
На рис. Р.6.8 показала структурная схема приемника, реали-
зующего алгоритм (Р.6.9). От схемы рис. Р.6.7 она отличается
наличием обратной связи по решению (ОСР) от блока УП до
блока БИФ, В последнем, помимо четырех опорных сигналов sr(t),
формируется также сигнал gOcT(0 =±£2 (0^(0- Знак этого сигна-
ла при анализе очередного символа определяется тем, были ли при
анализе предыдущего символа зафиксированы в УП 1 или 0.
6.1.15. Если имеется «идеальная» обратная связь по решению
и £> = 0, то на интервале анализа Га = Т две реализации сигнала,
соответствующие передаче 1 и 0, определяются так:
si(0=£i'(0; МО =—£1(0-
В это'М случае алгоритм оптимального приема
J[z(O±g2(0]gl(OdU 0 (Р.6.10)
о 0
реализуется линейной схемой рис. Р.6.9. Блок БИФ, охваченный
обратной связью по решению, формирует по результатам измере-
ния характеристик канала элементы gi(t) и gz(t). Знак при g2(f)
в (Р.6.10) определяется тем, были ли зарегистрированы при ана-
лизе предшествующего символа 1 или 0.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 6.2.
6.2.1. Согласно (6.13) импульсная переходная характеристика
согласованного фильтра является зеркальным отражением сигна-
ла относительно точки to. Следовательно, в данном случае
g(t)=k(T-t), 0<i<T.
График этой функции показан на рис. Р.6.10.
211
Рис. Р 6 10. Импульсная пе-
реходная характеристика
фильтра, согласованного с
линейно нарастающим сиг-
налом
Рис. Р.6.11. Структурная схема оптимального
приемника с согласованным фильтром для оди-
ночного прямоугольного импульса
6.2.3. Согласно (6.18) в момент окончания входного сигнала
на выходе согласованного фильтра получается напряжение, про-
порциональное сигналу на выходе интегратора корреляционного
приемника. Следовательно, оптимальное приемное устройство- при
точно известном сигнале можно реализовать на базе согласован-
ных фильтров.
Рассмотрим пример построения согласованного фильтра для
прямоугольного видеоимпульса, заданного в виде s(/)=X, при
s(/)=0 при /<0, t>T. Спектр по Фурье для такого им-
пульса определяется соотношением S(j(o) = (1—е-^т). На
основании (6.15) для коэффициента передачи согласованного
фильтра получим
К (j и) = —ЕЛ--(1 _ Г) e-/2nf т = (1 _ ту
—/2л f j2лf
Известно, что умножение на l/i(/2jif) в частотной области соответ-
ствует интегрированию в пределах от —оо до t во временной об-
ласти, а умножение на е-^2я^т соответствует задержке сигнала на
время Т. Следовательно, фильтр, согласованный с одиночным пря-
моугольным импульсом, состоит из интегратора «J », линии за-
держки ЛЗ на время Т и вычитающего устройства ВУ. Структур-
ная схема оптимального приемника с таким фильтром показана
на рис. Р.6.11. На схеме ЯП — ячейка памяти.
6.2.4. В рассматриваемом случае корреляционные устройства
в оптимальном приемнике должны быть заменены фильтрами, со-
гласованными с радиоимпульсами, имеющими частоты заполне-
ния ап и (02. В качестве примера найдем импульсную переходную
характеристику фильтра, согласованного с сигналом:
$1(0 = ^mCOS((OiZ + (pi),
и рассмотрим его возможную реализацию. Выбирая /о = Л соглас-
но (6.13) можно записать
S-(0 ~ aUтп COS ((01 to + —(010 > Т.
212
Такая характеристика может
быть реализована с помощью
высокодобротного (Q>*1) ко-
лебательного контура при ус-
ловии, что для частоты coi он
создает фазовый сдвиг
—Mito—фь Структурная схема
оптимального приемника пока-
зана на рис. Р.6.12. Ключ К в
момент t = tQ=T на очень ко-
роткое время закорачивает ем-
кость и разрывает цепь с ин-
дуктивностью для освобожде-
ния контура от накопленной
энергии и его подготовки к
приему следующих элементов
сигнала *.
Рис. Р.6.12. Реализация оптимально-
го по правилу максимального прав
доподобия приемника ЧМ-сигналов
на основе согласованных фильтров
6.2.5. Любую финитную функцию s(t) можно аппроксимиро-
вать последовательностью из п — Т^ прямоугольных импульсов
малой длительности Д и высоты ak (&=1, 2, ..., п) (рис. Р.6.13,а).
Величина Д^1/(2/?с) и определяется допустимой точностью ап-
проксимации.
Если на вход (точка Л) линии задержки с отводами через
интервалы Д подадим в момент t = 0 импульс с длительностью Д
единичной высоты и просуммируем с весами ah значения сигналов
в отводах линии (рис. Р.6.13,6), то на выходе сумматора получим
сигнал s(t). Фильтр нижних частот подавляет спектральные ком-
поненты, лежащие вне полосы сигнала Fc.
Если единичный импульс подвести к выходу линии (точка В),
отклик будет зеркальным отражением сигнала s(/), и схема рис.
Р.6.13,6 будет выполнять роль согласованного фильтра.
а)
Рис. Р.613 Реализация фильтра, согласованного с произ-
вольным непрерывным сигналом, на основе линии задержки
с отводами и блоками взвешивания:
а — сигнал: б — согласованный фильтр
* Такой вариант согласованного фильтра называется коммутируемым. В
принципе, можно построить согласованный фильтр и без коммутации парамет-
ров. В этом случае фильтр называют пассивным.
213
6.2.9. Пусть на вход линейной системы, осуществляющей обра-
т
ботку сигнала в соответствии с алгоритмом y(t)= J z(t)s(t)6/t,
поступает смесь сигнала и гауссовского стационарного шума
z(t) =s(t) +n(/)> причем s(0=#0 при В момент оконча-
ния сигнала t = T сигнальная компонента на выходе заданной ли-
т
нейной системы yd(O = J* s2 (x)dx = PcT—Е (Е — энергия сигнала
о
на входе). Шумовая компонента на выходе заданной линейной
т
системы yn(t) = $ n(x)s(x)dx представляет собой гауссовский про-
о _____________________
цесс с дисперсией y2rt(t) = N0E\/2 (No — спектральная плотность
мощности шума на входе). Отношение сигнал-шум на выходе за-
данной линейной системы в момент t = T
Рвых = У2с (П/О) = 2 E/No = 2h2 = 2Pc T/No = 2 FT (Рс/Рш)вх.
Полученный результат справедлив для согласованного фильтра и
коррелятора.
6.2.10. Согласно (6.16) выигрыш в отношении сигнал-шум, да-
ваемый согласованным фильтром, рвых/(Рс/Рш)вх:=2/?7, = 2-20Х
XI О-МО4 = 400.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 6.3.
6.3.1. Согласно решению задачи 6.1.1 правило решения прием-
ь4
ника имеет вид z^U0, где порог Uo = (o2/a)ln,[P(6i)/P(&2)]+0,5a.
b2
Отсчеты смеси детерминированного сигнала и шума z имеют гаус-
совское -распределение, дисперсию о2 и математическое ожидание
а (при передаче символа Ь2) или 0 (при передаче символа &i).
Условные плотности вероятности отсчетов при передаче символов
bi и Ь2 равны соответственно
w (z|6i) = (2ло2)-0’5ехр1(—0,5z2/<r2);
w (z| b2) = (2тео2)-°’5ехр(—0,5(z—a) W).
Найдем вероятности ошибочных переходов P(6i\b2) и P(62\bi):
P(b2\b1) = P(z->U0\b1)=J w(z\b1)dz =
и.
= (2no2)-°’s J* exp ( — 0,5z2/o2) dz = 0,5 [1 — Ф (U0/o)];
V»
V„
^(ММ = ^(г<^о16г) = J* w(z\b2)dz =
— oo
Vo
= (2 ла2)-0-5 j* exp [ — 0,5 (z — a)2/o2] dz =
— oo
= 0,5 [1 — Ф ([{/0 —a]/a)J.
214
Здесь Ф (х) — функция Крампа. Средняя вероятность ошибки
Рош = Р (bj Р (b^ + P (b2) Р (ЬМ =
= 0,5 {Р (bj [ I - Ф (t/0/o)] + Р (b2) [ 1 — Ф <[С70 - а]/о)]}.
6.3.4. Условия правильного приема символа Ь\ в многопозицио1Н-
ной системе, использующей ортогональные сигналы с активной
паузой, согласно решению задачи 6.1.7 такие:
f z(t)s1(t)dt> J z(t)st r = 2,3,4,...,m.
о 0
T T
Поскольку z(t) = Si(0 +n(t), J Si(/)si(0^ = 0 и j s2i(t)dt=E, to
0 0
T
эти условия можно записать так: J* n(t) ($i(/)—S{(\t)}dt>—E или
о
т
@г<®1+Е, где Qi = S Si(t)n(t)dt.
о
т
Случайная величина Qi= fSi(t)n(t)dt распределена по гаус-
6
совскому закону, имеет .нулевое математическое ожидание и дис-
персию &2i = NoE/2. Верояность выполнения неравенства 0i<0i +
+£ будет равна
1 / в? \
P(0i<61 + £) = J -тг== ехр -~±= ре,=
_те V 2 Л0? \ 2 )
1 / @2 \ ___
= з~/-дГр -f* ехр Ь)й0г = О,5[1+Ф(/+К2/12)],
ynN0E —со \ NqEJ
где f = 0x//yoE/2; h2 = E/NQ.
Вероятность того, что во всех ш—'1 ветвях значения 0* не пре-
высят значение 0Ь равна ('1/2)т-11[1+Ф(/+1/Г2/г?)]т“1. Усредняя
это выражение по всем возможным значениям 0Ь получаем веро-
ятность правильного приема
Рправ= -l— J е-^/2 (0,5 [1 + Ф(/ч-К27?)]}"1-1
—-оо
Вероятность ошибки в m-по'зиционной системе
Рош, тп ~ 1 Рправ = 1 ~~ Г е~*2/2 X
Т/2л Л
X [ Y + °’5 ф (1 + /2Л2)]т-‘ dt.
При больших значениях /г2 это выражение можно привести к
виду
Рош.т »0,5 (m- 1) [1-Ф/Л2].
215
bl
6.3.5. Согласно решению задачи 6.1.8 можно записать алгоритм
работы оптимального приемника двоичных сигналов:
J г(0 [s1(O-s2(/)]dZ i 0,5 Д
о ь2
'i-^ + TVoln^l .
1 2 ° P(&1)J
T
Здесь Ei= J s2i(t)dt — энергия сигнала Si(t).
Если действительно был передан символ bit то z(0=5i(0 +
+ n(t) и событию, заключающемуся в правильной регистрации пе-
реданного символа, будет соответствовать неравенство1
f п (/) К (0 - s2 (/)] dt > - 0,5 f [S1 (0 -
о о
- s2 (OF Л+ 0,5^ In .
p (&1)
Вероятность ошибки определится вероятностью выполнения обрат-
ного неравенства, т. е.
Jn(O [S1 (0-s2 (/)] dt
о
— s2 (0M + 0,52Voln P-^- .
2 \ /J ° p (6j)
-0,5 J [S1(0 -
0
т
T
Обозначим f n(/)[M0—S2(t)\dt=8-, J* («1(0—s2(t)]2dt=E3 и за-
fl о
пишем полученное неравенство' в виде
@< — 0,5 Ге8 + ЛГ01п .
TaR как шум в канале гауссовский и имеет нулевое математи-
ческое ожидание, то 0 является гауссовской случайной величиной
с пара метрами 0 = 0 и ог20=-^-£э. Теперь можно записать выра-
жение для вероятности Р(б21 &i):
_ Г Еэ+„0 ln LLM1
2 I Э P(*2)J
P(w =
w (0) d 0 =
_1_
2
/ Еэ + No In \
1-Ф 8 Р(ь2)
\ V2N0 Ед /_
Аналогично находим
P(W= Y
/ р „ р (*1)4
/ Ев- У01п ——-
1 — ф I ---------Р
\ V2N0Ea
216
Средняя вероятность ошибки
Рош = /’(&1)^- 1-Ф
+ Р(Ь2)-±- 1-Ф
„ , „ , Р (*1)
£э + У°1пГ^
У2ЛГ0£э
„ л; 1 Р(&1) \1
£э~^°1П P(Z>2) )
У2ЛГО£Э /_
Для системы с пассивной паузой (AM) si (t) У=0,
т
s2 (t) — О, Еэ = J sf (t) dt = Е±. При этом
о
1-Ф
2
„ , , Р (bi) \1
£1 + AJnFfaj ) +
Угл'оР! /]
У2^Я1 /
При использовании ортогональных сигналов Si (t) и s2(t) с оди-
наковыми энергиями £1 = Е2=£ (система с активной паузой)
имеем
Е9 = J [sx (0 - s2 (/)]2 dt = f sf (0 dt - 2 f sx (0 s2 (t) dt +
0 0 0
+ J* s2 (t)dt = 2E и
о
Р„-0.5Р(ад [1 -ф(2£ + ^'"^>"№1! \1 +
L \ ViV0E )]
+ 0,5Р(й2) \1
L \ 2Ум>£ Л
При использовании противоположных сигналов Si(/)=—s2(0
имеем
£э= f 4$2 (t)dt=4E и
о
Рош = 0,5 Р (&J
ф / 4 £ + In [?(/>!)/?(&,)] \1
\ 2У2^Е /J ”Г
4£-^ln[P(Z>1)/P(f>2)] \1
2 У 2AV? ) J ’
6.3.7. Согласно решению задачи 6.3.5 вероятность ошибки в
двоичной системе при точно известных сигналах и равновероят-
ных символах определяется выражением
рош = 0,5[1-Ф(УО,5Еэ/0
+ 0,5Р(&2) 1
217
и тем меньше, чем больше Еэ. При произвольных сигналах Si(t)
т
и s2(0 Еэ=\ —s2(t)]2dt. Определим условия, при которых
о
Еэ 'максимальна, полагая, что
£1= р2 (t)dt^E, E2=fs2 (/)Л<Е.
о о
т
Записав ЕЭ = 2Е1 + 2Е2—J [si(0+s2(0]2dt, заметим, что для
о
получения максимума этого выражения нужно сделать Ei и Е2 воз-
можно большими, а интеграл в правой части — как можно мень-
шим. Максимально возможные значения Ei и Е2 будут, если Ei =
=Е2 = Е.
т
Поскольку интеграл J [$f(/) + s2(t)]2dt принимает только поло-
о
житель,ные значения, его минимум равен нулю и достигается при
условии Si(/)=—s2(t), т. е. при противоположных сигналах. Та-
ким образом, в двоичном канале с постоянными параметрами и
аддитивным флуктуационным шумом минимальную вероятность
ошибки обеспечивает система с противоположными сигналами,
так как у них эквивалентная энергия максимальна (при фиксиро-
ванной энергии сигналов).
6.3.8. При приеме сигналов ОФМ по методу сравнения поляр-
ностей осуществляется когерентное (фазовое) детектирование сме-
си канального сигнала и шума с последующей перекодировкой
символов, которая осуществляется сравнением полярностей каж-
дого принятого символа с предыдущим. Очевидно, что вероятность
Рошофм ошибочной регистрации символов в системе ОФМ не сов-
падает с вероятностью появления искаженных знаков на выходе
фазового детектора или, что то же самое, с вероятностью ошибок
Рош фм в системе «классической» ФМ.
Очевидно, что ошибочная регистрация символов при приеме
методом сравнения полярностей возможна в результате одного из
двух несовместимых событий:
а) знак данного элемента принят ошибочно, а знак предыду-
щего — верно;
б) знак данного элемента принят верно, а предыдущего —
ошибочно1.
Каждое из этих событий имеет вероятность р0Шфм (1—Рошфм)-
Следовательно, Рошофм ~2рОШфм U—Рошфм)- В области малых
ошибок, когда рОшФМ<1, получаем рош0фМ^2рои1фМ=|1—Ф(]/2/12).
При Рс=0,5 Вт, k= 10“2, Т= 10 мс и jVo=1O-7 Вт/Гц имеем /г2 = 5
И РошОФМ = 10-3.
* 6.3.10. Сравнивая выражения для вероятностей ошибок, полу-
ченные в решении задачи 6.3.6, замечаем, что для сохранения ве-
роятности ошибки неизменной при переходе от AM. к ЧМ необхо-
димо выполнить условие /12чм = 0,5Й2ам или t/m4M = £4iam/V^2.
218
Изменение амплитуды колебания в ‘К2 раз приводит к измене-
нию пиковой мощности передатчика в 2 (раза. Отсюда следует, что
переход от AM к ЧМ при неизменной вероятности ошибки дает
выигрыш по пиковой мощности, равный 2. Аналогично находим,
что переход от ЧМ к ФМ дает выигрыш по пиковой мощности,
равный 2, а переход от AM к ФМ — 4.
При равновероятных сигналах в системе AM (система с пас-
сивной паузой) Рс — 0,5РМакс. В системах ЧМ и ФМ (системы с ак-
тивной паузой) Рс = Рмакс. Отсюда следует, что переход от AM к
ЧМ не дает выигрыша по средней мощности, при переходе от ЧМ
к ФМ выигрыш по средней мощности равен 2, при переходе от
AM к ФМ выигрыш по средней мощности также равен 2.
6.3.12. Полагая, что на вход приемника поступает процесс
z(t) +n(t), для напряжения на выходе интегратора получа-
ем
0 = (-l)f-i &£cos<p + & т/— J n(t) cos(<M + <p)<ft, i= 1,2.
г т о
Очевидно, что 0 является гауссовской -случайной величиной с
математическим ожиданием zne = (—IJ^^^icos <р и дисперсией
о% =F#0£i/2.
Условная плотность вероятности величины 0 при условии пе-
редачи сигнала Si(t)
1 1 V2nVk2ENQ/2
vexnf (0 + (-l/-1*£cos<p)»l . J2
X exp L kEih J ’ ~ ’
Используя методику решения задачи 6.3.5, после несложных
преобразований получаем для вероятности ошибки
Рош (ф) = 0,5 [1 - Ф (/2/Г2 cos ф)1 (Л2 = E/N9,
Ф (х) — функция Крампа).
Сравнивая полученное выражение с выражением, найденным
в задаче 6.3.5, легко заметить, что несинфазность принимаемого
сигнала и опорного колебания при ФМ ведет к энергетическому
проигрышу:
П= —^=-^. Прит)<1,1
Л- COS2 ф COS2 Ф
6.3.13. Полагая, что <р является случайной величиной, прини-
мающей в моменты t = nT (и=1, 2, 3, ...) значения на интервале
(—л, л), можно найти среднее значение вероятности ошибки
рош(ср), полученной в задаче 6.3.12, усреднив ее по всем возмож-
ным значениям (р:
(ф) = J* Рош (ф) (ф) dtp.
219
Подставляя сюда .выражения для рош('ф) из предыдущей задачи и
выражение ш1(ф), находим
Рош (ф) = 4" |1— J Ф (/2 Л2 cos <р) X
I —л
х Г_ке-о.5а’+ F (асозф) e-°'5<22sin,<₽l dw\ .
_2л “|/ 2л J )
Полученный интеграл в общем виде не вычисляется в элементар-
ных функциях. В частном случае при а= V2h2 имеем
^ош (ф) — ~
F (У 2 h cos ф) е~Лг sin2 <₽
। "1/2 h cos ф
V2F
d(p| = e~Zl2.
Полезно отметить, что при сделанных предположениях помехо-
устойчивость системы ФМ такая же, как и системы ОФМ при
приеме по 'методу сравнения фаз (см. задачу 6.4.7).
6.3.14. Используя алгоритм работы корреляционного приемни-
ка сигналов ФМ при точно известных параметрах канала (Р.6.6)
можно записать с учетом неточности синхронизации:
т-И 1
J* z(t)sou(t)dt * 0, = +
х О
Полагая, что на интервале (О, Г) передается сигнал Si(Z), а
на интервале (Г, 2Т) — сигнал записываем
т т-И 1
J [S1 (/) + п (/)] son (/) dt + J* [s2 (/) + п (/)] 50П (/) dt* 0.
х Т °
В данном случае ошибка будет иметь место при выполнении
условия
Т г+т
J* [S1 (0 + п (0] s0D (0 dt + J [s2 (0 + п (01 son (0 dt < 0.
о т
Подставляя сюда выражения сигналов Si(0, 5г(0 и son(t) и
осуществляя простые преобразования, получаем
j n(0]/2^/Tcos((ooZ + <po)d/<-E(l-2T/T).
X
Как и в задаче 6.3.12, величина интеграла в левой части нера-
венства представляет собой гауссовскую случайную величину с
дисперсией o2=ENq/2. Вероятность ошибки равна вероятности
выполнения полученного неравенства и определяется выражением
- Е(1- 2Х/Т) г-н ____
Рош= f w1(B)dQi где 0= j п(/) уг2Е/Гсов(й)о^ + фо)^/.
—оо' X
220
С учетом гауссовского распределения величины 0 получаем
Рош = 0,5 {1 -Ф [K2S7TV7(1-2т/Т)]} =
= 0,5 {1 - Ф [/27? (1 - 2 т/Т)]}.
Сравнивая полученное выражение для вероятности ошибки с вы-
ражением для случая точной синхронизации (т = 0) (см. задачу
6.3.6), замечаем, что неточная синхронизация приводит к энерге-
тическому проигрышу
Т] = Л2/' [ Л2 (1—2та/Г) ]2 = (1—2т/Т) -2.
При т]^ 1,1 т^2,5-10-27\
6.3.15, Легко показать, что в данном случае вероятность ошиб-
ки будет определяться соотношением
Рош = 0,5 {1 -Ф /27?cosф (1 — 2т/Т)]}.
Отсюда энергетический проигрыш т) = [созф(1—2т/Т)]“2. Зада-
ваясь величиной т) = 1,1 (потеря мощности передатчика составляет
10%), находим, что при т=0 ф=18° (этот результат получен
Л. М. Финком в [14]). Если положить ф=0, то т=0,025Т, т. е. до-
пустимая рассинхронизация составляет 2,5% от длительности эле-
ментарной посылки. Очевидно, что при ф#=0 и т=/=0 допустимые
погрешности будут соответственно меньше: 18° и 0,0257\ В табл.
Р.6.1 приведены значения ф и т/Т, при которых энергетический
ПрОИГрЫШ Т) = 1,1.
Таблица Р.6.1
<р 0° 6°48' 10°30' 13*24' 15°30' 18°
2,5-10—2 2-10—2 1,5-10—2 10“2 5.10—3 0
6.3.17. Воспользуемся алгоритмом работы когерентного прием-
ника, найденным в задаче 6.1.7. При передаче сигнала Si(/) ошиб-
т
ка произойдет в то-м случае, когда J z\t)sQn(t)dt<ZQ, где z(t) =
о
+n(t). Подставляя сюда значения Si(Z) и son(0> получаем
после очевидных преобразований
т _____________
j* п (1) У 2Е/Т cos [(о)о + До) t + ф] dt < — Е (Т До)”1 sin До Т.
о
С учетом сказанного в решении задачи 6.3.42 для вероятности
ошибки в данном случае можно записать
РошФМ = 0,5 [1—Ф(/2Л2 (АюТ)-1 sin А®Г)].
Для энергетического проигрыша в этом случае имеем т] =
='(ДоТ)28т~2Дсо7\ Задаваясь допустимой величиной т) = 1,1, полу-
чаем для допустимой величины частотной расстройки Дсо =
= ±0,54/Г.
221
6.3.19. Как показано в задаче 6.3.6, при корреляционном 'прие-
ме двоичной ФМ рош=0,5[1—Ф(К2Л2)]. Найдем вероятность
ошибки при интегральном приеме. При передаче сигнала s2(t) =
= pr2£'i/7’cos<oo^ на выходе интегратора имеем
0 = у V2E1T cos ®0 tdt+ у п (0 dt.
о о
Если 0>О, то фиксируется символ, соответствующий сигналу
в противном случае фиксируется символ, соответствующий
сигналу s2(t). Если при этом передавался сигнал Si(t), то произой-
дет ошибка. Таким образом, условием ошибки является выполне-
ние неравенства
J п (/) dt < — J У 2 Е/Т cos <в0 tdt
о о
или
J п (/) dt < — У 2 Е/Т ©о"' sin <в0 Т.
о
т
Величина А= $ п (t) dt является гауссовской, имеет нулевое мате-
о
магическое ожидание и дисперсию ст2 = O.STVoT'- Поэтому
— У 2Е/Т о”1 sin <оо Т
Рош = У ’ (*) =
—оо
= 0,5 {1 - Ф [У2ЁТГ (0,5АГо Т)-0,5 со?1 sin <оо Ш =
= 0,5 [1 - Ф(/2/?(оГ' Т~х sincoo Т)];
Т] = 0,5©2 72 sin-2 0)о 'Р
6.3.20. Аналогично решению задачи 6.3.12 можем записать для
условия ошибки при передаче сигнала $1 (/)
/z(i)son(i!)d/<0, где z(/) =
о
= У2Ё/Техр [ - Р8(t- 0,5Т)2] cos®01 + п(f)
или
ET~L / ехР [ - Р <f - О»57?] dt + У2Ё/Т уГп (0 cos ®о tdt < 0.
о о
После простых преобразований находим
У2Ё/Т уГп (/) cos ®0 tdt < - O.SE/jTT-1 Ф (Т Р//Г).
о
222
т ___________________
Учитывая, что J п(1)У 2Е)Т ^tdt представляет собой гаус-
о
совскую случайную величину с дисперсией (j2 = £Wo/2, находим ве-
роятность ошибки
Рош = 0,5 {1 - Ф [0,5 У2^ЁЦГ0 Ф (тр//Г)/ТРП =
= 0,5 {1 -Ф [0,5 /2^Ф(Т&V2)/Tр]).
Энергетический проигрыш по сравнению со случаем отсутствия
линейных искажений составляет величину т]= [0,5 ]^лФ(71р/]/2) /
Тр]-2. Например, при р = 0,1Т-1 т] = 1,89.
6.3.21. Квадрат модуля комплексного коэффициента передачи
«обеляющего» фильтра найдем как
№(©) =a/G0 (/) =0,5аа"1 [а2+ (©—<оо)2], a=const.
Спектральная плотность мощности шума на выходе «обеляющего»
фильтра #o='Go'(/;)-K2'(lco) =а.
Комплексный коэффициент передачи «обеляющего» фильтра
можно записать
Д' (/ <о) = ] z0,5a/a [а + j (<в — <в0)].
Учитывая, что умножение на /со .в частотной области эквива-
лентно дифференцированию во временной области, для сигналов
на выходе «обеляющего» фильтра получаем
si (0 = V 0,5a/a [a (f) + иг (/)!;
L dt \
s2 (0 = — VQ,5ala [a«1 (/) + ux (f) 1.
L dt J
Используя теперь формулу для вероятности ошибки при опти-
мальном когерентном приеме противоположных сигналов (см. за-
дачу 6.3.7), находим вероятность ошибки при использовании мето-
да выбеливания в заданных условиях:
Найдем теперь спектральную плотность мощности белого шу-
ма, имеющего в полосе fo±F такую же среднюю мощность, что
и заданный небелый шум:
1 fo+F
J »(М
f.-F
a f°fF_________d[________
F f*_P 4л* (/-/.)* +a»
=------arctg
2nF
2л F
a
223
Вероятность ошибки при оптимально-м когерентном приеме
Энергетический проигрыш, связанный с наличием небелого шума,
a + cojj/a 2лГ
т] = ———arctg-----
4nF a
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 6.4.
6,4.1. Подставив (6.25) в выражение функции правдоподобия,
найденное в задаче 3.1.16, после простых преобразований получим
для известных k и 0
(z| bi)k, е = /G. ехр Г(Yt cos 0 — Yt sin 0) —^-1
L No No -J
________ у? .
или, обозначив Vj= ]^Y2i + Y2i и щ = arctg —- >
Yi
w1(z\bi)k,e^K1exp Г-^-Угсо5(0-ф()--^Д].
L No No J
т т
Здесь Yi= ^z(t)si(t)dt\ Fj = \ z(t)st(t)dt\ Ki — нормирующий ко-
o . о
эффициент, не зависящий от I. Усреднив ш(г|&г-)л. е п0' всем зна-
чениям 0, при равномерном распределении фазы на интервале
(—л, л) получим
w(z\bi) = -±- J u)(z|6i)ft,ed0 = /C1exp(
2л \ No / \ No J
Здесь /о(х) — модифицированная функция Бесселя первого рода
нулевого порядка.
В соответствии с правилом максимального правдоподобия (6.4)
находим алгоритм оптимального приема при неопределенной фазе:
тах<[ь/0(-^Л-^а (Р.6.П)
L \ Nq J No J
Величины Yi и Yi можно получить на выходе корреляторов с опор-
ными сигналами Si(t) и Si(t) соответственно.
Структурная схема оптимального при неопределенной фазе
приемника на базе корреляционной техники показана на рис.
Р.6.14. На этой схеме Pi — генераторы опорных сигналов Si(t) с
точностью до фазы; фя /2 — фазовращатели на д/2 (генераторы
сопряженных сигналов); БОМ — блок определения модуля век-
тора Vi= V У2г + У2г по ортогональным компонентам; НУ — нели-
нейные устройства с характеристикой Ивых = 1п/0'[ (2&/Af0)uBx].
224
Рис. Р.6.14. Структурная схема
оптимального приемника при не-
определенной фазе сигнала (квад-
ратурная схема)
Как показано в решении
задачи 6.2.12, величины Vi
не зависят от начальной фа-
зы сигналов Si (Г) и опреде-
ляются огибающей (в мо-
мент окончания сигнала Т)
на выходе фильтра, согла- z(t)
сованного с сигналом Si(t).
Поэтому алгоритм (Р.6.11)
можно реализовать и на ба-
зе согласованных фильтров
в соответствии со схемой
рис. Р.6.15. Здесь СФ —
фильтр, согласованный с
сигналом Sj(O; Д — детек-
тор огибающей.
6.4.2. Указание к реше-
нию. Учтите монотонный ха-
рактер зависимости функ-
ции 1п/0(лг) от аргумента х.
6.4.3. Как показано в решении
задачи 6.2.12,
Vi
i Т ~ \2
+1 J z (/) Sj (/) dt j .
\о /
Если шум в канале отсутствует и передается символ bi, то
z(t) =k cosQsi(t)—k sin§i(t) и Vi=kyE.
В этом случае
lit Т \2
V}= у ( j‘/,cos0si (t)Sj(t)di — j* fcsinO st(t)Sj(f)dt j +
+ / j* & cos 0 s, (t)Sj(t)di— j* k sin 0 (t)sj(t)di
\o о
Согласно (6.25) наиболее помехоустойчивой является та систе-
ма, для которой при передаче символа значение Vi оказывается
наибольшим, а значения Vj^i — наименьшими. Так как У3-^0, то
минимально возможное значение Vj равно нулю. Нетрудно заме-
тить, что Vj будет равно нулю лишь при выполнении условий
т т
$ Si(t)s3-(t)di=O при i=£j, $ Si(t)sj(t)dt=^ при любых i, /. Но это
о о
есть не что иное, как условия ортогональности в усиленном смыс-
ле (см. § 2.5). Следовательно, в каналах с неопределенной фазой
8—53 225
Рис. Р.6.15. Реализация оптимального приемника при неопределенной
фазе сигнала на основе согласованных фильтров
максимальную помехоустойчивость будет иметь система с актив-
ной паузой и ортогональными в усиленном смысле сигналами.
Определим вероятность ошибки при приеме по алгоритму
bi
Vi Vj. При передаче символа bi
bi
Vt = ]^ (At +ХЕ)2+ (Ai + YE)2-, X — kcosQ, Y = ksinQ-
Vj = Ka/ + A/; At = $N(t)st(t)di; At = /N(t)st(i)dt.
° 9
Величины Ai, Л< имеют гауссовское распределение и нулевые
математические, ожидания. При ортогональных сигналах величины
A,, Aj с различными индексами независимы ,[8], независимы и ве-
личины Л,-, Ai вследствие взаимной ортогональности. Следователь-
но, независимы и величины Vi и Дисперсия величин Ai, Ai
равны NqE['2. Для плотностей вероятности величины Vi и Vj
имеем
wi (Vt) ~ ехр (
1 ” N9E f\
Л
N.B
EN0
\r (^L.\
/ °\ No )'
Вероятность ошибки для двоичной системы, одинаковая при
передаче любой позиции вследствие симметрии канала, опреде-
лится вероятностью невыполнения неравенства Vi>'Vj'-
P=j’^i(Vi)j,a’(b)dVidV/.
0 vi
Интегрируя по Vi, получаем
Q NqE \
Nq ' NqE J \ No J
226
Этот интеграл табличный [4] и равен
Рош = 0,5 ехр (- /г2/2); Zi2 = k* E/No = k* Рв/Рш.
Подставляя сюда числовые данные, получаем Л2 =10, рош=
=0,5ехр(—5) =3,37-10~3.
В канале с точно 'известными параметрами такая же ве-
роятность ошибки будет обеспечена п,ри А2 = 7,6. Следовательно,
незнание фазы сигнала приводит к энергетическому проигрышу
4 = 1,31.
6.4.6. Согласно результату задачи 6.4.2 алгоритм работы опти-
мального приемника m-позиционной системы с активной паузой,
ортогональной в усиленном смысле, при неопределенной фазе мож-
bi
но записать в виде Vi Vj.
ъ)
При передаче символа bi условием правильного приема являет-
ся выполнение системы т—1 неравенств Vi> Vj при всех /#=i. Ве-
роятность выполнения этих неравенств равна вероятности правиль-
ного приема:
ОО
Рпр, т = J^I (l^i)
0
Vt
^w1(Vj)dVj
о
dVt.
Вероятность ошибки, характеризующая помехоустойчивость систе-
мы при неопределенной фазе сигнала,
оо Г V. 1т—1
Poin.m=l-PnP,m = l-J,t2»i(VJ) dVf.
о [о
Подставив сюда плотности вероятности величин Vi и Vj из за-
дачи 6.4.3 и разложив после интегрирования по Vj величину {1—
—ехр[ V2t/(£Wo)]}m-1 по формуле бинома Ньютона, получим
Рош.т= 1- S (- 1)" С-_, -±- ехр - Л2 , Zt2 = E/AZ0.
п=0 п и 1 \ п "г 1 )
Отсюда при т = 2 следует результат, полученный в задаче 6.4.3
для двухпо-зиционной системы.
При больших отношениях сигнал-шум, заменяя обобщенное
распределение Рэлея гауссовским распределением с соответствую-
щими параметрами (см. решение задачи 6.4.8), получаем
Ропьт
1 00
—= f ехР
-оо
X
Wo*
X
(у2 1
---— dVt.
nbe/]
Используя для {1—ехр[—V\/ (N0E)]}m~' формулу бинома Ньюто-
на и ограничиваясь первым членом, находим, что в области малых
ошибок
рОш = 0,5(т—1)ехр (—й2/2) = (т—1)рош,
где рош — вероятность ошибки в двухпозиционной системе.
8* 227
6.4.7. При ОФМ информационный параметр сигнала определя-
ется двумя соседними посылками: (п—1)-й на интервале (О, Г)
и n-й на интервале (Т, 2Т). Поэтому оптимальный алгоритм, най-
денный .в задаче 6.4.2, можно в данном случае записать
тахг
z (0 st (t) dt
2
2Г Т2
J z(t)Si (t)dt
о
i = 1,2,
z/a= fzn-i(O при
U \zn(t) при T</<2T.
Если сигнал (n—1)-й посылки имеет'вид ^C/mcos((Oo/+0), где
0 — случайная начальная фаза, неизвестная на приеме, то систе-
му сигналов при ОФМ можно записать так: Si(t) = C/m со® (<dotf + 0)
при передаче 1 (п—1)-й посылкой (Os^^T),
k Um cos (<оо t + 0) при передаче 0 n-й посылкой
(Т</<2Т)
52 ~ —kUm cos (о)01 + 0) при передаче 1 n-й посылкой
(T^t^2T).
Эти сигналы являются ортогональными в усиленном смысле.
Поэтому с учетом выражения для рош из задачи 6.4.6 получаем
РошоФм=0,5ехр(—Л2), где учтено, что для реализаций сигналов
$i (/) и «2 (0 отношение энергии сигнала к спектральной плотности
шума на интервале 2Т равно удвоенному значению этого же отно-
шения при длительности элемента сигнала Т.
Полезно заметить, что полученное выражение совпадает с вы-
ражением для средней вероятности ошибки в системе ФМ при
учете фазовой нестабильности (см. задачу 6.3.13).
Согласно числовым данным й2 = 4, Рошофм =0,5е-4 = 9,15х
X Ю-3. Для обеспечения такой же вероятности ошибки при прие-
ме сигнала ОФМ в канале с точно известными параметрами (см.
задачу 6.3.10) необходимо иметь h2 = 3,5. Таким образом, переход
от когерентного приема двоичной ОФМ к некогерентному сопро-
вождается энергетическим проигрышем т}='1,14.
6.4.9. Функцию правдоподобия Wi(zlbt) запишем в виде
(2
—
xYt-yYi-^-^ + y2)
т т
где У<= $z(t)st(t)dt; Pj= J z(t)si(t)dt-, x=Acos0, y=kcosQ.
о о
Будем искать максимум функции
lntMzIM= (*2 + «/2)1 +1пЛ1.
No L 2 J
Согласно обобщенному правилу максимального правдоподобия
следует регистрировать символ если для всех j=/=i выполняют-
ся .неравенства
maxlnt0i(z|6i) >maxlnuh (z|&j),
228
где максимум ищется по параметрам х и у. Параметры, обращаю-
щие lnay (z|&?;) в максимум, определяются из условий:
^1па,1(г|6г) = — (Xt-xEi) = Q или x^YilEi-,
дх No
dlaw^bi) =2-(-yi-yEt)^0 или у= -Yt/Et.
ду N9
Найденные значения х и у называют максимально правдопо-
добными оценками этих величин. Учитывая их, получаем
у? I у? JZ?
1п^ (г|^)= +1п^= —1— +1П^.
Ei Nq EiN0
Отсюда оптимальный алгоритм принимает вид шах^ (У2г|/£г). Для
систем с активной паузой (Ei = E) найденный алгоритм сводится
к алгоритму (6.27).
6.4.10. В соответствии с решением задачи 6.4.3 вероятность
ошибки при оптимальном приеме сигналов с двоичной ЧМ в кана-
ле с неопределенной фазой
Рош=0,5 ехр'(—k2E/N0).
Для определения вероятности ошибки в случае замираний
амплитуды сигнала необходимо данное выражение усреднить по
всем значениям k:
Рош= 1 ехр ( —&2£Ж>) (k) dk.
о
Подставляя для Wtfk) обобщенное распределение Рэлея, полу-
чаем i[8]
ехр {— g2ft2/[2 (1-|-</2) + Л2]}
Рош = ---------=-------------11 . <7 = ар/°2-
2+ й2/(1 + 92)
Положив 72 = 5, получим
ехр( — 5Т2/(12+ Л2)
Рош ~ = •
2+ Л2/6
При рош=Ю_4 энергетический проигрыш равен 10 (10 дБ).
6.4.13. Если эффективная полоса пропускания разделительного
фильтра F3=nlT, п>1, а разнос между частотами нажатия и от-
жатия имеет порядок величины F3, то при передаче частоты нажа-
тия амплитуда сигнала на выходе ПФО определяется только поме-
хой в канале и имеет распределение Рэлея:
: / г2 \
Гл / 'О I
—2— ехр----------->
N0Fa 2N0Fa/
О»! Со) =
где N0F3 — дисперсия помехи на выходе фильтра.
9°—53 229
Амплитуда же сигнала на выходе ПФН обусловлена сигналом
и помехой и распределена по обобщенному закону Рэлея:
/ г? 1 7/2 \ . г» ч
----ехр - -У—-от- /0 (,
1 N0Fd 2N0F9 ) °\N0F9)
где Um — амплитуда сигнала на входе приемника. В этих услови-
ях при симметрии канала
Рош =]'“’! (гн) J* w (ro) dr0 dra.
о 'н
1 / \
Интегрируя, получаем рош= —ехр(------------------) •
2 \ i’iNoF^ ]
Обозначив h2 = U2mTI2No и учтя, что F3 = ib]T, получим
Рош=0,5 ехр>(—/г2/2л).
Эта величина больше вероятности ошибки при оптимальном не-
когерентном приеме в
Рош _ ехр (— Л2/2п)
^ош.опт ехр ( — Аа/2)
раз.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 7
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 7.1.
7.1.1. При гауссовском белом шуме функционал отношения
правдоподобия определяется соотношением
I (z|£) = exp
— f г (0 и (t, 0) dt - — 1
No No J
Т
где Е— $u2(t, Q)dt — энергия сигнала. Уравнение правдоподобия
о
(7.5) в этом случае выглядит так:
atlnZ('|fe)] = — f z (0 и (t, &)dt- — = 0.
dk No I ’ ’ No
Решением уравнения будет величина
k = — f г (f) и (t, @) dt,
E 0
которая и представляет собой максимально правдоподобную оцен-
ку коэффициента передачи канала при точно известном сигнале.
Оптимальный измеритель реализуется согласованным фильтром
или коррелятором (рис. Р.7.1).
230
Рис. Р.7.1. Структурная схема оптимального из-
мерителя коэффициента передачи канала при
точно известном сигнале
Так как z(/) = £м(Л 0) имеем
1 т
k = k+ — J n(t)u(t, 0) dt.
& о
Следовательно, ошибка измерения
8 = JL J ti (t) и (t, &)dt.
Е о
При гауссовском шуме с нулевым математическим ожиданием
и спектральной плотностью мощности NQ ошибка распределена
нормально, -имеет нулевое математическое ожидание и дисперсию
D[E]=N0/2E.
Следовательно, полученная оценка является несмещенной
(7И[Е]=0), состоятельной (Р[Е] = Nq/2E-+0 при Т->оо, £~>оо).
Поскольку при Т-+оо D[E}->0 оценка коэффициента передачи ка-
нала является асимптотически эффективной, так как значение
дисперсии ошибки, равное нулю, является минимально возмож-
ным.
7.1.2. Используя (3.13),-можно записать
г 1 т ч
w (z\k) = w (я) =/0^ ехр I — — j* [z (/) — ku(t)]2 dt\ .
( Л о о J
Учитывая, что анализ осуществляется в дискретные моменты ti,
находим
2 *40 + 2 z^kuiti)-
^0Г /=1
1 m
-----!— 2 k2u2(ti).
2N0F £
Составим уравнение правдоподобия:
Отсюда
k = 2 * (О и (tt) I 2 u2 (ti).
1=1 I 1=1
7.1.3. Указание к решению. Принять интервал между отсчетами
\t = Q,^IF и воспользоваться результатом задачи 7.1.2.
7.1.6. При неопределенной фазе сигнала функционал отношения
правдоподобия
Z (г|fc) = ехр (— k* E/No) Zo (2 k V/NJ,
9°*
231
где
i2
z (t) и (0 dt +
J z (t) 'll (t) dt 2
0
Составим уравнение правдоподобия по (7.4):
= ,/2» \ + , mi ехр (- _ о
дк I \ Л'. ) Н, 1 N, Л \ Л> )
так как din (х)/дх=Ц (х).
Отсюда ^=Vh(2^V/NQ)/EI^2^V/NQ).
Структурная схема измерителя (рис. Р.7.2) содержит согласо-
ванный фильтр, детектор огибающей, блоки, выполняющие опера-
ции умножения и деления, нелинейные операции г/1=Л(х), у2 =
= /о(х), вычитания. Оптимальная оценка амплитуды соответствует
тому значению ’множителя й, при котором на выходе вычитающего
устройства достигается нулевое значение напряжения.
7.1.7. Указание к решению. Представить огибающую
S г (tt) и &)
f=l
m "12
7.1.8. Указание к решению. Использовать оценку #, получен-
ную в решении задачи 7.1.6. Учесть, что при больших значениях
отношения сигнал-шум Л(х)^7о(х), 2kV/No'^>l, а обобщенное
распределение Рэлея удовлетворительно аппроксимируется гаус-
совским законом [40]:
w (V) = ~^= ехр [ - (V - k E)2/EN0].
у л ENq
7.1.9. При неопределенной фазе сигнала функционал отношения
правдоподобия можно записать в виде
Z(z/<p) = exp
Ио
т
cos qp J* z (0 и (/) dt —
о
Т
— sin ф j z (f) и (f) dt
о
k‘* Е]
Wo J ’
Рис. P.7.2. Струк-
турная схема on*
-тимального изме-
рителя коэффици-
ента передачи ка-
нала при неопре-
деленной фазе сиг-
нала
232
поскольку принимаемый сигнал s(t) =k cos yu(t)—ksinq>U(t). Сос-
тавим уравнение правдоподобия
d[lnZ(z|(p)]/dcp = O.
После дифференцирования получаем
— — sin <р Г z (t) и (t) dt = — cos ф J* z (/) и (t) dt
Wo о ^0 0
ИЛ1И
tg$= -У1/У2,
где
= j* z (0^(0 //2 (0 = p (0 u (0 dt.
о 0
Видно, что
уг = — kE sin ф + An y2 = kE cos ф + An
где ф — истинное значение фазы;
Л1 = р (Z) n (t) dt, Ai = j* и (/) n (t) dt,
о 0
tg Ф = tg Ф (1 — Ai/^F sin ф)/( 1 — AJkE cos ф).
В области больших значений отношения сигнал-шум, исклю-
чая пока из рассмотрения значения ф = &л/2 (& = 0, 1, 2, ...), можно
написать
tg ф = tg ф (1 — Aj/ftf sin ф)/( 1 — X-JkE cos ф) = tg ф — 82/cos2 ф,
где е= l/^E(Ai созф+Л1 sinq)). Величину tgcp—е2соз2ф можно счи-
тать первыми двумя членами разложения в ряд Тейлора функции
tg’(<p=<p—е) по малым приращениям е. Таким образом, в области
больших значений отношения сигнал-шум ф»ф—8*. Случайная
величина е имеет гауссовское распределение с нулевым математи-
ческим ожиданием и дисперсией е2 = Ао/2^2£'. Это означает, что
полученная оценка несмещенная, состоятельна и асимптотически
эффективна.
7.1.11. При равномерном распределении оцениваемого парамет-
ра алгоритм оценки, максимизирующий апостериорную вероят-
ность, не отличается от алгоритма, полученного по критерию мак-
симального правдоподобия. Функционал отношения правде подо-
бия
/[г(/)|ф, т] = ехрГ-^- ^z(f)a(t — т)соз(со/+ф)Л—
|_ Wo т Nо j
* Этот результат справедлив и для углов ф=£л/2.
233
V (т)=k у J "z (t) а (/—т) cos со tdt
Усредняя по фазе <р, которая считается распределенной равномер-
но, получаем для функционала отношения правдоподобия
/[г(/)|т]=К/о{2У(т)|/Уо],
где /С=ехр(—ktEINo),
' х+ти Т*
+ j* z(t)a(t— т)sinсо/Л .
Величина V(t) пропорциональна значению огибающей напря-
жения на выходе -фильтра, согласованного с сигналом в момент
/=т+ти, т. е. в момент окончания импульса сигнала на выходе
фильтра. Но к .моменту окончания сигнала на входе оптимально-
го фильтра напряжение на его выходе (при времени задержки
^о=ти) достигает максимума. Поскольку /о(х) — монотонная
функция от х, то при изменениях т максимум l[z(t) |т] совпадает
с максимумом 1/(т). Следовательно, оптимальная оценка времени
прихода т определяется моментом, при которо-м на выходе детек-
тора, подключенного к согласованному фильтру (рис. Р.7-3,а),
напряжение достигает максимума (рис. Р.7.3,б). Если этот мак-
симум достигается в момент £маКс, то т=/Макс—ти. Апостериорная
вероятность параметра т при неопределенной фазе
P(t|z)=^/o[2V(t)/#o]
(Ki определяется из условия нормировки).
При больших значениях отношения сигнал-шум У(т) велико,
и можно воспользоваться асимптотикой для /о'(х) =ех.р (х)/]/*2лх
[4]. Поскольку при изменениях т показатель экспоненты
ехр(2У(т)/Л^о] меняется несравненно быстрее, чем выражение, стоя-
щее в знаменателе, то можно написать
р (т I z) = к 2 ex.pi [ 2 V (т) \/N0 ]
(К.2 определяется из условия нормировки). Функция У(т) явля-
ется огибающей по <р функции
х+ти
|(т, <р)= J z(f)a(t — т) cos (со / + ф) d/,
т
где z(t) =a(t—To)cos(.(o/ + <po)/i(/—т) +n(t) (то, фо — истинные зна-
чения параметров т и ф сигнала на входе измерителя). В области
а)
Рис. Р.7.3. Оптимальный
измеритель времени при-
хода сигнала с неопреде-
ленной фазой (а) и от-
клик (б)
234
больших значений отношения сигнал-шум можно при определении
функции £(т, ср) пренебречь шумовым слагаемым в z(Z):
т+ти
g (т, <р) = J* a (t — т0) a (t — т) cos (со t + <р0) cos (со t + ф) h (t — т) dt.
На практике обычно выполняется условие соти^>1. Но тогда
можно в §(т, ф) положить ф0=0 и привести эту функцию -к виду
[ т+ти
£(т, ф)= 0,5 J* a(t — т0)а(/ — n)dt со$ф.
Следовательно, огибающая по ср
V (т) = 0,5 J a(t - т0) a (t - т) dt.
При большом значении отношения сигнал-шум погрешность изме-
рения т мала, р(т|г) имеет существенное значение лишь в облас-
ти, где т близко к то, т. е. при малых значениях разности Дт=т—
—то. Поэтому можно воспользоваться тремя первыми членами
разложения в ряд Тейлора: a(t—x)=a(t—т0)+я' (/—т0)Ат+
4-0,5а"(£—то)Дт2. Подставив a(t—т) под знак интеграла и выпол-
нив интегрирование по частям, получим [3]
V (т) = Е - 0,25 (Дт)2 /и[а' (t - т)]2 dt,
т
р(т|г) = К2ехр[ — 0,5 (т —т0)2/Р2], 02 = ЛГо / +^a[da(t — T)/dT]2dt.
I %
Условие нормировки дает /С2=!1/}/Г2лр2. Более правильный
результат для апостериорной вероятности
р СПZ) = ехр [ - 0,5 (т - Та)2/р2],
где тн — наивероятнейшее значение т, соответствующее максиму-
му кривой р(т|г). Его можно получить, если не пренебречь шумовой
компонентой n(t) в z(t) при вычислении §(т, ф), как это сделано
выше.
Из полученного результата следует, что при больших значениях
отношения сигнал-шум оценка времени прихода т несмещенная
(Л1[т]=тн), а дисперсия ошибки
D[x] = ^ = NqI
/ —оо
где |S(/(o) | — модуль комплексного спектра огибающей. Энергия
сигнала £ = 0,5 $a2(t)di = 0,5 ]*|5(j<о)|2df, поэтому
—оо —оо
£»[т] = Nj2Ev\ v2= J®2|S(/®)|2df / J|S(/®)|2df.
235
V (/) = k "I' j* г (/) cos со t dt
* о
Очевидно, lim D[t]=0 и, следовательно, полученная оценка
Т->оо(Е->ао)
является состоятельной и асимштотически эффективной.
7.1.12. Апостериорная вероятность частоты сигнала определя-
ется формулой P(f\z)=KiIo[2V(f)/No], а
2“
J* г (/) sin (dtdi —
_о
это огибающая по f колебания
5 (/, ф) = j* 2 (/) k cos (со t + <р) dt.
о
Величина V(/) для каждого значения частоты f пропорцио-
нальна значению огибающей (в момент t = T) колебания на вы-
ходе фильтра, согласованного с прямоугольным радиоимпульсом
$(/)=£ cos (со/+ф) с точностью до фазы ф. Так как структура сог-
ласованного фильтра зависит от частоты /=0,5со/л сигнала, то,
строго говоря, для оптимальной оценки частоты (т. е. выбора ве-
личины f, которая соответствует максимуму V(f)) следовало бы
располагать бесконечным набором таких фильтров для области
ЧаСТОТ ОТ /мин ДО /макс *•
На практике .вместо бесконечного набора фильтров можно ис-
пользовать п= (/макс—/мин)/А/ фильтров, где А/ — величина, мень-
шая ширины основной части спектра сигнала. По точкам функции
P(fk\z) (6=1, 2, 3, ...) можно более или менее точно построить
непрерывную (по /) кривую P(f\z). Структурная схема п-каналь-
ного измерителя частоты показана на рис. Р.7.4.
В области больших значений отношения сигнал-шум апостери-
орную вероятность можно определить так: Р(/|г) =^2ехр[—2У(/)/
Л/о]. При большом значении отношения сигнал-шум можно при
нахождении ]/(/) также считать z(t) =£cosсоо/, соо — истинное
значение частоты сигнала. Тогда
т
I (ft ф) = £2 J* cos со01 cos (со t + ф) dt =
о
т т
= cos ф J k2 cos со t cos соо tdt — sin ф J k2 cos co01 sin co t dt
о 0
и огибающая
V (/) = 1/ I k2 j cos coo/ cos co t dt I + [ k2 J cos coo t sin co t dt
При выполнении условий (/—/о)Г<С1, учитывая при-
ближения cosAco/^l—(Aco/)2/2, sin Дсо/«Асо/, получим
V(f)=E—0,5ft(со—coo)2, b=ET2/12.
* Если реализация z(t) может быть записана и сохранена на долгое время,
то вместо набора фильтров можно использовать один фильтр с перестраивае-
мой средней частотой / полосы пропускания.
236
Рис. Р.7.4. Структурная схема
оптимального измерителя час-
тоты сигнала с неопределен-
ной фазой
Апостериорная вероятность
Р (f Iг) = Язехр [— (со=®о) 2ЕТ2/12А0] •
Из 'полученного результата следует, что щри больших значениях
отношения сигнал-шум оптимальная оценка частоты несмещенная
(Af[f]=fo), а ее дисперсия D[f]=6N0/ET2. Полученная оценка
состоятельна ( lim £>[)] =0) и асимптотически эффективна.
Т->оо
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 7.2.
7.2.2. Оценки максимального правдоподобия координат Лг-, по-
лученные при анализе смеси z(t)=s(k, минимизируют
т
функционал d= j*[z(£)—s(X, t)]2dt, т. e. определяются из соотно-
о
шений (уравнений) правдоподобия
^-= —2 /[2(0 —0]-^— {s(b, t)}di=O. (Р.7.1)
vAj 0 и Aj
Если под действием слабой помехи n(t) принимаемое колеба-
ние z(t) получит приращение &z(t) =n(t), то координаты сообще-
ния на выходе приемника (детектора) получат приращения ДХ<.
Этим приращениям координат соответствует приращение каналь-
ного сигнала
Д«(Д1, 0 = S &(х’ ° ДЯ<- (Р.7.2)
1=1 dki
Средний квадрат отклонения колебания z(t)+Az(t) от сигнала
$(Х, 0+Д$(Д1, t) в пространстве Гильберта
т
d = J [z (0 + Д z (0 - s (X, 0 - Д s (ДХ, /)]2 dt. (Р.7.3)
о
Если оптимальные оценки координат удовлетворяют уравнению
Правдоподобия dd/dki=O, то из (Р.7.3) с учетом (Р.7.1) и (Р.7.2)
получаем
। Т д 1 Т а
V J «(0-^- [s(X, t)]dt= s дх^у OJX
1 о 1=1 1 о
х [s(X, (Р.1АУ
237
Если d[s(X. t)]/dXi с неодинаковыми индексами ортогональны
(что имеет место для всех анализируемых систем модуляции), то
из (Р.7.4) следует
A*i = vf 0]n(0^)/[^-[s(X, 0]f-
1 q v. u Ai J / [ О Л i j
Таким образом, величины AXf на выходе оптимального прием-
ника распределены по гауссовскому закону (при гауссовском рас-
пределении помехи п(0), не коррелированы при различных i
(вследствие взаимной ортогональности сигналов [s(X, /)])»
д hi
имеют нулевые математические ожидания и дисперсии:
X [s (X, 01 77- [s (X, 0)1 п (0 п (0) dtdtr.
и Ai
Так как п(0«(0) = (0 0) = О,5У\^о6 (0 —0, то с учетом фильтру-
ющего свойства d-функции находим
О2 = ДХ2 =о,5Уо
Так как при любых видах модуляции
{-A- [s(X, 01}2 = {-f- [s (X,/)]}’ ,
v 0A%i—1 О A%i J
то коэффициенты при синусах и косинусах одинакового аргумен-
та имеют одинаковые дисперсии: o22i-i = o22i.
В этих условиях е(/) =5АХ<ф<(0 представляет собой стацио-
i
парный гауссовский шум с нулевым математическим ожиданием
и средней мощностью (дисперсией) на частоте f=i!T, равной
o2(f)=2o22i_1 = 2(j22i.
Поскольку спектральные компоненты ряда Фурье сдвинуты по
частоте на Af=l/T, получаем
сВыхЮ=оч/)/а/=^о/{^чГ(х?о]У .
7.2.3. Для прямых систем модуляции с учетом ортогонального
разложения в ряд по функциям, заданным в задаче 7.2.1, находим
{^7 is (»т, ед}’ - {A (S (»и, о, -
'0 ) I 00 О Ai J
= ^{S [МО. /]}2 ФИО-
00
238
Частотный
д 2
спектр функции
лежит значительно выше
удвоенной верхней частоты спектра сообщения b(t) (функции
Ф2вс(0)- Так ка.к функции с неперекрывающимися спектрами ор-
тогональны, среднее значение их произведений равно произведе-
нию их средних значений. С учетом ортонор-мированности функций
Ф<(/) имеем
{ту- [S (Ь (0, /)] Г = М- [s (д (0, /)]) ф? (О =
ч О Л,} J ч ии J
-{^ [«(»(/). О!}1.
Подставляя это соотношение в формулу (7.10), получаем
бвых(/) = м> / .
7.2.6. Сигнал ОМ. в месте приема можно записать в виде
s (/) = kUmb (/)ооб (W+фо) —kVmb (/) sin (W+фо),
1 00
где b(t) — — Г b(t)/(t—x)dx — сигнал, сопряженный сообщению
Л **
— оо
b(t) *. Отсюда следует, что однополосную модуляцию нельзя стро-
го считать прямой.
Если записать
ь (t) = % Ki-i V2 sin (21 - 1) + %2I- /2 cos 2 i 1,
— oo < / < oo,
TO
~ Bc r— 2л
b(t)= s Ki-iV2COS(2i-l)^t-
i=i 1
— Kt V2 sin 2i t, — oo <2 t < oo.
Тогда
s(t) = kUm
2 Ki V2 cos (<i)ot + <po — 2i^- Л +
i=l V T J
+ S Ki-1 V2sin Г(2i — 1) / + (00/-ф0
i=i L T
* Фактически сообщение финитно и определено лишь на интервале одно-
го периода, а его преобразование Гильберта, строго говоря, отлично от напи-
санного.
239
= O,5No/Tk2U2m.
Дисперсия координаты шума на выходе оптимального прием-
ника
o2 = Alf = #о/2Т
7.2.8 Указание к решению. Ввести обозначение v(/) = $b(t)dt=
=2Хг J и учесть, что [J фг(/)б//]2= l/(02f.
7.2.11. Указание к решению. Принять опорное колебание синх-
ронного детектора
•Sno'(/) = 2 COS ((Оо/+ фо) •
7.2.12. Средняя мощность шума (дисперсия шума) на выходе
приемника с учетом решения задачи 7.2.6.
Рш.вых = Bco2i = 2Fc7o2i=N^k2 U2m.
Таким образом,
pBbIx = 62£/2m/n2WoFc.
Средняя мощность сигнала ОМ (см. задачу 7.2.6) Рс.вх =
_________ _____ ____ т
—k2U2mb2(t) = k2U2m/H21 поскольку &2(/)=52(/), a J*
о ____
Xsin(2coo/ + (p)d/ пренебрежимо мал по сравнению с b2(t). По-
этому pBX = k2U2m/n2N0FQ> так как при ОМ F=FC. Следовательно,
^ОМ = Рвых|/рвх= 1, § 0М=1«
7.2.17. Система АИМ относится к прямым системам модуля-
ции. В качестве переносчика в этой системе используется импульс-
ная последовательность (рис. Р.1.2,а), которую при отсутствии
модуляции на интервале длительности сообщения можно записать
0,5Г/Ги
f(t)= 2 F(t—iTB), где F(t) определяет форму импульса, а Ти==
(=-о,5г/ти •
= 0,5/'FH<C0,5//7c — период следования импульсов. Сигнал АИМ в
месте приема (рис. Р. 1.2,6) можно записать
s[b(t), t]=kb (/)№).
Средняя мощность этого сигнала
^с.вх={HROT2 = & k2 но/п2, а
(-^-{s [&(о, m .
\ ub )
Согласно (7.11)
= F_ kaf4t) IP = ~ 1 1 • *' =1
&АИМ p ’TV'/Ta P />'Z т F ’ ^аим
г c H k2 f2 (/) с ти c
240
7.2.18. Система ФИМ относится к прямым системам модуля-
ции, а сигнал ФИМ (,рис. Р.1.3) можно записать в виде
0.5 т/ти
s (0 = k S F (ti),
/=-0,5 Т/Ти
где ti = t—ГТц+МмаксЬ (1ТЯ) определяет временное положение мо-
дулируемого импульса; Д1макс6(/7’и) — мгновенное значение вре-
менного сдвига импульса от среднего положения; Д/Макс — макси-
мальное отклонение импульса, соответствующее &макс(/) = 1. Ве-
личина
*2 0*
ПЛ <4 __
Л,вх=[з(0]2= — Г F*(t)dt.
ТИ —0,5 т.,
и
Определим функцию — [$(0]:
— [s(/)] = = Д /макс k
db v ’ dtt db мак0
О15'/Г" dF(tl)
:=-0,5Т/Ти dti
I д F (t-) i2 I d F (i) I2
Так как при ФИМ у. I = I —j > число импульсов на
интервале Т равно Т/Ти и они не перекрываются, то можно запи-
сать
= Л^акс^7-
7 и
I OD )
0,5 Ти ГЛ Р (f\ "12
Г ^-^-1 dt.
-О.5ТИ L dt ]
С учетом этого результата находим
£фим —
Здесь
1 М/максу F . 1
П2Кф \ ТИ } Fc ’ ЬфИМ П2Яф
(Д /макс/^и)2.
коэффициент, определяемый формой импульса. Для обычно ис-
пользуемых импульсов плавной формы Лф«0,1, Fa 1/-ти. По-
скольку
А *макс < 0,5 Тв = 0,5/F„ < 0,25/Fc, то ( ^«Л2 А (2_\2.
\ ти ) 16 \Fc )
•Предельные значения выигрыша и обобщенного выигрыша при
ФИМ
0,6 t_F_\*' ' ~ 0,6 /_Р_Г
ёФИМ ла j , ёфИМ П2 \рс )
241
Рис. Р.7.5. Зависимость вы-
игрыша системы модуляции
от отношения сигнал-шум в
канале для идеальной
(-------) и для реальной
(-----) систем
О 10 20 50 40 50 60
7.2.19. Указание к решению. Принять__пик-фактор пром ежу точ-
ного сигнала при ЧМ и ФМ равным ПР'И AM — У2(1 +/и)/
У 2 +т2, при ОМ — П, при БМ — У 2П. Учесть, что на второй
ступени во всех системах осуществляется прямая модуляция.
7.2.20. Для идеальной системы связи при гауссовском источ-
нике и канале согласно) [7] выигрыш
g = 1(1 +Рвх)]а- 1]/РвХ.
Зависимость g(pBX) при некоторых значениях коэффициента
<i=F/Fc дана на рис. Р.7.5. Для всех рассмотренных нами ре-
альных систем модуляции при слабом шуме g=go не зависит от
рвх (непрерывные линии на рис. Р.7.5). Предельные минимально
возможные значения порога рПОр при заданном КР 'можно опреде-
лить как точки пересечения непрерывных и штриховых кривых
рис. Р.7.5 или из уравнения
[(1+РдОр) 1]/РпОр = й+
Для системы ОМ (без частотной избыточности, а=1) это со-
отношение удовлетворяется при любом значении рп0Р (в том чис-
ле при рПор = 0), т. е. для этой системы пороговый эффект отсутст-
вует. Для системы БМ а=2, go = 2, рпор=0.
При а^>1 (системы с большой частотной избыточностью) сле-
дует величина порога
Л Л fa
Рпор ~ g$ •
Отсюда видно, что с ростом частотной избыточности системы па-
дает порог, стремясь к 1 при а->-оо.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 7.3.
7.3.1. Коэффициент передачи оптимального фильтра
f/F при 0<7^Z
О при f>F
Согласно [12] энергетические спектры в полосе (О, F) равны:
для сигнала ошибки Ge(f) =Л (f/F—f2/F2), для полезного сигнала
Gys(f) = Af3/F3, для шума Gyn(f) =A(f2/F2—f3/F3).
242
Средняя мощность сигнала ошибки
= f G*(f) df = AF/6.
о
Средняя мощность полезного сигнала
£* = J Gya(f)df = AF/4.
о
Средняя мощность шума
У* = f GUn(f)df = AFl\2-, рвых = 3.
о
7.3.2. В полосе (О, F) энергетический спектр сигнала ошибки
Ge (f) = Ga (f) [К (о) - Ip + Gn (f) К2 (ш) = (Ко - 1) Af/F+
+ K*A(l-f/F).
Дисперсия сигнала ошибки
?= 0,5 AF [(Ко- 1)2 + Ко].
При /Со = 0,5 e2=AF/4 (это минимальное значение), что в
1,5 раза больше, чем для оптимального фильтра. Легко показать,
что рвых = У2з/у2п= 1- Эта величина в 3 раза меньше, чем для опти-
мального фильтра.
7.3.4. Пусть на входе заданной схемы действует напряжение с
комплексной амлитудой а на выходе tf2. Тогда передаточная
функция
кР (/ ®)=U./U.=((/, - и2) н а ^/и1=н а и)-н а о») fp а .
Отсюда
Н а со) = Fp (/ со)/[ 1 - Fp (/ (О)].
7.3.6. Указание к решению. Воспользоваться методикой реше-
ния задачи 7.3.4 для определения коэффициента передачи задан-
ной схемы.
7.3.7. Пусть S (/) — гауссовский случайный стационарный про-
цесс с корреляционной функцией B(ti, /2)=/>сехр(—a\t2—Л|), а
N (/)—стационарный белый шум со спектральной плотностью
Afo/2. Процесс 3(/) можно задать дифференциальным уравнением
1-го порядка [12]
dS/dt + ^S(t) = V2aPcV(t)t S(-oo) = 0.
Здесь V(/) —центрированный белый шум с единичной спектраль-
ной плотностью мощности.
Энергетический спектр
G (/)= - 2осРс--.
' а2 + 4л3/2
243
Сравнивая уравнение состояния для S(t) с (7.20), находим
g(f) = V2^:
В установившемся режиме уравнение (7.23) примет вид
0= — 2ак —к2-2/У0 + 2аРс.
Решая это квадратное уравнение, получаем
к = а(Уо/2) (/Т+Л- 1) = 0,5аNog(/),
где Л = 4Рс/аЛГ0.
С учетом полученного результата уравнение (7.20) принимает вид
dS/dt = - aS (t) + а (/Г+Л - 1) [z (t) - S (/)].
7.3.8. Указание к решению. Воспользоваться уравнением (7.23),
положив его левую часть равной нулю в установившемся ре-
жиме.
7.3.14. Пусть линейный фильтр имеет комплексный коэффици-
ент передачи /С(/со) =/С((о)ехр [/ср (со)]. При подаче на вход тако-
го фильтра сигнала $(/) известной формы с комплексным спект-
ром S(/(d)=S(co) ехр [/0(со)] для отклика фильтра получим
«вых (0 = (®) К (®) ехР {/ fat + 0 (со) + <р (со)]} df.
—оо
Если спектральная плотность белого шума на входе фильтра
¥0/2, то средняя мощность шума на выходе
Лп.вых = 0,5^0 ]K*(a))df.
— со
Предполагая, что пик полезного сигнала на выходе наблюда-
ется в некоторый момент /0, запишем
5вых (4) = J-S (®) К (ю) ехр {/ [co t0 + 0 (со) + ф (со)j} df.
—оо
Отношение пиковой мощности сигнала и средней мощности
шума
г2 15ВЫХ (Ml2 оо р (со) К (со) ехр {/ [со /0 + 0 (со) + <p (со)]} df —оо 2
г - р оо
ш.вых 0,5
—оо
Найдем максимум этой величины. Для этого воспользуемся
неравенством Буняковского — Шварца [12]:
?М*)М*) JlfiWPdr 1/ JU(*)№
—оо Г —оо * —оо
причем равенство достигается при f2(x) =afi(x), а — постоянная.
244 .
Примем/i(x) =S(co) ехр {/[а>о/+0(ы)+<р(®)]}, f2(x) = К(®). С
учетом неравенства Буняковского — Шварца имеем
/v0 —оо
оо
где j* S2 (<a)df=E=PsT— энергия сигнала. Поэтому
— 00
г» < 2E/N0 - 2РС T/No = г2акс, г2акс = 2Л’ = 2ри FT.
Величина г2 достигает максимума при f2 (х) =aft (х) или при
/С(/<д) =aS(®) ехр {/[(о/о + 0(со)+ф(«>)]}. Но это возможно лишь
при Ко(а>) =aS(i©) и ®/о+0(®)+фо(®)=О, т. е. при <ро(<о) =
= ——0(<в). Это означает, что комплексный коэффициент пере-
дачи оптимального фильтра
Ко (j a) = aS (со) ехр { - / [со t0 + 0 (о)]} = aS (—j со) ехр (— j <л t0),
где S(—/и)—комплексно-сопряженный спектр сигнала £(/).
Фильтр с таким комплексным коэффициентом передачи называют
согласованным с сигналом s(/) (см. § 6.2).
7.3.15. Комплексный спектр заданного сигнала
S(j<d) = k "f иехр( —/cof)df = — [1 — exp( — /<оти)1.
д
Коэффициент передачи согласованного фильтра
v /• \ с/ • \ I ak Г /<о(т+Д) /соД"I —jat,,
^с.ф(/®) = а5(-/®)ехр(-/©/0) = — е и -е |е °.
Потребуем /о=ти + А или получения пикового значения сигнала на
выходе фильтра в момент окончания входного сигнала (если А
меняется в пределах (О, Т—ти), то to меняется в пределах (ти, Т).
Тогда
W/®) = —[1-е~'“Ти].
/ со L J
Фильтр с такой передаточной функцией реализуется схемой
рис. 7.5,6.
Согласно решению задачи 7.1.1 максимально правдоподобная
оценка амплитуды видеоимпульса на фоне белого шума пропор-
циональна величине
Д-|-^и
K = k f
А
которая определяется напряжением на выходе согласованного
фильтра в момент ,tQ окончания сигнала на входе. Согласно свой-
ству согласованного фильтра в этот момент его выходное напря-
жение максимально. Следовательно, по максимуму этого напряже-
ния можно получить оптимальную оценку амплитуды независимо
от значения задержки А.
245
Оптимальная оценка положения фронта видеоимпульса должна
максимизировать величину
9Ь д+ти
J* Ь
#0 Д М)
Для любого значения k величина К\ максимизируется, если
д+ти
максимально j z(\t)dt. По моменту наблюдения максимума
д
этой величины /Макс можно найти оптимальную оценку А =
= ^макс—ти. Параметр г2 на выходе согласованного фильтра равен
г2 = 2Л2 = 2Рсти/^ = 262ти^0.
7.3.17. Указание к решению. Для решения задачи воспользо-
ваться теоремой об огибающей.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 8
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 8.1.
8.1.1. Согласно решению задачи 6.4.3 в заданных условиях
рош = 0,5ехр(—0,5А2). Если требуется обеспечить рОш^Ю-5, то в
системе без переприема (6=1) необходимо иметь h2 =—21п(2р) =
= 21,6. При использовании k ретрансляторов на каждом из них
необходимо обеспечить Р1^рОш/6 или h2 =—2 1п(2рош/6). Таким об-
разом, при 6=10 62 =—2 In (2-10-6) =26,2; при £=100 62 =
= — 2 In (2-10-7) =30,8; при 6=1000 h2 = — 2ln(2-10"8) =35.5.
8.1.4. Согласно (8.4) имеем PB/PR = 3(L—1)2/П2 = 3(128—
—1)2/3=16129 или 42,07 дБ.
8.1.5. Воспользовавшись соотношением (8.4), получим
Рв/Рв = 3 (2п - 1 )2/П2 = (28 - 1 )2/3 = 21675 или 43,4 дБ.
8.1.8. Воспользуемся соотношением (8.6). Легко заметить, что
сумма в этом выражении есть не что иное, как сумма первых чле-
нов геометрической прогрессии, знаменатель которой q = 4, а пер-
вый член равен 1. С учетом этого, приняв во внимание (8.4), на-
ходим
-у~ 4 4"-1 4 4п —1
= п-----------------= — л--------------.
ли (2п — 1)2 3 3 4« _ 2"+1 + 1
При р = 10~5 е2л.и= 1,35-10~5; при р = 10~6 е2л.и= 1,35-10-6; при
р = Ю-7 72Ги= 1,35-10-7.
8.1.10. Согласно (8.2) с учетом (8.4) находим е2 = 1/3(27—1)2 =
= 2,07-10-5. При р=10~5 и п = 7 е2л.и= 1,35-10-5 (см. решение за-
дачи 8.1.8). Суммарная мощность шума квантования и шума лож-
ных импульсов согласно (8.7) 822 =3,42-10-5. Полезно заметить,
246
что с уменьшением вероятности ошибки р влияние шума ложных
импульсов становится пренебрежимо малым. Величина отноше-
ния
Рв/Р82 = 1 /Па ф= 10в/3,42 • 3 « 9746.
8.1.12. При ширине спектра сообщения Рс минимальная частота
дискретизации согласно теореме Котельникова равна 2ЕС. Каждый
отсчет после квантования может принимать £ = 2ВМакс/А&+1 воз-
можных дискретных значений и заменяется при кодировании ком-
бинацией из n = logm/L /п-ичных импульсов. Длительность каждого
импульса не может быть больше, чем ти = 1/(2FClogm7<), а необхо-
димая полоса определяется как 1/ти = 2Ес logmL. При т=2
F'=2Fclog2L. Для заданного значения Ёс=3,1 кГц F'=6,21og2L
кГц.
8.1.15. Из заданного выражения для вероятности ошибки на-
ходим рвх = 21п(1/2р). Если допустить, что система ИКМ использу-
ется для передачи речевых сообщений, то ошибочный прием сим-
волов кодовой комбинации приводит к появлению отдельных
«щелчков». Если ошибок много, то отдельные «щелчки» переходят
в сильный шум. В системе ИКМ за одну минуту передается
2Есп-60 кодовых импульсов. При вероятности ошибки р на k рет-
рансляционных участках будет в минуту в среднем pk-120Fcn
ошибочно принимаемых импульсов. Если считать допустимым при
работе системы ИКМ один «щелчок» в минуту, то рдоп =
= 1/(120 knFc) и рвх = 21п(60 knFc).
8.1.16. Если примерно считать, что для телефонии с ИКМ FK —
=2nFc=2-7-3000 = 42000 Гц, то рвх = 2 In(60-42000k) «4,6 Ink +
+ 29,4. Если k=l, то ipBx«29,4. При пренебрежении ошибками на
выходе следует учитывать только шум квантования. В этом слу-
чае рВых = Рв/е2«5400 (согласно (8.4)). Выигрыш £икм-чм =
= 5400/29,4« 170, а обобщенный выигрыш ^'икм-чм =g/2n« 12.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 9
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 9.1.
9.1.1. Представим групповой сигнал согласно (9.1):
N 2N N
s(0=SM0~ 2 М0 = S^(0(Cfe-C^).
Легко заметить, что при Ck = Ck+N=/=0 s(t)=O.
Это означает, что при использовании сигналов биортогональ-
ной системы в качестве канальных переносчиков информации в
многоканальной системе связи нельзя осуществить однозначное
разделение сигналов. Этот вывод подтверждается и при проверке
условия (9.2).
247
В самом деле, для биортогональной системы
Грама
определитель
D =
Рп Р12 . . Pl.W “pl.tf-H — pl, W-i-2 . . . — Pl, 2N
Р21 Р22 . . Р2, N — P2, AH-l — P2, AH-2 . . . — P2, 2N
Pn, 1 PN, 2 . . . PN.N — P7V, АЧ-1 — Pn, N+2- . . ~ ptf, 2N
’ P27V, 1 Р2АГ, 2 . . . “P2W, N P2jV,JV4-l P2N, N4-2 . . . P2JV, 2JV
Легко показать, что линейным сложением элементов отдель-
ных строк или столбцов (что не изменяет величину определителя)
можно получить матрицу с нулевыми элементами по какой-либо
строке или столбцу, что приводит к результату D=0.
9.1.2. Для системы ортогональных функций {$л(0} определи-
тель Грама принимает вид
Pll 0 0 .. 0
0 P22 0 . .. 0 ^“P11P22 •• PNN
0 0 0 . .. pNN
1 т
Величина pkk=—^Sk(t)Sk(t)dt = Ek — энергия сигнала sh(t).
Т о
Если энергия хотя бы одной реализации Sk(t) будет равна ну-
лю, то определитель Грама О = рцр22... pjv№=0 и условие линейной
независимости не выполняется.
9.1.3. Составим определитель Грама. В данном случае
0,5а2 0,5 ах а2 cos Дф
0,5 а± а2 cos Дф 0,5 al
= 0,25 aj а2 (1 — cos2 Дф).
Замечаем, что £>—0 только при условии сов2Дф>=1 или при Дф=
=ikn(k = Q, 1, 2, ...).
Следовательно, однозначное разделение сигналов Si(t) и sz(f)
возможно при любых значениях Дф, кроме Дф=&гс.
9.1.4. Найдем опорные сигналы {т]л(/)}. Согласно (9.4) должны
выполняться следующие условия:
1 т . т
7 М (0 Th (0 -J- J s2 (/) П1 (0 d/==0;
1 о 1 о
1 Т 1 т
v J % (0 Th (0 Л-0, -у р2 (0 «2 (О Л=0,
1 о 1 о
т. е. опорный сигнал тр (0 ортогонален сигналу $2(0» а опорный
сигнал т)2 (0 ортогонален сигналу si (/). Так как ортогональность
248
можно обеспечить сдвигом сигналов тн(О и Sk(t) (i^=k) на угол
л/2, получим
т]х (0 = ~cos (®о t + Фо + Дф “ я'/2) •
sin Д<р
Яа (0 = cos Z + Фо + л/2)>
sinAcp
где Ai и А2 — постоянные коэффициенты.
Масштабные множители Xi/sin Аср и Дг/зшДф определяются из
условия (9.3).
При Дф = л/2 т)1 (t) =XiCOs((Oo^+<Po), Л2(0 =Л2соз((Оо^+фо+л;/2).
В этом случае опорные сигналы совпадают по фазе с сигналами
индивидуальных каналов.
9.1.5. Для данного случая определитель Грама
0,5 a1 a2cos Дфх
0,5 a2
0,5 a2 ал cos (Дф2 — Дфх)
D =
= 0,125 a2 a2 a2
0,5 a2
0,5 ax a2 cos Дфх
0,5 ar a3 cos Д<р2
0,5 ax a3 cos Дф2
- > 0,5 a2 a3 cos (Д<р2 — Дфх)
0,5 a23
X [ 1 + 2 cos Дфх cos Дф2 cos (Дф2 — Дфх) — cos2 Дфх — cos2 Дф2 —
— cos2 (Дф2 — Дфх)]-
Величина 0,125а21а22а2з¥=0 при ненулевых а&.
Найдем, чему равна величина совокупности слагаемых в скоб-
ках:
1 + 2 cos Дфх cos Дф2 cos (Дф2 — Дфх) — cos2 Дфх — cos2 Дф2 —
— cos2 (Дф2 — Дфх) = sin2 Дф2 cos2 Дфх — cos2 Дфх sin2 Дф2 = 0.
Поскольку при любых Дф1 и Дф2 определитель Грама для выб-
ранной системы сигналов равен нулю, эти сигналы являются ли-
нейно зависимыми и, следовательно, их однозначное разделение
невозможно.
9.1.6. При ортогональном ансамбле согласно (9.4) опорные сиг-
налы T]fe(/) =CfeSfe(Z), где Ck — коэффициент пропорциональности,
Подставляя в (9.3) вместо s(t) принимаемое колебание z(/) =
= s(t)+n(t) и выражение для т|ь(/)> получаем алгоритм обработки
в k-м канале:
Мг(0Ь= v J Ckz(t)sk(t)dt.
1 о
Если все реализации отдельных канальных сигналов Ak,iSh(t)
(i — номер реализации) известны в месте приема (а это возмож-
10—63 249
но при дискретном ансамбле {А/^}), то можно выбрать Ck,i —
=Ak,iT и в каждом канале реализовать алгоритм
L [2 (01 k = max
J z (t) Ch,{ sh (0 dt--!-J Al.i S1 (0 dt
.0 2 0
что обеспечивает минимум вероятности ошибки при стационарном
белом шуме в канале (см. гл. 6).
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 9.2.
9,2.1. Величину Fi найдем из условия, что в полосе fk±iFi со-
держится 95% мощности канального сигнала:
fk+F*
J* А ехр [ — Р2 (со — <oft)2] df = 0,95 A J* ехр [ — 02 (со — coj2] df .
После очевидных преобразований получим уравнение Ф(2лХ
ХЛУ2р) =0,95, где Ф(х) — функция Крампа.
По таблицам Ф(х) находим 2jiFiУ 2(5 = 1,96, откуда при р =
= 1,23*10-4 с получаем Л= 1,8 кГц.
Разнос между несущими частотами индивидуальных каналов
2Л = 3,6 кГц. Аналогичным образом находим величину F2, считая,
что в полосе fk±F2 сосредоточено 90% мощности канального сиг-
нала:
j* Аехр[ —Р2 (co-coft)2] # = 0,9А J* ехр [ - р2 (со - cofe)2] dt.
fk-F2
Отсюда получаем Ф(2]/2л772р) =0,9 и /72=1,5 кГц. Из условия
равенства коэффициента передачи фильтра 0,1 на частотах fk±Fi
находим полосу F3, на границе которой коэффициент передачи
фильтра обращается в нуль:
F3 = (Рг - F2)/0,9 + Г2, F3 = 1,83 кГц.
Определим мощность сигнала на выходе разделительного
фильтра &-го канала, полагая, что в полосе частот от fk + F2 до
fkA-Рз коэффициент передачи фильтра по мощности изменяется по
закону К2(со) = l-[f_(fft+F2)/(F3-F2)]:
Рс = 2 J* А ехр [ — р2 (со — coj8] d/+
+ 2 J A [ 1 - (f - fk - F2)/(F8 - F2)] exp [ - p2 (co - df.
fk+p>
250
После очевидных преобразований получаем
Ре = А (2 0 /л)-1 {Ф (2 /2 лр F3) + F2 (F3 - F2)-> x
X [Ф(2}<2лРГз)-Ф(2К2лРГ2)] + [2Р/5?(Г3-Г2)]-‘ x
X [exp (— P2 4 л2 F2) — exp (— P2 4 л2 F2)]} .
Вычисляя, находим Pc=10,9-10~3 Вт.
Мощность переходной помехи (заштрихованная область на
рис. 9.2) определим с некоторым превышением, полагая, что в
полосе fk±Fs характеристика фильтра равномерна, а переходная
помеха создается только двумя соседними каналами:
fk^2F^Fs
Ра.а = 2 J Д ехр [ — 02 (<о —<oft)2df = Д (2 0|^л)-1 х
fft+2F1-F,
X {Ф [2 /2 лр (2 Fx + F3)] - Ф [2 /2 лр (2 Fx - F3)]}.
После вычислений получаем РПп = 6,55-10-4 Вт. Отношение сигнал-
переходная помеха на выходе разделительного фильтра й-го кана-
ла Рс/Рп.п= 16,6.
9.2.2. Используя равенство Парсеваля [10], условие (9.5) мож-
но записать в виде
J Sk (j со) Si (— j со) ехр (/ сот) df = 0,
—оо
где Sfe(/(o) — комплексный спектр сигнала Si(—j(o) —
функция комплексно-сопряженная спектру сигнала si(t). <
Поскольку при классическом частотном разделении амплитуд-
ные спектры канальных сигналов не должны существенно пере-
крываться, то сформулированное условие действительно выполня-
ется (на практике приближенно). Следовательно, при частотном
разделении используются канальные сигналы, сохраняющие вза-
имную ортогональность при произвольных взаимных сдвигах.
Правда, это достигается существенным расширением занимаемой
полосы частот по сравнению с минимально возможной величиной.
9.2.9. Амплитудный спектр группового сигнала системы связи
показан на рис. Р.9.1. В данной системе спектры индивидуальных
сигналов существенно перекрываются.
Рис. Р.9.1. Амплитудный
спектр группового сигна-
ла многоканальной сис-
темы связи с ортогональ-
ными сигналами
10:
251
Для надежного разделения каналов на интервале анализа дол-
жно выполняться условие ортогональности индивидуальных сиг-
налов
J cos (2 л ftt + <pf) cos (2 л fh t + <Pfe) dt = 0, i =# k
о
или ^=(2г + ^/(2Та), 2 ...
Поскольку разнос между соседними канальными частотами
[2 (/—1) + N—21—TV] / (2Та) = 1/(2Та), получаем Та =
= 1/(2Л/) =7,04 мс. Интервал ЛГ=ГС—7\= 1,291 мс используется
для гашения колебаний соседних посылок.
9.2.10, Согласно условию разделения (9.5)
т
J* xk (0 cos (соо t + ф0) Xt (t + т) cos [соо (/ + т) + ф0] dt =
о
т т
= 0,5 cos соо т J* xk (0 xi (1 + т) dt + 0,5 J xk (/) xt (t +
о о
+ т) cos (2 соо t + соо т + 2 ф0) dt.
При Г^>2л/соо и узкополосных канальных сигналах (1/т<7о) вто-
рым интегралом можно пренебречь. В этом случае канальные сиг-
т
налы могут быть разделены при В/м(т) = j хь(/)х/(/+т)<#=0, т. е.
о
если двоичные последовательности, образующие «адреса» отдель-
ных каналов, ортогональны при произвольном взаимном сдвиге.
Если в качестве индивидуальных сигналов использовать после-
довательности Хаффмена с большим числом элементов за период
повторения Nk и Ni, то В^(т) = 1/(А/&М) ~0.
9.2.11. Заданной реализации ЧВМ. соответствует сигнал, пока-
занный на рис. 9.2,а. На выходе четырех амплитудных детекторов
выделяются видеоимпульсы, взаимное расположение которых по-
казано на рис. Р.9.2,б. Четыре линии задержки обеспечивают сов-
мещение во времени отдельных видеоимпульсов, а суммарный сиг-
нал с амплитудой 4й, превышая порог схемы совпадения, выдает
Л fi А Л
Рис. Р.9.2. Канальный
сигнал асинхронно-
адресной системы свя-
зи (а) и сигналы на
выходе амплитудных
детекторов (б)
252
на выходе рабочий импульс, по которому считывается информация
(при передаче аналоговой информации посредством ФИМ она со-
держится в положении импульса относительно точки отсчета).
9.2.12. Полагая, что в каждой адресной комбинации использу-
ются четыре импульса (занимающих определенные положения из
17 возможных) с различными мгновенными частотами, нетрудно
написать выражение для числа возможных кодовых комбинаций
(числа каналов): 4!-C3i^ = 24-560 = 13440, где C3i6 — это число
сочетаний, которое можно выполнить при фиксации первого им-
пульса (остается 16 свободных мест для размещения трех импуль-
сов); 4! — это число возможных перестановок из четырех, опре-
деляющее разнообразие взаимного размещения четырех импульсов
с различными мгновенными частотами.
9.2.13. Каждый импульс, несущий информацию об отсчете, пе-
редается в асинхронно-адресной системе посредством /-разрядной
кодовой комбинации. Для многоканальной системы с ФИМ долж-
но выполняться условие
N [А ^макс + (^ I) ти] “ ~ V(2 /^макс) •
Полагая N= 13440, FMaKc = 3400 Гц, А/Макс=128 ти, Z= 17, получаем
= 0,5/(FMaKC# [Z - 1 + 128]) = 7,6- 10-4 с.
Полоса сигнала F«2/th = 2,7-1010 Гц.
9.2.16. Графики первых шести функций Радемахера приведены
на рис. Р.9.3. Наименьшую длительность элементарного импульса
имеет функция г5(0). При переходе Г = 20 мс т=Г/32. Полоса час-
тот, которая требуется при передаче сообщений этими сигналами
1/т = 32/Т= 1600 Гц.
9.2.18. Согласно (6.22) вероятность ошибки в четырехпозици-
онной системе ДЧМ в гауссовском канале с неопределенной фазой
Рис. Р.9.3. Графики
функций Радемахера
253
Рис. Р.9.4. Векторная диаграмма сигнала
ДФМ
при больших значениях отношения
сигнал-шум и оптимальном некоге-
рентном приеме
Рош,4 1,5 ехр ( —Л2/2).
Из таблицы состояний (см. табл.
9.1) для ДЧМ следует, что лишь в
двух из трех случаев ошибочного
решения о переданной частоте груп-
пового сигнала символы в индиви-
дуальных каналах будут зарегистрированы ошибочно. Поэтому
вероятность ошибки в индивидуальном двоичном канале
Рош = 2Рош.4/3 ~ ехр (- h2/2).
9.2.19. Рассматривая рис. Р.9.4, можно заметить, что сигналы
отдельных позиций ДФМ можно представить как результат сум-
мирования двух независимых двоичных сигналов ФМ с амплиту-
дами 2, сдвинутых друг относительно друга на л/2. Средняя
мощность этих сигналов в 2 раза меньше, чем у суммарного сигна-
ла ДФМ. Следовательно, при оптимальном приеме в случае точно
известных параметров сигнала вероятность ошибки в каждом дво-
ичном канале р = 0,5[ 1—Ф(р^h2)]. __
Очевидно, что для системы ДОФМ р~ 1—Ф( У*h2).
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ГЛАВЫ 10
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 10.1.
10.1.1. Из соотношения (10.2) следует, что частотная эффектив-
ность изменяется от 0 при F = oo до оо при F = 0. С учетом этого из
соотношения (10.5) следует, что
Рмакс = lim р = lim (y/(2v — 1)) = 1 /1п 2 = 1,443 (1,59 дБ).
V->0 V~>o
10.1.2. Из (10.2) следует, что величина ум акс достигается при
^макс, которая, в свою очередь, равна logAf/T (Т — длительность
элементарного символа). С учетом этого умакс = 1о§АГ/7’/;'.
10.1.5. По графикам рис. 10.1 выигрыш по частотной и энерге-
тической эффективностям находим как разность соответствующих
абсцисс (Ду) и ординат (Др). Для заданных условий Ду = 5 дБ,
Др = — 6 дБ.
10.1.6. Используя графики рис. 10.1 и соотношение (10.4), име-
ем: для АМ2 г) = 0,23; для ЧМ2 t] = 0,15; для ФМ2 т] = 0,25.
254
10.1.7. Указание к решению. Использовать графики рис. 10.1.
10.1.8. Согласно формуле (10.6) с учетом (10.1) при # = const
ЭВг/;-= 10 lg (.
Принимая во внимание результат задачи 6.3.6, получаем,
ЭВАМ/ЧМ = Ю In 2 = 3,03 дБ; ЭВАМ/ФМ = 101g 4 = 6,06 дБ.
Очевидно, что полосы частот систем AM и ФМ одинаковы, а
полоса частот системы ЧМ вдвое превышает полосу частот систем
AM и ФМ. Поэтому ЛуАМ/ФМ=0 дБ; Лудм/чм =—3,03 дБ; Дучм/Фм^
= 3,03 дБ.
10.1.9. Известно [14], что для m-позиционной системы
рэ=1~(1-р0Ш,т)1/Ю^е
При
Рош»т 1 Рэ ~ Рот, т/1^22 •
Учитывая решение задачи 6.3.4, находим
рэ ж (m-1) poin/log2m.
Теперь можем записать
Рэ,1офм= тАк- °>5[1 -Ф(/25)1 = 8.15-10-5;
log2 10
Рэ.ючм= тА? 0.5(1 -Ф (1ЛТ2Г5)] = 6,32-10-3.
log2 10
Выигрыш по эквивалентной вероятности ошибки при переходе
от системы ЧМ к системе ФМ в данном случае 6чм/фм = 77,5.
10.1.11. Для двоичной системы ЧМ
Ч2чм = Л2= -21п2р=12.4 (при рэ= 10-3)
Для 5-позиционной системы при р = рэ = const, 7? = const
чм = -Г~Г 1П тЦ = 5>82 (при рэ = 10-3).
’° log25 log25
Энергетический выигрыш согласно (10.6)
ЭВ2 чм/5 чм = 3,28 дБ.
Полагая, что многопозиционная система с ортогональными сиг-
налами (ЧМ) создается путем использования отрезков гармони-
ческих сигналов с кратными величине 2л/Т частотами, можно счи-
тать, что полоса частот, занимаемая системой, пропорциональна
числу позиций. В этом случае выигрыш по полосе согласно (10.8)
Д?2 ЧМ/5 чм = — 4 дБ.
Полезно заметить, что переход от 2-позиционной к m-позицион-
ной системе ЧМ сопровождается выигрышем по эквивалентному
отношению сигнал-шум (коэффициент использования мощности пе-
редатчика повышается) и проигрышем по занимаемой полосе
частот.
255
10.1.12. Согласно [12] коэффициент использования пропускной
способности (10.3)
r] = log2m/(7,mC).
Величину С можно представить следующим образом:
С = F log (1 + р) = F log (1 + 2ВД,
так как р = Рс77(NQFT) = 2h2/B. Здесь B = 2FT—база сигнала.
Теперь для коэффициента использования пропускной способ-
ности можно записать
2log2 m
В log, (\+2h*/B) ’
При заданной скорости передачи информации R
R
Т]= -----------------------
^log2 (1 +Rh2s)/(F log m)
Величина
2 log2 m \ 2p3 log2 m
Теперь находим
300 -----------= 1,33-1 о-1.
6,69-300 \
6,2-103 J
Т) =
—-------In-----J--------- 6,69.
21og24 2-10 4log24
10.1.13. Вероятность того, что в (и—1) ветвях коэффициент пе-
редачи канала k<Z.ko, а в одной какой-либо ветви k = ko, опреде-
лится формулой
(kQ) dk0 = (k = kQ)
po
(k)dk
.0
n—1
= -^ exp (- k2/k2) [ 1 - exp (- ^2/Zj2)]"-1 dk0,
где Wi (k) = — exp(—k2!k2) — рэлеевское распределение коэф-
k2
фициента передачи канала (амплитуд).
Плотность вероятности для максимума коэффициента передачи
канала £Макс = &о получим, поделив w(kQ)dk0 на dk0:
w (*о) = Ио/^2) ехр (- kffi [ 1 — ехр (^/Г2)]"-1.
Для двоичной ЧМ в отсутствие замираний и при оптимальном
некогерентном приеме вероятность ошибки при k = k$
Рот (*о) = 0.5 ехР ( — 0>5 k20 Рс Т/No).
Рассматриваемая схема автовыбора эквивалентна схеме одинарно-
го приема, у которой коэффициент передачи меняется в соответст-
256
вии с найденной статистикой w\\ko). Следовательно, средняя веро-
ятность ошибки при n-кратном разнесении
Рош, П = (k0) w (k0) dk0 = (n/2k2)jk0 exp [ — (k2/k2) (1 +
о о
+ 0,5 h2)] [ 1 - exp (- kffiY1-' dk0,
где hz=№PcTIN0— отношение средней энергии посылки сигнала
в месте приема к спектральной плотности мощности шума.
Используя формулу бинома Ньютона, получаем
и!
Рош, п — ~ •
2 П а+Г2/2)
i=l
10.1.14, В области малых ошибок (при больших А2) из соот-
ношения для рОш,п» полученного в задаче 10.1.13, следует
Рош, 1 ~ 1/^р Рош, 2 ~ ~ 1/Р°ш» 1’
Й2 2/}ЛРош, 2«
При неизменной вероятности ошибки рош,1 = Рош,2 = Рош= Ю~4
энергетический выигрыш сдвоенного приема по сравнению с оди-
нарным
эв1/2= ioig(Kpош, 2 /2рош, 1) = 17 дБ.
10.1.16. Помехоустойчивость двоичной системы связи с ЧМ при
флуктуационной помехе определяется отношением /г2 = £/Л^о. Энер-
гия составного сигнала
тг n 32 N
£ = J S^mSin(iM + <pft) di=^Ek,
0 L &=1 . k=\
т
где Ek= S t/2msin2(cofe/ + (pfc)d/ — энергия элемента составного
о
сигнала. Поскольку энергии элементарных сигналов одинаковы,
можно записать
/г2= 2 Ek/NQ = E/N0.
Вероятность ошибки, равная в данном случае рош = 0,5[1—
- ф(Гл2)], не зависит от базы сигнала 2FT.
Коэффициент использования полосы частот y = R/F = 1/FT = 2/B.
При Т = 20 мс и 2V=2OOO т0= 10-6, Р=1/т0=Ю6Гц и у=10"4
бит/Гц. Из этого можно сделать вывод, что широкополосные систе-
мы связи с составными сигналами используют полосу частот весь-
ма неэффективно.
10.1.17. Можно считать, что при использовании сигналов с боль-
шой базой сосредоточенные помехи действуют так же, как флукту-
257
ационная помеха со спектральной плотностью, равной Gc.n=
=^Pc.tiIF, где F—полоса сигнала; SPCn — суммарная мощность
сосредоточенных помех в полосе сигнала.
Если в канале действует флуктуационная и сосредоточенные
помехи со спектральными плотностями No и Gcn, величина h2 мо-
жет быть определена как
й2 = E/(N0 + Gc.n) = Рс T/[Nq + &PC'B)/F].
Если A/o<CGcn, то h2^PcFTIlLPc.B. Этот результат свидетельст-
вует об ослаблении влияния сосредоточенных помех с ростом базы
сигнала.
10.1.18. Выигрыш ЭВ показывает, во сколько раз может быть
уменьшена мощность передатчика при переходе от одного метода
передачи к другому при сохранении качества передачи (средней
вероятности ошибки рош).
Средняя вероятность ошибки в двоичной системе модуляции
является однозначной функцией величины й2 = Рс77^о (Рс — сред-
няя мощность сигнала в подканале, Т — длительность элементар-
ной посылки):
рош = О, 5[1—Ф(]/пй2)] при когерентном приеме,
рош = 0,5[ехр(—0,5/гЛ2) ] при некогерентном приеме.
При ЧМ п=1, при ФМ (ОФМ) п = 2.
Таким образом, для сохранения качества связи (величины
Рош) необходимо поддерживать постоянной величину h2, т. е.
PqT = const.
В последовательной системе вся мощность передатчика Ро рас-
ходуется на один подканал: Pi = P0, макс,1 = Ро.
В параллельной системе средняя мощность передатчика рас-
пределяется между подканалами P2 = Po/R, Рмакс,2 = РоМх(О^Х^
^1). В последовательной системе длительность элементарной по-
сылки Ti = l/R (R— скорость передачи информации). В параллель-
ной системе 7,2 = n/7, = n/71i. Следовательно, PiI\ = Pq/R, Р2Т2 —
= P0/R — т. е. при сохранении средней мощности передатчика
(случай «а») выигрыш отсутствует (ЭВ = 1).
При фиксированной же пиковой мощности передатчика (слу-
чай «б»)
Р \ 7*1 = ^макс, P%F2~ Рмакс, %lRl&
и выигрыш
ЭВ = Рмакс t 1 Т^РМакс, 2^2 = 1 •
10.1.20. Распределение коэффициента передачи канала в одном
луче
(&i) = (2^i/^f) ехр ( - k2lk\).
При когерентном приеме по одному лучу
рош = 0,5[1-Ф(/2^Рс77ЛГ0)],
258
где Рс — мощность посылки; No — спектральная плотность мощно-
сти шума.
После усреднения полученного выражения по ki с учетом выра-
жения для w (ki) при больших h2i имеем [8] p^0,25//i2i.
При приеме по обоим лучам, если передача ведется по парал-
лельным каналам, 7\ =гг/7? = 20/1200« 16 мс, Та1 = 7\—А£=14 мс
и оба луча на протяжении 7\i сливаются в один также с рэлеев-
ским распределением коэффициента передачи, но с вдвое боль-
шим средним квадратом:
0У1 (k) = (kjtf) ехр ( - ^/2<).
При этом рош~0,125//г21.
Если передача ведется последовательным методом по одному
каналу, Т2 = 1/R = 1/1200 = 0,833 мс, Та2 = 7,24-А^ = 2,833 мс, оба лу-
ча не сливаются в один, а дополняют друг друга.
При больших h2i в этом случае pOUI~0,187/(/i2i)2 [8]. Таким
образом, для параллельной системы h\ «0,125/рош; для последо-
вательной Л21« уг0,187/рош.
Выигрыш перехода от параллельных систем к последователь-
ным
ЭВ = (0,125/рош)//о, 187/рош = 0,5/ /3^.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 10.2.
10.2.1. Используя формулу для т|, а также результаты задач
§ 7.2, найдем: для AM £ = 0,2, д = 0,42; для БМ g=2, т] = 0,5; для
ОМ g=\, т]=1; для ФМ ^=222, г| = 0,12; для ЧМ £ = 666, д = 0,17.
10.2.6. В соответствии с решением задачи 7.2.10 имеем
£АМ = 2m2/(m2 + П2) = 0,02.
Согласно решению задачи 7.2.13
£фм = Р П2 = 20 • 100/9 = 222.
По формуле (10.11) получаем
ЭВАМ/ФМ = 101g (222/0,02) ж 40 дБ.
10.2.8. По формуле (10.11)
ЭВФМ/ЧМ = 101g (^чм/^фм)-
Воспользовавшись результатами задач 7.2.15 и 7.2.13, найдем
ЭВФМ/ЧМ = 101g
Если полосы канальных сигналов одинаковы, то
ЭВфМ/чМ = 101g 3 = 4,7 дБ.
10.2.9. Так как в системе без модуляции g“=l, воспользовав-
шись результатом решения задачи 7.2.10, получаем по (10.11)
ЭВ = —14 дБ.
259
Таблица Р.10.1
Таблица Р.10.2
Ni 0,1 0,5 0,8 0,9 0,99 Система Значение Т)
при рвых—' =1 000 при Рвых= =5000
n2 0,20 0,75 0,96 0,99 А ПППО
U,УУУУ AM 0,34 0,56 1,0 0,41 0,29 0,34 0,54 1,0 0,21 0,18
Nt/Ni 2 1,5 1,2 1,1 БМ 1,01 ом ФМ
ФИМ—ОМ
10.2.10. Указание к решению. Воспользоваться решением задачи
7.2.11.
10.2.11. Указание к решению. Воспользоваться решением зада-
чи 7.2.12.
10.2.12. Указание к решению. Воспользоваться решением зада-
чи 7.2.13.
10.2.13. Указание к решению. Воспользоваться решением зада-
чи 7.2.18.
10.2.14. Указание к решению. Воспользоваться решением зада-
чи 7.2.17.
10.2.16. Ненадежность в отдельном параллельном канале
1—где Ni — надежность канала.
При приеме сигналов по п независимым каналам ненадежность
связи 1—Nn будет определяться вероятностью того, что одновре-
менно во всех каналах рВых<рпор, т. е. с учетом однородности ста-
тистики в отдельных каналах 1—Nn=(\—Ni)n или надежность
связи при n-канальном приеме Afn=l—(1—Ni)n. Интересующие
нас сведения сведены в табл. Р.10.1, из которой видно, что эф-
фективность параллельной передачи падает по мере улучшения
качества (надежности) работы одноканальной системы. Видно так-
же, что эффективность разнесенного приема падает по мере уве-
личения числа ветвей разнесения.
10.2.18. Полагая рвх = рвых/£, имеем расчетную формулу
fl — + Рвых)
F log (1 4- pBbix/g)
Значения т] сведены в табл. Р.10.2, из которой видно, что среди
сравниваемых систем наибольшее значение эффективности (ко-
эффициента использования пропускной способности канала) име-
ет система ОМ.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 10.3.
10.3.1. В системе с согласованными фильтрами при использо-
вании ортогональных в усиленном смысле реализаций отдельных
сигналов (для возможности приема в условиях неопределенной
фазы сигнала) можно выбрать минимальный разнос между час-
260
тотами Af=l/T=50 Гц. Поэтому в полосе =3100 Гц можно
разместить до 3100/50=62 реализаций, или до 31 двоичного ка-
нала.
10.3.4. Найдем сначала энергетическую цену разделения для
системы А. Индекс частотной модуляции рчм =А/2/Р2=Д/1/иЛ,
где АД — девиация частоты при одноканальном режиме; Fi— за-
нимаемая одним каналом полоса частот. Если мощность сигнала
на входе приемника остается неизменной, то отношение мощности
группового сигнала на выходе частотного детектора вых к
спектральной плотности мощности шума б0Вых пропорционально
Р2ЧМ и обратно пропорционально п2. Если среднюю мощность пе-
редатчика увеличить в п2 раз, то отношение Р2 вых/^овых останет-
ся неизменным. Но по определению энергетической цены разде-
ления должно оставаться неизменным отношение Pi вых
средней мощности канального сигнала на выходе приемника к
спектральной плотности мощности шума. При статистической не-
зависимости сигналов отдельных каналов Р\ъъ\х=Р^1п. Поэтому
энергетическая цена разделения системы A gp=n3. Поскольку в
системе А рост числа каналов не сопровождается расширением
полосы частот (так как девиация не меняется), то спектральная
цена разделения J>(A) = 1.
В системе Б будем считать, что девиация частоты меняется
пропорционально числу каналов п, но тогда (Р2/О0)Вых и вместе
с тем и рчм не зависит от п. Следовательно, для того чтобы сох-
ранить неизменным (Л/Go)вых (качество связи), достаточно уве-
личить среднюю мощность передатчика в многоканальном вари-
анте в п раз: £р = п. Спектральная цена системы Б gF(B)=n.
Согласно (10.17) энергетический выигрыш перехода от систе-
мы А к системе Б ЭВ а/б = 101g п2, что достигается проигрышем
в эффективности использования полосы частот в gF(B)/gF(A) =
= п раз.
10.3.5. При использовании синхронного детектора в системе фа-
зового разделения отношение сигнал-шум на выходе
рвых ==: 0,25Р макс /(ЛГо-РсП2!).
Для системы частотного разделения (при синхронном детекти-
ровании)
Рвых=== 0,5Р мак сД^оЛП21П%).
Отсюда получаем
ЭВа/б = 2х+74 = 2х~1.
В системе фазового разделения полоса группового сигнала рав-
на 2FC. В системе частотного разделения полоса группового сиг-
нала при разносе между канальными частотами 2FC равна 4FC.
Спектральный проигрыш при переходе от системы фазового
разделения к системе частотного разделения равен 2.
10.3.7. Очевидно, что пиковая мощность сигнала в системе ДЧМ
раВНа ПИКОВОЙ МОЩНОСТИ ПереДаТЧИКа Рмакс И h2дчм=Ллакс77М).
261
В двухканальной системе ЧМ пиковая мощность индивидуально-
го сигнала Рмакс,1=РМакс/2х. При строго линейном режиме пере-
датчика (х=2)
Рмакс, 1 = 0,25 Рмакс и ^2 ЧМ ~ ^ДЧМ'/4*
Следовательно, в этом случае ЭВ2чм/дчм=6 дБ. Если допустить
нелинейность в передатчике (%=1), то ЭВ2чм/дчм = 3 дБ. По-
скольку двухканальная система ЧМ занимает примерно ту же по-
лосу частот, что и система ДЧМ, коэффициент эффективности ис-
пользования полосы при одинаковых объемах передаваемой ин-
формации будет одинаков для этих систем.
10.3.8. Согласно (10.17) для систем, отличающихся только спо-
собом разделения, энергетический выигрыш перехода от одной си-
стемы к другой
ЭВг/; = 10 lg[^p (п) г'/£р(^) j] ,
где ^р(п)г — энергетическая цена разделения f-й системы. Для
системы ДОФМ gP(2)=2. Легко убедиться, что для двухканаль-
ной системы временного разделения £Р(2)=2, так как сокращение
длительности посылки в 2 раза требует увеличения мощности пе-
редатчика в 2 раза для сохранения неизменной верности. При час-
тотном разделении средняя мощность сигнала одного канала
уменьшается в 2 раза (для двухканальной системы) и gP(2)=2.
Следовательно, ЭВщ =0 дБ. Выигрыш по эффективности исполь-
зования полосы частот при переходе от двухканальной системы
частотного или временного разделения к системе ДОФМ равен 2,
так как полоса ДОФМ такая же, как и у одноканальной системы
ФМ, а у систем частотного и временного разделения она в 2 раза
больше.
10.3.9. Пропускную способность n-канальной системы в рас-
сматриваемом канале определим по формуле
п п г р
СХ = S Ck = 2 Fk log Г н---------—---------1
ktr L NtFk + K(n-l)Pch j
Средняя мощность в отдельном канале n-канальной системы
Рс k ~ ^макс/^П2 (п) = PMaiiC/f^ Пр
С учетом этого для пропускной способности n-канальной систе-
мы частотного разделения получаем
Р макс
Cs = nFftlog 14
П? [FkNQ + X (п - 1) Рмакс/пХ П?]
Если Х(п—1) Рсь<СА/о7ч (переходной помехой можно прене-
бречь), то при строго линейном режиме передатчика (%=2)
С2 = nFk log Г14
—-макс— = 4,8-105 бит/с.
J
262
Если %(n—то в указанных условиях
C2 = nFftlog[l + 1/X (n— 1)]
(это соответствует значению коэффициента %^>-VoFfe/[PCfe(^—1)]^
Например, при Х=10-1 С2 = 9,4-103 бит/ с.
10.3.10. Пропускная способность 20-канальной системы времен-
ного разделения
C2 = 20Ffelog Г1 4
________Р макс____________
nf [Л/о 20 Fk + X (п - 1) РМакс/П?]
Если пренебречь переходной помехой, то
С2 = 20Fft log [ 1 + РмаКс/ (П^О/Ш) ] = 1,6 • 106 бит/с,
что в 30 раз больше, чем при частотном разделении. При пере-
ходной помехе, существенно превышающей флуктуационный шум
в канале, пропускная способность этих двух систем одинакова.
10.3.11. Найдем пропускную способность системы передачи 20
независимых сообщений, каждое из которых занимает полосу
Рс=4000 Гц, при отношении сигнал-шум на выходе канала, рав-
ном 7:
Сс = 20Гс log [ I +рВых] = 2,4 -105 бит/с.
Коэффициент эффективности системы при использовании ка-
нала с частотным разделением (задача 10.3.9)
т] = Сс/С2 =0,5.
При использовании канала с временным разделением (задача
10.3.12)
т) = Сс/Сх = 0,15.
10.3.12. В данном случае пропускная способность системы
Сс=п/7,=8-104 бит/с.
Коэффициент эффективности системы, использующий канал с
частотным разделением (задача 10.3.9), т] = 0,167. Коэффициент
эффективности системы, использующей канал с временным раз-
делением (задача 10.3.10), ц = 0,05.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ § 10.4.
10.4.1. При декодировании с исправлением ошибок по миниму-
му расстояния по Хеммингу кодовая комбинация будет принята
с ошибкой, если в ней искажено более чем [п/2] кодовых симво-
лов (([п/2]— целая часть от п/2). Следовательно, вероятность оши-
бочного декодирования кодовой комбинации данного кода
Рк ~ S C/i Ро (1 Ро)
263
Эквивалентная вероятность ошибки согласно (10.21) р3 =
= 1—(1—pK)1/fe. Так как в данном случае число информационных
символов k = 1,
Рэ~ Рк~ 2 Сп Ро (1 Ро)
^=[«/2]+1
10.4.4. Воспользовавшись соотношениями для РЭ(7,4> и РЭ(п,п),
найденными в предыдущей задаче, определяем при P3=const
Л2э(7,4) = 1,75 In (1,31 /рэ); h23 (п>п) = 2 In (0,5/рэ).
Отсюда согласно (10.24)
рэ=10-2 ЭВ(П,п)/(7,4) = —0,045 дБ;
Рэ—Ю 3 ЭВ(п,п)/(7,4):= 0,37 дБ;
рэ=10“4 ЭВ(П.Л)/(7,4) = 0,11 дБ;
Рэ=10~5 ЭВ(П,п)/(7,4) = 0,21 дБ;
Рэ = 10~6 ЭВ(Л,п)/(7,4) = 0»27 дБ.
10.4.5. Коэффициент передачи канала с медленными рэлеевски-
ми замираниями имеет плотность вероятности
wx\(k) = (2klk2) ехр (—£2/£2).
Эквивалентную вероятность ошибки для кода (п,п) и кода (7,4)
находим, усредняя по всем значениям выражения, полученные в
задаче 10.4.3 с учетом (10.22):
Рэ (7,4) = 1,31 J ехр (—4£2РС/ (7 N0R)) w j (k) dk = 1,31 /(1 + 0,57ft2.),
Рэ (n,n) = 0,5 J exp (—0,5ft2Pc/ (NoR)) (k) dk = 1/ (2 + ft23),
где h23=^k2Pc/(NoR) — среднее значение h23.
Выигрыш по эквивалентной вероятности ошибки в данном слу-
б(п,п)/(7,4)= [1+4/12э/7]/1,31 (2 + /12э).
При
Ро = Рэ (п,п) == Ю 2
Ро~Рэ (п,п) = Ю 3
Ро = Рэ (п,п) == Ю 4
Ро==Рэ (п,п) = Ю 5
Ро — Рэ (п,п) =Ю 6
/Г2э = 98
Я = 998
Я=Ю4
Г2э=105
/Г2э=Ю6
6(П,п)/(7,4) = 0,4;
6(п,п)/(7,4) = 0,4;
6(п,п)/(7,4) = 0,4;
6(п,п)/(7,4) = 0,4;
6^п,п)/(7,4) = 0,4.
264
10.4.7. При быстрых замираниях коэффициент передачи кана-
ла случайно меняется от одной посылки к другой. В этом случае
средняя вероятность ошибки элементарного символа с учетом
(10.22)
Ро=0,5 J ехр (—Л2/2) w 1 (k) dk = 11 (2+kh^/n).
о
Следовательно, для кода (7,4)
Рэ(7,4) = 5,25/(2+0,57Л2э)2.
Для кода (п,и) Рэ(п,п)=1/(2+/г2э) и
6(п,п)/(7,4) = (2 + 0,57ft2,) 2/5,25 (2+Тг2э).
При
рэ (п,п) — 10“4 /12Г= ю4 б(п,п)/(7,4) = 622;
Рэ (п,п) =10 2 ft2,=98 6(п,п)/(7,4) = 6,4;
Рэ (п,п) =10 3 ft2,=998 6(п,п)/(7,4) = 61,9;
Рэ (п,п) =10 5 ft2,= 105 6(п,п)/(7,4) = 62200;
Рэ (п,п) =10 6 ft2,= 106 6(п,п)/7(,4) “ 62200.
10.4.9. Согласно решению задачи 10.4.2 при поэлементном
приеме
Рэ (п.п)= 0,75 exip (- —ft2,/3); ft2, = ЗЛ2.
При приеме в целом можно считать, что длительность сигна-
лов, ортогональных в усиленном смысле, равна ЗГ. В этом случае
вероятность ошибочного декодирования кодовой комбинации
рк = 0,5 ехр (—ЗЛ2/2);
рэ (п.ц) = рк = 0,5 ехр (—Л2э/2).
Выигрыш по вероятности ошибки
б(П.п)/(п.ц) = 0,75 ехр (—/г2э/3) /0,5 ехр (—й2э/2) = 1,5 ехр (й2э/6).
Энергетический выигрыш
ЭВ(п,п)/(п.ц) = 101g [ 1,5 In (0,75рэ) /1 п (0,5рэ) ].
При Ps<^i 1 ЭВ(п,п)/(п.ц)~ 101g 1,5= 1,76 дБ.
10.4.10. При роС1 эквивалентная вероятность ошибки кода
(n, k), исправляющего все ошибки кратности и не исправляю-
щего ошибок кратности 1 [14],
p3=np4«+1[k. _
При когерентном приеме ЧМ ро = О,5[1—Ф(|//г2)]. В случае
использования примитивного кода при той же скорости передачи
информации ро=О,5[1—Ф(]/ nh2fk)], так как длительность эле-
265
мента сигнала, а также и энергия его увеличиваются в n/k раз.
Используя асимптотическую формулу 0,5[—Ф(х)]=ехр(—х2/2)/
V2лх, находим
lim (ра/р0) = (n/k) ехр {1 /(1 - хк) -
Л2->оо
- qa - 1 ] Л2/2}/Г hq»+l .
Здесь хк= 1—kfn—избыточность кода. Если 1/(1—хк)>?и+1,
то lim (рэ/ро) = оо, т. е. рэ>Ро, и код (и, k) применять нецелесо-
,2
h -*оо
образно. Если 1/(1—хк)<<7и+1, то lim (рэ/ро)=О и при неко-
,2
h —оо
торых h2 рэ<р'о. Следовательно, корректирующий код (n, k) це-
лесообразно применять при условии
?и^Хк/( 1 Хк) •
10.4.14. Согласно графикам рис. 10.4 с ростом объема ансамб-
ля М при фиксированном п (п = 2) в системах ФМ и АФМ рас-
тет частотная эффективность у и уменьшается энергетическая эф-
фективность р.
10.4.15. Ортогональные, биортогональные и симплексные сиг-
налы образуют класс «разнесенных» сигналов, у которых с ростом
М увеличивается расстояние между сигналами, что приводит к
росту энергетической эффективности р. Ценой увеличения р явля-
ется снижение частотной эффективности (см. рис. 10.4).
10.4.19. Как следует из анализа диаграмм рис. 10.4, в непре-
рывном постоянном канале при р= 10_5 предельный энергетиче-
ский выигрыш Ар в системах с кодированием по сравнению с ФМ2
без кодирования составляет примерно 10 дБ. Так как применение
современной элементной базы существенно снизило затраты на
реализацию кодеров и декодеров, а стоимость энергетики канала
осталась практически неизменной, плата за выигрыш Др при ко-
дировании оказывается существенно меньше платы за тот же вы-
игрыш, полученный за счет увеличения энергетики канала (мощ-
ности сигнала или размеров антенн).
ОТВЕТЫ
Ответы к задачам главы 1
1.1.2. Для варианта 1: апЯогЯгз; ^11^12^23; «11^22^23; «11^32^23;
#11#42#23*, #U#52#23‘, ^11^62^23^ #11#72#23«
1.1.4. 1) 25; 2) 28; 3) 26; 4) 215; 5) 29; 6) 213; 7) 2n; 8) 210; 9) 212;
10) 217; 11) 214; 12) 219; 13) 221; 14) 220; 15) 225.
1.1.7. Для варианта!: Д = 0,4°, /С=46, М=846.
266
1.1.9. Число точек изображения в кадре «=520625; число воз-
можных кадров М= 17520625.
1.1.10. М= 1024520000.
1.1.13. 1) 10032; 2) 10025; 3) 15024; 4) 5012; 5) 20072; 6) 200180;
7) 100180; 8) 5016; 9) 3004; 10) 5072; 11) 5090; 12) 1006.
1.1.15. Для варианта 1: V’i/V2 = 3,7.
1.1.18. 1) 0,43 мВт; 2) 0,35 мВт; 3) 0,7 мВт; 4) 2,9 мВт; 5)
1,35 мВт; 6) 0,23 мВт; 7) 2 мВт; 8) 0,1 мВт; 9) 0,17 мВт; 10)
3,6 мкВт; 11) 0,71 мВт; 12) 0,33 мВт.
1.1.20. 1) 0,74; 2) 0,89; 3) 0,1; 4) 0,13; 5) 0,07; 6) 0,16; 7) 0,1;
8) 0,25; 9) 0,37; 10) 0,18; 11) 0,28; 12) 0,44.
1.1.23. 1) 3,7-107; 2) 1,35-107; 3) 1,49-107; 4) 7,7-107; 5) 1,4-107;
6) 1,03-107; 7) 2-107; 8) 4,3-107; 9) 8,43-107; 10) 9,9-106; 11)
5,1-107; 12) 2,7-107.
1.2.2 п=5; 2; 2; 1.
1.2.3. «мин=4; Ь1 = 0000; Ь2=0001; Ь3 = 0010; Ь4=0011; Ь5 =
=0100; Ь6 = 0101; Ь7 = 0110; Ь8 = 0111; Ь9= 1000; Ью = 1001.
Код является избыточным, так как число комбинаций N —
= 24= 16.
1.2.4. п=7.
1.2.5. Для двоичного кода я=4; 7; 6; 4; 9. Для восьмеричного
кода п=2; 3; 2; 3.
1.2.6. 101; 111; 11111; 100000; 1111111; 10000000; 10000001.
1.2.7. Для двоичного кода при К=8; 32; 256. Для троичного ко-
да при К=9.
1.2.10. о=200 Бод.
1.2.11. 7=20 мс; 10 мс; 5 мс.
1.2.12. 1) МОСКВА; 2) СЕКАМ; 3) МАСКА.
1.3.2. 1) 1,26 МГц; 2) 1,63 МГц; 3) 5,54 МГц; 4) 8,2 МГц;
5) 9,66 МГц; 6) 2,95 МГц; 7) 1,94 МГц; 8) 4,944 МГц; 10) 2,28 МГц;
11) 2,54 МГц; 12) 1,46 МГц.
1.3.4. 1) 218 кГц; 2)360 кГц; 3) 478 кГц; 4) 360 кГц; 5) 392 кГц;
6) 520 кГц; 7) 428 кГц; 8) 488 кГц; 9) 432 кГц; 10) 338 кГц; 11)
336 кГц; 12) 420 кГц;
{t
®2 (0 + ^ЧМ2.Р^т1
0
xd/х + ф! Л2 + ф2|; Л/= 8,4 МГц.
1.3.7. 1) 1,53 МГц; 2) 2,52 МГц; 3) 3,82 МГц; 4) 3,24 МГц;
5) 3,52 МГц; 6) 5,2 МГц; 7) 3,85 МГц; 8) 2,28 МГц; 9) 3,64 МГц;
10) 3,04 МГц; 11) 3,02 МГц; 12) 3,36 МГц.
1.3.13. 1) 600 кГц; 2) 1,5 МГц; 3) 300 кГц; 4) 375 кГц; 5)
150 кГц; 6) 75 кГц; 7) 33 кГц; 8) 50 кГц; 9) 100 кГц; 10) 42,8 кГц;
11) 500 кГц; 12) 750 кГц.
t
cos (01/4-^чм ip(^i)x
0
267
Ответы к задачам главы 2
„2
Я1
2.1.6. В четыре раза.
2.1.9. Wi (nJ = —7==- ехр I------------------I; (n2) = 77=^==
V 2nOj (0 у 2of (t) J V 2ла% (t)
(n2 \
-----— I. При 7?(т)=0 t<y2(ni, n2, r) = wl(nl)w1 (n2), что
2a2 G)/
доказывает независимость двух сечений случайного процесса.
2.1.10. W2(Z\, Z2, т) =-,...... X
2лУа2^)оЧ*2)[1-Я2(т)]
[zx Gi) — и Gi)P 2/? (т) ?1 GO z2 G2) |
a Gi) а G2)
хехр/------------ .
I 2[1—7?2(t)]l 2а2 (i,)
[22G2)~ a (^Ml
2o2G2) -И
2.1.11. При7?(т)=0 w (n2/«i) («a) = * - exp (—n22/2o22).-
V 2n<^
При R (т) = ± 1 w (n2/nx) = 6 («2—tiiR (t) 01/02) •
2.1.12. w3(nx, n2, n3; ti, t2) = — 1 ......X
2л у 2ло2 стз [1— R2 (ti)][1—/?2(t2)]
X ехр
Я1
°*
J__________
2 а2 [1 - Я2 (т2)]
— -----J------- (n2—nxR (ti) ffi/(T2—
2a2[l—Я2 (тх)]
- («3—«2# (T1Q02/03) j •
2.1.13. x=0; x2=l,2.
2.1.15. z(t)=mx cos ®(G+mySin a>ot; o22(Z) =o2x(/)cos2<oo^~F
-|-o2j/sin2<oo^> Bs(Л> t2) =0,5Bx(t)[coscoq/(t2—Л)-{-cos<bo(^i-|-/2)]-|_
+ 0,5-Sy (r) [cos coo (i2—ti) —cos coo (Л +12) ].
2.1.19. 1) 100 c; 460 c; 2) 10 c; 16,1 c; 3) 50 c; 115 c; 4) 25 c;
321 c; 5) 12,5 c; 23,7 c; 6) 16,7 c; 50 c; 7) 16,7 c; 28 c; 8) 50 c; 39 c;
9) 12,5 c; 50,5 c; 10) 12,5 c; 36 c; 11) 12,5 c; 126 c; 12) 50 c; 391 c.
2.1.21. Bx(tx, t2)=O,5No6(t2—tx).
2.1.22. По методу эквивалентного прямоугольника тк=У 0,5л/^=
= 125 с.
Из условия В(тк)=0,1В(0) т:к=]^—1пО,1/02= 151 с.
2.2.3. В(т)=#о51п2лГт/(2лВг); tk=0,5/F; F3 = F.
2.2.4. Гэ=р/4; ткВэ=1/4.
268
2.2.5. G(v) =B(0) ( ]/л/р)ехр(—©2/4p2); Вэ=р]Лл.
2.2.7. Gam (со) о= 0,5t/2m6 (со—соо) + 0,5&2amGx(co—соо)•
2.2.10. Вмл (т) = 0,5G2m (1— |т | /Т) cos coox+0,5G2m cos coot;
Gam (со) о=0,5G2m6 (со—соо) + 0,5U2mT siп2[ (со—со0) Т/2]/[ (со—соо) /Т/2]2.
2.2.11. Вчм (т) =0,5G2mcoscoi/ + 0,5G2mcosco2/ +
+ 0,5G2m(l— |т|/Т) cos co,r+0,5G2m(l— |т|/Т) cosco2x;
G4M (f)o=0,5t/2m6(co—co,) +0,5G2md(co—co2) + 0,5G2m7'X
X sin2[(co—co 1) T/2]f [ (co—co,) T/2]2+0,5U2mT sin2[ (co—co2) T/2]/
[(С0-<02)П2]2.
2.3.4. x (/) = Um (1 +mcos Qt) cos <j»o; У (/) — Um (1 + tn cos Qt) sin cpo-
2.3.5. \)r(t) = V U2i + U22 + UiU2cosQt-, cp(t) = arctg(G2 sin QZ)/
(I7i + t/2cosQ0; Q=<o2—co,; 2) r(0= У t721 + G22 + 2G1G2cos 2Q/;
cp(Z) =arctg[(t/2—Gi)tgfiZ/(t72+Gi)]; Q = O,5(co2—co,).
2.3.6. r(t) = Um; <р(0=Ш.
2.3.13. p=l—0,5/ra; при n=2 p = 0.75.
2.3.17. М[«нч] =k<jV^/2[l + U2m/2a2]I0(U2ml4o2) +
+ U2mh (U2m/4(J2) /2а2] exp (—t72TO/4o2); D [ынч] = 2k2c2+k2U2m—
-М2[«нч].
2.4.2 1) 15,7; 2) 20,8; 3) 6,7; 4) 15,6; 5) 14,8; 6) 16,4; 7) 14,6;
8) 17,4; 9) 14; 10) 15,6; 11) 6,7; 12) 18,6.
2.4.4. s,i = a,; s,2 = 6i; s,3 = 0; $,4=о!з; s,5=0; 521 = 0,; S22 = 0; s23 =
= &2i S24 = 0; 525 = ^з; d\S\, s2) = \f 621 + Й22 + О2з + Ь2з.
2.4.8. Xi = ai/V 2; х2=а2/У2; х3 = а3/У2; х^ЬиУ^-, х5=Ь21У2
Х6=Ь3/У2', ||s||= Р^О21 + О22 + О2з + Ь2| + &22 + Ь2з.
2.4.10. (s, s2) =o,a2sin /2при (со, + со2) (со,—со2)=Дсо;
a,//2=||s,||; ||s2||=a2/K2.
2.4.15. Сигналы АФМ образуют круговую сеть, изображенную
на рис. 0.2.1: d(s,, S4)=d(S2, S4)=d(s3, S4) = У 2Е.
d(si, s3) =d(s,, s2) =d(s2, s3) = У ЗЕ.
2.4.16. d(si, s2)=d(s2, s3)=d(s,, s3) = УЗЕ.
2.4.17. Пространство первичных сигналов при передаче показа-
но на рис. 0.2.2,о, при приеме — на рис. 0.2.2,б.
269
Рис О 2.1. К задаче 2.4 15
Рис. 0 22 К задаче 2.4.17
2.5.3. 1) 0,173 с; 2)0,183 с; 3) 0,592 с; 4) 0,151 с; 5) 0,223 с;
6) 0,288 с; 7) 1,11 с; 8) 0,237 с; 9) 0,42 с; 10) 0,634 с; 11) 0,126 с;
12) 0,634 с.
2.5.4. 30.
2.5.5. 1) 98; 2) 188; 3) 96; 4) 174; 5) 104; 6) 56; 7) 100; 8)50;
9) 104; 10) 50; 11) 104; 12) 142.
2.5.7. 1) 0,33; 2) 0,08; 3) 0,41; 4) 0,57; 5) 0,57; 6) 0,08; 7) 0,195;
8) 0,53; 9) 0,48; 10) 0,26; 11) 0,23; 12) 0,16.
2.5.10. 1) 0,23 с; 2) 0,7 с; 3) 0,17 с; 4) 0,28 с; 5) 0,14 с; 6) 1 с;
7) 0,19 с; 8) 0,05 с; 9) 0,12 с; 10) 0,26 с; 11) 0,39 с; 12) 0,58 с.
Ответы к задачам главы 3
3.1.1. Канал непрерывен по амплитуде, так как ее значение на
входе и выходе канала произвольно. По фазе канал дискретно-
непрерывен, поскольку на входе значения фазы равны 2ni/m (i=
= 1, 2,..., т), а на выходе — произвольны.
3.1.4. 8,3-10”8; 2) 1,7-10“5; 3) 1,6-10~8; 4) 2,2-10~16; 5) 3,4-10~27;
6) 2,2-Ю-4; 7) 5,7-10~6; 8) 1,4-10~28; 9) 1,3-10-26; 10) 9,4-10~13;
И) 1,7-10~9; 12) 4,4-10-25.
3.1.9. рправ= 1 Рош рс; рош== (т 1)ро; Рст-—• 1 Рправ рош*
3.1.11. 1) 0,42; 0,014; 0,5 2) 0,44; 0,03; 0,5; 3) 0,26; 0,012; 0,5;
4) 0,32; 0,025; 0,5; 5) 0,28; 0,012; 0,5; 6) 0,27; 0,025; 0,5; 7) 0,41;
0,5; 8) 0,23; 0,058; 0,5; 9) 0,35; 0,025 0,5; 10) 0,41; 0,027; 0,5; 11)
0,5; 0,071; 0,5; 12) 0,11; 0,032; 0,5.
3.1.13. Е [8]=01101101; 5; канал без памяти.
3.1.14. Е [8]=00111000; канал симметричный с памятью.
3.1.17. да(фг)=Кехр[-— f [z(0— Si(t)]2dt];K= (l//W)"^.
о
3.2.2. К (» =k ехр (—/2®Тс).
3.2.4. 1) 2 мс; 2) 18 мкс; 3) 0,75 мс; 4) 15 мс; 5) 0,3 мс;
6) 8,5 мкс; 7) 1,5 мс; 8) 1,5 мс; 9) 1,8 мс; 10) 5 мс; 11) 1,25 мс;
12) 7,5 мс.
3.2.7. 1) 20 Гц; 2) 800 Гц; 3) 10 Гц; 4) 340 Гц; 5) 2 Гц;
6) 997 Гц; 7) 80 Гц; 8) 120 Гц; 9) 100 Гц; 10) 200 Гц.
270
3.2.9. 1) 5; 2) 0,625; 3) 1,06; 4) 0,25; 5) 0,03; 6) 0,11; 7) 0,07;
8) 0,4; 9) 6,7; 10) 0,08.
3.2.12. Л/Рел=ехр(—/г2/2р), где р = PC/PUS=A^2U2U1- Af0H =
= 1—Ф (k/hV2).
3.2.14. 7<(/(о)кор= (ВоМо)ехр(юД)ехр(а2и2+ (а>—&)и).
3.2.18. Квадратичную характеристику корректирует нелиней-
ность вида x(t) — b
3.3.3. 1) 4,5-106; 2) 2,8-1016; 3) 6,1-10‘6; 4) 5,6-1015; 5) 3,7-106;
6) 5,1-106; 7) 1,02-10’7; 8) 5,08-1016; 9) 4,04-1016; 10) 5,6-1016;
11) 1,3-1017; 12) 1,8-1016.
3.3.5. 1) 1,9-10-7; 2) 4,2- 10~в; 3) 3,9-10~3; 4) 2,2-10~7; 5) 0,95;
6) 0,72; 7) 6,Ь10-29; 8) 0,8; 9) 0,72; 10) -0; 11) 0,75; 12) -0.
3.3.6. 5 (7 дБ).
3.3.10. 1) 0,999; 2) 0,999999; 3) 0,687; 4) 0,9998; 5) 0,769;
6) 0,998; 7) 0,999999; 8) 0,996; 9) 0,9999; 10) 0,998) 11) ~1; 12)
~1.
3.3.14. Рош=С2зР2и.п + С'3,зр2и.п»Зр2и.п. При примитивном кодиро-
вании Рош = РнП; Ри.п/3р2и.п ^ЗЗ.
3.4.2. Bv(t, /+т)=К(0К(^+т)Вх(т).
3.4.3. By(t,t+x)= ] |K(/©)|2Gx(Q)exp(M)df.
Ответы к задачам главы 4
4.1.1. 1) 2,33 бит; 2) 1,75 бит; 3) 1,33 бит; 4) 3,33 бит; Н (Л) =
= 1,86 бит/символ; хи=0,07.
4.1.9. Н(Л) =4,35 бит/символ; 77макс(Л)=5 бит/символ; хи =
=0,13. С учетом статистических связей хи=0,8.
4.1.10. И (Л) =4,043 бит/символ; 77макс(Л) =4,754 бит/символ;
Хи=0,15. С учетом статистических связей хи=0,52.
4.2.3. 1) 1200 бит/символ; 2) 5400 бит/символ; 3) 6900 бит/сим-
вол; 4) 3500 бит/символ; 5) 1200 бит/символ; 6) 3800 бит/символ;
7) 2000 бит/символ; 8) 2200 бит/символ; 9) 3200 бит/символ; 10)
2800 бит/символ.
4.2.5. 1) 7/(В|6) = 10 бит/символ; 77(6) =50 бит/символ;
/7/(В) = 1000 бит/с; И' (В | В) =500 бит/с; Г {В, В)=ЪЫ) бит/с;
Н'(8|В) =2000 бит/с.
4.2.7. 1) 959 бит/с; 2) 1742 бит/с; 3) 133 бит/с; 4) 2098 бит/с;
5) 982 бит/с; 6) 559 бит/с; 7) 1610 бит/с; 8) 4577 бит/с; 9) 2081 бит/с;
10) 2327 бит/с.
4.2.13. Граф кода Хаффмена приведен в табл. 0.4.1.
При таком коде гаСр = 3. При равномерном двоичном кодировании
27Г
Таблица 0.4.1
СимЬол p(a£) Граф кода Хаффмена Код
Oi az 04 05 Off O7 a8 1/4 1/4 1/8 1/8 1/16 1/16 1/16 1/16 /
/ П1
I Л - V- СЬ А Л — Z7- U ! 001 1 0010 00011 0001 0 00001 000 00
Таблица 0.4.2
«мин=log2K= 3. В данном случае экономия в числе разрядов рав-
на нулю.
4.2.14. Граф кода Хаффмена приведен в табл. 0.4.2.
Среднее число разрядов в кодовой комбинации лср=2,25;
Н(А) =2,21; [Пср—Н(А)]/Н(А) =0,018.
4.2.16. А->1; В->01; С->001; £>^0001; £->00001; F->00000;
лср=2,25; [«ср—Я (А) ] /Я (А) = 0,018.
4.2.17. а) А->1; В->01; С->001; £)->000; гасР=1,75; Я (А) = 1,75;
б) А->1; В->01; С->001; £>->000; лср=1,6; Я(А) = 1,53.
4.3.4. 1) 7,64 бит/отсчет; 2) 8,97 бит/отсчет; 3) 6,64 бит/отсчет;
4) 6,49 бит/отсчет; 5) 6,13 бит/отсчет; 6) 6,13 бит/отсчет;
7) 8,23 бит/отсчет; 8) 6,32 бит/отсчет; 9, 7,64 бит/отсчет;
10) 8,23 бит/отсчет.
4.3.5. h(Xp) = log рл12о2; h(Xu) =log 2aeo2; A/i=0,3 бит/отсчет.
4.3.6. /i(X)=log/2^72x; h(Y) = logV 2ле(о2х+о2п); h(X/Y) =
— log V 2neo2xo2n/ (<j2x+<J2n) •
272
4.3.10. Н'е (Хр) =2FC (log/ 12сг1 2 *х—log /2лео2п);
Н'в (Х„) = 2FC (log/2лео2ж—log V 2лео2п).
4.3.11. хи=1— log V12 рс — log Т/2 я е Рш
iog/P^
4.3.13. 1) 2,5-10-5; 2) 5,6-10-5; 3) 10~4; 4) 6,2-10~4; 5) 2,5-10~8;
6) 10-2; 7) 4-10-2; 8) 0,16; 9) 0,25; 10) 0,36.
4.4.2. 1) 2,27 бит/отсчет; 2) 3,04 бит/отсчет; 3) 2,05 бит/отсчет;
4) 2,2 бит/отсчет; 5) 3,1 бит/отсчет; 6) 2,4 бит/отсчет;;
7) 2,06 бит/отсчет; 8) 1,8 бит/отсчет; 9) 1,08 бит/отсчет;
10) 1,59 бит/отсчет.
4.4.4. 1) 336 бит/с; 2) 1581 бит/с; 3) 301 бит/с; 4) 1969 бит/с;
5) 1666 бит/с; 6) 1962 бит/с; 7) 116 бит/с; 8) 1003 бит/с;
9) 180 бит/с; 10) 1219 бит/с.
Ответы к задачам главы 5
5.1.3. хк = 0,3; Як=0,7. При га=8 хк=0,125, Як=0,875. При п=
= 12 хк = 0,417, Як = 0,533.
5.1.4. хк = 0,467; Як=0,533.
5.1.7. 1) хк=2/7; Як=5/7; 2) хк=1/3; Як=2/3; 3) хк = 0,248;
Як=0,752; 4) хк=0,197; Як=0,803.
5.1.8. 1) 0,5; 0,0625; 2) 0,875; 0,0625; 3) 0,9375; 4,88-10"4;
4) 0,9996; 9,76-10~4.
5.1.9. 0,5.
5.1.10. с?мин = 4.
5.1.11. <?и = 3.
5.1.12. а) с?мин=8; б) с?Мин=12.
5.2.2. хк=0,2; рпРав = C‘I25po (1— Ро) 124+C2i25p2o(l-po)123-
5.2.1. Код является линейным, dMHH = 2, хк=0,2.
5.2.3.
1 0 0 0 1 0 1
0 10 0 111
0 0 1 0 0 1 1
0 0 0 1 1 1 0
н =
1101100
0 1110 10
1 1 1 0 0 0 1
5.2.4. bStnv = bx®b2®b3\ &6,np = &i®&2®&4; Ь?,пр = Ь1®&з®^4;
н =
1110 10 0
110 10 10
10 110 0 1
273
Таблица 0.5.1
Синдром 001 01 0 011 100 101 по in
Разряд кодовой комбинации, подлежащий исправлению 7 6 1 5 2 3 4
5.2.6. Синдромы, соответствующие одиночным ошибкам в раз-
личных разрядах кодовых комбинаций, приведены в табл. 0.5.1.
5.2.10. Более просто реализуется второй код.
5.2.12. Ошибки имеются в комбинациях 110011, 0011010,
1000100, 0010101, ЮНОН, 0110010.
5.2.17. Правила формирования проверочных разрядов &5,пр=
= &]ФЬ2®Ь4; Ьв,пр = &1®&2®&з; &7,пр=Й2®&3®^4
1 0 0 0 1 1 0
0 10 0 111
0 0 1 0 0 1 1
0 0 0 1 1 0 1
110 110 0
1110 0 10
0 1110 0 1
н =
о
О)
2)
3)
4?
274
5.3.3. bi (x) =x5+x4+x3+x2+x; b2(x) =x4+x3+x2+x+1;
&з(х) =x6+x3+xz+x+1.
5.3.6. h (x) = x4+x3+x2+1.
5.3.7. h(x) =x5+x4+x+1.
5.3.11. 5.3.12. 1) <7„=1; 2) <?„ = !; 3) qB= 1.
5.4.3. ti==35\ A:= 16; с^мин===6.
5.4.4. K=C3z = 35; xk=0,265. Разрешенными являются комби-
нации, содержащие единицы в любых трех разрядах и нули в ос-
тальных разрядах: 1000110, 1110000 и т. д.
5.4.10. Рн.о=С1зро(1—Ро)2С'4ро(1-ро)3=12р2о(1—Ро)5; Хк =
= 0,268.
5.4.11. хк—0,5; Рн.о==р2о«
5.4.12. рн.о=С2пр40.
5.4.16. Для верхнего регистра /С=3, для нижнего — Я=2,
R=2/3.
5.4.17. Последовательность состояний регистра приведена на
рис. 0.5.1. Последовательность на выходе Ь=01101101.
5.4.21. = 1-|-£)2; Я8(2>(£>) = 1. Схема формирователя
синдрома приведена на рис. 0.5.2.
5.4.22. S= |1100011.
5.4.23. HsW(D) = l+D-[-Dz-, H8W(D) = 1+D2. Схема формиро-
вателя синдрома на рис. 0.5.3.
5.4.24. S=| 1110001.
Ответы к задачам главы 6
6.1.2. 1) 62; 2) 3) Ь2; 4) b2; 5) Ь2; 6) 62; 7) Ь2; 8) &i; 9) &2;
10) bi.
6.1.4. 1) 0,22 В; 2) —0,219 В; 3) —0,14 В; 4) 0,14 В; 5) —0,08 В;
6) 0,08 В; 7) —0,02 В; 8) 0,02 В; 9) —0,087 В; 10) 0,087 В.
6.1.9. Будет зарегистрирован символ 1, так как его апостериор-
ная вероятность больше.
6.2.11. 1) 8; 2) 8; 3) 10; 4) 10; 5) 12; 6) 12; 7). 14; 8) 14; 9) 16;
10) 16; 11) 16; 12) 16; 13) 16; 14) 16; 15) 16.
6.3.2. Рош=0,5[1—Ф(а/о)].
6.3.3. рош = 0,5 {Р (&!) [ 1—Ф {(U0-a) /о)} ] + Р (b2) [ 1 — Ф {(Uo +
+ а)}]}, где U0=(&/2a)ln[P(b2)/P(bi)].
6.3.6. При Р(&1) = Р(&2)=0,5 Рош=0,5[1—Ф(]Л£э/2Я0)];
Рошам=0,5[1—ФС/ед]; рошчм=0>5[1—Ф(/^)]; РошФМ =
= 0,5[1—Ф(]/2Л2)].
275
6,3.11. la) уменьшится в 12,5 раз; 16) останется неизменной;
2а) уменьшится в 3250 раз; 26) уменьшится в 12,5 раз; 3) умень-
шится в 200 раз.
6.3.16. Рошам = 0,5 cosф—0,5)J} ;
т]am = 0,25/ [ (1 —т/Г) cos ср—0,5]2;
Рошчм = 0,5{1-Ф [ ( J/T2 COS ф (1 -2-г/Т) ]};
П чм= Vcos2 ф (1—2т/Т)2.
6.3.1S. РошАМ = 0,5 {1— Ф [/ 2h2 (sin ДсоТ/ДшТ’—0,5) ]};
т)ам = 0,25/ (sin AqT/AwT—0,5);
Рошчм=0>5{1—Ф( V"/i2sinA(o7’/Att>7')};
т]чм= (A<nT)2/sin2 AoT.
bt
6.4.2. maXi(Vi) или V^Vj, i=/=j.
bi
6.4.4. Pc=—2Рш1п2рОш/^2.
6.4.5. F=—£2Рс/2#о1п2рош.
Ответы к задачам главы 7
ати (1 + со2/ос2)
4 а2
Д/л /1,4 (ати + 2,8/ати)
8асо« а2 п Л п)
7.1.15. (т2а= ----------5-------; при со = (йо о2а = 2о2/а.
(со — соо)2 + 4 а2 со2
7.1.16. От0 =* f- д. ; £= J s2 (f, т0) d%Q.
о,6 Е/No —со
7.1.17. о2 =(тЧи/1,4а£.
В п
7.2.1. b(t)= SC|%2ft_1/2sin(2^-l)^Z + X2feV2cos2A^-<
fc=i L т 1
b(t)= е
fe=i
e(0 =
/2 sin (2 k - 1)2^-1 + %2ft /2 cos 2 k 1
A%2ft_! /2 sin (2 k - 1) у t + Al2ft /2 cos 2k y-1
где = —Xfc.
216
7.2.7. g = F/П2 Рс.вх J A {s (Ь (0, /)} df,
о I d*k J
g' = FC/IF PCBIJ C UL {s (b (0,0} I"2 df.
o L^K J
f д л2 ( d U
H —ИИ0.0]} 77ls(*(0.0]}
7.2.8. g- f ’g~ n*P
v«Ba V«BX
7~d ?2 '~7'd i2
3F —[s(v(0,0]l 3 — [S(v(0,0]}
7.2.9. g = _____L^-----------L_ ; g> = _> ______________L_
4jiafcn2Pc.BX 4П2Г2П2Рсвх
7.2.10. gAn = 2m2l(m^+n2); g'^ = m2/(т2+П2).
7.2.11. gBM—2; g/BM=l.
7.2.13 g<t>}^ = F Рфм/Fc П2 ; g'&n = Р2фм/П2.
7.2.19. ^'чм-ам = 3 /п2 Р2чм/2 П2 (1 4- tn2/2); gzoM-AM ~
= tn21 ( tn2 + П2);
g OM-OM = 1 > g <!>M-OM = Р2фм/П2 ; gZ4M-OM = ЗР2чм/П2;
g^M- AM = ₽2ФМ т2Г№ (m2 + П2); g*HM-BM = 0,6 F2/!!2 ;
g'oM-Фм = ₽2фм/П2 ; g'AM-Фм = m2 Р2фм (2 + >n2)/2 (П2 + m2) X
X (1 +m)2;
g fiM-Фм = 02фм/2 П2; gZBM-AM ~ гг?1(.т2 + П2).
7.2.21. pnop=7.
7.2.22. ₽чмС/рвхП2/6рпор=Ю.
7.3.6. —------aS(t)+ а(/Т+Л—1) (z(t)-S(t)).
dt
7.3.17. 8/i2a[Si(x/2)]2/nx.
7.3.18. Д/опт=1,37ти; r2MaKC=0,82-2h2o.
Ответы к задачам главы 8
8.1.2. При k=\, й2=10,8; при £=10 й2=13,1; при £=100 Л2=
= 15,4; при £=1000 £2=17,8.
8.1.3. При £=1 Л2=8,95; при £=10 £2= 11,3; при £=100 £2=
= 13,5; при £=11000 £2= 15,7.
8.1.6. График зависимости Р JPB=f(L) приведен на рис. 0.8.1.
При удвоении числа уровней квантования Рг!Рв уменьшается при-
мерно на 6 дБ.
277
Рис. 0.8.1. К задачам 8.1.6,
8.1.7
Рис. 0.8.3. К задаче 8.1.13
Рис. 0.8.4. К задаче 8.1 Д4,
woX(p,8)=rbty
юа1(ЗД =г1(е)
well (2,8) =г2 (в)
walGVJ =1^(8) г2(8)
wal (4,8) =г^(8)
r.5(S)
^al(6,8)=rz(8) r5(8)
wal(7,8)=rf(8)r2(8) r3(8)
Рис. 0 9.1. Графики первых восьми функ-
ций Уолша (к задаче 9 2 18)
278
8.1.7. График зависимости Рe/PB—f (п) приведен на рис. 0.8.1.
Увеличение числа разрядов п на единицу уменьшает PJPb при-
мерно на 6 дБ. ____
8.1.9. Графики зависимости приведены на рис. 0.8.2.
8.1.13. График зависимости F'=f(tn) при L=128 приведен на
рис. 0.8.3.
8.1.14. График зависимости F'=f(L) приведен на рис. 0.8.4.
8.1.17. £икм-чм= 135; £'икм-чм —9,6.
Ответы к задачам главы 9
9.1.7. Отношение сигнал-шум в 6-канале ph=2Fh/-Nt>.
9.1.8. s(t) =Cil+C2t+ ... +CNtN.
9.1.9. G; C2. 9.2.3. -97,1 МГц.
9.2.4. -583 МГц.
9.2.5. n«HO; при тзащ=0 n—12.
9.2.6. 57,8 МГц.
9.2.8. Pn.n/Pc=tg2A.
9.2.17. Графики приведены на рис. 0.9.1. Г«400 Гц.
Ответы к задачам главы 10
10.1.3. Умакс=2 бит/с Гц; рмакс = —0,4 дБ.
10.1.4. уМакс=4 бит/с Гц; рмаКс= — 0,8 дБ.
10.1.10. 2,9-10-4; 3,2-10-6; 9,7-10~8; 5,4-10~16; 1,7-10~22.
10.1.12. г1=1,33-10-1.
10.1.19. 144.
10.2.2. Для ФИМ—AM £=666, г) = 0,17; для ИКМ—AM g=
=250; 71=0,23; для ИКМ—ЧМ £=500; п=0,32; для ИКМ—ФМ
£=1000, п = 0,47.
10.2.3. Ду = 6 дБ, Др = О дБ.
10.2.4. При рвых=30 дБ, Ду=3 дБ, Др = 6 дБ. При рВых=40дБ
Ду=3 дБ, Др=—6 дБ.
10.2.5. Ду=—4 дБ; Др = 7 дБ.
10.2.7. 50,5 дБ.
10.2.10. Др=3 дБ, Ду=—3 дБ,
10.2.11. Др=О дБ; Ду=0 дБ.
10.2.12. Д|р= 19 дБ; Ду=—11,6 дБ.
10.2.13. Др = 22,7 дБ; Лу= —11,5 дБ.
10.2.14. Др = 11,5 дБ; Ду=—11,5 дБ.
10.2.15. 99 %; 36 %; 0,0045 % •
10.2.17. М3/М2 = 1,16; при М1 = 0,5.
10.3.2. 10 каналов.
10.3.3. Для системы с согласованными фильтрами у=0,5 бит/Гц;
£к(га)=31; цп = 31; уп = 0,5 бит/Гц. Для системы с полосовыми
фильтрами •yi=0,17 бит/Гц, gF(ra) = 10; jxn=10; Лу=3.
279
10,3.6. F ЧМ.—ЧМ /Paa — 6,75-10 *; Тумаке Ал/-Рмакс ЧМ—ЧМ —9,1-103
(39,6 дБ).
10.3.13. В 25 раз.
10.4.3. 1) рэ=5,25-10-4,
2) рэ=5,25-10-8,
3) рэ=5,25-10-12,
10.4.6. ЭВ(П,п)/(7,4)=—4 дБ.
10.4.8. 1) 4 дБ; 2) 9 дБ; 3)
10.4.11. Целесообразно.
10.4.12. Нецелесообразно.
10.4.13. %к=0,5.
S(n,n)/(7,4)= 19;
d(n,n)/(7,4)= 1900;
S(n,n)/(7,4)= 190000.
14 дБ; 4) 19 дБ; 5) 24 дБ.
10.4.16. v=2; р=—9,6 дБ; т] = 0,47.
10.4.17. 1) АМ2; ЧМ2; 2) системы с корректирующими кодами;
3) многопозиционные системы ФМ и АФМ; 4) многопозиционные
системы ФМ и АФМ с корректирующими кодами.
10.4.18. Биортогональные сигналы с М=16.
СПИСОК ЛИТЕРАТУРЫ
1. Астанин Л. Ю., Дорский Ю. Д., Костылев А. А. Применение программируе-
мых калькуляторов для инженерных и научных расчетов. — Л.: Энергоатом-
издат, 1985. — 176 с.
2. Витерби А. Д., Омура Дж. К. Принципы цифровой связи и кодирования: Пер.
с англ./Под ред. К. Ш. Зигангирова. — М.: Радио и связь, 1982.— 526 с.
3. Горяйнов В. Т., Журавле в А. Г., Тихонов В. И. Статистическая радиотехни-
ка. Примеры и задачи: Учеб, пособие для вузов.—2-е изд., перераб. и доп.—
М.: Сов. радио, 1980. — 542 с.
4. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм рядов и произве-
дений.— 5-е изд., перераб. — М.: Наука, 1971.— 1108 с.
5. Дьяконов В. П. Справочник по расчетам на микрокалькуляторах. — 3-е изд.
перераб. и доп. — М.: Наука, 1989.—464 с.
6. Жуков В. П., Карташов В. Г., Николаев А. М. Задачник по курсу «Радиотех-
нические цепи и сигналы»: Учеб, пособие для вузов. — М.: Высшая школа,
1986. — 159 с.
7. Зюко А. Г. Помехоустойчивость и эффективность систем связи.—М.: Связь,
1972. — 359 с.
8. Кловский Д. Д. Передача дискретных сообщений по радиоканалам. — 2-е изд.,
перераб. и доп. — М.: Радио и связь, 1982. — 304 с.
9. Коржик В. И., Финк Л. М., Щелкунов К. Н. Расчет помехоустойчивости сис-
тем передачи дискретных сообщений: Справочник — М.: Радио и связь, 1981.—
231 с.
10. Левин Б. Р. Теоретические основы статистической радиотехники. — М..: Сов.
радио, 1974—1976. —Т. 1—3.
И. Помехоустойчивость и эффективность систем передачи информации/А. Г. Зю-
ко, А. И. Фалько, И. П. Панфилов, В Л. Банкет, П. В. Иващенко/Под ред.
А. Г. Зюко —М.: Радио и связь, 1985. — 279 с.
12. Теория передачи сигналов: Учебник для вузов/А. Г. Зюко, Д. Д. Кловский,
М. В. Назаров, Л. М. Финк.—2-е изд., перераб. и доп. — М.: Радио и связь,
1986 —304 с
13. Тихонов В. И. Оптимальный прием сигналов. — М.: Радио и связь, 1983 —
320 с
14. Финк Л. М. Теория передачи дискретных сообщений —М/ Сов радио,
1970. —727 с.
280